Л.В. ТАРАСОВ
МОСКВА
ФИЗМАТЛИТ
2004

УДК 530.1
ББК 22.3
Т19
Тарасов Л. В. Закономерности окружающего мира. В 3 кн. Кн. 2.
Вероятность в современном обществе. — М.: ФИЗМАТЛИТ, 2004. — 360 с. —
ISBN 5-9221-0516-7.
Данная книга демонстрирует принципиальную роль теории вероятностей в со-
современном обществе, которое основывается на высокоразвитых информационных
технологиях. Книга является достаточно популярным и в то же время строго науч-
научным развернутым введением в исследование операций и теорию информации. Она
имеет четко выраженный учебный характер; ее материал строго структурирован,
построен на доказательной основе, снабжен большим количеством графиков и схем;
приведено значительное количество задач, из которых часть разбирается в книге,
а часть предлагается читателю для самостоятельного решения. Являясь второй
книгой трехтомника автора с общим названием «Закономерности окружающего
мира» (первая книга: «Случайность, необходимость, вероятность», вторая книга:
«Вероятность в современном обществе», третья книга: «Эволюция естественно-
естественнонаучного знания»), данная книга рассматривается в качестве логического продол-
продолжения первой книги, хотя и представляет собой самостоятельный труд.
Для широкого круга читателей и в первую очередь для школьников старших
классов (начиная с 8-го класса), а также студентов техникумов и высших учебных
заведений.
© ФИЗМАТЛИТ, 2004
ISBN 5-9221-0516-7	© Л. В. Тарасов, 2004

Л.В. Тарасов
ВЕРОЯТНОСТЬ
В СОВРЕМЕННОМ
ОБЩЕСТВЕ

Книга вторая
Шк
/
,/

Оглавление
Вступительный диалог автора с читателем
ТЕМА 1. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ: ПРОБЛЕМЫ И ОСНОВНЫЕ
ПОНЯТИЯ, ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ	11
1.1	Чем занимается «исследование операций»?	11
1.2	Как оптимизировать решение в многокритериальных задачах?	16
1.3	Динамическое программирование	24
1.4	Беседа по поводу выбора решения в условиях неопределенности	30
ТЕМА 2. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ: МОДЕЛИРОВАНИЕ ОПЕРАЦИЙ
ПО СХЕМЕ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ	36
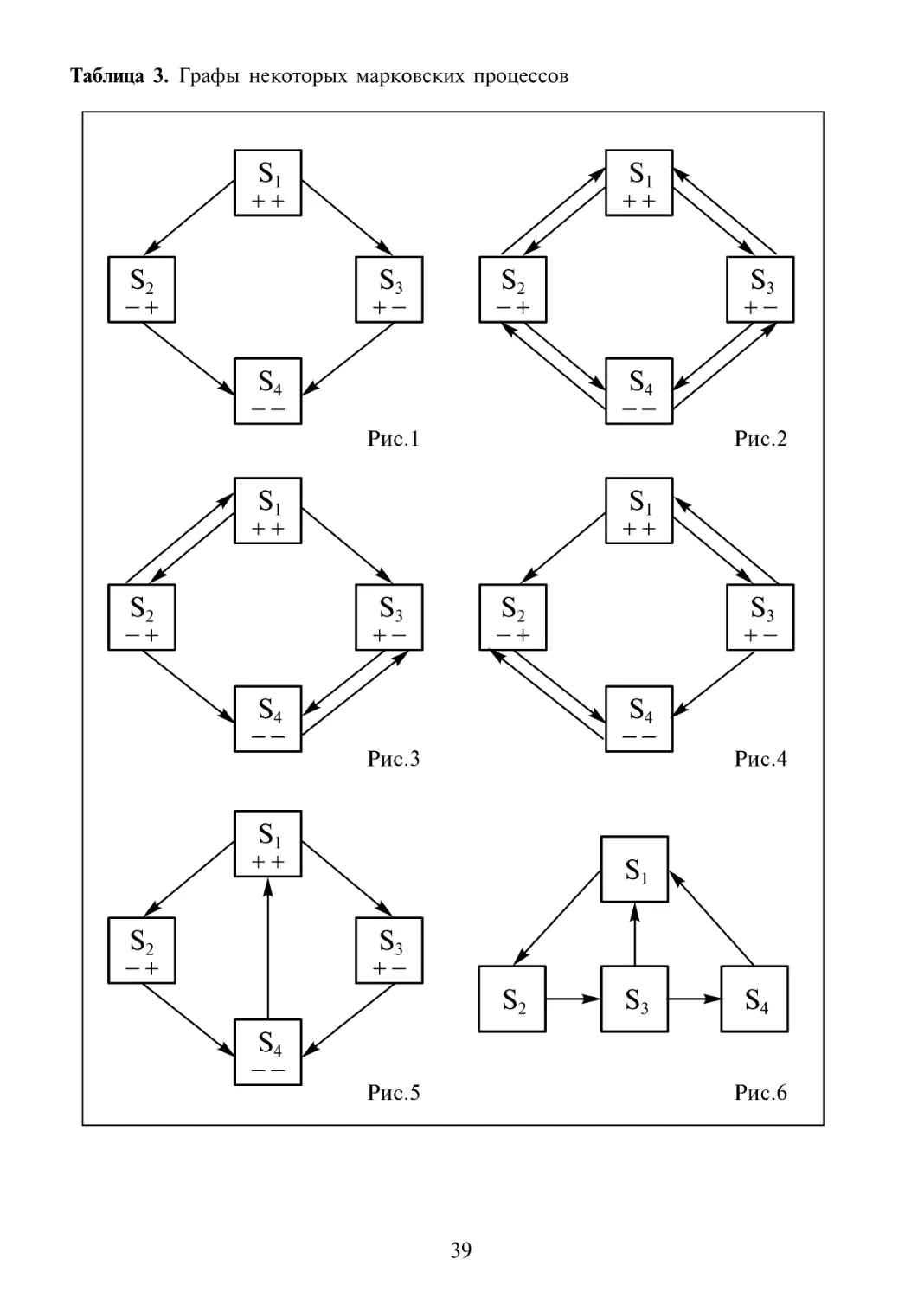
2.1	Марковские случайные процессы с дискретными состояниями
и графы	37
2.2	Марковские процессы с дискретными состояниями и дискретным
временем; переходные вероятности марковской цепи	41
2.3	Самая простая марковская цепь с дискретным временем	43
2.4	Сколько потребуется выстрелов для полного поражения цели?	45
2.5	Поток событий; интенсивность потока	48
2.6	Простейший (пуассоновский) поток событий	51
2.7	Непрерывная марковская цепь и пуассоновский поток событий	53
2.8	Уравнение Колмогорова для предельных вероятностей состояний	57
2.9	Какую рационализацию следует выбрать?	60
ТЕМА 3. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ:
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ	63
3.1	Проблемы массового обслуживания	64
3.2	Основные понятия, используемые в теории массового обслуживания 65
3.3	Виды систем массового обслуживания (СМО)	67
3.4	Схема гибели и размножения	70
3.5	Простейшая СМО — одноканальная система с отказами	74
3.6	Многоканальная СМО с отказами; формулы Эрланга	76
3.7	Сколько требуется каналов обслуживания?	78
3.8	Одноканальная СМО с ограниченной очередью	79
3.9	Насколько целесообразно увеличивать число мест в очереди?	82
3.10	Одноканальная СМО с неограниченной очередью	83
3.11	Какой штраф придется уплатить за ожидание в очереди?	84
3.12	Многоканальная СМО с ограниченной очередью	86
5

3.13	Пример с выбором научно обоснованного решения	89
3.14	Многоканальная СМО с неограниченной очередью	91
3.15	Две одноканальных системы или одна двухканальная?	92
ТЕМА 4. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ: ИГРА И ПРИНЯТИЕ РЕШЕНИЯ	95
4.1	Предмет математической теории игр и основные понятия	96
4.2	Платежная матрица игры, чистые стратегии, смешанные стратегии	100
4.3	Как происходит выбор игроком той или иной чистой стратегии
с заданной вероятностью?	104
4.4	Две такие похожие и такие различные игры	105
4.5	Принцип минимакса; нижняя и верхняя цена игры	107
4.6	Игра с седловой точкой; цена игры	111
4.7	Решение игры без седловой точки и оптимальные смешанные
стратегии	112
4.8	Как найти оптимальную смешанную стратегию для каждого
из игроков?	114
4.9	Геометрическое представление игр 2x2	118
4.10	Геометрическое представление игр 2хпи тх2	122
4.11	Игра «самолеты против зениток»	126
4.12	Упрощение игр. Заведомо невыгодные стратегии	129
ТЕМА 5. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ: ИГРЫ С «ПРИРОДОЙ»,
ИЛИ ПРИНЯТИЕ СТАТИСТИЧЕСКИХ РЕШЕНИЙ	135
5.1	Особенности игр с «природой»	135
5.2	Матрица рисков	138
5.3	Принятие решения, когда известны вероятности «стратегий природы» 139
5.4	Какой из участков следует выбрать под посадку картофеля?	142
5.5	Критерии выбора решения в отсутствие вероятностей «стратегий
природы»	143
5.6	Три критерия и задача с посадкой картофеля	145
5.7	Три критерия и задача с заказом товара	146
ТЕМА 6. «РАБОТАЮЩАЯ СЛУЧАЙНОСТЬ» (МЕТОД МОНТЕ-КАРЛО)	150
6.1	Что такое «метод Монте-Карло»?	151
6.2	Единичный жребий (розыгрыш) как основной элемент статистической
модели	157
6.3	Дискретные и непрерывные случайные величины; вероятность
и плотность вероятности	159
6.4	«Число R»	162
6.5	Как на практике разыгрывают «число R»	162
6.6	Разыгрывание дискретной случайной величины	164
6.7	Беседа о том, где и когда применяют метод Монте-Карло	166
6

ТЕМА 7. КОЛИЧЕСТВО ИНФОРМАЦИИ И ВЕРОЯТНОСТЬ:
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ И ОСНОВНЫЕ ПРИНЦИПЫ	187
7.1	Предварительные замечания об информации вообще и теории
информации в частности	188
7.2	Математическое отступление, посвященное логарифмической
функции	190
7.3	Игра «Бар-Кохба» — игра в вопросы, предполагающие ответы
только «да» или «нет».	194
7.4	Бит — двоичная единица измерения количества информации	200
7.5	Двоичная система счисления	201
7.6	Формула Хартли. Аддитивность количества информации	203
7.7	Сколько информации можно получить, задавая вопрос,
для которого ответы «да» и «нет» не равновероятны?	207
7.8	Формула Шеннона	210
7.9	Об использовании понятия «энтропия» в теории информации	213
7.10	От информации к выбору, от выбора к информации	215
ТЕМА 8. КОЛИЧЕСТВО ИНФОРМАЦИИ И ВЕРОЯТНОСТЬ:
ПЕРЕДАЧА ИНФОРМАЦИИ ПО КАНАЛУ СВЯЗИ	219
8.1	Общая схема канала связи	220
8.2	Передача сообщений по каналу связи (общие замечания)	224
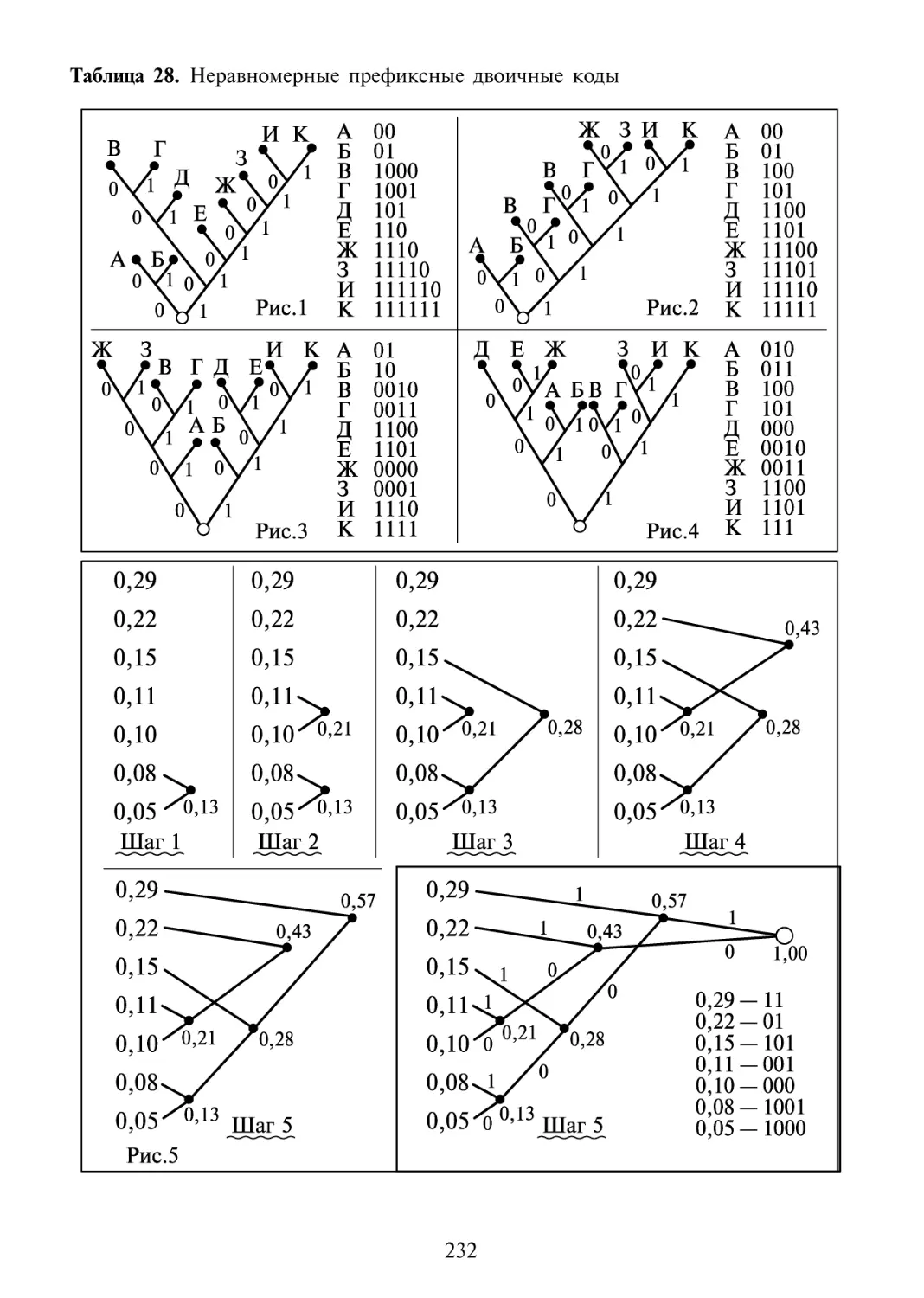
8.3	Кодирование с использованием равномерных двоичных кодов.
Код Бодо	229
8.4	Кодирование с использованием неравномерных префиксных
двоичных кодов	230
8.5	Энтропия «буквы» и среднее число двоичных цифр, приходящееся
на одну «букву»	233
8.6	Код Хаффмена	237
8.7	Эффективность канала связи с помехами. Взаимная информация
о сообщениях на входе и на выходе	239
8.8	Пропускная способность канала с помехами	246
8.9	Кодирование с целью уменьшения влияния помех и основная
теорема Шеннона	250
ТЕМА 9. ЭНТРОПИЯ В ТЕРМОДИНАМИКЕ	257
9.1	Три этапа в развитии понятия «энтропия»	257
9.2	Краткий экскурс в термодинамику	259
9.3	Цикл Карно	267
9.4	Энтропия как функция состояния макросистемы	269
9.5	Второе начало термодинамики как закон возрастания энтропии
замкнутой системы при необратимых процессах	272
9.6	Загадки термодинамики	274
7

ТЕМА 10. ЭНТРОПИЯ, ВЕРОЯТНОСТЬ, ИНФОРМАЦИЯ	276
10.1	Формула, объясняющая возрастание энтропии при расширении
теплоизолированного газа в пустоту	277
10.2	Микросостояния и макросостояния системы. Статистический вес
(термодинамическая вероятность) макросостояния	279
10.3	Формула Больцмана. Энтропия как мера беспорядка в системе	282
10.4	Статистическое объяснение второго начала термодинамики	283
10.5	Немного о флуктуациях случайных величин	285
10.6	Вероятностная природа второго начала термодинамики	291
Незапланированный диалог	292
10.7	«Демон», владеющий информацией	295
10.8	Формула Больцмана и формула Хартли. Связь между энтропией
и информацией	297
10.9	Формула Шеннона и формула Больцмана	299
10.10	Демонстрация антиэнтропийного (информационного) процесса
при формировании письменных текстов	301
10.11	Между абсолютным порядком и абсолютным беспорядком	308
ТЕМА 11. ЭНТРОПИЯ И ЖИЗНЬ	312
11.1	Краткий экскурс в биологию, посвященный метаболизму	312
11.2	Метаболизм как обмен энтропией (негэнтропией) организма
с окружающей средой	314
11.3	Энтропийные и антиэнтропийные процессы в живом организме	315
11.4	Генетический код; его универсальность	317
11.5	Эволюция жизни на Земле как глобальный антиэнтропийный процесс 320
ТЕМА 12. ЭВОЛЮЦИЯ РОЛИ ВЕРОЯТНОСТИ В ЧЕЛОВЕЧЕСКОМ ОБЩЕСТВЕ
(ОТ ИГРЫ В КОСТИ К НАУЧНО-ТЕХНИЧЕСКОЙ РЕВОЛЮЦИИ
И ИНФОРМАЦИОННОМУ ВЗРЫВУ)	330
Завершающая беседа: информатика и вероятность	336
Часть первая, в которой обсуждается весь спектр проблем, охватываемых
сегодня информатикой	336
Часть вторая, в которой вероятность снова оказывается в центре внимания	344
Часть третья, в которой сообщаются впечатляющие результаты
вычислительного эксперимента по прогнозу глобальных
климатических последствий ядерной войны	352
Список литературы	358

Вступительный диалог автора
с читателем
Какой шаг более важен — первый или второй ?
Без первого шага второй был бы невозможен.
Однако без второго первый шаг мог бы ока-
оказаться ненужным.
Восточная мудрость
Пвтор. В нашем разговоре о закономерностях окружающего мира пер-
первый шаг был сделан в предыдущей книге, озаглавленной «Случайность,
необходимость, вероятность».
'ЧиФнатель. Там этот разговор был всего лишь начат. Не более того.
А на самом деле упомянутая книга являлась развернутым введением в тео-
теорию вероятностей. Закономерностей окружающего мира она, по сути
дела, не рассматривала.
Пвтор. Можно сказать, что она их не рассматривала в явном виде.
Однако неявно она имеет к ним (к закономерностям мира) самое пря-
прямое и непосредственное отношение. Ведь именно вероятности явились
тем математическим аппаратом, который позволил сформулировать за-
закономерности, адекватно отражающие реалии окружающего нас мира.
Эти закономерности принято называть статистическими в отличие от
закономерностей динамических, которые, хотя и позволяют делать од-
однозначные предсказания, но дают весьма упрощенное представление о
мире, ограничиваясь рассмотрением идеализированных схем. Именно
через вероятности выражается присущее реальному миру диалектическое
единство таких противоположностей как необходимость и случайность.
Так что книгу «Случайность, необходимость, вероятность» следует рас-
рассматривать отнюдь не только как введение в теорию вероятностей, но и
как начало разговора о закономерностях окружающего нас мира (см.,
в частности, темы 1 и 2, имеющие названия: «Случайные события: про-
против и за» и «Порядок и беспорядок»).
'ЧиФИОФъель. По-видимому, теперь настало время сделать второй шаг —
поговорить о закономерностях окружающего мира обстоятельно и на-
напрямую?
9

Пвтор. Именно такова цель данной книги. Закономерности окружаю-
окружающего мира мы постигаем в процессе познания мира. Этот процесс тес-
теснейшим образом связан с развитием нашей способности активно и це-
целенаправленно действовать в реальном мире. Мир полон случайностей.
И чтобы познать его, человек должен был научиться учитывать эти слу-
случайности в своей целенаправленной деятельности, рассматривая их
не только в качестве своих противников, но также в качестве союзни-
союзников и помощников.
'Чининпель. В том, что мир полон случайностей, человек убедился
давно. Поэтому-то с давних времен он и относится к случайностям как
к фактору, препятствующему его целенаправленной деятельности. Воз-
Возможность же использовать случайности в качестве каких-то помощни-
помощников человек усматривал, пожалуй, лишь в гаданиях, толкованиях снов,
различных предметах. В основном он уповал на божий промысел. И впол-
вполне понятно, что издавна закономерности мира отождествлялись, по
большому счету, с законами религии.
Пвтор. Надо признать, что ничего другого и не оставалось делать
человеку в обществе, где понятие вероятности еще не родилось. Когда
же оно родилось, ситуация принципиально изменилась. Теперь вопрос
о постижении мира, его закономерностей, места человека в мире вы-
вышел, по сути дела, за религиозные рамки. Открылась возможность на-
научного рассмотрения этого вопроса, а именно возможность постижения
мира через вероятность, через вероятностные закономерности.
Мы намерены рассмотреть данную тему в двух аспектах, посвятив
им, соответственно, вторую и третью книги нашего трехтомника.
Первый аспект предполагает обращение к современному обществу.
Сегодня на дворе XXI-й век. Он начался с информационного взрыва.
Ему пророчат название века информации. Многообразные информацион-
информационные системы, как и само понятие количества информации (равно как и
понятие информационной энтропии), органически связаны с понятием
вероятности. Уже поэтому вероятность оказывается «ключевым словом»
в современном обществе. Об этом мы и поговорим во второй книге трех-
трехтомника, озаглавленной «Вероятность в современном обществе».
Второй аспект предполагает обращение к истории естествознания, а
точнее, к эволюции естественнонаучной картины мира, связанной с
постепенно углубляющимся процессом научного познания человеком
окружающего его мира. Этот процесс убедительно продемонстрировал
фундаментальность вероятностных (статистических) закономерностей,
которые стали сегодня подлинной основой научного миропонимания. Об
этом мы будем говорить в третьей книге трехтомника, озаглавленной
«От динамических закономерностей к вероятностным».
10

ТЕМА 1
ИССЛЕДОВАНИЕ ОПЕРАЦИЙ:
ПРОБЛЕМЫ И ОСНОВНЫЕ ПОНЯТИЯ,
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Потребности практики вызвали к жизни
специальные научные методы, которые удоб-
удобно объединять под названием «исследование
операций». Под этим термином мы будем
понимать применение математических, ко-
количественных методов для обоснования ре-
решений во всех областях целенаправленной
человеческой деятельности.
Е. С. Вентцелъ
1.1 Чем занимается «исследование операций»?
Jt5 самых общих чертах ответ на этот вопрос содержится в приве-
приведенном выше эпиграфе: исследование операций занимается применением
11

математики для принятия обоснованных решений в различных областях
человеческой деятельности.
Принимать решения всем нам приходится постоянно, изо дня в день.
На какое время завести будильник? Что выбрать на завтрак? Брать ли с
собой зонтик, выходя из дома? С кем сегодня связаться по телефону?
И так далее. Разумеется, все подобные решения принимаются без ка-
каких-либо специальных математических расчетов и не имеют отноше-
отношения к «исследованию операций». Нельзя считать «исследованием опе-
операций» и принятие более серьезных решений. Куда отправиться отдыхать
летом? Как уберечься от гриппа в период эпидемии? Как обезопасить
квартиру от грабителей? Как наладить хорошие отношения с родителями
жены (мужа)? Оптимизация подобных решений (т.е. выбор наиболее ра-
разумных и эффективных решений) происходит на основе жизненного
опыта, с учетом советов окружающих людей, информации, получаемой
из телевидения, журналов, газет. Математические расчеты тут не при-
применяются. Выбор не совсем удачного решения здесь не очень стра-
страшен — ведь он затрагивает интересы всего лишь одного или нескольких
человек. Как известно, на ошибках учатся.
Иное дело, если приходится принимать решения, затрагивающие ин-
интересы многих людей, а потому требующие весьма ответственного отно-
отношения. Допустим, требуется организовать в городе работу обществен-
общественного транспорта. Пусть это будут автобусы. В этом случае нужно принять
целый ряд решений. Какие маршруты выбрать? Как разметить останов-
остановки? Как выбрать частоту следования автобусов в зависимости от време-
времени суток? Сколько автобусов направлять по тому или иному маршруту?
Как организовать техническое обслуживание парка автобусов? Неопти-
Неоптимальный выбор совокупности подобных решений может существенно
усложнить нормальную жизнь горожан. Поэтому здесь было бы умест-
уместно воспользоваться соответствующими математическими расчетами, т. е.,
иначе говоря, заняться «исследованием операций». К сожалению, не-
нередко решения в таких случаях принимаются интуитивно, исходя из
опыта и соображений здравого смысла. И если у страдающего манией
собственной непогрешимости руководителя окажется недостаточно опы-
опыта и здравого смысла, то принятые им «волевые» решения вполне могут
«подарить» горожанам постоянную проблему с общественным транс-
транспортом. Да и не только с ним.
Чем сложнее, масштабнее планируемое мероприятие, тем менее по-
позволительны «волевые» решения. Тем более важными становятся пред-
предварительные математические расчеты, которые могут помочь выбрать
научно обоснованные оптимальные решения и предостеречь от ис-
12

пользования тех или иных неудачных вариантов (вариантов, менее вы-
выгодных в экономическом или социальном отношении). Именно такими
математическими расчетами и занимается наука, называемая «исследо-
«исследованием операций».
Под операцией понимается в этой науке любая совокупность дей-
действий (любое мероприятие), преследующих достижение какой-то цели.
Рассматривая конкретную операцию, мы ищем оптимальное (наиболее
разумное) решение, т. е. определяем такой набор зависящих от нас па-
параметров (факторов), который бы в наибольшей степени обеспечивал
достижение поставленной цели. В зависимости от выбора этих пара-
параметров принятые решения могут оказаться в той или иной мере менее
разумными или же вообще явно неудачными. Набор параметров, опре-
определяющих то или иное решение, образует множество элементов реше-
решения. Предположим, составляется план перевозок однотипных грузов из
пунктов отправления АХАЪ А3в пункты назначения Въ Въ Въ, В4я вы-
выбрано решение, согласно которому грузы из пункта Ах поступают в пунк-
пункты Въ Въ В3в количестве, равном, соответственно пц9 пи, я13, а грузы
из А2я ^43П0СТУпают в ^4В количестве, равном, соответственно, я24, Л34-
В данном случае числа ли, пп, я13, #24? пъа являются элементами выб-
выбранного решения.
Как оценивать степень разумности (лучше сказать, степень эффек-
эффективности) того или иного решения? Для этого вводят количественный
критерий, называемый показателем эффективности. Его выбирают, ис-
исходя из той цели, которая ставится в данной операции. Оптимальным
считается то решение, при котором показатель эффективности (его обыч-
обычно обозначают через W) окажется экстремальным — максимальным или
минимальным. Если, например, критерием эффективности выбран до-
доход от данной операции, то желательно, чтобы показатель эффектив-
эффективности оказался максимальным (записывают так: Ж^>тах). Если же
критерием выбраны затраты на проведение операции, то желательно,
чтобы показатель эффективности оказался минимальным (записывают:
W^> min).
Приведем несколько достаточно простых примеров.
Пример 1. Операция — снабжение ряда предприятий сырьем со скла-
складов с тем, чтобы потребности в сырье были обеспечены при минимуме
расходов на перевозки. Показатель эффективности W — расходы на
перевозки, скажем, за месяц; W^> min.
Пример 2. Операция — сооружение участка железнодорожной магист-
магистрали в минимально возможные сроки (необходимо распределить технику
и рабочих по участкам пути, продумать земляные работы, обеспечить
13

участки шпалами и рельсами, предусмотреть ремонтные работы и т. д.).
Показатель эффективности W — среднее ожидаемое время завершения
стройки; W^ min.
Пример 3. Операция — проведение медицинского обследования жи-
жителей некоторого района, где обнаружены случаи опасного заболева-
заболевания, с целью выявления заболевших и носителей инфекции (необходи-
(необходимо определить число медпунктов, разместить их по территории района,
установить последовательность осмотров специалистами, проведения
анализов и т. д.). Показатель эффективности W — средний процент вы-
выявленных больных носителей инфекции; W^ max.
Пример 4. Операция — проведение выборочного контроля изделий,
выпускаемых некоторым заводом, с целью обеспечения заданного ка-
качества изделий при минимальных расходах на контроль (необходимо
выбрать объем контрольной партии, набор соответствующих тестов,
правила браковки и т. д.). Показатель эффективности W— средние ожи-
ожидаемые расходы на контроль за единицу времени; W^ min.
Пример 5. Операция — продажа сезонных товаров с целью получе-
получения максимального дохода (необходимо определить число торговых то-
точек и характер размещения их с учетом спроса, учесть ассортимент то-
товаров, предусмотреть рекламу и т. д.). Показатель эффективности W —
средний ожидаемый доход по окончании распродажи; W^ max.
Заметим, что в четырех из пяти приведенных примеров показатель
эффективности имеет эпитет «средний». Дело в том, что при рассмот-
рассмотрении данных операций надо принимать во внимание различные слу-
случайные факторы. Как говорят, в подобных случаях решение принимается
в условиях неопределенности. Именно с такими случаями как раз и при-
приходится обычно иметь дело на практике. Поэтому позднее мы погово-
поговорим о них подробнее.
А пока отметим еще одну особенность приведенных примеров. Здесь
рассматривался всякий раз лишь один показатель эффективности. Од-
Однако эффективность операции, как правило, нельзя охарактеризовать
одним критерием. Особенно если речь идет о достаточно серьезных и
крупномасштабных операциях, направленных на достижение сразу не-
нескольких различных целей. В соответствующих задачах исследования опе-
операций приходится использовать не один, а несколько показателей эф-
эффективности. Такие задачи называют многокритериальными.
Допустим, организуется работа некоторого промышленного предприя-
предприятия. Конечно, хотелось бы получить максимальный возможный доход
Wi (Wi =^> max). В то же время хотелось бы минимизировать себестои-
14

мость продукции W2 (W^^>min). При этом желательно, чтобы оказа-
оказалась максимальной производительность труда W3 (Ж3^>тах).
Возвращаясь к примеру с продажей сезонных товаров, отметим, что
получение наибольшего дохода может являться отнюдь не единствен-
единственной целью, так что средняя ожидаемая прибыль Wx (Wi=> max) — это
всего лишь один из показателей эффективности. Возможно, что орга-
организаторы продажи заинтересованы также в том, чтобы время проведе-
проведения торгов было поменьше (ведь аренда торговых точек стоит недеше-
недешево); поэтому возникает еще один показатель эффективности — время
проведения торгов W2 (W2 =^> min). Чтобы побыстрее распродать това-
товары, надо позаботиться о хорошей рекламе, об увеличении числа торго-
торговых точек и продавцов. Все это потребует, конечно, дополнительных
расходов, которые хотелось бы минимизировать. В результате появля-
появляется третий показатель эффективности — расходы, связанные с органи-
организацией и проведением торгов JV3 (Ж3^>тах). Можно, наконец, пред-
предположить, что организаторы продажи, думая «на перспективу» (т. е.
заботясь об успешности распродажи товаров в последующие сезоны),
пожелают представить свои товары наибольшему количеству посетите-
посетителей (потенциальных покупателей). В связи с этим появляется четвер-
четвертый показатель эффективности — среднее число людей JV4, посетивших
в данном сезоне соответствующие торговые точки (^^>тах).
Итак, как правило, есть несколько показателей эффективности, одни
из которых желательно обратить в максимум, а другие, напротив, в
минимум. Выбор совокупности показателей эффективности — задача
не такая простая и, конечно же, не имеющая в каждом конкретном
случае однозначного решения. Как выбор показателей эффективности,
так и расположение их по степени важности существенно зависят от
того, с точки зрения чьих интересов оптимизируется решение в данной
операции.
Различают прямые и обратные задачи исследования операций. Обо-
Обозначим через Xмножество решений хъ хъ х3,..., хь хп,...9 которые воз-
возможны при рассмотрении некоторой конкретной операции. Выберем
какое-то решение xt из множества 1и выясним, чему равен показатель
эффективности для данного решения. Это есть прямая задача. При не-
необходимости ее следует рассмотреть для всех п возможных решений.
Другой подход к исследованию операций состоит в том, чтобы выявить
такое решение х* из множества X, при котором показатель эффектив-
эффективности примет экстремальное значение. Это есть обратная задача — за-
задача отыскания оптимального решения. Понятно, что обратная задача
сложнее прямой. Особенно, если она является многокритериальной.
15

Предположим, что число возможных решений, образующих множе-
множество X, относительно мало. В этом случае для решения однокрите-
риальной обратной задачи можно попросту рассмотреть прямую задачу
для каждого из решений хъ х2,..., хП9 получить, соответственно, п значе-
значений показателя эффективности W, сравнить их между собой и непо-
непосредственно указать один или несколько оптимальных вариантов. Та-
Такой способ отыскания оптимального решения называют способом простого
перебора.
Если учитываются несколько критериев, то надо рассмотреть пря-
прямую задачу для каждого из п возможных решений и каждого из показа-
показателей эффективности. При учете, например, трех критериев надо полу-
получить 3п величин: W{\ JV?,..., W?\ W\, W%,..., W?\ W\, Wf,..., Щ (здесь
и в дальнейшем нижний индекс фиксирует номер показателя эффек-
эффективности в многокритериальной задаче, а верхний индекс фиксирует
номер решения из множества X). Сравнивая друг с другом все эти
Ъп величин, можно попытаться выбрать то решение (или те решения),
которое представляется наиболее разумным.
Когда число возможных решений велико, метод простого перебора
даже в однокритериальных задачах может оказаться затруднительным
или вообще непригодным. В таких случаях используют методы направ-
направленного перебора вариантов. Все они основаны на том, чтобы отыскать
оптимальное решение путем последовательных «попыток» (последова-
(последовательных «приближений»), которые шаг за шагом приближают нас к ра-
разумному решению.
1.2 Как оптимизировать решение
в многокритериальных задачах?
'Чи&атель. Большинство задач исследования операций многокрите-
многокритериальные; они учитывают несколько показателей эффективности. Как
я понимаю, многокритериальное^ не создает особых проблем при рас-
рассмотрении прямых задач. На зато возникают серьезные проблемы с
обратными задачами, т. е. задачами на отыскание оптимальных реше-
решений. Можно ли полностью оптимизировать решение в многокрите-
многокритериальной задаче? Иначе говоря, существуют ли способы отыскания ре-
решения, которое являлось бы оптимальным сразу по всем показателям
эффективности, рассматриваемым в многокритериальной задаче?
Пвтор. Надо сразу сказать: такое невозможно в принципе. Решение,
обращающее в максимум (минимум) один из показателей эффектив-
16

ности, не может обеспечить экстремальные значения также и всех ос-
остальных показателей эффективности.
*Чи(*иипель. Однако нередко можно слышать призывы добиться мак-
максимального эффекта при минимуме затрат.
Пвтор. Это не более, чем красивая фраза. В математических расчетах
ее не надо принимать во внимание. Невозможно сделать так, чтобы,
как говорится, «и волки были сыты, и овцы были целы». Возьмем, к
примеру, уже обсуждавшуюся нами операцию по продаже сезонных
товаров. Мы рассматривали четыре показателя эффективности: сред-
среднюю ожидаемую прибыль Wx [Wx =^>max), время проведения торгов W2
(Ж^тт), расходы на их организацию и проведение W3 (Ж3^тт),
среднее число посетителей торговых точек W4 (W4=>max). Очевидно,
что, максимизируя прибыль, невозможно минимизировать расходы. Ми-
Минимизируя расходы, нельзя максимизировать прибыль. Стремясь уве-
увеличить число посетителей (потенциальных покупателей), мы, естествен-
естественно, должны увеличивать число торговых точек и число продавцов,
подумать о дополнительной рекламе. Значит, мы должны не умень-
уменьшать, а увеличивать расходы и, уж во всяком случае, не должны стре-
стремиться к сокращению времени проведения торгов. Легко видеть, что
оптимизация по одним показателям оказывается несовместимой с оп-
оптимизацией по другим показателям.
*Чипиииель. А нельзя ли свести многокритериальную задачу к одно-
критериальной, составив из различных показателей эффективности ка-
какой-то обобщенный показатель, который и следует максимизировать или
минимизировать?
Пвтор. Есть ли у Вас идея, как это сделать?
*Чи(*иипель. Да, такая идея есть. Почему бы не представить обобщен-
обобщенный показатель JVo6 в виде дроби? Числитель дроби — произведение
всех показателей эффективности, которые желательно максимизиро-
максимизировать, а знаменатель — произведение показателей, которые желательно
минимизировать. Оптимальным можно считать решение, обращающее
в максимум показатель JVo6, т. е. эту дробь. В нашем примере с прода-
продажей товаров показатель Wo6 можно было бы представить дробью
При увеличении ^и W4w уменьшении Ж2я JV3обобщенный показа-
показатель Wo6 будет, очевидно, возрастать. Вот и надо из всех возможных
решений выбрать то, для которого этот показатель окажется наиболь-
наибольшим. Оно и будет оптимальным решением.
Пвтор. На первый взгляд, такая идея может показаться разумной.
Однако рекомендовать ее не следует.
17

. Почему же?
Пвтор. По той простой причине, что из факта максимизация показа-
показателя Wo6 отнюдь нельзя заключить, что состоялась оптимизация по каж-
каждому из показателей Wh Wb W3, W4. Вы исходили из утверждения,
состоящего в том, что, если бы удалось максимизировать И^и И^и
минимизировать Ж2и Ж3, то произойдет максимизация JVo6...
Ъиниинелй. Простите, но разве это утверждение неверно?
Пвтор. Это утверждение верно. Но суть Вашей идеи заключается в
том, чтобы воспользоваться обратным утверждением. А вот оно-то не-
неверно. Нельзя утверждать, что, если произошла максимизация Wo6, то
удалось максимизировать Wln W4и минимизировать W2n W3. Мы встре-
встречаемся здесь с ситуацией, когда прямая теорема справедлива, а обратная
несправедлива.
g4u<StiuSU*&. Уточните, о каких теоремах идет речь.
Пвтор. Пусть обобщенный показатель эффективности есть дробь,
где числителем является произведение частных показателей, подлежа-
подлежащих максимизации, а знаменателем — произведение показателей, под-
подлежащих минимизации. Прямая теорема', если частные показатели эф-
эффективности максимизированы (минимизированы), то обобщенный
показатель в виде упомянутой дроби будет максимизирован. Эта теоре-
теорема справедлива, поскольку при увеличении числителя и уменьшения
знаменателя дроби сама дробь возрастает. Обратная теорема', если дроб-
дробный обобщенный показатель эффективности максимизирован, то част-
частные показатели эффективности будут максимизированы (минимизиро-
(минимизированы). Это теорема несправедлива.
ttufauSt&fib. Вообще-то следовало бы доказать последнее утверждение.
Пвтор. Дело в том, что увеличение числителя и уменьшение знамена-
знаменателя дроби есть достаточное, но отнюдь не необходимое условие возраста-
возрастания самой дроби. Дробь может расти, например, и при уменьшении чис-
числителя, если при этом знаменатель будет уменьшаться еще быстрее. Так,
в примере с продажей товаров может оказаться, что решение xt с наи-
наибольшим показателем Wo6 будет обеспечивать явно низкие показатели
Wln W4, если при этом показатели W2n W3будут особенно низкими.
Иначе говоря, максимум JVo6 вполне может быть достигнут при недости-
недостижении целей 1 и 4 (получение дохода и привлечение покупателей) за счет
«перевыполнения» по целям 2 и 3 (сокращение времени торгов и сокра-
сокращение расходов). Понятно, что в данном случае оптимизация по обоб-
обобщенному показателю отнюдь не решает проблемы оптимизации по всем
частным показателям. Коротко говоря, нельзя «компенсировать» непо-
неполучение доходов за счет сокращения расходов.
18

. Все-таки хотелось бы иметь доказательство несправедли-
несправедливости обратной теоремы в общем виде.
Пвтор. Воспользуемся методом доказательства от противного. Пред-
Предположим, что обратная теорема справедлива, т. е. из оптимизации по
обобщенному показателю эффективности следует оптимизация по всем
частным показателям. Это будет означать, что оптимизация одновре-
одновременно по всем частным показателям эффективности в принципе осу-
осуществима. Но такое невозможно. Следовательно, предположение о том,
что обратная теорема справедлива, не проходит и необходимо признать,
что эта теорема несправедлива.
*Чи(*иипель. Пожалуй, обобщенные показатели в виде дроби в самом
деле не годятся. А если попытаться скомбинировать частные показате-
показатели эффективности не в виде дроби, а как-то иначе?
Пвтор. Одна из таких попыток состоит в том, чтобы составить из
показателей Wb W2, W^ ..., Ws обобщенный показатель в виде «взве-
«взвешенной суммы»:
Wo6 = axWx + a2W2 + a3W3 + ... + asWs,	(**)
где аъ аъ я3,..., as — весовые коэффициенты, выбираемые с учетом
степени важности соответствующего показателя эффективности. Эти
коэффициенты положительны для показателей, подлежащих максими-
максимизации, и отрицательны для показателей, подлежащих минимизации.
*Чи(*иипель. Весовые коэффициенты — это разумно! Принимая реше-
решение с учетом различных факторов, мы часто взвешиваем мысленно все
«за» и все «против» и приписываем больший вес тем факторам, которые
представляются нам более важными. Формула (**) мне нравится.
Пвтор. Однако не спешите брать ее на вооружение. Различные пока-
показатели эффективности — это величины, имеющие, как правило, разные
размерности. Получается, что в (**) надо складывать слагаемые разной
размерности, что, очевидно, недопустимо. В примере с продажей това-
товаров пришлось бы, например, складывать деньги со временем и числом
покупателей.
'Читатель. Выходит, что с помощью математики можно оптимизиро-
оптимизировать решения лишь для однокритериальных операций, а в многокрите-
многокритериальных операциях следует ограничиваться только прямыми задачами?
Пвтор. Нет, это не так. Математический аппарат может быть с успе-
успехом применен также и к обратным многокритериальным задачам. Про-
Просто не надо пытаться заменить совокупность показателей эффективно-
эффективности неким обобщенным показателем — это заведомо тупиковый путь,
поскольку нельзя свести несколько различных целей к одной. Вместо
19

этого надо воспользоваться идеей компромисса — когда каждый из по-
показателей эффективности максимизируется (минимизируется) не в пол-
полной мере.
ёЧи<9ии9се*ь. Чтобы в какой-то мере были сыты волки и в какой-то
мере сохранялось поголовье овец?
Пвтор. Примерно так. Но прежде, чем искать компромиссное реше-
решение, целесообразно выявить из множества X возможных решений те
решения, которые уступают по всем рассматриваемым критериям хотя
бы одному решению из X. Эти решения как заведомо менее удачные можно
в дальнейшем не рассматривать. После отбрасывания заведомо менее
удачных решений множество X может существенно сократиться. Оста-
Останутся только те решения, среди которых не окажется ни одного, усту-
уступающего по всем показателям эффективности какому-либо из осталь-
остальных решений. Такие решения называют эффективными или паретовскими
(по имени итальянского экономиста Вилъфредо Парёто A848-1923),
который пытался математически обосновать концепцию взаимозависи-
взаимозависимости различных экономических факторов). Окончательное решение
выбирают из совокупности паретовских решений в процессе поиска
компромисса.
*Чипии*иль. Хорошо бы все это как-то проиллюстрировать.
Пвтор. Это удобно сделать, рассматривая некоторую задачу с двумя
показателями эффективности Wxyl W2 (двухкритериальную задачу). Пусть
для определенности оба показателя требуется максимизировать (Wx =^> max,
W2 =^> max). Решая прямую задачу, мы можем найти значения показа-
показателей Жхи Ж2для каждого из возможных решений. На рис. 1 в табли-
таблице 1 рассмотрены 4решения (хъ хъ х3, ха)- По оси ^отложены отве-
отвечающие этим решениям значения показателя Wx (они обозначены через
W{\ JV?9 JV?9 W{4), апооси W2 - значения показателя W2 {W\, Wl W\, W%)\
сами решения изображены в виде точек на плоскости Wx— W2 (точки
1, 2, 3, 4). Будем полагать, что всего для данной операции рассматрива-
рассматриваются 18 возможных решений — все они показаны точками на плоско-
плоскости Wi - JV2ua рисунках 2, Зи 4в таблице 1. Рассмотрим рисунок 2.
При условии Wi =^> max и W2 =^> max множество паретовских решений
состоит из решений 13, 2, 6, 9, 7. Любое из остальных тринадцати реше-
решений уступает по обоим показателям эффективности хотя бы одному из
пяти паретовских решений и может в дальнейшем не рассматриваться.
Например, решение 16 вытесняется (принято говорить «доминируется»)
решением 13 (Ж/6< Ж/3; W26 < W23), а решение 11 доминируется ре-
решением 9 (Ж/1 = Wl\ W\x < Wt).
20

Таблица 1. Двухкритериальные задачи исследования операций
W22
W23
w4
	1	f
II
11
! !
• 2
I 4
I I
Рис.1
W,3 W2W4
I i
I
W2
16*
1
*5
10
•
17
®-
13
3
•
12
15.
18*
14
2
Ni
4
§^
11 *\
•
47
8*
Рис.2
W,
w2
16
13
• •
AW,
f
„• I
Рис.3
W,
Рис.4
AW,
^4
2,
•6
w,
min
Рис.5 W2
f
• 3
•11
10
•9
w,
Wi ^> min
Рис.6 W2 => max
4.
/lO
<¦' I' w.
•11
W! =>max
Рис.7 W2 => min
21

. А если количество показателей эффективности будет боль-
больше двух? Предположим, рассматриваются четыре показателя, из кото-
которых три (Wi, Wb W$) надо максимизировать, а один (JV4) минимизиро-
минимизировать. Как быть в этом случае?
Пвтор. Представить ситуацию графически тут уже нельзя. Но можно
для каждого из п возможных решений (xl5 хъ х3,..., хп) отыскать четвер-
четверку показателей эффективности: {Wl, W\, W\, W\), {W\, W2, Wf, W%),...,
{W\y W", W", W%). Затем надо сравнить все п получившихся четверок
показателей между собой и забраковать каждую четверку (а значит, и
соответствующее решение), для которой найдется хотя бы одна среди
остальных четверок, доминирующая над этой четверкой. Иначе говоря,
если найдется хотя бы одна четверка, для которой показатели Wh Wb W3
больше, а показатель JV4 меньше по сравнению с данной четверкой.
&. Ну, хорошо. Допустим, мы выявили паретовские реше-
решения. Что делать дальше?
Пвтор. Возвращаемся к примеру с двухкритериальной задачей. Оце-
Оценив ситуацию, мы можем потребовать, чтобы показатель W2 был не меньше
некоторой определенной величины w2. Предположим, эта величина нахо-
находится между W2n W2 — см. рис. 2 в таблице 1. В этом случае паретов-
паретовские решения 9 и 7 следует исключить, а из оставшихся паретовских
решений (решений 13, 2 и 6) надо выбрать то, для которого окажется
наибольшим показатель Wx. Это есть решение 6.
ёЧи<9ии9се*ь. Как я понимаю, после того, как было наложено ограни-
ограничение w2ua показатель эффективности Wb задача стала, по сути дела,
однокритериальной и нам осталось оптимизировать по показателю Wx все
решения хь для которых W{^w2.
Пвтор. Совершенно верно. Мы могли бы, кстати говоря, и не отыс-
отыскивать паретовские решения, а сразу изъять из рассмотрения те реше-
решения xi9 для которых W{ < w2. тогда у нас остались бы решения 16, 1, 13,
12, 2, 6 — см. рис. 3 в таблице 1. Среди этих решений выбираем то, для
которого показатель ^является наибольшим. Получаем решение 6.
g4utftiuSU*b. Предположим, что мы считаем показатель Wx значительно
более важным, чем показатель W2. Наверное, в этом случае следует выб-
выбрать из паретовских решений (решений 13, 2, 6, 9, 7) то решение, для
которого показатель эффективности Wx наибольший, т. е. следует оста-
остановиться на решении 7. Не так ли?
Пвтор. Не совсем так. Существует метод отыскания компромиссно-
компромиссного решения, называемый методом последовательных уступок. Допустим,
показатель ^важнее показателя W2. Находим сначала решение, обра-
обращающее в максимум показатель Wx — это есть, как мы уже выяснили,
22

решение 7. Затем, исходя из практических соображений (из того, на-
насколько более важен показатель W{) назначаем некоторую «уступку» AWh
которую мы соглашаемся сделать, чтобы максимизировать показатель W2.
В связи с этим потребуем, чтобы выполнялось условие Wx > W± - AWX.
При таком условии выбираем из паретовских решений то, которое об-
обращает в максимум показатель W2. Это есть решение 9 — см. рис. 2
в таблице 1.
. По-видимому, мы могли бы воспользоваться данным ме-
методом, не тратя времени на поиск паретовских решений?
Пвтор. Да, могли бы. Из восемнадцати возможных решений xt надо
убрать из рассмотрения те, для которых W[ < Wl - AWX. Тогда останут-
останутся решения 8, 7, 11 и 9 — см. рис. 4 в таблице 1. Из этих решений выби-
выбираем решение с наибольшим W2; это есть решение 9.
*Чскп<14пель. Данный метод Вы назвали «методом последовательных
уступок». Какие последовательные уступки имеются здесь в виду?
Пвтор. Предположим, что рассматриваются не два, a s критериев.
Расположим s показателей эффективности в порядке постепенного убы-
убывания их важности: Wb W2, W$,..., Ws. Наиболее важен показатель Wb
наименее важен показатель Ws. После первой уступки (уступки AW{) мы
максимизировали показатель W2w нашли решение, для которого этот
показатель имеет значение W2. Далее назначаем вторую уступку вели-
величиной AWb ценой которой максимизируем показатель W3, и находим
решение с показателем W3. Затем назначаем третью уступку величи-
величиной в АЖ3, ценой которой максимизируем показатель Wx. И так да-
далее — до тех пор, пока не будет максимизирован показатель Ws.
^СшОаАел*. На рисунках 2, 3 и 4 рассматривались двухкритериальные
ситуации, когда Wx ^> max и W2 ^> max. Неплохо бы рассмотреть графи-
графически также ситуации: a) Wx ^> min, W2 ^> min, б) Wx ^> min, W2 ^> max,,
в) Wi ^> max, W2 ^> min.
Пвтор. Ситуации а), б), в) представлены графически, соответственно,
на рисунках 5, 6 и 7 в таблице 1. Паретовские решения изображены здесь
кружочками с точками внутри. Горизонтальные пунктирные прямые за-
задают ограничения на значения показателя эффективности W2. Попро-
Попробуйте самостоятельно выбрать окончательное (компромиссное) решение
в каждой из трех ситуаций двумя способами — учитывая ограничение по
показателю W2 и используя метод последовательных уступок.
*Чи(*иипель. Возвращаясь к проблеме компромисса, хотелось бы по-
поговорить о том, каким образом определяется степень важности того или
иного показателя эффективности в многокритериальных задачах.
23

Пвтор. Это решается отдельно для каждой конкретной операции и
является выбором, который должен сделать руководитель операции.
Именно за ним остается последнее (и подчас решающее) слово.
*4caftfufie*&. Получается, что здесь есть немало произвола?
Пвтор. Конечно. Важно, чтобы этот произвол не сводился к приня-
принятию решений наобум, а опирался на предварительные математические
расчеты. Понятно, что эти расчеты не приведут к жестким, однознач-
однозначным решениям. Однако они позволят избежать принятия заведомо не-
неудачных решений и подскажут решения, которые могут считаться дос-
достаточно разумными.
"ЧитОФнел^. Выходит, что исследование операций — это не просто
наука, но и в какой-то степени искусство?
Пвтор. Вы правы. Тут уместно привести шутливое высказывание од-
одного из зарубежных специалистов. Он заметил, что «исследование опе-
операций представляет собой искусство давать плохие ответы на те прак-
практические вопросы, на которые даются еще худшие ответы другими
методами».
1.3 Динамическое программирование
в
качестве конкретного примера оптимизации решения в детерми-
детерминированном случае (в случае, когда все условия операции известны зара-
заранее и не содержат неопределенности) рассмотрим одну из задач дина-
динамического программирования. Термин «программирование» является
данном случае синонимом термина «планирование»; его не надо путать
с программированием на ЭВМ. Под динамическим программированием
понимают метод оптимизации решений, применяемый в операциях,
которые можно разбить на последовательные «шаги». На каждом шаге
выбирается оптимальное решение, позволяющее получить максималь-
максимальный выигрыш в операции в целом.
Для иллюстрации метода динамического программирования рассмот-
рассмотрим следующую задачу с намеренно упрощенными условиями. Нужно
соорудить дорогу от пункта а до пункта со, лежащего к северо-востоку
от а. Для простоты полагаем, что весь путь от а до со разбит на восемь
отрезков (восемь «шагов») и что на каждом отрезке дорога идет или
строго на восток (горизонтальный отрезок), или строго на север (верти-
(вертикальный отрезок). Полагаем также, что из восьми отрезков пути четыре
отрезка являются горизонтальными и четыре — вертикальными. Все
24

возможные в нашей задаче отрезки можно видеть на рис. 1 в таблице 2.
Здесь прямоугольниками с латинскими буквами изображены точки на
местности, являющиеся границами отрезков, а числа показывают сто-
стоимость в некоторых условных единицах сооружения соответствующих
отрезков пути. Мы можем спланировать путь от а до со разными спосо-
способами, но всякий раз он будет иметь вид ступенчатой ломаной линии,
состоящей из четырех горизонтальных и четырех вертикальных отрез-
отрезков. Всего возможных путей столько, сколько существует выборок из
восьми по четыре, что составляет С84 = 70. Иначе говоря, существует
70 возможных решений при выборе пути от а до со.
Вот, например, четыре решения (четыре возможных пути а до со):
a-G2- F3- E3- DA-CA-B3- А2-ы	(путь 1),
a-Gl-Fl-El-D2-C2-B2-Al-a	(путь 2),
а - Gx - F2 - Е2 - Z>3 - С3 - В2 - А2 - со	(путь 3),
a-G2-F3-E3-D4-C3-B2-A2-co	(путь 4).
(*)
Советуем взять карандаш и наметить все эти пути на рисунке 1, а
заодно подсчитать для каждого из этих четырех вариантов стоимость
прокладывания пути от а до со. Она равна сумме чисел для соответству-
соответствующих восьми отрезков пути. Убедитесь, что стоимость пути составляет:
для пути	1:	11 + 10 + 9 + 10 + 13 + 10 + 14 + 10 = 87 единиц,
для пути	2:	10 + 8 + 11 + 10 + 13 + 10 + 14 + 10 = 86 единиц,
для пути	3:	10 + 9 + 10 + 7 + 11 + 8 + 11 + 10 = 76 единиц,
для пути	4:	11 + 10 + 9 + 10 + 11 + 8 + 11 + 10 = 80 единиц.
Ставится задача: найти оптимальное решение, при котором стоимость
прокладывания пути от а до со была бы наименьшей. Таким образом,
показателем эффективности является в данном случае стоимость со-
сооружения дороги; этот показатель требуется минимизировать.
Конечно, можно было бы рассмотреть все 70 возможных путей, по-
посчитать для каждого из них стоимость сооружения пути и найти наи-
наименьшую из семидесяти стоимостей. Тем самым будет выявлено иско-
искомое оптимальное решение. Это есть отмечавшийся в § 1.1 метод простого
перебора. Однако перебирать все 70 вариантов достаточно хлопотно;
поэтому попробуем поступить иначе.
Попробуем воспользоваться методом, который можно назвать ме-
методом простой пошаговой оптимизации. Первый шаг делается из пунк-
пункта а либо в пункт G2 (затраты: 11 единиц). Оптимизация этого шага озна-
означает выбор отрезка aGh поскольку 10 единиц меньше, чем 11 единиц.
25

Таблица 2. Пример решения задачи динамического программирования
5|	РИС.1
14
Рис.2
29 Сз
12
24 В3
I10
34 с4
Рис.4
Рис.3
Рис.5
26

В результате такого выбора мы окажемся в пункте Gj. Второй шаг дела-
делается из пункта б^либо в пункт Fx (затраты: 8 единиц), либо в пункт F2,
(затраты: 9 единиц). Оптимизируя этот шаг, выбираем отрезок G^F^ и ока-
оказываемся в пункте Fx. Оптимизируя третий шаг, выбираем отрезок РХЕХ и
оказываемся в пункте Ех. Оптимизируя четвертый шаг, выбираем отре-
отрезок E1D2n оказываемся в пункте D2. И так далее — до тех пор, пока не
окажемся в пункте со. В результате определится путь, показанный пунк-
пунктирными стрелками на рис. 1 в таблице 2. Это есть путь 2 из (*); стои-
стоимость его сооружения равна 86 единицам.
На первый взгляд, идея простой пошаговой оптимизации может по-
показаться привлекательной. Учитывая трудность оптимизации операции
в целом, мы разбиваем операцию на ряд шагов (на ряд маленьких опе-
операций) и оптимизируем один за другим каждый шаг. Все это представ-
представляется вполне разумным. Однако простая пошаговая оптимизация не
позволяет отыскать оптимальное решение, что видно уже из сопостав-
сопоставления стоимостей путей, представленных в (*). Легко видеть, что соору-
сооружение путей 3 и 4 оказывается менее дорогостоящим по сравнению с
сооружением пути 2, выбранного по методу простой пошаговой опти-
оптимизации. Не имеет смысла оптимизировать каждый шаг без учета по-
последующих шагов. Выиграв что-то на данном шаге, мы можем значи-
значительно больше потерять на последующих шагах.
Итак, планируя многошаговую операцию, надо выбирать управление на
каждом шаге с учетом последствий, к каким приведет этот выбор на
последующих шагах. Именно в этом и заключается идея динамического
программирования. Подчеркнем, что в отличие от простой пошаговой
оптимизации динамическое программирование предполагает оптими-
оптимизацию на каждом шаге, исходя не из выигрыша именно на данном шаге,
а из суммы выигрышей на данном и всех последующих шагах (в нашем
случае максимизация выигрыша означает минимизацию стоимости со-
сооружения пути). При использовании идеи динамического программи-
программирования весь процесс планирования разворачивают в обратном направ-
направлении — от конца к началу. Это означает, что планировать начинают не
с первого, а с последнего шага, последовательно перемещаясь к предше-
предшествующим шагам — до того, пока не выйдут на первый шаг.
Естественно, возникает вопрос: как можно планировать последний
шаг, если мы еще не знаем, чем окончится предпоследний шаг? Для это-
этого надо сделать возможные предположения о том, чем закончился предпос-
предпоследний шаг. И для каждого предположения надлежит выбрать условное
оптимальное управление для последнего шага. Здесь используется термин
«условное», так как выбор делается при условии, что предпоследний
27

шаг закончился соответствующим образом. Затем мы переходим к вы-
выбору предпоследнего шага и делаем возможные предположения о том,
чем закончился предпредпоследний шаг. Для каждого предположения
выбираем условное оптимальное управление для предпоследнего шага.
И так далее. Постепенно «пятясь назад», оптимизируем управление на
разных шагах — и в конечном итоге доходим до первого шага. В резуль-
результате выявляется искомое оптимальное решение; это есть решение, со-
состоящее из тех выборов, какие мы сделали в процессе нашего мыслен-
мысленного перемещения от конца многошаговой операции к ее началу.
А теперь проделаем все это на конкретном примере, обратившись к
нашей операции по минимизации затрат на сооружение пути от а до со.
Итак, начинаем с рассмотрения последнего (восьмого) шага — см. рис. 2 в
таблице 2. Если в результате предпоследнего (седьмого) шага мы оказа-
оказались в пункте Аъ то последний шаг будет состоять в сооружении отрез-
отрезка пути А^ы стоимостью в 14 единиц. Если в результате седьмого шага
мы оказались в пункте Аъ то последний шаг будет состоять в сооруже-
сооружении отрезка пути А2ю стоимостью в 10 единиц. Короче говоря, мы с
необходимостью отправляемся в со как из пункта Аъ так и из пункта А2
(см. на рисунке короткие стрелки). Тут нам пока выбирать нечего.
Далее рассматриваем предпоследний, т. е. седьмой шаг — см. рис. 3 в
таблице 2. Тут следует сделать три предположения. Первое: после шес-
шестого шага мы оказались в пункте Вх. Дальнейший путь в этом случае
предопределен, тут нам выбирать нечего. Это есть путь В1-А1- со; ука-
указываем его с помощью двух коротких стрелок — от В{к Аъ а затем от
А1к со. Сооружение данного пути имеет стоимость 12 + 14 = 26 единиц;
число 26 записываем в прямоугольнике Вх. Второе предположение: после
шестого шага мы оказались в пункте ^ Ив этом случае дальнейший
путь предопределен: В3-А2-ю (его стоимость: 14 + 10 = 24 единицы).
Третье предположение: после шестого шага мы оказались в пункте В2.
Вот теперь у нас появляется выбор: либо сооружать путь В2 - А1 - со стои-
стоимостью в 10 + 14 = 24 единицы, либо сооружать путь В2 -А2 - со стои-
стоимостью в 11 +10 = 21 единицу. Поскольку 21 меньше, чем 24, мы вы-
выбираем путь В2-А2-сд и отмечаем это на рисунке двумя короткими
стрелками — от В2 к Аъ а затем от А2 к со. Тем самым мы осуществили в
отношении седьмого шага условное оптимальное управление (оно осу-
осуществлено при условии, что после шестого шага мы оказались в В2).
Далее рассматриваем, продолжая «пятиться назад», шестой шаг —
см. рис. 4 в таблице 2. Тут следует сделать четыре предположения. Пер-
Первое: после пятого шага мы оказались в Q. В этом случае дальнейший
путь предопределен: С\ - В1 -А1 - со (его стоимость: 10 + 12 + 14 = 36 еди-
28

ниц). Второе предположение: мы оказались после пятого шага в С4. И в
этом случае дальнейший путь предопределен: С4-В3-А2-ю (его стои-
стоимость: 10 + 14 + 10 = 34 единицы). Третье предположение: после пятого
шага мы оказались в С2. Тут у нас есть выбор: либо из С2 отправиться в Въ
а затем в А1 и со (стоимость сооружения пути из С2: 11 + 12 + 14 = 37 еди-
единиц), либо из С2 отправиться в Въ а затем проследовать по уже выбран-
выбранному нами на седьмом шаге маршруту от В2к Аъ от А2к со (стоимость
сооружения такого пути из С2: 10+11 + 10 = 31 единица). Осуществляя
условное оптимальное управление, мы выбираем второй вариант, по-
поскольку 31 меньше, чем 37. Отмечаем сделанный выбор короткими стрел-
стрелками от С2к Въ от i?2K Аъ от А2 к со и записываем число 31 в прямо-
прямоугольнике С2. Четвертое предположение: после пятого шага мы оказались
в С3. Тут тоже есть выбор: либо путь С3- Въ-А2- со стоимостью в
12 + 14 + 10 = 36 единиц, либо путь С3- В2-А2-ю стоимостью в
8 + 11 + 10 = 29 единиц. Осуществляя условное оптимальное управле-
управление, выбираем второй вариант, поскольку 29 меньше, чем 36. Отмечаем
этот выбор короткими стрелками и записываем число 29 в прямоуголь-
прямоугольнике С3.
Аналогичным образом рассматриваем последовательно пятый, затем
четвертый, третий, второй, первый шаги. В итоге получаем схему, изоб-
изображенную на рис. 5 в таблице 2. Здесь число внутри того или иного
прямоугольника показывает суммарную стоимость прокладывания оп-
оптимального пути от данного прямоугольника (от данного пункта) до
конечного пункта со. Этот оптимальный путь прослеживаться по корот-
коротким стрелкам. Возьмем, к примеру, пункт Еъ. В соответствующем пря-
прямоугольнике стоит число 50. Значит, оптимальный (наиболее дешевый)
путь от Еъ к со имеет стоимость в 50 единиц. Этот путь прослеживается
по коротким стрелкам: от Е3к Z>4, от D4k С3, от С3к В2, от В2к Аъ от А2
к со A0+11 + 8 + 11 + 10 = 50).
Оптимальный путь из начального пункта а в конечный пункт со име-
имеет, как показано на рисунке 5, стоимость в 76 единиц. Проследив его по
коротким стрелкам, убеждаемся, что есть путь 3 из (*):
а - Gx - F2 - Е2 - D3 - С3 - В2 - А2 - со.
Так как это как раз и есть искомое оптимальное решение, изобразим
данный путь на рис. 5 с помощью толстых стрелок.
Метод динамического программирования применяют для оптимиза-
оптимизации решения в самых различных операциях — лишь бы их можно было
разбить на этапы (шаги). Понятие «этапа» (шага) в различных опера-
операциях может иметь разный смысл. В рассмотренном выше примере под
29

«этапами» понимались отдельные участки прокладываемого пути от а
к со. Восемь участков пути (восемь отрезков) — восемь этапов.
«Шагами» многошаговой операции часто бывают временные этапы.
Например, планируется на т лет работа двух групп предприятий, из
которых первая выпускает предметы потребления, а вторая ремонтиру-
ремонтирует и производит оборудование и механизмы для производства предме-
предметов потребления, т. е. обслуживает предприятия первой группы. Цель
операции — получение за т лет максимального объема выпуска пред-
предметов потребления. В соответствии с этим требуется оптимально опре-
определить долю капиталовложений в первую группу предприятий (а зна-
значит, и во вторую группу) на первый год, на второй год, на третий год и
так далее. Недальновидный руководитель в погоне за сиюминутным
выигрышем может вложить уже в первом году почти все выделенные
средства в предприятия первой группы, практически проигнорировав
поддержание и развитие предприятий второй группы. Дальновидный
руководитель воспользуется методом динамического программирования
и подсчитает, сколько средств следует вкладывать каждый год в пред-
предприятия первой группы и предприятия второй группы, чтобы в целом за
т лет (а не только в первые один-два года!) объем выпуска предметов
потребления оказался максимальным.
Укажем еще один пример многошаговой операции, которую можно
исследовать, используя метод динамического программирования. Рас-
Рассматривается вывод на орбиту многоступенчатой космической ракеты.
Пусть число ступеней равно т. Процесс вывода ракеты на орбиту со-
состоит из т этапов, каждый из которых завершается сбрасыванием оче-
очередной ступени. Динамическое программирование позволяет ответить
на вопрос: как надо распределить массу по т ступеням ракеты, чтобы
скорость ракеты при ее выходе на орбиту оказалась максимальной?
1.4. Беседа по поводу выбора решения
в условиях неопределенности
Пвтор. В общем случае показатель эффективности W (или совокуп-
совокупность таких показателей) зависит от трех групп факторов: заранее извест-
известных факторов (обозначим их всех через а), случайных факторов (обо-
(обозначим их через ?), решения х9 выбранного нами из множества X
возможных решений. Мы можем представить: W= W{a, ?; x). Если
фактор ? отсутствует, то говорят о выборе решения в детерминированном
30

случае. В общем же случае этот фактор присутствует — и мы имеем дело
с выбором решения в условиях неопределенности.
g4tuftiufie*b. Ранее мы рассматривали пример с распродажей товаров.
Давайте уточним, какие факторы входят здесь в группу а, а какие — в
группу ?. Ограничимся показателем эффективности W, связанным с полу-
получением прибыли от продажи. Этот показатель нужно максимизировать.
Пвтор. Под а здесь следует понимать выделенные средства на при-
приобретение товаров для продажи (или сами товары), средства на оплату
труда продавцов и на рекламу, предоставленные под торги помещения,
длительность торгов, сезон года и т. д. Под ? следует понимать количе-
количество покупок в день (оно изменяется случайным образом от одного дня
к другому), а также выбор покупателями тех или иных товаров (спрос
на те или иные товары колеблется во времени).
*Чипиинель. Поскольку факторы ? случайные, то должен быть случай-
случайной величиной и показатель эффективности W. Не так ли?
Пвтор. Совершенно верно.
*Чипиинель. А как можно максимизировать случайную величину? И
возможно ли такое в принципе?
Пвтор. Очевидно, что такое невозможно. Какое бы решение х мы ни
выбрали, величина W все равно остается случайной, а потому нельзя
гарантировать, что она окажется максимальной.
'ЧеаЯаЯе**. Какой же в таком случае смысл заниматься поиском оп-
оптимального решения? Да и какое решение надо теперь считать опти-
оптимальным?
Пвтор. В условиях неопределенности мы действительно не можем со
стопроцентной гарантией сделать показатель эффективности максималь-
максимальным (или минимальным). Однако за счет соответствующего выбора ре-
решения мы можем добиться этого с достаточно большой вероятностью.
"ЧитОФнел^. Значит, существуют все-таки приемы, используемые при
принятии разумных решений в условиях неопределенности?
Пвтор. Существуют. Самый простой прием состоит в замене случай-
случайных величин их средними значениями. Тем самым мы переводим факторы ?
в группу факторов а и фактически заменяем выбор решения в условиях
неопределенности выбором решения в детерминированном случае.
*Чи(*иипель. Как это могло бы выглядеть в примере с распродажей
товаров?
Пвтор. В этом случае следовало бы исходить из того, что ежеднев-
ежедневно делается такое-то число покупок и спрос на такие-то товары со-
составляет ежедневно такие-то проценты от общего спроса. Короче го-
говоря, колебания спроса и самого числа покупателей в течение всего
31

времени распродажи попросту игнорируются. Уместно заметить, что
такой прием широко используется в физических задачах. Ведь почти все
величины в таких задачах (температура, давление, электрическое со-
сопротивление и напряжение, сила тока, освещенность и т. д.) являются,
строго говоря, случайными величинами. Решая задачи, мы не учиты-
учитываем случайных изменений величин, обусловленных случайностями в
поведении элементарных частиц вещества и света, поскольку эти изме-
изменения незначительны по сравнению со средними значениями величин.
Случайные изменения силы тока, напряжения, сопротивления являют-
являются всего лишь очень малыми флуктуациями и в задачах не учитываются.
Мы используем известный закон Ома /= U/ R, не принимая во внима-
внимание флуктуации силы тока /, напряжения Е/, сопротивления R.
'ЧиФнатель. По-видимому, прием, состоящий в замене случайных ве-
величин их средними значениями, не будет удовлетворительно работать,
если отклонения случайных величин от средних значений (иначе гово-
говоря, флуктуации случайных величин) будут существенны? Полагаю, что
в примере с распродажей товаров мы имеем дело именно с таким слу-
случаем. Количество покупателей и спрос на те или иные товары могут
заметно флуктуировать во время распродажи.
Пвтор. Тут Вы правы. Отмеченные Вами факторы выступают как
существенно случайные факторы. Такое, кстати говоря, встречается и в
физических задачах. Например, при рассмотрении шумов в электрон-
электронной аппаратуре принципиально нельзя пренебрегать случайностями в
поведении электронных потоков.
ёЧи<9ии9се*ь. Как надо действовать тогда, когда замена случайных ве-
величин их средними значениями недопустима?
Пвтор. В таких случаях нередко используется прием, называемый
оптимизацией в среднем. Он состоит в том, чтобы в качестве показателя
эффективности рассматривать не саму случайную величину W, а ее ма-
математическое ожидание (W), и пытаться максимизировать (минимизи-
(минимизировать) именно (W). Напомним, что в примерах, приведенных в § 1.1,
имелся в виду именно этот прием. Там предполагалось минимизиро-
минимизировать не само время завершения стройки, а среднее ожидаемое время ее
завершения, не просто расходы на контроль качества изделий, а средние
ожидаемые расходы. Предполагалось максимизировать не доход от рас-
распродажи товаров, а средний ожидаемый доход от этой распродажи.
g4utftiuSU*b. Можно ли считать, что оптимизация в среднем устраняет
неопределенность?
Пвтор. Нет, так считать нельзя. Неопределенность, конечно, сохра-
сохраняется. Эффективность того или иного решения, выбранного при ис-
32

пользовании оптимизации в среднем, может весьма сильно отличаться
от ожидаемой эффективности. Однако мы можем надеяться, что после
многих повторений операции в итоге обязательно будем иметь выиг-
выигрыш. Дело в том, что оптимизация в среднем используется тогда, когда
выигрыши при повторении операции суммируются, так что «минусы» в
одних случаях могут компенсироваться «плюсами» в других. Так, опти-
оптимизация в среднем оправдана, когда стремятся повысить прибыль от
распродажи товаров. Прибыли, получаемые в разные дни, суммируют-
суммируются, так что случайно возникающие «неудачные» дни могут быть ском-
скомпенсированы случайно возникшими «удачными» днями.
*Чи4п<ипель. Но, однако, не всегда такая компенсация возможна! Пред-
Предположим, рассматривается эффективность работы службы неотложной
медицинской помощи большого города. В качестве показателя эффек-
эффективности выберем время ожидания врача по вызову. Это время жела-
желательно минимизировать. Очевидно, что в данном случае нельзя исполь-
использовать оптимизацию в среднем. Ведь слишком долгое ожидание врача
одним больным отнюдь не компенсируется быстрым обслуживанием
другого больного.
Пвтор. Вы правы. В подобных случаях выдвигают дополнительное
требование (ограничение). Пусть время ожидания врача Wне должно
превышать некоторого значения Wo. Поскольку Wслучайная величина,
то нельзя просто потребовать выполнения неравенства W<W$. Но мож-
можно потребовать, чтобы это неравенство выполнялось с достаточно боль-
большой вероятностью, например с вероятностью 0,9. Учет этого требова-
требования означает, что из множества X должны быть изъяты те решения х,
для которых рассматриваемое требование не удовлетворяется. Подоб-
Подобные требования называют стохастическими ограничениями (или, иными
словами, вероятностными ограничениями). Понятно, что использование
таких ограничений заметно усложняет проблему принятия решения.
'Чипиинель. Я вижу, что отыскивать разумные решения в условиях
неопределенности в принципе возможно. Хотелось бы теперь более кон-
конкретно познакомиться с тем, как это делается на практике.
Пвтор. Именно этим мы теперь и займемся. Сначала мы познако-
познакомимся со специальным типом случайных процессов, довольно часто
встречающихся на практике, — т. н. марковскими случайными процесса-
процессами с дискретными состояниями. Затем мы поговорим о системах массо-
массового обслуживания и о теории игр (игровых методах обоснования реше-
решения). Завершая знакомство с «исследованием операций», мы рассмотрим
моделирование операций методом статистических испытаний, извест-
известным как метод Монте-Карло.
33

ЗАДАНИЯ ПО ТЕМЕ 1
1.	В примере 2 в § 1.1 операция имеет один показатель эффективности. Укажите
возможные дополнительные показатели эффективности для данной операции.
2.	Такое же задание по отношению к операциям, представленным в примерах 1,
Зи4в §1.1.
3.	Попробуйте самостоятельно сформулировать одну или более конкретных опера-
операций и укажите для каждой операции несколько возможных показателей эффек-
эффективности.
4.	Рассмотрите внимательно рис. 2 в таблице 1 и укажите, какими решениями вы-
вытесняются (доминируются) следующие решения: а) 12, б) 15, в) 4, г) 16, д) 1,
е) 18.
Ответы: а) 2 и 6; б) 2, 6 и 9; в) 6, 11 и 9; г) 13; д) 13, 2, 12 и 6; е) 2, 15, 6, 9
и 11.
5.	Для двухкритериальной ситуации, представленной на рис. 5 в таблице 1, выбери-
выберите окончательное решение: а) учитывая ограничение по показателю И/2, б) ис-
используя метод последовательных уступок и считая при этом, что показатель
И/± важнее, чем И/2.
Ответы: а) 9, б) 7.
6.	Такое же задание для ситуации, представленной на рис. 6 в таблице 1.
Ответы: а) 2, б) 2.
7.	Такое же задание для ситуации, представленной на рис. 7 в таблице 1.
Ответы: а) 9, б) 10.
8.	Используя схему на рис. 1 в таблице 2, подсчитайте в принятых здесь условных
единицах стоимость сооружения пути от пункта а до пункта со при выборе следую-
следующих решений (следующих возможных путей):
а)	а - G± - F2 - Е3 - D4 - С4 - В3 - А2 - со;
б)	a-G2-F3-E4-D4-C3-e2-/\1-co;
в)	a- G±- F±- Е2- D3- С3- В3- А2- со;
г)	а - G2 - F2 - Е3 - D3 - С3 - В2 - А2 - со.
Ответы: а) 85 единиц, б) 86 единиц, в) 84 единицы, г) 86 единиц.
9.	Приступив к сооружению дороги от а до со (см. таблицу 2), руководитель строи-
строительства, не будучи знаком с динамическим программированием, избрал метод
простой пошаговой оптимизации. Он успел соорудить два отрезка пути, после
чего его заменили другим руководителем (который был знаком с динамическим
программированием) и предложили ему завершить сооружение дороги. Во сколько
в итоге обошлось государству строительство дороги от а до со?
Ответ: 77 единиц.
10. Во сколько бы обошлось государству строительство дороги от а до со, если бы
замена руководителя в предыдущей задаче произошла после сооружения не двух,
а трех отрезков пути?
Ответ: 83 единицы.
34

11. Начав сооружение дороги от а до со (см. таблицу 2), руководитель применил ди-
динамическое программирование, но успел соорудить лишь два отрезка пути, пос-
после чего был отправлен на повышение. Дорогу достраивал новый руководитель,
который о динамическом программировании даже не слышал и действовал по-
попросту — по методу простой пошаговой оптимизации. Во сколько в итоге обо-
обошлось государству сооружение дороги от а до со?
Ответ: 81 единица.
12.	После того, как в процессе сооружения дороги от а до со (см. таблицу 2) строители
оказались в пункте D4, явился руководитель, знакомый с динамическим програм-
программированием, который и достроил дорогу. Во сколько обошлось государству соору-
сооружение дороги от а до со: а) в наилучшем возможном случае, б) в наихудшем случае
(когда строительство от а до D4 велось по наиболее дорогостоящему варианту)?
Ответы: аO8 единиц, б) 83 единицы.
13.	Предложите одну или более ситуаций с выбором решения в условиях неопреде-
неопределенности, когда оптимизацию в среднем применять не следует, а надо ввести
стохастическое ограничение.
35

ТЕМА 2
ИССЛЕДОВАНИЕ ОПЕРАЦИЙ:
МОДЕЛИРОВАНИЕ ОПЕРАЦИЙ ПО СХЕМЕ
МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Многие операции, которые приходится
анализировать под углом зрения выбора оп-
оптимального решения, развиваются как слу-
случайные процессы, ход и исход которых за-
зависят от ряда случайных факторов... Для
математического описания многих операций,
развивающихся в форме случайного процес-
процесса, может быть с успехом применен матема-
математический аппарат, разработанный в теории
вероятностей для так называемых марковс-
марковских случайных процессов.
Е. С. Вентцелъ
Справка. Андрей Андреевич Марков A856-1922) — выдающийся российский мате-
математик, один из учеников П.Л. Чебышева A821-1894). Понятие «цепи Маркова» ока-
оказалось весьма ценным в различных приложениях, например, в теории диффузии,
теории массового обслуживания, теории надежности, а также в квантовой механике
и генетике. Развитие идеи марковской цепи привело к созданию важного раздела
теории вероятностей — теории случайных процессов, в которой исключительную роль
сыграли труды АК Колмогорова A903-1987) и А.Я. Хинчина A894-1959).
36

2.1 Марковские случайные процессы
с дискретными состояниями и графы
в
книге «Случайность, необходимость, вероятность» тема 11 была у
нас посвящена испытаниям Бернулли — независимым испытаниям с
двумя исходами, образующими полную группу событий («успех» и «не-
«неудача»). Независимые испытания Бернулли можно рассматривать как
частный случай цепей Маркова. Последние представляют собой последо-
последовательность испытаний, в каждом из которых появляется одно не из двух,
аизп образующих полную группу несовместных событий AhA2,A3,..., АП9
причем испытания теперь не являются полностью независимыми, а свя-
связаны между собой в определенного рода цепь. Конкретно: вероятность
наступления того или иного события Аъ А2,...9 Ап при очередном испы-
испытании (пусть это будет k-ot испытание) зависит от результата предыду-
предыдущего испытания (результата (k-l)-ro испытания) и только от него. Упо-
Упомянутая вероятность не зависит от результатов более ранних испытаний:
(?-2)-го, (?-3)-го, (?-4)-го и др.
Рассмотрим терминологию, которая обычно используется при изло-
изложении цепей Маркова. Упомянутым выше п независимым событиям
Аь А2,..., Ап сопоставляют п состояний Sh S2, S$,..., Sn, в одном из кото-
которых находится в данный момент времени некоторая система. Итак, пусть
Sh S2, S3,...9 Sn — возможные дискретные состояния некоторой систе-
системы. В любой момент времени система находится в каком-то из этих
состояний. В некий момент может произойти изменение состояния сис-
системы, после чего система окажется в каком-то другом из возможных
состояний. Таким образом, событие теперь — это нахождение системы в
соответствующем состоянии, а испытание связывается с изменением со-
состояния. Если состояние системы меняется во времени случайным обра-
образом, то говорят, что в системе протекает случайный процесс, в связи с чем
цепь Маркова называют также марковским случайным процессом. Точнее
говоря, марковским случайным процессом с дискретными состояниями.
Специфика марковского случайного процесса состоит в том, что веро-
вероятность системе оказаться (в результате очередного изменения состояния,
т. е. при очередном испытании) в некотором состоянии Sj зависит только
от того, в каком состоянии St она (система) находилась непосредственно
перед данным испытанием, и не зависит от того, когда и каким образом
система пришла в состояние Si9 т. е. в каких состояниях она побывала
ранее. Таким образом, марковский случайный процесс можно определить
как случайный процесс, в котором для каждого момента времени t0 вероятность
того или иного состояния системы в будущем (т. е. при t > /q) зависит от ее
состояния в настоящем (при t=t0) и не зависит от развития процесса в
37

прошлом {при t<t0). Иногда это свойство системы называют отутствием у
нее долговременной «памяти»; система запоминает только свое последнее
состояние, но напрочь «забывает» о всех более ранних.
В общем случае состояния системы могут меняться непрерывным
образом, плавно. Так, процесс изменения напряжения в электросети
является случайным процессом с непрерывными состояниями. Но мы
ограничимся рассмотрением процессов с дискретными состояниями —
когда возможные состояния системы (Sh Sb S3,...) можно перенумеро-
перенумеровать одно за другим. При этом сам процесс состоит в том, что время от
времени система скачком (мгновенно) переходит (можно сказать: пере-
перескакивает) случайным образом из одного состояния в другое. Для про-
процессов с дискретными состояниями удобно пользоваться геометричес-
геометрической схемой, называемой графом состояний. Граф геометрически
изображает возможные состояния системы (в виде, например, квадра-
квадратиков, кружков или просто точек) и соединяющие эти состояния стрел-
стрелки, показывающие возможные переходы из одного состояния в другое.
Графы некоторых марковских процессов показаны на рисунках в таб-
таблице 3. На рисунках 1-5 даны графы состояний для системы, представ-
представляющей собой некоторое техническое устройство, имеющее два узла.
Si — оба узла работают,
$2 — первый узел отказал, он не работает; второй работает,
$з — второй узел отказал, он не работает; первый работает,
S4 — оба узла не работают.
На графе показаны четыре стрелки: S{^> Sb S2^> S4, S{^> S3, S3 -> S4.
В какой-то момент вследствие каких-то случайных факторов первый
узел отказал — система перескочила в этот момент из состояния ?\в
состояние S2. Через некоторое время отказал также и второй узел —
система перескочила из состояния S2b состояние S4. Возможен также
иной вариант: сначала отказал не первый, а второй узел и система пере-
перескочила из ?\в S3. Затем отказал первый узел и система перескочила из
?3в S4. На рисунке нет стрелки Si~>S^9 поскольку вероятность того,
что оба узла откажут вдруг точно в один и тот же момент времени,
равна нулю (какой-то из узлов откажет хотя бы чуть-чуть раньше).
На рис. 2 рассматриваются следующие состояния системы:
Si — оба узла работают,
$2 — первый узел отказал, он ремонтируется; второй работает,
$з — второй узел отказал, он ремонтируется; первый работает,
S4 — оба узла ремонтируются.
На графе показаны восемь стрелок. Стрелки Si~>S2, S2^ S4, Si—>S$,
S3 -> S4 связаны с отказами узлов, а стрелки S4^S2, S2^Sh S4^S3,
S3 —> Si связаны с ремонтом узлов. Допустим, система оказалась в
38

Таблица 3. Графы некоторых марковских процессов
/
s2
Ч
/
/
ч
ч
Si
s4
4
4
4
+s3
x"
Л
s2
X
X
ч
^4
Si
s4
\
s3
;/
Рис.1 Рис.2
/*
s2
Ч
s2
—ь
X
ч.
ч
/
/
+s+
s4
Si
\ г-
Ч
4
4
4
4
4
+s3
Рис.3
4
s3
/
X
/
Si
s4
Si
s4
s2
у
\
^4
s3
X
Рис.4
s3
s4
У
Рис.Ь Рис.6
39

состоянии ?4 (оба узла ремонтируются). В какой-то момент времени
один из узлов (например, второй) начинает работать — в этот момент
система перескакивает из S4b S2. Через некоторое время заканчивается
ремонт также и первого узла — система перескакивает из S2b 6\. Другой
вариант соответствует тому, что сначала завершается ремонт первого
узла (S4 -> S3), а затем также и второго (S3 -> S{).
На рис. 3 граф содержит шесть стрелок. Рассматриваются состояния:
Si — оба узла системы работают,
$2 — первый узел отказал, он ремонтируется; второй работает,
53	— второй узел отказал и не ремонтируется (предполагается, что ремонт вто-
второго узла в принципе невозможен); первый узел работает,
54	— оба узла не работают; первый узел ремонтируется.
С ситуацией, граф которой изображен на рис. 4, читатель вполне
может разобраться самостоятельно.
В ситуации на рис. 5 предполагается, что ремонтировать узлы по-
порознь в данной системе нельзя, а надо ремонтировать их одновремен-
одновременно — уже после того, как они оба выйдут из строя. Состояния Sh S2, S3
здесь такие же, что и на рис. 1. Состояние S4 — °ба узла не работают и
одновременно ремонтируются (по окончании ремонта они начнут функ-
функционировать одновременно).
На рис. 6 дан граф устройства, которое может находиться в следую-
следующих состояниях:
51	— устройство нормально функционирует,
52	— устройство вышло из строя; оно ожидает квалифицированного осмотра,
$з — устройство осматривается и ремонтируется на месте,
S4 — устройство доставлено в ремонтную мастерскую, где оно подвергается
более серьезному ремонту.
Различают два типа марковских случайных процессов с дискретны-
дискретными состояниями. Первый тип: цепи Маркова с дискретным временем —
изменение состояний системы происходит случайным образом в фик-
фиксированные моменты времени: th t2, t3,..., th... Второй тип: цепи Марко-
Маркова с непрерывным временем — изменения состояний системы происходят
случайным образом в случайные моменты времени.
Заметим, что на практике чаще всего приходится иметь дело с мар-
марковскими случайными процессами с непрерывным временем. Все при-
примеры, приведенные на рисунках в таблице 3, относятся, как нетрудно
сообразить, именно к таким процессам.
Ниже мы подробнее познакомимся с обоими типами марковских
процессов. И начнем с процессов с дискретными состояниями и диск-
дискретным временем.
40

2.2 Марковские процессы
с дискретными состояниями
И ДИСКРЕТНЫМ ВРЕМЕНЕМ;
ПЕРЕХОДНЫЕ ВЕРОЯТНОСТИ МАРКОВСКОЙ ЦЕПИ
J Ьш марковского процесса с дискретным временем существует после-
последовательность фиксированных моментов времени
когда как раз и совершаются переходы (перескоки) системы из состоя-
состояния в состояние. Можно сказать, что именно в эти моменты осуществ-
осуществляются испытания', исходом испытания является попадание системы в
то или иное состояние. Фиксированные моменты времени принято на-
называть «шагами» или «этапами» процесса.
Допустим, данная система может находиться в одном из четырех воз-
возможных состояний: Sh S2, S$, S4. Конкретный смысл этих состояний,
равно как и самой системы, пока не уточняем. Происходящий в систе-
системе процесс может иметь, например, такой вид:
Si~> S2-> S2-> S^-> S^-> Si~> ...
Эту запись надо понимать так: на первом шаге (т. е. в момент t{) сис-
система перескочила из состояния 6\ в состояние S2; на втором шаге (в мо-
момент t2) состояние системы не изменилось (система задержалась в со-
состоянии S2); на третьем шаге (в момент Ц) система перескочила из S2
в S3. И так далее. Процесс является случайным', поэтому возможны, в
принципе, различные его реализации:
Si~> S2-> S$-> S$-> S^-* S^-* ...
S^-> S^-> S2-> S^-> S^-> S^-> ...
Si —> 6*2 —> S3 —> S4 —> Si —> Si -> ...
Характеристикой процесса в данной системе служит набор вероят-
вероятностей перескакивания системы из одного состояния в другое (вероят-
(вероятность перехода системы из St в Sj будем обозначать через Ptj) и вероят-
вероятностей задержки системы в том или ином состоянии (вероятность
задержки системы в состоянии St будем обозначать через Ри). Приме-
Применительно к системе с четырьмя состояниями указанный набор вероят-
вероятностей можно представить в виде матрицы 4x4:
41

P\l P\2 Р\Ъ Р\4
Г)	Г)	Г)	Г)
Г21 Г22 Г2Ъ Г24
р р р р
ГЪ\ ГЪ2 ГЪЪ ^34
Р\\ Р^2 Аз Р44
В общем случае, когда число возможных состояний системы равно п
(Sb S2, S3,..., Sn), надо рассматривать матрицу пхп:
Рп
Рп
Рп
Рп
Рщ
(ем
Рп
Р22
Р32
Рп
Р
± п2
^13
Ргз
Аз
Рп
р
± пЪ
обозначать
... Ру
... Ру
... Ру
р
р
как \\Ру
••• Ры
- Pin
... Р3п
... Pin
. Веро*
A)
Вероятности, входящие в
матрицу A), называют переходными вероятностями процесса.
Случайная последовательность, образованная событиями (состояния-
(состояниями) Sh S29 ?3,..., ^п> может рассматриваться как марковская цепь (как
марковский случайный процесс), если для любого шага вероятность Ptj
не зависит от того, когда и как система пришла в состояние St. Именно
так можно сформулировать определение марковского случайного про-
процесса с дискретными состояниями и дискретным временем; поэтому,
сторого говоря, здесь следует вместо слова «если» употребить словосо-
словосочетание «тогда и только тогда, когда» (напомним в связи с этим нашу
беседу о необходимости и достаточности в § 8.4 в книге «Случайность,
необходимость, вероятность»).
Как уже отмечалось, возможные состояния системы образуют пол-
полную группу событий. Значит, на любом шаге должна равняться единице
вероятность перехода системы из любого состояния St или в состояние Sh
или в состояние S2, или в состояние S$, ..., или в состояние Sn (задержку
в состоянии Sj рассматриваем формально как переход St —> St). Таким
образом,
у=1
(/ = 1,2,3,...,й).
42
B)

Будем обозначать через Pi(k) вероятность того, что после к-го шага
система окажется в состоянии St. Предположим, что перед первым
шагом система находилась в состоянии Sm. В результате первого шага
она перейдет в одно из состояний Sh S2, S3,...9 Snc вероятностью, рав-
равной, соответственно, РтЪ РтЪ Рт$,..., Ртп. Следовательно, вероятности
состояний системы после первого шага таковы:
Л A) = РтЪ Pi A) = РтЪ Ръ A) = Д,3>-> Рп A) = Ртп-	(*)
Чтобы найти вероятности состояний системы после второго шага,
воспользуемся формулой полной вероятности (мы рассматривали эту
формулу в § 10.2 в книге «Случайность, необходимость, вероятность»),
учитывая, что Ptj есть не что иное, как условная вероятность Ps.(St) —
вероятность системе оказаться в состоянии St при условии, что она ра-
ранее находилась в состоянии Sj. По формуле полной вероятности нахо-
находим, что вероятности состояний системы после второго шага определя-
определяются соотношениями:
jj	(/ = 1,2,3,...,я),	C)
у=1
где Pj{\) даны в (*).
Нетрудно сообразить (надо снова воспользоваться формулой полной
вероятности), что после третьего шага вероятности состояний системы
будут определяться соотношениями:
Л C) = 5>у B)fy	(/ = 1,2,3,...,я),	D)
у=1
а после k-го шага — соотношениями:
Pi(k)=^Pj(k -\)Pjt	(i =1,2,3,...,п).	E)
2.3 Самая простая марковская цепь
с дискретным временем
Рассмш
лрим предельно упрощенную систему с двумя состояниями
на примере предприятия, выпускающего какую-то продукцию. Пред-
Предположим, что по окончании каждой недели производится подсчет объема
43

выпущенной продукции. Условимся считать: если план по недельному
объему продукции окажется выполненным (перевыполненным), то си-
система переходит в состояние 6\ (или задерживается в состоянии 6\);
если план не будет выполнен, то система переходит в состояние S2 (или
задерживается в состоянии S2). Таким образом, фиксированные момен-
моменты времени (иначе говоря, шаги) — это моменты tb гъ t3,..., tk,..., где
tk — окончание ?-ой недели (к-й шаг). На рис. 1 в таблице 4 схемати-
схематически представлены различные возможные реализации рассматривае-
рассматриваемой марковской цепи. Здесь последовательные шаги разделены равны-
равными промежутками времени (неделей). В общем случае равенство
промежутков времени между последовательными шагами отнюдь не
обязательно.
Предположим, что после к-то шага (по окончании к-ой недели) сис-
система оказалась в состоянии ?\. Значит, за к-ю неделю план был выпол-
выполнен (перевыполнен), все этим удовлетворены и нет необходимости пред-
предпринимать в течение предстоящей недели какие-либо дополнительные
действия. Пусть в этом случае вероятность того, что план выпуска про-
продукции за неделю будет выполнен (перевыполнен), равна 0,5 и, соот-
соответственно, равна 0,5 вероятность не выполнить план; таким образом,
Рп = 0,5 и Рп = 0,5. Предположим теперь, что после к-то шага система
оказалась в состоянии S2. Значит, за к-ю неделю план не был выполнен
и в связи с этим требуется предпринять какие-то действия (возможно,
предусмотреть на (к+ 1)-ой неделе сверхурочную работу). Мы не будем
обсуждать эти действия, а просто отметим, что благодаря им вероят-
вероятность выполнить недельный план повысилась до 0,7, а вероятность не
выполнить его понизилась до 0,3; таким образом, Р21 = 0,7 и Р22 = 0,3.
Матрица переходных вероятностей имеет вид:
21 р22
0,5 0,5
0,7 0,3
На рис. 2 в таблице 4 изображен граф состояний нашей системы. Числа
вблизи стрелок — это соответствующие переходные вероятности. Граф,
на котором указаны значения переходных вероятностей, называют раз-
размеченным графом.
Найдем, чему равны вероятности состояний ?\ и S2 после пятого шага,
если перед первым шагом система находилась в состоянии 6\. Зная мат-
матрицу переходных вероятностей, заключаем, что после первого шага ве-
вероятности состояний Si и ?2 будут равны:
44

Таблица 4. Марковские процессы с дискретным временем
1-й шаг 2-й шаг 3-й шаг 4-й шаг
45

После второго шага вероятности состояний 6\и S2 можно легко найти,
используя соотношения C):
р1B) = р1A)Рп+р2A)Р21 =0,5-0,5 + 0,5.0,7 = 0,6;
Л B) = ЛA)Р12+ЛA)Р22= 0,5-0,5 + 0,5-0,3 = 0,4.
После третьего шага (с учетом соотношений D)):
ЛC) = ЛB)РП+ЛB)Р21= 0,6-0,5 + 0,4-0,7 = 0,58;
ЛC) = ЛB)Р12+ЛB)Р22= 0,6-0,5+ 0,4-0,3 = 0,42.
После четвертого шага:
Л D) =ЛC)РП+ЛC)Р21 =0,58-0,5+0,42-0,7=0,584;
Л D) =Л C)^2+^C)^22 =0,58-0,5+0,42-0,3 =0,416.
После пятого шага:
Л E) =Л D)^+^2D)^21 =0,584-0,5+0,416-0,7 =0,5832;
р2 E) = plD)Pn+p2 D)Р22= 0,584-0,5 +0,416-0,3 =0,4168.
Теперь найдем вероятности р\E) и р2E) состояний ?\и S2после пя-
пятого шага, если перед первым шагом система находилась не в состоя-
состоянии Sh а в состоянии S2. После первого шага имеем:
ЛA) = Р21=0,7 и ^A) = Р22=0,3.
Предлагаю читателю самостоятельно убедиться в том, что искомые ве-
вероятности имеют значения:
р[ E) = 0,5835 и р'2 E) = 0,4165.
Мы видим, что независимо от того, каково было состояние системы
перед первым шагом (?\или S2)9 через несколько шагов ситуация впол-
вполне стабилизируется — в состояние 6\ система будет попадать с вероят-
вероятностью около 0,58.
2.4 Сколько потребуется выстрелов
ДЛЯ ПОЛНОГО ПОРАЖЕНИЯ ЦЕЛИ?
11о некоторой цели производятся выстрелы в моменты времени
th гъ f3,... Возможные состояния системы (точнее говоря, цели) таковы:
Si — цель невредима,
$2 — цель повреждена не очень существенно,
46

S3 — цель повреждена существенно,
?4 — цель полностью поражена (не может функционировать).
Размеченный граф состояний представлен на рис. 3 в таблице 4. Здесь
числами показаны вероятности соответствующих переходов; они обра-
образуют матрицу:
ОД	0,4	0,3	0,2
0	0,3	0,4	0,3
0 0	0,4	0,6
0 0 0	1
(*)
Обратим внимание на то, что для каждой строки матрицы сумма пере-
переходных вероятностей равна 1 — в полном согласии с соотношением B).
Учитывая этот факт, будем показывать на графе вероятности переходов
лишь между разными состояниями, а переходы из любого состояния в
это же состояние вообще не будем изображать на графе. В результате
изображение графа заметно упростится (см. рис. 4 в таблице 4). Вероят-
Вероятности не показанных на графе переходов St —> St легко вычисляются с
помощью соотношения B) (например, Рп = 1- (Р12 + Р13 + Р\^)-
До того, как начались выстрелы, система (цель) находилась в состоя-
состоянии Sx. После первого выстрела (после первого шага) вероятности со-
состояний системы определяются из первой строки матрицы (*):
Pl A) = 0,1, р2 A) = 0,4, р3 A) = 0,3, р4 A) = 0,2	(**)
Таким образом, после первого выстрела вероятность полного пора-
поражения цели составляет всего лишь 0,2.
Поставим вопрос: сколько надо сделать выстрелов, чтобы вероятность
полного поражения цели оказалась не менее 3/4?
Делаем второй шаг (второй выстрел). Используя C), а также (*) и
(**), находим:
PlB) =pl(l)Pn
= 0,10,1+0 + 0 + 0 = 0,01;
P2B)=pl(l)Pu+p2(l)P22+p3(l)P32+p4(l)P42 =
= 0,1 ¦ 0,4 + 0,4 ¦ 0,3 + 0 + 0 = 0,16;
РзB) =аA)Лз +ЛA)^23 +ЛA)*$з +ЛA)Лз =
= 0,1 0,3 + 0,4 • 0,4 + 0,3 • 0,4 + 0 = 0,31;
p4B)=pl(l)Pl4+p2(l)P24+p3(l)P34+p4(l)P44 =
= 0,1 ¦ 0,2 + 0,4 • 0,3 + 0,3 ¦ 0,6 + 0,2 = 0,52.
47

Итак, после второго выстрела вероятности четырех возможных состоя-
состояний системы распределяются следующим образом:
рх B) = 0,01, р2 B) = 0,16, р3 B) = 0,31, р4 B) = 0,52. (***)
Мы видим, что вероятность полного поражения цели равна теперь 0,52.
(Хороший способ проверить правильность расчетов — убедиться, что сумма
полученных вероятностей равна 1, как того требует соотношение B)).
Делаем третий шаг (третий выстрел). Используя D), а также (*) и
(***), находим:
ЛC) =р1B)Рп +Р2B)Р21 + Р3B)Р31 + р4B)Р41 =
= 0,01 0,1+ 0 + 0 + 0 = 0,001;
Р2C) =Р1B)Рп + р2B)Р22 + РзB)Р32+р4B)Р42 =
= 0,01 • 0,4 + 0,16 • 0,3 + 0 + 0 = 0,052;
РзC) = PlB)P13 +p2{2)P23 +Рз{2)Р33 +Р4B)Р43 =
= 0,01 • 0,3 + 0,16 • 0,4 + 0,31 • 0,4 + 0 = 0,191;
р4(Ъ) = plB)Pu +Р2B)Р24 +Р3B)Р34 +р4B)Р44 =
= 0,01 • 0,2 + 0,16 • 0,3 + 0,31 • 0,6 + 0,52 = 0,756.
Итак, после третьего выстрела вероятности состояний распределяются
следующим образом:
АC) = 0,001, р2{Ъ) = 0,052, р3C) = 0,191, р4 C) = 0,756. (****)
Мы видим, что вероятность полного поражения цели равна теперь 0,756,
т. е. больше 3/4. Значит, требуется сделать три выстрела, чтобы веро-
вероятность полного поражения цели превысила 3/4?
2.5 Поток событий; интенсивность потока
1 Хрежде чем начать знакомиться с марковскими процессами с непре-
непрерывным временем, познакомимся с понятием «поток событий». Потоком
событий называется последовательность однородных событий, следующих
одно за другим в какие-то случайные моменты времени. Примеры потоков
событий: поток вызовов на АТС, поток заказов такси по телефону, поток
вызовов, поступающих в пункт неотложной медицинской помощи, по-
поток клиентов, посещающих предприятие бытового обслуживания или
магазин, поток неисправностей (сбоев) в работе некоторого устройства,
48

поток восстановлений (окончаний ремонтов) этого устройства, поток
заряженных частиц, регистрируемых счетчиком Гейгера, и т. д.
Предположим, в каком-то таксомоторном парке фиксируют момен-
моменты поступления заказов такси в течение определенного промежутка вре-
времени, например от 12.00 до 14.00. Обозначая эти моменты с помощью
кружочков на оси времени, получили картину, показанную на рис. la в
таблице 5. Это есть одна из реализаций потока заказов такси для рас-
рассматриваемого промежутка времени. Еще три реализации потока собы-
событий показаны на рисунках 16, 1в, 1г; они зафиксированы в другие дни.
Моменты появления событий в каждой реализации потока случайны.
Однако полное число событий на рассматриваемом двухчасовом про-
промежутке времени слабо меняется от одной реализации потока к другой:
числа событий в представленных на рисунках реализациях равны 19,
20, 21, 19. Это говорит о том, что поток событий обнаруживает стати-
статистическую устойчивость.
Наличие статистической устойчивости — веский аргумент в пользу
применения методов теории вероятностей. Но вычислять вероятность
того или иного исхода случайного события в потоке событий, очевид-
очевидно, не имеет смысла. Ведь все события в потоке являются однородными:
они не отличаются друг от друга. Любой заказ такси есть всего лишь
одна из заявок, которая сама по себе ничем не отличается от других
заявок. Тут надо рассматривать иные вероятности — например, вероят-
вероятность того, что на некотором участке времени (скажем на участке от t
до t + x, выделенном на рис. 1) событие наступит столько-то раз. Или
наступит хотя бы один раз. Или вообще не наступит.
Важной характеристикой потока событий является его интенсивность X.
Это есть среднее число событий, приходящееся на единицу времени. Воз-
Возвратимся к примеру, представленному на рис. 1 в таблице 5, и предпо-
предположим, что зафиксированы не четыре реализации потока заказов такси,
а п реализаций (рассмотрены п разных дней), причем п » 1.
Пусть количество заказов, приходящихся на участок времени от t до
t+x, образовали для п дней последовательность тъ тъ ..., тп. Интен-
Интенсивность потока заказов такси X(t) может быть определена с помощью
соотношения:
Здесь принято во внимание, что интенсивность потока зависит от t, т. е.
от того, где именно на протяжении суток выбирается участок времени
длительности т. Вполне очевидно, что, если бы этот участок времени
49

Таблица 5. Пуассоновский поток событий
О	12 3 4 5 6
Х=1мин'1
7	8 мин
Рис.2
50

был выбран не днем между 12.00 и 14.00, а, например, глубокой ночью
где-то между 2.00 и 4.00, то интенсивность потока заказов такси была
бы значительно ниже.
Поток событий называется стационарным, если вероятность появле-
появления того или иного числа событий на участке времени G; t + x) зависит
только от т и не зависит от t (не зависит от того, где именно на оси
времени расположен данный участок протяженностью т). Понятно, что
интенсивность стационарного потока событий не зависит от t; она яв-
является постоянной величиной. Стационарным можно считать, например,
поток сбоев в работе некоторой непрерывно функционирующей техни-
технической системы, в частности, некоторого электронно-вычислительного
комплекса. Поток частиц, регистрируемых счетчиком Гейгера, также
является стационарным. Многие нестационарные потоки событий (в том
числе и поток заказов такси) можно считать стационарными, если рас-
рассматривать их на ограниченном промежутке времени. Именно так, за-
заметим, обстоит дело со многими физическими процессами, которые
принято считать стационарными.
Следует иметь в виду, что стационарность потока событий отнюдь не
предполагает строгой регулярности следования событий. В стационар-
стационарном потоке событий (коль скоро рассматриваются случайные события)
обязательно наблюдаются местные «сгущения» и «разрежения»; они
случайны и не носят закономерного характера. При этом среднее число
событий, происходящих в единицу времени, остается одним и тем же
во всем интервале времени, в пределах которого поток может считаться
стационарным.
2.6 Простейший (пуассоновский) поток событий
дальнейшем мы ограничимся рассмотрением потоков событий,
называемых простейшими (а также пуассоновскими) потоками, поскольку
именно они обусловливают марковские процессы с непрерывным вре-
временем. Простейшим (пуассоноеским) называют поток событий, который
наряду со свойством стационарности обладает еще двумя свойствами —
отсутствием последействия и свойством ординарности.
Отсутствие последействия означает, что вероятность появления того
или иного числа событий на любом участке времени не зависит от того,
появлялись или не появлялись события в моменты времени, предше-
предшествующие началу рассматриваемого участка. Свойство ординарности
51

потока означает, что на любом участке времени, если он достаточно
мал (если Ад; = 1), может появиться не более одного события.
Примем без доказательства (оно приводится во всех систематичес-
систематических курсах по теории вероятностей) следующее утверждение: если по-
поток случайных событий является простейшим и характеризуется интен-
интенсивностью А, то вероятность Рт (т) появления т событий на любом участке
времени длительность определяется формулой Пуассона:
\	F)
Недаром простейший поток событий называют также пуассоновским
потоком.
На рис. 2 в таблице 5 даны графики функций Рт (т) для т = 0, 1, 2, 3, 4,
описывающих для пуассоновского потока с А = 1 мин вероятность по-
появления в интервале т (от т = 0 до т = 8 мин) одного события {т = 1),
двух событий (т = 2), трех событий [т = 3), четырех событий (т = 4), а
также вероятность непоявления события (т = 0). Заметим, что из F)
следует, например, что вероятность появления двух событий меньше
вероятности появления одного события в 4 раза для Ат = 0,5 и в 20 раз
для Ат = 0,1 (эти результаты можно получить, если воспользоваться таб-
таблицей 45 из книги «Случайность, необходимость, вероятность»).
Рассмотрим пуассоновский поток событий с интенсивностью А и про-
произвольно выберем на оси времени весьма малый (элементарный) участок
времени At, в пределах которого в силу ординарности потока практичес-
практически не может появиться более одного события (надо, чтобы выполнялось
неравенство АА^< 1). Найдем вероятность Pi(At) того, что участок време-
времени At не окажется «пустующим», т. е. что на этом участке появится ка-
какое-то событие. Обозначим через Po(At) вероятность того, что на участке
At никакого события не появится. Для ординарного потока:
и значит, P\{At) = 1 - PQ(Af). Используя F), находим отсюда:
Pl(At) = l-e-XAt	(**)
При АА^ < 1 можно приближенно представить:
е~ш -1-АД/,	(***)
после чего соотношение (**) принимает вид:
Рх (At) « АД/.	G)
52

Итак, для простейшего (пуассоновского) потока событий, характеризую-
характеризующегося интенсивностью А,, вероятность Pi(At) появления события на
очень малом (элементарном) участке времени At равна XAt. Этот резуль-
результат пригодится при рассмотрении марковских процессов с непрерыв-
непрерывным временем.
2.7 Непрерывная марковская цепь
и пуассоновский поток событий
Маг
арковские процессы с дискретными состояниями и непрерыв-
непрерывным временем кратко называют непрерывными марковскими цепями. Как
уже отмечалось, чаще всего на практике приходится иметь дело именно
с такими марковскими процессами (а не с процессами с дискретным
временем).
В основе рассмотрения непрерывных марковских цепей лежит про-
простая идея: перескоки системы из одних состояний в другие происходят под
действием соответствующих потоков событий (потоков вызовов, пото-
потоков отказов, потоков восстановлений и т. п.). В некоторый случайный
момент времени появляется событие из соответствующего потока — и
тут же (мгновенно) система совершает скачок из одного состояния в
другое. Непрерывные марковские цепи реализуются под действием про-
простейших (пуассоновских) потоков. Это связано с тем, что пуассоновский
поток характеризуется отсутствием последействия, — вероятность по-
появления события в этом потоке не зависит от «предыстории» процесса.
Понятно, что и вероятность вызванного таким событием перехода сис-
системы в новое состояние не будет зависеть от развития процесса в прош-
прошлом. А это и есть марковский процесс.
В случае марковских цепей с дискретным временем мы рассматривали
вероятности PtJ перехода системы из состояния St в состояние Sj; эти
переходы (перескоки) совершались в фиксированные моменты времени
под действием каких-то актов, происходивших в эти моменты (напом-
(напомним §2.2, 2.3, 2.4). В случае же непрерывных марковских цепей, когда
перескоки St —> Sj совершаются под действием событий, появляющихся в
случайные моменты времени, вероятность перескока системы точно в ка-
какой-то момент t0 равняется нулю (так же, как и вероятность того, что в
этот момент появится событие из соответствующего потока событий).
Напомним, что точно так же равна нулю вероятность любого конкрет-
конкретного значения непрерывной случайной величины. Как уже отмечалось
53

в книге «Случайность, необходимость, вероятность» (см. § 12.11), гово-
говорят не о вероятности Р(х) значения х непрерывной случайной величи-
величины, а о вероятности Р(х\ Ах) значений этой величины, попадающих в
промежуток (х; х + Ах). Предел
Ах
называется плотностью вероятности значения х непрерывной случай-
случайной величины — см. соотношение (*) в упомянутом выше § 12.11.
По аналогии с непрерывными случайными величинами рассматрива-
рассматривают для непрерывных марковских цепей не вероятность перехода из St в Sj
в тот или иной момент времени, а плотность вероятности перехода Xtj (t)
*T-
Здесь Py{t\ At) — вероятность того, что система, находившаяся в момент
tB состоянии Si9 перейдет в состояние Sj за время от t до t + At. Ограничи-
Ограничиваясь рассмотрением стационарных потоков событий, можем считать,
что вероятность Py{t\ At) (а значит, и плотность вероятности Xy(t)) не
меняется с изменением t. Учитывая это, упростим соотношение (8):
,?	(9)
J At^O At
Здесь Pjj(At) — вероятность перехода системы из St в^в течение про-
промежутка времени At, выбираемого произвольно на оси времени. Плот-
Плотность вероятности перехода XtJ является теперь постоянной величиной.
Каков «физический смысл» величины, называемой плотностью ве-
вероятности перехода? Его легко установить, если учесть, что при достаточно
малых At предел в (9) можно приближенно представить как Py(At) /At,
в результате чего соотношение (9) принимает вид:
ХуъР9(А1)/Ы.	A0)
Нам остается сопоставить A0) и G). Напомним: входящая в G) вероят-
вероятность P\{At) есть вероятность того, что на участке времени At появится
событие из соответствующего пуассоновского потока, характеризующе-
характеризующегося интенсивностью X. Если это есть тот самый поток событий, под
действием которого происходит переход системы из состояния St в со-
состояние Sj (т. е. если P\{At) = Py(At)), то соотношения A0) и G) можно
рассматривать как тождественные и, значит, Xtj- = X. Таким образом, плот-
плотность вероятности перехода из St в Sj есть не что иное, как интенсив-
54

ностъ пуассоноеского потока событий, под действием которого происхо-
происходит указанный переход.
Если положить At = 1, то Py(At) следует понимать как вероятность
перехода St -> Sj9 отнесенную к единице времени. При этом соотноше-
соотношение A0) принимает вид: Ху & Ру (At = 1). Следовательно, интенсивность
пуассоновского потока X можно рассматривать в равной мере и как
плотность вероятности перехода St —> Sp и как отнесенную к единице
времени вероятность этого перехода.
На рисунках 1-6 в таблице 3 были приведены графы нескольких мар-
марковских процессов с непрерывным временем. На рисунках 1-6 в табли-
таблице 6 приведены размеченные графы тех же процессов; здесь вблизи каж-
каждой стрелки указана интенсивность потока событий, под действием
которого происходит данный переход (интенсивность потока событий,
переводящего систему по данной стрелке).
На рисунках 1-4 в таблице 6:
Х1 — интенсивность потока отказов первого узла,
Х2 — интенсивность потока отказов второго узла,
jlxx — интенсивность потока окончаний ремонта первого узла,
\i2 — интенсивность потока окончаний ремонта второго узла.
На рисунке 5 в таблице 6:
Х{иХ2 — то же, что и на рисунках 1-4,
jLt — интенсивность потока восстановлений функционирования обоих узлов.
На рисунке 6 в таблице 6:
Х{ — интенсивность потока выходов из строя нашего устройства,
Х2 — интенсивность потока событий, представляющих собой квалифицирован-
квалифицированный осмотр устройства и ремонт на месте,
jljlx — интенсивность потока окончаний ремонта на месте, завершившихся вос-
восстановлением функционирования устройства,
Х2 — интенсивность потока событий, представляющих собой серьезный ремонт,
jll2 — интенсивность потока окончаний серьезного ремонта.
Примечания.
1.	Мы говорим о том, что переход системы из состояния St в состоя-
состояние Sj происходит под действием соответствующего потока событий.
На самом деле подразумеваем действие всего лишь одного события из
данного потока. Имеется в виду событие, которое появилось в потоке
первым после того, как система оказалась в состоянии St.
2.	Очевидно, что не имеет смысла рассматривать плотность вероят-
вероятности перехода из какого-либо состояния в то же самое состояние, по-
поскольку не может быть потоков событий, которые бы обусловливали
подобные переходы.
55

Таблица 6. Размеченные графы непрерывных цепей Маркова
\/
/
S2
- +
/УХх
s2
- +
х/
У
s2
— +
^2 \,
h
s,
h
s,
s,
I
s4
\x2 v\/y
+s3
Рис.1
+s3
s2
Рис.3
Ал/
s2
Рис.5
s4
s4
s,
s3
^2Ч
\
^4
+ -
Рис.2
1^2
+ -
Рис.4
\
s4
Рис.6
56

2.8 Уравнение Колмогорова
для предельных вероятностей состояний
ели известен размеченный граф непрерывной марковской цепи с
п состояниями, то можно вычислить вероятности p1(t),p2(t),p3(t),...,pn(t),
где pt{t) — вероятность того, что в момент времени t система будет
находиться в состоянии St. Поскольку в любой момент система должна
находиться в каком-то из п состояний, то
Заметим, что соотношение A1) выражает хорошо известное в теории
вероятностей правило: сумма вероятностей событий, образующих пол-
полную группу, равна единице. Кстати говоря, мы уже встречались с этим
правилом, знакомясь с марковскими процессами с дискретным време-
временем; нетрудно убедиться, что равна единице каждая из сумм в (**),
(***), (****) в § 2.4.
Выдающийся российский математик академик Андрей Николаевич Кол-
Колмогоров A903-1987) рассмотрел систему уравнений, позволяющую найти
вероятности Pi(t)9 P2{t), /J3@ v> Pn @ (так называемые уравнения Колмо-
Колмогорова). Эти уравнения являются дифференциальными уравнениями и по-
поэтому не могут быть рассмотрены в данной книге, ориентированной на
читателей, которые пока еще не познакомились с математическим ана-
анализом. Однако мы можем рассмотреть уравнения Колмогорова для пре-
предельной ситуации — когда по прошествии достаточно большого времени
(строго говоря, при ^^оо) устанавливаются постоянные, не зависящие
от времени и, в частности, от начальных условий вероятности состояний
системы. Это есть так называемый стационарный режим, достигнув кото-
которого, система, конечно, продолжает случайным образом менять свои со-
состояния, но при этом вероятности состояний от времени больше не за-
зависят. Теперь это уже не функции от времени Pi(t), /^(О* л@»-» Рп @>
а просто некоторые числа ръ ръ р3,..., рп (а потому уравнения Колмого-
Колмогорова теперь уже не дифференциальные, а алгебраические уравнения). Ве-
Вероятности состояний системы рь ръ ръ,..., рп называют предельными ве-
вероятностями (а также финальными вероятностями).
Предельную (финальную) вероятность pt состояния St можно рас-
рассматривать как среднее относительное время пребывания системы в со-
состоянии S;. Предположим, у системы есть четыре возможных состоя-
состояния F\, S2, S3, S4) и их предельные вероятности равны, соответственно,
57

0,3; 0,4; 0,1; 0,2. Это значит, что при установлении стационарного режи-
режима система в среднем три десятых времени будет находиться в состоянии Sh
четыре десятых времени — в состоянии S2, одну десятую — в состоянии S$,
две десятых — в состоянии S4. Если имеется достаточно большое коли-
количество N одинаковых систем, то произведение Npt можно рассматри-
рассматривать как число систем, находящихся в состоянии St.
Примем без доказательства утверждение, что отличные от нуля пре-
предельные вероятности устанавливаются со временем, если, во-первых,
число состояний системы конечно, и если, во-вторых, из каждого состо-
состояния можно попасть за то или иное число переходов в каждое другое со-
состояние. В случае, представленном на рисунке 1 в таблице 6 второе ус-
условие не выполнено. Так, нельзя попасть в ?\ни из S2, ни из S3, ни
яз S4. В данном случае при ^оо все системы «свалятся», в конечном
счете, в состояние S4n предельные вероятности будут иметь вид:
Pl=P2=P3=Q> P4=l-	(*)
А вот в случае, представленном на рис. 2 в таблице 6, выполнены оба
указанных выше условия. Поэтому представляется интересным полу-
получить в этом случае уравнения Колмогорова для предельных вероятнос-
вероятностей. Прежде всего рассмотрим состояние ?\. Из этого состояния воз-
возможны переходы в состояния ^2 и S3c отнесенными к единице времени
вероятностями А,} и А,2, соответственно. Следовательно, число уходов из
Si в единицу времени в коллективе из N систем равно
Npl(Xl+X2)	(**)
(число систем, находящихся в Sh равно Np{; мы умножаем его на отне-
отнесенную к единице времени суммарную вероятность Х{ + Х2 ухода из со-
состояния Si). Приходы в состояние ?\ совершаются из состояния S2 (с от-
отнесенной к единице времени вероятностью ^) и из состояния S3
(с вероятностью \i2). Число приходов в ?\в единицу времени равно
Np2iii+Np3ii2.	(***)
В стационарном режиме количества уходов и приходов для состояния S{
(как и для любого другого состояния системы) должны быть сбаланси-
сбалансированы. Следовательно, можно приравнять друг другу выражения (**) и
(***). В результате получаем для состояния ?\ уравнение:
(А,! + X2)Pi = VlP2 + V2P3-	(****)
Уравнение (****) демонстрирует общее правило:
Для каждого состояния системы сумма слагаемых, отвечающих выхо-
выходящим из данного состояния стрелкам, равна сумме слагаемых, отвечаю-
58

щих входящим стрелкам; при этом каждое слагаемое равно интенсивнос-
интенсивности потока событий, переводящих систему по данной стрелке, умножен-
умноженной на вероятность того состояния, из которого выходит стрелка.
Применив это правило к каждому из четырех состояний системы,
граф которой представлен на рис. 2 в таблице 6, получим следующую
систему уравнений для ръ ръ ръ, р4:
для состояния ibi :
для состояния S2 :
для состояния S3 :
для состояния S4 :
Нетрудно убедиться, что четвертое уравнение получается сложением
первых трех уравнений. К счастью, у нас есть соотношение A1), кото-
которое в данном случае имеет вид:
Р\+Р2+Ръ+Ра= 1-
Заменив четвертое уравнение в (****) соотношением A1), мы получим
систему уравнений Колмогорова:
A2)
(X2+\il)p2 =
Р1+Р2+РЗ+Р4 =1.
Читатель может без труда получить систему уравнений Колмогорова
для случая, который представлен в виде графа состояний на рис. 6 в
таблице 6. Эта система уравнений выглядит так:
Х2р2 =
Р1+Р2+Р3+Р4 =1.
A3)
Сформулированное выше правило в сочетании с соотношением A1)
позволяет без труда получить результат (*) для случая, представленного на
рис. 1 в таблице 6. В этом случае уравнения Колмогорова имеют вид:
=0;
Р1+Р2+РЗ+Р4 =1.
59

Из первого уравнения сразу видно, что рх = 0 и, следовательно, р2 = 0
ир3 = 0. Используя четвертое уравнение, заключаем отсюда, что р4=1.
Интересен случай, представленный на рис. 3 в таблице 6. Уравнения
Колмогорова имеют в данном случае вид:
(X2+\i1)p2 =
Р1+Р2+Р3+Р4 =1.
Решая эту систему уравнений, находим:
Pi =Pi = 0; Ръ = Hi / (h + Hi); P4 = h/ (h + Hi)-
Мы видим, что, войдя в стационарный режим, система «сосредота-
«сосредотачивается» лишь на состояниях S3n S4. В состоянии ?3она проводит
l^i / (^i + M^i)0 часть времени, а в состоянии S4 —Х{ / (к{ + ц^-ю часть.
Что же касается состояний 6\ и S2, то вероятность обнаружить систему
в этих состояниях равна нулю.
2.9 Какую рационализацию следует выбрать?
1 Хроанализируем конкретную ситуацию, используя уравнения A2)
(см. рис. 2 в таблице 6). Будем полагать, что каждый из двух узлов сис-
системы производит независимо друг от друга некоторую продукцию. Пред-
Предположим, что второй узел является более современным и имеет произ-
производительность вдвое более высокую, чем первый узел. Первый узел
приносит в единицу времени доход, равный, скажем, 5 условно выб-
выбранным единицам, а второй — 10 единицам. К сожалению, отказы вто-
второго узла происходят в среднем вдвое чаще, чем первого; положим А,} = 1,
Х2 = 2. Интенсивности потоков окончаний ремонтов узлов примем рав-
равными |и1 = 2 и ц2 = 3. Используя заданные интенсивности потоков отка-
отказов и окончаний ремонтов, перепишем A2) в виде:
Ърх =2р2+3р3;
Аръ =2pi +2p4;
Pi +Р2+Рз+Ра=1-
Решая эту систему уравнений, находим: р1 = 0,4, р2 = 0,2, ръ = 0,27,
^4 = 0,13. Получается, что в среднем 40% времени оба узла работают
одновременно (система находится в состоянии Sx), 20% времени ра-
60

ботает первый узел, а второй ремонтируется (состояние S2), 27% време-
времени работает второй узел, а первый ремонтируется (состояние S$), 13%
времени оба узла ремонтируются (состояние S4). Нетрудно подсчитать
доход, который дает наша система в единицу времени:
E + 10) • 0,4 + 5 • 0,2 + 10 • 0,27 = 9,7 единиц.
Допустим, что предлагается некоторая рационализация, позволяющая
вдвое сократить время ремонта либо первого, либо второго узла. По ряду
причин мы можем применить рационализацию лишь к одному из узлов.
Спрашивается, какой узел следует выбрать — первый или второй? Перед
нами конкретный пример практической ситуации, когда, пользуясь тео-
теорией вероятностей, надо научно обосновать принятие решения.
Предположим, мы выбрали первый узел. В результате рационализа-
рационализации интенсивность потока окончаний этого узла увеличивается вдвое,
так что теперь |и1 = 4 (остальные интенсивности остаются прежними:
А,} = 1, А,2 = 2, \i2 = 3). Уравнения A2) принимают теперь вид:
= 4р2+ Ъръ;
(**)
4ръ =2а+4/?4;
Р1+Р2+Р3+Р4 =1-
Решая эту систему, находим: а = 0?48; р2 = 0,12; ръ = 0,32; р4 = 0,08. С
учетом полученных предельных вероятностей определяем доход, кото-
который теперь будет давать наша система:
E + 10) • 0,48 + 5 • 0,12 + 10 • 0,32 = 11 единиц.
Если мы выберем не первый, а второй узел, то в результате рациона-
рационализации удвоится интенсивность потока окончаний ремонтов второго
узла — теперь \i2 = 6 (остальные интенсивности: А,} = 1, А,2 = 2, jll1 = 2).
Уравнения A2) принимают теперь вид:
= 4р2+ 6р3;
(***)
7/?з = 2 а + 2/?4?
Р1+Р2+Р3+Р4 =1.
Решая эту систему, находим: а = 0,5; р2 = 0,25; ръ = 0,17; р4 = 0,08. Под-
Подсчитываем доход:
E + 10) • 0,5 + 5 • 0,25 + 10 • 0,17= 10,45 единиц.
Мы видим, таким образом, что выгоднее применить рационализацию к
первому узлу.
61

ЗАДАНИЯ ПО ТЕМЕ 2
1.	Что представляют собой четыре состояния на графе, изображенном на рис. 4 в
таблице 3?
2.	Подсчитайте, чему будут равны после шестого шага вероятности состояний S±
hS2b системе, рассматривавшейся в §2.3. Предполагается, что перед первым
шагом система находилась в состоянии S±.
Ответы: р±F) = 0,58336, р2F) = 0,41664.
3.	Убедитесь, что, если система, рассматривавшаяся в § 2.3, находилась перед пер-
первым шагом в состоянии S2, то после пятого шага вероятности состояний S±
и S2будут равны, соответственно, 0,5835 и 0,4165.
4.	Сколько надо сделать выстрелов, чтобы вероятность полного поражения цели в
задаче из § 2.4 оказалась более 0,9?
Ответ: Не менее пяти выстрелов (р4D) = 0,8864, р4E) = 0,9497)
5.	Воспользовавшись соотношением F) определите значение Хх, при котором ве-
вероятность появления одного события на промежутке х точно равна вероятности
непоявления ни одного события на данном промежутке времени (рассматривает-
(рассматривается пуассоновский поток событий с интенсивностью X).
Ответ: Хх = 1.
6.	Такой же вопрос, но при условии, что вероятность появления одного события на
промежутке х равна вероятности появления на этом промежутке двух событий.
Ответ: Хх = 2.
7.	Такой же вопрос, но при условии, что вероятность появления на промежутке х
двух событий равна вероятности непоявления на этом промежутке ни одного со-
события.
Ответ: Хх = V2.
8.	Такой же вопрос, но при условии, что вероятность появления на промежутке х
двух событий в 100 раз меньше вероятности появления на этом промежутке од-
одного события.
Ответ: Хх =1/50.
9.	Подсчитайте предельные вероятности состояний S±, S2, S3, S4b случае, пред-
представленном на рис. 6 в таблице 6, полагая, что интенсивности потоков событий
имеют значения: Х± = 2, Х2 = 1, X3 = l, [i± = 3, jlx = 2.
Ответы: р± = 4 / 15, р2 = 8 / 15, Р3 = 2/ 15, Р4 = 1/15.
10.	Чему равны предельные вероятности состояний Slf S2, S3, S4b случае, представ-
представленном на рис. 4 в таблице 6?
Ответы: р± = р3 = 0, р2 = \i2 / (Х2 + |и2), р4 = Х2 / (Х2 + д2)
11.	Подсчитайте предельные вероятности состояний Slf S2, S3, S4b случае, пред-
представленном на рис. 5 в таблице 6, полагая, что Х± = 2, Х2 = 3, [i = 4.
Ответы: р± = 12 / 53, р2 = 8 / 53, р3 = 18/ 53, р4 = 15 / 53.
62

ТЕМА 3
ИССЛЕДОВАНИЕ ОПЕРАЦИЙ:
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
При исследовании операций часто прихо-
приходится сталкиваться с работой своеобразных
систем, называемых системами массового об-
обслуживания. Примеры таких систем: телефон-
телефонные станции, ремонтные мастерские, билетные
кассы, магазины, парикмахерские и т. п. Про-
Процесс работы системы массового обслуживания
представляет собой случайный процесс с дис-
дискретными состояниями и непрерывным вре-
временем. Состояние системы меняется скачком
в моменты появления каких-то событий — или
прихода очередной заявки, или окончания об-
обслуживания, или момента, когда заявка, кото-
которой надоело ждать, покидает очередь...
Е. С. Вентцелъ
Первоначально вопросы, приведшие к воз-
возникновению теории массового обслуживания
(теории очередей), появились в связи с эксп-
эксплуатацией телефонных сетей. Затем оказалось,
63

что подобные же задачи возникают при раци-
рациональной организации торговли, целесообраз-
целесообразной эксплуатации производственного обору-
оборудования, расчете пропускной способности
дорог, мостов, переездов, аэродромов, шлю-
шлюзов, морских портов и т. д.
Б. В. Гнеденко
3.1 Проблемы массового обслуживания
в
1 первой четверти ХХ-го столетия возникло и начало развиваться новое
направление в тории вероятностей, названное по предложению видного рос-
российского математика Александра Яковлевича Хинчина A894-1959) «теорией
массового обслуживания». А.Я. Хинчин не только подарил название ново-
новоявленной теории, но и внес весьма существенный вклад в ее развитие.
А началось все с работ сотрудника Копенгагенской телефонной компа-
компании датского ученого Агнера Эрланга A878-1929), который заинтересовал-
заинтересовался проблемами телефонных станций. В начале века телефонная техника
делала лишь первые шаги. В те годы на телефонных станциях напряженно
трудились телефонистки, которые по мере поступления вызовов должны
были быстро соединять одних абонентов с другими. Первая проблема за-
заключалась в том, что телефонные вызовы поступали в случайные моменты
времени. В течение малого промежутка могло поступить чрезмерно боль-
большое число вызовов и, наоборот, в течение какого-то времени вызовы
могли совсем не поступать. Вторая проблема заключалась в непредска-
непредсказуемости длительности каждого отдельного телефонного разговора. Про-
Продолжительность разговоров являлась случайной величиной. И вот в усло-
условиях такой «двойной случайности» необходимо было принимать решения
по проектированию телефонной системы, определять объем оборудова-
оборудования, количество телефонисток, режим их работы.
С того времени интерес к проблемам массового обслуживания начал
быстро расти. Стремление более эффективно обслуживать большие массы
людей потребовало изучения закономерностей образования очередей.
Очереди в магазинах, поликлиниках, парикмахерских, билетных кас-
кассах, на предприятиях общественного питания и бытового обслужива-
обслуживания — все они оказались в центре внимания теории массового обслужи-
обслуживания и дали ей второе название — теория очередей.
Скоро стало ясно, что задачи, рассматриваемые в данной теории, выхо-
выходят за рамки сферы услуг, имеют более широкую область применения,
предполагающую более широкую трактовку самого термина «обслужива-
64

ние». Возьмем, например, работу крупного морского порта, в который
прибывают суда из разных стран. Все эти суда требуется обслужить —
провести разгрузку, погрузку, ремонт, заправку и т. д. Для этого необходи-
необходимо организовать соответствующим образом работу порта, предусмотреть
оптимальные количества причалов, кранов, автопогрузчиков, рабочих. Все
решения приходится принимать в условиях неопределенности, обуслов-
обусловленных как случайностью времени прихода судов в порт, так и непредска-
непредсказуемости продолжительности обслуживания каждого конкретного судна.
При организации работы промышленного предприятия необходимо
учитывать, что различные его узлы и устройства время от времени вы-
выходят из строя и требуют обслуживания, представляющего собой прове-
проведение соответствующих ремонтных работ. Эта система массового об-
обслуживания также имеет дело с «двойной случайностью» — случайностью
моментов выхода из строя того или иного узла (устройства) и случайно-
случайностью моментов окончания ремонтных работ.
С теорией массового обслуживания мы встречаемся и тогда, когда
рассматриваем работу счетчика Гейгера. Он применяется в ядерной
физике для счета заряженных частиц. Когда частица попадает внутрь
счетчика Гейгера, там возникает разряд, по которому и фиксируется
появление частиц. Пока происходит разряд, новая частица не может
быть зарегистрирована (не может быть «обслужена») данным счетчи-
счетчиком. Случайны моменты появления частицы в счетчике, случайные
колебания испытывает длительность разряда (время «обслуживания»).
Налицо ситуация, характерная для систем массового обслуживания.
Итак, большие массы людей, массы судов в порту, массы техничес-
технических устройств, массы частиц — все они должны быть обслужены (в том
или ином смысле). Во всех подобных примерах случайны моменты нача-
начала обслуживания и случайны моменты окончания обслуживания. Этим
обуславливается случайный характер процессов, происходящих во всех
системах массового обслуживания. Во многих случаях эти процессы
можно представлять в виде марковских случайных процессов с дискрет-
дискретными состояниями и непрерывным временем.
3.2 Основные понятия, используемые
в теории массового обслуживания
G
>истема массового обслуживания (СМО) имеет одну или несколько
обслуживающих единиц — так называемых каналов обслуживания. Когда
вы, приходя в парикмахерскую, интересуетесь количеством работающих
65

мастеров, вы тем самым выясняете, чему равно в данном случае число
каналов обслуживания. В других ситуациях число каналов обслужива-
обслуживания есть число телефонов на переговорном пункте, число кассиров в
билетной кассе, число колонок на автозаправочной станции, число при-
причалов в порту и т. п. Приходя в поликлинику к определенному врачу,
мы имеем дело с одноканальной СМО.
Каждая СМО предназначена для обслуживания потока заявок, кото-
которые поступают в систему в случайные моменты времени. В роли заявки
может выступать появление пассажира в билетной кассе, пациента в
кабинете врача, клиента в парикмахерской, автомобиля на автозапра-
автозаправочной станции, судна в порту, частицы в счетчике Гейгера и т. д. Ин-
Интенсивность потока заявок X есть среднее число заявок, поступающих в
систему в единицу времени.
Важной характеристикой СМО является производительность канала
jll — среднее число заявок, которое может обслужить канал в единицу
времени. Величина ц есть интенсивность потока событий, являющихся
окончаниями обслуживания заявок (короче говоря, интенсивность по-
потока обслуживании). Этот поток рассматривается по отношению к тому
или иному каналу обслуживания.
Введем также величину 7^обсл — среднее время обслуживания каналом
одной заявки.
Поскольку среднее число заявок, обслуживаемых в канале в единицу
времени, есть ц, то ясно, что
^обсл = 1/М-	A)
Переходы СМО из одних дискретных состояний в другие происходят
случайным образом под действием указанных выше двух потоков собы-
событий — потока заявок и потока обслуживании. Будем полагать, что оба
эти потока простейшие (пуассоновские) и поэтому процессы в СМО
можно рассматривать по схеме марковских процессов с дискретными
состояниями и непрерывным временем. Обозначим через Р^аяв(т) ве-
вероятность появления в системе т заявок в промежутке времени т, а
через Р^бсл(т) обозначим вероятность обслуживания в рассматривае-
рассматриваемом канале системы т заявок (вероятность т обслуживания в канале) в
промежутке времени т. Так как потоки заявок и обслуживании про-
простейшие (пуассоновские), то, следовательно,
66

Чтобы судить об эффективности работы СМО, вводятся величины:
А — абсолютная пропускная способность системы (среднее число зая-
заявок, которые система может обслужить в единицу времени); q — отно-
относительная пропускная способность системы (средняя доля поступивших
заявок, которую может обслужить система, или, иными словами, вероят-
вероятность того, что поступившая в систему заявка будет обслужена)', Р0ТК —
вероятность того, что поступившая в систему заявка не будет обслуже-
обслужена (иными словами, это есть средняя доля необслуженных заявок, ко-
которые поступили в систему).
Очевидно, что
А = qX	B)
и что
P0TK=l-q.	C)
Казалось бы, зная ц, можно найти А с помощью простого равенства
А = (jJV, где N — число каналов обслуживания в системе. Так бы оно и
было, если бы каждый канал был занят обслуживанием все время. Од-
Однако обычно часть времени различные каналы «простаивают»; поэтому
нужно в указанном выше равенстве использовать не N, а среднее число
занятых каналов N:
А = \lN.	D)
Будем рассматривать еще две характеристики системы:
Гсист — среднее время пребывания заявки в системе,
f — среднее число заявок, находящихся в системе.
Эти величины связывает друг с другом соотношение (так называемая
формула Литтла):
ТСЖТ=7/Х,	E)
которое мы приводим без доказательства. Среднее время пребывания
заявки в системе равно среднему числу заявок в системе, деленному на
интенсивность потока заявок.
Вычисляя те или иные характеристики различных СМО (например,
q, TV, 7^сист), мы будем рассматривать стационарный (установившийся)
режим и будем использовать предельные вероятности состояний системы.
3.3 Виды систем массового обслуживания
11режде всего отметим, что СМО подразделяются на одноканаль-
ные (N=1) и многоканальные (N> 1). Как те, так и другие бывают
67

двух видов: системы с отказами и системы с очередью (или, иными сло-
словами, системы с ожиданием).
Если заявка поступает в систему с отказами в тот момент, когда все
каналы системы заняты, то она получает «отказ» и покидает систему не
будучи обслуженной. С подобными системами мы все знакомы на при-
примере обычного телефона. Если абонент занят, ваша заявка получает
отказ, и вы можете повесить трубку. Повторно набирая номер абонен-
абонента, вы тем самым посылаете новую заявку.
Более часто на практике встречаются системы с очередью, называе-
называемые также системами с ожиданием. Недаром теорию массового обслу-
обслуживания называют также теорией очередей. В таких системах заявка,
появившаяся в момент, когда все каналы обслуживания заняты, встает
в очередь и ожидает, пока не освободится какой-то из каналов. Суще-
Существуют системы с неограниченной очередью (стоящая в очереди заявка
рано или поздно будет обслужена; при этом число мест в очереди не
ограничено) и системы с ограниченной очередью. Используются также
термины «система с неограниченным ожиданием» и «система с ограни-
ограниченным ожиданием».
Ограничения могут быть разными:
-	по числу заявок, одновременно стоящих в очереди (в очереди долж-
должно быть не более некоторого количества заявок; всякая дополнитель-
дополнительная заявка получает отказ);
-	по времени пребывания заявки в очереди (после некоторого срока
пребывания в очереди заявка, если она не начала обслуживаться, поки-
покидает систему);
-	по времени работы системы (прием заявок к обслуживанию проис-
происходит в течение определенного времени, по истечении которого все заяв-
заявки в очереди, которые не начали обслуживаться, покидают систему).
Может учитываться также дисциплина обслуживания. Обычно заяв-
заявки обслуживаются в порядке их поступления в систему (раньше при-
пришла — раньше обслуживается). Возможно также обслуживание в слу-
случайном порядке. Нередко встречается так называемое обслуживание с
приоритетом — когда некоторые заявки обслуживаются вне очереди.
При этом заявка с более высоким приоритетом, поступив в систему,
может оборвать уже начавшееся обслуживание заявки с меньшим прио-
приоритетом, но может дождаться окончания предыдущего обслуживания.
В первом случае говорят об абсолютном приоритете, а во втором — об
относительном.
Заметим, что для СМО с неограниченной очередью несущественны
как абсолютная, так и относительная пропускная способность системы.
68

Ведь каждая поступившая заявка будет обслужена рано или поздно.
Зато для таких СМО весьма важными характеристиками являются:
г — среднее число заявок в очереди и
Тож — среднее время ожидания заявки в очереди.
Очевидно, что
г=ХТ0Ж.	F)
Теперь среднее время пребывания заявки в системе G"сист) складывает-
складывается из среднего времени ожидания в очереди (Тож) и среднего времени
обслуживания (То6сл), умноженного на вероятность обслуживания, т. е.
на относительную пропускную способность системы (q):
** сист ^ ож ~г ^ обсл ' О.%	\' )
Среднее число заявок в системе (f) складывается теперь из среднего
числа заявок в очереди (г) и среднего числа заявок, находящихся под
обслуживанием, т. е. среднего числа занятых каналов
f=r+N.	(8)
Для СМО с ограниченной очередью представляют интерес обе груп-
группы характеристик: как характеристики ожидания, так и абсолютная и
относительная пропускная способности системы.
Системы массового обслуживания всегда являются многокритериаль-
многокритериальными. Они характеризуются набором показателей эффективности. В ка-
качестве таковых могут выступать:
-	среднее число заявок, которое может обслужить система в единицу
времени,
-	среднее число занятых каналов обслуживания,
-	среднее число заявок, находящихся в очереди,
-	среднее время ожидания заявки в очереди,
-	средняя доля необслуженных заявок из тех заявок, которые посту-
поступили в систему,
-	вероятность того, что поступившая в систему заявка начнет немед-
немедленно обслуживаться.
Возможны также другие показатели эффективности.
Представляется естественным, что при организации работы той или
иной СМО следует стремиться к сокращению среднего числа заявок,
находящихся в очереди, к сокращению времени ожидания обслужива-
обслуживания. Хотелось бы максимизировать вероятность того, поступившая в сис-
систему заявка начнет немедленно обслуживаться, а долю необслуженных
69

заявок хотелось бы свести к минимуму. Для этого надо повышать про-
производительность системы (уменьшать время обслуживания заявки), ра-
рационализировать режим работы системы, увеличивать число каналов
обслуживания. Однако при увеличении числа каналов неизбежно сни-
снижается такой показатель как среднее число занятых каналов. Это озна-
означает, что возрастает время, в течение которого тот или иной канал не
будет занят обслуживанием, будет простаивать.
Таким образом, возникает необходимость оптимизации работы сис-
системы. Число каналов обслуживания не должно быть чрезмерно малым
(чтобы не возникали длинные очереди и не возрастало число необслу-
женных заявок), но оно не должно быть слишком большим (чтобы не
возрастали число и длительность простоев в каналах обслуживания).
Отметим, что оптимизация работы СМО может производиться как с
точки зрения интересов владельцев (организаторов) СМО, так и с точ-
точки зрения интересов обслуживаемых клиентов. С первой точки зрения
желательно «выжать все, что возможно» из системы и добиться, чтобы
ее каналы были предельно загружены. С точки зрения клиентов жела-
желательно уменьшение очередей. Разумный подход к оптимизации СМО
предполагает комплексное и по возможности полное рассмотрение всех
последствий каждого решения.
Построение и анализ математической модели позволяет достаточно
разумно (с учетом различных «за» и «против») подойти к проблеме
оптимизации СМО. Поэтому не будем выделять в задачах массового
обслуживания какого-либо одного показателя эффективности, а бу-
будем сразу рассматривать эти задачи как многокритериальные. Для
многих систем массового обслуживания подходит математическая мо-
модель, известная как «схема гибели и размножения». Познакомимся с
ней поближе и получим для нее предельные вероятности состояний
системы в общем виде, не интересуясь конкретным содержанием сис-
системы и ее состояний.
3.4 Схема гибели и размножения
ГТепрерывные марковские цепи, моделируемые по схеме гибели и
размножения, могут быть достаточно разнообразными в отношении со-
содержания. Не вникая пока в конкретное содержание процессов, рас-
рассмотрим схему гибели и размножения в общем виде, представив ее гра-
графом состояний, показанным в таблице 7.
70

Таблица 7. Схема гибели и размножения
So
A
s,
s2
s,
10
4 A*j9 /_iA/_i? /_2 ... A32A21A10 °
l34 •• -^n-2,n-l^n-l,n
A2)
A3)
| ^01^12 ¦ ^01^12^23 |	| ^01^12 •••^п-1,п
71

Особенность графа состояний для схемы гибели и размножения в
том, что состояния (пусть их число равно п + 1) можно представить в
виде цепочки (S$- S±- S2- S3-...- Sn), в которой каждое из состояний
Sh S2, S3, S4,...9 Sn_{связано парой входных и парой выходных стрелок с
левым и правым соседями — состояниями, ближайшими к данному со-
состоянию. Так, из состояния 6\ выходят стрелки к состояниям S$n S2
(интенсивности потоков — А,1Ои Хи соответственно) и входят в состоя-
состояние 6\ стрелки из состояний Son S2 (интенсивности потоков — А,01
и Х21 соответственно). Что касается двух крайних состояний (Son Sn)9 то
каждое из них связано входной и выходной стрелками только с одним
из соседей (или левым, или правым).
Термин «схема гибели и размножения» имеет биологическое про-
происхождение — подобной схемой моделируют процессы, связанные
с изменениями численности популяции. Если под St понимать со-
состояние, в котором численность популяции равна /, то переход
?,•—> *У/+1 означает возрастание популяции на единицу (процесс раз-
размножение), а переход St^ St_{ означает уменьшение популяции на
единицу (процесс гибели).
Будем исходить из размеченного графа состояний, данного в табли-
таблице 7, и воспользуемся правилом, сформулированным в § 2.8. Рассмот-
Рассмотрев п состояний (SQ, Sh S2,..., Sn_{), получим следующие п уравнений
для п + 1 предельных вероятностей /?0, ръ р^~^ Рп:
(рассматриваем
состояние^)
(состояние Sx) Хпрх + Xi0Pi = Х01р0 + Х21р2;
(состояние S2) ^2±р2 +
(состояние S3) X34p3 + Х32р3 = Х23р2 + Х43р4;	[ (9)
(состояние St) kii+lpt + XUi_iPi = h-uPi-i + h+vPi+ъ
(сОСТОЯНИе 5J K-l,nPn-l+K-l9n-2Pn-l = ^n-2,n-\Pn-2+^n,n-lPn-
В качестве (л+1)-го уравнения воспользуемся соотношением A1)
из §2.8:
Р0+Р1+Р2+Р3+ - + />/!=!•	(Ю)
72

Легко видеть, что с учетом первого уравнения второе уравнение в (9)
приводится к виду:
С учетом (*) третье уравнение из (9) приводится к виду:
(**)
С учетом (**) четвертое уравнение из (9) приводится к виду:
И так далее.
Последнее уравнение из (9) приводится к виду:
В результате получаем следующую систему п уравнений для предельных
вероятностей р0, ръ р2,..., рп\
= Х54р5;
A1)
Эту систему уравнений надо дополнить (п + 1)-м уравнением — уравне-
уравнением A0).
Рассматривая последовательно (начиная с 1-го и кончая п-м) уравне-
уравнения A1), мы можем выразить каждую из вероятностей^ (/= 1, 2, 3,..., п)
через вероятность р0 — см. своеобразную «пирамиду» равенств в табли-
таблице 7 (соотношения A2)). А чтобы найти р0, надо воспользоваться соот-
соотношением A0) — в результате получаем для /?0 соотношение A3) (оно
также приведено в таблице 7).
Соотношения A2) и A3), полученные при использовании графа со-
состояний для схемы гибели и размножения, будут использованы ниже —
при рассмотрении некоторых задач теории массового обслуживания.
73

3.5 Простейшая СМО — одноканальная система
с отказами
ХЭудем рассматривать данную СМО как систему, которая может на-
находиться в двух состояниях:
50	— канал обслуживания свободен, система готова к обслуживанию,
51	— канал обслуживания занят, система обслуживает заявку.
Переход So -> S{ происходит под действием потока заявок, характе-
характеризующегося интенсивностью X. Переход ?\ -> ^0 происходит под дей-
действием потока обслуживании с интенсивностью ц.
Граф состояний данной СМО может рассматриваться как частный
случай графа, данного в таблице 7. Нужно оставить на том графе только
состояния So и Si и две стрелки — для перехода So -> S{ (теперь А,01 есть
интенсивность X потока заявок) и для перехода Si —> So (теперь А,10 есть
интенсивность ц потока обслуживании). В результате получим очень
простой граф состояний — см. рис. 1 в таблице 8. Соотношениям A3) и
A2) отвечают теперь соотношения:
1
Ро =т
А = — Ро =
A4)
Предельная вероятность р0 состояния ^0 есть вероятность того, что по
установлении стационарного режима (при t —> оо) наша система будет
находиться в состоянии ^0 и поступившая в систему заявка будет обслу-
обслуживаться. Иными словами, это есть не что иное, как относительная
пропускная способность системы q. Итак, для рассматриваемой одно-
канальной СМО с отказами можем записать:
д = ро=11/(Х + [1).	A5)
С учетом B) получаем отсюда абсолютную пропускную способность
нашей системы:
А = qX =
Вероятность отказа:
Предположим, что в некотором поселке есть единственная теле-
телефонная линия, характеризующаяся интенсивностью потока вызовов
74

Таблица 8. Системы массового обслуживания с отказами
Одноканальная СМО с отказами
S»
	>
-^
Si
So "" канал обслуживания свободен,
S^ ~ канал обслуживания занят, система
обслуживает заявку.
Рис.1
Многоканальная СМО с отказами
(система имеет N каналов обслуживания)
А 	 А 	 А	А
So
s,
s2
s3
Ц	Z[i	3[i	4|Ll	N|Ll
Sq ~~ все N каналов свободны,
Оi — занят один канал (под обслуживанием одна заявка),
52	~~ заняты два канала (под обслуживанием две заявки),
53	~ заняты три канала (под обслуживанием три заявки),
Sfl — заняты все N каналов (под обслуживанием N заявок).
Интенсивность потока обслуживании для каждого канала — |Ы
Если заняты (находятся в работе) / каналов, то интенсивность
потока обслуживании системы — i\x
Рис.2
75

X = 0,8 мин !. Учитывая, что линия единственная, власти ввели ограни-
ограничение — длительность телефонного разговора не должна превышать
одной минуты. Благодаря этому ограничению среднее время обслужи-
обслуживания заявки To6cjl оказалось равным 50 с. Следовательно, интенсив-
интенсивность потока обслуживания равняется ц = 1 / То6сл =1: 5/6=1,2мин.
С учетом A5) заключаем, что
0=1,2 /@,8 + 1,2) = 0,6.
Это означает, что в установившемся режиме система обслуживает око-
около 60% поступающих вызовов, а 40% поступивших заявок получают
отказ.
Для снижения вероятности того, что поступившая в систему заявка
получит отказ, надо или еще больше ограничивать допустимое время
телефонного разговора (уменьшать Гобсл и тем самым увеличивать ц),
или просить пореже пользоваться телефоном (уменьшать X). Если не пред-
предпринимать мер принуждения, то в этом случае надо увеличивать число
каналов обслуживания, т. е. создать несколько телефонных линий.
3.6 Многоканальная СМО с отказами; формулы Эрланга
Рассмотрим TV-канальную систему массового обслуживания с отка-
отказами. Занумеруем возможные состояния системы по числу занятых ка-
каналов, или, иначе говоря, по числу заявок, находящихся под обслужи-
обслуживанием. Состояния рассматриваемой системы:
6*0 — все каналы свободны,
Si — занят один канал (под обслуживанием одна заявка),
$2 — заняты два канала (под обслуживанием две заявки),
?3 — заняты три канала (под обслуживанием три заявки),
SN — заняты все N каналов (под обслуживанием N заявок).
Граф состояний системы представлен на рис. 2 в таблице 8. По стрел-
стрелкам в направлении слева направо систему переводит поток заявок с
интенсивностью X. Этот поток переводит систему из любого левого со-
состояния в соседнее правое. С интенсивностями потоков обслуживании
все обстоит намного сложнее. Пусть система находится в состоянии 6\
(занят один канал). Как только закончится обслуживание заявки, нахо-
находящейся под обслуживанием в этом канале, система перейдет из ^в^.
Предположим, что поток событий, переводящий систему по стрелке
Si -> 6*0 имеет интенсивность ц. Рассмотрим теперь систему в состоянии S2
76

(заняты два канала). Чтобы системе перейти из S2b 6\, нужно, чтобы
либо закончил обслуживание первый канал, либо закончил обслужива-
обслуживание второй канал. Суммарная интенсивность потоков обслуживании
двух каналов равна 2ц; поэтому полный поток событий, переводящий
систему по стрелке S2—>Si, имеет интенсивность 2ц. Понятно, что пол-
полный поток событий, переводящий систему по стрелке S$—>S2, имеет
интенсивность Зц. И вообще: полный поток событий, переводящий
систему по стрелке St —> S^i и имеет интенсивность /ц.
Чтобы найти предельные вероятности р0, ръ ръ Рз,---9 Ры воспользу-
воспользуемся результатами A2) и A3), положив там Xt_i t = X и Xt t_i = i\i для
/= 1, 2, 3,..., N. Мы получим:
Ро =
1
\l) 2!
a/
K
J
1 p //'
1 , ,
3,+- +
TV
? '
1
/V!
-i
A6)
Вводя обозначение X/\i = p, где р — так называемая «приведенная ин-
интенсивность» потока заявок, перепишем A6) в виде:
Pi =P Po
Po =
/=1, 2,
-1
A7)
Соотношение A7) называют формулами Эрланга.
Заявка получает отказ, если приходит в момент, когда все N каналов
заняты. Вероятность этого равна:
= Pn=pnpJn\.
A8)
Отсюда следует, что вероятность принятия заявки к обслуживанию (ины-
(иными словами, относительная пропускная способность q) равна
Абсолютная пропускная способность:
A9)
B0)
Среднее число занятых каналов N найдем, воспользовавшись соотно-
соотношениями D) и B0):
= 9(\-9N Po/N\).	B1)
77

Ранее мы ввели такую характеристику системы как среднее число зая-
заявок, находящихся в системе /. Для многоканальной СМО с отказами:
37 СКОЛЬКО ТРЕБУЕТСЯ КАНАЛОВ ОБСЛУЖИВАНИЯ?
11редположим, что на станцию телефонного обслуживания поступа-
поступают в среднем 1,5 заявки в минуту, а среднее время обслуживания одной
заявки любым каналом составляет 2 мин. Значит, р = А,/ц=1,5/A/2) = 3.
Пусть число каналов обслуживания (число телефонных линий) равно
N=3. Используя соотношения A7), находим:
р0 =
=1/12 «0,08.
Учитывая этот результат и используя A9), определяем вероятность того,
что поступившая в систему заявка будет обслужена (определяем отно-
относительную пропускную способность системы):
q = \- р3р0/6 « 1 - 27 • 0,08/6 « 0,64.
При этом среднее число занятых каналов равно, с учетом B1):
3.0,64 = 1,92,
что составляет 64% от всего числа каналов.
Итак, вероятность отказа составляет 0,36 (в среднем 36% поступаю-
поступающих в систему заявок к обслуживанию не принимаются). Это многова-
многовато. Поэтому мы принимаем решение увеличивать число каналов обслу-
обслуживания.
Попробуем добавить еще один, четвертый, канал. В этом случае под-
подсчитываем:
]1= 1/15,38 ^0,065
и, значит, q = 1 - р% / 24 « 1 - 81 • 0,065 / 24 « 0,78. При этом число за-
занятых каналов становится равным 7V^2,34, что составляет 59% от все-
всего числа каналов.
По-видимому, решение о добавлении четвертого канала являлось
вполне обоснованным, поскольку при сравнительно небольшом сни-
снижении доли занятых каналов (с 64% до 59%) происходит довольно зна-
значительное увеличение вероятности обслуживания — с 0,64 до 0,78.
78

Дальнейшее увеличение числа каналов может оказаться невыгодным
из-за снижения эффективности использования СМО вследствие про-
простоев в каналах. Здесь необходим более детальный анализ с учетом стои-
стоимости каждого канала.
3.8 ОДНОКАНАЛЬНАЯ СМО С ОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ
простая СМО с ожиданием (с очередью) — это одноканаль-
ная система (N= 1), у которой число мест в очереди ограничено; пусть
оно равно т. Предположим, что в систему поступает поток заявок с
интенсивностью X (т. е. в среднем X заявок в единицу времени.) Интен-
Интенсивность потока обслуживании обозначим через ц (непрерывно заня-
занятый канал обслуживает в среднем ц заявок в единицу времени). Заявка,
поступившая в систему в момент, когда канал занят, становится в оче-
очередь и ожидает обслуживания. Если заявка пришла в момент, когда в
очереди уже стоят т заявок, она покидает систему необслуженной.
Состояние системы будем нумеровать по числу заявок, находящихся
в системе. Граф состояний показан на рис. 1 в таблице 9. Изображен-
Изображенная на рисунке схема есть, как легко видеть, схема гибели и размноже-
размножения, представленная в таблице 7, в которой надо положить:
^ij-\-l = А», кi+ii = \Х [I = U, 1, Z, J,..., J71 +1) .	(*)
Используя A2) и A3), находим, с учетом (*):
I р0 (/=1,2,3,..., /и + 1);
J	B2)
Введя обозначение р = А, / ц, преобразуем B2) к виду:
Pi=9lPo (i =1,2,3,...,т + 1);
B3)
п-1
Р0=\' ' '
Здесь мы учли, что стоящая в квадратных скобках сумма есть геометри-
геометрическая прогрессия с первым членом 1 и знаменателем р.
Заметим, что при р = 1 второе соотношение в B3) принимает осо-
особенно простой вид:
р0 =1/(/и + 2).	(**)
79

Таблица 9. Одноканальные системы массового обслуживания с очередью
Одноканальная СМО с ограниченной очередью
(имеются т мест в очереди)
Очереди нет
~Х N XXX
So
—>
-<—
s,
—>
-<—
s2
—>
-<—
s3
So — канал свободен,
\Ъ\ — канал занят, очереди нет,
52	~~ канал занят, одна заявка стоит в очереди,
53	~~ канал занят, две заявки стоят в очереди,
~ канал занят, т заявок стоят в очереди (все места
в очереди заняты).	рис
Одноканальная СМО с неограниченной очередью
Очереди нет
А 	 А 	 А 	 А	А 	 А
So
—>
-<—
s,
—>
-<—
s2
—>
-<—
s3
S,
—	канал свободен,
—	канал занят, очереди нет,
— канал занят, /-1 заявок стоят в очереди
(/ = 2, 3,4, 5,...).
Стационарный режим устанавливается
при условии X < Ц .
Если X > |Ы, то стационарный режим не
устанавливается и очередь при t^oo растет
неограниченно.	рис ^
80

Очевидно, что поступившая в нашу систему заявка получает отказ
тогда, когда канал занят и при этом заняты также все т мест в очереди,
т. е. когда система находится в состоянии Sm+i. Значит, вероятность
отказа равна
)	B4)
Относительная пропускная способность системы:
а-\-Р -1-РAр)
Интересно найти среднее число г заявок, находящихся в очереди. С
вероятностью р2 в очереди стоит одна заявка. С вероятностью ръ в оче-
очереди стоят две заявки, с вероятностью р4 — три заявки, с вероятностью
pt — / - 1 заявок. Величину г можно определить, подсчитав сумму:
г = ?(/-1)Л.	B6)
С учетом B3) перепишем B6) в виде:
m+l	m+1	m
r=po^2(i-i)pi=pop2^2(i-i)pi-2=pop2j2kPk-1. (***)
/=2	/=2	?=1
(мы ввели по ходу дела обозначение k=i - 1). Без вывода приведем
соотношение:
Используя это соотношение, получаем из (***):
A-Р)
или, с учетом того, что р0 = A - р) / A - рт+2),
81

Среднее время ожидания заявки в очереди Тож равно среднему числу
заявок в очереди г , деленному на интенсивность потока заявок — см. F).
Следовательно,
г p[l + P(mp-m-l)]
°Х *	A)A«+2) •	< ^
Результат B9) можно было бы получить также из следующих рассуж-
рассуждений. Вот в какой-то момент времени в систему поступает заявка. Ве-
Вероятность того, что в этот момент канал будет занят, а все места в
очереди свободны, есть вероятность/^. В этом случае заявка будет ждать
начала обслуживания в течение времени 1 / ц. Вероятность того, что в
момент поступления заявки в систему канал занят и занято одно место
в очереди, есть вероятность р2. В этом случае заявка будет ждать начала
обслуживания в течение времени 2 / ц. Вероятность того, что в момент
поступления заявки в систему канал занят и заняты /- 1 мест в очереди,
есть вероятность pt. В этом случае заявка будет ждать начала обслужи-
обслуживания в течение времени //ц. Нетрудно сообразить, что
^ож =Pl-+P2 -+-+Pi ^+'
Отсюда можно получить результат B9).
3.9 Насколько целесообразно увеличивать
число мест в очереди?
предпринимателей задумали построить на обочине некоторо-
некоторого шоссе автозаправочную станцию. Они оценили, что на данном учас-
участке шоссе следует ожидать поток заявок с интенсивностью X = 1 мин
(в среднем одна машина в минуту будет заворачивать на автозаправоч-
автозаправочную станцию). Длительность обслуживания машины, по оценкам пред-
предпринимателей, будет составлять в среднем 2 мин (ц = 0,5 мин). Для
начала было решено построить станцию с одной заправочной колонкой
и с двумя местами в очереди (заметим, что станция будет находиться на
обочине шоссе, так что для каждого места ожидания нужно заасфаль-
заасфальтировать определенную площадь).
Прежде чем начать строительство, предприниматели подсчитали ве-
вероятность отказа Ротк и время ожидания в очереди Тож. Итак, N= I, m = 2,
82

А, = 1 мин \ ц = 0,5 мин \ р = X/ ц = 2. Используя B4), они получили
Ротк = 8 / 15 = 0,533, а используя B9), получили Тож = 20 / 15 = 1,33 мин.
Вполне справедливо предприниматели рассудили, что вероятность
отказа 0,533 довольно высока и желательно ее снизить. Первый пред-
предприниматель считал, что для этого достаточно увеличить число мест в
очереди, тогда как второй предлагал запланировать строительство еще
одной колонки.
Допустим, что по-прежнему N= 1, но зато теперь т = 3. Исполь-
Используя B4) и B9), находим: Ротк = 16 / 31 = 0,516; Тож = 68 / 31 = 2,2 мин. Мы
видим, что при добавлении одного места в очереди вероятность отказа
в самом деле уменьшилась, однако не очень заметно (была 0,533, стала
0,516). Зато время ожидания Тож возросло более, чем в полтора раза.
Добавим еще одно (четвертое) место в очереди; теперь m = 4. Исполь-
Используя B4) и B9) находим: Ротк= 32/63 = 0,508; Тож= 196/63 = 3,1 мин.
Просматривается тенденция: при увеличении числа мест в очереди вре-
время отказа уменьшается все незначительнее, а вот время ожидания про-
продолжает заметно возрастать. При дальнейшем увеличении m эта тен-
тенденция подтверждается. Расчеты дают такую таблицу:
m
^отк
Тож, мин
2
0,533
1,3
3
0,516
2,2
4
0,508
зд
0,
5
504
4
0,
6
502
5
0
8
,5005
7
В результате было принято предложение второго предпринимателя и
решено было построить еще одну колонку.
ЗЛО ОДНОКАНМЬНАЯ СМО С НЕОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ
1 Хредположим, что в одноканальной СМО число мест в очереди не
ограничено; оно, в принципе, может быть сколь угодно большим
(/и -> оо). Граф состояний такой системы показан на рис. 2 в таблице 9.
До сих пор мы рассматривали системы с конечным числом состояний.
Теперь же мы имеем систему, у которой число дискретных состояний
бесконечно. Возникает вопрос: можно ли говорить о стационарном ре-
режиме (и, значит, о предельных вероятностях состояний) для такой сис-
системы? Оказывается, можно. Но при условии, что р < 1 (т. е. при усло-
условии, что А, < ц). Если это условие выполнено, то входящая в B3) сумма
l + p + p2+p3+... +
83

превращается при m^oo в сумму бесконечной убывающей геометри-
геометрической прогрессии, и мы можем записать:
1 + р + р2 +р3 +... = 1/A-р).	(*)
В результате соотношения B3) преобразуются к виду:
Pi =PiPo (| = 1,2Д...);|
ро=1-р.	J	C1)
Если же условие р < 1 не выполнено, стационарный режим не устанав-
устанавливается; очередь при ^^оо растет неограниченно.
Будем полагать, что р < 1. Переходя в B4) к пределу при т^оо,
получаем:
Итак, Ротк = 0 и, следовательно, q= 1. Этого следовало ожидать, посколь-
поскольку при неограниченном числе мест в очереди отказа никому не будет.
Рассмотрим теперь, чему равно среднее время ожидания заявки в
очереди Тож. Переходя в B9) к пределу при т^оо (и учитывая при
этом, что lim рт = 0), находим:
T°*=W^-y	C2>
Отсюда следует, что среднее число заявок, стоящих в очереди:
г=^ож=р2/A-р).	C3)
Как уже отмечалось (см. G)), среднее время пребывания заявки в СМО
Гсист равно среднему времени ожидания в очереди Тож плюс среднее
время обслуживания 7"обсл, умноженное на q. Для нашей системы q=\;
поэтому с учетом C2) можем записать:
В1	i		C4)
3.11 Какой штраф придется уплатить
за ожидание в очереди?
JL) качестве одноканальной СМО с неограниченной очередью рас-
рассмотрим разгрузочный пункт, к которому время от времени прибывают
84

автомобили с грузом. Если при подъезде к пункту разгрузки автомобиль
обнаруживает очередь ожидающих обслуживания (разгрузки) автомо-
автомобилей, то он становится в конец очереди и начинает ждать, пока будут
последовательно обслужены все стоящие впереди автомобили. А тем
временем позади нашего автомобиля могут появиться новые автомоби-
автомобили, прибывшие для разгрузки. Число мест в очереди не ограничено;
рано или поздно каждый автомобиль будет обслужен. Если интенсив-
интенсивность потока заявок X (интенсивность потока прибывающих на пункт
автомобилей) меньше интенсивности потока обслуживании ц и если
оба потока событий являются пуассоновскими, то, как уже отмечалось,
установится стационарный режим, характеризующийся постоянным (не
зависящим от времени) средним временем ожидания автомобиля в оче-
очереди, определяемым соотношением C2).
Разгрузочный пункт обязан уплачивать штраф в размере А рублей за
каждый час ожидания в очереди каждого автомобиля. Если в час к пункту
прибывают в среднем X заявок (автомобилей), то средняя величина штра-
штрафа в час (обозначим ее через М) может быть подсчитана по формуле:
М = ХТ0ЖА руб.	(*)
Предположим, что на наш разгрузочный пункт поступает пуассонов-
ский поток автомобилей с интенсивностью X = 2 ч (в среднем 2 авто-
автомобиля в час) и что разгрузка автомобиля происходит в среднем в тече-
течение времени То6сл= 1/Зч (ц = 3ч), так что р = 2/3. Требуется
подсчитать М.
Если бы поток заявок (автомобилей) был строго регулярным (иначе
говоря, если бы автомобили подъезжали разгружаться по расписанию —
через каждые полчаса) и если бы время разгрузки каждого автомобиля
составляло точно 1/3 часа, то в этом случае очередь автомобилей, оче-
очевидно, не возникала бы и никакого штрафа пункту не начислялось бы.
Однако и поток заявок, и поток обслуживании являются потоками слу-
случайных событий. Поэтому неизбежно существование очередей автомо-
автомобилей, а значит, неизбежен штраф за простой этих автомобилей.
Поскольку потоки событий здесь пуассоновские, то можно говорить
о непрерывной марковской цепи, рассматривать граф состояний, изоб-
изображенный на рис. 2 в таблице 9, и использовать соотношение C2). В
результате находим, что Тож = 2 / 3 ч; поэтому, согласно (*): М = 4 А / 3 руб.
В сутки набегает 32 А руб.
Чтобы снизить размер штрафа за простой автомобилей, стоящих в
очереди на обслуживание, следует или уменьшить время разгрузки ав-
автомобиля (увеличить ц), или увеличить число каналов обслуживания
(число разгрузочных модулей), или сделать и то, и другое.
85

3.12 Многоканальная СМО с ограниченной очередью
Рассмотрим систему массового обслуживания с ^каналами, у кото-
которой число мест в очереди равно т. В систему поступает поток заявок с
интенсивностью А,; интенсивность потока обслуживании для каждого
канала равна ц. Состояния системы будем нумеровать по числу находя-
находящихся в системе заявок — как тех, что находятся под обслуживанием,
так и тех, что стоят в очереди на обслуживание. Легко сообразить, что
полное число дискретных состояний системы равно N+m+ 1. Граф
состояний системы показан на рис. 1 в таблице 10.
Изображенная на этом рисунке схема есть схема гибели и размноже-
размножения, представленная на таблице 7, в которой следует положить:
X (i = 0,1, 2, 3, 4,..., N + т)\
/> (/ = 0,1, 2, 3,4,..., AT);
(*)
Используя A2) и A3), находим с учетом (*) следующие выражения для
предельных вероятностей р$, plf р2, р^,,---, Pn+w состояний нашей систе-
системы (попутно введем обозначение р = Х/ц):
Р\ =1
pN+l=pN+lp0/(N.Nl);
PN+2=pN+2Po/(N2-N\);
pN+i=pN+2p0/(N'.Nl);
PN+m=pN+mPo/(Nm-Nl).
C5)
P0 =
N
N-
-1
(**)
Сумма в круглых скобках в (**) есть сумма т членов геометрической
прогрессии с первым членом р / N и знаменателем р / N:
N
N1 N'
¦ + ... + ¦
р_ l-(p/N)
N ' 1 - p/N
86
э/N - (p/N)
1 -p/N
т+\
(***)

Таблица 10. Многоканальные системы массового обслуживания с очередью
Многоканальная СМО с ограниченной очередью
(N каналов, т мест в очереди)
Очереди нет
So
S,
л X
Sn+i
2|Ll N|Ll	NjLi	N|Ll	N|Ll N|Ll
!Sq "" все канале свободны,
О i — занят один канал, остальные свободны,
So ~~ заняты два канала, остальные свободны,
~~ заняты N каналов, свободных каналов нет, очереди нет,
r заняты N каналов, одна заявка стоит в очереди,
SN+y заняты N каналов, две заявки стоят в очереди,
~ заняты N каналов, т заявок стоят в очереди (все места
в очереди заняты),	рис
S»
S,
Многоканальная СМО с неограниченной очередью
(N каналов, мест в очереди неограниченно)
Очереди нет
X X
sN
SN+1
Njlx
2]x Njlx
Oq — все каналз свободны,
IS^ ~ занят один канал, остальные свободны,
N|i
~ заняты N каналов, свободных каналов нет, очереди нет,
S ~ заняты N каналов, / заявок стоят в очереди (/= 1,2,3,4,...),
Рис.2
87

Используя (***), перепишем (**) в виде:
Ро =
1 р р
1+Р+4т +-*гт
p/N-(p/N)
m+l
N*.N\
l-p/N
-l
C6)
Поступившая в систему заявка получает отказ в обслуживании тогда,
когда заняты все N каналов и все т мест в очереди, т. е. когда система
находится в состоянии SN+m. Значит, вероятность отказа Р0ТК равна ве-
вероятности pN+m:
C7)
Относительная пропускная способность системы (вероятность того, что
поступившая в систему заявка будет обслужена):
Nm.Nl).
C8)
Абсолютная пропускная способность системы (среднее число заявок,
которое система может обслужить в единицу времени):
А = Xq = X[l - pN+mp0/(Nm -TV!)].
C9)
Среднее число занятых каналов N есть, согласно D), N =A/\i. Под-
Подставляя C9), находим:
= p[l-pN+mp0/(Nm-N\)].
D0)
Среднее время ожидания заявки в очереди Тож найдем, воспользовав-
воспользовавшись суммой C0), в которой, однако, будем рассматривать pt не для
/= 1, 2, 3,..., т, а для i = N, N+ 1, N+ 2, N+ 3,..., N+m- 1, и вместо ц
будем использовать
Т°ж =
(****)
С учетом C5) перепишем (****) в виде:
т _
ож
1 + 2
PNPo m
¦ k=\
N
_Р_
+ 4
k-\
m-\
D1)

Стоящая здесь сумма — это не что иное, как сумма в B7), в которой
вместо р используется р / N. С учетом B7) соотношение D1) принима-
принимает вид:
т	pN Ро 1 + кш(тк — тп — 1)
ож = лу\п A_кJ '
где введено обозначение к = р / N. Наконец, из D2) находим, с учетом F),
среднее число заявок в очереди г :
о 1 + к1" (/як - m -1)
В заключение обратим внимание, что если на рис. 1 в таблице 10 при-
принять N= 1, то мы получим граф с m + 2 состояниями, представленный
на рис. 1в таблице 9. Соотношение (**) из § 13.2 принимает при
N=1 вид:
т. е. мы приходим к соотношению для /?оиз B3). Легко видеть, что при
N= 1 формулы C7) и D2) переходят в B4) и B9), соответственно.
3.13 Пример с выбором научно обоснованного решения
-Оернемся к тем двум предпринимателям из § 3.9, которые собирают-
собираются построить автозаправочную станцию на обочине шоссе. Напомним,
что по предварительным оценкам ожидается интенсивность потока зая-
заявок Х= 1 мин, а длительность обслуживания заявки предполагается в
среднем 2 мин (ц = 0,5 мин), так что р = 2. Наши предприниматели
уже поняли, что для того, чтобы сделать вероятность отказа меньше 0,5,
бесполезно увеличивать число мест в очереди при наличии одной един-
единственной колонки. И вот они решили ограничить очередь тремя места-
местами (т = 3), но предусмотреть не одну, а две колонки (N= 2), т. е. пе-
перейти к двухканальной СМО.
Итак, они рассмотрели СМО с N=2, т = 3,Х=1 мин, р = 2. Прежде
всего подсчитали вероятность р0. При этом нельзя было воспользовать-
p/N-{p/N)m+l
ся соотношением C6), потому что при p/^V= 1 дробь 	. _ ,„
89

дает неопределенность вида -~ . Поэтому воспользовались исходным со-
соотношением (**) из §3.12, которое для рассматриваемой СМО выгля-
выглядело так:
Ро =
(*)
Подставляя в (*) р = 2, получили р0 = 0,091.
Затем с помощью C7) подсчитали вероятность отказа в обслужива-
обслуживании; нашли, что Ротк = 0,182. С помощью D0) определили среднее чис-
число занятых каналов: 7V=1,64. Отсюда следовало, что каждый канал
обслуживания (каждая колонка) будет работать 82% времени (ведь
1,64 : 2 = 0,82), а простаивать будет всего лишь 18% времени. Наконец,
было подсчитано среднее время ожидания в очереди Тож по форму-
формуле D1); оказалось, что Тож= 1,1 мин. Таким образом, результаты полу-
получились совсем неплохими. (Напомним, что при N= I, m = 3 было под-
подсчитано: Ротк = 0,516и Гож = 2,2мин).
Второй из предпринимателей предложил снова увеличить число ка-
каналов обслуживания, не меняя при этом числа мест в очереди. Иначе
говоря, он предложил рассмотреть СМО с N= 3, m = 3, А,= 1мин~1,
р = 2. Для такой системы подсчет привел к результатам:
ротк = 0,094, N/N = 0,6, Тож = 0,8 мин.
Как мы видим, и Ротк, и Тож существенно сократились, что, конечно,
хорошо. Однако при этом существенно (более, чем в два раза) возросло
среднее время простаивания каждого канала — оно стало составлять
40% (вместо прежних 18%). А это, разумеется, нежелательно. Какой
смысл тратиться на сооружение третьей колонки, если при этом каналы
обслуживания будут простаивать 40% времени?
Первому из предпринимателей пришла в голову мысль оставить два
канала обслуживания, но увеличить не единицу число мест в очереди,
т. е. рассмотреть СМО с N= 2, m = 4, X = 1 мин, р = 2. Расчеты для
такой СМО дали результаты:
Ротк = 0,154, N/N = 0,85, Тож = 1,54 мин.
Эти результаты очень хорошие. Колонки теперь простаивают всего лишь
15% времени. Средняя доля заявок, не принятых к обслуживанию тоже
невелика A5,4). И время ожидания Тож тоже уменьшилось: с 2,2 мин
(при N= 2, m = 3) до 1,54 мин.
90

Именно такую автозаправочную станцию и решили построить наши
предприниматели. Так было выбрано научно обоснованное решение,
принятое в условиях неопределенности — когда и поток заявок, и по-
поток обслуживании представляют собой потоки случайных событий.
3.14 Многоканальная СМО с неограниченной очередью
Х\ак и в §3.10, посмотрим, что будет, если число мест в очереди
станет сколь угодно большим (/и—>оо). Граф состояний системы с N
каналами обслуживания и неограниченной очередью представлен на
рис. 2 в таблице 10. Без доказательства примем, что стационарный ре-
режим устанавливается в такой системе при выполнении условия к < 1
(т. е. при условии p/N< 1). При этом р не обязано быть меньше 1.
Предельные вероятности состояний системы, находящейся в стаци-
стационарном режиме, можно получить из C5) и C6) при переходе к пределу
при т —> оо:
Ро =
1 + р
2! 3!
Р2=^П
P
N\
N+1
Pi = PPo',
PN+i=pN+lPo/(N-N\y,
Pn+2=PN+2Po/(N2-N\);
PN+3=pN+3Po/(N3-Nl);
N\(N-p)
-l
n
D4)
Поскольку каждая заявка рано или поздно будет обслужена, то можем
записать:
Ротк=0; g = l; A = Xq = X; N = A/[i = p.	D5)
Среднее время ожидания в очереди Тож найдем из D2) при m —> оо:
T —
± 0Ж ~~
Среднее число заявок в очереди г :
г =
N -NKI-kY
91
D6)
D7)

3.15 Две одноканальных системы или одна двухканальная?
Оернемся к разгрузочному пункту, о котором мы говорили в § 3.11.
Предположим, что на этот пункт прибывают автомобили из двух райо-
районов — района А и района Д причем в среднем прибывают в час два
автомобиля из района А и два автомобиля из района В. Район А решил
построить в разгрузочном пункте еще один канал обслуживания (вто-
(второй разгрузочный модуль), но при этом выдвинул условие, чтобы этот
второй канал обслуживал исключительно автомобили из района А. При
таком условии мы имели бы дело с двумя одноканальными СМО с
неограниченной очередью, для каждой из которых А, = 2ч~1, |и = 3ч,
р = 2 / 3. Используя соотношение C2), получаем, что в этом случае вре-
время ожидания в очереди Тож = 2 / 3 = 0,67 ч. Отсюда следует, что среднее
число стоящих в очереди автомобилей г =4/3=1,33.
Однако специалист в области исследования операций посоветовал так
не делать, а создать одну двухканальную систему с неограниченной оче-
очередью. Это означало, что по прибытии к разгрузочному пункту все авто-
автомобили (как из района А, так и из района В) выстраиваются в общую
очередь и очередной автомобиль ставится на обслуживание в том из ка-
каналов, который раньше освободится. В этом случае СМО с неограничен-
неограниченной очередью имеет характеристики: N= 2, А, = 4 ч, ц = 3 ч, р = 4 / 3,
к=рIN=2/3. Поскольку к< 1, то можно говорить об установлении
стационарного режима и использовать соотношения, полученные в § 3.14.
При N=2 первое соотношение из D4) принимает вид:
р
Ро = " ' ~ ' ¦ '
3
2! 2-B-р)
-1
(*)
Подставляя в (*) р = 4/ 3, получаем/?0 = 0,2. Затем из D6) находим сред-
среднее время ожидания в очереди: Тож = 0,27 ч. Отсюда следует, что
г =\Т0Ж =1,08.
Как видим, при переходе от двух одноканальных систем к одной
двухканальной заметно снижается как среднее время ожидания в оче-
очереди (с 0,67 ч до 0,27 ч), так и среднее число автомобилей в очереди
(с 1,33 до 1,08). Оказывается, специализированное обслуживание (когда
в одном канале обслуживаются автомобили из района А, а в другом — из
района В) менее эффективно по сравнению с неспециализированным об-
обслуживанием. Оно и понятно. Ведь при неспециализированном обслу-
обслуживании освободившийся канал не будет простаивать в ожидании, ког-
когда поступит «подходящая» заявка, а начинает обслуживать любую
поступившую в систему заявку.
92

ЗАДАНИЯ ПО ТЕМЕ 3
1. Докажите равенство A), воспользовавшись соотношением (**) из § 3.2 и учиты-
вая, что
/с=0
Подсказка. Надо найти среднее число т обслуживании в канале, приходящееся
на промежуток времени т, используя соотношение:
5>
2.	Вернитесь к «пирамиде» соотношений в A2) (см. таблицу 7).
Используя систему уравнений (9), убедитесь в правильности соотношений, пред-
представленных в этой «пирамиде». Найдите закономерности в расположении множи-
множителей Ху в числителях и в знаменателях указанных соотношений.
3.	Имеется одноканальная система с отказами; Х = 0,5 мин. Каким должно быть
среднее время обслуживания заявки, чтобы система могла обслуживать не ме-
менее 80% поступающих заявок.
Ответ: Не более 0,5 мин.
4.	В примере с телефонными линиями, рассмотренном в § 3.7, подсчитайте q и
N/N для двух случаев: а) N=5, б) N=6.
Ответы: a) q = 0,88, N/N =53%; q=0,93, б) q = 0,93, N/N =47%.
5.	В ОТК цеха работают три контролера. Если деталь поступает в цех, когда все
контролеры заняты обслуживанием (проверкой) ранее поступивших деталей,
то она проходит непроверенной. Среднее число деталей, поступающих в ОТК в
течение часа, равно 24. Среднее время, затрачиваемое контролером на про-
проверку одной детали, равно 5 мин. Какова вероятность того, что деталь пройдет
ОТК необслуженной? Какую часть времени (в процентах) простаивает каждый
контролер?
Ответы: 0,21; 27%.
6.	Возвращаясь к предыдущей задаче, поставим следующие два вопроса. Сколько
следует иметь контролеров, чтобы вероятность того, что деталь будет обслужена
(проверена) в ОТК, превысила 0,95?
Какую часть времени будет при этом простаивать каждый контролер?
Ответы: Л/=5; 61%.
7.	Выведите соотношение B9), используя C0) и B7).
8.	Автозаправочная станция имеет одну колонку и три места в очереди. В дневное
время интенсивность потока заявок Х = 0,8 мин, а в ночное — Х = 0,4 мин.
Интенсивность потока обслуживании от времени суток не зависит, она равна
jlx = 0,5 мин. Подсчитайте вероятность отказа и среднее время ожидания заяв-
заявки в очереди для дневного и вечернего времени.
Ответы: днем — 0,415, 2,4 мин; ночью — 0,122, 2,15 мин.
93

9. Те же вопросы, что и в предыдущей задаче, но при условии, что теперь среднее
время обслуживания заявки сократилось с 2 минут до 1,5 минут.
Ответы: днем — 0,279, 1,9 мин; ночью — 0,056, 1,3 мин.
10.	Обратимся к примеру, рассмотренному в § 3.11. Желая сократить время ожида-
ожидания автомобиля в очереди, руководитель разгрузочного пункта увеличив количе-
количество рабочих и тем самым вдвое снизил среднее время обслуживания 7"обсл каж-
каждой заявки. Во сколько раз уменьшится средняя величина штрафа, начисляемого
пункту за простой автомобилей в очереди?
Ответ: в 8 раз.
11.	Автозаправочная станция с двумя колонками имеет три места в очереди;
X = 2 мин, jlx = 0,5 мин. Подсчитайте для данной СМО вероятность отказа Ротк,
относительную пропускную способность q, абсолютную пропускную способность А,
среднее число занятых колонок N , среднее число автомобилей в очереди 7,
среднее время ожидания в очереди для каждого автомобиля 7"ож.
Ответы: Ротк = 0,512, q= 0,488, А = 0,976 мин, N =1,95, 7 =2,18, 7;ж =
= 1,09 мин.
12.	Вернемся на автозаправочную станцию, рассмотренную в предыдущей задаче.
На сколько снизится вероятность отказа и на сколько сократится время ожида-
ожидания в очереди, если среднее время обслуживания одной заявки будет сокращено
с 2 минут до 1,5 минут?
Ответы: на 0,13; на 0,18 мин.
13.	Убедитесь, что соотношения C5) и C6) превращаются при в соотношения C1),
а соотношения D6) и D7) — в соотношения C2) и C3), соответственно.
14.	Самостоятельно разберитесь в ситуации, рассматривавшейся в § 3 со случаем,
когда Л/= 2, гп = 5, Х= 1 мин, р = 2.
94

ТЕМА 4
ИССЛЕДОВАНИЕ ОПЕРАЦИЙ:
ИГРА И ПРИНЯТИЕ РЕШЕНИЯ
Игр теория — раздел математики, в кото-
котором изучаются математические модели при-
принятия оптимальных решений в условиях кон-
конфликта... Схемы теории игр охватывают как
собственно игры (шахматы, домино, карты
и т. д.), так и различные ситуации, возника-
возникающие в экономических, военных и других
вопросах.
Большой энциклопедический словарь,
Москва — Санкт-Петербург, 1997.
Теория игр ценна прежде всего самой по-
постановкой задач, которая учит, выбирая ре-
решение в конфликтной ситуации, не забы-
забывать о том, что противник тоже мыслит.
Пусть рекомендации, вытекающие из игро-
игрового подхода, не всегда определённы и не
всегда осуществимы — все же полезно, вы-
выбирая решение, ориентироваться, в числе
других, и на игровую модель.
Е. С. Вентцелъ
95

4.1 Предмет математической теории игр
и основные понятия
Пс
шнятие «игра» часто используется в нашей жизни; оно имеет весьма
широкое толкование. Вспомним: «вся наша жизнь — игра!» Психологи
исследуют игру как специфическую форму деятельности, выделяя раз-
различные ее стороны и виды. В частности, они рассматривают игру как
деятельность, в которой складывается и совершенствуется управление
поведением. Мы еще более сузим предмет рассмотрения, имея в виду
поведение, связанное с принятием решения в тех или иных конфликтных
ситуациях.
«Конфликт» в переводе с латинского означает «столкновение». Сле-
Следует понимать столкновение сторон, мнений, сил. В общем случае под
конфликтной ситуацией понимают любую ситуацию, в которой эффек-
эффективность решения, принимаемого одной из сторон, зависит от действий
другой стороны (других сторон). Различают антагонистические и неан-
неантагонистические {кооперативные) конфликтные ситуации. Конфликт-
Конфликтная ситуация рассматривается как антагонистическая, если увеличение
выигрыша одной из сторон приводит к уменьшению выигрыша другой
стороны (других сторон). В данной книге будут рассматриваться только
антагонистические конфликты.
Подобные конфликты встречаются довольно часто. Они характерны
для военных операций и игровых видов спорта. Каждая из конфликтую-
конфликтующих сторон борется за то, чтобы обеспечить наибольший собственный
успех и воспрепятствовать достижению успеха другой стороне (другим
сторонам). С такими ситуациями мы имеем дело также в сфере экономи-
экономики при наличии рыночных отношений, при проведении предвыборных
кампаний, в арбитражных спорах — везде, где происходит столкновение
противостоящих друг другу интересов.
Участникам антагонистических конфликтных ситуаций приходится
принимать решения с учетом не только состоявшихся, но и возможных
действий со стороны других участников. Так, шахматист, принимая вся-
всякий раз то или иное решение, исходит не только из расположения фигур
на доске в данный момент, но старается предвидеть возможные действия
другого игрока, а также свои возможные ответы на эти действия. Реше-
Решение о проведении той или иной военной операции принимается с учетом
не только сложившейся обстановки, но и возможных ответных действий
противника. Принимая решение об установлении цены товара, продавец
на рынке учитывает не только общую конъюнктуру, но и возможную
реакцию покупателей, а также других продавцов на эту цену.
96

Конфликтные ситуации (как антагонистические, так и неантагонис-
неантагонистические) можно анализировать с привлечением математического ап-
аппарата, в частности, аппарата теории вероятностей. В этом случае мы
приходим к математической теории игр или, короче, к теории игр. Воз-
Возникновение теории игр принято связывать с именами двух американ-
американских ученых — Джона фон Неймана A903-1957) и Оскара Моргенштерна
A902-1977), которые опубликовали в 1944 году монографию «Теория
игр и экономическое поведение». С тех пор и началось бурное развитие
теории игр.
Коротко говоря, теория игр — это математическое моделирование
различных конфликтных ситуаций, анализируемых по определенным, зара-
заранее условленным правилам. Цель теории игр состоит в выработке для
каждого из участников конфликта рекомендаций по рациональному
образу действий. Точнее сказать, теория игр разрабатывает методы обо-
обоснования оптимальных решений в конфликтных ситуациях, обладающих
свойством многократной повторяемости. Обратим внимание на слова
«многократная повторяемость». Дело в том, что сама по себе отдельная
игровая партия (однократная реализация данной игры), как правило,
не позволяет выработать те или иные рекомендации для участников
игры. Эти рекомендации вырабатываются и приобретают практическую
значимость лишь при многократных повторениях игры. Именно поэто-
поэтому теорию игр следует рассматривать как одно из применений теории
вероятностей.
В отличие от реального конфликта игра в теории игр проводится по
определенным правилам, четко определяющим как права и обязанности
участников игры, так и исход игры (выигрыш или проигрыш каждого
участника). Задолго до появления теории игр широко использовались
подобные упрощенные модели конфликтов — игры в буквальном смысле
этого слова (шахматы, шашки, домино, карточные игры, бильярд и т. д.).
Собственно говоря, отсюда и происходят как название самой теории,
так и многие термины, используемые в ней. Так, конфликтующие сто-
стороны называют игроками, одну реализацию игры партией, выбор игро-
игроком того или иного действия (в пределах правил) ходом и т. д. В каче-
качестве игроков могут выступать не только отдельные лица, но также
команды, предприятия, фирмы, воюющие стороны. В зависимости от
числа игроков различают игры парные (два игрока) и множественные
(больше двух игроков). Для простоты, мы ограничимся рассмотрением
парных игр. Точнее говоря, парных антагонистических игр.
Отметим, что парные антагонистические игры относятся к классу
так называемых игр с нулевой суммой. В таких играх сумма выигрышей
97

всех сторон равна нулю. В парной антагонистической игре один игрок
выигрывает ровно столько, сколько проигрывает другой игрок. Игры с
нулевой суммой наиболее разработаны в настоящее время.
Ходы в игре подразделяются на личные и случайные. Личный ход
предполагает сознательный выбор игроком того или иного действия,
разрешенного правилами данной игры. Случайный ход не зависит от
воли игрока — он может быть определен по результату бросания моне-
монеты или игрального кубика, вынимания карты из колоды и т. п. Игры,
состоящие только из случайных ходов, называются азартными. Харак-
Характерный пример — игра в лото. Игры, в которых имеются личные ходы
(в отсутствие или при наличии случайных ходов), называются страте-
стратегическими. Пример стратегической игры, состоящей только из личных
ходов, — шахматы. Пример стратегической игры, состоящей как из лич-
личных, так и из случайных ходов — многие карточные игры (например,
игра в преферанс). Отметим, что в играх с личными и случайными хо-
ходами неопределенность выступает как бы в двух обличьях — в виде
неопределенности результатов случайных ходов и в виде неопределен-
неопределенности поведения противника в его личных ходах.
Сразу подчеркнем: теория игр азартными играми не интересуется.
Она занимается стратегическими играми. Одним из основных понятий
в этой теории является понятие «стратегии».
В играх, где игроки делают всего лишь по одному личному ходу в
каждой конкретной партии (будем называть такие относительно про-
простые игры одноходоеыми), выбор стратегии определяется выбором иг-
игроком того или иного возможного действия. Здесь совокупность стра-
стратегий каждого игрока охватывает все его возможные действия,
предусмотренные правилами данной игры. В более сложных {многохо-
{многоходовых) играх понятия «стратегия игрока» и «вариант возможных дей-
действий игрока» отличаются друг от друга. Понятие стратегия значитель-
значительно шире: оно включает в себя выбор при каждом личном ходе данного
игрока тех или иных действий в зависимости от ситуации, сложившей-
сложившейся к данному ходу в процессе игры. Хороший пример многоходовой
игры — шахматы.
Простоты ради мы ограничимся ниже рассмотрением игр, где каж-
каждый игрок делает только один личный ход и где, следовательно, набор
стратегий игрока есть выбор его возможных личных ходов. При много-
многократном повторении игры игрок в каждой партии выбирает ту или иную
стратегию (делает тот или иной личный ход). В одной партии он может
выбрать одну стратегию, а в другой — другую (возможно, с учетом ис-
исхода предыдущей партии).
98

Игра называется конечной, если набор стратегий конечен как для од-
одного, так и для другого игрока. Если, например, у одного игрока имеет-
имеется т стратегий, а другого п стратегий, то такую игру называют игрой
тхп (или пхт). Если хотя бы у одного из игроков набор стратегий бес-
бесконечен, то игру называют бесконечной.
Казалось бы, что, соглашаясь участвовать в некоторой многоходовой
конечной игре, игрок должен ознакомиться со всем набором как соб-
собственных возможных стратегий, так и возможных стратегий противни-
противника. После этого он мог бы заранее, еще не приступая к игре, выбрать ту
или иную стратегию (в форме: «если противник сделает такой-то ход,
то я поступлю так-то»). Теоретически это возможно для любой конеч-
конечной игры. Практически же это трудно или даже невозможно осуще-
осуществить, если число ходов в игре достаточно велико, что приводит, как
легко догадаться, к сильному возрастанию количества возможных стра-
стратегий. Поэтому на практике выбор при каждом личном ходе принима-
принимается игроком не заранее, а в процессе игры, с учетом изменяющейся
ситуации. Именно так играют, например, шахматисты. Здесь предвари-
предварительный просчет всевозможных стратегий в силу их огромного количе-
количества практически невозможен. Во всяком случае он не под силу челове-
человеческому мозгу. В какой-то степени с этой задачей справляются лишь
ЭВМ, обучающие играть в шахматы.
Как уже отмечалось, цель теории игр — выработка рекомендаций
игрокам для принятия ими оптимальных решений в тех или иных конф-
конфликтных ситуациях. Теперь можно уточнить: речь идет о выработке ре-
рекомендаций для выбора каждым из игроков стратегии, которая являлась
бы для него оптимальной. Какую же стратегию следует считать опти-
оптимальной? Отвечая на этот вопрос, теория игр исходит из двух основных
принципов. Во-первых, каждый игрок должен считать другого игрока
столь же разумным, как и он сам, и не должен рассчитывать не его
промахи. В теории игр не учитываются просчеты и ошибки игроков,
равно как и элементы азарта. Во-вторых, каждый игрок должен быть
достаточно осторожным и должен придерживаться такой линии пове-
поведения, которая независимо от действий противника гарантировала бы
выигрыш не менее какой-то величины (или проигрыш не более какой-
то величины). Это есть т. н. принцип осторожности. Его называют так-
также принципом гарантированного результата и принципом минимакса.
Исходя из указанных принципов, определяется понятие «оптималь-
«оптимальной стратегии». Оптимальной стратегией называется такая страте-
стратегия, которая при многократном повторении игры гарантирует данному
игроку максимально возможный средний выигрыш (или, что то же самое,
99

минимально возможный средний проигрыш) независимо от действий
противника. Если, разумеется, эти действия не выходят за рамки пра-
правил для данной игры.
В теории игр доказывается, что оптимальные стратегии игроков об-
обладают своеобразным свойством «устойчивости». Если один из игроков
придерживается своей оптимальной стратегии, то другому игроку не мо-
может быть выгодно отступать от своей оптимальной стратегии. Основ-
Основная теорема теории игр (примем ее без доказательства), называемая
теоремой о существовании решения игры, утверждает: любая конечная
антагонистическая игра имеет решение, т. е. оптимальные стратегии для
обоих игроков, а также соответствующую цену игры. Поясним: ценой
игры называется выигрыш (проигрыш), соответствующий оптимальным
стратегиям игроков.
Забегая немного вперед, отметим, что решение конечной парной анта-
антагонистической игры лежит в области чистых или смешанных стратегий.
Решение в чистых стратегиях наблюдается в играх с седловой точкой. Если
игра не имеет седловой точки, то существует решение в смешанных стра-
стратегиях. Все эти понятия мы рассмотрим в следующих параграфах.
4.2 Платежная матрица игры, чистые стратегии,
смешанные стратегии
ХЭудем рассматривать антагонистические игры с двумя игроками (иг-
(игроками А и В). Иными словами, будем рассматривать парные игры с
нулевой суммой. Выигрыш одного игрока равен проигрышу другого. Так
как проигрыш игрока В можно представить как выигрыш игрока А, взя-
взятый с обратным знаком, то мы можем интересоваться только выигрышем а
игрока А. Будем отождествлять себя мысленно с игроком А, а игрока В
будем считать нашим «противником». Нам желательно максимизировать
наш выигрыш а, а противнику желательно его минимизировать.
Предположим, что рассматривается игра тхп. Конкретное содержа-
содержание игры пока не имеет значения. У нас (у игрока А) есть т стратегий;
обозначим из через Аъ Аъ А3,...9 Ат. У нашего противника (у игрока В)
есть п стратегий: Въ Въ Въ,..., Вп. Если игра состоит только из личных
ходов, то выбор каждым из игроков той или иной стратегии однознач-
однозначно определяет исход игры, т. е. величину нашего выигрыша. Будем
обозначать через atj наш выигрыш, реализуемый в том случае, если мы
выбрали стратегию Аь а наш противник выбрал стратегию Bj. He будем
100

забывать, что слово «выигрыш» следует понимать здесь расширительно:
проигрыш — это тоже «выигрыш», но взятый со знаком «минус». Если
известны выигрыши а у для всех / от 1 до т и для всех у от 1 до я, то
можно представить игру в матричной форме, т. е. в виде прямоугольной
таблицы (матрицы), изображенной на рис. 1 в таблице 11. Это есть пла-
платежная матрица игры. Ее называют также матрицей выигрышей.
Заметим, что приведение к матричной форме той или иной игры
(особенно если в каждой партии игроки должны сделать не один, а
несколько личных ходов) может представлять весьма трудную или даже
практически невыполнимую задачу из-за огромного количества возмож-
возможных стратегий. Если, тем не менее, удается привести некую многоходо-
многоходовую игру к матричной форме, то тем самым, как нетрудно сообразить,
это многоходовая игра сводится фактически к одноходовой. Ведь те-
теперь от каждого игрока требуется сделать один ход — выбрать ту или
иную стратегию из стратегий, указанных в платежной матрице.
Чтобы поближе познакомиться с платежной матрицей, рассмотрим
три весьма простых одноходоеых игры в качестве конкретных примеров.
Пример 1: игра с монетой. Игроки А и Д не глядя друг на друга,
кладут на стол по монете либо вверх орлом, либо вниз орлом, по своему
усмотрению. Если окажется, что оба игрока положили монету одной и
той же стороной (или обе орлом вверх, или обе орлом вниз), то игрок А
получает от игрока В плату, например один цент. Если же окажется, что
монеты положены разными сторонами, то игрок А выплачивает один
цент игроку В. У нас (т. е. у игрока А) есть две стратегии: А1 — положить
монету орлом вверх, А2 — положить монету орлом вниз. У противника
(у игрока В) тоже есть две стратегии, причем такие же, как у нас: В1 —
положить монету орлом вверх, В2 — положить монету орлом вниз. Зна-
Значит, данная игра есть игра 2x2 и ее платежная матрица имеет элементы:
ап = ^22 = 1 (цент), аи = я21 = ~1 (цент). Эта матрица приведена на рис. 2
в таблице 11.
Пример 2: игра «два пальца». Игроки, не глядя друг на друга, показы-
показывают либо один, либо два пальца. Величина выигрыша или проигрыша
равна в каждой партии общему числу показанных пальцев. Если это
число четное, то соответствующее количество центов игрок А получает
от игрока В. Если это число нечетное, то соответствующее количество
центов игрок А выплачивает игроку В. Стратегия игрока А: А1 — пока-
показать один палец, А2 — показать два пальца. Такие же стратегии у игрока В:
Вх — показать один палец, В2 — показать два пальца. Перед нами игра
2x2. Ее платежная матрица приведена на рис. 3 в таблице 11.
101

Таблица 11. Платежная матрица игры
102

Пример 3: игра «три пальца». Она похожа на предыдущую игру, толь-
только теперь каждый из игроков располагает тремя стратегиями: показать
один палец (стратегии А1я В{), показать два пальца (стратегии А2ж В2),
показать три пальца (стратегии А3я Въ). Это игра 3x3. Ее платежная
матрица приведена на рис. 4 в таблице 11.
Вернемся к самому простому из рассмотренных примеров — к игре с
монетой. Уже этот простой пример дает возможность затронуть некото-
некоторые существенные для теории игр идеи. Прежде всего заметим, что,
если игра выполняется только один раз, то не имеет смысла говорить
каких-то более разумных или менее разумных «стратегиях» игроков. Иное
дело, если игра повторяется много раз. Допустим, мы выбрали страте-
стратегию Аг (класть монету орлом вверх) и придерживаемся ее от одной партии
к другой. Тогда по результатам нескольких партий противник может
догадаться о нашей стратегии и начнет выбирать стратегию В2 (класть
монету орлом вниз). Чтобы по результатам многих партий нам не ока-
оказаться в проигрыше, мы должны менять стратегию — в каких-то партиях
выбирать стратегию ^, ав каких-то — стратегию А2. Если мы будем
чередовать стратегии, придерживаясь какого-то порядка, то рано или
поздно противник это уловит. Поэтому надежнее всего чередовать стра-
стратегии Ах и А2 случайным образом.
Эти нехитрые рассуждения подвели нас к одному из важнейших поня-
понятий теории игр — понятию смешанной стратегии. Такая стратегия пред-
представляет собой случайное чередование с определенными частотами всех или
некоторых стратегий, указанных в платежной матрице игры. В отличие от
смешанных стратегий, стратегии, указанные в платежной матрице, назы-
называют чистыми стратегиями. Как будет показано позднее, именно среди
смешанных стратегий можно найти оптимальное для обоих игроков реше-
решение в игре с монетой (а также в играх «два пальца» и «три пальца»).
Имея в виду в общем случае игру тхп, будем обозначать смешанные
стратегии игрока А следующим образом:
SA=\ 1 2 3'" т или, проще, SA = (рьр2, р3,...,рт), A.А)
\Р\ Pi РЗ'"Рт)
где ph ръ Рз,..., рт — вероятности выбора игроком А соответствующих
чистых стратегий (Аъ Аъ Аъ,..., Ат). Аналогично обозначаются смешан-
смешанные стратегии игрока В:
SB =
В2В3...Ва
или, проще, SB = (qb g2, g3,..., gn), (l.B)
103

где qh q2, ft,.--? Qn ~ вероятности выбора игроком В соответствующих
чистых стратегий {Въ Въ Въ,..., Вп). Очевидно, что
Р1+Р2+Р3+ ••• + Рт = 1; Q\ + Qi + 4з + ••• + 0/1=1-	B)
Заметим, что среди вероятностей ръ р2,..., Рт и 4ъ ?2v> ?л некоторые
могут быть равны нулю. Это означает, что соответствующие чистые стра-
стратегии в создании данных смешанных стратегий не участвуют. Заметим
также, что, например, чистая стратегия А1 может рассматриваться как
смешанная стратегия SA, для которой р1 = 1, р2=р3 = ... =рт = 0.
При очень большом количестве партий вероятность pt практически
равна относительной частоте выбора игроком А стратегии At. Анало-
Аналогично: вероятность qj фактически равна относительной частоте выбора
игроком В стратегии Bj. Поэтому о вероятностях pt и qj нередко говорят
как о частотах применения игроками соответствующих чистых страте-
стратегий. Говорят также о «частотах, в которых смешиваются чистые страте-
стратегии». Отсюда и термин «смешанная стратегия».
4.3 Как происходит выбор игроком той
или иной чистой стратегии с заданной вероятностью?
ь. Я понимаю, что на протяжении большого числа партий
каждый из игроков должен менять свою стратегию случайным образом,
поскольку в противном случае другой игрок сможет соответствующим
образом сориентироваться и увеличить собственный успех.
Пвтор. Совершенно верно. Именно поэтому могут пригодиться сме-
смешанные стратегии — когда игрок (как один, так и другой) случайным
образом чередуют свои чистые стратегии.
ttufauSt&fib. Как только что было сказано, игрок чередует их «с опреде-
определенными частотами». Иными словами, игрок выбирает ту или иную стра-
стратегию Аг (если это игрок А) с определенной вероятностью pt. По правде
сказать, я этого не понимаю. Мне понятно, когда говорят: «игрок А выбрал
стратегию А{». Но как понимать фразу: «игрок А выбрал стратегию Ах с
вероятностью ръ стратегию А2 с вероятностью ръ а стратегию Аъ с вероят-
вероятностью ръ»1 Как в действительности совершается такой «выбор»?
Пвтор. Дело в том, что такой выбор игрок А (это же относится и к
игроку В) делает перед началом каждой партии, бросая жребий. Он бро-
бросает жребий и выбирает ту из своих чистых стратегий, которая при этом
случайным образом выпадет. Можно сказать, что игрок как бы «пере-
«передоверяет» свой выбор фактору случайности, обращаясь перед каждой
партией к какому-то механизму случайного выбора.
104

Но как тут учитываются вероятности pp.
Пвтор. Чтобы их учесть, нужно организовать бросание жребия соот-
соответствующим образом. Иными словами, надо воспользоваться соответ-
соответствующим механизмом случайного выбора.
Здесь без конкретного примера, наверное, не разобраться.
Пвтор. Предположим, что игрок А намерен придерживаться вот та-
такой смешанной стратегии:
л2 а
/6 1/3 11
Как я понимаю, ему предстоит выбирать стратегию Ах с ве-
вероятностью 1/6, стратегию А2с вероятностью 1/3, стратегию А3с веро-
вероятностью 1 / 2. И как же в этом случае происходит бросание жребия?
Пвтор. Можно взять мешок, внутри которого находятся шесть оди-
одинаковых наощупь шаров, из которых один красный, два желтых, три
синих. Вероятность вытащить наугад из мешка красный шар равна 1/6,
вероятность вытащить желтый равно 1/3, вероятность вытащить синий
равна 1 /2. И вот перед каждой партией игрок вытаскивает наугад шар
из мешка. Допустим, он вынул синий шар. Значит, в данной партии
ему следует выбрать стратегию Аъ. После этого вынутый шар возвраща-
возвращается обратно и мешок с шарами основательно встряхивается.
g4utftiuSte*&. Я понял. Перед каждой партией игрок А вынимает наугад
шар из мешка, после чего выбирает стратегию Аь если шар окажется
красным (ведь вероятность вынуть красный шар равна 1/6), выбирает
стратегию А2, если шар окажется желтым (вероятность вынуть желтый
шар 1/3), выбирает стратегию Аъ, если вынутый шар окажется синим
(вероятность вынуть синий шар 1/2). Это и означает, что игрок А при-
придерживается смешанной стратегии (*)?
Пвтор. Да, это как раз и означает, что игрок выбирает стратегии Аъ
Аъ А3с вероятностью 1/6, 1/3, 1/2, соответственно.
"Читателе Тут можно поступить проще. Закрасим одну из граней ку-
кубика красным, две грани желтым, а остальные красным. Перед каждой
партией игрок подбрасывает кубик и смотрит, какого цвета выпала грань.
4.4 Две такие похожие и такие различные игры
Ое
/бе игры (игра 1 и игра 2) на одну и ту же тему. В нашем распоря-
распоряжении три вида вооружения {Аь А2, А3), а у противника три вида само-
самолетов (Bh Въ Въ). Противник посылает всякий раз (в каждой партии)
105

какой-то самолет, а мы, используя тот или иной вид вооружения, пытаем-
пытаемся сбить его. Всякий раз мы выбираем вид вооружения, не имея информа-
информации о том, какого вида самолет будет послан противником. Элемент пла-
платежной матрицы пу — это вероятность того, что мы добьемся успеха в случае,
когда мы выбрали стратегию At, а противник выбрал стратегию Bj. Пла-
Платежная матрица для игры 1 приведена на рис. 5 в таблице 11, а платежная
матрица для игры 2 приведена на рис. 6 в той же таблице.
Рассматриваемые две игры действительно похожи одна на другую.
В чем же заключается различие? Понятно, что оно связано с тем, что в
одной игре применяются одни виды вооружения и самолетов, а в дру-
другой игре — другие, вследствие чего платежные игры 1 и игры 2 описы-
описываются разными наборами вероятностей atj. Принципиально ли это раз-
различие? Оказывается, принципиально.
Обратимся к платежной матрице игры 1 (рис. 5 в таблице 11) и не-
немного порассуждаем. Предположим, что мы выбрали стратегию Ах. Тогда
в зависимости от того, какую стратегию выберет противник {Въ В2шш
2?з), мы добьемся успеха с вероятностью либо 0,5, либо 0,6, либо 0,8.
Наименьшая из этих вероятностей равна 0,5 (она отвечает выбору про-
противником стратегии В{). Выбирая стратегию Аь мы обеспечиваем свой
успех с вероятностью не ниже 0,5. Предположим далее, что мы выбрали
стратегию А2. Теперь в зависимости от выбора стратегии противником
мы добьемся успеха с вероятностью либо 0,9, либо 0,7, либо 0,8. Наи-
Наименьшая из этих трех вероятностей равна 0,7 (она отвечает выбору про-
противником стратегии В2). Наконец, предположим, что мы выбрали страте-
стратегию Аъ. В зависимости от выбора, сделанного противником, мы добьемся
успеха с вероятностью либо 0,7, либо 0,5, либо 0,6. Наименьшая из этих
вероятностей равна 0,5. Итак, для нас наилучшая стратегия — это страте-
стратегия А2: она гарантирует нам успех с вероятностью не ниже 0,7. Это боль-
больше, чем гарантированные вероятности успеха в случае выбора нами стра-
стратегии А1 (не ниже 0,5) и стратегии Аъ (тоже не ниже 0,5).
Теперь встанем на точку зрения противника. Если он выберет стра-
стратегию Въ то в зависимости от нашего выбора он будет сбит с вероятно-
вероятностью либо 0,5, либо 0,9, либо 0,7. Наибольшая из этих вероятностей
равна 0,9. Выбирая стратегию Bh противник «терпит неудачу» с вероят-
вероятностью не более 0,9. Если он выберет стратегию 53, то в зависимости от
нашего выбора «потерпит неудачу» с вероятностью либо 0,6, либо 0,7,
либо 0,5. Наибольшая из этих вероятностей равна 0,7. Если противник
выберет стратегию В3, то в зависимости от нашего выбора, он «потер-
«потерпит неудачу» с вероятностью либо 0,8, либо 0,6. Наилучшая стратегия
для противника — это стратегия В2: она дает ему гарантию, что неудача
постигнет его с вероятностью не более 0,7 (а это меньше, чем 0,8 или 0,9).
106

Итак, в игре 1 минимальный гарантированный успех для одной сто-
стороны (для нас) и максимальная неудача для другой стороны (для про-
противника) оцениваются одной и той же вероятностью: а22 = 0,7.
А вот в игре 2 мы встречаемся с принципиальной иной ситуацией.
Используя платежную матрицу, представленную на рис. 6 в таблице 11,
мы заключаем, что успех нам гарантирован либо с вероятностью не ниже
0,2 (если мы выберем стратегию Л1или стратегию А$), либо с вероятнос-
вероятностью не ниже 0,3 (если мы выберем стратегию А2). Очевидно, нам выгод-
выгоднее выбрать стратегию А2. В этом случае наш минимальный гарантиро-
гарантированный успех оценивается вероятностью ап = 0,3. Теперь займемся нашим
противником. Ему гарантирована неудача либо с вероятностью не более
0,9 (если он выберет стратегию В{)9 либо с вероятностью не более 0,7
(при выборе стратегии В2), либо с вероятностью не более 0,8 (при выборе
стратегии В3). Понятно, что противнику выгоднее всего выбрать страте-
стратегию В2. В этом случае максимальная возможная неудача оценивается
вероятностью аЪ2 = 0,7. Как видим, в игре 2, в отличие от игры 1, мини-
минимальный гарантированный успех для одного игрока и максимальная воз-
возможная неудача для другого оцениваются разными вероятностями. Ниже
мы обсудим, насколько принципиален этот факт.
4.5 Принцип минимакса; нижняя и верхняя цена игры
Ллстал момент обстоятельно поговорить об объявленном еще в § 4.2
принципе минимакса {принципе гарантированного результата). Тем бо-
более, что фактически мы уже начали знакомиться с этим принципом,
обсуждая игру 2 в § 4.4.
Будем рассматривать в общем случае игру тхп. Элемент atj ее пла-
платежной матрицы определяет наш выигрыш в случае, когда мы выбрали
стратегию At, а наш противник выбрал стратегию Bj. У нас есть т воз-
возможных стратегий, а у противника — п стратегий (стратегии Аъ Аъ
А3,...9 Атя Въ Въ В3,..., Вп соответственно).
Сначала попробуем найти нашу наиболее разумную стратегию. Бу-
Будем перебирать мысленно все наши стратегии — от А1 до Ат. Для каж-
каждой из них найдем тот элемент платежной матрицы, который является
наименьшим. Обозначим такие элементы через аъ аъ я3,..., ат:
а, = min ац (/ = 1, 2, 3,..., т)	C)
(знак min читается так: «минимум по всему от 1 до п»; ос, — это мини-
\<j<n
мальный по отношению ко всем j от 1 до п выигрыш atj для случая,
107

когда мы выбрали стратегию Аг). Выпишем числа ocz рядом с платежной
матрицей в виде добавочного столбца справа — см. рис. 1 в таблице 12.
Итак, выбирая стратегию Аь мы выиграем не менее ocz. Можно ска-
сказать, что при таком выборе нам гарантирован выигрыш не менее ocz. Есте-
Естественно, что из т имеющихся у нас возможных стратегий целесообраз-
целесообразно выбрать ту стратегию, для которой число ocz является наибольшим.
Обозначим это число через а:
а = max а,-.	D)
\<i<m
Объединяя C) и D), запишем:
а = max min аЛ.	E)
\<i<m \\<j<n J
Величину а называют нижней ценой игры, а также максиминным выигры-
выигрышем (проще: максимином). Число а находится в некоторой строке пла-
платежной матрицы. Стратегия игрока А, соответствующая этой строке,
называется максиминной стратегией. Для нас (для игрока А) максимин-
ная стратегия является в определенном смысле наиболее разумной. Это
осторожная (можно сказать, перестраховочная) стратегия. Если мы бу-
будем ее придерживаться, то при любом поведении противника нам гаран-
гарантирован выигрыш, во всяком случае не меньший, чем а. Отсюда и назва-
название «нижняя цена игры».
А теперь поставим себя на место противника. Он тоже перебирает
мысленно возможные стратегии — стратегии от В1 до Вп. Для каждой из
них он находит наибольший элемент матрицы и обозначает такие эле-
элементы через р1? р2, р3,..., Р„:
Ру = max *fr. (у = 1,2,3,...,л).	F)
Здесь ру- — наибольший по отношению ко всем / от 1 до т выигрыш atj в
случае выбора стратегии Bj (числа Ру записываем рядом с платежной
матрицей в виде добавочной строки внизу — см. рис. 1 в таблице 12).
Выбирая стратегию Bj, противник ограничивает наш выигрыш величи-
величиной Ру; иными словами, теперь он проиграет не более Ру. Естественно,
что из п имеющихся у него стратегий противник выберет ту, где число
ру наименьшее. Обозначим это число через р:
Р= min p/y.	G)
\<j<n
108

Таблица 12. Принцип минимакса. Игра с седловой точкой
min max djj — верхняя цена
j i
Рис.1
са
т
в2
©©©L
©®@L
а/
Рис.4
Рис.5
109

Объединяя F) и G), запишем:
/	Г"
(8)
В = min max afi .
\<j<n\\<i<m Jl
Величину C называют верхней ценой игры, а также минимаксом. Придер-
Придерживаясь минимаксной стратегии, противник, конечно, перестраховал-
перестраховался; но зато он получил гарантию: независимо от наших действий он во
всяком случае проиграет не более р.
Принцип, согласно которому игрок А выбирает максиминную стра-
стратегию, а игрок В выбирает минимаксную стратегию, — это и есть прин-
принцип минимакса (он же принцип осторожности, или принцип гарантиро-
гарантированного результата).
На рисунках 2, 3, и 4 в таблице 12 наглядно показано, как найти
нижнюю и верхнюю цену в играх с монетой, «два пальца» и «три паль-
пальца», соответственно. Матрица не рис. 5 получена из матрицы на рис. 4
путем прибавления числа 6 к каждому элементу исходной матрицы —
для того, чтобы все элементы платежной матрицы стали положитель-
положительными. С точки зрения анализа оптимальных стратегий обе матрицы
эквивалентны.
Возвращаясь к игре 2 в §4.4 (см. рис. 6 в таблице 11), отметим, что
здесь нижняя цена игры равна 0,3 (игрок А должен придерживаться
стратегии А2), а верхняя цена игры равна 0,7 (игрок В должен придер-
придерживаться стратегии В2). На примере этой игры продемонстрируем неус-
неустойчивость минимаксных (максиминных) стратегий. Допустим, мы от
партии к партии придерживаемся максиминной стратегии Аъ а против-
противник придерживается минимаксной стратегии В2; в результате наш вы-
выигрыш составляет 0,6. Он больше нижней, но меньше верхней цены
игры. Как долго это будет продолжаться? — Очевидно, лишь до тех пор,
пока один из игроков не догадается о стратегии, какой придерживается
другой игрок. Как только противник поймет, что мы придерживаемся
стратегии Аъ он скорее всего, не удержится от того, чтобы не ответить
нам стратегией Въ в результате чего наш выигрыш снизится до 0,3 (т. е.
до нижней цены игры). Ясно, что и эта ситуация не может долго про-
продолжаться. На стратегию противника Вх мы можем ответить стратегией
Ах и тем самым увеличить вероятность собственного успеха до 0,9. И
так далее. Как мы видим, ситуация и в самом деле неустойчивая — она
меняется, как только один из игроков начинает понимать стратегию дру-
другого игрока.
ПО

4.6 Игра с седловой точкой; цена игры
Существует, однако, игры, для которых минимаксные (максимин-
ные) стратегии оказываются устойчивыми. Это игры, для которых ниж-
нижняя цена и верхняя цена равны:
ос = р.	(9)
Общее значение нижней и верхней цены называют ценой игры (а также
чистой ценой игры). Будем обозначать ее через v.
В игре 1 в § 4.4 нижняя и верхняя цена игры одна и та же: 0,7 (и,
значит, цена игры v = 0,7). Это хорошо иллюстрирует рис. 6 в табли-
таблице 12. Элемент а22 = 0,7, выделенный в платежной матрице, является
одновременно минимальным в своей строке и максимальным в своем
столбце. Точка на поверхности, соответствующая минимуму по од-
одной координате и максимуму по другой, называется в геометрии седло-
вой точкой — см. рис. 7 в таблице 12 (изображенная на этом рисунке
поверхность в самом деле напоминает седло; точка С — седловая точ-
точка). По аналогии термин «седловая точка» применяют также в теории
игр. Говорят, что игра, для которой выполняется условие (9), есть игра
с седловой точкой. Рассматриваемая нами игра 1 — пример игры с сед-
седловой точкой. Элемент а22 = 0,7 платежной матрицы этой игры есть сед-
седловая точка матрицы.
Напомним (см. §4.1), что оптимальной стратегией игрока называет-
называется такая стратегия, которая при многократном повторении игры обес-
обеспечивает данному игроку максимум успеха (минимум неуспеха) незави-
независимо от действий другого игрока. Стратегия игрока, содержащая седловую
точку (точнее говоря, стратегия, при которой среди возможных элемен-
элементов матрицы присутствует седловая точка матрицы), как раз и есть его
оптимальная стратегия. Это относится в равной мере как к игроку А,
так и к игроку В. Совокупность оптимальных стратегий обоих игроков
называют решением игры. Чтобы найти решение игры с седловой точ-
точкой, нужно найти седловую точку платежной матрицы; решение игры
есть совокупность стратегий At и Д, определяющих эту точку.
Если в игре 1 в § 4.4 игрок А придерживается своей оптимальной стра-
стратегии (стратегии А2), а игрок В придерживается своей оптимальной стра-
стратегии (стратегии В2), то игрок А будет иметь в среднем минимальный
гарантированный выигрыш, равный цене игры v = 0,7 (его выигрыш не
может быть меньше 0,7). При этом игрок В будет иметь в среднем мак-
максимальный гарантированный проигрыш, тоже равный цене игры v = 0,7
(его проигрыш не может превысить 0,7).
111

Пусть игрок А придерживается своей оптимальной стратегии Аъ а
игроку В вдруг захотелось отойти от своей оптимальной стратегии и
выбрать, например, стратегию Вх. В этом случае выигрыш игрока Л
оказывается больше цены игры (он теперь равен 0,9). Соответственно
увеличивается и максимальный гарантированный проигрыш игрока В
(теперь ему уже не гарантирован проигрыш не более 0,7; теперь ему
гарантирован проигрыш не менее 0,9).
Мы убеждаемся, что в игре с седловой точкой всякое отклонение
одного из игроков от своей оптимальной стратегии идет во вред этому
игроку и, напротив, полезно для противника. Таким образом, опти-
оптимальные стратегии как одного, так и другого игрока характеризуются
устойчивостью — ни одному из игроков не может быть выгодно откло-
отклоняться от собственной оптимальной стратегии. Понятно, что в игре с
седловой точкой (в отличие от игры без седловой точки) нет необходи-
необходимости скрывать свои намерения. И нет необходимости в случайных из-
изменениях стратегии.
Если игра имеет седловую точку, то можно сказать, что ее исход
заранее предрешен. Строго говоря, такая игра имеет смысл только для
лиц, которые не знают ее решения (которым неизвестна седловая точка
игры). В теории игр доказывается, что седловую точку имеет любая игра
с полной информацией. Так называют игру, в которой каждый игрок при
каждом личном ходе знает результаты всех предыдущих ходов. К играм
с полной информацией относятся, в частности, шахматы. Правда, ре-
решение шахматной игры до сих пор не найдено из-за исключительно
большого числа возможных стратегий. Практически невозможно соста-
составить платежную матрицу этой игры и найти ее седловую точку.
4.7 Решение игры без седловой точки
и оптимальные смешанные стратегии
1 Л
оговорим об играх, не имеющих седловой точки (для них а < C).
Как мы уже выяснили (см. § 4.5), если в такой игре игрок А будет при-
придерживаться максиминной стратегии, то ему гарантирован выигрыш не
менее а. А если игрок В будет придерживаться минимаксной стратегии,
его проигрыш не превысит р. Мы выяснили также, что эти стратегии
неустойчивы. Как только, например, игрок Л поймет, что его против-
противник намерен придерживаться минимаксной стратегии, он тут же найдет
более выгодную для себя стратегию, отличающуюся от максиминной.
112

Такова общая ситуация в игре без седловой точки, когда оба игрока
придерживаются только чистых стратегий. Предположим теперь, что от
партии к партии оба игрока свои чистые стратегии случайным образом
меняют с определенными вероятностями. Это означает, что каждый иг-
игрок придерживается некоторой смешанной стратегии, в которой все или
некоторые его чистые стратегии «смешаны» в соответствии с опреде-
определенными вероятностями. Возникает вопрос: можно ли найти такую
смешанную стратегию S/ (для игрока А) и такую смешанную стратегию
SB* (для игрока В), которые были бы оптимальными стратегиями и как
таковые обладали бы устойчивостью? Иными словами, можно ли, вос-
воспользовавшись смешанными стратегиями, найти решение (а значит, и
цену) игры без седловой точки?
Положительный ответ на этот вопрос дает основная теорема теории
игр. Вот ее краткая формулировка: каждая конечная игра имеет по край-
крайней мере одно решение (возможно, в области смешанных стратегии). Эта
теорема была впервые доказана фон Нейманом в 1928 году.
Как и при игре с седловой точкой, средний выигрыш, получаемый в
случае, когда найдено решение игры, называют ценой игры. Из основ-
основной теоремы следует, что каждая конечная игра имеет цену. Легко сооб-
сообразить, что цена игры v должна удовлетворять соотношениям:
a<v<p.	A0)
В самом деле, a — это наш наибольший гарантированный выигрыш,
если применяем только свои чистые стратегии. Поскольку смешанные
стратегии включают в себя, в частности, чистые стратегии, то, приме-
применяя кроме чистых еще и смешанные стратегии, мы не можем ухудшить
свое положение; следовательно, v > а. Аналогичные рассуждения, от-
относящиеся к нашему противнику, позволяют заключить, что v < р. В
результате приходим к соотношениям A0).
Оптимальные смешанные стратегии в играх без седловой точки, как
и оптимальные чистые стратегии в играх с седловой точкой, характери-
характеризуются устойчивостью. Если один из игроков придерживается своей оп-
оптимальной смешанной стратегии, то другому игроку невыгодно отсту-
отступать от собственной оптимальной смешанной стратегии. В этом случае
каждый игрок имеет в среднем выигрыш (проигрыш), равный цене
игрыу.
В игре тхп у игрока А есть т возможных чистых стратегий, а у
игрока В— п чистых стратегий. Оказывается, что в оптимальные смешан-
смешанные стратегии S/ и SB* могут входить не все, а только некоторые из имею-
имеющихся у игроков чистых стратегий. Эти некоторые стратегии называют
113

активными (или полезными). В теории игр доказывается теорема: если
один из игроков придерживается своей оптимальной смешанной страте-
стратегии, то его выигрыш (проигрыш) остается неизменным и равным цене игры
независимо от того, что делает другой игрок — лишь бы он не выходил за
пределы своих активных стратегий. Он может, например, воспользо-
воспользоваться любой из своих активных стратегий по отдельности, но может
также смешать их в любых пропорциях. Данная теорема играет важную
роль в теории игр. Мы воспользуемся ею в следующем параграфе.
4.8 Как найти оптиммьную смешанную стратегию
для кадцого из игроков?
1 Хокажем, как отыскать оптимальные смешанные стратегии S/ и
SB*9 т. е. как найти цену игры v, а также вероятности чистых стратегий,
если известны элементы atj- платежной матрицы. Простоты ради мы не
станем рассматривать в общем случае игру тхп, а ограничимся играми
2x2 и 3x3.
Начнем с игры 2x2. Нам известны элементы платежной матрицы:
ап, а1Ъ а2Ъ а22. Надо найти v и вероятности ръ ръ qh #2ДЛЯ оптималь-
оптимальных смешанных стратегий. Допустим, мы выбрали оптимальную сме-
смешанную стратегию S/ = (ph р2), а противник выбрал чистую стратегию Вх.
В этом случае наш средний выигрыш при многократном повторении
игры будет anpi + а2Хр2. Согласно теореме, сформулированной в конце
предыдущего параграфа, указанный выигрыш должен равняться цене
игры v:
<*uPi+<*2iP2 =v-	(*)
При выборе нами стратегии S/ и выборе противником стратегии Въ
мы получим средний выигрыш апрх + а12ръ который, согласно упомя-
упомянутой выше теореме, тоже должен равняться цене игры v:
апР\ + а22Р2 = v-	(**)
В итоге можем записать систему уравнений, которая позволяет найти
Ръ Р2> v:
(ПА)
anpl+a22p2 =v;
Р1+Р2 =1
114

Используя первое и второе уравнения из A1.А), запишем:
а\\Р\ +a2lP2 = а\2Р\ + «22^2-
(***)
Учитывая, что р2 = 1 - Р\, преобразуем (***) к уравнению относительно
р±. В результате получаем:
Р\ =
«11+«22 -«12 -«21
«11 -«12
«11 +«22 -«12 -«21
«11«22 ~«21«12
«11 +«22 -«12 -«21
A2.А)
Теперь предположим, что наш противник выбрал оптимальную стра-
стратегию SB* = (qh q2), а мы выбираем либо стратегию Аь либо стратегию А2.
По аналогии с A1.А) получаем следующую систему уравнений, которая
позволяет найти qlf и q2 (цена игры v уже найдена):
qx+q2 = 1.
(П-В)
Отсюда находим:
«1 =
v-«i2
«2 =l-«i =
«11 +«22 -«12 -«21 '
«11 -«21
«11 +«22 -«12 -«21 '
A2.В)
Обратимся к игре с монетой (см. рис. 2 в таблице 11). В этой игре:
«и = «22 = 1> «12 = «21 = -1- Подставляя эти значения в A2.А) и A2.В),
получаем
v = 0, рх =р2 = 1 / 2, qx = q2 = 1 / 2.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
Цена игры равна нулю. Значит, в данной игре ни игрок А,
ни игрок В в среднем (за много партий) ничего не выигрывают!
115

Пвтор. Но для этого игроки должны придерживаться оптимальных
смешанных стратегий S/ и SB*.
ttutftiuSU**. Поскольку р1 = р2 = 1 / 2 и q1 = q2 = 1 / 2, то каждый из иг-
игроков должен одинаково часто прибегать то к одной, то к другой из
двух своих чистых стратегий. Иначе говоря, каждый игрок должен в
половине всех партий класть монету орлом вверх, а в половине партий
орлом вниз. Проще всего, наверное, чередовать стратегии: «орлом вверх»,
«орлом вниз», «орлом вверх», «орлом вниз» и т. д.
Пвтор. Нет, так не годится. Дело не только в том, чтобы в половине
партий была выбрана одна стратегия, а в половине другая. Принципи-
Принципиально важно, чтобы этот выбор производился случайным образом. Мож-
Можно поступить, например, так: перед каждой партией каждый игрок под-
подбрасывает монету. Если подброшенная монета упадет орлом вверх, то
игрок и кладет ее на стол орлом вверх, т. е. выбирает стратегию Ai(B{).
Если подброшенная монета упадет орлом вниз, то игрок и кладет ее на
стол орлом вниз, т. е. выбирает стратегию А2(В2). Можно также бросать
игральный кубик, условившись, что при выпадении грани с нечетным
числом очков монета кладется орлом вверх, а при выпадении грани с
четным числом очков — орлом вниз. Мы используем тот факт, что
вероятности выпадения четной грани и нечетной грани равны.
Продолжая рассматривать игры 2x2, обратимся к игре «два пальца»
(см. рис. 3 в таблице 11). В этой игре: ап = 2, аи = а2\ = -3, а22 = 4. Под-
Подставляя эти значения в A2.А) и A2.В), получаем:
=
А Л2\ * = ( вх в2
7/12 5/12/ в [7/12 5/12
Итак, в данном случае цена игры v = -1 /12. Значит игра не выгодна
игроку А. Придерживаясь оптимальной смешанной стратегии, игрок
должен выбирать стратегию Лхс вероятностью 7/12, а стратегию А2с
вероятностью 5/12. Так же должен поступать со своими стратегиями
игрок В. На практике это означает, что перед очередной партией каж-
каждый игрок должен наугад вынуть шар из мешка, в котором находятся
7 белых и 5 черных шаров. Если вынутый шар окажется белым, игрок
выбирает стратегию А1 (В{), а если черным, то стратегию А2 B?2). Мож-
Можно также воспользоваться правильным двенадцатигранником (додекаэд-
(додекаэдром), у которого семь любых граней белые, а остальные пять граней
черные. Перед каждой партией игрок подбрасывает додекаэдр и выби-
выбирает ту или иную из двух своих чистых стратегий в зависимости от
цвета грани, оказавшейся верхней.
116

Рассмотрим теперь игру 3x3, полагая, что все три чистые стратегии
как игрока А, так и игрока В участвуют в создании оптимальных смешан-
смешанных стратегий, т. е. являются активными стратегиями. Цену игры и веро-
вероятности рь р2, ръ, q\, q2, q3 оптимальных смешанных стратегий можно
найти с помощью систем уравнений, аналогичных системам A1.А) и A1.В):
S*AnB2:
апрх +а21р2
+а22р2
+a2ip2
= v;
= v;
= v;
P1+P2+P3 =1-
SB и Ax : anql +anq2 +al3q3 = v;
с* л
uB И A2 : ^21^1 ~r^22^2 ~r ^23^3 ^ ^'
^5 и ^3 : a31g! +a32g2 +«33^3 = v;
A3.A)
A3.B)
Обратимся к игре «три пальца». Подставляя в A3.А) элементы пла-
платежной матрицы, представленной на рис. 4 в таблице 11, получаем сис-
систему уравнений:
= v;
= v;
A +i>2 +Л =1-
Исключим v, приравняв левые части 1-го и 2-го, а также 1-го и 3-го урав-
уравнений из (****):
р3 = -Ърх + 4^2 - 5^3;
^3 = 4/>х - Ърг + б^з-
Мы получили систему трех уравнений с тремя неизвестными:
2рх - Зр2
2рх - Ър2
р\ +Р2 -Рз =0;
Р1+Р2+РЗ =1-
117

Подставляя в первые два уравнения ръ = 1 - рх - ръ приходим к системе
двух уравнений с двумя неизвестными:
4pi+l6p2 = 9;
2р2 = 1.
В результате получаем: v = О, S*A = * 2 3
Используя v = 0 и систему уравнений A3.В), нетрудно получить:
* _ вх в2 въ
в 1/4 1/2 1/4
Чтобы реализовать полученные оптимальные смешанные стратегии
на практике, можно, например, воспользоваться мешком, внутри кото-
которого находятся один красный, один желтый и два синих шара. Можно
также воспользоваться додекаэдром, у которого три каких-то грани
выкрашены в красный цвет, три грани в желтый и шесть граней в си-
синий. Перед каждой партией каждый игрок либо вынимает наугад шар
из мешка, либо подбрасывает додекаэдр.
4.9 Геометрическое представление игр 2x2
JHLaM известны элементы платежной матрицы некоторой игры 2x2:
ап, ап, а>гъ а22- Требуется найти цену игры v и оптимальные стратегии
игрока А и игрока В. Рассматривая общий случай, будем полагать, что
игра не имеет седловой точки (случай с седловой точкой может рас-
рассматриваться как частный случай). В отсутствие седловой точки опти-
оптимальные стратегии игроков надо искать в области смешанных страте-
стратегий. Нам предстоит найти вероятности р1и р2дш оптимальной
смешанной стратегии S/ игрока А и вероятности qx и q2 для оптималь-
оптимальной стратегии SB* игрока В. Покажем, как с помощью геометрических
построений можно найти v и упомянутые вероятности.
Проведем отрезок прямой, длина которого равна 1. Концы отрезка
обозначим через Ах и А2. Восстановим из концов отрезка перпендикуля-
перпендикуляры и отложим на них отрезки АХВ[ = ап и A2B{f = а2\ — см. рис. 1 в таб-
таблице 13 (масштаб длин для отрезка АхА2ж упомянутых перпендикуляров
различен). Напомним, что ап — наш выигрыш, если мы выберем стра-
стратегию Аъ а противник выберет стратегию Вх. Соответственно, а21 —
118

наш выигрыш при выборе нами стратегии А2ж выборе противником
стратегии Вх.
Соединим отрезком прямой точки В{ и В{!. Теперь можно геометри-
геометрически найти выигрыш, который мы получим, применив смешанную
(А А)
стратегию SА =	, при условии, что противник по-прежнему
[Pi Pi)
выбирает стратегию Вх. Для этого надо фиксировать на отрезке ^4р42 точку
SA — такую, чтобы отрезок AXSA имел длину ръ а отрезок 6^42 ~~ длину
рх. Восстановим перпендикуляр к отрезку АхА2т> точки SA. Длина от-
отрезка SAB{" как раз и будет равна нашему выигрышу при применении
А1 А2
Ж Pi,
стратегии Вх. Известно, что этот выигрыш должен равняться апрх + а2Хр2.
Докажем, что именно такую длину имеет отрезок SAB{". Для этого дос-
достаточно рассмотреть треугольник, заштрихованный на рисунке 1, и тре-
треугольник B{B('L. Треугольники подобные; поэтому для их катетов мож-
можно составить пропорцию:
нами смешанной стратегии SA =
и применения противником
LBX SABx-an
Перепишем ее в виде:
Pi+Pi _ Pi
ап ~ ап bABi - ап
Отсюда находим:
(A +Pi)sab\ ~anPi ~anPi = ai\Pi ~а\\Ръ
или
= ^11^1+^21^2-
Так как р1 + р2 = 1, то SAB{" = anpi + tf^ife что и тРебовалось доказать.
На рисунке 2 в таблице 13 выполнены аналогичные рисунку 1 по-
построения, но для случая, когда мы выбираем ту же, что и раньше, сме-
А\ А2
шанную стратегию SА =
, а противник выбирает теперь страте-
Р\ Pi
гию не 5Ь а В2. В этом случае наш выигрыш составит:
S АВ2 = anpi + а22р2.
119

Таблица 13. Геометрическое представление игр 2x2
Рис.1
В
Рис.2
Рис.3
Рис.4
о
о
7
6
в;<
4
3
в;«
1
Ail
-*	г
в;1
/
м\ 111 ITT
V

	^-
в;
.Til
А2
120

Для доказательства приведенного равенства надо составить пропорцию
для катетов двух подобных треугольников — треугольника B2LB2 и тре-
треугольника, заштрихованного на рис. 2.
Понятно, что при произвольном разбиении единичного отрезка АХА2 на
отрезки длиной р1 и р2 смешанная стратегия SA не может рассматривать-
рассматриваться как оптимальная для игрока А. Как хорошо видно из сравнения ри-
рисунков 1 и 2,
Это означает, что, используя одну и ту же смешанную стратегию
о А А2
SA=	, мы получаем различные выигрыши — в зависимости от
Pi Pi
того, какой из своих стратегий (^или В2) воспользуется наш против-
противник. Естественно, такая стратегия не может быть оптимальной. Необхо-
Необходимым условием того, что SA есть оптимальная смешанная стратегия для
игрока А (будем обозначать такую смешанную стратегию как S/), явля-
является условие:
а\\Р\ + ^21^2 = a\lP\ + ^22^2-	(*)
Напомним, что с этим равенством мы уже имели дело — см. соотноше-
соотношение (***) в предыдущем параграфе.
Чтобы с помощью геометрии найти оптимальную для игрока А сме-
смешанную стратегию S/ (т. е. чтобы найти соответствующие вероятности
Pi и р2), надо на единичном отрезке АХА2 построить трапецию А1В{В{/А2 и
трапецию АхВ{В%А2ж найти точку пересечения их боковых сторон, т. е.
отрезков В{В{' и В{В{. Отрезки В{В{' и В{В{ будем рассматривать как
геометрическое представление стратегии BjH стратегии В2, соответ-
соответственно. Точка пересечения М стратегий B1n i?2nOKa3aHa на левом чер-
чертеже на рис. 3 в таблице 13. На этом рисунке геометрически представ-
представлена конкретная игра 2x2 с платежной матрицей, приведенной на том
же рисунке. Точка пересечения М позволяет ответить на интересующие
нас вопросы — надо только опустить из нее перпендикуляр MS/ на
отрезок АХА2. Длина отрезка MS/ есть цена игры v, длины отрезков
AXS/ и S/A2 — соответственно вероятностир2жрь задающие оптималь-
оптимальную смешанную стратегию игрока А. С помощью штриховки на данном
чертеже выделена ломаная линия B{MB{f, определяющая величину наи-
наименьшего гарантированного выигрыша А при выборе им той или иной
пары вероятностей рх и р2. Эту линию называют нижней границей выиг-
выигрыша. Обратим внимание на то, что цена игры v определяется по наи-
наивысшей точке нижней границы выигрыша.
121

На правом чертеже на рис. 3 показаны соответствующие геометри-
геометрические построения, которые выполняет наш противник, когда он отыс-
отыскивает свою оптимальную смешанную стратегию SB*. Точка пересечения
N отрезков А{А" и А2А2 (иными словами, точка пересечения стратегии
А1я стратегии А2) определяют цену игры v (она равна длине отрезка
NSB*; понятно, что NSB* = MS/) и вероятности q1 и q2, задающие опти-
оптимальную смешанную стратегию игрока SB* (длины SB*B2w BXSB, соот-
соответственно). Штриховкой выделена ломаная линия A2NA{, определяю-
определяющая величину максимального гарантированного проигрыша нашего
противника, — так называемая верхняя граница проигрыша. Заметим, что
цена игры может быть определена по наинизшей точке верхней границы
проигрыша.
В рассматриваемой игре нижняя цена игры а = А2В2 = 4, а верхняя
цена игры C = ВХА{ = 6. Как и следовало ожидать (это хорошо видно на
рис. 3), а < v < р.
Условие (*) является, как отмечалось выше, необходимым условием
оптимальности смешанной стратегии SA. Но оно не является достаточ-
достаточным условием. В этом можно убедиться, обратившись к рис. 4 в табли-
таблице 13. Предложим читателю самостоятельно исследовать левый и пра-
правый чертежи на этом рисунке. Особенность рассматриваемой ситуации
в том, что данная игра есть игра с седловой точкой', поэтому она решает-
решается в чистых стратегиях игроков. Их оптимальные стратегии: А2дш иг-
игрока А и В2 для игрока В. Седловая точка матрицы: а22 = 6, v = а = C = 6.
Как и в предыдущей игре, цену игры можно определить по наивысшей
точке нижней границы выигрыша, которая в данном случае есть не точка
пересечения стратегий В1я Въ а точка В2. Цену игры можно опреде-
определить также по наинизшей точке верхней границы проигрыша, которая в
данном случае не есть точка пересечения стратегий А1 и А2 (эти страте-
стратегии здесь вообще не пересекаются), а точка А2.
4.10 Геометрическое представление игр 2хп и тх2
в
теории игр доказывается следующая теорема: у любой конечной
игры тхп имеется решение, для которого число активных стратегий как
игрока А, так и игрока В не превосходит наименьшего из чисел тж п.
Из этой теоремы следует, что в играх 2хп и тх2 оптимальные смешан-
смешанные стратегии каждого игрока образуются с использованием только двух
его чистых стратегий. Остальные стратегии в решении игры не участву-
122

ют; их можно вычеркнуть из платежной матрицы. Это означает, что
игры 2хп и тх2 сводятся фактически к играм 2x2. Ниже мы убедимся в
справедливости этих утверждений, воспользовавшись геометрическим
представлениям таких игр.
В игре 2хп мы (игрок А) располагаем двумя чистыми стратегиями
А1и Аъ а наш противник (игрок В) имеет п чистых стратегий: Въ Въ
Въ,..., Вп. Платежная матрица игры состоит из двух строк и п столбцов.
На рис. 1 в таблице 14 приведена в качестве примера платежная матри-
матрица для некоторой игры 2x5. Там же дано геометрическое представление
такой игры, рассматриваемое с точки зрения игрока А. Мы поступаем
здесь аналогично тому, как поступали в предыдущем параграфе, рас-
рассматривая игру 2x2 (напомним левый чертеж на рис. Зв таблице 13).
Только теперь на чертеже будут изображаться отрезками прямых не две,
а пять стратегий игрока В. Имеются в виду отрезки: В{В{' (стратегия В{)9
ЩЩ (стратегия В2),...9 В^В? (стратегия В5). Определяем нижнюю гра-
границу выигрыша — ломаную линию, выделенную на рисунке с помо-
помощью штриховки. Отыскиваем на этой линии наивысшую точку; это есть
точка М. Опускаем из М перпендикуляр на отрезок АХА2. Длина перпен-
перпендикуляра MS/ есть цена игры v. Отрезки S/A2n A^/ определяют веро-
вероятности р1и р2для оптимальной смешанной стратегии игрока А:
SA*A2=p1,A1SA*=p2.
В рассмотренном случае наивысшая точка нижней границы выигры-
выигрыша определяется пересечением стратегий В2ж В4. Поэтому именно эти
две стратегии являются в данной игре активными стратегиями
игрока В. Вычеркивая в платежной матрице игры столбцы Въ В3, В5, мы
приходим к игре 2x2 с матрицей:
3 9
6 3
Подставляя в A2.А) и A2.В) элементы этой матрицы (ап = 3, аи = 9,
а21 = 6, а22 = 3), находим решение рассматриваемой здесь игры 2x5:
Итак, оптимальные смешанные стратегии:
^"'.1/3 2/3J' °5"[2/3 1/3
Игрок А должен выбирать стратегию Ах с вероятностью 1 / 3 и стратегию А2 с
вероятностью 2/3. Игрок В должен выбирать стратегию В2с вероятностью
123

Таблица 14. Геометрическое представление игр 2хи и тх2
Рис.1
\
Ах
А2
Bi
©
®
в2
©
®
В3
©
©
в4
@
©
в5
®
©
Рис.3
\
А!
А2
Bi
@
@
в2
©
D)
В3
0
@
В4
С8)
Рис.2
Рис.4
124

2 / 3 и стратегию В4с вероятностью 1 / 3, а стратегии Въ В3, В5 он вооб-
вообще не должен применять. Заметим, что в качестве «механизма случай-
случайного выбора» в данной игре можно использовать, например, игральный
кубик, у которого две произвольные грани как-то закрашены, а осталь-
остальные четыре грани оставлены незакрашенными.
В игре тх2у нас т стратегий (Аъ Аъ А$,..., Ат), у противника две
стратегии (^и В2); платежная матрица состоит из т строк и двух стол-
столбцов. На рис. 2 в таблице 14 можно видеть платежную матрицу и гео-
геометрическое представление (с позиции игрока В) некоторой игры 7x2.
По аналогии с правым чертежом на рис. 3 в таблице 13 изобразим здесь
в виде отрезков прямых семь стратегий игрока А (от ^до А7)9 выявим
верхнюю границу выигрыша (она выделена на рисунке штриховкой) и
отыщем на ней наинизшую точку. Это есть точка N. Опускаем из N пер-
перпендикуляр на ВХВ2. Длина перпендикуляра NSB* есть цена игрыу. От-
Отрезки SbB2ia B^SB определяют, соответственно, вероятности ^и q2RJin
оптимальной смешанной стратегии SB* игрока В.
Как видно из рис. 2, наинизшая точка верхней границы выигрыша
определилась в результате пересечения стратегий А4и А6. Значит, имен-
именно эти две стратегии являются активными стратегиями игрока А. Вы-
Вычеркивая в платежной матрице строки Аь Аъ Аъ, А5, А7, приходим к игре
2x2 с матрицей:
8 11
13 3
Подставляя в A2. А) и A2. В) элементы этой матрицы (ап = 8, ап = 11,
а21 = 13, а22 = 3), находим решение игры 7x2:
v = 9,2, рх = 10 / 13, р2 = 3 / 13, q{ = 8 / 13, q2 = 5 / 13.
Итак, оптимальные смешанные стратегии:
А4 А6 \ * ( Вх В2
10/13 3/13J' в [8/13 5/13
Игрок А должен выбирать стратегию А4с вероятностью 10/ 13 и страте-
стратегию А6с вероятностью 3/13, а стратегиями Аъ Аъ Аъ, А5, А7оя вообще
не должен пользоваться. Игрок В должен выбирать стратегию Вх с веро-
вероятностью 8 / 13 и стратегию В2с вероятностью 5/13.
Рассмотрим особый случай — игру 2x4, платежная матрица и гео-
геометрическое представление которой даны на рис. 3 в таблице 14.
Особенность данной игры в том, что ломаная линия, изображающая
125

нижнюю границу выигрыша (см. штриховку на рисунке), включает в
себя отрезок, ориентированный горизонтально. Это отрезок М'М". На
первый взгляд, в данном случае у игрока В не две, а три активных стра-
стратегии: Bh Въ В3. Но это не так; у игрока В (как и у игрока А) имеются
две активные стратегии. Просто у игрока В есть две альтернативы: он
может выбрать в качестве активных либо стратегии В1 и Въ либо страте-
стратегии В2ж Въ. Точнее говоря, он должен выбрать в качестве оптимальной
стратегии чистую стратегию В2и не смешивать ее ни со стратегией Въ
ни со стратегией В3. Что же касается игрока А, то его оптимальная
стратегия лежит в области смешанных стратегий, причем у него не одна,
а бесконечно много оптимальных смешанных стратегий. К ним относит-
ся любая смешанная стратегия SA =	, для которой р2 попадет в
\Р\ Pi)
интервал значений от р{ до р{ (см. рисунок), а вероятность
/^определяется всякий раз из соотношения Р\ = \ -р2. Ясно, что цена
игры v = 4. Чтобы найти р{, надо рассмотреть пересечение стратегий Вх и
Въ а чтобы найтир2 — пересечение стратегий В2ж Въ. Нетрудно подсчи-
подсчитать, что р{=1 /3 я p{f = 3 / 4.
4.11 Игра «самолеты против зениток»
в
§§ 4.9 и 4.10 задавались, а затем анализировались платежные мат-
матрицы игр. При этом не рассматривалось, каким образом появилась та
или иная платежная матрица, какую конкретную игровую ситуацию она
выражает. В данном параграфе мы рассмотрим конкретную игру под
названием «самолеты против зениток». Мы получим платежную матри-
матрицу этой игры и, используя ее, найдем решение игры — определим ее
цену и оптимальные стратегии игроков.
Мы (нападающая сторона А) посылаем два самолета-бомбардиров-
самолета-бомбардировщика с целью уничтожить некий объект, а противник (обороняющаяся
сторона В) старается с помощью четырех зенитных орудий сбить наши
самолеты. Оговорим условия игры. Имеются четыре коридора (I, II, III, IV),
по которым могут подлететь к объекту наши самолеты, и именно в этих
коридорах противник размещают свои орудия. Если хотя бы один из
наших двух самолетов-бомбардировщиков прорвется к объекту, тот обяза-
обязательно будет уничтожен. Каждое орудие может обстрелять только один
самолет, пролетающий в пределах коридора, в котором находится это
орудие. Обстрелянный самолет оказывается сбитым с вероятностью 1.
126

Мы не знаем, где и как размещены четыре орудия противника. Против-
Противник не знает, откуда прилетят наши два самолета-бомбардировщика.
У нас есть две стратегии:
Ах — послать по одному самолету в двух разных коридорах (безраз-
(безразлично, в каких именно),
А2 — послать два самолета в каком-то одном из коридоров.
У противника есть пять стратегий:
81	— выставить по орудию в каждом коридоре,
82	— выставить по два орудия в двух разных коридорах,
Въ — выставить два орудия в одном из коридоров и по одному ору-
орудию в двух других коридорах,
84	— выставить три орудия в одном из коридоров и одно орудие в
каком-то другом коридоре,
85	— выставить все четыре орудия в одном из коридоров.
Стратегия i?4 является заведомо невыгодной, поскольку ни в одном
из коридоров не появятся три самолета (у нас есть только два самоле-
самолета), так что три орудия в одном коридоре — это ненужное излишество.
Тем более невыгодна стратегия В5. Таким образом стратегия В4 и В5 надо
исключить, после чего у противника останутся только три стратегии
B?l5 В2, 2?з), и мы приходим к игре 2x3. Найдем элементы платежной
матрицы этой игры, т. е., иными словами, найдем вероятности уничто-
уничтожения объекта при выборе игроками тех или иных стратегий.
Предположим, что мы выбрали стратегию Ах — посылаем по одному
самолету в разных коридорах. Если при этом противник выберет страте-
стратегию Въ то, как легко сообразить, ни один из наших двух самолетов не
сможет прорваться к объекту. Вероятность уничтожения объекта в этом
случае равна нулю: ап = 0. Допустим, что противник выбрал стратегию В2
и разместил два орудия в коридоре I и два орудия в коридоре П. У нас
есть шесть равновероятных вариантов выбора пар коридоров, по которым
мы можем направить наши самолеты: I—II, I—III, I-IV, II—III, II—IV, III—IV.
Из этих шести вариантов проигрышным для нас является только один
вариант; в данном случае это вариант I—II. Если бы противник разместил
две пары орудий как-то иначе, например в коридорах I и IV, то и в этом
случае из шести указанных выше вариантов проигрышным для нас ока-
оказался бы только один вариант (вариант I-IV). Таким образом, вероятность
уничтожения объекта при выборе стратегий Ах и В2 есть ап = 5 / 6. Предпо-
Предположим теперь, что противник выбирает стратегию Въ — размещает два
орудия в одном из коридоров и по одному орудию в других коридорах, в
результате чего один из коридоров остается незащищенным. Пусть это бу-
будет коридор I. Как и в предыдущих случаях, наши самолеты могут выбрать
127

шесть равновероятных вариантов. В половине вариантов (варианты I—II,
I—III, I-IV) в незащищенном коридоре I окажется самолет; он уничтожа-
уничтожает объект. Значит вероятность уничтожения объекта при выборе страте-
стратегий А1 и Въ есть а13 = 1 / 2.
Разберемся теперь с вероятностями уничтожения объекта при усло-
условии, что мы выбрали стратегию А2 — по какому-то одному из коридо-
коридоров направили оба самолета. Пусть это будет коридор I (с равным успе-
успехом можно было бы выбрать любой другой коридор). Допустим,
противник при этом выберет стратегию В1 — защитит каждый коридор
одним орудием. Ясно, что для пары самолетов такая защита недоста-
недостаточна: один самолет будет, конечно, сбит, зато другой достигнет объек-
объекта. Значит, объект обязательно будет уничтожен: ап = 1. Допустим, про-
противник выбрал стратегию В2. У него шесть вариантов размещения пар
орудий по коридорам: I—II, I—III, I-IV, II-III, II—IV, III—IV. В половине
вариантов наши оба самолета будут сбиты (варианты I—II, I—III, I-IV), a
в половине вариантов оба самолета достигнут объекта (варианты II—III,
II—IV, III—IV). Следовательно, вероятность уничтожения объекта будет
равна «22 = 1 / 2. Наконец, предположим, что противник выбрал страте-
стратегию В3. Мы посылаем самолеты не поодиночке, а парами; поэтому про-
противник выиграет только в том случае, если наша пара самолетов ока-
окажется в коридоре, защищенном двумя орудиями. Вероятность того, что
это произойдет, равна 1/2. Значит, вероятность нашего выигрыша в
данном случае (вероятность уничтожения объекта) есть а1Ъ = 3 / 4.
Итак, мы нашли элементы платежной матрицы игры 2x3, в которой
два самолета-бомбардировщика выступают против четырех зенитных ору-
орудий. Эта платежная матрица, а также геометрическое представление дан-
данной игры, рассматриваемое с точки зрения нападающей стороны А, даны
на рис. 4 в таблице 14. Далее, как говорится, дело техники. Построив
соответствующие отрезки для стратегий противника Вь Въ Въ, выявляем
верхнюю границу выигрыша (ломаная B{MB{) и ее наивысшую точку
(точка М). Оказывается, активными стратегиями игрока В являются стра-
стратегии ВхжВъ так что столбец Въможно вычеркнуть из полученной ранее
платежной матрицы, после чего мы придем к матрице:
0	5/6
1	1/2
Подставляя в A2.А) и A2.В) ап = О, ап = 5 / 6, а1Х = 1, я22 = 1 / 2 нахо-
находим решение рассматриваемой игры:
5/8,1' 5=Ц/4 3/4
128

При многократном повторении игры нам выгодно выбирать стра-
стратегию А1 с вероятностью рх = 3 / 8 и стратегию А2 с вероятностью р2 = 5 / 8.
Противнику же выгодно выбирать стратегию Вх с вероятностью q1 = 1 / 4
и стратегию i?2c вероятностью д2 = 3 /4, а стратегии i?3> Ди ^5В0°бще
не следует применять. Цена игры v = 5 / 8 (вероятностью уничтоже-
уничтожения объекта есть 5 / 8, а вероятность его сохранения есть 1 -5/8 = 3/8).
Любое наше отклонение от оптимальной смешанной стратегии S/
нам невыгодно — оно может лишь привести к тому, что вероятность
уничтожения объекта окажется меньше 5/8. Любое отклонение про-
противника от оптимальной смешанной стратегии SB* ему невыгодно —
оно может лишь привести к тому, что вероятность сохранения объекта
окажется меньше 3/8. Если каждая из сторон желает действовать
целесообразно, то она должна придерживаться своей оптимальной сме-
смешанной стратегии.
4.12 Упрощение игр. Заведомо невыгодные стратегии
-Играя в «самолеты против зениток», мы существенно упростили
игру, исключив сразу же стратегии В4 и В5 как стратегии, заведомо не-
невыгодные для игрока В. С заведомо невыгодными стратегиями мы встре-
встречались также в играх, представленных на рисунках в таблице 14. Так,
заведомо невыгодны для игрока В стратегия В5яа рис. 1 и стратегия В4
на рис. 3. Заведомо невыгодны для игрока А стратегии Аь Аъ А3яа
рис. 2.
Нетрудно сообразить, что, если в платежной матрице все элементы
некоторой строки, определяющей стратегию At, не больше соответству-
соответствующих элементов какой-либо другой строки, то стратегия At является
заведомо невыгодной для игрока А. О стратегии, определяющей упомяну-
упомянутую «другую строку», говорят, что она доминирует над стратегией At.
Выбрав стратегию Ai9 игрок получит выигрыш, который будет меньше
или, в крайнем случае, будет равен выигрышу при выборе доминирую-
доминирующей стратегии. Ясно, что такой выбор заведомо невыгоден.
Если все элементы некоторого столбца, определяющего стратегию Bj,
не меньше соответствующих элементов какого-либо другого столбца,
то стратегия Bj является заведомо невыгодной для игрока В. О страте-
стратегии, определяющей «другой столбец», говорят, что она доминирует над
стратегией Bj.
129

Предположим, что нам удалось формализовать игру, т. е. привести ее
к матричной форме (составить платежную матрицу игры). После этого
следует проверить, совпадают ли нижняя и верхняя цена игры, т. е.
имеется ли в данной игре седловая точка. Если она имеется, то решение
игры определяется немедленно — это те стратегии игроков, в пересече-
пересечении которых находится седловая точка матрицы. Если игра не имеет
седловой точки, то нужно попробовать упростить ее, вычеркнув из пла-
платежной матрицы те строки и столбцы, которые отвечают заведомо не-
невыгодным стратегиям (если, конечно, таковые просматриваются). Кро-
Кроме того надо проверить, не имеются ли дублирующие стратегии, т. е.
такие стратегии, для которых все элементы одной строки равны соот-
соответствующим элементам другой (или все элементы одного столбца рав-
равны соответствующим элементам другого). Из дублирующих стратегий
достаточно сохранить в платежной матрице только одну стратегию (без-
(безразлично, какую именно).
Только после того, как произведено упрощение игры, начинается
поиск оптимальных смешанных стратегий игроков и определяется цена
игры. Иными словами, отыскивается решение игры.
Рассмотрим в качестве примера следующую платежную матрицу для
игры 4x7 (конкретная игровая ситуация, соответствующая такой матри-
матрице, в данном случае не обсуждается):
А
А2
Аз
А4
В\
2
2
4
3
В2
6
5
5
4
Вз
2
1
4
4
Я4
4
3
6
5
5
4
8
6
6
5
5
4
57
3
3
2
1
Для данной игры: ос = 2, р = 3. Следовательно, это есть игра без седло-
вой точки. Попробуем ее упростить прежде, чем начнем искать реше-
решение игры.
Легко видеть, что стратегия Ах доминирует над стратегией Аъ а стра-
стратегия Аъ доминирует над стратегией А4. Значит, стратегия А2 и А4 являются
заведомо невыгодными для игрока А. Вычеркивая эти стратегии, при-
приходим к матрице:
Аз
в,
2
4
6
5
#з
2
4
В4
4
6
5
8
Be
6
5
3
2
130

Сравнивая элементы столбцов, обнаруживаем несколько заведомо не-
невыгодных для игрока В стратегий. Это стратегии Въ В4, В5, В6; вычерки-
вычеркивая их, получаем матрицу:
А
Bi
2
4
в,
2
4
в7
3
2
Стратегии Вх и В3 оказались дублирующими; убираем одну из них, на-
например, стратегию В3. В результате мы свели игру 4x7 к игре 2x2:
А
А
в,
2
4
в7
3
2
Теперь совсем нетрудно найти решение игры — достаточно воспользо-
воспользоваться соотношениями A2.А) и A2.В). Решение игры:
= 8/3,
А А,
2/3 1/3
в, в7
1/3 2/3
Итак, оптимальная смешанная стратегия игрока А предполагает выбор им
стратегии Ах с вероятностью 2 / 3 и стратегии А 3 с вероятностью 1/3 (страте-
(стратегии А2кА4 применять не надо). Оптимальная смешанная стратегия игрока В
предполагает выбор им стратегии В{с вероятностью 1/3и стратегии В7
с вероятностью 2/3 (стратегии Въ Въ, В4, В5, В6применять не надо).
ЗАДАНИЯ ПО ТЕМЕ 4
1.	Найдите нижнюю цену а и верхнюю цену р игры и укажите максиминную страте-
стратегию игрока А и минимаксную стратегию игрока Б в играх, платежные матрицы
которых представлены на рисунках 1-7 в таблице 15.
Ответы: на рис. 1: ос = 3,	Р = 5;	стратегии А3\л В±;
на рис. 2: а = —1,	Р = 1;	стратегии А2 и Б2;
на рис. 3: а = 0,4,	Р = 0,5;	стратегии А±\л Б3;
на рис. 4: а = -5,	р = 4;	стратегии А±, А2, В±;
на рис. 5: а = 5,	Р = 16;	стратегии А±, В±, Б2;
на рис. 6: а = 4,	Р = 5;	стратегии Аъ и Б5;
на рис. 7: а = 0,8,	Р = 1,2;	стратегии Л5и Б4.
2.	Укажите заведомо невыгодные стратегии: а) на рисунке 6 в таблице 15 и) на
рисунке 7 в таблице 15.
Ответы: а) А2, А6, Б3; б) А±, А6.
131

Таблица 15. Каковы нижняя и верхняя цена игры?
\
А!
А2
А3
в.
©
©
в2
©
©
Вз
©
©
\
Ai
А2
А3
в.
©
(а)
@
в2
©
©
©
В3
©
©
©
\
Ах
А2
А3
В
<$,
1
5)
3)
6)
В
(?
2
8)
4)
2)
В
3
4)
5)
3)
Рис.1
\
А2
Аз
А4
в,
©
©
©
©
в2
©
©
©
®
В3
©
©
®
©
в4
©
®
©
®
Рис.4
\
Ах
А2
Аз
А4
А5
А,
А7
вх
©
©
©
©
©
©
©
в2
©
©
©
©
©
©
©
в,
0
©
©
©
©
©
©
в4
©
©
©
©
©
©
©
Вз
©
©
©
©
©
©
©
Рис.2
Рис.3
\
А,
А2
А3
А4
А5
В!
©
®
©
©
в2
©
©
©
©
Bj
®
@
©
©
®
в4
©
@
©
®
©
в5
®
©
®
©
®
Рис.5
Рис.6
Рис.7
132

3.	Присмотритесь внимательнее к матрице на рисунке 4 в таблице 15. Не сможете ли
предложить игру, для которой эта матрица могла бы служить платежной матрицей?
Ответ: игра «четыре пальца».
4.	Можно ли считать, что матрица на рисунке 5 в таблице 15 есть платежная матри-
матрица игры «пять пальцев»?
Ответ: можно; но при подсчете цены игры придется вычесть 10 из полученного
результата.
5.	Найдите цену игры и оптимальные смешанные стратегии для игры 2, сформулиро-
сформулированной в § 4.4.
Подсказка. Для удобства умножьте на 10 все элементы матрицы, приведенной
на рисунке 6 в таблице 11.
Ответ: v = 0,535.
Q* — ( 1	2	3 ) ,
Л~A9/52 29/52 4/52)''
5/13 7/13 1/13J1
(В, В2 В31
(9/26 6/13 5/26J'
6. Найдите цену игры и оптимальные смешанные стратегии в игре, платежная мат-
матрица которой представлена на рисунке 4 в таблице 15.
Ответ: v = О,
,*_ А
1/8 3/8 3/8 1/8
* _ в1 в2 в3 в4
1/8 3/8 3/8 1/8
7. Найдите решение игры в играх с седловой точкой, заданных следующими набора-
наборами элементов платежной матрицы:
а) э^у — 5,
а21 = 8,
а31 = 9,
б) аи = 4,
а21 = 5,
а31 = 6,
а41 = 4,
а51 = 5,
а12 = 4,
а22 = 1,
а32 = 4,
а12 = 4,
а22 = 4,
а23 = 5,
а24 = 3,
а25 = 2,
а13 = 6,
а23 = б-
а33 = 5,
а13 = 2,
а23 = 3,
а33 = 2,
а43 = 2,
а53 = 3,
а14 — 8,
а24 = ^,
а34 = 3-
а14 = 2,
а24 = 6,
а34 = 3,
а44 = 2,
а54 = 1.
а15 = 3,
а25 = 4,
а35 = 2,
а45 = 4,
а55 = 5,
Ответы: a) v = 6, оптимальные стратегии: Д2и Б3;
6) v = 3, оптимальные стратегии: Л2и Б3.
8. Найдите решение следующих игр 2x2 аналитически и графическим способом:
d} d л л — kj щ с& л о — / ¦	d о ¦I — ^^ ¦	d о о — I
о) a1:L = 2, а12 = 7,	а21 = 8,	а22 = 2;
/ 11 — ' 12 — '	21 — '	22 —
Ответы: a) v = 6,
2/3 1/3
S*B =
В, В2
1/2 1/2J'
6) v = 52/ll,
S* _
6/11 5/11
f
15/11
133

б) v = 22 / 7,
2/7 5/7J"
[4/7 3/7
9. Найдите решение следующих игр 2x4 аналитически и графическим способом:
a2'i —— о, а22 —— о,	а23 —— т",	а24 —— ^,
6) а±1 = 3, а12 = 6,	а13 = 6,	а14 = 9;
	  о 	 С\	о 	 О о 	 Л •
21 — ' 1 2.1. — '	23 — '	24 — '
б) а±1 = 4, a12 = 5f	a13 = 6f	a14 = 8;
э^л —— о, а22 —— т",	а23 ^— и,	а24 ^— ^.
Ответы: a) v = 5,
6) v = 21/5f
б) v = 9/2f
1/3 2/3J'
7/10 3/10J"
Б2 Б3
.1/2 1/2J'
?* _ | B2 B3
.3/5 2/5
A A
3/4 1/4
; s* =
"Si ^
3/4 1/4J'
10. Найдите решение следующих игр 4x2 аналитически и графическим способом:
/ 11 — ' 21 ^~ ' 31 ^~ ' 41 ^~ '
а12 = 6, а22 = 5, а32 = 4, а42 = 4;
б) а±1 = 0, а21 = 5, а31 = 8, а41 = 9,
а ^8 а ^8 а =6 а =2"
Ответы: a) v = 5,
6) v = 34 / 5,
б) v = 25 / 6,
1/2 1/2/
А А
2/5 3/5
А М
5/6 1/6.
в, в2
.1/4 3/4
2/5 3/5
В, В2
.5/12 7/12
134

ТЕМА 5
ИССЛЕДОВАНИЕ ОПЕРАЦИЙ: ИГРЫ
С «ПРИРОДОЙ», ИЛИ ПРИНЯТИЕ
СТАТИСТИЧЕСКИХ РЕШЕНИЙ
Близкой по идеям и методам к теории игр
является теория статистических решений. От
теории игр она отличается тем, что неопре-
неопределенная ситуация не имеет конфликтной
окраски — никто никому не противодейству-
противодействует, хотя элемент неопределенности налицо...
Соответствующие ситуации часто называют
«играми с природой». «Природа» мыслится
как некая незаинтересованная инстанция,
«поведение» которой неизвестно, но во вся-
всяком случае не злонамеренно.
Е.С. Вентцелъ
5.1 Особенности игр с «природой»
Как
уже говорилось, теория игр не интересуется азартными играми
(играми, в которых нет личных ходов); она интересуется играми страте-
стратегическими. Недаром одним из основных понятий этой теории является
135

понятие стратегии игрока. В антагонистических парных играх каждый
из противоборствующих игроков придерживается разумной стратегии —
он предпринимает именно те действия, которые наиболее выгодны ему
и наименее выгодны противнику.
К теории игр примыкает так называемая теория статистических ре-
решений. Здесь тоже есть игрок Л, заинтересованный в получении некоего
максимально возможного выигрыша. Однако теперь ему «противосто-
«противостоит» не игрок В, желающий максимально уменьшить выигрыш игрока А
и за счет этого обеспечить собственный успех, а некая объективная дей-
действительность, которую в данной теории принято называть природой.
При этом игрока А называют просто игроком, а также статистиком.
Можно ли, однако, говорить о противостоянии статистика и природы?
Строго говоря, противостояния как такового здесь нет, поскольку нет
двух заинтересованных сторон с противоположными целями. Есть только
одна заинтересованная (а потому активно действующая) сторона — ста-
статистик. Другая же сторона (природа) является незаинтересованной ин-
инстанцией. Ее «поведение» (точнее сказать: реализация ею тех или иных
возможных состояний) неизвестно статистику (игроку), так что тот
вынужден принимать решение в условиях неопределенности. Однако, во
всяком случае, «поведение» природы не содержит какой-либо нарочи-
нарочитой враждебности и сознательного противодействия. Это только в худо-
художественных произведениях природа иногда выступает как «сила», враж-
враждебная человеку. Вспомним у Баратынского:
Чья неприязненная сила,
Чья своевольная рука
Сгустила в тучи облака
И на краю небес ненастье зародила?
Будем полагать, что у игрока есть т возможных стратегий: Аь А2, Лъ,
А4,..., Ат, а у природы есть п возможных состояний: Nh N2, N3, N4,...,Nn.
Эти состояния будем условно называть стратегиями природы. У игрока
есть цель — выбрать такую чистую стратегию At (или такую смешанную
стратегию), которая бы обеспечивала ему наибольший выигрыш. У при-
природы, разумеется, никакой цели нет.
В принципе можно представить ситуацию в матричной форме — со-
составить матрицу выигрышей тхп (матрицу
(*)
А
А2
Ат
N1
«и
«21
«ml
N2
«12
«22
«m2
^3
«13
«23
«я,3
«14 •
«24 ¦
am4
•• «i«
¦• «2«
amn
136

Здесь atj есть выигрыш, который получит в том случае, если он выберет
стратегию Ai9 а природа реализует состояние Nj (или, условно говоря,
выберет стратегию Nj).
Казалось бы, при таком подходе теория статистических решений
превращается в некоторый вариант теории игр (ведь матрицу Ця^-Ц в (*)
можно рассматривать как платежную матрицу игры). Однако это не
так. Принципиальное отличие от теории игр связано с незаинтересо-
незаинтересованностью нашего «противника»; природа не вредит нам целенаправ-
целенаправленно и не отыскивает выгодные для себя стратегии (возможные состо-
состояния). Конечно, можно и должно говорить о том, что для природы
может быть полезно, а что вредно, и в этом смысле выгодно или невы-
невыгодно. Однако понятия собственной осознанной выгоды для природы не
существует (в отличие, разумеется, от нас, т. е. от статистика).
Отсюда следуют два важных отличия теории статистических реше-
решений от теории игр. Во-первых, здесь нам проще принять решение (коль
скоро никто нам целенаправленно не противодействует). Во-вторых,
здесь нам труднее обосновать свой выбор (именно потому, что нет це-
целенаправленного противодействия и мы не догадываемся, чего же до-
добивается наш «противник», т. е. матушка-природа). Целенаправленность
действий сознательного противника в теории игр в какой-то мере умень-
уменьшает для нас степень неопределенности. В теории же статистических
решений мы имеем дело с неопределенностью в «полной мере». Тут
возможны разные варианты. Один крайний вариант отвечает ситуации,
когда нам известны вероятности состояний природы. Будем обозначать
п
эти вероятности через Ръ Р2, Р^,..., Рп\ очевидно, что z2^j = 1- ДРУг°й
крайний вариант отвечает ситуации, когда мы ничего не знаем о вероят-
вероятностях состояний природы или, более того, когда даже понятие вероят-
вероятности, строго говоря, неприменимо. Оба эти варианта неопределеннос-
неопределенности мы обсудим позднее.
Формулируя кратко сущность различия между теорией игр и теорией
статистических решений, говорят, что в теории игр каждый игрок при-
принимает решение в условиях стратегической неопределенности, а в тео-
теории статистических решений игрок принимает решение в условиях
стохастической неопределенности. Последняя обусловлена не непред-
непредсказуемыми действиями другого игрока, а отсутствием у нас точных
знаний о тех или иных условиях проведения операции. Так, например,
мы можем не знать заранее, как сложатся погодные условия, каков бу-
будет покупательский спрос на данную продукцию, каков будет объем
перевозок или объем поставок и т. д.
137

Начиная работать с матрицей Ця^-Ц мы должны предварительно ее
«почистить», т. е. вычеркнуть заведомо невыгодные стратегии (если они
есть). В отличие от теории игр здесь могут оказаться заведомо невыгод-
невыгодными лишь какие-то из стратегий At. Что же касается «стратегий при-
природы» Nj, то они принципиально не могут быть выгодными или невы-
невыгодными. Так что теперь мы можем вычеркивать только строки матрицы
выигрышей, но никак не столбцы.
В заключение сделаем одно важное замечание. По большому счету,
задача принятия решения в играх с природой должна быть не однокри-
териальной, а многокритериальной. Мы должны учитывать не только,
насколько та или иная стратегия выигрышна для нас (экономический
критерий), но и насколько выбор той или иной нашей стратегии может
навредить природе (экологический критерий). Игры с природой должны
быть отнюдь не чисто экономическими играми, а играми эколого-эконо-
мическими. Простоты ради, мы ограничимся ниже однокритериальны-
ми играми.
5.2 Матрица рисков
теории статистических решении применяют наряду с матрицей
в
выигрышей \atj | также матрицу рисков
Поскольку игрок, выбирая ту или иную стратегию, не знает, какую
стратегию «выбрала» природа, он, естественно, в какой-то мере риску-
рискует. Величина риска зависит от того, какое из п возможных состояний
природы на самом деле реализуется при том или ином выборе игрока.
Если, например, реализуется состояние Nj9 то риск игрока, связанный
с выбором им стратегии At, принимается равным
ru = $j-
где
р • = max av .	B)
J \<i<m J
Если бы игрок знал заранее, что реализуется состояние Nj, то он выбрал
бы такую стратегию At, для которой выигрыш а у был бы наибольшим из
всех выигрышей ву-м столбце матрицы Ця^-Ц, т. е. был бы равен (Зу. В этом
случае не было бы никакого риска или, иными словами, риск сводился
бы к нулю: Гу= 0. Выбирая наугад стратегию At игрок, разумеется, рис-
рискует; при этом величина риска rtj- будет тем больше, чем меньше atj- no
сравнению с max au
\<i<m J
138

Сравните две приведенные ниже матрицы 4x6. Левая матрица — это
матрица выигрышей \\а^-\\. Правая матрица — матрица рисков Цг^Ц. Она
получена из левой матрицы с помощью соотношения A).
А
А
А,
АА
N\
2
3
6
5
N2
3
4
5
6
5
3
6
7
NA
7
8
7
6
5
2
3
6
6
5
4
5
Лз
АА
N1
4
3
0
1
N2
3
2
1
0
^3
2
4
1
0
N4
1
0
1
2
1
4
3
0
0
1
2
1
Поясним понятие риска на конкретном примере данной игры. Если
бы игрок знал, что реализуется, например, состояние N4, то в этом слу-
случае он, конечно, выбрал бы стратегию А2 и получил бы наибольший для
такого состояния природы выигрыш а24 = 8. Но игрок не знает, какое
состояние реализуется, и поэтому он принимает решение рискнуть и
выбрать стратегию наугад. (В последующих параграфах будет показано,
что наугад выбирать стратегию все-таки не нужно, поскольку можно
воспользоваться вероятностями состояний или, в крайнем случае, оп-
определенными критериями выбора). Допустим, что игрок выбрал страте-
стратегию Ах. При таком выборе его риск будет равен:
гп = 4, если окажется, что реализуется состояние Л^;
гп = 3, если окажется, что реализуется состояние N2;
г13 = 2, если окажется, что реализуется состояние N3;
гы= 1, если окажется, что реализуется состояние N4;
г15= 1, если окажется, что реализуется состояние N5;
г16 = 0, если окажется, что реализуется состояние N6.
Допустим, игрок выбрал стратегию А4. При таком выборе его риск ра-
равен нулю для трех состояний природы из шести, а для остальных состо-
состояний он равен либо 1, либо 2. При выборе стратегии А4 игрок рискует
меньше, чем при выборе стратегии Ах. Уже отсюда видно, что не следу-
следует выбирать наугад, т. е. случайным образом.
5.3 Принятие решения, когда известны вероятности
«стратегий природы»
]К1грая с природой, мы не знаем точно, какую именно из своих стра-
стратегий «выбрала» в том или ином случае природа. Приходится прини-
принимать решение в условиях неопределенности (точнее, стохастической
139

неопределенности). Однако в ряде случаев нам могут быть известны
вероятности Ръ Ръ Р^—, Рп возможных состояний (стратегий) приро-
природы. Они могут быть известны, например, на основе данных статисти-
статистических наблюдений. Если вероятности состояний известны, то опти-
оптимальная стратегия выявляется относительно просто — это есть стратегия,
соответствующая наибольшему (по сравнению с другими стратегиями) сред-
среднему значению выигрыша. Среднее значение выигрыша при выборе иг-
игроком стратегии At:
(а,-) = ааРх +ai2P2 +ai3P3 + ... +ainPn =Y;aiJPJ'
y=i
Максимальный средний выигрыш (цена игры с природой):
C)
а = max (а,-) = max
\<i<m	\<i<m
п
2JV;
D)
Оптимальной стратегией можно считать также ту стратегию, которая
соответствует наименьшему (по сравнению с другими стратегиями) сред-
среднему значению риска. Среднее значение риска при выборе игроком стра-
стратегии At:
г-) -
i/ —
г Р
v J*
E)
У = 1
Минимальный средний риск:
г = min (rf) = min
\<i<m	\<i<m
F)
Убедимся, что оптимальная стратегия, определенная по максимуму
выигрыша, и оптимальная стратегия, определенная по минимуму рис-
риска, — это одна и та же стратегия. Рассмотрим сумму <az) + (rt). Исполь-
Используя C), E), A), находим:
где через С обозначена постоянная величина. Отсюда видно, что, если
<az) обращается в максимум, то (rt) принимает минимальное значение.
140

Воспользуемся матрицами \\ay\\ и ||г^|| из предыдущего параграфа. Для
простоты предположим, что все состояния системы имеют одну и ту же
вероятность (такое предположение принято называть принципом недо-
недостаточного основания Лапласа). Итак, Р{ = Р2 = Р3 = Р4 = Р5 = Р6 = 1/6.
В этом случае значения <az) для Аь Аъ Аъ, А4 равны, соответственно,
4,67; 4,17; 5,17; 5,83; max (а,) = 5,83 . Оптимальная стратегия есть стра-
1</<4
тегия А4\ выбирая ее, игрок получает выигрыш 5,83. Значения (rt) для
Аъ Аъ Аъ, А4 равны, соответственно, 1,83; 2,33; 1,33; 0,67; min (rt) = 0,67 .
l</<4
Как видим, и при рассмотрении матрицы риска оптимальная стратегия
есть стратегия А4\ выбирая ее, рискуем меньше всего.
Обратим внимание на то, что полученная оптимальная стратегия яв-
является чистой стратегией. Есть правило: если известны вероятности
состояний природы, то пользоваться смешанными стратегиями игроку
нет смысла — любая смешанная стратегия обеспечит игрока средним
выигрышем, который не будет превышать (а скорее всего окажется
меньше) среднего выигрыша, получаемого при выборе оптимальной чи-
чистой стратегии. Это правило нетрудно доказать. Возьмем какую-нибудь
(Ах А2 ... Ат
смешанную стратегию SA =
\Р\ Pi '" Рт
выигрыш а, усредненный не только по п возможным состояниям при-
природы, но и по т чистым стратегиям игрока:
и рассмотрим средний
а = (а1)р1+(а2)р2+(а3)р3+... + (ат)рт.
Пусть оптимальная чистая стратегия есть стратегия Ах и, значит,
= max (aj) =oc.
\<i<m
Учитывая это, перепишем G) в виде:
а = сфх +(ос2)/?2 +(а3)/?3
Поскольку а > <а2), а > <а3),..., а > <ат), то, заменив дроби (ос2}/ос, (ос3}/а,
..., (а2}/а на единицы, мы можем лишь увеличить или, в крайнем слу-
случае, оставить без изменения выражение в скобках в (*). Следовательно,
Pi (ос2)/а + ръ (а3)/а +... + рт (ат>/а) <
<a(pi +p2 +... + рт) = а.	(**)
141

Сопоставляя (*) и (**), находим, что
а < а = max (а,) .	(8)
\<i<m
Это и требовалось доказать.
5.4 Какой из участков следует выбрать
под посадку картофеля?
]К1меются четыре участка, одинаковые по площади, но разные по
степени влажности почвы: участок I с повышенной влажностью,
участок II со средней влажностью, участок III с пониженной влажнос-
влажностью, участок IV с особенно низкой влажностью. Нам предстоит выб-
выбрать участок под посадку картофеля. У нас четыре стратегии: Ah Аъ Аъ, А4,
отвечающие выбору участков I, II, III, IV, соответственно. Для получе-
получения хорошего урожая картофеля требуется определенное количество
влаги в почве в период вегетации. При излишней влажности картофель
может частично сгнить на корню и, кроме того, может быть сильно
забит сорняками. При недостатке влаги в почве картофель будет плохо
развиваться. Выделим три состояния природы: N{ — в период вегета-
вегетации выпало много осадков, заметно больше нормы; N2 — осадки в нор-
норме; N3 — осадков заметно меньше нормы. Средняя урожайность карто-
картофеля на одном аре, т.е. на ста квадратных метрах, различна для разных
участков и для разных погодных условий. Усреднение здесь предпола-
предполагается по площади участка, которая может измеряться большим числом
аров. Предположим, что указанная средняя урожайность картофеля
описывается следующей матрицей \\aif\\:
А
А2
Аз
А4
1
1,2
2
1,8
N2
2
2,3
2,2
1,4
2,4
2
1
0,5
(*)
Здесь ау — средняя урожайность картофеля в центнерах на ар для /-го
участка при условии, что погода реализовала состояние Nj.
Стратегия А4 (выбор участка IV) является заведомо невыгодной стра-
стратегией; над ней доминирует стратегия А3. Значит, сажать картофель на
142

А
А2
А
1
1,2
2
N2
2
2,3
2,2
N2
2,4
2
1
участке IV заведомо невыгодно. После вычеркивания стратегии А4 мат-
матрица (*) упрощается:
(**)
Теперь стратегия N2 формально доминирует над стратегией Nx (все
элементы 2-го столбца больше соответствующих элементов 1-го столб-
столбца). Однако считать стратегию Nx заведомо невыгодной (и на этом ос-
основании вычеркнуть ее) нельзя, поскольку это есть стратегия природы,
а природа, как уже отмечалось, не различает выгодные и невыгодные
стратегии.
Предположим, что многолетние метеонаблюдения в данной местно-
местности позволяют оценить вероятности состояний Nh Nb N3. Пусть Рх = 0,2,
Р2 = 0,3, Р3 = 0,5. В этом случае находим с учетом (**) следующие сред-
средние (усредненные по состояниям природы) значения выигрыша:
при выборе стратегии Ах\ (о^} = 2
при выборе стратегии А2\ (а2) =1,93,
при выборе стратегии Аъ\ <а3) = 1,52.
Оптимальной стратегией является, таким образом, стратегия Ах. Следу-
Следует принять решение засадить картофелем участок I. Определенно не
следует выбирать участок III.
Предположим, что Рх = 0,3, Р2 = 0,4, Ръ = 0,3. В этом случае: (о^} = 1,82;
(а2) = 1,88; (ос3) = 1,72. Значит, следует выбрать под посадку картофеля
участок П.
5.5 Критерии выбора решения
в отсутствие вероятностей «стратегий природы»
ели вероятности состояний природы нам не известны даже при-
приблизительно (или понятие вероятности состояний в данной ситуации
вообще неприменимо), можно рискнуть выбрать разумную стратегию,
используя критерии, называемые в теории статистических решений кри-
критериями Вальда, Гурвица, Сэвиджа.
5.5.1. Максиминный критерий Вальда. В качестве наиболее разумной
стратегии этот критерий предлагает стратегию, которая гарантирует
143

игроку (статистику) наибольший выигрыш в наихудших возможных усло-
условиях. Этот выигрыш выражается уже знакомой нам формулой:
а = max min ajh	(9)
\<i<m \<j<n J
определяющей не что иное, как максиминную стратегию игрока. Ве-
Величина а играет роль нижней цены игры с природой. Используя дан-
данный критерий, игрок придерживается позиции «крайнего пессимиз-
пессимизма» (хуже этого не будет!). Такая позиция игрока понятна, если он
очень боится проиграть и, не желая рисковать, предпочитает пере-
перестраховаться.
5.5.2. Критерий пессимизма-оптимизма Гурвица. Конечно, крайнему
пессимизму можно противопоставить крайний оптимизм и выбирать ту
стратегию, для которой выигрыш может оказаться (при счастливом рас-
раскладе состояний природы) наибольшим как для всех п состояний, так и
для всех т возможных чистых стратегий игрока:
а' = max min afi.	A0)
\<i<m \<j<n J
Такой оптимизм выглядит весьма легкомысленным (авось повезет!).
Поэтому подобный критерий выбора решений практически не приме-
применяется. Зато применяется критерий «умеренного оптимизма», который
называют критерием пессимизма-оптимизма Гурвица (а также критерием
обобщенного максимума). Он рекомендует выбирать стратегию, для ко-
которой выигрыш у удовлетворяет соотношению:
у = max
\<i<m
X min aif + (l-X) max a
\<j<n J	l<j<n
A1)
где X — некоторый параметр @ < X < 1), задаваемый подчас из сообра-
соображений правдоподобия, здравого смысла или просто из интуитивных со-
соображений. Его называют коэффициентом пессимизма. При X = 0 соот-
соотношение A1) превращается в A0) (у=ос'; это соответствует позиции
крайнего оптимизма). При Х= 1 соотношение A1) превращается в (9)
(у = а; это соответствует позиции крайнего пессимизма). Чем больше
игрок желает подстраховаться при выборе разумной стратегии, тем бли-
ближе к единице задает он X.
Итак, допустим, что X выбран. После этого мы должны для каждой
стратегии At (/= 1, 2, 3,..., т) выполнить две операции: найти для всех
п состояний наибольший выигрыш max аИ и найти для всех п состоя-
\<j<n J
144

ний наименьший выигрыш min я,7. Затем вычисляем для выбранного
\<j<n J
значения X величину
/ = X min an +A-X) max an
\<j<n J	l<j<n J
A2)
и, наконец, отыскиваем ту из т стратегий, для которой ^ оказывается
наибольшим, т. е. равным у = max ?,-. Вот эту стратегию и рекомендует
\<i<m
выбирать критерий Гурвица.
5.5.3. Критерий минимаксного риска Сэвиджа. Этот критерий, как и
критерий Вальда, нужно отнести к крайне пессимистическому. Просто
он рекомендует ориентироваться при выборе наиболее разумной стра-
стратегии не на выигрыш, а на риск. Точнее говоря, он рекомендует выби-
выбирать ту стратегию, при которой величина риска будет минимальной даже
в наихудших условиях, т. е. будет равна
г — mm max rz7.
\<i<m \<j<n J
A3)
5.6 Три критерия и задача с посадкой картофеля
)ернемся к задаче выбора стратегии, обсуждавшейся в § 5.4. Пред-
Предположим, что мы не располагаем данными о вероятностях состояний
погоды (или просто не доверяем этим данным). Будем пользоваться
приводившейся в § 5.4 платежной матрицей (**).
Сначала обратимся за помощью к критерию Вальда. Для стратегий Аь
Аъ Аъ величина min atj принимает значения 1, 1,2 и 1, соответственно.
Наибольшее из этих значений равно 1,2; оно получается для стратегии
А2. Значит, рекомендуемой по Вальду стратегией является стратегия А2.
Далее обратимся к критерию Гурвица. Выбирая А,, не будем отдавать
предпочтения ни пессимизму, ни оптимизму и положим X = 0,5. Впрочем,
не помешает немного подстраховаться и рассмотреть также случай с X = 0,7.
Используя платежную матрицу (**) из § 5.4, составим следующую таблицу:
min а и
1</<3 J
max a a
1</<3 J
t,i для X = 0,5
\i для X - 0,7
Ai
1
2,4
1,7
1,42
А2
1,2
2,3
Аз
1
2,2
1,6
1,36
145

Мы видим, что при X = 0,5 критерий Гурвица рекомендует выбрать стра-
стратегию А2. Такую же стратегию рекомендует этот критерий и при X = 0,7.
Наконец, воспользуемся критерием Сэеиджа. Предварительно выпи-
выпишем матрицу рисков |rJ , исходя из матрицы (**) и используя A):
А
А2
А2
1
0,8
0
N2
0,3
0
од
0
0,4
1,4
Величина max rfi принимает для /= 1, 2, 3 значения, равные, соответ-
1</<3
ственно, 1, 0,8, 1,4. Наименьшее значение равно г =0,8. Такой риск
соответствует выбору стратегии А2.
Итак, в рассмотренной «картофельной» задаче все три критерия с
завидным единодушием рекомендуют выбрать стратегию Аъ т. е. реко-
рекомендуют выбрать под посадку картофеля участок П.
5.7 Три критерия и задача с заказом товара
руководству некоторого универмага нужно принять решение о за-
заказе того или иного количества экземпляров некоторого изделия для
продажи в универмаге. Специалисты по маркетингу утверждают, что
спрос на это изделие лежит в пределах от 6 до 10 экземпляров. Покупа-
Покупательский спрос выступает в данном случае в качестве «природы», кото-
которую можно охарактеризовать пятью состояниями: Nx = 6, N2 = 7, N3 = 8,
N4 = 9, N5 = 10. Руководству предстоит принять решение, сколько именно
экземпляров рассматриваемого изделия надо заказать: шесть (соответ-
(соответствует выбору стратегии А{), семь (стратегия А2), восемь (стратегия А$),
девять (стратегия А4), десять (стратегия А5). Если спрос окажется меньше
заказанного (и потому имеющегося в наличии) количества экземпляров,
то нереализованный товар поступит на склад; его хранение обойдется
универмагу в 1 условную денежную единицу за каждый нереализован-
нереализованный экземпляр изделия. Если спрос, напротив, окажется больше зака-
заказанного количества экземпляров, то потребуются срочный дополнитель-
дополнительный заказ и доставка недостающих экземпляров. Это обойдется
универмагу в 2 условных денежных единицы за экземпляр. Руководство
универмага заинтересовано в том, чтобы минимизировать выплаты за
хранение на складе, а также за срочный заказ и доставку изделий.
146

Нетрудно составить платежную матрицу \\afj | и соответствующую ей
матрицу рисков ||г^|| для данной «игры с природой» (точнее, «игры» руко-
руководства универмага с потребительским спросом). Эти матрицы таковы:
А
А2
Аъ
АА
А,
Ni
0
-1
-2
-3
-4
N2
-2
0
-1
-2
-3
-4
-2
0
-1
-2
N4
-6
-4
-2
0
-1
-8
-6;
-4
-2
0
\ы\
А
А2
Аз
А4
А5
*i
0
1
2
3
4
^2
2
0
1
2
3
^3
4
2
0
1
2
6
4
2
0
1
8
6
4
2
0
Здесь \\cijj\\ — количество условных денежных единиц, выплачиваемых
универмагом в том случае, если руководство универмага выбрало стра-
стратегию At, а покупательский спрос «выбрал» стратегию Nj. Впрочем, лучше
говорить не о «выборе стратегий» покупательским спросом, а о реали-
реализации того или иного «состояния» покупательского спроса.
Посмотрим, какие стратегии должно выбрать руководство универма-
универмага, используя тот или иной критерий. Предварительно составим на ос-
основе представленных выше матриц
а А и
г А следующую таблицу:
max пц
1<У<5 J
min a a
l</<5 J
max Гц
1<У<5 J
Ах
0
-8
8
-8А,
А2
0
-4
6
-4А,
Аз
0
-2
4
-2Х,
А4
0
-з
3
-ЗА,
0
-4
4
-4А,
Нетрудно убедиться, что на основании критерия Вальда следует выб-
выбрать стратегию Аъ (заказать 8 экземпляров изделия), поскольку именно
для этой стратегии величина min aif достигает максимума (он равен
1<у<5
-2). На основании критерия Сэеиджа следует выбрать стратегию А4 (за-
(заказать 9 экземпляров изделия), поскольку именно для этой стратегии
величина max rn обращается в минимум (он равен 3). На основании
l</<5 J
критерия Гуреица предпочтительна стратегия Аъ, причем при любых А,,
удовлетворяющих неравенствам 0 < X < 1. Понятно, что руководство уни-
универмага будет считать оптимальной стратегию Аъ и закажет 8 экземпля-
экземпляров изделия.
147

Заметим, что, если бы мы предположили равновероятность покупки
шести, семи, восьми, девяти и десяти изделий (т.е. исходили бы из прин-
принципа недостаточного основания Лапласа), то пришли бы к любопытно-
любопытному выводу. В этом случае все пять стратегий At оказались бы в равной
мере «оптимальными». Такой вывод следует из того, что max au = О
1<У<5
для всех Аг . Специалисты по маркетингу будут, естественно, категори-
категорически не согласны с ним. И будут правы.
ЗАДАНИЯ ПО ТЕМЕ 5
1. Дана следующая матрица рисков в игре 2x3:
Известно, что Р± = 3, Р2 = ~2, Р3 = 1- Постройте платежную матрицу.
Подсказка. Согласно A), можем представить: а/;= Р;- г/;. Воспользуйтесь этим со-
соотношением.
Ответ:
2.	Элементы платежной матрицы игры 2x2 таковы: а1± = 5, а12 = 3, а21 = 4, а22 = 6.
Найдите вероятности состояний природы Р± и Р2, если известно, что при исполь-
использовании оптимальной стратегии игрок получает выигрыш, равный 11/2. Найди-
Найдите также оптимальную стратегию.
Ответ: Р± = 1/4, Р2 = 3/4. Оптимальная стратегия — стратегия А2.
3.	Платежная матрица ||а/7| имеет вид:
3
1
-6
-2
-2
1
А
А2
Аз
А4
А5
Л/1
7
2
3
4
5
Л/2
7
3
2
5
3
Л/3
9
5
5
6
4
А/4
4
6
3
6
5
5
3
4
7
3
л/6
3
5
6
5
6
Найдите заведомо невыгодные стратегии, если таковые имеются. Определите
оптимальную стратегию, если известно, что вероятности всех шести состояний
равны.
Ответ: А2 — заведомо невыгодная стратегия. Оптимальная стратегия — страте-
стратегия А±; при выборе ее игрок получает средний выигрыш 5,83.
4. Платежная матрица имеет вид, представленный в задании 3. Известно, что
Р± = Р6 = 1/24, Р2 = Р3 = Р5 = 1 / 6. Подсчитайте средние выигрыши, получае-
получаемые при выборе различных стратегий. Найдите оптимальную стратегию.
Ответ: (а±) = 5,59; (а2) = 4,63; (а3) = 3,54; (а4) = 5,88; (а5) = 4,21.
Оптимальная стратегия — стратегия А4.
148

5.	Платежная матрица имеет вид, представленный в задании 3. Вероятности состоя-
состояний природы неизвестны. Найдите оптимальные стратегии из критерия Вальда и
из критерия Сэвиджа.
Ответы: из критерия Вальда — оптимальная стратегия есть А4;
из критерия Сэвиджа — оптимальные стратегии — A±v\ A4.
6.	Платежная матрица имеет вид, представленный в задании 3. Используя крите-
критерий Гурвица, найдите оптимальные стратегии:
а) при Х = 0,5, б) при Х = 0,8.
Ответы: а) стратегия А±, б) стратегия А4.
7.	В игре, рассмотренной в § 5.4, найдите оптимальную стратегию, используя кри-
критерий Гурвица при Х = 0,2. Вычислите ^ (/= 1, 2, 3)
Ответ: стратегия А±; ?± = 2,12, ^2 = 2,08, ^3 = !>96-
149

ТЕМА 6
«РАБОТАЮЩАЯ СЛУЧАЙНОСТЬ»
(МЕТОД МОНТЕ-КАРЛО)
В чем суть метода Монте-Карло? Если
очень коротко, то она заключается в исполь-
использовании случайности для расчетов.
Л.А. Растригин
При моделировании случайных явлений
методом Монте-Карло мы пользуемся самой
случайностью как аппаратом исследования,
заставляем ее «работать на нас»...
Е. С. Вентцелъ
Во-первых, метод Монте-Карло позволяет
моделировать любой процесс, на протекание
которого влияют случайные факторы. Во-
вторых, для многих математических задач,
не связанных с какими-либо случайностя-
случайностями, можно искусственно придумать вероят-
вероятностную модель, позволяющую решать эти
задачи. Таким образом, можно говорить о
методе Монте-Карло как об универсальном
методе решения математических задач.
ИМ. Соболь
150

6.1 Что такое «метод Монте-Карло»?
lVloHTe-Карло — это город в крохотном (площадью всего в 2 км2)
княжестве Монако, расположенном в Средиземноморье на берегу Ли-
Лигурийского моря на границе Франции и Италии. Монте-Карло широко
известен крупнейшими в мире игорными домами со знаменитой рулет-
рулеткой. Никакими математическими исследованиями этот город никогда
не славился. Однако в 1949 году в одном из научных журналов появи-
появилась статья с кратким названием «Метод Монте-Карло». Ее авторы,
американские математики Н. Метрополис и С. Улам, так назвали пред-
предложенный ими метод решения математических задач при помощи мо-
моделирования случайных величин, имея в виду монте-карловскую рулет-
рулетку — прекрасный генератор случайных чисел. Такое экстравагантное
название научного метода прижилось и вскоре стало широко использо-
использоваться в научной литературе.
Наряду со «строгими» названиями данного метода: метод статисти-
статистического моделирования и метод статистических испытаний. Иногда спра-
спрашивают: «Помогает ли метод Монте-Карло выигрывать в рулетку?» От-
Ответ однозначен: нет, не помогает и не может помочь. Более того, вообще
не занимается этим.
Что же представляет собой метод Монте-Карло (он же: метод стати-
статистических испытаний и метод статистического моделирования)?
В книге автора «Случайность, необходимость, вероятность» немало
говорилось о том, что случайность должна рассматриваться не только в
качестве нашего противника (нарушителя наших планов, разрушителя
порядка), но также в качестве нашего союзника. Метод Монте-Карло —
хороший тому пример, поскольку он основывается на использовании слу-
случайности для решения тех или иных математических задач. Можно ска-
сказать, что, применяя этот метод, мы заставляем случайность «работать
на нас», используем ее в роли нашего активного помощника при реше-
решении различных задач.
Конечно, прежде всего (и главным образом) имеются в виду задачи,
в которых рассматриваются случайные факторы; будем называть их ве-
вероятностными задачами. Вместе с тем метод Монте-Карло может ис-
использоваться также и при решении многих задач, не связанных с каки-
какими-либо случайностями. Одну из таких задач мы подробно рассмотрели
в книге «Случайность, необходимость, вероятность» — см. там § 7.5,
пункт 7.5.2 («Случайные числа и число л»). Правда, мы не упоминали там
о методе Монте-Карло и рассматривали задачу нахождения числа тг через
вычисление площади четверти круга как пример, иллюстрирующий одно
151

из возможных применений таблицы случайных чисел. А между тем эта
задача решалась именно методом Монте-Карло. Мы определили про-
программу единичного розыгрыша: надо было получить {разыграть) случай-
случайную точку в квадрате и проверить, попадет ли она в четверть круга.
Розыгрыш мог быть организован по-разному. Можно, например, слу-
случайным образом бросить песчинку на лист бумаги с чертежом квадрата
и вписанной в него четвертью круга. Но можно (и это много удобнее)
воспользоваться таблицей случайных чисел, взяв оттуда координаты
случайной точки. Именно такой розыгрыш и производился в упомяну-
упомянутом пункте 7.5.2. Разумеется, сам по себе единичный розыгрыш (единич-
(единичное испытание) проблемы не решает. Метод Монте-Карло предполагает
многократное повторение однотипных розыгрышей. Он предполагает
многократные испытания. Недаром этот метод называют также методом
статистических испытаний. В упомянутом пункте 7.5.2 испытания вы-
выполнялись 100 раз, в результате чего для числа тг было найдено значе-
значение 3,12. При большем числе испытаний метод Монте-Карло позволил
бы найти значение числа тг с большей точностью.
Таблица 16 — это заготовка для самостоятельного нахождения чита-
читателем числа л по методу Монте-Карло. Выполните сначала 15, а потом
150 испытаний; сравните результаты.
Итак, определение программы единичного розыгрыша (единичной
случайной реализации моделируемого явления) и затем многократное
повторение розыгрыша, выполняемое или в физическом опыте, или с
использованием таблицы случайных чисел — вот два принципиальных
момента, характеризующих метод Монте-Карло. Именно при много-
многократном повторении розыгрыша неуправляемая случайность начинает
фактически «работать на нас». Легко сообразить, что это полностью
согласуется с неоднократно отмечавшейся идеей об обнаружении зако-
закономерности (необходимости) в «толпе случайностей». Напомним так-
также, что на этой идее основывается понятие статистической устойчиво-
устойчивости и, как следствие, закон больших чисел.
Пример с числом тг — это не более как демонстрация возможности
использовать метод Монте-Карло для нахождения площади фигуры. На
практике для вычисления площади плоских фигур этот метод не ис-
используют; применяют иные методы, хотя и сложные, но зато более точ-
точные. Впрочем приведенный пример позволяет понять, в принципе, как
с помощью метода Монте-Карло можно было бы найти объем тела и,
более того, «объем тела» в многомерном пространстве. В таких случаях
метод Монте-Карло оказывается единственным численным методом,
позволяющим решить задачу.
152

Таблица 16. Самостоятельный поиск числа п методом Монте-Карло
4467
4889
2335
4862
4635
3187
6727
7013
1562
0754
1392
6301
4153
9849
9785
8453
5161
8951
9764
9565
4105
2851
4171
5765
8791
2302
2423
5228
1402
3497
4558
8269
7489
8081
5081
9828
3961
9123
3384
3145
0944
1281
9690
9115
6447
5320
4647
6993
6919
2254
1596
0368
8288
0756
2013
9651
0650
4125
5579
4471
9224
8144
6006
9910
2627
7802
7956
8851
5392
0466
6265
1863
6650
0159
8900
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
6271
8638
1736
7791
7959
3180
2304
9928
2986
7526
7877
9182
8567
2260
7852
2523
0010
0063
2837
8865
6859
0604
6560
6346
0927
1023
5998
6380
9844
3724
0709
4331
6157
3135
5704
9403
4746
4785
5761
0830
8922
0400
9854
4171
2873
3384
7429
0174
5848
0653
4312
5580
4631
9869
2222
4413
2611
2544
9886
5678
2607
0307
3775
8941
3682
4499
8417
2439
2018
6610
4733
9032
5045
1314
5843
0655
5255
6314
3157
9052
4105
1437
4064
1037
5718
5127
9401
4064
5458
2461
9265
7516
9284
7730
1970
6692
7264
9659
3333
7300
3756
0653
1014
7894
9307
6675
1126
1787
6256
627S
559С
0247
1863
8967
6298
2436
551S
0228
905С
3371
7989
6345
2391
1303
6307
2455
0583
0532
3383
6673
2408
9720
5460
1378
3243
3759
5059
5618
4081
4977
6463
7942
3199
0639
5951
5707
4745
3294
3756
4738
4320
3466
9313
5179
ЗОЮ
9599
4242
3585
5950
8462
0456
0672
5163
4995
6751
5592
4576
4245
6503
7935
3963
7679
6313
3016
6406
4477
0111
2835
2220
2958
2545
9926
2464
3361
3300
8740
6247
5014
0276
6582
3058
8697
0413
5273
4991
4436
7429
2575
0109
9979
6666
4911
6328
4503
8605
2545
5409
3043
1293
6458
3431
7746
0146
4754
0501
1609
2482
7619
2007
7427
5441
7979
3674
9795
3996
—*..
0,1
—-—
--—
0,2
0,3
0,4
0,5
\
\
0,6
ч
\
Ч
\
0,7
Ч
\
\
0,8
\
\
\
\
\
0,9
V
\
\
\
1
153

Как уже отмечалось, основная область применения метода Монте-
Карло — это задачи, в которых присутствуют случайные факторы. Ве-
Вероятностные задачи могут быть решены либо аналитически (с примене-
применением аппарата теории вероятностей), либо численно (с применением
метода Монте-Карло). В качестве конкретного примера рассмотрим
следующую достаточно простую задачу.
Производится сборка изделия из четырех одинаковых деталей. Дета-
Детали изготавливают цех I и цех П. Цех I изготавливает детали с неболь-
небольшим отрицательным отклонением их размера от номинала, а цех II — с
небольшим положительным отклонением. Известно, что 60% всех дета-
деталей поставляет цех I, а 40% — цех П. Все детали складываются в беспо-
беспорядке в один большой ящик, откуда сборщик берет наугад всякий раз
по четыре детали. Если все четыре или три детали из четырех оказыва-
оказываются с положительным отклонением от номинала, то собранное из них
изделие нормально функционировать не будет. Какова вероятность сбор-
сборки нормально функционирующего изделия?
Сначала рассмотрим аналитическое решение данной задачи. Вероят-
Вероятность того, что наугад вынутая из ящика деталь будет иметь положитель-
положительное отклонение, есть р+ = 0,4, а отрицательное отклонение — р_ = 0,6.
Вероятность того, что все четыре детали будут с положительным откло-
отклонением, есть р+. Вероятность того, что из четырех наугад взятых дета-
деталей три окажутся с положительным отклонением, а одна с отрицатель-
отрицательным, есть С}р1р_, где С43 — число сочетаний из четырех по три.
Вероятность того, что собранное из четырех наугад взятых деталей из-
изделие не будет нормально функционировать, есть р+ + С^р+р_. Значит,
искомая вероятность р есть
Подставляя сюда /?+ = 0,4 и /?_ = 0,6, находим:
р = 1 - @,44 + 4 • 0,43 • 0,6) = 1 - 0,1792 = 0,8208.
А теперь решим эту же задачу методом Монте-Карло. Нам нужно
организовать розыгрыш так, чтобы его условный результат имел вероят-
вероятность, равную вероятности соответствующего случайного события. Та-
Таким событием в данном случае будем считать событие А — случайно
вынута деталь с положительным отклонением от номинала; вероятность
события А есть р+ = 0,4. Событие, представляющее собой случайное
вынимание детали с отрицательным отклонением, можно рассматри-
рассматривать как противоположное событие А; его вероятность есть р_ = 0,6.
154

Розыгрыши организуем с помощью таблицы случайных чисел. Условим-
Условимся считать, что цифры 0, 1, 2, 3, 4, 5 в таблице соответствуют деталям
с отрицательным отклонением, а цифры 6, 7, 8, 9 — деталям с положи-
положительным отклонением. Каждая цифра появляется в таблице случайно с
вероятностью ОД. Следовательно, вероятность появления в таблице или
нуля, или единицы, или двойки, или тройки, или четверки, или пятер-
пятерки равна 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 = 0,6. Это есть вероятность на-
наступления события А . Вероятность появления в таблице или шестерки,
или семерки, или восьмерки, или девятки равна 0,1 + 0,1 + 0,1 + 0,1 = 0,4.
Это есть вероятность наступления события А.
Воспользуемся таблицей случайных чисел, приведенной на рис. 1 в
таблице 17. Весьма кстати то, что все цифры здесь разбиты на группы
по четыре цифры в каждой группе. Ведь для сборки каждого изделия
нужны четыре детали. В целом процесс разыгрывания организуется
следующим образом. Берем четверку цифр из нашей таблицы и смот-
смотрим, каким деталям соответствуют цифры, встречающиеся в данной
четверке. Если три раза или все четыре раза встречаются цифры, соответ-
соответствующие деталям с положительным отклонением, то данное изделие
будем считать бракованным. Мы обнаруживаем, что в нашей таблице
такие четверки (и, следовательно, бракованные изделия) встретились
49 раз — см. подчеркнутые четверки на рис. 1 в таблице 17. Всего
здесь имеем 300 четверок. Поделив 49 на 300, получаем 0,1633. От-
Отсюда находим, что искомая вероятность р приблизительно равна
/?« 1 — 0,1633 = 0,8367. (Напомним, что аналитическое решение дало
результат 0,8208.)
По-видимому, уместно напомнить нашу беседу в § 4.3, где использо-
использовалось понятие жребия. Там рассматривались разные способы бросания
(лучше сказать: разыгрывания) жребия в связи с проблемой организации
на практике случайного выбора той или иной стратегии с той или иной
вероятностью. Случайный розыгрыш, условный результат которого ре-
реализуется с определенной вероятностью, — это и есть как раз разыгры-
разыгрывание соответствующим образом организованного жребия.
Но вернемся к нашей задаче со сборкой изделия из четырех деталей.
Мы решили ее двумя способами. Наверное, читатель сделает вывод не в
пользу метода Монте-Карло. Проверять 300 четверок цифр — занятие
достаточно утомительное. А результат, как видим, не блещет точнос-
точностью. Значительно проще (и к тому же абсолютно точно) можно вычис-
вычислить вероятность р аналитическим способом с использованием соот-
соответствующих правил теории вероятностей.
155

Таблица 17. Метод Монте-Карло
156

Читатель совершенно прав. Мы привели здесь оба метода решения
конкретной вероятностной задачи лишь для того, чтобы более наглядно
представить сущность метода Монте-Карло. Разумеется, если не со-
составляет особого труда решить вероятностную задачу аналитически,
никто не станет прибегать к методу Монте-Карло. К сожалению, не-
нередко аналитическое решение или необычайно затруднено, или прак-
практически вообще невозможно из-за необходимости учитывать большое
число разных факторов. Вот тогда приходится применять метод Монте-
Карло (как правило, в сочетании с теми или иными аналитическими
расчетами). При этом для организации розыгрыша применяют на прак-
практике не таблицу случайных чисел, предполагающую работу вручную, а
современные быстродействующие компьютеры. Именно благодаря раз-
развитию современной электронной вычислительной техники метод Мон-
Монте-Карло находит в наши дни весьма широкое применение.
6.2 Единичный жребий (розыгрыш) как основной элемент
СТАТИСТИЧЕСКОЙ МОДЕЛИ
^Действуя по методу Монте-Карло, мы многократно разыгрываем жре-
жребий. Не будет лишним дать дополнительные разъяснения по поводу того,
как организуется такой акт.
Начнем с цитаты, взятой нами из книги Е.С. Вентцель «Исследова-
«Исследование операций: задачи, принципы, методология» (М.: «Наука», 1980):
«Основным элементом, из совокупности которых складывается статис-
статистическая модель, является одна случайная реализация моделируемого
явления... Отдельная реализация разыгрывается с помощью специаль-
специально разработанной процедуры, в которой важную роль играет «бросание
жребия». Каждый раз, когда в ход явления вмешивается случай, его
влияние учитывается не расчетом, а жребием».
Чтобы разыграть жребий, нужно воспользоваться каким-нибудь ме-
механизмом случайного выбора — бросанием монеты или игрального куби-
кубика, выниманием наугад шарика из мешка или барабана лототрона, вы-
выбором цифры или групп цифр из таблицы случайных чисел и т.п.
Допустим, мы разыгрываем жребий с целью выяснить, произошло
или не произошло некоторое случайное событие А, имеющее вероят-
вероятность р. Непосредственно за самим событием мы в данном случае не
следим; имеется в виду имитация данного события с помощью соответ-
соответствующего розыгрыша. В данном случае нужно организовать розыгрыш
157

так, чтобы его условный результат имел вероятность/?. Если, например,
вероятность наступления события А равна 1/2, то можно воспользо-
воспользоваться бросанием монеты (условившись считать, что событие А насту-
наступило, если монета выпала, скажем, орлом вверх) или бросанием иг-
игрального кубика (условившись считать, что событие А наступило, если
кубик выпал, скажем, гранью с нечетным числом очков). Можно было
бы воспользоваться также таблицей случайных чисел, условившись счи-
считать, что событие А наступило, если мы попали, например, на нечет-
нечетную цифру. Если событие А имеет вероятность 1/3 (или 2/3, или 1/6,
или 5/6), то для розыгрыша (для бросания жребия) очень подходит
бросание игрального кубика. Если событие А имеет вероятность р = т/ п,
где т и п — натуральные числа, то в качестве механизма случайного
выбора удобно выбрать мешок, внутри которого находятся т белых и п
черных шаров. Вместо мешка можно воспользоваться вращающимся
барабаном с перенумерованными шариками (шарики надо перенумеро-
перенумеровать от 1 до т + п).
Розыгрыш со случайным исходом, называемый единичным жребием,
позволяет ответить на следующие принципиальные вопросы.
Вопрос первый: произошло или не произошло случайное событие А! Этот
вопрос можно сформулировать иначе: какое из двух событий произош-
произошло — событие А или противоположное событие А ? Предполагается, что
известна вероятность р события А. В задаче со сборкой изделия (см.
предыдущий параграф) было показано для конкретной ситуации, как
можно получить ответ на такой вопрос.
Вопрос второй: какое из случайных событий Аъ Аъ Аъ,..., Ak произошло?
Предполагается, что эти события имеют вероятности ръ ръ р3,..., рк и
образуют полную группу. Напомним, что для полной группы событий:
Р1+Р2+Рз+- + Рк =!•	(*)
Отвечая на первый вопрос, мы разыгрываем взаимно противополож-
противоположные события. Отвечая на второй вопрос, мы разыгрываем полную группу
событий, состоящую из к событий. Легко сообразить, что первый во-
вопрос представляет собой частный случай второго вопроса (этот част-
частный случай соответствует к =2).
Как мы уже знаем, разыгрывать события можно разными способами,
с использованием различных механизмов случайного выбора. Однако
есть стандартный способ, с помощью которого можно разыграть любую
разновидность жребия. Этот способ заключается в разыгрывании так
называемого «случайного числа от 0 до 1», обычно для краткости име-
именуемого «числом R» (от английского RANDOM — случайный). Этим
158

«числом» называют непрерывную случайную величину, принимающую зна-
значения от 0 до 1 с плотностью вероятности, равной единице. По-видимо-
По-видимому, все это требует разъяснения; поэтому сделаем небольшую паузу и
напомним, чем отличается непрерывная случайная величина от диск-
дискретной случайной величины.
6.3 Дискретные и непрерывные случайные величины;
вероятность и плотность вероятности
в
книге «Случайность, необходимость, вероятность» мы достаточ-
достаточно подробно познакомились с дискретными случайными величинами
(см. там тему 12). Напомним, что дискретная случайная величина опи-
описывается законом распределения, который можно представить в виде таб-
таблицы из двух строк: первая строка содержит возможные значения xt
дискретной величины X, а вторая — соответствующие этим значениям
вероятности Pt:
л
Pi
х3
Рз
х4
Ра
х5
Р5
Ч
Рк
Вероятности подчиняются соотношению:
A)
На рис. 2 в таблице 17 в качестве примера представлена графически
дискретная случайная величина, имеющая закон распределения:
1
0,06
2
0,11
3
0,2
4
0,26
5
0,20
6
0,11
7
0,06
Возможные значения х непрерывной случайной величины X изменя-
изменяются непрерывно, например от некоторого значения а до некоторого
значения Ъ. Напомним (см. §12.11 в книге «Случайность, необходи-
необходимость, вероятность»), что для непрерывной случайной величины не имеет
смысла рассматривать вероятности ее значений, поскольку эти вероят-
вероятности равны нулю (для любого значения х от а до Ь). Непрерывную
случайную величину характеризуют не вероятностями ее значений, а
функцией /(х), называемой плотностью вероятности значения х. На
159

рис. 3 в таблице 17 в качестве примера приведен график функции/(х)
для некоторой непрерывной случайной величины. Площадь S (а; Ь) под
графиком fix), рассматриваемая на промежутке от а до Ъ (эта площадь
на рисунке заштрихована вертикальными линиями), равна вероятности
того, что будет реализовано хотя бы какое-то значение нашей случай-
случайной величины из промежутка от а до Ъ. Следовательно, эта площадь
равна единице:
S(a;b) = L	B)
Обратим внимание, что соотношение B) является аналогом соотно-
соотношения A). Площадь, заштрихованная на рис. 3 косыми линиями, есть
вероятность Р(х{; х2) того, что наша случайная величина примет ка-
какое-то значение из промежутка от х± до х2 (точки х± и х2 выбраны
произвольно):
S{xl;x2)=P{xl;x2).	C)
Полезно заметить, что
Р{а;х1)+Р{х1;х2)+Р{х2,Ъ)=1.	D)
Этот результат повторяет, очевидно, результат B).
Обратим внимание: вероятность Р(х) любого конкретного значения х
непрерывной случайной величины равна нулю, но не равна нулю веро-
вероятность Р(х; х + Ах) того, что значение непрерывной величины реализу-
реализуется где-то внутри промежутка от х до х + Ах. Коротко говоря, вероят-
вероятность попадания непрерывной случайной величины в точку равна нулю,
а вероятность ее попадания в какой-либо промежуток не равна нулю.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
ticaStiude**. Но позвольте! Получается какой-то парадокс! Вероятность
в точке х равна нулю, а вероятность на промежутке от х до х + Ах не
равна нулю! Но ведь вероятность на промежутке складывается (соглас-
(согласно правилу сложения вероятностей) из вероятностей в различных точ-
точках промежутка, т. е. складывается из нулей. Разве сумма нулей на рав-
равна нулю?
Пвтор. Сумма нулей, конечно, равна нулю. Но только при условии,
что число слагаемых в сумме конечное. Число точек на любом проме-
промежутке (как бы он ни был мал) бесконечно велико. Фактически речь
идет об умножении нуля на бесконечность. Такое произведение вполне
может иметь конечное численное значение, отличное от нуля.
160

Какое же именно?
Пвтор. Какое именно, в общем случае сказать нельзя. Это зависит от
конкретной задачи.
g4utftiuSte*&. Нельзя ли привести какой-нибудь пример?
Пвтор. Рассмотрим, например, следующие две бесконечные число-
числовые последовательности:
ап=1/3, 1/6, 1/9, 1/12, 1/15,..., 1/Зя,...
Ьп = 2, 4, 6, 8, 10,..., 2л,...
Легко видеть, что lim ап — 0, lim Ъп — оо.
Это означает, что при п^оо первая последовательность стремится к
нулю, а вторая к бесконечности. А теперь сообразим, к чему будет стре-
стремиться последовательность, члены которой являются произведением
членов последовательностей ап и Ьп? Короче говоря, к чему будет стре-
стремиться последовательность anbn?
'Чийии&ел*. Но апЪп = — • 2п = 2/3 . Значит, последовательность апЪп
есть 2/3, 2/3, 2/3, 2/3, 2/3, ...И так до бесконечности.
Пвтор. Вот мы и получили, что в данном конкретном примере:
0-ос = 2/3.
'Чипиинель. Признаться, я никогда над этим не задумывался...
Возвращаясь к разговору о вероятности попадания непрерывной слу-
случайной величины в промежуток от х до х + Ах, предположим, что про-
промежуток весьма мал — см. рис. 4 в таблице 17. Если Ах достаточно мал,
то можно приближенно полагать, что
S(x;x + Ax)^ f(x)Ax.	E)
В этом соотношении слева стоит площадь под графиком f(x) на проме-
промежутке от х до х + Ах, а справа стоит площадь прямоугольника со сторона-
сторонами/(х) и Ах (она на рис. 4 заштрихована). Чем меньше Ах, тем точнее
равенство E). Таким образом, произведение f(x)Ax можно считать при-
приблизительно равным вероятности Р(х; х + Ах) того, что наша случайная
величина примет какое-нибудь значение из промежутка от х до х + Ах:
Р(х;х + Ах)ъ f(x)-Ax.	F)
Это соотношение нам уже знакомо (см. соотношение (*) в §12.11 в
книге «Случайность, необходимость, вероятность»).
Рассмотрим теперь непрерывную случайную величину (обозначим ее
через R) которая принимает значения хота = 0доЬ=1я для которой
161

плотность вероятности f(x) = 1 — см. рис. 5 в таблице 17. Величина R
как раз и есть то, что ранее было объявлено как «случайное число от О
до 1», или как «число R».
6А «Число R»
JHLa рис. 5 в таблице 17 выбрано некоторое значение р, попадающее
в промежуток от 0 до 1. Вероятность Р@; р) того, что непрерывная
случайная величина R (иначе говоря, «число R») примет какое-нибудь
значение в промежутке от 0 до р, равна, согласно C), площади 5@; р);
эта площадь на рис. 5 заштрихована. Вычислить данную площадь не
составляет труда: S @; р) = 1 • р=р. Таким образом, вероятность того,
что значение случайной величины R окажется в промежутке от 0 до р)
равна р.
Теперь понятно, как можно использовать величину R для выяснения
того, произошло или не произошло событие А, имеющее вероятность р.
Надо разыграть эту величину (воспользовавшись, например, таблицей
случайных чисел) и, если ее значение х окажется меньше р, то можно
считать, что событие А произошло (см. рис. 6а в таблице 17). Если же
полученное при разыгрывании значение х величины R окажется боль-
больше р, то можно считать, что событие А не произошло, а произошло собы-
событие А (см. рис. 66 в таблице 17).
Наконец, покажем, как можно воспользоваться разыгрыванием вели-
величины R («числа R») для выяснения того, какое произошло событие из
совокупности событий Лъ Аъ А$,...9 Аь образующих полную группу и об-
обладающих вероятностями ph ръ р3,..., рь соответственно. Будем рассмат-
рассматривать конкретный пример, когда к = 4. Разобьем промежуток от 0 до 1 на
четыре частичных промежутка (промежутки А1? А2, A3, А4) так, чтобы дли-
длины этих промежутков равнялись рь ръ ръ, р4, соответственно — см. рис. 7
в таблице 17. Разыгрываем «число R» и, если окажется, что значение*
попало, например, в промежуток А3, то это будет указывать на наступле-
наступление события Аъ. Именно этот случай показан на рис. 7.
6.5 Как на практике разыгрывают «число R»
1.то6ы разыграть «число 7?», можно воспользоваться, например, вра-
вращающимся барабаном, внутри которого находятся перенумерованные
162

шарики. Допустим, мы хотим разыграть «число R» с точностью до 0,0001.
Тогда надо заложить в барабан 10 000 шариков с номерами от 1 до 10 000.
Приводим барабан во вращение и после остановки вынимаем из него
первый попавшийся шарик. Читаем его номер и мысленно делим на
10 000 — это будет первое значение «числа 7?», разыгранное нами с точ-
точностью до 0,0001. Оно будет иметь вид десятичной дроби с четырьмя
знаками после запятой.
Однако у нас нет под рукой вращающегося барабана с десятью тыся-
тысячами шариков. Зато есть таблица случайных чисел, в которой все встре-
встречающиеся цифры разбиты на группы по четыре цифры. Мы имеем в
виду таблицу случайных чисел, представленную на рис. 1 в таблице 17.
Каждую четверку цифр а, Ь, с, d будем сопоставлять с десятичной дро-
дробью 0, abed. Она как раз и есть одно из значений «числа 7?», разыгран-
разыгранных с точностью до 0,0001.
Выполним следующее несложное задание. Используя упомянутую ра-
ранее таблицу случайных чисел, требуется разыграть 20 жребиев для неко-
некоторого случайного события А, имеющего вероятность 0,485.
Прежде всего выберем из таблицы на рис. 1 какие-нибудь 20 чет-
четверок и образуем для них 20 десятичных дробей вида 0, abed. Пред-
Предположим, мы выбрали все четверки, находящиеся в первом столбце
таблицы. Мы тем самым получили следующие 20 случайных значе-
значений «числа R»:
0,0655;	0,5255;	0,6314;	0,3157;	0,9052;
0,4105;	0,1437;	0,4064;	0,1037;	0,5718;
0,5127;	0,9401;	0,4064;	0,5458;	0,2461;
0,4320;	0,3466;	0,9313;	0,5179;	0,3010.
(*)
Если дробь оказывается меньше 0,485, то это означает, что событие А
наступило. Если же дробь оказывается больше 0,485, то событие А не
наступило, а наступило противоположное событие А. Сравнив с 0,485
все дроби из (*), мы получим следующую последовательность событий:
А, А, А, А, А, А, А, А, А, А, А, А, А, А, А, А, А, А, А, А.
Вот так мы разыграли на практике 20 испытаний с целью выяснения,
наступило или не наступило событие А, для которого вероятность на-
наступления равна 0,485.
Если статистическое моделирование осуществляется не вручную, а с
использованием компьютера, то применение таблиц случайных чисел
163

оказывается нерациональным, поскольку они чрезмерно перегружают
память компьютера. В этом случае для розыгрыша «числа R» применя-
применяют специальные датчики, которыми оснащены многие современные
компьютеры. Используются как «физические датчики» случайных чи-
чисел, основанные на преобразовании случайных электрических сигналов
(например, при случайным образом меняющемся напряжении), так и
вырабатываемые самим компьютером так называемые псевдослучайные
числа.
Рассмотрим один из наиболее простых способов получения псевдо-
псевдослучайных чисел, предложенный Нейманом. Его называют методом сред-
средних квадратов. Берем произвольную десятичную дробь вида 0,abed. Пусть
для конкретности, это будет дробь 0,3452. Рассматриваем ее в качестве
первого случайного значения «числа R». Возводим 0,3452 в квадрат —
получаем 0,11916304. Подчеркнем группу из четырех цифр, оказавших-
оказавшихся здесь на среднем месте @,11916304) и образуем из нее дробь 0,9163,
которую рассматриваем в качестве второго значения «числа R». Возведя
0,9163 в квадрат, получим 0,83960569. Используя подчеркнутую группу
цифр, образуем дробь 0,9605 — третье значение «числа R». Далее по-
поступаем аналогичным образом:
0,96052 = 0,92256025 -> 0,2560 — четвертое значение «числа R»;
0,25602 = 0,06553600 -> 0,5536 — пятое значение «числа R»;
0,55362 = 0,30647296 -> 0,6472 — шестое значение «числа R»;
0,64722 = 0,41886784 -> 0,8867 — седьмое значение «числа R»
Этот способ генерации псевдослучайных чисел достаточно прост и лег-
легко может быть реализован в компьютере.
6.6 Разыгрывание дискретной случайной величины
азыгрывание дискретной случайной величины а, заданной зако-
законом распределения
(*)
производится с целью ответить на вопрос: какое значение приняла слу-
случайная величина X в том или ином испытании?
164
л
Pi
хз
Ръ
х4
А
...
...
Ч
Рк

Предварительно разбивают промежуток от 0 до 1 на к частичных
промежутков Д1? Д2, А3, А4,..., А^:
Д^ от 0 до Pi (длина промежутка равна Р{);
А2: от Р1 до Р1 + Р2 (длина промежутка равна Р2);
А3: от Р1 + Р2 до Р1 + Р2 + Р3 (длина промежутка Р3);
А4: от Р\ + Р2 + Рз до Рх + Р2 + Р3 + Р4 (длина промежутка Р4);
Xj
Pi
3
0,2
5
0,35
2
0,15
6
0,3
Ак: Р\ + Р2 + ... + Рк-\ ДО 1 (длина промежутка Рк).
Затем разыгрывают «число R» и смотрят, в какой из частичных про-
промежутков попало то или иное значение «числа R». Если в некотором
испытании значение «числа R» оказалось внутри промежутка Az, то это
означает, что в данном испытании разыгрываемая дискретная случай-
случайная величина X приняла значение xt.
Допустим, требуется разыграть десять возможных значений дискрет-
дискретной случайной величины X, заданной законом распределения:
(**)
Сначала разобьем промежуток от 0 до 1 на частичные промежутки с
длинами 0,2; 0,35; 0,15 и 0,3, равными значениям соответствующих ве-
вероятностей Pt. Вот начальные и конечные точки этих участков:
А{: от 0 до 0,2;	А2: от 0,2 до 0,55;
А3: от 0,55 до 0,7;	А4: от 0,7 до 1.
Затем воспользуемся уже знакомой нам таблицей случайных чисел (см.
рис. 1 в таблице 17) и разыграем десять значений «числа 7?», представ-
представленных десятичными дробями с четырьмя знаками после запятой. Вы-
Выберем, например, четверки цифр, оказавшиеся в верхней половине чет-
четвертого столбца таблицы. Мы могли бы, конечно, выбрать любой другой
набор из десяти четверок цифр, но выбрали в данном случае такой. Для
выбранного набора четверок цифр получаем следующую последователь-
последовательность случайных значений «числа R»:
0,3384; 0,7429; 0,0174; 0,5848; 0,0653;
0,4312; 0,5580; 0,4631; 0,9869; 0,2222.
Выясняем, в какие из четырех частных промежутков попадают эти дро-
дроби. Получаем такую последовательность промежутков:
А2, А4, А1? А3, А1? А2, А3, А2, А4, А2,
165

Теперь мы можем сказать, какие значения случайной величины X и в
какой последовательности реализовались в десяти рассмотренных ис-
испытаниях:
5, 6, 3, 2, 3, 5, 2, 5, 6, 5.
Вот так, воспользовавшись десятикратным розыгрышем «числа R» на
основе имеющейся в нашем распоряжении таблицы случайных чисел,
мы разыграли десять возможных значений xt дискретной случайной ве-
величины, заданной законом распределения (**).
Нетрудно сообразить, что разыгрывание полной группы случайных со-
событий Аь Аъ А$,..., Аь характеризующихся вероятностями Рь Ръ Р^,—, Рк>
можно свести к разыгрыванию дискретной случайной величины, заданной
законом распределения:
(***)
Действительно, можно считать, что наступило событие Аь если при
разыгрывании дискретной случайной величины, заданной законом рас-
распределения (***), реализовалось значение xt= i.
В заключение заметим, что разыгрывание взаимно противоположных
событий (события А с вероятностью Р и события А с вероятностью
1 - Р) можно свести к разыгрыванию дискретной случайной величи-
величины, заданной законом распределения:
xi
Pi
1
2
Pi
3
Ръ
4
—
к
Рк
Pi
1
Р
0
1 - Р
(По аналогии с (***) здесь надо бы вместо 0 поставить 2. Просто нуль
хорошо ассоциируется с событием А , означающим тот факт, что собы-
событие А не наступает).
6.7 Беседа о том, где и когда применяют
метод Монте-Карло
g4u<StiuSU*&. Насколько я понял из того, о чем говорилось, метод Мон-
Монте-Карло — это какой-то всемогущий метод. Он помогает решать не
только задачи, где случайных факторов нет, но также и всевозможные
вероятностные задачи. Он позволяет каким-то образом учитывать раз-
различные случайные факторы и отыскивать, несмотря на наличие таких
166

факторов, решение задачи. Получается что-то вроде «панацеи от всех
бед». Однако чудес не бывает и поэтому возникает вопрос: За счет чего
обеспечивается такая универсальность метода Монте-Карло? В чем тут
секрет?
Пвтор. Весь секрет в том, что, применяя метод Монте-Карло, мы
против случайности используем саму же случайность. Мы не стараемся
проникнуть в глубь сложных случайных процессов, не утруждаем себя
тем, чтобы смоделировать и аналитически рассмотреть эти процессы.
Вместо этого мы как бы предлагаем самой же случайности «разобраться»
в тех сложностях, которые она породила. Случайность усложняет кар-
картину, случайность же используется как инструмент, помогающий отыс-
отыскать в этой картине ответы на те или иные вопросы. Существенно, что
при этом не нужно ограничиваться рамками каких-либо предположе-
предположений, допущений, упрощений и вообще моделей. Этим и объясняется
универсальность метода Монте-Карло.
'Чиниикель. «Случайность против случайности» — звучит красиво. Но
как это понять практически? Как на практике случайность, используе-
используемая в методе Монте-Карло, «разбирается» со случайностями, присут-
присутствующими в конкретной задаче?
Пвтор. Вспомним задачу о сборке изделия из четырех деталей; мы
рассматривали ее в § 6.1. В задаче присутствовали случайности, связан-
связанные с тем, что рабочий выбирает четыре детали наугад (случайным об-
образом); при этом деталь с положительным отклонением размера от но-
номинала подворачивается ему под руку с вероятностью 0,4, а деталь с
отрицательным отклонением — с вероятностью 0,6. Эта задача допус-
допускала аналитическое решение, требовавшее знания комбинаторики и
правил умножения и сложения вероятностей. При использовании ме-
метода Монте-Карло мы можем обойтись без этих знаний, разыграв 300
(или более) случайных комбинаций из четырех цифр, содержащихся в
таблице случайных чисел. Случайный характер этих комбинаций — это
и есть та случайность, которую мы использовали против случайностей,
содержавшихся в рассматриваемой задаче.
'Чипиинель. Приведенный Вами пример вполне понятен. Однако он
не очень убедителен, поскольку случайности, содержащиеся в той зада-
задаче, были достаточно просты. Использование против них других случай-
случайностей не представлялось необходимым.
Пвтор. Рассмотрим более интересный пример. Он имитирует в пре-
предельно упрощенном виде задачу о вычислении вероятности того, что
нейтроны, рождающиеся в активной зоне атомного реактора, не прой-
пройдут сквозь защитную стенку и, таким образом, не окажутся в рабочем
167

зале атомной электростанции. Как я уже сказал, задача будет предельно
упрощена и может рассматриваться как задача-игра. Мы назовем ее
«Разыгрыванием «судьбы» отдельных нейтронов».
РАЗЫГРЫВАНИЕ «СУДЬБЫ» ОТДЕЛЬНЫХ НЕЙТРОНОВ
Пусть «защитная стенка» состоит всего из трех слоев атомных ядер — внутрен-
внутреннего, среднего, наружного (реальная стенка, разумеется, значительно толще). Дви-
Движение нейтрона будем полагать одномерным — перпендикулярно к слоям (в дей-
действительности же нейтроны могут распространяться в самых разных направлениях).
Подлетая к тому или иному из трех слоев, нейтрон может либо пролететь сквозь
слой (обозначим это событие буквой С — от слова «сквозь»), либо отразиться от
слоя назад (событие О — от слова «отразиться»), либо поглотиться одним из атом-
атомных ядер слоя (событие 77— от слова «поглощение»). Предельно упрощая реаль-
реальную ситуацию, будем считать, что каждое из этих событий наступает с определен-
определенной вероятностью — Рс, Ро, Рп, соответственно. Поскольку в данном случае у нас
игра, мы вправе задать произвольно значения этих вероятностей. Пусть в нашей
игре Рс = 0,52, Ро = 0,25, Рп = 0,23 (события образуют полную группу, поэтому
р + Р + Р = I)
± с * ± о * ± п L)•
В задаче-игре требуется найти вероятность Р того, что находящийся в актив-
активной зоне нейтрон, не преодолеет нашу трехслойную стенку. Если бы «стенка»
состояла из одного слоя атомных ядер, то искомая вероятность вычислялась бы
весьма просто:
Р = 1-Рс = Р0+Рй=0,48.	(*)
Но у нас три слоя; случайности подстерегают нейтрон в каждом слое до кото-
которого он доберется. Тут имеется много вариантов, так что рассчитать искомую
вероятность аналитически весьма сложно.
Поэтому воспользуемся методом Монте-Карло и устроим многократное разыг-
разыгрывание «судьбы» отдельного нейтрона (или, что то же самое, разыграем «судьбу»
многих нейтронов по отдельности). Пусть этих нейтронов будет тридцать. Все
тридцать розыгрышей представлены в таблице 18. Для каждого из разыгрываемых
нейтронов приведены используемые при розыгрыше «числа R» четверки цифр из
таблицы случайных чисел и схематически показано движение нейтрона от момен-
момента его подлета к внутреннему слою до момента, когда он будет либо поглощен,
либо вылетит назад в активную зону, либо вылетит за внешний слой.
Процедура разыгрывания нам уже известна. Разбиваем промежуток от 0 до 1 на
три частичных промежутка:
промежуток Ас: от 0 до 0,52 (длина промежутка равна Рс),
промежуток Ао: от 0,52 до 0,77 (длина промежутка равна Ро),
промежуток Ап: от 0,77 до 1 (длина промежутка равна Рп).
Покажем, как был разыгран жребий, например для нейтрона 1. Вот нейтрон под-
подлетает к внутреннему слою «стенки». Что с ним произойдет? Ответ дает первое
168

Таблица 18. Задача-игра «Разыгрывание "судьбы" отдельных нейтронов»
1
0,0655
5255
6314
3157
9052
4105
1437
4064
1037
5718
С
0
0
с
п
16
0,8922
0400
9854
4171
2873
6675
1126
1787
6256
6279
4-
п
Аг
Ао
Ап
2
0,8453
5161
8951
9764
9565
4105
2851
4171
5765
8791
4-
п
17
0,1023
5998
6380
9844
3724
7989
6345
2391
1303
6307
Ж
с
О
О
п
: 0
: 0
: 0
3
0,4467
4889
2335
4862
4635
3187
6727
7013
1562
0754
С
с
с
18
0,6265
1863
6650
0159
8900
5592
4576
4245
6503
7935
о
,52-
,77-
4
0,3384
7429
0174
5848
0653
4312
5580
4631
9869
2222
1
С
с
с
19
0,7877
9182
8567
2260
7852
3759
5059
5618
4081
4977
4-
п
5
0,5320
4647
6993
6919
2254
1596
0368
8288
0756
2013
¦*-
О
20
0,4733
0032
5945
1314
5843
3431
7746
0146
4754
0501
1
г
с
с
о
с
-0,52
-0,77
¦од
о
11
6
0,0709
4331
6157
3135
5704
9403
4746
4785
5761
0831
к
С
С
о
с
о
п
21
0,9599
4242
3585
5950
8462
0456
0672
5163
4995
6751
4-
п
7
0,2523
0010
0063
2837
8865
6859
0604
6560
6346
0927
С
с
с
22
0,9828
3961
9123
3384
3145
0944
1281
9690
9115
6447
4-
п
8
0,9224
8144
6006
9910
2627
7802
7956
8851
5392
0466
4-
п
23
0,8740
6247
5014
0276
6582
3058
8697
0413
5273
4991
4-
п
9
0,6271
8638
1736
7791
7959
3180
2304
9928
2986
7526
¦*-
О
24
0,0666
4911
6328
4503
8605
2545
5409
3043
1293
6458
V
с
с
о
с
п
10
0,2607
0307
3775
8941
3682
4499
8417
2439
2018
6610
С
с
с
25
0,6692
7264
9659
3333
7300
3756
0653
1014
7894
9307
О
11
0,5127
9401
4064
5458
2461
4320
3466
9313
5179
ЗОЮ
±
С
п
26
0,5590
0247
1863
8967
6298
2436
5519
0228
9050
3371
О
12
0,2302
2423
5228
1402
3497
4558
8269
7489
8081
5081
С
с
о
с
с
27
0,2455
0583
0532
3382
6673
2408
9720
5460
1378
3243
С
с
с
13
0,1392
6301
4153
9849
9785
2545
9926
2464
3361
3300
С
о
с
28
0,3963
7679
6313
3016
6406
4477
0111
2835
2220
2958
1 к
1
С
0
о
с
о
с
14
0,4413
2611
2544
9886
5678
4436
7429
2575
0109
9979
С
с
с
29
0,6463
7942
3199
0639
5951
5707
4745
3294
3756
4738
У-
О
15
0,9651
0650
4125
5579
4471
9265
7516
9284
7730
1970
4-
п
30
0,1609
2482
7619
2007
7427
5441
7979
3674
9795
3996
Ч Л
Ч
С
с
о
с
о
11
169

значение «числа R» — 0,0655. Оно попало в промежуток Ас; значит, наш нейтрон
пролетел сквозь внутренний слой и достиг среднего слоя. Что произойдет с ним
теперь? Ответ дает второе значение «числа R» — 0,5255. Оно попало в промежуток Ао;
значит, нейтрон отразился от среднего слоя и вернулся к внутреннему слою. Тре-
Третье значение «числа R» @,6314) попало в Ао; значит, нейтрон снова отразился и
вернулся к среднему слою. Четвертое значение «числа R» @,3157) попало в Ас;
значит, нейтрон пролетел сквозь средний слой и достиг наружного слоя. Пятое
значение «числа R» @,9052) попало в Ап; нейтрон поглощен одним из ядер в
наружном слое. На этом «история» нейтрона 1 завершилась.
Как можно видеть из таблицы 18, чрезвычайно короткой оказалась «история»,
во-первых, у нейтронов 2, 8, 15, 16, 19, 21, 22, 23 и, во-вторых, у нейтронов 5, 9,
18, 25, 26, 29. Первые поглотились ядрами атомов сразу же, как только подлетели
к внутреннему слою, а вторые сразу отразились от внутреннего слоя назад в актив-
активную зону. В нашем случае пять нейтронов из тридцати (нейтроны 3, 7, 10, 14, 27)
прошли сквозь трехслойную защиту. Получается, что искомая вероятность есть
Р=\ — 5/30 = 0,83. Это примерно вдвое больше вероятности (*). Впрочем, ре-
результат 0,83 следует считать приблизительным — ведь мы рассмотрели всего лишь
30 случайных реализаций моделируемого процесса. Для получения относительно
точного результата следовало бы разыграть «судьбу» не тридцати, а, по крайней
мере, трехсот нейтронов.
'Чсннсиъель. Задача-игра с нейтронами мне понравилась. Ее интерес-
интересно было бы разыграть с участием тридцати (или более) участников,
каждый из которых мог бы «изображать» отдельный нейтрон и, пользу-
пользуясь таблицей случайных чисел, мог бы разыграть свою «судьбу». Одна-
Однако все это — детская игра, не более того.
Пвтор. Тем не менее в эту «детскую игру», называемую разыгрыва-
разыгрыванием случайных реализаций по методу Монте-Карло, всерьез «играют»
ученые, стремящиеся обеспечить безопасность людей, работающих на
атомной электростанции или на подводном атомном крейсере. Конеч-
Конечно, им приходится решать существенно более сложную задачу, чем та,
которую мы только что рассмотрели. Им приходится иметь дело со
многими процессами, насыщенными случайностями. Случайны энергия
и направление движения каждого нейтрона в момент его перехода из
активной зоны реактора в защитную стенку, случайна длина пробега
нейтрона до его столкновением с каким-то ядром вещества стенки, слу-
случаен результат столкновения (поглощение нейтрона или его рассеяние
на тот или иной угол), случайны энергия и направление движения рас-
рассеянного нейтрона и т.д.
g4tuftfufie*b. He могу себе представить, каким образом можно анали-
аналитически просчитать все эти процессы. Какой же неимоверно сложной
должна быть аналитическая модель такой задачи!
170

Пвтор. Совершенно справедливо. Поэтому ученые вынуждены огра-
ограничиться упрощенной (а значит приближенной) аналитической моде-
моделью, а для практических расчетов использовать метод Монте-Карло.
Они вводят в компьютер данные о потоке нейтронов, входящем в стен-
стенку, данные о веществе стенки, а главное, ряд вероятностей, полученных
на основе статистических измерений в сочетании с теоретическими рас-
расчетами. Сюда входят вероятность реализации той или иной длины про-
пробега нейтрона от одного столкновения с ядром атома до другого, веро-
вероятность поглощения нейтрона при столкновении, вероятность его
рассеяния на тот или иной угол. Затем ученые, используя быстродей-
быстродействующий компьютер, многократно разыгрывают «судьбу» отдельного
нейтрона с учетом упомянутых данных и вероятностей. Такой розыг-
розыгрыш выполняется с момента попадания нейтрона внутрь защитной стен-
стенки вплоть до момента его выхода из игры (т.е. до его поглощения ядром
либо до его возвращения обратно в активную зону, либо до его вылета
в рабочий зал). В итоге получают множество возможных траекторий
нейтронов внутри защитной стенки — вроде тех, что схематически по-
показаны на рисунке 3 в таблице 29 в книге «Случайность, необходи-
необходимость, вероятность». Каждая траектория — исход какого-то одного испы-
испытания, представляющего собой розыгрыш «судьбы» отдельного нейтрона.
Огромный набор таких испытаний, проведенных не с реальными, а с
воображаемыми нейтронами компьютерного датчика псевдослучайных
чисел, дает в целом картину прохождения нейтронов через защитную
стенку и позволяет выработать практические рекомендации, касающие-
касающиеся выбора состава и толщины стенки.
^СшОаАел*. Пожалуй, теперь действительно начнешь уважать метод
Монте-Карло. Однако, как известно, за все надо платить. Преимуще-
Преимущество метода Монте-Карло в его универсальности, в возможности при-
применения для изучения практически любых процессов. А в чем заключа-
заключаются недостатки метода? Чем приходится расплачиваться за его
универсальность?
Пвтор. Во-первых, метод Монте-Карло весьма трудоемок, коль скоро
он предполагает многократные розыгрыши, многократные реализации
моделируемого процесса. Во-вторых, слабым местом здесь является не
слишком высокая точность, которая немедленно дает о себе знать, если
количество случайных реализаций оказывается не слишком большим.
"ЧитОФнел^. А как велико должно быть число реализаций для получе-
получения достаточно точных результатов методом Монте-Карло?
Пвтор. Мы не будем сейчас обсуждать этот вопрос. Замечу только, что
на практике для получения результата с точностью до 8 = 0,01 нужно
171

разыграть число реализаций N, измеряемое на десятками и не сотнями,
а тысячами. Приблизительно можно полагать:
N^l/г2.	(**)
В § 6.1 упоминалось о вычислении числа к с помощью метода Монте-
Карло. В результате разыгрывания N= 100 реализаций было получено
значение к = 3,12. Таким образом, число к было получено с точностью
до 0,1. Это согласуется с соотношением (**).
ёЧи<9ии9се*ь. Чтобы получить число тг = 3,14, надо обеспечить точность
8 = 0,01. Согласно (**), в этом случае число реализаций должно быть
порядка 10 000. Значит, чтобы получить число тг не с одним верным
знаком после запятой, а с двумя верными знаками, нужно выполнить
уже не 100, а примерно 10 000 реализаций! Действительно, точность в
методе Монте-Карло достигается с большим трудом!
Пвтор. Все это подводит нас к двум выводам. Во-первых, метод Мон-
Монте-Карло может использоваться для серьезных расчетов лишь при приме-
применении современных быстродействующих компьютеров. Во-вторых, метод
Монте-Карло должен сочетаться (везде, где это целесообразно) с при-
применением аналитических методов расчета с использованием теории ве-
вероятностей.
g4u<StiuSU*&. Но как понимать оговорку «везде, где это целесообраз-
целесообразно»? Чем определяется тут целесообразность]
Пвтор. Есть простой критерий. Чтобы применение метода Монте-
Карло было более целесообразным по сравнению с аналитическими
методами, надо, чтобы вся процедура розыгрыша была проще, а не слож-
сложнее применения аналитических методов.
&. Наша беседа подходит к концу. И хотелось бы спросить
напрямик: В каких ситуациях применяют на практике метод Монте-
Карло?
Пвтор. Я бы выделил три группы ситуаций. Во-первых, в ситуациях,
когда аналитический расчет весьма затруднен или просто невозможен.
Сюда относятся ситуации, когда случайные процессы не являются мар-
марковскими и не поддаются разработанным вероятностным методам рас-
расчета. Сюда относятся также ситуации, когда надо рассматривать не-
несколько взаимосвязанных случайных процессов, вследствие чего задача
весьма усложняется (как, например, при расчете защитной стенки атом-
атомного реактора). Сюда относятся, наконец, ситуации, когда имеющаяся
в нашем распоряжении информация о происходящих процессах недо-
недостаточна или попросту ненадежна. Во-вторых, метод Монте-Карло при-
172

меняют при необходимости проверки того, насколько корректны те или
иные аналитические модели. Всякий математический аппарат исполь-
использует те или иные допущения и упрощения. Метод Монте-Карло — един-
единственная возможность проверить корректность этих допущений и упро-
упрощений. По образному выражению Е.С. Вентцель, «метод Монте-Карло
в задачах исследования операций играет роль своеобразного Отдела тех-
технического контроля». В-третьих, метод Монте-Карло весьма ценен в
ситуациях, когда начинаются исследования принципиально новых опе-
операций, на стадии начальных поисков, проектирования. Его ценность
заключается в том, что он дает возможность как-то корректировать на-
направление поисков. В заключение отмечу, что метод Монте-Карло ши-
широко используется при апробировании деловых игр, моделирующих
различные производственные процессы.
*Чи(*иипель. Удивительно, но факт: случайность, этот разрушитель по-
порядка, может выступать в роли универсального инструмента в исследо-
исследовании операций! И даже может помогать корректировать поиск неведо-
неведомого! Получается, что случайность способна помочь в оптимизации самого
процесса поиска оптимальных решений. Интересно, как это происходит
на практике?
Пвтор. Вы коснулись проблемы случайного поиска, интенсивно разра-
разрабатываемой в наши дни. Со временем мы специально поговорим об этом.
ЗАДАНИЯ ПО ТЕМЕ 6
(Выполняя задания, будем пользоваться таблицей случайных чисел,
разбитой на блоки 00-59, — см. таблицу 19)
1.	Рабочий собирает изделие, состоящее из четырех одинаковых деталей. Он берет
детали наугад; вероятность того, что при этом попадется деталь с положитель-
положительным отклонением размера от номинала, равна 0,4, а с отрицательным отклонени-
отклонением — 0,6. Чтобы изделие нормально функционировало, нужно, чтобы все четыре
детали оказались с отрицательным отклонением от номинала. Какова вероятность
сборки нормально функционирующего изделия?
Найти как аналитическое решение задачи (вероятность РА), так и решение по
методу Монте-Карло с использованием всех блоков с 00 по 59 таблицы случайных
чисел (вероятность Рмк).
Ответ: РА -0,1296, Рмк = 48/300 = 0,16.
2.	Такое же, что и задание 1, но теперь будем полагать, что изделие нормально
функционирует, если в нем не более одной детали отклоняется от номинала в
положительную сторону.
Ответ: РА -0,4752, Рмк= 152 /300 = 0,507.
173

Таблица 19. К заданиям по теме 6
00
165!
5255
0655 8453
02
4467
4889
2335
3157 9764 4862
6314 8951
9052 9565
10 11
4105 4105
1437 2851
4064 4171
1037 5765
5718 8791
20
5127
9401
4064 5228
5458
2461
30
4320
ЗОЮ
40
50
45!
0672
6751
01
145
5161
4635
21
2302
2423
1402
3497
22
1392
6301
4153
9849
9785
31
5458
3466 8269
9313 7489
5179 8081
5081
41
9599 9828
4242 3961
3585 9123
5950 3384
8462 3145
0456 0944
51
194
1281
5163 9690
4995 9115
6447
12
3187
6727
7013
1562
0754
32
2545
9926
2464
3361
3300
42
8740
6247
5014
0276
6582
52
3058
8697
0413
5273
4991
03
3384
7429
0174
5848
0653
13
4312
5580
4631
9869
2222
23
4413
2611
2544
9886
5678
33
4436
7429
2575
0109
9979
43
6666
4911
6328
4503
8605
53
2545
5409
3043
1293
6458
04
5320
4647
6993
6919
2254
14
1596
0368
8288
0756
2013
24
9651
0650
4125
5579
4471
34
9265
7516
9284
7730
1970
44
6692
7264
9659
3333
7300
54
3756
0653
1014
7894
9307
05
0709
4331
6157
3135
5704
15
9403
4746
4785
5761
0830
25
8922
0400
9854
4171
2873
35
6675
1126
1787
6256
6279
45
5590
0247
1863
8967
6298
55
2436
5519
0228
9050
3371
06
2523
0010
0063
2837
8865
16
6859
0604 7956
6560
6346
0927
26
1023
5998
6380
9844
3724 8900
36
7989
6345
2391
1303
6307
46
2455
0583
0532
3382
6673
56
2408
9720
5460
1378
3243
07
9224 6271
8144
6006
9910
2627
17
7802
8851
5392
0466
27
6265
1863
6650
0159
37
5592
4576
4245
6503
7935
47
3963
7679
6313
3016
6406
57
4477
0111
2835
2220
2958
08
8638
1736
7791
7959
18
3180
2304 0307
9928
2986
7526
28
7877
9182
8567
2260
7852
38
3759
5059
5618
4081
4977
48
6463
7942
3199
0639
5951
58
5707
4745
3756
4738
09
2607
0307
3775
8941
3682
19
2607
3775
8941
3682
29
4733
9032
5045
1314
5843
39
3134
7746
0146
4754
0501
49
1609
2482
7619
2007
7427
59
5441
7979
3294 3674
9795
3996
0,1
0,4
1 х
Рис.2
У
Аналитическое решение "Задачи о встрече"
Двое договорились о встрече в некотором определенном месте.
Они условились, что каждый появляется в том месте в произволь-
произвольный момент от t = 0 до t= Ту ждет в течение времени Т и сразу
уходит. Какова вероятность Р того, что встреча состоится?
На рисунке х — момент прихода на место
встречи одного участника, а у — момент
прихода другого. Точка с координатами
х, у — одна из случайных реализаций. Реа-
Реализации, для которых встреча состоялась,
попадают в заштрихованную область.
Вероятность Р равна отношению заштри-
заштрихованной площади к площади квадрата:
22
«т,
X
р_ TZ-(T-XJ _
(Задача о встрече обсуждалась в §6.9 в книге автора "Случайность,
необходимость, вероятность")
174

3.	Такое же, что и задание 1, но теперь будем полагать, что для нормальной работы
изделия нужно, чтобы не менее одной детали отклонялось от номинала в отрица-
отрицательную сторону.
Ответ: РА -0,9744, Рмк = 290/300 = 0,967.
4.	Такое же задание, что и задание 1. Однако теперь изделие собирается не из
четырех, а из двух деталей. Оно нормально функционирует, если обе детали от-
отклоняются от номинала в отрицательную сторону.
Замечание. Каждую четверку цифр в таблице случайных чисел разбиваем на ле-
левую и правую двойки. В результате полное число случайных реализаций становит-
становится равным 600.
Ответ: РЛ = 0,36, Рт = 232/600 = 0,387.
5.	Такое же, что и задание 4, но теперь полагаем, что изделие нормально функцио-
функционирует, если хотя бы одна из двух деталей отклоняется от номинала в отрицатель-
отрицательную сторону.
Ответ: РЛ = 0,84, Рмк= 507 /600 = 0,845.
6.	Двое друзей договорились встретиться в новогоднюю ночь в парке под елкой.
Они условились, что каждый приходит на место встречи в любой момент между
0.00 и 1.00 и ждет ровно 5 минут (иными словами, 0,1 часа), после чего немед-
немедленно уходит. Какова вероятность того, что два друга встретятся под елкой? Дай-
Дайте аналитическое решение (вероятность РА) — см. рисунок 1 в таблице 19. Най-
Найдите также решение по методу Монте-Карло (вероятность Рмк), воспользовавшись
блоками с 00 по 39 таблицы случайных чисел.
Подсказка. Разбиваем каждую четверку цифр а, Ь, с, с/ в таблице на две двойки:
а, Ь и с, с/. Момент времени 0, аЬ (час) — момент появления под елкой одного из
друзей, а момент времени 0, cd (час) — момент появления другого. Друзья встре-
встретятся, если будет выполнено соотношения:
|0,аЬ-0,сс/|<0,1.	(*)
Ответ: РЛ = 0,19, Рмк = 45/200 = 0,225.
7.	В задании 6 предлагается найти Рмк, используя блоки с 10 по 49 таблицы случай-
случайных чисел.
Ответ: Рмк = 43/200 = 0,215.
8.	В задании 6 предлагается найти Рмк, используя блоки с 20 по 59 таблицы случай-
случайных чисел.
Ответ: Рмк = 43/200 = 0,215.
9.	Такое же, как задание 6. Но теперь каждый из двух друзей ждет другого под
елкой не 0,1 часа, а 0,4 часа B4 минуты). Дайте аналитическое решение (веро-
(вероятность РА) — см. рисунок 2 в таблице 19. Найдите также решение по методу
Монте-Карло (вероятность Рмк), воспользовавшись блоками с 00 по 29 таблицы
случайных чисел.
Ответ: РА = 0,64, Рмк = 102 /150 = 0,68.
175

10.	В задании 9 предлагается найти Рмк, используя все блоки с 00 по 59 таблицы
случайных чисел.
Ответ: Рмк = 201/300 = 0,67.
11.	Используя блоки с 50 по 53 таблицы случайных чисел, разыграйте 20 жребиев
(случайных реализаций) для некоторого случайного события А, наступающего с
вероятностью 0,341.
Ответ: А, А, А , А , А , А, А, А , А , А , А, А , А, А , А , А, А , А, А.
12.	Используя те же блоки, разыграйте 20 жребиев для случайного события А, на-
наступающего с вероятностью 0,659.
Ответ: А, А, А, А, А , А, А, А , А , А, А, А , А, А, А, А, А, А, А, А.
13.	Используя блоки с 56 по 59 таблицы случайных чисел, разыграйте 20 случайных
реализаций для полной группы событий А±, А2, А3, А4, имеющих вероятности, рав-
равные, соответственно, 0,25, 0,35, 0,22, 0,18.
Подсказка. Разбейте промежуток от 0 до 1 на четыре частичных промежутка (от
О до 0,25, от 0,25 до 0,6, от 0,6 до 0,82, от 0,82 до 1) и посмотрите, в какой из
них попадет то или иное из двадцати значений «числа /?».
ОТВет: /\^, /\^, /\^, /\^, /\^, г\^, /ij_» /\^, /\^, /\^, /\21 А21 /i2> ^2' ^2' ^2' 3' 2' 4' ^2"
14.	Дискретная случайная величина задана законом распределения:
20
0,08
15
0,12
10
0,33
5
0,47
Разыграйте 25 значений этой случайной величины, используя блоки с 05 по 09
таблицы случайных чисел.
Ответ: 20, 10, 5, 10, 5, 10, 20, 20, 10, 5, 5, 5, 5, 5, 10, 5, 5, 15, 5, 5, 10, 20, 10,
5, 10.
15. Монету подбрасывают 4 раза. Случайная величина — число выпадений орла в
четырех бросаниях (возможные значения: 0, 1, 2, 3, 4). Случайная величина
задается биномиальным законом распределения:
Р,= С4'/16
0
0,0625
1
0,25
2
0,375
3
0,25
4
0,0625
Разыграйте 10 значений данной случайной величины, используя блоки 24 и 25
таблицы случайных чисел.
Ответ: 4, 1, 2, 2, 2, 3, 0, 4, 2, 1.
16.	Используя калькулятор, получите из числа 0,4248 десять псевдослучайных чи-
чисел методом средних квадратов.
Ответ: 0,0455, 0,2070, 0,2849, 0,1168, 0,3642, 0,2641, 0,9748, 0,0235, 0,0552,
0,3047.
17.	Вернитесь к задаче-игре, рассмотренной в § 6.7. Повторите эту игру (найдите с
помощью метода Монте-Карло вероятность Р того, что нейтрон преодолеет трех-
трехслойную «защиту») при условии, что теперь Рс = 0,41; Р0 = 0,19; РЛ = 0,4. При
разыгрывании тридцати нейтронных «судеб» воспользуйтесь случайными значе-
значениями «числа /?», применявшимися в рассмотренной ранее задаче-игре.
176

Интермцция: возможен ли случайный поиск?
Интермедия — небольшая легкая пьеса,
исполняемая между действиями спектакля.
Из Энциклопедического Словаря
Случайный поиск обобщает детермини-
детерминированный, а всякий детерминированный
поиск является лишь частным случаем од-
одного или нескольких алгоритмов случайно-
случайного поиска.
Л.А. Растригин — доктор техничес-
технических наук, руководитель лаборатории
случайного поиска
Пвтор. Тема нашей беседы: возможен ли случайный поиск?
ёЧи&А&е*&. И в самом деле: возможен ли? Случайная находка, разу-
разумеется, возможна. А как что-то искать с помощью случайностей? По-
моему, поиск всегда предполагает целенаправленность. А целенаправ-
целенаправленность не согласуется со случайностями.
Пвтор. Почему же не согласуется? Предположим, наша цель — най-
найти оптимальное решение некоторой задачи в условиях неопределенно-
неопределенности. Разве мы не можем в процессе поиска такого решения действовать
случайным образом?
*Чипиинель. Поиск, осуществляемый случайным образом? Так это же
есть известный метод проб и ошибок! Разве можно относиться серьезно
к попыткам найти оптимальное решение наугад? Действуя случайным
образом, мы можем вообще не найти оптимального решения. Думаю,
что скорее всего именно так оно и будет.
Пвтор. Согласитесь, что действовать наугад и действовать случай-
случайным образом по определенной схеме — это далеко не одно и то же. А
относительно Вашего замечания о том, что при случайном поиске мож-
можно случайно вообще не найти оптимального решения, я бы заметил
следующее. Вероятность найти решение при случайном поиске можно
сопоставить, например, с вероятностью того, что при многократном
бросании монеты орел когда-нибудь непременно выпадет. Вероятность
того, что он ни разу не выпадет, уже при двадцати бросаниях оказыва-
оказывается меньше одной миллионной (туг надо учесть, что A/2J0 = 1/1048576).
'Чиниикель. Сравнение с бросанием монеты представляется мне не-
некорректным. Одно дело — бросание монеты, а другое — случайный
поиск оптимального решения.
177

Пвтор. Согласен. Однако не будем забывать, что в отличие от моне-
монеты, где «поиск» орла действительно производится наугад, случайный
поиск оптимального решения в той или иной задаче предполагает сле-
следование какой-то определенной схеме.
g4utftiuSU*b. Хотелось бы познакомиться с какими-нибудь примера-
примерами, доказывающими, что случайный поиск практически возможен. В
том смысле, что он может быть результативен.
Пвтор. За примерами далеко ходить не нужно. Ими могут служить
любые живые организмы. Еще в XIX столетии французский физиолог
Клод Бернар A813-1878) высказал идею о том, что в живых организмах
должны происходить физиологические процессы, поддерживающие
постоянство внутренней среды организма несмотря на случайные воз-
воздействия внешней среды. Эту идею позднее подтвердил и развил аме-
американский физиолог Уолтер Кеннон A871-1945). В 1929 году он пред-
предложил использовать термин «гомеостаз» (от греческих «гомос» и «статис»,
означающих соответственно «подобное» и «состояние» для характерис-
характеристики процессов, обеспечивающих динамическое постоянство состава и
свойств внутренней среды организма (например, постоянство темпера-
температуры тела птиц и млекопитающих, постоянство артериального давле-
давления и так далее).
'Чиниинель. Но причем тут случайный поиск?
Пвтор. Можно сказать, что живой организм, подвергшийся какому-
либо неожиданному воздействию внешней среды, немедленно предпри-
предпринимает случайный поиск необходимых в данной ситуации решений
(механизмов регуляции), обеспечивающих ему (организму) устойчивость
его состояния. Живой организм — это самоорганизующаяся на основе
случайного поиска система^ благодаря этому поиску она способна при-
приспосабливаться [адаптироваться) к окружающей среде с ее разнообраз-
разнообразными изменениями. В известном смысле, организм все время находит-
находится в процессе случайного поиска целесообразного состояния.
g4u<StiuSU*&. Живой организм — это объект живой природы. А может
ли человек создать техническое устройство, которое было бы способно
к самоорганизации на основе случайного поиска?
Пвтор. Может. Вот, например, автопилот — устройство для автома-
автоматической стабилизации и управления полетом авиалайнера. Оно немед-
немедленно реагирует на случайные воздействия на авиалайнер со стороны
внешней среды и быстро отыскивает необходимые решения, позволяю-
позволяющие удерживать авиалайнер на заданном курсе.
'Чийии&ел*. Когда впервые появились устройства, осуществляющие
случайный поиск?
178

Пвтор. В начале 50-х годов прошлого столетия. Впервые самоорга-
самоорганизующееся устройство на основе случайного поиска было сконструи-
сконструировано английским ученым Уильямом Эшби A903-1972) в 1948 году.
Эшби назвал свое устройство гомеостатом.
'Чиниипель. Как устроено и как функционирует это устройство?
Пвтор. Для этого надо познакомиться с рисунками 1, 2, 3 в табли-
таблице 20. На рис. 1 схематически показан электромагнитный измеритель-
измерительный прибор, который может использоваться, например, в качестве ам-
амперметра. На основе такого прибора конструируется электромагнитный
блок гомеостата; он частично изображен на рис. 2 (катушка электро-
электромагнита и ферромагнитный сердечник здесь не показаны). Обратим
внимание: при повороте стрелки ползунок скользит по обмотке реоста-
реостата, подключенной к электромагниту, вследствие чего изменяется сила
тока в обмотке катушки электромагнита. В целом гомеостат Эшби пред-
представлен схематически на рис. 3. Здесь S — система из четырех элект-
электрически взаимосвязанных электромагнитных блоков (четырех элект-
электромагнитов с кольцевыми реостатами). Углы поворота сердечников (углы
ос1? ос2, ос3, ос4) являются параметрами системы S. Блок Р — генератор
случайных изменений параметров ocz, включающийся как только ползу-
ползунок любого из четырех кольцевых реостатов случайно достигнет край-
крайнего положения (либо Л, либо В). На рис. 3 этот генератор представлен
четырьмя шаговыми переключателями (i?1? R2, R^, R^). Возможны до
400 000 комбинаций положений переключателей, им соответствует
столько же комбинаций параметров ос1? ос2, ос3, ос4.
Пока система ? находится в состоянии устойчивого равновесия, стрелки
ее электромагнитных блоков неподвижны (они фиксируют конкретный
набор равновесных параметров системы). При этом переключатели ге-
генератора Р бездействуют. Но вот, предположим, на систему оказано
какое-то воздействие извне, нарушившее ее равновесие.
*Чи(*иипель. Но каким образом?
Пвтор. Например, внезапно изменилась сила тока, питающего элек-
электромагниты. Тотчас сердечники электромагнитов придут в движение и,
значит, придут в движение ползунки кольцевых реостатов. В какой-то
момент какой-то из ползунков достигнет крайнего положения {А или В).
Немедленно начнут действовать шаговые переключатели генератора Р.
Это означает, что гомеостат начал случайный поиск новой комбинации
параметров системы S, соответствующей ее новому состоянию устой-
устойчивого равновесия. Как только этот поиск успешно завершился, конт-
контролирующий блок F подаст команду управляющему блоку V и тот ос-
остановит работу генератора случайных изменений параметров системы.
В системе наступит покой — вплоть до нового воздействия на нее.
179

Таблица 20. Гомеостат Эшби
Рис.1
При протекании тока по обмот-
обмотке катушки 1 электромагнита
ферромагнитный сердечник 2
втягивается внутрь катушки;
ось 3 и стрелка 4 при этом пово-
поворачиваются. Когда ток в обмотке
катушки прекращается, пружина
5 поворачивает ось и возвращает
стрелку в исходное положение.
0
Рис.2
На стрелке, поворачивающей-
поворачивающейся на оси 3, закреплен пол-
ползунок 6 кольцевого реостата 7,
включенного в общую цепь
с обмоткой катушки электро-
электромагнита. Через А и В обозна-
обозначены крайние положения пол-
ползунка кольцевого реостата.
180

Все это напоминает поведение спящей кошки. Если ее толкнуть,
потревожить, она проснется, предпримет своеобразный случайный по-
поиск (поищет новое удобное положение) и снова заснет. Гомеостат, «про-
«проснувшись» в результате внешнего воздействия, осуществляет случай-
случайный поиск новых значений равновесных параметров и, найдя их, как
бы снова «засыпает».
'Чинигнмль. Чувствую, что придется отказаться от сомнений по пово-
поводу возможности реализации результативного случайного поиска в тех-
технике. Однако насколько такой поиск целесообразен? Разве регулярный
поиск не привлекательнее? Разве он не быстрее приводит к цели?
Пвтор. Вы предлагаете сопоставить случайный поиск и поиск регу-
регулярный (последний лучше называть детерминированным). Не будем рас-
рассматривать относительно несложные задачи. Там предпочтительность
детерминированного поиска вполне очевидна. Иное дело сложные мно-
многокритериальные задачи, характеризующиеся многими факторами (в том
числе случайными). Здесь преимущество на стороне случайного поиска.
'Чийии&ел*. И в чем же оно заключается?
Пвтор. Во-первых, любой детерминированный метод по самой при-
природе своей является узко специализированным. Он работает лишь в рам-
рамках определенных ситуаций и вне этих рамок оказывается несостоя-
несостоятельным. Оно и понятно, коль скоро он предлагает строго определенные
действия. Случайный же поиск самой своей сути не ограничен выбором
задач. Случайность может «работать» (и помогать находить оптималь-
оптимальное решение) практически в любых ситуациях. Включая ситуации дос-
достаточно сложные и запутанные. Практически неограниченные возмож-
возможности случайного поиска объясняются просто: Его Величество Случай
есть, в конечном счете, источник всех и всяческих возможностей. В том
числе и тех, которые требуются для отыскания оптимального решения
в той или иной ситуации.
Во-вторых, случайный поиск в определенном смысле ничего не стоит.
^СшОаАел*. Простите, как это «ничего не стоит»? А современные ком-
компьютеры? А составление программ?
Пвтор. Я заметил, что не стоит «в определенном смысле». Имелись в
виду затраты на исследование той или иной конкретной ситуации вме-
вместе с ее различными модификациями, требующими использования раз-
различных приборов и устройств. В детерминированных методах учет ка-
какого-либо изменения той или иной ситуации неизбежно потребует
дополнительных затрат. А при применении случайного поиска подоб-
подобных затрат нет. По-прежнему нужен только компьютер и соответствую-
соответствующее программное обеспечение.
181

Думаю, Ваши аргументы в пользу случайного поиска до-
достаточно убедительны.
Пвтор. Но это еще не все аргументы. Отметим, в-третьих, что эф-
эффективность случайного поиска с ростом числа параметров системы
при ее усложнении снижается существенно медленнее, чем в случае лю-
любого детерминированного поиска. Пусть число параметров системы
равно п. Установлено, что трудоемкость решения задачи детерминиро-
детерминированным методом в лучшем случае пропорциональна п. Для случайного
же поиска она пропорциональна 4п . Именно поэтому при принятии
решений в достаточно сложных задачах (с большим числом парамет-
параметров) целесообразнее обращаться к случайному поиску.
Наконец, в-четвертых, не следует забывать, что в условиях неопреде-
неопределенности мы не всегда в состоянии оценить даже приблизительные ве-
вероятности тех или иных параметров. В этих случаях детерминирован-
детерминированными методами можно пользоваться лишь на отдельных этапах поиска.
В целом же картина может быть рассмотрена только в ходе случайного
поиска.
'ЧиФиатель. «Всемогущество» случайного поиска имеет, как я пони-
понимаю, те же корни, что и «всемогущество» метода Монте-Карло. По-
видимому, случайный поиск сродни методу Монте-Карло?
Пвтор. В обоих случаях мы заставляем случайность «работать на нас».
В обоих случаях исследователь прибегает к случайным шагам или, ины-
иными словами, к розыгрышу случайной реализации.
g4tufi€Ufie*b. Остается рассмотреть, как на практике осуществляется
случайный поиск. Гомеостат Эшби — это всего лишь частный пример.
Наверное, есть какие-то общие приемы, касающиеся технологии слу-
случайного поиска?
Пвтор. В небольшой беседе невозможно сколь-либо подробно обсу-
обсудить технологию случайного поиска. Ограничимся тремя основными
алгоритмами случайного поиска.
^Читатель. Термин «алгоритм» впервые появляется в наших беседах...
Пвтор. Алгоритм (или, иначе, алгорифм) — это перечень последова-
последовательных действий, которые следует предпринять, чтобы перейти, в ко-
конечном счете, от исходных данных к искомому результату. Понятие
алгоритма — одно из основных понятий математики и кибернетики.
Слово «алгоритм» («алгорифм») происходит от имени арабского мате-
математика IX-го столетия Мухаммеда алъ-Хорезми, описавшего правила
выполнения арифметических действий, которые можно рассматривать
как один из первых алгоритмов в истории математики.
182

. Значит, алгоритм случайного поиска — это последова-
последовательность действий, которые надлежит выполнять в процессе поиска?
Пвтор. Верно. Начнем с алгоритма случайного поиска, называемого
алгоритмом с линейной тактикой. Он представлен на рис. 1 в табли-
таблице 21. После того как сделан случайный шаг (это действие изображено в
виде прямоугольника «Random»), производится изображаемое по тра-
традиции в виде ромба контролирующее действие — проверка результата на
предмет выполнения условия AW> 0. Здесь A W — приращение показа-
показателя эффективности W, который в данном случае желательно максими-
максимизировать. Если в результате выполнения действия «Random» произош-
произошло приращение показателя эффективности (иначе говоря, если AW> 0),
то сделанный случайный шаг следует признать удачным, а если AW< 0,
то случайный шаг считается неудачным. В первом случае надо следовать
далее по стрелке с надписью «Да», а во втором случае — по стрелке с
надписью «Нет» — см. рисунок. Следуя по стрелке «Да», приходим к
новому действию, представленному на рисунке в виде прямоугольника
«Repeat». Это действие: «повторить предыдущий шаг». Следуя же по стрел-
стрелке «Нет» (в случае неудачного случайного шага), мы возвращаемся к
действию: «сделать случайный шаг». После действия «Repeat» снова про-
проверяем результат, т.е. проверяем условие AW> 0. Если проверка напра-
направит нас по стрелке «Да», то возвращаемся к действию: «повторить пре-
предыдущий шаг». Если же проверка направит нас по стрелке «Нет»,
возвращаемся к действию: «сделать случайный шаг».
'Чийии&ел*. Получается, что, следуя линейной тактике, мы повторяем
удачные шаги (когда AW> 0), а после неудачного шага всякий раз обраща-
обращаемся к случаю — снова делаем случайный шаг.
Пвтор. Такое поведение характерно для животных: в случае удачи
повторяется то действие, которое привело к удаче, а в случае неудачи
отыскивается какой-нибудь случайный ход. Следует согласиться с мне-
мнением Л.А. Растригина о том, что здесь «проявилась мудрость природы».
«Чем хороша здесь случайность? — Прежде всего тем, что она содержит
все возможности, в том числе и хорошие, которые приводят к удаче (и
последующему повторению удачного поведения)» (см. Л.А. Растригин,
«По воле случая», М.: «Молодая гвардия», 1986, стр. 166).
*Чи(*иипель. Алгоритм с линейной тактикой мне понравился.
Пвтор. Однако он имеет и свои слабые стороны. Одна из них заклю-
заключается в том, что здесь исследователь, активно используя удачные шаги
(повторяя их), ничего не предпринимает в отношении неудачных ша-
шагов. Он как бы предоставляет случаю разбираться с ними, что чревато
возможным накоплением (пусть даже временным) неудачных шагов.
183

Таблица 21. Алгоритмы случайного поиска
Random
Нет
Да
Repeat
Нет
Рис.1
Random
Back
Нет
->V
Да
Repeat
Нет
Рис.3
Back
1**	,
Random
TT
Рис.2
Random
¦ делаем случайный шаг;
Repeat
¦ повторяем предыдущий
шаг;
Back
¦ делаем шаг, обратный
предыдущему шагу;
- проверяем условие
AW>0
184

Накопление неудачных шагов исключено при использовании алгорит-
алгоритма с нелинейной тактикой. Он представлен на рис. 2 в таблице 21. Здесь
при неудаче делается не случайный шаг, а шаг, обратный предыдущему
шагу, это действие изображено на рисунке в виде прямоугольника «Back».
Тем самым восстанавливается предыдущая ситуация. И уже после этого
снова делается случайный шаг.
^СшОаАел*. Из рис. 2 следует, что в случае удачи предлагается вер-
вернуться к случайному шагу. В этом есть какая-то нелогичность.
Пвтор. Такая тактика, состоящая в том, чтобы не повторять удачных
шагов (кстати, именно поэтому ее называют нелинейной), имеет свой
смысл. Особенно если мы находимся уже недалеко от цели, когда надо
быть предельно осторожным и не слишком доверять предыдущему опыту,
даже если он был удачным.
*Чи(*иипель. И все-таки не хотелось бы отказаться от тактики повто-
повторения удачных шагов. Может быть, можно совместить обе тактики (ли-
(линейную и нелинейную) и использовать плюсы как той, так и другой?
Пвтор. Именно это и предлагает алгоритм случайного поиска, пред-
представленный на рис. 3 в таблице 21 (назовем его алгоритмом, сочетаю-
сочетающим линейную тактику с нелинейной). Здесь удачный шаг повторяется, а
неудачный поправляется.
*Чипиинель. Вернемся к проблеме случайного шага. Как я понимаю,
сделать случайный шаг — это все равно, что бросить жребий, разыграть
одну из реализаций случайного события. Но, как известно, розыгрыш
случайного события выполняется обычно не наугад, а с учетом его ве-
вероятности. Значит, можно (даже не можно, а нужно) говорить о том,
что случайные шаги делаются с учетом неких вероятностей? Может быть,
следует учитывать некие вероятностные свойства случайных шагов.
Пвтор. Хорошее замечание. Действительно, учитывая вероятност-
вероятностные свойства случайных шагов, можно существенно улучшить эффек-
эффективность случайного поиска.
'Чипиинель. Но как это делается практически?
Пвтор. Допустим, случайный шаг заключается в случайном выборе
того или иного направления в пространстве или того или иного воз-
возможного значения какого-то параметра х (если он представляет собой
дискретную случайную величину). Как направление в пределах того или
иного угла, так и возможные значения параметра х мы можем выби-
выбирать, делая случайные шаги не наугад, а с учетом вероятностей. Суще-
Существенно, что эти вероятности можно в ходе случайного поиска корректи-
корректировать, изменяя их так, чтобы количество удачных шагов возрастало.
185

. Это похоже на самообучение^. Значит, алгоритм случайно-
случайного поиска способен к самообучению?
Пвтор. Вот именно. Самообучение — это привилегия случайного поис-
поиска. Оно происходит в процессе корректировки вероятностей случайных
шагов. При детерминированном поиске оно (самообучение) принципи-
принципиально невозможно.
'гСи*к<инел<к. Однако в гомеостате Эшби вероятности случайных ша-
шагов не корректировались.
Пвтор. И тем не менее система в результате случайного поиска адап-
адаптировалась к изменившимся условиям. Процесс такой адаптации и есть
самообучение. Это отмечал «отец кибернетики» известный американс-
американский ученый Норберт Винер A894-1964). В связи с выходом в свет в
1952 году книги Эшби «Конструкция мозга» Винер писал: «Машина
доктора Эшби в известной степени способна обучаться, коль скоро она
может приспособляться формами своего поведения к устойчивому рав-
равновесию с окружением».
186

ТЕМА 7
КОЛИЧЕСТВО ИНФОРМАЦИИ
И ВЕРОЯТНОСТЬ:
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
И ОСНОВНЫЕ ПРИНЦИПЫ
Процесс получения и использования ин-
информации является процессом нашего при-
приспособления к случайностям внешней сре-
среды и нашей жизнедеятельности в этой среде.
Норберт Винер
Информация проникает во все поры жиз-
жизни людей и обществ... Жизнь невозможна
ни в вещественно-энергетическом, ни в ин-
информационном вакууме.
Аксель Иванович Берг,
российский академик A893-1979)
С одной стороны, мы понимаем под ин-
информацией конкретную информацию (сооб-
(сообщение), с другой — ее численную меру, то
есть выраженное в битах количество абст-
абстрактной информации, содержащейся в ин-
интересующей нас конкретной информации.
Название «информация» удобно сохранить
187

только за конкретной информацией, а чис-
численную меру абстрактной информации, содер-
содержащуюся в конкретной информации, назы-
называть «количеством информации»...Когда нам
необходимо измерить количество информации
и выразить его числом, то мы умышленно и
вполне сознательно оставляем без внимания
содержание и значение информации.
Альфред Ренъи,
венгерский математик A921-1970)
7.1 Предварительные замечания об информации вообще
и теории информации в частности
1 Лрактически каждому человеку знаком нынче термин «информа-
«информация». В наше время он употребляется необычайно широко. Широта
применения, естественно, приводит к размытости термина. Поэтому
необходимо отграничить от «информации вообще» ту информацию,
которой занимается хотя и очень молодая, но весьма быстро развиваю-
развивающаяся наука, называемая теорией информации.
Начнем с цитаты, взятой из книги Е.А. Седова «Одна формула и весь
мир» (М: «Знание», 1982): «До создания теории информации в понятие
«информация» никто не пытался вкладывать строгий научный смысл.
Слово «информация» толковалось как простое осведомление о чем-либо.
Факты, новости, сведения, полученные путем общения, чтения или
наблюдения, и все подобное этому объединялись в одном слове «ин-
«информация» практически во всех толковых словарях и энциклопедичес-
энциклопедических справочниках. Такое определение информации казалось вполне
исчерпывающим как для науки, так и для повседневной практики до
тех пор, пока не возникла необходимость в количественном измерении
всех этих новостей, сведений, знаний...».
Подчеркнем слова «необходимость в количественном измерении». Да,
такая необходимость действительно возникла и сделалась достаточно
острой, начиная примерно с середины ХХ-го столетия. Она выражала
требования научно-технического прогресса. Появились такие понятия
как «массив информации», «информационные потоки», «информаци-
«информационный взрыв». Возникла проблема переработки и передачи огромных
массивов информации, хранения их в памяти компьютеров. Понятно,
что говорить об «огромных массивах информации», их переработке,
188

хранении, передаче можно лишь при условии, что информация количе-
количественно измеряется.
Мы не умеем количественно измерять ценность той или иной конк-
конкретной информации, ее значимость в зависимости от того или иного
содержания, поскольку все подобные оценки по необходимости субъек-
субъективны. Поэтому первое, что нужно было сделать для того, чтобы на-
научиться измерять количество информации, — это абстрагироваться от
конкретного содержания информации и не обсуждать ее ценность и зна-
значимость для тех или иных потребителей информации.
Именно так и поступил создатель теории информации известный
американский математик и инженер Клод Элвуд Шеннон A916-2001),
занимавшийся в середине прошлого столетия в лаборатории компании
«Белл систем» проблемами математической теории связи. Рождение
теории информации связывают с выходом в свет в 1949 году моногра-
монографии Шеннона «Математическая теория связи». В течение ряда после-
последующих десятилетий именно с математической теорией электрической
связи ассоциировалось понятие «теория информации».
Говоря о создании Шенноном теории информации, отметим два прин-
принципиальных шага, сделанных создателем этой теории, который, следует
заметить, вряд ли сам осознавал в то время, к каким серьезным послед-
последствиям все это приведет в ближайшем будущем.
Первый шаг состоял в отказе от рассмотрения конкретного содержа-
содержания информации, что позволило сосредоточить внимание на ее объек-
объективных свойствах, которые можно было описывать математическим
языком на основе использования теории вероятностей. При этом Шен-
Шеннон ввел единицу измерения количества информации — бит.
Второй шаг Шеннона состоял в том, что для подсчета количества
информации он предложил воспользоваться вероятностной формулой
энтропии, введенной в термодинамике еще в 1877 году выдающимся
австрийским физиком Людвигом Болъцманом A844-1906). В этом ока-
оказался глубокий смысл, поскольку объективные (количественные) ха-
характеристики информации — одни и те же не только в канале связи,
книге, памяти человека или компьютера, но также в живой клетке, кри-
кристалле и вообще в любых объектах и системах окружающего мира. Ве-
Вероятностную формулу энтропии математики и кибернетики называют
сегодня формулой Шеннона, а физики и биологи — формулой Болъцмана.
Нередко ее называют также формулой Болъцмана-Шеннона, что пред-
представляется справедливым, поскольку Шеннон не просто воспользовал-
воспользовался готовой формулой, но фактически превратил ее из «формулы для
термодинамики» в формулу, работающую практически во всех областях
знания — от физики и кибернетики до языкознания и психологии.
189

Отмеченные два шага Шеннона как раз и оказались теми основопо-
основополагающими шагами, которые привели к возникновению теории инфор-
информации. Как справедливо отмечает Е.А. Седов, «благодаря этому случи-
случилось неожиданное даже для самого Клода Шеннона великое чудо: наука
приобрела инструмент для исследований информационно-энтропийных
соотношений, справедливых для всех форм информации, существую-
существующих в мире, будь то информация книг, радио, телевидения, газет и
журналов или информация, циркулирующая по нервным тканям и по
цепям электронных машин». Оценивая теорию информации с самых
общих позиций, подчеркнем, что она является теорией математичес-
математической, в основе которой лежит теория вероятностей. Как отмечает Джон
Пирс в книге «Символы, сигналы, шумы: закономерности и процессы
передачи информации» (перевод с англ., М.: «Мир», 1967), «пользо-
«пользоваться теорией информации могут и инженеры, и психологи, и физики,
однако она остается теорией математической, а не физической, психо-
психологической или инженерной».
Родившись как математическая теория электрической связи, теория
информации давно уже вышла за рамки проблем электрической связи
или, точнее сказать, проблем передачи сигнала по каналу связи. Это,
конечно, не означает, что упомянутые проблемы в какой-либо мере
остались без внимания. Значительный вклад в исследования проблемы
распространения неизвестных сигналов определенного типа по каналу
связи с шумом (иначе говоря, со случайными помехами) внесли Норберт
Винер и выдающийся российский математик академик Андрей Николае-
Николаевич Колмогоров A903-1987).
В темах 7 и 8 мы познакомимся с информацией под углом зрения
идей, разработанных Клодом Шенноном и другими учеными на основе
исследований по математической теории связи. В теме 10 мы погово-
поговорим об информации под более широким углом зрения, включающем
идеи Людвига Болъцмана. Иными словами, рассмотрим информацию с
точки зрения так называемого информационно-энтропийного подхода.
12 Математическое отступление, посвященное
логарифмической функции
11режде всего напомним, что такое показательная функция. Так на-
называют функцию вида у = а*, где число а, называемое основанием, поло-
положительно и не равно единице. Частным случаем показательной функ-
190

ции является экспонента', для нее основанием выбрано число е = 2,71828...
(график этой функции мы приводили в § 11.10 в книге «Случайность,
необходимость, вероятность» — см. рис. 2 в таблице 45). По определе-
определению, логарифм числа х по основанию а (записывается: log^ х) есть пока-
показатель степени, в которую надо возвести основание а, чтобы получить х;
основание а логарифма положительно и не равно единице. Из опреде-
определения логарифма следует, что
alo^x =x.	A)
Логарифмическая функция у = log^ x является обратной функцией по от-
отношению к показательной функции у=ах. Графики этих функций зер-
зеркально симметричны; ось симметрии — биссектриса угла уОх, т. е. пря-
прямая, для всех точек которой у = х. На рис. 1 в таблице 22 приведены
графики функций у = 2х и у = log2x, а на рис. 2 — графики функций
A)х
у = — и у = log!/2 х. Пунктиром на обоих рисунках показана ось
симметрии графиков показательной и логарифмической функций.
Отметим свойства показательной функции у = ах:
-	область задания функции: -оо < х < оо;
-	на всей области задания функция принимает положительные зна-
значения;
-	при а>\ функция у = ах — возрастающая функция, а при 0 < а < 1 —
убывающая;
-	при х = 0 функция у = ах принимает значение 1 при любом а;
-	при любом основании: ах • az = ах+2\ ах/ а2 = ax~z; (ax)z = axz.
Отметим свойства логарифмической функции у = log^ x:
-	область задания функции: 0 < х < оо;
-	при а>\ функция положительна, если х > 1 и отрицательна, если
0<х< 1;
-	при 0 < х < 1 функция положительна, если 0 < х < 1 и отрицатель-
отрицательна, если х> 1;
-	при а> 1 функция y = logax — возрастающая функция, а при
0 < а < 1 — убывающая;
-	при х = 1 функция у = log^ х обращается в нуль при любом а.
Особо отметим следующие свойства логарифма:
\oga (xz) = logfl х + logfl z	B)
(логарифм произведения равен сумме логарифмов сомножителей);
logfl (x/z) = logfl х - logfl z	C)
(логарифм частного равен разности логарифмов числителя и знаменателя);
191

Таблица 22. Логарифмическая функция
/
/
/ y = log2x
Рис.1
а>\
Рис.2
у=ах y = \ogax
0<й<1
Рис.3
О ОД 0,2 0,3037 0,3 0,6 0,7 0,8 0,9 1
192

\oga[xc) = c-\ogax	D)
(логарифм степени равен произведению показателя степени на лога-
логарифм основания).
Следствием из C) является соотношение:
*.	E)
Для перехода от logахк logbx используют соотношение:
\ogbx = \ogba • \ogax.	F)
Это соотношение легко вывести, используя A) и D). Действительно, из
равенства x = alogaX получаем logb x = logb(alogaX). С учетом D) мо-
можем записать: log ь ас = с • log ь а. Положив с = log a х9 преобразуем пос-
последнее равенство к виду:
logb(alogaX) = loga x -logb а.
Таким образом,
log а х = log^ (aloga x) = log^ a • loge x,
что и требовалось получить.
Положив в F) х = Ъ и учтя, что \ogb Ъ = 1, получим еще одно полез-
полезное соотношение:
\ogbaAogab = \.	G)
Заметим, что логарифм по основанию е является обратной функцией
по отношению к экспоненте. Его называют натуральным логарифмом и
используют для него специальное обозначение: lnx
Наиболее часто применяют логарифмы по основанию 10 (десятич-
(десятичные логарифмы); для них тоже есть специальное обозначение: \gx.
Широко используются таблицы десятичных логарифмов.
В теме 7 мы будем пользоваться логарифмами по основанию 2 [дво-
[двоичными логарифмами). На рис. 3 в таблице 22 сопоставляются графики
функций у = lg х и у = log2 х. Для перехода от десятичных логарифмов к
двоичным можно воспользоваться соотношением F), положив в нем
я=10и6 = 2и учтя, что log 2 10 = 1 /lg 2 = 3,32:
log2 x = log2 10 • lgx = 3,321gx.	(8)
Для любого х > 0 значение log 2 х легко найти из lg x, умножив lg x на
3,32 (см. рис. 3 в таблице 22).
193

В дальнейшем нам понадобится функция/(х) = х log 2 A / х). Эта функ-
функция определена на промежутке 0 < х < оо. Поскольку в качестве х мы
будем рассматривать вероятность, то нам достаточно знать функцию
f(x) лишь для х, не превышающих 1. График этой функции на проме-
промежутке от 0 до 1 представлен на рис. 4 в таблице 22. В таблице 23 эта же
функция представлена в табличной форме (для значений х от 0,001 до
0,999 приведены значения функции/ (х) с точностью до четвертого знака
после запятой). Заметим, что в точке х= 0 функция/(х) не определена,
но это в данном случае не страшно, поскольку
limxlog2(l/x) = 0.	(9)
О
7.3 Игра «Бар-Кохба» — игра в вопросы,
предполагающие ответы только «да» или «нет»
в
135 г. н.э. в Иудее вспыхнуло восстание против владычества рим-
римлян. Предводителем восставших был человек по имени Бар-Кохба. По-
Посланный им в лагерь римлян лазутчик был схвачен и подвергнут пыт-
пыткам, после чего тому отрезали язык. Лазутчику удалось бежать; однако,
будучи без языка, он не мог рассказать Бар-Кохбе о том, что удалось
высмотреть в стане противника. Тогда Бар-Кохба стал задавать лазут-
лазутчику такие вопросы, на которые надо было отвечать только либо «да»,
либо «нет». Например, посредством кивка или отрицательного покачи-
покачивания головой. Действуя так, Бар-Кохба сумел выведать у немого лазут-
лазутчика все нужные сведения и тем самым получить ценную информацию
о противнике.
Официальные исторические источники умалчивают о таком эпизоде
Иудейской войны. Возможно, что все это не более, чем легенда, сочи-
сочиненная много позднее. Однако для нас это несущественно. Важна идея
получения информации за счет ответов «да-нет». Заметим, что эту идею
использовал Александр Дюма A802-1870) в своем романе «Граф Мон-
те-Кристо». Один из героев романа, старик Нуартье, разбит параличом;
он не может ни говорить, ни двинуть рукой. Тем не менее родственни-
родственники общаются с ним, предлагая ему лишь такие вопросы, на которые
требуется ответить «да» или «нет». В первом случае Нуартье закрывает
глаза, а во втором несколько раз мигает.
Итак, ту или иную конкретную информацию можно представить в
виде набора ответов «да-нет» на соответствующим образом поставленные
194

Таблица 23. Значения функции f{x) = xlog2 — для х от 0,001 до 0,999
1 Л 1
Z?lO2 1 / D
-i О 0 / if
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,0S
0 09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0.20
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,30
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0 78
0,79
0,80
0,81
0,82
0,83
0,84
0,85
0,86
0,87
0,83
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
0

0,0664
0,1129
0,1518
0,1858
0,2161
0,2435
0,26S6
0,2915
0,3127
0,3322
0,3503
0,3671
0,3820
0,3971
0,4105
0,4230
0,4346
0,4453
0,4552
0.4644
0,4728
0,4806
0,4877
0,4941
0,5000
0,5053
0,5100
0,5142
0,5179
0,5211
0,5238
0,5260
0,5278
0,5292
0,5301
0,5306
0,5307
0,5304
0,5298
0,5288
0,5274
0,5256
0,5236
0,5211
0,5184
0,5153
0,5120
0,5083
0,5043
0,5000
0,4954
0,4906
0,4854
0,4800
0,4744
0,4684
0,4623
0,4558
0,4491
0,4422
0,4350
0,4276
0,4199
0,4121
0,4040
0,3957
0,3871
0,3784
0,3694
0,3602
0,3508
0,3412
0,3314
0,3215
0,3113
0,3009
0,2903
0,2796
0,2637
0,2575
0,2462
0.234S
0,2231
0,2113
0,1993
0,1871
0Д743
0,1623
O,1VJ6
0,1363
0,1238
0,1107
0,0974
0,0339
0,0703
0,0565
0,Gi26
0.02S6
0.0140
1
0,0100
0,0716
0,1170
0,1554
0.18S9
0,2190
0,2461
0,2709
0,2937
0,3147
0,3341
0,3520
0,3687
0,3841
0,3985
0,4118
0,4242
0,4357
0,4463
0,4562
0,4653
0,4736
0,4813
0,4883
0,4947
0,5006
0,5058
0,5105
0,5146
0,5132
0 5214
0 5240
0,5262
0,5280
0,5293
0,5302
0,5306
0!5307
0,5304
0 5297
0,5286
0,5272
0,5255
0,5233
0,5209
0,5181
0,5150
0,5116
0,5079
0,5039
0,4996
0,4950
0,4901
0,4849
0,4795
0,4738
0,4678
0,4616
0,4551
0,4484
0,4415
U.4343
0,4268
0,4192
0,4113
0,4032
0,3948
0,3862
0,3775
0,3685
0,3593
0,3499
0,3403
0,3304
0,3204
0,3103
0,2999
0,2893
0,2735
0,2676
0,2564
0,2451
0,2336
0,2220
0,2101
0,1931
0,1359
0,1735
0,1610
0,1434
0Д355
0,1225
0,1094
0,0960
0,0826
0,0689
0,0552
0,0412
0,0271
0,0129
2
0,0179
0,0766
0Д211
0,1589
0,1921
0.221S
0,2487
0,2733
0,2959
0,3167
0,3359
0,3537
0,3703
0,3856
0,3999
0,4131
0,4254
0,4368
0,4474
0,4571
0,4661
0,4744
0,4820
0,4890
0,4954
0,5011
0,5063
0,5109
0,5150
0,5136
0,5217
0,5243
0,5264
0,5281
0,5294
0,5302
0,5307
0,5307
0,5303
0,5296
0,5285
0,5271
0,5253
0,5231
0,5206
0,5178
0,5147
0,5112
0,5075
0,5034
0,4991
0,4945
0,4896
0,4844
0,4789
0,4732
0,4672
0,4610
0,4545
0,4477
0.4408
0,4335
0,4261
0,4184
0,4105
0,4023
0,3940
0,3854
0,3766
0,3676
0,3583
0,3489
0,3393
0,3295
0,3194
0,3092
0,2988
0,2882
0,2774
0,2664
0,2553
0,2440
0,2324
0,2208
0,2039
0,1969
0,1847
0,1723
0 1593
0,1471
0Д342
0,1212
0,1080
0,0947
0,0812
0,0676
0,0533
0,0393
0,0257
0,0115
3
0,0251
0,0815
0,1252
0,1624
0,1952
0,2246
0,2513
0,2756
0,2980
0,3187
0,3378
0,3555
0,3719
0,3871
0,4012
0,4144
0,4266
0,4379
0,4484
0,4581
0,4670
0,4752
0,4828
0,4897
0,4960
0,5016
0,5068
0,5113
0,5154
0,5189
0,5220
0,5245
0,5266
0,5283
0,5295
0,5303
0,5307
0,5307
0,5303
0,5295
0,5284
0,5269
0,5251
0,5229
0,5204
0,5175
0,5144
0,5109
0,5071
0,5030
0,4987
0,4940
0,4891
0,4839
0,4784
0,4726
0,4666
0,4603
0,453S
0,4471
0,4401
0,4328
0,4253
0,4176
0,4097
0,4015
0,3931
0,3845
0,3757
0,3666
0,3574
0,3480
0,3383
0.3285
0,3184
0,3032
0,2978
0,2871
0,2763
0,2653
0,2542
0,2428
0,2313
0,2196
0,2077
0,1957
0,1834
0,1711
0,1535
0,1458
0,1329
0,1199
0,1067
0,0933
0,0793
0,0662
0,0524
0.03S4
0,0243
0,0101
4
0,0319
0,0362
0,1291
0,1659
0,1933
0,2274
0,2533
0,2750
0,3002
0,3207
0,3398
0,3571
0,3734
0,3836
0,4026
0,4156
0,4277
0,4390
0,4494
0,4590
0,4678
0,4760
0,4835
0,4903
0,4966
0,5022
0,5072
0.511S
0,5153
0,5192
0,5222
0,5247
0,5268
0.52S4
0,5296
0,5304
0,5307
0,5307
0,5302
0,5294
0.52S3
0,5267
0,5249
0,5226
0,5201
0,5172
0,5140
0,5105
0,5067
0,5026
0,4982
0,4935
0,4886
0,4833
0,477S
0,4720
0,4660
0,4597
0,4532
0,4464
0,4393
0,4321
0,4246
0,4163
0,4089
0 4007
0,3922
0,3836
0.374S
0,3657
0,3565
0,3470
0,3373
0,3275
0,3174
0,3071
0,2967
0,2861
0,2753
0,2642
0,2531
0,2417
0,2301
0,2184
0,2065
0,1944
0,1822
0,169S
0,1572
0,1445
0,1316
0,1186
0,1054
0,0920
0,0785
0,0G4S
0,0510
0,0370
0,0230
0,0086
5
0,0382
0,0909
0Д330
0,1693
0,2013
0,2301
0,2563
O.2S03
0,3023
0,3226
0,3414
0,3538
0,3750
0,3900
0,4040
0,4169
0,4289
0,4400
0,4504
0,4599
0,4687
0,4763
0,4842
0,4910
0,4971
0,5027
0,5077
0,5122
0,5161
0,5196
0,5225
0,5250
0,5270
0.52S6
0,5297
0,5304
0,5307
0,5306
0,5302
0,5293
0.52S1
0,5266
0,5246
0,5224
0,5193
0,5169
0,5137
0,5102
0,5063
0,5022
0,4978
0,4930
0,4880
0,4828
0,4772
0,4714
0,4654
0,4591
0,4525
0,4457
0,4386
0,4313
0,4238
0,4160
0,40S0
0,3993
0,3914
0,3828
0,3739
0,3648
0,3555
0,3461
0,3364
0,3265
0,3164
0,3061
0,2956
0,2850
0,2741
0,2631
0,2519
0,2405
0,2290
0,2172
0,2053
0,1932
0,1810
0,1686
0,1560
0,1432
0,1303
0,1173
0,1040
0,0907
0,0771
0,0634
0,0496
0,0356
0,0214
0,0072
6
0,0443
0,0955
0,1369
0,1727
0,2043
0,2329
0,2588
0,2S26
0,3044
0,3246
0,3432
0,3605
0,3766
0,3915
0,4053
0,4181
0,4301
0,4411
0,4514
0,4608
0,4695
0,4776
0.4S49
0,4916
0,4977
0,5032
0,5082
0,5126
0,5165
0,5199
0.522S
0,5252
0,5272
0.52S7
0.529S
0,5305
0,5307
0,5306
0,5301
0,5292
0,5230
0,5264
0,5244
0 5222
0^5195
0,5166
0,5133
0,5098
0,5059
0,5017
0,4973
0,4926
0,4875
0,4822
0,4767
0,4708
0,4648
0,4584
0,4518
0,4450
0,4379
0,4306
0,4230
0 4153
0,4072
0,3990
0,3905
0,3819
0,3730
0,3639
0,3546
0,3451
0,3354
0,3255
0,3154
0,3051
0,2946
0,2839
0,2731
0,2620
0,2503
0,2394
0,2273
0,2160
0,2041
0,1920
0Д797
0,1673
0,1547
0Д419
0,1290
0,1159
0Д027
0,0893
0,0758
0,0621
0,0482
0,0342
0,0201
0,0058
7
0,0501
0,0999
0,1407
0,1760
0,2073
0,2356
0,2613
0,2848
0,3065
0,3265
0,3430
0,3622
0,3781
0,3929
0,4066
0,4194
0,4312
0,4422
0,4523
0,4617
0,4704
0,4783
0,4856
0,4923
0,4983
0,5038
0,5087
0,5130
0,5169
0,5202
0,5230
0,5254
0,5273
0,528S
0,5299
0,5305
0,5307
0,5306
0,5300
0,5291
0.527S
0,5262
0,5242
0,5219
0,5193
0,5163
0,5130
0,5094
0,5055
0,5013
0,4968
0,4921
0,4870
0,4817
0,4761
0,4702
0,4641
0,4578
0,4512
0,4443
0,4372
0,4298
0,4223
0,4145
0,4064
0,3982
0,3897
0,3810
0,3721
0,3430
0,3536
0,3441
0,3344
0,3245
0,3144
0,3040
0,2935
0.2S28
0,2720
0,2609
0,2497
0,2382
0,2266
0,2149
0,2029
0,1903
0Д785
0,1661
ОД534
0,1407
0,1277
0,1146
0,1014
0,0880
0,0744
0,0607
0,0468
0,0328
0,0186
0,0043
8
0,0557
ОДО43
0Д444
0,1793
0,2103
0,2383
0,2637
0,2871
0,3086
0,3284
0,3468
0,3638
0,3796
0,3943
0,4079
0,4206
0,4323
0,4432
0,4533
0,4626
0,4712
0,4791
0,4863
0,4949
0,4989
0,5043
0,5091
0,5134
0,5172
0,5205
0,5233
0,5256
0,5275
0,5289
0,5299
0,5305
0,5307
0,5305
0,5300
0,5290
0,5277
0,5260
0,5240
0,5217
0,5190
0,5160
0,5127
0,5090
0,5051
0,5009
0,4964
0,4916
0,4865
0,4811
0,4755
0,4697
0,4635
0,4571
0,4505
0,4436
0,4365
0,4291
0,4215
0,4137
0,4056
0,3973
0,3888
0,3801
0,3712
0,3621
0,3527
0,3432
0,3334
0,3235
0 3133
0,3030
0,2925
0,2318
0,2709
0,2598
0,2485
0,2371
0,2255
0,2137
0,2017
0,1896
0,1773
0Д648
0,1522
0,1394
0,1264
0,1133
0,1000
0,0866
0,0730
0,0593
0,0454
0,0314
0,0172
0,0029
10
0,0612
0,1086
0,1481
0,1825
0,2132
0,2409
0,2661
0,2893
0,3106
0,3303
0,3485
0,3654
0,3811
0,3957
0,4092
0,4218
0,4335
0,4443
0,4543
0,4635
0,4720
0,4798
0,4870
0,4935
0,4994
O.504S
0,5096
0,5138
0,5176
0.520S
0,5235
0,5258
0,5277
0,5290
0,5300
0,5306
0,5307
0,5305
0,5299
0,5289
0,5275
0,5258
0,5238
0,5214
0,5187
0,5157
0,5123
0,5087
0,5047
0,5004
0,4959
0,4911
0,4860
0,4806
0,4750
0,4691
0,4629
0,4565
0,4498
0,4429
0,4357
0,4383
0,4207
0,4129
0,4048
0,3965
0,3880
0,3792
0,3703
0,3611.
0,3518
0,3422
0,3324
0.3225
0,3123
0,3019
0,2914
0,2807
0,2698
0,2587
0,2474
0,2359
0,2243
0,2125
0,2005
0,1884
0,1760
0,1635
0,1509
0,1381
0Д251
0Д120
0,0987
0,0853
0,1717
0,0579
0,0440
0,0300
0,0158
0,0014
195

вопросы. Именно эта идея и используется в игре «Бар-Кохба», появив-
появившейся в начале ХХ-го столетия сначала в Венгрии, а затем в других стра-
странах. Один игрок что-то загадывает (задумывает). Он может, например,
загадать некое пожелание, слово, целую фразу. Другой должен выяснить,
что же именно задумал партнер. Для этого он задает партнеру различные
вопросы, на которые тот честно отвечает. Существенно, чтобы задавае-
задаваемые вопросы предполагали лишь ответы «да» или «нет».
Предположим, что первый игрок загадал слово «вероятность». Пред-
Предположим также, что игроки условились заранее рассматривать только
существительные, не являющиеся к тому же именами собственными
(заметим, что в принципе этого можно было не делать). Как выбрать
загаданное слово из всех существительных, встречающихся в русском
языке? У второго игрока исключительно богатый выбор. Понятно, что
необходима информация, которая позволила бы сделать нужный выбор.
Чтобы получить эту информацию, наш игрок начинает задавать вопро-
вопросы. Разыграем следующую возможную картину.
Вопрос 1-й: Это существительное одушевленное? Ответ: Нет.
Вопрос 2-й: Оно начинается с согласной буквы? Ответ: Да.
Вопрос 3-й: Эта согласная находится в последней пятерке букв русского алфа-
алфавита? Ответ: Нет.
Вопрос 4-й: Она находится в первой пятерке? Ответ: Да.
Вопрос 5-й: Это буква «б»? Ответ: Нет.
Вопрос 6-й: Эту буква «в»? Ответ: Да.
Вопрос 7-й: Вторая буква загаданного слова гласная? Ответ: Да.
Вопрос 8-й: Это буква «а»? Ответ: Нет.
Вопрос 9-й: Эту буква «е»? Ответ: Да.
Вопрос 10-й: Третья буква слова согласная? Ответ: Да.
Вопрос 11-й: Она находится в первой половине алфавита? Ответ: Нет.
Вопрос 12-й: Она среди первых пяти согласных букв? Ответ: Нет.
Вопрос 13-й: Она во второй пятерке согласных букв? Ответ: Нет.
Вопрос 14-й: Это буква «п»? Ответ: Нет.
Вопрос 15-й: Это буква «р»? Ответ: Да.
Вопрос 16-й: Четвертая буква слова согласная? Ответ: Нет.
Вопрос 17-й: Это «а», «и», «е» или «о»? Ответ: Да.
Вопрос 18-й: Эту буква «и» или «е»? Ответ: Нет.
Вопрос 19-й: Это буква «о»? Ответ: Да.
Используя информацию, содержащуюся в ответах на 19 заданных вопросов, а
также знание букв русского алфавита, второй игрок выяснил, что заветное слово
начинается с «веро».
Вопрос 20-й: Пятая буква слова согласная? Ответ: Нет.
196

Итак, после «веро» идет какая-то гласная буква. Теперь выбор становится до-
довольно ограниченным. Надо подумать. «Вероотступник»? «Вероисповедание»? «Ве-
«Вероятие»? «Вероятность»?
Вопрос 21-й: Есть ли в слове мягкий знак? Ответ: Да.
Вопрос 22-й: Было загадано слово «вероятность»? Ответ: Да.
Уместно задать вопрос: Можно ли оценить, насколько велико коли-
количество информации, необходимое для выявления в процессе игры «Бар-
Кохба» того или иного загаданного слова? Невольно напрашивается
ответ: Это количество информации можно оценить по числу вопросов с
ответами «да-нет», которое потребовалось для разгадывания. Чем бо-
богаче у второго игрока выбор, тем более велико количество информации, в
котором он нуждается, и тем больше, следовательно, он должен задать
вопросов. Впрочем, вопросы можно задавать по-разному. По-видимо-
По-видимому, от характера вопросов также зависит, больше или меньше придется
их задать, чтобы получить нужную информацию.
Дальнейшее обсуждение проблемы будем проводить, используя сле-
следующий конкретный и притом простой пример игры «Бар-Кохба». В
списке 16 фамилий, значащихся под номерами 0, 1, 2, ..., 15. Первый
игрок загадывает одну из фамилий (один из номеров), а второй игрок
должен разгадать эту фамилию, т.е. произвести выбор определенного {за-
{загаданного) элемента из множества, содержащего 16 элементов. Как уже
говорилось, чтобы произвести правильный выбор, необходимо распо-
располагать соответствующим количеством информации. Уместно заметить,
что, если выбора нет, то никакой информации не требуется; иными
словами, «соответствующее» количество информации равно нулю. Сле-
Следует заметить также, что существование какого-то выбора в том или
ином опыте говорит о неопределенности опыта. Естественно связывать
необходимое для выбора количество информации со степенью неопределен-
неопределенности опыта.
В нашей игре «Бар-Кохба» с шестнадцатью фамилиями (в нашем
опыте) второй игрок может по-разному сконструировать систему воп-
вопросов с ответами «да-нет». Рассмотрим три возможных варианта.
Вариант 1:
Вопрос 1-й: Загаданный номер (загаданная фамилия) находится среди номеров
с 0 по 7? Ответ: Нет.
Значит, номера с 0 по 7 можно исключить из дальнейшего рассмотрения.
Вопрос 2-й: Загаданный номер среди номеров с 8 по 11? Ответ: Да.
Вопрос 3-й: Загаданный номер — это или 8, или 9? Ответ: Да.
Значит, исключаются также номера Шили 11.
Вопрос 4-й: Загаданный номер — это 8? Ответ: Нет.
197

Значит, была загадана фамилия под номером 9. Игра окончена.
Потребовалось задать четыре вопроса, на которые были последовательно полу-
получены ответы:
нет-д а-д а-нет.	(*)
Вариант 2:
Вопрос 1-й: Загаданный номер среди номеров с 0 по 3? Ответ: Нет.
Исключаем номера с 0 по 3.
Вопрос 2-й: Загаданный номер среди номеров с 12 по 15? Ответ: Нет.
Исключаем также номера с 12 по 15.
Вопрос 3-й: Загаданный номер среди номеров с 4 по 7? Ответ: Нет.
Исключаем также номера с 4 по 7.
Вопрос 4-й: Загаданный номер — это или 8, или 11? Ответ: Нет.
Вопрос 5-й: Загаданный номер — это 9? Ответ: Да.
Игра окончена. Теперь потребовалось задать пять вопросов, на которые была
получена цепочка ответов:
нет-нет-нет-нет-д а.	(* *)
Вариант 3:
Вопрос 1-й: Загаданный номер среди номеров с 0 по 2? Ответ: Нет.
Вопрос 2-й: Он среди номеров с 3 по 5? Ответ: Нет.
Вопрос 3-й: Он среди номеров с 6 по 8? Ответ: Нет.
Вопрос 4-й: Он среди номеров с 9 по 11? Ответ: Да.
Вопрос 5-й: Это номер 9 или 10? Ответ: Да.
Вопрос 6-й: Это номер 9? Ответ: Да.
Игра окончена. Теперь пришлось задать шесть вопросов, на которые была по-
получена цепочка ответов:
нет-нет-нет-д а-д а-д а.	(* * *)
Возможны, разумеется, и другие варианты опыта (игры).
Рассмотренные три варианта иллюстрирует рис. 1 в таблице 24. Строки
соответствуют разным вопросам. Перечеркнем те номера (те фамилии в
списке), которые после ответа на данный вопрос (и всех предшествую-
предшествующих ответов) должны быть исключены из дальнейшего рассмотрения.
Как мы убедились, число вопросов с ответами «да-нет», приводящее
к разгадыванию задуманного другим игроком номера, изменяется от
одного варианта опыта к другому. Однако степень неопределенности и
определяемое ею количество информации, необходимое для отыскания
задуманного номера, не могут меняться от опыта к опыту. Возникает
естественный вопрос: действительно ли можно по числу заданных воп-
вопросов (точнее говоря, по числу полученных ответов «да-нет») судить о
количестве информации, необходимой для осуществления выбора? От-
Ответ на этот вопрос дан в следующем параграфе.
198

Таблица 24. Единица измерения количества информации — 1 бит
Вопрос 1-й
Вопрос 2-й
Вопрос 3-й
,Вопрос 4-й
Вопрос 1-й
Вопрос 2-й
Вопрос 3-й
Вопрос 4-й
IВопрос 5-й
Вопрос 1-й
Вопрос 2-й
Вопрос 3-й
Вопрос 4-й
Вопрос 5-й
.Вопрос 6-й
О 1 2 3 4 5 6 7 8 9 10 1112 13 14 15
х
х
х
X
х
X
X
X
X
X
X
X
X
X
х
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
х
х
X
х
х
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
х
х
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
х
х
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
х
X
X
X
X
X
X
X
х
X
X
X
X
X
X
X
X
х
х
X
X
х
х
X
X
X
X
х
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
000 001
I III
010 011 100 101
ЦП IIV IV IV!
А
Рис.2
ПО 111
IVII IVIII
в
t
199

7.4 Бит — двоичная единица
ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ
'твет на заданный выше вопрос таков: Да, можно, но при условии,
что для каждого вопроса ответы «да» или «нет» равновероятны. В этом
случае каждый ответ (либо «да», либо «нет») сообщает спрашивающему
количество информации в 1 бит. Слово «бит» происходит от словосо-
словосочетания binary digit, что в переводе с английского означает «двоичная
цифра».
Сформулируем определение двоичной единицы измерения количества
информации, именуемой «битом»:
Бит — количество информации, которое содержится в ответе на
вопрос, допускающий два равновероятных ответа.
Условие равновероятности ответов «да» или «нет» для всех заданных
вопросов выполнятся лишь в первом из трех рассмотренных в § 7.3 ва-
вариантов. Что же касается второго и третьего вариантов, то указанное
условие нарушается уже при первом вопросе. Вот, например, задан во-
вопрос: Находится ли загаданный номер среди номеров с 0 по 3? Ясно,
что ответ «да» имеет вероятность 1/4 (поделив четыре упомянутых в
вопросе номера на полное число номеров, получаем 4 / 16 = 1/4); соот-
соответственно, ответ «нет» имеет вероятность 3/4. Заметим, что для вто-
второго вопроса в варианте 2 ответ «да» имеет вероятность 1/3 (надо поде-
поделить четыре на число номеров, оставшихся для рассмотрения, т. е. на
число 12).
В варианте 1 второй игрок получает из ответов первого игрока ин-
информацию в 1 бит после каждого своего вопроса. Задав четыре вопроса,
он получил информацию в четыре бита, вследствие чего смог выбрать
загаданный номер. Таким образом, для выбора одного определенного эле-
элемента из множества, содержащего 16 элементов, потребовалось количе-
количество информации, равное 4 бит. Эту информацию можно представить в
виде цепочки (*):
нет-да-да-нет,
но лучше закодировать ее с помощью двух цифр: 1 («да») и 0 («нет») —
и представить в виде:
0 110.	(****)
Здесь каждая цифра @ или 1) содержит ровно один бит информации.
Цифр всего две, поэтому бит называют двоичной единицей измерения
количества информации.
200

Заметим, что подобное кодирование цепочек (**) и (***) не имело
бы смысла, поскольку в вариантах 2 и 3 не все ответы «да-нет» являлись
равновероятными; следовательно, не все они содержали по одному биту
информации.
Понятие бита информации можно наглядно продемонстрировать на
следующем примере. Железнодорожная станция имеет 8 путей: I, II,
III, IV, V, VI, VII, VIII. Предположим, к станции приближается поезд.
Диспетчер, осуществляя дистанционное управление, может направить
поезд на любой из восьми путей (будем считать, что все пути свободны,
так что диспетчер может выбрать для прибывающего поезда любой путь).
У диспетчера под рукой три переключателя (А, В, С), каждый из кото-
которых может быть поставлен либо в левое, либо в правое положение. Пе-
Переключатель А подает управляющий сигнал на входную стрелку а. Пе-
Переключатель В подает управляющий сигнал одновременно на стрелки Ъх и
Ъ2. Переключатель С подает управляющий сигнал одновременно на стрел-
стрелки с1? с2и с3. Схема железнодорожных путей с указанием всех входных
стрелок показана на рис. 2 в таблице 24. Закодируем сигнал, подавае-
подаваемый постановкой переключателя в левое положение, цифрой 0, а в пра-
правое положение — цифрой 1. Если на стрелку подается сигнал 0, она
открывает перед поездом левый путь, а если подается сигнал 1, то пра-
правый путь. Ставя переключатель в левое либо правое положение, диспет-
диспетчер всякий раз посылает управляющий сигнал @ или 1), содержащий
информацию в 1 бит. Поставив в соответствующие положения все три
переключателя, диспетчер сформирует управляющий сигнал, который
направит поезд на тот или иной из восьми путей. Восемь путей — восемь
управляющих сигналов, каждый из которых содержит 3 бита информа-
информации. Вот кодовая запись этих сигналов:
Путь
I
000
Путь
II
001
Путь
III
010
Путь
IV
011
Путь
V
100
Путь
VI
101
Путь
VII
ПО
Путь
VIII
111
Кодовые записи (****) и (*****) — примеры кодирования информа-
информации с использованием двоичной системы счисления. Уместно, по-види-
по-видимому, напомнить, что такое двоичная система счисления.
7.5 Двоичная система счисления
11роще всего сразу обратиться к конкретному примеру. Возьмем,
например, число 235. Оно представлено в привычной для нас десятич-
десятичной системе счисления, где для записи различных чисел используются
201

десять цифр: О, 1, 2, 3, 4, 5, 6, 7, 8, 9. Вот мы произносим «двести
тридцать пять» и, как правило, не задумываемся над тем, что перед
нами сумма двух сотен, трех десятков и пяти единиц:
235 = 2 • 102 + 3 • 101 + 5 • 10°.
Это же число можно представить в двоичной системе счисления, т. е. с
помощью всего двух цифр — 0 и 1. Оно будет выглядеть так:
1110 10 11,
что следует рассматривать как сумму:
1 • 27 +1 • 26 +1 • 25 + 0 • 24 +1 • 23 + 0 • 22 +1 • 21 + 0 • 2°.
1110 10 11
В самом деле, 27 = 128, 26 = 64, 25 = 32, 23 = 8, 21 = 2.
2° = 1, так что представленная в (*) сумма есть
128 + 64 + 32 + 8 + 4 + 1 = 235.
Покажем ход рассуждений, когда нужно записанное в десятичной системе чис-
число закодировать в двоичной системе счисления. Пусть это будет число 1349. Прежде
всего находим наибольшее натуральное число п, для которого 2п < 1349. Нетрудно
сообразить, что п= 10; ведь 210 = 1024, а 211 = 2048. Значит, в двоичной системе
число 1349 является 11-значным числом (оно состоит из одиннадцати нулей и
единиц). Представим:
1349= 1-210+ а-29 + b ¦ 2s + с ¦ 27 + d-26 +
+ е- 25 +/• 24 + g. 23 + h ¦ 22 + /• 21 + у • 2° =
= 1024 + 512я+ 256Й+ 128с + 64d + 32е + 16/+ 8g+4/* + 2/+/
Здесь буквы равны либо 0, либо 1. При а= 1 сумма 1024 + 512 превысит 1349.
Значит, а = 0. Понятно, что Ъ = 1, поскольку A024 + 256 = 1280) < 1349. Разность
1349- 1280 равна 69. Она меньше 128 (и, значит, с = 0), но больше 64 (и, значит,
d= 1). Разность 69-64равна 5. Она меньше 32, 16 и 8 (и, значит, e=f=g= 0), но
больше 4 (и, значит, h = 1). Поскольку 5-4 = 1, то ясно, что /= 0, иу= 1. Таким
образом, число 1349 в двоичной системе имеет вид: 10101000101.
Вернемся к обсуждавшемуся выбору загаданного номера из списка с
шестнадцатью фамилиями. Количество битов информации, необходи-
необходимое для осуществления выбора, определялось числом вопросов, задан-
заданных таким образом, чтобы ответы «да» и «нет» были равновероятными.
Это число, как оказалось, равно четырем. При этом второй, третий и
четвертый вопросы задавались после того, как был получен ответ на
202

предыдущий вопрос, и учитывали эти и предыдущие ответы. Оказы-
Оказывается, однако, что можно разгадать нужный номер, задав сразу четыре
вопроса и уже потом (после того, как все они заданы) рассмотрев отве-
ответы на них. Для этого следует воспользоваться двоичной системой счис-
счисления и предварительно закодировать в этой системе все шестнадцать
номеров
0	-> 0 @000),
1	-> 1 @001),
2	-> 10 @010),
3^ 11 (ООП),
4	-> 100 @100),
5	-> 101 @101),
6^ ПО (ОНО),
7^ 111 @111),
8 -> 1000,
9^ 1001,
10-> 1010,
11 -> 1011,
12-> 1100,
13-> 1101,
14-> 1110,
15-> 1111.
(Каждый из номеров с 0 по 15 закодирован четырехзначным числом из
нулей-единиц; поэтому в номерах с 0 по 7 пришлось добавить слева
соответствующее число нулей).
Теперь мы можем задать обещанную четверку вопросов. Она такова:
Верно ли, что в двоичной записи загаданного номера равна единице первая
слева цифра?Вторая цифра? Третья цифра? Четвертая цифра?Предпо-
цифра?Предположим, что мы получим на эти четыре вопроса такую цепочку ответов:
да-нет-нет-да, или, другими словами, 1001. Отсюда следует, что был
загадан номер 9 (в двоичной системе это как раз и есть 1001).
7.6 Формула Хартли.
Аддитивность количества информации
О § 7.3 мы выбирали загаданную фамилию из списка, содержавшего
#=16 фамилий (выбирали определенный элемент из N= 16 равноверо-
равновероятных элементов). Мы выяснили, что для этого нужно задать 4 вопроса
203

с равновероятными ответами «да-нет». Отсюда следовало, что необхо-
необходимое для выбора количество информации равно Н= 4 бит (будем обо-
обозначать буквой Н степень неопределенности опыта и, соответственно,
количество информации, необходимое для избавления от этой неопреде-
неопределенности; величина i/измеряется в битах).
Если N= 1, то, очевидно, Н= 0.
При N=2 (две фамилии в списке) нужно задать всего один вопрос,
так что в этом случае Н=\ бит.
При N= 4 нужно задать 2 вопроса с равновероятными ответами «да-
нет»; в этом случае Н=2 бит.
При Л^=8нужно задать 3 вопроса с равновероятными ответами
«да-нет»; в этом случае Н= 3 бит.
Нетрудно самостоятельно убедиться, что если N= 32, то для выбора
загаданной фамилии нужно задать 5 вопросов с равновероятными отве-
ответами «да-нет»; следовательно Н= 5 бит.
Нетрудно также убедиться, что при N= 64 понадобятся 6 вопросов с
равновероятными ответами «да-нет» и, значит, 6 бит информации.
Составим следующую таблицу:
(*)
В таблице (*) выбраны числа N, равные 2п где п = 0, 1, 2, 3, 4, 5, 6... Для
каждого N в этой таблице количество информации Н, выраженное в
битах, равно п. В связи с этим можно записать:
N
Н, бит
1 = 2°
0
2 = 2*
1
4 = 22
2
8 = 23
3
16 = 24
4
32 = 25
5
64 = 26
6
*>#
Откуда немедленно следует, что
Н = log2 N
A0)
(И)
Формулу A1) принято называть формулой Хартли — по имени амери-
американского инженера-связиста Р.В.Л. Хартли A888-1970). В 1928 году он
предложил характеризовать степень неопределенности опыта с N рав-
равновероятными исходами числом log2^. Понятно, что выбор загаданной
фамилии из списка с N фамилиями — один из примеров подобной
ситуации.
Формула A1) не вызывает сомнений в случаях, когда N= 2n. Логич-
Логично полагать, что она работает также и для прочих натуральных чисел N.
Докажем, что это предположение верно, с помощью следующих рас-
рассуждений.
204

Пусть Н— количество информации, которое необходимо, чтобы выб-
выбрать определенный элемент из множества \|/ содержащего N равноверо-
равновероятных элементов. Иными словами, Н есть степень неопределенности
опыта, заключающегося в выборе определенного элемента из множества \|/,
т. е. в осуществлении определенного исхода из ^равновероятных исхо-
исходов. Понятно, что Н есть некоторая функция от N, или H(N). Относи-
Относительно функции H(N) можно сразу сделать два утверждения:
#A) = 0,	A2)
Н (N2) > Н ТО, где N2 > N{.	A3)
Утверждение A2) означает, что если множество \|/ состоит всего из
одного элемента, то выбор однозначен, тут никакой информации не
требуется. Утверждение A3) означает, что чем больше элементов в мно-
множестве \|/, тем больше степень неопределенности опыта, тем больше
количество информации, необходимое для нахождения конкретного эле-
элемента этого множества.
Предположим теперь, что есть два множества: \|/ и Q. Множество \|/
состоит из N равновероятных элементов, а множество Q — из М эле-
элементов. Каково количество информации Н', необходимое для того, чтобы
выбрать два определенных элемента, один из которых находится в мно-
множестве \|/, а другой в множестве Q? Естественно считать, что
Н' = H{N) + H(M).	(**)
А теперь образуем множество Q, каждый элемент которого представля-
представляет собой пару, составленную из какого-либо элемента множества \|/ и
какого-то элемента множества Q. Всего в множестве Q будет, очевидно,
MN элементов. Упомянутые выше «два определенных элемента» явля-
являются одним из элементов множества Q: следовательно,
Н1' = H{NM).	(***)
Из (*) и (***) следует, что
Н (NM) = H(N) + Н(М).	A4)
Итак, функция H(N) удовлетворяет двум условиям: A2), A3), A4).
Всем этим условиям удовлетворяет функция
logaN, гдея>1.	A5)
В самом деле, log^ 1 = 0 и log^ х при а > 1 является возрастающей функ-
функцией. Так что условия A2) и A3) выполнены. А выполнение условия
205

A4) следует из свойства логарифма произведения — см. B). Можно
доказать (мы этого делать не станем), что совокупности условий A2),
A3) и A4) удовлетворяет только функция A5).
Выбор основания логарифма а связан с выбором единицы измере-
измерения количества информации Н. Обычно полагают а = 2, что соответ-
соответствует использованию двоичной единицы измерения — бита. Если по-
положить а = 10, то будет использоваться десятичная единица измерения
количества информации, называемое дитом. Чтобы найти соотноше-
соотношение между дитом и битом, воспользуемся тем, что
lg TV дит = log2 N бит	A6)
и, следовательно,
1 дит = (log2 NI lg N) бит.
С учетом (8) находим отсюда:
1 дит = C,32 • lg N/ lg N) бит = 3,32 бит.	A7)
Результат A5) подтверждает справедливость формулы Хартли A1) для
любого натурального числа N. Эту формулу можно озвучить так:
Количество информации, необходимое для выбора определенного ва-
варианта из N равновероятных вариантов, равно log2Nбит.
Отсюда получаем, что для выбора загаданного номера из списка, содер-
содержащего, например, N= 100 номеров, требуется информация
Н= Iog2100 = 3,32 • 2 = 6,64 бит.
Если, например, N= 650, то
Н= log2 650 = 3,32 • lg 650 = 3,32 • 2,813 = 9,34 бит
(результат lg 650 = 2,813 взят из справочника с таблицей десятичных
логарифмов).
В заключение отметим, что соотношение A4) указывает на аддитив-
аддитивность количества информации. Аддитивность (от лат. aditivus — прибав-
прибавление) — это свойство величин, означающее, что значение величины,
соответствующее всему объекту, равно сумме значений этой величины,
соответствующих всем частям, на которые каким-либо образом разбит
объект. Так, информация, необходимая для отгадывания фамилии из
одного списка и фамилии из другого списка, равна сумме количеств
информации, из которых одно необходимо для отгадывания фамилии
из первого списка, а другое — для отгадывания фамилии из другого
списка. Пусть а — опыт с выбором фамилии из первого списка, C —
206

опыт с выбором фамилии из второго списка, а у — опыт с выбором
одной фамилии из первого списка и одной из второго. Естественно
считать, что неопределенность, характеризующая опыт у, складывается
из неопределенностей, характеризующих опыты аир.
7.7 Сколько информации можно получить,
ЗАДАВАЯ ВОПРОС, ДЛЯ КОТОРОГО ОТВЕТЫ «ДА» И «НЕТ»
НЕ РАВНОВЕРОЯТНЫ?
ХЧогда в § 7.4 говорилось, что в ответе на вопрос, предполагающий
равновероятные ответы «да-нет», содержится информация в один бит, у
читателя должен был невольно возникнуть вопрос: А сколько инфор-
информации содержится в ответе на вопрос в том случае, когда ответы «да» и
«нет» не равновероятны0! Пришло время разобраться с этим вопросом.
Сразу можно сказать: если событие А имеет существенно меньшую
вероятность, чем противоположное событие Л, то неопределенность
опыта, заключающегося в наблюдении того, какое из событий А я А
произойдет, должна быть существенно меньше бита. Утверждение, что
дворовая футбольная команда проиграет команде высшей лиги, содер-
содержит фактически нулевую информацию. Это и так ясно. Неопределен-
Неопределенность опыта (а значит, и количество информации, которое может лик-
ликвидировать эту неопределенность) равна нулю, если одно из событий А
и А является достоверным (его вероятность равна 1), а другое невоз-
невозможным (вероятность равна нулю).
Пусть вероятность ответа «да» на поставленный вопрос равна р, а
вероятность ответа «нет» равна, соответственно, \-р. Количество ин-
информации, которое мы получим, задав такой вопрос, есть
H = p\0g2	h(l
P
A8)
Примем это соотношение без доказательства. Определяемая данным
соотношением функция Н (р) представлена на рис. 1 в таблице 25. При
желании, читатель может самостоятельно построить график функции Н
(р), воспользовавшись таблицей 23.
Из A8) немедленно следует, что если ответы «да» и «нет» равноверо-
равновероятны, т.е. если р = 1 / 2, то
Н = Ilog2 2 + ^-log2 2 = 1/2 + 1/2 = 1 бит.
207

Таблица 25. Неравновероятные ответы «да-нет»
,бит
H=plogA/p+
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1Х р
Рис.1
1
2
3
4
5
6
Вопросы
1. Загадан или 1, или
2. Загадан 1?
1. Загадан или 1, или
2. Загадан 2?
1. Загадан или 2, или
2. Загадан 2?
1. Загадан или 2, или
2. Загадан 3?
1. Загадан или 2, или
Z.
1. Загадан 2?
^¦-
2?
2?
3?
3?
3?
Ответы^
Да
Нет
Да
Да
Да
Да
Да
Нет
Да
Да
Н, бит
1
0,918
1
0,918
1
0,918
1
0,918
0,918
Рис.2
208

Если р = 1 или р = О, то оба слагаемые в A8) обращаются в нуль (тут
необходимо принять во внимание (9)).
Рассмотрим, например, случай, когда р=1/3. Воспользовавшись
таблицей 23, находим, что в этом случае Н= 0,918 бит, так как Н=
= 0,333 • Iog2( 1/0,333)+ 0,667 • Iog2(l/0,667) = 0,5283 + 0,3897 = 0,918.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
*Чи(*иипель. Ваш пример с р = 1/3 побудил меня заняться небольши-
небольшими подсчетами. Предлагаю сыграть в короткую игру «Бар-Кохба» и найти
количество информации Н, необходимое для выбора загаданного номе-
номера в списке, где всего три номера: 1, 2, 3.
Пвтор. Как, по-Вашему, могла бы проходить такая игра?
ль. Например, вот так:
Вопрос 1-й: Загаданный номер есть 1? Ответ: Нет.
Вопрос 2-й: Загаданный номер есть 2? Ответ: Да.
Игра окончена. Мы выяснили, что был загадан номер 2. И вот я хочу
воспользоваться соотношением A8) и подсчитать, сколько информа-
информации мне понадобилось, чтобы выяснить загаданный номер. Я задал два
вопроса. Для первого вопроса вероятность ответа «да» равна, очевидно,
1/3; значит, согласно A8), этот вопрос позволил мне получить инфор-
информацию, равную 0,918 бит. Для второго вопроса вероятность ответа «да»
(как и ответа «нет») равна 1/2 (ведь после исключения номера 1 из даль-
дальнейшего рассмотрения остается сделать выбор между двумя равноверо-
равновероятными исходами — 2 и 3). Значит, второй вопрос позволил мне полу-
получить информацию в 1 бит. Получается, что задав два вопроса и разгадав
тем самым номер, который был загадан, я использовал информацию
Я = 0,918 + 1 = 1,918 бит.	(*)
Однако я мог бы подсчитать Н, воспользовавшись формулой Хартли
A1) для N=3:
#=log23 = log210 . lg3 = (l/lg2)lg3.
Я выписал из справочника значения lg 3 и lg 2:
Ig3 = 0,4771; Ig2 = 0,3010.
В результате я получил:
Н= 0,4771 / 0,3010 = 1,585.	(**)
Результат (**) весьма сильно отличается от результата (*). Какой же из
них верен?
209

Пвтор. Верен результат (**). Кстати, он прекрасно ложится на гра-
график функции у = log2x — см. рис. 3 в таблице 22.
'Читсниель. А как быть с результатом (*)? Он получен с использова-
использованием формулы A8). В чем тут дело?
Пвтор. Дело в том, что опыт, в котором задаются вопросы с целью
выяснения загаданного номера, можно реализовать в данной ситуации
(при N= 3) в шести случаях, причем (это как раз и важно!) в четырех
случаях количество информации, получаемое при ответах на вопросы,
равно 1,918 бит, а в двух случаях — всего 0,918 бит. Это поясняет рис. 2
в таблице 25. Чтобы получить искомое количество информации, нужно
выполнить усреднение по шести постановкам опыта:
Н= D • 1,918 + 2 • 0,918) / 6 = 9,508 / 6 = 1,585 бит.	(***)
Как видите, результат (***) точно совпадает с результатом (**).
7.8 Формула Шеннона
§ 7.6, обсуждая формулу Хартли, мы с помощью рассуждений до-
достаточно общего характера убедились в аддитивности количества ин-
информации (полная информация складывается из «частичных» инфор-
информации) и пришли к весьма важному заключению, которое удобно
сформулировать так:
количество информации, связанное с реализацией определенного ва-
варианта из N равновероятных вариантов, равно log2N бит.
Словосочетание «связанное с реализацией определенного варианта» мож-
можно понимать по-разному. Например, как «необходимое для реализации
(иначе говоря, выбора) какого-то конкретного варианта». Или как «со-
«содержащееся в сообщении о том, какой именно вариант оказался реализо-
реализован (выбран)».
Функция H(N) = log2^— возрастающая функция. Чем больше число
вариантов N, тем больше неопределенность опыта, предполагающего
выбор определенного варианта, тем больше количество информации,
связанное с этим выбором. При N=1 нет проблемы выбора, нет нео-
неопределенности.
Предположим теперь, что рассматриваются N неравновероятных ва-
вариантов. Каково количество информации, связанное с выбором опре-
определенного варианта в этом случае? Ответ на этот вопрос дал в 1948 году
Клод Шеннон (и независимо от него Норберт Винер). Шеннон и Винер
показали, что
210

количество информации, связанное с реализацией определенного ва-
варианта из N вариантов, характеризующихся вероятностями ръ ръ
N	^
р3,..., pN, равно У2Pi l°?i— бит.
Соотношение
N
/-1	Pi
A9)
называют в теории информации формулой Шеннона. Она имеет, по сути
дела, такой же вид, что и знаменитая формула Больцмана, в которой Н
рассматривается как термодинамическая энтропия в вероятностном пред-
представлении. Разумеется, Шеннон не просто использовал готовую фор-
формулу Больцмана, но вывел ее, применив теорию вероятностей, само-
самостоятельным образом. Можно сказать, что Шеннон (а также Винер)
сначала вывел соотношение A9), а уже потом обнаружил сходство его с
формулой Больцмана. Мы не станем воспроизводить этот вывод, а вот
причины упомянутого сходства мы, конечно обсудим. И сделаем это в
теме 10.
Учитываемые в формуле Шеннона ^вариантов исчерпывают все воз-
возможные для рассматриваемой ситуации варианты. Поэтому
N
B0)
Если N=2, то A9) принимает вид:
ТТ	1	1	1	1
Н = рх log2 — + р2 log2 —.
Pi	Pi
B1)
Обозначая рх через р и учитывая B0), получаем из B1) уже знакомое
нам соотношение A8).
Если все N^ вариантов равновероятны, т.е. если
Pi=Pi=P3= - = Pn= l/N>	B2)
то из A9) получаем:
N
1
1
log2 N + log2 N +... + log2 N
N слагаемых
= log2 N.
211

Легко видеть, что в частном случае, когда выполняется B2), формула
Шеннона превращается в формулу Хартли A1).
Обратим внимание на то, что неравновероятность вариантов снижа-
снижает степень неопределенности опыта; поэтому количество иноформации,
связанное с реализацией определенного варианта, уменьшается. На при-
примере с N=2 мы в этом наглядно убедились, познакомившись с графи-
графиком зависимости Н от вероятности р (см. рис. 1 в таблице 25).
Рассмотрим в качестве примера случай с N= 5 вариантами, имею-
имеющими следующие вероятности реализации:
рх = 0,15; р2 = 0,2; р3 = 0,25; р4 = 0,1; р5 = 0,3.
Количество информации, которое мы получаем, когда нам сообщают,
какой именно из пяти вариантов реализован, не зависит от варианта, а
определяется по формуле A9). Применяя эту формулу и используя дан-
данные таблицы 23, запишем:
Н = 0,15.1og2 0^5+0,2.^^ + 0,25.1082^ + 0,1.1082^- +
+ о,31og2-^- = 0,4105 + 0,4644 + 0,5 + 0,3322 + 0,5211=2,228 бит.
и, j
Если бы пять вариантов были равновероятными, то в этом случае по
получении сообщения о том, какой именно вариант реализован, мы
получили бы, согласно A1), количество информации:
Яравн = log2 5 = 3,32 • lg 5 = 2,321 бит.
Мы убеждаемся, что Н< #равн.
Формулу Шеннона удобно интерпретировать, рассматривая дискрет-
дискретную случайную величину, принимающую N значений. Пусть некая дискрет-
дискретная случайная величина X задана законом распределения:
Р\
Pi
хъ
Ръ
...
xN
Pn
Иными словами, случайная величина Xпринимает Означений хъ хъ
хъ, ..., xN с вероятностями, равными, соответственно, ръ ръ ръ,..., pN.
Опыт, состоящий в наблюдении над данной случайной величиной, выявля-
выявляет некоторое определенное значение этой величины. Количество ин-
информации Н, которое мы получаем в результате произведенного наблю-
N
дения, есть Н = ^/?/ log2 (УPi) бит.
212

То же самое можно выразить немного иначе. Величина Хможет при-
принимать либо значение xl5 либо х2, либо х3, ..., либо xNc вероятностями,
соответственно, ръ ръ р^—, Pn- Налицо неопределенность, и степень
этой неопределенности равна Н бит, где Н определяется по формуле
Шеннона. Именно такое количество информации устраняет упомяну-
упомянутую неопределенность в опыте, состоящем в наблюдении над случай-
случайной величиной X.
Обратим внимание на то, что определяемое формулой Шеннона ко-
количество информации Н не зависит от того, какие именно значения
принимает в том или ином испытании случайная величина, или какие
именно варианты реализованы. Содержание возможных значений слу-
случайной величины или возможных вариантов вообще не рассматривают-
рассматриваются. Все определяется исключительно вероятностями значений случай-
случайной величины или вариантов.
В связи со сказанным подчеркнем еще раз два принципиальных мо-
момента, относящихся к понятию количества информации, используемо-
используемому в теории информации. Во-первых, это понятие абстрагируется от
конкретного содержания информации. Во-вторых, это понятие форми-
формируется исключительно на основе понятия вероятности. Благодаря имен-
именно этим двум моментам теория информации смогла стать сегодня в
полном смысле слова всеобъемлющей теорией.
Уберите понятие вероятности и тем самым вы уничтожите теорию
информации. В своем постепенно углубляющемся (и расширяющемся)
изучении окружающего мира человечество вышло сегодня на уровень,
когда невозможно обойтись без широкого применения теории информа-
информации в самых разных областях человеческой практики. А это означает, что
сегодня научное исследование окружающего мира невозможно без обра-
обращения к вероятности и ее закономерностям. Иными словами, постиже-
постижение мира на современном этапе — это постижение его через вероятность.
7.9 Об использовании понятия «энтропия»
в теории информации
ёЧи*п<г*пель. Насколько мне известно, Шеннон называл величину Нв
своей формуле энтропией.
Пвтор. Вы правы. Он рассматривал некий опыт, в результате кото-
которого могли реализоваться исходы Аъ Аъ Аъ, ..., AN с вероятностями
РъР2>Рз> ---•> Pn- Существование ^возможных исходов опыта, каждый
213

из которых можно предсказать лишь с какой-то вероятностью, говорит
о наличии в опыте неопределенности. Вот меру этой неопределенности
{степень неопределенности опыта) Шеннон и предложил называть энт-
энтропией опыта и обозначать буквой Н.
'Чи&а&елй. Мы называли эту величину количеством информации. И
мне это больше нравится.
Пвтор. Связь количества информации со степенью неопределеннос-
неопределенности опыта мы достаточно подробно обсудили. Тем самым мы фактичес-
фактически обсудили связь количества информации с понятием энтропии, вве-
введенным в теорию информации Шенноном.
ёЧи*п<г*пель. Получается, что одна и та же величина имеет целых три
названия: «количество информации», «степень неопределенности опы-
опыта», «энтропия опыта». Не многовато ли названий? Тут нетрудно запу-
запутаться. Тем более, что понятие энтропии родилось еще в XIX веке как
одно из понятий термодинамики и статистической физики.
Пвтор. Действительно, понятие энтропии впервые ввел в науку (в тер-
термодинамику) в 1865 году известный немецкий физик Рудольф Клаузиус
A822-1888), а в 1877 году Людвиг Больцман дал этой энтропии вероят-
вероятностное толкование. Больцман предложил для энтропии формулу, ко-
которую примерно через столетие снова вывел Шеннон, используя тео-
теорию вероятностей. Возможно, именно сходство формулы, выведенной
для измерения степени неопределенности опыта, с формулой Больцма-
на побудило Шеннона использовать термин «энтропия».
'Чи&а&ел*. Вот и возникает вопрос: Как связаны друг с другом (не с
точки зрения структуры формулы, а с точки зрения содержания) энтро-
энтропия Шеннона и энтропия Больцмана-Клаузиуса? Насколько существенна
и глубока эта связь?
Пвтор. Связь есть и притом глубокая. Однако, знакомясь с теорией
информации, целесообразно, по-видимому, последовать совету, данно-
данному Джоном Пирсом в его книге «Символы, сигналы, шумы»: «Чтобы
понять, что такое энтропия в теории информации, лучше выкинуть из
головы все, что хоть как-то связано с понятием «энтропия», применяе-
применяемым в физике. А разобравшись в том, что собой представляет энтропия
в теории информации, можно попробовать связать ее и с энтропией в
физике». Продолжая в теме 8 знакомиться с теорией информации, мы
воспользуемся советом Пирса и не будем касаться энтропии в физике.
'Чи&а&ел*. Значит, пока для нас энтропия — это всего лишь неопре-
неопределенность опыта при наличии выбора, или, иначе говоря, количество
информации, связанное с этим выбором?
214

Пвтор. Совершенно верно. В теме 8 мы познакомимся с теорией ин-
информации с точки зрения той проблемы, которая как раз и породила
саму эту теорию. Я имею в виду проблему передачи сообщений по каналу
связи. Здесь уместно еще раз процитировать Джона Пирса: «В матема-
математической теории связи рассматривается источник сообщений, например
человек, который в определенной ситуации может создать любое из
множества возможных сообщений. Количество информации, которое
несет в себе сообщение, возрастает при увеличении неопределенности
относительно того, из скольких возможных сообщений производится
выбор. Одно из десяти возможных сообщений несет в себе меньшее
количество информации, чем одно из миллиона. Энтропия в математи-
математической теории связи есть мера этой неопределенности, и эта неопреде-
неопределенность или (что то же самое) энтропия, берется в качестве меры ко-
количества информации, которое несет в себе сообщение от данного
источника».
ь. Как я понимаю, мы все-таки будем пользоваться поняти-
понятием «энтропия» в рамках теории информации?
Пвтор. Будем. Но не будем пока обсуждать связь этой энтропии с
той энтропией, которая используется в физике. Об этом в теме 10.
7.10 ОТ ИНФОРМАЦИИ К ВЫБОРУ, ОТ ВЫБОРА К ИНФОРМАЦИИ
'Чи&а&ель. В самом начале § 7.8 сделаны два уточнения словосоче-
словосочетания «количества информации, связанное с реализацией определен-
определенного варианта». Получается, что, с одной стороны, количество инфор-
информации — это то, что нам необходимо иметь для того, чтобы реализовать
определенный выбор (выбор определенного элемента из некоторого мно-
множества). А с другой стороны, количество информации — это то, что мы
получаем после того, как определенный выбор реализован. По-моему,
речь идет о разных вещах.
Пвтор. Не торопитесь с таким заключением. Допустим, рассматри-
рассматривается количество информации, связанное с выбором определенной фа-
фамилии из списка, содержащего 16 фамилий. Известно, что это количе-
количество информации равно четырем битам.
ёЧи*п<г*пель. Данную ситуацию мы уже обсуждали. И притом доволь-
довольно подробно.
Пвтор. Вот потому я сейчас и обращаюсь к ней. Некто загадал ка-
какую-то фамилию из шестнадцати и тем самым создал неопределенность,
215

измеряемую четырьмя битами. Чтобы устранить эту неопределенность,
я должен выявить (выбрать) загаданную фамилию и для этого (т. е. для
того, чтобы реализовать нужный выбор) мне понадобится информация
в четыре бита, которую я могу получить от загадавшего фамилию по-
посредством соответствующим образом сконструированных вопросов к
нему. Итак, я использую полученную из ответов на мои вопросы ин-
информацию для того, чтобы устранить неопределенность и сделать нуж-
нужный выбор.
ёЧи*п<г*пель. Вот и получается, что количество информации — это то,
что необходимо иметь, чтобы реализовать определенный выбор.
Пвтор. Простите, я еще не закончил. Теперь я действительно знаю
загаданную фамилию. Я владею информацией и количество этой ин-
информации равно четырем битам. Однако другие-то пока этой информа-
информацией не владеют! (Для чистоты картины полагаем, что обмен вопроса-
вопросами и ответами происходил в отдельной комнате, а не на виду у всех).
Эти «другие» должны наблюдать, как я буду делать выбор, указав зага-
загаданную фамилию. И в результате наблюдения за моим выбором они
получат, в свою очередь, ту же самую информацию в четыре бита. Те-
Теперь количество информации — это то, что получают после того, как
определенный выбор реализован (сделан, показан, объявлен).
Обратите внимание: здесь все время идет разговор об одном и том же
количестве информации.
*. Я бы сказал, что речь идет о передаче одного и того же
количества информации — от загадавшего фамилию к Вам и затем от
Вас к «наблюдателям».
Пвтор. Вы нашли весьма точное выражение: «передача количества
информации». Именно этому мы и посвятим тему 8.
ЗАДАНИЯ ПО ТЕМЕ 7
1.	Чему равна разность A / 2)log22 - 2log2(l / 2)?
Ответ: 2,5.
2.	Чему равно значение функции f(x)=x Iog2(l/x) в точках х=2, х=4, х=8,
х= 16? Начертите график функции на промежутке от 0 до 8.
Ответ: -2, -8, -24, -64.
3.	Выразите log2x через натуральный логарифм In x.
Ответ: log2x= log2 e ¦ \пх= (Ige/lg2)- In x= 1,44 • In x.
4.	Поиграйте с партнером в игру «Бар-Кохба». Можно предложить ему отгадать ка-
какое-нибудь задуманное Вами существительное, состоящее, скажем, из восьми
букв. А потом пусть он загадает существительное из такого же числа букв. Кому
из вас потребуется меньшее число вопросов для выявления загаданного слова?
216

5.	В списке 64 фамилии. Загадана одна из них. Покажите, как надо сконструиро-
сконструировать систему вопросов с ответами «да-нет», чтобы каждый вопрос позволял полу-
получить информацию в один бит.
6.	Имея в виду рисунок 1 в таблице 24, найдите вероятность ответа «да»: а) для
каждого из пяти вопросов в варианте 2, б) для каждого из шести вопросов в
варианте 3.
Ответы: а) 1 / 4, 1 / 3, 1 / 2, 1 / 2, 1 / 2;
б) 3 / 16, 3 / 13, 3 / 10, 3 / 7, 2 / 3, 1 / 2.
7.	Представьте в десятичной системе счисления следующие числа, закодирован-
закодированные в двоичной системе: а) 1111111, б) 1010101, в) 0101010, г) 1001001,
д) 1100011.
Ответы: а) 1111111 -> 127, б) 1010101 -> 85, в) 0101010 ^42, г) 1001001 -> 73,
д)	1100011 -> 99.
8.	Укажите, какое число следует сразу после представленных здесь в двоичной сис-
системе чисел: 11111, 11001, 10011, 11011, 10101.
Ответы: 11111 -> 100000, 11001 -> 11010, 10011 -> 10100, 11011 -> 11100,
10101 -> 10110.
9.	Закодируйте в двоичной системе счисления следующие числа, представленные в
десятичной системе: а) 38, б) 60, в) 75, г) 100, д) 110, е) 203.
Ответы: а) 100110, б) 111100, в) 1001011, г) 1100100, д) 1101110,
е)	11001011.
10.	Попробуйте закодировать в троичной системе счисления следующие числа, пред-
представленные в десятичной системе: а) 46, б) 100, в) 200.
Подсказка: 46 = 1 • З3 + 2 • З2 + 0 • З1 + 1 • 3° -> 1201.
Ответы: а) 1201, б) 10201, в) 21102.
11.	Таинственный незнакомец находится в списке, состоящем из Л/фамилий. Под-
Подсчитайте, какое количество информации мы получаем, когда нам сообщают фа-
фамилию таинственного незнакомца в случаях:
а) Л/= 10, б) Л/= 100, в) Л/= 1000.
Ответы: а) 3,32 бит, б) 6,64 бит, в) 9,96 бит.
12.	Дискретная случайная величина задана законом распределения:
р,
х±
0,12
х2
0,24
*з
0,26
0,15
0,23
Подсчитайте, воспользовавшись данными таблицы 23, чему равно количество
информации, которое мы получим в результате наблюдения над этой случайной
величиной, позволившего определить значение, которое она приняла.
Ответ: 2,265 бит.
13. Насколько меньше подсчитанное в задании 12 количество информации по срав-
сравнению со случаем, когда все пять значений случайной величины равновероятны?
Ответ: На 0,056 бит.
217

14.	В двух мешках находятся по 25 шаров. В первом мешке находятся 10 белых,
8 красных и 7 синих шаров. Во втором мешке находятся 9 желтых, 11 синих и
5 зеленых шаров. Опыт состоит в том, что из каждого мешка вынимают наугад
один из шаров. Подсчитайте, чему равно количество информации, которое мы
получим из сообщения о том, какого цвета шар оказался вынутым: а) в опыте с
первым мешком, б) в опыте со вторым мешком. Исход какого из опытов следует
считать более неопределенным?
Ответы: а) 1,569 бит, 2) 1,516 бит. Более неопределенным является исход опы-
опыта с первым мешком.
15.	Из многолетних наблюдений над выпадением осадков в некотором заданном
пункте известно, что 1 ноября вероятность дождя там равна 0,3, а вероятность
выпадения снега — 0,15. А вот 20 ноября вероятность дождя равна 0,15, а вы-
выпадение снега — 0,45. В какой из двух указанных дней погода в данном пункте
оказывается более неопределенной? На сколько битов более велика степень нео-
неопределенности?
Ответ: 20 ноября; на 0,52 бит.
218

ТЕМА 8
КОЛИЧЕСТВО ИНФОРМАЦИИ
И ВЕРОЯТНОСТЬ: ПЕРЕДАЧА
ИНФОРМАЦИИ ПО КАНАЛУ СВЯЗИ
Центральной проблемой теории инфор-
информации является проблема передачи инфор-
информации по каналу связи с помехами.
Альфред Репьи
Когда адресат принимает сообщение, пе-
переданное по каналу с шумом, он знает, ка-
какое сообщение он принял, но не может быть
уверен, что именно это сообщение было по-
послано отправителем. Таким образом, неопре-
неопределенность относительно того, какой сим-
символ был выбран отправителем, устраняется
не полностью даже после приема. Эта оста-
остаточная неопределенность зависит от веро-
вероятности того, что принятый символ будет
отличаться от отправленного. Указанная ве-
вероятность характеризует шум (помехи) в
данном канале связи.
Джон Пирс
219

8.1 Общая схема канала связи
Ка
шнал связи служит для передачи сообщений (информации) от от-
отправителя к адресату. Отправителя следует рассматривать в качестве
источника сообщений (источника информации), а адресата — в качестве
приемника сообщений (приемника информации).
Каналы связи чрезвычайно многочисленны и разнообразны. Вот,
например, первый человек обращается с какими-то словами ко второ-
второму. Здесь источник сообщений — первый человек. В качестве канала
связи (точнее сказать: линии связи) выступает воздушная среда, в кото-
которой сообщения распространяются благодаря звуковым волнам. Прием-
Приемник сообщений — второй человек (тот, что слушает). Звуковые сигна-
сигналы, несущие определенную информацию, достигают уха слушающего
человека и воздействуют на барабанную перепонку.
Если первый человек и второй человек находятся на большом рас-
расстоянии друг от друга, то для передачи информации от одного к друго-
другому используется телефонная связь. В этом случае работа канала связи
осуществляется либо посредством переноса электрических сигналов по
обычному телефонному кабелю, либо посредством переноса световых
сигналов по оптическому волоку, либо посредством сигналов, распро-
распространяющихся в виде электромагнитных волн (радиотелефон).
Вот мы читаем книгу, смотрим на телеэкран или просто рассматри-
рассматриваем то, что находится перед нами. Во всех этих случаях мы оказываем-
оказываемся частью канала связи, а точнее говоря, адресатом, принимающим
информацию, поступающую к нам благодаря электромагнитным вол-
волнам оптического диапазона, т. е. в виде световых изображений-сигна-
изображений-сигналов. Затем полученная информация поступает в следующий канал свя-
связи — канал, где линией связи является живой нерв (зрительный нерв),
а приемником сообщений — сетчатка глаза. По зрительному нерву нерв-
нервные импульсы (импульсы возбуждения) передаются от сетчатки глаза в
затылочный отдел головного мозга, где они превращаются в зритель-
зрительные образы.
Канал связи может быть весьма сложным (как, например, канал, бла-
благодаря которому мы можем видеть, т. е. получать информацию посред-
посредством зрения), но может быть и простым (например, пересылка письма
по обычной почте). Знакомиться с передачей информации по каналу
связи начинают, как правило, обращаясь к электротелеграфной связи.
Математическая теория связи (т. е. теория информации) возникла в
результате изучения именно электросвязи. Сначала телеграфной, а за-
затем также телефонной.
220

Справка. В 1837 году американский художник и изобретатель Сэмюэл Морзе
A791-1872) придумал первый электромеханический телеграфный аппарат. В
1838 году аппарат был усовершенствован и приспособлен для передачи сообщений
посредством кода Морзе (азбуки Морзе). В 1874 году телеграфную связь существен-
существенно усовершенствовал выдающийся американский изобретатель и предприниматель
Томас Эдисон A847-1931). В числе его многочисленных изобретений есть, в частно-
частности, фонограф (он был изобретен в 1877 году). История науки и техники отмечает
видную роль, которую сыграл в изобретении телефона и телефонной связи шотлан-
шотландец Александер Белл A847-1922), работавший, начиная с 1871 года в США. Упомя-
Упомянем также имя американского физика Гарри Найквиста A889-1976), внесшего су-
существенный вклад в развитие телеграфной и телефонной связи.
Рассмотрим общую схему канала связи. Она приведена на рис. 1 в
таблице 26. Одним из главных элементов канала связи является линия
связи. Именно по ней происходит передача информации в виде элект-
электрических или световых сигналов-импульсов, нервных импульсов или
просто писем, пересылаемых по почте. Отметим, что процесс передачи
информации по линии связи — это материальный процесс, связанный
с переносом вещества или энергии. В качестве линии связи могут вы-
выступать электрический кабель, оптическое волокно, нерв, а также про-
просто пространство, разделяющее отправителя и адресата.
Распространяясь по линии связи, информационный сигнал неизбежно
трансформируется: он в той или иной мере ослабляется и искажается.
Это происходит вследствие неустранимых помех (шумов), имеющих ста-
статистический характер. Они связаны с происходящими как внутри ка-
канала, так и вокруг него случайными процессами, в основном тепловыми.
Идеальных каналов связи (каналов без помех) не существует; всякая
реальная линия связи как-то ослабляет и искажает передаваемый по
ней информационный сигнал. Проблема повышения точности сигнала
на выходе канала связи по отношению ко входному сигналу — важней-
важнейшая проблема теории информации.
На входном конце канала связи находится кодирующее устройство, с
которым имеет дело отправитель информации, а на выходном конце
канала — декодирующее устройство', с ним имеет дело адресат. В коди-
кодирующем устройстве сообщение на входе (будем обозначать его через ф)
преобразуется в последовательность «элементарных сигналов» — сигнал
на входе (обозначим его через \|/). Именно сигнал \|/ и поступает в линию
связи. Кодирование — это операция отождествления сообщения на вхо-
входе с последовательностью элементарных сигналов (с сигналом на вхо-
входе), приспособленных для передачи по данной линии связи. На выход-
выходном конце канала связи происходит обратная операция — принятая
221

Таблица 26. Общая схема канала связи
Отправитель
Отправитель
Сообщение Сигнал
на входе
ф
Рис.1
на входе
Кодирование
Помехи
Линия связи
Сигнал Сообщение
на выходе j на выходе
I
Q
со
.Кодирование.
I
ГОРЕ
ИДЕАЛЬНЫЙ КАНАЛ
ГОРЕ
а)
3429
\
I
3429
110101100101
Рис.2
I
110101100101
I
б)
ГОРЕ
КАНАЛ С ПОМЕХАМИ
МОРЕ
3429
\
а)
I
3557
110101100101
Рис.3 I
110111100101
I
б)
222

адресатом последовательность элементарных сигналов (будем называть
ее сигналом Q) преобразуется в декодирующем устройстве в сообщение
на выходе (обозначим его через со).
Возьмем для примера обычную телефонную связь. Входное сообще-
сообщение ф реализовано в виде звука (в виде определенных колебаний давле-
давления воздуха). Кодирующее устройство — микрофон; он преобразует звуки
в электрические сигналы \|/, распространяющиеся по линии связи —
телефонному кабелю. Та часть телефонной трубки, которую мы подно-
подносим к уху, выполняет роль декодирующего устройства. В нем выходные
электрические сигналы Q преобразуются обратно в звуки (в сообщение
на выходе со).
На этом процесс передачи информации не заканчивается. Выходя-
Выходящие из телефонной трубки звуки играют роль входного сообщения для
другого канала связи — канала, функционирующего у нас в голове. Во
внутреннем ухе человека звуковое сообщение кодируется, превращаясь
в последовательность нервных импульсов; эти импульсы передаются по
слуховому нерву в височный отдел головного мозга, и там происходит
операция декодирования, преобразующая нервные импульсы в слухо-
слуховые образы.
Приведенный пример показывает, что понятия «отправитель» и «ад-
«адресат» могут иметь условный смысл. Они не всегда должны пониматься
буквально и связываться с разными людьми (разными участниками про-
процесса передачи информации).
Рисунок 2 в таблице 26 иллюстрирует идеальный канал связи (поме-
(помехи в линии связи предполагаются отсутствующими), а рис. 3 — анало-
аналогичный канал связи, но с помехами. На обоих рисунках представлены
два случая: а) сообщение ф — буквенный текст (точнее говоря, одно
слово), последовательность входных элементарных сигналов \|/ — по-
последовательность символов азбуки Морзе: точек, тире, пауз между бук-
буквами; б) сообщение ф — число в десятичной системе счисления, \|/ —
последовательность единиц и нулей, представляющих число ф в двоич-
двоичной системе.
В идеальном канале связи сигнал на выходе Q точно повторяет сиг-
сигнал на входе \|/. А вот в канале с помехами соответствие сигнала Q
сигналу \|/ оказывается неточным. Мы видим, что при передаче инфор-
информации в канале с помехами (см. рис. 3) была случайно утеряна точка в
коде Морзе для буквы «Г». Вместо посланной отправителем последова-
последовательности элементарных сигналов
223

адресат принял последовательность сигналов
в результате сообщение «ГОРЕ» на входе канала превратилось в сооб-
сообщение «МОРЕ» на выходе.
При кодировании числа 3429 была сформирована последовательность
элементарных двоичных сигналов:
110101100101.
Из-за помех в линии связи второй слева сигнал «0» случайно превратил-
превратился в сигнал «1», так что адресат принял последовательность двоичных
сигналов:
110111100101.
В результате сообщение «3429» на входе канала превратилось в сообще-
сообщение «3557» на выходе.
8.2 Передача сообщений по каналу связи
(общие замечания)
8.2.1. Передача дискретных сообщений. Разнообразие каналов связи
обусловлено прежде всего разнообразием характера сообщений, кото-
которые требуется передать по каналу. Сообщения на входе могут быть как
дискретными, так и непрерывными.
Передачу дискретного сообщения можно рассматривать как передачу
«буке» какого-то «алфавита». Это могут быть буквы русского, латин-
латинского, греческого или какого-либо другого алфавита. В качестве «букв»
могут выступать также отдельные слоги, слова, словосочетания, циф-
цифры, числа.
Каждая «буква» сообщения кодируется набором элементарных сигна-
сигналов', этот набор называют кодовым обозначением «буквы» (применяется
также термин «кодовое слово»). Цепочка элементарных сигналов образу-
образуется из кодовых слов, представляющих последовательно все «буквы»
данного сообщения.
Чаще всего используются двоичные элементарные сигналы. Каждый
такой сигнал — это либо импульс электрического тока длительностью т
(он кодируется единицей), либо пауза длительностью т (кодируется ну-
нулем). Импульсам длительностью 2т, Зт, 4т, и т.д. соответствуют 11, 111,
1111 и т. д. Аналогично паузам длительностью 2т, Зт, 4т, и т.д. соответ-
224

ствуют 00, 000, 0000 и т.д. На рис. 1 в таблице 27 представлено в виде
соответствующих импульсов тока и пауз некое сообщение, закодиро-
закодированное последовательностью двоичных элементарных сигналов, имею-
имеющей следующий вид:
10 1110 10 0001101.	(*)
Передача данного сообщения занимает время, равное 15т.
Кодовая запись (*) содержит 15 двоичных цифр. Однако из этого не
следует, что соответствующее сообщение содержит 15 битов информа-
информации. Можно утверждать только, что оно содержит не более 15 битов ин-
информации. А вот на сколько меньше пятнадцати битов — это зависит от
того, как было закодировано сообщение на входе канала.
Предположим, что по данному каналу связи за одну секунду можно
передать не более С двоичных элементарных сигналов и, следователь-
следовательно, не более С битов информации, подаваемой на вход. Величину С,
имеющую размерность бит/с, называют пропускной способностью (ина-
(иначе говоря, емкостью) данного канала связи. Заметим, что здесь пока
имеется в виду линия связи без помех (идеальный канал связи). Если
же говорить о реальном канале связи (учитывать помехи в линии свя-
связи), то для оценки емкости канала следует рассматривать не просто
количество информации, которое подается на вход (т. е. создается ис-
источником сообщений), а количество информации относительно сигнала
на входе, содержащееся в сигнале на выходе. Это понятие мы обсудим в
свое время (см. §8.7 и §8.8). Отметим, что лишь при условии отсут-
отсутствия помех в линии связи количество информации в сигнале на выхо-
выходе совпадает с количеством информации в сигнале на входе.
8.2.2. Передача непрерывных сообщений. Весьма часто сообщение не
входе является непрерывно изменяющимся во времени. Например, разго-
разговорная речь или музыка представляют собой непрерывные изменения
давления воздуха, воспринимаемые ухом слушающего. В телефонном
канале связи изменения давления воздуха, представляющие собой ре-
речевые сообщения, преобразуются в непрерывные изменения во време-
времени электрического напряжения.
В теории информации при передаче непрерывных сообщений ис-
используют так называемую теорему отсчетов. Она утверждает, что не-
непрерывный сигнал можно отобразить достаточно точно в виде после-
последовательности отсчетов его величины, взятых через равные промежутки
времени. На рис. 2а в таблице 27 изображен некий непрерывный сиг-
сигнал, а на рис. 26 этот сигнал представлен в виде совокупности отсче-
отсчетов, изображаемых вертикальными отрезками. Отсчеты берутся через
225

Таблица 27. Кодирование дискретных и непрерывных сообщений
0
т
////
X
1
0
i
1
ш
1
1
0
1
15х
0
0
0
0
1
i
1
0
1
1
Рис.1
Время-
Й
гч Время ¦
5788653235
100110111111101100010001010100
Рис.2
1-000
2-001
3-010
4-011
5-100
6-101
7-110
8-111
а
б
в
г
Д
е,ё
ж
3
00000
00001
00010
00011
00100
00101
00110
00111
и
й
к
л
м
н
о
п
01000
01001
01010
01011
01100
01101
01110
01111
р
с
т
У
Ф
X
Ц
ч
10000
10001
10010
10011
10100
10101
10110
10111
ш
щ
ы
ь,ъ
э
ю
я
—
11000
11001
11010
10011
11100
11101
НПО
11111
Рис.3
226

достаточно малые промежутки времени (меньше половины периода,
соответствующего наивысшей частоте, имеющейся в данном сигнале).
Так, для речевого сигнала, содержащего частоты до 4000 Гц, нужно
брать не менее 8000 отсчетов в секунду. В телевизионном сигнале при-
присутствуют частоты до 4 МГц; тут нужно брать до 8 000 000 отсчетов в
секунду.
Отсчеты отличаются друг от друга по амплитуде. Естественно, что
амплитуда отсчета может иметь любое значение от нуля до некоторого
максимального для данного сигнала значения U. В связи с этим выпол-
выполняют так называемое квантование отсчетов — делят (/на 100 и прибли-
приближенно представляют каждый отсчет двузначным числом, равным коли-
количеству отрезочков длиной G/100, укладывающихся на амплитуде данного
отсчета. В результате непрерывный сигнал преобразуется в набор дву-
двузначных чисел от 00 до 99. Таким образом, непрерывный сигнал оказы-
оказывается представленным в виде дискретного сообщения, в котором роль
«букв» играют указанные выше двузначные числа. Данное дискретное
сообщение содержит столько «букв», сколько взято отсчетов.
В целях иллюстрации идеи квантования отсчетов первые десять отсче-
отсчетов на рис. 26 в таблице 27 проквантованы в упрощенном варианте —
максимальное значение сигнала делится здесь не на 100, а на 8. Если при
этом амплитуда отсчета оказывается, например, между 4 и 5, то ей при-
приписывают значение 5. В результате такого квантования десяти отсчетов
возникает следующая последовательность десяти однозначных чисел:
578865323 5.
Воспользовавшись двоичной системой счисления, преобразуем эту пос-
последовательность однозначных чисел в цепочку двоичных элементарных
сигналов:
100 ПО 111 111 101 100 010 001 010 100.
Так как непрерывное сообщение можно в принципе отобразить в
виде дискретного сообщения, ограничимся в дальнейшем рассмотре-
рассмотрением только дискретных сообщений на входе канала связи. При этом
будем использовать для кодирования только двоичные элементарные
сигналы {двоичные коды).
8.2.3. Условия передачи сообщений. Отметим условия, которые долж-
должны быть выполнены при передаче сообщений по каналу связи.
Прежде всего необходимо, чтобы полученная при кодировании со-
сообщения цепочка элементарных сигналов (цепочка единиц и нулей)
могла быть правильно «прочитана» адресатом, т. е. однозначно преоб-
преобразована при декодировании в сообщение, посланное отправителем.
227

Коротко говоря, нужно кодировать сообщение на входе таким образом,
чтобы не возникало проблем при его декодировании на выходе канала.
Адресат должен уверенно распознавать, где в принятой им цепочке еди-
единиц и нулей кончается одна «буква» посланного отправителем сообще-
сообщения и где начинается следующая. (Напоминаем, что пока мы не учиты-
учитываем наличие помех в линии связи).
Максимальная скорость ввода информации в канал связи должна быть
согласована с его пропускной способностью. Допустим, что отправитель
вводит «буквы» сообщения в канал связи с некоторой постоянной ско-
скоростью, равной v «буквам» в секунду. Обозначим через Н энтропию
«буквы», т. е. рассматриваемую в расчете на одну «букву» сообщения
степень неопределенности, скрывающую в себе соответствующее коли-
количество информации, предназначенное для адресата (Н имеет размер-
размерность бит/«буква»). Энтропия Н отражает статистические свойства со-
сообщения, передаваемого по каналу связи; подробнее об этом понятии
мы поговорим в § 8.5. Если С бит/с — пропускная способность (ем-
(емкость) данного канала связи, то требование согласования скорости вво-
ввода информации в канал с емкостью канала можно представить в виде
соотношения:
v<C/H.	A)
Знак «=» определяет максимальную скорость ввода информации при
заданных С и Н.
Есть условия не столь обязательные, но весьма желательные. По ним
судят об эффективности кодирования сообщения. Речь идет, во-пер-
во-первых, об экономности кода. Общее пожелание: используемый код должен
быть максимально экономным. Иными словами, важно, чтобы для коди-
кодирования было использовано поменьше элементарных сигналов и тем
самым было сокращено, насколько это возможно, время, затрачивае-
затрачиваемое на передачу этого сообщения. Напомним, что время, затрачивае-
затрачиваемое на передачу сообщения, состоящего из N двоичных сигналов, рав-
равно jYt, где т — длительность однократного импульса или однократной
паузы (см. рис. 1 в таблице 27). Заметим однако, что в действительнос-
действительности вопрос об экономности кода отнюдь не прост. Необходимо прини-
принимать во внимание, что разные «буквы» сообщения могут кодироваться
разным числом двоичных сигналов и при этом могут иметь разную ве-
вероятность появления. Об этом будет разговор в § 8.5, где и будет сфор-
сформулировано условие наибольшей экономности кода.
Во-вторых, весьма важно, чтобы используемый код обеспечивал мак-
максимально возможную помехозащищенность передачи сообщения. Жела-
228

тельно кодировать так, чтобы насколько это возможно снизить вероят-
вероятность искажений передаваемой по данному каналу информации, обус-
обусловленных помехами в линии связи. При этом можно, в частности,
пожертвовать в какой-то мере экономностью кода, передавая, напри-
например, каждую «букву» сообщения два или даже три раза. В § 8.9 мы по-
познакомимся с тем, как можно бороться с помехами за счет использова-
использования соответствующего кодирования сообщения на входе.
8.3 Кодирование с использованием
равномерных двоичных кодов. Код Бодо
11ри использовании равномерных кодов каждая «буква» сообщения
представляется кодовым обозначением (кодовым словом), состоящим
из одного и того же количества п элементарных сигналов. При этом
автоматически выполняется условие уверенного декодирования адреса-
адресатом принятой им цепочки единиц и нулей. Адресату надо просто раз-
разбить эту цепочку на «кусочки» по п двоичных цифр. Каждый такой
«кусочек» есть кодовое слово, представляющее соответствующую «бук-
«букву» сообщения.
Примером равномерного двоичного кода является код Бодо, сопос-
сопоставляющий каждой букве алфавита кодовое слово из пяти двоичных
цифр. Почему именно пяти? Дело в том, что, комбинируя п двоичных
цифр, можно составить 2п различных кодовых слов. Если, например,
п = 2, то существует четыре кодовых слова:
00, 01, 10, 11.
Если п = 3, можем составить восемь кодовых слов:
000, 001, 010, 011, 100, 101, ПО, 111.
Если п = 4, то можно составить шестнадцать кодовых слов:
0000, 0001, 0010, ООП, 0100, 0101, ОНО, 0111,
1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
При п = 5 существует 25 = 32 кодовых слова. В греческом алфавите 24 бук-
буквы, в латинском — 27 буквы, в русском 33 буквы. Буквы каждого из
этих алфавитов можно кодировать, используя код Бодо. В том числе и
буквы русского алфавита, если не делать различия между «е» и «ё», а
также между «ь» и «ъ» (при этом останется кодовое слово для обозначе-
обозначения пробела между словами). Недаром двоичный код Бодо (именно он,
229

а не азбука Морзе) чаще всего применяется в современных буквопеча-
буквопечатающих телеграфных аппаратах.
Код Бодо для букв русского алфавита представлен на рис. 3 в табли-
таблице 27 (здесь тире означает пробел между словами). Он получен с помо-
помощью двоичной системы счисления. Буквы алфавита были по порядку
перенумерованы от 0 до 30, а затем каждый из номеров был записан в
двоичной системе счисления. Чтобы каждое кодовое слово содержало
пять двоичных цифр, там, где это потребовалось, были приписаны нули
слева. Например, номер 5 (буква «е») получил в качестве кодового сло-
слова не 101, а 00101.
Познакомившись с кодом Бодо, мы можем возвратиться к кодовой
записи (*) в § 8.2 и декодировать ее, разбив 15 двоичных цифр на три
кодовых слова, состоящих из пяти цифр:
10111 - 01000 - 01101.
Закодированное кодом Бодо слово есть, как легко убедиться, слово
«ЧИН».
В качестве примера закодируем кодом Бодо поговорку «ДЕЛО ДЕЛУ
УЧИТ». В закодированном виде эта поговорка выглядит так:
00100001010101101110111110010000101010
11100111111110011101110100010010.
8.4 Кодирование с использованием неравномерных
префиксных двоичных кодов
У1вляется ли равномерный двоичный код достаточно экономным? —
Вряд ли. Обратим внимание на то, что, например, буквы «ц», «щ», «ш»,
«э», «ф» кодируется пятью двоичными цифрами наряду с буквами «о»,
«а», «е», «и», «н». Однако вторая пятерка букв встречается в тексте зна-
значительно чаще (более, чем в 10 раз!), чем первая пятерка. Из соображе-
соображений экономности кода следовало бы буквы второй пятерки кодировать
более короткими кодовыми словами, нежели относительно редко встре-
встречающиеся в тексте буквы первой пятерки. Тем самым мы приходим к
идее неравномерных кодов — когда длина кодового слова может разли-
различаться для разных «букв».
Однако сможет ли адресат уверенно декодировать цепочку единиц и
нулей в случае использования неравномерного кода? — Да, сможет,
если неравномерный код будет удовлетворять условию: никакое кодовое
230

слово не совпадает с началом какого-либо другого более длинного кодового
слова. Если это условие выполнено, то, просматривая слева направо
цепочку единиц и нулей и имея перед собой список всех кодовых слов,
адресат сможет точно распознать, где кончается кодовое обозначение
одной «буквы» и начинается обозначение следующей. Данное условие
называют префикс-условием, а удовлетворяющие ему двоичные коды —
префиксными двоичными кодами.
Как получить префиксный код? — На этот счет есть простое прави-
правило. Надо построить дерево кода с числом свободных вершин, равным
числу «букв», подлежащих кодированию. Дерево кода строится следую-
следующим образом. От некоторой точки {исходной точки) проводим две вет-
ветви; левую ветвь помечаем нулем, а правую единицей. Одну из ветвей
или обе «расщепляем» на две вторичных ветви и снова помечаем левую
ветвь нулем, а правую единицей. От вторичных ветвей могут рождаться
пары третичных ветвей, от третичных — пары четверичных ветвей и так
далее. После каждой развилки левую ветвь помечаем нулем, а правую
единицей. Процесс ветвления прекращается, когда число свободных
вершин станет равным числу «букв», которые предстоит закодировать.
Каждой из этих вершин соответствует «буква» сообщения; кодовое обо-
обозначение (кодовое слово) этой буквы есть совокупность единиц и ну-
нулей, которые встречаются последовательно на пути от исходной точки
дерева к данной свободной вершине.
Понятно, что для одного и того же количества «букв» можно постро-
построить разные кодовые деревья и, следовательно, составить разные пре-
префиксные двоичные коды. Предположим, что сообщение состоит из де-
десяти «букв», которые условно будем обозначать как А, Б, В, Г, Д, Е, Ж,
3, И, К. На рисунках 1-4 в таблице 28 представлены четыре варианта
дерева для кодирования этих «букв». Там же показаны соответствую-
соответствующие префиксные двоичные коды.
Префиксный код на рис. 1 содержит 2 двузначных кодовых слова, 2 трехзнач-
трехзначных, 3 четырехзначных, 1 пятизначное, 2 шестизначных.
Общее число двоичных цифр:
М! = 2-2 + 2-3 + 3-4+1-5 + 2-6 = 39.
Префиксный код на рис. 2 содержит 2 двузначных кодовых слова, 2 трехзначных,
2 четырехзначных, 4 пятизначных. Общее число цифр:
М2 = 2-2 + 2-3 + 2-4 + 4-5 = 38.
Префиксный код на рис. 3 содержит 2 двузначных кодовых слова и 8 четырехзнач-
четырехзначных. Общее число двоичных цифр:
Мъ = 2 ¦ 2 + 8 • 4 = 36.
231

Таблица 28. Неравномерные префиксные двоичные коды
в
\
0N
ж
\
о\
х
0
0
0
0
0
0
0
Г
s/f Д
JvTV
o\/i
3
/в г
А\ /
\ 0Мл
К/ А
\
о\
Ъ
,29
,22
,15
,11
ДО
,08^
,05 ^0Д
jnarj
0
0
0
0
0
0
0
,29
,22	.
,15.
,08 vs/
,05^
Рис.5
И
ж\о/
vO/1
Л
Рис
И
Д Е\
J?v /
Б V/
у
/1
Рис
3
0,29
0,22
0,15
ОДО
0,08
0,05
К
1
К
/
3
>о,
jnar2^
—¦
	с
< /
1 /0,28
/
3 jnarj_
*3 /
/
А
Б
В
Г
Ж
3
И
к
А
Б
В
Г
д
Е
Ж
3
И
К
21
13
0,57
7
00
01
1000
1001
101
по
1110
НПО
111110
111111
01
10
0010
ООП
1100
1101
0000
0001
1110
1111
0,29
0,22
0,15
0,11
ОДО
0,08
0,05
0
0
0
0
0
0
0
А
(К
(
д
/у
0
•^0,21
•у/
/одз
Шаг
,29-
,22-
Д5Х
11 1
ДО'О
,080
,05^0
В
\
3 V
Е
v ° У
X
о\
/
3
1—¦—
¦	*
1
><
0,21
/
/
0,13
в
У
ж
/
'а
о\
о\
— —1
— —
у
о
ш
Ж 3
\о>
Г\1
А °)
оЧ/ч
3
БВ Г
/ioVi
oV
/
ч/
о
18
о,
о,
о,
о,
о,
о,
о,
1
0,43
0,28
и
0)
к
' 1
Рис.2
И
о/
у/1
(Л/
У
А
к
/
/л
Г1
Рис.4
29
22-
15.
1Ь
10'
08 >
05'
0,
2
/¦—
у
А
Б
В
Г
Д
1
Ж
3
и
к
А
Б
В
Г
д
Е
Ж
3
И
К
1 ?
/
ДПаМ
57
0,
о,
о,
о,
о,
- —
29-
22-
15-
11-
10-
0,08-
0,05-
00
01
100
101
1100
1101
11100
11101
НПО
11111
010
011
100
101
000
0010
ООП
1100
1101
111
0,43
*0,28
=О
1,00
11
01
101
001
000
1001
1000
232

Префиксный код на рис. 4 содержит 6 трехзначных кодовых слов и 4 четырехзнач-
четырехзначных. Общее число двоичных цифр:
М4 = 6 • 3 + 4 • 4 = 34.
Если бы мы применили равномерный код, то, учитывая, что 23 < 10 < 24, должны
были бы каждую из десяти наших «букв» кодировать четырьмя двоичными цифра-
цифрами. Общее число цифр равнялось бы Мщвп = 10 • 4 = 40.
Сравнивая МЩШ1 с Мь М2, Мъ, М4, мы поневоле приходим к выводу,
что неравномерный код более экономный, нежели равномерный. Со-
Согласитесь, что использовать для кодирования сообщения из десяти «букв»
34 двоичных цифры вместо сорока — это явная экономия времени, за-
затрачиваемого не передачу данного сообщения. Действительно, неравно-
неравномерный код экономнее равномерного, чем и объясняется предпочтитель-
предпочтительность использования неравномерных двоичных кодов (разумеется,
префиксных). Однако вопрос о степени экономности кода определяет-
определяется отнюдь не только общим числом М двоичных цифр в кодовой це-
цепочке. Необходимо принимать во внимание также статистические свой-
свойства сообщения, т. е. вероятности появления в нем тех или иных «букв».
Иными словами, надо учитывать, насколько часто используются те или
иные «буквы». На первый взгляд, может показаться, что код не рис. 4
более экономен, чем код на рис. 1. Это, однако, зависит от вероятнос-
вероятностей «букв». Вполне может оказаться, что более экономен код на рис. 1,
в чем мы как раз и убедимся в следующем параграфе.
8.5 Энтропия «буквы» и среднее число двоичных цифр,
приходящееся на одну «букву»
в
предыдущих параграфах, где было дано общее представление о
канале связи и об операции кодирования, мы фактически не обраща-
обращались к понятию вероятности. Поэтому вряд ли можно было понять,
какую роль в проблеме передачи сообщений по каналу связи играет
теория информации. Пришло время поговорить об этом.
Отправитель, используя некий «алфавит», создает сообщение на вхо-
входе канала, представляющее собой некоторую последовательность «букв»
«алфавита». Появление в сообщении той или иной «буквы» (выбор от-
отправителем той или иной «буквы») вносит в сообщение на входе какое-
то количество информации Н, которое принято называть энтропией (точ-
(точнее: энтропией «буквы» сообщения). С точки зрения адресата, Н — это
степень неопределенности, отнесенная к одной «букве». Адресат знает, ка-
каким «алфавитом» пользуется отправитель, но он пребывает в неведении
233

относительно выбранных отправителем «букв». Эта неопределенность
будет устранена, когда адресат примет присланное ему по каналу связи
сообщение, в результате чего он получит количество информации, рав-
равное Н (в расчете на одну «букву» сообщения). Собственно говоря, цель
и результат процесса передачи информации по каналу связи как раз и
состоят в устранении указанной выше неопределенности. Устранение не-
неопределенности будет полным в случае идеального канала связи и непол-
неполным в случае канала связи с помехами. В первом случае адресат получа-
получает количество информации, в точности равное Н9 а во втором случае —
количество информации, равное Н— Н1', где Н1 — количество инфор-
информации (в расчете на «букву» сообщения), потерянное в канале связи
вследствие случайных помех.
О частичной утрате информации в канале с помехами мы поговорим
в § 8.7, а пока вернемся к разговору об Н — энтропии «буквы» сообще-
сообщения на входе канала. Понятно, что чем богаче выбор «букв», тем боль-
больше неопределенность и, следовательно, больше энтропия Н «буквы».
Если «алфавит» содержит N «букв» и если все «буквы» равновероятны,
то Н определяется (в битах) по уже знакомой нам формуле Хартли:
Н = log2 N.	B)
Во многих случаях, однако, различные «буквы» характеризуются раз-
разной вероятностью появления. Пусть хъ хъ х3,..., xN— ^различных «букв»,
образующих данный «алфавит», и пусть ръ ръ ръ,..., pN — вероятности
N
этих «букв». Понятно, что ^2 Pi = 1. Совокупность вероятностей pt как
раз и выражает статистические свойства сообщения, передаваемого по
каналу связи. В соответствии с формулой Шеннона (с которой мы также
уже знакомы) энтропия «буквы» сообщения есть
-|-.	C)
P
Наряду с энтропией «буквы» в теории информации рассматривают
среднее число двоичных цифр, приходящееся на одну «букву». Будем обо-
обозначать это среднее число через X. Легко сообразить, что X есть не что
иное, как средняя длина кодового слова (кодового обозначения «бук-
«буквы»). Она определяется через вероятности р{.
М,	D)
234

где /z — длина кодового слова для /-ой «буквы». Подчеркнем, что именно
X характеризует степень экономности кода. Чем меньше средняя длина
кодового слова, тем более экономен код.
Пусть М — общее число двоичных цифр, соответствующее совокуп-
совокупности всех N различных «букв» данного «алфавита». Понятно, что
N
(*)
Если каждая «буква» имеет одну и ту же вероятность (равную, очевид-
очевидно, 1 / N), то в этом случае соотношение D) принимает простой вид:
E)
i=\
А
0,3
Б
0,25
В
0,06
г
0,04
д
0,12
Е
0,12
Ж
0,04
3
0,02
И
0,02
К
0,03
В этом (и только в этом) случае экономность кода полностью определя-
определяется общим числом двоичных цифр в кодовой записи сообщения. Если
бы в примерах, которые иллюстрируют рисунки 1-4 в таблице 28, «бук-
«буквы» А, Б, В, Г, Д, Е, Ж, 3, И, К характеризовались одной и той же
вероятностью (вероятностью 1/10), то мы могли бы уверенно утверждать,
что код на рисунке 1 более экономен, чем равномерный код (поскольку
4 > 39/ 10) степень экономности кодов на рисунках 1, 2, 3, 4 постепен-
постепенно возрастает от кода к коду (это следует из неравенств: 39 / 10 > 38 / 10 >
> 36/10 > 34/10).
Теперь предположим, что наши десять «букв» имеют вероятности:
(**)
Сравним для данного случая неравномерные коды на рис. 1 и на
рис. 4. Для кода на рис. 1 находим:
Х{ = @,3 + 0,25) • 2 + @,12 + 0,12) • 3 + @,06 + 0,04 + 0,04) • 4 +
+ 0,02 • 5 + @,02 + 0,03) • 6 = 2,78
Для кода на рис. 4 находим:
Х4 = @,3 + 0,25 + 0,06 + 0,04 + 0,12 + 0,03) • 3 +
+ @,12 + 0,04 + 0,02 + 0,02) • 4 = 3,2.
Итак, неравномерный код на рис. 1 оказывается для вероятностей
(**) существенно более экономным, чем неравномерный код на рис. 4.
235

В первом случае А,} = 2,78 элементарных сигналов (двоичных цифр) на
«букву», а во втором случае Х4 = 3,2 сигнала на «букву». Для сравнения
подсчитаем энтропию «буквы» с учетом вероятностей (**). Соотноше-
Соотношение C) принимает вид:
. - -,.	^ 0,12	'	OZ0,02 '	OZ0,03*
Используя данные таблицы 23, получаем:
Н= 2,75 бит/«буква».
Итак, Х{ = 2,78 двоичная цифра/«буква» и Н= 2,75 бит/«буква». Мы
видим, что неравномерный код на рис. 1 оказывается для рассматривае-
рассматриваемой совокупности вероятностей pt весьма экономным. При использо-
использовании этого кода каждая двоичная цифра содержит в среднем почти
целый бит информации (ведь 2,78 « 2,75). Этого отнюдь не скажешь о
коде на рис. 4; он в значительной мере менее экономен.
Рассмотрим теперь в качестве «алфавита» русский алфавит, а в каче-
качестве «букв» буквы этого алфавита плюс пробел между словами (при
этом не будем различать буквы «е» и «ё», а также «ь» и «ъ»). В данном
случае N= 32 и, если бы мы использовали равномерный двоичный код,
то имели бы X = 5. Его неэкономность вполне очевидна. Поэтому имеет
смысл поискать достаточно экономный неравномерный двоичный код
(разумеется, префиксный). Набор вероятностей pt мы позаимствуем из
книги A.M. Яглома и И.М. Яглома «Вероятность и информация» (М.:
«Наука», 1973):
пробел — 0,174
о - 0,090
е, ё - 0,072
а - 0,062
и - 0,062
т - 0,053
н - 0,053
с - 0,045
р - 0,040
в - 0,038
л - 0,035
к - 0,028
м — 0,026
д - 0,025
п - 0,023
у - 0,021
я - 0,018
ы - 0,016
з - 0,016
ь, ъ - 0,014
б - 0,014
г - 0,013
ч - 0,012
й - 0,010
х - 0,09
ж - 0,007
ю - 0,006
ш - 0,006
ц - 0,004
щ - 0,003
э - 0,003
ф - 0,002
F)
Предварительно подсчитаем с учетом вероятностей F), чему равна
энтропия одной буквы русского алфавита. Воспользуемся формулой
Шеннона C) и данными таблицы 23. Подсчет показывает, что с учетом
236

пробела между словами буква русского алфавита имеет энтропию (ин-
(информацию):
Н= 4,35 бит.	(***)
Теперь предстоит рассмотреть для заданных вероятностей F) наибо-
наиболее экономный неравномерный двоичный код. Таким кодом является
код Хаффмена. Покажем, как его можно построить.
8.6 Код Хаффмена
всего сразу рассмотреть конкретный пример. Он приведен
на рисунках 5 и 6 в таблице 28. Здесь «алфавит» состоит из семи «букв»,
имеющих вероятности: 0,29; 0,22; 0,15; 0,11; 0,10; 0,08; 0,05. Код Хаф-
Хаффмена строится путем постепенного (шаг за шагом) конструирования
соответствующего дерева кода, причем процесс конструирования дере-
дерева развивается не от исходной точки к свободным вершинам, а наобо-
наоборот, от свободных вершин к исходной точке. В качестве свободных вер-
вершин на рисунках рассматриваются вероятности соответствующих «букв»
нашего «алфавита». Выпишем в столбец все семь вероятностей в поряд-
порядке их постепенного убывания — от 0,29 до 0,05, после чего приступим к
конструированию хаффменовского дерева кода.
На 1-м шаге (см. рис. 5) находим две наименьшие вероятности из семи; это
вероятности 0,05 и 0,08. Складывая их, получаем на будущем кодовом дереве
«развилку», которой соответствует вероятность 0,05 + 0,08 = 0,13. В результате
такого сжатия «алфавита» у нас остаются шесть вероятностей: 0,29; 0,22; 0,15;
0,11; 0,10; 0,13.
На 2-м шаге находим две наименьшие вероятности из шести; это вероятности
0,10 и 0,11. Складывая их, получаем «развилку», которой соответствует вероят-
вероятность 0,10 + 0,11 = 0,21. В результате очередного сжатия «алфавита» у нас остают-
остаются пять вероятностей: 0,29; 0,22; 0,15; 0,21; 0,13.
На 3-м шаге находим две наименьшие вероятности из пяти; это вероятности
0,15 и 0,13. Складывая их, получаем «развилку», которой соответствует вероят-
вероятность 0,15 + 0,13 = 0,28. В результате остаются четыре вероятности: 0,29; 0,22;
0,21; 0,28.
На 4-м шаге находим две наименьшие вероятности из четырех; это вероят-
вероятности 0,22 и 0,21. Складывая их, получаем «развилку», которой соответствует
вероятность 0,22 + 0,21 = 0,43. В результате остаются три вероятности: 0,29;
0,43; 0,28.
На 5-м шаге находим две наименьшие вероятности из трех; это вероятности
0,29 и 0,28. Складывая их, получаем «развилку», которой соответствует вероятность
237

0,29 + 0,28 = 0,57. В результате остаются всего две вероятности: 0,57 и 0,43. Сло-
Сложив их на 6-м шаге, мы приходим, наконец, к исходной точке дерева, которой
соответствует, как и полагается, вероятность 1.
В отличие от кодовых деревьев, представленных на рисунках 1-4 наше дерево
как бы положено набок; поэтому вместо выходящих из развилок левых и правых
ветвей будем рассматривать здесь верхние и нижние ветви. Условимся все верхние
ветви обозначать единицей, а все нижние — нулем (см. рис. 6).
Перемещаясь теперь по дереву кода от его исходной точки к той или иной
свободной вершине, будем фиксировать последовательно все встречающиеся на
нашем пути единицы и нули. В результате получим кодовое слово для той «бук-
«буквы», которая соответствует данной свободной вершине.
На рис. 6 показан рядом с построенным деревом код Хаффмена для «букв»
нашего «алфавита»; последние представлены здесь своими вероятностями.
Используя полученный код Хаффмена, подсчитаем среднюю длину
кодового слова для «буквы» нашего «алфавита»:
X = @,29 + 0,22) • 2 + @,15 + 0,11 + 0,10) • 3 + @,8 + 0,5) • 4 = 2,62.
Для сравнения подсчитаем по формуле Шеннона C) с использованием
таблицы 23 энтропию «буквы» нашего «алфавита»:
1 = 0,29-log2-J^+ 0,22-log,-J^ +
Как видим X « Н, что свидетельствует о высокой экономности кода Хаф-
Хаффмена.
Нетрудно понять, почему код Хаффмена оказывается весьма эко-
экономным (более того, специалисты считают, что он наиболее эконо-
экономен). Дело в том, что, конструируя дерево кода, мы начинали переме-
перемещаться к исходной точке дерева сначала от «букв» с самыми малыми
вероятностями, постепенно включая в процесс «буквы» с увеличиваю-
увеличивающимися вероятностями. Поэтому весь путь вдоль дерева от «буквы» до
исходной точки (а значит, и длина кодового слова) получался более
длинным для менее вероятных «букв» и более коротким для более
вероятных «букв».
Теперь можно построить код Хаффмена для русского алфавита с уче-
учетом вероятностей букв, представленных в F). Это построение показано
в таблице 29 (там изображено соответствующее дерево кода). После того,
как мы познакомились с технологией построения кода Хаффмена на
238

примере «алфавита» с семью «буквами», нетрудно понять, как было скон-
сконструировано кодовое дерево Хаффмена в случае 32-буквенного русско-
русского алфавита.
Используя D), F) и дерево кода, изображенное в таблице 29, под-
подсчитаем среднюю длину кодового слова:
X = @,174 + 0,090) • 3 + @,072 + 20,062 + 20,053) • 4 + 0,260 • 5 +
+ 0,134 • 6 + 0,028 • 7 + 0,007 • 8 + 0,005 • 9 = 4,40.
Сравнивая этот результат с энтропией буквы русского алфавита, рав-
равной, как мы уже знаем, 4,35 бит, убеждаемся еще раз в высокой эко-
экономности кода Хаффмена.
8.7 Эффективность канала связи с помехами.
Взаимная информация о сообщениях на входе и на выходе
p сих пор, говоря о сообщении, передаваемом по каналу связи,
мы употребляли термины «алфавит» и «буква». Используя терминоло-
терминологию теории вероятностей, можно заменить эти термины терминами «дис-
«дискретная случайная величина» и «значение случайной величины». Вмес-
Вместо вероятности появления той или иной «буквы» следует рассматривать
теперь вероятность реализации того или иного значения дискретной
случайной величины.
Итак, будем говорить, что на вход канала связи поступает дискрет-
дискретная случайная величинаX, значения которой хъ х2, х3,..., .% реализуются
с вероятностями, равными, соответственно, ръ ръ /?3,..., Pn- На выходе
канала принимается дискретная случайная величина Z, значения кото-
которой гъ гъ 23,..., ^реализуются с вероятностями, равными, соответствен-
соответственно, qh qb #3,..., Qn- Можно сказать, что отправитель посылает дискретную
случайную величину X, а адресат принимает случайную величину Z. Мож-
Можно также говорить, что отправитель посылает сообщение X, содержащее
сигналы хъ хъ х3,..., xNc вероятностями ръ ръ ;?3,..., pN, а адресат прини-
принимает сообщение Z, содержащее сигналы гъ гъ 23,..., zNc вероятностями
ql9 q2, ft,-, qN.
Замечания. 1. Помехи воздействуют на сигналы, передаваемые по линии связи. А
по линии связи передаются элементарные сигналы, сформированные в результате
кодирования. Поэтому под используемым здесь понятием «сигнал» понимается
значение элементарного сигнала.
239

Таблица 29. Кодирование букв русского алфавита по методу Хаффмена
0,174
0,090
0,072-
0,062-
0,062
0,053-
0,053-
0,045-
0,040-
0,038-
0,035-
0,028-
0,026-
0,025-
0,023-
0,021-
0,018-
0,016-
0,016-
0,014-
0,014-
0,013-
0,012-
0,010
0,009-
0,007-
0,006-
0,006-
0,004-
0,003-
0,003-
0,002-
0,094
•0,005
о
е
а
и
т
н
'0,011
-	0,174
-	0,090
-	0,072
-	0,062
-	0,062
-	0,053
-	0,053
111
001
1011
1010
1001
0111
ОНО
-	0,045
-	0,040
-	0,038
-	0,035
-	0,028
-	0,026
-	0,025
-	0,023
-	0,021
-	0,018
-	0,016
-	0,016
-	0,014
-	0,014
-	0,013
-	0,012
-	0,010
-	0,009
-	0,007
-	0,006
-	0,006
-	0,004
-	0,003
-	0,003
-	0,002
11011
11010
11001
10001
01011
01001
00011
00010
110001
110000
100001
010101
010100
010001
000011
000010
000001
1000001
0100001
0100000
0000001
10000001
10000000
000000001
000000000
240

2. Полагаем для простоты, что число сигналов в сообщении Z совпадает с
числом N сигналов в сообщении X (как если бы рассматривался идеальный канал
связи). В общем случае для канала с помехами указанные числа совпадать не
обязаны.
В отсутствие помех в линии связи можно считать, что, если отправи-
отправитель послал сигнал xi9 то адресат будет наблюдать сигнал zt (/ = 1, 2, 3,..., N).
Тут вся неопределенность связана исключительно с энтропией Н{Х)
посланного сообщения; она обусловлена тем, какой из сигналов хъ хъ
х3,..., xN выбирает отправитель. Напомним, что энтропия Н (X) опреде-
N	j
ляется формулой Шеннона: Н{Х) = Y^Pi log 2 — •
При наличии помех в линии связи ситуация становится более не-
неопределенной. Теперь отправитель, послав сигнал xi9 не может сказать с
уверенностью, какой из сигналов гъ гъ 23,..., 2/,..., zN будет принят
(будет наблюдаться) адресатом. Отправитель послал сигнал xi9 а адресат
может наблюдать в принципе любой из сигналов гъ гъ 23,..., zj9...9 zN —
см. рис. 1 в таблице 30. В связи с этим рассматривается условная веро-
вероятность Рх (zj). Это есть вероятность наблюдения адресатом сигнала Zj
при условии, что был послан сигнал xt. Строго говоря, речь идет не об
одной, а об N2 условных вероятностях, т. е. о матрице Рх (г
PXlBl)PXlB2)...PXl{2j)...PXlBN)
PX2Bl)PX2B2)...PX2{2j)...PX2BN)
РхЛг,)РхАг2)...Рх(гЛ...Р:
xNBN
G)
При наличии помех в линии связи адресат тоже ни в чем не уверен.
Приняв сигнал zj9 он не может сказать с определенностью, какой из
сигналов хъ хъ х3,..., xi9 xN6hm послан отправителем. Адресат принял
сигнал zj9 а отправитель мог послать в принципе любой из сигналов
хъ хъ х3,..., xi9 xN — см. рис. 2 в таблице 30. В связи с этим рассматри-
рассматривается условная вероятность Pz\xt). Это есть вероятность посылки
отправителем сигнала xt при условии, что адресатом принят сигнал Zj.
Строго говоря, речь идет о (NxN)-матрице условных вероятностей
\Рг. (х/)|, аналогичной матрице G).
Вероятности Рх. (z^ и Р2 (xf) связаны друг с другом. В этом легко убедиться,
вспомнив основы теории вероятности. Пусть At — случайное событие, состоящее в
посылке отправителем сигнала xi9 a Bj — случайное событие, состоящее в приеме
241

Таблица 30. Неопределенности, обусловленные случайными помехами в линии
связи
Рис.2
Неопределен-
Неопределенность для
адресата
Рис.1
Неопределен-
Неопределенность для
отправителя
Oz2
242

адресатом сигнала Zj. Обозначим: P{At) — вероятность наступления события xi9
P(Bj) — вероятность наступления события Zj, РА. (Bj) — вероятность наступления
события Bj при условии наступления события Ai9 Рв (At) — вероятность наступ-
наступления события Аг при условии наступления события Bj9 P(AtnBj) — вероятность
совместного наступления событий At и Bj. Из теории вероятности следует (см.,
например, §9.4 в книге автора «Случайность, необходимость, вероятность»):
PAl {Bj) • Р(Д.) = РВ. (A,) -P{Bj) = Р(Д-) П Bj). .	(8)
У нас Р(Д.) = Pi; P(Bj) = q/, PAj {Bj) = Рщ (гу); PBj (A,) = Рг.(х,.).
Поэтому равенства (8) можно переписать в виде:
PXl(zj)-Pt =PZj(xi)-gJ=P{AinBj).	(9)
Подчеркнем, что условные вероятности Рх [zj) и P2.(xf) (имеются в
виду, конечно, матрицы \\РХ. [zj)\\ и |PZ. (xf) ) обусловлены случайными по-
помехами е линии связи; они являются статистическими характеристика-
характеристиками помех. В отсутствие помех (для идеального канала связи):
PXi{zJ) = Pgj(xi)=&(i9	A0)
где Ьу — так называемый символ Кронекера: 8^- = 0 при / ^j и 8^- = 1 при
Из-за помех в линии связи адресат, наблюдая сообщение Z, полу-
получает количество информации, которое меньше количества информа-
информации, содержавшегося в посланном сообщении X и определявшегося
энтропией Н(Х). Будем обозначать количество информации о послан-
посланном отправителем сообщении X, содержащееся в принятом адресатом
сообщении Z, через Н(Х9 Z) и будем называть кратко это количество
информации взаимной информацией о сообщениях X и Z (этот термин
поясним немного позднее). Как только что было отмечено, Н(Х9 Z) <
< Н{Х). Разность
Hr = H{X)-H{X,Z)	A1)
следует рассматривать, очевидно, как количество информации, поте-
потерянное при передаче вследствие случайных помех. Понятно, что, чем больше
взаимная информация Н(Х9 Z) (точнее сказать: чем она ближе к Н(Х))9
тем меньше количество информации, потерянное при передаче, и тем,
следовательно, больше эффективность данного канала связи.
Отметим два предельных случая. В первом случае канал связи макси-
максимально эффективен. Это означает, что в принятом адресатом сообщении
243

содержится полностью то количество информации, которое послал от-
отправитель: Н(Х, Z) = Н{Х). В данном случае Н' = 0. Мы имеем здесь
дело с каналом связи без помех.
Во втором предельном случае канал связи совершенно неэффективен
(можно сказать, что его эффективность равна нулю). Это означает, что
в принятом адресатом сообщении не содержится вовсе количества ин-
информации, которое послал отправитель: Н(Х, Z) = 0. В данном случае
Н' = Н{Х) — вся посланная информация утрачена из-за помех.
Приведем без доказательства соотношение, выражающее Н(Х, Z) че-
через вероятности pt и qj и условные вероятности Рх
A2)
Мы простоты ради опустили вывод соотношения A2). Зато покажем,
что в отсутствие помех в линии связи правая часть этого соотношения
действительно превращается в энтропию Н{Х). Если нет помех, то ус-
условные вероятности принимают вид A0). Для всех у, не равных /, имеем
Р (г-)
Рх (г^ = 0 и, соответственно, Рх {Zj)pt log2 ——— = 0 (поскольку
lim (wlog2 w) =0). Таким образом, в A2) остаются только слагаемые с
i =j9 в результате чего это соотношение принимает вид:
Так как, в соответствии с A0), Рх Bt) =1, то получаем
В отсутствие помех адресат принимает в точности то сообщение, какое
послал отправитель, так что gi = pi9 и таким образом, правая часть ра-
равенства (*) превращается в ^^^- log2 — = Н(Х). Итак, при исчезнове-
i	^l
нии помех взаимная информация Н{Х> Z) становится равной энтропии
Н{Х) посланного сообщения, что и требовалось доказать.
244

Найдем количество информации Н', утраченное при передаче сооб-
сообщения X из-за случайных помех в линии связи. Используя A1) и A2),
запишем:
'=Е Pt iog2j- -ЕЕд, (zM iog2 Ц^.
(**)
Далее учтем, что для наступления события Аг нужно, чтобы наступило
или событие Atr\Bh или событие А(Г\В2, или событие ^П^,..., или со-
событие Atr\BN9 а поскольку все события AjCiBj (/= 1, 2, 3,..., N) попарно
несовместны, то
N
A3)
У=1
(это есть не что иное, как формула полной вероятности', см., например,
§ 10.2 в книге «Случайность, необходимость, вероятность».
Учитывая, что P(At) =pt и что, согласно (9), P(At [)Bj) = Px. (zj)- pt,
перепишем A3) в виде:
N
Pi =^PXi{zj)Pi.	A4)
y=i
С учетом A4) соотношение (**) преобразуется следующим образом:
Поскольку
1
log2 —-log2
Pi
то окончательно получаем:
^ = Ю82 "
PXi{2j)-Pi
A5)
В заключение объясним, почему Н(Х, Z) называют взаимной инфор-
информацией о сообщениях Хж Z. Напомним, что через Н{Х, Z) мы обозна-
обозначили количество информации о посланном отправителем сообщении X,
245

содержащееся в принятом адресатом сообщении Z. Обозначим теперь через
Н(Х, Z) количество информации о принятом адресатом сообщении Z, со-
содержащееся в посланном отправителем сообщении X. Из соображений
симметрии соотношение для Н(Х, Z) должно получаться из соотноше-
соотношения для Н(Х, Z), если в последнем заменить Рх (<гу) на Р2.(хг-),а также
поменять местами pt и qj% В результате соотношение A2) превратится в
соотношение:
A6)
Поскольку, в соответствии с (9) Р2 {xf)qj = Рх. [г^рг, откуда немед-
немедленно следует, что Р2 (*/)//>/ = Рх (Zj)fqj , то из сравнения правых ча-
частей A2) и A6) можно придти к заключению:
H(X,Z)=H(Z,X).	A7)
Это равенство можно выразить словами: наблюдение случайной вели-
величины (сообщения) Z дает такое же количество информации о случай-
случайной величине (сообщении) X, какое наблюдение случайной величины
(сообщения) X дает о случайной величине (сообщении) Z. Отсюда и
термин «взаимная информация».
8.8 Пропускная способность канала с помехами
пропускной способности С канала связи (иначе говоря, о емкости
канала) мы уже упоминали в § 8.2, где выяснили, в частности, что еди-
единица измерения С есть бит/с. Настало время уточнить содержание это-
этого понятия и рассмотреть его применительно не только к идеальному
каналу связи, но и к каналу с помехами.
Для идеального канала связи пропускная способность канала опре-
определяется просто как наибольшее количество единиц информации (би-
(битов), которое можно в единицу времени ввести в линию связи и, соот-
соответственно, получить на приемном конце линии. В случае канала с
помехами ситуация усложняется — теперь отнюдь не все количество
информации, поступающее на вход линии связи, принимается на ее
выходе и тем самым оказывается переданным по линии связи. Пере-
Переданное по линии связи количество информации в расчете на один при-
принятый адресатом элементарный сигнал равно теперь не Н{Х) (как это
246

было в отсутствие помех), а Н(Х, Z). Нас интересует, однако, не просто
H(X9Z)9 а самое большое количество взаимной информации по отно-
отношению к различным наборам вероятностей pt и qj. Иначе говоря, нас
интересует наибольшее количество информации, которое можно полу-
получить на выходе канала с помехами при приеме одного элементарного
сигнала: с = max H{X, Z) (с измеряется в единицах бит /элементарный
сигнал). Чтобы выразить пропускную способность С канала с помеха-
помехами, нам остается умножить с на число L элементарных сигналов, пере-
передаваемых в единицу времени (L = 1 / т, где т — длительность одного
элементарного сигнала, например, паузы или импульса тока):
С = cZ =
A8)
Из A1) следует, что
= max
H{X)-H'
Отсюда видно, что в отсутствие помех (т. е. при Нг = 0):
C=Zmax Н(Х).	(**)
Энтропия Н{Х) в общем случае описывается формулой Шеннона C).
Ее максимум достигается, как мы уже знаем, когда все ^возможных
значений элементарного сигнала равновероятны; он составляет, согласно
формуле Хартли B), log2^Vбит/элементарный сигнал. Таким образом, в
отсутствие помех пропускная способность канала связи есть
= Llog2N.
A9)
Как и следовало ожидать, этот результат представляет собой частный
случай соотношения A8).
Рассмотрим простой пример канала с помехами. Его линия связи
есть так называемая двоичная симметричная линия связи. Она представ-
представлена схематически на рис. 1 в таблице 31. По данной линии можно
передавать двоичный элементарный сигнал; здесь хх = 1, х2 = 0, zx = 1,
z2 = 0. Вероятность безошибочного приема как сигнала 1, так и сигна-
сигнала 0 равна 1 - р, а вероятность принять сигнал 0 вместо посланного
сигнала 1 или принять сигнал 1 вместо посланного сигнала 0 равна р.
Таким образом, матрица условных вероятностей G) имеет в данном
случае вид:
\-р
Р
Р
\-р
B0)
247

Таблица 31. Пропускная способность канала с помехами
X	Ро(О) = 1-/> Z
C/L, бит/элем, сигнал
1-/?
\-р
Рис.1
Рис.2
О ОД 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Р
^^
^^
X
\-p
^^
\-p
^—^
J—W
z
Рис.3
248

Найдем пропускную способность такого канала связи. Используя A8),
A2) и B0), представим:
С = Lc = L max
log2 (л g* +pPl log2
В нашем случае N=2, поэтому max H(X) = log2 2=1 бит. Указанный
максимум достигается при р1 = р2 = 1 / 2. Полагая, что при этом также
qx = q2 = 1 / 2, можно убедиться (мы этого делать на будем), что Н1 не
зависит от Pj и #/ • Итак, максимум выражения, стоящего в квадратных
скобках в (***), достигается при условии, что
Р1=р2 = д1 = д2=\ /2.	(****)
Используя (****), преобразуем (***) к виду:
С = Lc = L
1 - p log2 — - A - p) log2 —
B1)
Обратим внимание на то, что С/L= I — Н(р), где Н{р) — хорошо
знакомая нам функция; ее график приведен на рис. 1 в таблице 25. За-
Зависимость С/ L от р изображена на рис.2 в таблице 31. Наибольшее
значение, равное 1 бит/элемент, сигнал, C/L принимает, во-первых,
при р = 0 (т. е. в отсутствие помех) и, во-вторых, при р=\.Ъ последнем
случае помехи переводят каждый сигнал 1 в сигнал 0, а каждый сиг-
сигнал 0 в сигнал 1; такие помехи нисколько не мешают понять, какой
сигнал передавался, и фактически соответствуют случаю отсутствия
помех. При р = 1 / 2 пропускная способность канала обращается в нуль.
Действительно, для любого из двух сигналов на входе мы в этом случае
получаем на выходе с вероятностью 1/2 сигнал 1 и с вероятностью 1/2
сигнал 0, так что принятый сигнал не будет содержать какой-либо ин-
информации о том, какой сигнал посылал отправитель. С тем же успехом
адресат мог бы попросту подбрасывать монету и считать, что при выпа-
выпадении, скажем, орла он принял сигнал 1, а при выпадении решки —
сигнал 0.
Заметим, что уже при сравнительно небольших отклонениях/? от нуля
или от единицы пропускная способность нашего канала связи заметно
снижается. Допустим, что в секунду передаются 100 элементарных сиг-
сигналов, и подсчитаем для нескольких значений р пропускную способ-
способность канала, используя формулу B1). Получаем, что при/? = 0,01 (когда
249

в среднем только 1 элементарный сигнал принимается с ошибкой) про-
пропускная способность канала снижается со 100 бит/с до 92 бит/с; при
р = 0,05 (искажаются 5 из 100 передаваемых сигналов) пропускная спо-
способность канала снижается до 71 бит/с; при /? = 0,1 (искажаются 10 из
100 сигналов) пропускная способность канала снижается до 53 бит/с.
Рассмотрим еще один простой пример канала с помехами — линию
связи со «стиранием». Она показана схематически на рис. 3 в табли-
таблице 31. Подаваемые на вход линии сигналы 1 и Олибо с вероятностью
\—р передаются по линии без искажения, либо с вероятностью р «сти-
«стираются», что связано с появлением на выходе некоего третьего сигнала ?,
который нельзя расшифровать. Матрица условных вероятностей есть в
данном случае Bx3)-матрица; она имеет вид:
7 ,° Р ¦	B2)
0 \-р р
Приведем без вывода выражение для пропускной способности рассмат-
рассматриваемого канала (см. рис. 4 в таблице 31):
C = Lc = L{\-p).	B3)
Из L посылаемых отправителем элементарных сигналов Lp сигналов «сти-
«стираются» (они не переносят информации), а остальные L{\ -р) сигналов
будут правильно расшифрованы на приемном конце линии связи.
8.9 Кодирование с целью уменьшения влияния помех
и основная теорема шеннона
. В энциклопедии в статье «Кодирование» я прочитал: «Ко-
«Кодирование в теории информации применяют для достижения следую-
следующих целей: во-первых, для уменьшения так называемой избыточности
сообщений и, во-вторых, для уменьшения влияния помех, искажающих
сообщения при передаче по каналам связи». Насколько я понимаю,
использование экономных кодов (например, кода Хаффмена) как раз и
предназначено для уменьшения избыточности сообщений за счет умень-
уменьшения средней длины кодового слова (кодового обозначения «буквы»
сообщения). А это, в свою очередь важно для сокращения времени,
затрачиваемого на передачу сообщения. Тут мне все ясно. А вот каким
образом за счет выбора соответствующего кодирования можно умень-
уменьшить влияние помех на передачу сообщения по каналу связи?
250

Пвтор. Это можно сделать довольно просто. Можно, например, каж-
каждую двоичную цифру сообщения передавать по линии связи дважды.
Например, вместо того, чтобы передавать последовательность цифр
10 11010100,	(*1)
отправитель посылает последовательность цифр
1100111100110011000 0.	(*2)
Предположим теперь, что одна из цифр последовательности (*2) пере-
передана неправильно. Скажем, вместо единицы, стоящей на 5-м месте в
(*2), прошел по линии связи нуль, так что адресатом была принята
последовательность цифр
1100 0111001100110000.	(*3)
Адресат должен сразу заметить непорядок в цифрах, выделенных в пря-
прямоугольнике. Именно здесь случайным образом появилась ошибка.
*Чи(*иипель. Но как исправить эту ошибку? Адресат вправе считать,
что была послана как последовательность цифр (*2), так и последова-
последовательность цифр
1100001100110011000 0.	(*4)
Какую ему выбрать, чтобы выявить, какая именно цифра передана не-
неправильно?
Пвтор. Вообще-то в данном случае адресат может попросить отправи-
отправителя повторить посылку сообщения. Но возможен и иной вариант. Что-
Чтобы адресат мог не только обнаружить факт появления ошибки при пере-
передаче сообщения, но и имел возможность исправления ошибки, можно
каждую двоичную цифру передавать трижды. Так, вместо последова-
последовательности цифр (*1) отправитель может передавать последовательность:
11100011111100011100011100000 0.	(*5)
Предположим теперь, что адресат принял последовательность цифр
111000011111000110000111010000.	(*6)
"Т" "~2~" "Т" "Т" "~5~" "~6~" "~7~" "Т" "~9~" "Т6~"
Разбив принятую последовательность цифр на тройки, он увидит, что
вместо нуля в 3-й и в 6-й тройках должна быть единица, а вместо еди-
единицы в 9-й тройке должен быть нуль. Ошибки однозначно установлены
и могут быть исправлены. Лишь бы в пределах одной и той же тройки
не появились сразу две или три ошибки.
251

. Все это напоминает ситуацию, когда в телефонном раз-
разговоре какое-нибудь незнакомое слово передают «по буквам». Напри-
Например, передавая слово «каптоприл» (название одного из лекарств), про-
произносят в телефонную трубку набор слов: «Кузьма, Андрей, Петр,
Татьяна, Ольга, Петр, Роман, Иван, Леонид».
Пвтор. Вы совершенно правы. Тут действительно есть аналогия с
повторением каждой передаваемой двоичной цифры несколько раз.
*Чи(*иипель. Однако такой способ уменьшения влияния помех в кана-
канале связи существенно увеличивает избыточность сообщения, а значит, и
время, затрачиваемое на передачу сообщения. Получается, что умень-
уменьшение вероятности ошибки при приеме сообщения достигается ценой зна-
значительного снижения скорости передачи сообщения.
Пвтор. Да, это так.
^СшОаАел*. В таком случае цели кодирования следовало бы сформу-
сформулировать немного иначе, чем это сделано в энциклопедии. Надо было
бы говорить, что кодирование применяют либо для уменьшения избы-
избыточности сообщения (с целью увеличения скорости передачи информа-
информации), либо для уменьшения влияния помех в канале связи (за счет уве-
увеличения избыточности сообщения).
Пвтор. Можно было бы Вам сразу возразить. Почему бы сначала не
уменьшить насколько возможно среднюю длину кодового обозначения
(с помощью, например, кода Хаффмена), а уже затем все двоичные
цифры удвоить или утроить? Однако в любом случае утроение переда-
передаваемых по линии связи двоичных цифр существенно снизит скорость
передачи сообщения. Так что поневоле возникает мысль: существенно
уменьшить вероятность ошибки при приеме сообщения в принципе невоз-
невозможно без значительного увеличения избыточности сообщения.
ь. Я именно это имел в виду.
Пвтор. Так же думали и ученые до того, как Клод Шеннон доказал в
начале 40-х годов прошлого столетия свою знаменитую «основную тео-
теорему о кодировании при наличии помех». Согласно этой теореме, для
обеспечения сколь угодно малой вероятности ошибки при приеме со-
сообщения отнюдь не обязательно идти по пути простого увеличения из-
избыточности сообщения; возможен другой и притом более эффектив-
эффективный путь — использование специальных «помехоустойчивых кодов».
'Читатель. Сразу возникают два вопроса. Первый: Как отражается на
скорости передачи сообщения использование «помехоустойчивых» ко-
кодов? Второй вопрос: Что представляют собой «помехоустойчивые» коды?
Пвтор. Отвечая на первый вопрос, я просто приведу одну из форму-
формулировок основной теоремы Шеннона'.
252

Для любой линии связи с помехами всегда можно подобрать специ-
специальный код, позволяющий передавать сообщения по этой линии с за-
заданной скоростью, сколь угодно близкой к максимально возможной
скорости v = СIH, так, чтобы вероятность ошибки в определении
каждой переданной буквы оказалась меньше любого заранее заданно-
заданного числа 8.
. А если это «любое заранее заданное числе 8» очень мало?
Скажем, равно 0,001; или 0,00001; или еще меньше? Неужели и тогда
можно подобрать такой специальный «помехоустойчивый» код, кото-
который позволил бы, не снижая скорости передачи сообщения, обеспечить
столь незначительную вероятность ошибки при приеме сообщения?
Пвтор. Да, именно это утверждает основная теорема Шеннона, до-
доказательство которой мы, естественно, опустим.
'Чиниипель. Однако все это похоже на чудо!
Пвтор. Недаром теорема Шеннона в свое время буквально потрясла
инженеров и математиков, занимавшихся теорией связи.
*Чи(*иипель. Что же представляют собой эти волшебные «помехоус-
«помехоустойчивые» коды? Как они выглядят? Как их строить применительно к
тем или иным значениям вероятности ошибки?
Пвтор. Сама теорема Шеннона ответа на этот вопрос не дает. Она
утверждает лишь, что существует возможность построения таких ко-
кодов. Благодаря тому, что такая возможность была доказана, возникло
и стало интенсивно развиваться новое научное направление в теории
информации — так называемая теория кодирования. Эта теория как
раз и занимается разработкой кодов, обнаруживающих и исправляю-
исправляющих ошибки, связанные со случайными помехами в каналах связи. Из
первых «помехоустойчивых» кодов упомянем коды Хэмминга, разрабо-
разработанные в 1950 году.
*Чи(*иипель. Какова общая идея построения подобных кодов?
Пвтор. Общая идея заключается в том, чтобы использовать кодиро-
кодирование не отдельных букв, а сразу достаточно длинных «блоков» из боль-
большого числа букв.
'Чинигниль. Признаться, такое пояснение ничего мне не дает. Я не
представляю, как следует кодировать какие-то блоки из элементарных
сигналов с тем, чтобы можно было обнаружить и исправить ошибоч-
ошибочный сигнал, случайно появившийся внутри блока.
Пвтор. Тут нам поможет весьма простой пример. Пусть блок состоит
из 16 двоичных цифр, образующих такую последовательность:
101110001100100 1.	(*7)
253

Кодирование данного блока состоит в том, что к последовательности
цифр (*7) добавляют 8 т. н. проверочных двоичных цифр: 0110110 0. В
результате по линии связи вместо последовательности цифр (*7) будет
передаваться последовательность:
10111000110010010110110 0.	(*8)
Адресату известно, что в каждом блоке из 24 двоичных цифр первые
16 цифр несут информацию о передаваемом сообщении {информацион-
{информационные цифры), а остальные 8 цифр являются проверочными.
'Чиниипель. Предположим, что при передаче какая-то из цифр в (*8)
оказалась переданной неправильно (единица «превратилась» в нуль или
нуль «превратился» в единицу). Каким образом адресат обнаружит и
исправит ошибку?
Пвтор. Адресат должен превратить принятую им последовательность
из 24 двоичных цифр в такую таблицу:
ф
ф
(Ш
(Ш
(Ш
1
1
1
1
ф
0
0
1
0
ф
1
0
0
0
1
0
0
1
(*9)
Здесь внутри квадрата выписаны четыре четверки информационных
цифр, а кружочками выделены проверочные цифры. Адресат подсчи-
подсчитывает суммы цифр для каждого столбца и каждой строки квадрата
(включая цифры в кружочках). Если окажется, что каждая из восьми
сумм четная @, 2 или 4), то это будет означать, что все цифры последо-
последовательности (*8) переданы правильно, ошибок нет. Именно этот случай
демонстрирует таблица (*9). Если окажется, что для одного из четырех
столбцов и для одной из четырех строк сумма получилась нечетной, то
это будет означать, что передана неправильно та информационная цифра,
которая находится на пересечении данного столбца и данной строки.
Если окажется, что только для одного столбца сумма цифр получилась
нечетной, то это будет означать, что передана неправильно та провероч-
проверочная цифра, которая попадает в данный столбец. Если окажется, что
только для одной строки сумма цифр получилась нечетной, то это будет
означать, что передана неправильно та проверочная цифра, которая
попадает в данную строку.
254

. Действительно, проверка на четность столбцов и строк
позволяет выявить в данном блоке неправильную цифру (если она там
появилась). Это впечатляет.
Пвтор. Правда, тут принципиально важно, чтобы в каждом блоке только
одна из 24 цифр могла оказаться неправильной. Этим замечанием мы и
завершим нашу беседу, оставляя в стороне более сложные примеры.
ЗАДАНИЯ ПО ТЕМЕ 8
1.	Число 4651 было представлено в двоичной системе счисления и в таком виде
передано по каналу связи. Четвертая, считая слева, двоичная цифра оказалась
переданной неправильно. Какое число в результате этой ошибки было принято
адресатом?
Ответ: 4139.
2.	В результате квантования второго десятка отсчетов на рисунке 26 в таблице 27
получена следующая последовательность однозначных чисел: 654333578 7.
Выпишите соответствующую цепочку двоичных цифр.
Ответ: 101100011010010010100110111110.
3.	Докажите, что, комбинируя п двоичных цифр, можно составить 2п различных
кодовых слов.
4.	Адресат получил следующую цепочку двоичных цифр, составленную с использова-
использованием кода Бодо:
0000100101100000010100011010001111110111001011000110
010110111111110001011000111001011011100010010011.
Выполните декодирование и прочтите переданную отправителем фразу.
5.	«Алфавит» состоит из пяти «букв», характеризующихся вероятностями: 0,3; 0,25;
0,2; 0,15; 0,1. Выполните три задания:
а)	постройте два варианта кода Хаффмена; выпишите для каждого варианта
кодовые слова для «букв» по мере уменьшения вероятностей «букв»; б) убеди-
убедитесь, что для обоих вариантов средняя длина кодового обозначения одна и та
же (подсчитайте ее); в) подсчитайте, чему равна энтропия «буквы» нашего «ал-
«алфавита».
Ответы: а) первый вариант: 11, 10, 01, 001, 000; второй вариант: 11, 01, 00,
101, 100;
б)	2,25;
в)	2,228 бит.
6.	«Алфавит» состоит из восьми «букв» с вероятностями 0,32; 0,2; 0,16; 0,12; 0,08;
0,05; 0,04; 0,03. Чему равны: а) энтропия «буквы»? б) средняя длина кодового
слова для «буквы» при использовании кода Хаффмена? в) длина кодового слова
для «буквы» при использовании кода Бодо?
Ответ: а) 2,203 бит, б) 2,24; в) 3.
255

7.	Закодируйте кодом Хаффмена фразу: «ДО ПОРЫ ДО ВРЕМЕНИ НЕ СЕЮТ СЕМЕ-
СЕМЕНИ». Подсчитайте полное число двоичных цифр, необходимое для передачи дан-
данной фразы с использованием кода Хаффмена. На сколько меньше это число чис-
числа двоичных цифр, которое потребовалось бы при использовании кода Бодо?
Ответ: 138; на 27.
8.	Такое же задание применительно к фразе: «ДОБРОЕ ДЕЛО БЕЗ НАГРАДЫ НЕ
ОСТАНЕТСЯ».
Ответ: 155; на 25.
9.	Рассматривая линию связи, представленную на рисунке 1в таблице 31, сравни-
сравните пропускную способность С± (при р = 0,3) с пропускной способностью С2 (при
Р = 0,6).
Ответ: С±/С2 = 4,1.
9. Адресат принял следующие блоки из 16+8 двоичных цифр A6 информационных
и 8 проверочных цифр):
а)	0100 ООН 1011 01011111,
б)	1010 0001111110111101 0111,
в)	1100 0010 1001 ОНО ООН 0100,
г)	1110 01011010 ООН 0010 1000.
Проверяя каждый из этих блоков на четность, выясните, появилась ли при прие-
приеме ошибка в том или ином блоке. Если ошибка появилась, то укажите какая имен-
именно двоичная цифра передана неправильно.
Ответы: а) неправильно передана 6-я цифра из последовательности информаци-
информационных цифр;
б)	неправильно передана 11-я цифра из последовательности информационных
цифр;
в)	неправильно передана 3-я цифра из последовательности проверочных цифр;
г)	в данном блоке ошибок нет.
256

ТЕМА 9
ЭНТРОПИЯ В ТЕРМОДИНАМИКЕ
Чтобы рассмотреть принцип получения
движения из тепла во всей полноте, надо его
изучить независимо от какого-либо опреде-
определенного механизма...
Сади Карно
Второе начало термодинамики говорит, что
в природе для каждой системы тел существует
величина, обладающая следующим свойством:
при всех изменениях, которые затрагивают
только эту систему, она или остается посто-
постоянной (обратимые процессы), или увеличива-
увеличивается (необратимые процессы). Величина эта,
по Клаузису, называется энтропией системы.
Макс Планк
9.1. Три этапа в развитии понятия «энтропия»
в
своем развитии понятие «энтропия» прошло три этапа.
Первый этап следует назвать термодинамическим. Как мы уже отме-
отмечали, энтропию ввел в науку Рудольф Клаузиус в 1865 году. Это понятие
257

(Клаузиус обозначал его через S) появилось в контексте теории тепловых
машин и выступало наряду с внутренней энергией тела Е в качестве од-
одной из функций состояния макроскопических объектов, исследовавшихся
термодинамикой. Клаузиус писал: «Если искать для S характерное наи-
наименование, то подобно тому, как мы говорили о величине Д связывая ее
с тепло- и работосодержанием, можно говорить и о величине S, связывая
ее с превращениями теплоты и работы. Учитывая всю важность величи-
величины ?для естествознания, необходимо придумать и соответствующее наи-
наименование для нее». Клаузиус предложил назвать S энтропией тела, ис-
исходя из греческого слова evxpojuoc, означающего «превращение». Он
заметил: «Слово "энтропия" я намеренно подобрал ближе к слову «энер-
«энергия», так как обе соответствующие этим выражениям величины настоль-
настолько близки по своему смыслу, что они, по моему мнению, требуют одно-
однородного обозначения. Состояние тела, независимо от способа, каким оно
приходит в данное состояние, определяется энергией и энтропией».
С самого начала было понятно, что энтропию, как и энергию, невоз-
невозможно ограничить рамками теории тепловых машин. Уже в цитирован-
цитированной выше работе Клаузиуса содержится вот такая предельно краткая
формулировка первого и второго начал термодинамики: «1) энергия мира
постоянна, 2) энтропия мира стремится к максимуму». Едва появившись
в научном обиходе, понятие «энтропия» уже рассматривалось как поня-
понятие, равнозначное понятию «энергия». Известный швейцарский астро-
астрофизик и геофизик Роберт Эмден A862-1940) отмечал в своих воспоми-
воспоминаниях: «Будучи студентом, я с пользой прочел небольшую книгу Вальда
«Царица мира и ее тень». Имелись в виду энергия и энтропия. Достиг-
Достигнув более глубокого понимания, я пришел к выводу, что их надо поме-
поменять местами. В гигантской фабрике естественных процессов принцип
энтропии занимает место директора, который предписывает вид и тече-
течение сделок. Закон сохранения энергии играет лишь роль бухгалтера,
приводящего в равновесие дебет и кредит».
Однако на термодинамическом этапе своего развития понятие энт-
энтропии, оставаясь в области динамических (жестко определенных) законо-
закономерностей, не могло обнаружить своего физического смысла и выгляде-
выглядело как хотя и весьма важное, но, по сути дела, достаточно загадочное
понятие. Физическая сущность энтропии раскрылась на более глубо-
глубоком уровне ее понимания — на уровне статистических (вероятност-
(вероятностных) закономерностей. В 1877 году Людвиг Болъцман привел вероятност-
вероятностную трактовку энтропии и тем самым обосновал второе начало
термодинамики. Он подчеркивал: «Второе начало является законом ве-
вероятностным и поэтому его вывод только посредством одних уравне-
уравнений динамики невозможен... Его аналитическое доказательство возможно
258

только на таких основаниях, которые предполагают применение исчис-
исчисления вероятностей».
Формально именно с этого времени следует отсчитывать второй этап
в развитии понятия энтропии — когда она стала рассматриваться как
мера числа возможных микросостояний в макросостоянии системы, или,
выражаясь проще, как мера «внутреннего беспорядка», характеризующе-
характеризующего макросистему. Фактически этот этап (его можно назвать статисти-
статистическим этапом) начался несколько позднее появления знаменитой ра-
работы Больцмана «Об отношении второго начала механической теории
теплоты и исчисления вероятностей в соответствии с теоремами о теп-
тепловом равновесии» (октябрь, 1877). Потребовалось время для преодоле-
преодоления учеными старых стереотипов, в результате чего возникла новая
физическая наука — статистическая физика.
Переход от термодинамического понимания энтропии к статисти-
статистическому (вероятностному) — это выход на более глубокий уровень позна-
познания. А выход на более глубокий уровень является, как правило, одно-
одновременно выходом на более широкий уровень. Ведь по мере углубления
процесса познания неизбежно раздвигаются и рушатся всевозможные
«перегородки» в наших понятиях, расширяется область применения бо-
более глубоких понятий.
Именно это и произошло с понятием «энтропия». В 40-х годах прошло-
прошлого столетия начался третий этап в развитии этого понятия после работ
Клода Шеннона и Норберта Винера, который естественно назвать информа-
информационным этапом. Теперь энтропия выходит за рамки исследования микро-
микроявлений и становится мерой неопределенности, которую можно измерить
соответствующим количеством информации. На этом уровне энтропия ока-
оказывается одним из важнейших понятий, позволяющим осмысливать гло-
глобальные проблемы эволюции. В ходе такого осмысления выявляется вся
важность взаимодействия энтропийных процессов (процессов, связанных
с увеличением энтропии и уменьшением информации) и антиэнтропий-
антиэнтропийных, или, иначе говоря, информационных процессов (процессов, связанных
с уменьшением энтропии и увеличением информации).
9.2. Краткий экскурс в термодинамику
9.2.1. Первое начало термодинамики. Совершим небольшой экскурс в
термодинамику — раздел физики, где с наиболее общих позиций ис-
исследуются процессы обмена энергией между макроскопическим объектом
(будем называть его макросистемой, или, проще, системой) и окружаю-
окружающей средой (между данной макросистемой и другими макросистемами).
259

Термодинамика рассматривает разные способы обмена энергией (раз-
(разные каналы энергообмена). Ограничимся, для простоты, двумя канала-
каналами: 1) через передачу теплоты и 2) через совершение работы при переме-
перемещениях внешних по отношению к данной макросистеме тел. Если
макросистема (например, газ) перемещает внешние тела в процессе сво-
своего расширения, то при этом она совершает работу. Если внешние тела,
перемещаясь, сжимают систему, то при этом над ней совершается рабо-
работа. Заметим, в частности, что при расширении газа в пустоту работа не
совершается.
Предположим, что система находилась в состоянии 1 и характеризо-
характеризовалась внутренней энергией Ех. Системе передана теплота Q, и одно-
одновременно система совершила работу А. В результате она (система) пере-
перешла в состояние 2 с внутренней энергией Е2. В этом случае справедливо
равенство:
E2-El=Q-A.	A)
Равенство A) выражает первое начало термодинамики и представляет
собой не что иное, как закон сохранения энергии, учитывающий возмож-
возможность энергообмена по двум каналам.
Обратим внимание на существенное отличие величины is от величин Q
и А. Энергия Е является функцией состояния системы: она изменяется
при переходе системы из одного состояния в другое и при этом (что
принципиально!) изменение величины Е не зависит от того, как совер-
совершатся переход. В отличие от ^величины QuAue являются функциями
состояния системы. Не имеет смысла говорить, что в данном состоя-
состоянии у системы имеется столько-то теплоты или столько-то работы. Теп-
Теплота Q и работа А — это просто изменения энергии системы, осуществ-
осуществляемые по двум разным каналам.
Напомним, что энергия системы Е однозначно связана с ее абсо-
абсолютной температурой Т (если система находится в состоянии термоди-
термодинамического равновесия, вследствие чего можно говорить о какой-то
определенной для всей системы температуре).
Отметим в качестве примера случай изотермического расширения, т. е.
расширения, при котором температура, а значит, и энергия системы не
изменяются. Согласно A), в этом случае:
Q=A.	B)
Теплота, полученная системой, полностью превращается в работу сис-
системы, совершаемую ею над внешними телами.
9.2.2. Термодинамическое равновесие. Обратимые и необратимые про-
процессы. Термодинамическое равновесие — одно из важнейших понятий в
термодинамике. Предположим, что на систему как-то подействовали, а
260

затем поместили в условия, в которых систему можно считать замкнутой
(изолированной). Иначе говоря, начиная с какого-то момента времени,
система оказалась изолированной от среды и предоставленной самой себе.
(Напомним, что система называется замкнутой, или изолированной, если
между ней и средой нет обмена энергией.) Предоставленная самой себе
макросистема придет, спустя некоторое время, в характерное для нее как
целого состояние и будет оставаться в этом состоянии сколь угодно дол-
долго; это есть состояние термодинамического равновесия.
Рассмотрим две макросистемы, каждая из которых в отдельности
находится в состоянии термодинамического равновесия. Приведем эти
системы в контакт друг с другом; иными словами, нарушим замкну-
замкнутость каждой из систем, предоставив им возможность энергообмена друг
с другом. При этом будем полагать, что в целом пара систем остается
изолированной от окружающей среды и представляет собой замкнутую
систему. Будем говорить, что имеется замкнутая система, состоящая из
двух подсистем.
Предположим, что наблюдается некомпенсированный энергообмен
между нашими подсистемами: передача энергии от одной подсистемы
к другой не компенсируется передачей энергии в обратном направле-
направлении. Наличие такого энергообмена свидетельствует о том, что до при-
приведения в контакт подсистемы не находились в равновесии по отношению
друг к другу. Спустя некоторое время после приведения в контакт не-
скомпенсированный энергообмен прекратится — подсистемы придут в
равновесие по отношению друг к другу. Это будет означать, что вся
система в целом пришла в состояние термодинамического равновесия.
Пусть некоторая подсистема А находится в равновесии с подсисте-
подсистемой Б и одновременно с подсистемой В. Опыт показывает, что в этом,
случае будет наблюдаться равновесие также между подсистемами Б я В.
Отсюда следует, что должны существовать какие-то физические пара-
параметры, которые будут количественно характеризовать состояние термо-
термодинамического равновесия системы (подсистемы). У всех подсистем,
находящихся в равновесии друг с другом, соответствующие параметры
должны быть одинаковыми. Указанные параметры называют термодина-
термодинамическими параметрами (а также интенсивными параметрами).
Число таких параметров определяется числом каналов энергообмена
данной системы со средой. В нашем случае (когда рассматриваются только
два канала — через передачу теплоты и совершение работы) термодина-
термодинамическими параметрами являются температура Тж давление Р. Темпера-
Температура играет роль «регулятора» энергообмена через передачу теплоты, а
давление «регулирует» энергообмен через совершение работы. Если сис-
система находится в термодинамическом равновесии, то как температура,
261

так и давление должны иметь одно и то же значение для всех ее подси-
подсистем. В этом случае можно говорить, что каждый термодинамический
параметр имеет определенное значение для всех точек системы и, таким
образом, характеризует систему как целое. Заметим, что под «точкой
системы» следует, строго говоря, понимать соответствующую подсисте-
подсистему, хотя и весьма малую с точки зрения наших масштабов, но все-таки
макроскопическую.
Переход макросистемы из одного равновесного состояния (назовем
его начальным) в другое равновесное состояние (назовем его конеч-
конечным) может происходить двумя принципиально разными способами;
а) кеазистатически (если внешние условия изменяются относительно
медленно) и б) некеазистатически (если внешние условия изменяются
быстро). В первом случае макросистема все время находится в термоди-
термодинамическом равновесии, переходя постепенно из одних равновесных со-
состояний в другие — пока не достигнет конечного состояния. Во втором
случае макросистема в результате быстрого изменения внешних усло-
условий (в результате «возмущения») выводится из начального равновесно-
равновесного состояния, становится термодинамически неравновесной и затем при-
приходит к равновесию в новом (конечном) состоянии.
Благодаря медленному изменению внешних условий в случае квази-
квазистатического перехода макросистемы имеется возможность «руководить»
процессом перехода на всех его промежуточных стадиях. Отсюда следу-
следует, что квазистатический процесс можно обратить вспять — осуществить
его в обратном направлении. Поэтому квазистатические процессы на-
называют обратимыми процессами.
В случае же неквазистатического перехода говорить об обратимости
принципиально невозможно. Выведя макросистему из исходного рав-
равновесного состояния, мы затем предоставляем ей самой придти к ново-
новому равновесному состоянию (как если бы она стала замкнутой). Мы не
можем контролировать процесс в замкнутой системе и, в частности, не
можем обратить его вспять. Поэтому неквазистатические процессы на-
называют необратимыми процессами (а также неравновесными процессами).
Допустим, в результате неодинакового нагрева частей макросистемы
возникло некоторое распределение значений температуры по ее объе-
объему. Система как целое оказалась термодинамически неравновесной. Ее
можно представить в виде большого числа подсистем, которые по от-
отдельности находятся в термодинамическом равновесии, причем каждая
при своей температуре. Если в какой-то момент прекратить нагрев си-
системы и предоставить ее самой себе (изолировать ее), то в системе нач-
начнется перенос теплоты от более нагретых подсистем к менее нагретым.
Этот процесс, называемый теплообменом, приведет к тому, что через
262

некоторое время распределение температуры по системе выровняется
(все подсистемы окажутся при одной и той же температуре) и система
как целое придет в состояние термодинамического равновесия.
Процесс теплообмена (переход теплоты от нагретого тела к холодно-
холодному) — один из примеров необратимого процесса. Необратимыми явля-
являются также, например, процесс расширения газа в пустоту или процесс
перемешивания двух разных газов, оказавшихся в общем объеме. Все
эти процессы протекают самопроизвольно, без управления извне. В то
же время не наблюдается самопроизвольный переход теплоты от холод-
холодного тела к нагретому. Не происходит самопроизвольное разделение
газовых компонентов из смеси газов. Не было случаев, чтобы газ вдруг
самопроизвольно сжался. Следует подчеркнуть: всякий необратимый
процесс характеризуется определенной направленностью. Он развивается
в каком-то одном направлении и не развивается в обратном. Какое
направление развития процесса оказывается дозволенным, а какое за-
запрещенным, — этими вопросами ведает второе начало термодинамики.
9.2.3. Второе начало термодинамики. Обращаясь ко второму началу
термодинамики, традиционно приводят две его формулировки. Одна
принадлежит Рудольфу Клаузиусу:
Теплота сама собой не может переходить от тела холодного к
телу нагретому.
Другая формулировка известна как формулировка Кельвина—Планка:
Невозможно построить такую машину, которая могла бы только
за счет поглощения теплоты из некоторого резервуара совершать
эквивалентное количество работы, не вызывая при этом никаких
других эффектов.
Справка. Лорд Кельвин, он же Уильям Томсон A824-1907) — выдающийся анг-
английский физик; являлся автором многих работ по термодинамике и теории элект-
электрических и магнитных явлений; предложил абсолютную шкалу температур (шкала
Кельвина).
Макс Планк A858-1974) — выдающийся немецкий физик, один из основопо-
основоположников квантовой механики; автор работ по термодинамике и теории относи-
относительности.
Согласно формулировке Клаузиуса, менее нагретое тело не может
самопроизвольно передавать часть своей внутренней энергии более на-
нагретому телу за счет передачи теплоты. Согласно формулировке Кель-
вина-Планка, невозможен двигатель (по сути дела, вечный), который
работал бы только за счет получения некоторого количества теплоты от
другого тела (например, от Мирового океана).
263

На рисунках 1 и 2 в таблице 32 схематически представлены оба за-
запрещенных процесса. Процесс на рис. 1 запрещен согласно формули-
формулировке Клаузиуса. Процесс на рис. 2 запрещен согласно формулировке
Кельвина—Планка. На рисунках кружком показано рабочее тело тепло-
тепловой машины или холодильника. С помощью штриховки показаны тер-
термостаты — макросистемы, сохраняющие свою температуру постоян-
постоянной даже при наличии энергообмена с рабочим телом (для этого
макросистемы должны быть достаточно велики).
Принципы, содержащиеся в формулировках Клаузиуса и Кельвина-
Планка, внешне выглядят различными. В действительности же обе фор-
формулировки эквивалентны. Любая из них может служить формулировкой
второго начала термодинамики.
На рисунках 3 и 4 в таблице 32 схематически представлены процес-
процессы, не запрещаемые вторым началом термодинамики. На рис. 3 пока-
показан т.н. холодильник Карно (обращенная машина Карно): при условии
получения работы А рабочее тело может «забрать» у холодильника (тер-
(термостата с температурой Т2) теплоту Q2 и передать нагревателю (термо-
(термостату с температурой 7\; Тх > Т2) теплоту Qh равную Q2 + А. На рис. 4
показана машина Карно: рабочее тело может совершить работу А за счет
полученной от нагревателя теплоты Q1 при условии передачи холодиль-
холодильнику теплоты Q2, равной Q1 — A.
Справка. Сади Карно A796-1832) — талантливый французский физик и инже-
инженер, один из основателей термодинамики; рассмотрел идеальную тепловую маши-
машину с коэффициентом полезного действия, равным (Т{ - Т2) / Тх — см. § 9.3.
9.2.4. Обратимое изотермическое расширение идеального газа. В даль-
дальнейшем нам придется обратиться к необратимому изотермическому рас-
расширению идеального газа (расширение теплоизолированного газа в пу-
пустоту). В связи с этим предварительно рассмотрим обратимое
изотермическое расширение газа (когда газ квазистатически расширя-
расширяется, отодвигая поршень и тем самым совершая работу). О теплоизоли-
рованности газа в данном случае не может быть и речи — ведь соверша-
совершаемая газом работа берется за счет передачи теплоты газу от внешней
среды (см. соотношение B)).
Напомним современную запись уравнения состояния идеального газа,
находящегося в термодинамическом равновесии {уравнения Клайперо-
на—Менделеева):
PV = ЖТ.	C)
Здесь Ри V — термодинамические параметры (давление и температура),
V — объем газа, N — число молекул газа в данном объеме. Величина
264

Таблица 32. Экскурс в термодинамику
У///////////Л
Q
(Ti>T2)
т2
Y///////////A 1 рис.1
У///////////Л
Y//////////A
У///////////Л,
У///////////Л
Рис.2
Y///////////A
Т2 Рис.4
Р=const
V
V,
Рис.5
= NkT(l/V)
V2 Рис.6
2 Изотермы
265

к — универсальная физическая постоянная, называемая постоянной
Болъцмана (к= 1,381 • 10~23 Дж/град = 3,296 • 104 кал/град).
Из C) следует, что состояние термодинамического равновесия иде-
идеального газа с N молекулами можно задать, указав любую пару величин:
или Р и V, или Ки Т, или РжТ. Таким образом, состояние газа можно
задать точкой на любой из плоскостей P—V, V—T, Р—Т, а обратимый
процесс — как линию на этой плоскости.
Если обратимый процесс рассматривается на плоскости Р— V, то ра-
работу, совершаемую газом в этом процессе при расширении от Vx до V2,
можно найти как площадь под графиком зависимости Р от V на отрезке
абсциссы от Vx до V2. Это утверждение легко доказывается в случае изо-
изобарического расширения газа, т. е. расширения, при котором давление
газа поддерживается постоянным:
A = P.(V2-V1).	D)
Данный случай представлен на рис. 5 в таблице 32.
Заметим, что изобарическое расширение осуществляется, если уве-
увеличение объема будет сопровождаться пропорциональным возрастани-
возрастанием температуры. В самом деле, из C) видно, что давление постоянно
{Р = const), если NkT/ V= const, откуда следует, что в данном случае
V^ T {закон Гей-Люссака).
При изотермическом расширении зависимость Р от F является обрат-
обратно пропорциональной: Р~ 1/ V {закон Бойля-Мариотта). Это немед-
немедленно следует из C), если учесть, что при изотермическом процессе
температура газа постоянна G'= const). Работа, совершаемая газом при
изотермическом расширении от Vx до V2, равна заштрихованной пло-
площади на рис. 6 в таблице 32. Чтобы найти эту площадь, нужно проин-
проинтегрировать от Vx до V2 функцию P{V) = NkT/ V. Для тех, кто незна-
незнаком с интегрированием, сообщим результат:
А=ЖТЫ^	E)
(через In обозначается, напомним, натуральный логарифм, т. е. логарифм
по основанию е).
С учетом B) заключаем отсюда, что количество теплоты, полученное
газом при изотермическом обратимом расширении от Vx до V2 при тем-
температуре F, есть
Q=NkT]n^.	F)
Именно это соотношение нам и понадобится в дальнейшем.
266

9.3 Цикл Карно
в
1824 году в Париже вышла книга 28-летнего инженера Сади Кар-
Карно «Размышления о движущей силе огня и о машинах, способных раз-
развивать эту силу». Глубина мыслей, изложенных в этой книге, была оце-
оценена лишь много лет спустя, уже после смерти автора. Карно исследовал
вопросы, связанные с получением работы в тепловых машинах. Он по-
показал, что для получения работы недостаточно иметь только нагретое
тело; требуется еще и второе тело, имеющее более низкую температуру
(первое тело называют нагревателем, второе — холодильником). Кроме
нагревателя и холодильника необходимо рабочее тело (жидкость, пар,
газ), которое передает теплоту от нагревателя к холодильнику и попут-
попутно совершает полезную работу (см. рис. 4 в таблице 32). Отметим, что
идея о невозможности создания вечного двигателя, работающего толь-
только за счет передачи теплоты от некоторого резервуара, была осознана
Карно за четверть века до исследований Кельвина (Томсона) и Клаузиуса
и, по сути дела, предопределила эти исследования.
Выбрав в качестве рабочего тела идеальный газ, Карно рассмотрел
цикл, представленный для плоскости Р-Кна рис. 7 в таблице 32. Цикл
Карно состоит из четырех обратимых процессов:
-	изотермического расширения при температуре нагревателя 7\ (про-
(процесс 1 —>2);
-	адиабатического расширения, приводящего к охлаждению газа до
температуры холодильника Т2 (процесс 2^3);
-	изотермического сжатия при температуре холодильника Т2 (про-
(процесс 3^4);
-	адиабатического сжатия, приводящего к нагреванию газа до тем-
температуры нагревателя 7\ (процесс 4 —> 1).
Итак, цикл состоит из двух изотерм и двух адиабат.
Напомним, что адиабатическими называются процессы, при кото-
которых можно пренебречь теплообменом системы с окружающей средой.
Этого можно достичь, когда система специально теплоизолирована
или когда процесс протекает достаточно быстро, так что передача теп-
тепла просто не успевает произойти (впрочем, при всей быстроте адиаба-
адиабатического процесса он должен быть достаточно медленным, чтобы про-
процесс можно было рассматривать как квазистатический, т. е. обратимый).
При адиабатическом расширении система совершает работу за счет
своей внутренней энергии; поэтому температура системы уменьшает-
уменьшается. При адиабатическом сжатии работа совершается над системой и
увеличивает ее внутреннюю энергию; поэтому температура системы
повышается.
267

Но вернемся к циклу Карно для идеального газа. В процессе 1 —> 2
газ, расширяясь от Vx до V2 получает от нагревателя теплоту Qh равную,
согласно F),
Q^NkT^n^.	(*1)
За счет этой теплоты он совершает работу А{.
Ах = Qv	(*2)
В процессе 2^3 газ, расширяясь от V2 до F3, совершает работу А2 за
счет уменьшения внутренней энергии, равного Ех- Е3\
Е\ - Е3 = А2	(*3)
(поясним: Е{-Е3 = (Е{ - Е2) + (?2 - ?3) = 0 + (?2 - Еъ) = 0 + Л2).
В процессе 3^4 газ сжимают от V3 до ^ и тем самым совершают
над ним работу А3, равную, согласно E),
А3 = ЖТ21п^.	(*4)
Эта работа тут же передается газом холодильнику в виде теплоты Q2:
Q2=A3.	(*5)
В процессе 4 —> 1 газ сжимают от V4 до ^ и тем самым совершают
над ним работу А4, которая идет на увеличение внутренней энергии:
А4 = Ех - Е3.	(*6)
Коэффициент полезного действия г| тепловой машины, работающей
по циклу Карно, есть отношение полезной работы за цикл, равной
А1+А2-А3- А4, к теплоте Qh полученной газом от нагревателя:
Л = —	^7Г^		(*7)
(полезная работа за цикл численно равна площади внутри контура, об-
образованного изотермами и адиабатами цикла на плоскости P-V). С
учетом (*2), (*3), (*5), (*6) перепишем (*7) в виде:
ц = Qi+(El-E3)-Q2-(El-E3) = Qx-Q2	(?)
Из (*1) следует, что
Из (*4) и (*5) следует, что
(*9)
n
268

Докажем, что
п п
(8)
т2
учитывая, что для обратимого адиабатического процесса:
PVy = const,	(9)
где у зависит от числа атомов в молекуле газа (для газов с одноатомны-
одноатомными молекулами у = 1,67; для газов с двухатомными молекулами у= 1,4).
Доказательство. Для адиабатического расширения 2^3 запишем, с учетом (9):
(P2V2) -V2y = P3VJ. Это соотношение перепишем в виде:
1-	(*ю)
Так как, согласно C), P2V2 = NkTb P3V3 = NkT2, то из (*10) следует:
х	\	(*п)
Аналогично для адиабатического сжатия 4 —> 1 запишем: Ру? = P4V4 • Переписав
это соотношение в виде {РУ\)У^~1 = (P4V4)V4y~l и воспользовавшись уравнением
C), получаем:
Туу =T2VJ-1.	(*12)
Разделив (*11) на (*12), приходим к соотношению (У2/У{У~1 =(F3/F4)Y~1, откуда
следует, что V2 / V{ = V3 / V4 и, значит,
ln-^ = ln^.	(*13)
У I	У 4
Используя (*13), получаем из (*8) и (*9) соотношение (8), что и требовалось доказать.
Соотношение (8) позволяет переписать выражение G) для коэффи-
коэффициента полезного действия машины Карно в виде:
_т1-т2
A0)
Это есть наибольший возможный коэффициент полезного действия
для тепловых машин. В реальных тепловых машинах коэффициент
полезного действия всегда меньше — из-за неизбежных необратимых
процессов.
9.4 Энтропия как функция состояния макросистемы
Хабота рано ушедшего из жизни Сади Карно, в которой был рас-
рассмотрен идеальный обратимый цикл (названный впоследствии циклом
269

Карно), долгое время не привлекала должного внимания со стороны
ученых. В 1865 году, спустя сорок лет после появления работы Карно,
Рудольф Клаузиус, размышляя над установленным Карно соотноше-
соотношением (8), усмотрел в нем своеобразный закон сохранения: «отобран-
«отобранная» рабочим телом у нагревателя величина Qx / 7\ равна «передан-
«переданной» затем холодильнику величине Q2 / T2. Что это за величина?
Клаузиус сначала даже присвоил ей специальное название; он назвал
ее «приведенной теплотой». Но затем он пришел к мысли, что Q/ Т
лучше рассматривать как происходящее в изотермическом процессе
при температуре Т изменение некоторой величины, являющейся функ-
функцией состояния тела. Эту величину Клаузиус обозначил через S и дал
ей название «энтропия».
Если рабочему телу (в данном случае идеальному газу) передается
теплота Q при температуре Т9 то энтропия тела S возрастает; при этом
приращение энтропии S определяется соотношением:
Если от рабочего тела отбирается теплота Q, при температуре Т, то
энтропия тела S уменьшается. В этом случае приращение энтропии яв-
является отрицательной величиной (будем говорить об отрицательном
приращении):
-f.	A2)
Из A1) немедленно следует формула для возрастания энтропии твер-
твердого тела в результате его плавления, а также формула для возрастания
энтропии жидкости в результате кипения. Ведь оба эти процесса тепло-
теплопередачи происходят при определенных (постоянных) температурах.
Плавление увеличивает энтропию тела на величину
^	A3)
^ пл
где qi — удельная теплота плавления, М — молярная масса (масса веще-
вещества, взятого в количестве одного моля), Тил — температура плавления.
Кипение увеличивает энтропию жидкого тела на величину
^	A4)
^ КИП
где q2 — удельная теплота парообразования при температуре кипения,
Гкип — температура кипения при заданном давлении. Изменение энт-
энтропии в A3) и A4) рассматривается по отношению к одному молю
270

(это означает, что число молекул N в теле равно числу Авогадро
7VA=6,02- 1023).
Заметим, что энтропия имеет размерность энергия/градус, как это вид-
видно, например, из A1). Она измеряется в единицах Дж/Кили кал/К (К —
Кельвин, градус шкалы Кельвина). Заметим также, что 1 кал = 4,187 Дж.
Обратим внимание на то, что формулами A3) и A4) описывается
также уменьшение энтропии тела при соответствующих обратных фазо-
фазовых переходах — когда теплота не передается телу, а напротив, отбира-
отбирается от него.
Согласно тепловой теореме Нернста, называемой также третьим на-
началом термодинамики, при стремлении температуры к абсолютному нулю
энтропия системы стремится к нулю, так что
S(T = 0) = 0.	A5)
Третье начало термодинамики было установлено в 1906 году немецким
физико-химиком Вальтером Нернстом A864-1941).
Вернемся к циклу Карно, представленному на рис. 7 в таблице 32. В
процессе 1 —> 2 происходит приращение энтропии газа Д?\ = Qx / Т. В про-
процессе 2^3 приращение энтропии газа равно нулю (поскольку нет пе-
передачи теплоты). В процессе 3^4 происходит отрицательное прира-
приращение энтропии газа А^2 = - (?2 / ^2- В процессе 4 —> 1 приращение
энтропии газа равно нулю. Суммарное изменение (приращение) энтро-
энтропии газа за весь цикл равно, таким образом,
С учетом (8) получаем отсюда, что
^цикл=0,	A6)
т. е. в целом за обратимый цикл (в результате перехода из данного со-
состояния в это же состояние) энтропия газа не изменилась. Можно было
бы доказать (мы этого делать не будем), что результат A6), установлен-
установленный в данном случае для цикла Карно, в действительности справедлив
для любого обратимого цикла. Так оно и должно быть, коль скоро энт-
энтропия является функцией состояния системы. Разумеется, то же отно-
относится и к любой другой функции состояния системы, например к
внутренней энергии. Так, для внутренней энергии идеального газа име-
имеем в случае цикла Карно, представленного на рис. 7 в таблице 32:
271

Обратим внимание на то, что процессы в цикле Карно — это процес-
процессы, при которых либо не изменяется внутренняя энергия газа, а его
энтропия изменяется (изотермы), либо не изменяется энтропия газа, а
его внутренняя энергия изменяется (адиабаты). Энтропия макросисте-
макросистемы может быть определена как такая функция ее состояния, которая
сохраняется при адиабатических процессах. Соответственно, внутреннюю
энергию можно рассматривать как функцию состояния макросистемы,
которая сохраняется при изотермических процессах.
9.5 Второе начало термодинамики как закон возрастания
энтропии замкнутой системы при необратимых процессах
]К1спользуя формулировку второго начала термодинамики, данную
Клаузиусом, легко получить из A1) и A2) весьма важный результат:
необратимый процесс в замкнутой (изолированной) макросистеме сопро-
сопровождается возрастанием энтропии макросистемы.
Пусть некая замкнутая система состоит из подсистем 1 и 2, имеющих
температуры Тх и Тъ соответственно; причем Тх > Т2. Обозначим через
AQ весьма малое количество теплоты, которое в необратимом процессе
теплопроводности передается от нагретой подсистемы (от подсистемы 1)
к холодной подсистеме (к подсистеме 2). Величина AQ мала настолько,
чтобы можно было считать, что температуры подсистем при таком теп-
теплообмене не изменились. В этом случае энтропия подсистемы 1 умень-
уменьшается или, иными словами, получает отрицательное приращение, рав-
равное, согласно A2),
а энтропия подсистемы 2 увеличивается, т. е. получает приращение, рав-
равное, согласно A1),
AS2 =-^-.	(**)
Поскольку энтропия — величина аддитивная, то AS=AS{ + AS2 и, сле-
следовательно,
[± J^	(***)
Так как 7\ > Тъ то из (***) следует, что
AS>0.	A7)
272

Мы убедились, что необратимый процесс передачи теплоты от нагретой
подсистемы к холодной действительно сопровождается возрастанием
энтропии замкнутой систем, состоящей из рассматриваемых подсистем.
Обобщая полученный результат, отметим, что любой необратимый
процесс в замкнутой системе идет таким образом, чтобы энтропия сис-
системы при этом возрастала. Возрастание энтропии происходит до тех
пор, пока система не придет в состояние термодинамического равнове-
равновесия. Все это справедливо, в частности, для процессов расширения газа
в пустоту и взаимного перемешивания двух различных газов, попавших
в общий объем. Второе начало термодинамики можно, таким образом,
трактовать как закон возрастания энтропии замкнутой системы при не-
необратимых процессах.
А если система не является замкнутой? Если происходит теплообмен
между системой и средой? — Этот случай уже рассматривался в § 9.4.
Поэтому ответ ясен: при передаче системе при температуре Т теплоты
AQ в систему поступает энтропия AS = AQ/ Т, а при передаче теплоты
AQ от системы с температурой Тв окружающую среду происходит уда-
удаление из системы энтропии AS= AQ/ Т. Значит, у незамкнутой (точнее
сказать, нетеплоизолированной) системы энтропия может как возрас-
возрастать, так и уменьшаться.
В общем случае следует рассматривать приращение энтропии AS си-
системы в виде двух слагаемых:
AS = А^внутр + А^внеш.	A8)
где А^внутр — количество энтропии, которое производится внутри систе-
системы при необратимых процессах, а А*Увнеш — количество энтропии, по-
поступающее в систему из внешней среды в процессе передачи теплоты.
Поскольку А5внугр > 0 (согласно A7)), a ASmGni = AQ/T9 то A8) можно
преобразовать к виду:
AS>
AQ
A9)
Здесь знак «больше» относится к необратимым процессам, а знак ра-
равенства — к обратимым.
Выражение A9) есть не что иное, как формулировка второго начала
термодинамики. Именно в таком виде сформулировал Клаузиус второе
начало в работе «Об определении энергии и энтропии тел», опублико-
опубликованной в 1867 году. (Приведенная в 9.2.3 первоначальная формулиров-
формулировка второго начала была дана Клаузиусом в 1850 году и была им названа
«тепловой аксиомой».)
273

9.6 Загадки термодинамики
v> помощью понятия энтропии соотношение A9) дает математи-
математически лаконичную формулировку второго начала термодинамики. Но мож-
можно ли считать, что тем самым второе начало получило объяснение? Пред-
Предписывая определенную направленность процессов в природе, это начало
ввело принципиальную необратимость. Однако первопричины этой
необратимости оставались по-прежнему необъясненными, поскольку
оставалась невыясненной физическая сущность самой энтропии.
В рамках классической термодинамики необратимость наблюдаемых
в природе процессов всего лишь констатировалась. Уже одно это было,
по сути дела, огромным достижением, поскольку ранее ученые рассмат-
рассматривали процессы, всегда предполагая их обратимость. О какой-либо не-
необратимости вообще не было речи. Обнаружившаяся в рамках термоди-
термодинамики необратимость процессов, конечно же, нуждалась в объяснении.
Почему выведенная из термодинамического равновесия система сама
по себе (самопроизвольно, спонтанно) возвращается в равновесное со-
состояние и сама по себе из него не выходит? Почему теплота переходит
от нагретого тела к холодному, а обратно сама по себе не переходит?
Почему газ не сжимается самопроизвольно? Почему, оказавшись в од-
одном и том же объеме разные газы перемешиваются, тогда как самопро-
самопроизвольного разделения компонентов смеси газа не происходит? Нас не
удивляет некоторое повышение температуры наковальни, когда по ней
ударяет молот. Но почему, сколько бы мы ни нагревали наковальню с
лежащим на ней молотом, мы не можем добиться обратного эффекта —
отскакивания молота от наковальни?
Подобных «почему» можно было бы предложить очень много. Клас-
Классическая термодинамика не отвечает на все эти «почему». Для нее это —
загадки, остающиеся без ответов. Ответы дала молекулярно-кинетичес-
кая теория вещества, которая показала, что второе начало термодинами-
термодинамики является не динамической, а статистической закономерностью и что
энтропия должна рассматриваться как понятие вероятностной природы.
ЗАДАНИЯ ПО ТЕМЕ 9
1. Докажите эквивалентность принципов, содержащихся в формулировках Клаузиу-
са и Кельвина-Планка для второго начала термодинамики.
Указание. Убедитесь, что отказ от первого принципа приводит к отказу от второ-
второго принципа и наоборот: отказ от второго принципа приводит к отказу от первого
принципа.
274

2.	Выведите соотношение D).
Подсказка. Работа по перемещению поршня на расстояние / равна F- /, где F—
сила, действующая на поршень со стороны газа.
3.	Рассматриваются три случая сжатия газа, находящегося под поршнем: 1) не-
необратимое сжатие, 2) обратимое изотермическое сжатие, 3) обратимое адиаба-
адиабатическое сжатие. Расположите эти случаи в порядке уменьшения скорости дви-
движения поршня, сжимающего газ.
Ответ: 1; 3; 2.
4.	Соотношением PVy = const для обратимого адиабатического процесса в идеаль-
идеальном газе удобно пользоваться, если рассматривать процесс на плоскости P-V.
Найдите соотношение для адиабатического процесса, которым удобно пользо-
пользоваться, рассматривая процесс: а) на плоскости V—T, б) на плоскости Р—Т.
л	ч т,/Y-i const _ч Ту const
Ответы: а) Л/у = ; б) —— =
5. Подсчитайте увеличение энтропии в расчете на 1 моль при плавлении: а) льда,
б) свинца, в) алюминия. Воспользуетесь таблицей:
лед
свинец
алюминий
М(г)
18
207
27
q^ (кал/г)
79,7
5,9
94,5
Гпл (°С)
0
327
659
Ответы: а) 5,25 кал/К, б) 2,04 кал/К, в) 2,74 кал/К.
6. Подсчитайте увеличение энтропии в расчете на 1 моль при кипении: а) водорода,
б) метана, в) воды, г) бензола. Воспользуйтесь таблицей:
водород
метан
вода
бензол
М(г)
2
16
18
78
q2 (кал/г)
108
138
540
94
Гкип (°С)
-253
-159
100
80
Ответы: а) 10,8 кал/К, б) 19,37 кал/К, в) 26,06 кал/К, г) 20,77 кал/К.
7.	Сравните результаты, полученные при выполнении заданий 5 и 6. Что можно за-
заключить из этого сравнения и как это объяснить?
8.	Обратимый цикл для идеального газа из /V молекул состоит из трех процессов:
изотермического расширения от V± до V2, изобарического сжатия, адиабатичес-
адиабатического сжатия. Изобразите этот цикл на плоскости P—V. Каково изменение энтро-
энтропии газа при изобарическом сжатии в данном цикле?
Ответ: энтропия газа возрастает на величину, равную Nk\n(V2/ Ц_).
9.	Докажите, почему две адиабаты не могут пересекаться друг с другом.
Указание. Предположите, что это возможно и рассмотрите на плоскости P—V
обратимый цикл из двух адиабат и одной изотермы.
275

ТЕМА 10
ЭНТРОПИЯ, ВЕРОЯТНОСТЬ,
ИНФОРМАЦИЯ
Энтропия стала мерой беспорядка, ца-
царящего в системе, и, следовательно, мерой
неопределенности наших знаний о внутрен-
внутренней структуре системы.
77. Шамбадалъ
(«Развитие и приложения понятия энтро-
энтропии» Пер. с французского. М.: «Наука»,
1967)
Благодаря теории информации наука
стала исследовать энтропию не только не-
незримых микропроцессов, но и таких дос-
доступных для непосредственных наблюдений
объектов, как изображение на телеэкране
или печатный текст.
ЕЛ. Седов
(«Одна формула и весь мир: книга об
энтропии». М.: «Знание, 1982)
276

10.1 Формула, объясняющая возрастание энтропии
при расширении теплоизолированного газа в пустоту
]К1спользуя соотношения F) и A1) из темы 9, получаем, что при
обратимом изотермическом расширении газа от объема Vx до объема V2
энтропия газа возрастает на величину
A)
где N — число молекул в газе. Таково изменение энтропии при квази-
квазистатическом (обратимом) переходе газа из состояния (F1? T) в состоя-
состояние {уъ Т). Энтропия является функцией состояния газа; следователь-
следовательно, ее изменение при переходе (F1? Т) —> (F2, T) не зависит от того,
как происходит переход — обратимо или необратимо. Значит, соотно-
соотношение A) справедливо также для необратимого изотермического про-
процесса — расширения газа в пустоту от объема Vx до объема V2 при усло-
условии, что газ теплоизолирован (и, следовательно, согласно первому началу
термодинамики, его начальная температура Г не изменяется).
Итак, есть два разных процесса. Первый: обратимое изотермическое
расширение газа от Vx до V2 (газ совершает работу за счет получаемой
извне теплоты). Второй процесс: необратимое расширение от Vx до V2
теплоизолированного газа (газ не совершает работы и не обменивается
теплотой с окружающей средой). Процессы разные, но в обеих энтро-
энтропия газа возрастает на одну и ту же величину AS, определяемую соотно-
соотношением A). «Природа» этого возрастания энтропии различна. Если вос-
воспользоваться соотношением A8) из темы 9, то можно отметить, что для
первого процесса:
= 0, А^ВНеШ = Nk In ^,	(*)
а для второго процесса:
А^внутр =Nk\n-±, А?внеш = 0.	(**)
у\
Короче говоря, в первом процессе энтропия AS поступает в газ из окру-
окружающей среды, тогда как во втором процессе энтропия AS производится
внутри газа.
Сейчас нас интересует второй процесс. Чтобы его реализовать, надо
воспользоваться теплоизолированной полостью (обозначим ее объем
через Vq) с перегородкой. По одну сторону перегородки находится газ; он
занимает объем Vx. По другую сторону перегородки находится вакуум.
277

Убирая перегородку, мы предоставляем газу возможность расширяться
в пустоту. Представим себе, что в процессе расширения объем газа уве-
увеличился от начального значения Vx до некоторого значения V2. В этом
необратимом процессе будет произведена в газе энтропия, величина
которой нам известна — она определяется соотношением A).
Благодаря чему, спрашивается, состоялась эта генерация энтропии?
Ответ напрашивается сам собой: благодаря тому, что объем газа увели-
увеличился от Vi до V2. Причем не просто «благодаря тому», а «только благо-
благодаря тому», поскольку при этом никакого энергообмена газа со средой
не происходит. Почему же таким важным оказалось в данном случае
увеличение объема газа от Vx до V{1 И почему, достигнув объема Vb газ
продолжал расширяться, а не стал сжиматься к объему V{t
Людвиг Больцман предположил, что все дело в вероятности молеку-
молекуле газа оказаться в том или ином объеме. Эта вероятность тем больше,
чем больше объем. В нашем примере с полостью объема Vo вероятность
молекуле оказаться в объеме Vx равна Vx / Fo, а вероятность оказаться в
объеме V2 равна V2/ Vo. Всего в газе N молекул. Вероятность того, что
все они окажутся в объеме Nh равна
а вероятность всем им оказаться в объеме V2 равна
) •	B'б>
Теперь соотношение A) можно переписать в виде:
Согласно C), изменение энтропии газа в рассматриваемом необра-
необратимом процессе его расширения от Vx до V2 равно помноженному на к
логарифму отношения вероятностей w2/w1. Поскольку w2>wb то
AS>0, что означает возрастание (генерацию) энтропии. Возрастание
энтропии получает, таким образом, простое объяснение: газ переходит из
менее вероятного состояния (когда весь газ собирается в пределах объе-
объема V{) в более вероятное состояние (когда газ собирается в объеме V2).
Обратный процесс, соответствующий самопроизвольному сжатию газа,
а значит, уменьшению его энтропии, предполагал бы переход газа из
более вероятного состояния в менее вероятное.
Итак, следуя идеям Больцмана, мы пришли к формуле C), которая
благодаря обращению к вероятностям \юхж\ю2 вполне объяснила, почему
278

возрастает энтропия теплоизолированного газа при его расширении в
пустоту. Естественным образом возникает мысль, что не только измене-
изменение энтропии, но и сама энтропия газа должна выражаться через лога-
логарифм вероятности. Имеется в виду вероятность состояния, в котором
находится газ. В самом деле, почему бы не принять, что состояниям
газа с вероятностями wx и w2 соответствуют значения энтропии газа,
равные, соответственно,
Sl = k\nwl и S2 = klnw2?	D)
Ведь это согласовывалось бы с формулой C), поскольку AS = S2 - S± и,
значит, из D) следовало бы, что
AS = к (In w2 - In w2) = к In
Щ
Ничего не имея против соотношения C), мы, тем не менее, не можем
согласиться с соотношениями D). Чтобы понять, в чем тут дело, мы
должны предварительно познакомиться с понятием «число микрососто-
микросостояний в данном макросостоянии». Это понятие Больцман именовал «чис-
«числом комплексий». В настоящее время для данного понятия используют
два термина: «термодинамическая вероятность макросостояния» и «ста-
«статистический вес макросостояния».
10.2 Микросостояния и макросостояния системы.
Статистический вес (термодинамическая вероятность)
макросостояния
Jl ассмотрим для начала крайне простую систему, состоящую всего
из четырех частиц, каждая из которых с равной вероятностью может
находиться в одном из двух состояний. Можно представить себе по-
полость, мысленно разделенную на две одинаковые половины (левую и
правую), и всего четыре молекулы внутри полости. Каждая молекула с
равной вероятностью может быть обнаружена в левой или правой поло-
половине полости. В данном случае возможны пять макросостояний систе-
системы; будем различать их по числу п молекул в одной из половин полости
(например, в левой половине). Вот эти пять макросостояний:
п = 0 — в левой половине молекул нет;
п = 1 — в левой половине одна молекула;
п = 2 — в левой половине две молекулы;
279

п = 3 — в левой половине три молекулы;
п = 4 — в левой половине все четыре молекулы.
Различные макросостояния могут быть реализованы разным числом рав-
равноправных (равновероятных) способов. Иными словами, различным мак-
макросостояниям соответствуют разные числа Wn микросостояний. Это вид-
видно на рис. 1 в таблице 33, где для молекул использованы четыре разных
изображения. Видно, что макростояния 0 и 4 могут быть реализованы
каждое одним способом; каждому из них соответствует одно микросос-
микросостояние (Wo = Cl = 1; W4 = С\ = l). Макросостояниям 1 и 3 соответству-
ют по четыре микросостояния [W^ — С\ — 4; W^ — С\ — 4 . Макросос-
тоянию 2 соответствуют шесть микросостояний (W2 = C4 = 6]. Всего в
данном случае имеется 16 микросостояний. Все они равновероятны.
В общем случае вероятность п-vo макросостояния (обозначим ее че-
через wn) пропорциональна числу Wn микросостояний, которые соответ-
соответствуют данному макросостоянию (реализуют данное макросостояние):
W
».-^.	E)
где со — полное число микросостояний. В нашем простом примере со = 16
и, следовательно,
Наиболее вероятным оказывается в данном случае макросостояние 2
(когда «газ» из четырех молекул «заполнил» весь объем полости). Наи-
Наименее вероятны макросостояния 0 и 4 (когда «газ» собрался полностью
либо в первой, либо во второй половине объема полости).
Число Wn микросостояний, соответствующих я-му макросостоянию,
называют статистическим весом, или, иначе, термодинамической веро-
вероятностью п-то макросостояния. Согласно E), термодинамическая ве-
вероятность макросостояния пропорциональна его вероятности w, но от-
отнюдь не равна ей. Вероятности принимают, как хорошо известно, любые
значения от 0 до 1, а термодинамическая вероятность принимает значе-
значения: 1, 2, 3, ... Чтобы не путать термодинамическую вероятность с веро-
вероятностью, лучше всего избегать пользоваться не очень удачным терми-
термином и применять термин «статистический вес».
Рассмотрим теперь газ из N молекул, полагая 7V> 1. Пусть при расши-
расширении газа в пустоту его первоначальный объем V увеличивается вдвое.
Используя формулу C), где теперь следует принять w2/ w1 = wK0Il / ьишч =
280

= 2V/ V= 2 (через ьишч и ьикоя обозначены начальное и конечное мак-
макросостояния газа, соответственно), получаем
AS = kln^^ = kln2.	U)
Как выразить в данном случае отношение вероятностей ьикоя / ьият че-
через числа микросостояний (через статистические веса) начального и
конечного макросостояний газа? — Будем рассуждать так же, как мы
только что делали в примере с четырьмя молекулами.
Делим мысленно объем 2 V газа на две равные половины и обозначаем
макросостояния газа числом п молекул в левой половине; я=1,2,3,...,Ж
Число макросостояний равно N+1, но, конечно, единицей здесь можно
пренебречь и полагать, что число макросостояний есть N. Поэтому мож-
можно считать, что
и/^	^	F)
л=0
Начальное состояние газа, характеризующееся вероятностью ьишч = w0,
есть макросостояние с п = 0 (в левой половине объема 2Кнет ни одной
молекулы, все они находятся в правой половине). Конечное макросос-
макросостояние характеризуется вероятностью м;кон = wN/ 2. Это есть состояние
с п = N12 — когда молекулы заняли весь объем 2 V (при очень больших
N можно, очевидно, считать, что N— четное число). Воспользовавшись
F), представим формулу C) в виде:
\2Г\2Г
Для JV> 1 справедливо соотношение (т. н. формула Стирлинга):
\nN\ = N\nN.	G)
Используя G), преобразуем (**) к виду:
AS = k
2
= k
2 2
= kln2.
Таким образом, мы пришли к результату (*) и тем самым на конкрет-
конкретном примере необратимого увеличения объема газа вдвое подтвердили
281

общее положение: при необратимом переходе газа из пгто макросостоя-
макросостояния в nTt макросостояние происходит самопроизвольное увеличение
(генерация) энтропии газа:
W
Sn2-Sni=kln-^.	(8)
yvn2
10.3 Формула Больцман.
Энтропия как мера беспорядка в системе
Соотношение (8) справедливо в общем случае — для необратимого
процесса в любой макросистеме (газе, жидкости, твердом теле). При не-
необратимом переходе макросистемы из макросостояния со статистичес-
статистическим весом We более вероятное макросостояние со статистическим весом
W энтропия макросистемы возрастает на величину
W1
kln^.	(9)
Само по себе это соотношение совпадает с C). Однако, в отличие от
формулы C), оно позволяет перейти от AS к S, если принять, что для
макросостояния со статистическим весом, равным единице, энтропия
равна нулю:
S(JV = l) = 0	A0)
(что, кстати говоря, согласуется с третьим началом термодинамики;
см. A5) из темы 9). Из соотношений (9) и A0) следует:
\S = klnW.\	A1)
Перед нами знаменитая формула Болъцмана, высеченная на камен-
каменном памятнике, установленном на могиле ученого в Вене. Энтропия S
системы, находящейся в макросостоянии со статистическим весом W,
равна klnJV.
Как следует из E), статистический вес макросостояния тем больше,
чем больше вероятность макросостояния. Значит, энтропия системы
должна возрастать по мере ее перехода из менее вероятных в более веро-
вероятные макросостояния. Мы убеждаемся, таким образом, что энтропия
имеет статистическую (вероятностную) природу.
Здесь обнаруживается, заметим, принципиальное различие между
энтропией и энергией. Оно вполне отвечает приводившемуся в §9.1
282

образному сопоставлению энтропии с директором предприятия, а энер-
энергии — с бухгалтером. Если бухгалтер должен точно подсчитывать дебет
и кредит, то директор должен иметь свободу выбора, позволяющую ему
принимать решения, обладающие более высокой вероятностью успеха.
Вспоминая рис. 1 в таблице 33, обратим внимание на то, что макро-
макросостояния с « = 0ис /1 = 4 четко выявляют определенную структуру
системы: в одной половине системы находятся молекулы, а в другой
половине молекул нет. Макросостояние с п = 2, напротив, структуры
не выявляет — все молекулы одинаковым образом распределены по
обеим половинам системы. Наличие определенной внутренней струк-
структуры связывают с порядком в системе, тогда как отсутствие структуры
указывает на беспорядок. Чем выше степень упорядоченности макросо-
макросостояния, тем меньше его статистический вес (тем меньше число соот-
соответствующих микросостояний). Достаточно сильно разупорядоченные
макросостояния со слабо выраженной внутренней структурой имеют
большой статистический вес; они могут быть реализованы многими
способами, иначе говоря, многими микросостояниями.
Все это позволяет рассматривать энтропию как меру беспорядка в си-
системе. Чем больше беспорядок в данном макросостоянии, тем больше
его статистический вес и тем, следовательно, больше энтропия систе-
системы, находящейся в рассматриваемом макросостоянии.
10.4 Статистическое объяснение второго начала
термодинамики
'ормула Больцмана позволила весьма просто объяснить постули-
постулируемое вторым началом термодинамики возрастание энтропии при не-
необратимых процессах в замкнутой системе. Возрастание энтропии объяс-
объясняется тем, что система переходит из менее вероятных в более вероятные
состояния. Рассмотренный выше пример с расширением газа в пустоту
хорошо это продемонстрировал.
Реально протекающие в природе процессы — это, строго говоря, не-
необратимые процессы; обратимость следует рассматривать как некую идеа-
идеализацию, соответствующую некой упрощенной схеме. Представляется
естественным, что природным процессам соответствуют переходы в более
вероятные состояния. Больцман подчеркивал: «Во всех случаях, где при-
применим закон больших чисел, т. е. в явлениях природы, обнимающих ог-
огромное число молекул, всякое изменение, которое может произойти само
283

Таблица 33. Вероятностная природа второго начала термодинамики и флуктуации
Wn =
= 1/16
= 1/4
0
О
W2 = 6
002 = 3/8
s
I
и
Г
1г
r
V-
jnl
г U
а)
100<Е>
б)
Рис.2
ЕГО
W3 =
О
W4 = l
Ю4 = 1/16
Рис.1
7
и
A
\
1
A
4
\
\
1 ^
V
s
\
/
^5
\
<¦
ж
?
Й
у
у
V^
>
s
s
¦**'
\
Рис.3
\
i
J
i
1
\
J
/
•
7
i
L
1
\
\
X
л
ж
\
Рис.4
284

собой (т. е. без компенсации), есть переход от менее вероятного состоя-
состояния к более вероятному состоянию». Планк в своей книге «Теория теп-
теплового излучения» A906), характеризуя сущность второго начала термо-
термодинамики, связывал ее с тем, что «в природе отдается предпочтение более
вероятным состояниям по сравнению с менее вероятными».
При вероятностном подходе энтропия выступает как мера беспоряд-
беспорядка в системе. Поэтому закон возрастания энтропии в замкнутых систе-
системах можно рассматривать как закон увеличения степени беспорядка в этих
системах. Иначе говоря, переход из менее вероятных в более вероятные
состояния соответствует переходам «порядок —> беспорядок». Когда,
например, молот ударяет по наковальне, упорядоченная составляющая
движений молекул молота, связанная с поступательным движением
молота как целого, переходит в неупорядоченное тепловое движение
молекул наковальни и молота.
Количество энергии в замкнутой системе с течением времени не из-
изменяется. Однако изменяется качество энергии. Уменьшается ее спо-
способность совершать работу. Возрастание энтропии в замкнутой системе
есть, по сути дела, постепенное разрушение системы, постепенная ее
деградация. Всякая замкнутая система со временем неизбежно деградиру-
деградирует, разупорядочивается. Изоляция системы отдает ее во власть разруша-
разрушающих случайностей, направляющих систему по пути к беспорядку. Как
выразился известный французский физик Леон Бриллюэн A889-1969)
«второе начало термодинамики говорит о смерти вследствие изоляции».
Чтобы поддерживать или, тем более, повышать степень упорядочен-
упорядоченности системы, необходимо ею управлять, для чего нужно, прежде все-
всего, чтобы не было изоляции системы, чтобы система была открытой.
Конечно, после того как система лишается «защитной оболочки», от-
открывается доступ к ней для различного рода внешних дезорганизующих
факторов. Однако наряду с этим открывается доступ и для управляю-
управляющих факторов. Действие последних может приводить к уменьшению
энтропии системы.
10.5 Немного о флуктуациях случайных величин
п,
LpepBeM на короткое время обсуждение второго начала термодина-
термодинамики и поговорим о флуктуациях случайных величин.
10.5.1. Флуктуации микровеличин и макровеличин. Напомним, что
случайная величина может принимать различные значения, характеризую-
характеризующиеся либо вероятностью (если величина дискретная), либо плотностью
285

вероятности (если величина непрерывная); см., например: «Случайность,
необходимость, вероятность», тема 12. Следя за случайной величиной,
можно наблюдать случайную смену ее значений; эти случайные изме-
изменения и называют флуктуациями. Говорят, что случайная величина флук-
флуктуирует (колеблется) около своего среднего значения.
Будем обозначать через (X) математическое ожидание случайной ве-
величины X. Полагая, что число испытаний, реализующих всякий раз
то или иное значение величины, достаточно велико, будем отождеств-
отождествлять математическое ожидание величины с ее средним значением. В ка-
качестве меры отклонения случайной величины от ее среднего значения
(математического ожидания) рассматривают дисперсию D(X) случайной
величины, являющуюся математическим ожиданием квадрата отклоне-
отклонения величины Хот ее математического ожидания (X):
D(X) = ([X-(X)]2) = (X2)-(XJ.	A2)
Дисперсию D (X) называют квадратичной флуктуацией величины X. От-
Отношение sjD(X) к (X) называют относительной флуктуацией величи-
величины; обозначим относительную флуктуацию через ?:
Рассматривая флуктуации в макросистеме, содержащей большое число
молекул, различают флуктуации микровеличин и флуктуации макровели-
макровеличин. Микровеличины — это случайные величины, характеризующие
отдельные молекулы. Например, скорость v или энергия е поступательно-
поступательного движения молекулы. Макровеличины — это случайные величины,
относящиеся к макросистеме из большого числа N молекул. Например,
внутренняя энергия Е или энтропия S макросистемы.
Для примера рассмотрим ^е и \Е — относительные флуктуации соот-
соответственно для еи? термодинамически равновесного идеального газа.
Энергия молекулы е является непрерывной случайной величиной; она
характеризуется плотностью вероятности
^кТ	A4)
На всякий случай поясним, что вероятность молекуле иметь энергию в
интервале от е до е + Де (обозначим ее через ю{г\ Ае)) равна /(е)Ае при
условии достаточной малости Ае. Строго говоря,
^M.	A5)
286

Примечание. Мы не будем выводить соотношение A4). Заметим лишь, что это
соотношение вытекает из соотношения для плотности вероятности скорости мо-
молекулы, полученного в 1859 году выдающимся английским физиком Джеймсом
Клерком Максвеллом A831-1879) и известного ныне как максвелловское распреде-
распределение скоростей молекул газа. Это распределение имеет вид:
.( m \3/2
\2nkTJ '
где m — масса молекулы.
Используя A5), можно получить:
3?7\
A6)
Оба эти результата мы приводим без вывода.
Из A7) и A8) следует (с учетом A2) и A3)):
В(г) =
Ъ[кТ)
2
~2
\ 2
A7)
A8)
A9)
B0)
Как видим, «размах» флуктуации микровеличины (в данном случае энер-
энергии молекулы идеального газа) оказывается примерно равным средне-
среднему значению микровеличины — см. рис. 2а в таблице 33.
Теперь будем рассматривать не одну молекулу, а макросистему из
N
Л^молекул. Ее внутренняя энергия is есть сумма Е = /_2ei и' следовательно,
/=1
E = N(e).	B1)
Дисперсию D(E) = ([Е — (Е)} ) можно преобразовать, с учетом B1), сле-
следующим образом:
N
N
N
где через 8ez обозначена разность 58/ =8/ — (е).
Выражение
N
представим в виде:
N	2 N	N N
287

Таким образом,
IN
Выполняя усреднение, получаем:
iJ) = N([ei-(e)]2) = ND(e);	(**)
N N
ijbZj) = 0,	(***)
так как при i^j: Ee/88y) = E8/)Eey) (математическое ожидание произ-
произведения независимых случайных величин равно произведению матема-
математических ожиданий этих величин) и так как (8et) = ([?; — (е)]) = (г) — (е) = 0.
Используя (*), (**), (***), заключаем, что
D (Е) = ND (г) =	\—}—.	B2)
Из B1) и B2) следует (с учетом A3) и B0)), что
B3)
Итак, как мы убедились, относительная флуктуация внутренней энер-
энергии газа из N молекул пропорциональна \/4W. В кубическом санти-
сантиметре газа при нормальном давлении содержится около 1019 молекул.
Значит, для газа объемом порядка 10 см3 относительная флуктуация
внутренней энергии составляет всего лишь 10~10, т. е. ничтожно мала.
На рис. 2,6 в таблице 33 сделана попытка изобразить графически харак-
характер изменения величины Е со временем. Полезно сопоставить рис. 2,а
и 2,6. В отличие от энергии молекулы внутренняя энергия газа, содер-
содержащего большое число молекул, может рассматриваться не как случай-
случайная величина, а как величина с определенным значением. Оно равно
математическому ожиданию (среднему значению) (Е).
Таково общее положение: если число N молекул в системе достаточ-
достаточно велико, то для ее макровеличин:
**и	B4>
что позволяет на практике пренебрегать, как правило, флуктуациями мак-
макровеличин и оперировать с их средними значениями. Глядя, например, на
уравнение Клапейрона-Менделеева PV= NkTwm на закон Ома /= U/ R,
288

многие даже не подозревают, что все присутствующие в этих формулах
буквы (за исключением постоянной Больцмана к) обозначают, строго
говоря, случайные величины, которые представлены здесь своими сред-
средними значениями.
Однако следует помнить, что в действительности все макровеличины
(не только внутренняя энергия, но также энтропия, давление, темпера-
температура, электрическое напряжение и пр.) флуктуируют около своих сред-
средних значений и эти флуктуации могут становиться существенными при
уменьшении N.
10.5.2. Броуновское движение и голубой цвет неба — примеры, нагляд-
наглядно демонстрирующие существование флуктуации в макросистемах. В
1827 году английский ботаник Роберт Броун A773-1858) обнаружил с
помощью обычного микроскопа хаотическое движение мелких частиц
(пыльцы растений), взвешенных в воде. «Движение это, как я убеж-
убежден, — писал Броун, — обусловлено не потоками в жидкости, не посте-
постепенным ее испарением, а принадлежит самим частицам». Объяснение
природы броуновского движения дал в 1905 году Альберт Эйнштейн. Он
показал, что причиной броуновского движения является хаотическая бом-
бомбардировка взвешенных мелких частиц молекулами окружающей жид-
жидкости, находящимися в тепловом движении.
Представим себе взвешенный в жидкости маленький диск (диамет-
(диаметром, скажем 10~4см). Отнесенное к единице времени число ударов мо-
молекул жидкости по одной стороне диска равно в среднем числу ударов
по другой стороне. Но равенство соблюдается только в среднем. В дей-
действительности же число ударов по одной из сторон диска в течение
какого-то малого промежутка времени может оказаться заметно боль-
больше числа ударов по другой стороне. В результате диск получит неском-
пенсированный импульс и совершит в соответствующем направлении
скачок. Можно сказать, что причиной скачков диска являются флуктуа-
флуктуации давления, оказываемого молекулами жидкости на разные стороны
диска. В пределах объема 10~4 х 10~4 х 10~4 = 10~12 см3 эти флуктуации
оказываются достаточно ощутимыми.
На рис. 3 в таблице 33 представлена картина броуновского движе-
движения трех частиц гуммигута в воде, наблюдавшаяся французским физи-
физиком Жаном Батистом Перреном A870-1942). Точками отмечены по-
положения частиц через каждые 30 с. Радиус частиц 0,5-10м;
расстояние между делениями сетки на рисунке 3,4 • 10м. Отметим,
что выполненные Перреном исследования броуновского движения
позволили экспериментально определить постоянную Больцмана и
число Авогадро.
289

Теперь о голубом цвете неба. Цвет неба мы воспринимаем вследствие
рассеяния солнечных лучей в земной атмосфере. Мысленно разобьем
воздушное пространство атмосферы на маленькие ячейки-кубики с дли-
длиной ребра, соответствующей длине световой волны (около 0,5 • 10~6м).
Хаотическое движение молекул воздуха приводит к тому, что число
молекул в пределах кубика будет случайно изменяться от одного кубика
к другим. Оно будет случайно изменяться также в пределах одного и
того же кубика, если производить наблюдения в разные моменты вре-
времени. На этих флуктуациях плотности воздуха, достаточно существен-
существенных в пределах каждого кубика (ввиду его малости), и происходит рас-
рассеяние света.
Согласно современной теории, интенсивность света, рассеянного
объемом воздуха АКпри температуре Т, пропорциональна AVT/X4, где
X — длина волны света. Отсюда видно, что рассеяние света происходит
тем интенсивнее, чем меньше длина световой волны. Поэтому спектр
рассеянного в атмосфере света оказывается смещенным в коротковолно-
коротковолновую область, что и объясняет наблюдаемый нами голубой цвет неба.
10.5.3.	Формула Найквиста. Из закона Ома следует, что если в элект-
электрической цепи нет электродвижущей силы, то ток в ней идти не будет.
Это, однако, не совсем верно. Дело в том, что флуктуации, связанные с
тепловым движением электронов в проводнике, приводят к возникно-
возникновению флуктуационных токов, так что можно говорить о наличии флук-
туационной электродвижущей силы.
В 1928 году американский физик Найквист показал, что на концах
проводника с сопротивлением 7?, имеющего температуру Т, возникает
флуктуация напряжения U, дисперсия которого D (U) = ([U — (?/)] ) опи-
описывается формулой:
D(U)~ RT.	B5)
Флуктуации электрических величин играют важную роль в современ-
современных приборах и устройствах. Они являются принципиально неустрани-
неустранимым источником шума (помех) в каналах связи. Они определяют пре-
пределы чувствительности различных измерительных приборов.
10.5.4.	Флуктуации и абсолютная температура. Обратим внимание на
то, что в соотношения B2) и B5) входит абсолютная температура Т.
Мы видим, что квадратичная флуктуация макровеличин возрастает с
ростом Т. Чем выше абсолютная температура тела, тем сильнее флук-
флуктуируют его физические параметры.
Известно, что абсолютная температура тела может рассматриваться как
мера средней энергии молекул тела (это хорошо видно на примере идеаль-
идеального газа — см. A7)). Следует, однако, помнить, что это справедливо лишь
290

при условии, что тело находится в термодинамическом равновесии. Если
же состояние некоего коллектива частиц существенно неравновесно
(предположим, рассматривается космический ливень или пучок частиц
из ускорителя), то в этом случае средняя энергия частиц уже не может
измеряться температурой.
Более общий подход к понятию температуры тела предполагает ее
связь не со средней энергией частиц, а с флуктуациями физических
параметров тела. При этом температура может рассматриваться как
мера флуктуации. Измеряя флуктуации, можно, в принципе, измерять
абсолютную температуру тела. Для такой цели весьма подходят флуктуа-
флуктуации электрических величин.
Связь температуры с флуктуациями указывает, в частности, на то,
что понятие температуры, строго говоря, не имеет аналога в классичес-
классической механике. Температура предполагает наличие вероятностных про-
процессов, она выступает в качестве меры дисперсии случайных величин.
10.6 Вероятностная природа второго начала
термодинамики
11родолжим наш разговор о втором начале термодинамики. Мы вы-
выяснили, что предписываемые этим началом необратимые процессы
имеют статистическое объяснение — это есть процессы, связанные с
переходом системы из менее вероятных состояний в состояния, харак-
характеризующиеся более высокой вероятностью.
Зададимся вопросом: являются ли требования второго начала термо-
термодинамики абсолютно жесткими! Иными словами, означает ли это на-
начало, что процессы обязательно должны идти в направлении от менее
вероятных к более вероятным состояниям? Ответ на этот вопрос отри-
отрицателен. Переходы системы в более вероятные состояния происходят
не в обязательном порядке, а всего лишь с некоторой вероятностью.
Диктуемое вторым началом термодинамики направление развития не-
необратимых процессов не является в действительности жестко предоп-
предопределенным. Это есть лишь более вероятное направление.
Нарушения второго начала термодинамики в принципе возможны.
Обычно мы не наблюдаем их лишь по той причине, что они оказыва-
оказываются весьма маловероятными. Газ самопроизвольно расширяется в пус-
пустоту. Это есть наиболее вероятное направление процесса. Однако в
принципе возможна ситуация, когда скорости молекул в газе окажутся
291

вдруг (иными словами, случайно) ориентированными таким образом,
чтобы газ самопроизвольно сжался. Такая ситуация маловероятна для
макрообъема газа, содержащего огромное число молекул. Но она может
стать вполне вероятной в малом объеме газа.
Самопроизвольное сжатие газа следует рассматривать как флуктуа-
флуктуацию его плотности. Чем больше молекул в газе, тем меньше относи-
относительная флуктуация плотности (напомним, что она пропорциональ-
пропорциональна l/>fW)9 тем, следовательно, меньше вероятность наблюдать такую
флуктуацию в макроскопических масштабах. Допустим, однако, что
некоторое явление наблюдается в микромасштабе, т. е. требует учас-
участия относительно небольшого числа молекул. В этом случае уже не-
нетрудно наблюдать различного рода флуктуации, свидетельствующие
о нарушениях второго начала. В предыдущем параграфе мы говорили
о флуктуациях плотности воздуха в пределах достаточно малого объе-
объема, линейные размеры которого соответствовали длине световой вол-
волны. Эти флуктуации проявляются в самопроизвольных сжатиях и
разрежениях воздуха, которые и обусловливают наблюдаемый нами
голубой цвет неба.
Для броуновской частицы наиболее вероятно получить в единицу
времени одинаковое число ударов молекулы жидкости с той и с другой
(противоположной) стороны. Однако вследствие малости размеров ча-
частицы вполне вероятны флуктуации давления, связанные с нескомпен-
сированностью ударов с разных сторон. В результате частица совершает
скачки в тех или иных направлениях. Совершая очередной скачок, бро-
броуновская частица наглядно демонстрирует самопроизвольное превра-
превращение теплоты, отбираемой от жидкости, в кинетическую энергию своего
поступательного движения.
Следует заключить, таким образом, что второе начало термодинами-
термодинамики имеет вероятностную природу. Рассматриваемые в рамках этого на-
начала закономерности являются не динамическими (жестко детермини-
детерминированными), а статистическими (вероятностными). Это убедительно
подтверждает существование флуктуации, демонстрирующих вероятност-
вероятностную природу необратимых процессов.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
*Чит<1(пел<к. Вот Вы произнесли слова «вероятностная природа не-
необратимых процессов». Я понимаю, что если процесс стохастический
(т. е. случайный, вероятностный), то он должен быть необратимым. Как
292

известно, развивающаяся случайным образом система утрачивает свою
предысторию и уже по этой причине ее развитие оказывается необрати-
необратимым. Короче говоря, из стохастичности процесса следует его необрати-
необратимость. Однако можно ли утверждать, что из необратимости процесса
следует его стохастичность?
Пвтор. Прежде, чем ответить на Ваш вопрос, я хотел бы сделать
некоторые замечания общего характера. В математике, кроме прямой и
обратной, рассматриваются также противоположная теорема и теорема,
обратная противоположной.
'ЧеаЯаЯе**. О противоположных теоремах я не слышал.
Пвтор. Прямая теорема: если есть А, то есть Б.
Обратная теорема: если есть Б, то есть А.
Противоположная теорема: если нет А, то нет Б.
Теорема, обратная противоположной: если нет Б, то нет А.
Впрочем, не все эти теоремы требуется доказывать. Если, например,
верна противоположная теорема, то будет верна и обратная теорема.
'Чиниипель. Откуда это следует?
Пвтор. Предположим, дано: если нет А, то нет Б. Докажем, что если
есть Б, то есть А. Предположим противное: допустим, что Б есть, но А
нет. Мы тут же «приходим в тупик», поскольку нам дано, что если нет
А, то не должно быть и Б. «Выход из тупика» ясен — надо отказаться от
сделанного допущения и принять, что если есть Б, то есть А.
&. Но зачем нам все эти доказательства? Какое они имеют
отношение к стохастичности и необратимости процессов?
Пвтор. Пусть утверждение А таково: данный процесс является сто-
стохастическим. Утверждение Б: данный процесс является необратимым.
Тогда прямую теорему можно сформулировать так: если процесс стоха-
стохастический, то он необратимый. А как Вы сформулируете противопо-
противоположную теорему?
. Если процесс нестохастический, то он не является нео-
необратимым.
Пвтор. Верно. Только это можно сформулировать получше: если про-
процесс динамический (жестко детерминированный), то он обратимый. Надо
ли доказывать эту теорему?
*Чи(*иипель. Думаю, что не надо. Вполне очевидно, что всякий жест-
жестко детерминированный процесс можно заставить идти в обратном на-
направлении.
Пвтор. Вы правы. Это хорошо иллюстрируют процессы, рассматри-
рассматриваемые в рамках классической механики. Итак, противоположная тео-
теорема верна. А как в нашем случае выглядит обратная теорема?
293

Если процесс необратим, то он стохастический.
Пвтор. Вот Вам ответ на вопрос, который Вы задавали. Как видите,
из самых общих соображений следует, что коль скоро из стохастичнос-
ти (случайности) процесса можно заключить о его необратимости, то
точно так же из необратимости процесса можно сделать вывод о его
стохастичности.
Мы пришли к весьма важному выводу: в основе необратимости про-
процессов в природе лежит стохастичность, т. е. вероятностный характер
этих процессов. Все это подсказывает нам, что именно вероятностные
закономерности (отражающие необратимые процессы) являются фун-
фундаментальными, тогда как динамические закономерности (отражаю-
(отражающие обратимые процессы) оказываются при ближайшем рассмотре-
рассмотрении некоторым упрощением, идеализацией. Эту мысль мы надеемся
развить в третьей части данной книги. А пока отметим лишь, что об-
обнаружившиеся благодаря второму началу термодинамики необрати-
необратимые процессы (например, теплопроводность диффузия, вязкость) впер-
впервые в истории естествознания заставили ученых рассматривать наряду
с динамическими закономерности иной природы — статистические за-
закономерности.
В заключение приведем отрывок из речи Макса Планка «Динами-
«Динамическая и статистическая закономерность», произнесенной им в Бер-
Берлинском университете в августе 1914 года:
«Во всей совокупности физических явлений нет более резко выраженного раз-
различия, чем то, которое существует между обратимыми и необратимыми процесса-
процессами. К первым принадлежат явления, зависящие от тяготения, механические и
электрические колебания, акустические и электромагнитные волны. Все их нетруд-
нетрудно подвести под один динамический закон — принцип наименьшего действия, ко-
который содержит в себе также и принцип сохранения энергии. К необратимым явле-
явлениям относятся теплопроводность, электропроводность, трение, диффузия, а также
химические реакции. Для этих явлений Клаузиус вывел свое необычайно плодо-
плодотворное для физики и химии второе начало термодинамики, значение которого
состоит в том, что оно предписывает каждому необратимому процессу определен-
определенное направление. Но лишь Больцману впервые удалось, введя атомистические
представления, установить глубокие основы содержания второго начала и вместе с
тем всей совокупности необратимых процессов, своеобразие которых представля-
представляло непреодолимые трудности для общего динамического объяснения... Для физи-
физика не остается никаких сомнений: материя состоит из атомов, теплота есть движе-
движение молекул и теплопроводность, равно как и все остальные необратимые процессы,
управляется не динамическими, а статистическими законами, т. е. законами веро-
вероятности (курсив наш. — Автор).
294

10.7 «Демон», владеющий информацией
в
1871 году Джеймс Максвелл в своем труде «Теория теплоты», об-
обсуждая второе начало термодинамики, рассмотрел воображаемую ситуа-
ситуацию, в которой второе начало не работает. Для этого ему пришлось при-
придумать некое «существо со столь изощренными способностями, что оно
в состоянии следить за каждой отдельной молекулой во всех ее движени-
движениях». (Это придуманное Максвеллом существо Уильям Томсон заменил
позднее термином «демон Максвелла»). Максвелл поручил этому суще-
существу управлять клапаном (задвижкой, дверцей) в отверстии перегородки,
разделяющей два равных объема (А и Б) с газом — см. рис. 4 в табли-
таблице 33. «Пусть существо, способное различать отдельные молекулы, — писал
Максвелл, — открывает и закрывает попеременно отверстие в перего-
перегородке таким образом, чтобы только более быстрые молекулы могли пе-
переходить из А в Б и только более медленные молекулы могли переходить
из Б в А. Такое существо без затраты работы повысит температуру в Б и
понизит ее в А — вопреки второму началу термодинамики».
Демон Максвелла, коль скоро он способен различать отдельные мо-
молекулы, мог бы также открывать дверцу в отверстии перегородки перед
молекулами, подлетевшими к этому отверстию из объема А, и, напро-
напротив, закрывать дверцу перед молекулами, подлетевшими к отверстию
из объема Б. Тем самым происходило бы самопроизвольное возраста-
возрастание плотности газа в объеме Б — наблюдался бы эффект самопроиз-
самопроизвольного сжатия газа. Тоже вопреки второму закону термодинамики.
Демон Максвелла мог бы сортировать молекулы в смеси двух разных
газов, пропуская через отверстие в одном направлении молекулы одно-
одного компонента смеси, а в обратном направлении — другого компонента
смеси. В результате происходило бы самопроизвольное разделение ком-
компонентов смеси — в одном объеме накапливались бы молекулы одного
газа, а в другом объеме молекулы другого газа. Опять-таки вопреки
второму началу термодинамики.
Итак, возникала парадоксальная ситуация: демон Максвелла опро-
опровергал второе начало термодинамики. Этот парадокс обсуждало несколь-
несколько поколений физиков. Было высказано немало соображений по пово-
поводу неосуществимости устройства, которое действовало бы подобно
демону Максвелла. Указывалось, например, что флуктуации должны
были бы приводить к случайному открыванию и закрыванию дверцы,
что неизбежно нарушило бы действие всей системы. Указывалось так-
также, что для того, чтобы демон мог различать молекулы, нужно было бы
освещать молекулы с помощью какого-то источника излучения, что
295

потребовало бы затраты энергии. Это означало бы, что вопреки мне-
мнению Максвелла активность демона не могла быть даровой и, значит,
нельзя было рассматривать вызываемые действиями демона процессы
самопроизвольными (иначе говоря, внешний источник излучения на-
нарушал бы замкнутость системы, а в открытой системе второе начало не
обязано работать).
На самом деле попытки доказать, что демон Максвелла не может су-
существовать (в виде какого-либо хитроумного устройства), особого инте-
интереса не представляют. По сути дела, нет смысла заниматься «изгнанием»
этого демона по двум причинам. Во-первых, демон Максвелла отнюдь не
опровергает второе начало термодинамики, а только доказывает, что это
начало имеет не жестко детерминированную, а вероятностную природу.
Во-вторых, проблема, поставленная Максвеллом, касалась не возможно-
возможности или невозможности существования такого демона, а смысла тех дей-
действий, которые он мог бы производить, если бы существовал.
Надо признать, что смысл действий демона Максвелла был осознан
по-настоящему только в ХХ-м столетии. Как подчеркивал Бриллюэн в
книге «Наука и теория информации» A956), «проблема демона Макс-
Максвелла представляет прекрасный случай для применения теории инфор-
информации и ясно указывает на связь между информацией и энтропией» (кур-
(курсив наш. — Автор). Впервые на существование такой связи указал
венгерский физик Лео Сцилард A898-1964) в 1929 году. Впрочем, эта
связь проглядывается уже в словах самого Максвелла, который указы-
указывал, что придуманное им «существо» способно «следить за каждой от-
отдельной молекулой». Ведь фактически это означает, что такое «существо»
должно владеть информацией. Только имея необходимую информацию
о молекулах, движущихся слева и справа от отверстия в перегородке,
демон Максвелла может предпринимать действия, приводящие к умень-
уменьшению энтропии системы.
В общих чертах смысл действий демона Максвелла можно сегодня
объяснить следующим образом. В отсутствие демона система (напри-
(например, газ) существенно разупорядочена, имеет максимальную энтропию
и минимальное количество информации. Обладая каким-то количеством
информации, демон Максвелла вносит в систему соответствующее ко-
количество отрицательной энтропии (информации), соответствующим
образом снижает энтропию системы и тем самым уменьшает степень
беспорядка в системе. Как отмечал Норберт Винер (в книге «Киберне-
«Кибернетика, или управление и связь в животном и машине», 1961), «демон
способен действовать лишь на основании принимаемой информации, а
эта информация представляет собой отрицательную энтропию».
296

10.8 Формула Больцмана и формула Хартли,
связь мещу энтропией и информацией
Ч^ормула Больцмана (соотношение A1) в данной теме):
Читается: энтропия системы в некотором состоянии есть произведение
постоянной Больцмана на натуральный логарифм числа равновероят-
равновероятных микросостояний, соответствующих данному состоянию системы.
Формула Хартли (соотношение (И) в теме 7):
Н = log2 N
Читается: количество информации, связанное с реализацией (выбором)
определенного варианта из N равновероятных вариантов, равно log2^.
На первый взгляд может показаться, что речь идет о двух разных
формулах, не имеющих связи друг с другом. К тому же величина S
измеряется в единицах Дж/К (имеет размерность энергия/температу-
энергия/температура), тогда как Н измеряется в битах (иначе говоря, Н безразмерна).
Легко, однако, заметить два обстоятельства, являющиеся общими для
рассматриваемых формул:
1)	В обе формулы входит логарифм (использование логарифмов с раз-
разными основаниями непринципиально; ведь lux = In 2 • log2x = 1,44 log2x).
2)	В обеих формулах под знаком логарифма стоят числа равновероят-
равновероятных вариантов. В формуле Больцмана речь идет о равновероятных ва-
вариантах данного состояния макросистемы (варианты отождествляются
с микросостояниями), а в формуле Хартли равновероятные варианты
вообще не уточняются (просто указывается их количество N).
При более пристальном рассмотрении обнаруживается, что отмечен-
отмеченные обстоятельства принципиальны, причем не только в математичес-
математическом отношении (в обоих случаях используется логарифм), но также в
физическом отношении. Так что S и Н оказываются по сути своей вза-
взаимосвязанными величинами.
Начнем с формулы Хартли. Как понимать используемые в этой фор-
формуле слова «количество информации, связанное с реализацией (выбо-
(выбором) определенного варианта»? В § 7.8 мы обращали внимание на то, что
это можно понимать двояко. Во-первых, как количество информации,
которое надо внести в систему, чтобы произошел выбор в системе какого-то
конкретного варианта. Так, чтобы направить прибывающий на станцию
297

поезд на какой-то конкретный из N путей, диспетчер должен послать
соответствующий управляющий сигнал, обладающий информацией, рав-
равной log2^ битам. Во-вторых, речь может идти о количестве информации,
содержащемся в сообщении о том, какой именно вариант был выбран в
системе. Так, выяснив, на какой из N путей был направлен поезд, мы
получаем количество информации, равное log2 N битам.
В обоих случаях величина Н, равная log2^, характеризует степень
неопределенности опыта. Как опыта, состоящего в посылке управляю-
управляющего сигнала, так и опыта, состоящего в отыскании поезда на станци-
станционных путях. Чем больше число равновероятных вариантов (чем боль-
больше N), тем выше степень неопределенности. И, соответственно, тем
больше то количество информации, которое содержится как в управля-
управляющем сигнале диспетчера, так и в сообщении о том, где находится
прибывший на станцию поезд. Поэтому естественно рассматривать Н
одновременно и как меру степени неопределенности, и как количество
информации, которое устраняет неопределенность.
Наличие неопределенности связывают с наличием беспорядка (точ-
(точнее сказать, разупорядоченности), а устранение неопределенности — с
упорядочиванием. Тут уместно вспомнить, что энтропия состояния си-
системы может рассматриваться как мера разупорядоченности (беспоряд-
(беспорядка) для данного состояния. В формуле Больцмана степень разупорядо-
разупорядоченности измеряется числом микросостояний в состоянии системы (если
имеется только одно микросостояние, то W= 1 и, следовательно, S= О —
случай «полной упорядоченности»). В формуле Хартли степень разупо-
разупорядоченности измеряется числом равновероятных вариантов (если име-
имеется только один вариант, то N=\ и, следовательно, Н= О — случай
«полной упорядоченности»). Сообщение системе количества информа-
информации H=log2N приводит к соответствующему уменьшению степени ее
неопределенности, что отвечает повышению энтропии системы на ве-
величину S = k In W, если в качестве равновероятных вариантов рассмат-
рассматривать равновероятные микросостояния. Мы приходим к важному за-
заключению: величина Н в формуле Хартли (измеряющая степень
неопределенности опыта, или, что то же самое, количество информа-
информации, связанное с этим опытом) может интерпретироваться как энтро-
энтропия, рассматриваемая с более общей точки зрения — когда равновероят-
равновероятные варианты не сводятся только к равновероятным микросостояниям
физической макросистемы.
Итак, с более общей точки зрения, процесс получения информации
соответствует процессу упорядочивания, и следовательно, процессу по-
понижения энтропии. И напротив, процесс повышения энтропии связан с
298

процессом разупорядочивания и, следовательно, процессом потери ин-
информации, «Процессы, ведущие к потере информации, — писал Винер, —
весьма сходны с процессами, ведущими к росту энтропии». Подчеркнем,
что все эти утверждения имеют общий характер и не ограничиваются
рассмотрением каких-либо физических макросистем. Именно поэтому
можно говорить, что в теории информации энтропия выходит на новый
этап своего развития, связанный с исключительно широким примене-
применением этого понятия.
Возвращаясь к рассмотрению физических макросистем, будем теперь
пользоваться, наряду с понятием энтропии, понятием информации,
понимая под последней информацию, которой мы располагаем относи-
относительно микроструктуры данной системы. Винер называл эту информа-
информацию отрицательной энтропией, а Бриллюэн — негэнтропией. Когда энт-
энтропия системы возрастает, негэнтропия системы уменьшается. Закон
возрастания энтропии в замкнутых системах может теперь интерпрети-
интерпретироваться как закон уменьшения негэнтропии в таких системах. Изоляция
системы чревата не только возрастанием энтропии, но и потерей содер-
содержащейся в системе информации. Обратим внимание на то, что теперь
энтропия физической макросистемы — это не только мера ее разупоря-
доченности, но и мера неопределенности нашего знания внутренней
структуры макросистемы, или, по выражению Бриллюэна, «мера недо-
недостатка информации о действительной структуре системы».
10.9 Формула Шеннона и Формула Больцмана
Обобщением формулы Хартли на случай, когда N вариантов не
являются равновероятными, а характеризуются вероятностями ръ ръ
ръ, ..., pN, является формула Шеннона (соотношение A9) в теме 7):
N
1
N
Неравновероятность вариантов, как уже отмечалось в § 7.8, снижает
степень неопределенности и тем самым уменьшает количество информа-
информации Н. В зависимости от того, каков набор из j? вероятностей/?z, коли-
количество информации Н может варьироваться от 0 до log2 N. Если одна из
вероятностей равна единице, а все остальные равны нулю, то Н=0.
Если каждая из ^вероятностей равна 1 / N, то Н= log2N. В первом случае
299

реализован (или может быть реализован) только один вариант — тот,
для которого вероятность равна единице. Тут выбора нет, неопределен-
неопределенность отсутствует и, следовательно, энтропия Н как мера «недостатка
информации» равна нулю. Во втором случае, напротив, степень не-
неопределенности максимальна. Ведь тут не только возможны все N ва-
вариантов, но, кроме того, тут нельзя отдать предпочтение каким-либо из
этих вариантов. Поэтому во втором случае энтропия Н максимальна и,
следовательно, максимально то количество информации, которое тре-
требуется для выбора любого конкретного варианта.
В предыдущем параграфе проводилось сопоставление формулы Хартли
с ее «предшественницей» — формулой Больцмана. Это сопоставление
позволило нам обсудить связь энтропии с информацией. У формулы
Шеннона также есть «предшественница» в теории Больцмана. Соответ-
Соответствующее выражение можно вывести из нижеследующих достаточно
несложных (хотя и несколько упрощенных) рассуждений.
Пусть макросистема содержит N молекул и пусть в данном состоя-
состоянии макросистемы пх молекул имеют энергию в интервале 1 (от 0 до
Де), п2 молекул имеют энергию в интервале 2 (от Де до 2Де), пъ молекул
имеют энергию в интервале 3 (от 2Де до ЗДе) и т. д. Число таких интер-
интервалов, в каждом из которых находится достаточно большое число моле-
молекул, обозначим через т. Обозначим через wt вероятность молекуле ока-
оказаться в /-м интервале, т. е. в интервале значений энергии от (/ - 1)Де до
/ • Де. Понятно, что
Число микросостояний, соответствующее макросостоянию, характери-
характеризующемуся вероятностями wh wb w3, ..., wm обнаружить молекулу в ин-
интервалах соответственно 1, 2, 3, ..., т, равно
w = —Г-Г1	г	B6)
пх\п2\пъ\...пт\
(микросостояния различаются перестановками молекул внутри каждо-
каждого из интервалов; на рассматриваемое макросостояние системы эти пе-
перестановки, очевидно, не влияют). Таким образом, согласно формуле
Больцмана A1), энтропия данного макросостояния системы есть
= klnW = k
(**)
300

Учитывая, что все числа молекул, входящие в выражение B6), много
больше единицы и применяя в связи с этим формулу Стирлинга G),
перепишем (**) в виде:
(***)
С учетом (*) представим:
т
V	>
>
т
> щ In — = N > wt In
т
л т	т	л
— Ywi =NYivAn—-NlnN.
Используя этот результат, перепишем (***) в виде:
л
Соотношение B7), являющееся одним из представлений формулы Больц-
мана A1), аналогично формуле Шеннона и действительно может рас-
рассматриваться в качестве ее «предшественницы».
В случае, когда все вероятности wt равны и, значит, wt= 1 / т (i= 1, 2, 3, ..., , m),
из B7) получаем:
S = kN In m.	(****)
Этот же результат получается из соотношения S= klnW, если учесть, что в дан-
данном случае для всех / имеем щ = N/ т, и поэтому вместо B6) следует рассматривать
W =
\т
Используя (*****), получаем
?-=\nW = \nN\-m\n[—)\ = NlnN-m — In— = NlnN-NlnN+ Nlnm.
к	\ m I	mm
10.10 Демонстрация антиэнтропийного
(информационного) процесса при формировании
письменных текстов
Ч^твлечемся от каких-либо физических систем и поговорим об об-
общих закономерностях взаимодействия энтропии и информации. Для
301

этой цели весьма удобным объектом оказывается письменный текст.
Его формирование позволяет буквально воочию видеть и даже искусст-
искусственно изменять энтропию (и следовательно, также информацию). Клод
Шеннон продемонстрировал это, работая с английскими текстами. По-
Подобными исследованиями с русскими текстами занимался математик
Р.Л. Добрушин.
В работе Р.Л. Добрушина «Математические методы в лингвистике»
A961) дан энтропийно-информационный анализ текста, построенно-
построенного с использованием 32 букв русского алфавита (буквы «е» и «ё», а
также «ь» и «ъ» не различаются, зато учитывается в качестве еще од-
одной буквы пробел между словами). Представим себе урну с тридцатью
двумя карточками-буквами. Извлекая наугад из урны всякий раз ка-
какую-то карточку (с последующим возвращением ее в урну) и записы-
записывая соответствующую букву, Добрушин получил, в частности, вот та-
такой текст:
Текст № 1
СУХЕРРОБЬДЩ ЯЫХВЩИЮАЙЖТЛФВНЗАГФОЕНВШТЦР
ПХГБКУЧТЖЮРЯПЧЬКЙХРЫС
Каждая буква здесь (включая пробел) появляется с одной и той же ве-
вероятностью, равной 1 / 32. Согласно формуле Хартли, энтропия (сте-
(степень неопределенности) буквы равна Нх = log2 32 = 5 бит. Так как веро-
вероятности появления всех букв в данном опыте равны, то энтропия Щ
есть максимальная энтропия буквы; она соответствует наибольшему бес-
беспорядку в системе «текст на основе русского алфавита». Понятно, что
такой «текст» ни в какой мере не похож на обычный текст, который
используется на практике. Его даже озвучить невозможно, не говоря
уже о явной бессмысленности написанного.
Теперь предположим, что учтены вероятности появления различных
букв в русскоязычном тексте — эти вероятности даны в F) в § 8.5. В
этом случае в опыте с урной пришлось бы использовать не 32, а гораздо
больше карточек — с тем, чтобы выполнялись пропорции nt/ nj = pt/pj,
где щ и nj — числа карточек соответственно с /-й и у'-й буквами, —
характеризующимися вероятностями pt и pj. Вынимая наугад карточки
из этой урны и записывая извлеченные буквы, можно сформировать
текст, подобный следующему тексту, полученному Добрушиным:
Текст № 2
ЕЫНТ ЦИЯЬА ОЕРВ ОДНГ ЬУЕМЛОЛЙК ЗБЯ ЕНВТША
302

В данном случае можно было бы обойтись без урны с карточками, а
просто выбирать наугад буквы из текста какой-либо русской книги,
например, сочинения Льва Толстого. Можно, раскрыв книгу наугад,
выписывать, скажем, каждую десятую букву из первой, второй, третьей
и так далее строк, считая буквой пробел, но не принимая во внимание
знаки препинания.
По сравнению с текстом № 1, текст № 2 несколько более похож на
обычный текст: исчезли ненормально длинные «слова», наблюдается
вполне правдоподобное распределение числа гласных и согласных. Но,
конечно, тут еще очень далеко до разумного текста.
Используя F) из § 8.5 и формулу Шеннона, несложно вычислить
энтропию буквы в тексте № 2: Н2 = 4,35 бит (этот результат мы приво-
приводили в §8.5). Как видим, энтропия буквы несколько снизилась — с
5 бит до 4,35 бит. Это произошло благодаря использованию информа-
информации, содержащейся в наборе вероятностей в F) из § 8.5.
Впрочем, те вероятности рассматривались в предположении, что ве-
вероятность появления в тексте той или иной буквы не зависит от того,
какая буква ей предшествовала. На практике это предположение не
выполняется. Если, например, появилась в тексте гласная, то велика
вероятность появления на следующем месте согласной. Вероятность по-
появления буквы «ь» сразу после пробела или гласной равна нулю. Как и
вероятность появления «й» сразу после согласной. Равна нулю также
вероятность появления букв «ы», «ю», «я» сразу за буквой «ч». Скорее
всего после «ч» появятся буквы «и», «е», «а», «у», но не «о». Таких при-
примеров можно привести очень много.
Чтобы учесть вероятность появления в тексте той или иной пары
букв, можно выполнить следующий опыт. Надо взять 32 урны, обозна-
обозначив каждую одной из букв алфавита (включая пробел). В каждую урну
надо поместить карточки с различными двухбуквенными сочетания-
сочетаниями, которые начинаются с буквы, обозначенной на данной урне. Чис-
Числа карточек с определенными парами букв должны быть пропорцио-
пропорциональны вероятностям появления в обычном русскоязычном тексте
соответствующих двухбуквенных сочетаний. Выбираем произвольно
любую урну, например, урну «а», и извлекаем наугад карточку из нее.
Допустим, это есть карточка «ав». Записываем вторую букву карточ-
карточки — букву «в». Затем подходим к урне «в» и извлекаем наугад кар-
карточку из нее. Допустим, это есть карточка «вр». Записываем вторую
букву карточки — букву «р». Затем подходим к урне «р» и извлекаем
наугад карточку из нее. Допустим, это есть карточка «ра». Записываем
вторую букву карточки — букву «а». Затем подходим к урне «а»... И
303

так далее. Вот у нас уже начал формироваться текст из последователь-
последовательно записанных букв: «вра...».
Рассмотренный опыт можно видоизменить, весьма существенно уп-
упростив его. Не будем заготавливать карточки-буквосочетания и не бу-
будем (что особенно приятно!) заниматься выяснением вероятностей по-
появления в обычных текстах различных буквенных пар. А просто
воспользуемся снова какой-нибудь русской книгой. Текст, учитываю-
учитывающий вероятности появления тех или иных буквенных пар, будем фор-
формировать следующим образом. Наугад извлечем из текста книги какое-
нибудь сочетание из двух букв. Допустим, это есть «вр». Записываем
«р» и начинаем скользить взглядом по строке, начав с только что вы-
выбранного сочетания «вр», — до тех пор, пока не наткнемся на букву «р».
Смотрим, какая буква в тексте книги следует сразу после этой «р». До-
Допустим, следует буква «а». Записываем «а». Продолжаем скользить взгля-
взглядом по строке (переходя при необходимости на следующую строку),
пока не обнаружим букву «а». Смотрим, какая буква в тексте следует за
этой «а». Допустим, следует буква «с». Записываем «с» и продолжаем
далее скользить по строке... И вот у нас уже начал формироваться текст
из записанных букв: «рас...»
Выполнив описанный опыт, Добрушин получил вот такой текст:
Текст № 3
УМАРОНО КАЧ ВСВАННЫЙ РОСЯ НЫХ КОВКРОВ НЕДАРЕ
Нетрудно заметить, что текст № 3 является более упорядоченным и
более легко произносимым по сравнению с текстом № 2. Здесь уже
попадаются привычные сочетания букв (например, «мар», «оно», «ван-
«ванный», «рос», «ных», «кров», «еда», «дар»). Хотя, конечно, это еще не
разумный текст.
Введение в нашу систему некоторого количества информации, пред-
представленной, в частности, правилами грамматики (причем введение не
продуманное, а посредством случайного поиска, осуществляемого с
помощью урн или текста книги), приводит к дополнительному умень-
уменьшению энтропии буквы. Как показали исследования с использованием
компьютера, теперь энтропия буквы равна Н3 = 3,52 бит, что почти на
целый бит ниже энтропии буквы в тексте № 2.
Можно пойти еще дальше и счесть, что в нормальном тексте вероят-
вероятность появления каждой буквы зависит не только от предыдущей бук-
буквы, но и от сочетания двух предыдущих буке. Соответствующий опыт
потребовал бы использования 32 х 32 = 1024 урн, каждая из которых
304

должна быть обозначена каким-нибудь двухбуквенным сочетанием и
должна содержать в соответствующих количествах всевозможные трех-
трехбуквенные сочетания, начинающиеся с данной пары букв. Такой опыт
реализовать безумно хлопотно. Поэтому Добрушин воспользовался тек-
текстом, взятым из некоторой русской книги. Предоставим читателю са-
самому сообразить, как надлежит работать с текстом книги в данном слу-
случае, и ограничимся тем, что просто приведем один из примеров
сформированного Добрушиным текста:
Текст № 4
ПОКАК ПОТ ДУРНОСКАКА НАКОНЕПНО ЗНЕ СТВОЛОВИЛ
СЕ ТВОЙ ОБНИЛЬ
Обратим внимание на то, что текст стал еще более походить на обыч-
обычный текст. Тут даже появились известные слова («пот» и «твой»). В
получившихся непонятных «словах» можно разглядеть такие извест-
известные слова, как «пока», «нос», «носка», «кон», «ствол», «ловил». Как
показали машинные расчеты, энтропия буквы в данном случае равна
#4 = 3,01 бит.
Еще более упорядоченным становится текст, когда принимается во
внимание тот факт, что вероятность появления той или иной буквы
зависит также от сочетания трех предшествующих буке. Соответствую-
Соответствующий опыт предполагает извлечения из 32 х 32 х 32 = 32 768 урн карто-
карточек, содержащих различные четырехбуквенные комбинации. Значительно
более предпочтителен опыт, аналогичный описанному выше экспери-
эксперименту с русской книгой. Подобный опыт позволяет сформировать текст,
подобный следующему тексту:
Текст № 5
ВЕСЕН ВРАТЬСЯ НЕ СУХОМ И НЕПО И КОРКО
Этот текст состоит из «почти русских» слов и претендует на некото-
некоторую осмысленность. Согласно приблизительным оценкам, энтропия
буквы равна в данном случае Н5^2,5 бит.
Дальнейшее введение информации в систему приведет рано или
поздно к формированию нормального литературного текста. Оценки
показывают, что в литературном тексте энтропия буквы равна
Ялит « 1 бит.
Итак, мы продемонстрировали антиэнтропийный (иными словами,
информационный) процесс на примере постепенного формирования
305

письменного текста. Этот процесс можно воочию наблюдать; он связан
с переходами:
[Текст 1| -> [Текст 2| ->[Текст 3| ->[Текст 4| ->[Текст 5| -> Лит*
текст
Н{ ^ Н2 ^ Н3 ^ Н4 -»> Я5 -»> Ялит B8)
5 бит 4,35 бит 3,52 бит 3,01 бит 2,5 бит 1 бит
В данном процессе энтропия буквы в тексте (а значит, и энтропия всего
текста) постепенно уменьшается; степень упорядоченности текста воз-
возрастает и вместе с этим увеличивается количество информации (не-
гэнтропии), содержащейся в тексте; он постепенно приближается к
осмысленному тексту.
Обратный процесс {энтропийный процесс) можно наблюдать, рас-
рассматривая последовательность текстов в обратном порядке — от лите-
литературного текста к тексту № 1. В этом процессе энтропия буквы в тек-
тексте возрастает; растет беспорядок в тексте и соответственно уменьшается
содержащаяся в нем информация. Текст постепенно приближается к
полнейшей абракадабре в виде текста № 1, которую даже просто озву-
озвучить не представляется возможным.
Важно отметить, что все энтропии от Нх до Нлш могут быть последо-
последовательно получены из формулы Шеннона
qg24
в процессе постепенно увеличивающейся дифференциации вероятностей —
когда какие-то вероятности всё более и более возрастают, причем, ра-
32
зумеется, за счет уменьшения других вероятностей, коль скоро
Энтропия Нх получается, когдар1=р2=р3 = ... =/?з2? т- е- когда диффе-
дифференциации вероятностей вообще нет. Энтропия И2 получается, когда
вероятности ph ръ ръ, ..., р32 описываются соотношением F) из § 8.5,
учитывающего безусловную вероятность появления той или иной буквы
в тексте, т. е. вероятность безотносительно от вероятности появления
других букв. Последующие энтропии учитывают условные вероятности
появления букв; для них наборы рь ръ ръ, ..., рЪ2 становятся постепенно
все более и более дифференцированными.
306

Если в антиэнтропийном процессе энтропия системы уменьшилась от
ЛдоЧг,
/	Pi	i	Pi
то это означает, что в системе произошло накопление количества ин-
информации (негэнтропии), которое равно Н1 - Н11; оно может быть пред-
представлено формулой:
н1 -н11 = Y.P? iog2 р? -Ел1 1о§2 р\-	C0)
В частности, поскольку при переходе от текста № 1 к литературному
энтропия буквы уменьшается с 5 битов до одного, то это означает, что
произошло накопление информации в тексте, равное 4 битам в расчете
на одну букву.
Заканчивая данный параграф, коснемся вопроса о сочинении пись-
письменных текстов компьютерами. Многочисленные эксперименты пока-
показали, что компьютеры могут печатать вполне осмысленные (на наш
взгляд) тексты, в которых энтропия буквы оказывается равной двум
битам или даже менее того. Для этого надо вложить в компьютер соот-
соответствующее количество информации — снабдить его достаточным за-
запасом слов и «познакомить» с различными грамматическими правила-
правилами. «Познакомив» компьютер с правилами стихосложения, можно
получить от него нечто вроде поэтического текста. Вот одно из машин-
машинных стихотворений, опубликованное в журнале «Автоматика и телеме-
телемеханика» в 1977 году:
ДОБРЫЙ РЕЕТ ШЕЛЕСТ
ПЛАЧЕТ ПУСТОТА
СЛУШАЮТ КАЧЕЛИ
И ПОЕТ БЕДА
СТАНЬ ПОКОРНО ГОРЕ
ТОМНО ЛИШЬ ЛЕТИТ
И ПРОЗРАЧНО МОРЕ
ТАЙНО ШЕЛЕСТИТ
И БЕЖИТ ЗЕМНАЯ
НЕЗАМЕТНО ТЕНЬ
МЕДЛЕННО ЛЕСНАЯ
СЛАВИТ ВЛАЖНЫЙ ДЕНЬ.
Бесполезно обсуждать, какой «смысл» вкладывал компьютер в этот текст.
Не обладают компьютеры мышлением. Но сравнить такой текст с текстом
307

№ 5 достаточно интересно. В отличие от текста № 5 здесь значительно
больше упорядоченности и, соответственно, меньше энтропии. Отдель-
Отдельные строки машинного стихотворения мы можем осмысленно воспри-
воспринимать, хотя, конечно, можно заметить, что качели не могут слушать,
пустота не может плакать, тишь (тишина) не может летать и к тому же
томно. И непонятно, кто же славит влажный день. Впрочем, не следует
забывать об аллегориях и метафорах...
10.11 МЕЩУ АБСОЛЮТНЫМ ПОРЯДКОМ
И АБСОЛЮТНЫМ БЕСПОРЯДКОМ
На
примере письменных текстов мы наглядно продемонстрировали
два противоположных типа процессов — антиэнтропийный {инфор-
{информационный) и энтропийный. В первом случае энтропия системы умень-
уменьшается, а негэнтропия (содержащееся в системе количество информа-
информации) возрастает. Во втором случае всё происходит наоборот. Фактически
эти два типа процессов мы уже рассматривали ранее — в книге «Слу-
«Случайность, необходимость, вероятность» (см. тему 2, озаглавленную
«Порядок и беспорядок»). Антиэнтропийные процессы выступали там
под именем конструктивных процессов; они приводили к переходам
беспорядок —> порядок. Энтропийные процессы выступали под именем
деструктивных процессов; они приводили к переходам порядок —> бес-
беспорядок.
В упомянутой теме 2 из предыдущей книги параграф 2.2 имел загла-
заглавие «Абсолютный беспорядок и абсолютный порядок — две нелепые
крайности». Нелепость воображаемого мира абсолютного беспорядка
аргументировалась тем, что в таком мире должны были бы отсутство-
отсутствовать какие-либо причинно-следственные связи, так что всё должно было
бы «выглядеть» как мгновенная сиюминутная данность, не обусловлен-
обусловленная прошлым и не влияющая на будущее (что эквивалентно исчезнове-
исчезновению самого понятия времени). Нелепость воображаемого мира абсо-
абсолютного порядка, на первый взгляд, не столь очевидна. Жесткая
предопределенность и абсолютная упорядоченность может многими
восприниматься позитивно несмотря на то, что это исключает полнос-
полностью какое-либо развитие. Убедительное свидетельство нелепости мира
абсолютного порядка появляется после того, как устанавливаются па-
параллели между беспорядком и асимметрией, а также между порядком и
308

симметрией (см. § 4.5 в книге «Случайность, необходимость, вероят-
вероятность»). Абсолютно упорядоченный мир оказывается абсолютно сим-
симметричным миром, т. е. миром, где все сохраняется при любых преобра-
преобразованиях, в частности, геометрических — отражениях в зеркале,
поворотах, переносах. Очевидно, что в таком мире принципиально невоз-
невозможно существование каких-либо конкретных объектов; ведь требование
полной симметрии (симметрии относительно любых преобразований)
могло бы выполняться разве лишь для абсолютно однородной «каши»,
заполняющей все пространство. Понятно, что ни о каком развитии, ни
о какой эволюции не может быть и речи как в абсолютно беспорядоч-
беспорядочном, так и в абсолютно упорядоченном мире.
Возвращаясь снова к антиэнтропийному процессу формирования
письменных текстов, подумаем над тем, к чему в пределе при Н^О
должен приводить этот процесс. Мы наблюдали, как по мере уменьше-
уменьшения энтропии буквы текст становился все более осмысленным, и зна-
знаем, что при Н^\ бит на букву реализуется текст, соответствующий обыч-
обычному литературному тексту. Понятно, что продвижение от текста № 1 к
литературному тексту рассматривается как некий позитивный процесс,
к которому относятся эпитеты «упорядочивающийся», «конструктив-
«конструктивный», «информационный». Давайте же доведем этот позитивный про-
процесс до логического завершения, продолжая накапливать информацию и
упорядоченность или, иными словами, продолжая уменьшать степень
беспорядка и неопределенности (т. е. энтропию).
При некотором уменьшении Н ниже одного бита на букву мы перей-
перейдем от литературных текстов к текстам специализированным, понятным
лишь для соответствующих специалистов. Возрастание степени диффе-
дифференциации вероятностей букв в этих текстах связано с увеличением час-
частоты применения каких-то определенных слов и словосочетаний, сло-
словесных штампов. При этом уменьшается степень вариативности языка
за счет снижения степени его образности и эмоциональности. Текст
становится более информационным, более строгим, более упорядочен-
упорядоченным. И в то же время (правильнее сказать: по той же причине) он
становится более непонятным для непосвященных (иначе говоря, не-
недостаточно информированных) потребителей этого текста.
Продолжая антиэнтропийный процесс дальше, мы, в конечном сче-
счете, придем к ситуации, отвечающей предельно большой дифференциации
вероятностей букв — когда одна из букв (например, буква А) имеет ве-
вероятность 1, а все остальные буквы имеют нулевую вероятность. Оче-
Очевидно, это как раз и будет предельная ситуация абсолютного порядка,
309

при которой энтропия обращается в нуль. Согласно формуле Шеннона,
имеем в данном случае:
32	,
Я = 1. log 1 + X)° 'log2 77 = 1 • 0 + 310 = 0.
Вот мы и убедились (теперь уже на «языке» теории информации), что
абсолютный порядок (когда Н=0) выглядит как нелепость. Процесс
постепенного упорядочивания письменного текста привел нас в преде-
пределе к тексту:
Текст № 6
ААААААААААААААААААААААААААААААААААААААААА...
Итак, в предельном случае полного беспорядка мы имели текст № 1.
И вот, потратив немало усилий на то, чтобы все более и более упорядо-
упорядочить текст, мы пришли в предельном случае полного порядка к тек-
тексту № 6. Плохо, когда энтропии очень много, и плохо, когда ее очень мало.
Мы убедились в этом на примере письменных текстов. Но данный вы-
вывод справедлив и в общем случае — для систем любой природы. Чрез-
Чрезмерное увеличение энтропии (чрезмерное увеличение беспорядка в си-
системе) приближает нас к миру хаоса — абсолютно энтропийному миру,
характеризующемуся отсутствием причинно-следственных связей. Чрез-
Чрезмерное увеличение негэнтропии (чрезмерное увеличение порядка в си-
системе) приближает нас к абсолютно упорядоченному миру, который
можно назвать абсолютно антиэнтропийным миром. В нем полностью
отсутствует какое-либо разнообразие, какой-либо выбор.
Реальный мир, окружающий нас, — это мир, где диалектически со-
сочетаются порядок и беспорядок, мир систем, характеризующихся нали-
наличием как негэнтропии, так и энтропии. Негэнтропия обеспечивает опре-
определенную стабильность системы, ее устойчивость при взаимодействиях
с окружающей средой. Энтропия обеспечивает динамичность системы,
возможность ее развития, адаптации к непредсказуемо изменяющимся
условиям. Об этом надо напоминать любителям чрезмерного упорядо-
упорядочивания, чрезмерной унификации.
В реальном мире совершаются как антиэнтропийные, так и энтро-
энтропийные процессы. Это хорошо наблюдается в живых организмах. Ко-
Конечно, письменный текст и живой организм — весьма разные системы.
То, что их можно рассматривать с общих позиций (позиций энтропий-
энтропийно-информационного подхода), указывает на общезначимость такого
подхода.
310

ЗАДАНИЯ ПО ТЕМЕ 10
1. Объем Vразделен перегородкой на объемы V± и V2. В объеме ^находится газ 1
при температуре 7" и давлении Р. В объеме V2 находится газ 2 при температуре Т
и давлении Р. Перегородку убирают, и газы 1 и 2 смешиваются. Используя соот-
соотношение A), найдите увеличение энтропии системы из двух газов, происходя-
происходящее в результате их смешивания.
Р
Ответ: AS =?
' V М	* 2
2.	Подсчитайте количество макросостояний, их статистические веса и вероятности
для системы из восьми частиц, каждая из которых с равной вероятностью может
находиться либо в состоянии 1 либо в состоянии 2.
Указание. Макросостояния системы нумеруем по числу / частиц, находящихся в
состоянии 1.
Ответ: Система имеет 9 макросостояний, поскольку / = 0,1, 2, ..., 8. Статистичес-
Статистические веса макросостояний равны, соответственно, 1, 8, 28, 56, 70, 56, 28, 8, 1.
Вероятности макросостояний: 1/256, 1/32, 7/64, 7/32, 35/128, 7/32, 7/64,
1/32, 1/256.
3.	Подсчитайте, чему равна энтропия системы, рассмотренной в предыдущем зада-
задании, для /-го макросостояния в случаях: а) /= 0, б) /= 2, в) /= 4.
Ответы: а) 0, б) 1,1 • 103 кал/К, в) 1,4 • 103кал/К.
4.	Воспользовавшись каким-либо литературным текстом, сформируйте собственный
текст № 2, состоящий в общей сложности из 50 букв.
5.	Воспользовавшись каким-либо литературным текстом, сформируйте собственный
текст № 3, состоящий в общей сложности из 50 букв.
311

ТЕМА 11
ЭНТРОПИЯ И ЖИЗНЬ
Средство, при помощи которого организм
поддерживает себя постоянно на достаточно
высоком уровне упорядоченности (на доста-
достаточно низком уровне энтропии), в действи-
действительности состоит в непрерывном извлече-
извлечении упорядоченности из окружающей среды.
Эрвин Шрёдингер
11.1 Краткий экскурс в биологию,
посвященный метаболизму
ЛХивой организм — открытая (незамкнутая, неизолированная) сис-
система, которая в течение всей жизни обменивается с окружающей средой,
во-первых, веществом и, во-вторых, энергией. Этот обмен называют ме-
метаболизмом и рассматривают как основу жизнедеятельности организма,
как главную отличительную особенность живого.
Одна из главных сторон метаболизма — питание организма, которое
расширительно трактуется как извлечение организмом из окружающей
среды как вещества (в частности, углерода), так и энергии. Различают
312

два основных вида питания — аетотрофное (его называют фотосинте-
фотосинтезом) и гетеротрофное. Соответственно подразделяют организмы на две
группы — аетотрофы и гетеротрофы.
Автотрофы добывают углерод, поглощая содержащийся в атмосфере
диоксид углерода (углекислый газ), а гетеротрофы добывают углерод,
поглощая различные органические соединения, содержащиеся в авто-
трофах и других гетеротрофах. Для обеспечения себя энергией автотро-
автотрофы используют световую энергию солнечного излучения, а гетеротро-
гетеротрофы — химическую энергию, т. е. энергию, накопленную в химических
связях поглощенных гетеротрофами органических соединений. К авто-
трофам относятся растения и некоторые бактерии. К гетеротрофам от-
относятся все животные и все грибы, а также большинство бактерий.
Итак, организмы-автотрофы забирают из среды только неорганичес-
неорганические вещества (в частности, диоксид углерода и воду) и синтезируют из
этих веществ органические соединения (прежде всего глюкозу, из кото-
которой затем формируются цепочки полисахаридов — крахмала, гликогена,
целлюлозы). Забирая из среды световую энергию, автотрофы использу-
используют ее для синтеза органических соединений, и тем самым превращают
световую энергию в химическую энергию, «упаковывая» последнюю в
химических связях синтезируемых соединений.
В отличие от автотрофов, гетеротрофы не синтезируют органических
соединений из неорганических веществ, а используют соединения, син-
синтезированные другими организмами — автотрофами или другими гете-
гетеротрофами. Прежде, чем синтезировать собственные белки, углеводы,
липиды, гетеротрофы расщепляют соединения, синтезированные дру-
другими организмами. За счет освобождающейся при расщеплении энер-
энергии гетеротрофы и осуществляют собственный синтез. Если автотрофы
превращают световую энергию в энергию химических связей, то гете-
гетеротрофы превращают энергию одних химических связей в энергию других
химических связей.
Метаболизм реализуется в виде большой совокупности процессов.
Все эти процессы разделяют на две группы. В одну группу относят про-
процессы анаболизма {ассимиляции) — когда в живых организмах синтези-
синтезируются сложные органические соединения из достаточно простых мо-
молекул. Примеры анаболизма: фотосинтез (из молекул воды и диоксида
углерода синтезируются органические соединения — углеводы) и био-
биосинтез белка (из молекул аминокислот «собираются» цепочки молекул бел-
белков). В другую группу относят процессы катаболизма {диссимиляции) —
когда в организме сложные органические соединения расщепляются на
более простые молекулы. Пример катаболизма: процессы дыхания. Про-
Происходящее в организмах-гетеротрофах расщепление поглощенных ими
313

органических соединений также является катаболизмом. Процессы ана-
анаболизма нуждаются в получении энергии извне; они превращают ее в
энергию химических связей синтезируемых соединений, В процессах
катаболизма происходит высвобождение химической энергии расщепля-
расщепляемых соединений.
11.2 Метаболизм как обмен энтропией
(негэнтропией) организма с окружающей средой
У1\И1
1вые организмы — это обладающие низкой энтропией весьма
упорядоченные системы. Упорядоченность тем больше, чем выше уро-
уровень их организации. Человек, например, — в значительной мере более
упорядоченная система, чем, скажем, червь или, тем более, амеба.
Смерть и последующее разложение организма следует рассматривать
как его постепенный переход в состояние термодинамического равнове-
равновесия. Но пока организм живет, он пребывает в неравновесном состоянии
при достаточно низкой энтропии, поддерживая это состояние благодаря
метаболизму. Как отмечал в своей книге «Что такое жизнь с точки зрения
физика» выдающийся австрийский физик Эрвин Шрёдингер A887-1961),
«живой организм питается отрицательной энтропией, чтобы тем самым
компенсировать увеличение энтропии, производимое им в процессе жиз-
жизни, и таким образом поддерживать себя на постоянном и достаточно низ-
низком уровне энтропии». Можно сказать, что живой организм — это откры-
открытая неравновесная система, непрерывно черпающая порядок (негэнтропию)
из окружающей среды. Иными словами, эта открытая неравновесная систе-
система благодаря метаболизму постоянно освобождается от энтропии, кото-
которую она столь же постоянно производит всю свою жизнь.
Таким образом, метаболизм представляет собой не просто обмен орга-
организма со средой энергией и веществом; благодаря метаболизму орга-
организм получает от среды негэнтропию или, иными словами, передает в
среду энтропию.
В определенном смысле, борьба за существование — это борьба за
негэнтропию. Степень успешности борьбы определяется, в частности,
тем, насколько эффективно организм противодействует различным разу-
порядочивающим факторам, в том числе факторам, вызывающим забо-
заболевания. Отметим в этой связи способность живого организма адаптиро-
адаптироваться к изменениям внешней среды, оперативно и гибко реагировать
на случайные изменения. Эта способность тем выше, чем выше уро-
уровень организации того или иного живого организма.
314

Автотрофы получают негэнтропию, поглощая энергию солнечного
света; гетеротрофы извлекают негэнтропию из живых организмов, в том
числе из организмов-автотрофов. И всегда пища, потребляемая орга-
организмом, имеет более низкую энтропию, чем отходы данного организма.
Первоисточником негэнтропии для живых организмов является, в
конечном счете, солнечный сеет. Так что Солнце с полным основанием
следует рассматривать как первоисточник информации. Воображение
рисует глобальный канал передачи информации (канал связи), где от-
отправителем является Солнце, а адресатом — все живые организмы на
Земле. По меткому выражению Е.А. Седова, «не люди придумали ин-
информацию; информацией их снабжает природа, а человек изобрел только
способы получения информации и ее обработки». Добавим сюда спосо-
способы передачи, хранения и практического использования информации.
11.3 Энтропийные и антиэнтропийные процессы
в живом организме
Y1так, с самой общей точки зрения, живые организмы являются
системами, в которых энтропийные процессы, вызывающие старение и
приводящие в конечном итоге к смерти, сочетаются с антиэнтропий-
антиэнтропийными процессами, противостоящими старению. В первых процессах
происходит накопление энтропии в организме, а во вторых процессах
происходит освобождение организма от энтропии.
При более детальном подходе обнаруживается сочетание в организме
энтропийных и антиэнтропийных процессов в виде сочетания непре-
непрерывно происходящих в нем процессов, соответственно, катаболизма и
анаболизма. Катаболизм — это диссимиляция, разрушение, расщепле-
расщепление. Понятно, что процессы катаболизма — это энтропийные процессы;
они сопровождаются возрастанием энтропии организма. Анаболизм —
это ассимиляция, созидание, синтез. Понятно, что процессы анаболиз-
анаболизма — это антиэнтропийные процессы; они сопровождаются уменьшени-
уменьшением энтропии организма. Пока организм живет, в нем происходят одно-
одновременно как те, так и другие процессы. Так что жизнедеятельность следует
рассматривать одновременно и как созидание, и как разрушение.
Как уже отмечалось, примером катаболизма является дыхание. На
«языке» химических формул дыхание можно проиллюстрировать с по-
помощью реакции окисления глюкозы:
С6Н12О6 + 6О2 -> 6Н2О + 6СО2.	A)
315

Противоположным процессом (процессом анаболизма) является фото-
фотосинтез. Если опустить промежуточные стадии и рассматривать лишь
начальные и конечные продукты, то реакцию фотосинтеза можно пред-
представить в следующем виде:
6Н2О + 6СО2 -> СН12О6 + 6О2.	B)
В реакции A) происходит разрушение относительно сложной молекулы
глюкозы С6Н12О6; в результате образуются простые молекулярные струк-
структуры, характеризующиеся более низкой организацией. В реакции B), на-
напротив, из простых молекул «собирается» (синтезируется) относительно
сложная молекула С6Н12О6. Повышение энтропии в процессе описывае-
описываемом реакцией A), связано не только с возрастанием степени молекуляр-
молекулярной неупорядоченности в системе, но и с понижением качества энергии
при превращении энергии химических связей молекулы С6Н12О6 в тепло-
тепловую энергию молекул Н2О и СО2. Соответственно, понижение энтропии в
реакции B) связано как с уменьшением степени молекулярной разупоря-
доченности, так и с превращением «малокачественной» тепловой энергии
молекул в «высококачественную» химическую энергию, которая оказыва-
оказывается «упакованной» в химических связях молекулы глюкозы.
Ярким примером сочетания энтропийных и антиэнтропийных про-
процессов служит пищеварительный процесс, протекающий в организме
животных (в частности, человека). Попадающие с пищей в пищевари-
пищеварительный тракт животного полимерные молекулы белков или углеводов
расщепляются, превращаясь, соответственно, в молекулы аминокислот
и глюкозные мономеры. Эти процессы расщепления являются, очевид-
очевидно, энтропийными процессами. Затем организм синтезирует из образо-
образовавшихся мономерных молекул собственные полимерные органичес-
органические соединения, что нужно отнести к антиэнтропийным процессам.
Отметим, что энтропийные процессы катаболизма и антиэнтропий-
антиэнтропийные процессы анаболизма происходят как в организме в целом, так и в
отдельных его клетках. В каждой клетке организма есть, например, ма-
маленькие образования (размером 1-10 мкм), называемые митохондрия-
митохондриями. Они выполняют обе функции — энтропийную и антиэнтропийную.
Энтропийная функция заключается в том, что в митохондриях реализу-
реализуется процесс клеточного дыхания. Химическая реакция для этого про-
процесса может быть описана уже знакомой нам формулой A). Антиэнтро-
Антиэнтропийная функция митохондрии заключается в том, что она синтезирует
так называемые молекулы ЛТФ (молекулы аденозинтрифосфорной кис-
кислоты) и при этом превращает освободившуюся в процессе дыхания теп-
тепловую энергию в энергию химических связей молекул АТФ. Именно
316

эта «упакованная» в химических связях молекул АТФ энергия и ис-
используется клеткой в процессе ее жизнедеятельности. Недаром мито-
митохондрии нередко называют «внутриклеточными энергостанциями». Ко-
Количество митохондрий в одной клетке измеряется тысячами (доходит
до 100 тысяч).
11.4 Генетический код; его универсальность
Гс
оворя об антиэнтропийных процессах внутри клеток организмов,
нельзя не коснуться хотя бы вкратце биосинтеза белка — процесса
синтезирования молекул-цепочек белка из молекул аминокислот. Этот
антиэнтропийный процесс совершается на вкрапленных в большом
количестве в цитоплазму каждой клетки весьма маленьких (всего
20 нм = 2 • 10~5 мм в поперечнике) образованиях, называемых рибосо-
рибосомами. Количество рибосом в клетке доходит до 100 тысяч. Каждая ри-
рибосома «собирает» белковую молекулу-цепочку, образующую длинную
последовательность молекул аминокислот. Число «звеньев» белковой
цепочки может превышать тысячу, но все они имеют всего 20 разно-
разновидностей B0 типов аминокислот), чередующихся по длине белковой
цепочки определенным образом.
Процесс «сборки» белковой цепочки управляется соответствующей
молекулой-цепочкой РНК (молекулой рибонуклеиновой кислоты). Мо-
Молекула РНК дублирует всю наследственною информацию, «записанную»
в двойной спирали молекулы ДНК (молекулы дезоксирибонуклеиновой
кислоты), находящейся в ядре клетки. Заметим, что каждая молекула
ДНК — это основа соответствующей хромосомы. Непосредственно уп-
управлять «сборкой» белковых цепочек молекулы ДНК не могут, так как
не выходят за пределы ядра клетки. Они «поручают» управление моле-
молекулам РНК. «Прибыв на место», т. е. приблизившись к какой-то рибо-
рибосоме, молекула РНК начинает подобно некой ленте протягиваться сквозь
рибосому. По мере того, как эта «лента» протягивается, рибосома «счи-
«считывает» содержащуюся в молекуле РНК информацию (полученную от
молекулы ДНК) и, руководствуясь ею, постепенно «собирает» соответ-
соответствующую белковую цепочку из находящихся вокруг молекул амино-
аминокислот. Эта «сборка» напоминает процесс нанизывания бусинок на нить;
бусинками здесь служат молекулы аминокислот.
Мы имеем здесь дело со своеобразным каналом связи, где отправителем
является ядро клетки, а адресатом — одна из великого множества риб-
рибосом, находящихся в клетке (правильнее говорить о множестве каналов
317

связи). Обращаясь к схеме канала связи, изображенной на рис. 1 в таб-
таблице 26, заметим, что сообщению на входе \|/ соответствует в данном слу-
случае наследственная информация, записанная в молекуле ДНК. Каждая из
двух цепочек-спиралей молекулы ДНК содержит последовательность
«звеньев», называемых нуклеотидами. Они различаются молекулами т. н.
азотистых оснований. В молекуле ДНК чередуются вдоль каждой из
спиралей в некотором определенном порядке четыре типа азотистых
оснований; они имеют названия: Ц — цитозин, Г — гуанин, А — аденин,
Т — тимин. Всего в одной молекуле ДНК (и значит, в одной хромосо-
хромосоме) насчитывается свыше десяти тысяч нуклеотидов. Значит, используя
четыре различных нуклеотида, можно «записать» на одной хромосоме
количество информации не менее log2 410000 = 20 000 бит. Заметим, что
число хромосом в клеточном ядре может равняться нескольким десят-
десяткам; например, у человека в каждой половой клетке {гамете) имеются
23 хромосомы, а в каждой соматической (неполовой) клетке — 46 хро-
хромосом. Заметим также, что отдельные участки хромосомы (и следова-
следовательно, молекулы ДНК), «ответственные» за те или иные наследствен-
наследственные признаки, называют генами. Каждая хромосома содержит несколько
сотен генов.
Но вернемся к схеме канала связи на рис. 1 в таблице 26. Сигнал на
входе Ч* содержится в молекуле РНК, которой предстоит отправиться от
ядра клетки к рибосоме-адресату — такова в данном случае линия связи.
Молекула-цепочка РНК точно копирует порядок чередования четырех
типов нуклеотидов в одной из спиралей молекулы ДНК; только везде
«звено» с азотистым основанием Т (тимином) заменяется в молекуле
РНК «звеном» с другим азотистым основанием — урацилом (У). Так что
сигнал *Р представляет собой некоторую последовательность четырех
элементарных сигналов (Ц, Г, А, У).
Наш канал связи может считаться идеальным, т. е. не подвергаю-
подвергающимся действию случайных помех. Адресат-рибосома принимает сиг-
сигнал на выходе Q, тождественный сигналу XF, и должна, приступая к «сбор-
«сборке» белковой цепочки из молекул аминокислот, выполнять декодирование
сигнала Q в сообщение на выходе со, представляющее собой последова-
последовательность аминокислот двадцати типов. Таким образом, выполняя де-
декодирование выходного сигнала, требуется перевести информацию, за-
закодированную четырьмя элементарными сигналами (Ц, Г, А, У), в
информацию, закодированную двадцатью элементарными сигналами
(двадцатью типами аминокислот).
Как же природа решила эту проблему? Как она реализовала переход
от четырехбуквенного алфавита РНК (и ДНК) к двадцатибуквенному
318

алфавиту белка? Ответ на этот вопрос был найден в 1961-1963 годах груп-
группой биохимиков, возглавляемой американским биохимиком Маршаллом
Ниренбергом (род. 1927). Оказывается, природа «придумала» генетический
код, в котором «буквы» алфавита белка (т. е. аминокислоты) кодируются
тройками (триплетами), составленными из «букв» алфавита РНК. Из
четырех «букв» (Ц, Г, А, У) можно образовать 4 х 4 х 4 = 64 триплета.
Этого с избытком хватает для кодирования двадцати аминокислот. Бо-
Более того, почти все аминокислоты кодируются не одним, а нескольки-
несколькими триплетами (от двух до шести триплетов на одну аминокислоту).
При этом три триплета используются в качестве «знаков препинания»,
показывающих, когда начинается и когда заканчивается последователь-
последовательность триплетов, кодирующих информацию, хранящуюся в данном гене.
Посмотрите, как выглядит Таблица генетического кода. В таблице в
левом столбце даны все двадцать аминокислот (их названия и сокра-
сокращенные обозначения). В правой стороне таблицы даны триплеты нук-
леотидов, кодирующие соответствующую аминокислоту. Ученые назы-
называют эти триплеты кодонами (от глагола «кодировать»).
Таблица генетического кода
Аминокислота
Алании
Аргинин
Аспарагин
Аспарагиновая
кислота
Валин
Гистидин
Глицин
Глутамин
Глутаминовая кислота
Изолейцин
Лейцин
Лизин
Метионин
Пролин
Серии
Тирозин
Треонин
Триптофан
Фенил аланин
Циестеин
Знаки препинания
ала
арг
асн
асп
вал
гис
гли
глн
глу
иле
лей
лиз
мет
про
сер
тир
тре
трп
фен
цис
ГЦУ
ЦГУ
ААУ
ГАУ
ГУУ
ЦАУ
ГГУ
АУУ
ЦУУ
ццу
УЦУ
УАУ
АЦУ
УУУ
УГУ
Кодирующие триплеты —
гцц
цгц
АЦЦ
ГАЦ
ГУЦ
ЦАЦ
ГГЦ
АУЦ
ЦУЦ
ЦЦЦ
УЦЦ
УАЦ
АЦЦ
УУЦ
УГЦ
ГЦА
ЦГА
ГУА
ГГА
ЦАА
ГАА
АУА
ЦУА
ААА
ЦЦА
УЦА
АЦА
УГА
ГЦГ
ЦГГ
ГУГ
ГГГ
ЦАГ
ГАГ
ЦУГ
ААГ
АУГ
ЦЦГ
УЦГ
АЦГ
УГГ
УАГ
кодоны
АГА АГГ
УУА УУГ
АГУ АГЦ
УАА
319

Совсем нетрудно научиться пользоваться данной таблицей. Допустим, цепочка
РНК представлена вот такой последовательностью десяти кодов:
гцц
ГАА
УУЦ
АЦА
АУА
ГАГ
ААЦ
ГУЦ
УЦУ
ААГ
Первым идет кодон ГЦЦ. Смотрим в таблицу. Видим, что этим кодоном коди-
кодируется аминокислота аланин. Записываем: «ала». Затем идет следующий кодон:
ГАА. Тут надо заметить, что кодоны следуют по цепочке друг за другом, не пере-
крываясь и не оставляя промежутков в один или более нуклеотидов. Согласно
таблице, кодону ГАА соответствует аминокислота «глу». И так далее. И вот перед
нами белковая цепочка из десяти аминокислот:
ала
глу
фен
тре
иле
глу
асн
вал
сер
ЛИЗ
Обратим внимание на удивительный факт. Оказывается, что у всех
организмов (у человека, собаки, бабочки, инфузории, бледной по-
поганки, моркови и т. д.) наследственная информация записана в мо-
молекулах ДНК с использованием одних и тех же четырех нуклеотидов,
а белковые молекулы собраны из одних и тех же двадцати аминокис-
аминокислот. При этом во всех случаях реализуется универсальная схема пере-
перевода четырехбуквенного алфавита нуклеиновых кислот в двадцати-
буквенный алфавит белков. Иначе говоря, приведенная выше таблица
генетического кода является одной и той же для всех организмов на
Земле. Это есть, наверное, самое убедительное доказательство един-
единства происхождения всех живых организмов. Это потрясающее обсто-
обстоятельство внутренне роднит нас, людей, со всеми, кто живет вместе с
нами на планете, — со всеми животными, растениями, грибами, бак-
бактериями.
11.5 Эволюция жизни на Земле как глобальный
АНТИЭНТРОПИЙНЫЙ ПРОЦЕСС
11.5.1. Решающая роль мутаций. Эволюция жизни на Земле представ-
представляет собой глобальный антиэнтропийный процесс. Существенно, что имен-
именно энтропия является необходимым условием существования этого про-
процесса. Ведь в основе эволюции лежат мутации — неупорядоченные
(случайные) изменения наследственных свойств организма в результате
непредвиденных перестроек и различного рода нарушений в хромосо-
хромосомах и генах. Как известно, эволюция происходит путем естественного
отбора случайно возникающих мутаций. Естественный отбор формирует
320

комбинации признаков и свойств, обеспечивающих адаптацию орга-
организмов к условиям внешней среды.
Отдельная мутация — это флуктуация. Она может быть вызвана теп-
тепловым движением молекул живого вещества, а также различными внеш-
внешними факторами (т. н. мутагенными факторами). К мутагенным факто-
факторам относятся различные излучения (например, радиоактивное) и многие
химические вещества. Допустим, произошла такая флуктуация в зиготе
(клетке, образующейся при слиянии мужской и женской гамет). В ре-
результате в зиготе появились гены-мутанты, изменяющие как-то свой-
свойства организма. По мере развития данного организма произойдут мно-
многократные деления его клеток, и в итоге ген-мутант будет продублирован
примерно 1015 раз. Если мутация наградила данный организм свойства-
свойствами, помогающими ему адаптироваться к внешним условиям, то увели-
увеличится вероятность этому организму выжить и дать потомство, которое
унаследует благоприобретенные свойства.
С точки зрения эволюции, мутации, безусловно, полезные — более
того, они необходимы. Огромное разнообразие генов у каждого вида, а
также многообразие существующих на Земле видов (около двух миллио-
миллионов) — все это есть следствие многочисленных мутаций, которые про-
происходили на протяжении многих миллионов лет (происходят и поны-
поныне). С точки же зрения отдельного организма, мутации, как правило,
вредны; в отдельных случаях даже смертельны. Как следствие длитель-
длительной эволюции, организм появляется на свет со сложным генотипом,
достаточно хорошо приспособленным к условиям обитания. Случайное
изменение генотипа скорее всего вызовет какие-то нарушения в отла-
отлаженном биологическом механизме.
Появление мутаций в половых клетках организмов способствует рас-
расширению фонда генов, которым обладает тот или иной вид, что делает
вид более многообразным и может приводить к появлению новых ви-
видов. Опасно, если у данного вида мутации будут возникать слишком
редко. В этом случае повышается вероятность того, что при каком-ни-
каком-нибудь внезапном и значительным изменении внешних условий данный
вид не сумеет приспособиться к новым условиям и погибнет. Напри-
Например, мамонты не сумели приспособиться к резкому похолоданию во
время очередного ледникового периода, оказавшегося особенно мощ-
мощным, и в итоге вымерли. Опасно также, если мутации будут возникать
слишком часто (например, вследствие радиоактивного заражения среды
обитания). В этом случае может сильно повыситься смертность многих
организмов, что тоже может привести к гибели тех или иных видов.
321

11.5.2. Многообразие видов как результат длительной эволюции. На-
Наблюдаемое ныне многообразие видов, где наряду с простейшими со-
сосуществуют и весьма сложные виды, есть результат эволюции, длив-
длившейся более трех миллиардов лет. Примерно 3,5 миллиарда лет назад
сформировались первые одноклеточные организмы, не имевшие ни
ядра, ни митохондрий, ни других внутриклеточных образований (уче-
(ученые называют их прокариотами). Первичными прокариотами были
анаэробные гетеротрофы; они питались накопившимися в древних во-
водоемах органическими соединениями, расщепляя их и затем синтези-
синтезируя из продуктов расщепления свои собственные структуры. Процесс
расщепления происходил в отсутствие свободного кислорода; это было
бескислородное {анаэробное) расщепление (такой процесс называют также
гликолизом).
Отметим, что эволюция жизни на Земле не привела к исчезновению
анаэробных гетеротрофов. Они сохранились в виде бактерий, играю-
играющих весьма важную роль в природе, превращая органику в неорганику
в результате процессов брожения и гниения. Если бы на Земле не было
анаэробных бактерий-гетеротрофов, то куда бы девались останки жи-
животных и прекратившие жизнедеятельность растения?
Возвращаясь на 3 миллиарда лет назад, отметим, что в те времена
запасы органической пищи в водоемах постепенно всё более истоща-
истощались, и анаэробным гетеротрофам грозило вымирание. Но развитие жиз-
жизни не зашло в тупик. Примерно 3 миллиарда лет назад эволюция нашла
выход: появились бактерии, способные превращать с помощью солнеч-
солнечного света неорганические вещества в органические. Эти были первич-
первичные автотрофы (бактерии-фотосинтетики). С их появлением на Земле
возник фотосинтез.
Сначала зародились бактерии-фотосинтетики, которые не выделяли
кислорода в атмосферу. Такой фотосинтез называется аноксигенным, т. е.
бескислородным. Одними из первых бактерий-фотосинтетиков были зе-
зеленые серобактерии, потреблявшие сероводород (H2S) и диоксид углеро-
углерода (СО2) из продуктов извержения многочисленных вулканов. Как и
обычный фотосинтез (с выделением кислорода) фотосинтез у серобак-
серобактерий имел две стадии (две фазы) — световую, которая протекала с
помощью солнечного света, и темновую, которая не нуждалась в свете.
В световой фазе бактерии поглощали сероводород и расщепляли его
молекулы на атомы, используя энергию света. В темновой фазе бакте-
бактерии поглощали диоксид углерода и вырабатывали глюкозу и воду. При
этом некоторые продукты, появившиеся в световой фазе, поглощались
в темновой фазе. Не рассматривая по отдельности реакции, протекав-
322

шие в световой и в темновой фазах, приведем реакцию, выражающую
суммарный результат:
12H2S
6СО2
Поглощается Поглощается
бактериями бактериями
12S
Выделяется
бактериями
С6Н12О6 + 6Н2О
t
Выделяется
бактериями
в световой фазе в темновой фазе в световой фазе в темновой фазе
C)
Аноксигенный фотосинтез
Как бы ни старались вулканы, однако рано или поздно запасы серо-
сероводорода на Земле должны были истощиться. Назревал новый кризис в
развитии жизни. Он был преодолен благодаря появлению примерно
2,3 миллиарда лет назад синезеленых водорослей. Название «водоросли»
не должно вводить в заблуждение, так как фактически это не растения,
а бактерии (т.н. цианобактерии). В отличие от серобактерий синезеле-
ные водоросли «научились» расщеплять молекулы воды (что, кстати,
значительно труднее, чем расщеплять молекулы сероводорода). При
фотосинтезе синезеленых водорослей в атмосферу стал выделяться кис-
кислород. Такой фотосинтез называют оксигенным, т. е. кислородным. Все
зеленые растения участвуют именно в оксигенном фотосинтезе. Сум-
Суммируя реагенты, участвующие в световой и темновой фазах оксигенно-
го фотосинтеза, получаем следующее уравнение (оно работает при фо-
фотосинтезе не только синезеленых водорослей, но и вообще всех зеленых
растений):
12Н2О
6СО2
6О2 + С6Н12О6 + 6Н2О
t
Поглощается Поглощается
бактериями бактериями
Выделяется
бактериями
Выделяется
бактериями
в световой фазе в темновой фазе в световой фазе в темновой фазе
D)
Оксигенный фотосинтез
Фактически реакция D) нам уже знакома (см. B)).
После того, как синезеленые водоросли начали подпитывать зем-
земную атмосферу кислородом, настал черед возникновения прокариот,
323

способных поглощать кислород. Такие прокариоты появились примерно
2 миллиарда лет назад; это были аэробные бактерии.
Таким образом, в результате эволюции прокариот на Земле возникли
несколько разных типов одноклеточных организмов. Наряду с самыми
первыми прокариотами (анаэробными гетеротрофами) существовали бак-
бактерии-фотосинтетики (в том числе синезеленые водоросли) и аэробные
бактерии. И тут эволюция сделала два важных хода.
Первый ход заключался в том, что первичные прокариоты и аэроб-
аэробные бактерии вступили в симбиоз. Таким термином принято называть
взаимополезное «сожительство». Аэробные бактерии внедрились внутрь
первичных прокариот, поскольку жизнь внутри другой клетки имеет свои
преимущества с точки зрения обеспечения питанием. Первичные про-
прокариоты при этом тоже выиграли — они могли пользоваться энергией,
запасенной в химических связях молекул аэробных бактерий. Со вре-
временем аэробные бактерии внутри клетки превратились в митохондрии
(«внутриклеточные энергостанции»). Симбиоз двух столь разных про-
прокариот потребовал единого управления новой (объединенной) клеткой,
поэтому начало формироваться внутриклеточное ядро — прокариоты
стали превращаться в эукариоты. Так эволюция привела к возникнове-
возникновению примерно 1,7 миллиарда лет назад одноклеточных эукариот-гете-
ротрофов. Это были далекие предки животных и грибов.
Далее эволюция сделала второй важный ход. Некоторые эукариоты-
гетеротрофы вступили в симбиоз с синезелеными водорослями. Точнее
говоря, синезеленые водоросли внедрились внутрь эукариот-гетеротро-
фов и со временем превратились в хлоропласты (органеллы раститель-
растительных клеток, в которых как раз и происходят процессы фотосинтеза). В
результате эукариоты-гетеротрофы перешли на автотрофный тип пита-
питания. Так возникли примерно 1,5 миллиарда лет назад одноклеточные эука-
риоты-автотрофы — далекие предки растений.
Схема возникновения одноклеточных эукариот с гетеротрофным
питанием и с автотрофным питанием на основе симбиоза прокариот
разного типа представлена на рис. 1 в таблице 34.
Возникнув полтора миллиарда лет назад, одноклеточные эукариоты
долгое время не формировали многоклеточных организмов. Можно
предположить, что первые многоклеточные эукариоты появились лишь
спустя 500 миллионов лет, т. е. примерно 1 миллиард лет назад. А до
того происходил процесс постепенного совершенствования эукариот-
ной клетки: приживались к новой «обстановке» аэробные бактерии и
синезеленые водоросли, превращаясь, соответственно, в митохондрии
324

Таблица 34. Эволюция жизни на Земле
Бактерии-фотосинтетики
Одноклеточные
эукариоты
Анаэробные^
гетеротрофы
(первичные
прокариоты)
Рис.1
Аэробные
бактерии
1	— Клеточное ядро;
2	— Митохондрия; 3 — Хлоропласт
Животные
Рис.2
ЭРА
ПЕРИОД
Наступают ледники. Появился человекL
о
в в
Вымирает большинство
" " ПЦ] рептилий
Образуется мел в
морских отложениях
леса отступили
| к экватору.
Вымерли многие
земноводные
Много тепла и дождей,
возникают пышные леса,
образуется уголь
Растения и животные
заселяют сушу
Образуются горы, море отступает,
сухо и жарко
325

и хлоропласты, формировалось клеточное ядро, отрабатывался меха-
механизм деления клетки.
Без сомнения, все многоклеточные эукариоты возникли в ходе эво-
эволюции из одноклеточных эукариот благодаря естественному отбору,
поскольку многоклеточностъ давала много преимуществ живому орга-
организму. Она привела к специализации клеток внутри организма и к
появлению у организма различных органов, выполняющих те или иные
функции.
Рассматривая зарождение и развитие жизни на Земле, ученые выде-
выделяют два периода — криптозой (в переводе с греческого «скрытая жизнь»)
и фанерозой («явная жизнь»). Криптозой начался более 4 миллиардов
лет назад (еще до появления первичных прокариот) и завершился
570 миллионов лет назад. Затем начался фанерозой, продолжающийся
и поныне.
Эволюция многоклеточных эукариот в криптозое происходила ис-
исключительно в водоемах. По-видимому, наблюдались различные пути
эволюционных превращений первых многоклеточных. Некоторые пе-
перешли к сидячему образу жизни и превратились в организмы типа гу-
губок. Другие ползали, перемещаясь по дну с помощью ресничек; от них
произошли плоские черви. Третьи сохранили плавающий образ жизни,
приобрели ротовое отверстие и дали начало кишечнополостным. Ника-
Никаких скелетов — ни внутренних, ни внешних — у организмов, обитав-
обитавших в морях криптозоя, не было. Скелеты появились позднее — в нача-
начале фанерозоя.
Весь фанерозой разбивают на три эры — палеозой, мезозой и кайно-
кайнозой. Эры подразделяют на периоды. Всего выделяют 12 периодов — см.
рис. 2 в таблице 34. Числа в кружочках на этом рисунке показывают,
сколько миллионов лет назад начался тот или иной период. Используя
их, легко подсчитать длительность каждого периода в миллионах лет.
На этом же рисунке можно видеть, что постепенно в ходе эволюции из
менее сложных организмов возникали более сложные.
Конечно, процесс эволюции нельзя рассматривать как простой пе-
переход от менее сложных видов и организмов к более сложным. Наибо-
Наиболее простые организмы — прокариоты (бактерии) и одноклеточные эука-
эукариоты — до сих пор существуют на Земле, равно как существуют
беспозвоночные, рыбы, земноводные и др. Строго говоря, эволюция
шла (и идет) не от простого к сложному, а от менее приспособленного к
более приспособленному, поскольку именно так действует естественный
отбор. И главным результатом такого процесса является увеличение чис-
числа видов, все большее и большее их разнообразие.
326

Тем не менее в целом можно констатировать постепенное появление
в ходе эволюции всё более и более сложных видов, так что эволюция
жизни на Земле должна рассматриваться как глобальный антиэнтропий-
антиэнтропийный процесс.
11.5.3. Почему эволюция вдет в целом в направлении постепенного услож-
усложнения видов? Мы приблизились, наконец, к самому острому вопросу.
Почему эволюция жизни на Земле идет в целом в направлении посте-
постепенного усложнения видов? Иными словами, почему, несмотря на реша-
решающую роль энтропии, эволюционный процесс оказывается в целом гло-
глобальным антиэнтропийным процессом?
Попытаемся ответить на этот вопрос. Прежде всего заметим, что ис-
исторически первыми были не сложно организованные, а простые и, бо-
более того, простейшие организмы и виды. Уже отсюда следует, что обус-
обусловленное случайными факторами (т. е. мутациями) появление новых
видов не могло обойтись без появления более сложных видов. При об-
общем возрастании разнообразия адаптированных к условиям среды видов
неизбежно случайное появление видов с более высокими уровнями орга-
организации.
Далее отметим, что случайный характер возникновения видов пре-
предопределяет не только их уникальность (невосполнимость в случае ги-
гибели), но и необратимость всего эволюционного процесса. Так, возникно-
возникновение на каких-то этапах амфибий от рыб, рептилий от амфибий,
млекопитающих от рептилий — это процессы необратимые. Обратные
переходы (от млекопитающих к рептилиям, от рептилий к амфибиям,
от амфибий к рыбам) принципиально невозможны. Вернувшись в вод-
водную среду, некоторые позвоночные (такие рептилии как ихтиозавры
или такие млекопитающие как киты) отнюдь не превращались в рыб.
Отметим, наконец, еще одно немаловажное обстоятельство. Более
высокие уровни организации обладают более значительным количеством
негэнтропии (информации), помогающей более оперативно и гибко при-
приспосабливаться к внешним условиям и тем самым повышают вероятность
выживания при тех или иных изменениях внешних условий.
Казалось бы, вполне понятно, почему эволюционный процесс ока-
оказывается в целом антиэнтропийным процессом. И тем не менее было
бы преждевременно ставить точку. Почему бы не принять точку зре-
зрения, согласно которой эволюционный процесс, являясь на начальных
этапах по необходимости антиэнтропийным, становится с течением
времени в какой-то степени сбалансированным — когда возникнове-
возникновение более сложных видов как бы уравновешивается возникновением
327

менее сложных видов? Почему бы не допустить, что если более слож-
сложные виды выживают за счет своей более высокой организации, то ме-
менее сложные виды выживают за счет более быстрого и массового раз-
размножения?
В этой связи уместно вспомнить выступление эстонского академика
Густава Наана на Всесоюзной конференции по философским вопро-
вопросам естествознания в Москве в 1959 году. «При анализе совокупности
фактов, известных науке, — говорил академик, — трудно избавиться от
подозрения, что список фундаментальных законов природы существенно
не полон, что в нем не хватает по крайней мере одного очень общего
закона. В самом деле. Мы имеем законы, ответственные, грубо говоря,
за стабильность. Это законы сохранения, прежде всего закон сохране-
сохранения энергии. Мы имеем закон, ответственный за направленность про-
процессов природы, — второй закон термодинамики. Он говорит об уни-
универсальной эволюции в направлении всё большего беспорядка. Между
тем мы наблюдаем в природе разнообразные процессы антиэнтропий-
антиэнтропийного характера — процессы возникновения сложного из более просто-
простого. Быть может, возникновение звезд, планет, галактик, происхождение
жизни и ее эволюция именно потому с трудом поддаются раскрытию,
что нам неизвестен соответствующий общий закон, и мы находимся во
власти сильно укоренившегося представления о том, что все эти явле-
явления могут получить объяснение только как достаточно редкое исключе-
исключение из общего правила».
ЗАДАНИЯ ПО ТЕМЕ 11
1. Цепочка РНК представлена следующей последовательностью кодонов:
ЦУУ
ЦЦУ
ГГА
ГЦА
АГЦ
ААА
ГАЦ
ГУУ
УУУ
ЦАГ
ЦГУ
ААУ
УГУ
УГГ
ГАА
ЦАУ
Напишите соответствующую последовательность аминокислот.
Ответ: лей-про-гли-ала-сер-лиз-асп-вал-фен-глн-арг-асн-цис-трп-глу-гис.
2.	Используя четыре нуклеотида (А, Г, Ц, У), составьте все возможные их пары.
Ответ: АА, ГА, ЦА, УА, АГ, ГГ, ЦГ, УГ, АЦ, ГЦ, ЦЦ, УЦ, АУ, ГУ, ЦУ, УУ.
3.	Подсчитайте, сколько различных четверок (квартетов) можно образовать, ис-
используя четыре разных нуклеотида.
Ответ: 256.
4.	Предположим, что нуклеотидный алфавит состоял бы не из четырех, а из пяти
«букв». Сколько кодирующих триплетов можно было бы составить в этом случае?
Ответ: 125.
328

5.	В целом процесс фотосинтеза — это процесс анаболизма. Однако в нем есть
составляющая, которую следует отнести к катаболизму. В чем заключается эта
составляющая?
Ответ: Эта составляющая — расщепление молекул воды, происходящее в свето-
световой фазе.
6.	Откуда берется свободный кислород при оксигенном фотосинтезе — из воды или
из диоксида углерода?
Ответ: из воды, как это хорошо видно из реакции D).
7.	Используя данные, представленные в 11.5.2, оцените, во сколько раз длитель-
длительность существования на Земле бактерий больше длительности существования на
ней; а) рыб, б) земноводных, в) пресмыкающихся, г) млекопитающих.
Ответы: а) 8, б) 9, в) 10, г) 14.
8.	Почему случайность возникновения новых видов живых организмов обусловли-
обусловливает необратимость процесса видообразования (процесса эволюции)? Выскажи-
Выскажите свои соображения на этот счет.
329

ТЕМА 12
ЭВОЛЮЦИЯ РОЛИ ВЕРОЯТНОСТИ
В ЧЕЛОВЕЧЕСКОМ ОБЩЕСТВЕ
(ОТ ИГРЫ В КОСТИ
К НАУЧНО-ТЕХНИЧЕСКОЙ
РЕВОЛЮЦИИ
И ИНФОРМАЦИОННОМУ ВЗРЫВУ)
Замечательно, что наука, которая нача-
началась с рассмотрения азартных игр, обещает
стать наиболее важным объектом человечес-
человеческого знания.
Пьер Симон Лаплас
Хаскроем поэму Данте A265-1321) «Божественная комедия». В той
ее части, которая называется «Чистилище», есть такие строки (см. на-
начало песни шестой):
Когда кончается игра в три кости.
То проигравший снова их берет
И мечет их один в унылой злости...
Перед нами свидетельство того, что уже в XIV столетии была извест-
известна игра в кости. Есть основания полагать, что играть в кости люди
330

начали гораздо раньше. Ну кто бы мог тогда предположить, что эти
безобидные развлечения приведут со временем к подлинному перево-
перевороту в представлениях людей о закономерностях окружающего мира?
В современных автомобилях используются, в частности, карданные
механизмы — шарнирные механизмы, обеспечивающие вращение двух
валов под переменным углом. Прообразом карданного механизма явля-
является подвес, изобретенный в XVI столетии итальянцем Джероламо Кар-
дано A501-1576). Этот талантливый итальянец был также врачом, фи-
философом, математиком. После кончины Кардано в его бумагах была
найдена работа, озаглавленная «Книга об игре в кости». Есть основа-
основания считать, что именно с этой работы и началась теория вероятностей.
Классического определения вероятности, да и самого этого понятия в
данном труде мы не находим — там просто подсчитываются величины
ставок и шансы игроков. Но эти подсчеты фактически предвосхитили
как теорему сложения вероятностей для несовместных событий, так и
теорему умножения вероятностей для независимых событий.
Становление и первые шаги теории вероятностей как математичес-
математической науки связывают с такими видными учеными XVII столетия как
Влез Паскаль A623-1662), Пьер Ферма A601-1665), Христиан Гюйгенс
A629-1695), Якоб Бернулли A654-1705). Дальнейшее развитие теории
вероятностей происходило в XVIII-XIX столетиях благодаря трудам
многих видных математиков, среди которых следует особо отметить
выдающихся представителей французской науки Пьера Симона Лапласа
A749-1827) и Симеона Дени Пуассона A781-1840) и Петербургской ма-
математической школы Пафнутия Львовича Чебышёва A821-1894), Андрея
Андреевича Маркова A856-1922), Александра Михайловича Ляпунова
A857-1918). Во второй половине XIX-го столетия теория вероятностей
проникает в физику (благодаря работам Джеймса Клерка Максвелла
A831-1879), Людвига Больцмана A844-1906), Джозайи Уилларда Гиббса
A839-1903)), а также в биологию (благодаря не получившим должного
признания современников работам Грегора Иоганна Менделя A822-1884)).
В ХХ-м столетии весьма существенный вклад в развитие теории вероят-
вероятностей внесли российские ученые: Сергей Натанович Бернштейн A880—
1968), Александр Яковлевич Хинчин A894-1959), Андрей Николаевич Кол-
Колмогоров A903-1987), Борис Владимирович Гнеденко A912-1995).
В своем развитии теория вероятностей прошла долгий путь, на кото-
котором ей пришлось испытать весь спектр оценок — категорическое не-
неприятие, сомнения по поводу корректности получаемых результатов,
предсказания огромного успеха. Известный английский философ Джон
331

Толанд A670-1722) утверждал: «Величайшей нелепостью представляет-
представляется мне обожествление случайного, этой противоположности всякому
порядку, разуму и плану». Известный английский химик Джозеф Пристли
A733-1804) высказывался столь же категорично: «Согласно установ-
установленным законам природы ни одно событие не могло произойти иначе,
чем оно произошло или произойдет; все явления в прошедшем, насто-
настоящем и будущем в точности таковы, как задумал их Творец природы».
Выдающийся французский математик и физик Жан Лерон Д'Аламбер
A717-1783) опубликовал работу, озаглавленную «Сомнения и вопросы
относительно теории вероятностей». В одном из своих трудов A761)
Д'Аламбер прямо заявлял, что теорию вероятностей «нельзя отнести к
точным и верным исчислениям ни по принципам, ни по результатам».
А вот знаменитый Лаплас, живший в те же годы, совсем иначе оцени-
оценивал значение теории вероятностей. Вот некоторые из его высказыва-
высказываний: «Большей частью важнейшие жизненные вопросы являются на
самом деле лишь задачами из теории вероятностей... Нет науки более
достойной наших размышлений и результаты которой были бы более
полезны».
Эти пророческие слова произнесены где-то в начале XIX-го века. И
только сто лет спустя пророчество Лапласа начало сбываться. А до того
вероятность в широкой общественной практике по сути дела не применя-
применялась, серьезным отношением со стороны общественного мнения не пользо-
пользовалась, в рамках общего среднего образования не изучалась. Вспомним, что
блестящие исследования Больцмана, Гиббса, Менделя не нашли при-
признания и поддержки у их современников. И даже великий Эйнштейн,
немало сделавший в свое время для становления статистической физи-
физики (мы имеем в виду его теорию броуновского движения и квантовую
статистику, известную ныне как статистика Бозе—Эйнштейна), пытал-
пытался до конца жизни «освободить» физическую науку от вероятностей,
заявляя, что «Бог не играет в кости».
Двадцатый век награждают разными эпитетами. По нашему мнению,
наиболее правильно было бы называть его «веком вероятностей», или,
точнее говоря, «веком осознания человеческим обществом принципи-
принципиальной и исключительной важности вероятности». Причем важности
как для процесса познания человеком окружающего мира, так и для
конкретной практической деятельности людей, реализующей то, что
именуют научно-техническим прогрессом. Проще говоря, двадцатое
столетие — это столетие, в котором люди стали, наконец, по-настояще-
по-настоящему осознавать, какие широкие возможности таятся в теории вероятно-
вероятностей, в вероятностных подходах, моделях, системах. Человеческий ра-
332

зум стал, наконец, преодолевать веками складывавшийся стереотип не-
негативного отношения к случайному.
Итак, в двадцатом столетии вероятность, образно выражаясь, вышла
в жизнь, в человеческую практику. Можно считать, что этот «выход в
жизнь» в существенной мере связан с развитием исследований в трех
областях. Во-первых, отметим активно развивающуюся, начиная с пер-
первой четверти столетия, область научно-технической деятельности, на-
называемую исследованием операций, или, иначе говоря, теорию принятия
решений. Во-вторых, отметим состоявшийся в первой трети столетия
мощный прорыв физики в изучении свойств материи. Этот прорыв оз-
ознаменовался возникновением квантовой механики, от которой затем
родились квантовая электродинамика, квантовая электроника, кванто-
квантовая химия, квантовая теория твердого тела. В-третьих, отметим созда-
создание в сороковых годах первых компьютеров на электронных лампах,
последовавшее затем бурное развитие компьютерной техники, появле-
появление кибернетики и, наконец, информатики.
Работы в области исследования операций показали, что обращение к
вероятности позволяет решать многие практически важные задачи пла-
планирования, проектирования, управления в разных сферах человеческой
деятельности с учетом реальных условий, предполагающих наличие раз-
различного рода неопределенностей. Применение теории вероятностей дало
возможность моделировать случайные процессы и, в частности, про-
просчитывать системы массового обслуживания и разрабатывать игровые ме-
методы обоснования оптимальных решений. Выяснилось, что теория вероят-
вероятностей позволяет успешно использовать против случайностей сами же
случайности и находить решения в сложнейших ситуациях с помощью
метода Монте-Карло.
Уже сказанного достаточно для того, чтобы признать исключитель-
исключительную полезность вероятности для человеческой практики и найти ей
место в рамках современного общего образования. Однако ценность
вероятности этим отнюдь не исчерпывается. Идеи Максвелла, Больц-
мана, Гиббса о фундаментальной роли вероятностных закономернос-
закономерностей в физике вещества получили в первой трети ХХ-го века мощное
развитие, которое привело к созданию квантовой механики — новой
физической теории, причем теории принципиально вероятностной. В
определенном смысле все новейшее естествознание (начиная с середи-
середины ХХ-го столетия) опирается на квантовую механику или, более ши-
широко, на квантовую физику. В третьей части книги мы уделим идеям и
принципам квантовой механики достаточное внимание. А пока отме-
отметим лишь, что построенная на вероятностных принципах квантовая
333

физика оказалась теоретической основой современного учения о структу-
структуре и свойствах материи.
Не будет преувеличением сказать, что именно появление и развитие
квантовой физики привело к тому, что в середине XX-го столетия наука
превратилась в ведущий фактор развития общественного производства.
Это «превращение» принято называть научно-технической революцией
(сокращенно: НТР). Как отмечал академик Б.М. Кедров, «самая важная
особенность НТР в том, что развитие науки опережает развитие техни-
техники, как бы прокладывая путь для дальнейшего ее развития» (курсив
наш. — Автор).
Вспомним промышленную революцию XIX-го столетия, связанную
с изобретением паровой машины. В тот период техника опережала в
своем развитии науку, заставляя последнюю заниматься обоснованием
технических достижений (вспомним, что термодинамика возникла по-
поначалу как «теория паровых двигателей»). В случае же НТР мы имеем
качественно иную ситуацию — когда ведущим (движущим) фактором
научно-технического прогресса оказывается наука. Во многом это объяс-
объясняется тем, что достижения в области квантовой физики позволили не
только вычислять те или иные параметры вещества, но и создавать ве-
вещества с наперед заданными свойствами. Нелишне подчеркнуть при
этом, что все расчеты тех или иных параметров вещества проводились
на основе вероятностных закономерностей.
Отметим три выдающихся изобретения, во многом предопределив-
предопределивших НТР, — ядерный реактор A942), транзистор A948), лазер A960).
Благодаря этим трем изобретениям возникли, соответственно, ядерная
энергетика, полупроводниковая техника, лазерная техника. Существен-
Существенно, что и физика ядерного реактора, и физика транзистора, и физика
лазера являются, по большому счету, разделами квантовой физики.
Говоря об НТР, нужно особо отметить появление и весьма быстрое
развитие компьютеров:
-	в 1953-1954 годах на электронных лампах (с быстродействием до
104 операций в секунду),
-	в 1958-1960 годах на транзисторах (до 106 операций в секунду),
-	в 1965-1966 годах на полупроводниковых малых интегральных схе-
схемах (до 107 операций в секунду),
-	в 1976-1979 годах на больших интегральных схемах (до 108 опера-
операций в секунду).
-	в 1990-1992 годах на сверхбольших интегральных схемах (до
1012 операций в секунду).
334

Мы отметили здесь лишь пять первых поколений компьютеров. От-
Отметим также, что если мировой парк компьютеров в 1960 году состав-
составлял всего 5000 штук, то в 1975 году парк компьютеров вырос до
300 000 штук, а в 1992 году — превысил 100 000 000 штук.
Бурное развитие компьютерной техники во второй половине ХХ-го
столетия вывело НТР на новый уровень — привело к развитию космо-
космонавтики и кибернетики. Впрочем, дело тут не только в появлении все
более и более совершенных компьютеров. Другим решающим факто-
фактором явилось превращение теории электрической связи в теорию информа-
информации. И тут вероятность еще раз (и притом особенно громко) заявила о
себе — само понятие количества информации, как выяснилось, выража-
выражается через вероятность, а задачи кодирования, передачи и обработки
информации являются вероятностными задачами. Как тут не вспом-
вспомнить пророческие слова Лапласа, сказанные сто лет назад!
О кибернетике и информатике мы поговорим в беседе, которая за-
завершит вторую часть данной книги. А пока подчеркнем главное (если
не главнейшее) достижение человечества в конце ХХ-го столетия —
весьма и весьма многообещающий «симбиоз» в виде взаимовыгодного
тесного союза вычислительной техники и основанной на вероятности тео-
теории информации. Наблюдаемый сегодня информационный взрыв можно
рассматривать как апофеоз вероятности, которая, наконец, явила чело-
человеческому обществу свою подлинную значимость.
335

ЗАВЕРШАЮЩАЯ БЕСЕДА:
ИНФОРМАТИКА И ВЕРОЯТНОСТЬ
...Человечество вступило в пору инфор-
информационной революции и встало на путь пе-
перехода к информационному обществу. Ко-
Конечно, овладение информацией невозможно
без появления науки о ней. Информатика
играет такую же фундаментальную роль, как
те науки, которые помогли человечеству про-
проникнуть в тайны вещества и энергии. По-
Поэтому информатику по праву называют ца-
царицей наук в информационном обществе.
ДА. Поспелов, академик, Президент
Ассоциации искусственного интеллекта
Часть первая,
в которой обсуэдается весь спектр проблем,
охватываемых сегодня информатикой
Наша беседа посвящена информатике. Хотелось бы прежде
всего уточнить, что же сегодня называют информатикой. И чем она
отличается от кибернетики. В книге В.Д. Пекелиса «Кибернетика от А до
Я: Маленькая энциклопедия» (Москва: «Детская литература», 1990) о
кибернетике говорится, что это есть «наука о процессах управления в
сложных динамических системах», а об информатике говорится, что
это есть «комплексная научная и инженерная дисциплина, изучающая
все аспекты разработки, проектирования, создания, функционирова-
функционирования систем переработки информации». Короче говоря, кибернетика —
это наука об управлении в разных системах, а информатика — наука о
системах переработки информации, т. е. наука о компьютерах. Но вот я
336

заглянул в более поздний литературный источник — Большой энцик-
энциклопедический словарь, изданный в 1997 году в научном издательстве
«Большая российская энциклопедия». Там написано, что информати-
информатика — это «отрасль науки, изучающая структуру и общие свойства инфор-
информации, а также вопросы, связанные с ее сбором, хранением, поиском,
переработкой, преобразованием, распространением и использованием
в различных сферах деятельности». Кибернетику же Большой энцикло-
энциклопедический словарь определяет как «науку об управлении, связи и пе-
переработке информации». Там же отмечается, что «теоретическое ядро
кибернетики составляют теория информации, теория алгоритмов, тео-
теория автоматов, исследование операций, теория оптимального управле-
управления, теория распознавания образов». Кроме того, в Словаре говорится,
что «кибернетика разрабатывает общие принципы создания систем уп-
управления и систем для автоматизации умственного труда».
Пвтор. Что же Вам тут непонятно?
'Чинигнмль. Многое. Почему, например, информатика в Словаре име-
именуется отраслью науки? Какой именно науки? Если информатика изу-
изучает структуру и общие свойства информации, а также занимается ее
переработкой, то почему она «отдает» кибернетике теорию информа-
информации? Почему в одной книге кибернетика занимается только процесса-
процессами управления, а в другой — также и переработкой информации? В чем
отличие переработки информации в кибернетике от переработки ин-
информации в информатике? Наконец, я заглянул в Энциклопедию
для детей издательства «Аванта+» (том 11: Математика; издан в 1998 году).
Там я прочитал: «Совокупность наук об информационных процессах
называют информатикой. Одна из них — наука об измерении и переда-
передаче информации — называется теорией информации». И теперь я уже не
в состоянии разобраться, где работает информатика и где работает ки-
кибернетика.
Пвтор. Итак, нам с Вами следует прежде всего разобраться с поняти-
понятиями «информатика» и «кибернетика». Как Вы поняли, четкого разграни-
разграничения этих понятий в настоящее время нет. Однако вполне просматри-
просматривается точка зрения, которой сегодня придерживается большинство
ученых. Прежде чем ее сформулировать, вспомним, когда возникли
понятия «кибернетика» и «информатика» и какой смысл вкладывался в
эти понятия первоначально.
*Чи(*иипель. Я знаю, что сначала возникло понятие «кибернетика». В
первой половине XIX-го столетия французский физик Ампер предло-
предложил назвать так науку управления людьми. Он исходил из греческого
слова «кибернетикос», что означает «искусный в управлении». Термин
337

«кибернетика» возродил в середине ХХ-го столетия Норберт Винер, на-
написавший книгу под названием «Кибернетика, или управление и связь в
животном и машине»; книга была издана в 1948 году. А что касается
термина «информатика», то, насколько мне известно, он стал исполь-
использоваться в научной литературе позднее — где-то в 60-х годах прошлого
столетия.
Пвтор. Действительно, термин «информатика» впервые вошел в науч-
научный обиход в 60-х годах. Он родился во Франции и может рассматривать-
рассматриваться как соединение двух слов: information («информация») и automatique
(«автоматика»). Таким образом, «информатика» означала автоматичес-
автоматическую обработку информации, или, более широко, применение средств
вычислительной техники для работы с информацией. В знаменитой
Французской энциклопедии Ларусса издания 1985-1987 гг. информа-
информатика определяется как «совокупность дисциплин, способствующих ав-
автоматической и рациональной обработке информации». В США и Ве-
Великобритании аналогичное научно-техническое направление получило
название computer science, что переводится как наука о вычислительной
технике, или, дословно, вычислительная наука.
g4tuftfufie*b. Итак, информатика родилась как автоматическая обра-
обработка информации или, иными словами, как наука о вычислительной
технике. А как складывались (и как в конце концов сложились) взаи-
взаимоотношения этой новоявленной науки с кибернетикой?
Пвтор. Очевидно, что корни информатики лежат в кибернетике. В
известном смысле информатика выросла из кибернетики. Некоторые
исследователи придерживаются той точки зрения, что «отпочковавшая-
«отпочковавшаяся» от кибернетики информатика превратилась в науку, которая, хотя и
взаимодействует тесным образом с кибернетикой, но тем не менее су-
существует самостоятельно. Согласно такой точке зрения, кибернетика
рассматривается как теоретическая наука о переработке информации в
целях управления системами, а информатика — прикладная дисциплина,
изучающая использование компьютеров для переработки информации.
Короче говоря, сама информация изучается кибернетикой, а перераба-
перерабатывается информация информатикой. Своеобразное «разделение труда».
ttcuSUuSie**. Достаточно четкое «разделение труда», по-моему.
Пвтор. Однако такая точка зрения все больше и больше уступает
место другой точке зрения, согласно которой информатика — это не
«ответвление» кибернетики, решающее свои собственные задачи, а су-
существенно более общий Феномен. Это действительно совокупность наук
об информационных процессах. И в эту «совокупность наук» входят, в
338

частности, кибернетика, теоретические аспекты вычислительной тех-
техники, программное обеспечение компьютеров. Принципиально, что
научные и научно-технические направления, объединяемые ныне ин-
информатикой, с одной стороны, не растворились в ней, а с другой сторо-
стороны, не оказались автономными, сугубо самостоятельными образовани-
образованиями под общим названием. Как составляющие части общей науки —
информатики — все эти направления теснейшим образом взаимодей-
взаимодействуют друг с другом и открывают в таком взаимодействии новые воз-
возможности для своего собственного дальнейшего развития. Именно это
взаимодействие является главной чертой, определяющей современный
облик информатики.
'Чиниикель. И как же структурно выглядит этот современный облик
информатики?
Пвтор. Представить достаточно полно структуру информатики невоз-
невозможно в одной беседе. Относительно полно структура информатики как
«совокупности наук об информационных процессах» представлена в книге
«Информатика: энциклопедический словарь для начинающих» под ре-
редакцией академика ДА. Поспелова (Москва: «Педагогика-Пресс», 1994).
А мы наметим здесь лишь основные контуры этой структуры. Инфор-
Информатика включает в себя шесть основных направлений: 1) теоретическая
информатика, 2) кибернетика, 3) искусственный интеллект, 4) програм-
программирование, 5) вычислительная техника (без разработки элементной базы
компьютеров), 6) информационные системы. Отдельно отмечают инфор-
информатику в природе и информатику в обществе.
'Чиниипель. Наверное, нужно хотя бы кратко охарактеризовать каж-
каждое из перечисленных направлений.
Пвтор. Начнем с теоретической информатики. Рассматривая общие
свойства информации, проблемы, связанные с ее рождением, кодиро-
кодированием, обработкой, передачей, потерей, теоретическая информатика
объединяет целый ряд теоретических дисциплин, в том числе матема-
математическую логику, теорию информации, теорию кодирования. Она иссле-
исследует информационные математические модели различных объектов и
разрабатывает алгоритмы обработки информации для этих моделей. Тем
самым теоретическая информатика охватывает такие дисциплины, как
исследование операций (включая системы массового обслуживания, тео-
теорию игр, теорию статистических решений), имитационное моделирова-
моделирование, системный анализ, теория алгоритмов. Отдельно отметим исследо-
исследования, выполняемые с помощью компьютеров на математических
моделях; такие исследования называют вычислительным экспериментом.
339

. Однако Большой энциклопедический словарь объявляет
теорию информации, теорию кодирования, исследование операции раз-
разделами кибернетики.
Пвтор. Надо признать, что это — несколько устаревшая классифи-
классификация. До середины 70-х годов вообще не использовался термин «тео-
«теоретическая информатика», а использовался термин «теоретическая ки-
кибернетика», или, иначе, «математическая кибернетика».
*Чи(п<14пель. Чем же должна заниматься кибернетика теперь, когда
она стала одним из направлений информатики?
Пвтор. Именно теми проблемами, с которых и начиналась в свое
время. Я имею в виду проблемы организации эффективного управления
в системах различных типов на основе обработки информации с помо-
помощью компьютеров. Естественным образом кибернетика подразделяется
на дисциплины, соответствующие разным типам управляемых систем:
техническую кибернетику, биологическую кибернетику (включая нейро-
кибернетику), медицинскую кибернетику, экономическую кибернетику,
математическую лингвистику. Особенно активно развивается техническая
кибернетика, включающая в себя, в частности, системы автоматичес-
автоматического регулирования и автоматического управления, гомеостатику, техни-
техническую диагностику. Сила кибернетики именно в том, что она рассмат-
рассматривает закономерности управления, общие для самых разных систем.
Уместно напомнить, что многие оппоненты Винера заявляли в свое
время, что принципиально недопустимо искать какие-то общие про-
процессы в таких разных системах как животное и машина. В этом была
причина первоначального неприятия кибернетики рядом ученых. Как
пишет Л.Л. Растригин в книге «Этот случайный, случайный, случайный
мир» (Москва: «Молодая гвардия», 1974), «до появления кибернетики
процессы управления в электрическом генераторе рассматривались элект-
электротехникой, управление движением часового маятника исследовалось в
механике, управление динамикой популяций — в биологии. Винер впер-
впервые указал на универсальность управления и показал, что процесс упо-
упорядочения объекта можно производить стандартными приемами, т. е.
применять методы кибернетики независимо от физических особеннос-
особенностей объектов».
ёЧи<9ии9се*ь. Наверное, в техническую кибернетику следует включить
также робототехнику?
Пвтор. Давайте прежде всего уточним, что такое робототехника се-
сегодня. Это наука, занимающаяся созданием специальных технических
систем (роботов), которые, во-первых, способны функционировать в
реальной среде и, во-вторых, способны в той или иной степени заме-
340

нить человека в некоторых сферах его деятельности. При этом имеется
в виду деятельность не только чисто механическая (выполнение тех или
иных производственных операций), но и интеллектуальная. Выделяют
четыре типа роботов: программные, адаптивные, интеллектуальные, ин-
интегральные. Самые простые роботы — это программные роботы; они
многократно повторяют те или иные действия в соответствии с некото-
некоторой жесткой программой (например, взял заготовку, положил под пресс,
включил пресс, вынул изделие из-под пресса, перенес его в другое ме-
место). Адаптивные роботы, в отличие от программных, имеют своеобраз-
своеобразные «органы чувств» в виде тех или иных (световых, тактильных, тем-
температурных и др.) датчиков. В такие роботы встраивают компьютер,
который обрабатывает сигналы от датчиков и формирует соответствую-
соответствующие управляющие сигналы. Адаптивные роботы способны подстраи-
подстраиваться под изменения, возникающие в окружающей среде (способны в
определенной мере адаптироваться к изменениям среды). Интеллекту-
Интеллектуальные роботы способны в какой-то мере распознавать образы, в ка-
какой-то мере обучаться, принимать решения и даже составлять планы.
Интегральные роботы (их называют также суперроботами) — это авто-
автономные роботы, способные самонастраиваться и менять программу своих
действий в зависимости от обстоятельств. Согласно новейшей класси-
классификации, интеллектуальные и тем более интегральные роботы (а зна-
значит, и в целом робототехнику, если понимать ее в широком смысле)
относят к третьему направлению современной информатики — направ-
направлению, именуемому искусственным интеллектом.
'Чиниипель. По-видимому, термин «искусственный интеллект» надо
понимать условно? Ведь не может же компьютер в самом деле мыслить!
Пвтор. Дискуссии на тему «Может ли компьютер мыслить?» ведутся
довольно давно — с середины 50-х годов. Высказывались различные
точки зрения, в том числе самые крайние.
'Чинигнмль. С тех пор прошло полвека. Прекратились ли эти дискус-
дискуссии? Какие точки зрения возобладали? Родилась ли истина в споре?
Пвтор. Спор отнюдь не обязательно завершается «рождением исти-
истины» (если под «рождением истины» понимать получение определенно-
определенного ответа на вопросы, волновавшие спорящих). Довольно часто в споре
рождаются новые вопросы, требующие дальнейшего анализа постав-
поставленной проблемы.
*Чи(*иипель. Но, наверное, появились какие-то разумные, а также кон-
конструктивные соображения, определяющие направление (или направле-
направления) нынешних исследований в области искусственного интеллекта?
341

Пвтор. Весьма разумно высказался Уильям Эшби еще несколько де-
десятков лет назад. В своей статье «Что такое разумная машина» этот
большой энтузиаст исследований по искусственному интеллекту под-
подчеркнул: «Разум машины ограничивается количеством информации,
которое мы в нее внесли. Мы можем получить от машины столько ра-
разума, сколько мы хотим, но только при условии, что в нее заложено
соответствующее количество информации». Конструктивный подход к
проблеме искусственного интеллекта требует различать две разные цели.
Одна цель (ее можно назвать дальней целью) — это создание компью-
компьютеров, способных воспроизводить те мыслительные процессы, которые
совершаются в человеческом мозгу. Здесь речь идет о возможности со-
создания искусственного мозга, который мог бы успешно конкурировать
с мозгом человека. Другая цель (ее можно назвать ближней целью) —
это создание компьютеров, способных имитировать не самый процесс
мышления, а всего лишь некоторые интеллектуальные действия челове-
человека, которые тот совершает в результате своей мыслительной деятельно-
деятельности. Такие компьютеры могут принимать оптимальные решения в слож-
сложных ситуациях, характеризующихся неопределенностью. Причем могут
делать это быстрее, чем человек, поскольку способны быстро переби-
перебирать и анализировать огромное число вариантов. Сразу отметим, что
«ближняя цель» во многих случаях уже достигается. С помощью компью-
компьютеров и соответствующих программ автоматизируются многие виды че-
человеческой деятельности из тех, которые называют интеллектуальными
и традиционно считают доступными лишь человеку. Сегодня компью-
компьютеры могут хорошо играть в шахматы, осуществлять перевод письмен-
письменного текста с одного языка на другой, распознавать образы, имитируя
процесс осознанного восприятия, моделировать рассуждения, плани-
планировать поведение, общаться с человеком в диалоговом режиме и т. д.
Всеми этими проблемами как раз и занимаются теоретически и на прак-
практике сегодняшние специалисты по искусственному интеллекту.
'Чипинъель. Какие дисциплины входят в направление, называемое
искусственным интеллектом?
Пвтор. Среди этих дисциплин отметим распознавание образову компью-
компьютерную лингвистику (анализ, синтез, понимание текстов, зрительное
«оживление» текстов), представление знаний (формализация и ввод в
память компьютера знаний из различных областей), экспертные систе-
системы (моделирование рассуждений), диалоговые системы и, конечно, ро-
робототехнику.
Однако все это не решает проблему моделирования мозга.
342

Пвтор. Конечно, специалисты по искусственному интеллекту не за-
забывают о дальней цели — создании искусственного мозга. Проблема
упирается прежде всего в создание соответствующих программ. Одни
специалисты полагают, что надо совершенствовать программы, оттал-
отталкиваясь от программ, которые используются в существующих компью-
компьютерах. Другие считают, что этот путь бесперспективен и что надо созда-
создавать принципиально новые программы — не для игры в шахматы или
перевода текстов, а для моделирования тех реальных процессов, кото-
которые протекают в нашем мозгу. Вот только сами эти процессы во мно-
многом еще не известны. Не надо забывать, в частности, что два полуша-
полушария мозга человека функционально различны. Если левое полушарие
ответственно за абстрактно-логическое мышление, то образным мыш-
мышлением «заведует» правое полушарие. Можно пытаться «запрограмми-
«запрограммировать» процессы в левом полушарии мозга, но как подступиться к пра-
правому полушарию? Можно ли в принципе использовать в этом случае
технические структуры, применяемые в существующих компьютерах?
Может быть, следует обратиться к нейрокибернетике и пойти по пути
создания нейрокомпьютеров на основе моделирования нервной систе-
системы живых организмов? Все эти и многие подобные вопросы остаются
пока без ответа.
'Чиниикель. Остаются еще три направления информатики — програм-
программирование, вычислительная техника, информационные системы.
Пвтор. Отмечу, что эти три направления как раз и охватывают тот
спектр проблем, которым ограничивалась информатика поначалу —
тогда, когда она рассматривалась только как «наука о вычислительной
технике» и еще не образовала симбиоза с кибернетикой. Говоря о про-
программировании, или, иными словами, о программном обеспечении компью-
компьютеров (просьба не путать с линейным программированием или с дина-
динамическим программированием!), отметим создание разнообразных языков
программирования и специальных программ (так называемых транслято-
трансляторов), позволяющих программу, написанную на том или ином языке
программирования, переводить на язык команд компьютера. Особо ос-
остановимся на направлении информатики, имеющем название «инфор-
«информационные системы». Фактически это направление начало развиваться
еще до появления компьютеров (имеются в виду документалистика, а
также сбор и анализ научно-технической информации). Сегодня в рам-
рамках данного направления осуществляются: а) анализ и прогнозирова-
прогнозирование потоков разнообразной информации, циркулирующей в обществе;
б) исследование способов представления, хранения и быстрого извлече-
извлечения информации; в) создание компьютерных сетей хранения, обработки
343

и передачи информации. Каждая компьютерная сеть представляет со-
собой группу компьютеров и их периферийных устройств, соединенных
линиями связи. За последние тридцать лет в мире созданы десятки и
сотни тысяч больших и малых компьютерных сетей. В 1973 году про-
произошло объединение компьютерных сетей Великобритании и Норвегии,
положившее начало процессу формирования глобальной компьютерной
сети, образованной десятками тысяч локальных сетей (миллионами
больших и малых компьютеров). Сегодня такая глобальная компьютер-
компьютерная сеть, объединяющая сети многих стран мира, существует. Эта «сеть
сетей» получила название Интернет (от английских international — «меж-
«международный» и net — «сеть»). Интернет обладает общим (единым) инфор-
информационным полем, которым может воспользоваться в принципе любой
человек.
. Наверное, единое информационное поле Интернета можно
сравнить с радиоэфиром или телевизионным эфиром?
Пвтор. Конечно, можно. Однако тут есть принципиальная особен-
особенность — в этом «эфире» (в Интернете) информация может храниться и
каждый пользователь может, при желании, ее востребовать.
Часть вторая,
в которой вероятность снова оказывается
в центре внимания
Пвтор. Как видите, сегодня в понятие «информатика» вкладывается
существенно большее содержание по сравнению с тем, какое вкладыва-
вкладывалось в него тридцать или даже двадцать лет назад. Сегодня информати-
информатика — это не просто «наука о вычислительной технике», а наука, рассмат-
рассматривающая весь комплекс проблем, связанных с анализом, моделированием
и практическим применением многообразных информационных процессов
в современном обществе. В этот комплекс входят как проблемы, отвечаю-
отвечающие нынешнему уровню развития науки и техники, так и проблемы,
рождающиеся в ходе научно-технического прогнозирования, проблемы
информационного общества XXI-го столетия.
'Чи&атель. По-видимому, к последним проблемам относится, в част-
частности, проблема создания искусственного мозга, который по своим
возможностям превосходил бы человеческий мозг.
Пвтор. Не будем гадать, насколько реально решение в ближайшем
будущем такой проблемы, как и некоторых других проблем, относя-
344

щихся к сфере искусственного интеллекта. Но в любом случае можно
утверждать, что одним из принципиальных условий при рассмотрении
таких проблем является решительный выход за рамки жесткой детер-
детерминированности и опора на вероятностные подходы и методы теории
вероятностей.
*Чипиииель. Означает ли это, что информатику следует рассматривать
как принципиально вероятностную (статистическую) науку?
Пвтор. Именно так и надо относиться к информатике в ее сегод-
сегодняшнем понимании. Ведь ее «теоретическим ядром» является теория
информации. А основным понятием в этой теории является понятие
количества информации, которое «конструируется», согласно формуле
Шеннона, из соответствующих вероятностей. Можно напомнить так-
также, что степень неопределенности того или другого опыта измеряют
количеством информации, необходимым для устранения этой неопре-
неопределенности. Обо всем этом мы уже неоднократно говорили.
'Чийии&ел*. Но информатика — это не только теория информации.
Хорошо бы почувствовать, насколько глубока связь с вероятностью
информатики в целом.
Пвтор. Мы живем в мире, насыщенном случайностями. Чтобы ус-
успешно функционировать в этом мире, достигать тех или иных целей,
управлять какими-то процессами, мы постигаем в ходе научного позна-
познания различные закономерности окружающего мира, разрабатываем на
их основе и затем проверяем на практике различные алгоритмы своего
общения с миром. И все это вместе взятое может быть названо по боль-
большому счету процессом получения и использования информации. Вероятно-
Вероятностная природа мира, естественно, предопределяет вероятностную сущ-
сущность этого процесса. Кратко, образно, емко это выразил Норберт Винер;
он писал в своей книге «Кибернетика и общество» A954): «Процесс
получения и использования информации является ничем иным, как
процессом нашего приспособления к случайностям внешней среды и
нашей жизнедеятельности в этой среде».
'Чиниикель. Да, вероятность и в самом деле играет в информатике
принципиальную роль.
Пвтор. Это становится еще очевиднее, если учесть, что «процесс
нашего приспособления к случайностям внешней среды и нашей жиз-
жизнедеятельности в этой среде» во многих случаях означает на практи-
практике принятие оптимального решения в условиях неопределенности.
Сегодня буквально на каждом шагу мы обнаруживаем вероятност-
вероятностный облик информатики — в системах массового обслуживания,
345

игровых моделях для отнюдь не игровых ситуаций, методах приня-
принятия статистических решений в «играх с природой», в широком при-
применении в самых различных областях метода статистических испы-
испытаний (когда мы используем против случайностей внешней среды
сами же случайности).
'Чинигтель. Лучше, наверное, противопоставлять случайностям внеш-
внешней среды соответствующим образом организованное управление?
Пвтор. Да, лучше. Если, конечно, мы всякий раз в состоянии его
организовать. Как раз этим и занимается кибернетика, исследуя воз-
возможность эффективного управления в самых различных системах (от
машин и живого организма до промышленного объединения, экономи-
экономики отрасли, биосферы в целом). Управление — это процесс упорядочива-
упорядочивания, иначе говоря, негэнтропийный (информационный) процесс. Он
противостоит энтропийным процессам разупорядочивания, происходя-
происходящим благодаря действию «случайностей внешней среды».
g4u<StiuSU*&. Наверное, можно сказать, что осуществляя управление,
принимая то или иное решение, мы вносим в окружающую среду ка-
какое-то количество информации и тем самым уменьшаем в какой-то
мере энтропию среды, иначе говоря, степень ее неупорядоченности.
Пвтор. Совершенно верно. Винер говорил, что при этом возникает
«локальная зона организации в мире, общей тенденцией которого яв-
является разрушение». Подчеркивая роль информационных процессов,
он говорил: «В мире, где энтропия в целом стремится к возрастанию,
существуют местные и временные островки уменьшающейся энтропии, и
наличие этих островков дает возможность некоторым из нас доказы-
доказывать наличие прогресса».
g4«uSiatfie*&. Кибернетика исследует информационные процессы управ-
управления, благодаря которым возникают в мире «локальные зоны организа-
организации», «островки уменьшающейся энтропии». Короче говоря, управление
действует против случайностей. Оно противостоит случайностям. Мож-
Можно ли утверждать, что в гипотетической ситуации абсолютного управ-
управления мы должны были бы придти к миру без случайностей, иначе
говоря, к абсолютно упорядоченному (абсолютно детерминированно-
детерминированному) миру?
Пвтор. В наших беседах мы уже приходили к заключению о принци-
принципиальной невозможности (более того, бессмысленности) абсолютно
упорядоченного мира. Что же касается противостояния управления слу-
случайностям и хаосу, то нужно принять во внимание, что сама возмож-
возможность осуществления управления предполагает существование случайнос-
346

тей. Чтобы управлять, надо иметь выбор, иметь неопределенность. Нет
смысла выбирать то или иное решение, если все предопределено. Избе-
Избежать предопределенности помогают как раз случайности. Именно они
делают возможным управление. В этом лишний раз проявляется диа-
диалектическое единство необходимого и случайного в реально существую-
существующем мире. И выражается это единство на математическом языке через
вероятность.
'Чипиинель. Я понимаю: в абсолютно беспорядочном мире управле-
управление невозможно, а в абсолютно упорядоченном мире оно просто не нужно.
Пвтор. На рис. 1 в таблице 35 представлена общая схема управления в
кибернетической системе. Она включает в себя четыре принципиаль-
принципиальных элемента: управляемую систему [W — выходной сигнал, рассматри-
рассматриваемый как результат управления системой), управляющее устройство
{V — управляющее воздействие на систему), линию прямой связи, линию
обратной связи. Система подвергается действию случайных возмущений.
Чтобы управляющее устройство было в состоянии при этом корректи-
корректировать управляющий сигнал V, оно должно все время получать инфор-
информацию о результатах управления. Для этого и служит линия обратной
связи. Любая реальная схема управления предполагает наличие обратной
связи. Управление без обратной связи не только неэффективно, но и
фактически всегда нежизнеспособно.
. Как показано на рисунке, случайности воздействуют не
только на управляемую систему; они создают также помехи в обеих
линиях связи — прямой и обратной.
Пвтор. Всё это и обусловливает стохастический (случайный) харак-
характер процесса управления в кибернетических системах.
. А вот в схеме на рис. 2 в таблице 35 нет каких-либо слу-
случайных воздействий или помех.
Пвтор. Просто они там не показаны. Схема на этом рисунке есть
схема так называемого ситуационного управления. Допустим, в результа-
результате управления система должна реализовать некую ситуацию, которой
отвечает выходной сигнал W. В силу различного рода случайных воз-
воздействий и, в частности, вмешательства внешней непредусмотренной
ситуации наша система может «выдать» нештатную ситуацию. Необхо-
Необходима оперативная корректировка управляющего воздействия V. Поэто-
Поэтому информация о выходном сигнале системы вместе с информацией о
внешней ситуации передается по линии обратной связи в «Анализа-
«Анализатор», который определяет, необходима или нет корректировка управля-
управляющего воздействия. Если она необходима, то информация передается в
347

Таблица 35. Случайность в кибернетических системах
Случайные воздействия
V
>
со
3
3
о
О
Управляемая
система
I
С
я
о
Управляющее
устройство
W
i
i
о
ю
о
Рис.1
V
^-
Решатель
i
t
к 1
Управляемая
система
Внешняя ситуация
—->
W
г
Анализатор
Имитатор
\
Классификатор
и
База данных
Рис.2
v Случайные связи J
It
Рис.3
Рис.4
Случайные воздействия
PQ
о
348

«Классификатор», связанный с «Базой данных». В памяти последней
хранятся данные о различных типах ситуаций и соответствующие им
необходимые решения. «Классификатор» отыскивает нужное решение
и передает информацию о нем в «Решатель», который и осуществляет
корректировку управляющего воздействия. Если в «Классификаторе»
отсутствует готовое нужное решение, то он сообщает об этом «Решате-
«Решателю» и тот пытается подобрать приемлемое решение с помощью «Ими-
«Имитатора». «Имитатор» хранит в своей памяти всю необходимую инфор-
информацию об управляемой системе и пытается спрогнозировать управляющее
воздействие, перебирая разные варианты. Наиболее подходящий вариант
он сообщает «Решателю».
'Чиниикель. Я вижу, что если в схеме на рис. 1 надо рассматривать
всего два информационных потока (по линии прямой и линии обрат-
обратной связи), то в схеме на рис. 2 число информационных потоков замет-
заметно больше. Их здесь восемь, если судить по числу стрелок.
Пвтор. Теперь обратимся к рис. 3 в таблице 35. Здесь представлена в
упрощенном виде схема наиболее простого технического устройства для
распознавания образов. В данном случае имеется в виду распознавание
букв в письменном тексте.
'Чийии&ел*. Разве распознавать буквы в тексте трудно?
Пвтор. Речь идет о распознавании той или иной буквы с учетом ее
различных возможных изображений, положений, размеров. Иначе го-
говоря, необходимо распознать объект с учетом неопределенности его
представления. В общем способность распознавать образы связывают с
осознанным восприятием — когда воспринимаются некие общие, харак-
характерные для данного образа (объекта) признаки, а конкретные частные
признаки как бы отступают на второй план. Благодаря этой способно-
способности человек относит воспринимаемый объект к какой-то категории,
определенному понятию (это — яблоко, это — собака и т. д.).
'Чинигнмль. Но можно ли говорить об осознанном восприятии в при-
применении не к человеческому мозгу, а к техническому устройству?
Пвтор. Вот об этом сейчас и идет речь. Для распознавания букв аме-
американский кибернетик и психолог Фрэнк Розенблат A928-1971) скон-
сконструировал еще в 1957 году техническое устройство, названное им пер-
септроном (от латинского perceptio, что означает «восприятие»). Оно-то
и представлено схематически на рис. 3. Персептрон Розенблата можно
рассматривать как весьма упрощенную модель системы «глаз — мозг».
Роль глаза, а точнее, сетчатки глаза, выполняет экран 1, составленный
из большого числа светочувствительных элементов (рецепторов). На
349

экран проецируется изображение. Рецепторы преобразуют световые
сигналы в электрические, которые поступают по многочисленным ли-
линиям связи к экрану-анализатору 2, разбитому на большое число ассо-
ассоциативных элементов — формальных нейронов с управляемым усиле-
усилением. Каждый формальный нейрон имитирует живой нейрон; он способен
возбуждаться и передавать сигнал возбуждения по искусственному ак-
аксону. Формальные нейроны являются изобретением американского ней-
нейрофизиолога Уоррена Мак-Каллока A898-1969); они широко применя-
применяются в нейрокибернетике. В персептроне Розенблата сигналы от
нейронов передаются по линиям связи решающим элементам 3, фикси-
фиксирующим результаты операции распознавания.
ttcuSUuSie**. Все это хорошо бы пояснить немного подробнее.
Пвтор. В этом нет необходимости. Сам по себе персептрон Розен-
Розенблата сегодня уже не представляет особого интереса. Я обратил на него
внимание лишь для того, чтобы отметить весьма любопытное и прин-
принципиальное обстоятельство: электрические связи между рецепторами и
формальными нейронами, а также между нейронами и решающими
элементами имеют случайный характер. Мы наблюдаем здесь случайную
структуру связей между элементами технического устройства.
g4tuftfufie*b. Получается, что рецепторы и нейроны, а также нейроны
и решающие элементы соединяют провод очками, используя таблицу
случайных чисел?
Пвтор. Фактически так оно и есть.
g4u*ftiuSU*b. Но как же может работать техническое устройство на
основе полной «неразберихи» соединений между его элементами? Оно
же никуда не годно!
Пвтор. Поначалу персептрон и вправду не годен. Его предстоит
обучить — настроить на распознаваемые образы. И именно случай-
случайный характер связей в персептроне делает возможным такое «обуче-
«обучение». Не вникая в процедуру «обучения», отметим лишь, что оно
происходит в процессе подбора величины усиления для различных ней-
нейронов при многократных предъявлениях персептрону распознаваемых
образов.
g4utftiufU*&. Насколько я понимаю, случайности выступают здесь уже
не в роли возмущения и помех, а в роли позитивного фактора, позволя-
позволяющего реализовать в техническом устройстве восприятие, аналогичное
человеческому осознанному восприятию. Значит, можно говорить, что
сделан хотя бы первый шаг на пути создания модели мозга!
Пвтор. И заметьте (это особенно важно!), что уже первый шаг ука-
указывает на стохастическую природу модели мозга. Чтобы рассчитывать
350

на какой-то успех, мы должны выбрать путь стохастического моделиро-
моделирования мозга.
*Чи(*иипель. Стохастическое моделирование... Но мне всегда казалось,
что для моделирования системы нужно иметь определенную информа-
информацию об ее внутреннем устройстве.
Пвтор. Вы неправы. В кибернетике применяется моделирование слож-
сложных систем на основе использования модели «черного ящика». Так назы-
называют любую управляемую систему, в которой исследуются только реак-
реакции ее выходных сигналов на входные воздействия и при этом не
рассматривается внутреннее устройство системы. «Черный ящик» ус-
условно изображен на рис. 4 в таблице 35. Современные системы оказы-
оказываются все более и более сложными, а их функциональные возможнос-
возможности (то, что они могут делать) становятся все более богатыми. Понятно,
что в этих условиях на первый план выдвигается исследование именно
функциональных возможностей систем. Исследование же внутренней
структуры систем отступает на второй план. Тем более что во многих
случаях такое исследование в полном объеме оказывается практически
невозможным из-за сложности систем. Подобное смещение акцентов
приводит нас к качественно новой точке зрения, когда главной задачей
становится изучение общих закономерностей процессов управления и
самоуправления независимо от конкретного устройства тех или иных
управляемых систем. Именно эта точка зрения и привела к кибернетике
как науке об управлении (самоуправлении) в сложных системах. Оказа-
Оказалось, что отнюдь не обязательно вникать во все детали внутренней струк-
структуры системы. Более того, расчленение сложной системы на составные
части может даже приводить к утрате принципиально важной инфор-
информации. В этой ситуации модель «черного ящика» приобретает принци-
принципиальное значение.
*Чи(*иипель. Моделирование на основе «черного ящика» оставляет «за
кадром» информацию о внутреннем устройстве системы; эта информа-
информация не используется. Иными словами, такое моделирование выполня-
выполняется при наличии в системе соответствующего количества энтропии
(неопределенности). Стохастическое моделирование, предполагающее
наличие в системе случайных связей, также выполняется, несмотря на
присутствующую в системе неопределенность. На мой взгляд, просмат-
просматривается связь моделирования на основе «черного ящика» и стохасти-
стохастического моделирования.
Пвтор. Действительно, связь просматривается. Если моделирова-
моделирование на основе «черного ящика» показывает, что можно обойтись без
351

информации о детальном устройстве сложной системы, то стохастичес-
стохастическое моделирование исходит из того, что не только можно, но и в извес-
известном смысле нужно обходиться без указанной информации. Давно под-
подмечено, что для достаточно надежного функционирования сложных
систем необходимо отсутствие в их внутренних связях жесткой детер-
детерминированности. В сложной системе много элементов. И если все они
будут жестко взаимосвязаны, то выход из строя любого из них может
нарушить функционирование всей системы. Коротко говоря, чем слож-
сложнее система, тем опаснее ее жесткая детерминированность. Сложная
система будет достаточно надежной только при условии ее стохастично-
сти, т. е. при наличии в ней случайных связей. «Как доказано киберне-
кибернетикой, — пишет Е.А. Седов в своей книге "Одна формула и весь мир", —
случайный, стохастический энтропийный характер внутрисистемных
связей является необходимым условием надежности сложных систем.
Только при наличии гибких, недетерминированных (вероятностных)
связей между элементами система приобретает возможность перестраи-
перестраивать свои элементы, перераспределять их функции, если вышел из строя
какой-нибудь элемент. Благодаря этому свойству существуют не только
организмы, но и вообще все живое».
Часть третья,
в которой сообщаются впечатляющие результаты
вычислительного эксперимента по прогнозу глобальных
климатических последствий ядерной войны
Пвтор. Информатика позволяет нам не только «приспособиться к
случайностям внешней среды», но и прогнозировать глобальные послед-
последствия многих наших серьезных решений. Как известно, на ошибках
учатся. Подразумеваются ошибки, которые уже были сделаны. Но с
возрастанием технических возможностей общества увеличивается опас-
опасность необратимых последствий допущенных ошибок. Поэтому весьма
важно переходить от обучения на тех ошибках, которые уже совершены,
к обучению на ошибках, которые пока не совершены, но могут быть
совершены. Такое обучение предполагает проведение вычислительных
экспериментов — когда математически моделируются и анализируются
вероятные последствия принятия людьми того или иного серьезного
решения.
352

Хорошо бы привести конкретный пример такого экспе-
эксперимента.
Пвтор. Познакомимся с результатами вычислительного экспери-
эксперимента по прогнозу глобальных климатических последствий ядерной
войны, выполненного в 1980-1984 гг. в Вычислительном центре АН
СССР под руководством академика Никиты Николаевича Моисеева
A917-1998). Была создана система «Гея», включающая в себя гидро-
гидродинамическую модель общей циркуляции атмосферы (тропосферы и
стратосферы) и термодинамическую модель верхних слоев Мирового
океана. Наряду с относительно устойчивыми факторами (такими, как
глобальные ветры у поверхности Земли и вблизи границы тропосфе-
тропосферы) ученые постарались учесть значительное число факторов, харак-
характеризующихся большой степенью неопределенности: движение цик-
циклонов, образование облачности, дыхание наземной растительности,
колебания концентрации углекислого газа в атмосфере и др. Было вы-
выполнено большое число вероятностных расчетов с использованием
электронно-вычислительной машины БЭСМ-6. В расчеты заложили
предположительный сценарий ядерной войны, согласно которому на
ряд крупных городов в Северном полушарии были сброшены в тече-
течение одних суток атомные бомбы общей мощностью порядка 100 мега-
мегатонн в тротиловом эквиваленте.
&. Это много или мало?
Пвтор. Ядерный взрыв одного килограмма урана-235 или плуто-
ния-239 эквивалентен по количеству выделившейся энергии химичес-
химическому взрыву 20 тысяч тонн тротила. О такой атомной бомбе говорят,
что она обладает мощностью в 20 килотонн в тротиловом эквивален-
эквиваленте. Именно такова была мощность каждой из двух атомных бомб, сбро-
сброшенных 5 августа 1945 года американскими летчиками на Хиросиму и
Нагасаки. Водородная бомба примерно таких же размеров обладает
мощностью в 20 раз большей; следовательно, мощность сравнительно
небольшой водородной бомбы можно оценивать в 0,5-1 мегатонну.
Ядерная война мощностью 100 мегатонн предполагает, как мы видим,
использование 5000 атомных бомб типа тех, что были сброшены на
японские города, или всего 100-200 не очень крупных водородных
бомб.
ь. Как я понимаю, именно к такой войне применим извест-
известный термин «ограниченная ядерная война».
Пвтор. И тем не менее результаты расчетов оказались весьма впечат-
впечатляющими. Прежде всего отметим, что в результате нанесения такого
353

«ограниченного» ядерного удара по нескольким крупным городам Се-
Северного полушария должна будет полностью перестроиться циркуляция
воздушных масс в тропосфере. Как можно видеть на рис. 1 в таблице 36,
эта циркуляция, рассматриваемая в меридиональнальной плоскости,
характеризуется в настоящее время шестью циклами (шестью «ячейка-
«ячейками») — тремя в Северном полушарии и тремя в Южном. На рисунке
буквой Н отмечены области широт с пониженным давлением (в этих
областях воздушные массы поднимаются от Земли к границе тропосфе-
тропосферы), а буквой В отмечены области широт с повышенным давлением
(эти области на рисунке заштрихованы; здесь воздушные массы опус-
опускаются к поверхности Земли). Не вникая в детали, заметим, что образо-
образование таких «ячеек» обусловлено двумя факторами — конвекцией воз-
воздушных масс и вращением Земли вокруг своей оси. В результате ядерной
бомбардировки все эти ячейки исчезнут и установится циркуляция воз-
воздушных масс, изображенная на рис. 2. В Северном полушарии из-за
массовых пожаров возникнут грандиозные облака сажи, которые дос-
достаточно быстро распространятся в направлении к Южному полюсу и в
конечном счете накроют сплошным черным покрывалом весь земной
шар. На рис. 3 видно, как постепенно на Земле наступит «ядерная ночь»:
а — первые сутки после бомбардировки, б — через неделю, в — через
две недели, г — через три недели. На несколько месяцев Земля будет
окутана сплошным черным покрывалом из сажи, практически не пропус-
пропускающим солнечное излучение. Верхние слои тропосферы разогреются до
сотен градусов, зато у поверхности Земли существенно похолодает —
наступит «ядерная зима». Установившиеся через месяц после ядерной
бомбардировки среднесуточные температуры на Земле (впрочем слово
«среднесуточные» излишне, поскольку смены дня и ночи не будет)
показаны в виде изотерм на рис. 4 в таблице 36. Везде на суше темпе-
температуры будут ниже О °С, местами опускаясь до 40-50 градусов ниже
нуля; в приповерхностных водах океанов тоже понизится, хотя и в
меньшей степени (благодаря большой теплоемкости воды) — она опу-
опустится примерно до 0 °С. Но это еще не все. Вследствие сильного
нагрева верхних слоев тропосферы начнется активное таяние вечных
снегов и ледников в высокогорных местностях. Образовавшаяся ог-
огромная масса воды устремится в низовья и там превратится в ледяной
массив, который накроет почти всю площадь Европы, Северной Аме-
Америки, Азии. В итоге замерзнут все источники пресной воды и погибнет
земная растительность. Вследствие большой разницы температур по-
поверхности суши и поверхности океанов возникнут многочисленные
354

Таблица 36. Вычислительный эксперимент: прогноз глобальных климатических
последствий ядерной войны
Полярная ячейка
Ячейка Ферелла
355

свирепые штормы в прибрежных районах. Кроме того, может заметно
повыситься уровень Мирового океана из-за таяния снегов и льдов на
высокогорьях Антарктиды.
ёЧи<9ии9се*ь. Страшная картина. А ведь ядерная бомбардировка может
оказаться более мощной, — например, до 1000 или 10 000 мегатонн.
Пвтор. Накопленных на Земле сегодня ядерных боезапасов с из-
избытком хватило бы для более мощной бомбардировки. Разумеется, в
этом случае последствия оказались бы еще более катастрофичными.
Похолодание было бы более глубоким, все океаны покрылись бы льдом.
На рис. 5 в таблице 36 показаны температуры поверхности Земли в
случае ядерной бомбардировки мощностью 10 000 мегатонн не через
месяц, а через восемь месяцев. Можно видеть, что сохранились глубо-
глубокие низкие температуры на суше и, кроме того, сохранилась отрица-
отрицательная температура на большей части Мирового океана. Были вы-
выполнены расчеты на период в 380 дней после ядерной бомбардировки.
Обнаружено, что к концу года произойдет существенное повышение
температуры Земли вследствие передачи теплоты от нагретых сажевых
облаков в нижние слои тропосферы. Тогда наступит настоящий все-
всемирный потоп.
g4utftiuSU*b. А какова вероятность человечеству выжить?
Пвтор. Даже в случае «ограниченной» ядерной войны человечество
вряд ли выживет. Добавьте к гибели растительности, глобальному про-
промерзанию всех источников пресной воды, всемирному оледенению, от-
отсутствию солнечного света еще и такие губительные для жизни факто-
факторы, как мощное радиоактивное заражение земной поверхности,
изменение химического состава атмосферы, разрушение практически
всех производственных объектов, а также медицинских учреждений —
и после этого судите сами, сколь ничтожны шансы уцелеть человече-
человечеству даже в виде немногочисленных одичавших групп.
'Чинигтель. А как же насчет ответного ядерного удара возмездия, о
котором и поныне говорят некоторые политики?
Пвтор. Он попросту не понадобится. Ведь погибнут не только те, кто
подвергнется ядерной бомбардировке, но также и те, кто эту бомбарди-
бомбардировку предпринял. «Ядерная зима» и радиоактивное заражение — это
не локальные, а глобальные бедствия. Они не пощадят никого.
'Чснна&ель. То, что последствия ядерной войны будут катастро-
катастрофичны, признается всеми. Но считалось (а кто-то, может быть, счи-
считает до сих пор), что они катастрофичны лишь для непосредствен-
непосредственных участников ядерного конфликта. А остальное человечество могло
356

бы «находиться на холме и оттуда наблюдать, как тигры дерутся в
долине».
Пвтор. Как показал вычислительный эксперимент (проведенный не
только в СССР, но также и в США), такое представление — это всего
лишь иллюзия. Никому не удастся «отсидеться на холме». Благодаря
возможностям современной информатики человечество получило серьез-
серьезное предупреждение. Это предупреждение звучит так: существует вероят-
вероятность того, что информационное общество, едва сформировавшись на пла-
планете Земля, может самоуничтожитъся, взорвав хотя бы сравнительно
небольшую часть тех ядерных боеприпасов, которыми оно сегодня распо-
располагает. Ядерная война, если она будет кем-либо развязана, окажется
той последней ошибкой, на которой больше некому будет учиться. Воз-
Возможно, что этот мрачный прогноз является наиболее важной информа-
информацией, которой мы сегодня обладаем.
357

СПИСОК ЛИТЕРАТУРЫ
Популярные издания
1.	Л. А. Растригин. Этот случайный, случайный, случайный мир. М.: Молодая
гвардия, 1974.
2.	Л.А. Растригин. По воле случая. М.: Молодая гвардия, 1986.
3.	Е.С. Вентцелъ. Элементы теории игр. М.: Физматгиз, 1961.
4.	Е.С. Вентцелъ. Исследование операций: Задачи, принципы, методология. М.:
Высшая школа, 2001.
5.	Т.А. Платонов, М.А. Файнберг, М.С. Штилъман. Поезда, пассажиры и... мате-
математика. М.: Транспорт, 1977.
6.	И.М. Яглом. Теория информации. М.: Знание, 1961.
7.	Дэн:. Пирс. Символы, сигналы, шумы: Закономерности и процессы передачи
информации. Пер. с англ. М.: Мир, 1967.
8.	А. Ренъи. Трилогия о математике (Записки студента по теории информации).
Пер. с венгерского. М.: Мир, 1980.
9.	Е.А. Седов. Одна формула и весь мир: Книга об энтропии. М.: Знание, 1982.
10.	Дж. Фен. Машины, энергия, энтропия. Пер. с англ. М.: Мир, 1986.
11.	Г.Н. Алексеев. Энергия и энтропия. М.: Знание, 1978.
12.	Н. Винер. Кибернетика и общество. Пер. с англ. М.: ИЛ, 1958.
13.	А.Я. Лернер. Начала кибернетики. М.: Наука, 1967.
14.	Л.П. Теплое. Очерки о кибернетике. М.: Московский рабочий, 1963.
15.	В.Д. Пекелис. Кибернетика от А до Я: Маленькая энциклопедия. М.: Дет-
Детская литература, 1990.
16.	И.И.Артоболевский, А.Е. Кобринский. Знакомьтесь — роботы. М.: Молодая
гвардия, 1979.
17.	КН. Моисеев. Экология человечества глазами математика. М.: Молодая гвар-
гвардия, 1988.
18.	Информатика: Энциклопедический словарь для начинающих. Под ред.
Д.А. Поспелова. М.: Педагогика-Пресс, 1994.
19.	Л.В. Тарасов. Мир, построенный на вероятности. М.: Просвещение. 1984.
Научные издания
1.	Е.С. Вентцелъ. Исследование операций. М.: Советское радио, 1972.
2.	А.Я. Хинчин. Работы по математической теории массового обслуживания. М.:
Физматгиз, 1963.
3.	Б.В. Гнеденко, И.Н. Коваленко. Введение в теорию массового обслуживания.
М.: Наука, 1966.
4.	Л.А. Овчаров. Прикладные задачи теории массового обслуживания. М.: Ма-
Машиностроение, 1969.
358

5.	А.Кофман, Р. Крюон. Массовое обслуживание: Теория и практика. Пер. с франц.
М.: Мир, 1965.
6.	А. Кофман, Р. Фор. Займемся исследованием операций. Пер. с франц. М.:
Мир, 1966.
7.	Н.П. Бусленко, Ю.А. Шрейдер. Метод статистических испытаний. М.: Физ-
матгиз, 1961.
8.	Теория прогнозирования и принятия решений. Под ред. С. Саркисяна. М.:
Высшая школа, 1977.
9.	К. Шеннон. Работы по теории информации и кибернетике. Пер. с англ. М.:
ИЛ, 1963.
10.	A.M. Яглом, И.М. Яглом. Вероятность и информация. М.: Наука, 1973.
11.	А.Д. Урсул. Информация: Методологические аспекты. М.: Наука, 1971.
12.	Р. Фано. Передача информации: Статистическая теория связи. Пер. с англ.
М.: Мир, 1965.
13.	Л. Бриллюэн. Наука и теория информации. Пер. с англ. М.: ГИФМЛ, 1960.
14.	Л. Бриллюэн. Научная неопределенность и информация. Пер. с англ. М.:
Мир, 1966.
15.	П. Шамбадалъ. Развитие и приложения понятия энтропии. Пер. с франц.
М.: Наука, 1967.
16.	Н. Винер. Кибернетика или Управление и связь в животном и машине. Пер.
с англ. М.: Советское радио, 1968.
17.	У.Р. Эшби. Введение в кибернетику. Пер. с англ. М.: ИЛ, 1958.
18.	М. Аптер. Кибернетика и развитие. Пер. с англ. М.: Мир, 1970.
359

Учебное издание
ТАРАСОВ Лев Васильевич
ЗАКОНОМЕРНОСТИ ОКРУЖАЮЩЕГО МИРА
Книга 2
ВЕРОЯТНОСТЬ В СОВРЕМЕННОМ ОБЩЕСТВЕ
Редактор Ю.Г. Рудой
Оригинал-макет: О.А. Пелипенко
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 04.08.04.
Формат 70x100/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 29,17. Уч.-изд. л. 25. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru; http://www.fml.ru
Отпечатано с диапозитивов
в ОАО «Чебоксарская типография № 1»
428019, г. Чебоксары, пр. И. Яковлева, 15
ISBN 5-9221-0516-7
9 78592205163