Иванов М. А., Чугунков И. В.
Теория, применение и оценка
КАЧЕСТВА ГЕНЕРАТОРОВ
ПСЕВДОСЛУЧАЙНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
"КУДИЦ-ОБРАЗ"
Москва • 2003
ББК 32.811.4
Иванов М. А., Чугунков И. В.
Теория, применение и оценка качества генераторов псевдослучайных по-
следовательностей. - М.: КУДИЦ-ОБРАЗ, 2003. - 240 с. - (СКБ - специа-
листу по компьютерной безопасности)
ISBN 5-93378-056-1
ISBN 5-93378-047-2 (серия)
Книга состоит из трех глав. В главе 1 рассматриваются основы теории
генераторов псевдослучайных последовательностей (ПСП). В главе 2 подробно
описаны генераторы, функционирующие в конечных полях. Эти устройства
используются в качестве строительных блоков при проектировании крипто-
стойких генераторов ПСП. В главе 3 рассматриваются принципы проектирова-
ния и свойства стохастических генераторов ПСП. Обладая всеми достоинствами
криптографических генераторов, устройства этого класса допускают эффектив-
ную программную и аппаратную реализацию. В главе 4 дается обзор статисти-
ческих тестов, используемых для исследования ПСП, описываются существую-
щие методики оценки качества ПСП.
Книга рассчитана на широкий круг читателей, интересующихся вопросами
защиты информации. Может быть полезна студентам и аспирантам вузов ком-
пьютерных специальностей, разработчикам и пользователям компьютерных
систем.
М. А. Иванов, И. В. Чугунков
Теория, применение и оценка качества генераторов псевдослучайных после-
довательностей.
Учебно-справочное издание
Корректор Т. Елизаветина
Макет А. Ширкевич
Лицензия ЛР № 071806 от 2.03.99. НОУ «ОЦ "КУДИЦ-ОБРАЗ"».
119034, Москва, Гагаринский пер., д. 21, стр. 1. Тел.: 333-82-11; ok@kudits.ru
Подписано в печать 22.04.2003.
Формат 60x90/16. Бум. офсетная. Печать офс.
Усл. печ. л. 15. Тираж 3000. Заказ 225
Отпечатано с готовых диапозитивов в типографии "Профиздат".
109044, Москва, ул. Крутицкий вал, д. 18.
ISBN 5-93378-056-1	© М. А. Иванов, И. В. Чугунков, 2003
ISBN 5-93378-047-2	© Макет НОУ «ОЦ "КУДИЦ-ОБРАЗ”», 2003
Введение
Сфера применения генераторов псевдослучайных последова-
тельностей (ПСП) чрезвычайно широка. Можно выделить, на-
пример, следующие области их использования:
•	космическая связь;
•	коды, обнаруживающие и исправляющие ошибки;
•	встроенное самотестирование СБИС;
•	защита информации и др.
Качественные псевдослучайные последовательности, являясь
по своей сути детерминированными, обладают тем не менее
практически всеми свойствами реализаций истинно случайных
процессов и успешно их заменяют, так как случайные последова-
тельности чрезвычайно сложно формировать.
Настоящая работа посвящена в первую очередь генераторам
ПСП, ориентированным на использование в системах защиты
«информации от случайных и умышленных деструктивных воз-
действий. В первой главе рассматриваются общие принципы про-
ектирования непредсказуемых генераторов ПСП, требования
к таким устройствам, описываются основные строительные бло-
ки, используемые при их создании. Уделяется внимание конгру-
энтным генераторам, регистрам сдвига с линейными (LFSR)
и нелинейными обратными связями. Во второй главе рассматри-
вается важнейший класс ПСП, а именно последовательности,
формируемые генераторами, функционирующими в конечных
полях. Третья глава целиком посвящена теории стохастических
генераторов ПСП (RFSR), основными достоинствами которых
являются эффективная программная и аппаратная реализация,
высокое быстродействие. По этим параметрам RFSR очень незна-
чительно уступают LFSR, при этом в отличие от последних явля-
ются нелинейными и обладают всеми свойствами криптографи-
ческих генераторов ПСП. В четвертой главе описываются суще-
ствующие подходы к оценке качества генераторов ПСП. Приво-
дятся сведения о разработанном авторами программном комплек-
се, предназначенном для анализа статистической безопасности
алгоритмов генерации ПСП и криптоалгоритмов.
4
Теория,, применение и оценка качества генераторов псевдослучайных последовательностей
Авторы выражают признательность С. А. Осмоловскому за ин-
терес к настоящей работе, многочисленные ценные советы и реко-
мендации по выбору направлений исследований и разработок.
Книга рассчитана на широкий круг читателей, интересующих-
ся вопросами криптографической защиты информации. Может
быть полезна студентам и аспирантам вузов компьютерных спе-
циальностей, разработчикам и пользователям компьютерных
систем.
Данная книга является второй в серии «Безопасность компью-
терных технологий». Первая содержала описание шифра Rijndael,
принятого в 2001 г. после проведения открытого международного
конкурса в качестве американского стандарта криптографической
защиты AES - Advanced Encryption Standard, а также изложение
основ теории конечных полей (полей Галуа), на математическом
аппарате которой построен шифр. AES принят на замену мораль-
но устаревшему DES - самому распространенному криптоалго-
ритму в мире, де-факто многолетнему мировому стандарту крип-
тозащиты.
Ближайшие книги серии:
•	Современные поточные шифры.
•	Криптоанализ блочных шифров.
•	Стеганогафические методы защиты информации.
•	Теория кодирования и криптография.
•	Защита информации в банковском деле и электронном бизнесе.
ГЛАВА 1
Принципы построения
и свойства генераторов
псевдослучайных
последовательностей
1.1.	Функции генераторов
псевдослучайных последовательностей
в системах защиты информации
Генераторы псевдослучайных последовательностей (ПСП) яв-
ляются неотъемлемыми элементами любой системы защиты, они
используются для решения следующих задач:
•	генерации гаммирующих последовательностей при преобразо-
вании информации по схеме, наиболее близкой к схеме абсо-
лютно стойкого шифра, т. е. при построении синхронных по-
точных шифров;
•	хеширования информации;
•	построения самосинхронизирующихся поточных шифров;
•	формирования ключевой информации, на секретности и каче-
стве которой основывается стойкость криптоалгоритмов;
•	формирования случайных запросов при реализации большого
числа криптографических протоколов, например протоколов
выработки общего секретного ключа, разделения секрета,
подбрасывания монеты, привязки к биту, аутентификации,
электронной подписи и др.;
•	внесения неопределенности в работу защищаемых аппаратно-
программных средств;
•	внесения неопределенности в работу средств защиты, например,
при реализации концепции вероятностного шифрования, при ко-
ь
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
тором одному и тому же исходному тексту при одном и том же
ключе соответствует огромное множество шифротекстов.
Степень защищенности компьютерной системы можно повы-
сить даже за счет всего лишь простой замены //-разрядных счетчи-
ков команд и адреса на генераторы ПСП с числом состояний 2N.
1.1.1. Шифрование информации
Наиболее эффективным и перспективным методом защиты ин-
формации является ее криптографическое преобразование (шиф-
рование для обеспечения секретности информации или формиро-
вание контрольного кода для проверки аутентичности информа-
ции). Более того, в некоторых случаях этот метод является единст-
венно возможным.
В общем случае процессы зашифрования и расшифрования
могут быть описаны следующим образом
Ек‘- Р —С, Dk‘. С —> Р,
где Ek, Dk, к,Р тлС соответственно функции зашифрования и рас-
шифрования, секретный ключ, пространство открытых текстов и
пространство шифротекстов. При этом для любого х справедливо
DkCE/fyc)) = х.
На рис. 1.1, а показана схема абсолютно стойкого шифра.
Шифрование информации по этой схеме суть наложение на
входную информационную последовательность р ключевой по-
следовательности к. Операция наложения, называемая гаммиро-
ванием, осуществляется с помощью некоей функции F (в качест-
ве которой очень часто используется операция XOR). Иными сло-
вами, для каждого элемента с, зашифрованной последовательно-
сти с справедливо
с, = Ftp., к.),
где pt, к, - г-е элементы соответственно исходной информацион-
ной последовательности р и ключевой последовательности к,
i = l,m, т- длина последовательностей р, с и к. Расшифрование
осуществляется с использованием функции F1, обратной F:
Pi = F\d, ki),
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
7
Абсолютная стойкость криптосхемы объясняется отсутствием
каких-либо закономерностей в зашифрованных данных. Против-
ник, перехвативший шифротекст, не может на основе его анализа
получить какую-либо информацию об исходном тексте. Это
свойство достигается при выполнении трех требований:
•	равенство длин ключа и исходного текста;
•	случайность ключа;
•	однократное использование ключа.
Дополнительные требования, предъявляемые к этой схеме, де-
лают ее слишком дорогой и непрактичной. В результате на прак-
тике применяется схема, показанная на рис. 1.1, б, надежность
которой определяется качеством используемого генератора ПСП.
Функция генератора ПСП состоит в том, чтобы, используя корот-
кий секретный ключ к как зародыш, сформировать длинную
псевдослучайную последовательность у. Каждый элемент р, ис-
ходной последовательности р шифруется независимо от других с
использованием соответствующего элемента у, ключевой после-
довательности у:
Ct = F(pb у,), pi = F\ch у,).
При использовании схемы гаммирования с обратной связью
(рис. 1.2) результат шифрования каждого элемента входной по-
следовательности зависит от всех ее предшествующих элементов.
Ключ
к
Ключ
к
Исходная
Зашифрованная jr
информация с
Расшифрованная
информация р
Рис. 1.1. Использование генераторов ПСП при шифровании информации:
а - схема абсолютно стойкого шифра;
б - схема гаммирования (синхронное поточное шифрование).
G - генератор ПСП, F - линейная (например, X0R или mod р) или
нелинейная функция
8
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Рис. 1.2. Схема гаммирования с обратной связью
(самосинхронизирующееся поточное шифрование); FB - функция
обратной связи, Q - элементы памяти генератора ПСП
1.1.2.	Хеширование информации
Важную роль в системах защиты играет хеширование
информации, одна из возможных схем которого показана на рис.
1.3. Хеш-функция Л(х) принимает на входе массив данных р
произвольной длины и формирует на выходе хеш-образ й(р)
фиксированной длины. Хеш-преобразование используется:
•	при формировании контрольных кодов, обеспечивающих про-
верку целостности (CRC-коды) или аутентичности (MDC-
коды) информации; проверку правильности хода выполнения
программ;
•	при организации парольных систем;
•	при реализации протоколов электронной подписи.
Функция Л(х) должна удовлетворять следующим требованиям:
•	результат ее действия должен зависеть не только от всех битов
исходного массива данных, но и от их взаимного расположе-
ния; иными словами, результат действия й(р) хеш-функции
должен быть чувствителен к любым изменениям входной ин-
формационной последовательности р;
•	она должна быть вычислительно необратимой, т. е. подобрать
массив данных под заданный хеш-образ можно только путем
полного перебора по пространству возможных значений р;
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
9
•	она не должна иметь коллизий, т. е. задача нахождения для
заданной последовательности р другой последовательности р',
рФ р, такой, что h(p') = h(p), должна быть вычислительно
неразрешимой.
Рис. 1.3. Хеширование информации:
а - схема формирования хеш-образа массива данных произвольной
длины;
б - принцип действия хеш-функции.
Pi - элементы (блоки) исходного массива разрядности n<N,t<N-
разрядность хеш-образа разрядность генератора ПСП
а
Сущность процесса контроля целостности с использованием
контрольных кодов заключается в следующем. Генератор конт-
рольного кода инициализируется фиксированным начальным
значением. Анализируемая двоичная последовательность преоб-
10
ТЕОрИЯл ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
разуется в относительно короткий (обычно длиной от 2 до 32
байт) двоичный код - хеш-образ. Значение полученного кон-
трольного кода сравнивается с эталонным значением, получен-
ным заранее для последовательности без искажений. По резуль-
татам сравнения делается вывод о наличии или отсутствии иска-
жений в анализируемой последовательности.
1.1.3.	Криптографические протоколы
Целью построения криптографического протокола является
решение какой-либо практической задачи, возникающей при
взаимодействии удаленных абонентов. Последние для информа-
ционного обмена используют открытые каналы связи. Протокол
включает в себя:
•	распределенный алгоритм, определяющий характер и после-
довательность действий участников;
•	спецификацию форматов пересылаемых сообщений;
•	спецификацию синхронизации действий участников;
•	описание действий при возникновении сбоев.
На рис. 1.4 показана схема симметричной аутентификации
(проверки подлинности абонентов А и В) с использованием
третьей, доверенной стороны С. Арбитр С использует свой гене-
ратор ПСП для формирования сеансовых ключей кАВ, с использо-
ванием которых происходит взаимодействие абонентов А и В,
изначально не доверяющих друг другу. Абонент А использует
свой генератор ПСП для формирования случайных запросов хА,
используемых в процессе взаимной аутентификации А и В. IDA,
IDB - идентификаторы соответственно абонентов А и В\ кАс -
секретный ключ, разделяемый А и С, кве - секретный ключ, раз-
деляемый В и С; ЕАС{р) - результат шифрования сообщения р на
ключе кАС, Евсф) - результат шифрования сообщения р на ключе
кве, Еав(р) - результат шифрования сообщения р на ключе кАВ-
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
11
Рис. 1.4. Схема симметричной аутентификации
1.1.4.	Вероятностное шифрование
Одной из функций генераторов ПСП в системах криптографи-
ческой защиты информации может быть внесение неопределен-
ности в работу средств защиты, например выбор элементов веро-
ятностного пространства R при вероятностном шифровании
Ек: Р х R С,
где Ек, к, R, С - соответственно функция зашифрования, секрет-
ный ключ, пространство открытых текстов и пространство шиф-
ротекстов. Главная особенность вероятностного шифрования -
один и тот же исходный текст, преобразованный на одном и том
же ключе, может привести к появлению огромного числа различ-
ных шифротекстов.
Схема одного из возможных вариантов вероятностного сим-
метричного блочного шифрования в режиме простой замены по-
казана на рис. 1.5, где на вход функции зашифрования Ек посту-
пает «расширенный» блок р[, полученный в результате конкате-
нации блока открытого текста р, разрядности п и двоичного набо-
ра г, разрядности т с выхода генератора ПСП. В результате за-
шифрования получается блок с, закрытого текста разрядности п + т.
При расшифровании часть г, блока, полученного на выходе
функции Dk, просто отбрасывается.
12
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Рис. 1.5. Пример вероятностного шифрования. Ек и Dk - функции
шифрования симметричной или ассиметричной криптосистемы
Можно выделить следующие достоинства вероятностного шифра:
•	повышается надежность и расширяется область использования
режима простой замены;
•	при шифровании используется секретная информация (после-
довательность г), известная только отправителю информации;
•	появляется принципиальная возможность увеличения времени
жизни сеансовых ключей;
•	использование качественного генератора ПСП позволяет при
использовании симметричных криптосистем уменьшить число
раундов шифрования, а значит, увеличить быстродействие
криптоалгоритма;
•	при использовании рассматриваемой схемы в криптосистемах
с открытым ключом противник лишается возможности вычис-
лять значение функции шифрования интересующих его тек-
стов и сравнивать их с перехваченным шифротекстом;
•	отношение длин блока открытого текста р, и соответствующе-
го ему элемента г, вероятностного пространства может высту-
пать в качестве параметра безопасности.
Недостаток у рассматриваемой схемы лишь один - шифро-
текст всегда длиннее соответствующего ему открытого текста. .
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей 15
1.2.	Принципы построения генераторов ПСП
Можно выделить два подхода при использовании в составе
генераторов ПСП нелинейных функций: это использование нели-
нейной функции непосредственно в цепи обратной связи (рис.
1.6, а) и двухступенчатая структура (рис. 1.6, б), в которой задача
первой ступени (по сути счетчика) заключается всего лишь в
обеспечении максимально большого периода при данной разряд-
ности N используемого регистра Q.
Рис. 1.6. Два варианта построения генератора ПСП:
а - с нелинейной внутренней логикой (режим 0FB - Output
FeedBack);
б - с нелинейной внешней логикой (режим Counter);
в - входной и преобразованный вектор ошибок.
Q - элементы памяти генератора, FB - линейная или нелинейная
функция обратной связи, Fk - нелинейная функция, к - ключ, у, -
элемент выходной последовательности, е - входной вектор ошибок,
содержащий 1 в разрядах, соответствующих измененным
(искаженным) битам, е' - преобразованный (выходной) вектор ошибок
Pi e~Pi®Pi Рг
в
14
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1.3.	Требования к генераторам ПСП.
Криптостойкость
Качественный генератор ПСП, ориентированный на использо-
вание в системах защиты информации, должен удовлетворять
следующим требованиям:
•	криптографическая стойкость;
•	хорошие статистические свойства, ПСП по своим статистиче-
ским свойствам не должна отличаться от истинно случайной
последовательности;
•	большой период формируемой последовательности: например,
при шифровании для преобразования каждого элемента вход-
ной последовательности необходимо использовать свой эле-
мент псевдослучайной гаммы;
•	эффективная аппаратная и программная реализация.
При использовании криптостойкого генератора ПСП три сле-
дующие задача для противника вычислительно неразрешимы:
•	определение (i - 1)-го элемента Ум последовательности на
основе известного фрагмента гаммы YiYi+iYi+2... Yi+*-i конечной
длины Ь\
•	определение (i + 1)-го элемента последовательности на
основе известного фрагмента гаммы Yi-i+i... Y1-2Y1-1Y1 конечной
длины Ь',
•	определение ключевой информации по известному фрагменту
гаммы конечной длины.
Справедливо следующее утверждение. Непредсказуемый влево
генератор ПСП является криптостойким. Криптоаналитик,
знающий принцип работы такого генератора, имеющий возмож-
ность анализировать фрагмент
YiYi+iYi+2—Yi+a-D
выходной последовательности, но не знающий используемой
ключевой информации, для определения предыдущего вырабо-
танного элемента последовательности у -1 не может предложить
лучшего способа, чем подбрасывание жребия.
[лава 1 . Принципы ПОСТРОЕНИЯ И СВОЙСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
15
В рамках другого подхода к построению качественного гене-
ратора ПСП предлагается свести задачу построения криптогра-
фически сильного генератора к задаче построения статистиче-
ски безопасного генератора. Статистически безопасный генера-
тор ПСП должен удовлетворять следующим требованиям:
•	ни один статистический тест не обнаруживает в ПСП каких-
либо закономерностей, иными словами, не отличает эту по-
следовательность от истинно случайной;
•	нелинейное преобразование Fk , зависящее от секретной ин-
формации (ключа к), используемое для построения генератора
(рис. 1.6), обладает свойством «размножения» искажений - все
выходные (преобразованные) вектора е' возможны и равнове-
роятны независимо от исходного вектора е\
•	при инициализации случайными значениями генератор поро-
ждает статистически независимые ПСП.
1.4.	Классификация генераторов ПСП
1.4.1.	Криптографические генераторы ПСП
На рис. 1.7 приведена классификация генераторов ПСП. Роль
нелинейной функции Ft может выполнять функция зашифрования
Ек одноключевой (классической) или двухключевой криптосисте-
мы, при этом использование криптостойких функций Ек автомати-
чески придает аналогичное свойство и генератору ПСП. Стой-
кость функций Ек современных криптосистем основывается на
недоказуемом предположении о том, что у противника не хватит
ресурсов (вычислительных, материальных, временных и т.п.), для
того чтобы инвертировать эту функцию при неизвестном к.
Симметричные криптоалгоритмы (криптоалгоритмы с секрет-
ным ключом) делятся на три большие группы: поточные, блоч-
ные и комбинированные.
Особенности поточного шифрования (рис. 1.1, 1.2):
•	каждый элемент исходной информационной последовательности
шифруется на своем элементе ключевой последовательности;
•	результат преобразования отдельных элементов зависит от их
позиции в исходной последовательности;
16
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
•	высокое быстродействие - шифрование осуществляется прак-
тически в реальном масштабе времени сразу при поступлении
очередного элемента входной последовательности;
•	эффективная программная реализация.
Рис. 1.7. Классификация генераторов ПСП
Особенности блочного шифрования:
•	шифрованию подвергаются порции информации фиксирован-
ной длины (блоки);
•	каждый блок исходной последовательности шифруется неза-
висимо от других на одном и том же ключе;
•	низкое быстродействие, так как функция шифрования любого
современного блочного криптоалгоритма суть многократное
повторение одной и той же раундовой операции.
Глава 1. Принципы построения и свойства ГЕНЕрлюров псевдослучайных последовательностей
17
Недостатки блочного шифрования:
•	одинаковым блокам открытого текста соответствуют одинако-
вые блоки шифротекста и наоборот;
•	нечувствительность криптосхемы к выпадению или вставке
целого числа блоков;
•	существование проблемы последнего блока неполной длины.
В результате на практике чаще всего используется комбини-
рованный подход, при котором шифрование осуществляется либо
с использованием операции сцепления блоков (режим СВС), либо
с использованием генераторов ПСП по схемам, показанным на
рис. 1.1 (режимы OFB и Counter) и рис. 1.2 (режим CFB). При
этом в качестве нелинейных функций генераторов ПСП (рис. 1.6)
используются функции зашифрования соответствующих блочных
криптоалгоритмов.
Особенности шифрования методом гаммирования (поточное
или комбинированное шифрование в режимах OFB и Counter):
•	наличие у противника, даже не знающего ключевой информа-
ции, возможности внесения предсказуемых изменений в за-
шифрованную информацию при ее хранении или передаче;
•	жесткие требования к синхронизации генераторов ПСП ис-
точника и приемника информации - выпадение или вставка
элемента зашифрованной последовательности при ее хранении
или передаче приводит к необратимым искажениям всех по-
следующих элементов после расшифрования.
Эти не очень приятные особенности отсутствуют при шифро-
вании в режиме гаммирования с обратной связью (поточное или
комбинированное шифрование в режиме CFB).
На рис. 1.8 показан генератор ПСП ГОСТ 28147-89, который
функционирует в режиме Counter, где , i = 1,32, - раундовые
ключи. Разрядность блока данных ГОСТа равна 64 битам, число
раундов преобразования равно 32. Функция Ек построена с ис-
пользованием схемы, которая носит название сбалансированной
сети Фейстеля. Схема раундовой функции F показана на рис. 1.9.
Ключевая информация ГОСТа - собственно ключ, состоящий из
восьми 32-разрядных элементов Ко, К\, ..., Кт, и таблица замен
18
ТЕОрИЯ, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
размерностью 4x16x8 бит, определяющая логику работы восьми
4-разрядных блоков замены (5-блоков). Последовательность ис-
пользования ключевых элементов при построении функции Ек
имеет вид
Ко, Кь К], Ко, К\, ..., Ку, Kq, Ki, ..., Ку, Ку, Ко, ..., Ко.
1-й раунд
31-й раунд
32-й раунд
Рис. 1.8. Генератор ПСП ГОСТ 28147-89
Таким образом, в состав раунда ГОСТа входят следующие
преобразования 32-разрядных двоичных наборов:
•	сложение правой половины 7?-блока данных с раундовым ключом;
•	разбиение результата на восемь 4-битовых элементов и замена
каждого из них по таблице замен;
•	циклический сдвиг результата на 11 разрядов влево;
•	поразрядное сложение по модулю 2 (XOR) результата с левой
половиной L блока данных;
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
19
•	новое значение элемента L становится равным R, новое значе-
ние элемента R становится равным результату предыдущей
операции.
32-й раунд отличается от остальных - в нем отсутствует по-
следняя операция.
32
32 /
32
Циклический сдвиг
влево на 11 разрядов
32 У
Рис. 1.9. Раундовая функция ГОСТ 28147-89
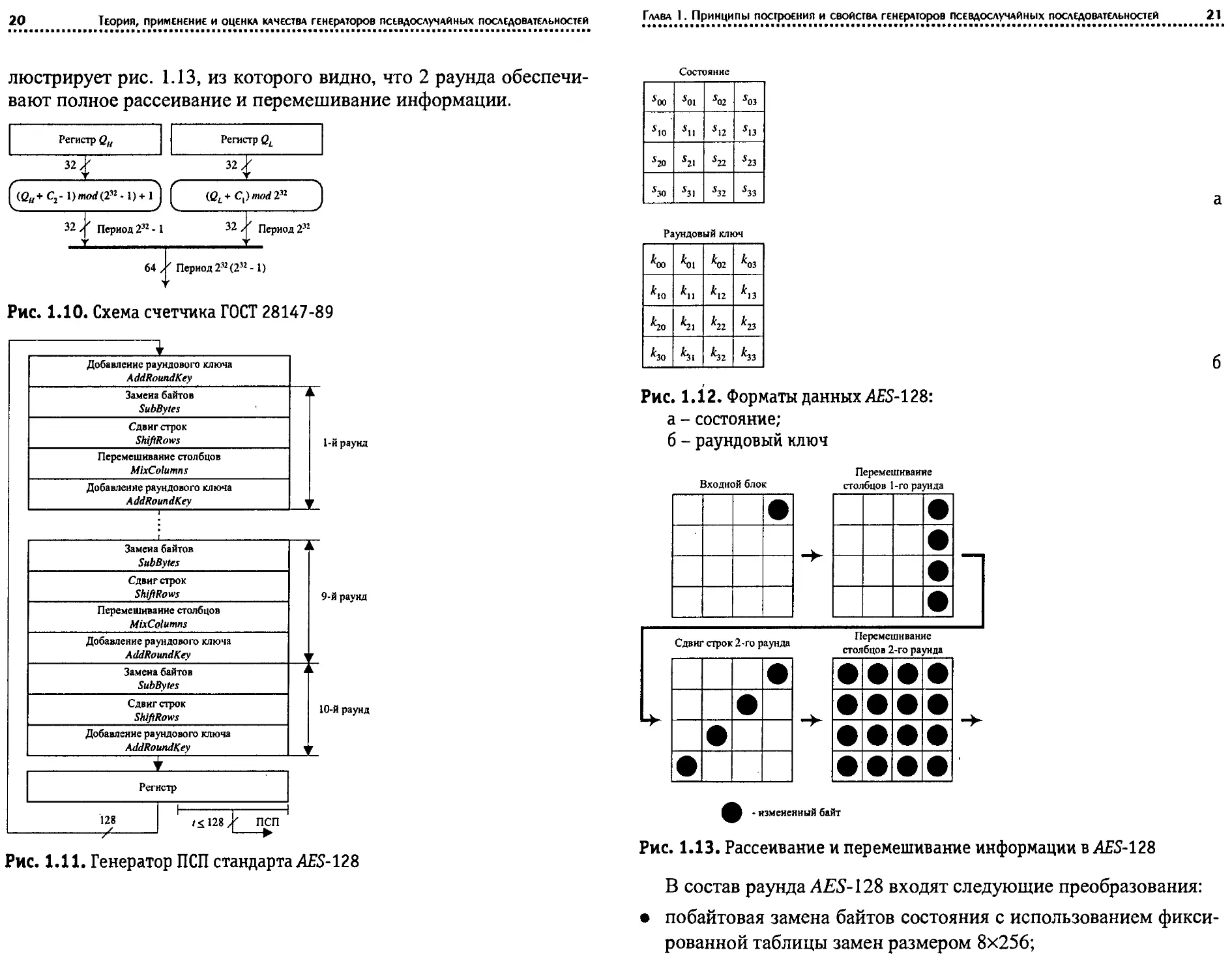
На рис. 1.10 показана схема счетчика ГОСТа, который состоит
из двух независимых счетчиков со взаимно простыми числами
состояний соответственно 232 и 232 - 1. В результате период по-
следовательности на выходе схемы оказывается равным произве-
дению 232(232 - 1). Константы Ci = OlOlOlOlh и С2 = 01010104b
подобраны таким образом, чтобы каждое следующее состояние
счетчика отличалось от предыдущего в каждом байте.
На рис. 1.11 показан генератор ПСП, построенный в соответ-
ствии с принятым в 2001 г. американским стандартом AES-128
[4]. Разрядность блока данных AES-128 равна 128 битам, число
раундов преобразования равно 10. Функция ^ построена с ис-
пользованием новой архитектуры "Квадрат". Промежуточные
результаты преобразований, выполняемых в рамках криптоалго-
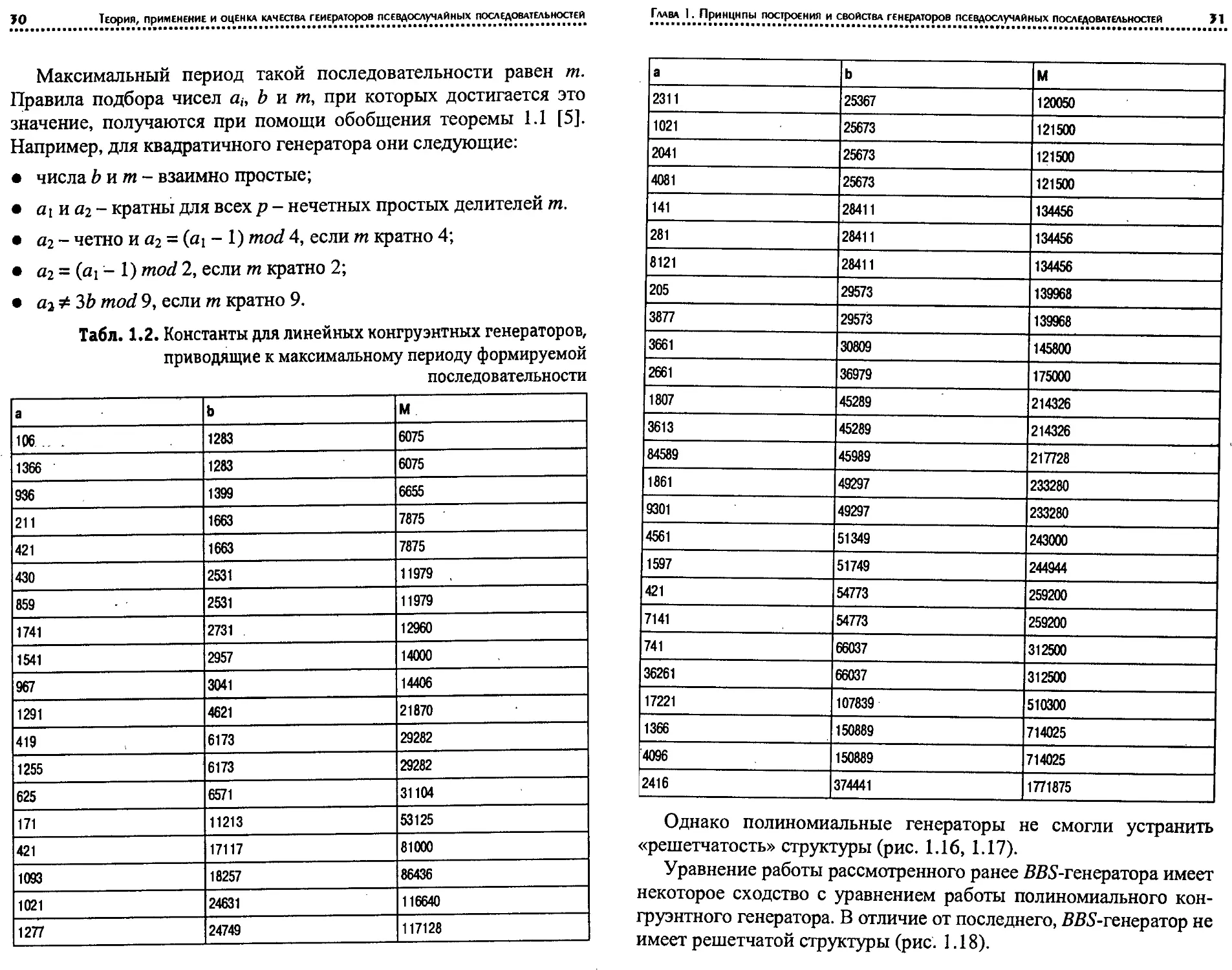
ритма AES-128, называются состояниями. Состояние (рис. 1.12,
а) и раундовые ключи шифрования (рис. 1.12, б) можно предста-
вить в виде квадратного массива байтов, имеющего 4 строки и
4 столбца. Разрядность исходного секретного ключа, из которого
формируются раундовые ключи, равна 128. Свойства шифра ил-
20
ТЕОРИЯ, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
люстрирует рис. 1.13, из которого видно, что 2 раунда обеспечи-
вают полное рассеивание и перемешивание информации.
Рис. 1.10. Схема счетчика ГОСТ 28147-89
Рис. 1.11. Генератор ПСП стандарта 4ES-128
Глава 1. Принципы построения и свойства генерлюров псевдослучайных последовательностей
21
а - состояние;
б - раундовый ключ
- измененный байт
а
Рис. 1.13. Рассеивание и перемешивание информации в AES-128
В состав раунда АЕ5-128 входят следующие преобразования:
•	побайтовая замена байтов состояния с использованием фикси-
рованной таблицы замен размером 8x256;
22
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
•	побайтовый циклический сдвиг строк результата - г-я строка
сдвигается на i байтов влево, i = 0,3 ;
•	перемешивание столбцов результата;
•	поразрядное сложение по модулю 2 (XOR) результата с раун-
довым ключом.
10-й раунд отличается от остальных - в нем отсутствует пред-
последняя операция.
Основные особенности AES-128:
•	новая архитектура «Квадрат», обеспечивающая быстрое рас-
сеивание и перемешивание информации, при этом за один ра-
унд преобразованию подвергается весь входной блок;
•	байт-ориентированная структура, удобная для реализация на
8-разрядных МК;
•	все раундовые преобразования суть операции в конечных по-
лях, допускающие эффективную аппаратную и программную
реализацию на различных платформах.
В отличие от блочных шифров, функции Ек которых, как уже
отмечалось, строятся по итерационному принципу, при проекти-
ровании поточных шифров используется огромное множество
приемов и методов, классифицировать которые очень сложно.
Можно выделить все же следующие [6]:
•	работа по принципу stop-and-go\
•	перемешивание двух ПСП под управлением третьей;
•	многоступенчатая структура;
•	использование 5-блоков с изменяющейся в процессе работы
таблицей замен;
•	использование блоков пространственного сжатия информации;
•	использование в качестве строительных блоков генераторов,
функционирующих в конечных полях.
Одним из лучших поточных шифров является 7?С4 - шифр
с переменным размером ключа, разработанный Р. Ривестом.
Криптоалгоритм работает в режиме OFB, т. е. поток ключевой
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
2>
информации не зависит от открытого текста. Используются два
8-разрядных счетчика (21 и Q2 и 8-разрядный блок замены (5-
блок) (рис. 1.14), таблица замен имеет размерность 8 х 256 и яв-
ляется перестановкой (зависящей от ключа) двоичных чисел от О
до 255.
Рис. 1.14. Схема генератора ПСП ЙС4
Рассмотрим алгоритм работы 8-разрядного генератора ПСП
RC4, точнее, процедуру генерации очередного байта гаммы.
Пусть S(i) и у - содержимое ячейки с адресом i таблицы замен S-
блока и очередной байт гаммы.
Один такт работы генератора ПСП RC4:
1)	Такт работы первого счетчика:
QI = «21 + 1) mod 28.
2)	Такт работы второго счетчика:
Q2 = (Q2 + 5(Q1)) mod 2й.
24
Теория, применение и оценка качества генерлгоров псевдослучайных последовательностей
3)	Ячейки таблицы замен 5-блока с адресами <21 и Q2 обменива-
ются своим содержимым:
S(Q1)^S(Q2).
4)	Вычисление суммы содержимого ячеек таблицы замен 5-блока
с адресами (И и Q2:
r=(S((21) + 5((22)) mod 2*.
5)	Считывание содержимого ячейки таблицы замен 5-блока с
адресом Т\
4 = S(T).
Таблица замен 5-блока медленно изменяется при использова-
нии, при этом счетчик Q1 обеспечивает изменение каждого эле-
мента таблицы, a Q2 гарантирует, что элементы таблицы изме-
няются случайным образом.
Криптографически стойкие генераторы ПСП могут быть по-
строены на основе использования в цепи обратной связи так на-
зываемых односторонних функций. Понятие односторонней
функции является базовым для нового направления - криптогра-
фии с открытым ключом [2].
По заданному аргументу х е X легко вычислить значение та-
кой функции F(x), в то же время определение х из F(x) трудновы-
числимо, т. е. нет алгоритма для решения этой задачи с полино-
миальным временем работы. Теоретически х по известному зна-
чению F(x) можно найти всегда, проверяя по очереди все воз-
можные значения х до тех пор, пока соответствующее значение
F(x) не совпадет с заданным. Однако практически при значитель-
ной размерности множества X такой подход неосуществим.
Односторонней функцией называется функция F: X —> У, об-
ладающая двумя свойствами:
•	существует полиномиальный алгоритм вычисления значений
F(x)\
•	не существует полиномиального алгоритма инвертирования
функции F.
До сих пор ни для одной функции, кандидата на звание одно-
сторонней, не доказано свойство 2.
Глава 1. Принципы построения и свойства генердторов псевдослучайных последовательностей
29
Примером кандидата на звание односторонней функции являет-
ся модульное возведение в степень, т. е. функция F(x) = (О1 mod р,
где р - большое простое число, о - примитивный элемент поля
GF(p) [4].
Задача вычисления функции, обратной модульному возведе-
нию в степень, называется задачей дискретного логарифмирова-
ния. На сегодняшний день неизвестно ни одного эффективного
алгоритма вычисления дискретных логарифмов больших чисел.
Односторонняя функция в качестве функции зашифрования
неприменима, так как, хотя Fix') - надежно зашифрованное сооб-
щение х, никто, в том числе и законный получатель, не сможет
восстановить х. Обойти эту проблему можно с помощью одно-
сторонней функции с секретом [2]. Такова, например, функция
Fk'. Х->. Y, имеющая обратную Ff1: Y —» X, однако узнать обрат-
ную функцию только по Fk без знания секрета к невозможно.
Таким образом, односторонней функцией с секретом к, назы-
вается функция Fk- X —» Y, зависящая от параметра к и обладаю-
щая тремя свойствами:
•	при любом к существует полиномиальный алгоритм вычисле-
ния значений ^(х);
•	при неизвестном к не существует полиномиального алгоритма
инвертирования Fk\
•	при известном к существует полиномиального алгоритма ин-
вертирования Fk.
Функцию Fk можно использовать для зашифрования инфор-
мации, а обратную ей функцию Fk'1 - для расшифрования.
При этом подразумевается, что тот, кто знает, как зашифровы-
вать информацию, вовсе не обязательно должен знать, как рас-
шифровывать. Так же как и в случае с односторонней функцией,
вопрос о существовании односторонних функций с секретом от-
крыт. Для практической криптографии найдено несколько функ-
ций, кандидатов на звание односторонней функции с секретом.
Для них второе свойство не доказано, однако известно, что задача
инвертирования эквивалентна некоторой хорошо изученной и
давно известной трудной математической задаче. Это означает,
что второе требование к односторонней функции с секретом за-
гь
Теория, применение и оценил качества геиерлторов псевдослучайных последовательностей
меняется более слабым условием: при неизвестном к, вероятно,
не существует полиномиального алгоритма инвертирования
Рассмотрим так называемый 555-генератор, получивший свое
название в честь авторов Э, Блюм, М. Блюма и М. Шуба, осно-
ванный на криптосистеме Блюма [1].
Пусть р и q - два больших простых числа примерно одинако-
вого размера, причем
р = 3 mod. 4,q = 3 mod 4.
Тогда число п = pq называется целым числом Блюма. Пусть
Z* - множество целых положительных чисел, меньших п, кото-
рые не делятся ни на р, ни на q. Пусть QRn - подмножество Z*,
состоящее из квадратичных вычетов по модулю п. Число элемен-
тов множества Z* равно (р - l)(q - 1), причем в точности четвер-
тую их часть составляют элементы подмножества QRn. Каждый
элемент QRn имеет ровно четыре различных квадратных корня в
Z*, из них лишь один, называемый примитивным, принадлежит
QRn.
Задача определения примитивных квадратных корней по мо-
дулю числа п вычислительно эквивалентна задаче разложения
этого числа на множители. Таким образом, получаем кандидата
на одностороннюю функцию с секретом, так как функция
F(x) = х2 mod п
эффективно вычисляется, а произвести обратное преобразование
может лишь тот, кто знает секрет - разложение п на множители.
Пусть п - целое число Блюма.
Генератор ПСП Э. Блюм - М. Блюма - М. Шуба
1) Выберем в качестве инициализирующего вектора случайное
число хо £ QRn- Для этого возьмем случайное число х, такое,
что (х, п) = 1, и вычислим
хо = х2 mod п.
2) Искомой последовательностью бит длиной т будет являться
последовательность
BBSn, m(x0)=boblb2..Fi..Fm_l,i = 0,(rn-l),
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
27
где Ь( - младший бит числа х„
х, +1 = х2 mod п.
Важным достоинством этого генератора является то, что при
знании разложения п на множители он допускает прямое опреде-
ление отдельных бит, которые в нем вырабатываются. Имеем
Xj = х0 mod и.
По теореме Эйлера
а значит,
2'mod(p-l)(q-l)	,
Ji} •” Aq	iilUU ft,
т. е. с помощью двух операций модульного возведения в степень,
которые эффективно вычисляются, любое число xt может быть
найдено исходя лишь из начального вектора xq и индекса i.
Аналогичным образом можно построить генератор ПСП на
основе другой односторонней функции с секретом, например,
лежащей в основе криптосистемы RSA, т. е. на основе функции
F(x) = xe mod п,
где п = pq\ pviq- простые числа, причем р * q\ а е взаимно про-
стое с (р- 1)(#- 1).
Генератор RSA
1) Выберем в качестве инициализирующего вектора случайное
число х0 е Z*.
2) Искомой последовательностью бит длиной т будет являться
последовательность
RSAn, rn (*о) = bobib2 bi" bm-x, i = о, (m -1),
где Ь, - младший бит числах,,
x, +1 =x,e mod n.
1.4.2.	Конгруэнтные генераторы ПСП
Общая схема линейных конгруэнтных генераторов была пред-
ложена Д. Г. Лехмером в 1949 году.
Выберем 4 числа (табл. 1.1).
28
Теория, применение и оценка качества генерлторов псевдослучайных последовательностей
Табл. 1.1. Числа, определяющие структуру линейного
конгруэнтного генератора
т	Модуль	Л7>0
a	Множитель	0< а< т
ь	Приращение	0 < />< т
*	Начальное заполнение	0<^< т
Сформируем последовательность {хп} такую, что
хл+1 = (ах„ + b) mod т,
или, обобщая:
хп+к =
к 1 >
к	1 ,	,
а х. +-----b mod т.
п	1
а-1
Эта последовательность называется линейной конгруэнтной
последовательностью. Максимальный период такой последова-
тельности равен т. Следующая теорема позволяет определить,
возможно ли достижение максимального периода для данного
конгруэнтного генератора.
Теорема 1.1. Линейная конгруэнтная последовательность, опре-
деленная числами т, а, b и х0, имеет период длиной т тогда и
только тогда, когда:
•	числа Ьнт- взаимно простые;
•	а - 1 кратно р для каждого простого р, являющегося делите-
лем т;
•	а - 1 кратно 4, если т кратно 4.
В табл. 1.2 приведены некоторые такие значения.
Кроме периода, линейные конгруэнтные генераторы характе-
ризуются потенциалом.
Определение 1.1. Потенциалом линейной конгруэнтной последо-
вательности с максимальным периодом называется наименьшее
целое число s, такое, что
(а - l)s = О mod т.
В работе [5] утверждается, что последовательности с потен-
циалом 5 и выше обладают достаточно хорошими статистиче-
скими свойствами.
Глава 1. Принципы построения н свойства генераторов псевдослучайных последовательностей
29
Следует отметить, что линейные конгруэнтные генераторы,
хотя и обладают хорошими статистическими свойствами, не яв-
ляются криптостойкими, что связано в том числе с «решетчато-
стью» их структуры. На рис. 1.15 показан результат теста «рас-
пределение на плоскости» для одного из линейных конгруэнтных
генераторов. Суть теста подробно рассмотрена в главе 4.
Рис. 1.15. Распределение на плоскости для генератора
хл+1 = (430хп + 2531) mod 11979
В разное время предпринимались различные попытки видоиз-
менить структуру этих генераторов. Одной из первых таких по-
пыток было создание так называемых полиномиальных конгру-
энтных генераторов, уравнение работы которых имеет вид
хп+1 =(а,-Х, + ...+ ахх„ +b) mod т.
КО	Теория, применение и оценка качества геиерлторов псевдослучайных последовательностей
Максимальный период такой последовательности равен т.
Правила подбора чисел a,-, bum, при которых достигается это
значение, получаются при помощи обобщения теоремы 1.1 [5].
Например, для квадратичного генератора они следующие:
•	числа b и т - взаимно простые;
•	ai и а2 - кратны для всех р - нечетных простых делителей т.
•	а2~ четно и а2 = (ai - 1) mod 4, если т кратно 4;
•	а2 = (ai - 1) mod 2, если т кратно 2;
•	a2*3b mod9, если т кратно 9.
Табл. 1.2. Константы для линейных конгруэнтных генераторов,
приводящие к максимальному периоду формируемой
последовательности
а	Ь	М
106 .. .	1283	6075
1366	1283	6075
936	1399	6655
211	1663	7875
421	1663	7875
430	2531	11979 ,
859	2531	11979
1741	2731	12960
1541	2957	14000
967	3041	14406
1291	4621	21870
419	6173	29282
1255	6173	29282
625	6571	31104
171	11213	53125
421	17117	81000
1093	18257	86436
1021	24631	116640
1277	24749	117128
Глава 1. Принципы построения и свойства генерлторов псевдослучайных последовательностей
51
а	b	М
2311	25367	120050
1021	25673	121500
2041	25673	121500
4081	25673	121500
141	28411	134456
281	28411	134456
8121	28411	134456
205	29573	139968
3877	29573	139968
3661	30809	145800
2661	36979	175000
1807	45289	214326
3613	45289	214326
84589	45989	217728
1861	49297	233280
9301	49297	233280
4561	51349	243000
1597	51749	244944
421	54773	259200
7141	54773	259200
741	66037	312500
36261	66037	312500
17221	107839	510300
1366	150889	714025
4096	150889	714025
2416	374441	1771875
Однако полиномиальные генераторы не смогли устранить
«решетчатость» структуры (рис. 1.16, 1.17).
Уравнение работы рассмотренного ранее ВВ5-генератора имеет
некоторое сходство с уравнением работы полиномиального кон-
груэнтного генератора. В отличие от последнего, ВВ5-генератор не
имеет решетчатой структуры (рис. 1.18).
12
Теория, применение и оценю» качества генераторов псевдослучайных последовагельносгей
Рис. 1.16. Распределение на плоскости для генератора
хп +1 = (994 + 430хп + 2531) mod 11979
Рис. 1.17. Распределение на плоскости для генератора
хп + 1 = (ЗбЗхп + 994 + 430хп + 2531) mod 11979
Глава 1. Принципы построения и свойства генердторов псевдослучайных последовательностей 77
Рис. 1.18. Распределение на плоскости для генератора
хп +! = mod 28565461
Следующие попытки сводились к тому, чтобы формируемый
элемент сделать зависимым от нескольких предыдущих элемен-
тов последовательности. Это было сделано в аддитивном гене-
раторе Фибоначчи и аддитивном генераторе Фибоначчи с за-
паздыванием, уравнения работы которых имеют соответственно
вид
хп +1 = {х„ + xn-i) mod тихп = (хп_р + xn_q) mod т,
где т - четное.
74	Теория, применение н оценка качества генераторов псевдослучайных последовательностей
Теорема 1.2. Если многочлен xq + х? + 1 является примитивным
над GFQ), то последовательность, формируемая аддитивным
генератором Фибоначчи с запаздыванием, имеет максимальный
период, который равен 2/о?2т-1(29-1).
В аддитивных генераторах Фибоначчи (как в простом, так и с за-
паздыванием) отсутствует «решетчатая» структура (рис. 1.19,1.20).
Рис. 1.19. Распределение на плоскости для генератора
xn + i = (xn+Xn-i) mod 11979
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей 75
Рис. 1.20. Распределение на плоскости для генератора
Хп = (Хп-з+хп-7) mod 256
Дж. Марсалья предложил заменить сложение в формуле для
аддитивного генератора умножением, получив тем самым муль-
типликативный генератор Фибоначчи с запаздыванием:
хп = (хп-р -Xn-q) mod т,
где т - четное, а хо,..., х9 _ i - целые нечетные числа, сравнимые с
1 по модулю 4.
Теорема 1.3. Если многочлен xg + х? + I является примитивным
над GF(2), то последовательность, формируемая мультиплика-
тивным генератором Фибоначчи, имеет максимальный период,
который равен 2'"А'У"‘3(2'7-1).

Теория, применение и оценка качества генердторов псевдослучайных последовательностей
Кроме уменьшения периода, замена сложения на умножение
привела к тому, что в мультипликативном генераторе Фибоначчи
вновь появилась «решетчатая» структура (рис. 1.21).
Рис. 1.21. Распределение на плоскости для генератора
Xn = (Xn-4+xn-n) mod 256
Идея зависимости формируемого элемента от нескольких пре-
дыдущих нашла свое продолжение в генераторе, уравнение кото-
рого имеет вид
•хл — (^i Хп ~р + ... + Ок х„ - к) mod р,
где р - простое число.
Глава 1. Принципы построения и свойства генерлторов псевдослучайных последовательностей
77
Теорема 1.4. Если константы аь ак таковы, что многочлен
- а\^л - ... - ак является примитивным над GF(p) и хотя бы
один из элементов х0, •••>** не равен нулю, то период генератора
равен рк - 1.
Последовательности, формируемые данным генератором, по-
прежнему имеют решетчатую структуру (рис. 1.22).
Рис. 1.22. Распределение на плоскости для генератора
хп = (4xn-i + 9Хп.г) mod 11
Генератор данного вида является простейшим представителем
важнейшего класса генераторов ПСП - генераторов, функциони-
рующих в конечных полях, которые будут рассмотрены в главе 2.
У8
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Еще один вариант построения - инверсивный конгруэнтный
генератор, уравнение работы которого имеет вид
xn+i = (ах'\ + b) modр,
где р - простое число, хх-1 = 1 (О'1 = 0).
Теорема 1.5. Последовательность, формируемая инверсивным
конгруэнтным генератором, определенным числами а,Ьир, име-
ет максимальный период, равный р + 1, тогда и только тогда,
когда многочлен Дх) = х - сх - а обладает следующими свойст-
вами:
•	xp+1 mod Дх) равняется отличной от нуля константе;
•	х(р+1)/'7 mod fix) имеет степень 1 для каждого простого q, деля-
щего р + 1.
Значение р + 1 является исключительно теоретическим, так
как получается в предположении, что О"1 = °® и °о-1 = 0. На прак-
тике обычно полагают О-1 = 0, в этом случае максимальный пери-
од равен р.
В инверсивных генераторах отсутствует «решетчатая» струк-
тура (рис. 1.23).
Рис. 1.23. Распределение на плоскости для генератора
хп +! = (5830Х;1 + 402) mod 8191
Глава 1. Принципы построения и свойства ГЕнерАюров псевдослучайных последовательностей 79
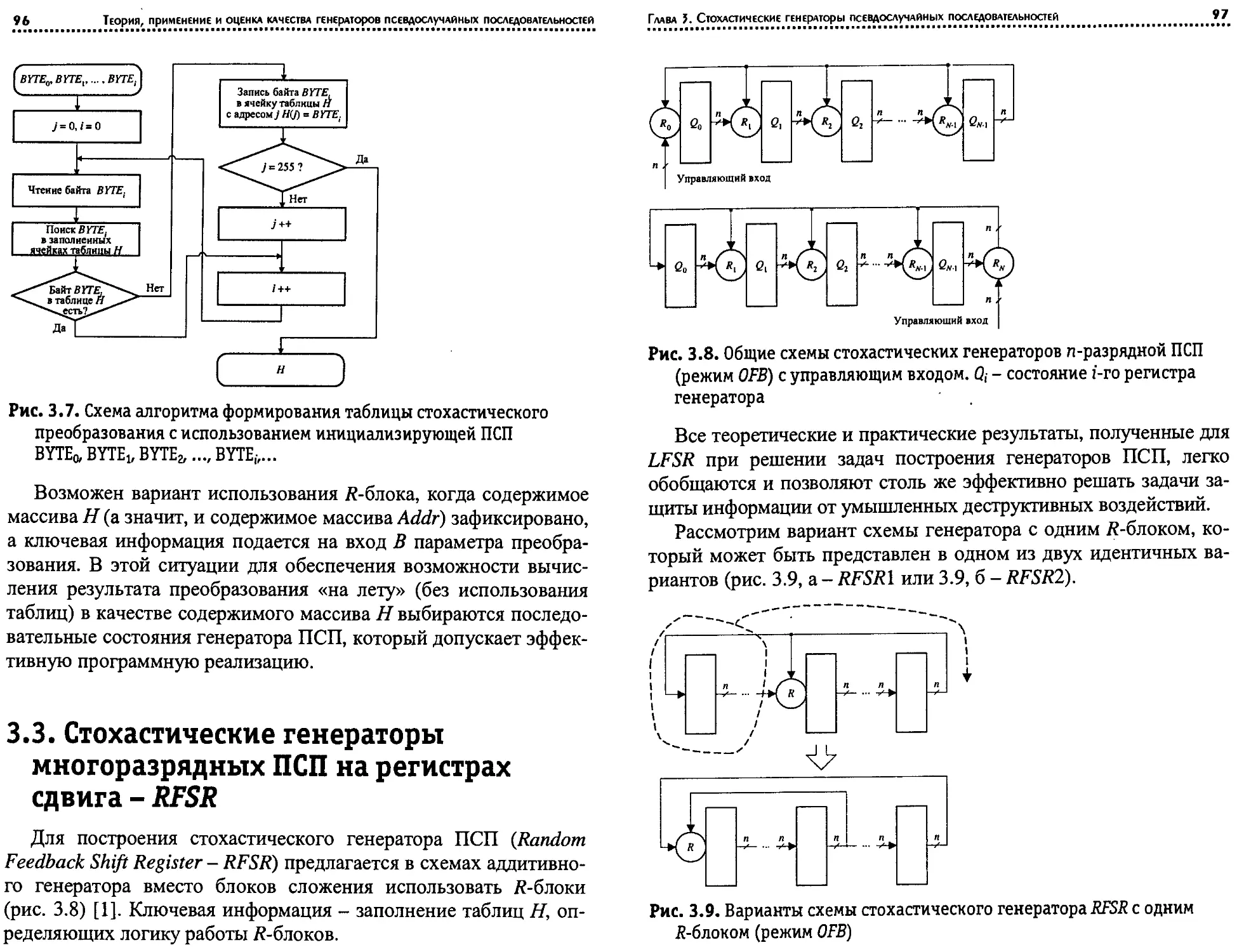
1.4.3.	Генераторы ПСП на регистрах сдвига
с линейными обратными связями
Важнейшим классом ПСП являются последовательности,
формируемые генераторами на основе регистров сдвига с линей-
ными обратными связями - LFSR (Linear Feedback Shift Register).
Используемый при их анализе математический аппарат - теория
линейных последовательностных машин и теория конечных по-
лей (полей Галуа) [4]. Основными достоинствами этих генерато-
ров являются:
•	простота аппаратной и программной реализации;
•	максимальное быстродействие;
•	хорошие статистические свойства формируемых последова-
тельностей;
•	возможность построения на их основе генераторов, обладаю-
щих свойствами, ценными при решении специфических задач
защиты информации (формирование последовательностей про-
извольной длины, формирование последовательностей с пред-
периодом, формирование ПСП с произвольным законом рас-
пределения, построение генераторов, обладающих свойством
самоконтроля и т. п.).
LFSR, к сожалению, не являются криптостойкими, поэтому
применяются при решении задач защиты информации от умыш-
ленных деструктивных воздействий лишь в качестве строитель-
ных блоков.
Наиболее известные примеры использования LFSR и матема-
тического аппарата полей Галуа:
•	С7?С-коды - идеальное средство контроля целостности ин-
формации при случайных искажениях информации;
•	реализация концепции самотестирования БИС и СБИС;
•	поточные шифры А5, PANAMA, SOBER, SNOW и др.;
•	блочный шифр RIJNDAEL, принятый в 2001 г. в качестве
стандарта криптографической защиты XXI века - AES.
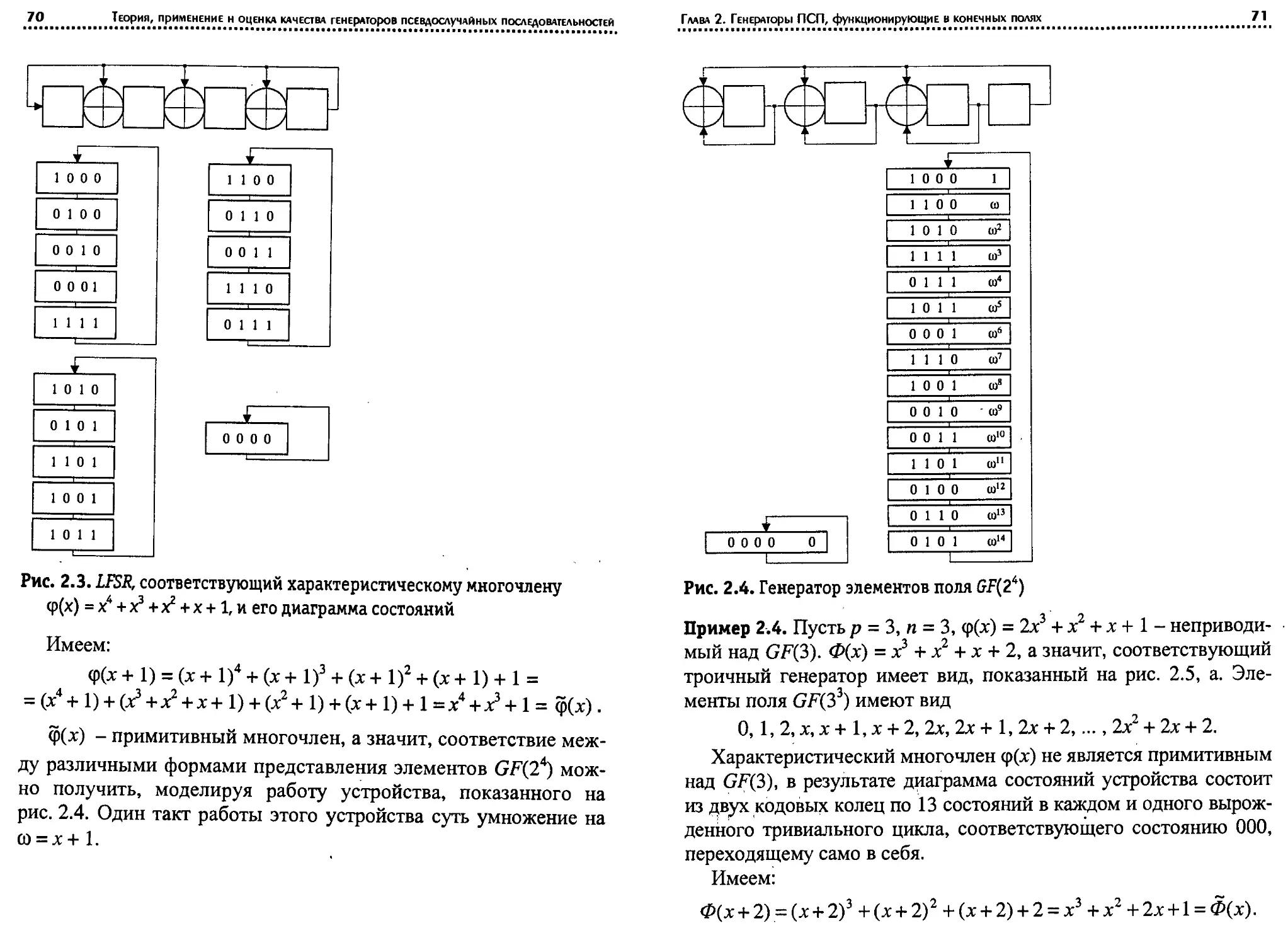
Исходная информация для построения двоичного LFSR - так
называемый образующий многочлен. Степень этого многочлена
40
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
определяет разрядность регистра сдвига, а ненулевые коэффици-
енты - характер обратных связей. Так? например, многочлену
Ф(х) — х + х7 + х5 + х7, + 1
соответствуют два устройства, показанные на рис. 1.24 и 1.25.
В общем случае двоичному образующему многочлену степени N
N	_______
Ф(х) = ^а‘х‘ > aN =ao=i’ aje {°д}> j = t(N~ 1)
i=0
соответствуют устройства, показанные на рис. 1.26, a (LFSR1 -
схема Фибоначчи) и б (LFSR2 - схема Галуа).
Рис. 1.24. Генератор Фибоначчи (LFSR1), соответствующий
Ф(х) = х8 + х7 + х5 + х3 +1, и его диаграмма состояний
Глав* 1. Принципы построения и свойства генерлторов псевдослучайных последовательностей
41
1	
1	0 0	0 0	0 0 0	
0	1 0	0 0	0 0 0	
0	0 1	0 0	0 0 0	
0	0 0	1 0	0 0 0	
0	0 0	0 1	0 0 0	
0	0 0	0 0	1 0 0	
0	0 0	0 0	0 1 0	
0	0 0	0 0	0 0 1	
1	10	10	10 0	
0	11	0 1	0 10	
0	0 1	10	10 1	
1		 *  1	
1	0 1	0 1	0 0 1	
г		
10	0 0	0 0 о о о |
Рис. 1.25. Генератор Галуа (LFSR2), соответствующий
Ф(х) = х8 + х7 + х5 + х3 + 1, и его диаграмма состояний
Рассмотренные устройства могут использоваться только для
генерации битовых ПСП. Если необходима «-разрядная последо-
вательность, можно предложить два варианта действий. В первом
случае выбираем образующий многочлен степени N > п (еще
лучше N » п), выбираем схему LFSR1 или LFSR2 и считываем
очередной «-разрядный двоичный код с соседних разрядов реги-
стра сдвига каждые « тактов работы LFSR. Во втором случае син-
тезируем схему устройства, работающего в « раз быстрее исход-
ного LFSR (иначе говоря, выполняющего за один такт своей ра-
боты преобразования, которые в исходном LFSR выполняются за
п тактов). Этот вариант особенно эффективен в тех случаях, ко-
гда образующий многочлен генератора Фибоначчи имеет вид
Ф(х) = х? + х' + 1, a i кратно п (рис. 1.27).
42
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Рис. 1.26. Общий вид LFSR, соответствующих
Ф(х) = Xя + aN. ix"'1 +... +	+... + а?*2 + агх +1:
a - схема генератора Фибоначчи;
б - схема генератора Галуа.
БУ - блоки умножения на ц е {0,1}; qj(t) е {0,1};
при aj = 1 умножение на а, равносильно наличию связи;
при а, = 0 умножение на а,- равносильно отсутствию связи
Общий вид генератора двоичных последовательностей, соот-
ветствующего уравнению
еа+1) = т* Q(t),
где <2(0 и <20+1) - состояния регистра генератора ПСП соответ-
ственно в моменты времени t и t + 1 (до и после прихода синхро-
импульса); Т - квадратная матрица порядка N вида
	ах а2 ... aN_{ aN		о о о &
	1	0 ...	0	0		1 ... 0 0 aN^
т\ =	0	1 ...	0	0	или Т2 =	
			0 ... 1 0	«2
	0 0 ...	1	0		0 ... 0 1
[лава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей 4J
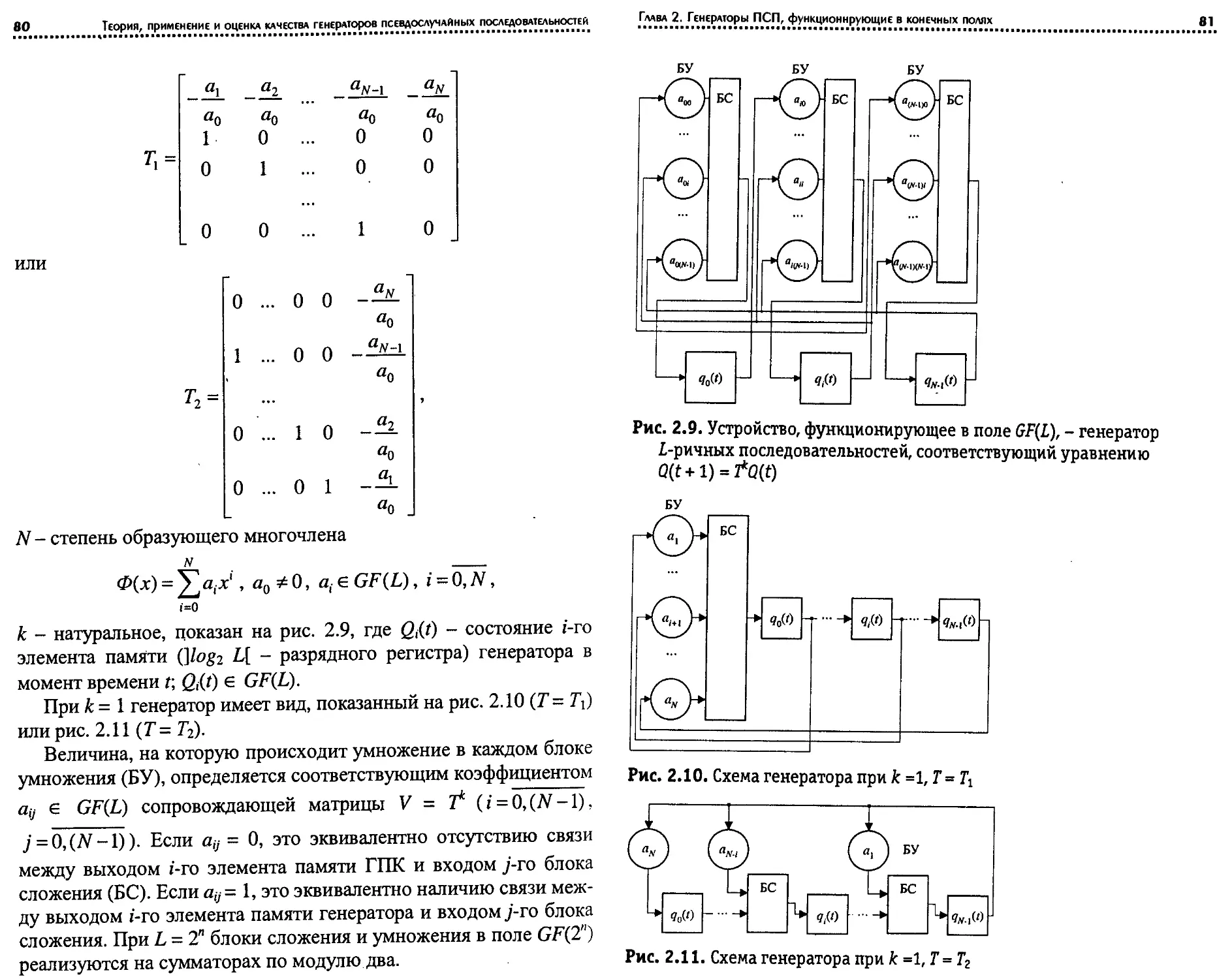
N - степень образующего многочлена
_______
Ф(х) = ^а,х', aN-aQ-\, а;е{0,1}, j = 1,(W-1),
t=o
к - натуральное, показан на рис. 1.28. В частном случае при к =1,
получаем либо схему генератора Фибоначчи (Т = Т\), либо схему
генератора Галуа (Т = Тг).
Л65
Рис. 1.27. Байтовый генератор ПСП:
а - битовый генератор Фибоначчи, соответствующий многочлену
Ф(х) = х65+х32 + 1;
б - байтовый генератор Фибоначчи, соответствующий
Ф(х) = х65 + Х32 +1.	____
<7, - состояние г-го разряда LFSR1, i = 0,64
44
Теория, применение и оценил качества генерлторов псевдослучайных последовательностей
БУ
БУ
БУ
Рис. 1.28. Генератор двоичных последовательностей, соответствующий
уравнению Q(t+1) = 7* Q(t)
Величина, на которую происходит умножение в каждом блоке
умножения (БУ), определяется соответствующим коэффициентом
ау 6 {0,1} сопровождающей матрицы.
V=Tk(i = 0yN-lyj = 0yN-l).
Если ау-= 0, это эквивалентно отсутствию связи между выхо-
дом i-го разряда регистра генератора и входом у'-го сумматора по
модулю два. Если ау = 1, это эквивалентно наличию связи между
выходом i-го разряда регистра генератора и входом у-го суммато-
ра по модулю два.
Так как нулевое состояние регистра ГПК является запрещен-
ным, максимально возможное число состояний устройства, а зна-
чит, и максимально возможная длина формируемой двоичной
последовательности, снимаемой с выхода любого из триггеров,
равны 2n - 1. В этом случае диаграмма состояний генератора со-
стоит из одного тривиального цикла и цикла максимальной дли-
ны 2Л'-1.
Многочлен Ф(х) степени N называется примитивным, если он
не делит нацело ни один многочлен вида xs - 1, где 5 < 2N - 1.
Примитивные многочлены существуют для любого N. Показате-
Глава 1. Принципы построения и свойства генерлюров псевдослучайных последовательностей
49
лем многочлена Ф(х) называется наименьшее натуральное число
е, при котором хе - 1 делится на Ф(х) без остатка.
Пусть Ф(х) - примитивный многочлен степени N, тогда спра-
ведливо следующее утверждение.
Свойство 1.1. Формируемая последовательность имеет макси-
мальный период S = 2n - 1 тогда и только тогда, когда наиболь-
ший общий делитель чисел S и к равен 1 (т. е. S и к взаимно про-
сты).
Следствие. При к = 1 примитивность Ф(х) является необходимым
и достаточным условием получения последовательности макси-
мальной длины.
Последовательность максимальной длины принято называть
М-последовательностью, а формирующий ее генератор - гене-
ратором М-последовательности. Именно генераторы ЛА-после-
довательностей обычно используются для формирования ПСП.
Каждая матрица V имеет характеристический многочлен
(р(х), которым является определитель матрицы V - хЕ, т. е.
(р(х) - | V - хЕ |, где Е - единичная матрица. Многочлен Ф(х)
определяет только структуру генератора, свойства же последнего
зависят именно от <р(х).
Свойство 1.2. Каждая квадратная матрица удовлетворяет своему
характеристическому уравнению, т. е. <р(У) = 0.
Свойство 1.3. Характеристический и образующий многочлен ге-
нератора связаны следующим соотношением:
<р(х) = ФСх1')^,
т. е. являются взаимно обратными.
Примитивность <р(х) автоматически означает примитивность
Ф(х) и наоборот.
Децимацией последовательности {</,(0} по индексу к называет-
ся формирование новой последовательности {q*i(f)}, состоящей
из к-х элементов {дД)}, т. е. q*i{f) = q^kf). Если период последо-
вательности, полученной в результате децимации ЛАпоследова-
тельности, равен максимальному, децимация называется собст-
венной или нормальной.
46
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Последовательность, снимаемая с выхода i-го триггера генера-
тора, изображенного на рис. 1.28, является децимацией по индек-
су к последовательности, снимаемой с выхода i-го триггера гене-
раторов, изображенных на рис. 1.26. Если Q - начальное состоя-
ние генератора, то последовательности состояний, в которых
будут находиться устройства в следующие моменты времени,
имеют вид
Q, QV, QV2, QV3,...
(для устройства, изображенного на рис. 2.8) и
Q, QT, QT1, QT3,...
(для устройств, изображенных на рис. 1.26, где Т = 1\ (а) или
Т =	(б)). Учитывая, что V = 7*, можно сделать вывод, что в ге-
нераторе, показанном на рис. 1.28, за один такт осуществляются
преобразования, которые в генераторах, показанных на рис. 1.26,
происходят за к тактов. Таким образом, устройство, показанное
на рис. 1.28, в котором содержимое первых к триггеров (при
k<N) полностью обновляется в каждом такте, может использо-
ваться для генерации последовательности ^-разрядных двоичных
кодов, что нельзя сказать про устройства, показанные на рис.
1.26, которые формируют лишь сдвинутые копии одной и той же
двоичной последовательности.
Пример 1.1. Пусть
# = 4, Ф(х) = х4 + х3+ 1, Т=Тьк = 1.
Этой ситуации соответствует генератор, схема и диаграмма
состояний которого показана на рис. 1.29. Если начальное со-
стояние устройства равно 1000, на выходе первого триггера q0
формируется периодическая последовательность
100 1 10 10 1 1 1 1 00 0...,
удовлетворяющая рекуррентному соотношению
<7о(^+4) = <7о(^-ь1) © ^о(О-
С выходов триггеров qi, q2 и q3 снимаются сдвинутые копии
той же последовательности.
Гмва 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
47
Рис. 1.29. Генератор двоичной .^-последовательности,
. соответствующий Ф(х) = х4 + х3 +1, Т = 7\,к = 1; и его диаграмма
состояний
Уравнения работы генератора имеют вид:
9оО+1) = О’9о(О © 0-91(0 © 1 -9г(0 © 1 -9з(0
91(Г+1) = 1-9о(О © 0-91(0 © 0’92(0 © 0’9з(0
9г(/+1) = О-9о(О © 1-91(0 © °-9г(0 ©0-9з(0
9з(Г+1) = О-9о(О © 0’91(0 © 1-9г(0 © 0’9з(0,
или в матричной форме:
90(? + 1)		0 0 11	9о(0
9i(' + l)		10 0 0	91(0
92(Т +1)		0 10 0	9 г (0
9з(Г + !)		0 0 10	9з(0
48
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Пример 1.2. Пусть
N = 4, Ф(х)=х4 + ?+ 1, 7’=7’1Д = 2.
Этой ситуации соответствует генератор, схема и последова-
тельность переключений которого показана на рис. 1.30. Если
начальное состояние устройства равно 1000, на выходах первого
и второго триггеров формируется периодическая последователь-
ность двухразрядных двоичных кодов
10 1 1 1 1000 100 1 10...
00 100 1 10 10 1 1 1 10...
или
103113202122330...
t—~
| 1000 j
| 0010 I
| 1100 I
| 1011 I
| 1010 I
I 11/0 I
| 0 1'11 I
| 000 1 I
| 0 100 I
| 100 1 I
| 0110 I
| 0 10 1 I
I “‘о* I
I I
| 0011 I
V
| 0000 I
Рис. 1.30. Генератор двоичной ^-последовательности,
соответствующий Ф(х) = х4 + х3 +1, Т = Ть к = 2; и его диаграмма
состояний
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
49
Уравнения работы генератора имеют вид:
7оО+1) = O-qo(t) © 1-710) © 1 -qiit) © 0-7з0)
<71(7+1) = О’7о(О © 0^1(0 © 1-72(0 © 1'7з0)
7г(Т+1) = Г7оО) © 0-71(0 © 0-71(0 © 0-7з0)
7з0+1) = О-7о(О © 1-71(0 © 0-7г(0 © O-73O),
или в матричной форме:
eo+n=veo),
где
1 1 0
0 1 1
0 0 0
1 о о
Пример 1.3. Пусть
N= 4, Ф(х) = х4 + х3 + 1, Т = Ть к = 4.
Этой ситуации соответствует генератор, схема и диаграмма
состояний которого показаны на рис. 1.31.
Уравнения работы генератора имеют вид:
7оО+1) = 1-7о(О © 0-71(0 © 1-7г(0 © 1'7з(0
710+1) = 1-7о(О © l-7i(0 © 0-71(0 © 0-7з(0
72O+I) = О-7о(О © 1-71(0 ® 1-7г(0 © 0-7з(0
7з(Г+1) = О-7о(О © 0-71(0 © 1-7г(0 ® 1’7з(0,
или в матричной форме: <20+1) = V Q(f), где
0 1 1
1 0 0
1 1 0 ‘
0 1 1
Пусть Т= Т2, к = 1, F(x) - примитивный многочлен. Генерато-
ры, образующий многочлен которых имеет вид
Ф(х) = (х + l)F(x),
обладают свойством самоконтроля: при правильной работе уст-
ройства свертка по модулю для содержимого всех триггеров не
меняет своего значения.
50
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
•f----
|  1 000 I
| 1100 |
| 1010 I
I 0 1'11 1
| 0100 I
| 0 1'10 I
| ООН I
| 0010 I
। ‘в** 1 *-!
I I
| О 001 I
| 1001 I
| 0101 I
I 11'11 I
| 0000 I
Рис. 1.31. Генератор двоичной ^-последовательности, соответству-
ющий Ф(х) = х4 + х3 +1, Т = Тьк = 4; и его диаграмма состояний
Пример 1.4. Пусть
7V = 5,F(x)=x4 + x3 + 1, Т=Т2,к = 1,
Ф(х) = (х + 1)(х4 + X3 + 1} = X5 + X3 + X + 1.
Этой ситуации соответствует генератор, схема и диаграмма
состояний которого показаны на рис. 1.32.
Уравнение работы генератора имеет вид <20+1) = Т2 Q(t), где
о
о
о
о
о
о
О О
1 О
Т2 = (} 1
О 0 1 о
1
о
1
о
0 0 0 1 1
Уравнение самоконтроля
q^t) © q2(f) © <7з(О © q^f) © q5(f) = const.
Глава 1. Принципы построения и свойства генерлторов псевдослучайных последовательностей Я
4	4
1 IP 00 9. 1	| 11000 |
1 Q1000 1	1 01100 I
[ 001ooj	| ooiio |
l_ooo_ioj	|_00° i i |
1 00001 1	| 10100 |
1 i_oioi_J	| 01010 |
L 11 L1 U	| 00101 |
1 Lio.10— 1	[ 10111 |
L_ 0 1 1 0 1_|	l_i 11!.° 1
1 i .9 о 11 |	| 01111 |
1 niooj	| 10010 I
1 0111 ° 1	| 01001 I
| 0£ l 1 1_ ]	| 10001 1
[ 1 ° 1 1 о J	1 _!.11Q.1 1
[ 01011 1	| 11011 |
1			1	
4-	4
| 11001 |	I ooooo |
1	1
Рис. 1.32. Генератор двоичной последовательности с самоконтролем,
соответствующий Ф(х) = х5 + х3 + х +1, Т = Тг; и его диаграмма
состояний
1.4.4. Генераторы двоичных
последовательностей произвольной длины
Исключение запрещенного нулевого, состояния всех триггеров
генератора позволяет увеличить период формируемой последова-
тельности и сделать его максимально возможным, равным 2 ,
и повысить ее качество, так как вероятности появления 0 и 1 ста-
новятся равными 1/2. Последовательности длиной 2N называются
последовательностями де Брейна (De Bruijn). Уравнения работы
генератора последовательности длиной 2N при к = 1 и Т = Тх мо-
гут, например, иметь вид
________________ N
qQ (t + Y) = q0 (t) ql(t)-..  qN_2 (/) © £	(0 (mod 2)
i=l

92
Теория, применение и оценка качества генерАюров псевдослучайных последовательностей
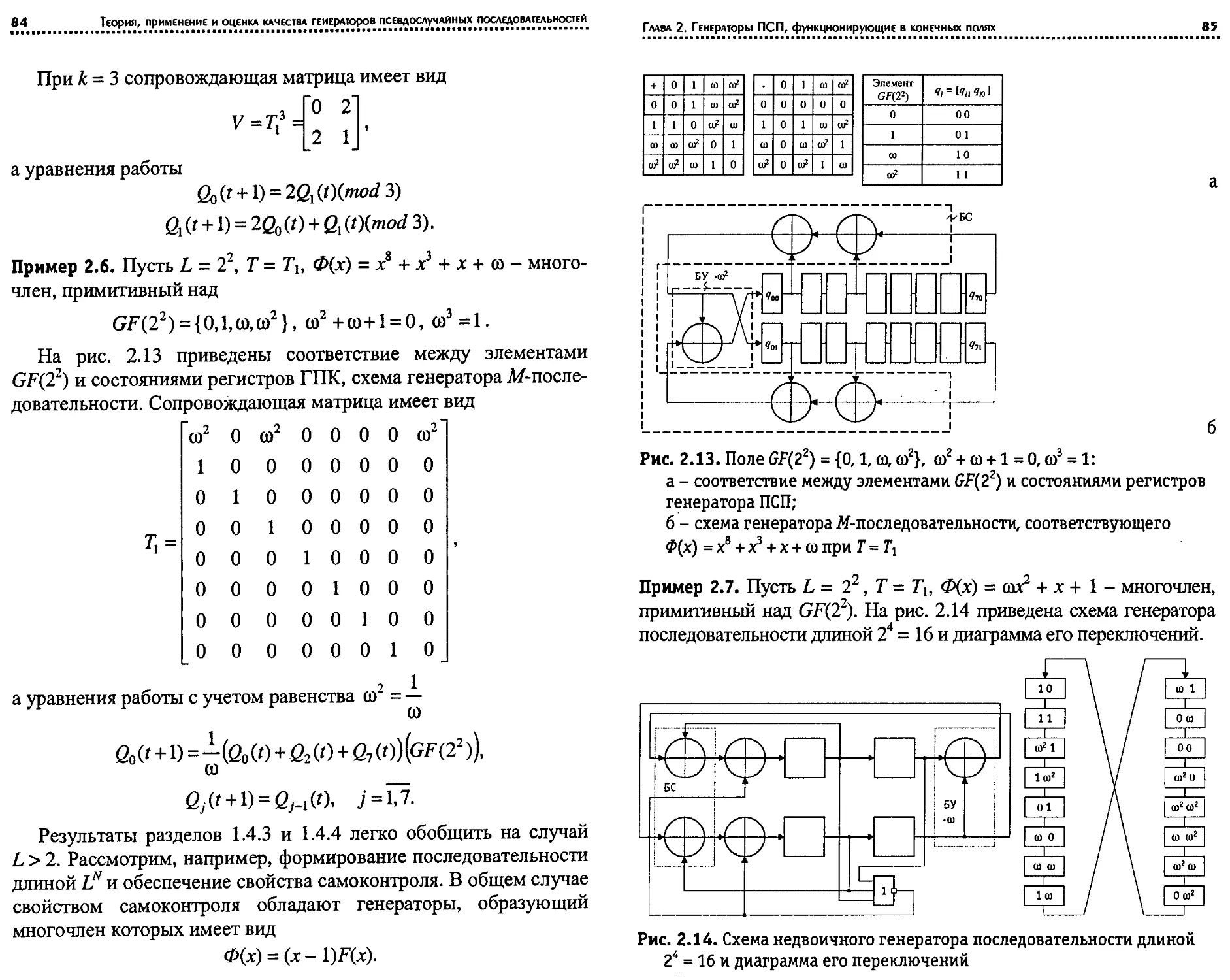
Пример 1.5. Пусть Ф(х) = х4 + х3 + 1, Т= Т\, к = 1. Схема генера-
тора периодической последовательности длиной 16 и диаграмма
его состояний приведены на рис. 1.33. Уравнения работы генера-
тора имеют вид
9о 0 +1) = 90 0) ’ 91W ’ 9г (') ® 9г (') ® 9з (О
9jO + 1) = 9j-iO)J = * 1> 2,3.
| 1000 I
| 0Ю0 I
| 0010 I
| 1001 I
| 1100 I
| 0110 I
I 1о'и I
| 0101 I
| 1010 I
I 11'01 I
I ч'10 I
I 411 |
I 01'11 I
| 0011 I
| oo'oi I
| 0000 I
Рис. 1.33. Четырехразрядный генератор последовательности де Брейна
Генератор последовательности произвольной длины 2N'1 < S <
<2N - 1 строится следующим образом. Выбирается примитивный
многочлен Ф(х) степени N. Фиксируется произвольное ненулевое
состояние Qo генератора. Моделируется t = 2N - S тактов работы
ГПК и определяется состояние Q,. Выполняется поразрядная опе-
рация XOR над кодами <21 и Qt. Единичные биты результата опре-
деляют номера тех триггеров ГПК, сигналы на D-входах которых
необходимо инвертировать, когда генератор находится в состоя-
Глава 1. Принципы построения и свойства генерлторов псевдослучайных последовательностей 57
нии Qo. Управляемые инверторы реализуются на дополнительных
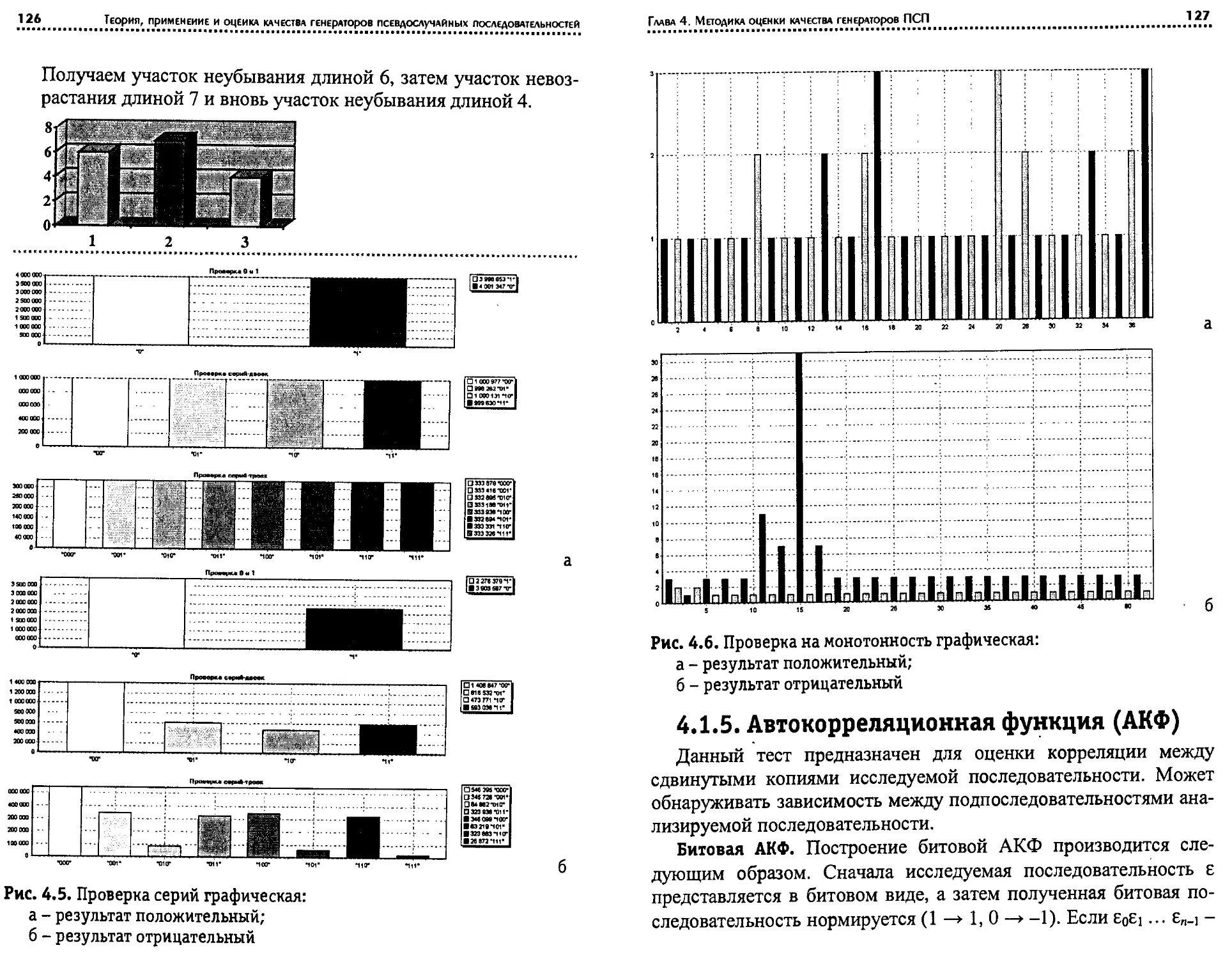
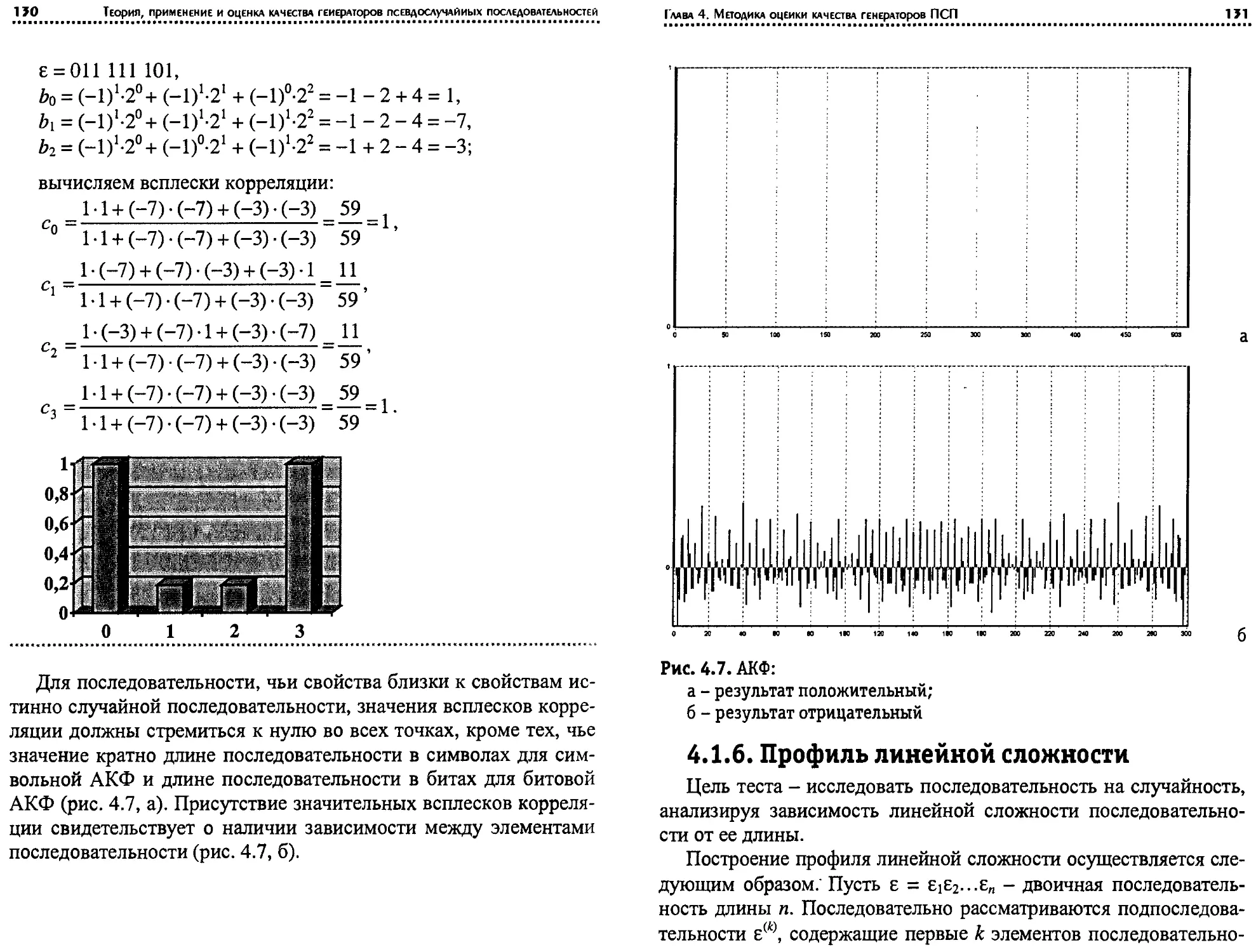
элементах XOR, число которых и место в схеме генератора опре-
деляются результатом операции <21 © Qi-
Пример 1.6. Пусть
Ф(х) = х4 + х3 + 1, Т= Т\,к = l,s= 10.
Выберем Qo = 0001. Тогда Qt = 1000, Qt = Q6 = 0110, <2i © <2t =
= 1110. Схема генератора периодической последовательности
длиной 10 и предпериодом длиной 6, а также диаграмма его со-
стояний приведены на рис. 1.34.
I 0000 |
I 1000 |
I 0100 |
I 0010 |
I 1001 |
I 1100 |
----►
''___
I 0110 |
I 1011 |
I 0101 |
I 1010 |
I 1101 |
Рис. 1.34. Схема генератора периодической последовательности
длиной 10 и предпериодом длиной б и диаграмма его состояний
Пример 1.7. Пусть
Ф(х)=х4 + х3 + 1, Т=Т\,к= 1.
На рис. 1.35 показано универсальное устройство, которое мо-
жет формировать последовательность любой длины, меньшей
или равной 16. Эта длина зависит от того, к каким входам управ-
ления режимом (УР) подключен выход изменения режима (ИР).
Так, например, если все входы УР подключены к шине лог. «0»,
формируемая последовательность имеет длину 16; если выход ИР
54
]ЕОРИЯ, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
подключен к первому входу УР, а оставшиеся входы управления
режимом к шине лог. «О», формируемая последовательность име-
ет длину 15 и предпериод длиной 1; если выход ИР подключен ко
второму входу УР, а оставшиеся входы управления режимом к
шине лог. «О», формируемая последовательность имеет длину 14
и предпериод длиной 2 и т. д.
Рис. 1.35. Схема четырехразрядного универсального генератора
двоичных последовательностей
1.4.5. Другие схемы генераторов ПСП
Генераторы ^-последовательностей, обладающие при боль-
ших значениях N практически идеальными статистическими ха-
рактеристиками, к сожалению, не являются непредсказуемыми.
Например, анализируя принцип формирования М-последователь-
ностей (рис. 1.36), можно сделать вывод, что, для того чтобы оп-
ределить характер обратных связей устройства разрядностью не
более N, иначе говоря найти коэффициенты а„ i = l,N, образую-
щего многочлена Ф(х), достаточно иметь фрагмент гаммы всего
лишь длиной 2N.
Пример 1.8. Пусть N < 4. Известен фрагмент последовательности
QiQt+ iQi+zQi+iQi+iQi+sQi+eQi+i 0 1 1110 10...,
полученный с выхода LFSR . Необходимо найти коэффициенты
ah i = 1,4, образующего многочлена Ф(х).
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей 99
На основе рис. 1.36 составим систему из 4 линейных уравнений:
Si+4 = aiQi+3 ® alQi+2 ® Язб|+1 ® aiQi
Qi+5 = alQt+4 ® alQi+3 ® Язб|+2 ® aiQi+l
Qi+й = aiQi+S ® aiQi+i ® fl30i+3 ® fl4(2i+2
б,+4 = а1б1+б © Я2б;+5 © азб<+4 ® a4Si+3’
подставляя в которую известные значения элементов последова-
тельности, получим
1 = аг ®а2 ©а3
О = fl] ©	®	© ^4
1 = а2 © а3 ® а4
О = Я] ©п3 ©а4.
М2
Рис. 1.36. Принцип формирования последовательности {QJ
$6
Теория, применение и оценка качества генердюров псевдослучайных последовательностей
Сложив первые два уравнения системы, найдем а4 = 1. Сложив
второе и третье уравнения, найдем af = 1. Сложив второе и чет-
вертое уравнения, найдем аг = 1. Наконец, подставив в первое
уравнение найденные значения а{ и аг, определим аз = 0. Таким
образом, заданный фрагмент последовательности получен с вы-
хода LFSR, образующий многочлен которого имеет вид
Ф(х) = х4 + х + I.
Рассмотрим схемотехнические приемы, повышающие крипто-
стойкость генераторов ПСП. Гамма может быть, например, ре-
зультатом действия функции усложнения, входными переменны-
ми для которой являются элементы последовательностей, форми-
руемых на выходах генераторов, в качестве последних могут ис-
пользоваться регистры сдвига как с линейными (LFSR), так и
нелинейными обратными связями (NLFSR). Простейшие примеры
NLFSR были уже рассмотрены выше. Выходы некоторых генера-
торов в общем случае могут управлять схемой синхронизации,
обеспечивающей формирование импульсов сдвига. Схема син-
хронизации может обеспечивать, например, работу генераторов
по принципу «stop-and-go», с разной частотой и т. п. Ключевой
информацией являются параметры схемы синхронизации и
функции усложнения, а также начальное заполнение генераторов.
При оценке качества подобных схем используется понятие ли-
нейной сложности выходной последовательности, под которой
понимается минимальная разрядность LFSR, на выходе которого
может быть сформирована точно такая же последовательность.
Однако независимая от ключа линейная сложность является не-
обходимым, но недостаточным условием получения качествен-
ной ПСП.
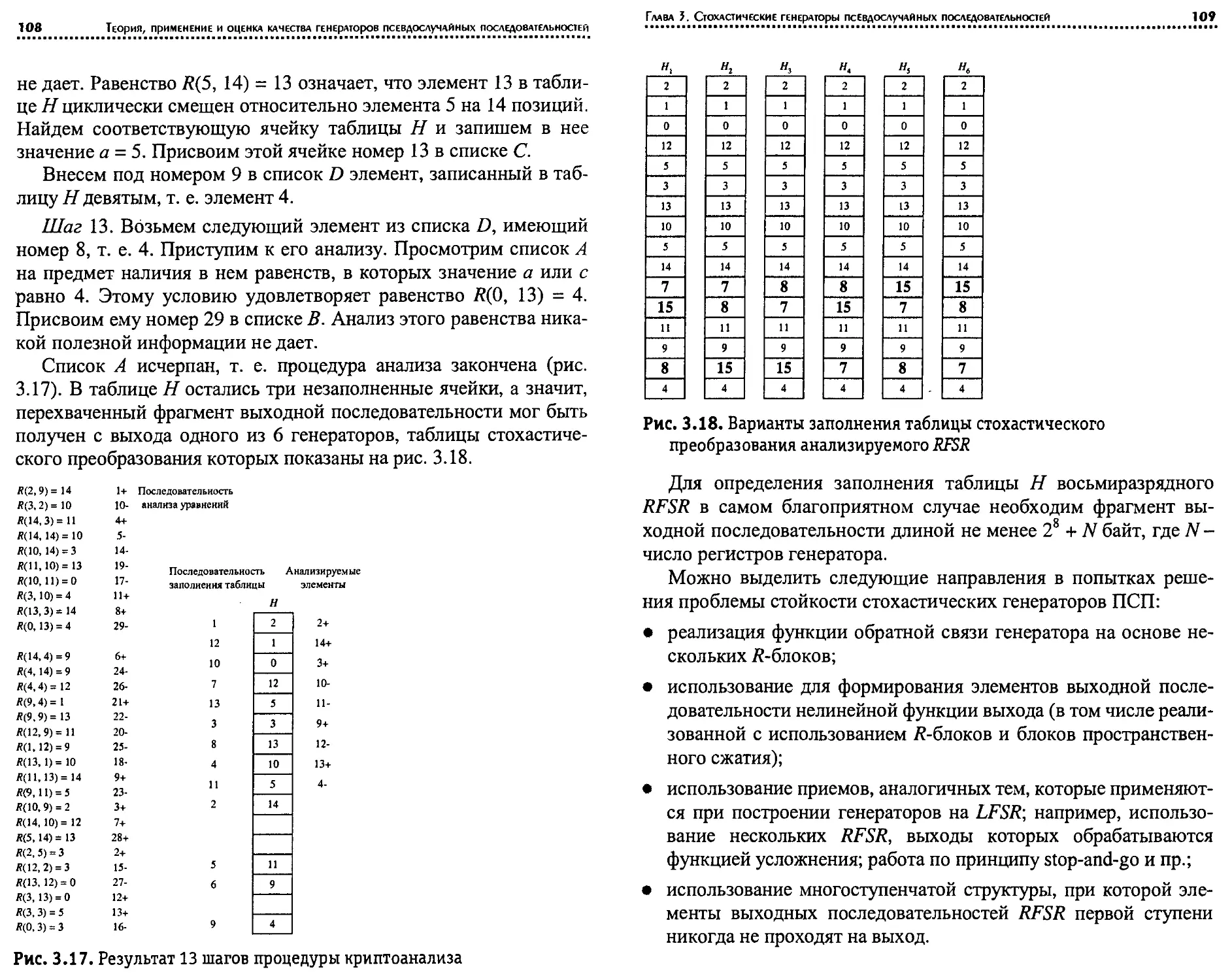
Рассмотрим некоторые наиболее известные схемы генерато-
ров на основе LFSR. Генератор Джиффи обеспечивает переме-
шивание двух последовательностей X] и хг с выходов LFSR 1 и 2
под управлением последовательности х3 с выхода LFSR 3. Пере-
мешивание осуществляется с помощью функции усложнения
F(x1, х2, Х3 ) = X] х3 + х2х3 =? х3 ® х{х2 © х2х3,
которая может быть реализована с помощью мультиплексора
2—^1, как показано на рис. 1.37.
Глава 1. Принципы построения и свойства генерлторов псевдослучайных последовательностей 57
В том случае, когда периоды S, последовательностей {5,(0}
попарно взаимно просты, период результирующей последова-
тельности у(Г) равен произведению SiS2Si- Функция F выдает на
выход информацию о состояниях LFSR 1 и 2, так как вероятность
совпадения элемента выходной последовательности со значением
xi или х2 равна 3/4, иначе говоря,
P(F(X] , х2, х3) = X]) = /’(F(x1, х2, х3) = х2) = 3/4.
Возможны другие варианты представленной схемы. Так, на-
пример, использование
F(X], х2, х3) = хгх3 © Х]Х2 © х2х3
позволяет получать последовательности с более высокой линей-
ной сложностью.
При формировании «-разрядной последовательности можно
добиться более эффективного перемешивания двух п-разрядных
ПСП за счет использования функции усложнения на основе п
одноразрядных мультиплексоров 2 —> 1.
В схеме генератора Д. Голлманна, в работе которого исполь-
зуется принцип «stop-and-go» (рис. 1.38), каждый генератор LFSR
i управляет синхронизацией двух последующих LFSR (i + 1) и
LFSR (1 + 2). Выход последнего LFSR является выходом генера-
тора. Если разрядность каждого LFSR равна N, линейная слож-
ность системы из т LFSR равна
^(2^-I)"1-1.
Криптографы советуют применять m > 15, а при равных зна-
чениях mN отдавать предпочтение варианту с большим числом
коротких LFSR, а не варианту с меньшим числом длинных LFSR.
Нория, применение и оценка качества генераторов псевдослучайных последовательностей
Рис. 1.38. Генератор Голлманна
Развитием описанной идеи является схема, предложенная
У. Дж. Чамберсом, одна ступень которой показана на рис. 1.39.
На вход ступени поступает последовательность М-разрядных
двоичных чисел. Несколько этих бит (к на рис. 1.39) управляет
сдвигом LFSR разрядности N. Например, при к = 2 предлагается в
зависимости от значения этих двух битов сдвигать LFSR на 1, 2,4
или 5 разрядов. В первой ступени 'движение LFSR равномерное.
Значение N одинаковое для всех ступеней, многочлены обратной
связи могут различаться. М выходов LFSR суммируется пораз-
рядно по модулю два со входным значением каскада и поступает
на вход 5-блока, выход которого и является выходом ступени.
Автором выбрано значение М = N. Для каскада из m ступеней
период достигает величины (2N - I)"1.
Рис. 1.39. Схема одной ступени каскада с неравномерным движением
Чамберса. СС - схема синхронизации
Сжимающий (shrinking) использует другую форму управления
синхронизацией. В схеме генератора, предложенного сотрудни-
ками IBM Д. Копперсмитом, X. Кравчиком и Й. Мансуром, ис-
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей 59
пользуются 2 LFSR. Тактовые импульсы поступают на оба LFSR.
На выход генератора проходят только те биты с выхода LFSR 2,
которым соответствует «1» на выходе LFSR 1. Пусть
с = c0cic2... -
последовательность с выхода LFSR 1,
b = ЬоЬ\Ьг--- -
последовательность с выхода LFSR 2. Результирующая последо-
вательность
Z = Z0Z1Z2— ~
включает в себя те биты bh для которых соответствующие, биты с,
равны «1». Остальные биты последовательности b игнорируются.
Иными словами, для всех j = О, 1,2,... имеем
где ij - позиция j-й «1» в последовательности с. Эта же идея мо-
жет быть применена к любой паре источников ПСП.
Пусть периоды последовательностей с и b равны соответст-
венно Sc и Sb, а разрядность соответствующих LFSR - Nc и /V*.
Авторами идеи было доказано следующее утверждение, справед-
ливое как для фиксированных, так и переменных точек съема
сигналов обратной связи. Если Sc и Sb имеют максимальную дли-
ну, а взаимно просты, т. е. (Sc, Sb) = 1 то сжатая последователь-
ность z имеет период
(2Nb -1)2^'*
и линейную сложность LC, удовлетворяющую условию
Nb-2Nc~1 <LC<Nb-2Nc~\
Недостатками сжимающего генератора являются понижение
скорости формирования последовательности по сравнению со
скоростью работы LFSR и. непостоянная скорость выдачи битов
выходной последовательности. Для решения этой проблемы
можно использовать буферизацию.
Очень эффективна с точки зрения производительности схема,
называемая аддитивным генератором (рис, 1.40). Самостоятель-
ного значения эти генераторы в силу своей криптографической
слабости не имеют, но могут использоваться в качестве строи-
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
тельных блоков при создании стойких генераторов ПСП. Генера-
тор состоит из N регистров разрядностью М каждый и сумматора
по модулю 2м. Начальным заполнением (ключом) генератора
является массив
Qo(P)Qi(P)-Qn-i(P)
Л/-битовых слов. Уравнения работы генератора имеют вид
Q0(t + l) = '^aiQi_l(t)mod2M,
где Qi(t) - состояние г-го регистра в момент времени t, а а(- - ко-
эффициенты двоичного прймитиваного многочлена Ф(х) степени
N. Начальное заполнение выбирается таким образом, чтобы хотя
бы в одном из регистров младший бит содержал «1». В этом слу-
чае младшие биты регистров образуют генератор двоичной
ЛГ-последовательности и период аддитивного генератора дости-
гает максимального значения 2м ~ l(2N - 1). Учитывая, что при
большом числе ненулевых коэффициентов Ф(х) быстродействие
схемы снижается, возможна модификация схемы генератора с
распределением двухвходовых блоков сложения по модулю 2м
между регистрами, как это имеет место в случае генераторов,
функционирующих в недвоичных полях GF(L).
Пусть, например, Ф(х) = х5 + х3 + 1. Тогда генератор формиру-
ет рекуррентную последовательность в соответствии с формулой
Qi=(Qi-5 + Qi_i)mod2M.
На рис. 1.41 показан суммирующий (summation) генератор, в
котором выходная последовательность суть результат действия
функции усложнения, реализованной с использованием дополни-
Глава 1. Принципы построения и свойства генераторов псевдослучайных последовательностей
61
тельной памяти т и сумматора SM. Совокупность сигналов с вы-
ходов LFSR прибавляется как целое число к содержимому допол-
нительной памяти т для получения суммы Q. Бит четности
Q mod 2 в качестве элемента гаммы поступает на вход устройст-
ва, а старшие биты LQ/2J записываются в память. Для анализа
формируемых ПСП необходим совершенно иной математический
аппарат, а именно арифметика р-адических (p-adic) чисел [6].
Рис. 1.41. Суммирующий генератор
1.5.	Структурная схема генератора
случайных последовательностей
Можно перечислить следующие принципы проектирования
качественного генератора случайных последовательностей (СП).
•	Простота встраивания в уже готовые системы.
•	Простота использования, позволяющая квалифицированному
программисту, даже не имеющему знаний в криптографии,
безопасно работать с ним.
•	Использование существующих сильных криптографических
примитивов.
На рис. 1.42 показана схема генератора, применяемая на прак-
тике [8]. В схеме используются два криптографических примити-
ва - хеш-функция в блоках хеширования и блочный шифр (в ре-
62
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
жимах OFB или Counter) в блоке генерации. Безопасность устрой-
ства определяется в первую очередь безопасностью этих крипто-
графических примитивов.
Рис. 1.42. Структурная схема генератора СП
Ключ, используемый функцией зашифрования блочного крип-
тоалгоритма, регулярно обновляется на основе текущего значе-
ния и информации, поступающей от источников энтропии (кла-
виатура, мышь, таймер, жесткие диСки и пр.). Информация с вы-
хода последних после преобразования в первом блоке хеширова-
ния собирается в накопителях. Задача блока хеширования не дать
противнику возможности предсказывать значения выборок из
накопителей, используемых для обновления ключа. При выклю-
чении питания желательно хранить часть внутреннего секретного
состояния блока генерации или ключ в энергонезависимой памя-
ти. Это позволит генератору при перезапуске оказаться в непред-
сказуемом состоянии. В промежутке между соседними обновле-
ниями ключа устройство суть генератор гаммы поточного режи-
ма блочного шифра.
Глава 1. Принципы построения н свойства генераторов псевдослучайных последовательностей
61
Синхронизацию работы всех блоков генератора, а также опре-
деление моментов инициирования процедуры обновления ключа
обеспечивает блок управления. Процедура обновления иниции-
руется при накоплении достаточного количества энтропии и воз-
никновении одного Из трех событий:
•	наступило время планового обновления ключа;
•	блок генерации оказался в «слабом» состоянии, из которого в
течение длительного времени самостоятельно не может выйти;
•	обнаружены нарушения статистической безопасности выход-
ной последовательности.
Функции блока оперативного и тестового контроля:
•	проверка работоспособности (методом сравнения с Эталоном)
устройства в заданные моменты времени (при включении пи-
тания, по запросу пользователя, периодическая и т. п.у,
•	анализ статистической безопасности формируемых фрагмен-
тов выходной последовательности, в том числе анализ корре-
ляции между соседними фрагментами;
•	анализ ключа и внутреннего состояния блока генерации на
предмет попадания в пространство «слабых» значений;
•	информирование блока управления о проблемах в работе бло-
ка генерации, например о необходимости обновления ключа.
64
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Литература к главе 1
1)	Брассар Ж. Современная криптология: Пер. с англ. М.: ПОЛИМЕД,
1999.
2)	Введение в криптографию / Под общ. ред. В. В. Ященко. М.:
МЦНМО, «ЧеРо», 1998.
3)	Винокуров А. Ю. ГОСТ не прост ... , а очень прост! // Монитор,
1995. № 1. С. 60-73.
4)	Зензин О. С., Иванов М. А. Стандарт криптографической защиты
XXI века - AES. Теория конечных полей / Под ред. М. А. Иванова.
М.: КУДИЦ-ОБРАЗ, 2002.
5)	Кнут Д. Искусство программирования для ЭВМ: В 3 т. 3-е изд. Т. 2.
Пер. с англ. М.: Мир, 1998.
6)	Поточные шифры. Результаты зарубежной открытой криптологии.
http://www.ssl.stu.neva.ru/psw/crypto.html.
7)	Daemen J., Rijmen V. AES Proposal: Rijndael. 1999.
8)	Kelsey J., Schneier B., Ferguson N. Yarrow-160: Notes on the Design
and Analysis of the Yarrow Cryptographic Pseudorandom Number
Generator. 2000.
9)	Menezes A., van Oorshot P., Vanstone S. Handbook of Applied
Cryptograthy. CRC Press, 1997.
10)	Schneier B. Applied cryptography, 2nd Edition, John Wiley & Sons
(1996). [Имеется перевод: Шнанер Б. Прикладная криптография.
http://ww w. ssl .stu.neva.ru/ps w/crypto .html.]
11)	Stahnke W. Primitive Binary Polinomials. Mathematics of Computation,
1973. V. 27. № 124. P. 977-980.
ГЛАВА 2
Генераторы ПСП,
функционирующие
в конечных полях
2.1.	Введение
Устройства, рассмотренные ранее в разделе 1.4.3, являются
простейшим частным случаем при L = 2 генераторов, функцио-
нирующих в конечных полях GF(L). При L > 2 генераторы фор-
мируют L-ричные последовательности, свойства которых качест-
венно отличаются от свойств двоичных последовательностей
с выходов LFSR.
2.2.	Основы теории конечных полей
Поле - это множество элементов, обладающее следующими
свойствами:
•	в нем определены операции сложения, вычитания, умножения
и деления;
•	для любых элементов поля а, (3 и у должны выполняться соот-
ношения (свойства ассоциативности, дистрибутивности и ком-
мутативности)
а + ₽ = ₽ + а, а(3 = Ра, а + (Р + у) = (а + Р) + у,
а(Ру) = (аР)у, а(Р + у) = ар + ау;
•	в поле должны существовать такие элементы 0, 1, -а и (для
а Ф 0) а"1, что
0 + а = а, а + (-а) = 0, 0а = 0, 1а = а, а(а-1) = 1;
ьь
Теория, применение и оценил качества генерлторов псевдослучайных последовательностей
•	все ненулевые элементы конечного поля могут быть представ-
лены в степени некоторого фиксированного элемента поля со,
называемого примитивным элементом.
Конечное поле содержит конечное число элементов. Поле из L
элементов обозначается GF(L) и называется полем Галуа в честь
первооткрывателя Эвариста Галуа (1811-1832).'
Простейшие поля получаются следующим образом. Пусть р -
простое число. Тогда целые числа 0, 1, 2, ...(р - 1) образуют
поле GF(p), при этом операции сложения, вычитания, умножения
и деления выполняются по модулю р. Более строго, GF(p) - это
поле классов вычетов по модулю р, т. е.
GF(p) = {0,1, 2,..., (р-1) },
где через 0 обозначаются все числа, кратные р,, через 1 - все чис-
ла, дающие при делении на р остаток 1, и т.-д. С учетом этого
вместо р - 1 можно писать - 1. Утверждение а = 0 в GF(p) озна-
чает, что а - 0 делится на р или что а сравнимо с 0 по модулю р,
т. е.	J
а = fi(mod р).
Поле, содержащее L = рп элементов, где р - простое число,
ап - натуральное, не может быть образовано из совокупности
целых чисел по модулю L. Например, в множестве классов выче-
тов по модулю 4 элемент 2 не имеет обратного, так как 2-2 = 0.
Таким образом, хотя это множество состоит из 4 элементов, оно
совсем не похоже на поле GF(L). Чтобы подчеркнуть это разли-
чие, обычно вместо GF(4) пишут GF(22).
Элементами поля из р" элементов являются все многочлены
степени не более и - 1 с коэффициентами из поля GF(p). Сложе-
ние в GF(pn) выполняется по обычным правилам сложения мно-
гочленов, при этом операции приведения подобных членов осу-
ществляются по модулю р. Многочлен с коэффициентами из
GF(p} (т. е. многочлен над полем GF(p~)'), не являющийся произве-
дением двух многочленов меньшей степени, называется неприво-
димым. Примитивный многочлен автоматически является непри-
водимым. Выберем фиксированный неприводимый многочлен
ф(х) степени и. Тогда произведение двух элементов поля получа-
ется в результате их перемножения с последующим взятием ос-
Глава 2. Генерлторы ПСП, функционирующие в конечных полях
67
татка после деления на ф(х). Таким образом, поле GF(pn) можно
представить как поле классов эквивалентности многочленов над
GF(p). Два таких многочлена объявляются эквивалентными, если
их разность делится на ф(х). Конечные поля порядка рп сущест-
вуют для всех простых р и всех натуральных п.
Пример 2.1. Рассмотрим
GF(5) = {0,1,2, 3,4}.
Типичные операции сложения, вычитания, умножения и деле-
ния в этом поле выглядят так:
2 + 4 = 6 = 1 mod 5,
1 -4 = -3 = 0-3 = (5 -3) mod5 = 2,
4-2 = 8 = 3 mod 5,
3 _ (0 + 3) _ (5 + 3) mod 5 _
2" 2	2	"
Все ненулевые элементы этого поля можно представить в виде
степени 2 или 3, т. е. 2 и 3 - примитивные элементы GF(5):
2° =1, 21 =2 , 22=4, 23=3;
3° =1, З1 =3, 32 = 4, З3=2.
Пример 2.2. Пусть
р = 2, п = 4, ф(х) = х4 + х + 1
- примитивный над GF(2). Элементы поля GF(2i) имеют вид
0,1,х, х + 1,... ,х3 + х2 + х+ 1.
Так как ф(х) - примитивный, ему соответствует устройство,
диаграмма состояний которого состоит из цикла максимальной
длины 24 - 1 и одного тривиального цикла, включающего состоя-
ние 0000, переходящее само в себя (рис. 2.1). Таким образом, в
качестве со можно взять корень ф(х), а устройство, для которого
ф(х) = х4 + х + 1 является характеристическим многочленом, объ-
явить генератором ненулевых элементов поля. В результате соот-
ветствие между различными представлениями элементов поля
имеет вид, представленный на рис. 2.2. Состояния генератора
определяют список элементов GF(24) в порядке возрастания сте-
пеней со, т. е. один такт работы устройства, соответствующего
68
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
характеристическому многочлену ср(х), суть умножение текущего
состояния устройства на со = х.
Типичные операции сложения, умножения и деления в поле
GF(24) в рассматриваемом случае выглядят следующим образом:
(х3 + х2 + 1) + (х2 + Х+ 1) = х3 + х,
или
1101+0111 = 1010;
(х + 1)(х3 + х) = со4  со9 = со13 = х3 + X2 + 1,
или
(х + 1)(х3 + х) = х4 + х3 + х2 + x(mod ср(х)) = х3 + х2 + 1,
или
0011-1010= 1101;
(X2 + х + 1): (х3 + х2) = со10 : со6 = со4 = х + 1,
или
0111:1100 = 0011.
Рис. 2.1. LFSR, соответствующий характеристическому многочлену
ср(х) = х4 + х +1, и его диаграмма состояний
Глава 2. Генераторы ПСП, функционирующие в конечных полях
69
0 0 0 1 = 1	= (!>”= 1
Рис. 2.2. Соответствие между различными формами представления
элементов поля Gf(24)
Пример 2.3. Пусть
р = 2, п = 4, ф(х) = х4 + х3 + х2 + х + 1
- неприводимый над GF(2).
На рис. 2.3 показано устройство, соответствующее характери-
стическому многочлену <р(х) = х4 + х3 + х2 + х + 1. Диаграмма со-
стояний устройства состоит из трех циклов длиной 5 и одного
тривиального цикла, а значит, данное устройство, один такт ко-
торого суть умножение на х по модулю <р(х), не может использо-
ваться в качестве генератора элементов поля. Такая ситуация
всегда имеет место, когда ф(х) - неприводимый. Определим
структуру устройства (генератора элементов поля); позволяюще-
го сопоставить каждому ненулевому элементу поля соответст-
вующую степень примитивного элемента.
70
Теория, ПРИМЕНЕНИЕ Н ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Рис. 2.3. LFSR, соответствующий характеристическому многочлену
ср(х) = х4 + х3 + х2 + х +1, и его диаграмма состояний
Имеем:
<р(х + 1) = (х + 1 )4 + (х + 1 )2 + (х + 1 )2 + (х + 1) + 1 =
= (х4+ 1) + (х3+х2 + х+ 1) + (х2+ 1) + (х+ 1) + 1 = х4 + х3 + 1 = ф(х).
ф(х) - примитивный многочлен, а значит, соответствие меж-
ду различными формами представления элементов GF(24) мож-
но получить, моделируя работу устройства, показанного на
рис. 2.4. Один такт работы этого устройства суть умножение на
со = х+ 1.
Глава 2. Генераторы ПСП, Функционирующие в конечных полях
71
ООО
1 -	0	0	° 1 1	
1 	1	0 0		СО 1
1 1	0	1	0	0)2!
1 1	1	1	1	(Я3 |
1 0	1	1	1	О)4 |
1 1	0	1	1	о/ I
I	0_	0 0		1	О)6 |
L1	1	1	0	О)7 |
1 1	0 0		1	О)8 |
|_ 0 0		1	0	 ш’ |
1 0 0		1	1	а>‘°|
1 1	1	0	1	О)11 |
1 0	1	0 0		О)12 |
1 0	1	1	0	0)13|
1 0	1	0	1	О)14 |
О 0 |
Рис. 2.4. Генератор элементов поля ff£(24)
Пример 2.4. Пусть р = 3, п = 3, ф(х) = 2х3 + х2 + х+1- неприводи-
мый над GF(3). Ф(х) = х3 + х2 + х + 2, а значит, соответствующий
троичный генератор имеет вид, показанный на рис. 2.5, а. Эле-
менты поля GF(33) имеют вид
0,1, 2, х, х + 1, х + 2, 2х, 2х + 1, 2х + 2,..., 2х2 + 2х + 2.
Характеристический многочлен ф(х) не является примитивным
над GF(3), в результате диаграмма состояний устройства состоит
из двух кодовых колец по 13 состояний в каждом и одного вырож-
денного тривиального цикла, соответствующего состоянию ООО,
переходящему само в себя.
Имеем:
Ф(х + 2) = (х + 2)3 +(х + 2)2 + (х + 2) + 2 = х3 +х2 + 2х + 1 = Ф(х).
72
Теория, применение и оценка качества генердторов псевдослучайных последовательностей
Ф(х) является примитивным над GF(3), а значит, в качестве
генератора элементов поля GF(33) можно взять устройство, такт
работы которого эквивалентен умножению на х + 2 по модулю
ср(х). Схема генератора элементов поля, соответствующего урав-
нениям
Q0(t +1) = 2<2О(Т) + Q2(t)(mod 3),
£(' + 1) = бо« + 2^(0 + Q^t)(mod 3),
с2а+1)=С1Ют
показана на рис. 2.5, б. В матричной форме логика работы уст-
ройства может быть записана следующим образом:
са+1)=г2с(о+2б(о,
т. е. операция умножения на со может быть описана матрицей
2 0 1
1 2 1
О 1 О
Состояния генератора элементов поля определяют список
элементов GF(33), которые в виде последовательных степеней со
и в виде коэффициентов (при х°, х1, х2) троичных многочленов
степени не более 2 показаны на рис. 2.5, в.
Типичные операции сложения, умножения и деления выглядят
следующим образом:
(х2 + х + 2) + (2х2 + х) = 2х +2,
или
112 + 210 = 022;
(х2 + х + 1) (2х) = со2 • со5 = со7 = х2 + х +2,
или
(х2 + х + 1) (2х) = 2х3 + 2Х2 + 2x(mod ср(х)) = х2 + х + 2,
или
111 -200= 112;
(х2): (2х2 + х) = (О10 : (О6 = (О4 = х2 + 1,
или
100:210= 101.
Глава 2. Генераторы ПСП, Функционирующие в конечных полях
7?
Конечные поля порядка рп существуют для всех простых р
и всех натуральных п.
1 0 0	1
2 1 0	0)
1 1 1	СО2
0 1 1	(О3
1 0 1	со4
0 2 0	(О5
0 1 2	со6
2 1 1	со7
2 2 1	со8
2 1 2	со’
0 0 1	со10
1 1 0	со11
2 0 1	со12
I о о о о |
2 0 0	со13
1 2 0	со14
2 2 2	(О15
0 2 2	СО16
2 0 2	(О17
0 1 0	СО18
0 2 1	со1’
1 2 2	10ю
1 1 2	(О21
1 2 1	id22
0 0 2	(О23
2 2 0	(О24
1 0 2	10“
а
б
в
Рис. 2.5. Поле Gf(33):
а - устройство, соответствующее Ф(х) = х3 + хг + х+2;
б - генератор элементов поля GF(33);
в - диаграмма состояний генератора элементов поля GF(33)
2.3. Сложение и умножение в поле GF(2n)
Элементами поля GF(2”) являются двоичные многочлены сте-
пени меньшей п, которые могут быть заданы строкой своих ко-
эффициентов, т. е. в виде «-разрядных двоичных кодов.
Сложение в поле GF(2") - это обычная операция сложения
многочленов с использованием операции XOR при приведении
подобных членов; или операция поразрядного XOR, если элемен-
ты поля представлены в виде строки коэффициентов соответст-
74
Теория, ПРИМЕНЕНИЕ Н ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
вующих многочленов. Например, в поле GF(28), элементами ко-
торого являются двоичные многочлены, степень которых меньше
восьми, байту 01010111 ({57} в шестнадцатеричной форме) соот-
ветствует многочлен
Х^ + X4 + X2 + X + 1.
Пример выполнения сложения в поле GF(28):
{57}+ {83} = {04},
так как
(хб + х4 + X2 + х + 1) + (х7 + X + 1) = X7 + X6 + X4 + X2,
или
01010111+10000011=11010100.
В конечном поле для любого ненулевого элемента а сущест-
вует обратный аддитивный элемент - а, при этом а + (-а) = 0.
В GF(2") справедливо а + а = 0, т. е. каждый ненулевой элемент
является своей собственной аддитивной инверсией.
В конечном поле для любого ненулевого элемента а существу-
ет обратный мультипликативный элемент а'1, при этом аа-1 = 1.
Умножение в поле GF(2") - это обычная операция умножения
многочленов со взятием результата по модулю некоторого не-
приводимого двоичного многочлена ф(х) n-й степени и с исполь-
зованием операции XQR при приведении подобных членов. Ум-
ножение в GF(2”) также можно выполнять, рассматривая ненуле-
вые элементы поля как степени некоторого примитивного эле-
мента со.
Программная реализация операции умножения двух элемен-
тов а и Р поля GF(2”) может быть выполнена двумя способами:
табличным и вычислением результата аР «на лету».
Если элементы поля а и Р представлены в виде степени при-
митивного элемента, т.е.
а = С1)'иР = йУ,
то их произведение аР может быть вычислено по формуле
ар =
Именно этот факт используется при реализации умножения
табличным способом. Формируются два массива Elem и Addr.
Первый массив состоит из 2” - 1 ненулевых элементов поля
Глава 2. Генераторы ПСП, Функционирующие в конечных полях
75
(«-разрядных двоичных кодов), расположенных в порядке воз-
растания степеней примитивного элемента. Например, содержи-
мое ячейки массива Elem с адресом 0 равно coQ= 1, т. е.
Elem [0] = £0°;
содержимое ячейки массива Elem с адресом 1 равно со1 = со, т. е.
Elem [1] = (!)' ит. д.,
содержимое ячейки массива Elem с адресом i равно со1, т. е.
Elem [i] = со1; где I = 0, (2” - 2).
Второй массив формируется для ускорения поиска нужного
элемента в массиве Elem, в каждой ячейке массива Addr с адре-
сом j содержится адрес элемента поля j в массиве Elem,
j =1,(2"-1),т. е.
Elem[i\ = а <=> AcZcZr[a] = i, ае GF(2"), а Ф 0.
Процедура определения результата оф умножения двух эле-
ментов поля
a = со'и Р = со7
с использованием массивов Elem и Addr основана на нахождении
в массиве Elem элемента а и считывании результата умножения
из ячейки массива Elem, циклически смещенной в сторону стар-
ших адресов относительно ячейки, содержащей а, на j позиций,
т. е.
aP = Elem [(i + j) mod 2” -1] = Elem [(АйИг[а] + AtZdrfp]) mod 2" - 1].
Рассмотрим поле GF(24), порожденное многочленом
cp(x) = х4 + х + 1. На рис. 2.6 показан пример умножения двух эле-
ментов поля а = 0111иР = 0010:
0111-0010=1010.
На рис. 2.7 показан пример умножения двух элементов поля a
= 1101 ир = 0011:
1101-0011 = 0010.
76
Теория, применение и оценка качества генерАторов псевдослучайных последовательностей
Addr	Addr	Elem
о X			
1	0 0 0 0		
2	0	0	0 1
3	0	1	0 0
4	0	0	1 0
5	1	0	0 0
б	0	1	0 1
7	1	0	1 0
8	0	0	1 1
9	1	1	1 0
10	1	0	0 1
11	0	1	1 1
12	0	1	1 0
13	1	1	0 1
14	1	0	1 1
15	1	1	0 0
0	
1	0 0 0 0
2	0 0 0 1
3	0 10 0
4	0 0 10
5	10 0 0
6	0 10 1
7	10 10
8	0 0 11
9	1110
10	10 0 1
11	0 111
12	0 110
13	110 1
14	10 11
15	110 0
mod 15
2
2
_2
2
4_
_5
£
7_
2
2
10
и
12
13
14
0 0 0 1
0 0 10
0 10 0
10 0 0
0 0 11
0 110
110 0
10 11
0 10 1
10 10
0 111
1110
1111
110 1
10 0 1
9
Рис. 2.6. Пример умножения двух элементов поля GF(24)
Addr	Addr
0	3X1
1	0 0 0 0
2	0 0 0 1
3	0 10 0
4	0 0 10
5	10 0 0
6	0 10 1
7	10 10
8	0 0 11
9	1110
10	10 0 1
11	0 111
12	0 110
13	110 1
14	10 11
15	110 0
0	
1	0 0 0 0
2	0 0 0 1
3	0 10 0
4	0 0 10
5	10 0 0
6	0 10 1
7	10 10
8	0 0 11
9	1110
10	10 0 1
11	0 111
12	0 110
13	110 1
14	10 11
15	110 0
Elem
0	0 0 0 1
1	0 0 10
2	0 10 0
3	10 0 0
4	0 0 11
5	0 110
6	110 0
7	10 11
8	0 10 1
9	10 10
10	0 111
11	1110
12	1111
13	110 1
14	10 0 1
Рис. 2.7. Пример умножения двух элементов поля 6Р(24)
Пусть, например, для построения поля GF(2S) выбран
ф(х) = х8 + х4 + х3 + х + 1
- неприводимый многочлен показателя 51. Диаграмма состояний
соответствующего ему устройства (рис. 2.8, а), один такт работы
которого суть умножение на х по модулю ср (х), имеет 5 кодовых
колец по 51 состоянию в каждом и один вырожденный тривиаль-
ный цикл, соответствующий состоянию {00} (hex), переходяще-
му самому в себя. Определим структуру устройства (генератора
Глава 2. Генераторы ПСП, функционирующие в конечных полях
77
элементов поля), позволяющего сопоставить каждому ненулевому
элементу поля соответствующую степень примитивного элемента.
а
Рис. 2.8. Поле (Щ28):
а - LFSR, соответствующий характеристическому многочлену
ср(х) = х8 + х4 + х3 + х +1;
б - генератор элементов GF(28)
Имеем:
ср(х +1) = (х +1)8 + (х +1)4 + (х + I)3 + (х + 1) + 1 =
= (х8 +1) + (х4 +1) + (х3 + х1 2 + X +1) + (х + 1) +1 =
= х8 + х4 + х3 + X2 +1 = ф(х).
ф(х) - примитивный многочлен, а значит, соответствие между
различными формами представления элементов GF(28) можно
получить, моделируя работу устройства, показанного на рис. 2.8, б:
0 000000 1- {01} (со°=1)
000 0001 1 - {03} (со)
00000 10 1-{05} (со2)
00001 1 1 1 - {Of} (со3)
0 001 0 00 1-{11} (со4)
001 100 1 1 - {33} (со5)
0 1 0 1 0 1 0 1 - {55} (со6)
1 1 1 1 1 1 1 1 - {ff} (со7)
000 1 1 0 1 0-{1а} (со8)
001011 1 0- {2е} (со9)
1 1 1 1 0 1 1 l-{f7} (со25)
00000010 - {02} (со26)
Глава 2. Генераторы ПСП, функционирующие в конечных полях	;	79
?8	Теория, применение и оценка качества геиерАЮров псевдослучайных последовательностей
000001 1 О-{06} (со27)
1 10001 1 1-{с7} (со252)
0 10 1001 0-{52} (со253)
1 1 1 101 1 0-{f6} (со254)
00000001-{01} (со255 = 1).
Пример выполнения операции умножения в рассматриваемом
поле:
(х6 + х4 + х2 + х + 1) (х7 + х + 1) =
= х13 + х11 + х9 + х8 + хб + х5 + х4 + х3 + 1 =
= (х7 + х6 + 1) mod <р(х),
или
СО98.(О8О=(О178,
а значит,
{57}{83} = {с1}.
В GF(28) справедливо
со255 = 1,
а значит, ненулевые элементы со1 и оУ (т Ф j) являются взаимно
обратными тогда и только тогда, когда
i+j = 255.
Например,
со4со251 = со255,
т. е.
{11}-{Ь4} = 1,
или
(х4 + 1) (х7 4-х5 + х4 + х2) = 1.
Умножая произвольный многочлен
а(х) = а7х7 + а6хб + а5х5 + а4х4 + а3х3 + а2х2 + atx + а0
на х, получим в общем случае многочлен 8-й степени
а7х8 + а6х7 + д5х6 + а4х5 + а3х4 + а2х3 + Д]Х2 + аох.
Если а7 = 0, мы сразу получаем результат умножения; если
«7=1, необходимо взять результат по модулю <р(х), что в рас-
сматриваемой ситуации, очевидно, эквивалентйо вычитанию из
результата <р(х). Таким образом, умножение а(х) на х на байтовом
уровне - это либо результат циклического сдвига в сторону
старших разрядов байта
(а7д6а5а4а3а2а1ао)»
если а7 = 0; либо поразрядный XOR результата циклического
сдвига байта
( а1 аб а5 а4 а3 а2 а\ ао )
в сторону старших разрядов с вектором обратной связи {1b}
(рис. 2.8, а), если а7 1.
Пусть
xTime(a)
- операция умножения элемента поля а на х. Тогда умножение на
х" можно осуществить путем n-кратного повторения операции
xTime(a).
В результате произведение двух элементов поля {57} и {13}
можно вычислить следующим образом:
{57}-{02} = xTime(5T) = {ае},
{57} • {04} = xTime(ae) = {47},
{57}-{08} =xTime(47)= {8е},
{57}-{ 10} = xT/zne(8e) = {07},
{57}-{ 13} = {57}-({01}Ф{02}Ф{10}) = {57}®{ae}®{07}={fe}.
2.4. Устройства, функционирующие
в GF(£), L > 2
Пусть L > 2 - степень простого числа, GF(L) - поле Галуа из L
элементов. Общий вид генератора L-ричных последовательно-
стей, соответствующего уравнению
<2(^+1) =/т
где Q(t') и Q(t+1) - состояния генератора соответственно в момен-
ты времени г и г + 1 (до и после прихода синхроимпульса); Т -
квадратная матрица порядка N вида
80
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
£Т.“..?;.^Е“ЕрМ?.р“.95'П' Функционирующие в конечных полях
81
aN-l	aN
а0	а0
О	О
О	О
1	0
«о
aN-l
ао
«О
_^L
«о .
N - степень образующего многочлена
Ф(х) = У^а,х', а0 Ф 0, а,€ GF(L), i = O,N,
i=0
к - натуральное, показан на рис. 2.9, где gi(0 - состояние i-ro
элемента памяти (\log2 L[ - разрядного регистра) генератора в
момент времени t; Qt(t) е GF(L).
При к = 1 генератор имеет вид, показанный на рис. 2.10 (Т = Ti)
или рис. 2.11 (Т = Т2).
Величина, на которую происходит умножение в каждом блоке
умножения (БУ), определяется соответствующим коэффициентом
Ду е GF(L) сопровождающей матрицы V = 7* (i = 0,(N-1),
j = 0,(У -1)). Если «у = 0, это эквивалентно отсутствию связи
между выходом i-ro элемента памяти ГПК и входом j-ro блока
сложения (БС). Если Оу = 1, это эквивалентно наличию связи меж-
ду выходом i-ro элемента памяти генератора и входом j-ro блока
сложения. При L = 2Л блоки сложения и умножения в поле GF(2")
реализуются на сумматорах по модулю два.
Рис. 2.9. Устройство, функционирующее в поле GF(i), - генератор
I-ричных последовательностей, соответствующий уравнению
Q(t +1) = Z*Q(t)
БУ
Рис. 2.10. Схема генератора при к =1, Т=
Рис. 2.11. Схема генератора при к =1, Т=Тг
82
Теория, применение н оценил качества генерлторов псевдослучайных последовательностей
Максимально возможное число состояний устройства, а зна-
чит, и максимально возможная длина формируемой L-ричной
последовательности, снимаемой с выхода любого из элементов
памяти, равны LN - 1. В этом случае диаграмма состояний генера-
тора состоит из одного тривиального цикла и цикла максималь-
ной длины LN - 1.
Многочлен Ф(х) степени У с коэффициентами из GF(L) назы-
вается неприводимым, если он не делится ни на один другой мно-
гочлен степени, меньшей У и большей 0. Многочлен Ф(х) степе-
ни N с коэффициентами из GF(L) называется примитивным, если
он не делит нацело ни один многочлен вида xs - 1, где S < LN - 1.
Число примитивных многочленов степени N равно
<P(L"-D
N ’
где ф(«) - функция Эйлера (число натуральных чисел, меньших п
и взаимно простых си).
Пусть Ф(х) - образующий многочлен степени N, примитивный
над GF(L), тогда справедливо следующее утверждение.
Свойство 2.1. Формируемая последовательность имеет макси-
мальный период S = Ln - 1 тогда и только тогда, когда наиболь-
ший общий делитель чисел S и к равен 1 (т. е. S и к взаимно про-
сты).
Пример 2.5. Пусть L = 3, Т = Тх, Ф(х) = х2 + х + 2 - многочлен,
примитивный над GF(3). На рис. 2.12 приведены правила сложе-
ния и умножения по модулю 3, соответствие между элементами
GF(3) и состояниями регистров генератора ПСП, схемы генера-
торов и диаграммы состояний при к = 1 и к = 3. Последователь-
ность переключения устройства при к = 1 показана сплошной
линией, при к = 3 - пунктирной. При приведенном соответствии
между элементами GF(3) и состояниями регистров генератора
умножение на 2 по модулю 3 эквивалентно простой передаче
сигналов с первого и второго входов БУ соответственно на вто-
рой и первый выходы блока. При к = 1 сопровождающая матрица
имеет вид
Глава 2. Генерлторы ПСП, функционирующие в конечных полях
87
а уравнения работы
Qo(t +1) = Q0(t) + Qx{t)(mod 3)
6ia+D=<^(/)-
Элемент GF(3)	е,=[»„«„]
0	00
1	01
2	10
a
6
г
Рис. 2.12. Поле GF(3):
а - правила сложения и умножения по модулю 3, соответствие между
элементами £?F(3) и состояниями регистров генератора ПСП;
б и в - схемы генераторов троичной /^-последовательности (Т = Тх,
Ф(х) = х2 + х + 2) соответственно при к = 1 и к = 3;
г - диаграммы состояний генераторов
84
Теория, применение и оценка качества геиерлторов псевдослучайных последовательностей
При к = 3 сопровождающая матрица имеет вид
з Г° 21
v=r3 =
L2 к
а уравнения работы
е0(Т + 1) = 2е1(Г)(/п^З)
е1(т+1)=2ео(о+е1(о(^з).
Пример 2.6. Пусть L = 22, Т = Tit Ф(х) = xs+x3+x + (a - много-
член, примитивный над
GF(22) = {0,1,со,со2}, со2+(0+1 = 0, (о3=1.
На рис. 2.13 приведены соответствие между элементами
GF(22~) и состояниями регистров ГПК, схема генератора ЛАпосле-
довательности. Сопровождающая матрица имеет вид
со2	0	со2	0	0	0	0	(о2
1	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0
т= 0 0 100000
’"о	0	0	1000	о’
0	0	0	0	1	0	0	0
0	0	0	0	0	1	0	0
0	0	0	0	0	0	1	0
-	2	1
а уравнения работы с учетом равенства со = —
(О
Q0(t +1) = -(е0(0 + Q2 (0 + 67 (C)(GF(22)),
со
еуа+1)=бл1(о. ;=й-
Результаты разделов 1.4.3 и 1.4.4 легко обобщить на случай
L > 2. Рассмотрим, например, формирование последовательности
длиной Ln и обеспечение свойства самоконтроля. В общем случае
свойством самоконтроля обладают генераторы, образующий
многочлен которых имеет вид
Ф(х) = (х-l)F(x).
Глава 2. Генерлторы ПСП, функционирующие в конечных полях
8$
Рис. 2.13. Поле GF(22) = {0,1, со, со2}, <в2 + +1 = 0, о? = 1:
а - соответствие между элементами GF(22) и состояниями регистров
генератора ПСП;
б - схема генератора ^-последовательности, соответствующего
Ф(х) =х8 + х3 + х + юпри Г=Гг
а
б
Пример 2.7. Пусть L = 22, Т = Тх, Ф(х) = сох2 + х + 1 - многочлен,
примитивный над GF(22). На рис. 2.14 приведена схема генератора
последовательности длиной 24 = 16 и диаграмма его переключений.
Рис. 2.14. Схема недвоичного генератора последовательности длиной
24 = 16 и диаграмма его переключений
86
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Пример 2.8. Пусть
L = 22, Т = Тг, Ф(х) = (х + 1) F(x),
F(x) = сох8 + х7 + х5 + 1 - многочлен, примитивный над GF(22). На
рис. 2.15 приведена схема ГПК с самоконтролем с учетом того,
что
Ф(х) = (ОХ9 + (О2Х8 + X7 + X6 + X5 + X + 1.
Рис. 2.15. Схема недвоичного ГПК с самоконтролем
Уравнение самоконтроля:
9
(t)(mod 2) = const, i = 0,1.
;=i
2.5.	Свойства генераторов
^-последовательностей
Основные свойства и структурные особенности последова-
тельностей максимальной длины [7, 8]:
1)	каждому многочлену Ф(х) степени N, примитивному над
GF(p), соответствует множество О(Ф(х)) из pN - 1 сдвинутых
копий ^/-последовательности;
2)	сумма по модулю р двух ^/-последовательностей из П(Ф(х))
также является .^-последовательностью из О(Ф(х));
3)	если
б= QoQiQ2"Qpn-2
- это ^/-последовательность из £2(Ф(х)), а а - ненулевой эле-
мент поля GF(p), то а<2 также является .^-последователь-
ностью из £2(Ф(х));
Глава 2. Генераторы ПСП, Функционирующие в конечных полях
87
4)	в ^/-последовательности 0 встречается pN 1 - 1 раз, а каждый
ненулевой элемент поля GF(p) - pN~x раз;
5)	^/-последовательность имеет следующую структуру:
Q = Ь, ыЬ, (й2Ь,(j)p~2b,
где b - последовательность длины
(/-1)/(р-1),
а со — примитивный элемент поля GF(p), т. е. период Л/-по-
следовательности всегда можно разделить на (р - 1) частей,
причем элементы каждой последующей можно получить пу-
тем умножения соответствующих элементов предыдущей час-
ти на со;
6)	пусть а - ненулевой элемент поля GF(p\ па(1) и «о(0 - число
серий длиной I из элемента а и из Z нулей соответственно, то-
гда
па(1) = л0(1) = рм-3(р-1)2,
па(2) = «0(2) = рл,-4(р-I)2,...,
ла(А-2) = п0(А-2) = (р-1)2,
na(N-l) = p-2,
n0(N-l) = p-l,
zia(2V) = l, /io(2V) = O;
7)	в ^/-последовательности имеется равное число серий из эле-
ментов поля GF(p), это число равно
PN-2/(p-iy,
8)	частота появления символа а за период ^/-последовательности
равна
PN~1I(P-1),
частота появления нуля равна
(pN~x - l)/(pN - 1).
Автокорреляционная функция (АКФ) ^-последовательности
может быть записана следующим образом:
88
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
т РК~2
Р i=0
На практике удобнее пользоваться АКФ центрированной
.^-последовательности
для получения которой следует произвести изоморфное отобра-
жение множества
{0,1,2,.., (р-1)}
на множество
(о,1,2,..,-^,--.., -2, -11.
[22	J
На рис. 2.16 и 2.17 показаны АКФ центрированных Л/-после-
довательностей соответственно для случаев:
р = 2, Ф(х) = х5 + х3 + 1, замена 0 —» -1;
р = 7, Ф(х) = Зх3 + х + 6, замена 6 —> -1, 5 —» -2, 4 —> -3.
Рис. 2.16. АКФ центрированной Я-последовательности для случая р = 2,
Ф(х) = х5 + х3 +1
Глава 2. Генердторы ПСП, функционирующие в конечных полях
89
ад
2
4------о..................
171
-в-----------------------------
S	S	2S
3	2	3	____________
5	5S	S = 73-l
7	7
1
171
Рис. 2.17. АКФ центрированной ^-последовательности для случая р = 7,
Ф(х) = Зх3 + х + б
90
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Литература к главе 2
1)	Алексеев А. И., Шереметьев А. Г., Тузов Г. И., Глазов В. И. Тео-
рия и применение псевдослучайных сигналов. М.: Наука, 1969.
2)	Аршинов М. Н., Садовский Л. Е. Коды и математика (рассказы
о кодировании). М.: Наука. Главн. ред. физ.-мат. лит., 1983.
3)	Болл У., Коксетер Г. Математические эссе и развлечения: Пер.
с англ. / Под ред. И. М. Яглома. М.: Мир, 1986.
4)	Бурдаев О. В., Иванов М. А., Тетерин И. И. Ассемблер в задачах
защиты информации / Под ред. И. Ю. Жукова. М.: КУДИЦ-ОБРАЗ,
2002.
5)	Гараков Г. А. Таблицы неприводимых полиномов над полем GF(p)
(р < 11). Математические вопросы кибернетики и вычислительной
техники. Ереван: Изд. Арм. ССР, 1970. С. 112-142.
6)	Зензин О. С., Иванов М. А. Стандарт криптографической защиты
XXI века - AES. Теория конечных полей / Под ред. М. А. Иванова.
М.: КУДИЦ-ОБРАЗ, 2002.
7)	Доценко В. И., Фараджев Р. Г. Анализ и свойства последователь-
ностей максимальной длины И Автоматика и телемеханика. 1969.
№ 11, С. 119-127.
8)	Доценко В. И., Фараджев Р. Г., Чхартишвили Г. С. Свойства по-
следовательностей максимальной длины с Р-уровнями И Автоматика
и телемеханика. 1971. № 8, с. 189-194.
9)	Макуильямс Ф. Дж., Слоан Н. Дж. А. Псевдослучайные последо-
вательности и таблицы // ТИИЭР. 1976. № 12. С. 80-95.
10)	Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.: Мир,
1976.
11)	Элспас Б. Теория автономных линейных последовательных сетей И
Кибернетический сборник. 1963. Вып. 7. С. 90-128.
12)	Arvillias А. С., Maritsas D. G. Toggle-Registers Generating in Parallel к
hh Decimaitions of m-Sequences x? + x + 1 Desighn Tables. IEEE
Transaction on computers. V. C-28. № 2. 1979. P. 89-100.
13)	Pradhan D. K., Hsiao M. Y., Patel A. M., Su S. Y. Shift Registers
Designed for on-line Fault Detection. Proceedings of 8th International
Conference on Fault-Tolerant Computing, 1978. P. 173-178.
ГЛАВА 3
Стохастические
генераторы
псевдослучайных
последовательностей
3.1.	Стохастическое преобразование
информации
В качестве одного из алгоритмов нелинейного преобразования
элементов х, «-разрядной информационной последовательности
X = Xi Х2 Хз ... Xi ... хт
длиной т под управлением ключевой «-разрядной последова-
тельности
Y = Yi УгУз У/Ym
такой же длины и качественного генератора псевдослучайных
последовательностей (ПСП) с числом состояний 2" можно пред-
ложить следующий (рис. 3.1). Для каждого элемента х,- (i = l, т)
повторяем нижеприведенную последовательность действий:
• очередной элемент х, входной последовательности загружаем
в память генератора ПСП;
•	выполняем Yi тактов работы генератора;
•	состояние генератора после у, тактов работы при начальном
состоянии X, объявляем результатом у, преобразования элемен-
та Х|.
После преобразования всех элементов исходной последова-
тельности будет получена результирующая последовательность
У = У1У2 Уз ••• Ут
длиной т, для каждого элемента которой справедливо
yi=R(Xi,yi).
92
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Данное преобразование может эффективно использоваться для
решения различных задач, связанных с защитой информации.
Впервые оно было предложено С. А. Осмоловским для реализа-
ции стохастического кодирования информации [2, 3]. В данной
главе рассматривается его применение для построения генерато-
ров ПСП.
Элемент входной
информационной
последовательности
Генератор
ПСП
Результат
преобразования
«, У,= Я(<Л,)
/ »
Y,
Параметр преобразования
(число тактов работы генератора)
Рис. 3.1. Стохастическое преобразование информационной
последовательности {х(}
3.2.	Я-блок
Схема одного из возможных вариантов построения блока R
стохастического преобразования (Random) и его условное графи-
ческое обозначение показаны соответственно на рис. 3.2 и 3.3.
Ключевая информация R-блока - характер заполнения таблицы
Н = {H(m)},m = Q, (2"-1),
размерности п х 2”, содержащей элементы GF(2n), перемешанные
случайным образом, т. е. Н(т) е GF(2n). Результат Rh(A, В) пре-
образования входного л-разрядного двоичного набора А зависит
от заполнения таблицы Н и параметра преобразования В, задаю-
щего смещение в таблице относительно ячейки, содержащей зна-
чение А, следующим образом:
RH (А, В) = н((тА + В) mod 2п),
Глава 5. Стохастические генераторы псевдослучайных последовательностей
»>
где тА - адрес ячейки таблицы Н, содержащей код А, т. е.
= А. Другими словами, результат работы Л-блока суть счи-
тывание содержимого ячейки таблицы Н, циклически смещенной
на В позиций в сторону старших адресов относительно ячейки,
содержащей код А.
Основной
массив
Вспомогательный
массив (адресный)
Адрес Addr	Адрес Н
Рис. 3.2. Логика работы Л-блока
Рис. 3.3. Условное графическое обозначение Л-блока
Для ускорения преобразования в состав jR-блока вводится
вспомогательный адресный массив
Addr-{Addr(j)}
размерности п х 2”, причем
V;=0,(2"-1) Addr(J) = mj-
Иными словами, ячейка с адресом j в массиве ADDR хранит
адрес ячейки массива Н, содержащей код/
Заслуживают внимания следующие факты:
•	при Addr = {0, 1, 2,..., (2" - 1)}, т. е. при записи в каждую ячей-
ку массива Addr ее собственного адреса, и п = 4 результат пре-
94
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
образования в точности совпадает с результатами работы двух
тактов (сложение с 4 битами ключа и замена в соответствую-
щем узле замены) одной секции раундовой функции российско-
го стандарта криптографической защиты, ГОСТ 28147-89;
•	в частном случае при Addr = {0, 1, 2,(2" - 1)} и В = 0 полу-
чаем классический S-блок (блок замены) с таблицей замен /7;
•	при записи в каждую ячейку массивов Н и Addr ее собственно-
го адреса получаем классический сумматор по модулю 2", а
значит, с полным на то основанием Я-блок может быть назван
стохастическим сумматором',
•	по такому же принципу (заменой сумматора по модулю 256 на
операцию поразрядного XOR) может быть построен стохас-
тический сумматор в поле GF(2S) (стохастический XOR), а
также другие элементы (AND, OR, mod рит. п.);
•	требует дополнительного исследования схема стохастического
преобразования, показанная на рис. 3.4, где функция F - сум-
матор по модулю 28 или поразрядный XOR (а возможно и дру-
гие операции AND, OR, mod. рит. п.).
Рис. 3.4. Вариант схемы блока стохастического преобразования
(RF-блок)
Ключевая информация, необходимая для работы 7?-блока, -
содержимое таблицы Н стохастического преобразования. Алго-
ритм замены ключевой информации, т. е. «перемешивания» или
«взбивания» таблиц Н, показан на рис. 3.5. Каждая очередная
пара байтов
BYTE,, BYTEM
инициализирующей последовательности меняет местами два со-
ответствующих элемента массива Н, т. е. выполняется операция
Глава Стохастические генераторы псевдослучайных последовательностей
9$
H(BYTE^ о H(BYTEM\ i = 0, 2, 4,
где H(f) - элемент массива Н, расположенный в ячейке с адресом
j. Алгоритм формирования вспомогательного массива Addr пока-
зан на рис. 3.6.
Рис. 3.5. Схема алгоритма «переме-
шивания» таблицы стохастического
преобразования с использованием
инициализирующей ПСП
BYTEo, BYTEj, BYTE?,BYTE,-, BYTEi+1(.
Рис. З.б. Схема алгоритма
формирования адресного
массива Addr по
известному массиву Н
Можно предложить еще один возможный алгоритм формиро-
вания таблицы стохастического преобразования, его схема при-
ведена на рис. 3.7. Для создания таблицы Нможет быть применен
также любой из известных алгоритмов создания таблицы замены,
например алгоритм, реализованный в поточном шифре RCA.
Учитывая, что циклически сдвинутые таблицы стохастическо-
го преобразования эквивалентны, существует 255! различных
вариантов заполнения таблицы И.
9b
Теория, применение и оценка качества генердторов псевдослучайных последовательностей
Рис. 3.7. Схема алгоритма формирования таблицы стохастического
преобразования с использованием инициализирующей ПСП
BYTEo, BYTEV BYTE?,BYTE,-,...
Возможен вариант использования Я-блока, когда содержимое
массива Н (а значит, и содержимое массива Addr) зафиксировано,
а ключевая информация подается на вход В параметра преобра-
зования. В этой ситуации для обеспечения возможности вычис-
ления результата преобразования «на лету» (без использования
таблиц) в качестве содержимого массива Н выбираются последо-
вательные состояния генератора ПСП, который допускает эффек-
тивную программную реализацию.
3.3. Стохастические генераторы
многоразрядных ПСП на регистрах
сдвига - RFSR
Для построения стохастического генератора ПСП (Random
Feedback Shift Register - RFSR) предлагается в схемах аддитивно-
го генератора вместо блоков сложения использовать Я-блоки
(рис. 3.8) [1]. Ключевая информация - заполнение таблиц Н, оп-
ределяющих логику работы Я-блоков.
Глава 5. Стохастические генераторы псевдослучайных последовательностей
97
Рис. 3.8. Общие схемы стохастических генераторов n-разрядной ПСП
(режим 0FB) с управляющим входом. О,- - состояние i-го регистра
генератора
Все теоретические и практические результаты, полученные для
LFSR при решении задач построения генераторов ПСП, легко
обобщаются и позволяют столь же эффективно решать задачи за-
щиты информации от умышленных деструктивных воздействий.
Рассмотрим вариант схемы генератора с одним Я-блоком, ко-
торый может быть представлен в одном из двух идентичных ва-
риантов (рис. 3.9, а - RFSR1 или 3.9, б - RFSR2).
Рис. 3.9. Варианты схемы стохастического генератора RFSR с одним
^-блоком (режим OFB)
98
Теория, ПРИМЕНЕНИЕ Н ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
При соответствующем выборе таблицы стохастического пре-
образования выходная ПСП по сути - это нелинейная М-
последовательность, т. е. последовательность максимальной дли-
ны, по своим статистическим свойствам превосходящая класси-
ческую ^/-последовательность с выхода LFSR той же разрядности
(рис. 3.10-3.11).
3 1
О 3
3 о
2 3
О 2
2 О
3 2
3 3
1 3
2 1
2 2
1 2
0 1
F
1 о
2 1
О 2
2 0
1 2
_£
1 о
2 1
2 2
1 2
3 I
3 3
2 3
О 2
2 0
3 2
0 3
3 0
I 3
Г
1 о
3 1
3 3
О 3
3 о
2 3
2 2
3 2
1 3
3 1
2 3
2 2
3 2
О 3
3 О
3 3
1 3
0 1
1 о
о 1
2 1
О 2
2 0
1 2
0 1
Рис. 3.10. Стохастический генератор при N= 2:
схема генератора - а;
возможные таблицы преобразования и соответствующие им
диаграммы переключений - б
а
б
На рис. 3.10 и 3.11 показаны примеры генераторов стохасти-
ческой ^/-последовательности длиной соответственно 15 и 63.
На рис. 3.12 приведен пример преобразования стохастического
генератора, диаграмма состояний которого состоит из трех циклов
длиной 22, 25, 16 и одного тривиального цикла, состоящего из
Глава 5. Стохастические генераторы псевдослучайных последовательностей
99
состояния ООО, переходящего самого в себя, в генератор последо-
вательности длиной 64. Преобразование потребовало включения
в состав устройства сумматора и элемента ИЛИ-HE, выход которо-
го соединен со входом переноса сумматора. Переходы исходного
генератора на рис. 3.12 показаны пунктирной линией.
| ООО I
Рис. 3.11. Стохастический генератор при N= 3:
схема генератора и таблица стохастического преобразования - а;
диаграмма его переключений - б
а
На рис. 3.13 приведена схема генератора ПСП с непрерывно
изменяющейся таблицей стохастического преобразования. В каж-
дом такте работы такого RFSR слово (BYTEM, BYTE,) с выхода
управляющего генератора меняет местами содержимое двух яче-
ек таблиц Н:
H(BYTEM)<^H(BYTEi).
100
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
а
													1				
	1 0 0			2 0 3			2 0 0			3 1 0			3 0 0			3 2 1	
	0 1 0			3 2 0			0 2 0			1 3 1			0 3 0			1 3 2	
	1 0 1			2 3 2			2 0 2			0 1 3			3 0 3			2 1 3	
	2 1 0			2 2 3			1 2 0			2 0 1			3 3 0			2 2 1	
	1 2 1			0 2 2			2 1 2			2 2 0			3 3 3			1 2 2	
	1 1 2			3 0 2			0 2 1			2 2 2			1 3 3			3 1 2	
	0 1 1			1 3 0			1 0 2			3 2 2			1 1 3			0 3 1	
	3 0 1			3 1 3			1 1 0			3 3 2			2 1 1			0 0 3	
	2 3 0			2 3 1			1 1 1			2 3 3			1					
	3 2 3			0 2 3			3 1 1			1 2 3							
	0 3 2			0 0 2			3 3 1			0 1 2		г					
							0 3 3			0 0 1						0 0 0	
							1 0 3					। ।						
б
Рис. 3.12. Стохастический генератор ПСП длиной 64:
схема генератора и таблица стохастического преобразования - а;
Рис. 3.13. Схема генератора ПСП с непрерывно изменяющейся таблицей
стохастического преобразования
Глава 5. Стохастические гЕньрдторы псевдослучайных последовательностей
101
3.4. Криптоанализ RFSR
Рассмотрим процедуру определения таблицы Н стохастиче-
ского преобразования RFSR с одним 1?-блоком по перехваченно-
му фрагменту длиной т выходной последовательности на приме-
ре криптоанализа четырехразрядного стохастического генерато-
ра, соответствующего Ф(х) = х4 + х3 + 1 (рис. 3.14). Таблица Н
стохастического преобразования имеет размерность 4 х 16 и со-
держит все 4-разрядные двоичные коды, перемешанные случай-
ным образом, а число N регистров RFSR равно 4. Уравнение фор-
мирования очередного элемента y(z) выходной последовательно-
сти у имеет вид:
у(0 = ад-3),у(Г-4)).
/1(2.9) =14	Я(4,0) = 4
Я(12,2) = 3
Рис. 3.14. Пример четырехразрядного RFSR, соответствующего
Ф(х) = х4 + х3 +1, и фрагмент его выходной последовательности
Предположим, был перехвачен фрагмент длиной т = 35:
92 3 14 14 10 11 103 13 0 4 14 4 49 9 12 1 13 11 9 10 14 52 12
13 3 3 00530.
Шаг 1. «Перемещая» уравнение у(г) = R(y(t - 3), y(t - 4)) вдоль
перехваченного фрагмента у, получим список А из 31-го равенст-
ва вида R(a, b) = с (рис. 3.15, а), где а, b и с - элементы фрагмента
у. Равенство R{a, b) = с означает, что в искомой таблице Н эле-
мент с циклически смещен в сторону старших адресов относи-
102
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
тельно элемента а на b позиций. В общем случае число этих ра-
венств равно m-N.
Шаг 2. Проанализируем список А и исключим из него повто-
ряющиеся строки, а также равенства вида R(a, 0) = а, не содер-
жащие никакой полезной информации. Исключив из списка А
равенства 1?(4, 0) = 4 и 1?(0, 0) = 0, получим новый список А, со-
держащий 29 равенств (рис. 3.15, б).
Шаг 3. Организуем еще три списка: В, С и D. Список В опре-
деляет последовательность анализа равенств из списка А (рис.
3.15, в). Равенствам R(a, b) = с, которые будут анализироваться
первым, вторым, третьим, ... в списке В будут соответствовать
номера 1, 2, 3, ... . Список С определяет последовательность за-
полнения таблицы Н (рис. 3.15, г). Ячейкам таблицы Н, которые
будут заполнены первой, второй, третьей, ... , в списке С будут
соответствовать номера 1, 2, 3, ... . Список D последовательно
заполняется анализируемыми элементами таблицы Н (рис. 3.15, е).
Шаг 4. Начнем анализ первого равенства R(2, 9) = 14 в списке
А. Запишем в верхнюю ячейку таблицы Ни в список D анализи-
руемых элементов значение а = 2. Присвоим верхней ячейке таб-
лицы Н номер 1 в списке С.
Шаг 5. Начнем анализ элемента 2 из списка D. Просмотрим
список А на предмет наличия в нем равенств, в которых значение
а = 2. Этому условию удовлетворяют равенства R(2, 9) = 14 и R(2,
5) = 3. Присвоим им номера соответственно 1 и 2 в списке В.
Просмотрим список А на предмет наличия в нем равенств, в ко-
торых значение с = 2. Этому условию удовлетворяет равенство
1?(10, 9) = 2. Присвоим ему номер 3 в списке В.
Равенство 2?(2, 9) = 14 означает, что элемент 14 в таблице И
циклически смещен относительно элемента 2 на 9 позиций. Най-
дем соответствующую ячейку таблицы Н и запишем в нее значе-
ние с = 14. Присвоим этой ячейке номер 2 в списке С. Равенство
1?(2, 5) = 3 означает, что элемент 3 в таблице Н циклически сме-
щен относительно элемента 2 на 5 позиций. Найдем соответст-
вующую ячейку таблицы Н и запишем в нее значение с = 3. При-
своим этой ячейке номер 3 в списке С. Равенство 1?(10, 9) = 2 оз-
начает, что элемент 2 в таблице И циклически смещен относи-
Глава 5. Стохастические генераторы псевдослучайных последовательностей
10?
тельно элемента 10 на 9 позиций. Найдем соответствующую
ячейку таблицы Н и запишем в нее значение а = 10. Присвоим
этой ячейке номер 4 в списке С.
/?(2,9)= 14
Я(3, 2) = 10
Я(14, 3)= 11
/?(14, 14)= 10
Я(10, 14) = 3
Я(11, 10) = 10
Я(10, 11) = 0
Я(3, 10) = 4
/?(13, 3) = 14
Я(0,13) = 4
Я(4, 0) = 4
Я(14, 4) = 9
Я(4,14) = 9
Я(4,4) = 12
Я(9, 4) = 1
/?(9,9)= 13
/?(12,9)= 11
/?(1, 12) = 9
/?(13, 1)= 10
Я(11,13)= 14
/?(9, 11) = 5
Я(10,9) = 2
/?(14,10) = 12
Я(5,14)= 13
/?(2,5) = 3
Я(12,2)= 3
Я(13,12) = 0
Я(3, 13) = 0
/?(3,3) = 5
ад 3) = з
Я(0,0) = 0
Я(2, 9) = 14
/?(3, 2)= 10
Я(14,3)= 11
Я(14,14)= 10
/?(10, 14) = 3
/?(11,10)= 10
Я(10,11) = 0
ад, ю) = 4
Я(13,3)= 14
ад 13) = 4
Я(14, 4) = 9
Я(4, 14) = 9
/?(4, 4) = 12
/?(9, 4) = 1
Я(9, 9) = 13
Я(12,9)= 11
Я(1, 12) = 9
Я(13, 1)= 10
Я(11,13)= 14
/?(9, 11) = 5
Я(10, 9) = 2
Я(14,10)= 12
Я(5,14)= 13
Я(2,5)=3
/?(12,2) = 3
Я(13,12) = 0
ад, 13) = о
ад,3) = 5
ад, 3) = з
б
1+ Последовательность
анализа уравнений
4+/V
5-
Анализируемые
элементы
	Н	
8+	1 6+ 7 3 8 4 9- 2 3+ 7+ 2+	5 6 Последовательность заполнения таблицы	2	2+ 14+
		
		
	12	
		
	3	
	13	
	10	
		
	14	
		
		
	И	
	9	
		
		
Рис. 3.15. Результат б шагов процедуры криптоанализа;
исходный список А равенств вида R(a, b)=c- а;
модифицированный список А - б;
список Б, т. е. последовательность анализа равенств из списка А - в;
список С, т. е. последовательность заполнения таблицы И - г;
таблица Н- д;
список D, т. е. последовательность анализируемых элементов
таблицы Н - е
Анализ элемента 2 и соответствующих ему равенств в списке
А закончен. Внесем под номером 2 в список D элемент, записан-
ный в таблицу Н вторым, т. е. элемент 14.
104
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Шаг 6. Возьмем следующий элемент из списка D, имеющий
номер 2, т. е. 14. Приступим к его анализу. Просмотрим список А
на предмет наличия в нем равенств, в которых значение а = 14.
Этому условию удовлетворяют 4 равенства 1?(14, 3) = 11, /?(14,
14) = 10, 1?(14, 4) = 9 и 1?(14, 10) = 12. Присвоим им номера соот-
ветственно 4, 5, 6 и 7 в списке В. Просмотрим список А на пред-
мет наличия в нем равенств, в которых значение с = 14. Этому
условию удовлетворяют 2 равенства 1?(13, 3) = 14 и 2?(11,13) = 14.
Присвоим им номера соответственно 8 и 9 в списке В.
Равенство 1?(14, 3) = 11 означает, что элемент 11 в таблице Н
циклически смещен относительно элемента 14 на 3 позиции.
Найдем соответствующую ячейку таблицы Н и запишем в нее
значение с = 11. Присвоим этой ячейке номер 5 в списке С. Ра-
венство 1?(14, 14) = 10 означает, что элемент 10 в таблице //цик-
лически смещен относительно элемента 14 на 14 позиций. Этот
факт уже отражен в таблице, т. е. равенство никакой полезной
информации не дает. Равенство /?(14, 4) = 9 означает, что элемент
9 в таблице Н циклически смещен относительно элемента 14 на 4
позиции. Найдем соответствующую ячейку таблицы Н и запишем
в нее значение с = 9. Присвоим этой ячейке номер 6 в списке С.
Равенство /?(14, 10) = 12 означает, что элемент 12 в таблице Н
циклически смещен относительно элемента 14 на 10 позиций.
Найдем соответствующую ячейку таблицы Н и запишем в нее
значение с = 12. Присвоим этой ячейке номер 7 в списке С.
Равенство /?(13, 3) = 14 означает, что элемент 14 в таблице Н
циклически смещен относительно элемента 13 на 3 позиции.
Найдем соответствующую ячейку таблицы Н и запишем в нее
значение а = 13. Присвоим этой ячейке номер 8 в списке С. Ра-
венство 2?(11, 13) = 14 означает, что элемент 14 в таблице Н цик-
лически смещен относительно элемента 11 на 13 позиций. Этот
факт уже отражен в таблице, т. е. равенство никакой полезной
информации не дает.
На рис. 3.15 отражена ситуация на этот момент, при этом зна-
ком «+» помечены те элементы списков В и D, анализ которых
дал результат, а знаком «-» - те элементы списков В и D, анализ
которых оказался безрезультатным.
(лава 5. Стохастические генераторы псевдослучайных последовательностей
10$
Анализ элемента 14 и соответствующих ему равенств в списке
А закончен. Внесем под номером 3 в список D элемент, записан-
ный в таблицу Н третьим, т. е. элемент 3.
Шаг 7. Возьмем следующий элемент из списка D, имеющий
номер 3, т. е. 3. Приступим к его анализу. Просмотрим список А на
предмет наличия в нем равенств, в которых значение а = 3. Этому
условию удовлетворяют 4 равенства 1?(3, 2) = 10, /?(3, 10) = 4,
/?(3, 13) = 0,1?(3, 3) = 5. Присвоим им номера соответственно 10,
11, 12 и 13 в списке В. Просмотрим список А на предмет наличия
в нем равенств, в которых значение с = 3. Этому условию удовле-
творяют 3 равенства /?(10, 14) = 3, /?(12, 2) = 3 и 1?(0, 3) = 3. При-
своим им номера соответственно 14, 15 и 16 в списке В.
Равенство 7?(3, 2) = 10 означает, что элемент 10 в таблице Н
циклически смещен относительно элемента 3 на 2 позиции. Этот
факт уже отражен в таблице, т. е. равенство никакой полезной
информации не дает. Равенство 1?(3, 10) = 4 означает, что элемент
4 в таблице Н циклически смещен относительно элемента 3 на 10
позиций. Найдем соответствующую ячейку таблицы Н и запишем
в нее значение с = 4. Присвоим этой ячейке номер 9 в списке С.
Равенство 1?(3, 13) = 0 означает, что элемент 0 в таблице //цик-
лически смещен относительно элемента 3 на 13 позиций. Найдем
соответствующую ячейку таблицы Н и запишем в нее значение с
- 0. Присвоим этой ячейке номер 10 в списке С. Равенство /?(3, 3)
= 5 означает, что элемент 5 в таблице Н циклически смещен от-
носительно элемента 3 на 3 позиции. Найдем соответствующую
ячейку таблицы Ни запишем в нее значение с = 5. Присвоим этой
ячейке номер 11 в списке С.
Равенство /?(10, 14) = 3 означает, что элемент 3 в таблице Н
циклически' смещен относительно элемента 10 на 14 позиций.
Равенство /?(12, 2) = 3 означает, что элемент 3 в таблице Н цик-
лически смещен относительно элемента 12 на 2 позиции. Равен-
ство /?(0, 3) = 3 означает, что элемент 3 в таблице Н циклически
смещен относительно элемента 0 на 3 позиции. Все эти факты
уже отражены в таблице, т. е. равенства никакой полезной ин-
формации не дают.
106
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Анализ элемента 3 и соответствующих ему равенств в списке
А закончен. Внесем под номером 4 в список D элемент, записан-
ный в таблицу Н четвертым, т. е. элемент 10.
Шаг 8. Возьмем следующий элемент из списка D, имеющий
номер 4, т. е. 10. Приступим к его анализу. Просмотрим список А
на предмет наличия в нем равенств, в которых значение а = 10.
Этому условию удовлетворяет равенство /?(10, 11) = 0. Присвоим
ему номер 17 в списке В. Просмотрим список А на предмет нали-
чия в нем равенств, в которых значение с = 10. Этому условию
удовлетворяет равенство 1?(13, 1) = 10. Присвоим ему номер 18 в
списке В. Анализ этих равенств никакой полезной информации
не дает.
Внесем под номером 5 в список D элемент, записанный в таб-
лицу Н пятым, т. е. элемент 11.
Шаг 9. Возьмем следующий элемент из списка D, имеющий
номер 5, т. е. 11. Приступим к его анализу. Просмотрим список
А на предмет наличия в нем равенств, в которых значение а или
с равно 11. Этому условию удовлетворяют два равенства
1?(11, 10) = 13 и R(12, 9) = И. Присвоим им номера соответствен-
но 19 и 20 в списке В. Анализ этих равенств никакой полезной
информации не дает.
Внесем под номером 6 в список D элемент, записанный в таб-
лицу Я шестым, т. е. элемент 9.
Шаг 10. Возьмем следующий элемент из списка D, имеющий
номер 6, т. е. 9. Приступим к его анализу. Просмотрим список А
на предмет наличия в нем равенств, в которых значение а или с
равно 9. Этому условию удовлетворяют пять равенства 1?(9,4) = 1,
2?(9, 9) = 13, 2?(9, И) = 5, 2?(4, 14) = 9 и 2?(1, 12) = 9. Присвоим им
номера соответственно 21, 22, 23, 24 и 25 в списке В.
Равенство R(9, 4) = 1 означает, что элемент 1 в таблице Н цик-
лически смещен относительно элемента 9 на 4 позиции. Найдем
соответствующую ячейку таблицы Н и запишем в нее значение с -
1. Присвоим этой ячейке номер 12 в списке С. Анализ остальных
равенств никакой полезной информации не дает.
На рис. 3.16 отражена ситуация на этот момент.
Глава 5. Стохастические генераторы псевдослучайных последовательностей
107
Я(2, 9) =14	1+
Я(3,2)=10	10-
Я(14, 3)=11	4+
Я(14, 14) =10	5-
Я(10, 14) = 3	14-
Я(11т 10) =13	19-
Я(10, П) = 0	17-
/?(3, 10) = 4	11 +
Я(13, 3)=14	8+
/?(0,13) = 4
Я(14,4) = 9	6+
Я(4,14) = 9	24-
Я(4,4)= 12
Я(9, 4) = 1	21+
Я(9,9)=13	22-
Я(12, 9) =11	20-
Я(1, 12) = 9	25-
Я(13, 1)=10	18-
Я(11, 13)= 14	9+
Я(9,11) = 5	23-
/?(10, 9) = 2	3+
Я(14, 10) =12	7+
Я(5, 14)= 13
Я(2,5) = 3	2+
/?(12,2)= 3	15-
Я(13, 12) = 0
Я(3, 13) = 0	12+
Я(3,3) = 5	13+
Я(0,3) = 3	16-
Последовательность
анализа уравнений
Последовательность Анализируемые
заполнения таблицы элементы
	Н	
1	2	2+
12	1	14+
10	0	3+
7	12	10-
		11-
3	3	9+
8	13	
4	10	
11	5	
2	14	
		
		
5	11	
6	9	
		
9	4	
Рис. 3.16. Результат 10 шагов процедуры криптоанализа
Внесем под номером 7 в список D элемент, записанный в таб-
лицу Я седьмым, т. е. элемент 12.
Шаг 11. Возьмем следующий элемент из списка D, имеющий
номер 7, т. е. 12. Приступим к его анализу. Просмотрим список А
на предмет наличия в нем равенств, в которых значение а или с
равно 12. Этому условию удовлетворяет равенство 1?(4, 4) = 12.
Присвоим ему номер 26 в списке В. Анализ этого равенства ника-
кой полезной информации не дает.
Внесем под номером 8 в список D элемент, записанный в таб-
лицу Я восьмым, т. е. элемент 13.
Шаг 12. Возьмем следующий элемент из списка D, имеющий
номер 8, т. е. 13. Приступим к его анализу. Просмотрим список А
на предмет наличия в нем равенств, в которых значение а или с
равно 13. Этому условию удовлетворяют два равенства 7?(13, 12) = 0
и 1?(5, 14) = 13. Присвоим им номера соответственно 27 и 28 в
списке В. Анализ первого из них никакой полезной информации
108
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
не дает. Равенство R(5, 14) = 13 означает, что элемент 13 в табли-
це Н циклически смещен относительно элемента 5 на 14 позиций.
Найдем соответствующую ячейку таблицы Н и запишем в нее
значение а = 5. Присвоим этой ячейке номер 13 в списке С.
Внесем под номером 9 в список D элемент, записанный в таб-
лицу Я девятым, т. е. элемент 4.
Шаг 13. Возьмем следующий элемент из списка D, имеющий
номер 8, т. е. 4. Приступим к его анализу. Просмотрим список А
на предмет наличия в нем равенств, в которых значение а или с
равно 4. Этому условию удовлетворяет равенство 2?(0, 13) = 4.
Присвоим ему номер 29 в списке В. Анализ этого равенства ника-
кой полезной информации не дает.
Список А исчерпан, т. е. процедура анализа закончена (рис.
3.17). В таблице Н остались три незаполненные ячейки, а значит,
перехваченный фрагмент выходной последовательности мог быть
получен с выхода одного из 6 генераторов, таблицы стохастиче-
ского преобразования которых показаны на рис. 3.18.
Я(2,9) = 14	1+	Последовательность
Я(3,2) = 10	10-	анализа уравнений
Я(14, 3) = 11	4+	
Я(14, 14)= 10	5-	
Я(10, 14) = 3	14-	
Я(11,10)= 13	19-	Последовательность Анализируемые
Я(10,11) = 0	17-	заполнения таблицы	элементы
/?(3,10) = 4	11+	Я
Я(13, 3)= 14	8+	
/?(0,13) = 4	29-	1	2	2+
		12	1	14+
Я(14,4) =9	6+	10	0	3+
Я(4,14) = 9	24-	
Я(4,4)= 12	26-	7	12	10-
Я(9,4) = I	21+	13	5	11-
Я(9,9) = 13	22-	3	3	9+
Я(12, 9) = 11	20-	
Я(1,12) = 9	25-	8	13	12-
Я(13, 1)= 10	18-	4	10	13+
Я(11, 13)= 14	9+	11	5	4-
Я(9,11) = 5	23-	
Я(10,9) = 2	3+	2	14
Я(14, 10)= 12	7+	
Я(5,14) = 13	28+	
Я(2, 5) = 3	2+	—	
Я(12, 2) = 3	15-	5	И
Я(13, 12) = 0	27-	6	9
Я(3, 13) = 0	12+	
*(3.3) = 5	13+	—
Я(0,3) = 3	16-	9	4
Рис. 3.17. Результат 13 шагов процедуры криптоанализа
Глава 5. Стохастические генераторы псевдослучайных последовательностей
109
Н1	"г			Н,		Н.		Hs		
2		2		2		2		2		2
1		1		1		1		1		1
0		0		0		0		0		0
12		12		12		12		12		12
5		5		5		5		5		5
3		3		3		3		3		3
13		13		13		13		13		13
10		10		10		10		10		10
5		5		5		5		5		5
14		14		14		14		14		14
7		7		8		8		15		15
15		8		7		15		7		8
11		11		11		11		11		11
9		9		9		9		9		9
8		15		15		7		8		7
4		4		4		4		4		4
Рис. 3.18. Варианты заполнения таблицы стохастического
преобразования анализируемого RFSR
Для определения заполнения таблицы Н восьмиразрядного
RFSR в самом благоприятном случае необходим фрагмент вы-
ходной последовательности длиной не менее 28 + N байт, где N -
число регистров генератора.
Можно выделить следующие направления в попытках реше-
ния проблемы стойкости стохастических генераторов ПСП:
•	реализация функции обратной связи генератора на основе не-
скольких 2?-блоков;
•	использование для формирования элементов выходной после-
довательности нелинейной функции выхода (в том числе реали-
зованной с использованием 2?-блоков и блоков пространствен-
ного сжатия);
•	использование приемов, аналогичных тем, которые применяют-
ся при построении генераторов на LFSR:, например, использо-
вание нескольких RFSR, выходы которых обрабатываются
функцией усложнения; работа по принципу stop-and-go и пр.;
•	использование многоступенчатой структуры, при которой эле-
менты выходных последовательностей RFSR первой ступени
никогда не проходят на выход.
110
Теория, применение и оценил клчествл генерлторов псевдослучайных последовлгельностен
3.5.	Двухступенчатые стохастические
генераторы многоразрядных ПСП
Генераторы ПСП, схемы которых приведены на рис. 3.9,
функционируют в режиме OFB. На рис. 3.19 показаны схемы
двух вариантов формирования ПСП в режиме Counter. В состав
устройства на рис. 3.19, а входят два генератора, байтовые ПСП
с выхода которых поступают на входы 2?-блока.
Рис. 3.19. Варианты схемы стохастического генератора ПСП:
выходная последовательность у суть результат стохастического
преобразования последовательности хг под управлением
последовательности х2 - а;
выходная последовательность у суть результат перемешивания двух
ПСП под управлением третьей - б (режим Counter)
а
б
Первая ступень устройства на рис. 3.19, б - генератор ПСП,
формирующий три пары поразрядных последовательностей, каж-
Глава Стохастические ГЕНЕрдторы псевдослучайных последовательностей
111
дая из которых поступает на входы соответствующего 7?-блока.
Последовательности, формируемые на выходах первого и второ-
го 2?-блоков, перемешиваются под управлением последователь-
ности с выхода третьего /?-блока. Перемешивание обеспечивают
п одноразрядных мультиплексоров 2 —> 1. Включение в состав
устройства блоков пространственного сжатия (БПС) информации
п* —> п позволяет исключить появление на выходе генератора
двоичных наборов с выходов 2?-блоков.
Рассмотрим случай, когда п* = п. Для получения «-разрядной
выходной последовательности
Y=ЪЪЪ-Ъ-
используется три «-разрядных 2?-блока, каждому из которых со-
ответствует своя таблица i = 1, 2, 3, причем
т = 0,(2п -1), Я,.(т)е GF(2").
Пусть
W) =	-
«-разрядный двоичный набор на выходе z-ro F-блока в момент
времени t, r^f) G {0, 1}, i = 1, 2, 3, j = 0,(«-l). Тогда уравнения
работы генератора имеют вид
'ВД = RH,	= 1ДЗ,
Yr = £ 2? j (')гз j W v r2j W>r3j
или
'/?,(/) = Я,.((/«& 2(г) + e2i._1(0)«lOJ 2"),/ =1,2,3,
Yr = £ 2 ? (0r3J (t) v r2j (t)r3 j)
j=o
где Qi(f) - «-разрядный код на l-м выходе ГПК в момент времени
t, 0 < I < 5.
112
Теория, применение н оценил качества генерлторов псевдослучайных последовательностей
3.6.	Стохастические генераторы ПСП
с многораундовой функцией обратной
связи
Одной из типовых структур, использующихся для построения
многораундовых функций обратной связи генераторов ПСП, яв-
ляется квадрат (см. главу 1). Рассмотрим вариант схемы с по-
добной структурой на основе 1?-блоков. Входной блок разрядно-
стью 128 бит и все промежуточные результаты его преобразова-
ния представляются двумерным массивом байтов размерностью
4x4, вид этого массива показан на рис. 3.20, а, где <2У- - элемент
массива (байт), находящийся на пересечении i-й строки и J-го
столбца, i = 0, 3, j = 0, 3 . Преобразование (рис. 3.20, б) суть мно-
гократное повторение одного и того же раунда, состоящего из
трех операций:
•	перемешивание строк;
•	перемешивание столбцов;
•	стохастическое преобразование байтов блока с использовани-
ем элементов (байтов) раундового ключа.
На рис. 3.21 показана схема операции стохастического пре-
образования байтов ау с использованием блоков стохастическо-
го преобразования, параметрами преобразования являются
соответствующие байты ку раундового ключа, i = 0,3, j = 0,3, i -
номер строки, j - номер столбца, а у - преобразованный байт, т. е.
<2 у = l?i(4Zy, ку).
На рис. 3.22 показаны варианты 4-тактного перемешивания
строк
Я|3 <2/2 <2|1 «Ю, I = 0,3 ,
с использованием блоков R2 - Rs- На рис. 3.23 - варианты
4-тактного перемешивания столбцов
аз, a2j aij aoj, j = 0,3,
с использованием блоков R6 - R9. Начальное состояние Q2 Q2 QiQo
регистров при преобразовании строк (столбцов) равно байтам
Глава 5. Стохастические генераторы псевдослучайных последовательностей
11>
строки (столбца) или соответствующим байтам ключа. Байты
ключа в первом случае или байты строк (столбцов) во втором
случае поступают на вход схем последовательно: в первом такте
3-й байт, во втором - 2-й, в третьем - 1-й и в четвертом 0-й.
Данные	Ключ
	“и	°01	аоо
Л13	а\1	«и	Я10
"а	ап	«2,	Я20
«в		“31	азо
Начальное
состояние
	*02	*01	*00
*13	*12		*ю
*13	*22	*21	*20
*33	*32	*31	*30
°™ I
128-разрядный регистр
Функция
обратной связи
генератора ПСП
£4
м
Стохастическое преобразование
байтов
Перемешивание строк
Перемешивание столбцов
Стохастическое преобразование
___________байтов__________
Перемешивание строк
Перемешивание столбцов
Стохастическое преобразование
байтов
।
1-й
раунд
2-й
раунд
Перемешивание строк
Перевешивание столбцов
Стохастическое преобразование
байтов
tf-й
раунд
б
Рис. 3.20. Принцип построения функции обратной связи генератора ПСП:
структура блока данных - а;
процедура преобразования блока данных - б
Рис. 3.21. Раундовая операция стохастического преобразования байтов
114
Теория, ПРИМЕНЕНИЕ Н ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Рис. 3.22. Варианты раундовой операции стохастического
преобразования строк
На рис. 3.24, а показана схема формирования раундовых клю-
чей из исходного 128-разрядного ключа, где к, - 32-разрядные
элементы ключа (столбцы); начальное заполнение генератора
раундовых ключей равно кз кз к\ ко, т. е. исходному ключу. Функ-
ция F обратной связи зависит от индекса i: при i = 4п - 1, где п -
натуральное, схема преобразования F показана на рис. 3.24, б, где
сопзг сопгг conir соп0г - байты 32-разрядной константы (г - номер
128-разрядного ключевого элемента), в противном случае блок F
осуществляет простую передачу 32-разрядного входного набора
на выход без изменения. В качестве r-й константы можно исполь-
зовать, например, состояние 32-разрядного LFSR в r-м такте его
работы.
Глава 5. Стохастические генераторы псевдослучайных последовательностей
11$
Рис. 3.23. Варианты раундовой операции стохастического
преобразования столбцов
Можно предложить следующие варианты заполнения таблиц
Н1-Н9:
•	фиксированные таблицы стохастического преобразования;
•	таблицы, перемешанные с использованием исходной ключе-
вой информации одним из указанных в разделе 3.2 способов.
При отсутствии особых требований к быстродействию рас-
смотренного генератора для повышения его криптостойкости
можно дополнительно рекомендовать во втором случае переме-
шивание таблиц преобразования 2?-блоков после каждого их ис-
пользования.
116
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
а
Рис. 3.24. Формирование раундовых ключей:
схема формирования - а;
схема 4-тактного преобразования F - б
3.7.	Выводы
1.	Рассмотренная схема 8-разрядного блока стохастического
преобразования (7?-блок) может эффективно использоваться
для генерации ПСП.
2.	Основным достоинством блоков стохастического преобразо-
вания и генераторов ПСП на их основе является эффективная
программная и аппаратная реализация при приемлемой для
большинства приложений криптостойкости.
3.	Ключевая информация, необходимая для работы 8-разрядного
блока стохастического преобразования, суть характер запол-
нения массива размерности 8x256. Всего существует 255! ва-
риантов заполнения этого массива.
Глава 5. Стохастические генераторы псевдослучайных последовательностей
117
Литература к главе 3
1)	Жуков И. Ю., Иванов М. А., Осмоловский С. А. Принципы по-
строения криптостойких генераторов псевдослучайных кодов //
Проблемы информационной безопасности. Компьютерные системы.
2001. № 1.С. 55-65.
2)	Осмоловский С. А. Стохастические методы передачи данных. М.:
Радио и связь, 1991.
3)	Стохастическая защита информации кодами Осмоловского.
http://stocos.ru
ГЛАВА 4
Методика оценки качества
генераторов ПСП
Пройдя в кабинет, я сел на свое ме-
сто и принялся за кофе. Вульф, ут-
кнув нос в средний ящик стола,
подсчитывал пробки от пивных
бутылок, чтобы знать, сколько он
выпил с воскресенья.
- Ну нет, этого не может быть...
Статистика всегда врет, - про-
ворчал он, закрывая наконец ящик.
Р. Стаут. Снова убивать
Генераторы ПСП являются важнейшими элементами любой
системы защиты, надежность последней в значительной степени
определяется именно свойствами используемых генераторов.
В данной главе рассматриваются тесты, используемые для анали-
за статистической безопасности генераторов ПСП, а также мето-
дика интерпретации полученных результатов.
Для исследования ПСП применяются две группы тестов.
•	Графические тесты. Статистические свойства последова-
тельностей отображаются в виде графических зависимостей,
по виду которых делают выводы о свойствах исследуемой по-
следовательности.
•	Оценочные тесты. Статистические свойства последователь-
ностей определяются числовыми характеристиками. На основе
оценочных критериев делаются заключения о степени близо-
сти свойств анализируемой и истинно случайной последова-
тельностей.
Глава 4. Методика оценки качества генераторов ПСП
119
4.1. Графические тесты
К данной категории можно отнести, например, следующие тесты:
•	гистограмма распределения элементов последовательности;
•	распределение на плоскости;
•	проверка серий;
•	проверка на монотонность;
•	автокорреляционная функция;
•	профиль линейной сложности;
•	графический спектральный тест.
4.1.1.	Гистограмма распределения элементов
Данный тест позволяет оценить равномерность распределения
символов в исследуемой последовательности, а также определить
частоту появления конкретного символа.
Строится гистограмма следующим образом. В исследуемой по-
следовательности Е подсчитывается, сколько раз встречается каж-
дый элемент, после чего строится график зависимости числа появ-
лений элементов от их численного представления (ASCII-значение
для байтов).
Пример 4.1.
Вход:
£ = 0 12132 1.
Тест:
преобразуем исходную последовательность байтов в последо-
вательность ASCII-значений символов:
Е = 48 49 50 49 51 50 49;
теперь подсчитаем, сколько раз встречается каждое значение:
«48 = 1,
«49 = 3,
«50 = 2,
«51 = 1-
120
Теория, применение и оценка качества геиерлторов псевдослучайных последовательностей
48 49 50 51
Для того чтобы последовательность удовлетворяла свойствам
случайности, необходимо, чтобы в ней присутствовали все возмож-
ные элементы рассматриваемой разрядности, при этом разброс час-
тот появления символов стремился к нулю (рис. 4.1, а). В противном
случае последовательность не является случайной (рис. 4.1, б).
Рис. 4.1. Примеры гистограмм:
а - результат положительный;
б - результат отрицательный
а
Глава 4. Методика оценки качества генераторов ПСП
121
Данный тест может принести пользу также в тех случаях, ко-
гда оценивается качество последовательности с законом распре-
деления, отличным от равномерного, либо последовательности,
в которой некоторые символы вообще отсутствуют (рис. 4.2).
Рис. 4.2. Пример гистограммы последовательности с законом '
распределения символов, близким к нормальному
4.1.2.	Распределение на плоскости
Данный тест предназначен для определения зависимостей ме-
жду элементами исследуемой последовательности.
Построение распределения на плоскости осуществляется сле-
дующим образом. На поле размером (2я - 1) х (2я - 1) (R - раз-
рядность чисел исследуемой последовательности) наносятся точ-
ки с координатами (е,; e(+i), где е, - элементы исследуемой после-
довательности Е, i = 1, (п -1), п - длина последовательности.
Пример 4.2.
Вход:
е = 2 3 54 3.
Тест:
получаем точки:
точка 1 (2; 3),
точка 2 (3; 5),
122
Теория, применение и оценка качества гЕнерлторов псевдослучайных последовательностей
точка 3 (5; 4),
точка 4 (4; 3).
Далее анализируется полученная картина. Если между эле-
ментами последовательности отсутствуют зависимости, то точки
на поле расположены хаотично (рис. 4.3, а). Если на поле присут-
ствуют зависимости, наблюдаются «узоры» - последовательность
не является случайной (рис. 4.3, б). Для последовательностей
большой длины хорошим результатом является абсолютно чер-
ное поле (рис. 4.4).
а
б
Рис. 4.3. Распределение на плоскости:
а - результат положительный;
б - результат отрицательный
Глава 4. Методика оцеики качества генераторов ПСП
12>
Рис. 4.4. Распределение на плоскости (положительный результат для
последовательности большой длины)
4.1.3.	Проверка серий
Данный тест позволяет оценить равномерность распределения
символов в исследуемой последовательности на основе анализа
частоты появления нулей и единиц и серий, состоящих из к бит.
Построение осуществляется следующим образом. Подсчиты-
вается, сколько раз встречаются нули, единицы, серии-двойки
(00, 01, 10, 11), серии-тройки (ООО, 001, 010, ОН, 100, 101, ПО,
111) и т. д. в битовом представлении исследуемой последова-
тельности е. Полученные результаты представляются в графиче-
ском виде.
Пример 4.3.
Вход:
е = 264718 3.
Тест:
представляем исходную последовательность в битовом виде:
Е = 0010 0110 0100 0111 0001 1000 0011;
подсчитываем число единиц и нулей:
Е = 0010011001000111000110000011,
124
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
п0=17,
П] = 11;
0	1
подсчитываем число серий-пар каждого вида:
е = 00 10 01 10 01 00 01 1100 01 10 00 0011,
«оо - 5,
«01 = 4,
«ю = 3,
«и = 2;
*00'	'01'	'Ю*	'11'
подсчитываем число серий-троек каждого вида (последний бит
отбрасывается, так как он не входит в состав тройки):
е = 001 001 100 100 011100 011 000 001 1,
«ооо = 1,
«оо1 = 3,
«ою = 0,
«он = 2,
«юс = 3,
«Ю1 = 0>
«по = О,
«ш = 0.
Глава 4. Методика оцеики качества гЕиерАТоров ПСП
и;

-T^gr-jBggau

У последовательности, чьи статистические свойства близки к
свойствам истинно случайной последовательности, разбросы меж-
ду числом появлений нулей и единиц, между числом появлений
серий-пар каждого вида и между числом появлений серий-троек
каждого вида должны стремиться к нулю (рис. 4.5, а). В противном
случае последовательность не является случайной (рис. 4.5, б).
4.1.4.	Проверка на монотонность
Данный тест позволяет оценить равномерность распределения
символов в исследуемой последовательности на основе анализа
длин участков невозрастания и неубывания элементов последова-
тельности.
Построение производится следующим образом. Исследуемая
последовательность е графически представляется в виде следую-
щих друг за другом непересекающихся участков невозрастания и
неубывания элементов последовательности.
У последовательности, чьи статистические свойства близки к
свойствам истинно случайной последовательности, вероятность
появления участка невозрастания (неубывания) определенного
размера зависит от его длины: чем больше длина, тем меньше
вероятность (рис. 4.6, а). В противном случае последовательность
не является случайной (рис. 4.6, б).
Пример 4.4.
Вход:
Е = 1 234555443222 1 234 5.
Тест:
разобьем последовательность на участки невозрастания и не-
убывания:
Е = 123455544322212345.
126
Теория, применение и оценка клчествд гснсрдторов псевдослучайных последовлтельностей
Получаем участок неубывания длиной 6, затем участок невоз-
растания длиной 7 и вновь участок неубывания длиной 4.
1 оси ОСО
000000
000000
•00 000
200000
о
9900000
3000 000
2000 000
2000 000
t SOO 000
1000 000
000 000
о
□ээзотэчосг
□ ззэ ме w
□ 332808*010*
□ 333188-011"
Взм&эетосг
 332804*101*
 339 331*110*
 333 328*111*
1200000
1000000
500 000
500000
400 000
200000
Рис. 4.5. Проверка серий графическая:
а - результат положительный;
б - результат отрицательный
□546 30$ ЧОО*
□ 34$ 720*001*
□ 84 002 *О10*
□ 323 838-011-
 346089100"
 83 210 101*
 323 8вЗЧ’(Г
26 972*111*
а
б
Глава 4. Методика оценки качества генераторов ПСП
127
Рис. 4.6. Проверка на монотонность графическая:
а - результат положительный;
б - результат отрицательный
4.1.5.	Автокорреляционная функция (АКФ)
Данный тест предназначен для оценки корреляции между
сдвинутыми копиями исследуемой последовательности. Может
обнаруживать зависимость между подпоследовательностями ана-
лизируемой последовательности.
Битовая АКФ. Построение битовой АКФ производится сле-
дующим образом. Сначала исследуемая последовательность е
представляется в битовом виде, а затем полученная битовая по-
следовательность нормируется (1 —> 1, 0 —> — 1). Если e0Ei ... En_i -
128
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
двоичная запись исследуемой последовательности, то нормиро-
ванная последовательность bobi ... bn_i получается следующим
образом:
Ь( = (-1)‘Л 1 = 0,(л-1).
После этого вычисляются всплески корреляции:
п-1
'^a+j)modn
где п - длина нормированной битовой последовательности,
J=0, п.
Пример 4.5.
Вход:
е = 3 5.
Тест:
битовое представление последовательности:
Е = 011 101;
приводим последовательность к нормированному виду:
е = -1 111-11;
вычисляем всплески корреляции:
(-1) • (-1) + 1-1 + 1-1+ 1-1+ (-1)-(-1)+ 1-1 6 ,
0 (-1)-(-1) + 1-1 + 1-1 + 1-1 + (-1)-(-1) + 1-1 6
_ (-1)1 + 1-1 +1-1 + 1-(-1) + (-1)-1 +1-(-1) _ -2 _ 1
1	6	6	3
_(-1)-1 + Ы + 1-(-1) + Ы + (-1)-(-1) + 1-1_2_ 1
2	6	6 3
_(-1)-1 + 1-(-1) + 1-1 + 1-(-1) + (-1)-1 + 1-1_-2_ 1
3	6	6	3
(-1)-(-1) + 1-1 + 1-(-1) + 1-1 + (-1)-1 + 1-1 2 1
Сд	6	6 3’
Глава 4. Методика оценки качества генераторов ПСП
129
(-1)-1 + 1-(-1) + 1-1 + 1-1 + (-1)-1 + 1-(-1) -2	1
с =----------------------------------------------— — = —
5	6	6	3
6	6	6
0	1	2	3	4	5	6
Символьная АКФ. Построение сймвольной АКФ производится
следующим образом. Сначала исследуемая последовательность е
нормируется. Пусть аЛ_]аЛ_2...ао (R - разрядность числа) - двоич-
ная запись z-го элемента исследуемой последовательности. Тогда
нормированное значение этого элемента есть
Л-1
7=0
После этого вычисляются всплески корреляции:
п-1
’^(1+/) mod п
п-1	’
1=0
где п - длина исследуемой последовательности, j = 0, п .
Пример 4.6.
Вход:
Е = 3 7 5.
Тест:
приводим последовательность к нормированному виду:
170
Теория, применение и оценка качества геиерАторов псевдослучайных последовательностей
Е = 011 111 101,
Ьо = (-1)‘-20+ (-l)1^1 + (-1)°-22 = -1 - 2 + 4 = 1,
br = (-1)‘-2°+ (-l)1^1 + (-1)‘-22 = -1 - 2 - 4 = -7,
b2 = (-1)1-2° + (-1)°-2‘ + (-1)‘-22 = -1 + 2 - 4 = -3;
вычисляем всплески корреляции:
1  1 +(-7) - (-7) 4-(-3) • (-3) 59
° 1 • 1 + (-7) • (-7) + (-3)  (-3) 59
с _ 1 • (-7) + (-7)  (-3) + (-3) • 1 _ 11
С‘ 1 • 1 + (-7) • (-7) + (-3) • (-3) 59’
с _ 1 • (-3) + (-7) • 1 + (-3) • (-7) _ 11
Сг 1 • 1 + (-7)  (-7) + (-3) • (-3) 59’
с _ 1 • 1 + (-7) • (-7) + (-3) • (-3) _ 59 _ г
Сз 1 • 1 + (-7) • (-7) + (-3) • (-3) 59
Для последовательности, чьи свойства близки к свойствам ис-
тинно случайной последовательности, значения всплесков корре-
ляции должны стремиться к нулю во всех точках, кроме тех, чье
значение кратно длине последовательности в символах для сим-
вольной АКФ и длине последовательности в битах для битовой
АКФ (рис. 4.7, а). Присутствие значительных всплесков корреля-
ции свидетельствует о наличии зависимости между элементами
последовательности (рис. 4.7, б).
Глава 4. Методика оцеики качества генераторов ПСП
1>1
Рис. 4.7. АКФ:
а - результат положительный;
б - результат отрицательный
а
4.1.6. Профиль линейной сложности
Цель теста - исследовать последовательность на случайность,
анализируя зависимость линейной сложности последовательно-
сти от ее длины.
Построение профиля линейной сложности осуществляется сле-
дующим образом. Пусть е = Е1Е2...еп - двоичная последователь-
ность длины п. Последовательно рассматриваются подпоследова-
тельности Еда, содержащие первые к элементов последовательно-
172
Теория, применение и оценка качества генерАТоров псевдослучайных последовательностей
сти, и строится график зависимости линейной сложности L от
длины подпоследовательности N.
Пример 4.7.
Вход:
£ = 001101110.
Тест:
Е(1) = 0, L = 0,
e(2) = 00,L = 0,
е(3) = 0 0 1, L = 3,
е(4) = 0 0 1 1, L = 3,
е(5) = 0 0 1 1 0, L = 3,
Е(6) = 001 101,£ = 3,
е(7) = 00 1 1 0 1 1,L = 3,
е(8) = 0 0 1 1 0 1 1 1, L = 5,
е(9) = 0 0 1 1 0 1 1 1 О, L = 5.
L 6-1----------------
123456789
У последовательности, чьи свойства близки к свойствам ис-
тинно случайной последовательности, линия графика должна
стремиться к линии L = N/2 (рис. 4.8, а). В противном случае по-
следовательность не является случайной (рис. 4,8, б).
Глава 4. Методика оценки качества генераторов ПСП
1»
а
Рис. 4.8. Профиль линейной сложности:
а - результат положительный;
б - результат отрицательный
4.1.7. Графический спектральный тест
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа высоты вы-
бросов преобразования Фурье.
Пусть Е = Е1Е2...еп - двоичная последовательность длины п.
Преобразуем ее в последовательность х = xix2...xn, где х, = 2е, - 1
(т. е. 1 —» 1, 0 —> -1). Теперь применим к х дискретное преобразо-
вание Фурье и получим последовательность гармоник
S = DFT(x).
Изобразим графически первые п/2 гармоник.
114
Теория, применение и оценил качества генерлторов псевдослучайных последовательностей
Пример 4.8.
Вход:
E = 1001010011,
n= 10.
Тест:
x — 1,-1,-1, 1,-1, 1,-1,-1, 1, 1,
S = DFT(x),
10 k=\	f 2я	Л . . f 2 COS 	(л-1) +Т-5ТИ — UO	J u	
10 $*2 = k=\	соя	'2n-2 Л . . ( 	(л-l) +i-szn <10	J I
10 5'з=2л t=l	соя	27f3z7 , A . . f: 	(л-l) +T-szn - 10	J	v
10 k=l	cos^	2я-4	Л . . ( 	(л-l) +t-sin 10	J <
10 S 5 = У\хк k=l	cos	(2ti	. (2 —(л-l) +i-sin — lio ) u
(*-1)
= 1.618-1.175/,
-2	)
——(k-Xn =1.381-4.253/,
10	)
1 jr . 3	)
—(£-1) =-0.618-1.902/,
10	J
2я-4	1
(£-1) = 3.618+2.628/,
10	J
(Лг-1) =-2-7.04-IO’19/,
Mi = modulus (1.618 - 1.175z) = 2,
M2 = modulus (1.381 - 4.253/) = 4.472,
M3 = modulus (-0.618 - 1.902/) = 2,
M4 = modulus (3.618 + 2.628/) = 4.472,
Глава 4. Методика оценки качества генераторов ПСП
1 >5
У последовательности, чьи свойства близки к свойствам ис-
тинно случайной последовательности, число гармоник, чьи дли-
ны значительно превышают среднюю длину гармоники, должно
стремиться к 0 (рис. 4.9, а). В противном случае последователь-
ность не является случайной (рис. 4.9, б).
Рис. 4.9. Спектральный тест:
а - результат положительный;
б - результат отрицательный
а
б
1>6
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
4.2. Оценочные тесты
В отличие от графических тестов, где результаты интерпрети-
руются пользователями, вследствие чего возможны различия в
трактовке результатов, оценочные тесты характеризуются тем,
что они выдают численную характеристику, которая позволяет
однозначно сказать, пройден тест или нет.
В табл. 4.1 приведена информация по наиболее известным
подборкам статистических тестов, применяемых для анализа ге-
нераторов, ориентированных на использование в системах крип-
тографической защиты.
Табл. 4.1. Наборы статистических тестов
Автор	Где описан или где реализован
Д. Кнут (Стэнфордский Университет)	Искусство программирования. Том 2. Получисленные алгоритмы [1]
Дж. Марсалья (Флоридский Государст- венный Университет, США)	DIEHARD [4]
X. Густафсон и др. (Куинсландский Технологический Университет, Австралия)	CRYPT-S [3]
А Менезис и др.	Руководство по прикладной криптографии [5]
А Рухин и др. (Национальный Институт Стандартов и Технологий США - НИСТ)	Руководство по статистическому тестированию генера- торов ПСП (в дальнейшем Руководство НИСТ) [7]
4.2.1. Сведения из теории вероятностей
и математической статистики
Биномиальные коэффициенты суть
х(х-1)... (х-п + 1)
п\	’ для п > °;
= <	1,	для п = 0;
, п
47	0,	дпяжО.
Числа Стирлинга суть
а
>
и/
1, если а = b либо b = 1 и а > 0;
если 6 = 0 либо а < 6;
во всех остальных случаях.
Глава 4. Методика оценки качества генераторов ПСП
1 >7
Критерий £ (chi-square). Пусть результаты испытаний тако-
вы, что их можно разделить на к категорий. Проводится п незави-
симых испытаний, где п - достаточно большое число. Пусть ps -
вероятность того, что результат испытания попадет в s-ю катего-
рию, a Ys - число испытаний, которые реально попали в s-ю кате-
горию.
Сформируем статистику:
2г г ч V* (X ~nPs?
X (obs) = 2,-^-----5—.
Zf nPs
Для оценки полученного результата используются таблицы
распределения %2. В строках этих таблиц расположены степени
v свободы, а в столбцах - вероятности р. Смысл таблиц в сле-
дующем. Если в таблице в строке V и колонке р находится число
х, то это означает, что значение y2(obs) будет больше х с вероят-
ностью р.
Например, дляр = 5% и v = 10 табл. 4.2 дает значение х = 18.31;
это означает, что %2(obs) >18.31 только в 5% всех случаев.
Табл. 4.2. Распределение %2 с числом степеней свободы, равным 10
	Р						
	99%	95%	75%	50%	25%	5%	1%
у=10	2.558	3.940	6.737	9.342	12.55	18.31	23.21
Дополнительный интеграл вероятностей (Complementary
Error Function) суть функция
e-“2du,
2 л 2
где erf(x) = —f= е~и du - функция ошибок.
х/Л J
У О
Поскольку данный интеграл является недифференцируемым,
т. е. его нельзя выразить через элементарные математические
функции, для вычисления erfc(x) применяется разложение в ряд
функции erfixy.
178
Теория, применение и оценка качества геиердторов псевдослучайных последовательностей
v " о
Таким образом,
х3	1 ?	1 х1
г--------1-------------+
3	2! 5	3! 7
? 1 / lx7
3 2!Т-3!Т
2
erfc(x) = \—т= х------+
УЯ <	3
Неполная гамма-функция (Incomplete Gamma Function) суть
rx(p) = \tp-1e~‘dt.
о
При вычислении статистики теста используется функция
igamc(a, х) = 1 - Р(а, х),
Г* (а}
где Р(а, х) = ——F(a)=\ta~1e~,dt -гамма-функция.
Г(а) J
Стандартное нормальное распределение (Standard Normal
Function) суть функция
. X и2
Ф(х)=~г==
л/2л
ли	1
J е 2 du =— 1 + erf
x
Дискретное преобразование Фурье (Discrete Fourier
Transform) DFT(x) суть получение функций по гармоникам для
нормированной битовой последовательности х =	. хп.
k=l
Для упрощения вычислений предлагается использовать сле-
дующую формулу:
2nj . (2ltj ,
е " =cos—-k +i-sin -к
\ п J \п
Таким образом,
п
fj=lLxk
k=l
f 2tti z j ,. । , , । 2tti 1 ।
cos---(£-1) +i-5in----(£-1) .
I» J I n J
Глава 4. Методика оцеики качества гЕИЕрлторов ПСП
1>9
4.2.2. Подборка тестов Д. Кнута
В состав своей подборки Д. Кнут включил тесты, которые тра-
диционно применяются для исследования статистических свойств
ПСП.
Проверка несцепленных серий. Цель теста - исследовать по-
следовательность на случайность, анализируя длины несцеплен-
ных серий различной длины.
Пусть е = Е1Е2...еп - двоичная последовательность длины п и
т - длина серии. Подсчитывается число появлений v, , всевоз-
можных непересекающихся серий длиной т (лишние биты от-
брасываются) и вычисляется статистика:
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным 2т - 1.
Пример 4.9.
Вход:
Е= 110010010000 Ш 111 ОН 010101000100 010 000101 10100011,
п = 50,
т = 3.
Тест:
Vooo = 4,
Vooi = 0,
Voio = 4,
Von = 1,
V100 = 1,
Vioi = 3,
Vno = 1,
Viu = 2.
140
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
xXobs} = ((4 - 2)2 + (0 - 2)2 + (4 - 2)2 + (1 - 2)2 + (1 - 2)2 +
+ (3 - 2)2 + (1 - 2)2 + (2 - 2)2)/2 = 8.
(4 - 2)2 + (4 - 2)2 + (4 - 2)2 + (4 - 2)2
Проверка интервалов. Данный тест проверяет равномерность
распределения символов в исследуемой последовательности,
анализируя длины подпоследовательностей, все элементы кото-
рых принадлежат определенному числовому интервалу.
Пусть е = EiE2...En - последовательность m-разрядных чисел.
Пусть а и Р - два целых числа, таких, что 0<а<Р<2'"-1. Под-
считываются длины интервалов между числами, лежащими в
промежутке [а; Р]. После этого определяется число интервалов
V,, i = 0,z, длины 0, 1, 2,..., t и рассчитывается статистика:
%2(оЬ)
где Г| =	- общее число интервалов.
i=0
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным t.
Пример 4.10.
Вход:
£ = 054 1 046 1,
т = 3,
а = 0,
Р = 2.
Тест:
v0 = 2: {0}, {10};
Vi =0;
v2 = 2: {0541}, {0461};
Глава 4. Методика оценки качества генераторов ПСП
141
Т| = 2 + 2 = 4.
7 I 4)	41	4)	-П ч;
z’(oto) = ^-^+l------.............. ...J ,5.
л1	. 2 . 2 )
4 —
4
Проверка комбинаций. Данный тест проверяет равномерность
распределения символов в исследуемой последовательности,
анализируя различные комбинации чисел в подпоследовательно-
стях.
Пусть е = Е1Е2...£я - последовательность m-разрядных чисел
длины п. Разобьем ее на подпоследовательности длиной t каждая
(лишние биты отбрасываются). Подсчитывается число подпосле-
довательностей v(-,i = l, г, содержащих i различных чисел, и
вычисляется статистика:
V, - - Pi
X2 Cobs') =

J = 2m-1, 
где р,. =
dk
- числа Стирлин-
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным г - 1.
Пример 4.11.
Вход:
£=015013222301023111110333512,
и = 27,
т = 3,
/ = 5.
142
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Тест:
Vi = 1 {1 1 1 1 1},
v2= 1 {3 222 3},
v3 = 2 {0 1 5 0 1} и {0 3 3 3 5},
v4 = 1 {0 1 0 2 3},
d=23- 1=7,
51
> = 0.0004,
1J
7
л=7
7-6 [5
Р2 75 I2.'
= 0.037,
\2
•0.0004
2
•0.0004
•0.037
= 503.
Тест собирателя купонов. Данный тест проверяет равномер-
ность распределения символов в исследуемой последовательно-
сти, анализируя различные комбинации чисел в подпоследова-
тельностях.
Пусть е = Е1Е2---Ея - последовательность т-разрядных чисел
длины п. Подсчитывается число V, подпоследовательностей дли-
ны г, г = 2т, t, содержащих полный набор чисел от 0 до 2т - 1, и
вычисляется критерий:
Глава 4. Методика оценки качества ГЕИЕрлюров ПСП
14?
-12
V,
где pr= —
d
%2(obs)= £
i=d
dl fr-1
Pi
-, r = d,(t-l), pt =1-
d
d\ p-f
d
>, d = 2m-l.
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным t - 2т + 1.
Пример 4.12.
Вход:
6=01201322230102311103212,
т = 2,
t = 6.
Тест:
v4= 1 {0 2 3 1},
V5 = l {1 1 03 2},
v6 = 2 {0 1 20 1 3} и {22230 1},
6
=14-14-2 = 4,
J=4
d = 22 - 1 = 3,
3! [4-1
3-1
3! (5-1
3-1/
3! /6-1
Рб ~	36’1 3
 = 0.22,
Р*=-у
- = 0.17,

} = 0.38,
= (1-4-0.22)^ (l-4.0.17)^.(l-4.Q.38)i =
v '	4-0.22	4-0.17	4-0.38
144
Теория, применение и оценка качества генераторов псевдослучайных посаедоватеаьиостей
Следует отметить, что «собиратель купонов» является специ-
фическим тестом и рассчитан на определенный тип последова-
тельностей. В нем, по существу, происходит анализ не всей по-
следовательности целиком, а наборов по t m-разрядных чисел.
Проще всего проходят этот тест ПСП, для подпоследовательно-
стей длины d которых вероятность появления каждого числа из
интервала [0; J-1] близка к 1.
Проверка перестановок. Данный тест проверяет равномер-
ность распределения символов в исследуемой последовательно-
сти, анализируя взаимное расположение чисел в подпоследова-
тельностях.
Пусть е = Е1Е2...Е„ - последовательность m-разрядных чисел
длины п. Разобьем ее на подпоследовательности длиной t чисел
каждая (лишние биты отбрасываются). В каждой такой подпос-
ледовательности возможно г! вариантов относительного распо-
ложения чисел. Подсчитывается, сколько раз встречается каждое
такое расположение vt, i = 1, ?!, и вычисляется статистика:
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным Л' - 1.
Пример 4.13.
Вход:
£ = 35421461 0,
п = 9,
/ = 2.
Тест:
£ = 354214610,
Vi (первое число меньше второго) = 2,
v2 (первое число больше второго) = 2,
Глава 4. Методика оценки качества генерАТоров ПСП
145
%2(о^) =
V Го Г9
 +2-------
2j 2!j
= 0.
2 2!
Проверка на монотонность. Данный тест проверяет равно-
мерность распределения символов в исследуемой последователь-
ности, анализируя участки невозрастания и неубывания элемен-
тов последовательности.
Пусть Е = Е1£2...8л - последовательность m-разрядных чисел.
Пусть v(, i = 1, t, - число участков невозрастания (неубывания)
длиной i.
Вычисляется статистика:
X2(obS) = %
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным t - 1.
Пример 4.14.
Вход:
Е = 3 5 4 21461 0.
Тест:
Участки невозрастания:
е = 354214610,
Vi = 1,
v2 = 0,
v3 = 2,
146
Теория, применение и оценка качества генерАТоров псевдослучайных последовательностей
3
= Vj+v2+v3 =3,
;=i
1	1	1
1	1	2!	2
1	1	1
2	21	31	3
1 1 1
3! 4! 8 ’
( 1Y ( 1Y ( 1Y
1-3--	0-3--	2-3- —
x2 (obs)=k—2L+k—2L+k—AL=ю.5.
Участки неубывания:
£ = 354214610,
v,=2,
V2 = 2,
2
£v.=V1+.V2=4,
2=1
Г2-4-Т
%2(ofo)=k—AL
4--
2
3
Проверка корреляции. Данный тест проверяет взаимонезави-
симость элементов последовательности.
Пусть £ = £0£|...£n-i - последовательность m-разрядных чисел
длины п. Вычисляется статистика
п ' '^n-2^(n-2+f)mod п ’^^n-L^(n-l+j)mod п) fefl "^1
«(Go +Е[ +.. -+£„4) — (Ед +Е1 +•. -+£^-1)
Для любого j значение Су должно лежать в интервале
[рп ~ 2,43сг„; рп + 2,43сг„],
Глава 4. Методика оценки качества генераторов ПСП
147
где
=____1_	2_ П2
n-Г G" (и-1)2(и-2)
Пример 4.15.
Вход:
£= 1 3 232,
п = 5,
J = 2.
Тест:
С _ ^'(1'2 + 3-3 + 2-2 + 3-1 + 3-3)-(1 + 3 + 2 + 3 + 2)2
2	5-(12 +32 + 22 +32 + 22)-(1 + 3 + 2 + 3 + 2)2	" ’
ц5 =----- = -0.25,
5	5-1
7	52
о2 =-------------= 0.52.
(5-1)2(5-2)
Выводы
В целом подборку можно признать очень многообещающей.
Д. Кнутом предложен ряд оригинальных алгоритмов, позволяю-
щих значительно ускорить время выполнения тестов.
К недостаткам данной подборки можно отнести 3 факта.
•	Отсутствие рекомендуемых параметров тестирования. Не совсем
корректный выбор некоторых значений может привести к тому,
что ряд тестов (проверка на монотонность, тест собирателя купо-
нов) будет зависеть от длины исследуемой последовательности
или, что еще хуже, браковать все последовательности.
•	Спорной представляется методика оценки результатов. Д. Кнут
предлагает считать последовательности, для которых вероят-
ность появления данного результата лежит в интервалах [0;
0.01] и [0.99; 1], неслучайными, (0.01; 0.1] и [0.9; 0.99) - по-
дозрительными на случайность, (0.1; 0.9) - случайными. Та-
ким образом, для истинно случайной последовательности ве-
148
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
роятность должна стремиться к 0.5, хотя, как представляется,
на самом деле она должна стремиться к 0.
• Отсутствие программной реализации описанных алгоритмов.
4.2.3.	Система оценки статистических свойств
«DIEHARD»
Данная программа была предложена Дж. Марсалья для иссле-
дования статистических свойств разработанных им же конгру-
энтных генераторов.
Проверка промежутков между «Днями рождения» (The
Birthday-Spacings Test). Цель теста - проверить равномерность
распределения символов в исходной последовательности, анали-
зируя длины интервалов между так называемыми «Днями рожде-
ния» (ДР).
Пусть е = £1£2...ел - последовательность m-разрядных чисел.
Отсортируем числа в порядке неубывания, образовав тем самым
последовательность ДР: Y = У1У2---Уп- Сформируем последова-
тельность W промежутков между ДР:
У2 - Уь Уз - У2, • •; Уп - Уп-1, У1 + 2т - уп.
Пусть Hi, i = 0, к, - число промежутков, имеющих i дублика-
тов. Вычисляем статистику:
x=(<,fc)=2;<2LW,
to "Pi
__	2
Полученный результат анализируется при помощи критерия %
с числом степеней свободы, равным к.
Пример 4.16.
Вход:
£= 12345,
п = 4,
т = 4.
Глава 4. Методика оценки качества генераторов ПСП
149
Тест:
У=34 5 12,
W= 1 1 7 6,
По = 2 (7 и 6),
«1 = 1(1),
п>2 = О,
р0 =^- = 0.368,
0!
Х-е’1
р, = ———— = 0.368,
1 1!
/?>2 =1-р0- =1-0.368-0.368 = 0.264,
2 b (2-4-0.368)2 (1-4-0.368)2 (0-4-0.264)2
Х ° S) 4-0.368 + 4- 0.368 +	4-0.264
К большому сожалению, данный тест очень трудно применять
к последовательностям большой длины из-за сложности выбора
тип. Поскольку значение X должно стремиться к 1 (в противном
случае значения р, будут стремиться к 0, что сразу приведет к
отрицательному результату прохождения теста), значение п це-
ликом и полностью зависит от т, что, как видно из приведенной
ниже табл. 4.3, значительно уменьшает размер тестируемой по-
следовательности.
Табл. 4.3. Соотношение между т, п и X
m	п	Л = пЩт
8	16	2
16	64	2
25	512	1
32	4096	4
Из-за этих ограничений данный тест в программе «DIEHARD»
проверяет только первые 500 32-разрядных чисел (точнее, наборы
по 24 бита из этих чисел: 1-24, 2-25, ..., 9-32). Минимальная длина
последовательности для тестирования равна 500 • 32 = 16000 байт.
150
Теория, применение и оценка качества генерАТоров псевдослучайных последовательностей
Проверка пересекающихся перестановок (The overlapping
k-permutation test). Цель теста - проверить равномерность рас-
пределения символов в исходной последовательности, анализи-
руя частоты появления наборов из т чисел.
Пусть Е = EiE2...E„ - последовательность /«-разрядных чисел.
Представим ее в виде N =
п-1
к-1
пересекающихся наборов по к
чисел. Лишние числа отбрасываются. В каждом таком наборе
возможно kl относительного расположения чисел. Пусть V, - чис-
ло появлений г-го состояния в наборах
Vi:E><Ey+i<... <£j + k-i,
v2: £/ < ^j + k-2 < £у +1 < ••• < £у+*-з< Ey + *-b
. бу + t -1 < 6y + к - 2 < • • • < £y>
где j = 1, (n - к +1) - индекс первого элемента набора.
Примечание. В данном тесте предполагается, что в одном на-
боре нет равных между собой чисел, точнее, вероятность появле-
ния данного события настолько мала, что даже если оно все-таки
имеет место, то это никак не сказывается на результатах тестиро-
вания (данный набор просто выбрасывается из рассмотрения).
Вычисляем статистику:
к\
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным к\ - 1.
Пример 4.17.
Вход:
Г-1 I—I I—I I—I I—I I—I I—I
Е = 0 2 4	7 3 5 1	6 2 0 5	1 4 6 3	0 6 3 5	6 3 2 1	6 7 3 7	2,
п = 28,
Глава 4. Методика оценки качества ГЕНЕрлторов ПСП
1Я
т - 3,
к = 3.
Тест:
28-1
= 13,
{О, 2, 4} {4, 7, 3} {3, 5, 1} {1, 6, 2} {2, 0, 5} {5, 1, 4} {4, 6, 3}
{3,0,6} {6, 3,5} {5, 6,3} {3, 2, 1} {1,6,7} {7, 3,7},
Vi=2: {0, 2,4} и {1,6, 7},
v2=l: {1,6,2},
v3 = 2: {2, 0,5} и {3, 0,6},
v4 = 2: {5, 1,4} и {6, 3,5},
v5 = 4: {4, 7,3}, {3, 5, 1}, {4, 6,3}, {5, 6,3},
v6=l: {3,2,1}.
Примечание. Набор {7, 3, 7} не рассматривался, так как в нем
встречаются два одинаковых числа.
z	\ 2	/ х 2	/
2_»	j.»	2_*3
13
3!
В системе «DIEHARD» анализируемая последовательность
представляется в виде двух подпоследовательностей, состоящих
из 1 000 000 пересекающихся наборов по пять 32-разрядных чи-
сел (отсюда минимальная длина тестируемой последовательности
должна быть 2 • 4 • (1000000  4 + 1) = 32000008 байт).
Проверка рангов матриц (The binary rank test). Цель теста -
проверить равномерность распределения символов в исходной
последовательности, анализируя частоты появления матриц раз-
личных рангов.
152
Теория, применение и оценка качества геиерАторов псевдослучайных последовательностей
Пусть Е = £1£2...е„ - последовательность m-разрядных чисел.
Представим ее в виде N =
п
~Q^R
двоичных матриц. Лишние
числа отбрасываем.
Пример 4.18. Разбиение на матрицы.
£ = A25Ch24BlhE923h,
или в двоичном представлении:
£= 1010 0010 0101 1100 0010 0100 1011 0001 1110 1001
0010 0011.
Предста А25Сй=	вим каждое 10 10 0 0 10 0 10 1 110 0	ЧИСЛО В Е 24В1Л =	шде матрш 0 0 10 0 10 0 10 11 0 0 0 1	(Ы 4 х 4: E923U	1110 10 0 1 0 0 0 1 0 0 11	
Подсчитываем ранги матриц. Пусть v(- - число матриц ранга г,
г = 1, min(Q, R). Вычисляем статистику:
min(Q.R) , Л, ,2
/>м= s
м	Npi
Р = 21(С+л-о-^ jj (1-2>-6)(1-2>-д)
7=0	1-27
Полученный результат анализируется при помощи критерия %2
с числом степеней свободы, равным min(Q, R) - 1.
В системе «DIEHARD» реализовано 3 разновидности данного
теста.
Проверка рангов матриц 32x32. Последовательность 32-раз-
рядных чисел рассматривается как 40000 матриц размером
32x32. Формирование матриц происходит следующим образом:
берутся наборы по 32 числа, двоичное представление первого
числа - первая строка матрицы, второго - вторая и т. д. Анали-
Глава 4. Методика оценки качества генераторов ПСП
15?
зируются следующие ранги матриц: 32, 31, 30 и меньшие либо
равные 29. Минимальная длина последовательности равна
40000 • 32 • 4 = 5 120000 байт.
Проверка рангов матриц 31x31. Последовательность 32-раз-
рядных чисел рассматривается как 40000 матриц размером
31x31. Формирование матриц происходит следующим образом:
берутся наборы по 32 числа, первые 31 бит первого числа - пер-
вая строка матрицы, первые 31 бит второго - вторая и т. д. Ана-
лизируются следующие ранги матриц: 31, 30, 29 и меньшие либо
равные 28. Минимальная длина последовательности равна
40000  32 • 4 = 5 120000 байт.
Проверка рангов матриц 6x8. Последовательность 32-раз-
рядных чисел рассматривается как 100000 матриц размером 6x8.
Формирование матриц происходит следующим образом: берутся
наборы по 6 чисел, первые 8 бит первого числа - первая строка
матрицы, первые 31 бит второго - вторая и т. д. Анализируются
следующие ранги матриц: 6, 5 и меньшие либо равные 4. Мини-
мальная длина последовательности равна 100000 - 6 - 4 = 2400000
байт.
Буквенные тесты (The Monkey Tests). Цель тестов - проверить
равномерность распределения символов в исследуемой последо-
вательности на основе анализа отсутствующих в ней подпоследо-
вательностей.
Столь странному названию («обезьяньи») данные тесты обя-
заны своему автору - Дж. Марсалья, который предложил рас-
сматривать генератор как обезьяну, печатающую на машинке
с определенным набором символов, и анализировать количество
пропущенных слов в выдаваемой последовательности.
Пусть е = Е1Е2...£л - последовательность m-разрядных чисел.
Преобразуем ее в строку е*, состоящую из N слов. Каждое слово
состоит из к /-разрядных букв (буквы и слова в исходной после-
довательности Е не обязательно следуют друг за другом). Тогда
число отсутствующих слов в строке Е* аппроксимируется с нор-
мальным распределением со средним
1Я
Теория, применение и оценил клчествл геиерлторов псевдослучайных последовательностей
и отклонением
N
ц = 2е 2
где nt
1, если буква, равная 2‘, присутствует в слове;
О, если буква, равная 2‘, отсутствует в слове.
Вычисление ст является в ряде случаев проблематичным, по-
этому на практике используют либо табличные значения, либо
значения, полученные в результате ряда экспериментов.
В системе «DIEHARD» реализованы следующие 4 представи-
теля данной группы тестов.
Проверка потока бит (The bitstream test). Представим исход-
ную последовательность £ = £i£2...£n в виде последовательности
бит b = bib2...b32n- Преобразуем b в строку, состоящую из 20-бук-
венных пересекающихся слов (1 буква - 1 бит). Получим:
bib2...b2o b2b2...b2i ... ^32л-19^32и-18---^32п-
Тогда в строке, состоящей из 221 пересекающихся 20-буквен-
ных слов, число отсутствующих слов аппроксимируется с нор-
мальным распределением с р = 141909 и <7= 428. Тест повторяется
20 раз (1-й раз отсчет начинается с 1-го бита, 2-й - с (221 + 1)-го
и т. д. до 20-го).
Следуя введенным обозначениям, N = 221, к = 20,1 = 1.
Минимальная длина тестируемой последовательности равна
221-20 бит = 5 242 800 байт.
Пример 4.19.
Вход:
£ = 5 20 7,
N = 10,
к = 3,
1=1.
Глава 4. Методика оценки качества ГЕИЕрлюров ПСП
155
Тест:
Ь= 101 010 000 111.
Слова: {101}, {010}, {101}, {010}, {100}, {000}, {000}, {001},
{011},{111}.
Число отсутствующих слов равно 1 - {ПО}.
Проверка разреженных пересекающихся пар (OPSO -
Overlapping-Pairs-Sparse-Occupancy). Пусть £ = £i£2...£n - исход-
ная последовательность 32-разрядных чисел. Из каждого числа
выбираем 10 бит (букву) и образуем 2-буквенные слова. Тогда
в строке из 221 пересекающихся слов число отсутствующих слов
аппроксимируется с нормальным распределением с р. = 141909
и о = 290. Тест повторяется 23 раза (1-й раз выбираются биты
с 1-го по 10-й, 2-й - со 2-го по 11-й и т. д. до 23-го).
Следуя введенным обозначениям, N = 221, к = 2,1 - 10.
Минимальная длина тестируемой последовательности равна
(221+ 1) • 4 = 8388 612 байт.
Пример 4.20.
Вход:
£ = 15 1207 94 1 13 10 843 0 8,
#=13,
к = 2,
1 = 2.
Тест:
1-й раз выбираются первые 2 бита:
b = 1111 1100 0000 0111 1001 0100 0001 1101 1010 1000 0100
0011 0000 1000.
Слова: {1111}, {1100}, {0001}, {ОНО}, {1001}, {0100},
{ООП}, {1110}, {1010}, {1001}, {0100}, {0000}, {0010}.
Число отсутствующих слов равно 5 - {0101}, {0111}, {1000},
{1011}, {1101}.
1»6
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Проверка разреженных пересекающихся четверок (OQSO -
Overlapping-Quadruples-Sparse-Occupancy). Пусть е = £i£2...£„ -
исходная последовательность 32-разрядных чисел. Из каждого
числа выбираем 5 бит (букву) и образуем 4-буквенные слова. Тогда
в строке из 221 пересекающихся слов число отсутствующих слов
аппроксимируется с нормальным распределением с ц = 141909 и
а = 339. Тест повторяется 28 раз (1-й раз выбираются биты с 1-го
по 5-й, 2-й - со 2-го по 6-й и т. д. до 28-го).
Следуя введенным обозначениям, N = 221, к = 4,1 = 5.
Минимальная длина тестируемой последовательности равна
(221 + 3) • 4 = 8 388 620 байт.
Пример 4.21.
Вход:
£ = 760342065421047 3,
N = 5,
fc = 4,
Z=l.
Тест:
1-й раз выбираются первые 3 бита:
b = 111 ПО ООО 011 100 010 000 ПО 101 100 010 001 000 100
111011.
Слова: {1100}, {0100}, {0111}, {1000}, {ОНО}.
Число отсутствующих слов равно 16-5 = 11.
Проверка разреженных пересекающихся десяток (DNA). Пусть
Е = £i£2. . .£„ - исходная последовательность 32-разрядных чисел. Из
каждого числа выбираем 2 бита (букву) и образуем 10-буквенные
слова. Тогда в строке из 221 пересекающихся слов число отсутст-
вующих слов аппроксимируется с нормальным распределением с
ц = 141909 и ст = 339. Тест повторяется 31 раз (1-й раз выбирают-
ся биты с 1-го по 2-й, 2-й - со 2-го по 3-й и т. д. до 31-го).
Следуя введенным обозначениям, N = 221, к = 2,1 = 10.
Минимальная длина тестируемой последовательности равна:
(221 + 9) • 4 = 8388644 байт.
Глава 4. Методика оценки качества гЕИЕрАторов ПСП
157
Подсчет 1 в потоке байт (The count-the-1 's test on a stream of
byte). Цель теста - проверить равномерность распределения сим-
волов в исследуемой последовательности на основе анализа час-
тоты появления байтов с различным числом единиц.
Пусть е = eie2...e„ - исходная последовательность 32-разряд-
ных чисел. Представим ее в виде последовательности байт b = Ь\
bz.-.bin. Каждый байт может содержать от 0 до 8 единиц с вероят-
ностями 1/256, 8/256, 28/256, 56/256, 70/256, 56/256, 28/256, 8/256,
1/256 соответственно. Введем следующие обозначения: если байт
содержит от 0 до 2 единиц, обозначим его А, 3 единицы - В,
4 единицы - С, 5 единиц - D, от 6 до 8 единиц - Е. Соответствую-
щие вероятности равны: р(А) - 37/256, р(В) = 56/256, р(С) = 70/256,
p(D) = 56/256, р(Е) = 37/256. Представим последовательность b в
виде строки из N пересекающихся ^-буквенных слов. Пусть
V-, i = 1, 5k , - число появлений слова конкретного типа (напри-
мер, Vj- число появлений слова ААААА, ..., Уз125- число появле-
ний слова ЕЕЕЕЕ). Вычисляем статистику:
X2
Np*
Np^
которая аппроксимируется с распределением %2 с числом степе-
ней свободы, равным 5к - 5к~ (р\ - вероятность появления слова
V-).
В системе «DIEHARD» используются следующие параметры:
N - 256000, к = 5. Минимальная длина тестируемой последова-
тельности равна 256000 - 4+ 1 = 1024001 байт.
Пример 4.22 формирования слов.
Вход:
£ = C700h A4C9h 2367h E4B7h,
k=3,
N=3.
1*8
Теория, применение и оценка качества геиердторов псевдослучайных последовательностей
Формирование слов:
b = 11000111 0000000 10100100 11001001 00100011 01100111
11100100 10110111,
Z> = EABCBDCE.
Слова: {EAB}, {ВСВ}, {BDC}.
Примечание. Почему бы просто не посчитать количество байт
с различным числом единиц и не применить критерий %2 с чис-
лом степеней свободы, равным 7?
Подсчет числа единиц в определенных байтах (The count-the-
1 ’s for specific bytes}. Данный тест является расширением преды-
дущего. Рассматривается последовательность 32-разрядных чи-
сел и из каждого числа выбирается 8 бит, которые затем участ-
вуют в образовании слов. Тест повторяется 25 раз (1-й раз выби-
раются биты с 1-го по 8-й, 2-й - со 2-го по 9-й и т. д. до 25-го).
Минимальная длина тестируемой последовательности равна
4 • (256 000 • 4 + 1) = 4 096 004 байт.
Пример 4.23. формирование слов.
Вход:
е = C700h A4C9h 2367h E4B7h 4D20h 128Ah BB47h 98C3h
3AC6h,
k = 3,
N = 2.
Формирование слов:
/>= 11000111 00000000 10100100 11001001 00100011 01100111
11100100 10110111 01001101 00100000 00010010 10001010
10111011 01000111 10011000 11000011 00111010 11000110.
Слова: {DBC}, {CEC}.
Выводы
Можно перечислить следующие недостатки системы «DIE-
HARD».
• Описания некоторых тестов «DIEHARD» (а именно a parking
lot test, the minimum distance test, 3Dsphears test, the SQEESE
Глава 4. Методика оценки качества ГЕИЕрлюров ПСП
159
test, the overlapping sums, the runs test и the craps test), приве-
денные автором, не позволяют понять смысл этих тестов.
•	Параметры тестирования жестко заданы, например, размер
области тестирования - независимо от размера файла анализи-
руется определенное число байт.
•	Полностью отсутствует справочная служба и методика трак-
товки результатов.
•	Большинство тестов основано не на теоретических расчетах, а
на результатах испытаний.
4.2.4. Руководство НИСТ
4.2.4.1.	Общие положения
Различные статистические тесты могут применяться к ПСП,
для того чтобы сравнить ее с истинно случайной последователь-
ностью. Случайность - вероятностное свойство; это означает, что
свойства случайной последовательности могут быть охарактери-
зованы и описаны в терминах вероятности. Вероятный результат
статистических тестов, применяемых к истинно случайной по-
следовательности, известен априорно и может быть описан в ве-
роятностных терминах. Существует бесконечное число возмож-
ных статистических тестов, оценивающих присутствие или от-
сутствие «образца», который при обнаружении указал бы, что
последовательность неслучайна. Поскольку существует так мно-
го тестов, оценивающих, является ли последовательность слу-
чайной или нет, никакой определенный конечный набор тестов
не считают «законченным». Кроме этого, результаты статистиче-
ского теста должны интерпретироваться с некоторой осторожно-
стью и предостережением, чтобы избежать неправильных заклю-
чений об определенном генераторе (см. Приложения).
Статистический тест формулируется для проверки определен-
ной нулевой гипотезы Но о том, что проверяемая последователь-
ность является случайной. С этой нулевой гипотезой связана аль-
тернативная гипотеза На о том, что последовательность неслучай-
на. Для каждого применяемого теста получают заключение о
принятии или отклонении нулевой гипотезы, основываясь на
сформированной исследуемым генератором последовательности.
160
Теория, применение и оценил качества генерлторов псевдослучайных последовательностей
Для каждого теста должна быть выбрана подходящая стати-
стика случайности для принятия или отклонения нулевой гипоте-
зы. Согласно предположению о случайности, такая статистика
имеет распределение возможных значений. Теоретическое эта-
лонное распределение этой статистики для нулевой гипотезы
определяется математическими методами. Из этого эталонного
распределения определяется критическое значение. Во время
проведения теста вычисляется значение тестовой статистики. Это
значение сравнивается с критическим значением. Если значение
тестовой статистики превышает критическое значение, нулевая
гипотеза для случайности отклоняется. В противном случае нуле-
вая гипотеза принимается.
Проверка статистических гипотез работает, потому что эта-
лонное распределение и критическое значение зависят и генери-
руются согласно предварительному предположению о случайно-
сти. Если предположение о случайности последовательности
истинно, то результирующее значение тестовой статистики для
нее будет иметь очень низкую вероятность превышения критиче-
ского значения (например, 0.01).
С другой стороны, если расчетное значение тестовой стати-
стики превышает критическое значение (т. е. происходит событие
с низкой вероятностью), то с точки зрения проверки статистиче-
ской гипотезы событие с низкой вероятностью не может встре-
титься естественно. Поэтому, когда расчетное значение тестовой
статистики превышает критическое значение, делается заключе-
ние, что первоначальное предположение о случайности является
подозрительным или ошибочным. В этом случае делается заклю-
чение об отклонении Но (случайность) и принятии На (неслучай-
ность).
Проверка статистической гипотезы - процедура генерации за-
ключения, которая имеет два возможных результата - или при-
нять Но (данные случайны), или принять На (данные неслучай-
ны). Табл. 4.4 связывает истинное (неизвестное) состояние дан-
ных с заключением, полученным процедурой проверки.
Глава 4. Методика оценки качества генераторов ПСП
161
Табл. 4.4. Принятие заключений по результатам проведения
статистических испытаний
Ситуация	Заключение	
	Принять Ц>	Принять Н,
Данные случайны (/4 истинна)	Нет ошибки	Ошибка 1-го рода
Данные неслучайны (Н, истинна)	Ошибка 2-го рода	Нет ошибки
Если данные на самом деле случайны, то заключение об от-
клонении нулевой гипотезы (т. е. что данные неслучайны) будет
приниматься крайне редко. Это заключение называется ошибкой
первого рода. Если данные неслучайны, то заключение о приня-
тии нулевой гипотезы (т. е. что данные случайны) называется
ошибкой второго рода. Заключения о принятии Но, когда данные
действительно случайны, и отклонении Но, когда данные неслу-
чайны, являются правильными.
Вероятность ошибки 1-го рода называется уровнем значимо-
сти теста. Эта вероятность может быть установлена до испыта-
ния и обозначается как а. Для теста а суть вероятность того, что
тест укажет на неслучайность последовательности, тогда как на
самом деле она является случайной. То есть на то, что последова-
тельность имеет неслучайные свойства, даже если ее произвел
хороший генератор.
Вероятность ошибки 2-го рода обозначается как р. Для теста Р
есть вероятность того, что тест укажет на случайность последова-
тельности, тогда как это не так; т. е. плохой генератор произвел
последовательность, которая, как кажется, имеет случайные
свойства. В отличие от а, Р не является фиксированным значени-
ем; Р могут принимать множество различных значений, потому
что существует бесконечное число ситуаций, когда поток данных
может быть неслучаен, и каждая из них выдает различные р. Вы-
числение ошибки 2-го рода является более сложным из-за мно-
жества возможных типов неслучайности.
Одной из основных целей нижеописанных тестов является
минимизация вероятности ошибки 2-го рода, иначе говоря, ми-
нимизация вероятности принятия последовательности, произве-
денной плохим генератором, за последовательность, произведен-
ную хорошим генератором. Вероятности а и Р связаны друг с
другом и с длиной п проверяемой последовательности: если два
162
Теория, применение и оценил качества генерАТоров псевдослучайных последовательностей
из этих значений определены, третье определяется автоматиче-
ски. На практике обычно выбирают размер п и значение для а
(вероятности ошибки 1-го рода). Тогда критическая точка для
данной статистики выбирается так, чтобы получить наименьшее
значение Р (вероятность ошибки 2-го рода).
Каждый тест основан на вычислении значения тестовой стати-
стики, которое является функцией данных. Если значение тесто-
вой статистики есть S, a t - критическое значение, то вероятность
ошибки 1-го рода и 2-го рода есть соответственно
Р(5 > 11| Но истинна) = Р(отклонить Но | Но истинна),
P(S < 11| Но ложна) = Р(принять Но | Но ложна).
Тестовая статистика использует вычисление значения P-value,
которое констатирует силу доказательства против нулевой гипо-
тезы, иначе говоря, P-value есть вероятность того, что совершен-
ный генератор случайных чисел произвел бы последовательность
менее случайную, чем исследуемая, для типа неслучайности,
проверяемого тестом. Если P-value для теста равно 1, то последо-
вательность абсолютно случайна. P-value, равное 0, указывает,
что последовательность абсолютно неслучайна. Для теста следу-
ет выбрать уровень значимости а. Если значение P-value больше
или равно а, то принимается нулевая гипотеза, т. е. последова-
тельность кажется случайной. Если значение P-value меньше а,
то нулевая гипотеза отклоняется, т. е. последовательность кажет-
ся неслучайной. Параметр а обозначает вероятность ошибки 1-го
рода. Как правило, а выбирается в интервале [0.001, 0.01].
•	Значение а, равное 0.001, говорит о том, что из 1000 случай-
ных последовательностей не прошла бы тест лишь одна. При
P-value > 0.001 последовательность рассматривается как слу-
чайная с доверительностью 99.9 %. При P-value < 0.001 после-
довательность рассматривается как неслучайная с доверитель-
ностью 99.9 %.
•	Значение а, равное 0.01, говорит о том, что из 100 случайных
последовательностей не прошла бы тест лишь одна. При
P-value > 0.01 последовательность рассматривается как слу-
чайная с доверительностью 99 %. При P-value < 0.01 последо-
Глава 4. Методика оценки качества гЕнерлторов ПСП
16?
вательность рассматривается как неслучайная с доверительно-
стью 99 %.
По отношению к исследуемым последовательностям можно
сделать следующие предположения.
•	Равномерность. В любой точке при генерации последователь-
ности случайных или псевдослучайных битов 0 и 1 равноверо-
ятны и вероятности их появления равны 1/2. Ожидаемое число
нулей (или единиц) равно лг/2, где п - длина последовательно-
сти.
•	Масштабируемость. Любой тест, применимый к последова-
тельности, может также применяться к произвольной подпос-
ледовательности. Если последовательность случайна, то любая
ее подпоследовательность должна также быть случайна. Сле-
довательно, любая подпоследовательность должна пройти все
тесты на случайность.
•	Полнота. Поведение генератора ПСП связано с начальным
заполнением, поэтому неверно делать заключение о качестве
генератора, основываясь на результатах анализа последова-
тельности при каком-то одном начальном заполнении. Анало-
гично неверно делать заключение о генераторе случайных чи-
сел, основываясь только на результатах анализа одного произ-
веденного им фрагмента последовательности.
Итак, оценка статистических испытаний основана на проверке
гипотезы о случайности исследуемой последовательности нулей
и единиц. Табл. 4.5 показывает пошаговый процесс, позволяю-
щий оценить конкретную двоичную последовательность.
Табл. 4.5. Процедура оценки
Номер шага	Пошаговый процесс	Комментарии
1.	Постановка гипотезы	Предполагаем, что последовательность является случайной
2.	Вычисление тестовой статистики последовательности	Проводим тестирование на битовом уровне
3.	Вычисление P-value	P-value е [0;1]
4.	Сравнение P-value с а	Задаем а, где а е[0.001; 0.01]. Если P-value > а - тесты пройдены
164
Теория, применение и оценка качества генердторов псевдослучайных последовательностей
В табл. 4.6 даны общие характеристики каждого статистиче-
ского теста НИСТ.
Табл. 4.6. Статистические тесты НИСТ
№	Статистический тест	Определяемый дефект
1.	Частотный тест	Слишком много нулей или единиц
2.	Проверка кумулятивных сумм	Слишком много кулей или единиц в начале последо- вательности
3.	Проверка «дырок» в подпоследова- тельностях	Отклонения в распределении подпоследовательно- стей единиц
4.	Проверка «дырок»	Большое (малое) число подпоследовательностей нулей и единиц свидетельствует, что колебание потока бит слишком быстрое (медленное)
5.	Проверка рангов матриц	Отклонение распределения рангов матриц от соот- ветствующего распределения для истинно случайной последовательности, связанное с периодичностью подпоследовательностей
6.	Спектральный тест	Периодические свойства последовательности
7.	Проверка непересекающихся шаб- лонов	Непериодические шаблоны встречаются слишком часто
8.	Проверка пересекающихся шабло- нов	Слишком часто встречаются /w-битные последова- тельности единиц
9.	Универсальный статистический тест Маурера	Сжимаемость (регулярность) последовательности
10.	Проверка случайных отклонений	Отклонение от распределения числа появлений подпоследовательностей определенного вида
11.	Разновидность проверки случайных отклонений	Отклонение от распределения числа появлений подпоследовательностей определенного вида
12.	Проверка аппроксимированной энтропии	Неравномерность распределения да-битных слов. Малые значения означают высокую повторяемость
13.	Проверка серий	Неравномерность распределения да-битных слов
14.	Сжатие при помощи алгоритма Лемпела-Зива	Большая сжимаемость, чем истинно случайная последовательность
15.	Линейная сложность	Отклонение от распределения линейной сложности для конечной длины (под)строки
4.2.4.2. Частотный (монобитный) тест (Frequency
(Monobit) Test)
Цель теста - проверить равномерность появления 0 и 1 в ис-
следуемой последовательности.
Пусть Е = EjE2---Е„ - двоичная последовательность длины п.
Вычисляем разницу между числом появления единиц и нулей:
Sn = п\ - «о-
Глава 4. Методика оценки качества генераторов ПСП
169
Вычислим статистику
и значение P-value
s(obs) =
P-value = erfc
scobs')'
< V2 ,
Значение P-value должно быть больше 0.01.
Рекомендуемая длина последовательности - не менее 100 бит.
Пример 4.24.
Вход:
Е = 110010010000111111011010101000100010000101101000110
0001000110100110001001100011001100010100010111000,
п - 100.
Тест:
^100 = п\ - по = 42 - 58 = - 16,
s(pbs) = '	=1.6,
7100
1.6
P-value = erfc
= 0.109598 > 0.01 - тест пройден.
4.2.4.3. Частотный тест в подпоследовательностях
(Frequency Test Within a Block)
Цель теста - проверить равномерность появления 0 и 1 в под-
последовательностях.
Пусть Е = Е1Е2.. -Еп - двоичная последовательность длины п. Ра-
п
М
зобьем ее на N =
непересекающихся Л/-битных подпосле-
довательностей. Лишние биты отбрасываем. Определим долю
единиц в каждой подпоследовательности:
166
Теория, применение и оценил качества генераторов псевдослучайных последовательностей
М
X Е('-1)л/+;
л, -----------, l<i<M.
‘ М
Вычислим статистику
м
x4obs} = 4M^’n.i-Q.5)2
i=l
и значение Р - value
. .	. (N z4obs)\
Р-value = igamc —, L------- .
\ 2 2 /
Значение P-value должно быть больше 0.01.
Рекомендуемая длина последовательности - не менее 100 бит.
п> MN, М> 20, М >0.01п, N < 100.
Пример 4.25.
Вход:
е=110010010000111111011010101000100010000101101000110
0001000110100110001001100011001100010100010111000,
п = 100,
М= 10.
Тест:
N= 10,
4
61 = 1100100100 л, = —,
' 1 10
7
е2 = 00ШШ01 я, = —,
2 10
4
Е3= 1010101000 л3= —,
3 10
е4 = 1000100001 л4 = —,
4 10
65 = 0110100011 л5 = —,
5 10
Глава 4. Методика оценки качества генераторов ПСП
167
з
е6 = 0000100011 л, = —,
6 10
4
е7 = 0100110001 л7 = ——,
7 10
4
е8 = 0011000110 л„= —,
8 10
4
е9 = 0110001010 л9 = —,
9 10
4
Ею = 0010111000 л,0 = —,
10 10
X2(obs) = 4 • 10 • [(0.4 - 0.5)2 + (0.7 - 0.5)2 + (0.4 - 0.5)2 +
+ (0.3 - 0.5)2 + (0.5 - 0.5)2 + (0.3 - 0.5)2 + (0.4 - 0.5)2 +
+ (0.4 - 0.5)2 + (0.4 - 0.5)2 + (0.4 - 0.5)2] = 7.2,
(10 7.2^
P-value = igamc —, — = 0.706438 > 0.01 - тест пройден.
4.2.4.4.	Тест «дырок» (Runs Test)
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа количества
появлений «блоков» - подпоследовательностей, состоящих из
одних единиц, и «дырок» - подпоследовательностей, состоящих
из одних нулей.
Пусть Е = EiE2...En - двоичная последовательность длины п.
Сначала определим предтестовую статистику л - долю единиц в
рассматриваемой последовательности:
п
л = -—
п
।	।	2
Если л-0.5 >Т = -т=г, то тест считается непройденным.
ум
В противном случае вычислим статистику (количество блоков
и дырок):
168
Теория, применение и оценил качества генерлторов псевдослучайных последовательностей
vn(ofo) = 2y(£) + l,
к=1
где г(к) = 0, если Е* = E*+i и r(k) = 1, если е* / е*_ ь
и значение P-value
P-value = erfc
| Уп(оЬз)-2пя(1-я) |
Значение P-value должно быть больше 0.01.
Рекомендуемая длина последовательности - не менее 100 бит.
Пример 4.26.
Вход:
Е = 11001001000011111101101010100010001000010110100011
00001000110100110001001100011001100010100010111000,
п = 100.
Тест:
2
т = -Д= = 0.2,
7100
42
п = — = 0.42 >0.2,
100
iWoto) = 52,
|52-2-100-0.42-(1-0.42)|
2-л/2-100-0.42-(1-0.42)
P-value = erfc
= 0.50079 > 0.01 -
тест пройден.
4.2.4.5.	Тест «блоков» в подпоследовательностях
(Test for the Longest Run of Ones in a Block)
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа количества
появлений «блоков» в подпоследовательностях.
Пусть Е = Е]Е2...е„ - двоичная последовательность длины п.
п
М
Разделим ее на N =
непересекающихся Л/-битных подпос-
ледовательностей. Лишние биты отбрасываем.
Глава 4. Методика оценки качества ГЕиЕрлторов ПСП
169
Распределим число появлений подпоследовательностей с мак-
симальной длиной «блока», равной I, по категориям (табл. 4.7).
Табл. 4.7. Распределение по категориям в зависимости от длины
«блока»
V|	М=Ъ	М= 128	М= 10*
Vo	/< 1	/<4	/< 10
Vi	/=2	/=5	/= 11
v2	/=3	/=6	/=12
v3	/>4	/=7	/=13
v4		/=8	/= 14
V5		/>9	/= 15
V6 -			/> 16
Вычислим статистику:
2/ , х V (v, -^,.)2
Xz(obs) = 2^ '	‘ 
Значения К определяются из табл. 4.8.
Табл. 4.8. Соотношение между М и К
М	8	128	10*
К	3	5	6
Значения л, берутся из табл. 4.9.
Табл. 4.9. Значения itj для различных М и vf
47=8													
Vo			v.				v2				v3		
0.2148			0.3672				0.2305				0.1875		
М= 128													
Vo		Vi-			v2		v3		v4			v5	
0.1174		0.2430			0.2493		0.1752		0.1027			0.1124	
47=10*													
Vo	V«			v2		v3		v4		v5			v6
0.0882	0.2092			0.2483		0.1933		0.1208		0.0675			0.0727
170
Теория, применение и оценка качества генЕрлторов псевдослучайных последовательностей
Вычислим значение P-value
_ ,	. [К X\obs)
P-value = igamc —, -
2
Значение P-value должно быть больше 0.01.
Рекомендуемая длина последовательности - не менее 100 бит.
Значение М выбирается в соответствии с табл. 4.10.
Табл. 4.10. Соотношение между Я и минимальной длиной
последовательности
minn	128	6272	750000
м	8	128	104
Пример 4.27.
Вход:
е = 11001100000101010110110001001100Ш000000000001001
001101010100010001001111010110100000001101011111001100
111001101101100010110010,
п = 128,
М = 8,
к=з.
Тест:
Ei = 11001100, максимальная длина «блока» = 2;
Ег = 00010101, максимальная длина «блока» = 1;
£3 = 01101100, максимальная длина «блока» = 2;
е4 = 01001100, максимальная длина «блока» = 2;
Е5 = 11100000, максимальная длина «блока» = 3;
е6 = 00000010, максимальная длина «блока» = 1;
£7 = 01001101, максимальная длина «блока» = 2;
Ев = 01010001, максимальная длина «блока» = 1;
Ед = 00010011, максимальная длина «блока» = 2;
Ею = 11010110, максимальная длина «блока» = 2;
Е] ] = 10000000, максимальная длина «блока» = 1;
е12 = 11010111, максимальная длина «блока» = 3;
ei3 = 11001100, максимальная длина «блока» = 2;
Глава 4. Методика оценки качества ГЕИЕрлторов ПСП
171
Eu = 1И 00 И 0, максимальная длина «блока» = 3;
Би = 11011000, максимальная длина «блока» = 2;
Е16 = 10110010, максимальная длина «блока» = 2;
Vo = 4, V] = 9, v2 = 3, v4 = 0,
у2(obs} = (4-16-0.2148)2 + (9-16-0.3672)2 *
16-0.2148	16-0.3672
(4-16-0.2305)2 (0 -16 • 0.1875)2 _
Ч----------------1---------------4.оо2о,
16-0.2305	16-0.1875
D Z	4.8826^ л 1ОЛСЛ ЛЛ1
P-value = igamc\—, —-—1 = 0.18059 >0.01-
тест пройден.
4.2.4.б.	Проверка рангов матриц (Binary Matrix Rank
Test)
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа количества
появлений матриц различных рангов.
Пусть Е = Е]Е2...ЕП - двоичная последовательность длины п.
Разделим ее на
непересекающихся подпоследова-
тельностей. Лишние биты отбрасываем. Теперь представим каж-
дую такую подпоследовательность как бинарную матрицу разме-
ром MxQ.
Пример 4.28.
£ = 010110'01001010101101,
п - 20,
M=Q = 3.
Разбиение				
	0 1 0		0 1 0	
	1 1 0	и	1 0 1	
	0 1 0		0 1 1	
172
Теория, применение и оценил качества генерлторов псевдослучайных последовательностей
Определим ранг каждой матрицы. Пусть
FM - число матриц с рангом М,
FM_\ - число матриц с рангом М- 1,
N- FM- FM-i - число оставшихся матриц.
Вычислим статистику
-.2/	(Тм-0.2888N)2 , (FM_,-0.5776N)2
Х	0.28887V	0.5776W
, (2V-FM -FM,-0.13367V)2
O.13367V
и значение P-value
P-value = igamc 1,

Значение P-value должно быть больше 0.01.
Рекомендуемая длина последовательности - не менее 38ЛЛ<2
бит.
4.Z.4.7. Спектральный тест (Discrete Fourier Transform
(Spectral) Test)
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа высоты вы-
бросов преобразования Фурье.
Пусть £ = Е^г-.-Еп - двоичная последовательность длины п.
Преобразуем ее в последовательность х = xix2.. .хп, где х, = 2е, - 1
(т. е. 1 —> 1, 0 —> -1). Теперь применим к х дискретное преобразо-
вание Фурье и получим последовательность гармоник:
S = DFT(x).
Пусть S' - подпоследовательность S, содержащая первые п/2
элементов S. Для каждого элемента 5' найдем модуль:
М, = modulus (S'i) (S', является комплексным числом). Последова-
тельность М даст нам последовательность высот выбросов пре-
образования Фурье.
Глава 4. Методика оценки качества генераторов ПСП
177
Найдем
Т = 4^п,
..	0.95л
N»= —
Вычислим Ni - число элементов М меньших, чем Т.
Вычислим статистику
п
2
и значение P-value
P-value = erfc
Значение P-value должно быть больше 0.01.
Рекомендуемая длина последовательности - не менее 1000
бит.
Пример 4.29.
Вход:
Е=1001010011,
п = 10.
Тест:
х= 1, -1, -1, 1,-1, 1, -1, -1, 1, 1,
S = DFT(x),
=	cos^^(&-l)^ + Z-s/n^“(&-l)j =1.618-1.175/,
S'2 = ^xk	+	=1.381-4.253/,
= -0.618-1.902/,
S3 ~У\хк
ы
174	Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Глава 4. Методика оценки качества генераторов ПСП
175
10
$ 5 = Хк
к=1
=-2-7.04 10~19i,
Mi = modulus (1.618 - 1.175г) = 2,
М2 = modulus (1.381 -4.2531) = 4.472,
М3 = modulus (-0.618 - 1.902г’) = 2,
M4 = modulus (3.618 + 2.628г) = 4.472,
Ms = modulus (-2 - 7.04-10”19i) = 2,
T = TTTO = 5.47,
n0 == 4.75,
0	2
шаблона в битах. Начинаем сканировать j-ю подпоследователь-
ность. Если рассматриваемый набор
Ещ-1) + к, , EN(j-l)+k + m-l, к = 1, (М - т + 1),
совпадает с шаблоном, то значение v7 увеличиваем на 1 и рас-
сматриваем набор
EN(j- 1) + к + т,   •> E/V(/- 1) + 1: + 2т- 1,
в противном случае значение v7 не изменяем и рассматриваем
набор
En(J- Г) + к + 1, , EN(j-l) + k + m-
Сканирование прекращаем, когда часть элементов набора вы-
ходит за пределы рассматриваемой подпоследовательности.
Находим
M = 5,
d =	5~4-75 .=0.51,
Jo.95 — 10
V 2
IM
V2
М-т + 1
ц =---
г 2т
о2=М-(—
\2т
2т -1
21т
P-value = erfc
= 0.61 > 0.01 - тест пройден.
Вычислим статистику
2( h \ V1
X (pbs)=y-+—2—
^7 о
4.2.4.8. Проверка непересекающихся шаблонов
(Non-overlapping Template Matching Test)
и значение P-value
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа частоты
встречаемости заранее определенных шаблонов.
Пусть Е = Е1Е2 -  -Еп - двоичная последовательность длины п. Ра-
Vi 	\ N X2(obs)
P-value = igamc -
2 )
Значение P-value должно быть больше 0.01.
Рекомендуемые параметры тестирования: N < 100, М > 0.01л.
п
зобьем ее на N =
М
непересекающихся Л/-битных подпосле-
довательностей. Лишние биты отбрасываются.
Пусть у, - количество появлений шаблона (подпоследователь-
ности определенного типа) в j-й подпоследовательности (j = 1, N ).
Поиск осуществляется следующим образом. Пусть т - размер
Пример 4.30.
Вход:
е= 1010010010111001011010,
п = 22,
М= 10,
т = 3,
шаблон равен 001.
176
Теория, ПРИМЕНЕНИЕ Н ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Тест:
'22'
W = — = 2,
|_10 J
Е1 = 1010010010,
е2= 1110010110.
Позиции битов	е, = 1010010010		£2=1110010110	
	Биты	V,	Биты	v2
1-3	101	0	111	0
2-4	010	0	110	0
3-5	100	0	100	0
4-6	001	K+D	001	K+D
5-7	Пропуск	1	Пропуск	1
6-8	Пропуск	1	Пропуск	1
7-9	001	2(+1)	011	1
8-10	010	2	110	1
о2=1оГ-4"
<23
2-3-1
22-з
= 0.46875,
X2(ofo) =
(2-1)2 । (1-1)2
0.46875 0.46875
= 2.1(3),
P-value = igamc
2 2.1(3)
2’ 2
= 0.3441 >0.01 - тест пройден.
4.2.4.9. Проверка пересекающихся шаблонов
(Overlapping Template Matching Test)
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа частоты
встречаемости заранее определенных шаблонов.
Пусть Е = Е]Е2.. .Е„ - двоичная последовательность длины п. Ра-
зобьем ее на N = —
LmJ
непересекающихся ЛЛбитовых подпосле-
довательностей. Лишние биты отбрасываем.
Глава 4. Методика оценки качества генераторов ПСП
177
Пусть V, - число подпоследовательностей, в которых шаблон
появляется i раз (i = О, К , К- число степеней свободы, в запи-
сывается число подпоследовательностей, в которых шаблон
встречается К и более раз). Поиск осуществляется следующим
образом. Пусть т - размер шаблона в битах. Начинаем сканиро-
вать j-ю подпоследовательность, j = 1, N . Рассматриваем пере-
секающиеся наборы по т бит.
Находим
. М -т + 1	к
л =--------, т] = —.
2т	2
Вычисляем статистику:
X2(ofo)
у (у,- -Мс,)2
где
-q i Л; _ А „II
е ' X-1 1 1 Л
Л/ = —~ 7	— ,
и значение P-value
P-value = igamc
Х2(оЬз)
2
Значение P-value должно быть больше 0.01.
Рекомендуемые параметры тестирования: п > MN, N  тт(лд > 5,
X = 2, т ~ logiM, К ~ 2/1.
.aaa»a«aa<aaaa>a>a»aa<a<««a>a<*aaaaxaai»aaaaaaaaa<aa>aair»»l>><aa«aaaaaaaaaaa»a>«>a:aaaaaaaaaa»aaa(>aa>aaaaaaa>
Пример 4.31.
Вход:
Е = 101110111100101101000111СЮ101110111110000101101001101,
п = 53,
М = 10,
т = 2,
шаблон равен И,
К = 5.
178
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Тест:
v0 = О, V] = 0, v2 = 0, v3 = 0, v4 = 0, v5 = 0.
e, =1011101111		
Позиции битов	Биты	Число появлений шаблона
1-2	10	0
2-3	01	0
3-4	11	1(+1)
4-5	11	2(+1)
5-6	10	2
6-7	01	2
7-8	11	3(+1)
8-9	11	4(+1)
9-10	11	5(+1)
Vo = 0, v, = 0, v2 = 0, v3 = 0, v4 = 0, v5 = 1		
После тестирования оставшихся четырех подпоследователь-
ностей
v0 = 0, v, = 2, v2 = 0, v3 = 1, v4 = 1, v5 = 1,
10-2 + 1 904
H = —-----= 2.25,
2-25 , 1лс
n =----= 1.125,
2
-ц 0
0
Л1='2Г^
z i=i
712 =^rL
/-1
-1 l = fM
1-1} l\
nz	e’”
— = n— = n
1-1} l\ 2
"1125 = 0.324652,
-------= 0.182617,
2
-.2 \ -n
T| j e .
= -— П + —| = Л-—01 + 2) =
1-1} 1\	4	2	8
2	'8
-1.125
= 1.125—у—(1.125 + 2) = 0.142670,
Глава 4. Методика оценки качества генераторов ПСП
179
2	3 А
Л , Л
е V
7C3=^tL
£	/-1
= 1.125—
8
2 V
<=. V - 1J к-
,-1125 fl-125^
6
е~г'
8
г| + 2—+— =т|-— —+ п + 1 =
2 3!	8 6	1
2 3!
+ 1.125+1 =0.106645,
е V
7C4=TrL
z 1=1
П2 . аЛ\ Л'
О А	-п
$ Л _________ nj-т'1 и."?'1	11
—--------Т) + 5----И 3----1---
Z-1J 1\ 16	2!	3! 4!
2! ’ 3! 4!
е
8
е
3
+ —-1.125 + 1 =0.077147,
2
= 1.125—
16
—п / „3	о
е 1 п	л	3
= п------— + — +—п + 1 =
16 24	2	2	J
•1125^1.1253 1.1252
	1	
24-------------2
л5 = 1 -тс0 -Ttj - л2 - л3 -л4 =1-0.324652-0.182617-
- 0.142670 - 0.106645 - 0.077147 = 0.166269,
2	(0-5-0.324652)2 (2-5-0.182617)2 (0-5-0.14267Q)2
Х °	5-0.324652 + 5-0.182617 + 5-0.142670
(1-5-0.106645)2 (1-5-0.077147)2 (1-5-0.166269)2
_|--------------1----------------1--------------_ 5.6656,
5-0.106645	5-0.077147	5-0.166269
( 2 2 1ГЗ)Л
P-value = igamc\ —, —-—1 = 0.3441 >0.01-тест пройден.
4.2.4.10. Универсальный тест Маурера (Maurer's
«Universal Statistical» Test)
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа расстояний
между шаблонами.
Пусть Е = Е]Е2...Е„ - двоичная последовательность длины п. Ра-
зобьем ее на два сегмента: инициализирующий и тестовый. Пер-
вый состоит из Q блоков по L бит, второй - из К = [nlL\ - Q бло-
ков по L бит. Лишние биты отбрасываем.
180
НорИЯ, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Инициализирующий сегмент используется для создания таб-
лицы Т. Для i = О, Q Tj = i, где j есть десятичное представление
i-го L-ричного блока.
После этого переходим к сканированию тестового блока. Про-
веряем каждый из К блоков и определяем расстояние в блоках от
последнего появления данного i-го блока (т. е. i - 7}), одновре-
менно обновляя таблицу: 7} = i.
Вычисляем статистику
, е+х
Л i=e+i
и значение P-value
P-value = erfc
fn - expectedValue(L)
41c
-3
КL Ivariance(L)
__ _
Значения expectedValue и variance берутся из табл. 4.11.
Табл. 4.11. Значения expectedValue и variance
L	ExpectedValue	Variance
1	0.7326495	0.690
2	1.5374383	1.338
3	2.4016068	1.901
4	3.3112247	2.358
5	4.2534266	2.705
6	5.2177052	2.954
7	6.1962507	3.125
8	7.1836656	3.238
9	8.1764248	3.311
10	9.1723243	3.356
11	10.170032	3.384
12	11.168765	3.401
13	12.168070	3.410
14	13.167693	3.416
15	14.167488	3.419
16	15.167379	3.421
Глава 4. Методика оценки качества генераторов ПСП
181
Значение P-value должно быть больше 0.01.
Рекомендуемые параметры тестирования указаны в табл. 4.12.
Табл. 4.12. Рекомендуемые параметры тестирования
п	L	0=10-2'
>387 840	6	640
>904 960	7	1280
> 2 068 480	8	2 560
2:4654080	9	5120
2 11 342 400	10	10 240
> 22 753 280	11	20 480
>49643 520	12	40 960
> 107 560 960	13	81920
>231 669760	14	163 840
2 496 435 200	15	327 680
2 1 059061 760	16	655360
Пример 4.32.
Вход:
е = 010110100111010101110,
п = 21,
L = 2,
6 = 4.
Тест:
Инициализирующий сегмент:
ея = 01011010. 
Заполняем таблицу:
То = 0, Т1 = 2, Т2 = 4, Т3 = 0.
Тестовый сегмент:
ЕГ=011101010111,
i = 5. Значение блока = 1,
sum = log 2(5 - 2) = 1.5849,
Л = 5;
182
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
I = 6. Значение блока = 3,
sum = 1.5849 + log2 (б - 0) = 4.1699,
7’3 = 6;
1=1. Значение блока = 1,
sum = 4.1699 + log2 (7 - 5) = 5.1699,
Л =7;
7=8. Значение блока = 1,
sum = 5.1699 + /og2(8 - 7) = 5.1699,
Ti = 8;
7=9. Значение блока = 1,
sum = 5.1699 + log2(9-8) = 5.1699 ,
Л =9;
7 = 10. Значение блока = 3,
sum = 5.1699 + log2 (10 - б) = 7.1699,
Т\ = 10;
а =
-з
0.7-^ + f4 + ^£i
2 I 2) 15
=0.184,
6
„ ,	, (1.195-1.537Л
P-value = erfc —7=-------
< V2-0.184 J
= 0.063 > 0.01 - тест пройден.
4.2.4.11. Проверка сжатия при помощи алгоритма
Лемпела-Зива (Lempel-Ziv Compression Test)
Цель теста - проверить равномерность распределения 0 и 1 в
исследуемой последовательности на основе анализа степени сжа-
тия последовательности.
Пусть е = Е1Е2...Еп - двоичная последовательность длины п.
Выделим из нее последовательные непересекающиеся и неповто-
ряющиеся «слова», которые образуют «словарь».
Глава 4. Методика оценки качества ГЕНЕрлторов ПСП
18?
Пример 4.33.
Е = 010110010.
Позиция бита			
1	Бит	Новое слово?	Слово
2	0	Да	0(бит 1)
3	1	Да	1 (бит 1)
4	0	Нет	
5	1	Да	01 (биты 3-4)
6	1	Нет	
7	0	Да	10 (биты 5-6)
8	0	Нет	
9	1	Нет	
			
Подсчитываем число слов в словаре WObs и вычисляем значе-
ние P-value-.
P-value =
—erfc , 0DS
2 v2o2 ,
Для вышеприведенного примера WObS = 5 (0, 1, 01, 10, 010).
В настоящее время не существует теоретических способов для
нахождения Ц и о2. Для данного теста эти значения получают,
используя генератор с функцией SHA-1 в цепи обратной связи
или генератор Blum-Blum-Shub.
Значение P-value должно быть больше 0.01.
Рекомендуемая длина последовательности: п > 1000000.
4.2.4.12. Проверка линейной сложности (Linear
Complexity Test)
Цель теста - исследовать последовательность на случайность,
анализируя линейные сложности ее подпоследовательностей.
Пусть е = EiE2...En - двоичная последовательность длины п. Ра-
п
М
зобьем ее на W =
непересекающихся подпоследовательно-
стей длиной М. Лишние биты отбрасываем.
184
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАЮрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Определим линейную сложность L„ i = 1, N, каждой подпос-
ледовательности (т. е. минимальную длину LFSR, необходимую
для генерации данной подпоследовательности). Для вычисления
линейной сложности можно использовать алгоритм Берлекампа-
Месси.
Находим среднее значение:
рИ 2'
= М , (9 + (-l)M+1) U+9y
И 2	36 2м
и вычисляем статистику для каждой подпоследовательности:
т;.=(-1)Л/(л-ц)+|.
Значения 7} распределяются на К + 1 категорий Vo, ..., vfc и
вычисляется статистика:
2, , . 57 (у,- -Ml,)2
%2(оМ = У/ .. ' 
to Nni
Разработчики теста не указали алгоритм разбиения. В качестве
одного из вариантов разбиения можно использовать разбиение,
приведенное в примере 4.34.
Значения л, определяются следующим образом:
‘=1.2.-;
Вычисляем значение P-value
„ i . (К x\obs)
P-value = igamc —---------
2
Значение P-value должно быть больше 0.01.
Глава 4. Методика оценки качества генераторов ПСП
Рекомендуемые параметры тестирования:
«> 1000000,
500 <М< 5000,
#>200.
Пример 4.34.
Вход:
Е = 1101011110001,
п = 13,
1И = 13,
# = 1.
Тест:
Минимальная длина LFSR, необходимого для генерации дан-
ной последовательности, равна 4 (рис. 4.10 ), т. е. L\ = 4.
<13 2А
— + -
Т]=(-1)13(4-6.77) + | = 3.
Рис. 4.10. LFSR длиной 4, формирующий последовательность е
186
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Разбиение на категории произведем следующим образом:
если Т, < -2, Vq увеличиваем на 1,
если - 2 < 7} < -1, Vi увеличиваем на 1,
если - 1 < 7} < 1, V2 увеличиваем на 1,
если 1 < Tt < 2, v3 увеличиваем на 1,
если Ti > 2, v4 увеличиваем на 1.
Таким образом, получается Vo = 0, Vi = 0, v2 = 0, v3 = 0, v4 = 1.
Соответствующие вероятности равны:
л0=Р(Г<-2) = —^ = 0.0416,
л, = Р(Т < -1) - л0 = з	- 0.0416 = 0.125,
п4 = Р(Т > 2) - Р(Т = 2) =	= 0.0208,
лз = Р(Т > 1) - л4 =-- 0.0208 = 0.3125,
□	* 3 22
л2 =1-л0-л1-л3-л4 =1-0.0416-0.125-0.3125-0.0208=0.5,
2, , . (0-1-0.0416)2 (0-1-0.125)2 (0-1-0.5)2
1-0.0416	1-0.125	1-0.5
+ (0-1-0.3125)2 + (1-1-0.0208)2 =
1-0.3125	1-0.0208	’ ’
P-value = igamc	= 1-8 ’ Ю 8 < 0-01 -
тест не пройден.
4.2.4.13.	Проверка серий (Serial Test)
Цель теста - исследовать последовательность на случайность,
анализируя длины серий различной длины.
Пусть £ = EiE2. . .Еп - двоичная последовательность длины п и m -
длина серии. Сформируем последовательность е' = Ei£2- • .EnEiE2.. .e„,_i,
добавив к концу последовательности Е первые m - 1 битов той же
самой последовательности. Подсчитаем число появлений v, ,
Глава 4. Методика оценки качества генераторов ПСП
187
всевозможных пересекающихся серий длиной т, vt , 1 - длиной
т - 1 и V,	- длиной т - 2.
Вычислим статистики


Vv* =v2m
V2^=^-2Vt>+vt2
и значения P-value
P-valuei = igamc(2m 2, V\|/2),
P-value? = igamc (2m-3, V2\j/2).
Значения P-value^ и P-value? должны быть больше 0.01.
Рекомендуемые параметры тестирования: т < [log?n] - 2.
Пример 4.35.
Вход:
е=0011011101,
п = 10,
т = 3.
Тест:
т = 3: 
е' = 001101110100,
Vqoo = 0, Vooi = 1» Voio = 1» Von = 2, Vwo = 1, Vioi = 2, Vno = 2,
Vin = 1;
m = 2:
e' = 00110111010,
Voo = 1, Voi = 3, Vio = 3, Vn = 3;
188
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
т = 1:
е' = 0011011101,
v0 = 4, Vi = 6;
93
v2=—(О2 + 12 +12 + 22 +12 + 22 + 22 +12)-10 = 2.8,
3 1()к
v2=— (I2 +32+ 32 +32)-10 = 1.2,
2 10
v2=—(42+62)-10 = 0.4,
1()v
V^=V32-V2=2.8-1.2 = 1.6,
V2\|/2 =\|/з-2-\|/г+ Yi2 = 2.8-2-1.2 + 0.4 = 0.8,
/	1 6^
P-value^ = igamcl 23~2, — =0.808 > 0.01,
k 2 J
( . , 0 8^
P-valuei = igamc 2 , — = 0.67 > 0.01 - тест пройден.
I 2 J
4.2.4.14.	Проверка аппроксимированной энтропии
(Approximate Entropy Test)
Цель теста - исследовать последовательность на случайность,
анализируя длины серий различной длины.
Пусть е = Е1Е2.. .еп - двоичная последовательность длины п и т -
длина серии. Сформируем последовательность е' = EiE2. . .EnEiE2-  .Em-i,
добавляя к концу последовательности Е первые т - 1 битов той
же самой последовательности. Рассмотрим пересекающиеся серии
длиной т. Пусть #i (i = 0, 2т ) - число появлений серий типа i.
Вычислим:
п
1=0
(Нарушая все правила, считаем, что 0 • /и(0) = 0.)
Глава 4. Методика оценки качества генераторов ПСП
189
Аналогично поступим с пересекающимися сериями длиной
т + 1.
Вычислим статистику
X2(oZ>s) = 2пЦп2-<р(т) + ^(т+1))
и значение P-value
P-value = igamc 2я*"1
Х2(о^)'
2
Значение P-value должно быть больше 0.01.
Рекомендуемые параметры тестирования: т < [log2n] - 2.
Пример 4.36.
Вход:
е = 0100110101,
п = 10,
т = 3.
Тест:
т-3'.
е' = 010011010101,
#	000 = 0, #001 = 1, #010 = 3, #011 = 1, #100 = 1, #101 = 3,
#110= 1,#111 =0;
с^оо =0, С3т =0.1, С310 =0.3, С3П =0.1, С3» =0.1, С301 =0.3,
С3о=О.1,С3п=О;
(p(3)=0-Zn0 + 0.1-Zn0.1 + 0.3-Zn0.3 + 0.1-Z«0.1 + 0.1Zn0.1 +
+ 0.3-Zn 0.3 + 0.1 • Zn 0.1 + 0 • Zn 0 = -1.6434;
т = 4:
е' = 0100110101010,
#	0000 = 0, #0001 = 0, #0010 = 0, #0011 = 1, #0100 = 1,
#	0101 = 2, #0110= 1, #0111 = 0, #1000 = 0, #1001 = 1,
#	1010 = 3, #1011 = 0, #1100 = 0, #1101 = 1, #1110 = о,
#	1111 =0;
190
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Оюоо = G)001 = 0’ QoiO = 0’ ^0011 = 0-1’ Q100 = 0-1’
Q)ioi = 0-2, С0110 = 0.1, Coni = 0, Qooq-O, С]оо1=О. 1,
Оою =0-3, С1011 =0, Сцоо =0, С11о1 = 0.1, С111о =0, СШ1 =0;
(p(4)=0-Zn0 + 0Zn0 + 0Zn0 + 0.1Zn0.1 + 0.1-Z«0.1 +
+ O.2-Z«O.2 + O.l-ZnO.l + OZ«O + O-ZnO + O.l-ZnO.l + O.3-ZnO.3 +
+ 0-/n0 + 0Zn0 + 0.1Zn0.1 + 0-Zn0 + 0-Zn0 = -1.8343,
%2(oZw)=2 • 10- (Zn2 - ср(3) + ср(4))=20- (Zn2+1.6434-1.8343)=10045,
P-value = igamcl 23-1,	= 0.2618 > 0.01 - тест пройден.
4.2.4.15.	Проверка кумулятивных сумм (Cumulative
Sums (Cusum) Test)
Цель теста - исследовать последовательность на случайность,
анализируя максимальное отклонение суммы элементов норми-
рованной последовательности от нуля.
Пусть е = EiE2...En - двоичная последовательность длины п.
Преобразуем ее в последовательность X: х, = 2е, - 1 (т. е. 1 —> 1,
0->-1).
Найдем максимальное значение суммы: Zi = max	.
k=l, п V ,=1	?
Вычислим значение P-value:
^-i
___
4
P-value = 1 - У,
-^+1
к=^~
4
Глава 4. Методика оценки качества генераторов ПСП
191
п '
Аналогичные вычисления проведем для z2 = тах / ,х,
*=1, " v=n-t+i >
почему
случаи
(двигаемся от конца последовательности). Непонятно,
разработчики Руководства НИСТ не рассматривают
< П А
и z4 = min	V xt
к=1, п  ,
\i=n-k+l J
z3 = min V
*=i."
к=1, п
; по значимости
они не
уступают Zi и Z2 (zi и Z2 обнаруживают преобладание единиц, a zi
и Z4- преобладание нулей).
Значения P-value для zi, Z2, Z3 и z4 должны быть больше 0.01.
Рекомендуемая длина последовательности: п > 100.
Пример 4.37.
Вход:
е = 1011010111,
п = 10.
Тест:
Х = 1,-1, 1, 1,-1, 1,-1, 1, 1, 1.
Проход вперед:
Si = l,
S2 = 1 + (-1) = 0,
S3=l + (-1) +1 = 1,
S4 = 1 + (-1) +	1 + 1	= 2,
55 = 1 + (-1) +	1 + 1	+ (-1) = 1,
S6= 1 + (-1) +	1 + 1	+ (-1) + 1 =	2,
S7 = 1 + (-1) +	1 + 1	+ (-1) + 1 +	(-1)	= 1,
S8 = 1 + (-1) +	1 + 1	+ (-1) + 1 +	(-1)	+ 1=2,
S9=l + (-1) +	1 + 1	+ (-1) + 1 +	(-1)	+ 1 +	1=3,
Sio = 1 + (—1) + 1 + 1 + (—1) + 1 + (—1) +1 + 1 + 1= 4,
z, = max St = 4,
1<Ш0
192
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
= 0.4118 > 0- для прохода вперед тест пройден.
4.2.4.16.	Проверка случайных отклонений - 1
(Random Excursions Test)
Цель теста - исследовать последовательность на случайность,
анализируя отклонения суммы элементов нормированной после-
довательности от нуля.
Пусть е = Е1Е2...еп - двоичная последовательность длины п.
Преобразуем ее в последовательность X: х, = 2е( - 1 (т. е. 1 —> 1,
0 —> -1). Сформируем последовательность:
7=1
Сформируем последовательность:
S' = 0, SbS2, 0.
Разделим ее на блоки, имеющие вид
{0, Sj, Sj+1,..., Sj+k, 0 },
т. е. на подпоследовательности, у которых первый и последний
элементы равны нулю, а все остальные отличны от нуля.
Считаем, что состояние любого ненулевого элемента х блока
может принимать одно из значений: (-4), (-3), (-2), ... , 3, 4, т. е.
хе {(-4), (-3), (-2),..., 3, 4}.
Глава 4. Методика оценки качества генераторов ПСП
19>
Пусть vk(x) - число блоков, в которых значение х встречается
ровно к раз, к = 0, 5. Число появлений, превышающее 5, фикси-
5
руем в v5(x). Если общее число блоков равно J, то 2V*U) = J.
*=0
Вычислим статистики для каждого х:
5
X2(obs)x = ^
к=0
(vt(x)~ JTCt(x))2
Jnk (х)
Значения пк(х) берутся из табл. 4.13.
Табл. 4.13. Таблица значений я^(х)
X	лоМ	М4	лИл)	Лз(л)	я«(л)	Я5(Л)
±1	0.5	0.25	0.125	0.0625	0.0312	0.0312
±2	0.75	0.0625	0.0469	0.0352	0.0264	0.0791
±3	0.8333	0.0278	0.0231	0.0193	0.0161	0.0804
±4	0.8750	0.0156	0.0137	0.0120	0.0105	0.0733
Вычислим значения Р-value:
'5

P-valuex = igamc
Значения P-value для каждого x должны быть больше 0.01.
Рекомендуемая длина последовательности: п > 10б.
Примечание. На самом деле, состояния х должны принимать
значения от min Si до max St. Разработчики Руководства НИСТ,
1=1, п 1=1, п
выбрав другую формулу, выиграли в простоте, но проиграли (хо-
тя совсем немного) в точности.
Пример 4.38.
Вход:
Е = 0110110101.
Тест:
Х=-1, 1, 1,-1, 1, 1,-1, 1,-1, 1,
Si =-1,
s2 = -1 + 1 = о,
194
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
$3 = -1 + 1 + 1 = 1,
S4 = -1 + 1 + 1 + (-1) = О,
S5 = "l + 1 + 1	+ (-1) +	1	=	1,
$б = -1 + 1 + 1	+ (-1) +1	+	1=2,
$7 = -1 + 1 + 1	+ (-1) +	1	+	1 + (-1) =	1,
S8 = -1 + 1 + 1	+ (-1) +	1	+	1 + (-1) +1=2,
S9 = -1 + 1 + 1	+ (-1) +	1	+	1 + (-1) +	1 + (-1) = 1,
S10 = -1 + 1 + 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1=2,
S = -l,0, 1,0, 1,2, 1,2, 1,2,
S'= 0,-1,0, 1,0, 1,2, 1,2, 1,2, 0,
J= 3: {0, -1, 0}, {0, 1, 0}, {0, 1, 2, 1, 2, 1, 2, 0}.
Состояниеx	Блок1 {0,-1,0}	Блок 2 (0,1,0}	БлокЗ (0,1,2,1,2,1,2,0}
—4	0	0	0
-3	0	0	0
-2	0	0	0
-1	1	0	0
1	0	1	3
2	0	0	3
3	0	0	0
4	0	0	0
v0(-4) = 3,	Vi(-4)	= v2(-4)	= v3(—4)	= v4(-4)	= v5M)	= 0,
v0(-3) = 3,	V1(-3)	= v2(-3)	= v3(-3)	= v4(-3)	= v5(-3)	= 0,
v0(-2) = 3,	V1(-2)	= v2(-2)	= v3(-2)	= v4(-2)	= v5(-2)	= 0,
vo(-l) = 2,	V1(-l)	= v2(-l)	= v3(-l)	= v4(-l)	= v5(-l)	= 0,
v0(l)=l,	V!(l)	= l, v3(l)=l, v2(l) = v4(l) = v5(l) = 0,
v0(2) = 2,	v3(2)	= 1, V1(2) = v2(2) = v4(2) = v5(2) =	0,
v0(3) = 3,	vi(3)	= v2(3) = v3(3) = v4(3) = v5(3) = 0,
v0(4) = 3,	V1(4)	= v2(4) = v3(4) = v4(4) = v5(4) = 0.
Для x = 1:
V2(obs} Jl-3-0.5)2 , (1-3-0.25)2 t (0-3-0.125)2 ,
1	3-0.5	3-0.25	3-0.125
(1-3-0.0625)2 (0-3-0.0312)2 [ (0-3-0.0312)2 _ „
3-0.0625	3 0.0312	+	3-0.0312
<5 49^
P-value = igamc\ — = 0.42 > 0.01 - для x = 1 тест пройден.
Глава 4. Методика оценки качества генераторов ПСП
195
4.2.4.17.	Проверка случайных отклонений - 2
(Random Excursions Variant Test)
Данный тест является расширением предыдущего.
Пусть е = £1£г...£п - двоичная последовательность длины п.
Преобразуем ее в последовательность X: х, = 2е( - 1 (т. е. 1 —> 1,
О —> -1). Сформируем последовательность:
7=1
Сформируем последовательность:
S' — 0, Si, S2, •••, Sn, 0.
Разделим ее на блоки, имеющие вид
{0, Sj, Sj+i,Sj+t, 0 },
т. е. на подпоследовательности, у которых первый и последний
элементы равны нулю, а все остальные отличны от нуля.
Считаем, что состояние любого ненулевого элемента х блока
может принимать одно из значений: (-9), (-8), (-7),... , 8, 9, т. е.
хе {(-9), (-8), (-7),..., 8, 9}.
Пусть J - общее число блоков и £(х) - число появлений со-
стояния х во всех J блоках.
Вычислим значения P-value для каждого х:
P-valuex= erfc
j2J(4|x|-2)?
Значения P-valuex для каждого х должны быть больше 0.01.
Рекомендуемая длина последовательности: п > 10б.
Примечание. Как и в предыдущем тесте, разработчики Руко-
водства НИСТ упростили значения х. На самом деле, состояния х
должны принимать значения от min St до max S(.
/=1, п	i=l, п
Пример 4.39.
Вход:
Е = 0110110101.
196
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Тест:
х = —1, 1, 1,-1, 1, 1,-1, 1,-1, 1,
5i=-l,
Sy — — 1 + 1 = О,
$3 = -1 + 1 + 1 = 1,
S4 = —1 + 1 + 1 + (—1) = О,
$5 = -1 + 1 + 1 + (-1)4-1 = 1,
S6 =-14-14-14-(-1)4-14-1=2,
Sy — —1 4- 1 4- 1 4- (—1) 4-14-14- (—1) = 1,
Sg = —1 4-14-14- (—1) 4-14-14- (—1) 4-1=2,
S9 = -1 4- 1 4- 1 4- (-1) 4- 1 4- 1 4- (-1) 4- 1 4- (-1) = 1,
S10 = -1 + 1 4- 1 + (-1) 4- 1 4- 1 4- (-1) 4- 1 + (-1) +1=2,
S = -l,0, 1,0, 1,2, 1,2, 1,2,
S'=0,-l,0, 1,0, 1,2, 1,2, 1,2,0,
J = 3: {0, -1, 0}, {0, 1,0}, {0, 1,2, 1,2, 1,2,0),
£(-l) = l,
£(D = 4,
£(2) = 3,
£(-9) = £(-8) = £(-7) = £(-6) = £(-5) = £(-4) = £(-3) = £(-2) =
= ^(3) = £(4) = £(5) = £(6) = £(7) = £(8) = £(9) = 0.
Длях- 1:
P-value i = erfc
j2-3(4-|l -2)j
0.683 >0.01-
для х = 1 тест пройден,
4.3.	Другие тесты
В данном разделе рассматриваются еще два существующих
теста, не вошедшие в упомянутые выше подборки, при этом пер-
вый из них является наиболее сильным (как показали исследова-
ния, даже чересчур сильным) из всех рассмотренных в данной
работе.
Глава 4. Методика оценки качества генераторов ПСП
197
4.3.1.	Посимвольная проверка
Проверяется равномерность распределения символов в иссле-
дуемой последовательности на основе анализа частот появления
каждого символа.
Пусть е = Е1Е2.,.Е„ - последовательность m-разрядных чисел
длины п. Подсчитываем, сколько раз V,, г = О, (2"1 -1), встреча-
ется каждое число. Значение V, должно лежать в интервале
п-2.58^п(2т - У) п + 2.58^п(2т -V)
Пример 4.40.
Вход:
£ = 3542 1 46 1,
п = 8,
т = 3.
Тест:
v0 = 0, Vi = 2, v2 = 1, v3 = 1, v4 = 2, v5 = 1, v6 = 1, v7 = 0.
8 — 2.58-^/8(23 — 1) _ in 8 + 2.58-^8(23-1) =зя
23	‘ ’	23
Все значения v( принадлежат интервалу [-1.41; 3.41].
4.3.2.	Проверка частот
Проверяется равномерность распределения символов в иссле-
дуемой последовательности.
Пусть е = EiE2...e„ - последовательность m-разрядных чисел
длины п. Подсчитываем, сколько раз v,, i = 0, (2m -1), встреча-
ется каждое число, и вычисляем статистику:
2т 2”-1f
Xz(obs) = —£
п
1=0 к
198
Теория, ПРИМЕНЕНИЕ и ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
которая анализируется с помощью критерия %2 с числом степеней
свободы, равным 2"1.
Пример 4.41.
Вход:
£ = 3542 146 1,
п = 8,
т = 3.
Тест:
v0 = 0, Vi = 2, v2 = 1, v3 = 1, v4 = 2, v5 = 1, v6 = 1, v7 = 0.
n 8
— — т = 1,
2W £
x2 (pbs) = (o -1)2 + (2 -1)2 + (1 -1)2 + (1 -1)2 + (2 -1)2 + (1 -1)2 +
+ (1-1)2+ (0-l)2 =4.
4.4.	Оценка результатов тестирования
Процесс исследования статистических свойств генератора ПСП
состоит из следующих шагов:
•	генерация последовательностей для тестирования;
•	исполнение набора статистических тестов;
•	анализ прохождения статистических тестов;
•	принятие решения о свойствах генератора.
4.4.1.	Генерация последовательностей для
тестирования
Для заданного генератора формируется т последовательно-
стей длины п.
=ЕрЦ1\..е(1\
е<2) = е(2Ц2’...42’,
Глава 4. Методика оценки качества генераторов ПСП
199
P(m)
t -tl t2 —fcn •
Длина последовательности n выбирается таким образом, что-
бы все тесты могли быть пройдены.
4.4.2.	Исполнение набора статистических
тестов
Каждая из т последовательностей проверяется каждым из t
тестов набора. Результатом работы каждого теста является вы-
числение тестовой статистики scobs'). Таким образом, после про-
верки всех последовательностей получается mt тестовых стати-
стик, как показано в табл. 4.14.
Табл. 4.14. Результаты выполнения набора статистических тестов
Последовательность	Тест 1	Тест 2	...	ТестТ
е'Ч		s^'1! o6s)		s/'V/is)
е(2)	S,,2|(O&5)			s)2|(oZ«)
				
ew		shafts)		
4.4.3.	Анализ прохождения статистических
тестов
Анализ прохождения статистических тестов начинается с ана-
лиза тестовой статистики. Существует три варианта оценки тес-
товой статистики.
1)	Пороговые значения. Если тестовая статистика больше (мень-
ше) порогового значения, последовательность считается не-
случайной.
2)	Фиксированные интервалы. Если тестовая статистика выходит
за пределы заданного интервала, последовательность считает-
ся неслучайной.
3)	Вероятностные значения. Для тестовой статистики вычисля-
ется P-value. Под P-value понимается вероятность того, что
совершенный генератор случайных чисел произвел бы после-
довательность менее случайную, чем исследуемая, для типа
неслучайности, проверяемого тестом. Для теста выбирается
200
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
уровень значимости а. Если значение P-value больше либо
равно а, то последовательность считается случайной.
Поскольку для первых двух способов необходимо заранее рас-
считывать пороговые значения и фиксированные интервалы, вы-
числение P-value представляется наиболее эффективным вариан-
том оценки тестовой статистики.
Таким образом, вычисляются значения P-value для тестовых
статистик s(pbs) как показано в табл. 4.15.
Табл. 4.15. Результаты вычисления значений P-value для тестовых
статистик s(pbs)
Последовательность	Тест 1	Тест 2	...	Тест/
е'"	P-value{']	P-value^		P-value^
£UI	P-value^	P-value^		P-value*'
				
е(и|	P-va/uef1*	P-value^		P-value')’*
Существует два варианта оценки прохождения т последова-
тельностями i-ro теста, z = l, t.
1) Анализ числа появлений значений P-value.
Множество значений P-value [0; 1] разбивается на к категорий
с вероятностями, равными Ик в каждой категории, после чего
подсчитывается v„ i = 1, к , - число последовательностей, зна-
чения P-value которых принадлежат z-й категории.
Вычисляется статистика:
к /	\2
v-ч т\
х2<°ь,)=	„
к
которая анализируется при помощи критерия %2 с числом сте-
пеней свободы, равным к - 1.
Одним из преимуществ данного варианта является то, что он
позволяет косвенным образом определить значение т, по-
скольку эмпирическое правило [1] для критерия %2 гласит, что
значение т/к должно быть больше либо равным 5, то т > 5к.
Глава 4. Методика оценки качества генераторов ПСП
201
2) Анализ значений P-value. Подсчитывается доля последователь-
ностей, прошедших данный тест (т. е. доля последовательно-
стей, для которых P-value > а). Значение этой доли должно
лежать в интервале
Результаты тестирования набора из т последовательностей
каждым из t тестов могут быть сведены в таблицу, аналогичную,
например, табл. 4.16.
Табл. 4.16. Результаты тестирования m последовательностей
набором из t статистических тестов
Последователь- ность	Тест 1	Тест 2	...	Тест/
	прошла/не прошла	прошла/не прошла		прошла / не прошла
е»>	прошла / не прошла	прошла/не прошла		прошла / не прошла
				
Е(«|	прошла / не прошла	прошла/не прошла		прошла/не прошла
Результат проверки генератора ПСП	прошел /не прошел	прошел / не прошел		прошел / не прошел
Непрохождение какого-либо теста свидетельствует о стати-
стических слабостях в структуре генератора.
4.5. Анализ статистической безопасности
криптоалгоритмов
Одним из требований, предъявляемых к надежным криптоал-
горитмам, является их пригодность к использованию в качестве
генераторов ПСП. Это означает необходимость исследования
выдаваемых ими последовательностей на статистических тестах.
Для блочных шифров, например с разрядностью блока и раз-
рядностью раундового ключа равными п, можно перечислить
следующие последовательности, которые должны удовлетворять
требованиям случайности:
202
Теория, применение и оценка качества генерлторов псевдослучайных последовательностей
•	гаммирующая последовательность на выходе криптоалгорит-
ма (режимы OFB и Counter) при случайном ключе;
•	последовательность, полученная в результате поразрядного
XOR двух последовательностей, в исходном состоянии со-
стоящих из одинаковых «-разрядных блоков (проводятся три
типа экспериментов - соответственно для нулевых блоков,
блоков высокой и низкой плотности), отличающихся только в
одном z-м бите (0 < i < п - 1) и зашифрованных с использова-
нием набора случайных «-разрядных ключей;
•	последовательность, полученная в результате поразрядного
XOR двух последовательностей, в исходном состоянии со-
стоящих из случайных «-разрядных блоков и зашифрованных
с использованием фиксированного «-разрядного ключа (про-
водятся три типа экспериментов - соответственно для нулевых
ключей, ключей высокой и низкой плотности), отличающихся
только в одном z-м бите (0 < i < « - 1);
•	последовательность, полученная в результате шифрования в
режиме СВС набора нулевых «-разрядных блоков с использо-
ванием случайного ключа;
•	последовательность, полученная в результате поразрядного
XOR последовательности, состоящей из случайных «-разряд-
ных блоков, и результата ее шифрования на наборе случайных
«-разрядных ключей.
Глава 4. Методика оценки качества генераторов ПСП
20>
Литература к главе 4
1)	Кнут Д. Искусство программирования для ЭВМ: В 3 т. 3-е изд. Т. 2.
Пер. с англ. М.: Мир, 1998.
2)	Чугунков И. В., Жуков Ю. И. Генератор паролей. Научная сессия
МИФИ-2001. Сборник научных трудов: В 14 т. Т. 12. Компьютерные
системы и технологии. М.: МИФИ, 2001. С. 68-69.
3)	Gustafson Н. et. al. A computer package for measuring strength of
encryption a algorithms. Journal of Computers and Security. Vol. 13.
No. 8 1994 P. 687-697.
4)	Marsaglia G. DIEHARD Statistical Tests.
5)	Menezes A,, van Oorshot P., Vanstone S. Handbook of Applied
Cryptography. CRC Press, 1997.
6)	Schneier B, Applied cryptography, 2nd Edition, John Wiley & Sons
(1996). [Имеется перевод: Шнайер Б. Прикладная криптография.
http://www.ssl.stu.neva.ru/psw/crypto.html.]
7)	A Statistical Test Suite for the Validation of Random and Pseudorandom
Number Generators. NIST Special Publication 800-22. http://csrc.nist.gov
Вместо заключения
Система оценки
статистической
безопасности алгоритмов
генерации ПСП
и криптоалгоритмов
Для исследования статистической безопасности алгоритмов
генерации ПСП и криптоалгоритмов авторами разработан ком-
плекс, включающий в себя следующее ПО:
•	универсальную систему оценки качества генераторов ПСП для
проведения графических и оценочных тестов, описанных в гл. 4;
•	программу оценки корреляции двоичных последовательностей;
•	программные модели конгруэнтных генераторов; генераторов,
функционирующих в конечных полях; BBS-генератора; гене-
раторов, используемых в поточных шифрах А5 и ВС4; генера-
торов, построенных на основе блочных шифров ГОСТ 28147-
89иАЕ5-128;
•	программные модели RFSR и стохастических генераторов
ПСП с многораундовыми функциями обратной связи.
Цели исследования:
•	оценка статистической безопасности наиболее известных ге-
нераторов ПСП;
•	исследование свойств стохастических генераторов ПСП;
•	ранжирование оценочных тестов по их силе;
•	исследование зависимостей качества т-разрядных ПСП, сни-
маемых с выхода ^-разрядного генератора, от т, 1 < т < г,
•	поиск методов выявления периодичности в исследуемой по-
следовательности.
Вместо заключения. Оценка 6езопасности Алгоритмов генерации ПСП и крипгаллгоритмов
205
Наиболее важные результаты исследования:
•	статистическая безопасность генераторов ПСП поточных
шифров А5 и RC4 оказалась выше, чем предполагалось до на-
чала исследования;
•	статистическая безопасность ВВ5-генератора, генераторов
ПСП на основе блочных шифров оказалась ниже, чем предпо-
лагалось до начала исследования;
•	значимость большинства графических тестов оказалась выше,
чем предполагалось до начала исследования;
•	качество стохастических генераторов ПСП оказалось не хуже,
чем качество генераторов, построенных на основе стандартов
криптозащиты ГОСТ 28147-89 и AES',
•	качество стохастических генераторов ПСП можно дополнитель-
но существенно повысить за счет перемешивания таблиц стохас-
тического преобразования после каждого их использования;
•	дефект исследуемой последовательности, связанный с наличи-
ем периодичности, очень трудно обнаружить; наиболее удобен
для этой цели графический тест вычисления АКФ;
•	очень часто /-разрядные последовательности с выходов /-раз-
рядного ПСП, показывающие хорошие результаты, при иссле-
довании их качества при разрядности меньшей / оказываются
полностью непригодными для использования для решения ка-
ких-либо задач защиты информации;
•	практически каждый отдельно взятый графический или оце-
ночный тест можно «обмануть», т. е. заставить признать слу-
чайной заведомо некачественную последовательность (в том
числе очень сильные тесты проверки линейной сложности и
посимвольной проверки).
Наиболее важные выводы:
•	гарантированно большой период генератора ПСП при любом
значении ключевого параметра - неотъемлемое свойство каче-
ственного генератора ПСП;
•	делать выводы о качестве /-разрядной ПСП можно только по
результатам комплексного исследования по значительной со-
206	Теория, применение и оценкл качсства генерлторов псевдослучайных последовательностей
вокупности тестов с обязательным исследованием качества
т-разрядных ее подпоследовательностей, 1 < т < V,
•	графические тесты очень удобны при исследовании рассеи-
вающих и перемешивающих свойств криптоалгоритмов, при
исследовании запаса их прочности, а также при сравнении ра-
ундовых преобразований различных блочных шифров.
Некоторые результаты исследования генераторов ПСП приве-
дены в приложении.
Приложения
Приложение 1
Неприводимые многочлены над GF(p),
р - простое
Примечания
1.	Многочлены заданы набором их коэффициентов a^i—^2
«1 ад. Например набор 1021 соответствует многочлену х3 + 2х +1.
2.	В скобках указан показатель многочлена, т. е. наименьшее
положительное число е, при котором хе -1 делится на данный
многочлен без остатка.
3.	Многочлены f*(x), для которых справедливо соотношение
f*(x) = axNf(x~'), где а е GF(p), а Ф 0, /(х) - многочлен степе-
ни N, уже имеющийся в списке, не приводятся.
Неприводимые многочлены над GF(2)
N=1	11(1)	N=7	10000011 (127)	N=S	100011011 (51)
N=2	111 (3)		10001001 (127)		100011101 (255)
N=3	1011 (7)		10001111(127)		100101011 (255)
			10011101(127)		100101101 (255)
N=4	10011 (15)		10100111(127)		100111001 (17)
	11111 (5)		10101011(127)		100111111 (85)
H=5	100101(31)		10111111 (127)		101001101(255)
	101111 (31)		11001011(127)		101011111 (255)
	110111 (31)		11101111 (127)		101100011 (255)
A*=6	1000011 (63)				101110111 (85)
	1001001(9)				101111011 (85)
	1010111 (21)				110000111 (255)
	1011011 (63)				110001011 (85)
	1100111 (63)				110011111 (51)
					111001111 (255)
					111010111 (17)
208
Теория, применение и оценил качества генераторов псевдослучайных последовательностей
Неприводимые многочлены над GF(3)
N=1	11(2) 12(1)	V=4	1 0012(80) 10022(80)	/V=5	100021 (242) 100022(121)	102211 (242) 102221(22)
N=2	101 (4)	10102(16)		100112(121)	110012(121)
	112(8)	10111(40)		100211 (242)	110021 (242)
N=3	1021 (26)	10121 (40)		101011 (242)	110111 (242)
	1 vb 1 \b-V/ 1022(13)	11021(20)		101012(121)	110122(121)
	1 Vta. | 1 \J j 1112(13)	11111(5)		101102(121)	111121 (242)
	1191 (26)	11122 (80)		101122(121)	111211 (242)
	114 1 \CAJJ	12112(80)		101201 (242)	111212(121)
		12121(10)		101221 (242)	120212(121)
				102112(121)	120221 (242)
				102122(11)	121112(121)
Неприводимые многочлены над GF(5)
N= 1 11 (2)	N=3	1011(62)	1131 (62)
12(4)		1014(31)	1134(31)
14(1)		1021 (62)	1141 (62)
H=2	102(8)		1024(31)	1143(124)
111(3)		1032(124)	1213(124)
112(24)		1033 (124)	1214(31)
123(24)		1042(124)	1223 (124)
124(12)		1043(124)	1312(124)
141 (6)		1113(124)	1323(124)
		1114(31)	1341 (62)
Неприводимые многочлены над GF(7)
11(2)	N=3 1002(18)	1124(342)	1235(171)	1432(342)
12(6)	1003(9)	1126(57)	1245(171)	1434(342)
13(3)	1011 (114)	1131(38)	1251 (114)	1453(171)
16(1)	1016(57)	1135(171)	1261 (114)	1461 (114)
101 (4)	1021 (38)	1143(171)	1262 (342)	1513(171)
102(12)	1026(19)	1146(57)	1264(342)	1532(342)
113(48)	1032 (342)	1151 (114)	1325(171)	1534(342)
114(24)	1035(171)	1152(342)	1334(342)	1552(342)
116(16)	1041 (114)	1153(171)	1336(19)	
123(48)	1046 (57)	1154(342)	1341 (38)	
125(48)	1052(342)	1163(171)	1343(171)	
131 (8)	1055(171)	1165(171)	1352(342)	
136(16)	1062 (342)	1214(342)	1354(342)	
141 (8)	1065(171)	1216(57)	1413(171)	
145(48)	1112(342)	1223(171)	1416(19)	
152(24)	1115(171)	1226(57)	1425(171)	
Приложения
209
Неприводимые многочлены над GF(ll)
N=\	11(2)	Л/=2	101 (4)	124(30)	147(120)	161(12)
	12(5)		103(20)	125(60)	148(40)	172(120)
	13(10)		105(20)	126(120)	149(60)	175(30)
	15(10)		Ш(3)	12А(24)	151 (12)	183(60)
	17(5)		114(60)	136(120)	152(120)	192(40)
	1А(1)		116(40)	138(120)	153(15)	1А1(6)
			117(120)	139(15)	157(40)	
			118(120)	13А{8)	15А(24)	
Приложение 2
Примитивные многочлены над GF(2)
Примечание. Многочлены заданы индексами N, i, 0 своих не-
нулевых коэффициентов, например строка 89 38 0 соответствует
многочлену х89 + х38 + 1.
1 0	24 4 3 1 0	49 9 0	7416 15 1 0
2 1 0	25 3 0	50 27 26 1 0	7511 10 1 0
3 1 0	26 8 7 1 0	51 1615 1 0	76 36 35 1 0
4 1 0	27 8 7 1 0	52 3 0	7731 30 1 0
5 2 0	28 3 0	531615 1 0	78 20 19 1 0
6 1 0	29 2 0	54 37 36 1 0	79 9 0
7 1 0	3016 15 1 0	55 24 0	80 38 37 1 0
8 6 5 1 0	31 3 0	562221 1 0	81 4 0
9 4 0	322827 1 0	57 7 0	82 38 35 3 0
10 3 0	33 13 0	5819 0	834645 1 0
11 2 0	341514 1 0	592221 1 0	8413 0
12 7 4 3 0	35 2 0	60 1 0	85 28 27 1 0
13 4 3 1 0	3611 0	61 1615 1 0	861312 1 0
13 4 3 1 0	37 12 10 2 0	62 57 56 1 0	8713 0
141211 1 0	38 6 5 1 0	63 1 0	887271 1 0
15 1 0	39 4 0	64 4 3 1 0	89 38 0
16 5 3 2 0	40 21 19 2 0	6518 0	901918 1 0
17 3 0	41 3 0	66 10 9 1 0	918483 1 0
18 7 0	42 23 22 1 0	67 10 9 1 0	92 13 12 1 0
19 6 5 1 0	43 6 5 1 0	68 9 0	93 2 0
20 3 0	44 2726 1 0	692927 2 0	94 21 0
21 2 0	45 4 3 ГО	701615 1 0	9511 0
22 1 0	46 21 20 1 0	71 6 0	964947 2 0
23 5 0	47 5 0	72 53 47 6 0	97 6 0
	482827 1 0	73 25 0	9811 0
Примитивные многочлены вида + х1 + 1
где # - число Мерсенна
17 11 0	89 380	521 363 0	1279 1063 0
1712 0	127 64 0	521 473 0	2281 1252 0
17140	127 90 0	521 489 0	2281 13660
31 180	127 97 0	6073340	2281 1566 0
31240	127112 0	607 460 0	3217 2641 0
31250	127 1200	607 502 0	321731500
3128 0	521 353 0	1279 861 0	
Примитивные многочлены вида xN + х1 + 1
где i = 8,16,32,64,128
15 8 0	81 16 0	127 64 0	177 8 0
39 8 0	97 64 0	135 16 0	225 32 0
63 32 0	105 16 0	159 128 0	521 32 0
65 32 0	119 8 0	175 16 0	
Примитивные многочлены вида xN + х1 + 1
где (z, 2n - 1) = 1
15 7 0	52 19 0	84 13 0	111 49 0
18 7 0	52 21 0	87 13 0	113 9 0
20 3 0	55 24 0	94 21 0	113 15 0
23 5 0	57 7 0	95 110	113 30 0
23 9 0	57 22 0	95 17 0	118 33 0
25 3 0	58 19 0	97 6 0	118 45 0
25 7 0	60 11 0	97 12 0	119 38 0
28 3 0	63 5 0	97 33 0	121 18 0
28 9 0	63 31 0	97 34 0	129 5 0
28 13 0	65 18 0	98 11 0	129 31 0
33 13 0	68 9 0	98 27 0	129 46 0
36 11 0	68 33 0	100 37 0	130 8 0
39 14 0	71 6 0	103 9 0	132 29 0
41 3 0	71 9 0	103 13 0	134 57 0
41 20 0	71 18 0	103 30 0	135 11 0
47 5 0	71 20 0	103 31 0	135 22 0
47 14 0	71 35 0	105 17 0	140 29 0
47 20 0	73 25 0	105 37 0	142 21 0
47 21 0	73 28 0	105 43 0	145 52 0
49 9 0	73 31 0	105 52 0	145 69 0
49 12 0	79 9 0	106 15 0	148 27 0
49 15 0	79 19 0	108 31 0	150 53 0
49 22 0	81 35 0	111 10 0	151 3 0
Приложения
211
151 9 0	194 87 0	258 83 0	396 109 0
151 15 0	198 65 0	266 47 0	396 169 0
151 31 0	201 14 0	268 25 0	396 175 0
151 39 0	201 17 0	268 61 0	404 189 0
151 43 0	201 59 0	270 53 0	412 147 0
151 45 0	201 79 0	270 133 0	428 105 0
151 51 0	202 55 0	282 35 0	436 165 0
151 63 0	207 43 0	282 43 0	460 61 0
151 66 0	212 105 0	284 119 0	462 73 0
151 67 0	218 11 0	286 69 0	475 15 0
151 70 0	218 15 0	286 73 0	476 141 0
159 31 0	218 71 0	292 97 0	484 105 0
159 34 0	218 83 0	294 61 0	508 109 0
159 40 0	225 74 0	300 7 0	524 167 0
161 18 0	225 88 0	300 73 0	532 37 0
161 39 0	225 97 0	300 91 0	540 1 79 0
161 60 0	225 109 0	316 135 0	540 211 0
170 23 0	231 26 0	322 67 0	564 163 0
172 7 0	231 34 0	332 123 0	588 151 0
174 13 0	234 31 0	350 53 0	588 253 0
175 6 0	234 103 0	364 67 0	708 278 0
175 18 0	236 5 0	366 29 0	708 301 0
175 57 0	250 103 0	378 43 0	756 119 0
177 22 0	252 67 0	378 107 0	756 349 0
17788 0	255 52 0	380 47 0	780 299 0
178 87 0	255 55 0	390 89 0	804 295 0
183 56 0	255 82 0	396 25 0	828 205 0
Приложение 3
Примитивные многочлены над
GF (22) = {0,1, со, со2}, со2 + со + 1 = 0, со3 = 1
и GF(23) = {0,1, со, со2, со3, со4, со5, со6},
со3 + со2 + 1 = 0, со7 = 1
Примечания:
1. Многочлены заданы набором своих коэффициентов, например
набор 101 coco2 соответствует многочлену х4 + хг + сох + со2, где
со - примитивный элемент поля.
212
корня, применение и оценка качества генераторов псевдослучайных последовательностей
2. Многочлены /*(х), для которых справедливо соотношение
f*(x) = адЛ /(х-1), где а е GF(L), а # О, f(x) - многочлен степе-
ни N, уже имеющийся в списке, не приводятся.
Gf(22) (Я< 10)
col	colOOOl	со 1 1 0 0 0 0 0 0 1
coll	collOOOl	со со со 1 000000 1
colli со2со100001
со2со011 со 1 0 1 0 0 0 0 1
Gf(23) (N<3)
col	со31001	со3со1ОООО1
со со 1 со31 1 0 0 1
со 1 0 1 со 1 0 0 0 0 1
Gf(23)(tf=2)
со со 1	со со61	со2 со31	со31 1	со3 со61
со со51	со2 со21	со2 со51	со3 со21
Приложение 4
Использование JK-триггеров при
проектировании LFSR
В ряде случаев при проектировании генераторов псевдослу-
чайных кодов на основе LFSR удается существенно упростить
аппаратную реализацию этих устройств за счет использования
Т-триггеров.
Такая возможность появляется, например, в следующих си-
туациях:
•	проектирование TV-разрядных LFSR, логика работы которых
описывается уравнением
еа+1)=г1Лге(0;
•	проектирование LFSR, осуществляющих в каждом такте ум-
ножение нах + 1;
Приложения
21>
•	проектирование LFSR, логика работы которых описывается
уравнением
ea+i)=TxkQ(f),
при выборе в качестве образующего многочлена вида
<Z>(x)=Z+... + ?+ 1.
Во всех этих случаях и программная реализация этих уст-
ройств может быть существенно упрощена.
На рис. П4.1 показаны два примера использования /АГ-тригге-
ров при проектировании генераторов псевдослучайных кодов на
LFSR.
а
б
в
Рис. П4.1. Использование ЛГ-триггеров при построении LFSR:
D- и JZ-триггеры и их условное графическое обозначение - а;
вариант реализации генератора ^-последовательностей,
изображенного на рис. 1.31, - б;
схема генератора байтовой псевдослучайной последовательности,
соответствующего образующему многочлену Ф(х) = х39 + х8 + 1, - в
214
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Приложение 5
Алгоритм Берлекампа-Масси
Алгоритм Берлекампа-Масси является эффективным средст-
вом определения линейной сложности L двоичной последова-
тельности е = Eo£i...En_ 1 длины п. Алгоритм использует п итера-
ций, причем A-я итерация (А < п) определяет линейную слож-
ность подпоследовательности Е^, состоящей из первых А бит по-
следовательности е.
Алгоритм
1.	Инициализация:
C(D)<- 1,L<-O,w<— 1, B(D) <— 1, А«—0.
2.	Пока А < п, выполнить п.2.1-2.3.
2.1. d<r-
(	L
I	i=l
Ci£N-l
mod 2.
2.2.	Если d = 1, выполнить n. 2.2.1, 2.2.2.
2.2.1.	ДО) <- C(O), C(O) <- C(D) +
2.2.2.	Если L < A/2, to L <- A + 1 - L, m <- A, 5(0) <- ДО).
2.3.	A<—A+ 1.
3.	Возвратить значение L.
Пример
£ = 001101110,
и = 9.
	d	T(D)	C(D)	L	m	8(D)	N
—	—	-	1	0	-1	1	0
0	0	—	1	0	-1	1	1
0	0	—	1	0	-1	1	2
1	1	1	1 + D3	3	2	1	3
1	1	1 + D3	1 +D+D3	3	2	1	4
0	1	\+ D+D3	1 +£>+ D3 + D3	3	2	1	5
1	1	\ + D+Dl + D3	l+D+D1	3	2	1	6
1	0	] + D+D3 + D3	\+D+D3	3	2	1	7
1	1	1 + D+D3	1 +D+D3+D5	5	7	1 + D+D3	8
0	1	1 + D+D3 + D5	1 + D3 + D5	5	7	\+D+D3	9
Линейная сложность L равна 5.
Приложения
215
Приложение 6
Формула Лапласа
Пусть задана последовательность символов е = E]E2 ... е„ и пусть
V, - число появлений z-ro символа. Тогда вероятность того, что
отклонение экспериментальной частоты появления символа
v;	1
рэ = — от теоретического значения рТ = — не превышает за-
данного числа £ > 0, приближенно равна удвоенной функции
Лапласа:
v; 1
р —<г =2Ф,
* ь
п 2т
п
—fl—-
)ГП I 2W
Полагая
(V 1 I
Р ------<£ =99%,
I п 2т
получаем:
2ФЬ
п
2т I 2т
= 2ФЬ ^-2т-
= 0.99.
Отсюда
ф£ ^2т-
= 0.495.
П
2т-1
Используя таблицу значений функции Лапласа, получаем:
^.2т. —— =2.58,
V2m-1
£ 2.58 /2т -1
2т \ п
Таким образом, с вероятностью 99%
216
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
у,-	11 2.58 /2m-l
п	2т У п '
Отсюда
1 2.58 l2m-l 1 2.58 /г" -1
2m 2m V п п 2т 2т У п
или
п-2.58-Jn-(2m-Г) < <n + 2.58-7«-(2m-l)
Приложение 7
Система генерации паролей
Система генерации паролей предназначена для выработки па-
ролей, удовлетворяющих требованиям случайности.
Системные требования
•	Pentium 100;
•	RAM 32 МВ;
•	550 Кб на диске для файла программы;
•	ОС: Windows 9х, NT, 2000, ME, ХР.
Запуск программы
После запуска программы выполняется проверка работоспо-
собности системы. При отрицательном результате проверки вы-
водится диагностическое сообщение (рис. П7.1).
Ошибка тестирования
Рис. П7.1. Диагностическое сообщение при неправильной работе
программы
Если проверка прошла успешно, система ищет в текущей ди-
ректории файл gen5.ini, который используется для хранения час-
Приложения
217
ти ключевой информации. Если файла не существует, то система
предлагает создать новый или выйти из программы (рис. П7.2).
Не найден или поврежден файл 'genB.ini' >
✓ Создать новый [ У.ЖвыйТйиз программы |
Рис. П7.2. Диагностическое сообщение при отсутствии файла
инициализации
После инициализации пользователь получает доступ к систе-
ме. Управление процессом генерации осуществляется при помо-
щи специальной панели (рис. П7.3).
Генерация | Пельзователй;| Тесты .Настройки , |'
Рис. П7.3. Панель управления процессом генерации
Кнопка «ГЕНЕРАЦИЯ»
Данная кнопка активизирует окно генерации (рис. П7.4).
О Готовность системы
О Начальное заполнение
• Генерация
•	Тестирование
•	Запись паролей в файл
- Режим-----------;
г автомат & ручной j
г Запись в файл-----
। выкл. ₽ ркл’ |
СТАРТ |
НЗ |
ТЕСТ I
й| Выходной файл. D \Test\parol1
Рис. П7.4. Панель генерации
В этом окне пользователь может выбрать следующие режимы
работы:
•	Автоматический - генерация ПСП производится до получения
положительного результата (т. е. до удовлетворения требова-
ниям статистической безопасности);
218
Теория, применение и оценил качества генерлторов псевдослучайных последовательностей
•	Ручной - генерация производится один раз, и пользователь
решает сам - использовать или нет полученный фрагмент
ПСП для формирования паролей.
В этом же окне пользователь может выбрать файл, куда будут
записываться пароли.
Кроме того, имеется три кнопки:
•	Старт - начать генерацию;
•	НЗ - установить новые начальные значения;
•	Тест - проверка работоспособности системы.
Кнопка «ПОЛЬЗОВАТЕЛИ»
При нажатии этой кнопки появляется список пользователей
(рис. П7.5).
N* п/п	Фамилия И.О.	I N> карточки	пароль
1 X	Иванов ИИ.	 1	TAMQ0IL8YJGMIKMV
2	Петров П.П.	2	YJGMIKMVTILGV562
	Сидоров С.С.	3	TILGV562CCQ9HY5J
|( Добавить i	Печать таблицы
Удалить	Печать карточек
Чтение	Настройка принтера
Запись	
Рис. П7.5. Панель пользователей
Для модификации списка используются следующие кнопки:
•	Добавить - вставить новую запись;
•	Удалить - удалить запись;
•	Чтение - читать список из файла;
•	Запись - записать список в файл;
•	Печать таблицы - печать всего списка;
•	Печать карточки - печатать карточку с паролем для каждого
пользователя;
•	Настройка принтера.
Приложения
219
Кнопка «ТЕСТЫ»
В данном окне содержится статистика прохождения тестов
(рис. П7.6).
ТЕСТЫ	npovtaei и
- Отчет--------------------у-i 'г--------?•
г Полный ff Краткий	.^91
Рис. П7.6. Результаты прохождения тестов
Пользователь имеет возможность вывести отчет в двух видах:
• Краткий - выводится совокупный результат (тесты пройдены /
тесты не пройдены);
• Полный - выводится результат прохождения каждого теста с
указанием числовых характеристик (рис. П7.7).
Проверка 0 и 1	прошел
Критерий	Вероятность
2.048	(5%.25%]
Рис. П7.7. Пример полного отчета для теста «Проверка 0 и 1»
Кнопка «НАСТРОЙКИ»
При нажатии на данную кнопку пользователь получает воз-
можность изменять значения границ для статистики тестов. Для
тестов, чьи статистики сравниваются с нижней границей, имеется
специальная панель для выбора нижней границы (рис. П7.8).
Нижняя граница - -
~ 1% ~ 5096
- 5% г 75% " 99% :
г 25% ~ 95%
Рис. П7.8. Пример выбора нижней границы для тестовой статистики
220
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Для тестов, чьи статистики лежат в определенных интервалах,
имеется специальная панель (рис. П7.9).
' т| 5Л<7 Значение критерия для биграмм <=, ' |9
Рис. П7.9. Пример задания интервала для тестовой статистики
Приложение 8
Система оценки качества генераторов
псевдослучайных последовательностей
(версия 3.06.7.beta)
Руководство пользователя
Система оценки качества (в дальнейшем - СОК) предназначе-
на для исследования статистических свойств генераторов ПСП и
анализа статистической безопасности криптоалгоритмов. В со-
став системы входит два вида тестов:
•	Графические тесты. Пользователь получает определенные
графические зависимости и по их виду делает вывод о свойст-
вах анализируемой последовательности.
•	Оценочные тесты. Система на основе оценочных критериев
выдает заключение о степени близости статистических свойств
анализируемой и истинно случайной последовательности.
Системные требования
•	Pentium 100;
•	RAM 32 Мб;
•	6,5 Мб на диске для файлов программ и справочной службы;
•	50 Мб свободного пространства на диске;
•	ОС: Windows 9х, NT, 2000, ME, ХР.
Приложения
221
Установка программы
Для установки программы необходимо запустить программу
установки COK_SETUP.EXE или, в случае отсутствия дистрибу-
тива, скопировать файлы программы и справочной службы на
жесткий диск.
Запуск программы
Для начала работы программы необходимо запустить файл
СОК.ЕХЕ. На экране появится окно программы (рис. П8.1).
Рис. П8.1. Начальное окно программы
Тестирование
Процесс тестирования состоит из следующей последователь-
ности шагов:
•	создание нового запроса;
•	выбор исследуемых файлов;
•	выбор тестов;
222
Теория, применение и оценка качества генердторов псевдослучайных последовательностей
•	настройка параметров тестирования;
•	запуск тестов;
•	просмотр результатов.
Создание нового запроса
Создание нового запроса осуществляется при помощи выбора
пункта меню «Файл | Новый запрос». При этом появляется окно
запроса (рис. П8.2).
При создании нового запроса все установки предыдущего запро-
са будут либо удалены, либо установлены в исходные значения.
Выбор файла
Выбор файла осуществляется при помощи пункта меню «Файл
| Добавить файл». На экране появляется диалоговое окно выбора
файла (рис. П8.3).
Приложения
225
-ZJxl
Папка: | Q AES
3 о © С*
3^1 AES.100K._4R
j|AES_100K_6R
§AES_100K_8R
Имя Файла: |aES_100K_10R
Тип Файлов. [
3
Открыть
Отмена
Рис. П8.3. Окно выбора файлов
Выбор директории
Выбор директории осуществляется при помощи пункта меню
«Файл | Добавить директорию». На экране появляется диалоговое
окно выбора директории (рис. П8.4).

Диск 3,5 (А:)
Д-ра Локальный диск (С:)
; Й-ра Локальный диск (D:)
ЕВО Локальныйдиск(Е:)
i Й Компакт-диск (F:)
\ tM?NEW(H:)
Е-(§LMoe сетевое окружение
OK I Отмена
Рис. П8.4. Выбор директории
224
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
При выборе директории отсутствует принцип вложенности,
т. е. поддиректории, входящие в рассматриваемую директорию,
не тестируются.
Выбор тестов
Выбор тестов осуществляется при помощи пункта меню «Тес-
тирование | Выбор тестов» (рис. П8.5).
Выбор те с т о в
« Графические тесты - ------
< Быстрые
। р Гистограмма
1 Р Распределение на плоскости
[ Р Проверка серий	t
, Медленные	|
I р Проверка на монотонность
j р Байтовая АКФ	!
। р Битовая АКФ
Р Спектральный тест
, р Профиль линейной сложности 1
L_J
Оценочные тесты	*	- ------।
р Быстрые,,	4	*'-
।	& РроёёркаОи"!	,
|	р Проверка 0 и 1	в гкмпослцд	J
| р Проверка несяепленных серий
 Р Проверка сеепленных серий
। Р Проверка "дырок**
| Р Проверка "дырок" в подпослед.
| Р Проверка непересек шаблонов '
! р Проверка пересек, шаблонов
I Р Проварка частот
р Посимвольная проверка
Р Проверка интервалов
р Проверка перестановок
! р Проверка на монотонность
Р Универсальный тест Маурера
। р Проверка рангов матриц 32*32 ;
р Проверка кумулятивных сумм
Р Проверка случайных отклонений ;
Р Проверка линйной сложности
Медленные
Р Проверка сжатия (Лемпелл-Зив)
Рис. П8.5. Выбор тестов
Приложения
229
Настройки параметров тестирования
Настройки параметров тестирования осуществляются при по-
мощи пункта меню «Тестирование | Настройка тестов» (рис.
П8.6).
в4 тестов
.........in II1
включить	С отключить
Р” |Тестировать’то ль коперио д!
Прпверка нп мпнотонность
Размер области тестирования в байтах рОО
Внимание! Увеличение области тестирования
увеличивает время тестирования и может привести
к зависанию компьютера
Размер области не должен превышать 100.000 байт
Байтовая АКФ
Размер области тестирования в байтах |500	I
Внимание! Увеличение области тестирования
увеличивает время тестирования и может привести
к зависанию компьютера
Размер области не должен превышать 100.000 байт |
. I-----------------------______----------------J J j
Исходные |	| if ОК |
Рис. П8.6. Настройка параметров тестирования
После выполнения вышеперечисленных шагов исходные дан-
ные для тестирования будут отображены в окне запроса (рис.
П8.7).
226
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Тестируемые файлы:
ОДТез^Исследоеанмв AES\AES_10QK_4R
ОДТевГ\Исследование AES\AES_10Q*L8R
О:\Твд(\Исследоеание AES\AESJ0QK_16R
Тестируемый файл.
Оценочные
Проверка 0 и 1
Проверял В м 1 в пмпосмд.	 I
Проверяв несаепмннмм Ьермй
Проверка смплммьв серий
Проверка "дырок"
Проверка "дырок" в подлосяед.
Проверка мнеросек wdaotiui
Проверка пересек ниблом*
Проверка «агтот
Поеммволымл проверял	|
Проверка итрвалоа	 j
Проверка пороет анодов
Проверка на монотонность
litiliд	I
Рис. П8.7. Отображение выбранных параметров в окне запроса
Запуск тестов
Запуск тестов осуществляется при помощи пункта меню «Тес-
тирование | Старт». Тестирование можно прервать нажатием на
кнопку «Стоп» на панели кнопок. (Примечание. Тестирование
при нажатии на кнопку «Стоп» закончится лишь после заверше-
ния выполнения текущего теста).
Для ускорения процесса тестирования перед запуском тестов
рекомендуется скрыть панель индикаторов. Сделать это можно
при помощи пункта меню «Тестирование | Скрыть индикаторы».
Просмотр результатов
Просмотр результатов выполнения отдельного теста осущест-
вляется при помощи пункта меню «Результаты | Название тре-
буемого теста» (рис. П8.8).
Приложения
227
Результаты Помощь	|
Г истограмма
Распределение на плоскости
Проверка серий графическая
Проверка на монотонность графическая
Байтовая АКФ	I
Битовая АКФ	I
Спектральный тест	:
Профиль линейной сложности	|
Проверка 0 и 1	I
Проверка 0 и 1, в подпоследовательностях	;
Проверка несцепленных серий	.
П роверка сцепленных серий
Проверка "дырок"	;
П роверка' 'дырок'' в псдпоследоваге льностях	|
Проверка непересекающихся шаблонов	|
Проверка пересекающихся шаблонов	I
Проверка частот	1
Посимвольная проверка
Проверка интервалов	I
Проверка перестановок
Проверка на монотонность
U ниверсальный тест М аурера
П роверка рангов матриц 32'32
Проверка кумулятивных сумм
Проверка случайных отклонений
Проверка линейной сложности
Проверка сжатия (Лемпелл-Зив)
Ша Общий отчет	;
Рис. П8.8. Просмотр результатов тестирования
Также имеется возможность просмотреть общий отчет тести-
рования при помощи пункта меню «Тестирование | Общий отчет»
(рис. П8.9).
Данные общего отчета можно сохранить на диск при помощи
пункта меню «Файл | Сохранить отчет» или распечатать при по-
мощи пункта меню «Файл | Печать отчета».
228
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
I Общий отчет							
							
	!______ 		Результаты тестирования файла: Р:\ТевЪ\Иооледование AES\AES_10k Размер файла: 10000 Период: 10000 Тестируется: 10000 	it			_____ 1		
	।	 1 1		Тесты	1	1 | Гэксп |	1 Гтеор |		1 Результат | __ _ 1		
	1 [ Проверка	0 и 1	-1		1 | 2,33280 1		 _ । 6,63500 |	— _ ।		
	[_	 | Проверка ।		0 и 1 в подпослед.	_[—	1 | 0,44542 |			[. 0,01000 |	““  	1 _	____।		
	।	 | Проверка [_		не оцепленных серий	।		1 1	1		 1 1		1		
	।	 | Проверка t	оцепленных серий	_|		 j 1	1		1 1		1		
	। | Проверка дырок		_ ।		 । | 0,41949 |		[. 0,01000 ।				1		
	। | Проверка । 		дырок в подпослед.	_ ।	1 | 0,59132 |			 1 0,01000 1	-		1		
	। 	 | Проверка ।		___	кепереоек. шаблонов	"1 “	I" | 0,99999 |		1 0,01000 |	1		
	। 	 | Проверка	пересек, шаблонов	-| 1	1	1		 [- 0,01000 I	1		
	। | Проверка частот [_____ — 			।	 । | 243,276 |		1- 310,900 1		 _ _ ।		
	।	 	 | Посимвольная проверка [_		__ _			। 	। 1	1	_	1 - 1		 ।		
	।	 		 | Проверка интервалов [______, _______ __ _____________		_|		1 1	1	1 - 1		1		
	।	 - _ —			 | Проверка перестановок		।		1 1	1			 _ 1 _ 1		1		
	। | Проверка t			на монотонность	- —।_ 1	1		|- 1	— _ ।		
	। 	 | Проверка । 				рангов матриц 32*32	-1 -	-	1	- | 0,17772 | ।	 _ । _		1 0,01000 1 		 1_	1 		।		
		| у/	'0К |			IKj	
Рис. П8.9. Пример общего отчета
Приложения
229
Приложение 9
Тест «распределение на плоскости» для
LFSR, соответствующего Ф(х) = х9 + х* + 1
Рис. ПЭЛ. Битовый генератор Рис. П9.2. Байтовый генератор
Приложение 10
Линейные блоки пространственного
сжатия информации 8 -> 3,9 -> 8
Пусть Ф(х) = х3 + х2 + 1, тогда логика работы БПС 8 —> 3 мо-
жет быть описана матрицей
1
1
0 0 1
0 1 0
1 0 0
1
0
1
1 0 1
1 1 1
1 1 о
иначе го-
0
воря, уравнения работы БПС имеют вид
а0 = а0 © а3 © а4 © а5 © а7;
 flj = а0 © а2 © «5 © а6 © а7;
а2 = ах ©й4 ®а5 ©а6;
где at,i - 0,7, - входы, , i = 0,2, - выходы блока.
2J0
Теория, ПРИМЕНЕНИЕ Н ОЦЕНКА КАЧЕСТВА ГЕНЕрАЮрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Пусть Ф(х) = х8 + х7 + х5 + х3 + 1, тогда логика работы БПС 9 —>
8 может быть описана матрицей	
	11110 10 0 1
	0 0 0 1 1 1 0 1 1
	0 0 1110 110
	1 0 0 0 0 0 1 0 1
	0 0 0 0 0 1 0 1 0
	11111110 1
	1111110 10
	111110 10 0
иначе говоря, уравнения работы БПС имеют вид
а0 = а0 © й] © а2 © а3 © а5 © а8;
= а3 © а4 © а5 ® а7 © й8;
а2 = а2 © а3 © а4 © а6 © а2;
Г
а3 = а0 © а6 © а8;
а4 = а5 © а7;
а5 = а0 © а6 © а8;
а6 =а0@а5®а7;
а7 =а0 ©я4 ©а6;
где а( ) i = 0,8, - входы, а;., i = 0,7, - выходы блока.
Приложения
2Я
Приложение 11
Результаты анализа статистической
безопасности алгоритмов генерации ПСП
В таблицах П11.1-П11.9 приведены результаты исследований
генераторов ПСП, а точнее, число успешно пройденных оценоч-
ных статистических тестов. Длина анализируемой последова-
тельности во всех случаях равна 220 бит, число экспериментов
равно 1000 для каждого теста. Исходное заполнение для некрип-
тографических, таблицы преобразований 2?-блоков для стохасти-
ческих и исходный ключ для криптографических генераторов для
каждого эксперимента формировались случайным образом. Что-
бы тест мог считаться пройденным, из 1000 экспериментов ус-
пешно должно закончиться не меньше 980. Для некоторых п-
разрядных генераторов в таблицах дополнительно указывается
разрядность t исследуемой ПСП, t < п.
Табл. ПИЛ. Условные обозначения (У0) генераторов ПСП
УО	| Генератор
Конгруэнтные генераторы	
CG-1	Х„= (2147001325-4., + 715136305) mod232
CG-2	Хп=^Ш-Х„.^У}гшх!2п
CG-3	Х„ = (3141592651 -Х„_, + 1) mod232
CG-4	4 = (4-24+4-55)®^232
CG-5	Х„ = (4- 24 -4-s)mod^
CG-6	4= (14288-4.+ 758634) mod!?'-У)
ДДО-генератор	
BBS-У	4 = 4.,2ото</33433457
BBS -2	4 = 4./^23878703773
LFSR с образующим многочленом приведенного вида	
LFSR-У	X32 + ^26+J23+J22+Z,e+Z,2 + X,, + Z,0 + 4! + Z7 + 4! + Z4+>r2 + Z+1
LFSR-2	/"ъГ32*!
8-разрядный RFSRс образующим многочленом Х+Х+ 1	
RFSR-У	Обратная связь задает параметр преобразования Яблока
RFSR-2	Обратная связь задает преобразуемое значение
Стохастический генератор с 1О-раундовой функцией обратной связи	
Rgen-У	Преобразуемый блок (массив байтов размерности 4x4) - 128 бит; раундовые функции - стохастическое преобразование байтов, стохастическое преобразо- вание строк и столбцов
272
Теория, применение и оценка качества генерАюров псевдослучайных последовательностей
Табл. П11.2. Результаты исследований конгруэнтных генераторов
ПСП (начало)
	Проверка 0 и 1	Проверка 0 и 1 в подпослед.	Проверка несцепл.серин	Проверка сцепл. серий	Проверка «дырок»	Проверка «дырок» в подпослед.	Проверка частот	Посимвольная проверка	Проверка интервалов	Проверка перестановок	Проверка на монотонность	Гест Маурера	Проверка рангов матриц	Проверка кумулятивных сумм	Проверка случайных отклонений
	1	2	3	4	5	6	7	В	9	10	11	12	13	14	15
CG-1															
32 бита	1000	1000	1000	1000	998	994	1000	760	964	907	882	936	992	1000	915
8 бит (0-й байт)	1000	1000	1000	1000	1000	0	1000	1000	0	0	0	0	0	1000	0
8 бит (1-й байт)	1000	1000	1000	1000	1000	1000	1000	1000	1000	1000	1000	1000	719	1000	302
8 бит (2-й байт)	997	976	969	972	986	986	998	108	953	883	900	983	994	992	893
8 бит (3-й байт)	990	990	975	975	988	993	988	95	965	887	874	990	995	987	911
4 бита	1000	1000	1000	1000	1000	0	0	0	0	0	0	0	0	1000	0
2 бита	1000	1000	0	0	1000	0	0	0	0	0	1000	0	0	1000	0
1 бит	1000	1000	0	0	0	0	0	0	0	0	1000	0	0	1000	0
Табл. П11.3. Результаты исследований конгруэнтных генераторов
ПСП (продолжение)
	11	[2	3	4	5 |б		7	[в		10		I12	13	14	|7Г
CG-2															
32 бита	1000	1000	1000	1000	1000I989		1000|767		0	898	0	969	992	1000|920	
07-3															
32 бита	0_ 1°		0	0	0	534	0	о	970	858	643	971 |508		0	720
CG -4															
32 бита	986	992	978	975	992	989	995	109	963	887	866	991	993	984	922
16 бит	993	989	972	972	989	983	990	109	958	869	897	988	987	988	904
8 бит (0-й байт)	993	984	975	975	988	990	984	91	959	880	888	988	989	994	909
8 бит (1-й байт)	991	984	970	966	991	993	992	93	964	872	906	993	996	988	909
8 бит (2-й байт)	990	991	980	977	998	989	989	97	963	891	911	985	988	986	912
8 бит (3-й байт)	989	990	973	972	987	989	994	91	967	886	875	986	987	979	907
4 бита	990	991	971	966	983	993	995	95	971	890	878	984	991	987	897
2 бита	991	985	976	972	991	986	988	88	970	882	894	990	994	987	910
1 бит	988	991	975	971	989	987	988	91	954	890	888	991	992	991	910
Приложения
277
Табл. П11.4. Результаты исследований конгруэнтных генераторов
ПСП (окончание)
	1	2	з	4	5,	6	7	8	9|	10	11	12	13	14	15
CG-5															
32 бита	991	997	0	0	0	420	0	0	963	171	887	972	0	990	469
16 бит	993	1000	0	0	0	0	0	0	960	439	889	920	0	994	117
8 бит (1-й байт)	998	1000	0	0	0	0	0	0	962	0	0	0	0	998	32
8 бит (2-й байт)	992	994	978	977	988	992	993	101	959	890	873	994	990	983	898
8 бит (3-й байт)	991	991	968	979	987	993	987	116	949	862	866	992	986	988	906
8 бит (4-й байт)	992	989	982	974	987	982	991	93	966	862	869	993	993	990	913
4 бита	1000	1000	0	0	0	0	0	0	1000	0	0	0	0	0	0
2 бита	1000	1000	0	0	0	0	0	0	0	0	0	0	0	1000	0
1 бит	1000	1000	0	0	0	0	0	0	0	0	0	0	0	1000	0
CG-6															
8 бит	990	988	965	970 |989 |993 |995				86	962	889	887	992	988 |981 |904		
Табл. П11.5. Результаты исследований BBS-генераторов
	1	2	з	4	5	6	7	8	9	10	11	12	13	14	15
															
16 бит	992	991	959	961	989	986	981	130	936	857	882	993	991	991	911
8 бит	990	994	966	972	994	972	973	168	951	883	867	989	989	987	900
4 бита	988	991	941	904	962	966	862	80	891	859	840	985	990	984	910
2 бита	988	979	903	919	992	930	891	102	891	807	883	966	993	990	902
1 бит	964	968	827	797	943	819	882	107	910	897	882	973	989	964	895
BBS-2															
32 бита	968	988	902	947	982	987	937	71	907	788	821	988	988	963	928
16 бит	965	996	894	945	991	960	924	73	883	870	891	988	989	947	907
8 бит	927	976	894	883	988	946	821	107	892	883	882	988	988	924	888
4 бита	954	993	657	472	933	883	872	69	872	660	557	957	980	954	903
2 бита	928	992	883	383	957	883	701	10	883	780	875	923	985	922	902
1 бит	935	969	257	14	4	896	791	0	881	764	897	924	993	935	898
Табл. П11.6. Результаты исследований LFSR
	1	2	з	4	5	6		8	9	10	11	12	13	14	15
LFSR-}															
32 бита	992	991	978	969	989	985	987	108	957	893	886	989	0	989	887
16 бит	989	991	970	972	990	992	984	102	957	872	883	986	0	986	901
8 бит	982	987	968	971	987	990	995	94	970	868	876	990	0	978	913
4 бита	985	994	982	981	994	989	995	94	945	877	890	994	0	983	911
254
Теория, ПРИМЕНЕНИЕ И ОЦЕНКА КАЧЕСТВА ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
2 бита	992	991	978	969	989	985	987	108	957	893	886	989	0	989	887
1 бит	990	984	977	975	994	994	995	97	962	891	884	986	3	987	902
LFSR-2															
вбит	994	987	978	974	983	989	995	94	960	863	878	991	990	988	900
1 бит	989	992	980	970	993	992	991	102	972	885	878	989	992	986	900
Табл. П11.7. Результаты исследований RFSR
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RFSR-У															
8 бит	988	992	973	966	985	986	987	103	950	884	865	988	991	985	930
4 бита	990	988	982	974	992	991	993	99	965	797	869	992	990	988	922
2 бита	990	991	968	969	988	984	992	97	967	653	733	990	991	985	909
1 бит	988	994	979	974	995	990	884	73	963	889	899	990	987	986	919
RFSR-2															
вбит	982	987	961	966	979	985	992	96	937	884	856	990	985	976	921
4 бита	987	980	964	963	993	991	990	94	955	879	867	985	990	983	915
2 бита	993	992	971	964	988	989	989	99	965	805	847	991	993	986	921
1 бит	990	995	969	969	991	987	863	52	968	881	892	989	991	988	908
Табл. П11.8. Результаты исследований криптографических
генераторов ПСП (начало)
	1	>2		4		6		8	9	ю	!ц	12	Из	14	115
>45															
1 бит	994	982	!976	976	991	984	992	88 |963		869	886	993	991	988	908
RM															
вбит	987	991	967	965	988	988	994	121	954	883	877	991	990	984	904
4 бита	995	989	977	974	990	987	990	93	978	888	891	991	989	993	914
2 бита	991	991	977	972	987	985	995	103	963	879	879	985	993	987	899
1 бит	991	994	975	965	991	984	989	90	958	885	882	990	998	988	915
ГОСТ 28147-89															
64 бита	990	990	979	973	991	990	994	99	968	891	894	986	987	988	922
32 бита	998	1000	983	992	998	1000	997	98	994	915	926	999	998	997	922
16 бит	993	993	970	970	991	988	993	104	962	893	884	988	991	990	909
вбит	987	987	965	968	985	990	987	97	970	867	876	983	988	985	922
4 бита	991	991	969	981	987	987	988	90	966	876	897	992	990	988	905
2 бита	993	994	979	980	993	993	989	93	976	881	889	989	993	986	898
1 бит	988	983	976	971	992	981	990	91	961	885	886	986	990	986	917
Приложения
2»»
Табл. П11.9. Результаты исследований криптографических
генераторов ПСП (начало)
		2	3		[5	[6		8	|9		LLL	J2	[13	114	J5
Л£У-128															
128 бит	991	989	977	980	993	992	990	104	974	866	885	986	989	987	918
64 бита	987	995	972	975	988	991	996	95	954	888	892	987	990	985	901
32 бита	986	994	974	966	985	992	990	79	968	892	888	983	992	984	910
16 бит	990 '	986	974	976	993	990	987	103	962	868	884	987	984	989	918
8 бит	995	988	971	965	985	984	991	101	964	860	889	988	988	990	909
4 бита	989	995	977	969	991	994	992	91	961	875	903	985	990	988	923
2 бита	992	992	983	977	995	990	985	105	960	883	883	989	990	990	919
1 бит	994	991	978	981	996	986	989	100	972	878	874	990	985	988	921
Rgen-\															
128 бит	992	991	966	970	995	983	990	108	969	876	891	987	993	987	900
64 бита	983	987	967	965	990	982	991	95	958	886	892	987	989	984	910
32 бита	986	987	982	971	996	995	985	108	963	872	908	989	990	984	916
16 бит	988	991	970	968	988	985	988	112	950	898	903	989	991	985	918
8 бит	991	994	965	974	987	989	988	95	966	886	880	983	992	986	914
4 бита	989	987	975	973	990	995	989	84	959	873	884	980	991	988	905
2 бита	991	989	965	966	989	990	995	102	966	881	879	989	983	987	923
1 бит	990	989	976	974	991	989	991	122	970	880	886	987	986	989	890
Примечание. Последовательности с младших разрядов кон-
груэнтных генераторов CG1 (табл. 11.2) и CG2 (табл. 11.3) не
проходят тест проверки периодичности.
Содержание
Введение...........................................................5
ГЛАВА 1. Принципы построения и свойства генераторов
ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ............................... 5
1.1.	Функции ГЕНЕрАТОрОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
В СИСТЕМАХ ЗАЩИТЫ ИнфорМАЦИИ................................. 5
1.1.1.	ШифровдниЕ информации..................................6
1.1.2.	Хеширование информАции.................................8
1.1.5.	КриптогрАфичЕскиЕ протоколы................................10
1.1.4.	Вероятностное шифровАниЕ...................................1 1
1.2.	Принципы ПОСТРОЕНИЯ гЕНЕрдторов ПСП...............................1 5
1.5.	ТрЕбовдния к гЕНЕрдтордм ПСП. Криптостойкость....................1 4
1.4.	Классификация ГЕНЕрдторов ПСП....................................1 5
1.4.1.	КрИПТОГрдфИЧЕСКИЕ ГЕНЕРАТОРЫ ПСП....................... 1	5
1.4.2.	КонгруэнтныЕ генераторы ПСП...........................27
1.4.5.	Генераторы ПСП на регистрах сдвига с линейными обрдтными связями.5 9
1.4.4.	Генераторы двоичных последовательностей произвольной длины.5 1
1.4.5.	Другие схемы ГЕНЕрдторов ПСП....................‘.....54
1.5.	Структурндя СХЕМА ГЕНЕрДТОрА СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ.......6 1
ЛиТЕрАТурА К ГЛАВЕ 1 ..................................................64
ГЛАВА 2. Генераторы ПСП, Функционирующие
в конечных полях.................................................6 5
2.1.	Введение.........................................................6 5
2.2.	Основы теории конечных полей.....................................65
2.5.	Сложение и умножение в поле G7{2'v).........................75
2.4.	Устройства, функционирующие в 67{Z), Z > 2..................79
2.5.	Свойства ГЕНЕрдторов /^-последовательностей......................86
ЛитЕрдтурд к главе 2...................................................90
ГЛАВА 5. Стохастические генераторы псевдослучайных
ПОСЛЕДОВАТЕЛЬНОСТЕЙ..............................................9 1
5.1.	Стохастическое	прЕобрдзовдниЕ информдции.........................9 1
5.2.	/?-блок..........................................................92
5.5.	Стохастические ГЕНЕрдторы многордзрядных ПСП на регистрах
сдвига - RFSR....................................................9 6
5.4.	Криптоанализ RFSR................................................1 01
Содержание
217
5.5.	Двухступенчатые стохастические генераторы
многоразрядных ПСП.................................................1	10
5.6.	Стохастические гЕНЕрдторы ПСП с многордундовой
Функцией обрдтной связи............................................1	1	2
5.7.	Выводы.......................................................1	1	6
Литература к главе 5.....................................................1	1	7
ГЛАВА 4. Методика оценки качества генераторов ПСП..................1	1	8
4.1.	ГрдфиЧЕСКИЕ ТЕСТЫ............................................ 1 1 9
4.1.1.	Гистограмма распределения элементов.........................1 1 9
4.1.2.	Распределение на плоскости..................................121
4.1.5.	Проверил серий..............................................125
4.1.4.	ПровЕркд на монотонность....................................1 2 5
4.1.5.	Автокорреляционная функция (АКФ)............................127
4.1.6.	Профиль линейной сложности..................................1 5 I
4.1.7.	ГрдфичЕский спектральный тест...............................I 5 5
4.2.	Оценочные тесты..............................................1 5 6
4.2.1.	Сведения из теории вероятностей	и математической статистики.1	56
4.2.2.	ПодборкА тестов Д. Кнутд....................................1	59
4.2.5.	Система оценки статистических свойств «DIEHARD».............1	48
4.2.4.	Руководство НИСТ............................................1	59
4.5. Другие тесты..................................................1 96
4.5.1. Посимвольная проверка.......................................1	9 7
4.5.2. ПровЕркд частот.............................................1	97
4.4.	Оценка результатов тестирования..............................1 98
4.4.1.	Генерация последовательностей для тестирования..............1 98
4.4.2.	Исполнение ндборд статистических тестов.....................I 99
4.4.5.	Анализ прохождения статистических тестов....................I 99
4.5.	Анализ статистической 6езопасности криптодлгоритмов..........201
Литература к главе 4...............................................205
Вместо заключения. Система оценки статистической
бЕЗОПАСНОСТИ Алгоритмов ГЕНЕРАЦИИ ПСП
И КРИПТОАЛГОРИТМОВ...................................................204
Приложения...........................................................207
Приложение 1.........................................................207
Неприводимые многочлены над	Cf\p], р - простое.................207
Неприводимые многочлены над	С7(2)..............................207
Неприводимые многочлены над	С7(5)..............................208
Неприводимые многочлены над	С/(5)............................  208
Неприводимые многочлены над	Cf\l}..............................208
Неприводимые многочлены над	CF{ I 1)..'........................209
278
Теория, применение и оценка качества генераторов псевдослучайных последовательностей
Приложение 2..........................................................209
Примитивные многочлены над С7{2).................................209
Примитивные многочлены вида аЛ + V +	I,	где	/V - число	Мерсенна..2 1 О
Примитивные многочлены вида аЛ +а/+	I,	где	1=8, 16,	52, 64,	128.210
Примитивные многочлены вида аЛ+ а/ч-	1,	где	(4 2W - 1)	= 1.......21 О
Приложение 5..........................................................2 1 1
Примитивные многочлены над СЛ22) = {0, 1, <п, со2}, от2 + от + 1 = 0, со’ = 1
и С/(2 ’) = {О, 1, со, со2, со’, со4, со5, со6}, со’ + со2 + 1 = О, Со7 = 1.21 1
Приложение 4. Использование У/СтриггЕров при
проектировании LFSR...........................................2 1 2
Приложение 5. Алгоритм Берлекампа-Масси..........................................21 4
Алгоритм.......................................................................21	4
Приложение 6. Формулд Лапласа....................................................21 5
Приложение 7. Система генерации	паролей......................................21 6
Системные трЕбовдния........................................................21 6
Здпуск прогрдммы............................................................21 6
Кнопка «ГЕНЕРАЦИЯ............................................................217
Кнопка «ПОЛЬЗОВАТЕЛИ........................................................21 8
Кнопка «ТЕСТЫ................................................................219
Кнопка «НАСТРОЙКИ»...........................................................219
Приложение 8. Система оценки качества генераторов
псевдослучайных последовательностей (версия 5.06.7.Бета)........220
Руководство пользователя.....................................................220
Системные требовАния.........................................................220
Установка прогрдммы..........................................................221
Здпуск прогрдммы.............................................................221
Тестирование.................................................................221
Создание нового запроса......................................................222
Выбор Файла..................................................................222
Выбор директории.............................................................225
Выбор тестов.................................................................224
Ндстройки параметров тестирования............................................225
Здпуск тестов................................................................226
Просмотр РЕЗУЛЬТАТОВ.........................................................226
Приложение 9. Тест «распределение на плоскости» для LFSR,
соответствующего Ф(л] = л9 + л4	+ 1.....................229
Приложение 10. Линейные блоки пространственного сжатия
информАции 8 —> 5, 9 —> 8.......................................229
Приложение 1 1. Результаты анализа статистической 6езопасности
Алгоритмов ГЕНЕРАЦИИ ПСП........................................251
издательство «ОН КУДИН-ОБРАЗ»
Тел.: (0951333-82-11; ok@kudits.ru, ttp://www.kudits.ru/publish |
КНИГИ В ПРОДАЖЕ________________________________ ________________________
Бурдаев О. В., Иванов М. А., Тетерин И. И.
Ассемблер в задачах защиты информации. 320 с.
ISBN 5-93378-038-3	Оптовая цена 96,8 руб.
В книге рассмотрен язык Ассемблера для процессоров семейства Intel 80x86, а также
различные аспекты применения этого языка в области защиты информации.
Книга состоит из трех частей. Глава 1 суть учебное пособие для начинающих по програм-
мированию на Ассемблере, она содержит описание архитектуры компьютера IBM PC, системы
команд, способов адресации данных, системных функций, некоторых приемов программирова-
ния. Вторая и третья главы книги рассчитаны на более подготовленного читателя. Глава 2
содержит описание криптографических методов и возможные способы решения задач контроля
целостности и обеспечения секретности информации. Глава 3 посвящена специфическим
применениям Ассемблера, таким как защита программ от статического и динамического иссле-
дования, борьба с вирусами, "изощренное" программирование.
Книга рассчитана на широкий круг читателей, в том числе и не являющихся профессио-
нальными программистами. Может быть полезна программистам, инженерам, студентам вузов.
Зензин О. С., Иванов М. А.
AES - стандарт криптографической защиты. Конечные поля. Книга 1 серии "СКВ -
специалисту по компьютерной безопасности". 176 с.
ISBN 5-93378-047-2	Оптовая цена 55 руб.
Книга состоит из трех глав. В главе 1 рассматриваются основы криптографии с сек-
ретным ключом. В главе 2 дается описание шифра Rijndael, принятого в 2001 г. в качестве
американского стандарта криптографической защиты AES - Advanced Encryption Standard.
AES принят на замену морально устаревшему DES - самому распространенному крипто-
алгоритму в мире. Rijndael полностью построен на математическом аппарате теории
конечных полей, которая рассматривается в главе 3.
Книга рассчитана на широкий круг читателей, интересующихся вопросами крипто-
графической защиты информации. Может быть полезна студентам и аспирантам вузов
компьютерных специальностей, разработчикам и пользователям компьютерных систем.
ОЖИДАЕМЫЕ КНИГИ СЕРИИ "СКБ - СПЕЦИАЛИСТУ ПО КОМПЬЮТЕРНОЙ
БЕЗОПАСНОСТИ"
ISBN 5-93378-047-2
Асосков А. В., Иванов М. А., Кривенко А. В., Мирский А. А., Рузин А. В.,
Сланин А. В., Тютвин А. Н., Чугунков И. В.
Поточные шифры. Книга 3.
М.А. Деднев, Д.В. Дыльнов, М.А. Иванов.
Защита информации в банковском депе и электронной коммерции. Книга 4.
М.А.Иванов, В.А.Суханов.
Стеганографические методы защиты информации. Книга 5.
М.А.Иванов.
Стохастические методы защиты информации в компьютерных системах и сетях.
Книга 6.
ИЗДАТЕЛЬСТВО
«ОЦ КУДИЦ-ОБРАЗ»______________________________________
Тел.: (095) 333-82-11; ok@kudits.ru, http://www.kudits.ru/publish |
ПРИОБРЕТАЙТЕ КНИГИ У	НАШИХ ПАРТНЕРОВ
Барнаул Социалистический пр-т, 117а, (3852) 38-18-72 Великий Новгород ул. Б. Санкт-Петербургская, 44 тел. (81622) 73-188 доб. 34 Екатеринбург "Книжный мир", ул. 8 Марта, 8г, (3432) 71-18-87 Краснодар "Мир книги", ул. Буденного, 147 Москва	Ростов-на-Дону "Мир книги", Ворошиловский пр-т, 33, (8632) 62-54-61 Санкт-Петербург "Санкт-Петербургский Дом книги" Невский проспект, 28, тел. (812) 312-01-84 издательство "Наука и Техника" пр. Обуховской Обороны, 107, тел. (812) 567-70-25,567-70-26 Саратов "Книжный Мир”, пр-т Кирова, 32, (8452) 32-98-14
"0ПТИМА+” Розничная торговля м. Тульская, Варшавское ш., 9, книжная ярмарка "Центральная", зеленая линия, павильон 412-57 Оптовая торговля (095)333-65-67 Нижний Новгород "Нижегородский Дом книги”, ул. Советская, 14, тел. (8312) 44-22-73 Новосибирск "Книжный пассаж", ул. Ленина, 10а, (3832) 29-50-30 "Сибирский Дом Книги", Красный пр-т, 153,(3832) 26-62-39 "Книжный мир", пр-т К.Маркса, 51 Омск "Книжный Мир", ул. Ленина, 17/19, (3812) 24-32-54	Ставрополь "Книжный Мир", ул. Мира, 337, (8652) 35-47-90 Томск "Книжный Мир",ул. Ленина, 141, (3822) 51-07-16 Уфа 000 ПКП "Азия", тел./факс: (3472) 50-39-00 Оптовая торговля Ул. Зенцова, 70 Розничная торговля Магазин "Оазис", ул. Чернышевского, 88 Магазин "Книжник", пр. Октября, 106 Ханты-Мансийск Магазин "Книги", ул. Ленина, 39 Челябинск "Книжный Мир", ул. Кирова, 90, (3512) 33-19-58 Ярославль Магазин "Наука", ул. Володарского, 63, (0852) 25-95-04
ЗАКАЗ КНИГ НАЛОЖЕННЫМ ПЛАТЕЖОМ
Издательство «ОЦ КУДИЦ-ОБРАЗ» осуществляет рассылку книг по почте.
Заказы принимаются по адресу: 121354, Москва, а/я 18; или через интернет-магазин
http://www.books.kudits.ru
Условия рассылки: Сумма наложенного платежа складывается из оптовой цены книг,
накладных расходов «ОЦ КУДИЦ-ОБРАЗ» на пересылку (30% от стоимости книг)
и почтовых расходов (по тарифам почты РФ).
Заказы из регионов России с авиадоставкой, а также заказы из стран ближнего и дальнего
зарубежья обслуживаются только по предварительной оплате