Автор: Нефёдов Ю.М. Балицкая Т.Ю.
Теги: вычислительная математика численный анализ математика оптимизация
ISBN: 966-1571-590-02-9
Год: 2006
Текст
1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ
УНИВЕРСИТЕТ ИМЕНИ ВЛАДИМИРА ДАЛЯ
Ю.М . НЕФЁДОВ
Т.Ю . БАЛИЦКАЯ
МЕТОДЫ ОПТИМИЗАЦИИ
ПРАКТИКУМ
Учебное пособие
Луганск 2006
2
ББК 22.18
Н58
УДК 519.6
Рекомендовано Вченою Радою СНУ ім. В.Даля
як навчальний посібник
Рецензенти:
Грібанов В.М ., доктор технічних наук, професор, завідувач кафедри прикладної
математики Східноукраїнського національного університету
імені Володимира Даля.
Арлінський Ю.М ., доктор фізико - математичних наук, професор завідувач кафед-
ри математичного аналізу Східноукраїнського національного
університету імені Володимира Даля.
Нефьодов Ю.М., Балицька Т.Ю.
Н 58 Методи оптимізації. Практикум: Навчальний посібник. – Л у-
ганськ: Вид-во НЦППРК “Ноулідж”, 2006. – 30 4 с.
ISBN 966-1571-590-02 -9
В навчальному посібнику викладені основні теоретичні положення та методи
розв'язання типових задач оптимізації. Послідовно розглянуті методи та алгорит-
ми лінійного програмування, чисельні методи та алгоритми одномірної, богатомір-
ної і умовної богатомірної оптимізації. Наведено наочні ілюстрації, конкретні при-
клади та задачі до самостійного розв'язання.
Для студентів математичних та інженерно-технічних спеціальностей вузів.
ББК 22.18
УДК 519.6
ISBN 966-1571-590-02 -9
© Нефьодов Ю.М., Балицька Т. Ю.
© НЦППРК “Ноулідж”, 2006
3
ОГЛАВЛЕНИЕ
Предисловие ................................................................ 5
1. УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИЙ ...................... 7
1.1. Постановка задачи оптимизации и основные определения.
7
1.2. Безусловный экстремум ...........................................
14
1.3. Условный экстремум при ограничениях равенствах ........
24
1.4. Условный экстремум при ограничениях неравенствах .....
42
1.5. Условный экстремум при смешанных ограничениях........
56
Задачи для самостоятельного решения .............................. 71
2. МЕТОДЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ............... 75
2.1. Основные понятия и определения ................................ 75
2.2. Симплекс-метод Данцига .......................................... 84
2.3. Двойственный симплекс-метод.................................... 97
2.4. Специальные задачи линейного программирования.......... 107
2.4.1. Транспортные задачи ......................................... 107
2.4.2. Параметрические задачи .................................... 119
2.4.3. Дробно-линейные задачи .................................... 128
2.4.4. Целочисленные задачи. Метод Гомори .................. 132
Задачи для самостоятельного решения ................................ 136
3. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ
ОПТИМИЗАЦИИ ......................................................... 141
3.1. Постановка задачи и принципы одномерной оптимизации.. 141
3.2. Методы нулевого порядка .......................................... 145
3.2.1. Метод равномерного поиска ............................... 145
3.2.2. Метод деления отрезка пополам ........................... 148
3.2.3. Метод дихотомии ............................................. 152
3.2.4. Метод золотого сечения ..................................... 154
3.2.5. Метод Фибоначчи ............................................. 158
3.2.6. Метод квадратичной аппроксимации ..................... 162
3.3. Методы первого и второго порядка ............................... 165
3.3.1. Метод средней точки ......................................... 166
3.3.2. Метод хорд ...................................................... 168
3.3.3. Метод Ньютона ................................................ 171
Задачи для самостоятельного решения ............................... 174
4
4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МНОГОМЕРНОЙ
ОПТИМИЗАЦИИ .......................................................... 177
4.1. Общие принципы построения численных методов
многомерной оптимизации .......................................... 177
4.2. Методы нулевого порядка ........................................... 181
4.2.1. Метод конфигураций ......................................... 182
4.2.2. Метод деформируемого многогранника .................. 188
4.2.3. Метод сопряженных направлений ......................... 196
4.2.4. Адаптивный метод случайного поиска ................... 199
4.3. Методы первого порядка............................................. 204
4.3.1. Метод наискорейшего градиентного поиска ............ 205
4.3.2. Метод Гаусса – Зейделя ...................................... 211
4.3.3. Метод сопряженных градиентов ........................... 217
4.4. Методы второго порядка ............................................ 223
4.4.1. Метод Ньютона ................................................ 224
4.4.2. Метод Макварда ............................................... 229
4.4.3. Квазиньютоновский метод .................................. 235
Задачи для самостоятельного решения ............................... 240
5. ЧИСЛЕННЫЕ МЕТОДЫ УСЛОВНОЙ МНОГОМЕРНОЙ
ОПТИМИЗАЦИИ.......................................................... 245
5.1. Принципы построения численных методов поиска
условного экстремума .................................................. 245
5.2. Метод штрафных функций .......................................... 251
5.3. Метод барьрных функций .......................................... 260
5.4. Метод множителей ................................................... 267
5.5. Метод проекции градиента.......................................... 274
5.6. Метод Зойтендейка ................................................. 292
Задачи для самостоятельного решения ............................... 294
Литература........................................................................ 302
5
ПРЕДИСЛОВИЕ
Никто не обнимет необъятного.
Козьма Прутков.
В настоящее время требования к математической подготовке инжене-
ра достаточно высоки. В частности, от него требуется умение грамотно
переводить на математический язык технические, экономические, естест-
веннонаучные и другие прикладные задачи, анализировать зависимость их
решений от условий, режимов, параметров реальных процессов и выби-
рать наилучшие варианты, т.е. обладать навыками математического моде-
лирования и оптимизации реальных объектов. Поэтому дисциплине “Ме-
тоды оптимизации” отводится значительная роль в математической подго-
товке студентов вузов. Поскольку в большинстве практически важных
случаев аналитическое решение задач оптимизации затруднительно или
невозможно, инженер-исследователь должен владеть численными метода-
ми, рассчитанными на применение современных компьютеров.
Данное учебное пособие написано на основании многолетнего чтения
лекций и проведения семинарских занятий для студентов различных спе-
циальностей. Основное внимание уделено практическому применению
численных методов оптимизации. Каждая глава содержит основные теоре-
тические сведения, алгоритмы методов, детально разобранные примеры и
задачи для самостоятельной работы.
В первой главе описаны общие критерии существования безусловно-
го и условного экстремума многомерных функций. Критерии условного
экстремума рассмотрены при различных видах ограничений: равенствах,
неравенствах и смешанных ограничениях. При этом условия Куна-Таккера
приведены как для обобщенной, так и для классической функций Лагран-
жа. Поиск и исследования экстремальных точек проиллюстрированы мно-
жеством примеров.
Вторая глава содержит основные методы решения задач линейного
программирования. Рассмотрены алгоритмические особенности двойст-
венного симплекс-метода и его применение для решения параметрических
и целочисленных задач линейного программирования. Приведены разно-
образные примеры использования методов.
В третьей главе рассмотрены численные методы одномерной оптими-
зации, которые широко используются в алгоритмах методов минимизации
6
многомерных функций. Каждый метод представлен алгоритмом и приме-
ром.
Четвертая глава посвящена основным методам нулевого, первого и
второго порядка безусловной минимизации функций нескольких перемен-
ных. Дана сравнительная характеристика методов. Алгоритмы и подробно
разобранные примеры позволяют оценить особенности каждого метода.
Пятая глава содержит методы условной многомерной оптимизации,
которые построены на различных идеях и подходах к решению задач оп-
тимизации с ограничениями. В практике используется множество модифи-
каций этих методов. Однако в учебном пособии рассмотрены некоторые
наиболее интересные и важные с методологической точки зрения методы.
Каждая глава содержит набор задач для самостоятельного решения с
соответствующими ответами.
Для усвоения материала книги достаточно знаний в пределах дисцип-
лин математического анализа и линейной алгебры университета.
7
Глава 1
УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИЙ
1.1 . Постановка задачи оптимизации и основные
определения
В общем виде задачу поиска оптимального решения можно сформу-
лировать следующим образом: минимизировать (максимизировать) целе-
вую функцию с учетом ограничений на переменные.
Задача оптимизации содержит:
–
целевую функцию (x)
f ,где
1
x ( ,...,
)T
n
x
x
, определённую на n -
мерном евклидовом пространстве
n
R . Её значения характеризуют степень
достижения цели, во имя которой поставлена или решается задача;
–
множество допустимых решений
n
XR
, среди элементов кото-
рого осуществляется поиск.
Следовательно, требуется найти такой вектор x
из множества до-
пустимых решений, которому соответствует минимальное значение целе-
вой функции на этом множестве:
x
(x) min (x)
X
f
f
.
Замечание 1.1. Задача поиска максимума функции (x)
f сводится к
эквивалентной задаче поиска минимума (и наоборот) путем замены знака
перед функцией на противоположный:
x
x
(x) max (x)
min (x)
X
X
f
f
f
.
Задача поиска минимума и максимума целевой функции (x)
f назы-
вается задачей поиска экстремума:
x
(x ) extr (x)
X
f
f
.
Если множество допустимых решений X задаётся ограничениями
(условиями), накладываемыми на вектор x , то решается задача поиска
8
условного экстремума. Если
n
XR
, т.е. ограничения (условия) на вектор
x отсутствуют, то решается задача поиска безусловного экстремума.
Решением задачи поиска экстремума является пара (x , (x ))
f
,
включающая точку x
и значение целевой функции в этой точке.
Множество точек минимума (максимума) целевой функции (x)
fна
множестве X обозначается X
.
Оно может содержать конечное число
точек (в том числе одну), бесконечное число точек или быть пустым.
Определение 1.1. Точка x
X
называется точкой глобального (аб-
солютного) минимума функции (x)
f на множестве X , если функция
достигает в этой точке своего наименьшего значения, т.е.
(x) (x)
f
f
xX
.
Определение 1.2. Точка x
X
называется точкой локального (от-
носительного) минимума функции (x)
f на множестве X , если сущест-
вует
0
,такое,чтоеслиx X
и||xx||
,то (x)(x)
f
f
.
Здесь
2
2
2
1
2
||x||
...
n
x
x
x
–
евклидова норма вектора x .
В определении 1.1 точка x
сравнивается со всеми точками множе-
ства допустимых решений X , а в определении 1.2 – только с принадле-
жащими - окрестности.
Если в определениях 1.1 и 1.2 знак неравенство заменить на , то
получатся определения глобального (абсолютного) и локального (относи-
тельного) максимумов.
Глобальный экстремум всегда является одновременно локальным, но
не наоборот.
Определение 1.3. Поверхностью уровня функции (x)
f называется
множество точек, в которых функция принимает постоянное значение, т.е.
(x) const
f
. Если
2
n , поверхность уровня изображается линией уров-
ня на плоскости
2
R.
Пример 1.1
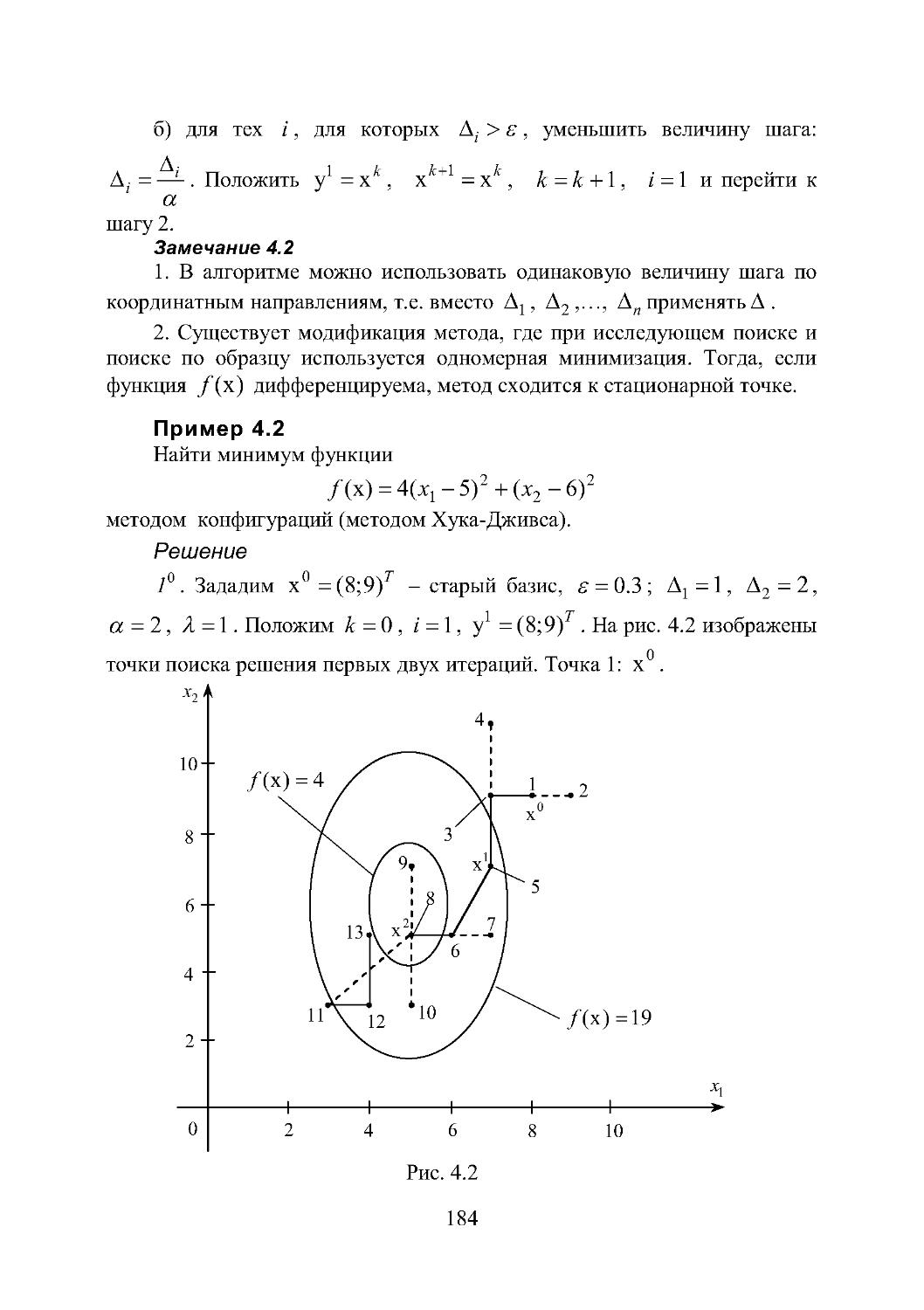
На рис. 1.1 изображены линии уровня некоторой функции. Числа ука-
зывают значение функции (x)
f на соответствующей линии. Точкам A и
B соответствуют значения функции ( ) 5
fA и
()10
fB
.
Требуется
классифицировать эти точки.
Решение
Функция рассматривается на множестве
2
R , т.е. решается задача по-
иска безусловного экстремума. В точке A с координатами (1; 2) достига-
9
ется локальный и глобальный минимум одновременно; в точке B с коор-
динатами (2;1) достигается локальный минимум; в точке C нет ни ми-
нимума, ни максимума, так как по одним направлениям функция убывает,
а по другим возрастает. Заметим, что изображенная структура линий уров-
ня типична для так называемых многоэкстремальных задач.
Определение 1.4. Градиентом (x)
f
непрерывно дифференцируе-
мой функции (x)
f в точке x называется вектор-столбец, элементами
которого являются частные производные первого порядка, вычисленные в
данной точке:
1
2
(x) (x)
(x)
(x)
;
;...;
T
n
ff
f
f
x
x
x
.
Градиент функции направлен по нормали к поверхности уровня (см.
определение 1.3), т.е. перпендикулярно к касательной плоскости, прове-
денной в точке x , в сторону наибольшего возрастания функции в данной
точке.
Определение 1.5. Матрицей Гессе (x)
H дважды непрерывно диф-
ференцируемой в точке x функции (x)
f называется матрица частных
производных второго порядка, вычисленных в данной точке:
1
x
20
1
()10
fB
()5
fA
2
x
2
C
A
15
B
30
Рис.1.1
2
1
0
40
10
2
2
11 12
1
2
1
1
21 22
2
2
2
1
2
2
1
(x)
(x)
...
...
...
(x)
...
...
...
...
...
...
(x)
(x)
...
...
n
n
n
n
n
nn
n
n
f
f
hhh
x
xx
hhh
H
f
f
hhh
xx
x
,
где
2
(x)
ij
ij
f
h
xx
,
,
1,...,
ij
n
.
Матрица Гессе является симметрической размера ( )
nn
.
Вместе с градиентом можно определить антиградиент, равный по
модулю градиенту, но противоположный по направлению. Он указывает в
сторону наибольшего убывания функции в данной точке.
С помощью градиента и матрицы Гессе, используя разложение в ряд
Тейлора, приращение функции (x)
f в точке x может быть записано в
форме
2
1
(x) (x
x)
(x) (x) x
x
(x)x||x||
2
T
T
ff
f
f
H
,
где
2
|| x||
–
сумма всех членов разложения, имеющих порядок выше
второго; x (x) x
T
H
– квадратичная форма.
Пример 1.2
Для функции
2
4
1
2
(x)
fxx
вычислить градиент и найти матрицу
Гессе в точках
(0)
x
(0; 0)T
,
(1)
x
(1; 1)T
.
Решение
Согласно определениям 1.4 и 1.5 имеем:
3
1
2
(x)2;4
T
f
xx
,
2
2
20
(x)
012
H
x
;
(0)
(x) 0;0
T
f
,
(0)
20
x
00
H
;
(1)
(x) 2;4
T
f
,
(1)
20
x
012
H
.
Определение 1.6. Квадратичная форма x
(x) x
T
H
(а также соот-
ветствующая матрица Гессе (x)
H ) называется :
11
–
положительно определенной ( (x) 0
H ), если для любого ненуле-
вого x
выполняется неравенство x
(x)x0
T
H
;
–
отрицательно определенной ( (x) 0
H ), если для любого ненуле-
вого x
выполняется неравенство x
(x)x0
T
H
;
–
положительно полуопределенной ( (x) 0
H ),еслидлялюбого x
выполняется неравенство x
(x)x0
T
H
и найдется отличный от нуля
вектор x
, для которого x
(x)x0
T
H
;
–
отрицательно полуопределенной ( (x) 0
H ),еслидлялюбого x
выполняется неравенство x
(x)x0
T
H
и найдется отличный от нуля
вектор x
, для которого x
(x)x0
T
H
;
–
неопределенной ( (x) 0
H ), если существуют такие векторы x
,
x
, что выполняются неравенства x
(x)x0
T
H
,x
(x)x0
T
H
;
–
тождественно равной нулю ( (x) 0
H ),еслидлялюбого x
вы-
полняется x
(x)x0
T
H
.
Пример 1.3
Классифицировать квадратичные формы и матрицы Гессе, получен-
ные в примере 1.2:
1.
20
00
H
. Выпишем квадратичную форму
1
2
1
2
1
2
20
x
x
;
2
00
T
x
H
xx
x
x
.
Очевидно, x
x0
T
H
для любого вектора x
иx
x0
T
H
для
10
x
илюбых
20
x
. Согласно определению 1.6 квадратичная
форма (матрица Гессе) положительно полуопределённая.
2.
20
012
H
. Выпишем квадратичную форму
1
2
2
1
2
1
2
2
20
x
x
;
2
12
012
T
x
H
xx
x
x
x
Очевидно, x
x0
T
H
для любого ненулевого вектора x
.Со-
гласно определению 1.6 квадратичная форма (матрица Гессе) положитель-
но определённая.
12
Определение 1.7. Множество X называется выпуклым, если оно со-
держит всякий отрезок, концы которого принадлежат X , т.е . если для лю-
бых
(1) (2)
x,x
X
и0
1
справедливо
(1)
(2)
x
(1)xX
.
Определение 1.8. Функция (x)
f , определенная на выпуклом мно-
жестве X , называется выпуклой, если
(1)
(2)
(1)
x
(1 )x
x
f
f
(2)
(1)x
f
(1) (2)
x,x
X
,0
1
.
Определение 1.9. Функция (x)
f , определенная на выпуклом мно-
жестве X , называется строго выпуклой, если
(1)
(2)
x
(1 )x
f
(1)
(2)
x
(1)x
f
f
(1) (2)
x,x
X
,
(1) (2)
x
x
,0
1
.
Определение 1.10. Функция (x)
f , определенная на выпуклом мно-
жестве X , называется сильно выпуклой с константой 0
l ,если
2
(1)
(2)
(1)
(2)
(1)
(2)
x
(1 )x
x
(1)x
(1)xx
2
l
f
f
f
(1) (2)
x,x
X
,
(1) (2)
x
x
,0
1
.
Геометрическая интерпретация определений 1.8 – 1.9 состоит в сле-
дующем:
–
функцию (x)
f называют выпуклой, если она целиком лежит не
выше отрезка, соединяющего две ее произвольные точки;
–
функцию (x)
f называют строго выпуклой, если она целиком ле-
жит ниже отрезка, соединяющего две ее произвольные, но не совпадаю-
щие точки.
Замечание 1.2. Если функция сильно выпуклая, то она одновременно
строго выпуклая и выпуклая. Если функция строго выпуклая, то она одно-
временно выпуклая.
Замечание 1.3. Выпуклость функции можно определить по матрице
Гессе:
–
если (x) 0
H
x
n
R
, то функция выпуклая;
–
если (x) 0
H
x
n
R
, то функция строго выпуклая;
–
если
(x)
H
lE
x
n
R
, где
0
l ; E – единичная матрица, то
функция сильно выпуклая.
При решении задач удобно использовать следующие свойства выпук-
лых функций (доказательство см. в [3]):
13
1. Если (x)
f выпуклая функция на выпуклом множестве X , то вся-
кая точка локального минимума является точкой ее глобального минимума
наX.
2. Если выпуклая функция достигает своего минимума в двух раз-
личных точках, то она достигает минимума во всех точках отрезка, соеди-
няющего эти две точки.
3. Если (x)
f строго выпуклая функция на выпуклом множестве X ,
то она может достигать своего глобального минимума на X не более чем
в одной точке.
Пример 1.4
Исследовать выпуклость функции
2
2
1
2
(x)
fxx
на множестве
2
R.
Решение
Матрица Гессе, построенная согласно определению 1.5, удовлетворя-
ет условию
20
10
(x)
02
01
H
l
при 0
2
l.
Следуя замечанию 1.3, можно сделать вывод о сильной выпуклости
функции. Одновременно она является строго выпуклой и выпуклой (см.
замечание 1.2)
Определение 1.11. Функция ( )
f x , удовлетворяет условию Липшица
наотрезке[;]
abR
, если существует такое число
0
L (константа Лип-
шица), что
(1)
(2)
(1) (2)
()()
fxfx
Lxx
(1) (2)
,
[,]
xx
ab
.
(1.1)
Если неравенство (1.1) выполняется с константой L , то оно справед-
ливо для бесконечного множества констант, больших L . Как правило,
представляет интерес минимальная из констант Липшица.
Замечание 1.4. Из условия (1.1) следует непрерывность функции
(x)
f наотрезке[;]
a b .Есликрометогофункцияимеетна [;]
a b непре-
рывную производную, то константа Липшица
[,]
max
()
xab
L
fx
.
Условие (1.1) означает, что модуль углового коэффициента любой
хорды графика функции (x)
f не превосходит L .
Пример 1.5
Проверить, удовлетворяют ли условию Липшица следующие функ-
ции: а) (x) sin
f
x
на отрезке [0; ]
;б)(x)
f
x
на отрезке [0;1] .
Решение
Воспользуемся определением 1.11 и замечанием 1.4:
14
а) функция (x) sin
f
x
удовлетворяет условию Липшица на отрезке
[0; ]
с константой
[0; ]
max|cos|1
x
L
x
;
б) функция (x)
f
x
не удовлетворяет условию Липшица на отрез-
ке [0;1] , так как при
0
x угловой коэффициент касательной к графику
неограниченно возрастает, а переходя в (1.1) к пределу
(1) (2)
0
x
x
,
можно заключить, что если в некоторой точке существует касательная к
графику функции (x)
f , то модуль ее углового коэффициента не может
превышать L .
1.2 . Безусловный экстремум
Дана дважды непрерывно дифференцируемая
функция (x)
f , определенная на множестве допус-
тимых решений
n
XR
, т.е. на всем пространстве
n
R.
Требуется исследовать функцию (x)
f на экстремум, т.е. определить
точки x
n
R
ее локальных минимумов и максимумов на
n
R:
x
(x) min (x)
n
R
f
f
;
x
(x) max (x)
n
R
f
f
.
Для решения задачи находятся точки x
локальных экстремумов с помощью не-
обходимых условий первого и второго порядка (порядок условий опреде-
ляется порядком используемых производных), а также достаточных усло-
вий безусловного локального экстремума. Вычисляются значения (x )
f
функции в найденных точках локальных экстремумов.
Теорема 1.1 (необходимые условия экстремума первого порядка).
Пусть x
n
R
есть точка локального минимума (максимума) функ-
ции (x)
f на множестве
n
Rи(x)
f дифференцируема в точке x
. Тогда
градиент функции (x)
f вточке x
равен нулю, т.е.
(x) 0
f
(1.2)
или
(x)
0
i
f
x
,
1,..,
i
n
.
(1.3)
Определение 1.12. Точки x
, удовлетворяющие условию (1.2) или
(1.3) называются стационарными.
Постановка задачи
Стратегия решения задачи
15
Теорема 1.2 (необходимые условия экстремума второго порядка).
Пусть точка x
есть точка локального минимума (максимума)
функции (x)
f на множестве
n
R и функция (x)
f дважды дифференци-
руема в этой точке. Тогда матрица Гессе (x )
H функции (x)
f , вычис-
ленная в точке x
является положительно полуопределенной (отрица-
тельно полуопределенной), т.е .
(x) 0
H
(x) 0
H
.
Теорема 1.3 (достаточные условия экстремума).
Пусть функция (x)
f вточке x
n
R
дважды дифференцируема, ее
градиент равен нулю, а матрица Гессе является положительно опреде-
ленной (отрицательно определенной), т.е.
(x) 0
f
и
(x) 0
H
(x) 0
H
.
Тогда точка x
является точкой локального минимума (максимума)
функции (x)
f на множестве
n
R.
Определение 1.13. Рассмотрим определитель матрицы Гессе (x )
H
,
вычисленной в стационарной точке
11 12
1
21 22
2
1
2
...
...
det (x)
...
...
...
...
...
n
n
n
n
nn
hh
h
hh
h
H
hh
h
.
Определители 1
11
h
,
11 12
2
21 22
hh
hh
,...,
11
1
1
...
...
...
...
...
n
n
n
nn
hh
hh
назы-
ваются угловыми минорами.
Определители m -го порядка (
)
mn
, получающиеся из определите-
ля матрицы (x )
H
вычеркиванием каких-либо (
)
nm
строк и (
)
nm
столбцов с одними и теми же номерами, называются главными минорами.
Для проверки выполнения достаточных условий экстремума и необ-
ходимых условий второго порядка используются два способа.
Первый способ (с помощью угловых и главных миноров).
I. Критерий проверки достаточных условий экстремума (критерий
Сильвестра).
16
1. Для того чтобы матрица Гессе (x )
H была положительно опреде-
ленной( (x) 0)
H
и точка x
являлась точкой локального минимума,
необходимо и достаточно, чтобы знаки угловых миноров были строго по-
ложительны:
10
,20
,...,
0
n
.
2. Для того чтобы матрица Гессе (x )
H была отрицательно опреде-
ленной( (x) 0)
H
и точка x
являлась точкой локального максимума,
необходимо и достаточно, чтобы знаки угловых миноров чередовались,
начиная с отрицательного:
10
,20
,30
...,(1)
0
n
n
.
II. Критерий проверки необходимых условий экстремума второго
порядка.
1. Для того чтобы матрица Гессе (x )
H была положительно полуоп-
ределенной ( (x ) 0)
H
и точка x
может быть являлась точкой локаль-
ного минимума, необходимо и достаточно, чтобы все главные миноры оп-
ределителя матрицы Гессе были неотрицательны.
2. Для того чтобы матрица Гессе (x )
H была отрицательно полуоп-
ределенной ( (x ) 0)
H
и точка x
может быть являлась точкой локаль-
ного максимума, необходимо и достаточно, чтобы все главные миноры
четного порядка были неотрицательны, а все главные миноры нечетного
порядка – неположительны.
Второй способ (с помощью собственных значений матрицы Гессе).
Определение 1.14. Собственные значения i
, 1,...,
i
n
матрицы
(x)
H размера( )
nn
находятся как корни характеристического уравне-
ния (алгебраического уравнения n -ой степени):
11
12
1
21
22
2
1
2
...
...
(x)
0
...
...
...
...
...
n
n
n
n
nn
h
h
h
hh
h
H
E
h
h
h
.
(1.4)
Собственные значения симметрической матрицы (x )
H
веществен-
ны.
Оба способа проверки достаточных и необходимых условий экстре-
мума второго порядка приведены в таблицах 1.1 и 1.2
17
Критерии проверки достаточных условий второго порядка
в задаче поиска безусловного экстремума при (x ) 0
f
Таблица 1.1
No
(x)
H
Первый способ
Второй способ
Тип стационар-
ной точки x
1.
0
10
,...,
0
n
10
,...,
0
n
Локальный
минимум
2.
0
10
,...,(1)
0
n
n
10
,...,
0
n
Локальный
максимум
Критерии проверки необходимых условий второго порядка
в задаче поиска безусловного экстремума при (x ) 0
f
Таблица 1.2
No (x)
H
Первый способ
Второй способ
Тип стационарной
точки x
1.
0
Все главные миноры
det (x)
H
неотрица-
тельны
10
,...,
0
n
Может быть
локальный min ,
требуется допол-
нит. исследование
2.
0
Все главные миноры
det (x)
H
четного
прядка неотрицательны,
а нечетного – неположи-
тельны
10
,...,
0
n
Может быть
локальный max ,
требуется допол-
нит. исследование
3.
0
Матрица Гессе состоит
из нулевых элементов
10
,...,
0
n
Требуется допол-
нительное иссле-
дование
4.
0
Не выполняются все пре-
дыдущие усл овия
i
имеют разные
знаки
Нет экстремума
Алгоритм
1. Записать необходимые условия экстремума первого порядка в
форме (1.3) и найти стационарные точки x
в результате решения систе-
мы n алгебраических уравнений с n неизвестными. Для численного ре-
шения системы уравнений (в общем случае нелинейных) могут использо-
ваться известные численные методы: простой итерации, Зейделя, Ньютона
и др.
2. В найденных стационарных точках x
проверить выполнение дос-
таточных (табл.1.1), а если они не выполняются, то – необходимых усло-
вий второго порядка с помощью одного из двух способов (табл.1.2).
18
3. Вычислить значения (x )
f
в точках экстремума.
Замечания 1.5
1. Если требуется определить глобальные экстремумы, то они нахо-
дятся в результате сравнения значений функции в точках локальных ми-
нимумов и максимумов с учетом ограниченности функции на
n
R.
2. Для случая функции (x)
f одной переменной ( 1)
n можно сфор-
мулировать правило, заменяющее п.2 алгоритма:
–
если функция (x)
f и ее производные непрерывны, то точка x
яв-
ляется точкой экстремума тогда и только тогда, когда число m – четное,
где m – порядок первой не обращающейся в нуль в точке x
производ-
ной. Если
()()0
m
fx
,товточкеx
–
локальный минимум, а если
()()0
m
fx
,товточкеx
–
локальный максимум. Если число m нечет-
ное, в точке x
нет экстремума.
3. Часто на практике, особенно при применении численных методов
поиска экстремума, рассматриваемых в последующих разделах, требуется
проверить, выполняются ли необходимые и достаточные условия экстре-
мума в некоторой точке. Такой анализ необходим, так как многие числен-
ные методы позволяют найти лишь стационарную точку, тип которой тре-
бует уточнения.
Пример 1.6.
Найти экстремум функции
2
2
1
2
(x)
fxx
на множестве
2
R.
Решение
1. Запишем необходимые условия экстремума первого порядка:
1
1
(x)
20
f
x
x
,
2
2
(x)
20
f
x
x
.
В результате решения системы получаем стационарную точку x (0; 0)
.
2. Проверим выполнение достаточных условий экстремума и необхо-
димых условий второго порядка.
Первый способ. Матрица Гессе имеет вид
20
(x)
02
H
. Так как
11120
h
,
2
20
40
02
, то достаточные условия экстре-
мума не выполняются (табл. 1.1, строки 1 и 2). Проверим выполнение не-
обходимых условий второго порядка. Главные миноры первого порядка
19
(1
m ) получаются из 2
в результате вычеркивания
211
nm
строк и столбцов с одинаковыми номерами: 2
, 2 . Главный минор второ-
го порядка ( 2
m ) получается из
2
в результате вычеркивания
0
nm
строк и столбцов, т.е. совпадает с 2
:4
. Отсюда следует, что
необходимые условия экстремума второго порядка не выполняются (табл.
1.2, строки 1 и 2). Так как матрица Гессе не является нулевой, то можно
сделать вывод о том, что в точке x
нет экстремума (табл. 1.2, строка 4).
Второй способ. Найдем собственные значения матрицы Гессе, ис-
пользуя (1.4):
2
0
det(
)
(2)(2)0
0
2
HE
.
Отсюда120
,
2
20
, т.е. собственные значения имеют разные
знаки. Поэтому точка x
не является точкой минимума или максимума
(табл. 1.2, строка 4), а является седловой точкой.
3. Так как экстремум не достигается ни в одной точке, то (x )
f
не
вычисляется.
Пример 1.7.
Найти экстремум функции
2
4
1
2
(x)
fxx
на множестве
2
R.
Решение
1. Запишем необходимые условия экстремума первого порядка:
1
1
(x)
20
f
x
x
,
3
2
2
(x)
40
f
x
x
.
В результате решения системы получаем стационарную точку
x
(0; 0)T
.
2. Проверим выполнение достаточных условий экстремума и необхо-
димых условий второго порядка. Матрица Гессе имеет вид
2
2
20
20
(x)
00
012
H
x
.Таккак11120
h
,
2
20
0
00
,
то достаточные условия экстремума не выполняются (табл. 1.1, строки 1 и
2). Проверим выполнение необходимых условий второго порядка. Получа-
ем главные миноры первого порядка: 2 ; 0 , и главный минор второго по-
рядка: 0 . Так как все главные миноры неотрицательные, то в точке x
может быть минимум и требуется дополнительное исследование (табл. 1.2,
строка 1).
20
3. Вычислим значение целевой функции в точке x
: (x)0
f
и
рассмотрим - окрестность точки x
, а также поведение функции (x)
f
на множестве
2
R . При любых
2
xR
имеем: (x) (x ) 0
ff
, что со-
ответствует не только определению 1.2, но и определению 1.1. Поэтом у
точка x
является точкой глобального минимума.
Пример 1.8.
Найти экстремум функции
2
22
1
2
1
(x)(1)10(
)
f
x
x
x
на мно-
жестве
2
R.
Решение
1. Запишем необходимые условия экстремума первого порядка:
2
1
12
1
1
(x)
2(1)40(
)0
f
x
xx
x
x
,
2
2
1
2
(x)
20(
)0
f
x
x
x
.
В результате решения системы получаем стационарную точку x (1; 1)T
.
2. Проверим выполнение достаточных условий экстремума первым
способом.
Матрица Гессе имеет вид
82 40
(x)
40 20
H
.
Так как
1820
,
282204040400
,товточкеx
локальный ми-
нимум (табл. 1.1, строка 1) и ( x ) 0
H
. Следовательно функция является
строго выпуклой. Поэтому точка x
–
точка глобального минимума.
3. Вычислим значение функции в точке глобального минимума x
:
(x) 0
f
.
Пример 1.9.
Найти экстремум функции
2
2
2
1
2
3
1
12
3
(x)
2
f
x
x
x
x
xx
x
на множестве
3
R.
Решение
1. Запишем необходимые условия экстремума первого порядка:
1
2
1
(x)
21
0
f
x
x
x
,
2
1
2
(x)
2
0
f
x
x
x
,
3
3
(x)
220
f
x
x
.
В результате решения системы получаем стационарную точку
21
x
;;1
33
T
.
21
2. Проверим выполнение достаточных условий.
Первый способ. Матрица Гессе имеет вид
210
(x)120
002
H
.
Так как 1
20
,
2
21
30
12
,
3(2)360
, т.е.
знаки угловых миноров чередуются, начиная с отрицательного, следова-
тельно точка x
–
точка локального максимума (табл. 1.1, строка 2).
Второй способ. Найдем собственные значения матрицы Гессе, ис-
пользуя (1.4):
2
1
0
det(
)12
0
0
0
02
HE
.
Отсюда
2
(2)(2)10
и
1
20
,
2
10
,
3
30
.
Так как все собственные значения матрицы Гессе отрица-
тельны, то в точке x
локальный максимум (табл. 1.1, строка 2).
3. Вычислим значение функции в точке
21
x
;;1
33
T
локаль-
ного максимума:
4
(x)
3
f
.
Пример 1.10.
Найти экстремум функции
3
2
2
1
2
3
23
1
2
(x)
362
fxxxxxxx
на множестве
3
R.
Решение
1. Запишем необходимые условия экстремума первого порядка:
2
1
1
(x)
330
f
x
x
,
2
3
2
(x)
2
60
f
xx
x
,
3
2
3
(x)
2
0
f
xx
x
.
В результате решения системы получаем две стационарные точки:
(1)
x
(1; 4; 2)T
,
(2)
x
(1; 4;2)T
.
2. Проверим выполнение достаточных и необходимых условий второ-
го порядка в каждой стационарной точке двумя способами.
22
Исследуем точку (1)
x
(1; 4; 2)T
.
Первый способ. Матрица Гессе имеет вид
(1)
600
(x)021
012
H
. Так
как160
,
2
60
120
02
,3180
, то точка
(1)
x
является
точкой локального минимума (табл. 1.1, строка 1).
Второй способ. Найдем собственные значения матрицы Гессе, ис-
пользуя (1.4):
(1)
2
6
00
(x)
02
1
(6)(2)10
0
12
H
E
.
Отсюда160
,
230
,
310
иточка
(1)
x
является точкой
локального минимума (табл. 1.1, строка 1).
Исследуем точку (2)
x
(1; 4;2)T
.
Первый способ. Матрица Гессе имеет вид
(1)
600
(x) 021
012
H
. Так
как 1
60
,
2
60
120
02
,3
180
, то достаточные
условия экстремума не выполняются (табл. 1.1). Проверим необходимые
условий экстремума второго порядка. Главные миноры первого порядка
(1)
m
получаются из
3
600
021
012
в результате вычеркивания
312
nm
строк и 2 столбцов с одинаковыми номерами: 6
, 2,2.
Главные миноры второго порядка ( 2)
m
получаются из 3
в результате
вычеркивания
321
nm
строк и столбцов с одинаковыми номера-
ми: 3, 12
,
12
. Главный минор третьего порядка ( 3)
m
получается
из3
в результате вычеркивания
330
nm
строк и столбцов, т.е .
совпадает с 3
18
. Отсюда следует, что необходимые условия экстре-
23
мума второго порядка не выполняются (табл. 1 .2, строки 1 и 2). Так как
матрица Гессе не является нулевой, то можно сделать вывод о том, что в
точке
(2)
x
нет экстремума (табл. 1.2, строка 4).
Второй способ. Найдем собственные значения матрицы Гессе:
2
6
00
02
1
(6)(2)10
0
12
.
Отсюда 1
60
,
230
,
310
, т.е. собственные значения
имеют разные знаки. Поэтому в точке
(2)
x
нет экстремума (табл. 1.2,
строка 4).
3. Вычислим значение функции в точке
(1)
x
локального минимума:
(1)
(x)12
f
.
Пример 1.11.
Найти экстремум функции
6
5
4
3
165
()536
60 36
2
fxxx
x
x
на множестве R .
Решение
1. Запишем необходимые условия экстремума первого порядка:
5
4
3
2
2
()30180330180 30(1)(2)(3)0
dfx
x
x
x
x
xx
x
x
dx
.
Отсюда получаем стационарные точки:
(1) 0
x
,
(2) 1
x
,
(3) 2
x
,
(4) 3
x
.
2. Проверим выполнение достаточных условий экстремума:
2
4
3
2
2
()150 720 990 360
dfx
x
x
x
x
dx
;
(1)
()0
fx
,
(2)
()600
fx
,
(3)
()1200
fx
,
(4)
()5400
fx
.
Поэтому в точках
(2)
x
,
(4)
x
–
локальный минимум, а в точке
(3)
x
–
ло-
кальный максимум (табл. 1.1, строки 1 и 2). В точке
(1)
x
достаточные ус-
ловия не выполняются (табл. 1.2, строка 3), поэтому вычислим третью про-
изводную:
(1)
3
3
2
3
0
( ) (600 2160 1980 360)
360
x
dfx
x
x
x
dx
.
24
Так как эта производная отлична от нуля и имеет нечетный порядок, то в
точке
(1)
x
нет экстремума (п.2 замечаний 1.5).
3. Вычислим значение функции в точках экстремума:
(2)
()27.5
fx
,
(3)
()44
fx
,
(4)
()4.5
fx
.
При x и x
()
f x , следовательно функция не имеет
точки глобального максимума. Точка
(4) 3
x
является точкой глобально-
го минимума.
Пример 1.12.
Найти экстремум функции
6
()(1)
fxx
на множестве R .
Решение
1. Запишем необходимые условия экстремума первого порядка:
5
()6(1)0
dfx
x
dx
.
Отсюда стационарная точка
1
x
.
2. Проверим достаточные условия экстремума с учетом п.2 замечаний
1.5. Первая не равная нулю производная имеет порядок
6
m:
(6)()6!0
fx
. Так как m четное, то функция достигает в точке
1
x
локального минимума.
3. Вычислим значение функции в точке минимума: ( ) 0
fx
.
1.3 . Условный экстремум при ограничениях равенствах
Даны дважды непрерывно дифференцируемые на
множестве
n
R целевая функция
1
(x) ( ,...,
)n
ffxx
и функции ограничений
1
(x) ( ,...,
)
i
i
n
g
gxx
,
1,...,
i
m
. Система огра-
ничений (x) 0
i
g,1,...,
i
m
определяет множество допустимых реше-
нийX.
Требуется исследовать функцию (x)
f на экстремум, т.е. определить
точки x
X
ее локальных минимумов и максимумов на множестве X :
x
(x) min (x)
X
f
f
,
(1.5,а)
где
x: (x) 0, 1,...,
;
i
X
g
i
mmn
.
(1.5,б)
Находится точка x
локальных
экстремумов с помощью необходимых и
достаточных условий минимума и максимума первого и второго порядка
Постановка задачи
Стратегия решения задачи
25
при ограничениях типа равенств (порядок условий определяется порядком
используемых производных). Вычисляются значения
(x)
f функции в
найденных точках локального экстремума.
В классическом математическом анализе для определения условного
экстремума в задаче (1.5) применяется метод множителей Лагранжа.
Этот метод позволяет свести задачу поиска условного экстремума к задаче
поиска безусловного экстремума.
Определение 1.15. Функция
0
0
1
(x, ,λ)
(x)
(x)
m
ii
i
L
f
g
(1.6)
называется обобщенной функцией Лагранжа, числа 0 1 2
,
,
, ...,
m
–
множителями Лагранжа,
12
λ(,,...,
)T
m
.
Если01
,тофункция
(1.6) называется классической функцией Лагранжа:
1
(x, λ) (x)
(x)
m
ii
i
L
f
g
.
(1.7)
Определение 1.16. Градиентом обобщенной (классической) функции
Лагранжа по x называется вектор-столбец, составленный из ее частных
производных первого порядка по j
x,
1,...,
j
n
:
0
0
x
0
1
(x, ,λ)
(x, ,λ)
(x, ,λ)
,...,
T
n
L
L
L
x
x
,
(1.8)
x
1
(x, λ)
(x, λ)
(x, λ)
, ...,
T
n
L
L
L
x
x
.
Определение 1.17. Вторым дифференциалом обобщенной (классиче-
ской) функции Лагранжа
0
(x, ,λ)
L
(x, λ)
L
называется функция
2
2
0
0
11
(x, ,λ)
(x, ,λ)
n
n
ij
ij
ij
L
dL
dx dx
xx
,
(1.9)
2
2
11
(x, λ)
(x, λ)
n
n
ij
ij
ij
L
dL
dx dx
xx
.
Определение 1.18. Первым дифференциалом функции ограничения
(x)
i
g называется функция
1
(x)
(x)
n
i
i
j
j
j
g
dg
dx
x
,
1,...,
i
m
.
(1.10)
26
Определение 1.19. Градиенты ограничений 1(x)
g ,...,
(x)
m
g
явля-
ются линейно независимыми в точке x
, если равенство 1 1 (x )
g
2 2(x) ...
(x) 0
m
m
g
g
выполняется только при 1
2 ...
...
0
m
.
Если существуют числа 1 ,...,
m
одновременно не равные
нулю, для которых равенство выполняется, то градиенты линейно зависи-
мы. В этом случае один из них является линейной комбинацией осталь-
ных. Один вектор
1(x )
g
тоже образует систему векторов: при
1(x) 0
g
линейно независимую, а при
1(x) 0
g
линейно зависи-
мую. Система векторов, содержащая нулевой вектор, всегда линейно зави-
сима.
Если
1
2
(x) (x)... (x)
m
rang A rang g
g
g
m
, то система
векторов линейно независима. Если rang A m
, то система линейно за-
висима.
Теорема 1.4 (необходимые условия экстремума первого порядка).
Пусть x
есть точка локального экстремума в задаче (1.5). Тогда
найдутся числа 0 1
,
, ...,
m
, не равные одновременно нулю и такие, что
выполняются следующие условия:
–
условие стационарности обобщенной функции Лагранжа по x :
0
(x, ,λ)
0
j
L
x
,
1,...,
j
n
;
(1.11,а)
–
условие допустимости решения:
(x) 0
i
g
,
1,...,
i
m
.
(1.11,б)
Если при этом градиенты
1(x )
g
,...,
(x)
m
g
в точке x
линей-
но независимы (выполняется условие регулярности), то 0 0
.
Условие (1.11,а) можно записать в векторной форме:
x
0
(x, ,λ) 0
L
.
Система (1.11) содержит n m
уравнений с
1
nm
неизвестными
0
,
1
λ(;...;)T
m
,
1
x
( ;...; )T
m
x
x
.
Точки x
, удовлетворяющие
системе при некоторых 0
,λ
называются условно стационарными.
Точка экстремума, удовлетворяющая системе (1.11) при 0 0
,на-
зывается регулярной, а при 0 0
–
нерегулярной. Случай 0 0
отража-
ет вырожденность ограничений. При этом в обобщенной функции Ла-
27
гранжа исчезает член, содержащий целевую функцию, а в необходимых
условиях экстремума не используется информация, представляемая гради-
ентом целевой функции.
Замечание 1.6. При решении задач проверка условия регулярности
затруднена, так как точка x
заранее не известна. Поэтому, как правило,
рассматриваются два случая: 0 0
и00
.Если00
, в системе
(1.11,а) полагают 0 1
. Это эквивалентно делению системы уравнений
(1.11,а) на 0
и замене
0
i
наi
. При этом обобщенная функция Ла-
гранжа становится классической, а сама система (1.11) имеет вид
1
(x)
(x,λ)
(x)
0
m
i
i
i
j
j
j
g
L
f
x
x
x
,
1,...,
j
n
;
(1.12,а)
(x) 0
i
g
,
1,...,
i
m
.
(1.12,б)
Здесь число уравнений равно числу неизвестных.
Система (1.12) отражает тот факт, что антиградиент целевой функции
в регулярной точке экстремума x
является линейной комбинацией гра-
диентов ограничений. Действительно, с учетом (1.7) можно переписать
условие (1.12,а) в форме
1
*
*
x
x
0
m
i
i
i
f
g
Отсюда
1
*
*
x
x
m
i
i
i
f
g
.
(1.13)
Условие (1.13) имеет определенный геометрический смысл: в точке
x
антиградиент целевой функции
(x)
f
является линейной комбина-
цией градиентов
(x)
i
g
(нормалей к поверхностям (x) 0
i
g).
На рис. 1.2 приведена иллюстрация этого факта для задачи (1.5) при
2
n,
1
m . Пунктиром изображены линии уровня целевой функции
(x)
fc
. Вточкеx
векторы
(x)
f
и
1(x )
g
коллинеарны. В точ-
ках x из достаточно малой окрестности точки x
, удовлетворяющих ус-
ловию 1(x) 0
g , выполняется неравенство (x) (x )
ff
. Точка x
ус-
ловного экстремума (максимума) является точкой касания линии уровня
целевой функции и кривой, описывающей ограничение (рис. 1.2). Очевид-
но,
(1)
x
является точкой локального условного минимума, а
(2)
x
–
ло-
28
кального максимума (x)
f при ограничении 1 (x) 0
g
.
Стационарная
точка функции Лагранжа
(3)
x не является точкой локального условного
экстремума, так как из нее можно сместиться, оставаясь на линии
1(x) 0
g так, что значение функции (x)
f изменится в ту или иную сто-
рону по сравнению с
(3)
(x)
f.
Теорема 1.5 (необходимые условия экстремума второго порядка).
Пусть x
–
регулярная точка минимума (максимума) в задаче (1.5) и
имеется решение (x , λ )
системы (1.12). Тогда второй дифференциал
классической функции Лагранжа, вычисленный в точке (x , λ )
, неотри-
цателен (неположителен):
2
(x,λ) 0
dL
2
(x,λ)0
dL
(1.14)
для всех x
n
dR
таких, что
1
(x)
(x)
0
n
i
i
j
j
j
g
dg
dx
x
,
1,...,
i
m
.
(1.15)
Теорема 1.6 (достаточные условия экстремума).
Пусть имеется точка (x , λ )
, удовлетворяющая системе (1.12).
Если в этой точке
2
(x,λ) 0
dL
2
(x,λ)0
dL
для всех ненулевых
x
n
dR
таких, что
1
x
1(x) 0
g
3
(x)
fc
2
(x)
fc
1
(x)
fc
2
x
(x)
f
1(x )
g
1
2
3
cc
c
(1)
x
(2)
x
x
(3)
x
Рис.1.2
11
(x)
(x)
f
g
29
1
(x)
(x)
0
n
i
i
j
j
j
g
dg
dx
x
,
1,...,
i
m
,
то точка x
является точкой локального минимума (максимума) в задаче
(1.5).
Необходимые и достаточные условия в задаче поиска условного
экстремума при ограничениях типа равенств
(при условии x
0
(x, ,λ) 0
L
,
(x) 0
i
g
,
1,...,
i
m
)
Таблица 1.3
No
п/п
00
,
2
(x,λ)
dL
(x)
i
dg
,
1,...,
i
m
Тип условно стационарной
точки x
1
2
3
4
1
0
0,x0
d
Условный локальный
минимум
2
0
0,x0
d
Условный локальный
максимум
3
0
0
Может быть условный ло-
кальный минимум.
Требуется дополнительное
исследование
4
0
0
Может быть условный ло-
кальный максимум.
Требуется дополнительное
исследование
5
0
0
Требуется дополнительное
исследование
6
0
0
Нет экстремума
Замечание 1.7. Достаточные и необходимые условия экстремума
второго порядка проверяются в условно стационарных точках, которые
удовлетворяют системе (1.11) при 0 0
или системе (1.12), так как для
практики безусловно представляет интерес случай, когда в функции Ла-
гранжа присутствует целевая функция, экстремум которой ищется.
Алгоритм
1. Составить обобщенную функцию Лагранжа:
0
0
1
(x, ,λ)
(x)
(x)
m
ii
i
L
f
g
.
30
2. Записать необходимые условия экстремума первого порядка:
а)
0
(x, ,λ)
0
j
L
x
,
1,...,
j
n
;
б)(x)0
i
g
,
1,...,
i
m
.
3. Решить систему уравнений п.2 для двух случаев:
1)00
;
2)00
(поделить условие «а» на 0
и заменить
0
i
наi
).
В результате найти условно-стационарные точки x
, выделив из них
полученные при 0 0
(они могут быть регулярными точками экстрему-
ма).
4. Для выделенных на шаге 3 точек проверить достаточные условия
экстремума:
а) записать выражение для второго дифференциала классической
функции Лагранжа в точке (x , λ )
:
2
2
11
(x,λ)
(x,λ)
n
n
ij
ij
ij
L
dL
dx dx
xx
б) записать систему (1.15) в точке x
:
1
(x)
(x)
0
n
i
i
j
j
j
g
dg
dx
x
,
1,...,
i
m
;
в) из предыдущей системы выразить любые m дифференциалов
j
dx через остальные (
)
nm
и подставить в
2
(x,λ)
dL;
г) если
2
(x,λ)0
dL
при ненулевых x
d,товточкеx
–
услов-
ный локальный минимум. Если
2
(x,λ)0
dL
при ненулевых x
d,тов
точке x
–
условный локальный максимум. Если достаточные условия экс-
тремума не выполняются, следует проверить выполнение необходимых
условий второго порядка (см. теорему 1.5), следуя аналогичной процедуре.
Если они выполняются, то требуется дополнительное исследование, а если
не выполняются, то в точке x
нет условного экстремума.
5. Вычислить значения функции в точках условного экстремума.
Условия экстремума в задаче (1.5) приведены в таблице 1.3.
31
Замечание 1.8. Иногда удается проверить условие линейной незави-
симости градиентов ограничений на множестве X (см. определение 1.19.) .
Если оно выполняется, то на шаге 1 следует записать классическую функ-
цию Лагранжа (1.7), на шаге 2 можно записывать сразу систему (1.12), а на
шаге 3 отсутствует случай 0 0
.
Пример 1.13
Найти экстремум функции
2
2
1
2
(x)
fxx
на множестве X , которое
образуется условием 1
1
2
(x)
20
g
xx
.
Решение
Проверим условие регулярности. Так как
1(x) (1;1) 0
g
то усло-
вие выполняется (см. определение 1.19). Поэтому будем пользоваться
классической функцией Лагранжа (1.7).
1. Составим функцию Лагранжа:
2
2
1
1
2
11
2
(x, )
(
2)
L
x
x
xx
.
2. Выпишем необходимые условия экстремума первого порядка:
а)
1
1
1
1
(x, )
2
0
L
x
x
, т.е.
1
1
2
x
;
1
2
1
2
(x, )
2
0
L
x
x
, т.е.
1
2
2
x
;
б)1
1
2
(x)
20
g
xx
.
3. Решение системы: 1
21
x
x
,
1
2
–
условно стационарная
точка.
(x) 2
f
2
x
1
x
x
(1,1)T
1
1
0
Рис. 1.3
(x) 8
f
(x) 1
f
1(x)
g
32
4. Проверим достаточные условия экстремума:
а)
2
2
2
1
1
2
(x,)2
2
dL
dx dx
,
т.
к.
2
2
1
1
2
2
1
2
(x, )
(x, )
2
L
L
x
x
,
2
2
1
1
12
21
(x, )
(x, )
0
L
L
xx
xx
;
б)1
1
2
(x)
0
dg
dx dx
, т.к.
1
1
1
2
(x) (x)
1
g
g
x
x
;
в) выразим дифференциал 1
dx через 2
dx: 1
2
dx dx
и подставим
в
2
dL;
г)
2
2
1
2
(x,)4
0
dL
dx
при
20
dx ,товточкеx
(1,1)T
–
регулярный
локальный условный минимум (табл. 1 .3, строка 1). Графическое решение задачи приве-
денонарис.1.3.
Пример 1.14
Найти условный экстремум в задаче
1
2
(x)
extr
fxx
;
2
2
1
1
2
(x)
20
g
x
x
.
Решение
Проверим условие регулярности. Так как
1
1
2
(x)(2;2)0
T
g
xx
длявсехx X
, то условие выполняется (см. определение 1.19). Поэтом у
будем пользоваться классической функцией Лагранжа.
1. Составим функцию Лагранжа:
2
2
1
1
2
11
2
(x, )
(
2)
L
xx
x
x
.
2. Выпишем необходимые условия экстремума первого порядка:
а)
1
11
1
(x, )
12
0
L
x
x
или 1
1
1
2
x
,
1
12
2
(x, )
12
0
L
x
x
или 2
1
1
2
x
;
б)
2
2
1
1
2
(x)
20
g
x
x
.
3. Решением системы являются две условно-стационарные точки:
A:11
x
,
21
x
,
1
1
2
;B:1
1
x
,
2
1
x
,
1
1
2
.
33
4. Проверим достаточные условия экстремума:
а)
2
2
2
1
11
12
(x,)2
2
dL
dx
dx
, так как
2
2
1
1
1
2
2
1
2
(x,λ)
(x,λ )
2λ
L
L
x
x
,
2
2
1
1
12
21
(x,λ)
(x,λ )
0
L
L
xx
xx
;
б)1
11
22
(x) 2
2
0
dg
xdx
xdx
, так как
1
1
1
(x)
2
g
x
x
,
1
2
2
(x)
2
g
x
x
.
в) Исследуем точку A . Получаем
1
1
2
()2 2
0
dgA dx dx
, отку-
да
1
2
dx dx
.
С учетом полученного соотношения
2
()
dLA
2
2
2
1
2
2
2
0
dx dx
dx
при
20
dx .Поэтомувточкеx
(1; 1)T
–
регулярный условный локальный максимум (строка 2 в табл. 1.3).
Исследуем точку B . Получаем
1
1
2
()22
0
dgB
dx dx
, откуда
1
2
dx dx
.
С учетом полученного соотношения
2
2
2
1
2
()
dLB dx dx
2
2
2
0
dx
при
20
dx .Поэтомувточкеx
(1; 1)T
–
регулярный
условный локальный минимум (строка 1 в табл. 1.3).
4. Подсчитаем значения функции в точках экстремума: ( ) 2
fA,
()2
fB
. Графическое решение задачи изображено на рис. 1.4.
Пример 1.15
Найти условный экстремум в задаче
1
(x)
extr
fx
;
3
2
1
1
2
(x)
0
g
x
x
.
1(x) 0
g
2
x
1
x
A
B
(x) 2
f
(x) 0
f
1
1
0
Рис. 1.4
1
1
(x) 2
f
2
2
2
2
34
Решение
Проверим условие регулярности. Так как
2
1
1
2
(x)(3;2)0
T
g
x
x
в точке x (0;0)T
, то условие не выполняется (см. определение 1.19). Бу-
дем пользоваться алгоритмом с использованием обобщенной функции Ла-
гранжа.
1. Составим обобщенную функцию Лагранжа:
3
2
01
01
11
2
(x,,)
(
)
L
x
x
x
.
2. Выпишем необходимые условия экстремума первого порядка:
а)
2
01
0
11
1
(x,,)
3
0
L
x
x
,
01
12
2
(x,,)
2
0
L
x
x
;
б)
3
2
1
1
2
(x)
0
g
x
x
.
3. Решим систему для двух случаев.
В первом случае 0 0
.
Тогда 1 0
,таккаквтеореме1.4все
множители Лагранжа не могут быть одновременно равны нулю. Отсюда
1
20
x
x
,
00
.
Во втором случае 0 0
. Поделим уравнения приведенной в п.2 сис-
темы на 0
с заменой
1
0
на1
:
2
11
13
0
x
;
12
2
0
x
;
3
2
1
20
x
x
.
Рассмотрим второе уравнение.
Если10
, то система несовме-
стна. Если 2 0
x,то10
x исис-
тема тоже несовместна. Как видно,
применение классической функции
Лагранжа не дает результата.
4.Таккак 0 0
, достаточ-
ные условия экстремума не прове-
ряются. Точка x
со значением
целевой функции (x ) 0
f
являет-
ся точкой нерегулярного локально-
го и глобального миним ума, как
следует из рис. 1.5.
2
x
1
x
2
3
2
1
0
x
x
(x) 0
f
1
Рис. 1.5
(x) 1
f
2
0
(x) 2
f
*
x
35
Пример 1.16
Найти условный экстремум в задаче
2
2
1
2
(x)( 2)( 2) extr
f
x
x
;
2
2
1
1
2
(x)
20
g
x
x
.
Решение
Будем следовать алгоритму, не проверяя условие регулярности.
1. Составим обобщенную функцию Лагранжа:
2
2
2
2
01
0
1
2
11
2
(x,,)
(2)(2)
(
2)
L
x
x
x
x
.
2. Выпишем необходимые условия экстремума первого порядка:
а)
01
01
11
1
(x,,)
2(2)2
0
L
x
x
x
,
01
02
12
2
(x,,)
2(2)2
0
L
x
x
x
;
б)
2
2
1
1
2
(x)
20
g
x
x
.
3. Решим систему для двух случаев.
В первом случае 0 0
. Из п.2 следует:
11
2
0
x
,
12
2
0
x
,
2
2
1
220
x
x
.
Так как согласно теореме 1.4 1 0
, то из первых двух уравнений: 1 0
x,
20
x
. Однако при этом третье уравнение (ограничение) не удовлетворя-
ется: 1(x) 2 0
g
. Следовательно, система несовместна.
Во втором случае 0 0
. Перепишем систему, приведенную в п.2,
поделив уравнения на 0
с заменой
1
0
на1
:
1
1
11
1
1
2
12
2
2
2
1
1
2
(x, )
2(2)2
0,
(x, )
2(2)2
0,
(x)
20.
L
x
x
x
L
x
x
x
g
x
x
(1.16)
36
Система уравнений (1.16) имеет два решения, т.е. найдены две усл ов-
но стационарные точки:
A:1
21
xx
,
11
;B:1
2
1
xx
,
1
3
.
4. Проверим достаточные условия экстремума, используя условия
теоремы 1.6:
а)
2
2
2
1
1
1
1
2
(x,)(22)(22)
dL
dx
dx
;
б)1
11
22
(x) 2
2
0
dg
xdx
xdx
.
в) Исследуем точку A :
1
1
2
()2 2
0
dgA dx dx
,
откуда
1
2
dx dx
и
2
2
2
2
1
2
2
()4 4
8
0
dLAdxdxdx
при
20
dx .Поэтомув
точке A – регулярный условный минимум (табл. 1.3, строка 1).
г) Исследуем точку B : 1
1
2
()22
0
dgB
dx dx
, откуда
1
dx
2
dx
и
2
2
2
2
1
2
2
()44
8
0
dLA
dx dx
dx
при
20
dx .Поэтомув
точке B – регулярный условный максимум (табл. 1.3, строка 2).
5. Подсчитаем значения функции в точках экстремума: ( ) 2
fA,
()18
fB
. Графическое решение задачи изображено на рис. 1.6.
Пример 1.17
Найти условный экстремум в задаче
2
2
1
2
(x)
extr
fxx
;
2
2
1
1
2
(x)
10
g
x
x
.
Решение
1. Составим обобщенную функцию Лагранжа:
1(x) 0
g
2
x
(2, 2)
1
x
A
B
(x) 2
f
(x) 18
f
1
1
0
Рис. 1.6
37
2
2
2
2
01
01
2
11
2
(x,,)
(
)(
1)
L
x
x
x
x
.
2. Запишем необходимые условия экстремума первого порядка:
а)
01
01
11
1
(x,,)
2
2
0
L
x
x
x
,
01
02
12
2
(x,,)
2
2
0
L
x
x
x
;
б)
2
2
1
1
2
(x)
10
g
x
x
.
3. Решим систему для двух случаев.
В первом случае 0 0
.Тогда10
в силу утверждения 1.4. По-
этому из первых двух уравнений следует: 1
20
xx
. Однако условие «б»
при этом не выполняется. Следовательно, система несовместна.
Во втором случае 0 0
. Перепишем систему, приведенную в п.2,
поделив уравнения на 0
с заменой
1
0
на1
:
1
1
1
1
1
2
1
2
2
2
1
1
2
(x, )
2(1)0,
(x, )
2(1)0,
(x)
10.
L
x
x
L
x
x
g
x
x
(1.17)
Пусть 1
1
.Тогда20
x,а1
1
x .Пусть11
.Тогда 1 0
x,а
2
1
x . Других решений система не имеет. Таким образом, система (1.17)
имеет четыре условно-стационарные точки:
A:11
x
,
20
x
,
1
1
;B:1
1
x
,
20
x
,
1
1
;
C:10
x
,
21
x
,
11
;D:10
x
,
2
1
x
,
11
.
4. Проверим достаточные условия экстремума. Воспользуемся систе-
мой (1.17):
а)
2
2
2
1
1
1
1
2
(x,)2(1)
2( 1)
dL
dx
dx
;
б)1
11
22
(x) 2
2
0
dg
xdx
xdx
.
38
в,г) Исследуем точку A :
1
1
()2
0
dgA dx
, откуда
10
dx
и
2
2
2
()4
0
dLA
dx
при
20
dx . Поэтому в точке A – регулярный ло-
кальный условный максимум (строка 2 в табл. 1.3).
Исследуем точку B :
1
1
()2
0
dgB
dx
, откуда
10
dx
и
2
2
2
()4
0
dLB
dx
при
20
dx . Поэтому в точке B – регулярный ло-
кальный условный максимум (табл. 1.3, строка 2).
Исследуем точку C :
1
2
()2
0
dgC dx
, откуда
20
dx
и
2
2
1
()4
0
dLC dx
при
10
dx . Поэтому в точке C – регулярный ло-
кальный условный минимум (табл. 1.3, строка 1).
Исследуем точку D :
1
2
()2
0
dgD
dx
, откуда
20
dx
и
2
2
1
()4
0
dLD dx
при
10
dx . Поэтому в точке D – регулярный ло-
кальный условный минимум (табл. 1.3, строка 1).
4. Вычислим значение функции в точке условного экстремума:
()()1
fAfB
,
()()1
fCfD
.
Графическое решение приведено
на рис. 1.7.
Пример 1.18
Найти условный экстремум в задаче
2
2
2
1
2
3
(x)
extr
fxxx
;
2
2
1
1
2
3
(x)
0
g
x
x
x
,
2
1
2
3
(x)
40
g
xxx
.
Решение
1. Составим обобщенную функцию Лагранжа:
1(x) 0
g
2
x
1
x
A
B
(x) 1
f
(x) 1
f
0
Рис. 1.7
(x) 1
f
(x) 1
f
C
D
39
2
2
2
2
2
012
01
2
3
11
2
3
11
2
3
(x,,,)
(
)(
)(
4)
L
x
x
x
x
x
x
xxx
.
2. Запишем необходимые условия экстремума первого порядка:
а)
012
01
11
2
1
(x,,,)
2
2
0
L
x
x
x
,
012
02
12
2
2
(x,,,)
2
2
0
L
x
x
x
,
012
03
1
2
3
(x,,,)
2
0
L
x
x
;
б)
2
2
1
1
2
3
(x)
0
g
x
x
x
,
2
1
2
3
(x)
40
g
xxx
.
3. Решим систему для двух случаев.
В первом случае 0 0
. Тогда из п.2 следует система уравнений:
11
2
2
0
x
,
12
2
2
0
x
,
1
20
или
1
2
,
2
2
1
2
30
x
x
x
,
1
2
340
xxx
.
Первые два уравнения системы перепишутся в виде
1
1
(21)0
x
,
1
2
(21)0
x
.
Если10
,то20
, что противоречит требованиям теоремы
1.4. Если 1 0
,то1
1
2
x
,
2
1
2
x
. Из двух последних уравнений сис-
темы получаем 3
1
2
x
и3
1
2
4
5
x
xx
, т.е. имеется противоречие и
система несовместна.
Во втором случае 0 0
. Перепишем систему, приведенную в
п.2, поделив уравнения на 0
с заменой
1
0
,
2
0
на1
,2
:
12
1
1
2
1
(x,,)
2(1)
0
L
x
x
,
12
2
1
2
2
(x,,)
2(1)
0
L
x
x
,
40
12
3
1
2
3
(x,,)
2
0
L
x
x
;
2
2
1
1
2
3
(x)
0
g
x
x
x
,
2
1
2
3
(x)
40
g
xxx
.
Из первых трех уравнений имеем:
2
1
2
1
2(1 )
xx
;
1
2
3
2
x
.
Подставляя полученные соотношения в последние два уравнения и решая
их, получаем:
1
2
3
,
2
10
3
;
1
20
3
,
2
68
3
.
Таким образом, получены две условно-стационарные точки:
A:11
x
,
21
x
,
32
x
,
1
2
3
,
2
10
3
;
B:1
2
x
,
2
2
x
,
38
x
,
1
20
3
,
2
68
3
;
4. Проверим достаточные условия экстремума:
а)
2
2
2
2
12
1
1
1
2
3
(x,,)2(1)
2(1 )
2
dL
dx
dx dx
;
б)1
11
22
3
(x) 2
2
0
dg
xdx
xdx dx
,
2
1
2
3
(x)
0
dg
dxdxdx
;
в) выразим дифференциалы 1
dxи 3
dx через 2
dx:
2
1
2
1
12
12
x
dx
dx
x
,
1
2
3
2
1
2(
)
12
xx
dx
dx
x
;
г) исследуем точку A :
1
2
dx dx
,
30
dx,
2
2
2
2
2
2
2
()21()21
0
3
3
dLA
dx
dx
при
20
dx.
Поэтому в точке A – регулярный локальный условный минимум (табл.
1.3, строка 1).
Исследуем точку B :
1
2
dx dx
,
30
dx,
2
2
2
2
2
20
20
()21()21
0
3
3
dLB
dx
dx
при
20
dx.
Поэтому в точке B – регулярный локальный условный максимум (табл.
1.3, строка 2).
41
5. Значение функции в точках экстремума: ( ) 6
fA,()72
fB
.
Покажем, что множитель Лагранжа i
характеризует чувствитель-
ность оптимального значения f
в задаче (1.5) к изменениям правой части
ib в i -м ограничении (1.5,б). Рассмотрим задачу условной минимизации в
пространстве
2
R с одним ограничением:
12
(,) min,
fxx
112
1
(,)
gxxb
.
Пусть стационарная точка
1
(x; )
классической функции Лагранжа
1
11
1
(x, )
(x)
(x)
L
f
g
b
является решением этой задачи. Так как
1
1
(x)
g
b
и
1
(x, )
(x)
fL
f
то, очевидно, оптимальные значе-
ния x
,
1
иf
связаны функциональной зависимостью с величиной 1b .
Выразим частную производную
1
f
b
с помощью правила дифференциро-
вания сложной функции:
1
2
1
1
1
2
1
x
x
ff
f
b
x
bxb
.
(1.18)
С другой стороны, из условия 1 1 2
1
(,)
gxxb
получаем:
1
1
1
2
1
1
2
1
10
gx
gx
xb
x
b
.
(1.19)
Умножим обе части равенства (1.19) на 1
и прибавим к (1.18):
2
1
1
1
1
1
1
j
j
j
j
x
g
f
f
b
x
x
b
.
Так как
1
(x, )
–
стационарная точка функций Лагранжа, то с уче-
том (1.12,а) получаем:
1
1
f
b
.
Таким образом, скорость изменения
оптимального значения f
, вызываемого изменением правой части в ог-
раничении 1 1 2
1
(,)
gxxb
, определяется значением множителя Лагранжа.
Для задачи на условный экстремум с m ограничениями
(x)
i
i
g
b
,
1,...,
i
m
.
Аналогично можно получить:
i
i
f
b
.
42
1.4 . Условный экстремум при ограничениях неравенствах
Даны дважды непрерывно дифференцируемые на
множестве
n
R функция
1
(x) ( ,...,
)n
ffxx
(це-
левая функция) и функции ограничений
1
(x) ( ,...,
)0
i
i
n
g
gxx
,
1,...,
i
m
, определяющие множество допустимых решений X .
Требуется исследовать функцию (x)
f на экстремум, т.е. определить
точки x
n
XR
ее локальных минимумов (максимумов) на X :
x
(x) min (x)
X
f
f
;
x
(x) max(x)
X
f
f
,
(1.20)
где
x: (x) 0, 1,...,
i
X
g
i
m
.
Для решения задачи находятся точки x
локального экстремума с помощью не-
обходимых и достаточных условий минимума и максимума перв ого и вто-
рого порядка при ограничениях типа неравенств (порядок условий опреде-
ляется порядком используемых производных). Вычисляются значения
(x)
f функции в найденных точках локального экстремума.
Определение 1.20. Ограничение
(x) 0
i
g называется активным в
точке x
, если
(x) 0
i
g
. Если
(x) 0
i
g
, то ограничение называется
пассивным.
Если допустимое множество X удовлетворяет так называемому ус-
ловию регулярности (условию Слейтера), то существует точка
(0)
x
n
XR
, такая, что
(0)
(x)0
i
g
при всех
1,...,
i
m
. Это означает, что
у множества X есть хотя бы одна внутренняя точка.
Теорема 1.7 (необходимые условия минимума (максимума) первого
порядка).
Пусть x
–
точка локального минимума (максимума) в задаче (1.20).
Тогда найдется такое число 0 0
и вектор
1
λ ( ,...,
)T
m
, не рав-
ные одновременно нулю и такие, что выполняются следующие условия:
–
условие стационарности обобщенной функции Лагранжа по x :
0
(x, ,λ)
0
j
L
x
,
1,...,
j
n
;
(1.21,а)
–
условие допустимости решения:
(x) 0
i
g,
1,...,
i
m
;
(1.21,б)
Постановка задачи
Стратегия решения задачи
43
–
условие неотрицательности для условного минимума:
0
i
,
1,...,
i
m
;
(1.21,в)
( условие неположительности для условного максимума :
0
i
,
1,...,
i
m
):
–
условие дополняющей нежесткости:
(x) 0
ii
g
,
1,...,
i
m
.
(1.21,г)
Если при этом градиенты активных в точке x
ограничений линейно не-
зависимы (выполняется условие регулярности), то 0 0
.
Точки x
удовлетворяющие системе (1.21), называются условно ста-
ционарными.
В отличие от случая ограничений типа равенств необходимые усло-
вия экстремума первого порядка формулируются отдельно для максимума
и минимума. Теорема 1.7 была доказана Ф. Джоном (F. John), а при 0 0
Куном и Таккером (H.W. Kuhn, A.W. Tucker).
Если в решаемой задаче ограничения записаны в форме
(x) 0
i
gто
их необходимо переписать в виде, используемом в (1.20): (x) 0
i
g
.
Далее будем использовать множество индексов ограничений, актив-
ных в точке x
, которое обозначим через a
I.
При решении задач поиска условного максимума можно использовать
необходимые и достаточные условия минимума, применяя преобразова-
ние, описанное в замечании 1.1.
Замечание 1.9. Так как точка x
заранее неизвестна, то проверка
условия регулярности затруднена, поэтому рекомендуется следовать алго-
ритму, описанному в замечании 1.6.
Точка экстремума, удовлетворяющая системе (1.21) при 0 0
,на-
зывается регулярной, а при 0 0
–
нерегулярной. Случай 0 0
отража-
ет вырожденность ограничений.
Условие (1.21,а) в регулярной точке экстремума x
отражает тот
факт, что антиградиент целевой функции является неотрицательной (непо-
ложительной в случае максимума) линейной комбинацией градиентов
функций, образующих активные ограничения в точке x
. Действительно,
условие (1.21,а) с учетом (1.21,г) можно переписать в форме
44
1
(x)
(x)
(x)
a
m
i
i
i
i
i
iI
f
g
g
.
На рис. 1.8 в точке x
достигается минимум и выполняется приве-
денное равенство. В других точках это равенство не выполняется.
Замечание 1.10. При 0 0
справедливы два важных утверждения:
1) если функции (x)
f,(x)
i
g,
1,...,
i
m
, выпуклые, то условия
теоремы 1.7 являются одновременно и достаточными условиями глобаль-
ного минимума;
2) если функции
(x)
f
,
(x)
i
g,
1,...,
i
m
, выпуклые, то условия
теоремы 1.7 являются одновременно и достаточными условиями глобаль-
ного максимума.
В обоих случаях множество допустимых решений X выпукло.
Условие допустимости решения, являющееся следствием постановки
задачи (1.20), включено в (1.21) для удобства формирования алгоритма
решения задачи.
Замечание 1.11. Из условия дополняющей нежесткости следует, что
если ограничение в точке x
пассивное, т.е. (x ) 0
i
g
,то
0
i
,аесли
–
активное, т.е. (x ) 0
i
g
,то
0
i
(для минимума) и
0
i
(для мак-
симума).
3(x) 0
g
1(x) 0
g
1
1(x)
g
2(x) 0
g
3
(x)
fc
2
(x)
fc
1
(x)
fc
U
x
-
(x)
f
1(x )
g
2(x)
g
2
2(x)
g
Рис. 1.8
1
2
3
cc
c
45
Теорема 1.8 (достаточные условия минимума (максимума) первого
порядка).
Пусть имеется точка (x ; λ )
, удовлетворяющая системе (1.21) при
00
, число активных ограничений в точке x
совпадает с числом n
переменных (при этом условие регулярности выполняется). Если
0
i
для всех
a
iI
,тоточкаx
–
точка условного локального минимума. Ес-
ли
0
i
для всех
a
iI
,тоx
–
точка условного локального максимума
в задаче (1.20).
Терема 1.9. (необходимое условие минимума (максимума) второго
порядка).
Пусть x
–
регулярная точка минимума (максимума) в задаче (1.20)
и имеется решение (x ; λ )
системы (1.21). Тогда второй дифференциал
классической функции Лагранжа, вычисленный в точке (x ; λ )
, неотри-
цателен (неположителен):
2
(x,λ)0
dL
(2(x,λ)0
dL)
(1.22)
для всех x
n
dR
таких, что
(x) 0
i
dg
,
a
iI
,
0
i
(
0
i
);
(x) 0
i
dg
,
a
iI
,
0
i
.
Теорема 1.10. (достаточные условия экстремума второго порядка).
Пусть имеется точка (x , λ )
, удовлетворяющая системе (1.21) при
00
. Если в этой точке
2
(x,λ)0
dL(2(x,λ)0
dL)длявсех
ненулевых x
n
dR
таких, что
(x) 0
i
dg,
a
iI
,
0
i
(0)
i
;
(x) 0
i
dg
,
a
iI
,
0
i
,
то точка x
является точкой локального минимума (максимума) в задаче
(1.20).
Замечания 1.12. В рассматриваемой задаче замечание 1.3 и замеча-
ние 1.4 также справедливы с учетом замены (1.13) на (1.21).
Алгоритм
1. Составить обобщенную функцию Лагранжа:
0
0
1
(x, ,λ)
(x)
(x)
m
ii
i
L
f
g
.
46
2. Записать необходимые условия минимума (максимума) первого
порядка
а)
0
(x, ,λ)
0
j
L
x
,
1,...,
j
n
;
б)(x)0
i
g , 1,...,
i
m
.
в)
0
i
,
1,...,
i
m
(для минимума),
0
i
,
1,...,
i
m
(для
максимума);
г)(x)0
ii
g
,
1,...,
i
m
.
3. Решить систему для двух случаев:
1)00
;
2)00
(при этом поделить условия, записанные на шаге 2, на 0
и заменить
0
i
наi
).
В результате найти условно-стационарные точки x
, выделив из них
полученные при 0 0
(они могут быть регулярными точками экстрему-
ма). В каждом из двух случаев следует начинать с рассмотрения 2
m
вари-
антов удовлетворения условия «г» дополняющей нежесткости.
4. Для выделенных на шаге 3 точек проверить достаточные условия
экстремума первого или второго порядка.
Для проверки достаточных условий первого порядка следует:
а) определить число l активных в точке x
ограничений;
б)еслиl n
и
0
i
для всех
a
iI
,товточкеx
–
локальный
минимум. Если l n
и
0
i
для всех
a
iI
,товточкеx
–
локальный
максимум. Если l n
или соответствующие множители Лагранжа не
удовлетворяют достаточным условиям первого порядка, проверить доста-
точные условия второго порядка.
Для проверки достаточных условий второго порядка следует:
а) записать выражение для второго дифференциала классической
функции Лагранжа в точке (x , λ )
:
2
2
11
(x,λ)
(x,λ)
n
n
ij
ij
ij
L
dL
dx dx
xx
;
б) записать условия, накладываемые на первые дифференциалы ак-
тивных ограничений:
47
1
(x)
(x)
0
n
i
i
j
j
j
g
dg
dx
x
,
a
iI
;
0
i
(
0
i
);
1
(x)
(x)
0
n
i
i
j
j
j
g
dg
dx
x
,
a
iI
;
0
i
;
в) исследовать знак второго дифференциала функции Лагранжа для
ненулевых x
d , удовлетворяющих системе (1.23). Если
2
(x,λ)0
dL
,
товточкеx
–
условный локальный минимум. Если
2
(x,λ)0
dL
,тов
точке x
–
условный локальный максимум.
Если достаточные условия первого и второго порядка не выполняют-
ся, следует проверить выполнение необходимых условий второго порядка
(теорема 1.9), следуя аналогичной процедуре. Если они выполняются, то
требуется дополнительное исследование, а если нет, то в точке x
нет ус-
ловного экстремума.
5. Вычислить значения функции в точках условного экстремума.
Алгоритма удобно применять с учетом необходимых и достаточных
условий экстремума приведенных в таблицах 1.4 и 1.5.
Необходимые и достаточные условия первого порядка в задаче
поиска условного экстремума при ограничениях типа неравенств
Таблица 1.4
No
Необходимые условия
x
0
(x, ,λ)0
L
;
(x) 0
ii
g
,
1,...,
i
m
Достаточные условия
0
0
Число активных ограничений l n
1
(x)
i
g
1,...,
i
m
00
,
i
,
1,...,
i
m
i
,
a
iI
Тип условно
стационарной
точки x
2
0
0
0
Условный локальный
минимум
3
0
0
0
Условный локальный
максимум
(1.23)
48
Необходимые и достаточные условия второго порядка в задаче
поиска условного экстремума при ограничениях типа неравенств
(при условии x
0
(x, ,λ) 0
L
,
(x) 0
ii
g
,
1,...,
i
m
)
Таблица 1.5
No
2
(x,λ)
dL
(x)
dgi
,
a
iI
0
i
(0
i
)
(x)
dgi
,
a
iI
0
i
Тип условно стационарной
точки x
10
(0
)0,x0
d
0
Условный локальный
минимум (максимум)
20
(0
)
0
0
Может быть условный
локальный min ( max ).
Требуется дополнительное
исследование
3
0
0
0
Требуется дополнительное
исследование
4
0
0
0
Нет экстремума
Пример 1.19
Найти условный экстремум в задаче
1
2
(x)
extr
fxx
;
2
2
1
1
2
(x)
10
g
x
x
.
Решение
1. Составим обобщенную функцию Лагранжа:
2
2
01
01
2
11
2
(x,,)
()(
1)
L
xx
x
x
.
2. Выпишем необходимые условия экстремума первого порядка:
а)
01
0
11
1
(x,,)
2
0
L
x
x
,
01
0
12
1
(x,,)
2
0
L
x
x
;
б)22
1
210
x
x
;
в)10
(для минимума, 1 0
(для максимума);
г)
2
2
11
2
(
1)0
x
x
.
3. Решим систему для двух случаев.
В первом случае 0 0
. Тогда согласно теореме 1.7 требуется, чтобы
10
.Приэтом 1
10
xx
и не удовлетворяется условие «г» допол-
няющей нежесткости.
49
В втором случае 0 0
. Поделим уравнение системы, приведенной в
п.2, на 0
и заменим
1
0
на1
:
а)
1
11
1
(x, )
12
0
L
x
x
,
1
12
1
(x, )
12
0
L
x
x
;
б)22
1
210
x
x
;
в)10
(для минимума, 1 0
(для максимума);
г)
2
2
11
2
(
1)0
x
x
.
Из условия «г» дополняющей нежесткости следуют два варианта:
1)10
. Тогда условие «а» не выполняется;
2)10
.Тогда
2
2
1
210
x
x
и система имеет два решения
(рис.1.9):
точка A: 1
2
2
2
x
x
,
1
2
2
(в точке A может быть мини-
мум);
точка B: 1
2
2
2
x
x
,
1
2
2
(в точке B может быть мак-
симум).
4. Проверим достаточные условия экстремума. В точках A и B ог-
раничения являются активными, но
1
2
l
n
. Поэтому условия перво-
го порядка не выполняются. Проверим условия второго порядка:
2
2
2
1
11
12
(x,)2
2
dL
dx
dx
,
1
11
22
(x) 2
2
0
dg
xdx
xdx
.
В точках A и B выполняется
1
2
dx dx
. Так как
2
2
11
()4
dLA
dx
2
2
22
0
dx
при
20
dx , то в точке A – регулярный локальный ус-
ловный минимум (строка 1 в табл. 1.5). Так как
2
2
12
()4
dLB
dx
2
2
22
0
dx
при
20
dx , то в точке B – регулярный локальный ус-
ловный максимум (табл. 1.5, строка 2). С другой стороны, функции (x)
f
и
1
2
(x)
f
xx
–
выпуклые и ограниченные (см. определения 1.7 и
1.8), поэтому в точках A и B достигается глобальный экстремум (замеча-
ние 1.10). Достаточные условия первого и второго порядка проверялись
для демонстрации методики.
50
5. Вычислим значения функции в точках условного экстремума:
()2
fA
,
()2
fB
. Графическое решение задачи изображено на рис.
1.9.
Пример 1.20
Найти условный максимум в задаче
1
(x)
max
fx
;
1
2
(x)
0
g
x
,
3
2
2
1
(x)
(1)0
g
x
x
.
Решение.
1. Составим обобщенную функцию Лагранжа:
3
012
01
1
2
22
1
(x,,,)
()
(1)
L
x
x
x
x
.
2. Выпишем необходимые условия максимума первого порядка:
а)
2
0
0
2
1
1
(x, ,λ)
3(1)0
L
x
x
,
0
1
2
2
(x, ,λ)
0
L
x
;
б)20
x
,
3
2
1
(1)0
x
x
;
в)10
,
20
;
г)1
2
()0
x
,
3
22
1
(1)0
x
x
.
3. Решим систему для двух случаев.
2
2
1(x) 0
g
2
x
1
x
A
B
(x) 2
f
(x) 0
f
Рис. 1.9
(x) 2
f
2
2
0
51
В первом случае 0 0
,тогда 1 1
x
,
20
x
. Приэтом 1
20
,
например,
1
2
1
.
Получили условно стационарную точку
x
(1; 0)T
,
00
.
На рис.1.10 показано, что в точке x
(1; 0)T
достигается нерегуляр-
ный локальный и глобальный максимум. В ней условие линейной незави-
симости градиентов
1(x ) (0; 1)T
g
,
2 (x ) (0;1)T
g
не выполняется,
и антиградиент целевой функции не может быть представлен в виде непо-
ложительной линейной комбинации градиентов активных ограничений.
Условие «а» выполняется только при 0 0
. Покажем это.
Во втором случае 0 0
. Тогда разделим уравнения системы, приве-
денной в п.2, на 0
и заменим
1
0
на1
,
2
0
на2
. Имеем:
2
2
1
13(1)0
x
,
1
20
;
20
x
,
3
2
1
(1)0
x
x
;
10
,
20
;
1
2
()0
x
,
3
22
1
(1)0
x
x
.
Рассмотрим четыре варианта выполнения условия дополняющей не-
жесткости:
1
1
1(x )
g
2
x
1
x
(x) 1
f
(x)
f
Рис. 1.10
1
2
(x)
0
g
x
(x) 0.5
f
x
0
2(x)
g
2(x) 0
g
X
52
1)120
. Из первого уравнения следует, что система несовме-
стна;
2)10
,20
. Из первого уравнения также следует, что система
несовместна;
3)10
,20
. Из второго уравнения получаем, что 1
20
,
т.е . имеется противоречие;
4)10
,20
,Тогда 2 0
x,11
x и первое уравнение не удов-
летворяется.
Новых условно стационарных точек не найдено. Поэтому в задаче
имеется только одна точка x
(1; 0)T
нерегулярного максимума с
(x) 1
f .
Пример 1.21
Найти условный экстремум в задаче
2
2
1
2
(x)( 2)( 3) extr
f
x
x
;
2
2
1
1
2
(x)
520
g
x
x
.
Решение
1. Составим обобщенную функцию Лагранжа:
2
2
2
2
01
0
1
2
11
2
(x,,)
(2)(3)
(
52)
L
x
x
x
x
.
2. Выпишем необходимые условия экстремума первого порядка:
а)
01
01
11
1
(x,,)
2(2)2
0
L
x
x
x
,
01
02
12
2
(x,,)
2(3)2
0
L
x
x
x
;
б)22
1
2520
x
x
;
в)10
, (для минимума),
10
(для максимума);
г)
2
2
11
2520
x
x
.
3. Решим систему для двух случаев.
В первом случае 0 0
.Тогда10
согласно теореме 1.7. Поэтому
10
x,20
x и не выполняется условие «г» дополняющей нежесткости.
Во втором случае 0 0
. Поделим уравнения системы, приведенной
вп.2,на 0
с заменой
1
0
на1
:
53
а)
1
1
11
1
(x, )
2(2)2
0
L
x
x
x
,
1
2
12
2
(x, )
2(3)2
0
L
x
x
x
;
б)22
1
2520
x
x
;
в)10
(для минимума),
10
(для максимума);
г)
2
2
11
2520
x
x
.
Рассмотрим два варианта выполнения условия «г» :
1)10
.Тогда12
x,23
x и выполняются необходимые условия
и для минимума, и для максимума (табл. 1.4, строка 1 и 2). Имеем условно
стационарную точку A : 1 2
x
,
23
x
,
10
;
2)10
.Тогда
2
2
1
2520
x
x
и система имеет решение, которое
определяется точкой B : 1 4
x
,
26
x
,
1
1
2
иточкойC: 1
4
x
,
2
6
x
,
1
3
2
.Таккак10
в обеих точках, то в них минимума
нет, но может быть максимум.
4. Проверим достаточные условия экстремума. В условно стационар-
ных точках B и C ограничение превращается в равенство, т.е. активно.
Так как число активных ограничений 1 2
l
n
, то условия первого
порядка не выполняются. Так как функция
2
2
1
2
(x)(2)(3)
f
x
x
не является выпуклой (см. определение 1.8), то необходимые условия не
являются достаточными (замечаний 1.10). Проверим условия второго по-
рядка:
2
2
2
1
1
1
2
(x,λ)(22) (22)
dL
dx
dx
.
В точке A ограничение не является активным. Так как 1 0
,то
2
2
2
1
2
(x,λ)2
2
0
dL
dx dx
при
0
dx . Поэтому в точке A – услов-
ный локальный минимум (строка 1 в табл. 1.5). Так как целевая функция
(x)
f выпуклая и множество допустимых решений выпукло (рис. 1.11), то
можно заключить, что в данном случае необходимое условие минимума
является достаточным. В точке A – глобальный минимум (замечаний
1.10). В точках
BиC
ограничение активно. Поэтому
54
1
11
22
(x) 2
2
0
dg
xdx
xdx
.
ВточкахBиC
выполняется
1
2
3
2
dx
dx
. Так как
2
2
2
2
2
3
()
0
2
dLB
dx
dx
при
20
dx,а
1
1
0
2
, то достаточные условия максимума не выполняются (табл.
1.5, строка 1). Так как
2
()0
dLB привсех
2
dx , то и необходимое усло-
вие максимума второго порядка в точке B не выполняется (табл. 1.5,
строка
2). Поэтому
в
ней
нет
экстремума.
Так как
2
2
2
2
2
3
()
0
2
dLC
dx
dx
при
20
dx , то достаточные условия
максимума выполняются. В точке C условный локальный максимум
(строка 1 в табл. 1.6).
5. Вычислим значения функции в точках экстремума ( ) 0
fA,
()117
fC
.
Пример 1.22
Найти условный минимум в задаче
1
2
(x)
min
fxx
,
2
2
1
1
2
(x)
(1)10
g
x
x
,
2
1
(x)
0
g
x
,
3
2
(x)
0
g
x
.
1(x) 0
g
2
x
1
x
2
A
B
Рис. 1.11
4
C
52
4
6
()117
fC
3
()13
fB
()0
fA
55
Решение.
Решаем задачу графическим методом. Геометрическая интерпретация
решения представлена на рис. 1.12.
Как следует из рис.1.12, глобальный минимум достигается в точке A :
1
20
x
x
.
В точке A все три ограничения активны и их градиенты линейно за-
висимы, так как
1()(0;2)T
gA
,
2() (1;0)T
gA
,
3()(0;1)T
gA
и
010
2
3
201
rang
m
(см. определение 1.19). Условие регулярности в теореме 1.4 не выполняет-
ся. Условие (1.21 а) в ней имеет вид
0
11
22
33
()
()
()
()
fA
gA
gA
gA
или
0
1
2
3
1
0
1
0
1
2
0
1
.
Если00
, то не существует таких неотрицательных 1
,2
,3
,
чтобы сумма, стоящая справа, равнялась нулю. В этом случае условно ста-
ционарных точек нет.
Если00
, можно поделить равенство на 0
, заменяя
1
0
на1
,
2
0
на2
,
3
0
на3
. При этом равенство будет справедливо при
1
1()
gA
1
x
()
fA
Рис. 1.12
2
1
(x)
0
g
x
(x) 0
f
2
A
1(x) 0
g
3
2
(x)
0
g
x
1
2
x
3()
gA
2()
gA
1
56
1
1
2
,
21
,
30
. Это свидетельствует о том, что первое и второе
ограничения активны: 1 ( ) 0
gA,2()0
g A , а третье не является актив-
ным. Заметим, что третье ограничение в задаче является «лишним», так
как его добавление не меняет множества допустимых решений. Хотя усло-
вие регулярности в точке A не выполняется, она является точкой регуляр-
ного минимума, так как 0 0
.
Приведем условия оптимальности Куна - Таккера в задаче выпуклого
программирования (1.20) для недифференцируемых функций.
Определение 1.21. Точка (x ; λ )
называется седловой точкой клас-
сической функции Лагранжа задачи (1.20), если
(x,λ) (x,λ) (x,λ)
L
L
L
длявсехx U
ивсех
1
λ ( ,...,
)m
, где
0
i
, 1,...,
i
m
.
Доказано [7], что необходимыми и достаточными для седловой точки
функции Лагранжа задачи (1.20) являются следующие условия:
x
(x,λ) min(x,λ)
n
R
L
L
;
(x) 0
ii
g
,
1,...,
i
m
.
Теорема 1.11. (о седловой точке классической функции Лагранжа).
Для того чтобы точка x
n
R
была решением задачи выпуклого
программирования (1.20), допустимое множество которой удовлетворя-
ет условию регулярности, необходимо и достаточно, чтобы существовал
вектор λ
m
R
,
0
i
, 1,...,
i
m
,такой,что(x;λ)
–
седловая точ-
ка классической функции Лагранжа этой задачи.
1.5 . Условный экстремум при смешанных ограничениях
Даны дважды непрерывно дифференцируемые
целевая функция
1
(x) ( ,...,
)n
ffxx
и функции
ограничений типа равенств и неравенств: (x) 0
i
g,1,...,
i
k
;(x)0
i
g,
1,...,
ik
m
, определяющие множество допустимых решений X .
Требуется исследовать функцию (x)
f на экстремум, т.е. определить
точки x
X
ее локальных минимумов (максимумов) на множестве X :
x
(x) min (x)
X
f
f
;
x
(x) max(x)
X
f
f
,
(1.24)
Постановка задачи
57
где
(x) 0, 1,..., ,
;
x:
(x) 0,
1,...,
;
i
i
g
i
kkn
X
g
ik
m
.
Для решения задачи (1.24) находятся
точки x
локального экстремума с по-
мощью необходимых и достаточных условий минимума и максимума пер-
вого и второго порядка при смешанных ограничениях (порядок условий
определяется порядком используемых производных). Вычисляются значе-
ния (x)
f функции в найденных точках локального экстремума.
Теорема 1.12 (необходимые условия минимума (максимума) первого
порядка).
Пусть x
–
точка локального минимума (максимума) в задаче (1.24).
Тогда найдется такое число 0
и вектор
1
λ ( ,...,
)T
m
, неравные од-
новременно нулю и такие, что выполняются следующие условия:
–
условие стационарности обобщенной функции Лагранжа по x :
0
(x, ,λ)
0
j
L
x
,
1,...,
j
n
(1.25,а)
–
условие допустимости решение.
(x) 0
i
g
,
1,...,
i
k
;(x)0
i
g,
1,...,
ik
m
;
(1.25,б)
–
условие неотрицательности для условного минимума:
0
i
,
1,...,
ik
m
(1.25,в)
(условие неположительности для условного максимума:
0
i
,
1,...,
ik
m
);
–
условие дополняющей нежесткости:
(x) 0
ii
g
,
1,...,
ik
m
.
(1.25,г)
Если при этом градиенты активных ограничений-неравенств и огра-
ничений-равенств в точке x
линейно независимы (выполняется условие
регулярности), то 0 0
.
Точки x
удовлетворяющие системе (1.25), называются условно ста-
ционарными.
Необходимые условия экстремума первого порядка формулируются
отдельно для максимума и минимума.
Если в решаемой задаче ограничения записаны в форме
(x) 0
i
gто
их необходимо переписать в виде, используемом в (1.24): (x) 0
i
g
.
Стратегия решения задачи
58
Далее будем использовать множество индексов ограничений, актив-
ных в точке x
, которое обозначим через a
I.
При решении задач поиска условного максимума можно использовать
необходимые и достаточные условия минимума, применяя преобразова-
ние, описанное в замечании 1.1.
Так как точка x
заранее неизвестна, то проверка условия регулярно-
сти затруднена, поэтому рекомендуется следовать алгоритму, описанному
в замечании 1.2.
Условие (1.25 а) в регулярной точке экстремума ( 0 0
) отражает
тот факт, что антиградиент целевой функции является неотрицательной
(неположительной в случае максимума) линейной комбинацией градиен-
тов функций, образующих активные ограничения-неравенства в точке x
и ограничения-равенства.
Замечания 1.13. При 0 0
справедливы два важных утверждения:
1) если функции (x)
f,(x)
i
g,
1,...,
ik
m
, выпуклые, а функции
(x)
i
g , 1,...,
i
k
, линейные, то условия теоремы 1.12 являются одновре-
менно и достаточными условиями глобального минимума;
2) если функции
(x)
f
,
(x)
i
g,
1,...,
ik
m
, выпуклые, а функции
(x)
i
g , 1,...,
i
k
, линейные, то условия теоремы 1.12 являются одновре-
менно и достаточными условиями глобального максимума.
В обоих случаях множество допустимых решений X выпукло.
Следует подчеркнуть, что условия дополняющей нежесткости и зна-
коопределенности множителей Лагранжа записываются только для огра-
ничений-неравенств.
Условие допустимости решения, являющееся следствием постановки
задачи (1.24), включено в (1.25) для удобства формирования алгоритма
решения.
Из условия дополняющей нежесткости (1.25 г) следует, что если ог-
раничение-неравенство в точке x
пассивное, т.е. (x ) 0
i
g
,то00
,а
если – активное, т.е. (x ) 0
i
g
,то00
, (для минимума) и 0 0
(для
максимума).
Теорема 1.13 (достаточные условия минимума (максимума) первого
порядка).
Пусть имеется точка (x ; )
, удовлетворяющая системе (1.25) при
00
, суммарное число активных ограничений-неравенств в точке x
и
ограничений-равенств совпадает с числом n переменных (при этом усло-
59
вие регулярности выполняется). Если
0
i
для всех
a
iI
,тоточкаx
–
точка условного локального минимума в задаче (1.24). Если
0
i
для
всех
a
iI
,тоx
–
точка условного локального максимума.
Теорема 1.14 (необходимые условия минимума (максимума) второго
порядка).
Пусть x
–
регулярная точка минимума (максимума) в задаче (1.24)
и имеется решение (x ; )
системы (1.25). Тогда второй дифференциал
классической функции Лагранжа, вычисленный в точке (x ; )
, неотри-
цателен (неположителен):
2
(x,λ) 0
dL
2
(x,λ)0
dL
для всех x
n
dR
таких, что
(x) 0
i
dg
,
1,...,
i
m
и
a
iI
,
0
i
(
0
i
);
(x) 0
i
dg,
a
iI
,
0
i
.
Необходимые и достаточные условия первого порядка в задаче
поиска условного экстремума при смешанных ограничениях
Таблица 1.6
Необходимые условия
x
0
(x, ,λ)0
L
;
(x) 0
ii
g
,
1,...,
im
p
(x) 0
i
g
,
1,...,
i
m
Достаточные условия
0
0
Число ограничений l n
No
п\п
(x)
i
g
1,...,
im
p
00
,
i
,
1,...,
i
m
i
,
a
iI
Тип условно стацио-
нарной точки x
1
0
0
0
Условный локальный
минимум
2
0
0
0
Условный локальный
максимум
60
Теорема 1.15 (достаточные условия экстремума второго порядка).
Пусть имеется точка (x ; )
, удовлетворяющая системе (1.25) при
00
. Если в этой точке
2
(x,λ) 0
dL
2
(x,λ)0
dL
для всех
ненулевых x
n
dR
таких, что
(x) 0
i
dg
,
1,...,
i
m
и
a
iI
,
0
i
(
0
i
);
(x) 0
i
dg,
a
iI
,
0
i
,
то точка x
является точкой локального минимума (максимума) в задаче
(1.24).
Необходимые и достаточные условия второго порядка в задаче
поиска условного экстремума при смешанных ограничениях
(при условии x
0
(x, ,λ) 0
L
,
(x) 0
ii
g
,
1,...,
i
m
)
Таблица 1.7
No
п\п
2
(x,λ)
dL
(x)
dgi
,
a
iI
0
i
(0
i
)
(x)
dgi
,
a
iI
0
i
Тип условно стационарной
точки x
10
(0
)0,x0
d
0
Условный локальный
минимум (максимум)
20
(0
)
0
0
Может быть условный
локальный min ( max ).
Требуется дополнительное
исследование
3
0
0
0
Требуется дополнительное
исследование
4
0
0
0
Нет экстремума
Алгоритм
1. Составить обобщенную функцию Лагранжа:
0
0
1
(x, ,λ)
(x)
(x)
m
ii
i
L
f
g
.
2. Записать необходимые условия минимума (максимума) первого
порядка:
а)
0
(x, ,λ)
0
j
L
x
,
1,...,
j
n
;
61
б)(x)0
i
g
,
1,...,
i
k
;
(x) 0
i
dg,
1,...,
ik
m
;
в)00
,
1,...,
ik
m
(для минимума), 0 0
,
1,...,
ik
m
(для максимума);
г)(x)0
iig
,
1,...,
ik
m
.
3. Решить систему для двух случаев:
1)00
;
2)00
(при этом поделить условия «а», «в», «г» на 0
и заме-
нить
0
i
наi
).
В результате найти условно стационарные точки x
, выделив из них
полученные при 0 0
(они могут быть регулярными точками экстрему-
ма). В каждом из двух случаев следует начинать с рассмотрения 2
mk
ва-
риантов удовлетворения условия «г» дополняющей нежесткости.
4. Для выделенных на шаге 3 точек проверить достаточные условия
экстремума первого или второго порядка.
Для проверки достаточных условий первого порядка следует:
а) определить число l ограничений-равенств и активных ограниче-
ний-неравенств;
б)если l n
и
0
i
для всех
a
iI
, т.е. для всех активных ограни-
чений неравенств, то в точке x
–
локальный минимум. Если l n
и
0
i
для всех
a
iI
,товточкеx
–
локальный максимум. Если l n
или соответствующие множители Лагранжа не удовлетворяют достаточ-
ным условиям первого порядка, проверить достаточные условия второго
порядка.
Для проверки достаточных условий второго порядка следует:
а) записать выражение для второго дифференциала классической
функции Лагранжа в точке (x ; )
:
2
2
11
(x,λ)
(x,λ)
n
n
ij
ij
ij
L
dL
dx dx
xx
;
б) записать условия, накладываемые на первые дифференциалы огра-
ничений равенств и активных в точке x
ограничений неравенств:
1
(x)
(x)
0
n
i
i
j
j
j
g
dg
dx
x
,
1,...,
i
k
и
a
iI
;
0
i
(
0
i
); (1.26)
62
1
(x)
(x)
0
n
i
i
j
j
j
g
dg
dx
x
,
a
iI
;
0
i
;
в) исследовать знак второго дифференциала функции Лагранжа для
ненулевых x
d удовлетворяющих (1.26). Если
2
(x,λ) 0
dL
товточке
x
–
условный локальный минимум. Если
2
(x,λ) 0
dL
,товточкеx
– условный локальный максимум. Если достаточные условия экстремума
не выполняются, следует проверить выполнение необходимых условий
второго порядка (теорема 1.14), следуя аналогичной процедуре. Если они
выполняются, то требуется дополнительное исследование, а если нет, то в
точке x
нет условного экстремума.
5. Вычислить значения функции в точках условного экстремума.
Условия экстремума в задаче (1.24) приведены в табл. 1.6, 1.7.
Достаточные и необходимые условия экстремума второго порядка
проверяются в условно стационарных точках, которые удовлетворяют сис-
теме (1.25) при 0 0
, так как для практики безусловно представляет ин-
терес случай, когда в функции Лагранжа присутствует целевая функция,
экстремум которой ищется.
Рассмотрим пример на идентификацию точек с помощью этих усло-
вий.
Пример 1.23.
Сделать заключение об оптимальности следующих точек:
(1)
x
(0; 0)T
,
(2)
1
x
1;
2
T
и
(3)11
x
;
36
T
для задачи
2
2
1
2
(x)
2
min
fxx
;
2
2
1
2
1
2
5,
221.
x
x
x
x
Решение.
1. Составим классическую функцию Лагранжа:
2
2
2
2
1
2
11
2
2
1
2
(x, λ)
2
(
5)(221)
L
x
x
x
x
x
x
.
2. Выпишем необходимые условия экстремума первого порядка
(1.25):
1
11
2
1
(x, λ)
22
2
0
L
x
x
x
,
(1)
2
12
2
2
(x, λ)
42
20
L
x
x
x
,
(2)
63
2
2
1
250
x
x
,
(3)
1
2
2210
x
x
,
(4)
10
,
(5)
2
2
11
2
(
5)0
x
x
.
(6)
3. Проверим точку (1)
x
(0; 0)T
. Условие (4) не удовлетворяется, т.е.
точка не принадлежит области допустимых решений (ОДР). Этого доста-
точно, чтобы сделать вывод о том, что точка
(1)
x не является точкой экс-
тремума.
Точка
(2)
1
x
1;
2
T
принадлежит ОДР, т.к. удовлетворяются усло-
вия (3) и (4). Из условия (6) следует: 1 0
,т.к.
2
2
1
250
x
x
. Из усло-
вий (1) и (2) находим 2
1
и21
соответственно (что не является
решением). Следовательно, условия теоремы 1.12 не удовлетворяются, и
точка
(2)
x не является точкой экстремума.
Точка
(3)11
x
;
36
T
принадлежит ОДР, т.к. удовлетворяются ус-
ловия (3) и (4). Из условия (6) следует, что 1 0
. Тогда из условий и (1),
и (2) следует: 2
1
3
. Следовательно, условия теоремы 1.12 удовлетво-
ряются и точка
(3)
x является точкой минимума целевой функции, значе-
ние которой
(3)
min
1
x
6
f
.
Пример 1.24
Найти условный экстремум в задаче
2
1
2
(x)
extr
fxx
;
1
1
2
(x)
60
g
xx
,
2
1
(x) 1
0
g
x
,
2
2
3
1
2
(x)
260
g
x
x
.
Решение.
1. Составим обобщенную функцию Лагранжа:
2
2
2
0
01
2
11
2
2
1
31
2
(x, ,λ) (
)(
6)(1)(
26)
L
x
x
xx
x
x
x
.
2. Выпишем необходимые условия экстремума первого порядка:
а)
0
01
1
2
31
1
(x, ,λ)
2
2
0
L
x
x
x
,
64
0
0
1
32
2
(x, ,λ)
2
0
L
x
x
;
б)1260
xx
,
1
1
0
x
,
2
2
1
2260
x
x
;
в)20
,
30
(для минимума),
20
,
30
(для максимума);
г)2
1
(1)0
x
,
2
2
31
2
(
26) 0
x
x
.
3. Решим систему для двух случаев.
В первом случае 0 0
. Тогда условие «а» имеет вид
1
2
31
2
0
x
,
1
32
2
0
x
.
Рассмотрим два варианта удовлетворения условия «г» дополняющей
нежесткости:.
1)20
,30
.Тогда10
и не удовлетворяются условия тео-
ремы 1.12;
2)20
,30
.Тогда10
и20
, что противоречит условию
20
;
3)20
,30
.Тогда
2
2
1
2260
x
x
,
1
260
xx
,
1
31
2
0
x
,
1
32
2
0
x
.
Из двух последних уравнений следует:
32
1
2(
)0
xx
.Таккак30
,
то1
2
xx
. Из двух первых уравнений следует:
11
x,25
x;
15
x,21
x;
т.е. 1
2
xx
. Поэтому система несовместна;
4)20
,30
.Тогда
2
2
1
2260
x
x
,
1
1
0
x
1
260
xx
.
Система удовлетворяется в точке 1 1
x,25
x
. Условия «а» примут вид
1
2
3
20
,
1
3
100
.
65
Отсюда 1
3
10
и2
3
8
.Таккак30
,то2
и 3 имеют раз-
ные знаки, что противоречит условию и минимума, и максимума.
Во втором случае 0 0
. Поделим уравнения системы, приведенной
вп.2,на 0
и заменим
1
0
на1
,
2
0
на2
,
3
0
на3
. Условие «а» при-
нимает форму
1
1
2
31
2
2
0
x
x
,
1
32
1
2
0
x
;
Условия «б» – «г» сохраняют вид. Рассмотрим четыре варианта выполне-
ния условий «г» дополняющей нежесткости:
1)20
,30
.Тогда11
, 1
1
2
x
, что не удовлетворяет огра-
ничениям «б»;
2)20
,30
.Тогда11
x,25
x,11
,23
. Получена ус-
ловно стационарная точка A : 1 1
x
,
25
x
,
11
,23
,вкоторой
удовлетворяются необходимые условия минимума;
3)20
,30
.Тогда
2
2
1
2260
x
x
,
1
260
xx
,
1
1
31
2
2
0
x
x
,
1
32
1
2
0
x
;
Отсюда получаем точки с координатами 1 1
x,25
xи15
x,21
x .В
первой точке имеем
1
3
2
20
,
1
3
1
100
,
откуда 1
11
4
,
3
3
8
. Во второй точке
1
3
10
100
,
1
3
1
20
,
откуда 1
15
4
,3
11
8
.
Получены условно стационарные точка A :
11
x
,
25
x
,
1
11
4
,
20
, 3
3
8
, в которой удовлетворяются
66
необходимые условия минимума, и точка B : 1 5
x
,
21
x
,
1
15
4
,
20
,3
11
8
, в которой удовлетворяются необходимые условия мак-
симума;
4)20
,30
.Тогда
2
2
1
2260
x
x
,
1
1
0
x
1
260
xx
выполняется в точке 1 1
x,25
x
. Условия «а» принимает вид
1
2
3
2
20
,
1
3
1
100
.
Отсюда 1
3
110
и
3
2
38
0
.Таккак20
и30
,атакже
они должны быть одного знака, то последнее равенство выполняется толь-
копри 20
,30
,вчастности,при 3 0.1
,22.2
.
При этом
10
. Получили ту же условно стационарную точку A : 1 1
x
,
25
x
,
10
,2 2.2
,30.1
.
4. Проверим достаточные условия экстремума первого порядка. Ог-
раничение-равенство в точках A и B естественно выполняется. В точке
A активно второе ограничение и, следовательно,
2
l
n
.
Так как
230
, то в точке A активно третье ограничение и поэтом у
2
l
n
. Таккак 3
3
0
8
, то в точке A – условный локальный ми-
нимум. В точке B активно третье ограничение и, следовательно,
2
l
n
.
Так как 3
11
0
8
, то в точке B – условный локальный
максимум (табл. 1.6, строка 2).
Проверим выполнение достаточных условий экстремума второго по-
рядка (из методических соображений):
2
2
2
3
1
32
(x,λ)(22)
2
dL
dx
dx
.
В точке A активно второе ограничение:
1
1
2
()
0
dgAdxdx
,
2
1
()
0
dgA dx
.
67
Отсюда
1
20
dx dx
и
2
()0
d L A . Поэтому требуется дополнительное
исследование (табл. 1.7, строка 3).
В точке A активно третье ограничение:
1
1
2
()
0
dgAdxdx
,
3
11
22
1
2
()2
2
2
10
0
dgA
xdx
xdx dx dx
.
Отсюда
1
20
dx dx
и
2
()0
dLA
. Поэтому требуется дополнительное
исследование (табл. 1.7, строка 3).
В точке B активно третье ограничение:
1
1
2
()
0
dgBdxdx
,
3
11
22
1
2
()2
2
10
2
0
dgB xdx
xdx
dx dx
.
Отсюда
1
20
dx dx
и
2
()0
d L B . Поэтому требуется дополнительное
исследование (табл. 1.7, строка 3).
В точке A активны второе и третье ограничения:
1
1
2
()
0
dgA dxdx
,
2
1
()
0
dgA
dx
,
3
1
2
()210
0
dgA
dx dx
.
Поэтому
1
20
dx dx
,
2
()0
dLA
и требуется дополнительное иссле-
дование (табл. 1.7, строка 3).
Из рис. 1.13 следует, что в точках A и B – соответственно глобаль-
ные минимум и максимум.
6
1
x
Рис. 1.13
2
1
(x) 1
0
g
x
(x) 0
f
1
A
1(x) 0
g
3(x) 0
g
6
2
x
0
(x) 24
f
(x) 4
f
B
68
Теперь исследуем свойства целевой функции и ограничений. Ограни-
чение-равенство – линейное. Так как целевая функция и функции второго
и третьего ограничений удовлетворяют условиям
20
(x)
0
00
fH
,
2
00
(x)
0
00
g
H
,
3
20
(x)
0
02
g
H
,
то они выпуклы (замечание 1.13).
5. Значения функции в точках условного экстремума:
()4
fA ,
()24
fB
.
Пример 1.25
Найти условный экстремум в задаче
2
2
1
2
(x)( )
extr
f
x
x
,
2
2
1
1
2
(x)
10
g
x
x
,
2
1
(x)
0
g
x
при
2
и
1
.
Решение
1. Составим обобщенную функцию Лагранжа:
2
2
2
2
0
0
1
2
11
2
2
1
(x, ,λ)
()
(
1)()
L
x
x
x
x
x
2. Выпишем необходимые условия экстремума первого порядка:
а)
0
01
11
2
1
(x, ,λ)
2(
)2
0
L
x
x
x
,
0
02
12
2
(x, ,λ)
2
2
0
L
x
x
x
;
б)22
1
210
x
x
,
10
x
.
в)20
, (для минимума),
20
, (для максимума);
г)2
1
()0
x
.
3. Решим систему для двух случаев.
В первом случае 0 0
. Тогда условие «а» имеет вид
11
2
2
0
x
,
12
2
0
x
.
Рассмотрим два варианта удовлетворения условия «г».
69
Если20
,топри 10
не удовлетворяется утверждение 1.12, а
при10
получаем: 1
20
xx
. Тогда не удовлетворяется ограничение-
равенство в условии «б».
Если20
,то10
xи20
, т.е. имеется противоречие.
Во втором случае 0 0
. Поделим уравнения системы, приведенной
вп.2,на 0
с заменой
1
0
на1
,
2
0
на2
. Условие «а» принимает фор-
му
а)
1
11
2
1
(x, λ)
2(
)2
0
L
x
x
x
,
2
12
2
(x, λ)
22
0
L
x
x
x
;
Рассмотрим два варианта удовлетворения условия «г»:
1)20
. Тогда
1
11
2(
)2
0
x
x
,
2
12
2
1
22
2(1)0
x
x
x
,
2
2
1
210
x
x
.
Из второго уравнения следует: 1
1
или20
x
.При11
первое
уравнение несовместно, так как
0
.При20
x получаем 1
1
x .Ог-
раничению «б» удовлетворяет 1 1
x .Тогда1
1
. Получили услов-
но-стационарную точку A : 1 1
x
,
20
x
,
1
1
;20
;
2)20
.Тогда 1 0
x,2
1
x .Изусловия«а»следует 1
1
,
2
2
. Получили две условно-стационарные точки:
B:10
x
,
21
x
,
1
1
;22
;
C:10
x
,
2
1
x
,
1
1
;22
.
При
0
в точках может быть максимум, так как 2 0
,апри
0
–
минимум.
4. Проверим достаточные условия экстремума. Начнем с условий
первого порядка. В точке A ограничение-неравенство не является актив-
ным, поэтому 1
2
l
n
и условия не выполняются. В точках B и C
ограничение-неравенство активное:
2
l
n
.
При
2
получаем
70
2
40
, поэтому в точках B и C – условный локальный максимум
(табл. 1.6, строка 2). При
1
получаем 2 2 0
и поэтому в точках
B и C – условный локальный минимум (табл. 1.6, строка 1).
Проверим достаточные условия экстремума второго порядка.
Исследуем точку A . В ней ограничение-неравенство не является ак-
тивным:
2
2
2
1
1
1
2
()(22) (22)
dLA
dx
dx
,
2
1
11
22
1
()2
2
2
0
dgA xdx
xdx dx
.
Отсюда
10
dx
и
2
2
1
2
()(22)
dLA
dx
.
При
2
получаем
11
и
2
2
2
()4
0
dLA dx
при
20
dx , следовательно, в точке A –
условный локальный минимум (табл. 1.7, строка 1). При
1
получаем
1
2
и
2
2
2
()2
0
dLA
dx
при
20
dx . Поэтому в точке A – услов-
ный локальный максимум (табл. 1.7, строка 1). Исследуем точки B и C
(их можно было бы и не проверять, так как вывод уже сделан). В них огра-
ничение-неравенство
активное.
Так
как
1
1
,
то
2
2
() ()0
dLB dLC
. Т ребуется дополнительное исследование (табл. 1.7,
строка 3). Так как ограничение-равенство не является линейным, нельзя
сделать вывод о глобальном минимуме и максимуме (замечание 1.3). Гра-
фическое решение свидетельствует о том, что в точках B и C при
2
достигается глобальный условный максимум, а при
1
–
глобальный
условный минимум (рис. 1.14).
1(x) 0
g
Рис. 1.14
1(x) 0
g
2
x
1
x
2
A
B
C
2
(x) 5
f
1
(x) 1
f
2(x) 0
g
X
2
x
1
x
1
A
B
C
1
(x) 4
f
(x) 2
f
2(x) 0
g
X
а
б
71
Задачи для самостоятельного решения
1. Найти точки экстремума функции
2
2
2
1
(4)
(x)(1)
16
x
f
x
на
множестве
2
R.
Ответ: в точке x
(1;4)T
–
одновременно локальный и гло-
бальный безусловный максимум.
2. Найти точки экстремума функции
2
2
1
12
2
(x)
4
4
fxxxx
на
множестве
2
R.
Ответ: так как
2
1
2
(x)( 2)
f
x
x
, то во всех точках прямой с урав-
нением 1
2
2
x
x
достигается одновременно локальный и глобальный ми-
нимум.
3. Проверить знакоопределенность матрицы Гессе целевой функции
3
3
1
2
12
(x)
3
fxxxx
вточке (0;0).
Ответ: матрицы Гессе и соответствующая квадратичная форма не-
определенные.
4. Проверить знакоопределенность матрицы Гессе целевой функции
2
2
1
12
2
(x)
4
4
fxxxx
, Исследовать ее на выпуклость.
Ответ: матрицы Гессе положительно полуопределенная, функция
выпуклая.
5. Найти безусловный экстремум функции
2
2
1
2
12
1
(x)434
f
x
x
xxx
.
Ответ: в точке x
(316; 18)T
–
локальный и одновременно
глобальный минимум.
6. Проверить, является ли точка x
(0; 0; 0)T
точкой безусловного
экстремума функции
2
2
2
1
2
3
12
13
23
(x)
236
8
4
fxxxxxxxxx
.
Ответ: не является, так как в ней не выполняются необходимые ус-
ловия экстремума второго порядка.
7. Найти безусловный экстремум функции
3
2
2
1
12
12
2
(x)24
10
f
x
xx
xxx
.
Ответ: в точке x
(1; 1)T
–
локальный минимум; в точке
x
(0; 0)T
нет экстремума, так как не выполняются необходимые усло-
вия экстремума второго порядка.
72
8. Найти безусловный экстремум функции
3
2
1
12
2
1
2
(x)
234
fxxxxxx
.
Ответ: в точке x
(12; 54)T
–
локальный минимум; в точке
x
(13; 53)T
нет экстремума, так как не выполняются необходи-
мые условия экстремума второго порядка.
9. Найти безусловный экстремум функции
4
2
1
2
(x)(1)(3)
f
x
x
.
Ответ: в точке x
(1; 3)T
выполняется необходимое условие экс-
тремума второго порядка, т.е.
(x) 0
H .Таккакдлялюбых
2
xR
справедливо: (x ) 0 (x)
f
f
, то по определению 1.1 точка x
является
точкой глобального минимума.
10. Найти безусловный экстремум функции
22
2
2
1
1
(x) (
)(1)
f
xx
x
.
Ответ: в точке x
(1; 1)T
–
локальный минимум.
11. Проверить, является ли точка x
(1; 1)T
точкой безусловного
минимума функции
22
2
2
2
1
1
2
(x) (
)(1)10(1)
f
xx
x
x
.
Ответ: является.
12. Найти безусловный экстремум функции
2
2
12
12
12
(x) 3
f
xx xx
xx
.
Ответ: в точке
(1)
x
(1; 1)T
–
локальный максимум; в точке
(2)
x
(0; 0)T
нет экстремума.
13. Найти условный экстремум в задаче
1
2
(x)
extr
fxx
,
2
2
1
1
2
(x)
80
g
x
x
.
Ответ: в точке
(1)
x
(2; 2)T
–
локальный минимум; в точке
(2)
x
(2; 2)T
–
условный максимум.
14. Решить задачу
2
2
1
2
(x)
min
fxx
,
2
2
1
1
2
(x)
280
g
x
x
.
73
Ответ: в точках
(1)
x
(0; 2)T
и
(2)
x
(0; 2)T
–
условный мини-
мум.
15. Решить задачу
2
2
1
1
2
2
(x)44
85extr
f
x
xx
x
,
1
1
2
(x) 2
60
g
xx
.
Ответ: в точке x
(2.25; 1.5)T
–
условный максимум.
16. Найти условный экстремум в задаче
2
2
1
2
(x)( 2)( 2) extr
f
x
x
;
2
2
1
1
2
(x)
10
g
x
x
,
2
1
(x)
0
g
x
,3
2
(x)
0
g
x
.
Ответ: в точке
(1)
x
(0; 0)T
–
условный минимум, а в точке
(2)
x
(22; 22)T
–
условный максимум.
17. Решить задачу
2
2
1
2
(x)
(4)min
fxx
,
2
2
1
1
2
(x)
4
g
x
x
,
2
2
2
1
2
(x) 4
4
g
x
x
.
Ответ: в точке x
(0; 2)T
–
условный минимум.
18. Решить задачу
2
2
1
2
(x) 2
min
f
x
x
,
2
2
1
1
2
(x)
4
g
x
x
,
2
2
2
1
2
(x) 4
4
g
x
x
.
Ответ: в точках
(1)
x
(1; 0)T
и
(2)
x
(1;0)T
–
условный мини-
мум.
19. Решить задачу
2
1
1
2
(x) 6
max
f
xx
x
,
1
2
2324
x
x
,
1
2
215
x
x
,
1
2
3224
x
x
,
10
x,20
x,24
x.
Ответ: в точке x
(3; 4)T
–
условный максимум.
20. Найти условный экстремум в задаче
2
2
1
2
(x)
extr
fxx
;
74
1
1
(x)
10
g
x
,
2
1
2
(x)
20
g
xx
.
Ответ: в точке
(1)
x
(1; 0)T
–
условный локальный минимум; в
точке
(2)
x
(1; 1)T
–
условный локальный максимум (после дополни-
тельного исследования).
21. Найти условный экстремум в задаче
2
1
2
(x)
extr
fxx
;
1
1
2
(x)
10
g
xx
,
2
2
2
1
2
(x)
50
g
x
x
.
Ответ: в точке
(1)
x
(3 2;12)T
–
условный локальный максимум
и
(1)
(x)54
f
; в точке
(2)
x
(2; 1)T
–
условный локальный минимум
(после дополнительного исследования) и
(2)
(x)1
f
;вточке
(3)
x
(1; 2)T
–
условный глобальный минимум (после дополнитель-
ного исследования) и
(3)
(x)5
f
.
75
Глава 2
МЕТОДЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача линейного программирования является наиболее полно иссле-
дованным частным случаем задач математического программирования.
Основными методами решения задачи линейного программирования яв-
ляются симплекс-метод Данцига и его модификация – двойственный сим-
плекс-метод.
2.1. Основные понятия и определения
Общая форма математической модели задачи линейного програм-
мирования имеет следующий вид:
1
(x)
max
n
jj
j
f
cx
,
(2.1,а)
1
n
ijj
i
j
axb
, 1,...,
i
k
;
(2.1,б)
1
n
ijj
i
j
axb
,
1,...,
ik
m
;
(2.1,в)
0
jx,
1,...,
j
n
.
(2.1,г)
Функция (2.1,а) называется целевой функцией. Ограничения (2.1,б) –
(2.1,г) образуют множество допустимых решений
n
XR
.
Искомое ре-
шение
12
x
( , ,...,
)T
n
xx
x
X
задачи (2.1) называется оптимальным
решением.
Замечание 2.1. Задача поиска минимума функции (x)
f сводится к
эквивалентной задаче поиска максимума путем замены знака перед функ-
цией на противоположный:
x
x
(x) min (x)
max
(x)
X
X
f
f
f
.
76
Симплекс-метод применим только к канонической форме математи-
ческой модели. Математическая модель называется канонической, если в
(2.1) ограничения (2.1,б) – (2.1,в) являются равенствами, т.е. k m
.
Замечания 2.2. С помощью эквивалентных преобразований любую
форму математической модели можно привести в каноническую:
1. В каждое ограничение-неравенство со знаком вводится допол-
нительная неотрицательная переменная со знаком «+», а в каждое ограни-
чение-неравенство со знаком вводится дополнительная неотрицатель-
ная переменная со знаком «–». И наоборот, для перехода от уравнения к
неравенству неотрицательная базисная переменная отбрасывается, т.е.
11
11
...
,
...
,
0;
i
inn
ni
i
i
inn
i
ni
ax
ax
x
b
ax
axb
x
11
11
...
,
...
,
0.
i
inn
ni
i
i
inn
i
ni
ax
ax
x
b
ax
axb
x
2. Если по исходной задаче какая-либо переменная неограниченна по
знаку, например n
x , то ее можно представить в виде
1
2
n
n
n
xx
x
, где
дополнительные переменные
10
n
x ,
20
n
x .
Таким образом, с учетом замечаний 2.2 любая общая форма матема-
тической модели может быть преобразована в каноническую форму.
Каноническая форма математической модели имеет следующий вид:
1
(x)
max
n
jj
j
f
cx
;
(2.2,а)
1
n
ijj
i
j
axb
, 1,...,
i
m
,
(2.2,б)
0
jx,
1,...,
j
n
,
(2.2,в)
где (2.2,а) – целевая функция, (2.2,б) – система ограничений, (2.2,в) – усло-
вия неотрицательности.
Система ограничений (2.2,б) представляет собой систему линейных
алгебраических уравнений. Поэтому в симплекс-методе для поиска реше-
ния используется метод Жордана – Гаусса решения систем уравнений.
Определение 2.1. Решением системы уравнений (2.2,б) называется
вектор
12
x(,,...,
)T
n
xx
x
, для которого все уравнения (2.2,б) являются
верными числовыми равенствами.
Система уравнений (2.2,б) совместна, если у нее есть хотя бы одно
решение. Совместная система определенна, если она имеет единственное
77
решение, и неопределенна, если имеет бесконечное множество решений.
Две системы уравнений эквивалентны (равносильны), если любое решение
первой системы является решением второй и любое решение второй явля-
ется решением первой.
Процесс решения системы уравнений основан на эквивалентных пре-
образованиях исходной системы в систему, решения которой очевидны. В
классическом методе Жордана - Гаусса используются следующие форму-
лы преобразований:
,
rj
rj
rk
a
a
a
r
r
rk
b
b
a
,
ir
;
(2.3,а)
,
rj ik
ij
ij
rk
aa
a
a
a
rik
i
i
rk
ba
bb
a
,
ir
,
(2.3,б)
где
(0)
rk
a
–
разрешающий элемент, относительно переменной xk ко-
торого выполняются преобразования по формулам (2.3); ,
iji
ab
– новые
значения соответствующих коэффициентов и свободных членов системы
уравнений (2.2).
Формуле (2.3,б) соответствует так называемое правило прямоугольни-
ка: на разрешающем rk
aи
преобразуемом ij
a элемен-
тах, как концах одной из
диагоналей прямоугольни-
ка, определяется вторая
диагональ,
соединяющая
элементы ik
aиrj
a . Далее
из текущего значения ij
a
вычитается произведение
элементов ik
aиrj
a , деленное на разрешающий элемент rk
a (рис. 2.1).
Получается новое значение ij
a.
Алгоритм метода Жордана–Гаусса
1. Выбрать в левой части системы уравнений (2.2,б) элемента
0
rk
a , который называется разрешающим элементом. Строка и столбец,
на пересечении которых находится этот элемент называются соответст-
венно разрешающими.
2. Пересчитать элементы разрешающей строки по формулам (2.3,а).
rk
a
ik
a
rj
a
ij
a
Рис. 2.1
,
rj ik
ij
ij
rk
aa
a
a
a
78
3. Пересчитать все остальные элементы системы уравнений (2.2,б) по
формулам (2.3,б). Переменная k
x становится базисной. Вычисления за-
кончить, если построен единичный базис или, если система несовместна,
иначе перейти к шагу 1.
Замечания 2.3
1. Система уравнений несовместна (т.е. не имеет решения), если в ре-
зультате выполнения очередной итерации хотя бы в одном уравнении все
коэффициенты при переменных равны нулю, а свободный член этого урав-
нения не равен нулю.
2. Совместная система уравнений линейно зависима, если в результате
выполнения очередной итерации хотя бы в одном уравнении все коэффи-
циенты при переменных и свободный член становятся равными нулю.
В процессе решения совместная линейно независимая система урав-
нений (2.2) с помощью метода Жордана – Гаусса приводится к следующе-
му виду:
1
n
i
ijj
i
jm
x
x
,
1,...,
i
m
,
(2.4)
где ij
,i
– значения преобразованных коэффициентов системы уравне-
ний. Переменные 1, ...,
m
x
x называются базисными, переменные
1 ,...
m
x
...,
n
x – небазисными (или свободными).
Частное решение системы (2.4) называется базисным решением, если
все свободные переменные принимаются равными нулю, т.е .
i
i
x
,
1,...,
i
m
;
1 ...
0
m
n
x
x
.
Определение 2.2. Опорным планом задачи линейного программиро-
вания в канонической форме называется неотрицательное базисное реше-
ние системы уравнений (2.4).
Определение 2.3. Оптимальным опорным планом называется опор-
ный план, при котором целевая функция (x)
f достигает экстремального
значения.
Определение 2.4. Опорный план называется невырожденным, если
все базисные переменные положительны. Задача при этом называется не-
вырожденной. Если хотя бы одна базисная переменная равна нулю, то
опорный план и соответственно задача называются вырожденными.
79
Пример 2.1
Решить систему уравнений методом Жордана – Гаусса и выполнить
одно преобразование однократного замещения:
1
2
3
4
1
2
3
4
1
2
3
4
3
42,
26,
2
3.
x
x
x
x
x
x
x
x
x
x
x
x
Решение
Решение системы уравнений выполняется в таблицах с использовани-
ем формул (2.3). В каждой таблице клетка с разрешающим элементом вы-
делена двойной линией. На каждой итерации появляется новая базисная
переменная. Процесс решения приведен в таблицах 2.1.
1
.
1 Выбираем произвольно разрешающий элемент
0
rk
a .Напри-
мер,
211
rk
a
a
.
2
.
2 Согласно (2.3,а) пересчитаем вторую строку табл. 2.1,а.
1
.
3 По формуле (2.3,б) (или по правилу прямоугольника) пересчитаем
первую и третью строки табл. 2.1,а:
–
для первой строки табл. 2.1,а имеем:
12
11
3
4
1
a
,
13
11
1
0
1
a
,
14
21
4
6
1
a
,
1
61
2
4
1
b
.
–
для третьей строки табл. 2.1,а имеем:
32
12
1
3
1
a
,
33
12
1
1
1
a
,
34
22
1
3
1
a
,
3
62
3
15
1
b
.
Таблицы 2.1,а
Баз.пер.
1
x
2
x
3
x
4
x
i
b
-
1
–3
1
–4
2
-
1
1
1
2
6
-
2
–1
1
1
–3
Результаты пересчета приведены в табл. 2.1,б. Переходим к шагу 1.
2
.
1 Выбираем разрешающий элемент в первой или второй строках
табл. 2.1,б
0
rk
a . Например,
33
1
rk
a
a
.
Таблицы 2.1,б
Баз.пер.
1
x
2
x
3
x
4
x
i
b
-
0
–4
0
–6
–4
1
x
1
1
1
2
6
-
0
–3
–1
–3
–15
80
2
.
2и
2
.
3 Пересчитаем по формулам (2.3) все элементы табл. 2.1,б.
Таблицы 2.1,в
Баз.пер.
1
x
2
x
3
x
4
x
i
b
-
0
–4
0
–6
–4
1
x
1
–2
0
–1
–9
3
x
0
3
1
3
15
Результаты пересчета приведены в табл. 2.1,в. Переходим к шагу 1.
3
.
1 Выбираем разрешающий элемент в первой строке табл. 2.1,в
0
rk
a . Например,
12
4
rk
a
a
.
3
.
2и
3
.
3 Пересчитаем по формулам (2.3) все элементы табл. 2.1,в.
Таблицы 2.1,г
Баз.пер.
1
x
2
x
3
x
4
x
i
b
2
x
0
1
0
1.5
1
1
x
1
0
0
2
–7
3
x
0
0
1
–1.5
12
Результаты пересчета приведены в табл. 2.1,г. Система решена отно-
сительно переменных 1x , 2
x,3
x (базисные переменные), через перемен-
ную 4
x (свободная переменная).
Итак, система уравнений неопределенна. Общее решение системы:
1
4
72
x
x
,
2
4
1 1.5
x
x
,
3
4
12 1.5
x
x
.
Базисное решение системы x ( 7; 1; 12; 0)T
.
Для проверки правильности решения системы уравнений общее ре-
шение подставляется в левую часть каждого уравнения системы. Получа-
ются тождества:
4
4
4
4
(72)3(11.5)(121.5)4 2
x
x
x
x
,
22
;
4
4
4
4
(72)(11.5)(121.5)2 6
x
x
x
x
,
66
;
4
4
4
4
2(72)(11.5)(121.5)
3
x
x
x
x
,
33
.
Преобразование однократного замещения представляет собой замену
одной базисной переменной свободной переменной в результате чего по-
лучается новое базисное решение.
81
В табл. 2.1,г выбираем, например, разрешающий
242
rk
a
a
. Пере-
считаем по формулам (2.3) все элементы табл. 2.1,г. Результаты пересчета
приведены в табл. 2.1,д.
Таблицы 2.1,д
Баз.пер.
1
x
2
x
3
x
4
x
i
b
2
x
–0.75
1
0
0
6.25
4
x
0.5
0
0
1
–3.5
3
x
0.75
0
1
0
6.75
Новое базисное решение системы x (0; 6.25; 6.75; 3.5)T
.
Решение задач линейного программирования осуществляется в евк-
лидовом пространстве.
Определение 2.5. Линейное векторное пространство
n
R называется
евклидовым пространством, если для любых двух векторов x, y
n
R
определено их скалярное произведение:
1
x,y
n
ii
i
xy
.
Понятие скалярного произведения позволяет ввести понятие длины
вектора
1
2
|x|
x,x
i
n
ix
.
Определение 2.6. Если вектор x
n
R
выражается через векторы
(1) (2)
()
x,x
,...,x
k
n
R
в виде
()
1
x
x
k
i
i
i
,
iR
, то говорят, что
x
n
R
есть линейная комбинация векторов
(1) (2)
()
x,x
,..., x
k
n
R
.
Далее будем использовать следующее обозначение i -го вектора:
()
() ()
()
12
x
( , ,...,
)
i
i
i
iT
n
xx
x
,
()
x
i
n
R
.
Определение 2.7. Векторы (1)
()
x ,...,x
k
n
R
называются линейно не-
зависимыми, если равенство
(1)
(2)
()
1
2
x
x
...
x
0,
k
k
выполняется
лишь при 1
2 ...
0
k
. Если же это равенство может выполнять-
ся и в том случае, когда не все числа 1 2
,
, ...,
k
равны нулю, то векто-
ры (1)
()
x ,...,x
k
n
R
называются линейно зависимыми.
82
Определение 2.8. Пространство
n
R называется n - мерным, если в
нем найдется система n линейно независимых векторов, но любые ( 1)
n
векторов линейно зависимые.
Определение 2.9. Совокупность n линейно независимых векторов
n -мерного пространства
n
R называется базисом этого пространства.
Определение 2.10. Выпуклой комбинацией векторов
()
x
i
n
R
,
1,...,
i
k
называется множество вида:
()
1
1
x
|x
x,
1,
0, 1,...,
k
k
n
i
i
i
i
i
i
X
R
i
k
.
Определение 2.11. Множество
n
XR
называется выпуклым, если
вместе с любыми двумя точками этого множества оно содержит и отрезок,
соединяющий эти точки, т.е. если
(1) (2)
x,x
X
,
(1)
(2)
1
2
x
x
x
,
1
21
,10
и20
,тоx X
.
Пример 2.2
Показать, что множество точек
2
12
x(,)
T
xx
R
полуплоскости
12
1
2
{(,)|
}
T
X
xx
axbxc
выпукло.
Решение
Пусть
(1)
(1) (1)
1
2
x
(,)
T
xx
X
и
(2)
(2) (2)
1
2
x
(,)
T
xx
X
,а
12
x(,)
xx
(1)
(2)
1
2
x
x
при 1
21
,10
и20
точки отрезка, соеди-
няющего точки
(1)
xи
(2)
x или
(1)
(2)
1
1
2
1
1
x
x
x
и
(1)
(2)
2
1
2
2
2
x
x
x
.
Покажем, что x X
. Имеем:
(1)
(2)
(1)
(2)
1
2
1
2
1
2
1
1
2
2
(
)(
)
ax bx
ax
x
bx
x
(1)
(1)
(2)
(2)
1
2
1
2
1
2
(
)(
)
ax
bx
ax
bx
.
Используя неравенства
(1)
(1)
1
2
ax
bxc
и(2)
(2)
1
2
ax
bxc
(т.к. точки
(1)
xи
(2)
x принадлежат допустимой полуплоскости X ), получим:
1
2
1
2
ax bx
c
cc
,т.е.xX
.
Аналогично можно показать, что полупространство
n
XR
выпук-
ло.
Теорема 2.1. (о пересечении выпуклых множеств).
Пересечение конечного числа выпуклых множеств является множе-
ством выпуклым.
83
Следовательно, множество допустимых решений задачи линейного
программирования является выпуклым множеством.
Определение 2.12. Крайней точкой x
n
XR
выпуклого множе-
ства X называется такая точка, которая не может быть выражена в виде
выпуклой комбинации других точек
()
x
i
X
,
1,...,
i
k
()
x
x
i
.
Определение 2.13. Множество
(0)
(0)
{x:|x x| ;x,x
}n
S
R
называется - окрестностью точки
(0)
x.
Определение 2.14 . Точка
(0)
x
X
называется внутренней точкой
множества X , если существует такая ее -окрестность, все точки которой
принадлежат X .
Определение 2.15. Точка
(0)
x
X
называется граничной точкой
множества X , если любая ее окрестность содержит как точки, принадле-
жащие множеству X , так и точки, не принадлежащие множеству X .
Определение 2.16. Множество
n
XR
называется ограниченным,
если существует такая константа C , что | x | C
,длялюбого x X
.
Теорема 2.2. (об опорном плане)
Опорному плану
12
x(,,...,
, 0,..., 0)T
m
b
системы (2.2,б) соот-
ветствует крайняя (угловая) точка многогранника решений
n
XR
и
при этом одному опорному плану соответствует одна крайняя точка.
Теорема 2.3. (об экстремальной точке)
Если функция (x)
f в задаче (2.1) или (2.2) достигает максимума на
множестве допустимых решений X , определяемом ограничениями и ус-
ловиями неотрицательности, то она достигает его по крайней мере в
одной крайней точке этого множества. Если она достигает его в не-
скольких крайних точках, то она достигает его на любой выпуклой ком-
бинации этих крайних точек [29].
С учетом утверждений теорем 2.2 и 2.3 о том, что экстремальное ре-
шение достигается в угловой точке многогранника решений и опорном у
плану соответствует угловая точка, можно сделать следующий вывод:
перебором всех угловых точек многогранника решений можно определить
оптимальный опорный план. Симплекс-метод содержит процедуру целе-
направленного перебора опорных планов для поиска оптимального опор-
ного плана.
Метод нахождения начального опорного плана
Каноническая форма задачи может не иметь опорного плана. Тогда
для построения исходного опорного плана, как начальных условий для
применения симплекс-метода, осуществляется переход к так называемой
84
М-задаче. Для этого используются искусственные базисные переменные, в
результате чего получается вспомогательная задача или М-задача.
В каждое уравнение канонической формы математической модели, не
содержащего элемента опорного плана вводится новая неотрицательная
переменная (см. зам. 2.2), которая называется искусственной. Пусть кано-
ническая форма (2.2) не имеет ни одного элемента опорного плана. Тогда
М-задача будет построена в следующем виде:
1
1
(x)
max
n
m
jj
ni
j
i
f
cx
Mx
;
(2.5,а)
1
n
ijj
ni
i
j
ax
x
b
,
0
i
b , 1,...,
i
m
;
(2.5,б)
0
jx,
1,...,
j
n
;
0
ni
x , 1,...,
i
m
,
(2.5,в)
где ni
x – искусственные базисные переменные,
0
M – достаточно
большое число. Опорный план задачи (2.5):
1
x (0,..., 0,
,...
)T
n
nm
bb
.
Замечание 2.4. Назначение слагаемого
1
m
ni
i
Mx
в (2.5,а) состоит в
том, чтобы в ходе решения задачи (2.5) вывести искусственные перемен-
ные ni
x из состава базисных. Если в результате решения задачи окажет-
ся, что искусственные переменные входят в состав базисных переменных
оптимального опорного плана и их значения не равны нулю, то это означа-
ет, что ограничения (2.2,б) несовместны и область допустимых решений
задачи (2.2) пустая.
2.2 . Симплекс-метод Данцига
Требуется найти оптимальное решение x
и мак-
симум линейной функции в канонической форме
математической модели
1
(x)
max
n
jj
j
f
cx
;
(2.6,а)
1
n
ijj
i
j
axb
, 1,...,
i
m
,
(2.6,б)
0
jx,
1,...,
j
n
.
(2.6,в)
Стратегия поиска решения задачи (2.6)
симплекс-метода Данцига (Dantzig G. B.)
основана на свойствах этой задачи. Множество
Постановка задачи
Стратегия решения задачи
85
1
x:
,
1,...,
;
0, 1,...,
n
ijj
i
j
j
X
ax bi
mx
j
n
допустимых решений задачи, определяемое ограничениями (2.5,б), (2.5,в),
есть выпуклое множество, которое геометрически представляет собой вы-
пуклый многогранник, имеющий конечное число крайних (угловых) точек.
Теоремы 2.2 и 2.3 определяют стратегию решения задачи, реализо-
ванную с помощью симплекс-метода, – это направленный перебор опор-
ных планов, определяющих крайние точки многогранника, при котором
значение целевой функции (x)
f последовательно улучшается.
Направление поиска оптимального решения и окончание процесса
поиска (если оптимальное решение найдено) в симплекс-методе опреде-
ляют оценки оптимальности:
b
bb
j
jijj
jJ
cac
,
1,...,
j
n
,
(2.7)
где bJ – множество индексов базисных переменных; bj – индекс базисной
переменной, расположенной в i -м уравнении;
bjc – коэффициенты целе-
вой функции при текущих базисных переменных; ij
a – элементы столбца
коэффициентов при переменной jx в системе уравнений, соответствую-
щей текущему базису; jc – коэффициент целевой функции при перемен-
нойjx.
При переходе от одного опорного плана к другому в базис вводится
та переменная k
x , для которой
min{
0}
c
c
c
k
j
jJ
,где cJ –множество
индексов свободных (небазисных) переменных.
Новая переменная k
x вводится на место переменной rx , удаляемой
из числа базисных, номер r , который определяется из условия
min
,
0
i
r
ik
iI
ik
rk
b
b
a
a
a
,
(2.8)
где ib – значение координаты текущего базисного решения, соответст-
вующей i -й строке; ik
a – коэффициент при координате k
x.вi-йстроке.
Рассматриваются только неотрицательные отношения.
В результате выбирается разрешающий элемент rk
a , относительно
которого выполняются преобразования по формулам (2.3) всех коэффици-
86
ентов и свободных членов системы уравнений. Получается новый опор-
ный план с большим значением функции (x)
f.
Теорема 2.4. (Основная теорема симплекс-метода)
1. Опорный план x
задачи (2.6) является оптимальным, если все
оценки
0
j
, 1,...,
j
n
. (Признак оптимальности опорного плана).
2. Если x
–
оптимальный опорный план и хотя бы одна оценка сво-
бодной переменной
0
j
, то этот план не единственный. (Признак не-
однозначности оптимального решения).
3. Если найдется такой номер
1
km
, для которого оценка
0
k
ивсе
0
ik
a,1,...,
i
m
, то целевая функция max
f намно-
жестве допустимых решений
n
XR
.
(Признак неограниченности об-
ласти допустимых решений).
4. Если для опорного плана x найдется такой номер
1
km
,для
которого оценка
0
k
и хотя бы один элемент
0
ik
a,1,...,
i
m
,то
существует такой новый опорный план x , которому соответствует
(x) (x)
f
f
. (Признак улучшаемости опорного плана).
Процедура вычислений связана с использованием симплекс-таблиц,
каждая из которых соответствует текущему опорному плану (табл.2.2).
Таблица 2.2
1
c
2
c
...
M
Баз.
пер.
bjc
ib
1
x
2
x
...
nm
x
i
ik
b
a
1
n
x
M
1
n
b
11
a
12
a
...
0
...
...
...
...
...
...
...
...
nm
x
M
nm
b
1
m
a
2
m
a
...
1
()
fc
1
1
...
0
–
f–
()
fM1()
M
1()
M
...
0
–
Алгоритм
1. Построить каноническую форму (2.2) математической модели на
основании замечаний 2.1 и 2.2.
2. Построить исходный опорный план (если его нет) с помощью ис-
кусственных базисных переменных (М-задача) (2.5).
87
3. Заполнить исходную симплекс-таблицу (табл.2.2) с оценками оп-
тимальности, вычисленными по формуле (2.7) и значением целевой функ-
ции
0
1
(x)
m
ii
i
f
cbc
. Заметим, что для базисных переменных оценки
оптимальности равны нулю (в этом легко убедиться при непосредственном
их вычислении).
4. Выбрать разрешающий столбец k по наименьшей отрицательной
оценке оптимальности:
min{ 0, 1, ..., }
k
j
j
n
,
–
если отрицательных оценок нет, то получен оптимальный опорный
план (теорема 2.4, п.1);
–
если оптимальный опорный план неоднозначен (теорема 2.4, п.2),
то определить все оптимальные опорные планы и построить множество
оптимальных решений в виде выпуклой комбинации оптимальных опор-
ных планов;
–
если получен оптимальный опорный план М-задачи и хотя бы одна
искусственная базисная переменная не равна нулю, то исходная задача не
имеет решений (замечание 2.4);
тогда вычисления закончить, иначе перейти к шагу 5.
5. Выбрать разрешающую строку r согласно условию (2.8):
min
,
0, 1,...,
k
i
ik
rk
ik
b
b
a
i
m
a
a
.
Если все
0
ik
a,1,...,
i
m
, то оптимального опорного плана нет, т.к.
область допустимых решений неограниченная (теорема 2.4, п.3). Тогда
вычисления закончить, иначе перейти к шагу 6.
6. Преобразовать симплекс-таблицу по формулам Жордана – Гаусса
(2.3) относительно разрешающего элемента rk
a . Получается новый опор-
ный план x , для которого (x) (x)
f
f
. Перейти к шагу 4.
Замечания 2.5
1. Если в задаче (2.6) в каждом уравнении имеется неотрицательная
базисная переменная, то на шаге 2 нет необходимости делать линейные
преобразования или вводить искусственные базисные переменные.
2. Если решается задача поиска минимума, то стратегия симплекс-
метода аналогична, только в базис вводится переменная, которой соответ-
ствует наибольшая положительная оценка
k
. Итерационный процесс
88
заканчивается, когда найден такой опорный план, что все оценки
0
j
,
1,...,
j
n
.
Сходимость
Теорема 2.5. (о сходимости симплекс-метода)
При условии невырожденности задачи линейного программирования
симплекс-метод сходится за конечное число шагов [29].
Утверждение базируется на том, что число вершин выпуклого много-
гранника конечно, а требование строгого возрастания функции при пере-
ходе от вершины к вершине исключает прохождение одной и той же вер-
шины дважды.
Пример 2.3
Решить симплекс-методом задачу
1
2
(x)42
max
f
x
x
;
1
24
xx
,
1
2
2
2
xx
,
10
x,20
x.
Решение
.
1 Построим каноническую форму:
1
2
(x)42
max
f
x
x
;
1
2
34
xx
x
,
1
2
4
2
2
xx
x
,
0
jx,
1,..., 4
j
.
.
2 Построим опорный план. Каноническая форма задачи имеет опор-
ный план, так как в каждом уравнении есть неотрицательная базисная пе-
ременная. Начальный опорный план x (0; 0; 4; 2)T
,где1xи2
x – свобод-
ные переменные, 3
xи4
x – базисные переменные.
.
3 Заполняем табл. 2.3,а согласно п.3 алгоритма с учетом п.1 реше-
ния.
Вычислим оценки оптимальности j
, 1,2,3,4
j
:
1
010(2)(4)4
,
2
0(1)0122
,
30
,
40
и значение целевой функции (x) 0 4 0 2 0 0
f
. Занесем их в табл.
2.3,а.
89
Таблица 2.3,а
–4
2
0
0
Баз.
пер.
bjc
ib
1
x
2
x
3
x
4
x
i
ik
b
a
3
x
0
4
1
–1
1
0
–
4
x
0
2
–2
1
0
1
2
f–
0
4
–2
0
0
–
1
.
4 Проанализируем оценки оптимальности. Оценка
2
20
наименьшая (единственная) отрицательная оценка. Столбец с этой оцен-
кой выбираем разрешающим. Свободная переменная 2
x вводится в базис.
1
.
5 Определим переменную, выводимую из базиса. Наименьшее не-
отрицательное отношение i
ik
b
a
равно 2 во второй строке. Поэтому из бази-
са выводим переменную 4
x . Таким образом, разрешающий элемент rk
a
211
a
(табл. 2.3,а).
1
.
6 Пересчитываем симплекс-таблицу по формулам Жордана-Гаусса
(2.3) относительно разрешающего элемента 21
a . Результаты пересчета
приведены в табл. 2.3,б.
Таблица 2.3,б
–1
4
0
0
Баз.
пер.
bjc
ib
1
x
2
x
3
x
4
x
i
ik
b
a
3
x
0
6
–1
0
1
1
–
2
x
4
2
–2
1
0
1
–
f–
4
0
0
0
2
–
Получаем новый опорный план x (0; 2; 6; 0)T
и(x)4
f
.
Переходим к шагу 4.
2
.
4 Проанализируем оценки оптимальности. Отрицательных оценок
нет. Следовательно, получено оптимальное решение (см. теорему 2.4(1) ):
x
(0; 2; 6; 0)T
. Оптимальное решение неоднозначно, т.к . оценка свобод-
ной переменной 1x равна нулю, т.е. 1 0
(см. теорему 2.4(2) ). Еще один
оптимальный опорный план получить невозможно, т.к . в разрешающем
столбце нет положительных элементов (см. теорему 2.4(3) ). Для получе-
ния множества оптимальных решений введем вектор ( )
x в следующем
виде:
90
,
1, ...,
;
=
,
;
0,
1, ..., ,
,
i
ik
i
bai
m
x
ik
im
nik
где
0
k
и
0
ik
a длявсех
1,...,
i
m
.
Очевидно, что все компоненты ( ) 0
ix,т.к.
0
и
0
ik
a .Под-
становка x( ) в систему ограничений (2.6,б) дает тождество.
Вданнойзадачеx() (;22;6 ;0)T
,
0
является мно-
жеством оптимальных решений. Легко проверить, что это решение удов-
летворяет системе ограничений и (x ( )) 4
f
. Геометрически это соот-
ветствует множеству точек луча, начало которого в точке при
0
:
x ( ) (0;2;6;0)T
.
Пример 2.4
Найти максимум в задаче
1
2
(x)
46max
f
x
x
;
1
22
xx
,
1
24
xx
,
10
x,20
x.
Решить графическим методом и симплекс-методом.
Решение
Решим задачу графическим методом, используя геометрическую ин-
терпретацию элементов математической модели.
4
Рис. 2.2
C
1
2
2
xx
2
x
1
x
B
1
f
0
1
2
2
3
X
max
5
f
(x) 2
f
3
4
A
(x) 6
f
1
24
xx
D
91
Используя систему ограничений и условия неотрицательности исход-
ной математической модели, построим множество допустимых решений
X (четырехугольник ABCD с внутренней штриховкой) (рис.2.2).
Целевая функция
12
11
22
(,)
fxx cxcx
графически изображается
множеством параллельных прямых, называемых линиями уровня, каждой
линии соответствует определенное значение целевой функции.
Градиент целевой функции
12
12
12
1
1
(,)(
,
)
;
(;)
T
T
fxxfxx
f
cc
x
x
обладает следующими свойствами:
–
направление градиента указывает направление роста целевой функ-
ции;
–
линии уровня целевой функции перпендикулярны градиенту;
–
модуль градиента определяет скорость роста целевой функции в
точке его построения.
Градиент целевой функции
1
2
(x)
46
f
x
x
задачи имеет вид:
( 1;4)T
f
.
Перпендикулярно градиенту f через начало координат проводим
линию уровня (пунктирная линия), которой соответствует значение
6
f
. Так как градиент направлен в сторону наискорейшего возраста-
ния функции в данной точке, то в точке
x
(1; 3)T
C
достигается мак-
симум max
(x) 5
ff
(рис.2.2).
Замечание 2.6. При поиске минимума функции (x)
f линия уровня
перемещается в направлении противоположном направлению градиента до
крайней точки области X . В задаче минимум достигается в точке
(4; 0)T
D
.
Решим поставленную задачу симплекс-методом.
.
1 Построим каноническую форму:
1
2
(x)
46max
f
x
x
;
1
2
3
2
xx
x
,
1
2
44
xx
x
,
0
jx,
1,..., 4
j
.
.
2 Построим опорный план. Каноническая форма задачи имеет опор-
ный план, так как в каждом уравнении есть неотрицательная базисная пе-
92
ременная. Начальный опорный план x (0; 0; 2; 4)T
,где1xи2
x – свобод-
ные переменные, 3
xи4
x – базисные переменные. Опорному плану соот-
ветствует точка A на рис. 2.2.
.
3 Заполняем табл. 2.4,а согласно п.3 алгоритма с учетом п.1.
Вычислим оценки оптимальности j
, 1,2,3,4
j
:
1
0(1)01(1)1
,
2
010144
,
30
,40
и значение целевой функции
0
1
(x)
6
b
m
ji
i
f
cbc
(табл. 2.4,а).
Таблица 2.4,а
–1
4
0
0
Баз.
пер.
bjc
ib
1
x
2
x
3
x
4
x
i
ik
b
a
3
x
0
2
–1
1
1
0
2
4
x
0
4
1
1
0
1
4
f––6
1
–4
0
0
–
1
.
4 Проанализируем оценки оптимальности. Оценка
2
40
наименьшая (единственная) отрицательная оценка. Столбец с этой оцен-
кой выбираем разрешающим. Свободная переменная 2
x вводится в базис.
1
.
5 Определим переменную, выводимую из базиса. Наименьшее не-
отрицательное отношение
i
ik
b
a
равно 2 в первой строке. Поэтому из базиса
выводим переменную 3
x . Таким образом, разрешающий
121
rk
a
a
(табл. 2.3,а).
1
.
6 Пересчитываем симплекс-таблицу по формулам Жордана-Гаусса
(2.3) относительно разрешающего элемента 12
a . Результаты пересчета
приведены в табл. 2.4,б.
Таблица 2.4,б
–1
4
0
0
Баз.
пер.
bjc
ib
1
x
2
x
3
x
4
x
i
ik
b
a
2
x
4
2
–1
1
1
1
–
4
x
0
4
2
0
0
–1
2
f–
2
–3
0
0
4
–
93
Получаем новый опорный план x (0; 2; 0; 4)T
и
(x) 2
f
.
Этому
опорному плану соответствует точка B на рис. 2.2.
Переходим к шагу 4.
2
.
4 Проанализируем оценки оптимальности. Оценка
1
30
наименьшая (единственная) отрицательная оценка. Столбец с этой оцен-
кой выбираем разрешающим. Свободная переменная 1x вводится в базис.
2
.
5 Определим переменную, выводимую из базиса. Единственный
положительный элемент во второй строке. Поэтому из базиса выводим
переменную 4
x . Таким образом, разрешающий
212
rk
a
a
(табл. 2.4,б).
2
.
6 Пересчитываем симплекс-таблицу по формулам Жордана-Гаусса
(2.3) относительно разрешающего элемента 21
a (табл. 2.4,в).
Таблица 2.4,в
–1
4
0
0
Баз.
пер.
bjc
ib
1
x
2
x
3
x
4
x
i
ik
b
a
2
x
4
3
0
1
0.5
0.5
–
1
x
–1
1
1
0
–0.5 0.5
–
f–
5
0
0
2.5
1.5
–
Отрицательных оценок нет. Поэтому получаем оптимальный опор-
ный план x
(1;3; 0; 0)T
, на котором достигается максимум целевой
функции max (x) 5
f (теорема 2.4, п.1). Этому опорному плану соответст-
вует точка C на рис. 2.2.
Таким образом, в процессе применения процедуры симплекс-метода
произошел направленный перебор вершин множества допустимых реше-
ний. Переход из вершины A в вершину B , а затем в C связан с последо-
вательным увеличением значения целевой функции.
Пример 2.5
Решить задачу симплекс-методом:
1
2
3
(x)16312
max
f
x
x
x
;
1
28
x
x
,
1
2
3
45
80
x
x
x
,
1
24
x
x
,
0
jx,
1,2,3
j
.
Дать геометрическую интерпретацию решения.
94
Решение
Решим поставленную задачу симплекс-методом.
.
1 Построим каноническую форму:
1
2
3
(x)16312
max
f
x
x
x
;
1
2
4
8
x
x
x
,
1
2
3
45
80
x
xx
,
1
2
54
x
x
x
,
0
jx,
1,..., 5
j
.
Базисное решение x (0; 0;80; 8; 4)T
не является опорным планом, т.к.
40
xи50
x.
.
2 Строим начальный опорный план. Используя искусственные ба-
зисные переменные, строим M - задачу:
1
2
3
6
7
(x)16312
max
f
x
x
xMxMx
;
1
2
4
6
8
x
x
x
x
,
1
2
3
45
80
x
xx
,
1
2
5
74
x
x
x
x
,
0
jx,
1,..., 7
j
с опорным планом x (0, 0, 80, 0, 0, 8, 4)T
и значением целевой функ-
ции
960 12
f
M
.
.
3 Заполняем табл. 2.5,а согласно п.3 алгоритма.
Таблица 2.5,а
–16
3
12
0
0
–M
–M
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
5
x
6
x
7
x
6
x
–M
8
1
1
0
–1
0
1
0
3
x
12 80
4
5
1
0
0
0
0
7
x
–M
4
1
–1
0
0
–1
0
1
f
–
960 64 57
0
0
0
0
0
()M
–
–12М
–2М
0
0
М
М
0
0
Вычислим оценки оптимальности j
, 1,...,7
j
:
–
оценки свободных переменных
1
()1124()1(16) 2 64
M
M
M
,
95
2
()1125( )(1)(3)57
M
M
,
4M
,5M
–
оценки базисных переменных всегда равны нулю: 3 0
,60
,
70
.
Значение целевой функции:
0
1
(x)
()81280()40 12 960
b
m
ji
i
f
cbc
M
M
M
.
Оценки и значение целевой функции занесем в последние две строки
табл. 2.5,а.
1
.
4 Проанализируем оценки оптимальности. Оценка
10
наи-
меньшая (единственная) отрицательная оценка. Столбец с этой оценкой
выбираем разрешающим. Свободная переменная 1x вводится в базис.
1
.
5 Определим переменную, выводимую из базиса. Наименьшее не-
отрицательное отношение
i
ik
b
a
равно 4 в третье строке. Поэтому из базиса
выводим переменную
7
x . Таким образом, разрешающий элемент
311
rk
a
a
(табл. 2.5,а).
1
.
6 Пересчитываем симплекс-таблицу по формулам Жордана-Гаусса
(2.3) относительно разрешающего элемента 31
a (табл. 2.5,б).
Таблица 2.5,б
–16
3
12
0
0
-M
-M
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
5
x
6
x
7
x
6
x
-М
4
0
2
0
–1
1
1
–1
3
x
12 64
0
9
1
0
4
0
–4
1
x
–16
4
1
–1
0
0
–1
0
1
f
-
70401210
0
64
0
–64
()M
-
–4М
0–2М0
М–М
0
2М
Текущее решение: x (4, 0, 64, 0, 0, 4, 0)T
и
704 4
f
M
.
Переходим к шагу 4.
2
.
4 Проанализируем оценки оптимальности. Наименьшая отрица-
тельная оценка 2 121 2 0
M
. Столбец с этой оценкой выбираем
разрешающим. Свободная переменная 2
x вводится в базис.
96
2
.
5 Определим переменную, выводимую из базиса. Для этого выби-
раем
122
rk
a
a
из условия
1
1
2
12
12
22
464
min
,
min
,
29
b
bb
a
a
a
.
В
первой строке базисная переменная 6
x . Она выводится из базиса. Разре-
шающий элемент
122
rk
aa
(табл. 2.5,б).
2
.
6 Пересчитываем симплекс-таблицу по формулам Жордана-Гаусса
(2.3) относительно разрешающего элемента 12
a (табл. 2.5,в).
Таблица 2.5,в
–16
3
12
0
0
-M
-M
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
5
x
6
x
7
x
2
x
3
2
0
1
0 –0.5 0.5 0.5
–0.5
3
x
12 46
0
0
1
4.5
–0.5
–4.5 0.5
1
x
–16
6
1
0
0 –0.5
–0.5 0.5 0.5
ff
–
462 0
0
0 60.5 3.5
–60.5
–3.5
()M
–
0
0
0
0
0
0
М
М
Переходим к шагу 4.
3
.
4 Проанализируем оценки оптимальности. Отрицательных оценок
нет и все искусственные переменные равны нулю (т.е. 6 0
xи70
x).
Согласно теореме 2.4(1) и замечанию 2.4 получено оптимальное решение
исходной задачи: 1 6
x
,
22
x
,
346
x
и значение целевой функции
max
462
f
.
960
f
2
x
1
x
(1)
(3)
f
0
10
20
(2)
10
X
max
f
max
462
f
x
(6, 2)
x
15
Рис. 2.3
A
5
97
Геометрическая интерпретация решения приведена на рис. 2.3. Под-
ставляя 3
1
2
8045
x
x
x
второго ограничения в целевую функцию и
отбрасывая 3
x из ограничения-равенства, получаем эквивалентную форму
исходной задачи:
1
2
(x) 64 57 960 max
f
x
x
;
1
28
x
x
,(1)
1
2
4580
x
x
,(2)
1
24
x
x
,(3)
10
x,
20
x.
Используя систему ограничений (1) – (3) и условия неотрицательно-
сти, строим область допустимых решений X .
Градиент целевой функции имеет вид:
( 64, 57)T
f
. В произ-
вольном масштабе он построен на рис. 2.3.
Перпендикулярно вектору градиента
f через начало координат
проводим линию уровня (пунктирная линия), которой соответствует зна-
чение
960
f
.
Перемещая линию уровня параллельно самой себе в пределах области
допустимых решений в направлении градиента до крайней точки области
X , получаем оптимальное решение в точке А (рис. 2.3). Эта точка образ у-
ется пересечением прямых (1) и (3). Решая соответствующую им систем у
уравнений:
1
28
xx
,(1)
1
24
xx
,
(3)
находим оптимальное решение: x
(6; 2)T
и
max
(x)
462
f
f
.
2.3 . Двойственный симплекс-метод
Каждой задаче линейного программирования (на-
зовем ее прямой) можно поставить в соответствие
двойственную задачу линейного программирования.
Пусть прямая задача имеет вид:
1
(x)
max
n
jj
j
f
cx
;
(2.9,а)
1
n
ijj
i
j
axb
, 1,...,
i
m
,
(2.9,б)
Элементы теории
98
0
jx,
1,...,
j
n
.
(2.9,в)
Определение 2.17. Следующая задача поиска минимального значе-
ния целевой функции:
1
(y)
min
m
ii
i
g
by
;
(2.10,а)
1
m
ijij
i
ayc
,
1,...,
j
n
,
(2.10,б)
0
i
y, 1,...,
i
m
.
(2.10,в)
называется двойственной по отношению к прямой (2.9).
Замечания 2.7
1. Пара двойственных задач вида (2.9) и (2.10) называется симмет-
ричной. Если система ограничений (2.9,б) смешанная или (и) условия не-
отрицательности (2.10,в) распространяется не на все переменные, то такие
задачи называются несимметричные. С помощью эквивалентных преобра-
зований возможен переход от несимметричных задач к симметричным.
2. Из определения 2.17 следует правило построения двойственных
задач:
а) установить соответствие между целевой функцией (2.9,а) и сис-
темой ограничений (2.9,б), т.е., если
max
f
, то все неравенства приво-
дятся к неравенствам со знаком « »; если
min
f
–
то приводятся к
неравенствам со знаком « »;
б) каждому неравенству (2.9,б) соответствует двойственная пере-
менная
0
iy ( 1,...,
i
m
) и наоборот;
в) коэффициентами целевой функции двойственной задачи явля-
ются свободные члены системы ограничений прямой задачи; при этом,
если целевая функция прямой задачи задается на максимум, то целевая
функция двойственной задачи (2.10,а) – на минимум, и наоборот;
в) главная матрица системы ограничений двойственной задачи яв-
ляется транспонированной матрицей прямой задачи.
Теорема 2.6. (О допустимых решениях взаимодвойственных задач)
Если
0
jx ( 1,...,
j
n
)и
0
i
y ( 1,...,
i
m
) – допустимые реше-
ния прямой (2.9) и двойственной (2.10) задач, то значения целевой функ-
ции прямой задачи не превышают значений целевой функции двойственной
задачи, т.е. (x) (y)
fg
.
99
Теорема 2.7. (Об оптимальных решениях двойственных задач)
1. Если x
иy
–
допустимые решения взаимодвойственных задач и
(x) (y)
f
g
,тоx
иy
–
оптимальные решения этих задач.
2. Если целевая функция одной из пары двойственных задач не огра-
ниченна, т.е. (x)
f((y)
g ), то область допустимых решений
другой задач пустая.
Теорема 2.8. (О дополнительной нежесткости).
Для оптимальности опорных планов x
иy
пары двойственных за-
дач необходимо и достаточно, чтобы они удовлетворяли следующим сис-
темам уравнений (условиям дополнительной нежесткости):
1
0
n
i
ijj
i
j
y
axb
,
1,...,
i
m
;
(2.11)
1
0
m
j
iji j
i
x
ayc
,
1,...,
j
n
.
(2.12)
На основании теоремы 2.8 можно установить соответствие между пе-
ременными взаимодвойственных задач (2.9) и (2.10). Для решения этих
задач симплекс-методом необходимо каждую из них привести в канониче-
скую форму с помощью введения соответствующих дополнительных не-
отрицательных переменных. Тогда системы ограничений каждой из взаи-
модвойственных задач принимают вид:
1
n
ijj
ni
i
j
axx
b
,
0
ni
x ,
1,...,
i
m
;
(2.13)
1
m
iji
mj
j
i
ayy
c
,
0
mj
y ,
1,...,
j
n
.
(2.14)
Теорема 2.9
Положительным компонентам оптимального решения одной из взаи-
модвойственных задач соответствуют нулевые компоненты оптималь-
ного решения другой задачи, т.е . для любых 1, ...,
i
m
и
1,...,
j
n
: если
0
jx
,то
0
mj
y
;если
0
ni
x
,то
0
iy
; и аналогично, если
0
iy
,то
0
ni
x
;если
0
mj
y
,то
0
jx
.
Из теоремы 2.9 следует соответствие между переменными взаимо-
двойственных задач, представленное в следующей таблице:
100
Переменные исходной задачи
Первоначальные
Дополнительные
1
x
...
jx
...
n
x
1
n
x
...
ni
x
...
nm
x
1
m
y
...
mj
y
...
mn
y
1
y
...
jy
...
m
y
Дополнительные
Первоначальные
Переменные двойственной задачи
Рассмотрим применение двойственного симплекс-метода для реше-
ния задач линейного программирования.
Требуется найти оптимальное решение x
и мак-
симум линейной функции в канонической форме
математической модели, содержащей начальное базисное решение
1
(x)
max
n
jj
j
f
cx
;
(2.15,а)
1
nm
ijj
nmi
i
j
ax
x
b
,
1,...,
i
m
,
(2.15,б)
0
jx,
1,...,
j
n
,
(2.15,в)
где j
x ( 1,...,
j
nm
) – свободные переменные; n m i
x ( 1,...,
i
m
)–
базисные переменные.
Стратегия двойственного симплекс-
метода принципиально не отличается от
стратегии симплекс-метода Данцига (раздел 2.2). При этом достаточно
наличия начального базисного решения в канонической форме математи-
ческой модели. Опорный план строится алгоритмически. Если базисного
решения нет, то, используя метод Жордана-Гаусса, его можно построить.
Алгоритм
1. Построить каноническую форму математической модели с базис-
ным решением (2.15).
2. Построить симплекс-таблицу с соответствующими оценками опти-
мальности j
(2.7) и значением целевой функции.
3. Выбрать разрешающую строку r :
–
если есть хотя бы один элемент
0
i
b , то строка выбирается по
наименьшему отрицательному значению базисной переменной:
min{ 0, 1, ..., }
r
i
b
b
i
m
;
Постановка задачи
Стратегия решения задачи
101
–
если все
0
i
b , 1,...,
i
m
, то перейти к шагу 6.
4. Выбрать разрешающий столбец k :
–
если есть хотя бы один элемент
0
rj
a , то столбец выбирается по
наибольшему отношению элементов оценочной строки к отрицательным
элементам разрешающей строки:
max
,
0, 1,...,
j
k
rj
rk
rj
a
j
n
a
a
;
перейти к шагу 5.
–
если в разрешающей строке нет ни одного отрицательного элемен-
та, то задача не имеет допустимых решений (признак пустой области до-
пустимых решений). Решение закончить.
5. Преобразовать симплекс-таблицу по формулам Жордана – Гаусса
относительно выбранного разрешающего элемента rk
a . Перейти к шагу3.
6. Выбрать разрешающий столбец по наименьшей отрицательной
оценке оптимальности:
min
0, 1, ...,
k
j
j
n
,
–
если отрицательных оценок нет, то получен оптимальный опорный
план;
–
если оптимальный опорный план неоднозначен, то определить все
оптимальные опорные планы и построить множество оптимальных реше-
ний в виде выпуклой комбинации оптимальных опорных планов;
вычисления закончить, иначе перейти к шагу 7.
7. Выбрать разрешающую строку согласно условию:
min
,
0, 1,...,
i
r
ik
rk
ik
b
b
a
i
m
a
a
.
Если все
0
ik
a,1,...,
i
m
, то оптимального опорного плана нет, т.к.
область допустимых решений неограниченна, т.е. (x)
f (теорема 2.4,
п.3), тогда вычисления закончить. Иначе перейти к шагу 6.
8. Преобразовать симплекс-таблицу по формулам Жордана–Гаусса
относительно разрешающего элемента rk
a . Перейти к шагу 6.
Замечания 2.8
Шаги 3 – 5 алгоритма повторяются до получения опорного плана или
процесс решения заканчивается согласно признаку пустой области допус-
тимых решений. Шаги 6 – 8 совпадают с шагами 4 – 6 алгоритма сим-
плекс-метода Данцига (раздел 2.2).
102
Пример 2.6
Решить задачу двойственным симплекс-методом:
1
2
3
(x)16312
max
f
x
x
x
;
1
28
x
x
,
1
2
3
45
80
x
xx
,
1
24
x
x
,
0
jx,
1,2,3
j
.
(см. пример 2.5)
Решение
.
1 Построим каноническую форму так, чтобы система имела полный
набор базисных переменных:
1
2
3
(x)16312
max
f
x
x
x
;
1
2
4
8
x
x
x
,
1
2
3
45
80
x
xx
,
1
2
5
4
x
x
x
,
0
jx,
1,..., 5
j
.
Базисное решение x (0; 0;80; 8; 4)T
.
.
2 Заполняем табл. 2.6,а с вычисленными оценками оптимальности
j
, 1,...,5
j
.
Таблица 2.6,а
–16
3
12
0
0
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
5
x
4
x
0
–8
–1
–1
0
1
0
3
x
12
80
4
5
1
0
0
5
x
0
–4
–1
1
0
0
1
f
–
960
64
57
0
0
0
Оценки оптимальности свободных переменных
1
0112401(16) 64
,
2
011250(1)(3)57
.
Оценки базисных переменных равны нулю.
Значение целевой функции:
0
1
(x)
0(8)12800(4) 0960
b
m
ji
i
f
cbc
.
103
1
.
3 Проанализируем базисные переменные. Начального опорного
плана нет, т.к. 4
80
xи5
40
x
. По наименьшей отрицательной
базисной переменной 4
x выбираем разрешающую строку 1
r.
1
.
4 Выбираем разрешающий столбец согласно п.4 алгоритма:
2
12
64 57
max
;
11
k
rk
a
a
. Разрешающий столбец
2
k
. Таким
образом, разрешающий элемент
12
1
rk
a
a
(табл. 2.6,а). Переменная
2
x вводится в базис вместо переменной 4
x.
1
.
5 Пересчитываем симплекс-таблицу по формулам Жордана-Гаусса
(2.3) относительно разрешающего элемента 12
a (см. табл. 2.6,б).
Таблица 2.6,б
–16
3
12
0
0
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
5
x
2
x
3
8
1
–1
0
–1
0
3
x
12
40
-1
0
1
5
0
5
x
0
–12
–2
0
0
1
1
f
–
504
7
0
0
57
0
Текущее базисное решение x (0; 8; 40; 0; 12)T
.
Значение целевой
функции (x) 504
f
. Переходим к п.3.
2
.
3 Проанализируем базисные переменные. Начального опорного
плана нет, т.к. 5
120
x
. По этой базисной переменной 5
x выбираем
разрешающую строку 3
r
.
2
.
4 Выбираем разрешающий столбец. Единственный отрицательный
элемент
31
2
rk
a
a
становится разрешающим (п.4 алгоритма). Разре-
шающий столбец
1
k . Переменная 1x вводится в базис вместо перемен-
ной 5
x (табл. 2.6,б).
2
.
5 Пересчитываем симплекс-таблицу 2.6,б по формулам Жордана-
Гаусса (2.3) относительно разрешающего элемента 31
a . Результат преобра-
зования – в табл. 2 .6,в.
104
Таблица 2.6,в
–16
3
12
0
0
Баз.
пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
2
x
3
2
0
1
0
–0.5 0.5
3
x
12
46
0
0
1
4.5
–0.5
1
x
–16
6
1
0
0
–0.5
–0.5
f
–
462
0
0
0
60.5 3.5
Текущее базисное решение x (6; 2; 46; 0; 0)T
. Значение целевой функ-
ции (x) 462
f
. Переходим к п.3.
3
.
3 Проанализируем базисные переменные. Все базисные перемен-
ные неотрицательны. Согласно п.3 алгоритма переходим к п.6
1
.
6 Проанализируем оценки оптимальности. Отрицательных оценок в
таблице 2.6,в нет. Согласно п.6 алгоритма получен оптимальный опорный
план x
(6; 2; 46; 0; 0)T
и max (x) 462
f
.
Пример 2.7
Решить задачу двойственным симплекс-методом:
1
2
(x)84
max
f
x
x
;
1
23
x
x
,
1
2
4212
x
x
,
0
jx,
1,2
j
.
Решение
.
1 Построим каноническую форму, вводя в неравенства дополни-
тельные неотрицательные переменные:
1
2
(x)84
max
f
x
x
;
1
2
3
3
xxx
,
1
2
4
42
12
x
x
x
,
0
jx,
1,..., 4
j
.
.
2 Заполняем симплекс-таблицу 2.7,а с вычисленными оценками оп-
тимальности j
, 1,...,4
j
.
105
Таблица 2.7,а
8
4
0
0
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
3
x
0
–3
–1
–1
1
0
4
x
0
12
4
2
0
1
f
–
0
–8
–4
0
0
Начальное базисное решение x (0; 0; 3; 12)T
. Значение целевой функ-
ции: (x) 0
f
.
1
.
3 Проанализируем базисные переменные. Начального опорного
плана нет, т.к. 3
30
x
. Разрешающая строка
1
r.
1
.
4 Выбираем разрешающий столбец согласно п.4 алгоритма:
1
11
84
max
;
11
k
rk
a
a
. Разрешающий столбец
1
k . Таким
образом, разрешающий элемент
11
1
rk
a
a
(табл. 2.7,а). Переменная
1
x вводится в базис вместо переменной 3
x.
1
.
5 Пересчитываем симплекс-таблицу по формулам Жордана-Гаусса
(2.3) относительно разрешающего элемента 11
a . Результат преобразования
приведен в таблице 2.7,б.
Таблица 2.7,б
8
4
0
0
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
1
x
8
3
1
1
–1
0
4
x
0
0
0
–2
4
1
f
–
24
0
4
–8
0
Текущее базисное решение x (3; 0; 0; 0 )T
. Решение вырожденное, т.к .
базисная переменная 4 0
x (подчеркнута). Значение целевой функции
(x) 24
f
. Переходим к п.3.
2
.
3 Проанализируем базисные переменные. Базисное решение явля-
ется опорным планом, т.к. все базисные переменные неотрицательны. Пе-
реходим к п.6.
1
.
6 Проанализируем оценки. Опорный план не оптимален, т.к. есть
одна отрицательная оценка 3
80
. Разрешающий столбец
3
k
.
106
1
.
7 Выбираем разрешающую строку согласно п.7 алгоритма. Разре-
шающая строка
2
r
. Разрешающий элемент
234
rk
a
a
(табл. 2.7,б).
1
.
8 Преобразуем элементы симплекс-таблицы по формулам Жордана-
Гаусса (2.3) относительно разрешающего элемента 23
a . Результат преоб-
разования приведен в таблице 2.7,в.
Таблица 2.7,в
8
4
0
0
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
1
x
8
3
1
0.5
0
0.25
3
x
0
0
0
–0.5
1
0.25
f
–
24
0
0
0
2
Текущее базисное решение x (3; 0; 0; 0 )T
. Решение вырожденное, т.к .
базисная переменная 3 0
x (подчеркнута). Значение целевой функции
(x) 24
f
. Переходим к п.6.
2
.
6 Проанализируем оценки. Получен оптимальный опорный план,
т.к . нет отрицательных оценок. Одна из оценок свободных переменных
20
.
Следовательно,
(1)
x
(3; 0; 0; 0)T
и max(x) 24
f
.
Можно по-
строить еще один оптимальный опорный план, выбирая разрешающий
столбец
2
k
.
2
.
7 Выбираем разрешающую строку. Разрешающая строка
1
r .Раз-
решающий элемент
12 0.5
rk
a
a
(табл. 2.7,в).
2
.
8 Преобразуем элементы симплекс-таблицы по формулам Жорда-
на-Гаусса (2.3) относительно разрешающего элемента 12
a . Результат пре-
образования приведен в таблице 2.7,г.
Таблица 2.7,г
8
4
0
0
Баз.
пер.
bjc
i
b
1
x
2
x
3
x
4
x
2
x
4
6
2
1
0
1
3
x
0
3
1
0
1
0.5
f
–
24
0
0
0
2
Оптимальный опорный план (2)
x
(3; 0; 0; 0)T
и max(x) 24
f
.
Оптимальное решение задачи определяется как выпуклая комбинация
двух опорных планов
(1)
x
и
(2)
x
:
107
(1)
(2)
1
2
1
2
2
x
x
x
(3 ;6 ;3 ;0)T
,
10
,20
,1
21
.
2.4 . Специальные задачи линейного программирования
К специальным задачам линейного программирования относят зада-
чи, для решения которых кроме симплекс-метода применимы методы, от-
личающиеся от классического алгоритма симплекс-метода.
2.4 .1. Транспортные задачи
Транспортная задача формулируется в терминах
классической транспортной задачи, но подобную
математическую модель могут иметь и другие задачи распределительного
типа [21].
Пусть некоторый однородный продукт находится в m пунктах, его
необходимо доставить потребителям в n пунктов. Известны следующие
параметры:
i
a – количество (ед.) продукта в i -м пункте,
0
i
a,
1,...,
i
m
;
jb – потребность (ед.) в продукте в j -м пункте,
0
jb,
1,...,
j
n
;
ij
c – стоимость доставки единичного количества продукта из i -го
пункта в j -ый пункт,
0
ij
c;
ij
x – количество (ед.) продукта, доставляемого из i -го пункта в j -ый
пункт.
Предполагается, что суммарные запасы равны суммарным потребно-
стям (условие разрешимости транспортной задачи):
1
1
m
n
i
j
i
j
a
b
.
(2.16)
Математическая модель транспортной задачи имеет вид:
11
(x)
min
mn
ij ij
ij
f
cx
;
(2.17,а)
1
n
ij
i
j
x
a
, 1,...,
i
m
,
(2.17,б)
1
m
ij
j
i
xb
, 1,...,
j
n
,
(2.17,в)
0
ij
x, 1,...,
i
m
,
1,...,
j
n
.
(2.17,г)
Постановка задачи
108
Требуется определить оптимальный опорный план x
на основании
системы ограничений (2.17,б) – (2.17,в) и условий неотрицательности
(2.17,г), которому соответствует минимальное значение целевой функции
(2.17,а).
Поставленная задача является частным
случаем задачи линейного программиро-
вания, поэтому стратегия решения аналогична:
1. Находится начальный опорный план. Для построения начального
опорного плана чаще всего используются метод северо-западного угла
или метод минимальной стоимости (2.17,а).
2. Выполняется улучшение опорного плана, т.е. переход от одного
плана к другому, с последовательным уменьшением значения целевой
функции (т.е. суммарной стоимости перевозок). Для улучшения начально-
го плана применяется метод потенциалов (как один из методов решения
транспортных задач). При этом используется табличная форм математиче-
ской модели (табл. 2.8).
Методы построения начального опорного плана
Ранг матрицы системы ограничений (2.17,б) – (2.17,в) всегда равен
(1)
mn
. Поэтому число базисных переменных: (
1)
mn
.
Метод северо-западного угла
Построение начинается с левой верхней клетки транспортной табли-
цы, т.е. 11
11
min{,}
x
ab
и заканчивается в правой нижней клетке mn
x .На
каждом шаге остаток по строке (или по столбцу) помещается в соседнюю
клетку, но так, чтобы не нарушались ограничения (2.17,б) и (2.17,в). Если
на некотором шаге (не на последнем) остаток оказался равным нулю, то в
соседнюю клетку (вниз или вправо) записывается базисный нуль и клетка
соответствует базисной переменной, а опорный план оказывается вырож-
денным.
Стратегия решения задачи
mn
c
1n
c
jb
1
b
n
b
1
a
i
a
m
a
1n
x
11
c
11
x
mn
x
...
...
...
...
1
m
c
1
m
x
...
...
...
Таблица 2.8
109
Пример 2.8
Найти начальный опорный план методом северо-западного угла в
транспортной задаче, заданной таблицей 2.9.
(Табл.2.9 содержит ответ поставленной задачи).
Решение
Начинаем с северо-западного угла, т.е. 11 min{210,150} 150
x
.
Тогда в пункте
1
b потребности удовлетворены и, следовательно,
21310
x
x
(в таблице 2.9 соответствующие клетки свободны). Первый
столбец исключается из рассмотрения.
Продолжаем
с
северо-западного
угла,
т.е.
12 min{(210 150),160}
x
60
. Тогда запасы в пункте 1
a исчерпаны и
1314150
xxx
. При этом первая строка исключается из рассмотрения.
Продолжаем с северо-западного угла:
22 min{(160 60),100} 100
x
.
Потребности в пункте 2
b удовлетворены и запасы в пункте 2
a ис-
черпаны. Поэтому исключаем из рассмотрения вторую строку или второй
столбец (не имеет значения). Например, исключаем второй столбец. Тогда
320
x.
Продолжаем с северо-западного угла оставшейся части таблицы. Так
как запасы 2
a исчерпаны, используем базисный нуль, т.е. 23 0
x . Соответ-
ственно свободные переменные 24 25 0
x
x
.
Заполняем последнюю строку:
33 min{600, (200 0)} 200
x
,
34 min{(600 200), 100} 100
x
,
35 min{(600 200 100), 300} 300
x
.
Таким образом, получен начальный опорный план в виде матрицы:
Таблица 2.9
jb
600
210
i
a
300
100
150
100
4
6
160
8
200
1
8
7
12
3
7
5
7
15
1
2
3
150
60
100
0
200
100
300
110
15060000
x
0100000
0 0 200100300
.
Этому опорному плану соответствует следующее значение целевой
функции:
(x) 8150 660 7100120 7200151001300 5460
f
.
Метод минимальной стоимости. В методе северо-западного угла
при построении начального опорного плана не учитываются стоимости и
поэтому в общем случае план далек от оптимального. В методе минималь-
ной стоимости учитываются затраты на перевозку. Как следствие, соответ-
ствующий начальный план, как правило, ближе к оптимальному.
Построение начинается с клетки с минимальной единичной стоим о-
стью ij
c . В эту клетку помещается меньшее из двух чисел, связанных с
ней, т.е.
min{,}
ij
ij
x
ab
. Разность по строке (или по столбцу) помещает-
ся в клетку с минимальной стоимостью без нарушения ограничений
(2.17,б) и (2.17,в). Эта процедура выполняется на каждом шаге до полного
распределения запасов.
Если на некотором шаге (не на последнем) остаток оказался равным
нулю, то в клетку с наименьшей стоимостью по строке (или по столбцу)
записывается базисный нуль и эта клетка соответствует базисной перемен-
ной, а опорный план оказывается вырожденным.
Пример 2.9
Найти начальный опорный план методом минимальной стоимости в
транспортной задаче, заданной таблицей 2.10 (см. пример 2.8).
(Табл.2.10 содержит ответ поставленной задачи).
Решение
Заполняем клетку с наименьшей стоимостью 14 1
c (или с клетки
(3,5), в которой 35 1
c):14
14
min{ , } min{210, 100} 100
x
ab
.
Тогда
Таблица 2.10
jb
600
210
i
a
300
100
150
100
4
6
160
8
200
1
8
7
12
3
7
5
7
15
1
2
3
100
110
100
150
90
60
300
111
потребности в пункте 4
b удовлетворены и 24 34 0
x
x
(в табл. 2.10 эти
клетки свободны). Четвертый столбец исключается из рассмотрения.
Из оставшихся клеток первой строки находим клетку с наименьшей
стоимостью и заполняем ее: 13 min{(210 100), 200} 110
x
.
Тогда
запасы в пункте 1
a исчерпаныи 11 12 15 0
xxx
. При этом первая строка
исключается из рассмотрения.
Из оставшихся клеток третьего столбца находим клетку с наимень-
шей стоимостью и заполняем ее: 33 min{(200 110), 600} 90
x
. Тогда
потребности в пункте 3
b удовлетворены и 23 0
x . Третий столбец исклю-
чается из рассмотрения.
В третьей строке последовательно заполняются
клетка (3,5): 35 min{(600 90), 300} 300
x
;и250
x;
клетка (3,1): 31 min{(600 90 300), 150} 150
x
;и210
x;
клетка (3,2): 32 min{(600 90 300 150), 160} 60
x
.
Запасы в пункте 3
a исчерпаны и 34 0
x (свободная переменная).
И наконец, 22 min{(160 60), 100} 100
x
.
Таким образом, получен начальный опорный план в виде матрицы:
001101000
x
0100000
15060900300
.
Этому опорному плану соответствует следующее значение целевой
функции:
(x) 41101100 71003150 560 7901300 2920
f
.
Метод потенциалов
Метод основан на следующей теореме:
Теорема 2.10. (Основная теорема метода потенциалов)
Опорный план транспортной задачи оптимален, если найдутся та-
кие m чисел i
u,
1,...,
i
m
, называемые потенциалами строк, и такие n
чисел j
v,
1,...,
j
n
, называемые потенциалами столбцов, что будут
выполнены следующие соотношения:
(1)ij
ij
uvc
для базисных переменных ij
x;
(2) (
)0
ij
i
j
c
uv
для свободных переменных ij
x.
Условие (2) теоремы 2.10 является признаком оптимальности опорно-
го плана. Это условие используется для построения оценок оптимально-
112
сти:
()
ij
ij
i
j
c
uv
. Наличие отрицательных оценок свидетельствует
о том, что опорный план транспортной задачи неоптимальный и его можно
улучшить, вводя в базис свободную переменную с отрицательной оценкой.
Введем следующие понятия.
1. Цикл – замкнутая ломаная с вершинами в клетках и звеньями, рас-
положенными вдоль строк и столбцов матрицы перевозок. В каждой вер-
шине встречаются два звена, причем одно из них располагается по строке,
а другое – по столбцу. Число вершин цикла четно. Цикл может быть само-
пересекающейся ломаной, но точки ее самопересечения не могут быть вер-
шинами цикла.
2. Означенный цикл – цикл, в котором каждой вершине приписаны
чередующиеся знаки ( )
или()
.
3. Сдвиг по циклу на число
0
. При этом значения ij
x , стоящие в
вершинах цикла со знаком ( )
, увеличиваются на число , стоящие в
вершинах со знаком ( )
, уменьшаются на число .
Алгоритм
1. Найти начальный опорный план методом северо-западного угла
или методом минимальной стоимости.
2. Определить потенциалы строк iu и столбцов j
v . Для каждой ба-
зисной клетки составить уравнение i
jij
uvc
.
Так как эти уравнения
образуют систему (
1)
mn
уравнений с (
)
mn
неизвестными (систе-
ма имеет бесконечное множество решений), то для определенности следу-
ет положить 1 0
u
.
Тогда все остальные потенциалы находятся одно-
значно.
3. Вычислить оценки оптимальности ij
свободных переменных (сво-
бодных клеток) по формуле
()
ij
ij
i
j
c
uv
.
4. Проанализировать оценки оптимальности:
а) если все оценки неотрицательны, т.е .
0
ij
, то получен опти-
мальный опорный план;
б) если получен оптимальный опорный план и хотя бы одна оцен-
ка свободной переменной равна нулю, то оптимальное решение неодно-
значно. При этом можно построить еще один оптимальный опорный план
и определить оптимальное решение в виде выпуклой комбинации опти-
мальных опорных планов, закончит вычисления;
в) если среди оценок ij
свободных переменных есть отрицатель-
ные, найти среди них наименьшую отрицательную оценку и пометить зна-
ком()
. Перейти к шагу 5.
113
5. Для свободной клетки ( , )
i j с выбранной оценкой ij
, помеченной
знаком ( )
, построить означенный цикл (или цикл пересчета). Все его
вершины, кроме расположенной в клетке ( , )
i j , должны находиться в ба-
зисных клетках.
6. Выполнить сдвиг циклу, построенному на шаге 5, на величину ,
равную наименьшему из чисел, стоящих в отрицательных вершинах, При
этом числа, стоящие в положительных вершинах, увеличить на , а числа,
стоящие в отрицательных вершинах, уменьшить на .
Если наименьшее значение в нескольких отрицательных вершинах
цикла, то при сдвиге следует поставить базисный нуль во всех таких вер-
шинах, кроме одной. Опорный план получается вырожденный.
Элементы матрицы, не входящие в цикл, остаются без изменений.
Перейти к шагу 2.
Замечания 2.9
1. При решении задач может возникнуть ситуация, в которой
0
.
Тогда при сдвиге свободная клетка становится базисной (ставится базис-
ный нуль), а базисная с
0
становится свободной.
2. Значения суммарной стоимости перевозок при переходе от одного
опорного плана к другому связаны соотношением
1
()()
k
k
ij
fxfx
,
где k – номер итерации, и ij
находятся на шагах 3 и 6 алгоритма.
Пример 2.10
Решить транспортную задачу с исходными данными примера 2.8 (или
примера 2.9) методом потенциалов, построив начальный опорный план
методом минимальной стоимости (табл. 2.11).
jb
600
i
u
210
i
a
jv
300
100
150
100
4
6
160
8
200
1
8
7
12
3
7
5
7
15
1
0
2
4
1
2
0
5
3
100
110
90
150
60
100
()
()
()
()
300
Таблица 2.11,а
2
3
–
114
Решение
Решаем по алгоритму (стр. 109).
.
1 Найдем начальный опорный план методом минимальной стоимо-
сти (табл. 2.11,а). Подробности построения в примере 2.9. (x) 2920
f
.
1
.
2 Определяем потенциалы строк и столбцов. Для каждой базисной
клетки составляем уравнение i
jij
uvc
:
1
34
uv
,1
41
uv
,3
37
uv
,
3
25
uv
,2
27
uv
,313
uv
.
Полагая 1 0
u , последовательно находим: 3 4
v,41
v,33
u,
22
v,25
u,10
v
,
5
2
v
(табл. 2.11,а).
1
.
3 Для каждой свободной клетки вычислим оценки оптимальности
по формуле
()
ij
ij
i
j
c
uv
:
11
11
11
( )8(00)8
c
uv
,
12
12
1
2
( )6(02)4
c
uv
,
15
15
1
5
( )8(02)10
c
uv
,
21
21
2
1
( )2(50)3
c
uv
,
23
( )12(54)3
ij
i
j
c
uv
,
24
24
2
4
( )3(51)3
c
uv
,
25
25
2
5
( )7(52)4
c
uv
,
34
34
3
4
( )15(31)11
c
uv
.
1
.
4 Проанализируем оценки оптимальности. Условие окончания не
выполнено, т.к . 21
30
и24
30
. Выбираем наименьшую от-
рицательную оценку, например 21
(или 24
,т.к. 21
24
).
1
.
5 Для клетки (2, 1) строим означенный цикл. По углам цикла рас-
ставляем чередующиеся знаки ( )
и()
,начинаяс()
в клетке (2, 1)
(табл. 2.11,а).
1
.
6 Найдем число
min{100,150} 100
, равное наименьшему из
чисел, стоящих в отрицательных вершинах цикла. Выполним сдвиг по
циклу на число
100
: числа, стоящие в клетках с ( )
, увеличиваются
на 100, а числа, стоящие в клетках с ( )
, уменьшаются на 100. Элементы
матрицы, не входящие в цикл, остаются без изменений. Результат преобра-
зования опорного плана представлен в табл. 2.11,б.
115
Значение целевой функции (x) 2620
f
.
Перейдем к шагу 2.
2
.
2 Определяем потенциалы строк и столбцов. Для каждой базисной
клетки составляем уравнение i
jij
uvc
и, полагая 1 0
u , определяем
все потенциалы: 2 2
u,33
u,10
v,22
v,34
v,41
v,5
2
v
(табл. 2.11,б).
2
.
3 Для каждой свободной клетки вычислим оценки оптимальности
по формуле
()
ij
ij
i
j
c
uv
:118
,124
, 1510
,
223
,
236
,240
,257
,3411
.
2
.
4 Проанализируем оценки оптимальности. Отрицательных оценок
нет, следовательно получен оптимальный опорный план. Значение целевой
функции (минимальная стоимость перевозок) min 2620
f
.
Одна оценка свободной переменной 24 0
. Согласно п.4(б) алго-
ритма опорный план не единственный. Построим новый опорный план.
2
.
5 Для клетки (2, 4) строим означенный цикл. По углам цикла рас-
ставляем чередующиеся знаки ( )
и()
,начинаяс()
в клетке (2, 4)
(табл. 2.11,а).
2
.
6 Найдем число
min{100,150} 100
, равное наименьшему из
чисел, стоящих в отрицательных вершинах цикла. Выполним сдвиг по
циклу на число
100 t
(где
[0;1]
t
): числа, стоящие в клетках с ( )
,
увеличиваются на 100 t , а числа, стоящие в клетках с ( )
, уменьшаются
на 100 t . Элементы матрицы, не входящие в цикл, остаются без измене-
ний. Таким образом, построено общее оптимальное решение в виде вы-
пуклой комбинации:
jb
600
i
u
210
ia
jv
300
100
150
100
4
6
160
8
200
1
8
7
12
3
7
5
7
15
1
0
2
4
1
2
0
2
3
100
110
90
50
160
100
3
2
()
()
()
300
()
()
()
Таблица 2.11,б
–
116
0
0 11090100900
x
100 90
0
0
90
0
50 90 160
90 90
0
300
t
t
t
t
t
t
.
Задаваясь конкретным значением параметра t от 0 до 1, можно пол у-
чить частное оптимальное решение при том же значении целевой функции
min 2620
f
.При0
tи
1
t получаем два оптимальных опорных плана
с тем же значением целевой функции.
Замечание 2.10
Задачи с нарушенным балансом (2.16) решаются путем сведения к за-
дачам, удовлетворяющим условию баланса. Далее задача решается как
обычная задача (2.17). Оптимальный опорный план новой задачи содержит
оптимальный опорный план исходной задачи.
Возможны два случая.
Первый случай. Суммарные запасы больше суммарных потребностей:
1
1
m
n
i
j
i
j
a
b
.
В этом случае следует:
–
ввести фиктивный пункт потребления
1
n с потребностью
1
1
1
m
n
n
i
j
i
j
b
a
b
;
–
положить стоимости перевозок единицы груза в фиктивный пункт
потребления равным нулю: , 1 0
in
c,
1,...,
i
m
.
Второй случай. Суммарные запасы меньше суммарных потребностей:
1
1
m
n
i
j
i
j
a
b
.
В этом случае следует:
–
ввести фиктивный пункт хранения
1
m с запасом груза, равным
1
1
1
n
m
m
j
i
j
i
a
b
a
;
–
положить стоимости перевозок единицы груза из фиктивного пунк-
та хранения равным нулю:
1,
0
m
j
c
,
1,...,
j
n
.
Пример 2.11
На двух базах хранится груз в количествах: 1 200
a
,
2 100
a
.
117
Этот груз необходимо перевезти в три пункта назначения в следую-
щих количествах: 1 150
b,2
05
b,3150
b
.
Стоимости перевозок единицы груза ij
c заданы следующей матри-
цей:
624
865
c
.
Начальный опорный план построить методом северо-западного угла и
решить методом потенциалов.
Решение
Поставленная задача является задачей с нарушенным балансом. По-
скольку суммарные запасы меньше суммарных потребностей, то вв одится
фиктивный пункт хранения 3 410 300 110
a
единиц. Стоимость пе-
ревозок из фиктивного пункта хранения полагается равной нулю. Получа-
ем задачу, в которой выполняется условие баланса (табл. 2.12,а).
Результаты решения содержатся в табл. 2.12,а – 2.12,в.
Значение целевой функции (x) 1680
f
.
Оценки оптимальности:
134(01)3
,
218(46)2
,
310(16)5
,
320(12)1
.
Относительно клетки (3,1) с наименьшей отрицательной оценкой выпол-
няем преобразование опорного плана. Сдвиг по циклу осуществляем на
величину
31 min{180, 60,110} 60
x
.
Новый опорный план – в табл.
2.12,б. Значение целевой функции (x) 1380
f
.
Оценки оптимальности :
134(06)2
,
218(16)3
,
226(12)5
,
320(62)4
.
()
()
jb
110
i
u
200
i
a
jv
180
100
4
2
80
6
150
6
5
0
0
1
6
2
1
0
4
110
40
20
60
180
0
8
()
()
()
()
Таблица 2.12,а
–
118
Сдвиг по циклу на величину
13 min{120, 50} 50
x
.
Новый опорный план представлен в табл.2 .12,в.
Значение целевой функции (x) 1280
f
.
Оценки оптимальности :
218(16)1
,
226(12)3
,
320(62)4
,
330(64)2
.
Отрицательных оценок нет, вычисления окончены. Оптимальный опорный
план:
120800
x
0 0100
и
min
(x ) (x) 1280
f
f
.
На величины 31 60
x
и3350
x
в пунктах 1
bи3
b соответственно не
будут удовлетворены потребности.
Транспортные задачи, соответствующие второму случаю (см. зам.
2.10), решаются аналогично первому случаю.
jb
110
i
u
200
i
a
jv
180
100
4
2
80
6
150
6
5
0
0
6
6
2
4
0
1
110
100
80
50
70
0
8
Таблица 2.12,в
–
()
()
jb
110
i
u
200
i
a
jv
180
100
4
2
80
6
150
6
5
0
0
6
6
2
6
0
1
50
100
80
60
120
0
8
()
()
Таблица 2.12,б
–
119
2.4 .2. Параметрические задачи
Задачи линейного программирования, в которых
коэффициенты целевой функции и (или) свобод-
ные члены системы ограничений зависят от неко-
торого параметра, называются задачами параметрического программиро-
вания.
Математическую модель такой задачи можно представить в следую-
щем виде:
1
(x, )
(
) max
n
jjj
j
ft
c ctx
;
(2.18,а)
1
()
n
ijj
i
i
j
ax
bbt
,
1,...,
i
m
;
(2.18,б)
0
jx , 1,...,
jn
,
(2.18,в)
12
[;]
ttt
.
(2.18,г)
Решение параметрической задачи заклю-
чается в том, чтобы при каждом значении
параметра
12
[;]
lt
tt
было определено решение задачи. Это может быть
оптимальное решение, пустая или неограниченная область допустимых
решений. Практически решение задачи сводится к выделению подынтер-
валов изменения
11
12
[;][;]
l
l
ll
tTtt
tt
, на которых определенное ре-
шение устойчиво. Для решения параметрических задач используется
двойственный симплекс-метод.
Алгоритм
1. Построить симплекс-таблицу с указанием параметра t согласно ал-
горитму двойственного симплекс-метода (см. разд. 2.3).
2. Выбрать значение
12
[;]
l
tttt
. При этом параметр в таблице ос-
тается в общем виде.
3. Решить задачу двойственным симплекс-методом, анализируя ре-
зультаты с учетом значения lt и всех признаков типа решения.
4. Определить множество lT значений параметра, содержащее lt . Для
выделения этого множества (подынтервала) решить систему неравенств,
состоящую из условий оптимальности и условий допустимости опорного
плана. Получить
11
12
[;][;]
l
ll
Ttt
tt
.
5. Задать новое значение параметра
1
l
l
tt
(или
1
l
l
tt
).
Перейти к шагу 3.
Постановка задачи
Стратегия решения задачи
120
Процесс решение (шаги 3 – 5) продолжается до тех пор, пока не будут
исследованы решения задачи при всех значениях параметра
12
[;]
ttt
.
Замечания 2.11
1. Множество подынтервалов lT , 1,...,
l
k
должно удовлетворять
условиям
12
1
[;]
k
l
l
Ttt
и
1
k
l
l
T
.
2. Для решения параметрической задачи на шаге 3 можно использо-
вать симплекс-метод с искусственным базисом. При этом на каждой ите-
рации необходимо строить новую М-задачу.
Пример 2.12
Решить параметрическую задачу
1
2
(x,)(8)(2)
max
ft
tx
tx
;
1
2
326
x
x
,
1
22
x
x
,
1
2
24
x
x
,
1
2
0,
0
x
x
;
(;)
t.
Решение
.
1 В соответствии с двойственным симплекс-методом строим кано-
ническую форму математической модели:
1
2
(x,)(8)(2)
max
ft
tx
tx
;
1
2
3
32
6
x
x
x
,
1
2
52
x
x
x
,
1
2
4
2
4
x
x
x
,
0
jx , 1,...,5
j
;
(;)
t.
Строим симплекс-таблицу 2.13,а. Все построения выполняем согласно ал-
горитму двойственного симплекс-метода (см. разд. 2.3).
Таблица 2.13,а
8t
2t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
3
x
0
6
–3
2
1
0
0
4
x
0
–4
–1
–2
0
1
0
5
x
0
2
1
1
0
0
1
f-
0
8t
2t
0
0
0
121
Начальное базисное решение: x (0; 0; 6; 4; 2)T
.
.
2 Выбираем значения
10
t
. Фиксированное значение параметра
можно выбирать достаточно произвольно в пределах исходного заданного
интервала.
1
.
3 Решаем задачу двойственным симплекс-методом с учетом
10
t
. При
10
t
в табл. 2.13,а разрешающий элемент
22
2
rk
a
a
.
Результат преобразований представлен в табл. 2.13,б.
Таблица 2.13,б
8t
2t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
3
x
0
2
–4
0
1
1
0
2
x
2t
2
0.5
1
0
–0.5
0
5
x
0
4
1.5
0
0
–0.5
1
f-
42t
9 0.5t
0
0
1 0.5t
0
При
10
t
в табл. 2 .13,б получен оптимальный опорный план:
(1)
x
(0;2;2;0;4)T
;max142
f
t
.
1
.
4 Определяем интервал 1
T изменения параметра t , в котором оп-
тимальное решение
(1)
x
устойчиво. Используем условие оптимальности
опорного плана:
1
4
90.50,
10.50.
t
t
Откуда следует, что
1(;2]
tT
.
1
.
5 Задаем новое значение параметра так, чтобы нарушилось одно ус-
ловие (табл. 2.13,б). В этом случае конец интервала 1
T совпадет с началом
следующего интервала. Пусть
0
t
. Перейдем к шагу 3.
2
.
3 Решаем двойственным симплекс-методом с учетом
0
t
. Тогда в
табл. 2.13,б отрицательная оценка
4
1
.
Разрешающий элемент
141
a . Результат преобразований представлен в табл. 2.13,в. При 0
tв
табл. 2.13,в получено оптимальное решение:
(2)
x
(0;3;0;2;5)T
;max263.
f
t
2
.
4 Определяем интервал 2
T изменения параметра t , в котором оп-
тимальное решение
(2)
x
устойчиво. Используем условие оптимальности
опорного плана:
122
52.50,
10.50.
t
t
Отсюда следует, что
2[2;2]
tT
.
Таблица 2.13,в
8t
2t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
4
x
0
2
–4
0
1
1
0
2
x
2t
3
–1.5
1
0.5
0
0
5
x
0
5
–0.5
0
0.5
0
1
f-
63t
5 2.5t
0
1 0.5t
0
0
2
.
5 Задаем новое значение параметра. Пусть
3
t
. Нарушается одно
условие оптимальности 1 5 2.5 3 2.5 0
. Перейдем к шагу 3.
3
.
3 При всех значениях
2
t оценка 1 0
и разрешающий столбец
с этой оценкой не содержит положительных элементов: 1 0
i
a,1,2,3
i
,
что соответствует неограниченному росту целевой функции (теорема 2.4,
п.3). Следовательно, при
3[2;)
tT
задача не имеет оптимального
решения из-за того, что max
f .
Решение окончено.
Таким образом, получено следующее решение задачи:
(;2]
t
:
(1)
x
(0;2;2;0;4)T
,
max142
f
t
.
[2; 2]
t:
(2)
x
(0;3;0;2;5)T
,
max263
f
t
.
[2; )
t:
max
f .
Пример 2.13
Решить параметрическую задачу
1
2
(x)36
max
f
x
x
;
1
2(8)
xx
t
,
1
2(2)
xx
t
,
10
x,20
x;
[ 20; 20]
t
.
Решение
.
1 В соответствии с двойственным симплекс-методом строим кано-
ническую форму математической модели:
1
2
(x)36
max
f
x
x
;
1
2
3
(8 2),
xx
x
t
123
1
2
4 (2);
xx
x
t
0
jx , 1,...,4
j
;
[ 20; 20]
t
.
Строим симплекс-таблицу 2.14,а. Все построения выполняем согласно ал-
горитму двойственного симплекс-метода (см. разд. 2.3).
Таблица 2.14,а
3
6
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
3
x
0
82t
1
1
1
0
4
x
0
2t
–1
1
0
1
f-
0
–3
–6
0
0
.
2 Выбираем значение
0
t
. В табл. 2.14,а нельзя выбирать
4
t ,
т.к . это соответствует признаку пустой области, но наличие отрицательных
оценок 1
3
и2
6
не позволяет установить истинный интервал
1
T существования пустой области.
1
.
3 Решаем двойственным симплекс-методом. При
0
t
в табл.
2.14,а разрешающий элемент:
21
1
rk
a
a
.
Результат преобразований
представлен в табл. 2.14,б.
Таблица 2.14,б
3
6
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
3
x
0
63t
0
2
1
1
1
x
3
2t
1
–1
0
–1
f-
63t
0
–9
0
–3
При 0
t в табл. 2.14,а разрешающий элемент:
122
rk
a
a
. Результат
преобразований представлен в табл. 2.14,в.
Таблица 2.14,в
3
6
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
2
x
6 31.5t
0
1
0.5
0.5
1
x
3 50.5t
1
0
0.5
–0.5
f - 3310.5t
0
0
4.5
1.5
В табл.2.14,в получен оптимальный опорный план:
124
(1)
x
(5 0.5 ; 3 1.5 ;0;0)T
t
t
и max1 33 10.5
f
t
. Переходим к шагу 4.
1
.
4 Определяем интервал 1
T изменения параметра t , в котором оп-
тимальное решение
(1)
x
устойчиво. Используем условие допустимости
опорного плана:
1
2
50.50,
31.50.
x
t
x
t
Откуда следует, что
1[2;)
tT
.
1
.
5 Задаем новое значение параметра так, чтобы нарушилось одно ус-
ловие (табл. 2.14,в). В этом случае конец интервала 1
T совпадет с началом
следующего интервала. Пусть
3
t
. Перейдем к шагу 3.
2
.
3 Выбираем разрешающую строку по отрицательной базисной пе-
ременной 1
r ,т.к.
(1)
2
31.50
x
t
при
2
t
. Разрешающая строка
не содержит отрицательных элементов, это соответствует признаку пустой
области (см. алгоритм двойственного симплекс-метода). Признак сохраня-
ется при всех
2
t
.
Решение окончено. При
2(;2)
tT
область
допустимых решений пустая.
Таким образом, получено следующее решение задачи по интервалам:
1[2;)
tT
:
(1)
x
(5 0.5;3 1.5;0;0)T
t
t
и max1 33 10.5
f
t
;
2(;2)
tT
: ОДР .
Пример 2.14
Решить параметрическую задачу
1
2
(x,)(6)(3)
max
ft
tx
tx
;
1
2(8)
xx
t
,
1
2(2)
xx
t
,
1
24
xx
,
1
2
0,
0;
x
x
(;)
t.
Решение
.
1 В соответствии с двойственным симплекс-методом строим кано-
ническую форму математической модели:
1
2
(x,)(6)(3)
max
ft
tx
tx
;
1
2
3
(8)
xx
x
t
,
1
2
4
(2)
xx
x
t
,
1
2
54
xx
x
,
0
jx,
1,..., 5
j
;
(;)
t.
125
Заполняем симплекс-таблицу 2.15,а. Все построения выполняем со-
гласно алгоритму двойственного симплекс-метода (см. разд. 2.3).
Таблица 2.15,а
6t
3t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
3
x
0
8t
1
1
1
0
0
4
x
0
2t
–1
1
0
1
0
5
x
0
4
–1
1
0
0
1
f
-
0
6t
3t
0
0
0
.
2 Выбираем значение
0
t
.
1
.
3 Решаем двойственным симплекс-методом. При
0
t
в табл.
2.15,а разрешающий элемент:
21
1
rk
a
a
.
Результат преобразований
представлен в табл. 2.15,б.
Таблица 2.15,б
6t
3t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
3
x
0
6+2 t
0
2
1
1
0
1
x
6t
2–t
1
–1
0
–1
0
5
x
0
6–t
0
0
0
–1
1
f
-
2
128tt
0
–9
0
6t
0
В табл. 15,б выбираем разрешающий элемент
122
rk
a
a
по наи-
меньшей отрицательной оценке 2
9
и единственному положительно-
му элементу в разрешающем столбце. Результат преобразований представ-
лен в табл. 2.15,в.
Таблица 2.15,в
6t
3t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
2
x
3t
3t
0
1
0.5
0.5
0
1
x
6t
5
1
0
0.5
–0.5
0
5
x
0
6t
0
0
0
–1
1
f
-
2
39tt
0
0
4.5
1.5 t
0
126
В табл. 2.15,в выбираем разрешающий элемент
14 0.5
rk
a
a
по от-
рицательной оценке 4
1.5 t
и единственному положительному эле-
менту в разрешающем столбце. Результат преобразований – в табл. 2 .15,г.
Таблица 2.15,г
6t
3t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
4
x
0
62t
0
2
1
1
0
1
x
6t
8t
1
1
1
0
0
5
x
0
12t
0
2
1
0
1
f
-
2
482tt
0
32t
6t
0
0
В табл.2.15,г получен оптимальный опорный план:
(1)
x
(8 ;0;0;6 2;12 )T
t
t
t
и
2
max1 48 2
f
tt
.
Переходим к шагу 4.
1
.
4 Определяем интервал 1
T изменения параметра t , в котором оп-
тимальное решение
(1)
x
устойчиво. Используем условия допустимости и
оптимальности опорного плана:
620,320,
8
0,6
0,
12
0.
t
t
t
t
t
Откуда следует, что
1 [3;1.5]
tT
.
1
.
5 Задаем новое значение параметра слева (или справа) от 1
T так,
чтобы нарушилось одно из условий (табл. 2.15,г). Пусть
2
t
. Перейдем к
шагу 3.
2
.
3 Решаем двойственным симплекс-методом. При
2
t
в табл.
2.15,г разрешающий элемент:
122
rk
a
a
. В результате преобразований
табл. 2.15,г получаем табл.2.15,в, в которой при 2
t получен оптималь-
ный опорный план:
(2)
x
(5;3 ;0;0;6 )T
t
t
,
2
max2 39
f
tt
.
Переходим к шагу 4.
2
.
4 Определяем интервал 2
T изменения параметра t , в котором оп-
тимальное решение
(2)
x
устойчиво. Используем условия допустимости и
оптимальности опорного плана:
127
50,
4.5 0,
3
0, 1.5
0.
6
0,
t
t
t
Откуда следует, что
2 [1.5; 6]
tT
.
2
.
5 Задаем новое значение параметра 6
t так, чтобы нарушилось
одно из условий (табл. 2.15,в). Пусть
7
t
. Перейдем к шагу 3.
3
.
3 Решаем двойственным симплекс-методом. При
7
t
в табл.
2.15,в разрешающий элемент:
34
1
rk
a
a
.
В результате преобразова-
ний табл. 2.15,в получаем табл.2.15,д, в которой при 7
t получен опти-
мальный опорный план:
(3)
x
(2 0.5;6 0.5;0; 6 ;0)T
t
t
t
; max3 30 8.5
f
t
.
Таблица 2.15,д
6t
3t
0
0
0
Баз.
Пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
2
x
3t
6 0.5t
0
1
0.5
0
0.5
1
x
6t
2 0.5t
1
0
0.5
0
–0.5
4
x
0
6t
0
0
0
1
–1
f
-
30+8.5 t
0
0
4.5
0
1.5 t
Переходим к шагу 4.
3
.
4 Определяем интервал 3
T изменения параметра t , в котором оп-
тимальное решение
(3)
x
устойчиво. Используем условия допустимости и
оптимальности опорного плана:
20.50,
4.5 0,
60.50,1.5
0.
6
0.
t
t
t
t
Откуда следует, что
3[6;)
tT
.
3
.
5 Задаем новое значение параметра слева от 1
T (табл. 2.15,г). Пусть
4
t
. Перейдем к шагу 3.
4
.
3 При
4
t
значение 4 0
x . Тогда, в разрешающей строке
1
r
нет отрицательных элементов, поэтому, согласно признаку пустой области
допустимых решений двойственного симплекс-метода, при всех
3
t
задача не имеет решений. Решение закончено.
Таким образом, получено следующее решение задачи:
(;3)
t
:
ОДР .
[ 3; 1.5]
t
:
(1)
x
(8 ;0;0;6 2 ;12 )T
t
t
t
;
2
max1 48 2
f
tt
.
128
[1.5; 6]
t
:
(2)
x
(5;3 ;0;0;6 )T
t
t
;
2
max2 39
f
tt
.
[6; )
t :
(3)
x
(2 0.5;6 0.5;0;6 ;0)T
t
t
t
; max3 30 8.5
f
t
.
Замечание 2.12.
Значения параметра t на концах подынтервалов называются крити-
ческими точками. Значения целевой функции в критических точках смеж-
ных подынтервалов должны быть равны:
1.5
t
:
(1)
x
(9.5; 0; 0; 9; 13.5)T
,
max 1 42.75
f
;
(2)
x
(5; 4.5; 0; 0; 4.5)T
,
max 2 42.75
f
;
–
решение в этой точке альтернативное (неоднозначное);
6
t:
(2)
x
(5;9;0;0;0)T
,
max2 81
f;
(3)
x
(5;9;0;0;0)T
,
max3 81
f;
–
решение в этой точке вырожденное. Базисные переменные,
равные нулю, подчеркнуты.
2.4 .3. Дробно-линейные задачи
Задача, в которой целевая функция дробно–
линейна, а множество допустимых решений X
определяется линейными ограничениями и условиями неотрицательности
переменных, называется задачей дробно–линейного программирования :
0
1
0
1
(x)
max
n
jj
j
n
jj
j
cx
c
f
dxd
;
(2.19,а)
1
n
ijj
i
j
ax
b
,
1,...,
i
k
;
(2.19,б)
1
n
ijj
i
j
ax
b
,
1,...,
ik
m
;
(2.19,в)
0
jx,
1,...,
j
n
,
(2.19,г)
где
1
c ( ,...,
)n
n
c
c
R
и
1
d ( ,...,
)n
n
ddR
–
фиксированные векторы;
0
c,0
d – свободные члены целевой функции. Предполагается, что знаме-
натель целевой функции в X :
0
1
0
n
jj
j
dxd
. Такое условие не нару-
Постановка задачи
129
шает общности задачи, поскольку в том случае, когда эта величина отри-
цательна, знак минус можно отнести к числителю. Случай, когда знамена-
тель
0
1
0
n
jj
j
dxd
в пределах области допустимых решений, требует
дополнительного исследования. Система ограничений (2.19,б) – (2.19,в) и
условия неотрицательности (2.19,г) такие же, как в общей задаче линейно-
го программирования (2.1).
Задача (2.19) сводится к задаче линейно-
го программирования с помощью введе-
ния новых переменных.
Необходимо убедиться, что на допустимом множестве X знамена-
тель целевой функции (2.19,а) сохраняет знак, т.е.
0
1
0
n
jj
j
dxd
для
всехx X
. Вводится новая переменная
0
0
1
1
n
jj
j
y
dxd
.
(2.20)
Очевидно, что 0 0
y привсехx X
. Вводятся новые переменные:
0
j
j
yyx
,
1,...,
j
n
.
С новыми переменными задача (2.19) принимает следующий вид:
0
(x)
max
n
jj
j
f
cy
;
(2.21,а)
0
1
0
n
ijj
i
j
ayby
,
1,...,
i
k
;
(2.21,б)
0
1
0
n
ijj
i
j
ax by
,
1,...,
ik
m
;
(2.21,в)
0
1
n
jj
j
dy
;
(2.21,г)
0
jy,
0,1,...,
j
n
.
(2.21,д)
Задача (2.21) является задачей линейного программирования, которая эк-
вивалентна дробно-линейной задаче (2.19), и решается симплекс–методом.
Стратегия решения задачи
130
Алгоритм
1. Ввести новую переменную 0 0
y (2.20) и соответственно ввести
новые переменные
0
j
j
yyx
,
1,...,
j
n
, переходя от дробно-линейной
задачи (2.19) к линейной задаче (2.21).
2. Построить каноническую форму математической модели и началь-
ное базисное решение.
3. Решить двойственным симплекс-методом, определив оптимальное
решение
0
y ( ,...,
)T
n
yy
и max
(y)
f
.
4. Перейти к решению исходной дробно-линейной задачи с помощью
равенств
0
j
j
y
x
y
,
1,...,
j
n
и max
max
(x)
(y)
f
f
.
Пример 2.15
Решить следующую задачу дробно–линейного программирования:
1
2
1
2
2
(x)
max
21
xx
f
x
x
;
1
2
3
2
2
x
x
x
,
1
2
4
2
6
xx
x
,
0
jx,
1,..., 4
j
.
Решение
.
1 Вводим дополнительную переменную 0
1
2
1
(21)
y
x
x
и пере-
ходим к новым переменным
0
j
j
yyx
,
1,..., 4
j
. Получим задачу ли-
нейного программирования:
1
2
(y) 2
max;
f
yy
1
2
3
0
2
20
yyy
y
,
1
2
4
0
2
60
yy
yy
,
1
2
0
2
1
yy
y
,
0
jy,
0,1,..., 4
j
.
.
2 Задача п. 1 – в канонической форме, но не имеет базисного реше-
ния. Для применения симплекс-метода построим базисное решение разре-
шим систему ограничений относительно переменной 0y , исключая эту
переменную из первого и второго уравнений. Это целесообразно сделать,
т.к.00
y по определению:
131
1
2
(y) 2
max;
f
yy
1
2
3
32
2
yyy
,
1
2
4
813
6
y
y
y
,
1
2
0
2
1
yy
y
,
0
jy,
0,1,..., 4
j
.
.
3 Решаем задачу симплекс-методом. Заполняем симплекс-таблицу и
выполняем необходимые преобразования для получения результата.
Таблица 2.16,а
2
–1
0
0
0
Баз.
пер.
ic
i
b
1
y
2
y
3
y
4
y
0
y
3
y
0
2
3
2
1
1
0
4
y
0
6
8
13
0
0
0
0
y
0
1
1
2
0
0
1
f-
0
–2
1
0
0
0
Разрешающий элемент:
113
rk
a
a
(см. разд. 2.3). Результат преобразо-
вания представлен в табл. 2.16,б.
Таблица 2.16,б
2
–1
0
0
0
Баз.
пер.
ic
i
b
1
y
2
y
3
y
4
y
0
y
1
y
2
23
1
23 13
0
0
4
y
0
23
0
233 83
1
0
0
y
0
13
0
43 13
0
1
f-43
0
73 23
0
0
В табл. 2.16,б получен опорный план:
0
1
3
y
,
1
2
3
y
,
20
y
,
30
y
,
4
2
3
y
и max
4
3
f
.
.
4 Переходим к решению исходной задачи согласно п. 4 алгоритма:
x
(2; 0; 0; 2)T
,
max
4
3
f
.
Замечание 2.13
Задачу (2.21) можно решать симплекс-методом с искусственным ба-
зисом (М-задача) (см. разд.2.2).
132
2.4 .4. Целочисленные задачи. Метод Гомори
Найти оптимальный целочисленный опорный
план задачи линейного программирования, пред-
ставленной в канонической форме:
1
(x)
max
n
jj
j
f
cx
;
(2.22,а)
1
n
ij
i
j
j
axb
,
1,...,
i
m
;
(2.22,б)
0
jx,
1,...,
j
n
;
(2.22,в)
jx – целые,
1,...,
j
n
.
(2.22,г)
Замечание 2.14
Требование целочисленности (2.22,г) может быть наложено не на все
переменные j
x,алишьначасть.
Задача (2.22) решается двойственным
симплекс-методом без учета требований
на целочисленность переменных. Если пол ученный оптимальный опорный
план
1
x
( ,...,
)n
x
x
является целочисленным, то решение задачи окон-
чено. В противном случае дальнейшие действия состоят в формировании
путем построения дополнительных ограничений нового множества допус-
тимых решений, которое:
–
содержало бы все целочисленные точки исходной задачи (2.22);
–
не содержало бы оптимальное нецелочисленное решение x
.
Таким требованиям удовлетворяет отсечение Гомори:
1
{}{}
n
rj
j
r
j
x
,
(2.23)
где{ }
rj
и{}
r
– дробные части соответствующих коэффициентов r -го
уравнения.
Теорема 2.11. (Теорема Гомори о правильном отсечении).
Пусть задача линейного программирования (2.22) имеет решение x
,
причем его r -я координата не является целой, а допустимое множество
целочисленной задачи (2.22) не пусто. Тогда ограничение (2.23) есть пра-
вильное отсечение допустимого множества X задачи (2.22,а) – (2.22,в)
[22].
Постановка задачи
Стратегия решения задачи
133
Замечание 2.15
Целой частью любого дробного числа r
является наибольшее целое
число, не превосходящее этого числа, тогда дробная часть числа
r
:
{}
[]
r
r
r
,где[]
r
– целая часть числа. Следовательно, дробная
часть любого дробного числа всегда положительна, т.е. { } 0
r
.Напри-
мер,
3.2
r
.Тогда[]4
r
и{}
[]3.2(4)0.8
r
r
r
.
Таким образом, при реализации метода Гомори в условие нецелочис-
ленной задачи линейного программирования последовательно добавляют-
ся новые ограничения вида (2.23) до тех пор, пока ее решение не станет
целочисленным или не будет обнаружено, что целочисленное решение
отсутствует.
Алгоритм
1. Привести исходные ограничения задачи (2.22) к целочисленном у
виду, т.е. к целочисленным коэффициентам.
2. Определить двойственным симплекс-методом оптимальный опор-
ный плана задачи (2.22) без учета требований на целочисленность пере-
менных. Если решение задачи целочисленно или задача не имеет решения,
то вычисления окончены. В противном случае перейти к шагу 3.
3. Выбрать в таблице с оптимальным решением нецелочисленную пе-
ременную с максимальной дробной частью { }
r
. Взять дробные части
всех коэффициентов { }
rj
и записать новое ограничение (2.23):
1
{}{}
n
rj
j
r
j
x
.
4. Записать новое ограничение в виде равенства
1
1
{}
{}
n
rj
jn
r
j
x
x
.
(2.24)
Расширить последнюю симплекс-таблицу на одну строку и один столбец и
записать в нее дополнительное ограничение (2.24). Перейти к шагу 2.
Замечание 2.16
Алгоритм метода Гомори является конечным, если множество допус-
тимых решений задачи (2.22) ограничено.
Пример 2.16
Решить целочисленную задачу методом Гомори
1
2
(x)45
max
f
x
x
;
1
2
356
x
x
,
1
25
xx
,
134
10
x,20
x;1x,2
x – целые.
Решение
.
1 Исходная задача содержит целочисленные коэффициенты. Перей-
дем к шагу 2.
1
.
2 Решаем задачу двойственным симплекс-методом. Для этого в со-
ответствие с алгоритмом (см. разд. 2.3) строим каноническую форму ма-
тематической модели:
1
2
(x)45
max
f
x
x
;
1
2
3
35
6
x
x
x
,
1
2
45
x
x
x
,
0
jx,
1,..., 4
j
.
Решение представлено в табл. 2.17,а и 2.17,б.
Таблица 2.17,а
–4
–5
0
0
Баз.
пер.
ic
i
b
1
x
2
x
3
x
4
x
3
x
0
–6
–3
–5
1
0
4
x
0
5
1
1
0
1
f04500
Таблица 2.17,б
–4
–5
0
0
Баз.
пер.
ic
i
b
1
x
2
x
3
x
4
x
2
x
–5
1.2 0.6 1
–0.2 0
4
x
03.80.400.21
f–61
0
1
0
В табл. 2.17,б получен оптимальный опорный план x
(0; 1.2; 0; 3.8)T
,
который не является целочисленным. Перейдем к шагу 3.
1
.
3 Выбираем вторую строку, т.к . переменная 4
x имеет наибольшую
дробную часть 4
{}0.8
b
. На основании второй строки строим дополни-
тельное ограничение (2.23):
1
3
0.4 0.2 0.8
x
x
.
1
.
4 Строим новое ограничение в виде равенства (2.24)
135
1
3
5
0.4 0.2
0.8
x
xx
и дописываем в симплекс-таблицу (табл. 2.18,а).
Таблица 2.18,а
–4
–5
0
0
0
Баз.
пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
2
x
–5
1.2 0.6 1
–0.2 0
0
4
x
03.80.400.21
0
5
x
0 –0.8
–0.4 0
–0.2 0
1
f––61
0
1
0
0
Переходим к шагу 2.
2
.
2 Решаем задачу двойственным симплекс-методом. Выбираем раз-
решающий элемент
31
0.4
rk
a
a
. Результат преобразования представ-
лен в табл. 2.18,б.
Таблица 2.18,б
–4
–5
0
0
0
Баз.
пер.
ic
i
b
1
x
2
x
3
x
4
x
5
x
2
x
–5
0
0
1
–1
0 1.5
4
x
0
3
0
0
0
1
1
1
x
–4
2
1
00.50
–2.5
f––80
00.502.5
Получено оптимальное целочисленное решение
12
x
,
20
x
,
max
8
f
.
Замечание 2.17
В методе Гомори признаком пустой области допустимых решений за-
дачи (2.22) является нарушение условия
1
{}{}
n
rj
j
r
j
x
, т.е. при
{}0
r
все{}0
rj
,
1,...,
j
n
.
136
Задачи для самостоятельного решения
Задачи линейного программирования 1-5 решить
– графическим методом;
– сим пл ек с-методом Данцига;
– двойственным симплекс-методом.
1.
1
2
3
(x)38
max
f
x
xx
;
1
2
23
6
x
x
1
34
x
x
,
1
2
6
x
x
,
0
jx,
1,2,3
j
.
Ответ: 1 2.4
x
,
2 3.6
x
,
3 1.6
x
; max
(x) 23.2
f
.
2.
1
2
3
(x) 9
min
f
xx
x
;
1
2
2
8
x
x
,
1
2
2
4
x
x
,
1
2
35
xx
x
,
20
x,30
x , 1x – произвольная переменная.
Ответ: 1
2
x
,
23
x
,
30
x
; min(x) 15
f
.
3.
1
2
3
(x) 4
2
max
f
xx
x
;
1
2
2
10
x
x
,
1
2
3
2
4
x
x
x
,
1
2
2
x
x
,
0
jx,
1,2,3
j
.
Ответ: (1)
x
(0; 10; 24)T
; (2)
x
(4; 2; 12)T
; max
(x) 38
f
.
Общее решение в виде выпуклой комбинации точек
(1)
x
и
(2)
x
:
2
1
2
1
2
x
(4;102;2412)T
,
1
21
,10
,20
.
4.
1
2
3
(x)
6
max
f
x
xx
;
1
2
8
8
x
x
,
1
2
2
10
x
x
,
1
2
3
3
6
x
xx
,
0
jx,
1,2,3
j
.
137
Ответ: задача не имеет решения, т.к. область допустимых решений
пустая.
5.
1
2
3
(x)38
max
f
x
xx
;
12
2
xx
,
1
2
3
2
4
xxx
,
1
2
2
4
x
x
,
0
jx,
1,2,3
j
.
Ответ: задача не имеет решения, т.к . область допустимых решений
не ограниченная и max
(x)
f .
Транспортные задачи 6-8 решить методом потенциалов. На-
чальный опорный план построить
– м ет одом северо-западного угла;
–
методом минимальной стоимости.
6. Даны запасы груза 1 100
a
,
2 200
a
,
3 150
a
и потребности
1 150
b,2100
b,3150
b,450
b
. Найти оптимальный план x
дос-
тавки груза от поставщиков потребителям при минимальной суммарной
стоимости затрат. Известна матрица
1,2 ,3
1,. .., 4
C{}i
ijj
c
стоимости перевозки
единицы груза из пункта ia ,
1,2,3
i
в пункт jb , 1,2,3,4
j
:
6231
C5459
5367
.
Ответ:
005050
x
10001000
5010000
;
min (x) 1750
f
.
7. Даны запасы груза 1 100
a
,
260
a,3150
a
и потребности
150
b,2120
b,380
b
. Найти оптимальный план x
доставки груза
от поставщиков потребителям при минимальной суммарной стоимости
затрать. Известна матрица
1,2,3
1,2,3
C{}i
ijj
c
стоимости перевозки единицы
груза ij
c изпункта ia,
1,2,3
i
в пункт jb , 1,2,3
j
:
833
C556
214
.
Ответ:
02080
x
000
501000
;
138
Запасы п. 2
a не использованы.
min (x) 500
f
.
8. Даны запасы груза 1 160
a
,
2 160
a
и потребности 1 80
b,
2 120
b,3180
b,340
b
. Найти оптимальный план x
доставки груза
от поставщиков потребителям при минимальной суммарной стоимости
затрать. Известна матрица
1,2
1,. .., 4
C{}i
ijj
c
стоимости перевозки единицы
груза из пункта ia ,
1,2
i
в пункт jb , 1,2,3,4
j
:
8347
C
1534
.
Ответ:
0140200
x
800800
;
Пункты 3
bи4
b не получат 60 и 40 (ед.);
min (x) 820
f
.
Параметрические задачи 9-12 решить с использованием
двойственного симплекс-метода.
9.
1
2
(x,)(6)(8)
max
ft
tx
tx
1
2
2
4
x
x
,
1
220
x
x
,
1
2
210
x
x
,
10
x,20
x;
(;)
t
.
Ответ: ( ; 22]
t
:
(1)
x
(2; 0)T
; max(1) (x) 12 2
f
t
;
[22;8]
t:
(2)
x
(0; 4)T
; max(2) (x) 32 4
f
t
;
[ 8; 1.33]
t
:
(3)
x
(0; 5)T
; max(3) (x) 40 5
f
t
;
[1.33; )
t
:
(4)
x
(0; 5)T
; max(4) (x) 20 20
f
t
.
10.
1
2
4
(x,)8(4)(12)
max
ft
x
tx
tx
;
1
2
3
28
x
xx
,
1
2
4
3
20
x
x
x
,
0
jx , 1,...,4
j
;
[ 20; 20]
t
.
Ответ: [ 20; 4]
t
:
(1)
x
(28; 0; 0; 48)T
; max(1) (x) 800 48
f
t
;
[4; 20]
t
:
(2)
x
(52; 24; 0; 0)T
; max(2) (x) 512 24
f
t
.
139
11.
1
2
3
4
(x) 2
max
f
xxxx
12
3
(10 2)
xxx
t
,
1
2
4
2
(4)
xx
x
t
,
0
jx , 1,...,4
j
;
(;)
t
.
Ответ:
(;4]
t
:
(1)
x
(0; 4 ;14 ;0)T
t
t
; max(1) (x) 10 2
f
t
;
[4;5]
t
:
(2)
x
(0;0;10 2;4 )T
t
t
; max(2)(x) 6 3
f
t
;
[5; )
t : область допустимых решений – пустое множество.
12.
1
2
3
(x,)(4)(8)
max
ft
tx
txx
1
2
3
23
(24 )
x
xx
t
,
1
2
4 (4)
xx
x
t
,
1
2
56
xx
x
;
0
jx , 1,...,5
j
;
(;)
t
.
Ответ: ( ; 5.33)
t
: область допустимых решений – пустая;
[ 5.33; 2]
t
(1)
x
(4 ;0;16 3;0;10 )T
t
t
t
,
2
max(1) (x) 32 3
f
tt
;
[2; )
t:
(2)
x
(12 0.5;0;0;8 1.5;18 0.5)T
t
t
t
,
2
max(2) (x) 48 14 0.5
f
t
t
;
Дробно-линейные задачи 13-15 решить методом замены пе-
ременных с использованием двойственного симплекс-метода.
13.
1
2
1
2
2
(x)
max
xx
f
xx
;
1
2
27
x
x
,
1
2
2
7
xx
,
11
x,21
x.
Ответ: 1 3.5
x
,
20
x
; max
(x) 3.5
f
.
14.
1
2
1
2
3
(x)
max
2
xx
f
xx
;
1
23
xx
,
140
1
2
2
10
xx
,
10
x,20
x.
Ответ: 1 5
x
,
20
x
; max
15
(x)
7
f
.
15.
1
2
1
2
2
(x)
max
xx
f
xx
;
1
2
2
11
x
x
,
1
2
8
x
x
,
1
2
3
3
9
x
xx
10
x,20
x,30
x.
Ответ: 1 9
x
,
21
x
;315
x
; max
(x) 1.9
f
.
Целочисленные задачи 16-18 решить методом Гомори с ис-
пользованием двойственного симплекс-метода.
16.
1
2
(x) 4
max
f
xx
;
1
2
20
x
x
,
1
2
1
xx
,
1
2 3.2
xx
10
x,20
x;1x,2
x – целые.
Ответ: 1 2
x
,
21
x
;
max
(x) 7
f
.
17.
1
2
(x)22
max
f
x
x
;
1
2
24
x
x
,
1
2
3214
x
x
,
10
x,20
x;1x,2
x – целые.
Ответ: 1 2
x
,
23
x
; max
(x) 2
f
.
18.
1
2
(x)
max
fxx
;
1
2
436
x
x
,
1
2
2
6
x
x
,
10
x,20
x;1x,2
x – целые.
Ответ: (1) (1; 3)T
x
и
(2) (2; 2)T
x
; max
(x) 4
f
.
141
Глава 3
ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ
ОПТИМИЗАЦИИ
3.1. Постановка задачи и принципы одномерной
оптимизации
Требуется найти безусловный минимум функции ( )
f x одной пере-
менной, т.е. такую точку x R
,что()min()
xR
fx
fx
.
Поставленная задача одномерной минимизации может быть решена с
помощью необходимых и достаточных условий безусловного экстремума
(см. разд. 1.2). Однако проблема получения решения уравнения
()0
dfx
dx
может оказаться весьма сложной. Более того, в практических задачах
функция ( )
f x может быть не задана в аналитическом виде или часто не-
известно, является ли она дифференцируемой. Поэтому получение реше-
ния поставленной задачи численным методом является актуальным.
Замечания 3.1
1. Для методов одномерной минимизации типично задание априорной
информации о положении точки минимума с помощью начального интер-
вала неопределенности
0
00
;
Lab
(рис. 3.1). Предполагается, что точка
минимума x
принадлежит интервалу 0L , т.е.
0
xL
R
.
2. Большинство известных методов одномерной минимизации приме-
няется для класса унимодальных функций.
Определение 3.1. Функция ( )
f x называется унимодальной на ин-
тервале
0
00
;
Lab
, если она достигает глобального минимума на
00
;
a b в единственной точке x
, причем слева от x
эта функция строго
убывает, а справа от x
строго возрастает. Если 0
a
yzx
,то
() ()
fyfz
,аесли
0
x
yzb
,то()
()
fyfz
(рис. 3.1).
142
Отметим, что непрерывная строго выпуклая функция является уни-
модальной. Однако определению 3.1 могут удовлетворять и функции, не
являющиеся непрерывными и выпуклыми (рис. 3.1, б).
3. Методы одномерной минимизации широко применяются в числен-
ных методах многомерной оптимизации.
Существуют две принципиально различные стра-
тегии выбора точек, в которых производится вы-
числение значений функции. Если все точки задаются заранее, до начала
вычислений, – это параллельная (пассивная) стратегия. Если эти точки вы-
бираются последовательно в процессе поиска с учетом результатов преды-
дущих вычислений, – это последовательная стратегия. Примером реализа-
ции пассивной стратегии является метод равномерного поиска.
Последовательную стратегию можно реализовать следующими спо-
собами:
а) применением квадратичной и кубической интерполяции, где по не-
скольким вычисленным значениям функции строится интерполяционный
полином, а его минимум указывает на очередное приближение искомой
точки экстремума;
б) построением последовательности вложенных друг в друга интер-
валов, каждый из которых содержит точку минимума.
Стратегия поиска включает в себя три этапа:
1. Выбор начального интервала неопределенности. Границы 0
a,0
b
интервала должны быть такими, чтобы функция ( )
f x была унимодаль-
ной.
2. Уменьшение интервала неопределенности.
Стратегия поиска
0
a
0
b
z
0
L
x
x
y
y
()
fx
z
а)
0
a
0
b
0
L
x
x
()
fx
б)
Рис. 3.1
143
3. Проверку условия окончания. Поиск заканчивается, когда длина
текущего интервала неопределенности
;k k
a b оказывается меньше уста-
новленной величины.
Ответом является множество точек, принадлежащих последнему ин-
тервалу неопределенности, среди которых каким-либо образом выбирается
решение задачи x
.
Замечание 3.2
В некоторых методах заранее задается или находится количество n
вычислений функции. В этом случае продолжительность поиска ограниче-
на.
Для эвристического выбора начального интервала неопределенности
можно применить алгоритм Свенна (Swann W. H.):
1) задать произвольно следующие параметры: 0
x – некоторую точку,
0
t – величину шага. Положить
0
k
.
2) вычислить значение функции в трех точках: 0
xt
,
0
x,0
xt
;
3) проверить условие окончания:
а) если
0
0
0
()()()
fxtfxfxt
, то начальный интервал не-
определенности найден:
00
0
0
;
;
ab
xtxt
;
б) если
0
0
0
()()()
fxtfxfxt
, то функция не является
унимодальной (см. определение 3.1), а требуемый интервал неопределен-
ности не может быть найден. Вычисления при этом прекращаются (реко-
мендуется задать другую начальную точку 0
x);
в) если условие окончания не выполняется, то перейти к шагу 4;
4) определить величину :
а) если
0
0
0
()()()
fxtfxfxt
,то
t
,0
0
ax
,
1
0
xxt
,
1
k;
б) если
0
0
0
()()()
fxtfxfxt
,то
t
,
0
0
bx
,
1
0
xxt
,
1
k;
5) найти следующую точку
1
2k
k
k
x
x
;
6) проверить условие убывания функции:
а) если
1
()()
k
k
fx fx
и
t
,то0
k
ax
;
если
1
()()
k
k
fx fx
и
t
,то0
k
bx
;
в обоих случаях положить
1
kk
и перейти к шагу 5;
144
б) если
1
()()
k
k
fx fx
, процедура завершается. При
t
по-
ложить 0
1
k
bx
,апри
t
положить 0
1
k
ax
. В результате имеем
00
;
a b – искомый начальный интервал неопределенности.
Уменьшение интервала неопределенности, осуществляемое при ис-
пользовании последовательной стратегии, производится на основании вы-
числения функции в двух точках текущего интервала. Свойство унимо-
дальности позволяет определить какой из возможных подынтервалов со-
держит точку минимума.
Пусть в точках y и z интервала
,
a b вычислены значения функ-
ции:
()
fyи()
fz . Если
() ()
fyfz
,то
;
x
ay
и поэтому
;
x
yb
(рис. 3.2,а). Если
() ()
fyfz
,то
;
x
zb
и поэтому
;
x
az
(рис. 3.2,б). Иными словами, в качестве нового интервала бе-
рется «гарантирующий интервал», наверняка содержащий точку миниму-
ма. Если
() ()
fyfz
, в качестве нового интервала берется интервал
;yz.
Для оценки эффективности алгоритмов уменьшения интервала неоп-
ределенности при заданном числе n вычислений функции введем крите-
рий.
Определение 3.2. Характеристикой ( )
R n относительного умень-
шения начального интервала неопределенности называется отношение
длины интервала, получаемого в результате n вычислений функции, к
длине начального интервала неопределенности:
0
() nL
Rn
L
.
а
Рис. 3.2
a
b
z
()
fx
x
x
()
fy
y
()
fz
Новый интервал
Текущий интервал
a
b
z
()
fx
x
x
()
fy
y
()
fz
Новый интервал
Текущий интервал
б
145
Пример 3.1
Найти начальный интервал неопределенности для поиска минимума
функции
2
()(5)
fxx
.
Решение
Воспользуемся алгоритмом Свенна.
0
.
1 Зададим 0 1
xи
1
t . Положим
0
k
.
0
.
2 Вычислим значения функции в точках
0
0
xt
,
01
x,
0
2
xt
:
(0) 25
f,(1)16
f,(2)9
f
.
0
.
3 Условия окончания не выполняются.
0
.
4 Так как (0) (1) (2)
fff
,то
1
t
,01
a,1
0
2
xxt
,
1
k.
0
.
5 Найдем следующую точку 2 1 2 4
xx
.
0
.
6 Так как
2
1
()1()9
fx
fx
и
1
,то 0
12
ax
. Положим
2
k иперейдемкшагу5.
1
.
5 Найдем следующую точку 3
248
xx
.
1
.
6 Так как
3
2
()9()1
fx
fx
и
1
t
, то поиск завершен и
правая граница 0
38
bx
. Поэтому начальный интервал неопределенно-
сти имеет вид
00
;
2;8
ab
.
3.2 . Методы нулевого порядка
Методы, использующие только значения функции ( )
f x в заданных
точках, называются методами нулевого порядка (или прямыми методами)
минимизации. Достоинством методов нулевого порядка является то, что от
целевой функции не требуется дифференцируемости и, более того, она
может быть не задана в аналитическом виде.
3.2 .1. Метод равномерного поиска
Метод равномерного поиска (или метод перебора) является простей-
шим из методов нулевого порядка минимизации.
Требуется найти безусловный минимум унимо-
дальной функции ( )
f x одной переменной, т.е.
найти такую точку x R
,что()min()
xR
fx
fx
.
Постановка задачи
146
Метод относится к методам с пассивной
стратегией. Задается начальный интервал
неопределенности
0
00
;
Lab
и количество вычислений функции n .
Вычисления производятся в n равноотстоящих друг от друга точках (при
этом интервал 0
L делится на
1
n равных интервалов). Путем сравнения
величин ( )i
fx,
1,...,
i
n
находится точка k
x , в которой значение функ-
ции наименьшее. Искомая точка минимума x
считается заключенной в
интервале
1
1
[;]
k
k
xx
(рис. 3.3).
Алгоритм
1. Задать начальный интервал неопределенности 0
00
[;]
Lab
,n–
количество вычислений функции.
2. Вычислить точки
0
0
0
()
1
i
ba
xai
n
,
1,...,
i
n
равноотстоящие
друг от друга.
3. Вычислить значения функции в n найденных точках:
()i
fx,
1,...,
i
n
.
4. Среди точек ix ,
1,...,
i
n
найти такую, в которой функция прини-
мает наименьшее значение:
1
()min()
k
i
in
fx
fx
.
5. Точка минимума x
принадлежит интервалу
1
1
[;]
k
k
n
x
x
x
L
,
на котором в качестве приближенного решения может быть выбрана точка
k
x
x
.
Стратегия решения задачи
2
x
Рис. 3.3
0
a
0
b
1x
()
fx
N
x
x
1
kx
kx
1
kx
1
()k
fx
1
()k
fx
()k
fx
147
Сходимость
Для метода равномерного поиска характеристика относительного
уменьшения начального интервала неопределенности находится по фор-
муле
2
()
1
Rn
n
, где n – количество вычислений функции.
Замечание 3.3
Погрешность определения точки минимумах x
функции ( )
fx ме-
тодом равномерного поиска не превосходит величины
0
0
()
n
ba
n
.
Действительно, предположим, что k
x является внутренней точкой
разбиения отрезка 0 0
[;]
a b ,т.е.1
1
kn
. Тогда с учетом свойства уни-
модальных функций следует что:
а)
1
()()
k
k
fxfx
, т.е.
10
[;]
k
x
x
b
;
б)
1
()()
k
k
fxfx
, т.е.
0
1
[;]
k
x
ax
.
Отсюда получаем, что
1
1
1
1
[;][;][;]
k
k
k
k
x
x
bax
x
x
.
Длина
последнего отрезка равна
2()
ba
n
,аточкаk
x является его серединой.
Поэтому
0
0
(
)
|
|
k
n
ba
xx
n
.
Таким образом, чтобы обеспечить требуемую точность определе-
ния точки x
, число отрезков разбиения n необходимо выбрать из усло-
вия
0
0
(
)
n
ba
n
,т.е.
0
0
()
ba
n
.
Пример 3.2
Найти минимум функции
2
()212
fxxx
методом равномерного
поиска.
Решение
Воспользуемся алгоритмом метода равномерного поиска.
1. Найдем начальный интервал неопределенности методом Свенна
(см. стр. 140):
а) зададим начальную точку 0 5
x,шаг
5
t
. Положим
0
k;
б) вычислим значение функции в трех точках: 0
0
xt
;05
x;
0
10
xt
:
0
()0
fxt
;
0
()10
fx
;
0
( )80
fxt
;
148
в) так как
0
0
0
()()()
fxtfxfxt
то начальный интервал не-
определенности найден: 0 [0; 10]
L
.
Зададим
9
n так,чтобы 0
L со-
держал 1 10
n равных подынтервалов.
2. Определим точки вычисления функции:
(10 0)
0
10
ix
i
i
,
1,..., 9
i
.
3. Вычислим значения функции в девяти точках:
(1) 10
f
,
(2) 16
f
,
(3) 18
f
,
(4) 16
f
,
(5) 10
f
,
(6) 0
f,
(7) 14
f,(8)32
f,(9)54
f
.
4. В точке
33
x
функция принимает наименьшее значение:
3
()18
fx
.
5. Искомая точка минимума после девяти вычислений принадлежит
интервалу:
9
[2; 4]
x
L
, в котором выбирается точка
33
x
x
.
Заметим, что характеристика относительного уменьшения начального
интервала неопределенности
9
0
||42
()
0.2
||100
L
Rn
L
.
3.2 .2. Метод деления отрезка пополам
Требуется найти безусловный минимум унимо-
дальной функции ( )
f x одной переменной, т.е.
найти такую точку x R
,что()min()
xR
fx
fx
.
Метод относится к последовательным
стратегиям и позволяет исключить из
дальнейшего рассмотрения на каждой итерации в точности половину те-
кущего интервала неопределенности. Задается начальный интервал неоп-
ределенности, а алгоритм уменьшения интервала, являясь, как и в общем
случае, «гарантирующим» (см. рис. 3.2), основан на анализе величин функ-
ции в трех точках, равномерно распределенных на текущем интервале (де-
лящих его на четыре равные части). Условия окончания процесса поиска
стандартные: поиск заканчивается, когда длина текущего интервала неоп-
ределенности оказывается меньше установленной величины.
Алгоритм
1. Задать начальный интервал неопределенности 0
00
[;]
Lab
и
0
– требуемую точность.
2. Положить
0
k
.
Стратегия решения задачи
Постановка задачи
149
3. Вычислить среднюю точку
2
c
k
k
k
ab
x
,
2
||kkk
L
ba
,
()c
k
fx.
4. Вычислить точки:
2
||
4
k
k
k
L
ya
,
2
||
4
k
k
k
L
z
b
и
()k
fy,
()k
f z . Заметим, что точки ky ,
c
kx , kz делят интервал на четыре равные
части.
5. Сравнить значения ( )
k
fyи()
c
k
fx:
а) если
()()c
k
k
fy fx
исключить интервал ( ; ]
c
kk
x b , положив
1
c
k
k
bx
,
1
k
k
a
a
. Средней точкой нового интервала становится точка
ky:
1
c
k
k
x
y
(рис. 3.4, а). Перейти к шагу 7;
б)если ( )
()c
k
k
fy fx
, перейти к шагу 6.
6. Сравнить значения ( )
k
fzи()
c
k
fx:
а) если
()()c
k
k
fzfx
исключить интервал [ ; )c
kk
a x , положив
1
c
k
k
a
x
,
1
k
k
bb
. Средней точкой нового интервала становится точка
kz:
1
c
k
k
x
z
(рис. 3.4, б). Перейти к шагу 7;
б)если ( )
()c
k
k
fzfx
, исключить интервалы [ ; )
kk
ay,(;]
kk
zb,
положив
1
k
k
a
y
,
1
k
k
bz
.
Средней точкой нового интервала стано-
вится точка
c
kx:
1
c
c
k
k
x
x
.
7. Вычислить
2( 1)
1
1
|
||
|
k
k
k
L
ba
и проверить условие оконча-
ния:
а) если 2( 1)
|
|
k
L
, процесс поиска завершается и
2( 1)
k
xL
1
1
[;]
k
k
a
b
. В качестве приближенного решения можно взять середину
последнего интервала:
1
c
k
x
x
;
б) если 2( 1)
|
|
k
L
, то положить
1
kk
и перейти к шагу 4.
Сходимость
Для метода деления интервала пополам характеристика относитель-
ного уменьшения начального интервала неопределенности находится по
формуле
2
1
()
2n
Rn
, где n – количество вычислений функции.
150
Замечания 3.4
1. Средняя точка последовательно получаемых интервалов всегда
совпадает с одной из трех пробных точек, найденных на предыдущей ите-
рации. Следовательно, на каждой итерации требуются два новых вычисле-
ния функции.
2. Если задана величина ( )
R n , то требуемое для достижения желае-
мой точности количество вычислений функции находится как наименьшее
целое, удовлетворяющее условию
2ln()
ln 0.5
Rn
n
.
3. Текущие интервалы имеют четные номера 0
L,2
L,4
L ,..., где ин-
декс указывает на сделанное количество вычислений функции.
Пример 3.3
Найти минимум функции
2
()212
fxxx
методом деления отрезка
пополам.
Решение
0
.
1 Зададим начальный интервал неопределенности 0 [0; 10]
L
(см.
п. 1 примера 3.2). Пусть
1
.
0
2 . Положим
1
k.
0
.
3 Вычислим 0
010
5
2
c
x
,
0
|||100|10
L
,
0
()10
c
fx
.
0
.
4 Вычислим
0
0
0
||2.5
4
L
ya
,
0
0
0
||7.5
4
L
z
b
и
0
()17.5
fy
,
0
()22.5
fz
.
Рис. 3.4
()
fx
()k
fz
()c
k
fx
kz
ky
c
kx
kb
ka
()k
fy
x
Новый интервал
Текущий интерва л
а
()
fx
()k
fz
()c
k
fx
kz
ky
c
kx
kb
ka
()k
fy
x
Новый интервал
Текущий интерва л
б
151
0
.
5 Сравним
0
()
fyс
0
()c
fx .Таккак
0
0
()17.5()10
c
fy
fx
,
то положим 1
00
aa
,
1
05
c
bx
,
1
0 2.5
c
x
y
. Переходим к шагу 7.
0
.
7 Получим 2 [0; 5]
L
,
2
||51
L
Переходим к шагу 4.
1
.
4 Вычислим
2
11
||1.25
4
L
ya
,
2
11
||3.75
4
L
zb
;
1
( ) 11.875
fy
,
1
( ) 16.875
fz
.
1
.
5 Сравним
1
()
fyс
1
0
()()
c
fx fy
.
Так как
1
( ) 11.875
fy
1
()17.5
c
fx
, то перейдем к шагу 6.
1
.
6 Сравним
1
()
fzс
1
()c
fx .Таккак
1
1
()16.875 () 17.5
c
fz
fx
,
то положим: 2
1 1.25
ay
,
2
1 3.75
bz
,
2
1 2.5
c
c
x
x
.
1
.
7 Получим 4 [1.25; 3.75]
L
,
4
||2.5
1
L
. Положим
2
kи
переходим к шагу 4.
2
.
4 Вычислим
4
2
2
| | 1.875
4
L
ya
,
4
2
2
| | 3.125
4
L
z
b
;
2
( ) 15.47
fy
,
2
( ) 17.97
fz
.
2
.
5 Сравним
2
()
fyс
2
1
()()
c
c
fxfx
.
Так как
2
( ) 15.47
fy
2
()17.5
c
fx
, то переходим к шагу 6.
2
.
6 Сравним
2
()
fzс
2
()c
fx.Таккак
2
2
()17.97 ()c
fz
fx
17.5
; то положим 3
2 2.5
c
ax
,
3
2 3.75
bb
,
3
2 3.125
c
x
z
.
2
.
7 Получим 6 [2.5; 3.75]
L
,
6
||1.25
1
L
. Положим
3
kи
переходим к шагу 4.
3
.
4 Вычислим
6
33
||2.81
4
L
ya
,
6
3
3
||3.43
4
L
z
b
;
3
( ) 17.93
fy
,
3
( ) 17.62
fz
.
3
.
5 Сравним
3
()
fyс
3
2
()()
c
fxfz
.
Так как
3
( ) 17.93
fy
3
( ) 17.97
c
fx
, то перейдем к шагу 6.
3
.
6 Сравним
3
()
fzс
3
()c
fx.Таккак
3
3
()17.63 ()c
fz
fx
17.97
, то положим 4
3 2.81
ay
,
4
3 3.43
bz
,
4
3 3.125
c
c
x
x
.
152
3
.
7 Получим 8 [2.81; 3.43]
L
,
8
||0.62
1
L
;
8
xL
,
8
n
.В
качестве решения можно взять среднюю точку последнего интервала
3 3.125
c
x
x
,
min
( ) 17.97
ffx
.
3.2 .3. Метод дихотомии
Требуется найти безусловный минимум унимо-
дальной функции ( )
f x одной переменной, т.е.
найти такую точку x R
,что()min()
xR
fx
fx
.
Метод дихотомии относится к последо-
вательным стратегиям. Задается началь-
ный интервал неопределенности и требуемая точность. Алгоритм опирает-
ся на анализ значений функции в двух точках (см. рис. 3.2). Для их нахож-
дения текущий интервал неопределенности делится пополам и в обе сто-
роны от середины откладывается по
2
, где – малое положительное
число. Условия окончания процесса поиска стандартные: поиск заканчива-
ется, когда длина текущего интервала неопределенности оказывается
меньше установленной величины.
Замечание 3.5
Число итераций n метода дихотомии, необходимое для определения
точки x
с точностью , определяется неравенством
0
0
2
log
2
ba
n
.
Поэтому число выбирается из условия
2
.
Алгоритм
1. Задать начальный интервал неопределенности 0
00
[;]
Lab
,
0
–малое число,
0
– требуемую точность.
2. Положить
0
k
.
3. Вычислить
2
k
k
k
ab
y
,
()k
fy;
2
k
k
k
ab
z
,
()k
fz.
4. Сравнить ( )
k
fyс()
k
fz:
а)если ( )
()
k
k
fy fz
, положить
1
k
k
a
a
,
1
k
k
bz
и перейти
к шагу 5;
б)если ( )
()
k
k
fy fz
, положить
1
k
k
a
y
,
1
k
k
bb
.
5. Вычислить
2( 1)
1
1
|
||
|
k
k
k
L
ba
и проверить условие оконча-
ния:
Постановка задачи
Стратегия решения задачи
153
а) если
2( 1)
|
|
k
L
процесс поиска завершается и
2( 1)
k
xL
1
1
[;]
k
k
ba
. В качестве приближенного решения можно взять середину
последнего интервала:
1
1
2
k
k
a
b
x
;
б) если 2( 1)
|
|
k
L
, положить
1
kk
и перейти к шагу 3.
Сходимость
Для метода дихотомии характеристика относительного уменьшения
начального интервала неопределенности находится по формуле
2
1
()
2n
Rn
, где n – количество вычислений функции
Замечания 3.6
1. Текущие интервалы неопределенности 0
L,2
L,4
L ,... имеют чет-
ные номера, указывающие на количество сделанных вычислений функции,
как и в методе деления интервала пополам.
2. Эффективность метода дихотомии при малых и метода деления
интервала пополам можно считать одинаковой.
Пример 3.4
Найти минимум функции
2
()212
fxxx
методом дихотомии.
Решение
.
1 Зададим начальный интервал неопределенности 0 [0; 10]
L
(см.
п. 1 примера 3.2). Положим
0.2
,1
.
2. Положим
0
k
.
0
.
3 Вычислим
0
0
0
4.9
2
ab
y
,
0
0
0
5.1
2
ab
z
;
0
( ) 10.78
fy
,
0
()9.18
fz
.
0
.
4 Так как
0
0
()()
fy fz
,то1
00
aa
,
1
0 5.1
bz
.
0
.
5 Получим 2 [0; 5.1]
L
,
2
||5.1
1
L
. Положим
1
k ипе-
рейдем к шагу 3.
1
.
3 Вычислим
11
1
2.45
2
ab
y
,
11
1
2.65
2
ab
z
;
1
( ) 17.395
fy
,
1
( ) 17.755
fz
.
1
.
4 Так как
1
1
()()
fy fz
,то 2
1 2.45
a
y
,
2
1 5.1
bb
.
154
1
.
5 Получим 4 [2.45; 5.1]
L
,
4
||2.65
1
L
. Положим
2
kи
перейдем к шагу 3.
2
.
3 Вычислим
2
2
2
3.675
2
ab
y
,
2
2
2
3.875
2
ab
z
;
2
( ) 17.089
fy
,
2
( ) 16.469
fz
.
2
.
4 Так как
2
2
()()
fy fz
,то 3
2 2.45
aa
,
3
2 3.875
bz
.
2
.
5 Получим
6 [2.45; 3.875]
L
,
6
| | 1.425
1
L
.
Положим
3
k иперейдемкшагу3.
3
.
3 Вычислим
33
3
3.06
2
ab
y
,
33
3
3.26
2
ab
z
;
3
( ) 17.99
fy
,
3
( ) 17.86
fz
.
3
.
4 Так как
3
3
()()
fy fz
,то 4
3 2.45
aa
,
4
3 3.26
bz
.
3
.
5 Получим 8 [2.45;3.26]
L
,
8
||0.81
1
L
. Таким образом,
8 [2.45; 3.26]
xL
,
8
n и в качестве решения принимаем:
2.45 3.26
2.855
2
x
,
min
()
17.958
fxf
.
3.2 .4. Метод золотого сечения
Требуется найти безусловный минимум унимо-
дальной функции ( )
f x одной переменной, т.е.
найти такую точку x R
,что()min()
xR
fx
fx
.
Для построения конкретного метода одномерной минимизации, рабо-
тающего по принципу последовательного сокращения интервала неопре-
деленности, следует задать правило выбора на каждом шаге двух внутрен-
них точек (см. рис. 3.2). Число вычислений новых точек и значений функ-
ции должно быть минимальным. В методе золотого сечения в качестве
двух внутренних точек выбираются точки так называемого золотого сече-
ния.
Определение 3.3. Точка производит «золотое сечение» отрезка, если
отношение длины всего отрезка к большей части равно отношению боль-
шей части к меньшей.
На отрезке
00
[;]
a b имеются две симметричные относительно его
концов точки 0
yи0
z:
Постановка задачи
155
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
15
1.618
2
babyba
z
a
byya
z
a
bz
.
Кроме того, точка 0
y производит золотое сечение отрезка 0 0
[;]
az,а
точка 0
z –отрезка 0 0
[;]
y b (рис. 3.5).
Метод относится к последовательным
стратегиям. Задается начальный интер-
вал неопределенности и требуемая точность. Алгоритм уменьшения ин-
тервала опирается на анализ значений функции в двух точках (см. рис.
3.5). В качестве точек вычисления функции выбираются точки золотого
сечения. Тогда с учетом свойств золотого сечения на каждой итерации,
кроме первой, требуется только одно новое вычисление функции. Условия
окончания процесса поиска стандартные: поиск заканчивается, когда дли-
на текущего интервала неопределенности оказывается меньше установ-
ленной величины.
Алгоритм
1. Задать начальный интервал неопределенности 0
00
[;]
Lab
, точ-
ность
0
.
2. Положить
0
k
.
3. Вычислить:
0
0
0
0
35
()
2
ya
ba
,
0
0
0
0
z
aby
,
35
0.38196
2
.
4. Вычислить
()k
fy,()
k
fz.
5. Сравнить значения ( )
k
fyи()
k
fz:
а) если
()()
k
k
fy fz
, то положить
1
k
k
a
a
,
1
k
k
bz
и
1
1
1
k
k
k
k
y
a
by
,
1
k
k
z
y
. Перейти к шагу к шагу 6;
б)если ( )
()
k
k
fy fz
, положить
1
k
k
a
y
,
1
k
k
bb
и
1
k
k
y
z
,
1
1
1
k
k
k
k
z
a
bz
.
6. Вычислить
1
1
|
|
k
k
a
b
и проверить условие окончания:
Стратегия решения задачи
0z
0
y
0
b
0
a
x
Рис. 3.5
156
а) если
, процесс поиска завершается и
1
1
[;]
k
k
x
a
b
.В
качестве приближенного решения можно взять середину последнего ин-
тервала:
1
1
2
k
k
a
b
x
;
б) если
, положить
1
kk
и перейти к шагу 4.
Сходимость
Для метода золотого сечения характеристика относительного умень-
шения начального интервала неопределенности находится по формуле
1
( ) (0.618)n
Rn
, где n – количество вычислений функции.
Замечания 3.7.
1. Текущие интервалы неопределенности имеют следующий вид: 0
L,
2
L,3
L,4
L ,... Они отражают тот факт, что на первой итерации произво-
дится два вычисления функции, а на последующих – по одному.
2. Сокращение длины интервала неопределенности постоянно:
0
3
2
2
3
4
...
1.618
L
L
L
LLL
.
3. Если задана величина ( )
R n , то требуемое для достижения желае-
мой точности количество вычислений функции находится как наименьшее
целое число, удовлетворяющее условию
ln()
1
ln 0.618
Rn
n
.
Пример 3.5
Найти минимум функции
2
()212
fxxx
методом золотого сече-
ния.
Решение
.
1 Зададим начальный интервал неопределенности: 0 [0; 10]
L
(см.
п. 1 примера 3.2). Положим
1
.
.
2 Положим
0
k
.
0
.
3 Вычислим
0
0
0
0
0.382 (
) 0 0.382 10 3.82
ya
ba
;
0
0
0
0 0103.826.18
z
aby
.
0
.
4 Вычислим
0
( ) 16.65
fy
;
0
()2.22
fz
.
0
.
5 Сравним
0
()
fyи
0
()
fz .Таккак
0
0
()()
fy fz
,то 1
00
aa
;
106.18
bz
;111006.183.822.36
yaby
;103.82
z
y
.
157
0
.
6 Получим 2 [0; 6.18]
L
;2
||6.18
1
L
. Положим
1
kи
перейдем к шагу 4.
1
.
4 Вычислим
1
( ) 17.18
fy
(новое значение);
1
1
() ()
fzfz
16.65
(уже было вычислено на шаге
0
4).
1
.
5 Сравним
1
()
fyи
1
()
fz .Таккак
1
1
()()
fy fz
,то 2
10
aa
;
213.82
bz
;222103.822.361.46
yaby
;212.36
z
y
.
1
.
6 Получим 3 [0; 3.82]
L
;3
||3.82
1
L
.
Положим
2
k
и
перейдем к шагу 4.
2
.
4 Вычислим
2
( ) 13.25
fy
(новое вычисление);
2
1
()()
fz fy
17.18
(уже было вычислено на шаге
1
4).
2
.
5 Сравним
2
()
fyи
2
()
fz .Таккак
2
2
()()
fyfz
,то321.46
ay
;
323.82
bb
;322.36
yz
;33321.463.822.3622.92
zabz
.
2
.
6 Получим 4 [1.46; 3.82]
L
;4
| | 3.82 1.46 2.36
1
L
.По-
ложим
3
k иперейдемкшагу4.
3
.
4 Вычислим
3
2
()()17.18
fy fz
(уже было вычислено на шаге
2
4);
3
( ) 17.99
fz
.
3
.
5 Сравним
3
()
fyи
3
()
fz .Таккак
3
3
()()
fyfz
,то432.36
ay
;
433.82
bb
;432.92
yz
;44432.363.822.923.26
zabz
.
3
.
6 Получим 5 [2.36; 3.82]
L
;5
| | 3.82 2.36 1.46
1
L
.По-
ложим
4
k иперейдемкшагу4.
4
.
4 Вычислим
4
3
()()17.99
fy fz
(было известно на шаге
3
4);
4
( ) 17.86
fz
.
4
.
5 Сравним
4
()
fyи
4
()
fz .Таккак
4
4
()()
fy fz
,то542.36
aa
;
543.26
bz
;555 42.363.262.922.7
yaby
;5
4 2.92
z
y
.
4
.
6 Получим 6 [2.36; 3.26]
L
;6
| | 3.26 2.36 0.9
1
L
.Вы-
числения окончены:
6
xL
,
6
n
.
Решение:
3.26 2.36
2.81
2
x
,
min
( ) 17.93
ffx
.
158
3.2 .5. Метод Фибоначчи
Требуется найти безусловный минимум унимо-
дальной функции ( )
f x одной переменной, т.е .
найти такую точку x R
,что()min()
xR
fx
fx
.
Для построения эффективного метода одномерной минимизации, ра-
ботающего по принципу последовательного сокращения интервала неоп-
ределенности, следует задать правило выбора на каждом шаге двух внут-
ренних точек. Желательно, чтобы одна из них всегда использовалась в ка-
честве внутренней и для следующего интервала. Тогда количество вычис-
лений функции сократится вдвое. В методе Фибоначчи (L. Fibonacci) реа-
лизована стратегия, обеспечивающая максимальное гарантированное со-
кращение интервала неопределенности при заданном количестве вычисле-
ний функции и претендующая на оптимальность. Эта стратегия опирается
на числа Фибоначчи.
Определение 5.4. Числа Фибоначчи определяются по формуле
0
11
FF
,
1
2
k
k
k
FFF
,
2,3,4,...
k
.
Последовательность чисел Фибоначчи имеет вид 1,1 , 2 , 3 , 5 , 8 ,13 , 21 ,
34, 55 ,89,... .
Метод Фибоначчи относится к последо-
вательным стратегиям. Задается началь-
ный интервал непределенности и коли-
чество N вычислений функции. Алгоритм уменьшения интервала опира-
ется на анализ значений функции в двух точках (см. рис. 3.2). Точки вы-
числения функции находятся с использованием последовательности из
1
n чисел Фибоначчи. Как в методе золотого сечения, на первой итера-
ции требуются два вычисления функции, а на каждой последующей –
только по одному. Условия окончания процесса поиска стандартные: по-
иск заканчивается, когда длина текущего интервала неопределенности ока-
зывается меньше установленной величины.
Алгоритм
1. Задать начальный интервал неопределенности 0
00
[;]
Lab
,
0
–
допустимую длину конечного интервала,
0
– константу различимо-
сти.
2. Найти количество n вычислений функции как наименьшее целое
число, при котором удовлетворяется условие
0
||
n
L
F
, и числа Фибо-
наччи 0
F,1
F, ...,
n
F.
Постановка задачи
Стратегия решения задачи
159
3. Положить
0
k
.
4. Вычислить
2
0
0
0
0
(
)
n
n
F
ya
ba
F
;
1
0
0
0
0
()
n
n
F
z
a
ba
F
.
5. Вычислить ( )
k
fyи()
k
fz.
6. Сравнить ( )
k
fyи()
k
fz:
а)если ( )
()
k
k
fy fz
, положить
1
k
k
a
a
;
1
k
k
bz
;
1
k
k
z
y
;
3
1
1
1
1
(
)
nk
k
k
k
k
n
F
ya
ba
F
.
Перейти к шагу 7;
б)если ( )
()
k
k
fy fz
, положить
1
k
k
a
y
;
1
k
k
bb
;
1
k
k
yz
;
2
1
1
1
1
1
(
)
nk
k
k
k
k
nk
F
z
a
ba
F
.
7. Проверить условие окончания и в случае необходимости сделать
заключительное n -е вычисление функции для получения решения:
а) если
3
kn
, положить
1
kk
и перейти к шагу 5;
б) если
3
kn
, то всегда
2
2
2
2
(
)
2
n
n
n
n
a
b
y
z
, т.е. от-
сутствует точка нового вычисления функции. Следует положить:
1
2
2
n
n
n
y
y
z
;
1
1
n
n
z
y
В точках
1
n
yи
1
n
z вычисляются
значения функции и находятся границы конечного интервала неопреде-
ленности:
–
если
1
1
()()
n
n
fy fz
, положить
1
2
n
n
a
a
,
1
1
n
n
bz
;
–
если
1
1
()()
n
n
fy fz
, положить
1
1
n
n
a
y
,
1
2
n
n
bb
.
Процесс поиска завершается и
1
1
[;]
n
n
x
a
b
. В качестве прибли-
женного решения можно взять любую точку последнего интервала, на-
пример, его середину
1
1
2
n
n
a
b
x
.
Сходимость
Для метода Фибоначчи характеристика относительного уменьшения
начального интервала неопределенности находится по формуле
1
()
n
Rn
F
, где n – количество вычислений функции.
160
Замечания 3.8
1. При заданном количестве n вычислений функции метод Фибонач-
чи обеспечивает минимальную величину конечного интервала неопреде-
ленности по сравнению с методами, изложенными в разд. 3.2.1 – 3.2.4.
2. Нумерация интервалов неопределенности такая же, как в методе
золотого сечения: 0
L,2
L,3
L,4
L ,... (см. п.1 замечания 3.6).
3. На k -ой итерации длина интервала неопределенности сокращается
по правилу
1
nk
nk
F
F
.
Пример 3.6
Найти минимум функции
2
()212
fxxx
методом Фибоначчи.
Решение
.
1 Зададим начальный интервал неопределенности: 0 [0; 10]
L
(см.
п. 1 примера 3.2). Пусть
1
,
0.01
;
0
6
10
13
10
1
L
F
, поэто-
му6
n
.
.
2 Найдем числа Фибоначчи: 0
11
FF
,
22
F,33
F,45
F,
58
F,613
F
.
.
3 Положим
0
k
.
0
.
4 Вычислим
4
0
0
0
0
6
5
()0
10 3.846
13
F
ya
ba
F
;
5
0
0
0
0
6
8
(
)0
10 6.154
13
F
z
a
ba
F
.
0
.
5 Вычислим
0
( ) 16.57
fy
,
0
( ) 1.893
fz
.
0
.
6 Сравним
0
()
fyи
0
()
fz Таккак
0
0
()()
fy fz
,то1
00
aa
;
1 0 6.154
bz
;103.846
zy
;
63
11
11
61
3
( ) 0 6.154 2.308
8
F
ya
ba
F
.
0
.
7 Проверим условие окончания:
0
33
k
n
; 2 [0; 6.154]
L
.
Положим
1
k иперейдемкшагу5.
1
.
5 Вычислим значения
1
( ) 17.04
fy
,
1
( ) 16.57
fz
(уже было
вычислено на шаге
0
5).
161
1
.
6 Сравним
1
()
fyи
1
()
fz Таккак
1
1
()()
fy fz
,то 2
10
aa
;
2 1 3.846
bz
;212.308
zy
;
64
22
2
2
62
2
( ) 0 3.846 1.538
5
F
ya
ba
F
.
1
.
7 Проверим условие окончания:
1
33
k
n
; 2 [0; 3.846]
L
.
Положим
2
k иперейдемкшагу5.
2
.
5 Вычислим значения
2
( ) 13.73
fy
,
2
( ) 17.04
fz
(уже было
вычислено на шаге
1
5).
2
.
6 Сравним
2
()
fyс
2
()
fz .Таккак
2
2
()()
fy fz
,то
3
2 1.538
a
y
;323.846
bb
;322.308
yz
;
64
33
33
63
2
( ) 1.538 (3.846 1.538) 3.077
3
F
za
ba
F
.
2
.
7 Проверим условие окончания:
2
33
k
N
; 4 [1.538; 3.846]
L
. Положим
3
k иперей-
дем к шагу 5.
3
.
5 Вычислим значения
3
2
()()17.04
fy fz
(уже было извест-
но);
3
( ) 17.9884
fz
.
3
.
6 Сравним
3
()
fyс
3
()
fz .Таккак
3
3
()()
fy fz
,то
4
3 2.308
a
y
;433.846
bb
;433.077
yz
;
65
44
4
4
64
1
( ) 2.308 (3.846 2.308) 3.077
2
F
za
ba
F
.
3
.
7 Проверим условие окончания:
3
33
k
n
; 5 [2.308; 3.846]
L
.
Положим 5
4 4 3.077
yyz
;55
3.077 0.01 3.087
z
y
. Вычислим
5
( ) 17.9884
fy
(было вычислено на шаге
3
5);
5
( ) 17.985
fz
.
Так
как
5
5
()()
fy fz
,
то
5
4 2.308
aa
;553.087
bz
.
Поэтом у
6 [2.308; 3.087]
xL
;
6
| | 3.087 2.308 0.78
1
L
.
Заметим,
что
6
0
6
||
11
0.078
0.077
||
13
L
L
F
.
162
В качестве приближенного решения возьмем середину интервала 6
L:
2.308 3 .087
2.697
2
x
и min
( ) 17.816
ffx
.
3.2 .6. Метод квадратичной аппроксимации
Требуется найти безусловный минимум унимо-
дальной функции ( )
f x одной переменной, т.е.
найти такую точку x R
,что()min()
xR
fx
fx
.
Метод квадратичной интерполяции, или
метод Пауэлла (Powell M. J. D.), отно-
сится к последовательным стратегиям. Задается начальная точка и с по-
мощью пробного шага находятся три точки так, чтобы они были как мож-
но ближе к искомой точке минимума. В полученных точках вычисляются
значения функции. Затем строится интерполяционный полином второй
степени, проходящий через имеющиеся три точки. В качестве приближе-
ния точки минимума берется точка минимума полинома. Процесс поиска
заканчивается, когда полученная точка отличается от наилучшей из трех
опорных точек не более чем на заданную величину.
Алгоритм
1. Задать начальную точку 1x , величина шага
0
x
,1
и2
–ма-
лые положительные числа, характеризующие точность.
2. Вычислить 2
1
x
x
x
.
3. Вычислить
1
1
()
fxf
и
2
2
()
fxf
.
4. Сравнить
1
()
fxс
2
()
fx:
а) если
1
2
()()
fxfx
, положить 3
12
xx
x
(рис. 3.6,а);
б) если
1
2
()()
fxfx
положить 3
1
xx
x
(рис. 3.6,б).
5. Вычислить
3
3
()
fxf
.
6. Найти min
123
min{, ,}
F
fff
,
min
i
x
x
:
min
()i
fxF
.
7. Вычислить точку минимума интерполяционного полинома, постро-
енного по трем точкам:
2
2
2
2
2
2
2
31
3
12
1
23
2
31
3
12
1
23
(
)(
)(
)
1
2(
)()()
x
xf
x
xf
x
xf
x
xxf
xxf
xxf
,
и величину функции ( )
f x (рис. 3.6).
Постановка задачи
Стратегия решения задачи
163
Если знаменатель в формуле для x на некоторой итерации обращает-
ся в нуль, то результатом интерполяции является прямая. В этом случае
рекомендуется обозначить 1
min
xx
и перейти к шагу 2.
8. Проверить выполнение условий окончания:
min
1
()
()
F
fx
fx
,
min
2
x
x
x
.
Тогда:
а) если оба условия выполнены, процедура закончена и x
x
;
б) если хотя бы одно из условий не выполнено и
13
[;]
xxx
, выбрать
наилучшую точку ( min
x
или x ) и две точки по обе стороны от нее. Обо-
значить эти точки в естественном порядке и перейти к шагу 6;
в) если хотя бы одно из условий не выполнено и
13
[;]
xxx
,топо-
ложить 1x x
и перейти к шагу 2.
Замечание 3.9
Шаги 1 – 4 алгоритма позволяют выяснить направление убывания
функции, а в некоторых случаях определить интервал, на котором функ-
ция является унимодальной.
Пример 3.7
Найти минимум функции
216
()2
fxx
x
методом квадратичной
интерполяции.
()
fx
1
()
fx
2
()
fx
2
x
3x
x
1x
3
()
fx
x
а
()
Px
()
fx
3
()
fx
1
()
fx
1x
2
x
x
3x
2
()
fx
x
б
()
Px
Рис. 3.6
164
Решение
0
.
1 Зададим начальную точку 1 1
x , величину шага
1
x
,
1 0.003
и20.03
.
0
2 . Вычислим 2
1
2
x
x
x
.
0
.
3 Вычислим
1
1
() 18
fxf
;
2
2
()
16
fxf
.
0
.
4 Так как
1
2
()()
fxfx
,положим 3 1 2
123
xx
x
(рис.3.6).
0
.
5 Вычислим
3
3
()
23.33
fxf
.
0
.
6 Найдем min min{18; 16; 23.33} 16
F
; min
22
x
x
.
0
.
7 Вычислим точку минимума интерполяционного полинома:
1 (4 9)18 (9 1)16 (1 4) 23.33
1.714
2 (2 3)18 (3 1)16 (1 2) 23.33
x
; ()15.21
fx
.
0
.
8 Проверим условия окончания:
1
16 15.21
0.052
0.003
15.21
(не выполняется),
x – наилучшая точка, слева от нее точка 1 1
x,асправа2 2
x
. Обозна-
чим их в естественном порядке 1 1
x;2
1.714
x
x
;32
x
. Этим точ-
кам соответствуют следующие значения функции: 1 18
f;215.21
f
;
316
f
. Перейдем к шагу 6.
1
.
6 Найдем min min{18; 15.21; 16} 15.21
F
; min
2 1.714
x
x
.
1
.
7 Вычислим точку минимума интерполяционного полинома:
2
2
1 (1.714 4)18 (4 1)15.21 (1 1.714 )16
1.65
2 (1.714 2)18 (2 1)15.21 (1 1.714)16
x
;()15.142
fx
.
1
.
8 Проверим условия окончания:
1
15.21 15.142
0.0045
0.003
15.142
(не выполняется);
x – наилучшая точка, слева от нее точка 1 1
x ,асправа 2 1.714
x
. Обо-
значим их в естественном порядке 1 1
x;21.65
x
; 3 1.714
x
.
Этим
точкам
соответствуют
следующие
значения
функции: 1 18
f;
2 15.142
f
; 3 15.21
f
. Перейдем к шагу 6.
165
2
.
6 Найдем min min{18; 15.142; 15.21} 15.142
F
; min
2 1.65
x
x
.
2
.
7 Вычислим точку минимума интерполяционного полинома:
2
2
2
2
1 (1.65 1.714 )18 (1.714 1)15.142 (1 1.65 )15.21
1.6125
2 (1.65 1.714)18 (1.714 1)15.142 (1 1.65)15.21
x
;
( ) 15.123
fx
.
2
.
8 Проверим условия окончания:
1
15.142 15.123
0.0013
0.003
15.123
(выполняется);
2
1.65 1.6125
0.023
0.03
1.6125
(выполняется).
Поиск закончен. Решение
1.6125
x
x
.
Найдем аналитически координату точки минимума с помощью необ-
ходимых условий безусловного экстремума:
2
()
16
4
0
dfx
x
dx
x
Отсюда
3
4 1.5874
x
. В этой точке достаточные условия безус-
ловного минимума выполняются, т.е.
2
2
3
()
32
4
120
xx
dfx
dx
x
.
3.3 . Методы первого и второго порядка
Прямые методы (см. разд. 3.2) используются при минимальных тре-
бованиях к функции ( )
f x – она считается унимодальной и вычислению
доступны значения функции. Эти требования можно усилить, предполо-
жив,что ()
f x является дифференцируемой в произвольно выбранных
точках.
Методы первого порядка предполагают использование значений
функции и ее первых производных, а методы второго порядка – возмож-
ность использования значений и вторых производных функции ( )
fx.
Для выпуклой дифференцируемой функции равенство
()0
fx
яв-
ляется не только необходимым, но и достаточным условием глобального
минимума. Поэтому если известно, что x
является внутренней точкой
отрезка [ ; ]
a b , то приближенное равенство
()0
fx
или|()|
fx
,
где
0
– достаточно малое число, может служить условием окончания
вычислений.
166
3.3 .1. Метод средней точки
Дана непрерывно дифференцируемая унимодаль-
ная функция (x)
f , определенная на множестве
допустимых решений
[;]
XabR
.
Требуется найти локальный минимум функции ( )
f x одной перемен-
ной, т.е. найти такую точку x X
,что()min()
xX
fx
fx
.
Задается начальный интервал неопреде-
ленности
0
00
;
Lab
.
Вычисляется
значение
()
dfx
dx
в средней точке интервала
()
2
ab
x
.
Если
()0
dfx
dx
,
то точка x лежит на участке монотонного возрастания ( )
f x , поэтому
x
x
, и точку минимума следует искать на отрезке [ ; ]
a x , отрезок
[;]
x b исключается. При
()0
dfx
dx
точка минимума ищется на отрезке
[;]
xb,отрезок[;]
a x исключается (рис. 3.7). Такое исключение отрезков
требует на каждой итерации только одного вычисления производной и
уменьшает отрезок поиска точки x
вдвое. Равенство
()0
dfx
dx
означает,
что точка минимума найдена точно: x
x
.
Постановка задачи
Стратегия решения задачи
Рис. 3.7
()
fx
x
a
a
x
x
x
()0
fx
x
b
()
fx
b
a
b
x
x
()0
fx
x
x
x
а
б
167
Алгоритм
1. Задать начальный интервал неопределенности 0
00
[;]
Lab
и точ-
ность
|()|0
fx
. Определить выражение ( )
fx
.
2. Положить
0
k
.
3. Вычислить среднюю точку
2
k
k
k
ab
x
и значение производной
()k
fx
.
4. Проверить окончание поиска:
а)если| ( )|
k
fx
, то процесс поиска завершается и
k
xx
,
min
()
ffx
;
б)если | ( )|
k
fx
,топерейтикшагу5.
5. Сравнить ( )
k
fx
с нулем:
а) если
()0
k
fx
, то положить
1
k
k
bx
,
1
k
k
a
a
,
1
kk
и
перейти к шагу 3;
б) если
()0
k
fx
, то положить
1
k
k
a
x
,
1
k
k
bb
,
1
kk
и
перейти к шагу 3.
Пример 3.8
Найти минимум функции
4
()
x
fxxe
методом средней точки.
Решение
.
1 Зададим начальный интервал неопределенности 0 [0;1]
L
. Пусть
точность
0.02
. Определим
3
()4
x
fxxe
.
2. Положим
0
k
.
0
.
3 Вычислим
0
0
0
01
0.5
2
2
ab
x
и
3
0.5
(0.5) 4 0.5
0.107
f
e
.
0
.
4 Проверим окончание поиска точки минимума:
| (0.5) | 0.107
0.02
f
. Переходим к шагу 5.
0
.
5 Сравним
0
()
fx
с нулем. Так как
0
()0.1070
fx
,топола-
гаем 1
0 0.5
ax
,
1
01
bb
,
1
k . Переходим к шагу 3.
1
.
3 Вычислим
11
1
0.75
2
ab
x
и
1
( ) (0.75) 1.215
fxf
.
168
1
.
4 Так как
1
|()|1.215
0.02
fx
, то переходим к шагу 5.
1
.
5 Сравним
1
()
fx
с нулем. Так как
1
()1.2150
fx
, то полагаем
2
1 0.5
a
a
,
2
1 0.75
bx
,
2
k
. Переходим к шагу 3.
2
.
3 Вычислим
2
2
2
0.625
2
ab
x
и
2
( ) 0.441
fx
.
2
.
4 Так как
2
|()|0.441
0.02
fx
, то переходим к шагу 5.
2
.
5 Сравним
2
()
fx
с нулем. Так как
2
()0
fx
, то полагаем
3
2 0.5
aa
,
3
2 0.625
bx
,
3
k
. Переходим к шагу 3.
3
.
3 Вычислим
33
3
0.563
2
ab
x
и
3
( ) 0.142
fx
.
3
.
4 Так как
3
|()|0.142
0.02
fx
, то переходим к шагу 5.
3
.
5 Сравним
3
()
fx
с нулем. Так как
3
()0
fx
, то полагаем
4
3 0.5
a
a
,
4
3 0.563
bx
,
4
k
. Переходим к шагу 3.
4
.
3 Вычислим
4
4
4
0.531
2
ab
x
и
4
( ) 0.012
fx
.
4
.
4 Так как
4
|()|0.012
0.02
fx
, то процесс поиска токи ми-
нимального значения функции окончен и
0.531
x
,
min
()
0.6675
fxf
.
3.3 .2. Метод хорд
Дана непрерывно дифференцируемая унимодаль-
ная функция (x)
f , определенная на множестве
допустимых решений
[;]
XabR
. Требуется найти локальный мини-
мум функции ( )
f x одной переменной, т.е. найти такую точку x X
,
что()min()
xX
fx
fx
.
Равенство
()0
fx
является необхо-
димым и достаточным условием гло-
бального минимума выпуклой дифференцируемой функции ( )
fx(см.
разд. 1.2). Поэтому если на концах отрезка [ ; ]
a b производная ( )
fx
име-
ет разные знаки, т.е.
()()0
fafb
,тонаинтервале[;]
a b найдется точ-
ка, в которой ( )
fx
обращается в нуль, и поиск точки минимума ( )
fx на
Постановка задачи
Стратегия решения задачи
169
[;]
a b эквивалентен решению уравнения
()0
fx
,
(;)
xab
.
Любой
приближенный метод решения уравнения ( ) 0
fx
можно рассматривать
как метод минимизации выпуклой дифференцируемой функции ( )
fx на
отрезке [ ; ]
a b . Таким методом является метод хорд приближенного реше-
ния уравнения
()0
fx
наотрезке[;]
abпри()()0
fafb
.Этотме-
тод основан на исключении отрезков путем определения точки x пересе-
чения с осью 0 x хорды графика функции ( )
F x на очередном отрезке
(рис. 3.8).
На основании уравнения отрезка прямой, соединяющего две точки
;()
afa
и
;()
bfb
, записываем координату точки x , в которой
()0
fx
:
()()
() ()
fa
xa
ab
fafb
.
()
Отрезок дальнейшего поиска точки x
[;]
axили[;]
xb
выбирается
в зависимости от знака
()
fx
(см. разд. 3.3.1). На каждой итерации, кроме
первой, следует вычислять одно новое значение ( )
fx
.
Алгоритм
1. Определить выражение
()
fx
. Задать начальный интервал неопре-
деленности 0
00
[;]
Lab
так, чтобы удовлетворялось
0
0
()()0
fafb
,и
точность
|()|0
fx
.
2. Положить
0
k
.
3. Найти kx по формуле ( ):
()(
)
()()
k
k
k
k
k
k
k
fa
x
a
ab
fafb
.
x
()
fx
a
x
b
x
b
x
x
Рис. 3.8
170
4. Вычислить значение ( )
k
fx
.
5. Проверить окончание процесса поиска: если | ( ) |
k
fx
, то поло-
жить
k
xx
,
min
()
ffx
и поиск завершить, иначе – перейти к шагу 6.
6. Перейти к новому отрезку:
а)если()0
k
fx
, положить
1
k
k
a
a
,
1
k
k
bx
,
1
()()
k
k
fb fx
,
1
k k ;перейтикшагу3;
б)если ()0
k
fx
, положить
1
k
k
a
x
,
1
k
k
bb
,
1
()()
k
k
fafx
,
1
k k ;перейтикшагу3.
Замечание 3.10
При заданном интервале [ ; ]
a b и нарушении условия
()()0
fafb
точку x
можно указать сразу. Так, если
()0
fa
и()0
fb,то ()
fx
возрастает на [ ; ]
a b , следовательно, x
a
,апри()0
fa
и()0
fb
она убывает и x b
.
Вслучае ()
()0
fafb
,x
a
илиxb
в
зависимости от того, на каком из концов интервала [ ; ]
ab()0
fx
.
Пример 3.9
Найти минимум функции
4
()
x
fxxe
методом средней точки на
интервале [0;1] с точностью | ( ) | 0.05
fx
.
Решение
.
1 Определим
3
()4
x
fxxe
. Задано:
[0;1]
x
и
0.05
.
2. Положим
0
k
.
0
.
3 Вычислим
0
0
0
0
0
0
0
()(
)
()()
fa
x
a
a
b
fafb
1
1
0
(0 1) 0.216
1(4 )
e
.
0
.
4 Вычислим
3
0.216
0
()40.216
0.766
fx
e
0
.
5 Проверим окончание поиска минимума. Так как
0
|()|
fx
, пе-
реходим к шагу 6.
0
.
6 Перейдем к новому отрезку. Так как
0
()0
fx
, положить
1
0 0.216
ax
,
1
01
bb
;
1
0
() ()0.766
fafx
,
1
k . Переходим к
шагу 3.
171
1
.
3 Вычислим
1
1
1
11
1
1
()( )0.352
() ()
fa
x
a
ab
fafb
.
1
.
4 Вычислим
1
3
0.352
()40.352
0.528
fx
e
.
1
.
5 Проверим окончание поиска. Так как
0
|()|
fx
, переходим к
шагу 6.
1
.
6 Перейдем к новому отрезку. Так как
0
()0
fx
, положить
2
1 0.352
a
x
,
2
11
bb
,
1
0
() ()0.766
fafx
,
1
k . Переходим к
шагу 3.
Результаты вычислений на остальных итерациях – в табл. 3.1.
Таблица 3.1
Номер
итерации
k
a
k
b
k
x
()k
fx
Знак
()k
fx
2
0.352
1
0.435
–0.319
(–)
3
0.435
1
0.480
–0.175
(–)
4
0.480
1
0.504
–0.091
(–)
5
0.504
1
0.516
–0.046
0
|()|
fx
Таким образом,
0.516
x
,
min
( ) 0.6678
ffx
.
3.3 .3. Метод Ньютона
Дана дважды непрерывно дифференцируемая вы-
пуклая функция (x)
f , определенная на множестве
допустимых решений
[;]
XabR
.
Требуется найти минимум функции ( )
f x одной переменной, т.е.
найти такую точку x X R
,что()min()
xX
fx
fx
.
По условию функция ( )
f x дважды
дифференцируема, причем
()0
fx
(это гарантирует выпуклость ( )
f x ). Тогда корень уравнения
()0
fx
можно искать приближенно, используя метод касательных. Этот метод
решения уравнения
()0
fx
состоит в построении последовательных
приближений
,
0, 1,...
kx k
следующим образом. В точке k
x строится
линейная аппроксимация ( )
()()()
k
k
k
fxfxfxxx
функции ( )
fx
(т.е. касательная к линии
()
fx
) и точка, в которой линейная аппрокси-
мирующая функция обращается в нуль, используется в качестве следую-
Постановка задачи
Стратегия решения задачи
172
щего приближения
1
kx (рис. 3.9). В процедуре решения не требуется оп-
ределенный интервал [ ; ]
a b , поэтому для задачи безусловной оптимизации
предполагается X R
.
Описанная стратегия поиска точки минимума называется методом
Ньютона.
Замечания 3.11
1. Для квадратичных функций ( )
f x метод Ньютона гарантирует вы-
сокую скорость сходимости к точке минимума.
2. В общем случае, сходимость метода Ньютона зависит от начально-
го приближения 0
x (последовательность k
x,
0,1, 2,3,...
k
может ока-
заться расходящейся). Поэтому 0
x должно быть выбрано достаточно
близко к x
с помощью какого-либо другого метода.
Алгоритм
1. Определить выражения
()
fx
и
()
fx
. Задать начальную точку
0
x и точность решения
|()|0
fx
, как условие окончания поиска экс-
тремальной точки.
2. Вычислить значение
0
()
fx
.
3. Проверить является ли 0
x решением задачи: если
0
|()|
fx
,то
положить
0
xx
,
min
()
ffx
и окончить поиск, иначе перейти к шагу 4.
4. Положить
0
k
.
5. Вычислить значение
()k
fx
. Значение ( )
k
fx
уже известно.
6. Найти
1
kx по формуле
1
()
()
k
k
k
k
fx
x
x
fx
.
7. Вычислить значение
1
()k
fx
.
1
k
x
x
()
fx
x
k
x
Рис. 3.9.
1
()
()
k
k
k
k
fx
x
x
fx
173
8. Проверить окончание поиска экстремальной точки: если выполня-
ется условие
1
|()|
k
fx
, то положить
1
k
xx
,
min
()
ffx
и поиск
завершить, иначе
1
k k иперейтикшагу5.
Пример 3.10
Найти точку минимума функции
2
() arctg 0.5ln(1 )
fxxx
x
методом Ньютона с точностью
7
|()| 10
fx
.
Решение
.
1 Определим
( ) arctg
fx
x
и
2
1
()
1
fx
x
(()0
fx
). Выбе-
рем начальное приближение 0 1
x . Точность
7
10
задана.
2. Вычислим
0
( ) arctg1 0.785
fx
.
3. Так как
0
|()|0.785
fx
, то перейдем к шагу 4.
4. Положим
0
k
.
0
.
5 Вычислим
0
()0.5
fx
;
0
( ) 0.785
fx
.
0
.
6 Вычислим
0
1
0
0
( ) 0.785
1
0.570
()
0.5
fx
x
x
fx
.
0
.
7 Вычислим
1
( ) arctg( 0.570) 0.519
fx
.
0
.
8 Так как
1
|()|0.519
fx
,то
11
kk
иперейдемкшагу5.
1
.
5 Вычислим
1
2
1
()
0.755
1 ( 0.570)
fx
;
1
( ) 0.519
fx
.
1
.
6 Вычислим
1
2
1
1
()
0.519
0.570
0.117
()
0.755
fx
x
x
fx
.
1
.
7 Вычислим
1
( ) arctg(1.687) 0.519
fx
.
1
.
8 Так как
1
|()|0.519
fx
,то
12
kk
иперейдемкшагу5.
Результаты вычислений на остальных итерациях – в табл. 3.2.
174
Таблица 3.2
Номер
итерации
k
x
()k
fx
()k
fx
Точность
решения
2
0.117
0.116
0.435
2
|()|
fx
3
3
1.061 10
3
1.061 10
1
3
|()|
fx
4
8
9 10
8
9 10
1
4
|()|
fx
Таким образом,
8
910 0
x
,
min
()0
ffx
.
Замечание 3.11
Если в примере 3.4 положить начальное приближение 0 3
x ,топо-
лучим расходящуюся
последовательность:
1
9.5
x
,
2 124
x
,
3
23906
x
,
8
4 8.97 10
x
,
18
5
1.27 10
x
,...
Задачи для самостоятельного решения
1. Методом Свенна найти начальный интервал неопределенности для
решения задачи
2
()
614min
fxxx
при
0
0
x иразличныхt:
1
t; 0.1
t ; 0.01
t
.
Ответ: 0 [1; 7]
L
при 1
t ; 0 [1.5;6.3]
L
при 0.1
t;
0 [1.27; 5.11]
L
при 0.01
t
.
2. Методом Свенна найти начальный интервал неопределенности для
решения задачи
2
()
612min
fxxx
.
Ответ:
0 [8;4]
L
при
0
10
x
,
2
t;
0 [5;1]
L
при
01
x,
2
t;
0 [6;0]
L
при01
x,
1
t;
0[7;1]
L
при00
x,
1
t.
3. Методами равномерного поиска, деления интервала пополам, дихо-
томии решить задачу
2
()
614min
fxxx
,
0 [2;4]
L
.
Ответ:
метод равномерного поиска при 10
n
[2.364; 3.455]
x
;
175
метод деления интервала пополам: при 1
[2.50; 3.25]
x
,
при
0.1
[2.969; 3.063]
x
;
метод дихотомии: при
1
,
0.1
,
6 [2.425; 3.263]
xL
;
при
0.1
,
0.01
,
14 [2.960; 3.017]
xL
.
Точное решение
3
x
и()5
fx
.
4. Методами равномерного поиска, деления интервала пополам, дихо-
томии, золотого сечения, Фибоначчи решить задачу
2
()
612min
fxxx
,
0 [4;1]
L
.
Ответ:
–
метод равномерного поиска при 10
n:
[ 3.545; 2.636]
xL
;
–
метод деления интервала пополам: при 1
6 [ 3.375; 2.750]
x
L
;
–
метод дихотомии: при
1
,
0.2
6 [ 3.4; 2.6]
xL
;
–
метод золотого сечения: при
0.1
10 [ 3.033; 2.967]
xL
;
–
метод Фибоначчи:
5
n,
0.01
,
5 [ 3.375; 2.740]
xL
.
Точное решение
3
x
и()39
fx
.
5. Методом равномерного поиска решить задачу
4
()
min
x
fxxe
,
[0;1]
x
с точностью
0.1
.
Проверить унимодальность функции на отрезке [0;1] .
Ответ:
10
n,
0.5
x
,
()0.67
fx
.
6. Методом дихотомии решить задачу
4
()
min
x
fxxe
,
[0;1]
x
с точностью
0.1
.
Ответ:
0.02
,
10 [0.49; 0.633]
x
L
;
0.56
x
,
()0.67
fx
.
7. Методом золотого сечения решить задачу
4
()
min
x
fxxe
,
[0;1]
x
с точностью
0.1
.
Ответ:
5 [0.472; 0.618]
xL
,
0.55
x
,
()0.67
fx
.
8. Методом золотого сечения решить задачу
2
127
61
()
2 min
4
4
fx
x
x
,
при точности
0.15
. Интервал неопределенности определить методом
Свенна при начальной точке 0 0.25
x
и величине шага
0.25
x
.
176
Ответ:
0.25
x
и()0.1719
fx
.
9. Методом квадратичной интерполяции решить задачи
а)
2
127
61
()
2 min
4
4
fx
x
x
,
1 0.25
x
,
0.25
x
,
1 0.02
;
б)
4
()
min
x
fxxe
,
0 0.5
x
,
0.5
x
,20.02
Ответ: а)
0.2402
x
и()0.1688
fx
;
б)
0.5224
x
и()0.667
fx
.
10. Составить программы минимизации функции методами равно-
мерного поиска, деления отрезка пополам, дихотомии, золотого сечения,
Фибоначчи, используя какой-либо язык программирования. Проверить
работу этих программ, решив следующие задачи с точностью, выбранной
самостоятельно, и сравнить с ответом
а)
3
()
3sin
min
fxx
x
,
[0; 1]
x
;
б)
1
()
min
x
fxe
x
,
[0.5; 1.5]
x
.
Ответ: а)
0.8241
x
и()1.6421
fx
;
б)
0.7035
x
и()3.4423
fx
.
11. Методами средней точки, хорд и Ньютона решить задачу
2
()
min
x
fxxe
при заданном 0 [0; 1]
L
.
Воспользоваться компьютером, составив про-
грамму (на любом языке), сравнить полученные результаты с ответом.
Ответ:
0.3517
x
и()0.8272
fx
.
12. Методами средней точки, хорд и Ньютона решить задачу
2
()
sin
min
fxxxx
при заданном 0 [ 1; 0]
L
. Воспользоваться компьютером, составив про-
грамму (на любом языке), сравнить полученные результаты с ответом.
Ответ:
0.8354
x
и()0.8791
fx
.
177
Глава 4
ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ
МНОГОМЕРНОЙ ОПТИМИЗАЦИИ
4.1. Общие принципы построения численных методов
многомерной оптимизации
Применение необходимых и достаточных условий безусловного экс-
тремума, изложенных в первой главе, эффективно для решения ограни-
ченного числа примеров. Для решения большинства практических задач
они не могут быть рекомендованы по следующим причинам:
1. Целевая функция (x)
f может не иметь непрерывных производных
до второго порядка включительно.
2. Использование необходимого условия первого порядка (1.3) связа-
но с решением системы n в общем случае нелинейных алгебраических
уравнений, что представляет собой самостоятельную задачу, трудоемкость
решения которой сравнима с трудоемкостью численного решения постав-
ленной задачи поиска экстремума.
3. Возможны случаи, когда о целевой функции известно лишь то, что
ее значение может быть вычислено с нужной точностью, а сама функция
задана неявно.
Численные методы оптимизации относятся к классу итерационных,
т.е . порождающих последовательность точек в соответствии с предписан-
ным набором правил, включающим критерий окончания. При заданной
начальной точке
0
x методы генерируют последовательность
0
x,
1
x,
2
x ,... . Преобразование точки x
k
в
1
x
k
представляет собой итерацию.
Для численного решения задач безусловной минимизации:
x
(x) min (x)
n
R
f
f
(4.1)
разработано множество алгоритмов, использующих итерационные проце-
дуры вида
(1)
(0) (1)
(1)()
x
(x ,x
,...,x
,x)
k
k
k
,
(0)
x
n
R
,
(4.2)
178
позволяющие при определенных условиях построить последовательность
()
{x}
k
такую, что
()
lim(x)
inf (x)
n
k
k
R
f
f
f
.
(4.3)
Определение 4.1. Последовательность { x }
k
называется минимизи-
рующей, если
()
lim(x)
k
k
f
f
, т.е. последовательность сходится к ниж-
ней грани
x
inf (x)
n
R
f
f
.
Определение 4.2. Последовательность { x }
k
называется сходящейся
к точке минимума x
, если |x
x|0
k
приk.
Основное правило построения последовательности { x }
k
имеет вид
1
x
x
p
k
k
k
k
,
0,1,2,...
k
,
(4.4)
где точка
0
x – начальная точка поиска; k
– величина шага, p
k
–
прием-
лемое направление перехода из точки x
k
в точку
1
x
k
, обеспечивающее
выполнение условия
1
(x)(x)
k
k
f
f
,
0,1,2, ...
k
(4.5)
и называемое направлением спуска (поиска),.
Начальная точка поиска
0
x задается, исходя из физического содер-
жания решаемой задачи и наличия априорной информации о положении
точек экстремума.
Приемлемое направление спуска p
k
должно удовлетворять условию
(x),p 0
kk
f
,
0,1,2,...
k
,
(4.6)
обеспечивающему убывание функции (x)
f . Примером приемлемого на-
правления является направление вектора антиградиента: p
(x)
k
k
f
.
Величина шага
0
k
выбирается либо из условия (4.5), либо из ус-
ловия минимума функции вдоль направления спуска:
(x
p) min
k
k
k
k
f
.
(4.7)
Выбор шага k
из условия (4.7) делает спуск в направлении p
k
наиско-
рейшим.
Имеет место следующее свойство исчерпывающего спуска.
179
Теорема 4.1. Для дифференцируемой в
n
R функции (x)
f в итераци-
онном процессе (4.4) с выбором шага k
в соответствии с (4.7) для всех
1
k выполняется условие
1
(x),p0
k
k
f
.
(4.8)
Соотношения (4.8) можно проиллюстрировать геометрически в про-
странстве
n
R . При перемещении из точки x
k
вдоль прямой, задаваемой
вектором p
k
, в направлении убывания функции, происходит пересечение
линий уровня функции (x)
f до тех пор, пока либо не будет достигнута
стационарная точка
1
((x)0)
k
f
, либо прямая не коснется в точке
1
x
k
некоторой линии уровня функции (x)
f . Равенство (4.8) и есть усл о-
вие касания (рис. 4.1).
Сходимость последовательности { x }
k
при выборе приемлемого на-
правления p
k
и величины шага k
из условия (4.5) или (4.7) зависит от
характера функции (x)
f и от выбора начальной точки
0
x.
В зависимости от наивысшего порядка частных производных функ-
ции (x)
f , используемых для формирования p
k
иk
, численные методы
решения задачи безусловной минимизации (4.1) принято делить на три
группы.
1. Методы нулевого порядка, использующие только информацию о
значении функции (x)
f.
2. Методы первого порядка, использующие информацию о первых
производных функции (x)
f.
1
x
k
pk
x
k
1
(x)
k
f
2
x
1x
1
2
3
(x)
(x)
(x)
fc
fc
fc
1
2
3
cc
c
Рис. 4.1
180
3. Методы второго порядка, требующие для своей реализации зна-
ния вторых производных функции (x)
f.
Работоспособность метода еще не гарантирована доказательством
сходимости соответствующей последовательности – нужна определенная
скорость сходимости. Заметим, однако, что на практике результаты об-
щей теории сходимости должны использоваться с большой осторожно-
стью. Так, например, нельзя оценивать алгоритмы только по величинам
теоретических скоростей сходимости генерируемых ими последовательно-
стей – хотя эти скорости в определенной степени определяют эффектив-
ность методов, условия, при которых они достижимы, реализуются редко.
Точно так же нельзя пренебрегать алгоритмом лишь по той причине, что
теоремы о скорости его сходимости не доказаны: не исключено, что дока-
зательства нет просто потому, что провести его очень сложно.
Тем не менее, скорость сходимости является важной характеристикой
сходящихся последовательностей.
Рассмотрим последовательность { x }
k
, сходящуюся к x
. Предполо-
жим, что все ее элементы различны и ни одна из точек x
k
не совпадает с
x
.
Наиболее эффективный способ оценивания скорости сходимости со-
стоит в сопоставлении расстояния между x
k
иx
,т.е.||x
x||
k
,ирас-
стояния между
1
x
k
иx
, т.е.
1
||x x||
k
.
Определение 4.3. Последовательность { x }
k
называется сходящейся
с порядком r , если r – максимальное число, для которого
1
||x x||
0 lim
||x x||
k
k
r
k
.
Поскольку величина r определяется предельными свойствами { x }
k
,
она называется асимптотической скоростью сходимости.
Определение 4.4. Если последовательность { x }
k
сходится с поряд-
комr,точисло
1
||x x||
lim
||x x||
k
k
r
k
c
называется асимптотическим параметром ошибки.
Определение 4.5. Если
1
r,
1
c , то сходимость линейная, если
2
r , то сходимость квадратичная; если
1
r или
1
r,
0
c ,тосхо-
димость сверхлинейная.
181
Линейная сходимость является синонимом сходимости со скоростью
геометрической прогрессии.
Пример 4.1
Определить порядок сходимости последовательности:
12
k
k
x
,
0,1,2, ...
k
.
Решение
Последовательность
359
{}2,,,,...
248
k
x
сходится к
1
x
,при-
чем
1
11
lim
2
1
k
k
k
x
x
и
1
r . Сходимость линейная.
Замечание 4.1. Одним из критериев сходимости, часто используемым
при сравнении алгоритмов, является их способность эффективно миними-
зировать квадратичные функции. Это объясняется тем, что вблизи мини-
мума квадратичная функция может быть достаточно хорошей аппрокси-
мацией исследуемой функции. Таким образом, алгоритм, который не дает
хороших результатов при минимизации квадратичной функции, вряд ли
может быть с успехом использован в случае общей нелинейной функции,
когда текущая точка находится в окрестности минимума.
Установление факта сходимости последовательности { x }
k
и оценка
скорости сходимости дают существенную информацию об итерационном
процессе (4.4).
Конкретный вычислительный алгоритм на основе (4.4), в котором
может получаться, вообще говоря, бесконечная последовательность { x }
k
,
необходимо дополнять условием остановки вычислений (критерием окон-
чания счета). На практике часто пользуются следующими условиями:
1
1
||x x||
k
k
,
2
1
|(x) (x)|
k
k
f
f
,
3
|| (x )||
k
f
,
где 1
,2
,3
– заранее заданные параметры точности.
Алгоритмы, построенные на основании процедуры (4.4), т.е .
1
x
x
p
k
k
k
k
,
0,1,2,...
k
,
различаются способом построения вектора p
k
и выбора шага k
.
4.2 . Методы нулевого порядка
Методы решения задачи безусловной минимизации (x) min
f
,
x
n
R
, которые опираются только на вычисление значений функции
(x)
f , называются методами нулевого порядка (прямыми методами) ми-
182
нимизации. Важно отметить, что для их применения не требуется не толь-
ко дифференцируемости целевой функции, но даже аналитического ее за-
дания. Нужно лишь иметь возможность вычислять или измерять значения
(x)
f в произвольных точках. Такие ситуации часто встречаются в прак-
тически важных задачах оптимизации.
4.2 .1. Метод конфигураций
Требуется найти безусловный локальный мини-
мум функции (x)
f многих переменных, т.е. най-
ти такую точку x
n
R
,что
x
(x) min (x)
n
R
f
f
.
Метод конфигураций является модифи-
кацией метода циклического покоорди-
натного поиска [5]. Этот метод известен как метод Хука–Дживса (R.
Hooke, T. A. Jeeves) представляет собой комбинацию исследующего поиска
с циклическим изменением переменных и ускоряющего поиска по образцу.
Исследующий поиск ориентирован на выявление локального поведения
целевой функции и определение направления ее убывания вдоль «овра-
гов». Полученная информация используется при поиске по образцу при
движении вдоль «оврагов».
Исследующий поиск, начинается в некоторой начальной точке
0
x на-
зываемой старым базисом. В качестве множества направлений поиска
выбирается множество координатных направлений
i
e,
1,...,
i
n
. Задает-
ся величина шага, которая может быть различной для разных координат-
ных направлений и переменной в процессе поиска. Фиксируется первое
координатное направление и делается шаг в сторону увеличения соответ-
ствующей переменной. Если значение функции в пробной точке меньше
значения функции в исходной точке, шаг считается удачным. В противном
случае необходимо вернуться в предыдущую точку и сделать шаг в проти-
воположном направлении с последующей проверкой поведения функции.
После перебора всех координат исследующий поиск завершается. Полу-
ченная точка называется новым базисом
1
x . Если исследующий поиск с
данной величиной шага неудачен, то она уменьшается и процедура про-
должается. Поиск заканчивается, когда текущая величина шага станет
меньше некоторой величины.
Поиск по образцу заключается в движении по направлению от старого
базиса к новому (от точки
0
x через точку
1
x,източки
1
x через точку
2
x,из
2
x через
3
x и т.д.) . Величина ускоряющего шага задается уско-
Стратегия решения задачи
Постановка задачи
183
ряющим множителем . Успех поиска по образцу определяется с пом о-
щью исследующего поиска из полученной точки. Если при этом значение
в наилучшей точке меньше, чем в точке предыдущего базиса, то поиск по
образцу удачен, иначе поиск неудачен. Если поиск по образцу неудачен,
происходит возврат в новый базис, где продолжается исследующий поиск
с уменьшенным шагом.
При поиске по направлению
i
e меняется только переменная ix , а ос-
тальные переменные остаются зафиксированными.
Алгоритм
1. Задать начальную точку
0
x , число
0
для остановки алгорит-
ма, начальные величины шагов по координатным направлениям 1
,,
n
, ускоряющий множитель
0
, коэффициент уменьшения шага
1
. Положить
1
0
yx
,
1
i, 0
k
.
2. Осуществить исследующий поиск по выбранному координатном у
направлению:
а) если
(y
) (y)
i
i
i
i
f
e
f
, т.е.
1
1
( ,...,
, ...,
) ( ,...,
i
i
i
i
i
i
n
fyy
yfy
,...,
)
i
i
i
n
y y , то шаг считается удачным. В этом случае следует положить
1
yy
i
i
i
ie
иперейтикшагу3;
б) если в п. «а» шаг неудачен, то делается шаг в противоположном
направлении. Если
(y
) (y)
i
i
i
i
f
e
f
, т.е.
1
( ,...,
, ...,
)
i
i
i
i
i
n
fyy
y
1
( ,...,
, ...,
)
i
i
i
i
n
fyyy
, то шаг считается удачным. В этом случае следует
положить
1
y
y
i
i
i
ie
и перейти к шагу 3;
в) если в пп. «а» и «б» шаги неудачны, положить
1
yy
i
i
.
3. Проверить условия:
а)еслиi n
, то положить
1
i i и перейти к шагу 2 (продолжить
исследующий поиск по оставшимся направлениям);
б)если i n
, проверить успешность исследующего поиска:
–
если
1
(y)(y)
k
k
f
f
, перейти к шагу 4;
–
если
1
(y)(y)
k
k
f
f
, перейти к шагу 5.
4. Провести поиск по образцу. Положить
1
1
x
y
k
n
,
1
1
yx
k
1
(x x)
k
k
,ik
,
1
kk
и перейти к шагу 2.
5. Проверить условие окончания:
а)есливсе i
, то поиск закончить: x
x
k
;
184
б) для тех i , для которых
i
, уменьшить величину шага:
i
i
.
Положить
1
yx
k
,
1
x
x
k
k
,
1
kk
,
1
i и перейти к
шагу 2.
Замечание 4.2
1. В алгоритме можно использовать одинаковую величину шага по
координатным направлениям, т.е. вместо 1
,2
,...,
n
применять .
2. Существует модификация метода, где при исследующем поиске и
поиске по образцу используется одномерная минимизация. Тогда, если
функция (x)
f дифференцируема, метод сходится к стационарной точке.
Пример 4.2
Найти минимум функции
2
2
1
2
(x)4(5)(6)
f
x
x
методом конфигураций (методом Хука-Дживса).
Решение
0
1 . Зададим
0
x
(8;9)T
–
старый базис,
0.3
;11
,22
,
2
,
1
. Положим
0
k,1
i,
1
y (8;9)T
. На рис. 4.2 изображены
точки поиска решения первых двух итераций. Точка 1:
0
x.
9
4
2
x
1
x
0
x
2
7
5
6
3
1
10
8
6
6
4
4
10
8
2
2
0
1x
2
x
Рис. 4.2
8
10
11
12
13
(x) 19
f
(x) 4
f
185
0
.
2 Так как
1
1
1
0
1
(y
) (9;9) 73 (y) (x) 45
f
e
f
f
f
,то
этот шаг неудачен. Точка 2: (9; 9) .
Так как
1
1
1
0
1
(y
) (7;9) 25 (y) (x) 45
f
e
f
f
f
, то этот
шаг удачен:
2
1
1
1
yy
(7; 9)T
e
. Точка3: (7;9).
0
.
3 Поскольку 1 2
i
n
, то положим
12
ii
и перейдем к
шагу 2.
1
.
2 Так как
2
2
2
2
(y
) (7;11) 41 (y) 25
f
e
f
f
,тошагне-
удачен. Точка 4: (7; 11) .
Так как
2
2
2
2
(y
) (7;7) 17 (y) 25
f
e
f
f
, то этот шаг уда-
чен:
3
2
2
2
yy
(7;7)T
e
. Точка5:(7;7).
1
.
3 Поскольку 2 2
i
n
и
3
0
(y) 17 (x) 45
f
f
, то перейдем
к шагу 4.
0
.
4 Положим
1
3
x
y (7;7)T
–
новый базис,
1
i,
11
kk
,
найдем
11
1
0
y x 1(x x) (7;7) (7;7) (8;9) (6;5)
T
T
T
T
.
Точка 6:
1
y . Выполнен поиск по образцу. Перейдем к шагу 2.
2
.
2 Так как
1
1
1
1
(y
)(7;5)17(y)5
f
e
f
f
, то шаг неуда-
чен. Точка 7: (7; 5) . Так как
1
1
1
1
(y
)(5;5)1(y)5
f
e
f
f
,тошаг
удачный:
2
1
1
1
yy
(5; 5)T
e
. Точка8: (5;5).
2
.
3 Поскольку 1 2
i
n
, то положим
2
i иперейдемкшагу2.
3
.
2 Так как
2
2
2
2
(y
) (5;7) 1 (y) (5;5) 1
f
e
f
f
f
,тошаг
неудачен. Точка 9: (5, 7) . Так как
2
2
2
2
(y
)(5;3)9(y)1
f
e
f
f
,то
шаг неудачен, поэтому
3
2
y y (5;5)T
. Точка10:(5;3).
3
.
3 Поскольку 2 2
i
n
и
3
1
(y)1(x)17
f
f
, то поиск по
образцу на шаге
0
4 успешен. Точка
3
y (5;5)
становится новым бази-
сом, а точка
1
x
(7; 7)T
–
старым базисом. Перейдем к шагу 4.
1
.
4 Положим
2
3
x
y (5; 5)T
–
новый базис,
1
i,
12
kk
,
найдем
1
2
2
1
yx(x
x ) (5;5) (5;5) (7;7) (3;3)
T
T
T
T
.
Выпол-
нен поиск по образцу. Точка 11: (3; 3) . Перейдем к шагу 2.
186
4
.
2 Так как
1
1
1
1
(y
) (4;3) 13 (y) (3;3) 25
f
e
f
f
f
,то
шаг удачен:
2
1
1
1
yy
(4; 3)T
e
. Точка12: (4;3).
4
.
3 Поскольку 1 2
i
n
, то положим
2
i иперейдемкшагу2.
5
.
2 Так как
2
2
2
2
(y
)(4;5)5(y)13
f
e
f
f
, то шаг удачен:
3
2
2
2
yy
(4;5)T
e
. Точка13:(4;5).
5
.
3 Поскольку i n
и
3
2
(y)5(x)1
f
f
, то поиск по образцу на
шаге
1
4 неудачен. Переходим к шагу 5.
0
.
5Таккак11
,
22
, то уменьшим шаг:
1
1
0.5
2
,
2
2
1
2
.Положим
1
2
y x (5;5)T
,
3
2
x
x
(5;5)T
,
1
i,
13
kk
и перейдем к шагу 2 (конец второй итерации, рис. 4.2).
6
.
2 Так как
1
1
1
1
(y
) (5.5;5) 2 (y) 1
f
e
f
f
, то шаг неуда-
чен. Так как
1
1
1
1
(y
) (4.5;5) 2 (y) 1
f
e
f
f
, то шаг неудачен,
поэтому
2
1
y y (5;5)T
.
6
.
3 Поскольку 1 2
i
n
, то положим
2
i иперейдемкшагу2.
7
.
2 Так как
2
2
2
2
(y
) (5;6) 0 (y) (5;5) 1
f
e
f
f
f
,тошаг
удачен:
3
2
2
2
yy
(5; 6)
e
.
7
.
3 Так как
3
3
(y)0(x)1
f
f
, то переходим к шагу 4. Точка
3
y
становится новым базисом, а точка
3
x – старым. Перейдем к шагу 4.
2
.
4 Положим
4
3
x
y (5; 6)T
–
новый базис,
1
i,
14
kk
,
найдем
1
4
4
3
yx(x
x ) (5;6) (5;6) (5;5) (5;7)
T
T
T
T
.
Выпол-
нен поиск по образцу. Перейдем к шагу 2.
8
.
2 Так как
1
1
1
1
(y
) (5.5;7) 2 (y) (5;7) 1
f
e
f
f
f
,тошаг
неудачен. Так как
1
1
1
1
(y
) (4.5;7) 2 (y) 1
f
e
f
f
, то шаг неуда-
чен. Тогда
2
1
y y (5;7)T
.
8
.
3 Поскольку 1 2
i
n
, то положим
12
ii
и перейдем к
шагу 2.
187
9
.
2 Так как
2
2
1
2
(y
)(5;8)4(y)1
f
e
f
f
, то шаг неудачен.
Так как
2
2
1
2
(y
)(5;6)0(y)1
f
e
f
f
, то шаг удачен. Тогда
3
2
2
2
yy
(5; 6)T
e
.
9
.
3 Поскольку 2 2
i
n
и
3
4
(y) (x) (5;6) 0
f
f
f
, то поиск
по образцу неудачен. Переходим к шагу 5.
1
.
5Таккак1
,2
, то уменьшим шаг: 1 0.25
,
2 0.5
.
Положим
1
4
y x (5;6)T
,
5
4
xx
,
1
i,
15
k k иперейдемкшагу2.
10
.
2 Так как
1
1
1
1
(y
) (5.25;6) 0.25 (y) 0
f
e
f
f
,тошаг
неудачен. Так как
1
1
1
1
(y
) (4.75;6) 0.25 (y) 0
f
e
f
f
,тошаг
неудачен и
2
1
y y (5;6)T
.
10
.
3 Поскольку 1 2
i
n
,то
12
i i иперейдемкшагу2.
11
.
2 Так как
2
2
2
2
(y
) (5;6.5) 0.25 (y) 0
f
e
f
f
,тошагне-
удачен. Так как
2
2
2
2
(y
) (5;5.5) 0.25 (y) 0
f
e
f
f
,тошагне-
удачен и
3
2
y y (5;6)T
.
11
.
3 Поскольку 2 2
i
n
и
3
5
(y)0(x)0
f
f
, то исследую-
щий поиск неудачен. Переходим к шагу 5.
2
.
5 Таккак 1 0.25
0.3
,
20.5
, то уменьшим шаг 2
:
1 0.25
,
2 0.25
. Положим
1
5
y x (5;6)T
,
6
5
x
x
,
16
kk
,
1
i иперейдемкшагу2.
12
.
2 Так как
1
1
1
1
(y
) (5.25;6) 0.25 (y) 0
f
e
f
f
,тошаг
неудачен. Так как
1
1
1
1
(y
) (4.75;6) 0.25 (y) 0
f
e
f
f
,тошаг
неудачен и
2
1
y y (5;6)T
.
12
.
3 Поскольку 1 2
i
n
,то
12
i i иперейдемкшагу2.
13
.
2 Так как
2
2
2
2
(y
) (5; 6.25) 0.0625 (y ) 0
f
e
f
f
,тошаг
неудачен. Так как
2
2
2
2
(y
) (5; 5.875) 0.0625 (y ) 0
f
e
f
f
,то
шаг неудачен и
3
2
y y (5;6)T
.
13
.
3 Поскольку 2 2
i
n
и
3
6
(y)0(x)0
f
f
, то переходим
к шагу 5.
188
3
.
5 Таккак 1 0.25
0.3
и20.25
0.3
,топоискза-
вершен: x
(5; 6)T
,
min
(x)
0
f
f
.
4.2 .2. Метод деформируемого многогранника
Требуется найти безусловный локальный минимум
функции (x)
f многих переменных, т.е . найти та-
кую точку x
n
R
,что
x
(x) min (x)
n
R
f
f
.
В основу метода деформируемого мно-
гогранника положено построение по-
следовательности систем
1
n точек x
i
,
1,...,
1
i
n
, которые являются
вершинами выпуклого многогранника (симплекса). Точки системы на
(1)
k -ой итерации совпадают с точками системы на k -ой итерации,
кроме i h
, где точка x
h
–
наихудшая в системе точек на k -ой итерации,
т.е .
1
1
(x) max (x)
h
i
in
f
f
.
Точка x
h
заменяется на другую точку по спе-
циальным правилам, описанным ниже в алгоритме. В результате много-
гранники деформируются в зависимости от структуры линий уровня целе-
вой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя
направление в изогнутых впадинах и сжимаясь в окрестности минимума.
Построение последовательности многогранников заканчивается, когда
значения функции в вершинах текущего многогранника отличаются от
значения функции в центре тяжести системы x
i
,
1,...,
1
i
n
,ih
не
более чем на
0
.
Алгоритм
1. Задать координаты вершин многогранника
1
x ,...,
1
x
n
; параметры
отражения , сжатия , растяжения ; число
0
для остановки ал-
горитма. Положить
0
k (последующие шаги 2-6 соответствуют текуще-
му номеру системы точек k - ой итерации).
2. Среди вершин найти «наилучшую» x
l
и «наихудшую» x
h
, соот-
ветствующие минимальному и максимальному значениям функции:
1,...
1
(x)
min (x)
l
i
in
f
f
;
1,. ..
1
(x) max (x)
h
i
in
f
f
,
а также точку x
s
, в которой достигается второе по величине после макси-
мального значение функции (x )
s
f.
Стратегия решения задачи
Постановка задачи
189
3. Найти «центр тяжести» всех вершин многогранника за исключени-
ем наихудшей x
h
:
1
1
2
1
1,
1
1
x
xx
x
n
n
n
i
h
i
i
iih
n
n
.
4. Проверить условие окончания
а) если
12
1
2
2
1
1
(x)(x)
1
n
i
n
i
f
f
n
, процесс поиска
можно завершить и в качестве приближенного решения взять наилучшую
точку текущего многогранника x
x
l
;
б)если
, продолжать процесс.
5. Выполнить операцию отражения наихудшей вершины через центр
тяжести
2
x
n
(рис. 4.3):
3
2
2
x
x
(x x)
n
n
n
h
.
6. Проверить выполнение условий:
а) если
3
(x)(x)
n
l
f
f
, то выполнить операцию растяжения (рис.
4.3, б):
4
2
3
2
x
x
(xx)
n
n
n
n
.
Найти вершины нового многогранника:
–
если
4
(x)(x)
n
l
f
f
, то вершина x
h
заменяется на
4
x
n
(при
2
n многогранник будет содержать вершины
1
x,
3
x,
6
x ). Затем следу-
ет положить
1
kk
и перейти к шагу 2;
–
если
4
(x)(x)
n
l
f
f
, то вершина x
h
заменяется на
3
x
n
(при
2
n многогранник будет содержать вершины
1
x,
3
x,
5
x ). Далее
следует положить
1
kk
и перейти к шагу 2;
б) если
3
(x)(x)(x)
s
n
h
f
f
f
, то выполнить операцию сжатия
(рис. 4.3, в):
5
2
2
x
x
(xx)
n
n
h
n
.
Следует заменить вершину x
h
на
5
x
n
, положить
1
kk
и перей-
тикшагу2(при
2
n многогранник будет содержать вершины
1
x,
3
x,
7
x);
в) если
3
(x)(x)(x)
l
n
s
f
f
f
вершину x
h
заменить на
3
x
n
. При
этом следует положить
1
kk
и перейти к шагу 2;
190
г) если
3
(x)(x)
n
h
f
f
выполнить операцию редукции (рис. 4.3, г).
Формируется новый многогранник с уменьшенными вдвое сторонами и
вершиной x
l
:
x
x 0.5(x x)
i
l
i
l
,
1,...,
1
i
n
.
При этом следует положить
1
kk
и перейти к шагу 2.
Замечание 4.3. Нелдер и Мид (J.A. Nelder, R. Mead) рекомендуют ис-
пользовать параметры
1
,
0.5
,
2
; Павиани (D. Paviani) –
1
,0.4
0.6
,2.8
3
; Паркинсон и Хатчинсон (J.M. Parkinson,
D. Hutchinson) –
2
,
0.25
,2.5
. В последнем случае в рамках
операции отражения фактически выполняется растяжение.
Пример 4.3
Найти минимум следующей функции
2
2
1
2
(x)4(5)(6)
f
x
x
методом деформируемого симплекса (методом Нелдера-Мида).
2
x
x
h
1
x
x
l
4
2
x
x
n
3
1
x
x
x
n
s
5
3
x
x
n
а
6
4
x
x
n
1
xx
l
4
2
x
x
n
3
1
x
x
x
n
s
5
3
x
x
n
4
(x)(x)
n
l
f
f
4
(x)(x)
n
l
f
f
б
2
x
x
h
Рис. 4.3
1
xx
l
2
x
x
h
3
1
x
x
x
n
s
5
3
x
x
n
4
2
x
x
n
г
1
xx
l
2
x
x
h
3
1
x
x
x
n
s
5
3
x
x
n
4
2
x
x
n
в
7
5
x
x
n
191
Решение
0
.
1 Так как
2
n , зададим начальный треугольник с вершинами
1
x
(8; 9)T
,
2
x
(10;11)T
.
3
x
(8,11)T
.
Положим
1
,
0.5
,
2
;
0.2
,
0
k
.
0
.
2 Так как
1
(x) 45
f,
2
(x) 125
f,
3
(x) 61
f,то
1
xx
l
,
2
x
x
h
,
3
x
x
s
.
0
.
3 Найдем центр тяжести вершин
1
xи
3
x (середину стороны, про-
тивостоящей вершине x
h
):
4
1
3
1
1
x
(x x ) (8;9) (8;11)
(8;10)
2
2
T
T
T
,
4
(x) 52
f
.
0
.
4 Так как
12
2
2
2
1
(7739)
42.66
3
, то процесс про-
должается.
0
.
5 Выполним отражение:
5
4
4
2
x x 2(x x ) (8;10) (8;10) (10;11) (6;9)
T
T
T
T
;
5
(x) 13
f
.
0
.
6 Так как
5
1
(x) 13 (x) (x) 45
l
f
f
f
, в ыполним растяжение:
6
4
5
4
x
x 2(x x ) (8;10) 2 (6;9) (8;10) (4;8)
T
T
T
T
,
6
(x) 8
f
.
Так как
6
1
(x)8(x)(x)45
l
f
f
f
, то вершина
2
x заменяется на
6
x . Новый многогранник содержит вершины
2
x,
3
x,
6
x . Положим
11
kk
иперейдемкшагу2.
1
.
2 Имеем вершины
1
x
(8; 9)T
,
2
x
(4;8)T
,
3
x
(8;11)T
;
1
(x) 45
f,
2
(x) 8
f,
3
(x) 61
f;
2
xx
l
,
3
x
x
h
,
1
x
x
s
.
1
.
3 Найдем центр тяжести вершин
2
xи
1
x:
4
1
2
1
1
x
(x x ) (8;9) (4;8) (6; 8.5)
2
2
T
T
T
,
4
(x ) 10.25
f
.
1
.
4 Так как
12
2
2
2
1
(34.75 ( 2.25) 50.75 )
35.53
3
,то
процесс продолжается.
1
.
5 Выполним отражение:
5
4
4
3
x
x 1 (x x ) (6;8.5) (6;8.5) (8;11) (4;6)
T
T
T
T
;
5
(x) 4
f
.
192
1
.
6 Так как
5
2
(x)4(x)(x)8
l
f
f
f
, выполним растяжение:
6
4
54
x x 2(x x ) (6;8.5) 2 (4;6) (6;8.5) (2;3.5)
T
T
T
T
,
6
(x ) 42.25
f
.
Так как
6
2
(x) 42.25 (x) (x) 8
l
f
f
f
, то вершина
3
x
x
h
заменя-
ется на
5
x . Новый многогранник содержит вершины
1
x,
2
x,
5
x . Поло-
жим
12
kk
иперейдемкшагу2.
2
.
2 Имеем вершины
1
x
(8; 9)T
,
2
x
(4;8)T
,
3
x
(4; 6)T
;
1
(x) 45
f,
2
(x) 8
f,
3
(x) 4
f;
3
xx
l
,
1
x
x
h
2
x
x
s
.
2
.
3 Найдем центр тяжести вершин
2
xи
3
x:
4
2
3
1
1
x
(x x ) (4;8) (4;6) (4;7)
2
2
T
T
T
,
4
(x) 5
f
.
2
.
4 Так как
12
2
22
1
(4031)
23.2
3
, то процесс продол-
жается.
2
.
5 Выполним отражение:
5
4
4
1
x
x
(x x ) (4;7) (4;7) (8;9) (0;5)
T
T
T
T
;
5
(x) 101
f
.
2
.
6 Так как
5
(x) 101 (x) 45
h
f
f
, в ыполним редукцию:
1
1
x x 0.5(x x ) (4;6) 0.5 (8;9) (4;6) (6;7.5)
l
l
T
T
T
T
,
2
2
x
x 0.5(x x ) (4;6) 0.5 (4;8) (4;6) (4;7)
l
l
T
T
T
T
;
3
3
x
x 0.5(x x) x (4;6)
l
l
l
T
.
Положим
13
kk
иперейдемкшагу2.
3
.
2 Вычислим значения функции:
1
(x ) 6.25
f,
2
(x) 5
f,
3
(x) 4
f
. Поэтому
3
xx
l
,
1
x
x
h
,
2
x
x
s
.
3
.
3 Найдем центр тяжести вершин
2
xи
3
x:
4
2
3
1
1
x
(x x ) (4;7) (4;6) (4; 6.5)
2
2
T
T
T
,
4
(x ) 4.25
f
.
3
.
4 Так как
12
2
2
2
1
(2 0.75 ( 1/25) )
1.24
3
, то процесс
продолжается.
3
.
5 Выполним отражение:
5
4
4
3
x x (x x ) (4;6.5) (4;6.5) (6;7.5) (2;5.5)
T
T
T
T
;
5
(x ) 36.25
f
.
193
3
.
6 Так как
5
1
(x) 36.25 (x) (x) 6.25
l
f
f
f
, то выполним ре-
дукцию:
1
1
x x 0.5(x x ) (4;6) 0.5 (6;7.5) (4;6) (5; 6.75)
l
l
T
T
T
T
,
2
2
x
x 0.5(x x ) (4;6) 0.5 (4;7) (4;6) (4; 6.5)
l
l
T
T
T
T
;
3
x
x
(4; 6)
l
T
.
Положим
14
kk
иперейдемкшагу2.
4
.
2 Вычислим значения функции:
1
(x ) 0.5625
f
,
2
(x ) 4.25
f,
3
(x) 4
f
. Поэтому
1
xx
l
,
2
x
x
h
,
3
x
x
s
.
4
.
3 Найдем центр тяжести вершин
1
xи
3
x:
4
1
3
1
1
x
(x x ) (5; 6.75) (4; 6) (4.5; 6.375)
2
2
T
T
T
,
4
(x ) 1.14
f
.
4
.
4 Так как
12
1
(0.34 9.67 8 .18)
2.46
3
, то процесс
продолжается.
4
.
5 Выполним отражение:
5
4
4
2
x
x (x x ) (4.5; 6.375) (4.5; 6.375) (4; 6.5) (5; 6.25)
T
T
T
T
;
5
(x ) 0.0625
f
.
4
.
6 Так как
5
(x ) 0.0625 (x ) 0.5625
l
f
f
, то выполним растя-
жение:
6
4
5
4
x x 2(x x ) (4.5; 6.375) 2 (5;6.25) (4.5; 6.375)
T
T
T
(5.5; 6.125)T
,
6
(x ) 1.015
f
.
Так как
6
1
(x) 1.015 (x) (x) 0.5625
l
f
f
f
, то вершина
2
x
x
h
заменяется на
5
x . Положим
15
kk
иперейдемкшагу2.
5
.
2 Имеем вершины
1
x
(5; 6.75)T
,
2
x
(5; 6.25)T
,
3
x
(4; 6)T
;
1
(x ) 0.5625
f
,
2
(x ) 0.0625
f
,
3
(x) 4
f;
2
xx
l
,
3
x
x
h
,
1
x
x
s
.
5
.
3 Найдем центр тяжести вершин
1
xи
2
x:
4
1
2
1
1
x
(x x ) (5; 6.25) (5; 6.25) (5; 6.5)
2
2
T
T
T
,
4
(x ) 0.25
f
.
194
5
.
4 Так как
12
1
(0.098 0 .035 14.06
2.17
3
, то процесс
продолжается.
5
.
5 Выполним отражение:
5
4
4
2
x
x (x x ) (5; 6.5) (5; 6.5) (4;6) (6;7)
T
T
T
T
;
5
(x) 5
f.
5
.
6 Так как
5
3
(x)5(x)(x)4
l
f
f
f
, то выполним редукцию:
1
1
x x 0.5(x x ) (5; 6.25) 0.5 (5; 6.75) (5; 6.25) (5; 6.5)
l
l
T
T
T
T
,
2
x
x
(5; 6.25)
l
T
,
3
3
x
x 0.5(x x ) (5; 6.25) 0.5 (4; 6) (5; 6.25) (4.5; 6.125)
l
l
T
T
T
T
.
Положим
16
kk
иперейдемкшагу2.
6
.
2 Имеем вершины
1
(x ) 0.25
f,
2
(x ) 0.0625
f
,
3
(x ) 1.015
f
.
Поэтому
2
xx
l
,
3
x
x
h
,
1
x
x
s
.
6
.
3 Найдем центр тяжести вершин
1
xи
2
x:
4
1
2
1
1
x
(x x ) (5; 6.5) (5; 6.25) (5; 6.375)
2
2
T
T
T
,
4
(x ) 0.14
f
.
6
.
4 Так как
12
1
(0.01 0.006 0 .765
0.5
3
, то процесс
продолжается.
6
.
5 Выполним отражение:
5
4
4
1
x
x (x x ) (5; 6.375) (5; 6.375) (4.5; 6.125)
T
T
T
(5.5; 6.625)T
;
5
(x ) 1.39
f
.
6
.
6 Так как
5
(x) (x) 1.015
h
f
f
, то выполним редукцию:
1
1
x x 0.5(x x ) (5; 6.25) 0.5 (5; 6.5) (5; 6.25) (5; 6.375)
l
l
T
T
T
T
;
2
x
x
(5; 6.25)
l
;
3
3
x x 0.5(x x ) (5; 6.25) 0.5 (4.5; 6.125) (5; 6.25) (4.75; 6.18)
l
l
T
T
T
T
.
Положим
17
kk
иперейдемкшагу2.
7
.
2 Так как
1
(x ) 0.14
f,
2
(x ) 0.0625
f
,
3
(x ) 0.28
f ,тополу-
чим
2
xx
l
,
3
x
x
h
,
1
x
x
s
.
195
7
.
3 Найдем центр тяжести вершин
1
xи
2
x:
4
1
2
1
1
x
(x x ) (5; 6.375) (5; 6.25) (5; 6.31)
2
2
T
T
T
,
4
(x ) 0.09
f
.
7
.
4 Так как
12
1
(0.025 0.0007 0 .036)
0.14
0.2
3
,то
процесс решения закончен: x
x
(5, 6.25)
l
T
; (x ) 0.0625
f
.
Результаты расчетов начальных трех итераций (до шага
2
6 ) приведе-
ны на рис. 4.4. При этом приняты следующие обозначения x ( )
i
k,гдеi–
номер точки, k – номер итерации.
4
2
x(3) x(4)
2
x (0)
4
x (0)
6
2
2
x(0) x(1) x(2)
3
3
x(0) x(1)
1
1
1
x(0) x(1) x(2)
10
8
6
6
4
4
10
8
2
2
0
1x
2
x
5
5
3
x(1) x(1) x(2)
4
x (1)
5
x (0)
5
x (3)
6
x (1)
Рис. 4.4
196
4.2 .3. Метод сопряженных направлений
Требуется найти безусловный минимум функции
(x)
f многих переменных, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
.
Определение 4.6. Ненулевые векторы
1
p,..., p
k
называются сопря-
женными относительно матрицы H размера ( )
nn
( H – ортогональ-
ными), если скалярное произведение
p,p 0
ij
H
,ij
,,
1,...,
ij
k
.
Матрица H (матрица Гессе) является симметрической матрицей
вторых производных, определенных в данной точке.
Сопряженное направление может
быть построено алгоритмически. Выберем
некоторое направление
1
p и две точки
0
x
и
0
y такие, чтобы векторы
00
(x y)
и
1
p
были неколлинеарны (рис. 4.5). Выполнив
исчерпывающий спуск из точек
0
xи
0
yв
направлении
1
p , получим точки
1
xи
1
y.
По свойству исчерпывающего спуска в
точках
1
xи
1
y имеет место касание соответствующими прямыми (на-
правлениями убывания) линий уровня целевой функции. Направление
2
1
1
pxy
и направление
1
p являются H - сопряженными.
В методе сопряженных направлений или
методе Пауэлла (Powell M.J.D.) исполь-
зуется тот факт, что минимум квадра-
тичной функции может быть найден не более чем за n шагов при условии,
что поиск ведется вдоль сопряженных относительно матрицы Гессе на-
правлений. Так как достаточно большой класс целевых функций может
быть представлен в окрестности точки минимума своей квадратичной ап-
проксимацией, описанная идея применяется и для неквадратичных функ-
ций. Задается начальная точка и направления совпадающие с координат-
ными. Находится минимум (x)
f при последовательном движении по
(1)
n направлениям с помощью одного из методов одномерной миними-
зации. При этом полученная ранее точка минимума берется в качестве ис-
ходной для поиска по следующему направлению, а направление p
n
ис-
0
y
2
1
1
pxy
1
x
0
x
1
p
2
p
x
1
y
1
p
Рис. 4.5
Постановка задачи
Стратегия решения задачи
197
пользуется как при первом
0
(p p)n
, так и последнем поиске. Находится
новое направление поиска, сопряженное p
n
. Оно проходит через точки,
полученные при первом и последнем поиске. Заменяется
1
pна
2
p,
2
pна
3
p и т.д. Направление p
n
заменяется сопряженным направлением, после
чего повторяется поиск по ( 1)
n направлениям, уже не содержащим ста-
рого направления
1
p . Для квадратичных функций последовательность
2
n
одномерных поисков приводит к точке минимума (если все операции вы-
полнены точно). Построение сопряженного направления для квадратичной
функции при
2
n изображено на рис. 4.5. Оно проходит через точки
1
x
и
1
y , а также точку минимума x
.
Алгоритм
1. Задать начальную точку
0
x , число
0
для окончания вычисли-
тельного процесса, начальные направления поиска
1
p (1; 0;...; 0)T
,
2
p (0;1; 0;...; 0)T
,..., p (0;...; 0;1)
n
T
.
Положим
0
ppn
,
0
i,
0
0
yx
,
0
k
.
2. Найти
1
yx
p
i
i
i
i
,гдешаг i
находится в результате поиска
минимума функции (x
p)
i
i
i
f
поi
одним из методов одномерной
минимизации.
3. Проверить выполнение условий:
а) если
1
in
, положить
1
i i и перейтикшагу2;
б) если
1
in
, проверить успешность поиска по n первым на-
правлениям. Если
0
yy
n
, то поиск завершить: x
yn
, иначе положить
1
i i иперейтикшагу2;
в)еслиi n
, проверить успешность поиска по n последним на-
правлениям. Если
1
1
y
y
n
, поиск завершить:
1
x
yn
, иначе перейти к
шагу 4 для построения сопряженного направления.
4. Положить
1
1
x
y
k
n
и проверить условие окончания:
а) если
1
||x x||
k
k
, то поиск завершить:
1
x
x
k
;
б) иначе положить:
0
1
1
ppy
y
n
n
(новое направление);
1
pp
i
i
,
1,...,
1
i
n
(исключается старое направление).
198
Если при этом
1
rang(p ,..., p )n
n
, то новая система направлений
линейно независима. В этом случае положить: p p
i
i
,
0,1,...,
i
n
;
1
kk
,
0
i,
0
1
yx
k
и перейти к шагу 2.
Если
1
rang(p ,..., p )n
n
, то новая система направлений линейно
зависима. Тогда следует продолжать поиск в старых направлениях. Для
этого положить: p p
i
i
,
0,1,...,
i
n
;0
1
yx
k
,
1
kk
,
0
i иперей-
тикшагу2.
Замечание 4.4. В [5] изложена модификация алгоритма Пауэлла,
предложенная Зангвиллом (Zangwill W.I .) . Эта модификация гарантирует
линейную независимость направлений поиска и сходимость за конечное
число шагов.
Пример 4.3
Найти минимум функции
2
2
1
2
(x)4(5)(6)
f
x
x
методом сопряженных направлений (методом Пауэлла).
Решение
0
.
1 Зададим начальную точку
0
x
(8;9)T
,
1
p (1; 0)T
,
2
p (0;1)T
,
0.1
. Положим
0
2
ppp
n
;00
yx
,
0
i, 0
k
.
0
.
2 Получаем
1
0
0
0
0
0
yy
p (8;9)
(0;1) (8; 9 )
T
T
T
.
Най-
дем минимум функции
2
0
0
(8;9 )36(3 )
f
по0
. Очевидно,
0
3
,
1
y (8; 6)T
.
0
.
3 Имеем
02
i
n
поэтому
1
i i иперейдемкшагу2.
1
.
2 Получаем
2
1
1
1
1
1
yy
p (8;6)
(1;0) (8 ; 6)
T
T
T
.
Най-
дем минимум функции
2
1
1
(8;6)4(3)
f
по1
. Очевидно, он дос-
тигается при 1
3
,
2
y (5; 6)T
.
1
.
3 Имеем
1
1
i
n
,
2
0
yyy
n
поэтому
12
i i иперехо-
дим к шагу 2.
2
.
2 Получаем
3
2
2
2
2
2
yy
p (5;6)
(0;1) (5; 6 )
T
T
T
.
Най-
дем минимум функции
2
2
2
(5;6 )
f
по
2
. Очевидно,
20
,
3
2
y y (5;6)T
.
199
2
.
3 Имеем
2
i
n
,
3
1
yy
. Переходим к шагу 4.
0
.
4 Находим
1
3
x
y (5; 6)T
,
1
0
2
2
||xx||(85)(96)
4.24
. Положим
0
2
3
1
pppyy(5;6)(8;6)(3;0)
n
T
T
T
,
1
2
0
pp
1
. Так как
30
rang
2
01
n
, то система векторов линейно
независима. Положим
2
2
p p (3;0)T
,
1
1
p p (0,1)T
,
0
0
pp
( 3;0)T
,
1
kk
,
0
i
0
1
y x (5;6)T
и перейдем к шагу 2.
3
.
2 Получаем
1
0
0
0
0
0
yy
p (5;6)
(3;0) (53 ;6)
T
T
T
.
Найдем минимум функции
2
0
0
(53;6)36
f
по0
.Таккак 0 0
,
то,
1
0
y (5;6) y
T
.
3
.
3 Имеем
0
11
i
n
поэтому
11
i i иперейдемкшагу2.
4
.
2 Получаем
2
1
1
1
1
1
yy
p (5;6)
(0;1) (5; 6 )
T
T
T
. Ми-
нимум функции
2
1
1
(5;6 )
f
по1
достигается при 1 0
.
Тогда
при
2
1
0
y(5;6)yy
T
.
4
.
3 Имеем
1
1
i
n
,
2
0
yy
поэтому поиск завершается:
2
x
y (5; 6)T
,
min
(x) 0
ff
.
4.2 .4. Адаптивный метод случайного поиска
Требуется найти безусловный минимум функции
(x)
f многих переменных, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
.
Задается начальная точка
0
x . Каждая
последующая точка находится по форму-
ле
1
x
x
ξ
k
k
k
kt
, где
0
kt – величина шага; ξ k
–
случайный вектор
единичной длины, определяющей направление поиска; k – номер итера-
ции. На текущей итерации при помощи генерирования случайных векто-
ров
k
получаются точки, лежащие на гиперсфере радиуса
k
с центром
в точке x
k
(рис. 4.6). Если значение функции в полученной точке не
меньше, чем в центре, шаг считается неудачным (точки
1
y,
2
y при поиске
Постановка задачи
Стратегия решения задачи
200
из
0
x;
1
y,
3
y при поиске из
1
x ). Если число неудачных шагов из теку-
щей точки достигает некоторого числа M , дальнейший поиск продолжа-
ется из той же точки, но с меньшим шагом до тех пор, пока он не станет
меньше заранее заданной величины R . Если же значение функции в пол у-
ченной точке меньше, чем в центре, шаг считается удачным и в найденном
направлении делается увеличенный шаг, играющий роль ускоряющего
шага (как при поиске по образцу в методе конфигураций). Если при этом
значение функции снова меньше, чем в центре, направление считается
удачным и дальнейший поиск продолжается из этой точки (точки
3
1
z
x
при поиске из
0
x,
4
2
z
x
при поиске из
1
x ). Если же значение функции
стало не меньше, чем в центре, направление считается неудачным и поиск
продолжается из старого центра (в точке
2
y при поиске из
1
x функция
меньше, чем в
1
x,авточке
2
z уже не меньше, поэтому направление
2
1
(z x)
неудачное).
Алгоритм
1. Задать начальную точку
0
x , коэффициенты расширения
1
и
0
1
, M – максимальное число неудачно выполненных испытаний
2
z
1
y
3
y
4
2
z
x
3
1
z
x
0
x
2
y
1
y
4
y
1x
2
x
3
y
x
Рис. 4.6
2
y
201
на текущей итерации, 0 1
t
–
начальную величину шага, R – минималь-
ную величину шага, N – максимальное число итераций. Положить
0
k,
1
j.
2. Получить случайный вектор
1
ξ ( ,...,
)
j
j
jT
n
, где
j
i
– случайная
величина, равномерно распределенная на интервале [ 1;1]
.
3. Вычислить
ξ
yx
||ξ ||
j
jk
kj
t
, где
2
1
||ξ ||
()
n
j
j
i
i
.
4. Проверить выполнение условий:
а)если (y) (x)
j
k
f
f
, шаг удачный. Положить
z
x
(y
jk
j
x)
k
. Определить, является ли текущее направление
(y x)
jk
удачным:
–
если
(z) (x)
j
k
f
f
, направление поиска удачное. Положить
1
x
z
k
j
,
1
k
k
t
t
,
1
kk
и проверить условие окончания. Если
kN
, положить
1
j иперейтикшагу2.Если k N
, поиск завер-
шить: x
x
k
;
–
если (z) (x)
j
k
f
f
, направление поиска неудачное, перейти к
шагу 5;
б)если (y) (x)
j
k
f
f
, шаг неудачный и перейти к шагу 5.
5. Оценить число неудачных шагов из текущей точки:
а)если j M
, следует положить
1
j j иперейтикшагу2;
б)если j M
, проверить условие окончания:
–если kt R
, процесс закончить: x
x
k
,(x)(x)
k
f
f
;
–
если kt R
, положить k
k
t
t
,1
j иперейтикшагу2.
Замечания 4.5
1. Величина
j
i
, равномерно распределенная на интервале [ 1;1]
, ге-
нерируется обычно с помощью датчиков псевдослучайных чисел на ком-
пьютере. Вырабатывается случайная величина
j
i
, равномерно распреде-
ленная на [0;1] , а затем используется линейное преобразование:
21
j
j
i
i
.
2. Если выполнено условие окончания kt R
, то в качестве ответа
можно использовать любую точку внутри шара с радиусом kt и центром в
точке x
k
.
202
3. Существуют многочисленные варианты метода случайного поиска
[9]. Например, вариант метода с элементами обучения, при котором на-
правления убывания функции становятся более вероятными, а другие на-
правления – менее вероятными.
Пример 4.4
Найти минимум функции
2
2
1
12
2
(x) 2
f
x
xx
x
методом адаптивного случайного поиска.
Решение
0
.
1 Зададим начальную точку
0
x
(0.5; 1)T
;
1
;
0.5
;
3
M;
100
N
;
0.5
R;01
t . Положим;
0
k, 0
j
.
При
1
точка z
j не вычисляется на шаге 4 алгоритма, так как она совпадает с
точкой yj.
0
.
2 Получаем
1
ξ ( 0.875; 0.436)T
.
0
.
3 Вычисляем
1
1
0
01
ξ
( 0.875; 0.436)
yx
(0.5; 1) 1
( 0.395; 0.553)
0.977
||ξ ||
T
T
T
t
.
0
.
4 Так как
1
0
(y) 0.399 (x) 2
f
f
, шаг удачный. Так как
1
,
то
1
1
z
y
,
1
0
(z) (x)
f
f
.
Положим
1
1
1
x
z
y ( 0.395; 0.553)T
,
11
kk
,1
001
t
tt
,
1
j иперейдемкшагу2.
1
.
2 Получаем
1
ξ (0.199; 0.396)T
.
1
.
3 Вычисляем
1
1
1
11
ξ
(0.199; 0.369)
yx
( 0.395; 0.553) 1
(0.08; 1.43)
0.419
||ξ ||
T
T
T
t
.
1
.
4 Так как
1
1
(y) 2.17 (x) 0.399
f
f
, шаг неудачный.
0
.
5 Имеем
1
3
jM
, поэтому
12
j j иперейдемкшагу2.
2
.
2 Получаем
2
ξ (0.287; 0.763)T
.
2
.
3 Вычисляем
2
2
1
12
ξ
yx
||ξ ||
t
(0.287; 0.763)
( 0.395; 0.553) 1
( 0.04; 0.38)
0.815
T
T
T
.
203
2
.
4 Так как
2
1
(y) 0.16 (x) 0.399
f
f
, шаг удачный. Так как
1
,то
2
2
z
y
,
2
1
(z) (x)
f
f
.
Положим
2
2
x
z
( 0.04; 0.38)T
,
12
kk
,2
111
t
tt
,
1
j иперейдемкшагу2.
3
.
2 Получает
1
ξ ( 0.937; 0.831)T
.
3
.
3 Вычисляем
1
1
2
21
ξ
( 0.937; 0.831)
yx
( 0.04; 0.38) 1
( 0.79; 0.28)
0.815
||ξ ||
T
T
T
t
.
3
.
4 Так как
1
2
(y) 1.1 (x) 0.16
f
f
, шаг неудачный.
1
.
5 Имеем
1
3
jM
, поэтому
12
j j иперейдемкшагу2.
4
.
2 Получаем
2
ξ (0.692; 0.178)T
.
4
.
3 Вычисляем
2
2
2
22
ξ
(0.692; 0.178)
yx
( 0.04; 0.38) 1
(0.929; 0.63)
0.714
||ξ ||
T
T
T
t
.
4
.
4 Так как
2
2
(y) 1.54 (x) 0.16
f
f
, шаг неудачный.
2
.
5 Имеем
2
3
jM
, поэтому
13
j j иперейдемкшагу2.
5
.
2 Получаем
3
ξ (0.596; 0.05)T
.
5
.
3 Вычисляем
3
3
2
23
ξ
(0.596; 0.05)
yx
( 0.04; 0.38) 1
(0.956; 0.463)
0.598
||ξ ||
T
T
T
t
.
5
.
4 Так как
3
2
(y) 2.48 (x) 0.16
f
f
, шаг неудачный.
3
.
5 Имеем
3
jM
,но21
0.5
t
R
. Положим 2
2 0.5
t
t
,
1
j иперейдемкшагу2.
6
.
2 Получаем
1
ξ (0.08; 0.971)T
.
6
.
3 Вычисляем
1
1
2
21
ξ
(0.08; 0.971)
yx
( 0.04; 0.38) 1
(0.08; 0.118)
0.974
||ξ ||
T
T
T
t
.
6
.
4 Так как
1
2
(y) 0.036 (x) 0.16
f
f
, шаг удачный. Так как
1
,то
1
1
zy
,
1
2
(z) (x)
f
f
.
204
Положим
3
1
1
x
z
y (0.08; 0.118)T
,
13
kk
,3
2 0.5
t
t
,
1
j иперейдемкшагу2.
7
.
2 Получаем
1
ξ (0.343; 0.512)T
.
7
.
3 Вычисляем
1
1
3
31
ξ
(0.343; 0.512)
yx
(0.08; 0.118) 0.5
(0.358; 0.53)
0.616
||ξ ||
T
T
T
t
.
7
.
4 Так как
1
3
(y ) 0.727 (x ) 0.036
f
f
, шаг неудачный.
4
.
5 Имеем
1
3
jM
, поэтому
12
j j иперейдемкшагу2.
8
.
2 Получаем
2
ξ ( 0.218; 0.491)T
.
8
.
3 Вычисляем
2
2
3
32
ξ
yx
||ξ ||
t
( 0.218; 0.491)
(0.08; 0.118) 0.5
( 0.123; 0.34)
0.537
T
T
T
.
8
.
4 Так как
2
3
(y ) 0.187 (x ) 0.036
f
f
, шаг неудачный.
5
.
5 Имеем
2
3
jM
, поэтому
13
j j иперейдемкшагу2.
9
.
2 Получаем
3
ξ ( 0.715; 0.252)T
.
9
.
3 Вычисляем
3
3
3
33
ξ
yx
||ξ ||
t
( 0.715; 0.252)
(0.08; 0.118) 0.5
( 0.391; 0.284)
0.758
T
T
T
.
9
.
4 Так как
3
3
(y ) 0.275 (x ) 0.036
f
f
, шаг неудачный.
6
.
5 Имеем
3
jM
,
3 0.5
t
R
. Поэтому процесс завершается:
3
x
x
(0.08; 0.118)T
,
(x ) 0.036
f
.
4.3 . Методы первого порядка
Методы решения задачи минимизации (x) min
f
,x
n
R
, кото-
рые используют информацию о первых производных функции (x)
f ,на-
зываются методами первого порядка. В этом разделе рассмотрены методы
первого порядка, основанные на итерационной процедуре минимизации
вида:
205
1
x
x
p
k
k
k
k
,
0,1,2, ...
k
;0
x
n
R
,
(4.8)
где направление убывания p
k
определяется тем или иным способом с уче-
том информации о первых частных производных функции (x)
f ,авели-
чина шага
0
k
такова, что:
1
(x)(x)
k
k
f
f
,
0,1,2, ...
k
.
(4.9)
Так как функция предполагается дифференцируемой, то в качестве
критерия окончания вычислений в случае бесконечной итерационной по-
следовательности {x }
k
, как правило, выбирается условие || ( x ) ||
k
f
,
где
1
x
(x)
(x)
(x)
,...,
k
T
n
k
f
f
f
x
x
–градиент в точке x
k
.
Разумеется,
могут быть использованы и другие критерии.
4.3 .1. Метод наискорейшего градиентного спуска
Пусть дана функция (x)
f , ограниченная снизу на
множестве
n
R и имеющая непрерывные частные
производные во всех его точках.
Требуется найти локальный безусловный минимум функции (x)
fна
множестве допустимых решений
n
XR
, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
.
Стратегия решения задачи состоит в по-
строении последовательности точек
{x}
k
,
0,1, 2, ...
k
таких, что
1
(x)(x)
k
k
f
f
,
0,1, 2, ...
k
Точки по-
следовательности {x }
k
вычисляются по правилу
1
x
x
(x)
k
k
k
kf
,
где точка
0
x задается пользователем; величина шага k
определяется для
каждого значения k из условия
()x
(x)
min
k
k
k
k
k
f
f
.
(4.10)
Решение задачи (4.10) может осуществляться с использованием необ-
ходимого условия минимума
0
k
d
d
с последующей проверкой доста-
Стратегия решения задачи
Постановка задачи
206
точного условия минимума
2
2
0
k
d
d
. Такой путь может быть использован
либо при достаточно простой минимизируемой функции ( )
k
,либопри
предварительной
аппроксимации достаточно
сложной функции
()x
(x)
k
k
k
k
f
f
полиномом ( )
k
P (как правило, второй или
третьей степени), и тогда условие
0
k
d
d
замещается условием
0
k
dP
d
,
а условие
2
2
0
k
d
d
– условием
2
2
0
k
dP
d
.
Другой путь решения задачи (4.10) связан с использованием числен-
ных методов одномерной оптимизации, когда ищется min ( )
k
k
min x
(x)
k
k
k
k
f
f
. При этом степень близости найденного значе-
ния
k
к оптимальному значению
k
, удовлетворяющему условиям
0
k
d
d
,
2
2
0
k
d
d
, зависит от точности выбранного метода одномерной
минимизации [19].
Построение последовательности {x }
k
,
0,1, 2, ...
k
заканчивается в
точке x
k
, для которой
1
|| (x )||
k
f
,где1
– заданное число, или, если
kM
, M – предельное число итераций, или при двукратном одновре-
менном выполнении неравенств
1
2
||x x||
k
k
,
1
2
|(x)(x)|
k
k
f
f
,
где 2
– малое положительное число. Вопрос о том, может ли точка x
k
рассматриваться как найденное приближение искомой точки локального
минимума x
, решается путем дополнительного исследования.
Алгоритм
1. Задать
0
x,10
,20
, предельное число итераций M . Найти
градиент функции в произвольной точке
1
(x)
(x)
(x)
, ...,
T
n
f
f
f
x
x
.
2. Положить
0
k
.
3. Вычислить
(x)
k
f
.
207
4. Проверить выполнение критерия окончания
1
|| (x )||
k
f
,где
2
1
(x)
|| (x )||
n
k
i
i
f
f
x
:
а) если критерий выполнен, то расчет окончен и x
x
k
;
б) если критерий не выполнен, то перейти к шагу 5.
5. Проверить выполнение неравенства k M
:
а) если неравенство выполнено, то расчет окончен и x
x
k
;
б) если нет, то перейти к шагу 6.
6. Вычислить величину шага k
из условия
()x
(x)
min
k
k
k
k
k
f
f
7. Вычислить
1
x
x
(x)
k
k
k
kf
.
8. Проверить выполнение условий
1
2
||x x||
k
k
,
1
2
|(x)(x)|
k
k
f
f
;
а) если оба условия выполнены при текущем значении k и
1
kk
, то расчет окончен и
1
x
x
k
;
б) если хотя бы одно из условий не выполнено, то положить
1
kk
и перейти к шагу 3.
Геометрическая интерпретация метода для
2
n приведена на рис.
4.7.
Рис. 4.7
2
x
3
(x)
fC
1
2
3
CCC
1
x
0
x
0
(x)
f
1
(x)
fC
2
(x)
fC
1x
2
x
x
208
Сходимость
Теорема 4.2. Пусть функция (x)
f дифференцируема и отграничена
снизу на
n
R , а ее градиент удовлетворяет условию Липшица
|| (x) (y)|| ||x y||
f
f
L
,
x,y
n
R
, где
0
L . Тогда при произ-
вольной начальной точке
0
x
n
R
для метода градиентного спуска имеем
lim|| (x)|| 0
k
k
f
.
Теорема 4.3. Пусть функция (x)
f удовлетворяет условиям утвер-
ждения 4.2. Тогда при произвольной начальной точке
0
x
n
R
для метода
наискорейшего градиентного спуска имеем || ( x ) || 0
k
f
приk [20].
Замечания 4.6
1. Теорема 4.3 гарантирует сходимость последовательности {x }
k
к
стационарной точке x
, где
(x) 0
f
. Следовательно, найденная в ре-
зультате применения метода точка x
k
нуждается в дополнительном ис-
следовании с целью ее классификации.
2. Метод наискорейшего спуска гарантирует сходимость последова-
тельности {x }
k
к точке минимума для сильно выпуклых функций [20].
Скорость сходимости
Оценки скорости сходимости получены только для сильно выпуклых
функций, когда последовательность {x }
k
сходится к точке минимума
функции (x)
f со скоростью геометрической прогрессии (линейная схо-
димость):
1
||x x||
||x x||
k
k
k
Mm
Mm
,гдеMиm–оценкинаи-
большего и наименьшего собственных значений матрицы вторых произ-
водных (x)
H функции (x)
f [20].
Замечания 4.7
1. Точку x
k
необходимо проанализировать для того, чтобы устано-
вить, является ли точка x
k
найденным приближением решения задачи.
Следует провести проверку функции (x)
f на выпуклость в - окрестно-
сти точки x
k
, используя критерий выпуклости для функций
1
(x)
fC
:
функция (x)
f выпукла (строго выпукла) в том и только в том случае,
если
(x y) (x) (x),y
f
f
f
, x,y
n
R
(x y) (x) (x),y
f
f
f
.
209
Если функция (x)
f выпукла (строго выпукла), то x
k
есть найденное при-
ближение точки x
.
2. Если требуется найти глобальный минимум функции (x)
f ,тодля
строго выпуклой (x)
f решение этой задачи аналогично поиску локально-
го минимума функции. В случае, когда (x)
f имеет несколько л окальных
минимумов, поиск глобального минимума осуществляется в результате
перебора всех локальных минимумов.
Пример 4.5
Найти локальный минимум функции
2
2
1
12
2
(x) 2
f
x
xx
x
методом наискорейшего спуска. Проанализировать найденное решение.
Решение
.
1 Зададим
0
x,1
,2
,M:
0
x
(0.5; 1)T
;10.1
;20.15
;
10
M
. Найдем градиент функции в произвольной точке:
1
21
2
(x) (4
;
2)T
f
xxx
x
.
.
2 Положим
0
k
.
0
.
3 Вычислим
0
(x ) (3; 2.5)T
f
.
0
.
4 Вычислим
0
|| (x )|| 3.9 0.1
f
. Переходим к шагу 5.
0
.
5 Проверим условие k M
:
010
k
M
, переходим к шагу 6.
0
.
6 Следующая точка находится по формуле
1
0
0
0
0
0
0
xx
(x ) (0.5;1)
(3;2.5) (0.5 3 ;1 2.5 )
T
T
T
f
.
Подставим полученные выражения
1
1
0
0.5 3
x
,
1
2
0
1 2.5
x
для ко-
ординат точки
1
xв(x)
f:
2
0
0
0
0
()2(0.53)(0.53)(12.5)
2
0
(12.5)
. Найдем минимум функции (x)
fпо0
с помощью необ-
ходимых условий безусловного экстремума:
0
0
0
0
0
0
()12(0.53)3(12.5)2.5(0.53)5(12.5)
d
d
0
15.25 63.25 0
. Отсюда 0 0.24
. Так как
2
0
2
0
()63.250
d
d
,
то найденное значение шага обеспечивает минимум функции
0
()
по
0
.
210
Заметим, что можно получить формулу для вычисления наилучшей
величины шага 0
на любой итерации из условия
()x
(x)
min
k
k
k
k
k
f
f
.
Имеем
1
21
2
(x)(4
;
2)
k
k
kk
kT
f
x
xx
x
;
1
1
2
2
1
2
x
(x)
(4
);
(
)
T
k
k
k
k
k
k
k
k
k
k
k
f
x
x
x
x
x
x
;
2
1
1
2
1
1
2
2
1
2
()2
(4
)
(4
)
(
)
k
k
k
k
k
k
k
k
k
k
k
k
k
x
xx
x
xx
x
xx
2
2
1
2
(
)
k
k
k
k
x
x
x
.
Из условия
()0
k
k
d
d
получаем
2
2
1
2
1
2
2
2
1
2
1
21
2
1
2
(4
)(2)
4(4
) 2(4
)(2)2( 2)
k
k
k
k
k
k
k
k
kk
k
k
k
x
x
x
x
x
x
x
xx
x
x
x
.
Определим 0
:00.24
.
0
.
7 Найдем
1
0
0
0
x
x
(x)
f
(0.5; 1) 0.24 (3; 2.5) ( 0.22; 0.4)
T
T
T
.
0
.
8 Вычислим
1
0
||x x || 0.937 0.15
:
Вычислим
1
0
| (x) (x)| 1.83 0.15
f
f
.
Вывод: полагаем
1
k и переходим к шагу 3.
1
.
3 Вычислим
1
(x ) ( 0.48; 0.58)T
f
.
1
.
4 Вычислим
1
|| (x )|| 0.752 0.1
f
.
1
.
5 Проверим условие k M
:
110
k
M
.
1
.
6 Определим 1 0.546
(см. п.
0
6).
1
.
7 Найдем
2
1
1
1
x
x
(x)
f
( 0.22; 0.4) 0.546 ( 0.48; 0.58) (0.04; 0.08)
T
T
T
.
1
.
8 Вычислим
2
1
||x x||
,
2
1
|(x) (x)|
f
f
:
2
1
||x x || 0.41 0.15
,
2
1
| (x) (x)| 0.156 0.15
f
f
Полагаем
2
k и переходим к шагу 3.
211
2
.
3 Вычислим
2
(x ) (0.24; 0.2)T
f
.
2
.
4 Вычислим
2
|| (x )|| 0.312 0.1
f
.
2
.
5 Проверим условие k M
:
210
k
M
..
2
.
6 Определим
1 0.24
(см. п.
0
6).
2
.
7 Найдем
3
2
2
2
x
x
(x)
f
3
x
(0.04; 0.08) 0.24(0.24; 0.2) ( 0.0176; 0.032)
T
T
T
.
2
.
8 Вычислим
3
2
||x x||
,
3
2
|(x) (x)|
f
f
:
3
2
|| x x || 0.0749 0.15
,
3
2
|(x) (x)| 0.0116 0.15
f
f
Полагаем
3
k и переходим к шагу 3.
3
.
3 Вычислим
3
(x ) ( 0.012; 0.0816)T
f
.
3
.
4 Вычислим
3
|| (x )|| 0.082 0.1
f
.
Расчет окончен. Найдена
точка
3
x
( 0.0176; 0.032)T
,
3
(x ) 0.00127
f
.
Анализ точки
3
x . Функция
2
2
1
12
2
(x) 2
f
x
xx
x
является дважды
дифференцируемой, поэтому проведем проверку достаточных условий
минимума в точке
3
x . Для этого проанализируем матрицу Гессе
41
12
H
. Матрица постоянна и является положительно определенной
(т.е.
0
H ), т.к. оба ее угловых минора 1 4
и27
положительны,
а
функция
(x)
f – строго
выпуклой. Следовательно,
точка
3
x
( 0.0176; 0.032)T
есть найденное приближение точки x
(0; 0)T
глобального минимума функции (x)
f ,т.е.
min
(x)
0
f
f
.
4.3 .2. Метод Гаусса - Зейделя
Пусть дана функция (x)
f , ограниченная снизу на
множестве
n
R и имеющая непрерывные частные
производные во всех его точках.
Требуется найти локальный безусловный минимум функции (x)
fна
множестве допустимых решений
n
XR
, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
.
Постановка задачи
212
Стратегия метода Гаусса - Зейделя
(Gauss – Seidel) состоит в построении
последовательности точек {x }
k
,
0,1, 2, ...
k
таких, что
1
(x)(x)
k
k
f
f
,
0,1, 2, ...
k
Точки последовательности {x }
k
вычисляются по правилу
1
1
1xx
(x)
x
x
jk
jk
jk
k
k
k
f
e
x
,
где j – номер цикла вычислений,
0,1, 2,...
j
; k – номер итерации внут-
ри цикла,
0,1,...,
1
k
n
;1
ke – единичный вектор, ( 1)
k -я проекция
которого равна 1 ; точка
00
x задается пользователем, величина шага k
выбирается из условия
1
1xx
(x)
()x
min
k
jk
jk
k
k
k
k
f
f
e
x
.
Эта задача является задачей одномерной минимизации функции
()k
и может быть решена либо с использованием условий
0
k
,
2
2
0
k
, либо численно с использованием методов одномерной миними-
зации, как задача
[,]
()min
k
k
ab
.
Если уравнение
0
k
имеет высокую степень и корни его трудно
определить, можно аппроксимировать функцию
()k
полиномом
()k
P второй или третьей степени и определить k
из условий
0
k
P
,
2
2
0
k
P
.
При численном решении задачи определения величины шага степень
близости найденного значения k
к оптимальному значению k
, удовле-
творяющему условиям
0
k
,
2
2
0
k
, зависит от точности метода
одномерной минимизации [19].
Стратегия решения задачи
213
Легко видеть, что при фиксированном j за одну итерацию с номером
k изменяется только одна проекция точки x
jk
, имеющая номер 1
k,ав
течение всего цикла с номером j , т.е. начиная с
0
k икончая
1
kn
,
изменяются все n проекций точки
0
x
j . После этого точке x
jn
присваива-
ется номер
1,0
x
j
и она берется за начальную точку для вычислений в
(1)
j -м цикле.
Расчет заканчивается в точке x
jk
при выполнении по крайней мере
одного из трех критериев окончания счета:
1
|| (x )||
jk
f
,илиkM
,
или выполнения неравенств
1
2
||x x||
jk
jk
,
1
2
|(x)(x)|
jk
jk
f
f
.
Здесь 1
,2
– малые положительные числа, M – предельное число цик-
лов итераций. Вопрос о том, является ли точка x
jk
найденным приближе-
нием искомой точки, решается путем проведения дополнительного иссле-
дования.
Алгоритм
1. Задать
00
x,10
,20
; предельное число M циклов счета,
кратное n , где n – размерность вектора x . Найти градиент
(x)
f.
2. Задать номер цикла
0
j
.
3. Проверить условие j M
:
а)если j M
, то расчет окончен и x
x
jk
;
б)если j M
,топерейтикшагу4.
4. Задать
0
k
.
5. Проверить условие
1
kn
:
а) если
1
kn
, топерейтикшагу6;
б)если k n
, то положить
1
j j иперейтикшагу3.
6. Вычислить
(x)
jk
f
.
7. Проверить выполнение условия
1
|| (x )||
jk
f
:
а) если условие выполнено, то расчет окончен и x
x
jk
;
б) если нет, то перейти к шагу 8.
8. Вычислить k
из условия
1
1xx
(x)
()x
min
k
jk
jk
k
k
k
k
f
f
e
x
.
214
9. Вычислить
1
1
1xx
(x)
x
x
jk
jk
jk
k
k
k
f
e
x
10. Проверить выполнение условий
1
2
||x x||
jk
jk
,
1
2
|(x)(x)|
jk
jk
f
f
:
а) если оба условия выполнены в двух последовательных циклах с
номерами j и 1
j , то расчет окончен, найдена точка
1
x
x
jk
;
б) если не выполняется хотя бы одно условие, положить
1
kk
и перейти к шагу 5.
Пример 4.6
Найти локальный минимум функции
2
2
1
12
2
(x) 2
f
x
xx
x
методом Гаусса – Зейделя. Определить точку x jk
, в которой выполнен
хотя бы один критерий окончания расчетов.
Решение
.
1 Зададим
00
x,1
,2
,M:
00
x
(0.5; 1)T
;10.1
;20.15
;
10
M
. Найдем градиент функции в произвольной точке:
1
21
2
(x) (4
;
2)T
f
xxx
x
.
.
2 Зададим
0
j
.
0
.
3 Проверим выполнение условия j M
:010
j
M
.
0
.
4 Зададим
0
k
.
0
.
5 Проверим выполнение условия
1
kn
:
01
1
k
n
.
0
.
6 Вычислим
00
(x ) (3; 2.5)T
f
.
0
.
7 Проверим условие
00
1
|| (x )||
f
:
00
|| (x )|| 3.9 0.1
f
.
0
.
8 Определим величину шага 0
из условия
0
0
0
0
0
1
1xx
(x)
()x
min
j
j
f
f
e
x
.
При
0
k, 0
j:
00
01
00
0
1
1xx
(x)
x
x
f
e
x
.
215
Поскольку
00
00
1
2xx
1xx
(x)
4
213
f
xx
x
,
1 (1; 0)T
e
,
то
01
0
0
x
(0.5;1)
3 (1;0) (0.5 3 ;1)
T
T
T
или
01
1
0
0.5 3
x
,
01
21
x . Подставляя полученные выражения в (x)
f , имеем
2
0
0
0
()2(0.53)(0.53)11
.
Из необходимого условия экстремума
0
0
0
()3690
d
d
нахо-
дим 0 0.25
. Так как
2
0
2
0
()360
d
d
, то найденное значение шага
обеспечивает минимум функции
0
()
по0
.
0
.
9 Определим
00
01
00
0
1
1xx
(x)
x
x
( 0.25;1)T
f
e
x
.
0
.
10 Проверим условия
01
00
2
||xx||
,
01
00
2
|(x)(x)|
f
f
:
01
00
||x x || 0.25 0.15
,
01
00
| (x ) (x )| |0.875 2| 1.125 0.15
f
f
.
Полагаем
1
k , перехо-
дим к шагу 5.
1
.
5 Проверим условия
1
kn
:
1
1
k
n
.
1
.
6 Вычислим
01
(x ) (0; 1.75)T
f
.
1
.
7 Проверим условие
01
1
|| (x )||
f
:
00
|| (x )|| 1.75 0.1
f
.
1
.
8 Определим величину шага 1
из условия
1
1
1
1
1
2
2xx
(x)
()x
min
j
j
f
f
e
x
.
При 1
k, 0
j:
01
02
01
1
2
2xx
(x)
x
x
f
e
x
.
Поскольку
01
01
1
2xx
2xx
(x)
2
0.25 2 1.75
f
x
x
x
,
2 (0;1)T
e
,
то
02
1
1
x
( 0.25;1)
1.75 (0;1) ( 0.25; 1 1.75 )
T
T
T
или
02
1
0.25
x
,
02
2
1
1 1.75
x
. Подставляя полученные выражения в (x)
f , имеем
2
2
1
1
1
()2(0.25) (0.25)(11.75)(11.75)
.
216
Из необходимого условия экстремума
2
2
1
1
1
( ) 21.75
1.75 0
d
d
находим 1 0.5
. Так как
2
2
1
2
1
()21.75 0
d
d
, то найденное значе-
ние шага обеспечивает минимум функции
1
()
по1
.
1
.
9 Определим
01
02
01
1
2
2xx
(x)
x
x
( 0.25; 0.125)T
f
e
x
.
1
.
10 Проверим условия
02
01
2
||xx||
,
02
01
2
|(x)(x)|
f
f
:
02
01
||x x || 0.875 0.15
,
02
01
| (x ) (x )| |0.12 0.875| 0.755
f
f
0.15
. Полагаем
2
k , переходим к шагу 5.
2
.
5 Проверим условие
1
kn
:
2
k
n
.
Полагаем
1
j,
10
02
x
x
, переходим к шагу 3.
1
.
3 Проверим условие j M
:110
j
M
.
1
.
4 Зададим
0
k
.
3
.
5 Проверим условие
1
kn
:
01
1
k
n
.
3
.
6 Вычислим
10
02
(x ) (x ) ( 0.875; 0.00)T
f
f
.
3
.
7 Проверим условие
10
1
|| (x )||
f
:
10
|| (x )|| 0.875 0.1
f
.
3
.
8 Полагаем 0 0.25
. (см. п.
0
8).
3
.
9 Вычислим
10
11
10
0
1
1xx
(x)
x
x
( 0.03; 0.125)T
f
e
x
.
3
.
10 Проверим условия
11
10
2
||xx||
,
11
10
2
|(x) (x)|
f
f
:
11 10
||x x || 0.22 0.15
,
11
10
| (x ) (x )| |0.013 0.137| 1.124 0.15
f
f
.
Полагаем
1
k , пере-
ходим к шагу 5.
4
.
5 Проверим условие
1
kn
:
1
1
k
n
.
4
.
6 Вычислим
11
(x ) ( 0.005; 0.22)T
f
.
4
.
7 Проверим условие
11
1
|| (x )||
f
:
11
|| (x )|| 0.22 0.1
f
.
4
.
8 Зададим 1 0.5
. (см. п.
1
8).
4
.
9 Вычислим
11
12
11
1
2
2xx
(x)
x
x
( 0.03; 0.015)T
f
e
x
.
217
4
.
10 Проверим условия
12
11
2
||xx||
,
12
11
2
|(x) (x)|
f
f
:
12 11
||x x || 0.11 0.15
,
12
11
| (x ) (x )| | 0.0015 0.013| 0.0115 0.15
f
f
. Полагаем
2
k , пере-
ходим к шагу 5.
5
.
5 Проверим условие
1
kn
:
2
k
n
.
Полагаем
2
j,
20
12
x
x
, переходим к шагу 3.
2
.
3 Проверим условие j M
:210
j
M
.
2
.
4 Зададим
0
k
.
6
.
5 Проверим условие
1
kn
:
01
1
k
n
.
5
.
6 Вычислим
20
(x ) ( 0.105; 0)T
f
.
5
.
7 Проверим условие
20
1
|| (x )||
f
:
20
|| (x )|| 0.105 0.1
f
.
5
.
8 Зададим 0 0.25
. (см. п.
0
8).
5
.
9 Вычислим
20
21
20
0
1
1xx
(x)
x
x
( 0.004; 0.015)T
f
e
x
.
5
.
10 Проверим условия
21
20
2
||xx||
,
21
20
2
|(x)(x)|
f
f
:
21 20
||x x || 0.026 0.15
,
21
20
| (x ) (x )| |0.0002 0.0015| 0.15
f
f
.
Условия
1
2
||x x||
jk
jk
,
1
2
|(x)(x)|
jk
jk
f
f
выполнены
в двух последовательных циклах с номерами
2
j
и
11
j
.
Расчет
окончен, найдена точка
21
xx
( 0.004; 0.015)T
; (x ) 0.000197
f
.
Точка
21
x является найденным приближением точки глобального
минимума (x)
f , так как функция (x)
f строго выпуклая.
4.3 .3. Метод сопряженных градиентов
Пусть дана функция (x)
f , ограниченная снизу на
множестве
n
R и имеющая непрерывные частные
производные во всех его точках.
Требуется найти локальный безусловный минимум функции (x)
fна
множестве допустимых решений
n
XR
, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
.
Постановка задачи
218
Стратегия метод сопряженных градиен-
тов состоит в построении последова-
тельности точек {x }
k
,
0,1, 2, ...
k
таких, что
1
(x)(x)
k
k
f
f
,
0,1, 2, ...
k
Здесь рассматривается алгоритм метода Флетчера – Ривса
(Fletcher R., Reeves M.) Точки последовательности {x }
k
вычисляются по
правилу
1
x
x+p
k
k
k
k
,
0,1, 2, ...
k
;
(4.11)
1
1
p
(x)
p
k
k
k
k
f
;
(4.12)
0
0
p
(x)
f
;
(4.13)
2
1
12
|| (x )||
|| (x )||
k
k
k
f
f
.
(4.14)
Точка
0
x задается пользователем, величина шага k
определяется
для каждого значения k из условия
()(x+p)min
k
k
k
k
k
f
.
(4.15)
Решение задачи одномерной минимизации (4.15) может осуществ-
ляться либо из условия
0
k
,
2
2
0
k
, либо численно, с использова-
нием методов одномерной минимизации, когда решается задача
()min
k
k
.
При численном решении задачи определения величины шага степень
близости найденного значения k
к оптимальному значению k
удовле-
творяющему условиям
0
k
,
2
2
0
k
, зависит от точности исполь-
зуемого метода одномерной минимизации.
Вычисление величины
1
k
по формуле (4.14) обеспечивает для
квадратичной формы
11
(x)
nn
ijij
ij
f
axx
построение последовательно-
сти H -сопряженных направлений
0
p,
1
p ,...,
pk
,..., для которых
p,p 0
i
j
H
,
,
0,1, ...,
ij
k
,ij
. При этом в точках последователь-
Стратегия решения задачи
219
ности {x }
k
векторы-градиенты функции (x)
f взаимно перпендикулярны,
т.е .
1
(x),(x)0
k
k
f
f
, 0,1,...
k
.
Для квадратичных функций (x)
f с матрицей
0
H метод сопря-
женных градиентов является конечным и сходится за число шагов, не пре-
вышающее n – размерность вектора x .
Замечание 4.8. При минимизации неквадратичных функций метод
Флетчера-Ривса не является конечным, при этом следует отметить, что
погрешности в решении задачи (4.15) приводят к нарушению не только
перпендикулярности градиентов, но и H -сопряженности направлений.
Для неквадратичных функций, как правило, используется алгоритм Пола-
ка-Рибьера (Polak E., Ribiere G.) , когда в формулах (4.11) – (4.14) величина
1
k
вычисляется следующим образом:
1
12
1
(x), (x) (x )
,
,
|| (x )||
0,
,
k
k
k
k
k
f
f
f
kJ
f
kJ
где
{0, ,2 ,...}
J
nn
.
В отличие от алгоритма Флетчера-Ривса алгоритм
Полака-Рибьера предусматривает использование итерации наискорейшего
градиентного спуска через каждые n шагов. Построение последователь-
ности {x }
k
заканчивается в точке, для которой
1
|| (x )||
k
f
,где1
–
заданное число, или при k M
, M – предельное число итераций, или
при двукратном выполнении двух неравенств
1
2
||x x||
jk
jk
,
1
2
|(x)(x)|
jk
jk
f
f
,где2
– малое положительное число.
Алгоритм (Флетчера – Ривса)
1. Задать
0
x,10
,20
; M – предельное число итераций. Най-
ти градиент
(x)
f.
2. Положить
0
k
.
3. Вычислить
(x)
k
f
.
4. Проверить выполнение критерия окончания
1
|| (x )||
k
f
:
а) если критерий выполняется, то x
x
k
, расчет окончен;
б) если нет, то перейти к шагу 5.
5. Проверить условие k M
:
а) если неравенство выполняется, то расчет окончен и x
x
k
;
220
б) если нет, то при
0
k перейтикшагу6,апри 1
k перейти к
шагу 7.
6. Определить по (4.13) 0
0
p
(x)
f
.
7. Определить по (4.14)
2
1
12
|| (x )||
|| (x )||
k
k
k
f
f
.
8. Определить по (4.12)
1
1
p
(x)
p
k
k
k
k
f
.
9. Найти k
из условия ( )
(x+p)min
k
k
k
k
k
f
.
10. Вычислить
1
x
x+p
k
k
k
k
по формуле (4.11).
11. Проверить выполнение условий
1
2
||x x||
jk
jk
,
1
2
|(x)(x)|
jk
jk
f
f
:
а) в случае выполнения обоих условий в двух последовательных
итерациях с номерами 1
k и k расчет окончен, найдена точка x
k
;
б) если не выполняется хотя бы одно из условий, полагаем
1
kk
и переходим к шагу 3.
Геометрическая интерпретация метода для
2
n изображена на рис.
4.8.
0
0p
3
(x)
fC
Рис. 4.8
1
p
1
2
3
CCC
1
x
0
x
0
0
(x)
p
f
1
(x)
fC
2
(x)
fC
1x
2
x
x
221
Сходимость
Сходимость методов Флетчера-Ривса и Полака-Рибьера определяется
соответственно следующими теоремами.
Теорема 4.4. Если квадратичная функция
11
(x)
nn
ijij
ij
f
axx
сне-
отрицательно определенной матрицей A достигает своего минимально-
го значения на
n
R , то метод Флетчера-Ривса обеспечивает отыскание
точки минимума не более чем за n шагов [29].
Теорема 4.5. Если функция (x)
f ограничена снизу, а ее градиент
удовлетворяет условию
Липшица
|| (x) (y)|| ||x y||
f
f
L
,
x,y
n
R
, то в методе Полака-Рибьера lim || (x) || 0
k
k
f
[20].
Замечания 4.9
1. Теорема 4.5 гарантирует сходимость последовательности {x }
k
к
стационарной точке x
, где
(x) 0
f
. Следовательно, найденная в ре-
зультате применения метода точка x
k
нуждается в дополнительном ис-
следовании с целью классификации этой точки.
2. Метод Полака-Рибьера гарантирует сходимость последовательно-
сти{x}
k
к точке минимума для сильно выпуклых функций.
Скорость сходимости
Оценки скорости сходимости получены только для сильно выпуклых
функций, когда последовательность {x }
k
сходится к точке минимума
функции (x)
f со скоростью
2
||x x|| ||x x||
kn
k
C
,
{0, ,2 ,...}
knn
[29].
Пример 4.7
Найти локальный минимум функции
2
2
1
12
2
(x) 2
f
x
xx
x
методом Флетчера-Ривса. Определить точку x
k
, в которой выполнен хотя
бы один критерий окончания расчетов.
Решение
.
1 Зададим
0
x,1
,2
,M:
0
x
(0.5,1)T
;10.1
;20.15
;
10
M
. Найдем градиент функции в произвольной точке:
1
21
2
(x) (4
;
2)T
f
xxx
x
.
222
.
2 Положим
0
k
.
0
.
3 Вычислим
0
(x ) (3; 2.5)T
f
.
0
.
4 Проверим условие
0
1
|| (x )||
f
:
0
|| (x )|| 3.9 0.1
f
.
0
.
5 Проверим условие k M
:
010
k
M
.
0
.
6 Определим
0
0
p
(x ) (3; 2.5)T
f
.
0
.
9 Определим величину шага 0
из условия
0
0
0
0
(x+p) min
f
:
0 0.24
(первая итерация выполняется по методу наискорейшего спус-
ка, см. пример 4.5).
0
.
10 Вычислим
1
0
0
0
x
x + p ( 0.22;0.4)T
.
0
.
11 Проверим условия
1
0
2
||x x||
,
1
0
2
|(x) (x)|
f
f
:
1
0
||x x || 0.937 0.15
,
1
0
|(x) (x)| |0.17 2| 1.83 0.15
f
f
.
Полагаем
1
k , переходим к шагу 3.
1
.
3 Вычислим
1
(x ) ( 0.48; 0.58)T
f
.
1
.
4 Проверим условие
1
1
|| (x )||
f
:
1
|| (x )|| 0.752 0.1
f
.
1
.
5 Проверим условие k M
:
110
k
M
.
1
.
7 Определим
12
0
02
|| (x )||
0.0373
|| (x )||
f
f
.
1
.
8 Определим
1
0
0
0
p
(x) p
f
:
( 0.48; 0.58) 0.0373 (3; 2.5) (0.368; 0.673)
T
T
T
.
1
.
9 Определим величину шага 1
из условия
1
1
1
1
(x+ p) min
f
.
Воспользуемся формулой
2
1
1
1
1
x
x + p ( 0.22;0.4)
(0.368; 0.673)
T
T
1
1
( 0.22 0.368 ; 0.4 0.673 )T
.
Подставляя полученное выражение в (x)
f , имеем
2
1
1
1
1
( ) 2( 0.22 0.368 ) ( 0.22 0.368 )(0.4 0.673 )
2
1
(0.4 0.673 )
.
Применяя необходимое условие безусловного экстремума
223
1
1
1
1
( ) 4 ( 0.22 0.368 ) 0.368 0.368 (0.4 0.673 )
d
d
1
1
( 0.22 0.368 ) ( 0.673) 2 (0.4 0.673 ) ( 0.673) 0
,
находим 1 0.595
. Поскольку
2
1
2
1
()0.9520
d
d
, найденное значе-
ние шага обеспечивает минимум функции
1
()
по1
.
1
.
10 Вычислим
2
1
1
1
x
x + p (0.001; 0.000)T
.
1
.
11 Проверим условия
2
1
2
||x x||
,
2
1
2
|(x) (x)|
f
f
:
2
1
||x x || 0.456 0.15
,
2
1
| (x) (x)| 0.17 0.15
f
f
.
Полагаем
2
k , переходим к шагу 3.
2
.
3 Вычислим
2
(x)
f
:
2
(x ) (0.003; 0.006)T
f
.
2
.
4 Проверим условие
2
1
|| (x )||
f
:
2
|| (x )|| 0.0067 0.1
f
.
Расчет окончен. Найдена точка
2
x
(0.001; 0)T
;
2
6
(x) 210
f
.
С учетом того, что функция
2
2
1
12
2
(x) 2
f
x
xx
x
строго выпуклая,
она
имеет
единственный
минимум,
приближение
которого
2
x
x
(0.001; 0)T
найдено за две итерации.
4.4 . Методы второго порядка
Методы решения задачи минимизации (x) min
f
,x
n
R
, кото-
рые используют информацию о первых и вторых производных функции
(x)
f , называются методами второго порядка. В этом разделе рассмотре-
ны методы второго порядка, основанные на итерационной процедуре ми-
нимизации вида:
1
x
x
p
k
k
k
k
,
0,1,2, ...
k
;
0
x
n
R
,
(4.16)
где направление убывания p
k
определяется тем или иным способом с ис-
пользованием первых и вторых частных производных функции (x)
f,а
величина шага
0
k
такова, что:
1
(x)(x)
k
k
f
f
,
0,1,2, ...
k
.
(4.17)
В качестве критерия окончания вычислений, как правило, выбирают-
ся те же условия, что и в методах первого порядка.
224
4.4 .1. Метод Ньютона
Пусть дана функция (x)
f , ограниченная снизу на
множестве
n
R и имеющая непрерывные частные
производные во всех его точках.
Требуется найти безусловный локальный минимум функции (x)
fна
множестве допустимых решений
n
XR
, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
,
2
(x)
fC
.
Стратегия решения задачи методом
Ньютона ( Newton I.) состоит в построе-
нии последовательности точек {x }
k
,
0,1, 2, ...
k
таких, что
1
(x)(x)
k
k
f
f
,
0,1, 2, ...
k
Точки последовательности {x }
k
вычисля-
ются по правилу
1
x
x
p
k
k
k
,
0,1, 2, ...
k
где точка
0
x задается пользователем, а направление спуска p
k
определя-
ется для каждого значения k по формуле
1
p
(x) (x)
k
k
k
H
f
.
(4.18)
Выбор pk
по формуле (4.18) гарантирует выполнение требования
1
(x)(x)
k
k
f
f
при условии, что
(x) 0
k
H
. Формула (4.18) получена
из следующих соображений:
1. Функция (x)
f аппроксимируется в каждой точке последователь-
ности {x }
k
квадратичной функцией
1
(x) (x),p
p,(x)p
2
k
kk
k
kk
k
Ff
f
H
.
2. Направление p
k
определяется из необходимого условия экстрему-
ма первого порядка:
0
p
k
k
dF
d
. Таким образом, при выполнении требования
(x) 0
k
H
последовательность является последовательностью точек ми-
нимумов квадратичных функций kF , 0,1, 2, ...
k
(рис. 4.9). Чтобы обес-
печить выполнение требования
1
(x)(x)
k
k
f
f
,
0,1,2, ...
k
,дажев
тех случаях, когда для каких-либо значений матрица Гессе (x )
k
H
не ока-
жется положительно определенной, рекомендуется для соответствующих
Стратегия решения задачи
Постановка задачи
225
значений k вычислить точку
1
x
k
по методу градиентного спуска
1
x
x
(x)
k
k
k
kf
с выбором величины шага
k
из условия
x
(x) (x)
k
k
k
k
f
f
f
.
Построение последовательности {x }
k
заканчивается в точке x
k
, для
которой
1
|| (x )||
k
f
,где1
– заданное число, или, если k M
(M–
предельное число итераций) или при двукратном одновременном выпол-
нении двух неравенств
1
2
||x x||
k
k
,
1
2
|(x)(x)|
k
k
f
f
,где2
–
малое положительное число. Вопрос о том, может ли точка x
k
рассматри-
ваться как найденное приближение искомой точки локального минимума
x
, решается путем проведения дополнительного исследования, которое
описано ниже.
Алгоритм
1. Задать
0
x,10
,20
, M – предельное число итераций. Найти
градиент функции в произвольной точке
(x)
f
и матрицу Гессе (x)
H.
2. Положить
0
k
.
3. Вычислить
(x)
k
f
.
4. Проверить выполнение критерия окончания
1
|| (x )||
k
f
:
а) если неравенство выполнено, то расчет окончен и x
x
k
;
б) в противном случае перейти к шагу 5.
1
x
x
Рис. 4.9
2
x
1
F
0
F
0
x
()
fx
x
()
fx
226
5. Проверить выполнение неравенства k M
:
а) если неравенство выполнено, то расчет окончен и x
x
k
;
б) если нет, то перейти к шагу 6.
6. Вычислить матрицу (x )
k
H
.
7. Вычислить матрицу
1
(x)
k
H
.
8. Проверить выполнение условия
1
(x) 0
k
H
:
а) если
1
(x) 0
k
H
,топерейтикшагу9.
б) если нет, то перейти к шагу 10, положив p
(x)
k
k
f
.
9. Определить
1
p
(x) (x)
k
k
k
H
f
.
10. Найти точку
1
x
x
p
k
k
k
k
,
положив
1
k
,если
1
p
(x) (x)
k
k
k
H
f
, или
выбрав k
из условия
1
(x)(x)
k
k
f
f
,еслиp
(x)
k
k
f
.
11. Проверить выполнение условий
1
2
||x x||
k
k
,
1
2
|(x)(x)|
k
k
f
f
;
а) если оба условия выполнены при текущем значении k и
1
kk
, то расчет окончен и x
x
k
;
б) в противном случае положить
1
kk
и перейти к шагу 3.
Сходимость
Теорема 4.6. Пусть функция (x)
f дважды непрерывно дифферен-
цируемая сильно выпуклая с константой 0
l на
n
R и удовлетворяет
условию Липшица
|| (x) (y)|| ||x y||
H
H
L
,
x,y
n
R
,
где
0
L , а начальная точка такова, что
2
0
8
|| (x )||
lq
f
L
при
(0, 1)
q
.
(4.19)
Тогда последовательность{x }
k
сходится к точке минимума с квадра-
тичной скоростью
2
4
||x x||
k
k
lq
L
[29].
227
Замечания 4.10
1. Сходимость метода Ньютона доказана лишь для сильно выпуклых
функций и для достаточно хорошего начального приближения, определяе-
мого условием (4.19), практическое использование которого крайне за-
труднено, так как постоянные l и L , как правило, неизвестны или требу-
ют трудоемкого исследования для их определения. Поэтому при практиче-
ском использовании метода Ньютона следует:
а) анализировать матрицу
(x)
k
H
на выполнение условия
(x) 0
k
H
,
0, 1,...
k
и заменять формулу
1
1
x
x
(x) (x)
k
k
k
k
H
f
на формулу
1
x
x
(x)
k
k
k
kf
в случае его невыполнения;
б) производить анализ точки x
k
с целью выяснения, является ли она
найденным приближением искомой точки x
.
2. При решении задачи поиска безусловного максимума формула
(4.18) не изменяется, так как в этом случае (x ) 0
k
H
.
3. Для точки x
k
, в которой выполняется по крайней мере один крите-
рий окончания расчета, необходимо осуществить проверку выполнения
достаточных условий минимума (x ) 0
k
H
. Если условие выполнено, то
точка x
k
может рассматриваться как найденное приближение точки ми-
нимума x
. Проверку выполнения достаточных условий минимума можно
заменить проверкой (x)
f функции на выпуклость.
Пример 4.8
Найти локальный минимум функции
2
2
1
12
2
(x) 2
f
x
xx
x
методом Ньютона. Определить точку x
k
, в которой выполнен хотя бы
один критерий окончания расчетов.
Решение
.
1 Зададим
0
x,1
,2
,M:
0
x
(0.5; 1)T
;10.1
;20.15
;
10
M
. Найдем градиент функции
1
21
2
(x) (4
;
2)T
f
xxx
x
и мат-
рицу Гессе
41
(x)
12
H
.
.
2 Положим
0
k
.
0
.
3 Вычислим
0
(x ) (3; 2.5)T
f
.
228
0
.
4 Проверим условие
0
1
|| (x )||
f
:
0
|| (x )|| 3.9 0.1
f
. Пере-
ходим к шагу 5.
0
.
5 Проверим условие k M
:
010
k
M
. Переходим к шагу 6.
0
.
6 Вычислим
0
41
(x)
12
H
.
0
.
7 Вычислим
10
21
77
(x)
14
77
H
.
0
.
8 Проверим выполнение условия
10
(x) 0
H
.Таккак 1
2
0
7
,
2
1
0
7
, то согласно критерию Сильвестра
10
(x) 0
H
.
0
.
9 Определим
0
10
0
21
3
1
77
p
(x) (x)
2
5
14
1
2
77
H
f
.
0
.
10 Вычислим
1
x
0.5; 1
0.5; 1
0;0
T
T
T
.
0
.
11 Проверим выполнение условий
1
0
2
||x x || 1.12
0.15
,
1
0
2
|(x)(x)|2
0.15
f
f
.
Полагаем
1
k , переходим к шагу 3.
1
.
3 Вычислим
1
(x) (0;0)T
f
.
0
.
4 Проверим условие
0
1
|| (x )||
f
:
0
|| (x)|| 0 0.1
f
. Расчет
окончен.
В точке
1
x выполняется необходимое условие первого порядка, по-
этому она является стационарной точкой. Исходная функция
2
2
1
12
2
(x) 2
f
x
xx
x
является строго выпуклой, так как ее матрица вто-
рых производных положительно определенная (x)
H . Поэтому найденная
точка
1
x
(0; 0)T
есть точка локального и одновременно глобального ми-
нимума функции (x)
f:
1
x
x
(0; 0)T
и min
(x) 0
ff
.
229
Замечание 4.11. Одной из модификаций метода Ньютона является
метод Ньютона – Рафсона (Newton – Raphson), в котором точки последова-
тельности {x }
k
,
0,1, 2, ...
k
такие, что
1
(x)(x)
k
k
f
f
,
0,1, 2, ...
k
,
вычисляются по правилу
1
1
x
x
(x) (x)
k
k
k
k
kH
f
,
0,1, 2, ...
k
,
где начальная точка
0
x задается, а величина шага k
определяется из ус-
ловия
1
(x) min
k
k
f
.
4.4 .2. Метод Марквардта
Метод Марквардта (Marquardt D.W.), а также методы Левенберга-
Голдфилда (Levenberg K., Goldfeld S. M.) и Квондта-Тротера (Quandt R. E.,
Trotter H. F.), являются модификациями метода Ньютона. Метод Мар-
квардта представляет собой комбинацию метода наискорейшего спуска и
метода Ньютона и оказывается эффективнее каждого из них в отдельно-
сти.
Пусть дана функция (x)
f , ограниченная снизу на
множестве
n
R и имеющая непрерывные частные
производные во всех его точках.
Требуется найти безусловный локальный минимум функции (x)
fна
множестве допустимых решений
n
XR
, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
,
2
(x)
fC
.
Стратегия метод Маркуардта состоит в
построении последовательности точек
{x}
k
,
0,1, 2, ...
k
таких, что
1
(x)(x)
k
k
f
f
,
0,1, 2, ...
k
Точки по-
следовательности {x }
k
вычисляются по правилу
1
1
x
x
(x)
(x)
k
k
k
k
k
H
E
f
,
0,1, 2, ...
k
где точка
0
x задается пользователем, E – единичная матрица, k
–по-
следовательность
положительных
чисел,
таких,
что
матрица
1
(x)
k
k
H
E
положительно определена. Как правило, число 0
на-
значается как минимум на порядок больше, чем самый большой элемент
матрицы
0
(x)
H
, а в ряде стандартных программ полагается
4
010
[26]. Если
1
x
(x)
(x) (x)
k
k
k
k
k
f
H
E
f
f
,то
1
2
k
k
.В
Стратегия решения задачи
Постановка задачи
230
противном случае
12
k
k
. Легко видеть, что алгоритм Маркуардта в
зависимости от величины k
на каждом шаге по своим свойствам либо
приближается к алгоритму Ньютона, либо – к алгоритму градиентного
спуска.
Построение последовательности {x }
k
заканчивается, когда либо
1
|| (x )||
k
f
, либо число итераций k M
,где1
– малое положитель-
ное число, а M – предельное число итераций.
Вопрос о том, может ли точка x
k
рассматриваться как найденное
приближение искомой точки минимума, решается путем проведения до-
полнительного исследования.
Алгоритм
1. Задать
0
x,10
,00
, M – предельное число итераций. Най-
ти градиент функции
(x)
f
и матрицу Гессе (x)
H.
2. Положить
0
k,
0
k
.
3. Вычислить
(x)
k
f
.
4. Проверить выполнение критерия окончания
1
|| (x )||
k
f
:
а) если неравенство выполнено, то расчет окончен и x
x
k
;
б) если нет, перейти к шагу 5.
5. Проверить выполнение неравенства k M
:
а) если неравенство выполнено, то расчет окончен и x
x
k
;
б) если нет, то перейти к шагу 6.
6. Вычислить матрицу (x )
k
H
.
7. Вычислить матрицу (x )
k
k
H
E
.
8. Вычислить матрицу
1
(x)
k
k
H
E
.
9. Вычислить
1
p
(x)
(x)
k
k
k
k
H
E
f
.
10. Вычислить
1
1
x
x
(x)
(x)
k
k
k
k
k
H
E
f
.
11. Проверить выполнение условия
1
(x)(x)
k
k
f
f
:
а) если неравенство выполняется, то перейти к шагу 12.
б) если нет, перейти к шагу 13.
12. Положить
1
kk
,
1
2
k
k
и перейти к шагу 3.
13. Положить
12
k
k
и перейти к шагу 7.
231
Замечания 4.12
1. В окрестности точки минимума x
метод Маквардта обладает ско-
ростью сходимости, близкой к квадратичной [20].
2. Если достаточное условие минимума (x ) 0
k
H
выполнено, то
точка x
k
может рассматриваться как найденное приближение точки ми-
нимума x
. Проверку выполнения достаточных условий минимума можно
заменить проверкой функции (x)
f на выпуклость.
Пример 4.8
Найти локальный минимум функции
2
2
1
12
2
(x) 2
f
x
xx
x
методом Маквардта. Определить точку x
k
, в которой выполнен хотя бы
один критерий окончания расчетов.
Решение
0
.
1 Зададим
0
x,1
,M:
0
x
(0.5,1)T
;10.1
;
10
M
. Найдем градиент
функции
1
21
2
(x) (4
;
2)T
f
xxx
x
и матрицу Гессе
41
(x)
12
k
H
.
0
.
2 Положим
0
k,020
.
0
.
3 Вычислим
0
(x ) (3; 2.5)T
f
.
0
.
4 Проверим условие
0
1
|| (x )||
f
:
0
|| (x )|| 3.9 0.1
f
. Пере-
ходим к шагу 5.
0
.
5 Проверим условие k M
:
010
k
M
. Переходим к шагу 6.
0
.
6 Вычислим
0
41
(x)
12
H
.
0
.
7 Вычислим
0
0
241
(x)
122
H
E
.
0
.
8 Вычислим
1
0
0
0.0417 0.0019
(x)
0.0019 0.0455
H
E
.
0
.
9 Вычислим
1
0
0
0
0
p
(x)
(x)
H
E
f
( 0.119; 0.108)T
.
0
.
10 Вычислим
1
1
0
0
0
0
x
x
(x)
(x)
H
E
f
232
0.381; 0.892
T
.
0
.
11 Проверим условие
1
0
(x) (x)
f
f
:
1
0
(x) 1.438 2 (x)
f
f
.
0
.
12 Полагаем
1
k,
0
1
10
2
и переходим к шагу 3.
1
.
3 Вычислим
1
(x ) (2.41; 2.16)T
f
.
1
.
4 Проверим условие
1
1
|| (x )||
f
:
1
|| (x )|| 3.18 0.1
f
.
Пе-
реходим к шагу 5.
1
.
5 Проверим условие k M
:
110
k
M
. Переходим к шагу 6.
1
.
6 Вычислим
1
41
(x)
12
H
.
1
.
7 Вычислим
1
1
141
(x)
112
H
E
.
1
.
8 Вычислим
1
1
1
0.072 0.0059
(x)
0.0059 0 .084
H
E
1
.
9 Вычислим
1
1
1
1
1
p
(x)
(x)
H
E
f
( 0.160; 0.168)T
.
1
.
10 Вычислим
1
2
1
1
1
1
x
x
(x)
(x)
H
E
f
0.381; 0.892 (0.160; 0.168) (0.221; 0.724)
T
T
T
.
1
.
11 Проверим условий
2
1
(x) (x)
f
f
:
2
1
(x ) 0.791 1.438 (x )
f
f
.
1
.
12 Полагаем
2
k,
1
2
5
2
ипереходимкшагу3.
2
.
3 Вычислим
2
(x ) (1.60; 1.67)T
f
.
2
.
4 Проверим условие
2
1
|| (x )||
f
:
2
|| (x )|| 2.31 0.1
f
.Пе-
реходим к шагу 5.
2
.
5 Проверим условие k M
:
210
k
M
. Переходим к шагу 6.
2
.
6 Вычислим
2
41
(x)
12
H
.
233
2
.
7 Вычислим
2
2
91
(x)
17
H
E
.
2
.
8 Вычислим
1
2
2
0.113 0.016
(x)
0.016 0.145
H
E
2
.
9 Вычислим
1
2
2
2
2
p
(x)
(x)
H
E
f
:
( 0.155; 0.217)T
.
2
.
10 Вычислим
1
3
2
2
2
2
x
x
(x)
(x)
H
E
f
0.221; 0.724 (0.155; 0.217) (0.07; 0.51)
T
T
T
.
2
.
11 Проверим условий
3
2
(x) (x)
f
f
:
3
2
(x) 0.3 0.791 (x)
f
f
.
2
.
12 Полагаем
3
k,
2
3
2.5
2
и переходим к шагу 3.
3
.
3 Вычислим
3
(x ) (0.79; 1.09)T
f
.
3
.
4 Проверим условие
3
1
|| (x )||
f
:
3
|| (x )|| 1.34 0.1
f
.Пе-
реходим к шагу 5.
3
.
5 Проверим условие k M
:
310
k
M
. Переходим к шагу 6.
3
.
6 Вычислим
3
41
(x)
12
H
.
3
.
7 Вычислим
3
3
6.5 1
(x)
1 4.5
H
E
.
3
.
8 Вычислим
1
3
3
0.159 0.035
(x)
0.035 0 .23
H
E
3
.
9 Вычислим
1
3
3
3
3
p
(x)
(x)
H
E
f
( 0.078; 0.22)T
.
3
.
10 Вычислим
1
4
3
3
3
3
x
x
(x)
(x)
H
E
f
0.07; 0.51 (0.078; 0.22) ( 0.008; 0.29)
T
T
T
.
3
.
11 Проверим условий
4
3
(x) (x)
f
f
:
4
3
(x) 0.082 0.3 (x)
f
f
.
234
3
.
12 Полагаем
4
k,
3
4
1.25
2
и переходим к шагу 3.
4
.
3 Вычислим
4
(x ) (0.26; 0.57)T
f
.
4
.
4 Проверим условие
4
1
|| (x )||
f
:
4
|| (x )|| 0.62 0.1
f
. Пе-
реходим к шагу 5.
4
.
5 Проверим условие k M
:
410
k
M
. Переходим к шагу 6.
4
.
6 Вычислим
4
41
(x)
12
H
.
4
.
7 Вычислим
4
4
5.25 1
(x)
1 3.25
H
E
.
4
.
8 Вычислим
1
4
4
0.2039 0.0623
(x)
0.0623 0.327
H
E
4
.
9 Вычислим
1
4
4
4
4
p
(x)
(x)
H
E
f
( 0.017; 0.17)T
.
4
.
10 Вычислим
1
5
4
4
4
4
x
x
(x)
(x)
H
E
f
0.008; 0.29 (0.017; 0.17) ( 0.025; 0.12)
T
T
T
.
4
.
11 Проверим условий
5
4
(x) (x)
f
f
:
5
4
(x ) 0.012 0.082 (x )
f
f
.
4
.
12 Полагаем
5
k,
4
5
0.625
2
и переходим к шагу 3.
5
.
3 Вычислим
5
(x ) (0.02; 0.22)T
f
.
5
.
4 Проверим условие
5
1
|| (x )||
f
:
5
|| (x )|| 0.22 0.1
f
. Пе-
реходим к шагу 5.
5
.
5 Проверим условие k M
:
510
k
M
. Переходим к шагу 6.
5
.
6 Вычислим
5
41
(x)
12
H
.
5
.
7 Вычислим
5
5
4.622 1
(x)
1 2.622
H
E
.
235
5
.
8 Вычислим
1
5
5
0.236 0.09
(x)
0.09 0.416
H
E
5
.
9 Вычислим
1
5
5
5
5
p
(x)
(x)
H
E
f
(0.015; 0.090)T
.
5
.
10 Вычислим
1
6
5
5
5
5
x
x
(x)
(x)
H
E
f
0.025; 0.12 (0.015; 0.09) ( 0.01; 0.03)
T
T
T
.
5
.
11 Проверим условий
6
5
(x) (x)
f
f
:
6
5
(x ) 0.0006 0.012 (x )
f
f
.
5
.
12 Полагаем
6
k,
5
6
0.312
2
и переходим к шагу 3.
6
.
3 Вычислим
6
(x ) ( 0.01; 0.05)T
f
.
6
.
4 Проверим условие
6
1
|| (x )||
f
:
6
|| (x )|| 0.051 0.1
f
.
Расчет окончен.
Точка
6
x
( 0.01; 0.03)T
является найденным приближением точки
минимума x
, так как функция
2
2
1
12
2
(x) 2
f
x
xx
x
– строго выпуклая.
4.4 .3. Квазиньютоновский метод
Квазиньютоновский метод или метод Дэвидона – Флетчера – Пауэлла
(Davidon W. C., Fletcher R., Powell M. J. D.) , который часто называют
ДФП-метод, не использует вторые производные, но по мере увеличении
числа итераций сходится к методу Ньютона.
Пусть дана функция (x)
f , ограниченная снизу на
множестве
n
R и имеющая непрерывные частные
производные во всех его точках.
Требуется найти безусловный локальный минимум функции (x)
fна
множестве допустимых решений
n
XR
, т.е. найти такую точку
x
n
R
,что
x
(x) min (x)
n
R
f
f
,
2
(x)
fC
.
Постановка задачи
236
Стратегия ДФП-метода состоит в по-
строении последовательности
точек
{x}
k
,
0,1, 2, ...
k
таких,
что
1
(x)(x)
k
k
f
f
,
0,1, 2, ...
k
Точки последовательности {x }
k
вычисля-
ются по правилу
1
x
x
(x)
k
k
k
k
kAf
,
0,1, 2, ...
k
,
(4.20)
где
k
A – матрица размера ( )
nn
, которая вычисляется по правилу
1
k
k
k
A
AB
,
0
AE
,
(4.21)
x(x)
(g) g
x,g
g,g
k
kT
k
kT
kk
k
k
k
kk
k
A
A
B
A
,
(4.22)
где
1
x
x
x
k
k
k
,
1
g
(x)(x)
k
k
k
f
f
.
Точка
0
x задается пользователем, величина шага k
определяется из
условия
()x
(x)
min
(
)k
k
k
k
k
k
f
Af
.
(4.23)
Решение задачи (4.23) может осуществляться как из условий
0
k
d
d
,
2
2
0
k
d
d
или
0
k
dP
d
,
2
2
0
k
dP
d
,где()
k
P – полином, ап-
проксимирующий функцию ( )
k
, так и численно, т.е. путем поиска ре-
шения задачи ( ) min
k
k
методами одномерной минимизации.
Формулы (4.21), (4.22) при аналитическом решении задачи (4.23)
обеспечивают построение последовательности { }
k
A положительно опре-
деленных матриц, таких, что
1
(x)
k
AH
при k . Следствием
этого для квадратичной функции
1
(x)
x,x
b,x
2
f
H
,
0
H ,явля-
ется тот факт, что направления p
k
,
0,1, 2, ...
k
будут H - сопряженными
и, следовательно, алгоритм ДФП-метода сойдется не более чем за n ша-
гов.
Для неквадратичных функций (x)
f алгоритм перестает быть конеч-
ным и его сходимость зависит от точности решения задачи (4.23). Гло-
бальную сходимость алгоритма можно гарантировать лишь при его обнов-
лении через каждые n шагов, т.е. когда в формуле (4.20)
Стратегия решения задачи
237
1
1
,
;
{0, ,2 ,...},
,
.
k
k
k
EkJJ
nn
A
AB
kJ
Построение последовательности {x }
k
заканчивается в точке x
k
, для
которой
1
|| (x )||
k
f
,где1
– заданное число, или при k M
(M–
предельное число итераций), или при двукратном одновременном выпол-
нении двух неравенств
1
2
||x x||
k
k
,
1
2
|(x)(x)|
k
k
f
f
,где2
–
малое положительное число. Вопрос о том, может ли точка x
k
рассматри-
ваться как найденное приближение искомой точки минимума, решается
путем проведения дополнительного исследования.
Алгоритм
1. Задать
0
x,10
,20
, M – предельное число итераций. Най-
ти градиент функции в произвольной точке
(x)
f.
2. Положить
0
k,
0
AE
.
3. Вычислить
(x)
k
f
.
4. Проверить критерий окончания
1
|| (x )||
k
f
:
а) если критерий выполнен, то расчет окончен и x
x
k
;
б) если критерий не выполнен, то перейти к шагу 5.
5. Проверить условие k M
:
а) если неравенство выполнено, то расчет окончен и x
x
k
;
б) если нет, то перейти при
0
k кшагу10,апри 1
k кшагу6.
6. Вычислить
1
(x)(x)
k
k
k
g
f
f
7. Вычислить
1
x
x
x
k
k
k
.
8. Вычислить
x(x)
(g) g
x,g
g,g
k
kT
k
kT
kk
k
k
k
kk
k
A
A
B
A
.
9. Вычислить
1
k
k
k
A
AB
.
10. Определить p
(x)
k
k
k
Af
.
11. Вычислить k
из условия
()x
(x)
min
k
k
k
k
k
k
f
Af
.
12. Вычислить
1
x
x
(x)
k
k
k
k
kAf
.
13. Проверить условия
1
2
||x x||
k
k
,
1
2
|(x)(x)|
k
k
f
f
:
238
а) если оба неравенства выполняются в двух последовательных
итерациях с номерами k и 1
k , то расчет окончен и
1
x
x
k
;
б) в противном случае положить
1
kk
и перейти к шагу 3.
Сходимость
Теорема 4.7. Алгоритм ДФП-метода в применении к квадратичной
функции
1
(x)
x,x
b,x
2
f
H
с положительно определенной мат-
рицей Гессе H обеспечивает отыскание минимума
1
x
b
H
не более
чем за n шагов [29].
Замечания 4.13
1. Если (x)
f дважды непрерывно дифференцируема и (x ) 0
H
,то
ДФП-метод с обновлением сходится к точке локального минимума x
со
сверхлинейной скоростью [29].
2. Если в дополнение к условиям п.1 справедливо || ( x) y || || y ||
H
k
ynR
в окрестности точки x
, то последовательность {x }
k
сходится к
точке x
с квадратичной скоростью [29].
Пример 4.9
Найти локальный минимум функции
2
2
1
12
2
(x) 2
f
x
xx
x
методом ДФП. Определить точку x
k
, в которой выполнен по крайней ме-
ре один из критериев окончания расчетов.
Решение
.
1 Зададим
0
x,1
,2
,M:
0
x
(0.5,1)T
;10.1
;20.15
;
10
M
.
Найдем градиент функции в произвольной точке:
1
21
2
(x) (4
;
2)T
f
xxx
x
.
.
2 Положим
0
k,
0
AE
.
0
.
3 Вычислим
0
(x)
f
:
0
(x ) (3; 2.5)T
f
.
0
.
4 Проверим условие
0
1
|| (x )||<
f
:
0
|| (x )|| 3.9 0.1
f
. Перехо-
дим к шагу 5.
0
.
5 Проверим условие k M
:
010
k
M
, переходим к шагу 10.
0
.
10 Определим
239
0
0
0
0
0
(x)
(x)
(x ) (3; 2.5)T
p
Af
Ef
f
.
0
.
11 Вычислим 0
из условия
0
0
0
0
x
(x)
min
f
f
:
0
0
2
0
0
0
0
x
(x)2(0.53)(0.53)(12.5)
f
f
2
0
0
(12.5)
()
.
Из условия
0
0
d
d
находим 0 0.24
(см. пример 4.5), так как
первая итерация выполняется по методу наискорейшего спуска).
0
.
12 Вычислим
1
0
0
0
x
x
(x ) ( 0.22; 0.4)T
f
.
0
.
13 Проверим условия
1
0
2
||x x||
,
1
0
2
|(x) (x)|
f
f
:
1
0
||x x || 0.94 0.15
,
1
0
| (x) (x)| |0.17 2| 1.83 0.15
f
f
.
Полагаем
1
k , переходим к шагу 3.
1
.
3 Вычислим
1
(x ) ( 0.48; 0.58)T
f
.
1
.
4 Проверим условие
0
1
|| (x )||<
f
:
0
|| (x )|| 0.75 0.1
f
. Пере-
ходим к шагу 5.
1
.
5 Проверим условие k M
:110
k
M
, переходим к шагу 6.
0
.
6 Вычислим
0
1
0
(x) (x) (3.48; 1.92)T
g
f
f
.
0
.
7 Вычислим
0
1
0
x
xx
( 0.72; 0.6)T
.
0
.
8 Вычислим
0
0
0
0
00
0
0
0
0
0
0
x(x)
(g) g
x,g
g,g
T
T
A
A
B
A
0.72
10 3.48
10
( 0.72; 0.6)
( 3.48; 1.92)
0.6
01 1.92
01
3.48
10 3.48
( 0.72; 0.6)
( 3.48; 1.92)
1.92
01 1.92
0.625 0.305
0.305 0.134
.
0
.
9 Вычислим
1
0
0
0.375 0 .305
0.305 0 .866
AAB
.
1
.
10 Определим
1
1
1
p
(x ) (0.356; 0.648)T
Af
.
240
1
.
11 Вычислим 0
из условия
1
1
1
1
x
(x)
min
f
f
. Определяем
2
1
1
1
1
1
1
1
1
1
x
x
(x) x
p ( 0.22 0.356 ;0.4 0.648 )
Af
.
Под-
ставляя полученные выражения
2
1
1
0.22 0.356
x
,
2
2
1
0.4 0.648
x
в функцию (x)
f , получаем
2
2
1
1
1
1
1
( ) 2( 0.22 0.356 ) ( 0.22 0.356 )(0.4 0.648 ) (0.4 0.648 )
.
Применяя необходимое условие безусловного экстремума
1
1
1
1
( ) 4( 0.22 0.356 )0.356 0.356(0.4 0.648 )
d
d
1
1
( 0.22 0.356 ) ( 0.648) 2 0.648 (0.4 0.648 ) 0
или
1
0.8854 0.5467 0
, находим 1 0.6175
. Поскольку
2
1
2
()
k
d
d
0.8854 0
, найденное значение шага обеспечивает минимум функции
1
()
по1
.
1
.
12 Вычислим
2
1
1
1
x
x
(x ) (0.000; 0.000)T
f
.
1
.
13 Проверим условия
1
0
2
||x x||
,
1
0
2
|(x) (x)|
f
f
:
2
1
||x x || 0.45 0.15
,
2
1
| (x) (x)| 0.17 0.15
f
f
.
Полагаем
2
k , переходим к шагу 3.
2
.
3 Вычислим
2
(x)
f
:
2
(x ) (0.000; 0.000)T
f
.
2
.
4 Проверим условие
0
1
|| (x )||<
f
:
0
|| (x)|| 0 0.1
f
.
Расчет
окончен в точке
2
x
(0; 0)T
.
Функция
2
2
1
12
2
(x) 2
f
x
xx
x
является квадратичной формой с
положительно определенной матрицей Гессе. Следовательно точка
2
x
есть найденное приближение точки минимума x
(0; 0)T
.
241
Задачи для самостоятельного решения
1. Сделать 3 итерации методом конфигураций в задаче
2
2
1
2
(x)4(5)(6)min
f
x
x
при
0
x
(1, 2)T
,
0.1
,
1
2 0.5
,
1.5
,
1
.
Ответ: полученные точки
(1.5; 2)T
,
(1.5; 2.5)T
,
1
x (2;3)T
;
(2.5; 3)T
, (2.5; 3.5)T
,
2
x
(3.5; 4.5)T
; (4; 4.5)T
, (4; 5)T
,
3
x
(5.5; 6.5)T
.
Точное решение x
(5; 6)T
,
min 0
f
.
2. Сделать 4 итерации методом деформируемого многогранника в за-
даче
2
2
1
2
(x)4(5)(6)min
f
x
x
при
0.1
,
1
,
2
и
следующих вершинах начального многогранника: (4; 7)T
, (3; 2)T
, (6;7)T
.
Ответ: в результате трех последовательных редукций получены тре-
угольники, заданные своими вершинами. Первый треугольник: (4; 7)T
,
(5;7)T
,
(3.5; 4.5)T ;
второй
треугольник:
(4.5; 7)T
,
(5;7)T
,
(4.25; 5.75)T ; третий треугольник: (4.75; 7)T
, (5;7)T
, (4.625; 6.375)T
.
В результате четвертой итерации (растяжения) получен треугольник:
(4.938; 6.063)T
, (5;7)T
, (4.625; 6.375)T
.
3. Решить задачу методом сопряженных направлений
2
2
1
2
(x)4(5)(6)min
f
x
x
при
0
x
(1; 2)T
,
0.1
.
Ответ: решение получено за две итерации:
0 4.001
,
1
x
(1.000; 6.001)T
; 1 4.000
,
2
x
(5.000; 6.001)T
. Точное решение
x
(5; 6)T
,
min 0
f
.
4. Решить задачу
3
2
1
2
1
2
(x)
322min
fxxxx
методами деформируемого многогранника, конфигураций, сопряженных
направлений, адаптивного случайного поиска. Полученные решения срав-
нить с точным решением.
Ответ: точное решение x
(1;1)T
,
min
1
f
.
5. Решить задачу
2
2
2
2
1
2
1
2
(x) (
11) (
7) min
f
x
x
xx
242
методами деформируемого многогранника, конфигураций, сопряженных
направлений, адаптивного случайного поиска. Полученные решения срав-
нить с точным решением.
Ответ: точное решение x
(3; 2)T
,
min 0
f
.
6. Решить задачу
4
4
22
1
2
12
1
(x)
2
43min
fxxxxx
методами деформируемого многогранника, конфигураций, сопряженных
направлений, адаптивного случайного поиска. Полученные решения срав-
нить с точным решением.
Ответ: точное решение x
(1; 0)T
,
min 0
f
.
7. Решить задачу
2
2
2
1
2
3
(x)(2)(5)(2)min
f
x
x
x
методами деформируемого многогранника, конфигураций, сопряженных
направлений адаптивного случайного поиска. Полученные решения срав-
нить с точным решением.
Ответ: точное решение x
(2; 5; 2)T
,
min 0
f
.
8. Методами наискорейшего градиентного спуска, Гаусса-Зейделя и
сопряженных градиентов из начальных точек
0
x
(0.5; 0)T
и
0
x
( 0.1; 0.5)T
решить задачу:
2
2
2
2
2
1
1
2
(x)(1)
(1)
min
f
x
x
x
x
.
Ответ: точные решения:
(1)
x
(0; 1)T
из точки
0
x
(0.5; 0)T
;
(2)
x
(0; 1)T
из точки
0
x
( 0.1; 0.5)T
.
9. Методами наискорейшего градиентного спуска, Гаусса-Зейделя и
сопряженных градиентов из начальных точек
0
x
(0;3)T
и
0
x
(3; 0)T
решить задачу:
2
2
2
2
1
2
1
2
(x) (
1)(
1) min
f
x
x
xx
.
Ответ: точные решения:
(1)
x
(0;1)T
из точки
0
x
(0;3)T
;
(2)
x
(1; 0)T
из точки
0
x
(3; 0)T
.
10. Методами наискорейшего градиентного спуска, Гаусса-Зейделя и
сопряженных градиентов решить задачу:
3
2
1
12
2
1
2
(x)
234min
fxxxxxx
,
0
x
(0; 0)T
.
Полученное решение сравнить с точным решением.
Ответ: точное решение x
(0.5; 1.25)T
и min
6.4375
f
.
243
11. Методами наискорейшего градиентного спуска, Гаусса-Зейделя и
сопряженных градиентов решить задачу:
22
2
2
1
1
(x) (
)(1)min
f
xx
x
,
0
x
(0; 0)T
.
Полученное решение сравнить с точным решением.
Ответ: точное решение x
(1;1)T
иmin0
f
.
12. Методами наискорейшего градиентного спуска, Гаусса-Зейделя и
сопряженных градиентов из начальной точки
0
x
(0;1)T
решить задачу:
12
1
2
(x)
exp (
) min
f
xx
xx
.
Полученное решение сравнить с точным решением.
Ответ: точное решение x
(1;1)T
и min
0.1353
f
.
13. Аппроксимировать функцию
3
22
1
12
21
(x)
fxxxxx
в точке
0
x
(1;1)T
квадратичной функцией (x)
F.
Ответ:
2
2
1
2
1
2
12
(x)12
2
3
F
xx
x
x
xx
.
14. Является ли удачной начальная точка
0
x
(1; 2; 1; 1)T
для реше-
ния задачи
2
2
2
1
2
3
4
(x) (
)(
) min
f
x
x
xx
методом Ньютона?
Ответ: нет, так как матрица
0
(x)
H
не является положительно опре-
деленной.
15. В задаче
2
2
1
2
(x) 100
min
f
x
x
,
0
x
(0; 10)T
определить
координаты точки
1
x с помощью метода Ньютона.
Ответ:
1
x
(0; 0)T
.
16. В задаче
2
2
2
1
1
(x) 100(
)(1) min
f
xx
x
сделать 9 итера-
ций из точки
0
x
(2; 3)T
методом Ньютона.
Ответ: полученные точки:
1
x (1.996; 3.982)T
,
2
x
( 2.752; 14.969)T
,
3
x
( 2.751; 7.565)T
,
4
x
( 0.941; 2.385)T
,
5
x
( 0.938; 0.880)T
,
6
x
(0.472; 1.763)T
,
7
x
(0.473; 0.224)T
,
8
x
(1.123; 0.84)T
,
9
x
(1.122; 1.259)T
.
Точное
решение x
(1; 1)T
.
17. Решается задача
2
2
1
2
1
(x)
max
(1)
f
x
x
.
244
Указать, из какой точки решение задачи методом Ньютона потребует не
более одной итерации.
Ответ: из любой начальной точки, если решать эту задачу как задачу
поиска минимума функции
2
2
1
2
1
(1)
(x)
x
x
f
.
18. После десяти итераций по методу Макварда при решении задачи
22
2
1
2
1
(x)()(1)min
f
xx
x
программа остановилась в точке
x (1; 1)T
. Пояснить причину остановки.
Ответ: x (1;1)T
–
точка минимума.
19. Решить задачу
2
2
1
2
(x)4(5)(6)min
f
x
x
методом Ма-
кварда из точки
0
x
(8;9)T
;020
,10.1
,
2 0.1
.
Ответ: полученные точки:
1
x (7.143; 8.727)T
,
2
x
(6.190; 8.273)T
,
3
x
(5.458; 7.623)T
,
4
x
(5.109; 6.902)T
,
5
x
(5.015; 6.347)T
,
6
x
(5.001; 6.083)T
,
7
x
(5.000; 6.011)T
.
Расчет закончен по градиенту, так как
7
|| (x ) || 0.0223 0.1
f
.
20. Решить задачу
2
2
1
2
(x)4(5)(6)min
f
x
x
методом
ДФП (квазиньютоновским методом) из точки
0
x
(8;9)T
;10.1
,
2 0.1
. На каждой итерации величину шага определять методом равно-
мерного поиска (методом перебора) на интервале [0; 1] с параметром
999
N
. Повторить задание с
99
N
и сравнить результаты.
Ответ: при
999
N
полученные значения шага и точки:
0 0.131
,
1
x (4.856; 8.214)T
; 1 0.494
,
2
x
x
(4.997; 6.000)T
.
Расчет закончен по градиенту, так как
2
|| (x ) || 0.0229 0.1
f
.
21. Методом ДФП (квазиньютоновским методом) из начальных точек
0
x
(0;3)T
и
0
x
(3; 0)T
решить задачу:
2
2
2
2
1
2
1
2
(x) (
1)(
1) min
f
x
x
xx
.
Ответ: точные решения:
(1)
x
(0;1)T
из точки
0
x
(0;3)T
;
(2)
x
(1; 0)T
из точки
0
x
(3; 0)T
.
245
Глава 5
ЧИСЛЕННЫЕ МЕТОДЫ УСЛОВНОЙ
МНОГОМЕРНОЙ ОПТИМИЗАЦИИ
5.1. Принципы построения численных методов
поиска условного экстремума
Рассмотрим общую постановку задачи поиска условного экстремума
со смешанными ограничениями.
Даны дважды непрерывно дифференцируемые целевая функция
12
(x) (
, ...,
)n
ffxxx
и функции ограничений (x) 0
i
g,
1,..,
i
p
;
(x) 0
i
g,
1,..,
ip
m
, определяющие множество допустимых решений
n
XR
.
Требуется найти локальный минимум целевой функции на множестве
X,т.е.такуюточкуx X
что
x
(x) min (x)
X
f
f
,
(5.1)
(x) 0, 1,.., ;
x
(x) 0,
1, ..,
i
i
g
i
ppn
X
g
ip
m
.
Применение необходимых и достаточных условий условного экстре-
мума, изложенных в гл.1, эффективно для решения ограниченного числа
примеров, в которых вытекающие из этих условий соотношения имеют
аналитическое решение. Для решения большинства практических задач
используются численные методы, которые делятся на две группы:
1. Методы, использующие преобразование задачи условной оптими-
зации в последовательность задач безусловной оптимизации путем введе-
ния в рассмотрение вспомогательных функций: методы последовательной
безусловной минимизации.
2. Методы непосредственного решения задачи условной оптимиза-
ции, основанные на движении из одной допустимой точки, где выполнены
все ограничения, к другой допустимой точке с лучшим значением целевой
246
функции. Эти методы часто называются методами возможных направле-
ний.
Основная идея методов первой группы состоит в том, чтобы аппрок-
симировать исходную задачу условной оптимизации некоторой вспомога-
тельной задачей, решение которой менее сложно, чем решение исходной.
Естественно, что ограничившись одной вспомогательной задачей, можно
получить, вообще говоря, лишь приближенное решение. Если же исполь-
зовать последовательность задач, в определенном смысле "сходящихся" к
исходной, то искомое точное решение в большинстве случаев окажется
пределом соответствующей последовательности приближенных решений.
Идея преобразования задачи с ограничениями в надлежащим образом по-
строенную последовательность задач без ограничений представляется за-
манчивой главным образом в связи с наличием эффективных и надежных
методов безусловной минимизации, рассмотренных в главах 3 и 4.
На первый взгляд кажется странным, что предлагается решать беско-
нечную последовательность задач оптимизации, а не всего одну задачу.
Дело в том, что на практике для получения решения исходной задачи с
требуемой точностью достаточно бывает решить конечное (относительно
небольшое) число вспомогательных задач. При этом нет необходимости
решать их точно, а информацию, полученную в результате решения оче-
редной вспомогательной задачи, обычно удается эффективно использовать
для решения следующей.
В рамках единой методологии можно выделить несколько подходов к
решению задачи.
Первый – называется методом штрафов (внешних штрафов). В этом
методе к целевой функции добавляется функция, интерпретируемая как
штраф за нарушение каждого из ограничений. Метод генерирует последо-
вательность точек, которая сходится к решению исходной задачи.
Второй подход называется методом барьеров (внутренних штра-
фов). Здесь к целевой функции исходной задачи добавляется слагаемое,
которое не позволяет генерируемым точкам выходить за пределы допус-
тимой области.
Третий подход связан с добавлением штрафной функции не к целевой
функции, а к ее функции Лагранжа. В результате возникает модифициро-
ванная функция Лагранжа, а методы, использующие эту функцию, назы-
ваются методами множителей.
Четвертый подход базируется на введении так называемых точных
штрафных функций, позволяющих ограничиться решением лишь одной
задачи безусловной минимизации. Систематизированное описание моди-
фикаций метода точных штрафных функций имеется в монографии [8].
Методы непосредственного решения задачи условной оптимизации,
образующие вторую группу, связаны с нахождением предела x
последо-
247
вательности {x }
k
допустимых точек при k , таких, что
1
(x)(x)
k
k
f
f
,
0,1, ...
k
.
Последовательность {x }
k
строится по правилу
1
x
x
x
k
k
k
,
0,1, ...
k
,
где вектор x
k
определяется в зависимости от применяемого метода.
К описанной группе методов относятся метод проекции градиента и
метод возможных направлений Зойтендейка.
В методе Зойтендейка на каждой итерации строится возможное на-
правление спуска и затем проводится оптимизация вдоль этого направле-
ния.
Определение 5.1 . Ненулевой вектор d называется возможным на-
правлением в точке x X
, если существует такое
0
,чтоxtdX
для всех
(0; )
t
.
Определение 5.2. Вектор d называется возможным направлением
спуска в точке x X
, если существует такое
0
,что(x)(x)
ftdf
иxtdX
длявсех
(0; )
t
.
Рассмотрим частный случай задачи поиска условного минимума:
x
(x) min (x)
X
f
f
,
xx
,
x
X
AbCe
,
(5.2)
где A – матрица размера (
)
mn
,C –матрицаразмера( )
ln
,b –век-
тор( 1)
m ,e –вектор( 1)
l.
Теорема 5.1 (о возможном направлении спуска в случае линейных
ограничений). Пусть x – допустимая точка в задаче (5.2) и предполо-
жим, что 1
1
x
Ab
,
2
2
x
Ab
,где
1
2
A
A
A
,
1
2
b
b
b
. Тогда ненулевой
вектор d является возможным направлением в точке x в том и только
в том случае, если 1
0
Ad ,
0
Cd
. Если, кроме того,
(x)
0
T
fd
,то
d является возможным направлением спуска [5].
Пример 5.1
В следующей задаче
2
2
1
2
(x)(6)(2)min
f
x
x
;
1
2
24
x
x
,
248
1
2
3212
x
x
,
10
x
,
20
x
указать множество возможных направлений спуска в точке
(2;3)T
B
.
Решение
Первые два ограничения являются активными в точке
(2;3)T
B
.
Поэтому матрица 1
12
32
A
.
Следовательно, вектор d является воз-
можным направлением тогда и только тогда, когда 1
0
Ad т.е. если
1
2
20
dd
,
1
2
320
dd
.
На рис. 5.1 изображены совокупности возможных направлений: –
конус возможных направлений; – полупространство направлений спус-
ка; – конус возможных направлений спуска. Отметим, что если сдви-
нуться на небольшое расстояние от точки x вдоль любого вектора d ,
удовлетворяющего двум приведенным выше неравенствам, то точка оста-
ется в допустимой области. Если вектор d удовлетворяет в точке B нера-
венству
1
2
(x)
820
T
fddd
, то он является направлением спуска.
()
fB
(x) 17
f
1
2
3212
x
x
(6; 2)
B
Рис. 5.1
4
2
0
6
6
4
4
2
2
1x
2
x
(x) 4
f
1
2
24
x
x
249
Таким образом, совокупность направлений спуска определяется открытым
полупространством
12
1
2
{(,)|82 0}
dd
dd
Пересечение конуса воз-
можных направлений с этим полупространством задает множество
всех возможных направлений спуска .
Замечание 5.1. Естественный подход к построению возможного на-
правления спуска, как следует из теоремы 5.1, заключается в минимизации
(x)
T
fd
при условии 1
0
Ad ,
0
Cd
. Однако, если существует вектор
d
, такой, что
(x)
0
T
fd
,1
0
Ad
,
0
Cd
, то минимальное зна-
чение целевой функции в сформулированной задаче равно , так как
любой вектор d
, где – сколь угодно большое число, удовлетворяет
всем ограничениям.
Таким образом, в задачу должно быть включено условие, которое ог-
раничивало бы вектор d . Поэтому для нахождения возможного направ-
ления спуска требуется решить задачу
(x)
min
T
fd
,
1
0
Ad ,
0
Cd ,
(5.3)
||1
jd,
1,..,
jn
.
Рассмотрим задачу условной минимизации при ограничениях типа
неравенств
x
(x) min (x)
X
f
f
,
x
(x) 0, 1,...,
i
X
g
i
m
.
Теорема 5.2 (о возможном направлении спуска в случае нелинейных
ограничений). Пусть x – допустимая точка, a
a
I - множество индексов
активных в этой точке ограничений, т. е .
{| (x) 0}
a
i
Iig
.
Предпо-
ложим, что функции (x)
f,(x)
i
g,
a
iI
дифференцируемы в x , а функ-
ции (x)
i
g,
a
iI
непрерывны в этой точке. Если
(x)
0
T
fd
и
(x)
0
T
i
g
d
при
a
iI
, то вектор d является возможным направле-
нием спуска [5] .
На рис. 5.2 показана совокупность возможных направлений спуска в
точке x . Вектор d , удовлетворяющий равенству
(x)
0
T
i
g
d
, является
касательным к множеству {x | (x) 0}
i
g
. Так как функции (x)
i
g
нели-
нейны, движение вдоль такого вектора может привести в недопустимую
250
точку, что вынуждает требовать выполнения строгого неравенства
(x)
0
T
i
g
d
. На рис. 5.2 используются следующие условные обозначе-
ния: 1 – первое ограничение; 2 – второе ограничение; 3 – третье ограниче-
ние; 4 – четвертое ограничение; 5 – возможные направления спуска; 6 –
линии уровня функции.
Замечания 5.2
1. Чтобы найти вектор d , удовлетворяющий условиям теоремы 5.2,
естественно минимизировать максимум из
(x)
T
fd
и
(x)
T
i
g
d
для
a
iI
. Обозначим его через z . Кроме того, как и в случае линейных огра-
ничений, введем ограничения на вектор d (см. замечание 5.1). Поэтому
для нахождения возможного направления спуска требуется решить задачу
min
z
,
(x)
0
T
fdz
,
(x)
0
T
i
g
dz
,
a
iI
,
||1
jd,
1,..,
jn
.
Частным случаем задачи поиска условного экстремума является зада-
ча линейного программирования, в которой целевая функция и ограниче-
ния линейны по x . Эта особенность задачи отражается в специфике при-
меняемых для ее решения методов, рассмотренных в гл. 2. Область допус-
тимых решений представляет собой выпуклый многогранник, имеющий
конечное число вершин. Процедура поиска решения заключается в пере-
ходе от одной вершины к другой, так чтобы значение функции улучша-
3(x)
g
2
4 (x)
g
4
(x) const
f
X
5
1
3
Рис. 5.2
1x
2
x
(x)
f
6
251
лось. Процедура поиска завершается в случае, когда из текущей вершины
будет невозможен переход, связанный с улучшением функции.
2. Если текущая точка близка к границе, определяемой одним из ог-
раничений, и если это ограничение не используется в процессе нахожде-
ния направления поиска, то может случиться так, что удастся сделать
только маленький шаг и точка окажется на границе, определяемой этим
ограничением. Поэтому в качестве множества a
I активных ограничений
следует брать совокупность индексов почти активных ограничений, т.е.
,
{|
(x) 0}
a
i
I
i
g
,где
0
– достаточно малое число. При этом
решение задачи поиска возможного направления спуска даст вектор, кото-
рый обеспечивает сравнительно большие возможности для движения в
рамках допустимой области.
5.2 . Метод штрафных функций
Даны дважды непрерывно дифференцируемые
целевая функция
12
(x) (
, ...,
)n
ffxxx
и функ-
ции ограничений (x) 0
i
g,1,..,
i
p
;(x)0
i
g,
1,..,
ip
m
опреде-
ляющие множество допустимых решений X .
Требуется найти локальный минимум функции (x)
f на множестве
X , т.е. найти такую точку x
n
XR
, что
x
(x) min (x)
X
f
f
,
(x) 0, 1,.., ;
x
(x) 0,
1, ..,
i
i
g
i
ppn
X
g
ip
m
.
Идея метода заключается в сведении
задачи на условный минимум к решению
последовательности задач поиска безус-
ловного минимума вспомогательной функции:
x
(x, )
(x) (x, ) min
n
k
k
R
Fr
fPr
,
где (x, )
k
P r – штрафная функция,
k
r – параметр штрафа, задаваемый на
каждой k -й итерации. Это связано с возможностью применения эффек-
тивных и надежных методов поиска безусловного экстремума, изложен-
ных в главах 3 и 4. Штрафные функции конструируются, исходя из усло-
вий:
Постановка задачи
Стратегия решения задачи
252
при выполнении ограничений
при невыполнении ограничений,
0,
,
(x, )
0,
k
Pr
причем при невыполнении ограничений и
k
r , k справедливо
(x, )
k
P r .Чембольше
k
r , тем больше штраф за невыполнение огра-
ничений. Как правило, для ограничений типа равенств используется квад-
ратичный штраф (рис. 5.3,а), а для ограничений типа неравенств – квадрат
срезки (рис. 5.3,б):
2
2
1
1
(x, )
(x)
(x)
2
p
k
m
k
i
i
i
ip
r
Pr
g
g
,
где (x)
i
g
–
срезка функции:
если
если
(x) ,
(x) 0,
(x) max 0, (x)
0,
(x) 0.
i
i
i
i
i
g
g
g
g
g
Начальная точка поиска задается обычно вне множества допустимых
решений X . На каждой k -й итерации ищется точка x ( )
k
r
минимума
вспомогательной функции (x , )
k
Fr
при заданном параметре
k
r с помо-
щью одного из методов безусловной минимизации. Полученная точка
x()
k
r
используется в качестве начальной на следующей итерации, вы-
полняемой при возрастающем значении параметра штрафа. При неограни-
ченном возрастании
k
r последовательность x ( )
k
r
стремится к точке
условного минимума x
.
(x)
g
0
r
Рис. 5.3
1
r
1
0
r
r
0
r
1
r
(x, )
k
Pr
1
r
0
r
(x)
g
(x, )
k
Pr
1
0
r
r
a
б
253
Алгоритм
1. Задать начальную точку
0
x ; начальное значение параметра штрафа
0
0
r;число
0
C для увеличения параметра штрафа; малое число
0
для остановки алгоритма. Положить
0
k
.
2. Составить вспомогательную функцию
2
2
1
1
(x,)
(x)
(x)
(x)
2
p
k
m
kk
k
k
k
i
i
i
ip
r
Fr
f
g
g
.
3.Найтиточку x( )
k
r
безусловного минимума функции (x , )
k
Frпо
x с помощью какого-либо метода (нулевого, первого или второго поряд-
ка):
x
x( ),
min (x, )
n
kk
k
R
Frr
Fr
.
При этом задать все требуемые выбранным методом параметры. В качест-
ве начальной точки взять x
k
. Вычислить
x( ),
kk
Prr
.
4. Проверить условие окончания:
а) если
x( ),
kk
Prr
, процесс поиска закончить:
x
x()
k
r
,
(x)
x()
()k
f
fr
;
б) если
x( ),
kk
Prr
, положить
1
k
k
r
Cr
,
1
x
x()
k
k
r
,
1
kk
и перейти к шагу 2.
Сходимость
Теорема 5.3. Пусть x
–
локально единственное решение задачи по-
иска условного минимума, а функции (x)
fи(x)
i
g
непрерывно диффе-
ренцируемы в окрестности x
. Тогда для достаточно больших
k
r най-
дется точка x ( )
k
r
локального минимума функции (x , )
k
F r в окрестно-
сти x
иx( )
x
k
r
при
k
r [25].
Замечания 5.3
1. Так как сходимость метода обеспечивается при
k
r ,товозни-
кает вопрос о том, нельзя ли получить решение исходной задачи в резуль-
тате однократного поиска безусловного минимума вспомогательной функ-
ции с параметром
k
r , равным большому числу, например
20
10 . Однако
такая замена последовательного решения вспомогательных задач не пред-
ставляется возможной, так как с ростом
k
r функция (x, )
k
Fr
приобрета-
254
ет ярко выраженную овражную структуру. Поэтому скорость сходимости
любого метода безусловной минимизации к решению x ( )
k
r
резко пада-
ет, так что процесс его определения заканчивается, как правило, значи-
тельно раньше, чем будет достигнута заданная точность, и, следовательно,
полученный результат не дает возможности судить об искомом решении
x
.
2.Точки x ( )
k
r
в алгоритме – это точки локального минимума функ-
ции (x, )
k
F r . Однако функция (x, )
k
Fr
может быть неограниченной
снизу и процедуры методов безусловной минимизации могут расходиться.
Это обстоятельство необходимо учитывать при программной реализации.
3. В методах штрафных функций имеется тесная связь между значе-
ниями параметров штрафа и множителями Лагранжа для регулярной точки
минимума (см. разд.1.5):
()
x()
k
k
k
i
i
r
rg
r
,
1,...
i
m
;
()
x()
k
k
k
i
i
r
rg
r
,
a
iI
;
lim()
k
k
i
i
r
r
,
1,...
i
m
;
a
iI
.
4. Обычно выбирается
0
0.01; 0.1; 1
r
,а
[4; 10]
C
. Иногда начи-
нают с
0
0
r , т.е. с задачи поиска безусловного минимума.
5. При решении задач процедура расчетов завершается при некотором
конечном значении параметра штрафа
k
r . При этом приближенное реше-
ние, как правило, не лежит в множестве допустимых решений, т.е. ограни-
чения задачи не выполняются. Это является одним из недостатков метода.
С ростом параметра штрафа
k
r генерируемые алгоритмом точки прибли-
жаются к решению исходной задачи извне множества допустимых реше-
ний. Поэтому обсуждаемый метод иногда называют методом внешних
штрафов.
6. На практике для получения решения исходной задачи с требуемой
точностью достаточно бывает решить конечное (относительно небольшое)
число вспомогательных задач. При этом нет необходимости решать их
точно, а информацию, полученную в результате решения очередной вспо-
могательной задачи, обычно удается эффективно использовать для реше-
ния следующей.
Пример 5.2.
Найти минимум в задаче
2
2
1
2
(x)
min
fxx
,
1
1
2
(x)
20
g
xx
.
255
Решение
.
1 В поставленной задаче одно ограничение-равенство, ограничения-
неравенства отсутствуют. Решим задачу аналитически.
.
2 Составим вспомогательную функцию:
2
2
2
1
2
1
2
(x, )
(
2)
2
k
k
r
Fr
x
x
xx
.
0
.
3 Найдем безусловный минимум (x , )
k
Fr
по x с помощью необ-
ходимых и достаточных условий:
1
1
2
1
(x, )
2
(
2)0
k
k
Fr
xrxx
x
,
2
1
2
2
(x, )
2
(
2)0
k
k
Fr
xrxx
x
.
Вычитая из первого уравнения второе, получаем
1
2
xx
и
1
2
()()
1
k
k
k
k
r
xr
xr
r
. В табл. 5.1 приведены результаты расчетов при
1, 2, 10, 100, 1000,
k
r
, а на рис. 5.4 дана графическая иллюстрация
решения.
Таблица 5.1
k
k
r
1
2
()()
k
k
xr
xr
x( ),
(
)
k
k
Frr
1()
k
r
0
1
0.5
1
–1
1
2
0.667
1.333
1.333
210
0.909
1.81
1.818
3 100
0.990
1.98
1.980
4 1000
0.999
1.998
1.998
5
1
2
2
Так как матрица Гессе
2
x( ),
0
2
(
)=
k
k
kk
k
k
r
r
Hrr
r
r
при
0
k
r,
то достаточные условия минимума (x , )
k
F r удовлетворяются. При
k
r имеем
1
2
lim
1
1
k
k
k
r
r
x
x
r
;(x)2
f
. Одновременно нахо-
дится множитель Лагранжа:
256
1
1
1
2
2
lim()lim
()()2
lim
2
1
k
k
k
k
k
k
k
k
k
r
r
r
r
r
rxr
xr
r
.
Пример 5.3
Найти минимум в задаче
2
2
1
2
(x)
min
fxx
,
1
1
(x)
10
g
x
,
2
1
2
(x)
20
g
xx
.
Решение
1. В поставленной задаче два ограничения-неравенства, ограничения-
равенства отсутствуют. Решим задачу аналитически.
2. Составим вспомогательную функцию:
2
2
2
2
1
2
1
1
2
max
max
(x, )
{ [0;(1 )]} { [0;(
2)]}
2
k
k
r
Fr
x
x
x
xx
.
3. Найдем безусловный минимум (x , )
k
F r при фиксированном
k
r:
1
1
1
2
1
1
1
1
2
1
1
1
2
1
1
2
1
1
1
2
1
1
2
2,(1)0,(
2) 0,
2
(1),(1)0,(
2) 0,
(x, )
0
2
(
2),(1)0,(
2) 0,
2
(1)(
2),(1)0,(
2) 0;
k
k
k
k
k
x
x
xx
xrx
x
xx
Fr
x
xrxx
x
xx
xrx
rxx
x
xx
2
1
2
2
2
1
2
1
2
2,(
2) 0,
(x, )
0
2
(
2), (
2) 0.
k
k
x
xx
Fr
x
xrxx
xx
1
2
x
Рис. 5 .4
2
x (1)
1x
0
2
1
12
(x)
20
g
xx
x
(1;1)
1
x (2)
x (10)
257
Рассмотрим четыре случая:
1)
1
(1)0
x
,
1
2
(
2)0
xx
. Имеем 1
20
x
x
, но при этом
не удовлетворяется первое неравенство 1 (x) 0
g;
2)
1
(1)0
x
,1
2
(
2)0
xx
. Имеем
1
12
2
12
2
(
2) 0,
2
(
2) 0.
k
k
xrxx
xrxx
Отсюда 1
2
xx
и1
2
()()
1
k
k
k
k
r
xr
xr
r
. Однако
1
1
1()
0
1
k
k
xr
r
при
0
k
r , что противоречит первому неравенству;
3)
1
(1)0
x
,1
2
(
2)0
xx
. Имеем
1
1
2
2
(1)0,
20.
k
xrx
x
Отсюда 2 0
x
,
1()
2
k
k
k
r
xr
r
. Таккак
1
2
0
(),
0
02
k
kk
r
Hxrr
,
то достаточные условия локального минимума выполняются (табл. 1.1,
строка 1). Численные результаты приведены в табл. 5.2 и отражены на рис.
5.5;
4)1
(1)0
x
,1
2
(
2)0
xx
. Имеем
1
1
1
2
2
1
2
2
(1)(
2) 0,
2
(
2) 0.
k
k
k
xrx
rx
x
x
rx
x
Отсюда
2
1
2
()6
()
()64
k
k
k
k
k
r
r
xr
r
r
,
2
2
2
()4
()
()64
k
k
k
k
k
r
r
xr
r
r
.
x (10)
1
1
0
x
2
x
Рис. 5.5
2
x (1)
1x
0
2
1
220
xx
x
(1; 0)
1
x (2)
X
(x) 1
f
258
Однако 1
2
2
28
()()2
0
()64
k
k
k
k
k
r
xr
xr
r
r
при всех
0
k
r,т.е.
второе неравенство не выполняется.
В результате получаем решение задачи
1
lim
1
2
k
k
k
r
r
x
r
;20
x
;(x)1
f
.
Таблица 5.2
k
k
r
1()
k
xr
2()
k
xr
x( ),
(
)
kk
Frr
1()
k
r
2()
k
r
010.3330
0.556
0.6667
0
12
0.5
0
0.750
1
0
2100.8330
0.972
1.6667
0
3 100 0.980 0
0.9996
0.9608
0
4 1000 0.998 0
0.9999
1.9960
0
5
1
0
1
–2
0
Пример 5.4
Найти минимум в задаче
2
2
1
2
(x)
min
fxx
,
1
1
(x)
10
g
x
,
2
1
2
(x)
20
g
xx
.
Решение
1. В задаче одно ограничение-равенство и одно ограничение–
неравенства. Решим задачу аналитически.
2. Составим вспомогательную функцию:
2
2
2
2
1
2
1
1
2
max
(x, )
[( 1)] { [0;(
2)]}
2
k
k
r
Fr
x
x
x
xx
.
3. Найдем безусловный минимум (x , )
k
Fr
по x с помощью необхо-
димых и достаточных условий:
1
1
12
1
2
1
1
1
12
2
(1)(
2), (
2) 0,
(x, )
0
2
(1),(
2) 0,
k
k
k
k
xrx
rxx
xx
Fr
x
xrx
xx
2
1
2
1
2
2
2
1
2
2
(
2), (
2) 0,
(x, )
0
2,(
2) 0.
k
k
xrxx
xx
Fr
x
x
xx
259
Рассмотрим два случая:
1) Пусть 1
2
(
2)0
xx
. Вычитая из первого уравнения второе, по-
лучаем: 2
1
1
(1)
2
k
r
x
x
x
. После подстановки в первое уравнение имеем
2
1
2
()6
()
()64
k
k
k
k
k
r
r
xr
r
r
,
2
2
2
()4
()
()64
k
k
k
k
k
r
r
xr
r
r
.
Однако при всех
0
k
rимеем1
2
2
28
()()2
0
()64
k
k
k
k
k
r
xr
xr
r
r
,
что противоречит условию 1
2
(
2)0
xx
для рассматриваемого случая.
2) Пусть 1
2
(
2)0
xx
.Тогда20
x
,а1()
2
k
k
k
r
xr
r
.
В табл.
5.2 приведены результаты расчетов, а на рис. 5.6 дана графическая иллю-
страция.
Так как матрица Гессе
1
2
0
(),
0
02
k
k
k
r
Hxr
r
при всех
0
k
r , то достаточные условия минимума (x , )
k
F r удовлетворяются
(табл. 1.1, строка 1). При
k
rимеем 1( )lim
1
2
k
k
k
k
r
r
xr
r
,
20
x
,
(x) 1
f
.
Одновременно находятся множители Лагранжа:
x (10)
1
1
(x) 1
0
g
x
2
x
Рис. 5.6
2
x (1)
1x
0
2
1
220
xx
x
(1; 0)
1
x (2)
X
(x) 1
f
260
1
1
1
2
lim()lim [()1] lim
2
2
k
k
k
k
k
k
k
k
r
r
r
r
r
rxr
r
;
2
2
1
2
lim()lim
max{0,[()()2]}
k
k
k
k
k
k
r
r
r
r
xr
xr
lim max 0,
20
2
k
k
k
k
r
r
r
r
.
5.3 Метод барьерных функций
Даны дважды непрерывно дифференцируемые
целевая функция
12
(x) (
, ...,
)n
ffxxx
и функ-
ции ограничений-неравенств
(x) 0
i
g,1,..,
i
m
определяющие множе-
ство допустимых решений X .
Требуется найти локальный минимум функции (x)
f на множестве
X , т.е. найти такую точку x
n
XR
, что
x
(x) min (x)
X
f
f
,
x
(x) 0, 1, ..,
i
X
g
i
m
.
Идея метода заключается в сведении
задачи на условный минимум к решению
последовательности задач поиска безусловного минимума вспомогатель-
ной функции:
x
(x, )
(x) (x, ) min
n
k
k
R
Fr
fPr
,
где (x, )
k
P r – штрафная функция,
0
k
r – параметр штрафа.
Как правило, используются:
а) обратная штрафная функция
1
1
(x, )
(x)
m
k
k
i
i
Pr
r
g
(рис. 5.7,а);
б) логарифмическая штрафная функция
1
(x, )
ln (x)
m
k
k
i
i
Pr
r
g
(рис. 5.7,б).
Обратная штрафная функция была предложена Кэрролом (Carrol
С.W.), а логарифмическая Фришем (Frisch К.R.) .
Постановка задачи
Стратегия решения задачи
261
Обе штрафные функции определены и непрерывны внутри множества
X , т.е. на множестве
x
(x) 0, 1, ..,
i
X
g
i
m
, и стремятся к бес-
конечности при приближении к границе множества изнутри. Поэтому они
называются барьерными функциями. При
0
k
r штрафная функция, зада-
ваемая обратной функцией, положительна. Логарифмическая штрафная
функция положительна при 1 (x) 0
i
g
и отрицательна при
(x) 1
i
g , т.е. внутренним точкам области отдается предпочтение перед
граничными точками.
Начальная точка задается только внутри множества X . На каждой
k – й итерации ищется точка x ( )
k
r
минимума вспомогательной функ-
ции (x, )
k
Fr
при заданном параметре
k
r с помощью одного из методов
безусловной минимизации. Полученная точка x ( )
k
r
используется в ка-
честве начальной на следующей итерации, выполняемой при уменьшаю-
щемся значении параметра штрафа. При
0
k
r последовательность
точекx( )
k
r
стремится к точке условного минимума x
.
Барьерные
функции как бы препятствуют выходу из множества X , а если решение
задачи лежит на границе, то процедура метода приводит к движению из-
нутри области к границе.
Заметим, что согласно описанной процедуре точки x ( )
k
r
лежат
внутри множества допустимых решений для каждого
k
r . Этим объясняет-
ся то, что метод барьерных функций иногда называется методом внутрен-
них штрафов.
Рис. 5.7
()
gx
0
r
1
0
r
r
1
r
(,)
k
Pxr
а
0
r
1
r
1
0
r
r
1
(,)
k
Pxr
()
gx
б
262
Алгоритм
1. Задать начальную точку
0
x внутри области X ; начальное значе-
ние параметра штрафа
0
0
r ;число
1
C для уменьшения параметра
штрафа; малое число
0
для остановки алгоритма. Положить
0
k
.
2. Составить вспомогательную функцию:
1
1
(x, )
(x)
(x)
m
k
k
i
i
Fr
fr
g
или
1
(x, )
(x)
ln (x)
m
k
k
i
i
Fr
fr
g
.
3.Найтиточку x( )
k
r
минимума функции (x , )
k
Fr
поxспомо-
щью какого-либо метода (нулевого, первого или второго порядка) поиска
безусловного минимума с проверкой принадлежности текущей точки внут-
ренности множества X . При этом задать все требуемые выбранным мето-
дом параметры. В качестве начальной точки взять x
k
. Вычислить:
1
1
x( ),
x()
()
m
kk
k
k
i
i
Prr
r
g
r
или
1
x( ),
ln
x()
()
m
kk
k
k
i
i
Prr
r
g
r
.
4. Проверить выполнение условия окончания:
а) если
x( ),
kk
Prr
, процесс поиска закончить:
x
x()
k
r
,
(x)
x()
()k
f
fr
;
б) если
x( ),
kk
Prr
, положить
1
k
k
r
r
C
;
1
x
x()
k
k
r
,
1
kk
и перейти к шагу 2.
Сходимость
Теорема 5.4. Пусть функции (x)
fи(x)
i
g , 1,..,
i
m
выпуклы и
конечны, множество X
решений задачи поиска условного минимума не
пусто и ограничено, существует точка
0
x
X
такая, что
0
(x) 0
i
g
,
1,..,
i
m
. Тогда в методе барьерных функций
x
Arg min (x, )
k
k
X
Fr
,
функции (x , )
k
Fr
выпуклы, последовательность
0
x()
k
k
r
, порожден-
ная алгоритмом, ограничена и все ее предельные точки принадлежат
X
, причем
x()
(x)
()k
frf
,x
X
[25].
263
Замечания 5.4
1. Обычно выбирается
0
1, 10, 100
r
,а
10, 12, 16
C
.
2. При
0
k
r обеспечивается сходимость, однако с уменьшением
k
r функция (x, )
k
F r становится все более овражной. Поэтому полагать
k
r малым числом сразу нецелесообразно.
3. Так как большинство методов поиска безусловного экстремума ис-
пользует дискретные шаги, то вблизи границы шаг может привести в точ-
ку вне допустимой области. Если в алгоритме отсутствует проверка на
принадлежность точки множеству
x
(x) 0, 1, ..,
i
X
g
i
m
,тоэто
может привести к ложному успеху, т.е. уменьшению вспомогательной
функции в точке, где она теоретически не определена. Поэтому на шаге 3
алгоритма требуется явная проверка того, что точка не покинула допусти-
мую область. Процедура поиска обычно завершается при некотором малом
k
r , отличном от нуля. Однако приближенное решение принадлежит мно-
жеству допустимых решений. Это одно из преимуществ метода барьерных
функций.
4. Побочным продуктом вычислений в методе штрафных функций
является вектор множителей Лагранжа:
2
()
x()
()
k
k
i
k
i
r
r
g
r
,
1,..,
i
m
–
для обратной штрафной функции;
()
x()
()
k
k
i
k
i
r
r
g
r
,
1,..,
i
m
–
для логарифмической штрафной
функции;
0
lim()
k
k
i
i
r
r
.
Пример 5.5
Найти минимум в задаче
2
2
1
2
(x)(4)(4)min
f
x
x
,
1
1
2
(x)
50
g
xx
.
Решение
Решим задачу с применением разных штрафных функций.
А. Применение обратной штрафной функции.
1. В поставленной задаче одно ограничение-неравенство. Решим ее
аналитически.
2. Составим вспомогательную функцию:
264
2
2
1
2
(x,)(4)(4)(x,)
k
k
Fr
x
x
Pr
, где
1
2
(x, )
5
k
k
r
Pr
xx
.
3. Найдем безусловный минимум (x , )
k
Fr:
1
2
1
1
2
(x, )
2( 4)
0
(
5)
k
k
Fr
r
x
x
xx
,
2
2
2
1
2
(x, )
2( 4)
0
(
5)
k
k
Fr
r
x
x
xx
.
Вычитая из первого уравнения второе, имеем
1
2
xx
и
3
2
1
1
1
436105100
0
2
k
r
x
x
x
.
При
100
k
r
получаем
3
2
1
1
1
436105500
x
x
x
. Найдем корни по
формуле Кардана. Так как
4
a,
36
b
,
105
c
,
50
d
, то перепи-
шем уравнение в виде
3
320
ypyq
,где
1
13
3
b
yx
x
a
,
2
2
3
3
0.75
3
acb
p
a
,
3
3
3
2
2
12.25
273
bbcd
q
a
a
a
. Отсюда
0.25
p
,
6.125
q
; дискриминант
2
3
37.5 0
Dqp
, поэтому уравнение
имеет
один
действительный
корень:
1yuv
,
где
2
3
3
0.10845
u
qqp
,
2
3
3
2.3050
v
qqp
.
Тогда
1
2.4135
yuv
,
1 0.5864
x
.
Результаты расчетов приведены в табл. 5.3, где 1
2
1
()
x()
()
k
k
k
r
r
g
r
.
Таблица 5.3
kk
r
1()
k
xr
,
2()
k
xr
x( ),
()
k
k
Frr
x( ),
()
k
k
Prr
1x()
()k
gr
1()
k
r
0 100
0.5864
49.4341
26.1288
–3.8272 6.8271
110
1.7540
16.7914
6.7024
–1.4920 4.4922
21
2.2340
8.1172
1.8797
0.5320 3.5332
3 0.1
2.4113
5.6116
0.5637
0.1774 3.1775
4 0.01
2.4714
4.8480
0.1748
0.0572 3.0564
5 0.001
2.4999
4.6097
0.0549
0.0182 3.0189
60
2.5
4.5
-
0
3
265
Б. Применение логарифмической штрафной функции.
1. В поставленной задаче одно ограничение-неравенство. Решим ее
аналитически.
2. Составим вспомогательную функцию:
2
2
1
2
(x,)(4)(4)(x,)
k
k
Fr
x
x
Pr
,
где
1
2
(x, )
ln(5
)
k
k
Pr
r
xx
.
3. Найдем безусловный минимум (x , )
k
F r с помощью необходимых
и достаточных условий при фиксированном
k
r:
1
1
1
2
(x, )
2( 4)
0
(5
)
k
k
Fr
r
x
x
xx
,
2
2
1
2
(x, )
2( 4)
0
(5
)
k
k
Fr
r
x
x
xx
.
Вычитая из первого уравнения второе, получаем 1
2
xx
. С учетом этого
имеем
1
1
2( 4)
0
52
k
r
x
x
или
2
1
1
21320
0
2
k
r
x
x
.
Корни последнего уравнения: 1,2
1394
4
k
r
x
.
Корень 1x
2
1394
4
k
r
x
не удовлетворяет ограничению 1
250
xx
при
0
k
r .Поэтому 1
2
1394
()()
4
k
k
k
r
xr
xr
. Матрица Гессе
2
2
1
2
1
2
1
2
2
1
2
1
2
2
(5
)
(5
)
(),
0
2
(5
)
(5
)
k
k
kk
k
k
r
r
xx
xx
Hxrr
r
r
xx
xx
,
так как 1
2
1
2
2
0
(5
)
k
r
xx
,
2
2
1
2
4
4
0
(5
)
k
r
xx
, т.е. дос-
таточные условия минимума выполняются (табл. 1.1, строка 1). При
0
k
rимеем1
2
1
2
()()
2.5
k
k
xr
xr
x
x
,
(x) 4.5
f
.
Результаты расчетов приведены в табл. 5.4, где 1
2
1
()
x()
()
k
k
k
r
r
g
r
.
266
Таблица 5.4
kk
r
1()
k
xr
,
2()
k
xr
x( ),
(
)
kk
Frr
x( ),
(
)
kk
Prr
1x( )
()k
gr
1()
k
r
0 100 –1.8059 –147.8963 –215.31
–8.6118
11.61
1 10 1.5000 5.5685
–6.9315
–2.0000
5
2 1 2.3486 6.6489
1.1947
–0.3028
3.3
3 0.1 2.4835 4.9406
0.3411
–0.0330
3.03
4 0.01 2.4983 4.5669
0.0570
–0.0033
3.003
5 0.001 2.4998 4.5090
0.0080
–0.0003
3.0003
60
2.5
4.5
-
0
3
В. Решим задачу с помощью необходимых и достаточных условий
условного экстремума (см. разд. 1.4).
1. Составим обобщенную функцию Лагранжа:
2
2
01
01
2
11
2
(x,,)
(4)(4)(
5)
L
x
x
xx
.
2. Выпишем необходимые условия минимума первого порядка:
а)
01
01
1
1
(x,,)
2(4)
0
L
x
x
,
01
02
1
2
(x,,)
2(4)
0
L
x
x
;
б)1250
xx
;
в)10
;
г)11
2
(
5)0
xx
.
Решим систему для двух случаев.
В первом случае 0 0
.Тогда10
, что противоречит теореме 1.7.
Во втором случае 0 0
. Поделим систему на 0
и заменим 1
0
на1
.
Условие «а» примет вид
1
1
2( 4)
0
x
,
2
1
2( 4)
0
x
.
Из условия «г» дополняющей нежесткости следуют два случая:
1)10
.Тогда124
xx
, но при этом не выполняется условие «б»;
2)10
.Тогда
267
1
250
xx
,
1
1
28
0
x
,
2
1
28
0
x
.
Получим 1
2 2.5
x
x
;130
.
3. Проверим достаточные условия минимум:
2
2
2
1
2
(x,)2
2
dL
dx dx
,
1
1
2
(x)
0
dg
dx dx
.
Отсюда
1
2
dx dx
и
2
2
2
(x,)4
0
dL
dx
при
20
dx .Поэтомув
точке x
(2.5; 2.5)T
условный минимум (табл. 1.5, строка 1)
4. Значение функции в точке условного минимума: (x ) 4.5
f
.
5.4 . Метод множителей
Даны дважды непрерывно дифференцируемые
целевая функция
12
(x) ( , ,...,
)n
ffxxx
и функ-
ции ограничений (x) 0
i
g,1,..,
i
p
;(x)0
i
g,
1,..,
ip
m
, опреде-
ляющие множество допустимых решений
n
XR
.
Требуется найти локальный минимум функции (x)
f на множестве
X , т.е. найти такую точку x X
,что
x
(x) min (x)
X
f
f
,
(x) 0, 1,.., ;
x
(x) 0,
1, ..,
i
i
g
i
ppn
X
g
ip
m
.
Стратегия аналогична используемой в
методе внешних штрафов, только штраф-
ная функция добавляется не к целевой функции, а к классической функции
Лагранжа. В результате задача на условный минимум сводится к решению
последовательности задач поиска безусловного минимума модифициро-
ванной функции Лагранжа:
2
1
1
(x,λ,μ,)(x)
(x)
(x)
2
p
p
k
kkk
k
ii
i
i
i
r
L
r
f
g
g
2
2
1
1
max 0,
(x)
2
m
k
k
k
i
i
i
k
ip
rg
r
,
Постановка задачи
Стратегия решения задачи
268
где
1
λ ( ,...,
)
k
k
kT
p
,
1
μ ( ,...,
)
k
k
kT
p
m
–
векторы множителей; k
r–
параметр штрафа; k – номер итерации.
Задается начальная точка поиска
0
x . На каждой k -ой итерации
ищется точка минимума модифицированной функции Лагранжа при за-
данных λ
k
,μ
k
,
k
r с помощью одного из методов безусловной миними-
зации. Полученная точка x ( λ ,μ , )
kkk
r
используется в качестве началь-
ной на следующей итерации, выполняемой при возрастающем значении
параметра штрафа
k
r и пересчитанных определенным образом векторах
множителей λk
,μ
k
.
Для достижения сходимости в отличие от метода
внешних штрафов не требуется устремлять
k
r к бесконечности.
Метод множителей был предложен Пауэллом (Powell M.J.D.) и Хес-
тенсом (Hestenes M.R.) и имеет многочисленные модификации [8, 26].
Алгоритм
1. Задать начальную точку
0
x ; начальное значение параметра штрафа
0
0
r ;число
1
C для увеличения параметра штрафа; начальные значе-
ния векторов множителей
0
λ,
0
μ ; малое число
0
для остановки алго-
ритма. Положить
0
k
.
2. Составить модифицированную функцию Лагранжа:
2
1
1
(x,λ,μ,)(x)
(x)
(x)
2
p
p
k
kkk
k
ii
i
i
i
r
L
r
f
g
g
2
2
1
1
max 0,
(x)
2
m
k
k
k
i
i
i
k
ip
rg
r
,
3.Найтиточкуx(λ,μ , )
kkk
r
безусловного минимума функции по
x с помощью какого-либо метода (нулевого, первого или второго поряд-
ка):
x
(x,λ,μ,)min(x,λ,μ,)
n
kkk
kkk
R
L
r
L
r
.
При этом задать все требуемые выбранным методом параметры. В качест-
ве начальной точки взять x
k
.
4. Вычислить
x(λ,μ , ),μ ,
kkk
kk
P
r
r
,
где
2
2
2
1
1
1
x,μ ,
(x)
max 0,
(x)
2
2
p
k
m
kk
k
k
k
i
i
i
i
k
i
ip
r
P
r
g
rg
r
и
проверить выполнение условия окончания вычислений:
269
а) если
x(λ,μ , ),μ ,
kkk
kk
P
r
r
, процесс поиска закончить:
x
x(λ,μ , )
kkk
r
,
(x)
x(λ,μ , )
kkk
f
f
r
;
б) если
x(λ,μ , ),μ ,
kkk
kk
P
r
r
, положить:
1
k
k
r
Cr
–
пересчет параметра штрафа;
1
λ
λ
x(λ,μ , )
k
k
k
kkk
rg
r
–
пересчет множителей для огра-
ничений-равенств;
1
max 0,
x(λ,μ , )
k
k
k
kkk
i
i
i
rg
r
–
пересчет множите-
лей для ограничений-неравенств;
1
x
x(λ,μ , )
k
kkk
r
,
1
kk
и перейти к шагу 2.
Сходимость
Теорема 5.5 (о сходимости метода множителей в задаче с ограниче-
ниями типа равенств). Пусть функции (x)
fи(x)
i
g , 1,..,
i
m
непре-
рывны, последовательность {λ }k
ограничена,
1
0kk
r
r
привсехk,
причем
k
r,X
–
компактное изолированное множество точек ло-
кального минимума в исходной задаче. Тогда найдется подпоследователь-
ность {x }
k
K , сходящаяся к некоторой точке x
X
и такая, что ее
произвольный элемент x
k
,kK
является точкой локального минимума
функции (x, λ , )
kk
L
r .ЕслиприэтомX
состоит из единственной
точки x
, то можно указать последовательность { x }
k
и номер
0
k
такие, что x
x
k
иx
k
является точкой локального минимума функ-
ции(x,λ,)
kk
L
r
приk k
[8].
Замечания 5.5
1. Сходимость метода множителей в задаче со смешанными ограни-
чениями доказана в [8].
2. На каждой итерации желательно, чтобы найденная точка локально-
гоминимумаx(λ,μ , )
kkk
r
была бы ближайшей к x
. Метод корректен,
если начиная с некоторого k метод безусловной минимизации всякий раз
приводит в окрестность одной и той же точки x
условного локального
минимума. Это определяет описанная на шаге 3 алгоритма преемствен-
ность задач.
270
3. Обычно выбирается
0
0.1, 1
r
,а
[4;10]
C
. Целесообразно вы-
брать
0
λ,
0
μ,близкимик λ
,μ
, используя априорную информацию о
решении. Иногда выбирают
0
0
λμ0
. В этом случае первая вспомога-
тельная задача минимизации совпадает с решаемой в методе внешних
штрафов.
4. Методом множителей удается найти условный минимум за мень-
шее число итераций, чем методом штрафов. При этом для достижения
сходимости не требуется устремлять
k
r к бесконечности. Доказано, что
минимум модифицированной функции Лагранжа, начиная с некоторого
k
r , совпадает с минимумом в исходной задаче. Это приводит также к то-
му, что проблема увеличения овражности не является такой острой, как в
методе штрафов.
5. Найденная в результате точка x
удовлетворяет условиям Куна-
Таккера (утверждение 1.12 при
0
λ0
),аλ
λ
k
,μ
μ
k
[8].
Пример 5.6
Найти минимум функции (x)
f в задаче
2
2
1
2
(x)
min
fxx
,
1
1
2
(x)
20
g
xx
.
Решение
1. В поставленной задаче одно ограничение-равенство. Зададим
0.001
.
2. Составим модифицированную функцию Лагранжа:
2
2
1
2
(x,λ,)
(x,λ,)
kk
kk
L
r
x
x
P
r
2
2
2
1
2
11
2
1
2
(
2)
(
2)
2
k
k
r
x
x
xx
xx
.
3. Найдем минимум функции (x, λ , )
kk
L
r:
1
1
1
2
1
(x,λ,)
2
(
2)0
kk
k
k
L
r
x
rxx
x
,
2
1
1
2
2
(x,λ,)
2
(
2)0
kk
k
k
L
r
x
rxx
x
.
Вычитая из первого уравнения второе, имеем 1
2
xx
и11
(,)
kk
x
r
1
21
0.5
(,)
1
k
k
kk
k
r
x
r
r
.
Достаточные условия минимума удовлетво-
271
ряются, так как матрица Гессе
2
0
2
kk
k
k
rr
H
r
r
в силу того, что
12
0
k
r
,
2440
k
r
при
0
k
r . Формула пересчета мно-
жителей имеет вид
1
1
1
1
11
21
1
0.5
(,)(
,
)2
2
1
1
k
k
k
k
k
kk
kk
k
k
k
r
rx
r
x
r
r
r
.
Численные результаты для последовательности
k
r , используемой в
примере 5.2, и различных начальных значениях
0
1
приведены в табл. 5.5.
Расчеты остановлены при
1
1
x( ,),
,
0.001
kk
kk
P
r
r
.
Заме-
тим, что если
0
1
ближек 1
2
(см. пример 5.2), то сходимость быст-
рее. Если
0
1
1
2
, то решение находится на первой итерации:
1
2
1 0.5( 2)
1
11
x
x
.
Таблица 5.5
kk
r
1
k
1()
k
xr
,
2()
k
xr
P
1
k
1()
k
xr
,
2()
k
xr
P
01
0
0.5
0.5
–1
0.75
0.625
12
–1
0.8333
0.444
–1.5 0.9167
0.2777
2 10 –1.666 0.9848
0.058
–1.833 0.9924
0.0289
3 100 –1.969 0.9998
0.00079 –1.9853 0.99993 0.00029
В табл. 5.5 принято обозначение
1
1
x( ,),
,
kk
kk
PP
r
r
.
Пример 5.7
Найти минимум функции (x)
f в задаче
2
2
1
2
(x)
min
fxx
,
1
1
(x)
10
g
x
,
2
1
2
(x)
20
g
xx
.
272
Решение
1. В поставленной задаче одно ограничение-равенство и одно ограни-
чение-неравенство. Зададим
0.001
.
2. Составим модифицированную функцию Лагранжа:
2
2
2
1
2
1
1
(x,λ ,
,
)
(1)(1)
2
k
kkk
k
r
L
r
x
x
x
x
22
1
2
1
max 0,
(
2)
()
2
k
k
k
k
rxx
r
.
3. Найдем безусловный минимум (x, , , )
kkk
L
r
:
1
1
12
1
1
1
12
12
2
( 1),
(
2) 0,
(x,,,)
02
(1)
(
2),
(
2) 0;
k
k
k
k
kkk
k
k
k
k
k
k
x
rx
rxx
L
r
x
rx
x
rxx
rxx
2
12
2
2
12
12
2,
(
2) 0,
(x,,,)
0
2
(
2),
(
2) 0.
k
k
kkk
k
k
k
k
x
rxx
L
r
x
x
rxx
rxx
Формулы для пересчета множителей имеют вид
1
1(, ,)1,
k
k
k
kkk
rx
r
1
1
2
max 0,
(,,)(
,
,
)2
k
kk
kkk
kkk
rx
r
x
r
.
Рассмотрим два случая:
1) Пусть
12
(
2)0
kk
rxx
.Тогда20
x
,
1(,)
2
k
k
kk
k
r
x
r
r
.
2) Пусть
12
(
2)0
kk
rxx
. Тогда
2
1
2
22
2
()
(,,)
46()
k
k
k
kk
k
kkk
k
k
r
r
r
x
r
r
r
;
1
2
2(,,)
(,,)
2
k
kkk
k
kkk
k
r
x
r
x
r
r
.
Положим
0
0
,
0
1
,
0
1
r.
По формуле для первого случая
000
1
10
(,,)
0.333
21
x
r
,
20
x
.
273
При этом
0
0
000
000
1
2
(,,)(
,
,
)2 0.6660
rx
r
x
r
,
т.е.
условие выполняется.
По формуле для второго случая
000
1
22001
(,,)
0.0909
461
x
r
;
000
2
1 (2 0.0909) 1
(,,)
0.303
21
x
r
.
При этом
0
0
000
000
1
2
(,,)(
,
,
)2 0.6060
rx
r
x
r
,
что
противоречит условию.
При этом для первого случая
1
0
0
000
1( , ,)101(0.3331)0.666
rx
r
1
0
0
000
000
1
2
max 0,
(,,)(
,
,
)2
rx
r
x
r
max0,110.3332 0
.
Можно проверить, что аналогичная ситуация имеет место при других
значениях параметров, используемых при расчетах в данном примере. Чи-
словые результаты приведены в таблице 5.6.
Таблица 5.6
kk
r
k
k
1(,,)
kkk
x
r
2(,,)
kkk
x
r
P
01
0
1
0.333
0
–0.277
12–0.6660
0.666
0
0.333
2 10 –1.334 0
0.9445
0
0.0894
3 100 –1.889 0
0.9989
0
0.00213
4 1000 –1.999 0
0.99999
0
0.0005
В табл. 5.6 принято обозначение
x(,,),
,
,
kkk
kkk
PP
r
r
.
Сравнивая с примером 5.4, можно сделать вывод о том, что метод
множителей сходится быстрее метода штрафов, а
1
2
k
20
k
.
274
5.5 . Метод проекции градиента
Среди методов возможных направлений (или проективных методов)
наиболее известным является метод проекции градиента (метод Розена
(Rozen J. B.)) , который применяется в задачах поиска условного экстрему-
ма с ограничениями типа равенств и неравенств. Метод проекции градиен-
та учитывает ограничения в явной форме и реализуется по траектории,
обеспечивающей улучшение значений целевой функции и не выходящей
за пределы области допустимых решений.
Применение метода в задачах с ограничениями
типа равенств
Найти минимум дифференцируемой функции
(x)
f при ограничениях
(x) 0
i
g,1,..,
i
m
, т.е.
такую точку x
n
XR
, что
x
(x) min (x)
X
f
f
,
(5.4)
x
(x) 0, 1,..,
,
i
X
g
i
mmn
,
где функции (x)
i
g , 1,..,
i
m
, являются дифференцируемыми функция-
миx.
Стратегия поиска решения задачи (5.4)
методом проекции градиента состоит в
построении последовательности точек { x }
k
, вычисляемых по правилу
1
x
x
x
k
k
k
,
0,1, ...
k
,
(5.5)
где x
k
есть вектор, вычисляемый для каждого значения k . Приращение
x
k
определяется из условия проекции вектора
(x)
k
ktf
,
0,1, ...
k
на
аппроксимирующую плоскость, задаваемую уравнением
x
τ
k
k
k
A,
(5.6)
которая аппроксимирует в точке x
k
,
0,1, ...
k
, поверхность S , задавае-
мую уравнениями
(x) 0
i
g, 1,..,
i
m
.
Здесь k
A – матрица размера
()
mn
вида
Постановка задачи
Стратегия решения задачи
275
1
1
1
1
xx
(x) (x)
...
...
...
...
(x)
(x)
...
k
n
k
m
m
n
g
g
x
x
A
g
g
x
x
,
(5.7)
а τ k – вектор столбец,
1
τ
(x ), ...,
(x)
T
k
k
k
m
g
g
.
На рис. 5.8 в точке x
(1; 0.5)
k
T
построена аппроксимирующая пря-
мая для задачи:
2
2
1
2
(x)(4)(5)min
f
x
x
,
2
2
1
1
2
(x)
4160
g
x
x
.
Ее уравнение 1
2
29
x
x
, так как
1
2
(1; 0.5)
(2;8)|
(2; 4)
k
T
k
x
A
xx
;
112
2
1
2
x(
;
)(1;
0.5)
k
kT
T
xxx
x
x
x
;
1
xτ
(x)
k
k
k
A
g
и следо-
вательно
1
2
2(1)4( 0.5)14
x
x
.
Вектор x
k
определяется по формуле
1
2
x
x
x
k
k
k
,
(5.8)
где 1x
k
называется градиентной составляющей приращения; она равна
1
1x
(x)
x
k
T
T
k
k
k
kkk
k
k
tEAAA
Af
t
(5.9)
и обладает следующим свойством: градиентная составляющая приращения
1x
k
в линейном приближении не меняет вектор невязки условий связи.
Это означает, что под действием градиентной составляющей точка x
k
движется параллельно или по плоскости
x
τ
k
k
k
A (рис. 5.8). Состав-
ляющая 2 x
k
называется компенсационной составляющей приращения и
равна
1
2x
k
T
T
kkk
k
AAA
.
Эта составляющая обладает, в линейном
приближении, свойством компенсировать вектор невязки условий связи на
величину τ k . Под действием составляющей 2 x
k
осуществляется проек-
ция точки x
k
на плоскость
x
τ
k
k
k
A (рис. 5.8).
276
Величина шага kt может выбираться как из условия убывания (x)
f
при переходе из точки x
k
в точку
1
x
(x)
k
T
T
k
k
kkk
k
tEAAAAf
так и из условия
1
()x
(x)
min
k
k
T
T
k
k
k
kkk
k
t
t
f
tEAAA
Af
.
(5.10)
Задача (5.10) может решаться либо с использованием необходимых и
достаточных условий минимума:
()0
kt
,
()0
kt
, применяемых
непосредственно к функции ( )
kt
или к аппроксимирующим ее полино-
мам, либо с использованием численных методов.
Расчет заканчивается в точке x
k
, в которой||x||
k
,
2
||x||
k
,
где – заданная точность. В полученной точке x
k
требуется обязатель-
ная проверка выполнения достаточных условий минимума функции в за-
даче (5.4). Точное равенство
1
1x
(x) 0
k
T
T
k
k
kkk
k
tEAAA
Af
свидетельствует о точном выполнении необходимых условий экстремума,
при этом вектор множителей Лагранжа определяется по формуле
1
λ
(x)
k
T
k
kk
k
AAAf
.
(5.11)
Знание приближения λ
k
вектора λ
, определяемого формулой (5.11), по-
зволит осуществить проверку достаточных условий в точке x
k
.
1x
k
1
2
x
Рис. 5.8
9
2x
k
1x
0
4.5
2
2
1
1
2
(x)
4160
g
x
x
2
2
1
2
(x)(4)(5)
f
x
x
4
1
2
29
x
x
x
x
k
1
x
k
277
Замечание 5.6. Если в задаче (5.4) ограничения линейны, т.е. имеют
вид
1
n
ijj
i
j
ax
b
, 1,...,
i
m
, то матрица A постоянна. Это означает,
что в силу свойства составляющей 2 x
k
матрица вычисляется единст-
венный раз в точке
0
x . При этом начальная точка попадает в область
допустимых решений за одну итерацию. Дальнейший процесс построения
последовательности {x }
k
связан с вычислением составляющей 1x
k
.
Алгоритм
1. Задать начальную точку
0
x;
0
;числоитерацийM.
2. Положить
0
k
.
3. Проверить выполнение условия k M
:
а) если неравенство выполнено, то расчет окончен. Вычислить λ
k
,
проверить необходимые и достаточные условия минимума и оценить ре-
зультат;
б) если неравенство не выполнено, то перейти к шагу 4.
4. Вычислить матрицу
1
1
1
1
xx
(x) (x)
...
...
...
...
(x)
(x)
...
k
n
k
m
m
n
g
g
x
x
A
g
g
x
x
.
5. Вычислить
1
τ
g(x )
(x ),...,
(x)
T
k
k
k
k
m
g
g
.
6. Вычислить
1
2x
k
T
T
kkk
k
AAA
.
7. Вычислить
2
||x||
k
.
8. Вычислить
(x)
k
f
.
9. Вычислить
1
x
(x)
k
T
T
k
kkk
k
EAAAAf
.
10. Проверить выполнение условий || x ||
k
и
2
||x||
k
:
а)если|| x||
k
и
2
||x||
k
, то расчет окончен. Перейти к
вычислению λ
k
по формуле (5.11) и проверке достаточных условий ми-
нимума.
278
б)если || x||
k
,
2
||x||
k
, то положить 2x
0
k
иперей-
ти к шагу 11;
в)если|| x||
k
,
2
||x||
k
, то положить x
0
k
иперей-
ти к шагу 13;
г)если|| x||
k
,
2
||x||
k
, то перейти к шагу 11.
11. Получить точку x
x
k
k
kt
.
12. Определить kt
из условия (x
x) min
k
k
k
k
t
ft
.
13. Вычислить
1
2
x
x
x
x
k
k
k
k
kt
.
Положить
1
kk
ипе-
рейти к шагу 3.
Замечание 5.7. Если ограничения в задаче линейны, то при 1
k на
шаге 3 переходим к шагу 8. На шаге 10 следует положить
2
||x||0
k
.
Сходимость
Так как проекция вектора
(x)
k
ktf
осуществляется для каждого
значения k на множество
x|(xx)
,x
k
n
k
k
Q
A
R
, то алгоритм
метода проекции градиента сходится для выпуклых, дифференцируемых
на
n
R функций (x)
f , градиент которых удовлетворяет условию Липшица
(см. опр. 1.11).
Теорема 5.6. Пусть (x)
f выпуклая, дифференцируемая на
n
R
функция, градиент которой удовлетворяет на множестве Q условию
Липшица с константой L . Пусть множество Q – выпуклое и замкнутое
множество решений задачи
x
Arg min (x)
Q
X
f
не пусто, а
0
(2)
kt
L
.
Тогда x
x
k
X
и, если
(x)
f сильно выпукла,
x
x
k
со скоростью геометрической прогрессии [25].
Пример 5.8
Решить задачу методом проекции градиента:
2
2
1
2
(x)(4)(5)min
f
x
x
,
2
1
1
2
(x)
40
g
xx
.
279
Решение
.
1 Зададим
0
x
(0; 0)
;
0.05
;
5
M
.
.
2 Зададим
0
k
.
0
.
3 Проверяем условие k M
:
05
k
M
.
0
.
4 Вычисляем матрицу
0
0
2x
(1;2 ) (1;0)
A
x
.
0
.
5 Вычисляем 0
(004)4
.
0
.
6 Получаем
0
2x
(1;0) 14 (4;0)
T
T
.
0
.
7 Вычисляем
0
2
||x||4
.
0
.
8 Вычисляем
0
(x)(8;10)T
f
.
0
.
9 Вычисляем
0
101
8
0
x
0.5 (1; 0)
010
10 10
.
0
.
10 Проверяем выполнение условий
0
||x||
,
0
2
||x||
:
0
||x||10
0.05
,
0
2
||x||4
0.05
.
0
.
11 Получаем точку
0
0
0
0
x
x
(0; 10 )T
t
t
.
0
.
12 Определяем 0t
из
0
0
0
0
0
0
0
(x x)min(x
x)
t
ft
ft
:00.5
t
.
0
.
13 Вычисляем
1
0
0
0
0
2
x
x
x
x
(0;0) (0;5) (4;0)
T
T
T
t
(4;5)T
(Рис. 5.9). Полагаем
1
k , переходим к шагу 3.
1
.
3 Проверяем условие k M
:15
k
M
.
1
.
4 Вычисляем матрицу
1
1
2x
(1;2 ) (1;10)
A
x
.
1
.
5 Вычисляем 1
(4254) 25
.
1
.
6 Получаем
1
2 x ( 0.248; 2.48)T
.
1
.
7 Вычисляем
1
2
||x|| 2.49
.
1
.
8 Вычисляем
1
(x) (0;0)T
f
.
1
.
9 Вычисляем
1
x (0; 0)T
.
1
.
10 Проверяем выполнение условий
1
||x||
,
1
2
||x||
:
1
||x||0
0.05
,
1
2
||x|| 2.49
0.05
.
Переходим к шагу 13.
1
.
13 Вычисляем:
2
1
1
2
x
x
x (4;5) ( 0.248; 2.48) (3.752; 2.52)
T
T
T
(рис. 5.9).
Полагаем
2
k , переходим к шагу 3.
280
2
.
3 Проверяем условие k M
:
25
k
M
.
2
.
4 Вычисляем матрицу
2
2
2x
(1; 2 ) (1; 5.04)
A
x
.
2
.
5 Вычисляем 2
(3.752 6.32 4) 6.07
.
2
.
6 Получаем
2
2x
( 0.23; 1.16)T
.
2
.
7 Вычисляем
2
2
||x||1.18
.
2
.
8 Вычисляем
2
(x ) ( 0.496; 4.96)T
f
.
2
.
9 Вычисляем
2
1 0 0.038 0.19
0.496
0.475
x
01
0.19 0.69
4.96
0.103
.
2
.
10 Проверяем выполнение условий
2
||x||
,
2
2
||x||
:
2
|| x || 0.486
0.05
,
2
2
||x||1.18
0.05
.
Переходим к шагу
11.
2
.
11 Получаем
2
2
2
2
2
x
x
(3.752
0.475; 2.52
0.103)T
t
t
t
.
2
.
12 Определяем 2
0.138
0.585
0.236
t
.
3
x
0
x
2
1
1
2
(x)
40
g
xx
2
2
1
2
(x)(4)(5)
f
x
x
Рис. 5.9
5
3
1
2
5
6
4
1
1x
4
3
2
2
x
x
2
x
1
x
281
2
.
13 Вычисляем
3
2
2
2
2
2
xx
x
x
t
(3.752; 2.52) 0.585 ( 0.475; 0.103) ( 0.23; 1.16) (3.244;1.42)
T
T
T
T
(рис. 5.9). Полагаем
3
k , переходим к шагу 3.
3
.
3 Проверяем условие k M
:
35
k
M
.
3
.
4 Вычисляем матрицу
3
3
2x
(1; 2 ) (1; 2.84)
A
x
.
3
.
5 Вычисляем 3
(3.244 2.02 4) 1.264
.
3
.
6 Получаем
3
2x
( 0.139; 0.394)T
.
3
.
7 Вычисляем
3
2
||x|| 0.41
.
3
.
8 Вычисляем
3
(x ) ( 1.512; 7.160)T
f
.
3
.
9 Вычисляем
3
1 0 0.110 0.314
1.512
0.89
x
01
0.314 0.89
7.160
0.314
.
3
.
10 Проверяем выполнение условий
3
||x||
,
3
2
||x||
:
3
||x|| 0.94
0.05
,
3
2
||x|| 0.41
0.05
.
Переходим к шагу 11.
3
.
11 Получаем
3
3
3
3
3
x
x
(3.244 0.89 ; 1.42 0.314 )T
t
t
t
.
3
.
12 Определяем 3
0.445
0.5
0.89
t
.
3
.
13 Вычисляем
4
3
3
3
3
2
x
x
x
x
t
(3.244; 1.42) 0.5 ( 0.89; 0.314) ( 0.139; 0.394) (2.66;1.18)
T
T
T
T
.
Полагаем
4
k , переходим к шагу 3.
4
.
3 Проверяем условие k M
:
45
k
M
.
4
.
4 Вычисляем матрицу
4
4
2x
(1; 2 ) (1; 2.36)
A
x
.
4
.
5 Вычисляем 4
(2.66 1.39 4) 0.05
.
4
.
6 Получаем
4
2x
( 0.0076; 0.018)T
.
4
.
7 Вычисляем
4
2
|| x || 0.019
.
4
.
8 Вычисляем
3
(x ) ( 2.72; 7.64)T
f
.
4
.
9 Вычисляем
4
1 0 0.152 0.36
2.72
0.45
x
0 1 0.36 0.848
7.64
0.18
.
282
4
.
10 Проверяем выполнение условий
4
||x||
,
4
2
||x||
:
4
||x||0.48
0.05
,
4
2
|| x || 0.019
0.05
. Положим
4
2x
0
и
переходим к шагу 11.
4
.
11 Получаем
4
4
4
4
4
x
x
(2.66 0 .45 ; 1.18 0.18 )T
t
t
t
.
4
.
12 Определяем 4
0.09
0.39
0.237
t
.
4
.
13 Вычисляем
5
4
4
4
4
4
2
2
где
xx
x
x
(x0)
t
(2.66; 1.18) 0.39 ( 0.45; 0.18) (2.48; 1.25)
T
T
T
.
Полагаем
5
k , переходим к шагу 3.
5
.
3 Проверяем условие k M
:
5
k
M
.
Расчет окончен, вычислим
5
и проверим необходимые и достаточ-
ные условия минимума. Находим (5.11)
5
3.04
1
(1; 2.5)
3.001
7.5
7.25
.
Выпишем необходимые условия экстремума (разд. 1.3) с учетом вида
функции Лагранжа
2
2
2
1
2
1
2
(x,)(4)(5)(
4)
L
x
x
xx
:
1
2( 4)
0
x
,
2
2
2(5)2
0
x
x
,
2
1
240
xx
.
Будем считать, что необходимые условия выполнены, если абсолют-
ная величина невязки любого из этих равенств не превышает 0.1 . В ре-
зультате подстановки точки
5
xи
5
получаем
2(2.48 4) 3.001 0.04
,
2(1.25 5) 2 1.25 3.001 0
,
2
2.48 1.25 4 0.04
.
Отсюда следует, что необходимые условия выполняются. Проверим доста-
точные условия экстремума. Получаем
2
dL:
2
2
2
2
2
1
2
1
2
2
2(1 3)
2
8
dL dx
dxdxdx
.
Дополнительное условие 1
22
2
0
dx xdx
. Отсюда
2
2
2
20.5
0
dL
dx
.
Вывод: точка
5
x
(2.48; 1.25)T
является приближением точки ми-
нимума x
(табл.1.1, строка 1).
283
Применение метода в задачах с ограничениями
типа неравенств
Найти минимум дифференцируемой функции
(x)
f при ограничениях
(x) 0
i
g,1,..,
i
m
, т.е.
такую точку x
n
XR
, что
x
(x) min (x)
X
f
f
,
(5.12)
x
(x) 0, 1, ..,
i
X
g
i
m
,
где функции (x)
i
g , 1,..,
i
m
, являются дифференцируемыми функция-
миx.
Стратегия поиска решения задачи (5.12)
методом проекции градиента учитывает
тот факт, что решение x
может лежать как внутри, так и на границе
множества допустимых решений.
Для определения приближения решения x
строится последователь-
ность точек { x }
k
:
1
x
x
x
k
k
k
,
0,1, ...
k
, где приращение x
k
определяется в каждой точке x
k
в зависимости от того, где ведется поиск
–
внутри или на границе множества допустимых решений.
Решение задачи начинается с обхода границы допустимой области.
Обход границ множества допустимых решений связан с выявлением ак-
тивных в точке x
k
ограничений
1
( ,...,
)T
A
p
ggg
, аппроксимацией их
плоскостью
x
k
k
A
,
(5.13)
где
xx
k
i
k
j
g
A
x
–
матрица размера (
)
pn
,pn
;
(x)
k
k
A
g
,и
проекцией на нее вектора
(x)
k
ktf
. Для выявления неравенств, актив-
ных в точке x
k
, задается погрешность определения активных ограничений
10
. Активными считаются те ограничения, для которых
1
(x) 0
i
g
. Число p ограничений, активных в точке x
k
, не должно
превышать n – размерности вектора x .
Поиск ограничений, активных в точке x
k
, рассматривается как само-
стоятельная задача, которая может быть решена путем последовательных
Постановка задачи
Стратегия решения задачи
284
приближений. Задается точка x
k
и вычисляется
(x)
i
g , 1,..,
i
m
.
Если
1
(x)
i
g
, то выбираются любые p ограничений с наименьшими по аб-
солютной величине невязками
(x)
k
k
i
ig
в точке x
k
, строится матрица
k
A , вычисляется k
и находится точка
1
1
x
x
()
k
k
T
T
kkk
k
AAA
,
(5.14)
затем снова вычисляются невязки выбранных p ограничений. Уточнение
по формуле (5.14) осуществляется до тех пор, пока не будет найдена точка
x
k
, в которой 1
(x) 0
i
g
. Проекция вектора
(x)
k
ktf
в точке x
k
,в
которой активны p ограничений, определяется точкой
1
1
x
x
()
(x)
k
k
T
T
k
k
kkk
k
tEAAA
Af
,
(5.15)
где приращение
1
x
()
(x)
k
T
T
k
k
kkk
k
tEAAA
Af
осуществляет
движение по плоскости
x
k
k
A
в направлении убывания (x)
f . Вели-
чина kt выбирается так:
max
min
0;
0
k
k
k
t
t
t
, где kt
есть шаг, при
котором
1
1
x()minx()
k
k
k
k
k
t
f
t
f
t
(см. (5.15)),
а max
kt
–
наименьший шаг, при котором
1
max
x
()
(x) 0
k
T
T
k
i
k
kkk
k
g
t
EAAAAf
для всех ограничений, которые не были активными в точке x
k
. Разумеет-
ся, невязка ограничений в точке
1
x
k
изменяется, и поэтому вычислению
точки
2
x
k
должна предшествовать процедура выбора активных ограни-
чений, описанная выше.
Процедура вычисления точек последовательности { x }
k
обеспечивает
последовательное движение вдоль границы допустимой области. При вы-
полнении неравенства
1
2
||x||
()
(x)
k
T
T
k
kkk
k
EAAAAf
,
где 2
– заданное достаточно малое положительное число, вычисляется
приближение
k
вектора множителей Лагранжа
:
1
()
(x)
k
T
k
kk
k
AAAf
.
(5.16)
Если
0
k
,товточкеx
k
выполнены необходимые условия мини-
мума и в ней должны быть проверены достаточные условия. Если среди
285
множителей
k
i
есть отрицательные, то это означает, что x
k
не является
приближением точки x
, так как в ней не выполнены необходимые усло-
вия минимума (x)
f при ограничениях
(x) 0
i
g,1,..,
i
m
(см. теорему
1.7). Однако выбор шага kt позволяет говорить о том, что значение (x)
f
не может быть уменьшено при заданном составе активных ограничений и,
следовательно, процесс минимизации (x)
f необходимо продолжить,
уменьшив их число: в число пассивных переводится то из ограничений,
которому соответствует наибольший по абсолютному значению отрица-
тельный множитель
k
i
. Такая процедура поиска позволяет отыскать ре-
шение, лежащее как на границе, так и внутри множества допустимых ре-
шений.
Алгоритм
1. Задать
0
x,10
,20
,числоитерацийM.
2. Положить
0
k
.
3. Проверить выполнение условия k M
:
а) если неравенство выполнено, то расчет окончен, перейти к вы-
числению λ
k
и оценке результата;
б) в противном случае перейти к шагу 4.
4. Вычислить (x )
k
i
g
,
1,..,
i
m
.
5. Проверить выполнение условий 1
(x) 0
k
i
g
, 1,..,
i
m
:
а) если неравенство выполнено хотя бы для одного i , вычислить
(x)
k
f
.
Если
(x) 0
k
f
, перейти к шагу 7. Если
(x) 0
k
f
при
0
k ,перейтикшагу9,аесли
0
(x) 0
f
, то следует проверить точку
0
x на принадлежность области допустимых решений. Если
0
x
X
,пе-
рейти к шагу 9. В противном случае задать заново точку
0
x и перейти к
шагу 4;
б) если ни одно из условий не выполнено, перейти к шагу 6.
6. Вычислить точку x
, в которой будет выполнено условие
1
(x) 0
i
g
, по крайней мере для одного значения i : x
x
k
1
()
T
T
kkk
k
AAA
. Положить x
x
k
и перейти к шагу 7.
7. Вычислить
1
x
()
(x)
k
T
T
k
kkk
k
EAAAAf
.
286
8. Проверить условие
2
||x||
k
:
а) если неравенство выполняется, перейти к шагу 9;
б)еслинет–кшагу10.
9. Вычислить вектор
1
()
(x)
k
T
k
kk
k
AAAf
.
Если
0
k
,то
расчет окончен, проверить достаточные условия минимума. Если нет, то
исключить из состава активных ограничение (оно переводится в пассив-
ные), которому соответствует наибольший по модулю отрицательный
множитель, и перейти к шагу 7 (при этом из матрицы k
A удаляется стро-
ка, соответствующая исключаемому ограничению).
10. Получить точку
1
x
x
x
k
k
k
kt
.
11. Определить kt . Для этого следует:
а) вычислить kt
из условия
0
(x
x) min
k
k
k
k
t
ft
;
б) для всех пассивных в точке x
k
ограничений, кроме переведен-
ных в пассивные на шаге 9, определить величину
i
kt из условий
(x
x)0
k
k
i
k
g
t
,
0
kt (если условие
(x
x)0
k
k
i
k
g
t
выполняет-
ся только при
0
i
kt,то
i
kt не вычисляется);
в) найти величину max min { }
i
k
k
i
t
t
;
г) вычислить значение
max
min{; }
k
kk
t
tt
.
12. Вычислить
1
x
x
x
k
k
k
kt
. Положить
1
kk
и перейти к
шагу 3.
Сходимость
Теорема 5.7. Пусть (x)
f выпуклая дифференцируемая на
n
R функ-
ция, градиент которой удовлетворяет на множестве Q условию Липши-
ца с константой L . Пусть множество Q – выпуклое и замкнутое,
множество
x
Arg min (x)
Q
X
f
не пусто, а величина kt удовлетворяет
условию
2
0kt
L
.Тогдаx
x
k
X
и, если (x)
f сильно выпукла,
тоx
x
k
со скоростью геометрической прогрессии [25].
287
Пример 5.9
Найти минимум в задаче
2
2
1
2
(x)(4)(5)min
f
x
x
,
1
1
2
(x)
10
g
xx
,
2
1
(x)
0
g
x
,
3
2
(x)
0
g
x
.
Решение
.
1 Задаем
0
x
(0; 0)T
;10.1
;20
;
5
M
.
.
2 Полагаем
0
k
.
0
.
3 Проверяем условие k M
:
05
k
M
.
0
.
4 Вычисляем
0
1(x)10
g
;
0
2(x) 0
g
;
0
3(x) 0
g
.
0
.
5 В точке
0
x активны ограничения второе и третье ограничения
0
2(x) 0
g
,
0
3(x) 0
g
, они формируют матрицу 0A . Так как
0
(x)
f
(8;10) 0
T
, переходим к шагу 7.
0
.
7 Вычисляем
0
00
8
0
x
00100
,таккак 0
10
01
A
.
0
.
8 Проверяем условие
0
2
||x||
:
0
||x||0
, переходим к шагу
9.
0
.
9 Вычисляем
0
1
0
00
0
10
8
8
λ
()
(x)
01 10
10
T
AAAf
,
удаляем третье ограничение 3
2
(x)
0
g
x
(оно переходит в пассив-
ные), которому соответствует наибольший по модулю множитель 10
,и
переходим к шагу 7 (при этом из матрицы 0
A исключается вторая строка).
1
.
7 Вычисляем
0
10
1
8
0
x
10
01
0
10 10
, так
как
0
10
A
.
1
.
8 Проверяем условие
0
2
||x||
:
0
2
||x||10
0.1
, перехо-
дим к шагу 10.
0
.
10 Получаем точку
1
0
0
0
0
x
x
x
(0; 10 )T
t
t
.
288
0
.
11 Определяем
0
0 0max
min ;
t
tt
: величину 0t
находим из усло-
вия
0
0
0
0
0
0
0
0
(x
x)min(x
x)
t
ft
ft
:00.5
t
; так как первое ограни-
чение пассивно в точке
0
x , то из условий
0
1010
t
и00
t находим
1
0 0.1
t ; третье ограничение в аналогичной процедуре не участвует, по-
скольку переведено в пассивные на шаге 9; 0 max
0
min{ } 0.1
i
i
t
t
;
0 min{0.5; 0.1} 0.1
t
.
0
.
12 Вычисляем
1
0
0
0
x
x
x
(0;1)T
t
. Полагаем
1
k и перехо-
дим к шагу 3.
1
.
3 Проверяем условие k M
:
15
k
M
.
1
.
4 Вычисляем
1
1(x) 0
g
;
1
2(x) 0
g
;
1
3(x)10
g
.
1
.
5 Проверяем
1
1
(x) 0
i
g
:
1
1
1(x) 0
g
,
1
1
2(x) 0
g
,
1
3
1
(x)
g
. Активны первое и второе ог-
раничения, они формируют матрицу 1
11
10
A
;
0
(x) 0
f
. Перехо-
дим к шагу 7.
2
.
7 Вычисляем
1
1
1011
1111
11
80
x
0110
1010
10
80
.
2
.
8 Проверяем условие
1
2
||x||
:
1
||x||0
, переходим к шагу 9.
1
.
9 Вычисляем
1
1
1
11
1
11
11
88
()
(x)
12
10
80
T
AA Af
;
1
18
,
1
20
. Необходимые условия минимума выполнены.
Проверяем достаточные условия минимума:
2
2
2
1
2
2
2
0
dLdxdx
.
Дополнительные
условия
1
20
dx dx
,
10
dx
. Отсюда
1
20
dx dx
. Следовательно,
2
2
2
4
0
dL dx
. Точка
1
x
x
(0; 1)T
–
точка минимума функции (x)
f (табл. 1.5, строка 1).
289
Пример 5.10
Найти минимум в задаче
2
2
1
2
(x)(4)(5)min
f
x
x
,
2
1
1
2
(x)
40
g
xx
,
2
1
(x)
0
g
x
,
3
2
(x)
0
g
x
.
Решение
.
1 Задаем
0
x
(0; 0)T
;10.1
;20.1
;
5
M
.
.
2 Полагаем
0
k
.
0
.
3 Проверяем условие k M
:
05
k
M
.
0
.
4 Вычисляем
0
1(x) 4
g
;
0
2(x) 0
g
;
0
3(x) 0
g
.
0
.
5 Проверяем
0
1
(x) 0
i
g
:
0
1(x) 0
g
,
0
1
2(x) 0
g
,
0
1
3(x) 0
g
. Активны второе и третье ог-
раничения, они формируют матрицу 0A ;
0
(x) 0
f
. Переходим к шагу 7.
0
.
7 Вычисляем
0
00
8
0
x
00100
,таккак 0
10
01
A
.
0
.
8 Проверяем условие
0
2
||x||
:
0
||x||0
, переходим к шагу
9.
0
.
9 Вычисляем
0
1
0
00
0
10
10
8
8
λ(
)
(x)
01 01
10
10
T
AAAf
,
удаляем третье ограничение 3
2
(x)
0
g
x
(оно переходит в пассив-
ные), которому соответствует наибольший по модулю множитель 10
,и
переходим к шагу 7 (при этом из матрицы 0
A удаляется вторая строка).
1
.
7 Вычисляем
0
00
8
0
x
01
10 10
, так как
0
10
A
.
1
.
8 Проверяем условие
0
2
||x||
:
0
2
||x||10
0.1
, перехо-
дим к шагу 10.
0
.
10 Находим точку
1
0
0
0
0
x
x
x
(0; 10 )T
t
t
.
290
0
.
11 Определяем 0t : 0 0.5
t
; так как первое ограничение пассивно в
точке
0
x , то из условия
2
0
(10)40
t
и00
t находим
1
0 0.2
t;
третье ограничение в аналогичной процедуре не участвует, поскольку пе-
реведено
в
пассивные
на
шаге
9;
0 max
0
min{ } 0.2
i
i
t
t
;
0 min{0.5;0.2} 0.2
t
.
0
.
12 Вычисляем
1
0
0
0
x
x
x
(0; 2)T
t
(рис.5.10). Полагаем
1
k
и переходим к шагу 3.
1
.
3 Проверяем условие k M
:
15
k
M
.
1
.
4 Вычисляем
1
1(x) 0
g
;
1
2(x) 0
g
;
1
3(x)20
g
.
1
.
5 Проверяем
1
1
(x) 0
i
g
:
1
1
1(x) 0
g
,
1
1
2(x) 0
g
,
1
3
1
(x)
g
. Активны первое и второе ог-
раничения, поэтому 1
14
10
A
;
0
(x) 0
f
. Переходим к шагу 7.
2
.
7 Вычисляем
1
10
11
11
14
8
0
1
x
01
40
117
10
6
0
16
,
2
.
8 Проверяем условие
1
2
||x||
:
1
||x||0
, переходим к шагу 9.
1
.
9 Вычисляем
1
1
1
11
1
1.5
λ(
)
(x)
6.5
T
AAAf
.
Рис. 5.10
3
x
x
0
x
X
2
x
2
1
240
xx
1x
1
x
2
x
2
5
4
0
291
Удаляем первое ограничение 1 (x) 0
g (оно переходит в пассивные), ко-
торому соответствует наибольший по модулю отрицательный множитель,
и переходим к шагу 7 (при этом из матрицы 1
A исключается первая стро-
ка).
3
.
7 Вычисляем
1
10
1
80
x
10
01
0
66
,
так
как
1
1;0
A
.
3
.
8 Проверяем условие
1
2
||x||
:
1
2
||x||6
, переходим к
шагу 10.
1
.
10 Получаем точку
2
1
1
1
1
x
x
x
(0;2 6 )T
t
t
.
1
.
11 Определяем 1t : 1 0.5
t
; так как третье ограничение пассивно
в точке
1
x , но условия
1
(26)0
t
выполняется только при 1 0
t,по-
этому
3
1t не вычисляется; первое ограничение в аналогичной процедуре не
участвует, поскольку переведено в пассивные только на шаге 9; следова-
тельно, 1 max
t
не вычисляется и 1 1 0.5
tt
.
1
.
12 Вычисляем
2
1
1
1
x
x
x
(0; 5)T
t
(рис.5.10). Полагаем
2
k
и переходим к шагу 3.
2
.
3 Проверяем условие k M
:
25
k
M
.
2
.
4 Вычисляем
2
1(x) 21
g
;
2
2(x) 0
g
;
2
3(x) 5
g
.
2
.
5 Проверяем
2
1
(x) 0
i
g
:
2
1
1
(x)
g
,
2
1
2(x) 0
g
,
2
3
1
(x)
g
. Активно второе ограничение,
оно формирует матрицу 2A ;
2
(x) 0
f
. Переходим к шагу 7.
4
.
7 Вычисляем
2
0080
x
010
0
, так как
2
10
A
.
4
.
8 Проверяем условие
2
2
||x||
:
2
||x||0
.
2
.
9 Вычисляем
2
1
2
22
2
()
(x) 8
T
AAAf
.
Удаляем второе
ограничение 2 (x) 0
g и переходим к шагу 7.
5
.
7 Вычисляем
2
2
x
(x) 8;0
T
Ef
.
292
5
.
8 Проверяем условие
2
2
||x||
:
2
2
||x||8
, переходим к
шагу 10.
2
.
10 Находим точку
3
2
2
2
2
x
x
x
(8 ;5)T
t
t
.
2
.
11 Вычисляем 2 2 0.5
tt
.
2
.
12 Вычисляем
3
2
2
2
x
x
x
(4; 5)T
t
(рис.5.10). Полагаем
3
k и переходим к шагу 3.
3
.
3 Проверяем условие k M
:
35
k
M
.
3
.
4 Вычисляем
3
1(x) 25
g
;
3
2(x) 4
g
;
3
3(x) 5
g
.
3
.
5 Проверяем
3
1
(x) 0
i
g
:
3
1
1
(x)
g
,
3
2
1
(x)
g
,
3
3
1
(x)
g
. Вычисляем
3
(x) 0;0
T
f
. Пере-
ходим к шагу 9.
3
.
9 Вычисляем
3
:
3
10
,
3
20
,
3
30
.
Проверяем достаточные условия:
2
2
2
1
2
2
2
0
dLdxdx
. Дополни-
тельные условия отсутствуют, так как все три ограничения в точке
3
x пас-
сивны. Точка
3
(4; 5)T
x
x
–
точка минимума (табл. 1.5, строка 1).
5.6 . Метод Зойтендейка
Найти минимум дважды непрерывно дифференци-
руемой функции (x)
f при условии, что точка
x
n
R
удовлетворяет ограничениям
(x) 0
i
g, 1,..,
i
m
, в которых
функции (x)
i
g , 1,..,
i
m
также дважды непрерывно дифференцируемые
функции x , т.е . найти такую точку x X
,что
x
(x) min (x)
X
f
f
,
(5.17)
x
(x) 0, 1, ..,
i
X
g
i
m
.
Стратегия решения задачи (5.17) мето-
дом Зойтендейка (Zoutendijk G.) состоит
в построении последовательности допус-
тимых точек { x }
k
, таких, что
1
(x)(x)
k
k
f
f
,
0,1,2, ...
k
. Правило
построения точек последовательности { x }
k
:
1
x
x
k
k
k
ktd
,
0,1, ...
k
,
(5.18)
Постановка задачи
Стратегия решения задачи
293
где
k
d – направление спуска, точка x
k
–
допустимая и такова, что
(x) 0
k
k
ig
,
a
iI
,
(5.19)
a
I – множество индексов i активных ограничений, для которых выпол-
нено условие (5.19); величина шага
0
kt находится в результате решения
задачи одномерной минимизации:
(x
) min
k
k
k
ftd
,
(5.20)
(x
)0
k
k
i
k
g
td
, 1,...,
i
m
.
(5.21)
Задача (5.20), (5.21) может быть решена с использованием алгоритма
применения необходимых и достаточных условий условного минимума,
описанных в разд. 1 .4. Иначе величину kt следует выбирать из соотноше-
ния
min{ 0;
0}
k
k
k
t
t
t
,
(5.22)
где
величина
kt
определяется
из
условия
0
(x
)min(x
)
k
k
k
k
k
k
k
t
ftd
ftd
, а величина
min{ }
i
k
k
t
t
,
i
kt – удовле-
творяет условиям (x
)0
k
k
i
k
g
td
,
0
kt.
Направление спуска
k
d удовлетворяет системе неравенств
(x)
0
kTk
fd
,
(5.23)
(x)
0
kTk
i
g
d
,
a
iI
.
(5.24)
Возможное направление спуска
k
d , удовлетворяющее условиям
(5.23), (5.24), определяется из решения задачи линейного программирова-
ния (см. разд. 5.1 и разд. 2.2)
min
z
,
(5.25)
(x)
kTk
fdz
(x)
kTk
i
g
dz
,
a
iI
,
1
k
jd,
1,...,
j
n
.
Если решение z
задачи (5.25) меньше
k
, то для поиска нового воз-
можного направления спуска
1
k
d
полагают
1
k
k
. Если же
k
z
,
то расчет по усмотрению пользователя либо следует закончить, так как в
точке x
k
с точностью до k
выполняются условия минимума в задаче
(5.17), либо продолжить, с целью добиться более высокой точности, поло-
жив
1
k
k
q
,где0
1
q
.
294
Алгоритм
1. Задать 0
, предельное число итераций M , допустимую начальную
точку
0
x
X
, в которой
0
(x) 0
f
.
2. Положить
0
k
.
3. Проверить выполнение условия k M
:
а)еслиk M
расчет закончен;
б)если k M
, перейти к шагу 4.
4. Вычислить (x )
k
i
g
,
1,...,
i
m
.
5. Проверить выполнение условия
(x) 0
k
k
ig
,
1,...,
i
m
.
Сформировать множество a
I индексов i , для которых условие выполне-
но. Если условие выполнено хотя бы для одного
a
iI
, то перейти к шагу
6. В противном случае положить
2
k
k
и повторить вычисления на
шаге 5.
6. Записать систему неравенств
(x)
0
kTk
fd
,
(x)
0
kTk
i
g
d
,
a
iI
.
7. Сформировать задачу линейного программирования:
min
z
,
(x)
kTk
fdz
,
(x)
kTk
i
g
dz
,
a
iI
,
1
k
jd,
1,...,
j
n
.
8. Решить задачу линейного программирования, сформированную на
шаге 7. В результате находится искомое возможное направление спуска
k
dиz
–
минимальное значение z .
9. Вычислить шаг kt , решив задачу
(x
) min
k
k
k
ftd
,
(x
)0
k
k
i
k
g
td
,
1,...,
i
m
;
либо из соотношения (5.22), для чего следует:
а) найти величину kt
из условия
0
(x
)min(x
)
k
k
k
k
k
k
k
t
ftd
ftd
;
б) определить величину
i
kt , 1,...,
i
m
из условий (x
x)0
k
k
i
k
g
t
,
0
kt (если условие (x
x)0
k
k
i
k
g
t
выполняется только при
0
kt,то
295
i
kt не вычисляется). Если в точке x
k
ограничение с номером i активно и
0
kt , то значение
i
kt не вычисляется;
в) найти
min{ }
i
k
k
i
t
t
;
г) вычислить значение
min{;}
k
kk
t
tt
.
10. Найти точку
1
x
x
k
k
k
ktd
.
11. Вычислить величину
1
(x)
k
f
.
12. Проверить условие окончания:
а) если
k
z
, то расчет может быть либо закончен, если точ-
ность k
удовлетворительна, либо продолжен при
1
k
k
q
,0
1
q
.В
первом случае
1
x
k
–
искомое приближенное решение задачи (5.17), во
втором – следует перейти к шагу 3;
б) если
k
z
, то положить
1
k
k
,
1
k k иперейтикшагу3.
Замечания 5.7
1. Если задача (5.17) не является задачей выпуклого программирова-
ния, в которой не все функции (x)
f,(x)0
i
g,1,..,
i
m
выпуклые, то
алгоритм Зойтендейка сходится к точке x
, удовлетворяющей с точно-
стью k
необходимым условиям минимума функции многих переменных
при ограничениях типа неравенств (см. разд. 1.4) [20] . Следовательно, в
точке x
должны быть проверены достаточные условия минимума.
2. Если задача (5.17) – задача выпуклого программирования и ее мно-
жество допустимых решений
{x| x
,
(x) 0, 1,..,
}
n
i
X
Rg
i
m
имеет
внутренние точки, то найденная по алгоритму Зойтендейка точка x
есть
решение задачи (5.17) [20].
3. Скорость сходимости алгоритма Зойтендейка оценивается как низ-
кая по числу итераций [20].
Пример 5.11
Найти минимум в задаче
2
2
1
2
(x)(4)(5)min
f
x
x
,
1
1
2
(x)
10
g
xx
,
2
1
(x)
0
g
x
,
3
2
(x)
0
g
x
.
296
Решение
.
1 Задаем
0
x
(0; 0.95)T
,
0
(x) 0
f
;00.02
;
10
M
.
.
2 Полагаем
0
k
.
0
.
3 Проверяем условие k M
:
0
10
k
M
.
0
.
4 Вычисляем
0
1(x ) 0.05
g
;
0
2(x) 0
g
;
0
3(x ) 0.95
g
.
0
.
5 Проверяем выполнение условия
(x) 0
k
k
ig
, 1,...,
i
m
:
0
1
0
(x ) 0.05
0.02
g
,
0
2(x) 0
g
,
0
3
0
(x ) 0.95
0.02
g
.
Активным является ограничение 2
1
(x)
0
g
x
,2
a
i
I
.
0
.
6 Записываем систему неравенств:
0
0
(x)
0
T
fd
,
0
0
2(x )
0
T
g
d
.
Имеем
0
(x)(8; 8.1)T
f
;
0
2(x) ( 1;0)T
g
и
0
0
1
2
88.10
d
d
,
0
10
d
.
0
.
7 Записываем задачу линейного программирования
min
z
,
0
0
1
2
8 8.1
d
dz
,
0
1
dz
,
0
1
||1
d,
0
2
||1
d.
0
.
8 Решаем задачу линейного программирования. Для этого приво-
дим ее к каноническому виду (см. разд. 2.2), вводя следующие обозначе-
ния:
0
1
1
2
dxx
;0
2
3
4
dxx
;
5
6
zx
x
;1
6
,...,
0
x
x.
Имеем
5
6
min
xx
,
1
2
3
4
5
6
7
888.18.1
0
x
x
x
xxxx
,
1
2
3
4
5
6
8
00
0
xx
x
xxxx
,
1
2
3
4
5
6
9
0000
1
xx
x
x
x
xx
,
1
2
3
4
5
6
10
0000
1
xx
x
x
x
xx
,
1
2
3
4
5
6
11
00
00
1
x
x
xx
x
xx
,
1
2
3
4
5
6
12
00
00
1
x
xxx
x
xx
,
0
jx,
1,...,12
j
.
297
Решение задачи линейного программирования с использованием сим-
плекс-метода (см. разд. 2.2) имеет вид 1 1
x;20
x;31
x;40
x;
50
x;61
x;715.1
x
;80
x;90
x;102
x;110
x;122
x
. По-
этому
0
11
d;
0
21
d;
1
z
.
0
.
9 Вычислим шаг 0t из условия (5.22). Имеем
а)
0
0
2
2
0
0
0
(x
)(4)( 4.05) min
ftd
t
t
,
0
0
0
2(4)2(4.05)0
df
t
t
dt
; 0 4.025
t
;
2
2
0
40
df
dt
;
б)
0
0
1
0
0
0
(x
) 0.95
10
g
td
t
t
,
00
t;1
0 0.025
t
;
0
0
2
0
0
(x
)
0
g
td
t
,
00
t ; поскольку второе ограничение
активно и 0 0
t , величина
2
0t не вычисляется;
0
0
3
0
0
(x
)(0.95)0
g
td
t
,
00
t ; так как равенство вы-
полняется только при 0
0.95 0
t
, величина
3
0t не вычисляется;
в)0
0
min{ } 0.025
i
i
t
t
;
г)0
00
min{ , } 0.025
t
tt
.
0
.
10 Находим точку
1
0
0
x
x
(1;1)T
t
:
1
x
(0; 0.95) 0.025 (1;1) (0.025; 0.975)
T
T
T
.
0
.
11 Вычисляем
1
(x)
f:
1
0
(x) 31.8 32.4 (x)
f
f
.
0
.
12 Проверяем условие окончания. Так как
0
1
0.02
z
,
полагаем
11
kk
,1
0
и переходим к шагу 3.
1
.
3 Проверяем условие k M
:
10
kM
.
1
.
4 Вычисляем
1
1(x) 0
g
;
1
2(x) 0.025
g
;
1
3(x ) 0.975
g
.
1
.
5 Проверяем выполнение условия
(x) 0
k
k
ig
, 1,...,
i
m
:
0
0
1(x) 0
g
,
1
2
0
(x)
g
,
1
3
0
(x)
g
. Активным является ограниче-
ние
1
1
1
2
(x)
10
g
xx
,
1a
i
I
.
1
.
6 Записываем систему неравенств:
1
1
(x)
0
T
fd
,
1
1
2(x)
0
T
g
d
.
Имеем
1
(x ) ( 7.95; 8.05)T
f
;
1
1(x ) (1;1)T
g
и
298
1
1
1
2
7.95 8.05 0
d
d
,
1
1
1
10
dd
.
1
.
7 Записываем задачу линейного программирования
min
z
,
1
1
1
2
7.95 8 .05
d
dz
,
1
1
1
1
ddz
,
1
1
||1
d,
1
2
||1
d.
1
.
8 Решаем задачу линейного программирования. Для этого прив о-
дим ее к каноническому виду (см. разд. 2.2), вводя следующие обозначе-
ния:
1
1
1
2
dxx
;1
2
3
4
dxx
;
5
6
zx
x
;1
6
,...,
0
x
x.
Имеем
5
6
min
xx
,
1
2
3
4
5
6
7
7.95 7.95 8.05 8.05
0
x
x
x
xxx
x
,
1
2
3
4
5
6
80
xxxxxxx
,
1
2
3
4
5
6
9
0000
1
xx
x
x
x
x
x
,
1
2
3
4
5
6
10
0000
1
xx
x
x
x
xx
,
1
2
3
4
5
6
11
00
00
1
x
xxx
x
xx
,
1
2
3
4
5
6
12
00
00
1
x
x
xx
x
xx
,
0
jx,
1,...,12
j
.
Решение задачи линейного программирования с использованием сим-
плекс-метода (см. разд. 2.2): 1 0
x;21
x;30.99
x
;40
x;50
x;
6 0.01
x
;70
x;80
x;90
x;102
x;111.99
x
; 12 0.01
x
.
По-
этому
1
1
1
d ;
1
2 0.99
d
;
0.01
z
.
1
.
9 Вычислим шаг 1t из условия (5.22). Имеем
а)
1
1
2
2
1
1
1
(x
) ( 3.975) (0.99 4.025) min
ftd
t
t
,
1
1
1
2( 3.975) 2(0.99 4.025) 0
df
t
t
dt
;т.к. 1 0
t
, то величина 1t
не
вычисляется;
б)
1
1
1
0
1
1
(x
) 0.025
0.975 0.99 1 0
g
td
t
t
;1
10
t
–
по-
скольку первое ограничение активно, то в вычислениях не используется;
1
1
2
1
1
(x
) 0.025
0
g
td
t
,т.к.10
t,то
2
1 0.025
t
;
299
1
1
3
1
1
(x
) 0.975 0.99 0
g
td
t
,таккак10
t , то величина
3
1t не вычисляется;
в)1
1
min{ } 0.025
i
i
t
t
;
г)1
11
min{ , } 0.025
t
tt
.
1
.
10 Находим точку
2
1
1
x
x
( 1; 0.99)T
t
:
2
x
(0.025; 0.975) 0.025 ( 1; 0.99) (0; 0.99975)
T
T
T
.
1
.
11 Вычисляем
2
(x)
f:
2
0
(x) 32 32.4 (x)
f
f
.
1
.
12 Проверяем условие окончания. Так как
0
0.01
z
, то рас-
чет окончен, точка
2
x есть найденное приближение точки x
(0; 1)T
.
Задачи для самостоятельного решения
1. Методом штрафных функций решить задачу
2
1
2
2
(x)
24
max
fxxx
,
1
2
326
x
x
.
Ответ: в точке x
( 2.556; 0.833)T
–
условный максимум.
2. Методом штрафных функций решить задачу
2
1
1
2
(x)48
3 max
f
x
xx
,
1
22
xx
.
Ответ: в точке x
( 1.125; 0.875)T
–
условный максимум.
3. Методом штрафных функций решить задачу
2
2
1
1
2
2
(x)44
85min
f
x
xx
x
,
1
2
2
6
xx
.
Ответ: в точке x
(2.25; 1.5)T
–
условный минимум.
4. Методом штрафных функций решить задачу
2
2
1
2
(x)( 4)( 4) extr
f
x
x
,
1
2
2
2
xx
,10
x,20
x.
Ответ: в точке x
(0; 4)T
–
условный минимум, усл овного макси-
мума нет.
300
5. Методом барьерных функций решить задачу
3
1
2
1
(x)(1)
min
3
f
x
x
,
110
x
,
20
x.
Ответ: в точке x
(1; 0)T
–
условный минимум.
6. Методом барьерных функций решить задачу
1
2
1
2
49
(x)
min
f
xx
xx
,
1
26
xx
,10
x,20
x.
Ответ: в точке x
(2; 3)T
–
условный минимум.
7. Методом множителей решить задачу
2
()
4 min
fxxx
,
1()
10
gxx
. Точность
0.001
.
Ответ:
4
1000
r
,
4
1.997
,
44
1
( , ) 1.0000029
x
x
r
,
()3
fx
.
8. Методом множителей решить задачу
2
2
1
2
(x)
min
fxx
,
1
1
(x)
10
g
x
,
2
1
2
(x)
20
g
xx
. Точность
0.001
.
Ответ:
4
1000
r
,
4
1.999
,
4
0
444
111
(,,)0.999
x
r
,
444
211
(,,)0
x
r
,
(x ) 0.999
f
.
9. Методом множителей решить задачу
2
(x)
4 min
fxx
,
10
x
.
Ответ:
4
k
,
1000
k
r
,
1.997
k
,
( , ) 1.0000029
kk
x
r
.
Точное решение
1
x
,
()3
fx
.
10. Методом проекции градиента решить задачу
2
2
1
12
2
(x)34
5
min
f
x
xx
x
,
1
24
xx
,10
x,20
x.
Ответ: точное решение x
(3; 1)T
.
11. Методом проекции градиента решить задачу
301
2
2
1
2
(x)(4)(2)min
f
x
x
,
1
23
xx
,1
2
24
x
x
,10
x,20
x.
Ответ: точное решение x
(2.5; 0.5)T
.
12. Методом проекции градиента решить задачу
1
2
(x)
min
f
xx
,
2
2
1
225
x
x
.
Ответ: точное решение x
(2.5 2; 2.5 2)T
.
13. Методом Зойтендейка решить задачу
2
2
1
2
(x)(4)(5)min
f
x
x
,
1
21
xx
,10
x,20
x.
Ответ: 1x (0.025; 0.975)T
,
1
()31.8
fx
.
Точное решение
x
(0; 1)T
,
()32
fx
.
14. Методом Зойтендейка решить задачу
2
2
1
12
2
(x)34
5
min
f
x
xx
x
,
1
24
xx
,10
x,20
x.
Ответ: Точное решение x
(3; 1)T
,
()44
fx
.
15. Методом Зойтендейка решить задачу
2
2
1
2
(x)(4)(2)min
f
x
x
,
1
23
xx
,1
2
24
x
x
10
x,20
x.
Ответ: Точное решение x
(2.5; 0.5)T
,
()4.5
fx
.
302
ЛИТЕРАТУРА
1. Абрамов Л. М., Капустин В. Ф. Математическое программирова-
ние. – Л.: Изд-во Ленингр. ун-та, 1981.
2. Акулич И. Л. Математическое программирование в примерах и за-
дачах. - М.: Высшая школа, 1986.
3. Алексеев В. М., Галеев Э. М., Тихомиров В. М . Сборник задач по оп-
тимизации. – М.: Наука, 1984.
4. Аоки М. Введение в методы оптимизации. - М.: Мир, 1977.
5. Базара М., Шетти К. Нелинейное программирование. Теория и ал-
горитмы. – М.: Мир, 1982.
6. Банди Б. Методы оптимизации. Вводный курс. – М.: Радио и связь,
1988.
7. Банди Б. Основы линейного программирования.
–
М.: Радио и
связь, 1989.
8. Бертсекас Д. Условная оптимизация и методы множителей Ла-
гранжа. – М.: Радио и связь, 1987.
9. Васильев Ф.П. Численные методы решения экстремальных задач. –
М.: Наука, 1980.
10. Габасов Р., Кириллова Ф. М . Методы оптимизации. – Минск: Изд-
во БГУ, 1981.
11. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация.
–
М.:
Мир, 1985.
12. Деордица Ю. С., Нефёдов Ю. М. Исследование операций в плани-
ровании и управлении. – Киев: Вища шк., 1991.
13. Дэннис Дж., Шнабель Р. Численные методы безусловной оптими-
зации и решения нелинейных уравнений. – М.: Мир, 1988.
14. Евтушенко Ю.Г . Методы решения экстремальных задач и их при-
менение в системах оптимизации. – М.: Наука, 1982.
15. Зайченко Ю. П. Исследование операций. – К.: Вища шк., 1988.
16. Зуховицкий С. И., Авдеева Л. И. Линейное и выпуклое программи-
рование. – М.: Наука, 1964.
17. Карманов В.Г . Математическое программирование. – М.: Наука,
1975.
18. Ляшенко И. Н. и др. Линейное и нелинейное программирование. –
Киев: Вища шк., 1975.
303
19. Мину М. Математическое программирование. Теория и алгорит-
мы. - М.: Наука, 1990.
20. Моисеев Н. Н., Иванилов Ю. П., Столярова Е. М. Методы оптими-
зации. – М.: Наука, 1978.
21. Мухачева Э. А. , Рубинштейн Г. Ш. Математическое программиро-
вание. – Новосибирск: Наука, 1987.
22. Нефёдов Ю. М. Методы оптимизации: Учеб. пос. – Л уганск: Изд.
ВНУ им. В. Даля, 2004.
23. Нефёдов Ю. М., Таращанский М. Т. Сборник примеров и задач по
математическому программированию: Учеб. рос. – Л уганск: Изд. ВНУ им.
В. Даля, 2002.
24. Пшеничный Б. И., Данилин Ю. М . Численные методы в экстре-
мальных задачах. – М.: Наука, 1975.
25. Поляк Б.Т. Введение в оптимизацию. – М.: Наука , 1983.
26. Реклейтис Г., Рейвиндран А.; Рэгсдел К. Оптимизация в технике.
Т.1и2,в2-хт. – М.:Мир,1986.
27. Сборник задач по математике для втузов. Методы оптимизации.
Уравнения в частных производных. Интегральные уравнения / Под ред.
А.В. Ефимова. – М.: Наука, 1990.
28. Сергиенко И. В. Математические модели и методы решения задач
дискретной оптимизации. – Киев: Наук. думка, 1985.
29. Сухарев А. Г., Тимохов А. В., Федоров В. В . Курс методов оптими-
зации. – М.: Наука, 1986.
30. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Мето-
ды последовательной безусловной минимизации. – М.: Мир, 1972.
31. Химмельблау Д. Прикладное нелинейное программирование. – М.:
Мир, 1975.
32. Численные методы условной оптимизации / Под ред. Ф. Гилла, У;
Мюррея. – М.: Мир, 1977.
304
Навчальне видання
НЕФЬОДОВ ЮРІЙ МИХАЙЛОВИЧ
БАЛИЦЬКА ТЕТЯНА ЮРІЇВНА
МЕТОДИ ОПТИМІЗАЦІЇ
ПРАКТИКУМ
російською мовою
Навчальний посібник
Редактор
З. І . Андронова
Техн. редактор
Т. М. Дроговоз
Оригінал-макет
Т. Ю. Балицька
Підписано д о друку 10.04 .2006
Формат 60х84 1/16. Папір типограф. Гарнітура Times.
Друк лазерний. Умов. друк. арк. 17,67.
Тираж 300 екз. Ціна договірна
Видавництво НЦППРК “Ноулідж”
91050, м. Луганськ, кв. Комарова, 76