Текст
в
В. В. Амелькин
Т. и. Рабuевич
В. л. Тимохович
ШКОЛЬНАЯ
rEОМЕТРИЯ
L..
r-
в ЧЕРТЕЖАХ
И ФОРМУЛАХ
11
!
++
.иС
d:..4:'
%-"'- [ С I
...
. ....
,
,., i';'I.
_...
11111111111111 11 Sеаи 4
В. В. Амелькин
Т. и. Рабцевич
В. л. Тимохович
в ЧЕРТЕЖАХ
И ФОРМУЛАХ
в
<. ....: - . ...... .
.
.>::"/-" -.:.-:." :."......:
." " fl/JКО
ЬНАfilrЕОМЕrрц9. ..... __
;
!f
:
:'
::.
y
. ",,,,.-'
МИНСК
«Красико"Принт»
2008
Sea_
УДК 514.112 (075.3)
ББК 22.151.0я721
А61
р е Ц е н з е н т канд. физ.
мат. наук, доц. каф. rеометрии,
тополоrии и методики преподавания математики Бrу
с. r. Кононов
Амелькин, В. В.
А61 Школьная rеометрия в чертежах и формулах I
В. В. Амелькин, Т. и. Рабцевич, В. л. Тимохович.
Минск:
Красико
Принт, 2008.
80 с.
ISBN 978
985405464
3.
Пособие содержит тщательно отобранный и систематизирован
ный теоретический материал, который поможет учащимся не только
yrлубить свои знания, про верить и закрепить практические навыки
при систематическом изучении rеометрии, но и предоставляет xopo
шую возможность для эффективной подrотовки как к выпускному и
конкурсному экзаменам, так и к централизованному тестированию.
Предназначено школьникам, абитуриентам, учителям.
УДК 514.112 (075.3)
ББК 22.151.0я721
ISBN 978-985-405-464-3
@ Амелькин В. В., Рабцевич Т. Н.,
Тимохович В. Л., 2008.
@ Оформление
ИООО «Красико
Принт», 2008
Sea_
СОДЕРЖАНИЕ
][[)J
II
()IJII
...............................................................................
()lIlIl»le ()(i():lII
..
III1I1............................................................. ()
JlJl
II
JL. ][[JI
III1
e1r]JIIII..............................................................
Свойства yrлов И параллельных пряМых..........................
Свойства произвольноrо треyrольника ............................ 9
Свойства равнобедренноrо треyrольника ...................... 10
Свойства прямоyrольноrо треyrольника........................ 11
Равенство треyrольников .... ...... .... ... ..................... ........... 12
од()бие треyr()ЛI>НИК()В ................................................... 1
ропорциональные отрезки...... .................................... ... 1
ОКРУЖНОСТI>. Свойства хорд и yrлов............................... 17
ОКРУЖНОСTh. Касательная, касательные
и хорды, касательные и секущие..................................... 19
1\IIедиаIIJ>I ............................................................................ 20
BI>IC()TI>I............................................................................... 2
I>lfccelC1r}JlfCI>I ...................................................................... 2
Треyrольник. Вписанные, описанные
и вневписанные окружности.. .......... ........ ....................... 2
ар
ел()
аММ................................................................
2
ТрапецliJl............................................................................
Равн()б()l{ная трапеция......................................................
7
Вписанный четырехyrольник..........................................
писанная трапеЦIiJI .........................................................
1
писанный пар
елоrpамм.. ..........................................
1
Описанный чeThIрехyrольник..........................................
1
ОписаннаJl трапеция .........................................................
2
ОписаННI>IЙ . пар
ел()
амм...........................................
роизвольный ЧeThIрехyrольник ....................................
ll
yr()лl>ник .........................................................................
()
равlfJIl>нl>Iй ll
yr()лl>ник...................................................
7
]ElписаННI>IЙ ll
yr()JIl>ник.....................................................
7
ОписаНIII>IЙ ll
yr()JIl>lIик.........I...........................................
з
Seee_
()
(lДI> 1r}Je){lr()JII>IIIf]((l .....................................................LJ
()
(lдl> lle1rI>II>e){)f1l()JII>IIIfIC(l.............................................
()
(lДI> 1r}J(lIIe
IfIf.............................................................
()ll{(lдl> П(l}J(lJIJIеJI()
(lJVIJVI(l...............................................
ПЛОll{(lДI> описанноrо П
){lrольника ... ............ ....... .............
Площадь ПI>авильноrо п
yrольника .. ........ .... ............... ....
6
rрадусная и радианная меры )(lrла.
)C(JII1II(l дуrl1 .........................................................................
6
JI()щ(lДI> c;e}(1r()I>(l ...............................................................
()
л()
(lдl> c;erJVIelI1r(l .............................................................
6
Соотношения JVlежду площадяJVIИ фиryIJ..........................
7
JI
IJ
. c=:1reJJe()
1rJJIISI.............................................................()
араллелl>ные прямые, плоскости, ПРЯJVI(lЯ
11 IIJI()c;}()c;1r1> ........................................................................6
}J()еК
l1я ПЛ()С;}()11 фИryIJl>I ...............................................6
ПеРIIеНДИICулярные ПЛОС;КОС;ТI1, IIрЯJVIая
и ПЛ()С;}()С;1r1> ........................................................................6:J
()c;IC()c;1rI>, ПрЯJVI(lЯ If сфеI>(l...............................................6LJ
ПIf}J(lJVIlfд(l............................................................................()
П}JИ:JIv.[(l. П(lI>(LJIл
леIIIfIIеД..................................................()
П}J(lIJИЛl>lII>Iе Iv.[II()r()
(llIlIl1}(If.............................................()
IJLI(lp .....................................................................................71
ПраlJильная ПИР(lМИД(l, IJIIисаННЫI1
If ()IIl1c;(lllIII>II1 Ш(lРI>I ............................................................ 7
IfJIlfндр.............................................................................. 7LJ
K()lIYc; .................................................................................. 7
}Je){
(lllllI>Iii ){lr()JI..............................................................77
ЛIl1rе JJ а ryP
............................................................................................ 79
4
Seee_
ПРЕДИСЛОВИЕ
в этой небольшой книжке, кoroрую мыI предлaraeм читате.то,
приведены в чертежах и формулах основные reОМeIpические свойства
и coornошения IШОСКИХ и пространствеЮIЫХ фшур.
Цель, ПocтaRЛеlПIая авторами,
рассказать о школьном курсе
reoмeIpИИ по возможнОС1И исчерпывающе и систематизировано, но
коротко и ясно.
Решение тобой rеомeIpИЧеской задачи начинается с построения
чертежа. Правильно вьmолненный чертеж
это уже шar к решению
задачи, и поэтому к построению чертежа нужно ОТНОСИIЪся серьезно.
принятыIe в пособии обозначения помоJYf читаreто не только
правильно и быстро Bьтoтrnть чертеж, но и системаrnзировать YCBO
еШlые им фактыI. Исходные данныIe болышmства yrверждеНИЙ в по
собии указаны непосредcrвelШО в чертежах. Позroму дaшIое пособие
поможет читателю научиться <<ЧИraТЬ» чертежи, <qfiRЛекая» из них He
обходимую информaцmo, определяющую дальнеЙШИЙ ХОД решения.
Несмmpя на небольшой объем, книжка может быть использова
на yчиreлем при состаRЛении заданий для самостоятельной работы
учащихся с последующим КОН1рОлем учителя.
Возможно ее использование как зада'llIИКa для работы в классе и
.....
для домашних задании.
Эro пособие подходит и в качестве материала для повторения,
параллельноro изучению дрyrиx reM в llIКоле, а таюке в Kat.1ecтвe спра
ВО'llIИКa.
Авторы уверены в том, что приведеЮlые в книжке сведения по
зволят каждому усвоившему их llIКольнику, а заreм и абитуриеmy,
успеIШIО pennrrь reОМeIpические задачи как IllКольноro и KOнкypcHO
ro экзаменов по маreматике, так и rеОМeIpические задачи цеmpализо
вaшIОro тестирования.
Мы блaroдарны доцету с. r. Кононову за КОНС1рyкIИВные за
мечания и рекомендации по улучшению пособия.
В. В. Амелъкин
Т. и. Рабцевич
В. л. Тимохович
5
Seee_
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Если АВС
1реyroлышк, то ниже используются следующие
обозначения:
а=ВС, Ь=АС, с=АВ
Длинысторон(илипростоcroроны);
а = LCAВ, (3 = LЛВС, У = LВCA АВ
величиныI yrлов (или
просто yrлы);
ha, h b , hc
высоты, опущенные соответственно из верIШfН А, В,
С на стороны а, Ь, с (ИJШ их продолжения);
та, ть, те
медианы, проведенные соответственно из верпmн
А, В, С к сторонам а, Ь, с;
la, lIJ., lc
биссеюрисы, проведенные соответственно из вершин
А, В, С к сторонам а, Ь, с;
La, 4, 4:
внешние биссеюрисы, проведеШlые cooтвercтвeннo
из вершин А, В, С на продолжение сторон а, Ь, с;
T
радиус вписанной окружнocrn;
1
точка пересечения биссеюрис, ЯШIЯЮщаяся центром вписан
ной окружнocm (mщеmp);
"
т й"' Ть-, Те
радиусы вневписанных окружнocreи, касающихся
соответственно сторон а, Ь, с и продолжеНИЙ двух дрyrиx сторон;
lа, lь, lе
цетры вневписанных окружностей, КacaIOщихся co
oтвercтвeннo сторон а, Ь, с и продолжеНИЙ двух дрyrиx сторон;
R и О
радиус и cooтвercтвeннo цетр описанной окружнocrn;
М
ТОчка пересечения медиан (центроид, цетр масс);
Н
точка пересечения высот или их продолжеНИЙ (ортоцетр
или внеIШIИЙ ортоцеIПp);
( а+ь+с )
р
полупериме1р 1реyroльникa р == 2 ;
Pa=p
a, pь=p
b, pc=p
c;
S (SМEc)
ШIощадъ 1реyrольника.
Теперь о некоторых соrлашениях. В пособии мноmе свойства
reoме1рИЧеских фитур нумеруются с буквой Х (например, свойство
4Х). Эro означает, что такие свойства ЯШIЯЮТCЯ характеристическими,
6
Seee_
Т. е. кроме сформулированноro yrвepждения имеет место и yrвержде
ние, обратное приведенному.
Далее. На мноrиx чертежах равные 01резки: отмечaюrcя одина
ковым образом одной ИJШ несколькими черточками (СМ. например,
задачу 14, rде AD = DB, аВЕ =ЕС).
В тех случаях, коrда возможны разночтения (зro случаи пересе
чения равных отрезков дрyrими mpeзками или дyraми), концы paв
ных mpезков обозначаются или жирными точками, ИJШ буквами (см.
например, задачу 155, rде АК = КС, аВЕ =ED).
Теперь о том, как следует читать чертежи. Здесь ПРИIЩИПИальны
два случая. В первом из них информация из раздела <<дано» mpaжена
на чертеже полностью. Тоrда справа от чертежа просто формулирует
ся искомое свойcrвo. Так, например, остановимся на задаче 3. Ее П
чтение следующее: если две прямыIe пересекaюrcя 1:peТI>eЙ прямой и
yrол аl равен yrлу (31, то yrол а2 равен yrлу (32'
Во втором случае информация из раздела «дано» mpажена на
чертеже чacrnчно. Тоrда недостающая информация дается справа от
чертежа после слова «если» до слова <<1'0». Так, например, за.цача 5Х
читается следующим образом: если две прямые а и Ь пересекaюrcя
1:peТI>eЙ прямой и если а 11 Ь, то yroл а равен yrлу J3. Имеет мecro и
обраrnое yrверждение (задача с буквой Х): если две прямые а и Ь пе
ресекaюrcя третьей прямой и если yroл а равен yrлу (3, тоа 11 Ь.
7
Seee_
4Х
5Х
6Х
rЛАВА 1.
ТРИЯ
'"
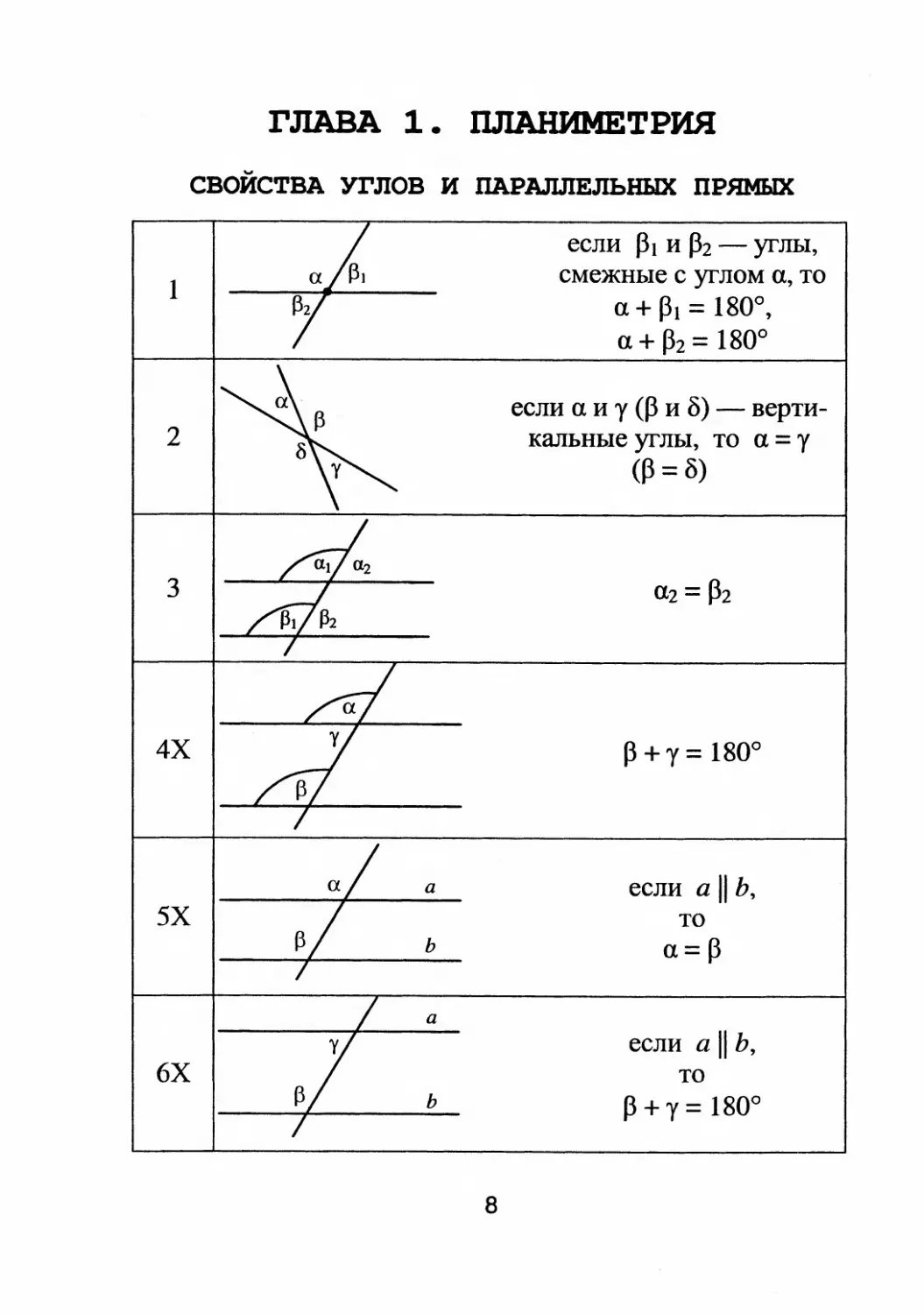
СВОИСТВА уrлов И ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
1
2
3
а
ь
а
ь
если Рl И Р2
yrлы,
смежные с yrлом 0., ТО
О. + Рl = 1800,
о. +
2 = 1800
если о. и у (Р и ь)
верти
кальные yrлы, ТО а = у
(Р = ь)
0.2 = Р2
Р + 'у = 1800
если а 11 Ь,
то
а.=р
если а 11 Ь,
то
р + у = 1800
8
7
8
10
12Х
2 lак. 1133
9
11
d,'
I а
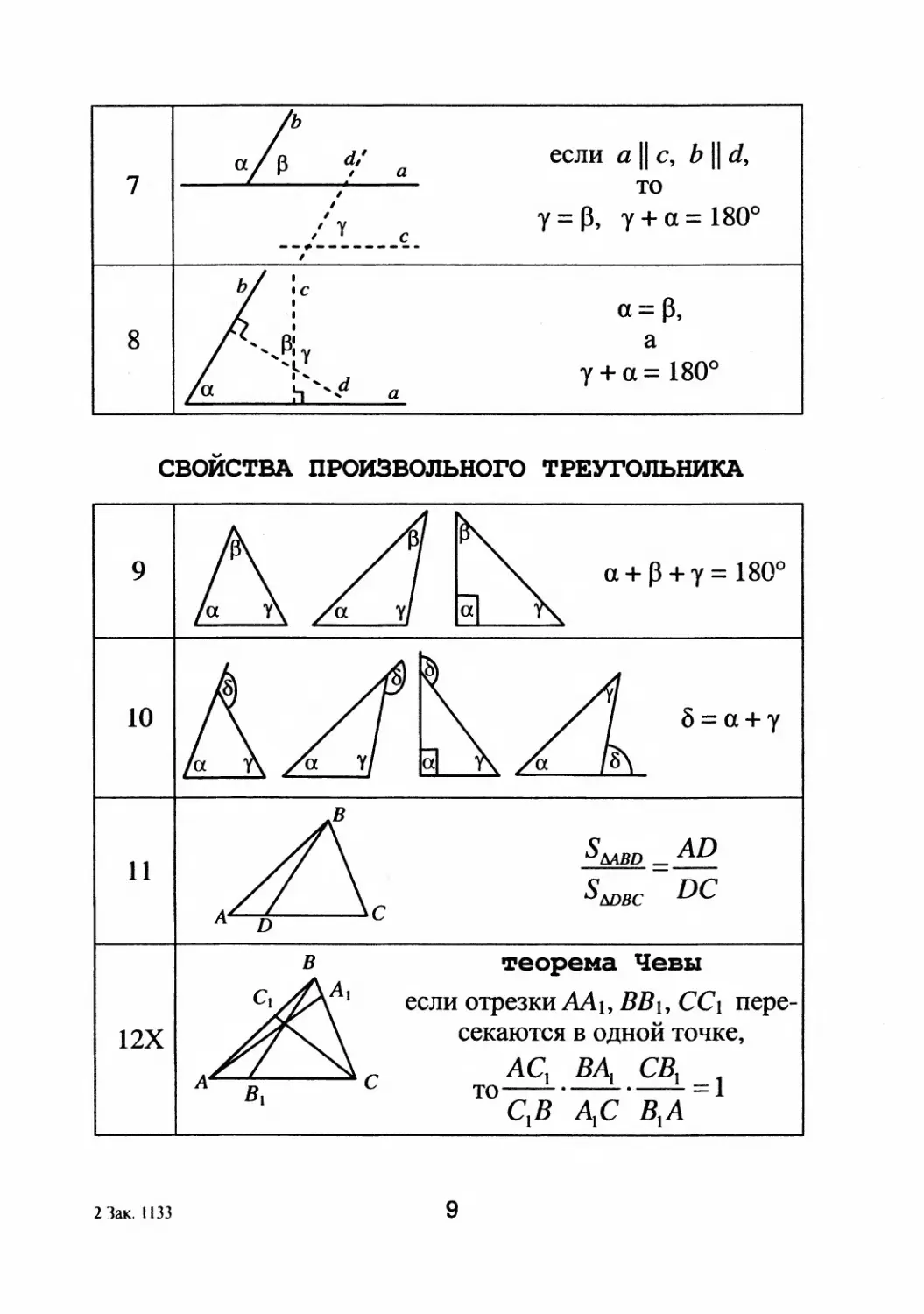
если а 11 с, Ь 11 d,
то
у =
, у + а = 1800
I
I
I
" 'у с
_.-",.--_..-..-
-
I
I
'С
I
I
I
.... А.
.... .... tJ. 'У
.......
1............ d
.... а
а=
,
а
у + а. = 1800
..,
СВОИСТВА пРоизвольноrо ТРЕYrОЛЬНИКА
а. +
+ у = 1800
б=а.+у
А
с
S MBD AD
S МJBC DC
в
'Z'еореиа чевы
если отрезки АА 1 , BB l , CC l пере
секаются в ОДНОИ точке,
С ТО АС! . B
. СВ! = 1
C1B A1C В 1 А
А
BI
9
13Х
14
15
16
в
А
теорема Менепаи
если точка Вl на продолжении
стороны АС является точкой
пересечения прямыхсc и C1A 1 ,
то АС.. B
. Сп. ==1
C1B
C BIA
DE 11 АС,
DE=!AC
2
если DE 11 АС,
то
ID=DA,IE=EC
с
если АС> АВ,
то
13>1
'"
СВОИСТВА РАВНОБЕДРЕнноrо ТРЕYrOЛЬНИКА
17Х
18
с Bl
в
А
с
в
А
А
а=у
А
lb = ть = h b
обратное утверждение:
каждое из трех указанных равенств
означает, что МНС
равнобед
ренный (АВ = ВС)
в
с
10
в
19
та=т е
А
с
в
20
la = le
А
с
в
21Х
если АВ = ЕС, ТО ha = he
А
с
СВОЙСТВА ПРЯМОYrольноrо ТРЕYrОЛЬНИКА
в
22
1
те = R =
с = ОС
2
А
ь
a+b
c
r=
23
2
а
с
24
r MDC + r I:!..CDB + r = he
А
в
D
11
с
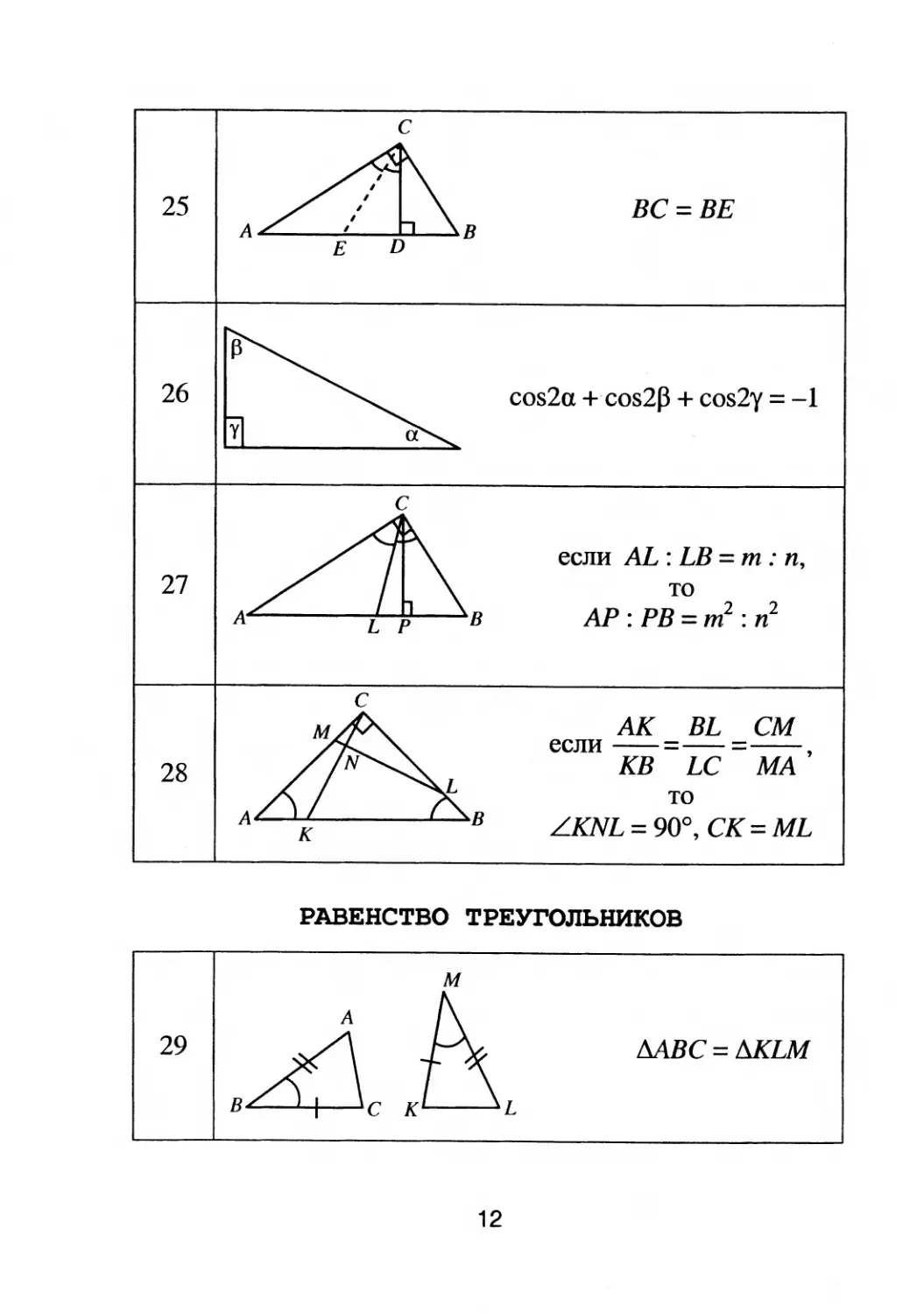
25 ве = ВЕ
А В
Е D
26 cos2a +
cos2p + cos2y =
1
27
28
29
А
с
L Р
в
с
А
к
в
если AL: LB = т : п,
то
АР : РВ = т 2 : п 2
если
АК BL
.....
.....
КВ LC
СМ
МА'
.....
.....
то
LKNL= 900, CK=ML
РАВЕНСТВО ТРЕуrольников
в
м
А
с к
12
МВС = MLM
L
30
31
32
33
34
35
36
в
в
А
в
в
в
в
с
в
А
к
с м
L
МВС = MLM
м
с L
к
МВС =
KLM
L
.
МВС = I:1KLМ
А кТ .
м
к
.
МВС = MLМ
А ML
. ...
?'--... L
к
МВС = MLM
А м А
L
L
МВС = MLМ
А к/ I
M
к
А L
м
МВС = MLM
13
37
38
39
40
41
42
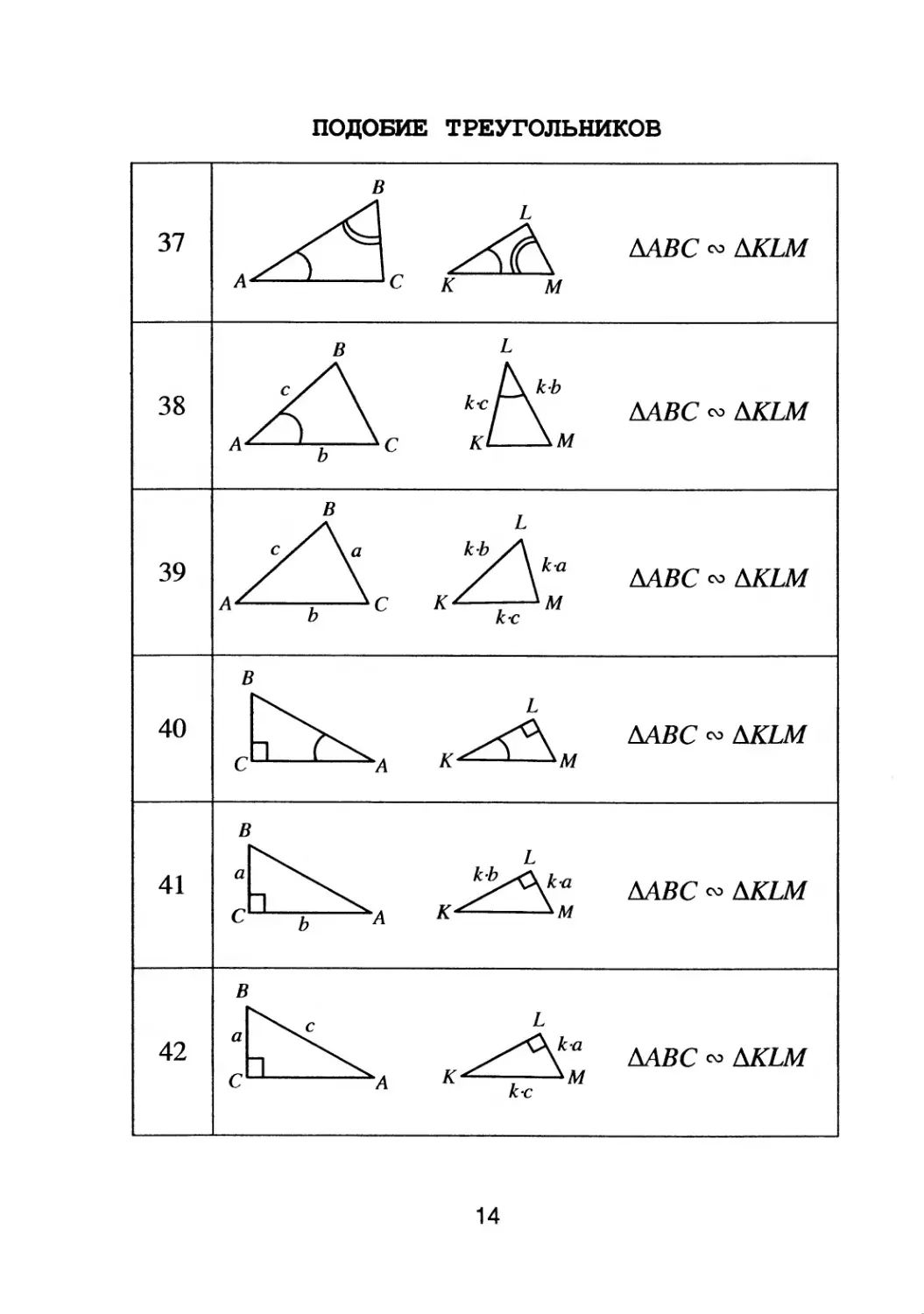
ПОДОБИЕ ТРЕyrольников
А
в
А
в
L
d\
с к м
мв С (\) MLM
L
с
МВС (\) MLM
к
м
А
в L
k.a МВС (\) MLM
с к м
k.c
в
в
а
в
а
с
А
L
K
M
МВС (\) MLM
А
L
к м
МВС (\) MLM
А
L
k
МВС (\) MLM
к k.c М
14
С 1 А 1
\ ,
\ , ,
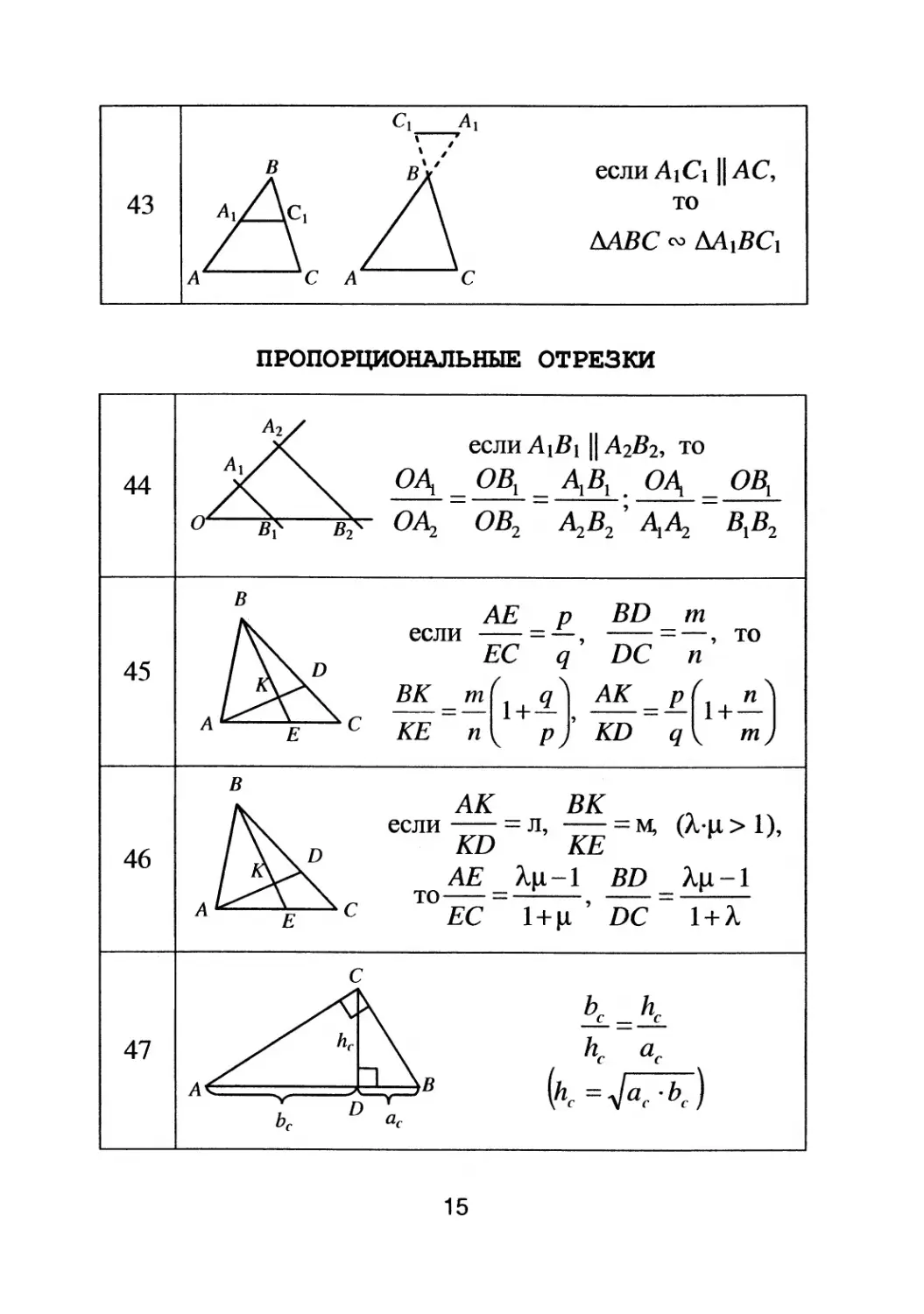
в \ , если A1C11I АС,
в
43 то
МВС ro М}ВС 1
А С А С
ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ
44
если AI B l 11 А2 В 2 , то
O
ОВ} А} В} O
ОВ}
.......... . ..........
,
OAz ОВ 2 AzB2 А}А2 В 1 В 2
о
в АЕ BD
р т
если
ТО
,
,
ЕС q DC п
45
А с ВК = т (l+
, АК =.E.(1+
J
Е КЕ п р KD q т
В
АК ВК (л.J,t> 1),
если = л = М,
KD ' КБ
46
АЕ л,J,t
1 BD ЛJl
1
то
А С , l+л
ЕС 1 + Jl DC
с
А
в
Ь с
hc
hc ас
(hc =
ac 'Ь с )
47
Ь С ас
15
с Ь с
Ь
ас а
48 Ь ,
с а с
А Ь с D ас В (ь=Д, a=h)
с
ас
а 2
49
Ь С Ь 2
А Ь с D ас В
С
50Х b
а
hc
в с а с Ь
А
с
теорема ПифаZ'ора
51Х 2 2 + ь2
с =а
с
в
eopeMa Ван
ОбепR
СК СВ} СА}
52 = + ,
KC 1 В}А А}В
с ВК ВС} ВА} АК АС} АВ}
А В} = + = +
, В.С
КВ} C1A А}С КА} С.В
в
eopeMa ЖерZ'онна
53 КА, + КВ, + КС, =1,
АА} ВВ} СС}
КА КВ КС =2
с + +
В. АА} ВВ} СС}
16
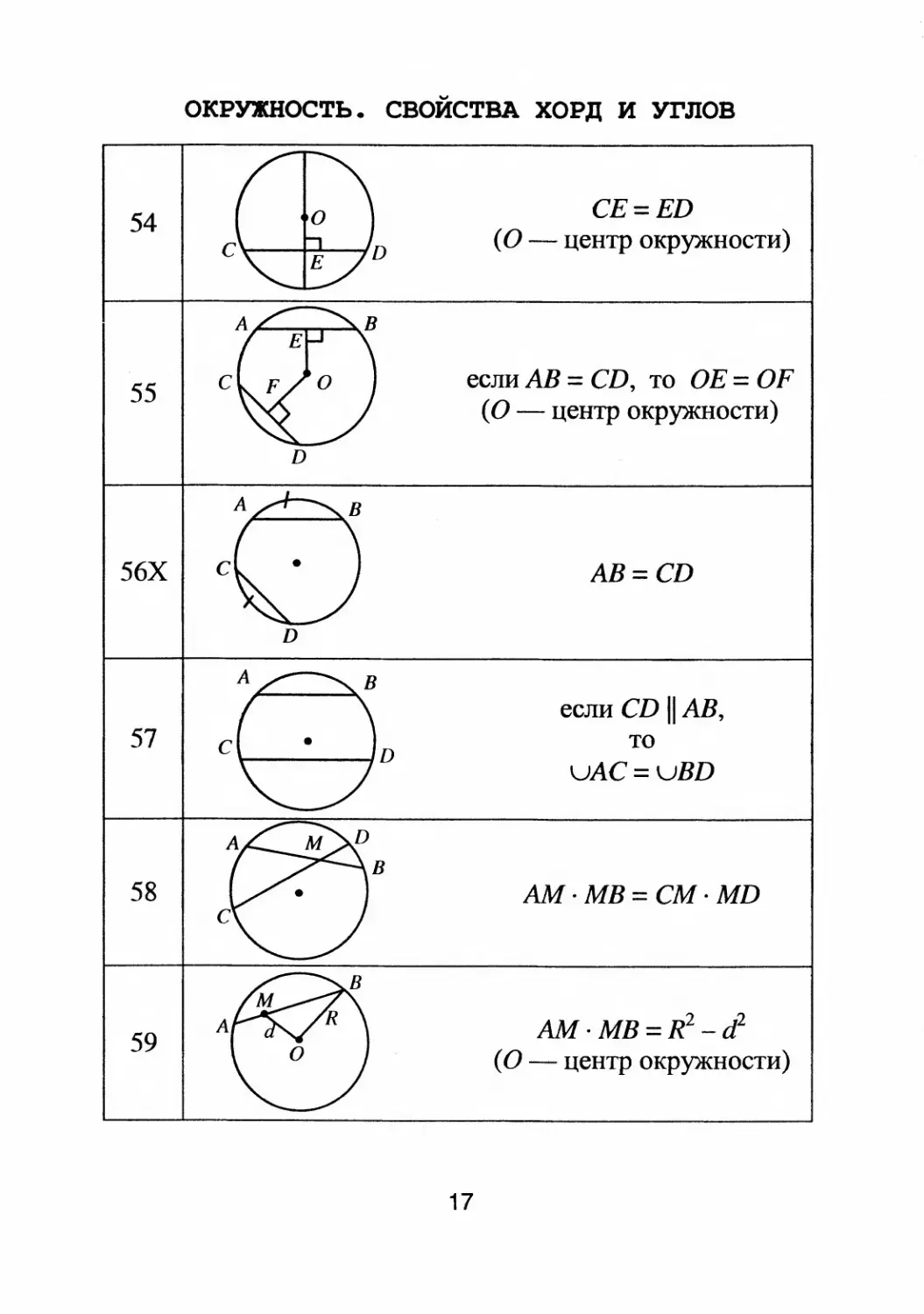
54
55
окружность. СВОЙСТВА ХОРД И ПЛОВ
СЕ = ED
(О
центр окружности)
если АВ = CD, то ОЕ = OF
(О
центр окружности)
с
D
56Х с
57
58
59
АВ = CD
D
D
если CD 11 АВ,
то
uAC = uBD
AМ.MB=CM.MD
АМ . МВ = R 2
d 2
(О
центр окружности)
17
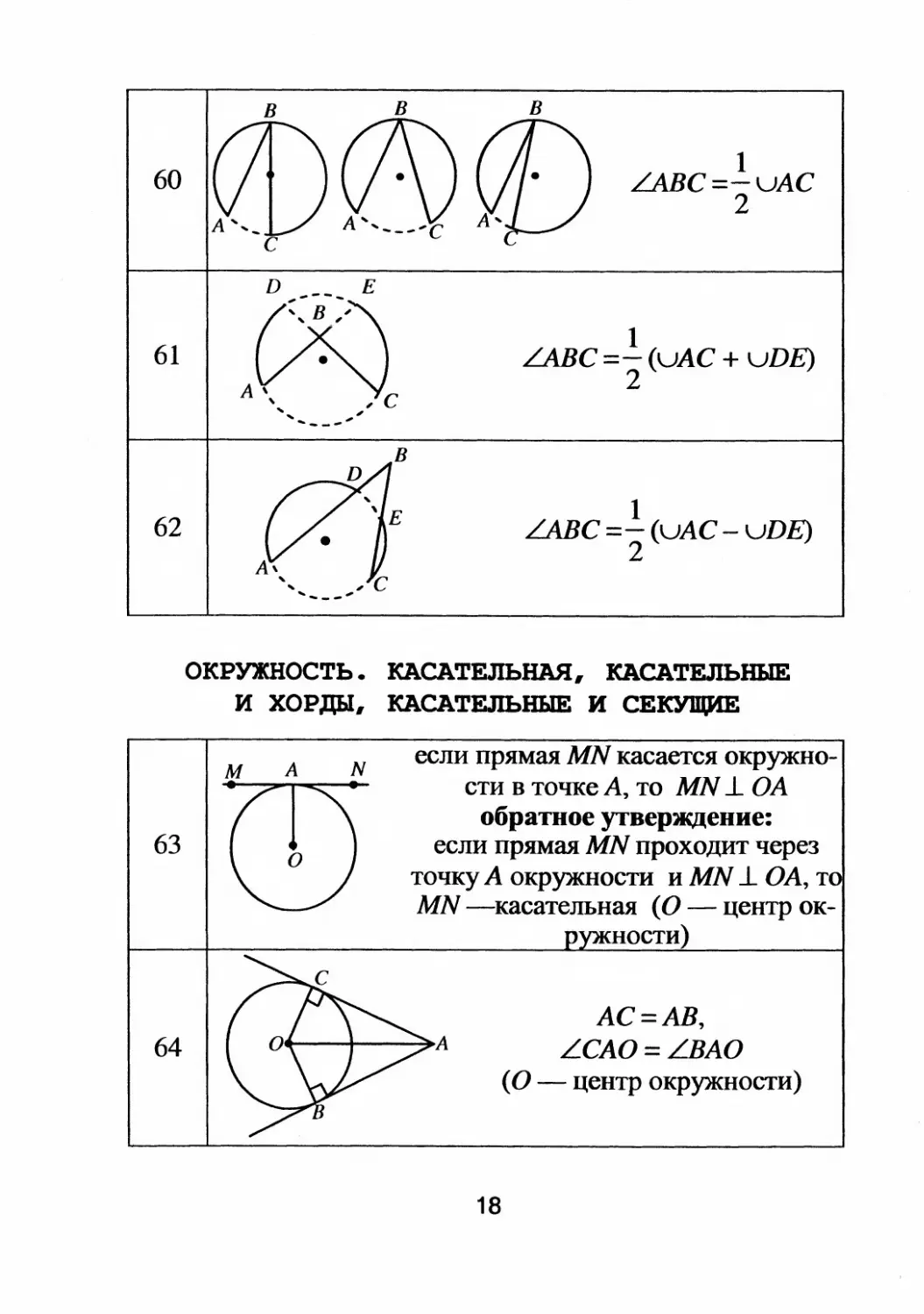
60
61
62
в
в
в
1
LABC=
uAC
2
1
LABC =
(uAC + uDE)
2
1
LAВC =
(uAC
uDE)
2
ОКРУЖНОСТЬ. КАСАТЕЛЬНАЯ, КАСАТЕЛЬНЫЕ
И xopды, КАСАТЕЛЬНЫЕ И СЕКУЩИЕ
63
64
если прямая MN касается окружно
сти В точке А, то MN
ОА
обратное утверждение:
если прямая MN проходит через
точку А окружности и MN
ОА, т
MN
касательная (О
центр OK
ности)
, с
,
..........--'
в
, с
" .,
--.
...
м А
N
А
АС = АВ
,
LCAO = LBAO
(О
центр окружности)
18
Е 1
LВAC=
uAEB
65 F 2 '
1
LBAD =
uAFB
с А D 2
66
67 А
68
69
м
19
МА .мв=мс 2 ,
МА . МВ = [2
R 2
(О
центр окружности)
ОВ 1.. DE
(О
центр окружности)
LBAC = 900
AB=2
R.r
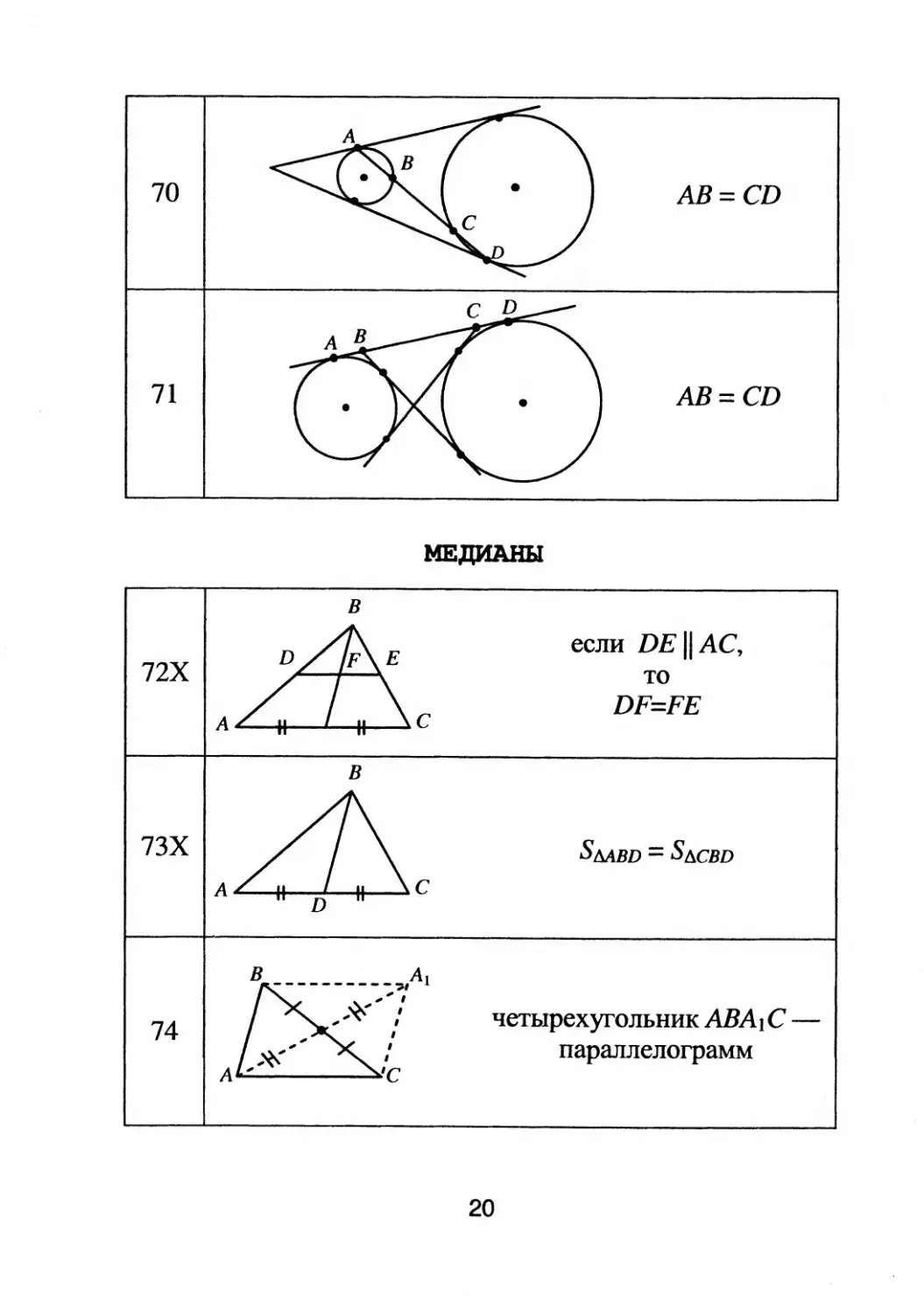
70
71
АВ = CD
с D
АВ = CD
МЕДИАНЫ
в
если DE 11 АС,
72Х то
DF=FE
А с
В
7ЗХ
74
А
с
5MBD = SACBD
в А
..__.......__...._
, 1
"
" ,
" ,
,," ,
,
,
I
'с
четырехyrольник АВА} С
параллелоrpамм
"
"
А ",,
20
75
76Х
77
78
79
в
А
с
медианы треyrольника пере
секаются в одно и точке;
АМ: МА 1 = ВМ: МВ} =
= СМ : МС} = 2 : 1
в
А
с
SMMB = SЫЗМС = SMMC
1 .J 2 2 2 1 .J 2 2 2
т =
2Ь +2с
a т b =
2с +2а
b
а 2 ' 2 '
1 .J 2 2 2
т е =
2а +2Ь
c
2
2
2 2 2 2
2 2 2
а =
-2ть + 2т с
тa , Ь =
-2т с + 2т а
тb ,
3 3
2
2 2 2
c=
2т +2т
т
3 а ь с
с
А
AL BN СК
если = =
LB NC КА'
то точки пересечения медиан
треyrольников АВС и LNK
в совпадают
L
21
80
81
82
83
с
А.
D
в
А
А
в
D
DM 2 =2. (DA 2 + DIf2 + DC)
3
2. (АВ 2 + ВС + СА 2 )
9
(D
произвольная точка
плоскости)
СА 2 + св 2 = 2СЕ. CD
с
если ВР: РЕ = т : п,
то
CD : DB = т : 2п
4
cosLACB =
,
5
1
cosLCAB = cosLCBA = L
""l0
22
84
85
86
высоты
НЬ
С}
}
В}
С}
В}
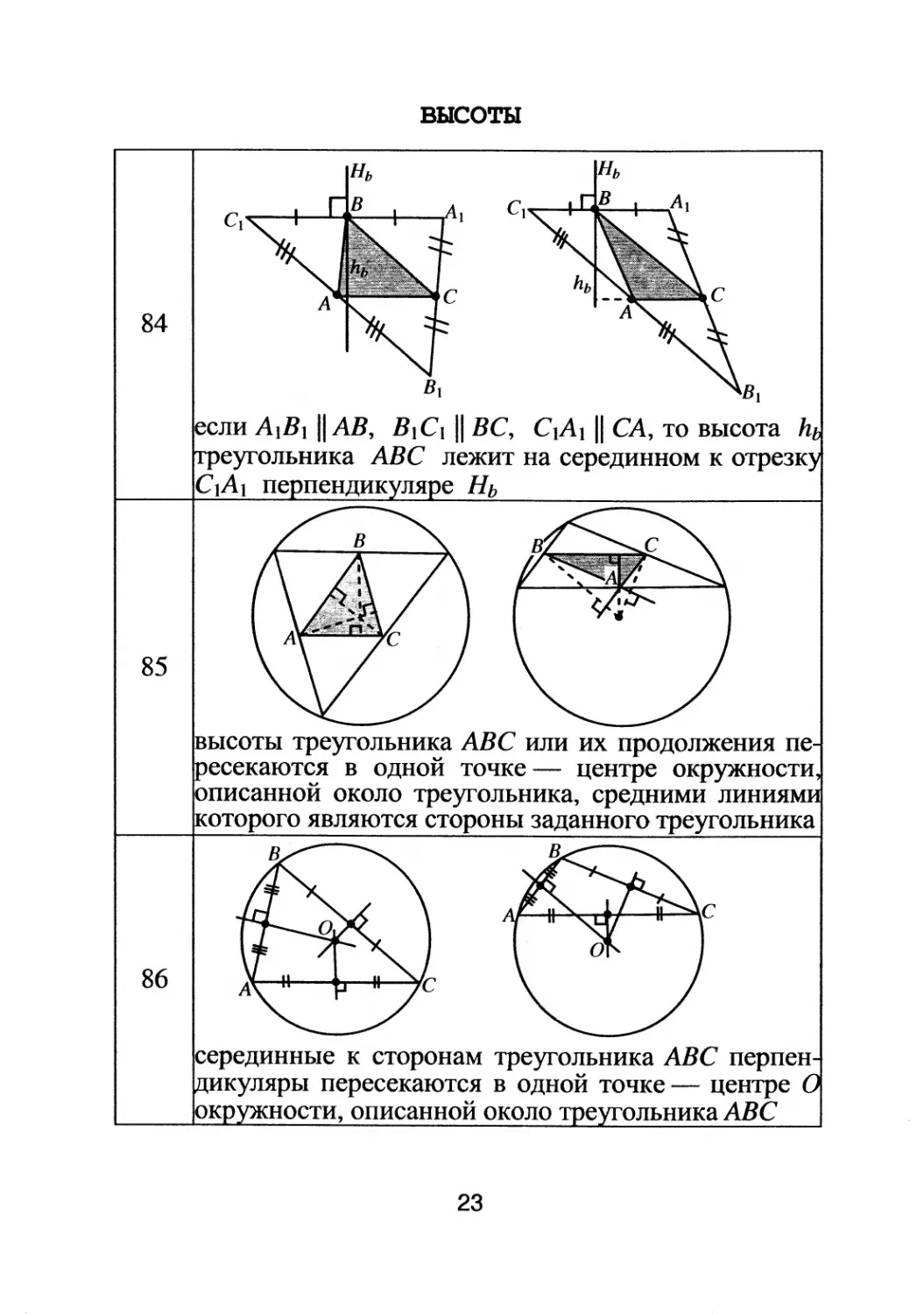
если AIBl 11 АВ, B1C 1 11 ВС, С 1 А 1 11 СА, то высота
еyrольника АВС лежит на серединном к отрезк
С 1 А 1 пе пендик ля е НЬ
высоты треyrольника АВС или их продолжения пе
есекаются в однои точке
центре окружности
описаннои около треyrольника, средними линия
KOToporo являются стороны заданноrо треyrольника
в в
серединные к сторонам треyrольника АВС перпен
икуляры пересекаются в однои точке
центре
ок ности, описанной около е ольника АВС
23
в
в
87
,
,
,
,
,
,
, ,
В , ,
1 '
, ,.
,
А С H
С
В 1
АН -НА 1 = ВН -HB 1 = СН -Н С},
АА 1 -НА 1 = ВА 1 .А 1 С, BBl -НВ} =ABl -В}С,
СС} - HCl = AC l . С 1 В
в
в
88
А 1
МВС N M1B1C,
LЛВС = LЛ}В}С,
LBAC= LB}A 1 C,
ВС АС
1 =.(
= ICOS rl
ВС АС
в
А
с
MBD N
CBD,
МВС N MBD,
МВС N
CBD
89
90 LABD= LCBE
А с
В
LC}A}A = LB 1 A}A,
LAIBIB = LC}B}B,
.
91 LВ]C1C = LA1C}C,
Н
центр окружности,
вписанной в 11 AIBl C 1
А. В 1 С
24
в
92
с
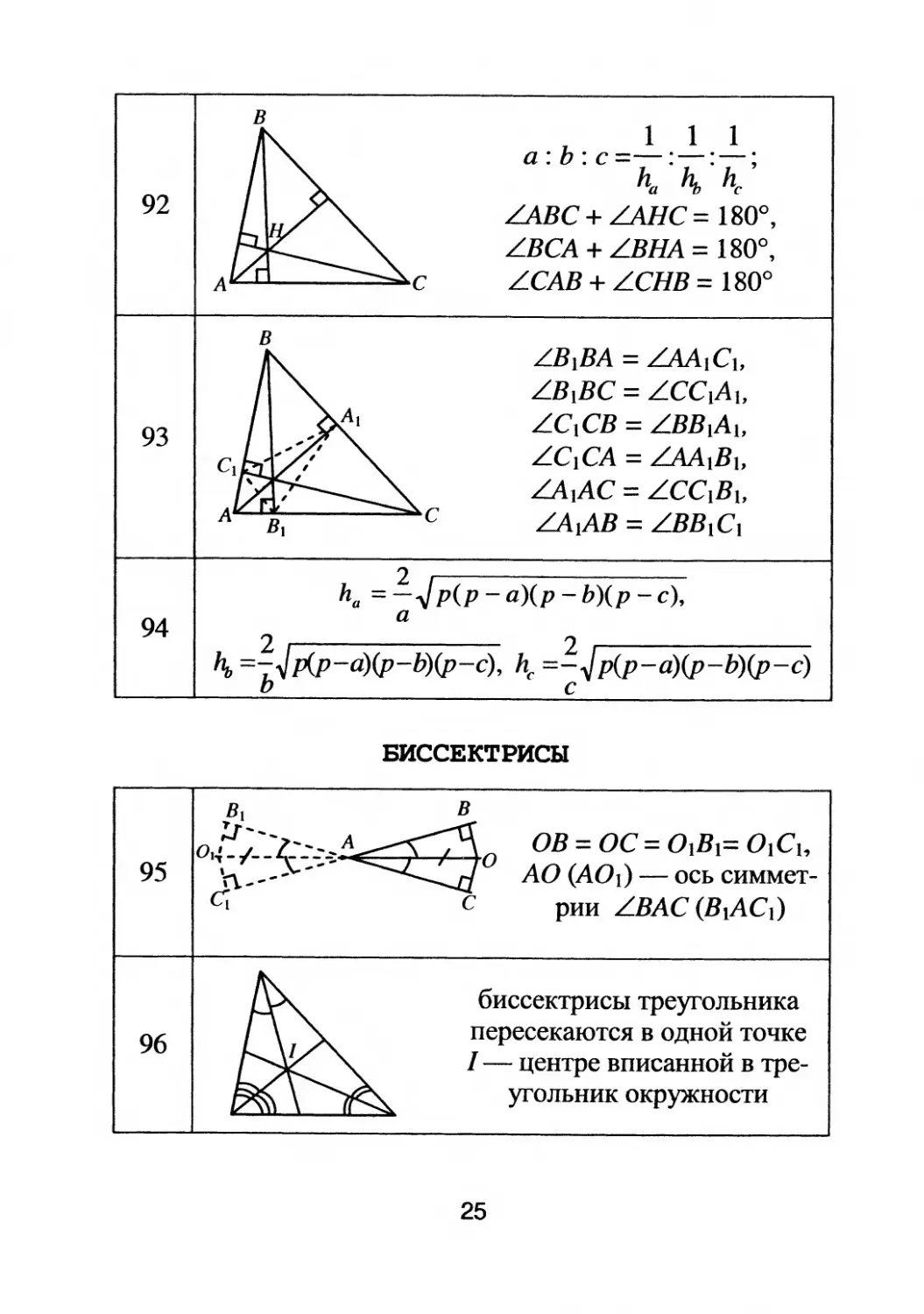
1 1 1
a . b . c =
.
.
.
.. ..,
ha h" hc
LЛВС + LЛНС = 1800,
LBCA + LBHA = 1800,
LCAB + LCHB = 1800
А
в
LBIBA = LAA 1 C t ,
LB1BC = LCC 1 A l,
93 LC1CB = LBB 1 A 1 ,
LC1CA = LAAtBl,
LAtAC = LCC 1 B 1 ,
А В I С LAIAB = LBB1C t
94
ha ='!.: .J p(p
a)(p
b)(p
c),
а
"ь =
N
a)(P
b)(p
C)' hc =
p(p
a)(p
b)(p
c)
БИССЕКТРИСЫ
В I
7',.....
,.." ... ... ... ... А
014 .. {.. .. i..
95 п
в
ОВ = ос = OtBl= OICl
О АО (АО})
ось симмет
с рии LBAC (B1AC 1 )
96
биссектрисы треyrольника
IU'
пересекаются в однои точке
1
центре вписанной в тpe
yrольник окружности
25
97
98
99
....
........
........
....
....
[с
центр вневписанной
окружности
с
........
....
........
............
BD .1 ВЕ
А
....
....
....
c
E
если D и Е
точки пересечени
окружности соответственно
внyrpенней и внешней биссек
трисами вписанноrо треyrольник
АВС, выходящими из одной вер
шины В, то DE
диаметр ок
ружности
D
В
AD АВ
,
100X DC ВС
5MBD АВ
S ЛСВD ВС
А D С
D
101Х DC АС
DB АВ
с
26
А
А/ Ь+с В/ а+с
,
,
/А 1 а /В 1 Ь
102
С/ а+Ь
/С 1 С
С В
103
а
2Ьс cos
2
lа == ,
Ь+с
2accos
2abcos у
lь == 2, lс == 2
а+с а+Ь
L
104
.
,
,
,
.
,
.
,
........
....
р к
....
........
........
....
....
........
Q
....
............ Q
-
------------
.
р
LQ =
ILK · LP
KQ · QI1
105 l;=ь{l
(ь:2сr). 1;=0 1 (0:2 су · 1,
=a{1
(a:2byJ
с LOAD = LEAD
106 (О
центр OK
ружности)
27
107Х
108
109
110
111
112
А
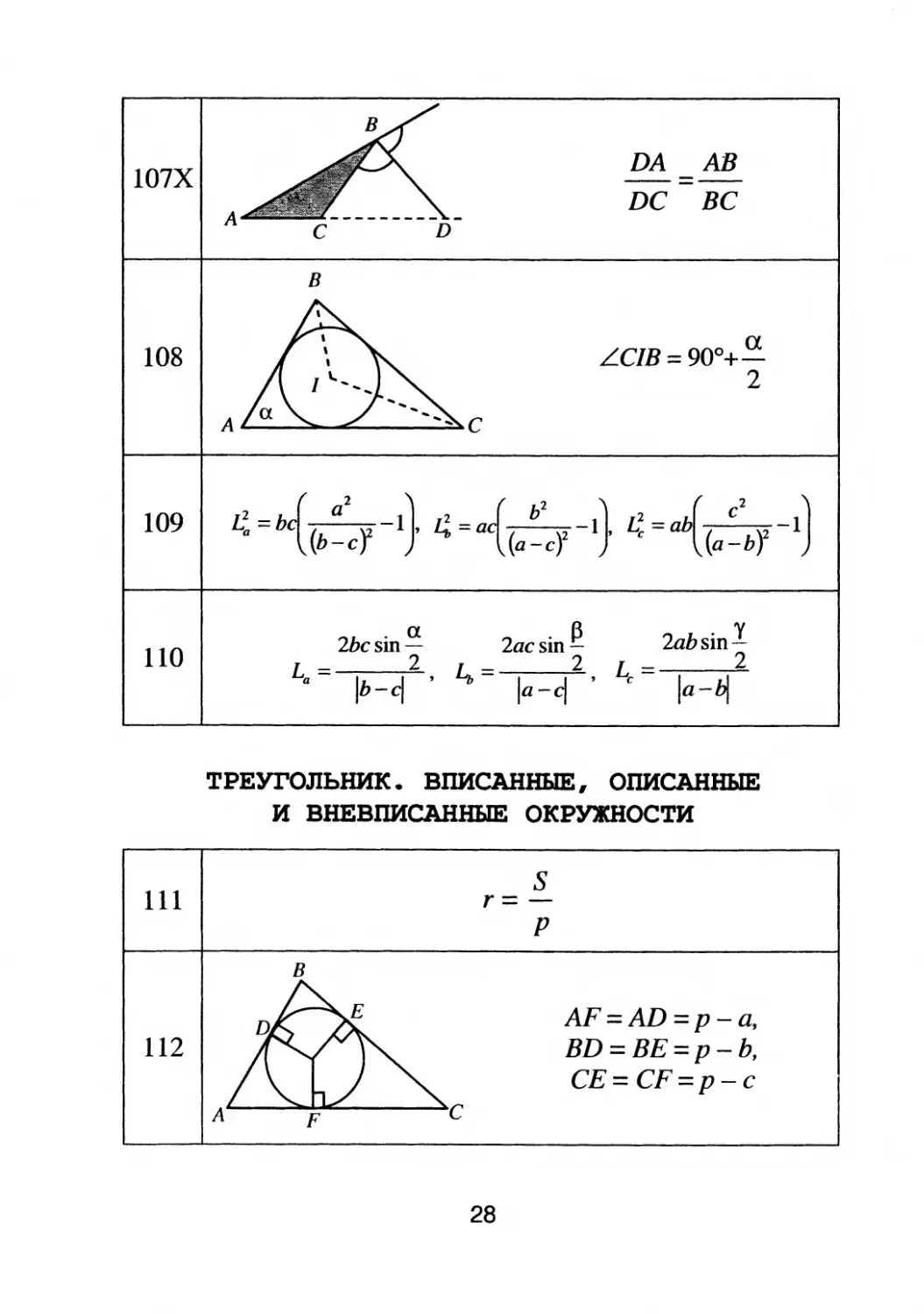
АВ
ВС
DA
DC
.---
--
----... -
с D
в
а
L-C/B = 900+
2
L
=Ь{(ь а 2 с)
1).
=а{(а Ь 2 с )
1} L; =а{(а с 2 ь )
1)
2Ьс sin а 2ас sin f3 2аЬ sin 'у
L
2 т
2 L
2
а
'Ь
CI '
'а
CI ' с
la
ТРЕYrОЛЬНИК. ВПИСАННЫЕ, ОПИСАННЫЕ
И ВНЕВПИCAННblE ОКРУЖНОСТИ
s
r=
р
в
А
с
AF=AD=p
a,
BD = BE=p
Ь,
СЕ= CF=p
c
F
28
113 у = (р
а) tg а = (р
Ь) tg В = (р
с) tg У
114
115
116
117
118
119
. б . r
SlD
SlD
r= с =с 2 2
б r . б+r '
ctg
+ ctg
SlD
222
а
r=
в r
ctg
+ctg
2 2
=а
. в . r
SlП
SlП
2 2
. в +r
SlП
, r =
2
. б . в
Sln
SlD
=Ь 2 2
б в . б+в
ctg
+ctg
SlD
222
R= аЬс
4S
ь
AD=p
А
s s s
, Уъ = , ус =
p
a p
b p
c
ra = р . tg а rb = р · tg t3 re = р · tg 1.
2
2' 2
Уа =
MN = а + с,
DQ=b
29
120
121
122
123
ra + rb + re = r + 4R
1 1 1 1 1 1 1
=
+
+
=
+
+
r Та Т ь Те ha h b hc
ТРИЛИСТНИК:
BD=DC=/D
формула ЭЙЛера
2
/0 =R
2rR
124 01; = R 2 + 2raR, 01; = R 2 + 2rbR, OI
= R 2 + 2TcR
125 11; = R (Уа
r), 11; = R (УЪ
У), 1 I
= R (У е
У)
126
теорема Карно
OD+ ОЕ+ OF=R + т
(О
центр окружности)
зо
127
128
129
130
131
теорема синусов
а Ь с
= = =2R
sin а sin f3 sin у
. а . f3 . 'у r
Sln
. Sln
. sln
=
2 2 2 4R
а
у р
cos
. cos
. cos
=
2 2 2 4R
01 D = 02 D
(D
точка отрезка ЕС, 01
и 02
центры окружно
ou'
стен, проходящих через
с тройки точек А, В, D и А,
С, D соответственно)
теорема косинусов
2 ь 2 2 Ь Ь 2 22 А
а = + с
2 с. cosa, = с + а
2са . cos....,
2 2 2
С = а + Ь
2аЬ . cosy
теорема косинусов в отрезках
в
в
132 А D
В
D rJ
А
С
вс 2 = Ав 2 + Ас 2
2АС · AD,
Ав 2 =Ас 2 +вс 2 +2АС. CD
31
ПАРАЛЛЕлоrрАММ
в с
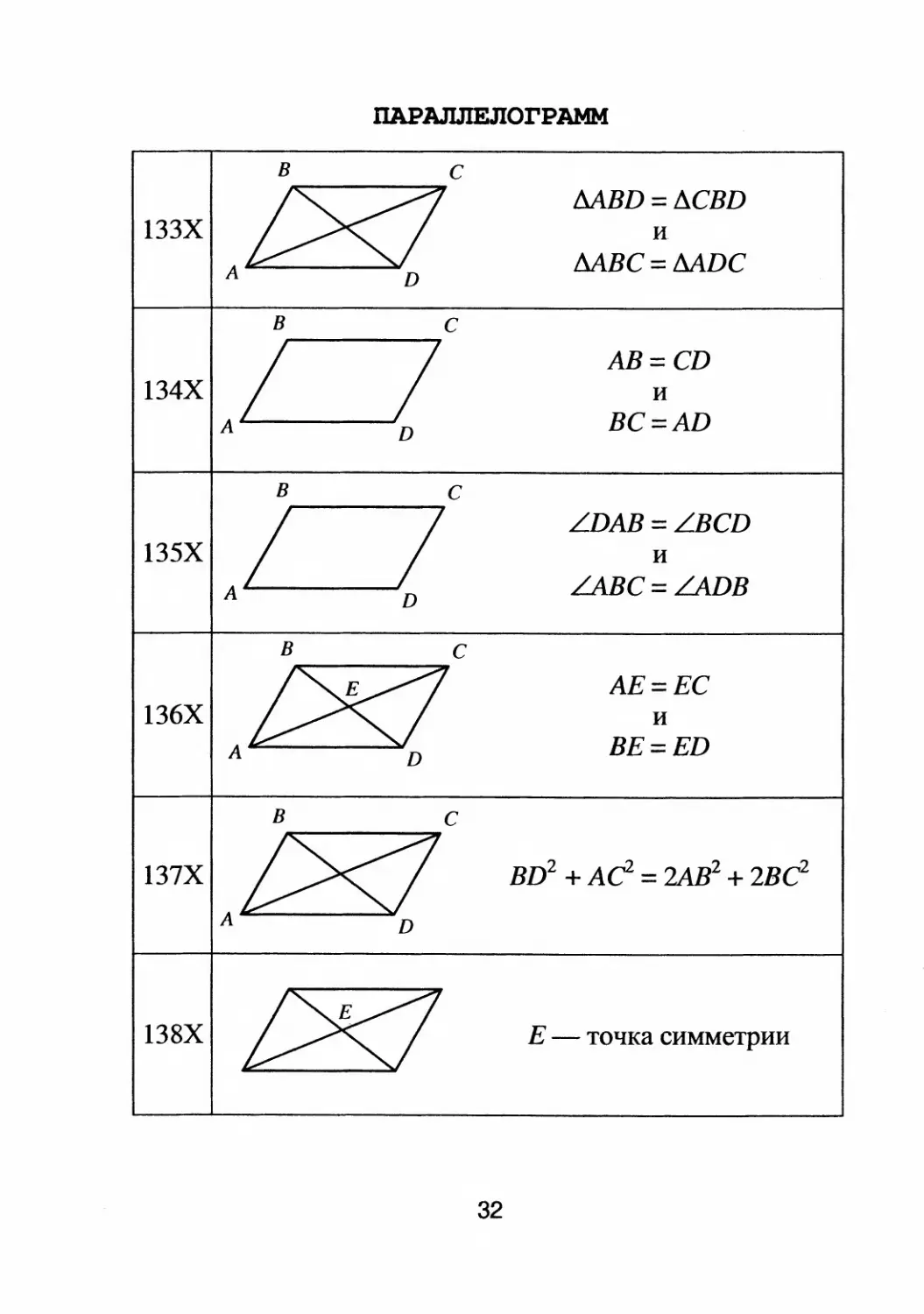
MBD = !lCBD
133Х и
А МВС = MDC
D
в С
АВ = CD
134Х и
А D ВС = AD
в с
LDAB = LBCD
135Х и
А D LЛВС = LADB
в с
АЕ = ЕС
136Х и
А D ВЕ = ED
в
с
137Х
BD 2 + Ас 2 = 2Ав 2 + 2вс 2
А
D
138Х
Е
точка симметрии
32
в G С
АЕ DF CG ВН
если .... .... ....
.... .... .... НА '
139 ED FC GB
то HEFG
параллело
А Е rpaMM
с
если NL 11 AD, PL 11 АВ,
140 то
точки К, L, С лежат на oд
А "" ""
НОИ прямои
141Х
142Х
143Х
144Х
в
с
А
D
р
N
в
А
в
А
АС = BD
KL и PN
оси симмет
рин
с
BD
АС
с
АС и BD
биссектрисы
yrлов
зз
145Х
146
147
148
149
,
,
,
,
" .,.
,
,
.,.
А .,.'"
А
с
ED
прямые АС и BD
оси
симметрии
с
BK=KN=ND
АВ. PF=AD. РЕ
(Р
произвольная
точка прямой АС)
с о EFKL
параллело
rpaMM, EF 11 LK 11 АС,
FK 11 EL 11 BD,
1
EF=
AC,
2
1
FK =......BD
2
Е
.,.
....
"1 '\ ........
, 1 '\ ........
, '\....
В' I '\ ........ С
1 '\
1 '\
1 '\
1 '\
I '\
'\
1 '\
'\
А
D
АЕ + Ес! = ВЕ + ED 2
(Е
произвольная точ
ка плоскости)
з4
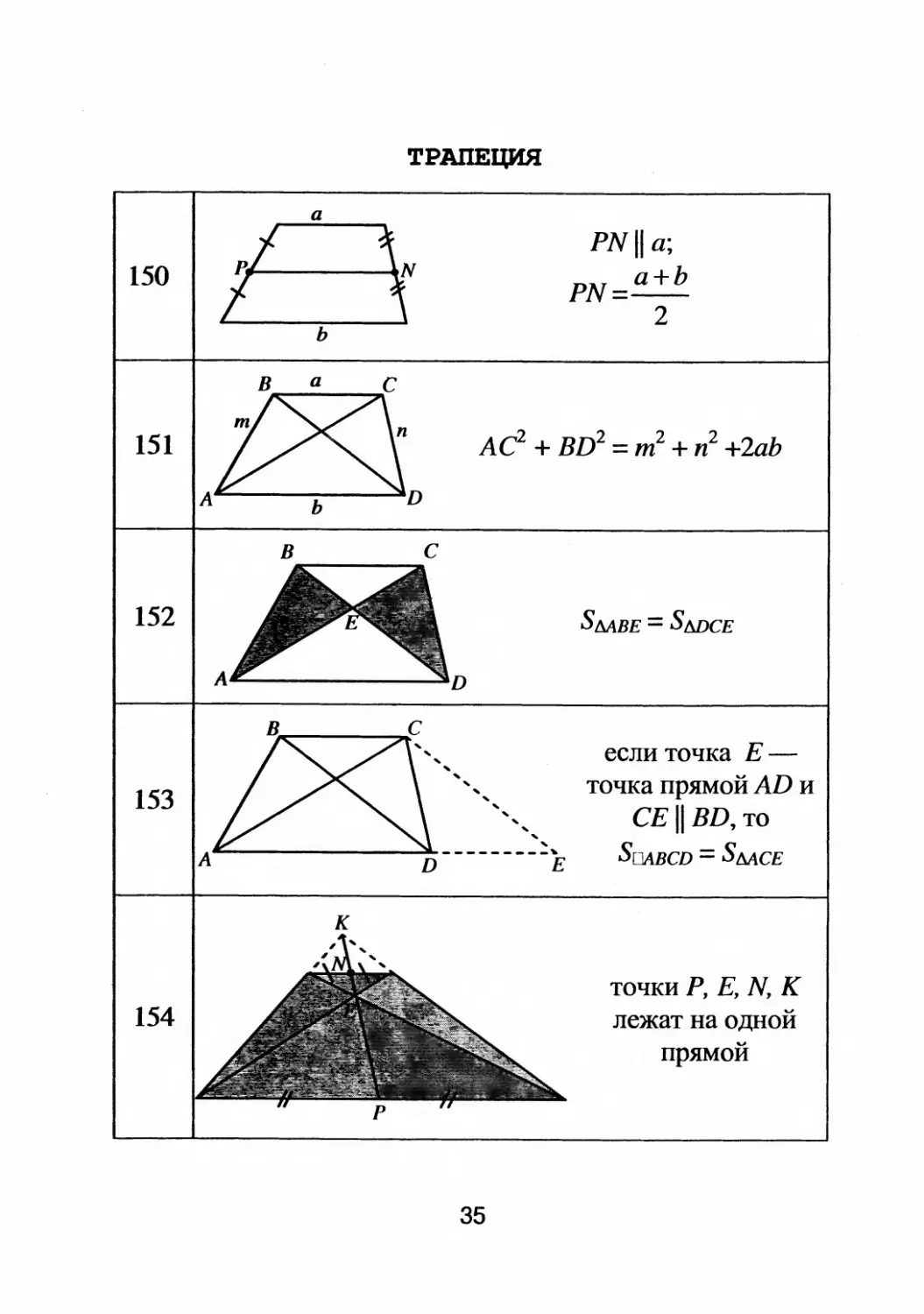
ТРАПЕЦИЯ
а
PN 11 а;
150 PN= а+Ь
2
ь
а
151
152
153
154
А
Ас 2 + BD 2 = т 2 + п 2 +2аЬ
ь
D
в
с
jf1;
.
'.. .
.
.
.
.
.
.
.
.
.
.. ....
. .
. .
=--:- =-
.
..<
:..:::;..
li.
:
-'O..7:..
.
;
{
:
=-
r
:i/
А
t
c
D
А
"
"
"
"
"
"
"
"
"
"
"
"
"
"
..
...._.._
D Е
к
, "
"
, "
, "
р
35
5MBE = SblJCE
если точка Е
точка прямой AD и
СЕ 11 BD, то
SOABCD = SMCE
точки Р, Е, N, К
"
лежат на одно и
"
прямои
155
точки Р, к, Е, N лежат
" "
на ОДНОИ прямо И
а
1
156 MN =
Ia
bl
2
ь
157
точки Р, К, N лежат на
" "
ОДНОИ прямои
а
если PN 11 а,
158 то PN = 2аЬ
а+Ь
ь
в а С
159 CN т
a
т .....
.....
ND b
т
А Ь D
В а
если SOPBCN = SDAPND,
160
а 2 + ь 2
то PN =
А Ь D 2
36
Р... А , N
... , ... ,
.... ... ,
....
... ... ,
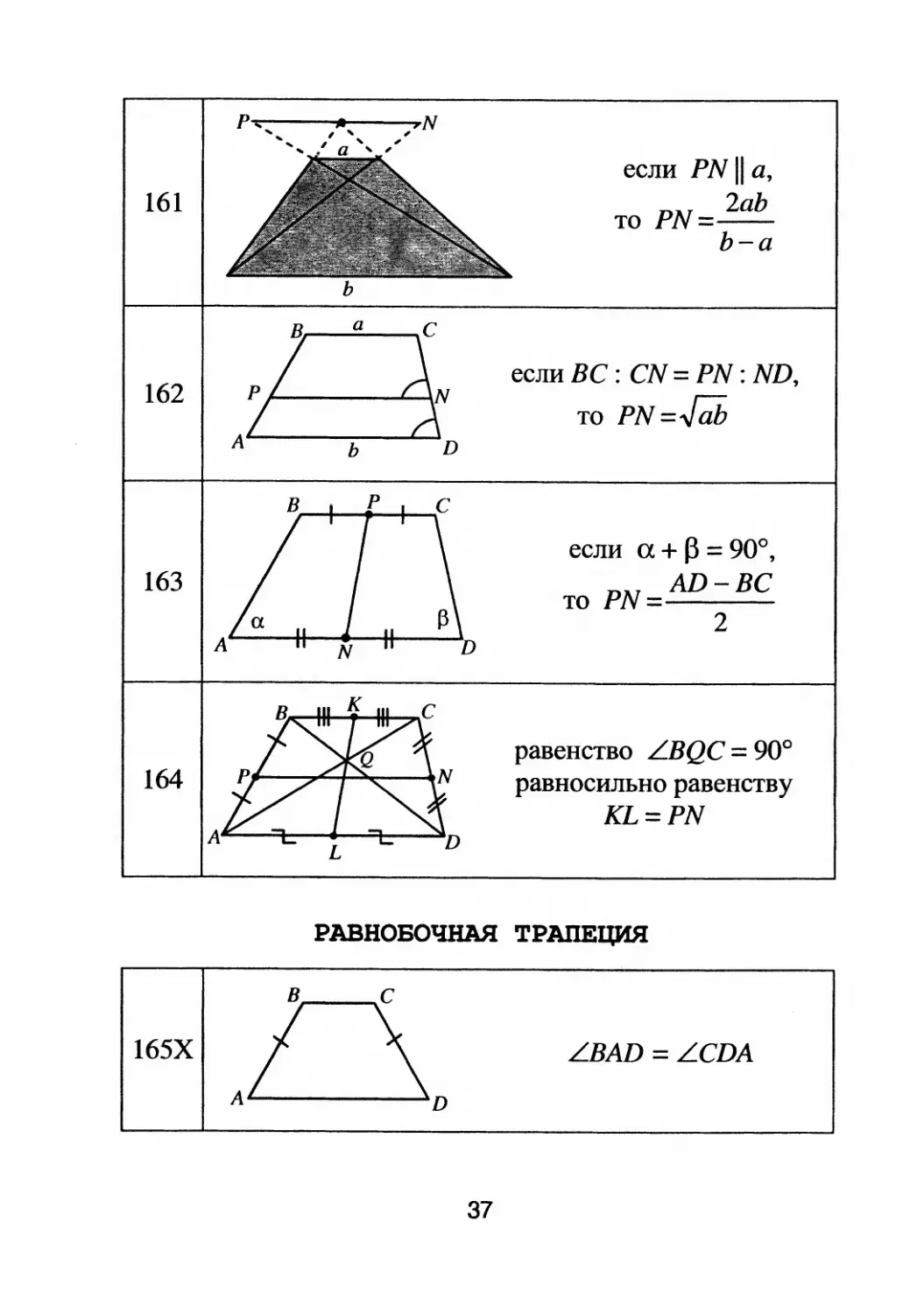
если PNII а,
161 то PN = 2аЬ
b
a
ь
а
если ВС : CN = PN : ND,
162 то PN = .Jab
А Ь D
163
если а + f3 = 900,
P IAT AD
ве
то lУ =
2
А
164
равенство LBQC = 900
равносильно равенству
KL = PN
А
L
РАВНОБОЧНАЯ ТРАПЕЦИЯ
165Х
LBAD = LCDA
А
D
37
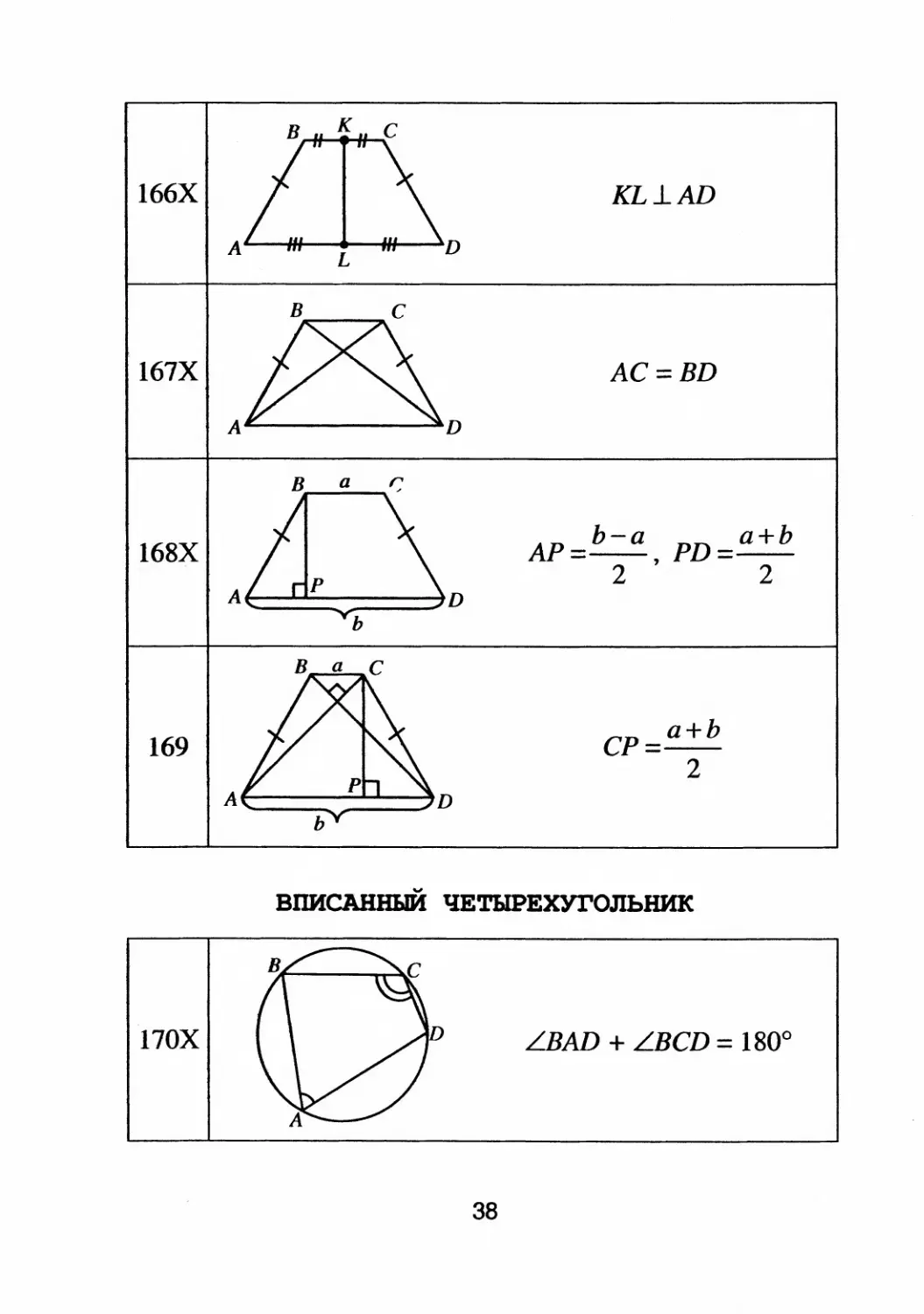
166Х
167Х
168Х
169
170Х
А
L
А
А
а
ь
А
D
ь
D
D
D
KL 1.. AD
АС = BD
AP=b
a PD=a+b
2 ' 2
СР = а + Ь
2
ВПИСАННЫЙ ЧЕТЫРЕХYrОЛЬНИК
38
LBAD + LBCD = 1800
171Х
172Х
173Х
174
175
D
D
D
в
39
LDAC = LDBC
АЕ . ЕС = ВЕ · ED
теорема П'Z'оnемея
АС · BD = ас + bd
BC=AB+DC
АВ 11 CD
176
177
178
179
А
.
\
\
АС ad+bc
,
BD ab+cd
АС sinLADC
BD sin LBAD
EN · ЕР = ЕК · EL
(Е
произвольная
точка на окружности)
радиус окружности
т2 +п 2
2пmcos<p
R=
2 sin <р
если О
центр окружности,
то
[lOKPN
параллелоrpамм
40
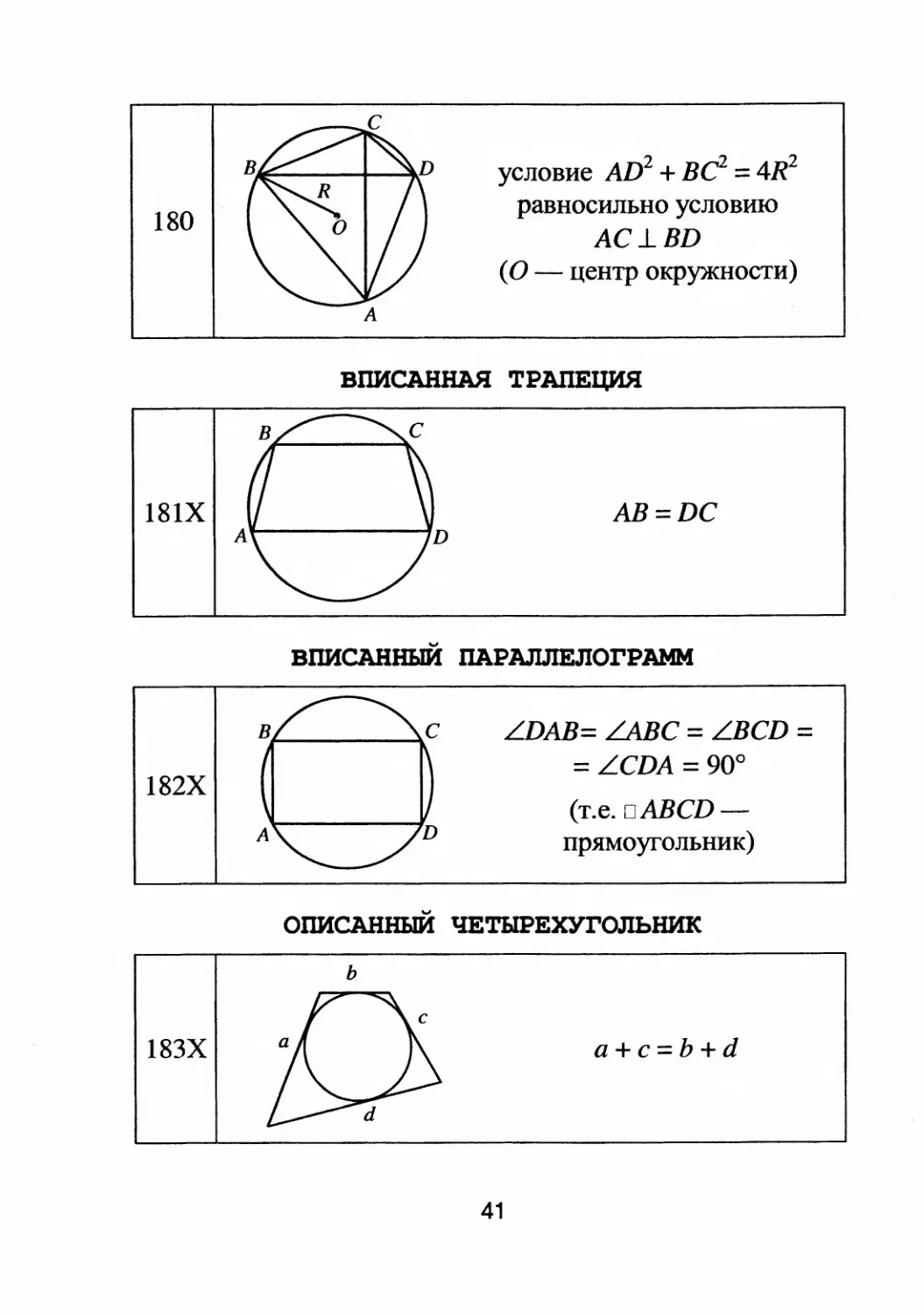
180
181Х
182Х
183Х
условие AD 2 + вс 2 = 4R 2
равносильно условию
АС ..l BD
(О
центр окружности)
ВПИСАННАЯ ТРАПЕЦИЯ
А
АВ = DC
ВПИСАННЫЙ ПАРАЛЛЕлоrрАММ
LDAB= LЛВС = LBCD =
= LCDA = 900
(т.е. oABCD
прямоyrольник)
ОПИСАННЫЙ ЧЕТЫРЕхуrольник
ь
a+c=b+d
41
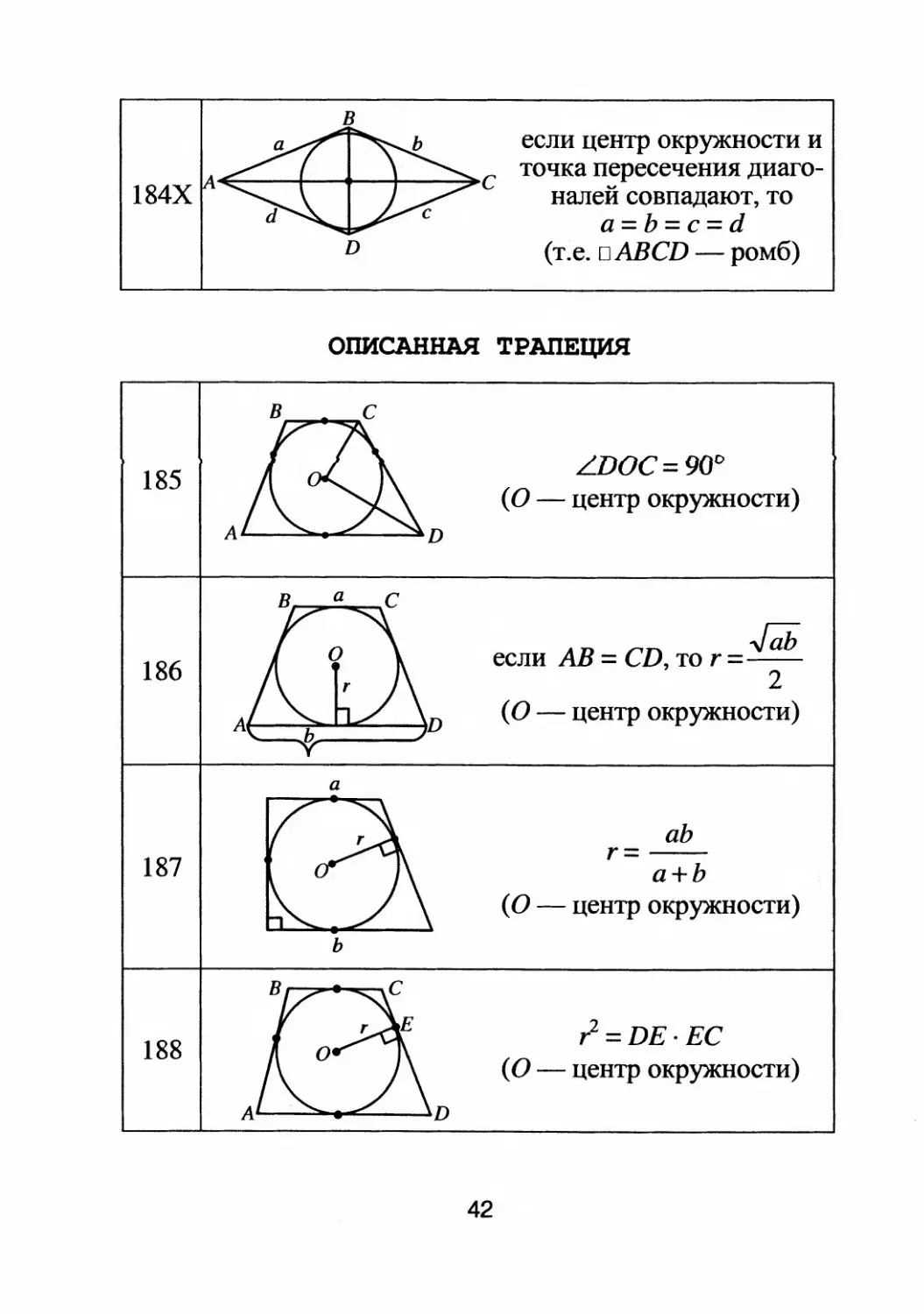
184Х
185
186
187
188
в
D
если центр окружности и
с точка п
ресечения диаrо
налеи совпадают, то
a=b=c=d
(т.е. oABCD
ромб)
ОПИСАННАЯ ТРАПЕЦИЯ
А
D
а
А
D
а
ь
А
D
LDOC = 900
(О
центр окружности)
.Jab
если АВ = CD, то r=
2
(О
центр окружности)
аЬ
а+Ь
(О
центр окружности)
r=
2
r = DE · ЕС
(О
центр окружности)
42
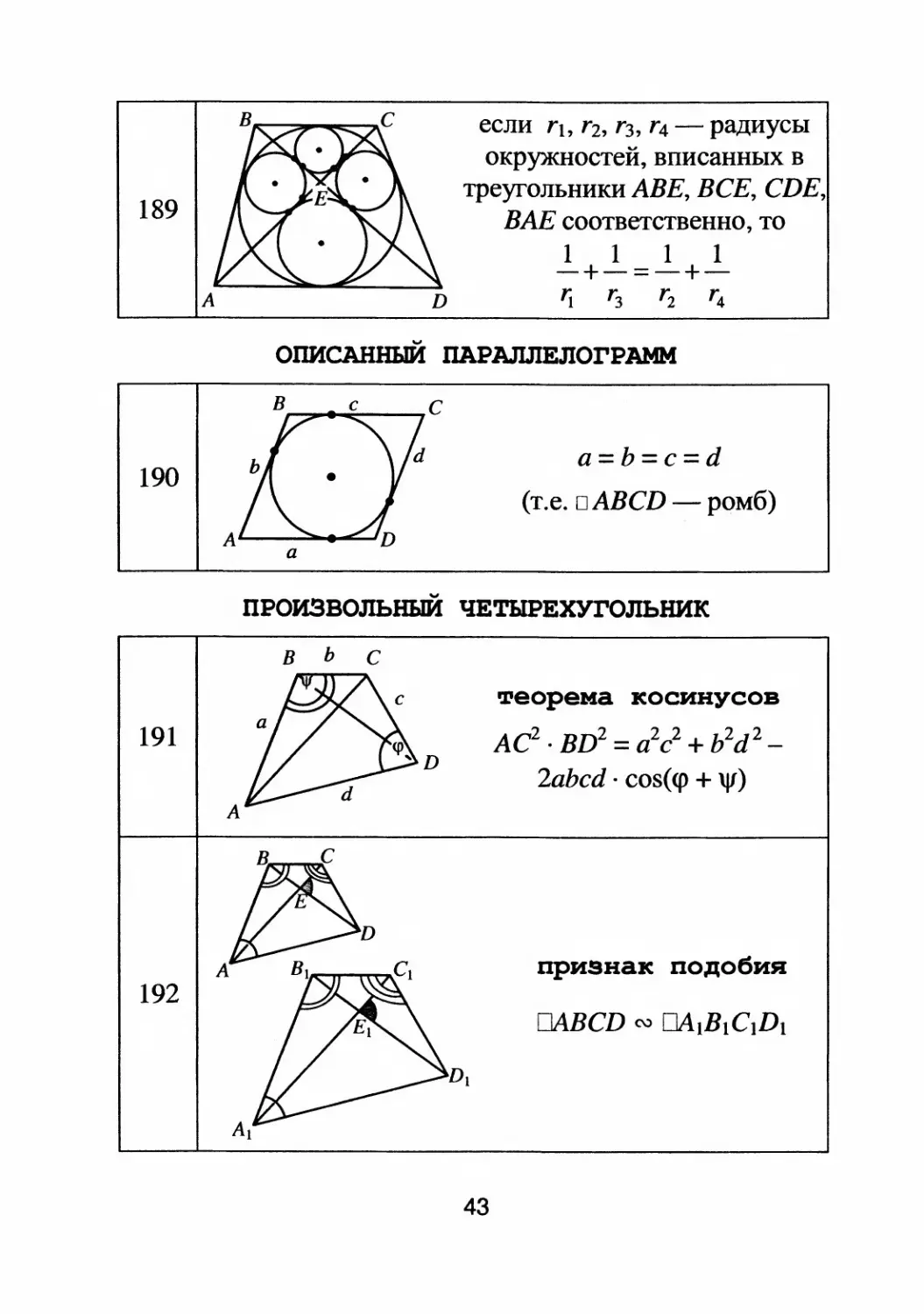
189
190
А
если Tl, Т2, Тз, Т4
радиусы
окружностей, вписанных в
треyrольники АВЕ, ВСЕ, CDE,
ВАЕ соответственно, то
1 1 1 1
+
=
+
D 'i r з Т 2 r 4
ОПИСАННЫЙ ПАРАЛЛЕлоrрАММ
А
a=b=c=d
(т.е. oABCD
ромб)
с
а
произвольНЫЙ ЧЕТLIPЕхуrольник
в ь С
А
eopeMa косинусов
191 Ас 2 . BD 2 = а 2 с 2 + b 2 d 2
2abcd . cos( <р + \11)
192
признак подобия
DABCD ro DAIBl C]D 1
Dl
Аl
43
. 193
194
195
196
с
А
D
в
с
в
D
,\\
L
с
oKLPN (\) oABCD
АВ 11 CD
(01 и 02
центры окруж
ностей)
точки касания окружно
стей с диаrональю BD
совпадают тоrда и только
тоrда, коrда а + с = Ь + d
(т.е. четырехyrольник
ABCD описанный)
четырехyrольник KLPN
"
вписанныи
44
197
198
199
200
201
А
F
А
в
р
45
D
если ВК : КЕ =
= DP : РЕ =
=AN: NF=
= CL : LF = 2 : 1,
то oKLPN (\) oABCD
KN=NL, EN=NF
BC+AD=AB + CD
(т.е. четырехyrольник ABCD
описанный)
AD 2 +DC 2 + св 2 +ВА 2 =
=Ас 2 + BD 2 + 4PN
Ас 2 + CD 2 + DB 2 + ВА 2 =
= AD 2 + вс 2 +
4PN
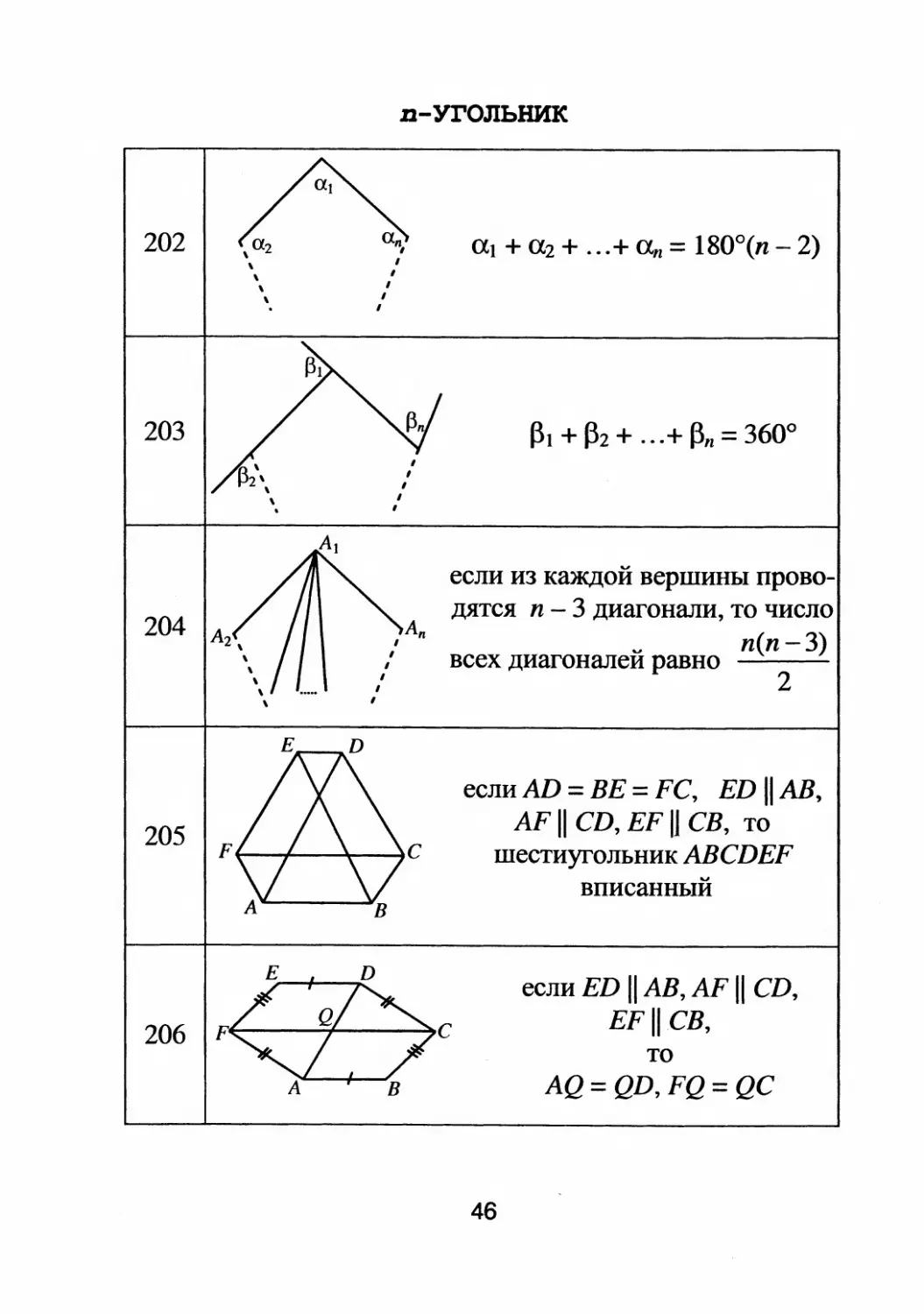
202
203
204
205
п--YrОЛЬНИК
.
А 2
\
\
\
\
\
\
А п
I
I
I
I
I
I
F
с
206 р
аl + а2 + ...+ а п = 180 0 (п
2)
(31 + 132 + ...+ f3n = 3600
если из каждой вершины прово
ДЯТСЯ п
3 диаrонали, то число
" п(п
3)
всех диaroналеи равно 2
если AD = ВЕ = FC, ED 11 АВ,
AF 11 CD, EF IJ СВ, то
шестиyrольник ABCDEF
v
вписанныи
с
если ED 11 АВ, AF 11 CD,
EF 11 СВ,
то
AQ = QD, FQ = QC
46
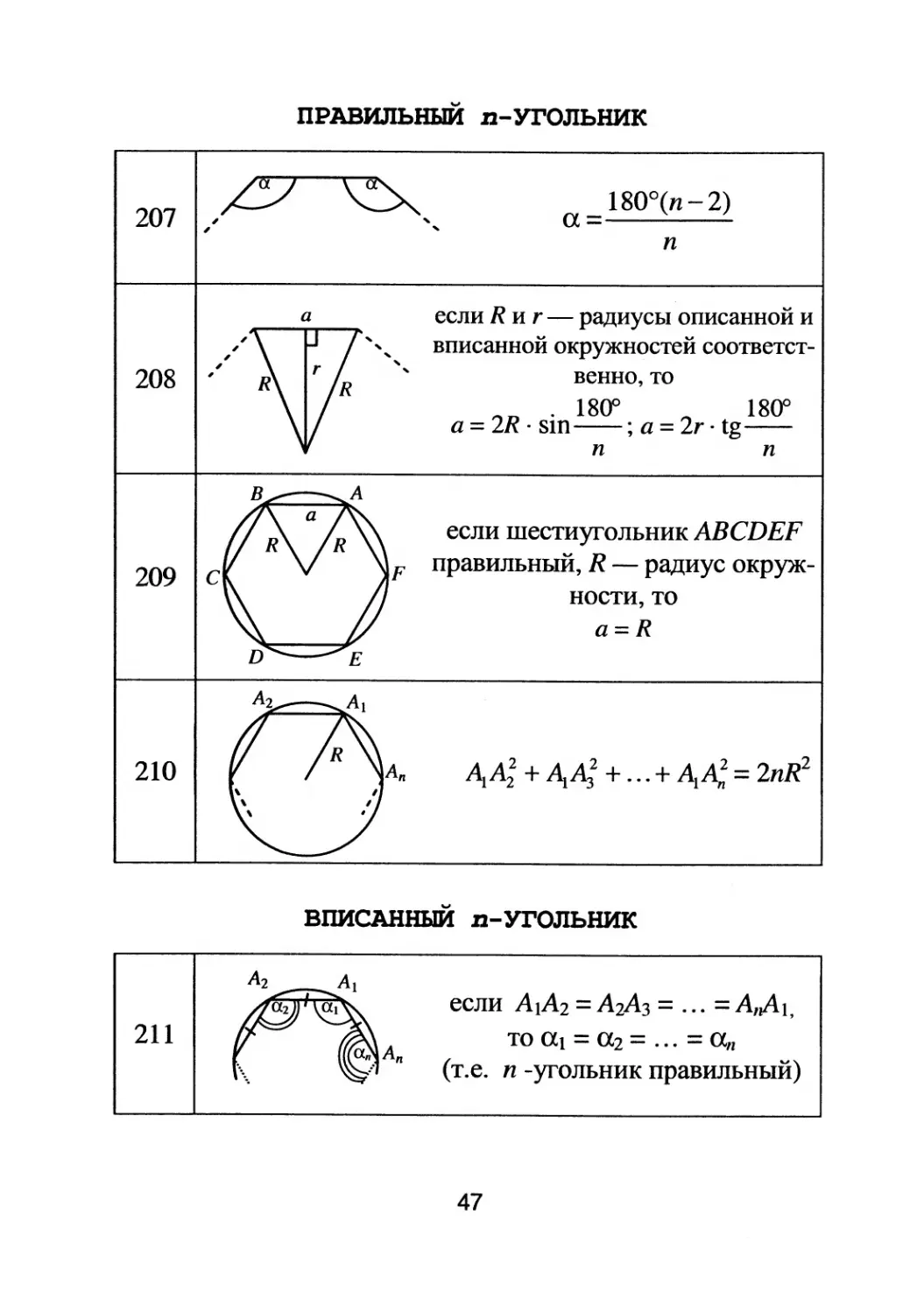
207 ,
,
208
""
ПРАВИЛЬНЫИ п--уrольник
а
,
,
,
,
,
"
"
"
"
"
"
"
1800(п
2)
а=
п
если R и r
радиусы описанной и
v' v'
вписаннои окружностеи COOTBeTCT
венно,ТО
. 1800 1800
а = 2R . Sln ; а = 2r . tg
п п
если шестиyrольник ABCDEF
F правильный, R
радиус окруж
НОСТИ,то
a=R
209 с
210
211
А п
AIAi + AIA; + ... + AIA; = 2nR 2
ВПИСАННЫЙ п--уrольник
А 2
если А 1 А 2 = А2Аз = ... = А,,л1,
то al = а2 = ... = а 1l
(т.е. п
yrольник правильный)
47
212
213
214
215
А 2
Al
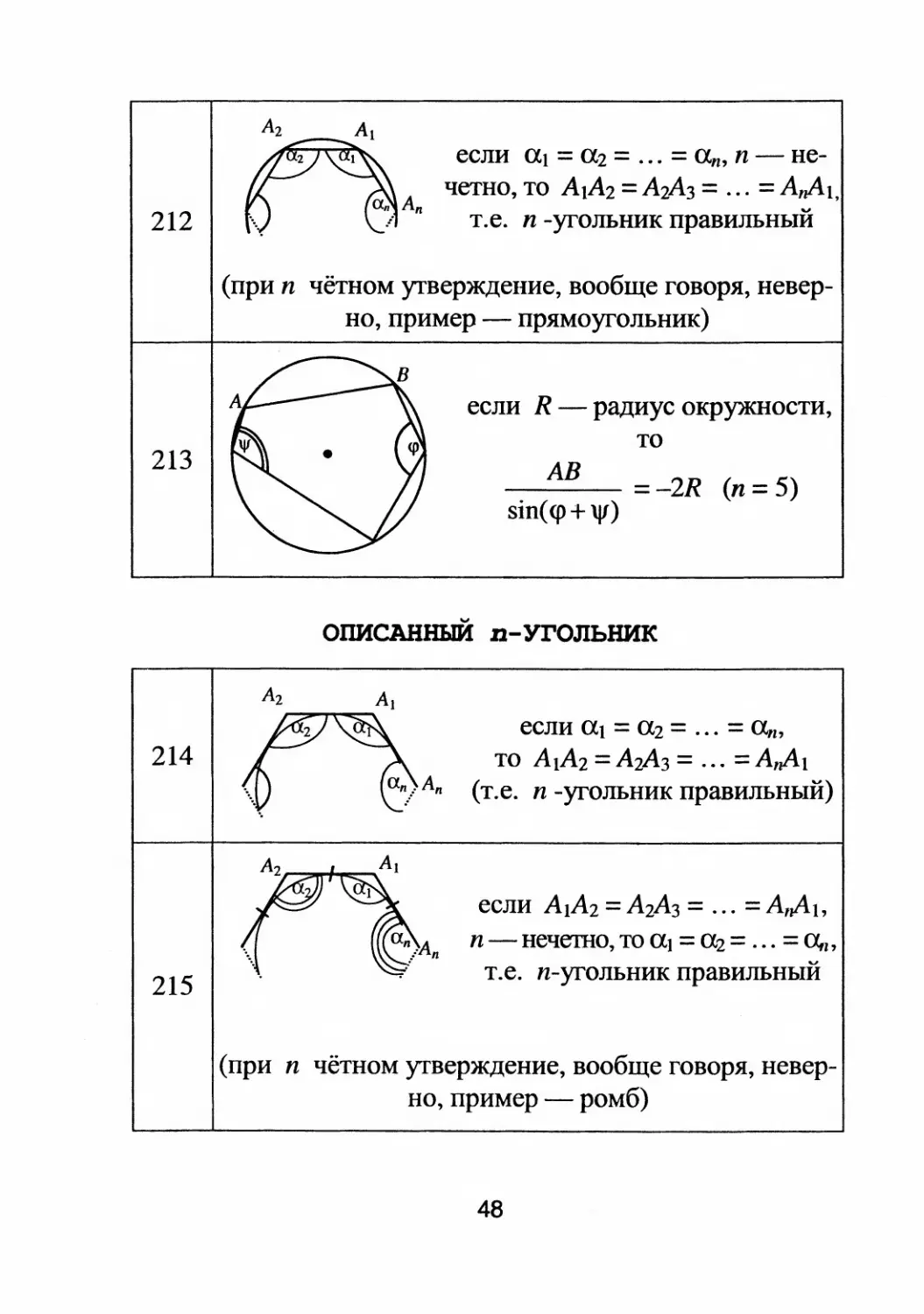
если а1 = а2 = ... = а п , п
He
четно, то АIА2 = А2Аз = ... = AnAl,
"
т.е. п
yrольник правильныи
(при п чётном yrверждеllие, вообще rоворя, HeBep
но, пример
прямоyrольник)
если R
радиус окружности,
то
АВ
=
2R (п = 5)
sin( <р + \11)
ОПИСАННЫЙ D--уrольник
А 2
А 1
если аl = а2 = ... = а п ,
то AIA2 =А2 А з = ... =AnAl
(т.е. п
yrольник правильный)
если А 1 А 2 = А2Аз = ... = А,,л1,
п
нечетно, m аl = а2 =... = а",
"
т.е. п
yrольник правильныи
(при п чётном yrверждение, вообще rоворя, HeBep
но, пример
ромб)
48
216
217
218
219
220
221
222
ПЛОЩАДЬ ТРЕуrольниКА
111
S =
а . ha
=
ь · hb =
с . he
222
S 1 Ь . 1 . А l Ь .
=
a. . slnY =
a . с · slnfJ =
. с . Slna
222
s = а 2 . sin в . sin у = Ь 2 . sin у . sin а
2 sin а 2 sin В
с 2 sin а . sin В
==
.
2
.
Sln у
s = 2R 2 · sina . sinf3 · siny
s =
. R 2 · (sin2a + sin2f3 + sin2y)
2
s = Р . r = Ра . ra = рь · rb = Ре · re
S = R . r .(sina + sinf3 + siny)
49
223
s=abc
4R
224
s =
. ha · hb =
. ha . hc =
. hb · hc
2 sin у 2 sin f3 2 sin а
225 S =.! h 2 . sin б =.! h 2 . sin rз =.! h 2 . sin у
2 а sin в . sin у 2 ь sin а . sin у 2 с sin а . sin f3
226
1 а. hb . sin f3 1 Ь. hc . sin у 1 с. ha . sin б
S
2 sin а 2 sin в 2 sin у
227
у f3 а
s = ra · rb · tg
= ra . rc . tg
= rb · rc . tg
222
228
2 f3 у а 2 у а f3
S = r . tg
. tg
. ctg
= rb · tg
. tg
. ctg
=
а 222 222
2 а f3 у
= rc · t g 2 . t g "2. ctg 2
229
а f3 у
S= r. ra. ctg
= r. rb. ctg
= r. rc. ctg
222
50
230
231
232
233
234
2 а f3 у
S = r . ctg
. ctg
. ctg
222
формула repOHa
S=
P.Pa.Pb.Pc
S= .J r.r .r, .r
а Ь с
S=.!
2R.h.h .h
2 а ь с
s==
1
(
+
+
J(
+
J(
+
J(
+
]
235 s =!
(ma +mь +mсХmь +mс
maXma +mс
mbXma +mь
mJ
3
236
2
S = r + 2r · R
51
237
238
239
240
lc
S = r · Тс
S = ra · rb
А
в
А
в
если DE 11 АВ, то
S
S
EC
MBC
S tillEC
А
если PN 11 АВ, КЕ 11 АС,
QL 11 СВ, ТО
5MBC =
= (
SMТL +
SмrrE +
S6.QTP )2
52
241
242
243
244
с
А
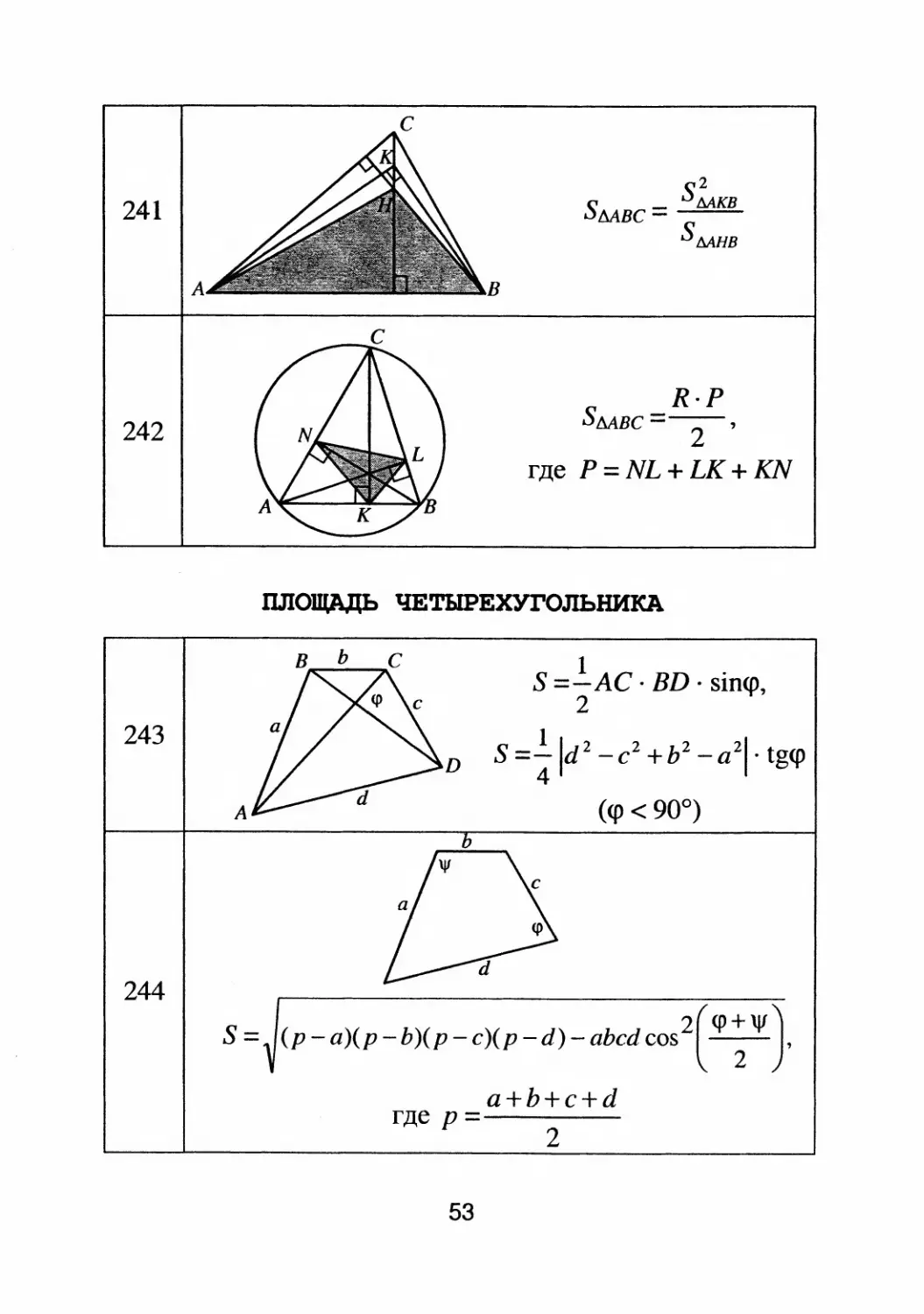
S .... s
KB
МВС .....
SMHB
.В
R.P
5MBC= 2 '
rде P=NL+LK +KN
ПЛОЩАДЬ ЧЕТЫРЕХYrОЛЬНИКА
А
.D
S =.!..АС · BD · sin<p,
2
S =
Id 2
c2 +ь 2
a21. tg<p
(<р < 900)
2 ( <P+W )
(р
а)(р
Ь)(р
с)(р
d)
abcd cos 2 '
a+b+c+d
rде р =
S=
53
2
245
246
247
248
249
ь
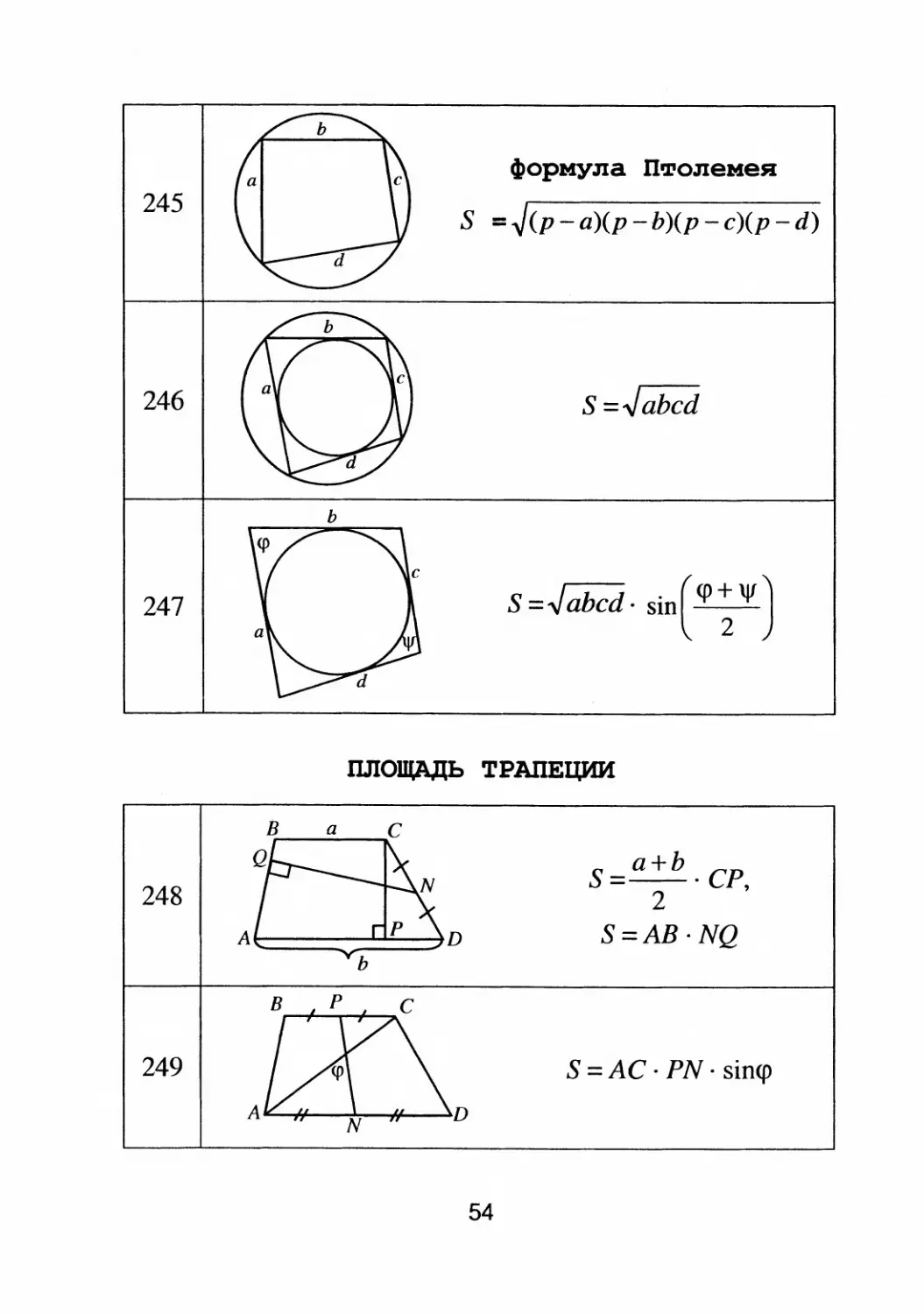
формула Птолемея
S =
(p
а)(р
b)(p
с)(р
d)
s =
abcd
s = .J abcd. Sin( <Р
\Jf J
ПЛОЩАДЬ ТРАПЕЦИИ
А
ь
А
D
s = а + Ь . ср
2 '
S =АВ. NQ
S = АС . PN . sin<p
D
54
250
251
252
253
254
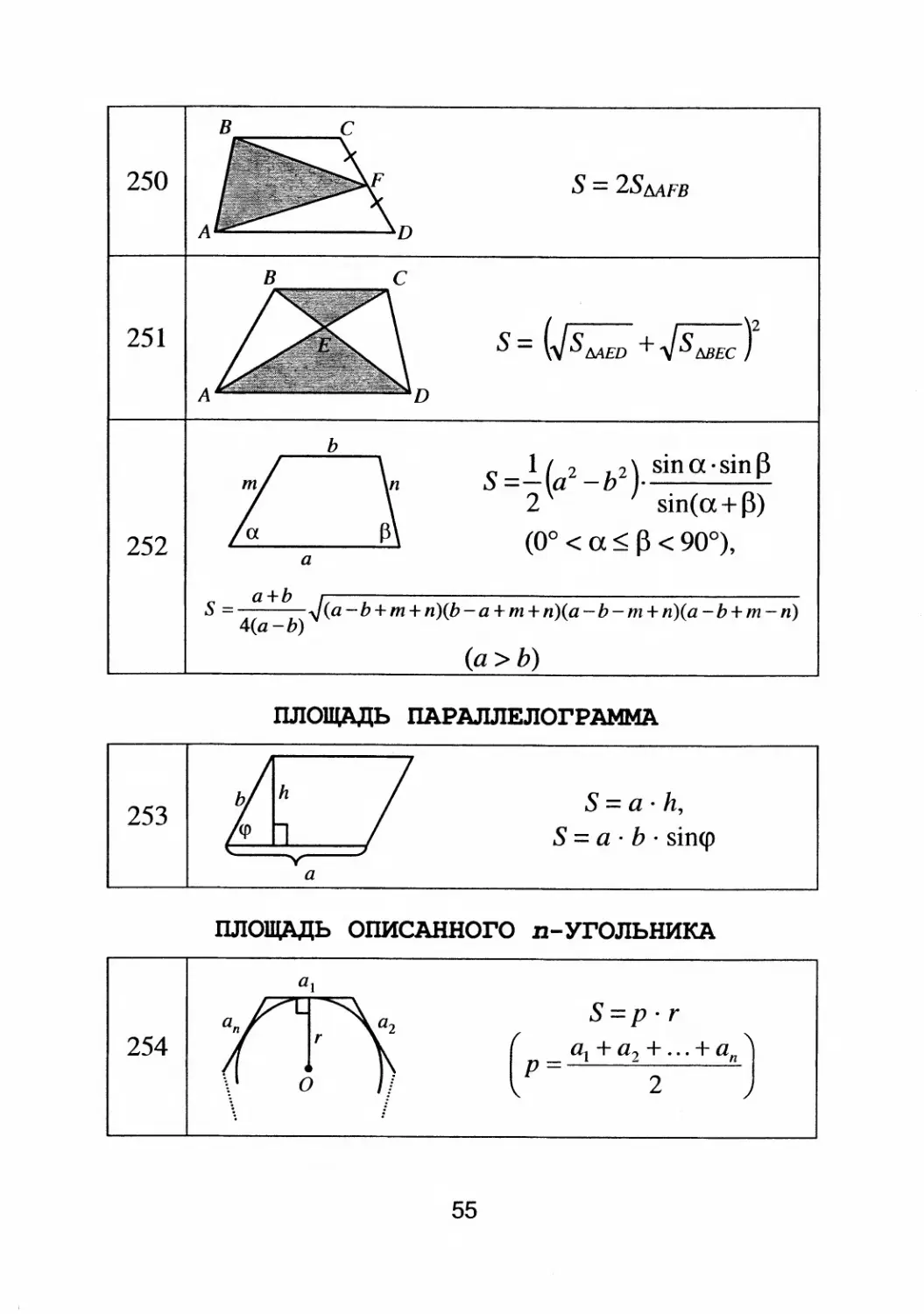
S = 2S MFB
А.
D
в
с
А
D
S = (.J SMED + .J SblJEC У
Ь
S =.!..(а 2
b2). sin а .sinJ3
2 sin(a+ fЗ)
(00 < а < f3 < 900),
а
а+Ь .J
s = (a
b+т+п)(b
a+т+п)(a
b
т+п)(a
b+т
п)
4(а
Ь)
(а>Ь)
ПЛОЩАДЬ ПАРАЛЛЕлоrрАММА
S = а . h,
S = а . Ь . sin<p
а
ПЛОЩАДЬ ОПИСАНноrо п...уrольниКА
а}
S=p.r
( р == а! + а 2
.. · + а п )
55
255
ПЛОЩАДЬ ПРАВильноrо п--YrОЛЬНИКА
rРАДУСНАЯ ИР' 11 "
256
257
258
180 О а
если LЛОВ = а радиан, то п =
1t
1
2 1800 1
S = r . п · t g S =
а · п · r.
п' 2 '
1 2 . 3600
S =
R . п · Sln
2 п
,. МЕРЫ YrЛА. ДЛИНА ДYrИ
,
пn
длина дyrи 1 = Ra = R ,
180
длина ок ности С = 2nR
ПЛОЩАДЬ СЕКТОРА
1
S=!..aR 2 = 1tn R 2 S=!..Z-R
2 360' 2 '
2
площадь Kpyra равна nR
ПЛОЩАДЬ CErмEHTA
1
1 2 1 2.
S =
R a
R Slna,
2 2
S пn 2 1 R 2. пn о
= R
sln ,
360 2 180
1 1 2. [
S =
R.[
R Sln
2 2 R
56
259
260
261
262
263
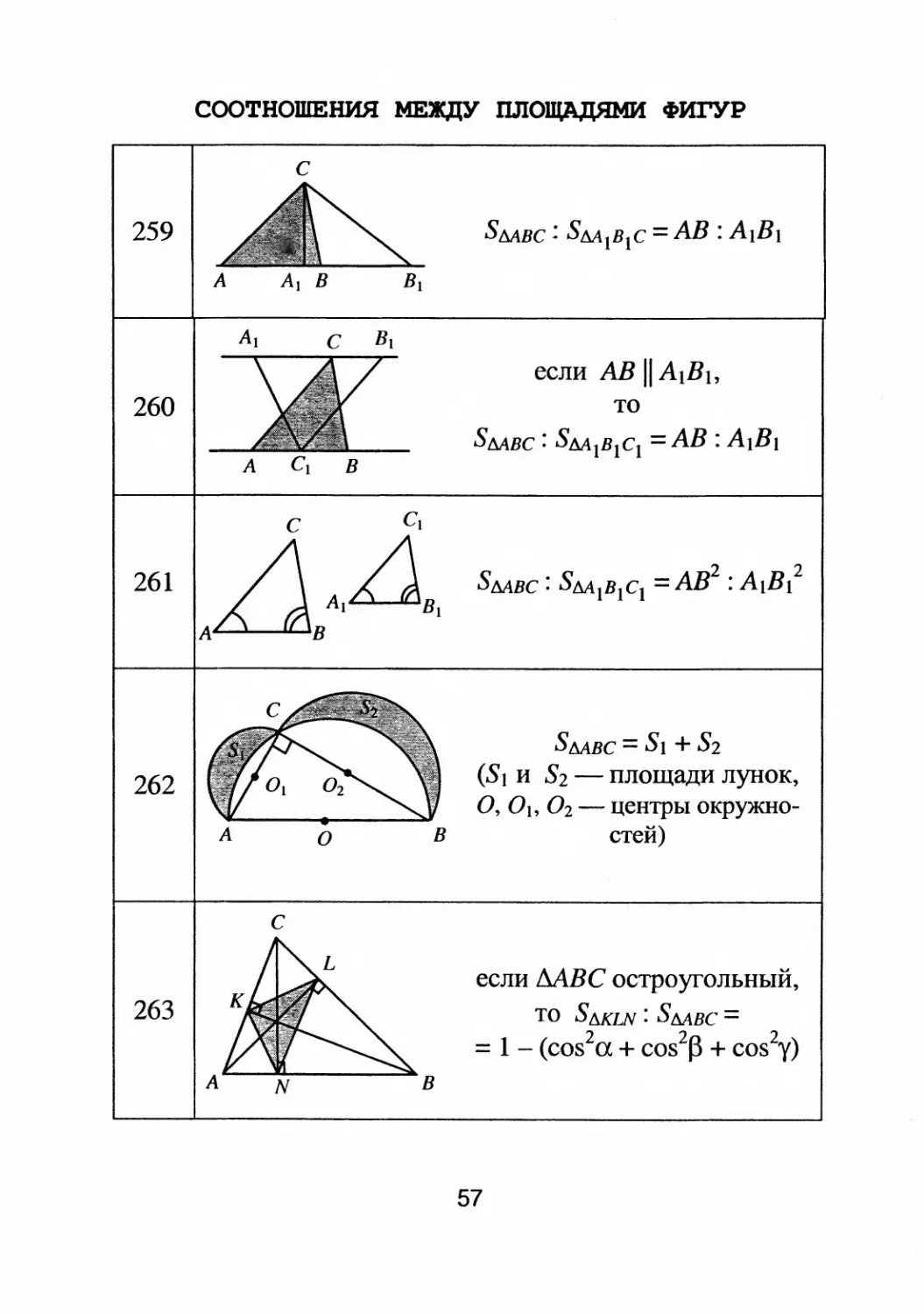
СООТНОШЕНИЯ МЕЖДУ ПЛОЩАДЯМИ ФИrYР
С
5MBC: SM 1 B 1 C = АВ : А 1 В 1
А А} В В 1
А 1 С 81
если АВ 11 А 1 В l,
то
5MBC: SM 1 B 1 C 1 =АВ: А 1 В]
А С 1 В
С С 1
./'\ 5MBC: SM1B1C 1 = А.В 2 : AI B 12
A1U B ]
А В
А
5MBC = Sl + S2
(SI И S2
площади лунок,
0,01, 02
центры ОКРУЖНО
в стей)
о
с
А
в
если МВС остроyrольный,
то S MLN : S МВС =
= 1
(cos 2 a + cos 2 B + cos 2 y)
N
57
264
265
266
267
268
к
.
.
.......
в
А
N
в
А
с
N
в
с
А
N
с
А
в
к
А
в
если МВС тупоyrольный,
то SMLN: 5MBC =
=cos 2 a + cos 2 f3 + cos 2 y
1
если АВ : ве : АС = р : q : 1,
то S !ИВС : S MLN =
(p+q)(p+l)(q+l)
2pql
SMLN 2 . а .
. у
= Sln
. Sln
. Sln
S МВС 2 2 2
АК BL
если КВ =р, LC =q,
S
ТО МВС = (р + 1) · (q + 1)
SMLC
АК BL CN
если = = ':F 1
,
КВ LC NA
то SMEK = SЫJPL = SЫiCQ,
S[JKEPB = SOLPQC = SCNQEA
58
269
270
271
272
273
с
А
в
А
D
А
А..
в р
к
D L
SЫJMC = SDAEMD
5MBD : SblJCD = АЕ : ЕС
S[]ABCD =2S0KLPN
1
SMED + SЫJEC =
SDABCD
2
(точка Е пересечения отрезков
KL и NF может не лежать на
АС (BD))
если PN 11 АС, KL 11 АС,
KN 11 BD, PL 11 BD,
то SOKLPN = 2S ОЛВСD
59
274
75
76
277
278
с
А
в
А
в
А Е
D
60
SOPKNL = SMLD + SЫJKC
если KN 11 АВ,
то
SMDC : 5MBD = 1 : 2
S
S МСВ · S MBD
DABCD
S
МВЕ
АЕ
ЕС
AB.AD SMDB
CD.CB Sf1CDB
если EL 11 АС, вк = KD,
то
SDABCE = Sl1ECD
279
280
281
282
А
N
А
а
А
с
Е D
А
SOAKNP= 5MBC
если о ABCD
параллело
С
rpaMM, а :1= Ь, то о KLPN
прямоyrольник,
1 Ь 2 .
SfJКLPN=2(a
) .sша,
SDABCD + SOKLPN =
а 2 + ь 2 .
· Slna
2
если о ABCD
трапеция,
00 < LADC < LDAB < 900, ТО
SNKPLE = SMKB + SЫJPC + S!:"CLD
SMED . SЫJEC = SMEB . SЫJEC
61
283
284
285
286
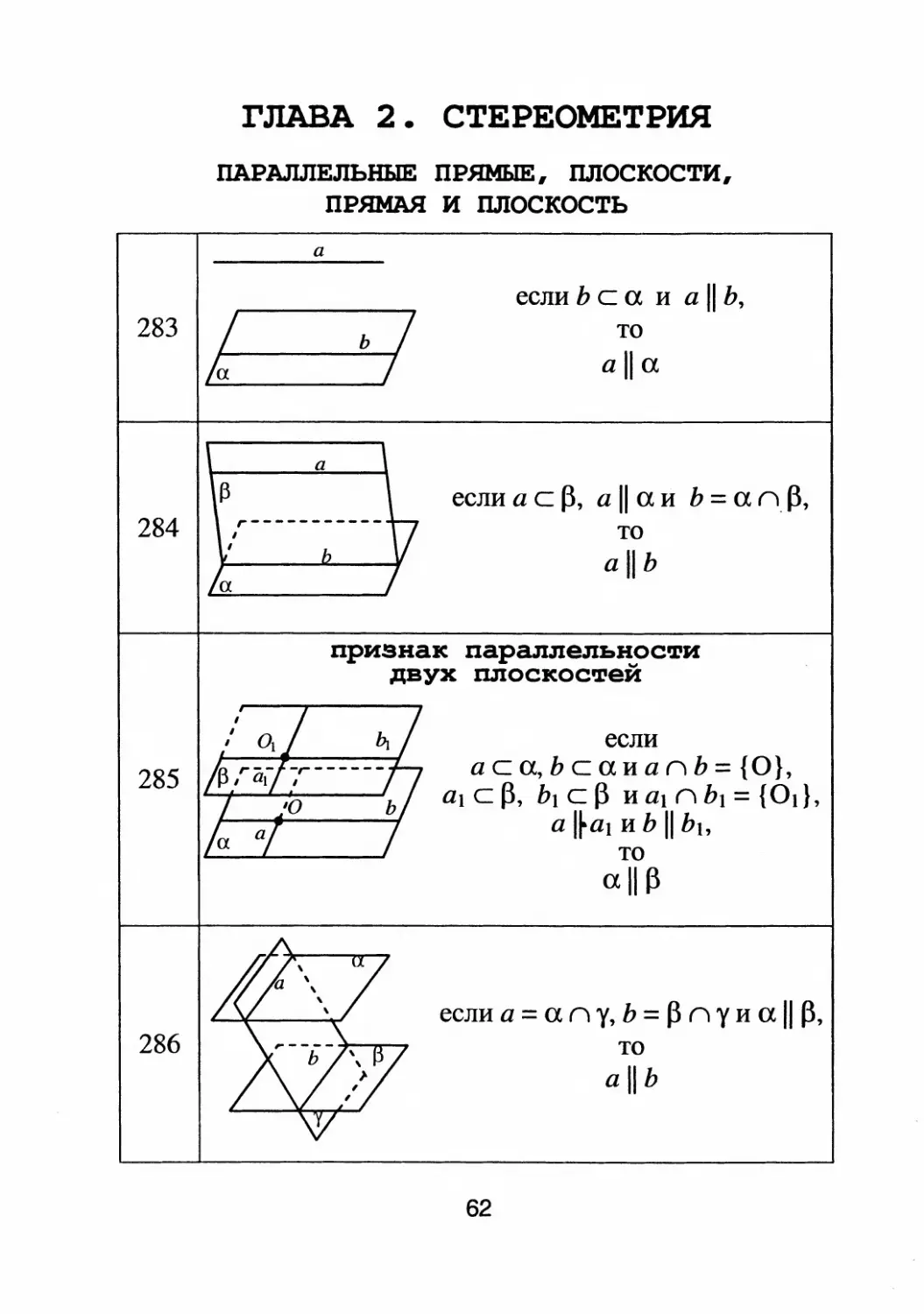
rЛАВА 2. СТЕРЕОМЕТРИЯ
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, ПЛОСКОСТИ,
ПРЯМАЯ И ПЛОСКОСТЬ
а
ь
а
J3
r..............-...........-
I
I
если Ь с а и а 11 Ь,
то
alla
если а C
, а 11 а и Ь = а ("\
,
то
а 11 ь
признак параллельности
""
двух ПЛОСКОС'.1'еи
если
аса,ЬсаиаnЬ= {О},
а} C
, Ь 1 С
И аl (\ Ь 1 = {01},
а I
al и ь 11 Ь 1 ,
ТО
а 11 J3
если а = а п у, Ь =
(\ у и а 11 J3,
то
а 11 ь
62
287
288
289
290
291
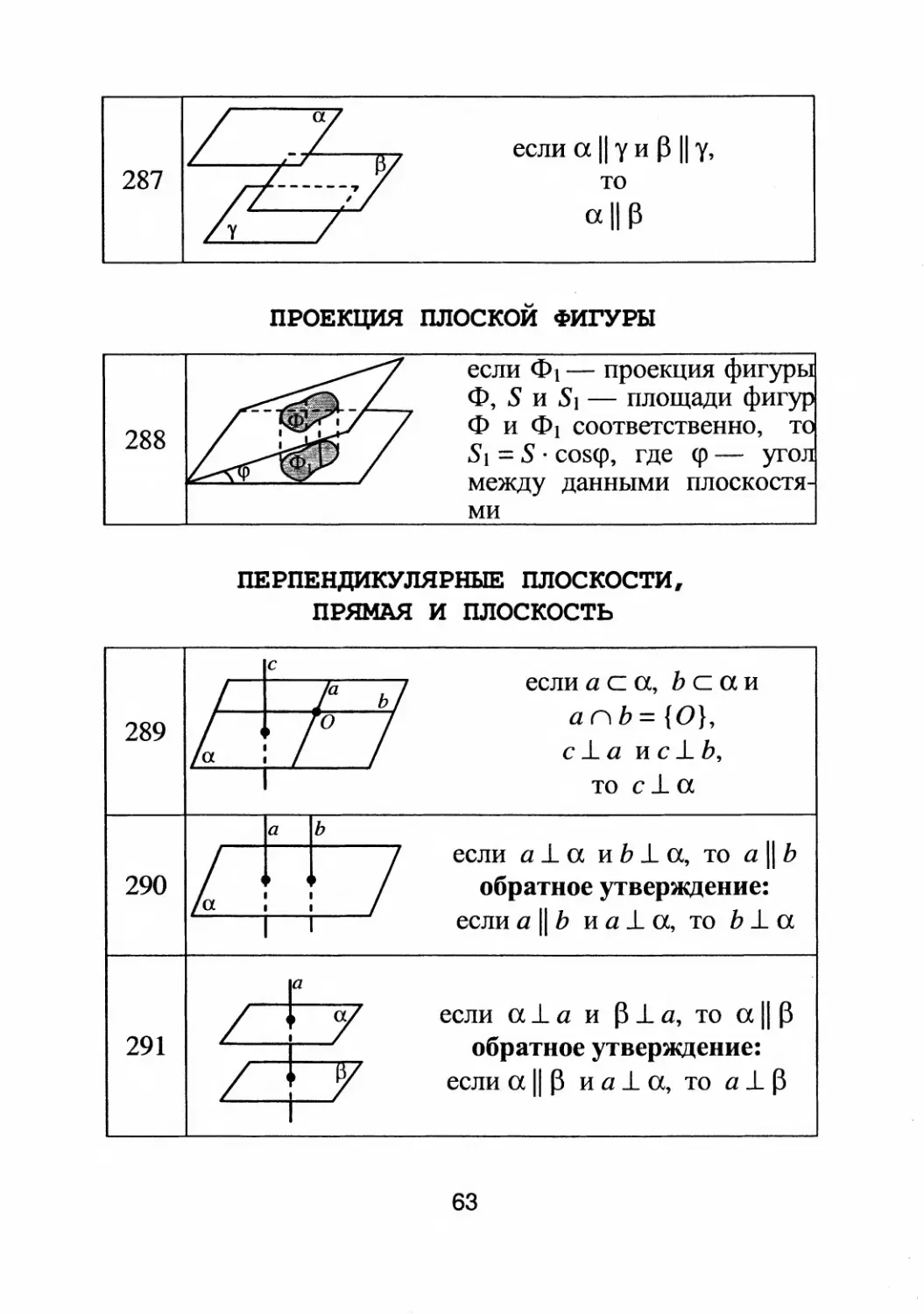
если а 11 у и
11 у,
то
all
ПРОЕКЦИЯ ПЛОСКОЙ ФИrYРЫ
если Ф 1
проекция фиrурь
Ф, S и S]
площади фиr
Ф и Ф 1 соответственно, т
Sl = S . cos<p, rде <р
yro
между данными плоскостя
ми
ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ,
ПРЯМАЯ И ПЛОСКОСТЬ
с
а
ь
а
если а С а, Ь с а и
апЬ= {О},
с
а и с
Ь,
то с
а
если а
а и Ь
<1, то а 11 ь
обратное утверждение:
если а 11 ь и а
а, то Ь
а
если <1
а и
а, то <1 11
обратное утверждение:
если а 11
и а
<1, то а
63
292
293
294
295
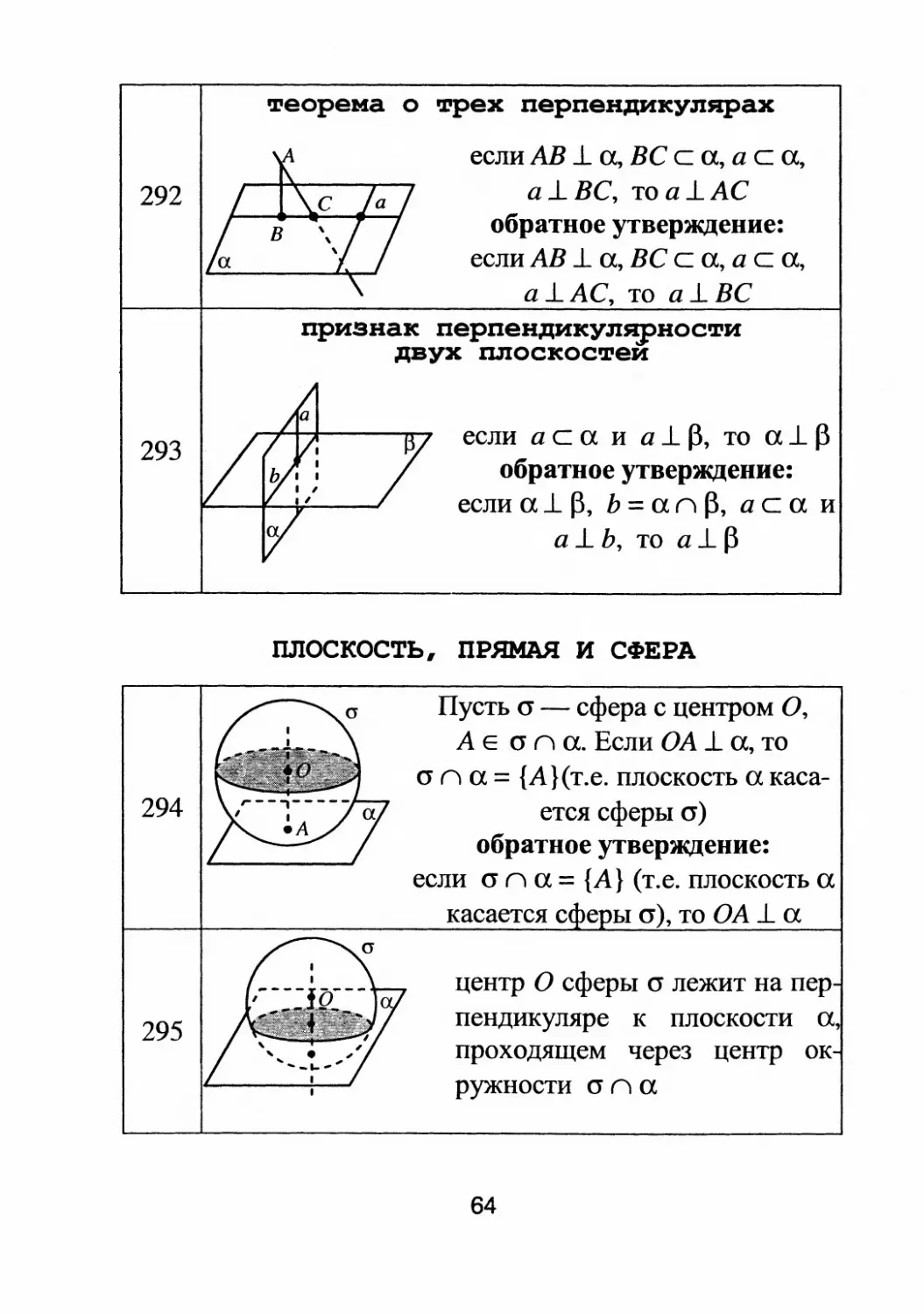
теорема о трех перпеидикупнрах
если АВ
а, ВС с а, а С а,
a
BC, тоа1.АС
обратное утверждение:
если АВ 1. а, ВС с а, а с а,
а
АС, то а 1. ВС
признак перпендикул
ности
двух плоскостеи
если а С а и а 1. f3, то а 1. f3
обратное утверждение:
если а 1.
, Ь = а п f3, а с а и
а 1. Ь, то а 1. f3
ПЛОСКОСТЬ, ПРЯМАЯ И СФЕРА
Пусть а
сфера с центром О,
А Е а п а. Если ОА 1. а, то
а п а = {А}(т.е. плоскость а Kaca
ется сферы а)
обратное утверждение:
если а n а = {А} (т.е. плоскость а
касается с е ы а), то ОА 1. а
центр О сферы cr лежит на пер
пендикуляре к плоскости а,
проходящем через центр ок
ружности cr п а
64
296
297
298
если п
yrольник AtA2.. .А,
лежит в плоскости а и вс
ero стороны касаются сфе
ры 0', то в п
yrольни
можно вписать окруж
ность, причем перпендику
ляр к плоскости (1" прохо
дящей через центр Q это
окружности, содержи
цен О с е ы
ПИРАМИДА
s
площадь боковой поверхности
Sбок
это сумма площадей ее бо
ковых rpанеи, площадь полнои
поверхности SПОЛН = Sбок + SOCH,
1
V =
SOCH · Н, rде SOCH
площадь
3
основания, Н = SO
высота
в
с
npавильиаи пир амид а
ирамида называется nравuльной, если в ее OC1l0вa
....
ии лежит правuльныи М1l020У20ЛЬ1lик u основа1lи
ысоты совпадает с центром этО20 М1l020У20льника
S
1
Sбок =
Р · h,
2
rде Р
периметр основания
пирамиды, h = SK ............ апофема
пир амиды
65
299
300
301
'"
«долька» npавипьнои пирамиды
s s если а = LOD8
yro
наклона боковоrо ребр
к плоскости основания
J3 = LOK8
yrол на
клона боковой rpани
плоскости основания
<р = LD8K
половин
к к yrла при вершине боко
вой rpани, у = LMNK
половина двyrpанноrо yrл
между соседними боковыми rpанями пирамиды,
= п = LDOK (этот yrол в правильной п
yrольной
п
пирамиде всеrда известен), то tga = tgJ3 . cosv,
g<p = cosf3 · tgv, sin<p = cosa . sinv, siny. cos<p = cosv
t = sina . t v, cos = sin . sinv
усеченная пир амид а
8 полн
площадь полной поверх
ности равна сумме площадеи все
ее rpанеи,
v= .!.(S\ +S2 + .J S\oS2).H, rде S]
3
и 82
площади оснований пира
с миды, Н = 01 О
высота
правипьная усеченная пирамида
площадь боковой поверхности
1
8бок=
(
+P2).h, rдеР 1 ИР2
2
периметры оснований, h
апо
81
82
фема; 8 бок = , rде 81
cosa
" 82
площади соответственн
D большеrо и меньшеrо основа
с ний, а
yrол наклона боково
ани
66
302
303
304
s
если SO
высота пирамиды
а LSA 1 0 = LSA 2 0 = ... = LSA"
или SA 1 = SA 2 = ... = SA п , то О
центр окружности, описанно
около основания пирамиды
обратное утверждение:
если основание О высоты SO
центр окружности, описанно
около основания пирамиды, т
LSA 1 0 = LSA20 = ... = LSA"O
SA 1 = SA 2 = ... = SA"
если SO
высота пирамиды, а вс
боковые rpани пирамиды наклонень
к плоскости основания под одни
yrлом а, то О
центр окружности
вписаннои в основание пирамиды
при этом SOCH = Sбок · cosa
обратное утверждение:
если основание О высоты SO
центр окружности, вписаннои в ос
нование пир амиды, то все боковы
rpани пирамиды наклонены к плос
кости основания под одним лом
если В 1 В 2 ...В"
сечение пира
миды SA 1 A 2 .. .А" плоскостью
параллельнои плоскости основа
ния а, h = SQ и Н= SO
высо
ты, V 1 И V2
объемы пирами
SB 1 B 2 .. .В" и SA 1 A 2 .. .А" соот
А п
s
Al
s
ветственно, то
2 , '-"t = (
) 3
V 2 Н
Sсеч
SOCH
67
305
306
307
ПРИЗМА. ПАРАЛЛЕЛЕПИПЕД
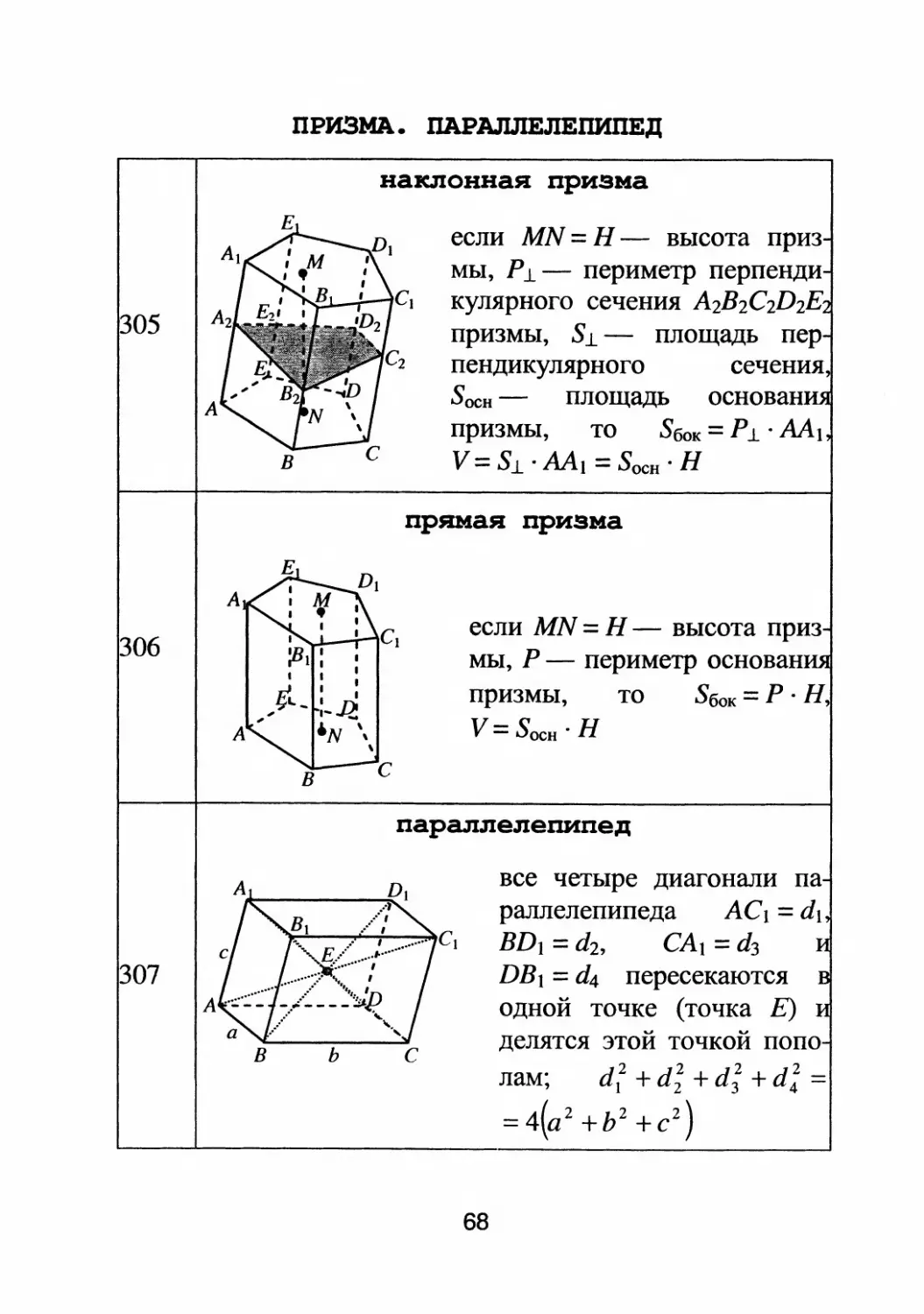
наклонная призма
если MN = Н
высота приз
мы, Р.1
периметр перпенди
С} кулярноrо сечения A 2 B 2 C2 D 2 E
призмы, S.1
площадь пер
пендикулярноrо сечения,
SOCH
площадь основан
призмы, то Sбок = Р.1 . АЛ}
V = S.1 · АЛ. = SOCH · Н
А
в
прямая призиа
А
I С}
:Вl: '
I I I
I I
L. I I
" ... ,...р
--
" .1. \
-N \
\
с
в
если MN = Н
высота приз
мы, Р
периметр основан
призмы, то Sбок = Р . н
V = SOCH . Н
параллелепипед
D 1
...)
.... ,
Вl .... ,
-.. ..., ........ с 1
С -- Е . ....
........ ..' ...,..,
....:........ ,
.........:....... '
........ .... "':'
А ........ ..' :::
. п
... ..
.. .. .......t;'
..' "-
..' '-
..' "
в
ь
с
все четыре диаrонали па
раллелепипеда АС 1 = d 1
BD 1 = d 2 , СА} = d з
DB} = d 4 пересекаются
одной точке (точка Е)
делятся этои точкои попо
лам. d 2 +d 2 +d 2 +d 2 =
, 1 2 3 4
= 4(а 2 + Ь 2 + с 2 )
68
D 1
'"
ПрНМОИ параппепепипед
если диаrонали прямоrо парал
лелепипеда BD} = d} и СА} = d 2
то d 1 2 = а 2 +ь 2 +с 2
2аЬ. cosa,
d; = а 2 +ь 2 + с 2 + 2аЬ. cosa;
Sбок = 2(а + Ь)с;
Sполн = 2(а + Ь)с + 2аЬ. sina;
V = 2аЬс. sina
1
в
308
....... ....
...... '.
I ..... -'.
I .....:ie;.... d 2
I .... ........
d . '.
:n 1 ... . '"
., ....
------
- __е С
, .
4. ....
, (J:' .....
А
в
'"
прнмоуrольныи параллелепипед
D 1
309
V = аЬс,
d= .J a 2 +b 2 +c 2
А
а
ПРАВИЛЬНЫЕ мноrоrрАННИКИ
М1l0202ра1lНИК llазывается правuльным, если все е20 2pa
1lи
правuлыlеe МНО20У20ЛЬ1lИКИ и все М1l0202ранные У2Лbl
равны.
Для правильных мноrоrpанников введем следующие обо
значения:
V
объем мноrоrpанника, S
площадь поверхности,
R
радиус описанной сферы, r
радиус вписанной сфе
ры, а
ребро мноrоrpанника.
:куб
S = 6а 2 V = а 3 , R = J3 а
, 2 '
r= a d=a J3
2'
...
......
....... d
...
. ...
...
. ...
I
,
--
--
310
,
,
,
а
69
311
312
313
пра:вильНЪIИ тетраэдр
имеет четыре rpани
равно
сторонние треyrольники,
S =.J3 а 2 V = .[2 а 3 R = J6 а
, 12' 4
J6 J6
r= а Н= а
12' 3
(Н
высота пирамиды)
правильныи октаэдр
имеет 8 rpаней
равных равно
сторонних треyrольников, 6 вер
шин, 12 ребер,
.J3 2 .[23
S =2 3 а V = а
, з'
.[2 J6
R= а r= а
2' 6
правильНЪIИ додекаэдр
имеет 12 rpаней
равных правиль
ных пятиyrольников, 20 вершин
30 ребер,
S =3
5(5+2.J5) а 2 ,
v= .!(15+ 7.J5)a 3 , R = .J3 (1 +.J5)a,
4 4
r =
1O(25+ 11.J5) а
20
70
314
315
316
""
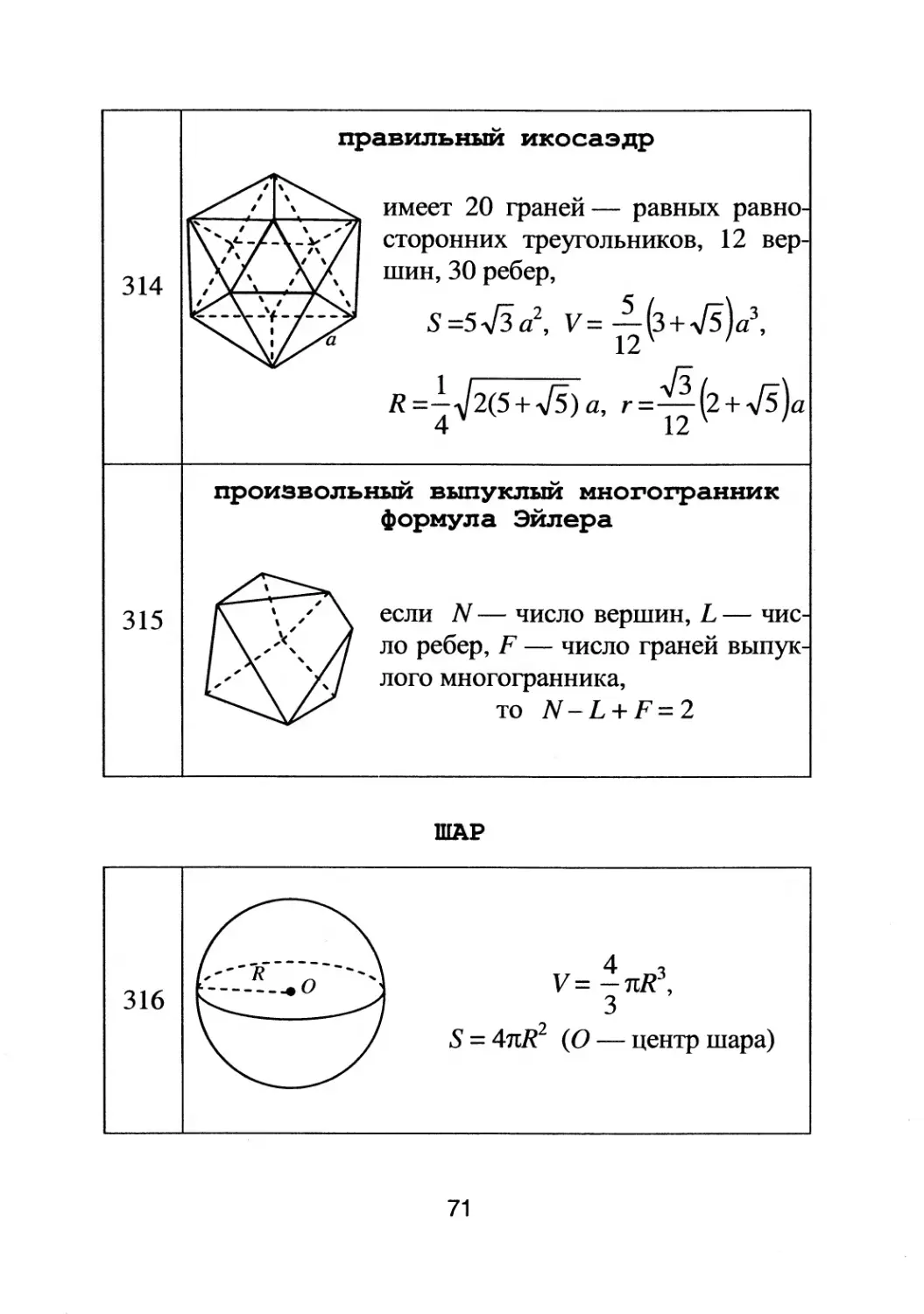
правильныи икосаэдр
имеет 20 rpаней
равных равно
сторонних треyrольников, 12 Bep
шин, 30 ребер,
S=5.J3a 2 , v= 2(з+.J5)а 3 ,
12
R =!
2(5 +.J5) а, r = .J3 (2 + .J5)a
4 12
"" ""
произвольныи выпуклым мно
о
анник
формула ЭЙЛера
если N
число вершин, L
чис
ло ребер, F
число rраней выпук
лоrо мноrоrpанника,
то N
L+F=2
ШАР
4
v=
'ЛR3
3 '
S = 4пR 2 (О
центр шара)
71
317
318
319
""
шаровом сеJ:1Иент
2 h 2
V = 7th (R
), а = h(2R
h),
3
Sбок = 21tRh,
Sполн = 41tRh
1th 2 = 1t(2Rh + а 2 )
(О
центр шара, h
высота
cerMeHTa)
""
шаровои сектор
v =3. nIfh,
3
Sполн = 1tR (2h + .J 2Rh
h 2 )
(О
центр шара, h
высота
соответствующеrо cerMeHTa)
"" ""
шаровои спои
1 3 1 ( 2 2 )
V =.......1th +
7t 'i + r 2 h,
6 2
Sбок = 2xRh
(О
центр шара, h = 0201
высота шаровоrо слоя)
72
320
321
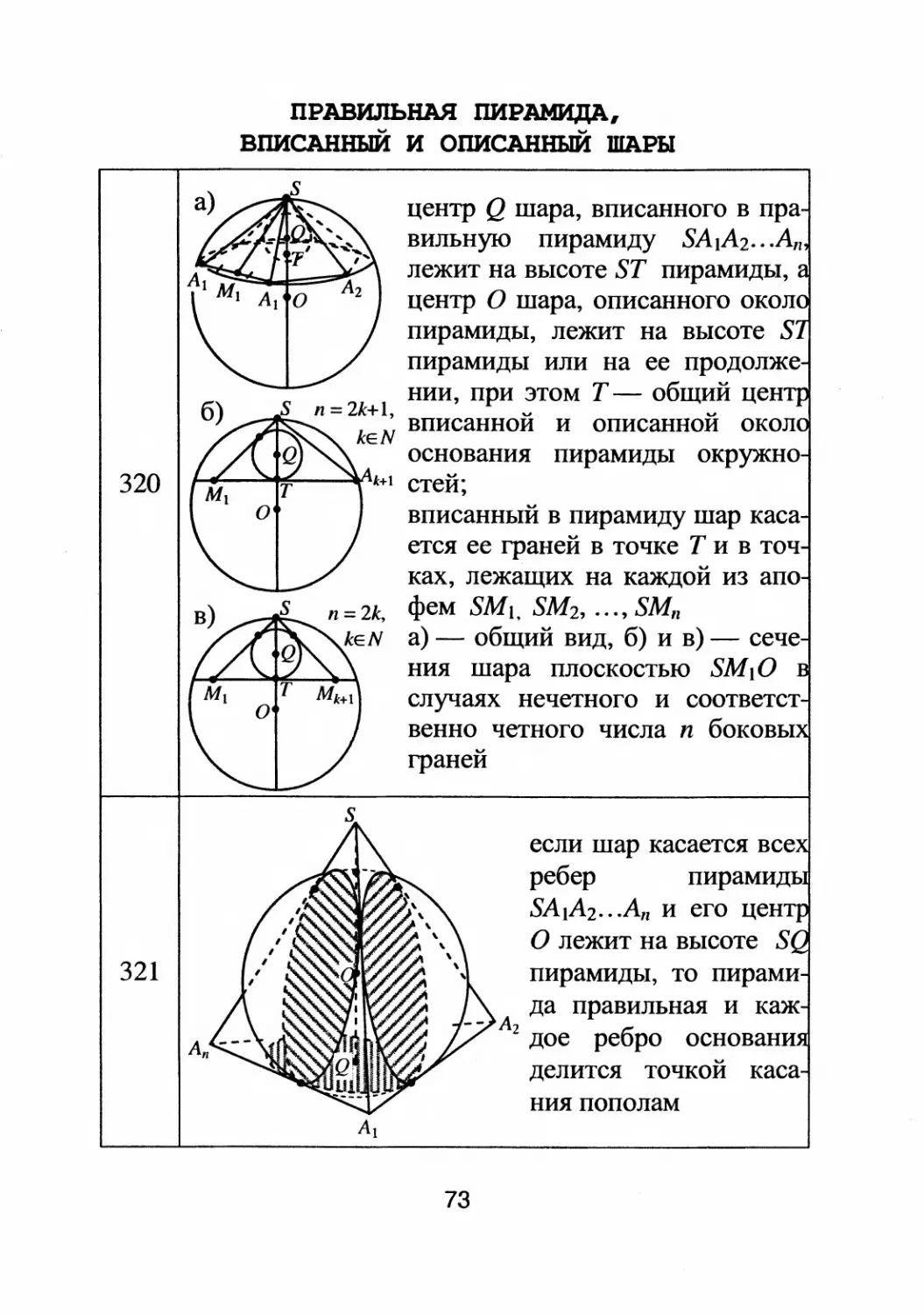
ПРАВИЛЬНАЯ ПИРАМИДА,
ВПИСАННЫЙ и ОПИСАННЫЙ ШАРЫ
центр Q шара, вписанноrо в пра
вильную пирамиду SA 1 A 2 .. .А 1l
лежит на высоте ST пирамиды,
центр О шара, описанноrо окол
пир амиды, лежит на высоте S
пирамиды или на ее продолже
нии, при этом Т
общий цен
S п = 2k+ 1,
keN вписаннои и описаннои окол
основания пирамиды окружно
k+l стей;
вписанныи в пирамиду шар каса
ется ее rpаней в точке Т и в точ
ках, лежащих на каждои из апо
фем SM 1 , SM 2 , ..., SM Il
а)
общий вид, б) и в)
сече
ния шара плоскостью SM 1 0
случаях нечетноrо и соответст
венно четноrо числа п боковы
rpанеи
S
S
S
А 1
73
если шар касается все
ребер пирамидъ
SA 1 A 2 .. .A ll И ero цен
О лежит на высоте S
пирамиды, то пирами
да правильная и каж
А
2 дое ребро основани
делится точкои каса
ния пополам
322
323
324
s
если центры вписанноrо
описанноrо llIаров для тре
yrольной пирамиды SAB
совпадают, то rpани пира
миды
равные треyrоль
ники (т. е.
МВС = J1.SAB = J1.SBC =
= J1.SAC)
ЦИЛИНДР
.
'h
I
I
2
V = nR h, Sбок = 2nRh,
SПОЛН = 2nR(h + R)
(R
радиус оснований,
h
высота)
v
вписаниыи цилиндр
центр О описанноrо около ци
линдра шара есть середина от
резка, соединяющеrо центръ
01, 02 оснований; при этом:
4/3 3 2/3 .J6
maxV= nR при h = R, r=
R;
933
RJ2
mаХSбок = 2пR 2 при h = R J2, r =
.
,
3
mахS полн = nR 2 (l +J5)
5
/5 5+/5
при h = 2R , r = R
10 10
74
325
326
327
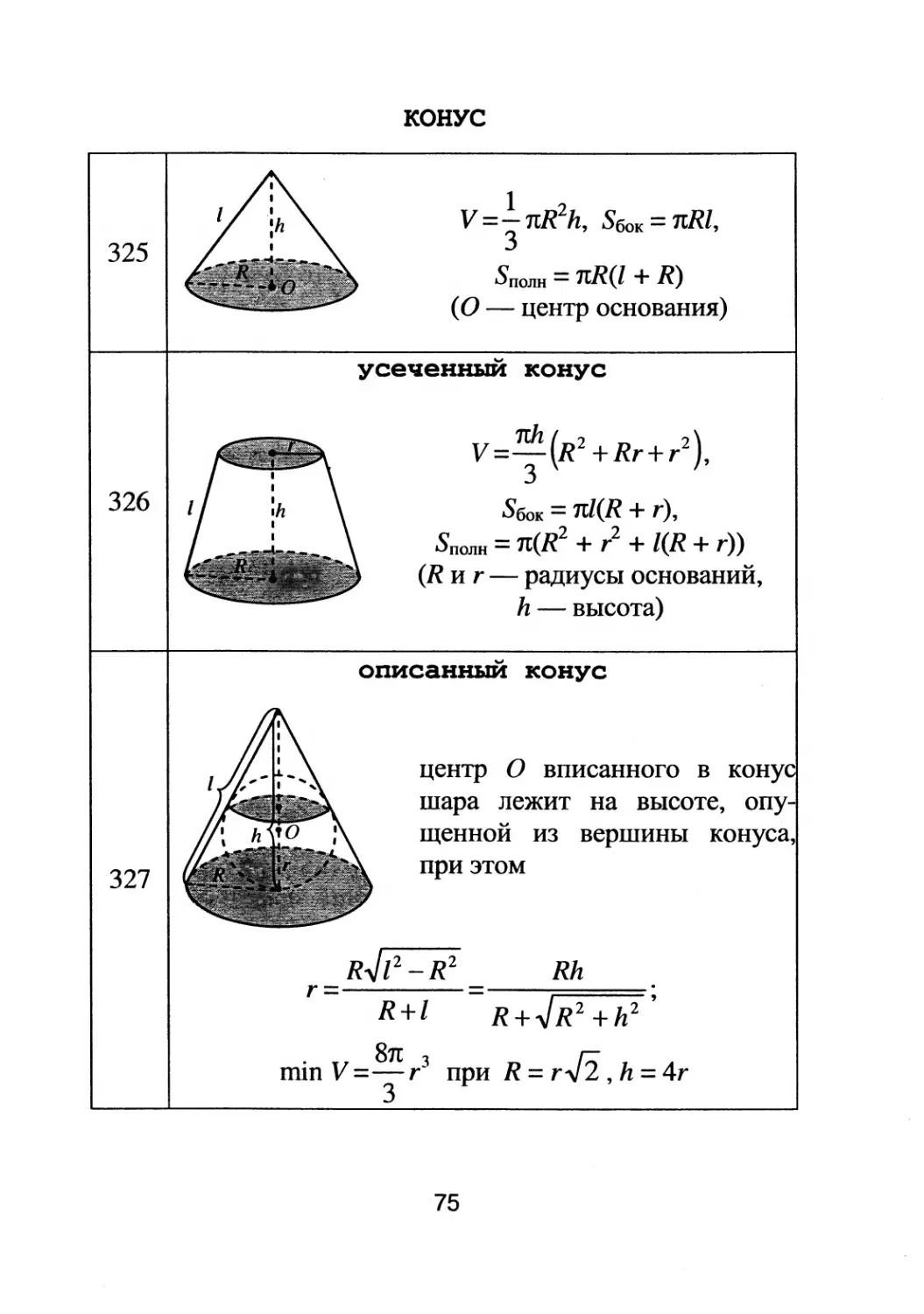
КОНУС
1 2
V =
nR h, Sбок = nRI,
3
Sполн = nR(1 + R)
(О
центр основания)
""
усеченНЪIИ :конус
nh ( 2 2 )
v=
R +Rr+r ,
3
Sбок = nl(R + r),
Sполн = n(R 2 + r 2 + I(R + r»
(R и r
радиусы оснований,
h
высота)
""
описанНЪIИ :конус
центр О вписанноrо в кону
шара лежит на высоте, опу
щеннои из вершины конуса,
при этом
R .J 1 2
R 2
r=
R+l
Rh
.
R+ .J R 2 +h 2 '
при R = r/2 , h = 4r
. V 8п 3
тlП =
r
3
75
328
329
330
"" ""
описаниыи усечениыи конус
центр О вписанноrо в усеченны
конус шара лежит на отрезке, со
единяющем центры основании.
при ЭТОМ r = -J Rl · R 2 , 1 = R] + Rz;
.п V = 2пr 3 при R 1 = R 2 = r (т.е. коrда
конус «превращается» В цилинд )
""
вnисаниыи :конус
усеченны
центр О описанноrо около конус
шара лежит на опущеннои и
вершины конуса высоте или на е
продолжении, при этом
32 3 4R 2RJ2
maxV=
nR П р и h =
r= ·
, ,
81 3 3
8/3 2 4R 2RJ2
mахSбок = nR при h =
, r =
933
"" ""
вnисаниыи усечениыи конус
центр О описанноrо около усе
ченноrо конуса шара лежит н
прямои, проходящеи через цен
""
тры основании, при этом
4/3 3 16
maxV= nR при rl = r2 =
R
9 3
2/3
h = R (т.е. коrда усеченны
3
конус «превращается» В
линд )
76
331
332
ТРЕхrрАННЫЙ пол
Трехrpанный yrол
фиrура,
образованная тремя лучами,
имеющими общую начальную
точку и не лежащими воднои
плоскости, И заключенными
между этими лучами частями
плоскости. Образно rоворя,
трехrpанный yrол
фиrура,
представляющая собой BO
ронку, склеенную (сшитую)
з трех плоских yrлов с общей вершиной, или, ина
е rоворя, трехrpанныи yrол
это треyrольная пи
амида с «бесконечно удаленным основанием».
лоские yrлы а, f3, у тpexrpaHHoro yrла называютс
.ero rpанями;
учи, по которым пересекаются rpани тpexrpaHHor
ла, называются ero ребрами;
лы между rpанями (LЛ, LB, LC) тpexrpaHHor
ла называются ero двyrpанными yrлами
""
своиства плоских и двуrpаниых y
пOB
TpexrpaHHO
O y
пa
1. а + f3 > у, а + у > f3, f3 + у> а.
2. а + f3 + у < 3600.
3. LA = LB тоrда и только тоrда, коrда а = f3
де а и
плоские yrлы тpexrpaHHoro yrла, а LA
В
противолежащие им двyrpанные yrлы.
77
4. Теорема косинусов:
LC cosy
cosa .COs
cos = .
sin а . sin
Следствие (теорема о трех косинусах):
332 LC = 900 тоrда и только тоrда, коrда
cosy = cosa . cos
.
5. Теорема синусов:
.
Slna
sin LA
sin
sin LB
.
slnY
sin LC
.
Seee_
ЛИТЕРАТУРА
1. АмеЛЬКUIl, В. В. rеометрия на плоскости: теория,
задачи, решения! В. В. Амелькин, В. л. Рабцевич,
В. л. Тимохович.
Минск: 000 «Асар», 2003.
592 с.
2. АмеЛЬКUIl, В. В. Планиметрия: теория и задачи!
В. В. Амелькин, В. л. Рабцевич, В. л. Тимохович.
Минск: 000 «Асар», 2005.
320 с.
3. ШЛblков, В. В. rеометрия: Учебник ДЛЯ 11
ro кл.!
В. В. Шлыков.
Минск: Нар. асвета, 2002.
269 с.
4. rеометрия: Учебник ДЛЯ 1()"",11 классов средней
школы! л. с. Атанасян [и др.].
М.: Просвещение,
1993.
207 с.
Seee_
Учебное издание
ШКОЛЬНАЯ rЕОМЕТРИЯ
в ЧЕРТЕЖАХ И ФОРМУЛАХ
Авторы:
Амелькин Владимир Васильевич
Рабцевич Татьяна Ивановна
Тимохович Владимир Леонидович
Редактор Т. И. Рабцевuч
Обложка Н. Л Навроцкой
Компьютерная верстка И. И. Fалицкиu
Корректор с. И Шердюкова
Подписано в печать с rотовых диапозитивов 22.04.2008 r.
Формат 60х84/16. Бумаrа офсетная. rарнитура Тайме. Печать офсетная.
Уел. печ. л. 4,65. Уч.
изд. л. 3,7. Тираж 3 100 экз. Заказ N5! 1133.
Издательское 000 «Красико
nринт». ЛИ N5! 02330/0150112 от 09.10.2007 [.
220035, Беларусь, [. Минск, ул. ТИМИРЯЗ.ева, 65 б, ПОМ. ]42.
Республиканское унитарное предприятие
«Издательство «Белорусский Дом печати». 220013, r. Минск, пр
т Независимости, 79.
ЛП 02330/0131528 от 30.04.2004 [.
Seee_
Цель, Поставленная aвтopaмn,
рассказать о школьном Курсе rеометрии
по возможности исчерпывающе и систе
матизировано, но коротко и ясно.
Решение любой rеометрической зада
чи начинается с ПОстроения чертежа.
Правильно ВЫполненный чертеж
это
уже шаr к решению задачи, и поэтому к
ПОстроению чертежа нужно ОТНоситься
серьезно.
Несмотря на небольшой объем, в данном
издании приведены в чертежах и Форму
лах все ОСНовные Свойства Плоских и про
странственных фиryр.
ЭТО ПОсобие ПОДХОдит в качеСтве и MaTe
риала для повторения, параллеЛЬноrо изу
чению дрyrих тем в школе, и справочника.
Авторы уверены в том, что приведен
ные в КНижке сведения ПОЗВОлят каждому
УСВОИвшему их школьнику, а затем и аби
туриенту успешно решить rеометри
ческие задачи как ШКОльноrо и KOHKypCHO
ro экзаменов по математике, так и цeHтpa
лизованноrо теСТИрования.
1
r
t:
+t ISBN
t-
ii
.t
.11..
111111 9
111111
11
4
11
>;-. '.. .,..;,,"-....b.,,
111111
11
..
.". ;
ом.. _"""'1'"
,'
. h Ч
. <.,
.
; .
.
:..: ..