СООТВЕТСТВИЕ МЕЖДУ ПУНКТАМИ УЧЕБНИКА И ЗАДАЧАМИ ТЕТРАДИ
Номера
пунктов
учебника
39, 40
41
42
43
44
45
46
47
48
49, 50
51
52
53
54
55
56, 57
58
59
60
61
62
63
64
66
67
68
69
70
71
72
73
74
75
76, 77
78
79
80, 81
82
83
84
85
Тема
Многоугольник. Выпуклый многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Трапеция
Задачи на построение
Прямоугольник
Ромб и квадрат
Осевая и центральная симметрии
Понятие площади многоугольника
Площадь квадрата. Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Пропорциональные отрезки. Определение подобных
треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
Синус, косинус и тангенс острого угла прямоугольного
треугольника
Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°
Взаимное расположение прямой и окружности
Касательная к окружности
Градусная мера дуги окружности
Теорема о вписанном угле
Свойства биссектрисы угла и серединного перпендикуляра к
отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Понятие вектора. Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Законы сложения векторов. Правило параллелограмма.
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Номера
задач
тетради
1 — 5
6, 7
8—14
15
16—18
19, 20
21 — 23
24
25, 26
27
28—32
33—35
36—41
42—44
45—48
49, 50
51 — 53
54
55—58
59
60
61—65
66-68
69, 70
71 — 73
74 — 77
78, 79
80—84
85, 86
87—94
95 — 102
103
104 — 108
109—111
112
113, 114
115, 116
117—121
122—128
129—133
134
135 — 137

ГЕОМЕТРИЯ
РАБОЧАЯ
ТЕТРАДЬ
КЛАСС
Пособие
для учащихся
общеобразовательных
учреждений
12-е издание
Москва
«Просвещение»
2010

УДК 373.167.1:514 ^
ББК 22.151я72 1Щ
ГЗб ^
Авторы:
Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина
Рабочая тетрадь является дополнением к учебнику «Геометрия, 7—9»
авторов Л. С. Атанасяна, В. Ф. Бутузова и др. и предназначена для организации
решения задач учащимися на уроке после их ознакомления с новым учебным
материалом. На этом этапе учащиеся делают первые шаги по осознанию
нового материала, освоению основных действий с изучаемым материалом. Поэтому
в тетрадь включены только базовые задачи, обеспечивающие необходимую
репродуктивную деятельность в форме внешней речи. Наличие текстовых
заготовок облегчает ученику выполнение действий в развернутой письменной
форме, а учителю позволяет осуществлять во время урока оперативный контроль
и коррекцию деятельности учащихся. Использование данной тетради для
организации других видов деятельности (самостоятельных работ, повторения, контроля
и т. д.) малоэффективно.
Учебное издание
Атанасян Левон Сергеевич
Бутузов Валентин Федорович
Глазков Юрий Александрович
Юдина Ирина Игоревна
ГЕОМЕТРИЯ
Рабочая тетрадь
8 класс
Пособие для учащихся
общеобразовательных учреждений
Зав. редакцией Т. А. Бурмистрова. Редактор Л. В. Кузнецова. Младший редактор
Н. В. Ноговицына. Художники В. А. Андрианов, В.В.Костин, О. П. Богомолова.
Художественный редактор О. П. Богомолова. Компьютерная верстка Е. А. Стрижевской,
О.С.Ивановой. Технический редактор Е.Н. Зелянина. Корректор Н.Д. Цухай.
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000.
Изд. лиц. Серия ИД №05824 от 12.09.01. Подписано в печать 20.04.10. Формат 70xl007i6-
Бумага писчая. Гарнитура Школьная. Печать офсетная. Уч.-изд. л. 3,27. Доп. тираж 50 000 экз.
Заказ № 30039.
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано в ОАО «Саратовский полиграфкомбинат».
410004, г. Саратов, ул. Чернышевского, 59. www.sarpk.ru
ISBN 978-5-09-022773-5 © Издательство «Просвещение», 1999
© Художественное оформление.
Издательство «Просвещение», 2006
Все права защищены

Глава V
Четырехугольники
Многоугольники
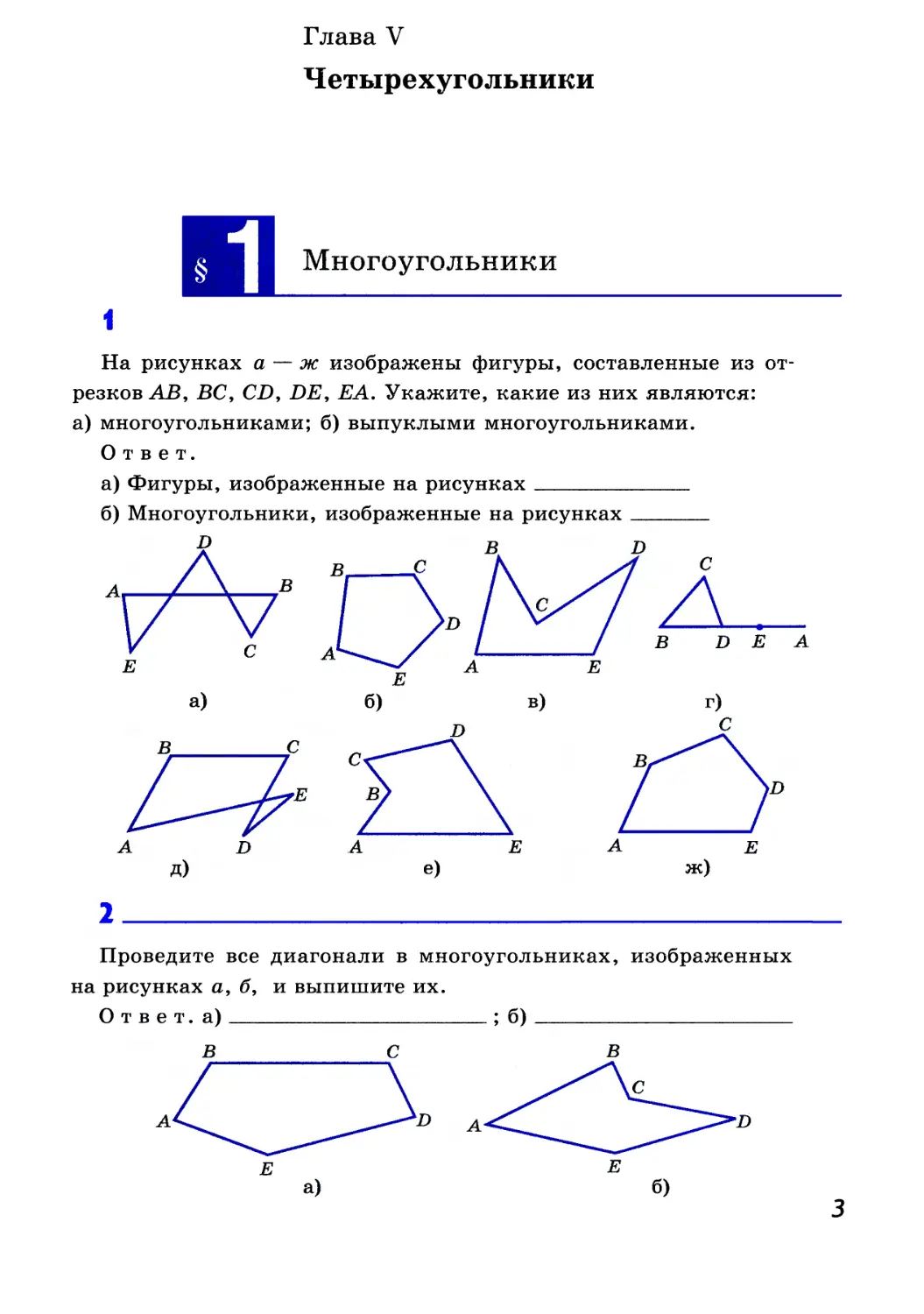
1
На рисунках а — ж изображены фигуры, составленные из
отрезков АВ, ВС, CD, DE, EA. Укажите, какие из них являются:
а) многоугольниками; б) выпуклыми многоугольниками.
Ответ.
а) Фигуры, изображенные на рисунках
б) Многоугольники, изображенные на рисунках
В D
А
В
В
Е
1_У
Л
В
D Е А
Е
Е
а)
б)
в)
е)
ж)
Е
Проведите все диагонали в многоугольниках, изображенных
на рисунках а, б, и выпишите их.
Ответ, а) ; б)
ВС В

Начертите выпуклый семиугольник
и из какой-нибудь его вершины
проведите все возможные диагонали.
а) Сколько при этом образовалось
треугольников?
б) Найдите сумму углов
семиугольника.
Ответ.
а)
б) °.
Используя формулу для вычисления суммы углов выпуклого
многоугольника Sn = 180°(n - 2), найдите сумму углов выпуклого:
а) одиннадцатиугольника: Sn = 180° • =
б) двадцатидвухугольника: S22 = 180° • =
Ответ.
а) °;
б) °.
Найдите число сторон выпуклого многоугольника, каждый угол
которого равен: а) 135°; б) 150°.
Решение.
а) Сумма всех углов выпуклого n-угольника, каждый угол
которого равен 135°, равна 135° • п; с другой стороны, она равна
(п - 2) • 180°. Таким образом, 135° • п = (п - 2) • 180°, или 135° • п =
=180° • п - 360°, откуда 45° • п = 360°, п = 8.
б)
Ответ.
а) п = 8;
б) п =

Найдите сторону ВС четырехугольника ABCD, если его периметр
равен 22 см, сторона АВ на 2 см больше стороны ВС и на 2 см
меньше каждой из сторон DA и CD.
Решение.
По условию PABCD = АВ + ВС + CD + DA = 22 см, ВС = АВ -
- , CD = DA = АВ +
Итак, 22 см = = ,
откуда АВ = , а ВС =
Ответ. ВС =
Найдите углы В, С и D выпуклого четырехугольника ABCD, если
АВ, Z.C = Z.DuZ.A = 35°.
Решение.
Так как по условию ZA=ZBhZA= 35°, то Z.A + /LB = 35° X
х 2 = 70°. Сумма углов выпуклого четырехугольника равна °,
поэтому Z.C + Z. D = - =
По условию ZC = ZD, значит, каждый из них равен
Ответ. АВ = ,ZC = , /. D =
Параллелограмм и трапеция
8
В параллелограмме ABCD найдите: а) стороны, если ВС на 8 см
больше стороны АВ, а периметр равен 64 см; б) углы, если Z.A = 38°.
Решение.
а) По свойству параллелограмма АВ = , ВС = и Z. А =
= Z , /. В = ^ По условию PABCD = 64 см, следовательно,
2 (АВ + ВС) = , откуда АВ + ВС = , но ВС на
больше АВ, поэтому АВ + = 32 см,
откуда АВ = , ВС = + 8 см =
б) По условию ZA = 38°, а так как /_А + /_В = °, то Z. В =
о qqo о
Ответ, а) АВ = = см, ВС — = см;
б) А С = °, АВ = А = °.

в
В параллелограмме ABCD диагональ АС, равная 24 см, образует
со стороной AD угол в 30°, О — точка пересечения диагоналей АС
и BDj ОЕ _L AD. Найдите длину отрезка ОЕ.
Решение.
Диагонали параллелограмма точкой
пересечения ,
поэтому АО = = см.
Треугольник АОЕ — прямоугольный с
гипотенузой и острым углом А,
равным °. Поэтому катет ОЕ,
лежащий против угла в °, равен
, т. е. ОЕ = см = см.
D
Ответ.
см.
10
Биссектриса угла А параллелограмма ABCD пересекает сторону
ВС в точке Р, причем ВР = PC. Найдите стороны
параллелограмма, если его периметр равен 54 см.
Решение.
1) Z. 1 = Z. 2, так как луч АР —
так как эти углы
при пересечении параллельных прямых
секущей .
Следовательно, Z. 1 = Z 3.
2) Треугольник АВР —
, так как его углы
1 и 3 равны, поэтому АВ =
3) По условию ВР = PC,
следовательно, ВС = ВР = АВ.
Итак, PABCD=2(AB + ) = АВ.
Так как периметр параллелограмма
равен 54 см, то АВ = 54 см,
откуда АВ = см и ВС = см.
D
Ответ. АВ = DC =
ВС = AD =
.см,
_см.

11
На рисунке в четырехугольнике
ABCD Z1 = Z3,Z2 = Z4.
Докажите, что четырехугольник
ABCD — параллелограмм.
D
Доказательство.
1) Так как Z 1 = Z 3, а эти углы —
при пересечении прямых и секущей , то прямые
и параллельны.
2) Так как Z 2 = Z 4, то прямые и также параллельны.
Итак, четырехугольник ABCD — параллелограмм, так как его
стороны
12
в
А
1 3
С
4
Является ли четырехугольник
ABCD на рисунке параллелограммом,
если:
а) Z. 1 = 75°, Z. 3 = 105°, Z2^Z4;
б) /_ 1 = Z. 2 = 70°, ^ 3 = 105°?
Решение.
а) В четырехугольнике ABCD две стороны АВ и CD
параллельны, так как Z1+ Z3= 75° + 105° = 180°, а эти углы —
односторонние при пересечении прямых АВ и DC секущей AD. Поскольку
АВ || DC, то /- 1 = /- 4 (как соответственные углы). Две другие
стороны AD и ВС четырехугольника ABCD не параллельны, так как
накрест лежащие углы 1 и 2 не равны (Zl = Z4 ^Z2).
Следовательно, четырехугольник ABCD не является параллелограммом.
б)
Ответ, а) Нет; б)

м
13
На рисунке в параллелограмме
ABCD на сторонах ВС и AD отмечены
точки М и JV так, что ВМ = DN.
Докажите, что четырехугольник AMCN —
параллелограмм.
Доказательство.
Так как по условию ABCD — параллелограмм, то его
противоположные стороны ВС и AD
и , т.е. II , = Так как МС =
N
D
, AN =
, и так как ВМ = DN, то
МС =
Таким образом, в четырехугольнике AMCN две
противоположные стороны и
( || , = ), следовательно, AMNC—
14
На сторонах параллелограмма
EFKP отмечены точки М, N, T, L
так, как показано на рисунке, причем
FM = РТ, EL =KN. Докажите, что
четырехугольник MLTN —
параллелограмм.
Доказательство.
1) Так как EFKP — параллелограмм, то по свойствам
параллелограмма Z.F = Z. , Z.E = Z. и EF = , ЕР = По ус-
К
ловию FM = PT, EL = KN и ЕМ = EF -
поэтому ЕМ = , PL =
КТ= РК-
2) Л MEL = Л .
по
Из равенства этих треугольников следует
равенство сторон ML и
3) Аналогично Л MFN = Л , откуда MN =
Итак, в четырехугольнике MLTN противоположные стороны
и , и попарно ,
следовательно, MLTN — параллелограмм.
8

15
На рисунке диагонали
параллелограмма MNPQ пересекаются в
точке О. Докажите, что четырехугольник
ABCD является параллелограммом,
если ОА =\ОМ, OB = Jew, ОС =^
О О О
N
Доказательство.
По свойству параллелограмма диагонали МР и NQ точкой
перет. е.
, аналогично ОВ =
и
2
сечения О
поэтому ОА = = — _
о t»
Итак, в четырехугольнике ABCD диагонали АС и BD точкой
пересечения О , поэтому ABCD —
Найдите углы М и Р трапеции MNPQ с основаниями MQ и NP,
если А N = 109°, a A Q = 37°.
Решение.
Углы М и JV, Р и Q — при пересечении
параллельных прямых MQ и NP секущими и , поэтому AM +
+ А N = °, АР + AQ = °. Так как по условию А N = 109°,
A Q = 37°, то AM = ° - AN = °, А Р = ° - A Q = °.
Ответ. А М =
_°, АР =
17
Один из углов равнобедренной трапеции равен 115°. Найдите
остальные углы трапеции.
Решение.
Пусть в равнобедренной трапеции ABCD, где AD и ВС —
основания, АВ = 115°. Так как углы при каждом основании
равнобедренной трапеции , то А С = А = °, а так
как сумма углов, прилежащих к боковой стороне трапеции,
равна °, то AA = AD = ° - А В = ° - 115° = °.
Ответ. AA = AD= °,AC= °.

18
Е
D
Найдите основание AD
равнобедренной трапеции ABCD, если ВС = 10 см,
АВ = 12 см, AD = 60°.
Решение.
В трапеции ABCD основания AD и
ВС параллельны, а боковые стороны
АВ и CD равны.
Проведем прямую С£, параллельную стороне АВ. Полученный
четырехугольник АВСЕ — , так как его
стороны попарно Поэтому АЕ = = см,
СЕ = = см, и так как CD = АВ, то СЕ = CD = см.
Треугольник CDE — ( = ) с
углом при основании в 60°, следовательно, этот треугольник —
и ED = = см. Значит, AD =
= АЕ
= 10 см +
см =
. см.
Ответ. AD =
см.
Задачи на построение
19
Постройте параллелограмм ABCD
так, чтобы его смежные стороны АВ и
AD были равны соответственно
данным отрезкам P]Q1 и P2Q2, а угол А
был равен данному углу hk (рисунок а).
Решение.
1) На рисунке б построим
треугольник ABD по
так, что
АВ = PXQV AD = P2Q2 и/_А = /_hk.
2) Построим треугольник BCD no
трем сторонам (сторона BD построена,
ВС = AD = P2Q2, CD=AB = PfiJ так,
чтобы точки А и С лежали по разные
стороны от прямой BD.
а)
б)
10

Четырехугольник ABCD — искомый. Действительно, так как по
построению АВ = и ВС = , то ABCD —
. А так как АВ = PXQV AD = и Z.A = Z. по
построению, то параллелограмм ABCD отвечает всем условиям задачи.
20
Разделите данный на рисунке
отрезок АВ на 5 равных частей.
Решение.
На рисунке проведем луч АХ, не
лежащий на прямой АВ, и на нем от
точки А отложим пять
друг другу отрезков ААг, АгА2,
AgA4, AjA5. Проведем прямую А5В и
построим прямые, проходящие через
точки Av A2, As, A4 и параллельные
прямой . Эти прямые пересекают
отрезок АВ в точках Bv B2, В3, ВА,
которые по теореме Фалеса (задача 385)
делят отрезок на л« *В
Прямоугольник, ромб, квадрат
21
Найдите периметр прямоугольника
ABCD, изображенного на рисунке,
если биссектриса угла В пересекает
сторону AD в точке Е и делит ее на
отрезки АЕ = 17 см и ED = 21 см.
Решение.
1) Так как ABCD — прямоугольник, то AD || и поэтому Z 2 =
= Z . Но Z2 = Z по условию, следовательно, Z 1 = Z
и А АВЕ — с основанием . Значит,
АВ = = см.
2)AD = АЕ + ED = + = ; PABCD = 2( +
+ ) = 2 ( см + см ) = 2 • см = см.
Ответ. PABCD = см.
11

22
В прямоугольнике ABCD сторона АВ равна 12 см, а диагональ BD
образует со стороной АВ угол в 60°. Найдите диагональ АС.
Решение.
1) В прямоугольном треугольнике
ABD А А = 90°, А В = 60°, поэтому
ZD = °, и по свойству катета,
лежащего ,
имеем: BD = 2 • = см.
2) Так как в прямоугольнике
диагонали , то АС = = см.
Ответ. АС =
см.
23
На рисунке в прямоугольнике ABCD
диагонали АС и BD пересекаются в
точке О, причем ААОВ = 40°.
Найдите A DAO.
Решение. А
1) Так как ABCD — прямоугольник, то его диагонали
и точкой пересечения , откуда следует, что
ААОВ — и А ВАО = • (180°- °) = °.
2) ADAO = АА — А.
Ответ. A DAO = _
= 90° -
24
Найдите периметр ромба ABCD,
изображенного на рисунке, если А В =
= 120°, а диагональ BD = 15 см.
Решение.
1) Так как диагонали ромба делят
, то A ABD =
= А = °.
2) В треугольнике ABD сторона АВ =
D
(так как стороны
ромба
_) и A ABD = °, следовательно, этот треугольник
иАВ = = = см.
12

= 4
. CM =
.СМ.
Ответ. PABCD =
. см.
25
На рисунке изображены
треугольник ABC и прямая /. Постройте
треугольник AlBlCl, симметричный
треугольнику ABC относительно прямой Z.
Решение.
Точка Av изображенная на рисунке,
симметрична точке А относительно
прямой Z, так как прямая / —
серединный перпендикуляр к отрезку ААГ
Через точки В и С проведем прямые,
к прямой Z,
и отметим на них точки Вх и Сх так,
чтобы прямая I была
к отрезкам ВВХ и .
Проведем отрезки AXBV BlCl, CjA1 и
получим искомый треугольник A^jCj.
26
На рисунке изображены отрезок АВ
и точка О. Постройте отрезок AJBV
симметричный отрезку АВ
относительно точки О.
Решение.
Проведем прямую АО и отметим на
ней точку Ах так, чтобы точка О была
отрезка АА1 (см.
рисунок). Точка Аг
точке А относительно точки О.
Аналогичным образом построим
точку Bv
точке В относительно .
Отрезок АХВХ — искомый.
/3

Глава VI
Площадь
EL
Площадь многоугольника
27
На рисунке четырехугольник
ABCD — параллелограмм, точка Е
симметрична точке А относительно
точки В. Докажите, что SABCD = SADE.
Доказательство.
1) Л BEF = Л CDF по стороне и
двум прилежащим к ней углам (АВ =
= = , Z. 1 = , Z3 = ,
так как эти углы
при пересечении
параллельных прямых и
секущими и ), поэтому SBEF =
2) SABCD
+ , поэтому S
9 ^ADE ^ABFD ^
ABCD
28
Найдите площадь квадрата, если его сторона равна:
а) 3,2 см;
б) 2V3 дм.
Решение.
Так как площадь S квадрата со стороной а равна а2, то:
а) S = ( см)2 =
б) S = ( дм)2 = дм2
см2;
Ответ,
а)
б) дм2
см2;
14

29
Найдите сторону а квадрата, если его площадь S равна: а) 64 см2;
б) 1,69 дм2.
Решение.
Так как площадь S квадрата со стороной а равна а2, то а = V
а) а = V см2 = см; б) а = V дм2 = дм.
Ответ, а) см; б) дм.
30
Смежные стороны прямоугольника равны 4,2 см и 3,5 см.
Найдите площадь S этого прямоугольника.
Решение.
S = см • см = _
см2.
Ответ.
см2.
31
Пусть а и 6 — смежные стороны прямоугольника, a S — его
площадь. Найдите сторону 6, если а = 12 см, a S = 192 см2.
Решение.
192 см2 = см • Ъ , откуда Ъ =
Ответ. Ь = см.
еж"
см =
см.
32
Площадь прямоугольника ABCD, изображенного на рисунке,
равна Q, точка М — середина стороны DC. Найдите площадь
треугольника ABE.
Решение.
1) Л ADM = Л ЕСМ по в СЕ
. (DM = по условию,
°, /_ AMD = , так
как эти углы
_), поэтому SADM =
SABE ~ SABCM
~ S
ABCM
Ответ. SABE=.
15

Площади параллелограмма,
треугольника и трапеции
33
Пусть а — основание, h — высота, S — площадь
параллелограмма. Найдите:
а) S, если а = 16 см, h = 9 см;
б) а, если h = 4,8 см, S = 48 см2;
в) h, если а = 3,5 дм, S = 14 дм2.
Решение.
а) S = • = см2;
б) 48 см2 = а • см, откуда а = см2 : см = см;
в) 14 дм2 = 3,5 дм • Л, откуда h = : = дм.
Ответ, a) S =
см2; б) а =
см; в) h =.
дм.
34
На рисунке изображен
параллелограмм ABCD с высотой BE.
Найдите SABCD, если АВ =13 см,
AD = 16 см, Z.B = 150°.
Решение.
1) /_ А = ° - 150° = _
Е D
, так как сумма углов,
равна .
2) А АВЕ — прямоугольный с острым углом А, равным
поэтому BE = = см.
ABCD
СМ2.
Ответ. S
ABCD
СМ2.
35
На рисунке изображен параллелограмм ABCD с высотой BE.
Найдите SABCD, если АЕ = ED, BE = 3,2 см, А А = 45°.
Решение.
1)ААВЕ — прямоугольный и /LA = 45°, следовательно, /LB =
= ° и Л АВЕ — Поэтому
.= BE = 3,2 см.
16

2) Так как по условию АЕ = ED, то
3) S
ABCD
Ответ. S
ABCD
Е
36
Пусть а — основание, h — высота, S — площадь треугольника.
Найдите:
а) S, если а = 5,4 см, h = 6 см;
б) Л, если а = 12 см, S = 42 см2;
в) а, если Л = 2,4 дм, S = 4,32 дм2.
Решение.
a)S = — а - h = -
2 2
б) ft = : а =
в) а = 2S : =
Ответ.
a) S = см2; б) h =
см2;
см; в) а =
см;
- ДМ.
дм.
37
На рисунке смежные стороны
параллелограмма ABCD, равные 6 см и
10 см, образуют угол в 30°. Найдите
площадь треугольника ABC.
Решение.
1) Пусть АВ = 6 см, AD = 10 см, АА = 30°. Так как диагональ
параллелограмма делит его на два ,
то Л ABC = Л , и поэтому SABC = = SABCD.
2) iSABCZ) = AD • BE, где BE — параллелограмма.
Остается найти BE. A ABE — прямоугольный и Z.A = 30°, поэтому
катет , лежащий , равен
SABCD = 10
СМ
, т. е. BE = -
см2, a S
АВС
см,
Ответ. SABC =
см2.
2 Рабочая тетрадь Геометрия, 8 кл
17

38
Площадь прямоугольного
треугольника равна 96 см2. Найдите катеты
этого треугольника, если известно, что
3
один из них составляет - другого.
4
Решение.
Пусть в прямоугольном
треугольнике ABC, изображенном на рисунке,
ВС=- АС.
4
Так как площадь прямоугольного треугольника равна поло-
1 1
вине произведения его катетов, то SAnr = - • = - X
ABC 2 2
ЧУ __
4
По условию SABC = 96 см2, поэтому 96 см2 = , откуда
АС2 = см2 и АС = см, а ВС = см.
Ответ. см и см.
39
На рисунке АС = 8 см, ВС = 12 см,
CD = 10 см, СЕ = 4 см, SABC = 48 см2.
Найдите SCDE.
Решение.
Треугольники ABC и CDE имеют по
равному углу (Z.ACB = /LDCE, так
как эти углы вертикальные), поэтому
по теореме об отношении площадей
треугольников, имеющих по равному углу, получаем SCDE : SABC =
= см • см : см • см = , откуда SCDE =
= &авс- ^ак как по условию SABC = 48 см2, то SCDE = X
X см2 = см2.
Ответ. SCDE = см2.
40
На рисунке точка М делит сторону АС треугольника ABC в
отношении AM : МС = 2:3. Площадь треугольника ABC равна 180 см2.
Найдите площадь треугольника АВМ.
18

Решение.
Треугольники ABM и ABC имеют
общую высоту BD, поэтому их
площади относятся как основания и
Так как по условию AM: МС =
= 2 : 3, то AM : АС = : и
• Q =
* °АВС -
SABC =
Ответ.
, откуда S
180 см2 =
ABM
CM2
41
На рисунке CN = -АС, СМ = -ВС,
SMNC = 18 СМ2.
Найдите SABC.
Решение.
По теореме об отношении площадей
треугольников, имеющих по равному
углу, S^c : SMNC = :
м
Так как по условию CM =-BC, CN = -АС и SMNC= 18 см2, то
3 2
АС ВС
SABC= 18 см2.
-ВС -АС
3 2
= 18 см
2 .
Ответ. SABC =
см'
см*
42
В трапеции ABCD, изображенной на
рисунке, АВ = 12 см, AD =15 см, ВС =
= 7 см, Z. А = 30°. Найдите площадь S
трапеции.
Решение. А
Проведем высоту ВН трапеции ABCD.
1) ААВН — прямоугольный, Z. Н = 90° по построению, АА = 30°
по условию, поэтому ВН = — = см.
2)SABCC = -2(ВС + ) • .!_ =
Ответ. см2.
D
см2 =
19

43
В прямоугольной трапеции ABCD,
изображенной на рисунке, АВ = ВС =
= 9 см, ZD = 45°.
Найдите площадь трапеции.
Решение.
Проведем CF ±AD.
1) ABCF — квадрат, так как у
прямоугольника ABCF смежные стороны
АВ и , поэтому AF =
CF =
см.
2) Л CFD — прямоугольный, Z. F = 90° по построению, /L.D =
= 45° по
ACFD —
условию, поэтому Z. DCF =
3)AD = AF
см +
Ответ.
см2.
см =
и, следовательно,
= см.
см и S
ABCD
СМ*
44
В равнобедренной трапеции ABCD,
изображенной на рисунке, ВН —
высота, А В = 135°, АН = 2,8 см, HD =
= 6,8 см.
Найдите площадь трапеции.
Решение.
Проведем СР _L AD.
1) Так как трапеция ABCD — равнобедренная, то DP = =
= см, поэтому HP = HD - = 6,8 см - см = см;
AD = АН + = см + см = см.
2) Четырехугольник НВСР — прямоугольник, поэтому ВС =
= = см.
3) /LHBC = 90°, а так как ААВС = 135°, то /L.ABH = /L.ABC-
- = Л АВН — прямоугольный (Z. Н = 90°, Z. Б = 45°)
и , поэтому ВН = = см.
4) SABCD = = СМ ' СМ = СМ2'
Ответ. см2.

Теорема Пифагора
45
В прямоугольном треугольнике а и 6 — катеты.
Найдите: а) 6, если а = 8, с = 12; б) с, если а = 4 V2, 6 = 7;
в) а, если 6 = Зл/3,с = 5л/3.
Решение. По теореме Пифагора с2 = а2 + б2.
а) б2 = с2- , откуда 6 = у]с2- =,/144- ~ = ^ = _
б) с2 = + , откуда с =,/ + ~ = ^j + =^ =
в) а2 = с2 - , откуда а = ^ - ~~ = ^ - " =
Ответ, а)
; б)
; в)
46
На рисунке в равнобедренном
треугольнике ABC основание АС = 16 см,
высота ВН = 6 см. Найдите боковую
сторону.
Решение.
1) Так как А АВС — равнобедренный с основанием АС, то АВ = ВС
и высота ВН является , значит, АН = — = см.
2
2) Из прямоугольного треугольника АВН по теореме Пифагора
находим: АВ =
Ответ.
+
4-
см:
см.
см.
47
По гипотенузе с = 14 и катету 6 = 7 прямоугольного
треугольника найдите высоту Л, проведенную к гипотенузе.
Решение.
1) Пусть а — второй катет прямоугольного треугольника, тогда
по теореме Пифагора а = J - = J - = J =
2) Площадь S прямоугольного треугольника равна —а
1 2
1
а с другой стороны, S = -с , поэтому а
h =
Ответ.
= с
откуда
21

48
На рисунке диагонали ромба ABCD
пересекаются в точке О, АВ = 13 см,
BD =10 см. Найдите АС и SilBCZ).
Решение.
1) Так как диагонали ромба взаимно
перпендикулярны, то BD J и
ААВО —
по условию, а катет ВО = —
, причем гипотенуза
1
= — • см =
2
= 13 см
ме Пифагора находим: АО =,
АС = 2 = 2 • см =
см. По
теоресм = см,
см.
2) Площадь ромба можно вычислить по формуле S Rrn = —AC'BD
(задача 476 учебника), откуда SABCD =-
2
Ответ. см2.
.см
ABCD
СМ =
. см2.
49
Найдите меньшую высоту треугольника со сторонами 15, 20 и 25.
Решение.
Так как 252 = 202 + 152 (625 = 400 + 225), то по теореме,
обратной , данный треугольник —
. Гипотенуза является наибольшей стороной этого
треугольника, а высота h, проведенная к гипотенузе,
Так как h • 25 = 15 • 20, то h = =
Ответ.
50
Найдите площадь четырехугольника ABCD, если АВ = 9 см,
ВС = 12 см, CD = 25 см, AD = 20 см, АС = 15 см.
Решение.
1) Так как 152 = 122 + 92 и 252 = 202 +
+ 152, то по теореме, обратной
, треугольники
ABC и DAC —
2 '
(СМ2).
Ответ.
22

Глава VII
Подобные треугольники
EL
Определение подобных
треугольников
51
Даны отрезки: АВ = 12 см, CD = 8 см, EF = 15 см, KL = 30 см,
MN = 16 см, PQ = 20 см. Найдите среди них пары
пропорциональных отрезков.
Решение.
-ч m АВ 12 4 MN 16 4 АВ MN
1) Так как = — = -, = — = -, то = , т. е.
EF 15 5 PQ 20 5 EF PQ
отрезки АВ и MN пропорциональны отрезкам EF и PQ.
очгр CD 8 1 EF 15 CD
2) Так как = — = -, = — = , то = , т. е.
MN 16 2 MN
отрезки CD и пропорциональны отрезкам MN и
оч т АВ 12 3 KL 30 3
3) Так как — = — = -, = — = -, то = =
7 CD 8 2 _ 2
т. е. отрезки и пропорциональны отрезкам и
Ответ.
52
Подобны ли треугольники ABC и DEF, в которых Z.A = 98°,
Z.B = 44°, Z.F = 38°, Z D = 98°, АВ = 12, АС = 21, ВС = 30,
DF = 7, £F =10, D£ = 4?
Решение.
1)/-А = /_ D = 98° по условию. В треугольнике ABC имеем:
Z.C = 180°- ( ° + °) = °, поэтому Z.C = Z. =
= °. В треугольнике DEF имеем: /_ Е = 180°-( ° +
+ °) = °, поэтому /_ В = Z. = °.
Итак, углы треугольников ABC и DEF соответственно равны.
23

2) Рассмотрим отношения сходственных сторон треугольников
лг>л ПР77 АВ 12 3 АС 21 3 ВС 30 3
ABC и DEF: — = — = -, — = — = -, — = — =-, поэтому
DE 4 1 DF 7 1 EF 10 1
АВ АС ВС лт>„
— = — = — , т. е. стороны треугольника ABC
DE DF EF
Итак, Л ABC ™ Л DEF no
Ответ.
Треугольники ABC и DEF
53
В подобных треугольниках ABC и EDF стороны АВ и ED, ВС и DF
являются сходственными. Найдите стороны АВ и АС треугольника
ABC, если ED = 3 см, DF = 5 см, EF = 7 см, ВС = 15 см.
Решение.
В подобных треугольниках ABC и EDF стороны ВС и DF
являются сходственными по условию, поэтому коэффициент k подобия
ВС г.
этих треугольников равен —, т. е. k = : =
Следовательно, АВ = k • = • см = см,
АС = k • = • см = см.
Ответ.
АВ = см, АС = см.
54
Площади двух подобных треугольников равны 35 дм2 и 315 дм2.
Одна из сторон первого треугольника равна 14 дм. Найдите
сходственную ей сторону второго треугольника.
Решение.
Пусть k — коэффициент подобия треугольников, тогда по
теореме об отношении площадей подобных треугольников получим:
k2 = дм2: дм2 = , откуда k = . Искомая
сторона а второго треугольника в раза больше сходственной ей
стороны первого треугольника, т. е. а = • 14 дм = дм.
Ответ. дм.
24

Признаки подобия треугольников
55
На рисунке DE \\ AC. Докажите, что
треугольники ABC и DBE подобны, и
найдите коэффициент подобия ft, если
АВ = 21 см, AD = 7 см.
Решение.
1) A ABC ™ ADBE по двум углам
(/. — общий, ZA = , так как
эти углы —
при пересечении параллельных
прямых и секущей ).
2) Так как коэффициент ft подобия треугольников ABC и DBE
равен отношению сходственных сторон, то ft = АВ :
DB = АВ - = см - см = см, и поэтому
ft = см : см =
Ответ.
56
На рисунке Z. PQC = Z. А, ВС = 18 см,
СР = 6 см, CQ = 4 см. Найдите
сторону АС.
Решение.
Л CPQ со Л СВА по
(Z. — общий, Z. PQC = Z. по
условию). Стороны СР и СВ, CQ и
— сходственные стороны этих
подобных треугольников, поэтому
коэффициент ft подобия равен
СР: = см : см = и
= , откуда АС=
см.
Ответ.
в
см.
25

57
AF 3
На рисунке А В = ZB, — = —
CF 2 />^ D
BF = 15 см. Найдите
Решение.
1) AABF со Л CDF по
(Z. = Z. по условию, Z.AFB =
= /_ , так как эти углы
2)AF и FC — сходственные стороны подобных треугольников
ABF и CDF, поэтому коэффициент ft подобия равен : =
3) Так как BF и DF тоже являются сходственными сторонами,
то BF : DF = , откуда DF = BF = см =
= см.
Ответ.
см.
58
Диагонали трапеции ABCD,
изображенной на рисунке, пересекаются в
точке О, ВО = 3,2 см, OD = 6,4 см,
ВС = 4,8 см. Найдите AD.
Доказательство.
1)AAOD со АСОВ по
(Z1 = А ,
/_ 2 = /. , так как эти углы —
при A D
пересечении параллельных прямых
и секущими и ).
2) OD и ОВ — сходственные стороны подобных треугольников
AOD и СОВ9 поэтому k = = см : см =
3) AD и ВС также сходственные стороны этих треугольников,
поэтому AD : ВС = ft, откуда AD = • = • см =
= см.
Ответ.
см.
26

59
На рисунке ВС = 18 см, СМ = 9 см, CN = 6 см, АС = 12 см.
Докажите, что треугольники ABC и MNC подобны.
Доказательство.
Z.C — угол треугольников и .
Рассмотрим отношения сторон, заключающих этот угол: AC:CN =
= см : см = , ВС : СМ = см : см = .
Эти отношения , поэтому стороны и
треугольника ABC
пропорциональны сторонам и
треугольника MNC. Следовательно,
Л ABC ™ Л по
признаку подобия треугольников. в N
60
Докажите, что треугольники MNP и CDE подобны, если
стороны MN = 7,5 см, МР = 4,5 см, PN = 6 см, DE = 24 см, ЕС = 18 см,
CD = 30 см.
Доказательство.
Так как MN : CD = см : см = , МР : СЕ =
= см : см = и NP : DE = см : см =
, то стороны MN,
треугольника
_ и треугольника MNP
сторонам , и
. Следовательно, по
Л MNP со Л CDE.
61
Применение подобия к решению
задач и доказательству теорем
Точки К и М — середины сторон AD
и ВС параллелограмма ABCD,
изображенного на рисунке. Отрезки КМ
и BD пересекаются в точке О.
Докажите, что КО — средняя линия
треугольника ABD.
м
к
D
27

треугольника
Доказательство.
Докажем, что точка О — середина стороны
ABD. По условию задачи DK = — и ВМ = .
Четырехугольник ABCD — параллелограмм, следовательно, AD =
= , поэтому и KD ВМ.
Так как AD || , то А 1 = А и A3 = А Следователь-
но, Л OKD = Л
. Отсюда получаем: OD =
Итак, точки К и О —
сторон AD и
тре-
угольника ABD, поэтому КО —его
и требовалось доказать.
линия, что
62
В треугольнике ABC отрезок ОТ —
средняя линия, А А = АС.
а) Докажите, что треугольник СОТ
равнобедренный.
б) Найдите периметр треугольника
СОТ9 если периметр треугольника
ABC равен 18 см.
Решение.
а) Так как ОТ —
то ОТ || , поэтому А СТО = Z. _
треугольник СОТ —
линия треугольника ABC,
= АС. Следовательно,
б) Так как ОТ — средняя
треугольника ABC,
то ОТ = -.
2
, со =
рсот =
ВС и СТ =
1
(АВ +.
= -АВ +
2
\ —
*АВС
. Следовательно,
+ =
см.
Ответ.
Точки Kj M, О, Г — середины
сторон четырехугольника ABCD.
а) Докажите, что четырехугольник
К МОТ — параллелограмм.
б) Найдите периметр
четырехугольника КМОТ, если АС = 12 см, BD =
= 16 см.
28

Решение.
а) Проведем диагональ АС четырехугольника ABCD. В
треугольнике ABC точки К и М — сторон АВ и ,
поэтому отрезок КМ — его средняя , и
следовательно, КМ || и КМ = АС.
Аналогично отрезок ОТ — линия
треугольника ADC, поэтому ОТ АС и ОТ = АС. Отсюда
следует, что КМ || ОТ и КМ ОТ, а значит, четырехугольник
КМОТ является
б) По доказанному КМ = АС = • 12 = (см) и
ОТ КМ = см. Проведем диагональ BD. В треугольниках
ABD и BCD отрезки КТ и МО — средние ,
следовательно, КТ = BD = см и МО = BD = см.
Итак, КТ = МО = см и КМ = ОТ = см, следовательно,
Ркмот = 2 • + 2 ' = см-
Ответ.
64
Площадь треугольника ABC равна 20
см2, АВ = 70°, точки Р, Г и О —
середины сторон. Найдите: a) А РТО;
б) площадь треугольника ОТ Р.
Решение.
а) Так как точки Р, Т, О —
сторон, то отрезки РТ, ТО
и РО — средние
вательно, РТ ||
и ТО
треугольника ABC, следо-
. Так как противоположные
стороны четырехугольника ВРТО попарно ,
то этот четырехугольник является ,
поэтому А РТО = А =
б) Так как отрезки РТ, ТО и РО — средние
треугольника ABC, то РТ = ВС, ТО = АВ и РО = АС,
т. е.
РТ
то
-, поэтому Л ОТР Л ABC с коэффициен-
ВС AC
том подобия k = . Следовательно, SOTP : SABC =
получаем: SnTP = SARC = • 20 = (см2).
; 6)SnT =_см2.
откуда
JOTP
Ответ, а) А РТО =
29

65
Точка Р — середина стороны АВ
треугольника ABC, РМ || АС.
Докажите, что отрезок РМ — средняя линия
треугольника ABC.
Доказательство.
Предположим, что отрезок РМ не
является средней
треугольника ABC, тогда точка М не
будет серединой стороны .
Пусть точка О — середина
есть линия треугольника ABC, и поэтому РО АС.
Итак, через точку Р проходят прямые (
параллельные прямой , что противоречит
ВС, тогда отрезок РО
и
аксиоме
прямых.
Следовательно, исходное предположение неверно, т. е. отрезок
РМ является линией треугольника ABC, что и
требовалось
В треугольнике ABC стороны АВ =
= ВС = 5 м, АС = 8 м, медиана АК и
биссектриса ВН пересекаются в
точке М. Найдите ВМ и АК.
Решение.
Так как АВ = ВС, то треугольник ABC — ,
а потому биссектриса ВН является также его высотой и
, следовательно, ВН АС и АН НС = м.
Медианы треугольника пересекаются в
точке и
делятся ею в отношении
ВМ = МН и AM = _
АВН имеем: ВН2 = АВ2 -
ВН = м. Поэтому МН =
: , считая от вершины, т. е.
МК. В прямоугольном треугольнике
__ = = (м2), откуда
ВН = м, ВМ = м.
В треугольнике АМН имеем: AM2
(м2), откуда AM = _
Ответ. ВМ = м, АК =
м. Следовательно, АК = -.
м.
м.
30

67
В треугольнике ОВМ, изображенном
на рисунке, Z. ВОМ = 90°, ОН ±ВМ,
ВМ = 26 дм, ВН = 18 дм. Найдите ОН
и ОБ.
Решение.
Так как ОН —
прямоугольного треугольника ОВМ,
проведенная из вершины
угла, то ОБ =,
м
(дм). Далее, МН = ВМ -
дм, поэтому ОН = q
= J : = (ДМ).
Ответ. ОБ = _
ОН =
ДМ,
ДМ.
68
Гипотенуза АВ прямоугольного
треугольника ABC равна 30 м, а
отношение катетов равно 3:4. Найдите
отрезки, на которые гипотенуза
делится высотой треугольника.
Решение.
Пусть АС = Зх, тогда ВС = 4х и
(Зх)2 + ( )2 = 302. Отсюда х2 =
= , X2 = И X = .
Следовательно, АС =
м и ВС =
м
. Но АС = yjAB~-

поэтому АС2 = •
= 30 • , откуда АН =
, или 182 = А
М,
а ВН = 30 -
(м).
Ответ. АН = м,
ВН = м.
31

69
Длина тени столба равна 10 м, а
длина тени человека, рост которого равен
1,8 м, равна 3,6 м. Найдите высоту
столба.
Решение.
Изобразим отрезками АВ и ОВ столб
и его тень, отрезками CD и OD покажем
человека и его тень. В треугольниках OCD и ОАВ угол О — общий,
Z ODC = Z. = 90°, следовательно, Л OCD Л ОАВ. Отсюда
ОВ-
получаем, что OD : CD = ОВ : , а значит, АВ =
О
D
Ответ. Высота
(м).
равна
. м.
OD
70
Постройте треугольник по двум
углам и медиане, проведенной из
вершины третьего угла.
Решение.
Пусть даны углы 1 и 2 и отрезок
PQ. Требуется построить треугольник
ABC, у которого Z. А = Z. 1, Z. В Z. 2,
а медиана СМ равна PQ.
Построим сначала треугольник,
подобный искомому. Для этого:
1) Проведем отрезок АХВХ.
2) От луча А1В1 отложим угол BjA^X,
равный углу 1, и от луча ВХАХ — угол
А1Б1У, равный углу , как
показано на рисунке. Точку пересечения
лучей АгХ и BXY обозначим буквой С.
3) Проведем медиану СМХ
полученного треугольника
4) На луче СМХ от точки
отложим отрезок СМ, равный данному
отрезку
а)
м
\
Q
В т
Мх
б)
32

5) Через точку М проведем прямую т, параллельную прямой
AjBj. Точки пересечения прямой т и лучей САг и обозначим
буквами А и В.
Треугольник ABC — искомый. Действительно, так как АВ
AjBj, то /.ВАС = А , ААМС = /. , следовательно,
ААМС ™ АА^МгС, а потому AM : AXMY = CM : Аналогично
Л ВМС Л В^^, а потому ВМ : = СМ : CMV
Следовательно, AM : АХМХ = ВМ : , но АгМх = , поэтому
AM ВМ, т. е. отрезок СМ — медиана треугольника и она
равна данному отрезку . Как было доказано, /L ВАС =
= Z_ , но А = /- 1, следовательно, /-ВАС Z1.
Аналогично /.ABC /_ 2. Поэтому треугольник ABC
удовлетворяет всем требованиям задачи.
I Соотношения между сторонами
' и углами прямоугольного треугольника
■■H-L
71
Найдите синус, косинус и тангенс угла М треугольника МРТ,
если /. Р = 90°, МР = 8, РТ = 15.
Решение.
Синусом острого прямоугольного треугольника
называется отношение катета к
. Против угла М лежит катет .
По теореме найдем гипотенузу: МТ2 =
= 82+ = > откуда МТ = Следовательно,
• л, рт 15
sin М = — = —.
Косинусом острого угла
треугольника называется отношение
к . К углу М прилежит
л/г МР
катет , следовательно, cos М = = =.
Тангенсом угла прямоугольного треугольника
называется противолежащего катета
к , т. е. tg М = =
Ответ.
33

72
Докажите, что в треугольнике ВСН с прямым углом Н
выполняются следующие равенства;
a) sin В = cos С;
sin В
в) sin2C + cos2C= 1.
Доказательство.
а) sin В = — cos С = ^г, следовательно, sin В cos С;
сн сн sinB сн-
б) sin В = —, cos Б = =, tgB = , поэтому ^g = — = tgB;
в) sin С = =, cos С = =, sin2 С -f cos2 С = ( )2 + ( )2 =
, cos С =
ВН2 +
ВС2 ВС2
= 1.
73
Гипотенуза АС прямоугольного треугольника АСЕ равна 50,
sin А = — . Найдите площадь треугольника.
25
Решение.
Синусом острого прямоугольного треугольника
называется отношение
к . Против угла А лежит
катет , следовательно, sin А = ==грг> откуда СЕ = АС • =
= 50 • =
Второй катет найдем, используя теорему
АЕ = yJAC2- =д/502- =
Площадь прямоугольного треугольника равна
произведения катетов, поэтому SACE = АЕ
Ответ.
34

74
В треугольнике ABC даны Z А = 90°, А В = 60°, АС = 9. Найдите
сторону АВ.
Решение.
По условию задачи Z.A = , следовательно, отрезок АС —
катет, противолежащий углу , и требуется найти катет,
прилежащий к углу
Отношение катета, противолежащего углу В, и катета,
прилежащего к этому углу, есть угла В, следователь-
АС
но,
A-LJ
Отсюда АВ = АС :
: tg60° =
Ответ.
75
В прямоугольном треугольнике гипотенуза равна с, а один из
острых углов равен а. Выразите катеты через с и а и найдите их
длины, если:
а) с = 12 дм, а = 30°;
б) с = 16 дм, а= 45°.
Решение.
Обозначим длину катета, противолежащего углу а, буквой а
и длину , прилежащего к углу а, буквой 6.
Тогда sina = =^= , cosa = =. Отсюда получаем: а= с • ,
Ъ =
. Подставляя числовые данные, получим:
а) а =
Ъ =
б) а =
Ь =
sin30° =
(дм);
(дм).
(дм);
(дм).
Ответ.
а)
б)
35

76
Найдите площадь равностороннего
треугольника со стороной а.
Решение.
Sabc ~ 2 АС
, где отрезок ВН —
треугольника. В
прямоугольном треугольнике АВН
гипотенуза АВ равна , Z. А =
= , ВН — ,
противолежащий углу А. Следователь-
вн
но, sin A =
х sin A =
', откуда ВН =
sin60°= •
Итак, SABC=-a
Ответ.
77
Найдите углы ромба ABCD, если
его диагонали АС и BD равны 4V3 м
и 4 м.
Решение.
Пусть Z ВАО = а. Диагонали ромба
делят его углы ,
значит, /L DAO = Z. = а.
Диагонали ромба взаимно
и точкой пересечения делятся , следовательно, в
прямоугольном треугольнике АВО катет АО равен м, а
катет равен м. Поэтому tga = = ,
откуда a =
,aZ BAD = 2
_, Z. ADC = Z.
Ответ.
36

Глава VIII
Окружность
Касательная к окружности
78
Проведите прямые через каждые
две точки. Сколько общих точек имеет
каждая из прямых с окружностью?
Ответ.
Прямая и окружность не
имеют общих точек.
Прямая и окружность имеют
только одну точку.
Прямые , , ,
и окружность имеют две общие
В
точки.
•D
79
В треугольнике ABC, изображенном
на рисунке, ZA = 90°, АВ = 5 см,
ВС = 13 см. Найдите радиус
окружности с центром С, если она имеет с
прямой АВ только одну общую точку.
Решение.
По условию задачи окружность и
прямая имеют только
общую точку.
Если бы радиус окружности был меньше расстояния от
окружности — точки — до прямой АВ,
то окружность и прямая имели бы
Если бы радиус
общие точки.
от точки
до
был больше расстояния
АВ, то окружность и прямая
общих точек.
37

Следовательно, радиус R окружности
от точки С до
Итак, R =
Ответ. Радиус окружности равен
расстоянию
АВ, т. е. равен катету
= J = (см).
см.
80
Дан прямоугольник ABCD, где АВ =
= 8 см, AD = 6 см. Какие из прямых
АС, ВС, CD и BD являются секущими
по отношению к окружности с
центром А радиуса 6 см?
Решение.
Прямая АС проходит через центр
— точку А,
следовательно, прямая АС является
по отношению к
окружности с А.
Так как /_В = 90°, то АВ ВС, поэтому расстояние от точки А
до ВС равно см, т. е. больше
окружности. Следовательно, прямая ВС
секущей по отношению к данной окружности.
Так как /L.D = 90°, то AD CD, поэтому расстояние от
А до CD равно см, т. е.
радиусу окружности. Следовательно, прямая CD
по отношению к данной окружности.
Чтобы найти расстояние от точки А до BD,
проведем из точки
лим его
перпендикуляр АН к прямой BD и вычис-
Находя двумя способами площадь
треугольника ABD, получим: -АВ -AD = -BD
2 2
. По теореме
Пифагора BD =
см. Поэтому АН =
см.
Итак, расстояние от точки А до прямой BD
радиуса окружности, следовательно, прямая BD
секущей по отношению к данной
Ответ. Секущими являются прямые
и
38

81
Какая из прямых АС, ВС, CD и BD из предыдущей задачи
является касательной к окружности с центром А радиуса б см?
Решение.
Касательной к называется ,
имеющая с окружностью только
и окружность имеют только одну
точку. Прямая
точку, если
расстояние от центра
до прямой равно
окружности. Это условие выполняется для прямой , значит,
касательной к данной является прямая
Ответ. Касательной является прямая
82
Прямая АВ — касательная в точке А
к окружности с центром О. Найдите
длину отрезка ОВ, если АВ = 24 дм, а
радиус окружности равен 7 дм.
Решение.
По условию задачи прямая АВ
является к данной
окружности, следовательно, прямая АВ
_^ к радиусу ОА, проведенному в _
касания. Поэтому треугольник АОВ —
По теореме Пифагора ОВ2 = ОА2 + , отсюда ОВ =
Ответ. ОВ =
дм.
дм.
83
Прямые АВ и АС касаются
окружности с центром О в точках Б и С.
Найдите угол ВАО, если АВ = ВС.
Решение.
Так как отрезки касательных к
окружности, проведенные из одной
точки, , то АВ = ,
следовательно, треугольник ABC —
, поэтому
Z ВАС =
39

Отрезки касательных к окружности, проведенные из одной
, составляют углы с прямой,
проходящей через эту точку и окружности,
следовательно, Z. ВАО = Z.
Ответ. АВАО =
= -А.
2
84
Прямая АС проходит через центр О
окружности, Z. МАО = Z. ОСМ= 30°.
Докажите, что прямая СМ является
касательной к данной окружности.
Доказательство.
Так как в треугольнике АОМ АО =
= , то Z. АМО = Z. =
В треугольнике АМС Z.AMC = 180° - (Z. MAC + Z.
- ( + ) = Поэтому АОМС = /.АМС -
) = 180° -
, т. е. СМ ОМ.
= 120° - = _
Итак, прямая СМ проходит через конец радиуса ,
лежащий на окружности, и перпендикулярна к этому радиусу. Поэтому
она является к данной окружности, что
и требовалось
Центральные и вписанные углы
85
Какие углы являются
центральными углами окружности с центром А?
Решение.
Центральным
окружности называется угол с вершиной в
. На
рисунке центр окружности — точка
служит вершиной углов МАЕ, ,
Эти
углы являются центральными углами
данной
Ответ.
40

86
Точка О — центр окружности,
Z. МОК = 105°, ^р# = ^МК. Найдите
градусную меру угла МОР.
Решение.
Угол МОК является
углом окружности, а дуга МК
меньше полуокружности, поэтому
Г= Z = . По условию
, и, значит, гра-
задачи ^>РК = ^
дусная мера дуги РК равна
>180°, т. е. дуга МКР больше полуокружности, поэтому
- Z. МОР, поэтому Z. МОР = -
Ответ. АМОР =
87
Какие из углов НАМ, НЕМ, ТСЕ
и НРМ являются вписанными?
Решение.
Вписанным углом называется угол,
вершина которого лежит на
, а стороны
окружность.
Точка А лежит на окружности, а
стороны угла НАМ
окружность. Следовательно, угол
Точка В лежит на
пересекают
вписанным.
, а стороны угла НЕМ
, следовательно, угол НВМ
Точка С
не пересекает
, а сторона СЕ угла ТСЕ
, следовательно, угол ТСЕ
Точка Р
вписанным.
на окружности, следовательно, угол НРМ
вписанным.
Ответ. Вписанными являются углы
и
41

88
На рисунке точка О — центр
окружности, Z.AOB = 92°. Найдите А АСВ.
Решение.
Угол АОВ является
углом данной окружности и равен
, следовательно, ^АМВ =
Угол АСВ является
и опирается на дугу , поэтому
ААСВ=-.
2
Ответ. А АСВ =
89
На рисунке ^МАР=120°. Найдите
A MAP.
Решение.
Угол MAP является
углом окружности и опирается на
дугу ^МВР = 360° - ^ =
= 360°- =
_ 1 _
2
Ответ. A MAP =
/.MAP =
90
На рисунке ААРМ=38°, А ВСМ=
= 32°. Найдите А АМР.
Решение.
Вписанные углы РАВ и ВСР
на одну и ту же
ВР, следовательно,
РАВ = Z.
Из треугольника AMP получим:
Z АМР = 180°- (Z. +А ) =
= 180°- ( + ) =
Ответ. Z. AMP =
42

91
Дана окружность с диаметрами АС
и BD. Докажите, что четырехугольник
ABCD — прямоугольник.
Доказательство.
Отрезок АС —
окружности, следовательно, дуга
ADC — полуокружность. Вписанный
угол ABC опирается на
, поэтому он
Аналогично углы ADC,
и
прямые.
Следовательно, четырехугольник ABCD является
92
Точки А, В, С лежат на одной окружности, /LABC = 80°. Лежит
ли центр окружности на отрезке АС?
Решение.
Если центр окружности лежит на отрезке АС, то отрезок АС
является этой окружности, а дуга АС является
. Тогда вписанный угол ABC
опирается на полуокружность, а потому он равен , но
по условию задачи Z. ABC =
окружности
Ответ.
Следовательно, центр
на отрезке АС.
93
Хорды КМ и РТ пересекаются в точке С, КС= 7 см, СМ = 4 см,
РТ = 16 см. Найдите отрезки PC и СТ.
Решение.
Хорды КМ и РТ пересекаются, следовательно, произведение
хорды КМ равно
отрезков хорды , т. е. PC • = КС • Обозначим
длину отрезка PC буквой х, тогда СТ = , следовательно,
х • ( ) = 7 • . Корни полученного квадратного
уравнения х
2 _
х +
, и тогда СТ =
= 0 равны
_ , либо PC =
и
Итак, либо PC =
, и тогда СТ =
Ответ. PC = см, СТ =
см или PC =
см, СТ = см.
43

94
Точки А, В и С лежат на одной окружности. Отрезки АВ и СН
пересекаются в точке М. Лежит ли точка Н на данной
окружности, если AM = 5 м, MB = 6м, СМ = 8 м, МН = 4 м?
Решение.
Если точка Н лежит на данной окружности, то отрезки АВ и
СН являются хордами этой , пересекающимися
в точке Поэтому должно быть верным равенство AM • =
= МН • Но так как 5 • 6 8-4, то точка Н
на данной окружности.
Ответ.
Четыре замечательные точки
треугольника
95
На рисунке ААВС= 120°, HBLBC,
ВН = 4 см. Вычислите расстояние от
точки Н до стороны ВА угла ABC.
Решение.
Проведем из точки
перпендикуляр НМ к прямой ВА, тогда
расстояние от точки Н до прямой равно
длине отрезка . По условию задачи А АВС=
т.е. Z. = 90°. Значит, /LABH= 120°- =
, НВ ВС,
В треугольнике НВМ Z. МВН =
Z. НМВ =
вательно, НМ = —.
2
4 =
, следо-
(см), т. е. расстояние от
точки
до прямой
равно.
.см.
Ответ.
96
Луч ME является биссектрисой угла ТМР. Верно ли, что:
а) точка А равноудалена от сторон угла ТМР;
б) точка В не равноудалена от сторон угла ТМР;
в) точка Н равноудалена от сторон угла ТМР;
г) точка С не равноудалена от сторон угла ТМР?
44

Решение.
а) Точка А лежит на биссектрисе ME
угла , поэтому она
от сторон этого
угла. Следовательно, данное
утверждение о точке А
б) Точка В лежит на
ME угла ТМР, поэтому она
от
этого угла. Следовательно, данное
утверждение о точке В
в) Если бы точка Н была равноудалена от
ТМР, то она лежала бы на
точка Н на биссектрисе угла
Следовательно, данное утверждение о точке Н
г) Если бы точка С была равноудалена от
, то она на биссектрисе этого
М
угла
этого угла. Но
Следовательно, данное утверждение о точке С
97
Биссектрисы углов А и С треугольника ABC пересекаются в
точке М. Найдите /.АВМ, если Z. MAC = 30°, Z. MCA = 20°.
Решение.
Биссектрисы треугольника
пересекаются в точке,
следовательно, луч ВМ —
_ угла ABC, т. е.
. По условию за-
дачи лучи AM и СМ
углов А и
поэтому
. Следовательно, Z. В = 180°-
) = 180°-(
, значит, Z. АВМ =
Ответ. Z. АВМ =
-+ А
45

98
На рисунке даны Z. ОКС = Z. ЕКО,
ОМ1.КС, ОМ = 7 см. Найдите
расстояние от точки О до прямой КЕ.
Решение.
По условию задачи луч КО является
угла ,
поэтому точка О
от сторон этого угла, т. е. от прямых
и
Расстоянием от точки О до прямой СК является длина
ОМ, проведенного из точки к этой
прямой, т. е. расстояние от точки до СК
равно
см. Поэтому расстояние от
_ КЕ равно см.
О до
Ответ.
99
В треугольнике ABC, изображенном
на рисунке, АС = ВС^АВ, ВМ = МС,
BT.LAC, Z.ACO = Z.BCO. Какая из
прямых AM, CO, ВТ является
серединным перпендикуляром к стороне
треугольника ABC?
Решение.
Прямая называется серединным
перпендикуляром к отрезку, если
она проходит через
По условию задачи ВМ =
лярна к
этого отрезка и
_ к нему.
, но прямая AM не перпендику-
ВС, так как в противном случае
отрезок AM был бы медианой и
ABC, а тогда были бы равны стороны АВ и
Следовательно, прямая AM
. треугольника
, что неверно.
серединным
к стороне ВС.
46

По условию задачи ВТ 1.
, но AT CT9 так как в
противном случае отрезок ВТ был бы высотой и
треугольника ABC, а тогда были бы
стороны АВ и ВС9
что неверно. Следовательно, прямая ВТ
серединным к стороне АС.
По условию задачи Z. АСО = Z.
отрезок СО является
и АС = , т. е.

равнобедренного треугольника, а потому он является также его медианой и
. Следовательно, прямая СО проходит через
отрезка АВ и к
этому отрезку, т. е.
серединным
к стороне
Ответ.
Серединным
ника ABC является прямая .
к стороне треуголь-
100
Точки А, В и С не лежат на одной
прямой; прямые ри g — серединные
перпендикуляры к отрезкам АВ и ВС.
Докажите, что прямые р и q
пересекаются.
Доказательство.
Предположим, что прямые р и q не
пересекаются. По условию задачи
р АВ, а из предположения следует,
что р || q, значит, по свойству
параллельных прямых АВ q. Итак, через
точку В проходят
прямые АВ и ,
перпендикулярные к прямой д, что невозможно.
Следовательно, наше предположе- а
ние неверно, а значит, серединные
к отрезкам АВ и ВС
47

101
Прямые р и q — серединные
перпендикуляры к отрезкам АВ и ВС.
Докажите, что АО = ОС.
Доказательство.
Так как прямая р —
перпендикуляр к
. Аналогично, так
АВ, то АО =
как прямая q — серединный
к отрезку ВС, то ОВ = Итак, АО = ОВ =
АО = , что и требовалось доказать.
поэтому
102
Прямая р — серединный
перпендикуляр к отрезку СЕ. Верно ли, что:
а) точка А равноудалена от концов
отрезка СЕ; б) расстояния от точки М
до точек С и £ не равны; в) точка Н
равноудалена от точек С и Е; г) точка Т
удалена на разные расстояния от
концов отрезка СЕ?
Решение.
а) Точка А лежит на
-
г
А
Т
С
-
Е
М
Н
•
Р
к отрезку СЕ, следовательно, она
цов этого отрезка, т. е. данное утверждение о точке А
б) Точка М лежит на серединном
перпендикуляре
от кон-
к
отрезку
, поэтому она
от концов
отрезка СЕ, а значит, расстояния от нее до точек С и
, т.е. данное утверждение о точке М
в) Если бы точка Н была равноудалена от точек С и Е, то она
лежала бы на серединном к отрезку
, но это не так, и поэтому данное утверждение о точке Н
г) Если бы точка Т была удалена на равные расстояния от точек
С и Е, то она лежала бы на серединном
к отрезку , что в данном случае не выполняется.
Следовательно, данное утверждение о точке Т
48

103
Отрезки АН и ВР — высоты треугольника ABC. Проведите с
помощью одной линейки (без делений) высоту из вершины С.
Решение.
Высоты треугольника пересекаются
в точке, поэтому ■?
третья высота треугольника проходит
через точку . С помощью линейки
проведем прямую и обозначим
буквой Т точку пересечения этой
прямой с прямой АВ. Отрезок —
искомая
треугольника ABC.
Вписанная и описанная
окружности
104
На каких рисунках а — д изображены многоугольник и
вписанная в него окружность?
Решение.
Окружность называется вписанной в
если стороны многоугольника _
окружности. Все
окружности на рисунках и
и
многоугольника касаются
_ , следовательно, многоугольник
в него окружность изображены на
рисунках и
Ответ. и
49

105
Достройте четырехугольник ABCD
так, чтобы он был описан около
данной окружности.
Решение.
Многоугольник описан около
окружности, если его стороны
касаются .
Проведем через точку А
к данной окружности, отличную от
AM, и обозначим буквой D
пересечения этой касательной и
прямой СР. Четырехугольник —
искомый.
106
Четырехугольник ABCD описан
около окружности. Докажите, что
AB + CD = BC+AD.
Доказательство.
Используя свойство отрезков
касательных к ,
проведенных из одной точки, получаем:
AB + CD = a + b+ + , ВС +
+ AD = . Следовательно,
АВ + = ВС + , что и
требовалось
d D
107
Окружность, вписанная в
треугольник ABC, касается его сторон в точках
Н, М и Г. Найдите периметр
треугольника ABC, если AM = 5 м, СН = 3 м,
6м.
Решение.
Отрезки касательных к
проведенные из А
В
50

одной
м, ВН =
, равны. Поэтому AT =
5 м, СМ =
м. Следовательно, РАВС = AM + МС +
+ СН +
= 2 • (AM +
(5 +
-) =
Ответ. РАВС =
м.
\
108
Найдите площадь треугольника
ABC, если его периметр равен 60 см, а
радиус г вписанной окружности равен
4 см.
Решение.
Соединим центр окружности с
вершинами треугольника и точками Н,
М и Е касания сторон треугольника и
окружности. Так как радиус,
проведенный в точку ,
На
Е
следовательно,
перпендикулярен к касательной, то ОН _1_
отрезок ОН — треугольника АОС. Аналогично
отрезок ОМ — высота
ВОС, отрезок ОЕ —
треугольника
■ Поэтому SAOB = -AB
Аналогично SRn = -ВС
Итак, SABC= SAOB
SB
-) =
(АВ
вое —
г + ВС- г
= - (АВ • ОЕ + ВС
_) =
(АВ
АС)г =
ABC
(см2).
Ответ.
109
На каких рисунках a — д изображены многоугольник и
описанная около него окружность?
Решение.
Окружность называется около
многоугольника, если вершины многоугольника на окружности.
51

в)
г)
Д)
Все вершины многоугольника на окружности на
рисунках и , следовательно, многоугольник и описанная
него окружность изображены на рисунках и
Ответ.
110
Достройте четырехугольник ABCD так, чтобы он был вписан в
окружность.
Решение.
Многоугольник вписан в
окружность, если его вершины
лежат на
Отметим на дуге АС точку D и
проведем отрезки AD и .
Четырехугольник искомый.
111
В треугольнике ABC /LA = 40°.
Найдите остальные углы треугольника,
если центр описанной около него
окружности лежит на стороне АС.
Решение.
Так как точки А, Б и лежат на
данной , а ее
центр — точка О — лежит на отрезке
, то отрезок АС —
данной окружности, а угол Б является
окружность и опирается на ее .
АВ = , a Z. С =180° -(40°+
Ответ. /LB = ,Z.C =
в эту
Поэтому
-) =
52

Глава IX
Векторы
Понятие вектора
112
На рисунке изображен ромб ABCD,
где АВ = 4, Z. BAD = 60°.
а) Началом каких ненулевых
векторов служит точка В?
б) Концом каких данных ненулевых
векторов служит точка А?
в) Как называется и обозначается
вектор с началом и концом в точке С?
г) Найдите длины (модули) векторов
ВС и BD.
д) Какой ненулевой вектор коллинеарен вектору ВА ?
е) Какие данные ненулевые векторы сонаправлены и какие
противоположно направлены?
ж) Равны ли векторы ВА и CD, ВС и DA, BA и BD, АО и АС,
АС и ВС, АО и ОС?
з) Какой вектор, равный вектору CD, отложен от точки В?
О т в е т. а) ВА, , ; б)
D
в) вектор с началом и концом в
и обозначается _
С называется
г)|БС| = __
д)вектору ВА
или
е) сонаправлены ненулевые векторы
противоположно
вектор
и
векторы
и
. и
ж) ВА CD, так как | ВА | | CD | и ВА 11 ; ВС DA, так
как ВС и не сонаправлены; ВА BD, так как ВА и BD
; АО АС, так как I АО | | АС \;
з)
53

113
а) Постройте ненулевой вектор с
началом в точке О:
кол линеарный вектору а;
сонаправленный с вектором 6;
противоположно направленный
вектору с?
б) Отложите от точки О вектор,
равный вектору с?
в) Сколько векторов, равных
вектору с! можно отложить от точки О?
Ответ, в) От точки О можно
отложить только вектор,
равный вектору с.
114
о
а
ч,
/
/
Стороны прямоугольника ABCD равны 3 дм и 4 дм. Найдите
длину вектора АС .
Решение.
Длина вектора АС — это длина
АС. Отрезок АС
является
вательно, АС = yJ32+_
Ответ.
прямоугольника ABCD, следо-
. (дм), т. е. | АС | = дм.
Сложение и вычитание векторов
115
Используя правило треугольника, найдите сумму векторов:
а) РМ и МТ\ б) СН и НС; в) АВ+О; г) О +СЕ.
Решение.
а) РМ+ МТ =
б) СН + НС = =
в) АВ + (Г= + ВВ=
г) (Г + СЕ = + СЕ =
Ответ, а) ; б) ; в) ; г)
54

116
Используя правило треугольника, постройте векторы ОА
= а + Ь и СВ = а + Ъ. Определите вид четырехугольника ОАВС.
Решение.
Отложим от точки О вектор ОМ =
= а и от точки М вектор МА =
= , тогда ОА = + .
Аналогично строим СК = а и ХВ =
= 6, тогда СВ =
Так как ОА = + и СВ =
= + , то ОА СВ,
следовательно, ОА || и ОА = ,
поэтому четырехугольник ОАВС —
Ответ. Четырехугольник ОАВС —
ъ
о
/
/а
\
С
117
Используя правило
параллелограмма, постройте векторы ОР = х + у и
СТ = у + х. Докажите, что ОС = РТ.
Решение.
Отложим от точки О векторы ОА =
= х и ОВ = у. Построим точку Р так,
чтобы четырехугольник ОАРВ был
,
тогда по правилу параллелограмма
ОР = + . Отложим от
точки С векторы СМ = у и СЕ = .
Построим
СМТЕ, тогда по правилу
СТ = +
\
У
о
с
СТ =
Так как ОР = +
+ (переместительныи закон
и
векторов), то ОР СТ. Следовательно, четырехугольник ОРТС —
, а потому ОС = , что и
требовалось доказать.
55

118
а) Постройте векторы ОТ = х + у и
РМ = ~y+~z.
б) Отложите от точки Н векторы
т = ОТ + z ъ~п = х + РМ.
в) Докажите, что т = п.
Доказательство.
Так как ОТ = х + , то т = ОТ +
+ г = ( +у) +2. Так как РМ = у +
, To7l=
В соответствии
ров выполняется равенство:
с сочетательным
_ сложения
вектоа значит, т
п, что и требовалось
X
/
р
У
Н
О
119
В трапеции ABCD, изображенной на
рисунке, AD \\ ВС, Л. ABC = 120°, AD =
= 6 см, АВ = 3 см.
Найдите | ВА + AD |.
Решение.
По правилу треугольника имеем:
ВА + AD = , следовательно,
\BA + AD\ = | |. Длина вектора
BD — это отрезка
, то Z. BAD =180°-
Так как AD \\
-Z. =
Проведем высоту ВН трапеции. В прямоугольном треугольнике
АВН имеем: ВН = АВ • sin = 3 • = (см),
АН = • cos = • = (см).
Из треугольника BHD по теореме Пифагора получаем:
BD2 = + (AD - )2 = + = (см2), откуда
BD = см.
Ответ.
56

120
Пользуясь правилами и законами сложения векторов, упростите
выражение МС + AM + СТ.
Решение.
= (AM +
) +СТ =
+ СТ =
Ответ.
121
Обоснование.
закон
закон
треугольника
правило
Пользуясь правилом многоугольника и законами сложения
векторов, упростите выражение ВН + НК + ТР + МТ + Ю\4.
Решение.
ВН + НК + ТР + МТ+ = + ТР + МТ+ =
+ + тр + мт = + мт + = + тр =
Ответ.
122
В трапеции ВСЕН, изображенной
на рисунке, ВН = 2СЕ, точка О —
середина ВН. Какие векторы с концом
и началом в отмеченных точках
являются противоположными вектору ОН?
Решение.
По определению противоположным
вектору ОН является вектор,
направление которого
, а длина длине вектора ОН.
О
направлению вектора
Противоположно направлены вектору ОН векторы НВ, ,
, . Из них имеют длину, равную
вектора ОН у векторы
Итак,
векторы ,
Ответ.
вектору ОН являются
57

123
Какой из векторов CM, СР, РМ, PC равен разности векторов
МСи МР?
Решение.
По определению разностью векторов МС и МР является вектор
х, такой, что 4- х =
Проверим, какой из данных векторов удовлетворяет этому
условию:
МР + СМ МС, следовательно, СМ * МС -
МР +СР МС, следовательно, СР МС - МР.
МР+РМ , т. е. РМ МС - МР.
МР + , т. е. PC МС- МР.
Ответ.
124
Докажите, что для любых трех точек X, У, Z верно равенство ХУ-
ZY =XY+YZ.
Доказательство. —► —► —►
По теореме о разности векторов а - Ъ = а + ( ), поэтому
XY— ZY = + ( ). Запись «-ZY» означает «вектор,
противоположный вектору », т. е. -ZY= . Следовательно,
^У= + (- ZY) = XY+ , что и требовалось
125
Упростите выражение (НВ + ВА-ТА) - (РХ-ТХ).
Решение.
(НВ +ВА-ТА) - (РХ- ) = ( - ТА) -
= НТ +
Ответ.
58

126
Отрезок AM — медиана
треугольника ABC. Выразите векторы ВМ, AM,
С А через векторы ВА = х и МС = у.
Ответ.
ВМ =
AM = -
СА =~~у- +
127
Найдите вектор х, если:
а)РО-7=РМ; б)Г-МА =РМ; в)СМ -~х=РМ.
Решение.
sl)PO~x=PM, следовательно, РО=РМ +
= РО- =РО + =
б) х - МА = РМ, откуда х = + =
, откуда х =
в) СМ - х = РМ, поэтому х = СМ -
Ответ, а) ; б) ; в)
= СМ +
128
В трапеции ABCD, изображенной
на рисунке, AD \\ ВС, Z.ABC = 120°,
AD = 6 м, АВ = 3 м. Найдите | АВ - аЬ |.
Решение.
АБ - AD = , следовательно,
\AB-AD\ = | 1 = Так как
AD II , то Z. BAD = 180°- Z1 =
Проведем высоту ВН трапеции. В треугольнике АВН имеем:
ВН=АВ- sin = • = (м), НА=АВ • =
(м). Тогда DH = AD -.
(м).
Из треугольника BHD по теореме Пифагора находим:
BD2 = + = ( + ) = (м2),
откуда BD = м.
Итак, \АВ - AD\ =
Ответ.
м.
59

Умножение вектора на число.
Применение векторов к решению
задач
129
Отложите от точки О векторы х = - а, у = 2с, z =- а + 2 с.
Решение.
Так как jT= - at то, согласно опреде-
лению произведения вектора на число,
х\\ и |х| = \а\. Отложим от
точки О вектор х.
Аналогично у 1: и | у \ = .
Отложим от точки О вектор
z =-a
2
Так как
векторы :? и отложены от точки
строить вектор z = х +
правилу
удобно по
Строим вектор
о
а
130
На рисунке изображен
параллелограмм ABCD, где DM = СМ, ~~^ "*
= 7Г,
Выразите:
а) векторы АС и СО через вектор п;
б) векторы DM и СМ через вектор а*;
в) вектор ВС через векторы а и п.
Решение.
D
а) Так как точка О является точкой пересечения
параллелограмма, то АО = , и, значит, \АС\ = ~
того, АС ТТ , следовательно, согласно определению
произведения вектора на число, АС = АО =
и СО АО , поэтому СО = АО = —
\АО\. Кроме
э произведе-
~п. Далее, \СО\ \АО\
60

б) Противоположные стороны параллелограмма
и , поэтому DC АВ = а. Далее,
DM\\ DC и | DM | = | DC |, следовательно, согласно определению
вектора на , DM = DC = а.
Так как CM || DC и \СМ\ = |Бс|, то СМ = DC =
в) По правилу треугольника ВС = ВА + . Но ВА = - =
= -а, АС = 2 л, следовательно, ВС = +
Ответ.
а)
б)
в)
131
Упростите выражение:
а) -0,5(12а)ц
б) 2,5Ь- 1,76;
в) 3(с%7) - Ьр;
г) 2(5]Г- 3<f) - 3(3^- 2q).
Решение.
а) - 0,5(12<Г) = ( • )~а =
б) 2,5Ь-1,7Ь= ( )Г=
—)-Ър= +
+ ( )?=
г)2(5р- )-3( -2q) = ?- ~q-
+ = + =
Ответ, а) ; б) ; в) ; г)
132
Докажите, что векторы с = 2(а + 1,5р ) - Зр и а коллинеарны.
Доказательство.
~с = 2(а + ) - Зр = 2а + - 3]Г = 2а + ( )р*= 2~а +
+ р = а*. По определению произведения вектора на
векторы а* и 2а ,
что и требовалось
61

133
Докажите, что для любого вектора а справедливы равенства:
а) 1 • а = а; б) (-1) • а = - а.
Доказательство.
Если а = 0, то обе части каждого равенства — нулевые векторы,
поэтому равенства справедливы. Пусть а ^ 0.
а) По определению произведения вектора на
| 1- а | = | | • | | = 1в| | = | |, а так как число 1
положительно, то векторы 1* а и а .
Следовательно, по определению равных векторов 1* а
б) По определению
а.
вектора
на число |(-
• а | =
а так как
-1 0, то векторы (-
и *Г противоположно
. По определению противоположного вектора | - а \ = \ а \
и -а\[ Следовательно, |(-1)а | \~а\ и (-1)а|| ,
т. е. (-1) • а - а.
134
Точки К и М — середины сторон АВ
и CD четырехугольника ABCD,
изображенного на рисунке, точки Р и Т —
середины диагоналей АС и BD.
Докажите, что середины отрезков КМ и РТ
совпадают.
Доказательство.
Пусть точка X — середина отрезка КМ, точка У — середина от-
а)
резка РТ. Тогда для произвольной точки О имеем:
ох = -(дк ом)
и
OY = (ОР + ОТ). (2)
По условию задачи точки К и М — середины отрезков АВ и
, следовательно, ОК = (ОА + ) и ОМ = (ОС+ ).
Аналогично ОР = (ОА + ОС) и ОТ = (ОВ + ).
Подставляя найденные выражения в формулы (1) и (2), получим:
ОХ = -(-(ОА + ОВ) +
2 2
OY = ( (ОА + ОС) + (ОВ +
(OC+OD)) = -(ОА + ОВ + ОС + ),
~* )) = (ОА + ОВ + +
62

Отсюда следует, что ОХ = OY. Так как от точки О можно
отложить только вектор, равный данному, то
точки X и совпадают, следовательно, совпадают середины
отрезков и , что и требовалось доказать.
135
В трапеции ABCD, изображенной
на рисунке, АХ = ХВ, СМ = MD, ВР =
= РХ, СТ = ТМ, ВС = 2 м, AD = 8 м.
Найдите РТ.
Решение.
Так как АХ = и СМ = ,
то отрезок ХМ — средняя
трапеции, следовательно, ХМ ВС и
ХМ = (ВС + ) = (2 + ) =
= —(м).
В четырехугольнике ВСМХ стороны ВС и ХМ
, а стороны ВХ и не параллельны,
следовательно, ВСМХ — По условию задачи ВР =
= и СТ = , поэтому отрезок РТ — средняя
трапеции ВСМХ, и, следовательно, РТ = (ВС + ) =
= = (м).
Ответ.
136
Прямая ОТ параллельна основанию
CD трапеции ABCD, причем АО = OD.
Докажите, что отрезок ОТ — средняя
линия трапеции.
Доказательство.
В соответствии с определением
средней трапеции
нужно доказать, что точка Т является
стороны ВС.
63

Предположим, что это не так, и пусть серединой стороны ВС
является точка X. Тогда отрезок ОХ — линия
трапеции, поэтому ОХ CD. Но по условию задачи ОТ CD.
Итак, через точку О проходят прямые, параллельные
прямой , что противоречит параллельных
прямых. Следовательно, точка Т —
ВС, т. е. отрезок ОТ —
что и требовалось
трапеции,
137
В трапеции ABCD отрезок РТ —
средняя линия, AD = 9 м, ВС = 5 м.
Найдите длину отрезка КМ.
Решение.
По свойству средней
трапеции РТ ВС и РТ = (AD +
+ ). В треугольнике ABC отрезки

следоваАР и РВ равны и прямая РК параллельна стороне
тельно, отрезок РК — линия треугольника
ABC (задача 65). Поэтому РК = ВС. Аналогично в
треугольнике BCD TM = ±
Итак, КМ = РТ-(РК +
+ ВС) = ВС + AD -
) = (ВС +
)-(-
+
= -(AD-
) = (9- ) =
Ответ.

ОГЛАВЛЕНИЕ
Глава V. Четырехугольники
§ 1. Многоугольники 3_
§ 2. Параллелограмм и трапеция 5_
§ 3. Прямоугольник, ромб, квадрат 11
Глава VI. Площадь
§ 1. Площадь многоугольника 14
§2. Площади параллелограмма, треугольника и трапеции 16
§3. Теорема Пифагора 21
Глава VII. Подобные треугольники
§ 1. Определение подобных треугольников 23
§ 2. Признаки подобия треугольников 25
§ 3. Применение подобия к доказательству теорем и решению задач 27
§ 4. Соотношения между сторонами и углами прямоугольного треугольника 33
Глава VIII. Окружность
§ 1. Касательная к окружности 37
§2. Центральные и вписанные углы 40
§ 3. Четыре замечательные точки треугольника 44
§4. Вписанная и описанная окружности 49
Глава IX. Векторы
§ 1. Понятие вектора 53
§ 2. Сложение и вычитание векторов 54
§3. Умножение вектора на число. Применение векторов к решению задач 60