Радиолокационные сигналы теория и применение - Кук Ч., Бернфельд М.

Автор: Кук Ч. Бернфельд М.

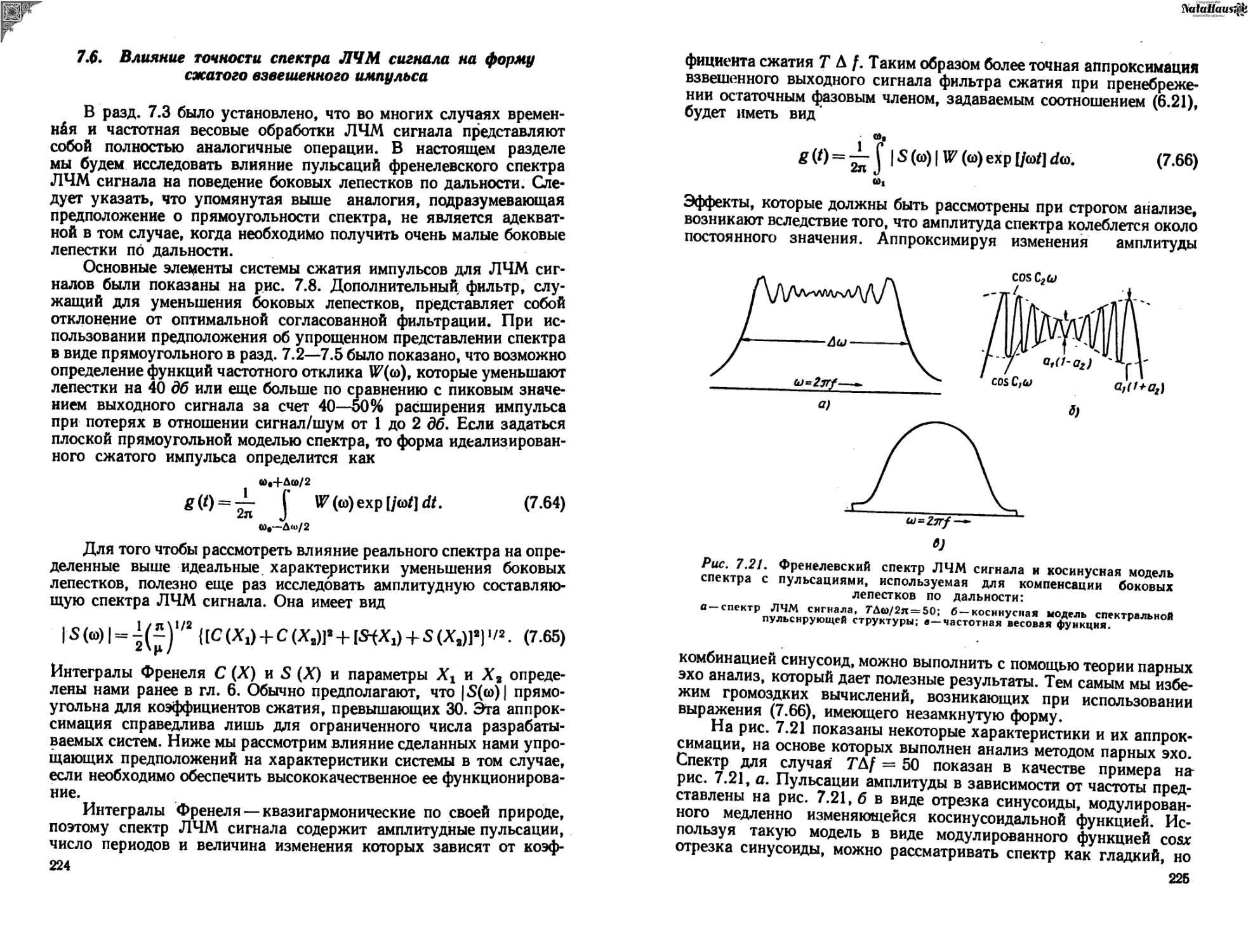
Теги: электротехника радиотехника радиостанции радиолокация радиосвязь советское радио радиолокационные сигналы

Год: 1971

Похожие

Основы радиолокации и радиолокационные устройства

Теория сложных сигналов

Радиолокационные отражатели

Применение цифровой обработки сигналов

Текст

Ч-КУК
М-БЕ РНФЕЛЬД
радио-
локационныЕ
сигналы
RADAR SIGNALS
AN INTRODUCTION TO THEORY AND APPLICATION
CHARLES E. COOK AND MARVIN BERNFELD
Advanced radar studies department
Sperry Gyroscope company
Great Neck, Long Island, New York
1967
ACADEMIC PRESS New York . London
Ч. КУК, М. БЕРНФЕЛЬД
РАДИОЛОКАЦИОННЫЕ
СИГНАЛЫ
ТЕОРИЯ И ПРИМЕНЕНИЕ
Перевод с английского под редакцией
В. С. КЕЛЬЗОНА
ИЗДАТЕЛЬСТВО «СОВЕТСКОЕ РАДИО»
МОСКВА—1971
УДК 621.396.96
Ч. Кук, М. Бернфельд. Радиолокационные
сигналы. Пер. с английского под ред. В. С. К е л ь з о н а.
М. Изд-во «Советское радиож, 19/1, стр. 568, тир. 8000 экз.,
ц. 2 р. 67 к.
В книге излагаются вопросы теории и практики при-
менения сложных радиолокационных сигналов, позволяющих
осуществлять сжатие импульсов. Рассматриваются основные
элементы теории согласованной фильтрации применительно
к ЧМ сигналам и системам сжатия импульсов, а также
функции неопределенности таких сигналов; описываются
системы с линейной и нелинейной частотной модуляцией
сжимаемых импульсов и системы с дискретным кодирова*
нием сигналов. Обосновываются требования к сигналам
для работы при наличии пассивных помех и оценивается
влияние искажений, вносимых при согласованной фильтра*
ции. Описан ряд конструктивных решений согласованных
фильтров на базе Т-образных звеньев и ультразвуковых ли-
ний задержки, а также оптические и СВЧ методы согласован-
ной фильтрации.
Книга будет полезна радиоспециалистам и разработ-
чикам радиолокационных станций, а также студентам и аспи-
рантам соответствующих специальностей.
14 табл., 320 рис., 341 библиогр. назв.
3-4-4
7-71
Предисловие редактора
Настоящая книга представляет собой серьезную монографию,,
в которой излагаются вопросы теории и практики сложных радио-
локационных сигналов, позволяющих осуществлять сжатие им-
пульсов.
Существенным достоинством книги является простота изло-
жения, сочетающаяся с большой глубиной рассмотрения и охватом
широкого круга вопросов современной радиолокации.
Большое внимание уделено проблемам обоснования и выбора
сигналов для работы в условиях различного рода пассивных помех,
вопросам влияния искажений в трактах радиолокационных станций
на характеристики сигнала, а также вопросам расчета и проекти-
рования согласованных фильтров для сжатия радиолокационных
сигналов с использованием ультразвуковых, СВЧ и оптических
методов.
Эта книга вместе со сравнительно недавно вышедшими пере-
водами книг: «Современная радиолокация» Р. Берковица и «Введе-
ние в технику радиолокационных систем» Д. Бартона в известной
мере отражает современный уровень радиолокационной техники
в США.
Техника сложных радиолокационных сигналов, как известно,
развивалась параллельно в ряде стран, в том числе и в Советском
Союзе. Однако в данной книге авторы ссылаются только на работы
ученых США, Англии и Германии. При переводе этот недостаток
частично исправлен и приведены ссылки на оригинальные работы
советских ученых.
В американском издании книги имеются отдельные неточности
и опечатки. На одну из них указано в работе Палса (см. «Зарубеж-
ная радиоэлектроника» № 2 за 1970 г.). При переводе сделаны
необходимые исправления.
Перечни литературных источников, помещенные после каждой
главы, воспроизведены так, как они даны в английском издании.
Работы, переведенные на русский язык, отмечены звездочкой и
приводятся дополнительно под теми же номерами после источников
на английском языке. Двумя звездочками отмечаются статьи из
журнала Proceedings IEEE, который с 1961 г. полностью перево-
дится на русский язык издательством «Мир» вначале под названием
ТИРИ и затем (с 1963 г.) как ТИИЭР.
Книга Кука и Бернфельда будет полезна широкому кругу
радиоспециалистов, разработчикам радиолокационных станций и
систем, а также студентам и аспирантам вузов.
Перевод книги выполнен М. К. Размахниным (главы 1—8 и
13—14) и Г. Н. Белобровым (главы 9—12).
В. С. Кельзон
5
Предисловие авторов
В настоящей книге рассматриваются основы теории и примене-
ния радиолокационных сигналов, получивших название сигналов
с большим значением произведения длительности на ширину полосы
частот, сигналов, позволяющих осуществлять сжатие импульса,
или сложных сигналов. Теория сигналов этого класса является
одним из краеугольных камней современной радиолокации, однако
до сих пор не опубликованы труды, где этот вопрос был бы рассмот-
рен достаточно полно и на сравнительно простом уровне, пользуясь
которыми студенты старших курсов и инженеры-практики могли
бы получить необходимые основы знаний для работы в этой области
радиолокации. При написании данной книги авторы пытались пред-
ставить в единой форме теоретические и практические аспекты
применения некоторых методов обработки радиолокационных сиг-
налов, которые освещены в целом ряде опубликованных работ.
Понимая необходимость создания пособия, где эта информация
была бы изложена в более доступной для читателя форме, авторы
подготовили для работников фирмы Sperry Gyroscope курс лекций.
Указанный курс был предназначен для слушателей вечерних курсов
повышения квалификации и охватывал вопросы теории применения
и формирования сигналов с большим значением произведения дли-
тельности на полосу частот. Этот курс и послужил в дальнейшем
основой для создания настоящей книги. Хотя в книге отсутствуют
примеры, специально предназначенные для проработки материала
различных глав, вопросы и задачи для проверки усвоения его
могут быть получены непосредственно из текста и приведены
в соответствие с запросами студентов в процессе изучения мате-
риала.
Практические потребности, связанные с военными применения-
ми радиолокации, послужили начальным толчком к проведению
исследований для изучения свойств и методов формирования слож-
ных радиолокационных сигналов как на протяжении второй миро-
вой войны, так и после нее. В этот период был достигнут быстрый
прогресс в понимании существа проблемы, а также в определении
и обосновании требований, предъявляемых к оптимальным линей-
ным методам обработки сигналов. В то же самое время развитие
техники подготовило почву для практической реализации методов,
опирающихся на развитую теорию; выдвигались многочисленные
предложения о путях построения систем, известных теперь как
системы со сжатием импульса или системы с кодированными сиг-
налами.
Работы Вилле, Вудворда — Дэвиса и Вудворда обеспечили
единую базу, основываясь на которой начинается второй этап кон-
центрированных усилий в определении ограничений, накладывае-
6
мых на вид функции неопределенности радиолокационных сигналов
и принципы реализации специфических радиолокационных систем
в результате выбора того или иного вида радиолокационного сиг-
нала. В течение некоторого времени упорно существовала надежда,
что может быть найден такой сложный сигнал, который был бы оп-
тимален для целого ряда различных приложений. После того, как
такие попытки, предпринимавшиеся в течение десятилетия, позво-
лили сформировать значительно более глубокое понимание суще-
ства проблемы, оказалось, что эта надежда была в значительной
мере иллюзорна. В этом отношении утверждение Вудворда, что
«основной вопрос, заключающийся в том, что (какой радиолокацион-
ный сигнал) следует передавать, остается по существу без ответа»,
было до некоторой степени пророческим. Несмотря на достигнутый
с тех пор большой прогресс (1953 г.), это заявление все еще содержит
элемент истины, если только не может быть дано очень точного
описания природы элементов окружающего мира, расположенных
в области, от которой отражается радиолокационный сигнал. В этом
случае может оказаться возможным оптимальное согласование
практически полученного радиолокационного сигнала с окружаю-
щей средой. Однако прогнозирование распределения и движения
отражающих поверхностей обычно связано с большей или меньшей
неопределенностью. При этих условиях разработчик радиолока-
ционной станции обычно стремится сформировать радиолока-
ционный сигнал (или сигналы) компромиссного типа, который,
как он думает, будет обеспечивать выполнение задачи в некото-
рых заранее заданных возможных ситуациях. Намерения авторов
книги как раз и состоят в том, чтобы обеспечить читателя знанием
теории и принципов, которые будут помогать его попыткам при
разрешении стоящих перед ним специфических проблем.
Изложение материала в книге сопровождается примерами раз-
личных типов радиолокационных сигналов. При этом было найдено,
что для многих задач наиболее подходящим и легко реализуемым
является сигнал с линейной частотной модуляцией (ЛЧМ сигнал).
В связи с этим указанные сигналы используются в качестве при-
мера во многих разделах, где рассматриваются практические
проблемы, связанные с радиолокационными системами, которые
используют сложные сигналы.
Интересно отметить, что сложные сигналы нашли применение
в таких различных областях как метеорология, сейсмология, ио-
носферное зондирование, портовая навигация, контроль движения
х в аэропортах, определение дефектов в металлах и эксперимен-
тальный анализ пограничных слоев между различными средами.
Следует ожидать, что с течением времени этот перечень будет
увеличиваться и мы надеемся, что настоящая книга внесет свой
вклад в расширение области использования этого класса сигналов.
Ч. Кук, М. Бернфельд
Список обозначений
2а — эффективная длительность (среднеквадратичное значение).
2₽ — эффективная ширина полосы (среднеквадратичное значение).
Ру (<о) — фазовая характеристика фильтра, в случае согласованного
фильтра Р/ (<о) = — Ф(<о).
Р^ (со) — групповая задержка фильтра dPy (w)/dco.
v — постоянная распространения (используется в главах 13 и 14).
о — длительность элементарного импульса в дискретном кодиро-
ванном сигнале.
бг — среднеквадратичная ошибка измерения дальности.
— среднеквадратичная ошибка измерения скорости.
6(0 — функция фазовой модуляции.
6Д0 — ошибка функции фазовой модуляции.
6'(0 — функция частотной модуляции, dti(t)/dt.
0О — фазовая постоянная (индекс фазовой модуляции).
61, 62 — обобщенные параметры сигнала (используются только в гл. 5).
6 (т» Ф) — симметричная функция неопределенности.
X — длина волны. »
р, — скорость изменения угловой частоты при ЛЧМ.
р — пространственно-частотная корреляция или коэффициент ча-
стотно-временной связи.
°Ф — среднеквадратичная ошибка измерения частоты.
Оф — дисперсия ошибки измерения частоты.’
ох — среднеквадратичная ошибка измерения времени.
ох — дисперсия ошибки измерения времени.
<р — допплеровский сдвиг частоты.
Ф(<о) — фазочастотная передаточная функция.
ф0 — фазовая постоянная фильтра.
X (т» ф) — функция отклика.
1х(т»Ф)18— функция неопределенности сигнала.
Хр (tZ’ Ф) — функция отклика на элементарный импульс дискретного ко-
дированного сигнала.
% (кб, <р) — функция отклика на дискретный кодированный сигнал при
целых значениях 6. *
ф(0 — комплексный сигнал.
V(f) — спектр комплексного сигнала.
<0 — угловая частота, 2nf.
u>d — угловая частота Допплера, 2nf.
a(t) — огибающая сигнала.
{ап} — последовательность с дискретным кодированием амплитуды.
{Ьп} — последовательность с комбинированным кодированием ампли-
туд и фаз по коду Хаффмана.
{cn}, {dn} — другие представления последовательностей с дискретным ко-
дированием фазы.
{6П} — последовательность фаз при дискретном кодировании.
{<оп} — последовательность угловых частот при дискретном кодиро-
вании.
Г ДО) — постоянная разрешения по частоте.
Fr(x) — обобщенная постоянная разрешения по частоте.
8
— комплексная передаточная функция фильтра.
Е — энергия действительного сигнала s(/).
М — число подымпульсов Pn(t) в дискретно-кодированном сиг-
нале.
N — число возможных размещений подымпульсов в кодированном
сигнале.
No — спектральная плотность мощности белого шума.
7V(co) — спектральная плотность мощности для небелого шума.
Рп(0 — импульс единичной, амплитуды фиксированной длительности.
P(D) — многочлен по степеням оператора единичной задержки D,
описывающий функционирование регистра сдвига.
P(s) — многочлен Хаффмана.
s(f) — действительный сигнал.
S(f) — спектр s(0.
Т — длительность сигнала.
ТД/ — произведение длительности сигнала на его полосу (база сиг-
нала).
Д/ — ширина спектра (пропорциональная 1 /Т для неполированного-
импульса).
Тг(0) — постоянная разрешения по времени.
Тг(<р) — обобщенная постоянная разрешения по времени.
u(t) — комплексная огибающая a(t) exp [/©(/) ].
£/(<о) — спектр u(t).
w(t) — временная весовая функция для уменьшения боковых лепест-
ков.
ИГ(<о) — частотная весовая функция для уменьшения боковых лепест-
ков.
ГЛАВА 1
ОСНОВНЫЕ ЭЛЕМЕНТЫ ТЕОРИИ
СОГЛАСОВАННОЙ ФИЛЬТРАЦИИ
И СЖАТИЯ ИМПУЛЬСОВ
1.1. Введение
В начале развития радиолокации было широко распространено
деление радиолокационных систем на две основные категории.
В соответствии с этим радиолокатор являлся либо системой с не-
прерывным излучением, обладающей большими возможностями по
измерению скорости (или допплеровского сдвига), либо импульсной
системой, эффективно измеряющей дальность и имеющей хорошую
разрешающую способность по дальности. В импульсных радиолока-
ционных системах параметры передаваемого импульса обычно пред-
ставляли собой компромисс между желанием получить лучшее раз-
решение по дальности (что связано с необходимостью иметь воз-
можно меньшую длительность импульса) и стремлением добиться
максимально возможной дальности обнаружения (что требует
максимизации энергии импульса за счет использования как мож-
но более длительных импульсов).
Попытки удовлетворить этим противоречивым требованиям
одновременного обеспечения разрешения по дальности и максималь-
ной дальности обнаружения часто заставляли идти на компромисс
при решении и других вопросов, связанных с разработкой радио-
локатора. Одним из примеров его является уменьшение скорости
обзора исследуемого пространства антенной радиолокатора с тем,
чтобы получить большее число импульсов, отраженных от объекта.
Максимальная дальность обнаружения при этом могла увеличивать-
ся за счет использования методов накопления импульсов (интегри-
рования).
Разработка радиолокационной системы1 обычно начинается
1 В списке литературы, помещенной в конце этой главы, можно найти
ряд недавно вышедших работ, посвященных рассмотрению общих принци-
пов построения радиолокационных систем.
10
^alatlausilk
знание без границ W *
с исследования ограничений, накладываемых уравнением дальности
радиолокации, которое имеет вид
р _ р* с*х*°
г (4л)аР4
ИЛИ
Р —Г PtGWo ]1/4
макс [ (4n)»SMHH J ’
(Ыб)
где Pt — передаваемая мощность; Рг — принимаемая мощность;
G — коэффициент усиления передающей и приемной антенн; X —
длина волны излучаемого сигнала; о — эффективная площадь
рассеяния объекта; R — расстояние между радиолокатором и от-
ражающим объектом; Ямакс — максимальная дальность обнаруже-
ния и SMHH — минимальный обнаружимый сигнал.
Используя уравнения (1.1а) или (1.16), разработчик радиолока-
тора может взвесить достоинства возможных компромиссных ре-
шений, которые позволяют достигнуть требуемых результатов.
С развитием радиолокационной техники наметился постепенный
переход от разработки устройств, единственным критерием каче-
ства которых была их работоспособность, к созданию систем, спо-
собных обеспечить оптимальную или близкую к ней обработку
сигналов. Возникли новые концепции, которые заложили основы
теории построения сигналов как неотъемлемой части теории радио-
локационных систем. Одним из примеров применения этой теории
для частной задачи служат импульсные допплеровские системы,
в которых была предпринята попытка обеспечить одновременное
точное измерение скорости (или разрешение по скорости) и разре-
шение по дальности. Это явилось предвестником более поздних
работ, основанных на использовании сложных сигналов в виде
последовательностей импульсов. Однако лишь в фундаментальной
монографии Вудворда [1] были систематизированы исследования
в различных областях теории радиолокационных сигналов, которые
начали развиваться в послевоенный период. Эта работа позволила
установить, что форма сигнала является дополнительным парамет-
ром при разработке радиолокатора и что такие характеристики
радиолокационной системы, как разрешение по дальности, могут
определяться не только средней излучаемой мощностью и длитель-
ностью излучаемого импульса, но и формой сигнала.
Применительно к уравнению радиолокации (1.1а) или (1.16)
основные идеи, развитые Вудвордом, означают, что длительность
излучаемого импульса может быть выбрана настолько большой,
насколько это необходимо для удовлетворения энергетических тре-
бований, предъявляемых к системе (например, для наиболее пол-
ного использования характеристик, имеющихся в мощных каскадах
передатчика ламп). После удовлетворения требований к характе-
11
ристикам обнаружения можно обеспечить условия для получения
необходимого разрешения по дальности за счет кодирования излу-
чаемого сигнала с помощью широкополосной модуляции. Одним
из наиболее важных вкладов Вудворда в развитие современной
радиолокации было установление того, что разрешение по дальности
и точность измерений определяются шириной полосы сигнала, а не
длительностью излучаемого импульса.
Для извлечения широкополосной информации, содержащейся
в сигнале описываемого типа, требуется использовать более слож-
ные приемные системы по сравнению с системами для простого им-
пульсного радиолокатора. Такие приемные системы получили наз-
вание систем обработки сигнала с помощью согласованных фильтров
или систем согласованной фильтрации сигнала. Термин «обработка
сигнала» в общем случае подразумевает операции, выполняемые
над принимаемым сигналом в высокочастотных каскадах или в кас-
кадах на промежуточной частоте радиолокационного приемника,
и отличается от термина «обработка данных», который обычно свя-
зан с операциями над продетектированным радиолокационным
сигналом.
Возможность варьировать и подбирать в соответствии с теми
или иными требованиями различные характеристики радиолока-
ционного сигнала является важным фактором развития современных
радиолокационных систем, использующих сложные методы обработ-
ки сигналов. Соответствующие современному уровню развития
радиолокационных систем методы обработки сигналов широко из-
вестны как методы сжатия импульсов, согласованная фильтрация
или методы кодирования сигналов [2—4]. Назовем некоторые из
основных практических соображений в пользу развития этих ме-
тодов, хотя такой перечень, конечно, не будет исчерпывающим. При
помощи этих методов достигается:
1. Более эффективное использование средней мощности, ко-
торую можно получить от радиолокационного передатчика, а иногда
и возможность избежать трудностей, связанных с ограничением
пиковой мощности в мощных каскадах радиолокационного передат-
чика.
2. Более высокая разрешающая способность как по дальности,
так и по скорости. При стремлении обеспечить высокую разрешаю-
щую способность по дальности с помощью использования методов
сжатия импульса можно обойти затруднения, связанные с генери-
рованием сигналов, имеющих очень крутые фронты импульсов и
высокую пиковую мощность.
3. Повышение помехоустойчивости по отношению к опреде-
ленным типам интерферирующих сигналов, свойства которых от-
личаются от свойств кодированных сигналов.
4. Извлечение информации из сигналов, поступающих на
вход приемника, что позволяет оценить такие важные параметры,
как дальность, скорость и, возможно, ускорение объектов, от ко-
^alaHausttk
знание без границ Ч *
торых отражены отдельные сигналы. Этот вид обработки радиоло-
кационных сигналов называется оценкой параметров.
На рис. 1.1 показана упрощенная форма радиолокационной
системы, в которой методы кодирования сигналов использованы
для реализации указанных выше возможностей. Поскольку задачей
настоящей книги является развитие идей и принципов, необходи-
мых для понимания и сознательного применения специфических
методов обработки радиолокационных сигналов (согласованная
фильтрация со сжатием импульса), мы особенно подробно рассмот-
рим теоретические вопросы, связанные с теми элементами схемы
Рис. 1.1. Блок-схема радиолокационной системы с кодирован-
ными сигналами.
на рис. 1.1, которые обозначены как «схема формирования кодов»
и «декодирующее устройство», а также возможные пути их реали-
зации.
Изложенный в книге материал может быть разбит на три ос-
новных части. В первых пяти главах рассматриваются общие теоре-
тические вопросы, связанные с методами согласованной фильтрации.
Изложена сущность принципа согласованной фильтрации и дана
история развития методов сжатия импульса; приведены различные
критерии качества функционирования системы, использование
которых приводит к необходимости применять согласованную
фильтрацию. Подробно рассматриваются: 1) принцип стационарной
фазы, имеющий большое значение и применяемый для вывода приб-
лиженных соотношений, связывающих частотно-модулированный
кодированный сигнал и согласованный с ним фильтр; 2) функция
неопределенности радиолокационного сигнала и ее применение
в качестве критерия при формировании радиолокационного сигнала;
3) теория оценки параметров и связь характеристик кодированного
сигнала с результатами радиолокационных измерений.
13
В гл. с 6 до 10 изложены вопросы, относящиеся к специфическим
радиолокационным сигналам. Особое внимание уделяется ЛЧМ
сигналам1, так как во многих отношениях именно они являются
каноническими сигналами, позволяющими осуществить сжатие
импульса с помощью согласованной фильтрации. Среди всех сигна-
лов с большим значением произведения длительности на полосу
частот, которые были предложены для использования в радиоло-
кации, ЛЧМ сигналы нашли наиболее широкое применение и им
уделено самое большое внимание при создании элементов устройств
для генерирования и приема сигналов.
Дискретно-кодированные сигналы, которые здесь противо-
поставляются непрерывным ЧМ сигналам, рассматриваются как
единый класс сигналов в гл. 8. Некоторые из них представляют
собой дискретную аппроксимацию хорошо известных ЧМ сигналов,
в то время как другие не имеют вообще никакой связи с классом ЧМ
сигналов. Теория оценки параметров как критерий при построении
сигналов исследуется в гл. 9, где теоретические соотношения,
полученные в гл. 5, применяются к некоторым сигналам, рассмотрен-
ным в других главах. Гл. 10 посвящена рассмотрению критериев
построения сигналов в некоторых задачах с множественными и
пространственно-распределенными целями. В последних четырех
главах (11—14-я) исследуются различные практические проблемы,
связанные с реализацией согласованных фильтров. Сюда входит
учет воздействия искажений, изучение методов обработки сигналов
при помощи линейных фильтров с задержкой сигнала на большие
отрезки времени и ультразвуковых линий задержки, а также при-
менение оптических и СВЧ методов для построения согласованных
фильтров.
Приведенный материал рассчитан на то, чтобы дать инженерам
и студентам основные понятия о принципах формирования радио-
локационных сигналов и, кроме того, обеспечить специалистов,
заинтересовавшихся этим вопросом, необходимым фундаментом
для последующего изучения более сложных задач в области иссле-
дования методов обработки сигналов и их приложений.
1.2. Принцип согласованной фильтрации
Основные принципы согласованной фильтрации были сформу-
лированы в результате исследований, направленных на оптимиза-
цию функционирования радиолокационных систем. По этим углуб-
ленным теоретическим представлениям необходимо было разработать
схемы, которые могли бы быть реализованы инженерами-практи-
ками. Метод согласованной фильтрации осуществляет оптимальную
1 Здесь и далее сокращение ЛЧМ сигналы обозначает линейно-частот-
но-модулированные сигналы. (Прим, перев.)
14
ftalcfflaus,
знание без границ
линейную обработку радиолокационных сигналов. При такой обра-
ботке исходная радиолокационная информация, поступающая на
вход приемника и искаженная согласно предположению белым
гауссовым шумом, преобразуется к виду, удобному для вынесения
оптимального решения об обнаружении (наличия или отсутствия
цели) или для оценки параметров цели (дальности, скорости и т. д.)
с'минимальной среднеквадратичной ошибкой, или для обеспечения
максимально возможного разрешения группы целей.
Характеристики согласованных фильтров могут быть описаны.
с помощью частотной либо временной функции отклика, кото-
рые связаны между собой преобразованием Фурье. В пространстве
частот переходная функция согласованного фильтра //(cd) есть ком-
плексно-сопряженная функция спектра сигнала, который должен
быть обработан оптимальным образом. Таким образом в общем
виде
Н (<о) = kS* ((d) ехр [—j<*>Td], (1.2)
где S(to) — спектр входного сигнала s(0 и Td — постоянная задерж-
ка, нужная для физической реализации фильтра. Нормирующий
коэффициент k и постоянная задержка, как правило, опускаются
при записи основных соотношений теории согласованной филь-
трации, которые обычно формулируются в виде
Н ((d) = S* (о). 1.3)
Соответствующая зависимость во временной области между
сигналом, который должен быть обработан, и характеристикой
согласованного фильтра получается в результате обратного преоб-
разования функции Фурье //((d). Это приводит к тому, что импуль-
сный отклик фильтра представляет собой обращенную во времени
копию известной временной функции, описывающей сигнал. Таким
образом, если импульсный отклик согласованного фильтра есть
h(t), то основное соотношение, эквивалентное равенству (1.2),
имеет вид
h(t) = ks(Td-t). (1.4)
Как и в предыдущем случае, произвольная задержка Td в записи
основного соотношения может быть опущена1:
Л(/) = &>(—О- (1.5)
Считается, что свойства оптимального приемника в зависимости
от параметров спектра сигнала для случая белого гауссового шума
[уравнение (1.2)] первым определил Норс [5]. Поэтому согласован-
ные фильтры называют также фильтрами Норса; однако Ван Флек и
1 В этом случае, однако, при записи уравнений нормирующий множи-
тель k будет сохранен, поскольку он необходим для определения коэффици-
ента передачи согласованного фильтра при единичном усилении.
15
ииит
ЦТ
Миддлтон [61 были, очевидно, первыми, кто использовал термин
«согласованный фильтр» по отношению к фильтрам, оптимизирую-
щим отношение сигнал/шум для импульсных сигналов. Вывод
требований, которым должен удовлетворять согласованный фильтр,
рассматривается в гл. 2 для законченности изложения, а также
с тем, чтобы помочь заинтересованному читателю глубже понять
сущность систем с согласованными фильтрами. На рис. 1.2 иллюст-
рируются соотношения, определяемые равенствами (1.3) и (1.5).
Рис. 1.2. Связь между характеристиками сигнала и согласован-
ного фильтра.
Импульсный от клин
согласованного фильтра Sf-tj
Исходные соображения для вывода условий, определяющих
оптимальное обнаружение сигнала, поясняются на рис. 1.3, где
дана упрощенная схема приемной системы. Выходной сигнал в точке
б представляет собой смесь сигнала с шумом. Целью разработчика
системы являетсй оптимизация вероятности обнаружения сигнала
на некотором интервале наблюдения, который может представлять
собой строб дальности. В других случаях этот интервал явно не
указан, мы просто фиксируем факт, что внимание наблюдателя
должно быть направлено на некоторую особую точку случайно
либо вследствие наличия априорных данных. 'Порог наблюдения
может быть четко зафиксированным, например, в автоматических
сигнализаторах тревоги, или устанавливаться подсознательно че-
ловеком-оператором, который по своим физиологическим свойствам
способен не учитывать даже сравнительно большие шумовые выб-
росы, не являющиеся истинными сигналами. Статистические харак-
теристики, используемые в процессе обнаружения, будут зависеть
от многих факторов, например от уровня порога и наличия априор-
ной информации относительно расположения сигнала.
16
NaiaHausiM
знание без границ “ w
Однако даже без учета существенных факторов из рассмотре-
ния рис. 1.3 мы можем заметить, что для. оптимизации процедуры
обнаружения, как подсказывает логика, следует попытаться мак-
симизировать пиковое значение сигнала по отношению к шуму.
Так как сигнал, по всей вероятности, присутствует редко (непре-
рывный сигнал по определению не может переносить полезной
информации), то при непрерывном наблюдении случайных флюктуа-
ций шумового сигнала мы будем концентрировать внимание на
кратковременных отклонениях от усредненного за длительный
период или среднеквадратичного значения шума. С этой точки
Вход Выход
Рис. 1.3. Критерий обнаружения сигнала.
зрения логично сделать вывод, что получение максимального
пикового значения сигнала по отношению к среднеквадратичному
значению шума будет приводить к нужной нам оптимизации, т. е.
< s \ __Максимальная мгновенная мощность выходного сигнала
< N /макс Выходная мощность шума
(16)
Читатель, которого интересует определение условий макси-
мизации отношения, задаваемого равенством (1.6), может найти
этот вывод в гл. 2, где рассматривается также статистический подход
к оптимизации характеристик систем обнаружения. Оба эти подхода
приводят к целесообразности использования согласованной филь-
трации, которая характеризуется равенствами (1.3) и (1.5). Найдено,
что в случае применения согласованного фильтра, который за-
дается этими выражениями, максимальное значение отношения
сигнал/шум на выходе фильтра при наличии белого гауссова
шума определяется соотношением
S _______ 2хэнергия принятого сигнала
N /макс Спектральная плотность шума, вт/гц
(1-7)
Равенство (1.7) для простого импульсного радиолокационного
сигнала может быть получено эвристическим путем при рассмотре-
17
|ЯГ
ции параметров, показанных на рис. 1.4. Энергия принимаемого
сигнала равна
£ = 4-Л«Т, (1.8)
а мощность шума определяется как
PN=Nobf, (1.9)
где No спектральная плотность мощности шума и Д/ — эф-
фективная полоса фильтра.
Рис. 1.4. Параметры импульсного
сигнала.
Оптималь-
ный фильтр
Ширина полосы f/T
Отношение пиковой мощности сигнала к мощности шума,
выраженное через энергию сигнала, равно
7_S\ Л« 2Е
\'N / макс TN0&f
(1.Ю)
Для получения равенств, описывающих оптимальную обработ-
ку, можно использовать известный вывод о том, что ширина полосы
фильтра связана с длительностью импульса приближенной за-
висимостью
bf = k!Tt
(1.11)
где значение k — всегда близко к единице. Предположим, что k = 1,
тогда отношение сигнал/шум, задаваемое равенством (1.10), све-
дется к
_______= Ц. (1.12)
\ N ,/макс NJ.
Этот результат означает для разработчика радиолокатора, что
«поскольку согласованный фильтр используется в додетекторных
18
каскадах приемной системы, то ее способность к обнаружению
зависит только от содержащейся в сигнале энергии и никоим обра-
зом не связана с формой сигнала, в которой он поступает на вход
приемника. Для того чтобы получить оптимальное отношение сиг-
нал/шум на выходе, фильтр должен быть согласован с сигналом.
Однако теория показывает, что если построение строго согласован-
ного фильтра окажется практически невыгодным или невозможным,
то обычно можно использовать разумную аппроксимацию, причем
это весьма слабо скажется на способности радиолокационной
системы к обнаружению сигнала.
•
1.3. Исторические предпосылки появления теории
сжатия импульсов
Принцип согласованной фильтрации был сформулирован в ре-
зультате поисков теоретического критерия, который позволил бы
независимо от практических ограничений оценить качество функ-
ционирования импульсных радиолокационных систем. Приблизи-
тельно в это же время инженеры, столкнувшись с недостатками
реальных радиолокаторов периода второй мировой войны, обра-
тились к исследованию методов, которые бы позволили улучшить
характеристики радиолокаторов (в эту группу уходили некоторые
всемирно известные физики и специалисты по математической теории
цепей, которые в соответствии с требованиями военного времени
занимались созданием радиолокационных систем). В ходе войны
по мере развития и совершенствования методов обработки радиоло-
кационных сигналов становилось очевидным, что главным препят-
ствием на пути радикального улучшения функционирования радио-
локаторов является ограничение fto мощности передатчиков, ко-
торые использовались в> радиолокационных системах.
Эта проблема имела двойственный характер. Пиковая мощность,
которая могла быт$> получена с помощью существовавших пере-
дающих ламп, была ограничена, а, кроме того, даже если бы в тот
момент можно было получить большую мощность, многие из эле-
ментов передатчика не могли бы работать при более высоких уровнях
мощности, чем те, на которые в то время онц рассчитывались.
Прямое решение проблемы лучшего использования возможностей
передающих ламп при ограниченной пиковой мощности состоит
в использовании импульсов большей длительности. Однако на этом
пути возникает конфликт в связи с требованием систематического
улучшения разрешающей способности радиолокатора, необходимой
для таких целей, как картографирование земной поверхности или
разрешение отдельных целей при наблюдении больших групп са-
молетов. Таким образом, самый простой и очевидный путь преодоле-
ния ограничений системы по мощности оказался неприемлемым
именно в той области, где имелась наибольшая необходимость.
2* ' 19
Метод решения рассмотренной выше двойственной проблемы
был предложен несколькими учеными [7— И]1. Существо этого
метода заключалось в использовании при передаче импульса боль-
шой длительности, несущая частота которого изменялась бы внутри
импульса по линейному закону. Интуитивно ясно, что это должно
приводить к появлению зависимости между временем и частотой,
которая должна использоваться в радиолокационном приемнике.
Для обработки такого сигнала был предложен фильтр, имеющий
линейную характеристику зависимости времени задержки от час-
тоты. При этом, очевидно, величина задержки для одного края
принимаемого импульса будет больше, чем для другого края,
что приведет к сжатию сигнала во времени и увеличению его пиковой
амплитуды (см. рис. 6.19). Вынесение каких-либо заключений
о приоритете при формулировке основной идеи принципа сжатия
импульса выходит за пределы настоящей работы. Однако тот факт,
что ученые, работавшие самостоятельно и находившиеся далеко друг
от друга, нашли более или .менее идентичное решение общей проб-
лемы, сам по себе достаточно красноречив.
Принций сжатия импульса был сформулирован слишком позд-
но, чтобы как-то повлиять на технический уровень вооружения,
использовавшегося во время второй мировой войны. Добавим
также, что в то время не были еще созданы специальные типы ламп,
такие, как высокомощные клистроны, которые требовались для
практической реализации этих интересных методов. Таким образом
методы обработки радиолокационных сигналов, использующие
сжатие импульса, остались лежать в досье патентных бюро как
любопытные предложения, оставшиеся в наследие от военного
времени.
Однако по мере развития техники необходимые элементы
передающих устройств были в конце концов разработаны, и в связи
с этим в среде специалистов возродился интерес к перспективным
принципам сжатия импульсов и согласованной фильтрации. В ре-
зультате к началу 50-х годов уже несколько наиболее крупных лабо-
раторий начали осуществлять программы исследований, посвящен-
ных внедрению в практику принципов сжатия импульсов [12—15).
1.4. Эвристическое определение основных параметров
сжатия импульсов
Основные идеи предложений, о которых мы упоминали в пре-
дыдущем разделе, можно понять из рассмотрения примеров, пока-
занных на рис. 1.5. Здесь изображен передаваемый импульс дли-
1 В Советском Союзе независимо было сделано предложение Я. Д- Шир-
маном. Авторское свидетельство № 146803 по заявке № 461977/40 от 25 ию-
ля 1956 г. <Бюллетень изобретений», 1962, № 9. (Прим, ред.)
20
^alaltaus^ii
знание без границ \ *
тельности Т (рис. 1.5, а), несущая частота которого изменяется по
линейному закону (рис. 1.5, б). Фильтр, сжимающий импульс
(связь задержки с частотой показана на рис. 1.5, в), задерживает
один конец принимаемого импульса относительно другого, что и
приводит к появлению на выходе фильтра более короткого импульса
с большей пиковой амплитудой (рис. 1.5, г и 1.5, д). Линейная
зависимость времени задержки в фильтре от частоты приводит
к тому, что задержка высокочастотных компонент в начале импульса
больше задержки низкочастотных компонент в конце импульса
Рис. 1.5. Идеализированные характеристики процесса сжатия
импульса:
а—огибающая импульса иа входе; б—функция модуляции несущей ча-
стоты; а—функция изменения задержки в фильтре; г—огибающая сжа-
того импульса; о — сравнение сигналов иа входе и иа выходе согласо-
ванного фильтра.
пропорциональные задержки будут иметь промежуточные частот-
ные компоненты. Результатом этого явится сжатие импульса. Так
как мы рассматриваем пассивный линейный фильтр, то справедлив
закон сохранения энергии и выигрыш в пиковой мощности сжатого
импульса должен быть пропорционален отношению длительностей
импульсов на входе и на выходе фильтра. Таким образом
(1.13)
где Pt — пиковая мощность входного импульса и — пиковая
мощность сжатого.
Заметим, что если длительность импульса тр такова, что обес-
печивает необходимое разрешение, то применение этого метода поз*
волит использовать радиолокационный импульс длительности 7,
с тем, чтобы впоследствии за счет сжатия повысить среднюю мош*
ность сигнала до значений, превышающих предельные.возможности
передатчика. Сжатие импульса и увеличение его эффективной пи*
ковой мощности осуществляются за счет частотной модуляции
21
сигнала, и таким образом преодолеваются существующие ограни-
чения по пиковой мощности для импульсных радиолокационных
систем. Это позволяет разработчикам получить необходимую энер-
гию в импульсе, нужную для достижения требуемой дальности об-
наружения при заданном значении разрешающей способности. Тем
самым обеспечивается решение задач, поставленных перед радио-
локационной системой.
Ниже путем эвристических рассуждений мы выведем установ-
ленные в предыдущих разделах фундаментальные соотношения,
что позволит получить приближенные выражения для описания
характеристик систем, использующих сжатие импульса. Итак,
пусть передаваемый импульс имеет прямоугольную огибающую
(как будет показано в гл. 3, это предположение не является обяза-
тельным, но при его выполнении мощность передатчика исполь-
зуется наилучшим образом), а закон изменения частоты выражается
через
<|)«=<оо + р/, |/|<Т/2. (1.14)
Если не учитывать влияния огибающей, то зависимость фазы
передаваемого сигнала от времени имеет вид
8(0= $<od/ = (i)o/ + ^4-Ср (1.15)
Отсюда видно, что фазовый угол 0 содержит квадратичный член
(1.16)
Если произведение длительности передаваемого импульса Т
на девиацию частоты Д/ — Д<о/2л = / 2 — велико, то при линей-
ном изменении несущей частоты от до амплитудный спектр
сигнала будет иметь практически прямоугольную огибающую.
На рис. 1.6 приведены основные характеристики импульса, полу-
ченные с помощью этих рассуждений.
Фильтр сжатия является^фильтром, имеющим линейную зави-
симость времени задержки от частоты, противоположную линейному
закону ЧМ сигнала. Эта функциональная зависимость может быть
представлена в виде
td=^2K^-^) + b. (1.17)
Так как обычно используются полосовые фильтры, то соответ-
ствующий фазовый сдвиг фильтра равен
Р/((о) = Jf</do = K(<o—(Oj)® + bin + Са. (1.18)
Следует иметь в виду, что при практической разработке фильтра
может быть синтезирована только часть фазовой функции, кото-
22
^alaHausA
знаниебезграниц Ч*
рая соответствует положительным временам задержки. Соотноше-
ния (1.17) и (1.18) иллюстрируются графиками, приведенными на
рис. 1.7.
Если постоянные р и К подобраны соответствующим образом,
то спектр сигнала на выходе фильтра сжатия по предположению
характеризуется прямоугольным амплитудным распределением и
плоской или линейной фазовой функцией. Зависимость амплитуды
Форма сигнала во времени
Амплитудный спектр
Рис. 1.6. Параметры широкого
импульса на входе фильтра ежа*
тия и предполагаемый вид ампли-
тудного и фазового спектров.
сжатого импульса от времени легко может быть определена через
спектральные параметры; огибающая сигнала имеет вид (sin х)/х,
а длительность импульса равна тр = 1/А/ при измерении на уровне
4 дб ниже пиковой амплитуды. Расстояние между первыми нулями
этой огибающей равно 2/Д/. Несущая частота сжатого импульса при
сделанных выше предположениях постоянна и равна /0, а пиковая
амплитуда составляет УТЩ, как показано на рис. 1.8.
Наши рассуждения не станут менее общими, если будем пред-
полагать что фильтр сжатий имеет прямоугольную полосу пропус-
кания Д/ с центром на частоте /0. При этом мы можем рассматривать
операцию сжатия импульса как согласованную фильтрацию по
Норсу, описанную в разд. 1.2.
В приведенных выше рассуждениях не учитывался ряд эф-
фектов второго порядка, которые могут оказаться важными для
разработчика систем. Они будут подробно рассмотрены в после-
дующих главах. Важным результатом, полученным с помощью
23
этого подхода, является связь между пиковой мощностью входного
и выходного сигналов и параметром сжатия импульса ГД/ или
произведением длительности на ширину полосы (что соответствует
терминологии, принятой в теории согласованной фильтрации).
Эта связь имеет вид
P0/Pt - Tlxp = Tbf. (1.19)
Следующим интересным результатом является вывод о том, что
сжатый импульс имеет форму функции (sin х)/х с характерными бо-
ковыми лепестками, тогда
как в упомянутых патен-
тах считалось, что выход-
ной сигнал соответствует
виду усеченной функции.
Этот результат под-
тверждается строгим ана-
лизом, проведенным в гл. 6,
и представляет значитель-
ный интерес для задач
Рис. 1.7. Функция изменения задержки и Рис. 1.8. Форма входного сиг-
фазового сдвига в фильтре сжатия. нала и сжатого импульса, по-
лученные при эвристическом
анализе.
радиолокационного наблюдения многих целей с большим динами-
ческим диапазоном эффективных площадей рассеяния. Ухудшение
наблюдения вследствие наличия боковых лепестков привело к не-
обходимости исследовать различные методы рассогласования ха-
рактеристик фильтров для уменьшения боковых лепестков времен-
ной функции (sinx)/x, или, как их еще называют, боковых лепестков
по оси дальности. Кроме того, в поисках сложных1 сигналов, для
1 Здесь и далее мы будем применять термин «сложный сигнал» вместо
используемого в оригинале громоздкого термина «сигнал, позволяющий осу-
ществлять сжатие импульса с помощью согласованного фильтра». (Прим, ред.)
24
которых форма сжатого импульса имеет более приемлемый вид,
рассматривались различные виды кодированных импульсных сиг-
налов с нелинейной ЧМ. В следующем разделе будет показано,
что такой эвристический подход на несколько более формальной
основе может быть применен и для исследования свойств общего
класса частотно-модулированных функций, позволяющих осущест-
влять сжатие импульса.
1.5. Характеристики согласованного фильтра для ЧМ
сигнала произвольного вида
В предыдущем разделе с помощью аналитического подхода,
при котором внимание сконцентрировано на наиболее важных ха-
рактеристиках сигнала и согласованного фильтра и не учитываются
эффекты второго порядка, были получены приближенные харак-
теристики согласованного фильтра, позволяющего осуществлять
сжатие импульса для ЛЧМ сигнала. Важным'результатом явилось
установление связи между законом линейной частотной модуляции
и распределением амплитудного спектра для случая прямоугольной
огибающей импульса. При этом предполагалось, что линейное из-
менение частоты несущей дает огибающую амплитудного спектра
прямоугольной формы. Так как общая ширина полосы зависит
от скорости изменения угловой частоты, выраженной в радианах
на секунду в квадрате, и общей длительности сигнала Т, то связь
между распределением спектральной плотности мощности и фазой
сигнала 0 при фиксированной длительности Т может быть выражена
в виде
М(а>,)|>~1/в"(0. (1.20)
Так как
Л»
то
0"(О = Н (1-21)
и
| Д((о„)|а^ 1/р.
В этих расчетах есть то значение угловой частоты, для которого
величина Л(<о) соответствует определенному значению 0. Прове-
денные выше рассуждения могут быть положены в основу более
формального рассмотрения. Это даст возможность приближенно
определить параметры спектра и согласованного фильтра для
сжатия обобщенного ЧМ сигнала, имеющего вид
s(/) = a(/)cos[(Do/ + 0(OJ, (1.22)
25
где dQ(t)!dt — функция частотной модуляции самого общего вида.
Метод анализа, который позволяет получить эти результаты, осно-
ван на принципе стационарной фазы, сформулированном Кель-
вином [16]. Этот принцип использован для исследования сложных
сигналов в работах [17—18]. В настоящей книге указанный метод
рассмотрен в гл. 3.
ЛИТЕРАТУРА
•1. Р. М. Woodward. Probability and Information Theory, with Appli-
cations to Radar, Pergamon Press, Oxford, 1953.
•2. G. L. T u r i n. An introduction to matched filters, IRE Trans. Inform.
Theory IT-в, 311-329 (1960).
3. E. N. F о w 1 e. The design of radar signals. The MITRE Corporation, Bed-
ford, Massachusetts, Spec. Rept. SR-98 (1963).
4. M. В e r n f e 1 d, С. E. С о о k, J. P а о 1 i 1 1 o, and С. A. Pa 1 m i e r i.
Matched filtering, pulse compression, and waveform design, Parts I—IV,
Microwave J. 7, № 10, 57—64, № 11, 81—90, № 12, 70—76 (1964); 8,
№ 1, 73—81 (1965).
5. D. O. North. Analysis of factors which determine signal-to-noise
discrimination in radar, RCA Laboratories, Princeton, New Jersey, Rept.
PTR-6c (June, 1943).
6. J. H. V a n V 1 e c k and D. Middleton. A theoretical comparison
of visual, aural, and meter reception of pulsed signals in the presence of
noise, J. Appl. Phys. 17, 940—971 (1946).
7. E. H u t t m a n. German Patent № 768, 068, March 22, 1940.
8. W. A. C a u e r. German Patent № 892, 772, December 19, 1950.
9. D. O. S p г о u 1 e and H. J. Hughes. British Patent № 604, 429,
July 5, 1948.
10. R. H. D i c k e. U. S. Patent № 2, 624, 876, January 6, 1953.
II. S. D a r 1 i n g t о n. U. S. Patent № 2, 678, 997, May 18, 1954.
12. С. E. С о о k. Analysis and experimental verification of the performance
of a network for time compressing a frequency modulated pulse. Unpub-
lished research notes (1954).
13. С. E. С о о k. Modification of pulse-compression waveforms, Proc. Natl.
Electron, Conf., 14, 1058—1067(1958).
14. J. E. C h 1 n and С. E. С о о k. The mathematics of pulse compression —
a problem in systems analysis, Sperry Eng. Rev., 12. 11 — 16 (1959).
•15. J. R. К 1 a u d e r, A. C. Price, S. Darlington and W. J. A 1-
b e r s h e i m. The theory and design of chirp radars, Bell Syst. Tech. J.
39, 745—808 (1960).
•16. S. Goldman. Frequency Analysis, Modulation and Noise, McGraw
Hill, New York, 1948.
17. E. L. К e у, E. N. F о w 1 e, and R. D. H a g g a r t y. .A method of pulse
compression employing nonlinear frequency modulation. MIT Lincoln
Lab., Lexington, Massachusetts, Tech. Rept. 207 (1959).
18. E. C. W a t t e r s. A note on the design of coded pulses, Proc. Pulse Com-
fress. Symp., Rome Air Dewelopment Center, New York, Tech. Rept.
R-59-161 (1959).
Работы* посвященные анализу радиолокационных систем
•I. М. I. S к о I п 1 к. Introduction to Radar Systems. McGraw-Hill, New
York, 1962.
•II. D. К. В a r t о n. Radar System Analysis. Prentice-Hall, Englewood
Cliffs, New Jersey, 1964.
26
^lalaHaus^l
знание Вез границ w *
*111. R. S. Berkowitz (ed.), Modern radar: Analysis, Evaluation, and
System Design. Wiley, New York, 1966.
IV. С. E. Фалькович. Прием радиолокационных сигналов на фоне
флюктуационных помех, изд*во «Советское радио», 1961.
1. Вудворд. Теория вероятности и теория информации с примене-
ниями в радиолокации, изд-во «Советское радио», 1955.
2. Турин. «Зарубежная радиоэлектроника», 1961, № 3, стр. 30.
15. Клауде р, Прайс и др. «Зарубежная радиоэлектроника», 1961,
№ 1, стр. 15.
15. Гольдман. Гармонический анализ, модуляция н шумы, Издательст-
во иностранной литературы, 1951.
I. С к о л н и к. Введение в технику радиолокационных систем, изд-во
«Мир», 1965.
II. Бартон. Радиолокационные системы, Воеииздат, 1967.
III. Современная радиолокация, изд-во «Советское радио», 1969.
Работы советских авторов, добавленные редакто-
ром перевода
Д. Е.В а к м а н. Сложные сигналы и принцип неопределенности в радио-
локации, изд-во «Советское радио», 1963.
В. И. Т и х о и о в. Статистическая радиотехника,изд-во «Советское радио»,
1968.
ГЛАВА 2
ОПТИМАЛЬНАЯ ДОДЕТЕКТОРНАЯ ОБРАБОТКА
И ТЕОРИЯ СОГЛАСОВАННЫХ ФИЛЬТРОВ
2.1. Введение
В гл. 1 было установлено, что оптимальной додетекторной
обработкой в радиолокационной системе при мешающем воздейст-
вии белого гауссова шума является фильтрация принимаемого
сигнала с помощью фильтра, импульсный отклик которого
ft(0 = s(—/), (2.1)
а соответствующая передаточная функция фильтра //(<о) равна
Я (о) = S* (to), (2.2)
где s(t)—сигнал на входе радиолокационного приемника и
S(co) — соответствующее преобразование Фурье этого сигнала.
Такой метод обработки сигнала получил название согласованной
фильтрации.
Свойства согласованного фильтра, определяемые равенствами
(2.1) и (2.2), могут быть выведены на основании нескольких раз-
личных критериев. Такими критериями являются:
1. Критерий отношения сигнал/шум.
2. Критерий отношения правдоподобия.
3. Критерий максимума апостериорной вероятности (обратной
вероятности).
Применение всех трех критериев дает один и тот же результат:
для наиболее эффективного извлечения передаваемой информации
в приемном устройстве необходимо использовать согласованный
фильтр, т. е. фильтр, обладающий приведенными выше характе-
ристиками.
При использовании критерия отношения сигнал/шум предпо-
лагают, что оптимальная додетекторная система обработки макси-
мизирует отношение сигнал/шум в один из моментов времени. Этот
подход был исследован несколькими учеными, главным образом
Норсом (11, а также Ван Флеком и Миддлтоном 12]. Критерий
28
NataHausiiiik
знание без границ Ч *
отношения правдоподобия определяет оптимальный додетекторный
фильтр как фильтр, который, обрабатывая принимаемый сигнал,
производит оценку отношения двух условных вероятностей для
принятого сигнала (т. е. вероятность при наличии суммы сигнала
и шума и вероятность при наличии только шума). Этот критерий
был сформулирован на основании теории статистических решений,
развитой Вальдом [3], Нейманом и Пирсоном [4] и др. Одними из
первых применение теории статистических решений к задаче приема
радиолокационных сигналов рассмотрели Маркум и Сверлинг
15], Лоусон и Уленбек 16], Миддлтон [7], Миддлтон и Ван Митер
(8, 9] и Петерсон и БирдсоллЛО]. Критерий обратной вероятности
описывает идеальный приемник как приемник, который, обрабаты-
вая принимаемый сигнал, образовывает на своем выходе апостериор-
ное распределение вероятностей (или какое-либо другое эквивалент-
ное представление). Этот подход основан на шенноновской теории
информации и впервые применялся для анализа радиолокационных
систем Вудвордом и Дэвисом [11]. Позднее он был расширен Вуд-
вордом [12].
В следующем разделе приведен вывод свойств согласованных
фильтров с точки зрения максимизации отношения сигнал/шум.
Остальные разделы настоящей главы посвящены рассмотрению
в общих чертах некоторых других вопросов теории обнаружения,
изучение которых возможно осуществить с помощью статистических
методов.
2.2. Критерий отношения сигнал/шум [/—2]
Отношение сигнал/шум, которое чаще всего используется при
рассмотрении радиолокационных систем, определяется как \
S __ Мгновенная пиковая мощность выходного сигнала
N Выходная мощность шума
В настоящем разделе мы определим свойства линейной системы
(фильтра), которая максимизирует отношение, задаваемое равенст-
вом (2.3).
Пиковая мгновенная мощность сигнала есть, по определению,
квадрат максимального напряжения выходного сигнала в отсутст-
вии шума, измеряемого на нормированной выходной нагрузке 1 ом.
В_этом случае напряжение сигнала может быть записано как
4-00
g (t) = ~ f 5 (со) Н (со) ехр [/со/] dco, (2.4)
—оо
где 5(<о) — спектр сигнала и //(со) — передаточная функция сис-
темы.
29
Рассмотрим момент времени Td, в который g(f) достигает мак-
симума, причем Td больше или равно длительности сигнала. Тогда
+*>
I (2.5)
Представим далее нормированную мощность шума на выходе филь-
тра в виде
4-00
J |Я(в)Н^, (2.6)
—оо
где No есть односторонняя спектральная плотность мощности шума
на входе фильтра, выраженная в ваттах на герц. Таким образом,
отношение сигнал/шум, задаваемое равенством (2.3), может быть
записано как
SlN=g'(Td)/a'. ’ (2.7)
Поскольку мы трактуем оптимизацию как нахождение наилучшей
Я(со) при условии, что все остальные параметры фиксированы
(т. е. входной сигнал и No), то для нахождения этой функции можно,
применить метод вычисления вариации, предполагая, что Я(ш)
может изменяться в окрестности соответствующей оптимальной
функции (если она существует).
При вычислениях удобнее использовать логарифм отношения
сигнал/шум, как это делал Норс, так что выражение, которое мы
будем рассматривать, имеет вид
\gS/N = 2\gg(Td)~- 1g о». (2.8)
Изменение отношения сигнал/шум вследствие вариации бЛ/(<о)
можно выразить через g (Td) и о8, в которые неявно входит Н (со),
следующим образом:
6 (1g s/ЛГ) = 6 [g (Г,)] + 5 [а«]. (2.«)
Из равенства (2.8) можно получить введенные выше частные
производные 1 в виде
^^ = —2—, (2.10а)
dg(Td) g(Td) '
(2.10б)
да* а*
1 Вычисление вариации 6F(x, у) подчиняется тем же самым правилам,
что и вычисление общих дифференциалов, за исключением того, что при этом
ие накладывается ограничений на величину б£(х, у) [1Б].
30
Ratafia и srdii
знание без границ * *
Подставляя их в равенство (2.9), получаем
«(igS/Я) = (2.11)
e(Td) o’
Использовав выражения для g(Td) и а® из равенств (2.5) и
(2.6) соответственно, приведем (2.11) к виду
2 J S(©) б [Н (со)] exp [/G)Td] dtaftn
8(lgS/*)- - ' ~g(7.,--------------------------
(ЛГ./2) f 6[H(w)H*(co)]d(o/2n
--------—--------------------• (2.12)
Так как вариация произведения равна
6 [Н (со) Я* (со)] = Я* (со) 6 [Я (со)] + Я (со) б (Я* (со)] =
= 2 Re Я* (<•>)« [Я (со)], (2.13)
то при дополнительно наложенном ограничении, что
+«»
$ 6 [Я (со)] ехр [/со^] Ясо = X (/) (2.14)
—00
есть действительная функция, можно показать
[ Я*(о>)5[Я(ш)]^ = f h(t)K(t)dt = f Я (о>) 6 [Я* (<•>)] — (2.15)
J 2л J J 2л
—оо — оо —оо
И) следовательно,
оо оо
2Re J Я* (со) 6 [Я (cd)] = 2 J Я*
—00 —оо
(«>) 6 [Я (<0)1 . (2.16)
[ХЛ
Применение формул (2.13) — (2.16) и подстановка результата
в выражение для 6(lg S/N) дают возможность вынести выражение,
содержащее вариацию б[Я(<о)1, за скобки, так что равенство (2.12)
примет вид
6(lgS/Af>= j [
2S (со) exp [Jco7\f]
g(r„)
_ <217)
31
Приравняв это последнее соотношение нул1р, можно получить ус-
ловия, определяющие стационарную точку в зависимости от отно-
шения сигнал/шум. Для того чтобы это нулевое значение сущест-
вовало и было независимым от вариационного изменения IAZ(co) 1,
должны удовлетворяться следующие условия:
2S (со) exp [/coTrf] No Ц* (со)
g (Td) ' 2а«
(2.18)
Так как g(Td), /Vo и оа постоянные величины, то это приводит
к выражению
Н (со) — kS* (со) ехр (— /coTj,
(2.19)
что совпадает с определением передаточной функции оптимального
фильтра, приведенным в гл. 1.
В качестве второго возможного подхода к определению свойств
оптимального фильтра покажем, что Н(о), задаваемое равенством
(2.19), действительно дает максимальное значение отношения сиг-
нал/шум, которое может быть получено при использовании следую-
щих эквивалентных выражений для g(Td) и о2, где через h(t) обоз-
начен импульсный отклик фильтра //(со):
Td
g(Td)= jj s(Td—x)h(x)d%
(2.20a)
и
oo
oa - f /i2(t)Jt,
At At
0
(2.206)
причем это последнее выражение можно получить из равенства
(2.6) путем применения теоремы Парсеваля, в соответствии с ко-
торой энергия сигнала может быть определена как через спектраль-
ную характеристику Я(со), так и через временную функцию Л(/).
Применение этих соотношений к равенству (2.3) приводит к следую-
щей форме определения отношения сигнал/шум:
s(Td — x)h(x) dx
N
OO
(No/2) J Л1 (т) dx
o
(2.21)
32
^alaHausA
знание без границ Ч
Используя неравенство Шварца \ получаем
J* sa (Та—т) dx J h* (т) dx
А < 5-------------2-------, (2.22)
(2Vo/2) f h»(T)dt
о
откуда следует, что отношение сигнал/шум будет максимальным
при
h(f) — ks(Td—t), (2.23)
которое представляет собой просто преобразование Фурье Я(ю).
Тем самым мы получили другое возможное определение согласован-
ного фильтра.
Из привёденных выше рассуждений очевидно, что максималь-
ное значение отношения сигнал/шум может быть выражено в виде
3* <та—X) dx
S_\ l_
N /макс
Отметим, что числитель в выражении (2.24) представляет собой
полную энергию сигнала Е. Это приводит к интересному выводу
о том, что возможность обнаружения сигнала произвольного вида
зависит только от содержащейся в сигнале энергии и не определяет-
ся временной структурой сигнала. Однако для практической реали-
зации этого Ьывода необходимо производить обработку сигнала
с помощью согласованного фильтра.
Подставляя полученные характеристики фильтра, оптимизи-
рующего выходное отношение сигнал/шум в два возможных выра-
жения для g(t), получим следующие соотношения:
t
g (t) - jj s (т-1) s (т-TJ dT (2.25)
b
и
oo
g(l)** jj |S((o)iaexp[/co/]d(i)/2jt. (2.26)
В первом из этих выражений можно узнать определение автокорре;
ляционной функции сигнала s(t), откуда следует эквивалентность
1 Одна из форм неравенства Шварца имеет вид
оо \ 2 4-оо
J f (*) g (х) dx I < J*
—00 / —oo
4-00
f*(x)dx у g*(x)dx.
— oo
33
согласованной фильтрации и корреляционной обработки. Связь
между характеристиками сигнала и согласованного фильтра гра-
фически показана на рис. 1.2.
Для того чтобы обосновать использование критерия отноше-
ния сигнал/шум, можно исследовать влияние этого отношения на
функционирование системы. В этом случае одной из лучших харак-
теристик функционирования системы является вероятность того,
что в процессе обнаружения будет сделана ошибка. Рассмотрим,
например, систему связи, предназначенную для передачи случай-
ных бинарных посылок с помощью включения и выключения сиг-
нала. В точке приема необходимо принять некоторое решение об
одном из двух возможных состояний посылки. Наличие шума,
однако, приведет к тому, что некоторые решения будут неправиль-
ными. Вероятность ошибки определяется выражением
где
ехр [—xa] dx
где b — пороговое напряжение (критерий решения), Л2/2оа —
отношение сигнал/шум и А — амплитуда принимаемого сигнала,
который представляет собой одно из состояний посылки. Это со-
отношение получено в предположении, что шум в системе гауссов,
что каждое из состояний посылки имеет равную вероятность
(т. е. Ро = Pi = 1/2), что решение принимается на основании
единственного выборочного значения сигнала и что процесс приня-
тия решения состоит в сравнении выборки сигнала с заранее уста-
новленным пороговым уровнем. Из равенства очевидно, что большее
значение отношения сигнал/шум соответствует меньшему значе-
нию вероятности ошибки. Отсюда делаем вывод, что при обработке
принимаемого сигнала следует максимизировать отношение сиг-
нал/шум.
Если мешающий шум гауссов, но не белый, и если ему может
быть приписана спектральная плотность мощности Л/(со), то ра-
венство (2.6) записывается в виде
оо
а2 = т f N <ш) Iн (<в) !* •
«too
(2.6а)
Вывод, аналогичный выводу соотношений (2.9) — (2.19), дает в этом
случае общее выражение для 7/(со), оптимизирующее отношение
сигнал/шум

kS* (<о) ехр [У<о7\Я
ЛЦю)
(2.19а)
34
Nataliauswk
знание без границ * *
2.3. Критерий отношения правдоподобия и статистическая
теория решений [5—5]
Из равенства (2.27) следует, что вероятность ошибки зависит
не только от величины отношения сигнал/шум, но также и от ис-
пользуемого критерия решения.
При
Л*у2с8 s= const (2.28)
это дает возможность минимизировать вероятность ошибки Ре*
Для условий, сформулированных в предыдущем разделе, это мини-
мальное значение Рв имеет место при b « Л/2 и составляет
Р£ = — 1—erf
2
Л
2^2 а
(2.29)
Можно показать, что решение, принимаемое на основе измерения
единственной выборки принятого сигнала и сравнения его с порогом
b = Л/2, эквивалентно принятию решения на основе критерия:
I »> 1; принимается решение о наличии сигнала
р° Ю амплитуды Л и шума,
Р, (v) (2«30)
Z ; ; < Г, принимается решение о наличии только
”• (°)] шума.
Здесь Pi(v) — условная вероятность того, что напряжение при-
нимаемого сигнала (о) будет лежать в интервале значений (v, v 4-
+ dv) при условии, если принимаемый сигнал является суммой
сигнала и шума. Аналогично, Р0(о) будет условной вероятностью
того, что напряжение принимаемого сигнала лежит в том же самом
интервале значений при условии присутствия на входе приемника
только шума. Отношение этих вероятностей, обозначаемое через
/, есть так называемое отношение правдоподобия; оно является
одной из основных формул теории статистических решений и теории
оценки параметров.
Вероятность ошибки всегда будет минимальной, если решение
о наличии сигнала амплитуды Л и шума принимается при
(2.31)
а решение о наличии только шума принимается когда
(2.32)
где Ро — вероятность того, что принимаемая посылка состоит
только из шума и Рг — вероятность того, что принятая посылка
35
состоит из суммы сигнала и шума. Этот критерий известен как ре-
шающее правило Байеса и основан на точке зрения введенного
Зигертом [6] «идеального наблюдателя», который минимизирует
общую вероятность ошибки. Однако, так как значения Ро и Рх
при приеме обычно не известны, как это имеет место в радиолока-
ции, то критерий, использующий отношение P0/Pi, заменяется
критерием решения, разработанным на основании теории проверки
статистических гипотез Неймана — Пирсона [4].
Основная идея этой теории заключается в сохранении фиксиро-
ванной вероятности ошибки для случая, когда принимаемый сигнал
состоит только из шума. Эта фиксированная вероятность получила
название вероятности ложной тревоги. Правило принятия решения
определяется при этом минимизацией вероятности ошибки для
случая, когда принимаемый сигнал представляет собой сумму сиг-
нала и шума; это эквивалентно максимизации вероятности обнару-
жения при фиксированной вероятности ложной тревоги. Найденный
в результате указанной процедуры статистический критерий должен
включать также использование отношения правдоподобия и ре-
шающего правила байесовского типа. Подробное рассмотрение
этого вопроса можно найти в работе Миддлтона [7].
До настоящего времени наше внимание было направлено на
применение статистических критериев для обнаружения сигналов
при использовании единственной выборки его с тем, чтобы облегчить
понимание путей развития важных статистических принципов.
Оптимальная додетекторная обработка в этом случае состоит в том,
чтобы выдать наблюдателю (человеку или какому-либо устройству)
принимаемый сигнал в его необработанной форме. В общем случае,
однако, для обнаружения используется более одной статистически
независимой выборки сигнала. Можно показать, что если состояние
посылки постоянно в интервалах между моментами времени, в ко-
торые берутся выборки, то оптимальной доДетекторной системой
является интегратор. Если, однако, состояние посылки изменяется
во времени на протяжении этого интервала, то таким оптимальным
додетекторным приемным устройством будет коррелятор. Ниже
мы исследуем этот вопрос подробнее.
В случае большого числа выборок, если известна точная форма
посылки сигнала, отношение правдоподобия записывается в сле-
дующем виде:
/(г = п,,
2.... 2ВГ") ₽<,(»=«,»,....°™тУ
(2.33)
Символ z — (vj, ^2» '•••. ^2вт0) можно рассматривать как точку,
лежащую в многомерном пространстве с 2ВТ0 координатами, где
В — полная полоса шума и То — интервал наблюдения. Координа-
тами точки в этом пространстве являются 2ВТ0 измеренных зна-
чений принимаемого сигнала, взятых через интервалы времени,
36
ftataSausilk
знание без границ Ч *
равные 1/В.для того чтобы обеспечить статистическую независимость.
Для высокочастотного сигнала в каждой точке наблюдения берутся
два ортогонально связанных выборочных значения, что дает 2ВТ
выборок. На рис. 2.1 показан способ определения выборочных зна-
чений видеосигнала. В этом случае выборки сигнала берутся через
интервалы времени 1/2/3, для того чтобы обеспечить статистическую
независимость. Исчерпывающее рассмотрение теории выборок мож-
но Найти в работе Вудворда 1121.
Рис. 2.1. Пример типичной реализации огибающей отра-
женного радиолокационного сигнала.
Показаны моменты отсчета выборочных значений t... <я.
Каждой точке пространства z выборочных значений соответст-
вуют единственные значения многомерных плотностей вероятности
р0 и р! и определяемые ими значения отношения правдоподобия.
В качестве примера на рис. 2.2 показан вид двумерной плотности,
соответствующей двум наблюдениям гауссова шума.
С помощью теоремы о выборках было показано, что эффектив-
ным методом обработки сигнала для получения на выходе отноше-
ния правдоподобия является корреляция этого сигнала с опорным
сигналом-копией передававшегося сигнала
т0
ст= jj v (/) s (/) dt.
’о
(2.34)
Если принятый сигнал v(t) содержит s(t), то результат вычисления
корреляции можно записать в виде
То То То
Jj v(t)s(t)dt = ^ si(t)dt + '^ (шум) s (t) dt.
b о b
(2.35)
37
Это выражение представляет собой энергию переданного сигнала
с небольшой добавкой, определяемой корреляцией между передан-
ным сигналом и шумом. Вспомним, что сигнал на выходе согласо-
ванного фильтра имеет вид,
t
= x)s(Td—x)dx. (2.36)
о
Рис. 2.2. Вид первого квадрата функции плотности совмест-
ной вероятности p[v(/t), о(/8)] для случая двух выбороч-
ных значений гауссова шума.
Точка г=о,. о, характеризует величину выборочных значений шума
в моменты времени tx и соответственно.
Следовательно, корреляция принятого сигнала равна выходному
сигнаЛу согласованного фильтра1 при t = Та. Кроме того, в этот
момент выходной сигнал y(f) достигает максимального значения.
2.4. Критерий отношения правдоподобия и теория
оценки параметров [11—14]
Если форма используемого сигнала точно известна, то очевидно,
что для его обработки лучше всего применять согласованный
1 В общем случае реализация согласованного фильтра представляет
собой менее сложную задачу, чем реализация корреляционного приемника.
Единственный согласованный фильтр дает на выходе все возможные значения
задержки по дальности для принимаемого сигнала. При корреляционном при-
еме необходимо иметь неискаженную задержанную копию переданного сиг-
нала для каждого значения задержки по дальности, которое представляет
интерес. Таким образом, может потребоваться большое число таких сигналов,
если нужно исследовать значительный интервал дальностей.
38
^alaHausnii
знание без границ Ч *
фильтр. Однако передаваемый сигнал часто переносит информацию
в виде изменения некоторого параметра сигнала. В случае радиоло-
кации, например, таким параметром может быть задержка принятого
сигнала относительно передаваемого сигнала. Если такие параметры
представляют интерес, то следует принять меры предосторожности
во избежание искажений этой информации в процессе обработки
принятого сигнала для принятия оптимального решения об обна-
ружении. Вудворд и ряд других авторов показали, что информация
о задержке сигнала сохраняется
при корреляции сигнала v(t) со
всеми возможными ожидаемыми
сигналами s(t — tx), где tx —
параметр задержки. Применяя
этот метод, можно извлечь ин-
формацию о задержке сигнала
и в то же самое время выполнить
условия, обеспечивающие опти-
мальное принятие решения об
обнаружении. Для достижения
этого необходимо обрабатывать
принятый сигнал с помощью
согласованного фильтра. В этом
случае только согласованный
фильтр обеспечивает эффектив-
ную обработку и таким образом
является идеальной додетек-
торной системой.
Когда особенности тактиче-
Рис. 2.3. Схема типичного набора
согласованных (оптимальных) доде-
текторных фильтров, выходные сиг-
налы которых позволяют оценить
такие параметры сигнала, как доп-
плеровский сдвиг.
ского применения радиолока-
ционной системы требуют оценки других параметров кроме задержки
сигнала, то один согласованный фильтр уже не оказывается эф-
фективным. В этом случае теория согласованной фильтрации дока-
зывает, что необходим набор согласованных фильтров, представ-
ленный на рис. 2.3, который при необходимости будет соответст-
вующим образом модифицирован с тем, чтобы перекрыть область
неизвестных параметров. Если параметром, который нужно оценить,
является, например, допплеровский сдвиг, то центральные часто-
ты согласованных фильтров (набора) выбираются так, чтобы при
этом обеспечивалось перекрытие всех ожидаемых сдвигов частот,
принимаемого сигнала. Основы теории оценки параметров и фун-
даментальные соотношения для оценки параметров радиолокацион-
ного сигнала, полученные исходя из этой теории, подробно рас-'
смотрены в гл. 5, а их приложение к специфическим радиолокацион-
ным сигналам обсуждается в гл. 9.
39
2.5. Критерий обратной (апостериорной) вероятности [11, 12}
В начале 50-х годов Вудворд и Дэвис применили шенноновскую
теорию информации для решения проблем, связанных с идеальным
приемником. Согласно их определению идеальным приемником яв-
ляется приемник, который должен выдавать на выходе всю доступ-
ную информацию о радиолокационных параметрах, переносимую
принятым сигналом. Эта информация принимает форму распределе-
ния вероятностей pv(x) для каждого измеряемого параметра при
условии, что сигнал был принят. Было высказано мнение, что нет
необходимости рассматривать наблюдателя как часть приемной
системы, как это делается в теории статистических решений, так
как наблюдатель не сможет сделать ничего большего, как определить
pv(x). Это распределение вероятностей получило название обрат-1
ной или апостериорной вероятности. Однако, в свою очередь, оно
может быть определено через функцию правдоподобия. Следова-
тельно, за исключением некоторых различий в постоянных коэф-
фициентах пропорциональности, структура идеального приемника
остается, по существу? той же, что и раньше.
Связь между обратной вероятностью и отношением правдоподо-
бия может быть получена с помощью байесовского правила для
условных вероятностей. Для вывода этого соотношения наиболее
удобно рассмотреть бинарный случай, причем символ 1 будет при-
писываться величинам, характеризующим прием при наличии сиг-
нала и шума, а символ 0 — величинам, показывающим прием при
наличии только шума. Соответствующие вероятности для сигнала и
шума или для приема только шума можно тогда записать в виде
р (1) = .^A(V) t р (0) = р°Ро(и) , (2.37)
' P(v)d(v)' 7 p(v)dv '
где Р} и Ро—априорные вероятности, определенные в соответ-
ствии с неравенствами, задаваемыми (2.31) и (2.32),
p(v)dv = P1P1(v) + P0P0(v), (2.38)
так что, делая соответствующие подстановки, получаем
Pv (1) = --------=----l.--- (2.39)
k ЛОО/РоОО+Ро/Рх /+(Po/Pi) v '
и
Pv (0) =----Po(t,)/P1 (t,)-=----!----. (2.40)
v Pa(f)/Pi(v) + />i//>0 Ц-ЦЛ/Ро) k
Как только приемник оценит Рс(1) и РДО), то тем самым вы-
полнится вся необходимая обработка сигнала. Значения этих двух
вероятностей представляют максимальную информацию, доступную
относительно двух возможных состояний передаваемого сигнала,.
40
^atattausKii
знание без границ Ч *
которая может быть извлечена из принимаемого сигнала. Если
эти вероятности определены, то процесс принятия решения стано-
вится автоматическим, поскольку всегда выбирается наиболее
вероятное состояние сигнала. Интересно отметить, что этот кри-
терий эквивалентен байесовскому решающему правилу. Это можно
видеть, если взять отношение Рр(1)/Рр(0) и предположить, что
пороговое значение равно единице. Тогда
= (2.41)
Р®(0) Ро
и когда
/ > Ро/Р1» выбираем состояние «1»,
а когда
1<.Ро!Рх, выбираем состояние «О».
Применение метода обратной вероятности к общим проблемам
радиолокации может быть проиллюстрировано на примере системы,
которая должна выполнять измерение задержки принимаемого
сигнала или дальности. С точки зрения Вудворда [ 121, идеальный
приемник не может сделать ничего больше, как подсчитать услов-
ную вероятность рс(т) того, что сигнал поступил в момент т при
условии, что принят сигнал v(f). Используя правило Байеса, можно
выразить совместную вероятность величин т и v(f) в виде
Р (т, v) = рх (v) р (т) = pv (т) р (0, (2.42)
где р(т) — априорное распределение вероятности сигнала, задер-
жанного на т сек, p(v) — априорное распределение вероятности
появления сигнала v(t), рх (и) — условное распределение вероят-
ности величины v(f) при заданном т и рс(т) — условное распреде-
ление вероятности величины т при заданном v(t).
Сигнал v(t) имеет вид
u(Z) = s(f-Q + n(/), (2.43)
где td— задержка сигнала и $(/) — вид передаваемого сигнала.
Условная вероятность px(v) может быть выражена через функцию
правдоподобия, которая в том случае, если v(t) представляет собой
ансамбль независимых случайных гауссовых переменных, равна
Рх (0 == k exp
т
J [и (/) — s(t — x)]2d/
(2.44)
Постоянная k есть нормирующий множитель, определяемый усло-
вием
$ Рх (v) dv = l.
(2.45)
41
Так как радиолокационный приемник должен вычислять рс(т),
то из уравнения (2.42) получаем
. . рх (о)р(т) /гр(т)
(т) = —---------= -- ехр
р(<0 р(Ю f
[о(0—s(t—т)]М/ . (2.46)
Если сигнал присутствует, то р(и) есть некоторая постоянная ве-
личина. Если мы предположим, что р(т) есть равномерное распреде-
ление, то оно также имеет постоянное значение. Обе эти константы
могут быть включены в k, так что выражение (2.46) перейдет в
р, (т) = £ехр
1
[0(0—s(t — т)]М/
(2.47)
или
рр (т) = £ехр
т
J о2 (0 dt
о
ехр
т
J s2(t—x)dt
о
х ехр
о (t)s(t—т) dt
(2.48)
Первые две экспоненты зависят от энергии принятого сигнала о(0 и
переданного сигнала s(0 соответственно. Следовательно, они —
постоянные величины и могут быть также включены в k. Тогда
можно заметить, что идеальным является приемник, который вы-
полняет операцию, описываемую интегралом
т т т
$ v(t)s(t—x)dt= J s(t—td)s(t—T)dt+ j —x)dt. (2.49)
о о 0
Этот интеграл принимает максимальное значение при т = td\
при этом значении т мы получаем максимальное значение pv (т) или
наиболее вероятное значение т. Вудворд указывает, что на самом
деле нет необходимости вычислять р„(т), так как с точки зрения
обработки информации достаточно просто выполнить операцию,
определяемую уравнением (2.49). Эффективный приемник, который
вычисляет (2.49), выполняет над v(f) ту же самую необратймую опе-
рацию, которая могла быть проделана идеальным приемником при
вычислении рр(т). Необратимость выполняемой приемником опера-
ции означает, что искомая информация в сигнале сохраняется, а не-
желательная информация разрушается. Кроме того, в случае иде-
ального приемника, как только будет определена рр(т), восстано-
вить структуру о(/) из этой функции уже невозможно.
42
^ataUaus^i
знание без границ У *
Сравнивая полученные соотношения с материалами предьщу-
щих разделов настоящей главы, можно отметить, что уравнение
(2.49) описывает корреляционный приемник или, что эквивалентно,
приемник, который содержит согласованный фильтр, рассмотрен-
ный в разд. 2.2. Эффективный приемник максимизирует отношение
сигнал/шум для случая белого гауссова шума, что эквивалентно
получению полного апостериорного распределения т. Основное
указание Вудворда заключается в том, что с точки зрения теории
информации от идеального приемника больше ничего требовать
нельзя. При этом подходе не принимаются во внимание такие
критерий апостериорной
Вероятности
Рис. 2.4. Обобщенное представление возможных методов
осуществления оптимальной додетекторной фильтрации.
Критерии принятия решения:
/—правило Байеса; 2 —минимаксный; 3— Неймаиа-Пирсона;
4—«идеального наблюдателям, Б— максимума правдоподобия.
вопросы, как структура решающего правила или вероятность ошиб-
ки в системе. Однако поскольку структура приемной системы,
которая максимизирует информацию на выходе приемника, иден-
тична структуре приемников, получаемых при использовании дру-
гих указанных выше критериев, то ясно, что различные критерии
оптимизации функционирования радиолокационных систем тесно
связаны между собой. |
На рис. 2.4 дано обобщенное представление трех общих теоре-
тических точек зрения на оптимальную додетекторную фильтрацию.
ЛИТЕРАТУРА
1. D. О. N о г t h. An analysis of the factors which determine slgnal-to-noise
discrimination in radar, RCA Lab. Princeton, New Jersey, Rept. PTR-6c
(1943) and Proc. IEEE 51, 1016—1027 (1963).
43
2. J. H. Van Vleck and D. Middleton. A theoretical comparison
of visual, aural, and meter reception of pulsed signals in the presence of
noise, J. Appl. Phys. 17, 940—971 (1946).
3. A. W a 1 d. Statistical Decision Functions, Wiley, New York, 1950.
4. J. N e у m a n and El S. Pearson. The problem of the most efficient
tests of statistical hypothesis, Phil. Trans. Roy. Soc. Ser. A231, 289—333
(1933).
*5. J. I.Ma rcum and P. S w e r 1 i n g. Studies of target detection by pul-
sed radar. IRE Trans. IT-6, 59—308 (1960). See also: Rand Research Me-
mos. RM 754 (December, 1947), RM 753 (July, 1948), RM-1217 (March,
1954).
*6. J. L. L a w s о n and G. E. U h 1 e n b e c k. Threshold Signals. McGraw-
Hill, New York, 1950.
7. D. M i d d I e t о n. Statistical criteria for the detection of pulsed carriers
in noise, J. Appl. Phys. 24, 371—379—391 (1953).
8. D. Middleton and D. VanMeter. Modern statistical approaches
to reception in communication theory. IRE Trans. IT-4, 119—145 (1954).
*9. D. M i d d 1 e t о n and D. Van Meter. Detection and extraction of
signals in noise from the point of view of statistical decision theory, J.
Soc. Ind. Appl. Math. 3, 192—253 (1955); 4, 88—119 (1956).
*10. W. W. Peterson and T. G. Birdsall. The theory of signal de-
tectability, Electronic Defense Group, Dept. EE, Univ, of Michigan, Ann.
Arbor, Michigan, Tech. Rept. 13 (June, 1953).
11. P. M. Woodward and I. L. D a v i e s. A theory of radar information,
Phil. Mag. 41, 1001 (1950).
*12. P. M. Woodward. Probability and Information Theory with' Appli-
cations to Radar. Pergamon Press, Oxford, 1953.
13. R. M a n a s s e. Range and velocity accuracy from radar measurements,
Lincoln Lab., M. I. T., Lexington, Massachusetts, Group Rept. 312—26
(February, 1955).
14. E. J. К e 1 1 у, I. S. R e e d, and W. L. R о d t. The detection of radar echo-
es in noise, J. Soc. Ind. Appl. Math. 8, 309—341, 481—507 (1960).
15. L. A. P i p e s. Applied Mathematics for Engineers and Physicists, p. 292—
298, McGraw-Hill, New York, 1946.
* ♦ *
5. Маркум, Сверлинг. «Зарубежная радиоэлектроника», 1960; «Сов-
Веменная радиолокация», изд-во «Советское радио», 1969.
ороговые сигналы, изд-во «Советское радио», 1952.
9. Прием импульсных сигналов в присутствии шумов, сборник перево-
дов под ред. Башаринова А. Е. и Александрова М. С., Госэнергоиз-
дат, 1960.
10. Теория обнаружения сигналов, сборник переводов под ред. Харкевича
А. А., Физмат, 1959.
12. Вудворд. Теория вероятности и теория информации с применениями
в радиолокации, изд-во «Советское радио», 1955.
^alatiausj^i
знание без ераниц Ч *
ГЛАВА 3
СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ЧМ СИГНАЛОВ
ПРОИЗВОЛЬНОГО ВИДА
3.1, Введение
Общее направление исследований, которым посвящена настоя-
щая глава, было уже определено в гл. 1 при обсуждении взаимо-
связи функции частотной модуляции и распределения амплитудного
спектра для ЛЧМ сигнала. Для того чтобы эвристические рассуж-
дения первой главы можно было повторить на более логичной и
строгой основе, целесообразно использовать принцип стационарной
фазы. Это позволяет интуитивные идеи и соображения, приведенные
в гл. 1, распространить на более широкий класс сложных ЧМ сигна-
лов произвольного вида, определяемых формулой
s (0 = a (0 cos [<оо t + 6 (/)], (3.1 >
где a(t) — огибающая передаваемого сигнала и соо + 0'(О —
функция частотной модуляции. В большинстве радиолокационных
задач предполагается, что огибающая импульса a(t) имеет пря-
моугольный вид, хотя общий анализ не ограничивается этим част-
ным случаем.
Сложные ЧМ сигналы с нелинейной ЧМ исторически были пред-
ложены в качестве средства улучшения вида сжатого импульса,
который для согласованного фильтра с линейным изменением час-
тоты имеет вид (sin х)/х. Однако этот подход приводит к некоторым
существенным ограничениям, которые должны быть наложены на
использование сигналов с нелинейной ЧМ. Некоторые другие,
более общие методы улучшения формы сигнала на выходе согласо-
ванного фильтра обсуждаются в гл. 7. Однако анализ широкого
класса сигналов произвольного вида, определенных равенством
(3.1), позволяет лучше понять сущность важной задачи построения
сложных ЧМ сигналов.
45
ir
3.2. Принцип стационарной фазы
При рассмотрении некоторых вопросов, связанных с анализом
временных и частотных функций, часто оказывается целесообразным
использовать комплексное представление сигнала. Если действи-
тельный сигнал задается равенством
s(O = a(Ocos(©o/ + 0(OJ, (3.2)
то эквивалентное комплексное представление имеет вид
и(О = а(0ехр[/0(0]. (3.3)
Преобразование Фурье этой комплексной времённбй функции за-
пишется следующим образом:
00
(/(<>) = J а(/)ехр(7{-т/+0(/)}]Л, (3.4)
— оо
где (d = 2nf. Функции U (со) и и (0 связаны теоремой Парсеваля,
так что
оо оо оо
j l"(OI’<«=i j |C/(®)|’da>= J |y(f)|»df = 2E, (3.5)
— 00 —oo —oo
где E — энергия действительного сигнала, задаваемого соотно-
шением (3.2)1. Наличие мнимого экспоненциального члена в (3.4)
указывает на то, что подынтегральное выражение в этом равенстве
представляет осциллирующую функцию, изменяющуюся со ско-
ростью
(3.6)
at
Отсюда видно, что спектр Фурье, задаваемый уравнением (3.4),
будет в основном определяться тем интервалом, на котором ско-
рость изменений колебаний минимальна. Это обстоятельство поз-
воляет рассматривать его в стационарной фазовой точке, которая
определяется уравнением
— [со/—в(0]=О или со—0'(О = О. (3.7)
dt
Данное выражение является параметрическим, так как оно свя-
зывает две независимые переменные со и t. Таким образом некоторое
конкретное значение /, которое удовлетворяет условию (3.7), может
.. 1 Использование угловой частоты со = 2nf удобно тем, что делает
обозначения в комплексной форме более компактными, хотя и приводит
к необходимости переписывать коэффициент (2л)—1 в интегральных выраже-
ниях, таких, например, как в равенстве (3,5).
46
^alattauswll
знание без ераниц * *
быть определено лишь после того, как сделано предположение
о значении со. Если только ©(f) не является постоянной, то момент
времени t, когда фаза стационарна, будет различным для каждой
из частот соА. Две составляющие экспоненты в равенстве (3.4) могут
быть представлены, как показано на рис. 3.1, в виде двух независи-
мо вращающихся векторов. Отсюда следует, что максимальное
влияние этих двух векторов на интегральное уравнение для (/(со)
будет иметь место в том случае, когда векторы вращаются с одной
и той же скоростью. Для некоторой фиксированной частоты соА,
Рис. 3.1. Векторное представление мнимых
компонент спектра, определяемого инте-
гралом в соотношении (3.4).
Рис 3.2. Критерий стационар-
ной фазы для частоты <оА.
указанной на рис. 3.1, это влияние будет преобладающим в мо-
мент f, для которого разность фаз coftf — 0(f) постоянна. Так как
cof есть вектор, вращающийся с постоянной угловой скоростью,
a 0(f) в общем случае с переменной скоростью, то существует неко-
торый момент времени fh, для которого скорость изменения раз-
ности фаз равна нулю. Это идентично условию, задаваемому равен-
ством (3.7).
На рис. 3.2 показана зависимость фазы от времени, соответст-
вующей каждому из этих двух векторов. Стационарная точка рас-
положена при f = fA, когда касательная к функции 0(f) параллельна
прямой линии <oAf. Так как крутизна этой прямой линии равна
(оА (частотному параметру), то можно еще раз убедиться, что момент
времени th, при котором имеет место стационарная точка, связан
с (0Л.
Обращаясь снова к рис. 3.2, заметим, что разность <&ht —
— ©(Сможет быть разложена в ряд Тейлора относительно th. При
этом получаем
CDhf-0(f)==(DA th-e(fft) +
+ К-е' (<*)] (t-thy+ ... (3.8)
47
Если в уравнении (3.8) временная разность (/ — th) = ±6 со-
храняется малой, то это равенство может быть достаточно точно пред-
ставлено своими первыми тремя членами. Таким образом, для
малых интервалов около точки th
<oh/-0(/) = (oftZh-e(/fc) +
+ К-е' (4)1 (/-4)- (<—4)2-
(3-9)
Так как по условию (3.7) coh—О'(/Л) = О, то уравнение (3.9) около
точки th сводится к
<oftz-0(0 = <oA4-e(4)--^-)(/-4)2. (3.10)
Подставляя это последнее соотношение в Фурье-преобразование
Z/(<o) и рассматривая а(/) как медленно меняющуюся величину по
сравнению со скоростью изменения фазы в точке видим, что
спектр частот может быть записан в виде
^Ю = а(4)
6" Uh)
2
(/-Л)2)р/. (3.11)
Именно этот последний результат и окажется полезным при выводе
приближенной связи между заданной функцией кодированного
сигнала и соответствующим согласованным фильтром.
3.3. Приложение принципа стационарной фазы к сложным
сигналам общего вида
Принцип стационарной фазы может быть применен к осцил-
лирующим функциям, которые имеют непрерывные первые произ-
водные. Некоторыми такими функциями описывается большой класс
сигналов, позволяющих осуществлять сжатие импульса с помощью
согласованных фильтров, построение которых основано на исполь-
зовании методов частотной модуляции. ЛЧМ сигналы представляют
собой частный случай сигналов этого общего класса.
Спектр сигнала, задаваемого формулой (3.1), равен
ос
S(g))= J а (0 cos [<о0/ -|-6(/)] ехр [ — jo)t]dt.
— оо
(3.12)
48
^alaltauswh
знание без границ - *•
Это выражение может быть переписано в виде
00
S(<о) = J a(0exp[j{(<00— <>)*+ 6(/)}]dt +
— оо
оо
+ 4“ f а(/)ехр[—/{(<00 + <0)/ + 0(0}]^ = S+(<o) + 5_((o),'(3.13)
—00
где S+(co) и 5_(<о) — соответственно положительная и отрица-
тельная части спектра. Будем предполагать, что соответствующие
центральные частоты S+((o) и S_(co) достаточно далеко разнесены
друг от друга, так что влияние S_(co) в положительной области
Рис 3.3. Положительная и отрицательная части спектра.
частот пренебрежимо мало. Это условие графически показано на
рис. 3.3. Здесь сигнал является узкополосным и может исполь-
зоваться комплексное представление сигнала. Из уравнения (3.4)
получаем, что £/(<о) = 2S-|_(co + <оо). Следовательно, результаты
предыдущего раздела могут быть применены для анализа узкопо-
лосных частотно-модулированных сигналов. Комплексный спектр
сигнала, задаваемого равенством (3.1), равен
оо
£/(<о) = J а(/)ехр[/{ — <о/ + 6 (/)}] dt.
— оо
(3.14)
Условия стационарной фазы для равенства (3.14) даны в уравнении
(3.7). Воспользуемся выкладками, приводящими к (3.11). В соот-
ношении (3.11) th является постоянной величиной. Следовательно,
члены, зависящие только от th, могут быть вынесены за знак ин-
теграла. Это приводит к выражению
С7 (со) = a (th) exp [ j { — a>th + Q (fA)}] X
X J exp — th)2 dt.
/A-fi
(3.15)
Произведем следующую замену переменных:
/—= H и
0" (4) 2 *У2
3 Зак. 1341
49
так что
В этом случае выражение для спектра вблизи точки th принимает
вид
*/(<>)= 2 V лехр [/ {—<о^ + 0 (fh)}] х
V 16'(/А) I
(Iе* ('*)l/«),/2ft
X J ехр р ~J dy. (ЗД6)
о
Интеграл в равенстве (3.16) есть одна из форм записи интеграла
Френеля и если верхний предел достаточно велик, то его можно
аппроксимировать выражением
jL-ехр[/-=-]. (3.17)
Подставляя (3.17) в равенство (3.16), получаем, что выражение для
спектра около точки th имеет вид
7/(ш) = 1<2я ——-— ехр[/ (—<>«*+ 6 (<»)+—П (3.18)
V I0'(**)l L ' V / 4 /J
Предполагая, что соотношение (3.17) выполняется при всех зна-
чениях th, получаем следующее выражение:
<ЗЛ9>
где обозначение cut указывает на зависимость используемой пере-
менной (частоты) от t. Вывод, который приводит к получению (3.19),
аналогичен выводу Кея и др. [1, 2], где принята точка зрения,
что переданный сигнал представляет собой выходной сигнал одного
из двух согласованных фильтров (один на передатчике и один на
приемнике, как показано на рис. 3.4, а). В комплексной форме этот
сигнал записывается так:
ОО ф
и W = ЯГ J ।и 1ехР И <ф (°) + “Ol du,
— оо
(3.20)
где Ф(со) есть фазовая функция спектра. Точка стационарной фазы
для (3.20) задается уравнением
ф'(<о)=— t.
(3.21>
50
^alaUausiffk
знание без ераниц “ *
Окончательное соотношение, эквивалентное равенству (3.19), ко-
торое может быть получено с помощью только что описанного метода
стационарной фазы, имеет вид
(3.22)
1 IУ («>) I*
2л |Ф*(со)|
Рис 3.4. Возможные схемы построения приемных и пере-
дающих устройств, использующих согласованные фильтры:
л— передающее устройство, использующее согласованный фильтр
с нелинейной ЧМ (вверху); приемное устройство, содержащее
согласованный фильтр с нелинейной ЧМ (внизу); б —активный
генератор сигнала с нелинейной ЧМ; в —возможная схема при-
емника.
Заменяя th на t в равенстве (3.18), видим, что фазовый спектр
<D(w) приближенно задается равенством
Ф (со) ~ — <0/4- 0 (О 4- -р (3.23)
Дифференцируя по со, получаем
Ф'(со)'^ — t— (со—(3.24)
k * \ dt ) da ' '
Применяя условие стационарной фазы, задаваемое равенством
(3.7), видим, что (3.24) принимает вид
Ф'(<о)^ —/.
(3.25)
51
Данное приближенное соотношение, полученное путем применения
метода стационарной фазы для анализа преобразования Фурье
временной функции, совпадает с определением точки стационарной
фазы, задаваемым равенством (3.21) для преобразования Фурье
спектральной функции. Это указывает на эквивалентность соотно-
шений, определяемых равенствами (3.19) и (3.22). Они представляют
собой набор параметрических равенств, которые могут быть ис-
пользованы для получения приближенных выражений для j (7(ю) |
(или |S((d) |) и Ф(со), если задан вид сигнала, или для нахождения
a(f) и 6(f), если задан спектр (/(со) вместе с фазовой функцией Ф(<о).
В большинстве случаев эти приближенные выражения могут быть
достаточно точными.
В обычном для радиолокации случае a(t) постоянно в течение
длительности сигнала и равенство (3.22) может быть непосредствен-
но использовано для нахождения временной зависимости задержки
согласованного фильтра, необходимой для определения вида модуля
спектра | {/(со) |. Системы согласованных фильтров на приемной и
передающей сторонах для этого случая показаны на рис. 3.4, а.
Импульсный отклик фильтра передатчика и есть искомый несжатый
модулированный по частоте сигнал1. Фильтры в передатчике и
приемнике можно взаимно поменять местами. Две возможных
функции для Ф(со), которые удовлетворяют требованиям равенства
(3.22), являются комплексно-сопряженными функциями. На пере-
датчике может быть использован и активный ЧМ генератор, как
показано на рис. 3.4, б, для того чтобы заменить один из двух
согласованных фильтров. Необходимая в этом случае функция
частотной модуляции получается из уравнения (3.19). В специальном
частном случае, когда О'(/) обладает нечетной симметрией, одна и
та же функция может быть использована и на передатчике, и в при-
емнике при условии, что применяется метод инверсии полосы ча-
стот, как это показано на схеме возможной структуры приемника
на рис. 3.4, в. Это и другие применения приемо-передающих согла-
сованных фильтров для ЧМ сигналов, позволяющих осуществлять
сжатие импульса, будут рассматриваться далее в гл. 6.
Из приведенного в гл. 1 примера ЛЧМ сигнала интуитивно
кажется очевидным, что функция частотной модуляции 0'(О и
функция групповой задержки согласованного фильтра Ф'(<о) свя-
заны обратной зависимостью. Это было’бы в случае, если бы ра-
венства (3.19) и (3.22) давали хорошее приближение для связей
между параметрами одного и того же сигнала. Следующие выкладки,
выполненные Фоулом [41, показывают, что в общем случае это за-
ключение справедливо. Рассмотрим условия стационарной фазы,
1 С практической точки зрения требования к функции, возбуждающей
фильтр передатчика, состоят в том, что это должен быть импульс, спектр
которого значительно шире полосы пропускания согласованного фильтра и
практически постоянен в пределах этой полосы.
52
NatatiausiSii
знание без араниц Ч *
определяемые в (3.7) и (3.21). Итак,
<о == 0'(/) и —/- Ф'(со). (3.26а)
Пусть
О' (/) — со (/) и Ф'(со)=-—Г (и).
Тогда условия (3.26а) перейдут в
to--to(/) Z-T(to). (3.266)
Из приведенного гыше рагенства получаем и — Т~1 (/) и, следо-
вательно,
to(/)- Т-'(/). (3.27)
Равенство (3.27) показывает, что закон изменения’мгновенной час-
тоты (о(/) и функция групповой временнбй задержки T(to) есть об-
Рис. 3.5. Соотношение между задержкой в согласо-
ванном фильтре и функцией частотной модуляции
I для сигнала с нелинейной ЧМ.
ратные функции. Это проиллюстрировано на рис. 3.5. Такое соотно-
шение может быть также выражено в виде
/(/) = ?-• (О, (3.28)
где <о (/) = 2л/ (/) и Т([)~Т (со/2л).
Следует заметить, что равенства (3.27) или (3.28) на самом деле
являются приближенными, как показывает выражение (3.24),
которое зависит от функций
и (О = a (0 ехр (/б (01
и
(/(и) = | U (to) | ехр [/Ф (со)],
связанных преобразованием Фурье. Так как анализ по методу
стационарной фазы приводит к приближенным соотношениям,
53
связывающим a(t), | (/(to) ), Ф(со) и 0(0, то и преобразование Фурье
также является приближенным и задается соотношениями
a (f)exp [/0(01 — — f IU (“) | ехр [/ {Ф (со) + со/}] dco, (3.29а)
2л J
— оо
оо
147(со) | ехр [/Ф (со)] с- J а (0 ехр [—j {at—0 (0)1 dt. (3.296)
— 00
Для большинства ЧМ сигналов качество приближения улучшается
с ростом произведения длительности сигнала на полосу частот.
Равенство (3.28) удовлетворяется с возрастающей точностью для
сигналов с большим произведением длительности на полосу частот.
Вопросы о том, насколько велико должно быть произведение
длительности на полосу частот, и как оно должно зависеть от типа
сигнала, обсуждаются в разд. 3.4.
При некоторых радиолокационных применениях может ока-
заться возможным модулировать передаваемый сигнал по ампли-
туде. В системах с высокой мощностью это должно привести к поте-
рям в передаваемой энергии. Если, однако, способность обнаруже-
ния не является наиболее важной характеристикой, то такая моди-
фикация может оказаться полезным методом, позволяющим осу-
ществлять сжатие импульса с малым уровнем боковых лепестков
[5]. Кроме того, существуют и другие области радиоэлектроники,
в которых возможность одновременного использования амплитуд-
ной и частотной модуляции передаваемого сигнала является по-
лезной. Метод построения сложных сигналов, в которых огибаю-
щая импульса a(t) и модуль спектра) U(a) |определены независимо,
подробно разработан Фоулом [4]. Ниже мы в общих чертах рас-
смотрим этот метод.
Из условия стационарности фазы (3.17) с помощью дифферен-
цирования получаем
|ф"(<о)|= ——, (3.30)
da
и отсюда путем подстановки в равенство (3.22)
ai(t)dt = — 1(со) |2 dco. (3.31)
2л
Используя соотношение между a(t) и U(со), определяемое в (3.5)
(теорема Парсеваля), получаем следующие интегральные выра-
жения х:
t 1
| a2(x)dT=-— f |47(Q)|*dQ (3.32)
J 2Л J
1 Пределы интегрирования в (3.32) и (3.33) не являются независимыми.
Как следует из приведенных выше рассуждений, t = /(со) или со = <о(/).
54
^alaHausA
знаниебезграниц Ч4*
ИЛИ
o2(T)dT= — £ |U (Q)I8dQ.
2л J
(3.33)
co
Равенства (3.32) и (3.33), каждое в отдельности, определяют воз-
можное решение для фазовых функций 0(/) и Ф(со). Как будет по-
казано, два решения для каждой фазовой функции являются ком-
плексно-сопряженными функциями. Фоул сделал следующие опре-
деления:
а2 (т) dx — P (/),
1 Г
j | U (Q) |2 dQ = Q (to),
(3.34)
(3.35)
<0
|4/(Q)|2dfi = 2£'—Q(co),
(3.36)
где P(—oo) = Q(—oo) = 0 и Q(oo) = 2£—энергия, соответствую-
щая комплексному сигналу [см. равенство (3.5)]. Из (3.32) по-
лучаем
/ = Р-'[(?(<•>)]. (3.37)
Применение равенства (3.21) дает в результате
Ф'(со)= - Р-« [Q(co)], (3.38)
и
Фг ((0) = — $ р-1 [Q (со)] Сх. (3.39)
Используя уравнение (3.33), получаем
ф'(ю)= —Р-* [2Е—Q(<o)] (3.40)
и
ф2 (ю) = - $ Р-1 [2P-Q (со)] + С2, (3.41)
где С\ и С2 — постоянные интегрирования.
Аналогичные соотношения для 6(/) могут быть получены с по-
мощью той же самой процедуры. В результате имеем
01(0 = f Q-1 [Р (01 dt+ С„ (3.42)
е.(0=$<г-Ч2£-Р(0)Л+С4. (3.43)
55
Решения для 6(0 и Ф(со) позволяют построить две пары прибли
женных преобразований Фурье:
| U ((d) |ехр [/Фх (о)] - {а (0 ехр [ /0х (0]}, (3,44а)
IU (<о) | ехр ]/Ф2 (со)] - £ {а (0 ехр [/0а (0]}. (3.446)
Мы'получим’условия согласованной фильтрации, выраженные через
огибающую ^автокорреляционной функции выходного сигнала сог-
ласованного фильтра, которая задается соотношением
оо
g(0=2F f l^((o)|aexp{—j(D0d(o.
— оо
(3.45)
Точность приближенных преобразований Фурье, задаваемых ра-
венствами (3.44а) и'(3.446), зависит от типа сигнала и величины
произведения длительности на полосу сигнала. В следующем раз-
деле приводятся примеры применений результатов, полученных
с помощью метода стационарной фазы для анализа и построения
сложных сигналов.
3.4. Приложение теории построения сигналов
к сложным ЧМ сигналам
Приведенные в этом разделе примеры построения сигналов взяты
из работ Фоула [4], Kenvil, 2] и Кука [61. Они иллюстрируют
применение различных соотношений, полученных с помощью ме-
тода стационарной фазы для анализа и построения некоторых
основных типов сложных сигналов.
Пример! [4 ]
Огибающая сигнала и модуль комплексного спектра определяются
гауссовыми функциями, которые задаются соотношениями:
... 1 Г ( 21 V
0(‘,= 7т ехр1'Чт)
|t/(f)l=75Fexp
(3.46)
(3.47)
Длительность и ширина спектра для этих функций определяются как интер-
вал между точками е-1 для Т или Д/ соответственно. Произведение длитель-
ности на полосу частот для этого сигнала равно TAf1. Огибающая импульса
и модуль спектра показаны иа рис. 3.6 как огибающая выходного сигнала * 56
1 Эти определения длительности и полосы частот отличаются от исполь-
зованных Фоулом. Обозначения, используемые -в примерах этой главы,
согласуются со стандартными обозначениями, принятыми в других главах.
56
'NdtaHausIU!
знание без ераниц Ч w
согласованного фильтра. Этот сигнал представляет собой преобразование
Фурье функции (3.47) и имеет вид
[л8 ДР Р 1
• (3>48)
о J
Используя уравнение (3.22), получаем
импульса
Рис. 3.6. Характеристики сигнала с гауссовой
огибающей и гауссовым спектром при его сжа-
тии в согласованном фильтре.
Пусть 2у^2 '(т/Т)«=у и 2V2 (О/2лД/) = г, тогда равенство. (3.49) при-
мет вид
2УТ(//Т) 2V2(f/bf)
J ехр[ —ya]dy^ J ехр( —г8]</г. (З.БО)
Прира внивая пределы в (3.50), находим
J________________________________/ со
Т “ Д/ “ До ’
где со "«2л/, Применение соотношения (3.26а) дает
• > Т<&
— ф (<o) = Pj (<о) = ——
' Ди

1 Т
Ф ((!)) = — ---- fi^+Ci.
2 дсо
(3.51)
(3.52)
(3.53)
57
Аналогично функция частотной модуляции принимает вид
= (3.54)
н
0(0=4 V(*+c” (3'85)
л» Л
Выражения (3.52) и (3.55) показывают, что согласованный фильтр имеет
линейную зависимость задержки от частоты и что применяется линейная
частотная модуляция сигнала. Амплитудный отклик согласованного фильтра,
есть, конечно, гауссова функция, согласованная с (3.47). Фоул сравнил эти
результаты с данными, полученными при использовании точного преобразо-
вания функции Фурье:
и№ = /ЬГеХР[~~(т’)2]еХР *’+Сз)] ' (3'56)
Сравнение показало, что для ТД/j = 40/л (один из вариантов определения
ГД/) модуль спектра и фаза, задаваемые соотношениями (3.47) и (3.53),
отличаются на доли процента от значений, полученных по точному преобра-
зованию функции по Фурье (3.56). Таким образом для Т&1, превышающих
примерно 10, уравнения (3.46), (3.47), (3.53) и (3.55) могут быть использованы
для определения пары преобразований Фурье с большой точностью. Как
правило, для сигналов с большими значениями произведения длительности
на полосу при определении огибающей импульса и модуля спектра получен-
ная функция 0'(/) описывает линейный закон ЧМ, а функция групповой за-
держки Р' ((о)’= — Ф'(о>) определяет линейную зависимость задержки от
частоты.
Пример 2(1, 2, 4]
В предыдущем примере a(t) и |С/(со)| были гладкими непрерывными функ-
циями. В данном примере о(0 будет прямоугольной функцией, т. е. не глад-
кой, a |t/(<o)| будет гладкой непрерывной функцией. Они задаются равенст-
вами
(3.57)
при других t,
V2 1
IU (<о)1 = —=^ г — -
/Дш/2 /1 +(2<о/Д<о)а
(3.58)
Эти функции показаны на рис. 3.7 Автокорреляционная функция выход-
ного сигнала согласованного фильтра, определяемая с помощью преобразо-
вания Фурье (3.58), равна
g(0 = exp[—лД/ |f Ц.
Применение равенства (3.33) дает
t оо
If, If 1 dco
— । ат= — I----------------------------.
Т J nJ 1 + (2<о/До)8 (Дсо/2)
0 со
(3.59)
(3.60)
58
ftalattauslisk
знание без границ “ *
Интегрируя (3.60), получаем уравнение
л 2со \
—— arctg—— ,
2 Дсо /
t______£
Г ~~ л
(3.61)
из которого можно найти
— Ф'1 (“)=₽; (co)=-^-fl —
\
2 , 2(0
— arctg —
л i
Дсо 1 ’
(3.62)
Огибающая передаваемого сигнала
s)
Ли)
U)ff
I
Спектр
сжатого импульса
в)
Рис. 3.7.Характеристики сигнала при его обработке в согласованном фильт-
ре с обратно тангенциальным законом изменения групповой задержки.
Использование соотношения (3.32) приводит к другой формуле:
t <0
1 Г 1 Г 1 dco
— I dx— — I------------------------------------
Т J, л J 1 + (2(о/Дсо)» (Дсо/2)
o.J -ж
и
, . Т ( 2 2ш \
-Ф2(со) =р2(со) = — arctg- —4-1
(3.63)
(3.64)
Функции групповой задержки —Ф| (со) и —Ф2(со) показаны на рис. 3,8.
При рассмотрении его и приведенных равенств можно заметить, что в ре-
Рис. 3.8. Два возможных реше-
ния для функции групповой за-
держки в согласованном фильтре
с обратно тангенциальным зако-
ном изменения задержки.
зультате мы получили функции Фг (со) и Ф2 (со), которые являются комплекс-
но-сопряженными, где
dw -|- Ci
(3.65)
59
Используя полученные ранее соотношения, функцию ЧМ можно определить
в виде
. Дсо
61 (0 = — arctg
л nt
~2~~Т
(3.66)
и
Дсо Г ( п nt \
6i(0=—I arctg —Jd/4-Сз. (3.67)
Кей и др. [2] с помощью численных методов нашли 6'(0 и а(0 для модуля
спектра и фазы, задаваемых равенствами (3.58) и (3.65) для значений ГД/,
равных 10/л и 100/л. Они показаны на рис. 3.9. Основываясь на этих данных,
можно сделать вывод, что для построения с хорошей точностью пары преоб-
разований Фурье для сигналов, существенные характеристики которых в
основном совпадают с приведенными в данном примере, необходимые значения
произведения ТД/должны быть больше 20 или 30. Этим требованиям удовлет-
воряет целый класс сложных сигналов, для которых a(t) либо Ц/(со)| имеют
разрывы, в то время как другая функция — гладкая и непрерывная.
Если необходимо, чтобы и a(t) и |(/(со)| имели вид прямоугольных
функций, то, как. указывалось при обсуждении ЛЧМ сигнала с прямоуголь-
ной огибающей в гл. 1, |1/(со)| не может быть хорошо аппроксимировано
прямоугольным распределением, если только не выполняется неравенство
7Д/ > 100. Это можно видеть на примере спектра, показанного на рис. 6.6.
Такое поведение вытекает из ограничения, что огибающая й спектр одновре-
менно не могут быть усеченными. Однако для достаточно больших ТД/
можно с приемлемой точностью считать, что огибающая импульса и спектр
одновременно являются усеченными. Отметим, что если желательно иметь
прямоугольный спектр для того, чтобы на выходе согласованного фильтра
получить функцию sin х/х,- то хорошая аппроксимация для этого случая
получается при ЛЧМ сигнале со значениями ТД^ > 20. Следовательно,
для получения такого сигнала не нужно добиваться очень точной аппрок-
симации прямоугольного спектра.
ПримерЗ [6]
Выходной сигнал согласованного фильтра в обоих предыдущих примерах
является гладкой непрерывной функцией, гауссовой или экспоненциаль-
ной соответственно. В случае гауссового выходного сжатого сигнала ампли-
туда сигнала на краях спадает только на —26 дб при t = ±1,8/Д£. Для
получения экспоненциального сжатого импульса, который формируется
при нелинейной ЧМ в примере 2, необходимо управлять функцией группо-
вой задержки согласованного фильтра в полосе, которая в несколько раз
превышает основную полосу Д/. Значения на краях сжатого импульса для
этого сигнала также спадают довольно медленно по отношению к величине,
обратной ширине полосы, необходимой для построения фильтра.
Во многих случаях бывает желательно, чтобы сжатый импульс в зави-
симости от времени быстро спадал до определенного уровня и затем оставал-
ся ниже его. Большинство сигналов, которые попадают в эту категорию,
имеют лепестковую структуру, аналогичную боковым лепесткам антенны
(т. е. здесь не происходит монотонного убывания амплитуды сигнала на его
краях). В общем случае приходится идти на компромисс между скоростью, с
которой спадает^амплитуда огибающей сжатого импульса, и допустимым мак-
симальным уровнем боковых лепестков на временной оси. При заданной
допустимой ширине полосы, в которой должна быть сконцентрирована груп-
повая задержка согласованного фильтра, наиболее эффективное использова-
ние этой полосы .при построении сложного ЧМ сигнала обычно может быть
достигнуто при сигналах описанного, выше типа. Сигналы одного из таких
60
^aiattausj^i
знание без границ Ч «Ь
. 3.9. Вычисленные функции огибающей растянутого импульса и частотной модуляции для со-
гласованного фильтра с обратно тангенциальным законом изменения задержки:
а— огибающие импульсов; б —функции частотной модуляции.
классов имеют прямоугольную огибающую и модуль спектра, задаваемый
соотношениями
|t/n (<о) 1а= лп cos" , I <о| < •
Дсо л 2
(3.68)
Используя равенство (3.22) и имея в виду, что длительность огибающей рав-
на Т, читатель может проверить путем прямого интегрирования, что зависи-
мость групповой задержки от частоты Тп(©) = ₽„(©) имеет следующий
вид (Лп получена путем оценки Тп(а>) в одной из конечных точек):
л—1,
л = 2,
Л (<*>)=4
л»
Л©
sin—— ,
ДсО}
2 л©
sin-----
Д©а
(3.69)
(3.70)
г. Т Г л© ( „ лю
п = 3, Т8(©) =— sin——< cosa------+ 2
4 L Д©з ( Д©3
(3.71)
1 2л©
— sin -— +
2л Д©4
2 л© л©
-f-— cos3---- sin--
Зл Д©4 Д©4
(3.72)
Это семейство функций групповой задержки изображено на рис. 3.10. По от-
ношению к сигналу sin х/х, прямоугольный спектр которого заполняет
интервал Д©, ширина сжатого импульса (на уровне —3 дб) для каждого
спектра, определяемого равенством (3,68), больше ширины импульса sin х/х
в 1,34 раза при п = 1, в 1,62 раза при п = 2, в 1,87 раза при п = 3 и в 2,09
раза при п = 4. Можно использовать денормализующий коэффициент для
Д© так, чтобы выходные сигналы согласованного фильтра имели равную
ширину импульса на уровне —3 дб.
Это показано на рис. 3.11, где денормализация выполнена по отноше-
нию к |1/(©))а для п = 1. Кроме того, здесь же приводятся уровни боковых
лепестков для сжатого импульса, соответствующего каждому такому спек-
тральному распределению. Отсюда можно видеть, что для достижения мало-
го уровня боковых лепестков на временной оси при приблизительно одинако-
вых значениях ширины спектра необходимо управлять краевой частью спект-
ра выходного сигнала на значительном интервале вне . основной области
сосредоточения спектральной энергии. Это в свою очередь означает, что не-
обходимо управлять функцией Tn(w) в том же самом интервале частот.
Для того чтобы уменьшить этот интервал и все еще получать сжатый
в согласованном фильтре импульс с низкими боковыми лепестками на времен-
ной оси, можно использовать (3.22), чтобы иметь такое Т(©), которое форми-
рует спектр вида косинус в квадрате с пьедесталом, определяемым соотноше-
нием
\Uk (<о) |а = ЛА
Д©А
(3.73)
Эта функция аппроксимирует спектр, взвешенный функцией Тейлора (см.
гл. 7) для k = 0,088. Групповая задержка, полученная из (3,73), равна
(© 1 — k © \
-— + —-----sin 2л —— ). (3.74)
Д©А 2л Д©А /
62
flatailausmk
знание Вез границ Ч *
Рис. 3.10. Функции групповой задержки для спектра мощности в виде cos".
0,4
1,0
0,8
0,6
1
2
3
4
О 0,2 0,4 0,6 4)/Дш
Рис. 3.11. Спектры мощности сигналов вида cos".
Тп (to) денормализовано таким образом, чтобы у всех импульсов была
длительность.
&4Jn
Ди><
1,00
1,21
1,40
1,57
уробень
бокобых
лепестков
-2305
-3205
4005
4755
равная
63
Тонкая структура функции, определяемой уравнением (3.74), вблизи Дсо/2
для аппроксимации Тейлора показана отдельно на вынесенном графике
рис. 3.10. Для k = 0,088 и Дсо^ = l.lAwj получается такая же ширина
импульса, как и для косинусквадратного спектра при пиковом уровне боко-
вых лепестков —40 дб. Аналитические выражения функции 6'(/) для клас-
са функций групповой задержки, использованных в этом примере, найти ока-
зывается сложно. Наиболее простой метод оценки функции Q'(t) в подоб-
ных случаях состоит в применении графических методов. С этой целью оси
Рис. 3.12. Растянутый импульс на выходе фильтров
с нелинейной и линейной задержкой.
Вверху: возбуждающий импульс и сигнал на выходе фильтра
с нелинейной задержкой; внизу: возбуждающий импульс
и сигнал на выходе фильтра с линейной задержкой.
на рис. 3.10 надо повернуть так, чтобы в качестве независимой переменной
вместо времени можно было использовать задержку и взаимно поменять
местами положительные и отрицательные значения частоты.
На рис. 3.12 показан импульсный отклик (т. е. несжатый импульс)
согласованного фильтра с нелинейным изменением задержки и со спектром
Ц/(ю)|, который приближенно описывается косинус-квадратным законом.
Форма несжатого импульса для согласованного фильтра с линейной групповой
задержкой при том же самом входном импульсе значительно больше отлича-
ется от прямоугольной, а сжатый импульс имеет более высокий уровень
боковых лепестков. Превышение средней амплитуды в каждом конце несжа-
того импульса при нелинейной ЧМ получается вследствие отклонения от
идеального закона задержки согласованного фильтра и амплитудного откли-
ка вблизи границ полосы фильтра.
64
ftalafiausi^
Приме p 4
В примерах 1—3 рассматривались случаи, когда огибающая a(t) имеет
прямоугольную форму, а 6'(/) есть нелинейная функция ЧМ, или когда a(t) —
амплитудно-модулированная функция, а 0'(О — линейная функция ЧМ.
Примером сигнала, для которого одновременно огибающая имеет модуляцию
по амплитуде и используется нелинейная ЧМ, может служить сигнал вида
/л nt \1/2
а(/) = cOS •
» • у о'р 71 /
Использование соотношения (3.32) дает
t
л Г jvr 2
— I cos — dx = ~
2T J T Af
-T/2
(3.75>
(3.76}
(3.77>
f cosa -^7 df,
J ДГ
-Af/2
Пусть y — nxIT и z = ntlbf, тогда уравнение (3.77) принимает вид
nt/т nf/bf
1 Г . 2 f
— I cos ydy = — I cos’ zdz.
2 J nJ
—n/2 -л/2
Выполняя интегрирование, получаем
1 Г nt ] f 1 2л1 1
s,n~ + l =“Г7Ч-~ sin—— J-—-
2 [ T J Д/ 2л A/ 2
и
T Г f 1 2лМ
t=* —arc sin - — J-—- sin —— .
л |_Af 2л Af J
(3.78>
(3.79}
(3.80}
Соотношение Ф'(со) = t позволяет найти функцию групповой задерж-
ки, показанную на рис. 3.13. Как и в предыдущем примере, 9'(0 проще -
всего определяется графическим методом. Кривизна этой функции частот-
ной модуляции лежит между кривизной ЛЧМ и нелинейной ЧМ, необходи-
мой для получения косинус-квадратного спектра мощности при прямоуголь-
ной огибающей импульса.
Побудительным мотивом исследования сигналов с нелинейной ЧМ яв-
ляется желание сформировать спектр сигнала так, чтобы улучшить форму
сжатого импульса на выходе согласованного фильтра (автокорреляционную
функцию) без ухудшения каких-либо энергетических характеристик системы,
которыми она обладает при передаче импульсов с прямоугольной огибающей.
Как только удается избежать ухудшения этих характеристик, то уменьше-
ние боковых лепестков по оси времени (или дальности) для автокорреляцион-
ной функции согласованного фильтра при таком подходе достигается за счет
увеличения уровня боковых лепестков выходного сигнала при наличии час-
тотного сдвига у принимаемого входного сигнала (случай движущегося отра-
жателя). Вследствие этого применение сложных сигналов с нелинейной
ЧМ обычно ограничивается случаями, в которых ожидаемый разброс скоро-
стей принимаемых сигналов относительно мал. Такой пример рассмотрен в
гл. 7.
65
Важный итог этого раздела, заключается в том, что, задавшись формой
ЧМ сигнала произвольного вида u(t) на входе согласованного фильтра,
с помощью принципа стационарной фазы можно получить достаточно хоро-
шие приближенные выражения для следующих параметров:
1. Ц/(<в) | , амплитудный
спектр сигнала и амплитуд-
ный отклик согласованного
фильтра.
2. |Ф(ы)|, фазовый спектр
и функция, сопряженная фазо-
вому отклику согласованного
фильтра.
Задержка для сигналов
Рис. 3.13. Функция групповрй
задержки для модулированно-
го по амплитуде сигнала с не-
линейной ЧМ, который рас- •
смотрен в примере 4.
3. — Ф'(ш), закон изменения групповой задержки согласованного
фильтра, как результат определения Ф(со).
Кроме того, могут быть получены и другие функции, связанные с сиг-
налом на выходе согласованного фильтра. Все это кратко описано в следую-
щем разделе.
3.5. Функция неопределенности согласованного фильтра
к
Амплитудный спектр сигнала на выходе согласованного фильтра
относится к числу функций, которые можно легко получить при
помощи метода стационарной фазы. Зная комплексный амплитуд-
ный спектр | £/(©) |, можно вычислить автокорреляционную функцию
согласованного фильтра:
ОО
g (0 = 2^- $ Iи И I2 ехР 1М1а<й-
— оо
(3.81)
Используя соотношения, связывающие импульсный отклик
с другими характеристиками сигнала, которые приведены в гл. 1,
получаем другую форму записи для сигнала на выходе согласован-
ного фильтра:
ОО
g(t)= j «(t)u(t—t)dx.
— оо
(3.82)
66
Ч\а1аНаи$Ж
знание Вез границ * ш
Эти два равенства могут быть записаны в более общей форме»
так что
00
g (t = 2Г J U (° + U* eXP d(0‘ <3’83>
— 00
00
g (*> ®d) = J w (t) u* (t—t) exp [j(od T]dT = % (—t, <od). (3.84)
oo
Функция g(t, (od) есть отклик согласованного фильтра на входной
сигнал, несущая частота которого имеет сдвиг. Эта более общая
функция, характеризующая выходной сигнал согласованного
фильтра, полезна для определения отклика фильтра (для узкополос-
ного случая) при приеме сигналов, отраженных от движущихся
объектов. Получающаяся при этом функция (отклик согласованного
фильтра) обозначается через | % | и носит название «радиолокацион-
ная функция неопределенности» [7, 8]. Функция неопределенности
радиолокационного сигнала, полученная из (3.83) или (3.84), обоз-
начается как | %(/, (dJ |2 или | %(/, <р) |2, где <р = (od/2n.
При формировании и анализе сигналов в системах с согласо-
ванными фильтрами введенная выше функция неопределенности
служит критерием, который может быть использован для определе-
ния пригодности того или иного сигнала либо для однократного
(за один импульс) измерения скорости движущегося объекта и
дальности до него, либо для разрешения по скорости и дальности
нескольких движущихся объектов. С этой точки зрения она имеет
большое значение при создании радиолокационных систем, приз-
ванных выполнять те или иные тактические задачи.
Функцию неопределенности часто представляют в трехмерной
форме. Функции | % | или | х |2 могут быть изображены как поверх-
ности над координатной плоскостью, по осям которой отложены
время или дальность и частотный сдвиг или скорость. На рис. 3.14
показана такая функция и некоторые типичные сечения ее поверх-
ности. Пик функции неопределенности всегда имеет координаты
t = 0 и <od = 0. Сечения функции неопределённости, параллельные
оси времени или дальности, представляют собой квадрат амплитуды
выходного сигнала согласованного фильтра при различных значе-
ниях сдвига частоты cod. Сечения, параллельные оси частот, пред-
ставляют собой изменение этой выходной величины в фиксированные
моменты времени; они определяют одну из основных характерис-
тик сигнала и(1) — пригодность его для измерения скорости.
Если функция | х I2 имеет резко выраженный пик в начале коорди-
нат, то говорят, что u(f) обладает хорошей разрешающей способ-
ностью по дальности и по скорости одновременно. Если пик функ-
ции неопределенности широкий и захватывает значительную пло-
щадь в частотно-временной плоскости, то сигнал не обладает хорошей
разрешающей способностью; при этом дальность и скорость невоз-
67
можно определить независимо друг о.т друга при изучении единст-
венного отраженного сигнала на выходе согласованного фильтра.
Все эти вопросы теории сигналов будут подробно исследованы
в главах, посвященных общим вопросам теории построения сигна-
лов. Здесь же мы будем рассматривать функцию неопределенности
как функцию, характеризующую ухудшение свойств сигналов при
сдвиге их несущих частот относительно частоты настройки согласо-
ванного фильтра. Основное ограничение, накладываемое на функ-
Рис. 3.14. Сечения функции неопределенности.
цию неопределенности, состоит в том, что объем, охватываемый ее
поверхностью, постоянен для всех входных сигналов с равными
энергиями. Эта функция играет важную роль при рассмотрении'
общих проблем построения сигналов для систем, использующих
согласованные фильтры. Особое значение имеет функция неопреде-
ленности для лучшего понимания преимуществ и недостатков тех
или иных подходов к построению специфических радиолокационных
сигналов. Следующая глава посвящена более подробному обсуж-
дению этой1 важной функции и ее свойств.
ЛИТЕРАТУРА
1. Е. L. К е у, Е. N. F o’w 1 е, and R. D. Н a g g а г t у. A method of pulse
compression employing nonlinear frequency modulation, Lincoln Lab.,
M. I. T., Lexington, Massachusetts, Tech. Rept. 207 (September, 1959).
2. E. L. Key, E. N. F о w 1 e, and R. D. H a g g a r t y. A method of de-
signing signals of large time-bandwidth product, IRE Intern. Conv. Re-
cord Pt. 4, 146—155 (1961).
3. E. N. F о w 1 e. A general method for controlling the time and frequency
envelopes of FM signals, Lincoln Lab., M. I. T., Lexington, Massachu-
setts, Group Rept. 41G-0008 (June, 1961).
68
WaiaHausiVii
знание без границ Ч *
*4. Е. N. F о w 1 е. The design of FM pulse-compression signals, IEEE Trans.
IT-10, 61—67 (1964).
5. E. N. Fowle. Private communication.
• 6. С. E. С о о k. A. class of nonlinear FM pulse-compression signals, Proc.
IEEE (Correspond.) 52, 1369—1371 (1964).
• 7. P. M. Woodward. Probability and Information Theory .with Appli-
cations to Radar, Pergamon Press, Oxford, 1953.
* 8. W. M. S i e b e r t. A radar detection philosophy, IRE Trans. IT-2, 204—
219 (1956).
♦ •
4. Ф о у л. «Зарубежная радиоэлектроника», 1966, № 6, стр. 49.
7. Вудворд. Теория вероятности и теория информации с применениями
в радиолокации, изд-во «Советское радио», 1955.
8. Зиберт. «Вопросы радиолокационной техники». 1957, стр. 41.
ГЛАВА 4
ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
РАДИОЛОКАЦИОННОГО СИГНАЛА
4.1. Введение
В гл. 2 было проведено общее рассмотрение проблемы оптималь-
ной обработки радиолокационных сигналов. Было показано, что»
если помеха представляет собой белый гауссов шум, то оптималь-
ный приемник может быть найден в классе линейных фильтров,,
которые характеризуются двумя соотношениями:
Н (со) = kS* (<о),
н н (4.1)
где 7/(<х>) и h(f) — передаточная функция и импульсный отклик
оптимального фильтра, a <S*(®) и s( — f) — сопряженный спектр и
зеркальное отображение (или обращенный во времени сигнал),
соответствующие сигналу s(t). Эти равенства представляют собой
условия согласованной фильтрации. Отсюда очевидно, что до реа-
лизации оптимальной системы обнаружения в первую очередь
должна быть определена конкретная форма сигнала, предназна-
чаемого для передачи. Наличие этого требования приводит к тому,
что перед разработчиком радиолокационных систем встает важная
задача найти предварительно для каждого случая применения сис-
тем соответствующий вид сигнала. Для разработчика, решающего
задачу повышения разрешения и точности, не менее важно, чтобы
этот сигнал после выполнения согласованной фильтрации содержал
наименьшую возможную неопределенность.
В этой главе более подробно рассматривается двумерная функ-
ция распределения амплитуд сигнала в зависимости от временной
задержки т и частотного сдвига <р, которая была кратко определена
в гл. 3. Такая функция в современной радиолокации является ос-
новой для систематических исследований и поиска наилучших сиг-
налов в тех или иных конкретных случаях использования РЛС..
70
flalaHausllSl
знание без границ W *•
Эту функцию общепринято называть функцией неопределенности.
Функция неопределенности записывается в виде %(т, <р) %*(т, <р),
где [11
оо
X (т, ф) = J и (/) u* (t + т) ехр [—/2жр /] dt. (4.2а)
— 00
В равенстве (4.2а) для записи сигнала s(/) использовано комплекс-
ное представление u(t), которое будет более подробно обсуждаться
в разд. 4.2. Хотя в этой главе в качестве параметров рассмотрены
только временная задержка и частотный сдвиг, принцип неопре-
деленности может быть расширен таким образом, что он будет вклю-
чать более двух параметров или различные пары параметров [2].
С помощью теоремы Парсеваля1 можно показать, что в дополнение
к форме, определяемой уравнением (4.2а), функция %(т, ф) выра-
жается через U(f), являющейся преобразованием Фурье u(t), в виде
оо
Х(Ьф) = f ^*(/)i/(/ + <p)exp[—/2л/тИ/. (4.26)
— оо
В настоящей книге мы будем называть %(т, <р) комплексной
частотно-временной функцией отклика или просто функцией откли-
ка. Причины для выбора такого названия будут становиться яснее
по мере изучения материала этой главы. Функция отклика была
введена Виллем [3], хотя на ее значение для радиолокации указы-
вал еще Вудворд 111. Большой вклад в изучение этой функции
внесли Зиберт [41 и Вилкокс [51, которые описали большинство
из ее фундаментальных свойств и рассмотрели соответствующие
теоремы. Кроме того, функции х(т, Ф) и | %(т, ф) |2 изучались и дру-
гими исследователями [6—101. Некоторые из этих работ посвящены
рассмотрению общих свойств %(т, ф), в то время как в других ана-
лизируются свойства х(т« ф) Для конкретных сигналов2.
Целью настоящей главы является фундаментальное изучение
функции неопределенности радиолокационного сигнала. Комплекс-
ное представление сигнала и допплеровская аппроксимация обсу-
ждаются в разд. 4.2 и 4.3. Далее в разд. 4.4 дается общее определе-
ние функции неопределенности и рассматриваются две точки зре-
ния, которые приводят к выводу функции неопределенности.
В разд. 4.5—4.11 приводятся важные свойства х(т, ф) и | х(т, ф) |2
1 Теорема Парсеваля имеет вид
р(0 и* (t) dt=§ V (f)U* (f) df.
Эта важная теорема еще будет использована в данной главе.
2 Клаудер [10] обнаружил аналогию функции неопределенности с ха-
рактеристической функцией распределения Винера, используемой в кван-
товой механике.
71
и связанные с ними теоремы. И, наконец, в разд. 4.12 и 4.13 об-
суждаются свойства функций неопределенности сигналов и при-
менение принципа стационарной фазы для анализа функций неоп-
ределенности.
4.2. Комплексное представление сигнала
Класс радиолокационных сигналов состоит из всех действи-
тельных сигналов, которые могут быть представлены в виде
s (/) = a (t) cos [2л/01 + 0 (/)!,
(4.3)
где огибающая a(f) и функция фазовой модуляции 0(0 являются
медленно изменяющимися функциями времени по сравнению
с cos [2л/0Л. Эти сигналы обладают тем общим свойством, что их
преобразование Фурье £(/) сконцентрировано главным образом
в окрестности несущей частоты /0. Более того, поскольку они
являются действительными функциями времени, то можно показать,
что
S(/) = S*(—/)-
(4.4)
Для теоретического исследования преобразований, включающих
только линейные операции над’ s(f) или над сигналом вида
Л(т—Z)s(f) (взвешенная функция времени), удобно представлять $(/)
в виде
$(0 = Ие{ф(/)},
(4.5)
где ф(/) — некоторая комплексная функция, действительная часть
которой, выделяемая с помощью оператора Re { ), равна $(/).
При такой записи сигнала вычисления в общем случае содержат
меньшее число операций, если s(t) заменить на ф(0 и использовать
оператор выделения действительной части после выполнения всех
линейных операций над ф(/). В принципе это значительно более
простая процедура, но, к сожалению, практически трудно, если
не невозможно, точно определить функцию ф(/), соответствующую
определенному виду сигнала.
Общий вид ф(/) часто выражается соотношением
Ф (0 = a (t) ехр [/ {2л/01 + 0 (/)}].
(4-6)
72
fttdaHaustti!.
знание Вез границ ' *
Однако если только s(0 не является «узкополосным сигналом»1,
форма, задаваемая равенством (4.6), так же неудобна для исполь-
зования, как и s(i). Правильная форма записи ф(0 для более
удобного анализа линейных систем задается равенством
<p(o=sw+/'v
я
t — т
(4.7)
Эта форма приписывается Габору [11]. Мы видим, что действитель-
ная часть, как и требуется, представляет собой s(f), в то время как
мнимая часть равна
s(t)
t — т
dr,
(4.8)
где s(0—гильбертовское преобразование s(f). Мнимую часть
ф(/)» заданной соотношением (4.7), можно сравнить с мнимой частью
(4.6), которая определяется просто как
Im {ф (0} = a (0 sin [2nf01 + 0 (/)],
(4.9)
где Im{ ) обозначает мнимую часть ф(^). В общем случае (4.6) и
(4.7) не будут равны.
Преимущества, которые мы получаем, используя комплексное
представление Габора, можно проиллюстрировать на примере вы-
числения энергии, содержащейся в s(t). Энергия сигнала s(t) опре-
деляется в виде
оо
Е = J s*(t)dt.
— оо
(4.Ю)
1 Узкополосный сигнал по определению есть сигнал, обладающий свой-
ствами:
S+(f) = O, 0>f,
S_(D = 0, 0<Д
где
s+(f)= f
—оо
+°O *
S_(f)= f exp [—j2jift]dt;
I X
—co
73
Читатель может сам убедиться в трудности вычисления Е из этого
равенства путем подстановки выражения для сигнала s(t) (4.3)
в (4.10). В общем случае при вычислениях придется учитывать
слагаемые разностной и суммарной частот. Можно легко показать,
что энергия, определяемая с помощью комплексного представления,
запишется как
J WW'l>(0+'l>,W'K0)d<
(4.11)
— оо
Использование для расчетов этого выражения может быть таким
же трудным, как и (4.10). Однако, если подставить в негоф(0=
— s(0 + /s (t), то соотношение (4.11) сведется к
(4.12)
— оо
Оператор Re { ) в равенстве (4.12) опущен, так как величина Е
всегда действительна. Очевидно, что это выражение более удобно,
чем (4.11). Оно сводится к этой простой форме, так как
ф (/) ф (/) dt — 0,
(4.13)
где ф (0 = s (/) + js (/). Этот результат также означает, что
оо оо
j s2(0^ = j s2(f)dt
— OO — 00
(4.14)
Г Г s(оS(т)
J J t—x
— оо
dt dx = O.
(4.15)
Для доказательства (4.13) применим- теорему Парсеваля и по-
лучим
у 1|>(оч>(о<«= У
(4.16>
где V (/)—преобразование Фурье, соответствующее ф(/). Правая
часть равенства очевидно исчезает, если
(4.17>
2
и
^(/)=о>
74.
^alaHauswk
знание без границ Ч*
Доказательство завершается записью следующей пары преобразо-
вания Фурье:
s(/)+/"s(O=*-'F(f)={2'So(_Z)’ (4.18)
В общем случае для других линейных операций над s(t), таких,
как интеграл свертки, можно показать, что
ос оо
J s<t) h (t—т) di: = Re J [ф (т) фА (т, f) + Ф (т) ф! (т, /)] du ,
— OO ( — co
(4.19)
где ф(т) и фЛ(т)— комплексное представление s(t) и h(—т)
соответственно. Когда ф(т) и фА(т) суть габоровские комплекс-
ные представления, то, преобразуя равенство (4.19) аналогич-
но (4.12), получаем
ОО
f s(t)/i(/—T)dx = -^-Re
С/ &
— ОО
оо
J Ф СО Фл (ь О
— оо
(4.20)
Отсюда видно, что если h(t—t) = s(t-}-/), то равенство (4.20)
описывает автокорреляционную функцию s(t).
В предварительных замечаниях этого раздела мы упоминали
о трудностях определения габоровского сигнала; они возникают
вследствие того, что обычно оказывается невозможным выразить
гильбертово преобразование в замкнутой форме. Поэтому практи-
чески при исследовании конкретных сигналов комплексное пред-
ставление Габора часто аппроксимируется соотношением (4.6).
Эта аппроксимация, однако, становится точным представлением,
если s(f) будет «узкополосным, сигналом». В общем случае ошибка
аппроксимации 6(f) задается как функция времени соотношением
(о
J S+ (f) ехр [j2nft] dt
— ОС
где
оо
$+(/)= j а(Оехр[-/{2л(/-и/-е(0}]Л.
— оо
(4.21)
(4.22)
Равенство (4.21) зависит, очевидно, только от характера изменения
S^(f) в области отрицательных частот; практически используемые
импульсные радиолокационные сигналы будут всегда связаны с не-
которым «заползанием» S+(f) в область отрицательных частот,
так как они всегда имеют конечную длительность. Однако если
Д/7/о мало (Д/ — полоса частот сигнала), то ошибка будет незна-
чительна. Для большинства радиолокационных сигналов данное
75
условие будет удовлетворяться, так что величиной 6(0 можно пре-
небречь. Но это не всегда справедливо для сигналов звуковых ло-
каторов, и поэтому следует более осторожно здесь использовать
комплексное представление (так же как и для некоторых радиоло-
кационных сигналов с очень большой полосой частот).
В остающейся части этой главы для записи сигналов мы будем
использовать их комплексные представления. Чтобы избежать
каких-либо недоразумений, будем предполагать, что для конкрет-
ных сигналов, которые рассматриваются в этой главе, комплексные
представления аппроксимированы при необходимости с помощью
соотношения (4.6). Однако для общего рассмотрения сигналов в этой
главе, так же как и в последующих главах, будем пользоваться
точным представлением Габора. Мы применим следующее описание
комплексного представления:
ф(0 = и(0ехр[/2л/о0, (4.23)
где
оо
2Ef0= J /|Т0|2^;
— оо
и(0 —а(0ехр[/0(0].
(4.24)
(4.25)
4.3. Допплеровская аппроксимация
Хотя в настоящее время общепринято аппроксимировать эффект
Допплера как смещение частоты, истинный допплеровский эффект
правильнее всего характеризовать умножением независимой пере-
менной — времени на некоторый масштабный множитель. Таким
образом, если перед передачей сигнал имел вид ф(0, то после отра-
жения от движущейся цели он будет иметь вид Уаф(а0. Мас-;
штабный множитель а — 1±2 v/c, где плюс (+) и минус (—) ис-
пользуются для характеристики скоростей v при приближении и
удалении цели, ас — скорость распространения радиоволн. Мно-
житель У а необходим для учета того, что энергия не изменяется
при преобразовании, вызванном допплеровским эффектом.
Для того чтобы получить предыдущий результат, постули-
руем простую, но часто используемую модель. Она состоит из то-
чечной цели, перемещающейся с постоянной скоростью и по радиаль-
ному направлению к радиолокатору (или от него). Если передан
сигнал ф(0, отраженный сигнал имеет вид ф(/ — 0). Задержка trJ
сама является функцией времени, определяемой равенством
d с ± и
(4.26)
76
ftataHaus№i
знание без ераниц Ч *
При выбранной модели дальность как функция времени имеет
вид
R(t) = R0±vt, (4.27)
где Ro—начальная дальность цели в момент / = 0. Подставляя
выражение для td и группируя члены, получаем
Ф(*— Q = ^(aZ “7^7)’ (4.28)
где 2Я0/(с±и)—номинальная задержка сигнала ф(0 на пути до
цели и обратно.
Представляющая для нас интерес пара по Фурье1 имеет вид
'=V(f/a). (4.29)
V l«l
Смысл этого соотношения заключается в том, что истинный
согласованный фильтр для принимаемого сигнала должен иметь вид
kW*(f/a) вместо обычно используемого kV* (f ± ср). Можно, однако,
показать, что, поскольку (2и/с)7,А/< 1, рассогласование, которое
при этом происходит, не имеет значения. Более того, при тех же
самых условиях анализ отклика согласованного фильтра для сигна-
лов с допплеровским сдвигом может быть также проведен и при
использовании ЛУ*(/ ± <р). Повсюду в этой книге допплеровский
сдвиг приближенно описывается с помощью простого смещения
частот, за исключением случаев, которые специально отмечены.
4.4. Общее представление функции неопределенности
Из нашего ежедневного жизненного опыта мы знаем, что раз-
личия в цвете, размерах и т. д. являются теми различиями, кото-
рые делают один предмет отличным от другого. Точно так же и для
радиолокатора возможность различения двух целей зависит от
различий в характеристиках сигналов, отраженных от этих целей.
В этом разделе обсуждаются - различия сигналов, возникающие
вследствие разного временного расположения (характеризуемого
задержкой т) и частотного сдвига (обозначаемого через <р). Мерой
различия, которая будет использоваться в настоящей работе,
явится «среднеквадратичное уклонение» между сигналами с раз-
личными параметрами [ 11. Оно задается соотношением
J |ф(0—Ф(^ + т, /+ф)|2^, (4.30)
— 00
1Две функции, связанные преобразованием Фурье, здесь и в дальней-
шем будем называть парой по Фурье или Фурье-парой. (Прим, перев.)
77
is иИТ'
Д'
г
где + т, f + <р) и ф(0 — сигналы со сдвигом и без него. Эта
мера различия имеет также и вторую возможную форму записи,
полученную при использовании теоремы Парсеваля в виде
$ + /4-T)|2df, (4.31)
— со
где ¥(/) — преобразование Фурье ф(/). Соотношения (4.30) и
(4.31) соответственно могут быть сведены к общим выражениям
функции неопределенности (4.2а) и (4.26). Однако для того чтобы
показать это, достаточно рассмотреть только одно из таких выра-
жений, поскольку без всякой потери общности теорема Парсеваля
может быть применена к полученной конечной формуле для полу-
чения другой формы записи функции неопределенности.
Рассматривая уравнение (4.30), получаем следующее выраже-
ние:
$ |Ф(0—Я’(^ + т. /+ф)|8<# = /г—2ReI § ф(0ф*(* + ь/+ф)<И •
— оо ( —оо
(4.32)
где k—постоянная, связанная с энергией сигнала соотношением
оо оо
* = J |M>(0l2<ft+ J 1Ч>0 + ь /+<Р)М. (4.33)
Так как интеграл, появляющийся в выражении (4.32), является
единственным членом, который изменяется с изменением т и ф, то
он, следовательно, и будет единственным существенным членом. Этот
интеграл существует, поскольку два сигнала ф(0 и ф(/ + т, f -h <р)
достаточно подобны; он представляет корреляционную функцию
при одновременном сдвиге по времени и частоте. В общем случае
этот член имеет тенденцию становиться малым для значений т и q>,
удаленных от начала координат, находящегося в точке т = <р = 0.
Начало координат для этого интеграла может быть расположено
так, как показано на рис. 4.1,- в любой точке прямоуголь-
ника, по осям которого отложены абсолютные значения задержки
td и частоты /0. Расположение начала координат определяется от-
носительной задержкой и частотой, которые предварительно выбра-
ны для ф(0. Плоскость т — ср можно рассматривать как частотно-
временное пространство, в котором определены представляющие
для нас интерес радиолокационные сигналы.
Одним из основных вопросов теории построения радиолока-
ционных сигналов является управление поведением этой двумерной
корреляционной функции. Следующий раздел посвящен рассмотре-
нию ограничений, связанных с этой проблемой. Там же будет по-
78
NataHaus,M
знание без границ * *
казано, что эта функция достигает своего максимального значения
при т = <р = 0. Однако, возможно, что она будет иметь пики в, точ-
ках, удаленных от начала координат.
Эти пики нельзя отличить от основных максимумов функций
ф(/) других сигналов, которые соответствуют этим точкам. Харак-
тер возникающих в таком случае затруднений ясен: оценки задержки
и частоты становятся не только в высшей степени неопределенными,
Рис. 4.1. Координаты, используемые для задания
функции неопределенности: плоскость (т, ср) и
плоскость (/, [).
но и, более того, в случаях, когда число целей неизвестно (предпо-
ложим, что эти цели могут существовать только в дискретных точ-
ках, где происходит совмещение сигналов), оказывается невозмож-
ным определить действительное число целей, которое наблюдается
радиолокатором. Будет ли эта потенциальная неопределенность
иметь значение при поисках подходящих сигналов или нет, зависит
от того, насколько вероятно такое расположение сигналов во вре-
мени и частоте. Указанная вероятность определяется возможностью
заранее построить точную модель пространства, в котором будет
функционировать радиолокатор. Этот вопрос обсуждается далее
в гл. 10.
Используя уравнение (4.21), можно показать, что
<30
J Ф (0 Ф* (*+ т, f+ф) dt = ехр [—/2л (f0+ф) т] х
— 00
X ( и(/)и*(/4-т)ехр[—/2лфП^/. (4 34)
г
Интеграл в правой части (4.34) представляет собой х(т, <р); с помощью
теоремы Парсеваля можно получить другую форму х(т, <р). Функция
неопределенности находится в виде. х(т» ф) Х*(т» Ф)» как это и Ука'
зывалось ранее.
Таким образом, функция неопределенности есть математиче-
ская концепция, которая, как мы надеемся, достаточно хорошо ха-
рактеризует меру неопределенности, присущую радиолокацион-
ному сигналу. Критерий «среднеквадратичного уклонения» есть
только один из большого числа возможных критериев, характе-
ризующих меру различия межДу двумя сигналами; однако обще-
Запаздыва -
ние
Опережение т
Опережение
Запаздыва- Т
ние
о) 6)
Рис. 4.2. Плоскости |(т, <р):
а—для функции неопределенности; б —для частотно-временнбй
функции отклика.
принято считать его наилучшим. Для того чтобы пояснить физи-
ческий смысл х(т» Ф)» мы сейчас проведем другой вывод этой функ-
ции. Он будет основан на том, что х(т» ф) рассматривается как
частотно-временнбй отклик согласованного фильтра.
Предположим, что W*(f) есть передаточная функция фильтра,
согласованного с сигналом ф(/). Легко показать, основываясь на
предварительно введенные определения U(f) в разд. 4.1, что
(4.35)
где f0 — опорная частота, показанная на рис. 4.1. Предположим,
кроме того, что входной сигнал представляет собой копию сиг-
нала ф(0, сдвинутого на допплеровскую частоту. Преобразование
Фурье для такого входного сигнала записывается в виде
^(/ + Ф) = ^(/-/О + Ф). (4.36)
Тогда можно показать, что выходной сигнал этого фильтра опре-
деляется соотношением
Г (т, <р) = ехр [j2nf0 т] J U* (f) U (f + <р) ехр [/2л/т] df (4.37)
— 00
«о
^ataUaus^k
знание без границ Ч *
или еще
Г(т, <р) = ехр [/2л/от] х (—т, <р). (4.38)
Это равенство означает, что выходной сигнал согласованного филь-
тра есть обращенная во времени функция неопределенности. Однако,
обозначая т через то/ и %mf соответственно для функции неопреде-
ленности и функции отклика, мы видим, что
W (4.39)
Это различие более ясно показано на рис. 4.2.
4.5. Свойства функции неопределенности
Изучению свойств функции х(т, <р) было посвящено большое
число работ с тех пор, как ее впервые ввели в качестве основы для
построения теории радиолокационных сигналов. Главной целью
этих исследований явилось определение необходимых и достаточных
условий для того, чтобы функция двух переменных могла быть
функцией неопределенности. Хотя полученные результаты не поз-
волили достигнуть этой цели, было получено много сведений об
общих свойствах х(т> <Р)- Эти свойства рассмотрены в настоящем
разделе1 * * 4. В дальнейшем изложении нам будет удобно описывать
свойства функции х(т» ф). с помощью функции 0(т, <р), которая
определяется выражением
Х(т, (р) = ехр [рирт] 0 (т, <р). (4.40)
Это соотношение получено введением в (4.2а) новой переменной
s = /-f-x/2 с целью получения симметричной формы
-(- оо
0(т, <р)— С u(t-—— ) и* 11 ] ехр [—j2nq>t]dt (4.41)
J \ 2 / \ 2 /
— оо
или путем замены р = /-Ь<р/2 в равенстве (4.26), с тем чтобы
получить
ехр [ — /2л/т] df. (4.42)
Эти преобразования не существенны для теории построения сиг-
налов, так как разработчик обычно интересуется только величиной
Х(т, <Р), а не ее фазовой структурой; в результате же использования
функции 0 может измениться только фазовая структура.
1 Приведенное изложение опирается в основном на работы Зиберта [4]
и Уилкокса 15]. Кроме того, в соответствующих местах этой главы исполь-
зуются и цитируются некоторые другие источники.
4 3.IK. 1.441 81
г
Свойство I: Симметрия относительно
начала координат
Из равенств (4.41) и (4.42) легко заметить, что
6(т, <р) = в*(—т, — <р), (4.43)
откуда следует
|0(т, ф)|а = |0(-т, — <р)|а. (4.44)
Кроме того, Штутт [6] установил также, что
|6(т, <р)|ехр[/т(т, Ф)1 = |0(—т, —<р)| ехр[—/у(—т, —<p)J.
(4лЬ)
Следовательно, фазовая функция у(т, <р) обладает нечетной сим-
метрией.
Свойство II: Наибольшее значение 0(т, ф)
ч Свое наибольшее значение функция неопределенности прини-
мает в начале координат при т = ф = 0, т. е.
|6(т, ф)Р<|©(0, 0)|«. (4.46)
Доказательство может быть получено применением неравенства
Шварца1.
Таким образом, применяя это неравенство, находим
то получаем неравенство (4.46).
Свойство III: Временной масштаб
Если 0(т, ф) соответствует «(/). то (1/| а |) 0 (ат, ф/а) соответ-
ствует u(at). Доказательство получают прямой подстановкой нового
переменного в (4.41).
1 Неравенство Шварца имеет вид
[j /* («) S (*) 2 < j* f («) f* («) dz f s (г) 8* (г) dz.
82
^alattausniit.
знаниеВезераниц ч*
Свойство IV: Параболиче сшк а я фаза
а) Время
Если 0(т, <р) соответствует «(/)» то 0(т, <р + Лт/л) соответствует
и(/)ехр [/Л/2]. Для доказательства производят прямую подстановку
в равенство (4.41). Широко известный пример получается, если
М0=М, И <772,
.0, |/|>Т/2.
(4.49)
Новый сигнал Л ехр [/Л/21 представляет собой ЛЧМ импульс.
б) Частота
Если 0(т, <р) соответствует u(f),то 0(т + Л<р/л, <р) соответствует
f/(f)exp j/й/2!. Доказательство получают прямой подстановкой
в (4.42).
Свойство V: Инвариантность объема
Если | %(т, <р) I1 есть функция неопределенности, то можно
показать, что
J J 1<Х (т»<Р) I2 = | % (0, 0) |2.
(4.50)
— оо
Это свойство обычно называют «принципом неопределенности ра-
диолокации» [4], или иногда «законом сохранения неопределен-
ности» |5]. Из него можно сделать вывод, что общая потенциальная
неопределенность одинакова для всех сигналов, обладающих одной
и той же энергией. Кроме того, это равенство представляет собой
необходимое условие для того, чтобы функция двух переменных
была функцией типа | Х(т, <р) |2. По-видимому, это наиболее важное
ограничение, накладываемое на функцию неопределенности, так
как оно означает, что все сигналы одинаково хороши (или плохи),
если они сравниваются без учета специфической радиолокационной
обстановки. Однако каждому из сигналов соответствует свое рас-
пределение неопределенности. На рис. 4.3 показаны распределения
неопределенности для некоторых имеющих большое значение ра-
диолокационных сигналов. Именно эта возможность варьировать
распределение неопределенности совместно с пониманием разработ-
чиком основ радиолокационных систем позволяет производить
систематическое изучение и поиск подходящих сигналов для пере-
дачи. Из этого следует, как показали Прайс и Хофштеттер [12],
что более общим условием является
$ j 1х(т» Ф)12р^(/ф = -1-|х(0, о);2,
(4.51)
— 00
где р—любое целое число, большее единицы.
4*
Сейчас мы проведем доказательство равенства (4.50), доказа-
тельство же равенства (4.51) можно найти в работе Прайса и Хоф-
штеттера [121. Заметим, что
Х*(т, ф) = J и*(0и(*4-т)ехр[/2лфП dt-
— оо
оо
- J и (f)U'(f 4- ф) ехр [j2nfx]df.
— оо
(4.52)
6)

Рис. 4.3. Примеры функций неопределенности. Вид контуров сече-
ний на некотором постоянном уровне относительно %(0, 0) :
а —короткий импульс с постоянной несущей; б —ЛЧМ импульс; в—одно-
родная последовательность импульсов (см.-гл. 8); в —импульсная после-
довательность. в которой несущая частота изменяется от импульса к им-
пульсу (см. гл. 8).
84
4\afaHaus7tiik
знание без границ * *
Следовательно,
% (т, ф) X* (т, ф) = |х (т, ф)|2 = jj § w (t) и* (/ + т) U (f)U'(f + ф) X
— оо
X ехр 1/2 л (/т — фО ] dt df (4.53)
и
J JI X (*. <Р) I2 dx dq = и (t)u* (t + т) U (t) U* (/ + ф) X
— оо —оо
хехр [/2л (fx— ф/)] dtdxdf dq>. (4.54)
Последнее равенство может быть упрощено с помощью следую-
щей пары преобразований Фурье:
оо
J н* (/+ т) ехр [/2л/т[ dx = ехр [—j2nft] U* (f)
— оо
(4.55)
и
ОО
(7* (f 4- ф) ехр [ — /2лфП dtp = ехр [j2nftj и* (t).
— оо
(4.56)
Подставляя эти выражения в правую часть (4.54), получаем, что
JjJ IX (т, ф) I2 dx </ф = и (t) и* (/) U (/) х
— оо — оо
xU'(f)dfdt = J |U(OM J \U(f)\2df.
— оо — оо
(4.57)
Гак как
оо оо
j \u(t)\*dt - J Rf)M=lx(0, 0)1,
(4.58)
то доказательство тем самым завершено.
Рассмотрим второй возможный подход к доказательству свой-
ства V, который приводит к получению некоторых важных интег-
ралов. Для этого подхода необходима следующая пара по Фурье:
J и (0 ехр [—/2л (f ,4- ф)] dt = U (f 4- ф).
(4.59)
86
Если эту пару по Фурье вместе с (4.55) применить к уравнению
(4.54), то в результате получим
$ $ lx(T, <p)|adrd<p= $$|1/(П|,|У(/+ф)М<*ф. (4.60)
— ОО —00
Отсюда видно, что внутренние интегралы равны. Эта связь рас-
смотрена в разд. 4.11. Используя теорему Парсеваля, можем
записать
со оо
У |V(f)|‘|y(f+v)|’<i/= j lx(r. 0)|*ехр(—/2жрт]Л. (4.61)
— 00 —00
Сейчас мы рассмотрим Другой подход к доказательству свой-
ства V, для чего необходима следующая пара по Фурье:
j U(f)exp[l2nf(t + x)]df = u(t + x).
— 00
(4.62)
Если эту пару совместно с (4.56) применить к уравнению (4.54),
то получим
|Х(Ь ф)Мф<^ =
— 00 —оо
\и (О I» I u(f4-T) |ad/dT. (4.63)
Мы снова видим, что внутренние интегралы равны. Используя
теорему Парсеваля, получаем следующее соотношение:
оо оо
J |ц (О I2 i и (*+*) М = j |%(0,ф) |аехр [/2лфт] t/ф. (4.64)
— оо — оо
Этот результат обсуждается далее в разд. 4.11.
Свойством инвариантности объема -также обладают рассогла-
сованные функции неопределенности; они возникают в том слу-
чае, если устройство обработки принимаемого сигнала не согласо-
вано с передаваемым сигналом. В качестве примеров можно ука-
зать на методы линейного рассогласования задержки и уменьшения
боковых лепестков по оси дальности, рассмотренные соответствен-
но в гл. 6 и 7. Как именно рассогласование приемника влияет на
распределение неопределенности в отдельных локальных областях
плоскости неопределенности будет зависеть от конкретной природы
внесенного рассогласования.
Свойство VI: Свойство самотрансформации
Если | %(т, ф) |я есть функция неопределенности, то
оо
§ § I х (т, ф) I2 ехР 1/2я “та)1 dTd<₽= lx (v* °) I2- <4-65)
— оо
вб
^alaHausA
знание без границ Ч
Доказательство этого свойства, по существу, совпадает с доказа-
тельством предыдущего свойства. Таким образом, левая часть
равенства (4.65) расшифровывается с помощью подстановки других
интегральных форм для %(т, <р), что дает в результате
X ехр [j2n {(V—t) ф—(а —f) т) J dt df dx dtp. (4.66)
Этот интеграл может быть сейчас упрощен с помощью следую-
щих пар преобразований:
J U* (f + ф) ехр [/2лф (v—/)] dtp « и* (t—v) ехр [j2nf (t—v)] (4.67a)
— 00
И
j u* (t + t) exp [—]2nx (a—f)J dx =
= U* (f—u) exp [—/2 л (/—о) /].
(4.676)
При введении переменных р = t—v n-q = f—и интеграл в равен-
стве (4.66) сводится к виду
jj $ и*(р)u(p+v)U*(q)U(q + о)ехр[/2л(up—47v)] dpdq. (4.68)
— 00
Легко заметить, что этот интеграл представляет собой произве-
дение
Х(°» v)x*(o, v) = Jx(o, v)|a. (4.69)
Свойство VII: Инвариантность по отноше-
нию к повороту
Функция неопределенности обладает свойством оставаться
инвариантной при преобразованиях, когда плоскость х — ф пово-
рачивается на угол 0, так что
Tl_[cos® —sinOirx'
ф'J [sin0 cosGJ [ф
(4.70)
Таким образом, если %(т, ф) есть функция неопределенности, ко-
торая соответствует u(f), то %(х\ ф') — также функция неопределен-
ности, соответствующая сигналу
V (0= I COS 0|1 /2 J df ехр I—j2nft] cos 6 j и (х) х
— 00 —00
X ехр/2лр*—dx. (4.71)
87
Для класса сигналов, называемых эрмитовыми, найдено, что
V (0 (4.72)
Дополнительная информация относительно этого класса сигналов
приводится в разд. 4.12 настоящей главы, где даны некоторые важ-
ные примеры функций неопределенности.
Свойство преобразования функции неопределенности при по-
вороте осей координат в другую функцию неопределенности было
обобщено Райсом [8]. Он установил, что если
°12
а22
соответствует сигналу
хрГ/2лап/
(4.73)
°21
то х (ап т + а1а ф, п21т4-аааф)
Н0 = |а„|,/2 7 d/<
X
-^х
2ан
Новая функция неопределенности %(т', <р') может быть выве-
дена с помощью последовательного использования свойств II,
IV,а и IV,б. Таким образом, если u(t) соответствует %(т, ф), то
z(f) = u(at)exp[jkt2] соответствует (1/|а|)%{ат,(1/а)[ф 4- kx/n]}.
Если теперь Z(f) есть преобразование Фурье z(t), то функция
неопределенности, которая соответствует сигналу со спектром
V(f) = 2(/)ехр[/Л/а], есть (1/|а' )%{аг 4- аЛф/л, kxlan 4-((р/а)[ I +
4-М/ла]} с характеристическим определителем
(4-74)
а
ah
п
k
ап
Свойство VIII:
Правило умножения
(4.75)
Если Хи(т» ф) есть функция неопределенности, соответствующая
«(/), а Хо(т» Ф) — функция неопределенности, соответствующая
v{t), то для z соответствующая функция неопре-
деленности Хио(т. ф) задается свзрткой хЛт> ф) и Х>(т, ф) отно-
сительно допплеровской оси
оо
Хш.(т, ф) = j х«(т, Х)хДт, Ф—X)dX. (4.76)
— оо
Аналогично, если Z(f)-U (/) V (f), то
оо
Хл(т» Ф)= J Ху (Л ф)Ху(т—Ф)^- (4.77)
88
NalaHausilk
знание без границ X
4.6. Теорема единственности
Для того чтобы некоторую функцию от двух переменных мож-
но было отнести к классу 8(т, ф) функций, необходимо и достаточно,
чтобы она преобразовывалась следующим образом [4, 5]:
ОО
и (х ——) и* (х + = f в (т, ф) ехр [/2лфх] dip.
\ 2 / \ 2 j J
— 00
(4.78)
При введении новых переменных р = х—т/2 и о = х-|-т/2 это
условие можно выразить в более удобной форме:
00
Ы(р)п*(о)= J 6(0—р, ф)ехр[/лф(р+о)]г/ф.
— 00
(4.79)
Можно показать, что если (4.78) справедливо для некоторой функ-
ции двух переменных, то
ОО
и (й) V (₽) = [ 6(т, й—Р) ехр |/п (И + ₽) т] dr. (4.80)
— оо
В результате получаем, что если 6и (т, ф) соответствует и (0, а 6
(т, ф)— функции v(t) и если 0„(т, ф)= 6р(т, ф), то из уравнения
(4.78) следует, что и (0 и о (0 могут отличаться лишь постоянным
множителем с, где | с | = 1 (т. е. v (t) = си (0).
Это свойство единственности следует из того, что поскольку
6ы(т, ф) = 6г(т, ф), то из (4.78) получаем
а (р) а* (о) = v (р) и* (о). (4.81)
Для того чтобы это равенство было справедливо, необходимо
выполнение условия
и (Р) (о) = си (р) с* и* (о). (4.82)
Следовательно,
[|с]|а-11МР)“*(<0=0, (4.83)
и так как м(0 не тождественно нулю, то следует, что |с|* = 1.
Аналогичное условие того, чтобы функция двух переменных
была функцией 16(т, ф) | ’, до сих пор еще не найдено.
89
4.7. Объем свободной области и средний уровень
боковых лепестков
Предположение, сделанное Грином, побудило Прайса и Хоф-
штеттера 112] доказать, что максимально возможный' объем сво-
бодной области, которая может окружать пик, расположенный
при т = ф = О, равен четырем. Это означает, что максимальная
область в координатах дальность — частота Допплера, которая
может быть исследована без неопределенности, равна единице.
Если V (Л) соответствует объему, охватываемому | х(т, ф) | * внутри
Рис. 4.4. Функция неопределенности Рис. 4.5. Функция неопределен-
бесконечной последовательности импуль* ности при повороте рядов «иго-
сов в виде рядов «иголок». лок».
границ центрально расположенной выпуклой симметричной обла-
сти А, с(А) — объему свободной области внутри этих границ,
а Уо — объему пика при т = ф = 0, то результат Прайса и Хоф-
штеттера можно представить следующим соотношением:
' (4.84)
4
Равенство в соотношении (4.84) имеет место только в том случае,
Когда с(Л)<4.
Этот результат показан на рис. 4.4 для последовательности
импульсов
и(0 = 2 б(/—пГ>> <4-85)
Л — — оо
где 6(0 определяет отдельные импульсы. Из рис. 4.4 видно, что
функция неопределенности для (4.85) состоит из ряда острых пиков
(«иголок») и имеет ярко выраженную прямоугольную область вокруг
центрального пика, площадь которой равна четырем. На рис. 4.5
показан свободный объем в виде эллиптической области, получаю-
90
NataHausmik
знание без границ * *
щейся при умножении (4.85) на ехр !/£/] для формирований сиг-
нала, описываемого равенством
«(0 = £ б(^-л7)ехр[/Л(п7)»].
Л "— оо
(4.86)
Так как функция неопределенности для (4.85) задается соотношением
Х(т, Ф) = 2 6
Л " — оо
т—пТ, <р
(4.87)
то, вспоминая свойство IV разд. 4.5, видим, что функция неопре-
деленности для (4.87) записывается в виде
оо z
X [т. Ф-Ь-^-—6 (т—л7, ф--------?- + — ). (4.88)
\ Znl •' \ П1 Л '
л «В —оо
Пусть k = (л/2) (1/и7)я. Это приводит к сдвигу импульсов в (4.87)
на величину <р = 1/27 вдоль линии постоянных т, определяемой
соотношением л = 2д — 1, так что получаем
X (ь Ч> + 2 6 ('С—"Т’ф~ 2^т) • (4-89)
Л» — оо
На рис. 4.5 показано, что объем свободной области для (4.89)
ограничен эллипсом, полуоси которого имеют размер |/^ Т вдоль
оси времени и 1/7 вдоль оси частот, а площадь составляет 3,6.
Обобщение теоремы об объеме свободных областей получено
путем оассмотрения аналогичных областей, для которых
| х(т, ф)|*<л« Прайс и Хофштеттерпоказали, что для этого случая
неравенство принимает вид .
V0+nc(4)> У(Л)>с-<^-У0. (4.90)
Это неравенство справедливо только при т) < Уо/4 и
(4.91)
В общем случае можно заметить, что чем больше становится т], тем
больше будет с(Л).
Прайс и Хофштеттер показали, что для функции неопределен-
ности, имеющей пик при т = ф = 0, когда усреднение производит-
ся по области, площадь которой значительно превышает четыре,
средний уровень боковых лепестков должен превосходить j/y
9)
где Vo — объем центрального пика. Этот средний уровень боковых
лепестков задается в виде
S2 = У(А)~У±. (4.92)
с (Л)
Для идеальной, так называемой «кнопочной», функции неопреде-
ленности, которая состоит из импульса объемом Vo, расположен-
ного в начале координат и окруженного плоским пьедесталом высо-
той Vo, найдено, что средний уровень боковых лепестков равен У Vo.
4.8. Обобщение теоремы о функциях неопределенности [5, 6]
Рассмотрим последовательность функций
МО. А(0. МО.......МО-
Если члены этой последовательности интегрируемы в
в пределах — оо< /<оо и если они ортогональны
определению
(4.93)
квадрате
согласно
J М')£(0Л = 6„„. (4.94)
— оо
где 8птп—дельта-символ Кронекера, то отсюда следует, что при
полноте последовательности fn (I), Втп (т» ф). которая определяет-
ся как
ВЛп(т, Ф)= f fn(t—^УГт(/ + ^-)ехр(-/2л(рЛЛ, (4.95)
также является членом полной ортогональной последовательнос-
ти, где
jj$ Втп (т. ф)Вр« (т, ф) dT d(f> = 6np 6mg. (4.96)
— oo
Если u(t) интегрируема в квадрате, то
«(0=2 «„ fn (D. (4.97)
л—0
где
о„ = J и dt (4.98)
— оо
и
i Kl2= J |и(0|а^- (4.99)
л=0 — <z>
92
^latattauSfVii
знание без границ ч *
Функция неопределенности для и (/) задается соотношением
в(т, <р)= 2 S anamBnm(x, <р), (4.100)
т яа О Л “Я О
где
cnm = anam--= JJe(T» Ч}В*Пт(^ <p)dxd(p (4.101)
— 00
и
2 2 |c„ml’= Z 1 аЛр. (4.102)
tn — 0 л — О Л— О
4.9. Функция неопределенности вблизи начала координат
Для значений т и ф, близких к началу координат, функция
неопределенности может быть описана двумя первыми членами
разложения |%(т, <р) |а в ряд Тейлора. Таким образом,
1х(т>ф)|> - II П к^х|
1х(0, 0)|« IX(0, 0)|« L
+ 2тфКе(^М +<Ра-г4] • (4.103)
( От дф) дф* ]т - <р — о
Оказывается возможным выразить (4.103) через величины, опре-
деляющие ширину полосы и длительность сигнала, и через так
называемый «коэффициент частотно-временной связи ошибок», ко-
торый^более подробно рассмотрен в гл. 5. Приступая к выводу
этого результата, рассмотрим в первую очередь коэффициент при
т1 в равенстве (4.103). Легко показать, что
*Х|
дт8 |т = <р - о
- J
— оо
(4.104)
Применяя теорему Парсеваля, получим
(4.105)
— ОО --or
Мы видим, что выражение в правой части уравнения (4.105) содержит
второй момент | U(f) |а. Это выражение используется для определе-
ния ширины полосы u(t), т. е. ширина полосы, обозначаемая здесь
через р, определяется как
оо
2Е₽2 = (2л)> J P|t7(f)|*4.
— оо
(4.106)
93
где Е обозначает энергию сигнала Re {и (/) ехр [Jcd0/]} и опреде-
ляется выражением
2
и (t)u* (/) dt.
(4.107)
Коэффициент при та может теперь быть представлен в виде
= -2£₽«.
ОТ1 Т — ф — о
(4.108)
Рассматривая далее коэффициент при <ра в равенстве (4.103),
получаем следующее соотношение:
дах
д<р*
ОО
= (2л/)а ? /а|м(0|МГ.
т-Ф — о _’оо
(4.109)
Интеграл в правой части уравнения (4.109) является, очевидно,
вторым моментом |а(/)|а; он будет использован для определения дли-
тельности1 сигнала u(t), обозначаемой здесь через а,’с помощью
следующего равенства:
ОО
2Еаа = (2л)а $ fa|u(0M.
—оо
(4.110)
Поэтому коэффициент при фа может быть выражен в виде
—х- = —2Еаа.
дф* т»ф-о
(4.1И)
Наконец, определяя коэффициент при 2т<р в равенстве (4.103),
получаем
Re L^Xj —2п Im
(дт дф)т — ф—о
оо
tu (0 [u* (t)]'dt
(4.112)
— 00
где Im{...} обозначает «мнимая часть...». В гл. 5 будет показано,
что параметр сигнала, называемый «коэффициентом частотно-времен-
ндй связи ошибок» и обозначаемый как р, может быть выражен через
величины, входящие в правую часть равенства (4.112). Таким обра-
зом,
2Ер —-----Im
f ар
tu (0 [и* (t)]’dt
(4.ИЗ)
1 Определения ширины полосы и длительности сигнала в виде (4.106)
и (4.110) дают среднеквадратичные значения этих величин и не обязательно
совпадают с обычно используемыми значениями ширины полосы или длитель-
ности огибающей на уровне 3 дб.
94
^ataHaus,^*
знание без границ Ч *
Поэтому коэффициент при 2т<р равен
Re(^-| = -2Еа₽р. (4.114)
(ОТ Оф)т-Ф“0
Заметив, что | X (0, 0) | = 2Е, выразим разложение в ряд Тей-
лора через параметры сигнала а, р и р в виде
=1 - IP***+2 (“₽) Рт(₽ I- «VI- (4.115)
Отсюда видно, что кривая, образованная пересечением |х (х, ф) I*
и плоскостью уровня вблизи максимума | х (0, 0) |а, определяется
уравнением
рат2 4- 2 (ар) ртф а2фа = уа. (4.116)
Эта кривая всегда представляет собой эллипс [51. Взяв уа =
= NJ8E, заметим, что равенство (4.116) описывает так называемый
Рис. 4.6. Эллипс неопределенности.
«эллипс неопределенности» [13], который
Ширина' этого эллипса вдоль оси т равна
₽|2E//V0
Ширина эллипса вдоль оси ср составляет
показан на рис. 4.6,
(4.И7)
(4.118)
Дф —------ .
а
Наиболее удаленные точки в обоих направлениях для эллипса
неопределенности имеют координаты
1
2₽ | 2Ё/Ъ
1
Г
Дт — 4-
* ма кс
(4.119)
95
I
I
и
= ±----------------
2a )/2E//Vo l
Величины, задаваемые равенствами с (4.117) по (4.120), будут
рассмотрены более подробно в гл. 5, где изучается проблема оценки
задержки и допплеровского сдвига принимаемого сигнала. Там же
показано, что эти равенства определяют наименьшие возможности
ошибки в среднеквадратичном смысле.
4.10. Обобщение принципа неопределенности сигнала
Обратная зависимость между длительностью сигнала и шири-
ной полосы его преобразования Фурье приводит к догадке, что
произведение длительности а и ширины полосы 0 не может быть сде-
лано сколь угодно малым. Габор |11] был первым, кто определил
нижнюю границу этого произведения с помощью неравенства
ар > л.
(4.121)
Это неравенство является одной из формулировок принципа неоп-
ределенности сигнала. Более общее выражение для неопределен-
ности сигнала задается другим неравенством
аяра 11 —р2] > л2,
(4.122)
которое получается из рассмотрения интеграла в правой части
(4.112). Мнимая часть его задается уравнением (4.113). Легко пока-
зать, что действительная часть этого интеграла равна
Re
с I 1
\ <«!(<) [и* (0)'dt =- т х (0, 0),
— оо )
(4.123)
откуда, комбинируя мнимую и действительную части, получаем
2
л2 + (а0р)а =
2л
1х (0,0) |«
оо
$ tu(t) [и* (01'4/
(4.124)
—оо
Используя неравенство Шварца, а затем теорему Парсеваля, сводим
уравнение (4.124) к (4.122). Из (4.122) видно, что нижняя граница
произведения а0 зависит от коэффициента частотно-временндй
связи р.
96
^alaHaus^!,
\
\
\
4.11. Постоянная разрешения no времени
Вудворд [ 1 1 впервые ввел • характеристику, которая могла
служить количественной основой для вынесения суждения о раз-
решающей способности радиолокационного сигнала. Он определил
величину, названную «(постоянной разрешения по времени», которая
используется при отсутствии допплеровского сдвига и задается
выражением
J 1х(т> 0) |« dx
TR(0) - . (4.125)
IX(0.0)|«
Будем считать, что сигнал, который обеспечивает наименьшее
значение для TR (0), обладает наибольшими возможностями для
разрешения двух сигналов во времени1. Отсюда видно, что 7р(0)
Рис. 4.7. Вид спектра, в котором чередуются занятые
и свободные участки спектра.
связана обратной зависимостью с полосой частот, «занимаемой»
сигналом. Чтобы понять, что означает термин «занимаемая полоса»,
рассмотрим следующий пример. Предположим, то спектр, со-
ответствующий сигналу u(t), задается соотношениями (рис. 4.7):
Vtf) = 0. + + (4.126)
</(D=0. fN+^<f.
где я=1, 2, ..., ЛЛ Полоса, занимаемая этим сигналом, в дан-
ном случае равна
2 (4.127)
Л = 1
1 В разд. 11.8 приведены некоторые примеры сигналов, для которых
это предположение' является недоказанным.
97
Для того чтобы продемонстрировать связь между Tr(Q) и суммой
занятых полос, применим теорему Парсеваля к (4.125) и получим
тк (0) =
J \иф\**Г
—оо
(4.128)
Подставляя в это равенство выражение для I/ (f), данное форму-
лой (4.126), находим
7>(0) =----(4.129)
ul V А/п
Отсюда видно, что
T«(0)=^J------. (4.130)
п ==0
Перегруппировывая сомножители в (4.129), получим другое вы-
ражение для Tr(0) в виде
7'«(0)=-J-, (4.131)
где Е обозначает энергию, определяемую соотношением (4.107).
Для сигналов с равными энергиями, которые имеют фиксированную
ширину полосы, равную сумме чередующихся коротких частотных
полос, занятых и незанятых спектром сигнала, величина Uo будет,
очевидно, достигать своего наименьшего значения, когда внутрен-
ний спектральный промежуток полностью заполнен. В соответствии
с этим из (4.131) получаем, что это также приводит к наименьшей
неопределенности.
Хорошо известное и важное заключение, получаемое из этого
результата, состоит в следующем: если априори известно, что сиг-
налы не будут претерпевать допплеровского сдвига, то при передаче
отдельных импульсов неопределенность будет меньше, чем при
передаче их последовательности. С помощью вариационных методов,
подбирая только форму огибающей спектра в пределах фиксиро-
ванной полосы частот, было найдено, что 77?(0) ДЬстигает мини-
мального значения в том случае, когда спектр имеет постоянную
огибающую и целиком заполняет разрешенную полосу. Импульс
с ЛЧМ, который имеет большое значение произведения полосы на
длительность (скажем >20), обладает приблизительно таким спект-
ром. Следовательно, с точки зрения Tr (0) импульсе ЛЧМ аппрокси-
98
^alaHausA
знаниебезграниц Ч4*
мирует оптимальный ограниченный по полосе сигнал для разреше-
ния нескольких сигналов, если только известно, что принимаемый
сигнал никогда не будет смещен относительно некоторой произволь-
ной опорной частоты1. Этот вывод впервые сделал Манассе в работе
[14].
Подход, использующий постоянную разрешения по времени,
был позднее расширен Уэстерфильдом и др. [15], хотя они и не
использовали такой термин. Эти авторы показали, какую важную
роль играет постоянная разрешения по времени, выраженная
как функция допплеровского сдвига <р в виде
f I Х(т, <р) I’dt
Г . (4.132>
1Х(0.0)|« '
Они также ввели интегральные соотношения
со оо
$ |Х(Ьф)12<1т= Jj |C/(0l*|t/(/4-4P)l2dq>. (4.133)
—оо —оо
оо оо
$ 1х(т, ф)|Мт = $ |%(т, 0)|»ехр[—/2лфт](/т. (4.134>
—оо —оо
Эти соотношения выведены выше в разд. 4.5.
Сделаем несколько замечаний относительно различных форм
определения Tr (ф). Первая форма, задаваемая равенством (4.132),
может быть интерпретирована как суммарная характеристика не-
определенности, наблюдаемой на выходе согласованного фильтра
при допплеровском сдвиге. Эта интерпретация представляет собой
расширение понятия постоянной разрешения по времени Вудворда.
Следующая форма, задаваемая равенством (4.134), ясно указывает,
что Tr (ф) связана с профилем функции неопределенности при ну-
левом допплеровском сдвиге через преобразование Фурье. И, нако-
нец, последняя форма, задаваемая (4.133), поддается более ясной
физической интерпретации. Если рассматривать [U(f) |2 как энер-
гетический отклик согласованного фильтра, то эту последнюю форму
можно трактовать как энергетический отклик согласованного филь-
тра на входные сигналы с допплеровским сдвигом. Для частного
случая, когда в интервале — оо< ф<сю каждому допплеровскому
сдвигу соответствует единственный сигнал, можно показать, ин-
тегрируя Tr (ф) в этих пределах, что суммарная энергия равна
I х(0. 0) I ’• Величина Tr (ф) будет далее рассмотрена в гл. 10 в ка-
1 Это ограничение можно опустить,' если система разрабатывается с
таким расчетом, чтобы использовать свойства ЛЧМ сигнала для определения
дальности, как это будет рассмотрено в разд. 9.5.
99
честве критерия для построения сигналов при наличии многих
целей и при плотном расположении отражателей в окружающей
среде.
Вудворд ввел также постоянную разрешения по частоте, опре-
деляемую соотношением
Fr (0) =
f 1х(0, <p)|’dq>
—00
IX (0,0) р
(4.135а)
Это определение постоянной разрешения по частоте было с тех пор
расширено с тем, чтобы оно отражало и зависимость от задержки
т [151. Обобщенное определение постоянной разрешения по частоте
имеет вид
Fr С0 =
f 1Х(т, <Р>1“Жр
—оо
1х(0,0)1»
(4.1356)
Равенства (4.63) и (4.64) определяют другие формы для (т).
Мера способности к одновременному разрешению по времени
и частоте для радиолокационного сигнала определяется произве-
дением (0) Fr (0). Для импульса с синусоидальным заполне-
нием и гауссовой огибающей Tr (0)F« (0) = 1, а с прямоугольной
огибающей Tr (0) Fr (0) = 2/3. Следовательно, так как прямоуголь-
ный ^импульс имеет меньшее значение произведения, то его, по-
видимому, предпочтительнее использовать в случаях, когда одно-
временно необходима разрешающая способность по времени и по
допплеровскому сдвигу.
4.12. Примеры функций неопределенности
В предыдущих разделах этой главы обсуждалось значение
функции неопределенности и описывалось ее общее поведение.
Рассматривая свойства этой функции, можно определить основные
правила построения сигналов, которые могут быть использованы
для передачи в радиолокационных системах. Игнорирование ре-
зультатов этих разделов может очень легко привести к серьезным
заблуждениям. Например, можно пытаться найти сигнал — па-
нацею от всех бед, — который бы давал единственный пик в на-
чале координат плоскости неопределенности. Однако интегральные
соотношения, вытекающие из свойства инвариантности объема,
сразу же показывают, что теоретически такой сигнал найти не-
возможно.
100
<\aiaHaus№k
знание без границ ч «Ь
Так называемая «кнопочная» функция неопределенности
(рис. 4.8) является наиболее близкой аппроксимацией поверхности
неопределенности с единственным пиком. Она состоит из единст-
венного узкого пика, окруженного однородным низким пьедеста-
лом. Размеры пика по ширине вдоль оси времени равны 1/0 и вдоль
оси частот 1/а. Основная часть объема, однако, лежит под пьеде-
сталом. В соответствии с теми интегральными соотношениями,
о которых мы сказали выше, этот объем ограничен, по существу
а единицами по оси времени и 0 единицами по оси частот. Высоту
пьедестала можно определить, используя свойство инвариантности
объема; она равна | %(0,0) | а/а0.
Хотя многие сигналы имеют ха-
рактеристики, близкие к харак-
теристикам кнопочной функции
неопределенности, однако до сих
пор не найдено сигнала, который
обеспечивал бы такую поверх-
ность неопределенности. Кроме
того, эта поверхность неопределен-
ности может оказаться полезной
далеко не для всех применений.
Как и для всех других поверхно-
стей, вопрос о ее полезности дол-
жен быть подвергнут тщательному
анализу. Все это обсуждается да-
лее в гл. 10.
т
Рис. 4.8. «Кнопочная> функция
неопределенности.
Некоторые дополнительные примеры поверхностей неопреде-
ленности приведены в табл. 4.1 [16]. Для каждого из них предпо-
лагалось, что соответствующие сигналы нормализованы
СО
(4.136)
Следовательно, все поверхности неопределенности, приведенные
в табл. 4.1, имеют в начале координат единичную высоту. Табл. 4.1
включает описание u(t), U(f) и j %(т, 0) |. Главные контуры | %(т, <р) |
вдоль оси времени и оси частот получаются в том случае, если
положить <р = 0 и т = 0 соответственно. Уровневые контуры
(для | х(т, ф) | с^0,7) некоторых этих поверхностей показаны на
рис. 4.3. Читатель может вспомнить из разд. 4.9, что вблизи пика
I Х(т > ф) i2 эти контуры обычно являются эллипсами. И только когда
рассматривают более низкие уровни, наблюдаются различные
контуры разрешения.
Ниже приведены некоторые общие характеристики поверх-
ностей неопределенности (табл. 4.1).
101
Примеры функций
U(t)
V (Ь
1. Гауссова огибающая
Монотонная (постоянная частота
заполнения) I—I ехр [—Л2/2]
\ л /
/2А2\
Линейная ЧМ I —) ехр [— (Л2—
\ л /
2л \
Л2 )
( 2Л2л V/4 Г —л2/2
^<+62/ expb2- jb +
1 ft2 1
+ / — arctg—
Параболическая ЧМ1
X ехр [—(Л2—jct)P]
Н'*х
\ п /
Xcos
2 (2л/) ^2 л
3 |/3c~ 2
где />0
2. Прямоугольная огибающая
Монотонная (постоянная частота
fi /Т ,
у sinnT/
пТ/
заполнения)
О, |/|>Т/2
Линейная L Jr ехР 1/^1» 1Л<772
ЧМ Г 1
О, |/|>Г/2
i №)4-(Si4-S2)’J /2X
ia ^2 ”1
_ ardg
Ci 4- C>> I
Хехр -
где
хп
Сп = [ cos ny2dy, Sn = | sin nipdy
о b
(n = 1,2)
к
’ =(2ТЛ/)‘/> ( -
х2 J \ 2
А/
102
ftaiaHausii®!.
знание без границ ч *
неопределенности
1 х (т. 0) I 1 X (0. ф) 1 1 X (Т. ф) |
Таблица 4.1
е ехр —^Л’т» Г 1 / 6’\ 1 лф1] f 1 у/< 1.1-F-(3c/2fc2)«Ta ' х Г Ь2т1 Г 1 л’ф1 ех4“ 2 *• Г 1 л«ф’ 1 е,РН 4» 1 ГлаФ» 1 ехрН *• ] Г 1 ехр[“2 ехр Л» \1+(2 1 / л1®* V (w+ *•)] — 2 |*“т> + / ^\2)1 ф+— \ я / J ?‘х 1с/2Л»)«т»/ - fe»Ta , 2/г«л«ф«
0. |т| I'-—'I к Т J sin bx [Г — | т <Т Т X |] sin лТф лТф sin лТф L \ 2 ‘Г4Л< Л | т | \ sin лфТ( к “ Т ) nq>T(\- 0, |т|>Т I’-y) sin [6т—лф] [Г Iх Г 1о Н н — 21 Д’ = — Ч » А ~ Ч -3 - 1—
Ьх [7 0, '-НИ И1 > 9 И1<т т лТф 0. | — лф][Т — т|>Т HI] ’ икт
103
«<0 UU)
Прямоугольная огибающая (про- должение) Параболическая ЧМ1 )/^exp[Jd«], |/|<Т/2 . 0, |/|>772 / 1 У/4 Г 2 (2л/Ла л \ 6Т»с// [3 /Зс 4J’ л t ЗсТа где 0 < f < оЛ
Косинусная функция ЧМ
1 Г~\ Г 2л/1
J/ ±ехр[удез1п— . I/K772
О, |/|>Т/2
ОО
m,/a 2
П ™—ОО
sin n(f — n/T)T
n(f-n!T)T
где x = 2Д0 sin —-
3. Эрмитовы сигналы
ехр [—л/«] Нп (2 )ZH?)
уп\
(л=0, 1, 2,...),
где
(-/)"«(/)
Нп (*) = (— 1)”ехр
* Вычисления спектров проведены с использованием принципа стационарной фазы»
104
^alaUaus^lj.
знание без границ ч *
Продолжение табл. 4.1
1 X (*. 0) I 1 Х(0. ф) | 1 X (t, Ф) 1
1 1 Т 1 'Де Сп = •$п = *1 1 х8 J 1 Т / Д «С1+С,)’+ ’ ост HSi + S»)*]4’, хп cos ny2dy *п [ sin ny2dy, л=1,2 'о -4i х(Т-И1) 2 </)Я^п(х)Х j >in лТф л7ф L/^[<c.+c.)+ H-CSi+Ss)’]1/’, |т|<7 0, |t|>7 *‘l ( n x2 / \ бет / n =—oo
Х(Т-|т|)Х s iп пТо) sin л (ф—л/Т) (T—| т |)
sin (лл/7)(7—|т|) (лл/7) (7 —| т |) 1т|< 0, |т|> » т т л7ф X л (ф—n/T) (T — |t|) |t| ЛТ гдех = 2Д0 sin -y- » <7
ехр -У” Ln (пт)2 ехр X Г л > (Т)2 2 £п (ЛФ8) X • ехр XLn(л| где Ln(x) > Л 1 — у (т’Н-ф’^х т® + фа|)(л-0,1,2,. 1 dn = уехр|х|^х <(xn exp [ —x))
105
4.12а. Сигналы с гауссовой огибающей и синусоидальным
или ЛЧМ заполнением
Мы видим, что вертикальные профили вдоль осей времени и
частоты, так же как и все профили, взятые параллельно этим осям,
имеют форму гауссовых кривых. Кроме того, профиль вдоль любой
линии, проходящей через начало координат, также будет иметь
гауссову форму. Для импульса с синусоидальным заполнением и
гауссовой огибающей уровневый контур (рис. 4.9) представляется
окружностью, если коэффициент Л* = л, в противном случаемой
Рис. 4.9. Контуры сечений функции неопределенности для сиг-
налов с гауссовой огибающей:
а—импульс с постоянной несущей частотой; б—ЛЧМ импульс.
будет эллипсом, главная ось которого совпадает с осью т, когда
k*>n, и с осью <р, когда Л’<л. Уровневый контур для ЛЧМ сиг-
нала будет эллипсом, главная ось которого совпадает с линией,
задаваемой уравнением
(4.137)
где 2Ь равно тангенсу угла наклона функции ЧМ (рис. 4.9).
4.126. Сигналы с прямоугольной огибающей
Для всех ЧМ сигналов, которые имеют прямоугольную огибаю-
щую, форма х(0, <р) задается равенством
X (О» <Р) =
sin лТф
лТф
(4.138)
106
^atallaus^k
знание без границ Ч’ь
где Т — длительность огибающей. Это становится очевидным, если
рассмотреть преобразование Фурье
7/2
Х(0, ф)—
—7/2
и (0 Iе ех р [—/2лфЛ dt,
(4.139)
где
IM0I
4.12в. Сигналы с прямоугольной огибающей
и с синусоидальным или ЛЧМ заполнением
Для этих сигналов х(т» ф) имеет профиль вида (sin х)/х вдоль
любой линии, параллельной оси ф. Профили достигают своего
максимального значения над осью т для импульса с синусоидаль-
ным заполнением рис. 4.10 и на линии, задаваемой равенством
(4.137) и проходящей через начало координат для ЛЧМ сигналов
рис. 4.11. Как видно из рисунка, эти максимумы взвешены функ-
цией

(4.140)
Общая структура неопределенности для этих сигналов показана
на рис. 4.12 и 4.13. ЛЧМ сигналы в случае прямоугольной огибаю-
щей обсуждаются далее в гл. 6.
4.12г. Сигналы с функцией ЧМ более высоких порядков
и прямоугольной огибающей
В предыдущих примерах было найдено, что вдоль всех линий,
параллельных оси ф, форма профилей поверхности неопределен-
ности задается функцией (sin х)/х. Для сигналов с ЧМ более высо-
ких порядков эта функция деформируется. При параболической
ЧМ функция неопределенности (см. табл. 4.1 и рис. 4.14) опреде-
ляется интегралами Френеля. В общем случае невозможно описать
структуру функции неопределенности в терминах простых порож-
дающих функций. Часто оказывается полезным в таких случаях
применить принцип стационарной фазы для получения прибли-
женных данных о характеристиках функции неопределенности.
Этот подход обсуждается в следующем разделе.
107
Рис. 4.10. Частотно-временная функция отклика для импульса с
постоянной несущей и прямоугольной огибающей:
а —профили постоянных т; б—профили постоянных ф.
Рис. 4.11. Функция отклика для ЛЧМ импульса с пря-
моугольной огибающей.
108
ftataHausiilk
знание без границ Ч *
Рис. 4.12. Импульсный сигнал с постоянной несу-
щей й соответствующая поверхность отклика:
a—вид сигнала; б—рассчитанный вид поверхности от-
клика; а—экспериментально полученный вид поверхности
отклика.
109
т
2
т
z
I
**?[№*]
Рис. 4.13. ЛЧМ импульс и
вид поверхности отклика при
ТА/ = 10:
а—вид сигнала; б —рассчитанный
вид поверхности отклика; в—экс-
периментально полученный вид по-
верхности отклика.
Z7 при других t
110
^lalaHausA
знание без границ Ч ш
«р при других t
\'С=0
Рис. 4.14. Импульс с параболическим законом ЧМ и
вид поверхности отклика при T&f, — 200:
а — вид] сигнала; б—экспериментально полученный вид по-
верхности отклика.
111
4.12д. Импульсы с V-образной ЧМ
Сигналы с линейной V-образной ЧМ и соответствующая функ-
ция неопределенности показаны на рис. 4.15. Для приведенного
здесь V-образного изменения частоты сигнал записывается в виде
u(0 = Ui (0 + «2(0.
— T<t<T
u(t) = Q при других t,
(4.141)
где
M0 = -=-exp[ —jbt*],
J2T
Ы8(О = —LrexpIjW],
)2Т
—T<t<o
о<е <т.
(4.142)
Функция неопределенности для такого сигнала состоит из четырех
частей: двух автокорреляционных члейов, соответствующих «1(0
и и2(0» и двух взаимокорреляционных членов, соответствующих
двум взаимным произведениям u^t) и u2(t). Выраженная через
эти компоненты полная функция неопределенности имеет вид
X (г, ф) = Хп (г, ф) + Х22 (г, Ф) + Хи (т, Ф) + Х21 (т. Ф)« (4-143)
Основной вклад в эту функцию вносят автокорреляционные члены
Хп(т»ф) и Х22(т» ф)- Они связаны1 следующим образом:
Х22(Ч Ф) = Х*1 (—Ь Ф), (4.144)
7.22 (г, ф) = Х11(Ч —ф)ехр[/2л<рт], (4.145)
где
Х11(т, ф)= ур —у^-]х
X
sin {л [ф —frr/л] [Т— | т |]}
л [ф— bn/я] [Т— | т |]
ехр [/ (л<р [Т + т] — ЬхТ],
(4.146)
Очевидно, что поскольку Х12 (0,ф) = X2i (0» ф)=0, то
Х(0, <₽) — 2 Re (Хп (0, <р)| = (4.147)
2л7ф
В общем случае сумма основных слагаемых быстро спадает до
уровня более низкого пьедестала, определяемого взаимокорреля-
1 Равенства (4.144) и (4.145) применимы ко всем сигналам, которые
имеют четные функции для огибающих и четные функции частотной модуля-
ции.
112
yulaHausvk
знание без границ Ч *
Рис. 4.15. Импульс с V-образной
ЧМ и вид поверхности отклика
при = 200:
a —вид сигнала; б—рассчитанный вид
поверхности отклика (пьедестал не
учитывался); в—экспериментально
полученный вид поверхности отклика.
*0 при других t
5 Зак. 1341
113
ционными членами Xi2(t, <р) и %21(т, <р). Можно показать, что эти
члены характеризуются интегралами Френеля. Каждый из них
заключен в одной половине плоскости т — <р между задержками,
ограниченными пределами 0< |т|< 2Т. Высоты %18(т, <р) и х81(т, <р)
изменяются в небольших пределах относительно уровня \l2[nlbTi}il*.
Это может быть выражено через произведение полосы на длитель-

б)2ТД/~500
Рис. 4.16. Автокорреляционные
функции сигналов с V-образной
ЧМ (отметим изменение высоты
пьедестала в зависимости от ве-
личины произведения длитель-
ности на полосу).
ность ТА/ для каждой 'линейной компоненты функции ЧМ, если,
по определению, b == nAf/T, где А/ — девиация частоты, показан-
ная на рис. 4.15. Заметим также, что пьедестал существует только
в интервале Т<|т|<2Т.
На рис. 4.16 показана автокорреляционная функция х(т> 0)
для V-образной ЧМ при различных значениях- произведения полосы
на длительность. Основной метод реализации согласованных филь-
тров для этих сигналов показан на рис. 4.17. Согласованный фильтр
для сигнала с двунаправленной ЧМ будет аналогичен двухканаль-
ной системе, в каждом канале которой имеется фильтр сжатия,
согласованный с соответствующим сегментом функции ЧМ.
141
^alaHausA
знание без границ Ч
Основное значение сигналов с линейной V-образной ЧМ состоит
в том, что они представляют собой наиболее характерный класс
сложных ЧМ сигналов, которые позволяют получить некоррели-
рованные измерения дальности и скорости (т. е. р = 0). Такое свой-
ство может быть связано с расщеплением выходного сигнала согла-
сованного фильтра на два отдельных сигнала, когда допплеровский
сдвиг вызывает рассогласование принимаемого сигнала с согласован-
ным фильтром.
а)
Задержка В канале V/
Задержка в канале
О 2Т
Сигнал на Выходе
канала t/2
27
Автокорреляционная
функция суммарного сигнала
2Т ЬТ
Сигнал на Выходе
канала t/f
Ч)
Рис, 4.17. Блок-схема согласованного фильтра для сигнала с V-образ-
ной ЧМ, показанного на рис. 4.15.
Этот допплеровский эффект показан на рис. 4.15, из которого
можно видеть, что сигналы, имеющие .допплеровский сдвиг, легко
могут быть распознаны. Однако если присутствует больше чем
один сигнал, то происходит возрастание неопределенности отно-
сительно числа целей, их действительных дальностей и скоростей.
Метод уменьшения неопределенности при отсутствии эффекта Допп-
лера для класса сигналов с V-образной ЧМ состоит в увеличении
кривизны каждой ветви функции ЧМ. Это приводит к уменьшению
амплитуд сигналов с допплеровским сдвигом, что и наблюдается
в случае параболической ЧМ. Уменьшение пиков сигналов с доп-
плеровским сдвигом хорошо видно на рис. 4.14 при <р = 0. Од-
нако оно достигается ценой увеличения боковых лепестков сигналов
на выходе согласованных фильтров как при <р =0,' так и при <р=/=0.
Здесь мы сталкиваемся с конкретным проявлением свойства инва-
риантности объема функции неопределенности.
5* 115
4.12е. Эрмитовы сигналы
Класс сигналов, которые инвариантны по отношению к пово-
роту плоскости неопределенности (см. разд. 4.5, свойство VI),
задается соотношением [5, 10]
ип(0 = -^-ехр(-п/ЧЯп(2рл/). (4.148)
/л!
где Нп(х) есть полином Эрмита п-ro порядка. Полиномы Эрмита
определяются по формуле
гг / \ / 1ч„ I х2 \ dn / хя \
Я„(х) = (-1уехр(—) —ехр(~—
(4.149)
где
Я0(х)-1,
A/j (х) = х,
//2(х) = х2-1,
* Я3(х)=х3—Зх,
Я4(х) = х4—6х2—3
Эти сигналы обладают свойством самотрансформируемости, т. е.
они переходят сами в себя при преобразовании Фурье
«n(0=*t/„ (ft = (-/)” «„(/)• (4 150)
Как легко показать, функция неопределенности для этих сигна-
лов имеет вид
Хп(т. ф) = ехр[—-^-(т2 + ф2)1 Ln [л (т2+ ф2)], (4.151)
где Ln(x)—полином Лаггера n-го порядка. Полиномы Лаггера
определяются формулами [17]
1 dn
L„(X) = ±e* £-„(*" е~'). (4.152)
п
<4153>
fe = o —R>‘ Rl
Примеры таких сигналов приведены Клаудером [10], который при-
водит и функцию неопределенности для нескольких порядков п, по-
казанных на рис. 4.18 и 4.19. Боковые лепестки этих функций не-
определенности спадают приближенно по закону тогда
как боковые лепестки ЛЧМ сигналов спадают по закону t~l.
116,
^alaltausfA
знание без границ ' *
Амплитуда сигнала.
Рис. 4.18.
117
Амплитуда сигнала
Рис. 4.18. (Л, Б, В). Эрмитовы сигналы (а) и соот-
ветствующие корреляционные функции (б) для раз-
ных значений п.
Рис. 4.19. Поверхность отклика х(т, <р) для эрмитова сигнала
при п = 10.
118
^lalaHaus^i
знание без границ Ч *
4.13. Применение принципа стационарной фазы для
анализа функции неопределенности
Свойства поверхности неопределенности, описанные в преды-
дущем разделе, могут быть получены при рассмотрении общего вы-
ражения функций неопределенности как результата преобразова-
ния Фурье произведения u(t) u*(t + т), причем т рассматривается
как параметр. Из принципа стационарной фазы следует, что
|х(т, ф)|~К2л
u(t)u'(t+x)
VI де*(о ।
»
*=/«₽)
(4.154)
где А6 "(О = 6*(0 — + т) есть разность между крутизной
функции ЧМ для сдвинутого во времени сигнала u(t + т) и несдви-
нутого сигнала u(t). Решение для t = так же как и координаты
стационарной точки, получается из уравнения
2лф — АО'(0 = О. (4.155)
Легко показать, что для импульса с синусоидальным заполнением
А0'(О = 0. Так как это выражение, несомненно, не зависит от
времени, то принцип стационарной фазы указывает, что х(т, ф)
сконцентрировано большей частью над осью т и что форма х(т» ф)
при постоянном т определяется преобразованием Фурье
| u(t)u*(t + т) |. Аналогично, для ЛЧМ импульса А0'(0 = ± и
функция х(т> ф) сконцентрирована при постоянном т вдоль пря-
мой ф = ± bx/л. Очевидно, что эвристическое предсказание формы
профилей ф), взятых вдоль линий постоянного т, может быть
осуществлено как только определена конкретная функция ЧМ.
Продемонстрируем еще раз применение принципа стационарной
фазы к анализу функции неопределенности на примере рассмотре-
ния функции неопределенности сигнала с параболической ЧМ, где
0(0 = ct3. Для этого сигнала АО'(0 = ± Зс[т2 + 2/т]. Ис-
пользуя равенство (4.153) для сигнала с параболической ЧМ и пря-
моугольной огибающей, показанного на рис. 4.14, видим, что
1Х(т,ф)|^Уй» ‘ (4.156)
Т /бет
Следует отметить хорошее совпадение этого результата с точной
формой, приведенной в табл. 4.1.
Нужно, однако, предостеречь от неосмотрительного примене-
ния принципа стационарной фазы. Использовать его необходимо
осторожно, поскольку I u(t)u*(t + т)| не всегда изменяется быстро
по сравнению с ехр[/{0(0— 0(/+т)}1. Для сигналов с прямоуголь-
ной огибающей это означает, что данный принцип не даст точных
результатов для значений т, близких к началу координат, так же
как и вблизи т = ± Т. Однако поскольку функция неопределен-
. 119
ности вблизи начала координат близка к единице, в то время как
около т = ± Т она очень мала, то это ограничение не очень серь-
езно влияет на полезность принципа стационарной фазы для ана-
лиза функции неопределенности. Так как для большинства ана-
лизируемых сигналов получение точно замкнутой формы описания
9С(т, ф) практически невозможно, то принцип стационарной фазы
является очень важным для анализа и построения сигналов.
4.14. Заключение
В современной радиолокации функция неопределенности яв-
ляется основой при систематических поисках оптимальных сиг-
налов для специальных применений. В настоящей главе приведен
полный обзор, включающий вывод важных соотношений, многих
аспектов функции неопределенности и ее характеристик, которые
представляют интерес для специалиста в области построения радио-
локационных систем. Хотя в различных разделах настоящей главы
мы не раз говорили о важности оценки сигналов для конкретных
радиолокационных применений, попыток глубже исследовать эти
возможности здесь не производилось. Обсуждение различных при-
меров радиолокационной обстановки и применений сигналов дается
в последующих главах.
Было показано, что функцию неопределенности можно рас-
сматривать как меру различия, в среднеквадратичном смысле,
между сигналом s(f) и сдвинутой во времени и по частоте копией
того же сигнала. Эта точка зрения была первоначально выдвинута
Вудвордом. Желающие получить более наглядное физическое объ-
яснение аналитических методов могут использовать другой подход
к трактовке функции неопределенности, а именно считать, что
функция неопределенности соответствует частотно-временнбй
функции отклика, наблюдаемой на выходе согласованного фильтра.
Для обоих этих подходов функция неопределенности является,
очевидно, мерой способности радиолокатора к различению в прием-
нике одинаково закодированных сигналов, если они отличаются по
времени поступления и/или частотному сдвигу. Следовательно,
функцию неопределенности можно трактовать так же, как меру
того, насколько точно и неоднозначно можно оценить скорость и
дальность единственной цели, а также насколько надежно могут
быть разрешены две цели при использовании этих параметров,
Неопределенность можно интерпретировать различными путя-
ми. На рис. 4.20 иллюстрируются проблемы, относящиеся к сигналам
с однонаправленной функцией ЧМ, которые имеют неизвестный
допплеровский сдвиг. Влияние допплеровского сдвига проявляется
во введении временного смещения (или ошибки в определении
дальности) .сжатых импульсов на выходе согласованного фильтра.
Величина временного смещения относительно истинного положения
120
4XalaHaus,Aii
знание Сез ераниц * «Ь
сигнала связана с отношением величины допплеровского сдвига
к ширине полосы и типом используемой функции ЧМ. В результате
возникает так называемая неопределенность дальность — доппле-
ровский сдвиг или частотно-временная связь. Зависимость между
модуляционными характеристиками радиолокационного сигнала и
теоретическими ошибками измерения, соответствующими этому
типу неопределенности, исследуется в следующей главе, а примеры
специфических сигналов приведены в гл. 9.
Второй тип неопределенности связан с относительной величиной
и распределением во времени ложных сигналов, которые появляются
на выходе согласованного фильтра. Эти ложные сигналы могут быть
Ro-истинная дальность
Г\ R - измеренная дальность
I | AR-ошибка В определении
I | дальности, связанная с
/ | допплеровским рассогласованием
mJ линейной ЧМ AR-(7/Af)y^
лк
Рис. 4.20. Неопределенность измерения дальности, вызван-
ная допплеровским сдвигом.

вызваны искажениями в системе (это обсуждается в гл. 11) или
являются откликами согласованного фильтра на входные сигналы
с допплеровским сдвигом. В случае многих сигналов, имеющих
большой динамический диапазон, наличие ложных сигналов, по-
явление которых связано с боковыми лепестками больших сигналов,
могут быть ошибочно приняты за реальные сигналы. Этот тип неоп-
ределенности, связанной с ложными целями, может быть более
опасным, чем шумовые ложные выбросы обычного типа, так как
сигналы от ложных целей ведут себя как детерминированные.
Третья форма неопределенности связана с количеством энер-
гии, содержащейся в структуре боковых лепестков по дальности
выходного сигнала согласованного фильтра. Если энергия боковых
лепестков относительно велика и они занимают значительный вре-
менной интервал, то более слабые сигналы, расположенные на дру-
гих дальностях, могут быть замаскированы интерферирующими бо-
ковыми лепестками. Это имеет особое значение при наличии многих
отражателей и большой плотности их в пространстве наблюдения.
Этот вопрос обсуждается в гл. 10.
Наиболее важным свойством функции неопределенности яв-
ляется то, что общая потенциальная неоднозначность, измеряемая
объемом под поверхностью, порожденной этой функцией, не зависит
от типа используемых радиолокационных сигналов, если только
все сигналы нормализованы так, чтобы содержащаяся в них энер-
121
F
гия была равной. Указанный результат хорошо известен как «прин-
цип неопределенности радиолокации» 14] или как «закон сохране-
ния неопределенности» 15]. Это означает, что в случае, если раз-
работчик радиолокатора не имеет абсолютно никаких априорных
сведений о специфике использования радиолокатора или характера
окружения, то все сигналы для него одинаково хороши (или плохи).
Однако каждый из сигналов будет давать различное распределение
неопределенности, как это было показано на примере распределе-
ния неопределенности для некоторых основных сигналов на
рис. 4.3 (так же как и другие примеры, рассмотренные в разд. 4.12).
Именно эти изменения в распределении неопределенности сов-
местно с грубыми, прикидочными оценками радиолокационной
системы и поддерживают нашу надежду, что разработчик радио-
локационной системы может в результате систематических поисков
найти подходящий сигнал.
Предпочтительной процедурой могла бы быть процедура под-
бора распределения неопределенности таким образом, чтобы обла-
сти максимальной потенциальной неопределенности попадали туда,
где параметры цели (задержка или частотный сдвиг) не ожидаются,
с последующим нахождением передаваемого сигнала по этому
распределению при помощи теоремы единственности1. К сожалению,
это потребует знания фазовой структуры %(т, <р).
Так как эта информация обычно недоступна, относительно нее
должны быть сделаны те или иные предположения. В этом случае
у нас нет гарантий, что получающийся в результате сигнал будет
физически реализуем. Поэтому процедура, которую обычно при-
меняют, состоит в исследовании функций неопределенности набора
сигналов и выбора такого сигнала, который обеспечивает наилуч-
шее приближение (после соответствующего выравнивания масштаба
длительности и полосы частот) к заданной (желательной) функции
распределения. Степень приближения является показателем того,
насколько хорошо будет функционировать радиолокационная сис-
тема в тех условиях, из которых мы исходим. Как и при любой
неидеальной ситуации, для этого, несомненно, придется прибег-
нуть к компромиссу. Это обычно достигается при изучении функ-
ционирования и стоимости всей системы в целом.
ЛИТЕРАТУРА
*1. Р. М. Woodward. Probability and Information Theory, with Ap-
plications to Radar, Perga mon .Press, Oxford, 1953.
**2. H. Ur kowi tz,G A. Hauer, and J. F. Koval. Generalized reso-
lution in radar systems, Proc. IRE 50, № 10, 2093—2105 (1962).
1 Области потенциальной неопределенности также определяют области
дальностей и допплеровских сдвигов, где интерферирующая энергия других
сигналов будет оказывать наиболее серьезное воздействие на характеристики
обнаружения.
122
ftaltfflauswk
знание без границ « *
3. J. V i 1 1 е. Theory and application of the notion of complex signal,
Cables Transmission 2, 61—74, 1948 [English Transl.: I. Selin, Rand
Rept. T-92 (August, 1958)].
4. W. M. S i e b e r t. Studies of Woodward’s uncertainty function, Mass.
Inst. Technol. Research Lab. Electronics, Quart. Progr. Rept (April, 1958).
5. С. H. W i 1 с о x. The synthesis problem for radar ambiguity functions,
Mathematical Research Center, U. S. Army, University of Wisconsin,
Madison, Wisconsin, Rept. 157 (April, 1960).
(See also: A mathematical analysis of waveform design problem. General
Electric Co., Schenectady, New York, Rept. R57 EMH54 (October, 1957).
6. C. A. S t u t t. The application of time/frequency correlation functions to
the continuous waveform encoding of message symbols, WESCON, Sect.
9/1 (1961).
7. N. DeClaris and E. T i t 1 e b a u m. Transformation of radar sig-
nals and ambiguity functions, Cornell University, Ithaca, New York, Re-
search Rept. EERL 26 (October, 1964).
8. F. B. R e i s. a linear transformation of the ambiguity function plane,
IRE Trans. (Correspond.) IT-8, 59 (1962).
9. C. S. S о г к i n. The theoretical design of waveforms for pulsed radar,
General Atronics Corporation, Bala Cynwyd, Pennsylvania, Rept. 770—
270—11 (July, 1960).
*10. J. R. Klauder. The design of radar signals having both high range
resolution and high velocity resolution. Bell System Tech. J. 39, 809—820
(1960).
11. D. G a b о r. Theory of communications. J. IEE (London) 93, 429—457
(1946).
12. R. P r i c e and E. M. H о f s t e t t e r. Bounds on the volume and height
distributions of the ambiguity function. IEEE Trans. IT-11, 207—214
(1965).
*13. С. M. H e 1 s t г о m. Statistical Theory of Signal Detection. Pergamon
Press, Oxford, 1960.
14. R. M a n a s s e. The use of pulse coding to discriminate against clutter,
Mass. Inst. TechnoL, Lincoln Lab., Lexington, Massachusetts, Group
Rept. 312—12 (August, 1957).
15. E, C. W es t e r f i e I d, R. H. P r a ger, and J. L. Stewart. Processing
gains against reverberation (clutter) using matched filters, IRE Trans.
IT-6, 342—348 (1960).
16. M. В e r n f e 1 d. Selection of appropriate signals by their ambiguity
functions, Unpublished notes.
47. E. J a h n к e and F. E m d e. Tables of Functions. Dover, New York,
1945.
* *
*
1. Вудворд. Теория вероятности и теория информации с применениями
в радиолокации, изд-во «Советское радио», 1955.
10. К л а у д е р. «Зарубежная радиоэлектроника». 1961, №1, стр. 50.
13. X е л с т р о м. Статистическая теория обнаружения сигналов, Изда-
тельство иностранной литературы, 1963.
17. Янке и Э м д е. Таблицы функций с формулами и кривыми, Физ-
матгиз, 1959.
ГЛАВА 5
ОЦЕНКА ПАРАМЕТРОВ
5.1. Введение
В гл. 1 было установлено, а в гл. 2 показано, что согласованная
фильтрация представляет собой наилучший метод обработки вход-
ных радиолокационных сигналов при наличии белого гауссова
шума, если целью обработки является получение сигнала, обеспе-
чивающего оптимальное принятие решения об обнаружении (от-
сутствие или наличие цели). Далее было показано, что согласован- ,
ная фильтрация представляет собой и наилучший метод обработки
тех же самых входных сигналов для получения максимально точ-
ных оценок (измерений) дальности, скорости и т. д., а также й для
эффективного разрешения множественных целей. Меры качества
такого разрешения обсуждаются в гл. 4.
Проблема оценки параметров, рассматриваемая в настоящей
главе, требует использования концепций, полученных в области
теории статистических оценок. Так, например, неравенство Кра-
мера — Рао применяется для получения границ минимальных
ошибок измерения, выраженных через некоторые основные пара-
метры радиолокационного сигнала, такие, как длительность, ши-
рина полосы и функция модуляции фазы или частоты. Интересно
отметить, что при определении границ минимальных ошибок можно
обойтись без детального описания конкретного метода обработки
сигналов. Однако оказывается, что метод максимального правдо-
подобия, который, как показано в гл. 2, реализуется с помощью
согласованного фильтра, приводит к ошибкам измерения, дости-
гающих границы Крамера — Рао при больших отношениях сиг-
нал/шум на выходе согласованного фильтра. Это последнее условие
обычно предполагается выполненным при исследовании проблем
оценки параметров.
Как будет показано в последующих разделах, вывод неравенства
Крамера — Рао зависит от условий регулярности, которым должен
удовлетворять сигнал. Однако для большинства сигналов, исполь-
зуемых в системах с согласованными фильтрами, огибающие которых
или функции фазовой модуляции не являются гладкими (т. е. имеют
124
^alaHausA
знание без границ Ч
прямоугольный вид), эти условия не удовлетворяются. Рассмотре-
ние этой проблемы по отношению к практически используемым
сигналам проводится в гл. 9, где результаты настоящей главы
применены к некоторым сложным сигналам с фазовой и частотной
модуляцией. Концепции классической теории оценки параметров
могут быть ценным методом получения сравнительных точностей
измерений для различных типов сигналов, если есть уверенность
в применимости их для данной задачи.
5.2. Параметры радиолокационного сигнала
I
Наряду с обнаружением отраженных от цели сигналов не
менее важной функцией радиолокационной системы является из-
влечение из отраженного сигнала информации, которая может быть
использована для определения дистанции до цели в пределах прямой
видимости, называемой дальностью, скорости цели и иногда ее
ускорения. Возможность вычислять эти параметры цели по отра-
женному сигналу объясняется влиянием, которое они оказывают
на переданный сигнал после его отражения целью.
Дальность цели определяется путем измерения времени между
моментом передачи радиолокационного сигнала и приемом отра-
женного. Если обозначить через s(/) передаваемый радиолокацион-
ный сигнал, начинающийся в момент t = 0, то s(/ — /0) будет отра-
женным радиолокационным сигналом, где t = /0 — время распро-
странения от передатчика до приемника. Связь между дальностью
R и t — t0 задается соотношением
/?-=с/0/2, (5.1)
где с — скорость распространения электромагнитных волн. Мно-
житель 2 введен в соотношение из-за того, что электромагнит-
ная волна проходит путь, равный удвоенной дальности.
Возможность определения скорости основана на использовании
воздействия эффекта Допплера. Для класса узкополосных сигналов,
к которому в общем случае относятся радиолокационные сигналы,
этот эффект обычно аппроксимируется смещением частоты отно-
сительно несущей переданного сигнала; существуют, однако, неко-
торые эффекты второго порядка, которые воздействуют на сигнал,
обсуждаемые в гл. 4. Мы предполагаем, что они пренебрежимо
малы для большинства основных радиолокационных применений.
Узкополосный сигнал может быть описан уравнением
s (/) - а (0 cos К14- О (ОЬ (5.2)
где огибающая а(/) и функция модуляции фазы 0(1) изменяются
медленно по сравнению с со» Несущая частота обозначается
126
через f0, где fo=<°o/2n. Влияние движения цеди на сигнал можно
записать в виде
sd (0 - а (П cos 12л (/0 + Ф) 14 0 (/)], (5.3)
где ф — допплеровский сдвиг частоты. С другой стороны, если
спектр передаваемого сигнала s(t) обозначить через S(f), то S(f 4- ф)
будет спектром отраженного радиолокационного сигнала. Связь
между скоростью и и допплеровским сдвигом ф задается соотно-
шением
v - сф/2/0. (5.4)
Заметим, что когда цель движется к радиолокатору, то допплеров-
ский сдвиг положителен, а когда в противоположном направлении,
то отрицателен.
Возможность определения ускорения цели в отличие от ука-
занных параметров не может основываться на использовании един-
ственного параметра сигнала. Воздействие ускорения цели при-
водит к искажению структуры сигнала. Вид и степень этого иска-
жения будут зависеть от структуры сигнала в течение передачи,
а также и от величины ускорения цели, Например, в случае простого
импульса с синусоидальным заполнением искажение проявляется
частично в виде появления дополнительного слагаемого с ЛЧМ.
Для большинства возможных ситуаций величина искажений
одиночного отраженного сигнала в результате ускорения цели будет
относительно мала» Следовательно, в случае цели с ускорением
обычно необходимо обработать более одного эхо-сигнала. Тогда
здесь лучше будет, видимо, выполнить косвенное извлечение данных
об ускорении путем вычислений, которые основаны на выборках
измерений дальности или скорости. В настоящей главе мы рассмат-
риваем возможности теоретической оценки параметров цели, осно-
ванной на информации, которая может быть извлечена из одиноч-
ного отраженного сигнала. Поэтому дальнейшее изложение не
будет затрагивать вопросы, связанные с определением ускорения
цели.
5.3. Проблема оценки параметров
Наличие шума в радиолокационном приемнике будет всегда
мешать получению точной оценки временного и частотного поло-
жения отраженного радиолокационного сигнала. В наилу чшем
случае значения параметров, которые получены при измерении
сигнала (в присутствии шума), представляют собой лишь оценки этих
параметров. Если все остальное зафиксировано, то эти оценки будут
изменяться случайным образом около истинных значений пара-
метров, как показано на рис. 5.1.
126
ftalaHauswk
знание без границ Ч *
Задачей радиолокационной системы является извлечение мак*
симально возможной информации об этих параметрах из входных
радиолокационных данных, что позволит получить наилучшие
оценки. Мерой качества оценки обычно является дисперсия ошибки,
так что слово «наилучшая» понимается в смысле минимальной дис-
персии ошибки относительно истинного значения параметра. В этой
главе дисперсия ошибки будет рассматриваться как мера качества
оценки. Следует, однако, заметить, что существуют другие точки
зрения относительно интерпретации слова «наилучший»; самым
Рис. 5.1. Пример дисперсии оценок при одновременном
измерении дальности и скорости.
Истиннные аиачення равны /, и соответственно.
общим является, по-видимому, подход Вальда, который использует
среднюю стоимость ошибки. Анализ этого подхода читатель может
найти в работах Хельстрома [1] или Миддлтона 12]. Другие/точки
зрения содержатся в интерпретации, основанной на теории ин-
формации, данной Вудвордом и Дэвисом 13] и Вудвордом 14], кото-
рая кратко обсуждается в гл. 2. ,
Наименьшую возможную дисперсию ошибки можно выразить
через эффективные меры таких параметров сигнала, как ширина
полосы и длительность.-Это может быть выполнено безотносительно
к методу обработки сигналов, который обеспечит наибольшую ин-
формацию о частотном и временнбм положении радиолокационного
отраженного сигнала. Указанные дисперсии, как будет показано
позднее, также зависят от отношения сигнал/шум в момент оценки
и от статистической связи между ошибками. Постоянно возрастаю-
щие требования к точности радиолокационных измерений, особенно
при наблюдении космических объектов и ракет, привели к тому,
что выражения для предельных дисперсий ошибок приобрели боль-
шое значение в теории построения радиолокационных сигналов.
127
5.4. Неравенство Крамера — Рао [5]
Неравенство^ Крамера — Рао устанавливает нижнюю границу
для дисперсии ошибки оценки параметров безотносительно ис-
пользуемого метода оценки. В настоящем разделе вывод этого не-
равенства будет проведен для случая единственного неизвестного
параметра. Позднее более общий результат, полученный Крамером,
применяется в специальном случае одновременной оценки радиоло-
кационных параметров дальности и скорости.
При единственном неизвестном параметре 6 неравенство имеет
вид
[ dm (6) ~|2
£•{(&—О)2) > ----------------Lf«J-----------------, (5.5)
ОО 4'00
I ( (dlogp(x; е) V - \ -
| •" 1 I-------------- p(x;e)dx
J J X W /
—оо —оо
где Е { } обозначает математическое ожидание, а 6 и 6 — соответ-
ственно неизвестный параметр и его оценку1, которая представляет
собой некоторую функцию статистических выборок х = xlt х2.........хп.
Кроме того, гп(О) есть среднее значение 0, которое в общем случае
будет некоторой функцией неизвестного параметра; когда щ(6) = 0,
то оценка называется несмещенной. Обозначение р(х; 0) представ-
ляет совместное распределение вероятностей случайной пере-
менной х при заданном неизвестном параметре. Оно называется
функцией правдоподобия и обозначается как Цх', 0), если х задано,
а 0 рассматривается как переменная. В действительности нера-
венство (5.5) корректно установлено через функцию правдоподобия.
Для того чтобы определить условия, при которых неравенство
(5.5) справедливо, и описать различные классификации оценок
параметров, приведем некоторые существенные этапы доказательства
этого неравенства, выполненного Крамером. Пусть статистическим
описанием оценки 0 служит р(0, 0); тогда
4’00
m(0) - бр(0; 0) do. (5.6)
—оо
Это равенство может быть переписано в следующем виде:
-1-00
m (0) = О -Ь $ (0 — 0) р (0; 0) dQ. (5.7)
—оо
1 Обобщенный параметр 0 не следует путать с 0(0 — обозначением
функции фазовой модуляции.
128
ftatafiausW
знание без границ * *
Интегральная часть этого выражения представляет собой смеще-
ние оценки. Выше мы уже указывали, что если эта часть равна
нулю, то оценка называется несмещенной. Сейчас для установления
условий регулярности вычислим производную от /п(в):
( (е — 0) др-& е) d0. (5.8)
d0 J 00
— OQ
Замечая, что
= (5.9)
dx v dx
перепишем (5.8) в виде
= J (O'-0) p(6; 0) 40. (5.10)
—oo
Уравнение (5.10) может быть представлено как
f (6-0)ГРde, (5.11)
—сю
где вместо р (0; 0) использовано р. Возводя обе части этого ра-
венства в квадрат и применяя неравенство Шварца, можно пока-
зать, что
-) оо -| оо
В соответствии с неравенством Шварца равенство в (5.12) имеет
место тогда и только тогда, когда существует некоторая вели-
чина К (6), такая что
= К(О)(б—0). (5.13)
Оо
Далее, если непрерывная плотность вероятности р (х; 0) может
быть единственным образом описана с помощью нового набора
случайных переменных, таких, что
р (х; 0)|/|= р(«; 0) р(у/б; 0), (5.14)
где |/| есть якобиан преобразования и б,у = уХ1 уг, ..., уп_\—
новый набор случайных переменных, то с целью определения
условий регулярности может быть показано, что
j ^.1прЯ о)^р (7. 0)d7= J р (й; 0) (5.15)
оо —сю
129
если р(у/&, б) не зависит от 0 для всех точек, для которых
р(ё;в)>о. Подставляя этот результат в (5.12) и замечая, что
первый интеграл в правой части (5.12) равен Е ((ё— 0)2], завер-
шаем доказательство уравнения (5.5).
Оценка 0 является регулярной оценкой 0, если р (х; 0) может
' быть записана в терминах новых случайных переменных 0, у и
удовлетворяет определенным условиям регулярности *.
Далее, оценка ё есть достаточная оценка 0, если в дополнение
к этому удовлетворяется условие, что р(у/ ё; 0) не зависит от 0 для
всех точек таких, что р(0; 0)>О. В таком случае оценка суммирует
всю полезную необходимую информацию, содержащуюся в выборке
х = Хр хя.....хп относительно неизвестного параметра. Наконец,
оценка является эффективной, если она будет несмещенной и для
нее выполняются условия равенства в соотношении (5.12). Такими
услориями будут: 1) оценка является достаточной и 2) существует
такая величина К(0), что К(0) (ё — 0) = д In р(ё; 0)/д0. Эффектив-
ная оценка обеспечивает наименьшую дисперсию ошибки. Однако
жесткие ограничения для существования этой оценки редко удов-
летворяются, и поэтому используют еще и другую классификацию
оценок. Это будет оценкой, которая сходится по вероятности к не-
известному параметру, когда число независимых выборок стремится
к бесконечности, и называется состоятельной оценкой 0. Смысл
здесь в том, что для бесконечно увеличивающегося числа выборок
плотность вероятности концентрируется в окрестности 0, так что
Для любого сг>0 вероятность того, что |ё—0|<о, стремится
к единице.
Несколько более сильный класс образуют оценки, для которых
р(0; 0) асимптотически нормальна при больших п. Среди этого
класса оценки, для которых дисперсия ошибки определяется ниж-
ней границей (5.5), называются асимптотически эффективными
оценками 0. Было показано, что подход к оценке параметров, из-
вестный как метод максимального правдоподобия, очень часто
обеспечивает асимптотически эффективные оценки. Метод макси-
мального правдоподобия обладает тем свойством, что когда эф-
фективная оценка существует, то она может быть найдена с помощью
этого метода. Приведенная выше классификация, которую исполь-
зует Крамер 15], была впервые введена Фишером 16], создавшим
теорию статистических оценок.
1 См., например, Б. Л. Вандер Варден. Математическая стати-
стика. Издательство иностранной литературы, 1960, или Г. Крамер. Мате-
матические методы статистики. Издательство иностранной литературы, 1948.
(Прим, ред.)
130
'iSatatfaus^
знание без границ * *
5.5. Пространство выборок
При последующем применении неравенства Крамера — Рао
и обсуждении метода максимального правдоподобия будет пред-
полагаться, что шум имеет гауссово распределение вероятностей и
одностороннюю спектральную плотность мощности, которая одно-
родна на интервале \f — /0| < №72 и равна Л/о. Наряду с этим
будем также предполагать, что ограниченный по полосе сигнал
может быть точно представлен на интервале Т конечным
числом отсчетов, размещенных на расстоянии 1/UZ друг от друга.
Так как в дальнейшем мы рассматриваем высокочастотные сигналы,
то каждая временная выборка будет давать два выборочных зна-
чения и всего 2WT выборок на интервале Т. Эти выборки статисти-
чески некоррелированы, а вследствие того, что шум гауссов, они
будут и статистически независимы.
<рто специальное выборочное пространство позволяет удобно
применять теорему выборок Шеннона 17]. В частности, метод взятия
выборок Шеннона будет использоваться для преобразования ре-
шений, которые появляются в форме дискретного суммиро-
вания с включением выборочных данных в интегральную форму.
С точки зрения строгого анализа эти преобразования не коррект-
ны, если только Т не стремится к бесконечности, потому что
они предполагают существование сигналов, которые одновременно
ограничены по длительности и по полосе, что теоретически невоз-
можно. Для удобства, однако, эта несовместимость игнорируется.
При более строгом анализе 18—10] теоретически возможно исполь-
зовать разложение Карунена—Лоэва, которое содержит собствен-
ные функции интегрального уравнения, ядром которого является
ковариационная функция шума.
5.6. Ошибки несмещенной совместной оценки параметров
радиолокационного сигнала
С точки зрения несмещенной совместной эффективной оценки
мы видим, что среднеквадратичная ошибка при совместной оцен-
ке двух статистических параметров 0;, / -- 1, 2, где 0; представ-
ляет временную задержку т, а допплеровский сдвиг <р задается
выражением (5], составляет
lnZ ОьОа)}8}
(5.16)
где р(бц 62) — коэффициент корреляции, отражакший статистиче'
скую связь оценок 0Х и Коэффициент корреляции определяет-
131
ся в виде
р(б,. Ог) =
/-1
' 2
п*
L/=i
772- (5-17)
В следующих разделах настоящей главы будет показано, что метод
максимального правдоподобия обеспечивает несмещенную асимпто-
тически эффективную оценку радиолокационных параметров т
и ф, когда отношение сигнал/шум становится очень большим
Функция правдоподобия
Рассмотрим конкретный пример. Пусть точечная цель переме-
щается по радиальному направлению относительно радиолокатора.
В этом случае на входе радиолокационного приемника помимо
шума будет находиться и сигнал, отраженный от цели. Как пра-
вило, описание сигнала наряду с параметрами т и ф включает и
«паразитные» параметры. В данной задаче такие параметры, содер-
жащие амплитуду и фазу сигнала, мы не будем учитывать. Это экви-
валентно предположению, что они известны и не влияют на оцен-
ку других параметров. Следовательно, общая форма сигнала на
входе приемника может быть записана в виде
х(0 = п(0+s(f,Oj, 02), (5.18)
где х(0 — сигнал на входе приемника, из которого должна быть
извлечена информация, п(0 — гауссов белый, ограниченный по
полосе шум, характеристики которого определены в разд. 5.5, и
s(/, 01. 62) — отраженный радиолокационный сигнал. Для опре-
деленности запишем s(t, 0lt 02) в виде
s(/, 0р 02) = а(/ — t)cos[2лф)(/—т)4-0(/—т)], (5.19)
где 0j и 02 заменены на т и ф.
Предполагаем, что функции х(0, п(0 и s(/) являются дейст-
вительными. Для удобства, однако, этот пример будет рассмотрен
с использованием соответствующих комплексных представлений,
предложенных Габором [11]. Таким образом, выполним следующие
подстановки:
х (/)->-у (/), n(/)->v(0, 5(/Г->ф(0^и(0ехр[/2л/о/1,
и в таком случае функция правдоподобия, выраженная через WT
комплексных выборочных значений радиолокационного входного
сигнала, определится соотношением
132
flatattauswih
знание без границ ч *•
WT
V Г 1 12М7Т/2 1 1
L(x;e„ е,)=-1- ехр—-1- 2 1Т|-*|(0».е^]*.(5.20)
[_ Zjl/V J */V
где JV = N0W. Произведя логарифмирование и взяв частную
производную по 0/, получаем
WT A.U* ‘
I-1
где Re означает действительную часть, звездочка — комплекс-
ное сопряжение. Теперь необходимо оценить величину (5.21) при
истинном значении параметра 0у. Так как коэффициент (yt — ф^)
может быть заменен на vt, то выражение (5.21) переходит в
wr ф
е. N £ ад,
(5.22)
где вертикальная черта с приписанным индексом 0/ означает,
что производная равенства (5.21) вычисляется при истинном зна-
чении параметра. Так как
£{v, v,}=0,
ч (°-
£|v'V/I = {2^
для всех i и /,
*=/=/•
» = /.
то непосредственные вычисления дают
(5.23)
Полученное выражение (5.23) представляет собой фундаменталь-
ный результат; впервые он, по-видимому, был получен Слепяном
[121. Интегральная форма равенства (5.23) может быть найдена
с помощью теоремы о выборках Шеннона. Итак, если ф (0 есть
функция с ограниченной полосой, так что
^(/) =
25(f),
О,
(5.24)
133
где S(f) есть преобразование Фурье s(0, то по теореме о выборках
получаем
I д In L
Лр(/; б’, 0°2)
дф (/; 6|. е°2)
dt, (5.25)
где производные вычисляются при истинном значении параметра.
Минимальная дисперсия ошибки измере-
ния временндй задержки
, Выражение (5.25) может быть использовано для определения
минимальной дисперсии ошибки измерения временнбй задержки.
Оно может также применяться для нахождения минимальной дис-
персии ошибки измерения допплеровского сдвига (это будет сдела-
но в следующем разделе). Читатель должен иметь в виду, что при
использовании одного лишь равенства (5.25), когда не учитывает-
ся множитель р(0ь 02), который появляется в неравенстве Краме-
ра—Рао, предполагается, что р(0ь 02) = 0 или что этот параметр
не будет измеряться, так как он известен. Последнее из этих двух
предположений представляется менее правдоподобным, чем первое;
оно означает, что мы имеем полную априорную информацию отно-
сительно этого конкретного параметра. Условия, при которых
p($i, 62) = 0, будут обсуждены в гл. 9.
Для того чтобы определить минимальную дисперсию ошибки
измерения задержки, необходимо в первую очередь отметить,
что задержанный по времени сигнал ф(0 имеет вид ф(/ — т). Таким
образом, используя правило дифференцирования сложных функ-
ций, находим, что
дх
(5.26)
Подставляя этот результат в (5.25), получаем
т- х
=4 I Ч>'(0 W (ОГ Л. (5.27)
1\ дх ) ) No J
— т
Применяя теорему Парсеваля, преобразуем интеграл в правой
части (5.27) к виду
Т оо
j (/) №* «)]' dt = - 12л/]» j /2Т tf) ¥•(/)<(/, (5.28)
о о
134
^alaHausA
знание без границ W *
где 'F(f) определяется равенством (5.24). Производя замену пере-
менных по формуле f = т) 4- /0, где f0 — центральная частота
| V |2, приводим (5.28) к виду
т
f
оо
= [2л]2 ( т]2 У (П + /о) У* (П + /о) dr) + [2nf0]2 2Е. (5.29)
-f.
Первое слагаемое в правой части этого равенства ранее использова-
лось для определения эффективной полосы 0 радиолокационных
сигналов [4]. Таким образом (5.28) принимает окончательный вид:
т
j Ф' (О 1ф* (ОГ dt = 2Е0Ч- [2л/0]2 2Е,
о
(5.30)
откуда следует
(2E/No) {₽> + [2л/о]2} ’
(5.31)
Для того чтобы получить оценку на основе (5.31), необходимо
иметь априорную информацию о фазе несущей частоты отраженного
радиолокационного сигнала, аналогично тому, как предполагалось
в первых параграфах этого раздела. Так как такая информация,
как правило, недоступна, то дисперсия ошибки будет значительно
превышать величину, которую дает (5.31), если только оценка не
усредняется по случайной фазе несущей частоты. Это эквивалент-
но выделению огибающей, которое производится после обработки
сигнала1. В этом случае дисперсия ошибки определяется формулой
£|(;-t)2i =
1
(2Е/М)₽2
(5.32)
Минимальная дисперсия ошибки измере-
ния допплеровской частоты
Для того чтобы определить минимальную дисперсию ошибки
Измерения допплеровской частоты, представим сигнал ф(/) в виде
Ф (0 = и (t) ехр [/2л (f0 4- (р) /], (5.33)
где u(t) называется «предогибающей» сигнала [13]. Отсюда по-
лучаем
/2л/ф (/). (5.34)
1 Этот вопрос рассмотрен в заключительной части разд. Б.8.
135
Подставляя этот результат в (5.25), будем иметь
0 In L \2)
ду J /

т-х
J /8Ф(0Ф*(0^.
—t
(5.35)
Выражение в правой части (5.35) ранее использовалось [4] для оп-
ределения эффективной длительности сигнала а. Напомним, что
это выражение имело вид
2Еа2 —(2л)2 j /2ф(0ф*(/)сИ.
Таким образом,
£ I / VI = 1
U 0Ф П (2£/JV0) а1
(5.36)
(5.37)
Равенство (5.37) аналогично равенству (5.32) для параметра р.
Связь между ошибками
Ошибки оценок в общем случае не будут независимы, если толь-
ко какой-либо параметр не известен априори и поэтому не измеря-
ется. Вследствие этого реальные дисперсии ошибок в общем случае
превысят те, которые задаются равенствами (5.32) и (5.37), посколь-
ку Р(еь 02) ¥= 0.
Для того чтобы выразить р(0п б2) через параметры сигнала, на-
помним, что
( a In Г dlnLI
£1 ар! ао, /
01п£ \2| Г/dlnL \2)1У2'
J£ К ае2 /)]
(5.38)
Так как знаменатель (5.38) был уже определен [см. (5.32) и (5.37)],
то задача состоит в том, чтобы выразить числитель этого выражения
через параметры сигнала. Используя (5.22), можно непосредствен-
но получить
WT •
= _L Re у —
2V ^0! йо 001 йо *
l«=l И2
(5.39)
136
NataHausii®!
знание без границ Ч *
Применяя еще раз теорему о выборках, получаем
pint pint) _ 1 СЭф*(О дф(О
Е[~ /“ТКе.]~"7ГЛ
О
(5.40)
Индексы, которые указывают, что производные должны вычислять-
ся при истинных значениях т и <р, в равенстве (5.40) для удобства
опущены, однако следует иметь в виду, что эта операция подразу-
мевается в равенстве (5.40).
Используя две формы представления ф(/), которые мы ввели
ранее, преобразуем (5.40) к окончательному виду
£{^^1 = —Г ( Л № (0 {♦* <0}'—*• (0 (01 Л. (5.41)
\ UX иф ) По I
— %
Величина ф(/) имеет общий вид
Ф (0 =- а (0 ехр [j {2nft 4- 0 (/)}]. (5.42)
Подставляя (5.42) в (5.41), получаем
Т-Х
f /|^|2[2л/4.е-(0|Л, (5.43)
( С/Т С/ф ) Nq J
где штрих обозначает дифференцирование. Этот результат может
быть представлен в виде суммы двух слагаемых
аит£|==2л г —(MV f (5>44)
( дх dtp ) Nq J Nq j
— t - X
Второе слагаемое в правой части (5.44) представляет собой первый
момент |ф(/) |2. Выбрав начало отсчета таким образом, чтобы пер-
вый момент был равен нулю, приводим выражение (5.44) к виду
£ F /е'|ф|2Л, (5.45)
( дх д(р ) Nq J
— X
Подставляя этот результат в (5.38) и используя (5.32) и (5.37),
получаем
Т-Х
Р(т, ф) = -^ [ /О'|ф|2а/. (5.46)
. .£CXJ> J
137
Вторая возможная форма записи для (5.46) может быть получена
с помощью теоремы Парсеваля и имеет вид
оо
Р (т, Ф) = f Ф' I у (/ + /о) I2 df, (5.47)
cotp J r
-f.
где Ф' (f 4- fo) есть производная преобразования Фурле фазовой
функции сигнала ф(0.
Так как результаты, полученные в данном разделе, имеют боль-
шое значение в теории построения сигналов, то мы суммируем их
для удобства ссылок при дальнейшем изложении:
1. Несущая частота
00
2£/0= J (5.48)
— оо
2. Ширина полосы
оо
2 г
J /21Ш/0)1Ч (5.49)
— оо
3. Длительность
Г 12 р
2£ 2^1 J /2|Ф(0М- (5.50)
J -ОО
4. Минимальная дисперсия ошибки измерения дальности
2 С*
°* ~ 4(2E/N0) Р’(1— р>) ’ t5,51)
5. Минимальная дисперсия ошибки измерения скорости
2 (г//о)а
°v~ 4(2Е/^)а«(1-р«) ‘
6. Коэффициент корреляции ошибок измерения (коэффи-
циент частотно-временнбй связи)
Р (Ь ф) = Т16' (/) I ф (0 |2 dt. (5.53)
EOtp v
— оо
Эти величины будут в дальнейшем рассмотрены в гл. 9, где
они используются при анализе некоторых конкретных сигналов.
138
ftataHausWil
знание без границ Ч *
5.7. Теоретическое значение эффективной полосы сигналов,
амплитудные и/или фазовые характеристики которых
имеют ступенчатую форму
I
Теоретическое значение эффективной полосы р сигнала, кото-
рая рассмотрена в разд. 5.6, определяется выражением
P2=-4f- J (5.54)
где U — спектр комплексной функции модуляции сигнала u(t) —
= a(t) ехр 1/6(01- Используя теорему Парсеваля, мы можем полу-
чить следующую альтернативную формулу:
4-00
Р2-— ~ J u*undt. (5.55)
Эта формула может быть расшифрована, если заметить, что z
ц* и" = {а" а—а2 62] + / [а2 6"+2аа' 6'] (5.56)
и что р есть действительная величина. Таким образом,
оо
₽•-- ,,'f ( (а"а-а2(0')2]Л. (5.57)
— ОО
I
Используя интегрирование по частям, получаем, наконец, выра-
жение для р2 в виде
оо
₽а = -2Ё J {!«')“ + ИТ) di.
---------------00
(5.58)
Этот результат указывает, что эффективная полоса становится бес-
конечной для сигналов, амплитудные и/или фазовые характеристи-
ки которых имеют разрывы. Заметим, что прямоугольные импуль-
сы всегда попадают в эту категорию независимо от вида используе-
мой функции ЧМ. Возникающие при этом проблемы и связь их с
точностью измерений для сигналов, обрабатываемых с помощью
согласованных фильтров, обсуждаются в гл. 9.
5.8. Метод максимального правдоподобия [5]
С помощью неравенства Крамера—Рао могут быть получены
выражения для предельной точности одновременной оценки парамет-
ров радиолокационного сигнала, выраженные через эффективные
значения таких параметров сигнала, как ширина полосы и длитель-
139
ность. Это рассмотрение было проведено независимо от метода оцен-
ки параметров. Таким образом нам остается доказать применимость
методов согласованной фильтрации для «наилучшей» оценки пара-
метров. Так как определение «наилучшей» в этой главе нами ранее
трактовалось в смысле минимума дисперсии ошибки, то примени-
мость будет доказана с помощью подхода, основанного на методе
максимального правдоподобия, ввиду того, что он обеспечивает
асимптотически эффективные оценки (см. разд. 5.4) для больших
отношений сигнал/шум в том случае, если шум имеет гауссов
характер.
Метод максимального правдоподобия является, вероятно, наи-
более общим методом оценки неизвестных параметров, которые
должны быть определены, с тем чтобы составить полное статистиче-
ское описание бесконечного множества случайных величин. Так как
общая постановка проблемы оценки параметров включает в себя
оценку нескольких неизвестных параметров, то метод максималь-
ного правдоподобия требует одновременного решения такого числа
уравнений, которое равно числу оцениваемых параметров. Эти урав-
нения имеют вид
.^.Uo) =0 , = 12.....т, (5.59)
dvi
где через L обозначена функция правдоподобия (см. разд. 5.3),
которая описывает изменение заданного распределения совмест-
ной вероятности р(х; 0) в данной точке выборочного пространства
х' = Xi, %2, ..., х’п через набор параметров 0 = 0Ь 02, ...» 0lt...
..., 0т. Так как In L и L достигают своего максимального значения
при одних и тех же значениях 0, то для удобства система (5.59)
заменяется системой
^ = 0. (5.60)
В данный момент графическая иллюстрация, возможно, помо-
жет читателю лучще представить себе сущность метода максималь-
ного правдоподобия. Предположим, например, что нам нужно
оценить среднее значение бесконечного множества случайных ве-
личин, имеющих гауссово распределение. Обозначим его через т.
Если одна величина представляет собой выборочное значение из
этого множества, то в соответствии с методом максимального прав-
доподобия она должна использоваться как оценка среднего зна-
чения, поскольку максимальная точка гауссового распределения
вероятности может быть выбрана таким образом, что попадет в эту
выборочную точку. Читатель заметит, что среднее значение гауссо-
вого распределения совпадает с точкой, в которой оно имеет макси-
мальное значение. Дисперсия ошибки для этой оценки среднего
140
вероятности, обозначаемое как
Рис. 5.2,. Графическая иллюстрация
оценки по критерию максимального
правдоподобия для двух выборок.
значения равна, очевидно, дисперсии о2 рассматриваемого мно-
жества величин.
Можно уменьшить дисперсию ошибки оценки, используя до-
полнительные выборочные значения множества в качестве основы
для оценки среднего значения. Предположим теперь, что из множе-
ства взяты две выборки, обозначенные через х[ и х2 соответственно.
Эти выборки можно рассматривать как реализации случайных
переменных хг и х2 соответственно. Такие случайные переменные
имеют распределение совместной
р(хх, х2; т). Оно может быть
представлено как поверхность
над координатной плоскостью,
на которой лежат координаты
хг и х2. Более того, две выборки
х\ и х2 являются координатами
некоторой точки на этой плос-
кости. Так как обе случайные
переменные имеют одно и то же
среднее значение т, то на коор-
динаты максимального значения
гауссовой 'поверхности теперь
накладывается ограничение, что
эта точка должна лежать на пря-
мой линии, определяемой урав-
нением хг — х2.
В соответствии с методом максимального правдоподобия оцен-
ка среднего значения получается из набора координат (т, т)
максимума поверхности, которая максимизирует распределение
совместной вероятности р(хх; х2; т) выборочной точки (хь х2).
Так как гауссова поверхность обладает симметрией вращения, то
координаты максимума поверхности, который максимизирует
р(х], х2; т), будут лежать, как показано на рис. 5.2, на пересече-
нии перпендикуляра, опущенного из выборочной точки (xj, х2) на
прямую хх = х2, с этой прямой.
Теперь мы можем выразить координаты максимума поверх-
ности, который максимизирует р(х\, х2; т) через координаты выбо-
рочной точки (xi, х2). Чтобы сделать это, достаточно просто выра-
зить длину линии хх = х2 до точки (т, т) через Xi и х2 и с другой
стороны через т. Оценка получается в том случае, если приравнять
эти величины друг к другу. Длина линии, выраженная через xi
и х2, равна
/? = у=-(х1+Х2), (5.61)
где множитель 1/J/2 есть направляющий косинус прямой. С дру-
141
гой стороны, длина отрезка прямой, выраженная через /и,
равна
R=V~2m. (5.62)
Следовательно, оценка среднего значения есть
Этот результат, конечно, хорошо известен. Нетрудно определить,
что дисперсия ошибки для такой оценки среднего значения рав-
на о2/2.
Отметим, что в данном конкретном случае метод наименьших
квадратов при оценке среднего значения дает тот же самый резуль-
тат. Оценка среднего значения с помощью метода наименьших
квадратов получается путем минимизации расстояния между выбо-
рочной точкой (xi, хг) и точкой (щ, т), определяющей максимум
поверхности. Однако эти два метода оценки параметра не всегда
дают одну и ту же оценку; это зависит от структуры совместной
вероятности.
Для того чтобы завершить графическую иллюстрацию метода
максимального правдоподобия, увеличим число выборочных зна-
чений до п. В этом случае ограничения, накладываемые на распо-
ложение максимума гиперповерхности для соответствующего мно-
гомерного гауссового распределения вероятности, будут иметь
вид Xj. = х2 — ... — хп. В соответствии с этим длина многомерной
линии составит
/? = ——* [xi 4-Х2+ •••
Уп
(5.64)
где, как и прежде, 1/у7Гесть направляющий косинус этой линии.
С другой стороны,
(5.66)
R = Y п т. (5.65)
Следовательно,
а х । + х2 + ... 4- хп
tn —----------------.
П
откуда нетрудно найти, что дисперсия ошибки равна о2/п.
Прежде чем перейти к рассмотрению специфических радио-
локационных задач, приведем формальный вывод для этой конкрет-
ной оценки. Однако для согласования этого вывода с последующим
рассмотрением удобнее несколько видоизменить постановку за-
дачи. Будем теперь предполагать, что нам необходимо оценить
неизвестный уровень постоянного напряжения, которое поступает
на вход приемного устройства совместно с белым гауссовым шумом.
142
^alallauswk
знание без ераниц * *
Нетрудно заметить, что обе-эти задачи эквивалентны. В последнем
случае, однако, п выборок будут представлять собой независимые
наблюдения временнбй последовательности1.
Пусть V есть неизвестный уровень постоянного напряжения,
тогда для независимых наблюдений временнбй последовательности,
обозначенных как х = xlt х2, ...» xt, ...» хп, причем выборки бе-
рутся в той последовательности, в которой они появляются, функ-
ция правдоподобия имеет вид
2WT
L = Д ехр ’ (5’67)
где о* = N0W, a No и W — плотность мощности шума и ширина
полосы соответственно. Вычислим логарифм этого выражения In L
и продифференцируем его по V, что даст
= (5.68)
Приравняв это выражение к нулю и разрешив его относительно
V, получаем оценку в виде
V=—— Ух (5.69)
2WT '
Нетрудно определить дисперсию этой оценки; она равна
е1(0-у)2|=^ = ^
(5.70)
Возвращаясь теперь к специфической радиолокационной за-
даче, предположим, что напряжение V есть некоторая заданная
функция времени, которая полностью известна, за исключением
ее временнбго и частотного расположения. Это напряжение будем
обозначать через s(f; 0lt 02) и считать, что оно представляет собой
отраженный радиолокационный сигнал. Как и в предыдущем
разделе, мы далее будем использовать Для удобства комплексное
представление s(t; 0Ь 02).
В графическом представлении последовательность входных
данных сводится к выборочной-точке в 2№Т-мерном пространстве.
Для случая единственного неизвестного параметра расположение
точек, которые связаны ограничениями, накладываемыми на мак-
симум гиперповерхности, определяет некоторую многомерную кри-
вую. Каждая точка на этой дуге определяет единственное значение
1 Временная последовательность определяется как одна из форм пред-
ставления стохастических процессов.
143
параметра. В случае двух параметров расположение точек, которые
связаны ограничениями, накладываемыми на максимум гиперпо-
верхности, определяет поверхность. Каждая точка на этой поверх-
ности представляет единственный набор значений параметров. Та-
кой подход может быть расширен на любое число неизвестных па-
раметров.
В отличие от предыдущего случая оценки параметров радиоло-
кационного сигнала нельзя получить точно через 21VT выборок
входной последовательности сигналов. Для оценки этих параметров
надо определить положение (на некоторой кривой, поверхности
или гиперповерхности в зависимости от конкретного рассматривае-
мого случая) максимума многомерного гауссового распределения
и максимизировать функцию правдоподобия. По существу, для это-
го необходимо вычислить корреляцию набора измерения выбороч-
ных значений с различными наборами выборочных значений для
всех возможных отраженных сигналов при отсутствии шума.
Соображения, приведенные в последнем параграфе, представ-
ляют собой эвристическое доказательство целесообразности приме-
нения согласованной фильтрации, так как обработка с помощью
согласованного фильтра эквивалентна корреляционной обработ-
ке (см. гл. 2). Аналогично рассмотренному выше примеру можно
получить и формальное доказательство этого результата. Исполь-
зуя комплексное представление сигнала, которое введено в
разд. 5.6, из равенства (5.20) получаем выражение для функции
правдоподобия:
, р . qWZr 1-1
Ь (х; 0х, 02) == —— ехр У 1?/—Ф/(0ц 62) |2. (5.7Г)
L zn/v j z/v j
С помощью равенства (5.71) нам необходимо составить набор пара-
метров 0Х и 02, определяющих временное и частотное положение
отраженного радиолокационного сигнала, которые максимизируют
L(x; 0Х, 02). Как было ранее замечено, независимо от того, где рас-
положен максимум L (х; 0ъ 02) в координатах 0Х и 02, максимум
логарифма In L расположен в той же самой точке. Следовательно,
lnt = -W'rin2«JV--l- У 1т,-(в,.е,)|«. (5.72)
2N
1 =!
Первое слагаемое в правой части (5.72) не зависит от параметров
0Х и 02 и, следовательно, его можно опустить. Далее, второе слагае-
мое в правой части (5.72) может быть записано в виде
WT WT
/=1 /=1
+ii v<^(ebe*)-
(5.73)
144
^ataHausiill
знание без границ Ч *
Первые два слагаемых в правой части уравнения (5.73) не зависят
от оцениваемых параметров и также могут быть опущены. Следо-
вательно, необходимо сосредоточить внимание на последнем слагае-
мом. Если учесть знаки всёх слагаемых в (5.73), то становится оче-
видным, что функция правдоподобия будет достигать максимума,
когда это слагаемое максимизировано по отношению к параметрам
0Х и 02. Математическая операция, которую описывает слагаемое,
представляет собой вычисление корреляции между входным сигна-
лом у, и сигналом фо изменяющимся в зависимости от 0Х и 62. Тем
самым мы получили формальное доказательство необходимости
применения согласованной фильтрации.
При этом рассмотрении игнорировался тот факт, что амплиту-
да, так же как и фаза принимаемого радиолокационного сигнала,
обычно не известна. Поскольку эти параметры не несут полезной
информации о положении цели, но могут влиять на точность оцен-
ки важных параметров, то, следовательно, необходимо учесть их
наличие путем включения в исходное определение функции правдо-
подобия. Учет этих «паразитных» параметров будет, естественно,
влиять на вид обработки, которую следует использовать. Было
показано, что включение указанных факторов изменяет предвари-
тельно рассмотренную методику обработки сигналов; в этом случае
выходной сигнал согласованного фильтра должен быть подан на
квадратичный детектор [9, 10, 14—16]. Максимальное значение
сигнала на выходе детектора при этом равно
WT 2
-у Sb’f'C'ei.ej. (5.74)
и используется для определения оценок 0Х и 02. На основе указан-
ного метода оценки параметров была получена линейная аппрокси-
мация дисперсии ошибок измерений, которая справедлива для
больших отношений сигнал/шум [9,10]. Этот результат может быть
выражен посредством функции неопределенности следующим обра-
зом:
£|(о;-еу)(0Л-еЛ)|=мА, (5.75)
где Mjh — элементы матрицы моментов ошибок, которые могут
быть определены через элементы обратной матрицы моментов
<5-76>
где индекс jk обозначает различные комбинации т и ф. Непосред-
ственная подстановка выражения для %(т, ф) в виде
оо
X (т» ф) = J и (/) и* (/ + т) ехр [—/2лф0 dt, (5.77)
— оо
где ф (0 = и (0 ехр [/2л/0 0 и и (0 = а (0 ехр 1/0(0],
6 Зак. 1341 145
приведет к получению тех же результатов, которые даны в конце
предыдущего раздела. Нетрудно заметить, что члены обратной
матрицы моментов ошибки являются коэффициентами при членах
второго порядка разложения %(т, <р) в ряд Тейлора [14]. Они были
определены в разд. 4.9.
ЛИТЕРАТУРА
•1. С. W. Н е 1 s t г о m. Statistical Theory of Detection. Pergamon Press,
Oxford, 1960.
•2. D. M i d d 1 e t о n. Introduction to Statistical Communications. McGraw-
Hill, New York, 1960.
3. P. M. Woodward and I. L. D a v i e s. A theory of radar information,
Phil. Mag. [7] 41. 1001—1017 (I960).
•4. P. M. Woodward. Probability and Information Theory with Appli-
cations to Radar. Pergamon Press, Oxford, 1953.
•6. H. C r a m e r. Mathematical Methods of Statistics. Princeton Univ. Press,
Princeton, New Jersey, 1946.
6. Полный список работ Фишера можно найти в библиографии к работе
Крамера |Б].
*7. С. A. Sha n no n. Communications in the presence of noise. Proc. IRE
37, 10—21 (1949).
•8. W. B. Davenport and W. L. Root. Random Signals and Noise,
McGraw-Hill, New York, 1948.
9. E. J. Kelly, I. S. R e e d, and W. L. R о о t. The detection of radar
echoes in noise. Parts I and II, J. Soc. Indust. Appl. Math. 8, 309—341,
481—507 (1960).
*10. E. J. К e 1 I y. The radar measurement of range velocity and acceleration,
IRE Trans. MIL-5, 51—57 (1961).
11. D. G a b о r. Theory of communications, J. Inst. Elec. Engrs. (London) 93,
Part III, 429—457 (1946).
12. D. S 1 e p i a n. Estimation of signal parameters in the presence of noise,
IRE Trans. IT-3, 68—89 (1954).
13. J. D u g u n d j i. Envelopes and pre-envelopes of real waveforms, IRE
Trans. IT-4, 53—57 (1958).
14. R. M a n a s s e. Range and velocity accuracy from radar measurements,
Mass. Inst. Technol., Lincoln Lab., Lexington, Massachusetts, Group Rept.
312—26 (February, 1955).
15. P. S w e r 1 i n g. Parameter estimation accuracy formulas, IRE Trans.,
IT-10, 302—314 (1964).
16. P. В e I I o. Joint estimation of delay, Doppler, and Doppler rate, IRE
Trans. IT-6, 330—341 (1960).
* *
*
1. Хелстром. Статистическая теория обнаружения сигналов, Издатель-
ство иностранной литературы, 1963.
2. Миддлтон. Введение в статистическую теорию связи, изд-во «Совет-
ское радио», 1962.
4. В у'д в о р д. Теория вероятности и теория информации с применениями
в радиолокации, изд-во <Советское радио», 1955.
Б. Крамер. Математические методы статистики. Издательство иностран-
ной литературы, 1948.
7. Шеннон. Работы по теории информации и кибернетике. Издательство
иностранной литературы, 1963.
8. Д а в е и п о'р т и Рут. Введение в теорию случайных сигналов и шу-
мов. Издательство иностранной литературы, 1960.
10. Келли. «Зарубежная радиоэлектроника», 1962, №2.
^alaHaussk
знание бег границ Ч
ГЛАВА 6
ЛЧМ СИГНАЛ И СОГЛАСОВАННЫЙ ФИЛЬТР
6.1. Введение
В гл. 1 с^помощью приближенных интуитивных рассуждений
были определены связи между характеристиками ЛЧМ сигнала и
согласованного фильтра, который осуществляет сжатие этого сиг-
нала. В гл. 3 рассматривался принцип стационарной фазы, который
помог нам расширить интуитивные рассуждения, с тем, чтобы они
охватывали более широкий класс кодированных сигналов, имею-
щих вид
s (/) = a (/) cos [<о01 + 6 (/)]. (6.1)
В этой и последующих главах более подробно будут рассмотрены
проблемы, связанные с согласованной фильтрацией ЛЧМ сигна-
лов, с точки зрения их использования в радиолокационных систе-
мах. Укажем на две основные причины, ^обусловливающие такой
подход:
1. ЛЧМ сигнал может быть использован в большинстве прак-
тических систем, поскольку он обладает рядом весьма полезных
свойств (включая простоту реализации) и, таким образом, важен
по своей сущности.
2. Подробное изучение свойств этого вида сложных сигналов
создает основу для изучения и сравнения свойств более сложных
по структуре сигналов, которые позволяют осуществлять сжатие
импульсов.
Таким образом, мы будем рассматривать ЛЧМ сигнал в качест-
ве характерного и полезного примера сигналов общего, более ши-
рокого класса, задаваемого равенством (6.1).
6.2. Согласованная фильтрация ЛЧМ сигнала
При обсуждении принципа согласованной фильтрации в гл. 1
было рассмотрено два основных подхода к определению характе-
ристик согласованного фильтра:
6* 147
а) Если спектр сигнала равен S(co), то частотная функция пе-
редачи фильтра Н((л), которая максимизирует отношение сигнал/шум
на выходе фильтра, представляет собой функцию, комплексно-
сопряженную со спектром сигнала, или Я((о) = S*(<o).
б) Если вид сигнала задается функцией $(/), то импульсный
отклик фильтра, удовлетворяющего условию а), равен h(t) =
= ks(—/), и вид сигнала на выходе фильтра можно найти с помо-
щью операции
ОО <
g(t)=k J s(x)s(/ — x)dx.
— оо .
Подход а) имеет значение при установлении свойств согласованно-
го фильтра, тогда как подход б) полезен в случае определения вида
сигнала на выходе согласованного фильтра.
При радиолокационных применениях удобно предположить,
что огибающая a(t) представляет собой постоянную по высоте
прямоугольную функцию. В этих условиях сигнал, формируемый
в передатчике радиолокатора, выражается как 11]
s(/) = cosj%/ + , — Т/2</<7'/2. (6.2)
Импульсный отклик фильтра, согласованного с этим сигналом,
равен
h (/) - k cos R1 — -^1, — Т/2 < t < Т/2. (6.3)
L 2 J
Если наложить условие, что коэффициент усиления согласованного
фильтра на частоте (о0 равен единице, то коэффициент k составляет
(6.4)
и сигнал на выходе согласованного фильтра имеет вид
___ +У/2
g (/) = 1/"^- f cos Lo т + ^-1 cos [<оо (/—т) — -] dx. (6.5)
г _/ j I I «ь I
— Г/2
Интегральное выражение (6.5) описывает оптимальный выходной
сигнал на выходе согласованного фильтра в смысле максимизации
отношения сигнал/шум. В реальных условиях сигнал, поступаю-
щий на вход радиолокационного приемника, не является точной
копией переданного сигнала, так как может быть подвержен раз-
личного рода искажениям. Наиболее общая форма искажений на-
блюдается в том случае, если сигнал отражается от объектов, ско-
рость перемещения которых имеет радиальную компоненту по от-
ношению к радиолокационной системе. Это приводит к допплеров-
148
знание без араниц W *
скому сдвигу центральной частоты отраженного сигнала, который
можно представить в виде
2с 2с t
(i)d= — <о0 или Ф = — fo
с с
(6.6)
где v — радиальная скорость; с — скорость света и ф = <od/2n.
Будем предполагать, что такое представление допплеровского сдви-
га полностью описывает искажение. ЛЧМ сигнала вследствие дви-
жения цели. При этом мы игнорируем некоторые эффекты второго
порядка, однако это представление является очень хорошей аппрок-
симацией произведения длительности на полосу или коэффициента
сжатия вплоть до значений 10 000. Применяя введенное прибли-
жение, запишем сигнал на выходе согласованного фильтра
__ ь
g(t,Vd) = j/ Jcos + +
a
HP-*)’.] dz,
2
(6.7)
XCOS <oo(/—т) —
Когда (dd = 0, to s(x) и /г(т) «согласованы» и g(t) есть автокорре-
ляционная функция входного сигнала. Если же o)d=^0, то g(t, wd)
будет взаимной корреляцией двух функций, представляющей
все возможные выходные сигналы согласованного фильтра при
движении отражающего объекта. Используя тригонометрическое
разложение произведения cos (a) cos (b) и замечая, что при подста-
новке его в выражение (6.7) слагаемые, содержащие высокочастот-
ные компоненты частоты (2cd0), могут быть опущены для большинст-
ва практически интересных случаев, перепишем выражение для
сигнала на выходе согласованного фильтра в виде
149
Оценивая выражение (6.9) для t > 0, получаем следующее вы-
ражение:
«1пГ<°»/+-^+-£(Т-<)]
I II J
®d + n*
Г Wd Т ц/
sin (M + o>d*— “Z-----о (г—О
L 4W X
»d + ^
Если прибавить и вычесть <od//2 в аргументе первого члена, то
получим
g (<•“«)=4-
sin Г( Ш.+ -^')/+-^(7'-O + J£(T-o|
I \ £t J Lt +t J
COd ~Ь
S "[(“•+ v) '--у(г-')-4(7’-°]
I \ “ / “ Lt J
<Od4~P^
Это выражение имеет форму
(6.И)
sin(a + P)—sin (a—0) =2 cos a sin 0,
где
«=(“»+ v)Z; ₽=^±Е'(Т-/).
\ Lt J **
Аналогичное выражение получается для /<0. Комбинируя эти
результаты, запишем сигнал на выходе согласованного фильтра

sin (Г-|< 1)1
®d + |^
(6.12)
Для частного случая <od = О равенство (6.12) сводится к определе-
нию автокорреляционной функции согласованного фильтра:
g(0= cosm„f, — T<t<T. (6.13)
Интересно отметить, что частотный сдвиг выходного сигнала
равен (od/2 при сдвиге частоты входного сигнала cud. Это можно
отнести за счет существенно прямоугольной частотной характери-
стики согласованного фильтра (как показано в следующем разделе),
которая определяет центральную частоту выходного спектра
(рис. 6.1). На рис. 6.2 и 6.3 приведено несколько примеров выход-
150
^alaHauswk
знание без границ Ч *’
u>a
Рис. 6.1. Выходной спектр,
формируемый при про-
хождении согласованного
фильтра:
a — полоса согласованного
фильтра; б — сдвинутый по ча-
стоте спектр входного сигна-
ла; с — результирующий спектр
выходного сигнала.

Рис. 6.2. Сигналы на выходе согласованного фильтра при ча-
стотном сдвиге входных сигналов.
Рис. 6.3. Вид автокорреляционных функций ЛЧМ сигналов при
ТД/ = 10 и ГД/ = 50.
Полоса нормирована, так что Af равно единице.
ных сигналов согласованного фильтра, которые показывают влия-
ние коэффициента сжатия (TAf) на вид автокорреляционной функ-
ции и на величину искажений, вызванных допплеровским сдвигом.
Искажения проявляются во временном сдвиге сигнала, уменьшении
Рис. 6.4. Рассчитанный вид
поверхности отклика для ЛЧМ
сигнала.
пиковой амплитуды и расширении импульса. Для <о(1 < Дсо/2
хорошее приближенное выражение для величины временного сдви-
га дает формула
/ __ . . ^<7 р
* р Дсо
На рис. 6.4 показана трехмерная модель (которая будет обсужде-
на ниже), иллюстрирующая влияние допплеровского сдвига на
выходной сигнал, а на рис. 6.5 приведена зависимость временного
сдвига и величины снижения амплитуды от ы(!1 Д(о или ф/Д/.
Можно заметить, что выходные сигналы согласованного
фильтра при допплеровском сдвиге ограничены треугольником с
основанием, занимающим отрезок от —Т до Т. Эта функция явля-
152
ftataHauswk
знание Вез грани» - w
ется автокорреляционной 'функцией прямоугольной огибающей
сигнала на входе согласованного фильтра, а замеченное соотноше-
ние есть одно из свойств ЛЧМ сигнала. Можно показать, что для
общего вида огибающей a(t) ЛЧМ сигналов выходные сигналы
согласованного фильтра ограничены автокорреляционной функ-
цией а(/). Для огибающей, имеющей значения от—772 до +772,
выходной сигнал идеального согласованного фильтра равен нулю
для моментов времени t < —Т и / > Т, т. е. g(t, со<;) — 0 для
\t[>T.
Во многих задачах ожидаемый диапазон допплеровских сдви-
гов составляет очень малую долю ширины полосы сигнала. В этом
случае ухудшение пиковой амплитуды выходного сигнала согласо-
ванного фильтра весьма незначительно. Таким образом, при малых
допплеровских сдвигах наблюдается лишь небольшое ухудшение
характеристик обнаружения ЛЧМ сигналов. Равенство (6.12)
определяет так называемую функцию отклика ЛЧМ сигнала. Функ-
ция отклика была введена в гл. 3 для описания характеристик со-
гласованного фильтра при наличии допплеровского сдвига частоты
входного сигнала.
На рис. 6.4 показана эта функция для ЛЧМ сигнала в виде
сложной составной трехмерной модели, характеризующей выходной
сигнал при наличии допплеровского сдвига. Форма «гребневой
линии» этой функции характеризует «неопределенность» при при-
еме только одного импульса без априорной информации о дальности
цели и ее скорости. Каждое сечение модели функции отклика пред-
ставляет собой выходной сигнал согласованного фильтра g(t, <od)
для последовательно возрастающих 'значений <od, причем любое
сечение смещено по частоте на 10% полосы сигнала, а центральное
сечение (т. е. (od = 0) представляет автокорреляционную функ-
цию.
Более подробно применение функции отклика или функции
неопределенности, которую можно рассматривать в качестве од-
ного из нескольких критериев принятия решения о ценности того
или иного конкретного сигнала, было рассмотрено в гл. 4.
6.3. Характеристики фильтра, согласованного с ЛЧМ.
сигналом
Анализ согласованной фильтрации ЛЧМ сигналов непосред-
ственно приводит к определению зависимости между сигналами
на входе и выходе согласованного фильтра в виде временных
функций. Такой анализ, однако, не дает, по существу, никаких
сведений о самом согласованном фильтре, между тем как именно
они и интересуют большинство инженеров. Для определения харак-
теристик фильтра, обеспечивающего согласованную фильтрацию,
лучше всего вернуться к основным соотношениям, полученным
153
Норсом. В соответствии с ними согласованный фильтр связан с
сигналом через передаточную функцию #(<о), которая комплексно
сопряжена со спектром сигнала. Отсюда мы делаем вывод, что при
полностью известном (идеальном) спектре сигнала мы имеем все
данные об идеальных амплитудных и фазовых характеристиках
согласованного фильтра.
Спектр ЛЧМ сигнала можно записать в виде 12—4]
7/5
С Г И*1
5(о) = J! cosI(d0/+~2-
— /•/2
ехр[—jut] dt =
(6.14)
Второй интеграл определяет спектр в области отрицательных
частот, и его влияние на спектральные характеристики в области
положительных частот пренебрежимо мало при большой величине
отношения центральной несущей частоты к ширине спектра. Су-
щественным здесь является предположение о том, что край спектра
отрицательных частот принимает исчезающе малые значения в
области положительных частот. Для достаточно больших значений
отношения ©в/А<о это предположение вполне правдоподобно и
обычно выполняется в практически работающих приемных систе-
мах. После дополнения членов в фигурных скобках в выражении
(6.14) до полного квадрата получаем следующее уравнение для
спектра:
(6.15)
Сделаем в выражении (6.15) замену переменных по формуле

(6.16)
так что
ftatattauswi',
знание безграниц Ч*
и спектр принимает вид
S(<o) = 4/^exp[-/(1^*)] f exp[/S-’px, (6.17)
—
где
цТ цТ
2 +(<0— ыо) у —1((0— (О0)
Х1 = --———, х2=--------—------
Улц
В результате получаем
S(<>)=4/vex₽
А г р», L \ / J
+ C(X2) + /S(X2)J, (6.18)
где
C(X)= C cos — dy и S(X)= fsin— dy
о 2 о 2
есть интегралы Френеля, обладающие свойством С(—X) = —С(Х)
и S(—X)= —S(X)1.
Спектр ЛЧМ сигнала обычно удобно представлять в виде
совокупности следующих трех главных компонент:
Амплитудный спектр*
| S (®) I = I ± {[С (X.) + С (Х,)]« + [S (X,)+5 (X,)]*}*'’. (6.19)
Квадратичный фазовый член
• (6.20)
Остаточный фазовый член
Ф, (ю) —arctgГs<x-)+s(Х8) 1 (6.21)
LC(X,) + C(X2)J ' '
Остаточный фазовый член Ф2 получил такое название потому, что
в общем случае при построении согласованного фильтра он опу-
скается. Для больших значений T&f
$(Хг) + $(Х2) j
С(Х1) + С(Х«)
1 Таблицы интегралов Френеля можно найти в нескольких математиче-
ских работах, приведенных в списке литературы в конце главы {5, 6].
1 При (О=(оо комбинация интегралов Френеля в равенстве (6.19) равна У^Г,
а | S (too) | = Уп/2р,. Отсюда можно найти коэффициент единичного усиле -
ния согласованного фильтра, определяемый равенством (6.4).
155
в интересующем нас интервале значений переменных. В этой области
Ф2 может быть приближенно заменено постоянным фазовым углом,
равным л/4. На рис"'6.6 показан вид функций Ф2 и |S(w)| для не-
скольких значений коэффициента сжатия. Интересно заметить,
что при замене переменных по формулам
Дсо . 2л пДсо ооч
, Л(о = — , (о — о)0=—— (о. 22)
аргумент в интегралах Френеля принимает вид
./= (6.23)
V т \ /2 / Г 7 \ /2 г
где п— теперь нормированный частотный параметр. Таким обра-
зом, спектр здесь зависит от коэффициента сжатия Т/т и (формаль-
но) не определяется конкретными значениями центральной несу-
щей частоты и ширины полосы.
Рис. 6.6. Спектр ЛЧМ сигналов при отбрасывании квад-
ратичного фазового члена.
Уже сейчас могут быть сделаны некоторые общие предположе-
ния о параметрах спектра, как это, например, проведено в следую-
щем разделе, однако для целого ряда практических применений
сложных сигналов в радиолокации важную роль играет детальная
структура спектра. Изучение этих вопросов мы отложим до гл. 7.
156
^alaHausTsk
знание без границ \ *
6.4. Сравнение идеализированного согласованного
фильтра и его практической реализации
В идеальном случае конструирование согласованного фильтра
для ЛЧМ сигнала с прямоугольной огибающей должно быть осно-
вано на использовании соотношения, которое мы приводили выше
Н (и) S* (со).
Компоненты S((d) определяются равенствами (6.19)—(6.21). Как уже
отмечалось, фазовый член Ф2 при построении фильтра можно опу-
стить. Предположим далее, что для больших коэффициентов сжа-
тия (т. е. для ТА/> 30) |S(<d)| можно приближенно заменить
прямоугольным распределением. При этом построение согласован-
ного фильтра сводится к созданию фильтра с существенно прямо-
угольной характеристикой (ширина полосы равна А/), фазовая
функция которого будет сопряженной с функцией
Фг (св) = (Р-вьР . (6.24)
2И
Согласованный фильтр должен в этом случае иметь квадратичную
фазовую характеристику
— Фх (со) = ₽z (w) = — (ю~<йо)2- (6.25)
или функцию изменения временной задержки
Т <,(<*) =
ар/
do
(D — (00
(6.26)
Для получения реализуемой задержки к величине, определяемой
равенством (6.26), необходимо добавить фиксированную постоян-
ную величину, так чтобы в ос-
новной части полосы пропуска-
ния мы получали положитель-
ные временные задержки. Таким
образом,
Td (<о) = — ^22^+ k. (6.27)
И
На рис. 6.7 показаны функции
задержки, определяемые равен-
ством (6.27), и вид кривой за-
держки, которая может быть
реализована практически.
(Функция, отражающая зави-
Снещенная идеальная
Рис. 6.7. Реализуемые характери-
стики фильтра, согласованного с
ЛЧМ сигналом.
симость задержки от частоты, называется дисперсионной функцией
задержек. Этот вопрос более подробно рассматривается в гл. 12
и 13.) Так как реализуемая линия задержки должна иметь нулевую
157
*
г
а}

S)
Рис. 6.8. Сжатие ЛЧМ сигналов в со-
гласованном фильтре:
а—ЛЧМ сигнал на входе; б —сигнал на вы-
ходе согласованного фильтра; а—сигнал на
выходе согласованного фильтра при растя-
нутой временнбй осн.
Рис. 6.9. Сигналы на выходе фильтра, согласован-
ного с ЛЧМ сигналом, при сдвиге частот^ вход-
ного сигнала wj.
158
NalaHausf№i
знание без границ Ч *
групповую задержку на нулевой частоте, то функция задержки,
которая может быть получена практически, будет в некоторой
степени отличаться от идеальной фазовой характеристики согла-
сованного фильтра. Однако, как показано на рис. 6.8, это ограни-
чение не является существенным. Вид выходного сигнала согласо-
ванного фильтра в основном подобен функции (sin х)/х и опреде-
ляется равенством (6.12). Отметим также влияние добавления по-
стоянной задержки k к линейной функции задержки.
Рис. 6.10. Блок-схема устройства для уменьше-
ния боковых лепестков сигналов на выходе со-
гласованного фильтра.
На рис. 6.9 показано влияние допплеровского сдвига, проявля-
ющееся в смещении центральной несущей частоты входного ЛЧМ
сигнала. Значительное отличие этих сигналов от сигналов вида,
данного в (6.12), проявляется в поведении боковых лепестков по
дальности. Отсюда, очевидно, можно сделать вывод, что на основа-
нии предположения о прямоугольности спектра и линейности функ-
ции задержки может быть построен фильтр, являющийся хорошей
аппроксимацией согласованного фильтра, осуществляющего сжатие
ЛЧМ сигнала.
Во многих практических случаях наличие больших боковых
лепестков по дальности у выходного сигнала ЛЧМ фильтра ограни-
чивает возможности радиолокатора по разрешению большого числа
целей при сколь-либо значительном динамическом диапазоне.
В этих случаях к согласованному фильтру добавляется схема рас-
согласования для уменьшения боковых лепестков. Пример такой
схемы приведен на рис. 6.10. При такой обработке сигнала предпо-
159
ложение о прямоугольном распределении спектра не всегда оказы-
вается справедливым; это подробнее рассмотрено в следующей
главе.
Применение систем сжатия импульсов в радиолокационных
системах определяется тем, что они функционируют как линейные
системы обработки сигналов. Очевидность этого иллюстрируется
Рис. 6.11. Разрешающая способ-
ность системы сжатия импульсов:
а — разрешение сигналов на выходе
согласованного фильтра при пере-
крытии входных сигналов; б —мини-
мальное разрешение сигналов на вы-
ходе согласованного фильтра.
на рис. 6.11, где показано, что разрешающая способность согласо-
ванного фильтра со сжатием импульсов при наличии многих целей
определяется длительностью сжатого импульса, а не входного (бо-
лее широкого). Это демонстрирует принцип суперпозиции, являю-
щийся одним из основных условий линейных систем.
6.5. Формирование ЛЧМ сигналов
Существуют два основных метода формирования ЛЧМ сигна-
лов, которые на приеме должны обрабатываться при помощи со-
гласованного фильтра с линейной функцией задержки. Первый из
них называется методом активного формирования сигнала, так как
основан на использовании управляемого по частоте генератора, уп-
равляющее напряжение для которого обеспечивает генератор со-
ответствующей модулирующей функции. Второй возможный метод
160
ftataHausifi',
знание без границ * w
известен под названием пассивного метода формирования частот-
но-модулированного сигнала, так как основным его принципом явля-
ется возбуждение импульсом схемы, сопряженной с согласованным
фильтром. Для последнего метода выходной сигнал сопряженного
фильтра можно рассматривать как импульсный отклик, который
согласован с характеристикой фильтра в приемнике.' Ниже мы
yvwvwwwvvvv
-л/ш-
низация
Рис. 6.12. Блок-схемы активного формирования ЛЧМ сигналов:
а —частотная модуляция; б — фазовая модуляция.
приведем описание некоторых методов формирования ЛЧМ сигна-
ла, хотя этр методы в несколько измененном виде могут быть при-
менены для формирования произвольных частотно-модулированных
сигналов, позволяющих осуществлять сжатие импульса с помощью
согласованного фильтра.
На рис. 6.12 показаны две схемы для активного формирова-
ния ЛЧМ сигнала. Частота управляемого напряжением генератора
на рис. 6.12, а пропорциональна напряжению на управляющем
элементе генератора, так что линейное нарастание напряжения
будет по необходимости вызывать линейное возрастание частоты во
времени. В такой схеме применен генератор с самовозбуждением,
имеющий соответствующий блок стробирования. Если необходимо
получить линейную ЧМ без искажений, то изменение частоты в ге-
161
нераторе может быть ограничено наиболее линейной частью харак-
теристики частота—напряжение. При необходимости иметь большие
значения девиации частоты можно использовать умножитель. В
генераторах такого типа могут применяться модуляторы с реактив-
ной лампой, клистроны, ЛОВ и т. д.
На рис. 6.12, б представлен второй возможный вариант схе-
мы активного формирования, в котором частота управляемого гене-
ратора пропорциональна производной напряжения на управляю-
щем элементе [7]. Таким образом, для того чтобы получить линей-
ное нарастание частоты во времени, необходим параболический или
К генератору,
управляемому
по фазе
Рис. 6.13. Две схемы формирования квадратичного управляющего
напряжения.
Приблизительно
пара бол и чес кая
форма
К генератору,
управляемому
по фазе
квадратичный закон изменения напряжения. Использование стро-
бирующих схем и умножения частоты служит для тех же целей,
что указывалось выше. На рис. 6.13 показаны две схемы формирова-
ния квадратичного напряжения для управления генератором, в
которых: 1) прямоугольные импульсы постоянной амплитуды про-
пускаются через два каскада линейного интегрирования или
2) происходит вырезание неискаженной синусоиды вблизи ее мак-
симального значёния (на этом отрезке форма кривой весьма близ-
ка к параболе) с дальнейшим линейным усилением. Обе эти схемы
позволяют получить напряжение желательной формы.
При любом из активных методов модуляции направление из-
менения частоты может быть изменено на обратное, для чего после
смесительного каскада выбирается та или иная боковая полоса вы-
ходного сигнала. Это может быть выполнено в передатчике или в
приемнике. Метод активного формирования сигнала можно приме-
нять в тех случаях, когда необходимо управление модуляционными
Характеристиками сигнала независимо от согласованного фильтра
в приемнике. Типичным примером этого является введение допол-
162
нительной функции модуляции для исключения влияния модуля-
ционных искажений, создаваемых в каких-либо каскадах передат-
чика, или формирование модифицированных линейных функций ЧМ,
рассмотренных в гл. 7. Если необходимо получить сигнал с нелиней-
ной ЧМ, то для управления переменной частотой генераторов тре-
буются другие типы генераторов управляющего напряжения.
На рис. 6.14 показаны выделенные в отдельные блоки основ-
ные элементы схемы пассивного формирования сигналов, позволяю-
щей осуществлять сжатие импульса с помощью согласованного
фильтра. Фильтр растяжения имеет дисперсионную характеристику
задержки, так что когда он возбуждается коротким импульсом,
h(t)
Фильтр рас-
тяжения Н(и>)
Фильтр
сжатия п(ш)
Рис. 6.14. Иллюстрация метода сопряженных фильтров.
то в результате на выходе фильтра появляется растянутый им-
пульс. Так как этот импульс должен переносить всю информацию,
содержащуюся в полосе узкого возбуждающего импульса, а по-
лоса растянутой огибающей значительно уже, то для передачи
информации должна быть использована частотная или фазовая
модуляция. Обозначая спектр возбуждающего импульса через S, (со),
мы можем* записать результат прохождения этого сигнала через
фильтры приемника и передатчика (пренебрегая искажениями в
среде распространения) следующим образом:
gR W = 2^ J 5‘ Н Н* ехР IMd(D =
= 7- f ИI H И I2 exp [/соП dm.
(6.28)
Если спектр gr(t) существенно прямоуголен и несколько шире
полосы пропускания //(со), то сигнал на выходе приемника за-
пишется
j | Н (со) |2 ехр [/со/] dco.
(6.29)
Тем самым мы показали возможность осуществления системы рас-
тяжения и сжатия импульса.
По практическим соображениям импульсную возбуждающую
функцию следует выбирать таким образом, чтобы основная часть
растянутого выходного импульса была сосредоточена в конечном
временном интервале. Вследствие неидеальности характеристик
задержки вне полосы частот Д/ (см. рис. 6.7) желательно также,
чтобы частотный спектр был ограничен. В силу этих соображений
импульсная функция [аппроксимированная выражением (6.12)1,
которая удовлетворяет данным условиям, имеет вид
М0 = Sinff-Lcos(°0<- (б-30)
Используя этот сигнал для возбуждения фильтра с линейной ха-
рактеристикой задержки, получаем на выходе фильтра растяжения
функцию времени вида
оо
(Н(со)5Д(о)ехр[/(о/]^о. (6.31)
—оо
Используя выражение для //(со) из (6.25)1 и применяя экспонен-
циальное представление функций, получаем
(Оо+цГ/2 2
#т(0=Цг I ехр Г/1 (м~Шо> + <i><)1d<o. (6.32)
Пределы интегрирования в этом равенстве получены в предполо-
жении, что спектр имеет прямоугольную форму в соответствии с
‘(6.30) и что ширина полосы равна р.71. Используя те же самые
выкладки, что и при нахождении спектра в разд. 6.3, преобразуем
равенство (6.32) к виду
где
Функция времени gT(t) может теперь быть записана как
gr(t}=a(t)exp / <оо/
(6.34)
1 Отметим, что мы используем представление Я (со) = ехр [ — /Р/(<о)1, а
временную задержку записываем в виде Td=dp/dw.
164
'\ataHausnk
знание без границ Ч *
Наиболее важные компоненты gT(t) могут быть представлены в
таком виде:
Огибающая
^([С(Х1) + С(Х2)Г+[5(Х1) + 5(Х2)р)1/2. (6.35)
1 г и
Функция линейной ЧМ1
d / , и/’ х
— (й01 — £— =(D0 — lit.
dt\ 2 ) ° Г
Остаточный член фазовой модуляции
02(О = —arctg
S(XQ + S(Xa)
С(Хг) + С(Х3)
(6.36)
(6.37)
Для больших значений ТА/ огибающая может быть аппроксими-
рована прямоугольной функцией, в то время как остаточный член
функции фазовой модуляции аппроксимируется постоянным фазо-
вым углом л/4. Выбор формы импульсной функции в виде (sin х)/х
приводит к тому, что растянутый импульс имеет, по существу,
амплитудные и фазовые свойства радиолокационного ЛЧМ сигнала.
На практике растянутому импульсу в дальнейшем следует придать
более прямоугольную форму с помощью ограничения и стробиро-
вания, и в результате спектр сигналена выходе передатчика будет
практически неотличим от спектра, полученного с помощью актив-
ной схемы.
Необходимая импульсная функция (sin х)1х может быть по-
лучена при пропускании узкого импульса (ширина полосы >»Af)
через полосовой фильтр с прямоугольной характеристикой (шири-
на полосы А/), который имеет линейную фазовую характеристику.
По существу, операция растягивания импульса сводится при этом
к согласованной фильтрации (сопряженной), при которой прибли-
женные характеристики выходного сигнала могут быть получены
с помощью принципа стационарной фазы. Однако равенство (6.35)
указывает, что огибающая растянутого импульса имеет френелев-
скую пульсирующую компоненту. Это может явиться весьма су-
щественным фактором, так как воздействие ограничения, которое
происходит в мощных радиолокационных передатчиках, будет при-
водить к тому, что пульсирующая структура временных функций
превращается при этом в пульсирующую структуру частотного
спектра. Воздействие этих эффектов на сжатие импульсов в радио-
локационных приемниках рассмотрено в гл. 7.
1 Характер частотной модуляции здесь противоположен характеру ча-
стотной модуляции в равенстве (6.2). Это иллюстрирует тот факт, что фильтр
сжатия, согласованный с ЛЧМ сигналом, имеющим положительный наклон
функции ЧМ, при использовании в качестве фильтра растяжения будет фор-
мировать сигнал с отрицательным наклоном функции ЧМ.
165
На рис. 6.15 приведен пример практической реализации радио-
локационной системы, содержащей сопряженные согласованные
фильтры. Система основана на преобразовании сигнала, имеющего
нечетно-симметричную функцию частотной модуляции, в сигнал,
Рис. 6.15. РЛС с согласованными фильтрами, использующая инвер-
сию полосы частот.
представляющий собой его временною инверсию. Осуществляется
это с помощью пропускания сигнала через смеситель, в котором вы-
ходная цепь настроена на разностную боковую полосу, а не на сум-
марную. Симметричная инверсия модуляции имеет место в том
А" МОЩНЫМ
каскадам
передатчика
Видеовыход
и
индикатор
Рис. 6.16. -Блок-схема системы, использующей принцип со-
пряженных фильтров с одним общим фильтром для пере-
датчика и приемника.
случае, если частота напряжения местного гетеродина, подаваемого
в смеситель, превышает любую частотную компоненту входного
сигнала. Так как такой метод приводит к появлению в приемнике
сопряженней временной функции, то фильтры, осуществляющие
166
Natifflauswil
знание без границ Ч «Ь
растяжение и сжатие сигнала, могут иметь идентичные характери-
стики, что позволяет избежать разработки двух различных филь-
тров.
На рис. 6.16 показано, как система с инверсией боковой по-
лосы может быть в дальнейшем преобразована для использования
лишь одного фильтра растяжения/сжатия, входящего как в схему
приемника, так и передатчика. Эти методы были рассмотрены Ку-
ком и Чином [8], Куком и Брокнером 19] и Рэмпом и Уингровом
ЦО]. Они могут применяться в любых системах сжатия импульсов
с помощью согласованного фильтра, которые используют нечетно-
симметричные функции частотной модуляции.
Рис. 6.17. Вид сигнале на
индикаторе типа А для си-
стемы с сопряженными со-
гласованными фильтрзми:
а —сжатые сигналы; б— несжа-
тые сигналы.
Рис. 6.18. Наложенные сжа-
тые и несжатые сигналы на
индикаторе кругового обзора.
Некоторые сложные радиолокационные сигналы, использован-’
ные в первых экспериментах, представлены на рис. 6.17 и 6.18.
Изображения сигналов на индикаторах типа А, показанные на
рис. 6.17, получены с помощью сопряженного фильтра (пассивное
формирование) для радиолокатора Ъ-см диапазона, расположенного
на крыше здания фирмы Sperry в Грейт-Нек (1955 г.). Сигналы на
индикаторе типа А указывают на наличие нескольких крупных
рассеивающих целей вблизи здания. Сигналы, прошедшие большое
расстояние и имеющие значительные амплитуды, являются отражен-
ными сигналами от уголковых отражателей, установленных на кры-
шах автомоблей, стоящих на дороге. Два более слабых сигнала, на-
ходящиеся между рассеивающими целями и уголковыми отражате-
лями, представляют собой отражения от автомобилей или грузови-
ков, проезжавших по дороге на этом участке. На рисунке наглядно
показано уменьшение вредного воздействия отражений от местных
предметов и улучшение разрешения в результате сжатия им-
пульсов.
167
Sr
На рис. 6.18 представлено изображение на экране индикатора
кругового обзора продетектированных сжатых и наложенных не-
сжатых сигналов. Сигналы на больших дальностях являются отра-
жениями от самолетов на местном аэродроме. Рисунок демонстрирует
более высокую эффективную пиковую мощность выходного сигнала
согласованного фильтра. На рис. 6.19 представлены последователь-
ные этапы сжатия ЛЧМ сигнала по мере его прохождения по каналу
сжатия. Верхний рисунок показывает форму сигнала на входе,
Рис. 6.19. Иллюстрация последова-
тельных этапов сжатия импульсов
при прохождении ЛЧМ сигнала
через канал сжатия, Т&f, — 70.
Рис. 6.20. Выделение сжатого сиг-
нала на фоне шумов при полностью
замаскированном шумом несжатом
сигнале.
а нижний на выходе фильтра сжатия, т. е. сжатый сигнал. Промежу-
точные сигналы иллюстрируют, как дисперсионная линия задержки
фильтра сжатия воздействует на сигнал в различных промежуточ-
ных точках. Рис. 6.20 показывает выделение сжатого импульса,
если несжатый полностью скрыт в шумах.
6.6. Влияние рассогласования линейного изменения
задержки на вид сжатого сигнала
Если фазовая характеристика согласованного фильтра для
сжатого сигнала неточно сопряжена с фазовым спектром передавае-
мого сигнала, то говорят, что произошло рассогласование. Обыч-
ным примером рассогласования для ЛЧМ сигнала может служить
случай, когда линейная характеристика задержки при приеме имеет
другой наклон, чем функция ЛЧМ передаваемого сигнала. Этот
случай называют рассогласованием линейной задержки или рассо-
168
ftalattausliik
знание без границ **
гласованием ЛЧМ. Такое рассогласование для линейной характе-
ристики задержки показано на рис. 6.21. Истинная линейная функ-
ция задержки для ЛЧМ сигнала, имеющего вид (6.2), равна
Рис. 6.21. Согласованная и
рассогласованная линейные
функции ЧМ.
_2n(f~2o)_+fei> (6.38)
Разность задержек для согласованного фильтра составляет Т '=
= 2лД/7р. Функция линейной задержки рассогласованного фильт-
ра сжатия имеет вид
И
(6.39)
где р' может быть больше или меньше, чем р. Разность задержек
для функции (6.39) равна Т' = 2лД//р'. Влияние этого рассогла-
сования функции линейной задержки на сжатый импульс можно
Рис. 6.22. Характеристики
фильтра с рассогласованной
функцией линейного изменения
задержки с частотой.
проанализировать, рассматривая идеальный согласованный фильтр,
за которым следует рассогласованный фильтр с линейной задерж-
кой, как показано на рис. 6.22.
169
Разность линейных задержек для рассогласованного фильтра
составляет
ДТ = 2лД/ ---------
Р'
2лД/
>
Рекв
(6.40)
где цвкв определяет наклон функции задержки для рассогласован-
ного фильтра и равна
Коэффициент рассогласования у = (р/ — р)/ р может быть вы-
бран так, что р8кв = р,/у. ДТ « уТ и коэффициент сжатия рассо-
гласованного фильтра равен |у| ТД/. Для коэффициентов сжатия
больших или равных 20 выходной сигнал идеального согласован-
ного фильтра, показанного на рис. 6.22, может быть приближенно
представлен в виде
в(0 = Г1/£ sln(^/2)-cos<V. (6.41)
, у 2л р/*/2
Из равенств (6.30)—(6.35) предыдущего раздела можно опреде-
лить выходной сигнал рассогласованного фильтра с линейной за-
держкой при входном сигнале (6.41) в виде
|/-b-dcw+c^F+isuo+s^n'^x
АТ у 2рвкв
X ехр j {<оо/ Нвкв *2 + 02 (/)}]» (6-42)
где 02(0 определяется уравнением (6.37) и
Л _ реквДТ[1Т(2//ДТ)]
2 Vлр8кв
С учетом параметров рассогласования фильтра, определенных
выше, переменные интегралов Френеля в равенстве (6.42) при-
нимают вид
Х|.,= ^ДТ"1. (6.43)
2 / улц
где п — 2t/yT и величина выходного сигнала с учетом искаже-
ний выражается равенством
!&(01 = 1/ 5r^-r (lC(Xi)+c(xs)]»+
V 2|||' —ц|
+ (5(Х1)+5(Х2)]2}|/21.
(6.44)
170
MatiauA
знание без границ \ *
Приближенная ширина импульса искаженного сигнала равна
т — уТ, а средняя амплитуда (для yT&f > 5) примерно составляет
(р7[||л'—р|)‘/« = 1/У|у|. Отношение амплитуды искаженного
сигнала на выходе рассогласованного фильтра к амплитуде выход-
ного сигнала идеального согласованного фильтра равно1 (для
средних амплитуд)
i/KlTl _ 1
/ГД/ KlviW ’
(6.45)
Искаженные временные функции, задаваемые уравнением (6.44),
напоминают спектр ЛЧМ сигнала при малых значениях произведе-
ния длительности на полосу частот. Примеры таких искаженных
Рис. 6.23. Вид нормированного сжатого ЛЧМ им-
пульса, искаженного вследствие рассогласования
задержки: уТ&1 = 2,5.
сигналов показаны на рис. 6.23—6.26. Нормированные значения
времени и амплитуды, указанные на этих графиках, можно пере-
считать в действительные временные и амплитудные коэффициенты
для определенных значений у, Т и ТА/. Таким образом, для ТА/ =
= 50, у = 0,1 и yTAf = 5 искаженный сигнал будет походить на
сигнал, изображенный на рис. 6.24. Ширина неискаженного им-
пульса на уровне 3 дб равна 0,9/А/. Из рис. 6.24 для ширины иска-
женного импульса на уровне 3 дб находим, что 2tlyT — ±0,67
или
/ - -4_ °>67УГ _ . 0.67уТД/ _ 0,67X5
2 ± 2Д/ ’ ± 2Д/ '
1 Если для вычисления этого отношения использовать пиковые зна-
чения, то оно будет меньше. Это следует из данных на рис. 6 24—5.26.
171
Рис. 6.24. Вид нормированного сжатого ЛЧМ импульса, искаженного вслед-
ствие рассогласования линейного изменения задержки: уТД/= 5.
Рис. 6.25. Вид нормированного сжатого ЛЧМ импульса, искаженного
вследствие рассогласования линейного изменения задержки: уТД/ = 7,5.
Рис. 6.26. Вид нормированного сжатого ЛЧМ импульса, искаженного вслед-
ствие рассогласования линейного изменения задержки: -угД/ = 10.
172
ftalattausisk
знание без ераниц * *
При этом отношение значений ширины импульса на уровне 3 дб
для искаженного и неискаженного импульсов равно 0,67*5/0,9 =
= 3,72, а отношение соответствующих амплитуд из уравнения (6.45)
составляет }/уТД/ = У5. На рис. 6.27 показано увеличение ши-
рины импульса на уровне 3 дб в зависимости от основного парамет-
ра уТД/. Как указывает этот график, по мере увеличения коэффи-
циента сжатия при одном и том же расширении импульса коэффи-
циент рассогласования у становится меньше. Когда полоса переда-
ваемого сигнала превышает ширину полосы фильтра, Д/' >. Д/, при-
Рис. 6.27. Воздействие рассогласо-
вания линейного изменения за-
держки (квадратичные фазовые
ошибки) на ширину сжатого им-
пульса по уровню 3 дб в зависи-
мости от произведения коэффициента
сжатия на коэффициент рассогласо-
вания, уТД/ .
веденный выше анализ может быть использован, если сначала
предположить, что идеальный согласованный фильтр обрабаты-
вает сигнал, у которого длительность и ширина полосы уменьшены
в Д/7Д/ раз. При этом мы получаем эффективное значение произ-
ведения длительности на полосу на входе согласованного фильтра,
равное ГД/ЧД^/Л/')2 = Т’(Д/)2/Д/:/. Скорость изменения частоты
рассогласованной ЧМ для такого случая составляет р' = 2лД/7Т.
Этот приближенный анализ может быть расширен на другие ком-
бинации рассогласований длительности и скорости изменения ча-
стоты входного сигнала для получения оценки формы рассогласо-
ванного сигнала на выходе фильтра сжатия.
Если после рассогласованного фильтра с линейной задержкой
ставится частотный весовой фильтр UZ(co), как это рассмотрено в
следующей главе, то искаженный выходной импульс в экспонен-
циальной форме может быть выражен как
<|>о4-Д<о/2
Л (/)=_!= Г (6.46)
У 2Л|1 J L I 2Ивкв JJ
со#—Дсо/2
173
Воздействие весовой функции на искаженный сжатый импульс
может быть показано на примере функции общего вида типа cos2
с пьедесталом, которая определяется формулой
№(ю) = £ + (1 — fc)cos2 — = (ехр [/—1 +
Лш 2 4 \ L Лео J
t* 2зхео ~| \
~/-т— (6.47)
А со JJ
Слагаемые в круглых скобках можно связать с сигналами парных
эхо, теория которых рассмотрена в гл. 11. Подставляя выражение
для 1Г((о) из (6.47) в (6.46) и используя вывод формулы, определяю-
щий форму искаженного невзвешенного импульса, приведенный
выше, в результате получаем
gd (t)={[С (X,)+с (Х2)р+[S (ХО+s(x,)i»},/!! X
х ехр Г/ Ц/ + х /«+ 0, (о)1 + ~ | [С(х;) + С (xi)]2 +
. I 2у j J 4 у 2у
+ l‘5(^i) + 5(X2)]2|1/2exp j f(oo (/ + 4?) +
L I • \ А/ / 2у \ Af)
+e«(<+^)j]+i7Tvl[c(x;)+c(x',)]4
+ [S(x;) + SIX,)]2|1'’exp[/{<o0(r-A) + X^_2-y +
(6л8)
где Хх и Х2 определены в уравнении (6.43) и
X' - УрТПТ2{Г+(1/АЛ}/Т]
1,2 2 У улц
х” __ТрТ[1Т2 {Г—(1/Л/))/П
. х,2--с------------ж----------
В областях, где функции от интегралов Френеля относительно по-
стоянны, два последних члена в уравнении (6.48) комбинируются
так, чтобы получить линейную частотную модуляцию, эквивалент-
ную модуляции, которую дает первый член, плюс члены, описываю-
щие пульсации функции ЧМ. В работе Клаудера и др. [4] было рас-
считано несколько примеров для k — 0,088 (уровень боковых ле-
пестков по дальности с учетом весовой обработки равен — 40 дб).
На рис. 6.28 проведено сравнение неискаженного взвешенного
импульса с искаженным импульсом для у ТА/ = 8. Для этой ве-
личины искажения рассогласования боковые лепестки возрастают
174
^ataHaus^k
знание без ераниц ч
лишь до —36 дб по сравнению со значительно более высоким уров-
нем лепестков, возникающих из-за искажений при отсутствии ве-
совой обработки. На рис. 6.29 показано ухудшение амплитудных '
Рис. 6.28. Влияние квадратичных фазовых искажений на взвешен-
ный импульс, уТД/ = 8:
a—при весовой обработке; б—без весовой обработки.
характеристик и расширение импульса для этого случая, получен-
ное на основе данных Клаудера и др., которые дают вывод, что
при уровне боковых лепестков сжатого сигнала, равном —40 дб
Рис. 6.29. Расширение импульса н уменьшение его амплитуды
при весовой обработке в случае рассогласования линейного
изменения задержки.
и весовой обработке значения уТД/ = 4 допустимы. На рис. 6.30
иллюстрируются реальные сжатые импульсы при весовой обработке
и без нее для различных значений уТД/. Рассогласование линейной
задержки может быть также представлено как квадратичная фазо-
175
F
вая ошибка, возникающая вследствие отклонения фазовых характе-
ристик от идеальных на краях полосы пропускания. Это фазовое
рассогласование на краях полосы можно выразить через коэффи-
циент рассогласования у и произведение длительности на полосу
сигнала в виде Ф = луТА//4.
Рис, 6.30. Искажения сжатого импульса при рассогласовании
линейной ЧМ:
а) уТМ = О; б) уТД| = 2; в) уТЩ = 6.
Вычисления, основанные на использовании уравнения (6.46),
могут стать очень сложными для весовых функций общего вида.
Если произведение длительности на полосу с учетом рассогласо-
Рис. 6.31. Влияние весовой обработки на форму
сжатого импульса на выходе фильтра с рассогласо-
ванным линейным изменением задержки.
вания у ТА/ сравнительно велико (больше 4), то искаженный вы-
ходной сигнал приближенно описывается той же самой функцией,
как и выходной сигнал при весовой обработке. Это показано на
рис. 6.31, где временной интервал АТ заменяет частотный интер-
176
^alatiausKk
знание без границ ' w
вал Д/. Такое приближение не учитывает уровень боковых лейест-
ков искаженного импульса» но оно полезно для подсчета расшире-
ния импульса, вызванного рассогласованием ЛЧМ или квадра-
тичными фазовыми ошибками при весовой обработке.
6.7. Методы обработки сигналов с большими значениями
произведения длительности на полосу
При использовании сигналов с большими значениями произве-
дения длительности на полосу построение согласованного филь-
тра приемника по методике, описанной в разд. 6.2—6.4, может
стать сложной задачей из-за появления таких факторов, как иска-
жение сигналов в длинных линиях задержки, а также потери и
ограничение ширины полосы. В настоящем разделе обсуждаются
два метода построения систем согласованной фильтрации ЛЧМ сиг-
налов с большим значением произведения длительности на полосу,
которые призваны разрешить эти проблемы.
а) Обработка в параллельных каналах
Основная схема согласованного фильтра с параллельными
каналами для обработки ЛЧМ сигналов показана на рис. 6.32.
В каждом канале имеется дисперсионный фильтр с коэффициентом
сжатия ТСД/С, где Тс — TIN и Д/с = &flN, причем Т — общая
длительность сигнала и Д/ — общая ширина полосы. Центральные
частоты каналов разнесены на величину &f/N и определяются со-
отношениями
= ,’о—( "-^+‘ ) . 1 < m < N. (6.49)
Если предположить, что входной сигнал каждого канала является
ЛЧМ сигналом с прямоугольной огибающей длительностью TIN
и девиацией частоты &f/N, то выходной сигнал каждого канала
имеет вид [11]

*/2 sin n&ft/N
COS
Jl.
L 4 J
(6.50)
Ширина сжатого импульса на уровне —4 дб равна тс = N/
на выходе каждого- канала. Постоянные линии задержки в каждом
канале обеспечивают временное совпадение соответствующих сиг-
налов. Кроме того, применяется управление фазой, чтобы согласо-
вать по фазе несущие частоты сигналов во всех N каналах при от-
сутствии допплеровского сдвига и совпадении пиков. Суммиро-
7 Зак. 134 I 177
вание выходных сигналов N каналов, как показано на рис. 6.32,
дает результирующий выходной сигнал, определяемый формулой
*/2 sin nkfi/N
nbft/N
sin лД//
sin n&ft/N
Xcos(2nf0/——cos (2nfot—~\ (6.51)
\ 4 / лД// \ 4 /
Равенство (6.51) указывает, что общее произведение длительности
на полосу в № раз превышает произведение для отдельного канала.
Оно же означает, что если произведение длительности на полосу
ПмопВые
Фиксированные
<£
а)
Рис. 6.32. Устройство сжатия импульсов с параллельными каналами
для обработки ЛЧМ сигналов, имеющих большую величину произве-
дения длительности на полосу:
«- блок-схема устройства; б — частотные характеристики полосовых фильтров.

равно ТДД то разделение согласованного фильтра на /V одинако-
вых каналов приводит к уменьшению величины произведения дли-
тельности на полосу для отдельного канала до TAfIN2. Такой при-
ем позволяет получить заметное упрощение дисперсионных линий
178
Nataliausl
знание вез границ
задержки^ для каждого канала по сравнению с созданием однока-
нального согласованного фильтра. Поскольку размеры дисперсион-
ного задерживающего фильтра прямо пропорциональны значению
произведения длительности на полосу (см. гл. 12—14), то число
или размер дисперсионных компонент, необходимых для создания
многоканального фильтра, приблизительно в Д' раз меньше, чем в
случае одноканального фильтра сжатия. Просачивание между сосед-
ними каналами, которое происходит вследствие перекрытия полосо-
вых характеристик, требует, чтобы линейная задержка в каждом
канале выдерживалась в полосе, превышающей &f/N. Следователь-
но, уменьшение размеров дисперсионных элементов задержки будет
несколько меньше чем 1/N. Такая экономия компонент частично
перекрывается необходимостью иметь фильтры с фиксированными
задержками и управлять фазой. Кроме того, необходимы более
сложные входные и выходные цепи.
Основное преимущество метода, использующего параллель-
ные каналы, состоит в том, что меньшие значения произведения дли-
тельности на полосу в каждом канале позволяют лучше контроли-
ровать искажения характеристик задержки в каждом дисперсион-
ном фильтре. Этот тип искажений, подробно рассмотренный в гл. 11,
играет все большую роль по мере увеличения произведения дли-
тельности на полосу дисперсионного фильтра. Фильтры сжатия в N
каналах могут относиться к любому тип) из рассмотренных в гл. 12—
14. Уменьшение уровня боковых лепестков можно выполнить с
помощью весовой обработки, проводимой после объединения кана-
лов, или посредством управления коэффициентами усиления в каж-
дом канале для получения ступенчатого взвешивающего отклика.
Для частного случая, когда в параллельных каналах использованы
узкополосные полосовые устройства, рассматриваемый метод поз-
воляет увеличить общую полосу частот.
Построение фильтра для сжатия ЛЧМ сигнала с коэффициентом
сжатия 1000 : 1, содержащего десять каналов, подробно рассмотре-
но Джакобусом 112]. Коэффициент сжатия для отдельного канала
равен 1000/№ или 10. Это устройство с равным успехом служило
как фильтром сжатия, так и растяжения. Сигналы, полученные с
помощью такого согласованного фильтра, представлены на рис. 6.33.
Рис. 6.33, а изображает растянутый импульс длительностью
1000 мксек. После инверсии боковой полосы для того, чтобы изме-
нить направление изменения частоты, тог же самый сигнал был
снова подан на параллельный многоканальный согласованный
фильтр с целью получения сжатого импульса длительностью 1 мксек
(ширина импульса на уровне — 4 дб), показанного на рис. 6.33, б.
При такой реализации в каждом канале использовались свои вход-
ные смесители и местные гетеродины, так что фильтры сжатия в
каждом канале работали на одной и той же центральной частоте, и,
следовательно, имели идентичное построение. Такие же местные
гетеродины и выходные смесители смещали спектральные составляю-
7* 179
щие отдельных каналов в их соответствующие Частотные позиций
(см. рис. 6.32, б) перед сложением отдельных импульсов из каждо-
го канала.
Этот метод построения, основанный на синтезе дисперсион-
ных характеристик многоотводных линий задержки, рассмотрен
Хэггерти 113]. Параллельный многоканальный метод может также
1000мксек —— ----
ft)
б)
Рис. 6.33. Форма сигналов на входе и выходе системы сжатия ЛЧМ импуль
сов с параллельными каналами при коэффициенте сжатия 1000 : 1.
а —несжатый импульс; б—сжатый импульс. Масштаб — 5 мксек/деление.
применяться для формирования нелинейных ЧМ сигналов. В этом
случае нелинейная ЧМ аппроксимируется набором смежных ЛЧМ
сегментов с различным наклоном. Каждый из этих ЛЧМ сег-
ментов обрабатывается в своем собственном канале с линей-
ной дисперсионной задержкой. Применение устройства такого
типа для обработки сложных сигналов с нелинейной ЧМ было опи-
сано Тором [14].
б) Метод обработки с помощью анализа-
тора спектра
Соотношение между временем и частотой для ЛЧМ сигнала
позволяет измерять дальность посредством гетеродинирования,
.180
т. ё. путем сравнения функции ЧМ принимаемого сигнала и сйЬЙА-
ла местного генератора, для которого функция ЛЧМ имеет такой
же наклон, что и передаваемый сигнал. При таком методе реализа-
ции приемного устройства момент запуска местного генератора с
согласованной ЛЧМ обычно задерживается на величину t0 после
момента передачи, но эта задержка должна быть меньше задержки
принимаемого сигнала на входе приемника. Сигнал местного гене-
ратора записывается в виде
cos^wz74--^-|i72j, 7>0, (6.52)
где / = / —/0.
Принимаемый сигнал поступает через Д/ сек после запуска
местного генератора и имеет вид
a (t—A/) cos I со, (t — Д/) + -Ь- И (t — Д/)2], Д/ < Г< Т + М. (6.53)
I I
Перемножение этих двух сигналов в смесителе, показанном на
рис. 6.34, дает в результате
a (t—A/)cos[pA//—6 (ДО] + слагаемое частоты 2соо, Д/<
</<Т4-Д/, (6.54)
где 6 (ДО = (оо Д/—р (ДО2.
Первый член в выражении (6.54) есть импульс постоянной
частоты длительностью Т, частота которого определяется времен-
ной задержкой (или дальностью) принимаемого сигнала относи-
тельно момента запуска местного генератора. Функция ЧМ для это-
го случая показана на рис. 6.35. Для того чтобы частота сигнала,
поступившего на вход в момент /0, не оказалась равной нулю,
сигнал местного генератора дополнительно смещается по частоте на
величину промежуточной частоты сопр. Выходной сигнал смесите-
ля в этом случае имеет вид
a (/—A/) cos |wnp7+ рД/7|, Д/ < / < Т 4-А/. (6.55)
Если огибающая а (/) имеет прямоугольный вид, то спектр сиг-
нала запишется
sin пТ ( f nT^f- Шпр рД \ 2л ' — . (6.56) соПр—рД/ \ 2л /
181
Рис. 6.34. Принцип приема сигналов с помощью анализа
тора спектра.
Рис. 6.35. Разрешение сигналов и способ
определения дальности при использовании
анализатора спектра ЛЧМ сигналов:
а — изменение частоты местного генератора и
двух принимаемых сигналов: б—вид спектр-
на входе анализатора.
182
Ширина этого спектра на уровне —4 дб равна 1/Т, она и опреде-
ляет величину элемента разрешения по спектру. Так как р =
= 2nAflT, то из (6.55) можно заметить, что второй сигнал с задерж-
кой по дальности Д / + 1/Д/, который размещается в соседнем эле-
менте разрешения по дальности при использовании сжатого импуль-
са, будет иметь сдвиг центральной частоты на выходе смесителя
р/2лД/ или 1/Т. Таким образом, процесс гетеродинирования при-
нимаемого сигнала с помощью местного генератора ЛЧМ сигнала
преобразует информацию, заложенную в разности задержек, ко-
торую можно было бы измерить на выходе фильтра сжатия, в ин-
формацию, выражающуюся в различии частот и обеспечивающую
разрешение по дальности, эквивалентное разрешению при сжатых
импульсах.
Реализация такой системы требует исследования выходных
сигналов смесителей с помощью анализатора спектра. Таким ана-
лизатором может быть набор узкополосных фильтров (ширина по-
лосы равна 1/Т), центральные частоты которых разнесены на МТ.
Описанная методика может стать более сложной, если необходимо
исследовать одновременно большое число элементов разрешения
по дальности. Более компактным устройство получается при ис-
пользовании когерентных запоминающих фильтров [15, 161, уст-
ройств с рециркуляционными линиями задержки, которые дают
возможность получать в реальном времени на выходе спектр боль-
шого числа одновременно поступающих сигналов [17]. В общем
случае при использовании анализатора спектра применяют слеже-
ние или рассматривают узкий строб по дальности, с тем чтобы из-
бежать затруднений, связанных с управлением линейностью ха-
рактеристик местного генератора при больших временных интер-
валах и очень широких пределах изменения частоты. В случае при-
менения слежения частотная информация с выхода смесителя по-
дается обратно в схему, управляющую запуском генератора линей-
но с возрастающей функцией ЧМ для сохранения постоянной цен-
тральной частоты выходного сигнала смесителя. Необходимая для
этого синхронизация запуска местного генератора осуществляется
с помощью данных слежения по дальности.
В работе Темеш и др. [18] описано применение системы такого
типа, в которой длительность передаваемого импульса равна
2000 мксек, девиация частоты составляет 4 Мгц, а произведение
длительности на полосу равно 8000. Если несколько сигналов по-
ступают практически одновременно, то боковые лепестки спектраль-
ных откликов более сильных сигналов могут замаскировать более
слабые сигналы. Боковые лепестки можно уменьшить посредством
весовой обработки или усечения огибающей принимаемого сигнала
до того, как он поступит на вход анализатора спектра. Это может
осуществляться путем управления частотной характеристикой
приемника еще до смесителя на рис. 6.34 или с помощью времен-
ной амплитудной модуляции огибающей принимаемого импульса.
Последний метод, исследованный Темешом, требует синхрониза-
ции временнбй весовой функции приемника со временем поступле-
ния принимаемых сигналов.
Весовая функция Хэмминга, описанная в гл. [7], может быть
непосредственно использована в амплитудном модуляторе приемни-
ка [18]. Однако временная весовая обработка в приемнике не явля-
ется оптимальным методом обработки, когда сдвиги во времени по-
ступления нескольких сигналов соизмеримы с длительностью пере- *
даваемого сигнала. Если принимаемые сигналы имеют допплеров-
ский сдвиг, то измерения дальности, основанные на применении
анализатора спектра, могут привести к ошибке. ЛЧМ сигналы при
этом автоматически корректируют ошибки определения дальности
при методах сопровождения по дальности, рассмотренных в
разд. 9.5.
Методы, в которых применяются анализаторы спектра, дают
наибольший эффект в том случае, если функции ЧМ передаваемого
сигнала и местного генератора строго линейны. В работе Темеша
и др. описан пушпульный метод умножения частоты для генериро-
вания линейных функций ЧМ с очень малыми искажениями.
Пиблс и Стивенс [19] рассмотрели другой метод, основанный на
формировании строго контролируемой лестничной ступенчатой
функции ЧМ и заполнении ступенек пилообразной ЧМ функцией;
при этом достигается нелинейность фазовой модуляции порядка
одного градуса.
6.8. Допплеровские искажения ЛЧМ сигналов с большим
значением произведения полосы на длительность
В разд. 6.2 мы предположили, что основное воздействие доп-
плеровского сдвига на ЛЧМ сигнал состоит в равномерном перено-
се его спектра, в то время как все остальные характеристики сиг-
нала остаются без изменений. Было отмечено, что такая аппрокси-
мация недостаточно точна для сигналов с очень большими значе-
ниями произведения полосы на длительность [20]. Для узкопо-
лосных сигналов допплеровский эффект может быть более точно
представлен, как показано в гл. 4, с помощью общего преобразо-
вания сигнала s(t) в сигнал sd(t)
S,/(O =
(6.57)
где а = 1 + 2v/c и v — радиальная скорость, которая считается
положительной для приближающихся целей.
Если s(t) имеет ограниченную длительность, то длительность
принимаемого импульса изменится в 1/а раз. Подставляя уравне-
18$
знание Вез границ “ ш
ние (6.57) в определение ЛЧМ сигнала, получаем
^-(*(“0’1 =
X I
2у
с
2и
(6.58)
2 \ с / J 2а 2а
Член 2v(aolc представляет допплеровский частотный сдвиг, выра-
женный в радианах, рассмотренный в разд. 6.2. В общем случае
воздействием скорости на амплитуду и длительность принимаемого
сигнала обычно пренебрегают. Для этого случая Рэмп и Уингров
[20] и Тор [14] предположили, что принимаемый.сигнал проходит
через сопряженный фильтр с линейной задержкой (т. е. пренебрег-
ли влиянием ограничения полосы согласованного фильтра), который
оптимален для сигнала с нулевым допплеровским сдвигом [см. урав-
нение (6.25)]. Спектр принимаемого сигнала (6.58) с большим зна-
чением произведения длительности на полосу практически прямо-
уголен в полосе Асо(1 + 2vlc), причем центральная частота равна
<оо + 2иш0/с. Квадратичный закон изменения фазы спектра при
допплеровских искажениях можно получить из уравнения (6.20),
обозначив ш0 = (1 + 2и/с)о)0 и р = р(1 + 2v/c)2. После обработ-
ки в фильтре с линейной задержкой спектр на выходе фильтра
имеет остаточный фазовый член, определяемый выражением (6.25);
его приближенно можно записать в виде

ФД(о) =
2v
---- CiXi)0
С
2и\2
1 + —
с 7
“о
з-
(6.59)
Последний член в уравнении (6.59) представляет постоянную фазу,
которая не влияет на форму выходного импульса. Средний член
представляет временной сдвиг, определяемый формулой
“о
С 7 <i>d | 4о G)d
р р с р ’
где cod = 2л<р. Член —(od/p = — (ур/указывает на
ной сдвиг на выходе согласованного фильтра для простой
симации допплеровского сдвига. Для большинства встречающих-
ся в практике радиолокации случаев вторым членом (6.60) можно
</Ф;
dtl)
(6.60)
времен-
аппрок-
185
йренебречь, так как 2и/с обычно имеет порядок 10~4 или менее.
Первый член уравнения (6.59) представляет квадратичный фазо-
вый член, который может быть сопоставлен с эквивалентным рассо-
гласованным фильтром, имеющим линейную задержку, аналогич-
но тому, как это было сделано в разд. 6.6. Искажения, вызванные
допплеровским сдвигом, зависящие от этого фазового члена, ана-
логичны искажениям в случае пропускания идеального сжатого
импульса вида (sin х)/х через фильтр с линейной задержкой, кото-
рый имеет закон изменения задержки
2v / 2v X t
— 2 +— (со-«0)
7--^-^-/-(<0-0^. (6.
41+v)
Общая разность задержек в этом фильтре приблизительно равна
|Д7| = —Т .
с
(6.62)
Для того чтобы использовать результаты разд. 6.6, положим
| 4v/c | = ур, где у0 есть эффективное рассогласование линейной за-
держки, обусловленное допплеровским сдвигом. С помощью рис. 6.27
можно теперь определить расширение импульса, вызванное этим
рассогласованием, вычислив для этого yvT^f. Таким образом,
для v — 7500 м/сек и TAf — 5 10б

4-7„5-103-5-10*
3-I08
= 5,
и коэффициент расширения импульса на уровне 3 дб вследствие
допплеровского эффекта равен 3,72. Форма искаженного импульса
будет похожа на форму импульса на рис. 6.24. Если мы примем
критерий, что коэффициент расширения импульса должен быть
меньше 1,1, то предельная величина произведения длительности
на полосу, которую можно использовать, определяется неравенст-
вами
ТА/ С 2 или
ТА/<1.
(6.63)
Критерий уравнения (6.58) согласуется с критерием, полученным
для случая согласованного фильтра общего вида несколькими ис-
следователями. Если в приемнике для уменьшения боковых лепест-
ков используется весовая обработка, то расширение импульса
вследствие допплеровского эффекта при заданном значении у0ТА/
может быть значительно уменьшено. В случае допустимого коэффи-
циента расширения импульса на уровне 3 дб, равном 2, на основе
рис. 6.29 получаем максимальное значение у0ТА/, равное 6,8. При
186
ftalaHausilik
этом предполагается, что величина смещения центральной частоты
2цй)0/с составляет менее 10% ширины полосы сигнала или что цен-
тральная частота полосы согласованного фильтра в приемнике сдви-
гается на величину 2исоо/с, как предполагали Кук и Хайесс [21].
Из приведенных рассуждений можно заметить, что значения
произведения длительности на полосу для ЛЧМ сигнала между
104 и 10б определяют верхний предел, за которым для преодоления
воздействия допплеровской дисперсии в радиолокационных задачах
необходимо применять специальные методы компенсации [14, 20).
Тор в работе [14] предложил использовать гиперболическую ЧМ
для случая очень больших произведений длительности на полосу
и показал, что 4юрма сжатого импульса, которая очень близка к
функции (sin х)/х, инвариантна при допплеровском сдвиге. Этим
же автором было найдено, что функция фазовой модуляции для это-
го сигнала, имеющая логарифмический вид, задается соотношением
<». t+е (/)=1 g I i —'-1‘-)=<o„z+± +... ~ <о„ t +
ц. \ <Во / 2 3(00
+тИ1+^г)- • (6-64>
Эта функция модуляции может быть более полезна для сонаров,
где отношение максимальных скоростей объекта к скорости распро-
странения сигнала в соответствующей среде значительно больше,
чем в случае радиолокации. Такое применение сигналов с гипербо-
лической ЧМ рассмотрено в работе Роландса [221, который анализи-
рует весомые функции для уменьшения боковых лепестков этих
сигналов в случае применения схем с многоотводными линиями за-
держки.
Если значение коэффициента велико и область допплеров-
ских сдвигов относительно узкая, то дисперсионная задержка со-
гласованного фильтра в приемнике может быть рассчитана таким
образом, чтобы компенсировать фазовый член Ф1 в уравнении (6.59).
При очень большом максимальном значении (значительно
превышающем 10) и равномерном распределении на интервале от
—имакс Д° + имакс ожидаемых скоростей может быть использован
метод, предложенный Бенджамином [23]. В этом случае фильтр
сжатия в приемнике имеет вид, показанный на рис. 6.36. Между
каждой из выходных ячеек в этой схеме используется добавочная
линия задержки. Сигнал, согласованный с правильной комбина-
цией линейных задержек, будет появляться на соответствующем
выходном отводе в виде оптимального сжатого импульса. Выход-
ные сигналы других отводов имеют дисперсионный (размазанный)
вид и уменьшенную амплитуду пика. Это обеспечит грубую индика-
цию скорости, если не слишком большое число сигналов участвует
в интерференционном сложении, формирующем сигнал на несо-
187
гласованных выходах. Соответствующая методика измерения ско-
рости описана в работе Кука и Чина [24].
Более точно влияние скорости на выходной сигнал согласован-
ного фильтра общего вида можно оценить, если рассматривать
выходной сигнал согласованного фильтра в виде
Xj (Ь <р) = /а f « (а/) u* (t 4-т) ехр [ —/2лф/] dt,
(6.65)
где пределы интегрирования равны —772а <Г772а для
2о/с>0 и—TI2<Zt<iTl2 для 2и/с<0. Рубин и Дифранко
[25] показали для этого случая, что произведение длительности на
Выходные сигналы с дискретно возрастающим
временем задержки
Рис. 6.36. Блок-схема, поясняющая способ приема ЛЧМ сиг-
налов с большим произведением длительности па полосу,
который позволяет компенсировать допплеровский сдвиг.
полосу сигнала У а и (at) при допплеровском сдвиге не изменяется.
Для ЛЧМ сигнала можно предположить, что в приемном фильтре
компенсируется перенос центральной частоты, но не рассогласо-
вание функции ЛЧМ. В этом случае, оценивая (6.65), получаем
следующее отношение пиковой амплитуды сжатого импульса при
допплеровских искажениях к оптимальному выходному сигналу
согласованного фильтра для условий (2v/c)T&f < 1 или yvTAf <2:
|1-*1(у^ГД//4)г||/г 2. _
/ 2о\1/2 ’ с '
V+ С 1 (6.66)
( 1 —<0,
\ с / с
где
Х(0.0)
Для максимального значения yvT&f = 2 минимальные значения
уравнения (6.66) приблизительно равны 0,88, что приводит к по-
терям, несколько превышающим 1 дб в отношении сигнал/шум на
выходе фильтра сжатия вследствие допплеровской дисперсии. Как
188
ftatatiausiiik
знание без ераниц * *
на это будет влиять наличие в приемнике фильтра весовой обра-
ботки для уменьшения боковых лепестков, пока неясно.
Дальнейшее искажение функции модуляции принимаемого
сигнала будет происходить в том случае, если кроме постоянной
радиальной скорости отражающий объект имеет также и ускорение.
При этом спектр сигнала при допплеровских искажениях будет со-
держать фазовые члены третьей и более высоких степеней. В ка-
честве возможной схемы построения приемника для этого случая
может быть предложена матрица различных комбинаций фильт-
ров, компенсирующих воздействие скорости и ускорения.
Применение теории построения радиолокационных сигналов
к этой сложной проблеме выходит за рамки данной книги, имею-
щей характер вводного курса, и рассматриваться здесь не будет.
Достаточно сказать, что ЛЧМ сигналы для большинства значений
коэффициента сжатия, которые могут встретиться при наиболее
общих применениях радиолокационных систем, имеют хорошее
свойство оставаться, по существу, полностью коррелированными
на выходе согласованного фильтра при допплеровском сдвиге.
Таким образом налицо очень малые потери в характеристиках
обнаружения для сигналов с допплеровским сдвигом на выходе
согласованного фильтра.. Влияние линейного смещения по дально-
сти в зависимости от допплеровского сдвига на точность измерения
дальности рассмотрено в разд. 9.6.
ЛИТЕРАТУРА
••I. С. Е. С о о k. A general matched-filter analysis of linear FM pulse comp-
ression, Proc. IRE (Correspondence) 49, 831 (1961).
2. J. E. C h i n and С. E. С о о k. The mathematics of pulse compres-
sion— a problem in systems analysis, Sperry Eng. Rev. 12. 11 — 16
(October, 1959).
* 3. С. E.Co о k. Pulse compression — key to more efficient radar transmis-
sion, Proc. IRE 48, 310—316 (1960).
* 4. J. R. Klauder, A. C. Price, S. Darlington, and W. J. Al-
ber s h e i m. The theory and design of chip radars, Bell System. Tech.
J. 39, 745—808 (1960).
* 5. E. J a h п к e and F. E in d e. Tables of Functions. Dover, New York,
1945.
6. Л V a n Wijngaarden and W. L. S c h e e n. Tables of Fresnel
integrals, Computation Dept., Math. Center., Amsterdam, Rept. R49
(1949).
7. L. В. Л г g u 1 tn b a u. Vacuum Tube Circuits. Wiley, New York, 1948.
8. С. E. Cook and J. E. C h 1 n. A radar system employing comple-
mentary pulse expansion and compression filters. Unpublished research
notes, 1956.
9. С. E. С о о к and С. E. В г о c h n e r. Pulse-compression system (pri-
vate communication), 1955.
*10. H. O. R a m p and E. R. W i n g г о v e, Jr., Principles of pulse compres-
sion, IRE Trans. MIL-5, 109—116 (1961).
**11. M. В e г n f e I d. Pulse-compression techniques, Proc. IEEE (Corres-
pondence) 51, 1261 (1963).
189
12. R. W. Jacobus. A" Inear FM 1000:1 pulse-compression system. The
MITRE Corporation, Bedford, Massachusetts, Tech. Memo. TM-3529
(January, 1963).
13. R. D. H a g g a r t y. Tapped delay line synthesis of large time-bandwidth
signals, The MITRE Corporation, Bedford, Massachusetts, Tech. Memo.
TM-3535 (January, 1963).
*14. R. С. T h о r. A large time-bandwidth product pulse-compression tech-
nique, IRE Trans. MIL-6, 169—173 (1962).
15. H. J. В i с к e 1. Spectrum analysis with delay-line filters, IRE WESCON
Conv. Record (Part 8), 59—67 (1959).
16. H. J. В i с к e 1 and R. I. В e r n s t e i n. Coherent Memory Filter, U. S.
Patent № 3, 013, 209.
17. J. Capo n. High-speed Fourier analysis with recirculating delay-line-
heterodyner feedback loops, IRE Trans. 1-10 (1961).
18. C. L. T e m e s. A. C i t r i n, M. A. L a v i о I a, H. К. В oy ce, and
J. P. Biggs. Pulse-compression subsystem for a down-range tracker.
IEEE Intern. Conv. Record (Part 8), 71—81 (1963).
19. P. Z. Peebles. Jr. and G. H. S t e v e n s. A technique for the gene-
ration of highly linear FM pulse radar signals, IEEE Trans. MIL-9, 32—
38 (1965).
•*20. H. O. Ramp and E. R. W i n g г о v e, Jr., Performance degradation
of linear FM pulse-compression systems due to the Doppler effect, Proc.
IRE (Correspondence) 49, 1693—1694 (1961).
**21. С. E. Coo k, W. H. Heis s,*H. O. R a m p and E. R. W i n g г о v e,
Jr., Linear FM Doppler distortion effects, Proc. IRE (Correspondence) 50,
1535—1536 (1962).
22. R. O. R о w 1 a n d s. Detection of a Doppler-invariant FM signal by
means of a tapped delay line, J. Acoust. Soc. Am. 37, 608—615 (1965).
23. R. В e n j a m i n. Recent developments in radar modulation and proces-
sing techniques, Proc. Inst. Elec. Engrs. (Londpn) 111, 2002—2015(1964).
24. С. E. С о о к and J. E. C h i n. Velocity Measuring Radar Apparatus
for High Speed Vehicles, U. S. Patent № 3, 105, 967, October, 1963.
**25: W. L. R u b i n and J. V. D i F r a n c o. The effects of Doppler disper-
sion on matched-filter performance. «Proc. IRE (Correspondence) 50,
2127—2128 (1962).
• •
♦
3. К у к. «Зарубежная радиоэлектроника», 1960, № 9, стр. 38.
4. Клауде р, Прайс и др. «Зарубежная радиоэлектроника», 1961,
№ 1, стр. 15.
5. Янке иЭмде. Таблицы функций с формулами и кривыми, Физмат-
гиз, 1959.
10. Рамп, У и н г р о в. «Зарубежная радиоэлектроника», 1962, № 9,
стр. 15.
14. Тор. «Зарубежная радиоэлектроника», 1963, № 12, стр. 31,
^ataHauswk
знание без границ Ч *
ГЛАВА 1
ПОДАВЛЕНИЕ БОКОВЫХ ЛЕПЕСТКОВ СИГНАЛОВ
НА ВЫХОДЕ СОГЛАСОВАННОГО ФИЛЬТРА
7.1. Введение
В гл. 6 было показано, что при подаче на вход согласованного
фильтра ЛЧМ сигнала форма сигнала на выходе будет определять-
ся функцией (sin х)/х, которая характеризуется наличием боковых
лепестков на оси дальности или времени по обе стороны от сжатого
импульса. Первый и наибольший на этих боковых лепестков по
дальности лишь на 13,2 дб ниже пикового значения сжатого импуль-
са, в то время как последующие боковые лепестки уменьшаются
приблизительно на 4 дб при переходе от лепестка к лепестку; между
лепестками сигнал спадает до нуля, причем для идеальной функции
(sin х)/х нули расположены на расстоянии 1/А/ друг от друга, где
А/ — номинальная ширина спектра. При наблюдении с помощью
радиолокатора, использующего сжатие импульса, большого числа
целей, имеющих широкий динамический диапазон отражающих по-
верхностей, упомянутые выше боковые лепестки по дальности пред-
ставляют собой источник интерференционных помех, которые могут
замаскировать более слабые сигналы.
Такой случай изображен на рис. 7.1 Успешное применение
методов сжатия импульсов с помощью согласованных фильтров
часто зависит, причем в некоторых случаях очень сильно, от того,
удастся ли получить на выходе согласованного фильтра сжатый
сигнал с низким уровнем боковых лепестков по дальности. Для
ЧМ сигнала общего вида, который мы ранее определили в виде
s(/) = a(/)cos[ciV + 0(Ob (7.1)
сигнал на выходе согласованного фильтра может быть записан
как
ОО
g(t)= f s(i:)s(T—t)dT, (7.2)
191
или
ОО 4-00
g (0 =j 5 (со) S* (о) ехр [jut] do = ~ J | S (w) |« ехр [fat]dv.
—оо —оо
(7.3)
Наличие нежелательных боковых лепестков по дальности определя-
ется интегральной записью сжатого сигнала; оно связано с модулем
спектра сигнала, как и следует из выражения (7.3). Для того чтобы
Слабый
сигнал
Время
б)
Рис. 7.1. Влияние боковых лепестков по дальности на
обнаружение слабых сигналов:
а —обычные импульсные сигналы; б —сигналы ия выходе согласо-
ванного фильтрп.
минимизировать воздействие этих нежелательных сигналов на функ-
ционирование системы, были предложены и рассмотрены различ-
ные методы управления модулем спектра сигнала. Они входят в
общий класс методов весовой обработки, т. е. формирование спектра
с помощью частотной фильтрации или формирование огибающей
сигнала как функции времени. Можно также применять управление
функцией ЧМ, как уже говорилось в гл. 3, для непосредственного
получения подходящего спектра сигнала. Методы компенсации с
помощью линий задержки, называемые трансверсальной фильтра-
цией, были также использованы для синтезирования эффективных
частотных передаточных функций с целью получения заранее за-
данного распределения амплитудного спектра на выходе согласо-
ванного фильтра.
Одним из важных аспектов всех этих общих методов является
отыскание оптимальных функций модуля спектра. Здесь «оптималь-
ности есть широко определенный термин, который обычно понима-
ется в смысле минимума средйих потерь в разрешающей способности
и характеристиках обнаружения сигнала при максимальном умень-
192
том случае, если конструктор
о)
^lataiLaus^!.
знание без границ “ w
шении помех, созданных боковыми лепестками. Однако определение
оптимальности может также включать и такие практические сооб-
ражения, как простоту реализации, чувствительность к изменениям
параметров модуля спектра (из-за допусков при расчете или слу-
чайных ошибок) и воздействие изменений несущей частоты входно-
го сигнала на уровень боковых лепестков по дальности. Скорость
спадания амплитуды боковых лепестков также может явиться пред-
метом тщательного рассмотрения в
системы решит использовать сиг-
нал, у которого ближние к сжато-
му импульсу лепестки будут отно-
сительно больше, за счет чего даль-
ние лепестки можно получать бо-
лее ослабленными, особенно если
при этом потери в разрешающей
способности или ухудшение отно-
шения сигнал/шум будут неболь-
шими.
В настоящей главе будут под-
робно рассмотрены различные ме-
тоды уменьшения уровня боковых
лепестков по дальности для клас-
са ЧМ сигналов, которые исполь-
зуются в системах с согласован-
ными фильтрами. Мы будем рас-
сматривать эти сигналы отдельно
от дискретных или фазомодулиро-
ванных сигналов с согласованной
фильтрацией, так как поведение
боковых лепестков по дальности
для каждого из этих классов сигналов имеет различный характер.
Боковые лепестки ЧМ сигналов обычно уменьшаются при удале-
нии от центра сжатого импульса, и, если форма спектра фиксирова-
на, их поведение относительно независимо от произведения полосы
на длительность или коэффициента сжатия. Таким образом в этом
случае особый интерес представляет уменьшение этих боковых лепе-
стков по дальности вблизи точки появления интересующего нас сиг-
нала. Уровень боковых лепестков дискретных или фазоманипулиро-
ванных кодов обычно зависит от произведения длительности на
полосу и обычно сохраняет практически постоянное значение на
интервалах ±7 сек по обе стороны сжатого импульса, где 7— дли-
тельность несжатого импульса.
Сравнение этих двух типов поведения боковых лепестков по
дальности приведено на рис. 7.2. Так как у фазоманипулирован-
ных сигналов боковые лепестки по дальности имеют большую дли-
тельность, то выделение слабых сигналов на их фоне часто бывает
более сложной задачей,чем при выделении на фоне боковых лепестков
193
Рис. 7.2. Два основных типа
структур боковых лепестков по
дальности сигналов на выходе
согласованного фильтра:
а — для сигналов с частотной модуля-
цией; б —для сигналов, построенных
па основе фазовых кодов.
ЧМ сигналов. Это становится особенно Важным при плотном лото*
ке целей, рассмотренном в гл. 10. Изучение фазоманипулированных
сигналов, используемых в системах с согласованными фильтрами,
проводится в гл. 8.
Один из главных выводов, который может быть сделан при
изучении вопросов, рассмотренных в настоящей главе, состоит
в том, что для большого числа практически интересных задач ЛЧМ
сигналы при дополнительной весовой обработке для уменьшения
боковых лепестков являются наилучшими. Поэтому мы рассмот-
рим некоторые специальные вопросы, относящиеся к сигналам
именно такого типа. В число их входит исследование функции предыс-
кажения частотной модуляции, которая может быть эффективно ис-
пользована для формирования ЛЧМ сигналов с низким уровнем
боковых лепестков.
7.2. Спектральные характеристики, обеспечивающие
необходимые свойства сложных сигналов
Если при определении свойств интересующих нас сигналов ис-
ходить из оптимального распределения амплитудного спектра, то,
естественно, следует обратить внимание на связанную с этой про-
блемой задачу формирования одномерной диаграммы направленно-
сти антенны. Конечной целью формирования диаграммы является
уменьшение пространственных боковых лепестков в дальней зоне
при минимальных расширениях луча и уменьшении коэффициента
направленности антенны. Это аналогично достижению минимально-
го временного расширения импульса и ухудшения отношения сиг-
нал/шум при максимальном уменьшении боковых лепестков по
дальности для сигналов на выходе согласованного фильтра. Для не-
прерывной антенны конечных размеров длины d (где d много боль-
ше длины волны излучаемого сигнала), в которой распределение
токов задается функцией IV'(z), интенсивность электрического поля
в дальней зоне как функция угла ср, задается интегралом Фурье
+<//2
Е (ф)~ f W'(z)exp[/2n(zA)sin<p]dz.
-5/2
(7.4)
Соотношение (7.3) описывает сигнал на выходе согласованного
фильтра в виде

dm.
194
'XahiUausW
знание без границ Ч *
При соответствующем выборе переменных приведенные выше соот-
ношения оказываются эквивалентными, так что квадрат модуля
спектра, определяемый функцией
|S(co)P-V7(z -<о), (7.5)
где W(z) — известная функция распределения по апертуре антен-
ны, при которой обеспечивается требуемая диаграмма излучения,
будет воздействовать на выходной сигнал согласованного фильтра.
Амплитуда сигнала зависит от времени подобно тому, как интен-
сивность излучения зависит от sin <р.
Рис. 773. Сравнение пространст-
венных параметров антенны и
сигналов на выходе согласован-
ного фильтра в зависимости от
времени.
Эти соотношения иллюстрируются рис. 7.3. Многие из возмож-
ных функций W(z) уже известны в теории антенн, некоторые же из
наиболее полезных функций еще раз рассматриваются в настоящем
разделе. В качестве основы для описания и сравнения между собой
различных сигналов будет использоваться идеализированный пря-
моугольный спектр и соответствующий сигнал (sin х)/х. Во многих
задачах предполагается, что спектральные распределения, которые
соответствуют сложным ЧМ сигналам, являются, по существу,
гладкими функциями без пульсаций. На практике это последнее усло-
вие часто не выполняется. Влияние его на действительное поведе-
ние боковых лепестков сигналов на выходе согласованного фильт-
ра будет рассмотрено в следующем разделе. Для идеальной систе-
мы с согласованными фильтрами выражение (7.5) будет спра-
ведливо и распределение спектра передаваемого сигнала можно
записать
|S(w)|t (7.6)
Это же самое соотношение описывает амплитудный отклик сог-
ласованного фильтра приемника |Н(<о)|. Для случая
|S(a>)|+-|H(<o)|
соотношение, эквивалентное (7.5), имеет вид
| S (<о) | • |//(<о) | — W" (<о). (7.7)
195
»-
При этом мы имеем несогласованный амплитудный отклик, и в
результате происходит ухудшение отношения сигнал/шум на вы-
ходе согласованного фильтра по сравнению со случаем идеального
согласованного фильтра. Однако такой подход может быть полез-
ным в целях уменьшения боковых лепестков, если | S(w)| , опре-
деляемое равенством (7.6), трудно воспроизводить или если это
амплитудное распределение указывает на согласованный фильтр,
который имеет нежелательные свойства при изменении параметров
сигнала, поступающего на его вход. В качестве примера укажем на
повышение уровня боковых лепестков выходных сигналов согласо-
ванного фильтра для некоторых нелинейных функций ЧМ при
допплеровском сдвиге частоты. Для интересующего нас IF(co) рас-
пределение спектра |S(w)| определяет отклик приемника | //(со) |
и в предельном случае прямоугольного спектра |//(со) | -- U/(co).
Сделаем основное предположение, что любое преднамеренное рассо-
гласование касается только спектрального распределения и ампли-
тудного отклика приемника и что фазовая передаточная функция
приемника и фазовый спектр остаются сопряженными функциями,
как рассматривалось в гл. 1.
В качестве основной процедуры будем использовать определе-
ние функции W'(co), необходимой для получения искомой временной
зависимости выходного сигнала от времени g(t) с помощью пре-
образования Фурье
СО
№(<•)) = J g (t) ехр [ —/(О/] dt. (7.8)
—во
Соответствующие методы уже были разработаны для синтеза на-
перед заданных диаграмм излучения антенны. Приходится, однако,
использовать более специфические методы, когда конечной целью
является получение наименьшей ширины луча (или длительно-
сти импульса) при заданном уровне боковых лепестков.
Распределение Дольфа —Чебышева
Решение задачи по определению распределения поля в раскры-
ве антенны, когда формируется наиболее узкий луч при заданном
уровне боковых лепестков, было получено Дольфом [ 1 ] для слу-
чая равномерно расположенных синфазных точечных источников,
функционирующих как решетка больших размеров. Используя для
определения диаграммы направленности излучения полиномы
Чебышева, Дольф определил оптимальную диаграмму антенны,
взяв в качестве критерия минимум ширины луча при заданном
уровне боковых лепестков. Полученная диаграмма антенны харак-
теризовалась тем, что все боковые лепестки имели равные амплиту-
ды. Когда число элементов в антенне с распределением Дольфа —
Чебышева возрастало, плотность тока в крайних элементах стано-
вилась очень большой, стремясь к бесконечности для непрерывной
196
NataHausii®!
знание без границ Ч <
антенны. Пример распределения Дольфа — Чебышева приведен на
рис. 7.4. Функция распределения для предельного случая непре-
рывного распределения была получена ван дер Маасом [2); она
имеет вид
2ш 1 \ ® / 2ю . . \ I 2л
-----1 -1 - О-----Г 1 -------
Aw / \ Аю /J АюсЬлД
где Щх)— функция единичного скачка; 6(х)— дельта-функция
Дирака; Л(х) — модифицированная бесселева функция первого
рода первого порядка и <о = 0 эквивалентно центральной частоте
спектра на промежуточной частоте.
Рис. 7.4. Пример непрерыв-
ного дольф-чебышевского рас-
пределения.
Рассматривая функцию Дольфа — Чебышева как спектральное
распределение выходного сигнала согласованного фильтра и вы-
полнив преобразование в частотную область, получаем выходной
сигнал в виде
g (Оо....”” - ,/|(А“/2п) , —oo</<qo. (7.10)
ch nA
Коэффициент А определяется заданным уровнем боковых лепест-
ков по следующей формуле:
20 1g (—1—= уровню боковых лепестков, дб. (7.11)
\ ch nA I
Сигнал, описываемый равенством (7.10), имеет постоянный уровень
боковых лепестков па всем протяжении оси времени, как показано
на рис. 7.5. Клаудер и др. 13], а также Темеш 14] указали на
197
физическую нереализуемость сигнала с такой структурой боковых
лепестков, так как энергия g(t)n здесь становится бесконечной. По
существу, такой результат следует из физической нереализуемости
самой непрерывной функции Дольфа• -Чебышева 1Г((о)£>, так как
для этого необходимо иметь бесконечное усиление на краях спек-
тральной полосы. При практическом применении систем сжатия
Рис. 7.5. Сравнение дольф-чебышевского и тейло-
ровского сигналов.
импульсов с помощью согласованных фильтров характеристики
дольфа-чебышевского сигнала используются как стандарт, с
которым сравниваются результаты других методов, используемых
для получения реализуемой аппроксимации функции Дольфа.
Распределение Тейлора
Аппроксимация распределения Дольфа — Чебышева, получен-
ная Тейлором 151, имеет вид
л— 1
U7 ((о)т = 1 4- 2 У Fm cos
2n/mo
(7.12)

198
ftatatiausw
знание безгоании Ч'
0,5 (-I)"11-' jz,1
Ш ~П~1 . к * 1
П л-1
где
п-2
°р т
Л«+(л-|/2)« ]’
Ширина импульса на уровне 3 дб по Тейлору_
Ширина импульса на уровне 3 дб по Дольфу—Чебышеву
Параметр А определяется равенством (7.11). Число членов, исполь-
зуемых при аппроксимации Тейлора, зависит от требуемой близо-
сти к оптимальной, но нереализуемой функции 1Г(<о)о. Когда уро-
вень боковых лепестков задан (тем самым определен коэффициент
Д) и выбрано число членов, используемое в равенстве (7.12), до-
полнительное расширение импульса по сравнению с функцией
Дольфа — Чебышева записывается
[Л» + (я-1/2)21,/2
(7.13)
Неравенство (7.13) устанавливает, что для получения более
низкого уровня боковых лепестков число членов в разложении
(7.12) должно быть увеличено настолько, чтобы сохранить величину
дополнительного расширения ир близкой к единице.
Сигнал на выходе согласованного фильтра при тейлоровской
весовой обработке задается соотношением
(/) — _sinj(Ao//2)_ р sin [(Дсо//2)-}-тл] .
2л AcoZ/2 ’ ' т (Ды//2) + /лл *"
V*1 р 1(А<о//2)—тп]
Д т bat/2—тя
(7.14)
которое представляет собой сумму сдвинутых по времени функций
(sin х)/х, умноженных на весовые коэффициенты Fm. Представле-
ние сигнала в такой форме приводит к заключению, что тейлоров-
ская частотная функция, так же как и другие функции отклика,
может быть синтезирована с помощью многоотводной линии задерж-
ки. Этот метод известен как трансверсальная фильтрация; он рас-
сматривается в разд. 7.8. Для тейлоровского сигнала характерен
постоянный уровень боковых лепестков в окрестности главного
максимума или сжатого импульса. Коэффициент п определяет про-
тяженность интервала, в котором это свойство сохраняется. Вне это-
го интервала уровень боковых лепестков уменьшается.
Из неравенства (7.13) можно заметить, что п определяет
также и коэффициент дополнительного расширения импульса ор.
199
Чем выше п, тем больше область постоянства уровня боковых ле*
пестков и тем меньше коэффициент расширения импульса. Если,
однако, л становится слишком большим, то тейлоровская функция
отклика №((о)г начинает проявлять некоторые черты, свойст-
венные дольф-чебышевскому отклику. Так, для больших п функция
Рис. 7.6. Весовые функции и нид сигналов при весовой обра-
ботке по Тейлору:
а —тейлоровские _частотные весовые функции; б —форма спектра и
вид сигнала при п-6, уровень боковых лепестков —25 дб; а—форма
спектранвид сигнала при л — 10, уровень боковых лепестков ра-
вен —20 дб.
отклика имеет пики на краях полосы, так же как и в ее центре.
Для малых значений п величина №(<о)т имеет максимум на централь-
ной частоте распределения и минимум на краях полосы при мо-
нотонно убывающем характере функции по мере удаления от цен-
тральной частоты к краям полосы. Этот последний вид функции
отклика предпочтителен с точки зрения попыток синтезировать ча-
стотную характеристику приемника для получения спектрального
200
ftalaHauswk
знание без границ Ч
распределения Тейлора. Однако для любого заданного уровня
боковых лепестков существует минимальное значение п, которое
должно быть использовано для получения результатов, определен*
ных Тейлором. В качестве примера укажем, что если заданный уро-
вень боковых лепестков на 25 дб ниже пйкового значения сигнала,
то минимальное значение п ~ 3, а если боковые лепестки на 40 дб
ниже пикового уровня, то необходимое значение п = 6.
На рис. 7.5 приведены результаты сравнения тейлоровской
и дольф-чебышевской временных весовых функций для уровня боко-
вых лепестков —40 дб и п — 6. На рис. 7.6 приведены некоторые
типичные функции распределения Тейлора для различных значений
уровня боковых лепестков и величин п. Коэффициент относитель-
ного расширения импульсов по сравнению с шириной импульса
(sin х)1х (прямоугольный спектр ширины Дсо) для функции Тейло-
ра и для функции Дольфа—Чебышева в зависимости от заданного
уровня боковых лепестков показан на рис. 7.15. Более подробное
рассмотрение этого вопроса можно найти в оригинальной работе
Тейлора.
Модифицированные функции Тейлора — ве-
совая обработка Хэмминга
Тейлоровские функции, показанные на рис. 7.5, получены
путем сложения взвешенной суммы косинусов с постоянной (или с
пьедесталом). Реализация функций, аппроксимирующих эти за-
висимости с помощью фильтров или амплитудной модуляции во
времени, может представлять значительные трудности. Несколь-
ко более простое выражение можно получить, опустив некоторые
члены более высоких порядков в выражении (7.12), для которых
значение коэффициента Fm очень мало. При реализации этого серьез-
ного влияния на вид сигнала (7.14) не отмечается. В качестве при-
мера рассмотрим случай, когда в разложении сохраняется только
первый член. Тогда усеченная функция Тейлора примет вид
- 1 4- 2FX cos — . (7.15)
Дсо
Для п равном 6 при уровне боковых лепестков минус 40 дб усечен-
ная функция Тейлора запишется
Wy? -= 1 4 0,84 cos . (7.16)
Дсо
При этой конкретной функции отклика уровень боковых лепестков
составит минус 40 дб» а ширина импульса будет лишь незначи-
тельно превышать ширину для точной тейлоровской функции на
уровне —3 дб.
Равенство (7.16) описывает более гладкую функцию, так что
аппроксимировать ее (с помощью каких-либо методов частотного
ЭД
г
или временнбго взвешивания оказывается проще. Нормализуя это
равенство для получения единичной амплитуды при со = 0 и при-
меняя стандартные тригонометрические тождества, получаем
- 0,088 + 0,912 cos» —. (7.17)
Д(о
Итак, мы получили косинус-квадратную весовую функцию с пье-
десталом. Хорошо известна весовая функция Хэмминга [41, кото-
рая близка к этой функции и определяется соотношением
1Г (со)я = 0,08 + 0,92 cos8 — . (7.18)
Дсо
Характеристики временной функции, соответствующей весовой
функции Хэмминга, обеспечивают пиковый уровень боковых ле-
пестков —42,8 дб и ширину импульса на уровне 3 дб, равную 1,47,
в то время как ширина тейлоровского импульса на уровне 3 дб
составляет 1,41 при уровне боковых лепестков —40 дб (ширина им-
пульса, соответствующая прямоугольному спектру шириной Дсо,
принята в качестве эталона ширины импульса и равна 1,0).
Формулы (7.17) и (7.18) можно рассматривать как частные
случаи более общей весовой функции, которая определяется как
U4<«))= * + (!—*) cos8— . (7.19)
Дсо
Эта функция представляет собой косинус-квадратный отклик,
взвешенный множителем (1 — k) и расположенный на пьедестале
высоты k, где 1. Ширина импульса и уровень боковых лепест-
ков по дальности, соответствующие этой весовой спектральной
функции, изменяются в зависимости от высоты пьедестала. Хэммин-
говское взвешивание (k = 0,08) обеспечивает наименьший уровень
боковых лепестков для этого класса функций. Сравнительные дан-
ные о весовых функциях, рассмотренных в настоящей главе, при-
ведены в разд. 7.5, где показано, что величина пьедестала весовой
функции может оказывать очень сильное влияние на выходной сиг-
нал согласованного фильтра. Отсюда следует, что формирование
тейлоровской или хэмминговской спектральных весовых функций
для получения боковых лепестков по дальности —40 дб требует
строгого контроля параметров весовых функций.
Весовая функция общего вида —функ-
ция косинуса в различной степени
Формула (7.19) дает возможность ввести весовую функцию еще
более общего вида, которая определяется как
1Г(со) -Д»4-(1 — k)cosn— .
Дсо
Если п есть целое число, то эта функция включает в себя весовые
функции степени косинуса, которые уже рассматривались в теории
(7.20)
NataUausiili
знание без границ \ **
антенн 16]. Функция временнбго отклика для такого класса функ
ций спектрального отклика задается соотношением
л
sin (Дсо//2) . 1 —fe Г
(Дсо//2) + п J
о
... Дсо .
R(t) —------ k
2л
cos'* и cos (~ ut du .(7.21)
\ « /
Были также проведены вычисления и для нецелых п при значениях
п от 1,8 до 2,2 и при различных величинах k для того, чтобы оценить
воздействие ошибок в задании хэмминговской функции отклика.
Эти данные позволяют также приближенно оценить влияние оши-
бок параметров для тейлоровской весдвой функции при уровне
боковых лепестков —40 дб.
7.3. Сравнение частотных и временных методов весовой
обработки с целью уменьшения боковых лепестков
ЛЧМ. сигналов
Методы формирования спектральной характеристики UZ(co)
с желаемой структурой боковых лепестков по дальности могут быть
основаны на амплитудной весовой обработке огибающей переда-
ваемого ЧМ сигнала или на амплитудном взвешивании частотного
Рис. 7.7. Уменьшение боковых лепестков по дальности при
временнбй весовой обработке передаваемого сигнала.
отклика согласованного фильтра приемника. В настоящем разделе
рассматривается применение этих двух методов к ЛЧМ сигналам.
ЛЧМ сигнал, взвешенный временной весовой функцией w (/),
может быть представлен в комплексной форме как
w(t) ехрГ/ f(oo/+ — ) 1, ——</< — ,
и (/) — L \ 2 /J 2 2 (7.22)
0 при других /,
где w(t)—действительная, четная функция. Предположим, что поло-
са фильтра приемника не ограничена, а фазовая характеристика
задается формулой (как показано на рис. 7.7)
«(<>) = ехр (7.23)
L 2н
203
Спектр сигнала на выходе фильтра имеет вид
Г/2
G (со) = Н (со) j w
—Т/2
а сам сигнал определяется соотношением
по / Т/2
~ f W(T)eXP[
-oo I -T/2
i И1’
w0T-lr-^-
ехр[ —/<от] dr, (7.24)
а
X exp [ — /on] dt exp [/co/ ] d(o.
(7.25)
Можно изменить порядок интегрирования в (7.25), чтобы ис-
пользовать интеграл
оо
J Я(о>)ехр [/со(/—т)] dan —
— । 2лр ехр / ((оо(/—т)
2
(7.26)
X
Соотношение (7.25) можно переписать следующим образом:
/--- Т/2
g(0=l/ ^"ехР Г/ — -^-1 ~)1 С ЬУ(т)ехр[/ит/]ат. (7.27)
Г 2П L\ Z 4 / J J
—Т/2
Так как w(t) была определена как действительная четная функ-
ция, то |g(/)| равно
1$(0 1 =
м>(т)ехр[/р.т/] dr.
(7.28)
Соотношение (7.28) определяет преобразование Фурье, связываю-
щее огибающие входного и выходного ЛЧМ сигналов при прохож-
дении через фильтр только с линейной задержкой. Если произведе-
ние длительности на полосу для ЛЧМ сигнала велико, то (7.28) яв-
ляется хорошим представлением сигнала, появляющегося на выходе
фильтра, согласованного с ЛЧМ сигналом, имеющим прямоуголь-
ную огибающую, когда на его вход поступает сигнал, взвешенный
функцией w(t). Это было показано в предыдущей главе для прямо-
угольной функции для которой выходной сигнал согласован-
ного фильтра, задаваемый (6.13), является близкой аппроксимаци-
ей сигнала (sin х)/х, определяемого, в свою очередь, соотношением
(7.28). Можно заметить, что приведенные выше рассуждения поз-
204
WalaHauslSk
знание без границ Ч
болякгг полупить выражение для сжатого сигнала, полностью ана-
логичное распределению поля, которое задается (7.4).
Если предположить, что спектр ЛЧМ сигнала имеет прямо-
угольное распределение, то вследствие функциональной эквива-
лентности частотного отклика И/(<о) и временнбй весовой функции
w(t) мы будем получать подобные по форме сигналы на выходе фильт-
ра сжатия. На рис. 7.8 показана одна из форм частотной весовой об-
работки ЛЧМ сигнала. Весовая функция приемника 1Г(<о) определе-
на на основе предположения об идеальности согласованного филь-
тра. Это приводит к ухудшению в отношении сигнал/шум для сжа-
того сигнала по сравнению с оптимальными условиями, что пред-
Рис. 7.8. Уменьшение боковых лепестков по дальности при ча-
стотной весовой обработке в приемнике.
ставляет собой ту цену, которую мы платим за применение частотной
весовой обработки для уменьшения боковых лепестков. Однако,
когда пиковая мощность передатчика ограничена, эти потери в
отношении сигнал/шум менее значительны, чем потери в принимае-
мой энергии для случая амплитудного взвешивания передаваемого
сигнала и согласованного по амплитудному отклику приемника.
Эквивалентность весовых функций w(t) и 1Г(<о), на которую
мы ссылались выше, в действительности является приближенной,
но степень этого приближения улучшается по мере увеличения про-
изведения длительности на полосу сигнала. Точное выражение для
частотной весовой функции, эквивалентной w(t), может быть полу-
чено, если взять отношение спектра (7.24) к спектру ЛЧМ сигнала
с прямоугольной огибающей S(w), где S(co) задается соотношения-
ми (6.19) — (6.21). Таким образом,
Т/2
J Мт)е*Р / (°)°т 1 ^)]ехр[—/(OTjdT. (7.29)
—Т/2
Из (7.29) получаем искомое выражение
. (7.30)
205
Пусть, например, временная весовая функция для ЛЧМ сигнала
имеет вид
u>(0 = *+(l—A)cos«y , —7/2</<Т/2. (7.31)
При этом получаем следующее выражение для спектра:
о (о>)=н («>) [ A±L s (ш)+-L-Л S (<о + )+-1=*. s (<0 - у.
(7.32)
Используя уравнение (7.30), получаем частотную весовую функ-
цию для этого класса сигналов
ц/ (ю) Н-1 _L l-а Г s [to + (2n/T)) + S(co-(2л/Т)]
S(CD)
(7.33)
4
Функция отклика фильтра, определяемая уравнением (7.33), будет
содержать фазовый член, так как //(со), задаваемая (7.23), не точно
согласована с фазовым членом спектра ограниченного по времени
ЛЧМ сигнала. При больших произведениях длительности на поло-
су влиянием этого фазового члена можно пренебречь, как было по-
казано Куком 17] для ЛЧМ сигнала с прямоугольной огибающей.
Для этого случая приближенное выражение для U7(<o) можно полу-
чить, если заметить, что искомый спектр выходного сжатого сигнала
должен иметь форму w(t) при замене времени на частоту. Таким
образом,
= (7.34)
так что для,временной весовой функции, задаваемой (7.31), экви-
валентная частотная весовая функция определится в виде
0°)прибл ~
fe4 (1 —fe) cos* [л (<00—<1))/Ды]
II S(®)||
(7.35)
На рис. 7.9 приведены эквивалентные П^(со) для хэмминговской
весовой обработки (k = 0,08) ЛЧМ сигнала при ТД/ = 50. Пуль-
сирующую структуру этой функции отклика трудно синтезировать
и, кроме того, она приведет к такой структуре боковых лепестков
сжатого импульса, которая чувствительна к сдвигу частоты вход-
ного сигнала. Практически более удобный подход состоит в удале-
нии или уменьшении выбросов ЛЧМ спектра, как это описано в
разд. 7.7, и в формировании гладкой функции частотного отклика,
которая имеет ту же самую форму, что и w(t).
Обычно весовую обработку огибающей передаваемого сигнала
в мощных радиолокаторах не применяют, так как оконечные ка-
скады усилителей, по существу, работают в режимах класса С и
в них нельзя управлять изменением амплитуды. Однако управление
206
ftataHausHil!.
знание Вез границ Ч *
временнбй огибающей ЛЧМ сигнала в маломощных лабораторных
приборах может представлять собой ценное средство для исследо-
вания влияния различных характеристик весовых функций и опре-
деления поведения боковых лепестков того или иного фильтра сжа-
тия. Это показано на рис. 7.10, где приведены данные о влиянии
весовой обработки на спектр ЛЧМ сигнала, структуру боковых
лепестков и ширину импульса сжатого сигнала.
Ча ст от и
Рис. 7.9. Пример частотной весовой функции,
необходимой для получения на выходе сигнала,
взвешенного по Хэммингу, при подаче на вход
ЛЧМ сигнала (пульсирующая структура опре-
деляется величиной коэффициента сжатия).
Другой пример приведен на рис. 7.11, где показан результат
временнбй весовой обработки в том случае, когда весовая функция
формируется путем независимого изменения параметров синусои-
дальных колебаний различных частот. Параметры каждого синусо-
идального колебания могли подбираться таким образом, чтобы да-
вать максимальное уменьшение боковых лепестков сигнала (sin х)/х
в определенном интервале. Если можно использовать достаточное
число синусоидальных компонент, то такая схема может применять-
ся в качестве аналогового вычислителя для определения наилучшей
комбинации уровней усиления выходных отводов. Это обеспечит
синтезирование частотной весовой функции трансверсального фильт-
ра, которая позволит компенсировать влияние искажения ампли-
туды в фильтре сжатия. Указанный метод использовался нами с тем,
чтобы продемонстрировать, что в ограниченном диапазоне заданных
уровней боковых лепестков можно получить лучшую аппроксима-
цию результатов весовой обработки по Дольфу-Чебышеву, чем это
позволяет метод весовой обработки по Тейлору.
207
Рис. 7.10. Весовая обработка оги-
бающей с нечетными гармониками
(треугольная аппроксимация),
k = 0,08:
а —взвешенный сжатый импульс нало-
жен на импульс (sin х)/х; б —взвешен-
ный ЛЧМ сигнал; а —спектр сигнала.
Рис. 7.11. Весовая обработка оги-
бающей, основанная на компен-
сации боковых лепестков за счет
вычитания сигналов парных эхо:
а —спектр сигналя; б —взвешенный
ЛЧМ сигнал; а —детальный вид струк-
туры боковых лепестков, позволяю-
щий видеть эффект компенсации;
г —структура боковых лепестков сжа-
того^нмпульса вида g(sln х)/х без ве-
совой обработки (ослаблено на 6 дб
по сравнению с рнс. 7.11, а).
2<»в
^alaHaus^!.
знание без границ ' *
7.4, Влияние весовой обработки на отношение сигнал/шум
на выходе согласованного фильтра
В предыдущем разделе было показано, что как временнбе взве-
шивание передаваемого сигнала, так и частотное взвешивание функ-
ции отклика приемника могут быть использованы для формирова-
ния идентичных сжатых сигналов на выходе согласованного филь-
тра. Общность этой процедуры не пострадает, если весовая обработ-
ка разделяется между передаваемым сигналом и приемником со
сжатием импульса, как это было бы в случае применения сопря-
женных согласованных фильтров в приемнике и передатчике. Для
Равная средняя мощность
°)
Ограниченная пикоВая мощность
Рис. 7.12. Сравнение огибающих импульса при весовой обра-
ботке и прямоугольной огибающей.
ЛЧМ сигнала временная весовая функция w(t) и частотная весовая
функция U/(co), необходимые для формирования одного и того же
выходного сигнала, по существу, идентичны.
Если используется временнбе взвешивание и средняя энергия
передаваемого сигнала может быть выбрана равной энергии не-
взвешенного сигнала (рис. 7.12, а), то отношение сигнал/шум на
выходе приемника не зависит от того, где производится весовая
обработка — в передатчике или в приемнике. Однако более реали-
стичным является условие, что предаваемый сигнал (взвешенный
или нет) всегда имеет ту же самую предельную пиковую мощность
(рис. 7.12, б). В этом случае предпочтительно всю весовую обра-
ботку проводить в приемнике. Такое заключение сделано на основе
рассмотрения четырех случаев временнбго и/или частотного взве-
шивания, показанного на рис. 7.13. В приведенных ниже рассуж-
дениях предполагалось, что невзвешенный спектр ЛЧМ сигнала
прямоуголен и занимает полосу До. Это позволяет использовать
функционально идентичные временнбй и частотный отклики* при
весовой обработке в приводимом ниже выводе соотношений, которые
для случаев I—III основаны на определении отношений сигнал/шум
на выходе фильтра сжатия для аналогичных сложных сигналов.
Во всех рассматриваемых случаях шум на входе приемника счита-
ется белым, имеющим плотность мощности в области положи-
тельных частот No.
8 Зйк. 1341
20Э
ш
Временные Весовые
функции
а)
частотные Весовые
функции
Рис. 7.13. Четыре основных случая при рассмотре-
нии отношения сигнал/шум на выходе согласованного
фильтра (нормировка по амплитуде).
Случай Г. Временная весовая обработка. Используя результат
уравнения (7.28), пиковое напряжение выходного сигнала при t =
= 0 запишем в виде
-- Т/2
£ f (7.36)
—Т/2
Средняя выходная мощность шума равна
Дсо/2
о« = ^ J №»(<•>+ <«>o)d<i). (7.37)
—Дсо/2
Для случая I (прямоугольная полоса пропускания приемника)
это дает
о? = N, . (7.38)
2л
210
flaiatiautflfy.
знание без зрении *
Таким образом, отношение сигнал/шум, Задаваемое формулой
\ _ (g (Омаке)*
IatJi oJ *
будет равно
w (0 dt
2
(7.39)
Случай II: Частотная весовая обработка. Частотная весовая
функция, эквивалентная временнбй весовой функции для случая
, равна
W (со) = w
<0 —(Ор
Н
(7.40)
где эквивалентность является следствием зависимости между ча-
стотой и временем для ЛЧМ сигнала
со = <о0 + р/.
Амплитуда спектра входного сигнала (спектр предполагается пря-
моугольным) равна
для нормированного принимаемого сигнала с единичной амплиту-
дой, так что изменение выходного напряжения во времени определя-
ется формулой
= ехр|/й/]<й; (7.41)
где со = (1)—со0. Сделав замену переменных
со/р, = х
и замечая, что
Асо/2 = р.Т/2,
находим выражение для максимального выходного
У---Т/2
g (Омаке = У J W(x)dx.
-Г/2
Найденное выше выражение эквивалентно (7.36).
8*
напряжения
(7.42)
211
Для этого случая средняя выходная мощность шума будет
(положив (оо = 0)
aJi =
Д<о/2
N. [
2л J
-Дщ/2
(7.43)
Таким образом отношение сигнал/шум на выходе
(S\
\ N ) П
w (х) dx
ДШ/2
I 1Г*((в)Жо
—Д<о/2
(7.44)
Случай III: Реализация согласованных фильтров— временнде
и частотное взвешивание. Аналогично случаю II можно показать,
что пиковое напряжение и в этом случае определяется формулой,
идентичной (7.42) (для упражнения доказательство этого предоста-
вим читателям). Однако в этом случае средняя выходная мощность
шума будет
Дш/2
о?п=А.( «7(<o)<fa>
2л J
—Д<0/2
(7.45)
и отношение сигнал/шум на выходе
/SX
\ JV / hi
Дш/2
No Г
2л J
—Д<о/2
IF (со) d<o
(7.46)
IP((i))d(0.
Нормируя интегралы в (7.39), (7.43) и (7.46), мы можем
записать соответствующие отношения сигнал/шум для каждого
из рассмотренных выше случаев в таком виде [отметим взаимоза-
меняемость w(t) и №(й))]:
[ S \
k aJi
W(y)dy
(7.47)
212
^alattausiM
знание без границ -
S
’ 1/2
TAf j W(y)dy
--I/2
2
(7.48)
N)u М2
N^f f W'(y)dy
-1/2
f 1/2
TAf I f F (y) dy
L\ _ L-1/2_______
\AM1H >/2
Wo if J (y)dy
-1/2
Из общих свойств функций частотного отклика приемника для этих
случаев следует, что
1/2
12
S
1/2
Поэтому
-1/2
-1/2
(S/tf)ii > (S/ЛОп, > (S/A/),.
(7.49)
(7.50)
(7.51)
Знаки равенства в соотношениях (7.50) и (7.51) применимы только
в случае, если весовые функции однородны [т. е. W(y) или ш(у) =
= 11. Когда же весовые функции неоднородны, что обычно имеет
место, если мы хотим добиться уменьшения боковых лепестков, то
применение весовой обработки в приемнике представляется наилуч-
шим из возможных методов с точки зрения сохранения характери-
стик обнаружения, даже несмотря на потери рассогласования, ко-
торые происходят из-за рассогласования отклика приемника с рас-
пределением амплитудного спектра.
Потери на рассогласование можно определить исходя из того,
что выходное отношение сигнал/шум для системы согласованной
фильтрации ЛЧМ сигналов с прямоугольной огибающей (случай
IV) дается формулой
/ S
I , (7.52)
k/V/iv MAf M
Отношение результатов для случаев II и IV определяет ухудшение
или потери на рассогласование, происходящие при весовой обра-
ботке в приемнике. Таким образом мы получаем
1/2
f W'Wdy
-М2 _
(SIN)n __
(S/Mjv
’ 1/2 12
Т/М J W(y)dy
.-1/2.
Т/М
1/2
f ^<y>dy
.-1/2________:
1/2
f W'(y)dy
-1/2
2
(7.53)
213
При использовании выражения (7.53) для подсчета потерь на рассо-
гласование для различных весовых функций следует помнить,
что W(y) представляет собой полосовую функцию отклика приемни-
ка, нормализованную к единичному параметру ширины полосы.
Для входного сигнала с прямоугольной огибающей произволь-
ной амплитуды А отношение пиковой амплитуды на выходе согласо-
ванного фильтра к шуму^ получаемое из уравнения (7.52), равно
(S/N)=^. (7.54)
Так как энергия этого входного сигнала на промежуточной частоте
Е = Я2 Т/2, (7.55)
то отношение сигнал/шум на выходе согласованного фильтра в об-
щем случае определяется как
(S/N)=2E/N0. (7.56)
Формула (7.56) представляет собой соотношение, применимое ко
всем сигналам, обрабатываемым с помощью согласованных филь-
тров 18]. Выражение (7.53) для потерь на рассогласование при ве-
совой обработке в приемнике также применимо к сигналу общего
вида, обрабатываемому с помощью согласованных фильтров, если
огибающая сигнала на входе приемника имеет прямоугольную
форму.
Вывод о том, что весовая обработка в приемнике является бо-
лее эффективным методом, чем весовая обработка в передатчике,
имеет важное практическое значение, так как управление огибаю-
щей на выходе мощных передатчиков в большинстве случаев не
осуществимо. Пример весовой обработки при использовании согла-
сованных фильтров в приемнике и передатчике для ЛЧМ сигнала
с гауссовой огибающей и приемника с гауссовой весовой обработ-
кой рассмотрен Фоулом и др. [9]. При лабораторных испытаниях
было показано, что этот сигнал имеет уровень боковых лепестков
равный —40 дб. Сравнение потерь в отношении сигнал/шум в прием-
нике для этого сигнала с потерями для ЛЧМ сигналов с прямоуголь-
ной огибающей при использовании частотной весовой обработки
при уровне боковых лепестков —40 дб приведено ниже.
При сравнении ЛЧМ сигнала, имеющего гауссову огибающую,
с другими сигналами были сделаны следующие предположения:
1. Возможно создание фильтра сжатия на основе дисперсион-.
ной линии задержки с дифференциальной задержкой То в полосе
А/. Это в основном определяет временнбй интервал То, в котором
и гауссова и прямоугольная огибающая могут быть использованы
для передаваемого сигнала.
2. Гауссов сигнал усечен в точках е~2, т. е. там, где его характе*
ристики несущественно влияют на характеристики сжатого сигна*
ла, как описано Фоулом и др. [9].
214
flataHausl^i
знание без границ * *
3. Все сигналы имеют одну и ту же ограниченную пиковую мощ-
ность.
Исходя из этих предположений, можно сравнить сигналы,
имеющие гауссову огибающую, с сигналами с прямоугольной оги-
бающей. Для случая TAf > 1 нормированное выражение для
гауссова сигнала, как показал Фоул и др. [9], приближенно
записывается в виде
и(/)№ехр —4

(7-57) .
2
Заметив, что эта функция равна е~2 при t = ± То/2, получаем
Т = Т„//2. (7.58)
Поскольку скорость изменения частоты для прямоугольного и гаус-
сова сигналов одна и та же, то
Д/ = ц772л. (7.59)
Используя функцию неопределенности, введенную Фоулом и др.,
можно показать, что огибающая гауссова сжатого импульса имеет
вид
lx(t.0)l = 41/-"-exp[-^
Z Г 2 |_ о
(7.60)
Сравнивая ширину импульсов на уровне 3 дб, получаем:
Гауссова огибающая: ширина сжатого импульса = 1,5/Af.
Прямоугольная огибающая: ширина сжатого импульса =
— 0,9/Af (без весовой обработки).
Весовая обработка по Хэммингу: ширина сжатого импульса =
= 1,3/А/.
На основе предположения (3) энергия гауссова импульса со-
ставляет
V2 Т/2
Е=-~ С
2 J
—У~2 Т/2
dt =
Т/2л
8
(7.61)
а энергия прямоугольного импульса равна
у 2 т/2 _
— f dt=^-
2 J 2
-/2 Т/2
(7.62)
215
Результаты сравнения даны в виде следующей таблицы:
Тип огибающей Относительная энергия сигнала, дб Потерн на рассо- гласование, дб Относительная эффективность сигнала, дб
Прямоугольная оги- бающая 0 1,34 (хэммин- говская весовая обработка) -1,34
Гауссова огибающая —3,53 0 —3,53
Таким образом, при определенных выше условиях сигнал с гауссо-
вой огибающей имеет проигрыш в 2,2 дб по характеристикам обна-
ружения для идеального уровня боковых лепестков —40 дб по срав-
нению с сигналом, имеющим прямоугольную огибающую.
7.5. Влияние частотной весовой обработки на характеристики
сжатого импульса
В настоящем разделе приведены данные о влиянии весовой ча-
стотной обработки сигналов в согласованных фильтрах на характе-
ристики выходного сжатого сигнала. На рис. 7.14 показана форма
некоторых сигналов при использовании весовых функций, рассмо-
тренных в разд. 7.2 (тейлоровские сигналы даны на рис. 7.5 и
7.6). Все рассмотренные весовые функции усечены на краях полосы
соо±Дй)/2. В сигналах, взвешенных функциями косинуса в степе-
ни (т. е. cos, cos2, cos8, cos4), при получающихся уровнях боковых
лепестков импульсы заметно расширяются. Этого можно избежать
путем добавления пьедестала с тем, чтобы получить весовые функции
вида
W = k + (1 — k) cos" Г-^=^-1. (7.63)
L J
Сжатый импульс, соответствующий такой функции, можно предста-
вить в виде суммы двух сигналов. Один из сигналов порожден ко-
синусной частью (1 — k)cosn функции 1Г((о). Другой
сигнал имеет вид (sin х)/х ширины т — \/&f, взвешенный множи-
телем k. В результате добавления взвешенного сигнала (sin х)/х
частично подавляются существующие боковые лепестки и сужается
центральный пик сжатого сигнала. Некоторые сигналы при весовой
обработке такого типа показаны на рис. 7.14, а. Так как эффект
подавления лепестков может быть связан с пьедесталом k, то сле-
дует ожидать, что уровень боковых лепестков будет значительно
изменяться вместе с изменением’высоты пьедестала. Можно считать,
что тейлоровские весовые функции принадлежат к тому классу
функций, для которых высота пьедестала является существенной
216
NataHausIM
знание без границ **
217
при определении уровня боковых Лепестков по дальности. На
рис. 7.14, б проведено сравнение (в логарифмическом масштабе)
структуры боковых лепестков при использовании в качестве вре-
менных взвешивающих функций косинуса в квадрате плюс пьеде-
стал и косинуса в кубе плюс пьедестал. Хэмминговская функция
Рис. 7.14, в. Влияние изменения величины п на структуру
лепестков сигнала при использовании частотной весовой функ-
ции вида (Л + (1 — fe)cos"l.
{k— 0,08) является оптимальной среди этого семейства, так как обес-
печивает оптимальную для него форму взвешенного импульса.
На рис. 7.14, в показано влияние изменения кривизны весовой
функции, полученной в результате изменения степени косинуса
в (7.63) относительно случая п = 2. Общее заключение, которое
можно сделать из рассмотрения этих результатов, состоит в том,
что временные весовые функции значительно более чувствительны
к изменениям высоты пьедестала, чем к изменениям формы весовой
функции.
218
^alatiauswii
знание без ераниц “ *
На рис. 7.15 приведены значения коэффициентов расширения
импульса для дольф-чебышевской и тейлоровской функций в зависи-
мости от уровня боковых лепестков по дальности. Приведены также
и экспериментальные данные, полученные при использовании мето-
дов временнбго взвешивания амплитуды сигналов, рассмотренных
в разд. 7.3. Интересно отметить, что в то время как тейлоровские
функции обеспечивают наилучшую однородную аппроксимацию
дольф-чебышевских характеристик во всем диапазоне уровней бо-
Рис. 7.15. Расширение импульса при весовой обработке
по сравнению с функцией (sin х)/х.
ковых лепестков, оказывается возможным с тем же самым числом
членов в выражении для весовой функции [см. (7.12)] получить
лучшие результаты для некоторых ограниченных областей значе-
ний уровня боковых лепестков и расширения импульса. Это дости-
гается путем подбора значений тейлоровских коэффициентов Fm,
что представляет собой один из возможных методов понижения
уровня боковых лепестков при использовании трансверсальных
фильтров. На рис. 7.16 приведены данные о потерях на рассо-
гласование при использовании тейлоровской весовой обработки в
приемнике с согласованным фильтром. Здесь же приведены потери
на рассогласование при использовании функции k + (1 — k) cosax.
На основе этого, а также данных, приведенных на рис. 7.17, можно
заметить, что для функции k + (1 — k) cos ах уровень боковых
лепестков, расширение импульса и потери на рассогласование не-
значительно отличаются от теоретических значений этих величин,
полученных для тейлоровской весовой обработки при уровне боко-
вых лепестков — 40 дб.
На рис. 7.18—7.20 приведены данные, относящиеся к весовым
функциям вида k + (1 — k) cosnx. Рис. 7.17 показывает влияние
высоты пьедестала на уровень боковых лепестков и рис. 7.18 —
219
Рис. 7.16. Потери на рассогласование при частотной
весовой обработке в приемнике.
Рис. 7.17. Влияние высоты пьедестала на уровень боко-
вых лепестков.
220
NalaHauswil
знание без орании Ч «Ь
на коэффициент расширения импульса для различных целых зна-
чений п. Рис. 7.19 иллюстрирует потери на рассогласование при
весовой обработке в приемнике для этих функций в зависимости от
высоты пьедестала k и рис. 7.20 — зависимость потерь на рассо-
гласование от степени функции косинус для различных значений
высоты пьедестала. Эти кривые могут быть использованы для оцен-
ки влияния на потери на рассогласование различных приближений
к искомой идеальной весовой функции. Таким образом, кривая при
k = 0,08 в области, около и = 2 характеризует влияние ошибок при
формировании характеристики вида cos4 для метода Хэмминга.
Эта конкретная кривая позволяет также приближенно оценить влия-
ние параметра k на результаты весовой обработки по Хэммингу
при уровне боковых лепестков —40 дб.
В табл. 7.1 прризводится сравнение численных данных для
некоторых весовых функций, рассмотренных в настоящей главе,
а в табл. 7.2 приведены данные о поведении уровня боковых лепест-
ков при изменении п вблизи оптимального значения п = 2 при не-
целых п для некоторых значений высоты пьедестала.
Таблица 7.1
Характеристики весовых функций1
Весовые функции Пиковый уровень бо- ковых ле- пестков, дб Коэффициент расширения импульса Потери иа рассогласо- вание, дб Скорость спа- дания лепест- ков в дальней зоне
Дольфа — Чебышева —40 1,35 — 1
Тейлора, л = 6 —40 1,41 — 1,2 1//
Л + (1— Л) cos'1
Хэмминга (k = 0,08, л = 2) -42,8 1,47 — 1,34 1//
Косинус в квадрате (^=0, л = 2) —32,2 1,62 —1,76 . 1/Г»
Косинус в кубе (Л = 0, л=3) —39,1 1,87 —2,38 I//4
л= 1, k = 0,04 —23 1,31 —0,82 lit
л = 2, Л=0,16 —34 1,41 —1,01 l/t
л=3, Л=0,02 —40,8 1,79 —2,23 I It
1 Все данные получены в предположении, что невзвешенный спектр
имеет прямоугольную форму.
Данные, приведенные в настоящем разделе, показывают, что
для получения уровня боковых лепестков порядка —40 дб при ми-
нимальном расширении импульса необходимо использовать весовые
функции, обладающие пьедесталом. Так как уровень боковых ле-
пестков может сильно изменяться, если значение пьедестала выбра-
но не совсем точно, то при реализации систем, использующих эти
весовые функции, полученные характеристики могут разочаровать
224
ИГ ’
г7"
Рис. 7.18. Влияние высоты пьедестала на ширину импульса.
Рис. 7.19 Влияние к на потери рассогласования.
Рис. 7.20. Влияние п на потери рассогласования.
^alaHausA
знание без границ Ч
Таблица 7.2
Значения отношения уровня максимального лепестка
к уровню боковых лепестков {дб) для весовых функций вида cos”
h n
1.8 1.9 2.0 2,1 2.2
0,07 35,3 38,0 41,8 43,7 43,0
0,08 35 9 39,5 42,8 42,1 41,5
0,09 36,6 40,6 41,5 40,8 40,0
инженеров, ожидающих получить результаты, предсказанные тео-
рией. Возможно, что для очень мощных систем более реалистич-
но предполагать уровень боковых лепестков равным —35 дб при
отсутствии тщательного и часто проводимого контроля весовой
функции. Если в системе, где требуется получить более низкий уро-
вень-боковых лепестков, надежность также является важным факто-
ром, то вместо оптимальных функций следует использовать «без-
опасные» весовые функции, которые менее критичны к изменениям
параметров. За это надо расплачиваться ббльшими потерями на рас-
согласование и большим расширением импульса. С потерями на рас-
согласование, по существу, ничего сделать нельзя. Расширение им-
пульса с точки зрения абсолютной разрешающей способности систе-
мы может быть компенсировано путем формирования более узкого
центрального максимума сжатого (невзвешенного) сигнала за счет
расширения полосы передаваемого сигнала.
В качестве последнего предостережения разработчику систе-
мы следует указать, на то, что все данные этого раздела основаны на
предположении о прямоугольном распределении амплитуд спектра
ЛЧМ сигнала. Амплитудные пульсации реального спектра могут
привести к появлению боковых лепестков вследствие искажений,
величина которых может значительно превышать уровень —40 дб.
Таким образом, для многих систем может быть слишком академич-
но говорить об уровне боковых лепестков —40 дб. Этот вопрос будет
более подробно рассмотрен в следующих разделах, где исследуют-
ся также методы сглаживания амплитудных пульсаций спектра
для получения низкого уровня боковых лепестков.
Другим аспектом проблемы получения низкого уровня боковых
лепестков являются попытки создать условия при разработке для
минимизации амплитудных и фазовых искажений сигнала в систе-
ме. Анализ искажений и методов коррекции выполнен в гл. 11. При
существующем в настоящее время уровне разработок систем и вы-
полнения отдельных ее компонентов для мощных радиолокационных
систем обеспечение уровня боковых лепестков —35 дб или даже
—30 дб при всех условиях эксплуатации представляет собой
серьезное достижение. t
223
7.6. Влияние точности спектра ЛЧМ сигнала на форму
сжатого взвешенного импульса
В разд. 7.3 было установлено, что во многих случаях времен-
ная и частотная весовые обработки ЛЧМ сигнала представляют
собой полностью аналогичные операции. В настоящем разделе
мы будем исследовать влияние пульсаций френелевского спектра
ЛЧМ сигнала на поведение боковых лепестков по дальности. Сле-
дует указать, что упомянутая выше аналогия, подразумевающая
предположение о прямоугольности спектра, не является адекват-
ной в том случае, когда необходимо получить очень малые боковые
лепестки по дальности.
Основные элементы системы сжатия импульсов для ЛЧМ сиг-
налов были показаны на рис. 7.8. Дополнительный фильтр, слу-
жащий для уменьшения боковых лепестков, представляет собой
отклонение от оптимальной согласованной фильтрации. При ис-
пользовании предположения об упрощенном представлении спектра
в виде прямоугольного в разд. 7.2—7.5 было показано, что возможно
определение функций частотного отклика №(<о), которые уменьшают
лепестки на 40 дб или еще больше по сравнению с пиковым значе-
нием выходного сигнала за счет 40—50% расширения импульса
при потерях в отношении сигнал/шум от 1 до 2 дб. Если задаться
плоской прямоугольной моделью спектра, то форма идеализирован-
ного сжатого импульса определится как
б).+Д®/2
#(/) = — Г W (со) ехр [/со/] dt. (7.64)
2л J
(Оф—Д<о/2
Для того чтобы рассмотреть влияние реального спектра на опре-
деленные выше идеальные, характеристики уменьшения боковых
лепестков, полезно еще раз исследовать амплитудную составляю-
щую спектра ЛЧМ сигнала. Она имеет вид
|5(ш)| = -|(-)'/2 ([C(X1) + C(X1)]> + [SfXi) + S(XI)l!)l/2- (7.65)
Интегралы Френеля С (X) и S (X) и параметры Хг и Х2 опреде-
лены нами ранее в гл. 6. Обычно предполагают, что |S(g>) | прямо-
угольна для коэффициентов сжатия, превышающих 30. Эта аппрок-
симация справедлива лишь для ограниченного числа разрабаты-
ваемых систем. Ниже мы рассмотрим влияние сделанных нами упро-
щающих предположений на характеристики системы в том случае,
если необходимо обеспечить высококачественное ее функционирова-
ние.
Интегралы Френеля — квазигармонические по своей природе,
поэтому спектр ЛЧМ сигнала содержит амплитудные пульсации,
число периодов и величина изменения которых зависят от коэф-
224
^Iaiattaus№ii
знание без грани» * *
фициента сжатия Т A f. Таким образом более точная аппроксимация
взвешенного выходного сигнала фильтра сжатия при пренебреже-
нии остаточным фазовым членом, задаваемым соотношением (6.21),
будет иметь вид'
1 г‘
g (0 = — I | S (со) | W (со) ехр [/со/] do.
Ь>1
(7.66)
Эффекты, которые должны быть рассмотрены при строгом анализе,
возникают вследствие того, что амплитуда спектра колеблется около
постоянного значения. Аппроксимируя изменения амплитуды
Рис. 7.21. Френелевский спектр ЛЧМ сигнала и косинусная модель
спектра с пульсациями, используемая для компенсации боковых
лепестков по дальности:
а —спектр ЛЧМ сигнала, ТД<о/2л = 5О; б —косинусная модель спектральной
пульсирующей структуры; е—частотная весовая функция.
комбинацией синусоид, можно выполнить с помощью теории парных
эхо анализ, который дает полезные результаты. Тем самым мы избе-
жим громоздких вычислений, возникающих при использовании
выражения (7.66), имеющего незамкнутую форму.
На рис. 7.21 показаны некоторые характеристики и их аппрок-
симации, на основе которых выполнен анализ методом парных эхо.
Спектр для случая T&f — 50 показан в качестве примера на
рис. 7.21, а. Пульсации амплитуды в зависимости от частоты пред-
ставлены на рис. 7.21, б в виде отрезка синусоиды, модулирован-
ного медленно изменяющейся косинусоидальной функцией. Ис-
пользуя такую модель в виде модулированного функцией соях
отрезка синусоиды, можно рассматривать спектр как гладкий, но
225
Имеющий соответствующую функцию ошибки. Таким образом,
основной исходной формулой будет
| S (со) [1 н-(d! cos Сх cd) (1Ь а2 cos Са со)], ci)x<(o<(i)2, (7.67)
где ах и а2 могут быть положительными или отрицательными в за-
висимости от конкретной природы интегралов Френеля, которые
должны быть аппроксимированы. Используя введенную выше
модель, представим взвешенный сжатый импульс в (7.66) как
£ ЪГ ।C0S 1 I °2 cos Q ®)1 W (<•>) ехР I^(О.
(7.68)
Множитель
(ах cos Ci со) (1 4- at cos С2 со)
(7.69)
может быть представлен в экспоненциальной форме, так что, вы-
полняя преобразования в (7.68), получим
£(/)= — f W (со) ехр (/со/) d(d 4- ~
Z V X
J W (со) ехр U (t -|- CJ cd] dco +
l“i
J U7 (со) ехр [/ (/-{-Cx4-C2)w]d(o4-
w, . “я
4-. j W (со) ехр [/ (t—Ci — Ct) со] dco 4- J W (co) exp I/(/4-Cx—C8)co]dco4-
“i “i
“i
4- j W (co) exp I/ (t — Ci 4- C2) co] dco
“i
(7.70)
Последние шесть членов в этом выражении представляют собой
смещенные во времени искажения типа парных эхо. Анализ с по-
мощью метода парных эхо позволяет определить удобный критерий
оценки искажений для систем обработки сигнала и сжатия импульса.
Он более подробно рассмотрен в гл. 11.
Предполагая, что путем соответствующего выбора Сх мы управ-
ляем частотой пульсаций амплитуды в центральной области спектра,
можно сделать следующие оценки постоянных в (7.67) для значений
коэффициента сжатия между 30 : 1 и 250 : 1:*
Ci = ^^~ периодов /А/,
2
С2 =1 период /А/,
ах = 0,06, а8 = 0,6—0,7.
226
^ataHaus^!.
знание без границ ' *
Отсюда мы получаем значения, приведенные в следующей таблице:
Расположение
парных ахо отно-
сительно центра
сжатого импульса
Приближенное
значение амплитуды
парных эхо, до
—40
-30
-40
Влияние этой тройки парных эхо на идеализированный уровень
боковых лепестков при весовой обработке сигналов с прямоуголь-
ным спектром показано на рис. 7.22. Спектральные составляющие,
возникающие из-за парных эхо, вычисленных по формуле (7.67),
Рис. 7.22. Вычисленные данные
о влиянии пульсаций спектра на
уровень боковых лепестков.
Идеализированный импульс получен
при хэммииговской весовой обработке
входного сигнала с прямоугольным
спектром.
Д/ 4/ Af Af Af Af
перекрываются и складываются векторно для вычисления струк-
туры боковых лепестков. При этом мы получаем сложное образо-
вание значительно более высокого уровня, чем полученное в пред-
положении о прямоугольном спектре.
Рис. 7.23 и 7.24 иллюстрируют поведение боковых лепестков по
дальности типа парных эхо, возникающих из-за пульсаций спектра,
227
и один из методов их ослабления. Левая осциллограмма на
рис. 7.23 показывает ЛЧМ сигнал с различной скоростью нараста-
ния и спадания огибающей. На средней осциллограмме дан отклик
схемы весовой обработки с уровнем боковых лепестков —40 дб на
ЛЧМ сигнал. Правая осциллограмма более подробно показывает
структуру боковых лепестков на выходе комбинированной схемы,
содержащей схему весовой обработки и фильтр сжатия.
Спектры, соответствующие этим сигналам, представлены на
рис. 7.24. Мы видим, что пульсации спектра уменьшаются по мере-
0tn к ли к схемы
весовой обработки
Сжатый импульс
и боковые лепестки
Рис. 7.23. Влияние крутизны фронтов ЛЧМ импульса иа выходной
сигнал схемы весовой обработки и уровень боковых лепестков сжа-
того сигнала:
а —время нарастания ХД/“0,67; б —время нарастания ХД/=»1,33; в—время
нарастания ХД/=2.67.
увеличения времени нарастания огибающей входного сигналам
С уменьшением амплитуды пульсаций спектра уменьшается и вы-
сокий уровень боковых лепестков по дальности, показанный на
правой осциллограмме рис. 7.23, а, так же как и импульсы на обоих
концах сигнала на выходе схемы весовой обработки. Когда спектр
приближается к гладкому распределению, боковые лепестки по
дальности у сжатого импульса достигают необходимого нам уровня
—40 дб. Влияние времени нарастания огибающей входного сигнала
согласованного фильтра на пульсации амплитуды френелевского
спектра ЛЧМ сигнала рассматривали Кук и Паолилло 110] и Йост
[11]. Причинные связи между пульсациями амплитуды спектра и
боковыми лепестками по дальности, определяемые соотношением
(7.70), поясняются примерами сигналов и спектров на рис. 7.23
и 7.24. Боковые лепестки по дальности типа парных эхо с отклоне-
ниями в пределах 1 дб от вычисленного по френелевской модели
спектра согласно уравнению (7.67) наблюдались экспериментально.
В следующем разделе описана методика предыскажения закона
228
^latattausj^
знание без границ -
ЧМ для регулирования величины пульсаций спектра ЛЧМ сигнала.
Это позволяет изменять боковые лепестки по дальности типа пар-
ных эхо, обусловленных этими пульсациями спектра. Такой метод
Спектр Лчм
импульса
Спектр сжатого
и м пульса
Рис. 7.24. Влияние' времени нарастания им-
пульса на спектр ЛЧМ сигнала и на спектр
сжатого импульса.
применяется в мощных системах, где обычно бывает невозможно
или нежелательно управлять временем нарастания передаваемого
импульса вследствие возникающих при этом потерь выходной мощ-
ности.
7.7. Предыскажение закона ЧМ
Для радиолокационных систем высокой мощности желательно
найти метод регулирования амплитудных пульсаций спектра,
который отличался бы от изменения огибающей передаваемого
импульса. Это можно достигнуть предыскажением закона фазовой
229
или частотной модуляции сигнала, так что передаваемый сигнал
имеет вид
sp(0=cos^0/+J^ + ep(0]. (7.71)
где 6р (t) — фазовая предыскажающая функция. Кук и Паолилло
[10] рассмотрели такую функцию предыскажения, показанную на
рис. 7.25. Эта функция была получена исходя из эквивалентности
6)

а)
Искажение
огибающей
б)
Искажения в законе
фазовой модуляции
Рис. 7.25. Получение предыскаженной линейной
ЧМ путем замещения искажений (т. е. уменьше-
ния пульсаций спектра), вызванных искажением
амплитуды (а) на эквивалентные фазовые иска-
жения (б) или частотные искажения (в), которые
получены при использовании монотонной функ-
ции ЧМ (г).
(для малых искажений) влияния искажений огибающей и фазовых
искажений, которые функционально аналогичны. Искажения
огибающей, показанные на рис. 7.25, а, приравниваются к искаже-
ниям фазовой модуляции, показанным на рис. 7.25, б. Для простоты
была рассмотрена квадратичная функция фазовой модуляции, ко-
торая приводит к предыскажению сегментов для линейной ЧМ,
показанных на рис. 7.25, в — |d(A0p/df]MaKC). При этом
получается монотонная функция частотной модуляции, изображен-
ная на рис. 7.25, г,
230
знание без ераниц ' *
Получающийся предыскаженный спектр определяется форму-
лой
Sp (о) = jSj (со) | ехр [/я)?! (w)] 4- |Sa (co) | x
X exp [/ф2 (to)] + |S3 (to) | exp ]/ф8 (to)], (7.72)
где Si(to) и Ss(to) — составляющие спектра, обусловленные конеч-
ными сегментами закона ЛЧМ, a S2 (to) — спектр согласованной
части ЛЧМ сигнала. Каждая составляющая функция представляет
собой френелевский спектр, определяемый соотношением (6.19),
а фазы фь ф2 и фз — формулами (6.20) и (6.21). Выражение (7.72)
есть векторная сумма комплексных спектров, которая не может
быть оценена с помощью прямых методов; его можно вычислить
только для конкретных значений параметров предыскажения 6
и Д/р. Любое такое вычисление должно удовлетворять условию фазо-
вой непрерывности на границах соответствующих сегментов за-
кона ЛЧМ.
Значения параметров предыскажения, полученные Куком и
Паолилло, равны Д/р = 0,75Д/ и б = 1/Д/, где А/— девиация
частоты неискаженного ЛЧМ сигнала, а 1/Д/ — номинальная ши-
рина сжатого импульса без весовой обработки. Экспериментальные
значения &fp и б, отличающиеся от этих величин не более чем на
20%, при коэффициентах сжатия 40 и 80 позволили существенно
уменьшить пульсации френелевского спектра, что привело к зна-
чительному уменьшению боковых лепестков сжатого сигнала типа
парных эхо, рассмотренных в разд. 7.6. При этом сопутствующим
эффектом было незначительное расширение спектра из-за увеличе-
ния девиации в результате использования предыскаженной функции
ЧМ.
На рис. 7.26 показаны сигналы на входе фильтра сжатия им-
пульсов для ЛЧМ и для предыскаженной ЛЧМ. Влияние функции
предыскажения на френелевский спектр при коэффициентах сжа-
тия 40 и 80 иллюстрирует рис. 7.27. На рис. 7.28 показано, как
указанное ослабление пульсаций спектра переносится на взвешен-
ный по временнбй функции сжатый импульс. Здесь хорошо видны
боковые лепестки типа парных эхо и их ослабление в результате
применения функции предыскажения.
На рис. 7.29 и 7.30 показано влияние предыскажения функ-
ции ЧМ, проявляющееся в сохранении низкого уровня боковых
лепестков при сдвиге частоты входного сигнала (т. е. аппрокси-
мация допплеровского сдвига). На рис. 7.29 иллюстрируется умень-
шение уровня искажений на несжатом выходном импульсе схемы
весовой обработки, когда на вход поступает сдвинутый по частоте
сигнал, который имеет предыскажения описанного выше типа. На
рис. 7.30 показано влияние частотного сдвига на предыскаженный
сигнал после того, как он прошел через фильтр сжатия. Сигналы,
изображенные слева, показывают, что кроме предсказанного изме- .
231
Рис. 7.26. ЛЧМ импульс и закон изменения частоты
при ЧМ (а); модифицированный ЛЧМ импульс и со-
ответствующая функция изменения частоты при ЧМ (б).
ТД}~ЧО 7&f~80
Рис. 7.27. Спектр модифицированного ЛЧМ сиг-
нала (а); спектр ЛЧМ сигнала (б).
232
^ataHauswk
знание без ераниц * *
нения положения импульса никаких заметных искажений формы
главного лепестка не происходит.
Боковые лепестки сжатого импульса изображены более де-
тально в правой части рис. 7.30. Частотный сдвиг на ±7,5% ши-
рины полосы сигнала вызывает изменение уровня боковых лепест-
ков, равного —40 дб при нулевом сдвиге частоты, не более чем на
3 дб. Рассматривая величины, входящие в (7.66), мы можем сказать,
что если произведение |S((o) \W (<о) остается относительно постоян-
ным на интервале интегрирования при сдвиге частоты, то его влия-
ние на взвешенный сжатый им-
пульс будет минимальным и бла-
годаря этому можно избежать
фазовых искажений. Линейность
характеристики задержки фильтра
сжатия в достаточно широкой
полосе, включающей все возмож-
ные допплеровские сдвиги, есть
одно из условий для минимизации
дополнительных фазовых иска-
жений » при допплеровском сдви-
ге. Возможны и другие функции
предыскажений, отличающиеся от
показанных на рис. 7.25, хотя
использование линейных сегмен-
тов ЧМ позволяет упростить ана-
Рис. 7.28. Уменьшение боковых
лепестков типа парных эхо при
коэффициенте сжатия 80 : 1.
литические выкладки при про-
граммировании функций предыскажения спектра для расчета на
ЦВМ. Принцип предыскажений в передатчике можно также рас-
пространить на компенсацию боковых лепестков, возникающих
из-за искажений, связанных не только с пульсациями спектра, но
и с другими факторами.
Величина пульсаций френелевского спектра в полосе схемы
весовой обработки может быть также уменьшена путем предна-
меренного расширения спектра ЛЧМ сигнала на входе схемы ве-
совой обработки или, напротив, сужением полосы пропускания
схемы весовой обработки. Сигнал с большим произведением полосы
на длительность, получающийся при первом методе, приводит
к более низкому уровню пульсаций спектра в частотной области,
охватываемой полосой схемы весовой обработки. Основной недо-
статок этого метода состоит в неэффективном использовании энер-
гии сигнала и ширины полосы по сравнению со случаем идеального
спектра. Эта неэффективность может быть выражена как потери
в отношении сигнал/шум, зависящие от отношения полос расши-
ренного спектра к идеальному спектру. В помещаемой ниже табли-
це приведены данные потерь, характеризующие этот метод. Все
они были получены экспериментально для коэффициентов сжатия
40 и 80 и схемы весовой обработки, предназначенной для обеспе-
233
Рис. 7.29. Уменьшение искажений’несжатого
ЧМ сигнала при весовой обработке при сдвиге
центральной частоты входного сигнала. Сиг-
налы , изображенные справа, имеют предыска-
женную функцию ЧМ:
a) f = f„ + 0.05&f-, б) f = f0; в) f=fo-0.05Af.
Рис. 7.30. Сжатые модифицированные ЛЧМ сигналы при сдви-
ге частоты входных сигналов (а); детальная структура боко-
вых лепестков, номинальный уровень равен —40 дб (6).
234
WataUausiM.
знание Вез границ “ **
чения уровня боковых лепестков (случай идеального прямоуголь-
ного спектра) на 40 дб ниже пикового значения сжатого импульса.
Коэффициент рас- ширения спектра Дополнительные потерн отношения сигнал/шум, дб Наблюдаемый уро- вень парных эхо. дб
1,00 0 —31
1,25 0,96 —34
1,50 1,76 -35
1,75 2,44 —37
2,00 3,00 —39
Критерий, используемый при разработке точного радиолока-
тора (т. е. радиолокатора с малыми искажениями), обсуждается
в гл. 11, где показано, что необходим строгий контроль за точностью
компонентов, определяющих амплитудные и фазовые характери-
стики системы. Материалы этого и предыдущего разделов показы-
вают, что тонкая структура спектра сигнала также может явиться
важным фактором при оптимизации функционирования системы.
7.8. Реализация весовой обработки с помощью
трансверсальной фильтрации
Соотношение (7.14) в разд. 7.2 указывает, что взвешенный по
Тейлору временной отклик выражается в виде суммы взвешенных
и сдвинутых во времени импульсов вида (sin х)/х. Если, как в случае
сигнала на выходе согласованного фильтра для ЛЧМ сигнала, сиг-
нал, поступающий на вход схемы весовой обработки для уменьше-
ния боковых лепестков с тейлоровской весовой функцией, также
имеет вид (sin х)/х (или близкий к нему, как при больших произве-
дениях длительности на полосу), то выходной сигнал представляет
собой сумму задержанных копий исходного входного сигнала.
Исходя из этого, можно найти другой метод синтеза выходной функ-
ции при весовой обработке по Тейлору, используя для этого линию
задержки с отводами.
Этот метод реализации весовой функции иллюстрируется на
рис. 7.31. Так как выполнение линейных операций над ансамблем
сигналов, которые перекрываются во времени, требует когерент-
ного сложения задержанных сигналов, то этот тип фильтра должен
быть синтезирован на промежуточной частоте, а не на видеочастоте.
Вследствие этого выходной сигнал трансверсального фильтра чув-
ствителен к изменению центральной частоты входного сигнала.
Даже умеренный сдвиг частоты узкополосного сигнала может при-
вести к тому, что задержанный сигнал и боковой лепесток в одном
235
и том же интервале времени будут складываться вместо того, чтобы
вычитаться.
Временная задержка между отводами трансверсального
фильтра равна ширине импульса на уровне 4 дб (или l/Af) для вход-
ного сигнала (sin х)/х и суммарный частотный отклик периодичен
в частотной области, причем частота обратно пропорциональна
Рис. 7.31. Принципиальная схема трансверсального фильтра
для полосовой весовой обработки по Тейлору.
ширине импульса на уровне 4 дб, как показано на рис. 7.32. Опре-
деление весовых коэффициентов по равенству (7.12) показывает,
что нечетные коэффициенты положительны, а четные — отрица-
тельны. В трансверсальном фильтре отрицательные коэффициенты
могут быть реализованы путем сложения взвешенных выходных
Номинальная ширима
полосы сигнала
Рис. 7.32. Частотная характеристика трансверсаль-
ного фильтра.
сигналов отводов с четными номерами и последующей инверсии или
изменения фазы несущей частоты на 180° посредством усилителя
или трансформатора. Так как взвешенные выходные сигналы на
отводах равномерно смещены относительно входного сигнала, то
физически реализуемый трансверсальный фильтр должен обладать
достаточной фиксированной задержкой, чтобы не потребовалось
отрицательных задержек. Величина этой фиксированной задержки
и, следовательно, физические размеры трансверсального фильтра
зависят от числа используемых коэффициентов Тейлора. По этой
236
WalaHauslSi
знание без ераниц » *
причине было бы желательно применять как можно меньшее число п
при тейлоровском представлении весовой функции или опустить
члены высших порядков при ее синтезе, как это рассматривалось
в разд. 7.2 для весовой обработки по Хэммингу или модифицирован-
ной тейлоровской обработки. Это приведет лишь к незначитель-
ному ухудшению уровня боковых лепестков и расширению импуль-
са по сравнению с идеальными значениями.
При практической реализации линии задержки трансверсаль-
ного фильтра должны быть предприняты меры для наиболее полной
развязки между отдельными отводами. Разработчик должен быть
Трансверсальная линия завержки

Инвер-
гтюрфазы
Инвер-
тор фазы
Регулирование фазы
tr г ujo
Регулирование амплитувы
К трансверсальному
суммирующему
усилителю
Рис, 7.33. Формирование квадратурного сигнала для регулировки
фазы сигналов на отводах трансверсального фильтра*
уверен, что существуют лишь минимально возможные взаимные
связи между отдельными отводами линии задержки. Для удовлет-
ворения этого требования обычно используют на отводах развязы-
вающие устройства, например усилители или направленные ответ-
вители. Конструкция самой линии задержки должна быть такой,
чтобы отражения от верхней и нижней граней линии и вызванные
ими рассогласования импеданса в точках расположения отводов
были меньше, чем желаемый уровень боковых лепестков в оконча-
тельном выходном сигнале.
Другим важным вопросом является обеспечение возможности
регулировки фазы несущей частоты в местах расположения отводов,
так как фаза несущей боковых лепестков, которые должны быть
подавлены, может и не соответствовать фазе по принятому пред-
положению, согласно которому на входе трансверсального фильтра
будет идеальный сигнал вида (sin х)/х, и вычитания не произойдет.
Это особенно важно в том случае, если боковые лепестки по даль-
ности сжатого сигнала комбинируются с искажениями типа парных
эхо. Метод обеспечения возможности этой необходимой регули-
ровки фазы в местах расположения отводов, который с успехом
использовался в эксперименте, показан на рис. 7.33. Фаза сигнала
. 237
в точке расположения отвода регулируется посредством сложения
синфазного и квадратурного сигналов на каждом отводе. Фаза комби-
нированного сигнала на отводе зависит от значений амплитуд и зна-
ков обеих составляющих и может изменяться в пределах 360°.
В схеме, показанной на рис. 7.33, квадратурная компонента полу-
чается благодаря введению второго отвода, для которого допол-
нительная временная задержка эквивалентна сдвигу фазы несущей
Рис. 7.S4. Вид сигналов при использовании трансверсального фильтра:
а —входной сигнал трансверсального фильтра, поступающий от фильтра сжатия
(заметны боковые лепестки, возникающие вследствие искажений); 0—взвешенный
выходной сигнал трансверсального фильтра (уровень боковых лепестков равен при*
\ близнтельно —30 дб).
частоты 90°. Второй возможный метод состоит в использовании
схемы сдвига фазы на 90° и расщеплении сигнала на выходе отвода
для получения синфазной и квадратурной компонент, которые за-
тем рекомбинируются, как указывалось выше. Можно заметить,
что при практическом построении трансверсального фильтра по-
требуется большое число независимых устройств для регулировки
фазы. По этой причине, а также из-за того, что трансверсальный
фильтр чувствителен к сдвигам частоты, использование указанного
метода для уменьшения боковых лепестков по дальности часто ока-
зывается нежелательным в тех системах, в которых вес и/или слож-
ность должны быть минимальными. На рис. 7.34 показан резуль-
тат применения трансверсального фильтра для уменьшения боковых
лепестков по дальности. Входной сигнал содержит как искажающие
сигналы типа парных эхо, так и нормальные боковые лепестки сжа-
того импульса. Боковые лепестки сигнала на выходе трансверсаль-
238
^alallausKk
знание без границ * *•
ного фильтра уменьшаются до уровня порядка —30 дб при коэф-
фициенте расширения импульса 1,25.
Теория весовой обработки по Тейлору основана на использова-
нии функций (sin х) / х, имеющих регулярно расположенные нули
и боковые лепестки, в которых фаза несущей частоты последова-
тельно сдвигается на 180°. Сигнал на выходе фильтра, согласован-
ного с ЛЧМ сигналом, является хорошей аппроксимацией функции
(sin х) / х только для сравнительно больших коэффициентов сжатия.
Реальный сигнал на выходе согласованного фильтра, задаваемый
выражением (6.13) для малых коэффициентов сжатия, имеет нере-
гулярно расположенные боковые лепестки, как показано на^рис. 6.3.
В случае такого сигнала с коэффициентом сжатия 10 : 1 Шрайт-
мюллер 112] вычислил, что значения тейлоровских весовых коэффи-
циентов для получения уменьшенных боковых лепестков могут быть
изменены. Для единственной пары отводов, расположенной вблизи
выхода Fo при интервале задержек 2/Af, а не 1/Д/, и модифици-
рованном значении — 0,15 уровень боковых лепестков оказался
равным —23 дб. Многоотводные линии задержки могут быть при-
менены для синтеза произвольных функций. Значения коэффициен-
тов можно подобрать таким образом, чтобы компенсировать нерегу-
лярные процессы в системе.
Трансверсальная фильтрация может также служить в качестве
дополнения к обычному полосовому весовому фильтру. При таком
построении схемы основное уменьшение боковых лепестков произ-
водится в полосовом весовом фильтре. Функция трансверсального
фильтра состоит в уменьшении дополнительных боковых лепестков,
вызванных амплитудными или фазовыми искажениями в системе.
Пратт [13] подробно обсуждает такое использование трансверсаль-
ной фильтрации, а также некоторые важные вопросы проектирова-
ния этих фильтров. Фундаментальное изложение теории трансвер-
сальной фильтрации можно найти в работе Кбллмана [14].
7.9. Согласованные фильтры с нелинейной ЧМ,
используемые для уменьшения боковых лепестков
Задача разработки ЧМ сигналов для систем согласованной
фильтрации с помощью принципа стационарной фазы рассматри-
валась в гл. 3. Было показано, что возможно построить сложные сиг-
налы с нелинейной ЧМ, для которых сжатый сигнал будет иметь
очень низкий уровень боковых лепестков. Так как такие сигналы
используются в системах с сопряженными согласованными филь-
трами, то при этом не происходит потерь на рассогласование, опи-
санных в разд. 7.4. Основное соотношение между спектром сигнала
и модуляционной функцией ЧМ, как было показано, имеет вид
|S(<o)[2~^^, (7.73)
1 1 10* (01
239
где О' (О — зависимость мгновенной частоты от времени для пере-
даваемого сигнала с нелинейной ЧМ. Так как используемые нами
частотные весовые функции являются четными симметричными функ-
циями, то из уравнения (7.73) следует, что 6"(0 также должна
быть четной симметричной функцией, и таким образом функция
О' (/) должна обладать нечетной симметрией. Некоторые сложные
ЧМ сигналы такого типа были рассмотрены в гл. 3. На рис. 3.4
показаны возможные схемы построения систем согласованной
фильтрации сигналов с нелинейной ЧМ. Выходной сигнал согласо-
ванного фильтра будем определять в виде
СО
^(0 = -^- J |S(to)|eexp[jto/]dto, (7.74)
— оо
где |5(<о) |2 = НДю), а №(<о) есть интересующая нас частотная ве-
совая функция. Построение дисперсионной нелинейной линии за-
держки ставит проблемы, которые нельзя решить так же эффектив-
но, как проблемы построения линейных линий задержки, хотя
возможности, предоставляемые ультразвуковыми и оптическими
методами фильтрации, могут обеспечить эффективные средства раз-
работки нелинейных линий задержки (см. гл. 13 и 14).
Использование фильтров сжатия импульсов с нелинейной ЧМ
для управления формой сжатого сигнала не лишено своих недо-
статков. Они проявляются главным образом в том случае, когда
входной сигнал имеет сдвиг по частоте. Это вызывает увеличение
боковых лепестков по дальности вследствие фазового рассогласо-
вания. В общем случае принимаемый спектр можно записать в виде
(ю) = A (to + wd) ехр f/Ф (со + со J], (7.75)
где cod = 2nq>, а переходная функция 'согласованного фильтра со-
ставляет
Н (со) = А (to) ехр [—/Ф (<•))]. (7.76)
спектр на выходе согласованного фильтра определится формулой
G (со) = S/? (to) Н (со) = A (to + toj А (со) ехр [/Ф^ (ю)], (7.77)
где Ф,(ю) ® Ф((о + tod) — Ф((о). Для ЛЧМ сигнала Фс/ (ю) пред-
ставляет в первую очередь разность двух квадратичных фазовых
функций и, следовательно, она является линейной функцией час-
тоты, имеющей наклон, пропорциональный знаку и величине <od.
Ее можно считать1 эквивалентной линейному временнбму сдвигу
выходного сигнала согласованного фильтра в зависимости от tod,
и это есть одно из свойств ЛЧМ сигналов при малых допплеровских
сдвигах, рассмотренных в гл. 6. Когда функция ЧМ нелинейна,
тогда Ф^ (to) может обладать нелинейностями, которые создают
эквивалентные боковые лепестки вследствие искажений на выходе
согласованного фильтра. В качестве примера укажем на сигнал
240
NalaHauswi!.
знание без границ * *
с нелинейной ЧМ, который имеет спектр |S(<o) |’ = cos’ (2л [©0 —
— со]/Дсо) в интервале частот Дсо. Дисперсионная характеристика
задержки для этого сложного сигнала, приведенная в гл. 3, имеет
вид
7» = Т
СОр—(О
Дсо
1 . . 2л(<оо—со)
— sin—— -
2л Дсо
(7.78)
Модуль спектра на выходе согласованного фильтра и характе-
ристика задержки для этого сигнала показаны на рис. 3.10 и 3.11.
Положим со = соо — ©, тогда фазовая функция, соответствующая
(7.78), определится формулой
₽/(“) =А. (7.79)
При наличии согласования фазовый спектр Ф,(со) равен взятому
со знаком минус фазовому спектру (7.79), так что получаем
Р/ (<о) + Фв (w) = 0. Если спектр сдвинут на величину cod, то фа-
зовый спектр на выходе согласованного фильтра для малых cod
принимает вид
P/И —+ [ — 2to(0d — (Dd] +
(7.80)
Первый член в уравнении (7.80) соответствует линейному сдвигу
во времени выходного сигнала согласованного фильтра. Второй
член представляет синусоидальную ошибку фазового спектра с час-
тотой, приблизительно равной одному периоду в полосе Дю. Это
будет вызывать появление эквивалентных временных искажений
типа парных эхо (см. гл. 11) на выходе согласованного фильтра.
Величина этой фазовой ошибки будет
sin для cod « Дсо, (7.81) *
2ла Дсо 2л
а величина соответствующего сигнала парных эхо
Л(ЬХ)^
&! __\Ttod
2 4л
(7.82)
Если эти искажающие боковые лепестки типа парных эхо должны
поддерживаться на"уровне 30 дб ниже пикового значения сжатого
импульса, то на cod накладывается ограничение
^;о,12л , ,0,06
< -4-. или, <р < -~
(7.83)
9 Зак. 1341
241
При уровне боковых лепестков—20 дб ограничение на iod сво-
дится к
. 0,4л 0,2
или Ф< —. (7.84)
Неравенства (7.83) и (7.84) показывают, что даже умеренный сдвиг
частоты принимаемого сигнала может привести к утрате преимуще-
ства, присущего сложному сигналу с нелинейной ЧМ при отсутствии
сдвига частоты (т. е. малых боковых лепестков по дальности авто-
корреляционной функции). Приведенные значения cod указывают
Рис. 7.35. Функция неопределенности сигнала с тангенциальной ЧМ при
коэффициенте сжатия 100 : 1 (сдвиг частоты для каждого выходного сигнала
равен 1/47’, где Т — длительность передаваемого импульса).
приближенно на частотную стабильность и/или ограниченный диа-
пазон допплеровских сдвигов, допустимый для этого сигнала, если
необходимо сохранять низкий уровень боковых лепестков по даль-
ности.
Такой вид поведения боковых лепестков по дальности подтверж-
дается детальным анализом сложных сигналов с обратно танген-
циальной характеристикой задержки [15]. На рис. 7.35 показана
модель функции неопределенности для обратно тангенциального
сигнала (тангенциальная функция ЧМ). Мы видим постепенное
увеличение боковых лепестков по дальности с одной стороны сжа-
того импульса при возрастании сдвига частоты входного сигнала
согласованного фильтра. Если знак сдвига частоты изменить на
обратный, то возрастающая структура боковых лепестков появ-
ляется с противоположной стороны сжатого импульса.
В приведенном выше рассмотрении мы предполагали, что со-
гласованные фильтры применяются в системах поиска или слеже-
ния, где надо чтобы отношение пикового напряжения сигнала на
выходе согласованного фильтра к боковым лепесткам по дальности
242
^alattaus^
знание без границ ч ш
оставалось сравнительно постоянным в некотором интервале доп-
плеровских сдвигов входных сигналов. Существуют и другие задачи,
в которых такое поведение выходного сигнала согласованного
фильтра нежелательно, и где могут использоваться определенные
типы сигналов с нелинейной ЧМ. Примеры таких задач рассмотрены
в гл. 9, в которой обсуждается применение сложных сигналов для
измерения или оценки параметров сигнала.
ЛИТЕРАТУРА
1. С. L. D о 1 р h. A current distribution for broadside arrays which opti-
mizes the relationship between beamwidth and sidelobe level. Proc. IRE
34, 335—348 (1946).
2. G. J.Van der Maas. A simplified calculation for Dolph—Tchebuc-
heff arrays, J. Appl. Phys. 25, 121—124 (1954).
*3. J. R. К1 a u d e r et al. The theory and design of chirp radars. Bell. Syst.
Tech. J. 39, 745—808 (1960).
*4. C. L. T e m e s. Sidelobe suppression in a range-channel pulse-compres-
sion radar, IRE Trans. Mll-6, 162—169 (1962).
5. T. T. Taylor. Design of line-source antennas for narrow beamwidths
and low sidelobes, IRE Trans. AP-3, 16—28 (1955).
•6. M. I. S k о 1 n i k. Introduction to Radar Systems, McGraw-Hill, New
York, 1962.
7. С. E. С о о k. Modification of pulse-compession waveforms, Proc. Nat.
Electron. Conf. 14, 1058—1067 (1958).
• 8. P. M. W о о d w a r d. Probability and Information Theory with Applica-
tions to Radar, Pergamon Press, Oxford, 1953.
* *9. E. N. F о w I e, D. R. С a г e y, R. E. Vander S c h u u r, and
R. C. Y о s t. A pulse-compression system employing a linear FM Gaus-
sian signal, Proc. IEEE 51, 304—312 (1963).
• •10. С. E. Cook and J. P а о 1 i 1 1 o. A pulse compression predistortion
function for efficient sidelobe reduction in a high power radar,Proc. IEEE
52, 377—389 (1964).
Г1. R. C. Y о s t. A linear FM radar pulse-compression system employing
thickness-tapered dispersive delay lines, Mass. Inst. Technol. Lincoln
Lab., Lexington, Massachusetts, Tech. Rept. 321 (July, 1963).
12. R. F. S c h г e i t m u e 1 1 e r. Notes on Taylor weignting. Unpublished,
memorandum (1959).
13. W. R. Pratt. Transverse equalizers for suppressing distortion echoes
in radar systems, Proc. Pulse Compression Svmp., p. 119—128, Rome Air
Development Center, Griffiss A. F. Base, New York, Tech. Document.
Rept. RADC-TDR-62-580 (April, 1963).
14. H. E. К a 1 1 m a n n. Transversal filters, Proc. IRE. 28. 302—310 (1940).
15. E. L. К e у, E. N. F о w 1 e, and R. D. H a g g a г t y, A method of de-
signing signals of large time-bandwidth product, IRE Intern. Conv. Re-
cord Pt. 4, 146—155 (1961).
3. Клауде p, Прайс и др. «Зарубежная радиоэлектроника», 1961, № 1,
стр. 15.
4. Тимс. «Зарубежная радиоэлектроника», 1963, № 5, стр. 23.
6. С ко л н и к. Введение в технику радиолокационных систем, изд-во «Мир»,
8. Вудворд. Теория вероятности и теория информации с применениями
в радиолокации, изд-во «Советское радио», 1955.
9*
243
ГЛАВА 8
ДИСКРЕТНО-КОДИРОВАННЫЕ СИГНАЛЫ
8.1. Введение
Радиолокационные сигналы, рассмотренные ранее в настоящей
книге, были построены главным образом на основе аналоговых ко-
дов с использованием непрерывной амплитудной и частотной (или
фазовой) модуляции. ЛЧМ импульс с прямоугольной огибающей
является одним из наиболее известных представителей сигналов
с аналоговым кодированием. В настоящей главе рассматриваются
некоторые дополнительные примеры сигналов, построенных на
основе дискретных кодов. В общем случае они представляют собой
упорядоченные последовательности х, которые воздействуют через
фиксированные интервалы времени * на амплитуду, фазу и частоту
когерентной непрерывной несущей.
Общее описание этих сигналов может быть дано в виде 8
Ф(0 =
2 anPn(Oexp[/{(o0+(on)/4-6n}]» 0<f<2V6,
л — I
при других /,
(8.1)
1 Упорядоченная последовательность обычно обозначается через {хп};
для амплитуды, фазы и частоты обозначения соответственно имеют вид
{ап), {ь>п} и {©„}.
3 Величины этого интервала должны быть выбраны в Соответствии с
требованиями, определяющими функционирование системы, и с практиче*
скими ограничениями, от которых зависит реализуемость системы.
8 Приведенное здесь описание сигнала не нормализовано, т. е.
J IM’COI2 dt =j= 1. Для нормализации необходимо умножить (8.1) на коэффи-
циент (1/6 2 ал),/2« При дальнейшем рассмотрении дли удобства он опущен,
что не оказывает влияния на общность рассуждений.
244
ftalaHauswk
знание Вез ераниц ' *
где п =* 1,2,..., # и Рп (0—импульс единичной амплитуды фик-
сированной длительности 6, так что
[Р(/-[п-1]6)=1,
Л>(0 =
(п—1)6 < t < «6,
при других t.
(8.2)
Подставляя (8.1) в формулу (4.2а) видим, что общее представление
функции отклика для дискретно-кодированных сигналов имеет
вид
N IN 4-оо
Х(т, ф)=2 2 f МО “«(*+*) ехр [—/2nq>/] Л, (8.3)
«=1 т»1 —оо
где
Ф (0 ехр [—/<00 Л = 2 «п (О- (8.4)
п—1
Общее представление х (т, ф) в уравнении (8.3) далее будет кон-
кретизировано для тех или иных специальных видов, дискретно-
кодированных сигналов.
Дискретно-кодированные сигналы, рассмотренные в настоя-
щей главе, можно разделить на три основные группы, характери-
зующиеся соотношениями:
Группа I: {6П} = (<•)„} = 0; (ап = 1, 0}.
Группа II: {(оп) = 0.
Группа III; (ап = 1,0); {0П} = 0.
Используя это деление, можно свести сигналы, рассмотренные
в этой главе, к основным сигналам. Они могут служить основой
для построения более сложных составных сигналов, которые поз-
воляют обеспечивать наилучшее функционирование радиолокацион-
ных систем в отдельных конкретных случаях. Графический мате-
риал, приведенный в этой главе, содержит большое количество
информации о характеристиках этих основных сигналов; приведены
экспериментальные данные и результаты вычислений на ЦВМ х.
8.2. Последовательности импульсов с постоянной
несущей частотой (группа I)
Кодированные сигналы, которые получаются при ограничении
величин элементов последовательности {ап} в группе I только зна-
чениями 1 .и 0, называются последовательностями импульсов с по-
1 Экспериментальные сигналы на основе импульсных последовательно-
стей были получены с помощью аналогового корреляционного вычислите-
ля, выход которого фиксировался на экране осциллографа.
245
стоянкой непрерывной несущей. Описание эуих сигналов получается
из соотношения (8.1) при отбрасывании <оп и 0П. Это приводит
к определению:
1>(0 =
2 апрп (0 ехр
Л»1
О
(8.5)
при других t.

Наиболее простая структура импульсной последовательности по-
лучается в том случае, если последовательность {ап} определяется
соотношениями:
ап=1, и—1—0 modp,
ап = 0, п—l^O modp, (8.6)
где р = 1, 2, ... и на него должно делиться без остатка N — 1,
давая в результате
М—1 = —-, (8.7)
Р
где М — число единиц в последовательности. Предполагается, что
первым и последним элементами последовательности всегда яв-
ляются единицы. В качестве примера рассмотрим случай, когда
N = 17 и р — 4. Тогда М = 5 и
{ап} = 10001000 1000 10001.
Сигналы, которые получаются на основе такой последовательности,
называются регулярными импульсными последовательностями.
Они нашли широкое применение в радиолокации при выполнении
ее основных задач, и их история восходит к самому началу развития
радиолокации. Однако лишь Вудворд [1] в 1953 г. впервые предло-
жил рассматривать регулярные импульсные последовательности
как кодированные радиолокационные сигналы. Изучение этих и
других сигналов типа импульсных последовательностей проведено
в работах Зиберта [21, Фоула и др. [31, Резника [41 и Рихачека [51.
Более удобно представлять регулярную импульсную последова-
тельность ф (0 в виде
m
М-1
Т }ехр[/<оо/], 0
(8.8)
ф(0 =
( 0 при других I,
-где Т — длительность последовательности между передними фрон-
тами первого и последнего импульсов. Структура огибающей этого
сигнала показайа на рис. 8.1. При представлении ф (/) в виДе (8-8)
не обязательно, чтобы период импульсной последовательности
246
Nalattausiiify
делился без остатка на длительность отдельного импульса б. Обыч-
но, однако, Т!(М — 1) > 26, и в этом случае
, лфТ
siting) [М — |fc|]
Это соотношение* получено подстановкой u(t) — ip (О ехр[—/ <о0Л
в общее выражение (8.1).
Рис. 8.1. Регулярная после-
довательность идентичных им-
пульсов, Т!(М — 1) = 56 (им-
пульсы расположены в пози-
циях: 1, 6, 11, 16, 21, 26, 31,
36).
а—последовательность импульсов;
б—выходной сигнал согласован-
ного фильтра (автокорреляцион-
ная функция); в—параметры им-
пульсов и их положение в после-
довательности.
б)
Заметим, что это выражение состоит из двух сомножителей.
Второй сомножитель есть периодическая по т функция на интер-
валах, определяемых величиной Т/(М — 1). Первый сомножитель
не зависит от т, но периодичен по ф в интервалах длительности
247
(М — 1)/Т. Спектр . регулярной последовательности импульсов
можно получить, положив т = k = 0. При этом имеем

sin я/fi
л/
(8.10)

Отклик согласованного фильтра (т. е. <р — 0) на регулярную после-
довательность импульсов равен
|Х(т, 0)| = Ж у [1—
Л--М
kT
М-1
(8.11)
Нетрудно заметить, что он состоит из периодической последова-
тельности треугольных импульсов с основанием, равным 26
(рис. 8.2), взвешенной функцией [1—|/г| /М]. На рис. 8.1,6
показан этот отклик согласованного фильтра, а на рис. 8.2 — не-
сколько вертикальных профилей (разрезов)
[Л4ф77 (М — 1) — 1, 2, 3, ..., М/2, ...» М—2, М—1, ЛП функции
I X (т, ф) |. Более подробный вид одного из профилей при нали-
чии допплеровского сдвига показан на рис. 8.3. На рис. 8.4 пред-
ставлены контуры сечения | %(т, ф) | на некотором постоянном
уровне (скажем на уровне 3 или 4 дб) ниже пикового значения
I X (0,0) |.
Важность регулярной импульсной последовательности опре-
деляется двумя ее свойствами, одно из которых связано с отсут-
ствием излучения между импульсами. ЭтЪ позволяет включать
приемник радиолокатора для обработки до того, как последова-
тельность импульсов будет полностью передана в эфир. Вторым
свойством является наличие свободной области (см. разд. 4.7),
которая окружает центральный максимум сжатого сигнала. Для
многих радиолокационных задач оказывается возможным так по-
добрать значения Тиб, что все сигналы, связанные с неоднознач-
ностями оценки параметров и потенциально неразрешимыми це-
лями (или пассивными помехами), будут априори сосредоточены
в некоторой подобласти теоретически свободной области, окружаю-
щей центральный пик. Однако существуют ситуации, когда этого
сделать нельзя. Для этих случаев периодические скачки неопре-
деленности, которые свойственны структуре неопределенности,
соответствующей сигналам типа регулярных импульсных последо-
вательностей, необходимо тщательно сравнить со структурой не-
определенности других сигналов.
Сигнал, который номинально будет хорошо подходить для
большого числа радиолокационных задач, можно получить путем
248
ftalatiauswk
знание без границ W *
Рис. 8.2. Сечения функции отклика для регулярной импульсной последова-
тельности вплоть до первого пика неоднозначности по допплеровскому сдвигу;
М = 8.
249
нарушения регулярной структуры импульсной последовательности
за счет размещения импульсов через неодинаковые интервалы.
Характеристики неопределенности для такой нерегулярной им-
Рис. 8.3, Форма сигнала на вы-
ходе согласованного фильтра при
подаче на его вход регулярной
последовательности из восьми
импульсов с допплеровским сдви-
гом частоты <р = 5(Л4 — 1)/Т
(Б-й пик неоднозначности):
а —выходной сигнал согласованного
фильтра; б—вид центрального им-
пульса выходного сигнала.
пульсной последовательности показаны на рис. 8.5 — 8.111.
Сигналы на рис. 8.5 и 8.6 получены при условиях, когда едини-
цы в последовательности {ап} могут быть расположены в пози-
Рис. 8.4. Контуры сечения
функции отклика однородной
импульсной последовательно-
сти на некотором постоянном
уровне.
Здесь М эквивалентно используе-
мой данной главе величине М— 1.
циях, отличающихся на —1, 0 или +1 от положения единиц в ре-
гулярной импульсной последовательности. Этот пример представ-
1 Для того чтобы сохранить основное свойство импульсных последо-
вательностей, позволяющего включать приемник до того, как сигнал передан
целиком, необходимо ввести дополнительный фиксированный интервал между
импульсами, который никогда может быть занят. Эти интервалы, однако,
можно опустить из последовательности (ап) при изучении основных свойств
неопределенности таких сигналов.
250
NalaHauswil
знание без орании Я «Ь
ляет частный случай более общего смещения положения импульсой,
которое рассмотрел Рихачек [5]. Конкретная последовательность,
изображенная на приведенных рисунках, содержит восемь ненуле-
вых элементов, положение которых задается соотношением
1, п = 1, 6, 10, 17, 21, 27, 30, 36,
0 при других п.
Пиковое значение наибольшего бокового лепестка при отсут-
ствии допплеровского сдвига достигает значенийХот 8 до 3. Эти
а)
2 Г
Рис. 8.5. Импульсная последовательность из восьми импульсов, в которой
положение импульсов может быть изменено на ±1 (номера позиций: 1, 6,
10, 17, 21, 27, 30, 36):
а —вид импульсного сигнала; б —выходной сигнал согласованного фильтра (авто-
корреляционная функция).
данные следует сравнить со свойствами неопределенности регуляр-
ной импульсной последовательности, представленными на рис. 8.1
и 8.2.

251
Рис. 8.6. Сечения функции отклика для импульсной последовательности
из восьми импульсов, положение которых изменено на ±1 позицию.
252
ftatallausffl!.
знание без ераниц Ч ’ь
На рис. 8.7 и 8.8 показаны свойства неопределенности для
нерегулярной импульсной последовательности, имеющей десять
ненулевых элементов, каждый из которых случайным образом рас-
положен в любой из 50 возможных позиций. Для этого случая
конкретная последовательность определялась соотношениями
( 1, л-1, 8, 11, 17, 27, 29, 32, 37, 45, 49
ten} =
( 0 при других п.
Последний пример, показанный на
нерегулярную импульсную по-
следовательность, где положе-
ния ненулевых элементов вы-
браны таким образом, чтобы
уровень боковых лепестков не
превышал единицы [6]. В этом
Рис. 8.7. Последовательность из де-
сяти импульсов, в которой положе-
ние импульсов изменено случайным
образом, Т = 506 (номера позиций:
1, 8, 11, 17, 27, 29, 32, 37, 45, 49)
a — импульсная последовательность;
б —выходной сигнал согласованного
фильтра (автокорреляционная функция).
рис. 8.9 и 8.10, иллюстрирует
6)
случае последовательность содержит семь единиц и определяется
следующим образом:
л==1, 4, 11, 17, 25, 29, 34
при других п.
На рис. 8.11 приводятся отклики на допплеровской оси (т. е.
при т = 0) для рассмотренных выше нерегулярных импульсных
последовательностей. Как и в случае регулярных импульсных по-
следовательностей отклики на допплеровской оси % (0, <р) имеют
такую же структуру, что и спектр сигнала. Это свойство ясно про-
слеживается на рис. 8.12, где сравнивается отклик на допплеров-
ской оси для семиимпульсной последовательности, приведенной
263
Рис. 8.8. Профили сечений функции отклика последовательности из десяти
импульсов, в которой положение импульсов изменено случайным образом,
254
^alaHausA
знание без границ Ч
27
б)
Рис. 8.9. Субоптимальная нерегулярная последовательность из семи им-
пульсов (номера позиций: 1, 4, 11, 17, 25, 29, 34):
a—последовательность импульсов; б—выходной сигнал согласованного фильтра (авто-
корреляционная функция); в—центральный импульс автокорреляционной функции.
выше с соответствующим выходным сигналом анализатора спектра.
Можно заметить, что смещение положения импульсов нарушает
периодичность отклика на допплеровской оси, а также периодич-
ность спектра и автокорреляционной функции.
Общее представление функции неопределенности для нере-
гулярной импульсной последовательности, полученное прямой
255
Рис. 8.10. Профили сечений функции отклика для субоптимальной нерегу-
лярной последовательности из семи импульсов.
256
ftaiaHausIliii
знание Вез грани» ч *
Рис, 8.11. Профили сечений функ-
ции отклика при т = 0 (т. е. от-
клик на оси допплеровских частот):
а —регулярная импульсная последова-
тельность, расстояние между максиму-
мами равно (М—\)/Т; б —при смещении
положений импульсов на ±1; в—для по-
следовательности^из десяти импульсов со
случайным смещением их положения;
а—для субоптимальной нерегулярной
последовательности из семи импульсов.

Рис. 8.12. Сравнение спектра суб-
оптимальной нерегулярной последо-
вательности из семи импульсов и
профиля сечения функции неопреде-
ленности при т = 0:
а—профиль сечения функции неопределен-
ности при Т = 0; б —спектр импульсной
последовательности (отметим различие
масштабов: ширина сигнала па верхнем
рнсуике соответствует центральной части
ннжнего рисунка).
257
подстановкой в (8.3), имеет вид
N-k
Х(т, <Р) = Хр«ф) 2 апап+Лехр[—/2лф(п—1)61 +
л
N-U+D
4-Х.0—ф) 2 anan+*+iexp[—/2лфп6],
п - 1
Т = £6 + т'»
где т' и k определяются соотношением
0<т'<6,
* = 0, 1, 2, ...,2V,
а ХР(Т\ ф) определяется формулой
Л-т'
ехр [—/2лфП dt, 0 < т
(8.12)
(8.13)
Хр« ф) =
6.
(8.14)
Форма хр (т', ф) эквивалентна односторонней (т. е. для 0 < т <
< оо) характеристике неопределенности, полученной для един-
ственного некодированного импульсного сигнала, который опре-
делен на интервале 0 t 6. Хотя функция (8.12) справедлива
только для т О, представление х (т, ф) можно расширить так,
чтобы оно включало всю плоскость т—ф и использовало специфи-
ческое свойство нерегулярной импульсной последовательности
(а также бинарных фазовых кодов, которые будут рассмотрены
в следующем разделе). Это свойство определяется соотношением
Х(т. Ф) = Х(—т, ф)ехр[—/2лфт].
(8.15)
Смысл уравнения (8.15) состоит в том, что | х (т» ф) । симметрична
относительно оси ф. Из рассуждений, приведенных в гл. 4 относи-
тельно свойств функции неопределенности, можно вспомнить, что
в общем случае
Х(т, ф) = Х*(—— ф)ехр(/2лфт]. (8.16)
Из уравнений (8.15) и (8.16) замечаем, что
Х(т, ф) = Х*(т» —Ф)- ' (8.17)
Очевидно, это соотношение означает, что |х(т»ф)1 симметрична
также и относительно оси т. Сочетание этих свойств делает нере-
гулярную импульсную последовательность очень привлекательной,
когда мы хотим получить сигналы с «кнопочной» характеристикой
неопределенностих. Резник [4] определил «оптимальную» нере-
1 Кнопочная функция неопределенности была рассмотрена в гл. 4 и
будет обсуждаться в гл. 10.
258
NalatiauslSb
знание без ераниц - *
гулярную импульсную последовательность как последовательность
неравномерно расположенных импульсов, для которой характе-
ристика неопределенности | %(т, 0) | обладает абсолютно однород-
ным уровнем боковых лепестков, равным единице, в интервале
6^|т|<Т (см., например, рис. 8.13)1. Такие нерегулярные
импульсные последовательности обеспечивают аппроксимацию,
очень близкую к аппроксимации кнопочной характеристики не-
определенности.
Для того чтобы получить эти характеристики, необходимо рас-
положить ненулевые элементы в нерегулярной последовательности
(ап) таким образом, чтобы набор расстояний между всеми воз-
Рис. 8.13. Автокорреляционная функция
оптимальной нерегулярной импульсной по-
следовательности.
можными парами ненулевых элементов был различимым и полным,
т. е. каждое расстояние, начиная с единичного расстояния и кон-
чая наибольшим возможным расстоянием N — 1, должно появлять-
ся однажды и только однажды. Эти последовательности будут в та-
ком случае содержать максимальное число ненулевых элементов
для заданной длины последовательности 2V. Так как каждый нену-
левой элемент должен образовывать пару с каждым другим нену-
левым элементом, то, очевидно, необходимым условием для полу-
чения оптимальной нерегулярной последовательности является
условие
(N—1)6-
(8.18)
1 Хотя последний из приведенных примеров нерегулярных импульс-
ных последовательностей (см. рис. 8.9 и 8.10) также обладает характеристи-
кой неопределенности 1х(х,<р)| с уровнем боковых лепестков, который ни-
когда не превосходит единицы, он на самом деле попадает под более широкое
определение субоптимальных нерегулярных [4] последовательностей, кото-
рые также обеспечивают единичные боковые лепестки, но не обладают наибо-
лее компактной структурой последовательности.
269
Из соотношения (8.18) можно заметить, что когда А1 > Ц то
М = /2ТД/ ,
(8.19)
где Д/ = 1/6 определяется как эффективная ширина полосы сиг-
нала. Отсюда отношение пикового значения к боковому лепестку
для. таких сигналов постоянно и равно y^TAf.
Оптимальные нерегулярные последовательности для М =2,
3 и 4 имеют соответственно вид
1. 1 1,
2. 110 1,
• 3. 110 0 10 1.
Других последовательностей не существует. Это значит, что не-
возможно, как показал Резник, найти оптимальную нерегулярную
последовательность^ для М > 4. Доказательство этого следует из
соотношения (8.18). Исходя из него, замечаем, что расстояния между
соседними ненулевыми элементами для оптимальной последова-
/ дЛ
тельности должны в сумме давать А— 1 = 1-^1. Этот результат
может быть получен только в том случае, когда соседние расстояния
между ненулевыми элементами последовательности состоят из всех
целых чисел от 1 до Af — 1. Это следует из того, что каждое рас-
стояние, состоящее из одной или двух единиц, может быть соседним
только с расстоянием в Af — 1 единиц. Отсюда расстояния в одну
и две единицы должны быть соседними (например, 1101) или же раз-
деляться расстоянием в три единицы (например, 1100101). Никакое
другое расположение невозможно, конечно, за исключением
(«„} = И, где имеется единственное расстояние в единицу. Однако
если ограничение, что структура боковых лепестков однородна,
исключается, то можно использовать более широкий класс субопти-
мальных нерегулярных последовательностей. Они обладают авто-
корреляционными функциями х (т, 0), у которых боковые лепестки
никогда не превосходят единицы, но иногда имеют и нулевые зна-
чения [6], как показано на рис. 8.9.
8.3. Бинарные фазовые коды (группа II)
Общее представление для бинарных фазовых кодов можно по-
лучить из соотношения (8.1), положив ап = 1 и опустив <оп. Оно
имеет вид
ч>'(0=
2 р„ (0 ехр I/ (<оо /+е„)1. 0 < t < W6,
л«= 1
0 при других t.
(8.20)
260
NalaHauStVii
знание Вез границ ' *
где 6П = <?» л. Для удобства в последующем рассмотрении ис-
пользован коэффициент сп, равный
сп = ехр[/6п]. (8.21)
Так как 0П = О, л, то можно заметить, что
сп = ±1. (8.22)
Бинарные последовательности {0П = 0,л} и {сп = ± 1} ока-
зываются таким образом взаимозаменяемыми. Бывают случаи,
особенно при исследовании свойств этих последовательностей,
когда бинарную фазовую кодовую последовательность удобнее
представлять в виде
dn = 0, 1. (8.23)
Существуют, таким образом, три различные пары элементов, с по-
мощью которых можно представить бинарную фазовую последо-
вательность. Они приведены в нижеследующей таблице х:
0/7 Сп dn
0 + О
7Г — 1
(8.24)
В соответствии с этой таблицей бинарных элементов можно опре-
делить два вида арифметических правил. Один из них основан на
использовании элементов сп и определяется следующей таблицей
перемножения:
(8.25)
1 Символы «+» и «—» означают соответственно «4-1» н «—1». Единица
обычно опускается.
261
Другой вид арифметических правил определен для элементов
dn и характеризуется следующей матрицей сложения по модулю 2:
D 1
0 0 1
1 1 0
(8.26)
Типичная бинарная фазовая последовательность {0П}, за-
данная, например, через элементы {сп}, имеет вид
К}= + + + - + -- + .
(8.27)
На рис. 8.14, аиб показаны видеосигнал и синусоидальный сигнал,
соответствующие последовательности (8.27). Отметим, что несущая
на рис. 8.14,6 непрерывна в точках инверсии фазы. Однако эта
непрерывность сохраняется только из-за того, что в данном примере
АААЛАМ/
б)
Рис. 8.14. Сигналы, построенные на
основе бинарных кодов:
а — модулированный по амплитуде видео-
сигнал; б — высокочастотный сигнал с фа-
зовой модуляцией, соответствующий ви-
деосигналу а.
использовано соотношение 6 = 1//0, выбранное только для удоб-
ства. Как правило, 6 += n/f0, где п — целый множитель 1//о- Сле-
довательно, так как несущая всегда когерентна, то тонкая струк-
тура в общем случае в точках инверсии фазы будет разрывной.
Общее описание функции отклика для бинарных фазовых ко-
дов, полученных из соотношения (8.3), имеет вид
N — k
Х(Ь ф) = Хр(т', ф) 2 спсп+Аехр[—/2лф(л—1)6] +
п=1
*-(*+!)
+ Хр(6—< Ф) 2 спсп+Л+1 ехр[ —/2гарп6], (8.28)
1
0<т<#6, —<’оо.
262
^alaHausA
знание без границ Ч
Это выражение, за исключением замены коэффициентов ап на сп,
было рассмотрено нами в связи с нерегулярными импульсными
последовательностями в предыдущем разделе. Можно заметить,
что для <р = О
Х(т, 0) = б[1
т1! 2 ^n+*+iTzi 2 с"Ся+‘+1 (8-29)
J л-1 И=1
и если ф = т' = 0, то
ЛГ-1Л1
Х(^6, 0) = 6 s cncn + k. (8.30)
П= 1
Функцию (8.30) удобно оценивать с помощью алгоритма Берн-
фельда [7, 8]. Он дает конструктивный метод вычисления произ-
ведения с помощью сложения элементов последовательности {сп}
и обратной к ней (или зеркальное отображение) последовательности
{с_Л. Возьмем, например, последовательность {сп}, задаваемую
(8.27), и, положив для удобства 6 = 1, получим х (^» 0) в следую-
щем виде:
ХМ'-
Этот метод полезен не только для бинарных последовательностей,
но и в более общем случае, когда сп являются комплексными чис-
лами. Очевидно, что х (т, 0) непосредственно определяется через
X (Л 6, 0). Функция (8.30), выраженная через dn при 6 = 1, может
быть представлена следующим образом:
ЛГ—I Л I
x(k, 0) = [N-\k\]-2 2 d„®4>+*. (8.31)
п = 1
где символ ф означает сложение по модулю 2 (доказательство
этого оставим в качестве самостоятельного упражнения для чита-
263
теля). Основное свойство % (k, 0) можно получить, представив
последовательность {сл} в следующем виде [8]:
{cn} = {Pn} + {qn}, (8.32)
где
Предположим, например, что {сп}= + -|-----Ь; тогда {рп}— 4-4-0-Н
a {qn} = 0 0—0. Если в функции (8.30) заменить {сп} йа {рп} + {gnJ,
то в результате получим
%(*, 0) = Х+(Л, 0)-| Х_(Л, 0), (8.33)
где
N-1 k |
%+(*» 0)= 2 [PnPn+* + <7n<M+*i; (8.34)
л = 1
ЛГ-I* I
Х-(£, 0)= 2 IPnQn+k + qnPn+k]- (8.35)
п— I
Мы видим, что х+(^» 0) всегда положительна, а Х-(^» 0) всегда
отрицательна. Образуем далее сумму, входящую в функцию
(8.30), заменяя {сп} на {pn}—{qn}- Это приводит к следующему
свойству:
2V-|^| = X+(^ О)-Х-(Л, 0) (8.36)
или
Х+ (ft, 0) = 4- 1х„,ке (*• 0) + X (ft. 0)J (8.37)
и
X—(ft, 0) = 4- (X(ft. 0)-x„„„c(ft. 0)1, (8.38)
где Хмакс (k, 0) = /V—Р|. Функция Хмакс(^» 0) Получается в том
случае, если не происходит инверсии знака в последовательности
fcn}-
Последовательности Баркера
Это семейство бинарных последовательностей характеризует-
ся соотношением
ло,-(Л.,8ж>
264
ftlataHautfSi!.
знание без ераниц **
Так же, как и оптимальные нерегулярные последовательности,
последовательности этой группы обладают свойством |х (А, 0) | < 1,
k =£ 0. Поэтому они также называются оптимальными. Однако
число последовательностей в этом семействе ограничено, так же как
и число оптимальных нерегулярных последовательностей.
Существуют всего девять таких последовательностей Баркера.
Они приведены в табл. 8.1. Сторер и Турин 110] показали, что
Таблица 8.1
N (г.)
г ♦ + 2 *
2 - 4 г -
з + 4 - 3 0-
Ч ♦ 4 - 4 Ч - 0 *
ч 4 4 4- к ♦ 0 “
5 + 4 4 - 4 5 0 * 0 *
7 4 4 4-4 10-0-0-
11 4 4 4 4 4 11 о - 0 - 0 - о - 0 -
13 ♦ ♦ - 4 л у*. 03 Оз ♦ оз ♦ 03 ♦ ♦ 4
хотя не имеется последовательности Баркера нечетной длины, пре-
восходящей 13, однако эта проблема остаётся нерешенной для ко-
дов четной длины. Было высказано предположение, что не суще-
ствует последовательности Баркера четной длины большей N = 4
[111. Это предположение подкрепляется тем фактом, что не было
найдено ни одной последовательности для N в интервале 4 < N <
< 6084. Если последовательность четной длины и существует, то
она должна быть полным квадратом. Это условие получается из
тождества [111:
- Т2 N— 1
2 с„ =%(0,0) + 2 2 Х(*.О) = Х(О, 0) +
,п-1 1
N— 1
-I- 2 (Х(*. 0) + Х(ЛМП 0)) (8.40)
k " 1
с учетом того, что для кодов четной длины (N > 2), % (Л, 0) +
+ % (N — | k |, 0) = 0. Необходимо также напомнить, что
X (0, 0) = N. В дополнение к тождеству (8.40), можно показать,
что когда (I) N нечетно, a (N — 1)/2 четно, то боковые лепестки
X (k, 0) всегда положительны (N = 5,13); (2) 2V нечетно и (N — 1)/2
четно, то боковые лепестки х (&> 0) всегда отрицательны (N =
= 3, 7, 11).
Эти свойства отражены в таблице последовательностей Баркера.
Элементы последовательностей Баркера нечетной длины связаны
между собой следующей рекуррентной формулой:
(8.41)
265
Кроме того, было показано, что для нечетных N
...Сп = Е12—. (8.42)
сп — 1 с2п-1
Наконец, было замечено, что когда N нечетно, a (N — 1)/2 четно,
то разность между числом знаков плюс и минус равна Y2N — 1.
Если же М нечетно и J(JV — 1 )/2 нечетно, эта разность равна единице.
Рис. 8.15. Сигнал, соответствующий коду Баркера длиной 13 элементов,
и поверхность отклика:
а — сигнал на входе согласованного фильтра; б—автокорреляционная функция иа
выходе согласованного фильтра; а—поверхность отклика.
На рис. 8.15 — 8.17 показаны различные полные харак-
теристики функций неопределенности для последовательностей
Баркера при N = 11 и М = 13. Модуль спектра последователь-
ности Баркера длиной 13 показан на рис. 8.17. Можно заметить,
что структура функции неопределенности для N = 13 имеет неко-
торое сходство со структурой профилей сигнала с V- образной ЧМ.
Это было также отмечено и для N = 11.
Последовательности максимальной
длины
Последовательности максимальной длины (или ЛЬпоследо-
вательности) образуют другой важный класс бинарных последова-
266
^alaHausA
знание без границ Ч
тельностей, которые могут быть использованы для фазового коди-
рования [2, 12—141. Эти последовательности образуются с помощью
рекуррентных формул, которые выбираются таким образом, чтобы
обеспечить генерирование максимального числа элементов после-
Рис. 8.16. Функция отклика согласованного фильтра |х(тф) |
для сигналов на основе кодов Баркера:
а—функция отклика для бинчриого фазового кода Баркера, №«!!;
б—функция отклика для бинарного фазового кода Баркера, ЛГ—13.
довательности, равного 2К — 1, прежде чем последовательность
циклически повторится. В общем случае, когда эти последователь-
ности записываются через элементы dn = 0,1, то для n > k каж-
дый элемент d/4.1 является суммой по модулю 2 определенных эле-
267
Рис. 8.17. Функция отклика и модуль спектра кода Баркера
длиной 13 элементов:
а —функция отклика; б—модуль спектра.

268
^alaHausA
знание без границ Ч
ментов, выбранных из предыдущих k элементов. Эта формула имеет
вид
d/4-1 =did|®(X|dj—1 @... а, (8.43)
где коэффициенты а равны либо нулю либо единице. Вторая
возможная форма записи через элементы сл, приводящая к экви-
валентной последовательности, задается соотношением
«Ж - П C1J- ж » (8-44)
/->
где показатели степени aj те же самые, что и коэффициенты a,j
в формуле (8.43).
Первые k элементов данных последовательностей, исключая
последовательность, состоящую только из нулей (или знаков плюс),
выбираются произвольным образом. Эти k элементов образуют ба-
зис для одной из 2* — 1 фаз, которая может быть получена для за-
данной последовательности а. Не все последовательности а, однако,
приводят к последовательности максимальной длины для элементов
dn (или сл). Условия для получения таких последовательностей
можно найти в нескольких работах [15—17], которые рекомендуют-
Рис. 8.18. Каноническая схема
регистра сдвига.
ся для дальнейшего изучения. Обширный список неприводимых и
примитивных полиномов, эквивалентных последовательностям а,
приведен в работе Питерсона [17].
Рекуррентная формула (8.43) оказывается особенно удобной
для реализации с помощью регистра сдвига. Каноническая схема
построения такого регистра показана на рис. 8.18. Она состоит из
трех основных элементов: 1) последовательно включенных элементов
задержки с единственным входом и единственным выходом, обозна-
ченных через D (оператор, введенный Хаффманом [18]; 2) переклю-
чателей обратной связи, обозначаемых через at (элементы последо-
вательности а), и 3) сумматоров по модулю 2. Такая схема обычно
синхронизируется с помощью (равномерно расположенных) син-
хроимпульсов. Для формирования каждого последующего им-
269
пульса хранящийся (накопленный) в элементе задержки импульс
сдвигается на один элемент вправо и вычисленное значение заносит-
ся в первый элемент задержки. Математическое описание регистра
сдвига обычно представляется в виде полинома P(D) по степеням
Вход
тактовых
импульсов
1234567
О
Рис. 8.19. Последовательные состояния регистра сдвига макси-
мальной длины для N - 7.
оператора единичной задержки D. Для того чтобы получить макси-
мальную длину последовательности прежде чем закончится цикл
регистра сдвига, этот полином должен быть неприводимым (нераз-
ложимым на множители) и примитивным (является делителем
Dm + 1 только при т > 2К — 1). Примером его может служить
полином
Р(О) — 1фОфОа,
(8.45)
270
NataHausiilk
знание без границ '
где через I, обозначена величина D°. Элементы последовательности
а, соответствующей полиному (8.46), равны ах = 1, ая = 0 и а8 =
= 1. Выбирая начальное состояние регистра сдвига в виде 010,
найдем, что последовательность максимальной длины, получаемая
при выбранной схеме построения регистра сдвига в соответствии
с (8.45), равна (рис. 8.19)
[dn}=... Ill, 0100111, 0100111, 010..., (8.46)
где N = 7. Другие фазы последовательности, определяемой (8.46),
могут быть получены, если исходить из различных наборов трех
начальных элементов (за исключением трех нулей). Остается шесть
таких наборов: 001, ОН, 111, 100, 101, 110.
Рис. 8.20. График полученной экспериментально автокорреляционной функ-
ции периодического псевдослучайного бинарного фазового кода.
Периодическая структура в виде (8.46) и соответствующие ей
полиномы были достаточно подробно изучены в работах [15—17].
Одним из важных результатов этого изучения явилось установление
свойства, что
( 2р—-1, k = 0 по mod (2р— 1),
-I, ^0 по mod (2-1), <8Л7>
где р использовано здесь для обозначения наивысшей степени поли-
нома P(D). Это свойство аналогично результату, полученному для
последовательностей Баркера. Однако в противоположность после-
довательностям Баркера, которые состоят из конечного числа эле-
ментов, для справедливости соотношения (8.47) структура последо-
вательности максимальной длины должна быть периодической.
Экспериментальная оценка х (Аг, 0) для N = 2₽ — 1 = 255 иллю-
стрируется графиком, приведенным на рис. 8.20.
271
N<5~
N-7
N6-
N=1S
N=31
Рис. 8.21.
рованных
усеченной
Автокорреляционные функции коди-
ло фазе сигналов, соответствующих
последовательности максимальной
длины.
Отметим влияние расположения элементов последо-
вательности на внд боковых лепестков.
Рис 8.22. Автокорреляционные функции кодированных
по фазе сигналов, соответствующих усеченным последо-
вательностям максимальной длины.
Отметим влияние расположения элементов последовательности
на внд боковых лепестков.
ю

Периодические последовательности максимальной длины нашли
применение в радиолокаторах с высоким разрешением [12—14].
Такой тип функционирования эквивалентен радиолокационным си-
стемам с непрерывным излучением и поэтому имеет ограничения
дальности, если только не обеспечена достаточная развязка передат-
чика относительно приемника. Для многих радиолокационных задач
последовательности конечной длины более предпочтительны, так
как при этом удается избежать проблем, связанных с непрерывно-
стью излучения. Кроме того, при этом нет необходимости связывать
максимальную дальность радиолокатора с интервалом времени
(2* — 1)6, характеризующим интервал неоднозначности периодиче-
ской последовательности максимальной длины. Примеры функций
Х(т, 0)для последовательностей максимальной длины, которые огра-
ничены одним периодом, показаны на рис. 8.21 и 8.22 для N = 7,15
и 31. Эти графики показывают, как структура боковых лепестков
X (т, 0) зависитот фазы этих усеченных последовательностей мак-
симальной длины. Кроме того, на рис. 8.23 приведена функция от-
клика х(т» ф), соответствующая N = 15 и 31. Для больших N
отношение пикового значения к боковому лепестку усеченной после-
довательности максимальной длины приближенно равно YN.
8.4. Многофазные коды (группа 11)
Общее описание многофазных кодов (за исключением упомя-
нутых в сноске1) также выводится из соотношения (8.1), если
положить ап — 1 и опустить <ол. Выражение для ф(0 задается (8.20),
однако 0„ не ограничивается лишь значениями 0 или л. В общем
случае последовательности {0л} будут многозначными, тем не менее
все же удобно заменить последовательности 0п последовательностями
сп, где сп определяется уравнением (8.21). Однако теперь сп будут
представлять собой комплексные коэффициенты, состоящие из дей-
ствительной и мнимой частей. Общее представление функции неопре-
деленности для многофазных кодов, получающееся из уравнения
(8.3), имеет вид (8.28), за исключением того, что члены и
в этом выражении являются сопряженными.
Многофазные последовательности Баркера
Последовательности, построенные из алфавита, содержащего
два или большее число фаз, и обладающие свойством | X (^» 0) | < 1,
образуют общий класс последовательностей Баркера, исследован-
ный Голомбом и Шольтцем [19], которые рассматривали построение
кодов с длинами от 1 до 19 при различных размерах алфавита.
_________ •
1 Получающееся выражение не описывает класс многофазных кодов,
которые известны как коды Хаффмана. В настоящем разделе они будут рас-
смотрены ниже.
274
Nalattausllk
знание без араниц — *
В этой работе также приведены исчерпывающие таблицы последо-
вательностей, полученных из алфавита с шестью элементами, и со-
ответствующие функции % (k, 0). Алфавит из шести элементов
оказывается уникальным, так как он образует последовательности
Баркера для каждой исследуемой длины вплоть до N •— 12; не суще-
ствует, по-видимому, теоретических ограничений, которые бы делали
невозможным существование более длинных последовательностей.
В общем случае алфавит, используемый для получения «обоб-
щенных последовательностей Баркера», состоит из р корней еди-
ницы (т. е. р°, р1 ехр 1/2л/р1,р2, ...,рр ')• Например, для N — 12
такая последовательность имеет вид
Ю -1, 1, р, р2, ря, р, р, р6, 1, ра, 1, р4,
где для рассматриваемого случая р = ехр |/2л/6]. Для этой после-
довательности получаем
k -и — 10 -У —8 —7 —6 —5 -4 -3 -2 — 1 0 1 2 3 4 5 6 7 8 9 10 11
0) р4 р‘ р3 0 1 0 р‘ рз РЯ РЬ Р 12 р‘ "1 Р4 ()3 Р 0 1 0 рз р 9 р’
(8.48)
где обозначение 0 в строчке х (Л, 0) означает отсутствие выходного
сигнала в этой точке.
Квантованные фазовые коды
Хеймиллер [201, Фрэнк и Задов [21 ] и Фрэнк [22] описали
метод, который может быть использован для построения многофаз-
ных кодов. В этом методе используется матрица [221, имеющая
следующую общую структуру. (Сигналы, которые формируются
с помощью этих последовательностей, называются квантованными
фазовыми кодами. Сигналы, основанные на приведенной ниже матри-
це, носят название многофазных кодов Фрэнка)
0 0 0 • • • • 0
0 1 2 • • • • А—1
0 2 4 • • • •
0 (А-1) 2(А-1) .... (/V—I)2.
Эту матрицу с одинаковым успехом можно читать как по строкам,
так и по столбцам. Элементы ее представляют собой коэффициенты-
Н)* 275
ж
сомножители основного фазового угла 2n.pl N, где р и М — целые
и взаимно простые числа. В нашем рассмотрении будем предпола-
гать, что р = 1. Реальная кодовая последовательность образуется
путем размещения строк или столбцов последовательно друг за
другом. При этом мы получаем последовательность, содержащую №
элементов. Предположим, например, ч7о N = 3, тогда с помощью
этой матрицы получаем последовательность 1
|^) =0,0,0; 0,1,2; 0,2,1, (8.49)
( 2л J
которая состоит из девяти элементов. Отметим, что элементы этой
последовательности представляют собой числа по модулю N и что
каждая из N групп начинается с нулевого элемента. Первая группа
из трех элементов в (8.49) указывает на факт отсутствия фазового
сдвига; в следующей группе из трех элементов коэффициенты отли-
чаются на единицу и соответствуют 0°, 120° и 240°; последняя трех-
элементная группа состоит из элементов, отличающихся на две
единицы, и соответствует 0°, 240°, 120° по модулю 360°.
Вследствие того, что нарастание фазового сдвига слева направо
имеет квадратичный характер, многофазные кодированные сигналы
Фрэнка, образованные на основе последовательностей, иногда рас-
сматриваются так же, как квантованные по фазе ЛЧМ сигналы.
Структуру этих сигналов можно сравнить со структурой сигналов
с линейно-ступенчатой ЧМ, которые являются другой квантован-
ной аппроксимацией аналоговых ЛЧМ сигналов (рассмотрение их
приведено в разд. 8.5). Ниже даются другие примеры таких после-
довател ьностей:
N №
2 4 а) 0,0/0,1 б) 0,0/1,0
4 16 0,0,0,0/0,1,2,3/0,2,0,2/0,3,2,1
5 25 0,0,0,0,0/0,1,2,3,4/0,2,4,1,3/0,3,1,4,2/0,4,3,2,1.
Последовательности для N — 2 также являются бинарными после-
довательностями Баркера.
Как периодические последовательности эти коды обладают
функциями % (Л, 0) с нулевыми боковыми лепестками для
k =/= 0 mod N2 [20, 21 ]. Такой оптимальный характер боковых ле-
пестков не сохраняется, если длина этих последовательностей огра-
ничивается одним периодом. Однако получающиеся при этом авто-
корреляционные характеристики обладают меньшими боковыми
лепестками, чем ЛЧМ сигналы. Общее описание сигналов, построен-
1 Эта последовательность и другие последовательности, состоящие из
кубичных корней единицы, были исследованы Делонгом [23].
276
^latdttausA
знание без границ * *
ных на основе усеченных последовательностей, удобно представ-
лять в виде суммы по двум индексам пит:
N N
ф(/)- 2 2 Ри—|(п—1)6 F(m—1)W6}[X
т=>1
Хехр Г/ |<оо/ +^(т—1) (п—1))1,
I /V j ]
(8.50)
где индекс п = 1,2, ..., N изменяется от элемента к элементу вплоть
до N элементов, а индекс т = 1,2,... изменяется от группы к группе
вплоть до /V-й группы. Общая длительность такого сигнала равна
№ 6, а эффективная ширина полосы составляет N (1/N 6). Произве-
дение длительности на ширину полосы равно таким образом №.
Спектральное представление такого сигнала, задаваемого соот-
ношением (8.50), определится в нормированных единицах как
п
// /и - Л sln nx/N V sinn[x-(n —1)]
U nx/N sin л [x—(л—1 )]/Л/ X
X exp Г —/2л(n — 1) (x — )1, (8.51)
где x = Nbf и U(f) = ф (f + f0). Из (8.51) очевидно, что U (x) со-
стоит из весовой функции, имеющей форму (sin у)/у, и векторной
суммы функций вида (sin Ny)/sin у, которые размещены через
единичный интервал на нормализованной шкале х или через ин-
тервалы \/N 6 на ненормализованной шкале частот. Более того,
также очевидно, что преобразование Фурье равно умноженной на N
весовой функции при целых значениях х, так как в этих точках на
оси х все векторные функционалы, кроме одного, исчезают. Вид
функции | U (х) |, вычисленной для некоторых случаев, включаю-
щих W = 6, 7 и 10, показан на рис. 8.24. Результаты эксперимен-
тального измерения спектра и автокорреляционной функции для
N = 6 показаны на рис. 8.25. Из этих иллюстраций видно, что | U (х) |
имеет структуру, характеризующуюся наличием пульсаций, кото-
рые изменяются в зависимости от произведения длительности на
полосу. Было высказано предположение, что поведение функции
неопределенности сигналов, образованных на основе кодов Фрэнка,
можно исследовать с помощью применения к пульсациям | U (х) |
метода парных эхо.
Общее выражение для функции отклика этих кодированных
сигналов удобно записывать с помощью переменных т = т' + рб -|-
4-&V6, где 0<t'<6 и т' представляет непрерывный сдвиг
времени в интервалах р6^т^(р + 1)6, а р является дискрет-
277
Ufx)
' N-Ю, произвр^ение ёлитрль*
1/7 пости но полису * ЮО
Рис. 8.24. Спектры сигналов на основе многофазных кодов Фрэнка:
а—проиэведеиие длительности на полосу равно 30; б—произведение длительности на
полосу равно 49; а—произведение длительности на полосу равно 100.
278
ftalaHauswk
знание без границ я ш
ным сдвигом времени в интервалах V) N& где
O^k^N — 1. Результирующая функция отклика имеет вид
%(т, <р) -= Х(тЧ pb \ kNb, ф) -- % (у', ф)[Р(р, k, Nq>)Q(p, k, ф) 4-
4-Р (p—N, Л-j-1, Мр) Q (N—p, Л-p 1, ф)] ехр [—/Q (р, k, ф)] 4-
+ Х(б—Л ф)(Р(р4-1, k, Nq>)Q(p 4-1, k,(f) -Ь
+ P(p-N+\, k+\, Л+1, ф)]Х
X exp[—jQ(p—1, k, Ф)],
где
Х(т', ф)--бГ1
sin Лфб
Лфб
exp —/лф
(8.52)
(8.53)
sinnfJV—Л] £- + ф^6
---------------p-'ехр
sinn 77 + фЛ^б
_/v J
(8.54)
Рис. 8.25. Экспериментально полученный сигнал на выходе согласованного
фильтра и спектр сигнала для многофазного кода Фрэнка длины 36: •
а — автокорреляционная функция на выходе согласованного фильтра; б—спектр сиг-
нала после детектирования.
279
sinnJJV—р] —+фв
Q(р, k, Ф) --=--z-т-ь—-—Lехр—/2 л (А— 1) ; (8.55)
sin я — -Ь.фб L J
L N J
й(р, k, ф)-[№—Nk—(p + 1)1 фб. (8.56)
Из соотношения (8.52) можно сделать следующие выводы:
1. Если т = 0, то
х(0.
я№фО
2. Если т' = р = 0 и ф = 0, то 1 (Nkb, 0) = 0.
3. Функция % (т, 0) имеет одно и то же абсолютное значение
при смещении j и (№ — /), если 1 < j < № (рис. 8.26).
Рис. 8.26. Автокорреляционные функции мно-
гофазных кодов Фрэнка.
4. Абсолютная величина корреляционной функции равна еди-
нице при смещении на единицу вправо или влево от значений, крат-
ных N [221.
5. Фрэнк [221 предположил, что максимальный боковой ле-
песток есть векторная сумма N/2 (при четном N) или (N -[- 1)/2
280
^lalaUauStO!.
знание без ераниц “ *
(при нечетном W) единичных векторов, причем вектора повернуты
относительно друг друга на 2л/N. Это означает, что для больших N
отношение пикового значения к боковому лепестку асимптотически
приближается к nN.
Характеристики неопределенности, соответствующие сигналу,
для которого N == 10, показаны на рис. 8.27. Величины дополни-
тельных характеристик (т. е. вторичный максимум и ложный сиг-
нал) и их зависимость от допплеровского сдвига представлены на
рис. 8.28. Из этих данных очевидно, что характеристика неопределен-
ности этого сигнала несколько напоминает характеристику ЛЧМ
сигналов, так как она имеет гребневой характер, часто соответствую-
щий ЛЧМ сигналу. Однако можно заметить, что они имеют также
большие (до 30% пикового значения выходного сигнала) цикличе-
ские скачки неопределенности в зависимости от допплеровского
сдвига. Такие черты делают эти конкретные квантованные фазовые
коды неподходящими, когда принимаемые сигналы могут иметь зна-
чительный допплеровский сдвиг. Для очень больших допплеровских
сдвигов характеристика функции неопределенности распадается на
два аналогичных сигнала, разделенных во времени интервалом,
равным длительности необработанного сигнала №6.
Коды Хаффмана
Предыдущие примеры, рассмотренные в настоящей главе под
названием кодов группы II, включали в себя только дискретные
фазовые последовательности. Наилучшее отношение пикового зна-
чения к боковому лепестку для % (k, 0) было равно /V. В каждом
случае, когда это достигалось, боковые лепестки распределялись
равномерно в интервале —N6 < т < N6. Отказавшись от ограни-
чения {ап = 1} и несколько жертвуя эффективностью использова-
ния времени, предназначенного для передачи, можно получить по-
следовательности, которые обладают свойством
Х(*,0) =
2£,
0,
±1»
/г = 0
|/г|=/=0, N—1
(8.57)
где Е — энергия сигнала. Метод, использованный для получения
этих последовательностей, был предложен Хаффманом [24]. Учи-
тывая свойства структуры х (к, 0) для таких последовательностей,
Хаффман назвал их «импульсно-эквивалентными» последователь-
ностями. В общем случае они состоят из пар величин амплитуды и
фазы {ап, 6П), которые могут принимать значения из некоторого
континуума. Для удобства эти пары значений последовательностей
мы будем обозначать через {Ьп}, где
bn = an ехр [/0п].
(8.58)
281
a)
юо
90
N-'0,Nl6= длительности
нодироданного сигнала
80
t/S
282
^alalfausiak
знание без ераниц W *
ВО
70
60
у>Т'2О
юо -во -60 -ьо -го о го <+о бо
80 100
t/<T
Рис. 8.27 г, д, е.
283
Рис. 8.27. Сигналы на выходе согласованного фильтра для
многофазного кода Фрэнка прн наличии допплеровского сдви-
га; произведение длительности на полосу равно 100; фТ есть
нормализованный допплеровский сдвиг.
Метод Хаффмана можно объяснить исходя из полинома
N- 1
r(s)“6x+ М+М’+ - +bNsN-'^bN П (s—г,), (8.59)
I» 1
где s — некоторая переменная величина. Полином, соответствую-
щий согласованному фильтру для последовательности (8.59), равен
P'(s) = 6,+ Z>2s-‘ + 63s-2+ ... +6A,s-<w-'>.
(8.60)
Рис. 8.28. Поведение существенных параметров, харак-
теризующих сигналы на основе многофазных кодов
Фрэнка, в зависимости от допплеровского сдвига;
произведеиие длительности на полосу равно 100,
2S4
ftatatiauswii
знание без границ Ч *
Отклик согласованного фильтра % (k, 0) можно получить из произ-
ведения РР*, которое записывается в виде
Р(s)bN s-(W-,’+ ... + (6,6,+
+ 6, 6, + ... + Ьн Ьн) s® + ••• 4"bi Ьн s —
6w(-s)-,N-'» п' г, "п1 ЬЧп+'ГЪ + гЛ1]. (8.61)
(«=1 / = 1
(8.62).
где х (Л» 0) — коэффициент при sK.
Для хаффмановских («импульсно-эквивалентных») последова-
тельностей это произведение сводится к
РР* = bl bN s~iN -1 ’ + 2Е + bl bN sN -1, (8.63)
где 2E = bi bx + ЬгЬг + ... +b;v bN представляет энергию коди-
рованного сигнала, полученного на основе этих последовательно-
стей. 2W—2 корней уравнения (8.63) лежат на двух концентриче-
ских окружностях с центром в начале координат, радиусы которых
определяются формулой
/?"-' = ~Е . (8.64)
bN
Нетрудно заметить, что эти радиусы взаимно обратны, если
|б, 6N| -=1. (8.65)
Для этого случая из (8.63) можно заметить, что отношение пико-
вого значения к боковому лепестку зависит только от энергии сиг-
нала Е. Кроме того, мы видим также, что
2Е > bt bi +bNbN= + 2 > 2. (8.66)
bN bN
Из 2N—2 корней произведения РР* одна половина лежит на вну-
тренней окружности, а другая при этих же радиусах — на внешней
окружности. В то же самое время одна половина этих корней, взя-
тых с любой окружности, может быть использована для формирова-
ния P(s), другая половина — для формирования сопряженного
полинома. Следовательно, существует 2Л/-1 возможных импульсно-
эквивалентных полинома, которые могут быть получены при за-
данном Е и длине последовательности /V. Коэффициенты этих поли-
номов обычно являются комплексными.
Полиномы с действительными коэффициентами могут быть
получены путем размещения сопряженных пар комплексных кор-
ней, выбранных для образования P(s), на одной и той же окружности.
286
Хотя некоторое уменьшение эффективности использования времени,
отведенного для передачи, с тем чтобы получить свойство (8.57)
можно допустить, тем не менее было бы неразумным не искать
для применения наиболее эффективную последовательность. Хаф-
фман установил, что наибольшая эффективность достигается при
максимизации отношения 2Е/1 max | Ьп |2. Это так называемое от-
ношение «эффективных энергий» имеет две степени свободы, а имен-
но: общую энергию кодированного сигнала 2Е и наибольшую вели-
чину коэффициентов P(s), обозначаемую тах|Ьп|2. Обращаясь
к соотношению (8.64), мы видим, что Е изменяется в зависимости от
радиуса концентрической окружности, на которой выбираются
корни P(s). Наибольшее значение | Ьп |2, однако, зависит от конкрет-
ного выбора N — 1 корней для P(s), так же как и от этих радиусов.
К сожалению, за исключением метода проб и ошибок не найдено
аналитического метода, который приводил бы к наиболее эффектив-
ной последовательности Хаффмана. При этом Хаффман предпола-
гал, что отношение энергий для импульсно-эквивалентной после-
довательности максимизируется; когда с каждой из окружностей
берется приблизительно по половине корней.
Общее представление кодированных сигналов Хаффмана, по-
лученное из выражения (8.1), имеет вид
ф(0-
N
2 5nPn(0expI/<M],
п = 1
О
0</<JV6.
(8.67)
при других t.
Общее представление функции неопределенности для этих сиг-
налов задается соотношением (8.28), за исключением того, что ве-
личины сп заменяются на Ьп и коэффициент сдвига является со-
пряженным.
Одна из примерных последовательностей Хаффмана длиной 14,
которая включает только действительные коэффициенты, имеет
следующий вид [25]:
[6П] - —0,57, 0,27, —0,56, 0,55, -0,14, —0,28, —0,31, —1,
— 0,43, 0,5, 0,037, —0,34, 022, 0,43.
Структура огибающей и характеристики неопределенности этой
последовательности показаны на рис. 8.29. Другая последователь-
ность длиной 9 элементов с почти постоянной амплитудой имеет
вид [25, 26]
|6п|-1 /180°, 0,97 /157,5°, 0,90 /76,5°, 0,95 /60,9°,
0,89 /195,9°, 0,90 /346,5°, 0,97 /202,5°.
286
^alaHausA
знание без границ Ч
Отношение энергий для этой последовательности равно 8,125. Инд-
жеян [26] изучал эту последовательность, но при этом положил
все величины равными единице и нашел, что отклонение ее свойств
Рис. 8.29. Сигналы на основе кодов Хаффмана и соответствующая
поверхность отклика; длина кода равна 14, отношение пикового
значения к боковому лепестку составляет 13,1:
а —сигнал на входе согласованного фильтра; б —автокорреляционная функ>
цня па выходе согласованного фильтра; а —полная поверхность отклика.
от свойства, описанного уравнением (8.57), пренебрежимо мало.
Отклик согласованного фильтра на последовательность Инджеяна
показан на рис. 8.30.
Отношение эффективных энергий является не единственным
важным фактором, определяющим выбор последовательностей Хаф-
фмана. Для этого Также может быть необходимо рассмотреть отно-
шение пикового значения к боковому лепестку. Поскольку эти тре-
бования обычно несовместимы, то окончательный выбор конкрет-
287
ной последовательности Хаффмана будет зависеть от того, какой
компромисс между этими требованиями допускает специфика кон-
кретной задачи.
Рис. 8.30. Сигналы на основе
кода Инджеяна длиной 9 эле*
ментов.
Входной сигнал имеет постоянную
амплитуду; автокорреляционна^
функция аналогична автокорреля-
ционной функции многофазного кода
Хаффмана:
а — сигнал иа входе согласованного
$нльтра; б —автокорреляционная
ункцня на выходе согласованного
фильтра.
Реальное применение указанных систем для сбора данных по
ионосферному зондированию изучали Колл и Сторей 127], которые
использовали как последовательности Хаффмана, так и бинарные
последовательности длиной 17. На рис. 8.31 ясно показано ослабле-
6)
____Л . А t . .1 4--< .
О 200 600 4000 мксек
Рис. 8.31. Сравнение уровня боковых лепестков для хаффманов-
ских и бинарных последовательностей.
Слева: хаффмановская последовательность; а —ложный отраженный сиг-
нал от слоя F,. возникший из-за бокового лепестка; б —нормальный
отраженный сигнал от слоя Ff; справа: втн же сигналы при бинарной
последовательности. ;
ние ложных сигналов, вызванных боковыми лепестками бинарных
сигналов, когда используются коды Хаффмайа. Отношение боко-
вых лепестков для бинарной последовательности, применяемой для
этих исследований, составляло 17/2.
288
^ataHaus^k
8.5. Дискретные частотные последовательности (группа 111)
Дискретные кодированные сигналы, полученные на основе
частотных последовательностей {<ол} образуют третью группу сиг-
налов, рассматриваемых в настоящей главе. Общее представление
этик сигналов имеет вид
N
Ф (О = 2 ип (0 ехр 1/(00 П, .(8.68)
п»! •
где
ып(0 = апРп(0ехр [/<опЛ;
Рп(0 = Р (/-(«-1)6], (п—1)6 </<п6;
( 0.
Конкретная структура последовательности, которая при этом
получается, обычно рассматривается как сигналы со ступенчатой
ЧМ, у которых частоты разнесены на 1/6 друг от друга. Для после-
довательности с возрастающими частотами элементы {<ол} задаются
соотношением
<от=2л
Гт-1 М-11
[б - 26 J’
(8.69)
где индекс m проходит все единицы в последовательности {ал} и М
равно общему числу единиц. Последовательность убывающих частот
получается при изменении знака в уравнении (8.69).
Преобразование Фурье, полученное для ф (/) при использо-
вании (8.69), если положить ап = 1 (т. е. М = Л/, сигнал с линей-
ной ступенчатой ЧМ) определяется формулой
(8.70)
Поучительно вспомнить спектральное описание (8.51) квантован-
ных фазовых кодов. За исключением весовой функции, не входящей
под знак суммирования (8.51), структурное сходство уравнений
(8.51) и (8.70) вполне очевидно. Одной из важных характеристик
является то, что произведение длительности на полосу частот обоих
сигналов равно ЛР, причем оно вычисляется в виде произведения
№6(Л//М6) для кода Фрэнка и в виде М6(Л//6) для сигнала со ступен-
289
®r
Рис. 8.32. Параллельный набор согласованных фильтров
для сигналов группы III.
Рис. 8.33. Выходные сигналы в параллельных каналах
и суммарный выходной сигнал согласованного фильтра
для последовательности пяти импульсов со ступенчатой
ЧМ.
290
WaldHausiSk
знание Вез границ * *
Рис. 8.34. Контуры сечения на заданном уровне
функций отклика сигналов со ступенчатой ЧМ:
а —непрерывная последовательность импульсов; б — по-
следовательность отстоящих друг от друга импульсов.
291
ДО
О)
юо
во
60
N=1O,N2=1OD
1(0 фТаО
-IS -го -15 -10 ’5 0 5
6)
60
40
10
I I I
15 го 25 30 tAf

-го -is
-<0 -6
0) Г100
-во
-60
- 40
-го
о 5 10 15 20 .
Нормированное врем я, tAf

<рТ'1О
—*---~~
ZfQ -5 о 5 10 15 20 25 30 35 tAf
^alaHausA
знание без границ Ч
г 100
-во
- 60
- 40
- 20
0
\ tpl'35
~4nrfJ 1 VVwVl I УУУУУ |У\^
10 15 20 25 30 35 40 45 50 55 tAf
Puc. 8.35. Сигналы на выходе согласованного фильтра для непрерывного
сигнала со ступенчатой ЧМ при допплеровском сдвиге N в 10.
293
чатой ЧМ, где N есть число групп в коде Фрэнка и число частот
в сигнале со ступенчатой ЧМ соответственно.
В общем случае отклик согласованного фильтра для сигналов
группы III может быть получен при схеме фильтра, показанной на
рис. 8.32, которая состоит из параллельного набора фильтров, при-
чем каждый фильтр согласован с одним подымпульсом ф (0, за ко-
торым следует схема когерентного сложения. На рис. 8.33 в общих
чертах показаны отдельные отклики таких фильтров и общий выход-
ной сигнал для последовательности импульсов со ступенчатой ЧМ
(N •= 5), разделенных расстоянием, равным длительности одного
импульса. Общий вид функции неопределенности, полученной
из уравнения (8.3) для сигнала со ступенчатой ЧМ без проме-
жутков между импульсами, задается формулой
Х(т, <р) -Г(т', k, <р)//« k, <р) +
+ Г(б—т', Л-} 1, ф)/7(т'-б, £+1, <р), (8.71)
ОСтСА^б, —ооСфСоо,
где т' и k определяются в виде т -- т' kb, 0 < т' < б,
k = 0, 1, 2... N — Г,
sin л [в—т']
Г(т', k, <р) (б-т') -r[- ------
л ф + ~ [б—т'1
k
Nb ,
(8.72)
sin л [7V— Л] 6 ф-|-
Н « k, ф) =

’+-45-
(8.73)
Следует отметить, что уравнение (8.73) определяет % (т, ф) только
для половины плоскости неопределенности. Выражение для другой
половины может быть получено при использовании свойства сим-
метрии
Х*(т» <Р)^Х(—— ф)ехр[—/2лфт]. (8.74)
Вывод выражения, аналогичного (8.71), которое может быть также
получено из уравнения (8.3) для случая последовательности с про-
межутками между импульсами, мы оставим читателям для упраж-
нения. Общая структура неопределенности как для непрерывной
последовательности, так и для последовательности с промежутками
между импульсами со ступенчатой ЧМ, показана в виде контуров
сечений % (т, ф) на определенных уровнях (рис. 8.34). Конфигурации
294
ftalattausttiil
знание без границ V *•
Рис. 8.36. Экспериментально полученные характеристики непрерывного
сигнала со ступенчатой ЧМ, N = 8:
а —отклик частотного дискриминатора на функцию модуляции сигнала; б —спектр;
в—профили сечений функции отклика.
295
б)
Рис. 8.37. Последовательность из четырех импульсов с линейно-сту-
пенчатой ЧМ: Л/п = 1/6, TIM = 7.
а —вид сигнала; б —функция изменения частоты.
Рис. 8.38. Сравнение структуры автокорреляционных функций для после-
довательностей четырех импульсов с постоянной частотой и линейно-сту-
пенчатой ЧМ (Д/п = 1/6):
а —центральный импульс; б—первый боковой лепесток, вносящий иеопределениость.
296
^alaHausA
знание без границ Ч
Рис. 8.39. Сигнал на выходе согла-
сованного фильтра для последова-
тельности четырех импульсов с ли-
нейно-ступенчатой ЧМ:
а —автокорреляционная функция; б —сиг-
нал на выходе согласованного фильтра
для ф==Л</27'; в —сигнал на выходе со-
гласованного фильтра для ф = Л//Г.
Рис. 8.40. Детальная структура
центрального отклика на выходе
согласованного фильтра для по-
следовательности четырех импуль-
сов с линейно-ступенчатой ЧМ в
зависимости от допплеровского
сдвига, Д/п = 3/0:
а) Ф = О; б) ф = Л//2Т; в) tp — M/T.
297
j
Щг
1 контуров характеризуют % (т, <р) на уровне приблизительно на 3
и 4 дб ниже пикового значения сигнала при %' -= ф -- 0. Рис. 8.35
показывает вычисленный отклик согласованного фильтра, полу-
ченный для непрерывной последовательности из 10 импульсов со
ступенчатым изменением частоты в соответствии с (8.69).
На рис. 8.36 приведены экспериментальные данные для непре-
- рывного сигнала с 8 ступенями изменения частоты. Хруя это и не
показано на рис. 8.34, а, тем не менее по форме сигнала рис. 8.35
можно заключить, что выходные сигналы также имеют цикличе-
скую структуру дополнительных пиков. Эти пики расположены

Рис. 8.41. Сигнал на ныходе согласованного фильтра для последова-
тельности четырех импульсов с линейно-ступенчатой ЧМ, Д/п » 3/6:
а — функция изменения частот»; б —автокорреляционная функция.
в точках <р = IN/2 Т[или / (X/26)J, где I — нечетное число. Однако
высота их много меньше уровня контурных сечений. % (т, ф), пока-
занных на рис. 8.34, а. Для сравнения укажем, что дополнитель-
ные пикц для последовательностей с разделенными импульсами
(рис. 8.37—8.40) значительно выше и включаются в контур на за-
данном уровне х (т, ф), показанный на рис. 8.34, б. Рис. 8.41—
8.42 иллюстрируют структуру сигнала для случая, когда частоты
разнесены на величину 3/6. Это — пример сигнала со ступенчатой
ЧМ, у которого высота частотных ступеней не согласована с дли-
тельностью отраженного импульса (т. е. — <ол > 2л/6) [51.
Увеличенная высота частотных ступеней снижает уровень допол-
нительных внецентральных пиков вдали от центрального максимума
за счет увеличения уровня дополнительных пиков в центральной
области.
Изменение структуры лепестков в центральной области в зави-
симости от допплеровского сдвига показано на рис. 8.42. Данные
рис. 8.43—8.44 соответствуют случаю, когда частоты, разделенные
на целые значения 1/6, случайно расположены в импульсной после-
довательности. Здесь показано, что порядок расположения частот
в последовательности не оказывает существенного влияния на цент-
298
Natatiauswk
знание без ерэниц W *
Рис. 8.42. Детальная структура центральной части сигнала на выходе ср*
гласованного фильтра для последовательности четырех импульсов с линейно*
ступенчатой ЧМ в зависимости от допплеровского сдвига, Д/п = 3/6:
а) ф==0; б) ф*=Л{/27; в) <р = М/Т. Треугольник представляет центральную часть от-
клика для однородной последовательности четырех импульсов без ступенчатой ЧМ.
299
ральный автокорреляционный отклик, но устанавливает распре-
деление неопределенности вне центральной области и при наличии
допплеровского сдвига.
Характерная гребнеподобная структура % (т, <р), соответ-
ствующая соотношениям (8.71)—(8.73) и показанная в иллюстра-
циях этого раздела, является наряду с формулой (8.70) дополни-

Рис. 8.43. Сигнал из пяти импульсов со случайно-ступенчатой ЧМ, А/Мии= 1 /6:
а — функция изменения частоты; б—автокорреляционная функция-
тельным аргументом в пользу того, что сигналы со ступенчатой
ЧМ наряду с квантованными кодами принадлежат к семейству
ЛЧМ сигналов. Эта аналогия делается более очевидной, если рас-
смотреть непрерывные фазовые функции, соответствующие анало-
говым ЛЧМ сигналам, и две дискретные функции настоящей главы.
Фазовую функцию для сигнала со ступенчатой ЧМ можно считать
первым порядком квантования параболической ЛЧМ фазовой функ-
ции. Квантованные фазовые коды в этом случае представляют собой
дополнительную степень квантования, которая усложнена большей
периодичностью в основной структуре сигнала. Таким образом, как
мы видим из иллюстраций, характеристики неопределенности для
этого метода кодирования в противоположность аналоговым сигна-
300
^alaHausA
знание без границ Ч
лам и сигналам со ступенчато-линейной ЧМ менее устойчивы к из-
менениям параметров и имеют более высокие изолированные допол-
нительные пики.
Рис. 8.44. Сигнал на выходе согласованного фильтра для по-
следовательности пяти импульсов со случайно-ступенчатой ЧМ:
а —структура центральной области автокорреляционной функции; б—
сигнал иа выходе согласованного фильтра при <р«=Л(/2Т; а —сигнал на
выходе согласованного фильтра, <р— 1/6.
301
8.6. Согласованные фильтры для дискретно - кодированных
сигналов
Дискретная природа сигналов, рассмотренных в этой главе,
позволяет использорать методы построения согласованных фильт-
ров и генерирования сигналов, которые основаны на применении
многоотводных линий задержки или цифровых методов. Методы,
применяющие дисперсионные линии задержки, которые недоста-
точно освещены в литературе, будут подробно изучены в гл. 12—14;
в противоположность этому методы обработки сигналов с помощью
многоотводных линий задержки и цифровых устройств, исследован-
ные в многочисленных опубликованных работах, в данной работе
полностью рассматриваться не будут. В этом разделе кратко опи-
сано их применение при разработке согласованных фильтров для
дискретных кодированных сигналов.
Для того чтобы упростить рассмотрение, мы будем предполагать,
что дискретные кодированные сигналы содержат либо фазовый код,
либо частотный код, т. е. в общей формуле для сигнала (8.1) либо
% либо 0Я не изменяются при переходе от одного элемента после-
довательности к другому. Будем также полагать, что длительности
элементов последовательности равны. Ни одно из вышеприведенных
предположений не создает существенных ограничений при построе-
нии сигналов, и методы, кратко рассмотренные ниже, могут быть
обобщены на случай, когда частота, фаза и длительность каждого
импульса, соответствующего элементу последовательности, изме-
няются в дискретной кодированной последовательности одновре-
менно.
Общая схема построения согласованного фильтра для случая
фазо-кодированной последовательности показана на рис. 8.45.
К выходу каждого отвода линии задержки подключены фазовраща-
тели, сдвигающие фазы сигналов для их сопряжения, а также
элементы, которые производят амплитудную весовую обработ-
ку. Так как длительности элементов последовательности рав-
ны, то в схеме необходимо иметь только один согласованный фильтр
для некодированного подымпульса. Он включен на выходе сумма-
тора, но с таким же успехом может быть и на входе, перед многоот-
водной линией задержки. В большинстве случаев, представляющих
практический интерес для радиолокационных приложений, ампли-
тудные весовые коэффициенты подымпульсов ап также должны быть
равны.
Если это выполняется, а фазовый код представляет собой би-
нарную последовательность, то показанный фильтр может служить
как согласованным фильтром, так и генератором кодированного
сигнала, так как каждая фазовая компонента (0 или 180 градусов)
сопряжена сама с собой (т. е. 180° = —180°). В этом случае для
формирования бинарного кодированного сигнала возбуждающий
импульс вводится с правой стороны многоотводной линии задержки.
302
^alaHausA
знание без границ Ч
Практически это может быть импульс на промежуточной частоте,
который имеет широкую полосу частот по сравнению с шириной
полосы подымпульса длительностью б. По мере распространения
импульса с правого конца линии на левый и поступления его через
отводы с кодировкой фазы на сумматор формируется сигнал дли-
тельностью JV6 = 1. Этот сигнал может быть обозначен как и (—0-им-
пульсный отклик согласованного фильтра, когда линия задержки
fo-fFfofrr#
Рис. 8.45. Общая схема построения согласованного фильтра для
сигналов на основе фазовых кодов.
Выход суммирующей схемы подключен к фильтру, согласованному с подымпульсами
ниже показан отклик этого фильтра.
возбуждается с обратного (или передающего) конца. Сигнал и (—t)
для бинарного фазового кода есть обращенный во времени импульс-
ный отклик согласованного фильтра, когда его рассматривают с при-
емного конца или с левой стороны. Следовательно, если фазо-коди-
рованный сигнал, генерируемый таким образом, поступает на
приемный конец, то условия «согласованной» фильтрации выпол-
няются, и на выходе мы получаем автокорреляционные и взаимо-
корреляционные функции, рассмотренные в разд. 8.3 Ч
Этот же самый тип фильтра может быть использован для повто-
ряющейся или периодической бинарной кодовой последователь-
ности. В этом случае более низкий уровень боковых лепестков уста-
навливается на выходе согласованного фильтра только после того,
1 При рассмотрении функционирования такой схемы читатель может
заметить из рис. 8.45, что подымпульс aiexp [/0J, представляющий собой
первую компоненту кодированного сигнала, поступает в линию задержки и
должен затем дойти до последнего отвода линии в согласованном фильтре,
с тем чтобы выполнялись условия согласованной фильтрации. В этом случае
кодированный сигнал полностью заполняет линию задержки, так что все от-
дельные импульсы согласованы и складываются в фазе в суммирующей схеме.
303
sr
г
как первый полный период последовательности поступит в линию
задержки, т. е. когда наступит устойчивое периодическое состояние
фильтра. Для более общего, небинарного, случая этот метод генери-
рования сигналов может применяться только при условии суще-
ствования отдельного набора сопряженных фазовращателей, под-
ключенных к отводам линии задержки, который может быть пере-
ключен после формирования кодированного сигнала для замены
фазовращателей, используемых в цикле генерации сигнала. Такая
Рис. 8.46. Схема построения согласованного фильтра с использованием со-
пряженных фазовращателей для формирования сигнала и его обработки в
случае небинарных сигналов.
Выход суммирующей схемы подключен к фильтру, согласоиннпому с подымпульсами.
схема показана на рис. 8.46. Здесь также можно применять либо
набор сопряженных фильтров, либо активный генератор, который
формирует сигнал, согласованный с фильтром приемника.
При конструировании согласованного фильтра с многоотводной
линией задержки должны быть приняты меры для минимизации
обратных отражений внутри многоотводной линии задержки в ме-
стах подключения отводов; может также появиться необходимость
развязки усилителей. Также важно контролировать и регулировать
точность фазы сигнала, поступающего в каждый отвод линии за-
держки. Лернер 1281 описал использование многоотводной магнито-
стрикционной линии задержки. Здесь отводы выполнены в виде
катушек, намотанных вокруг магнитострикционного стержня и
размещенных на равных расстояниях друг от друга. Положение
каждой катушки могло несколько изменяться, что давало возмож-
ность обеспечить требуемое управление фазой сигнала на выходе
отвода. I
Аналогичный метод, использующий свернутый в бухту замед-
ляющий кабель в качестве задерживающей среды, описан Бенд-
жамином 1291. Если применяется многоотводная линия задержки
с сосредоточенными параметрами, то можно осуществлять дискрет-
ный фазовый контроль на выходе каждой ячейки, присоединив не-
сколько отводов в каждом подынтервале задержки 6. В некоторых
304
4\alallaus7^!.
знание без границ “ w
случаях обработка сигнала с помощью согласованного фильтра про-
изводится на когерентной видеочастоте, а не на промежуточных
частотах, как предполагалось в приведенных выше рассуждениях.
При этом будет необходим квадратурный канал для того, чтобы из-
бежать ухудшения характеристик обнаружения с изменением фазы
принимаемого сигнала. Пример построения такого согласованного
Лильтра (его исследовали Колл и Сторей [27]) показан на рис. 8.47.
Алленом и Уэстерфилдом [30] было рассмотрено несколько методов
построения цифровых согласованных фильтров.
Фазочувствительный
демодулятор
Фильтр
ни жниX
частот
Многоотводная
линия задержки
2-ая па
300к гц
•— 300 нщ
\2двйг
тазы
на 90°
возведение
в квадрат
Возведение Т
в квадрат
Фильтр
► ни нс них -*
.{частот
Фазочувствительный
демодулятор
Многоотводная
линия задержки
Рис. 8.47. Схема обнаружения, использующая квадратурные согласованные
фильтры.
Согласованный фильтр на линии задержки с отводами для ди-
скретного частотно-кодированного сигнала, а также для сигнала со
ступенчатой ЧМ, может быть создан аналогично фильтру на оснбве
линии задержки для кодированного по фазе сигнала, который по-
казан на рис. 8.45. В этом случае вместо сопряженных фазовраща-
телей нужно использовать согласованные полосовые фильтры с раз-
личными центральными частотами. Недостатком подхода является
то, что полоса линии задержки здесь должна равняться полной ши-
рине полосы сигнала. Это требование часто приводит к затрудне-
ниям при синтезе линии, задержки, если полный спектр сигнала за-
нимает очень широкую полосу (это может произойти при попытке
сформировать либо однородно заполненный спектр, либо комби-
нированный спектр из набора дискретных полос).
Возможные пути преодоления этих конкретных трудностей по-
казаны на рис. 8.48. Полосовые фильтры на входе согласованного
фильтра разделяют отдельные частотные компоненты, каждая из
которых задерживается на соответствующую величину в своей
I I Зак. 134] 305
г
собственной узкополосной линии задержки. Выходные сигналы
каждой линии задержки поступают на суммирующее устройство.
В зависимости от расположения частотных компонент кодирован-
ного сигнала и характеристик входных полосовых фильтров может
оказаться полезным сформировать общий согласованный спектраль-
ный амплитудный отклик на выходе суммирующего устройства.
Рис. 8.48. Согласованный фильтр с параллельными каналами для дикретно-
кодированных по частоте сигналов.
Для сигнала с линейно-ступенчатой ЧМ, где \fn — fn-il = 1/6,
отклик n-го полосового фильтра будет иметь вид
</»(/)- • <8-75>
7СО (/—/п)
Из результатов разд. 8.5 можно заключить, что в этом случае для 7V
параллельных каналов значение произведения длительности на
полосу равно №. Это есть частный случай метода параллельной
многоканальной обработки ЛЧМ сигналов, рассмотренного в разд.
6.7, где N разнесенных по частоте параллельных каналов, каждый
из которых имеет коэффициент сжатия Tc&fc, позволяет получить
результирующее значение произведения длительности на полосу
№7'СД/С. Фильтр, схема которого показана на рис. 8.48, может
также использоваться в качестве генератора дискретного частот-
но-кодированного сигнала. Чтобы сформировать сигнал, согласо-
ванный с фильтром, показанным на рис. 8.48, фильтр, генерирую-
щий кодированный сигнал, должен иметь обратный порядок распо-
ложения фиксированных задержек по сравнению с фильтром
в приемнике. Один и тот же фильтр может быть использован для
генерирования и приема сигнала, если в схеме дополнительно вклю-
чено переключающее устройство для изменения порядка подсоеди-
нения фиксированных линий задержки на обратный после передачи
сигнала.
306
^lataHausX
знаниебезграниц **
Метод создания фильтров для сигналов в виде кодированных
или некодированных последовательностей импульсов непосредствен-
но следует из приведенных выше методов построения фильтров, если
некоторые конкретные значения амплитудных коэффициентов тож-
дественно равны.нулю. Таким образом в соответствующих точках
линии задержки отводы должны отсутствовать. Если каждый
импульс в последовательности имеет соответствующий частотный
или фазовый подкод, то согласованный фильтр на этот подкод дол-
жен содержать соответствующий отвод.
В некоторых задачах уровень боковых лепестков по дальности
для дискретных кодированных по фазе сигналов может быть слиш-
ком высок. Уменьшить этот уровень оказывается возможным с по-
мощью метода трансверсальной фильтрации подобно тому, как
кратко описано в разд. 7.8. Однако этот метод не может быть исполь-
зован для кодированных по фазе сигналов в той же самой степени,
что для ЛЧМ сигналов. В работе [311 показано, что для кода Бар-
кера длиной 13 элементов при использовании трансверсальной
фильтрации можно уменьшить уровень боковых лепестков от —22 дб
(отношение пикового значения к боковому лепестку 13 : 1) до
—32,4 дб (отношение пикового значения к боковому лепестку 42:1).
Суммарная задержка трансверсального фильтра равнялась 26 б при
13 отводах, разнесенных на 2'6. Выбранные авторами весовые ко-
эффициенты на отводах были таковы, что обеспечивали нулевой
уровень боковых лепестков в том временндм интервале, где. ранее
существовали боковые лепестки сигнала на выходе согласованного
фильтра при наличии остаточных боковых лепестков вне этой
области. Потери на рассогласование для этого метода составили
0,25 дб.
8.7. Допплеровская коррекция дискретно • кодированных
сигналов
В гл. 2и5 одновременное измерение дальности и скорости
радиолокационной цели (оценка параметров) рассматривалось как
одно из основных областей применения сигналов с большим зна-
чением произведения длительности на полосу. При этом величина
ошибки измерения минимальна, когда коэффициент частотно-вре-
менндй связи для сигнала равен нулю [см. уравнения (5.46) и (5.47) 1.
Коэффициент частотно-временной связи для различных классов
сложных сигналов рассмотрен подробно в гл. 9. Желательно, чтобы
функция отклика согласованного фильтра % (т, <р) была однородно
малой, за исключением основного пика при т = 0 и <р = 0. Эти тре-
бования удовлетворяются, если функция отклика обладает «кнопо-
чной» характеристикой, которая показана, например, на рис. 4.8.
Сигналам на основе апериодических усеченных бинарных фазовых
кодов максимальной длины (псевдослучайные последовательности)
И* 307
соответствуют отклик или функция неопределенности, которые
приближенно имеют такую же форму и, следовательно, их можно
рассматривать как пример сигналов, пригодных для оценки пара-
метров.
В общем случае устройство, необходимое для оценки парамет-
ров, представляет собой набор согласованных фильтров, показан-
ный на рис. 2.3 или на рис. 9.1 следующей главы. Центральные
частоты согласованных фильтров в наборе расположены таким
образом, чтобы перекрывать диапазон ожидаемых допплеровских
частот. При непрерывной полосе допплеровских частот номиналь-
ное частотное разнесение центральных частот равно 1/Г, т. е.
обратно' пропорционально длительности огибающей импульса
(предполагается, что форма импульса прямоугольна). При измене-
нии допплеровского сдвига принимаемого сигнала для формирова-
ния более равномерного нормализованного пикового выходного
сигнала на выходе набора согласованных фильтров иногда стре-
мятся расположить центральные частоты согласованных фильтров
ближе друг к другу. Так как каждый согласованный фильтр для
сигналов с большим значением произведения длительности на по-
лосу может представлять собой сложное и дорогое устройство, то
набор согласованных фильтров, видимо, явится частью радиолока-
ционного приемника, имеющей наибольшую стоимость.
Метод, позволяющий избежать излишних затрат и усложнения
аппаратуры при построении согласованного фильтра на полосовой
многоотводной линии задержки, состоит в использовании весовой
матрицы из сопротивлений и единственного согласованного фильтра
для моделирования полного набора согласованных фильтров. Та-
кая весовая матрица часто называется допплеровской. Характери-
стики этой весовой матрицы сопротивлений могут быть получены
на основе комплексного узкополосного представления принимае-
мого сигнала с допплеровским сдвигом, которое имеет вид
(0 = и (0 ехР !/2я (fo + ф) Л- (в.76)
Выделяя действительную часть сигнала (8.76), получаем
sd (0 = и (0 cos 2л (f04- <р) / =
и (/) cos 2л/01 cos 2лф/—и (/) sin 2л/01 sin 2лф/. (8.77)
Член w(/)cos2n/0Z представляет принятый сигнал при нулевом
допплеровском сдвиге. Класс бинарных фазо-кодированных сиг-
налов описывается соотношением
ц(/)-
2 u„(0. 0</<tf6,
Л «= 1
О при других /,
308
^lalaHaus/M.
знание без границ * *
где un(t) равно либо апРп (0ехр [/0], либо апРп(/)ехр[/л), а
Pn(t) определяется соотношением (8.2). Зная, что sin2n/0/ =
= —cos(2jtf0f 4-Л/2), мы можем переписать уравнение (8.77У
в окончательном виде
8</(0= «П (0 COS 2nfot COS 2лф/ +
л— I
+ nn(Ocos(2n/0/4-rt/2)sin2ji(pt (8.78)
л» I
Лернер в работе [28] указал, что для обычно встречающихся ин-
тервалов допплеровских сдвигов cos 2л<р/ и sin 2л<р/ изменяются
медленно по сравнению с длительностью подымпульса 6, так как ф,
как правило, измеряется в величинах, обратных общей длительности
последовательности, т. е. ф = тП\ 0. Поэтому уравнение
(8.78) приближенно может быть представлено в виде
N
»Л0= 2 «»(0 cos 2л/01 cos 2nmn/N +•
л-= 1
N
+ un (0COS (2nfof + n/2) sin 2nmnlN. (8.79)
n=l **
Операции, которые эквивалентны согласованной фильтрации такого
(гигнала, очевидны при изучении структуры функции (8.79). Чтобы
получить первую сумму в уравнении (8.79) для любого конкретного
допплеровского сдвига ф = m/Т, сигнал на выходе отвода фильтра,
согласованного с сигналом при нулевом допплеровском сдвиге, умно-
жается после соответствующего согласования фаз на коэффициент
cos2ntnnlN. Весовые коэффициенты, изменяющиеся в зависимости
от расположения отводов, образуют косинусную шину. Для обра-
зования второй суммы уравнения (8.79) те же самые выходные сиг-
налы отводов умножаются на коэффициенты sin 2nmnlNt сумми-
руются и сдвигаются по фазе на 90°. Затем эти два члена когерентйо
суммируются с целью восстановления эквивалентного отклика со-
гласованного фильтра для сигнала с допплеровским сдвигом.
Схема такой весовой обработки показана на рис. 8.49. Весовые
множители могут быть реализованы с помощью комбинации сопро-
тивлений. В случае тех отводов, для которых cQs2nmnlN или
sin2nmn/N отрицателен, выходные сигналы ячеек должны быть
сдвинуты на 180°. Это можно сделать при условии, если каждый
выход линии задержки выполнен в виде катушки со средней точкой,
с которой снимаются соответствующие реализации необходимых
положительных или отрицательных сигналов. Чтсбы перекрыть
ожидаемый диапазон допплеровских сдвигов (т. е. 1 < m < М),
требуется матрица сопротивлений размером М X N, которая имеет
указанные косинусные и синусные весовые последовательности
309
в каждой строке, соответствующей определенному допплеровскому
сдвигу. Лернер указывает, что если выходные сигналы с косинус-
ной или синусной шины непосредственно детектируются и сумми-
руются как видеосигналы, то при этом происходит незначительное
ухудшение по сравнению с идеальным случаем. Это устраняет не-
обходимость в фазовращателях на 90° и в когерентном сложении
составляющих сигналов в каждой строке допплеровской матрицы.
Рис. 8.49. Моделирование набора согласованных фильтров с помощью доп*
плеровской матрицы.
Входные сагнзлы к многоотводной линии задержки поступают через фильтр, согласо* .
• ванный с подыми ул ьсами.
Допплеровская матрица, описанная Лернером, заменяет на-
бор из 18 согласованных фильтров, содержащий канал с нулевым
допплеровским сдвигом для бинарного кодированного по фазе сиг-
нала (все ап равны), где N = 1000. Результаты, получаемые при
таком моделировании набора согласованных фильтров, очень близки
к теоретически достижимым для действительного набора согласован-
ных фильтров. Описанный выше метод использования доппллеров-
ской корректирующей матрицы может применяться при любых ти-
пах узкополосных сигналов, согласованный фильтр для которых
может быть реализован на основе многоотводной линии задержки.
Описанный метод допплеровской коррекции и моделирования
согласованного фильтра можно использовать в том случае, если ко-
эффициент допплеровской дисперсии (2и/с) ТД/ меньше единицы.
Влияние больших значений (2и/с) ТД/ на сжатый выходной сигнал
фильтра, согласованного с ЛЧМ сигналом, было рассмотрено
в разд. 6.8. Напомним, что когда (2о/с) TAf> 1, влиянием скоро-
310
NalattausliSk
знание без границ * *
сти цели на изменение временнбго масштаба принимаемого сигна-
ла нельзя пренебрегать. Для этого случая принимаемый сигнал
правильнее было бы записывать в виде
М0 =«(«О»
где
2v
(8.80)
а
с
и функция отклика сигнала имеет форму, определяемую соотноше-
нием (6.69). Влияние коэффициента а на выходные сигналы для раз-
личных типов дискретных кодированных сигналов не было иссле-
довано так подробно, как для ЛЧМ сигнала. Однако Ремли 132] вы-
числил влияние этой допплеровской дисперсии на сигнал, который
является большой, но конечной по величине выборкой стационарного
случайного процесса. Ремли сделал вывод, что такая формулировка
задачи приводит к результатам, которые в общем случае примени-
мы к классу псевдослучайных бинарных фазовых сигналов. Основ-
ным результатом этого исследования является представление мате-
матического ожидания значения функции отклика согласованного
фильтра в виде
Т/2
|£{Xd(T, Дф))| =
— f 0)ехр[—/2лД<рт]</т ,
Т —7/2
(8.81)
/2
где 6 = 2и/с/(1 + vic). Обозначение Дф указывает, что согласо-
ванный фильтр был предназначен для компенсации среднего доппле-
ровского сдвига ф и уравнение (8.81) характеризует отклик согла-
сованного фильтра, когда допплеровский сдвиг изменяется относи-
тельно среднего допплеровского сдвига на величину Дф. Как и
прежде, х (т, 0) есть автокорреляционная функция отклика со-
гласованного фильтра при нулевом допплеровском сдвиге, а Т —
длительность сигнала. Считая спектр сигнала прямоугольным
1т. е. х (ь 0) имеет вид функции (sin x)lx 1, Ремли вычислил влия-
ние допплеровской дисперсии на различные параметры выходного
сигнала согласованного фильтра. Результаты приведены на
рис. 8.50—8.52. Рис. 8.50 показывает уменьшение пикового напря-
жения выходного сигнала в зависимости от дисперсионного произ-
ведения TW |6|, где 6 определяется в (8.81), и W = Д/ — общая
мера ширины полосы, используемая в настоящей работе. Из гра-
фика следует, что для TW |6 | > 1 пиковое напряжение выходного
сигнала пропорционально \ITW 161.
На рис. 8.51 показано влияние коэффициента |6| на усиление
относительно шума приемника при обработке в согласованном фильт-
ре в зависимости от произведения длительности на полосу. Из при-
веденного следует, что максимально достижимое усиление приблизи-
тельно равно 1/16 | и достигается оно в том случае, когда WT161 = 1.
311
Рис. 8.50. Уменьшение пикового значения сигнала на выходе согласован-
ного фильтра вследствие допплеровской дисперсии.
Кривая вычислена в предположении о прямоугольной форме.
Рис. 8.51. Коэффициент усиления согласованного фильтра при допплеров-
ской дисперсии и прямоугольном спектре.
Рис. 8.52. Характеристика разреше-
ния по времени и частоте при различ-
ны* зиачеииях дисперсионного про-
изведения.
Дисперсионное произведение tV77<57
312
^laiaiLausi^ii
знание без границ ’ —
На рис. 8.52 показано расширение сечения на уровне 6 дб для функ-
ций % (т, 0) и х (0, Д Ф) в зависимости от w Т 161. Это характе-
ризует меру разрешающей способности по времени и частоте при
наличии допплеровских искажений. Вывод, который можно сде-
лать на основе этого графика, состоит в том, что"когда WT | 6 1
велико, то ширина искаженного импульса определяется формулой
Тр = |6| Т, а частотное разрешение •— соотношением Wp = |0|W.
Отсюда заключаем, что отношение площадей эллипса неопределен-
ности для случаев больших значений допплеровского дисперсион-
ного произведения и при отсутствии (или очень малой) допплеров-
ской дисперсии приближенно равно (№Т| 6 |)а.
Результаты Ремли очень, сходны, хотя и не идентичны с ре-
зультатами, полученными для ЛЧМ сигналов. Вычисленные точно
лишь для конкретного случая, тем не менее они подтверждают об-
щее заключение, что допплеровская дисперсия не оказывает зна-
чительного влияния на выходной сигнал согласованного фильтра,
когда (2 v/c) TAf или WT |61 меньше единицы. Если этот коэффи-
циент больше единицы, то результирующее влияние на отношение
сигналУшум на выходе согласованного фильтра и на разрешающую
способность может быть существенным. Все эти эффекты не зави-
сят от частоты передаваемого сигнала.
При больших WT | 6 [ разработчику радиолокатора целесооб-
разно использовать функции, характеризующие согласованный
фильтр приемника, которые удовлетворяют общему описанию, за-
даваемому равенством (4.29). При этом конструкция фильтров долж-
на быть такой, чтобы можно было компенсировать как допплеров-
ское смещение частоты, так и сжатие временнбго масштаба
сигнала (приближающаяся цель) либо расширение его (удаляющая-
ся цель). Построение согласованного фильтра такого типа рас-
смотрено в работах Бенджамина [29] и Келли и Вишнера [33].
8.8. Заключение
В этой главе было показано, что дискретные кодированные
сигналы предоставляют другую возможность для формирования
выходных сигналов согласованных фильтров. Различные виды
функции неопределенности, которые получаются с помощью ди-
скретных кодированных сигналов, подробно рассмотрены и пока-
заны на иллюстрациях настоящей главы. Как было показано, ха-
рактерной чертой таких сигналов является существование отдель-
ных областей с высоким уровнем выбросов; это свойство иногда
может быть полезным. На рис. 8.2 приведен пример, когда такие
характеристики оказываются полезными. Величина расстояния
между выбросами определяется тем, насколько велико разделение,
между элементами кода. Рассмотрение максимального объема сво-
бодной области в разд. 4.7 позволяет найти верхнюю границу сте-
пени разделения этих выбросов.
313
Использование дискретного кодирования позволяет получить
3 N степени свободы при кодировании, в противоположность ана-
логовым кодам, которые зависят от одного или, возможно, двух
параметров. 3 N степени свободы возникают вследствие возможности
выбирать независимо амплитудные, частотные и фазовые параметры
кода сигнала. Как эти 3 N степени свободы будут использованы,
определяется специфическими требованиями конкретной задачи.
Рис. 8.S3. Сравнение уровня боковых лепестков для
сигналов на основе различных фазовых кодов.
В этой главе была сделана попытка показать результаты различ-
ных способов использования указанных параметров. Так, коды
Баркера и нерегулярные импульсные последовательности пред-
ставляют собой примеры использования 7V из этих степеней свободы
для получения максимального отношения пикового значения к
боковому лепестку для х (<» 0). Результаты сравнения отноше-
ний пикового значения к боковому лепестку для различных ко-
дированных по фазе сигналов показаны на рис. 8.53. Коды
Хаффмана используют другие N степеней свободы, комбинируя
амплитудные и фазовые последовательности для достижения
«импульсно-эквивалентного» отклика х (т» 0). Каждый из этих
314
примеров, рассмотренных выше, является шагом к достижению
кнопочной функции отклика, что является решением большинства
задач, включающих одновременное измерение скорости и даль-
ности цели х.
Другим примером использования 3N степеней свободы являет-
ся случай, рассмотренный Венье [35], который исследовал ча-
стотно-кодированные нерегулярные импульсные последователь-
ности. Его целью было сохранение по возможности низким уровня
боковых лепестков % (т, 0) с одновременным обеспечением разде-
ления перекрывающихся входных сигналов с большим динамиче-
ским диапазоном в схеме, где ограничитель предшествует согласо-
ванному фильтру.
Для некоторых случаев, особенно когда преимущества, пдлу-
чаемые от цифровой реализации согласованного фильтра, являются
существенными, целью разработки может явиться аппроксимация
характеристик отклика заданного аналогового кодированного
сигнала, которая оказывается наиболее подходящей для конкретной
задачи. Ховард [36] рассмотрел использование ступенчатого ЧМ
сигнала и смещения положения импульсов для получения функций
неопределенности импульсной последовательности, центральный
пик которых в окрестности т = 0, <р = 0 аналогичен пику неко-
торых аналогичных ЧМ сигналов. Укажем также, что часто конеч-
ной целью разработки дискретных кодов является аппроксимация
характеристик ЧМ сигнала. Характерный гребнеобразный отклик
% (т, ср) ЛЧМ сигналов хорошо аппроксимируется сигналом со сту-
пенчатой ЧМ и квантованным фазовым кодом Фрэнка, которые были
рассмотрены в этой главе. Какова бы ни была задача, подход к раз-
работке сигналов, использующий дискретное кодирование, по-види-
мому, представляет дополнительные возможности, которые могут
быть полезными при формировании откликов согласованных
фильтров и реализации согласованной фильтрации.
В настоящей главе с единой точки зрения были рассмотрены
методы дискретного кодирования. Основной целью главы являлось
логическое математическое описание дискретных кодированных
сигналов и определение характеристик соответствующих выходных
сигналов согласованных фильтров. Следует отметить, что при сравне-
нии сигналов между собой особое внимание на это не обращалось.
Как и в других случаях при рассмотрении различных сигналов
в данной книге, основная идея настоящей главы состоит в том, что
все сигналы одинаково хороши (или плохи) до тех пор, пока не опре-
делена специфика конкретной задачи, для которой подбирается
1 Кейте рис и Рубин [34] рассмотрели метод достижения «кнопочной
функции неопределенности на видеочастоте» с помощью некогерентного ком-
бинирования выходных сигналов набора согласованных фильтров. Каждый
из них согласован с одним набором из ансамбля наложенных нерыулярных
импульсных последовательностей, где любая составляющая последователь-
ности по своему частотному спектру отличается от всех других.
316
сигнал. С этой точки зрения в гл. 9 и 10 рассматриваются некоторые
важные задачи, в которых уже характеристики сигналов являются
определяющими параметрами.
Читатель, который хочет использовать настоящую книгу для
решения некоторой конкретной задачи, может в этой главе найти
достаточную информацию, которая позволит ему сформировать
мнение о важности тех или иных достоинств отдельных сигналов.
Как минимум, читатель пополнит свои знания о некоторых важ-
ных методах дйскретного кодирования, которые могут быть исполь-
зованы в радиолокации или в других областях. Более того, имеется
надежда (в силу того, что здесь приведено большое количество ил-
люстраций, характеризующих различные дискретные кодирован-
ные сигналы), что читатель составит себе некоторое представление,
которое даст ему возможность сформировать с помощью методов
дискретного кодирования другие сигналы, которые удовлетворят
его специальные требования.
ЛИТЕРАТУРА
*1. Р. М. Wood ward. Probability and Information Theory with Appli-
cations to Radar, Perga mon Press, Oxford, 1953.
•2. W. M. S i e b e r t. A radar detection philosophy, IRE Trans. IT-2, 204-
221 (1956).
3. E. N. F о w 1 e, E. J. К e 1 I у and J. A. S h e e h a n, Radar system per-
formance in a dense target environment, IRE Intern. Conv. Record, Pt. 4,
136-145 (1961).
4. J. B. Resnick. High resolution waveforms suitable for a multiple
target environment, M. S. Thesis, Mass. Inst. Tech., Cambridge, Massa-
chusetts (June, 1962).
* *5. A. W. R 1 h a c z e k. Radar resolution properties of pulse trains, Proc.
IEE 82, 153-164 (1964).
• *6. С. К a 1 t e r i s and W. L R u bi n. Pulse trains with low residue ambi-
guity surfaces that minimize overlapping target echo suppression in li-
miting receivers, Proc. IEEE 54, 438—439 (1966).
* *7. G. J. S 1 m n>o n s. A factorization technique for binary autocorrelation
functions, Proc. IEEE (Letters) 54, 794—795 (1966).
• *8. M. В e rn f e 1 d. A property of binary sequences, Proc. IEEE (Corres-
pondence) 52, 744 (1964).
9. R. H. В a‘r k e r. Group synchronization of binary digital systems, in:
«Communication Theory» (W. Jackson, ed), p. 273—287, Academic Press,
New Jork and London, 1953.
10. J. E. S t о r e r and R. T u г у n. Optimum finite code groups. Proc. IRE
(Correspondence) 46, 1649 (1958).
•*11. R.Turyn. On Barker codes of even length, Proc. IRE (Correspondence)
51, 1256 (1963).
12. В. E I s p a s. A radar based on statistical estimation and resolution con- -
siderations, Stanford Electronips Lab., Stanford Univ., Stanford, Cali-
fornia, Tech. Rept. 361—1 (August, 1955).
13. S. E. Craig W. Fishbein, and О. E. R 1 t t e n b a c h. Conti-
nuous-wave radar with high range resolution and unambiguous velocity
determination, IRE Trans. MIL-6, 153-161 (1962).
14. T. Sakamoto, V. Takl, H. Miyakawa, H. Kobayashi,
and T. К a n d a, Coded pulse radar system, J. F a c. Eng. Univ. Tokyo
27, 119—181 (1964).
316
’’Xalallausitk
знание без ераниц «
.15 . S. W. G о I о m b. Sequences with randomness properties, Glenn L. Mar-
tin Co., Baltimore, Maryland Final Rept. on Contract SC-54-33611 (June,
1955). ,
16. N. Z 1 er 1 er. Linear recurring sequences, J. Soc. Ind. Appl. Math. 7,
31—48 (1959).
*17. W. W. P e t e г s о n. Error Correcting Codes, M. I. T. P r e s s, Cambrige,
Massachusetts/ 1961.
18. D. A. Huffman. The synthesis of linear sequential coding networks
in: «Information Theory.» (C. Cherry, ed), Academic Press, New York,
1956.
19. S. W. G о 1 о m b and R. A. S c h о 1 t z. Generalized Barker sequences,
IEEE Trans. IT-11, 533—537 (1965).
20. R. С. H e i m i 1 I e r. Phase shift codes with good periodic correlation
properties, IRE Trans., IT-7, 254 —257 (1961).
21. R. r r a n к and S. Z a d о f f. Phase shift codes with good periodic cor-
relation properties, IRE Trans. (Correspondence) IT-8, 381—382 (1962).
22. R. L. F r a n k. Polyphase codes with good nonperiodic correlation pro-
perties, IEEE Trans. IT-fl, 43—45 (1963}.
23. D. F. D e L о n g. Jr. Three phase codes, Mass. Inst. Technol. Lincoln
Lab., Lexington, Massachusetts, Group Rept. 47—28 (July, 1959).
24. D. A. H u f f m a n. The generation of impulse-equivalent pulse trains,
RE Trans. IT-8, S10—S16 (1962).
25. ^C. E. J a g g e r and R. H. M c L a u g h I i n. A compilation of ambigui-
Jy surfaces of some short codes, Canadian General Electric Co., Ltd., To-
ronto, Canada, Tech. Memo. RQ 65EE32 (August, 1965).
26. J. I n j e у a n. Generation of Huffman codes, Canadian General Elect-
ric Co., Ltd., Toronto, Canada, Tech. Memo RQ 65EE2 (October, 1965).
27. D. С. С о I I and J. R. Storey: Ionospheric sounding coded pulse
signals, J. Res. Natl. Bur. Std., Radio ScL, 68D, 1155—1159 (1964).
28. R. M. L e r n e r. A. matched-filter detection system for complicated Dop-
pler shifted signals, IRE Trans. IT-6, 373—385 (1960).
29. R. В e n j a ml n. Recent developments in radar modulation and pro-
cessing techniques, Proc. IEE (London) 111, 2002—2015 (1964).
30. W. B. Allen and E. C. Westerfield, Digital compressed-time
correlators and matched filters for active sonar, J. Am. Acoust. Soc. 36,
121 — 139 (1964).
31. E. L. К e у, E. N. F о w I e, and R. D. H a g g a r t y, A method of side-
lobe suppression in phase coded pulse compression systems, Mass. Inst.
Techno!.,. Lincoln Lab., Lexington, Massachusetts, Tech. Rept. TR-209
(August, 1959).
**32. W. R. R emley. Doppler dispersion effects in matched-filter detection
and resolution, Proc. IEEE 54, 33—39 (1966).
33. E. J. Kelly and R. P. W i s h n e r. Matched-filter theory for high
velocity accelerating targets, IEEE Trans. MIL-9, 56—69 (1965).
34. С. К a i t e r i s and W. L. R u b I n. A noncoherent signal design tech-
nique for achieving a low residue ambiguity function, IEEE Trans., AES-
г. 468—471 (1966).
35. G. О. V e n i e r. Pulse compression using frequency-coded nonuniform
pulse trains, Defence Research Board, Ottawa, Canada, DRTE Rept. 1149
(September, 1965).
36. T. В. H о w a r d. The application of some linear FM results to frequency-
diversity waveforms, RCA Rev. 26, 75—105 (1965).
* *
1. В у д в о p д. Теория вероятности и теория информации с примене-
ниями в радиолокации, изд-во «Советское радио», 1955.
2. Зиберт. «Вопросы радиолокационной техники», №5, 1957, стр. 41.
17. Питерсон. Коды, исправляющие ошибки, изд-во «Мир», 1964.
г
ГЛАВА 9
ТОЧНОСТИ ИЗМЕРЕНИЯ ПРИ ИСПОЛЬЗОВАНИИ
СЛОЖНЫХ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ И
КРИТЕРИЙ ВЫБОРА СИГНАЛОВ
9.1. Введение
Приведенное в гл. 4 рассмотрение функции неопределен-
ности показало, что для разработчика РЛС представляют ин-
терес три характеристики радиолокационного сигнала: разрешаю-
щая способность, неоднозначность и точность. Первые две из них
очень часто связаны между собой, ибо, как утверждает Вудворд,
требование о том, чтобы автокорреляционная функция сигнала
| х (т, 0) | имела минимальное значение всюду, за исключением
окрестности т = 0, представляет собой необходимое условие раз-
решения сигналов, пришедших с различных дальностей [1]. По-
этому особое значение придается синтезу сигналов, которые на вы-
ходе согласованного фильтра имеют вид узкого и острого пика
при т = 0 и чрезвычайно низкий уровень боковых лепестков по
дальности (зачастую противоречивые требования, которые должны
быть удовлетворены путем компромисса).
В гл. 4 уже рассматривались отдельные критерии оценки разре-
шающей способности и неоднозначности. С другой стороны, точ-
ность измерения обычно анализируется в предположении наличия
в приемнике одиночного сигнала и, как показано в гл. 5, опреде-
ляется отношением сигнал/шум и поведением двумерной корреля-
ционной функции х (т> ф) в окрестности т = 0, ф = 0. При ис-
пользовании хорошо известного в теории статистических оценок
неравенства Крамера — Рао в гл. 5 были сформулированы крите-
рии точности измерения. Было показано, что устройство, реализую-
щее соответствующие этим критериям дисперсии ошибок, представ-
ляет собой образованный совокупностью изображенных на рис. 9.1
согласованных фильтров приемник, который вычисляет максимум
функции правдоподобия.
Во многих применениях для разработчика РЛС представляет
интерес только один параметр — дальность, поскольку измерение
318
^alatiausiSk
знание без ераниц Ч *
скорости предполагается произвести вспомогательными методами,
не зависящими по своей природе от поведения сигнала на выходе
согласованного фильтра. При решении других задач проявляется0
большой интерес к возможности осуществления точных совмест-
ных измерений дальности и скорости. Как показано в гл. 5. в подоб-
ных случаях существенную роль начинает играть коэффициент
частотно-временнбй связи сигнала. Вообще, синтез сигнала по кри-
терию минимума ошибок измерения иногда, в частности при совмест-
ных измерениях дальности и скорости, не обеспечивает достижения
той степени разрешения и неоднозначности, которая необходима
при наличии в поле зрения РЛС многих целей.
Выходные сиеналы
согласованных
фильтров
Рис. 9.1. Набор согласованных фильтров, предназначенных для
измерения дальности и допплеровской скорости.
В данной главе сравниваются точности измерения координат,
обеспечиваемые некоторыми из рассмотренных в предыдущих гла-
вах сложных сигналов, и оценивается влияние коэффициента ча-
стотно-временнбй связи. В более широком смысле рассмотренные
ранее сигналы подразделяются на две категории: 1) сигналы, ко-
торые после их обработки согласованным фильтром сохраняют раз-
решающую способность по времени несмотря на наличие доппле-
ровского смещения частоты (их функции неопределенности напо-
минают острие ножа) и 2) сигналы, структура которых вследствие
допплеровского смещения полностью разрушается (их функции
неопределенности имеют кнопочную форму). Частотно-временнбя
связь у второго класса сигналов стремится к минимуму, а для ЧМ
сигналов наличие такой связи является общим условием. В даль-
нейшем, по мере рассмотрения различных примеров, станет ясно,
что развитая в гл. 5 общая теория оценки параметров вместо того,
чтобы быть средством получения количественной информации об
определенных радиолокационных сигналах, используется главным
образом при их качественном сравнении. Такое положение объяс-
няется тем, что математическое представление большинства радио-
локационных сигналов не удовлетворяет условию регулярности,
рассмотренному в гл. 5.
319
J(jF
Ж'
9.2. Минимальные дисперсии ошибок измерения времени и
частоты для некоторых радиолокационных сигналов с
большим произведением длительности на полосу
Выражения для минимальных дисперсий ошибок измерения
времени и допплеровского смещения частоты имеют вид (см. гл. 5).
(<J?)m«., = . (9.1)
(9.2)
где Е — энергия принятого сигнала; No — односторонняя спек-
тральная плотность шума, а 20 и 2а — эффективная ширина спектра
и эффективная длительность сигнала, определяемые соотношениями
4П« J /ч U(f)l‘df “
₽« -----j /’I у (О I’ df, (9.3)
f It/(fil’d/
—оо
4л« J <>| и (t) fdt *
а- =-----j /> | и (t) |2 dt, (9.4)
f | а (0 Iя Л
— оо
где и (0 — сигнал, представленный в комплексной форме .u(f) =
= a(t) ехр 1/0(0 1, а | U (f) | — модуль огибающей комплексного
спектра, равный 2 |S+(/ + /о) |, где S+ спектральная компонента
вещественного сигнала (предполагаемого узкополосным в смысле
определения, данного в гл. 4) в области положительных частот,
а /о — средняя частота спектра.
Из (9.1) и (9.2) получаем среднеквадратичные значения ошибок
при измерении дальности 6r = ^cot и скорости где X —
длина волны зондирующего сигнала, ас — скорость его распро-
странения. Параметры 0 иа выражены в радианах, поэтому значе-
ния эффективной полосы и длительности определяются соответ-
ственно как 20/2л и 2а/2л. Уравнения (9.3)’и (9.4) имеют вид мо-
ментов второго порядка и не эквивалентны стандартным определе-
ниям длительности сигнала и его ширины спектра ло уровню 3 дб.
Если учитываются только положительные частоты спектра
вещественного сигнала, то (9.3) принимает вид
оо
P> = ^f(/-M«|S(/)|«df. (9.5)
Е i
320
^alaHausKii
знание Без границ “ *
Выражения (9.1) и (9.2) для минимальных дисперсий ошибок
справедливы при условии, если один из параметров (<р либо т)
предполагается известным и следует оценить второй или если ко-
эффициент частотно-временнбй связи сигнала равен нулю. Выра-
жения для 0 и а позволяют произвести сравнение сигналов по точ-
ности измерения дальности и скорости. Однако в некоторых случаях
при интерпретации полученных значений необходимо проявлять
осторожность.
Относительно рассматриваемых ниже сигналов будем предпо-
лагать, что они имеют единичную амплитуду и длительность Т сек.
Энергия Е такого сигнала равна
7/2
£ = -i- I |и(«)|’Л = Г/2 . (9.6)
-Т/2
и поэтому
Т/2
I (9.7)
—772
Эти соотношения ‘справедливы для всех сигналов с прямоуголь-
ной огибающей независимо от функции фазовой модуляции 0(0.
В случае сигнала с прямоугольной огибающей спектра, ширина
которого ограничена величиной А/, получается аналогичный резуль-
тат р2 = л2А/2/3. Ранее было показано, что для 0“ имеет место дру-
гое выражение
Из уравнения (9.8) вытекает, что для любого сигнала с разрывной
огибающей, например прямоугольной, 0 = оо . При такой огибаю-
щей спадание спектра сигнала на краях происходит по закону 1//,
который, будучи подставленным в уравнение (9.3), привел бы к тому
же самому выводу. С точки зрения практики этот результат не имеет
никакого смысла, поэтому в качестве метода получения конечных
значений 0 в данном и следующем разделах на нескольких примерах
рассматривается модификация поведения спектра на краях.
В работе 12] Сколник описывает другой метод, основанный на
ограничении спектра сигнала определенным интервалом частот.
По существу, каждый из указанных методов представляет собой
прием, позволяющий приспособить теорию оценки параметров
к удобным в математическом отношении сигналам, которые, как
например, импульсы с прямоугольной огибающей, не удовлетворяют
условию регулярности.
Используя уравнения (9.3) или (9.5) и (9.4), можно вычислить
значения 0 и а для некоторых из рассмотренных в предыдущих гла-
321
вах сложных сигналов. На основании полученных значений далее
можно подсчитать минимальные среднеквадратичные ошибки изме-
рения дальности бг и скорости 6Г,. Первым рассмотрим ЛЧМ сиг-
нал с гауссовой огибающей [3], поскольку его как временная, так и
частотная зависимости являются регулярными функциями, которые
позволяют избежать решения проблему, поставленной уравнением
9.8).
Сигнал с гауссовой огибающей
и линейной ЧМ
Предположим, что рассматриваемый сигнал формируется путем
подачи короткого импульса на один из двух сопряженных фильтров
с гауссовой амплитудно-частотной характеристикой
|£/(f)| = 2exp(-4/W), -оо</<оо, (9.9)
последовательно с которым включена дисперсионная линия задерж-
ки на Т сек, обеспечивающая в полосе частот A f (определяемой
шириной спектра сигнала по уровню е-1) линейность группового
времени запаздывания— d<D(<o)/d(o = Tfl&f, гдеФ(со) — фазо-частот-
ная характеристика спектра сигнала. Согласно, работе [3] норми-
рованная огибающая сигнала на выходе такого устройства имеет вид
4f« 1
|м(/)|=ехр
16
(лД/)>
= ехр'
. (9.10)
Используя (9.9), получаем
(9.Н)
ОО
₽2 =
л»Д/а
4
(9.12)
Подобным же образом с учетом уравнения (9.10) будем иметь
16
я2 Т2 П1Т*
а2 =------=------
(лТД/)«
(9.13)
Величина произведения ^ характеризует предельную точность
одновременных измерений дальности и скорости, причем для полу-
чения точных совместных оценок дальности и скорости одним из
необходимых условий является достаточно большое значение произ-
ведения ра. В гл. 4 было показано, что 0а > л и что для радиоим-
пульса с гауссовой огибающей и фиксированной несущей здесь
имеет место знак равенства. Из уравнений (9.12) и (9.13), которые
322
Е = 2
о
и
4\alallausitii
знание без ераниц * *
представляют собой точные выражения параметров 0 и а для ЛЧМ
сигнала с гауссовой огибающей, произведение Ра равно
₽“ = -г(16+(лГД/)>]1/г. (9.14>
4
Отсюда вытекает, что 0а = л при ТД/ = 0. Для сложных частотно-
модулированных сигналов условие ТД/ = 0 соответствует предель-
ному случаю радиоимпульса с постоянной несущей, когда параметр
частотной модуляции Д/ можно считать равным нулю. При условии
Д/ = 0, понимаемом в указанном выше смысле, значение 0 опре-
деляется, конечно, преобразованием Фурье функции | и (/) |, а не
соотношением (9.12), которое было приведено в качестве примера для
импульса с гауссовой огибающей. Для ЛЧМ сигнала с гауссовой
огибающей эффективная ширина спектра на выходе согласованного
фильтра равна 20/2л = Д//2. По сравнению с номинальным опре-
делением ширины спектра по уровню 3 дб здесь имеется в виду
уровень е“’Ч соответствующий уменьшению спектральной ампли-
туды сигнала до значения 0,607.
Наиболее распространенные сложные радиолокационные сигна-
лы имеют прямоугольную огибающую, которая согласно уравне-
нию (9.8) приводит к равенству 0 = оо . Самым известным из них
является импульсный сигнал с прямоугольной огибающей и ли-
нейной ЧМ. I
Сигнал с прямоугольной огибающей
и линейной ЧМ
Из рис. 6.6 следует, что при больших значениях ТД/ спектр
ЛЧМ сигнала приближается к прямоугольному. Поэтому, прене-
брегая тем, что прямоугольная огибающая импульса теоретически
Рис. 9.2. Аппроксимация спектра ЛЧМ сигнала в краевой об-
ласти частот (f — |/| — А//2).
приводит к бесконечному значению 0, на основании уравнения (9.5)
получаем, что предельное значение параметра 0’ равно л2Д/’/3.
Ограничиваясь рассмотрением спектральной френелевской области
в пределах от Д//2 до —Д//2 (рис. 9.2), Сколник 12] доказывает,
323
что для ЛЧМ сигнала предельная величина параметра 0, вычислен-
ная для целых значений произведения ТД f, равна

3S (ЛТД/)] /г.
(2ТД/)3/2]/1
С(лГД/) ]
(2ТД/),/2 Г
(9.15)
где S(nTAf) и С(л7Д/) — обычные интегралы Френеля. Для значе-
ний ТА/ == 1,10 и 1000 расчет по формуле (9.15) дает соответственно
следующие величины параметра р2: 0,88 л2Д^2/3, 0,95 л2Д/2/3 и
0,965 л2Д/2/3. Нетрудно заметить, что в данном случае величина
параметра 02 стремится к своему предельному значению снизу. В тех
Рис. 9.3. Сравнение функции (9.16) со средним уровнем спектра
ЛЧМ сигнала в краевой области.
случаях, когда принимается во внимание частотно-временная связь
сигнала, это будет приводить к отрицательным значениям диспер-
сии ошибок измерения. Если же допустить, что 02 равна своему
предельному значений при той же величине частотно-временндй
связи, то это приведет к бесконечно большим значениям средне-
квадратичных ошибок измерений (см. разд. 9.3). Метод, позволяю-
щий выйти из этого положения, заключается в экстраполяции
спектральной характеристики сигнала вне интервала (—Д//2,
Д//2) такой функцией, которая была бы удобной при аналитических
расчетах и не приводила бы к тому, что 02 — оо . Одной из таких
функций, график которой показан на рис. 9.2 пунктиром, является
функция, определяемая соотношением
|S(0|= ±ехр[-^|/|
Д//2<|/|<оо.
(9.16)
л» ' I /
На рис. 9.3 приведены графики средней спектральной амплитуды
ЛЧМ сигнала с прямоугольной огибающей и функции (9.16) в крае-
вой области спектра, построенных для двух значений произведения
ТД/ = 30 и ГД/ = 90; здесь видно, что получается приемлемая
степень аппроксимации. Учет уравнений (9.5) и (9.16) в сочетании
321
ftalattauswk
знание без границ * *
с результатом Сколника дает следующее выражение для параметра
р2 сигнала с линейной ЧМ:
p2==p2_|_?Ll^. + 1. (9.17)
3 L (ТД/)3/2 4(ТД/),/2 J
При ТД/= 1 из уравнения (9.17) получаем Р2 = 6,2 л2Д/2/3,
а когда TAf -> оо , то параметр р2 стремится к величине л2Д/2/3
сверху. Этот результат в значительной мере соответствует интуитив-
ному представлению о поведении параметра Р2 ЛЧМ сигнала при
высоких значениях ТА/, основанному на предположении, что
в предельном случае импульса с постоянной несущей р2 должно
становиться большим.
Для того чтобы улучшить степень приближения, можно было
бы найти другие аппроксимирующие функции. Однако, как будет
показано в следующем разделе, рассмотренный метод также не дает
удовлетворительных результатов ,в тех случаях, когда требуется
вычислить коэффициент частотно-временнбй связи. В связи с этим
можно сделать вывод, что оба описанных в общих чертах метода
(т. е. усечение спектра или соответствующее изменение его краевых
частей) целесообразно использовать главным образом для полу-
чения приближенных значений Р2 и вычисления на их основе мини-
мальных значений среднеквадратичных ошибок измерения.
Сигнал с прямоугольной огибающей
и параболической ЧМ [4, 51
Этот сигнал первоначально был предложен для достижения
лучшего по сравнению с сигналом с V-образной ЛЧМ приближения
формы функции неопределенности к кнопочной. Его характеристики
как сигнала с однонаправленной ЧМ представляют интерес при
выяснении влияния кривизны нелинейной функции ЧМ на рас-
четные относительные точности измерения при некоторых слож-
ных импульсных сигналах с нелинейной ЧМ.
Сигнал с параболической однонаправленной ЧМ, пояснением
к которому служит рис. 9.4, определяется уравнением
s (/) = cos (coz 14- К (t 4- Т/2)8], — Т/2 < t < Т/2, (9.18)
в котором функция модуляции частоты будет
В предположении Д = coz/2n=0 при помощи метода стационарной
фазы можно вычислить спектр сигнала с параболической ЧМ, ко-
торый согласно [5] имеет вид
|S(/)|= -Г1'4. (9.20)
2 2 У. (Д/)1/2
325
где 0 < / < А/. Из уравнения (9.8) видно, что сигналы со сходными
по форме огибающими краевых областей спектра будут иметь оди-
наковые составляющие параметра 0®, обусловленные первым членом
этого уравнения. Поэтому при необходимости для рассматриваемого
сигнала можно было бы использовать ту же самую аппроксимирую-
щую функцию (9.16), которая применялась для ЛЧМ сигнала с пря-
моугольной огибающей. Предполагая распределение спектра на
Рис. 9.4. Параболические однонаправленные
функции ЧМ.
краях симметричным относительно частоты /о» из уравнения (9.20)
можно получить в чистом виде среднюю частоту спектра для пара-
болической ЧМ
Af Af
/, = у f %. (9.21)
Для спектра (9.20) определяемая основными спектральными ком-
понентами составляющая 0® равна
а/
₽’=8-^ f =
£ v
О
(Af А/ А/
= { f f/.df—WC f-l/2
(ДЬ‘,2Ц з r ' э $
16ла Д/1
“ 45
(9.22)
326
^atatiausKi'
знание без границ У *
Используем для краевых областей спектра экспоненциальную ап*
проксимирующую функцию (9.16); тогда для сигнала с однонаправ-
ленной параболической ЧМ, у которого произведение длительности
на полосу значительно больше единицы, параметр 0® запишется
в виде
1,067 +
3
3/2
4(ТДЛ,/2
(9.23)
Другие сложные импульсные сигналы
В гл. 3 и 7 были описаны некоторые методы коррекции формы
спектра сигнала на выходе согласованного фильтра, предназначен-
ные для уменьшения неоднозначности, обусловленной наличием
у сжатого импульса боковых лепестков по дальности. Они своди-
лись к операциям амплитудного взвешивания огибающей зондирую-
щего импульса, взвешивания частотной характеристики приемника
(метод рассогласования) или использовали нелинейную ЧМ для
сигнала с прямоугольной огибающей [6]. При употреблении этих
методов уменьшение уровня боковых лепестков по дальности со-
провождается расширением сжатого импульса. Это обстоятельство
отразится на рассчитанных значениях параметра 0®. В случае при-
менения операции взвешивания частотной характеристики рассо-
гласованного приемника множитель |S(f)|® в уравнении (9.5)
заменяется на | S(f) | W(f), где |S(f)|—спектр сигнала на входе
рассогласованного] фильтра, a W(f) — весовая функция. Примером
сигнала с нелинейной ЧМ является импульс, спектр которого на
выходе согласованного фильтра описывается функцией косинус в
квадрате (уровень его боковых лепестков по дальности не превы-
шает — 32 дб [71). Спектр этого сигнала (при = 0) определяется
следующим уравнением:
iSWI*-coe»i-±[l+cos^l, . (9.24)
af 2 [ Af J 2 2
Как и раньше, имеем а® = п®7^/3. Для рассматриваемого норма-
лизованного спектра E = Af, а 0® вычисляется на основании урав-
нения (9.5)
L.cosxdx = W1-U (9.25)
3 2л J 3 [ л®] '
—я
В табл. 9.1 приводятся значения 0® и а® для сигналов, у которых
| S(f) |® и |м(0| ® описываются либо функцией Хэмминга, либо ко-
синусом. Внесенные в табл. 9.1 значения 0® для сигналов с прямо-
327
й Таблица 9.1
00 Параметры, характеризующие точности измерения сжимаемых импульсных сигналов с однонаправленной ЧМ1
Функция Р* а* •^11 Предельная величина о* при больших зна- чениях произведения ТАГ»
А. Сигналы с линейнойЧМ
1. Огибающая rect (t/T) л’ А/’/З л’Т’/З n’TAf/3 (яТА/)« 2 18 мин
2. Гауссова огибающая:’ * •
? е—длительность импульса по уров-
_ 1 •
ню е
Л’л11 1 4 VI / лТА/V 2
А/—ширина спектра по уровню е л’ А/’М 4 [ ^\лТА/.) J к*ТЬ//4 4 ) °мнн
л’АЯ Г 5,5] л’Т’ Г 5,5] x'Tbf [ 5,5 1
3. Огибающая в виде корня квадрат- 1 — -1- , 1- , Не оценена
ного нз функции Хэмминга 3 L л’ 3 L л’ J 3 л’ J
Af—базисная ширина спектра
л’АЛ Г 6 ] л’П Г, 6 ] л’ТА/Г 6]
4. Косинусоидальная огибающая 3 L л’] 3 л2 J Не оценена
Af — базисная ширина спектра
Б. Сигналы с параболи-
ческой ЧМ и огибающей
rect (t/T) 16л’А/’/45 ' л’Т’/З rtTbf/3 16°МИН
Продолжение табл. 9.1
Функция Р» а* Предельная величина а* при больших значе- ниях произведения TAF*
В. Сигналы с нелиней- ной ЧМ
1. Косинусоидальный спектр мощ- ности, огибающая rect (t/T) n’Af* ГЗл’ —24 - л’ТА//4 100о2 МИН
з л’ - л’Т’/З
2. Косинус-квадратный спектр мощ- ности, огибающая rect (t/T) л’А/’ Г1- 61 л’Т’/З л’ТА/ Г 1- 15 1 мин
3 л’ 3 L 4л’ J
3. Спектр мощности, описываемый функцией Хэмминга, огибающая rect (t/T) n’Af1 I , 5,5 л’А/Т t —3,491 я’ J 17’7омин
з 1 я’ ] л’Т’/З з
4. Ограниченная во времени периоди- ческая импульсная последователь- ность Зависит от закона модуляции n’fe, Т’ — —
5. Сигнал со спектром в виде перио- дической последовательности пря- моугольных полос л2 Й2Т2 Зависит от вида временной функции —
6. Сигнал со скачкообразной ЧМ n’Af* [3-2fe] л’Т’/З л’ТА/ Г 3 - & 1 4 (3-2k) о2нн
3 3 L 2 J 4(3 — 2k) — (3— fc’)’
'i
* Предельная величина о* при больших значе- ниях произведения ТДЛ» « Такая же, как у ЛЧМ
м от < ь. L гд/ J
< ь. м к со
от 0 м ь.
и • ОТ 01 Такое же, как у ЛЧМ при больших ГД/
Функция 7. Сигнал с огибающей rect (t/T) и линейно-ступенчатой ЧМ
330
^alaHausA
знание без границ Ч
угольной огибающей и нелинейной ЧМ представляют собой пре-
дельные значения параметра, вычисленные при условии, что произ-
ведение длительности на полосу сигнала существенно больше еди-
ницы.
Регулярная последовательность
импульсов с прямоугольной огибающей
или сигналсо спектром в виде равномерно
смещенных полос
Для периодической последовательности, состоящей из N пря-
моугольных импульсов, показанных на рис. 9.5, величина параметра
а3 была получена Келли [8] в виде
а — п* kt T*t (9.26)
где
k — 1 [1 2т l2N т"
|Я" 3 N — l |/ Т + АГ+1 Т» ’
т — длительность отдельного импульса, а Т — общая длитель-
ность последовательности импульсов. При условии % = TIN полу-
чается огибающая в виде одного широкого прямоугольного импульса
Рис. 9.5. Периодическая по-
следовательность, состоящая
из /V импульсов (а); периоди-
ческая последовательность, со-
стоящая из N частотных по-
лос (б).
и выполняется равенство kt = 1/3. Это же самое значение величины
kt получается также при N -► оо, когда длительность каждого
импульса стремится к нулю.
Для сигнала, частотный спектр которого состоит из N равно-
мерно смещенных полос, аналогичных по форме изображенной на
рис. 9.5 импульсной последовательности, величина 0а запишется
в виде
Ра = лаЛ/Д/а, (9.27)
331
где
1 tf+1
i,= !—
< з tv— i
2Д/,
Af + +1 A/>
a Af, — ширина полосы частотного подынтервала. При N = 2
и (Д/,/Д/) = 0 параметр К} = 1, а 02 = л2Д/2. Это максимальная
величина параметра 02, которая может быть получена при ширине
спектра сигнала» ограниченной интервалом Д/. Аналогично этому
для сигнала, состоящего из двух узких импульсов, отстоящих друг
от друга на Т сек, имеем а2 = л2 Т2. Такому же значению равна
максимальная величина а2 для сигнала с ограниченным по времени
периодом Т. В двух последних случаях ограниченных по полосе или
длительности сигналов одинаковой энергии получаются теорети-
чески минимальные значения среднеквадратичных ошибок при изме-
рении соответственно дальности бг и скорости Sv.
9.3. Влияние коэффициента частотно-временной связи
на величину теоретических ошибок измерения
Коэффициент частотно-временндй связи, выражение для кото-
рого получено в гл. 5, может быть представлен в виде р = А12/₽а,
где
оо
2л J /6'(01 (01’^
А, = -^5------------------ = -§ J (01 и (t) |« dt (9.28)
J | и (t)12 dt -*
—оо
ИЛИ
„ 00
С \Uti) I’d/. (9.29).
, J af
—oo
Здесь 0(0 — функция фазовой модуляции сигнала; dB(f)/df =
= — 2лб/Ф(со4- <о0) / dco, a—dO((i))/d(o — групповая задержка в со-
гласованном фильтре.
Коэффициент частотно-временндй связи приобретает большое
значение в том случае, когда дальность и скорость необходимо оце-
нить одновременно. Тогда дисперсии ошибок измерения определяют-
ся соотношениями
g;=.. “° ,
т 2ЕР’(1-Р«)
а2 =-----.
‘Р 2Еа’(1—р»)
(9.30)
(9.31)
332
ftatatiausiiik
знание без ераниц * *
Ниже выясняется влияние величины А19 на теоретические
ошибки измерения при использовании рассмотренных в предыду-
щем разделе сигналов с однонаправленной ЧМ. В большинстве
случаев результирующие ошибки измерения будут получены для пре-
дельных условий, когда произведение длительности на полосу сиг-
нала достаточно велико. Как будет показано в дальнейшем, пред-
ложенная процедура аппроксимации поведения спектра на краях
применительно к ЛЧМ сигналу с прямоугольной огибающей может
дать приемлемое качественное описание зависимости величины 0
от ТА/, однако она непригодна для количественной оценки влияния
коэффициента частотно-временндй связи в условиях, когда коэффи-
циент сжатия увеличивается. Для того чтобы уравнения (9.30)
и (9.31) всегда давали положительные значения о* и oj, сигналы
должны удовлетворять следующему условию:
А2
1----->0.
р»а»
Неравенство (9.32) используется для контроля рассчитанных зна-
чений параметров 0, а и Д^1.
(9.32)
Сигнал с гауссовой огибающей
и линейной ЧМ
Значение Д1а для этого сигнала легче всего вычисляется из
(9.29), в котором необходимо принять dl}(f)ldf = +2л7у/А/. Тогда
Л1Я=——
£ J Д/ L A/*J 4
—оо
Из (9.12) и (9.13) получаем
i_p>=i_Jk=—1®—
г ₽>ая (лТД/)»+16
а отсюда выражениями для дисперсий ошибок будут
о2==/а2х (лТД/)»+16
1 \ Т/МИН 1g
о2 _. (о2 \ (лТД/)84- 16
<Р \ ЧМмин ]g
(9.33)
(9.34)
(9.35а)
(9.356)
в которых для вычисления величины (а2)Мин используются (9.12) и
(9.13).
1 Помимо (9.32) применяется доказанное в гл. 4 неравенство 0яа2 —
— А 2 2 > Ла.
333
При условии, что произведение длительности сигнала на по-
лосу больше 10, формулы (9.35) можно аппроксимировать соотно-
шением
2 ст2
мин
\ 4
(9.36)
Если необходимо рассчитать дисперсию ошибки при измерении
запаздывания, то
(с?) = W° , (9.37)
k т’мнн 2£лаД/“
что после подстановки в (9.36) дает
О2 = 1!Л_. (9.38а)
т 4 2Е ' '
Подобным же образом можно получить
О2 = ЛРГ«°.. (9.386)
• 4 2Е '
Формулы (9.38, а) и (9.38, б) показывают, что при нахождении
совместных оценок для дальности и скорости теоретические средне--,
квадратичные ошибки не зависят от величины произведения дли-
Рис. 9.6. Проекции функции |%(т, ф)|макс ЛЧМ сигнала
с гауссовой огибающей и большим значением произведения
Т&1 на вертикальные плоскости, проходящие через времен-
ную и частотную оси.
тельности сигнала на его полосу. Поэтому, если только'длительность
сигнала сделать постоянной, теоретическая среднеквадратичная
ошибка при измерении дальности не будет зависеть от ширины по-
лосы частотной модуляции сигнала, так же как это имело бы место
и в случае сигнала, у которого Л12 = 0. Интересно отметить, что
для ЛЧМ сигнала с гауссовой огибающей величины 7^/4 и Д/а/4
представляют собой моменты второго порядка показанных на рис. 9.6
проекций годографа максимальных значений функции отклика на
вертикальные плоскости, проходящие соответственно через времен-
331
WataUausA
знание без границ У *
н^ю и частотную оси диаграммы неопределенности. Это полезное
соотношение можно применить для оценки дисперсий ошибок дру-
гих ЛЧМ сигналов, обрабатываемых согласованным фильтром.
Сигнал с прямоугольной огибающей
и линейной ЧМ
Замечая, что для этого сигнала |и(/)| = 1 при 11Т/2,
2Е-Т и dO (t)/dt = 2nAft/T, нетрудно вычислить величину
На основании (9.28) получаем
Г/2
J (9.39)
—Т/2
Если использовать значение 0а, рассчитанное при условии экспонен-
циальной аппроксимации поведения спектра на краях, определяемой
формулой (9.17), то при больших значениях TAf для дисперсий
ошибок измерения получаются выражения
№ 4(ТДЛ2/2
х 2£р> 3 У2
(9.40а)
No 4(ТД/р/2
♦ 2£а» 3 V 2
(9.406)
Формулы (9.40 а) и (9.40 б) представляют интерес, хотя и не дают
ожидаемую зависимость дисперсий (отнесенных к омин) от пара-
метра TAf. Они иллюстрируют сложность проблемы, заключаю-
щейся в том, чтобы путем улучшения приближенного выражения
для 0 попытаться получить численные решения и в тех случаях,
когда огибающая зондирующего импульса имеет скачки. Если сде-
ланное ранее на основании (9.8) заключение (т. е. что 0 = оо )
понимать буквально, то независимо от значений TAf и 2E/N0
ошибка измерения дальности будет равняться нулю. Безусловно,
это следствие неудачного выбора в качестве меры ширины спектра
сигнала момента второго порядка функции |S (/) |а и является по-
водом для различных аппроксимаций параметра 0, предложенных
в работах Сколника 12] и Манасса [9] в предыдущем разделе. При-
мер экспоненциальной аппроксимации поведения спектра на краях
показывает, что подобная процедура позволяет получить хорошее
приближение к теоретическому спектру сигнала и удовлетворить
условию (9.32), однако при количественном определении свойств
совместной оценки она оказывается бесполезной.
В гл. 4 были описаны другие меры оценки для ширины спектра
и длительности сигнала, но они применялись главным образом при
анализе разрешения целей по дальности или частоте и не имели
336
отношения к задаче оценки параметров, в которой влияние коэф-
фициента частотно-временнбй связи является существенным. Прак-
тически параметр 0 никогда не может стать бесконечным, поскольку
реализуемые на практике огибающие сигналов не получаются раз-
рывно-ступенчатыми. Для большинства сигналов, у которых про-
изведение длительности на полосу существенно больше единицы,
имеется предельное распределение функции |S (/) |а, которое может
быть использовано для получения конечных значений 0 и сравне-
ния различных сигналов по достижимым точностям измерений.
Для ЛЧМ сигнала с прямоугольной огибающей можно полу-
чить более реалистичную зависимость дисперсий ошибок от пара-
Рис. 9.7. Проекции функции |%(т, <р)| макс для ЛЧМ
сигнала с прямоугольной огибающей.
метра ТД/, аналогичную полученной ранее для сигнала с гауссо-
вой огибающей и линейной ЧМ. В случае сигнала с прямоуголь-
ной огибающей проекция годографа максимальных значений функ-
ции отклика фильтра на вертикальную плоскость во временндм и
частотном измерениях представляют собой треугольные функции,
показанные на рис. 9.7. Моменты второго порядка этих функций
равны соответственно Та/6 и &р/6. При условии, что произведение
ГД/ велико (т. е. ТД/ > 10), и использовании (9.38 а) и (9.38 б)
получим
1 6 2£
(9.41а)
о2 = ДР
ф 6 2Е *
(9.416)
Заметим, что (а2)мин--=ЗЛГ0/2£лаД/а, а (о*)мин = 3/V0/2EлаТа;
тогда (9.41а) и (9.416) перепишутся в виде
д2 _ (лТДП»
т 18
Т/МВИ’
О2 OyTW. /а2 \
Ф 18 V Ф/мин*
(9.42а)
(9.426)
336
^alatlaus^!.
знание Сез границ “ *
Отсюда вытекает ожидаемая зависимость от параметра TAf, показы-
вающая, что путем применения линейной частотной модуляции
сигнала существующие теоретические погрешности измерений, опре-
деляемые формулами (9.41 а) и (9.41 б), уменьшить нельзя. Этот
вывод можно распространить на любой ЛЧМ сигнал, пропущенный
через согласованный фильтр, если определить геометрическое место
точек максимальных значений функции отклика, вычислить мо-
менты второго порядка проекции ее сечений, производимых вдоль
временндй и частотной осей, на вертикальную плоскость и затем
получить выражения, эквивалентные формулам (9.38) или (9.41).
Полученные формулы для дисперсий ошибок при использова-
нии ЛЧМ сигналов основываются на подразумеваемом предполо-
жении, что интервал допплеровских смещений частоты является'ве-
личиной того же порядка, что и ширина спектра сигнала. Однако
это условие выполняется редко. Если же диапазон допплеровских
частот много меньше ширины спектра сигнала, то ошибки при из-
мерении дальности для ЛЧМ сигнала с прямоугольной огибающей'
будут в значительной степени уменьшаться. Относящиеся сюда
вопросы рассматриваются в разд. 9.5.
Сигнал с однонаправленной
параболической ЧМ
Функция частотной модуляции для сигнала с однонаправлен-
ной параболической ЧМ определяется соотношением

, Т 2лД/ 1
’2/ 3 J
(9.43)
где (оо == <0/ + (2лД//3). Выражение в скобках . представляет собой
0'(О« Используя это обстоятельство, из (9.28) получаем
Аа=^-, (9.44)
т. е., как и в случае ЛЧМ сигнала1. Параболическая ЧМ, пока-
занная на рис. 9.4 пунктиром, также приводит к (9.44). Когда про-
изведение длительности сигнала на его полосу велико, то из (9.7)
и (9.22), последнее из которых дает предельную величину пара-
1 Зачастую утверждают, что критерием наличия линейной частотной
модуляции сигнала является большое значение величины Л f2/(<xP)a. Как
показывает пример с параболической ЧМ (для которого Л*2/(аР)“ = 0,933),
большое значение этого параметра является необходимым, но не достаточ-
ным условием того, чтобы преобладающей компонентой функции частотной
модуляции сигнала была линейная ЧМ. •
12 Зак. 1341 337
метра р при больших значениях Thf, вытекает следующее соот-
ношение между дисперсиями ошибки:
(9.45)
Отсюда видно, что у такого сигнала дисперсии ошибок являются
ограниченными (по отношению к Омин) величинами, а фактические
ошибки измерения с увеличением Т или Af будут уменьшаться.
Сигнал с нелинейной ЧМ,
спектр которого описывается функцией
косинус в квадрате
Для рассматриваемого сигнала с нелинейной ЧМ групповая
задержка по времени на выходе согласованного фильтра имеет вид
d<D (со-Нсор) _ у, г и _________1 sjn 2лсо
doo I Доо 2л Дсо
А (о
2
(9.46)
а поэтому
"<Й. = 2577. + г sin м,
df bf bf 2'2
Подстановка уравнения (9.-17) в (9.29) приводит к
(9.47)
Д//2 л
Л1а= — J P^f—J(^2cosx + xsinx)dx-f-
-Д7/2 -л
+ С sin«xdx = —-----------111 (9.48)
4л J 3 L 4л8 J
—л
На основании уравнений (9.7), (9.25) и (9.48) имеем 1 — р2 =
= 0,025, после чего получаем соотношение, справедливое при боль-
ших значениях ТА/
сг«--40а2ни. (9.49)
и в этом случае нелинейная ЧМ приводит к выражениям для диспер-
сий ошибок, которые являются ограниченными величинами отно-
сительно Омин- Появление более высокого по отношению к сигналу
с однонаправленной параболической ЧМ граничного значения ди-
сперсии можно отнести за счет значительной линейной компоненты,
которая содержится в нелинейной функции модуляции, приводя-
щей к косинус-квадратной форме спектра.
В табл. 9.1 приведены выражения для множителей, опреде-
ляющих коэффициент частотно-временндй связи для сигналов с пря-
моугольной огибающей и нелинейной ЧМ, спектры которых описы-
338
ftataHausiS!.
знание без границ ’ *
ваются функцией Хэмминга и косйнусом. Для этих сигналов ука-
заны также предельные значения дисперсий ошибок. Выражение
для производной dB/df сигнала, спектр которого описывается функ-
цией Хэмминга, можно вывести из (3.74), приняв k = 0,08.
9.4. Сигналы с нелинейной и скачкообразной ЧМ,
обеспечивающие малые среднеквадратичные ошибки измерения
При использовании определенных сигналов с нелинейной и
скачкообразной ЧМ можно получить достаточно малые среднеквад-
ратичные ошибки измерения. На рис. 9.8 показан типичный пример
такой модуляции. В случае, когда перепад частот достаточно велик,
Рис. 9.8. Пример «скачкообразной» функции ЧМ
с линейным перепадом девиации частоты.
спектральные составляющие сигнала, соответствующие отрезкам,
на. которых его частота постоянна, могут быть аппроксимированы
двумя узкими полосами, удаленными друг от друга на величину Д/.
Используя разложение Келли (8] [см. уравнение (9.27)], заклю-
чаем, что составляющая ра, обусловленная этой частью спектра
сигнала, пропорциональна произведению л®Д/а. Составляющая же
Р2, обусловленная отрезком, на котором частота сигнала изменяется
линейно, пропорциональна величине лаД/а/3. Коэффициенты про-
порциональности определяются конкретным соотношением энергий
различных частей сигнала, поэтому приближенное выражение для
Р2 запишется в виде
02=я^.[з_2*),
3
(9.50)
Замечая, что в первом интервале 6'(/) =—n&f> а в последнем
О'(/) = лД/, для величины Д12 получаем следующее выражение:
_ n'Tbf [3-fea]
18 3 [ 2 J ’
(9.51)
12»
339
На основании уравнений (9.50) и (9.51) для сигнала с прямоуголь-
ной огибающей получаем
о2 =,
4(3-2Л) —(3-*’)’ “ин
k<\.
(9.52)
В предельном случае, когда k = 0v о2 = 4о2Ин- Фотографии, пока-
занные на рис. 9.9, иллюстрируют форму авто- и кросскорреля-
ционной функций такого сигнала при k = х/3, а также и форму его
которого изображена на
рис. 9.8, • k = 1/3.

спектра. В этом случае а2 = 9,1 Омин- Нетрудно заметить, что для
сигнала с нелинейной ЧМ такого вида уменьшение ошибок измере-
ния приводит к возрастанию неоднозначности измерения. Для сиг-
налов, частота которых, скачкообразно изменяясь, принимает лишь
два значения f0 — &f/2 и f0 + Af/2, величину коэффициента ча-
стотно-временндй связи можно свести к нулю, если производить пе-
реключение частоты в моменты времени, показанные на рис. 9.10, а.
Этот и родственные ему сигналы подробно рассматриваются Швип-
пом в работе [10], где кроме того автор показывает, что данный класс
сигналов при измерениях дает результаты, не зависящие от уско-
рения. На рис. 9.10, в показана автокорреляционная функция такого
сигнала. Когда произведение длительности на полосу сигнала ве-
лико (т. е. Af значительно больше величины, обратной длительности
сигнала), эта функция на ограниченном временндм интервале по
своей форме приближается к рассмотренному Келли оптимальному
340
^iataUausA
знание без границ Ч *
в) V
г) *)
д}
з)
Рис. 9.10. Форма модулирующей функции, спектр сигнала, авто- и
кросскорреляционные функции для случая трех скачкообразных из-
менений частоты на величину А/:
а—функция частотной модуляции; б—спектр сигнала, а—автокорреляционная
функция при TAf-=I00; а—более подробное представление главного лепестка
автокорреляционной функции при ТД/-=100; д—более детальное представле-
ние правого бокового лепестка при TAf-=100; а—кросскорреляционная функ-
ция при ф7-=1.6 и ТД/-=100; ок—кросскорреляционная функция при <рг = б
и TAf-slOO; а—автокорреляционная функция при T&f-=20.
341
по точности измерения дальности сигналу, который ограничен по-
лосой частот А/ и имеет 02 = Ji2Af2.
Сложные импульсные сигналы с нелинейной ЧМ обычно дают
ограниченные (в функции параметра ТА/) ошибки измерения, ко-
торые по своей величине значительно меньше теоретических ошибок
измерения, получаемых при использовании сигналов с линейной
ЧМ. Тем не менее, пропущенным через согласованный фильтр
сигналам с нелинейной ЧМ, имеющим наименьшие теоретические
ошибки измерения, присущи недостатки, которые становятся оче-
видными при рассмотрении рис. 9.9 и 9.10.
Рис. 9.11. Зависимость пиковых значений функции откли-
ка сжимаемых импульсных сигналов с однонаправленной
ЧМ от величины допплеровского смещения частоты.
Нижняя кривая приведена для сигнала с функцией ЧМ, показан-
ной на рис. 9.8.
Как отмечалось ранее, значения дисперсий ошибок связаны
с поведением функции неопределенности вблизи начала координат.
Дисперсии ошибок меньше у тех сигналов, где функции неопре-
деленности в этой области спадают быстрее. Это обстоятельство ил-
люстрируется рис. 9.11, где для нескольких сигналов построены
графики зависимости пиковых значений функции отклика от нор-
мализованного допплеровского сдвига <p7\ В большинстве случаев
максимум кривой совпадает с пиком отклика согласованного фильтра
на смещенный по частоте сигнал. Это означает, что приведенные
в табл. 9.1 сравнительные данные согласуются с соответствующими
свойствами функции неопределенности.
9.5. Некоторые соображения относительно улучшения
точности измерения при использовании сигналов
с однонаправленной ЧМ
В предыдущем разделе было показано, что в рамках классиче-
ской теории оценок при использовании сигналов с линейной ЧМ
342
ftatafLausiM
знание без границ - *
ошибки измерения, отнесенные к своим минимальным значениям,
безгранично растут с увеличением произведения длительности на
полосу сигнала. При использовании сигналов с нелинейной ЧМ
среднеквадратичные ошибки измерения с ростом параметра ТД/
достигают конечных предельных значений. Эти результаты относи-
лись к случаю извлечения информации, переносимой одиночным
принятым сигналом. Ошибки измерения, получаемые при исполь-
Рис. 9.12. Влияние N наблюдений на величину среднеквадратичных оши-
бок измерения сжимаемых импульсных сигналов с однонаправленной ЧМ.
зовании классической схемы нахождения оценки параметра (т. е.
совокупности показанных на рис. 9.1 согласованных фильтров),
можно уменьшить при помощи процедуры с использованием зна-
чительно большего числа принятых сигналов. Если для измерения
используются N отраженных от цели импульсов, то дисперсии оши-
бок измерения становятся равными [11]
(о2)^ = o2//V. (9.53)
При этом предполагается, что измеряемый параметр и отношение
сигнал/шум 2EIN0 для каждого импульса не меняются на длитель-
ности всей последовательности; кроме того, считается, что наблюде-
ние каждого из N импульсов статистически независимо, а ошибка
распределена по. нормальному закону. Для некоторых из рассмо-
тренных в предыдущем разделе сигналов на рис. 9.12 построены
343
графики зависимости результирующих среднеквадратичных ошибок
от величины /V. Они дают заниженные верхние границы, так как
для некоторых сигналов с однонаправленной ЧМ, в особенности
для ЛЧМ сигналов \ можно предложить более целесообразные
критерии оценки погрешностей измерения. Они базируются на ис-
пользовании РЛС, спроектированных на других принципах, от-
личающихся от принципов системы на рис. 9.1 с классической схемой
получения оценки параметров. Ниже рассматриваются два пояс-
няющих примера.
Пример 1. Свойство ЛЧМ сигнала, позволяю-
щее прогнозировать дальность
Если функция модуляции ЛЧМ сигнала имеет положительный
наклон, то допплеровское смещение частоты <р на выходе согласо-
ванного фильтра (имеющего отрицательный наклон функции за-
держки) вызовет обусловленный фильтром относительный времен-
нбй сдвиг, равный ts = — Tq>/&f. Так как <р = 2vf0/c (v — скорость
объекта, f0 — несущая частота зондирующего радиоимпульса,
ас — скорость света), то временнбй сдвиг на выходе согласован-
ного фильтра запишется в виде
ta=-2TvfQ/cbf, (9.54)
а соответствующая ошибка по дальности составит
Д/? = с/в/2 = -сПо/Д/. (9.55)
Принимая в качестве приращения пути, покрываемого объектом за
время Д/, величину ДЯ = — иД/, Клаудер и др. [12] показали,
что для ЛЧМ сигнала с положительным наклоном функции частот-
ной модуляции ансамбль сигналов на выходе согласованного фильт-
ра точно соответствует положению движущихся объектов, которое
они занимает через Д/ сек после момента истинного отражения
сигнала, где
Д^ = Т/0/Д/. (9.56)
Соотношение (9.56), используемое в формуле Д/? = —v&t, пред-
ставляет собой константу, не зависящую от скорости.
Рихачек [13] указывает, что при измерении дальности эта ин-
терпретация, устраняя из оценки дальности неопределенность в ско-
рости, дает минимальное значение дисперсии ошибки, количествен-
1 Выражение (9.53) не отражает того дополнительного преимущества,
которое при измерении скорости проявляется в более продолжительном коге-
рентном наблюдении сигнала (по времени равном длительности сигнала),
состоящего из N импульсов. По существу, при выводе (9.53) предполагалось,
что энергия принятых импульсов увеличилась в N раз.
344
'NalaHausi
знание без араниц
но определяемое формулой (9.1) и относящееся к положению объек-
та, которое он занимает спустя А/ сек после фактического времени
приема сигналов. При этой оценке исходят из предположения,
что в интервале А/ скорости представляющих интерес объектов
остаются неизменными, а величина допплеровского смещения ча-
стоты ф составляет достаточно малую долю ширины спектра сигнала,
так что искажающее расширение импульса получается незначи-
тельным. Если эти предположения выполняются, то при исполь-
зовании ЛЧМ сигнала формула (9.56) представляет собой базис для
точного прогнозирования дальности, так как время упреждения
А/ может быть учтено вычислительным устройством, осуществляю-
щим сопровождение цели по дальности. Скорость в этом случае
будет определяться в качестве побочного продукта при осуществле-
нии программы сопровождения по дальности, получающей данные
о радиальной скорости посредством наблюдения изменения поло-
жения цели в пространстве N импульсов.
Если функция частотной модуляции зондирующего сигнала
имеет отрицательный наклон, то считается, что уравнения (9.55)
и (9.56) определяют истинное положение объекта, которое он за-
нимал за А/ сек до момента истинного отражения. В ряде примене-
ний важно определить, куда направляется объект, а не где он на-
ходился.
Пример 2. Ошибка определения дальности
при априори известном интер-
вале допплеровских частот
Если точно известно (или предполагается), что величина доппле-
ровского смещения частоты равномерно распределена в интервале
(—Af/2, А/72), то из сказанного выше вытекает, что время появле-
ния сжатого импульсного сигнала может быть равномерно распре-
деленной величиной в некотором интервале около положения, соот-
ветствующего истинному местонахождению цели, которое опре-
деляется соотношением
А/.^ТАф/А/. (9.57)
При большом отношении сигнал/шум и достаточно малом ин-
тервале допплеровских частот Аф по сравнению с А/ изменением
амплйтуды сжатого импульсного сигнала для любого заданного
допплеровского смещения частоты можно пренебречь. В таком
случае для априорной дисперсии флюктуаций оценки дальности
цели относительно истинного значения получается следующее выра-
жение:
‘а 12 12А/«
345
Отсюда среднеквадратичный интервал неопределенности по даль*
ности равен
л 1
сТДф
4 ^ЗД/ ’
(9.59)
Из уравнения (9.59) следует, что с ростом А/ ошибка измерения
дальности уменьшается и может быть, таким образом, сведена
к приемлемым значениям при достаточно большой величине Д/.
Если имеется возможность использования информации о радиаль-
ной скорости цели для уменьшения априорной ошибки дальности,
то измерение скорости можно было бы производить описанным в при-
мере 1 способом. Оба рассмотренных примера представляют собой
случаи, когда ЛЧМ сигнал может иметь приемлемые ошибки изме-
рения дальности. Во многих ситуациях применение этого сигнала
может быть предпочтительнее по сравнению с другим, имеющим
минимальную теоретическую ошибку измерения, но создающим
собственные помехи и обладающим неоднозначными характеристи-
ками.
9.6. Условия минимальности ошибок при совместных
оценках дальности и скорости
На примере рассмотренных в разд. 9.3 и 9.4 сигналов с одно-
направленной ЧМ было проиллюстрировано влияние определяемого
соотношениями (9.28) и (9.29) коэффициента частотно-временнбй
связи на рост теоретических среднеквадратичных ошибок измерения
в условиях, когда ищутся совместные оценки нескольких параметров
или когда производится оценка одного параметра при априорном
незнании других, влияющих на результат измерения параметров.
Если коэффициент связи равен нулю, среднеквадратичные ошибки
измерения минимальны. В этом отношении наиболее наглядным
примером является сигнал, у которого 0'(0 = 0, т. е. импульс с по-
стоянной несущей. Однако для такого типа сигнала измерения даль-
ности и скорости не могут быгь точными одновременно, хотя точ-
ность и может быть улучшена за счет измерения по нескольким отра-
женным сигналам. Для того чтобы получить хорошую точность изме-
рения как дальности, так и скорости, необходимо рассмотреть те
группы сложных сигналов, для которых выполняется условие
Т/2
— С /0'(/)1«(О1*ЛвО. (9.60)
£ J
-Т/2
При условии, что | и(0 | является четной функцией (обычно прямо-
угольной), это условие удовлетворяется, когда
0 Т/2
f /0;(/)df=— у (9.61)
—Т/2 0
346
ftataHauswk
знание без границ * *
т. е. при
о;(-о=о;(о.
(9.62)
Соотношение (9.62) означает, что закон модуляции частоты является
четной функцией времени. Свойство сигналов этого типа давать
оценки с минимальной ошибкой отмечалось несколькими авторами"
18, 9, 14]. Характерными приме-
рами, удовлетворяющими указан-
ному критерию, являются сигналы
eV-образной и квадратичной ЧМ.
Условие, налагаемое уравнением
(9.60), частным случаем которого
является (9.62), можно распростра
нить на более общий случай сиг-
налов с несимметричной, двуна-
правленной ЧМ. На рис. 9.13 по-
казано несколько примеров таких
сигналов. Их огибающая | u(t) |
имеет прямоугольную форму, а
функции ЧМ на двух временных
отрезках каждого сигнала являют-
ся идентичными (т. е. прямые ли-
нии, параболы и т. д.). Кроме
того, предполагается, что они
имеют одинаковую среднюю часто-
ту. Теперь в качестве условия ну-
левой связи имеем
л
£
О Т/г
[ л;(ол+J to'a(t)<u =о.
Рис. 9.13. Несимметричные дву-
направленные функции ЧМ.
(9.63)
где б! (0 и 02 (0 относятся к
средней частоте спектра. Для сиг-
нала, функция ЧМ которого представляет собой два отрезка пря-
мых, показанных на рис. 9.13, а, ниже выводятся удовлетворяющие
уравнению (9.63) соотношения между параметрами ДД, Д/2, Тиб,
смысл которых ясен из рис. 9.13. Функции ЧМ каждого отрезка,
отнесенные к соответствующим средним частотам, имеют вид
е;(0= (9.64а)
(0 = 4”r,l(2676>~nAf»- (9-64б>
347
Составляющая величины Л12, обусловленная функцией 6j (/),
равна
(Aa)i —
6
f tdt =
-Т/2
(9.65)
-8я fl [ (t-tb)dt—??^
7(7 + 26) J 7 Т
-Т/2
Т2т\т + 2б) 12Т& + 8бЧ =
= — 25^!l_(T + 26)a.
127 7
Используя (9.64, б) в (9.28), аналогичным образом получаем состав-
ляющую величины Л1Я для второго отрезка ЛЧМ
^^-(Т—26)а.
127 4 7
Обозначим длительность первого отрезка (Т/2 + 6) через 7\> а дли-
тельность второго отрезка (Т/2 — 6) через Т
(9.66) получаем следующее условие равенства нулю величины Л12:
А/а/Д/1=(Л/Л)а. (9-67)
Отсюда вытекает, что для рассмотренных отрезков произведения
длительностей на их полосы обратно пропорциональны отношению
их длительностей. Рассматривая в качестве второго примера пока-
занный на рис. 9.13, б сигнал с параболической ЧМ, получаем
соответствующие выражения для функций ЧМ:
(^1в)г —
(9.66)
2. Тогда из (9.65) и
е2 (о=8лд/2
/-6 ]2 2лД/,
3
2лД/а
3
T + 26J
Г t-N |2
(9.68а)
7 — 26
Т/2
(9.686)
о; (t)=sn^fl
6
или
О
8лД/2
t — T/2 12
7—26
Т/2,
(9.68в)
где Оз (0 — модулирующая функция, соответствующая параболи-
ческой ЧМ, показанной на рис. 9.4 пунктиром. Расчет величины Л12
с использованием этих соотношений приводит к тем же результатам,
которые били получены для сигнала с линейной ЧМ на отрезках,
т. е. к выражениям (9.656) и (9.66), а следовательно, и к (9.67).
Величина Л1в для любого из показанных на рис. 9.13 отрезков может
быть получена из общей формулы
И1.)я. »тр»ве = (Т ± 2«‘). (9.69)
348
ftataHausUk
знание без границ Ч *
где Д1в вычисляется для сигнала с прямоугольной огибающей и
однонаправленной ЧМ, девиация частоты которого производится
по тому же закону и в том же интервале частот, но за время Т.
Обращаясь к табл. 9.1, на основании (9.69) можно получить условие
равенства нулю коэффициента частотно-временнбй связи для раз-
личных комбинаций линейной и нелинейной ЧМ.
На рис. 9.14 показана несимметричная двунаправленная ЧМ,
удовлетворяющая условию отсутствия связи между оценками даль-
ности и скорости. Для сигнала с такой функцией ЧМ на рис. 9.15
показаны автокорреляционная
функция и функция взаимной кор-
реляции при наличии допплеров-
ского смещения частоты. Исходя
из этого рисунка, можно сделать
заключение, что функции неоп-
ределенности сигналов с несим-
метричной двунаправленной ЧМ
обладают свойством нечетной сим-
метрии. При достаточно больших
отношениях сигнал/шум это ин-
тересное свойство можно исполь-
зовать для различения в отдель-
Рис. 9.14. Несимметричная V-об-
разная функция ЧМ, сочетающая
линейный и параболический за-
коны изменения частоты.
ном канале сигналов с противопо-
ложными знаками допплеровского
смещения частоты (при условии,
что в окружающей среде плотность
мешающих отражателей невели-
ка). Если для получения информации о радиальной скорости пере-
мещающейся одиночной цели используется только один согласован-
ный фильтр, то мерой величины скорости является расстояние
между лепестками сигнала. Форма же лепестков, как показано на
рис. 9.15, служит индикатором направления радиальной скорости.
Для изолированных объ'ектов в качестве чувствительного к скорости
цели сигнала был предложен сигнал с V-образной линейной ЧМ.
При определенных условиях применение сигнала с несимметрич-
ной двунаправленной ЧМ предоставляет благоприятную возмож-
ность для извлечения дополнительной информации.
Используя полученные в данной главе общие соотношения,
можно оценить влияние на условие равенства нулю коэффициента
частотно-временнбй связи того обстоятельства, что отрезки функции
ЧМ сигнала имеют различные средние частоты. В таком случае
это условие сводится к следующему:
Ki T&f, г; _ K2T&fsTj 2п’f,TtT,T = 0
47’’ 4Г’ + Т*
(9.70)
, где fa — разность между средними частотами, а и — ко-
эффициенты, учитывающие форму спектра; для рассмотренных
349
в данной главе сигналов они могут быть определены исходя из
табл. 9.1. Уравнение (9.70) переходит в (9.67) при fa = 0 и при
использовании на отрезках одинаковых функций ЧМ (г. е., когда
Ki = К2).
О
рг - м
Рис. 9.15. Корреляционные функции сигнала с ча-
стотной модуляцией, показанной на рис. 9.14.
Если fa мало, то ее влиянием можно пренебречь. При fa
и fа Д/2 ситуация подобна случаю в ра5д. 9.4, где рас-
сматривался сигнал, спектр которого состоял из двух значительно
разнесенных узких полос. Отсюда можно сделать вывод, что влия-
ние fa на теоретические ошибки измерения невелико, хотя ее вели-
чина и будет оказывать решающее влияние на значение параметра
Ра и приводить к возникновению неоднозначности. Наконец, сле-
дует заметить, что если два отрезка сигнала излучаются не после-
довательно, а одновременно, то fa не влияет на величину коэффи-
350
ftalaUausMi
знание без ъраниц - *
циента связи. При этом, если оба отрезка достаточно продолжи-
тельны, а частота постоянна, то, как показал Келли [8], получается
сигнал, близкий по точности измерения дальности к оптимальному
в классе сигналов с ограниченным спектром. В этом случае вид
функции ЧМ в каждом отрезке будет оказывать слабое влияние
на точность измерения дальности, которая зависит от величины f,
при условии ft Afj и Afa. Однако при наличии у сигна-
лов допплеровского смещения частоты и при обработке их согласо-
ванным фильтром некоторые функции ЧМ могут способствовать
уменьшению неоднозначности, хотя в большинстве случаев сниже-
ние не столь уж значительно.
9.7. Коэффициент частотно - временной связи
для дискретно-кодированных сигналов
В гл. 8 были рассмотрены различные примеры дискретно-коди-
рованных сигналов. Представляет интерес оценить влияние формы
дискретной кодовой последовательности на теоретические точности
измерения, проявляющееся в изменении величины коэффициента
частотно-временндй связи. В гл. 8 было показано, что сигналы,
фаза которых кодирована двоичной последовательностью, имеют
функции неопределенности, которые при больших значениях про-
изведения длительности на полосу по своей форме приближаются
к кнопочной. Исходя из приведенных в предыдущих разделах сооб-
ражений, казалось бы, что величина Л1а для таких сигналов будет
автоматически равна нулю, так как в каждом кодовом интервале-
выполняется равенство 6'(0 = 0. Однако это рассуждение справед-
ливо не во всех случаях, поскольку оно также может быть приме-
нено к сигналу, кодированному многофазным кодом Фрэнка, кото-
рый очень напоминает ЛЧМ сигнал и, по-видимому, будет иметь
сравнительно большое значение величины Л1а.
На рис. 9.16, а поясняется метод рассмотрения сигналов, фаза
которых кодирована дискретной двоичной последовательностью.
Предположение о конечности времени переключения фазы из одного
состояния в другое обусловливает появление изображенной на
рис. 9.16, б импульсной функции ЧМ. Величина Л1а для такой
модели при использовании последовательного кода максимальной
длины можно записать в виде

/п+(6/2)
J
/п-(0/2)
(9.71)
где —(2*-1 — 1) < п < 2*-1 — 1, (2* — 1) — число элементов
кода, а (2* — 2) — число перескоков фазы. С ростом k определяемая
соотношением (9.71) величина Л1а становится малой и, следователь-
351
pF
но, этот вид кодированного сигнала удовлетворяет требованиям,
предъявляемым в тех случаях, когда измерения дальности и ско-
рости не должны быть связаны между собой, т. е. должны быть неза-
висимыми. Этот же вывод получается совершенно строго для всех
двоичных последовательностей на основании свойства симметрии,
присущего функции I х (*» ф) |> определенной в предыдущей главе
соотношениями (8.15) и (8.17).
Рис. 9.16. Кодирующая фазу двоичная последова-
тельность с конечным временем переключения (пунк-
тир) (а); эквивалентная импульсная функция ЧМ (б).
На рис. 9.17 обозначены параметры, используемые при анализе
коэффициента частотно-временнбй связи сигнала с линейно-ступен-
чатой ЧМ. Общее выражение для функции модуляции частоты такого
сигнала имеет вид
вл = 2л(/04-лЛ/п), (9.72)
причем моменты tn определяются из условия tn = nT/N, где
Т—общая длительность сигнала, a N—число ступенек, —(N—
— \)/2<n<(N—1)/2, N — нечетное или четное, Д/П = М/Т и
Д/ = NAfn=№/T. Произведение длительности на полосу такого
сигнала равно №. Величина Л1а, определяющая частотно-времен-
ною связь, находится по формуле
tn+(T/2N)
2л Г 2ллМп dt __ 4л*М ntn Т
Т 2d J Т ~ Т 2d N
п /п—(Г/2ЛО п
(9.73)
Заметим, что tn=nT/N и Д/=№Т; в таком случае уравнение
(9.73) принимает вид
А
_ л» TAf 12 v
з №
п
(9.74)
82
r\alaHaus№i‘,
знание без границ “ *
Можно показать, что в (9.74) сумма равна (№—2V)/12, так что
окончательно запишем
А ni™f г 1 ]_ [ТАЛ—!
11 3
(9.75>
№
3
Рис. 9.17. Линейно-ступен-
чатая функция ЧМ.
TAf
Когда № или ТА/ растет, величина АХ1 стремится к значению, ко-
торое она имеет для ЛЧМ сигнала. Считая, что величина р2 одна и
та же для обоих сигналов, на основании
(9.75) можно ожидать, что теоретиче-
ские точности измерения, обеспечивае-
мые сигналом со ступенчатой ЧМ, будут
немного лучше, чем у ЛЧМ сигнала.
Физически это можно объяснить поведе-
нием функций неопределенности каж-
дого сигнала около своего основного
пика. Из рис. 9.18 видно, что функция
отклика на сигнал со ступенчатой ЧМ с
ростом допплеровского смещения часто-
ты спадает гораздо быстрее. Как пока-
зано в гл. 8, это связано с переходом
энергии из центрального пика сигнала
на выходе согласованного фильтра в
периодические боковые лепестки, симмметрично расположенные со
сдвигом на*±М/Д/ единиц по обе стороны от центрального пика.

Рис. 9.18. Изменение пиков функции отклика на много-
фазный сигнал Фрэнка и сигналы с линейной и сту-
пенчатой ЧМ.
Многофазные коды Фрэнка представляют собой третий пример
дискретно-кодированных сигналов. Последовательность фаз в этом
сигнале показана на рис. 9.19, а, Используя для моментов переклю-
353
чения модель, аналогичную представленной на рис. 9.16, а,
получим эквивалентную импульсную функцию ЧМ для многофаз-
ного кода, показанную' на рис. 9.19, б. Если интервал 6 и общая
длительность сигнала с увеличением числа кодовых элементов
поддерживаются постоянными, функция на рис. 9.19, б будет стре-
миться к ступенчатой функции модуляции сигнала. На этом осно-
вании можно полагать, что общее их поведение будет одинаковым.
Проведенный в гл. 8 анализ показал, что при использовании
многофазных кодов сигналы на выходе согласованного фильтра при
Рис. 9.19. Нарастание фазы в сигнале Фоэнка (а);
эквивалентная импульсная функция ЧМ (б).
наличии допплеровского смещения частоты на входе имеют боль-
шее число периодических боковых лепестков. При увеличении доп-
плеровского смещения частоты это приводит к более высокой ско-
рости изменения функции неопределенности около начала коорди-
нат. Это и показано на рис. 9.18. Поскольку проведенный в разд. 9.5
анализ применим также и к двум последним сигналам, можно на-
деяться, что при использовании ЛЧМ сигналов, сигналов со ступен-
чатой ЧМ и сигналов с многофазным кодированием Фрэнка, замет-
ной разницы в точности практических измерений наблюдаться не
будет.
Возможно большое число вариантов кодирования фазы сигна-
лов и дискретного изменения его частоты. Используя описанные
в данном разделе методы точного или приближенного анализа,
можно изучить свойства коэффициента частотно-временндй связи.
Однако на многочисленных примерах данной главы было показано,
что сигналы, которые дают минимальные ошибки измерения, при
354
Aalalfauswii
знание без границ ' w
наличии допплеровского смещения частоты или при его отсутствии
зачастую обладают большой неоднозначностью. Поэтому, когда
принимаются во внимание все запланированные применения ра-
диолокационной системы, синтез сигнала по критерию минимальной
ошибки при одновременном измерении дальности и скорости не
всегда приводит к наиболее целесообразному сигналу.
Уместно сделать последнее замечание относительно использо-
вания критерия минимума ошибок измерения (в том виде, в каком
он был здесь рассмотрен) в качестве метода синтеза сигнала. Он пред-
ставляет собой один из многих критериев, которые могут быть при-
менимы к различным типам радиолокационных сигналов. Данный
критерий можно связать с поведением функции неопределенности
около начала координат плоскости неопределенности, где она имеет
максимальное значение (см. гл. 4 и 5). Поэтому критерий дает незна-
чительную информацию о поведении функции неопределенности
в других областях плоскости.
На нескольких примерах в данной главе было показано, что
сигналы, которые при измерении дают минимальные ошибки при
наличии или отсутствии допплеровского сдвига могут также иметь
существенно неоднозначные характеристики и в связи с этим будут
неприемлемыми при всех обстоятельствах, кроме случая одиночной
цели. При наличии в окружающей среде большого числа рассеива-
телей разработчик РЛС будет стремиться совместить необходимость
точного измерения по одиночному импульсу с требованием мини-
мизации взаимных помех на выходе согласованного фильтра, созда-
ваемых несколькими полезными сигналами. Круг вопросов, связан-
ных с работой РЛС при наличии большого числа плотно располо-
женных отражателей, рассматривается в следующей главе.
В любом случае тому факту, что радиолокационный сигнал
обладает или не обладает «хорошими» (в смысле неравенства Кра-
мера — Рао или родственного ему условия) возможностями для
точного измерения, нельзя придавать характер абсолютного суж-
дения. На самом деле некоторые из сигналов, в наименьшей степени
пригодные для обычного радиолокационного применения, теорети-
чески имеют оптимальные точности измерения. С другой стороны,
сигналы, считающиеся плохими с точки зрения условия Крамера —
Рао, оказываются гораздо более подходящими в том случае, когда
особое значение придается соображениям практической реализуе-
мости; примером этого является ЛЧМ сигнал, точность измерения
дальности которого рассматривалась в разд. 9.5. В отдельных слу-
чаях при выборе сигнала возможно придется пойти на многочислен-
ные компромиссы. При сравнительной оценке предполагаемых
к использованию в будущем сигналов критерий точности измерения
может дать полезную информацию. Однако, прежде чем сделать ра-
зумный выбор, необходимо учесть и другие факторы.
355
ЛИТЕРАТУРА
•1. Р. М. Woodward. Probability and Information Theory, with App-
lications to Radar, Pergamon Press. Oxford, 1953.
2. M. I. S к о 1 n i k. Theoretical accuracy of radar measurements, IRE
Trans. ANE-7, 123—129 (1960).
“•3. E. N. F о w 1 e, D. R. Carey, R. E. VanderSchuur, and
R. C. Y о s t. A pulse-compression system employing a linear FM Gausaian
signal, Proc. IEEE, 304—312 (1963).
4. F. P. C a 1 1 a h a h. Exposition of the theory of enhanced accuracy radar,
General Atronics Co., Philadelphia, Rept. 697-98-1391 (October, 1959).
5. D. R i c h m a n. Superresolution, Proc. Pulse-Compression Symposium,
Rome Air Development Center, Grlffiss A. F. Base, New York, RADC
TR—59—161 (September, 1959).
6. E. L. Key, E. N.Fowl e, and R. D. H a g g a r t y. A method of pulse
compression employing nonlinear frequency modulation, Mass. Inst. Tech-
nol., Lincoln Lab., Lexington. Massachusetts, Tech. Rept. 207 (August,
1959).
••7. С. E. Co о k. A class of nonlinear FM pulse-compression signals, Proc.
IEEE (Correspondence) 52, 1369—1371 (1964).
•8. E. J. К e 1 1 y. The radar measurement of range, velocity, and accelera-
tion, IRE Trans. MIL-5, 51—58 (1961).
9. R.Manass e. Range and velocity accuracy from radar measurements,
Mass. Inst. Technol., Lincoln Lab., Lexington, Massachusetts, Group
Rept. 312—26 (February, 1955).
10. F. C. S c h w e p p e. Radar frequency modulations for accelerating tar-
gets under a band-width constraint, IRE Trans. MIL-9, 25—32 (1965).
*11. H. Cramer. Mathematical Methods of Statistics, Princeton Univ.
Press, Princeton, New Jersey, 1946.
*12. J. R. Klauder, A. C. Price, S. Darlington, and W. J. Al-
ber s h e i m. The theory and design of chirp radars, Bell. Syst. Tech. J.
39, 745—807 (1960).
*13. A. W. R 1 h a c z e k. Range accuracy of chirp signals, Proc. IRE (Cor-
respondence) 53, 412—413 (1965).
14. P. В e 1 1 o. Joint estimation of delay, Doppler, and Doppler rate, IRE
Trans. IT-6, 330—341 (1960).
*
* •
1. Вудворд. Теория вероятностей и теория информации с применения-
ми в радиолокации. Изд-во «Советское радио», 1955.
8. Келли. «Зарубежная радиоэлектроника», 1962, № 2.
И. Крамер. Математические методы статистики, Издательство иност-
ранной литературы, 1948.
12. Клауде р, Прайс и др. «Зарубежная радиоэлектроника»,
1961, № 1, стр. 15.
^alatiausiik
знание без ераниц
ГЛАВА 10
КРИТЕРИЙ ВЫБОРА СИГНАЛА ДЛЯ РАБОТЫ
В УСЛОВИЯХ ПАССИВНЫХ ПОМЕХ
10.1. Введение
В предыдущей главе для нескольких видов сложных сигналов
были приведены данные относительно влияния их параметров (ши-
рины спектра, длительности функции модуляции) на точность изме-
рения дальности и скорости, которую теоретически можно полу-
чить для этих сигналов. Однако теория оценки параметра в том
виде, как она была применена для анализа радиолокационных си-
стем, основывается, в общем, на предположении, что на извлечение
информации об одиночной цели не оказывают влияние другие отра-
жающие объекты, находящиеся близ нее. На рассмотренных в пре-
дыдущей главе примерах было показано, что условиям независимо-
го измерения дальности и скорости могут удовлетворять многие
сигналы различного вида, прошедшие через согласованный фильтр.
Эти сигналы можно классифицировать как сигналы, чувствительные
к допплеровскому смещению частоты, поскольку их функции
неопределенности обычно имеют четко выраженный пик около
начала координат плоскости неопределенности.
. В некоторых случаях функции неопределенности этого обшир-
ного класса сигналов по своим очертаниям приближаются к кно-
почной форме (см. рис. 4.8), которая сама по себе является прибли-
жением к идеальной, но недостижимой пикообразной форме функ-
ции неопределенности. Применение чувствительных к допплеров-
скому смещению частоты сигналов, имеющих большое произведение
длительности на полосу, может привести (из-за боковых лепестков)
к размазыванию сигнала по области, находящейся на значительном
удалении от фактического его положения по дальности, оказывая
тем самым исключительно вредное влияние на обнаружение, разре-
шение и измерение параметров сигналов целей с другими дальностя-
ми. В таком случае, вероятно, возникнет вопрос, каким будет крите-
рий синтеза сигнала при условии, что радиолокационная станция
должна работать в среде сплошь или частично заполненной рассеи-
357
вателями? В теории синтеза сигналов к этой проблеме проявляется
постоянный интерес. Многие из предложенных критериев основаны
на исследованиях, выполненных для специфических применений,
и сильно зависят от предполагаемых статистических свойств окру-
жающей радиолокатор плотной рассеивающей среды (почвы, океана,
дипольных отражателей и т. д.), а также от размера и формы просма-
триваемой радиолокационной станцией зоны по дальности и ско-
рости. В данной главе рассматриваются .некоторые ситуации, с ко-
торыми может столкнуться разработчик РЛС при выборе сигнала
или сигналов для конкретной системы.
Одной из наиболее трудных и часто встречающихся проблем,
когда конструктивные параметры сигнала могут заметно влиять
на результаты работы станции, является задача выделения полез-
ного сигнала на фоне большого числа перекрывающихся мешающих
отражений или пассивных помех. Решение этой проблемы в общем
случае можно выразить в виде условий, которым должна удовлетво-
рять функция неопределенности радиолокационного сигнала. Дело
в том, что требуемые эксплуатационные характеристики и налагае-
мые функцией неопределенности ограничения, которые были рас-
смотрены в гл. 4, часто вступают в противоречие. Поэтому при вы-
боре сигнала разработчик РЛС возможно будет вынужден принять
компромиссное решение.
10.2. Некоторые соображения относительно сигнала для
случая протяженных распределений полуизолироеанных
движущихся рассеивателей
Чтобы показать возможную связь между окружающей радио-
локатор средой и различными параметрами синтезируемого радиоло-
кационного сигнала, рассмотрим основной пример. Имеется не-
который ансамбль полуизолированных отражающих объектов,
среднее расстояние между которыми меньше пути, проходимого
зондирующим сигналом за время Т (равное длительности несжатого
импульса), а диапазон дальностей представляющих интерес объек-
тов во много раз больше расстояния, соответствующего длитель-
ности Т. Предполагаем также, что объекты перемещаются друг от-
носительно друга. Требуется, чтобы система была в состоянии обна-
ружить и однозначно измерить дальности и скорости нескольких
объектов. Очевидно, что степень неоднозначности, обеспечиваемая
сигналом, состоящим из периодической последовательности импуль-
сов, является неудовлетворительной, и поэтому такой тип сигнала
из рассмотрения исключается. Следовательно, искомый сигнал
должен иметь непрерывную огибающую спектра (тонкой структурой,
обусловленной частотой повторения, пренебрегаем), а также и не-
прерывную огибающую по времени на интервале Т (т. е. прямо-
угольную, взвешенную функцию Хэмминга и т. д).
358
^atattausiik
знание без границ Ч "Ь
Если требуется измерять разность относительных скоростей,
то разработчик системы может выбрать один из чувствительных
к допплеровскому смещению частоты сигналов, как, например,
сигнал с V-образной или параболической ЧМ, сигнал с фазой, ко-
дированной двоичной последовательностью, и т. д. или избрать
. сигнал, который почти не чувствителен к допплеровскому, но чув-
ствителен к временндму сдвигу (сигналы с линейной и тангенциаль-
ной ЧМ)1. Для извлечения информации о скорости в последнем слу-
чае вместо наблюдения выходных сигналов набора согласованных
фильтров используют другие методы.
Рис. 10.1. Два сигнала, имеющие прямо противоположный характер чувст-
вительности к допплеровскому сдвигу частоты.
а— сигнал с кнопочной функцией неопределенности, амплитуда сигнала равна еди-
нице; б — ЛЧМ сигнал, амплитуда сигнала равна I //2ГД/ .
Если выполняется дополнительное условие, заключающееся
в том, что величина допплеровского смещения частоты принимаемых
сигналов мала по сравнению с шириной спектра сигнала (реали-
стичное допущение для широкополосных сигналов), то, по суще-
ству, все сигналы на выходе согласованного фильтра будут обла-
дать максимальной энергией, несмотря на различную форму их,
зависящую от вида сигнала и величины наблюдаемых допплеров-
ских сдвигов. Для иллюстрации допустим, что чувствительный
к допплеровскому смещению частоты вероятный сигнал имеет кно-
почную функцию неопределенности, пьедестал которой представ-
ляет собой постоянную функцию в интервале корреляции 2Т. На
рис. 10.1 показаны два предельных вида сигналов (в отношении
чувствительности к допплеровскому сдвигу частоты); это сигнал
с кнопочной функцией неопределенности и сигнал с линейной ЧМ.
1 Чувствительность к допплеровскому сдвигу в .употребленном здесь
смысле указывает на влияние допплеровского смещения частоты иа распре-
деление энергии сложного сигнала во времени на выходе согласованного
фильтра.
359
Если распределение энергии сигнала на интервале 27 предпола-
гается равномерным, то в первом случае уровень пьедестала, из-
меряемый относительно максимального значения сигнала на выходе,
получающегося при нулевом допплеровском смещении частоты,
равен (2 Л 7 Д ГД® k является функцией величины доппле-
ровского сдвига и формы функции спектральной плотности мощ-
ности.
На рис. 10.2 иллюстрируется влияние поведения этих сигна-
лов при допплеровском смещении частоты на взаимную интерфе-
ренцию между слабым и сильным сигналом. Если амплитуда по-
лезных сигналов может изменяться в диапазоне 40—50 дб, то нужно
Сигналы движущихся целей
♦
б)
Рис. 10.2. Влияние характера чув-
ствительности к допплеровскому
сдвигу частоты на взаимную интер-
ференцию между сигналами с раз-
личными дальностями.
было бы обеспечить произведение длительности на полосу порядка
10*—10е, чтобы средний уровень пьедестала для чувствительного
к допплеровскому смещению частоты сигнала, имеющего идеаль-
ную кнопочную функцию неопределенности, не превышал наимень-
шие значения пиков выходного сигнала при нулевом допплеровском
сдвиге на входе.
Проблемы, возникающие на практике при построении согла-
сованного фильтра для сигнала с таким значением произведения
длительности на полосу, могут оказаться слишком трудными. При
более умеренном диапазоне амплитуд сигнала, скажем, равном
30 дб или менее, и наличии в окружающей среде не очень плотно
размещенных отражающих объектов для разработчика РЛС воз-
можно окажется выгодным применить сигнал с кнопочной функцией
неопределенности х. Сигналы с функциями неопределенности про-
межуточного типа, например с V-образной и параболической ЧМ,
не пригодны для работы по многим целям в тех случаях, когда из-за
1 Иллюстрируемая рис. 10.2 кнопочная функция неопределенности не
удовлетворяет предъявляемому к функциям неопределенности требованию
двойственности (см., например, (7)) н поэтому не реализуема. При больших
значениях произведения длительности на полосу сигналы с фазой, кодирован-
ной двоичной М-последовательностью, имеют функцию неопределенности,
приближающуюся по форме к кнопочной.
360
ftalaHauA
знание без границ Ч
допплеровского смещения частоты на входе согласованного
фильтра возникает явление размазывания (переливание) энергии.
При этом имеет место неоднозначность в соседних элементах раз*
решения по дальности. Если два сигнала выбраны таким образом,
чтобы минимизировать прирост энергии в области боковых лепест*
ков одного сигнала при всех возможных расположениях по даль-
ности центрального пика другого, то их взаимное влияние оказы-
вается минимальным.
Возможности появления помех, порождаемых самим сигналом,
рассматриваются в разд. 10.4 и 10.5. При условии сохранения спо-
собности обнаружения слабого сигнала на дальностях, где отсут-
ствуют сильные сигналы, радиолокационная станция должна опре-
делить скорость по данным работы в режиме сопровождения по
дальности или при помощи других поимпульсных методов изме-
рения скорости. Как уже отмечалось в предыдущей главе, для та-
кого применения вполне подходит ЛЧМ сигнал.
Модификацией описанной выше среды является случай полу-
изолированных объектов, разбросанных по всему сравнительно
протяженному интервалу дальностей (>> 7)» где, кроме того, имеют-
ся области, плотно заполненные рассеивателями (например, дож-
дем), средняя скорость которых отлична от скоростей представляю-
щих интерес целей. Будем предполагать, что согласованный фильтр
или система фильтров настроены на частоту, учитывающую доппле-
ровское смещение полезных сигналов, так что выражение «нулевой
допплеровский сдвиг» относится к ожидаемому допплеровскому
смещению частоты интересующих сигналов. Кроме того, в данном
примере можно полагать, что минимальное расстояние между полу-
изолированными объектами либо меньше, либо больше расстояния,
определяемого длительностью Т\ мы выберем последний случай,
поскольку рассматриваемая в дальнейшем задача касается плотно
заполненных рассеивателями областей.
При условиях, которые подробно рассматриваются в следую-
щем разделе, соответствующий реальным рассеивающим областям
отраженный сигнал на выходе согласованного фильтра в функции
времени по своему характеру будет шумоподобным. В зависимости
от того, используется ли чувствительный или нечувствительный
к допплеровскому смещению частоты сигнал, эта шумоподобная
помеха может перемещаться, как показано на рис. 10.3, в соседние
области, создавая, в свою очередь, нежелательные помехи на
дальностях, значительно отличающихся от фактической дальности
областей, плотно заполненных отражателями. Когда радиолока-
ционная станция сопровождает объекты через области, содержащие
помехи, и при этом используется запоминающее устройство, то
любой сигнал помехи, переместившийся из соседней области, может
оказать вредное влияние при повторном захвате сопровождаемой
ранее цели за минимально возможное время. Разумеется, когда
протяженность насыщенной отражателями области становится го-
361
раздо больше расстояния, эквивалентного длительности сигнала,
то относительное влиянине этого фактора уменьшается.
В отличие от рассмотренных выше компактных сигналов им-
пульсные последовательности можно применять в том случае,
когда интересующий нас диапазон дальностей значительно меньше
расстояния, эквивалентного полной длительности сигнала.
Не следует считать, что из приведенного выше рассмотрения
можно сделать заключение о бесполезности чувствительных к доп-
плеровскому сдвигу частоты ожидаемых импульсных сигналов; на-
против, оно лишь подчеркивает, что при оценке потенциальных воз-
можностей сигнала с точки зрения условий окружающей среды,
Область помех от местных предметов
Рис. 10.3. Явление растекания пассивных помех, наблюдаемое
при использовании чувствительных к допплеровскому сдвигу
сигналов.
в которых предполагается функционирование радиолокатора, разра-
ботчик РЛС должен проявить рассудительность. Существует ряд
тактических требований, для удовлетворения которым с выгодой
можно применять одновременное измерение дальности и скорости
действительно разделенных объектов (разделение по времени
больше Т). В этом случае можно было бы использовать приемник
с набором согласованных фильтров, показанный на рис. 9.1.
10.3. Оптимизация сигнала при неподвижных или медленно
движущихся пассивных отражателях
В предыдущем разделе кратко был рассмотрен пример, радио-
локационной цели или целей, расположенных в области, сплошь
заполненной рассеивателями. Сейчас мы подробнее исследуем слу-
чай, когда относительное допплеровское умещение частоты между
полезными сигналами и сигналами, обусловленными плотной рас-
сеивающей областью, т. е. мешающими отражениями, имеет не-
большую величину. Это означает, что | фмакс | 1/Г, где <р — доп-
плеровское смещение частоты сигнала помехи относительно.средней
величины допплеровского сдвига полезных сигналов, а Т — дли-
тельность зондирующего импульса. В радиолокации эти условия
362
NataHauswih
знание без границ - *•
выполняются во многих случаях, когда длительность зондирующего
сигнала не слишком велика или когда различие относительных ско-
ростей не чрезмерно, например как при радиолокационном наблюде-
нии ракет. Считается, что радиолокационные цели находятся
«внутри» зоны помех, если соответствующие сигналы, отраженные
от цели и мешающих отражателей, попадают в приемник одновре-
менно. Физически цель может находиться в свободной от помех
области пространства (как, например, самолет, летящий над землей),
но из-за неблагоприятного относительного расположения радио-
локатора, целей и источника помех, ограниченных размеров антен-
ного луча и пространственной конфигурации боковых лепестков
антенны, все же возможно, что отраженный от цели сигнал окажется
замаскированным мешающими отражениями. В других случаях
физически цель может находиться непосредственно в области по-
мех, как, например, когда самолет пролетает через полосу дождя
или движется автомашина.
Будем полагать, что область, создающая мешающие отражения,
состоит из независимых широкополосных точечных рассеивателей,
причем размеры и координаты каждого взятого в отдельности рас-
сеивающего элемента являются случайными величинами. Кроме
того, предположим, что расстояние между отдельными рассеива-
телями гораздо меньше эффективной разрешающей способности
сигнала на выходе согласованного фильтра. При этих допущениях
вследствие перекрытия большого числа единичных сигналов ре-
зультирующий сигнал помехи в каждом элементе разрешения по
дальности имеет характеристики случайного шума. Если, кроме
того, не учитывать закон четвертной степени по дальности (вслед-
ствие ограниченной протяженности зоны помех либо значительной
удаленности ее от позиции радиолокационной станции), то поведе-
ние результирующего сигнала помехи, по существу, будет пред-
ставлять стационарный и гауссов случайный процесс.
Этот процесс не зависит от вида используемых сигналов (на-
пример, одного из рассмотренных в предыдущем разделе), так как,
если сигнал на входе согласованного фильтра имеет шумовой ха-
рактер, то передаточная функция согласованного фильтра суще-
ственно не изменит его шумоподобное состояние. Это согласуется
с предположением о неразрешимости отдельных рассеивателей на
выходе согласованного фильтра. Фоул и др. [1] отмечают, что
с увеличением разрешающей способности сигнала сигнал помехи
на выходе согласованного фильтра по своему характеру стремится
стать менее случайным, поскольку в каждом элементе разрешения
по дальности .уменьшается число образующих помеху сигналов.
Задачу оптимизации кодируемых параметров сигнала на основа-
нии описанной выше модели пассивных помех первым рассматри-
вал Манассе [2], который совокупность радиолокационного передат-
чика и пространства, содержащего источники пассивных помех,
представил в виде ряда возбуждаемых задающим импульсом фильт-
363
ров, показанных на рис. 10.4, а, где s (/) — импульсная характе-
ристика фильтра передатчика (т. е. кодированный сигнал),
a wc (0 — импульсная характеристика фильтра, представляю-
щего пространство, через которое распространяется излученный
и отраженный сигналы. Поскольку s(t) и wc (t) — сигналы на
выходе линейных фильтров, их порядок можно изменить так, как
Рис. 10.4. Модели согласованного фильтра, эквивалентного
передатчику, и фильтра, эквивалентного пространству целей.
показано на рис. 10.4, б. Для доказательства того, что сигнал на
входе приемника в изображенной на рис. 10.4 схеме имеет вид
v(0 = Xs(/-Q4-ne(0. (ЮЛ)
Манассе использует модель эквивалентного дробового шума, осно-
ванную на допущении, что рассеиватели, создающие пассивные по-
мехи, бесконечно малы по размеру, имеют неограниченную плот-
ность и равномерное распределение в пространстве. Первый член
уравнения (10.1) представляет собой полезный сигнал, маскируемый
пассивными помехами. Второй член обусловлен пассивными поме-
хами и является окрашенным гауссовым шумом со спектральной
плотностью мощности
Nc(f) = kc\S(f)\\ (10.2)
где S(f) — преобразование Фурье функции s (/)• Коэффициент
пропорциональности kc зависит от плотности отражателей и их
среднего размера. Когда белый гауссов шум приемника, имеющий
спектральную плотность No/2, суммируется с шумом, обусловлен-
ным пассивными помехами, наблюдаемая на входе согласованного
фильтра спектральная плотность результирующего шума равна
W(/) = W„/2+ftJStf)|«. (10.3)
364
'yalaHausr'ik
знание Сез ерениц Ч "ь
Рассмотренный в гл. 2 оптимальный приемник имеет передаточ-
ную функцию
= (10.4)
так что отношение сигнал/шум на выходе оптимального фильтра
при N (f), задаваемой выражением (10.3), равно
S_ = /a Г
N J (No/2)+*JS (/)|«’
—оо
(Ю.5)
Нетрудно заметить, что когда kc = 0 (т. е. мешающие отражения
отсутствуют), уравнения (10.4) и (10.5) приводятся к обычным для
согласованного фильтра соотношениям. При No = 0 H(f) =
= \lkc S (J) представляет собой инверсный фильтр, рассмотренный
Урковицем [3] для случая отсутствия тепловых шумов при опти-
мальном отношении сигнал/пассивная помеха. Манассе оптимизи-
ровал отношение сигнал/шум (10.5)' при условии, что ширина по-
лосы системы задана. Используя вариационное исчисление *, он
установил, что при таком ограничении оптимизирующая соотно-
шение (10.5) спектральная функция является плоской на всем ин-
тервале Af, так что
|S(/)la =
£/2А/,
0
f0—Af/2<|/|<f04-Af/2,
вне этой области.
(Ю.6)
Подстановка этой функции в уравнение (10.5) позволяет получить
выражение для оптимального отношения сигнал/шум
S \ = 2Л*£ = |2Л*£
АГ/опт”" No+kcE/bf ~ (М))ефф ‘
(Ю.7)
Уравнение (10.7) иллюстрирует важное значение, которое в данном
случае приобретает широкополосность сигнала с точки зрения ми-
нимизации влияния пассивных помех. Физически причину этого
можно понять, признав, что сигнал помехи ограничен по мощности
и зависит от энергии зондирующего импульса и среднего размера
создающих пассивные помехи частиц. Таким образом увеличение
ширины спектра сигнала при неизменной излучаемой мощности
приводит к снижению эффективной плотности мощности <шума»,
обусловленного пассивными отражателями; другими словами, та же
самая мощность <шума» распределяется по более широкой полосе
частот. Это равносильно утверждению, что суммарная плотность
пассивных помех, приходящихся на элемент разрешения по даль-
ности, уменьшается, когда разрешающая способность сигнала уве-
личивается. Разумеется, чтобы это обстоятельство можно было ис-
1 Другой, но связанный с этим способ вывода описан в разд.4.11.
365
пользовать, уровень полезных сигналов в элементе разрешения по
дальности должен быть выше среднего уровня помех.
Целесообразная величина предельной разрешающей способ-
ности достигается тогда, когда большинство полезных сигналов
обнаруживается или когда полученная разрешающая способность
приводит к тому, что на выходе согласованного фильтра полезные
сигналы распадаются на составляющие, которые имеют вид неза-
висимых отраженных сигналов от отдельных элементов искомых
радиолокационных целей. Сжимаемый импульсный сигнал с линей-
ной ЧМ позволяет приблизительно представить себе полученный
Манассе оптимальный сигнал с ограниченным спектром. Как было
установлено в первой главе, одним из основных преимуществ систе-
мы сжатия импульса является то, что она позволяет разработчику
* РЛС выбрать разрешающую способность системы независимо от
длительности зондирующего сигнала, которую затем можно опре-
делять, исходя из соображений максимизации энергии в импульсе.
Таким образом, при наличии в окружающей среде пассивных отра-
жателей описанного выше типа и аддитивности шумов приемника
ширину спектра сигнала можно практически увеличить до любой
необходимой величины без какого-либо ухудшения надежности
обнаружения.
10.4. Сравнение эффективности различных сигналов в
случае неподвижных или медленно движущихся
пассивных отражателей [4, 5]
При формулировке критерия оптимизации формы сигнала,
основанного на его спектральных характеристиках, Манассе отме-
чает, что этот критерий эквивалентен минимизации интеграла от
квадрата автокорреляционной функции сигнала. Если исходные
функции нормированы, то для сигнала с ограниченным спектром
эта операция представляет собой минимизацию постоянной разре-
шения по времени Вудворда Тг, определяемой соотношениями
J I X (т, 0) |« dx
(0,0)1» - W
J IS(O|M/
= (10.86)
f I S (/)!•<//
—oo
Физический смысл постоянной разрешения Тг заключается в том,
что она является мерой растекания энергии сигнала на выходе
согласованного фильтра за пределы окрестности т = 0. Если зна-
366
MaHaus»’
знание без ераниц ' *
чение Тг велико, то отсюда следует, что имеется повышенное раз-
мазывание энергии; другими словами, на всем интервале корре-
ляции 2Т появляются создаваемые сигналом собственные помехи.
Поскольку форма сжатого импульса sin х/х, получаемая при ис-
пользовании сигнала с прямоугольным спектром, в общем случае
не является желательной 1, интересно сравнить, пользуясь соот-
ношениями (10.8 а) или (10.8 б), относительные эффективности не-
которых из рассмотренных в гл. 7 (см. табл. 7.1) взвешенных им-
пульсных сигналов с пониженными уровнями боковых лепестков.
В табл. 10.1 приведены соответствующие данные для сигналов,
спектральная плотность мощности которых описывается функциями
(cos)n и обычной весовой k + (1 — k) cos’. Для взвешенного спектра
вида косинус в квадрате с пьедесталом, описываемого на выходе
согласованного фильтра соотношением
|5(/)|а = Л + (1-Л)со8а(л//А/),
нормализованная функция'разрешения по времени запишется в виде
MT = 3fe*+2fe + 3 1 r 2(fe« + 2fe + l) (10.9>
График этой функции изображен на рис. 10.5. Таблица 10.1 Сравнение разрешающей способности по времени сигналов с ограниченным спектром
Функция, описывающая спектральную плотность мощности сигнала Максимальный уро* вень боковых ле- пестков по даль- ности, дб Нормированная функция разреше- ния по времени i Длительность им- пульса по уровню -3 дб Нормированная функция разреше- ния по времени сигналов, приведен- ных к одной и той же длительности сжатого импульса по уровню — 3 дб
rect(f/Af) —13 1,00 1,00 1,00
cos (л//Д/) —23 1,23 1,34 0,918
cos* (л//Д/) —32 1,50 1,62 0,938
cos8 (л//Д/) —39 1,73 1,87 0,925
cos* (л//Д/) —47 1,93 2,2 0,877
0,08+0,92 cos’ (nf/bf) —42,8 1,36 1,47 0,92
0,16+0,84 cos’ (л//Д/) -34 1,26 1,41 0,89
1 Для случая нескольких целей большее значение имеют уровни боко-
вых лепестков, а не их общая энергия.
367
В последнем столбце табл. 10.1 приводятся эквивалентные зна-
чения Тг, вычисленные при условии, что ширина спектра каждого
взвешенного сигнала увеличивается таким образом, чтобы измеряе-
мые по уровню 3 дб длительности всех сжатых импульсов были оди-
наковыми. Очевидно, что при наличии мешающих отражений при-
веденные в таблице характеристики сигналов, спектры которых
описываются различными весовыми функциями, незначительно
различаются между собой. Если весовые функции ассоциируются
с расстроенным фильтром, включенным вслед за фильтром, согла-
сованным с ЛЧМ сигналом, имеющим прямоугольную огибающую,
Высота пьедестала, К
Рис. 10.5. Влияние высоты пьедестала на ве-
личину ТТ для сигнала, спектральная плот-
ность мощности которого описывается коси-
нус-квадратной функцией с пьедесталом.
то уменьшение отношения сигнал/пассивная помеха равно ухудше-
нию отношения сигнал/шум из-за рассогласования, оцененному
количественно в гл. 7 [см. уравнение (7.53) и табл. 7.1].
Это можно показать, исходя из того (см. рис. 10.4, б), что по-
ступающие на вход приемника пассивные помехи, по существу,
представляют собой белый гауссов шум, который вследствие конеч-
ности полосы пропускания рассогласованного приемника становится
окрашенным гауссовым шумом. Так как для рассматриваемой мо-
дели сигнал с плоской спектральной характеристикой является
оптимальным в классе сигналов с ограниченным спектром, потери
из-за рассогласования, обусловленные неоптимальностью фильтра,
можно трактовать как эквивалентное ослабление, возникающее
при наличии только белого гауссова шума приемника.
Эффективность других типов сигналов по отношению к мешаю-
щим отражениям можно оценить при помощи уравнения (10.8, б).
Так, например, для показанного на рис. 10.6 треугольного импуль-
са, который представляет собой напряжение на выходе согласован-
ного фильтра для сигнала с прямоугольной огибающей и фикси-
рованной несущей, получаем А/ Тг = 2/3. Это меньше приведен-
368
^alaHausA
знание без границ Ч
Af
Рис. 10.6. Автокорреляционная
функция прямоугольного им-
пульса.
кого в табл. 10.1 нормализованного значения для рассмотренного
Манассем оптимального сигнала. Здесь нет противоречия, поскольку
учтенные табл. 10.1 спектральные функции ограничены по ши-
рине, тогда как ширина спектра тре-
угольного импульса является беско-
нечной *.
На рис. 10.7 представлено два
типа автокорреляционных функций
кодированного сигнала, имеющих
растянутый по оси времени пьеде-
стал. Форма кривой, показанной на
рис. 10.7, а, приблизительно соот-
ветствует автокорреляционной функ-
ции сигнала, фаза которого кодиро-
вана двоичной последовательностью максимальной длины (Д[ТГ =
8/3). Приведенный на рис. 10.7, б сигнал имеет уровень пьеде-
стала (2ТА/)-' /2, а не (7Д/)“|/2 и соответствует рассмотренной
в разд.} 10.2 [идеальной кнопочной функции неопределенности.
Рис. 10.7. Автокорреляционные функции для двух
типов сигналов, имеющих кнопочные функции неопре-
деленности.
Нормализованный коэффициент эффективности по отношению
к помехам Л/ Тг для этого сигнала равен 5/3. Эти данные
означают, что в случае равномерно распределенных мешающих
отражателей отношение сигнал/пассивная помеха для сигналов
рассмотренного типа будет по крайней мере на 3—4 дб хуже, чем
для эквивалентного оптимального сигнала, ширина спектра кото-
рого ограничена (в этом случае Д/7Г = 1), плюс некоторое допол-
1 Величина &fTr -= 2/3, получена в предположении, что первые нули
функции sin х/х и треугольной функции расположены в точках ±1/Д/, при-
чем величина А/одна и та же для обоих сигналов. Если они построены таким
образом, что имеют одинаковую длительность по уровню 3 дб. то их постоян-
ные разрешения будут приблизительно равными.
13 Зак. 1341 369
нительное ослабление, обусловленное незначительными (<р 1/Т)
допплеровскими сдвигами частоты, которые приводят к снижению
пиковых значений напряжения на выходах согласованного фильтра
(т. е. кнопочная функция неопределенности).
На рис. 10.8 показана автокорреляционная функция периоди-
ческой последовательности максимальной длины. Если эта дли-
тельность превышает представляющий интерес диапазон дально-
ойнозна у ноет и
Рис. 10.8. Автокорреляционная функция сигнала с фа*
эой, кодированной двоичной периодической ^-последо-
вательностью.
стей, так что внимание можно сосредоточить лишь на определенном,
обозначенном на рисунке интервале, то вычисление по формуле
- (10.8) за один период автокорреляционной функции дает А/Тг =
— (2/3 + 1/N). При N[> 3 эта величина меньше единицы, поэтому
Рис. 10.9. Автокорреляционная функция периодической последова-
тельности импульсов.
в том случае, когда протяженность зоны действия пассивных помех
меньше длительности последовательности, данный сигнал можно
считать также пригодным. Вообще говоря, величину 1/Тг можно
принять в качестве меры способности РЛС работать при наличии
помех от неподвижных или медленно движущихся пассивных отра-
жателей.
Автокорреляционная функция периодической импульсной по-
следовательности показана на рис. 10.9. Если диапазон дальностей,
как и в рассмотренной выше ситуации, ограничен лишь определен-
370
ftaltfflauswk
знание без границ Ч *
ИЫМ интервалом, то AfTr = 2/3. Однако когда во внимание при-
нимается интервал корреляции целиком, то
Д/Л =
2 4/У«+2
3 SN
4W х
^-^-при больших
/V.
(10.10)
10.5. «Оптимальный» фильтр для'режекции
пассивной помехи [4, 5]
Фильтр, оптимизирующий отношение сигнал/помеха, в общем
случае сигнала с неплоским спектром на основе уравнения (10.4)
определяется соотношением
Рубин и Кейтерис [5] отмечают, что оптимальный фильтр с функ-
цией (10.11) эквивалентен показанной на рис. 10.10 цепочке, со-
стоящей из согласованного и режекторного фильтров. Фазовая ха-
рактеристика ее аналогична характеристике согласованного фильт-
Рис. 10.10. Структура оптимального фильтра для
режекции пассивной помехи.
pa. С другой стороны, Рихачек [4] аппроксимирует оптимальный
фильтр комбинацией параллельно соединенных согласованного
фильтра и фильтра Урковица; фильтр Урковица каскадно соединен
с полосовым пропускающим фильтром, ширина полосы пропуска-
ния которого равна 2 /с, где величина fc определяется из соотно-
шения ke |«S(/t)|* = Л70/2, а согласованный фильтр каскадно соеди-
нен с полосовым заградительным фильтром, имеющим такую же
ширину полосы.
Для сигнала с прямоугольным спектром согласованный фильтр
является и оптимальным фильтром. Из уравнения (10.11) видно,
что при конструировании оптимального фильтра в общем случае
13* 371
г
необходимо знать сотношение между шумами, обусловленными пас-
сивными помехами и шумами самого приемника. В большинстве
случаев его невозможно предсказать и построение оптимального
фильтра будет затруднительным (за исключением случая прямо-
угольного спектра сигнала). Для частного случая, когда спектр
сигнала описывается функцией

1+(7/л/)а ’
/
7=fo-f.
Но
Рис. 10.11. Характеристика потерь
при использовании согласованной
фильтрации вместо оптимальной.
Рихачек выясняет, какие потери возникают из-за применения со-
гласованного фильтра вместо оптимального. Для сигнала с таким
спектром на рис. 10.11 изображен график зависимости указанных
потерь от величины отношения уровня пассивной помехи к уровню
шумов приемника. Рубин и Кейтерис 151 рассматривают сигналы
с другой формой спектра, при
этом полученная зависимость
приблизительно аналогична по-
казанной на рис. 10.11 и изме-
няется лишь масштабный мно-
житель, величина которого зави-
сит от вида конкретного сигнала.
Кроме того, Рубин и Кейтерис
исследуют случай, когда режек-
торный фильтр рассчитывается
на некоторый средний ожидае-
мый уровень пассивных помех.
В условиях, когда помехи от-
сутствуют, этот тип фильтра по
сравнению с согласованным ра-
ботает плохо.
Сравнение оптимального и согласованного фильтров является
в некоторой степени академическим по ряду причин. Коэффициент
/гс, характеризующий двойства сигнала помехи, представляет собой
функцию разрешающей способности радиолокатора и разработчик
системы, для которого в большинстве случаев мешающие отраже-
ния являются незначительными, используя достаточно широко-
полосный сигнал, может подстраховать режим работы на нижнем
участке изображенной на рис. 10.11 кривой потерь (или эквива-
лентной ей кривой для других сигналов). Если для получения сиг-
нала на выходе согласованного фильтра с низкими боковыми ле-
пестками по дальности требуется произвести взвешивание спектра,
то, как отмечалось выше, несмотря на потери по сравнению с опти-
мальным фильтром, значения которых приведены в табл. 10.1,
и при любых отношениях уровня пассивных помех к уровню соб-
ственных шумов приемника рассогласованный ЛЧМ сигнал яв-
ляется лучшим для рассмотренного Рихачеком согласованного
372
фильтра с неплоской частотной характеристикой. В случае рассо-
гласованного сигнала с линейной ЧМ пассивные помехи и шумы
приемника в равной степени взвешиваются функцией, определяю-
щей форму спектра. Когда используется обычный согласованный
фильтр, сигнал помехи взвешивается функцией | S (/)|а, где
| S (/) | — амплитудно-частотная характеристика фильтра, тогда
как для собственных шумов приемника весовой функцией будет
При значительном возрастании коэффициента kc в уравнении
(10.11) оптимальный фильтр по своим свойствам приближается
к инверсному фильтру Урковица. Этот фильтр был известен и ранее
и использовался для увеличения полосы частот, чтобы получить
более высокую разрешающую способность [3, 51. Так как на прак-
тике при построении оптимального фильтра на разные уровни пас-
сивных помех* возникают затруднения, то обычно ограничиваются
применением согласованного фильтра. Согласованный фильтр будет
строго оптимальным, когда имеются только собственные шумы
приемника, и приблизительно оптимальным для широкого диапа-
зона условий, когда имеются пассивные помехи.
Было показано, что при наличии областей, плотно заполненных
рассеивателями, которые медленно движутся относительно пред-
ставляющих интерес целей (т. е. при ф 1/Т), сигнал должен быть
широкополосным. В классе сигналов с ограниченным спектром
форма спектральной характеристики должна быть прямоугольной,
хотя ухудшение работы вследствие применения сигналов с другой
формой спектра не будет значительным. Если взвешенный спектр
получается в результате пропускания ЛЧМ сигнала с прямоуголь-
ной огибающей через несогласованный фильтр, производимого
с целью получения низкого уровня боковых лепестков по дальности,
то степень ухудшения параметров по сравнению с характеристи-
ками оптимального фильтра не зависит от соотношения уровней пас-
сивных помех и шумов приемника.
Интересно отметить, что сигнал с неограниченной шириной
спектра, а именно прямоугольный импульс с фиксированной несу-
щей (имеющий автокорреляционную функцию в виде треугольного
импульса) при одинаковом определении ширины спектра сигнала
па выходе согласованного фильтра по первым нулевым точкам
спектральной характеристики был бы эффективнее сигнала, имею-
щего прямоугольный спектр. Физически это объясняется тем, что
прямоугольный импульс с фиксированной несущей совсем не имеет
боковых лепестков, из-за которых на более удаленных элементах
дальности могут появиться мешающие сигналы, аналогичные пас-
сивной помехе.
1 Когда нельзя пренебречь зависимостью интенсивности помех от даль-
ности, оптимальный фильтр становится фильтром с переменными во времени
параметрами, так же как и в том случае, когда плотность помех изменяется,
но времени.
373
Конечно, при использовании этого сигнала возникает проблема,
состоящая в том, что в случае дальнего обнаружения при наличии
только шумов приемника узкий импульс не может перенести доста-
точное количество энергии. При плотном заполнении окружающего
пространства пассивными отражателями применение согласованной
фильтрации вместо оптимальной для сигнала в виде периодической
последовательности импульсов или периодической последователь-
ности максимальной длины может также дать удовлетворительные
результаты, если эти отражатели расположены на определенном
интервале дальностей, соответствующем данным сигналам.
10.6. Соображения относительно структуры сигнала при
плотных распределениях движущихся рассеивателей
Когда плотная групповая цель или создающие хаотические
отражения объекты имеют значительное допплеровское смещение
частоты по отношению к представляющим интерес целям, то появ-
ляется дополнительная возможность максимизации отношения
сигнал/пассивная помеха на выходе приемника. Как показал на
основании (10.5) Рихачек [4], в этом случае отношение сигнал/шум
на выходе оптимального фильтра определяется соотношением
— -.Л’ [ -------|S(/)W------, (10.12)
н J (tf«/2) Mc|Sd(/)la
—оо
где Sd (f) — спектр пассивной помехи, обладающей допплеровским
смещением частоты. В большинстве интересных случаев доппле-
ровское расширение спектра обычно мало по сравнению с величиной
среднего допплеровского сдвига частоты, так что Sd //) можно за-
менить на S (/ + ср), где ф — величина среднего допплеровского
смещения частоты. В тех случаях, когда такая ситуация превали-
рует, отношение сигнал/шум максимизируют путем разделения S(f)
и S (/ 4- ф), т. е. максимумы спектральной характеристики сигнала
с допплеровским сдвигом располагаются в минимумах спектра по-
лезного сигнала или в их окрестностях.
Примером сигнала, который удовлетворяет этому требованию,
является периодическая последовательность импульсов при усло-
вии, что величину межимпульсного интервала АТ можно подстраи-
вать таким образом, чтобы выполнялось равенство ф = 1/2 АТ (ха-
рактеристика согласованного фильтра для периодической после-
довательности импульсов при ф = 1/2 АТ показана на рис. 8.2).
Оптимальный фильтр по-прежнему состоит из показанных на
рис. 10.10 согласованного и включенного вслед за ним режекти-
рующего помеху фильтров, причем заградительный фильтр теперь
374
ftataHauswk
знание без границ * ш
«настраивается» не на функцию, обратную к | S (f) |, как это было
в случае неподвижных помех, а на функцию, обратную к | S(f + ф) |.
К сожалению, мешающие отражения могут встретиться в несколь-
ких раздельных поддиапазонах или быть распределены по доста-
точно широкой полосе частот, так что, возможно, Не удастся синте-
зировать сигнал со спектром, который надлежащим образом отли-
чался бы от спектральной характеристики, сдвинутой на величину
допплеровского смещения пассивной помехи, сохраняя в то же время
другие требуемые в тактической обстановке характеристики сиг-
нала. Помимо этого, указанные выше остальные проблемы, свя-
занные с построением оптимального фильтра для случая движущихся
пассивных отражателей, не становятся сколько-нибудь проще.
Можно полагать, что в большинстве случаев будет применяться
именно согласованный, а не оптимальный фильтр.
В большинстве работ, где исследовались эти два типа фильтров
для конкретных сигналов и имеющих допплеровское смещение час-
тоты сигналов помехи, было показано, что с увеличением ширины
спектра зондирующего сигнала преимуществ оптимального фильт-
ра по сравнению с согласованным становится значительно меньше.
Это является опять-таки прямым следствием влияния ширины спект-
ра сигнала на коэффициент kc.
Общие выражения для отношения сигнал/пассивная помеха
при наличии в окружающей среде многих целей рассмотрены в ра-
ботах Стьюарта и Уэстерфилда 16], Уэстерфилда и др. 17] и Фоула
и др. [1 ]. Авторы этих работ показали, что в общем случае отноше-
ние сигнал/пассивная помеха тесно связано со свойствами сигнала
па выходе согласованного фильтра. Когда пассивные отражатели
или образующие плотную групповую цель объекты состоят из эле-
ментов, каждый из которых в отдельности невозможно разрешить,
то, вероятно, следует предположить, что результирующий сигнал
помехи на выходе согласованного фильтра зависит, вообще говоря,
от общего энергетического вклада каждого рассеивателя, а не от
поведения во времени отдельного, сдвинутого по частоте сигнала.
Поскольку сдвинутый по частоте нормализованный сигнал на вы-
ходе согласованного фильтра описывается сечением функции не-
определенности х (*, ф)» энергия сигнала на выходе согласованного
фильтра определяется уравнением
J |х(т,<р)|Мт = ГДч>), (10.13)
—00
где через Тг(ф) обозначена функция, являющаяся обобщением
введенной Вудвордом постоянной разрешения по времени (10.8 а)
в случае допплеровского смещения частоты. Однако необходимо
подчеркнуть, что по сравнению с Тт (6) функция ТГ (<р) имеет более
узкое толкование. Поскольку х (*, 0) принимает свое максималь-
ное значение при т О, Тг (0) определяет меру растекания энергии
375
сигнала % (т, 0) по удаленной от значения т = 0 области. Однако
для функции Тг (<р) зависимость такого вида вообще не существует.
Эта функция является мерой энергии, которую выделяет в требуе-
мом канале на выходе согласованного фильтра сигнал, являющийся
для него рассогласованным из-за допплеровского смещения частоты.
Уэстерфилд и др. [7] первыми специально отметили значение этой
функции при определении отношения сигнал/пассивная помеха
в общем случае1.
Функция Тг (<р) имеет большое значение для оценки эффектив-
ности подавления пассивных помех, создаваемых движущимися
отражателями, при использовании различных сигналов, обрабаты-
ваемых согласованным фильтром. Ниже приводятся различные
выражения для функции Тг (ф), которые были выведены в гл. 4:
Л(<Р)-
J 1Х(т. ф) I’dt
—оо
IX <0,0)1*
ОО
J
Л (<₽)“ —
х (т,0) )’ехр[/2лтф] dx
1х(0*0)
(10.14а)
(10.146)
(10.14в)
В случае нормализованного сигнала | % (0,0) | — J |S(f)|adf— 1.
— ОО
Уравнение (10.14 б) указывает на зависимость функции Тг(ф)
от автокорреляционной функции сигнала и, следовательно, от про-
тяженности спектра сигнала. Поэтому величину энергии сигнала
с допплеровским сдвигом на выходе согласованного фильтра неза-
висимо от автокорреляционной функции сигнала точно определить
невозможно. Эта связь, на которую впервые указали Уэстерфилд
и др. 17], может привести к некоторому противоречию в отношении
тонкой структуры полезного сигнала на выходе согласованного
1 Уэстерфилд и др. не дают специального обозначения для функции,
отмеченной здесь через Тг(ф). Авторы выбрали такое обозначение, чтобы
подчеркнуть его историческую зависимость от более ранней работы Вудвор-
да, в которой использовалось Тг(0). В своей оригинальной работе Ричман
[81 эту же самую функцию обозначил через Q(<p). При этом ее можно спутать
с хорошо известной в теории радиолокационного обнаружения Q-фуикцией.
Одним из первых Ричмэн систематически применял обобщенную функцию
разрешения по времени для исследования эффективности различных сигна-
лов при работе по движущимся плотным групповым целям.
376
СмциальиоОля
ftalaltausIM.
знание без границ * *
фильтра, которое можно учесть. Здесь подразумевается, что различ-
ные параметры сигнала (т. е. форма огибающей, вид функции фазо-
вой или частотной модуляции), которые комбинируют для полу-
чения определенной формы автокорреляционной функции, сами
по себе не оказывают влияния на функцию Тг(ф).
Рассматривая выражение для отношения сигнал/пассивная по-
меха, полученное в работе Фоула и др. [1] для случая большого
числа независимых широкополосных рассеивателей с разбросом по
дальности и скорости, можно показать, каким образом функция
Тг (ср) входит в определение эффективности сигнала в отношении
подавления пассивных помех. Для этого случая доказано, что
средняя мощность сигнала помехи на выходе согласованного фильт-
ра определяется соотношением
o.2a«.fo) = ^ П Р<т-f)IX('о + + <₽)IsЛdtf. (10.15)
где п — число рассеивателей; b — средняя эквивалентная, отра-
жающая поверхность рассеивателя, а р(т, ф) — совместная функ-
ция распределения рассеивателей по дальности и скорости; /0 и /0
представляют собой опорные значения временной задержки и час-
тоты сигнала на выходе согласованного фильтра. В частном случае
Рис. 10.12. Распределение'соз-
дающих сигнал помехи рассеи-
вателей в области R.
мы можем принять t0 — f0 — 0, т. е.
считать, что интересующий сигнал
имеет частоту /о» на которую на-
страивается согласованный фильтр, а
уравнение (10.15) описывает интер-
ференцию остальных сигналов, кото-
рые имеют разброс по времени отно-
сительно координаты Zo. соответст-
вующей истинному положению цели,
и мешают оценить характеристики
полезного сигнала. Если мощность
полезного сигнала на входе согласо-
ванного фильтра обозначить через
УЬт, то в момент t0 на выходе согла-
сованного фильтра ее квадрат будет равен Ьт\ % (0, 0)|а. Поскольку
предшествующее рассмотрение базировалось на нормализованной
функции неопределенности (т. е. | % (0, 0) |2 == 1), отношение мак-
симальной мощности полезного сигнала к средней мощности пас-
сивных помех запишется в виде
(10.16)
S =_______________Ьг_____________
1 nb |’f р (т,ф) | % (тер) |« dxdq
R-Д’ Д’
Ф
В уравнении (10.16) представляет показанную на рис. 10.12
область в пространстве параметров т и ф, в которой находятся рас-
377
сеиватели, создающие пассивную помеху. Фоул и др. аналогично
Уэстерфилду предполагают, что распределение пассивных помех
по дальности и скорости независимы, так что р (т, <р) = р(т) р (<р).
Кроме того, часто считают, что в ограниченном интервале дально-
стей Дт (>2Т) рассеиватели распределены равномерно (это допу-
щение включает в себя специально неоговариваемое предположение,
что зависимостью интенсивности отдельных мешающих сигналов
от дальности можно пренебречь). При этих условиях уравнение
(10.16) преобразуется к виду
-• = —---------. (10.17)
Z nb J р(<р) J lx(T,<p)|‘dTdq>
Дф дт
Учитывая уравнение (10.13), получаем
— - ьт^____________________ (10.18)
nb J р(<р) Тг (ф)t/ф
Аф
Если функция р (<р) постоянна на интервале Аф, то уравнение
10.18) преобразуется к виду
г ,* . (10.19)
1 пЬ$Тг(<№
Дф
При условии, что диапазон допплеровских частот представляет
собой узкую полосу около среднего значения допплеровского сдвига
<р, на основании (10.18) получим [5]
1 пЬТг(ч)
Уравнение (10.20) справедливо при условии, что функция 7\(ф)
существенно не изменяется в окрестности ф. Все приведенные выше
выражения указывают на важность обобщенной постоянной разре-
шения по времени Тг (ф). В связи с этим для разработчика РЛС
поведение функции Тг (ф) в зависимости от величины допплеров-
ского смещения частоты имеет первостепенное значение. На
рис. 10.13 приведены графики этой функции для трех типичных
образцов регулярных (т. е. сплошных) спектров, которые рассма-
тривались ранее в качестве сигналов на выходе согласованного
фильтра. Принимая функцию Тг (ф) сигнала с прямоугольным
спектром в качестве эталонной, видим, что для других сигналов эта
функция не может постоянно оставаться ни выше, ни ниже эталон-
378
^alattausjik
знание без границ ' ш
ной кривой при всех значениях ф. Это является следствием прин-
ципа неопределенности, поскольку
оо
([ 1Х(т.Ч>)1аЛй<р =
j Т, (ф) d<p - 4 Р,
— ОО
1 при нормализации.
(10.21)
Еще более поразительный пример приведен на рис. 10.14, а,
где изображена функция Тт (<р) регулярной импульсной последо-
вательности. Появляющиеся на выходе согласованного для этого
сигнала фильтра пассивные помехи имеют в зависимости от вели-
чины допплеровского сдвига чередующиеся максимумы и минимумы.
Такой сигнал обеспечит хорошее отношение SII, если диапазон
допплеровских частот сигналов пассивной помехи занимает узкую
полосу в окрестности нечетных значений, кратных <р = М / 2 Т
(М равно числу импульсов в последовательности)1. При четных,
кратных этой величине значениях на выходе согласованного фильтра
пассивная помеха становится очень большой, что является отраже-
нием многочисленных областей максимальной неопределенности,
присущих этому типу сигнала.
На рис. 10.14, б изображены функции ТГ (ф) для двух типов
сигналов, функции неопределенности которых приближаются
к кнопочной и которые сами являются типичными сигналами,
удовлетворяющими требованиям, предъявляемым при совместных
измерениях дальности и скорости. Нетрудно заметить, что при
умеренных значениях допплеровских частот и работе в условиях
плотных пассивных помех они имеют равномерно плохие характе-
ристики по сравнению с другими типами сигналов, рассмотренными
в разд. 10.2.
Если интересующие нас цели находятся в показанной на
рис. 10.15, а центральной однозначной области плоскости неопре-
деленности регулярной последовательности импульсов, то этот
сигнал можно использовать для обнаружения и разрешения в (огра-
ниченной) среде с плотным распределением источников пассивных
помех. В такой ситуации эквивалентная Тг (ф) функция в централь-
ной области имеет вид, показанный на рис. 10.15, б. Использование
такой регулярной последовательности импульсов в указанном част-
ном случае было рассмотрено Фоулом и др. 11]. Предложенный
ими метод заключается в таком подборе параметров импульсной
последовательности, чтобы межимпульсный интервал АТ соответ-
ствовал протяженности области, создающей помехи. Авторы ре-
1 Использованный здесь, и на рис. 10.14 и 10.15 параметр Л4 эквивален-
тен значению М—-1, фигурирующему в аналитическом описании регулярной
последовательности прямоугольных импульсов, приведенном в гл. 8.
379
BF
Рис. 10.13. Функция Тг(ф) для трех сигналов со сплошным
спектром.
Рис. 10.14. Поведение функции Tr(<jp) для различных сигналов:
а —функция Tf(<p) периодической последовательности импульсов; б — функция
Гг(ф) для сигналов с кнопочными функциями неопределенности (средние уровни).
380
^lataHauSiM
знание без границ * ш
койендуют взять такую несущую частоту, чтобы диапазон доппле-
ровских частот не превышал величину 1/ДТ, равную размеру изо-
браженной на рис. 10.15, а однозначной области по оси <р. Поэтому
f0 = c/2vrbT, (10.22)
где vr — величина, определяющая разброс радиальных скоростей
отражателей, создающих пассивные помехи.
Рис. 10.15. Свойства периодической последовательности импульсов:
а —центральная область функции неопределенности; б —функция Тг(<р) для цен-
тральной однозначной области. Высота квадрата равна 1/ДГ.
Условие (10.22) может привести к нереальным с практической
точки зрения значениям несущей частоты /0« Так, например, если
ДТ = 20 мксек, a vr = 300 м/сек, то f0 = 25 Ггц; такая частота
для большинства типов радиолокационных систем слишком высока.
При необходимости уравнение (10.22) можно использовать в случае
построения семейства кривых для различных сочетаний пара-
метров /о. vr и Д7\ Как уже отмечалось, во многих случаях оно не
381
Г'
дает реального с точки зрения практики решения, особенно если
величина ДТ должна быть очень большой.
Для разработчика РЛС интересно знать, какое количество объ-
ектов, несмотря на наличие в окружающей среде рассеивателей,
можно по отдельности обнаружить или разрешить. Исходя из урав-
нения (10.16), для случая равномерного распределения рассеива-
телей по дальности и скорости Фоул и др. получили выражение,
дающее ответ на этот вопрос:
Д. дт
ф
(10.23)
,1макс~.—, . , .
( b!Ьмин) (д’//)мин
И I X (т, <₽) I2 dx dq>
где 6МИ11 — минимальный размер цели, а (5//)МИ|1 — минимально
необходимое для обнаружения отношение сигпал/пассивная по-
меха.
Уравнение (10.23) справедливо при условии, что интенсивность
пассивной помехи намного выше интенсивности тепловых шумов
приемника. Для регулярной последовательности импульсов, пред-
назначенной для работы по целям, находящимся в указанной выше
однозначной центральной области, можно считать, что лмакс
равно числу элементов разрешения в этой области. Фоул показы-
вает, что в этом случае
Площадь свободной области _ 1 __М&Т , jq „44
м,кс Площадь центрального пика 6(1/Л4ДТ) б
Так как произведение М\Т является полной длительностью сиг-
нала, а б = 1/Д/, где Л/—номинальная ширина спектра, то п
определяется величиной произведения длительности на полосу
импульсной последовательности. Задаваемая соотношением (10.24)
величина лмак(, основывается на предположении, что групповые
цели, попадающие в одну и ту же ячейку на плоскости дальность —
частота Допплера, рассматриваются как одна цель. Если величина
нмаК(; в ожидаемой ситуации является недостаточной (т. е. слишком
много объектов не разрешается), то для получения требуемого раз-
деления целей по дальности и частоте Допплера можно сократить
длительность б элементарного импульса или увеличить число им-
пульсов в последовательности, либо выполнить то и другое вместе.
Вышеприведенное рассмотрение основывалось па предположе-
нии, что местонахождение и размеры области, в которой возникают
мешающие отражения, таковы, что зависимостью интенсивности
отраженного сигнала от дальности можно пренебречь. Ван Трисс
(91 анализирует случай, когда распределение интенсивности по
дальности нельзя считать постоянным, поэтому сигнал пассивной
помехи трактуется как нестационарный случайный процесс. Рас-
сматривая в качестве примера ДЧМ сигнал с гауссовой огибающей
(см. гл. 9), Ван Трисс оценивает различие характеристики обна-
382
iXalallauswk
знание без границ Ч *
ружения сигнала при использовании согласованного и оптималь-
ного фильтров.
Как и следовало ожидать на основании проведенного в преды-
дущих разделах анализа, различие становится меньше, когда
ширина спектра увеличивается. Рубин и Кейтерис [51 наряду
с оценкой специфического влияния зависимости интенсивности пас-
сивной помехи от дальности и от протяженности области с источ-
никами пассивных помех различного типа исследовали большое
число сигналов. Они тоже делают вывод, что при хорошо спроекти-
рованном сигнале качественные показатели согласованного фильтра
в общем приближаются к характеристикам оптимального фильтра.
При определении отношения сигнал/пассивная помеха в каждом
конкретном случае большое значение имеет поведение его обобщен-
ной постоянной разрешения по времени Тг (<р).
Сигналы, отраженные от рассеивателей или от протяженных
целей, при определенных условиях будут иметь вид импульсов на
фоне шума. Импульсные сигналы, которые по своему поведению
подобны полезным сигналам, могут порождаться имеющимися
в окружающей среде отдельными крупными объектами или возни-
кать за счет когерентного сложения сигналов, отраженных от более
мелких объектов, т. е.’ от частиц, создающих пассивные помехи
Степень, в которой эти коррелированные сигналы помех будут вы-
деляться на общем фоне пассивных помех, будет функцией ширины
спектра сигнала, несущей частоты передатчика и свойств экви-
валентной отражающей поверхности объектов, порождающих эти
сигналы. При выводе общего выражения для отношения сигнал/пас-
сивная помеха (10.16) эти сигналы можно было бы учесть. Однако
выражения, обобщающие эти соотношения на случай указанных
выше моделей, объясняющих появление сильной пассивной помехи,
являются очень громоздкими и были получены лишь для некоторых
применений и, вообще говоря, имеют ограниченную ценность.
1 Когда в приемнике имеется очень большой паразитный сигнал, раз-
работчик системы может предусмотреть применение ограничителя для его
подавления. Если ограничитель стоит перед согласованным фильтром, что
обычно требуется при эксплуатации, то существует опасность подавления
полезных сигналов на большом интервале дальностей, обусловленная тем,
что напряжение на выходе ограничителя регулируется сильными сигналами
с большим произведением длительности на полосу.
В работе [51 (см. гл. 14) имеются данные о потерях обнаружения, полу-
чающихся при перекрытии имеющихся на выходе ограничителя сигналов
с большим произведением длительности на полосу. В такой ситуации примене-
ние сигналов в виде импульсной последовательности с переменным межимпуль-
спым интервалом представляет собой метод минимизации подавления полез-
ных сигналов ограничителем путем выбора такого положения импульсов в
последовательности, что при любых относительных смещениях по времени
двух указанных сигналов наблюдается минимум совпадений отдельных им-
пульсов. Применение таких последовательностей рассмотрено в работах
[34 и 35] (в гл. 8).
383
10.7. Некоторые замечания относительно общей проблемы
• синтеза сигналов
В гл. 1 уже отмечалось, что в прогрессе методов проектирова-
ния радиолокационных сигналов большую роль сыграла моногра-
фия Вудворда [10]. Вудворд закончил свою работу замечанием,
что он испытывает некоторое разочарование, будучи неспособным
однозначно ответить на вопрос: «Каким должен быть радиолока-
ционный сигнал?> На протяжении десятилетия этот вопрос побуж-
дал научные изыскания, предпринимаемые с целью получить на
него окончательный ответ. Понятно, что в самом широком смысле
не существует ясного и окончательного ответа на этот вопрос, если
его не сопроводить ограничениями на окружающую среду, в кото-
рой предполагается использовать радиолокационный сигнал. Многие
из описанных в данной книге сигналов уже рассматривались в связи
с тем конкретным назначением, для которого они, по-видимому,
пригодны. Тем не менее, приведенные примеры наталкивают на
мысль, что в конкретной ситуации ни один из сигналов не является
строго оптимальным. Более вероятно, что в результате исследова-
ния обстановки выяснится, что не следует делать, а не то, чтд
лучше всего сделать.
Хорошей иллюстрацией к сказанному является пример, рас-
смотренный Уэстерфилдом и др. [7]. Они анализируют случай сиг-
нала с гауссовым спектром мощности, для которого функция
I X (т> 0) р имеет вид
| X (т,0) |а----ехр [—та], (10.25)
где W — номинальная ширина спектра в обозначениях Уэстер-
филда и др. Кроме того, они предполагают, что функция распре-
деления пассивных помех по дальности является равномерной, а по
скорости — гауссовой, так что
Р (Фс) = (1 /И^) ехр [—л<р2/№2], (10.26)
где фс = ф + ф — допплеровский сдвиг относительно средней
допплеровской частоты, з Wq — протяженность интервала доппле-
ровских частот.
Уэстерфилд и. др. проводили анализ влияния различных зна-
чений параметров сигнала и принятой пространственной модели
пассивных помех, а именно отношения средней допплеровской час-
тоты к величине интервала допплеровских частот ф/М^ и отноше-
ния ширины спектра сигнала к величине интервала допплеровских
частот W/Wq.
Полученные ими результаты для различных комбинаций этих
отношений графически показаны на рис. 10.16, где по оси ординат
отложен выигрыш в отношении сигнал/пассивная помеха за счет
384
WalatiauslVil
знание без границ * *
обработки в согласованном фильтре. Из рис. 10.16 видно, что когда
средняя допплеровская частота велика по сравнению-с интерва-
лам допплеровских частот, то наиЛучшим является сигнал большой
длительности, т. е. W/Wq <. 1. Если диапазон допплеровских час-
тот велик по сравнению со средним допплеровским сдвигом, т. е.
имеется малое (или вообще отсутствует) относительное допплеров-
ское смещение между полезным сигналом и помехой, то лучшими
характеристиками обладает сигнал с очень короткой длительностью,
т. е. W/Wq^> 1. Кривые ясно показывают, что имеется диапазон
значений, которого следует избегать. Иными словами, при проек-
тировании сигнала для случая плотного расположения целей необ-
ходимо стремиться к тому, чтобы иметь как можно меньше пересе-
чений между контурами неопределенности и областью, где в плоско-
сти дальность — частота Допплера распределены сигналы помех.
Сказанное поясняется рис. 10.17, где приводится пример двух
крайних случаев, рассмотренных выше. Когда величина среднего
допплеровского смещения частоты мала, то сигнал типа ЛЧМ
имеет приблизительно такие же характеристики, как и короткий
импульс.
Условие распределения неопределенности сигнала по тем об-
ластям плоскости (т, <р), где априори появления целей не ожидают,
является общим и надежным принципом проектирования. Однако,
если распределение целей в плоскости неопределенности имеет
вид разрывных или сложных по форме областей, то вследствие огра-
ничений, налагаемых условием реализуемости на форму функции
неопределенности, этот принцип может оказаться малополезным.
Обычно при проектировании сигнала стремятся получить больше
свободных областей в распределении неопределенности. В качестве
сигнала, обладающего таким свойством, была предложена периоди-
ческая последовательность импульсов. Однако большое количество
пиков неопределенности, присущих периодической последователь-
ности импульсов, является одним из ее неприятных свойств. Такой
ценой приходится платить за получение свободной области вокруг
центрального пика.
Различные методы уменьшения пиковых значений неопределен-
ности импульсной последовательности рассматривались в гл. 8,
где было показано; что при использовании таких методов, как из-
менение положения импульсов в последовательности, применение
в каждом импульсе кодирования фазы или ЧМ перераспределяется
объем неопределенности, соответствующий нежелательным вы-
бросам, по свободным областям плоскости неопределенности. Эти
методы приводят к созданию функции неопределенности, по своей
форме близкой к кнопочной, которая дает большое количество по-
мех, порожденных самим сигналом при всех практически инте-
ресных значениях дальности и допплеровского смещения частоты.
Поэтому, как отмечает Фоул 11], при условии плотного распре-
деления целей в компактной области применять их не рекомендуется.
386
ер'пишододдо шана at тлОапяд
Рис. 10.16. Выигрыш в отноше-
нии сигнал/пассивная помеха при
обработке гауссова импульса в
согласованном фильтре.
Область неопределен-
ности короткеео
инпульса
Рис. 10.17. Перекрытие области неопределенности с аоной
распределения пассивных помех.
Область неопределенности
/ при линейной им
Распределение пассивных
понек 8 плоскости
дальность - частота Допплера
386
Возможный способ устранения значительной неопределенности
заключается в изменении частоты заполнения каждого импульса
последовательности по линейному или случайному законам. При
этом в зависимости от величины изменения частоты во время пере-
хода от импульса к импульсу корреляция сигналов из областей
неопределенности, расположенных в интересующих интервалах
дальности и допплеровского сдвига, будет ослабляться. Однако
в этом случае широкой свободной области вокруг центрального
пика не получится. При Д/ = 3/6 влияние линейного закона изме-
нения частоты было рассмотрено в гл. 8, где показано, что централь-
ная часть функции неопределенности имеет мелкозернистую струк-
туру. Разрешение же различных сигналов будёт определяться,
вообще говоря, огибающей функции неопределенности, а не ее
мелкозернистой структурой. Поэтому устранение неопределенности
этим, методом достигается за счет увеличения полосы передатчика
и приемника без эквивалентного улучшения разрешающей способ-
ности по дальности, несмотря на ее практическую целесообразность.
Как отмечает Рихачек [12], в зависимости от конкретных обстоя-
тельств она может быть приемлемой или нет.
В свете высказанного в гл. 4 утверждения, что в отсутствие
всеобъемлющей предварительной информации относительно кон-
кретного применения радиолокатора или состояния окружающей
среды потенциально все сигналы следует считать одинаково хоро-
шими (или плохими), представляет интерес исследовать критерий
синтеза сигнала для общего случая плотного распределения целей.
Этот вопрос можно проиллюстрировать на примере описанной
в рЬзд. 10.2 кнопочной функции неопределенности и функции не-
определенности ЛЧМ сигнала, если предположить, что цели, плот-
ность которых в среде постоянна, равномерно распределены в об-
ласти плоскости неопределенности, определяемой неравенствами
—Т < т < Т по оси времени и —Д/ < <р < Д/ — по оси частот.
Здесь Т — длительность зондирующего сигнала, а Д/ определяется
полосой модуляции сигнала, а не среднеквадратичным значением 0,
которое, как указано в гл. 9, часто не совпадает с мерой ширины
полосы, обычно используемой радиоинженерами. То обстоятель-
ство, что длительность и полосу сигнала одновременно сократить
нельзя, в данном рассмотрении имеет второстепенное значение, по-
этому будем считать, что для указанных сложных сигналов на
плоскости неопределенности можно установить четко определенные
границы по обеим координатам.
Описанная в разд. 10.2 кнопочная функция неопределенности
относительно значения | %(0, 0) | = 1 имеет пьедестал величиной
(2А7,Д/)-’*/2. При установленных выше границах средняя величина
k — 2. Она определяется из условия равенства единице объема
I X I2 функции с пьедесталом, поскольку центральный максимум
имеет пренебрежимо малый объем. Средний уровень пиковой мощ-
ности сигнала от одиночной, расположенной в плоскости неопре-
387
деленности (за исключением центральной области) цели на выходе
согласованного фильтра равен 1/4ТД/. Так как имеется 27 А/ эле-
ментов разрешения по каждой из осей, то в плоскости неопределен-
ности будет (27 А/)8 ячеек разрешения. Если, кроме того, предпо-
лагается, что во. всех элементах разрешения отраженные сигналы
имеют одинаковую амплитуду, то наблюдаемое на выходе согласо-
ванного'фильтра при т = О, <р = 0 отношение полезного сигнала
к пассивной помехе равно
8 1
/ ТА/ ’
(10.27)
По существу, тождественный результат был получен Рихачеком
[12] для рассмотренной в разд. 4.12 функции неопределенности
с пьедесталом, который предполагается постоянным и протяженность
которого по времени и частоте определяется моментами второго
порядка а и 0, являющимися мерой длительности и ширины спектра
сигнала, а не упомянутыми выше величинами 2Т и 2Д/1.
Рассматривая затем ЛЧМ сигнал, характеристики которого
при наличии допплеровского смещения частоты взвешиваются по
амплитуде функцией 1 — | ф/А f |, получаем, что при распределении
целей, аналогичном предполагаемому выше, средний уровень оди-
ночного сигнала на выходе согласованного фильтра равен 1/2,
а средняя пиковая мощность составляет 1/4. Можно считать, что,
как показано на рис. 10.18, гребень функции неопределенности
ЛЧМ сигнала содержит приблизительно 27А/ целых ячеек разре-
шения и 47А/ полуячеек. Появляющиеся в любом из этих элементов
разрешения сигналы будут давать вклад в результирующую пассив-
ную помеху для ячейки разрешения, расположенной в начале коор-
динат плоскости неопределенности. Когда ЛЧМ сигнал исполь-
зуется при том же самом распределении целей, предположение, что
результирующее число ячеек разрешения под гребнем функции
неопределенности равно 47А/, приводит к выражению для отноше-
ния сигнал/пассивная помеха, тождественному соотношению (10.27).
Это эвристическое исследование показывает, что в рассматриваемом
случае, эквивалентном случаю отсутствия предварительной инфор-
мации о распределении целей, ни один из сигналов не имеет пре-
имуществ перед другими. Результат получаем аналитически, непо-
средственно основываясь на общих свойствах функции неопределен-
ности.
Существенной особенностью, следуемой из этих примеров,
является то, что увеличение произведения длительности на полосу
сигнала будет лишь благоприятствовать снижению отношения сиг-
нал/пассивная помеха, так как при этом увеличивается число ячеек
1 Если диапазон допплеровских частот Аф < А/, то (10.27) принимает
вид S/I « Аср/2ТАф, где — Дф < ф < Аф и АСр == 1 при Дф А/.
388
^alaUaus^i
знание без границ Ч *
разрешения, вследствие чего возрастает неопределенность в ячейке,
где производится наблюдение.
Согласно Фоулу и др. [11, единственным средством борьбы
с такой ситуацией является увеличение несущей частоты зонди»
рующего сигнала. В случае функции неопределенности ЛЧМ сиг-
нала это приводит к возрастанию величины допплеровского сдвига
частоты принимаемых сигналов и тем самым к перемещению их по
гребню функции неопределенности. Так как границы функции не-
определенности связаны с модуляционными параметрами сигнала,
Рис. 10.18. Определение числа ячеек разре-
шения, заключенных под гребнем функции
неопределенности ЛЧМ сигнала.
а не с несущей частотой, удвоение последней при том же самом
физическом распределении объектов в пространстве дальность —
скорость сократит наполовину число сигналов, которые* появятся
в задаваемой функцией неопределенности частотно-временндй об-
ласти. В результате уровень интерференционных помех, наблю-
даемых при т = 0 и <р = 0, снижается в два раза. Однако в любом
случае пропускная способность радиолокационной станции будет
все же весьма ограниченной. Если для рассматриваемого типа
окружающей среды с постоянной плотностью целей необходимо
получить приемлемое отношение полезного сигнала к помехе, то
из работ Фоула [1] и Рихачека [12] находим, что независимо от
используемого сигнала <эффективные> размеры ячейки разрешения
имеют порядок единицы, а не l/TAf.
Так как крайне маловероятно, чтобы диапазон допплеровских
частот был равен 2 ДД то обычно будут превалировать более уме-
ренные значения допплеровских частот, и здесь разработчик РЛС
может предпринять попытку перераспределить неопределенность
389
в области, не занятой сигналом. С другой стороны, как показано на
примере, рассмотренном в работе Уэстерфилда и др. [7], он может
попытаться сделать распределение неопределенности ортогональ-
ным к распределению целей по т и ф. При компактном распределении
целей можно попробовать те сигналы, которые, как, например,
периодическая последовательность импульсов, имеют в плоскости
неопределенности свободные области. Теоретически и для других
сигналов, имеющих функции неопределенности, близкие по форме
к кнопочной, тарке можно получить свободную область единичной
площади, окружающую начало координат (см. подробнее этот
вопрос в гл. 4 в и работе Рихачека [12]). Использование рассмотрен-
ных в гл. 8 оптимальных и близких к ним нерегулярных последова-
тельностей представляют собой один из способов получения функции
неопределенности такого вида.
В том случае, когда полезные сигналы и пассивные помехи
находятся в разрешимых узких допплеровских полосах, разработ-
чик системы для минимизации объема неопределенности в ограни-
ченных полосах, параллельных временнбй оси, может рассмотреть
возможность применения более сложных схем кодирования импульс-
ных последовательностей. Если требуемых для такой ситуации сиг-
налов имеется уравнительно мало, то возможно, что перераспре-
деление объема неопределенности по свободным зонам, получаемое
при помощи периодической импульсной последовательности, ока-
жется удовлетворительным с точки зрения ослабления влияния
помех. Сложный сигнал в виде кодированной последовательности
импульсов можно будет тогда использовать в диапазоне дальностей,
превышающем общепринятый для периодической пбследователь-
ности. Нетрудно показать, что при заданных длительности и пре-
дельной величине пиковой мощности сигнала импульсные последо-
вательности переносят энергию, которая меньше максимально воз-
можной. Поэтому такие сигналы найдут применение главным обра-
зом в том случае, когда прием ограничивается не шумами прием-
ника, а наличием пассивных помех.
Необходимо также предостерегать относительно использования
в качестве критерия проектирования сигнала его обобщенной по-
стоянной разрешения по времени Тг (ф). Было показано, что эта
функция имеет большое значение при определении характеристик
радиолокационной станции при наличии в окружающей среде плот-
ных пассивных помех. Результаты, полученные рядом исследова-
телей для этого случая, приводят к заключению, что сигнал с огра-
ниченной эффективной разрешающей способностью по допплеров-
ской частоте с линейной ЧМ, предпочтительнее сигнала, обладаю-
щего достаточным разрешением, но имеющего больший уровень
боковых лепестков. В группу сигналов, которые имеют функции
Тг (ф), сравнимые с аналогичной функцией ЛЧМ сигнала, входят
сигналы с линейно-ступенчатой ЧМ и многофазный сигнал Фрэнка.
Однако когда относительная плотность целей будет меньше (это
390
Ъ/ataUaus^l.
знание без границ Ч *
может произойти и вследствие применения сигнала с более широким
спектром), то отдельные боковые лепестки по дальности на выходе
согласованного фильтра, возникающие при наличии у сигнала доп-
плеровского сдвига, начинают приобретать более важное значение,
чем полная энергия всех боковых лепестков. Таким образом, разра-
ботчик РЛС должен тщательно исследовать предполагаемые усло-
вия окружающей среды в смысле ожидаемых значений допплеров-
ских сдвигов, прежде чем Сделать окончательный выбор между,
скажем, ЛЧМ сигналом со ступенчатой ЧМ или сигналом, исполь-
зующим многофазный код Фрэнка.
Как указывалось в гл. 4 и подразумевалось в данной главе,
Тг (0) является мерой разрешающей способности по дальности сиг-
нала на выходе согласованного фильтра, а также мерой относитель-
ного уровня порождаемых боковыми лепестками интерференцион-
ных помех. С практической точки зрения разрешающая способность
и уровень боковых лепестков тесно связаны между собой. При усло-
вии существенного изменения уровня принимаемого сигнала мини-
мально разрешаемое расстояние между двумя или более сигналами
будет зависеть от возможности обнаружения слабого сигнала на
фоне боковых лепестков по дальности более сильного сигнала.
Определяемая величиной Тг (0) мера разрешающей способности на
основе данной Вудвордом формулировки также называется «экви-
валентным прямоугольником разрешения!, поскольку она опреде-
ляет длительность прямоугольного импульса, который содержит
такое же количество энергии, как и | % (т, 0) |8.
Можно применять и другие аналитические меры разрешающей
способности, использующие функцию х (т, 0). Одной из них, имею-
щей важное значение, является временная протяженность отклика
согласованного фильтра, определяемая в виде квадрата стандарт-
ного отклонения <тр функции | X (т, 0) | :
J т’ | % (т,0) |Л
о£ = ==----------. (10.28)
f 1х(т» 0)| Л
—оо
Выражение (10.28) определяет эффективную полудлительность
функции | % (т, 0) | , так что 2ог является мерой общей длитель-
ности. В табл. 10.2 для некоторых простейших импульсов прово-
дится сравнение Тг (0), 2ог и длительности, определяемой по
уровню половинной амплитуды сигнала.
Основным недостатком выражения (10.28) является то, что оно
придает чрезмерно большой вес краям спектральной характери-
стики сигнала и дальним боковым лепесткам функции х (т» 0).
Поэтому, если область боковых лепестков произвольным образом
не исключается при расчетах, то оно, по-видимому, не будет подхо-
391
Таблица 10.2
Сравнение различных показателей разрешающей
способности по времени
Форма импульса TrW 2(1у Ширина импульса по уровню —вдб
rect (t/T) T 0,64 Т т
(1-1 Ч/n. 14 27/3 0,815 7 т
cos (л//27), 1t1 :.Т T 1,677 1,33 7
(sin at/T)/nt/T Т ОО 1,2 7
дящей мерой разрешающей способности сложных сигналов, у ко-
торых боковые лепестки занимают обширную область. При исполь-
зовании (10.28) для рассмотренного в разд. 10.4 варианта кнопочной
функции х (т, 0) читатель может убедиться в том, что имеется
сильная зависимость о? от величины произведения длительности
сигнала на его полосу. В противоположность этому ТГ(О) для
таких функций от произведения длительности на полосу не за-
висит.
Если наблюдаемым сигналом является не | X (т, 0) |,
a I X (т» 0) Iя» как» например, в случае включения устройства с квад-
ратичной характеристикой и с большим динамическим диапазоном,
то после согласованного фильтра формулу (10.28) также можно ис-
пользовать, заменив | % (т, 0) | на | X (т, 0) | а. Эта мера протяжен-
ности рассматривается далее в разд. 11.8 при анализе ухудшения
разрешающей способности сигнала, обусловленного искажениями.
В обоих случаях влияние протяженной области боковых лепестков
для многих сложных сигналов, представляющих интерес для разра-
ботчика РЛС, говорит не в пользу этих форм.
► В любом случае разработчик не будет полагаться исключи-
тельно на какой-либо из только что рассмотренных аналитических
критериев разрешающей способности, а присоединит к ним свой
собственный критерий, определяемый стоящей перед ним задачей.
В качестве последнего замечания скажем, что одним из наиболее
полезных свойств сигналов с линейной ЧМ является то, что в боль-
шинстве представляющих интерес диапазонов допплеровских частот
они сохраняют свою разрешающую способность по дальности (со-
гласно используемым на практике критериям разрешения).
Может показаться, что сигнал с линейной ЧМ, сигнал с фазой,
кодированной двоичной последовательностью, и периодическая
последовательность импульсов являются наиболее важными из
сложных сигналов, применяемых в радиолокации. Однако из рас-
392
смотренных в данной и предыдущей главах примеров должно быть
совершенно ясно, что при всевозможных обстоятельствах ни один
из сигналов не является идеальным для обнаружения, разрешения
и получения оценок параметров. Разработчик РЛС просто должен
определить для самого себя, какой вид распределения целей и ка-
кая часть плоскости неопределенности имеют для него основное
значение. Коротко их можно охарактеризовать так:
1. Плоскость неопределенности полностью (для всех практи-
ческих целей).
2. Ограниченные по дальности и величине допплеровского
смещения области.
3. Ограниченная по величине допплеровского смещения область
или области.
4. Ограниченная по дальности область или области.
5. Одиночная, групповая или плотно распределенные цели
для каждой из упомянутых категорий.
Для каждого из перечисленных применений могут подойти
один или несколько сигналов. Выбор может зависеть от того, предъ-
является или нет требование одновременного получения информа-
ции о дальности и скорости. Другими практическими факторами,
которые могут оказать влияние при выборе сигнала, являются:
простота его реализации, восприимчивость к искажениям, измене-
ниям плотности распределения целей и их характеристик, жела-
тельность использования нескольких типов сигнала, ограничения,
налагаемые передатчиком, стоимость и т. д. Поскольку невозможно
определить абстрактный «оптимальный! сигнал, можно надеяться,
что рассмотренные в предыдущих главах основные примеры дадут
разработчику РЛС систему отсчета, в которой он будет исполь-
зовать возникающие перед ним задачи и давать свое собствен-
ное решение. Авторы надеются, что они выполнили поставленную
перед собой цель снабдить разработчика РЛС сведениями о различ-
ных типах сигналов, находящихся в его распоряжении, а также
дать оценку некоторых теоретических и практических проблем,
связанных с их применением.
ЛИТЕРАТУРА
1. Е. N. F о w I е, Е. J. К е I I у, and J. A. S h е е h a n. Radar system per-
formance in a dense target environment, IRE Intern. Conv. Record, Pt. 4,
136—146 (1961).
2. R. M a n a s s e. The use of pulse coding to discriminate against clutter,
Mass. Inst. Technol., Lincoln Lab. .Lexington, Massachusetts, Rept. 312—
12 (August, 1957).
3. H. U г ко w I t z. Filters for detection of small signals in clutter, J. Appl.
Phys. 24, 1024-1036 (1953).
4. A. W. R i h a c z e k. Optimum filters for signal detection in clutter,
IEEE Trans. AES-1, 297—299 (1965).
5. W. L. R u b i n and С. К a i t e r i s. Waveform design for detection of
signals in clutter, Sperry Gyroscope Co., Great Neck, New York, Rept.
393
RD-5262-0611 (June, 196Б). To be published in Proc. 1EE (London),
(1967).
6. J. L, St e wa r t and E. C. Westerfield. A theory of active sonar
detection, Proc. IRE 47, 872-881 (1959).
7. E. C. W e s t e r f i e I d, R. H. P r a g e r and J. L. S t e w a r t. Pro-
cessing gains against reverberation (clutter) using matched filters, IRE
Trans. IT-6, 342 (i960).
8. D. R 1 c h m a n. Resolution of multiple targets in range, and range-rate,
Rome Air Develop. Center, Griffiss AF Base, New York, Rept. RADC-
TDR-62-580 (1963) (not generally available).
9. H. L. V a n Trees. Optimum signal design and processing for rever-
beration limited environments, IEEE Trans. MIL-9, 212—229 (1965).
*10. P. M. W о о d w a r d. Probability and Information Theory with Appli-
cations to Radar, Pergamon Press, Oxford, 1953.
**11. A. W. R ihaczek. Radar resolution properties of pulse trains, Proc.
IEEE 52, 153-164 (1964).
**12. A. W. R i h a c z e k. Radar signal design for target resolution, Proc.
IEEE 53, 116—128 (1965).
» ♦
*
10. Вудворд. Теория вероятностей и теория информации с примене-
ниями в радиолокации, изд-во «Советское радио», 1955.
WataHausiSk
знание без границ Ч *
ГЛАВА 11
ВЛИЯНИЕ ИСКАЖЕНИЙ ПРИ ОБРАБОТКЕ
СИГНАЛОВ СОГЛАСОВАННЫМ ФИЛЬТРОМ
11.1. Введение
Разработчики РЛС знают, что искажения и их нежелательные
последствия являются неизбежными. Задача, которую нужно
решить или свести к некоторому приемлемому компромиссу, заклю-
чается в том, чтобы установить источники искажения и затем до-
биться того, чтобы вклад каждого из них в результирующее иска-
жение сводился к минимуму. Из-за характера сигналов на выходе
согласованного фильтра, многие из которых имеют боковые лепестки
по дальности, иногда ошибочно полагали, что наблюдаемые-в ра-
диолокации искажения свойственны исключительно методам согла-
сованной фильтрации. Это, конечно, не верно, и в ранних, и даже
более поздних радиолокационных станциях влияние искажений,
несомненно, налагало сильные ограничения на динамический диа-
пазон, возможность обнаружения слабого сигнала или разрешаю-
щую способность станции. Можно утверждать, что характерной
особенностью систем, имеющих согласованный фильтр, является
то, что на его выходе помимо полезного сигнала зачастую можно
отдельно наблюдать последствия искажений функции временнбй
модуляции (амплитуды и фазы), получая в некоторых случаях до-
вольно интересные и специфические результаты.
В гл. 7 при рассмотрении вопроса о снижении уровня боковых
лепестков по дальности и расчетах взвешивающей функции было
показано, что пульсации спектральной функции могут привести
к появлению на выходе согласованного фильтра сигнала, эквива-
лентного боковым лепесткам. Именно присутствие боковых лепе-
стков по дальности на выходе согласованного фильтра возродило
интерес к искажениям как критерию качества проектирования
РЛС и к методу анализа искажений, который давно уже исполь-
зовался в телефонии и телевидении. В последующих разделах бу-
дет рассмотрен этот основной метод анализа искажений — метод
парных эхо и его использование при проектировании радиолока-
ционных систем и сигналов.
395
11.2. Кнализ искажений методом парных эхо
Во многих применениях желательно уменьшить самые боль-
шие боковые лепестки по дальности сжимаемого импульсного сигна-
ла на выходе согласованного фильтра до уровня —30 4-----40 дб
относительно максимального значения амплитуды сжатого импуль-
са. Ниже будет показано, что наличие искажений амплитуды и
фазы сигнала в приемнике может дать паразитные лепестки, или
так называемые парные эхо, подобные по внешнему виду боковым
Спектр Входною
г и г нала
Фильтр
без
искажении
а)
Спектр выходного
сигнала S(w)
Рис. 11.1. Представление при анализе идеального фильтра (а)
и фильтра с искажениями (б).
лепесткам по дальности, но которые нелегко устранить простыми
методами взвешивания. В связи с этим при практическом исполь-
зовании согласованного фильтра в РЛС бессмысленно говорить
о низких уровнях боковых лепестков по дальности, если не огова-
риваются допустимые уровни искажений во всех элементах системы,
или если в ее состав не входит аппаратура для компенсации иска-
жений.
Рис. 11.1, а иллюстрирует работу идеального фильтра без иска-
жений, через которые пропускается сигнал. На выходе он имеет
спектр S (со), так что неискаженный сигнал на выходе фильтра
в функции времени запишется
(/) = — f s ((о) ехр [/со/] do.
2л
—00
(11.1)
Уравнение (11.1) описывает идеальную форму сигнала без искаже-
ний. Если последовательно с идеальным фильтром соединить иска-
жающий фильтр, как показано на рис. 11.1. б, то характеристика
396
MaUausA
знание без араниц
искажающего фильтра будет оказывать влияние на выходной сиг-
нал, при этом
СО
si(0 = t- | S((o)A/((o)exp[/<o/]d(o.
2л J
—ОО
(Н.2)
Макколл [11 и Уиллер [2] предложили сделать допущение, что при
анализе искажений характеристики искажающего фильтра имеют
Рис. 11.2. Синусоидальные компоненты иска-
жающей функции Я(<о).
вид синусоидальных функций. Амплитуда и фаза спектральной
характеристики искажающего фильтра были выбраны соответствен-
но в виде
А (со) = a0 + flr cos Cj со, (11.3а)
В (<о) = Ьоа)—blsinCl(i). (11.36)
Поведение этих основных компонент искажения показано на
рис. 11.2. Результирующая искажающая функция принимает вид
Н (<о) = А (<о)ехр [ — /В (со)]. (П.4)
Подставляя уравнения (11.3) и (11.4) в выражение для искажен-
ного выходного сигнала, имеем
= “ f S(4o)(a04-a1cosC1(o)exp[/(o//4-/6iSinCi(o]dw,
2л •)
—00
(11.5)
где t' — f—b0. В элементарном случае &i = 0; тогда, представляя
член, определяющий амплитудные искажения, в виде
Ci cos Cj о = -у- (exp [/Cj co] exp [—/Cx co]), (11.6)
397
получаем выражение, которое справедливо только при аплитуд-
ных искажениях

J S(co)exp[/co/z]du)-| X
(ОО
-5- f S(m)exp[/m(f-{-C^ldm-)-
2л J
—оо
(11.7)
оо
J S (со) ехр [/со (f — С,)) dm
— 00
Замечая, что константа С\ в мнимой части экспоненты означает
сдвиг по времени начала отсчета, уравнение (11.7) можно записать
в виде
s, (0 = а„ s, (П + [s, (Г + С,) + s, (f - C,)J, (11.8)
где (Г + СО и Si (/' — Ci) представляют собой опережающую
и запаздывающую копии неискаженного сигнала, взвешиваемые
множителем ах12. Как следствие очевидной симметрии искажающих
членов в выражении (11.8), для их обозначения появился новый
термин «парные эхо>.
Когда имеются только фазовые искажения (т. е. av — 0), сигнал
на выходе искажающего фильтра определяется соотношением
ОО
s8 (/) = f S (<o) exp [/mf 1 exp [/6, sin m] dm.
2л J
—oo
(11.9)
Функцию, определяющую искажения фазы, можно заменить разло-
жением по бесселевым функциям
expl/7>i sinxl J0(6iH V Jn(^)( ехр|/лх] + (— l)"exp [ — /мх]|.
n-1
(ll.lt))
Подставим это выражение в соотношение (11.8) и осуществим тре-
буемое интегрирование
S8 (0 — а0 (^1) si (О 4“
+ A(M[Si(f 4 nC1) + (-l)"s1(r-nCi)l|. (11.11)
n-l J
398
ftalaHauswk
знание без границ ’ *
В случае чисто фазовых искажений существует бесконечный набор
парных эхо. Однако если Ьг мало, например менее 0,5 рад, то можно
приближенно принять
Л(М=1, Л(М = ^/2, Л(М = 0, п>2
и выражение (11.11) сводится к
S, (0 = а» («1 (О + ^- IS 0' + (i'-Qd. (11.12)
Таким образом, при условии относительно малых фазовых ошибок,
последствия фазовых искажений аналогичны результатам амплитуд-
ных искажений, за Исключением того, что члены, описывающие
эхо, имеют противоположную полярность. Выражения (11.8) и
(11.12) можно объединить так, что совместное влияние амплитудных
и фазовых ошибок, заданных соотношениями (11.3 а) и (11.3 б),
будет выражено следующим образом:
(11.13)
Если фазовые искажения не малы, то в таком случае интег-
рирование уравнения (11.5) дает
S, (0 - а, J, (Л,) |s, (Г -F С,) 4 s, (<' - С,)) 4; -ММ s, (Г) +
I- 2 Л (I),) |s, (Z- 4- nct) I (- 1)» s, (Z'-nC,) 4-
I
+ ^5. V J„ (6,) [S, (1- 4- «с, I- C.) 4- (-1 у s, (f -nCt 4- CJ] 4-
4- 2 J" (b'} |s* (<' + «с, - C.) 4- (- D" S, (/' - nC, - C,)jl,
( 1.14)
где, как и раньше, V = t—b0.
Преобразование выражений, стоящих под знаком суммы
в (11.14), приводит к комбинациям следующего типа:
[Л_1 (6.) 4-J„+1 (6,)] S, (/'±ПС,), (11.15)
£t
так что, применяя рекуррентную формулу для функций Бесселя
~ Л(^-Л-|(*)4-ЛЧ1(х), (11.16)
399
для искаженного выходного сигнала можно получить следующую
формулу:
«г (О = во ро (М «1 (*Э + 2 Л (М X
I 1
S, (Г + пС,) + (-1)"(1 --2ft) s, (Г -пС.) .
aQbiJ \ ааЬг/ J
(Н.17)
Она представляет собой общее выражение для искаженного сигнала
на выходе цепи, имеющей фазовые и амплитудные ошибки одина-
ковой частоты. В случае малых фазовых искажений выражение
(11.17) сводится к формуле (11.13), если использовать приведенные
выше аппроксимации для функции Бесселя.
Если искажающая функция цепи не выражается в виде простой
гармонической функции, ее можно рассматривать как сложную
функцию, состоящую из компонент разложения Фурье. В таком
случае сложную искажающую функцию можно представить в виде
N
Л (<о) = а0 4- 2 ап cos Сп о,
п=1
N
В ((й) = 60ш— 2 6nsinCn<o.
fl“ 1
(11. Зв)
(11.3г)
Для того чтобы получить компоненты Фурье, ап и Ьп, искажающей
функции, необходимо предположить, что она является функцией
с ограниченным спектром, и затем считать, что искажающие функции
являются периодическими в частотной области. Ограничения на
полосу пропускания функции и, следовательно, на ее искажения,
можно налагать в произвольных частотных пределах. Такими
пределами логично было бы выбрать частоты, на которых спектраль-
ная амплитуда сигнала спадает до половины значения, принимае-
мого на средней частоте спектра. Однако связанная с этим ошибка
будет зависеть от скорости спадания амплитуды спектральной
характеристики или от количества энергии, заключенной в отбра-
сываемой спектральной области (аналогичное рассмотрение сложных
функций с временными искажениями, применительно к импульсным
радиолокационным сигналам, приводит к ограниченным по времени
функциям, так что эта ошибка не имеет большого значения при ана-
лизе искажений во временной области). Путем надлежащего выбора
на оси частот опорных точек при разложении Фурье и введения
допущения о характере поведения искажающей функции за пре-
делами ограниченной области (т. е. нечетное или четное, симметрич-
ное ее поведение относительно граничных значений) можно полу-
чить разложения Фурье функций, описывающих искажения ампли-
туды и фазы, в виде, который будет соответствовать соотношениям
400
NalaHausMi
знание Вез границ ’» *
(11.Зв) и (11.3г), а также , и минимизировать число существенных
членов в разложении.
В случае амплитудных искажений отдельные компоненты иска-
жающей функции будут давать независимые группы парных эхо.
Однако при фазовых искажениях результирующий эффект заклю-
чается в перемножении синусоидальных функций, стоящих в мни-,
мой части экспоненты. В соответствии с выражением (11.10) это
приводит к перемножению рядов, состоящих из бесселевых функ-
ций. При малых фазовых ошибках (меньших 0,5 рад) можно счи-
тать, что воздействие различных составляющих фазовой ошибки
по существу независимо. При наличии больших фазовых ошибок
возможно появление значительных перекрестных составляющих.
В разделе, посвященном модуляционным искажениям, представ-
лены основные методы рассмотрения этой ситуации.
На частном примере использования согласованного фильтра
описанный выше аналитический метод может быть обобщен для
двух основных случаев, представляющих интерес. Первый из них
является следствием того, что характеристика задержки в согла-
сованном фильтре обычно выбирается независимо от какой-либо
амплитудной характеристики (см. гл. 12 и 13), так что частоты основ-
ных амплитудных и фазовых ошибок могут быть совершенно раз-
личными. Этот случай был рассмотрен Либмэном [31, и вытекает
непосредственно из описанной выше процедуры, причем схемные
искажающие функции теперь определяются соотношениями
А (<о) = 00 4-0! cos Cj to,
(^i Q.
В (о) = b0 to— bx sin Са со.
(11.18а)
(11.186)
Точное выражение выходного сигнала будет аналогичным (11.14),
за исключением того, что выражения для эхо? обусловленные фазо-
выми и амплитудными искажениями, смещены по времени на ве-
личину ±пСа; первые из них смещены относительно местоположе-
ния полезного сигнала, определяемого из условия Г =0, а вторые —
относительно моментов появления парных эхо, определяемых соот-
ношением t' =± Ci. Снова предполагая, что фазовые искажения
малы, получаем результирующее выражение для искаженного вы-
ходного сигнала:
s,(0 = a<,{si(O + -у !si(r + C2)-s,(/'-C2)] -Ь
+ г- [Si (<' + С,) + s, (Г-С,)1 +
+ hi (/' + С, + Cs)-s, (Г + C.-Q+
4G q
+ s1(f-CI+CJ-sl(f-C1-Ca)|l. (11.19)
14 Зак. 1341
401
Во многих случаях последние четыре члена будут пренебрежимо
малыми, при этом следует учитывать только пять первых (основной
сигнал плюс четыре эхо). Интересно отметить, что в предыдущем
рассмотрении, иллюстрирующем независимость положения парных
эхо и их формы от типа используемого сигнала, не было необходи-
мости конкретизировать форму сигнала s^t). Этого не требуется и
при рассмотрении ошибки временнбй модуляции произвольных
сигналов на выходе согласованного фильтра, хотя для ЛЧМ сиг-
нала, обработанного согласованным фильтром, связь между пар-
ными эхо, обусловленными модуляционными и схемными искаже-
ниями, становится однозначной.
Второй интересный случай также связан с тем, что характе-
ристика задержки в согласованном фильтре выбирается отдельно
от амплитудной характеристики системы. Вследствие этого нет
причин полагать, что фазовые ошибки имеют вид синусоиды, за-
даваемой соотношением (11.36). Более общее выражение для сину-
соидальной фазовой ошибки будет включать в себя произвольную
фазовую постоянную [41, так что
В(ш) — Ьош—(11.20)
Записывая напряжение на входе искажающего фильтра в виде
сигнала промежуточной частоты, т. е.
(/) = Sj (t) cos о)01, (11.21)
где Sj (/) означает огибающую сигнала на выходе согласованного
фильтра, можно определить влияние фазовой постоянной Фо.
В этом случае искаженный по фазе выходной сигнал можно пред-
ставить в комплексном виде
«2 (0 == 4“ ехр [/соо Л f S (со) ехр [f {cof 4- sin (Cx co + Фо)}] dco.
Zn J
(11.22)
Разложение по бесселевым функциям (11.10) теперь будет содержать
мнимые экспоненциальные члены
ехр[/п(С1(о4-Фо)1 и ехр[—/п^со + Фо)].
Используя это разложение, получаем выражение для искаженного
по фазе выходного сигнала, которое эквивалентно разложению
(И.Н):
S2 (0 = Uo (bi) Si (л ) COS юо /4-
4- 5 Л (bl) 4-nCJ cos (coo 14- пфо) 4-
+ (— 1)” Si(f—nCJ cos (coo t—лФ0)]). (11.23)
402
^alallauswk
знание без границ * *
Отсюда нетрудно заметить, что фазовая постоянная Фо переносится
в выражение для несущей частоты парных эхо в виде фазовых по-
стоянных ± пФ0. В зависимости от величин и Фо совокупность
перекрывающихся полезных сигналов и сигналов, порождаемых
искажениями, может приводить к эффектам несимметричного (отно-
сительно V = 0) ослабления и усиления сигналов. Вследствие ана-
логии модуляционных и схемных искажений для ЛЧМ сигнала,
показанные на рис. 11.12—11.17 формы сигналов, получающиеся
при модуляционных искажениях, можно рассматривать как ти-
Пиковые значения (разовых пульсаций
в градусах (
Рис. 11.3. Зависимость амплитуды первого пар-
ного эхо от величины амплитудных и фазовых
искажений.
личные примеры влияния схемных искажений на произвольный
выходной сигнал согласованного фильтра, поскольку было пока-
зано, что внешнее проявление схемных искажений не зависит от
вида используемого сигнала.
В тех случаях, когда для системы, использующей согласован-
ный фильтр, требуемый уровень боковых лепестков по дальности и
схема частотного взвешивания уже определены, парные эхо должны
быть не выше, а еще лучше, по крайней мере на 3 дб ниже уровня
боковых лепестков по дальности. Это условие устанавливает допу-
стимый уровень искажений в системе. На рис. 11.3 построен график
амплитуд парных эхо в децибелах, нормированных к максималь-
ному значению неискаженного сигнала, в зависимости от величины
амплитудных и фазовых искажений. Нетрудно заметить, что когда
уровень парных эхо составляет —30 дб относительно уровня по-
лезного сигнала или еще ниже, тогда имеют место лишь незначи-
тельные искажения.
И* 403
Тот факт, что парные эхо могут налагать серьезные ограниче-
ния на динамический диапазон станции вблизи принятого силь-
ного сигнала, иллюстрируется на рис. 11.4, с и б, которые позаим-
ствованы из фундаментальной работы по анализу искажений, вы-
полненной Дифранко и Рубином [51. Для идеальных прямоуголь-
ных импульсов здесь показано влияние парных эхо, обусловленных
амплитудными и фазовыми искажениями передаточных функций
цепей, которые обычно используются в приемных системах. Ширина
спектра сигнала по уровню 3 дб отмечена на рисунке интервалом
(—1, +1), а в графе «передаточные функции» приведены их значения
по уровню 3 дб (юзйб)- Полоса приемника, которая значительно
шире спектра сигнала, является чем-то необычным, особенно для
систем, использующих согласованный фильтр, у которых такой
элемент, как схема снижения уровня боковых лепестков за счет
изменения формы полосы пропускания определяет эффективный
сигнал и шумовую полосу системы. Для того чтобы устранить сиг-
налы, обусловленные искажениями, необходимо применять ампли-
тудную и фазовую коррекцию или компенсацию с использованием
трансверсального фильтра. Кроме того, возможно окажется необ-
ходимым прибегнуть к другому методу проектирования переда-
точной функции приемника.
11.3. Искажения временнбй задержки как мера
фазовых искажений
Проведенный в предыдущем разделе анализ эффектов искаже-
ния основывался на учете амплитудных и фазовых ошибок. Как
будет показано в гл. 12 и 13, для оценки свойств дисперсионной ли-
нии задержки, предназначенной для сжатия импульсов, чаще всего
измеряют ее групповое время запаздывания. В главах, посвящен-
ных конструированию дисперсионной линии задержки, в качестве
критерия проектирования предлагается использовать величину
ошибки временнбй задержки. Для того чтобы можно было исполь-
зовать эту ошибку в качестве средства для оценки уровня парных
эхо, обусловленных искажениями, необходимо преобразовать
ошибку временнбй задержки в ошибку по фазе. Для этого'исполь-
зуется следующее соотношение между групповым запаздыванием
и сдвигом фазы:
tg = dB((o)/da), , (11.24)
где tg — групповое запаздывание, а В(ю) — фаза, определяемая
соотношением (11.36). В свою очередь, пренебрегая постоянной
интегрирования, фаза сигнала может быть записана в виде
B(co) = J tgdu). (11.25)
404
ftalaHausIM
знание без границ “ *
Последовательное включение усилителей, передаточные
фукции которых икеют;
один полюс два полюса три полюса
405
Передаточные функции Анплитубно- - частотная характеристика Фазо- - частотная характеристика
1 । I +50° -1 -50°
0,4844(5 +2,0646) 10% пульсации (Чебышев) u38faZ И 1 1 1 I I I I
м о +1
1 L - +1 I ★50° -1 - -50°
6,3286(5+3,0429) 5°/о пульсации (Чебышев) изм~3. 1 1 1 1 I I I
-1 0 +1 •
1 L I
0,1425(5+7,0190) /% пульсации (Чебышев) и3дба7 1 I ★50°^ о*1.
1 1 I I ‘1 - -50*
-1 0 +1
sh Максимально плоская I CL ' 0**
амплитудно- частотная характеристика I I । । -1 ^50°
*386*7 -1 0 + 1
1 5+1 Максимально плоская I +1 । +50°
характеристика завертки, I I । -1 ^-50°
*здб*1 -1 0 +1
Передаточные функции 1 Амплитудмо - - частотная характеристика яазо- - частотная характеристика
I I 1 1 +100° - .1^1 и
0^688^+1,13705+1,1495)
10% пульсации (Чебышев) tJ396'S!'1^ I I । 1 1 1 1 7 +1 -1 -100°
1 1 + 1 । + 100°
0,6572(S2+1,48305+1,6004) 1 • 1 O^L
5% пульсации (Чебышев) “зм-^ 1 1 -1 i 1 1 I 7 +1 -1 Г4-100°
1 I 1*< г + 100°
0,2850(5г+2,48665+3,5452) 1 — — 1 1 о^_
1% пульсации (Чебышев) “звб9*2 1 i -1 I 1 1 7 +1 -1 ^-100°
1 51+1,41425+1 Максимально плоская \ ★100е -1
амплитудмо- частотная характеристика 1 ч 1 1 1 1 1 -1 -100°
*3дб~1 -1 7 + 1
1 ‘ 5г+35+3 Максимально плоская 1 1^, *' 1 I ★100° I
характеристика задержки *здва1^ 1 1 -1 ( I 7 Т/ -1 Г*4-100°
Однополюсные передаточные функции
Двухполюсные передаточные функции
I Передаточные I Функции Анплитудно - частотная характеристика Фаза- ча характе статная 1 оистика
[ t9376(53+1,02125^27155+0^161) Ю°/о пульсации (Чебышев) шзвба111 । । । । ( -1 *1 I I I 1 0 +1 +100\ ^0 < I
-1 \*f I
1_ 1,3144(5*+ 1,2984S!+t,5930S+0,760Sj 5% пульсации ( Чебышев) *3дб a I i I I । 1 +1 I I 1 1 1 + 1 ★100° 0 .
-1 \*f 1 '-100°
f а,5700(5*+2,00275г+2Д5535+1,7549) /% пульсации (Чедышев) ^Здба1^ г- — । । । 1 । _ -1 I ( 1 1 , 1 > +1 +100° 0 .
-1 -100 °
1 53+25г+25+1 Максимально плоская амплитудно - частотная характеристика ш38б~1 d 1 1 1 1 • +1 +100 е
•1 -100° [
15 53+65г+155+15 Максимально плоская д арактеристи к а задержки шзвб^1^ 1 1 1 1 -1 +1 1 1 1 + 1 +100° 7 .
-/ • I -100° I
Рис. 11.46.
приемника,
для расчета
рис. 11.4
Характеристики
использованные
показанных на
а сигналов.
Грех полюсные передаточные функции.
Предполагая, что кривая ошибки задержки может быть представлена
в виде комбинации конечного числа синусоидальных составляющих,
групповое запаздывание для каждой компоненты равно
(Un = cos Сп со, (11.26)
а соответствующая ей фазовая ошибка
Вп — bn sin Сп со, (11.27)
где Сп — число периодов составляющей ошибки в полосе сигнала
Дсо = 2лД/. Исходя из этого, координаты парных эхо можно опре-
делить точками ± Сп/Д/ секунд, расположенными по обе стороны
Рис. 11.5. Нормальные и искаженные функции за-
держки.
от полезного выходного сигнала. Величина паразитного сигнала
при максимальных фазовых ошибках Ьп, меньших 0,5 рад, равна
Ьп/2, или при измерении в децибелах амплитуда парных эхо равна
20 log (frn/2).
Из уравнения (11.26) нетрудно понять, что функция, описы-
вающая ошибки в групповом запаздывании, имеет большое значе-
408
'XaiaHauSfVii
знание без границ * w
ние в качестве критерия проектирования. Максимальная величина
ошибки . временной задержки равна

(11.28)
Хотя величина Ьп является решающим фактором при определении
амплитуды парных эхо, при коррекции ошибок задержки, предназна-
ченной для ослабления обусловленных фазовыми искажениями
сигналов, нет необходимости требо-
вать уменьшения пиковых значений
ошибки задержки, на что, казалось
бы, указывает приведенное выше со-
отношение, поскольку метод коррек-
ции, который в полосе Д/ дает увели-
ченное число периодов ошибки Сп,
будет уменьшать максимальное зна-
чение фазовой ошибки даже если
пиковое значение ошибки задержки
остается неизменным. Если коррек-
ция ошибки задержки уменьшает ее
пиковое значение и увеличивает число
ее периодов, то величина максималь-
ной фазовой ошибки будет умень-
шаться гораздо быстрее, чем вследст-
вие действия лишь одного фактора.
В гл. 12 описывается пример та-
кого метода коррекции ошибки за-
держки. Рис.. 11.5 и 11.6 иллюстри-
руют соотношение между величиной
задержки и фазовыми ошибками.
На рис. 11.5 показаны нормальные Рыс П6. влияние фазовых
и искаженные функции задержки искажений на сигнал,
фильтра сжатия с линейным измене-
нием задержки с частотой. Кривые, соответствующие задержке с
искажениями, были получены путем присоединения и отключения
соответствующих Т-образных мостовых звеньев, которые дают при-
близительно один период синусоидальной ошибки в полосе 1,6 Мгц.
Максимальные отклонения задержки от линейного закона изме-
нения оказались соответственно равными 0,67; 1,22 и 2 мксек.
Исходя из соотношения (11.28), максимальная ошибка фазы равна
b

п
где Сп = 1/(1,6 • 10е). Используя вышеприведенные значения мак-
симальных ошибок задержки, получим соответствующие им пико-
вые значения фазовых ошибок 1,07; 1,95 и 3,2 рад. Искажения формы
409
сигнала, которые получаются при наличии фазовых ошибок такой
величины, иллюстрируются на рис. 11.6, где наглядно показано
влияние рассматриваемых ошибок в согласованном фильтре или
в любой другой системе.
11.4. Модуляционные искажения, наблюдаемые на выходе
согласованного фильтра
Метод парных эхо, используемый при анализе искажений,
можно применить также для определения влияния модуляционных
искажений на форму сигналов на выходе согласованного фильтра.
Как будет показано при более общих условиях в следующем раз-
деле, при рассмотрении сигнала на выходе согласованного фильтра
возможно использовать функцию отклика согласованного фильтра
в качестве средства определения границ искажений, вызываемых
пассивными и активными источниками. Несмотря на то, что метод
анализа искажений аналогичен методу, использованному в преды-
дущих разделах данной главы, а некоторые из результатов по своей
форме подобны, можно считать, что парные эхо, обусловленные
модуляционными искажениями, существуют главным образом в ча-
стотной области в виде боковых полос модуляции. В большей или
меньшей степени эти боковые полосы модуляции, порождаемые
искажениями, имеются в любой системе. Однако в специальных
- случаях, требующих применения сложных сигналов и согласован-
ной фильтрации, сигналы на выходе согласованного фильтра, свя-
занные с этими боковыми полосами, часто можно наблюдать в виде
боковых лепестков по дальности, эквивалентных сдвинутым по вре-
мени парным эхо, которые сходны с реальными парными эхо, по-
являющимися при наличии схемных искажений.
В этом отношении сжимаемый ЛЧМ импульс является един-
ственным в своем роде сигналом, для которого имеется приблизи-
тельно однозначное соответствие между результатами модуляцион-
ного и схемного искажений, наблюдаемыми на выходе согласован-
ного фильтра. Модуляционные искажения амплитуды и фазы ЛЧМ
сигнала, которые легко моделируются и контролируются в лабо-
раторных условиях, дают на выходе согласованного фильтра сиг-
налы, подобные получающимся при схемных искажениях для про-
извольного сигнала, и по этой причине сжимаемый импульсный
ЛЧМ сигнал можно использовать как аналоговое устройство, поз-
воляющее анализировать любые схемные искажения. Детальный
анализ, производимый в данном разделе, в значительной степени
будет основываться на иллюстрирующих примерах, которые легко
получаются при помощи ЛЧМ сигнала.
Общий вид сигнала на выходе согласованного фильтра, под-
вергнувшегося модуляционным искажениям в передатчике РЛС,
410
^atalLaus,M
знание без границ ’
определяется соотношением
sm (/) = a (/) <(а0 + cos com, t) exp [j (ы01 + 6 (/) 4-
+ sin wmi 0]}, - T/2 < t < T/2,
(11.29)
где 0(0—кодированная функция модуляции, а шт( 2—частоты
искажающей модуляции.
1 Очевидно, что выражение (11.29) подобно (11.5). Рассматривая
последствия лишь амплитудной модуляции, член cos ®mt t мо-
жет быть представлен в экспоненциальной форме и тогда сигнал
с модулированной амплитудой можно записать в виде
«т (О = Оо (ехр [/ {(001 + 0 (0)1 + ехр [j {(соо + wm,) t + 6 (/)}] +
\ *^0
H ^exp[/{((00—(Dm,)/+ 0(0}]) ,
— T/2</< T/2,,. (11.30)
где a(t) = 1 для случая сигнала большой мощности.
Влияние синусоидальной амплитудной модуляции заключается
в образовании сигналов, соответствующих боковым полосам, и
в общем случае можно утверждать, что результатом модуляцион-
ного искажения являются парные боковые полосы. Амплитудная и,
как будет показано в дальнейшем, фазовая модуляции не оказы-
вают влияния на кодированную модулирующую функцию 0(0.
Как только сигнал (11.30) поступает в согласованный фильтр прием-
ника, сигнал на выходе согласованного фильтра будет определяться
его откликом на сдвинутые по частоте входные сигналы. Исходя
из функции отклика согласованного фильтра, можно рассмотреть
общий случай. В частном случае сжимаемых импульсных ЛЧМ сиг-
налов сигналы, обусловленные боковыми полосами, центры кото-
рых расположены в точках соо ± будут порождать выходные
сигналы, сдвинутые по времени на величину ± (comi/Aсо) Т сек,
где До — ширина интервала линейного качания частоты. Обозна-
чим через Si(f) огибающую сжатого сигнала. Тогда при условии,
что <omi мало по сравнению с Дсо, выходной сигнал можно прибли-
женно записать в виде
so(O = ao
s1(0cos<oo/ + ^-s1 cos(w0 + t +
\ Д(0 / \ 2 /

Рассматривая выражения для огибающих в этой формуле, можно
заметить определенное сходство с подобными членами соотноше-
411
ния (11.8), полученного для случая схемных амплитудных искаже-
ний. Это иллюстрирует аналогичную связь между влиянием моду-
ляционных искажений на форму сжатого импульсного ЛЧМ сигна-
ла, наблюдаемого на выходе согласованного фильтра, и эффектами
парного эхо для произвольного сигнала при схемных искажениях.
Рис. 11.7 показывает образование парных эхо для ЛЧМ сигнала при
Рис. 11.7. Парные эхо при двух
различных частотах амплитудной
модуляции.
Рис. 11.8. Влияние парных эхо при
амплитудной модуляции, когда щ
изменяется во времени.
двух различных частотах модуляции амплитуды. На рис. 11.8 видна
несимметрия амплитуд парных эхо, когда модуляционные искаже-
ния амплитуды на одном конце ЛЧМ сигнала больше, чем на другом.
Более сильные парные эхо появляются перед сжатым импульсом,
когда на начальном участке входного сигнала возникают интен-
сивные пульсации амплитуды и после сжатого импульса, если ин-
тенсивные пульсации возникают на конечном участке входного
сигнала. Анализ влияния модуляции сложной функцией можно
произвести, оперируя с основными компонентами Фурье функции
модуляции, при этом общая процедура аналогична рассматриваемой
ниже для случая модуляционного искажения фазы.
В случае использования мощного передатчика, в котором имеет
место эффект ограничения, можно полагать, что модуляционное
искажение амплитуды будет преобразовано в модуляционное иска-
жение фазы прежде чем сигнал будет излучен в пространство х.
Поэтому в выражении (11.29) можно положить равным нулю.
При этом условии общее выражение для временнбй функции, опи-
сывающей модуляционное искажение фазы (при использовании
экспоненциальной формы записи с целью упрощения последующего
анализа), имеет вид
sm (0 = S (0 ехр [/bi sin (<om t + 0O)J, (И .32)
где s(t) — неискаженный сигнал; — максимальное значение фа-
зовой ошибки (в радианах); = 2л/т — угловая частота фазовой
ошибки, а 0О — произвольная фазовая постоянная. .
Включение в выражение (11.32) фазового множителя 0О служит
той же самой цели, что и аналогичный фазовый множитель соот-
ношения (11.20),— сделать анализ модуляционного > искажения
фазы более общим. Пусть
s (0 = а (0 ехр [/ {о)01 + 0 (0)1,
где а(0 — огибающая сигнала. Используем формулу разложения
по бесселевым функциям (11.10); вытекающее из соотношения
(11.32) общее выражение для функции, описывающей модуляцион-
ные искажения фазы, которое эквивалентно определяемому соотно-
шением (11.23) выражению для схемных фазовых искажений, имеет
вид
sm (0 = а (0 Jo (6J ехр 1/ {<оо t + 0 (0)] +
+ а (0 2 Jn (bj (ехр [j {((оо+па)т) t +
л
+ 0(0+П0О}] + (—!)" ехр [/ {(€00—zi<om) t + 0 (0 - П0О}1). (11.33)
Как отмечалось ранее, погрешности функции фазовой модуля-
ции приводят к «парным боковым полосам», а не к «парным эхо»,
как, например, в случае схемных искажений, причем смещение
сигнала по времени заменяется смещением парных полос спектра
по частоте на величину n<om. Величина 0О определяет относительные
фазы несущих частот сигналов, связанных с появлением парных
полос спектра.
Для обыкновенного или некодированного импульсного сигнала
(т. е. 0(0 = 0) дополнительные сигналы, связанные с парными
боковыми полосами, появляются в течение того же временндго ин-
тервала, что и неискаженная функция времени s(0. При условии,
что s(0 — сжимаемый или кодированный сигнал, специфической
особенностью является то, что сигналы, соответствующие парным
1 Если имеется протяженный волноводный канал между оконечной
лампой передатчика и излучающей антенной, то амплитудная модуляция,
несмотря на эффект ограничения в передатчике, рее же может возникнуть
из-за рассогласований в волноводе [6].
413
1®)"
боковым полосам, вообще говоря, дисперсны во времени. При опре-
деленных условиях они полностью разделяются и, таким образом,
по отдельности наблюдаются и могут быть измерены.
Соотношение (11.33) можно применить к случаю, когда s(t)
представляет собой рассмотренный в гл. 6 сжимаемый импульсный
ЛЧМ сигнал. При наличии ошибок фазовой модуляции ЛЧМ сиг-
нала, используя соотношение (11.33), можно получить следующее
приближенное выражений для сигнала на выходе согласованного
фильтра:
«о (0 = Jo (bi) si (О cos “оt +
+ X kn J„ (6.)! Si ft + r) cos [ () t + ne„l +
( \ A co /Lx *• ) J
+ (_l)»Sip_"5sr)cosF(®,- (11.34)
\ Aco /Lx 2 / J
где s^t) — огибающая сжатого импульса; kn — весовой множитель
частотной характеристики фильтра; Т — длительность несжатого
импульса и Дсо/2я = Д/ — девиация частоты.
Более точное представление сигнала на выходе фильтра сжатия
включало бы видоизменения формы сигнала, основанные на функ-
циях взаимной корреляции сдвинутых по частоте сигналов, типа
искажения формы огибающей [7], которое наблюдалось бы при на-
личии парных сигналов на выходе фильтра (см. рис. 6.2). Однако
соотношение (11.34) оказывается полезным в большинстве практи-
ческих применений, включая случай, когда для уменьшения уровня
боковых лепестков используется взвешивание частотной харак-
теристики.
Соотношение (11.34) показывает, что имеется сигнал, по обе
стороны от которого симметрично и равномерно располагаются
разнесенные пары сигналов с амплитудами, определяемыми соот-
ветствующими функциями Бесселя Временнбй интервал
между ними можно определить в виде
р__fm р
A© Af
Поскольку (1/Af) приблизительно равно длительности сжатого
импульса т, этот интервал, выраженный через длительность сжа-
того импульса, равен
М-Л* (11.35)
Величина fm Т представляет собой число периодов функции, иска-
жающей функцию модуляции на интервале Т. Поэтому расстояние
между парными сигналами, выраженное в нормированных единицах
длительности сжатого импульса, зависит только от числа периодов
искажающей модуляцию функции в течение времени Т. Например,
414
Natdtlausfiiii*
знание без границ Ч »»
Рис. 11.9. Параметры модуляционного искажения»
Рис. 11.10. Градуировочные кривые, полученные в ла-
бораторных условиях.
415
bf-0 0,2 pad
Рис. 11.11. Форма сигналов и их спектров на
выходе фильтра сжатия при одной синусоидаль-
ной компоненте модуляции и условии fmT в 6.
а) ff)
Рис. 11.12. Влияние параметра 0О на перекры-
вающиеся и неперекрывающиеся парные эхо:
о —случай слияния; fm-»2 периода на длительности
входного импульса; б —случай неперекрывающихся
»хо; = 3 периода на длительности входного им-
пульса.
416
'XalaUausiM
знание без границ - *
если за время Т укладывается пять периодов, то наблюдаемая на
выходе фильтра сжатия первая группа парных сигналов будет
расположена приблизительно на расстоянии пяти длительностей
сжатого импульса от центра положения импульса (член Jo).
Величина 0О становится важной тогда, когда произведение
fmT таково, что первая группа сигналов перекрывает центральный
импульс. Эти взаимосвязанные сигналы будут смешиваться на вы-
ходе фильтра сжатия. В этом случае становится возможным полу-
чить различные варианты компенсации
или подчеркивания (усиления) сложных
сигналов в зависимости от величины
ошибки фазовой модуляции Ьх и значе-
ния 0О, определяющего начальную фазу
модуляции искажающей функции.
На рис. 11.9 показаны основные из
рассмотренных выше параметров моду-
ляционного искажения фазы. Кук [4, 81
обсуждает результаты лабораторных
экспериментов, в которых были исполь-
зованы простые и сложные функции
модуляционного искажения фазы ЛЧМ
сигналов. На рис. 11.10 сравниваются
гм
Jtn
fLT-ZO
Рис. 11.13. Сигналы, иллю-
стрирующие смещение пар-
ных эхо при изменении ча-
стоты функции фазовой
ошибки fm', bj 0,6 pad.
измеренные и расчетные амплитудные
вариации центрального сжатого им-
пульса [член Jo в уравнении (11.34) 1
и первой группы парных сигналов
(член Ji). Для получения уровня боко-
вых лепестков — 25 дб производилось
взвешивание сжатого сигнала. Нетрудно заметить, что весовой
множитель оказывал незначительное влияние на член Jp
Рис. 11.11 иллюстрирует форму спектров ЛЧМ сигнала при различ-
ных уровнях искажения функции модуляции, а также и соответ-
ствующие им сжатые импульсы. Влияние параметра 0О на выходной
сигнал фильтра для случая, когда величина fm Т мала, показано
на рис. 11.12, а смещение парных сигналов, когда произведение
fm Т увеличивается, показано на рис. 11.13. В отношении последнего
рисунка следует заметить, что расстояние между сигналами выра-
жено через длительности невзвешенного сжатого ЛЧМ импульса
(т. е. сигнала на выходе согласованного фильтра).
11.5. Сложные функции модуляционного искажения
Анализ элементарного случая синусоидальной фазовой моду-
ляции можно обобщить для более сложных функций, описывающих
модуляционные искажения, которые могут явиться результатом
действия нескольких источников искажения. Представленные ниже
417
примеры используются для того, чтобы указать аналитический метод
и содействовать применению принципа суперпозиции, который мо-
жет в значительной степени упростить любые оценки влияния по-
грешностей модуляции фазы, порождаемых активными источни-
ками.
В условиях, когда имеются два источника синусоидальной фа-
зовой модуляции различной частоты, сигнал с фазовыми искаже-
ниями можно представить (предполагая для .удобства 0(0 = 0)
в общем виде
sm (0 = а (0 ехр [/ (<оо1 + Ьг sin <ох t + b2 sin (о, 01. (11.36)
Применяя введенное ранее разложение для экспоненты, получим
равносильное (11.36) выражение
а (0 ехр [/хо0 0 (6J + 2 Jn (bj {ехр [jn^ 0 +
4- (— 1)« ехр [ —jna)! t]} j X (V+ S Jn X
X {exp [/Tuo, /1 + (— 1)" exp [ — /ncoa 0} j . (11.37)
Если blt bt^0,5 рад, то можно использовать приведенные ранее
аппроксимации для функции Бесселя. В этом случае sm(0 запи-
шется
a (t) ехр (/<оо 11 (1 + ~~ (ехр [/соа 0—ехр [—11)} X
X (1+-^-(ехр[/(0,0—ехр[—/соа0)] . (11.38)
\ X /
Раскрывая выражение (11.38), получаем
sm (0 = а (0 [ехр [/Ч 0 + ~ (ехр [/ (ю0 4- <Oj) 0 —
X
— ехр[/(<оо—coj)/])-{- -^-(ехр [/(<оо-|-<оа) /]—ехр [/(со0—<оа) /]) 4-
X
+ а (0 [-^ (ехр [/ (% + сог + со2) /1 — ехр [/ (соо—(0j + <оа) 0 +
I 4 \
4- ехр [/ (соо—соа — со2) t] — ехр [/ (u)0 |- (Gj—<оа) 0
(11.39)
Если, кроме того, налагается дополнительное ограничение,
заключающееся в том, чтобы важнейшие парные эхо не превышали
уровень —20 дб относительно пикового значения s(0, т. е. (Ь1/2)макв
418
^alatiausi^i.
знание без границ - *
и (^а/2)мако должны быть не более 0,1, то членом, содержащим их
взаимное произведение, для которого
(^1 ^а/4)макс 0,01,
можно пренебречь. При этом предположении последние четыре
члена выражения (11.39) опускаются. Поэтому при b < 0,2 рад
(односторонний пик, примерно равный 11,5°) каждая отдельная
компонента, искажающая модуляцию фазы, дает единственную
группу парных эхо (фактически парные боковые полосы), кото-
рые можно рассматривать независимо от других парных эхо.
Применительно к сжимаемому импульсному ЛЧМ сигналу,
функция модуляции которого имеет п компонент, в рассмотренном
выше случае получается следующее приближенное выражение для
выходного сигнала:
s0 (0 = Si(0 cos<o0H; V-у sx +
i
S+vV+9'l~
\ “ / I
n _______
— V —S1(/—- tUos[L0—oj, (11.
2 Ц До ) 1Д 0 2 / *J
где 0f — начальная фаза каждой компоненты искажающей моду-
ляции, имеющей частоту (о{. Из (11.40) видно, что каждые парные
эхо имеют следующие характеристики:
временной сдвиг ± —Т, частотный сдвиг ±—, начальная
Д<о 2
фаза ± 0/.
На рис. 11.14 показана полученная в лабораторных условиях
группа парных эхо, которая вызывается двумя синусоидальными
функциями, определяющими погрешности фазовой модуляции.
Частота второй синусоиды в два раза выше частоты первой. Макси-
мальная фазовая ошибка второго сигнала постоянна, тогда как
у первого сигнала она изменяется, обнаруживая меньшую, чем об
этом говорилось выше, независимость парных эхо ёигналов от пи-
ковых значений фазовых ошибок. При указанных условиях любую
сложную функцию, описывающую модуляционные искажения,
можно выразить через ее компоненты Фурье. Результирующий
искаженный сигнал можно затем получить на основании суперпо-
зиции искажений, вызываемых каждой компонентой. При более
высоких значениях максимальных фазовых ошибок следует ис-
пользовать более точные выражения (11.37) или* (11.39) при bt <
< 0,5 рад.
419
Результаты соотношения (11.40) можно обобщить на случай
показанных на рис. 11.15 искажающих функций, которые наблю-
даются на ограниченном интервале времени. Такую искажающую
функцию можно представить в виде ряда ее дискретных спектраль-
ных компонент, описываемых
формулой
i4nsin(2nn/r-f-6n), (11.41)
где fr — частота повторения сиг-
нала; 0n = 2ntonfr‘, t0 — задерж-
ка от начала линейного качания
частоты до центра искажающей
функции, а Ап—п-я Фурье ком-
понента спектра искажающей
функции.
Рис. 11.14. Сигналы на выходе
фильтра сжатия для функции моду-
ляции, состоящей из двух синусоид
(оа — 2 (Of
а —при б,«=0,1 рад, б,— 0,15 рад;
б —при bt «0,2 рад, Ь, —0,16 рад; в—при
hi«=0,26 рад, о»™0,1Б рад.
Функция модуляции фазы, связанная с каждой компонентой
в соответствии с (П-41), имеет вид
Ап
2nnft
cos (2nnfr t + fU-
Gl.42)
Для функции показанного на рис. 11.15 вида с ростом п пиковое
значение модуляции фазы спадает быстрее чем l/f, поскольку Ап
также уменьшается с ростом частоты. Поэтому в большинстве
случаев на основании принципа суперпозиции, так же как было
сделано при выводе выражения (11.40), в выражении для спектра
искажающей функции можно использовать конечное число членов.
Следует заметить, что операция инвертирования искажающей функ-
ции эквивалентна прибавлению к каждому 0л фазового сдвига
в 180°. Как показано на рис. 11.15, это приводит к тому, что на вы-
ходе согласованного фильтра некоторые области компенсации и
подчеркивания поменяются местами.
420
^alaHausX
знание без границ ч *
Хотя до сих пор подразумевалось, что в достаточно мощных
системах с жестким ограничением амплитудная модуляция должна
быть малой, имеются примеры применения согласованной фильтра-
ции там, где это условие не выполняется. Если встретится именно
а) б)
Рис. 11.15. Искажения сжатого импульса, обусловленные
локальными погрешностями функции ЧМ:
а —искаженная функция качания частоты импульса; б —неиска-
женный сжатый сигнал (вверху) и импульсы с искажениями.
такой случай, то вполне возможно, что будут существовать одно-
временно и амплитудная и фазовая модуляции. В предположении,
что величина фазовой модуляции столь мала, что в разложении
экспоненты по функциям Бесселя (11.10) можно ограничиться пер-
вой парой членов, выражение для излученного кодированного
сигнала сходно с первыми пятью членами выражения (11.19), полу-
ченного для случая комбинированных схемных искажений, и имеет
ВИД
Sm (0 = а (0 [ао {ехр [J {(оо t + 0 (/)}] +
+ ~ (ехР [/ {(<%+®j) t + е (0)1 + ехр [/ {(<00—<°х) t + 0 (0)] j +
+ ~ (ехр II «“о+®.) t+е (<)}] -ехр I/ t + е (0)1)1. (11.43)
421
В случае пропускания ЛЧМ сигнала через согласованный фильтр
сигнал на выходе (в предположении а0 = 1) запишется
Рис. 11.16. Влияние комбинирован-
ных модуляционных искажений,
когда частоты амплитудной и фазо-
вой модуляции различны:
а —только амплитудная модуляция;
б —комбинированная модуляция, <о >
т
Рис. 11.17. Влияние комбинирован-
ных модуляционных искажений,
когда частоты амплитудной и фа*
зовой модуляции одинаковы:
о —только амплитудная модуляция
б —комбинированная модуляция. <0^—
тн
422
^alallausvl!.
знание Вез границ “ ш
На рис. 11.16 приводится форма ЛЧМ сигнала на выходе согласо*
ванного фильтра для случая, когда искажения амплитудной и фа-
зовой модуляций происходят на различных частотах. При <ох ®
== <оа и равных величинах ах и Ьх может иметь место особый случай,
когда парные эхо полностью взаимно компенсируются по одну сто-
рону от полезного выходного сигнала и суммируются в фазе с дру-
гой стороны. Этот случай показан на рис. 11.1/. Изменение на 180°
начальной фазы для сох, либо для <ot приводит к тому, что области
полной компенсации и подчеркивания меняются местами. При про-
извольной начальной фазе могут возникнуть условия для частичной
компенсации или подчеркивания амплитуд парных эхо, которые
можно трактовать с помощью рассмотренных ранее общих методов.
11,6, Источники модуляционных искажений фазы
Источники модуляционного искажения, которые являются
опасными при использовании согласованной фильтрации для сжа-
тия импульсов, обычно возникают из-за меняющихся во времени
коэффициента усиления и величины задержки в цепи передатчика
большой мощности. Как уже отмечали Дифранко и Рубин (51,
этот процесс является мультипликативным. Однако если величина
максимальной фазовой ошибки не слишком велика, то при рассмо-
тренных выше условиях можно] применить принцип суперпозиции.
Обычно модуляционные искажения возникают вследствие наклона
плоской части импульса модулятора и наличия в ней пульсаций,
разряда накопительной емкости источников питания, несогласован-
ности следующих друг за другом каскадов и несоответствия импе-
дансов в формирующих цепях импульсного модулятора, пульсаций
в трансформаторе. Некоторые из перечисленных источников иска-
жений будут вызывать амплитудную модуляцию ЛЧМ сигнала.
Ограничивающее действие каскадов большой мощности в общем
случае преобразует амплитудную модуляцию в фазовую. Суммар-
ные эффекты различных источников фазовой ошибки будут зависеть
от чувствительности к ошибкам электронных устройств большой
мощности, применяемых в цепи передатчика. Либмэн [31 составил
таблицу (табл. 11.1) типичных источников искажения фазовой моду-
ляции в цепи передатчика.
Применение этих данных можно пояснить на примере ЛЧМ
сигнала и клистрона большой мощности, в котором напряжение
пучка, равное 100 кв, имеет пульсации, возникающие в формирую-
щей цепи импульсного модулятора пучка. Если электрическая длина
лампы равна ?0 рад, то максимальная величина пульсаций функции
фазовой модуляции составит
= 70 = 0,35 рад
2 100 г
423
Таблица lid
Фазовые пульсации в генераторных лампах
Тип лампы Приблизительная величина фааовых пульсаций bt
1. Клистрон 2 \ Е / 0'
2. ЛБВ ф Цд — со
3. Электронно-лучевые усилители со скре- щенными полями -1— 25 \ Е /
4. Триод __ / Д/ \ 50 ы
5. Тетрод (от 1 до 60) —
6. Амплитрон л / А/ \ 40 (т)
Примечание. 0/—электрическая длина лам-
пы; ДЕ/Е—относительные пульсации напряжения;
Д///—относительные пульсации тока.
или приблизительно 20°. Амплитуда парных эхо в децибелах равна
20 lg (fci/2)== —15 дб.
Предполагая, что на длительности зондирующего импульса имеется
шесть периодов пульсаций и что полоса качания частоты сигнала
составит 1 Мгц, получаем, что парные эхо будут появляться на
выходе согласованного фильтра со сдвигом ±6 мксек относительно
центра полезного сигнала. Ясно, что парные эхо такой величины
являются нежелательными. Один из методов уменьшения влияния
пульсаций напряжения пучка заключается в применении высоко-
вольтного ограничителя. Предполагая, что подобное устройство
сможет уменьшить пульсации напряжения пучка до 0,1 кв, уровень
парных эхо, появляющихся из-за искажений фазовой модуляции,
в этом случае составит
201g (0,035/2) =—35 дб.
Во многих применениях эта величина будет допустима.
424
ftataHausiMi
знание без ераниц > **
Как уже отмечалось, последствия искажений фазовой модуля-
ции, рассмотренные в предыдущих разделах, указывают на не*
обходимость установления жесткого контроля над источниками
модуляционных искажений в РЛС, использующих согласованный
фильтр. Последующие замечания относятся непосредственно
к ЛЧМ сигналу. При соответствующей модификации их также мож-
но отнести и к другим сложным сигналам, в частности к сигналам
с однонаправленной или кусочно-линейной ЧМ.
Число периодов синусоидальной искажающей функции моду-
ляции фазы, соответствующих длительности несжатого сигнала,
будет определять координаты порожденных искажениями импуль-
сов относительно номинального местоположения сжатого импульса.
Поэтому, если частота этой модуляции фиксирована, то увеличение
коэффициента сжатия системы (TAf) за счет увеличения Т будет
приводить к еще большему удалению обусловленных искажениями
парных эхо по оси времени от основного сигнала.
При выборе элементов станции разработчик должен особое
внимание обращать на характеристики элементов, влияющих на
искажения сигналов. Например, модулятор, создающий большую
частоту пульсаций на плоской части импульса, может оказаться
предпочтительнее модулятора с низкой частотой пульсаций, если
их амплитуды одинаковы. Вообще, более высокая частота моду-
ляционных искажений приводит к смещению соответствующих им
импульсов дальше от основного сигнала, и как следствие не создают-
ся помехи при обнаружении и разрешении импульсов, находящихся
вблизи основного сигнала. Помимо этого, более высокая частота
модуляционных искажений будет смещать мешающие импульсы за
пределы полосы пропускания согласованного фильтра, производя
дополнительное подавление паразитного сигнала. Если механизм
модуляции таков, что он приводит не к фазовой, а к частотной моду-
ляции, как, например, в случае пульсаций на ЛЧМ, то более высо-
кая частота модуляции вызовет меньшую фазовую модуляцию и
тем самым при фиксированной величине девиации даст меньшие
искажения. Кроме того, если осуществима точная регулировка пара-
метров модуляционного искажения blt fmT и Оо, то можно получить
частичное ослабление наиболее неприятных парных эхо. Однако
если модуляционных искажений достаточно, чтобы заметно исказить
сигнал, то следует подумать о другой конструкции элементов пере-
датчика или об ином их физическом расположении, так же как и
об использовании методов компенсации искажений.
а
11.7. Представление искаженных временных функций на
выходе согласованного фильтра для произвольных сигналов
Используя в качестве примера'сЖатый’импульсный^ЛЧМ сигнал
на выходе согласованного фильтра, в разд. 11.4—11.6 были при-
ведены иллюстрации, предназначенные также и для того, чтобы
425
показать виды искажения сигнала, которые могут встретиться при
наличии схемных искажений. Функция отклика радиолокатора,
кратко описанная в гл. 3 и более подробно в гл. 4, была использо-
вана Дифранко и Рубиным 15] как средство установления верхнего
предела для огибающей результирующего искаженного сигнала на
выходе согласованного фильтра. В разд. 11.2 было показано, что
при искажении частотной характеристики, которая эквивалентна
введению искажающего фильтра, форма сигнала на выходе согла-
сованного фильтра не зависит от вида кодирующей функции. Для
каждой компоненты амплитудных и фазовых искажений, существую-
щей в приемнике согласованного фильтра, искаженный выходной
сигнал можно представить в виде комбинации сдвинутых по времени
точных копий полезного сигнала. Можно считать, что каждый из
этих смещенных по времени сигналов представляет собой верти-
кальное сечение изображенной на рис. 11.18 функции отклика со-
гласованного фильтра |х (т, <р)|. Было показано, что при ограни-
чении спектра сложной искажающей функции можно получить ее
разложение в ряд Фурье, причем каждая компонента Фурье иска-
жающей функции даст группу парных эхо, или иначе, набор сдви-
нутых по времени вертикальных сечений функции отклика. Сече-
ние ансамбля функций отклика вдоль временнбй оси имеет общий
частотный параметр. Для определенной компоненты Фурье ампли-
тудных искажений ап парные вертикальные сечения функции от-
клика описываются соотношением
<р) , (11.45)
где ап — величина n-й компоненты амплитудных пульсаций;
па — число полных периодов пульсаций в полосе Д/, а | х (т, ф) | —
неискаженная функция отклика согласованного фильтра.
Аналогично этому для компонент фазового искажения в пред-
положении малых фазовых ошибок (т. е. Ьп < 0,5 рад) значения
каждой группы парных поперечных сечений функции отклика
определяются соотношением (при условии а0 = 1)
<Р. (П.46)
где Ьп — величина n-й компоненты пульсаций фазы, а пь — число
полных периодов пульсаций фазы в полосе частот Д/.
Подобным же образом в разд. 11.4 было показано, что в случае
временных модуляционных искажений возникают парные боковые
полосы, аналогичные парным эхо, которые обусловлены схёмными
искажениями. Каждый из этих сигналов, имеющих парные боковые
полосы, дает на выходе согласованного фильтра сдвинутый по ча-
стоте сигнал, который также можно выразить через функцию от-
клика. Иллюстрацией этому служит рис. 11.19. Для каждой состав-
429
ftatatiausllk
знание без границ * *
Рис. 11.18. Эскиз, иллюстрирующий функцию отклика при
частотных искажениях.
Рис. 11.19. Эскиз, иллюстрирующий функцию
отклика при временных модуляционных искажениях.
427
Ляющей амплитудной модуляции парные поперечные сечейия функ-
ции отклика получаются в виде
Ф±Ч)|,
Л»
(П.47)
а каждая пара сечений функции отклика, обусловленная фазовой
модуляцией, определяется (при Ьт < 0,5 рад) соотношением
^|Х(Г. <Р±К)|,
(11.48)
где ат—величина /n-й компоненты амплитудной модуляции;
Ьт—величина /n-й компоненты фазовой модуляции, fma—частота
т-й амплитудной компоненты, a fmb—частота m-й фазовой ком-
поненты.
Соотношения (11.45)—(11.48) основываются на предположении,
что искажения малы, так что члены, содержащие перекрестные
произведения амплитудных и фазовых искажений, так же как и
функции Бесселя более высокого порядка, связанные с фазовыми
искажениями, являются пренебрежимо малыми величинами. При
необходимости получить результирующее выражение для гранич-
ного значения вертикального сечения искаженной функции отклика,
соотношения (11.45)—(11.48) можно объединить. Обозначая эту
верхнюю границу искаженного сигнала на выходе согласованного
фильтра через | Xd I» получаем
ОО 00
|Х0(т, ч>)|< 2 С„|Х(т+л/ДЛ <р)| + 2 С„х
л-—оо лп«"—оо
X Iх(т. ф + /т)|,
(11.49)
где Сп — — (an-{-bn), Сп—С_п\ Ст — — (ат4- bm), Ст — С_т.
л» л»
В том, что это выражение действительно представляет собой верх-
нюю границу искаженного сигнала на выходе согласованного
фильтра, можно убедиться, если вспомнить, что по определению
подфункцией | % | понимается ее абсолютная величина, так что выра-
жение (11.49) представляет собой сумму положительных величин,
в то время как фактически наблюдаемые на выходе согласованного
фильтра сигналы, продемонстрированные в предыдущих разделах,
могут складываться и вычитаться в зависимости от относительных
428
^lalaHauStlii
знание без границ - w
фаз несущих Mactot парных эхо. Выражение (11.4$) позВоЛйет оце*
нить верхние границы влияния искажений на такие параметры
сигнала, как точность, неоднозначность и разрешающая способ*
ность *. Дифранко и Рубин указывают, что при наличии искажений
точность сигнала ухудшается из-за расширения главного лепестка
полезного сигнала на выходе согласованного фильтра. Это происхо-
дит при низкочастотных искажениях, которые приводят к тому,
что парные эхо сливаются с полезным сигналом. Такое обстоятель-
ство вызывает его расширение (в тех случаях, когда фазы парных
эхо таковы, что они складываются, а не вычитаются из полезного
сигнала на выходе согласованного фильтра). Характерный случай
квадратичных фазовых ошибок (т. е. линейное рассогласование за-
держки), рассмотренный в гл. 6 применительно к ЛЧМ сигналам,
представляет собой пример искажающего влияния низкочастотной
фазовой ошибки на выходной сигнал согласованного фильтра и свя-
занного с этим ухудшения разрешающей способности и точности.
Если искажающие парные эхо достаточно велики, превышают
порог обнаружения и могут быть приняты за полезные сигналы,
расположенные на дальностях, отличных от дальности истинного
сигнала, то возникает неоднозначность. При наличии в окружающей
среде многих целей это обстоятельство может явиться серьезной
проблемой. Подобным же образом разрешение ряда сигналов, имею-
щих различную амплитуду, может сильно ухудшиться, если иска-
жающие парные эхо окажутся достаточно большими, чтобы замаски-
ровать более слабые отраженные сигналы. Как отмечалось ранее,
каждое из этих соображений может служить поводом для уменьше-
ния искажений в радиолокаторе.
В ряде ситуаций, в которых возможно появление большого
числа перекрывающихся парных эхо, таких, например, как пока-
заны на рис. 11.15, выражение (11.19) может дать завышенную гра-
ницу и привести к установлению нереализуемых ограничений для
разработчика станции, поскольку дело идет о приемлемых допусках
на искажение. В этом случае возможно целесообразнее рассмотреть
среднее граничное значение для искаженного сигнала на выходе
согласованного фильтра. Эта средняя граница мож^т быть полу-
чена, исходя из среднеквадратичного значения функций, описы-
вающих парные отклики, которые образуют результирующие иска-
1 В реальной ситуации, заключающейся в том, что фазовые и амплитуд-
ные ошибки имеют одну и ту же частоту, Сп = (an±bn)/2 и С_п= (ап =рЬп)/2,
так что эти члены одновременно не будут равны. Условие, при котором значе-
ние одного из этих коэффициентов является более высоким, будет зависеть
‘>т относительной фазы (±90°) между составляющими амплитудной и фазовой
ошибок. В общем случае его нельзя предсказать, поэтому допущение
сп = С_п = (ап + Ьп)/2 во всех случаях обеспечивает максимальную верх-
нюю границу.
429
жения. Обозначая эту среднеквадратичную искаженную функцию
отклика согласованного фильтра через | Хо I » получим
|Хь(t> ф) = 1/ 2 сп х(т + ~» ф) 2+ 2 Ст| X(т»Ф+Ап) 1а-
Гло—оо \ Д/ / т=а — оо
(11.50)
11 .8. Оценки потерь в разрешающей способности при
случайных фазовых ошибках
На основании выражений (11.49) и (11.50) можно определить
положение максимальной верхней и средней границ по дальности
и частоте искажающих боковых лепестков на выходе согласованного
фильтра. При этом предполагается, что основные компоненты
Фурье искажающих функций известны. Когда искажения являются
произвольными или случайными функциями, тогда затруднительно
получить меру протяженности отклика, т. е. функции неопределен-
ности в области, окружающей центральный пик неопределенности.
Браун и Палермо рассмотрели две основные оценки потерь в раз-
решающей способности в результате влияния случайных фазовых
ошибок 19, 10]. Одна такая оценка основывается на моменте вто-
рого порядка или радиусе инерции искаженной функции неопре-
деленности. При наличии случайной ошибки 0,, (/) в функции фазо-
вой модуляции, искаженная функция отклика (на основании выра-
жения (3.83) 1 определяется соотношением
XD(T’ Ф); j w(0«*(rl т)ехр1—j |2лф/ —0e (/))] df. (11.51)
Браун и Палермо показывают, что оценка потерь в разрешающей
способности, основанная на радиусе инерции функции | %D |2, аппрок-
симируется выражением
2 f<P’l Х(т. <Р)|’^Ф , 2
Оф = ----------—------Ь О0'.
(11.52)
Первый член соотношения (11.52) представляет собой момент вто-
рого порядка (или эквивалентную полуширину в квадрате) неиска-
женной функции неопределенности в направлении оси ф. Второй
член есть дисперсия или средний квадрат ошибки по частоте 0е. (0
для функции частотной модуляции, связанной с ошибкой фазовой
модуляции Qe (/), т. е.
Се'Е| |e’(/)]2j — |Е [О, (/)]2| = среднему квадрату ошибки по ча-
' стоте, (11.53)
где Е {у} — математическое ожидание величины у.
430
^alallausx
знание Вез границ * *•
Обычно предполагается, что Е1ве(0] = 0, так что (ф =
£ {[0< (OF). В выражении (11.52) влияние сдвига среднего по-
ложения искаженной функции неопределенности не учитывается.
Обычно оно равно нулю для большинства распределений случайных
ошибок функции модуляции, у которых E{Qe (0}=0 для каждой вы-
борочной функции из ансамбля. При законах распределения оши-
бок, для которых условие Е{ве (0) = 0 выполняется только по
совокупности выборок, средняя ошибка положения будет стремиться
к нулю, если распределение спектра (/) окажется относительно
широким. Ошибки в положении на выходе согласованного фильтра
обычно обусловлены ее низкочастотными компонентами. Возможно,
что для функции модуляции фазы имеет место случайное распре-
деление низкочастотных ошибок, для которых условие Е {Ое(0} — 0
выполняется на протяженном временнбм интервале, но не на дли-
тельности каждого зондирующего импульса. Это будет приводить
к смещению положения сигнала на выходе согласованного фильтра
от импульса к импульсу относительно среднего положения, тогда
как случайные фазовые ошибки, имеющие широкий спектр для каж-
дого принятого импульса', будут приводить к размазыванию сигнала
на выходе согласованного фильтра.
При наличии случайной фазовой ошибки в согласованном
фильтре р(со) и при условии Е (pz(<i))} = 0 выражение для протя-
женности функции неопределенности аппроксимируется следующим
соотношением:
2 У т I х (т, ф) |« dt 2
0t = т-------------------h Он»
f 1x0*. ф)|’л
(11.54)
где op, = Е {[Р'((о)Р) —средний квадрат ошибки задержки.
Выражения (11.52) и (11.54) представляют дисперсию, так что раз-
брос функции неопределенности в направлении оси частот равен
2аф и в направлении временнбй оси 2стт. Используя выражения
(11.52) и (11.54) для любых значений смещения по дальности т
2
и скорости <р, можно получить соответствующие величины аф
и а; .
Другая оценка потерь в разрешающей способности, основан-
ная на рассмотренных в гл. 4 постоянных разрешения по времени
и частоте Вудворда, эквивалентна прямоугольнику разрешения по
дальности, определяемому уравнением
Тг = JI gt (О12 dtl | gd (0) I >, (11.55)
где ёа (0 — искаженный сигнал на выходе согласованного фильтра.
Как показано на рис. 11.20, это определение основывается на
приравнивании энергии эквивалентного прямоугольного импульса
энергии сигнала gd (/). На практике для большинства типов РЛС,
431
использующих согласованный фильтр, предположение о случай-
ности искажающих ошибок не является реалистичным х. Раз уж
конкретная РЛС, использующая согласованный фильтр, построена,
то, по-видимому, более соответствует реальности предположение,
что присущие ей искажения являются детерминированными и их
характеристики можно измерить. Используя это допущение, Ченг
определил верхнюю границу эквивалентного прямоугольника раз-
решения для сложных функций фазовых ошибок [11]. Ниже описы-
вается этот метод.
Рис. 11.20. Эквивалентный пря-
моугольник разрешения.
Рис. 11.21. Произвольная функция
фазовых искажений в согласованном
фильтре.
На рис. 11.21 изображена сложная функция, описывающая фа-
зовые ошибки. Максимальное значение величины р(2л /) относи-
тельно значения опорной фазы, равной нулю, составляет тр рад.
Искаженный сигнал на выходе согласованного фильтра gd (/) опи-
сывается соотношением
gM = f IS (/)I ’ ехр [/ {2nft + ₽ (2лЛ) ] df. (11 -56)
где | S(f) | — спектр зондирующего сигнала. Применяя теорему
Парсеваля, получаем выражение для энергии сигнала £d (/)
J 1&(01’Л = J I |S(f)|aexp[/₽(2nf)))’df = J\S(f)\‘df. (11.57)
Отсюда вытекает, что в действительности фазовые искажения не
изменяют энергию сигнала, а лишь влияют на ее распределение
во времени. Максимальное значение функции gd (/) получается из
выражения (11.56) при t = 0, т. е.
I gd (0) Is -1 j I s tf) I ’ exp [/₽ (2л/)] df I ’• (11.58)
1 Случайные фазовые ошибки могут также порождаться при распростра-
нении сигнала через среду с изменяющимися во времени и в пространстве ха-
рактеристиками пропускания. В этом случае среду можно рассматривать как
фильтр, для которого применим анализ Брауна и Палермо.
432
^alaHausA
знание без границ Ч
Если фазовые ошибки малы, то можно приближенно записать
ехр[/₽(2я/)] = 1 +/₽(2л/)—1₽’(2я/)+.... (11.59)
и тогда выражение (11.58) преобразуется к виду
IJ | S (0 |а ехр I/Р (2я/)] df |2—
={J|S(OIB[| - |₽’(2яп]а/}2+|j| S(/)P₽(2n/)dfp
Замечая, что | ₽(2л/) |макс =/пр и применяя к интегралам
о среднем, получаем
J|S(f)l2[l - J₽’(2«f)]
‘ 2
df
2 Т2 г л i2
f|S(/)|’d/].
Кроме того,
|j |S(f)|’₽(2n/)d/]2>0
(11.60)
теорему
(11.61)
(11.62)
и поэтому
|gd(O)P> [1-m?/2]2{f |S(f)|M]2- (11-63)
Подставляя (11.57) и (11.63) в выражение (11.55), приходим к по*
лученному Ченгом результату
[l-mJ/2]2 [{(SWIM]2 ’ V ’ '
Неравенство (11.64) дает верхнюю границу эквивалентного прямо-
угольника разрешения, которая имеет наименьшее значение когда
/ир = 0. Применительно к ЛЧМ сигналу единичной амплитуды,
для которого
IS (/) |2 ~ Т/2Д/, - ДZ/2 < f < Д//2, (11.65)
это соотношение дает
т _______WWW____________= ... 1W . (1 J .66)
[l-mJ/2|2(T2/W2)A/2 [1—m=/2]2
Если для уменьшения уровня боковых лепестков по дальности на
выходе согласованного фильтра используется взвешивающая функ-
ция W (/), то в приведенных выше соотношениях множитель 13(f) |а
заменяется на |S(f) | W(f). Если для ЛЧМ сигнала используется
косинусоидальная функция взвешивания (уровень боковых лепест-
ков при этом равен —23 дб), то (Тг)мин = 1,23/Д/, в то время как
ширина по уровню 3 дб составляет 1,34/Д/; при взвешивании функ-
Зак. 1341 433

цией cos2 получается (ТГ)МИ|, = 1,б/Д/, а ширина импульса по уров-
ню 3 дб— Поскольку соотношение
(Л)м„„=J|S(/)|‘d//[j |S(/)|«d/]2
выполняется для любого сигнала на выходе согласованного или
определенного выше несогласованного фильтров, выражение

(71 г) мин
(11.67)
представляет собой универсальную верхнюю границу при наличии
фазовых ошибок в согласованном фильтре. На рис. 11.22 графи-
чески изображена зависимость (11.67). В случае модуляционных
фазовых ошибок аналогичный анализ дает эквивалентное выраже-
ние для прямоугольника разрешающей способности по допплеров-
ской частоте, где
(/7ф)мин = JI и (014 dt / [ j | и (0 |2 и (0—огибающая зондирую-
щего сигнала
(11.68)

(11.69)
Определяемые соотношениями (11.64) и (11.66) верхние границы
неприменимы к произвольным функциям фазовых ошибок. Напри-
мер, если рассмотренная выше искажающая функция 0 (2л/) содер-
жит множество различных высокочастотных составляющих, то
искаженный сигнал на выходе согласованного фильтра может
иметь вид, показанный на рис. 11.23, а. Если одна из высокочастот-
ных искажающих компонент является доминирующей, то искажен-
ный выходной сигнал может принять форму, изображенную на
рис. 11.23, б. В приведенных примерах влияние фазового искаже-
ния проявляется в образовании интерферирующих сигналов по-
мехи или в появлении более сильного неоднозначного отклика при
отсутствии специфического эффекта размазывания главного отклика
согласованного фильтра. Основное влияние искажений в подобных
случаях заключается в ухудшении способности обнаруживать более
слабее сигналы, а не в потере разрешения сравнительно сильных
сигналов. Поэтому применять критерий эквивалентного прямо-
угольника разрешения следует с осторожностью и, по-видимому,
целесообразнее всего тогда, когда искажающие функции состоят
из низкочастотных компонент. Однако и здесь необходимо проявлять
некоторую осторожность при интерпретации результатов.
Показатель разрешающей способности, определяемый зависи-
мостью (11.67), не изменяется, если для снижения уровня боковых
лепестков применяется взвешивание, тогда как из рассмотрения
в гл. 6 случая низкочастотных квадратичных фазовых ошибок сле-
довало, что использование взвешивающей функции уменьшает
434
ftalaHausI
знание без границ
протяженность искаженного ЛЧМ сигнала на выходе согласован-
ного фильтра. По этим причинам, по-видимому, было бы целесооб-
разно попытаться определить, где это возможно, наиболее важные
компоненты искажающих функций с тем, чтобы получить более
точную картину влияния конкретной искажающей функции на рас-
сматриваемый выходной сигнал согласованного фильтра и приго-
товить базис для систематической компенсации искажений в прием-
нике.
ПикоОое значение разовой ошибки,тр
Рис. 11.22. Зависимость верхней
границы эквивалентного прямо-
угольника разрешения от пикового
значения фазовой ошибки тр.
Рис. 11.23. Искаженные согласован-
ным фильтром импульсы, для кото-
рых эквивалентный прямоугольник
разрешения является плохой мерой.
В ряде ситуаций искажения возможно возникают из-за изме-
няющихся во времени параметров аппаратуры РЛС. Сюда обычно
входят флюктуации напряжения питания и непостоянство длитель-
ности сигнала в передатчике, а также и в приемнике, если вместо
согласованного фильтра используется активный коррелятор.
И здесь разработчик может применять с рассудительной осторож-
ностью рассмотренные выше оценки потерь разрешающей способ-
ности. Если уровни искажений выше допустимых, то следует по-
думать о методах активной их компенсации, которые будут рас-
смотрены в следующем разделе.
11.9. Компенсация искажений
Несмотря на усилия разработчика системы, достижение требуе-
мого уровня допустимых искажений в передатчике путем прямого
контроля отдельных компонент может оказаться чрезмерно дорого-
,5* 435
ирг - — — —________ __________
ВТ''
г
стоящим. В таком случае наилучшей процедурой является кон*
струирование цепей компенсации искажений, которые вводят рав-
ные, но противоположные по знаку искажения с целью уничтоже-
ния искажений, возникающих в цепях передатчика большой мощ-
ности. Практически полного уничтожения искажающих компонент
добиться нельзя, однако снижение их величины на порядок в дей-
ствующих РЛС является реальным.
Компенсация искажений может основываться на методах, ис-
пользующих устройства с незамкнутой или замкнутой цепью обрат-
ной связи. Оба эти метода в общем виде были рассмотрены Дифран-
Рис. 11.24. Блок-схема устройства компенсации с не-
замкнутой цепью обратной связи.
ко и Рубиным в работе [5], откуда позаимствованы блок-схемы
устройств, изображенных на рис. 11.24 и 11.25. Принцип работы
показанной на рис. 11.24 схемы основывается на обнаружении ам-
плитудных пульсаций на выходе мощного оконечного каскада и
преобразовании данных этой амплитудной ошибки в сигнал преды-
скажения фазы, который подается к каскаду, предшествующему
оконечной лампе. Это устройство применимо в том случае, когда
можно обнаружить искажения амплитуды, связанные с искажениями
фазовой модуляции, и не пригодно, если оно само по себе является
источником искажений в виде боковых лепестков с уровнем выше
допустимого. Однако данный метод, основывающийся главным
образом на компенсации искажений, вносимых импульсным моду-
лятором оконечного каскада, трудно реализовать, тогда, когда
искажающие фазовую модуляцию компоненты будут иметь незна*
чительную, связанную с ней амплитудную модуляцию или вообще
не будут ее иметь.
Для корректирующей системы с незамкнутой цепью обратной
связи можно применить другой метод, если модуляционные ошибки
известны и повторяются от импульса к импульсу, или если требуется
компенсировать некоторую нежелательную и детерминированную
436
^alaUaus^k
знание без границ “ *
характеристику обыкновенного зондирующего сигнала на выходе
согласованного фильтра. В этом случае можно синтезировать не-
обходимую корректирующую функцию, т. е. функцию предыскаже-
ния, синхронизированную со временем появления сигнала и при-
ложенную в соответствующей точке схемы передатчика для дости-
жения требуемого результата. Рассмотренная в гл. 7 функция пре-
дыскажения ЛЧМ сигнала, предназначенная для уменьшения фре-
нелевских пульсаций спектра и уровня парных эхо, связанных
с этими пульсациями, является примером указанного метода ком-
пенсации искажений, использующего незамкнутую цепь обратной
связи 114].
Рис. 11.25. Блок-схема устройства компенсации
с замкнутой цепью обратной связи.
Работа показанной на рис. 11.25 схемы.коррекции искажений
с замкнутой цепью обратной связи основывается на отборе после-
довательных мгновенных значений сигнала с выхода мощного
оконечного каскада и на сравнении ошибочных девиаций его фазы
с фазой неискаженного опорного сигнала, получаемого от мало-
мощного генератора на выходе согласованного фильтра (он может
быть активным или пассивным). Оба сигнала вводятся после точной
временнбй и фазовой регулировки, осуществляемой путем уста-
новки на пути опорного сигнала задержки, равной запаздыванию
сигнала в канале мощного каскада. В тех случаях, когда эта за-
держка мала по сравнению с периодом наивысшей искажающей
компоненты корректируемого сигнала, тогда коррекция искажений
в течение длительности зондирующего импульса становится воз-
можной, а устройство наиболее простым. Если выравнивающая за-
держка не удовлетворяет этому требованию, то исправляющий
искажения сигнал может быть задержан на время, равное одному
периоду повторения, и использован для коррекции следующего
импульса, при условии, что в междуимпульсный период каких-либо
существенных изменений в соотношениях частот искажения не
произойдет.
437
Такие изменения могут возникнуть из-за нестабильности дли-
тельности синхронизирующего импульса или из-за порождаемой
уходом частоты нестабильности длительности сигнала в устройстве
пассивного формирования растянутого импульса. Этот метод можно
применять, если точка схемы передатчика, в которой производится
коррекция искажения, расположена после точки, где получают
информацию об искажении. Метод будет непригоден, если исправ-
ляющий ошибку сигнал поступает в устройство обратной связи,
которое уменьшает искажения в точке, откуда извлекается ин-
формация об искажениях. Де Лоренцо и Де Анджелис 112] рассма-
Рис. 11.26. Схема устройства сравнения фаз в реальном
масштабе времени.
тривают необходимые требования к аппаратуре, применяемой
в высокоточных РЛС, которая должна измерять ошибки фазовой
модуляции и формировать корректирующий их сигнал при ис-
пользовании устройства с замкнутой цепью обратной связи для
компенсации искажений в реальном масштабе времени. На рис. 11.26
поясняется один из описанных методов формирования сигнала
ошибки. Используемые для сравнения сигналы
s (/) = cos [<оо / | 0(/)1 (11.70)
являются неискаженными сигналами на выходе согласованного
фильтра, а искаженный сигнал на выходе передатчика запишется
sd (0 = cos ky + О (t) + 0. (0+ -5-1. (11.71)
I W I
где 0 (0 представляет собой кодированную функцию модуляции,
а (О —• функцию, искажающую фазовую модуляцию.
438
ftatattausilk
знание без грани» * ш
После усиления, ограничения и отфильтровывания высоко-
частотных составляющих сигнал на выходе изображенного на
рис. 11.26 видеоусилителя запишется в виде
о0 (0 « К cos Гбв (/) -F -^-1 = К sin [0в (01.
| 4М |
(11.72)
При малых значениях 0в(/) (т. е. меньших ±10°)» v0(t) можно
аппроксимировать следующим выражением:
v0(t)^KGe(t). (11.73)
Оно представляет собой корректирующее ошибку напряжение,
требуемое для применения в устройстве линейной фазовой моду-
ляции. Разработанный Де Лоренцо и Де Анджелисом способ можно
применить также для измерения фазовых искажений в частотной
области пассивных цепей и усилителей, если тест-сигналом служит
Sft)
К откалиброванному
индикатору
Рис. 11.27. Блок-схема устройства для измерения фазо-
вых искажений.
ЛЧМ сигнал, имеющий относительно большое значение произве-
дения длительности на полосу, и если ожидаемые фазовые ошибки
меньше ±10°.
На рис. 11.27 показана блок-схема испытательного макета
этого типа. ЛЧМ сигнал на выходе испытуемого устройства в функ-
ции времени будет содержать искажающую фазовую модуляцию,
которая почти идентична зависимости фазовой ошибки от частоты.
При правильно откалиброванном индикаторе напряжение ошибки,
полученное в показанной на рис. 11.27 схеме при вышеупомянутых
условиях будет служить весьма точной мерой фазовых искажений,
обуслойленных искажениями в частотной области. С точностью из-
мерения, равной 0, Г, были проведены лабораторные испытания
описанной выше аппаратуры на таких устройствах, как лампы бегу-
439
1®Г'
г
щей волны, СВЧ компоненты и усилители промежуточной частоты,
при этом было достигнуто снижение искажений фазовой модуляции
в реальном масштабе времени, превышающее 12 дб.
Радемахер и Рэндайс [13] исследовали требования и конструк-
тивные параметры цепи обратной связи, необходимой для подачи
корректирующего сигнала к одному из возможных преобразователей
напряжения в фазу в тракте с высоким уровнем мощности, например
к лампе бегущей волны. Рис. 11.28 иллюстрирует общую конфигу-
рацию цепи обратной связи в тракте передатчика рассматриваемого
типа, предназначенную для коррекции ошибки фазовой модуляции.
Требования к отдельным источникам ошибки и к выравнивающей
задержке отображены на рис. 11.29, а. Задержки т, связаны с ли-
нейной частью фазовой характеристики каждого устройства,
а Ф, (t, (о) — соответствующие фазовые ошибки в функции времени
и частоты. Когда частота является известной функцией времени,
как, например, в случае ЧМ сигналов, пропущенных через согласо-
ванный фильтр, то ошибка Ф, (/, со) может быть выражена как
Ф, (/), а используя преобразование Лапласа, система с обратной
связью может быть представлена в классической форме, показан-
ной на рис. 11.29, б.
Если преобразование Лапласа фазовых искажений в отсутствие
обратной связи равно ФС/ (s), а при наличии обратной связи ФГо (s),
то для случая, показанного на рис. 11.29, отношение этих двух чле-
нов, полученное исходя из общей теории цепей с обратной связью,
равно
_________________!_______ (1174)
Фс<(з) 1+B(s)exp[-T„s] ’ 1 }
где тп — задержка от точки приложения обратной связи до вы-
хода, а В (s) — преобразование Лапласа характеристики усилителя
в цепи обратной связи.
Требование к характеристике усилителя в цепи обратной связи
заключается в том, что величина коэффициента усиления | В (s) |
должна упасть ниже 0 дб раньше, чем значение фазы станет больше
180°. Разность между 180° и фактической фазовой характеристикой
усилителя, когда | B(s) | = 0 дб, представляет собой запас по фазе
в цепи обратной связи, а уровень усиления ниже 0 дб, когда фаза
составляет 180°, представляет Собой запас усиления системы обрат-
ной связи. Необходимость иметь каждый из этих запасов достаточно
большим для того, чтобы обеспечить стабильность работы системы
с обратной связью, налагает ограничение на величину произведения
коэффициента усиления на полосу системы и тем самым на эффек-
тивность уменьшения искажений. В этой связи Радемахер и Рэн-
дайс отмечают большое значение задержки тп, ибо она вводит допол-
нительный фазовый множитель в характеристику цепи обратной
связи.
440
MaUausi^t
знание Вез границ “ *
Рис. 11,28. Блок-схема СВЧ устройства «обратной связью
Рис. 11.29. Характеристики элементов устройства с обрат-
ной связью:
а—фазовые характеристики передаточных функций; б —схема уст*
ройства с обратной связью в классическом представлении, если на
вход поступает Ф__ (s).
Вл
441
Сказанное иллюстрируют показанные на рис. 11.30 характе-
ристики усилителя в цепи обратной связи. Для того чтобы поддер-
живать величину малой, необходимо подавать сигнал обратной
связи в точку, расположенную достаточно близко к оконечному
выходному каскаду. Это означает, что обратная связь должна быть
введена в точку, обладающую относительно высоким потенциалом,
тем самым увеличивая сложность и стоимость конструкции уси-
лителя в цепи обратной связи. Введение обратной связи в точку
с более низким потенциалом приведет, вообще говоря, к увеличению
Рис. 11.S0. Коэффициент усиления и фазо-частотная характери-
стика усилителя в цепи обратной связи.
значения тя и к уменьшению запаса усиления по фазе системы.
Результаты, полученные Радемахером и Рэндайсом для усилителя
в цепи обратной связи, сконструированного для работы в системе
с большим уровнем мощности, показывают, что когда тп = 0, за-
пас по Фазе в переходной точке усиления равен 95°. Однако когда
тл = 0,об мксек, запас по фазе составляет лишь 13°. Если тл велико,
то для того чтобы это компенсировать, необходимо снизить коэффи-
циент усиления. С другой стороны, результаты, полученные для
тл = 0,1 мксек, показали уменьшение фазовой ошибки в цепи пере-
датчика приблизительно в отношении 10 : 1, однако при тп =
= О.Зл/ссек коэффициент уменьшения ошибки упал до 5 : 1, так
как для поддержания стабильности системы необходимо было сни-
зить усиление.
ЛИТЕРАТУРА
1. L. А. М а с С о 1 1. unpublished manuscript referred to by C. R. Burrows,
Discussion of paired-echo distortion analysis, Proc. IRE (Correspondence)
27, 384 (1939).
2. H. A. Wheeler. The interpretation of amplitude and phase distor-
tion in terms of paired echoes, Proc. IRE 27, 359—386 (1939).
44 2
ftalaHausiiiii
знание без границ “ w
3. Р. М. L i е b m a n. The effect of distortion on pulsed radar residue level,
unpublished report, Sperry Gyroscope Company (1957).
4. С. E. Coo k. Effects of bhase modulation distortion on pulse-compres-
sion signals, IRE Intern. Conv. Record, Pt. 4, 174—184 (1962).
*5 . J. V. D i F r a n с о and W. L. Rubin. Signal processing distortion
in radar systems, IRE Trans. MIL-6, 219—225 (1962).
6. J. Reed. Long line effect in pulse-compression radar, Microwave J. 4,
99-100 (1961).
* *7. С. E. С о о k. A general matched-filter analysis of linear FM pulse compres-
sion, Proc. IRE (Correspondence) 49, 831 (1961).
8. С. E. Coo к. Transmitter phase -modulation errors and pulse-compres-
sion waveform distortion, Microwave J. 6, 63—69 (1963).
9. W. M. Brown and C. J. Palermo. Theory of coherent systems,
IRE Trans, MIL-6, 187—196 (1962).
10. W. M. Brown and C. J. Palermo. Effects of phase errors on the
ambiguity function, IEEE Intern. Conv. Record, Pt. 4, 118—123 (1963).
11. D. K. Cneng. Degradation effects of arbitrary phase errors on high-
resolution radar performance. Proc. IEE (London) 111, 1375—1378 (1964).
12. J. De Lorenzo and D. D e Л n g e 1 i s. Real time measurement and
correction of phase distortion in high fidelity radars, IEEE Intern. Conv.
Record, Pt. 8, 96—103 (1963).
13. P. Rademacher and D. R a nd Ise. An automatic phase-correc-
tion system, IEEE Inter. Conv. Record, Pt. 3, 179—186 (1963).
14. J. F. Cer a r and С. E. С о о k. Electronic means for supperessing range
side lobes of a compressed-pulse signal, U. S. Patent № 3, 281, 842, Octo-
ber, 1966.
5. P a °* Рубин. «Зарубежная радиоэлектроника!, 1963,
ГЛАВА 12
УСТРОЙСТВА С ДИСПЕРСИОННЫМИ
X АРАКТЕ РИСТИК АМИ.
ЦЕПОЧКИ Т-ОБРАЗНЫХ ЗВЕНЬЕВ
12.1. Введение
В гл. 3 было показано, что при реализации согласованного
фильтра сжатия ЧМ импульса общего вида, который должен обра-
батывать сигнал
s (/) --- а (/) [cos ю01-F 0 (/)], (12.1)
ущественную роль играет дисперсионная характеристика группо-
вого запаздывания —ФХ*0)» связанная обратным соотношением
с функцией ЧМ 0'(О- Требуемую функцию задержки с дисперсией
можно получить множеством способов, начиная от использования
волновода в диапазоне СВЧ до ультразвуковых линий задержки
(УЛЗ) на умеренно низких частотах. На основании имеющейся
в гл. 11 информации о влиянии искажений можно видеть, что сте-
пень, с которой фактически существующая задержка соответствует
функции —Ф'(*°), может быть весьма критической в тех примене-
ниях, которые требуют, чтобы сжатый импульс имел очень низкие
уровни боковых лепестков по дальности. В распоряжении разра-
ботчика системы сжатия импульсов, который должен установить
технические требования к тщательно контролируемой функции за-
держки с дисперсией, имеется три основных метода:
1) использование фильтров, основанных на применении мо-
стовых Т-образных звеньев с сосредоточенными постоянными,
которые эквивалентны фазосдвигающему фильтру на постоянных
сопротивлениях;
2) применение УЛЗ, работающих в дисперсном режиме с подав-
лением колебаний, не удовлетворяющих условию дисперсности.
Этот метод равносилен применению мостовых Т-образных звеньев
в диапазоне ультразвуковых частот;
3) методы оптической обработки сигнала, использующие ана-
логию пространства и частотной области, которая достигается при
помощи преобразований Фурье. Она позволяет синтезировать функ-
444
цию задержки с дисперсией не как частотные, а как пространствен-
ные функции.
Каждый из перечисленных методов имеет свои преимущества
и недостатки. Для того чтобы синтезировать необходимую задерж-
ку с дисперсией при помощи рассматриваемых в данной главе мо-
стовых Т-образных звеньев, требуется использовать большое число
таких четырехполюсников. Поскольку они критически зависят от
величины погрешности в настройке, фильтр, составленный из боль-
шого числа Т-образных звеньев, нуждается в тщательном контроле
допусков составляющих его индуктивностей и емкостей, а также и
в тщательной настройке. Несмотря на это, первый настоящий успех
в применении системы сжатия импульсов был достигнут при ис-
пользовании таких конструкций, и этот метод все еще применим
в системах, где требуется ширина полосы частот, превышающая
несколько мегагерц. Кроме того, описываемые в данной главе
схемы с сосредоточенными постоянными, а также подход к их
расчету, полезно применить для компенсации искажений в систе-
мах сжатия импульсов, рассчитанных с использованием других
методов. Поэтому, несмотря на то обстоятельство, что синтезиро-
ванные дисперсионные фильтры, использующие мостовые Т-образ-
ные звенья, во многих случаях вытесняются ультразвуковыми и оп-
тическими устройствами, описываемыми в последующих главах,
знакомство с основными свойствами цепей, составленных из мосто-
вых Т-образных звеньев, для разработчика РЛС может оказаться
полезным. (
12.2. Фазосдвигающие цепи
Имеется несколько справочных руководств, в которых описаны
основные свойства мостовых Т-образных звеньев, используемых
в согласованных фильтрах сжатия импульсов. Здесь мы следуем
в основном теории, изложенной в работе О' Мира [1] и работе 12].
Согласованный фильтр сжатия импульсов нуждается в харак-
теристике, приводящей к задержке по времени с дисперсией, т. е.
в характеристике, которая изменяется как функция частоты и об-
ладает свойством минимального ослабления сигнала в используемой
полосе частот. Это условие исключает возможность применения
большинства стандартных звеньев фильтров, дисперсионность ко-
торых максимальна в области, прилегающей к граничной частоте.
Отправным пунктом для разработки цепи требуемого типа служит
показанное на рис. 12.1 звено в виде скрещенного четырехполюс-
ника. Его характеристическое сопротивление равно
Z, = VTX (12.2)
а передаточная функция
£ =. x~YZalZb (12 3)
445
Если налагается условие
ZaZb-\ или Zb = l/Za,
то Zt — 1 (чисто активное нормированное сопротивление) и
Е,
£* 1 + /Za
l-Z„
l + za
ехр | a—j₽ I,
(12.4)
где a—функция ослабления, а 0—фазовая передаточная функция.
Если, кроме того, Za—чисто реактивное сопротивление, так что
zo^/xa, zb=/xb,
то
СХР1 ~' "-‘‘А.!. . ох р [ - 2 / arctg Х„|. (12.5)
1+/х« /1+х* схр 14- jarctgXal
Нетрудно заметить, что вышеприведенная передаточная функция
не дает ослабления сигнала (т. е. a = 0) и ее фазовая характери-
стика
0 = 2arctgXo.
(12.6)
Такой класс четырехполюсников называется фазосдвигающим
фильтрбм на постоянных сопротивлениях с задержкой по времени.
La
Рис. 12.1. Схема скрещенного четырехпо- Рис. 12.2. Реактивные ветви
люсника. фазосдвигающего скрещенного
четырехполюсника второго по-
рядка.
Наиболее общей моделью звена фазосдвигающего фильтра, ис-
пользуемого в качестве основы для синтеза схемы сжатия импульса,
является скрещенный четырехполюсник второго порядка, Za и Zb
которого показаны на рис. 12.2. Допустим, что
1/Со = 2о0 (12.7)
и
1/£оС„ —1 /Lb Cb = <oS.
446
^laiaHausi^i!.
знание без границ “ ш
тогда
, 2оо 1 2а0
Lb~20.‘ Сь~й‘' <12-8)
Выражения для Lb и Сь получают исходя из требования
Ьо/— Lbl Ca — 1 •
Поэтому
/со/С 2/а0 ш
—9 2 —2 2
(0Q — вГ (Од —(О
И
v 2ао<о
'‘•а —2 2 *
“о-®
На основании выражений (12.5) и (12.10) получаем
(12.9)
(12.10)
Р = 2 arctg
2(то<о
“о—<°2
(12.11)
Сигналы на выходе согласованного фильтра, которые будут затем
обрабатываться, являются сигналами промежуточной частоты,
другими словами, обладают некоторой полосой частот и поэтому
соответствующая им задержка является групповой задержкой по
времени. Она имеет вид
Т = = Х
D do) d<o
. 2аою
2 arctg ---j
®о—ш
(12.12)
4ao((og+(o2)
(w2-co2)2-{-4a2 о2
(12.13)
В следующем разделе выводится приближенное выражение для
величины То, которое при определенных условиях является весьма
точным и более простым при расчетах.
12.3. Приближенное выражение для задержки в
фазосдвиеающем фильтре
Подставляя выражение (12.9) для Zo в передаточную функцию
(12.5) и полагая
447
s = /со, sa = — со«, 1 /Св = 2о0,
7
получаем соотношение
2so0
Е,
£i
14-—i-
“о 4 s
(12.14)
//(s) =
которое сводится к виду
//(S)
= sg—2sqo + <og (s-sOfs-s,)
s24-2sgo4-<Oq (s—Si)(s—s4)
(12.15)
где slt S3 — нули функции H(s), a sa, s4 — ее. полюсы.
Используем формулу кррней квадратного уравнения для на-
хождения полюсов и нулей передаточной функции; она дает
sli3 = ofl±> —(о2 = а0±/%,
s2.4 = -^о ± “ ао ± Ч»
(12.16)
где со? — о? — со?. На рис. 12.3 показана диаграмма нулей и
полюсов в комплексной частотной плоскости. В теории цепей связь
между общей фазой передаточной функции и показанными на
приведенной выше диаграмме углами определяется соотношением
0=2₽«-2₽о.
(12.17)
где рж определяет направление вектора, исходящего из полюса
к произвольной точке с вещественной частотой со, а 0О — направ-
ление вектора, исходящего из нуля в произвольную точку с веще-
ственной частотой со.
Для рассматриваемого случая ₽ = 2S0X. Обращаясь к диа-
грамме нулей и полюсов, нетрудно заметить, что
₽S1=arctg^l!-t p.^ arctg^S- (12.18)
°о о0
и
₽ = 2
[arctgJ^ + arctgJi±^l.
L Оо O# J
(12.19)
О’Мира делает следующие предположения относительно пара-
метров: со0/ог0>3, |<о0—со | < О,3со0 (ширина полосы ±30%).
448
^lalaUausi^
знание без границ * w
В случае <о0/о0--3 второй член (12.19) принимает* следующие
значения:
w = 0,7<оо, arctg = arctg 5,1 = 78°55',
°0
<о = о>„, arctg— = arctg 6,0 = 80’33', (12.20)
°о
со= 1,3<о0, arctg-^5 = arctg 6,9 = 81° 47'.
Go
По сравнению в вариациями первого члена функции (12.19) вблизи
частоты со = <оо второй член можно аппроксимировать линейной
Рис. 12.8. Диаграмма нулей и полюсов фазо-
сдвигающего скрещенного четырехпЬлюсника.
функцией, так что при выполнении вышеупомянутых предположе-
ний относительно параметров величину р можно выразить в виде
Р = 2 arctg -J- k со + С. (12.21)
°о
449
В таком случае групповая задержка становится равной
-------------------------------(,222)
аш j । j w wo j uq
\ 00 /
Приведенные выше значения показывают, что k достаточно мало,
поэтому
(12.23)
\ °о /
Для целей нормализации полагаем со—(оо = х и
Off—1
(12-24)
где 2о“о представляет собой максимальную задержку по времени,
получаемую при х = 0. Выражение (12.24) является приближенной
V
V
У
V
V
У
V
О,*
о,г
о
О 0,5 1,0 1,5 2,0 2,5 3,0 3.5 4,0 4>5
х, pat/се*
Рис. 12.4. Кривые задержки для. Т-образной мостовой схемы, вы-
численные по приближенным формулам О'Мир».
По ординате отложена величина 0.6 сек, определяемая согласно формуле
формулой О'Мира для групповой задержки, получаемой в рассмот-
ренном звене фазосдвигающего фильтра с постоянным сопротивле-
нием.
460
NalaHauswk
знание без ераниц “
Для пояснения заметим, что:
©о — резонансная частота для импедансов ветвей четырехпо-
люсника;
<оо — частота, на которой наблюдается максимальная за-
держка (в соответствии с приближенной формулой для
Td), и <оо > со0.
Зависимость величины То от нормализованных параметров о0 и
(о — соо = х показана на рис. 12.4. Из этих кривых можно полу-
чить определенную информацию, необходимую для синтеза фильт-
ра. Эта процедура описывается в разд. 12.5.
12.4. Преобразование скрещенного четырехполюсника
к несбалансированному виду
Скрещенный тип четырехполюсника, показанный на рис. 12.1,
сам по себе, вообще говоря, не является желательным, так как он
несимметричен относительно точки заземления. В любой точке
схемы этого четырехполюсника Не имеется общего опорного напря-
Рис. 12.5. Преобразование
скрещенного четырехполюсни-
ка к Т-образной мостовой
схеме с продольной перемыч-
кой.
жения и он весьма критичен ко всякому рассогласованию импедан-
сов своих ветвей. Для того чтобы получить более удобную схему,
скрещенный четырехполюсник необходимо преобразовать к не-
сбалансированному эквиваленту.
Рис. 12.5 иллюстрирует преобразования к мостовой Т-образной
схеме с продольной перемычкой. Условия эквивалентности схем
имеют вид
1^1. 1
22О * z'a 2ZC
(12.25)
2 2
451
Для случая скрещенного четырехполюсника, ветвями которого
служат показанные на рис. 12.2 элементы, эквивалентная мостовая
Т-образная схема с продольной перемычкой и минимальным числом
элементов показана на рис. 12.6. Данный конкретный переход при-
водит к показанным на рисунке
значениям элементов. От емкости
21. а
\2СдСЬ
Сд-Сь
2
Рис. 12.6. Т-образная мостовая
схема с минимальным числом
элементов.
Рис. 12.7. Т-образная мостовая
схема с неминимальным числом
элементов.
Емкость конденсатора, параллельного
индуктивности 2 L , берется равной
Cfl(l-*)/2.
в параллельной, идущей к заземлению ветви, будет зависеть, при><
ведет ли такое преобразование к реализуемым значениям элемен-
тов схемы. Эта емкость определяется соотношением
Q __ ^Сд_______________________________
' (Са/Сь)-1
Денормализованные значения Са и Сь равны
С 1
а 2а0Р0 ’
г - |2°°
где /?0—требуемое полное сопротивление цепи. Поэтому
„ 2Са
(12.26)
(12.27а)
(12.276)
(12.28)
откуда можно видеть, что условие реализуемости состоит в выпол-
нении неравенства
<d0/<J0>2. (12.29)
Можно также применять изображенную на рис. 12.7 схему
с неминимальным числом элементов, значения которых указаны
452
^lalaHaus^i
знание безераниц Ч
Рис. 12.8. Области физической осуществимости при преобразовании к
Т-образным мостовым схемам:
а —Т-образная схема с минимальным числом элементов; б —Т-образная схема с
неминимальным числом элементов-
Рис. 12.9. Эквивалентные реактивные ветви Т-образного
моста с минимальным числом элементов:
а —последовательная ветвь; б—параллельная ветвь.
Рис. 12.10. Эквивалентные реактивные ветви Т-образного
моста с неминимальным числом элементов:
а —последовательная ветвь; б —параллельная ветвь.
453
на рисунке. В этом случае емкость в параллельной ветви равна
r 2kCa
а условие реализуемости имеет вид
й0/а0 > 2//Т.
(12.30)
(12.31)
Поскольку к<1, оно является более жестким требованием, чем
условие (12.29). На рис. 12.8 в виде заштрихованных областей
плоскости комплексной частоты изображены зоны, в пределах ко-
торых должны находиться нули и полюсы [выражение (12.16)]
передаточной функции четырехполюсников, показанных на
рис. 12.6 и 12.7. Схему с неминимальным числом элементов можно
применять тогда, когда схема с минимальным числом приводит
к таким значениям компонент, которые трудно выполнить кон-
структивно. Эквивалентные схемы ветвей мостовых Т-образных
фильтров, содержащих минимальное и неминамальное число реак-
тивных элементов, показаны на рис. 12.9 и 12.10.
12.5. Пример, иллюстрирующий расчет схемы
линейной задержки
Нормализованные графики задержек, полученные О'Мира
для мостовой Т-образной схемы и показанные на рис. 12.4, служат
основой при получении сложной характеристики задержки с диспер-
сией путем комбинирования нескольких таких взаимно рас-
строенных по центральной частоте денормализованных кривых.
О'Мира рассчитал несколько основных схем линейной задержки по
времени, составленных из 1, 2, 3, 4 и 6 мостовых Т-образных звеньев.
Эффективность построения схемы линейной задержки О'Мира
определил в виде
4^^100%, (12.32)
где N — общее число использованных звеньев. Для характеристик
линейной задержки, рассчитанных так, чтобы отклонение от ли-
нейности составляло приблизительно ± 1 %, эффективность в первом
приближении запишется как
т)~ 10п%,
где п — число звеньев в основной схеме. Количество звеньев опре-
деляет допустимый разброс параметров используемых индуктивно-
стей и емкостей и число пульсаций на кривой ошибки в задержке
по времени (и, следовательно, оказывает влияние на процесс кор-
рекции задержки). Для иллюстрации синтеза линейной* функции
454
па1аПаи$Ж
знание без границ *
задержки будут использованы данные, приведенные О'Мира для
схемы, состоящей из трех взаимно расстроенных звеньев.
В полученных нормализованных кривых были использованы
параметры o“J и х, где 2о~о — максимальная задержка при х = 0;
х = со — (оо — нормированная частота. Для схемы, состоящей
из трех мостовых Т-образных звеньев, О' Мира получает следующие
соотношения между этими параметрами [11:
хх = 0 аГ‘ = 1,00,
xt = 1 о?1 = 0,65,
х8 = 2,6 оГ1 =0,54.
На рис. 12.11 графически показана нормализованная результи-
рующая задержка для трехзвеньевой схемы О' Мира. Линейный
участок этой кривой простирается от х = 0,26 до х = 4,34, причем
Рис. /2.11. Аппроксимация линейной характеристики
задержки трехзвеньевой схемы (N = 3).
центр расположен при х = 2,3. Для того чтобы денормализовать
эту кривую с тем, чтобы она точно соответствовала конкретному
случаю, необходимо знать следующее:
fo — требуемую центральную частоту схемы; Д/ — полосу
частот, в которой должна обеспечиваться линейная задержка.
При наличии этих данных для определения фактической вели-
чины задержки трехзвеньевой схемы на произвольной частоте
вблизи f0 можно воспользоваться денормализирующим полосу
множителем 2nAflt±x по формуле
t
^фактич 2лД//Дх ‘
(12.33)
455
Значения денормализованных частот, на которых задержка макси-
мальна, относительно f0 получаются из соотношения
,(=/,_(*»=£!>^. = /,_(ж,_х,) (12.34)
2л, Дх Дх
В качестве примера можно рассмотреть следующие значения:
f0 = 5 Мгц, Д/ = 1,6 Мгц.
Поскольку в трехзвеньевой схеме О'Мира Дх = 4,08, а х0=2,3,
из соотношения (12.34) получаем значения максимально задер-
жанных частот для каждого звена:
/, = 5—(2,3-0)-1£- =4,098 Мгц;
4,08
f, = 5—(2,3-1)4£ =4,49 Мгц;
4,UO
/, = 5-(2,3-2.6)-^- = 5,112 Мгц.
На основании соотношения (12.16)
(12.35)
Денормализованные значения о, определяются соотношением
(12.36)
1 Дха~
так что:
/<,. = = 0,392 Мгц,
f„, = ^ =0,603 Мгц,
0,65
/а. = °^=0,726 Мгц.
0,54
Подставляя эти значения в (12.35), получаем следующие частоты
настройки трехзвеньевой схемы: _
= 4,10 Мгц,
f2 = 4,53 Мгц,
73 = 5,18 Мгц.
При наличии указанной выше информации, используя формулы
(12.7), (12.8)уи (12.26)—(12.30), можно рассчитать значения элемен-
тов основной трехзвеньевой схемы, показанных на рис. 12.6 и 12.7.
456
^alatiauStM
знание без границ * *
(12.37)
Эти значения будут соответствовать единичному импедансу. Как
только величина Ro установлена, фактические значения элементов
можно определить по расчетным формулам
т __ п т р _______Срдсчет
^фактич 0 ^расчет» '“'фактич о
Ко
Трехзвеньевая схема О' Мира будет иметь ошибку задержки по
времени, равную приблизительно 1% относительно полного диа-
пазона линейной задержки. Очевидно, это достаточно малая ошибка.
Однако, как показано в гл. 11, допустимая ошибка задержки осно-
вывается не на относительном, а на абсолютном значении отклоне-
ния задержки от линейной. Поэтому по мере того, как величина пол-
ного диапазона задержки увеличивается с целью получения более
высоких значений коэффициента сжатия, относительная ошибка
должна уменьшаться, чтобы сохранить ошибку в задержке и об-
условленные искажениями боковые лепестки на фиксированном
уровне. Здесь начинают действовать многие практические факторы,
такие, как накопленный эффект рассогласования импедансов в длин-
ной линии задержки, влияние паразитных индуктивностей и емко-
стей на теоретическую кривую задержки и последствия применения
компонент с заданным допуском. Вследствие этого на следующей
стадии нет необходимости заниматься улучшением теоретического
качества кривой задержки с целью еще большего уменьшения ошиб-
ки задержки. Ниже описывается метод, использующий рассмотрен-
ные выше схемы, который с успехом был применен для получения-
улучшенной линейности задержки.
На рис. 12.12 показаны результаты измерения задержки по
времени, которые были получены на трех трехзвеньевых схемах,
базирующихся на рассчитанных выше конструктивных параметрах.
Из-за упомянутых выше практических факторов ошибка задержки
возросла по сравнению с значениями ошибки, достигнутыми О' Мира
Чтобы получить более регулярную форму кривой задержки
в данной схеме рассчитывались незначительные изменения в ве-
личинах oi и Цель этой процедуры состояла в том, чтобы,
основываясь на методах частотного масштабирования, синтезиро-
вать вторую кривую задержки, имеющую пульсации, которые
в основном отличаются по фазе на 180° от пульсаций первой кри-
вой.
Сказанное иллюстрируется штриховой линией на рис. 12.12,
где показана кривая задержки, измеренная для последовательности
из трех основных трехзвеньевых схем, частоты которых были про-
порционально уменьшены в 1,02 раза. Сочетание двух таких кривых
задержки (измеренных для шести трехзвеньевых схем) также при-
ведено на рис. 12.12. Эффект уменьшения ошибки задержки, до-
стигнутый этим методом, является значительным. Несмотря на это,
в случае, когда производится каскадное соединение большого числа
комбинированных задерживающих устройств, результирующая
457
ошибка в задержке может оказаться все. же слишком большой и для
снижения ошибки, возможно, окажутся необходимыми дальнейшие
шаги. Это-t вопрос рассматривается в следующем разделе.
Оценку общего числа секций, необходимых для данного приме-
нения, можно получить из формулы
N =_____________
Д^(Дх/2лД/) ’
(12.38)
где ДТ — полная разность задержек, требуемая в полосе. Д/;
ДТ — нормализованная разность задержек, получаемая на основа-
нии данных О7 Мира, а 2лД/7Дх — денормйрующий множитель.
Рис. 12.12. Уменьшение ошибки задержки ме-
тодом частотного масштабирования исходных
расчетных данных.
Применяя это соотношение из вышерассмотренного примера к трех-
звеньевой схеме, в которой требуется получить общую задержку
50 мксек, находим
N — ————=50 трехзвеньевых секций.
(3,34—0,88)-----------
1 16,28X1.6
Рассмотрение окончательных технических требований к синтези-
руемым устройствам производится в следующем разделе.
458
NalallausX
знание без границ “ ш
/2.6. Коррекция ошибок согласованного фильтра
Описанный в предыдущем разделе метод групповой расстройки
может оказаться весьма полезным для компенсации некоторых
видов ошибок задержки. Тем не менее в процессе монтажа слож-
ного согласованного фильтра остаточная ошибка задержки может
достигнуть уровня, который превышает предельную границу, уста-
новленную для системы. Кроме того, после сборки сложного согла-
сованного фильтра сжатия импульсов имеются и другие источники
ошибок задержки. Поэтому возможно возникнет необходимость
включить в его состав устройство для результирующей коррекции
ошибок. При проектировании устройств результирующей коррек-
ции ошибок первым шагом является определение частотной зави-
симости ошибки для смонтированного фильтра в целом. Это делается
путем точного измерения задержки и нанесения на график разности
между измененной и заданной кривыми.
Сказанное поясняется рис. 12.13, где’информция об ошибке
в схеме, состоящей из 30 трехзвеньевых секций, рассмотренных
в примере синтеза в предыдущем разделе (кривая а), сравнивается
с частотной характеристикой идеальной задержки. Идеальная ча-
стотная характеристика показана штриховой горизонтальной ли-
нией, проходящей через; нулевую координату задержки. Схема
цепи коррекции задержки зависит от комбинации частотных харак-
теристик, полученных О' Мира. Для рассматриваемого случая была
применена комбинация на четырех таких * мостовых Т-образных
звеньев, дающих задержку по времени. Их индивидуальные и ре-
зультирующая функции задержки показаны на рис. 12.14. Резуль-
тат присоединения этой комбинации корректоров к фильтру показан
на рис. 12.13 (кривая б). Другая эталонная пунктирная линия отра-
жает результат сложения фиксированной задержки с первоначаль-
ной эталонной линией. Тем не менее, пока обе линии остаются па-
раллельными, такое сложение не влияет на свойства сжатия согла-
сованного фильтра, приводя лишь к дополнительной фиксированной
задержке сигналов на его выходе. В данном примере влияние этих
корректоров привело к снижению ошибки задержки в четыре раза.
Однако при этом возрастает также частота пульсаций, так что
наблюдается даже большее снижение фазовой ошибки, которая,
как показал проведенный в гл. И анализ парных эхо', фактически
является наиболее важным критерием. Если фазовая ошибка описы-
вается синусоидой
ре = б1 sin С(о, (12.39)
то обусловленная ею ошибка задержки равна
t' = = bt С cos Са. (12.40)
dco
459
I
LOO
I
§
I
-0,25
1,75
1,50 -
Заданный уровень задержки
после коррекции
б) Кри бая ошибки после коррекции
0,25
О
Заданный
уровень *
линейной
задержки
5,0
Частота, Мгц
6,0
Рис. 12.13. Величины ошибок линейной задержки.
Частота, Мец
Рис. 12.14. Синтез функции, корректирующей ошибки
задержки.
460
Nalattausjek
знание без границ - *
Отсюда можно видеть, что при фиксированном пиковом значении
ошибки задержки максимальная фазовая ошибка обратно пропор-
циональна С — числу периодов функции ошибки задержки во
всей полосе Д/. В конкретной практической разработке может по-
требоваться по отдельности или вместе метод групповой расстройки
и коррекция функции задержки. Однако предпринимаемые в дей-
ствительности шаги будут в значительной степени зависеть от
оценки разработчиком имеющейся информации о кривой ошибок.
При синтезе функции, корректирующей ошибки задержки,
полезнее использовать стандартизированную, а не нормализован-
ную кривую задержки. Из соотношений (12.27, а) и (12.24) для мак-
симальной задержки, получаемой в фазосдвигающих • фильтрах
с мостовыми Т-образными звеньями, можно найти связь между емко-
стью последовательной ветви Т-образного мостового четырехполюс-
ника и максимальной задержкой
Ca = tD9/4R0. (12.41)
Поскольку максимальная величина задержки определяет все дру-
гие параметры частотной характеристики задержки, значение
центральной частоты схемы не будет влиять на форму характери-
стики после того, как величина максимальной задержки уже вы-
брана. Поэтому из кривой ошибки задержки можно определить
приблизительную величину вклада пиковой задержки, требуемой
от каждого мостового Т-образного корректора, оценивая значение
частоты, на которой наблюдается максимальная задержка. Если
после рассмотрения кривой, корректирующей результирующую
задержку, потребуются дополнительные регулировки, то значения
центральных частот, на которых наблюдаются максимальные за-
держки, могут быть изменены. Вследствие только, что описанного
свойства это не повлияет на форму каждой составляющей частотной
характеристики задержки, поскольку максимальные значения за-
держки остаются неизменными. Для того, чтобы произвести синтез
таким способом, необходимо использовать стандартные частотные
характеристики задержки. В табл. 12.1 и на рис. 12.15 представлены
данные для нескольких таких стандартных характеристик задержки;
Как показано на примере рис. 12.14, если подходящая комби-
нация максимальных задержек и связанные с ними частоты уже
выбраны, то элементы каждого мостового Т-образного звена можно
рассчитать на основании соотношений (12.7) и (12.8). Поскольку
метод расчета приводит к значениям ot и ft (частоте, на которой
задержка максимальна), частота настройки каждого звена может
быть получена из соотношения (12.35).
Данные, приведенные в табл. 12.1, были рассчитаны для зна-
чений максимальной задержки, необходимых для использования
в рассмотренном примере синтеза. Если требуется получить набор
характеристик задержки, который охватывал бы широкую полосу
461
Таблица 12Л
Стандартные величины задержки (в микросекундах)
для частот |/0—f\ (в мегагерцах)
0,0 0,1 0,2 0,3 0,4 0,5 0.6 0,7 0,8 0,9 1.0
0,25 0,247 0,244 0,238 0,226 0,216 0,204 0,191 0,179 0,166 0,155
0,50 0,488 0,455 0,408 0,360 0,310 0,265 0,224 0,190 0,168 0,145
0,75 0,712 0,610 0,500 0,394 0,315 0,251 0,202 0,163 0,135 0,114
1,00 0,910 0,720 0,530 0,380 0,290 0,220 0,170 0,140 0,110 0,092
1,25 1,025 0,775 0,525 0,362 0,256 0,187 0,134 0,115 0,093 0,076
1,50 1,220 0,788 0,502 0,326 0,228 0,166 0,126 0,098 0,078 0,064
1,75 1,340 0,788 0,472 0,298 0,205 0,147 0,110 0,086 0,068 0,056
2,00 1,440 0,760 0,440 0,280 0,194 0,130 0,098 0,077 0,060 0,049
0,0 1.1 1,2 1.3 1.4 1 .Б 1.6 1.7 1.8 1.9 2,0
0,25 0,142 0,131 0,120 0,112 0,105 0,095 0,089 0,084 0,078 0,072
0,50 0,125 0,110 0,095 0,085 0,076 0,070 0,062 0,055 0,050 —
0,75 0,098 0,083 “0,071 0,063 0,055 0,049 0,044 0,039 —
1,00' 0,077 0,065 0,056 0,049 0,043 0,038 — — 1 — — —
1,25 0,064 0,054 0,046 0,042 •— — — — —
частот, то эти стандартные данные можно преобразовать для полу-
чения корректирующих задержку функций с меньшими (или боль-
шими) пиковыми значениями и в более широком (или в более узком)
частотном диапазоне. Это достигается путем умножения величины
пиковой задержки, и тем самым значения Са, на требуемый множи-
тель и деления частотных приращений на то же самое число. Так, на-
пример, если при использовании более широкой полосы требуется
вдвое меньшее значение максимальной задержки, каждое значение
задержки в требуемом ряду таблицы умножается на 1/2, а прира-
щения частот вместо 0,1 Мгц становятся равными 0,2 Мгц. Этот
метод можно считать вариацией метода О' Мира, реализованного
для конкретного применения. Установлено, что стандартные ча-
стотные характеристики задержки являются полезными для решения
проблемы коррекции ошибки задержки.
Второй основной причиной неидеальной реализации согласо-
ванного фильтра является неплоская амплитудно-частотная ха-
рактеристика фильтра сжатия. Она отражает результаты примене-
ния неидеальных компонент (т. е. компонент с конечными Q), в ко-
торых вследствие потерь наблюдается ослабление сигнала. Затуха-
ние этого вида может стать весьма большим в линии задержки, со-
462
’NataUauslM
знание без границ ' *
Рис. 12.15. Нормализованные кривые задержки
для скрещенного четырехполюсника второго по-
рядка, имеющего постоянное сопротивление
(в приближении О'Мира).
Рис. 12.16. Схема амплитудного корректора с постоянным со-
противлением.
Сопротивление в параллельной цепочке берется рапным (tn1— 1) R/2tn.
463
ставленной из многих звеньев. В общем виде влияние потерь опи-
сывается выражением, полученным Бодэ [31:
= (12.42)
Q da •
где АЛ — ослабление амплитуды, обусловленное потерями;
Q равно Q всех реактивных элементов (предполагаемых одинако-
выми), a dp/d(o — функция задержки фильтра.
Часто предполагается, что множитель о/Q сохраняется сравни-
тельно постоянным в достаточно узкой полосе частот, так что до-
полнительная функция ослабления связывается со значениями функ-
ции задержки по времени. В случае линейной функции задержки
ослабление должно быть приблизительно линейной функцией ча-
стоты, являясь наибольшим там, где задержка максимальна. Это
иллюстрируется изображенной на рис. 12.17 характеристикой
ослабления сигнала в схеме, рассчитанной ранее в качестве примера.
Для того чтобы скорректировать этот вид затухания, схему можно
дополнить устройством коррекции амплитудно-частотной харак-
теристики, т. е. выравнивателем. Для этой цели часто используется
показанная на рис. 12.16 схема амплитудной коррекции, имеющая
постоянное сопротивление. Вносимое цепью этого типа затухание
определяется выражением
ехр|2Д1 = 1+(1+'”)ауа , (12.43)
где т — cth Лоо, Лоо—максимальное затухание, а
v 7 aif—asP
' Примерная функция, описывающая вносимое затухание, по-
казана на рис. 12.16. Выбор т влияет на максимальную величину
вносимого затухания, а значения alt а3 и Ъг определяют критиче-
ские частоты Д и /2, и поэтому общую форму кривой. Значения
элементов Т-образной мостовой схемы с продольной перемычкой
связаны с этими параметрами соотношениями
— Ьа-1 ,
—» G2 = —------------, =. (12.44)
13 л 12 .. «1 , h i
4ла Lu — *
Яз аз
— = —= — = Яо (Яо—характеристическое сопротивление).
Сгз С 21 С12
На практике параметры функции вносимого затухания регу-
лируются так, что корректирующая амплитуду характеристика
располагается либо вблизи flt либо /2. Результат объединения
функции ослабления этого вида и амплитудно-частотной характе-
464
AalalfausA
знание без границ “ ш
ристики самой схемы сжатия, рассмотренной в качестве примера,
показан на рис. 12.17. Результирующая функция имеет требуемую
плоскую характеристику затухания в интервале Д/. На практике
общую характеристику амплитудной коррекции обычно реализуют
при помощи нескольких выравнивающих четырехполюсников,
которые могут быть распределены по всей сжимающей линии за-
держки.' Если полное вносимое затухание становится большим, то
через определенные интервалы в тракт линии задержки можно так-
же включить усилители. На практике часто объединяют амплитуд-
ный корректор и буферный усилитель в один конструктивный блок.
О
-1
дб
-2
X apa кт ери стика
корректора
S Амплитудно-
- частотная
характеристика
трехкаскадной
схемы
/Результирующая"^^***1
кридая
V $ ~690
Частота, Мщ
Рис. 12.17. Результирующие данные амплитудной
коррекции.
Необходимо отметить, что каждая из этих дополнительных цепей
будет оказывать влияние на кривую ошибок задержки и ее следует
принять во внимание при коррекции ошибки в соответствующей
части схемы. Большое* число вариантов корректирующих схем опи-
сано Цобелем 14] и Мидом [5].
Источниками ошибок при синтезе согласованного фильтра
являются не только неточности, связанные с приближенностью
расчета, но также и неточности изготовления компонент, рассогла-
сование импедансов и погрешности в настройке. Именно эта прак-
тическая сторона может беспокоить разработчика системы. Благо-
даря применению качественных компонент, точной измерительной
аппаратуры и аккуратности в работе зачастую можно обойтись
без излишних дополнительных усилий, связанных с коррекцией
фазы. Совокупное влияние допусков компонентов мостовой Т-об-
разной схемы на уровень обусловленных парными эхо боковых
лепестков сжатого импульса показано на рис. 12.18. Указанные
на графике величины допустимых отклонений представляют собой
среднеквадратичное значение допусков на компоненты [6].
Методы проектирования задержки с дисперсией и коррекции
ошибок, рассмотренные в данном и предыдущем разделах, основы-
16 Зак. 1341 465
вались на использовании результатов расчета линейной задержки,
проведенного в качестве примера. Тем не менее, общие методы плюс
конкретный подход к проблеме коррекции ошибок можно исполь-
зовать при решении задачи синтеза любого согласованного фильтра,
хотя саму по себе основную функцию задержки, возможно, при-
дется рассчитывать на ЦВМ, если это будет нелегко сделать при
помощи приближенных графических методов построения нелиней-
ных функций задержки. Проблема синтеза произвольной групповой
Рис. 12.18. Влияние величины
отклонения параметров компо-
нентов от заданных на уровень
искажающих боковых лепестков.
Отклонение частоты в 10 раз меньше
отклонений параметров компонентов.
задержки и фазовой характеристики была рассмотрена также
О' Мира [7]. Другие методы синтеза дисперсионной линии задержки
на сосредоточенных элементах, основанные на использовании фазо-
сдвигающих фильтров, описываются Брендоном 181 и Стьюардом
19].
12.7. Настройка мостовых Т-образных звеньев
- фазосдвигающего фильтра
В звене фазосдвигающего фильтра, являющемся скрещенным
четырехполюсником, элементы Za и Zb резонируют на частоте <d0-
Элементы звена в виде мостовой Т-образной схемы, которые экви-
валентны Za и Zb, также должны резонировать на этой частоте. Эти
элементы можно вычислить при помощи формул преобразования
(12.25)
-!-= 4 + — = Д- +/«>— (12.45)
2Za Za 2ZC J(i)2Lc 2
При резонансе Za приближается к бесконечности и в таком случае
фактическая величина резонансной частоты равна
То =---------—-------. (12.46>
(2л)’ (2ia) (С«/2)
466
yalullaustk
знание без араниц * w
Исходя из этого соотношения, нетрудно понять, что элементами,
эквивалентными Za, являются индуктивность 2La и емкость CJ2,
соединенные параллельно (см. рис. 12.9).
Элементы, эквивалентные Za, получаются аналогичным обра-
зом из формул (12.25):
_ •?' । ___ . Lfc ! 1 j 1
---— Lh “Г = / <0----------------+ ------.
2 2 1 2 /<oCe 2/toCa
(12.47)
При резонансе 2ь = 0 и фактическое значение резонансной час-
тоты равно
72 ________1_______
'° " /о и Lb с« 2С°
(2я)Т
(12.48)
Эквивалентные последовательные и параллельные элементы
для мостового Т-образного звена с минимальным числом элементов
показаны на рис. 12.9. Зачастую используется звено с неминималь-
ным числом элементов, так как в этом случае можно предусмотреть
настройку каждого элемента на резонансную частоту. Для схемы
этого звена на рис. 12.10 показаны эквивалентные последовательные
и параллельные элементы.
Настройку этих элементов на резонансную частоту можно про-
извести путем наблюдения относительной величины напряжения
на выходе Т-образного звена, когда оно подключено к изображенной
на рис. 12.19 контрольно-испытательной схеме. Генератор качаю-
щейся частоты используется для получения на экране осциллографа
зависимости напряжения сигнала от частоты, где резонанс опреде-
ляется по минимуму выходного напряжения, а требуемое значение
частоты f0 при помощи калиброванного генератора частоты, стаби-
лизированного кварцем.
Последовательный элемент можно настраивать, отсоединяя
катушку индуктивности Lbl2 от точки соединения двух конденса-
торов (kCa) и изменяя емкость конденсатора С2 или индуктивность
катушки 2La с тем, чтобы на определенной частоте получить мини-
мальное выходное напряжение. Однако если емкость между зазем-
лением схемы и заземлением цепи сигнала окажется достаточно
малой, то катушку индуктивности можно присоединить слева.
При этом условии схема, эквивалентная испытательной, также при-
ведена на рис. 12.19. Если отношение CJCX можно поддерживать
свыше 100, то суммарное влияние ошибки в частоте настройки не
превысит 0,2%.
Настройка параллельного элемента осуществляется путем
замыкания накоротко катушки 2La и подстройки конденсатора Се
или катушки индуктивности Lbl2 до получения минимального вы-
16* 467
ходного напряжения на определенной частоте. Эквивалентная схема
такой испытательной цепи показана на рис. 12.20.
Выходное напряжение определяется уравнением
. Са4~2Со \
2 V 2 + 2foCoCa /
^0 , / . , Са~\-2Са \
2 + V 2 + 2jG)CaCe '
0, когда «о2 =
С<+2СО ____ 2
-----------— (Оо-
2CeCa(Lb/2)
(12.49)
(12.50)
В этом случае отсчитываемая частота совпадает с фактической
резонансной частотой параллельного элемента. Однако, чтобы
исключить ошибки, обусловленные остаточными параметрами изме-
Рис. 12.19. Схема контрольно-испытательного устройства [для
настройки Т-образной мостовой схемы.
рительной цепи, при измерении напряжения на выводах параллель-
ного элемента необходимо принять меры предосторожности, ис-
пользуя короткие провода. Когда фильтр с дисперсионной задерж-
кой содержит много мостовых Т-образных звеньев, можно приме-
нить указанную на рис. 12.19 контрольную аппаратуру, используя
468
flalaHausiM
знание без ераниц * ш
испытательный пробник, с помощью которого быстро проверяются
отдельные Звенья, до того как будет произведено окончательное сое-
динение фильтра. Если соединение уже произведено, то для даль-
нейшей проверки точности на-
стройки исследуется поведение
входного и выходного импедансов.
Функцию входного импеданса
можно получить при помощи
устройства, блок-схема которого
показана на рис. 12.21, а. Вы-
ходной импеданс можно найти, по-
меняв местами входные и выход-
ные провода испытуемой схемы.
Частотные зависимости импедан-
Рис. 12.20. Эквивалентная схема
контрольно-испытательной цепи
при настройке параллельного
элемента.
сов, воспроизведенные на экране
осциллографа, показаны на
рис. 12.21, б. Из этих данных
можно получить КСВН и он должен
быть, в основном, одинаковым как для входа, так и для выхода.
В таком случае можно вычислить затухание сигнала при отражении
Входной импеданс Вьгходнои импеданс
Рис. 12.21. Контрольно-измерительное устройство для измере-
ния импедансов дисперсионной линии задержки:
а — схема измерений; б—сигналила экране осциллографа*
и распространении в прямом и обратном направлениях (26 дб при
КСВН = 1,1; 32 дб при КСВН= 1,05). Относительная амплитуда
паразитных выходных сигналов, обусловленных отражением, нахо-
469
дится путем добавления к затуханию при отражении потерь, вно-
симых при распространении в обоих направлениях, с учетом эф-
фекта рассогласования линейной задержки в тот момент времени,
когда отраженный сигнал достигает выхода, (см. разд. 6.6). При
значении КСВН в интервале 1,05—1,1 ложные отклики получают-
ся на 30—40 дб ниже уровня полезного сигнала. Если фильтр
сжатия содержит буферные усилители, то длина пути отраженного
сигнала равна тому участку фильтра, который расположен между
двумя соседними усилителями.
На более низких частотах также становится осуществимой
коррекция Q последовательных и параллельных элементов каждого
Т-образного мостового звена. Если Q2La <Z QLb/2, то это выпол-
няется путем включения последовательно с индуктивностью не-
большого переменного сопротивления и регулирования его до полу-
чения на выходе испытуемой схемы плоской характеристики во всей
полосе частот. При обратном условии Qslo > QLb/2 ту же самую
регулировку можно произвести, установив параллельно катушке
индуктивности 2La большое переменное сопротивление. Эта про-
цедура может снизить интегральное влияние фазовых ошибок и
ошибок из-за рассогласования.
Л И.ТЕРАТУРА
1. Т. R. О’М е а г a. The synthesis of «band-pass», all-pass time delay networks
with graphical approximation techniques (3rd. ed.), Hughes Aircraft Co.,
Res. Lab., Malibu, California, Rept. 114 (February 1962).
2. R. Bruch and С. E. С о о k. Summary of pulse-compression studies and
filter techniques, unpublished design data, Sperry Gyroscope Co., Great
Neck, New Vork (1961).
*3. H. W. В о d e. Network Analysis and Feedback Amplifier Design. Van Nos-
trand, Princeton, New Jersey, 1945.
4. O. J. Z о b e 1. Distortion correction in electrical circuits, Bell Syst. Techn.
J. 7, Ns 3, 438—534 (1928).
5. S. P. M e a d. Phase distortion and phase distortion correction, Bell. Syst.
Techn. J. 7, Ns 2, 195—224 (1928).
6. S. E. В о g о t c h and R. Brackenbury, private communication
(1962).
7. T. R. O’M e a r a. Maximally flat approximations to arbitrary group delay
and phase functions with Padd approximants, Hughes Aircraft Co., Res.
Lab. Malibu, California, Rept. 159 (November, 1960).
8. P. S. Brandon. The design methods for lump-constant dispersive net-
works suitable for pulse-compression radar, Marconi Rev. 28, 225—253 (1965).
9. K. W. F. S t e w a r d. A practical dispersive network system, Marconi Rev.
28, 254—272 (1965).
• «
♦
3. Боде. Теория цепей и проектированье усилителей с обратной связью.
Издательство иностранной литературы, 1948.
ftafalfausrffc
знание без границ ’
ГЛАВА 13
УСТРОЙСТВА
С ДИСПЕРСИОННЫМИ ХАРАКТЕРИСТИКАМИ.
УЛЬТРАЗВУКОВЫЕ ЛИНИИ ЗАДЕРЖКИ
13.1 Введение
Как было указано в предыдущей главе, разработка и конструи-
рование фильтров с дисперсионными характеристиками групповой
временной задержки могут быть осуществлены несколькими раз-
личными путями. Если разработка таких устройств основана на
использовании схем, состоящих из мостовых Т-образных секций,
то, как мы уже видели, процедура их согласования и проведение
измерений могут потребовать значительных усилий. Кроме того,
для построения необходимого числа секций потребуется большое
число катушек индуктивности и конденсаторов. Из примера, при-
веденного в разд. 12.5, видно, что для обработки ЛЧМ сигнала,
имеющего произведение длительности на полосу 80, необходимо
порядка 50 трехзвеньевых мостовых Т-образных секций (или 150
отдельных мостовых Т-образных звеньев). В данном примере при-
веденное число является, по-видимому, несколько оптимистичным,
так как в связи с требованиями к допустимой ошибке величины за-
держки уменьшается используемая ширина полосы разрабатывае-
мого фильтра.
Вследствие сложности и громоздкости схем с сосредоточенными
параметрами были предприняты поиски других возможных прин-
ципов построения дисперсионных линий задержки. Одним из наи-
более успешных методов в настоящее время с точки зрения их при-
менения в системах сжатия импульсов явилось построение диспер-
сионных ультразвуковых линий задержки (УЛЗ). Функционирова-
ние этих устройств основано на свойствах направленного распро-
странения волн в некоторых цилиндрических или прямоугольных
твердых стержнях. Обычно считалось, что такой тип УЛЗ обеспе-
чивает фиксированную задержку. Однако было известно, что в огра-
ниченном диапазоне частот тонкие проволочки обладают дисперсион-
ными свойствами для нескольких различных мод и типов распро-
471
странения волн [1]. Это свойство часто называют свойством геомет-
рической дисперсиойности, так как оно зависит от геометрии среды
распространения и ее соотношения с размерами длины ультразвуко-
вой волны, а не от свойств самой среды. Именно реализация этих
дисперсионных свойств проволочек и полосок в практических
устройствах позволила применить УЛЗ в радиолокационных си-
стемах, использующих сжатие импульсов.
В большинстве случаев разработчик фильтров для сжатия им-
пульсов не будет сам участвовать в непосредственном изготовлении
элементов УЛЗ, как например в случае использования мостовых
Т-образных звеньев. Однако разработчик системы будет обязан
определить требования к параметрам и рабочим характеристикам
линий, которые должны обеспечить изготовители УЛЗ, и точно
также он должен уметь оценить полученные результаты. Поэтому
разработчику следует понимать основные принципы работы таких
устройств и знать их существенные параметры. В следующих раз-
делах рассматриваются факторы, которые должны представлять
интерес для специалиста по оптимальным фильтрам и сжатию им-
пульсов. Основные работы в этой области выполнили Мейцлер
[2—4], Микер [5, 6], Мэй [7] и Фитч [8, 9]. Тщательное рассмотре-
ние теории распространения направленных волн в изотропной гомо-
генной среде выполнили Микер и Мейцлер [10]. Расчет, практи-
ческое построение и применение УЛЗ с направленным распростра-
нением волн (дисперсионных и недисперсионных) рассмотрены
Мэем .[11]. Обширную библиографию и соответствующие ссылки
можно найти в двух последних из упомянутых работ. Более поздние
методы применения УЛЗ в системах со сжатием импульсов основаны
на создании решеточных структур, у которых характеристики за-
держки зависят от частоты.
13.2. Распространение ультразвуковых волн
в изотропной упругой среде
Различают несколько видов распространения ультразвуковых
волн в упругой среде. Двумя основными типами волн являются
продольные (растяжение или сжатие) волны и волны сдвига (или
поперечные). При продольных волнах смещение частиц в упругой
среде происходит в направлении распространения волн; при попе-
речных волнах смещение частиц происходит в направлении, попе-
речном распространению волны. Это показано на рис. 13.1. Смеще-
ние частиц в среде происходит вследствие воздействия ультразвуко-
вого давления, вызванного каким-либо видом деформации (или
напряжения) внутри среды, как показано на рисунке. Для создания
этих двух основных типов механических волн в УЛЗ могут быть
использованы электромеханические преобразователи, которые
472
ftalatiauswi}
знание без границ ’ *
колеблются либо в поперечной, либо в продольной моде при подаче
на них электрического сигнала.
В упругой среде возможны также и другие виды волн, напри-
мер, волны изгиба в пластинке или полоске, как показано на
рис. 13.1, в, или крутильные волны в цилиндре или проволоке.
При разработке УЛЗ, применяющихся в системах сжатия импуль-
сов, обычно сталкиваются с наличием нежелательных мод распро-
странения и часто необходимы большие усилия и принятие мер
Направление распространения
Рис. 13.1. Типы распростране-
ния упругих волн в твердом
теле:
°—продольная волна; б—волна
сдвига; в—волна изгиба.
предосторожности для подавления их, так как энергия сигнала,
распространяющегося с этими модами, будет вызывать искажения
на выходе ультразвукового фильтра.
Свойства распространения упругих волн характеризуются
двумя независимыми упругими постоянными — модулем Юнга Е
и коэффициентом (или отношением) Пуассона о. Пусть однородный
цилиндрический стержень длиной L с площадью поперечного се-
чения А удлиняется на величину AL, если приложена растягиваю-
щая сила F. Модуль Юнга, или модуль продольной упругости, есть
коэффициент пропорциональности между приложенным давлением
(FM) и деформацией или растяжением (AL/L), т. е.
Е_ F/A
AL/L
(13.1)
Коэффициент Пуассона связан с изменением площади попереч-
ного сечения при продольной деформации стержня. Если диаметр
473
стержня равен d, а изменение диаметра равно Ad, то коэффициент
Пуассона определяется в виде
(13.2)
a=_^fL.
AI./L
Для большинства известных материалов 0,1 < о < 0,4. Параметры
£ и о являются постоянными в изотропном гомогенном твердом
теле, если только не превзойден предел упругости среды. Они не
зависят от размеров и формы образца и с их помощью можно опре-
делить все упругие свойства изотропного гомогенного твердого
тела. Коэффициент Пуассона является существенным фактором
при определении дисперсионных характеристик задержки в УЛЗ
с направленным распространением волны. Типичные значения и
для различных материалов приведены в табл. 13.1.
Таблица 13.1
Значения коэффициента Пуассона
для различных материалов
Материал о
Сталь .....................
Медь.......................
Алюминий.....................
Латунь ....................
Резина ....................
Стекло (специальные сорта) .
Плавленый кварц............
0,28
0,35
0,32—0,35
0,37
0,5
0.2
0,17
Двумя другими важными упругими постоянными являются
постоянные Ламе р и X. Постоянная р известна как модуль сдвига
и является коэффициентом пропорциональности между приложен-
ным сдвигающим усилием и получающейся при этом деформации
сдвига. Постоянная р может быть определена через модуль Юнга
и коэффициент Пуассона формулой
2(1+о)'
(13.3)
Другая постоянная Ламе связана с введенными выше постоянными
упругости соотношением
1==_^н_=—а*—. (1з.4)
1 —2о (14-о)(1—2о)
Постоянные упругости (£, и, р, X) входят в выражения, опреде-
ляющие скорость распространения «в свободном пространстве»
474
‘bataUausItk
знание Без границ ’
для продольных и поперечных волн. В бесконечном изотропном
теле скорость распространения Поперечных волн равна
(р -—плотность среды). (13.5)
Скорость распространения продольных упругих волн в бесконеч-
ном изотропном твердом теле равна
= V р(1 + а)(1—2а) *
В стержне скорость распространения продольных волн с нижней
граничной частотой равна
(13.7)
Скорость VB одна и та же как В случае бесконечной среды, так и
в случае тонкой полости или стержня. Используя выражения (13,3)
и (13.5), перепишем (13.6) в виде
Va = V‘V^- (13.8)
Равенство (13.8) чаще всего используется для характеристики соот-
ношения между скоростями продольной и поперечной волн в бес-
конечной среде.
При разработке дисперсионной УЛЗ параметрами, представ-
ляющими наибольший интерес, являются характеристики группо-
вой скорости и групповой задержки. Ниже будет показано, что они
связаны с основными постоянными упругости, которые мы опре-
делили выше, й с величинами Vt и Vd.
13.3. Дисперсионные характеристики задержки при
распространении поперечных волн в полосковой линии
Направленное распространение упругих поперечных волн
в тонкой пластинке бесконечной протяженности вполне аналогично
распространению направленной электромагнитной волны между
двумя параллельными проводящими бесконечными плоскими по-
верхностями. Единственное существенное различие состоит в том,
что в полосковой линии возможно существование моды нулевого
порядка, тогда как для электромагнитной аналогии это невозможно.
Теорию такого типа распространения ультразвуковых волн рас-
смотрели Бухвальд [12] и Мейцлер [2]. В работе Мейцлера также
описана экспериментальная дисперсионная УЛЗ с распростране-
нием поперечных волн. Было найдено, что если ширина тонкой
полоски из металла составляет от 10 до 20 длин волн, то измеренные
характеристики распространения, по существу, совпадают с ха-
рактеристиками, предсказанными теорией для тонкой пластинки.
475
Алюминиевый сплав 5052-Н32 нашел широкое применение в каче-
стве дисперсионного материала среды распространения, так как
он имеет очень низкую постоянную затухания. Кроме того, алю-
миниевый сплав обладает тем преимуществом, что из него легко
изготавливать тонкие полоски путем прокатывания.
Рис. 13.2. Движение частиц
при поперечных волнах в беско-
нечно тонкой пластинке.
На рис. 13.2 показано движение частиц и волн в бесконечной
тонкой пластинке. Поперечная волновая функция удовлетворяет
классическому волновому уравнению
, а*/г = 1 &ft_
дх* Ф ду\ V* д/«
(13.9)
Допуская, что амплитуда колебания частиц в твердом теле на второ-
степенных плоскостях (у — ±1/2 Л) равна нулю, получаем общее
решение уравнения (13.9) в виде
у, 0 = 21 (4»si п + вп cos ) ехР I/ (УпХ—<•)/) 1 ].
(13.10)
где Ап = 0 для п = 2, 4, 6..., и Вп = 0 для п = 1, 3, 5...
_^Оно описывает волну, распространяющуюся в направлении
осил, в которой смещение частиц вдоль оси г зависит от у. Для
п > 1 все моды распространения являются дисперсионными. Не-
дисперсионные моды существуют для п = 0 12]. Нижняя частота
среза для каждой моды определяется соотношением
(13.11)
откуда i»n = nJiVjh или fn=nVj2h.
476
^lalaMaus^
знание без ераниц ' *“
В алюминиевом сплаве марки 5052-Н32 Ve приближенно
равно 3,2-106 см1сек. Значения fn для образцов из этого материала
различной толщины приведены в табл. 13.2. Фазовая скорость
n-й моды определяется соотношением
(О X (О^
V„ = v- = V.J/ 1-^. (13.12)
Групповая скорость равна Un = d(a/dyn. Из уравнения (13.12)
получаем
<0 = /4 + VnVs2 (13.13)
и
(13.14)
* Уп 'П
Фазовые и групповые скорости оказываются равными для всех мод,
если переменная частота нормализована к частоте среза n-й моды.
Это показано на рис. 13.3, откуда следует, что дисперсионная ха-
рактеристика задержки \/Un нелинейна, причем наибольший наклон
кривая имеет в области вблизи частоты среза. Частота, нд которой
должна работать дисперсионная УЛЗ на поперечных волнах, долж-
на лежать между и для того, чтобы минимизировать энергию
посторонних мод.
Таблица 13.2
Зависимость частот^ среза от толщины'тонких полосок
из алюминиевого сплава
Толщина h, см Частота среза, Мвц
для первой моды для второй моды f,
0,25 0,63 1,26
0,2 0,788 1,575
0,15 1,05 2,10
0,1 1,575 3,15
0,05 3,15 6,30
На рис. 13.4 показана УЛЗ на поперечных волнах, использую-
щая тонкую пластинку, которая исследована в работе Мейцлера
[21. Преобразователи расположены таким образом, чтобы оптими-
зировать преобразование электрического входного сигнала в ультра-
звуковую волну поперечной моды. Концы полоски срезаны для
подавления недисперсионной нулевой моды, которая по порядку
величины была на 30 дб ниже уровня полезного сигнала (здесь не
учитывается влияние искажений на форму сжатого импульса).
477
Рис, 13.3, Фазовая и групповая скорости для поперечных
волн в тонкой пластинке:
в—фазовоя скорость и групповая скорость ип\ б —групповая
задержка.
Рис. 13.4. УЛЗ на поперечных волнах, использующая
тонкую пластинку.
6)
Гис. 13.5. Согласование функций изменения групповой задержки и частот-
ной модуляции, обеспечивающее оптимальные условия распространения по-
перечных волн:
а —функция изменения задержки; б —функция частотной модуляции.
478
^aiaHauSil^i
знание без границ * *
Найдено, что для подавления паразитных мод, вызванных отра-
жениями от второстепенных плоскостей, этим краям необходимо
придать клинообразную форму или располагать отводы вокруг
этих краев. Последний метод оказался более эффективным и он ис-
пользуется в качестве стандартного приема при изготовлении по-
лосковых УЛЗ. Применение дисперсионных УЛЗ с поперечными
волнами ограничено'случаями, когда необходимо получить нели-
нейную функцию частотной модуляции, показанную на рис. 13.5.
При разработке типичной УЛЗ можно исходить из следующих за-
данных параметров:
нормализованная ширина полосы пропускания Д/// = 0,5,
нормализованная центральная частота /о/Д = 1,55.
Используя эти данные и соотношения (13.12) и (13.14), полу-
чаем разность задержек на единицу длины, равную 1,13 мксек/см
и задержку в середине полосы, равную 4 мксек!см. Обе эти величины
не зависят от толщины полоски. Предполагая, что ширина полосы
пропускания равна 1 Мгц, находим, что fn = 2Д/. Используя
(13.11), для п. = 1 получаем толщину полоски h — 0,8 мм. Опре-
деляем также, что Д = 2,0 Мгц и f0 = 3,1 Мгц. При требуемом
коэффициенте сжатия 200 (длительность сигнала соответствует
200 мксек) длина линии равна 200/1,13 = 178 см и задержка в сере-
дине полосы пропускания равна 700 мксек. На практике при опре-
делении полосы частот, которую следует использовать, необходимо
учесть характеристики преобразователей и потери в материале.
13.4. Дисперсионные характеристики задержки при продольном
распространении в полосковых линиях
Продольные моды распространения упругих волн в тонких
пластинках мо^кно рассмотреть, пользуясь теорией распростра-
нения продольных упругих волн в бесконечной тонкой пластинке.
Соотношение, характеризующее распространение продольных волн
в бесконечной пластинке, задается частотным уравнением Ре-
лея—Лэмба [13, 14]. Обычная форма записи этого уравнения для
продольной моды распространения имеет вид

(А— толщина пластинки). (13.15)
(Та—п)а
Частота вводится в (13.15) при использовании связей между
постоянными распространения
^+£‘ = <0’/^, va+t)’ = «>/V2.,
(13.16)
479
где Vt и Vd определяются равенствами (13.5) и (13.8) соответст-
венно. Так как
у = со/ V,
(13.17)
где V—фазовая скорость упругой волны, то (13.15) можно пе-
реписать в виде
Трансцендентный характер этого уравнения не позволяет получить
решение, связывающее ю и V в явном виде, как это было сделано
для случая распространения поперечной моды в бесконечной
пластинке. Явное представление V8 и о в (13.18) в связи с определе-
нием Vd позволит вычислить поведение V в зависимости от со для
различных материалов, для которых эти упругие константы извест-
ны. Исчерпывающее исследование распространения упругих волн
в полосках и цилиндрах приведено в работе Холдена 115]
Разработка дисперсионной УЛЗ для систем сжатия импульсов
требует знания груйповой скорости Un используемой моды или
групповой задержки на единицу длины l/Un. Характеристика
групповой задержки имеет вид
или
d . . d . и \
dto “ dio \ V /
to dV
1 w dV V dto
V “ V« dto “ V
(13.19)
Микер 15, 61 приводит экспериментальные данные, которые пока-
зывают, что тонкая полоска толщиной h имеет характеристику за-
держки, очень близкую к характеристике, определяемой по урав-
нению Релея — Лэмба и соотношением (13.19), если ширина по-
лоски составляет от 10 до 20 длин волн х. Основная характеристика
групповой задержки для первой продольной моды показана на
рис. 13.6. На низких частотах задержка на единицу длины прибли-
зительно постоянна и равна (К,)-1, где Ур — скорость в тонкой
пластинке на нижней предельной частоте, определяемая формулой
V„ = V.V2/(l-0).’ (13.20)
. 1 При более широкой полоске можно применить больший по длине пре-
образователь, дающий более направленное излучение. В связи с этим меньше
становится возможность преобразования моды излучения в результате отра-
жения от неосновных поверхностей полоски.
480
ftalaHauslilk
знание Без границ
Например, для о = 0,35 Хр = 1,75 V,. Скорость на верхней пре-
дельной частоте для наинизшей продольной моды определяется ре-
леевской скоростью поверхностной волны Уд, где V/? приближенно
равно 0,9 V,. Между этими двумя областями задержка на единицу
длины зависит от частоты, как показано на рис. 13.5. Таким обра-
Рис. 13.6. Характеристики
групповой задержки для пер-
вой продольной моды в беско-
нечно тонкой пластинке.
зом оказывается возможным выбрать на этой кривой большую
область, в которой задержка имеет дисперсионный характер. На-
клон и*максимальное значение задержки этой дисперсионной области
зависят от пуассоновского отношения (коэффициента) о. Обе эти

a) 6)
Рис. 13.7. Зависимость частоты перегиба fi (а) и задержки на
частоте перегиба D/ (б) от пуассоновского отношения а.
величины возрастают при уменьшении о. Дисперсионная область
кривой групповой задержки для первой продольной моды имеет
точку перегиба на частоте ft. Частота перегиба зависит от пуассо-
новского отношения и толщины пластинки; эта зависимость пока-
зана на рис. 13.7, а. Задержка Dt (ft) на частоте перегиба зависит
только от пуассоновского отношения. Эта зависимость показана
на рис. 13.7, б. Измеренные значения области дисперсионной за-
держки для полоски из алюминиевого сплава марки 5052-Н32
481
,чс—FI'-
ten
iM"
r
(a = 0,35) приведены на рис. 13.8. Для этого значения а величина
ft = 0,703 VJh. Выбор используемой центральной частоты (в пред-
положении, что УЛЗ работает в области вблизи частоты перегиба)
определяет толщину h. Ширина полосы сигнала Af определяет отно-
шение по которому нд графике рис. 13.8 находится разность
задержек A/d на единицу длины, если используется алюминиевый
сплав. Длительность сигнала Т позволяет вычислить общую длину
полоски L = Tl&td. С помощью рис. 13.8 определяем, что задержка
в середине полосы частот равна приблизительно 4,3 L мксек, где L —
длина линии в сантиметрах.
Рис. 13.8. Зависимость нормированной задержки от
частоты для первой продольной моды в линии задержки
на алюминиевой полоске.
Существование точки перегиба на характеристике дисперсион-
ной задержки приводит к тому, что использование продольной моды
лучше подходит для аппроксимации линейной зависимости задерж-
ки от частоты, чем использование поперечной моды. Однако, как
показано на рис. 13.9, при этом имеют место отклонения от идеаль-
ной линейной функции изменения задержки (которую предпола-
гается использовать в системе сжатия ЛЧМ сигналов). Данные,
полученные Микером [61, показывают, что максимальное отклоне-
ние от линейности выше частоты перегиба 6РЛ больше, чем то же
отклонение ниже частоты перегиба 6DZ.
Эти отклонения становятся более симметричными по мере
уменьшения относительной ширины полосы Af/f, используе-
мого сигнала. Для 20%-ного отношения ширины полосы прибли-
женные значения &Dh и для полосковой линии из алюминиевого
сплава равна соответственно 0,035 и 0,0175. Путем сдвига опорной
функции задержки, как это сделано на рис. 13.9, оказывается воз-
можным сформировать почти симметричную кривую ошибок за-
держки, которая имеет приблизительно синусоидальную форму.
Зависимость Полученного при этих условиях среднего отклонения
482
Autaffauswij
знание без границ - w
задержки от линейной при изменении относительной ширины по-
лосы в процентах для о = 0,35 показана на рис. 13.10. Средняя
ошибка задержки больше для меньших значений о [61. Как указы-
валось в гл. 11, эффект искажения сигнала вследствие ошибок за-
держки такого типа зависит только от величины ошибки и не за-
висит от отношения ошибки к величине дисперсионной задержки
в процентах. Реально используемым критерием является макси-
Частота
Рис. 13.9. Отклонения от линейно-
сти групповой задержки при про-
дольной моде распространения.
Рис. 13.10. Средняя ошибка за-
держки для продольной моды рас-
пространения.
мальная фазовая ошибка в радианах. Для полосковой линии за-
держки с продольной модой распространения эта фазовая ошибка
приближенно определяется формулой
fcn = ?CcPA/ , (13.21)
Л
где л/Af — число периодов ошибки на ширину полосы сигнала.
Для полоски с постоянной толщиной л = 1. Если используется,
например, ЛЧМ сигнал с полосой 15%, Af = 500 кгц,
D = 200 мксек, то из графика на рис. 13.10 bDcJD = 0,013 и
Ьп = (0,013 • 200 • 10-в. 0,5-10®/1 = 1,3 рад. Фазовые ошибки та-
кой величины приводят к большим искажениям типа парных
эхо для сигналов. Как показывает этот пример, существуют
жесткие ограничения на величину произведения длительности на
ширину полосы при использовании в качестве согласованного
фильтра для ЛЧМ сигнала УЛЗ с постоянной толщиной при про-
дольной моде распространения.
Это ограничение может быть несколько снижено, если исполь-
зовать сам ультразвуковой фильтр в качестве пассивного частот-
ного генератора, в соответствии с методом, рассмотренным в гл. 6.
Полученная частотная модуляция будет близка к нечетно-симметрич-
ной (в зависимости от относительной ширины полосы в процентах)
483
слегка нелинейной ЧМ. Используя методы инверсии частоты, мы
можем обратить функцию ЧМ во времени, и после передачи, пре-
образования и приема сигнал может быть сжат с помощью 'УЛЗ
того же самого типа. Этот метод позволит получить лучшее согласо-
вание между передаваемым сигналом и фильтром приемника, чем
метод, использующий сигнал со строго линейной ЧМ. Проблема
больших ошибок задержки для дисперсионной линии с продольными
волнами была разрешена путем изменения толщины линии по ее
Длине. Этот метод был рассмотрен Фитчем [9]. Некоторые его особен-
ности описаны ниже.
Рассмотрим последовательное соединение нескольких различ-
ных сегментов с постоянной толщиной, причем для разных сегмен-
тов их толщина может принимать значения от до hn, а длины сег-
ментов принимают значения от до Ln. Получающееся при этом
устройство имеет сложную зависимость задержки от частоты. Она
может быть записана в виде
DT (/) = LX'DX (Л 4- L. D.(/) +... + Ln Dn (f), (13.22)
где Dt(f) — зависимость задержки на единицу длины от частоты
для сегмента толщиной ht. Равенство (13.22) показывает путь для
синтеза линейной функции задержки с меньшими ошибками задерж-
ки, чем это достигается с УЛЗ с постоянной толщиной. По существу,
такой метод аналогичен методу О’Мира [161 синтеза функций за-
держки с помощью мостовых Т-образных звеньев, который рас-
смотрен в предыдущей главе. В работе Фитча [9] приведена про-
грамма для разработки и расчета на ЦВМ линий задержки из сег-
ментов различной толщины и длины. Теоретически может быть
выбрано любое число сегментов, но на практике от 3 до 6 сегментов
обычно оказывается достаточным для формирования линейной функ-
ции задержки, обладающей значительно улучшенными характе-
ристиками по величине ошибки и относительной ширине полосы
частот по сравнению с УЛЗ постоянной толщины. Как только исход-
ные параметры будут выбраны, УЛЗ с переменной толщиной могут
быть изготовлены либо с помощью обработки полосы постоянной
толщины на прокатном стане, в котором толщина может регули-
роваться в соответствии с заданной функцией, либо с помощью ме-
тода химического травления, при котором толщина каждого отдель-
ного сегмента определяется временем, в течение которого сегмент
•погружен в травящий раствор. На рис. 13.11 приведены данные
толщины и длины четырех сегментов УЛЗ. Результирующая ха-
рактеристика задержки для этой конструкции может быть полу-
чена на основании нормированной кривой задержки на рис. 13.8
путем пересчета частотной ординаты и изменения масштаба функций
задержки. Частоты перегиба для каждого сегмента этой конструкций
приведены в табл. 13.3..
484
ftalaHausitiil
Таблица 13.3
Частоты перегиба для различных
сегментов УЛЗ со ступенчато
изменяющейся толщиной
Толщина сегмента, см Частота перегиба, Мсц<
/4—0,051 /1-4,43
Л,=0,043 /. — 5,21
/1,-0,039 5,90
h<-0,033 /<—6,81
На рис. 13.12 изображены кривые задержки для каждого от-
дельного сегмента и их суммарная кривая задержки. Была синте-
зирована линейная функция задержки, которая обеспечивает дис-
персионную задержку приблизительно в 28 мксек в полосе шириной
1,25 Мгц с центром на частоте 5 Мгц. Максимальный коэффициент
сжатия равен 35. Умножение длины каждого сегмента на постоян-
ный множитель увеличило бы общую дисперсионную задержку и,
Рис. 13.11. Размеры пластинки со ступенчато изменяющейся
толщиной для УЛЗ, состоящей из четырех сегментов.
Все размеры даны в миллиметрах.
следовательно, коэффициент сжатия. Эта функция может быть также
смещена вверх или вниз по шкале частот путем умножения толщины
всех сегментов на одну и ту же постоянную. Это приводит к увели-
чению или уменьшению ширины полосы устройства при повышении
или понижении центральной частоты. Использование большого
числа сегментов не только уменьшает величину ошибки задержки,
но приводит также к увеличению числа периодов функции ошибки
задержки. Это в свою очередь приводит к уменьшению соответствую-
щей фазовой ошибки, как указывает равенство (13.21).
Мейцлер [3] исследовал влияние изменения ширины УЛЗ
постоянной толщины вдоль ее длины. Было найдено, что при этом
преобразование энергии в нежелательные моды в полосковой УЛЗ
уменьшается, следовательно, улучшаются характеристики ампли-
тудного отклика. Было также показано, что этот метод дает в ре-
зультате узкополосные характеристики амплитудного отклика,
485
которые при соответствующей разработке конструкции могут быть
центрированы для совпадения с частотой перегиба, обеспечивая
тем самым одновременно и линейность. задержки, и взвешенный
амплитудный отклик.
Однако этот метод не получил широкого распространения.
Одной из причин, вероятно, были трудности точного управления
Рис. 1S.12. Частные характеристики сегментов
и результирующая функция задержки для УЛЗ
с переменной толщиной, состоящей из четырех
* сегментов.
узкополосной функцией отклика. Для изготовления УЛЗ постоян-
ной толщины для работы на более высоких частотах (30 Мгц и выше)
были использованы также различные марки стали. Сталь была вы-
брана в первую очередь потому, что из нее легче получать очень
тонкие ленты, чем из алюминиевого сплава. Однако изготовление
преобразователей для этих очень тонких высокочастотных линий
обычно труднее и такие ультразвуковые дисперсионные УЛЗ ха-
рактеризуются более высоким уровнем паразитных сигналов, вы-
званных преобразованием мод и паразитными отражениями, в ре-
486
Ма1аНаи$ж
знание без границ “ *
a)
б)
8)
Рис. 13.13 Вид сигналов, характеризующих работу УЛЗ постоянной тол*
щииы с центральной частотой 30 Мгц при коэффициенте сжатия 100:
а —растянутый импульс (стробированный): б —сжатый импульс; а —сжатый импульс
после весовой обработки, уровень боковых лепестков—32 дб.
487
зультате неправильной ориентации преобразователей и вследствие
взаимодействий, происходящих на второстепенных поверхностях
полосковой линии. Вносимые потери для высокочастотных УЛЗ
могут достигать 40—50 дб по сравнению с потерями от 10 до 15 дб
для <алюминиевых> УЛЗ, работающих на более низких частотах.
Несмотря на эти трудности, дисперсионные УЛЗ постоянной тол-
щины успешно использовались и на более высоких частотах. При-
мер этого показан на рис. 13.13, где изображены сигналы, сжатые
с помощью УЛЗ с центральной частотой 30 Мгц при коэффициенте
сжатия 100. С помощью этой УЛЗ было осуществлено растяжение
импульса, ограничение, частотная инверсия и сжатие импульса по
схеме, показанной на рис. 6.15.
13.5. Проволочные дисперсионные линии задержки
Теория распространения ультразвуковых волн в бесконечном
цилиндрическом стержне была независимо разработана Покхамме-
ром [171 и Чри [181. Частотное уравнение Покхаммера — Чри
определяет допустимые моды распространения и диапазоны частот
в бесконечно длинной цилиндрической проволоке. Эти параметры
могут быть вычислены, если заданы две упругие константы, напри-
мер пуассоновское отношение и модуль Юнга. Уравнение Покхам-
мера — Чри для цилиндра играет ту же роль, что и частотное урав-
нение Релея — Лэмба для бесконечной пластинки. Бэнкрофт [19)
приводит упрощенную форму уравнения Покхаммера — Чри в виде
(х—1)*ф(М—Ф(М] = 0. (13.23)
где x=(V/Vb)a(!_+£)._ ^(ha) = ha[J0(ha)/J1(ha)], а = радиусу про-
волоки, /i = y]/px—1, Р = (1 —2о)/(1—о), k = yY2x— 1. V, Vb,
о и у были определены ранее.
Равенство (13.23), как и в случае частотного уравнения Релея —
Лэмба есть трансцендентная функция, из которой фазовая скорость
V может быть вычислена для конкретных материалов. Первая про-
дольная мода распространения 1(0, 1) обладает дисперсионной
характеристикой, аналогичной характеристике, определенной для
полосковой линии. Мэй [7] приводит описание построения проволоч-
ной дисперсионной линии задержки. На рис. 13.14 показана функ-
ция дисперсионной задержки, вычисленная Мэем. Оказалось, что
измеренные характеристики проволочной линии задержки конечной
длины по существу ведут себя аналогично характеристикам, опре-
деляемым равенством Покхаммера — Чри. На рис. 13.14 показаны
первая и вторая паразитные изгибные моды распространения F (1, 1).
и г (1,2), а также изгибные и продольные моды более высоких поряд-
ков. График показывает, что возможно преобразование мод на ча-
стотах, где кривые фазовых скоростей различных мод пересекаются.
488
^atatiaus^k
знание без границ “ ш
Это приводит в результате к переходу энергий из полезных мод
в паразитные, которые вызывают на определенных частотах появ-
ление паразитных сигналов в выходном сигнале ультразвукового
фильтра сжатия. Это накладывает ограничения на относительную
ширину полосы, в пределах которой может быть получена линейная
характеристика задержки.
Такое явление существует и в проволочных, и в полосковых
линиях, но, как было показано, оно менее критично в полосковых
Рис. 13.14. Характеристики задержки для продольной и изгиб-
ной мод распространения упругих волн в проволоке.
линиях, действующих на первой продольной моде. Кроме того,
площадь поверхности преобразователей для дисперсионных линий
полоскового типа во много раз больше площади поверхности пре-
образователей для проволочных дисперсионных УЛЗ, имеющих
аналогичные характеристики. Это приводит в результате к более
низкому импедансу для полоскового преобразователя, что облег-
чает согласование импедансов в используемой полосе частот. Такое
свойство полосковой дисперсионной линии позволяет осуществлять
лучшее подавление отраженных сигналов, имеющих тройную за-
держку (трехкратное прохождение) на выходе линии. По этим
причинам при изготовлении линий, которые должны работать в си-
стемах сжатия импульсов на частотах порядка мегагерц, основное
внимание было уделено созданию дисперсионных УЛЗ на тонких
полосковых линиях, а не на тонких проволоках.
489
13.6. Характеристики преобразователей для тонких
полосковых линий задержки
Как уже говорилось выше, для построения дисперсионной
УЛЗ может быть использовано несколько мод распространения
волн в тонких полосковых линиях. Однако первая продольная мода
обладает наиболее подходящей формой для синтезирования линей-
ной зависимости задержки от частоты при использовании метода
изменения толщины, рассмотренного Фитчем 19].
Параметры конкретной моды распространения, возбуждаемой
в полосковой линии, могут изменяться при изменении поляризации
Механическая
свя 1ь через
/

^0 i
1^0 " I задерживаю-
। щую замедляу
| ющую среду ]
О * . * —- — —г 4
Входной Выходной
преобразователь а) преобразова’пель
с
Рис. 13.15. Эквивалентные схемы преобразова-
телей:
а — эквивалентная схема; б —эффективные параллель-
ные емкость и сопротивление.
и размеров преобразователя. При соответствующей разработке кон-
струкции, используя эти два параметра, можно возбуждать чистую
первую продольную моду, причем уровень других мод будет на
40—50 дб ниже. Асимметрия в конфигурации преобразователей
может привести к появлению паразитных сгибовых мод более вы-
сокого уровня. Мейцлер (20] указывает, что источником этого может
быть наклон концевых срезов преобразователя, неоднородности
слоев крепления и неоднородность материала преобразователей.
Амплитудные характеристики УЛЗ на полосковых линиях опре-
деляются конструкцией как преобразователей, так и самой ли-
нии. Считается, что абсолютная величина потерь складывается из
трех компонент: потерь на рассогласование, потерь в материале
и потерь при расширений луча. Форма амплитудной1 кривой, однако,
зависит1 как от указанных трех компонент, так и от механической
добротности Q преобразователей.
Преобразователь, нагруженный на линию вблизи резонанса,
может быть описан эквивалентной схемой, показанной на
рис. 13.15, а 121, 22]. На центральной частоте последовательная
цепочка, состоящая из R и С, находится в резонансе, что приводит
490
к минимуму потерь. Если параллельно входу подключить емкость
так, чтобы она совместно с внешней индуктивностью образовывала
антирезонансную цепь на центральной частоте, то суммарная форма
частотного отклика будет совпадать с его формой одной последова*
тельно настроенной цепи при изменении частоты в любую сторону
от резонанса. Значение сопротивления определяется постоянными
материала преобразователя, задерживающей среды и типом связи
между ними.
Так как потери в алюминиевой полоске возрастают прибли-
зительно как четвертая степень частоты, то максимально допусти-
мая частота для алюминия ограничена 6 Мгц. Столь быстрое воз-
растание потерь с частотой происходит в большей степени из-за
рассеяния акустического сигнала на границах зерен материала.
По мере приближения длины волны в материале к размеру зерен
оно становится очень большим.
В коротких УЛЗ, обычно используемых в системах сжатия
импульсов, потерями на расширение пучка можно пренебречь,
если длина преобразователя велика по сравнению с его шириной.
Таким образом, форма амплитудного отклика приближенно описы-
вается откликом единичного настроенного контура, соответствую-
щего контуру преобразователя.
При соответствующей конструкции преобразователей случай-
ные паразитные сигналы в УЛЗ на полосковой линии можно сни-
зить до уровня на 40 дб ниже полезного выходного сигнала. Отраже-
ние от концов УЛЗ вследствие рассогласования является основной
проблемой при рассмотрении паразитных сигналов в относительно
коротких линиях, где потери в материале малы. Такие сигналы
принято называть отражениями с тройной задержкой или сигналами
трехкратного прохождения, так как они появляются на выходе
с задержкой, в три раза большей чем задержка в линии, считая
с момента поступления входного сигнала. Они могут быть существен-
но уменьшены, если на концах линии импеданс окажется комплекс-
но-сопряженным импедансу преобразователей. Эквивалентная
схема, показанная на рис. 13.15, а, может быть преобразована
в схему с параллельными емкостью и сопротивлением, показанную
на рис . 13.15, б. Такие элементы в большинстве случаев могут быть
легко измерены с помощью стандартного оборудования. Отметим,
что значения этих параллельно включенных элементов зависят от
проводимостей данных двух схем. Для схемы на рис. 13.15, а
Y = /соСо + --------------, (13.24)
₽+j(coL-l/<oC)
а для схемы на рис. 13.15,6
У = J- + jaCE. (13.25)
491
Приравниваем действительные и мнимые части этих двух функций
проводимости и решаем относительно Re и Се. В результате полу-
чаем
с = Со----------(<*£—1/<»С)--- ’ (13.26)
Е . сй(₽« + [со£-1/соС1«) '
Эти функции приведены на рис. 13.16. На нем также показаны
практически полученные результаты, отлично совпадающие с теоре-
тическими кривыми. .
Рис. 13.16. Зависимость емкости и сопротивления в эквива-
лентной схеме преобразователя от частоты.
Для оптимальной режекции сигналов трехкратного прохожде-
ния, если схема работает с постоянным импедансом нагрузки, ис-
пользуется согласующая цепь. Эта цепь должна согласовывать со-
Рис. 13.17. Схема согласования преобразователя с на-
грузкой.
Насрузка
противление с постоянным значением нагрузки и емкость в преде-
лах частотной полосы, представляющей для нас интерес. Хорошие
результаты были получены при использовании с этой целью схемы,
показанной на рис. 13.17. Ее можно рассчитать графическим мето-
492
дом, подстраивая характеристики согласующей схемы к измерен-
ным зависимостям сопротивления и емкости преобразователя.
. Так как эта схема согласовывает преобразователь в полосе
частот, то она оказывает пренебрежимо малое воздействие на сум-
марный амплитудный отклик. Данный метод может быть использо-
ван для значений относительной ширины полосы вплоть до 40%
несущей частоты н обеспечивает уровень паразитных сжатых сиг-
налов трехкратного прохождения порядка 35—40 дб для коротких
полосковых линий задержки.
13.7. Требования к дисперсионным ультразвуковым линиям
задержки
В этом разделе суммированы некоторые из важных характе-
ристик, которые должны быть согласованы между поставщиком и
потребителем УЛЗ. Ри^. 13.18 иллюстрирует подход к определению
требований по задержке и ширине полосы. Идеальная кривая за-
держки определяется на основании ширины полосы и произведения
длительности на полосу. Требования должны допускать некоторые
расхождения наклона кривой задержки и наклона идеальной ха-
рактеристики. Эти расхождения можно определить при рассмотрении
рассогласования линейной задержки, описанного в гл. 6. Требова-
ния к функции ошибок задержки определяются исходя из наилуч-
шего среднеквадратичного приближения к измеренным значениям
времени задержки. В них должен быть задан ряд точек в области
линейной задержки, в которых будет измеряться временная задерж-
ка. Для измерения временндй задержки можно применить мето-
дику, предложенную Мэем [23], в которой используется высоко-
частотный импульс с гауссовой огибающей при ширине полосы,
узкой по сравнению с полосой. УЛЗ. На рис. 13.19 проиллюстри-
рован подход к определению требования к кривой ошибок задержки
и рассогласованию наклона линейного закона задержки. Так как
каждый из этих параметров может привести к ухудшению харак-
теристик выходного сигнала фильтра сжатия, то разработчик си-
стемы должен определить, который из них оказывает наибольшее
влияние в его конкретной задаче, и какая комбинация этих двух
параметров может быть приемлемой. Было установлено, что попытки
получить очень малую величину ошибки задержки в УЛЗ могут
привести к значительному увеличению стоимости устройства. В та-
ких случаях удобнее потребовать, чтобы величина ошибки задержки
была такой, которая приводит к проявлению боковых лепестков
типа парных эхо на уровне —25 дб, и затем произвести дополни-
тельную коррекцию ошибки задержки с помощью мостовой Т-образ-
ной корректирующей цепи, как это и было продемонстрировано
в предыдущей главе.
493
Страницы
отсутствуют
МаНаиА
знаниебезграниц Ч4*
BF'
Г
чению несжатого импульса должно составлять 10 1g ГД/ — Lt,
где Lt — номинальные вносимые потери в дисперсионной линии.
Сжатый импульс более подробно показан на рис. 13.22, б.
Если длительность и наклон линейной функции ЧМ входного сиг-
нала подобраны правильно, то наличие явно выраженных нулей
и правильная структура их распределения в выходном сигнале
будут служить одним из первых указаний на хорошее согласование
наклона характеристики задержки фильтра с сигналом. Если не
Рис. 13.21. Иллюстрация подхода к определе*
нию требований к вносимом потерям и характе-
ристикам амплитудного отклика для ультра-
звукового фильтра сжатия.
применяется специальных мер для уменьшения боковых лепестков,
то сжатый импульс будет иметь вид (sin х)/х, причем первый боко-
вой лепесток окажется на 13,2 дб ниже пикового значения сигнала.
Симметрия структуры боковых лепестков и четкое их определение
для нескольких интервалов по обе стороны от сжатого импульса
указывают на приемлемость кривой ошибок задержки. Однако воз-
действие более слабых искажений типа парных эхо не будет сказы-
ваться на форме сигнала вида (sin х)/х. Ширина сжатого импульса
должна составлять 1/Д/ на уровне —4 дб и 2/Д/ между первыми
двумя нулями в основании импульса. На рис. 13.22, в показана
область, в которой можно заметить сигнал с тройной задержкой.
Если конструкция удовлетворяет поставленным требованиям, то
этот сигнал и другие паразитные отклики не будут заметны при изу-
чении сжатого импульса при обычном усилении.
На рис. 13.22, г приведены те же самые сигналы, что и на
рис. 13.22, в, но только при значительно большем усилении. Здесь
496
^laiattaus,^.
знание без границ Ч *
17 Зак. 1341
497
сигнал с тройной задержкой виден очень отчетливо, и его уровень
более чем на 35 дб ниже пикового значения сжатого сигнала. Боко-
вые лепестки вокруг сжатого импульса спадают как показано выше;
они существуют в интервале относительно сжатого импульса.
Другие сигналы, расположенные между обычными боковыми ле-
пестками и сигналами с тройной задержкой, представляют собой
паразитные сигналы и наведенные сигналы от генератора, исполь-
зуемого для формирования рассматриваемых импульсов.
13.8. Дисперсионные устройства типа дифракционных решеток
Дисперсионные УЛЗ, рассмотренные в предыдущих разделах,
работают на принципе направленного распространения волн, но
это не единственно возможный принцип построения дисперсионных
устройств. Проведенные недавно исследования показали наличие'
дисперсионных свойств у ультразвуковых устройств типа дифрак-
ционных решеток. Они описаны в работах»Дункана и Паркера [24]
Рис. 13.23. Перпендикулярная дифракционная линия задержки:
а —геометрические характеристики; б —характеристики интерференции сигналов.
По оси х находится решетка иа N передающих элементов, а по оси у — решетка
из М приемных элементов.
и Коквина и Шу [25]. Дисперсионные свойства этих приборов воз-
никают вследствие создания эффективного пути задержки при рас-
пространении волны от входной решетки к выходной решетке пре-
образователей. Время задержки волны при этом зависит от частоты,
хотя само по себе распространение волны в среде определяется не-
дисперсионной поперечной модой. Примером УЛЗ типа решетки
такого вида является перпендикулярная дифракционная линия
задержки, описанная Коквином и Шу. Общий вид этого устройства
показан на рис. 13.23, а. Оно представляет собой решетку из N
излучающих источников и М приемных элементов, расположенных
498
’Xalallauswk
знание Вез границ **
на двух перпендикулярных друг другу сторонах образца, в которой
распространяются ультразвуковые волны (например, алюминий).
В нем N элементов-источников возбуждаются в фазе, а М приемных'
элементов соединены параллельно, причем М >W. Приемные эле-
менты находятся в ближней зоне поля диаграммы направленности
решетки источников.
Коквин и Шу рассмотрели основные свойства перпендикуляр-
ной дифракционной линии задержки с помощью интерференцион-
ного анализа х. Обратимся теперь к рис. 13.23, б. Источники Sn
и Sn-i расположены на оси х симметрично относительно точки хп,
расстояние между ними равно dn. Разность длин путей распростра-
нения между этими двумя источниками и точкой ут приближенно
равна (для dn rm>n)
?т,п rm,n—\ ~ dnCOSi)mtn — Хп dn/r(13.27)
Аналогично, для приемников Rm и Rm~\ разность длин путей
до точки хп равна
f fm—i ,п ~ dmCOS0mtn — ут dm! Гт.п'
(13.28)
Для частоты ft, излучаемой источниками Sn и 5Л_|, сложение
колебаний в результате интерференции происходит в приемни-
ках Rm и Rm-\ при удовлетворении следующего условия:
хп Ут^т pV„
Гт.п Гт,п fl
(13.29)
где р — порядок интерференции, a Ув — скорость распростране-
ния поперечных волн в среде. Если решетки приемников и источ-
ников расположены таким образом, что x„d„ = ут dm = С,
где С постоянная величина, и так что при увеличении х и у расстоя-
ние между преобразователями уменьшается, тогда все пары прием-
ник-источник, разделенные расстоянием rf, где
r^CfJpV» (13.30)
будут передавать с максимальной эффективностью сигналы, имею-
щие полосы частот с центрами на частотах ft. Для других пар прием-
ник — источник (S„_|, Sn-i) и (Rm, Rm-\), например, геометрия
задачи такова, что для более коротких длин путей из этих пар раз-
ность длин путей (dt cos 0,) больше. Таким образом, сигналы более
низких частот будут передаваться с меньшей задержкой в соответ-
1 Силвер [26] установил, что среднее значение интенсивности поля в
ближней зоне, созданного излучающей решеткой, может быть очень точно
вычислено на основании геометрической лучевой теории распространения.
17* 499
ствии с равенством (13.30), что приводит к линейной зависимости
задержки от частоты, имеющей вид
<*з.зо
Коэффициент С/(рУ?) определяет наклон функции задержки для
каждого порядка передачи. Верхний и нижний частотные пределы
для каждого порядка равны соответственно
= (13.32а)
= = . (13.326)
Важно, чтобы ни один из интересующих нас порядков не перекры-
вался по частоте. Для геометрии, показанной на рис. 13.23, б, это
условие удовлетворяется для первых р порядков, когда
г„> С,‘Р =, или г0>-52-. (13.33)
“ (p+I)V, (p+1)V. С р+1
Для рассматриваемого случая, когда источники и приемники
находятся на равном расстоянии относительно основных точек
хп и ут, для каждого тип справедливо следующее соотношение:
Ут dm = У™~ * ~ С’
(13.34)
Из (13.34) получаем общее соотношение для расположения элемен-
тов источника и приемника:
Хп = х\ + 2С(п — 1), l<n<2V, (13 35)
Ут=у* + 2С(т— 1), 1</л<М.
Свойства перпендикулярно-дифракционных линий задержки, най-
денные с помощью интерференционного анализа, можно, используя
равенства (13.32)—(13.32, б) и (13.35), суммировать в виде следую-
щего списка формул:
Центральная частота
(13.36)
Ширина полосы
* (13.37)
500
ftaltfflauswk
знание без границ Ч *
Дисперсионная задержка
Д/, = c_^.g=»
W v. 1 |(/.р+,1р)1
Лл
Произведение длительности на ширину полосы
у,== р (M—N) .
* с /ОР
(13.38)
(13.39)
Коэффициент С может быть записан в виде С = V% &td/ (f2—/х).
Если положить р = 1, то нижний частотный предел можно вы-
разить в виде
/? = (V./C)«[xi+»i+2C(tf-l)].
(13.40)
Таким образом, при заданных М, N и С приведенные выше соотно-
шения позволяют определить все существенные параметры перпен-
дикулярно-дифракционной линии задержки при использовании ее
в качестве фильтра сжатия ЛЧМ сигналов.
Условие отсутствия перекрывания порядков и выражения
(13.33) и (13.40) позволяют получить соотношение

Из (13.36) находим М = -^-(fip—flp) Afd + W, и границы для ве-
личины N, при котором ни один из первых р порядков не пере-
крывается, запишутся теперь в виде
N < 1 + (fl _ .
(13.41)
На практике было обнаружено, что существует оптимальное зна-
чение N, которое лежит ниже найденного выше верхнего предела.
Это объясняется тем, что при стремлении N к верхнему пределу
моды спадают недостаточно резко, так что не происходит полного
разделения смежных мод.
Коквин и Шу выполнили более строгий анализ, основанный
на дифракционной теории, который подтвердил результаты, полу-
ченные с помощью интерференционного анализа. На основании
проведенного рассмотрения были найдены типичные характеристики
отклика для моды первого порядка, которые показаны на рис. 13.24.
Отклонение характеристики задержки от линейной для N — 25
показано на рис. 13.25. Для конструкций такого типа (большие N)
относительная ширина полосы в каждой моде та же самая, как и
в суммарной дисперсионной характеристике задержки [см. равен-
501
ства (13.36) — (1'3.38)]. Ошибка задержки уменьшается при уве-
личении /V и стремлении его к оптимальному значению, выше ко-
торого ошибка задержки снова возрастает по причинам, которые
мы упоминали в предыдущем абзаце. Для кривой ошибок задержки,
приведенной на рис. 13.25, приближенная фазовая ошибка в соот-
ветствии с равенством (13.21) равна 0,4°, в предположении, что
6DCP,,„ = 0,3 мксек и Af == 0,5 х
h——н х 10~6/20.
Частота
Рис. 13.24. Функции амплитуд-
ного отклика и задержки для
«перпендикулярно- дифракционной
линии задержки.
Таким образом, здесь мы
имеем значительное улучшение по
сравнению с ошибками задержки,
которые могут быть получены с
помощью других методов построе-
ния УЛЗ или линий с сосредо-
точенными параметрами. Это га-
рантирует очень малые паразитные
сигналы. Они могут появляться
вследствие отражений от других
поверхностей устройства. Резуль-
таты испытаний на низкочастот-
ных устройствах показывают, что
этот уровень ошибок задержки
может быть достигнут и практи-
чески. Вносимые потери перпен-
дикулярно-дифракционных линий
задержки могут составлять 30 дб
или более. Однако класс устрой-
ств, основанных на дифракционных
принципах, позволяет обрабаты-
вать сигналы на значительно более
высоких частотах и с более широ-
кими полосами, чем другие ультразвуковые приборы. Кроме того,
преимуществом дифракционных устройств является низкий уровень
искажений задержки. Это иллюстрируется примером сигнала, пока-
занного на рис. 13.26, для которого ширина полосы сигнала равна
10 Мгц и произведение длительности на полосу равно 100.
Дополнительные данные по перпендикулярно-дифракционным
линиям задержки приведены в работе Эвелета [27], который ука-
зывает на потери порядка 60 дб для устройства с коэффициентом
сжатия 70 : 1 (Т — 12,8 мсек, Af = 5,5 Мгц), работающего на
центральной частоте 30 Мгц. В этом устройстве был получен уро-
вень паразитных сигналов, равный —45 дб по отношению к пико-
вому значению сжатого импульса на выходе. Эвелет описывает
также устройство с коэффициентом сжатия 400 : 1 (Т = 20 мсек,
= 20 Мгц), работающее на частоте 45 Мгц. Другой тип устрой-
ства, подобного дифракционной решетке, который был успешно про-
верен экспериментально, имел форму треугольного клина [28].
502
’NaliAaustWi
знание без границ * w
Решетка выходных дифракционных преобразователей размещена на
гипотенузе клина, а единственный длинный входной преобразова-
тель установлен на основании.
Конструкция такого устройства показана на рис. 13.27. Вы-
ходная решетка и в этом случае находится в ближней зоне поля из-
лучающего преобразователя. В таком типе устройства не исполь-
Рис. 13.25. Отклонение задержки перпендикулярно-дифрак-
ционной линии от линейной характеристики.
Рис. 13.26. Вид сигналов, характеризующих работу фильтра сжатия и рас-
тяжения сигналов с перпендикулярно-дифракционной линией задержки;
ТЩ — 100, f = 10 Мгц, центральная частота = 45 Мгц:
a—стробированный растянутый импульс, цена деления 2 мксек; б — невавешенный
сжатый импульс, цена деления 0.2 мксек.
503
г
эуются дифракционные принципы. Дисперсионная характеристика
клина определяется тем, что любые два смежных преобразователя
действуют как комбинированный резонансный преобразователь на
частоте, для которой пути задержки смежных преобразователей,
дисперсионной характеристикой за-
держки.
перпендикулярные к источнику,
различаются на одну длину вол-
ны. Следовательно, размещение
отдельных выходных преобразо-
вателей в виде решетки с пере-
менным шагом приводит в ре-
зультате к дисперсионной зави-
симости суммарной задержки от
частоты. Это происходит потому,
что резонансные частоты раз-
личных пар преобразователей
будут расположены в различ-
ных участках спектра широко-
полосного входного сигнала.
Клин будет обеспечивать либо
растяжение, либо сжатие импульса, в зависимости от того, поступает
ли на его вход широкополосный импульс или сигнал, функция ЧМ
которого согласована с характеристиками клина. В устройстве
такого типа может быть сформирована функция задержки с поло-
жительным и отрицательным наклоном, которая может быть и ли-
нейна* и нелинейна. Ошибка задержки для клина больше, чем для
перпендикулярно-дифракционной линии задержки. Эвелет приво-
дит результаты, полученные для согласованной пары дисперсион-
ных клинообразных линий при коэффициенте сжатия 70 : 1 с пара-
метрами, которые приведены выше.
В тех задачах, где первостепенное значение имеет низкий уро-
вень боковых лепестков по дальности, перпендикулярно-дифрак-
ционные линии задержки могут решить проблемы создания согла-
сованного фильтра с малыми искажениями для РЛС. В других
задачах, в которых приемлемы боковые лепестки по дальности по-
рядка —25 дб, низкая стоимость тонких пластинчатых УЛЗ с про-
дольной модой распространения (постоянной или переменной тол-
щины) сделает их, по-видимому, более подходящими, если только
с их помощью можно будет удовлетворить требования по ширине
полосы х. Во многих задачах экономически выгоднее использовать
линию переменной или постоянной толщины совместно с мостовыми
Т-образными корректирующими звеньями по методике, рассмотрен-
ной в гл. 12. Используя такой метод построения схем, разработчик
1 Дисперсионные УЛЗ могут быть использованы в многоканальных схе-
мах (с параллельными каналами) для обработки широкополосных сигналов.
Для этой цели могут быть использованы и другие устройства, работающие по
принципу дифракционной решетки, такие, как устройства с поверхностными
волнами, описанные в работе [29].
504
'NaldHausini
знание без границ - *
системы может считать, .что другие искажения амплитуды и задерж*
ки в приемнике устраняются схемой коррекции.
Еще одной интересной проблемой является влияние потерь,
вносимых фильтром сжатия, на динамический диапазон и характе-
ристики обнаружения приемной системы. Для линий с сосредото-
ченными параметрами общие вносимые потери могут быть компенси-
рованы путем разделения фильтра на блоки и подключения к каж-
дому блоку своего собственного усилителя, компенсирующего по-
тери. Но такую компенсацию возрастающих потерь трудно осуще-
ствить для дисперсионной УЛЗ, так как большая часть потерь про-
исходит во входных и выходных преобразователях. Когда вносимые
потери имеют порядок от 40 до 60 дб, как это может быть в некото-
рых ультразвуковых приборах, то может оказаться необходимым
компенсировать значительную часть этих потерь в предусилителе,
стоящем перед фильтром сжатия. Если усиление предусилителя
велико, тогда в линии может произойти насыщение для более силь-
ных принимаемых сигналов, что ограничит динамический диапазон
приемника.
ЛИТЕРАТУРА
1. W. Р. М а з о и. Physical Acoustics and the Property of Solids. Van. Nost-
rand, Princeton, New Jersey, 1958.
2. A. H. M e i t z 1 e r. Ultrasonic delay lines using shear modes in strips, IRE
Trans. UE-7, 35—43 (1960).
3. A. H. M e 1 t z 1 e r. Transmission characteristics of longftudfnal-mode
strip delay lines having asymmetrically tapered widths, IRE Trans. UE-9,
30-36 (1962).
4. A. H. M e i t z 1 e r. Mode coupling occurring in propagation of elastic pul-
ses in wires, J. Acoust. Soc. Am. S3, 435—445 (1961).
5. T. R. Mee ke r. Dispersive ultrasonic delay lines using the first longitudi-
nal mode in a strip, IRE Trans. UE-7, 53—58 (I960).
6. T. R. Mee ke r. The application of the theory of elastic waves in plates to
the design of ultrasonic dispersive delay lines, IRE Intern. Conv. Record,
Pt. 6, 327-333 (1961).
7. ,J. E. May, Jr. Wire-type dispersive ultrasonic delay lines, IRE Trans.
UE-7, 44—53 (1960).
8. A. H. F i t c h. A comparison of several dispersive ultrasonic delay lines
using longitudinal and shear waves in strips and cylinders, IRE Intern.
Conv. Record, Pt. 6, 284—292 (1960).
9. A. H. F i t c h. Synthesis of dispersive delay characteristics by thickness
tag er J ng in ultraSonic strip delay lines, J. Acoust. Soc. Am. 35, 709—714
10. V R. M e e k e r and A. H. M e i t z 1 e r. Guided Wave Propagation, in
Physical Acoustics, Principles and Methods (W. P. Mason, ed.), vol. 1, Part
A, p. Ill—167. Academic Press, New York, 1964.
11. J. E. M a y, Jr. Guided wave ultrasonic delay lines, ibid., p. 417—483.
12. V. T. В u c h w a 1 d. Transverse waves in elastic plates, Quart. J. Meek
Appi. Math. 2, 498—512 (1958).
13. Lord R а у 1 e i g h. On the free vibrations of an infinite plate of homoge-
neous, isotropic, elastic .matter, Proc. London Math. Soc. 20, 225—234
(1889).
50»
г
14. Н. Lamb. On waves in an elastic plate, Proc. Roy. Soc. (London)
A93, 114—128 (1917).
15. A. N. H о 1 d e n. Longitudial modes of elastic waves in isotropic
cylinders and slabs, Bell Syst. Tech. J. 30, 956—969 (1951).
16. T. R. O’M e a г a. The synthesis of «band-pass» all-pass time delay
networks with graphical approximation techniques, Hughes Aircraft Co.,
Res., Lab., Malibu, California, Res. Rept. 114 (June, 1959).
17. L. P о c h h a m m e r. Uber die Fortpflanzungsgeschwindigkeiten.
kleiner Schwingungen in einem unbergrenzten isotropen Kreiscylinder, J.
reine angew. Math. (Crelle) 81, 324—336 (1876).
18. С. C h г e e. The equations of an isotropic elastic solid in polar and
cylindrical coordinates, their solution and application, Trans. Cam. Phil.
Soc. 14, 250—269 (1889).
19. D. В a n с г о f t. The velocity of longitudinal waves in cylindrical bars,
Phys. Rev. 6», 588—593 (1941).
20. A. H. Me I tz I er. Selective attenuation of elastic wave motions in
strips of polycrystalline metals, J. Acoust, Soc. Am. 34, 444—453 (1962).
21. R. A. H e i s i n g. «Quartz Crystals for Electrical Circuits.» Van Nost-
rand, Princeton, New Jersey, 1948.
22. A. H. M e i t z I e r. A. procedure for determining the equivalent circuit
elements representing ceramic transducers used in delay lines, Proc. Elect-
ron. Components Symp. p. 210—219 (1957).
23. J. E. M a y, Jr. .Precise measurement of time delay, IRE Intern. Conv.
Record, P.t. 2, 134—142 (1958).
• •24. R. S. D u n c a n and M. R. P а г к e r, Jr. The perpendicular diffraction
delay line: a new kind of ultrasonic dispersive oivice, Proc. IEEE (Cor-
respondence) 53, 413—414 (1965).
• •25. G. А. С о q u i n and R. Tsu. Theory and performance of perpendicu-
lar diffraction delay lines, Proc. IEEE 53, 581-591 (1965).
• 26. S. S i 1 v e r. Microwave Antenna Theory and Design, p. 170. McGraw-
Hill, New York. 1948.
27. J. Eveleth. A survey of ultrasonic delay lines operating below 100
Mc/sec, Proc. IEEE 53, 1406-1428 (1965).
28. M. R. P a г к e r. U. S. patent application, filed June 11, 1964.
29. J. H. R о w e n. U. S. patent application, filed Dec., 24, 1963.
•30. V. A. К rja s i I ’ n 1 к о v. Sound and Ultrasound Waves, third ed.
(Transl.: N. К a n e r and M. Segal). Israel Programs for Scientific
Translations, Jerusalem, Israel, 1963.
26. Антенны сантиметровых волн, изд-во «Советское радио», 1950.
30. Красильников. Звуковые и ультразвуковые волны в воздухе,
воде и твердых телах, Физматгиз, 1960.
NalaHausllil
знание без границ “ *
ГЛАВА 14
ОПТИЧЕСКИЕ И СВЧ МЕТОДЫ СОГЛАСОВАННОЙ
ФИЛЬТРАЦИИ
14.1. Введение
В предыдущих двух главах были рассмотрены расчет, проекти-
рование и разработка линий задержки с сосредоточенными пара-
метрами и ультразвуковых дисперсионных' линий задержки. Эти
линии могут быть использованы в подавляющем большинстве
устройств, предназначенных для сжатия импульсов. Однако в не-
которых случаях радиолокационные сигналы обладают очень ши-
рокой полосой частот. Может оказаться также, что характер комп-
лексных функций модуляции не позволяет применить прямой метод
построения согласованных фильтров. В этих случаях обработка
сигналов с помощью обычных, сравнительно узкополосных, диспер-
сионных устройств часто оказывается невозможной.
Известным выходом из этого могут быть рассмотренные в гл. 6
методы, использующие схемы с параллельными каналами, позво-
ляющие применять узкополосные устройства для обработки широ-
кополосных сигналов. Методы построения СВЧ фильтров сжатия,
рассмотренные в некоторых опубликованных работах, характе-
ризуются более широкими полосами частот, чем ультразвуковые
линии или линии задержки с сосредоточенными параметрами, и
могут быть использованы там, где необходима обработка информа-
ции в реальном времени при высоком разрешении. Большинство
СВЧ методов позволяет получить лишь небольшие времена задерж-
ки. Поэтому такие методы не всегда оказываются оптимальными,
если необходимо обрабатывать сигналы, обладающие одновременно
как большой длительностью, так и широкой полосой частот.
В настоящей главе рассмотрены некоторые методы построения
СВЧ устройств с дисперсионными характеристиками задержки.
Разработчик, исходя из специфики радиолокационной системы и
используемых сигналов в состоянии определить, будет ли он при-
менять СВЧ методы, с помощью которых может быть получена ши-
рокая полоса частот, но малые по величине задержки, или же он
507
за счет некоторого усложнения системы применит один из методов
комбинирования узкополосных схем, который позволяет получить
и широкую полосу, и большие величины задержки. Детальное описа-
ние различных СВЧ компонент, которые могут быть использованы
при реализации конкретной системы, можно найти в литературе
[1, 2), поэтому нет необходимости рассматривать их в настоящей
книге.
Одним из наиболее интересных путей развития методов согла-
сованной фильтрации являются оптические методы обработки сиг-
налов. Функционирование оптических согласованных фильтров
определяется пространственно-частотной аналогией между систе-
мами оптической и электрической фильтрации. Можно считать,
что методы оптической обработки сигналов в основном характери-
зуются точно такими же значениями ширины полосы и произведе-
ния длительности на полосу, которые могут быть достигнуты и
в наиболее совершенных схемах с сосредоточенными параметрами
и ультразвуковых устройствах согласованной фильтрации. Наи-
более весомыми преимуществами, которые мы получаем при исполь-
зовании оптической обработки, являются: 1) более компактная
форма эквивалента набора согласованных фильтров и 2) устройство
оптической обработки, которое можно согласовывать с быстрыми
изменениями кодированных сигналов, посылаемых передатчиком.
Целесообразность применения .оптических устройств согласованной
фильтрации определяется в конечном счете проектировщиком, ко-
торый будет принимать окончательное решение, основываясь на
сочетании экономических и технических факторов, относительная
важность которых будет зависеть от конкретных условий.
14.2. Ленточная меандровая линия
Некоторые методы построения СВЧ дисперсионных линий за-
держки основаны на создании высокочастотного эквивалента мо-
стовой Т-образной схемы, рассмотренной в гл. 12. Ленточная меанд-
ровая линия [31 является одним из высокочастотных аналогов схем
с сосредоточенными параметрами, которые были успешно исполь-
зованы для получения дисперсионных характеристик задержки.
Разработка меандровой линии, применяемой для сжатия импульсов,
была выполнена Данном [4 ]. Это устройство в общих чертах пока-
зано на рис. 14.1, а, где изогнутая проводящая лента находится
между двумя боковыми плоскостями. Для крепления ленты в ра-
бочем положении используется диэлектрик. Основные физические
размеры устройства показаны на рис. 14.1, б. Длина линии L ве-
лика по отношению к промежутку s и основной модой является
суперпозиция волн ТЕМ, которые распространяются в направле-
ниях Требование, чтобы суперпозиция этих волн удовлетворяла
граничным условиям при у — ±L/2, приводит к следующему со-
508
NataHauStVi!
знание Без границ ч *
отношению для фазового сдвига р между соседними изгибами ленты
в зависимости от основной частоты <о = 2я/ для волны, которая
распространяется в направлении оси.*:
ctg1 =
с
(И.1)
Параметры у, у', у* и т. д. связаны со статической емкостью на
единицу длины между различными парами проводников бесконеч*
ной дЛины, которые имеют те же самые размеры поперечного сече*
Ф
Рис. 14.1. Обозначения размеров ленточной меандр
ровой линии.
ния, как и изогнутая лента. Данн показал, что для конфигурации,
приведенной на рис. 14.1, параметрами у', у" и т. д. можно пре-
небречь, если отношение dis 1,5. Подставляя у' = у" — О
в равенство (14.1), получаем следующее выражение для р:
р = агссоз
(14.2)
509
®r
где f0 = c/4L, или L равно четверти длины волны при частоте f0.
Дифференцируя соотношение (14.2) по со, получаем функцию груп-
повой задержки на один изгиб:
(14.3)
где

Общее поведение функции (14.3) показано на рис. 14.2 для различ-
ных значений у. Равенство (14.3) для f = f0 становится неопреде-
ленным и максимальное значение задержки можно получить с по-
мощью правила Лопиталя. Максимум задержки при f = f0 равен
!__1_
° V. V-I
(14.4)
Кривые, показанные на рис. 14.2, очень похожи на кривые, полу-
ченные в гл. 12 для схемы второго порядка из Т-образных мостовых
звеньев. Основное различие состоит в периодичности функции за-
держки меандровой линии, которое отличает эту функцию от функ-
ции задержки для мостовой схемы в краевых областях.
При определении характеристик дисперсионной задержки
ленточной меандровой линии важную роль играет параметр у. Ма-
лые значения у указывают, что соседние элементы изгибов ленты
сильно связаны, в то время как большие значения у указывают на
очень слабую связь (при отсутствии связи у = оо). Рассматривая
кривые на рис. 14.2, можно заметить, что для нашей задачи удобнее
использовать малые значения у. Данн нашел, что можно легко полу-
чить значения у в диапазоне 1,05 у 3,0, при которых пара-
метрами у', у" и т. д. можно пренебречь. Для устройств с плоским
проводником зависимость у от отношения размеров wls и d/s при-
ведена на рис. 14.3. Нормализованные функции временндй задерж-
ки для различных значений у показаны на рис. 14.4. Их можно
сравнить с функциями задержки для Т-образного моста, которые
получены в работе О' Мира и показаны на рис. 12.4.
Рассмотренные выше аналогии и взаимосвязи между различ-
ными методами построения линий задержки были использованы
Данном.для получения нескольких аппроксимаций линейных функ-
ций задержки как с положительным, так и отрицательным наклоном
характеристик.
510
^atatiaus^k
знание без границ ’ *
Рис. 14.2. Типичные характеристики
задержки и фазового сдвига на одни
изгиб ленты в меандровой линии.
Отметим периодичность кривых.
Рис. 14.3, Зависимость параметра у от отно-
шения w/s.
511
На рис. 14.5 приведен типичный пример характеристик такого
широкополосного устройства. Кривая задержки с отрицательным
наклоном нормализована по отношению к нижней частоте исполь-
зуемой полосы fb- Если наклон функции задержки отрицателен, то
периодичность основной характеристики задержки меандровой ли-
нии ограничивает область используемых частот, так что допустимые
Рис. 14.4. Зависимость задержки на один изгиб в
меандровой линии от частоты.
значения отношения наивысшей частоты к наинизшей могут быть
от 2 до 1. Значения нормализованных частот и коэффициента у
приведены на рис. 14.5. Для каждого нужного нам значения отно-
шения полос должны быть разработаны различные устройства, хотя
любое конкретное устройство может быть использовано и в случае
более узкой полосы чем та, на которую оно рассчитано. Такой под-
ход позволяет избежать сравнительно больших ошибок задержки,
которые обычно имеют место на краях полосы. Данн описал по-
строение фильтра с коэффициентом сжатия 50 : 1, обладающего ха-
рактеристиками, приведенными на рис. 14.5. Для определения необ-
ходимой полосы частот нормализованные частоты могут быть денор-
мализованы. Это позволяет определять величину реальной диспер-
512
ftataiia.usi$!i
знание без границ ' *
Сионной задержки на секцию, исходя из которой можно подсчитать
общее число необходимых секций. Дополнительные подробности
конструкции можно найти в работе Данна [4].
Меандровая линия не является точным аналогом фазосдвигаю-
щей Т-образной мостовой схемы с сосредоточенными параметрами.
Мнимый импеданс меандровой линии зависит от отношения разме-
ров dis и w/s и от диэлектрических свойств используемых материа-
Рис. 14.5. Аппроксимация характеристики' с
отрицательным наклоном в полосе от 2 до 1
для четырех секций линии задержки.
лов. Следовательно, может иметь место рассогласование между
секциями и между первой и последней секциями и импеданеами
нагрузок на входе и выходе. Количественной теоретической оценки
влияния этих факторов на функционирование меандровой линии
получено не было. Однако были достигнуты удовлетворительные
экспериментальные результаты. Это конкретное устройство предназ-
началось для применения в приемнике с быстрым сканированием
или анализаторе спектра. Сжатие импульсов в устройствах такого
типа рассмотрено в работе Кинхелоэ 15].
14.3. Расчет фазосдвигающего гибридного кольца
Обычно ленточная меандровая линия представляет собой замед-
ляющую структуру, нормализованная функция групповой задерж-
ки которой аппроксимируется функцией задержки низкочастотной
513
мостовой секции с сосредоточенными параметрами, рассмотренной
в гл. 12. Более точный структурный аналог обычной мостовой сек-
ции для СВЧ диапазона может быть построен при использовании
гибридного кольца на ЗЛ/2, показанного на рис. 14.6, хотя метод
построения не.ограничивается данной конкретной схемой. В области
Рис. 14.6. Гибридное кольцо на ЗК/2
в качестве полосового фазосдвигаю-
щего устройства.
структура
функционирует как гибридный
частот, в которой эта
элемент, использование двойственных импедансов, показанных на
рисунке, приводит к передаточной функции этого устройства:
£,1 — ZQ
£1 1+^а
Когда Za и Zb являются чисто реактивными, соотношение (14.5)
становится идентичным передаточной функции мостовой секции
с сосредоточенными параметрами постоянного сопротивления (14.5)
и, кроме того,
= ехр [—/2 arctg Ха] = ехр [—/₽ (со)],
.£>
где 0(<о) — фазовая передаточная характеристика.
На сверхвысоких частотах реактансы / Ха и j Хь могут быть
получены путем использования секции разомкнутых или замкну-
тых четвертьволновых или полуволновых резонансных линий. Если
Ха создается с помощью замкнутой полуволновой секции (т. е. цепи
с последовательным резонансом), то соответствующая функция
реактанса определится формулой
/Xo = /Z0tg^-,
©О
» <°е —<0
(14.5)
(14.6)
(14.7а)
/xe=/z„tg — = —/Z„tg«
(14.76)
В относительно узком интервале частот в окрестности <оо соотноше-
ние (14.7, б) можно аппроксимировать выражением
/X. = /«Z0^,
©О
(14.8)
514
^lataiLauSfil!.
знаниебезераниц ' *
а фазовую передаточную функцию в этом же интервале частот
мЬжно приближенно записать в виде
₽(<o) = 2arctg-^=^. ' (14.9)
(Oq/JIZq
Сравнивая с соотношением (12.21), которое определяет аппроксима-
цию О' Мира для фазовой функции мостовой схемы второго по-
рядка в виде
р (со) = 2arctg — ~~<0° + пренебрежимо малые слагаемые,
о0
мы можем заметить, что функция (14.9) идентична этому выраже-
нию, если coo/nZo представить как эквивалентную частоту СВЧ
диапазона о0- Следовательно, структура гибридного кольца может
быть использована для синтеза дисперсионных характеристик за-
держки СВЧ диапазона, причем при построении схем может быть
использована методика разработки низкочастотных мостовых схем
t сосредоточенными параметрами, если приведенные выше аппрок-
симации справедливы.
Практическая реализация СВЧ гибридной кольцевой мостовой
схемы рассмотрена в работе Фергюсона и Баррета [6]. Их схема
выполнена в виде полосковой структуры, показанной на рис. 14.7.
Рис. 14.7. Фазосдвигающая схема в СВЧ диапазоне.
Каждая показанная на рисунке полуволновая секция представляет
собой открытый резонатор. Однако четвертьволновые связывающие
элементы в местах расположения / Ха приводят к тому, что полу-
волновые секции ведут себя как соответствующие им двойственные
реактансы, или полуволновые короткозамкнутые секции.
Изменяя ширину полуволновых открытых секций и располо-
жение точек отводов Х/4 и Л/2 связывающих линий, можно регули-
ровать эффективное значение импеданса Zo в резонансных секциях.
Это позволяет получить необходимые значения эквивалентных ча-
стот о0, которые дают возможность перенести один из методов
О' Мира построения мостовых схем в диапазон СВЧ. Фергюсон и
Баррет описали счетверенные блоки из полосковых фазосдвигаю-
515

щих секций в \Q-cm диапазоне. Симметричная полосковая секция
была изготовлена путем фототравления. Устройство это показано
на рис. 14.8, причем каждый из указанных параметров оказывает
влияние на характеристический импеданс.
Измерения, проведенные на полосковых фазосдвигающих сек-
циях, указывают, что характеристики их дисперсионной задержки
и амплитудный отклик аналогичны соответствующим характери-
стикам, полученным на низких частотах в схемах с сосредоточен-
ными параметрами. Было найдено, однако, что на ошибки временнбй
задержки и рассогласование импедансов сильно влияют отклоне-
//////////////////// Металлическая пластина
, । XI—Ч Диэлектрическая облаеть, 8
t |‘ 6
Металлическая пластина
Непротравленная мебъ
Протравленная недь
Непротравленная мебь
Рис. 14.8. Устройство симметричной полосковой линии.
ния от расчетных размеров элементов гибридного кольца и секций
открытых резонаторов. В этом отношении полосковые секции про-
игрывают по сравнению с низкочастотными схемами, которые
можно подстраивать после сборки. Однако это компенсируется тем
преимуществом, что однажды созданная приемлемая схема, изго-
товленная методом фототравления, может копироваться с высокой
точностью. Как и в случае низкочастотных фазосдвигающих сек-
ций, необходимый коэффициент сжатия может быть получен путем
каскадного включения основных секций.
Отдельная гибридная кольцевая секция, изготовленная описан-
ным выше способом, имеет фиксированные потери и дополнительные
потери вследствие случайного рассеяния (равенство (12.42)] на
центральной несущей частоте кольца. Таким образом амплитудный
отклик счетверенного блока должен быть аналогичен отклику,
показанному на рис. 12.6. В этом случае также будут происходить
потери в цепях коррекции амплитудного отклика.
При использовании полосковых конструкций приходится огра-
ничиваться некоторой долей ширины полосы, в которой соотноше-
ния, характерные для гибридного кольца, являются справедливыми.
Кроме того, точная аналогия с функцией задержки мостовой схемы
О' Мира существует только в тех областях частот, где справед-
516
^alaUauswk
знание без границ * ш
лива аппроксимация импеданса резонансных секций, задаваемая
соотношением (14.8). Это приводит к- 15%-ному ограничению по-
лосы, получаемой в такой структуре, если СВЧ конструкция вы-
полнена на основе прямого метода частотного масштабного модели-
рования. Для сравнения укажем, что методы построения меандро-
вых линий, предложенные Данном, основаны на использовании
точных зависимостей времени задержки от частоты и позволяют
использовать значительно бдльшие участки ширины полосы. Ана-
логичные точные методы расчета и проектирования могут быть раз-
работаны и для гибридного кольца, так же как и других СВЧ ана-
логов фазосдвигающих схем.
14.4. СВЧ фильтры сжатия на основе многоотводных
линий задержки
Использования СВЧ компонентов, которые являются прибли-
женными аналогами низкочастотных фазосдвигающих схем с сосре-
доточенными параметрами, рассмотрено в разд. 14.2 и 14.3. Они
могут непосредственно применяться так же как низкочастотные
компоненты при создании согласованных фильтров для анало-
гичных классов кодированных ЧМ сигналов. Их можно применять
также для создания широкополосных схем обработки дискретных
кодированных сигналов, рассмотренных в гл. 8. В таких случаях
СВЧ аналоги низкочастотных многоотводных линий задержки,
полосовых фильтров и суммирующих схем могут использоваться
непосредственно, при этом осложнения возникают только из-за
способности их работать на более высоких частотах. Таким обра-
зом, СВЧ компоненты могут быть использованы для построения
согласованных фильтров для сигналов со ступенчатой ЧМ или для
создания фильтра на основе многоотводной линии задержки, рас-
смотренного в гл. 8.
Несколько отличный подход к построению фильтра сжатия
заключается в использовании компонентов с .фиксированными за-
держками для создания устройства обработки аналоговых ЧМ
сигналов. Примером этого может служить применение согласован-
ного фильтра со ступенчатой ЧМ для сжатия ЛЧМ сигналов, имею-
щих то же направление изменения частоты и частотную девиацию,
как и сигналы со ступенчатой ЧМ, с которыми согласован фильтр.
Такая обработка, очевидно, не является точной согласованной
фильтрацией. Но сам метод может оказаться полезным при построе-
нии фильтров на частотах, на которых недисперсионные (задержи-
вающие) компоненты удобнее использовать, чем компоненты ди-
сперсионного типа. Пример построения фильтра сжатия такого
типа приведен в работе Мюллера и Гудвина 17]. Их построение при-
ведено ниже в качестве иллюстрации общего метода, не входящего
в рассмотренные выше методы построения согласованных фильтров.
517
Он также является примером использования недисперсионных вы-
сокочастотных компонентов для устройств обработки кодирован-
ных сигналов. Хотя в приведенном примере рассматривается СВЧ
устройство, очевидно, что этот же самый метод может быть исполь-
зован для построения фильтров сжатия в частотных диапазонах,
которые мы выше рассматривали при изучении дисперсионных
УЛЗ и линий с сосредоточенными параметрами.
Фильтр сжатия, разработанный Мюллером и Гудвином, выпол-
няет разбиение фазовой характеристики идеальной линейной функ-
ции ЧМ на равные интервалы, что показано на рис. 14.9. Каждый
Рис. 14.9. Разбиение фазовой характеристики
согласованного фильтра на п равных сегментов.
Отметим раалнчие в раамерах частотных интервалов,
соответствующих каждому сегменту.
фазовый интервал соответствует различным интервалам на оси ча-
стот. Фильтр сжатия представляет собой многоотводную линию за-
держки, в которой расположение отводов с соответствующими за-
держками согласовано со средней задержкой каждого фазового
подынтервала. Таким образом, расположение отводов связано
с функцией фазовой модуляции. Минимальное число подынтервалов
фазы, необходимое для адекватного представления характеристики
фильтра сжатия, £авно корню квадратному из произведения дли-
тельности на полосу или коэффициента сжатия. При большем числе
отводов в линии задержки можно получить лучшую аппроксимацию
идеальной функции задержки согласованного фильтра. По суще-
ству этот метод основан на аппроксимации непрерывной зависимости
задержки от частоты с помощью дискретного набора фиксирован-
ных задержек. Фазовая функция ЛЧМ сигнала определяется фор-
мулой
е(0 = <о„/ + -1-(нН. 0<1<Т. (14.10)
518
ftataHausi
знание без границ
Представление выражения (14.10) исключает из рассмотрения отри-
цательные задержки в фильтре сжатия. Общее изменение фазы за
интервал времени Т равно
Д0(Т) = ш.Т + 4-(нП- (14.11)
Для п равных фазовых подынтервалов смещение фазы между отво-
дами линий задержки становится равным
()sp = де (T)/n. (14.12)
Располагая отвод линии задержки в средней точке каждого фазо-
вого интервала, получаем следующее выражение для нарастающей
фазы в точках расположения отводов:
Q Д6(Т) 2m —1 . ...
6m = ———о—’ !<"*<” (14.13)
л 2
Групповая задержка, соответствующая точке расположения от-
вода, может быть найдена из выражения (14.10) для фазовой функ-
ции и имеет вид
(14.14)
Значение частоты в средней точке, соответствующее каждой точке
расположения отвода, будет
= +
(14.15)
Фильтр, рассмотренный Мюллером и Гудвином, был рассчитан
на работу в диапазоне от 300 до 400 Мгц и осуществлял сжатие ЛЧМ
импульса длительностью 1 мксек при коэффициенте сжатия 100.
Использованная в эксперименте многоотводная линия задержки
имела 20 отводов (nttah = 10) и расположение их было равномер-
ным, так что задержка между соседними отводами была постоянной
по всей линии. В результате была получена структура лестнич-
ного типа, показанная на рис. 14.10. Для ввода и вывода сигнала
Вкод •
Направленные
♦
Полосовые__
фильтры и
аттенюаторы
Направленные
ответвители,
Вылов —
пооуоуоооопппппппопп
«а*
♦
Рис. 14.10. Упрощенная схема фильтра сжатия.
Слева область наивысших частот и минимальных задержек, справа — область
наиииэших частот и максимальных задержек.
Б19
в каждом отводе были использованы направленные ответвители.
Параметры схемы сжатия, вычисленные с помощью равенств'(14.14)
и (14.15) и полученные Мюллером и Гудвином, сведены в табл. 14.1.
Фильтр, построенный Мюллером и Гудвином, был предназначен
для сжатия импульса длительностью в одну микросекунду при из-
менении его частоты от 300 до 400 Мгц. Полосовой фильтр с частотой
302,9 Мгц был расположен в точке максимального приращения за-
держки относительно входной и выходной цепей. Приращения за-
держки и длины отрезков кабеля, приведенные в табл. 14.1 и 14.2,
вычислены для этого фильтра и подобраны таким образом, что син-
тезированная задержка уменьшается по линейно-ступенчатому
закону в интервале от 300 до 400 Мгц.
Параметры схемы сжатия импульсов1
Таблица 14.1
Центральная часто- та фильтра, Мец* Полоса фильтра, Мвц Приращение эадержки*, мксек Нараставшая аадержка*. мксек
302,9 8,0 0,02903 0,02903
ЗОв,6 7,9 0,05723 0,08626
314,2 7,8 * 0,05619 0,14245
319,8 7,7 0,05521 0,19766
325,2 7,6 0,05426 0,25192
330,5 7,4 0,05838 0,30530
335,8 7,3 0,05253 0,35783
341,0 7,1 0,05172 0,40955
346,0 7,0 0,05094 0,46049
351,1 7,0 0,05021 0,51070
356,0 6,9 0,04950 0,56020
360,9 6,8 0,04882 0,60902
365,7 6,7 0,04817 0,65719
370,5 6,6 0,04754 0,70473
375,2 6,6 0,04694 0,75167
379,8 7,6 0,04636 0,79803
384,4 6,4 0,04580 0,84383
388,9 6,3 0,04526 0,88909
393,4 8,2 0,04474 0,93383
397,8 6,1 0,04423 0,97806
1 Данные из работы Мюллера н Гудвина [7].
* /тд 300-|-100 fm в Мгц, tm в сек»
8 tmm —34- V94-0,175 (2л— 1) мксек, (1<т<20).
4 Нарастающая задержка отсчитывается от фильтра с центральной ча-
стотой 300 Мгц.
В качестве элементов фиксированной задержки был исполь-
зован коаксиальный кабель типа RC-213/U. При вычислении вели-
чин задержки или длины каждого отрезка кабеля были учтены
520
^ataHausi^i
знание Вез границ “ w
задержки в элементах соединений и направленных ответвителях.
Длины каждого отрезка кабеля, приведенные в табл. 14.2, выбраны
исходя из того, что каждый набор приращений задержки разделен
поровну между входной и выходной ветвями многоотводной линии
задержки. Всего было использовано приблизительно 195 м кабеля
типа RG-2X3IU. В качестве полосовых фильтров, использованных
в вводных и выводных направленных ответвителях; были применены
двухполюсные фильтры Бэттерворса. Значения ширины полосы из*
менялись от 6,1 до 8 Мгц\ эти значения приведены в табл. 14.1.
Пересечение характеристик происходит на уровне —1 дб относи-
тельно уровня отклика каждого фильтра на центральной частоте.
Для того чтобы избежать возбуждения в фильтрах, были нежела-
тельны резкие границы частотных характеристик полосовых
Таблица 14,2
Длины отрезков замедляющего кабеля в схеме сжатия импульсов1
Приращение эадержки между отводами, нсек Длина кабеля без соединительных элементов, слр'$ Приращение эадержки между отводами, нсек Длина кабеля без соединительных •лемёитов, слР'Ъ
57,2 543,6 48,8 460,3
56,2 533,4 48,2 454,2
55,2 523,2 47,5 449,6
54,3 513,1 46,9 441,2
53,4 505,6 46,4 436,4
52,5 497,1 45,8 430,3
51,7 488,9 45,3 425,2
50,9 481,1 44,8 420,4
50,2 474,2 44,2 414,3
49,5 467,7
1 Данные из работы Мюллера и Гудвина [7J.
8 Всего было по два кабеля длиной 543,Q, 533,4 523,2 см н т. Д-
Г 29,94 см td 1 / г
8 Длина кабеля равна А—--------—А__________,
/е
где td—приращение задержки, нсек; LdC — электрическая длина направлен
кого ответвителя (30,91 _сл<); Lc— электрическая длина двух соединительных
элементов (8,3 см); р е =1,503—квадратный корень из диэлектрической
постоянной данного типа кабеля; 29,94 см—это длина отрезка кабеля в
воздухе, обеспечивающего задержку в 1 нсек.
фильтров. Наконец, до и после каждого направленного ответвителя
были введены аттенюаторы для выравнивания общей характеристи-
ки потерь, а также для того, чтобы облегчить минимизацию влияния
отражений, вызванных рассогласованиями. Эти аттенюаторы мо-
гут быть также использованы для формирования частотного от-
клика с целью уменьшения боковых лепестков.
521
ael cnb WOA
С MA 408 В
Puc. 14.12. Зависимость вносимых потерь от частоты для фильтра сжатия.
Полная схема фильтра приведена на рис. 14.11. Амплитудный
отклик и вносимые фильтром потери показаны на рис. 14.12. Ука-
занные резонансные частоты были получены экспериментально;
их интересно сравнить со значениями, приведенными в табл. 14.1.
Фильтр был размещен в трех блоках, размеры каждого из них.
приближенно равны 48 х 48 х 51 см. Для формирования ампли-
тудного отклика был использован весовой фильтр, что позволило
получить уровень боковых лепестков по дальности порядка
—20 дб и увеличило ширину сжатого импульса по сравнению с опти-
мальным значением от 10 до 15 нсек. При этом функционирование
системы было наилучщим. Тот же самый общий метод построения,
что и рассмотренный выше, может быть применен для других функ-
ций ЧМ, или для согласованного фильтра со ступенчатой ЧМ [5].
Тот факт, что в общем случае все значения ширины полосы полосо-
вых фильтров могут быть различными, означает, что следует обра-
тить особое внимание на согласование их полосовых откликов для
получения плоской суммарной характеристики отклика.
14.5. Непрерывные дисперсионные структуры СВЧ диапазона
«
• СВЧ фильтры сжатия, рассмотренные в разд. 14.2—14.4, по
существу, построены по принципу кусочной аппроксимации задан-
ной функции задержки согласованного фильтра. Мы в данном слу-
чае рассматривали линейные характеристики задержки, хотя сами
по себе эти методы обладают достаточной гибкостью, что позволяет
применять их, в определенных пределах конечно, для формирования
произвольных зависимостей задержки от частоты. Второй возмож-
ный путь исследований состоит в использовании СВЧ структур,
которые имеют монотонные, нелинейные характеристики диспер-
сионной задержки, с последующим согласованием функции ЧМ пере-
даваемого сигнала с характеристикой задержки полученной струк-
туры. В некоторых случаях эти характеристики задержки прибли-
зительно линейны в узкой полосе частот и, следовательно, они
могут быть использованы в системах с ЛЧМ сигналами.
Нелинейная зависимость задержки от частоты для СВЧ струк-
тур этого типа таковы, что они обычно не могут быть использованы
в системах с сопряженными согласованными фильтрами (растяже-
ние/сжатие импульса), которые показаны на рис. 6.15. Их приме-
нение ограничивается теми случаями, где частотная модуляция
сигнала получается с помощью активных методов. Это последнее
соображение делает СВЧ структуры, рассматриваемые в настоящем
разделе, менее перспективными при использовании их в качестве
согласованных фильтров, так как для каждого типа структуры мы
должны применять специальную форму нелинейной частотной моду-
ляции, с тем чтобы получить оптимальное сжатие импульсов.
524
Ч\акг11аи$Ж
знание без ераниц * *
а) Однородный прямоугольный волновод
Наиболее известным типом СВЧ структуры, имеющей нели-
нейные дисперсионные свойства, является однородный прямоуголь-
Рис. 14.13. Групповая задержка в однородном
прямоугольном волноводе.
ный волновод, в котором распространяются волны вида ТЕ10
Фазовая функция для этого вида распространения будет
₽м=—i/i
с у \ co )
(14.16)
где с — скорость распространения; сос — критическая частота
(Ас *= 2с, где а — ширина волновода) и L — длина волновода.
Групповая задержка, найденная с помощью соотношения (14.16),
равна
Го(<0) = -^-=—/1/
dco с ! у \ со /
(14.17)
Зависимость, определяемая ~ равенством (14.17), изображена на
рис. 14.13. Эта функция аналогична функции задержки при рас-
пространении поперечных волн в полосковых УЛЗ (разд. 13.3).
Наибольшая величина дисперсионной задержки достигается в об-
ласти чуть выше <ое, а нижний предел со, используемой полосы
525
обычно определяется из соотношения сос/<о1 > 1. Ито [8] исполь-
зовал принцип стационарной фазы для исследования соотношений
между групповой задержкой в волновЬде, определяемой равенством
(14.11), и частотной модуляцией СВЧ сигнала на выходе волновода,
когда волновод действует как дисперсионный (т. е. растягивающий
узкие импульсы) фильтр при подаче на его вход очень узких импуль-
сов с длительностью порядка наносекунды. Ито описал применение
этого метода к системам сжатия импульса. В общем случае, частот-
ная модуляция импульса, подвергшегося дисперсии в однородном
волноводном фильтре, не будет подходящей для сжатия в том же
самом волноводе вследствие нелинейности характеристик волновода,
на что указывает рис. 14.13. Однако функция частотной модуляции,
необходимая для согласования задержки приемника, определяемой
равенством (14.17), также может быть получена с помощью метода
стационарной фазы, рассмотренного в гл. 3. Там было показано,
что если задержка согласованного фильтра есть 7d(o>), тогда согла-
сованная функция частотной модуляции ш(/) приближенно равна
обратной функции 77'(О- При известной нижней частоте со1 это
дает оптимальную функцию модуляции в виде
®(0 =----- “° --------- . (14.18)
]/ !_Г___________!________I2
где х
^макс = Td (<fy) 7d ( оо ).
Функции модуляции, определяемые соотношением (14.18), показа-
ны на рис. 14.14 вплоть до <о(/)=2(ос. Обычно длительность переда-
ваемого сигнала хорошо согласуется с этими пределами, если только
не требуется очень широкая полоса частот. Функции модуляции,
показанные на рис. 14.14, могут быть аппроксимированы с помощью
функций линейной ЧМ в определенных узких интервалах полосы
частот. Такой подход приводит к результатам, полученным Омэном
[91. Однако наиболее полезное применение эта волноводная струк-
тура получила при нелинейных функциях ЧМ, задаваемых соотно-
шением (14.18). В общем случае наилучшей частотной областью для
использования ЛЧМ сигналов является область больших значений
wz. Это приводит к значительному увеличению длины волноводов
при тех же самых основных параметрах сжатия, по сравнению с ис-
пользованием оптимальной функции модуляции совместно со зна-
чениями (oz, значительно более близкими к сос.
Свойства функции неопределенности сигнала, имеющего прямо-
угольную огибающую, и функция частотной модуляции, опреде-
ляемая соотношением (14.18), не были подробно изучены. Можно,
однако, предположить, что они должны быть аналогичны по свой-
526
^alattaus^ii
знание без границ ’ *
ствам сигналу однонаправленной параболической ЧМ, рассмотрен-
ной в гл. 9. Таким образом, форма сжатого импульса будет иметь
вид, приближенно напоминающий импульс (sin х)/х, но несколько
шире и будет обладать более высоким уровнем боковых лепестков
(см. рис. 4.14). Такой сжатый импульс наблюдал Уолтер [10] в за-
полненном водой акустическом волноводе, для которого дисперсион-
ная групповая задержка будет функционально эквивалентна за-
Рис. 14.14. Кривые для согласования нелиней-
ной ЧМ с характеристиками однородного пря-
моугольного волновода.
держке в однородном СВЧ волноводе. Зависимость пикового зна-
чения сигнала на выходе согласованного фильтра от нормализован-
ного допплеровского сдвига будет аналогична этой зависимости для
сигнала с однонаправленной параболической ЧМ, показанного на
рис. 9.11. Однако, так .как СВЧ сигнал может иметь чрезвычайно
широкую полосу, то во всех практических случаях зависимость его
характеристик от допплеровского’ сдвига не должна слишком силь-
но отличаться от поведения характеристик ЛЧМ сигнала с доп-
плеровскими сдвигами, очень малыми относительно полосы сигнала.
Потери в волноводе могут достигать 8 дб на 30, 48 м его длины.
Как только будут выбраны существенные определяющие параметры
волновода (wz/<oc, Ду и ATd), то ожидаемые вносимые потери можно
легко подсчитать с помощью известных характеристик потерь для
различных типов волноводов. Общие потери могут поддерживаться
на минимальном уровне путем выбора режима работы настолько
близким по частоте к сос, насколько это возможно (но так, чтобы при
527
работе не попасть на частоту <ос, что приведет к значительно боль»
шим потерям) и путем использования соответствующей нелинейной
функции ЧМ.
б) Клинообразный волновод
Дифференциальная задержка на единицу длины в волноводной
структуре может быть увеличена путем использования клинообраз*
ного волновода (волновод переменного сечения) с углом 20, который
имеет одну и ту же линейную скорость схождения клина и по ши-
рине и по высоте. Фазовая характеристика структуры такого типа
будет
Р(г) = -!у-1/Л 1—(14.19)
где coc(z) — критическая частота в каждой точке z.
Функция групповой задержки, найденная с помощью выраже-
ния (14.19), запишется в виде
Функция (14.20) изображена на рис. 14.15 в зависимости от L/z0
для различных значений ш1/и)с (0). Так как критическая частота
этой структуры возрастает с длиной волновода L, то выбор огра-
ничивает максимальное значение L/z0. На это указывает контур
критических частот на рис. 14.15. Нелинейная ЧМ, которая согла-
суется с групповой задержкой, определяемой равенством (14.20),
имеет вид
со (0 =---- - ..- —....... ,
/ . J______________1 , I2
V * “ \(c/L')TD ]COC(0)J — (e/Z?) / J
L' = £(1- /2z0).
(14.21)
Если произвести замену L >ca L', то можно заметить, что это выра-
жение идентично выражению (14.18). Таким образом одна и та же
функциональная форма нелинейной ЧМ может быть согласована
с характеристиками дисперсионной задержки как однородного,
так и клинообразного волноводов.
При использовании клинообразного волновода можно достиг-
нуть значительного уменьшения длины устройства. Используя
528
равенства (14.17) и (14.20), можно показать, что для сигнала, девиа-
ция которого занимает интервал от 1,05 до 1,20 со. (15% ширины
полосы нормализованной к критической частоте), необходимая
длина однородно сужающегося волновода составляет одну четверть
длины прямоугольного волновода с постоянным поперечным сече-
нием. Применение клинообразных волноводов в системах сжатия
импульсов и коррекции дисперсии рассмотрено Альбершаймом
Рис 14.15. Зависимость времени задержки от длины
клинообразно сужающегося волновода.
[11] . Тэнг [12] обсуждает построение неоднородно сужающегося
волновода, который позволяет получить большие линейные диспер-
сионные задержки. Кларрикоутс и др. [13] обсуждают применение
однородных и клинообразных диэлектрических нагруженных круг-
лых волноводов, работающих по принципу обратной волны, в радио-
локаторах со сжатием импульса сантиметрового диапазона. Методы
построения выравнивателей фазы и задержки с помощью клино-
образных волноводов рассмотрены Торгау [14].
в) Спиральная структура
Спиральная замедляющая структура получила наибольшую
известность вследствие ее использования в лампах бегущей волны.
В диапазонах частот, .представляющих интерес для этих применений,
свойства распространения в этой структуре описываются зависи-
18 зяк, 1341 529
иг
fir
1 мостью фазы от частоты, которая практически линейна и, следова-
тельно, не обладает дисперсионными свойствами на этих частотах.
Однако на более низких частотах существует область; в которой
фазовая характеристика имеет приблизительно параболический вид,
а функция групповой задержки приблизительно линейна. Фазовый
отклик спирали вдоль ее оси равен [15]
р (со) = (со/о) V(р/с)'+ у® ,
(14.22)
где о — фазовая скорость, а у — постоянная радиального распро-
странения.
14.16.
Зависимость между параметрами
постоянной радиального распро-
странения у.
Рис. 14.17. Фазовая харак-
теристика при распростра-
нении в спирали.
Рис.
спирали и
Рис. 14.18. Зависимость задержки от частоты
для спирального дисперсионного фильтра.
Оценка величины у позволяет вычислить функцию групповой
задержки обычным способом. К сожалений, выражение для у не
получено в явном виде; оно выведено Пирсом [15]
у .'ДТ»> *«,(*» a.JLctg*,
(14.23)
530
'NataHauswil
знание без границ Ч *•
где a •— радиус спирали; ф — угол наклона спирали; /0, h —
модифицированные функции Бесселя первого рода и /Со, Ki — моди-
фицированные функции Бесселя второго рода.
На рис. 14.16 изображена зависимость между со, а, у и ф. Фазо-
вая характеристика спирали показана на рис. 14.17. В дисперсион-
ной области задержка увеличивается с частотой, и, следовательно,
спираль может быть использована в качестве фильтра сжатия для
сигнала, который имеет отрицательный наклон функции модуляции.
Построение спирального фильтра сжатия описано Данном [161.
Этот фильтр имеет приблизительно линейную задержку, как пока-
зано на рис. 14.18. Использование фильтра сжатия такого типа
в приемнике со сканированием описал Кинхелоэ (5].
г) Д р у г и е СВЧ структуры и устройства
СВЧ структуры многих других типов могут быть использованы
в качестве широкополосных фильтров сжатия. Примером является
структура Кэрпа, одна из форм открытого гребенчатого волновода.
Волновод такого типа длиной 152,4 см был использован для полу-
чения коэффициента сжатия 16 на частоте около 1 Ггц Ц7].
Приведенные в настоящем разделе в качестве примеров струк-
туры в общем случае не обладают той гибкостью при построении
устройств с дисперсионной задержкой, которая может быть достиг-
нута с помощью СВЧ аналогов Т-образных мостовых схем или
с помощью методов, основанных на использовании многоотводных
линий задержки. Кроме того, волноводные структуры становятся
относительно громоздкими, когда необходимы дифференциальные
задержки сколько-нибудь значительной величины. Эти проблемы,
возможно, будут разрешены с помощью новых методов, которые
появятся в будущем. Дисперсионные свойства железо-иттриевого
граната; используемого в качестве среды распространения магнито-
упругих волн; позволяют рассматривать их как перспективный
материал для построения дисперсионных линий задержки в СВЧ
диапазоне 118, 19].
В экспериментах, проведенных Коллинзом и Нилсоном (191
было получено сжатие импульса длительностью 1 'мксек до 14 нсек
при использовании железо-иттриевой дисперсионной линии задерж-
ки при центральной частоте 2280 Мгц, причем время задержки воз-
растало в зависимости от частоты. Девиация частоты была равна
125 Мгц, что обеспечивало значение произведения длительности на
полосу для входного сигнала, равное 125. Ширина сжатого импульса
в 14 нсек была измерена на выходе такой схемы при использовании
весовой отработки по частоте. Боковые лепестки по дальности были
ниже уровня, соответствующего сжатому импульсу на выходе со-
18* 531
гласованного фильтра вида (sin х)1х. Устройство с железо-иттриевой
линией задержки, описанное Коллинзом и Нилсоном, представляло
собой стержень длиной 10 мм и шириной 3 мм, аксиально намагни-.
ченный в поле напряженностью 1050 эрст.
14.6. Оптическая обработка сигнала — пространственная
фильтрация
В радиолокации, когда необходимо выделить из принимаемого
сигнала одновременно информацию и о дальности до цели, и о ее
скорости, обычно используют набор согласованных фильтров. Такая
схема изображена на рис. 9.1. В некоторых случаях за единственным
согласованным фильтром последовательно включают схему компен-
' сации допплеровского сдвига, что позволяет работать в некотором
диапазоне допплеровских частот (пример этого для бинарных фазо-
кодированных сигналов был рассмотрен в разд. 8.7). Тем не менее,
рассмотренные ранее электрические фильтры имеют только одну
независимую переменную — время, и для обработки информации,
содержащейся во временных и частотных параметрах принимаемых
сигналов, необходимо большое число фильтров, отличающихся
центральными частотами. С другой стороны, оптические фильтры
могут быть построены так, чтобы иметь две независимые перемен-
ные; при соответствующем построении фильтра в качестве таких
переменных могут быть выбраны время и частота. Следовательно,
оптический фильтр позволяет создать набор согласованных фильтров
в одной компактной структуре. Связь оптической фильтрации с тео-
рией систем связи и теорией радиолокации была рассмотрена не-
сколькими авторами [20—261. Ряд примеров фильтрации оптиче-
ских сигналов в шумах привел О' Нейл [221.
Линзы обладают свойством (в первом приближении) выполнять
над сигналом преобразование Фурье, и это свойство может быть
использовано при синтезе согласованного фильтра. Двумерное
преобразование объекта, расположенного в передней фокальной
плоскости такой линзы, может быть получено в ее задней фокальной
плоскости [271. Это показано на рис. 14.19. Предполагается, что
используемые линзы отличаются высоким качеством и распола-
гаются в области вблизи оптической оси, где они позволяют полу-
чить наилучшее изображение. Линза £с служит для коллимирования
точечного источника монохроматического света (например, ртутная
лампа, помещенная за экраном с точечным отверстием), который
освещает объект (например, дифракционную решетку), расположен-
ный в передней фокальной плоскости линзы L\. Апертурная диафраг-
ма может быть использована для ограничения коллимированного
светового луча с тем, чтобы он падал на центральную область лин-
зы. Свет, пересекающий эту плоскость, пространственно когерентен;
это значит, что относительные пространственные фазы световых
532
^lataUaus^i
знание Сазараниц Ч*
волн в оптической системе не зависят от времени. В задней фокальной
плоскости Li распределение амплитуды и фазы света в направлении
оси х, в предположении, что угол дифракции линзы мал, определяет-
ся формулой
d/2
F(<i)J= \ /(xjexpf —KxJdXj,
-d/2
(14.24)
где | f(xi) |8 — передаточная функция в направлении оси х для
объекта, расположенного в передней фокальной плоскости; сох =
= 2jix2/Fal — пространственная частота в задней фокальной
плоскости; F — фокусное расстояние линзы и — длина волны
монохроматического света.
Диафрагма
Передняя
Фокальная
плоскость
Задняя
фокальная
плоскость
d _
2 ।
Оптичес-
кая ось
Пространст-
венный
,, Входная
дифракционная
'2
Рис. 14.19. Система линз, выполняющая оптическое преобразова-
ние Фурье.
Точечный
источник
монохромати-
ческого
излучения
В соотношении (14.24) можно узнать преобразование Фурье
«входной» функции длительностью d, расположенной в передней
фокальной плоскости. Если, например, /(х<) — постоянная функция
с однородной фазой на интервале d, то F(cox) определится выраже-
нием
sin 1/2 b)xd
\/2wxd
(14.25)
Если входная функция является двумерной и в нее входят обе коор-
динаты передней фокальной плоскости, то преобразование Фурье.
имеет вид
d/2
F (ых, %)= ff f(xlt f/i)exp[—/((OxXi + ^t/iJldXjdi/i. (14.26)
-d/2
18В Зак. 1341
533
Если |f(xi, yi) I* соответствует равномерному пропусканию череэ
круглое отверстие диаметра d, то преобразование Фурье имеет
форму 1
nd2
Г ((О-, (ои) =-----
' х v' 2lLF
J\ 1^/2}/ co^ + coy
d/2]/<o2-f-wj
(14.27)
Фотодетекторы .регистрируют интенсивность света, так что функ-
ции, наблюдаемые с помощью физических приборов, имеют вид
| F(iox) |2 и j F((ox, (Оу) |а соответственно для равенств (14.24) и
Входная
плоскость
Частотная
плоскость
Выходная
плоскость
Рис. 14.20. Система линз, выполняющая последователь-
ные преобразования Фурье.
(14.26). Эти два равенства можно рассматривать как описание
спектра пространственных частот либо одномерной, либо двумер-
ной функции входного сигнала.
Как и спектры временных функций, эти пространственные спект-
ры могут быть изменены путем использования фильтра Н(шх, ши)
в задней фокальной плоскости Ц, или «модулирующей» функции,
расположенной в передней фокальной плоскости. Введение, напри-
мер, в одномерном случае в переднюю фокальную плоскость на оси х
весовой функции такого типа, как мы рассматривали в гл. 7, будет
приводить к расширению спектрального распределения в задней
фокальной плоскости и понижению уровня боковых лепестков.
Спектр с модифицированным амплитудным и фазовым распреде-
лением в частотной плоскости определится выражением Sfco^Wy) =
= Г((оя, шу) X Н(шх, Шу). Вторая линза L2 в схеме на рис. 14.20
1 Равенства (14.25) и (14.27) представляют функции, которые должны
быть конечными вследствие физических ограничений, накладываемых сис-
темой линз и приближений, использованных в равенстве (14.24). В случае
согласованной фильтрации это эквивалентно предположению об одновремен-
ной ограниченности сигналов по длительности и полосе частот. Это не влечет
за собой серьезных последствий, если протяженность частотной плоскости
достаточна, чтобы в ней размещалась основная часть спектра.
534
5ValaHaas;lfe
знание без ераниц * *
формирует преобразование Фурье в задней фокальной плоскости Lt
(выходная плоскость)
s (х9, ‘ уа) = j j 5 К. wv) ex р I—/ (юя ха + <ov </а)1 dtox dtoy.
(14.28)
Равенство (14.28) не является обычным обратным преобразованием
Фурье, которое выполняется электрическим фильтром, а представ*
ляет собой дополнительное прямое преобразование Фурье. Однако
если иметь в виду инверсию координат, которая имеет место между
входной и выходной плоскостями, то выражение (14.28) можно пе-
реопределить как обратное преобразование. Оно представляет со-
бой инверсию нормального изображения, формируемую с помощью
системы изображающих линз. Если на вход поступает более одного
сигнала, то выходной сигнал представляет собой суперпозицию
выходных сигналов, получаемых при подаче на вход каждого из
поступающих сигналов отдельно, если только не происходит насы-
щения.
Согласованная фильтрация входного сигнала может быть полу-
чена в системе описанного выше типа путем размещения фильтрую-
щей функции в спектральной плоскости, причем эта функция
должна удовлетворять условию [23, 28]
як, = (14.29а)
JV (<0ж, (Оу)
где Я(<оя, wv) — пространственное распределение плотности мощ-
ности шума и k — нормализующий коэффициент согласованного
фильтра. Если шум белый и гауссов, то
Я(®ж, <ov) =• k'F* (<оя, ©v) = k'\F* (<оя, tov) | exp [j₽ (<ox, <£>„)]. (14.296)
Одним из преимуществ оптических систем является то, что ампли-
тудный и фазовый сомножители H(toxt tov) могут быть реализованы
отдельно; для электрических фильтров это, как правило, неосуще-
ствимо. | H(tox, toy) | можно получить путем изменения коэффициента
пропускания транспаранта, установленного в частотной плоскости,
а ₽(соя, cov) получается за счет изменения толщины транспаранта.
Второй метод создания оптического согласованного фильтра
состоит в размещении опорного сигнала h(xt\ yt) во входной плос-
кости (231, причем
h(Xi, yx)^f(-xu —yt). ‘ (14.30)
Согласованная фильтрация осуществляется путем физического
перемещения h(xt, yt) или f(xlt yj относительно другой функции
в передней фокальной плоскости Ц. Рассматривая выходную функ-
18В* 535
цию на оптической оси (т. е. сож = 0, <ои = 0) в задней фокальной
плоскости, получаем с учетом (14.26)
d/2
«(<• »;)= и/01Н(*;—i'i)dxid»r <14-з1>
где Xi, у\—переменные, описывающие смещение изображения.
Равенство (14.31) представляет собой обычное определение согла-
сованной фильтрации через интеграл свертки. Когда входная или
опорная функция скользит относительно неподвижной функции,
Скорость перемещениями^d/T
Рис. 14.21. Преобразование временных сигналов в
пространственные.
Т—длительность необработанного сигнала.
то непрерывное считывание | g(x\, у\) |2 может быть осуществлено
с помощью фотодетектора, расположенного на оптической оси.
Такое устройство эквивалентно согласованному фильтру, за кото-
рым следует квадратичный детектор. Этот последний способ являет-
ся основой важного метода построения согласованного фильтра
с помощью ультразвукового модулятора света.
Рассмотренный выше способ представляет, по-видимому, точ-
ный аналог электрической согласованной фильтрации, если про-
странственные координаты во входной плоскости могут быть пре-
образованы в эквивалентные временные единицы. Так как измене-
ние сигнала во времени характеризует одна координата, то для
создания временндго изменения электрический входной сигнал
фиксируется в виде непрерывной решетчатой функции на регистри-
рующей пленке, которая перемещается в направлении оси х, как
показано на рис. 14.21. Когда это выполнено, выходные сигналы,
полученные на основе описанных выше методов, являются функ-
циями времени.
Набор согласованных фильтров реализуется за счет исполь-
зования оси у для представления допплеровского сдвига, причем
536
^alaHausX
знаниебезграниц **
преобразования Фурье выполняются только по переменной х [23].
Это достигается за счет использования комбинации сферических и
цилиндрических линз, показанной на рис. 14.22. Так как операции,
выполняемые при фильтрации, включают только одномерные пре-
образования Фурье, то вместо точечного может быть использован
линейный источник. Входная Функция может иметь и дискретный
вид, как показано на рис. 14.23, причем каждая выборка опреде-
ляет пропускающую способность линии дифракционной решетки на
регистрирующей пленке, перемещаемой через входную плос-
кость.
Размещение набора функций согласованных фильтров в час-
тотной плоскости показано на рис. 14.23. Цилиндрические линзы
выполняют одномерное преобразование Фурье. Следовательно,
комбинация сферических и цилиндрических линз, показанная на
.рис. 14.22, выполняет двойное преобразование Фурье по оси у (или
не выполняет преобразования, за исключением инверсии оси у),
и только единственное преобразование Фурье по оси х. Преобразо-
вание входного сигнала с конкретным допплеровским сдвигом попа-
дает на все фильтрующие функции в частотной плоскости, однако
его фазовое и амплитудное распределение согласовано только с одним
фильтром в наборе. Сигналы на выходах фотодетекторов, располо-
женных друг за другом по оси у в выходной плоскости, будут изме-
няться во времени по мере перемещения пленки во входной плос-
кости, достигая максимального значения, когда сигнальная функция
заполнит входную плоскость. Один из фотодетекторов будет реги-
стрировать истинную автокорреляционную функцию, в то время
как другие выдавать взаимно-корреляционные функции или функции
с учетом допплеровского сдвига. Таким образом, это устройство
функционирует аналогично набору согласованных электрических
фильтров, показанному на рис. 9.1.
Другая схема может быть получена, если расположить необ-
ходимый набор опорных функций с допплеровским сдвигом во вход-
ной плоскости и считывать множественные сигналы согласованных
фильтров с фотодетекторов, соответствующим образом размещен-
ных за вертикальной целью, прорезанной вдоль оси у в задней фо-
кальной плоскости Li; эта операция является обобщением одномер-
ного случая интеграла свертки.
Для большинства радиолокационных задач важно, чтобы за-
пись входных сигналов была выполнена в реальном масштабе вре-
мени. Это значит, что в процессе записи нельзя допускать задержки,
превышающие максимальный интервал времени, в течение которого
регистрируемые входные сигналы еще остаются полезными как
информационный выход радиолокационной системы. В большин-
стве случаев такая задержка не должна превышать нескольких
секунд. Фотографическая пленка для регистрации входных сигна-
лов может быть использована лишь в тех случаях, когда время об-
работки пленки не ограничено.
537
Входная
плоскость
х1 - Время
/ -допплеровский
• сдвиг
Частотная
плоскость
(Dz - частота
и, -допплеровский
* * сдвиг
Яыкд&ная
плоскость
х3 - Время
у3-допплеровский
Рис. 14.22. Система линз, эквивалентная набору согласованных
фильтров.
ЛЛДЛАА
Электрический cut на л
Ожидаемый
допплеровский
интервал
Входной транспарант на пленке
F*(u)-ajd3)
F* (и>- 1иаг',
Г* (и>- сиа,)
F*fu>)
F*
F*(iu^Ud3)
Частотная плоскость транспаранта
Рис. 14.28. Дискретизация сигнала для регистрации
его на пленке с целью получения входного транспа-
ранта и характеристика набора согласованных фильт-
ров в частотной плоскости.
538
^alaHausiiik
знание без границ Ч*
Катрона и др. [23] вели запись входных функций непосредствен-
но с экрана электронно-лучевой трубки. Термопластические пленки
позволяют регистрировать сигналы и использовать входную ин-
формацию, по существу, в реальном масштабе времени [29]. Однако
допустимые скорости перемещения носителя для большинства мето-
дов регистрации таковы, что эти методы подходят лучше всего для
обработки относительно длительных и относительно узкополосных
сигналов. Поэтому если необходимо обработать сигналы с большим
значением произведения их длительности на полосу, то увеличение
этого произведения должно производиться за счет длительности.
Ламберт установил, что в настоящее время можно достичь скорости
перемещения носителя порядка 500 см/сек. Применение пленок и
ферромагнитных лент имеет то преимущество, что позволяет ис-
пользовать большое число опорных функций или каналов согласо-
ванной фильтрации, так как разрешающая способность этих видов
регистрации сигналов лежит обычно в пределах от 2000 до 10 000
линий на сантиметр [25]. Однако нестабильности вращения или де-
тонация механизма протяжки могут ограничить практическую раз-
решающую способность (или число линий на сантиметр) при боль-
ших скоростях перемещения носителя. Ультразвуковые модуляторы
света, которые могут быть использованы для получения согласо-
. ванных фильтров, работающих в реальном масштабе времени, будут
в дальнейшем рассмотрены в разд. 14.8.
В проведенном выше рассмотрении было сделано существенное
допущение о том, что оптические сигналы и фильтры можно рас-
сматривать как точные аналоги электрических сигналов и фильт-
ров. Это не совсем верно, так как оптические передаточные функции
должны быть всегда положительными. Влияние этого ограничения на
реализацию оптического согласованного фильтра кратко рассмот-
рено в следующем разделе.
14.7. Применение оптических согласованных фильтров
в радиолокации
Допустим, что сигнал на входе оптического согласованного
фильтра1 имеет вид импульса с постоянной несущей частотой и опре-
деляется формулой
f (0 = at cos соо t, — T/2<t<T/2. (14.32)
Равенство (14.32) задает форму сигнала, который должен воздей-
ствовать на устройство модуляции света, перемещаемое поперек
плоскости его входа. Так как на оптический транспарант можно
записать только положительные функции, то этот сигнал не может
быть непосредственно использован в качестве решетчатой дифрак-
ционной маски. Для преодоления этого ограничения к входному
сигналу добавляется смещение, так чтобы все части передаваемого
539
сигнала были положительны. Таким образом равенство (14.32)
можно переписать в виде
f (0 = Oo+fliCOS(o0/, a0>ai* (14.33)
Преобразователь электрического сигнала в оптический, исполь-
зующий, например, перемещение пленки, превращает этот входной
сигнал в пространственную функцию f (xi) (рис. 14.21). Простран-
ственный спектр появляется в задней фокальной плоскости Lt.
Эта спектральная функция имеет постоянную слагающую а0 плюс
две боковых полосы с амплитудой сц/2 (рис. 14.24). Интенсивности
равны ао для постоянной слагающей и а?/4 для боковых полос.
Рис. 14.24. Распределение амплитуды светового потока в ча
стогной плоскости в случае смещения входной функции.
Спектральные функции боковых полос в оптике называются диф-
ференционными порядками и для рассмотренного выше случая
мы имеем минус-первый порядок, нулевой порядок и плюс-первый
порядок. Для представления исходного сигнала [выражение
(14.32) ] необходима только одна из таких боковых полос, поэтому
с помощью диафрагм или полосовых фильтров в частотной плос-
кости, нулевой порядок и минус-первый порядок дифракционной
картины г устраняются. При этом свет, падающий на следующую
преобразующую плоскость, пропорционален комплексной форме
f(xi) (амплитуде и фазе). Опорная функция может быть размещена
в следующей преобразующей плоскости (временная плоскость)
для того, чтобы выполнить операцию свертки. Окончательный
выходной сигнал фильтра наблюдается при сох — 0 в следующей
преобразующей плоскости, как показано на рис. 14.25. Опорная
функция также должна быть записана со смещением. Световой поток,
исходящий из плоскости опорной функции, может быть представлен
в общих пространственных координатах в виде
f (*1— *i)l&o+bi £(*))» (14.34)
где Ьо 4- bt g(x) — смещенная опорная функция. Подставляя выра-
жение (14.34) в интеграл свертки (14.31), получаем выходную ампли-
туду, изменяющуюся по мере того, как f (xi) перемещается поперек
540
знание без границ “ *
входной плоскости. Так как выходной сигнал наблюдается в точке
выходной плоскости, где частота равна нулю, то член свертки, воз-
никающий вследствие bof(Xi — х\), следует рассматривать как
помеху, если f(x) имеет постоянную составляющую, которая накла-
дывается на интересующий нас выходной сигнал. В этом случае
такой дополнительный световой поток может быть смещен от точки
Входной Фильтр первою Опорная
сиснал порядка функция
Рис. 14.25. Система линз и экран в частотной плос-
кости для корреляции входного сигнала с опорной
функцией.
сож = О путем изменения представления входной и опорной функ-
ций с несущей пространственной частотой, так чтобы они приняли
вид
a04-aif fa—*i)cos<ocx и 60 + 6i£(x)cos(ocx.
Перемножение приведенных выше выражений в интеграле свертки
дает после отбрасывания члена, содержащего а0,
b0 f (х) cos <ос х4- f (xt—x't) g (х) Ц- + -1 cos 2<осxl. (14.35)
I W X I .
Теперь в положении <ох — 0 выходной плоскости будет появляться
только член, связанный с atbif(xi—x\)g(x), другие члены окажутся
смещенными относительно этой точки пропорционально и 2<ос.
Примеры обработки такого типа рассмотрены в работе Катрона
и др. [23]. При несколько более простой схеме построения входная
и опорная функции размещаются во входной плоскости, причем,
как и раньше, лишние порядки дифракции фильтруются в частот-
ной плоскости. Если либо f(x), либо g(x) заданы с пространственной
несущей частотой сос, тогда, наблюдая световой поток при сож = (ос
в частотной плоскости, изображенной на рис. 14.19, мы будем
получать в соответствии с выражением (14.24) [или (14.26) для
двумерного случая] на выходе интеграл свертки, аналогичный
(14.31). Этот выходной сигнал будет перемещаться на частотной
плоскости по мере перемещения входной функции относительно
опорной функции.
541
В большинстве случаев оказывается проще записать опорную
функцию на пленочный транспарант не как функцию, непрерывно
изменяющуюся между двумя крайними значениями, а в виде комби*
нации черных и белых полос, размещенных в соответствии с функ-
цией модуляции. Козма и Кэлли [30] показали, что «клиппирован-
ная» опорная функция такого типа приводит к потерям порядка
1,1 дб относительно коэффициента передачи согласованного фильтра,
получаемого при использовании в качестве опорной точной копии
принимаемой входной функции.
В качестве второго возможного подхода к проблеме согласо-
ванной фильтрации можно вместо вычисления интеграла свертки
ввести соответствующий согласованный фильтр в первую частотную
плоскость. Однако и в этом случае должны быть приняты специаль-
ные меры, обеспечивающие такое расположение транспаранта
фильтра, чтобы он воздействовал на соответствующую боковую
полосу распределения, задерживая в то же время другие спектраль-
ные компоненты. В особенности это относится к компоненте дробо-
вого шума максимума нулевого порядка с большой амплитудой,
который, попадая в выходной сигнал уменьшает контрастность или
динамический диапазон принимаемых сигналов. Хотя приведенные
выше примеры относились к простым импульсным функциям, оче-
видно, что этот общий подход одинаково применим и к сигналам
более сложного типа. Таким образом, в случае ЛЧМ сигнала по-
требуется опорная функция с линейной ЧМ и спектральные ампли-
туды будут определяться распределением Френеля, рассмотренным
в предыдущих главах. Пространственное распределение фазы в ча-
стотной плоскости будет практически квадратичным. Следователь-
но, при согласованной фильтрации для фазового замедления про-
странственного светового фронта в частотной плоскости необхо-
димо использовать линзы с параболической кривизной.
Одно из основных затруднений, возникающих при осуществле-
нии согласованной фильтрации в пространственно-частотной плос-
кости, связано с формированием линз, обладающих нужным фазовым
замедлением в том случае, если функция модуляции сигнала нели-
нейна или псевдослучайна по фазе или частоте. Метод формирования
сложной функции согласованного фильтра описал ван дер Люгт [28].
Этот метод основан на использовании интерферометра Маха —
Зендера для фиксации функции согласованного фильтра на фото-
графическую пленку, на которой можно регистрировать только по-
ложительные действительные функции. Схема, которую использо-
вал ван дер Люгт, показана на рис. 14.26. Световой поток, созда-
ваемый в выходной плоскости монохроматическим опорным пучком,
равен
/?(сох, oj = |Я(ых, cojexpl/^b^ + ccoj]. (14.36)
Фазовый множитель (14.36), который создается фазовой пластин-
кой в опорном пучке, линеен по оси х и по оси у выходной плоскости.
542
Сигнал f(x, у) с учетом рассмотренных ранее ограничений вводится
в переднюю фокальную плоскость линзы Lt, так что распределение
амплитуды света в плоскости Р2 от сигнала будет
F К, <oF) = | F (соя, ии) | ехр [/₽ (соя, со,)]. (14.37)
Таким образом, общий наблюдаемый выходной сигнал для точеч-
ного источника монохроматического света /?(шя, (и>и) = k = const
имеет вид
Источник
ЮК» |» = | R(<оя, co^ + FK, ю^РЧЯК, %)|‘+
+ I fK> ©^Р+Я’К» %)F((ox, wj + F* (соя, о,) Я К, %).
(14.38)
Опорный пцчок
Сие на л Lf
Выходная
плоскость
В -расщепитель
пучка
М-зеркало
Рис. 14.26. Схема модифицированного интерферометра Маха—
Зендера для регистрации комплексных пространственных
функций.

R(uJZyU)^
Вспоминая, что для белого гауссова шума характеристика сог-
ласованного фильтра Я(юя, %) = kF* (<ох, соД из (14.38) получа-
ем выражения
ЮК, <%)Р=?=Л((ОЯ, wy) + H*((0x, (ojexpl—/(д(0жч-ссор)]ч-
+ #К» <®lz)expI/(£xox4-c<ojr)],
(14.39)
где А (<оя, <о1/) = |/?((оя, <%)P + |F(<ox, (ov)p.
Последний член равенства (14.39) содержит нужную функцию со-
гласованного фильтра. Функция, задаваемая равенством (14.39),
полностью фиксируется на пленке и затем вводится в частотную
плоскость оптической системы такого типа, как показано на
рис. 14.20, причем сигнальная функция помещается во входной
543
плоскости. Выходная функция в соответствии с равенствами (14.38)
и (14.39) имеет вид
y>i = JP(<°х’ <^)«Pl/K*4-<M}l^»dM-
00
+ ~4^“П F^Xt <й1/)ехР1/{(х“-Ь)(Ох +
— 00
оо
+ (У—с) 1 rftox d(i)v 4- С [ F (шх, to) Н (tox, to ) х
4 Л* J J
— оо
X ехр [/ {(х + b) tox 4- (у + с) (Ov} 1 dtox dtoy. (14.40)
Последний член в уравнении (14.40) описывает искомый выходной
сигнал согласованного фильтра для записанного сигнала f(x, у)
с центром в точке с координатами х — —Ь, у — —с. Ван дер Люгт
Рис. 14.27. Схема модифицированного интерферометра Релея
для записи комплексных пространственных функций.
для удобства положил с = 0, так что искомый член может быть
отделен от других с помощью фотодетектора, расположенного
в точке х = —Ь, если b > хп, где хвх — общая пространственная
длительность входного сигнала.
Другая возможная схема интерферометра для регистрации
сложной функции фильтра на пленку рассмотрена в работе ван
дер Люгта и др. [31 ]. В этом методе используется интерферометр
Релея, показанный на рис. 14.27. Линза Lr фокусирует коллими-
рованный световой пучок в точке х = b в передней фокальной
плоскости линзы Li. При этом амплитуда света представляется
в виде дельта-функции Rb(x — b, у). Сигнал f(x, у) также вводится
544
в переднюю фокальную плоскость, так что пространственный спектр
в задней фокальной плоскости линзы Ц равен *
соу) ==/)[/(*, y)+Rb(x—Ь, «/)]ехр(/(wxx+wJ/t/)]dxd£/=
— 00
= F(cox, (оу) + /?ехр[/(охд]. (14.41)
Фотопленка, расположенная в задней фокальной плоскости Li,
регистрирует сигнал
| G (<ох, cov) |2 = |F (сох, cdJ |2 4- Я2 4- R exp [ —/сох Ь] X
xF(<ox, co^)4-/? exp [/<oxbl F*((ox, coy). (14.42)
Последний член в этом уравнении содержит функцию согласованного
фильтра, умноженную на постоянный и линейный фазовые члены.
Как и в случае интерферометра Маха — Зендера, зафиксированная
на пленке функция размещена в частотной плоскости устройства,
показанного на рис. 14.20, и в соответствии с приведенными выше
рассуждениями искомый выходной сигнал центрирован в точке
х = b выходной плоскости, при тех же самых условиях, относя-
щихся к величине Ь, как и в ранее рассмотренных случаях.
14.8. Ультразвуковой модулятор света
Использование фотопленки для регистрации и перемещения
сигналов относительно входной плоскости оптического согласован-
ного фильтра обычно не позволяет получить выходные сигналы,
которые можно было бы рассматривать как сигналы в реальном
масштабе времени. Класс оптических согласованных фильтров для
применения в радиолокации, которые функционируют в реальном
масштабе времени, может быть построен на основе использования
ультразвуковых модуляторов света для эквивалентного перемеще-
ния сигнала во входной плоскости.
Такой модулятор света представляет собой ультразвуковую
линию задержки, выполненную из прозрачного материала (обычно
это вода, кварц или стекло), которая устанавливается поперек
направления распространения коллимированного светового пучка,
как показано на рис. 14.28. Электрический сигнал, соответствую-
щий по форме входному сигналу, возбуждает электромеханические
преобразователи на входе ультразвукового модулятора света. Этот
сигнал обычно преобразуется в продольные ультразвуковые волны,
1 Пределы интегрирования в выражениях (14.40) и (14.41) конечны.
На практике они определяются конечными размерами линз, коллимирован-
ного светового пучка и отклонением входного сигнала.
545
которые распространяются в задерживающей среде снизу вверх.
По мере распространения ультразвуковых волн в линии задержки»
происходящие при этом изменения оптической плотности задержи-
вающей среды вызывают изменения коэффициента ее преломления,
которые пропорциональны возбуждающему сигналу [32]. Это,
в свою очередь, приводит к пространственной фазовой модуляции
коллимированного светового пучка, проходящего через ультразву-
ковой модулятор света. Такая фазовая модуляция прямо пропор-
циональна изменениям коэффициента преломления и следовательно,
изменениям функции сигнала, когда он проходит через некоторую
Поглотитель
Коллимированный
свет
Свет,
модулированный
по (разе
Входной сигнал,{(С}
Рис. 14.28. Схема ультразвукового модулятора света.
фиксированную точку линии задержки. Для входной функции
общего вида световой поток с пространственной фазовой модуля-
цией мон?ет быть записан в виде
f (х) = ехр [—/а0 {cos (ос х 4- 0 (х)}], (14.43)
где а0 — пиковое значение фазовой модуляции, зависящее от мощ-
ности входного сигнала, и 0(х) — функция модуляции сигнала.
Используя хорошо известное разложение по функциям Бес-
селя, запишем приведенное выше выражение в виде
00
f(x) = J0(a„) + 2 S /"'Jr.(“«)cos«K^ + e(x)|. (14.44)
п» 1
Учитывая свойства рассеянного светового потока, можно найти
такую пространственную область вблизи ультразвукового модуля-
тора, где члены равенства (14.44), содержащие Jo и Jit находятся
в фазе, а не в квадратуре. В этой области пространственное распре-
деление светового потока в направлении оси х является модулиро-
ванным по амплитуде, что эквивалентно существованию плюс-
первого, нулевого и минус-первого порядков, полученных с по-
мощью записанной на пленке решетчатой функции, которая содер-
жит исходный сигнал на входе, плюс смещение. Если а0 велико
546
^alatlauswk
знание без границ * --
то другими членами в равенства (14.44) нельзя пренебрегать, так
как в результате могут возникнуть модуляционные искажения, на
что указывалось в разд. 11.5 при рассмотрении случая перекрытия
входных сигналов.
В литературе описано несколько методов использования ультра-
звуковых модуляторов света в радиолокационных согласованных
фильтрах. Райх и Слободин [33, 341 применили их в системе общего
типа, показанной на рис. 14.28. Ламберт и др. (351, Арм и др. (361
и Слободин и др. [37] описали использование таких модуляторов
в устройствах обработки сигнала, действующих на основе свертки,
Опорная
Функция Ц
УльтразВукоВой
модулятор
Выход
Вход
Фото-
детектор
Коллимирующие
линзы
Экран д Выходной
Интегрирующие плоскости, ~
линзы пропускающий
1-й порядок одета
Рис. 14.29. Схема устройства для обработки сигналов с помощью
ультразвукового модулятора света.
которые содержат опорную согласованную функцию во входной
плоскости, как показано на рис. 14.29. Опорная решетчатая функ-
ция может быть расположена внутри или рядом с задерживающей
средой; в рассматриваемых случаях такой средой служила вода.
В оптическом фильтре, рассмотренном Слободиным, использовались
ЛЧМ сигналы и сигналы с псевдослучайной ЧМ при значениях про-
изведения длительности на полосу 120, при длительности сигнала
60 мксек и ширине полосы 2 Мгц. Ширина сжатого импульса со-
ставляла 0,5 мксек. Опорная решетчатая функция была получена
на основе фотографического метода и оптическая система была ис-
пользована для формирования кодированного сигнала путем по-
дачи импульсов на вход ультразвукового модулятора света.
На рис. 14.30, а показан растянутый ЛЧМ импульс, получен-
ный Слободиным, а на рис. 14.30, б — соответствующий ему сжа-
тый импульс. Сужающаяся по сторонам форма растянутого импульса
возникает вследствие неидеальности общих полосовых характери-
стик устройства обработки. На рис. 14.31, а и б показаны растяну-
тый и сжатый импульсы для сигнала с псевдослучайной ЧМ. Сжа-
тый импульс на выходе фотоэлемента содержит ультразвуковую не-
сущую, так что для,дальнейшего превращения его в видеосигнал
необходимо детектирование. В работе Арма и др. [361 обсуждается
547
Рис. 14.30. Осциллограммы, по-
лученные при обработке ЛЧМ
сигнала с помощью оптического
коррелятора на основе ультра-
звукового модулятора света:
а —растянутый нмпульс (I деление
шкалы равно 10 мксек); б —сжатый
нмпульс (1 деление шкалы равно
2 мксек).
Рис. 14.31. Осциллограммы, по-
лученные при обработке сигнала
с псевдослучайной ЧМ с помощью
оптического коррелятора на осно-
ве ультразвукового модулятора
света.
а —растянутый * сигнал (1 деление
шкалы равно 10 мксек); б —сжатый
импульс (1 деление шкалы равно
2 мксек).
а)

^1а1айаиз,Л.
знание без границ * *
использование приема рассогласования частоты опорного сигнала
с целью достижения большего разделения интересующего нас пер-
вого порядка дифракции от других компонент светового потока,
если интерференция между ними превышает допустимую. Это при-
водит к улучшению динамического диапазона сигналов на выходе
устройства обработки практически в пределах от 40 до 60 дб.
В частном случае использования ЛЧМ сигнала можно приме-
нять ультразвуковой модулятор света в качестве фильтра сжатия
при значительно более простой схеме его построения, при которой
Коллимированный *
монохроматический
свет
s' 1-й порядок света
Нулевой
порядок
света
1-й порядок света
Рис, 14.32. Дифракция света на решетке с линейной ЧМ.
отпадает необходимость использовать опорную решетчатую функ-
цию. Хоэфер (24] указывает, что первый порядок светового потока,
рассеянного на линейной ЧМ решетке, сходится как показано на
fine. 14.32. Это явление рассматривали также Гериг, и Монтегю
38), предложившие схему, показанную на рис. 14.33, в которой
использован этот эффект. Линза L2 фокусирует нулевой порядок
света на оптической оси. Свойство сходимости первого порядка
светового потока заставляет его фокусироваться в точке вне оптиче-
ской оси, и эквивалентное фокусное расстояние Гэкв определяется
формулой
1= J___________.
Р вив Р»
(14.45)
где Хо = кс2 Т/А(й — фокусное расстояние для первого порядка
светового потока в отсутствие линзы L2t k — волновое число свето-
вого потока в радианах, с — скорость распространения акустиче-
ских волн в ультразвуковых модуляторах света; Т — длительность
сигнала и Дсо — ширина полосы ЛЧМ сигнала в радианах.
549
По мере поступления ЛЧМ сигнала в ультразвуковой модуля-
тор света точка сходимости первого порядка светового потока пере-
мещается вниз по плоскости S2» совпадая с указанной фокальной
точкой лишь тогда, когда сигнал полностью войдет в линию за-
держки. Щель в экране, расположенном в плоскости S2, в этой
точке пропускает сходящийся пучок к фотодетектору, находящемуся
Кол/гцнируюьцие линзы
L-СДТ*4,5сн
Апертура
Ланпа
Зивеовыкод
II
BV
вход
фокусное расстояние равно Хб)
Апертура поля
Интерференцион-
ный фильтр
/Изображение от
нулевого порядка
света

Flfa-IC"
1 . 1 +
F)к8 ^Z *0
для Xq «/> (i-
Рис. 14.33. Схема устройства оптической обработки ЛЧМ сигналов, исполь
зующего дифракционные свойства решетки с линейной ЧМ.
за щелью. Фотодетектор превращает интенсивность падающего на
него света в выходное напряжение. Точка схождения светового
потока первого порядка скользит по щели в течение интервала вре-
мени, определяемого соотношением т = 2л/Дсо. Таким, образом
длительность пикового отклика от фотодетектора будет равна по
величине длительности сжатого импульса.
ЛИТЕРАТУРА
•1. С. G. Мо л tgomery, R. Н. Dicke, and Е. М. Р и г с е 1 1. Prin-
ciples of Microwave Circuits, McGraw-Hill, New Vork, 1948.
2. G. L. M a t t h a e i, L. Y о u n g, and E. M. T. J о n e s. Microwave Fil-
ters, Impedance Matching Networks, and Coupling Structures, McGraw-
Hill, New York, 1964.
3. A. L e В I о n d and G. M о u r i e r. Investigation of lines with periodic
bar structure for UHF valves, Parts I and II, Ann. Radioelec. 180, 311
(1954).
4. V. E. Dun n. Realization of microwave pulse-compression filters by
means of foldedtape meander lines, Stanford Univ., Stanford Electron.
Lab., Stanford, California, Rept. TR-557—3 (October, 1962).
550
Natattausini
знание без границ “ *
5. W. R. К 1 п с h е 1 о е, Jr. The measurement of frequency witji scanning
.spectrum analyzers, ibid., Rept. TR-557*2 (October, 1962).
<6. J. G. Ferguson and C. W. Barrett. Stripline all-pass networks
for pulse compression, Proc. Symp. Pulse-Compression Tech. Appl. TRR-
62-o80, Rome Air Develop. Center, New York (1963).
7. F. J. M u e 11 e r and R. L, G о о d w i n. A wideband microwave comp-
ressive receiver, IRE Intern. Conv. Record, Pt. 3, 103—119 (1962).
8. M. I t o. Dispersion of very short microwave pulses in wavequide, IEEE
Trans. MTT-13. 367—364 (1965).
9. G. P. О h m a n. Getting high range resolution with pulse-compression
radar, Electronics 28, 53—59 (October 7, 1960).
10. K. Walther. Pulse-compression in acoustic wavequide, J. Acoust.
Soc. Am. 28, 681—686 (1961).
11. W. J.« A 1 b e r s h e i m. Electronic wave equalization system, U. S. Pa-
tent № 2, 863, 127 (December 2, 1958).
12. С. С. H. T a n g. Delay equalization by tapered cutoff waveguides, IEEE
Trans. MTT-12, 607—615 (1964).
13. P. J. В. C 1 a r r i с о a t s, C. D. Hannaford, and А. К. В u n n.
Proposed microwave delay lines for pulse-compression radar, Electronics
Letters 1, 175—176 (1965).
14. E. N. T о r g о w. Equalization of waveguide delay distortion, IEEE Trans.
MTT-13, 756—762 (1965).
‘15 . J. R. Pierce. Traveling Wave Tubes. Van Nostrand, Princeton, New
Jersey, 1950.
16. V. E> D u n n. A time-compression filter employning am icrowave helix,
Stanford Univ., Stanford Electron. Lab., Stanford, California, Rept. TR —
557—1 (October, 1960).
17. A. К i i s. Microwave pulse-compression techniques, M. S. E. E. Thesis,
Polytechnic Inst. Brooklyn, New York (1962).
48. R. W. Damon and H. Van de Vaart. Spin waves and magne-
toelastic waves in YIG, Proc. IEEE 53, 348—354 (1965).
19. J. H. С о I 1 i n s and G. G. Neilson. Microwave pulse compression
utilizing an yttrium irongarnet delay line, Electronics Letters 1, 234
(1965).
20. P. E 1 1 a s. Optics and communication theory, J. Optical Soc. Am. 43,
229—232 (1953).
21. T. P. Cheatham and A. Kohlenberg. Optical filters-their
equivalence to and differences from electrical networks, IRE Intern. Conv.
Record, Pt. 4, 6—12 (1954).
22. E. L. O’N e i 1 1. Spatial filtering in optics, IRE Trans. IT-2, 56—65(1956)
"23. L. J. C u t г о n a, E. N. L e i t h, C. J. Palermo and L. J. P о r-
cello. Optical data processing and filtering systems, IRE Trans. IT-6,
386—400 (1960).
24. W. G. H о e f e r. Optical processing of simulated IF pulse Doppler sig-
nals, IRE Trans. MIL-6, 174—178 (1962).
'25. L. B. Lambert. Optical Correlation, in Modern Radar: Analysis,
Evaluation and System Design (R. S. Berkowitz, ed.), p. 245—273. Wi-
ley, New York, 1965.
26. J. W. G о о d m a n. The role of coherent optics in electrical engineering,
Proc. WESCON (1965).
27. J. Rhodes. Analysis and synthesis of optical images, Am. J. Physics
21, 337—343 (1953).
28. A. Vander Lugt, Signal detection by complex spatial filtering,
IEEE Trans. IT-10, 139-145 (1964).
29. W. E. G 1 e n n. Thermoplastic recording, J. Appl. Phys. 30, 1870—1873
(1959).
.30 . А. К о z m a and D. L. К e 1 1 y. Spatial filtering for detection of signals
submerged in noise, Appl. Optics 4, 387—392 (1965).
551
31. A. Vander Lug t, F. В. Rotz, and А. К I о о a t e r. Character**
reading by optical spatial filtering in «Optical-and Electro-optical In-
formation Processing (J. T. T i p p e t e t al., eds.), p. 125—141, M.
I. T. Press, Cambridge, Massachusetts, 1965.
32. А. В. В h a t i a and W. J. N о b 1 e. Diffraction of light by ultrasonic
waves, Proc. Royal Soc. A220, 356—385 (1953).
33. A. R e i c h and L. S 1 о b о d i n. Optical pulse expansion/compression,
E resented at Natl. Aerospace Electron. Conf., Dayton, Ohio (May, 1961).
.Slobodin and A. Reich. Expansion and compression of elect-
ronic pulses by optical correlation, U. S. Patent № 3, 189, 746 (June 15,
1965).
35. L. L a m b e r t, M. Arm, and I. Weissman. A radar technique
using an electro-optical two-dimensional filter, presented at Natl. Conv.
on Military Electron., Washington, D. C., 1960.
36. M. Arm, L. Lambert, and I. Weissman. Optical correlation
techniques for radar pulse compression, Proc. IEEE (Correspondence) 52,
842 (1964).
*37. L. S 1 о b о d i n. Optical correlation technique, Proc. IEEE (Correspon-
dence) 51, 1782 (1963).
*38. J. S. G e r i g and H. Montague. A simple optical filter for Chirp
radar, Proc. IEEE (Correspondence) 52, 1753 (1964)..
1. Теория линий передачи сверхвысоких частот, изд-во «Советское радио,
1951.
15. Пир с. Лампы с бегущей волной, изд-во «Советское радио», 1952.
23. Катрона и др. «Зарубежная радиоэлектроника», 1962, № 10, стр. 3.
25. Современная радиолокация, изд-во «Советское радио», 1969.
^alaUaus^i
знание без границ - *
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. S. Applebaum and Р. W. Н о w е 1 1 s. Waveform design for tomor
row’s radar, Space/Aeronaut. 32, 186—190 (1959).
•*2. E. D.'Ba nta. A generalized ambiguity criterion, Proc. IEEE (Corres-
pondence) 52, 976 (1964).
3. M. В e r n f e 1 d and С. E. С о о k. Matched filtering and pulse compres-
sion, Sperry Eng. Rev. 15, 44—53 (1963).
4. M. В e r n f e I d and С. E. Co о к. Measurement of radar parameters,
Electro-Technol., Sci. Eng. Ser. 78 (March, 1967).
5. S. E. В о g о t c h and С. E. С о о k. The effect of limiting on the detec-
tability of partially time-coincident pulse-compression signals, IEEE
Trans. MIL-9, 17—24 (1965).
6. E. В г о о к n e r. Optimum clutter rejection, IEEE Trans, IT-11, 597—
599 (1965).
7. E. Bro к ner. Effect of ionosphere on radar waveforms, J. Franklin
Inst. 280, 1—22 (1965).
8. F. С. Bequaert. Some limiting factors in radar measurement accu-
racy, Proc. Natl. Conv. on Mitit. Electron., 79—82 (1963).
**9. C. R. C a h n and J. E. S t a 1Id e r. Bounds for correlation peaks of pe-
riodic digital sequences, Proc. IEEE (Correspondence) 52, 1262—1263
(1964)
10. W. J. C a p u t i. A technique for the time-transformation of signals and
its application to directional systems, Radio Electronic Eng. 29, 135—
142 (1965).
11. J. J. С о n n о 1 y. Fundamental accuracy in the simultaneous measure-
ment of transverse and radial trajectories of radar targets, Proc. 1963 Natl.
Conv. Milit. Electron., 64—68.
**12. J. DeLorenzo and J. V. D i F r a n c o. Response of a linear FM
matched filter to gated noise, Proc. lEpE (Letters) 54, 905—906 (1966).
13. A. D e t a p e. Codage et decodage en phase d’impulsions longues affec-
tees d’effet Doppler, Ann. Radioelectricite' 20, (79) 3—13 (1965).
**14. J. V. D i F r a n c o. Closed form solution for the output of a finite-band-
width pulse-compression filter, Proc. IRE (Correspondence) 49, 1086
(1961).
15. C. W. Erickson. Clutter cancelling in autocorrelation functions by
binary sequence pairing, U. S. Navy Electron. Lab. Res. Rept. 1047 (June,
1961).
16. E. B. F e 1 s t e a d. Progress report on an optical matched filter for radar
signal processing, Canad. General Electric Co., Ltd., Toronto, Canada,
Tech. Memo. RQ65EE37 (September, 1965).
17. S. M. F о m e m к o. Signal processing system, U. S. Patent № 3, 211,
898, October, 1965.
**18. R. A. F о r d. A transversal filter for sidelobe reduction, Proc. IEEE (Let-
ters) 54, 703 (1966).
**19. D. F г у b e r g e r. On the use of pulse compression for the enhancement
of radar echoes from diffuse targets, Proc. IRE (Correspondence) 50, 1993—
1994 (1962).
20. D. A. George. Matched filters for interfering signals, IEEE Trans.
(Correspondence) IT-11, 153—154 (1965).
**21. W. G e r s c h. The limit of radar resolution for a distributed target, Proc.
IEEE (Correspondence) 51, 1787—1788 (1963).
22. N. R. G i 1 I e s p i e, J. В. H i g 1 e y, and N. MacKinnon. The
evolution and application of coherent radar systems, IRE Trans. MIL-5,
131—139 (1961).
19 Зак. 1341 553
23. M. G о 1 а у. Complementary seriea, IRE Trans. IT-7, 82—87 (1961).
24. R. О. H a r ger. An optimum design of ambiguity function, antenna pat-
tern and signal for side-looking radars, IEEE Trans. MIL-9, 264—278
(1965).
25. H. S. Hewitt. A design procedure for tapped-delay-line compression
filters, Stanford Electronics Lab., Stanford, California, Tech. Rept.
. 1965 — 1 (September, 1965).
••26. N. F. Izzo. Optical correlation technique using a variable reference
function, Proc. IEEE (Correspondence) 63, 1740—1741 (1965).
27. R. К г о n e r t. Impulsverdichtung, parts I and II, Nachrichtentechnik 7,
148—152, 162 (1957); 305—308 (1957).
28. R. M. L e r n e r. Signals with uniform ambiguity functions, IRE Intern.
Conv. Record, Pt. 4, 27—36 (1958).
29. R. M. L e r n e r. Means for counting «effective» numbers of objects or du-
rations of signals, Proc. IRE (Correspondence) 47, 1653 (1959).
30. R. M. L e r n e r. Signals having good correlation functions, Proc. 1961
W ESCON Conv. paper 9/3.
31. E. S. L u г i n. Digital pulse compression using polyphase codes, Proc.
IEEE (Correspondence) 51, 1262—1263 (1963).
•*33. T. Makimoto and T. S u e t a. A three-dimensional radar of fre-
quency-modulated pulse system. Proc. IEEE (Correspondence) 62, 727—
728 (1964).
••34. D. E. M i I I e r and M. R. P а г к e r. Dispersion by plane wave excita-
tion of piezoelectric transducer arrays, Proc. IEEE (Letters) 54, 891—892
(1966).
35. H. Miyakawa and M. A. H u s a у n. Design of transistorized flat
and linear delay circuits, Faculty of Eng., Univ. Tokyo, Japan (March,
1965).
**36. F. E. N a t ha nson. Time sidelobes in a combined phase-code and
pulse-Doppler system, Proc. IEEE (Correspondence) 53, 1775—1776
(1965).
37. N. J. N i 1 I s о n. On the optimum range resolution of radar signals in
noise, IRE Trans. IT-7, 245—253 (1961).
38. T. R. O'M e a г a. Some applications of matched-filter concepts to seismic
reflection profiling, Hughes Res. Lab., Malibu, California, Res. Rept. 304
(April, 1964).
39. T. R. O’M e a r a. The resonator-circulator all-pass network, part I, Hug-
hes Res. Lab., Malibu, California, Res. Rept. 334 (May, 1965).
40. К. M i 1 n e. The combination of pulse compression with frequency scan-
ning for three-dimensional radars, Radio Electronic Engr. 28, 89—106
(1964).
41. С. A. P a I m i er i. Radar waveform design, Sperry Eng. Rev. 15, 32—
—43 (1962).
*42. W. A. Penn. Signal fidelity in radar processing, IRE Trans. MIL-6,
2-218 (1962).
**43. A. W. R ihaczek. Doppler-tolerant signal waveforms, Proc. IEEE
54, 849-857 (1966).
44. W. L. R о о t. Radar resolution of closely spaced targets, IRE Trans. M1L-
6, 197-204 (1962).
45. W. L. R u b i n and J. V. D 1 F r a n c o. Analytic representation of wide-
band radio frequency signals, J. Franklin Inst. 275, 197—204 (1963).
46. F. C. Schweppe. On the accuracy and resolution of radar signals,
IEEE Trans. AES-1, 235—245 (1965).
47. F. C. Schweppe and D. L. Gray. Radar signal design subject to
simultaneous peak and average power constraints, IEEE Trans. IT-12,
13—26 (1966).
48. R. A. S I mo ne I I I. Generation of a phase-shift-keyed coded pulse
signal, Eng. Res. Lab., Corneil Univ., Ithaca, New York, Res. Rept. EERL
52 (June, 1966).
554
^atallaus^k
знание без границ ’
49. G. К. S t г о t h е г. Note on the possible use of ultrasonic pulse compres-
sion by bats, J. Acoust. Soc. Am. 33, 696—697 (1961).
50. C. A. S t u t t. Some results on real-part/imaginary-part and magnitude-
phase relations in ambiguity functions, IEEE Trans. IT-10, 321—32?
[1964).
51. 3. M. S uesma n. Least square synthesis of radar ambiguity functions,
IRE Trans. IT-8, 246—254 (1962).
52. R. G. S w e e t and W. R. К i n c h e 1 о e, Jr. A real-time scanning spec-
trum analyzer using a tapped sonic delay-line filter, Stanford Electron,
Lab., Stanford Univ., Stanford, California, Tech. Rept. 1967—1 (June»
1964).
53. P. S w e r 1 1 n g. Parameter estimation accuracy formulas, IEEE Trans.
IT-10, 302—314 (1964).
84. E. T 1 t I e b a u m. A generalization of a two-dimensional Fourier trans-
form property for ambiguity functions, IEEE Trans., (Correspondence)
IT-12, 80—81 (1966).
55. D. W. T u f t s. Matched filters and intersymboi interference, Cruft Lab.,
Harvard Univ., Cambridge, Massachusetts, Rept. 345 (July, 1961).
* *56. D. W. T u f t s. Nyquisvs problem—the joint optimization of transmit-
ter and receiver pulse amplitude modulation, Proc. IEEE 53, 248—259
(1965).
* *57. D. w. T u f t s and D. A. S c h n i d m a n. Optimum waveforms subject
to both energy and peak value constraints, Proc. IEEE 52, 1002—1007
(1964).
* *58. H. v a n de V a a r t. Pulse compression using X-band magnetoeiastic
waves in YIG rods, Proc. IEEE (Letters) 54, 1007—1008 (1966).
59. R. A. Wainwright. On the potential advantage of a smearing-des-
mearing filter technique in overcoming impulse-noise problems in data
systems, IRE Trans. CS-9, 362—366 (1961).
* *60. M. K. War d. Low-pass linear-slope delay filters for compression, Proc.
IEEE (Correspondence) 53, 497—498 (1965).
* •61. M. K. W a r a. Matched scan rate pulse-compression analysis. Proc. IEEE
(Letters) 54, 706—708 (1966).
* 62. G. R. W e 1 t i. Quaternary codes for pulsed radar, IRE Trans. IT-6,400—
408 (1960).
* *63. W. J. Williams and R. B. R u t I e d g e. A generalized distortion
analysis of a cross-correlation radar, Proc. IEEE (Correspondence) 53,
200—201 (1965).
64. M. J. W i t h e г s. Method of measuring phase errors in linear frequency-
modulated and pulse-compression radar systems, Electronics Letter 2, SO-
51 (1966).
65. M. J. Withers. Matched filter for frequency-modulated continuous-
wave radar systems, Proc. IEE (London) 113, 405—412 (1966).
66. J. M. Wozencraft and I. M. Jacobs. Principles of Communi-
cation Engineering. Wiley, New York, 1965.
67. R. C. Yost and E. B. Smith. Application of transversal equalizer
to radar receiver with emphasis on Doppler sensitivity, Mass. Ins. Tech-
nol., Lincoln Lab., Lexington, Massachusetts, Technical Report № 420
(June, 1966).
68. IRE Trans. IT-6, entire issue (1960).
69. N. Z i e r 1 e r. Several binary sequence generators, Proc. Am. Math. Soc.
7, 675-681 (1956).
42. Пен н. «Зарубежная радиоэлектроника», 1963, № 4, стр. 23.
62. Велти. «Зарубежная радиоэлектроника», 1961, №'4, стр. 3..
19*
АВТОРСКИЙ УКАЗАТЕЛЬ»
Альбершейм В. (Albershelm W. J.) 20,
[26]. 154. 174, [180]. 197. 198, [243],
334. [356]. 629. [551]
Аллен В. (Allen W. В) 305, [317]
Аргаймбо Л. (Arguimbau L. В.) 162, [190]
Арм М. (Arm М.) 547, [550]
Банн A. (Bunn А. К.) 529, [5511
Баркер Р. (Barker R. Н.) 265, [317]
Баррет К. (Barrett С. W.) 515, [551]
Бартон Д. (Barton D. К.) [26]
Белло П. (Bello Р.) 145, [146], 347, [356]
Бенджамин Р. (Benjamin R.) 188, [190],
304, 313, [317]
Берковиц Р. (Berkowitz R. S.) [27]
Бернфельд М. (Bernfeld М.) 12,[26], 37.
38, 43, 47. 51, 53, 68. 83. 101, 104,
118. [122-123], 161, 163, 166. 167.
168. 178. [189—190], 200, 216, 217,
218, 220, 263, 271, [316—317]
Бернштейн Р. (Bernstein R. I.) 184, [190]
Бнггс И. (Biggs J. Р.) 184, [189-190]'
Бикел X. (Bickel Н. 3.) 184, [190]
Бнрдсолл Т. (Birdsall Т. G.) 29. [44]
Богоч С. (Bogotch S. Е.) 466, [470]
Бойс X. (Воусе Н. К.) 184, [190]
Боуд X. (Bode Н. W.) 464, 470
Браун В. (Brown W. М.) 430, [443]
Брендон П. (Brandon Р. S.) 466, [470]
Брокиер К. (Brockner С. Е.) 166, [189]
Брух Р. (Bruch R.) 446. 463. [470J
Брэкенбери Р. (Brackenbury R.) 466, [470]
Бухвальд В. (Buchwald W. Т.) 475, [505]
Бхатья A. (Bhatia А. В.) 546. [550—551]
Бэнкрофт Д. (Bancroft D.) 488, [505]
Вайсман И. (Weissman I.) 547, [551]
Вальд A. (Wald А.) 29, 36, [43—44]
Ван де Ваарт X. (Van de Vaart Н.) 531,
[550-551]
Ван дер Люгт A. (Van der Lugt А.) 536,
542, 543, 544, [550-551]
Ван дер Маас Г. (Van der Maas G. J.)
197, [243]
Ван дер Шур Р. (Van der Schuur R. E.)
214, [243], 322, 356
Ван Внйнгаарден A. (Van Wljngaarden A.)
155, [190]
Ван Метер Д. (Van Meter D.) 29, [44]
Ван Трисс X. (Van Trees H. L.) 382,
[393], [394]
Ван Флек И. (Van Vleck J. H.) 16, [26],
[27]. 28. 29, [43]. [44]
Бенье Г. (Venter G. O.) 315, [317]
Вилле (Вайлл) И. Д. (Ville J.) 71,
[122-123]
Вишнер P. (Wishner R. P.) 313 [316-317]
Вудворд Ф. (Woodward P. M.) 11, [26],
29, 37. 38, 42. [431. [44], 67, 68. 71 .
97. [122], [123]. 127, 135, 136, [146].
214. [243]. 246. [316]. [317], 318.
[356]. 384. [393], [394]
Габор Д. (Gabor D.) 73, 95, 96, [122],
132. [146]
Гернг В. И. (Gerig J. S.) 549, 550. [551]
Глнн В. (Glenn W. E.) 539, [550]
Голдман C. (Goldman S.) 26, [26]
Голомб C. (Golomb S. W.) 269, 274, 280,
[316-317]
Гудвнн P. (Goodwin R. L.) 517, 520, 521.
Й2, 523, [551]
Гудмэн И. (Goodman J. W.) 531,[550—551]
Давенпорт В. (Davenport W. B.) 131, 146,
[1461
Дайк P. (Dicke R. H.) 21. 27, 507, 550
Данн В. (Dunn V. E.) 509, 510, Б11, 512,
513, 514, 515, 531, [551]
Дарлингтон C. (Darlington S.) 21, [26 —
27], 154, 175, [189-190], 197, 198.
[243], 344, [356J
Де Анджелес Д. (DeAngelis D.) 438. 439.
[442-443]
Деймон P. (Damon R..W.) 531. [551]
Де Кларнс H. (De Claris N.) 72, [122-123]
Де Лонг Д. мл. (De Long D. E. J. 276,
[310-317]
Де Лоренцо (De Lorenzo J.) 438, 439,
442-443
Джонс E. (Jones E. M. T.) 507, [550]
Дифранко И. (DI Franko J. V.) 188, [190],
403, 405, 406, 407, 423, 426, 436, 437,
[442-443]
Дольф К. (Dolph C. L.) 197, [243]
Дугунджн И. (Dugundji J.) 135, [146]
Дункан P. (Duncan R. C.) 499, [505]
Давне И. (Davies I. L.) 29, 39, [43—44],
128, [146]
Задов d. (ZadoffS.) 275, 276, [316-317]
Зиберт В. (Siebert W. M.) 67, [68], [69].
71. 81, 122, [123]. 246, 267, [316],
[317]
Инджеян И. (Injeyan J.) 288, [317]
Ито M. (Ito M.) 526, [551]
Йост P. (Yost R.) 215, 228, 243, 321, 322,
[356]
Кайтерис К. (Kalterls C.) 253, 255, 260,
313, [316, 317]. 371, 372, 373, 380,
383 Г393-—394]
Каллахан Ф. (Callahan F. P) 325, [356]
Канда T. (Kanda T.) 267, 272. 273, 274,
[317]
Катрона Л. (Cutrona L. J.) 541, 531, 535,
536, 537, [550]
1 Цифры без скобок указывают страницы, где приводятся ссылки на работы дан-
ного автора. Цифры в скобках указывают страницы, где помещена библиография
текущей главы. Там приведены полные данные указанной ссылки. Если на странице
мет непосредственной ссылки на работу того илн иного автора, то это означает, что
графический материал на этой странице заимствован из работы цитируемого автора.
(Прим, ред.)
556
ftalattauswli
знание без границ \ *
Кинхелоэ В. (Kincheloe W. R. J.) 613,
524, 631, [661]
Кнс А. (КН* А.) 531, [551]
Кларрикоутс П. (Clarricoats Р. J. В.) 629.
Клаудер И. (Klauder J. К.) 21, [26—27],
71, 115, 116, 117, 118,(123], 154. 175.
[189-190], 197, 198, [243], 344. [356]
Клустер A. (Kiooster А.) 544, 545, [551]
Кобаяси Г. (Kobayashi Н.) 267, 272, 273,
274, [317]
Коваль И. (Koval J. F.) [122-123]
Коэма A. (Kozma А.) 541, [550]
Коквин Г. (Coquin Q. А.) 498, 499, 502,
503, [505]
Койер В. (Cauer W. А.) 21, [27]
Коленберг A. (Kohlenberg А.) 532, [550]
Колл Д. К. (Coll D. С.) 288, 289. 305,
[317]
Коллинз И. (Collins J. Н.) 531, 532, [550]
Коллмаи Г. (Callman Н. Е. 239, [243]
Красильников В. (Krasilnikov V. А.) 473,
[505]
Крамер Г. (Cramer Н.) 128, 129, 131. 140,
[1461. 342. (3561
Крэйг С. (CralgS. Е.) 267, 271. [316-317]
Кук Ч. (Cook С. Е) 12, 20, 21, 23. 24,
[26—27], 37, 38, 39, 43, [44], 47, 51. 53,
56. 60, 63, 64, [68-69], 84, 1 15, 148,
151, 164, 156, 161, 163, 166, 167, 168,
176, 186. 187, [189-190], 200. 207,
217, 218, 219. 220, 222, 224, 225, 227,
228, 229, 230. 232, 233, 234, [243],
271, 327, [356], 402, 414, 415, 416,
417, 420, 421, 422, [442—443], 445,
463, [470]
Кэй Э. (Key Е.) 26, [26], 49. 56, 58, 69,
60. [68], 241, [243], 307. [317], 331,
[356]
Кайпон И. (Capon J.) 184, [190]
Квллн Д. (Kelly D. L.) 541, [551]
Квллн Э. (Kelly Е. J.) [43—44], 131, 145.
[146], 246, 313, [316—317], 327, 338,
347, 351, [366], 363, 375, 377, 379,
380, 387, 388, 389. [393, 394Л
Карей ^Carey D. R.) 215, [243], 321,
Лавнола М. (Laviola М. В.) 184, [190]
Ламберт Л. (Lambert L. В.) 532, 536,
539, 547, [551]
Леблоид A. (LeBIond А.) 508, [550]
Лейт Е. (Leith Е. N.) 532, 535, 536, 537,
541, [660-551]
Лернер Р. (Lerner R. М.) 304, 309, [317]
Либмаи П. (Llebman Р. М.) 401, 423,
[442-443]
Лоусон И. (Lawson J. L.), 29, 36, [43—44]
Лэмб Г. (Lamb Н.) 480, 505
Макколл Л. (MacColl L. А.) 397, [443]
Маклафлин Р. (McLaughlin R. Н.) 267,
287. [317]
Манассе Р. (Manasse R.) [43—44], 99,
U23]. [146], 335, 347, [356], 363,
Маркум И. ^Marcum J, I.) 29. 35. [43—44]
Маттхей Г. (Matthael О. L.) 507, [551]
Мейцлер A. (Meitzler А. Н.) 472, 475,
477, 478, 479, [505], 485, 490, 492
Мнд С. (Mead S. Р.) 465, [470]
Миддлтон Д. (Middleton D.) 16. [27].
28, 29. 36? [43-441. 127, [146]
Мнкер Т. (Meeker Т. R.) 472, 480, 481.
482, 483, [505]
Мнякава Г. (Miyakawa Н.) 267, 272, 273
274, [317]
Монтак Г. (Montaque Н.) 549, 550, [551]
Монтгомери К. (Montgomery С. О.) 508 „
аье Г. (Моиrier О.) 608, [650—561]
И. мл. (May J. Е. Jr.) 472, 488.
493, [506]
Мэйсон В. (Mason W. Р.) 472, [606]
Мюллер Ф. (Mueller F, J.) 617, 620, 521,
522, 523, [561]
Найлсон Г. (Neilson G. О.) 631, 532,
[550-551]
Нейман И. (Neyman J. J.) 29, 36, 37,
[43-44]
Норс Д. (North D. О.) 16, [26], 28, 29,
[43-44] •
Ноубл В. (Noble W. J.) 647, [651]
О’Мира Т. (O'Meara Т. R.) 445, 450, 454.
455, 466, [470], 484, [606]
Омэи Г. (Ohman О. Р.) 526, [650—551]
О’Нейл Е, (O’Neil Е. L.) 532, [651]
Пайпс Л. (Pipes L. А.) 30, [43], [44]
Палермо К. (Palermo С. J.) 430, [443],
532, 535, 536. 537, 541, [550—551]
Пальмьери К. (Palmieri С. А.) 12, [26].
37. 38. 43. 47. 51. 53. 68. 84. 117.
1 18, 161, 163, 166, 167, 168, 200, 217,
218, 219, 220, 271
Паолилло И, (Paollllo J.) 12, [26], 37,
38. 43. 47, 51, 53. 68, 84, 117, 118,
161, .163, 166, 167, 168, 200, 217, 218,
219, 220. 224, 225, 227, 228, 229, 230,
232, 233, 234, [2431, 271
Паркер М. мл. (Parker М. R. Jr). 498,
504, [505]
Питерсон У. (Peterson W. W.) 29. [43],
[44], 269. 270, [317]
Пиблс П. (Peebles Р. S.) 184, [190]
Пнрс И. (Pierce J. R.) 530, [650]
Пирсон Э. (Pearson Е. S.) 29, 36. 37.
[43-44]
Покхаммер Л. (Pochhammer L.) 488, [505]
Порчелло Л. (Porcello L. J.) 532, 535,
536, 537, 541, [550—551]
Прайс A. (Price А. С.) 21. [27], 154. 175,
[190], 197. 198, [243], 344, [356]
Прайс Р. (Price R.) 83, 84, 85, 90,
[122- 123]
Пратт В. (Pratt W. R.) 239, [243]
Прагер Р. (Prager R. М.) 99, 100, [123],
375, 376, 384. 386, 389, [394]
Пэрселл Е. (Purcell Е. М.) 508, [551]
Радемахер П. (Rademacher Р.) 440, 441,
(Reis F. В.) 71. 88, [122- 123]
Райх A. (Reich А.) 547, [551]
Резннк И. (Resnick J. В.) 246, 258, [316]
Ремлн В. (Remley W. R.) 312, 313.
[316-317]
Рид Д. (Reed J.) 413, [442 — 443]
Рид И. (Reed 1. S.) [43 — 44], 131. 145.
[146]
Рихачек A. (Rlchaczek A. W.) 246, 251,
294, [316]. 345, [356], 371, 372, 373,
374. 387. 388, 389, [393], [394]
Рихман Д. (Richman D.) 325, [356], 376,
[393-394]
Риттенбах О. (Rlttenbach О. Е.) 366, 274,
[316], [317]
Родс Д. (Rhodes J.) 532, [550 — 5511
Роланде Р. (Rowlands R. О.) 184, [190]
Ротц Ф. (Rotz F. В.) 544. 546, [551]
Роузи Д. (Rowen J. Н.) 504, [505]
Рубин В. (Rubin W. L.) 188, [190], 253,
255, 260, 313, [316-317], 371, 372,
373, 380, 383, [393 — 394], 403, 404,
405, 406, 407, 423, 426, 436, 437,
[442- 443]
557
РУТ В. (Root W. L.) [43-44], 131, 146,
[146]
Ралей (Rayleigh Lord) 479, [506] •
Рамп X. (Ramp Н. О.) 167, 184, 185, 187,
₽.та Д. (Randlse D.) 440, 441. [443]
Сакамото Т. (Sakamoto т.) 267, 272, 273,
274, [317]
Сверлннг П. (Swerllng Р.) 29, 36, [44],
145, [1461
Силвер С. (Silver S.) 499, [505]
Симмонс Г. (Simmons Q. J.) 263, [316],
[317]
Снтрин A. (Cltrln А.) 184, [190]
Сколинк М. (Skolnik М. I.) [26
203, [243], 321, 323, 335, П5«
Слепян Д. (Slepian D.) 133, Т141
Слободин Л. (Slobodin L.) 547, 5<8, 549,
550, [551]
Соркин К. (Sorkln С. S.) 71, [122 — 1231 128, Т146]
Спраул Д. (Sproule D. О.) 21, [26 — 27] Ховард Т. (И
Стивенс г. (Stevens О. НЛ 184, [1901 .Хоефер В. (Н
Сторей Д. (Storey J. R.) 288, 259, 305, “I [551]
[27].
Сторер Д. (Storer J. E.) 265, [3161, [317]
Стьюард К. (Steward К- W. F.) 466, [4 70]
СтьюартД. (Stewart J. L.) 99, lot, [122],
[1231, 375, 376, 377, 384, 386, 390,
[393]. [394]
Тайтлбаум E. (Titlebaum E.) 71, [122—123]
Такн Ю. (Takl Y.) 267, 272, 273, J74,
••*[317]
Темеш К. (Temos C. L.) 183, 184, [190],
197, 202, [2431
Top P. (Thor R. C.) 180, 184, 187, [190]
Торгау E. (Torgow E. N.) 529, [550-6511
Турин Г. (Turin Q. L.) 12, [26—27]
Турин P. (Turyn R.) 265, [316—317]
Тайлер T. (Taylor T. T.) 198, 200, [243]
Тэнг К. (Tang С. С. H.) 529, [550 — 551]
Уилер X. (Wneeler Н. А.) 397, [442]
Уилкокс К. (Wilcox С. Н.) 71, 81, 95,
118, 121, [122], [123]
Уннгров Е. мл. (Wingrove Е. R. Jr.) 167,
184, 185, 187, [190]
Уленбек Г. (Uhlепbeck О. [Ел 29, 36,
[43-44]
Уолтер К. (Walther К.) 527, [550—551]
Уоттерс Е. (Wattera Е. С.) 26, (271
Урковнц X. (UrkowltxH.) 71. [122], [123],
365, 373, [393], [394]
Уэсгерфильд Е. (Westerfield Е. С.) 99,
101, [122]. [1231. 305, [317]. 376, 376,
377, 384, 386, 390, [3931. [394]
Фергюсон Д. (Ferguson J. G.)]51o, [551]
Фнтч А. (Fitch А. Н.) 472, 484, 489, [505]
Фншбейи В. (Flshbein W.) 267, 271,
[316 — 317]
101,
Фишер Р. (Fisher R. А.) 131, [146]
Фоул Е. (Fowle Е. N.1 12, 26. [961. (271,
50, 52, 64, 56, 58, 59, 60, df. [68-69],
215, 242, (243], 246. 307, [4111-317f,
321, 322, 327, [356], 362? 374, 37?,
380, 387, 388, 369, [393 — 394]
Фраиклни В. (Franklin В.) 395, [442]
Франк Р. (Frank R.), 275, 276, 279, 280.
314, [316 — 317]
ХаЙесс В. (Helaa W. К.) 176. 187, [190]
Хаймнллер Р. (Heirailler R. С.) 276, 276,
[316 —*3171
Ханнафорд К. (Hannaford С. D.) 528, [550]
Хаттман Е. (Huttman ЕЛ 21, [27]
Xavap К. (Hauer С. А.И122 —123]
Хаффман Д. (Huffman D. А.) 269, 284,
Ж [316—317]
^Хейсинг Р. (Helslng R. А.) 490 [505]
-Хельстром К. (Helstrom С. W.) 94, [123],
128, [1461
“ 'Howard Т. В.)316, [317]
[Hoefer W. О.) 532, 548, 550,
' Холден A. (Holden A. N.) 481, [505]
Хофштеттер Е. (Hofstetter Е. Мл 83, 84,
85, 90. [122-123]
Хьюгс X. (Hughes Н. J.) 21, [27]
Хэггерти Р. (Haggarty R. D.) 26,
49, Ъб, 68, 59, 60, [68], 180,
241, [243], 307, [3171, 331, [366
Цирлер Н. (Zlerler N.) 269,
[516-317]
Цобель О. (Zobel О. J.) 465. [470]
Ченг Д. (Cheng D. К.) 432, 4$3, [4
Чин Д. (Chin J. Е.) 21. [27], 154,
188? [1891, [190]
Читам Т. (Cheathan
Чрн 1
Шаеппе Ф. (Scha
Ш<нн В. (Scheen
Г“ “ ' • '
[З93]?[394]
Шольтц Р. (Sc
[317]
Шрайтмюллер Р
238, [243]
Штатт К. (Stutt С. АЛ 71, [122 — 123]
Шу Р. (Tsu R.) 498, 499. 502, 503. [505]
Шеиион К. (Shannon С. А.) 131,,[146]
Введет П. (Eveleth J.) 503, [505]
Элиас ГЕ (Ellas Р.) 5!
ЭлспасВ.
Эм де Ф. (Е
Юнг Л. (Young L.) 508, ]
Яггер К. (Jagger С. ЕЛ
Якобус Р. (Jacobuc R. W
Хофштеттер L ._______
85, 90, [122-123]
Хьюгс X. (Hughes Н. J
Хэггерти Р. (Haggar
49, об, 58, 59, 60, [68], 1
241, [243], 307, [3171, 331,
Цирлер Н. (Zlerler N.) 2
[516-317]
Цобель О. (Zobel О. J.) 465, I
Ченг Д. (Cheng D. К.) 432, 43
Чи.|1Д г19!;!.п 21 • [27ь
м Т. (Cheatham Т. Р.) 532. [651]
К. (Cnree С.) 488 [505]
--------- “ ‘ F. С.) 343, [356]
— .------ ) 155, [189], [190 ]
Шихан Д. (Scheehan J. А.) 246, [316],
363, 374, 376, 377, 379, 387, 388, 389.
.......?:]
(Scholtz R. А.) 274, [316],
(261,
190].
274,
.) 503, [50h
^..Be r., u32, [551]
(Elspas ВЛ 267, 271, [310—3171
Emde F.) 118, [1231.155,(190]
*oung L.) 508, [551]
“ ’ 267, 287, [317]
____________________ (V.) 179, [190]
Янке E. (Jahnke E.) 118, [123], 156,(190]
^ataHausiili
знание без границ * *»
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Амплитудная коррекция 466
Баркера последовательности (см. Бинар-
ные фазовые коды)
Байеса решающее правило 36
Бинарные фазЪвые коды 260—274
— алгоритм построения Бернфельда 263
— генерация сигнала с помощью регистра
сдвига 273
— допплеровская коррекция 307
— общее определение 260
— общие свойства 265
— пары символов элементов 260
— последовательности Баркера 265—268
— последовательности максимальной дли-
ны 268—274
— согласованный фильтр с квадратурными
каналами 306
— схемы согласованной фильтрации 302—
306
— функции отклика 243
Боковых лепестков уменьшение (см. Весо-
вые функции)
.Борьба с помехами от местных предметов
— использование рассогласованного закона
ЧМ 369—372
— оптимальный фильтр 371—373
Весовая обработка амплитудного спектра
194-202
Весовая обработка в приемнике
— влияние на форму импульса 216—221
— потерн на рассогласоаание 213
Весовые функции
— дольф — чебышевские 196—198
— модифицированные тейлоровские 201—
202
— оптимальные 192
— отношение сигнал/шум 209—215
— реализация с помощью трансверсальной
фильтрации 235—239
— связь с весовой обработкой в антеннах
195
— случай несогласованных характеристик
195, 208-211
— случай согласованных характеристик
195. 212
— сравнение временной и частотной весо-
вой обработки 203—208
— тейлоровские 198
— точность задания ЛЧМ спектра 224—
227
функции вида cos " 202
— характеристики сжатого импульса 216—
223
— хэмминговекке 201
Гауссова огибающая ЛЧМ сигнала 102,
106. 215, 322
Генерация сигнала с помощью регистра
сдвига (см. Бинарные фазовые коды)
Г нльберта преобразование 72
Групповая задержка
— при одновременной частотной и вре-
менной модуляции 64
— при спектре мощности вида соа » 61. 62
— при тангенциальном законе ЧМ 59
Деформированные (нерегулярные) им*
пульсные последовательности 251—259
— деформация на одну позицию в обе сто-
роны 251
— оптимальная деформация 259
— свойство симметрии 256—259
— случайная деформация 252
— спектр 253
— субоптнмальная деформация 253—256
— функция отклика 253—256
Днскретно-коднрованные сигналы (см. Би-
нарные фазовые коды, дискретные час-
тотные последовательности, деформиро-
ванные импульсные последовательности,
многофазные коды, однородные импульс-
ные последовательности, Хаффмана ко-
ды)
— допплеровская коррекция 307—313
— общее определение 244, 245
— согласованные фильтры 302—307
— сравнение фазовых кодов 314
— степени свободы 313 •
— функция отклика 245, 246
Дискретные частотные последовательности
289-301
— импульсные со ступенчатой ЧМ 290—
291. 296-301
— сигналы со ступенчатой ЧМ 289—301
— согласованный фильтр 306
— спектр сигналов со ступенчатой ЧМ 289
— функция отклика при ступенчатом за-
коне ЧМ 289
Дисперсионные (ультразвуковые) линии
задержки (см. Ультразвуковые линии
задержки)
Дисперсионные линии, работающие по
принципу дифракционной решетки 498—
505
Длительность
— однородных импульсных последова-
тельностей 327
— Среднеквадратичное значение
----определение 94, 135, 320
----для сигналов с большим значением
произведения длительности на полосу
328
Додетекторная обработка (см. Согласо-
ванной фильтрации теория)
Дольф-чебышевская весовая обработка
196-198
Допплеровская дисперсия
— амплитудные потерн 186, 188, 311
— влияние на псевдослучайные сигналы
на основе фазовых кодов 310—312
Допплеровская матрица 308
Допплеровская чувствительность 358
Допплеровские искажения
— влияние на ЛЧМ сигналы с большим
произведением длительности на полосу
184-189
— коррекция функции ЛЧМ в приемнике
187
— коэффициент рассогласования функции
ЛЧМ 186
— остаточный фазовый член функции ЛЧМ
188
— уширение импульса 187, 311
5 59
Допплеровский \ масштабный коэффициент
Допплеровский сдвиг, инвариантность про-
изведения длительности на полосу 188
Допплеровской частоты измерения ошибка
135
Закона изменения задержки искажения,
мера фазовых искажений 404
Измерений ошибка при совместных оцен-
ках
— общие условия 347
— сигналы с нелинейной ЧМ 339—341
— сигналы с несимметричной ЧМ 346
— сигналы с четными функциями ЧМ 346
— условия получения минимальной ошиб-
ки 346—349
Измерений ошибки 320—331
Измерений точность
— как критерий построения сигнала 318,
356
— сигналы со скачком частоты 339
— сравнительные данные о сигналах 328
— улучшение при сигналах с однонаправ-
ленной функцией ЧМ 342—345
Импульсы с линейной V-образной ЧМ
112-118
— согласованный фильтр 118
Инверсия симметричной модуляции 166—
167
Ииджеяна коды 288
— функция отклика 285
Искажения
— анализ с помощью метода парных эхо
396-404. 410-417
— влияние на сложные сигналы 395
— компенсация с помощью
----замкнутой цепи петлн 434—441
---- разомкнутой цепи 433
----сигналов, корректирующих искаже-
ния 436
----цепи обратной связи 437—441
Квантованные фазовые коды (см. Много-
фазные коды)
Комплексное представление сигналов 72—
76
Корреляционный прием (см. Теория согла-
сованной фильтрации)
Косинусная весовая функция 203, 204
Коэффициент связи дальность — частота
Допплера
— при различии частот 351
----ошибки измерения 135—138, 332—340
— дискретно-кодированных сигналов 351—
354
— линейная ЧМ
----с гауссовой огибающей 333
----с прямоугольной огибающей 335—338
— линейио-ступенчатая ЧМ 352
— нелинейная ЧМ, спектр вида cos* 338
— параболическая ЧМ однонаправленная
337
Коэффициент усиления нормированный 148,
Крамера — Рао неравенство 128—130
Критерий построения сигналов
— движущиеся отражатели 374—383
— минимальные ошибки измерения (см.
также Точность измерения)
Коэффициент связи дальность — частота
Допплера 355
— обобщенная постоянная временного раз-
решения 376—379
— общие соображения 384—392
560
— плоскостное распределение неопреде,
ленностн 392
— распределение полунзолнрованных рас-
сеивателей 358—362
— случай большого числа плотно распо-
ложенных целей 357
— сравнение по временному разрешению
- сравнительная эффективность подавле-
ния пассивных помех 366—369, 379
— стационарная картина отражений от
местных предметов 362—366
Ламэ постоянная 474
Линейная функция ЧМ
— аналогичность воздействия искажений
фазовой и амплитудной модуляции 411
— генерация сигнала 160—168
— искажения при допплеровском сдвиге
184-189
— исключение неопределенности по скоро-
сти при измерении дальности 343
— метод приема с помощью анализатора
спектра 180—184
— ошибка при измерении дальности 344
— рассогласование наклона ЧМ 168—172
— свойство предсказания дальности 343
— сравнение временной и частотной весо-
вой обработок 203—208
— сравнение идеального и реального со-'
гласованных фильтров 157—160
— схема с параллельными каналами 178—
180
— теоретические ошибки нзмереинй 332—
339
— уменьшение боковых лепестков (см. Ве-
совые функции)
— функция отклика 150—152
— характеристики расширения импульса
163-165
— экспериментальная система 3-см диа-
пазона 166
Линейной задержки рассогласование 168—
176
— влияние амплитудной весовой обработ-
ки 173—176
— выходной сигнал 169
Логарифмическая фазовая модуляция
186
Максимального правдоподобия метод 139—
145
Максимальной длительности последова-
тельности
— вырезание одного периода 271
— генерирование с помощью регистра
сдвига 270
— порождающий полином 270
— рекуррентная формула 269
Методы обработки сигналов с большим
значением произведения длительности
на полосу 177—183
Минимальные ошибки измерения 320—33!
Многоотводные линии задержки
— данные о конструировании устройств,
с линейной задержкой 522
— согласованный фильтр для фазовых ко-
дов 302—306
— уменьшение боковых лепестков 235—238
Многофазные коды
— квантованные фазовые коды 275—284
---- спектры 277
---- Функция отклика 279
— кодирующая матрица Фрэнка 275
— многофазные последовательности Бар-
кера 274
Модуляционные искажения
— влияние фазовой постоянной 410—412
----сложный ЛЧМ сигнал 412—416
^lalatiausi^i
знание без границ Ч *
— источники возникновения искажений
423-425
— комплексные искажения 417—422
— симметрично расположенные боковые
полосы 411
Мостовая Т-обрааная схема
— аппроксимация закона изменения за-
держки 447—451
— влияние допусков в характеристиках
компонент 465
— компенсация 470
— оценка числа секций 457
— передаточная функция 445
— прнмененне в устройствах с линейной
задержкой 454—456
— согласование 466—470
— схема О’Мира 454
— трансформация в решетчатую 452—453
Нелинейная ЧМ
— в сочетании с весовой обработкой 54—
65. 64
— применение к формированию сигналов
56-66.,
— пример допплеровского рассогласова-
ния 230—942
— примеры точности измерений 325—327,
337—ЗМ
— спектр вида соз« 59—64
— тангенциальная функция ЧМ 58—59
— требования к согласованному фильтру
Неопределенности принцип 96
Неопределенности эллипс 95
Неопределенности функция 67
Несущая частота, определение 138
Обнаружения ошибка, вероятность 34
Обобщенная постоянная разрешения по
времени 99, 375
Обработка радиолокационных сигналов
11-15
Обработка сигналов с помощью анали-
затора спектра. ЛЧМ сигнал 180
Обратная вероятность (см. Согласованной
фильтрации теория)
Обратный (Урковица) фильтр 365, 371
Однородная последовательность импуль-
сов 245—249
— спектр 246
— функция отклика 246
— эффективная длительность 327
Оптимальный ограниченный по полосе
спектр 365
Оптимальный приемник, его передаточная
функция 35, 70, 364, 371
Оптимальный фильтр подавления отра-
жений от местных предметов 371
Оптические согласованные фильтры
— критерий согласованной фильтрации
535
— метод нспользования интерферометра
543—544
— набор 535—538
— пространственная фильтрация 507, 532—
534
— реализация в реальном времени 538—
644
— ультразвуковой модулятор света 545—
Отражения от местных предметов, оптими-
зации сигнала 362—365
Ошибки измерения задержки 134
Ошибок дисперсии минимальные 135, 320
Ошибок коррекция
— согласованный фильтр 459—466
— стандартные кривые задержки 462
Ошибок коэффициент связи 19, 22, 94, 135
— сигналов с большим произведением дли-
тельности на полосу 321
Параболическая ЧМ 104, 107, 120, 325—327,
337
Параметров оценка 12, 38, 124—146
— достаточная оценка 129
— несмещенная оценка 128
— ошибки совместного измерения 131—138,
346
— постановка проблемы 126—127
— пространство выборочных вначеннй 130
— функция правдоподобия 131, 142—145
Парные боковые полосы, эквивалентность
парным эхо 411
Парные эхо, выбросы спектра 224—228
Парных эхо анализ
— амплитудных искажений 396—400
— влияние фазовой постоянной 402
— сложных искажений 399
— фазовых искажений 400
Парсеваля теорема 46, 54, 73
Помехи от местных предметов (пассивные
помехи) 364
Помехи, создаваемые близко расположен-
ными целями 361
Последовательность импульсов. средне-
квадратичная длительность 327
Постоянная разрешения во времени 97—
100
— влияние частотной весовой обработки
366—370, 373
— критерий разрешения сигналов от близ-
ко расположенных целей 366
— критерий удержания целей на сопро-
вождении 369
— мера ухудшения разрешения нв-за фа-
зовых ошибок 430—433
Потерн в дисперсионных линиях задержки
464
Правдоподобия критерий (см. Согласован-
ной фильтрации теория)
Правдоподобия функция 131, 142—145
Предыскажения закона ЧМ 229—234
Пуассона отношение 474
Радиолокационное обнаружение 11
— критерий отношения сигнал/шум 17,
29-34
Радиолокационные параметры 125—126
Разложения теорема (см. Функция неоп-
ределенности )
Разрешение
— верхняя граница 434
— критерий постоянной временного разре-
шения 97—99
— критерий среднеквадратичного отклоне-
ния 77
— круговой критерий 430
— эквивалентный прямоугольник 431
Свойство предсказания дальности, линей-
ная ЧМ 344
Свойство симметрии, бинарные фазовые
коды 258
Сжатие импульсов
— вывод основных параметров 21—25
— в системе с параллельными каналами
177-181
— исторические предпосылки 19
— основные соотношения 21
Сигнал с линейной ЧМ 147, 332—334
Случайное рассеяние, энергетические по-
тери в дисперсионных линиях эадержки
464
Совместная оценка, коэффициент корреля-
ции 131
561
FT"
г
Согласованного фильтра характеристики
14. 24. 31
Согласованной фильтрации принцип 14
Согласованной фильтрации теория
— достаточный приемник 42'
— идеальный приемник 41
— корреляционный прием 37
— критерий максимума правдоподобия
35-39, 142-145
— критерий отношения сигнал/шум 29—34
— обратная вероятность 40—42
— статистическая теория решений 35—38
Согласованный фильтр
— отношение сигиал/шум
----влияние весовой обработки 209—216
----для белого шума 33
----для небелого шума 35
----при рассогласовании 209—211
— требования для произвольного ЧМ сиг-
нала 45—69
Согласованных фильтров набор 318
— оптических 535
Согласованные фильтры СВЧ диапазона
— волноводные структуры 524—528
— железо — итриевый гранат 531
— конструкция типа гибридного фазосдвн-
гающего кольца 513—516
— меандровая линия с изогнутой лентой
508-512
— многоотводная линия задержки 517—525
— спиральная структура 529—530
Сопряженные фильтры 51, 163
Спектр комплексный 49
Спектр ЛЧМ сигнала 153—156
— воздействие иа сжатый импульс при
весовой обработке 224—229
Спектра аппроксимация 323, 324
Статистическая теория решений (см. Со-
гласованной фильтрации теория)
Стационарной фазы анализ, параметры,
полученные с помощью 65
Стационарной фазы принцип 45—48
— применение к формированию сигналов
56-65
— применение к ЧМ сигналам в системе
сжатия 45—56
— связь мгновенной частоты и групповой
задержки 49
— структура преобразования Фурье 55
Ступенчатый закон ЧМ линейный, коэф-
фициент связи дальность — частота Доп-
плера 353
Тейлеровская весовая обработка 198—200
Теорема единственности (см. Функция не-
определенности)
Трансверсальная фильтрация 235—239, 307
•
Узкополосный сигнал
— определение 73
— ошибка приближения 74
Ультразвуковые волны в упругих средах
— скорость изгибиых воли 475
— скорость продольных волн 474
Ультразвуковые линии задержки
— изгибная мода 488
— применение для сжатия импульсов 471
— проволочные 488—489
— продольная мода
----при дискретно изменяющейся толщи-
не 483-489
в металлических полосках 479—483
— сдвиговая мода в металлических полос-
ках 475—479
— технические требования 493—498
— устройства типа дифракционной решет-
ки 498—501
562
— характеристики преобразователей 490—
492
Ультразвуковые модуляторы света 545—550
Уравнение дальности радиолокатора 10
Фазовые ошибки 430—434
Фазосдвигающая схема (см. Мостовая
Т-образиая схема)
Френеля интеграл 50, 155
Функция неопределенности
— изменение временного масштаба 82
— иивариаитность по отношению к вра-
щению 87
— ухудшение характеристик при сдвиге
частоты 68
— наибольшее значение 82
— обобщенный принцип неопределенности
96
— общая формулировка 77, 81
— определение 66. 70
— объем свободной области 90—92
— параболичиость фазы 83
— поведение вблизи начала координат
93-96
— постоянная разрешения по времени 97—
100
— постоянная разрешения по частоте 100
— правило умножения 88
— применение принципа стационарной фа-
зы 119-120
— примеры 100—119
— свойства 81—88
— свойство инвариантности объема 83
— свойство самотраисформации 86
— свойство симметрии 82 -
— симметричная форма 82
— соотношения для сигналов с четной
функцией ЧМ 112
— сигналов с гауссовой огибающей 102,
106
— сигналов с прямоугольной огибающей
102, 106
— сигналов с V-образной функцией ЧМ 112
— таблицы 102—105
— теорема единственности 89
— теорема о разложении 92
— частотно-временной отклик 79
— эрмитовых сигналов 104, 118
Функция неопределенности кнопочная 101,
385-387
— при плотном расположении отражате-
лей 358, 385-387
Функция отклика (см. Функция неопре-
деленности )
— ЛЧМ сигнала 150—152
— связь с сигналом иа выходе согласо-
ванного фильтра 80
Хаффмана коды 284—289
Хэмминга весовая обработка 202
Частотная весовая обработка 210
Частотная постоянная разрешения 101
Частотно-временное пространство сигна-
лов 79
Ширина полосы частот
— определение среднеквадратичного зна-
чения 93, 135, 320
— сигналов со скачками амплитудных и
фазовых характеристик 139
— сигналов в виде последовательностей
импульсов с постоянной несущей 327
— среднеквадратичное значение для сиг-
налов с большим значением произведе-
ния длительности ня полосу 328
Энергия сигнала 46. 73
Эпмнтовы сигналы 104, 118
Юнга модуль 473
NalaHaus№k
знание без границ ' *’
ОГЛАВЛЕНИЕ
Предисловие редактора ................................ ... 5
Предисловие авторов ....................................... 6
Список обозначений ........................................ 8
Глава 1. Основные элементы теории согласованной
фильтрации и сжатия импульсов............10
1.1. Введение..........................................10
1.2. Принцип согласованной фильтрации..................14
1.3. Исторические предпосылки появления теории сжатия им-
пульсов ............................................. 19
1.4. Эвристическое определение основных параметров сжатия
импульсов.............................................20
1.5. Характеристики согласованного фильтра для ЧМ сигнала
произвольного вида....................................25
Литература ................................................26
Глава 2. Оптимальная додетекторная обработка и тео-
рия согласованных фильтров.............28
2.1. Введение..........................................28
2.2. Критерий отношения сигнал/шум [1—2].......29
2.3. Критерий отношения правдоподобия и статистическая
теория решений [3—5]..................................35
2.4. Критерий отношения правдоподобия и теория оценки пара-
метров [11—141....................................... 38
2.5. Критерий обратной (апостериорной) вероятности [11, 12] . 40
Литература.................................................43
Глава 3. Согласованная фильтрация ЧМ сигналов про-
извольного вида........................................45
3.1. Введение..........................................45
3.2. Принцип стационарной фазы.....................46
3.3. Приложение принципа стационарной фазы к сложным сиг-
налам общего вида.....................................48
3.4. Приложение теории построения сигналов к сложным ЧМ
сигналам..............................................56
3.5. Функция неопределенности согласованного фильтра ... 66
Литература.................................................68
Глава 4. Функция неопределенности радиолокаци-
онного сигнала......................................• . . 70
4.1. Введение........................................ 70
4.2. Комплексное представление сигнала.................72
4.3. Допплеровская аппроксимация.......................76
4.4. Общее представление функции неопределенности .... 77
563
4.5. Свойства функции неопределенности..................81
4.6. Теорема единственности ................................. 89
4.7. Объем свободной области и средний уровень боковых ле*
пестков...............................................90
4.8. Обобщение теоремы о функциях неопределенности [5—6] 92
4.9. Функция неопределенности вблизи начала координат . . 93
4.10. Обобщение принципа неопределенности сигнала . . . • 96
4.11. Постоянная разрешения по времени..................97
4.12. Примеры функций неопределенности.................100
4.12а . Сигналы с гауссовой огибающей и синусоидальным или
ЛЧМ заполнением..........................................106
4.126. Сигналы с прямоугольной огибающей.....................106
4.12в. Сигналы с прямоугольной огибающей и с синусоидальным
или ЛЧМ заполнением......................................107
4.12г. Сигналы с функцией ЧМ более высоких порядков и пря-
моугольной огибающей.....................................107
4.12д. Импульсы с V-образной ЧМ.............................112
4.12е. Эрмитовы сигналы......................................116
4.13. Применение принципа стационарной фазы для анализа
функции неопределенности.................................119
4.14. Заключение.............................................120
Литература........................................................122
Глава 5. Оценка параметров.................................124
5.1. Введение....................................... 124
5.2. Параметры радиолокационного сигнала..............125
5.3. Проблема оценки параметров.......................126
5.4. Неравенство Крамера—Рао [5]......................128
5.5. Пространство выборок.............................131
5.6. Ошибки несмещенной совместной оценки параметров радио-
локационного сигнала..................................131
5.7. Теоретическое значение эффективной полосы сигналов,
амплитудные и/или фазовые характеристики которых
имеют ступенчатую форму...............................139
5.8. Метод максимального правдоподобия [5]............139
Литература.................................................146
Глава 6. ЛЧМ сигнал и согласованный фильтр . . .147
6.1. Введение..........................................147
6.2. Согласованная фильтрация ЛЧМ сигнала..............147
6.3. Характеристики фильтра, согласованного с ЛЧМ сигналом 153
6.4. Сравнение идеализированного согласованного фильтра и его
практической реализации...............................157
6.5. Формирование ЛЧМ сигналов.........................160
6.6. Влияние рассогласования линейного изменения задержки
на вид сжатого сигнала ...............................168
6.7. Методы обработки сигналов с большими значениями про-
изведения длительности на полосу......................177
6.8. Допплеровские искажения ЛЧМ сигналов с большим зна-
чением произведения полосы на длительность............184
Литература.................................................189
564
NataHaus,l$i
знание без границ У *
Глава 7. Подавление боковых лепестков сигналов на
выходе согласованного фильтра..............................191
7.1. Введение.........................................191
7.2. Спектральные характеристики, обеспечивающие необхо-
димые свойства сложных сигналов.......................194
7.3. Сравнение частотных и временных методов весовой обработ-
ки с целью уменьшения боковых лепестков ЛЧМ сигналов 203
7.4. Влияние весовой обработки на отношение сигнал/шум на
выходе согласованного фильтра.........................209
7.5. Влияние частотной весовой обработки на характеристики
сжатого импульса......................................216
7.6. Влияние точности спектра ЛЧМ сигнала на форму сжатого
взвешенного импульса..................................224
7.7. Предыскажение закона ЧМ..........................229
7.8. Реализация весовой обработки с помощью трансверсальной
фильтрации.......................................... 235
7.9. Согласованные фильтры с нелинейной ЧМ, используемые
для уменьшения боковых лепестков.................239
Литература.................................................243
Глава 8. Дискретно-кодированные сигналы . . . .244
8.1. Введение.........................................244
8.2. Последовательности импульсов с постоянной несущей ча-
стотой (группа I).....................................245
8.3. Бинарные фазовые коды (группа 11)................260
8.4. Многофазные коды (группа II)....................274
8.5. Дискретные частотные последовательности (группа III) 289
8.6. Согласованные фильтры для дискретно-кодированных си-
гналов ...............................................302
8.7. Допплеровская коррекция дискретно-кодированных сиг-
налов ................................................307
8.8. Заключение.......................................313
Литература.................................................316
Глава 9. Точности измерения при использовании слож-
ных радиолокационных сигналов и крите-
рий выбора сигналов ...................................... 318
9.1. Введение.........................................318
9.2. Минимальные дисперсии ошибок измерения времени и ча-
стоты для некоторых радиолокационных сигналов с боль-
шим произведением длительности на полосу..............320
9.3. Влияние коэффициента частотно-временндй связи на ве-
личину теоретических ошибок измерения.................332
9.4. Сигналы с нелинейной и скачкообразной ЧМ, обеспечиваю-
щие малые среднеквадратичные ошибки измерения .... 339
9.5. Некоторые соображения относительно улучшения точности
измерения при использовании сигналов с однонаправлен-
ной ЧМ ...............................................342
9.6. Условия минимальности ошибок при совместных оценках
дальности и скорости..................................346
9.7. Коэффициент частотно-временндй связи для дискретно-
кодированных сигналов.................................351
Литература ................................................356
565
Глава 10. Критерий выбора сигнала для работы в
условиях пассивных помех....................357
10.1. Введение......................................357
10.2. Некоторые соображения относительно сигнала для случая
протяженных распределений полуизолированных движу*
щихся рассеивателей.................................358
10.3. Оптимизация сигнала при неподвижных или медленно
движущихся пассивных отражателях....................362
10.4. Сравнение эффективности различных сигналов в случае
неподвижных или медленно движущихся пассивных от-
ражателей [4, 5J....................................366
10.5. «Оптимальный» фильтр для режекции пассивной помехи
(4, 5)............................................. 371
10.6. Соображения относительно структуры сигнала при плот-
ных распределениях движущихся рассеивателей . . . 374
10.7. Некоторые замечания относительно общей проблемы син-
теза сигналов.......................................384
Литература...............................................393
Глава 11. Влияние искажений при обработке сигналов
согласованным фильтром.......................395
11.1. Введение . . .................................395
11.2. Анализ искажений методом парных эхо...........396
Н.З. Искажения временидй задержки как мера фазовых иска-
жений ..........................................404
11.4. Модуляционные искажения, наблюдаемые на выходе со-
гласованного фильтра................................410
11.5. Сложные функции модуляционного искажения.......417
11.6. Источники модуляционных искажений фазы......423
11.7. Представление искаженных временных функций на выходе
согласованного фильтра для произвольных сигналов 425
11.8. Оценки потерь в разрешающей способности при случайных
фазовых ошибках.....................................430
11.9. Компенсация искажений.........................435
Литература...............................................442
Глава 12. Устройства с дисперсионными характеристика-
ми. Цепочки Т-образных звеньев......................444
12.1. Введение......................................444
12.2. Фазосдвигающие цепи...........................445
12.3. Приближенное выражение для задержки в фазосдвигаю-
щем фильтре.........................................447
12.4. Преобразование скрещенного четырехполюсника к не-
сбалансированному виду..............................451
' 12.5. Пример, иллюстрирующий расчет схемы линейной задержки 454
12.6. Коррекция ошибок согласованного фильтра.......459
12.7. Настройка мостовых Т-образных звеньев фазосдвигающего
фильтра.........................................466
Литература.................................... ...........470
566
^alaHaustlHi
знание без границ Ч «Ь
Глава 13. Устройства с дисперсионными характеристи-
ками. Ультразвуковые линии задержки . . 471
13.1. Введение......................................471
13.2. Распространение ультразвуковых волн в изотропной
упругой среде ................................. 472
13.3. Дисперсионные характеристики задержки при распростра-
нении поперечных волн в полосковой линии............475
13.4. Дисперсионные характеристики задержки при продольном
распространении в полосковых линиях.................479
13.5. Проволочные дисперсионные линии задержки......488
13.6. Характеристики преобразователей для тонких полосковых
линий задержки..................................490
13.7. Требования к дисперсионным ультразвуковым линиям
задержки............................................493
13.8. Дисперсионные устройства типа дифракционных решеток 498
Литература...............................................505
Глава 14. Оптические и СВЧ методы согласованной
фильтрации...................................507
14.1. Введение......................................507
14.2. Ленточная меандровая линия....................508
14.3. Расчет фазосдвигающего гибридного кольца......513
14.4. СВЧ фильтры сжатия на основе цногоотводных линий за-
держки .........................................517
14.5. Непрерывные дисперсионные структуры СВЧ диапазона 524
14.6. Оптическая обработка сигнала — пространственная филь-
трация .........................................532
14.7. Применение оптических согласованных фильтров в радио-
локации ............................................539
14.8. Ультразвуковой модулятор света................545
Литература...............................................550
Дополнительная литература................................553
Авторский указатель......................................556
Предметный указатель ....................................559
Кук и Бернфелъд
РАДИОЛОКАЦИОННЫЕ СИГНАЛЫ
Перевод с английского
под редакцией В. С. Кельзона
Редакторы Л. Б. Баскакова,
А. А. Кокушкин, А. И. Шестаков
Художественный редактор 3. Е. Вендрова
Художник О. В. Камаев
Технический редактор А. А. Белоус
Корректоры Е. П. Озерецкая, Г. М. Денисова
•
Сдано в набор 8/IX —70 г. Подписано в печать 1/111—71 г.
Формат 60X90/16. Бумага типографская № 2 Объем 35,5
усл. п. л., 35,217 уч.-изд. л. Тираж 8000 экз. Зак. 1341
Издательство «Советское радио», Москва, Главпочтамт,
п/я 693. Цена в пер. № 7 2 р. 67 к.
•
Московская типография № 4 Главполиграфпрома Комитета
по печати при Совете Министров СССР
В. Переяславская ул., 46