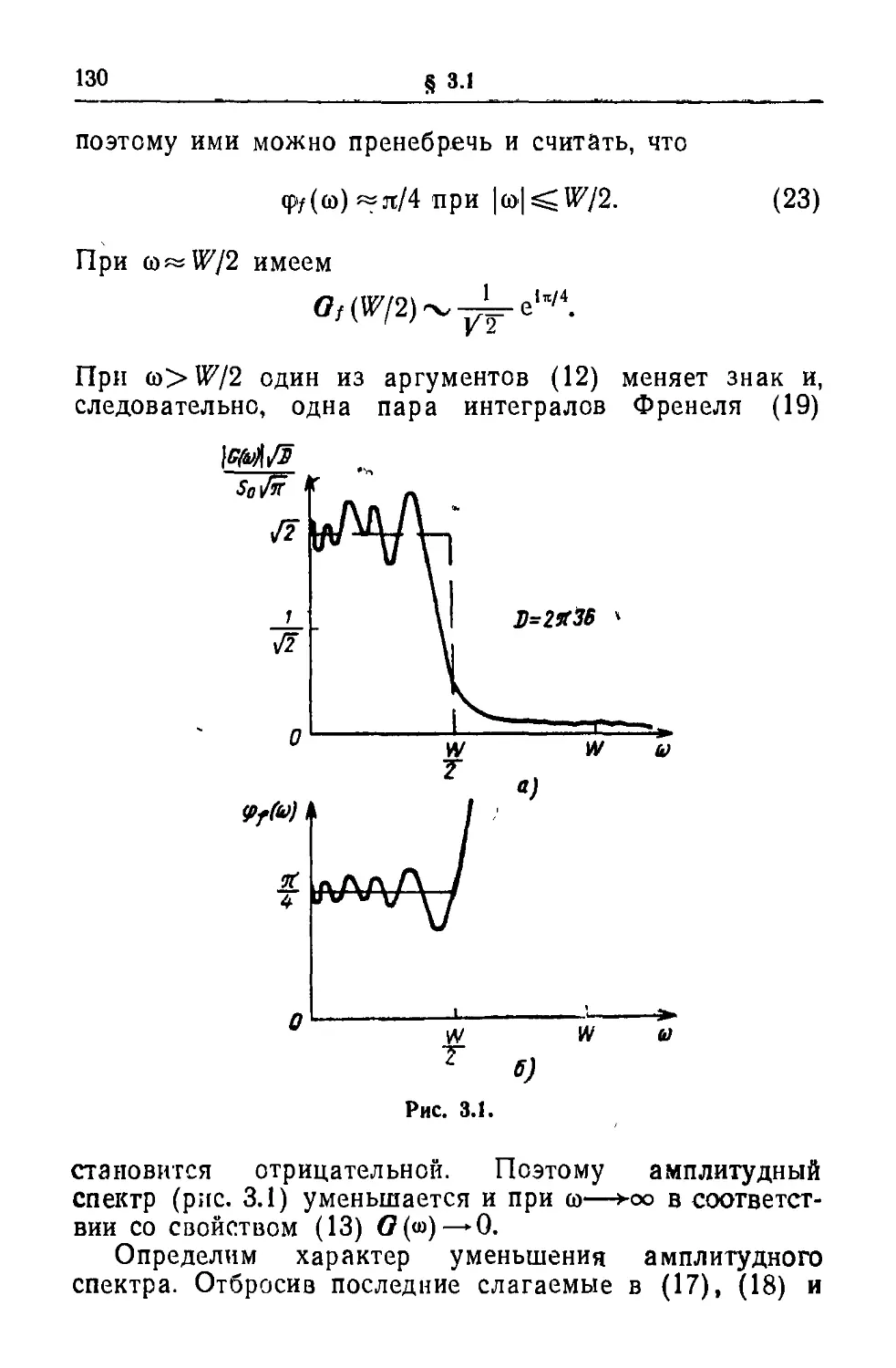
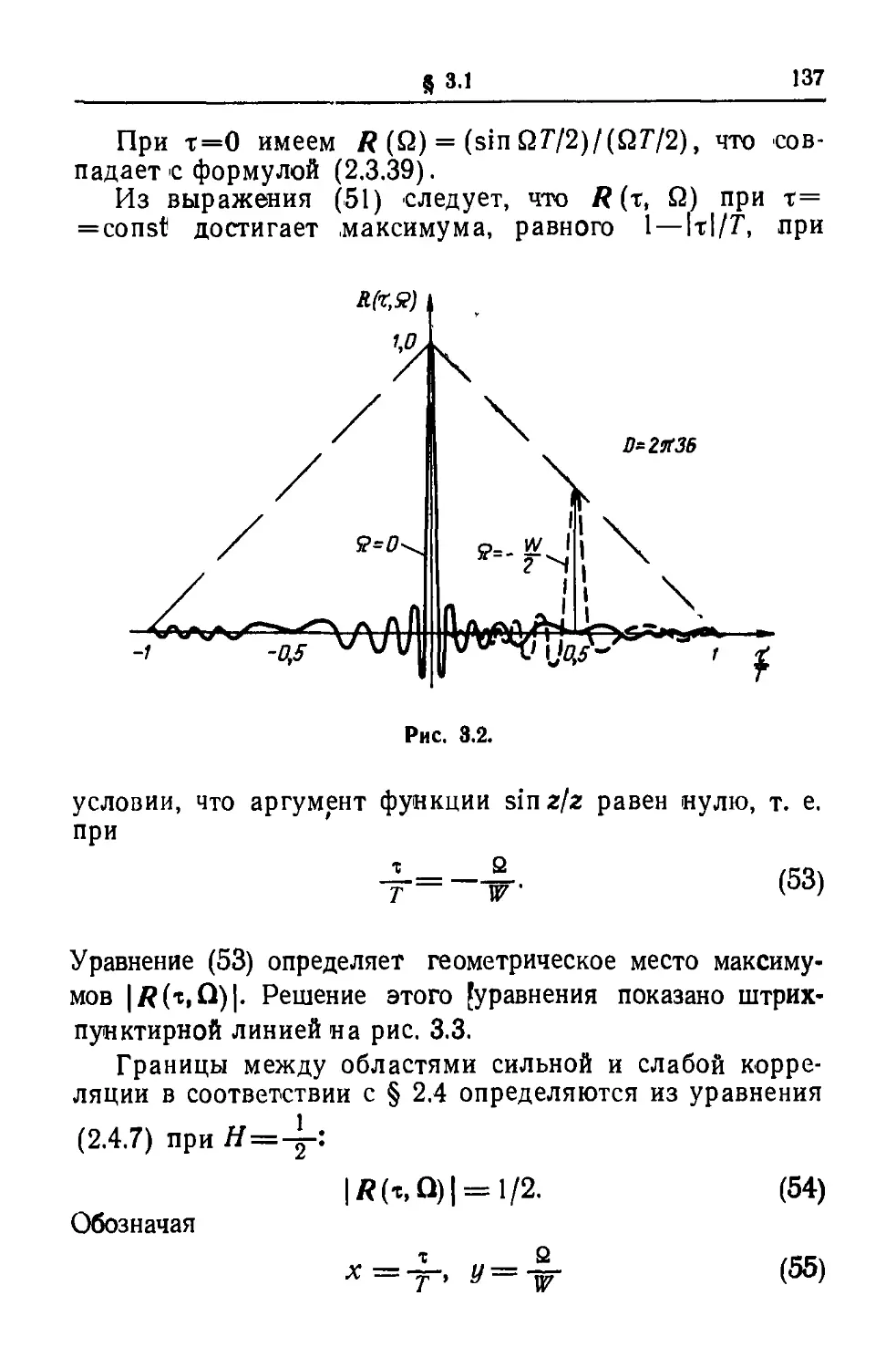
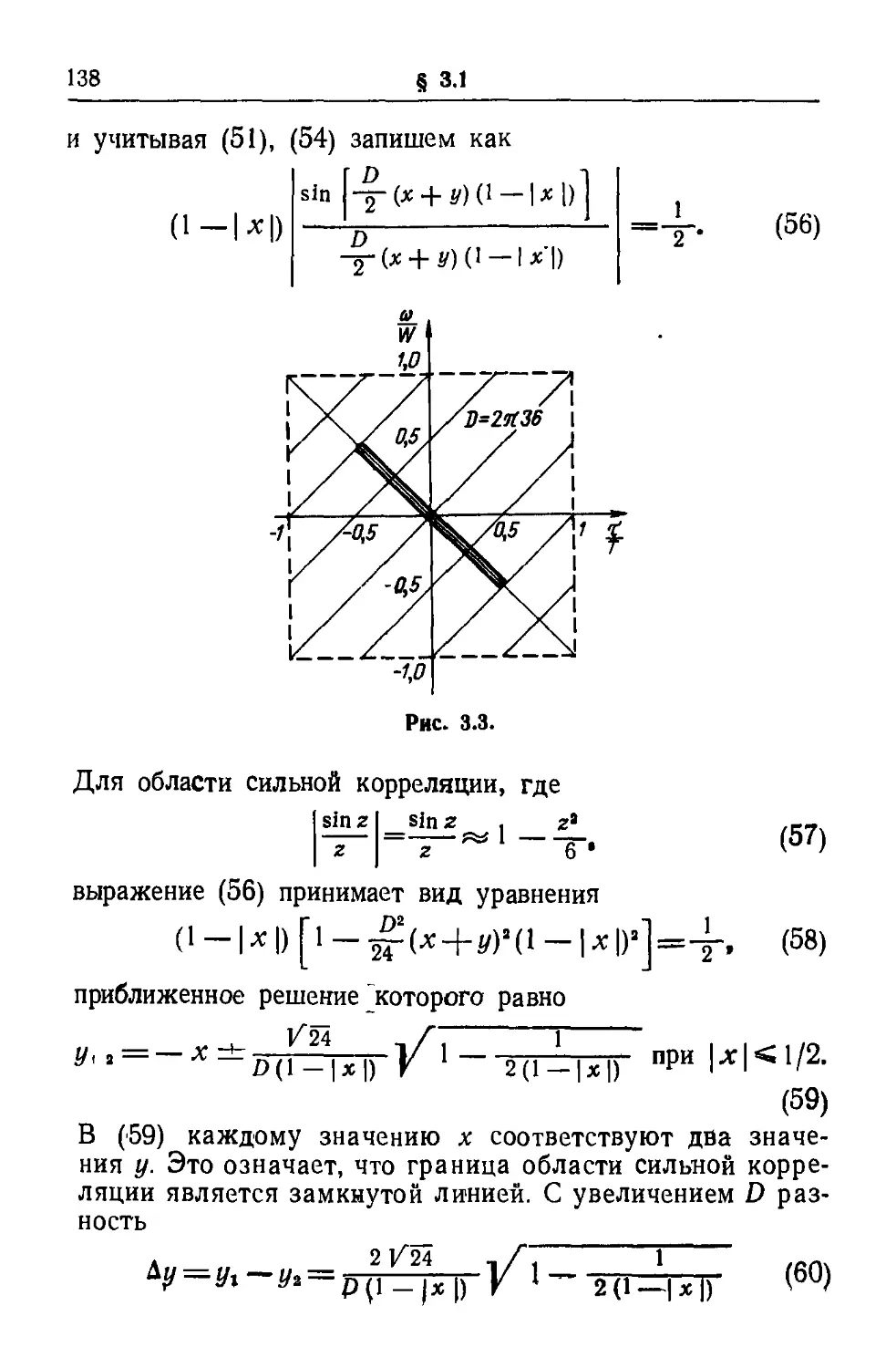
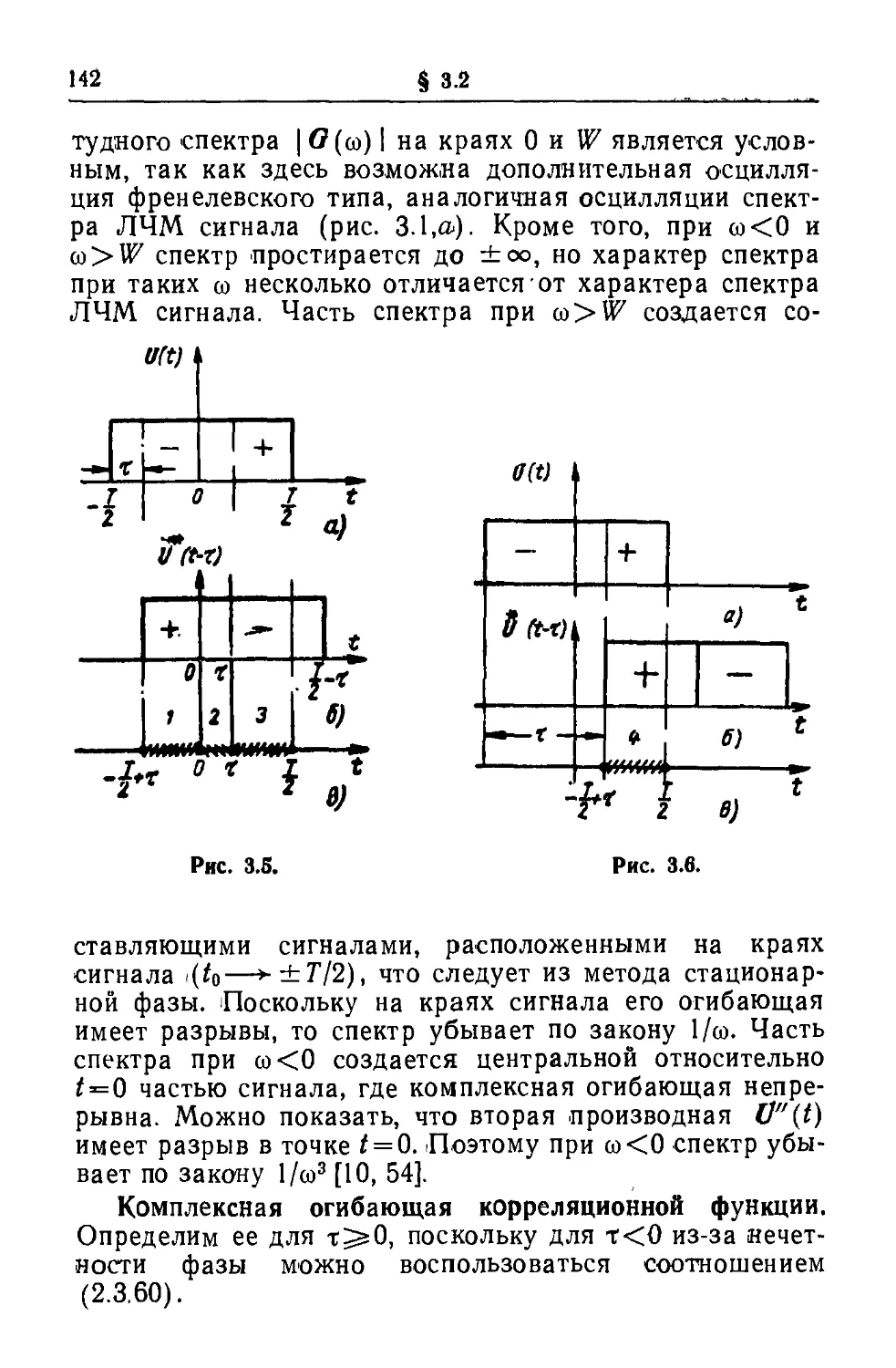
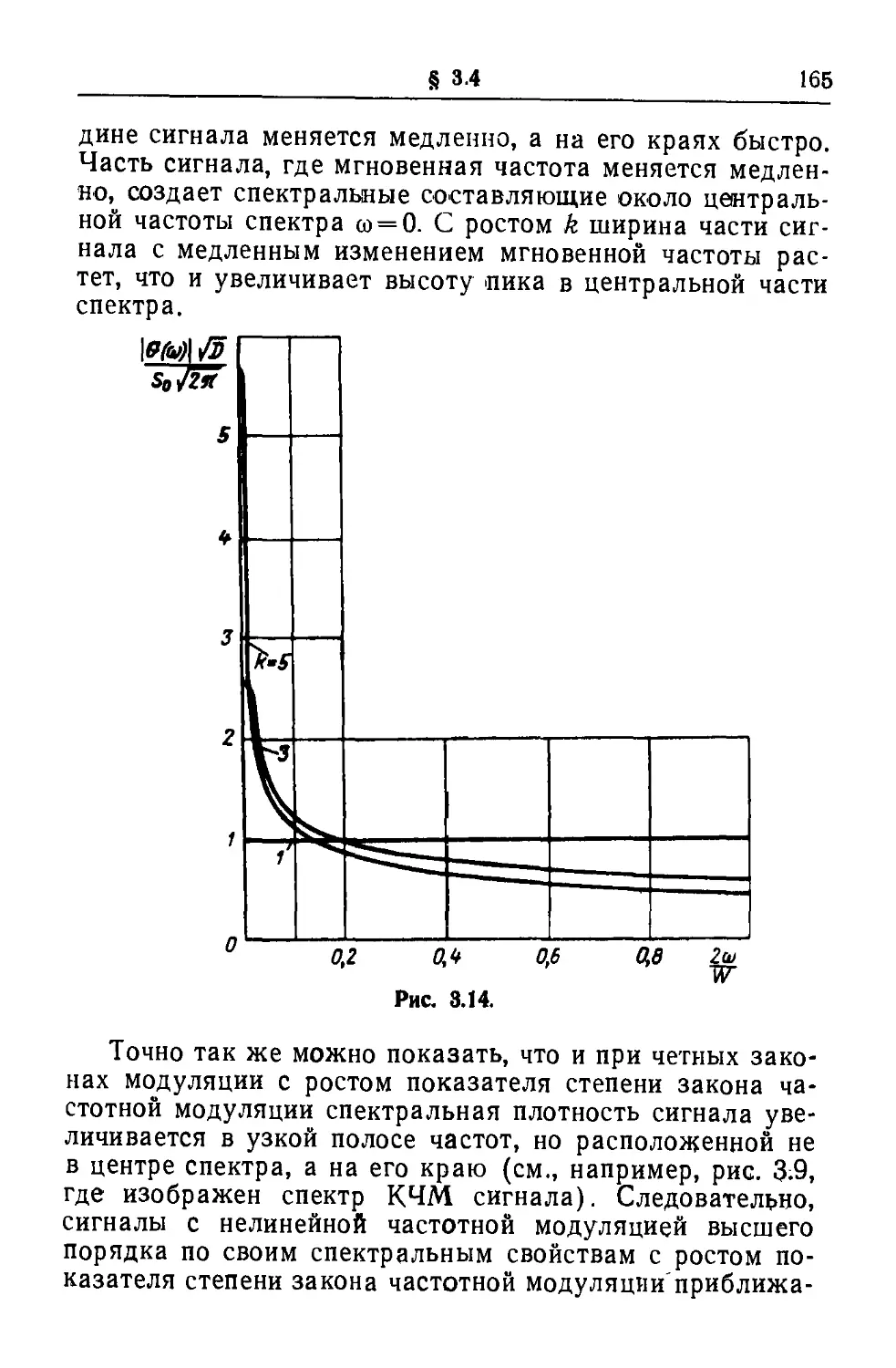
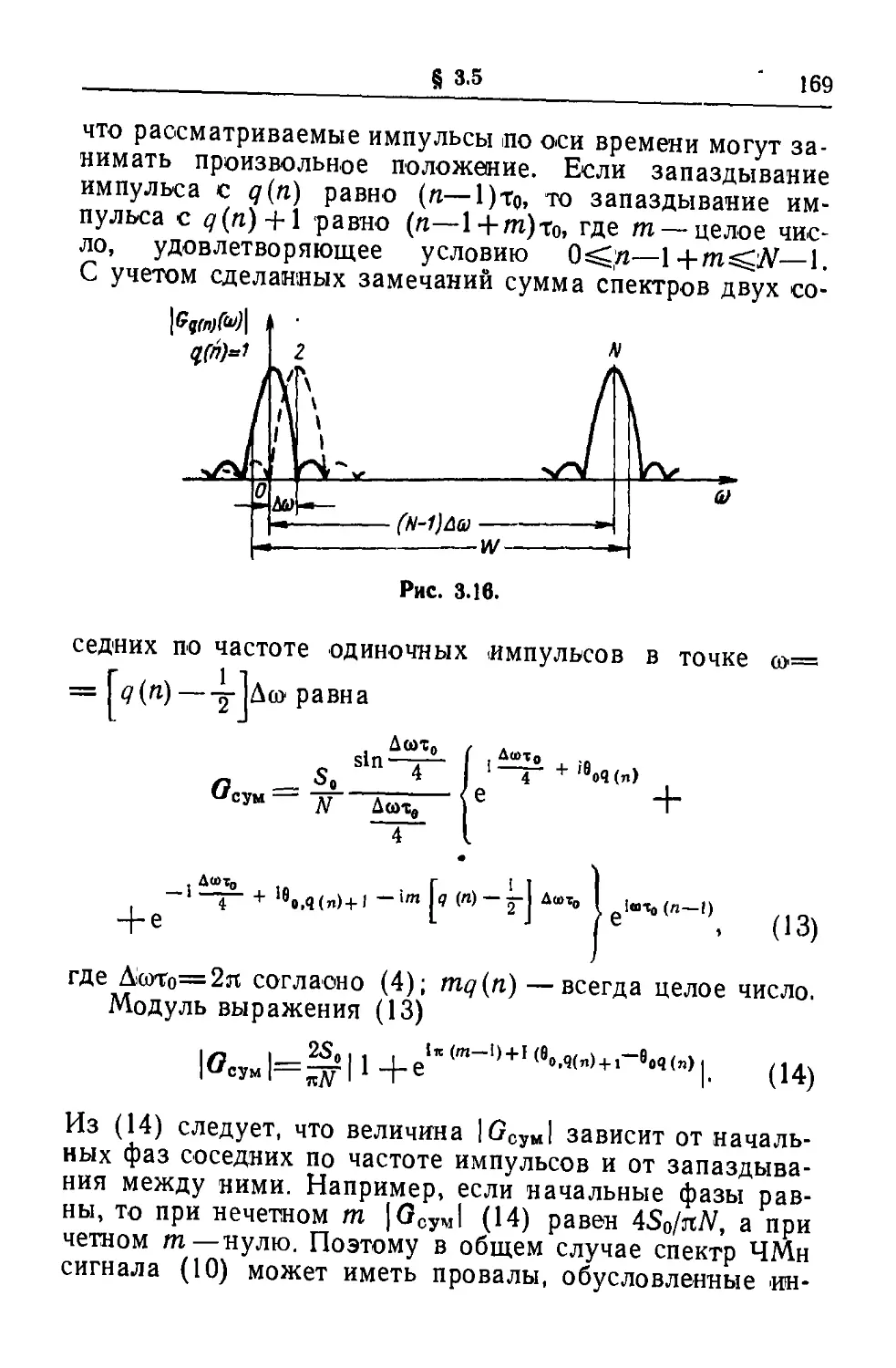
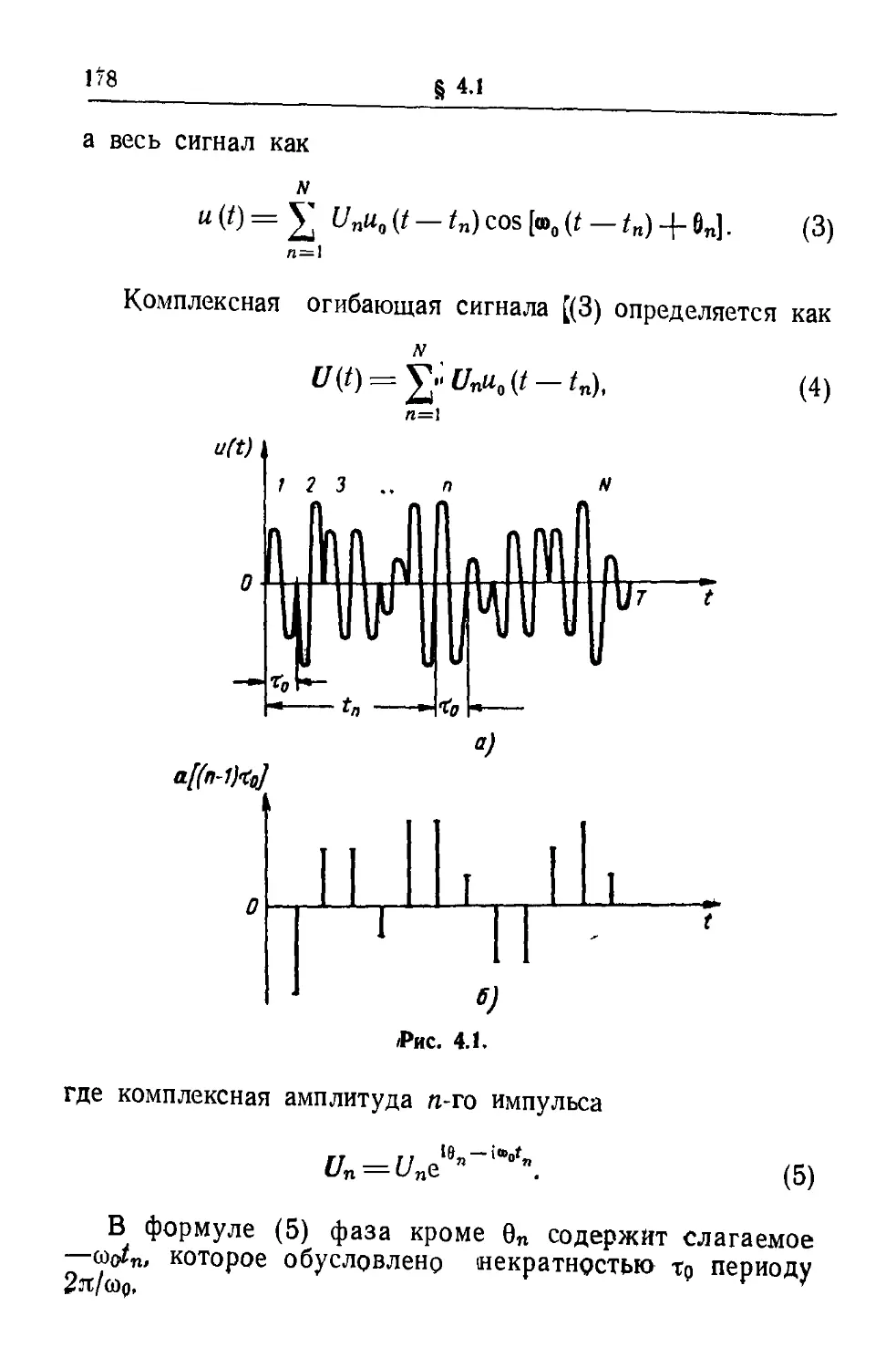
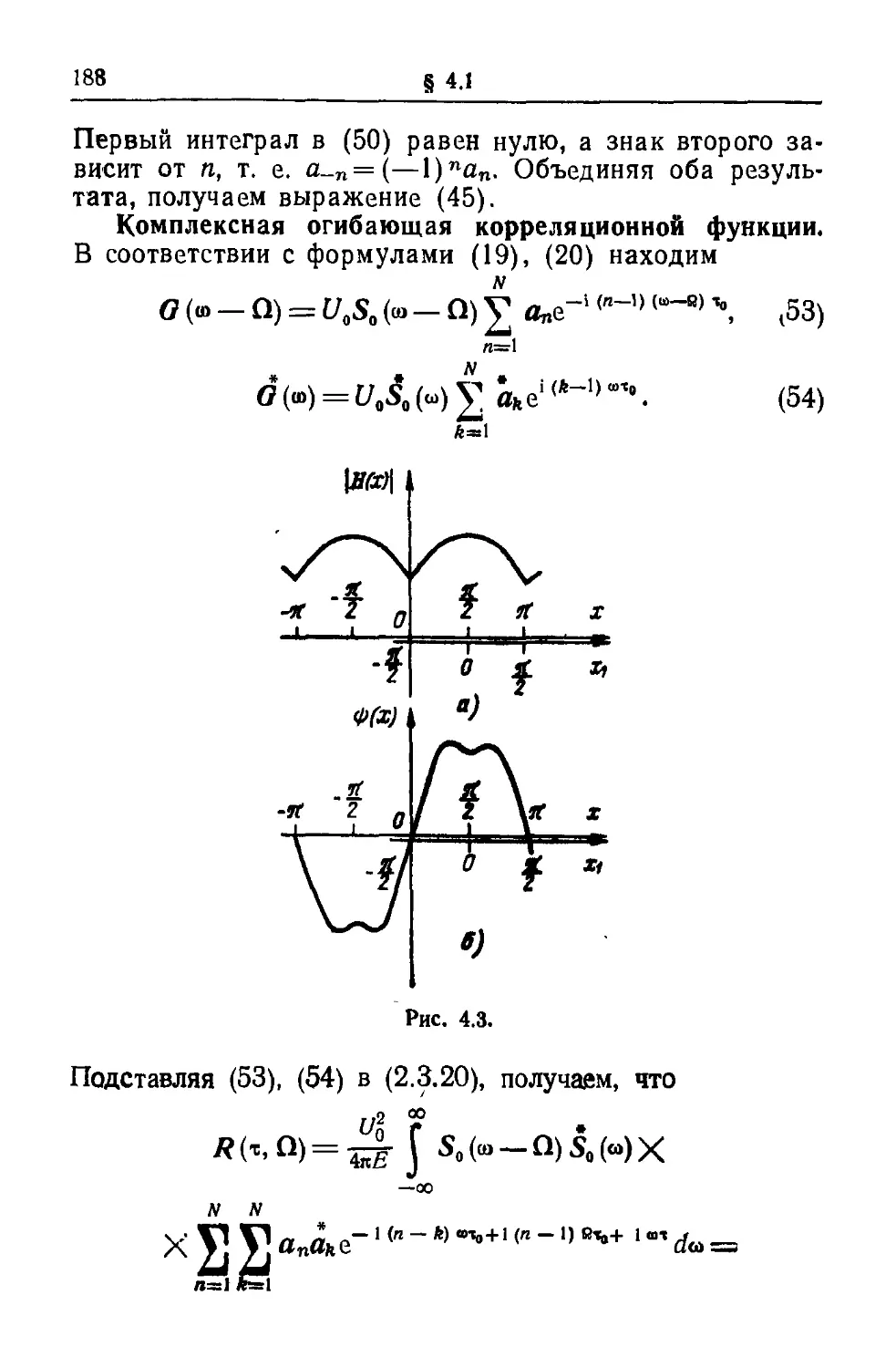
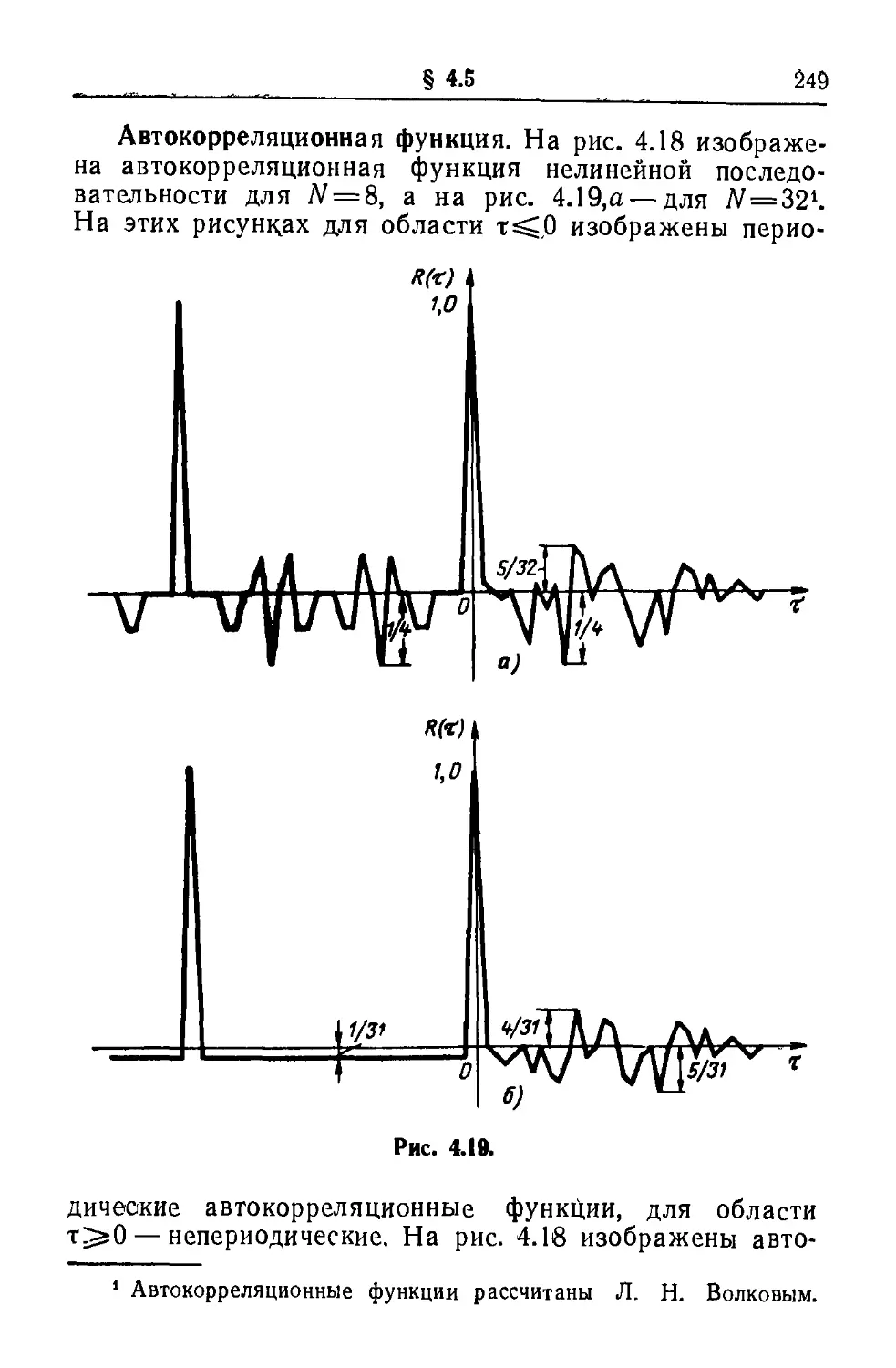
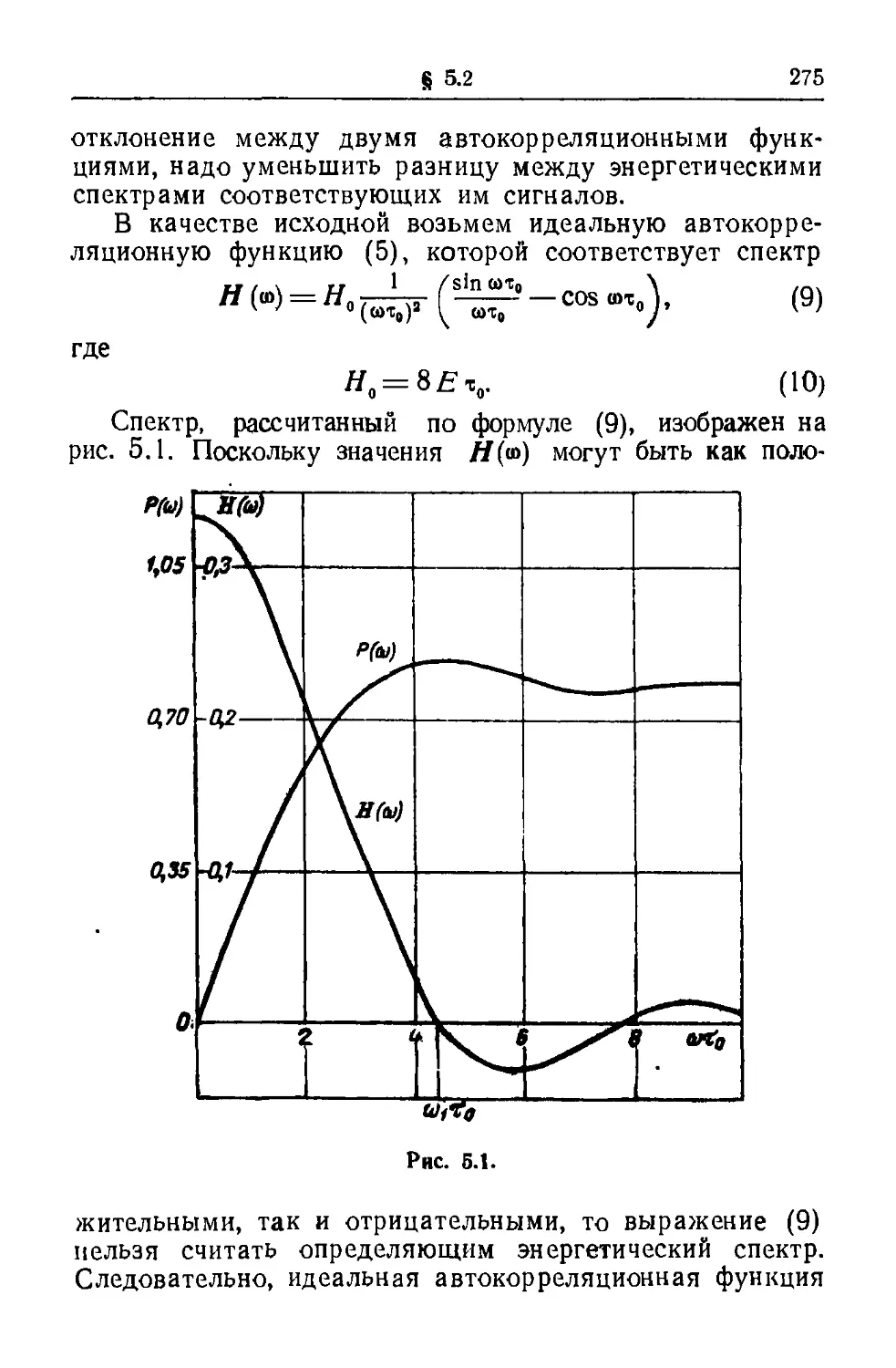
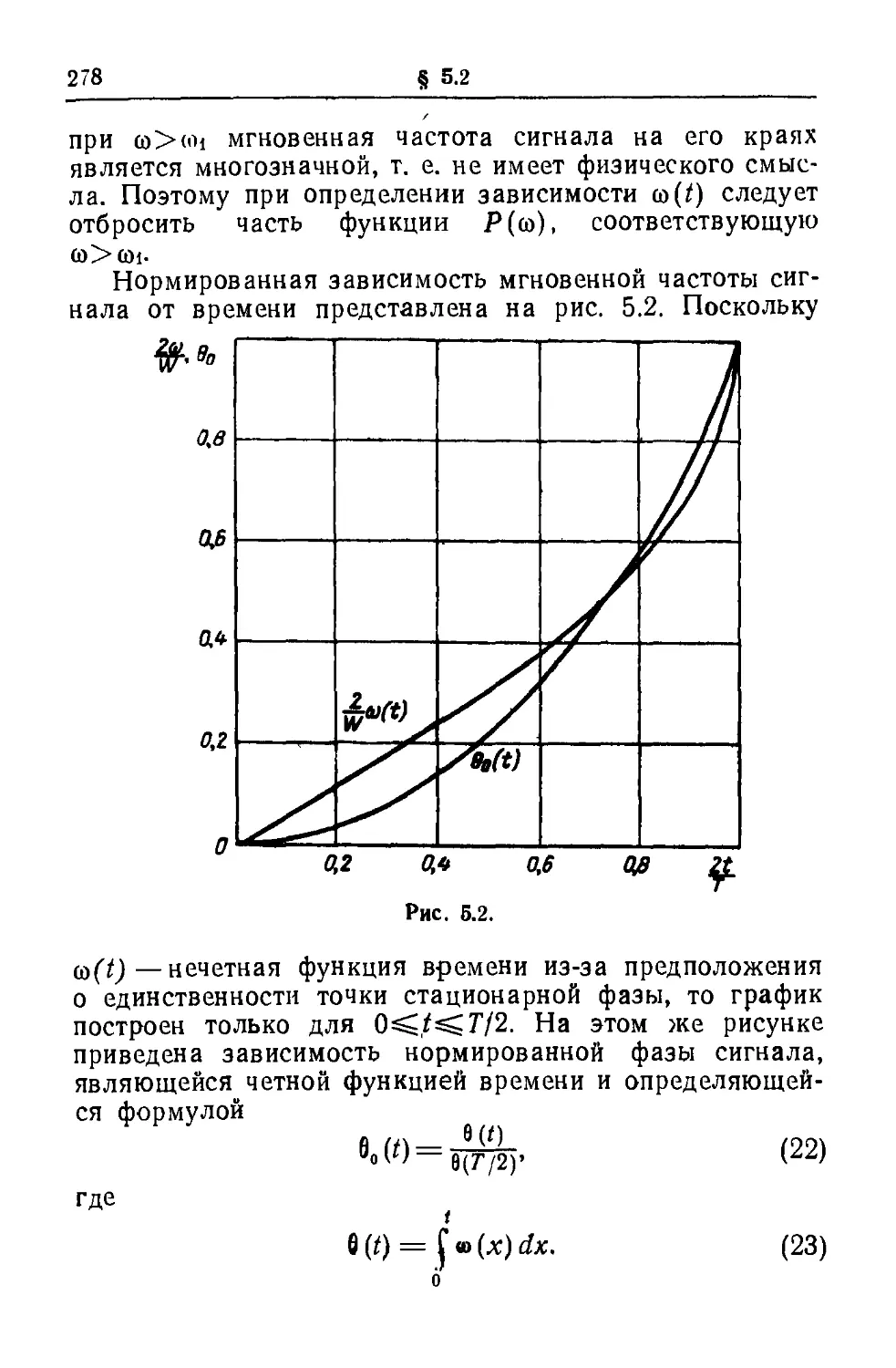
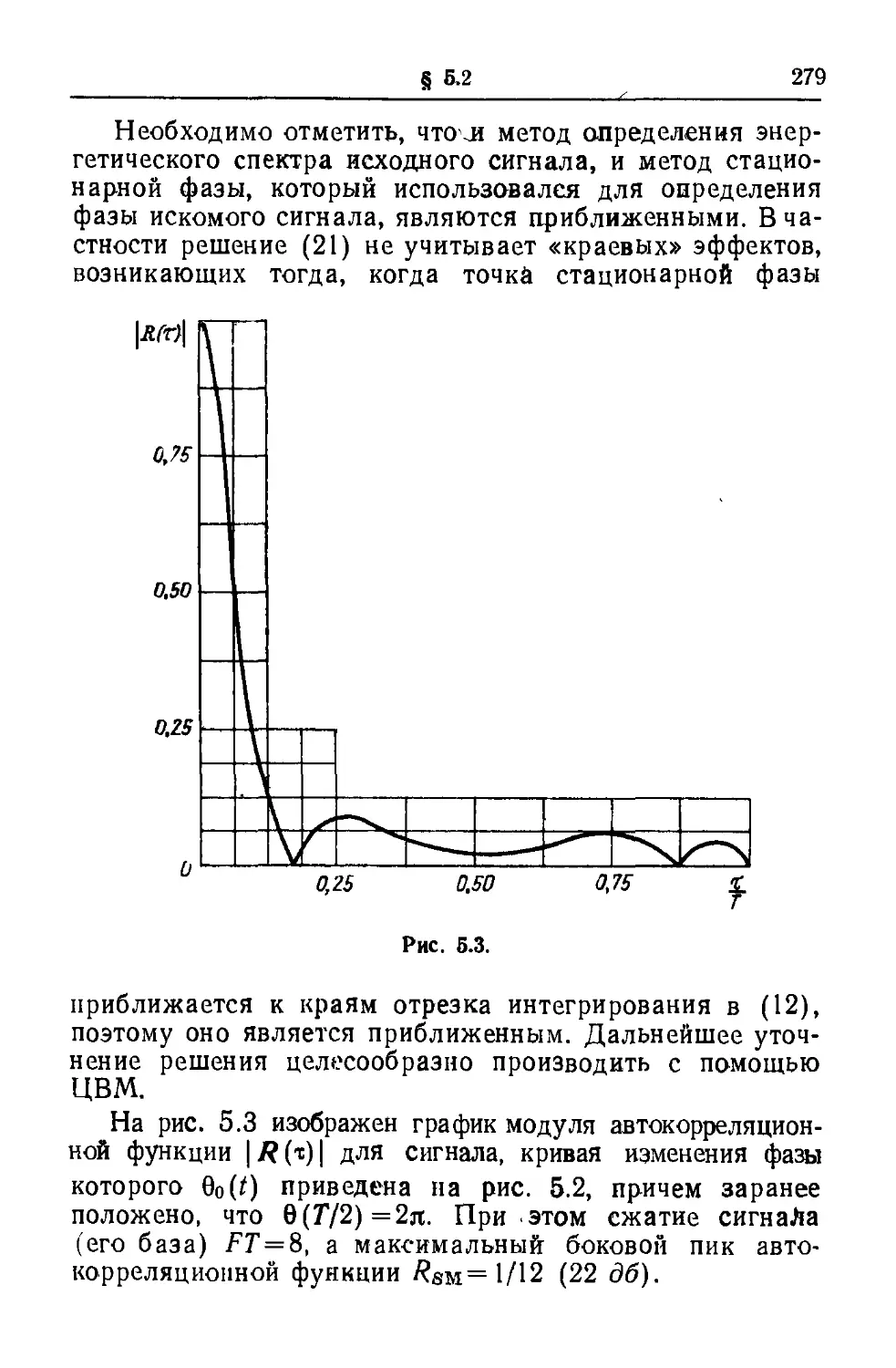
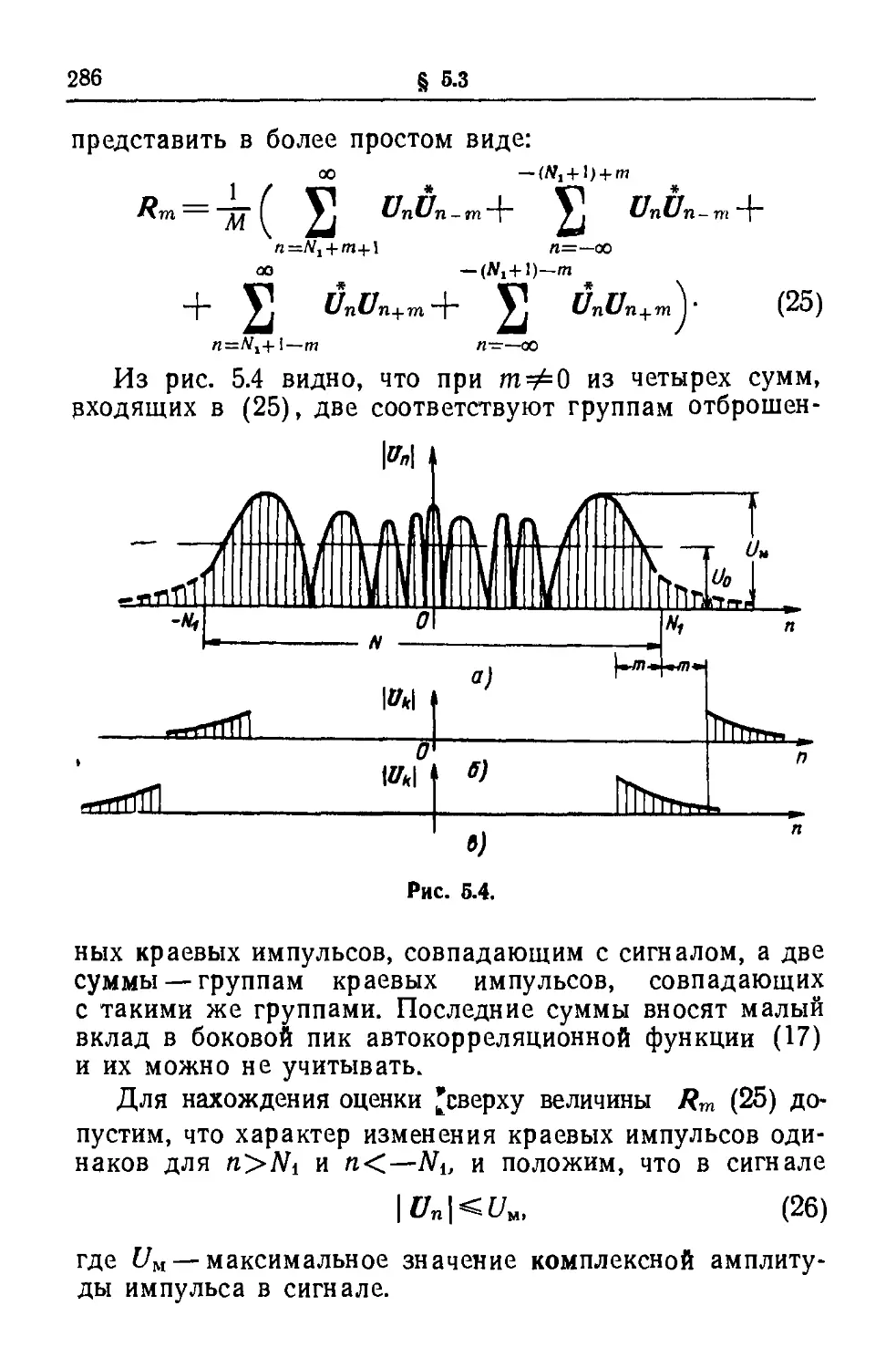
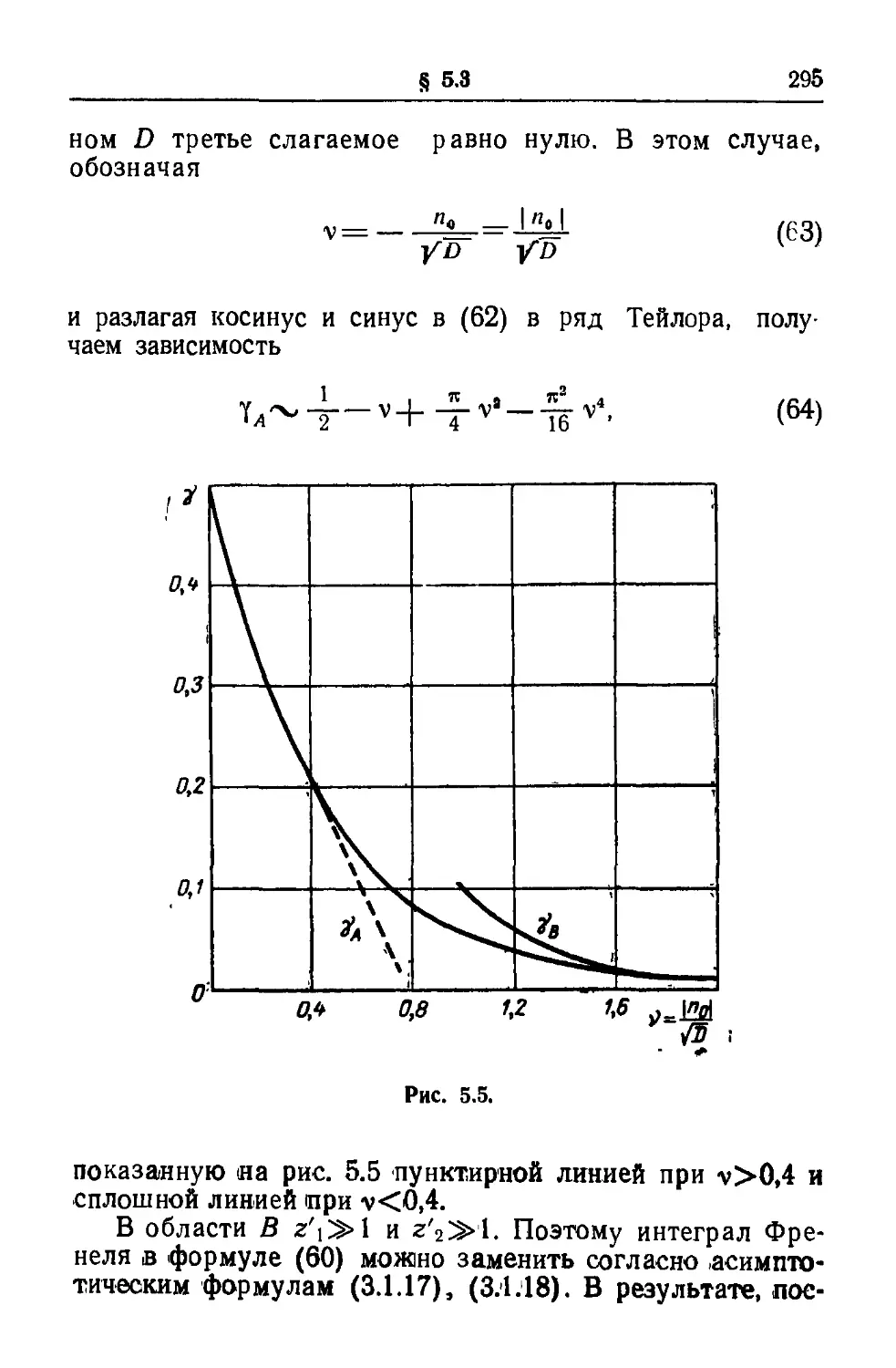
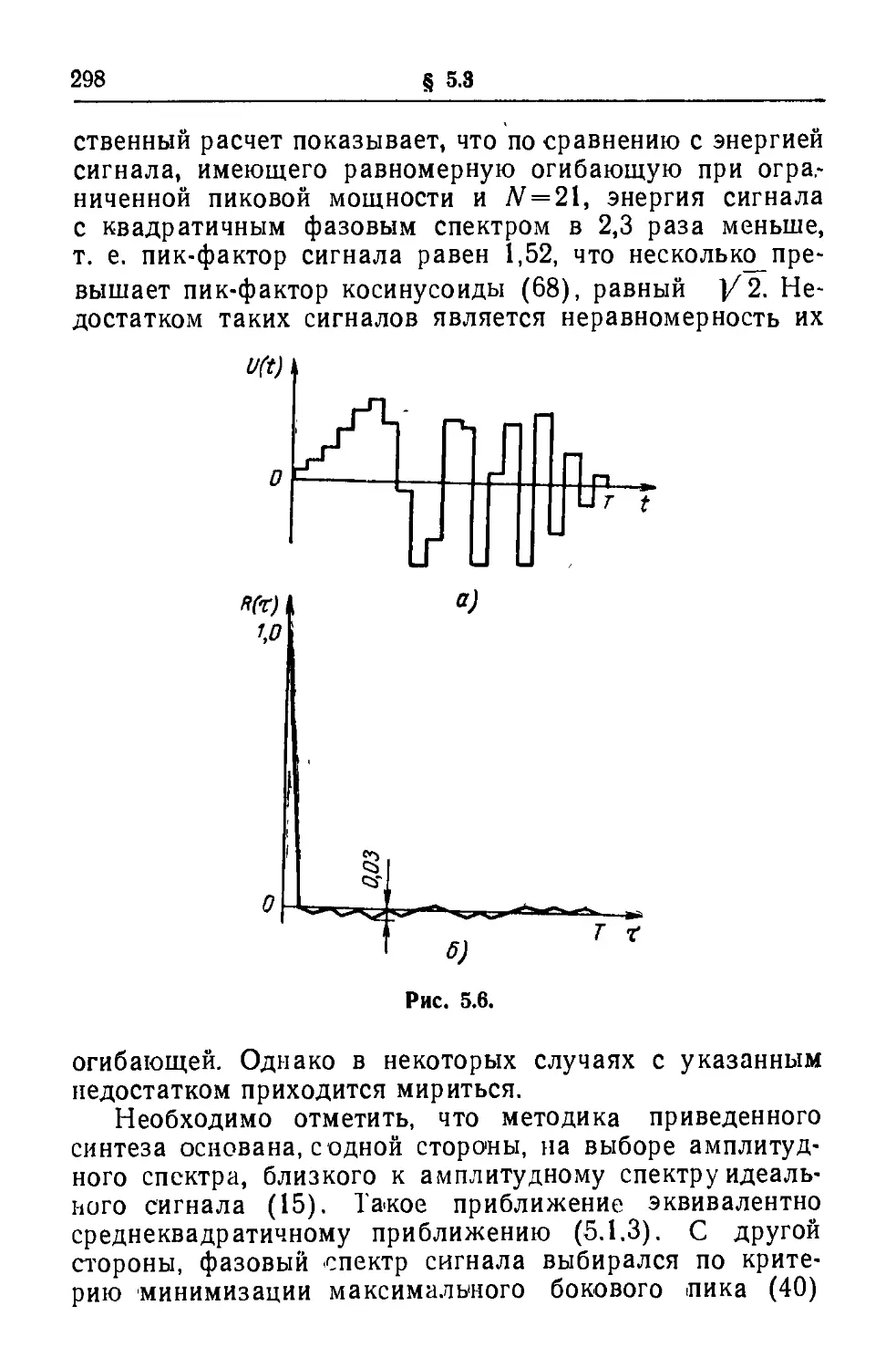
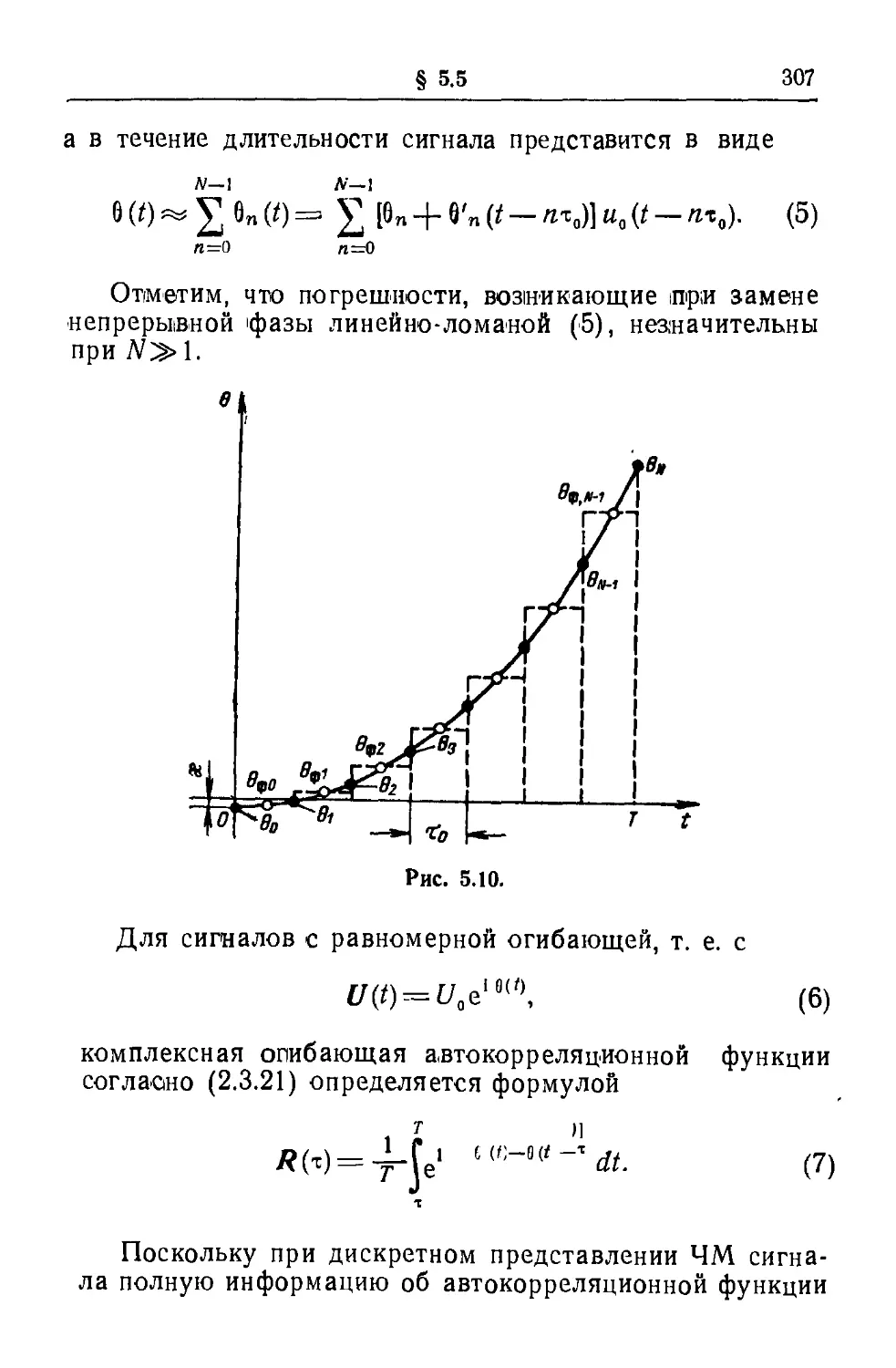
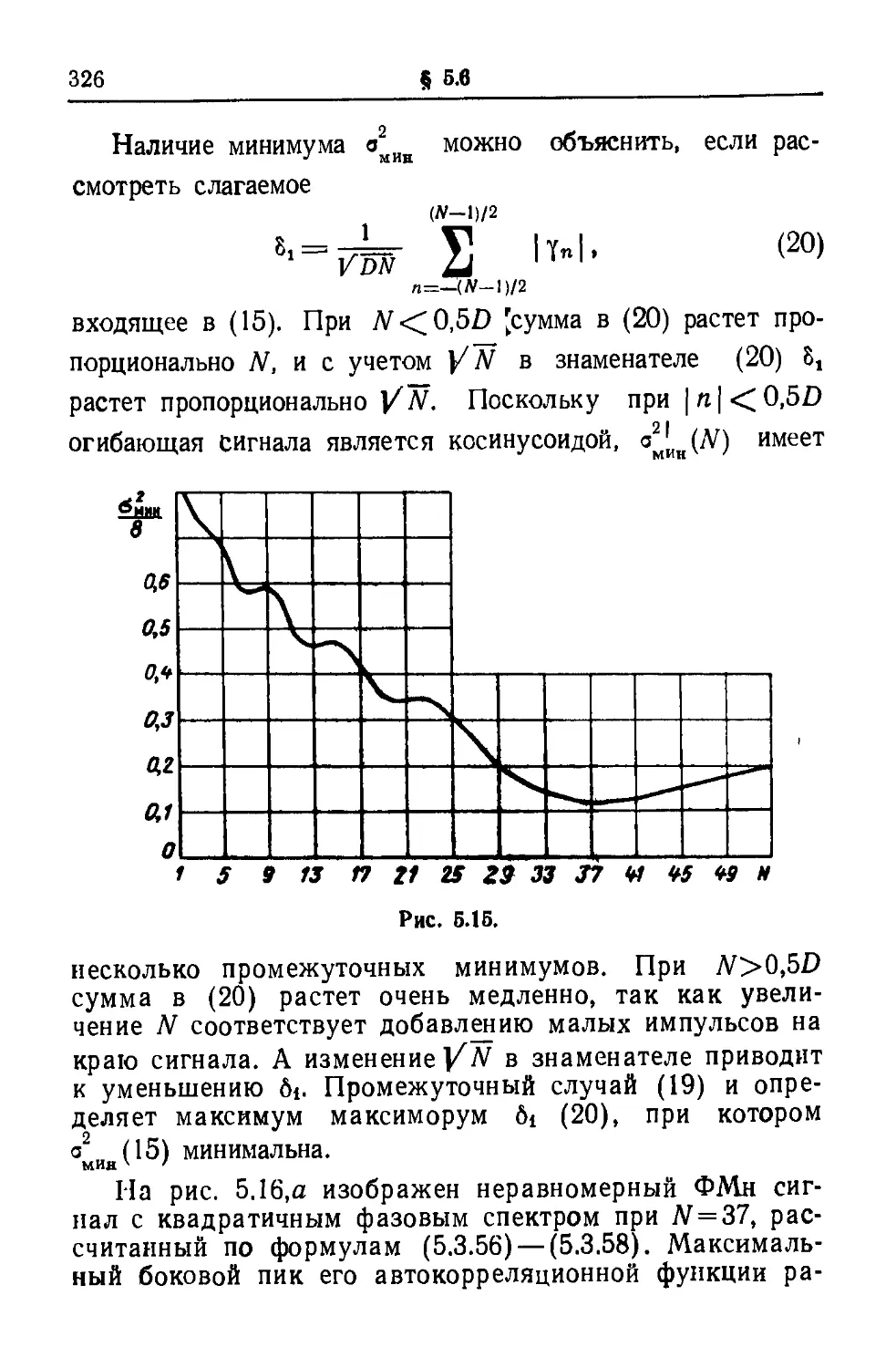
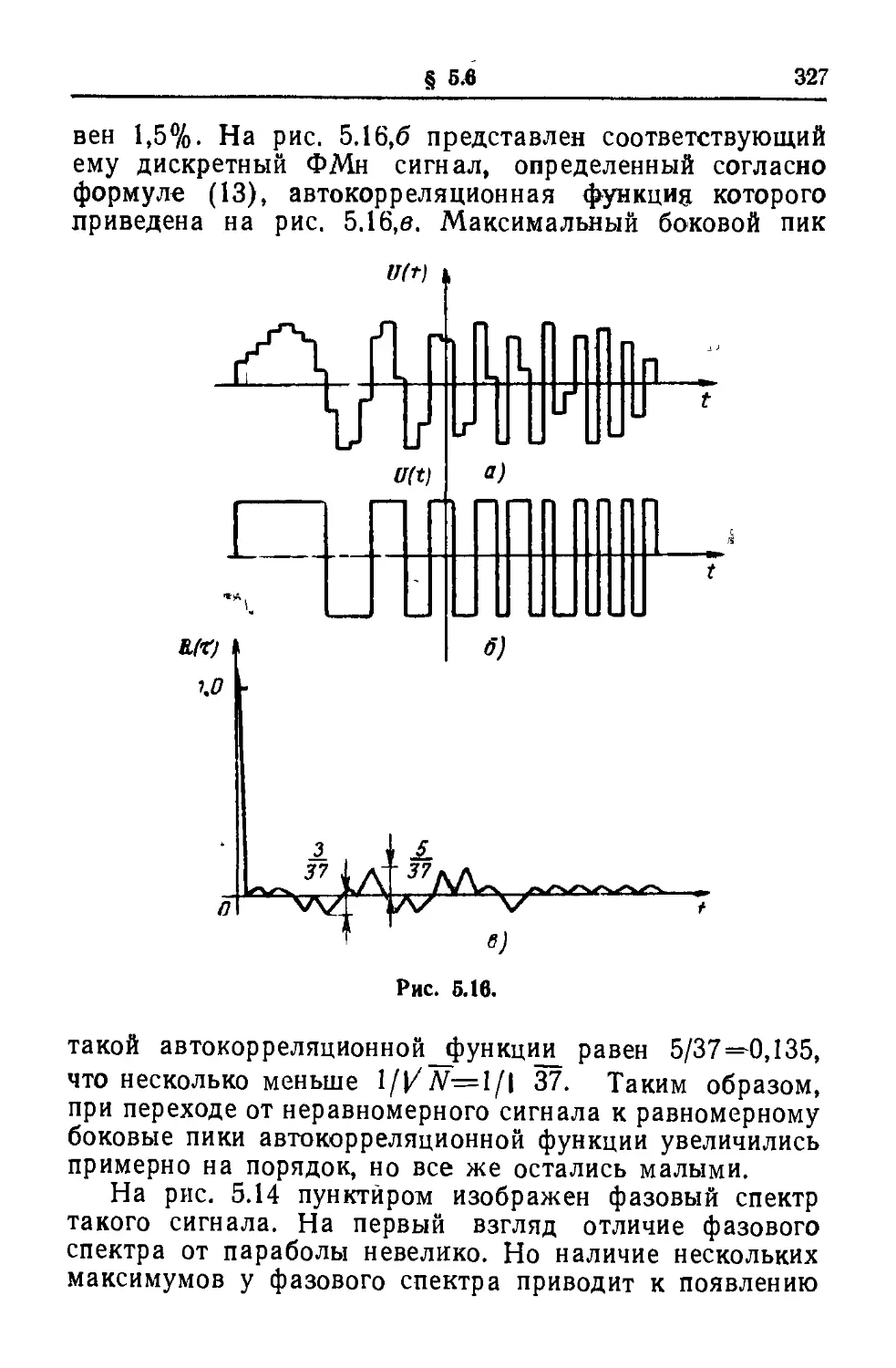
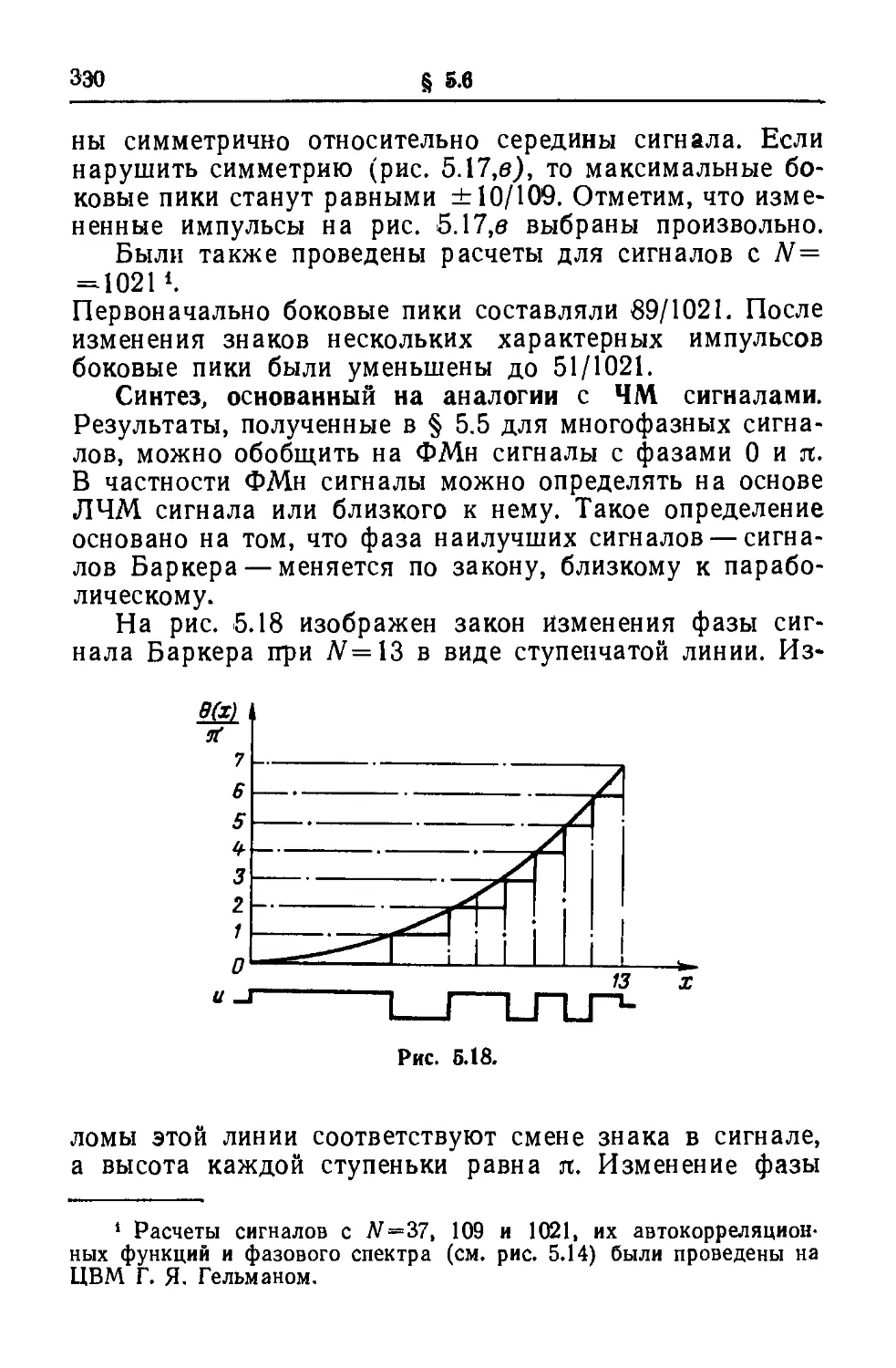
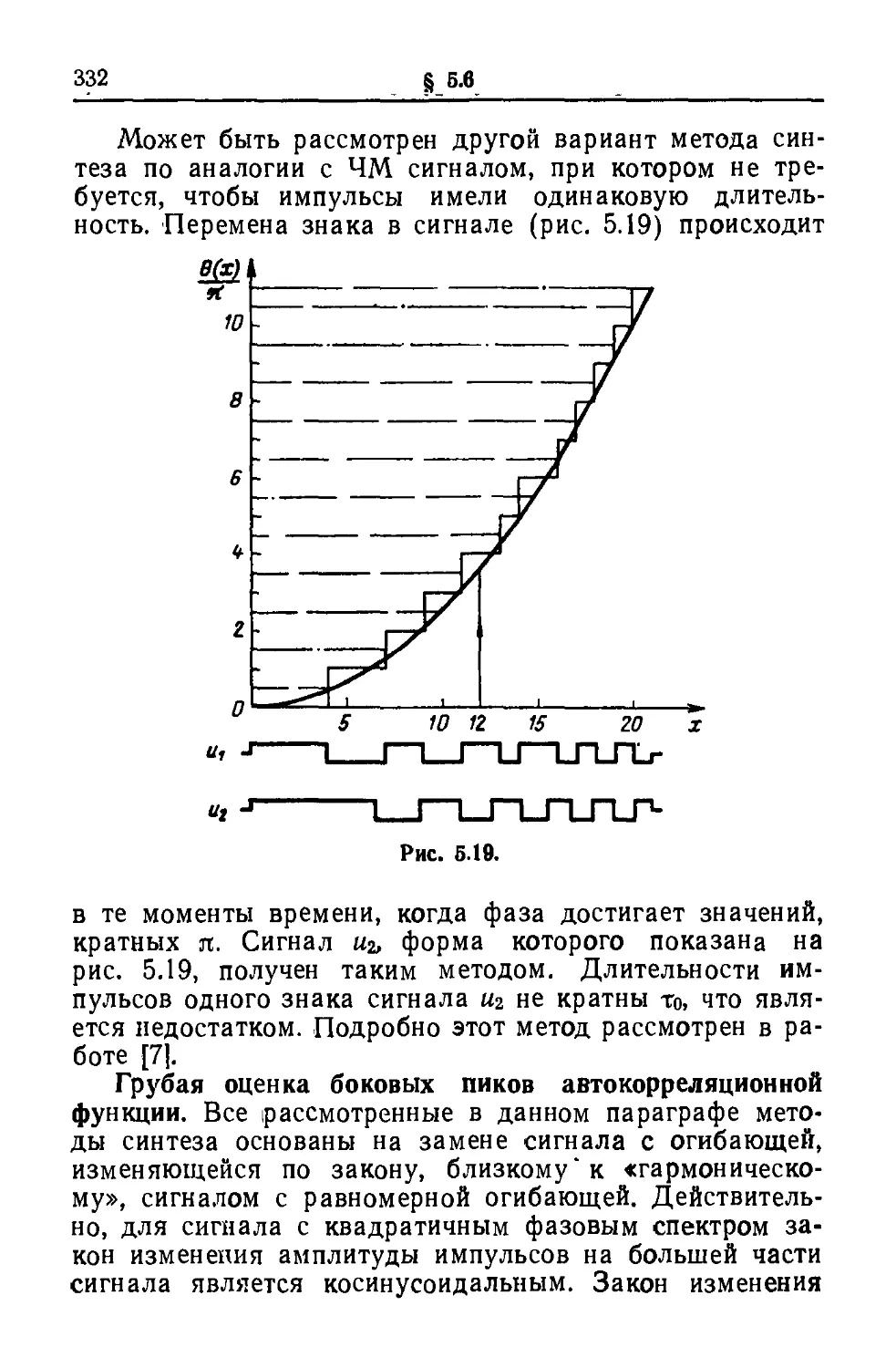
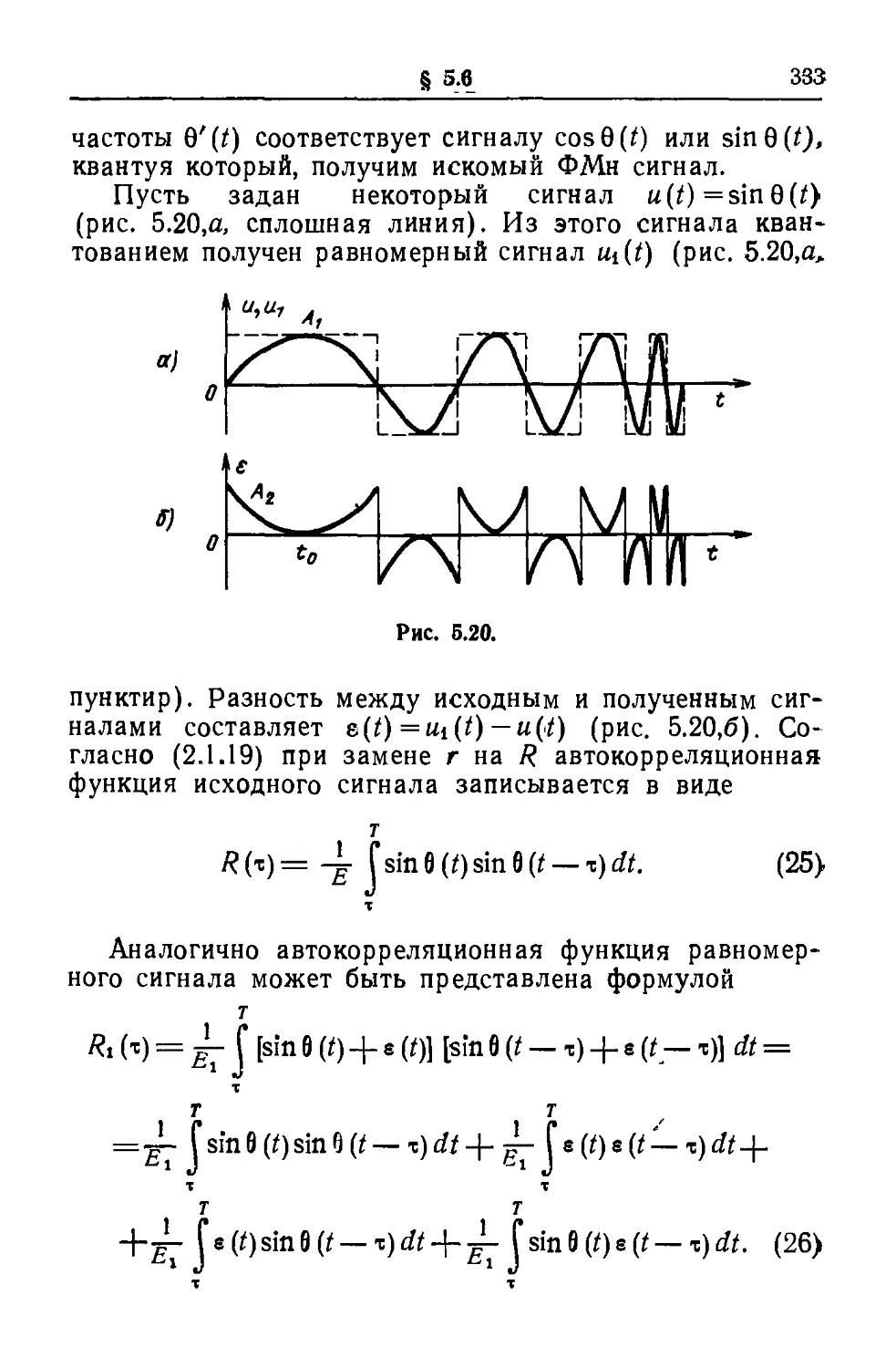
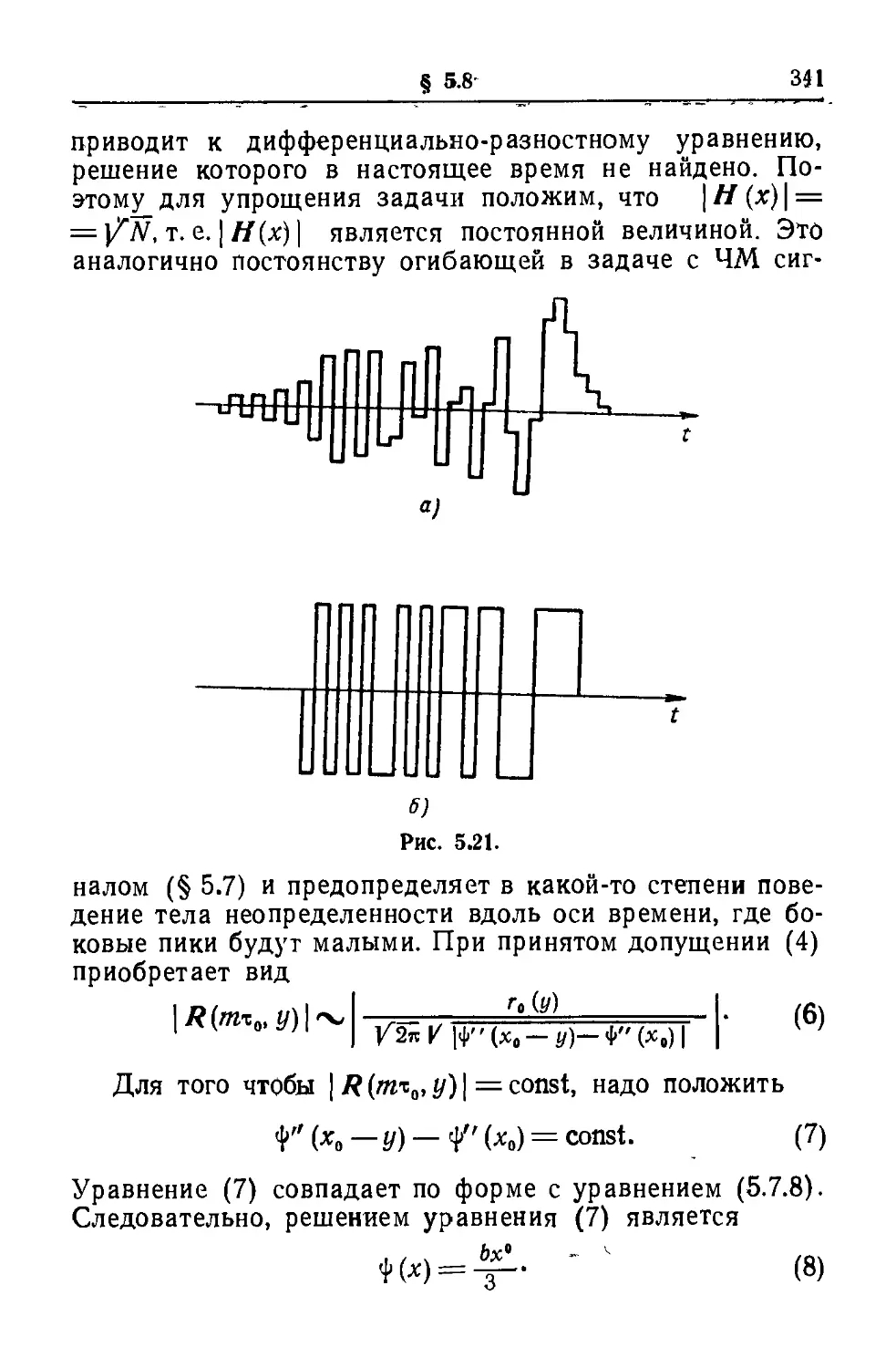
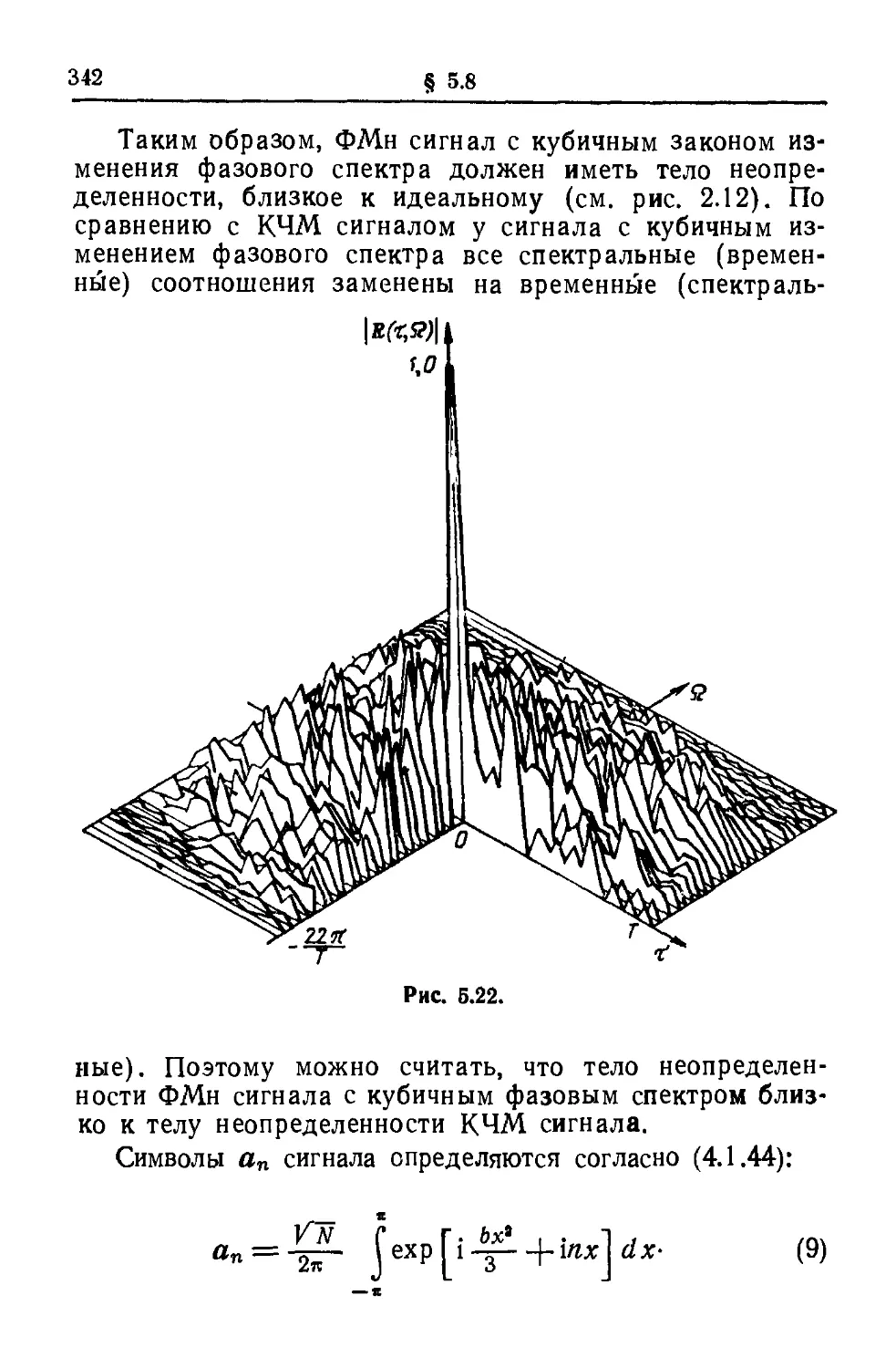
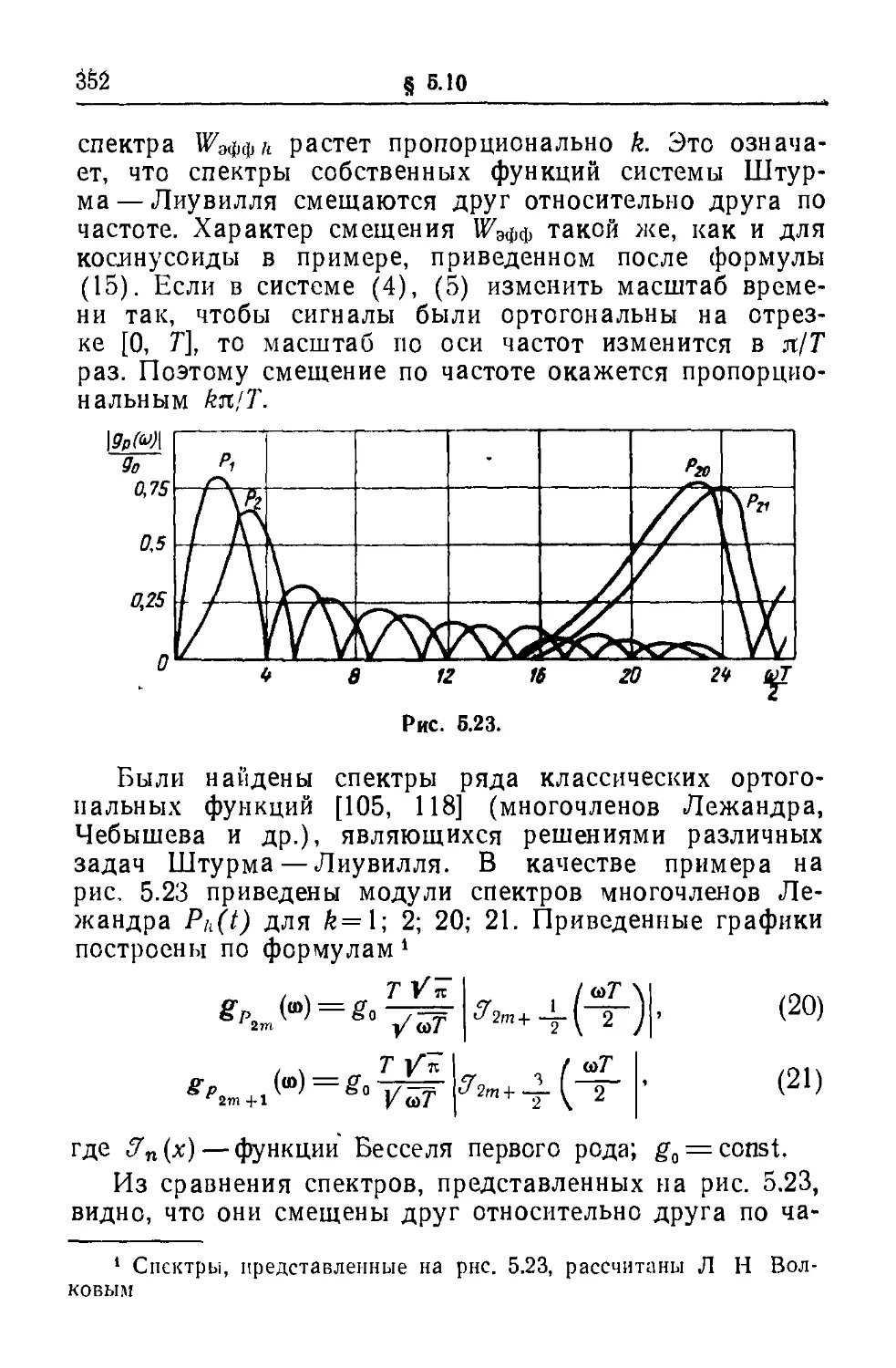
Текст
Л. Е. ВАРАКИН
ТЕОРИЯ
СЛОЖНЫХ
СИГНАЛОВ
«Советское радио»
Москва 1970
УДК 621.391.1
В а р а к и π Л Ε Теория сложных сигналов. Μ , Нзд-во «CoeetCKoe
радио», 1970, 376 стр , τ 12 000 экз , ц 1 ρ 28 к
В книге изложена теория сложных сигналов. Объяснены
причины применения сложных сигналов и приведены их
основные свойства. Подробно исследованы кореляционные
свойства сложных сигналов Рассмотрены различные
частотно-модулированные (с линейной и квадратичной ЧМ,
многочастотные и др) и фазсманипулированные (Λί-последоватсльностн,
последовательности Лежандра, нелинейные и др) сигналы.
Приведены решения задач синтеза частотно-модулированиых и
фазоманипулированных сигналов по их автокорреляционным
функциям и телам ьеопределенпости. Рассмотрены некоторые
вопросы построения систем ортогональных сигналов.
Книга предназначена для научных работников, инженеров,
аспирантов и студентов старших курсов радиотехнических
специальностей.
88 рис, 18 табл., библ. 120 назв.
3-3-12
8-70
Светлой памяти
Учителя — профессора
Геца Ароновичи
ЛЕВИНА
ПРЕДИСЛОВИЕ
Сложные сигналы находят все более широкое
применение в радиотехнических (локационных, связных и др.)
системах. Исследованию свойств сложных сигналов и
вопросам их применения посвящено большое число книг и
статей. Среди книг надо отметить книги Фальковича, Лс-
зина, Ширмана и Голикова, Вакмана, Башаринова, Го-
норовского, Тихонова [1—8]. Однако с момента издания
этих работ получено много новых результатов.
Обобщение и изложение этих результатов 'И является целью
книги.
Книга посвящена теории сложных сигналов. В первой
главе объясняются причины широкого использования
в радиотехнических системах сложных сигналов и
приводятся их общие свойства. Корреляционные свойства
сложных сигналов исследуются во второй главе.
Частотно-модулированные и фазоманипулированные сигналы
рассматриваются в третьей и четвертой главах
соответственно, а синтез сложных сигналов — в пятой. Вопросы
формирования и обработки сложных сигналов
излагаются, когда это необходимо для объяснения свойств
сигналов, очень кратко. Более подробно с этими вопросами
читатель может познакомиться в работах [4, б, 9].
Формулы, приведенные в книге, имеют нумерацию
внутри каждого параграфа. При ссылках внутри одного
параграфа указывается лишь номер формулы, при
ссылках на формулы других параграфов сначала указывается
номер параграфа.
Настоящая книга написана на основе лекций,
прочитанных автором в течение 1964—1968 гг. аспирантам,
инженерам и студентам Московского электротехнического
института связи. Инициатором лекций был учитель
автора— профессор Гец Аронович Левин.
Автор выражает искреннюю признательность
заведующему кафедрой радиотехнических систем МЭИС,
доц., канд. техн. маук А. И. Дымовой и проф.,докт. техн.
наук Б. Р, Левину за помощь и поддержку при
написании рукописи, а также рецензентам проф., докт. техн.
наук Ю. С Лёзину и докт. техн. наук Д. Е. Вакмаму за
ряд критических замечаадий, способствовавших
улучшению книги.
Автор сердечно благодарит Л. В. Варакину,
товарищей по работе — В. Н. Власова, Л. Н. Волкова, канд.
техн. наук И. М. Пышкина, канд. техн. наук И. X. Риз-
кина, а также студентов МЭИС (ныме инженеров),
охотно помогавших ему.
Все замечания и пожелания автор просит направлять
по адресу: Москва, п/я 693, изд-во «Советское радио».
глава ι ОБЩИЕ СВОЙСТВА
СЛОЖНЫХ СИГНАЛОВ
1.1. ПРОСТЫЕ И СЛОЖНЫЕ СИГНАЛЫ
Сигналом называется изменяющаяся физическая
величина, отображающая сообщение. Сигнал и,
являющийся функцией времени г, может быть записан в виде
u = u(t). (1)
Сигнал и его спектр giw)1 связаны преобразованиями
Фурье:
g»= j u(t)tTMdt, (2)
—оо
оо
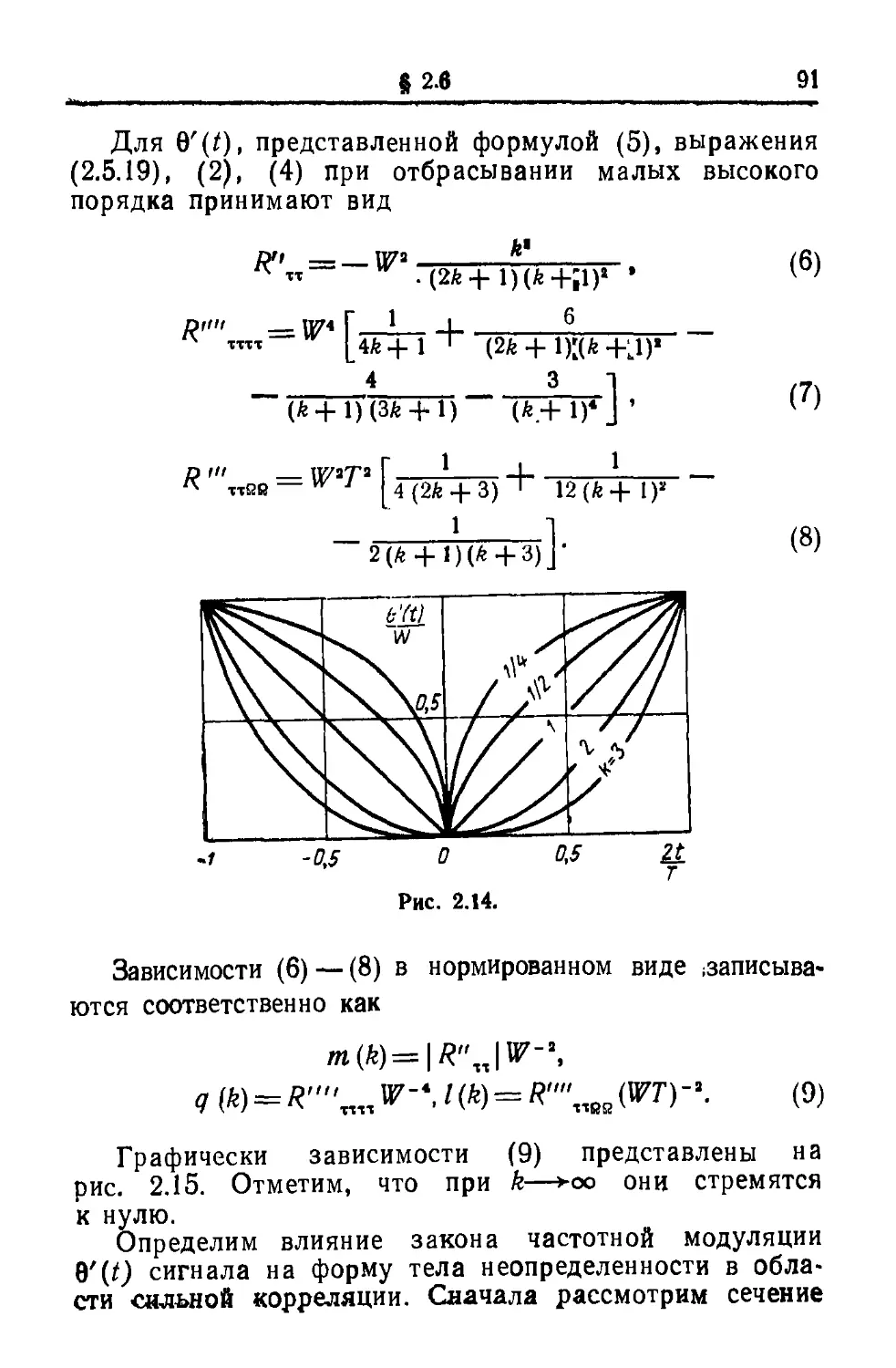
"(0=i Jff(«)e""dcD. (3)
—00
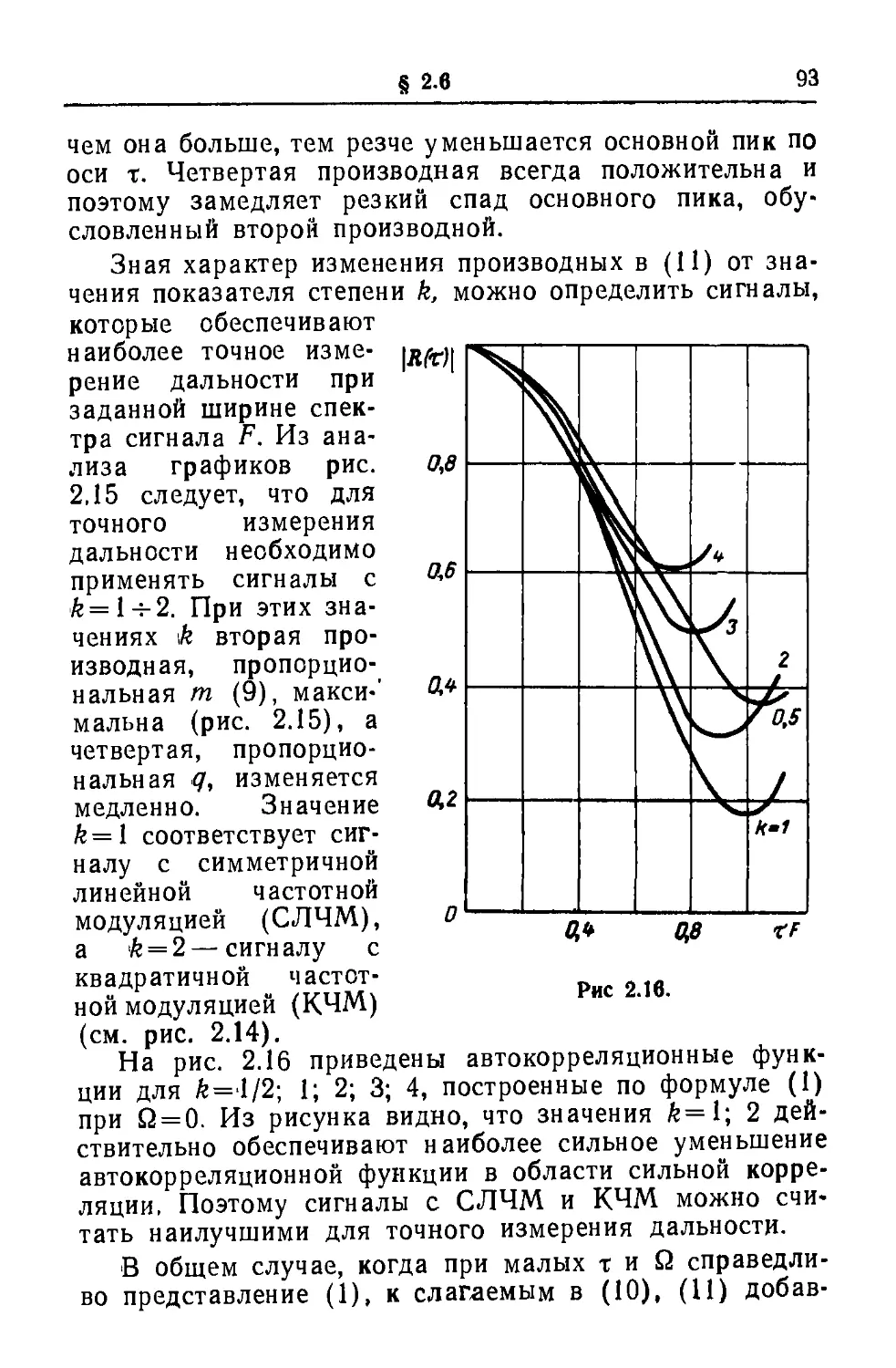
Пределы интегрирования в (2) и (3) определяются облас
тями существования функций и (ή и g(<o) соответственно.
Отметим, что реальные сигналы всегда являются
действительными функциями времени, а их спектры могут
быть комплексными функциями частоты.
Если функции u(t) или g(<o) заданы, то свойства
сигнала известны полностью. Но в ряде случаев нет
необходимости характеризовать сигнал исчерпывающим
образом, достаточно знать лишь его основные
характеристики. К таким характеристикам следует отнести энергию
сигнала, его длительность и ширину спектра. Энергия
сигнала определяет надежность приема
(помехоустойчивость), длительность — время, которое надо затратить на
передачу сигнала, ширина спектра—необходимую
полосу частот «анала передачи сигнала.
4 Здесь и в дальнейшем комплексные величины и функции
выделены полужирным шрифтом.
6
§ II
Если сигнал u(t) задан, то значение интеграла
00
Е= \ и1 (О Л (4)
—из
пропорционально энергии, выделяемой сигналом на
сопротивлении 1 ом. В дальнейшем величина Ε будет
называться энергией сигнала. Согласно равенству Парсеваля
00 00
f=ij 1гИГ^=4-|1гНГй»- (5)
—оо О
Длительность сигнала Τ и ширину его спектра F
целесообразно определять так, чтобы можно было
выяснить соотношение между свойствами сигнала и
характеристиками канала, по которому сигнал должен быть
передан. При этом надо иметь в виду следующее. Если
сигнал существует на некотором отрезке времени, а вне
этого отрезка тождественно равен нулю, то по оси
частот согласно преобразованиям Фурье (2), (3) он будет
занимать интервал (—оо, +оо). Аналогично, если спектр
сигнала занимает конечную полосу частот, то по оси
времени сигнал простирается от —оо до +оо.
Необходимо отметить, что реальные сигналы имеют начало и
конец и их длительность определяется этими моментами
времени, а ширина спектра — полосой частот, в которой
сосредоточено 99% энергии сигнала. Иногда совместно
использовать эти определения длительности и ширины
спектра бывает неудобно. Например, ширина спектра
прямоугольного видеоимпульса длительностью Τ часто
определяется первым нулем спектра, т. е. F=\/T (при
этом FT=l). Если же ширина спектра находится из
условия 99% энергии, то F я* 10/7 [10].
При теоретических исследованиях используются
различные определения длительности и ширины спектра
сигнала. Объясняется это тем, что то или иное определение
либо имеет больший физический смысл, либо упрощает
математические выкладки. Примеры таких определений
можно найти в литературе [5, 11, 12]. В дальнейшем
некоторые из этих определений будут использованы.
В теории сигналов [11] давно известно, что
независимо от определений длительности сигнала и ширины его
§ *.2
7
спектра, минимальное значение произведения FT
примерно равно единице. Такое значение FT получается для
прямоугольного, гауссова и ряда других импульсов,
которые описываются простыми функциями времени.
Поэтому можно назвать простыми сигналами такие, для
которых произведение FT (или база сигнала) примерно
равно минимальному значению.
В противоположность простым сигналам можно
назвать сложными сигналами такие сигналы, база
которых
В = /Т»1. (6)
Любой сложный сигнал можно представить в виде
суммы простых сигналов. Например, разложив сложный
сигнал в ряд Фурье или Котельникова, можно
представить его с допустимой степенью точности в виде
конечной суммы частотных или временных составляющих.
Сложные сигналы перед простыми обладают рядом
преимуществ, которые реализуются при оптимальных
методах обнаружения сигналов и выделения полезной
информации. Поэтому прежде чем изучать свойства
сложных сигналов, кратко остановимся на оптимальных
методах приема сигналов.
1.2. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
ОПТИМАЛЬНОГО ПРИЕМА СИГНАЛОВ'
Если на входе приемника действует сигнал x(t),
равный сумме полезного сигнала u(t) и помехи n(t) или
только помехе, то оптимальный приемник в случае
сигнала с полностью известными параметрами вычисляет
так называемый корреляционный интеграл, а затем
сравнивает его величину с порогом г0. Если помеха является
'нормальным случайным процессом, спектральная
плотность которого равномерна (белый шум), то
корреляционный интеграл имеет вид
τ
г= [x(t)u(t)dt. (1)
"J
Пределы интегрирования учитывают отрезок времени,
в котором может появиться обнаруживаемый сигнал.
1 Параграф 1 2 написан по материалам книг [2—4. 13—15],
a
§ 11.2
Для определенности этот отрезок выбран [О, Т]. Первый
множитель в (1) есть входной сигнал, а второй
множитель— сигнал, равный обнаруживаемому и формируемый
генератором в приемнике.
Значение корреляционного интеграла (1) находится
с помощью коррелятора или согласованного фильтра.
Основными элементами коррелятора, как следует из
выражения (1), являются переМ'НОЖ'Итель, генератор
сигнала и интегратор. На перемножитель поступают входной
сигнал x(t) и сигнал u(t) от генератора сигнала.
Произведение x(t)u(t) интегрируется с момента прихода (t =
= 0) и до момента окончания обнаруживаемого сигнала
(t=T). Отметим, что коррелятор является устройством
с переменными параметрами, так как режим его работы
зависит от изменения u(t) во времени. Поскольку
операции умножения и интегрирования линейны, то
коррелятор является линейным устройством. Имея в виду, что
он отфильтровывает сигнал от помех и является
линейным устройством с переменными параметрами, его
иногда называют активным фильтром {14] в отличие от
пассивных фильтров, параметры которых постоянны во
времени.
Найдем пассивный фильтр, который в момент
окончания сигнала создает напряжение, пропорциональное г.
Так как ζ (1) имеет размерность энергии, потребуем,
чтобы напряжение на выходе фильтра в момент
окончания сигнала равнялось ζ с точностью до постоянного
не зависящего от формы сигнала множителя, который
учитывает размерность г. Этот множитель может быть
учтен при определении порога и на характеристики
обнаружения не влияет.
Напряжение ν(ί) на выходе фильтра в момент t
можно найти с помощью интеграла Дюамеля
t
v(f)= \x(U)h(t-U)dU, (2)
—00
где h(t) —импульсная характеристика фильтра.
Пусть в момент окончания сигнала (t = T)
напряжение v(t) с точностью до постоянного множителя а
равняется г, т. е.
v(T)=az. (3)
§ 1.2
9
Подставляя в формулу ι('2) t = T и заменяя t\ 'на t,
'получаем
τ
υ(Τ)= С x(t)h(T — t)dt. (4)
—00
Отметим, 'что в интеграле '(4) нижний 'Предел можно
положить равным 0, поскольку сигнал начинается при t =
= 0. Сравнивая выражения (1) и '(4), видим, что
равенство (3) справедливо при следующем условии:
k(T—t)=au(t). (5)
Следовательно, импульсная характеристика искомого
фильтра должна иметь вид
h(t)=au{T—t). (6)
Полученная импульсная характеристика есть
зеркально отображенный сигнал с запаздыванием Т. Фильтр
с такой характеристикой называется согласованным.
Общим между коррелятором и согласованным
фильтром является равенство (с точностью до постоянной)
выходных напряжений в момент времени i = T. Это и
определяет их взаимную эквивалентность с точки зрения
обнаружения сигнала. Различие заключается в
следующем. Коррелятор является устройством с переменными
во времени параметрами, а согласованный фильтр —
устройством с постоянными 'параметрами. Следствием
этого является то, что согласованный фильтр
'инвариантен относительно задержки сигнала w его начальной
фазы (насколько эти величины изменятся в сигнале на
входе фильтра, настолько они изменятся и в сигнале на
выходе), а коррелятор 'не инвариантен.
Выбор между согласованным фильтром и
коррелятором в значительной степени зависит от особенностей
проектируемой системы. В настоящее время вопрос выбора
между этими устройствами окончательно не решен.
Можно только высказать предположение, что при
больших базах (Β;>5· 102) коррелятор предпочтительнее, так
как согласованный фильтр становится очень сложным
устройством.
Если сигнал имеет несколько неизмеряемых или
измеряемых случайных параметров, то структура опти-
10
§ 1.2
мального приемника 'Изменяется, но его основная часть
остается прежней, так как всегда должен быть
согласованный фильтр или коррелятор. Например, при
случайной начальной фазе сигнала в приемнике с
согласованным фильтром за фильтром должен следовать детектор
для выделения огибающей. В приемнике
корреляционного типа должны быть второй (квадратурный) канал и
схема выделения огибающей. Поэтому примем, что в
оптимальном приемнике всегда есть согласованный фильтр
или коррелятор, и в дальнейшем не будем подчеркивать,
известны или неизвестны параметры сигнала.
Преимущества сложных сигналов наиболее просто
объяснить на примере согласованного фильтра, основные
свойства которого и рассмотр-им.
Коэффициент передачи ft (ω) линейного фильтра с
постоянными параметрами и его импульсная
характеристика h(i) связаны преобразованиями Фурье
00
*(0 = i JftHe,l"'rfo), (7)
—00
*(ω)= lh(t)e~Mdt. (8)
—00
Подставляя в (8) определение импульсной
характеристики (6), получаем
ft (ω) = а | и (Т — t) e~'"' at = ае~ыт 1 и (t) еш at. (9)
—«О —00
Из выражения (1.1.2) ' находим
комплексно-сопряженный (*) спектр сигнала
έ(ω)= ]u(t)eMdt. (10)
— 00
Сравнивая (9) и (10), видим, что
Л(а)) = 4(а))е-1вГ. (11)
1 Здесь и в дальнейшем трехзначный номер означает ссылку на
формулу параграфа, номер которого определяется первыми двумя
цифрами-
§ 1.2
11
Формула (11) определяет коэффициент передачи
согласованного фильтра для сигнала, спектр которого равен
ί (ω).
Исключительная роль согласованного фильтра (или
коррелятора) в оптимальном приемнике объясняется тем,
что он максимизирует отношение сигнал/помеха ла
своем выходе. Это отношение при действии на входе
фильтра белого шума со спектральной плотностью Ν0 и
сигнала с энергией Ε >не зависит от формы сигнала и равно
Ч.= /Щ- (12)
При этом максимальное значение сигнала на выходе
фильтра равно аЕ, а среднеквадратическое значение
помехи — а \Z~ENJ2 . Результат (12) является частным
случаем, а более общим представляется случай воздействия
на -вход фильтра помехи с произвольным спектром, к
рассмотрению которого и перейдем.
Напряжение на выходе (отклик) фильтра с
коэффициентом передачи /г(<*>), когда на его входе действует сигнал
со спектром g(a>), равно
00
»(0=-^г ]"*(«»)*(«») *""<*«>■ (13)
— 00
Представим спектр сигнала и коэффициент передачи
фильтра в следующем виде:
£(«)·=!* Η |βΙφ(ω\ (14)
Λ(ϋ))=|Α>(ϋ))|θ,ψ("", (15)
где |β·(ω)| и φ(ω)—амплитудный и фазовый спектры
сигнала; ] к (ш)| и ψ(ω) — амплитудно-частотная и фазо-частот-
ная характеристики фильтра соответственно.
Тогда и момент t = T согласно (13) — (15) отклик
фильтра
00
°Μ=ΊΖ J" |£И|е,,Иш, + ,*(ш,+,шГ |*(ш)|</ш. (16)
—00
12
§ 1Ь2
При действии на входе фильтра помехи со
спектральной плотностью ΑΊ(.ω) мощность шомехи на выходе
фильтра
00
Л,выд= 2^г Г Ν (ω) | As (ω) |2 й?ш. (17)
δ1
Следовательно, отношение сигнал/помеха на выходе
фильтра в момент Τ равно
ν(Τ)
Я = >
К /" π в iii л
if Ιβ·(ω)|β^<ω' 4l*<e»+l,er|ft(»)|d»
V
/ij
W(ω)|ft (ω) ί 4ω
6
(18)
Для нахождения максимального значения q = qo
воспользуемся неравеиством Бугняковского— Шварца
* Г~ь Ъ
\\{x)p{x)dx< у J \f(*)\*d*^\p(x)\*dx, (19)
α α α
в котором равенство имеет место только при
p(x)=>cf(x), (20)
где с = const.
Тогда
00
1_ f L^i! 6!φ (->+ ΐφ(.) +1-г | Л((0) | /JvTWo
,7С J Κ«(ω)
Я =
2π
—00
|/ψ
(со) | ft (со) |2 dco
/00 00
ι С lg(to)la ι Ρ
— 5 ~
W(co)|ft(co)|2dco
^■JiV(»)|ft(»)|»d»
о
§ 11.2
13
/ι Ng(a>)i2
π J ЛЧсо)
Таким образом, максимальное значение отношения
сигнал/помеха
2
:ίίω· (21)
Отметим, что (21) справедливо при выполнении условия
(20) т. е.
\кП\1/7Щ'==:сМШ1е1*{Ш)+тш) + ''шТ- (22)
1 ν " ν ; У N (ш) ν
Левая часть равенства (22) ?гвляется действительной
я не отрицательной функцией частоты, Поэтому (22)
можно записать в виде двух равенств:
для модулей
i*Hi=cJf{ei' (И)
для фаз
ψ (ω) = _ ψ (ω) — <dT. (24)
Объединяя (23) и (24), получаем
Если шум белый, т, е. Μ(ω) =Νο= const, то (25)
совпадаете (11) при замене c/N0 на а, а отношение
сигнал/помеха (21) сводится к выражению (12).
Рассмотрим уравнения для модулей (23) и фаз (24).
Из (23) следует, что модуль коэффициента передачи
согласованного фильтра 'на любой частоте определяется
отношением спектральной плотности сигнала к
спектральной плотности помехи 'на соответствующей частоте.
Чем больше спектральная плотность сигнала, тем
больше модуль коэффициента передачи. С другой стороны,
14
§ 1.2
чем больше спектральная плотность помехи, тем
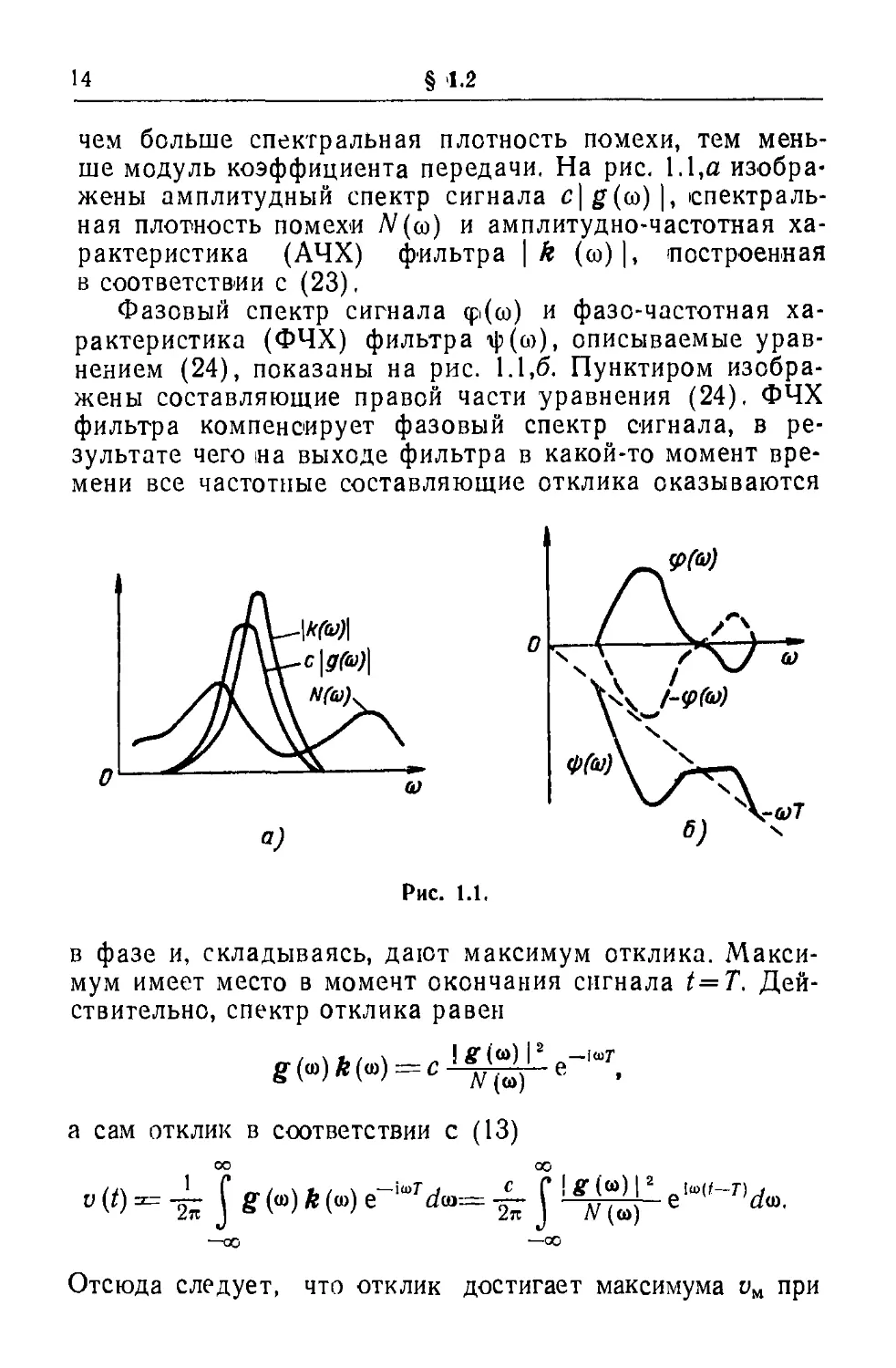
меньше модуль коэффициента передачи, На рис. 1.1,α
изображены амплитудный спектр сигнала c|g(co)|,
спектральная плотность помехи Ν(ω) и амплитудно-частотная
характеристика (АЧХ) фильтра \k (ω)|, построенная
в соответствии с (23),
Фазовый спектр сигнала φι(ω) и фазо-частотная
характеристика (ФЧХ) фильтра ψ (со), описываемые
уравнением (24), показаны на рис. 1.1,6. Пунктиром
изображены составляющие правой части уравнения (24), ФЧХ
фильтра компенсирует фазовый спектр сигнала, в
результате чего на выходе фильтра в какой-то момент
времени все частотные составляющие отклика оказываются
\к(ш)\
с\д(ш)\
_ ?>м
АЛ
ч\ /V
\
Φ(ω\ 4χ-\
\у ч\
ω
°)
Рис. 1.1,
в фазе и, складываясь, дают максимум отклика.
Максимум имеет место в момент окончания сигнала t = T.
Действительно, спектр отклика равен
g(m)k(u) = c
Iff (ω)
,—w
Λ'(ω)
а сам отклик в соответствии с (13)
00 00
ν (0 - i j g (ω) k (») е~шаш^ ±. j
g(to)|'
2π ] Л'(ω)
■00
.Ιω«-Γ)
do),
Отсюда следует, что отклик достигает максимума vH при
§ 1.2
15
ί = Γ и равен
—оо О
Необходимо отметить, что значение vM зависит от формы
сигнала, вида Ν(ω) и величины постоянной с. Если
помеха — белый шум, т. е. Ν(ω) = Ν0, то
00
w„ = w(D = ^-LjlirHI,rf<D==a£ (27)
о
и значение υΜ не зависит от формы сигнала и
определяется только его энергией Ε и величиной коэффициента
a — cjN0. Выясним влияние на абсолютную величину
максимума отклика произвольных постоянных а п с. Для
примера рассмотрим влияние а. Из (27) следует, что а
есть размерная величина. Чтобы определить размерность
а, выразим vM через модуль коэффициента передачи
фильтра. В соответствии с (13) запишем
00
»('0 = iJff(«)ftHelerd«. (28)
—00
Согласно (11)
*(«o) = -i-ft(«o)e-,er. (29)
Подставляя (29) в (28), находим
00
^irif IftHI1^· (30)
—00
Обозначим
αΰ οο
3 = i j |*(»)|'</ω= j А»(О Л. (31)
—00 ~oo
Последнее равенство записано согласно равенству Парсе-
16
§ 1-2
валя. Величина β определяет „энергию", заключенную в
импульсной характеристике фильтра. Из (30), (31)
получаем vu — $[a. Но согласно (27) vu = aE, поэтому
а=Кр, vu = \TjE. (32)
Если (§ = const, то согласно (27), (32) влияние а на νκ
состоит в том, что νκ пропорционально \/Е.
Когда на вход фильтра поступает сигнал, с которым
фильтр не согласован, максимальное значение отклика
всегда будет меньше величины, определяемой формулой
(32), что следует из неравенства Буняковского —
Шварца:
/00 00^
(33)
Равенство в (33) возможно только при согласовании
фильтра с сигналом. Из (33) следует, что из сигналов
с равными энергиями максимальный отклик создает
только тот, который согласован с фильтром. Можно
показать, что при увеличении рассогласований между сиг-
■налом и фильтром максимальное значение отклика
уменьшается по закону, график которого имеет вид
резонансной кривой. Причем, чем больше база сигнала, гем
острее резонансная кривая. Это дает основание
утверждать, что фильтр, согласованный с данным сигналом,
является для него резонатором '.
Отметив основные свойства согласованного фильтра,
рассмотрим более подробно отношение сигнал/помеха
(21), которое определяет помехоустойчивость приемника.
В общем случае оно зависит от свойств сигнала и
помехи. Выясним условия, при которых помеха наиболее
сильно уменьшает отношение (21), а затем покажем
преимущества сложных сигналов перед простыми.
1 Резонансные свойства согласованного фильтра были
доложены автором на XXII Всесоюзной научной сессии, посвященпой Дню
радно, секция общей радиотехнику, Москва, 1966.
§ !·3
17
1.3. ОТНОШЕНИЕ СИГНАЛ/ПОМЕХА
НА ВЫХОДЕ СОГЛАСОВАННОГО
ФИЛЬТРА ПРИ ПРОИЗВОЛЬНОЙ
ПОМЕХЕ
Если спектр помехи нерарномер'ный, то
коэффициент передачи согласованного фильтра определяется
формулой (1.2,25), а отношение сигнал/помеха — формулой
(1.2.21), которую запишем как
gl ^-L? lej;\rd„=±ll*£mdw. (1)
,0 я J JV(b) я J JV((0) v '
—00 О
Представляет интерес решение такой задачи: как
влияют изменения формы спектров в формуле (1) на
отношение сигнал/помеха при условии, что фильтр
всегда согласован с сигналом, Будем считать постоянными
энергию сигнала (1,1.5)
00
E = -±r^\g(»)\*d» (2)
о
и мощность помехи на входе фильтра
00
^^ij^H^· (3)
о
При изменении спектров сигнала и помехи могут быть
два случая. В первом случае задается спектр помехи N(u>),
а спектр сигнала выбирается так, чтобы получить
максимальное значение q20 , которое обозначим <7оМакс · ^° ВТ0Р0М
случае задается спектр сигнала, а спектр помехи
выбирается так, чтобы на выходе фильтра получить
минимальное значение Q0um· ^ обоих случаях с изменением
спектров фильтр перестраивается так, чтобы быть согласованным
в соответствии с формулой (1.2.25).
18
§ 1-3
Изменение спектра сигнала. Поскольку \g(u>)\2>0 и
iV(oi)X), то из формулы (1) получаем неравенство
о
Здесь /VMHH—-наименьшее минимальное значение
спектральной плотности помехи, поскольку в общем случае
минимумов TV (ад) может быть несколько. Чтобы q\ достигло
значения <7q hc ~2£"/УУмнн, необходимо сосредоточить спектр
сигнала в той области частот, где N(<d)—Nmwi или близко
к этому значению, что влечет за собой сужение спектра
сигнала.
Если ширина спектра помехи равна Fn = W„/2n и
мощность помехи (3) конечна, то средняя спектральная
плотность помехи
Л^р = 2лРп/№п. (5)
Для помехи с равномерным спектром всегда
выполняется равенство NMKli = Ncp = N0. Если в этом случае
помеха перекрывает сигнал по спектру (ширина спектра
сигнала F^.Fa), то максимальное значение отношения
сигнал/помеха дг0ткс = 2E[N0.
Для помехи с неравномерным спектром всегда
справедливо неравенство NMmi<Ncr,=N0.
Таким образом, любая неравномерность спектра
помехи дает принципиальную возможность увеличить
отношение сигнал/помеха в случае подстройки спектра
сигнала под помеху.
Изменение спектра помехи. Помеха подстраивается
под сигнал, а фильтр—под сигнал и помеху согласно
(1.2.25). Помеха выбирается так, чтобы получалось
минимальное значение отношения сигнал / помеха, т. е.
2 2
Чо ==^омин· Это вариационная задача на условный экстремум,
решение которой дано в работе [16]. Действительно,
изменяя Ν((ύ), надо минимизировать интеграл (1) при
условии, что мощность помехи (3) Pn = const. Такая
задача относится к изопериметрическим (17]. Для ее реше-
$ 1-3
lit
ния необходимо составить вспомогательный функционал
00
S = -~ {H(u>,N)d<» =
о
о
где λ>0 — множитель Лагранжа (постоянная величина).
Функция N (со), определяющая экстремум
функционала 3, находится из уравнения Эйлера [17]
dH(*.N)_() (7
ON ~~■ к '
Решение уравнения (7)
ЛГН = -^-|вг(со)|. (8)
Поскольку λ постоянная величина, спектральная
плотность помехи должна совпадать по форме с
амплитудным спектром сигнала. Интегрируя обе части
равенства (8) по частоте, получаем
00
1/Ί=.-^ j|g (ω) μω. (9)
о
При этом обязательным условием является
существование интеграла от правой части равенства (8). Отметим,
что для реальных сигналов данное условие всегда
выполняется. Можно показать, что решение (8)
соответствует м'Нннмуму интеграла (1).
Подставляя (8), (9) в (1),'Находим
г °°
L о
Для анализа выражения (10) предположим, что
сигнал и помеха сосредоточены в некоторой области частот
S, ширина которой равна W = 2nF. При этом энергия
сигнала и мощность помехи определяются выражениями
(2), (3), в которых пределы интегрирования определя-
(10)
20 § 1.3
ются областью S. Согласно неравенству Буняковского —
Шварца (1.2.19) из формулы (10) следует, что
2 I I Г j Ι Γι / мал Е^ 2HF /их
s s
Равенство в (11) согласно (1.2.20) выполняется только
при |g(u))|=const. В этом случае УУ(ш)— N0=PJF=const
и максимальное значение qQMIIH = 2£"/УУ0. Таким образом,
если помеха подстраивается под сигнал, то максимум
отношения сигнал/помеха будет тогда, когда спектр
сигнала является равномерным.
Выразим q0 через отношение мощностей сигнала и
помехи. 'Поскольку средняя мощность сигнала на входе
фильтра Pc = EjT, то максимальное значение ^„ш^
= 2FT\(PC/P11). Отсюда следует, что отношение
сигнал/помеха на выходе фильтра возрастает по сравнению с
отношением сигнал/помеха на его входе (Рс/Рц) в 2Ffpa3.
Таким образом, сложные сигналы, у которых база (В =
= FT) больше базы простых сигналов, позволяют
получить большие значения отношения сигнал/помеха, В этом
проявляется одно из преимуществ сложных сигналов
перед простыми.
Помеха в виде суммы белого шума и узкополосных
помех. Сказанное ранее относилось к случаям, когда
либо сигнал подстраивался под помеху, либо помеха —
под сигнал. На практике представляет интерес оценка
отношения сигнал/помеха для случая, когда помеха
равна сумме белого шума со спектральной плотностью N0
и узкополосных помех. Будем считать, что спектры
узкополосных помех не перекрывают друг друга. Пусть k-я
узкополосная помеха сосредоточена в полосе частот
Wh=<2nFh, а ее спектральная плотность постоянна в этой
полосе частот и равна Nk, Обозначим область частот, где
действует белый шум и k-я узкополосная помеха, через
Sft, а где только белый шум — через S0.
При таких предположениях из формулы (1)
получаем
S„ k S^
§ 1.3
21
Здесь суммирование производится по всем k.
Преобразуем выражение (12) к виду
«o=^iiffwr^+^SilffW|Mu)-
-Σ(^~·^^)ίι?(ω)|Μω· (13)
k Sh
Отметим, что в (13) сумма первых двух слагаемых равна
2E/N0. Обозначая
получаем
Допустим, что yVft>yV0. Тогда
Из выражения (16) следует, что отношение
сигнал/помеха зависит от отношения части энергии сигнала,
приходящейся на все частотные участки, где действуют
узкополосные помехи, к полной энергии сигнала.
Обозначая суммарную энергию всех узкополосных помех
через
£„ = £zfk, (17)
к
выражение (16) запишем в следующем виде:
«ί-τξ-('-■£■)· (18)
Таким образом, чем больше энергия сигнала Ε по
сравнению с суммарной энергией помех £п, тем больше
отношение сигнал/помеха.
22
§ 1.3
Оценим влияние на величину q0 множителя Nkl(Nh +
+ N0) в формуле (15). Пусть спектральные плотности
всех узкополосных помех одинаковы и равны Nho.
Полагая Nk0>N0, из (15) приближенно получаем, что
?0~ N» [1 Ε + NXtH J ^>
Третье слагаемое в (19), отсутствующее в (18),
обусловлено учетом множителя Nk/(Nk + No) в формуле (15).
Чем больше отношение Ν^ο/Νο, тем меньше влияние
этого слагаемого и, следовательно, множителя Nh/(Nh + N0)
в (15). Это объясняется тем, что с ростом Nh0IN0
коэффициент передачи фильтра на тех частотах, где есть
узкополосная помеха в (N0 + Nho) INo~Nho/No раз
меньше по сравнению с коэффициентом передачи .на тех
частотах, где помех нет. Чем больше Nh0/No, тем меньше
влияние тех частотных участков, где есть узкополосные
помехи. К такому оптимальному методу приема будет
близок неоптимальный, который сейчас и рассмотрим.
Неоптимальный прием. Допустим, что фильтр
согласован с сигналом, принимаемым па фоне белого шума,
а узкополосные помехи вырезаются полностью режек-
торными фильтрами. Максимум отклика фильтра
согласно (1.2.27) определяется как
υΗ-=α-±- Γ \g(w)\*dm. (20)
So
Мощность шума на выходе фильтра в соответствии
с (1.2.17) записывается в виде
^пгыХ = -^-||ё>)|^ш. (21)
So
Отношение сигнал/помеха на выходе фильтра
' = 7^=iHl*<->l,*B· (22)
So
Проведя те же преобразования, что и при получении фор-
§ 1.3
23
мулы (13), находим
2
«2 = ЛГ
или
^-jlffHl'^-^JlffHI
«2=Щ1-%^\ (23)
2Я / , yi /
ft
Сравнивая (15) и (23), замечаем, что разница
между ними определяется множителем Nh/(Nh + N0) в
формуле (15). С ростом отношения Nh/N0 эта разница
уменьшается.
Теперь допустим, что фильтр согласован с сигналом
в предположении, что помехой является белый шум,
а в действительности помеха обладает неравномерным
спектром Ν(ω). В соответствии с формулами (1.2.17),
(1.2.27) отношение сигнал/помеха определяется как
V о
1 N(m)dm ■ (24)
Допустим, что спектр сигнала является постоянным
в полосе частот W=2nF. Спектральная плотность
сигнала согласно (2) записывается в следующем виде:
G'l -r ъЕ/W - ΕβΓ. (25)
Подставляя (25) в (24) и учитывая (3), находим
q2=2EF/Pa. (26)
Если Ε и Ри постоянные величины, то отношение
сигнал/помеха увеличирается с ростом F независимо от
вида помехи. Для помехи с постоянным спектром Ν0 в
полосе сигнала мощность Pa=N0F. Тогда (26)
превращается в известное выражение q2='2E/N0.
Отношение сигнал/помеха (24) примет наименьшее
значение q тогда, когда интеграл примет максимальное
24
§ '·3
значение. Из неравенства Буняковского—Шварца (1.2.19)
имеем
оо
ij|g»l2yvH<b<
Г 00 ОО
<il/ flsHI4*»]^»*»- (27)
γ о ο
Равенство выполняется при условии
|g»|2 = WV(a)). (28)
Условие (28) означает, что спектральная плотность
наиболее мешающей помехи совпадает по форме с
энергетическим спектром сигнала. Интегрируя обе части
равенства (28), получаем
оо оо
о о
или
Ь = Е/2Ра. (29)
Подставляя (28), (29) в (24), запишем
Если допустить, что спектр сигнала является
равномерным в полосе частот F, то формула (30) сведется,
к (25), а так как в этом случае согласно (28) помеха
имеет тоже равномерный спектр, то дмии = 2E/N0.
Оценим, к каким потерям в отношении сигнал/помеха
приводит неравномерность спектра сигнала.
Предположим, что спектр сигнала сосредоточен в полосе частот от
О до W=2jtf, а энергетический спектр сигнала имеет вид
|g»|a = G;;-f xacos(2*/a)/U/). (31)
Здесь / — целое число, a κ2 — характеристик неравномер-
§ 1-4
25
ности спектра сигнала. Значение' G0 определяется из
формулы (2) и совпадает со значением (25). Очевидно, что
x2<Gg. Подставляя (31) в (30), получаем
2 2EF /, | т.* у ,ооч
W=-7sr(l+lorJ · (32)
Второй множитель в формуле (32) определяет потери
<7ЧИН, обусловленные неравномерностью спектра сигнала.
Если κ2= G0 (наихудший случай), то потери отношения
сигнал/помеха составят 1,78 дб. Отметим, что величина
потерь iHe зависит от формы спектра сигнала, так как
в формулу (32) .не входит величина /, определяющая
характер изменения спектра (31). Это связано с принятой
аппроксимацией спектра сигнала (31).
Необходимо отметить, что, если сигнал или помеха
в согласованном фильтре 'подстраиваются друг под
друга, то наиболее часто встречающимся на практике
является случай, когда сигнал и помеха обладают
равномерными спектрами в одной и той же полосе частот.
Именно такой случай и рассматривается в дальнейшем.
1.4. ВЫИГРЫШ В ПОМЕХОУСТОЙЧИВОСТИ
ПРИ ИСПОЛЬЗОВАНИИ СЛОЖНЫХ
СИГНАЛОВ
Шумовая помеха. Если на входе фильтра, согласо;
ваиного со сложным сигналом (/Т»1), действует
помеха с конечной мощностью, то при определенных
условиях отношение сигнал/помеха на выходе фильтра может
быть увеличено по сравнению с отношением
сигнал/помеха «а его входе.
Если мощность помехи ла входе фильтра равна Рп>
а ее спектр равномерно распределен в полосе частот
сигнала F, то спектральная плотность помехи записывается
как
Na=PJF. (1)
Средняя мощность сигнала, имеющего длительность Г
26
§1.4
и энергию Ε на входе фильтра равна
Рс = Е/Т. (2)
Отношение· сигнал/помеха по мощности на выходе
фильтра согласно формуле (1.2.12) определяется как
<7о =ΐνΓ- (3)
поскольку спектральная плотность помехи в пределах
полосы частот, занимаемой сигналом, равномерна.
Величина q задается исходя из условий обнаружения
сигнала. Если в (3) заменить Nu и Ε согласно (1) и (2), то
получим,что
£=Ъ,2РГ. (4)
* Π
Из формулы (4) следует, что увеличение (выигрыш)
отношения сигнал/помеха на "выходе фильтра по
сравнению с отношением на его входе составляет [18]
Например, если по условию дй должно быть равно 20,
то при 2/Т = 200 отношение сигнал/помеха по мощности
на входе фильтра может быть равно Рс/Рц = 0,\, т. е.
сигнал на входе приемника может быть скрыт помехой
и в то же время с помощью согласованного фильтра
надежно обнаруживаться. Чем больше база сложного
сигнала, тем меньшее отношение сигнал/помеха на входе
фильтра можно допустить при заданной надежности
обнаружения.
База сигнала растет, если увеличивается или
длительность сигнала, или ширина его спектра. С
увеличением Τ при заданной энергии Ε средняя мощность
сигнала Рс уменьшается, а помеха остается неизменной.
Поэтому отношение Рс/Рц на входе уменьшается и
обнаружение сигнала без знания его формы становится
затруднительным, т. е. повышается скрытность передачи
сигнала. Когда Т = const, a F растет, то ширина спектра
помехи Fn тоже растет, так как F=Fn.
§ 1-4
27
Рост Fn при Ра-= const приводит к уменьшению
спектральной плотности помехи ΝΏ и, следовательно, к
увеличению qQ (3). Если q'Q задано, то при больших Fn можно
допустить меньшее значение PJPa.
Таким образом, характер роста ρ (5) оказывается
различным при увеличении Τ и F. В тех случаях, когда
повысить энергию 'сигнала невозможно, q2a (3) можно
увеличить путем повышения F, так как при этом
уменьшается Nu (1).
Кроме сосредоточенных помех (ширина спектра F„
равна ширине спектра сигнала F) на согласованный
фильтр могут действовать и другие помехи:
узкополосные, импульсные м т. д. Рассматривая эти помехи,
следует учитывать действие собственного шума приемника.
Последний нельзя отнести к помехам с конечной
мощностью, так как его спектральная плотность Nm
постоянна, а ширина спектра практически бесконечна.
Сумма помехи и собственного шума приемника
[19]. Сначала учтем шумовые помехи, ширина спектра
которых
Fn<F, (6)
т. е, как узкополооные (F„<g.F), так и сосредоточенные
помехи (FU^>F), Предположим, что сигнал обладает
равномерным амплитудным спектром в полосе частот F.
Спектральную плотность сигнала обозначим через G0.
Тогда максимальное значение сигнала на выходе
фильтра согласно формуле (1.2.27) запишется
OHr=aE = 2aGlF, (7)
поскольку E — 2G\F (1.3.25). Мощность ji спектральная
плотность помехи на входе фильтра связаны соотношением
Pn = NnFn, (8)
а мощность шума, попадающего в полосу пропускания
согласованного фильтра, определяется как
pa = NuSF.
(9)
28
§ 1.4
Суммарная мощность помехи и шума на входе
согласованного фильтра согласно (8), (9)
Pnm = M„Fi1 + NmF. (10)
Как следует из формулы (,1.2.11), модуль
коэффициента передачи согласованного фильтра в полосе спектра
сигнала равен aGQ. Поэтому суммарная мощность
помехи и шума на выходе фильтра может быть представлена
следующим выражением:
P,mrb^ = a2Gl(NaFn-^NmF). (11)
В соответствии с (7), (11) отношение сигнал/помеха
на выходе фильтра
"I 40л F2
q — Р„*вих~ NnFn + NUiF (ΙΔ>
Поскольку E-=2G\ F, to согласно (2) и (8)
Pr 2FT Pc 2FT
f — pi l+NmF/N„F„ ~PV \+N„F/Pn ' (13)
Формула (13) позволяет сделать следующие выводы.
Во-первых, если \Nm = 0 (т. е. собственные шумы
приемника не учитываются), то q2 зависит ме от ширины
спектра помехи, а лишь от ее мощности. Это значит, что
в рассматриваемом случае ее имеет значения, является
ли помеха узкополосной (Fa<g.F) или сосредоточенной
(Fa^F). Во-вторых, при ЫшФО с увеличением F рост q*
замедляется, Предельное значение
v=ilVa=^r· (14)
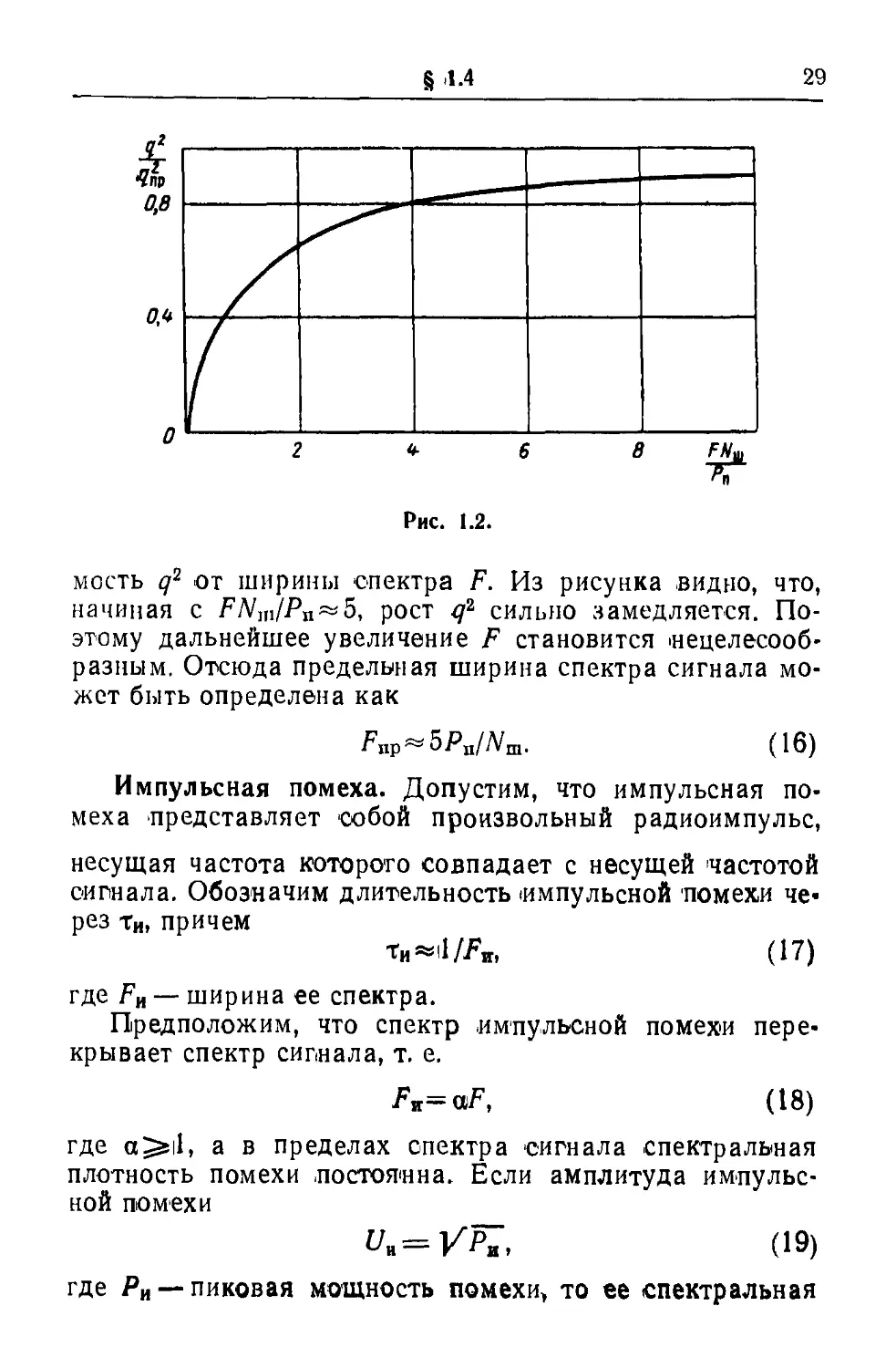
На рис. 1.2. изображена зависимость
<?2 _ Nu,F/Pn
4 > +адя.
(15)
полученная при делении (13) «а (14). В качестве
аргумента взята величина FNoJP. При Nm=iconst и Pn=iconst
отношение (15} характеризует относительную зав и си-
§,1.4
29
Рис. 1.2.
мость q2 от ширины спектра F. Из рисунка видно, что,
начиная с FyVm/Pn~5, рост q2 сильно замедляется.
Поэтому дальнейшее увеличение F становится
'нецелесообразным. Отсюда предельная ширина спектра сигнала
может быть определена как
пр-
<5ΡΏ/Να
(16)
Импульсная помеха. Допустим, что импульсная
помеха представляет собой произвольный радиоимпульс,
несущая частота которого совпадает с несущей частотой
сигнала. Обозначим длительность импульсной помехи
через ти, причем
Ти^и/Чг, (17)
где F„ — ширина ее спектра.
Предположим, что спектр импульсной помехи
перекрывает спектр сипнала, т. е.
Лг= oiF,
(18)
где α^ιΐ, а в пределах спектра сигнала спектральная
плотность помехи лостоя'нна. Если амплитуда
импульсной помехи
U*=VP~, (19)
где Р„ — пиковая мощность помехи, то ее спектральная
30
§ il.4
плотность может быть определена как
£„И = Он = OtyJT^ = 0,5^ 7УЛ,. (20)
При действии импульсной помехи напряжение на
выходе согласованного фильтра определяется в
соответствии с формулой (1.1.3) как
оо
—ОС
оо
ЪГ J ?W« '*»■ (21)
—00
Второй интеграл в (21) получен из первого с учетом
(20) и определения согласованного фильтра (1.2.11). Он
описывает импульсную характеристику фильтра h(t),
т. е. зеркально отображенный сигнал. Поэтому
vir(t)=aG„u(T—t). (22)
Если максимальное значение сигнала
ин = К/К (23)
где К — отношение максимального значения сигнала
к его среднеквадратичному, то на выходе согласованного
фильтра максимальное значение напряжения,
обусловленного импульсной помехой, равно
νηΜ = αΟηκνΚ (24)
Отношение сигнал/помеха на выходе согласованного
фильтра равно квадрату отношения максимума отклика
к максимальному значению помехи на выходе и в
рассматриваемом случае согласно (7), (24) может быть
записано в виде
Заменяя Е, FK, (?и определяющими их выражениями (2),
§ 1.4
31
(18), (20) соответственно, получаем
Величина а/К обычно близка к единице, поэтому
^„-■ft-W- (26)
Согласно (26) можно записать, что
?»=-iwr=(2FTr> с27)
т. е. выигрыш в помехоустойчивости при действии
импульсной 'помехи в 2FT раз больше, чем при действии
шумовой помехи (5).
Сравнение действия пом«х. Определим различие
в фильтрации шумовой и импульсной помех. Сначала
рассмотрим прохождение полезного сигнала через
согласованный фильтр. Разлагая сигнал длительностью Τ и
с шириной спектра F в ряд Фурье, представим его в
виде гармоник, число которых 2FT. Поскольку все
гармоники обладают одинаковой мощностью (по
предположению Go = const), то мощность /-Й гармоники на выходе
фильтра
Pcj = P</2FT. (28)
Проходя фильтр, каждая гармоника усиливается в aG0
раз и увеличивает свою мощность в a"G^ раз. Напомним,
что согласованный фильтр устраняет все фазовые
сдвиги между гармониками. Поэтому на выходе фильтра
гармоники складываются по амплитуде
vl = Р^аЮ] (2FT)> =- Pc2FTa> G" . (29)
С другой стороны, мощность /-й гармоники
сосредоточенной шумовой помехи на входе фильтра
Pni=Pa/2FT.
(30)
32
§ 1.4
Поскольку фильтр не компенсирует фазовые сдвиги
между гармониками помехи и их начальные фазы
случайны, то на выходе фильтра гармоники помехи
суммируются по мощности. Следовательно, мощность помехи
на выходе фильтра
Ра вы* = Р^аЮ20 2FT = РааЮ20. (31)
Здесь a?G\ — коэффициент усиления фильтра по
мощности.
Разделив (29) на (31), получим формулу (4).
Отметим, что формула (4) остается справедливой и для
узкополосной помехи, 'поскольку число гармоник в
окончательный результат (30) не входит.
При разложении в ряд Фурье импульсной помехи
следует иметь в виду, что все ее гармоники в какой-то
момент времени совпадают по фазе. В этот момент
импульсная помеха достигает максимума, т. е. создается
импульс. При образовании импульса все гармоники
суммируются по амплитуде. Поэтому мощность /-й
гармоники импульсной помехи равна
P„3- = /y(2F7V. (32)
Проходя через фильтр, гармоники импульсной
помехи получают дополнительные фазовые сдвиги,
вследствие чего на выходе фильтра они суммируются по
мощности. Мощность импульсной помехи на выходе фильтра
Л, ям = Ρ,Ρ'Οΐ 2FT = РиаЮ20 /2FT. (33)
Разделив (29) на (33), получим формулу (27).
Таким образом, на выходе согласованного фильтра
мощность сигнала возрастает в a'Gg 2FT раз, шумовой помехи
— в аЮ20, а импульсной — в a2G20/2FT раз. Это означает,
что согласованный фильтр позволяет получить больший
выигрыш υ случае действия на его входе импульсной
помехи, чем в случае шумовой помехи.
Возможность увеличить помехоустойчивость при
использовании сложных сигналов в условиях действия по-
§ l.S
33
мех с конечной мощностью обусловила широкое
применение сложных сигналов как в радиолокационных
системах, так и в системах передачи информации.
Однако следует отметить, что при решении каждой
конкретной задачи необходимо предварительно сделать
тщательный анализ характера помех, чтобы быть
уверенным, что применение сложных сигналов
действительно дает отмеченный ра-нее выигрыш в отношении
сигнал/помеха. Например, если помеха является
заградительной, т. е. она занимает гораздо большую полосу
частот, чем сигнал, то использование сложных сигналов
выигрыша не дает, так как помеха в полосе сигнала
обладает постоянной спектральной плотностью.
1.5. СЖАТИЕ СЛОЖНЫХ СИГНАЛОВ
Сложные сигналы и их спектры, как было отмечено
ранее, описываются сложными функциями времени и
частоты соответственно. При обработке сигналов эти
функции упрощаются. Например, в § 1.2 показано, что
согласованный фильтр компенсирует фазовый спектр сигнала.
Следовательно, отклик согласованного фильтра может
быть описан более простой функцией. При обработке
сложных сигналов имеет место сжатие сигналов.
Возможно сжатие во времени, осуществляемое линейным
четырехполюсником с постоянными параметрами
(согласованный фильтр) и по частоте, осуществляемое
линейным устройством с переменными параметрами
(коррелятор). Сначала рассмотрим сжатие во времени.
Найдем, как зависят минимальная и максимальная
длительности сигнала от его амплитудного и фазового
спектров.
Минимальная длительность сигнала. «Эффективная»
длительность сигнала определяется как
ос
^зфф^-Е- JC-'cpWOd'· (1)
—оо
Формула (1) описывает момент инерции функции
u2(t)/E относительно центра тяжести, координата
которого
3—2366
34
§ 1.5
tcp=± j" tu*(t)dt. (2)
—oo
За начало отсчета по оси времени выберем точку /Ср=0.
Тогда выражение (1) примет вид
во
71фф=х J ^В,(0Л· (3)
—со
Запишем формулу (3) через спектр и производные
спектра функции u(t). Спектр сигнала определяется
формулой (1.1.2). Дифференцируя эту формулу по ω,
получаем
со
g'(m) = — Г itu{t)&~imidt. (4)
—со
Применяя к выражению (4) обратное преобразование
Фурье, находим, что
со
-itu(t) = ± f g'(<o)eMd<o. (5)
—со
Согласно равенству Парсеваля
со со
р'и'(/)Л=^вг|»|»Л>. (6)
—со —со
Следовательно,
со
C-ssrJ If'МИ л». (7)
—со
Покажем, при каких условиях Τ принимает
минимальное значение [20]. Запишем спектр сигнала в
следующем виде:
ίΗ=ΙίΗΙβ,,(")=α(ω)β"(·). (8)
Дифференцируя (8), получаем
δ·'((Β)=[α'(α))4-ίφΉ«Μ]ε'φ(<0)· (9)
§ 1.5
35
Поскольку α (ω) и ψ (ω) являются действительными
функциями частоты, квадрат модуля выражения (9) можно
записать как
|g>)|2=[a>)]2+l?>)«Hla- (Ю)
Тогда формула (7) принимает вид
—оо —оо
Подынтегральные выражения обоих интегралов
являются неотрицательными функциями. Следовательно, для
уменьшения Т2 необходимо, чтобы они стремились к 0.
Рассмотрим снач'ала второй интеграл. Он равен нулю,
если или α(ω)=0, или φ'(ω) =0, т. е. φ(ω) =const. Таким
образом, условие, прм котором второй интеграл
обращается в нуль, 'принимает следующий вид:
φ'(ω) = 0 на тех частотах, где α((»)=έΟ,
φ'(ω) ^ 0 на тех частотах, где α(ω) = 0.
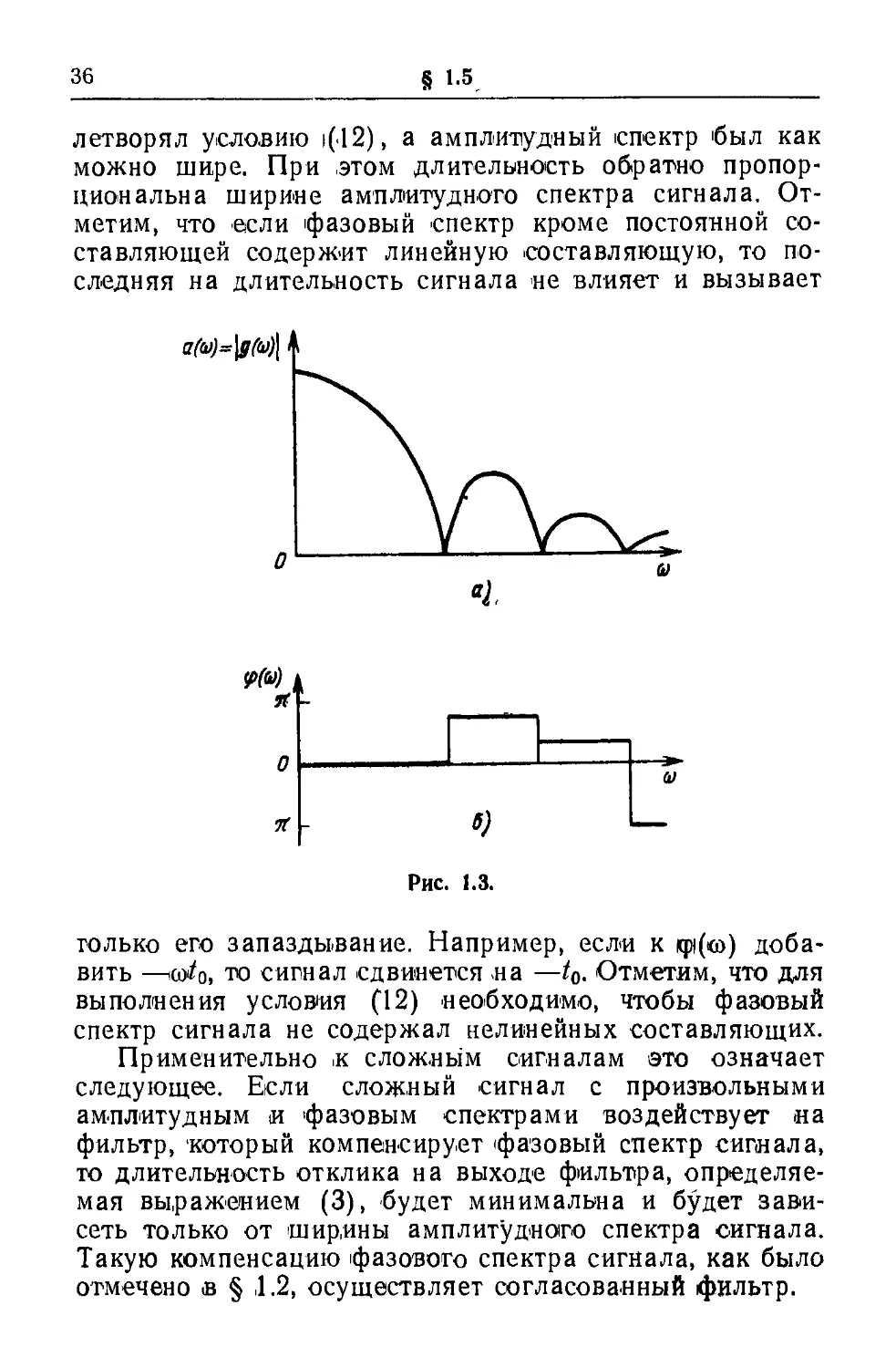
Амплитудный и фазовый спектры, удовлетворяющие
условию (12), изображены на рис. 1.3.
Первый интеграл в (11) равен нулю, если α'(ω)=0,
т. е. αι(ω) = const для всех частот от —оо до +оо. Это
совпадает с известным фактом, что чем шире
амплитудный спектр импульса, тем короче сам импульс. Можно
показать [20], что, если спектр сигнала сосредоточен
в полосе частот W=2nF, то при £ = constyT" достигает
минимального значения, если1
α(ω)= αοcos (πω/2№) при |ω|^№,
где а0=const. При этом
7эфф = я/2№=1/4^. (13)
Следовательно, для получения минимальной
длительности сигнала необходимо, чтобы его фазовый спектр удов-
1 Здесь и в дальнейшем запись }(х)ф0 при а^х^Ь означает
что f(x) eQ при х<а и х>Ь.
(12)
36
§ 1.5.
летворял условию ι(·12), а амплитудный спектр был как
можно шире. При этом длительность обратно
пропорциональна ширине амплитудного спектра сигнала.
Отметим, что если фазовый спектр кроме постоянной
составляющей содержит линейную составляющую, то
последняя на длительность сигнала не влияет и вызывает
а(ш)=\д(ш)\ А
φ(ω) ι
0
Я
I
в)
Рис.
1.3.
,
•
L
только его запаздывание. Например, если к κρι(ιω)
добавить —ωίο, то сигнал сдвинется на —10. Отметим, что для
выполнения условия (12) необходимо, чтобы фазовый
спектр сигнала не содержал нелинейных составляющих.
Применительно ικ сложным сигналам это означает
следующее. Если сложный сигнал с произвольными
амплитудным и фазовым спектрами воздействует на
фильтр, который компенсирует фазовый спектр сигнала,
то длительность отклика на выходе фильтра,
определяемая выражением (3), будет минимальна и будет
зависеть только от ширины амплитудного спектра сигнала.
Такую компенсацию фазового спектра сигнала, как было
отмечено в § ,1.2, осуществляет согласованный фильтр.
ς 1.5
37
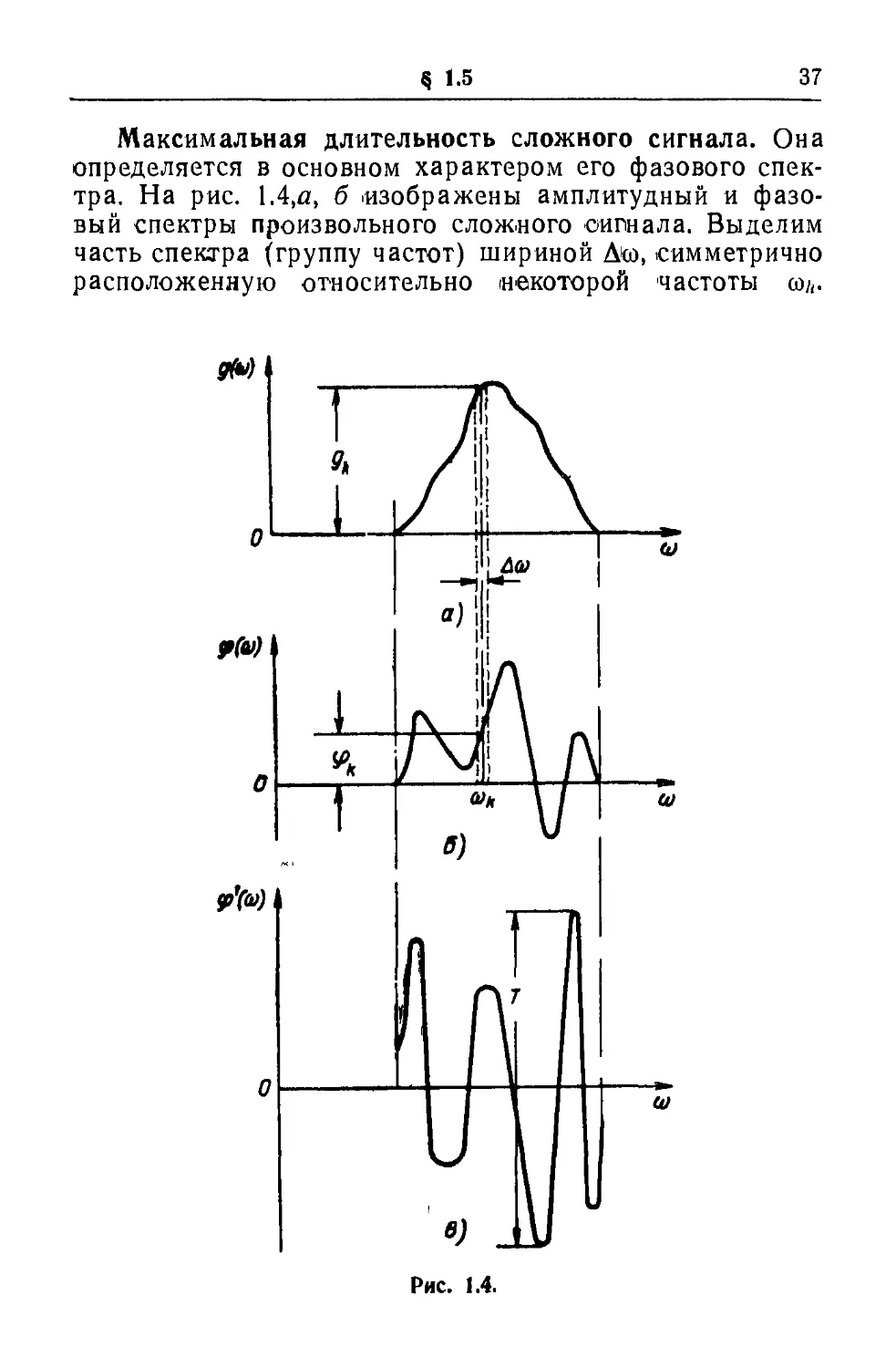
Максимальная длительность сложного сигнала. Она
определяется в основном характером его фазового
спектра. На рис. \Л,а, б изображены амплитудный и
фазовый спектры произвольного сложного сигнала. Выделим
часть спектра (группу частот) шириной Δίο, симметрично
расположенную относительно некоторой частоты ω;,.
38
§ 1-5
В пределах группы частот можно положить амплитудный
спектр постоянным и равным |g(<o)|=gfc, а фазовый
представить в виде суммы φ&+(ω—®h)th, где
k=?»L=.· (14)
Тогда в пределах области частот Δω спектр сигнала
запишется как
gk И => gk exp [i φΛ + i (ω — <ok) tk] при ωΛ—Δω/2 < ω <
< <oft-f Δω/2. (15)
Составляющие группы частот образуют часть сигнала,
которую можно найти с помощью обратного
преобразования Фурье
, оо оо
"*(0 = "ST J 2* W*™ά» = Re 4" J**И e"°' d" =
—оо О
ш +Дш/2
= Re&- f e"^"—^'^""ί/ω. (16)
со — Δω/2
Вычисляя интеграл (16), получаем
/^ gkb<o sin [Δω(/ 4-ik)/2] . , . . ,._,
М0 = ^ Δω(/+Χ)/2 «*Κ'+τ>)· (17)
Максимальное значение огибающей функции (17) во
времени запаздывает «а —tk относительно /=0. Если
выделить группы частот с различными значениями ίχ, то
соответствующие им части сигнала во времени будут
сдвинуты друг относительно друга и их максимальные
значения не совпадут. Можно считать, что сдвиг между
соответствующими частями сигнала достаточен для
различения их, если максимум последующей приходится на
первый нуль предыдущей, т. е., если
tk+\— ift>'2n/Ab=l/AF. (18)
§ 1.6 39
В общем случае групповое время запаздывания согласно
(14), (17) определяется первой производной фазового
спектра сигнала, т. е.
Т(<й)=— φ'(ω). (19)
Первая производная фазового спектра сигнала
изображена на рис. 1.4,в. Экстремальные значения φ'(ω)
определяют границы, внутри которых сосредоточен
сигнал. Поэтому можно считать, что приближенно
длительность сигнала
Τ »| Τ («We - Τ (ш)мин | = \ψ' (ш)макс-<р'Нмин |. (20)
Таким образом, чем сильнее изменяется фазовый
спектр (больше разность между экстремальными
значениями его производной), тем больше длительность
сигнала.
Сжатие во времени. Длительность сложного сигнала,
как было отмечено ранее, зависит от скорости
изменения фазового спектра. Следовательно, выбором
последнего можно достичь больших значений длительности
сигнала. Пропуская сложный сигнал через
согласованный фильтр, который компенсирует фазовый спектр
сигнала, получаем на его выходе отклик, длительность
которого определяется энергетическим спектром сигнала
|g(cu)|2. Чем шире амплитудный спектр сигнала, тем
шире его энергетический спектр и короче отклик.
Напомним, что энергетический спектр сигнала является
амплитудным спектром отклика. Следовательно,
длительность отклика на выходе фильтра может быть
получена значительно меньше, чем длительность сигнала на
его входе. Таким образом, происходит сжатие сложного
сигнала во времени. Отметим, что возможность сжатия
сигнала основывается на независимом выборе фазового
и амплитудного спектров сигнала.
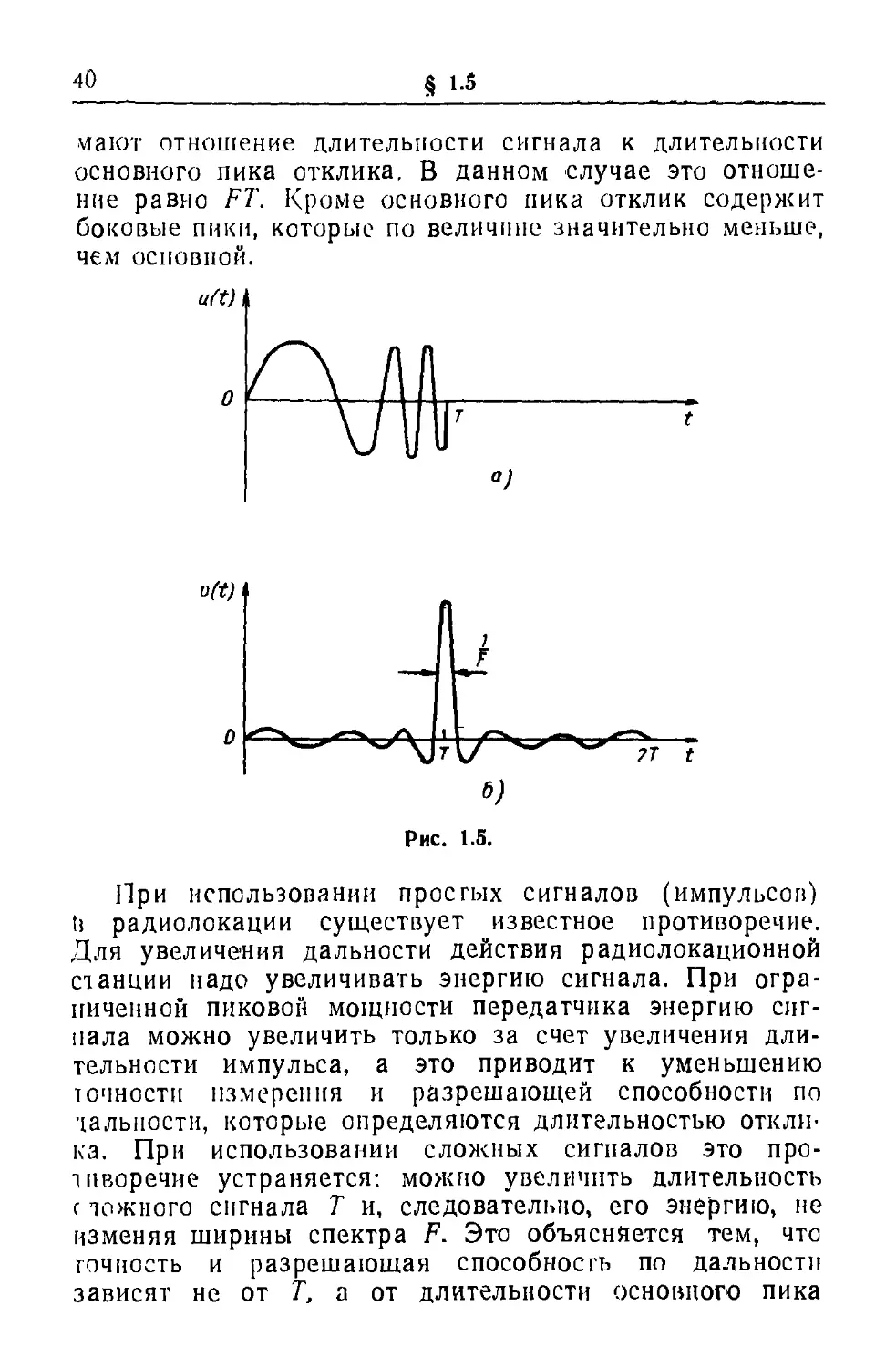
На рис. 1.5,а изображен сложный сигнал u(t)
длительностью Т, а на рис. 1.5,6 — отклик v(t)
согласованного фильтра на этот сигнал.
Полная длительность отклика равна 27".
Длительность центрального импульса, который называется
основным пиком, определяется шириной спектра
сигнала. Чем шире спектр, тем короче основной пик.
Отметим, что под сжатием сигнала во времени пони-
40
§ 1.5
мают отношение длительности сигнала к длительности
основного пика отклика. В данном случае это
отношение равно FT. Кроме основного пика отклик содержит
боковые пики, которые по величине значительно меньше,
чем основной.
и ft) к
vft)
Рис. 1.5.
При использовании простых сигналов (импульсов)
ti радиолокации существует известное противоречие.
Для увеличения дальности действия радиолокационной
станции надо увеличивать энергию сигнала. При
ограниченной пиковой мощности передатчика энергию
сигнала можно увеличить только за счет увеличения
длительности импульса, а это приводит к уменьшению
точности измерения и разрешающей способности по
чальности, которые определяются длительностью
отклика. При использовании сложных сигналов это
противоречие устраняется: можно увеличить длительность
с 10жного сигнала Τ и, следовательно, его энергию, не
изменяя ширины спектра F. Это объясняется тем, что
точность и разрешающая способность по дальности
зависят не от Т, а от длительности основного пика
§ 1.5
41
отклика, которая равна \/F. Поэтому, увеличивая Т,
можно увеличивать энергию сигнала. При этом
максимальная длительность сигнала огра'ничивается
допустимой мощностью передатчика. Для повышения точности
измерения и разрешающей способности по дальности
можно увеличивать F. Отметим, что все сказанное
будет справедливо только при условии, что боковые
пики отклика много меньше основного. В противном
случае возникает неоднозначность отсчета.
В настоящее время благодаря возможности сжатия,
во времени сложные сигналы широко применяются не
только в радиолокации, ио и в различных системах
передачи информации1.
Сжатие по частоте. Сжатие сигналов по частоте
рассмотрим исходя из свойства двойственности частотно-
временных представлений. Известно, что любой сигнал
можно описать временными функциями, вида
'u(t) = U(t) cos В(t) при 0<i<J. (21)
Здесь U(t)—огибающая, θ(/)—фаза сигнала.
Сложность сигнала определяется в основном характером
изменения его фазы. Чем сильнее изменяется фаза
сигнала, тем шире его спектр. Ширина спектра будет
минимальной в том случае, если фаза сигнала удовлетворяет
условиям (12), записанным для функции времени.
Чтобы сжать сигнал по частоте, надо скомпенсировать
фазу сигнала Q(t). После компенсации фазы ширина
спектра определяется только характером изменения
огибающей. Так, сигнал длительностью Τ после сжатия
по частоте имеет ширину спектра, примерно
равную 1/7".
Отметим, что сжатие во времени осуществляется
согласованным пассивным фильтром с постоянными во
времени параметрами, а сжатие по частоте —
коррелятором (активным фильтром с переменными во времени
параметрами). Необходимость изменения во времени
параметров фильтра вызывается тем, что компенсации
подлежит функция, изменяющаяся во времени (21).
1 В Советском Союзе впервые принципы сжатия сигналов были
разработаны под руководством Я. Д. Ширмана [2]. Обзор ранних
зарубежных работ по этому вопросу можно найти в статье [18].
глава 2 КОРРЕЛЯЦИОННАЯ
ФУНКЦИЯ И ТЕЛО
НЕОПРЕДЕЛЕННОСТИ
2.1. КОРРЕЛЯЦИОННЫЕ СВОЙСТВА
СИГНАЛОВ
Для описания свойств сигналов недостаточно знать
только их временные и частотные характеристики,
необходимо знать еще корреляционные характеристики.
Смысл последних можно пояснить, рассмотрев отклик
фильтра.
Пусть фильтр согласован с сигналом ui(t), т. е.
импульсная характеристика фильтра
hi(t)=au,(T—t), (1)
а на вход фильтра воздействует сигнал um(t). Отклик
фильтра в произвольный момент времени to находится
с помощью интеграла Дюамеля
к
tw(O)= [um(t)hi(t0 — t)dt =
—оо
к
= а <jum(t)ui(t — t0 + T)dt. (2)
—оо
Сигнал ui(t—to + T) оканчивается в момент времени
t—U, поэтому при t>to подынтегральное выражение
Um(t) Щ (t—ίο + Τ1)—О И верхний предел интеграла to
можно заменить на оо. Обозначая
x=to—T, (3)
записываем выражение (2) в следующем виде:
Omi(* + T) = a'tam(t)Ui(t — t)ctt. (4)
— оо
Величину Т, поскольку она является постоянной, можно
§ 2.1
43
опустить. Тогда
vnl{t) = a j um(t)ui(t — i)dt. (5)
—oo
Первый множитель под знаком интеграла (5)
является входным сигналом, а второй — импульсной
характеристикой фильтра. Отметим, что пределы
интегрирования в общем случае определяются областью
существования произведения um(t)u.i(t—τ). Если сигналы
имеют ограниченную длительность, то с изменением
т изменяются и пределы интегрирования. Это должно
учитываться при рассмотрении конкретных сигналов.
Пользуясь неравенством Буняковского — Шварца
(1.2.19), получаем, что
/оо оо
\ujt)dt §u](t)dt =a\>'EmEi. (6)
—оо —оо
Нормированный отклик фильтра, определяемый как
оо
rml(-t)=^^w=—^=[un(f)ul(t—t)dt1 (7)
а V EmEi У tmEt J
—оо
называется взаимокорреляционной функцией сигналов
Um(t) И Ui(t).
При равенстве энергий сигналов, т. е. при
Em=Ei=E, из (7) получаем, что
оо
rni(t)]=-^ ^um(t)Ul(t-z)dt. (8)
—оо
Взаимокорреляционная функция. Она характеризует
реакцию фильтра, согласованного с сигналом ui(t),
на воздействие сигнала um(t). Так как импульсная
характеристика фильтра (1) определяется через сигнал
ih{t), то взаимокорреляционная функция зависит от
двух сигналов. При этом она является интегральной
(средней) совместной характеристикой этих сигналов.
44
§ 2.1
При фиксированном τ значение rmi(x) является
функционалом двух переменных: um(t) и ui(t—τ), что
отмечается индексами т и /.
Взаимокорреляционная функция определяет
взаимосвязь между двумя сигналами. Смысл слова
«взаимосвязь» можно пояснить на следующем примере. Если
взять два тождественно равных сигнала, то можно
утверждать, что они максимально связаны друг с
другом: значения одного точно равны значениям другого
в совпадающие моменты времени. Если изменить форму
одного из сигналов, то «взаимосвязь» между ними
должна уменьшиться, поскольку значения одного могут
не совпадать со значениями другого в совпадающие
моменты времени. Таким образом, слово «взаимосвязь»
характеризует близость двух сигналов по форме.
Определим количественно меру (оценку) близости двух
сигналов по форме. Предварительно рассмотрим
графический пример.
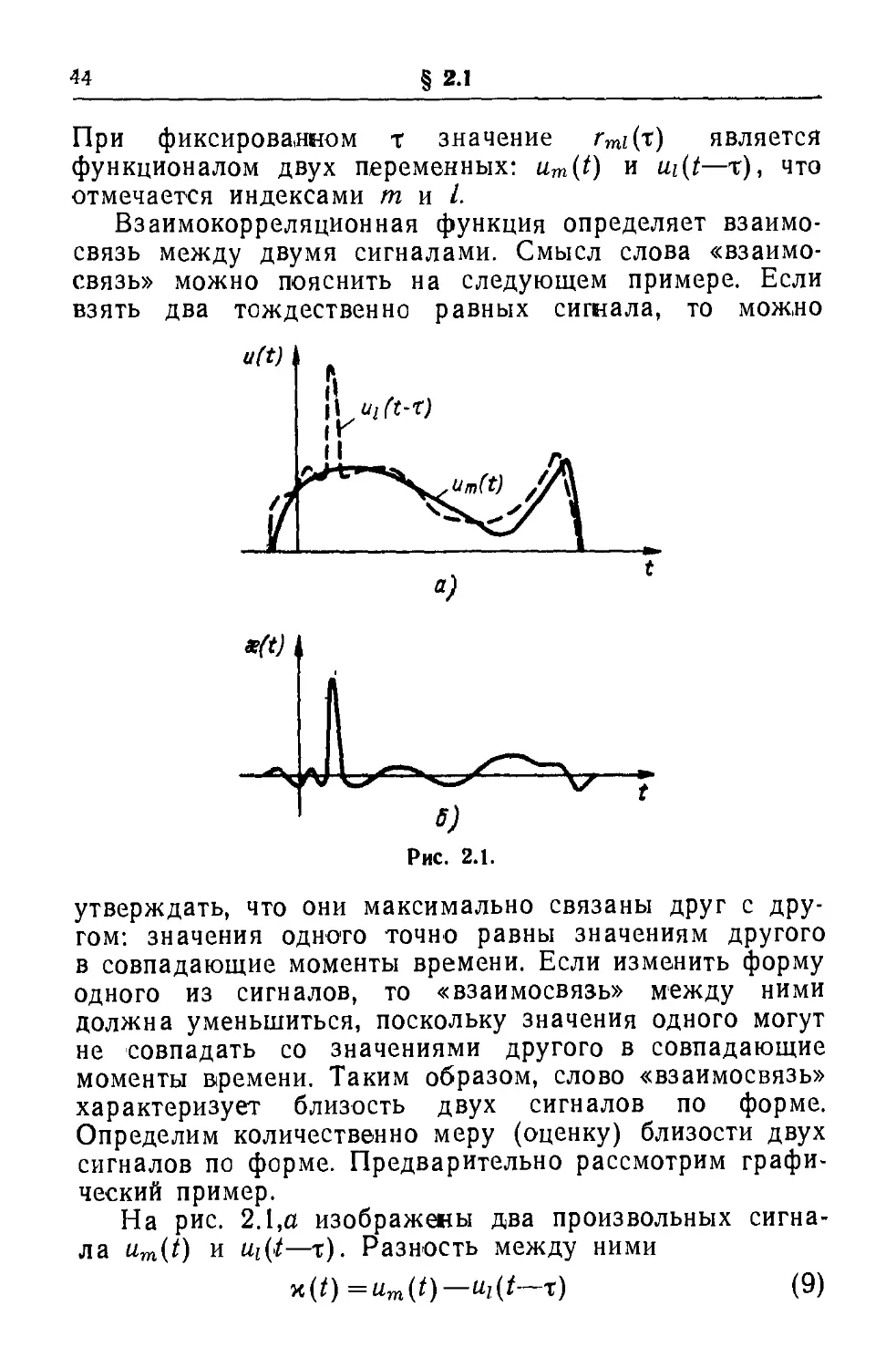
На рис. 2.1,α изображены два произвольных
сигнала um(t) и Ui(i—τ). Разность между ними
x(t)=um(t)—ul(t—x) (9)
§ 2.1
45
представлена на рис. 2.1,6. На рис. 2.1 видно, что
выбранные сигналы в целом близки друг к другу по
форме, так как разность x(t) мала по сравнению
с самими сигналами почти для всей области задания
этих сигналов. Но в точке, в которой имеется выброс
сигнала ui(t—τ), между сигналами существует сильное
различие. Из рассмотренного примера следует, что
оценка близости двух сигналов по форме должна
обязательно учитывать отличие между сигналами на
всем отрезке существования сигналов, т. е. должна быть
средней или интегральной оценкой.
Чтобы интегральная оценка не обращалась в нуль
вследствие знакопеременности разности κ(ί),
интегрируется (усредняется) функция κ2(ί). Поскольку
сигналы оцениваются по форме, то необходимо исключить
влияние их амплитуд на оценку близости. Например,
сигналы urn(t) и Xum(t) при λφ\ одинаковы по форме,
но не равны тождественно. Поэтому необходимо
сравнивать нормированные сигналы, определяемые как
«ж (0 ιΐι(( — τ) . „
Учитывая все ранее сказанное, в качестве оценки
близости двух сигналов можно взять
среднеквадратичную разность:
р- (,) = Т| «=^Щ— ««_<£==^1 Iя rfi. (ii)
Раскрывая квадрат разности в (П), используя
выражение (7) и определение энергии сигнала (1.1.4),
получаем, что
ρ·(τ) = 2[1->ΙΒ|(τ)]. (12)
Определим экстремальные значения г^ и р2.
Используя неравенство Буняковского — Шварца, из (7)
находим
— 1<Γ„ι(τ)<1. (13)
Равенство в правой части выражения (13)
выполняется только для совпадающих по форме сигналов,
4В
§ 2.1
т. е. для um(t)=tii(t—τ). При этом значение
среднеквадратичной разности ρ2(τ)=0 и является
минимальным, так как подынтегральное выражение в (11) не
может быть отрицательным. Равенство в левой части
(13) выполняется только для противоположных
сигналов, т. е. для um(i)=—tii(t—τ). При этом значение
Р2(т)=4 и является максимальным.
Очевидно, что при условии нормирования (10) и
задании одного из сигналов все возможные формы
другого занимают промежуточное положение между
формой, совпадающей с заданным сигналом, и противо-
полож'ной ей. Таким образом, степень близости между
двумя сигналами определяется взаимокорреляционной
функцией rmi(x) или ее эквивалентом ρ2(τ).
Из всех сигналов, занимающих промежуточное
положение между совпадающими и противоположными,
необходимо отметить ортогональные сигналы.
Ортогональными называются сигналы, которые удовлетворяют
условию.
$"η.(0Μί—*)Λ = 0, (14)
—оо
г. е.
Γ«ι(τ)=0, ρ2(τ)=2. , (15)
Среднеквадратичная разность (11) для ортогональных
сигналов равна их среднеквадратичной сумме.
Следовательно, энергия суммы двух ортогональных
сигналов равна сумме энергий слагаемых. Это означает, что
ортогональные сигналы суммируются по мощности.
Рассмотрим геометрический образ
взаимокорреляционной функции [7, 14]. Сигнал с конечной энергией
может быть представлен точкой в вещественном,
бесконечномерном, гильбертовом пространстве. Длина
сигнального вектора (норма), соединяющего начало
координат с сигнальной точкой, равна
||u||=J/ \u*{t)dt =γΕ. (16)
—оо
Расстояние между ^точками, представляющими сигналы
§ 2.1
47
um(t) и ut(t — τ), определяется как
d = \[um — ul[[—y J [МО —"ι ('-*)]**· (17)
—oo
Используя определения энергии сигнала и
взаимокорреляционной функции (1.1.4), (7), получаем, что
d* = Ет — 2 V EmEirnl (τ) + Еь (18)
Согласно формуле (18) d2 является квадратом стороны
треугольника, две другие стороны которого, равные j/'Em и
У Ей образуют угол а. Косинус этого угла равен г„(1 (τ).
Следовательно, угол α зависит от величины т. При
rmi(t) = l угол а=0 и сигнальные векторы совпадают
по направлению, а при rmi(x) = —1 угол α = π и
направления сигнальных векторов являются
противоположными. При rmi(x)=Q угол α=π/2 и сигнальные
векторы будут взаимно перпендикулярными.
Таким образом, взаимокорреляционная функция
характеризует разность углов между геометрическими
образами сигналов.
Отметим, что нормированные сигналы (10)
обладают единичной энергией. Следовательно, концы
сигнальных векторов (10) лежат на поверхности
единичной гиперсферы. При этом значения сР (18) и ρ2(τ)
(12) совпадают.
Автокорреляционная функция. Если воздействующий
на вход фильтра сигнал и фильтр согласованы (т = 1),
то из (7), отбрасывая индексы т и /, получаем
оо
r{x)~~^u{t)u{t — t)dt. (19)
—оо
Функция г(х), определяющая взаимосвязь между
сигналом и его сдвинутой во времени копией,
называется автокорреляционной. Согласно выражению (19)
r(0)=rMWQ=\.
(20)
8
§ 2.1
oft)
«)
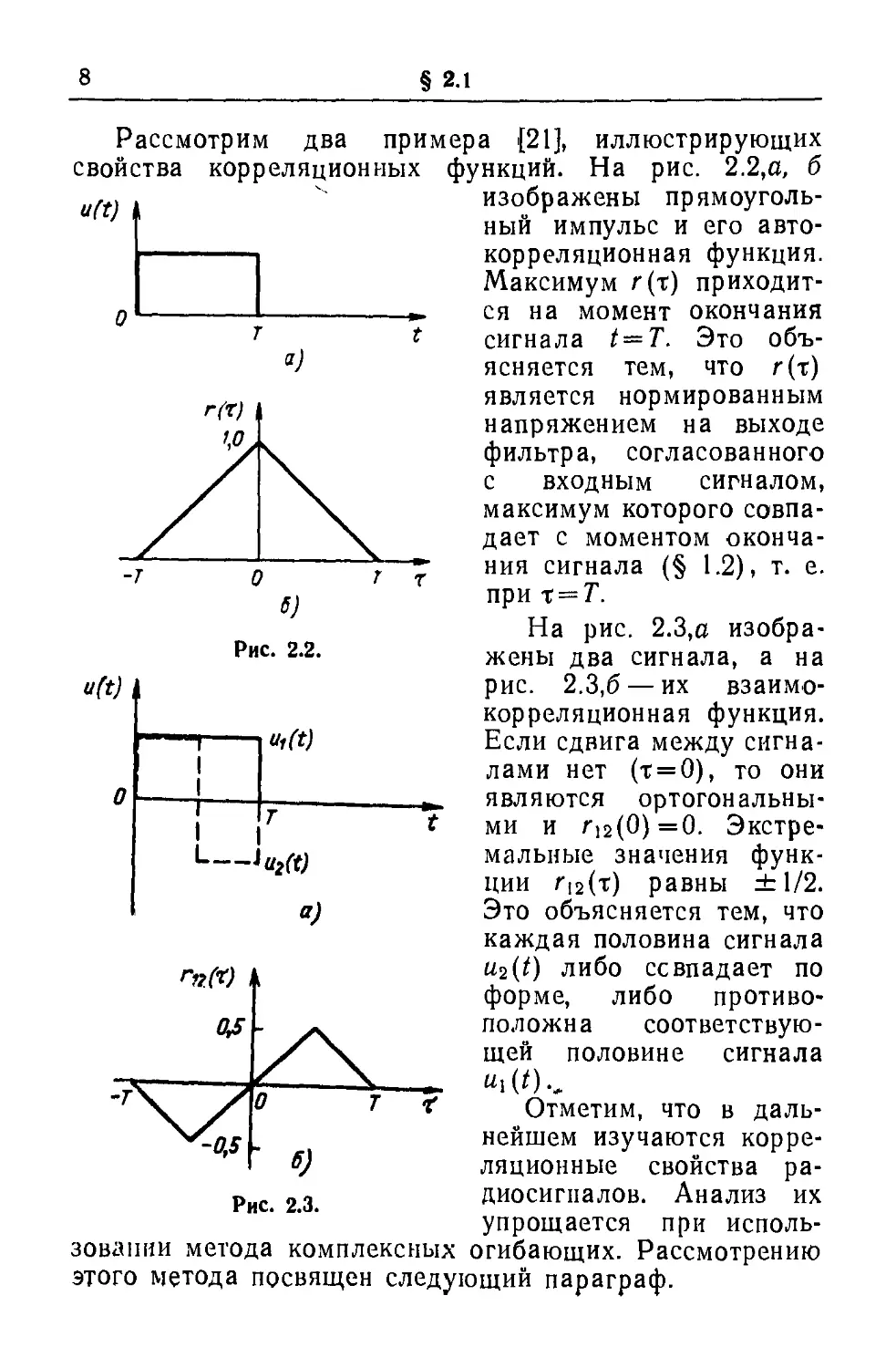
Рассмотрим два примера {21], иллюстрирующих
свойства корреляционных функций. На рис. 2.2,а, б
ц,^ . ч" изображены прямоуголь-
* ный импульс и его
автокорреляционная функция.
Максимум г (τ)
приходится на момент окончания
сигнала ί = Τ. Это
объясняется тем, что г(х)
является нормированным
напряжением на выходе
фильтра, согласованного
с входным сигналом,
максимум которого
совпадает с моментом
окончания сигнала (§ 1.2), т. е.
при х — Т.
На рис. 2.3,а
изображены два сигнала, а на
рис. 2.3,6 — их
взаимокорреляционная функция.
Если сдвига между
сигналами нет (т = 0), то они
являются
ортогональными и г12(0)=0.
Экстремальные значения
функции Г|2(т) равны ±1/2.
Это объясняется тем, что
каждая половина сигнала
u2(t) либо совпадает по
форме, либо
противоположна
соответствующей половине сигнала
МО·.
Отметим, что в
дальнейшем изучаются
корреляционные свойства
радиосигналов. Анализ их
упрощается при
использовании метода комплексных огибающих. Рассмотрению
этого метода посвящен следующий параграф.
«tft)
L—la2(t)
"J
ПгСг)
OJS
\У
v-v
Pi
ι
/\
k в)
ic. 2.3.
δ 2.2
49
2.2. КОМПЛЕКСНАЯ ОГИБАЮЩАЯ СИГНАЛА
И ЕЕ СПЕКТР
Произвольный сигнал u(t) можно записать в
следующем виде:
u(t) = U(t) cos@{t). (1)
Огибающая U(t) и фаза Θ(ί) однозначно
определяются с помощью сопряженного сигнала Ui(t):
t/(o=iAi«(o+u?(o, (2)
0(O = arctg^. (3)
Сигнал u(t) и сопряженный с ним u-i{t) связаны
преобразованиями Гильберта [3]:
—оо
—оо
Фаза сигнала Θ(ί) спязана с его мпюнешюи
частотой ω(/) следующим выражением:
αϊ d%(i) 'd г . . н, (/) ι ...
"W = -iI = -Sr["ctg-^ilJ (4)
и может быгь записана как
θ(ί)=ωοί + θ(0+Οο, (">)
где ωο—несущая частота;
θ (0—нелинейное слагаемое;
θο — начальная фаза.
Таким образом, произвольный сигнал iv\i)aciio (1)
может быть записан как
4—2366
50
§ 2.2
ll(t) = U(t) COS [»J + ba + b(t)]. (6)
Поскольку в дальнейшем Θ(ί) не используется, то
фазой сигнала будем называть Q(t), в которой учтем
величину θο· При этом
u(0 = t/(0cos[ro0i + e(0]. (7)
Представление сигнала в виде (6) или (7) справедливо
для любого сигнала u(t), но применять его имеет
смысл только для узкополосных сигналов, у которых
ширина спектра много меньше несущей частоты. Этому
условию удовлетворяют многие применяемые на
практике радиосигналы, независимо от значения базы FT.
Комплексная огибающая. В дальнейшем полагаем,
чго все сигналы можно представить в виде (7).
Несущая частота ωο в выражении (7) не влияет на форму
сигнала, она только смещает его спектр по оси частот
аналогично тому, как запаздывание смещает сигнал
по оси времени. Форма сигнала зависит только от
функций u(t) и Q(t). Поэтому целесообразно
представить сигнал в таком виде, который учитывает только
U(t) и Q(t) Для этого введем понятие аналитического
сигнала и его комплексной огибающей.
Аналитический сигнал определяется как
u(t) = U(t)e"", (8)
где
U{t) = U(t)eleit) (9)
— комплексная огибающая сигнала.
Можно показать, что аналитический сигнал
tt(t)=u(t)+iui(t),
где Ui(t) —сопряженный с u(t) сигнал. Отсюда следует,
что сигнал u(t) равен действительной части
аналитического, т. е.
u{t)=Reu(t). (10)
§2i
Si
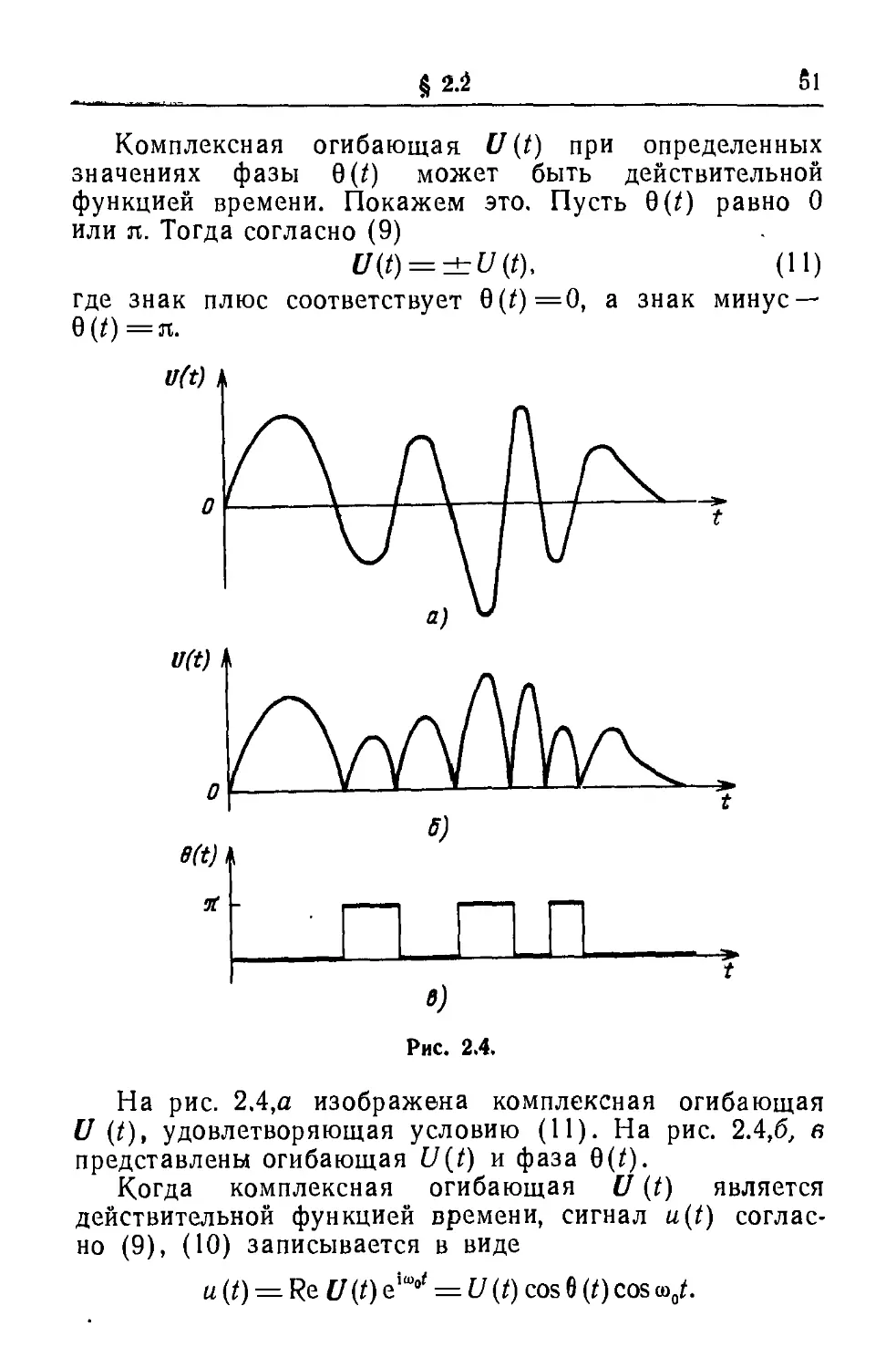
Комплексная огибающая U(t) при определенных
значениях фазы Q(t) может быть действительной
функцией времени. Покажем это. Пусть 0(0 равно О
или п. Тогда согласно (9)
U(t) = + U(t). (11)
где знак плюс соответствует θ(ί)=0, а знак минус —
θ(ί)=π.
На рис. 2А,а изображена комплексная огибающая
U (t), удовлетворяющая условию (11). На рис. 2.4Д в
представлены огибающая U(t) и фаза Q(t).
Когда комплексная огибающая U (t) является
действительной функцией времени, сигнал u(t)
согласно (9), (10) записывается в виде
и (t) = Re U(t) е'ш°' = U (t) cos θ (t) cos ω0ί.
52
§ 2.2
Отсюда следует, что сигнал обладает амплитудной
модуляцией и фазовой манипуляцией. Амплитудная
модуляция определяется огибающей >U\(t), а фазовая
манипуляция— сомножителем cos0(i). так как при θ(ί),
равном 0, или π, cos θ (if) = ±1.
Если β(ί) = :i-n/2, το U(t) является мнимой функцией
времени, т. е.
U(t) = iU(t)smb(t) = U(t)smb(t)eM2. (12)
Сигнал в этом случае записывается как
и (0 = Re U(/) eiV = — t/ (/) sin θ (t) sin ш0/
и тоже обладает амплитудной модуляцией и фазовой
манипуляцией, определяемой сомножителем sin0(i) =
= ±1.
В общем случае комплексная огибающая может быть
представлена как
U(t) = Ua(t)-\-W,.(t) = U(t)cosb(t) + \U(t)smb (t), (13)
где индекс α означает действительную часть, а индекс
г—мнимую. Из выражения (13) следует, что
U(t) = Vu'2a(t) + U2r(t). (Η)
e(0 = arctg^-· (15)
Если комплексная огибающая U{t) (13) содержит
и действительную Ua(t), и мнимую U,(t) составляющие,
то Q(t) является произвольной функцией времени и,
следовательно, сигнал u(t) будет обладать частотной
(угловой) модуляцией.
Отметим, что сумма двух комплексно-сопряженных
огибающих
Ut(t) = U(t)+U(t) = 2U(t)cosQ(t) (16)
является действительной функцией времени и благодаря
множителю cos0(0—фазоманипулированным сигналом.
§ 2·2
53
Спектр комплексной огибающей сигнала. Обозначим
его О (ш). Согласно прямому преобразованию Фурье
00 —Ι<οί
0(ω)=(|/(/)β di. (17)
—оо
Обратное преобразование Фурье записывается как
оо
U^ = ~L· f 0(»)ele'rf». (18)
—оо
Спектр g(a>) сигнала u(t) выражается через О (ω)
следующим образом:
оо
*(») = jM(0e-,wrf/ = 4-O(»-«0) +
—00
+ 4-О(-»-»0). (19)
Необходимо отметить, что спектр комплексной огибаю'
щей О (со) является произвольной функцией частоты, а
спектр £(ω) — нет. Запишем О (со) в следующем виде:
0(со) = |0(со)|е'ф(ш). (20)
Амплитудный |0(со)|и фазовый φ (со) спектры
комплексной огибающей произвольного сигнала изображены на
рис. 2.5, а, б.
Спектр g(co) реального сигнала u(t) запишем
аналогично выражению (20):
*(») = ! *Н|е','Н, (21)
где φ^(ω)—фазовый спектр сигнала.
Из формулы (19) можно показать, что если и(1) —
действительная функция времени, то должны
выполняться следующие соотношения:
1*(-»)| = 1*(»)|. (22)
?*(—») = —?*(»)■ . (23)
54
§ 2.2
Выражения (22), (23) означают, что амплитудный
спектр сигнала является четной функцией частоты,
а фазовый — нечетной функцией.
Амплитудный и фазовый спектры сигнала u(t),
построенного в соответствии с (22), (23), представлены
на рис. 2.5,0, г.
1Ш1
1 -й>а
\дм\
\ о
Ι φι(ω)
\У
I
а>о ι α>
А
! j/ί
ω0*ω„
')
Рис. 2,5.
Из-за взаимной связи обоих слагаемых в спектре (19)
достаточным для расчетов является знание функции
О (ω — св0), являющейся спектром аналитического сигнала
Я (f)(8). Действительно,
Ju(t)e-iatdt= f £/(0е-|<—-"Л = (7(»-«0), (24)
§ 2.2 55
а согласно обратному преобразованию Фурье
«(')=--^|0(ш-шо)е'Ш'^· (25)
—оо
Рассмотрим прохождение сигнала u(t) через фильтр
с коэффициентом передачи k(ω). Аналитический отклик
определяется аналогично выражению (25):
оо
ν (0 = -L Г Q (ю _ ш0) ft (ω) е,ш' </». (26)
—оо
Если фильтр согласован с радиосигналом, т. е.
пропускает полосу частот около ω=ωο, то его коэффициент
передачи записывается как
*(») = #(»-»„). (27)
Тогда (26) принимает вид
оо
ц(/) = 1[0(ш-шД(ш-ш0)е,ш' dco = V(/)eK/ , (28)
—оо
где комплексная огибающая отклика
оо
V(t)^~ Го(»)/Г(ш)е1в"</а>. (29)
—00
Отклик в соответстви с (10)
υ {t) = Rev {t), (30)
Свойства симметрии. Рассмотрим особенности 0(ш)
при симметрии U(t) относительно t = 0. Допустим, что
огибающая — четная функция времени, т, е.
U(-t) = U(t), (31)
Отметим, что большинство реальных сигналов
удовлетворяет условию (31),
56
§ 2.2
Подставляя в (17) определение (9) и разлагая
экспоненты по формулам Эйлера, получаем
О (ω) = Г и (t) cos θ (t) cos wtdt —
— i С U(t) cos6 (t) sin wtdt-\- [U(t)smQ(t)smu>tdt-\-
—oo —oo
+ i f U (t) sin b(t) cos a tdt. (32)
—oo
Допустим, что фаза сигнала является четной функцией
времени, т. е.
θ(—t)=Q(l). (33)
Тогда в формуле (32) второй и третий интегралы равны
нулю и формула принимает вид
об
0(ю)= f U(t) cos6 (/) cos wtdt +
—00
oo
+ i f t/(0sine(0cosro/i/i. (34)
—00
Так как частота ш входит в аргумент косинуса, С? (ω) при
условии (33) является четной функцией частоты, т. е.
0(— ю) = 0(ю). (35)
Согласно (20) соотношение (35) можно представить
в виде двух равенств:
для модулей
|0(-а,)| = |0(»)|. (36)
для фаз
φ(—ω)=(ρ(ω). (37)
Отсюда следует, что амплитудный и фазовый спектры
комплексной огибающей — четные функции частоты.
Теперь допустим, что фаза — нечетная функция
времени, т. е.
θ(—0 =—6(0- (38)
§ 2.2
57
Тогда в формуле (32) второй и четвертый интегралы
равны нулю и 0(ω) является действительной функцией
частоты:
О (ω) = f U (i) cos θ (t) cos wtdt +
—ее
oo
+ f t/(i)sine(0sinarfctt. (39)
—oo
Спектр <?(со) комплексной огибающей произвольного
сигнала, удовлетворяющего выражению (39), может бьгть
представлен графиками, приведенными на рис. 2.4, при
замене U(t) на О (ω), U(t) на |0(ω)|, θ (t) Гна φ (ω) и t на ш.
Рассмотрим особенности комплексной огибающей
£/(ί), если ее спектр обладает симметрией. Из (18)
аналогично (32) получаем, что
оо
U(t) = γ- Ι Ι Ο (ω) I COS φ (co)cos wtd<a-\-
—oo
oo
+ i -K^ f | О (ш) I COS φ (со) sin tatdm —
—oo
eo
— ~2π I I ^ (ш) I Sin f (ш)C0S ω^ω ~Γ~
—oo
oo
+' 'L· \\№ ^ ιsin ψ ^cos ω Wt°- (40)
Допустим, что амплитудный спектр комплексной
огибающей — четная функция частоты, т.е.
|0(-»)| = |0(»)|.
Если фазовый спектр — тоже четная функгшя частоты,
т. е.
φ(—ω)=φ(ω), (41)
58 § 2.3
то из (40) получаем, что
U{t) — j- \ | О (ω) | cos φ (ω) cos wtdw -\-
—оо
оо
+ i -^ I I О (со) | sin φ (со) cos со tdw. (42)
—оо
Поскольку U{t) содержит и действительную и мнимую
Составляющие, то сигнал u(t) согласно (13) будет
частотно-модулированным, а его фаза согласно (15) —
четной функцией времени.
Если фазовый спектр — нечетная функция частоты,
т. е.
φ(— ω)=—φ(ω), (43)
то из (40) следует, что комплексная огибающая сигнала
оо
£/(ί) = _ Г | 0 (ев) | COS 9 (со) COS coWco — .
—оо
оо
—2^" II О (ω) | sin ψ (со) sin со tdw (44)
—оо
— действительная функция времени, т. -е. сигнал фазо-
манипулированцый.
2.3. КОМПЛЕКСНАЯ ОГИБАЮЩАЯ
КОРРЕЛЯЦИОННОЙ ФУНКЦИИ И ЕЕ
ОСНОВНЫЕ СВОЙСТВА
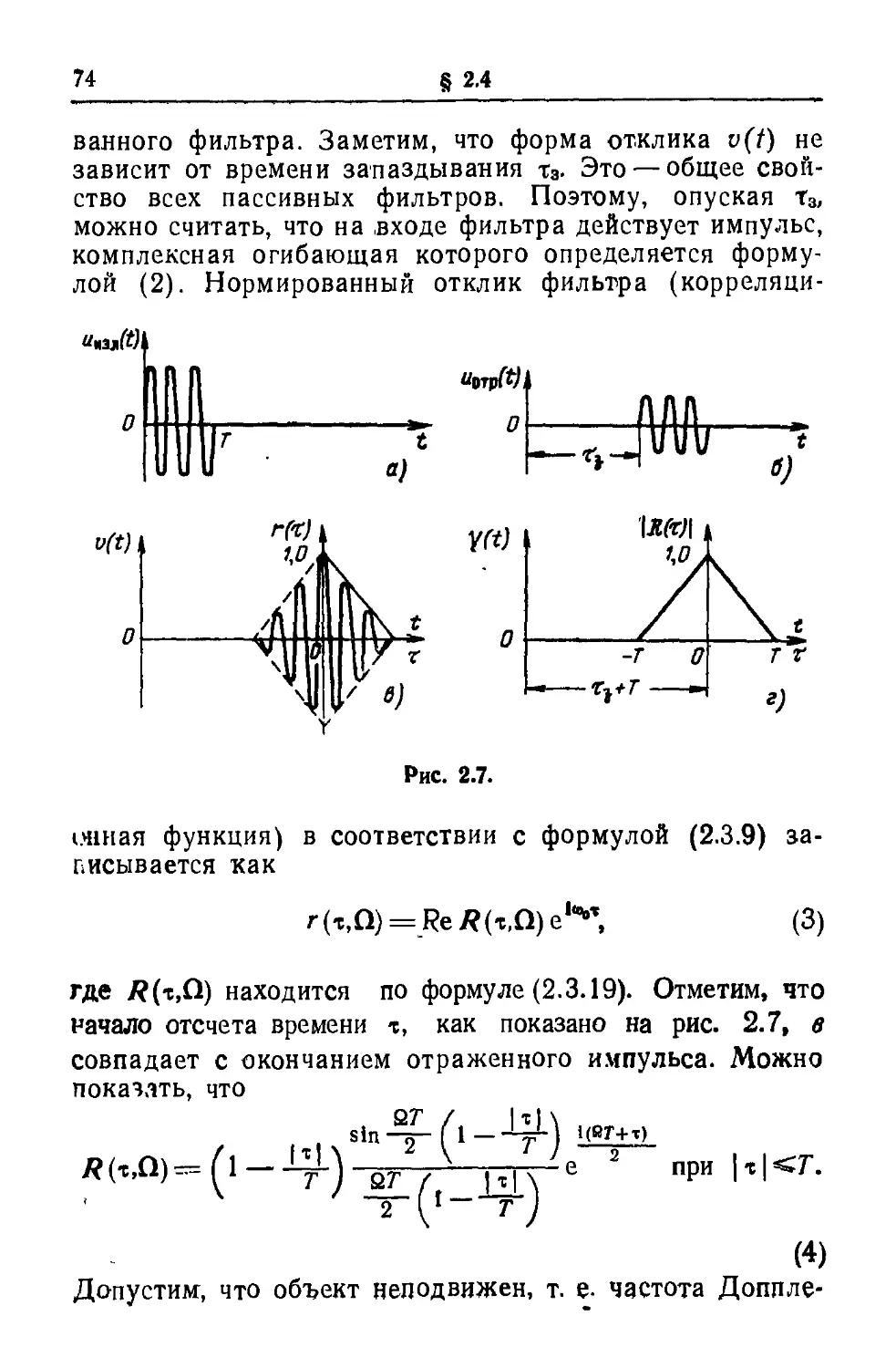
Рассмотрим формулу (2.1.7), определяющую
взанмокорреляционную функцию двух сигналов. Пусть
нд входе фильтра действует сигнал
"m(0 = £/m(0«>sKf + flm(0]. (I)
а фильтр согласован с сигналом
M0 = tM0cosK* + ei(0]. (2)
δ 2.3
59
Подставляя (1), (2) в (2.1.7), получаем, что
Гт1 (τ)= ~у=\ j Vm (t) COS [ω0ί + 9m (ί)] Χ
—оо
Xt/i(i —τ) cos [ω0(ί —τ) + βι(ί —τ)] Λ =
оо
= ^= j £/« (0 Uι(t - τ) cos [β„ (0 + ω0τ -h{t-
—оо
оо
- τ)] (it + ^у= J ^m (0 t/, (ί - τ) COS [2ω0ί -
_ ω,τ + β,^ο + Μ* —Ό]Λ· (3)
С учетом определения комплексной огибающей
сигнала (2.2.9) выражение (3) записывается как
(оо
^у^=, j Um (t) hi (t - ■«) e"°oT л +
== J £7m (0 I/, (i - τ) e' 2ω»ί-' -'Λ J · (4)
2 /£„,£
—оо
Введем обозначения;
оо
Rnil(z) = —-L= Г Um(W(t-*)dt, (5)
2 уЬтЬ1 J
—оо
оо
Qm, (τ) = —"- f £/„, (0 Ut (t - τ) e'2V Λ. (6)
—оо
Тогда формула (4) запишется в виде
/■„,(*) = Re [Rmi(i) e'^'+Qwii') е"' ш°1 (7)
Отметим, что подынтегральное выражение в (5)
равно произведению сопряженных комплексных
огибающих, а в (6) равно произведению несопряженных
комплексных огибающих и быстроперемен'ного множителя
60
§ 2.3
exp (ϊ2ω0ιί)· Поэтому, если ширина спектра сигнала
значительно меньше несущей частоты, то по крайней мере
из-за множителя ехр (ΐ2ωο0> выполняется неравенство
\Rm(t)\>\Qmib)\. (8)
В этом случае
rmi(x) = ReRmi(x)'el°'\ (9)
Из (9) следует, что Rmi{t) является комплексной
огибающей взаимокорреляционой функции.
Таким образом, если выполняется неравенство (8),
то взаимокорреляционная функция определяется
соотношением (9). Однако возможны случаи, когда
неравенство (8) не выполняется. В частности, если ω0—>-0,
то значение Qmt соизмеримо со значением Rmi- Поэтому
в общем случае для расчетов взаимокорреляционной
функции следует использовать соотношение (7).
В некоторых случаях в процессе распространения
сигнала его несущая частота ωο может изменяться.
Например, в радиолокации несущая частота сигнала,
отраженного от движущегося объекта, принимает
значение, равное ωο+Ω, где Ω называется частотой Доп-
плера. Дополнительную фазовую составляющую Ωί,
возникающую при отражении, при Ω<§;ωο можно
отнести к комплексной огибающей сигнала и можно
считать, что на входе фильтра действует сигнал с
комплексной огибающей вида
Um(t)eat. (Ю)
Подставляя (10) в (5), получаем, что комплексная
огибающая взаимокорреляционной функции зависит
от двух аргументов, а именно:
оо
Λ^(τ,Ω) = -π4=Γί/„(Οί7,(ί-τ)βιβ'Λ. (И)
—оо
Энергия любого сигнала, например m-го, по
определению (1.1.4) записывается как
§ 2.3
61
Em= J um (t) dt = j U2m (t) cos2 Ы + К (О] Л.
—oo —oo
После тригонометричесих преобразований получаем
оо
—00
оо
+4" j ul (0cos 2 К'+Θ'» (01 Λ· (12)
—оо
Для узкополосных сигналов, ширина спектра
которых намного меньше ωο, второе слагаемое в (12)
намного меньше первого, поскольку подынтегральное
выражение второго слагаемого содержит бысгропеременный
косинусоидальный множитель. Для таких сигналов
можно считать, что энергия
оо оо
Em = -L^U2Jt)dt = -±-^\Um(t)\>dt (13)
—оо —оо
и не зависит от фазовой структуры сигнала.
При ωο—>-0, т. е. при соизмеримости несущей
частоты с шириной спектра сигнала в (12) надо учитывать
оба слагаемых.
В дальнейшем полагаем Ет=Е. В этом случае
в соответствии с (13) выражение (11) принимает вид
<а
/?„, (τ, Ω) = ± | Um (t)U, (t - τ) e,ffii dt. (14)
—oo
Подставляя (2.2.18) в (14), находим
00 00
Лш(х, Q) = 2F | -яг Г От И е"* dw χ
—00 —00
Xij&We^'-^e'0'^
—оо
^flOmi^dm^l^^^dt^^dxdy. (15)
62
§2.3
Внутренний интеграл в (15) есть дельта-функция [22]:
4x) = i^ixzdz. (16)
—оо
Она обладает следующим фильтрующим свойством:
ь (f(x0) при а<х0<Ь,
и(х)Ъ(х— x0)dx=>) l/2f(x0) при х0 = а, или ха = Ь, (17)
а [0 при л0<а, л0>6.
Используя фильтрующее свойство дельта-функции,
формулу (15) представим в виде
оо
i?mi(t.Q) = 4SE"f От(Щ-0)0,Не!и(1В. (18)
—оо
Отметим, что формулы (14), (18) остаются
справедливыми й для фильтра, согласованного с сигналом
um(t), т. е. при т=/. В этом случае указанные формулы
описывают комплексную огибающую корреляционной
функции1 (2.1.19), для которой индексы т и / могут
быть опущены:
оо
R(x,Cl) = ±. Г υ(ί)ύ(ί-τ)έ*άί, (19)
—оо
ИЛИ
оо
R(t,Q)=-~ f 0(и> — Ω)σ(ω)ε!<οτίίω. (20)
—оо
Если частота Допплера Ω = 0, то согласно (19),
(20) комплексная огибающая автокорреляционной
функции запишется как
оо
/?w=2^J£/;(ow:-*)^,· (21)
—оо
1 Отметим, что в дальнейшем для корреляционной функции
Л? (τ, Ω), так же как и для автокорреляционной Л? (τ), индексы
опущены. Следует, однако, помнить, что первая всегда является
функцией двух аргументов, а вторая — одного.
§2.3.
63
ИЛИ
*(*) = ii-J|G(«)|1e,eTrf«o. (22)
—оо
Подынтегральные выражения в (14), (18) — (20)
имеют несимметричный вид относительно аргументов
первых двух множителей. Можно произвести их
симметризацию заменой переменных: t\ = t—τ/2, κοι = ω—Ω/2.
Введя индекс симметрии «с», из (14), (18) — (20)
получим
оо
/?сы (τ,Ω) = ^ j Um (t + -f) fr (' - -f) eiffii dt. (23)
—оо
ИЛИ
оо
RCmi (τ, Ω) = JL j Om f» - -§-) Οι U + -§-) e"01 dm, (24)
—оо
оо
Rc(x, 0) = -^- j U (*+-f) ΰ(* —г) e'°' Λ· (25>
—oo
ИЛИ
oo
Rc (t, Q) = 5^· J О (« - -§-) О («o + -§-) е- do,, (26)
—oo
При этом
Rand*, Ω) = Янн (τ. Ω) exp (— i Ωι/2), (27)
/?c (τ, Ω) = R (τ, Ω) exp (— i Ωτ/2), (28)
Ami(t. Q)| = | i?mi(*. Ω)| и |/?c(x, Ω)| = /?|(τ,Ω)|. (29)
Для комплексной огибающей автокорреляционной
функции (21) имеем
оо
/?с (τ) = Я (τ) = -±- J |/^+ -f) £ (/ - -1. j rf/. (30)
—oo
64
§ 2.3
Основные свойства комплексной огибающей
корреляционной функции.
1. Из (11) согласно неравенству Буняковского—
Шварца (1.2.19) получаем
Х|/ Ι Ιί;'"(/)«ΡΡβ„(/)-ίβι(/-τ) +
(31)
Равенство Rmi(t. Ω)=1 выполняется при
Um (/) ехр [/вт (/) — i bi (t — τ) 4- i Ω/] =α£/2 (/—τ),
что эквивалентно условию
Um(t)filat = aUi(t-T). (32)
Из условия (32) следует тождественность сигналов по
форме. А это означает, что фильтр согласован с
сигналом на его входе с учетом сдвига сигнала по частоте Ω
и запаздывания τ. Если сигналы удовлетворяют
равенству (32), то т = 1 и максимальное значение
комплексной огибающей корреляционной функции
Л(0,0)=1. (33)
2. Комплексная огибающая автокорреляционной
функции (22) является преобразованием Фурье
энергетического спектра комплексной огибающей сигнала и
не зависит от фазового спектра. Согласно обратному
преобразованию Фурье запишем
00
|0(а))|2 = 2£ ΓΛ(τ)β-,βΤίίτ. (34)
§ 2.3
65
Например, если /?(т) = г(т) (рис. 2.2,6), то
(ω? \2
sin — \
Заменяя в (21)τ на—τ, получаем
Я(—τ) = ΐ?(τ)· (36)
Из (22) находим, что
*(τ)=4ΪΤ J |σ(ω)|408ω^ω;+
~оо
оо
+ ί4^|ΐ£7Η|'8ίηω^ω. (37)
—оо
Если |0(<о)|а— четная функция частоты, то второй
интеграл равен нулю и /?(τ) является действительной
функцией τ. Кроме того, из (36) следует, что |/?(τ)| —
четная функция.
3. Согласно (Ί9) комплексная огибающая
корреляционной функции при τ = 0 определяется как
00
Я(й)=~- ^U*(t)el/Udt. (38)
—оо
Выражение (38)—преобразование Фурье от квадрата
огибающей сигнала. Оно не зависит от фазы сигнала
θ(0, а определяется только его огибающей. Например,
на рис. 2.6,а изображен прямоугольный имлульс U(t)
длительностью Г, а на рис. 2.6,6 — сечение комплексной
огибающей корреляционной функции (38), которое
имеет вид
ОТ
sln_2~
/?(Ω) = —^—-. (39)
2
4. Если в определении комплексной огибающей
корреляционной функции (19) изменить знаки на обратные,
5—2366
66
§ 2.3'
TO
oo
Λ(-τ,-Ω)=.±- [(J{t) U(t-\-t)e~lt>idt. (40)
—oo
Вводя новую переменную t1=t-\-z, выражение (40)
записываем в виде
00
/?(-τ,_.Ω) = εί13τ_!_ Γ U(t)(J(t-T)e~ls>idt. (41)
—00
U(t)\
тот t
а) · д)
Рис. 2.6.
Сравнивая полученное выражение (41) с исходным (19),
замечаем, что
/?(-τ,-Ω)=Λ(τ,Ω)εί13τ. (42)
Из (42) следует, что
|/?(-τ,-Ω)| = |*(τ,Ω)|, (43)
т. е. перемена знаков у обоих аргументов комплексной
огибающий корреляционной функции не меняет
величины ее модуля. Соотношение (42) с учетом (28)
принимает вид
/?ο(-τ,-Ω) = 4(τ,ΓΩ). (44)
Отметим, что свойство симметрии (44) выполняется
для произвольных сигналов.
9 2,3
67
5. Изменив знак у τ в формуле (26) на обратный,
получаем
л(-^41с(-т)*('+т)'"1,,й=
—оо
]|0(„_4-)||0(» + А)|ехр[,>(»-|-)-
-оо
— ίφ ίω -|- -g-J — i ωτ 1 dm. (45)
4π£
При замене переменной <о1 = — ω выражение (45)
принимает вид
оо
—оо
+4-)|6Χρ[ί(ρ(-ω>--§-) ~ ί(ρ(-ω>+-§-)-^
—J— i «otx Ί rff»!· (46)
Допустим, что амплитудный спектр комплексной
огибающей— четная функция частоты, а ее фазовый спектр —
нечетная, т. е.
|<7(-«)| = |<7Н|. (47)
?(—■) = — ?(■)·
(48)
В этом случае
| О (- щ - -§-)| I О (- щ + 4)1= | О (т, +
+τ)ΙΙβ(--τ)|· <*»
68
§ 2.3
С учетом (49) и (50) выражение (46) запишем как
Λ(-*.Ω)=-4^ί|σ(-—?-)||σ(··+-§-)|χ
Хехр Г,- φ Л», — -|")— ' * (ωι +~) + 'ωιτ] da)l· (51)
ИЛИ
/?с(— τ, Ω) = /?0(τ,Ω). (52)
Таким образом, если спектр сигнала удовлетворяет
условиям (47), (48), то значения корреляционной
функции для ±т совпадают. Свойством симметрии (52)
обладают фазоманипулированные сигналы, которые
удовлетворяют условиям (47), (48).
6. Если в соотношении (25) изменить знак у Ω на
обратный, то
оо
/?c(,,_q)=JL j u(t+-tyu(t—zTy~is>tdt=
—оо
=ж] υ ('+-f)υ (;--г>*р[» (Ч-f)-
—оо
-ϊβ(ί 1Λ-1£*]Λ. (53)
Сделав замену переменного ^ = — /, получим, что
оо
*,(,, _ Q)=-^ j С/(_*, + ■£■) С/(-f»--J-)X
—оо
Хехр [i θ ^— ί. 4—J-)— i β (— Λ £-)+*£*,]#,. (54)
Допустим, что огибающая сигнала — четная функция
времени, а фаза — нечетная функция, т. е.
U(—t) = U(t), ■ (55)
β (-*) = -β (f). (56)
§ 2.3
69
В этом случае
(57)
+6(^ + -г)· <58)
С учетом (57) и (58) формула (54) записывается как
—оо
Χβχρρβ^+^-Ιβ^-^ + ίΟί,]*,. (59)
или
/?c(t,— Q) = /?c(t,Q). (60)
Из соотношения (60) видно, что, если комплексная
огибающая сигнала удовлетворяет условиям (55), (56),
то значения комплексной огибающей корреляционной
функции .при противоположных значениях Ω совпадают.
Свойством симметрии (60) обладают
частотно-модулированные сигналы, которые удовлетворяют условиям
(55), (56).
7. Двойной интеграл от квадрата модуля
комплексной огибающей корреляционной функции равен
единице [23], т. е.
оо
-^|Λ(τ,Ω)|·<ΜΩ=1. ■ (61)
*—оо
Докажем это. Подставляя в левую часть равенства
(61) определение (19), запишем эту часть равенства
в виде
оо
1
ЯЯи{х) **{х ~τ) **{у) и{у ~τ)χ
70
§2,3
Интегрируя по Ω и используя свойства дельта-функции,
находим,
00
4£Γ^\υ(Χ)\'\υ(Χ-τ)\'άχάτ.
—<ю
Разделяя переменные и используя (13), получаем
соотношение (61), что и требовалось доказать.
8. Возьмем четыре различных сигнала и отметим их
индексами m,l,p,q. Рассмотрим взаимокорреляционные функ^
ции /?cm2(x,Q) и Rcpg(x,Cl)t В работе [24] доказано, что
двумерное преобразование Фурье от произведения Rcv ι
*
Rcpq удовлетворяет соотношению
00
/?cwKA)£cpm(*i, ΩΟ = -L·- Γ f /?„Η(τ,Ω) Χ
—οο
Х/?ср?КО)е1(ЙТ,~й,Т) dxdCl. (62)
Подробное доказательство формулы (62) можно найти
также в работе [5].
Правая часть соотношения (62) представляет
среднее значение произведения исходных взаимокорреляци-
онных функций, ;взятое с экспоненциальным весом на
плоскости (τ, Ω).
В частном случае, когда m = l=p = q, из (62)
получаем
00
| R (τ,,Ω.) |» = ^ j j \R (τ,Ω)|» е' (Βτ^°'τ) dxdd. (63)
—00
Равенство (63) означает, что двумерное преобразование
Фурье функции | R (τ, Ω)|2 на плоскости (τ, Ω) равно
значению этой же функции в точке (Γι, Ωι). Кроме того,
соотношение (63) определяет следующее свойство
корреляционной функции: произвольная функция является
«©^реляционной, если двумерное преобразование Фурье
«вадрата ее модуля — неотрицательная функция двух
.аргумента» (t и Ω).
$ 2.3 71
Преобразуем соотношение (62). Умножая обе его
части на ехр(—izti) и интегрируя по ть получаем
00 00
j Ran ΚΑ) koPm (τ,,Ω.) ε"1"' dzx = -L· f ff Rcml (τ,Ω) χ
—00 —00
X kcpq (τ,Ω) е-'°'т е1(°-г)т' dzdQd^. (64)
Интегрируя правую часть (64) по Γι и' используя
фильтрующее свойство дельта-функции, запишем (56) в пнде
оо оо
j/?c?2(ti,a)^m (т1(а)е~1гт' </τι = Г /?сыМ)Х
—00 — -с
ХЛс^(т,г)е-|й'т£Ь. (65)
Рассмотрим частные случаи выражения (65).
а. Пусть p = q = m = l, а г = 0. Тогда
J| ΛΚ,Ω.) Г Л, = J\R(xfe-la'dx. (66)
—00 —00
Из .соотношения (66), так же как и из соотношения (63),
следует, что произвольная функция от τ является
автокорреляционной, если преобразование Фурье квадрата
ее модуля — неотрицательная функция. Соотношение
(66) Отражает следующее свойство корреляционных
функций. Интеграл по τι от квадрата модуля
комплексной огибающей корреляционной функции при
произвольном значении частоты Ωι совпадает с преобразованием
Фурье от квадрата модуля автокорреляционной
функции сигнала. Следовательно, для описания
интегрального характера комплексной огибающей корреляционной
функции достаточно знать только автокорреляционную
функцию сигнала.
б. Пусть p=<q, m=l, 2 = 0. Тогда
00 00
[|/?pmKA)|a^i= $4рЫ/?ст(т)е-'Й'ТЛ. (67)
72
§ U
При Ω! = 0 формула (59) принимает вид
оо оо
У|/?ртЫ|аЛ1= $Лс,ЫЛстЫЛ. (68)
—оо ' —оо
Подобное соотношение приведено ,в работе [25].
в. Пусть ζ = Ωι=0. Тогда (65) запишется как
оо оо
^ Rcql Ы Rcpm Ы dxr = £/?
cml (τ) Hcpq
(τ) dt. (69)
—00 —00
Полученные соотношения (65) — (69) определяют
«интегральные» (т. е. усредненные) характеристики
корреляционных функций на плоскости время —частота. Из
интегральных соотношений (65) — (69) можно найти
оценки средних значений корреляционных функций.
Отметим, что в данном параграфе рассмотрены
только основные свойства корреляционных функций.
Известны также и другие свойства, которые подробно
исследованы в работах [5, 24, 26—36].
!, 2.4. ТЕЛО НЕОПРЕДЕЛЕННОСТИ
Корреляционная функция, определенная в § 2.1,
2.3, является одним из наиболее важных понятий в
теории сигналов. Объясняется это следующим. Передача
и прием сигналов необходимы для получения полезной
информации. Так, в радиолокации надо получить
данные о движении объекта, т. е. измерить его дальность,,
скорость и некоторые другие параметры. Дальность
измеряется по времени запаздывания отраженного от
объекта сигнала, скорость — по его частоте Допплера.
Измерить параметры можно только после уверенного
обнаружения сигнала. Процесс обнаружения сводится к
оптимальной обработке сигнала согласованным фильтром
или коррелятором. Для извлечения полезной
информации может использоваться только напряжение на
выходе согласованного фильтра, так как только пройдя через
фильтр, сигнал в значительно^ мере освобождается от
помех. Поэтому с точки зренид измерения полезных
параметров сигнала в первую очередь интерес предетав-
δ 2.4
73
ляет сигнальная составляющая напряжения на выходе
фильтра (отклика фильтра). А отклик фильтра является
корреляционной функцией сигнала.
При распространении сигнала от передатчика к
приемнику начальная фаза сигнала может изменяться
случайным образом, Случайная составляющая начальной
фазы сигнала полезной информации не несет, поэтому
ее можно исключить из отклика согласованного
фильтра. Это осуществляется детектором, расположенным
после фильтра. Если нормированное напряжение на
выходе согласованного-фильтра описывается
корреляционной функцией r(t), то на выходе линейного детектора—
модулем комплексной огибающей корреляционной
функции \R (t)\, а на выходе квадратичного детектора —
функцией |/? (0|2· 'По этой причине модулю
комплексной огибающей корреляционной функции уделяется
большое внимание. Именно он позволяет судить о точности
измерения полезных параметров сигнала.
Для пояснения ранее сказанного рассмотрим случай
радиолокационного наблюдения за объектом с
индикацией объекта на экране электронного индикатора. При
этом способе наблюдения сигнала напряжение с выхода
детектора поступает на вертикальные отклоняющие
пластины электронно-лучевой трубки.
Предположим, что был излучен, радиоимпульс
(рис. 2.7,а)
«κΗ,(ί)"»#«»(ωοί+θο) для р<*<7\ (1)
где U—амплитуда;
ωό — несущая частота;
θο — начальная фаза;
Τ — длительность сигнала.
Комплексная огибающая радиоимпульса согласнр (2.2.9)
записывается как
Ue% для 0<t<T: (2)
Отраженный импульс μ0τρ(ί) (рис. 2.7,6) 'запаздывает
относительно излученного на время τ3, величина
которого определяется дальностью до объекта. Допустим,
что помех нет. Найдем напряжение на выходе согласо-
74
§2.4
ванного фильтра. Заметим, что форма отклика v(t) не
зависит от времени запаздывания τ3. Это — общее
свойство всех пассивных фильтров. Поэтому, опуская т3,
можно считать, что на входе фильтра действует импульс,
комплексная огибающая которого определяется
формулой (2). Нормированный отклик фильтра (КОрреЛЯЦИ-
ЯиЭлДО
Φ) к
а)
w#,,
=^Рг
')
YCt)
η
/
-τ о
——χ-ι+τ —-
\
V
τ ν
*)
Рис. 2.7.
(.чшая функция) в соответствии с формулой (2.3.9)
записывается как
r(t,Q) = Re/?(t,Q)eKr,
(3)
где /?(τ,Ω) находится по формуле (2.3.19). Отметим, что
начало отсчета времени τ, как показано на рис. 2.7, в
совпадает с окончанием отраженного импульса. Можно
покаэять, что
sln^AllL\1(Br+T)
*(τ,0)=(ΐ--ψ-) QT Х м. е 2 при |τ|<7\
(4)
Допустим, что объект неподвижен, т. е. частота Доппле-
§ 14 7δ
pa Ω = 0. Тогда (4) записывается как
/? (τ) == ι —LiL ПрИ f τ | < г, (5)
и выражение (3) принимает вид
г(т)=А— ilHcosovc при \τ\<Τ. (6)
Из (6) следует, что при Ω=0 автокорреляционная
функция имеет вид треугольного радиоимпульса,
изображенного на рис. 2.7,в. Линейный детектор устраняет
радиочастотное заполнение и выделяет модуль
комплексной огибающей |/?(τ, Ω)|. Поэтому на выходе
детектора напряжение имеет форму треугольного
видеоимпульса (рис. 2.7,г_), который и увидит наблюдатель на
экране индикатора. Положение максимума этого
импульса во времени (запаздывание ха) определяется
дальностью до цели.
Разрешающая способность по дальности определяется
шириной |]/?(τ)|. Если расстояние ^между двумя соседними
объектами таково, что соответствующее ему
запаздывание отраженных импульсов будет больше
длительности Г, то отраженные от объектов импульсы будут
видны на экране индикатора раздельно.
Если цель движется с неизвестной скоростью (Ω^=0),
то комплексная огибающая корреляционной функции (4)
изменяется в зависимости от значения Ω, так как фильтр
перестает быть согласованным с сигналом на его входе
вследствие расстройки по частоте на величину Ω.
Соответственно изменяется и |/? (τ, Ω)|. В этом случае
наблюдатель увидит видеоимпульс, отличающийся от
треугольной формы.
На рис. 2.8 изображены |^(τ,Ω)| при Ω = 0,Ω = π/7\
Ω = 2π/7\ Из рисунка видно, что чем больше
рассогласование по частоте между сигналом и фильтром (больше Ω),
тем меньше максимум |/?(τ,Ω)|. Следовательно, для двух
объектов, движущихся с разными скоростями,
разрешающая способность по скорости будет зависеть от скорости
7α
§ 2.4
изменения |/?(τ,Ω)| при изменении Ω. Чем быстрей
уменьшается максимум | R (τ,Ω)| с ростом Ω, тем выше
разрешающая способность по скорости (частоте Допплера).
Действительно, пусть фильтр согласован с сигналом,
отраженным одним из двух движущихся объектов. Тогда,
полагая Ω4=0, будем считать, что другой объект
движется, со скоростью ιΩ,2=2π/Γ, для которой отраженный
сигнал и фильтр не согласованы. В этом случае от первого
объекта на экране осциллографа наблюдается
треугольный видеоимпульс (Ώ = 0 на рис. 2.8), а от второго —
двойной сглаженный импульс с меньшей амплитудой
(β = 2π/7Ήβ рис. 2.8).
Поэтому эти объекты
можно разделить по скорости.
Отметим, что чем
больше Г, тем быстрей
происходит спад
максимумов, тем лучше
разрешающая способность на-
-"- блюдаемых объектов по
скорости.
Таким образом, из рис.
2.8 можно заключить, что
набор модулей |/?(τ,Ω)| как функций τ при различных Ω
позволяет судить о разрешающих способностях
радиолокационной станции по дальности и скорости. Однако
необходимо отметить, что при этом всегда существует
вероятность того, что выбранные значения Ω только
частично характеризуют разрешающую способность по обеим
координатам. Чтобы устранить такой недостаток,
связанный с конечным числом различных Ω, строят
поверхность | R (τ, Ω) | от двух непрерывно изменяющихся
аргументов τ и Ω. Эта поверхность носит название
поверхности неопределенности.
На рис. 2.9 изображена поверхность
неопределенности прямоугольного радиоимпульса. Она образуется
модулем комплексной огибающей корреляционной
функции | R(x, Ω) I при непрерывном изменении Ω от —оо.
до +оо. Тело, образованное поверхностью
неопределенности и плоскостью координат (τ, Ω), называется телом
§2.4
77
неопределенности. В сечении тела неопределенности
вертикальной плоскостью, проходящей через ось τ,
получается треугольный импульс (рис. 2.8, Ω = 0), в сечении
вертикальной плоскостью, проходящей через ось Ω,—
функция |sin (ΩΓ/2)/(Ω772) | в соответствии с
формулами (2.3.39), (4). В любом сечении тела
неопределенности вертикальной плоскостью, параллельной оси τ,
получается форма напряжения на выходе детектора при
данном значении Ω.
Рис. 2.9.
С точки зрения измерения дальности и скорости
объектов интерес представляет центральная часть тела
неопределенности— основной пик. Его размеры по оси
времени т и оси частот Допплера Ω определяют
разрешающие способности и точности измерений дальности и
скорости.
Оптимальным методом измерения параметра
является такой, при котором отсчет параметра производится
по максимуму напряжения на выходе детектора. При
наличии помех положение максимума становится
случайным. Так как параметр измеряется на, выходе
согласованного фильтра, где уровень помехи много меньше
отклика, то смещение максимума будет малым. Обычно
смещение максимума не превосходит размеры основного
пика. Но и в этом случае при измерении параметров
7S $ 2.4
вследствие действия помех возникают ошибки, которые
приводят к неопределенности отсчета точного значения
параметра. Ошибки зависят от размеров основного
пика, т. е. от вида его поверхности |/? (τ, Ω)|. Именно
поэтому поверхность |/?(τ, Ω) | и получила название
поверхности неопределенности.
Если боковые пики поверхности неопределенности
намного меньше основного, то они на процесс
измерения непосредственно не влияют. Если боковые пики
соизмеримы с основным, то при наличии помех нельзя
с большой достоверностью выделить основной пик.
В этом случае возникает так называемая
неоднозначность отсчета.
Из сказанного ясно, что наибольшее значение для
измерения параметров имеет основной пик. Это
справедливо, если боковые пики относительно малы. Для
такого упрощенного представления поверхности
неопределенности нет необходимости в полном построении
тела неопределенности, что иногда представляет
значительные графические трудности.
Выделить наиболее характерные части тела
неопределенности можно с помощью топографических
диаграмм. Топографические диаграммы строят, используя
линии одинакового уровня, которые определяются из
уравнения
|/?(τ,Ω)| = # = const. (7)
Решая уравнение (7) для различных значений Н,
получаем семейство-линий одинакового уровня на
плоскости (т, Ω). При этом тело неопределенности
изображается аналогично представлению местности на
топографической карте. Однако для характеристики сигнала
с точки зрения разрешающей способности и точности
измерений достаточно выделить несколько линий уровня,
которые соответствуют наиболее характерным
значениям #. В дальнейшем будет использоваться одна
линия уровня (# = 0,5), разделяющая тело
неопределенности на область сильной корреляции |/?|>0,5 и на
область слабой корреляции |/?|<0>5.
На рис. 2.10 изображена линия уровня #=0,5- для
прямоугольного радиоимпульса. Внутри этой линии (гу-
δ 2.4
79
часть (τ>7\
соответствует
стая штриховка) расположена область сильной корреля-
дии, в которой производится измерение, а вне этой
линии— область слабой
корреляции (редкая *'
штриховка). Нсзаштри-
хованная
х<—Т)
1*1 =0-
Из рис. 2.10 видно,
что для прямоугольного
радиоимпульса границы
области сильной
корреляции определяются по
оси времени
длительностью импульса Т, а по
оси частот — величиной
1,19-2:лс/Т~2я7\
Следовательно, чем больше
длительность импульса, тем
больше размер области
сильной корреляции по
оси времени, но тем
меньше ее размер по оси
частот Ω, и наоборот.
Таким образом, для
прямоугольного радиоимпульса
разрешающие
способности по дальности и
скорости зависят друг от
друга. При этом с увели- -г
чением одной из них
другая уменьшается.
Отметим, что такая
взаимосвязь характерна для всех
простых сигналов.
Если используются
сложные сигналы, то
можно повысить
разрешающую способность по
дальности благодаря сжатию их во времени.
Действительно, ширина основного пика, автокорреляционной
Рис. 2.11.
§ 2-4
функции сложного сигнала по оси времени равна
приблизительно \/F=2n/W (см. рис. 1.5). При постоянной
длительности сигнала Т, расширяя W, можно получить
малую длительность основного пика по оси времени.
В то же время ширина основного пика по оси частот
определяется длительностью сигнала и равна 2п/Т.
Поэтому, увеличивая базу сигнала FT, можно получить
основной пик малых размеров. Топографическая
диаграмма для этого случая приведена на рис. 2.11. Чтобы
исключить неоднозначность отсчета, желательно иметь
нулевые боковые пики
в квадрате со сторонами
2Т, 2W. Вне этого квадра-
ра боковые пики равны
нулю, поскольку полная
длительность отклика
(см. рис. 1.5) не может
превышать 2Т, а
смещение спектра сигнала по
частоте на ±iW приводит
к тому, что спектр
сигнала не попадает в полосу
пропускания приемника.
Однако получить
тело неопределенности с
нулевыми боковыми
лепестками невозможно, так как существует
ограничение, которое не позволяет произвольно менять
форму тела неопределенности. Это ограничение
(свойство 7 в § 2.3) получило название принципа
неопределенности [23]. Суть его заключается в том, что объем,
заключенный между поверхностью |/?(τ, Ω)|2 и
плоскостью (т, Ω), не зависит от формы сигнала и равен
единице. Математически это записывается в виде
соотношения (2.3.61). Таким образом, объем тела
неопределенности является постоянным. Поэтому при
одновременном измерении дальности и скорости необходимо
стремиться к такой форме тела неопределенности, при
которой все боковые пики равны и равномерно
распределены в квадрате (2Г, 2W), так как в этом
случае рни минимальны по амплитуде. Тело неопределен-
Рис. 2.12.
ς 2.4
81
ности такой формы изображено на рис. 2.12. Узкий
основной пик стоит на основании высотой Rb. Величина
Rb при равномерном распределении боковых пиков
может быть найдена из формулы (2.3.61). Объем
основания равен
R2S2№T. (8)
Объем части основного пика, выступающей над
основанием, поскольку размеры основного пика равны
2n/W и 2п/Т (см. р_ис. 2.11), определяется следующим
выражением:
О-**)'-£--Τ--Ϊ-. <9>
Множитель π/4 обусловлен тем, что сечение основного
пика в области сильной корреляции близко к эллипсу.
'Суммируя с учетом множителя 1/2π (8), (9) и
учитывая, что
W=2nF, (10)
получаем
tf|4Fr + (l_/y»_£_=l. (П)
Поскольку с ростом FT второе слагаемое в левой
части (11) уменьшается, то при больших значениях FT
им можно пренебречь. Тогда выражение (11) принимает
вид
_1_
2 γ FT'
**=ο-^ϋ· (12)
Из (12) следует, что чем больше база сигнала, тем
меньше боковые пики.
Отметим, что тело неопределенности, изображенное
на рис. 2.12, иногда называют идеальным.
Из сказанного в данном параграфе следует, что
корреляционная функция и тело неопределенности являются
основными понятиями в теории сигналов, так как они
характеризуют сигнал с точки зрения точности
измерений дальности и скорости и разрешающих способностей
82
9 2.5
по этим координатам. Ширина области сильной
корреляции тела неопределенности характеризует точность
измерений и разрешающие способности, область слабой
корреляции — однозначность измерений. Однако этим не
исчерпывается полностью полезность этих понятий.
Известно, что воздействие на вход приемника различного
рода помех (например, пассивных), распределенных по
времени и частоте, оценивается на основе
использования этих понятий.
Более подробно особенности тела неопределенности
и его поверхности рассмотрены в § 2.5 — 2.9.
2.5. СОВМЕСТНОЕ ИЗМЕРЕНИЕ ДАЛЬНОСТИ
И СКОРОСТИ. ПОВЕРХНОСТЬ ВТОРОГО
ПОРЯДКА
Рассмотрим, чем определяются ошибки
совместного измерения дальности и скорости объекта наблюдения.
Необходимо отметить, что обнаружение сигнала,
отраженного от объекта, и определение его параметров
должны производиться одновременно. При наличии
помех задача обнаружения сигнала и измерения его
параметров является статистической. В большинстве случаев
для получения оценки параметров используется метод
максимального правдоподобия (или метод обратных
вероятностей) {23, 37]. В работах [13, 38] показано, что при
большом отношении сигнал/помеха в точке измерения
многие оптимальные методы оценки параметров
сводятся к методу максимального правдоподобия.
Согласно методу максимального правдоподобия
вычисляется отношение правдоподобия или, что
эквивалентно, апостериорная вероятность того, что в принятом
приемником колебании случайные параметры имеют
вполне определенные значения. Если наряду с
полезными случайными параметрами (запаздывание τ3, частота
Допплера Ω) сигнал содержит паразитные, т. е. не
подлежащие измерению, случайные параметры (например,
случайная начальная фаза)> то по этим паразитным
параметрам необходимо произвести усреднение. Известно
[13], что, если помеха представляет нормальный случай-
$ 15 ИЗ
ный процесс с равномерной спектральной плотностью N0,
то апостериорная вероятность того, что в принятом
колебании χ(ί) полезные параметры равны т3 и Ω,
определяется выражением
Ш[хв> Ω |*(/)] = fc.q^ii^.j. (1)
- постоянная величина;
модифицирова'нная функция Бесселя
нулевого порядка;
-огибающая напряжения на выходе
согласованного фильтра. Поскольку постоянная
составляющая задержки на оценку параметра
не влияет, то в общем случае можно
записать:
шЬ,О|*(0] = и[^Г"]· (2)
Далее Ζ (τ, Ω) представляется в виде суммы
сигнальной (отклик) и шумовой составляющих и находятся
ошибки, к которым приводит действие помехи. Но
поскольку помеха вызывает ошибку при измерении
параметров, постольку можно предположить, что на вход
согласованного фильтра поступает сигнал со
случайными параметрами, отличными от тех, для которых фильтр
согласован. Такой подход [39] справедлив, если
отношение сигнал/помеха в точке измерения намного
превышает единицу, т. е. при точных измерениях. Предположив,
что фильтр согласован с сигналом, имеющим параметры
τ = 0, Ω = 0, получим, что для входного сигнала с
параметрами хфО, ΩΦ0 огибающая напряжения на выходе
согласованного фильтра равна Е\ R (τ, Ω) |. В этом
случае выражение (2) записывается как
ю[х,0|х(/)] = М,[-^|ЛМ1)|]. (3)
где τ, Ω — случайные параметры с нулевыми средними
значениями.
Предположим, что 2ΕΙΝ0~^>\. Тогда функцию Бесселя
можно приближенно представить в виде экспоненты;
Здесь ki
Io-
Z(t3, Ω) -
84 $ 2.5
w\z,Q\x(/)] = Кехр [Щ-1R(τ,Ω)|], (4)
где fe2 — постоянная величина.
В дальнейшем исследование апостериорной
вероятности (4) проводится с учетом свойств модуля
комплексной огибающей \R (τ, Ω) |. Отметим, что при малой
помехе ошибки измерений малы и всегда меньше
размеров основного пика тела неопределенности. Поэтому,
рассматривая только область сильной корреляции,
поверхность неопределенности в окрестности точки
максимума (τ=0, Ω = 0) приближенно можно представить
параболоидом вида
| R (τ,Ω) | ~ 1 + -Ι" *"« Έ° + R' VQ + "Г ^'»»Q!' <5>
где принятое обозначение частных производных
(/+*) раз
D ._еК'+*)|^(т,В)|
(6)
τ=0, 0=0
будет использовано и в дальнейшем.
Формула (5) представляет ряд Тейлора, в котором
слагаемые третьего и более высокого порядка малости
отброшены. В общем случае в формулу (5) входит
линейный член, зависящий от τ· Для сложных сигналов
с большой базой в области сильной корреляции он
намного меньше остальных членов в формуле (-5) и им
можно пренебречь.
Подставляя (5) в (4), получаем
ш [τ,Ω | *(/)] = *, ехр 0£-)χ
X ехр [А- (/?''„ ,· + 2ЯVQ + /ГййО°)]. (7)
Сравнивая выражение (7) с двумерным нормальным
законом распределения {40], имеющим вид
§2.5
85
χ?
1 Γ χι ι
w(Xt,x2)= , exp — ψ -\-
,2
ι fXiXa *2
+ , —
(1— /-2)β,β, 2(1 —/·2)β|
(8)
получаем, что апостериорная вероятность (7) является
двумерным нормальным законом распределения
случайных величин τ и Ω. Введя обозначение
q'0 = 2E(N„ (9)
дисперсии, второй центральный смешанный момент и
коэффициент корреляции случайных величин т и Ω
запишем в следующем виде [1]:
(10)
(И)
(12)
Отметим, что при определении σχ0 было использовано
соотношение σχΒ = Γσχσ0.
Отметим общие особенности соотношений (10) — (12).
Из этих соотношений следует, что чем больше отношение
сигнал/помеха q\ , тем меньше дисперсии оценок.
Дисперсии оценок зависят от формы тела неопределенности,
так как в (10) — (12) входят частные производные
выражения (5). При заданных R'\T и R"aa дисперсии оценок
являются минимальными, если га = 0. При этом равна нулю
вторая смешанная производная /?"хВ и смешанная диспер-
2
1
2
°β —
2
°хй
г =
<7о*'\т
ίο^'Όο
г"
<7о*"хй (1
*"*
1
О
1
(1
—
-г·)
-г»)
г')'
86 § 2.5
сия στ8. Поэтому оценки τ и а оказываются независимыми-
В работе [1] отмечено, что г2=0, если линии уровня
| R (τ, Ω) Ι —Η на плоскости (τ, Ω) симметричны
относительно осей координат. Однако не показано, как
следует выбирать сигнал, удовлетворяющий этому
условию. Чтобы ответить на этот вопрос, необходимо
определить частные производные формулы (5).
Отметим, что в (5) входят производные модуля
комплексной огибающей корреляционной функции (2.3.19). Если
/?(τ,Ω) — действительная функция, то в области сильной
корреляции производные от |/?(τ,Ω)| и от /?(τ,Ω)
совпадают, но это не будет иметь места для сигналов,
характеризуемых телами неопределенности, близкими к
идеальному (см. рис. 2.12). Поэтому в общем случае
следует брать производные от функции |/?(τ, Ω)|,
которая может быть записана как
|Λ(τ,Ω)|=[α*(τ>Ω) + *,(τ,α)Γ/2, (13)
где α(τ,Ω) и 6(τ,Ω)— действительная и мнимая части
Λ(τ,Ω).
Наиболее часто на практике применяется сигнал с
постоянной огибающей U (i) = U0=const, т. е.
U(t)=U0emt) при | /1 < Г/2. (14)
Подставляя (14) в формулу (2.3.19), получаем, что при
τ^Ο действительная и мнимая части функции /?(т, Ω)
(13) записываются в следующем виде:
772
a(x,U)=-y- \ cos[fl(/) —θ(/ —τ)-|-Ω/]<//, (15)
-772 +τ
772
6(τ,Ω) = -}τ ί βίη [θ (^) — β(/— τ)4-Ω/1Λ. (16)
-772+τ
Отметим, что
α(0, 0) = Ι, 6(0, 0)=0. (17)
§ 2.5
87
Взяв производные выражения (5) в точке т=0, Ω = 0
и учитывая (17), получаем
При дифференцировании а(х, Ω) (15) и Ь(т, Ω) (16)
по τ в общем случае необходимо учитывать, что нижний
предел интегрирования в (15), (16) зависит от
переменной т. В области сильной корреляции (т<1//г) эта
зависимость является слабой. Докажем это.
Найдем погрешность, возникающую при
отбрасывании τ в нижних пределах интегралов (15), (16).
Переменная т, входящая в предел интегрирования, влияет,
в основном, на форму сечения тела неопределенности
вертикальной плоскостью, проходящей через ось τ, т. е.
на форму модуля автокорреляционной функции, которую
и рассмотрим.
С учетом малых величин, обусловленных переменным
нижним пределом интегрирования в формулах (15), (16)
модуль автокорреляционной функции [может быть записан
в виде |/?(т)|яа 1 -|-/?'ττ + 0,5/?"τττ'. По сравнению с
формулой (5) здесь появился линейный член, в котором
коэффициент при τ равен /?'τ =з α'τ Φ 0. Дифференцируя по
параметру τ соотношение (15), получаем, что производная
/?', = -1/7\
Вблизи границы области сильной корреляции, где
Я (τ) |^0,5, а τ^Ι/2/7, слагаемое 0,5R'\zt" ~ — 0,5.
Линейное слагаемое R\x при том же τ л* l[2F равно— lf2FT.
Если 2/Т;М, то линейным слагаемым в разложении
модуля автокорреляционной функции можно
пренебречь. Следовательно, с погрешностью, примерно
равной l/2Fr«C0,5, переменный нижний предел
интегрирования в формулах (15), (16) может быть заменен
постоянным, равным —Т/2,
(18)
88
§ 2.5
Полагая, что фаза θ(^) «епрерывна и имеет
непрерывные производные, из формул (15) — (18) находим
Г/2 Г/2
R"«=—y- f bn(t)dt-\-\-±r (b'(t)dtY, (19)
—Т/2 —Г/2
Я"»^-7,2/^, (20)
77 2
Я"хВ = -4г j Л'(О Л. (21)
—Г/2
Из формулы (21) следует, что #"τΟ=0, если
функция, описывающая частотную модуляцию сигнала Q'(t),
является четной функцией времени. Поэтому согласно
(10) — (12) сигналы с четной частотной модуляцией
обеспечивают минимальные дисперсии оценок. При этом
линии уровня будут симметричны относительно осей τ, Ω.
Действительно, если θ'(^) — четная функция, то 6(0—
— нечетная функция и |/?(τ,Ω)| = | /?(τ —Ω)| (2.3.60).
Кроме того, для любых б' (t) | R (τ,Ω) | = | /? (— τ, — Ω) | (2.3.43).
Полученный результат о влиянии вида частотной
модуляции на форму тела неопределенности в области
сильной корреляции имеет простое геометрическое
объяснение. Если в (5) положить \R (т, Ω) | =# = const, то
получим уравнение линии уровня, которое является
уравнением эллипса. При ϋ"τβΦ0 большая ось
эллипса наклонена к оси τ под углом -γ (рис. 2.13, пунктир),
который определяется соотношением
tg2Y = 2tfV(tf''„-tf''OB).
Наклон осей эллипса к осям координат (τ,Ω)
определяется взаимной зависимостью оценок дальности и скорости
при их совместном измерении. Если /?"хВ = 0, то оси
эллипса яараллельны осям координат (рис. 2.13, сплошная
линия) и оценки становятся независимыми. Последнее
позволяет измерять параметры независимо друг от
друга. Отметим, что таким свойством обладают все
сигналы с θ'(—t)=Q'(t).
Это означает, что индивидуальные особенности сиг-
§2.6
89
налов оказывают малое влияние на форму тела
неопределенности в области сильной корреляции. Чтобы
доказать это, перейдем к более детальному представлению
поверхности тела неопределенности в области сильной
корреляции, а именно к поверхности четвертого порядка.
Рис. 2.13.
2.6. ОБЛАСТЬ СИЛЬНОЙ КОРРЕЛЯЦИИ.
ПОВЕРХНОСТЬ ЧЕТВЕРТОГО ПОРЯДКА
Поверхность тела неопределенности в области
сильной корреляции имеет вид
| R (τ,Ω) |=1+4 (/?V· + *"ΒΒΩ') +
Слагаемое, содержащего /?"χΒ, нет, так как здесь и в
дальнейшем рассматриваются сигналы только с четной
функцией θ'(ί). Члены третьего порядка, а также #""хВВВ и
#""хххВ равны нулю вследствие симметрии функции |/?(τ,Ω)ι
относительно осей τ, Ω.
Проводя четырехкратное дифференцирование
выражения (1) и отбрасывая слагаемые, равные нулю и вы-
90 § U
сокого порядка малости, получаем, что
R"" =а"" — 6а" Ш Υ — 3 ψ )4 4-
4 χτχχ χτχχ χχ \ χ' \ χ/ Ι
Γ/2
+ 4ί//"χ„ = -1- | [β"(0-3θ""(0-4β'(0β"'(ί)]Λ +
—Γ/2
Γ/2 . Γ/2 Γ/2
4-6-τ- f e'W(-f- f вчол)'— 3(4" [β'(0Λι*4-
—Γ/2 —Γ/2 —Γ/2
Γ/2 Γ/2
4-4 (-f j θ' (0 Λ) -f j [θ'" (0 - θ" (01 dt, (2)
—Γ/2 —Γ/2
*"'«« = «""■« = 7780. Ο)
7/2 Γ/2
= ^. р«вм(0Л4-^-(-у- j в'(Ол)'—
—Γ/2 —Г/2
Г/2 Г/2
— 2-Jr Γβ'ίΟΛ-τ- f ^'(0*· (4)
—Г/2 —Г/2
Степенная модуляция. Анализ формул (2) —(4) и
(2.5.19) в общем виде затруднителен. Можно доказать
только, что /?"„<0. Для дальнейшего анализа
необходимо определить в общем виде закон частотной модуляции
О' (/). Положим что
β'(ί) = -^-|ί»| при |/1<Г/2. (5)
Нормирующий множитель в выражении (5) выбран
таким образом, что ширина спектра сигнала F=WI2n
равна девиации частоты. Показатель степени k может быть
любым числом ^0.
На рис. 2.14 изображены графики θ'(0.
построенные в соответствии с (5) для наиболее часто
встречающихся случаев четной частотной модуляции,
«2.6
91
Для Q'{t), представленной формулой (5), выражения
(2.5.19), (2), (4) при отбрасывании малых высокого
порядка принимают вид
R/> =~W1
&
-(2* + i)(*+;i)« *
Dim _ ψ* [_J ι 6
(Л+1)(3* + 1) (fe.+ l)4J'
RwrMt = WTt
4(2fe + 3) ' \2(k+ I)2
~~2(A + 1)(A+3)J-
ι\\ίί
//
Is Ν
^
I
-f
-V
Рис.
7
2.14.
0,5
Τ
(6)
(7)
(8)
Зависимости (6) — (8) в нормированном виде
записываются соответственно как
m{k)=\R"JW-\
<!(k) = R""„„W-\l(k) = R">>(WT)
(0)
Графически зависимости (9) представлены на
рис. 2.15. Отметим, что при k—»-оо они стремятся
к нулю.
Определим влияние закона частотной модуляции
θ'(0 сигнала на форму тела неопределенности в
области сильной корреляции. Сначала рассмотрим сечение
92
9 2.6
поверхности тела неопределенности (1) вертикальной
плоскостью, проходящей через ось Ω, т. е. |#(Ω)|.
Согласно (1)
| R (Ω) | = 1 + 4" *"*«Qa + -W *""йййй°4· <10)
Обе производные в формуле (10) согласно (2.5.20) и (3^
не зависят от b'(t), а определяются только длительностью
сигнала Т. Это следует из того, что |/?(Ω)| зависит
только от огибающей сигнала U(t) (2.3.39) и не зависит
от фазы Q(t).
m,q,l Ι Ι Ι I I
1 2 3 ч- к
Рис. 2.15.
Теперь рассмотрим сечение поверхности тела
неопределенности вертикальной плоскостью, проходящей через
ось τ, т. е. |/?Ы|. Из (1) получаем, что
Здесь вт,орая производная (6) отрицательна. Поэтому,
S 2.β
93
чем она больше, тем резче уменьшается основной пик по
оси τ. Четвертая производная всегда положительна и
поэтому замедляет резкий спад основного пика,
обусловленный второй производной.
Зная характер изменения производных в (11) от
значения показателя степени k, можно определить сигналы,
которые обеспечивают
наиболее точное изме- \цщ
рение дальности при
заданной ширине
спектра сигнала F. Из
анализа графиков рис.
2,15 следует, что для
точного измерения
дальности необходимо
применять сигналы с
fe = I -н2. При этих
значениях \k вторая
производная,
пропорциональная т (9), макси·'
мальна (рис. 2.15), а
четвертая,
пропорциональная q, изменяется
медленно. Значение
k=l соответствует
сигналу с симметричной
линейной частотной
модуляцией (СЛЧМ),
а к = 2 — сигналу с
квадратичной
частотной модуляцией (КЧМ)
(см. рис. 2.14).
На рис. 2.16 приведены автокорреляционные
функции для k=\\2; 1; 2; 3; 4, построенные по формуле (1)
при Ω = 0. Из рисунка видно, что значения k=l; 2
действительно обеспечивают наиболее сильное уменьшение
автокорреляционной функции в области сильной
корреляции, Поэтому сигналы с СЛЧМ и КЧМ можно
считать наилучшими для точного измерения дальности.
В общем случае, когда при малых τ и Ω
справедливо представление (1), к слагаемым в (10), (11)
добавив
0,6
а*
0,2
/*
X3
г
To.s
Η·1
я*
Ofi
tr
Рис 2.16.
94 § 2.6
ляется член со. смешанной производной, Так как эта
производная положительна {l(k) на рис. 2.15] тс она
расширяет произвольное вертикальное сечение тела
неопределенности при хфО и ΩφΟ. Минимум l(k) равен
нулю для немодулированного импульса (k=0). Но
такой сигнал не позволяет получить малые размеры
области высокой корреляции по оси τ. Поэтому можно
считать, что сигналы с k=l+2 будут лучшими для
совместного измерения дальности и скорости объекта,
поскольку в этой области значений k производная /?"ττ
максимальна, a l(k) и q(k) слабо изменяются с
изменением k. Из анализа графиков, приведенных на
рис. 2.15, следует, что индивидуальные свойства
сигналов слабо влияют на область сильной корреляции,
поскольку при fe>0,5 коэффициенты т, I, q меняются
медленно.
Этот вывод может быть получен также при
исследовании поверхности четвертого порядка (1) с помощью
линий уровня. Уравнение линии уровня записывается
в виде
|Я(х,0)| =tf = const, (12)
где | /?(τ,Ω) | определяется выражением (1).
Обозначая
R"" \R" I
L=6 « ххйп M = VW JUJlL. (14)
/1Я''"„хх1|Я""ВЙВй1 V\*""™\
Ν = γΤ—^=^,Λ=1-Η, (15)
У * ββοο
получаем уравнение линии уровня в канонической форме:
y* + Ly3x3 + x* — Ny3 — Жла + а = 0. (16)
Алгебраическое уравнение (16) описывает кривую
четвертого порядка. Необходимо отметить, что
уравнение кривой (16) не может быть сведено к известным
[41] при любых значениях коэффициентов L, М, N.
§ 2.6 95
Поскольку уравнение (16) является биквадратным
относительно у, то
у = ± -~= [(N — Lx*) =t γ{Ν—Ljca)a+4(jc*+ Меа—α)]1/2.
(17)
Опуская подробности исследования кривой (17),
перейдем к топографическим диаграммам. На рис. 2.17,а
изображены линии уровня при различных а=\—Η для
k=\, а на рис. 2.17,6 для /г = 2. На этих рисунках по-
0,5 ifi χ 0,5 U0 χ
α) δ)
Рис. 2.17.
казан только один квадрант, поскольку линии уровня
симметричны относительно осей χ и у. В зависимости от
параметра а линия уровня может состоять из
различного числа овалов (двух или шести). При α=Ό
центральный овал, стягивается в точку (максимум тела
неопределенности). С точки зрения формы тела
неопределенности интерес представляет только центральный овал.
На рисунках этот овал изображен утолщенными
линиями. Остальные овалы расположены при таких
значениях χ и у, при которых представление (1) не является
справедливым. При малых *a(l^//^Q,5) центральный
овал (область сильной корреляции) близок к эллипсу*
хотя и не является им. Эллипс на рис. 2.17 изображен
пунктиром для а = 0,4. Из сравнения центральных ова-
96
9 2.6
лов видно, что овалы при а=0,2; 0,4 для k=\\ 2 по
форме практически не отличаются друг от друга.
Следовательно, индивидуальные свойства сигналов почти не
сказываются на форме поверхности тела
неопределенности в области сильной корреляции. Однако следует
учитывать, что на рис. 2.17 масштаб по оси χ (13)
зависит от значения k, так как R""„„ есть функция к (7)#
Но это разница между масштабами по оси χ будет не-
1*1
0,75
0,50
0,26
О
Я-0
\г
*-Д
0,5 1
\Я\
0,75
0,50
0,2S
О
V
s=wf
> 2
к-1
0,5$. \/2
W
■0,75
0,50
0,25
О
Ζ=\Νψ
f-*^k=1
2
В)
v/2Vf
0,5\/5 \/5
з) ^tF
Рис. 2.18.
значительная: для k=\ имеем x = Q,\bWx, а для k =
= 2 имеем x = 0,\6Wt.
Рассмотрим теперь некоторые сечения тел
неопределенности сравниваемых сигналов {k=\ и k = 2). Как
будет показано в § 3.2, для сигнала с СЛЧМ (к=\) тело
неопределенности с точностью до малых высокого
порядка описывается выражением
где
[Я (τ,Ω) | = 4" YR\ + Rl + 2R*R* cos -T~ '
2хГ — Q.T . 2tW + QT
sln-
sln-
/?, = ■
2-zW — QT
» #2 =
2tW + QT
(18)
(19)
На рис. 2.18 сплошными линиями изображены
сечения тела неопределенности сигнала с СЛЧМ для Ω = 0;
9 24
97
Q = Wr/T, Q = 2WxjT. Пунктиром изображены
соответствующие сечения для сигнала с КЧМ, которые, как
будет показано в § 3.4, описываются выражением
|/?(τ,Ω)|=4-/-^-Χ
Χ Υ \С (ζ,) - С (г,)]2 + \S (ζ,) ^Ъ'Щ''
где С (ζ) и S(z)—интегралы Френеля [42];
/WT ( χ . Q.T V
/2Wi Л τ Q.T
(20)
(21)
Из сравнения сечений, приведенных на рис. 2.18,
видно, что в области сильной корреляции (|/?| з* 0,5) разница
между ними для обоих сигналов незначительна.
Существенное различие появляется только'при |/?|<0,5.
Анализ области сильной корреляции, проведенный
в § 2.5, 2.6, был основан на использовании
приближенных выражений (2.5.5), (1).
Поясним границы
применимости этих формул на примере
КЧМ сигнала.
На рис. 2.19 оплошной
линией изображено сечение тела
неопределенности для сигнала
с КЧМ при Q = WxlT,
построенное по точным формулам (20),
(21). Пунктиром изображено
сечение, соответствующее
квадратичному представлению
(2.5.5), а штрих-пунктиром —
сечение поверхности
четвертого тюрядка (1). Из
рисунка видно, что квадратичное
приближение справедливо
в области 1^|/? |^0,8. Использование приближения
четвертого порядка позволяет расширить область пред-
Ц5/2 s/lKf
Рис. 2.19.
98
§2.7
ставления тела неопределенности до значений
1 >|1?1>0(5.
Все, что было сказано в § 2.5, 2.6, справедливо для
сигналов, фаза которых непрерывна и имеет
непрерывную первую производную, и не справедливо для
сигналов, фаза которых дискретна (фазоманнпулированные
сигналы). Но, как будет показано в гл. 4, фазовый
спектр таких сигналов является непрерывной функцией
частоты. Поэтому для определения производных
\R (τ, Ω) I можно пользоваться частотным
представлением комплексной огибающей корреляционной
функции (2.3.20).
2.7. СОВМЕСТНОЕ ИЗМЕРЕНИЕ ДАЛЬНОСТИ,
СКОРОСТИ И УСКОРЕНИЯ
Неравномерное движение объекта. В большинстве
случаев движение объекта относительно точки приема
отраженного сигнала нельзя считать равномерным.
Характерным примером является пролет летящего с
постоянной скоростью объекта над радиолокационной
станцией (РЛС). В этом случае радиальная скорость
объекта, определяемая первой производной дальности по
времени, является функцией времени. Траектория
движения объекта относительно РЛС определяется не
только радиальной скоростью, но и производными
дальности по времени более высокого порядка. Все эти
производные влияют на структуру отраженного сигнала.
Если фильтр согласован с сигналом без учета движения
объекта, то неизбежно рассогласование между
отраженным сигналом и фильтром. Это рассогласование
приводит к уменьшению величины основного пика отклика
фильтра, т. е. к уменьшению отношения сигнал/помеха,
и к искажению формы пика, т. е. к ухудшению
разрешающих способностей по дальности и скорости.
Возможно также смещение основного пика относительно
исходного положения, что приводит к грубым ошибкам
при измерении параметров движения объекта.
Следовательно, необходимо определить величину потерь в отно-
§ 2.7
99
шении сигнал/помеха и характер искажений, вызванных
высшими производными дальности по времени.
Ютметим, что если искажения значительны, то их
можно использовать для измерения высших
производных дальности, что позволяет уточнять траекторию
движения объекта. Но при этом возникают проблемы
выбора схемы оптимального измерителя, определения
потенциальных точностей измерения и влияния формы
сигнала на точность измерения.
Исследование влияния большого числа производных
высокого порядка на обнаружение отраженного сигнала
представляет сложную математическую задачу. Поэтому
обычно учитывается только ускорение, т. е. вторая
производная дальности по времени. Пока скорости
объектов и длительности сигналов были относительно
невелики, ускорение объектов было тоже относительно мало
и его величина не сказывалась на результате
обработки сигналов. Это имело место даже для некоторых
космических объектов. Однако с увеличением
длительностей сигналов, обрабатываемых когерентно, ускорение
стало приводить к ощутимым дополнительным потерям
в отношении сигнал/помеха. Поэтому в случаях
ускоренного движения объекта необходимо учитывать его
ускорение1.
Рассмотрим сигнал, отраженный от движущегося
объекта. Пусть для излученного сигнала
иЦ)Ф0 три 0<Й<7\ (1)
Отраженный сигнал запаздывает относительно
излученного. Поскольку объект движется, то время
запаздывания τ3 в общем случае является функцией времени, т. е.
Xa=ta(t)· Поэтому отраженный сигнал без учета
изменения амплитуды имеет вид
a[t-r3(t)}. (2)
Определим влияние скорости и ускорения объекта
на характер изменения хл во времени. Передний фронт
сигнала (1) излучается в момент времени t = 0, в мо-
1 Совместному измерению дальности, скорости и ускорения
посвящены ооновополагающие работы [43—49]. Отдельные аспекты
этой проблемы рассмотрены в [50, 51].
100
§ 2.7
мент ί=τ3ο/2 он отражается от объекта и в момент t =
—Хза приходит в приемник. Измеренное значение
задержки переднего фронта сигнала τ3ο определяет дальность
до объекта в момент времени ί=τ3ο/2. Поэтому время
задержки любой части отраженного сигнала в общем
случае определяется из следующего функционального
соотношения:
:ψ = ±0^-2ψ.γ (3)
где с — скорость света;
D — дальность.
Левая часть выражения (3) представляет момент
отражения произвольной части сигнала от объекта,
правая часть — тот же момент времени, но выраженный
через дальность до объекта D в момент отражения.
Траектория движения реальных объектов не может
значительно измениться за время, равное длительности
сигнала. Поэтому зависимость τΒ(ί) в окрестности
точки ί=τ3ο можно представить функцией вида
Мг) = *зо+Р(г-0+а(г-х3„)8+... (4)
Определим коэффициенты β и а. Дифференцируя по t
(4) и полагая t=Xso, получаем
Ρ = τ',(τΒο), (5)
α = 0,5τ"8(τΒο). (6)
Дифференцируя по t соотношение (3), находимτ'η(ί)
и х"з(Ь- Подставляя найденные производные при ί=»
=Тао в (5), (б), получаем
β = 2υ (0,5τΒο) [ί + ο (0,5τΒ0)].-«« 2ν (0,5τΒο)/£, (7)
α = с'а (0,5хао) [с+υ (0,5τΒο] ~* « а (0,5твв)/с, (8)
где радиальная скорость
v(t)=D'(t), (9)
а ускорение
α(/)-0"(ί). (10)
§2.7
101
Отметим, что приближенные равенства в формулах (7),
(8) получены при условии и<с, что всегда имеет место
для реальных объектов. Например, если ^^20 км/сек,
то г>/с<10~4. Формулы (7), (8) определяют
коэффициенты β и α в момент отражения переднего фронта
сигнала от объекта.
Подставляя (4) в (2) и записывая отраженный
сигнал в виде аналитического, получаем
« Ιί — х3(01 = «Ιί — т30 — β(ί — xso) — α(ί — х3о)я]. (Π)
Поскольку аналитический сигнал согласно ('2.2.8)
определяется как
tf(i)=£/(i)exp(i<V), (12)
то
U [t — τ3 (t)] = U[t—xa (t)] exp {ίω0 [t — τ3 (t)]} =
= U\t — τ30— Щ — xao) — a{t — zsoy] exp {— i<o0 [τΒο +
+ β('-τ3„) + α(ί-τ3„)4 + 40· (13)
Аналогично (2.2.9) комплексная огибающая отраженного
сигнала (И) записывается в виде
£/[(l.-P)(i-W-«(i — *э0)а]ехр{-1<о0[тао +
+ β (^ — -»зо) -Ь α (ί — χ3ο)2]}. (14)
Перейдем к рассмотрению прохождения сигнала
с комплексной огибающей (14) через согласованный
фильтр.
Корреляционная функция. Допустим, что фильтр
согласован с сигналом, параметры которого равны тзс, ас,
βο Комплексная огибающая такого сигнала согласно
(14) имеет вид
• £/[(1 — рс) (t — тас) — ас (/— x3c)aJ exp {— ΐω0 [твс +
+ Pc(i-t8c)4-«c(i-Ma]}· (15)
Подставим (14), (15) в формулу (2.3.5) для комплексной
огибающей корреляционной функции двух сигналов, подра>
зумевая под Um{t) комплексную огибающую отраженного·
сигнала (14)( а под Ui{t)>— комплексную ©рибающую сиг-
102
§ 2.7
нала, с которым фильтр согласован (15). Обозначая
произвольную задержку τ в (2.3.5) через хь получаем
оо
/?(т„ т30, β, α, тзс> рс, ас)==2^_ j £/[(1 - β)(ί-
—оо
- τ30) - α (ί - τ 30)2j £[( 1 - рс) (ί - тзс - τ,)-
- ас (ί — тзс — τ,)2] exp {— ίω0 [τ30 + β (ί — τ3ο) +
+ α (ί — τ3ο)2] + К 1тзс + Рс (ί — τ3ε — τ,) + ас (ί — t3c —
-τ,)2]}^· (16)
Здесь Ε0, £с— энергии, соответствующие сигналам
с комплексными огибающими (14), (15) и
определяющиеся как
£ο = £/(1-β), £с = Я/(1-Рс). (17)
Произведя замену переменных (ti = t—τ30) и обозначив
τ = τ30—Тзо+Ть (18)
запишем (16) в виде
оо
/?(х,р,рс,а,ас)= ^^4=: J |/1(1 — β)ί —«ί·Ι ί/[(1 - β0)χ
—00
X (t — τ) — ас (t — τ)2] exp {— ίω0 (τ30 — тзс) —
- ίω0 ψ + α*») + ίω0 [β0 (ί - τ) + ас (ί -τ)»]} at (19)
Корреляционная функция (19) зависит от пяти
параметров: задержки τ (18), коэффициентов β, рс,
которые пропорциональны скоростям (7), и коэффициентов
а, ас, которые пропорциональны ускорениям (8). В (19)
имеются фазовые множители, не зависящие от t и не
влияющие на точность измерения параметров τ, β, α.
Поэтому эти множители можно опустить. Тогда формула
(19) примет вид
оо
Я(т,р.ре.«.ас)=_1= j £/[(]_ β)г-аО']*7[(1-рс)Х
—оо
X (t — t) — ае (t — τ)2] exp К фс — β) t + ίω„ <ас — α) ί2 —
— ίω„2α0τί] fifi, (20)
$ 2.7
103
Из (20) следует, что скорости и ускорения влияют на
комплексную огибающую корреляционной функции как
через фазовый множитель, так и через аргументы
комплексных огибающих сигналов. Когда аргументы
комплексных огибающих сигналов зависят от времени,
происходит изменение масштаба времени. При ас ?^0, а=?^0
изменение масштаба по оси времени является
нелинейным.
Рассмотрим равномерное движение объекта, т. е.
ас = а=0. В этом случае (20) записывается как
оо
Л(*>Ш = — *==- $17[(1-Р)*]£П(1-Рс)(*-х)]Х
—оо
XexpK(pc-p)i]rfi. (21)
Введем новую переменную
·*, = (!-?)* (22)
и обозначим
,„=(1-0),. (23)
Тогда с учетом (17) формула (21) примет вид
- ~°°
Xexp(i4^ii)^i. (24)
Как было отмечено ранее, для всех реальных
объектов υ<ί, τ. е.
β<1, 'Рс«1. ■ (25)
Тогда величинами β и рс в множителе, стоящем перед
интегралом, можно пренебречь по сравнению с
единицей. Это объясняется тем, что β и gc влияют, причем
слабо, только на амплитуду и не влияют на форму
огибающей /?(,„, β, рс)
104
§ 2.7
Аналогично можно поступить с величиной β" в
знаменателе показателя экспоненты. Обозначая
Δβ = рс — β, (26)
множитель в аргументе огибающей U в (24) с учетом (25)
можно представить в виде
(1-βο)/(1-β)^1-Δβ. (27)
Подставляя (26), (27) в (24) и опуская индексы у it и
τ„, получаем
00
/?(τ,Δβ)=---^ j £/(0 £>[(1 — Δβ)(ί — χ)] Χ
—οο
Xexp(i«vWi.· (28)
Определим, 'при каких значениях скоростей объектов
можно пренебречь изменением масштаба времени, т. е.
слагаемым Δβ в аргументе комплексной огибающей сигнала
U по сравнению с единицей. Множитель 1 —Δβ входит
•
как в огибающую сигнала U\{\—Δβ)(ί— τ)], так и в его
фазу θ[(1—Δβ) (t—τ)]. Расчеты показывают, что'
влияние Δβ в огибающей на значение R (τ, Δβ) значительно
слабее по сравнению с влиянием Δβ в фазе. Поэтому,
пренебрегая Δβ в огибающей по сравнению с единицей,
приближенно запишем (28) в следующем виде:
оо
Л (τ, т^ш \U(t)U(t-x)exp{ib(t)-
—оо
- ίθ [(1 — Δβ) (t - τ)] + i ω0Δβί} dt. (29)
При Δβ < 1
θ[(1— Δβ)(ί — τ)]^6(ί — τ) — Δβ(ί — τ) θ' (ί — τ). (30)
§2.7
105
С учетом (30) выражение (29) принимает вид
/?(τ,,Δβ)~2-^ \u(t)U(t — τ) exp (i ω0Δβί) exp [ι Δβ (ί —
—эо
ОО
-τ)θ'(ί-τ)]Λ~2-^ J£/(0i/(i-T)eK^ [1 +
—αο
-J- i Δβ (ί — τ)θ'(ί — τ)] Λ. (31)
Обозначая
Ω = Δβω0, (32)
формулу (31) запишем в следующем виде:
/?(τ,Δβ)^/?(τ,Ω) + ΔΛ(τ,Δβ), (33)
где корреляционная функция /?(τ, Ω) определяется
формулой (2.3.19), а
оо
Δ/?(τ,Δβ) = ^- Ut-x)V{t-z)U{t)U{t-z)ewdt. (34)
—оо
Изменение комплексной огибающей корреляционной
функции (34) обусловлено изменением масштаба
времени.
Оценим максимальное значение Δ/?(τ, Δβ). Допустим,
что
Θ'(0μΒκο<^ = 2^, (35)
где F-~г- ширина спектра сигнала. Пользуясь
неравенством Буняковского — Шварца и полагая, что U(t) мало
изменяется за время, равное длительности сигнала Т,
приближенно получаем, что Δ R (τ, p)^i2ApF7\ Тогда
согласно (33) запишем, что
| R (τ, Δβ) Ι < IR (τ, Ω) + i A$2FT1 < | R (τ, Ω) | -4- Δβ2/Τ. (36)
В области сильной корреляции | R(x, Ω)| =s 1. Поэтому,
если выполняется неравенство
Ff<l/2Ap\ (37)
то изменением масштаба времени можно пренебречь.
106 § 2.7
Предположим, что изменение величины тела
неопределенности из-за изменения масштаба времени не
превосходит заданной величины ε (потери в отношении
сигнал/помеха). Тогда допустимая база сигнала
/Τ=ε/2Δβ. (38)
Например, если с = 20 км/сек, то Δβ= 1,33· Ю-4.
Положив 6=10% (потери приблизительно 1 дб),
получаем /Т«400. Если v=l км/сек, то при том же ε
допустимое /Т = 8 000. Из этих примеров следует, что при
допустимых базах сигнала порядка нескольких сотен —
тысяч (в зависимости от скорости объекта) при
расчетах можно не учитывать изменение масштаба времени.
Неравенство (37) можно получить непосредственно
из (31), если предположить, что изменение фазы,
обусловленное аргументом Δβ(ί—τ)θ'(ί—τ), намного
меньше π. Поскольку i—τ<Τ, а θ'(ιί—t)^W, то
Δβ(ί—τ)θ'(ί—τ)<ΔβΓ№. (39)
Полагая, что
Δβ7ΊΤ«π,
и используя равенство W=2nF, получаем
/Τ<1/2Δβ, (40)
что совпадает с (37) Скорость движения объекта
определяется величинами β, ιβ0, Δβ [формулы (7), (26)].
Задавая базу сигнала FT, согласно неравенству (37) или
равенству (38) можно найти величины β, β0ι ΙΔβ, а
соответственно и скорость, при которой с изменением
масштаба времени можно не считаться.
Рассмотрим движение объекта, для которого
ускорение не равно нулю (20). Определим условия, при
которых можно пренебречь изменением масштаба
времени в комплексных огибающих из-за ускорения. Можно
показать, что ускорение, котооое входит в аргументы
*
комплексных огибающих U и U, приводит в основном
к изменению фазы
—atzQ'(t)+ac(t—ΐ)2θ'(ί—τ). (41)
§ 2.7
107
Чтобы изменением масштаба времени в (20) можно
было пренебречь, достаточно положить, чтобы изменение
фазы (41) было много меньше π. Поскольку —at2Q'(t) +
+ αϋ(ί-τ)2θ'(ί-τ)<2αΓ%, то, полагая
2aTzW<^n, (42)
'получаем
FT<l/4aT. (43)
Выясним, что означает условие (43). Так как α — α/c
(8)- т0 „ „
4«7'«l^=a-ZL*!L· (44)
С V С v '
Для реальных объектов, как было отмечено ранее,
v/c<^l. Обычно скорости объектов таковы, что и 4о/с<^С
<1. Величина aTjv также меньше единицы. Если
предположить, что αΤ=υ, то за время, равное
длительности сигнала, скорость объекта должна стать вдвое
больше начальной, что вряд ли возможно для реальных
объектов. Даже полагая aT/v = l, из (43), (44)
получаем
FT < isp- («)
Неравенство (45) аналогично неравенству (40), так как
Δβ определяет скорость объекта [формулы (7), (26)].
Следовательно, при базе сигнала, удовлетворяющей
неравенству (40) или (45), можно не учитывать в
подынтегральном выражении интеграла (20) изменения
масштаба времени при равномерном и равноускоренном
движениях объекта. В дальнейшем будем
рассматривать случай, когда изменение масштаба времени можно
не учитывать. Поэтому из (20) имеем
R (τ, Ω, μ, цс) = 2F f U(t) U(t » τ) exp (i Ot +
—00
+ i |if ■ — i 2μ0τί) at, (46)
где
μ = Κ — «)ωο. (47)
V-e = «c°>o (48)
108
lit
— величины, пропорциональные ускорениям, которые
будем для простоты называть ускорениями.
Как следует из (46), корреляционная функция
зависит не только от разности ускорений (47), но и от
абсолютного значения μ0 (48). Для случая полного
согласования фильтра с отраженным сигналом (τ = 0, Ω = 0, μ=.
=0) корреляционная функция
Л(0,0.0,щ.)=1. (49)
Перейдем к анализу точности измерений величин τ,
Ω, μ, входящих в формулу (46).
Точность измерений дальности, скорости и ускорения.
Предварительно сделаем следующие замечания.
Известно [47], что наибольшая точность измерения дальности
до объекта при ограниченной ширине спектра сигнала
может быть достигнута при использовании в РЛС
сигнала, спектр которого имеет вид двух дельта-функций
(два узких импульса на оси частот — двухчастотный
сигнал). Но в этом случае имеет место неоднозначность
отсчета. Аналогично, наибольшая точность измерения
скорости при ограниченной длительности сигнала
достигается при сигнале, состоящем из двух коротких
импульсов, расположенных на краях отведенного под
сигнал отрезка времени. Поскольку ускорение есть
приращение скорости, то для его измерения недостаточно
двух импульсов. Необходим сигнал, состоящий из трех
Импульсов. Он позволяет по двум измерениям
скорости найти ее приращение [45]. Однако подобные
сигналы обладают существенными недостатками. Во-первых,
при ограниченной пиковой мощности использование
коротких импульсов на большом временном интервале
невыгодно, так как уменьшается излучаемая энергия
сигнала. Во-вторых, имеет место неоднозначность
измерений скорости и ускорения, так же как и при измерении
дальности двухчастотным сигналом. Чтобы устранить
эти недостатки, необходимо излучать сигнал, полностью
занимающий отведенный отрезок времени. Будем
полагать, что его огибающая постоянна, т. е. U(t) = Uo при
§2.7
105
\t\^.T/2. Тогда согласно (46) запишем
Г/2
Λ(τ,Ω,μ,|ΐβ)=τ- f exp{i[6(0— β(ί —τ) + Οί +
—Γ/2
+ μί2 — 2μβτί]}Λ. ' (50)
Отметим, что пределы интегрирования в (50)
постоянны, так как рассматривается только область
сильной корреляции.
В соответствии с методикой, изложенной в § 2.5,
апостериорную вероятность (2.5.4.) запишем в виде
«0[τ.α|ΐ.μβ|*(Ο]=*.βΧρ ρ^-|/?(τ,Ω,μια0)|]. (51)
Представим | /?(τ, Ω, μ, μ0)] усеченным рядом Тейлора по
трем переменным τ, Ω, μ в окрестности точки максимума
(τ=>0, Ω = 0, μ = 0). Этот ряд имеет вид
|/?(τ)Ω,μ,μ0)|=1+0,5/?ν2 + 0.5^"ΒβΩί+0.5/?ν° +
+ *νΩ+/?"βμΩμ + /?'>τ· (52)
Напомним, что частные производные модуля
комплексной огибающей корреляционной функции в (52)
определяются в точке (τ=0, Ω=0, μ = 0) в соответствии с
формулой (2.5.6). Слагаемые с первыми производными
отсутствуют, так как при τ = 0, μ = 0, Ω = 0 выражение (50)
имеет максимум, равный единице.
Обозначая ς20 = 2Ε[Να и подставляя (52) в (51),
получаем
w (τ, Ω, μ, μ01 χ (ή\ = k3 exp q\ exp l0,5tf"„xa + 0,5/?"йй^ +
+ 0.5R "^ + /?"χβτΩ + /?"βμΩμ + /?"μχμτ]. (53)
Полагая, что вследствие действия помех параметры
сигнала τ, Ω, μ являются случайными величинами, сравним
выражение (53) с распределением трех случайных
коррелированных величин, распределенных по нормально-
по
§2.7
му закону с нулевыми средними, которое имеет вид[40]
[~
^3 (-"-1> %2г -"-з) ^3 6ХР КГ" 2 1 2 "^2
'~ ri2 v2 , 2(ru —ггага1) ι
где
х3Хз+ 2(Г,,~'"Г,,) *.*»]. (54)
Δ = 1 — г*2— 4— Гз,+ 2г1агазг3>; (55)
°м σ2 ■ °з — дисперсии случайных величин;
Гц. ''гз. ''si— коэффициенты корреляции.
Сравнивая (53) и (54), замечаем, что если обозначить
х1 = х1, Q = xa, μ=χ3. то
° = 5 j . (56)
σ1 = --^— ±^L, (57)
ϊο«".
г 1 1 — '12
О = 5 X · (58)
Используя определение второго смешанного момента [40]
а1Ч=ГРЧвР?Я· (59)
запишем совместные дисперсии рассматриваемых величин
в виде
σ
(60)
_г 1 Гц (Гц —ftxrxi) /ftl \
■*~ΊΪ*%—5—· ( >
_г ' r>\ \rt\ — г\гггх) 1М\
-~^v 1 " ( }
§2.7
111
Коэффициенты корреляции в (60) — (62) с учетом (59)
определяются через параметры распределения (53) с
помощью следующих уравнений:
(/•li-ra3r3l)a(l-4)"1(l-''3.)-1 = ^"J2(^"^"00)-1.
(63)
(гм —г»г„)"(1 -й)-(1 -ΓΪ2)-' = (/?"^» (/?"„/?"„»)"·
(64)
(ΓΗ-Γ,Λ^ίΐ-^-ίΐ-Γ^-^ί/?';,)1^"^'^)-1·
(65)
Отметим особенности результатов (56) — (58) и (60) —
(65). Если все смешанные производные в разложении
(53) равны нулю, то из уравнений (63) — (65) следует,
что все коэффициенты корреляции г равны нулю. При
этом Δ=1 и совместные дисперсии (60) — (62) равны
нулю, т. е. оценки параметров τ, Ω, μ являются
независимыми. Из формул (56) — (58) следует, что дисперсии
оценок параметров определяются только формой тела
неопределенности \R (τ, Ω, μ, μ0) | в сечении,
проходящем через ось измеряемого параметра, т. е.
°:=- -як-· (66)
где ν = τ, Ω, μ. Следовательно, чем больше вторая
производная R"v (короче область сильной корреляции), тем
меньше а".
V
Перейдем к анализу вторых производных /?"v для
сигнала вида f/(f) = t/0exp [ίθ(ί)]ι тело неопределенности
которого описывается формулой (50). Запишем (50) в
следующем виде:
|/?(τ, Ω,μ,μ0)| = (α»+^),/2, (67)
где
Г/2
α=,α(τ, Ω, μ, μ0) = -i- Γ cos [θ (t) — θ (t — τ) -f
-Τ/2
-(- Ωί 4- V-t" — 2μ0τί] dt (68)
112
§ 2.7
— действительная часть;
Т/2
6 = ί>(τ,Ω,μ,Μ = -Τ j 8ίη[ί(ί)-β(ί-τ) +
— Т/2
+ Ωί + μί2—2μ0τί]Λ (69)
— мнимая часть.
Отметим, что
а(0,0,0,[хс)=1, 6(0,0,0,^) = 0. (70)
Последовательно дифференцируя (67) и учитывая (68)—
(70), получаем
Т/2 / Т/2 \а
/?"„=- 4- J ΙΘ'(0-2μΛ2Λ+[4- | в'(ОЛ).
— Г/2 ^ —Г/2 '
(71)
*"т = -ТЧ12, (72)
/?"μμ = -74/180· (73)
Г/2
Я"хй = - ^- j ίβ'ίΟ^ + ^νβ. (74)
— Г/2
*V = °· (75)
Г/2 Т/2
/?'V* = -t- j ^'(О^+тг j β'(0Λ· (76)
—Т/2 —Г/2
Отметим особенности формул (71)—(76),
обусловленные ускорением объекта. Во-первых, точность
измерения дальности (71) зависит от истинного значения
ускорения μ0. Во-вторых, точность измерения ускорения
(73) повышается с увеличением длительности сигнала 7\
В-третьих, смешанная производная по τ и Ω (74)
зависит от истинного значения ускорения μ0. В-четвертых,
появилась смешанная производная по μ и τ (76).
δ 2.7
113
Найдем границу области сильной корреляции по
ускорению μ. Полагая в (52) τ=0, Ω = 0 и используя (73),
находим
| R (О, 0, μ, цс) | = 1 + 0,5R"^ = 1 - 7V/360. (77)
Определяя границу области сильной корреляции из
уравнения | R\ = 0,5, получаем
н = У№Т->=*±(2<х[Ту. (78)
Из (78) следует, что чем больше Т, тем меньше область
сильной корреляции по μ.
Теперь оценим влияние μ0 на значения частных
производных (71), (74). Положим, что закон частотной
модуляции θ'(0 является четной функцией времени,
т. е.
Q'(-<t)=Q'(t). (79)
Интегрируя (71) с учетом (79), получаем, что в /?"„
добавляется слагаемое —μ02Τ2/3. Оценим вклад этого
слагаемого в значение тела неопределенности на
границе области сильной корреляции по τ, когда
Из (52) получаем, что этот вклад равен
К^Р^/б. (80)
Подставляя в (80) выражения (8) и (48), находим, что
«-(T-f-.'O'w· (81)
.По определению частота Допплера Ω = 2ϋωο/£.
Допустим, что Ω^Ξ2№. Тогда
«<(ν)'~'·5(ν)'· ^
Поскольку для реальных объектов
α77ϋ«1, (83)
то из (82) следует, что «< 1. В области сильной
корреляции имеет место неравенство: 0,5 ■< | R (τ, Ω, μ, μ,.) | < 1.
Поэтому изменением тела неопределенности, обусловленным
114
§ 2.7
величиной μ0, входящей в R"n (71), можно пренебречь.
Если выполняется неравенство (83), то в формуле (74)
также можно не учитывать ускорение μ,.. В этом случае
с учетом (79)/?"тй = 0.
Теперь оценим смешанную производную по μ и τ (76).
Эта производная равна нулю только при нечетном
законе частотной модуляции. Поскольку производная (74)
обращается в нуль при четном законе частотной
модуляции, то при любой симметричной модуляции всегда будет
отличной от нуля одна из двух смешанных производных,
определяемых выражениями (74), (76). Пользуясь
неравенством Буняковского — Шварца, найдем оценку
смешанной производной (76):
\Κ"μτ\<ΓΨ[36. (84)
Отметим, что /?'' х<0.
Для четных законов частотной модуляции R" (76)
Не равна нулю, поэтому она вызывает расширение
области сильной корреляции по
μ и τ. При Ώ = 0
топографическая диаграмма тела
неопределенности имеет вид,
представленный на рис. 2.20.
Линия уровня является
эллипсом. Это объясняется
тем, что из-за ускорения
появляется дополнительная
линейная частотная
модуляция (фаза μί2) в аргументе
корреляционной функции
(50).
В тех случаях, когда
скорость движения объекта
известна, а измеряется его
ускорение, необходимо
использовать сигналы с
нечетным законом частотной модуляции. При этом смешанная
производная по μ и τ равна нулю и тело
неопределенности имеет узкую область сильной корреляции, которая
изображена пунктиром на рис. 2.20,
Рис. 2.20.
§ 2.7
115
Обнаружение сигнала при неизвестном ускорении.
Допустим, что все параметры обнаруживаемого сигнала,
за исключением ускорения, известны. При этом можно
положить τ=0, Ω=0, μο = 0, μ^Ο. Найдем потери в
отношении сигнал/помеха. Они будут равны уменьшению
максимального значения основного пика тела
неопределенности. Обозначая это уменьшение через ζ, в соответствии
с (77) получаем
ζ=μ2Γ4/360. (85)
Пусть ζ = 0,11 (потери равны 1 дб). Тогда μΓ2«2π.
Если μ (47) выразить через несущую частоту сигнала
/ο=ωο/2π и положить /<>= Ю10 Щ, ускорение взять равным
а=Л03 м/сек2, то длительность сигнала, при которой
потери ζ=0,11, равна Г«5 мсек. Отметим, что столь
большое ускорение (a=»100g) возможно в случае близкого
пролета объекта над РЛС. Например, если v~
= 103 м/сек, расстояние пролета D=103 м, то a=v2/D=·
= 103 м/сек2.
Измерение дальности при неизвестном ускорении.
Пусть τφΟ, Ω = 0, μ=^0. Допуская, что частотная
модуляция четная (2.6.5), формулу (52) запишем в виде
| R (τ, 0, μ, 0) | = 1 — a.WW — β7V — Ί^Τ'τμ, (86)
где
a = feV(fe+l)a(2fe+l)2; β =1/360;
γ = */6(*-μ 1)(* + 3). (87)
Неизвестное ускорение μ приводит к смещению
максимума |/?| по оси х, т. е. вызывает ошибку в
измерении дальности. Найдем ее величину. Дифференцируя
(86) по τ и приравнивая нулю полученную
производную, находим величину смещения максимума,
обусловленную незнанием ускорения μ:
,Ατ=-ΊΤ2μ/2αΨ. (88)
Найдем смещение ιΔ'τ для частного примера. Пусть
k=2 (сигнал с квадратичной частотной модуляцией),
Г = 5 мсек, α = Ί03 м/сек2 (μ = 2π105/3 сект1). Для этих
данных \tttF а*0,2. Если ширина основного пика xo^l/F,
8*
m
§г.8
то смещение из-за ускорения не превосходит ширины
основного пика.
Оценим теперь потери в отношении сигнал/помеха.
Можно показать, что сумма двух последних слагаемых
в (86) на границе области сильной корреляции равна
0,26, т. е. потери в отношении сигнал/помеха из-за
незнания величины ускорения могут достигать 2,5 дб.
При совместном измерении дальности и скорости
неизвестное ускорение влияет так же, как и при
измерении одной дальности, поскольку скорость и ускорение
не связаны друг с другом (75).
2.8. ОБЛАСТЬ СЛАБОЙ КОРРЕЛЯЦИИ
В предыдущих параграфах были приведены
некоторые результаты, характеризующие поведение
автокорреляционной функции в области сильной
корреляции. Перейдем к рассмотрению области слабой
корреляции. При совместном измерении дальности и
скорости желательно иметь идеальное тело
неопределенности, у которого область слабой корреляции
представляет равномерно распределенные боковые пики
(см. рис. 2.12). Из анализа области сильной
корреляции следует, что вблизи ее границ тело
неопределенности реальных сигналов изменяется более или менее
плавно. Это означает, что боковые пики вблизи области
сильной корреляции будут больше того значения,
которое определяется из условия ограниченности объема,
•расположенного под поверхностью |/?(τ, Ω) |а (2.4.12):
Возникает вопрос, можно ли принципиально найти
сигнал, тело неопределенности которого является
идеальным. Для ответа на этот вопрос рассмотрим
свойства сечений тела неопределенности при t=const.
Функция сечения. Введем функцию
°°
<&(*)= 5Г |ΐ*(τ-Ω)|ΜΩ, (2)
—оо
которую назовем функцией сечения.
§2.8 117
Подставляя в (2) определение корреляционной функции
*
/?(τ,Ω) (2.3.19) и учитывая, что |/?|а = /?/?, получим
—оо
X U(у) U(y-x) e~m dxdydd. (3)
Выделяя в формуле (3) экспоненты во внутренней
интеграл по Ω, замечаем, что внутренний интеграл
представляет дельта-функцию. Используя ее фильтрующее
свойство при у=х, получаем [1]
оо
S(r) = ^r ^U>(t)U'(t-t)dt. (4)
—оо
Функция $(х) не зависит от фазы сигнала b(t), а
определяется только его огибающей U(t). Поэтому сигналы
с различными законами изменения фазы, но с
одинаковыми огибающими, имеют одинаковую функцию &(х).
Например, для сигнала с постоянной огибающей
U(t) = Uo при \t\ ^772 функция 3 (τ) согласно (4) имеет
вид
<g(t)=4-(1-1f1) при М<г· <5>
Графически функция (5) представлена на рис. 2.21
сплошной линией для τ^Ο. С увеличением τ функция
Q (τ) уменьшается линейно.
В свою очередь фаза сигнала θ(0 определяет вид
сечения тела неопределенности вертикальной плоскостью
T=const при изменении Ω от — оо до +оо.
Следовательно, различным 0(0 соответствуют различные
сечения.
Оценка боковых пиков по функции сечения.
Предположим, что найдена такая фаза сигнала Q(t), которая
дает равномерное распределение |/?(τ, Ω)|=#β вдоль
сечения τ=const. Максимальная ширина сечения не
может превышать удвоенной ширины спектра сигнала
118
§ 2.8
2W—4nF. В соответствии с формулой (2) запишем
g(z) = Rss2F. (6)
Приравнивая правые части выражений (5) и (6), находим
Rs=-~=,Vl — \-l\fT .
yiFT
(7)
Из (7) следует, что уровень боковых пиков
(основания на рис. 2.12) при равномерном распределении
боковых пиков в вертикальном сечении тела неопределен-
W>|S
ности, имеющим максимальную длительность (длину),
зависит от τ.
Согласно (7) на рис. 2.22 построена зависимость
RSVFT от |τ|/Τ (сплошная линия). Пунктиром
изображена зависимость уровня боковых пиков от τ,
построенная согласно формуле (1) для идеального тела
неопределенности. Отметим, что соотношение (1) имеет место
только для |τ|/Γ=0,5. При меньших \χ\\Ύ уровень
боковых пиков будет больше, чем в идеальном случае.
Следовательно, для реальных сигналов с прямоугольной
огибающей сигнала при значениях |τ|/7,<0,5 не может
быть получен уровень боковых пиков, соответствующий
формуле (1).
§ 2.8
119
Это является следствием зависимости <§(τ) от τ. Чем
меньше τ, тем больше $(х), причем это справедливо для
любых огибающих сигнала. Максимальное значение β(χ)
согласно неравенству Буняковского — Шварца
определяется как
оо
выЛжс = в(0) = -^Г [U*{t)dt. (8)
—оо
Если огибающая сигнала U(t) не является постоянной,
то при небольших τ (0<| τ|/Τ<0,25) значения функции
$(х) будут больше, чем определяемые по формуле (5).
Следовательно, при той же ширине спектра сигнала
значения R& будут сильней отличаться от значений,
определяемых формулой (1), чем в случае сигнала
с прямоугольной огибающей. Для примера на рис. 2.21
пунктиром изображена функция &{t) для сигнала с
огибающей
£/(*) = £/„cos(πί/Γ) при \t\<T/2. (9)
Она описывается формулой
а, ч 1 Г Л Ы\Л ι 1' 2м \| 3 . 2π|τ||
<3W=t[(1-T1J(1 +ΊΓ005—) + 4Г5Ш^[
(10)
Следует отметить, что при косинусоидальной
огибающей (9) скорость изменения β(χ) больше, чем в случае
сигнала с постоянной огибающей.
Кроме того, всегда найдется такое сечение тела
неопределенности (особенно вблизи области сильной
корреляции), высота которого будет больше, чем
определяемая формулой (7). Это следует из того, что
формула (7) была получена при условии равномерного
распределения боковых пиков на максимальную длину,
равную 2F. Но возможны сечения, длина которых
меньше 2F. Их высота больше, чем определяемая
формулой (7). Следовательно, получить идеальное тело
неопределенности (см. рис. 2.12) не представляется
возможным.
120
9 2.8
Оценка боковых пиков по автокорреляционной
функции. Воспользуемся соотношением (2.3.66), которое
запишем как
J|*(t,Q)|»rft= J|/?(t)|se-|0Vt. (11)
—оо —оо
Будем рассматривать сечения с Ω^Ο. Допустим,
что длительность сигнала равна Т, а боковые пики
в произвольном сечении Ω=^=0 постоянны в пределах
максимального отрезка времени 27\ В этом случае
левая часть выражения (11) равна
^(Ω)2Γ= J|/?(t,Q)|Vt. (12)
—оо
Оценим Λ?β(Ώ) для нескольких видов
автокорреляционной функции R(x).
А. Автокорреляционная функция R (т) близка
к идеальной настолько, что ее боковыми пиками можно
пренебречь. Предположим, что
/?(τ) = 1 — \x\F при 0^|t|^,1/F. (13)
Подставляя (13) в правую часть равенства (11),
получаем, что
||Λ(τ,Ω)|«£/τ = 4γ//7, (14)
—00
где
u sin (Q/F)
Q/F
Y = Y(Q/F) = ^ . (15)
Q/F
Приравнивая (12) и (14), находим
1
^(Ω)=^Κυ(ω/^)· (16)
Нормированная зависимость Rs(d) (16) приведена на
рис. 2.23 сплошной линией. При малых Ω, т. е. вблизи
области сильной корреляции, Rs стремится к величине
\(Y"iFT, поскольку 1ΐπιγ(Ω//;,)=1/6. Это значение R
8-*Q δ
8 2.8
121
несколько превышает уровень боковых пиков для
идеального тела неопределенности (1), который
представлен на рис. 2.23 пунктиром.
Б. Допустим, что для τ^Ο
/1 приО<т<1/2Л
1 1 л — 1/?,. при l/2F<t<
\Я5апри l[2F<x<T.
(17)
Подставляя (17) в правую часть равенства (И) с
учетом симметрии |/?(τ)| (2.3.36) ивдачисляя интеграл, находим
RAO)-
4=,/:
Y2FT у
(1
Da slnQ/2f
' Кча)
Q/2F
■2FTR'
a slnQ?
Sa QT
(18)
Полагая /?$α=1/2/·Τ<1, опускаем Rsa в первом
множителе и при 2/·Ύ>·1 пренебрегаем вторым слагаемым
в (18) по сравнению с первым. В этом случае выраже-
fts/Ff
/2/3
1//2
0,6
ОЛ
0,2
О
^.
\
\
\
\
2 3
Рис. 2.23.
Ψ
мне (18) принимает вид
slnQ/2F
Q/2F
(19)
Зависимость (19) приведена на рис. 2.23 штрнх-пунктн-
ром. Следует отметить, что (19) справедливо только
для Q/2F^2n (т. е. Ω<№), когда функция sin*/*>0.
122
§2.9
Если положить RSa=> \\Y1FT, то
Rs(Ω) ~ 72T7 у -ΟΤΣρ-+ΊΣΓ-· (2°)
Опять-таки здесь надо иметь в виду только те
значения Ω, при которых выражение под корнем больше или
равно нулю. Можно заметить, что в данном случае
Rs(Q) имеет колебательный характер, т. е. может
меняться от нуля до \\\/П\
Таким образом, в случае равномерного
распределения боковых пиков на отрезке 2Т (12) уровень боковых
пиков вблизи области сильной корреляции может
превышать идеальный уровень (1) в два раза. Это следует
из сравнения (1) с (20) при Ω = 0. Если учесть, что
равномерное распределение боковых пиков для реальных
сигналов в некоторых сечениях невозможно обеспечить,
то всегда уровень боковых пиков будет больше, чем
\\YFT.
2.9. ВЛИЯНИЕ ШИРОКОПОЛОСНОСТИ
СИГНАЛОВ НА УРОВЕНЬ БОКОВЫХ
пиков корреляционной функции
Под широкополосными сигналами будем понимать
такие, ширина спектра W которых соизмерима с
несущей частотой сигнала ωο. Любой сигнал можно сделать
широкополосным, если его спектр сместить в область
видеочастот. Корреляционная функция широкополосных
сигналов в соответствии с (2.3.7) содержит два
слагаемых и может быть записана в виде (2.1.7). Обозначим
индексом / сигнал, с которым согласован фильтр
(несущая частота сигнала равна ωο), а индексом m
—отраженный от объекта сигнал с несущей частотой ωο+Ω.
Произведя преобразования, аналогичные тем, с помощью
которых было найдено соотношение (2.3.3), получим
корреляционную функцию широкополосного сигнала'·
r(t,Q) = Re{/?(t,Q)el<0»x+Q(t>Q)e-iv}, (1)
§2.9
123
где
/?(τ,Ω) = ^= ^U{t)U(t-z)^'dt, (2)
—оо
оо
Q(x,Q)=_^= ^U(t)U(t-*)eHa+™dt; (3)
—oo
oo
£,„ = £ + 4- f^a(0cos2[(o)0 + Q)i + e(i)]^; (4)
—X)
oo
£, = £+-!" UP(t) cos 2 [<o0t + b(t)]dt; (5)
—oo
oo
£ = -*- ^U>(t)dt. (6)
—00
Для узкополосных сигналов величиной Q (3) и вторыми
слагаемыми в (4), (5), как было отмечено в § 2.3,
можно пренебречь. Для широкополосных сигналов ими
пренебречь нельзя, так как они совместно с R (τ, Ω)
определяют уровень боковых пиков корреляционной
функции.
Увеличение боковых пиков. Рассмотрим фазоманипу-
лированные сигналы, у которых b(t) равна 0 или π. По·
*
скольку для этих сигналов огибающая U(t) = U{t) и
является действительной функцией времени, то из (2), (3)
следует, что
Q (τ,Ω) = Λ(τ, Ω + 2·0). (7)
Максимум функции Q имеет место при τ = 0 и Ω=—2ω0
и равен единице. Пусть u>0=-tt?/2. Область слабой
корреляции функции /?(τ, Ω) по Ω лежит в пределах от Ω =
= — W др Ω=>Ψ, а функции Q(τ, Ω) от — 2W до 0.
Поэтому в области значений частот Допплера, определяемых
неравенством — ΙΡ<[Ω<0, происходит наложение боковых
124
§ 2.9
пиков функций /?(ι,Ω) и Q(t, Ω). В результате боковые
пики корреляционной функции г (τ, Ω) могут быть вдвое
большими, чем у /?(τ,Ω). Среднеквадратичное значение
боковых пиков г (τ, Ω) увеличивается примерно в у"2 , так
как при суммировании R и Q учитываются экспоненты
выражения (1).
При нахождении г (τ, Ω) необходимо помнить, что
Ет и Ει зависят от ωο и Ω. Если положить, что U(t) =
=1/0 при 0^ί^,7\ то для фазоманипулированных
сигналов выражения (4) — (6) принимают вид
Ε=υ\τμ. (Ю)
Максимальные значения энергий (8), (9) равны 2Е.
Если <(йе~п2л1Т, где η — целое число, то Ει=Ε. Кроме
того, при Ω=& 2л/Т, где k — целое число, и Ет=Е.
Рассмотрим пример расчета боковых пиков. Для
сигнала Баркера {52] с числом импульсов N — 5 было
рассчитано тело неопределенности1 в дискретных точках
τ—№τ0 для т~0, >±1, ..., ±5; И~к2я/Т для k=0,
±1, ..., ±5; xo = T/N. Расчеты были проведены по
точной формуле^ (1). Несущая частота сигнала была
выбрана равной π/το, т. е. период равен удвоенной
длительности одного импульса.
В табл. 2.1 приведены расчетные значения модуля
автокорреляционной функции для 0^1/п^5. Каждая
строка таблицы — сечение тела неопределенности при
постоянном значении частоты"Допплера, равном 2nkJT.
Каждый столбец — сечение тела неопределенности при
постоянной задержке mTfN=mt0.
Как следует из таблицы, максимальное значение
основного пика получается при т=0 и &=0."Боковые
пики относительно центральной строки А=»0 не сим-
1 Расчеты выполнены В. И. Шустовым/
δ 2.9
125
Таблица 2.1
Номер
сечения по
частоте
k
5
4
3
2
1
0
—1
—2
—3
—4*
—5
m=0
0
0
0
0
0
1
0
0
0
0
1
-·
Номер сечения по времени
т=\
0
0,08
0,05
0,08
0,48
0
0,72
0,18
0,18
0,72
0
т=2
0
0,01
0,16
0,28
0,06
0,2
0,09
0,65
0,65
0,09
0,2
т=3
0
0,03
0,12
0,21
0,21
0
0,28
0,48
0,48
0,28
0
т=4
0
0,03
0,06
0,11
0,16
0,2
0,23
0,25
0,25
0-23
0,2
т=5
0
0
0
0
0
0
0
0
0
0
0
метричны, что характерно для корреляционной функции
широкополосного сигнала. Эта асимметрия вызвана
наложением /? и Q в (1). Максимальная разность
между боковыми пиками с координатами т~\, k~\ и
m=l, k=—1 равна 0,24. Максимальный боковой пик
R (t, Ω) согласно (2) соответствует значениям т=1 и
&=±1 и равен 0,58. Для широкополосного сигнала
максимальный боковой пик равен 0,72.
Объем тела неопределенности. Для широкополосных
сигналов объем тела неопределенности равен
J^jr'K Ω) dicta.
—оо
Он ие является постоянной величиной и зависит от
значения ωο и формы сигнала. Однако эта зависимость
слабая, что и не позволяет произвольно менять объем
тела неопределенности.
глава з СИГНАЛЫ С ЧАСТОТНОЙ
МОДУЛЯЦИЕЙ
3.1. СИГНАЛ С ЛИНЕЙНОЙ ЧАСТОТНОЙ
МОДУЛЯЦИЕЙ
Сигнал с линейной частотной модуляцией (ЛЧМ)
был первым сложным сигналом, примененным в
радиолокации [2, 18, '53]. Комплексная огибающая ЛЧМ
сигнала определяется как
ί/(;) = ^οεχρ[ί4(τ-)2] при |i|<7-/2, (1)
где
D=WT. (2)
Если считать, что ширина спектра сигнала W=2nF
совпадает с полным диапазоном изменения мгновенной
частоты сигнала (девиацией частоты), а фаза сигнала
согласно (1)
6^=Т-(т-У ПРИ т<7'/2. (3)
то закон изменения мгновенной частоты сигнала запишется
как
*'(f) = 7i=W-L, (4)
где
w= е'иакс (о - е'иин (о = θ' (-£-) -г- θ' (--L). (5)
Подставляя в (3) .значения ί = rt 7"/2 и ί = 0, получаем
еИаКс=е(±-^)=4' ^ (б)
е«иЯ=θ (0) == о.
8 3.1
127
Как следует из формулы (6), изменение фазы
сигнала за время, равное его длительности,
пропорционально D.
Спектр комплексной огибающей. Согласно формуле
(2.2.17) спектр комплексной огибающей ЛЧМ сигнала
записывается как
ψ ι £.£-'·'
О(о)) = С/0 ) е 2 р dt. (7)
—Υ/2
Дополнив показатель экспоненты в (7) до полного
квадрата, после преобразований получим
G(*) = U0e 2 И J е 2 Ут wUt. (8)
-Г/2
Разбивая интеграл (8) на два с пределами интегрирования
— 7/2-7-0, 0-г-Г/2 и используя интегралы Френеля [42]
г , π
;1 —XI
C(z)ztiS(z) = je 2 rfx, (9)
получаем
<?(«)= A>j*_ {[С (ζ,)-К (*,)] +
+ i[S(Zl) + S(za)]}e 2lr/, (10)
где
S0 = t/07- (11)
— .площадь" огибающей сигнала;
— аргументы интегралов Френеля в формуле (10).
Определим характер изменения спектра сигнала (10)
при изменении отношения ω/W, когда Ь>1. Отметим,
что выражение (Ю) содержит экспоненциальный
множитель с показателем —0,5 D((u/W)z.
12ё
*ъл
При (ύ = Ψ/2 фазовый сдвиг, обусловленный этим
множителем, равен —Zty8<C—1.
Вклад в G((u) сомножителя, заключенного в
фигурные скобки, определяется свойствами интегралов
Френеля.
Приведем основные из этих свойств:
С(оо)=0,5, 5(оо) =0,5, (13)
С(—z)--C(z), S(— z) = -S(z); (14)
при малом аргументе (z<4)
C(z)~z-±(^.yz\ (15)
S(z)^^z>-±(^-y^ (16)
при большом аргументе (ζ>1) справедливы
асимптотические формулы:
c(z)~4-+^sl'n-rza--i*-cos-i-zi' <17)
s(z)^4~ircos-rza-w-sin-i-zi· <18)
Сомножитель в (10), содержащий интегралы Френеля,
обозначим как
σ/(ω)=|σ/(ω)|ε,ν«»= ,
= [С (ζ,) + С (z,)] + i [S (z.) + S%(Zi)). (19)
Согласно свойствам интегралов Френеля функция Of (ω)
симметрично зависит от ζι и z% и поэтому спектр
комплексной огибающей сигнала (10) является четной
функцией частоты ω, τ. е.
0 (_ ω) = 0 (со), (20)
что соответствует формулам (2.2.34), (2.2.35).
Для центральной области частот спектра сигнала
(|а>/№|<1/2) согласно (12) Zi«z2« 0,5 YD\%.
§ 3.1
129
Поскольку πσ'условию £)^>1, то с учетом (17), (18)
C(zi) ~5(ζ4) ~0,5 и (19) преобразуется к виду
При этом выражение (10) записывается как
OH~Syfe"^(f)a + ii щщ\»\<^- (21)
При увеличении или уменьшении относительно нуля
частоты ω один из аргументов (12) увеличивается,
другой уменьшается. При этом в выражении (19) одиа
пара интегралов Френеля, содержащих возрастающий
аргумент, мало отличается от 0,5. Другая пара, которой
соответствует уменьшающийся аргумент, дает
возрастающий осциллирующий вклад в (19), приводящий
к осцилляции амплитудного и фазового спектров (10).
Hajpnc. 3.1 изображен амплитудный спектр |<?(ω)| и
составляющая фазового спектра φ/(ω) при D=2jt36,
т. е. при /Т = 36. Поскольку согласно (20) спектр
сигнала является четной функцией частоты, то на рисунке
приведены зависимости только для ω^Ο. При (&<^W/2
амплитудный спектр осциллирует относительно
значения S0[/2n/D, а фазовый — относительно π/4.
При ω—*-W/2 согласно (12) Ζι—>-0, г2>1 и, как
следствие, C(zi)—Я) (15), Sfa)—Я) (16), С(г2) ~0,5
(17), S(zi) ~0,5 (18). В этом случае выражение (19)
приобретает вид
Of (ω) ^ [С (г,) + 0,5] +j [5(2.) +0,5]. (22)
Из анализа (22) следует, что при больших значениях
D изменение D в (12) влияет только на частотный
масштаб и не влияет на глубину осцилляции спектра на
краях области частот (|ω|«№/2).
Можно показать, что на краях области частот
(ω«ΗΡ/2), так же как и в середине (ω»0),
составляющая фазового спектра φ/(ω) незначительно отклоняется
от величины π/4. Отклонения не превышают 10—15°,
130
§ 3.1
поэтому ими можно пренебречь и считать, что
ψ/(ω)~π/4 при |ω|^^/2. (23)
При (ύ~Ψβ имеем
При (ύ>Ψ/2 один из аргументов (12) меняет знак и,
следовательно, одна пара интегралов Френеля (19)
So fir f
D=2*36
Рис. 3.1.
становится отрицательной. Поэтому амплитудный
спектр (рис. 3.1) уменьшается и при ω—м» в
соответствии со свойством (13) <?(«·)) — 0.
Определим характер уменьшения амплитудного
спектра. Отбросив последние слагаемые в (17), (18) и
§ 3.1
131
подставив полученные при этом выражения в (19),
запишем
Подставляя (24) с учетом обозначения (19) в (10),
получаем
sin <2W
a((o)^,S0—■5^~ при | ω Ι > W(2. (25)
Таким образом, при |ω|»№/2 спектр сигнала
убывает по гиперболическому закону вида 1/ω.
Полученный результат можно объяснить тем, что
в области больших значений частоты ω спектр
сигнала определяется поведением сигнала на его краях
при t=±T/2, где огибающая сигнала имеет разрыв.
Известно [10, 54], что если Л-я производная имеет
разрыв, то спектр убывает по закону 1 /1 ω|ft+1. Разрыв
функции в рассматриваемом случае соответствует
А-0.
Из рис. 3.1,α видно, что девиация частоты сигнала
характеризует ширину спектра сигнала. При |ω|»±№/2
значения амплитудного спектра много меньше значений
при ω«0.
При больших D можно в первом приближении
пренебречь осцилляциями амплитудного спектра и
полагать, что он равномерен в пределах от —W/2 до
W/2 (штрих-пунктир на рис. 3.1,а). В этом случае
O(«)«S0j/g5e а И + 4 при.Н<№/2· (26)
Из (26) следует, что фазовый спектр описывается
квадратичной функцией частоты.
Соотношение (26) можно получить также, вычисляя
интеграл (7) асимптотическим методом стационарной
фазы. В дальнейшем этот метод будет широко
использоваться при анализе и синтезе сложных сигналов.
132
§ 3.1
Метод стационарной фазы. Метод стационарной фазы
[55] основан на том, что величина интеграла
«7(D) = |/(0е1О<р"'Л (27)
—00
при большом параметре D»l определяется в основном
только той частью подынтегрального выражения, в
которой фазовая функция φ(ί) меняется медленно. Там же,
где φ(/) изменяется быстро, осциллирующий множитель
cos[D«pl(i)] + i sin[D<p(i)] приводит к тому, что интеграл
мало отличается от нуля.
Наиболее медленно ψ(ί) изменяется около точки to,
в которой
φ'(0|,=<β=Υ(Ό) = Ο. (28)
Уравнение (28) определяет точку стационарной фазы
to. Разлагая фазовую функцию φ(ί) в ряд Тейлора около
точки i—4o и учитывая (28), имеем
? С) = ? С.) Ч-*^1 (*-*.)■ + ··· (29)
В разложении (29) ограничимся двумя первыми
слагаемыми. Подставляя их в (27) и полагая, что в окрестности
точки стационарной фазы f(t) меняется медленно,
находим
Sr(D)^fl(i,)ell"(<J Je 2 ' at. (30)
—во
Поскольку
Je 2 dx = Y2*e 4. (31)
—оо
а (Н - , . f (ϋ" ' -1' (32)
где знак перед π/4 совпадает со знаком ψ"(ί0).
Таким образом, интеграл (27) определяется
асимптотическим соотношением (32), где точка стационарной
фазы ί9находится ИЗ уравнения (28).
8 3.1
133
Отметим, что уравнение (28) в общем случае может
иметь несколько решений, т. е. несколько точек
стационарной фазы tok:
φ'(Μ=0. (33)
Если точки стационарной фазы удалены друг от друга,
то
, ^ /(ye'l^^L (34)
ff(D)^
Мерой близости точек стационарной фазы является
радиус влияния [56], который в принятых в книге
обозначениях выражается как
P = -=L=. (35)
/О IT" CO I
Следует отметить, что вклад точки стационарной фазы
в Уф) согласно (34) прямо пропорционален р. Если
расстояние между соседними точками стационарной фазы
ΔΙίιι,ь—ι=ioh—tfo,fc-4>p, то их вклады надо суммировать.
Практически суммировать можно при Mh.k-i1** (2-f-3)p.
Когда точки стационарной фазы расположены ближе,
расчет интеграла ϋ (D) усложняется.
Бели пределы в интеграле (27) конечны, т. е.
V.W=$№elD¥f)dt, (36)
а
то формулы (32), (34) остаются справедливыми, если
точки стационарной фазы расположены не близко
к краям интервала интегрирования (а, Ь). Мерой
близости точек стационарной фазы остается радиус
влияния р.
Иногда по условиям задачи большой параметр
входит в показатель экспоненты интеграла (27) в неявном
виде, т. е.
gr= Jf(t)el*mdt. (37)
—оо
Тогда точки стационарной фазы находятся из уравнения
φΊ№*) = 0, (38)
134
§ 3.1
интеграл (34) записывается как
У-νΣ ?,. ДЦе'К'^], (39)
*
*Ί ?". С.Ч)
а (35) принимает вид
Рь = _±=_ (40)
к I ?", (ioh) I
В качестве примера определим спектр ЛЧМ сигнала
(7). Фазовая функция согласно (7), (37)
Ti(0 = ^—'· (41)
Дифференцируя (41), согласно (38) получаем уравнение
^-«=0, (42)
из которого находим, что
-ίϊ-=— ί43ϊ
Из (43) следует, что при изменении ω от —W/2 до W/2
точка стационарной фазы t0 перемещается от —Т/2 до
Г/2. Согласно (7), (37)
f(M = l· (44)
Подставляя (43) в (41), фазовую функцию в точке
стационарной фазы запишем в виде
Дифференцируя дважды (41) и подставляя t~t0,
согласно (43) находим
φ"ι(ί.) = Τϊ· (46)
Подставляя (44) —(46) в формулу (39) и учитывая
множитель и0 перед интегралом в (7), а также обозна-
§ 3.1
135
чение (11), получаем выражение для спектра сигнала
. D Ι ω \ί π
OH^S0 y^&'^W) + " при |ω|< \, (47)
совпадающее с (26). Формула (47), как следует из
метода стационарной фазы, справедлива, если точка
стационарной фазы не располагается близко к краям
сигнала. Однако характер спектра описывается этой
формулой вполне удовлетворительно йри всех возможных
положениях точки стационарной фазы (штрих-пунктир иа
рис. 3.1).
При использовании метода стационарной фазы
следует помнить, что он дает только первое приближение
решаемой задачи и поэтому грубо определяет характер
искомой функции. В качестве примера срарним
амплитудный спектр ЛЧМ сигнала, построенный по точной
формуле (10) (сплошная линия на рис. 3.1), со
спектром, который получается на основе метода
стационарной фазы (штрих-пунктир). Различие между ними на
краях спектра, где непосредственно пользоваться
методом стационарной фазы нельзя, действительно большое.
Методы уточнения асимптотических решений даны в
работах [57, 58].
Рассмотрим спектры комплексных огибающих вида
U0 е'е(". По определению спектра (2.2.17)
Г/2
0(») = С/О \ ет~ш(И, (48)
-Г/2
где фазовая функция φι(0=θ(0—ωί. Отсюда
уравнение точки стационарной фазы t0 записывается как
ω = θ'(ί0). (49)
Согласно (49) спектр на частоте ω определяется точкой
стационарной фазы t0, в которой мгновенная частота
θ'(ί) совпадает с а>.
Корреляционная функция комплексной огибающей,
Подставляя выражение для комплексной огибающей (1)
136
§ 3.1
в формулу (2.3.19), находим для τ^Ο
„2 Г/2 . D I t \* . D /ί—х\а , ,„.
*(,0)=4 { .'τ(τ)-τ(τ)+-Λι (50)
—772 +τ
где в соответствии с (2.3.13) энергия \Ε — ϋ\Τβ.
Интеграл (50) выражается через функцию вида
sin zfz, поскольку показатель экспоненты содержит t
в первой степени. Аналогично формуле (50)
записывается выражение для R (τ, Ω) при τ^Ο. При этом
подынтегральное выражение не изменяется, а пределы
интегрирования становятся равными —7/2 и Τ/2+τ.
Объединяя результаты решений интегралов для τ^Ο,
получаем
е|В\
(51)
Согласно (51) автокорреляционная функция
„„rjp- л _ϋχ)ΐ
«w-0-^) %ϊψ) ■ (52>
Автокорреляционная функция, построенная по
формуле (52) при D=2n36, т. е. при FT=36, изображена на
рис. 3.2 сплошной линией. Ширина основного пика
между первыми нулями равна 4nW, что получается при
аргументе во втором множителе правой части (52), равном
/±π. На уровне 0,5 ширина основного пика равна το»
«'2π/№. Функция 1 — \x\jT — огибающая
автокорреляционной функции прямоугольного импульса длительностью
Τ показана на рис. 3.2 штрих-пунктиром.
Пунктиром на рис. 3.2 изображено сечение функции
R (τ, Ω) при Ω =—W[2. Следует отметить, что в этом
случае согласно (51) при τ<0 уровень /?(τ, Ω)
пренебрежимо мал.
93.l
137
При τ=0 имеем R (Ω) = (sin ΩΓ/2)/(Ω7/2), что
совпадает с формулой (2.3.39).
Из выражения (51) следует, что R (τ, Ω) при τ=
= const достигает максимума, равного 1 — ΙτΙ/Γ, при
А(%я)
в-глзб
Рис. 3.2.
условии, что аргумент функции sin ζ/ζ равен нулю, т. е.
при
(53)
τ
Ύ
w
Уравнение (53) определяет геометрическое место
максимумов |/?(τ,Ω)|. Решение этого [уравнения показано штрих-
пунктирной линией на рис. 3.3.
Границы между областями сильной и слабой
корреляции в соответствии с § 2.4 определяются из уравнения
(2.4.7) при Я=4-:
| R (τ, Ω)| = 1/2. (54)
Обозначая
х = γ-, У = -ψ (55)
138
§ 3.1
и учитывая (51), (54) запишем как
(1-1*1)
sin
=4-· (56)
Для области сильной корреляции, где
[sin ζ
sin ζ
1 — —
6'
(57)
выражение (56) принимает вид уравнения
(l-H)[l-~(x + i/)a(l-|x|)']=4-' (58)
приближенное решение которого равно
y"=-X-D(l-\x\)V '- 2(l-|*l) "РИ И^1/2'
(59)
В (59) каждому значению χ соответствуют два
значения у. Это означает, что граница области сильной
корреляции является замкнутой линией. С увеличением D
разность
§ 3.2 139
уменьшается, т. е. область сильной корреляции сужается.
Решение (59) справедливо только для —1/2^*^,1/2,
так как при больших \х\ модуль | R (х, г/)|<1/2. При
Ы = 1/2 разность Ау = 0. Решение (59) изображено на
рис. 3.3 сплошной линией в виде овала.
3.2. СИГНАЛ С СИММЕТРИЧНОЙ ЛИНЕЙНОЙ
ЧАСТОТНОЙ МОДУЛЯЦИЕЙ
Закон изменения частоты сигнала с симметричной
линейной частотной модуляцией (СЛЧМ) показан на
рис. 2.14 (k=\) и записывается как
β'(ή = 2ψψ- при \t\<T/2, (1)
где №=6'маКс—10'мин — девиация частоты.
Интегрируя (1) и находя закон изменения фазы,
получаем выражение для комплексной огибающей СЛЧМ
сигнала:
(U0exp(iD£) при 0<t<T/2,
U(t) = \ ) μ\ η (2)
[U0expf—iDfrj при —T/2<t<0.
Спектр комплексной огибающей. Согласно формулам
(2.2.17), (2) спектр комплексной огибающей представим
в виде
<?(«,) = <?,(«,) + <?», (3)
о,Н =
<?,(«>) =
/» ID
0
•υ. J."
t'
Τ'
-ID
— 1<о
it
ι
dt,
dt
-772
(4)
С помощью замены переменной it=—t во втором
интеграле (4) можно показать, что
<?,(«>)=&(«,). (5)
140
§3.2
Если Οι (ев) = \Q1{w) I ехр^Оо)], то
<?(■) = 2|Ot(«)|cos ?,(■). (6)
т. е. для определения спектра комплексной огибающей
достаточно найти только (?ι(ω)·
Сравнивая формулу (4) для <?ι(») с (3.1.7), следует
отметить, что последняя отличается от (4) лишь нижним
пределом интегрирования и множителем 1/2 в показателе
экспоненты. Поэтому φ (ев) можно выразить через
интегралы Френеля аналогично соотношению (3.1.10). Однако,
полагая, что D> 1, перейдем к асимптотическому
выражению Οι (»). Фазовая функция согласно (3.1.37)
9i(t) = DT£—t. (7)
Согласно (3.1.38), находя первую производную фазовой
функции (7) и приравнивая ее нулю, при замене D на
WT получаем уравнение для точки стационарной фазы t0:
2i0fT=wfW. (8)
Точка стационарнойГфазы t0 согласно области
определения спектра <?i(cb) (4) [может [изменяться в пределах от 0
до Г/2. При этом в соответствии с уравнением (8) точка
стационарной фазы определяет Ох («в) в диапазоне частот
(0—W). В этом заключается отличие спектра <?i(cb) от
спектра ЛЧМ сигнала, который располагается по оси
частот от —W/2 до W/2.
Вторая производная фазовой функции (7)
φ'Ί(0=^-· (9)
Заменяя в (7) и (9) аргумент t на ί0 из (8) и
подставляя полученные выражения в асимптотическую
формулу (3.1.39), получаем
O.(-)~S0|/^exp(-i^- + i-J-) при 0<«в<«7.
(10)
Согласно (10) спектр комплексной огибающей сигнала
§ 3.2
141
(6) можно записать в виде
<?(«)~2S0/^coe(^—^-)приО<«<^. (11)
Отметим основные особенности спектра СЛЧМ
сигнала. Во-первых, как следует из (6), (11), О (ω)
является действительной функцией частоты, что соответствует
результатам § 2.2 для сигналов с нечетной фазой (2.2.39).
Во-вторых, амплитудный спектр (11) является
осциллирующей функцией, поскольку (11) содержит косинусои-
If·
\
, L-
■W
\
/
Φ) ° -Т/2 -t0 0 t0 Т/2 t
Рис. 3.4.
дальний множитель. Осцилляции имеют место потому,
что спектр (11) представляет собой сумму спектров двух
сигналов. Первый сигнал занимает временной интервал
от —Г/2 до 0, второй — от 0 до 7/2, при этом мгновенная
частота каждого сигнала изменяется в пределах от 0 до
W, увеличиваясь относительно ί=ϋ {формула (1) и
рис. 3.4]. Поэтому для рассматриваемого полного спектра
существуют две точки стационарной фазы i0 и —U,
которые определяют спектр на одной и той же частоте ω =
= Q'(t). Расстояние между ними по мере увеличения to
увеличивается. В результате на некоторых частотах
происходит синфазное сложение вкладов точек стационарной
фазы в спектр сигнала, а на некоторых — противофазное.
Следовательно, в амплитудном спектре (11) возникают
максимумы и нули (рис. 3.4).
Отметим, что асимптотические соотношения (10), (11)
справедливы, когда точка стационарной фазы t0 не
близка к краям временного интервала (0, Г/2), т. е. когда ω
расположена не близко к 0 и W. Изображение ампли-
142
§ 3.2
тудного спектра | О (ω) I на краях 0 и W является
условным, так как здесь возможна дополнительная
осцилляция френелевского типа, аналогичная осцилляции
спектра ЛЧМ сигнала (рис. 3.1,0-). Кроме того, при ω<0 и
ω>Ψ спектр простирается до ±оо, но характер спектра
при таких ω несколько отличается от характера спектра
ЛЧМ сигнала. Часть спектра при ω>Ψ создается со-
art).
Ί
τ
Л
г
·/·
«-
1 +
_
о Ι τ t
1 *>
U(t-X)
I
+.
0
1
τ <
χ
г
? \
~
t
■И
з б)
г ι
;
t
0(t)
—
ΰ ft-τ)
—t-
\
+
+
тлш
')
—
e>
t
t
Рис. З.5.
:f* ί θ) t
Рис. 3.6.
ставляющими сигналами, расположенными на краях
сигнала i(t0—*-±Т/2), что следует из метода
стационарной фазы. Поскольку на краях сигнала его огибающая
имеет разрывы, то спектр убывает по закону l/ω. Часть
спектра при ω<0 создается центральной относительно
ί = 0 частью сигнала, где комплексная огибающая
непрерывна. Можно показать, что вторая производная 0"(t)
имеет разрыв в точке t = 0. Поэтому при ω<0 спектр
убывает по закону 1/ω3 [10, 54].
Комплексная огибающая корреляционной функции.
Определим ее для т^О, поскольку для т<0 из-за
нечетности фазы можно воспользоваться соотношением
(2.3.60).
§ 3.2
143
При вычислении /?(τ, Ω) по формулэ (2.3.19) следует
*
обратить внимание на то, что произведение U(t)U(t — τ)
записывается различными выражениями для различных
областей изменения t и τ. На рис. 3.5, а, б условно изображены
*
комплексные огибающие U{t) и U(t— τ) для 0 < τ < if/2;
знаки внутри огибающих соответствуют знакам их фазовых
множителей. На рис. 3.5, в заштрихована область, где про-
*
изведение U(t) U(t — τ) отлично от нуля. Она разделена
на три отрезка, в каждом из которых фазовые
множители при изменении t не меняют знака. При х>Т/2
(рис. 3.6) существует всего одна область, в которой
перемножаются составляющие одного знака.
Таким образом, для Ο^τ^Γ/2 согласно формуле
(2.3.19) комплексная огибающая корреляционной
функции описывается выражением
о
R(z,Q)=-L f expi[-D^+D-^1!-+Qi]^ +
-г/а+т
+ -^j'expi[D^-+D-i^-+Qi]ifi +
о
Г/2
+4" Jexpi[D£-D-£^£-+a]<«. (12)
В первом и третьзм интегралах (12) в показателях
Экспонент члены с f взаимно уничтожаются. В результате эти
интегралы (обозначим их jlt J,) выражаются через
функции вида sin zfz:
'--И·-г) х
4 { Τ W Д1 ~ T J
144
§ 32
-Г4(»Ч)0-Е)] t.fr»?*3) (l4)
Отметим, что в (13), (14) по сравнению с (3.1.51) стоит
дополнительный множитель 1/2.
Второй интеграл в (12), который обозначим &^, в
показателе экспоненты содержит слагаемое с ί2. Поэтому его
можно выразить через интегралы Френеля. Однако, как
будет показано далее, величина &г мала при D^>1.
Поэтому этот интеграл проще определить методом
стационарной фазы. Вынося из-под знака интеграла Уа
множитель, не зависящий от ί, найдем фазовую функцию
b(t) = 2DT£— 2D£+at. (15)
Согласно (3.1.38), беря первую производную (15) и
приравнивая ее нулю, при замене D на WT получаем
уравнение точки стационарной фазы ί0·'
«Le.Hl__l. (16)
В соответствии с пределами интегрирования в &г точка
стационарной фазы ίο может изменяться в пределах от О
до τ. Когда ί0 равно нижнему пределу интегрирования,
т» е. ίο=0, то (16) преобразуется в уравнение
—=—. (17)
На плоскости (τ, Ω) решение уравнения (17)
представлено линией / (рис. 3.7). При изменении τ От 0 до 7/2
частота Допплера Ω меняется от 0 до W.
Когда ί0 совпадает с верхним пределом
интегрирования, т. е. ίο=τ, то (16) записывается в виде уравнения
§3.2
145
которому соответствует
линия 2 на рис. 3.7. Точка
стационарной фазы при τ =
= const и Q=var
перемещается между линиями / и
2, т. е. 3ft определяет /?(τ,Ω)
в заштрихованной части
плоскости (τ, Ω).
Вторая производная
фазовой функции (15) равна
4D
?"ι(*.)=ΤΓ·
(19)
Подставляя выражение
(19) в асимптотическую
формулу (3.1.39), получаем
\&Л^
Yw
Рис. 3.7.
Очевидно, что при D>\
модуль | ^а | пренебрежимо
мал по сравнению с
единицей.
При 7/2^τ^,Τ согласно рис. 3.6 и формуле (2.3.19)
имеем
Г/2
3rt = R(i, Ω) =4- f expi[D-£+D-£^-+Qf]rff.
—Г/2+х
(21)
При вычислении интеграла (21) методом стационарной
фазы при 7'/2<х<7 получим асимптотическое равенство
|V4| ~~ ν%ΙΊΌ= 1/2J/FF, совпадающее с равенством (20).
Поэтому <74 определяет R (χ, Ω) на части плоскости (χ, Ω)_
ограниченной линиями 3 и 4, уравнения которых записи,
ваются
(22)
1 Т — 2W
Таким образом, внутри области с границами /—3 и
2—4 модуль корреляционной функции, определяемый &г
и ^4, примерно равен ]Лс/20. Следовательно, чем болше
D, тем меньше J Λ (χ, Ω)|.
146
§ 3.2
Основной вклад в корреляционную функцию вносят
интегралы -7, и .7, [формулы (13), (14)]. Если τ = const,
интеграл Uχ максимален при условии τ/Τ = Ω/2Ψ,
совпадающем с уравнением (17). Поэтому изменение <71макс при
изменении τ отображается линией / на рис. 3.7. Аналогично,
если τ = const, <7а максимален при условии ι/Τ — — 0./2W,
совпадающем с уравнением (18). Изменение <7ЗМакс при
изменении τ отображается на рис. 3.7 линией 2. Решение
каждого из интегралов ,7,, 7а в сечении тела
неопределенности горизонтальной плоскостью дает овал, близкий
к эллипсу (сравните с рис. 3.3), большой осью которого
является либо линия /, либо линия 2.
На рис. 3.8 изображено сечение тела неопределенности
вертикальной плоскостью при t = const<r/4 вдоль оси
частот Допплера Ω. Сплошными линиями показаны
составляющие тела неопределенности, определяемые интегралами
<7X и <7„, а пунктиром —составляющая, определяемая
интегралом «7а.
В области сильной корреляции сумма .7, и ,78 дает
основной пик тела неопределенности, который не имеет
направляющих вдоль линий / и 2 на рис. 3.7. Это
показано в § 2.6, где приведен анализ области сильной
корреляции. Для сигнала с СЛЧМ граница области сильной
корреляции является овалом (рис. 2.16,а).
Автокорреляционная функция согласно (12) при Ω = 0
с точностью до величины 1 /2 Υ FT определяется суммой Зх
и .7,, т. е.
ЯЫ« (l--^)X
X ^,V 2^'] е при0<,<7у2. (23)
2 (1— Τ )
При D>1 и τ/Τ < 1 в (23) можно отбросить множители
1—2τ/7\ Тогда первый нуль функции (1(τ) равен 2ic/W,
что совпадает с результатом, полученным для ЛЧМ
сигнала. Следовательно, ширина основного лепестка
автокорреляционной функции обоих сигналов — и ЛЧМ, и
СЛЧМ — одинакова.
§ 3.3
14?
При τ = 0 сумма Я\ + 5Ί. дает R (Ω) = sin (0,5ОТ)(0,5ОТ.
что совпадает с точным результатом для сигнала с
прямоугольной огибающей. Это является следствием того, что
при τ = 0 ^2 = 0(20).
\Xfr,S)\
ZWt 2WT
Рис. 3.8.
3.3. СИГНАЛ С КВАДРАТИЧНОЙ ЧАСТОТНОЙ
МОДУЛЯЦИЕЙ
Сигнал с квадратичной частотной модуляцией
(КЧМ) характеризуется телом неопределенности,
близким по форме к идеальному (рис. 2.12)1. Мгновенная
частота такого сигнала определяется как
9'(0 = «>£при \t\<T[2,
где D-
WT;
■β'
Θ'(±7γ2) —θ'(0).
(1)
(2)
Квадратичный закон изменения частоты (1) изображен
на рис. 2.14 (k = 2). Интегрируя (1), получаем что фаза
меняется по кубичному закону, т. е.
6(')=т-(-г)8при W<TI2' (3)
причем
бмакс = θ (Г/2) = D/6. 6МИ„ = θ (-7/2) = - D/6. (4)
1 Некоторые сведения о сигнале с КЧМ приведены в [34, 59]
148
§ 3.3
а диапазон изменения фазы за длительность сигнала
составляет D/3.
Комплексная огибающая КЧМ сигнала определяется
как
U(t)=Ufi 3 1Г; при \t\<Tf2. (5)
Спектр комплексной огибающей сигнала. В
соответствии с формулами (5), (2.2.17) .спектр комплексной
огибающей КЧМ сигнала записывается в виде
Г/2 iD ( t γ
<?(ω) = U0 j e v ' dt. (6)
-Г/2
Асимптотическое решение интеграла, аналогичного
(6), но с бесконечными пределами приведено в [60], для
случая конечных пределов и косинусоидальной
огибающей— в [61], а для случая конечных пределов и
постоянной огибающей — в [62]. Фазовая функция согласно
(3.1.37), (6) имеет вид
Точки стационарной фазы, определяемые из уравнения
(3.1.38), выражаются через параметры сигнала
следующим образом:
t01i3 = ±^-VV, (8)
где
— относительная частота.
При изменении ν от единицы до нуля точки
стационарной фазы tol и t02 движутся от краев сигнала (t =
= ±7/2) к середине (t=0), при v = 0 они сливаются, а
при v<0 превращаются в седловые. В случае v<0
следует использовать метод перевала [55]. Нахождение
интеграла (6) методом перевала достаточно громоздко [61].
Для нахождения интеграла (6) воспользуемся тем,
что его значение при проведении пути интегрирования
§ 3.3
149
через точку стационарной фазы или седловую точку при
большом параметре D определяется малой окрестностью
этих точек. Если эти точки расположены не близко
к краям отрезка интегрирования, чему соответствует
значение относительной частоты ν<1, то можно от конечных
пределов интегрирования перейти к бесконечным. Это,
в свою очередь, позволяет выразить интеграл (6) через
функцию Эйри (55, 60]. Однако при v«*l такой метод
применять нельзя, так как точки стационарной фазы
близки к краям отрезка (—7/2, 7/2]. В этом случае
фазовую функцию можно заменить параболой [61] и интеграл
(6) выразить через интегралы Френеля. Отметим, что
полученный при этом результат будет справедлив в
окрестности точки v=l, где 11—vl<Cl. Наконец, при ν>1
точки стационарной фазы выходят за пределы отрезка
[—7/2, 7/2]. Тогда следует воспользоваться разложением
интеграла (6) в асимптотический ряд [55, 61] и
ограничиться первым членом этого ряда.
Таким образом, процесс вычисления интеграла (6)
можно разбить на три этапа в соответствии с областями
изменения относительной частоты ν:
ν<1, ν«1, ν>1. (10)
Рассмотрим каждый случай отдельно. Пусть ν<Ί.
В соответствии со сказанным заменим конечные
пределы в интеграле (6) на бесконечные:
0(«) = С/. |е 3 1Г^ Ш dt. (11)
—оо
Введя новую переменную интегрирования
5=*Цг-« (12)
и используя мнимую часть υ (ζ) функции Эйри, которая
может быть записана как [55]
00
o(z) = iJLJcos(-!r+2*)d*. (13)
о
150
§ 3.3
выразим интеграл (11) через функцию ν (ζ):
O(v) = G0t;(-D2/32-2/3v), (14)
где
G0 = t/07V/221/3D~1/3. (15)
Приведем асимптотические формулы [55],
характеризующие поведение О (ν) при больших отрицательных и
положительных значениях аргумента функции Эйри для
ν<1.
Для отрицательных частот (ν<0, ω<0) аргумент
функции Эйри положителен и поведение спектра
определяется следующей асимптотической формулой:
О (v) ^ G02-5'6D-·"6 (- ν)" "4ехр [ --J- (_ ν)3'2] .(16)
Из формулы (16) следует, что при отрицательных
относительных частотах спектр затухает очень быстро. Это
вызвано наличием экспоненциального множителя.
Для положительных значений частоты справедливо
следующее выражение:
<?(v)^G.21/6D-1/6v-1/4cos (-|-v3/2 -JL\ при 0<v< 1.
(17)
Спектр в этом случае имеет осциллирующий характер,
определяемый косинусоидальным множителем. Кроме того,
с ростом ν спектр О (ν) затухает по закону ν~1/4.
Отметим также, что фаза косинусоиды промодулирована по
закону Dv3/2 /3. Следовательно, с ростом ν уменьшается
расстояние между соседними нулями спектра.
На рис. 3.9 изображен спектр сигнала с квадратичной
частотной модуляцией, рассчитанный по формуле (14),
для D = 9-102 при v<0,8. Огибающая спектра (штрих-
пунктир) построена по формуле
GMaKC = G02"6D-1/6v-1/V (18)
равной огибающей правой части выражения (17).
§ 3.3
151
Перейдем к случаю ν« 1, 11 —v| <С 1 ■ При этом
согласно ранее отмеченному, учтем влияние конечных пределов
интегрирования в (6) на результат интегрирования.
Разобьем интеграл (6) на два с пределами —7/2 и 7/2 так,
чтобы в каждом могла быть только одна точка
стационарной фазы. Тогда, разлагая фазовую функцию (7)
в окрестности точки стационарной фазы (например, toi)
Во
0,5-
)
1
Г
ч
^
0.25
0.5
Рис. 3.9.
0.75
W
в ряд Тейлора и отбрасывая малые высокого порядка
получаем
?,(0=MU+J^riiI('-Wa>
где
D
4D 1/2
?i(*.i) = -i-vd"; φ". (*..) = 7т ^
(19)
(20)
Член, содержащий φΊ(ίοι), отсутствует в (19) согласно
определению точки стационарной фазы. Аналогично (19)
записывается выражение для фазовой функции около
точки t02-
После замены фазовой функции в каждом интеграле
(6) параболами типа (19) оба интеграла можно
выразить через интегралы Френеля (3.1.9). Суммируя
результаты вычислений обоих интегралов, получаем
ОИ^2./э0?А,щ {[C(Zl)-C(z3)]cos-f-v3/2 -f
+ [S(z1)-S(za)]sin-^-v3/2lnpH ,W|, (21)
152
§ 3.3
где
z1 = /-£V'*; za = j/_£_v'/V'2-l). (22)
На рис. 3.9 согласно выражению (21) построен спектр
КЧМ сигнала для значений 0,8^v^,l,2. Огибающая
спектра рассчитана по формуле
°макс = ^з^б^ ^[С(21)-С(2а)]а + [5(21)-5(2а)]а.
(23)
Из рисунка видно, что огибающие спектра, построенные
по формулам (18) и (23) и соответствующие двум
различным участкам ν, достаточно хорошо сопрягаются на
границе участков (ν«0,9). Согласно формуле (18) при
ν = 0,9 огибающая спектра равна 0,370^ а согласно
формуле (23)—0,36 G0. Ошибка в сопряжении огибающих
спектра не превышает 3%', что вполне допустимо для
технических расчетов.
При ν>1 используем разложение интеграла (6)
в асимптотический ряд, получаемый последовательным
интегрированием по частям [55, 61]. Если интеграл в
общем виде может быть записан как
V{D) = \i{x)^wdx, (24)
а
то асимптотический ряд имеет вид
ft=o
где fh(x) определяются рекуррентными соотношениями:
f.(■«) = /И, №)=£\1ψ$-\ W
Если в исследуемом интеграле (6) заменить
переменную (x=it/T) и учесть (9), то интеграл (6) запишется как
G(v)c=U0T j e v ' dx. (27)
-1/2
9 3.3
153
Сравнивая интегралы (24) и (27) и учитывая (26),
замечаем, что
/(■*) = /,(*)= 1; ψ(χ) = ~Ι-χ'-νχ; ν'(χ) = 4χ>-ν. (28)
Подставляя соотношения (28) в ряд (25) и сохраняя
в нем только первый член (fe = 0), получаем
w^M^Y —^~ · (29)
Остальные члены с k>0 в формуле (25) можно
отбросить, так как в знаменателе к-то члена стоит Dh, a Z)» 1.
Согласно формуле (29) при больших ν спектр убывает
по закону 1/ν и имеет колебательный характер, причем
частота колебаний постоянна. Огибающая спектра
определяется соотношением
<w=^(4f^. (30)
На рис. 3.9 изображена часть спектра, построенная
по формуле (29) для \>\,2. При ν =1,2 огибающая
спектра согласно формуле (30) равна 0,049 Go, а согласно
формуле (23)—0,048 Go, т. е. ошибка сопряжения двух
соседних участков по огибающим не превышает 3%'.
Проанализируем полученные результаты. Во-первых,
следует отметить, что согласно (17), (21), (29) спектр
КЧМ сигнала имеет осциллирующий характер,
обусловленный тем, что сигнал (5) состоит из двух импульсов,
которые зеркально симметричны относительно начала
координат (/=0). Спектры этих импульсов содержат
одинаковые спектральные составляющие с различными
фазами. Интерференция между этими составляющими
приводит к появлению нулей в спектре сигнала.
Во-вторых, спектр О (ν) является действительной функцией
частоты вследствие нечетности фазы (2.2.39).
Рассмотрим неравномерность амплитудного спектра
КЧМ сигнала в пределах области 0<v<l (0<to<W),
т. е. при условии, что точки стационарной фазы лежат
на отрезке [—7/2, 7/2]. Вклад точки стационарной фазы
154
§ 3.3
в значение искомого интеграла определяется ее радиусом
влияния, который для данной задачи согласно (3.1.40)
равен
_ 1 _ 1 Τ
Р ~Vh'\(U)\ ~ Л/Щ^" 2D'/2v,/4 ' (31)
С ростом частоты ν радиус [влияния уменьшается
пропорционально νι/4 , т. е. в создании спектра на частоте ν
при ее увеличении участвует все меньшая доля сигнала.
Поэтому с ростом частоты спектральная плотность
уменьшается. Следует отметить, что все сигналы с нелинейной
частотной модуляцией должны иметь неравномерный
амплитудный спектр, так как радиус влияния с
перемещением точки стационарной фазы не остается
постоянным. Равномерный амплитудный спектр можно получить
только для сигнала с линейной частотной модуляцией,
поскольку для него вторая производная фазовой
функции будет постоянной.
Теперь обратимся к поведению спектра КЧМ
сигнала при ν>1 (ω>Ψ) и ν<0 (ω<0). В случае ν>1
асимптотическое поведение спектра определяется в основном
свойствами амплитудной огибающей сигнала вблизи
краев сигнала, которая при t=±T/2 терпит разрыв. Как
было сказано ранее, если функция терпит разрыв, то ее
спектр убывает пропорционально 1/v, о чем
свидетельствует формула (30), в знаменателе которой при v»l
можно пренебречь единицей. Действительно, как было
отмечено ранее, с ростом частоты ν точки стационарной
фазы перемещаются к краям сигнала и при ν>1 именно
края сигнала и определяют поведение спектра. При ν = 0
точки стационарной фазы сливаются и совпадают с
серединой сигнала, а затем при ν<0 они превращаются
в седловые. Поскольку поведение спектра при ν<0
определяется центральной областью сигнала, где сигнал и
все его производные непрерывны, то спектр быстро
затухает (16).
Комплексная огибающая корреляционной функции.
Подставляя комплексную огибающую (5) в (2.3.19), по-
§ з.з
155
лучаем для τ^Ο
1-555- 1 Γ ' "ρ·1 "ρ""")'
Λ (τ, Q) = e -г J e dt- С32)
-Г/2+τ
Дополняя показатель экспоненты (32) до полного
квадрата и вводя нормированные задержку и частоту Доп-
плера, равные соответственно
Χ = ·γ, ν = -ψ' (33)
получаем следующее выражение для комплексной
огибающей корреляционной функции
Г/2
K-M^vlf)]'
χ+ Г eT»r-l">-Krr|]ft (34)
-Т/2+хТ
где
<·(*.«= Y+f-тСг (35!
Введем новую переменную
при которой формула (34) преобразуется к виДу
Я{х.у) = *1*1'-')У^]еЬ''11г, (37)
где
156
§3.3
Используя определение интегралов Френеля (3.1.9),
формулу (37) можно записать как
X {[С (za) - С (ζ,)] + i [S (z2) - S (z,))} e,D" <*· "λ (40)
Рассмотрим сначала автокорреляционную функцию,
т. е. в (40) положим у = 0. При этом Ζι =—ζ2 и в силу
нечетности интегралов Френеля автокорреляционная
функция примет вид
R (■*) = У Ш [С (ζ.) +15 (г,)] е · (41)
Используя усеченные ряды Тейлора для интегралов
Френеля (3.1.15), (3.1.16) и учитывая, что S(z)<^C (z) при
ζ—-0, можно показать, что C(za)—»ζ,—► j/^D-xr/n, т. е.
R(x)—>1 при л: —0. Соответственно (41) модуль
автокорреляционной функции определяется формулой
1*(*)Н1/а/с,(г'> + 5'(^ · (42)
Рассмотрим зависимость модуля автокорреляционной
функции от нормированной задержки, рассчитанную по
формуле (42) для D=2n· 13, т. е. для iFT= 13, и
изображенную сплошной линией на рис. 3.10. В начале
координат имеется узкий основной пик, который согласно (42)
сужается по мере увеличения FT. Боковые пики убывают
медленно относительно среднего значения, но следует
отметить, что их величина близка к величине боковых
пиков идеального тела неопределенности (2.4.12).
Действительно, предположим 2гЗ>1, что справедливо при D^>1
и х, не стремящимся к нулю, т. е. вне области сильной
корреляции. Тогда из асимптотических формул (3.1.17),
(3.1.18) имеем C(z2)—*1/2 и S(z2)—»1/2. Это означает,
что
[/?(x)'K-^L== J_ при х>0. (43)
1 v " 2 YDx Y&FTx , '
Зависимость, рассчитанная по формуле (43), изображена
§ 3J
157
на рис. ЗЛО пунктиром. Из рисунка видно, что при х>
>0,05 отличие между точной кривой (42) и
асимптотической (43) незначительно. Из (43) следует, что при х—
= 1/2 значение |/?(*)1 совпадает со значением боковых
пиков идеального тела неопределенности.
Покажем, что формула (43) может быть получена
непосредственно из определения комплексной огибающей
0,8 1
ο,6 4
пи.
*'
ц*
V
^С
у\
FT-13
.
\
ν
L
ч:
^»
>С
^_
JS;
■?*
-Ч-
0,2
о,* 0,6
Рис 3.10.
Οβ
χ -
корреляционной функции (32). Фазовая функция
согласно (3.1.37), (32)
(44)
<Ρι (0 = -jr t* — (-ψ— Q J *■
Точка кггационарной фазы с учетом обозначений (33)
согласно (3.1.38) определяется из уравнения
Вторая производная фазовой функции
„" (t\ — *I*
(45)
(46)
158
§ 3.3
Используя (3.1.39), (34), получаем
\Я(х,у)\^
2УШ
при х>0, г/>0.
(47)
Формула (47) показывает, что в сечении х = const модуль
\R(x, y)\ при изменении у остается постоянным. Это
постоянство сохраняется приблизительно в пределах суще-
ствования точки стационарной
фазы. Из интеграла (32) видно,
что пределы существования точки
стационарной фазы равны 772 и
—Т/2 + х. Подставляя эти
значения в уравнение (45), получаем
уравнение линий на плоскости
(*. У)
у=±4(х*—х), (48)
между которыми точка
стационарной фазы вносит вклад (47)
в тело неопределенности.
Параболы, описываемые
уравнением (48), представлены на
рис. 3.11. Внутри парабол
согласно (47) уровень корреляционной
функции при *=const остается
примерно постоянным и опреде-
Рис. З.п. ляется величиной D и
значением х.
На рис. 3.12 изображены сечения тела
неопределенности, построенные в соответствии с (40) для FT=25 при
различных значениях y=mjFT (m = 0; 1; 5; 10). Такие
значения у соответствуют Q = m2n/T. Как видно из
рис. 3.12, при *>0,2 уровень всех сечений примерно
одинаков.
На рис. 3.13 представлено тело неопределенности,
построенное в соответствии с (40) для D = 9-102, т. е.
для FT=\43. Поскольку при больших значениях FT
уровень осцилляции мал по масштабу, то эти осцилляции не
приведены на рисунке. Вблизи основного пика боковые
пики больше уровня боковых пиков для идеального тела
9 3.4
159
неопределенности, но в целом тело неопределенности
КЧМ сигнала близко к идеальному.
Область сильной корреляции КЧМ подробно
исследована в § 2.6.
\*Гх.У)\
0,8
0,6
ОЛ
0,2
\\
г
h
1 Су*
\~Г
/ ,
т- -А
Г
У
)
>
=0
Лч
^с*«
FT
1
5FT
·/
^^^
/1
FT
1
OFT
\.
=25
—"■ "
<Z
\
<%
0,2
Ο,ϊ 0,6
Рис. 3.12.
0,8
3.4. СИГНАЛЫ С НЕЛИНЕЙНОЙ ЧАСТОТНОЙ
МОДУЛЯЦИЕЙ ВЫСШЕГО ПОРЯДКА
В § 3.2, 3.3 были рассмотрены сигналы с
нелинейной частотной модуляцией при четном законе изменения
частоты. Эти сигналы согласно § 2.5, 2.6 обеспечивают
160
§ 3.4
независимость оценок дальности и скорости при их
совместном измерении. !В области слабой корреляции тела
неопределенности этих сигналов приближаются к
идеальному (см. рис. 2.12). Наилучшим с точки зрения
приближения к идеальному следует считать КЧМ сигнал.
Кроме рассмотренных законов .нелинейной частотной
модуляции существует большое число других законов.
Рис. 3.15.
Например, пусть изменение мгновенной частоты
описывается полиномом
e'(0 = S^ft при |ί|<Γ/2, (1)
в котором коэффициенты аь выбраны так, чтобы
выполнялось условие
е'макс-е'„и„г=^. (2)
необходимое для адекватного сравнения различных
сигналов. Если К>2, то выражение (1) описывает
нелинейную частотную модуляцию высшего порядка.
Естественно, что выражением (1) не исчерпываются все
возможные законы нелинейной частотной модуляции.
§ 3.4 ,
161
Определим особенности сигналов с нелинейной
частотной модуляцией высшего порядка. Интегрируя (1),
получаем выражение для фазы
•W = SsTTifc+1· (3)
£=0
где а0 — начальная фаза.
Комплексная огибающая сигнала определяется как
U{t) = U^{t) при \t\<T/2, ■ (4)
где Q(t) представляется выражением (3).
Основные особенности спектра. Спектр комплексной
огибающей рассматриваемых сигналов может быть
определен с помощью выражения (2.2,17), Поскольку для
сложных сигналов D=WT^$>1, то для определения
спектра комплексной огибающей целесообразно использовать
метод стационарной фазы. При этом согласно (3.1.49)
необходимо найти точки стационарной фазы, решая
уравнение
θ'0ί№)·=ω. (5)
Из уравнения (5) следует, что спектр сигнала на
частоте ω определяется той частью сигнала, для которой
мгновенная частота θ'(0 совпадает с ω.
Для определения вклада каждой точки стационарной
фазы в спектр необходимо найти вторую производную
Q"(toh) и воспользоваться асимптотическим равенством
(3.1.39). Однако θ\(?) может иметь несколько
экстремумов, в которых θ"(0 =φ"ι(ί) =0. Поэтому от
квадратичного приближения фазовой функции (3.1.29) следует
перейти к приближению третьего порядка [55]. В общем
случае может оказаться, что в точке стационарной фазы
производные фазовой функции
Такая точка называется точкой стационарной фазы
порядка т [63]. При этом для фазовой функции в окрест-
162 § 3.4
ности такой точки следует использовать приближение
высшего порядка. Найдем вклад точки стационарной
фазы высшего порядка в спектр комплексной огибающей
сигнала.
Согласно (3.1.37), (2.2.17) из (5) фазовая функция
Φι(0 = θ(Ο—«Л (6)
Представим фазовую функцию (6) в окрестности точки
стационарной фазы to порядка т усеченным рядом
Тейлора:
^ = ^ο)+4^(ί~ίοΓ+1· (7)
где
т;т+,,(*0) = в(т+,,('.)при«>р, (8)
а первая производная удовлетворяет уравнению (5).
Подставим фазовую функцию (6) и (7) с учетом (8)
в выражение для спектра комплексной огибающей
сигнала (2.2.17). Полагая, что другие (если они есть) точки
стационарной фазы достаточно удалены от ίο, расширяем
пределы интегрироиания до бесконечности. В результате
получаем
О (·) <х, С/, ехр [щ (i.) ] J exp [i ^У)? {t ~ ίβΓ+' ] dU
—00
(9)
Осуществляя в (9) замену переменных
_ι ι_
2 = K±l)|ee»+,)(gDm + ' [(«+1)!] m+\t~U), (10)
где знак перед единицей определяется знаком 9(m+1)(i0),
получаем
0{^и^\Ж^\^ Jexpi-fc—)*.. (11)
—00
Определим интеграл
j(m-\-\)= jexp.(±iz«+1)ii2. (12)
—оо
9 3.4
163
входящий в (11). Пусть т-\-\ четно. Тогда
00 00
ff(m + \)—2 [ cos zm+1iiz ±12 J sin zm+ldz. (13)
ό о
Используя табличные значения интегралов (13) [64],
получаем
ff(m + l)-.
2г(^т) *'5ΤΪΤΪ)
т +
(14)
где Т(х) — гамма-функция.
Аналогично, при нечетном m -f-1
°° 2Г f^-χτ)
У (m + I) = 2 Г cos z™+xdz = —A—1-^
cos
2(»+I)
(15)
В табл. 3.1 приведены значения [7(m-\-l)\ для
различных τη. Можно показать, что
Уп
Ι^(» + ΐ)Ι
lim ^(/n -f
m-*oo
1
Κ"ί= 1,77
2
1,52
■1) = 2.
3
1,81
4
1,74
(16)
Таблица 3.1
5
1,95
6
1,89
Согласно (11) и (12) имеем
|ад|-^[^ж1Гт+,|-7^+1^^><
В качестве примера нахождения спектра комплексной
огибающей сигнала рассмотрим сигнал со степенным за-
164
8 3.4
коном частотной модуляции. Пусть
eW = iiFTn^+1' β'(') = ^" при \t\<T/2. (18)
где k=\, 3, 5, т. е. закон частотной модуляции нечетный.
-Поэтому точка стационарной фазы единственная и ее
можно найти из уравнения (5):
<.=4 (£)'"· <19>
Значение спектра комплексной огибающей сигнала
в точке ω = 0 определяется точкой стационарной фазы
порядка к при t0 = 0. Для расчета \0 (0) | в формуле (17)
достаточно заменить т на k. После преобразований
получаем
k—\ ι_
|<?(0)|^2 k+l S.(j^ k+i F(fc+l)l. (20)
где, как обычно,
D=WT; S0=U0T.
При ω^Ο порядок точки стационарной фазы т=\.
В этом случае, пользуясь формулой (3.1.39) [или, что
то же самое, формулой (17) при т=\], получаем
\OH\^Sy2i(kDril2(^-) 2* · (21)
На рйс. 3.14 изображены амплитудные спектры
комплексной огибающей сигнала, рассчитанные по
асимптотическим формулам (20), (21), для k=l, 3, 5 и £) =
= 2π·100, τ. е. для iT=100. Отметим, что спектры
построены только для соС^О, так как они четны
относительно ω=0 согласно (2.2.36).
Анализируя зависимости, приведенные на рис. 3.14,
отметим следующее. Характерным является увеличение
высоты пика в центральной части спектра (около ω=0)
с ростом k. Это объясняется тем, что при нелинейной
частотной модуляции (k>l) мгновенная частота в сере-
δ 3.4
165
дине сигнала меняется медленно, а на его краях быстро.
Часть сигнала, где мгновенная частота меняется
медленно, создает спектральные составляющие около
центральной частоты спектра ω = 0. С ростом k ширина части
сигнала с медленным изменением мгновенной частоты
растет, что и увеличивает высоту пика в центральной части
спектра.
0,2 0,U 0,6
Рис. 3.14.
Точно так же можно показать, что и при четных
законах модуляции с ростом показателя степени закона
частотной модуляции спектральная плотность сигнала
увеличивается в узкой полосе частот, но расположенной не
в центре спектра, а на его краю (см., например, рис. 3.9,
где изображен спектр КЧМ сигнала). Следовательно,
сигналы с нелинейной частотной модуляцией высшего
порядка по своим спектральным свойствам с ростом
показателя степени закона частотной модуляции'приближа-
166
δ 3.5
ются к смодулированному сигналу. Это означает, что и
корреляционные свойства таких сигналов аналогичны
корреляционным свойствам немодулированного сигнала.
3.5. СИГНАЛЫ С ЧАСТОТНОЙ
МАНИПУЛЯЦИЕЙ
Пусть сигнал длительностью Τ состоит из
радиоимпульсов (рис. 3.15), следующих друг за другом. Дли-
Рис. 3.15.
тельность одиночного импульса
το=Τ/Ν.
(1)
Несущие частоты всех импульсов отличаются друг от
друга на величину, кратную единичному сдвигу по
частоте Δω. Частотный сдвиг «-го импульса зависит от
номера импульса η и равен [q{n)—1]Δω, где
q(n) = \,2 Ν (2)
— целочисленная функция от п.
На рис. 3.15 под номерами импульсов η указаны
соответствующие им значения q(n). Минимильный
частотный сдвиг равен нулю, максимальный (Ν—1)Δω. Если
частотный сдвиг равен примерно ширине спектра
радиоимпульса, то полоса частот, занимаемая таким
сигналом, равна
Ψ=ΝΔ&, (3)
§ 3.5
167
Обычно
Δω = 2π/το. (4)
Поэтому W = 2nN/x0. Умножая выражение для W (3)
на длительность сигнала Τ = Ντ0 и учитывая (4),
получаем
WT=2nN\ или FT=N2. (5)
Например, если FT=100, то сигнал должен состоять из
10 импульсов.
Комплексная огибающая импульса с частотным
сдвигом [q(n)—ΙΙΔω определяется выражением
Uq(n) (t) = U0u0 (t) e'« (n)-] Ш+"« '"'при 0< t< ν (6)
где θο9(η) — начальная фаза; Uq — амплитуда.
Сигнал (рис. 3.15) состоит из импульсов вида (6).
Запаздывание относительно начала координат «-го
импульса равно (п—l)to. Для упрощения аналитической
записи выражения (6) определим единичный импульс
и0(0 = 1 при 0^/^То. (7)
Тогда выражение (6) может быть записано как
£/?(n)(0 = ^o(Oei[,('г)-|]Δω'+lθ'ч(",. (8)
Поскольку импульсы в сигнале запаздывают на
величину (п—l)to относительно начала координат, то
комплексная огибающая сигнала рис. 3.15 имеет вид
£Д0=£ идЫ) [t-(n-l)x0] =
=,U0^u0[t-(n-\)^]ei4ln)~l]&ait-in-i)4]+^· (9)
Если начальные фазы всех импульсов сигнала с
частотной манипуляцией одинаковы, то различие между
импульсами сводится к различным частотным сдвигам.
168
9 3.5
Такой сигнал можно назвать частотно-манипулирован-
ным (ЧМн). Если же и начальные фазы различны, то
сигнал можно назвать частотно-фазоманипулированным
(ЧФМн).
Особенности спектра. Спектр комплексной огибающей
ЧМн сигнала (9) как спектр последовательности
импульсов определяется следующим выражением:
0(-) = £ ^Ие-""-'»""0, (Ю)
где
О«(п)Н=]|7,(п)(0е"~,"/Л (11)
— спектр комплексной огибающей одиночного
импульса (8).
Подставляя в (11) значение Vq{n)(t) (8), после
преобразований получаем
<??(n)H=jX
sin {ω - [q (ή) - 1] Δω} ~- - !{«,_ tt (η)-ΐ] дш} £ +Ιθ„,(η)
χ —e . <12>
{»-Η/ι)-1]Δ»}-£
гдeSo=C/o7,.
Из выражения (12) следует, что положение спектра
«-го импульса на оси частот зависит от величины его
частотного сдвига [q{n)—1]Διω. На левом краю спектра
сигнала находится импульс с q(n) = l (рис. 3.16), а на
правом — с q(n) =N.
Спектр (10) определяется не только характером
спектра одиночного импульса (12), но и фазовым
сдвигом «-го импульса (η—1)ωτο, вызванным запаздыванием
импульсов. В подтверждение сказанного рассмотрим
сумму спектров двух соседних по частоте одиночных
импульсов с q(n) и q(n)+l в точке, лежащей посередине
частотного интервала между максимумами этих
спектров, Влиянием спектров других одиночных импульсов
из-за их малости в данной точке пренебрежем. Отметим,
§ 3.5
169
что рассматриваемые импульсы по оси времени могут
занимать произвольное положение. Если запаздывание
импульса с q(n) равно (п—1)tq, to запаздывание
импульса с q(n) + l равно (п—1+т)х0, где m — целое
число, удовлетворяющее условию О^/г—l+m^N—1.
С учетом сделанных замечаний сумма спектров двух со-
Рис. 3.16.
седних по частоте одиночных .импульсов в точке о>=
1
= \у(п)—2"|Δα> равна
"сум —
_- «.
Δωτ0 , Δ
sin—т— I i=2ji + i(
oq(n)
<=ум— N Δωτβ
+
+ e ί
e.^(«-0) (13)
где Δωτο=2π согласно (4); mq(n) — всегда целое число.
Модуль выражения (13)
\0,
сум
ι— 2S»i ι ι J"(m-1)+,((W>+i-W>i
(14)
Из (14) следует, что величина |<3Сум1 зависит от
начальных фаз соседних по частоте импульсов и от
запаздывания между ними. Например, если начальные фазы
равны, то при нечетном т |0Сум1 (14) равен 4S0lnN, а при
четном т—нулю. Поэтому в общем случае спектр ЧМн
сигнала (10) может иметь провалы, обусловленные «н-
170
δ 3.5
терференцией спектральных составляющих разных
импульсов. Характер спектра в целом определяется
начальными фазами импульсов θο9(η) и распределением
импульсов по частоте q{n).
Для сигнала с линейной частотной манипуляцией
(ЛЧМн), являющегося дискретным аналогом сигнала
с ЛЧМ, функция
q{n)=n. (15)
В этом случае в формулах (13), (14) т=\ и при
одинаковых начальных фазах импульсов |GcyM| (14) равен
4So/nN, т. е. в спектре ЛЧМн сигнала провалов до нуля
не будет.
Особеииости корреляционной функции. Подставляя
определение комплексной огибающей ЧМн сигнала (9)
в формулу (2.3.19), получаем комплексную огибающую
.корреляционной функции для ЧМн сигнала в следующем
виде:
τ ν ν
л(т.о)=4-|5]5]и.р-(я-1к]х
Хи0 ['-(*-1К-'] expi {[<?(«)-1] Δω [ί-(«-1)τ0]-
- [q\k)- 1] Δω [t-{k- 1).τ0 - τ] + θ0? (η) - θοί(Λ) + Ш}dt.
(16)
Меняя местами порядок суммирования и интегрирования
и вынося за знак интеграла множители, не зависящие от
переменной интегрирования t, получаем
N N
где
00
Λ. Κ. Ωι) = -^- JM0(0"o('-*i)e10''d/ (18)
—оо
— комплексная огибающая корреляционной функции
единичного импульса (7).
ξ 3.5
1?1
Пределы интегрирования в (18) учитывают область
определения u0{t) и знак т. Отметим, что
Л.(О, 0)=1; (19)
τ,=τ — (П— k)ia (20)'
— смещенная задержка;
Ω, = Ω+[?(η)-?(*)] Δω (2ί)
— смещенная частота Допплера;
γ = q(k)(k — η) Δωτ0 — (η — k) Δωτ0 -\-[q(k)—\\ Δωτ-f
+ e*(«)-fl*(k) + ("-l)Qv (22)
Согласно формуле (2.4.4) выражение (18) можно
записать в виде
Λ.(τ„ Ωι)=(ΐ_ίΑ!.)χ
Согласно (17) комплексная огибающая корреляционной
функции ЧМн сигнала представляется суммой слагаемых
вида /?0(ti, Ω^εχρΟγ). Местоположение максимального
значения (19) любого слагаемого из суммы (17) на
плоскости (τ, Ω) находится из уравнений
ti = 0, Ωι = 0, (24)
которые в соответствии с (20), (21) преобразуются
к виду
x = (n-k)x0, (25)
a = —[q(n) — q(k)]ba. (26)
Следует отметить, что согласно (17), (19) величина
максимума любого слагаемого равна 10. Местоположе-
172
§ 3.5
ние максимумов характеризуется как разностью (п—k)
(25), так и разностью q{n)—q(k) (26).
Рассмотрим слагаемые в формуле (17) в
зависимости от соотношения η и k. При n = k согласно (20) —
(22) q(n)=q(k), τ/= τ, Ω, = Ω,
a
γ = [?(η)-1]Δα« + (η-1)Ων (27)
Из уравнений (25), (26) следует, что максимумы
слагаемых с n^k расположены в начале координат (τ=0, Ω =
= 0), т. е. слагаемые в формуле (17) с n = k составляют
центральную часть корреляционной функции ЧМн
сигнала. Выделяя эти слагаемые из корреляционной
функции (17), запишем их сумму.
N
/?η=Λ(τ, Ω) = /?„(*, fl)^Jel"("bll4"' + ""-1,i". (28)
ra=i
Из (28), полагая τ = 0, Ω = 0, получаем, что
*n-k(0, 0) = Λ(0, 0)=1. (29)
Размеры области сильной корреляции в соответствии
с результатами, приведенными в гл. 2, должны быть
примерно равными 2n/W по оси τ и 2π/Τ по оси Ω. В то же
время множитель /?0(τ, Ω) перед суммой в (28)
определяет корреляционную функцию единичного импульса
(7), размеры которой по этим осям равны 2π/Δω и 2π/το,
поскольку Δ>ωτο=2π. Очевидно, что сумма в выражении
(28) является множителем, определяющим сжатие
корреляционной функции по оси частот.
Рассмотрим соотношение (28) при τ=0. В этом
случае согласно определению суммы геометрической
прогрессии
ve.-i)0.=_^_e » . (30)
*■■. sin —г—
8 3.5
ί73
Подставляя (30) в (28) и учитывая (23), получаем
Rn^(Cl)=-^-e =-^-е ■ (31)
2 2
Ширина центрального пика функции (31) между
максимумом и первым нулем равна 2я/Т. Отметим, что на
поведение корреляционной функции (17) вдоль оси Ω
оказывают влияние только слагаемые с n = k. Поэтому
(31) точно определяет (17) при τ=0. При Ω = 0 из (28)
с учетом (23) получаем
/?n=ft(x)=(i-41)4-i3ei[?(ra,~i]AMX· <32>
п—\
Чтобы вычислить сумму в (32), надо знать функцию
q(n), т. е. форму сигнала. В качестве примера
рассмотрим сигнал с ЛЧМн (15). Для такого сигнала сумма
в (32) в соответствии с (30) равна
*„-*(*)=(i-ш) 4|ге 2 · <33>
2
При Ы<СТо, разлагая второй множитель в (33) в ряд
Тейлора и беря модуль, получаем
|/?η=Λ(τ)|^1|--1-(Λ/Δω)ν=1-^-^ν, (34)
т. е. ширина области сильной корреляции обратно
пропорциональна ]/2ifW м 2m(W.
Рассмотрим теперь слагаемые в (17) с пф%
Максимумы этих слагаемых могут быть расположены только
при τ, кратном το (25), и при Ω, кратном ιΔΙω (26).
Решения уравнений (25), (26) приведены на рис. 3.17
(пунктирные линии). Максимумы слагаемых с пфк
могут находиться только на пересечениях пунктирных ли-
1"4 9 3.5
w
r ι ι ι
-4- -1-4-
4
■+■ -
ний, т. е. в узлах. Для примера на рис. 3.17 темными
точками отмечены положения максимумов слагаемых
с пфк для сигнала, представленного на рис. 3.15.
Отметим, что для данного сипнала для пфк нет ни одного
случая совпадения положений максимумов. Это
объясняется таким выбором функции q(n), при котором
минимальное значение максимумов боковых пиков равно
1/УУ=1/5.
Так как N = У FT, то боковые пики корреляционной
функции равны 1/J/KT. [Для [того чтобы получить такие
боковые пики, надо найти соответствующую функцию
q{n). /Например, для сигнала с ЛЧМн q(n)=n и
слагаемые с η—k = const (в 15) дают
совпадающие максимумы в
"1 | j | точке с координатами τ= (η —
— k)x0, Ω = — (η—Λ)Δω. На
рис. 3.17 этим максимумам
соответствуют светлые точки.
Выбор функции q(n), при
которой все максимумы с
пфк не совпадают друг с
другом, позволяет получить
минимально возможные боковые
пики для ЧМн сигналов. В
настоящее время еще
неизвестно, при каких N задача
определения 4(п) при
минимальных боковых пиках имеет ре-
1 ι I шение. Покажем, что на
плоскости (τ, Ω) можно разме-
Рис. 3.17. стить все максимумы без
взаимного наложения.
Действительно, число слагаемых в формуле (17)
равно Ν2. Согласно (28) N из них приходится на начало
координат. Половина оставшихся Ν2—N слагаемых
приходится на правую полуплоскость (τ, Ω) для τ>0, а
половина— на левую для τ<0, т. е. правой полуплоскости
(т, Ω), показанной на рис. 3.17, соответствуют (Ν2—Ν)/2
слагаемых. Слагаемые в (17) с пфк могут
соответствовать всем узлам, за исключением находящихся на пере-
-44+4~
D у
-ИЛ
-t--M-f-
__U-L
-<?—I—
-Г-Г4-+·
Τ t
δ 3.5
175
сечении линий τ = 0; Τ и Ω = 0; ± W. Поэтому общее
число свободных узлов равно 2(Л/—I)2. Очевидно, что
2(N— 1)2>(JV2—Ν) β, (35)
т. е. число свободных узлов на плоскости (τ, Ω) больше
числа импульсов с пфк.
В заключение отметим одну особенность 'некоторых
ЧМн сигналов. Рассмотрим плоскость время—частота
для ЧМн сигнала при N = 7 (рис. 3.18). Заштрихованные
Рис. 3.18.
квадраты на этой плоскости соответствуют размещению
отдельных импульсов по времени и частоте. Для
рассматриваемого сигнала функция <7(«) = 3, 4, 1, 6, 2, 5, 7.
Можно получить еще три сигнала, которые, обладают
минимальным распределением боковых пиков. Этим
сигналам соответствуют квадраты, повернутые относительно
исходного (рис. 3.18) на 90, 180, 270°. Таким образом
получены четыре сигнала, функции q(n) которых
записываются как:
3, 4, 1, 6, 2, 5, 7
5, 3, 7, 6, 2, 4, 1
1, 3, 6, 2, 7, 4, 5
7, 4, 6, 2, 1, 5, 3. (36)
176
§ 3.5
Кроме отмеченных четырех сигналов, могут быть
получены еще четыре-инверсных сигнала с функциями q{n)
вида:
7, 5, 2, 6, 1, 4, 3
1, 4, 2, 6, 7, 3, 5
5, 4, 7, 2, 6, 3, 1
3, 5, 1, 2, 6, 4, 7, (37)
т. е. всего может быть получено восемь сигналов. Однако
отмеченной особенностью обладают не все ЧМн сигналы.
177
глава 4 ФАЗОМАНИПУЛИРОВАННЫЕ
СИГНАЛЫ
4.1. ОБЩИЕ СВОЙСТВА
ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ
Фазоманипулированными (ФМн) называются
сигналы, 'которые представляют последовательность
импульсов одинаковой формы, следующих друг за другом с
интервалом το- Импульсы могут отличаться амплитудами и
начальными фазами.
На рис. 4.1,α изображен ФМн сигнал, состоящий из
радиоимпульсов. Для простоты на рисунке в каждом
импульсе укладывается один период несущей частоты.
Амплитуда, фаза и запаздывание относительно
начала координат п-то импульса обозначаются
соответственно U„, θ„, tn= (η—1)το. Число импульсов в сигнале N.
По форме все импульсы совпадают с единичным
импульсом Uo(t). Наиболее часто используются
прямоугольные единичные импульсы:
u0(it) = l при Ο^ιί^ΐο, (1)
длительность которых- равна интервалу ΝΤο между
импульсами сигнала (интервалу задержки). При любой
другой форме единичных импульсов будем считать, что
энергия произвольного единичного импульса равна
энергии прямоугольного единичного импульса, т. е. £ι = τ<>.
Если используются прямоугольные единичные
импульсы, то длительность сигнала
Τ=Ντ0. (2)
Первый импульс сигнала записывается как
САМО cos («„г+'60,
«-Й импульс —
U„u0 (t — tn) cos К (t — tn) -f S„],
1/8
§ 4.1
а весь сигнал как
N
«(')=£ */««.(* —*n)cos К(* — /„)+ А„]. (3)
л=1
Комплексная огибающая сигнала [(3) определяется как
U{t)^^Unua(t-tn),
п=\
affn-fjttj
Τ
π
(Рис. 4.1.
(4)
где комплексная амплитуда «-го импульса
(5)
В формуле (5) фаза кроме θη содержит слагаемое
—ωοίη« которое обусловлено некратностыо τρ периоду
2π/ωρ,
§ 4.1 179
ФМн сигнал образуется не только путем задержки
относительно друг друга импульсов одинаковой формы,
как сигнал, определяемый формулой (3), но и
«вырезанием» из непрерывного колебания coscoc^ импульса
с последующей амплитудной и фазовой манипуляциями.
В последнем случае ФМн сигнал записывается как
«(*)=£ ί/η"ο U - tn) COS (CD,/ + β„), (6)
а комплексная амплитуда «то импульса
Un = Ue\ (7)
Отметим, что формула (7) отличается от (5)
дополнительным слагаемым —iootn в фазовой функции
формулы (5). Это различие не является существенным,
поскольку величину —ωοίη всегда можно учесть в θη·
Поэтому в дальнейшем будем пользоваться
определением (7).
Так как комплексная огибающая «-го импульса
Un(t) = Unu0(t-tn), (8)
то комплексная огибающая сигнала записывается в виде
п=\
Наибольшее распространение получили ФМн
сигналы, фазы которых θη могут принимать только два
значения: 0 или π. Если в сигнале используется большее
число значений фаз θη в пределах 0—2π, то такие
сигналы называются многофазными. Амплитудная модуляция
ФМн сигналов обычно нежелательна, так как она
уменьшает излучаемую энергию при ограниченной пиковой
мощности передатчика. Поэтому в большинстве случаев
i/n = t/0= const. В дальнейшем будем пользоваться
нормированной комплексной амплитудой импульса (или сим-
180
9 4.1
волом), которая определяется как
an=U7-U7e ' (10)
где средняя амплитуда С/0 связана с энергией сигнала
выражением
г— ι/Σί/«τ» г—*—
и.-/?-} ^=J ^vl- (1„
Если Un=>U0, а θη = 0; π, то согласно (10)
a„ = cos6„ = ±l. (12)
Последовательность
{αη} = «ι, аа,..., а„,..., а„, (13)
составленную из символов ап, будем называть кодовой
последовательностью. Она полностью характеризует сигнал,
так как символы ап определяют нормированные
комплексные амплитуды импульсов, образующих ФМн сигнал.
Решетчатая функция. Кодовая последовательность
(13), изображенная на рис. 4.1,6, может быть описана
решетчатой функцией а[(п—1)то], значения которой
определяются только в дискретные равноотстоящие
моменты времени, т. е.
«1("-1Κ1 = Σ a„8[i-(n-l)tj, (14)
где δ (χ) — дельта-функция. Ординаты решетчатой
функции ап называется дискретами.
Спектральные свойства ФМн сигналов. Согласно
(2.2.17) спектр комплексной огибающей ФМн сигнала (4)
τ ν
О (■) = f £ £/„и0 (t - tn) e~ ш dt. (15)
О п=1
Меняя порядок суммирования и интегрирования в (15), и
9 4.1
181
обозначая через S0(m) спектр единичного импульса:
$,(■)= ]и0«)<гшса, (16)
—00
получаем
N
0(m) = S,(m) £ £/„e " ». (17)
Так как
ίη = (η-1)τ„ (18)
£/n = «nt^o согласно (10), то (17) можно записать как
/ν
0(«)=S(«)£ One-1 (я_|)"^, (19)
где
5(«)=1Ш«) (20)
— спектр единичного импульса со средней амплитудой С/0.
Обозначая
НМ^ап^^"*, (21)
п=\
запишем (19) в виде
0(<o) = SH//(co). (22)
Η (ω) будем называть спектром кодовой
последовательности. Рассмотрим его свойства.
1. Спектр кодовой последовательности является
спектром решетчатой функции. Действительно, согласно
(2.2.17) спектр решетчатой функции равен
11>п8и-("-1К]е-1<0'Л = £
О га=1 п=\
ίΣ e„8U-(n-l),Je-1"'rfi = 2 ane-1<n->)^ = H(«).
(23)
Для кодовой последовательности справедливо и обрат-
182
δ 4.1
ное преобразование Фурье, т. е.
оо N
[ ^(α))β1ωίίίω=^Ληδ[ί-(«-1)τβ1. (24)
2π
—00 П=\
2. Спектр кодовой последовательности —
периодическая функция с периодом 2π/το, т. е. для целых чисел /
//(ω + ί^)=//(ω)· (25)
Действительно, обозначая
*=»т,, (26)
согласно (21) получаем
N
Щх) = %апе-Цп-их. (27)
п=\
Из (27) следует, что спектр кодовой последовательности
Н(х) является периодической функцией с периодом 2*.
3. Подставляя (10) в (27) и разделяя действительную
и мнимую части, находим, что
N N
Η (х)= JJ gs- cos Ιβ„—(я— 1) js] +i JJ gs. Sin [β„—(n— 1 )x] =
— Y]^ lcos6„cos(«— l).x:-f-sin6„sin(« — l)x] +
n=l
/V
+ i V g^ Isin θ„ cos (я — 1) χ — cos θ„ sin (я — 1) x]. (28)
Если θ„ = 0; л, то sin6n = 0 и согласно (10) символ
Оп = ап = g=-cos9n (29)
является действительной величиной.
В этом случае (28) запишется в виде
Я(х)=|Я(х)|е1ф(х) =
Ν Ν
2j a„cos(«— Ι) χ—i 2^ a„sin(«— \)x. (30)
щи
183
Соответственно (30) модуль спектра кодовой
последовательности
|Я(*)| =
(31)
Г Ν Ν
= V Σ Σ ««<
;aftcos(« — k) χ,
n=\ k=l
т. е. амплитудный спектр кодовой последовательности
фазоманипулированного сигнала является четной
функцией:
\Н(-х)\=\Н(х)\. (32)
Фазовый спектр кодовой последовательности ψ (χ)
согласно (30) определяется как
N
V д„ sin (я — 1) χ
Щ(Х) = -!# . (33)
2, йп COS (/2— \)Х
Из (33) следует, что
га=1
ψ(-χ) = -ψ(χ),
(34)
т. е. фазовый спектр кодовой последовательности
является нечетной функцией частоты.
На рис. 4.2, α изображен \Н{х)\—четная функция
относительно х=0—для произвольного сигнала.
Пунктиром представлен амплитудный спектр единичного
прямоугольного импульса. На рис. 4.2,6 изображен фазовый
спектр ψ(*) —нечетная функция относительно *=0.
4. В общем случае, когда θη принимает любое
значение в интервале (0н-2я), соотношения (32) и (34) не
имеют места. Исключение составляют сигналы, у
которых
βη —«#_„.,, (35)
при этом равенство (32) выполняется.
184
§ 4-i
Действительно, согласно определению модуля
комплексной величины из (27) получаем
/Ν Ν
ΣΣ
ОлЯце
—1 (га—*) χ
(36)
га=1 *=1
В двойной сумме имеется N2 слагаемых. Сгруппируем их
попарно и найдем суммы вида
Оп«це
—1 (га—*) χ
~Т aN-n + iaN-k + ie
-1 K/V-ra + O-tN-A + I)! *
ОД,
/
^./
-3it -ZK -it О
\
\^ — -
Я" 2ч( ЗК
X
о)
ф(х)
А.
-Згг Лгк -it /И
U
7Г
/1*
зя τ
I
б)
Рис. 4.2.
которые в соответствии с (35) запишутся как
Опк 1е~' ("-*> х + е1 {n~k) х] = Чйпк cos (η - k) x. (37)
Из (37) следует, что все слагаемые в выражении (36)
являются четными функциями относительно х.
Следовательно, четным будет и \Н{х)\. Отметим, что в этом
случае фазовый спектр может и не быть нечетным
относительно х.
§4.1
185
5. Символы (дискреты) ап могут быть найдены из (27)
путем умножения обеих частей равенства на функцию
expi(fe—\)х и последующего интегрирования этих
частей в пределах от —π до π, τ. е.
π
θη=·§-τ f H(x)ei{n~Uxdx для « = 1,2, ..., Ν. (38)
6. Приведем основные соотношения, связывающие
комплексную огибающую сигнала, кодовую
последовательность и ее спектр, если начало отсчета времени
соответствует середине сигнала. Если N — нечетно, начало
отсчета приходится на середину среднего импульса. Его
номер обозначим через « = 0, при этом единичный
прямоугольный импульс определим как
и, (0=1 Для \t]<xJ2. (39)
Тогда согласно (4), (13), (18), (21), (38) получаем, что
комплексная огибающая сигнала
N~\
2
U(t)= £ Unu0(t-t„), (40)
N—\
n= g-
кодовая последовательность
χβη/^β ν—1 · ·"* "-»»· ···» "-ι> "0ι βρ ···, Ο,ηι ···< ";ν—1 '
J2- ~~Τ~
(41)
время задержки «-го импульса
i«=«V (42)
спектр кодовой последовательности
ы-\
Н(х)= £ \ап^пх, (43)
186
§4.1
rt-И СИМВОЛ
ап =
n = i [H{x)zmxdx. (44)
—π
7. Если при θη = 0; π амплитудный и фазовый спектры
кодовой последовательности на интервале (0, π) четны
относительно х — л\2, то
α_η = (— 1)ηα„. (45)
Согласно (30) выражение (44) можно записать как
π
αη = ^· 11 Η (x)\costy(x)cosnxdx-\-
— π
π
"Ι"'"ST ί |Я (х)|51Пф(л:)С05Лл:^л:+
—π
π
-|-i-2^ \ \H{x)\cos<]i(x)smnxdx —
—π
π
~~~ϊπ \\ Η {x)\sm<lf (x) sin nxdx. (46)
—π
Так как при θ„ = 0; π выполняются равенства (32), (34),
го выражение (46) в этом случае принимает вид
π
αη = α„=-2^ С \ Η (χ) \ cos ty (x) cos nxdx—
—«
π
— ~ i'| Я (χ) | sin ψ (χ) sin nx dx. (47)
—π
В силу четности подынтегральных выражений
относительно л:=0 получаем, что
π
α„ = — \\Н (x)\casty(x)cosnxdx —
о
π
— -i- f ] И(χ) I sin ψ (x) sin nx dx. (48)
§ 4.1
187
Вводя новую переменную
*ι = * γ, (49)
т. е. смещая начало отсчета времени в точку д; = ic/2,
переписываем (48) в виде
π/2
ап = 4* \ |# (^ι + τ^Ι^ψΓ-^ + τΜχ
-π/2
X cos (nxx -f- « -5-) d*i —
-HV(xi+^)isin*(xi+^)x
-π/2
X sinf rt^j + η~γ) d*r (50)
Если
Я(х)| = |Я(1с — χ)\, ψ (χ) = ψ (it — χ) для 0 ·£*<«, (51)
то первые два множителя в интегралах (50) являются
четными функциями относительно Х\.
На рис. 4.3 изображены \Н(х)\ и ψ (χ),
удовлетворяющие условию (51). Отметим, что условия (32), (34) также
выполняются.
Рассмотрим влияние на характер подынтегральных
выражений в (50) последних множителей ^ (ηχι+ηπ/2).
Пусть η — четное число. Тогда cos («^ι +«π/2) = ±cos«*i;
s\n(nxi + nn/2) = ±sinnxu где знак определяется
величиной η и не зависит от знака п. Второй интеграл в (50)
равен нулю в силу нечетности его подынтегрального
выражения относительно Х\. В свою очередь- первый
интеграл является четной функцией п. Поэтому αη=α_η при
четном п.
Пусть η — нечетное число. Тогда
cos (nxl -f- «ic/2) — =t sin nxu
sm(njei +л«/2) = (— Ι)1"' (±совл*,). (52)
188
§4.1
Первый интеграл в (50) равен нулю, а знак второго
зависит от п, т. е. а.-п={—\)пап. Объединяя оба
результата, получаем выражение (45).
Комплексная огибающая корреляционной функции.
В соответствии с формулами (19), (20) находим
О (ω - Ω) = С/А (ш - Ω) £ One"1 (η-" (ω-°> \ t53)
ra=l
G>) = t/0S0H£aftei(ft-1><"'. (54)
ft=l
Рис. 4.3.
Подставляя (53), (54) в (2.3.20), получаем, что
ΛΚΩ) = ώ \ 50(ω-Ω)50(ω)χ
Ν Ν
X
J V «пине
— 1 (га — ft) βΤο + l (га — 1) 0·»,+ 1 ωτ
§4.1
189
. Ν Ν
^ο VI ¥"1 «. ~ J («— Ο ot»
:-2i2j2janafte χ
η=1 ft=I
x-k J 5» (ω - Ω) Д> Иe'ω ["(η~Α> τβ1 ^ω· (55)
—00
Обозначим комплексную огибающую
корреляционной функции единичного импульса как
оо
г-0(т, Ω)= -g^L- jS0(«D-Q)S0(")ei<oVw. (56)
—оо
В дальнейшем Γ0(τ, Ω) будем называть единичным
откликом. Для прямоугольного единичного импульса (1)
единичный отклик с точностью до постоянного
множителя совпадает с выражением (2.4.4) и равен
r0KQ)-(i—^j χ
Хе 2 при |τ|<ν (57)
Как следует из (57), г0 (τ, Ω) принимает максимальное
значение, равное единице, при τ = 0, Ω=0, т. е. г0(0, 0)=1.
Ширина области сильной корреляции по τ равна τ0, а по
Ω — 2π/τ0, причем Γ0(τ, Ω)==0 при |τ|>τ0.
Подставляя (56) в (55) и учитывая (1), (11), получаем
Ν Ν
R (τ, Ω) = ±- JJ JJ OnW1 <"-') β V. [τ-(η- k) τ0, Ω]. (58)
ra=I *=I
Число слагаемых в двойной сумме выражения (58)
равно N1. Каждой паре чисел η и k соответствует слагаемое
*
с комплексной амплитудой an^expi (η — 1) Ωτ0. Форма
слагаемого совпадает с формой единичного отклика,
максимум которого достигается при х=(п—&)το, Ω = 0.
На рис. 4.4 изображена плоскость (τ, Ω), на которой
выделена полоса (п—k— 1)το<τ<,(η—k+l)x0, где ела-
190
§4.1
гаемое с η—& = const, входящее в (58), отлично от нуля.
Эта область построена для единичного прямоугольного
импульса, который будем рассматривать в дальнейшем.
Все слагаемые в выражении (58) с постоянной
разностью η—k = const занимают одну и ту же полосу на
плоскости (τ, Ω). Поэтому целесообразно сгруппировать
вместе такие слагаемые. Обозначив
m = n—k, (59)
Рис. 4.4.
запишем (58) в следующем виде:
m=—(N— I) n=m + l
(60)
В (60) внутренняя сумма определяет сумму всех
слагаемых в полосе при т = const (рис. 4.4). Выражение (60)
справедливо для любых — (/V— l)<m< (N— 1). Но
необходимо отметить, что при т<0 оно справедливо, если
\п—т\ не превышает N.
Для ФМн сигналов с θ„ = 0; π справедливы равенства
(32), (34) и поэтому в соответствий с формулой (2.3.52)
корреляционная функция ФМн сигнала будет четной
относительно оси Ω = 0. Следовательно, чтобы определить
§ 4.1 191
/?(τ, Ω), достаточно найти ее значение только для
Если используется единичный прямоугольный импульс,
то /?(τ, Ω) при τ = /ητ0 зависит только от слагаемых с
данным т, так как соседние слагаемые с m±z 1 на линии
z = m-z0 равны нулю. Поэтому /?(τ, Ω) при т = ти0
определяется только внутренней суммой слагаемых с m=const
(60):
N
Λ(«τ0,Ω)=4-Γ0(Ω) J] a„an-me,(n-,)a,°. (61)
/?(mx0, Ω) определяет сечения корреляционной функции
вдоль линии τ = ηΐτ0 при изменении т от — (Ν—I) до
(Ν—1). При m = ±JV комплексная огибающая /?(±JVt„
Ω) = 0.
Если т = 0, то согласно (61)
/?(Ω)=-^|]|α„|°ε,(η-,>β\ (62)
ra=I
Основной пик сечения (62) имеет максимум при Ω = 0.
Согласно (57) при τ = 0 и Ω=0 максимум единичного
отклика равен единице. Поэтому
N
№ 0) = 4-J],an|a=1· (63)
га=1
Автокорреляционная функция. При Ω=0
автокорреляционная функция ФМн сигнала согласно (60)
записывается как
\—ι ν
ΧΜ = ΊΓ J] J] а„ап.тг0{т-^тх0). (64)
т=— (\—I) га=т + 1
При х = отх0 формула (64) принимает вид
N
pm = R(mT0)-=-~ V anan-m· (65)
ra=m + I
Согласно (2.3.44), (65) для произвольных фазоманипу-
К» § 4.1
лированных сигналов получаем
*
а для ФМн сигналов с θ„ = 0; π—
" - т = Rrti·
(66)
(67)
Автокорреляционная функция ФМн сигнала полностью
характеризуется последовательностью {Rm}· Характер зави-
uft)k
о
W—г
а)
LL
6)
τ -с
Рис. 4.5.
симости значений Rm от т определяется свойствами
кодовой последовательности {ап}. Значения Rm, отложенные по
оси времени τ через интервалы τ0, образуют решетчатую ■
функцию. По известной решетчатой функции можно
построить автокорреляционную функцию, если около каждого
значения Rm построить единичный отклик г0'(х) с
амплитудой, равной Rm.
На рис. 4.5,а изображена комплексная огибающая
(в данном случае действительная функция времени) фа-
зоманипулированного сигнала с единичным
прямоугольным импульсом для N=5, на -рис. 4.5,6 — решетчатая
функция ФМн сигнала, на рис. 4.5,в — решетчатая
автокорреляционная функция. Тонкими линиями на
рис. 4.5,в показана автокорреляционная функция ФМн
сигнала. Для прямоугольных единичных импульсов
единичный отклик Го(т) имеет вид треугольного импульса,
поэтому для построения автокорреляционной функции
ФМн сигнала достаточно соединить между собой
соседние значения Rm.
§ 4.1
193
Вычисление Rm (65) может быть сведено к составлению
квадратной матрицы (табл. 4.1), элементы которой равны
*
произведениям типа апа^. Каждый элемент матрицы
* N
||en«k|l| , расположенный на пересечении я-й строки и fe-ro
столбца, равен произведению элемента ап верхней строки
* *
и элемента а* левого столбца (табл. 4.1). При {tffc} =
*
={а„} получается матрица для вычисления
автокорреляционной функции.
&„
а»
Таблица 4-.1
. . . Ощ-1 ан
.a.n-iu.1 «A
ч
я»а„ ага.п ·\ ·<*α*η ·Ν 'Я/цйп ajlr,
ν ч \
α)ΒΝ агам . . .Unit . . .α#-/2* я*5* ч^
%
\
Сумма элементов главной диагонали (след матрицы) рай-
*
на NR0, поскольку апа„=|ап|а и т—0. Элементы главной
диагонали в таблице соединены сплошной линией. Сумма
элементов боковых диагоналей (элементы соединены
пунктирными линиями) равна NjRm. Переходя последовательно
с диагонали на диагональ, получаем значения Rm для
— (N—l)^m^N—I. Главная диагональ определяет
величину основного (главного) пика, боковые диагонали —
194
§ 4.1
величину боковых пиков автокорреляционной функции
ФМн сигнала.
* *
Если кодовая последовательность {а*} ф- {ап}, то
значения Rm в таблице соответствуют взаимокорреляционной
функции сигналов с кодовыми последовательностями {ап}
и {ал}· В частности, подставляя в матрицу табл. 4.1
вместо ап значение anexpi(«—1)Ωτ0 и проводя указанные
ранее операции, получаем сумму в (61).
* N
Рассматривая структуру квадратной матрицы ||anafc||,
(табл. 4.1), можно заметить, что она получается при
перемножении матрицы-столбца
а2
а*.
(68)
aN
на матрицу-строку
|| а^,... «п...atf || (69)
С последующим изменением порядка сомножителей в эле-
* ·
ментах матрицы в соответствии с равенством aftan = а-пОц
Щ.
Свойство симметрии автокорреляционной функции.
Перенесем начало отсчета импульсов в сигнале в
середину сигнала. Пусть N — нечетное число. Введем индекс
суммирования
* = п-£^1 (70)
При изменении η от 1 до N значение k меняется от
— (Л'--1)/2 до {N—\)j2, принимая и значение £=0.
Тогда а соответствии с (65) получаем
Rm —
Ν
Σ.
ffftflfc-
(71)
ft=m—
Ν— I
§ 4.1
195
Рассмотрим особенность /?m (71) при выполнении
соотношения (45). Выделим Rm с нечетным т. Поскольку
число слагаемых в сумме (71) равно N—т, то при
принятых условиях (N—т)—четно. Выделим из суммы (71)
слагаемые, симметрично расположенные относительно
k = 0:
flkak_t(1 + a_ka_(k_m). (72)
Слагаемые в сумме (72) являются действительными
функциями, так как соотношение (45) справедливо при
θη = 0; π. Для четного k a-h = ah (45), a_(ft_m) = —aft_m,
поскольку (k—m) — нечетное число. Следовательно,
сумма (72) равна нулю. Для нечетного k разность
(к — т) —четное число, а-ъ. = —ah, aft_m = a_ft_m и,
следовательно, сумма (72) равна нулю. Собирая все
слагаемые в (71) попарно, получаем, что при нечетных т и
выполнении условия (45)
/?т = 0. (73)
Связь между решетчатой корреляционной функцией
и кодовой последовательностью. Из (61), (65) видно, что
аначения комплексных огибающих авто- и
корреляционной функций при х=тх0 не зависят от свойств
единичного отклика, а определяются в основном символами
*
&п И Йп-т·
Последние зависят только от спектра кодовой
последовательности Н(х) (44). Поэтому R(m%0, Ω) и Rm можно
выразить через Η (χ). Найдем интеграл
π
^ = ij H(x-y)H(x)elnxdX, (74)
—π
где
0 = Ωτο. (75)
Подставляя определение спектра кодовой
последовательности (27) в (74), получаем
17= Σ Σ """^ ("_,) у я ίе'(~n+ft+m) x dx' (76)
ra=I k—\ —η
196
§ 4.1
Так как
ι С ei {-п+ь+т) χ άχ = Г1 при т = η - k,
2π J ΙΟ при тфп — k,
— 1С
то
gr= £ anan.mei(n-^. (78)
ra=m + l
Сравнивая выражения (74), (78) с-(61), замечаем, что
π
/? («,„ Ω) = -^ f Η (χ-у) Η (χ) e,mx dx. (79)
—π
*
В выражении (79) Η (χ), Η (χ — у) — периодические
функции и подынтегральное выражение отлично от нуля
на отрезке [—и, π].
Если ιΩ = 0, τ. е. у = 0, то автокорреляционная
функция (79) записывается как
π
*«-' = W j" I #(*) Г *""*<**■ (8°)
Корреляционная функция периодического сигнала.
В некоторых случаях можно считать, что сигнал
излучается периодически. В случае фазоманипулированных
сигналов кодовая последовательность, соответствующая
интервалу времени от —оо до оо, записывается как
■■•"β;ν_ι> Я;у> «b «а. ■·■> «η, ···. eJV_I, aw. «ι ■■■ (81)
Пусть фильтр согласован с сигналом длительностью
в один период последовательности (81). Можно
показать, что корреляционная и автокорреляционная
функции ФМн сигнала при f = mto имеют вид
Я(тт0, Ω) = -^f- J[ а„а„.те! «"-'>·ΰ\ (82)
N
Rm=*lT У] "nOn-m. (83)
л=1
§4.2
197
Отличие формул (82), (83) от формул (61), (65)
заключается в том, что в суммах (82), (83) всегда имеется
N слагаемых. Это объясняется тем, что при сдвиге
импульсной характеристики согласованного фильтра на т
символов всегда имеется N ие равных нулю
произведений символов благодаря периодическому характеру
излучаемого сигнала.
4.2. СИГНАЛЫ БАРКЕРА
Кодовая последовательность Баркера |[52] состоит
из символов ап=±\ и характеризуется
автокорреляционной функцией вида
для т = О,
1
D-J О
Am— '
\— N
ДЛЯ
ДЛЯ
/я=2Ц-1,
т = 21,
(1)
где / = 0, 1, .·.,
М- 1
Знак в последней строке (1) зависит от величины N.
В табл. 4.2 приведены известные кодовые
последовательности Баркера1. В последнем столбце таблицы при-
Таблица 4.2
N
3
4
5
7
11
13
ап
1
а
II
е
СО
II
е
— 1
I
—1
1Л
II
е
1
-1
-1
1
е
1
-1
—1
II
е
-1
1
— 1
СО
II
е
—1
1
II
е
-1
1
о
li
е
1
—1
li
е
—1
1
li
е
-1
li
е
1
R2l
-1/3
±1/4
1/5
-1/7
-1/11
1/13
1 В табл. 4.2 не приведена кодовая последовательность {1, —1},
которую иногда относят к последовательностям Баркера. Для
некоторых N существует две последовательности. Например, для N=3
имеем {1, -1, 1}, {1, 1, -1}, для W=4-{1, 1, 1, -1}, {1, 1, -1, 1}.
198
δ 4.2
веден уровень боковых пиков автокорреляционной
функции (1).
Комплексные огибающие сигнала Баркера для N=5
и его автокорреляционной функции изображены на
рис. 4.5.
Кодовые последовательности, обладающие свойством
(1), для М>13 не найдены '.
Спектр кодовой последовательности. Амплитудный
спектр \Й {х)\ кодовой последовательности может быть
найден непосредственно из выражения (4.1.27).
Энергетический спектр согласно (4.1.27) равен
\H(x)\s=yif)anahQ~iln-k)x. (2)
Заменяя в выражении (2) η — k = m, записываем
W-1 N
ι"wia= Σ Σ α"α"-'
„—I mx
.e =
m=— (N— 1) n=m+\
/V—1 , N
^~» / „—\mx
m=—(/V—1)
(3)
e V anan-m )·
n=m + l J,
Внутренняя сумма в (3) согласно (4.1.65) равна NRm,
поэтому
\H(x)\* = N V /?me-imx. (4)
т=_(ЛГ—1)
Подставляя (1) в (4), получаем
l+/?5tie"'to+e,to)
1 = 1
где RB = ±\fN. Формулу (5) перепишем в следующем
виде:
\H(x)\' = N
(5)
Ν—Ι
2
|/ВД|2 = ЛМ 1+2/?β£ cos
2lx
(6)
;=ι
1 Поискам последовательностей Баркера для Л/'>113 (четным и
нечетным) посвящен ряд работ, например [66—72].
§ 4.2
199
Используя табличное значение [64], получаем
slnx /
\Η(χ)\' = Ν (l_/?fi + /?£
При RB=\[N выражение (7) принимает вид
\H(x)\> = n(\
JL.4—L slnJV*
Ν "Γ N sin
Vx\
τ}
а при RB = — IfN
|Я(х)|- = ЛГ(1 + 4-1^).
(7)
(8)
(9)
На рис. 4.6,α изображены зависимости f| Η (χ) |/|/ Ν ,
рассчитанные по формулам (8), (9) для N=11; 13. Из
рисунка видно, что амплитудные спектры при х = 0; я
Яш т «'*тмтяг а ■
/\ -.. /\
W9
яг
If
7
it
Л
Ό
Ι' >
/
AWf
\
^
*)
ж
г
Ю
Рис. 4.6.
имеют или провал, или пик. Фазовые спектры для
сигналов Баркера были рассчитаны численно и изображены
на рис. 4.6,6 для тех же Ν, что и амплитудные спектры'.
1 Расчеты спектров рис. 4.6 были произведены Г. Я. Гельманом.
200 § 4.2
Фазовые спектры рис. 4.6,6 соответствуют сигналам,
у которых номера импульсов отсчитываются от середины
сигналов1.
Тело неопределенности. На рис. 4.7 и 4.8
изображены |/?(τ, Ω)| для N=11; 13, построенные в соответствии
с формулой (4.1.61) при
Ω = ^- для /=0, +1 ±Ν. (10)
Дискретные значения |/?(τ, Ω)|, полученные для /=const
Рис. 4.7.
и m=var, соединены прямыми линиями. Как видно из
рис. 4.7, 4.8, основной пик тела (неопределенности
окружен довольно большими боковыми пиками. Вдоль оси Ω
боковые пики не изображены, так как при выбранном
смещении частоты (10) сечения |/? (τ, Ω) | проходят
через нули сечения /?(Ω) = 5ίπ(Ω7'/2)/(Ω7'/2) (2.3.39).
Для N=11 максимальное значение бокового пика
1 Методика расчета амплитудного спектра сигналов Баркера
приведена также в работе [73], а спектры сигнала с W=13 можно
найти в книге [6]. Отметим, что формулы (8), (9) непригодны для
расчета спектра сигнала с /V = 4, так как его автокорреляционная
функция (табл. 4.2) имеет боковые пики разных знаков.
§ 4.3
201
равно 0,53 (m±3, /=±1), для N=13
максимальное значение бокового пика — 0,378 (m=±2, /=±1).
Наличие относительно больших боковых пиков 1на
плоскости ι(τ, Ω) представляется естественным, так как
сигналы Баркера 1(табл. 4.2) похожи на ЛЧМ сигнал: чем
больше время (аргумент сигнала), тем чаще происходит
смена знаков импульсов. Однако боковые пики сигналов
Баркера меньше, чем в случае ЛЧМ сигнала. Объясня-
Рис. 4.8.
ется это свойством фазоманипулированных сигналов
(2.3.52): если есть один боковой пик определенной
величины, то таких пиков на плоскости (т, Ω) должно быть
по крайней мере 4 вследствие симметрии тела
неопределенности относительно осей τ и Ω.
4.3. ^-ПОСЛЕДОВАТЕЛЬНОСТИ
Основные свойства. Среди фазоманипулированных
сигналов особое место занимают сигналы, кодовые
последовательности которых являются последовательностями
202 § 4.3
максимальной длины или М-последовательностями '.
Такие последовательности обладают следующими
основными свойствами:
1. М-ггоследовательность является периодической
с периодом, состоящим из N импульсов (символов).
2. Боковые пики периодической автокорреляционной
функции сигналов, образованных М-последователь-
ностью, равны —\/N.
3. М-последовательность в общем случае состоит из
нескольких видов импульсов (например, импульсы могут
отличаться начальными фазами, «есущими частотами
и т. д.). Импульсы различного вида встречаются в
периоде примерно одинаковое число раз, т. е. все
импульсы распределяются в периоде равновероятно. Вследствие
этого М-последовательности называют часто
псевдослучайными.
4. Формируются М-последовательности с помощью
линейных переключательных схем на основе сдвигающих
регистров. При этом, если применяется регистр с k
разрядами и в М-последовательности используются ρ
различных видов импульсов (отличающихся, например,
фазами), то
N = ph—\. , (1)
Число разрядов регистра k = log (N+l)[logp.
Следовательно, значительное увеличение числа импульсов N
в периоде М-последовательности вызывает
незначительное увеличение числа разрядов регистра, так как
зависимость k от N является логарифмической.
5. Автокорреляционная 'функция усеченной
М-последовательности, под которой понимается непериодическая
последовательность длиной .в период N, имеет величину
боковых 'пиков, .близкую к il/j/ΛΛ Поэтому с ростом N
величина боковых пиков уменьшается.
Благодаря своим свойствам М-последовательности
широко применяются в радиотехнических системах. Для
пояснения этих свойств рассмотрим .пример.
Допустим, что сдвигающий регистр (рис. 4.9) состоит
1 Λί-последователышсти были найдены несколькими
исследователями [74. 75]. Основные свойства этих последовательностей рписа-
ны в (74—84).
§ 4.3
203
из трех триггерных ячеек 7\, Ts, T3, которые выполняют
роль дискретных элементов задержек, и сумматора. На
триггеры поступают сдвигающие импульсы, которые на
рис. 4.9 не показаны. Они следуют с тактовой частотой
I/to. Каждый тактовый импульс вызывает изменение
состояния (напряжения на выходе) всех триггеров. При
этом напряжение на выходе каждого триггера (символ)
становится равным напряжению (символу) на его входе
» г, —■- тг —г· т3
Рис. 4.9.
для предыдущего такта. Символы могут 'принимать два
значения, которые условно обозначим 0 и ,1. При
суммировании любых комбинаций входных символов на
выходе сумматора получаются только символы 0 и 1.
Правило суммирования символов в двоичной системе
счисления i(c двумя .возможными значениями символов) по
модулю 2(mod2) определяется табл. 4.3.
Таблица 4.3
Θ
0
1
0
0
1
1
1
0
Выясним, в каких состояниях может находиться
схема, представленная на рис. 4.9. Предположим, что в
исходном состоянии символ на одном из выходов
триггеров отличается от нуля, например символ ма выходетриг-
гера Ту имеет значение 1, а на выходе Т2 и Т3 —
значение 0. Тогда исходное состояние сдвигающего регистра
характеризуется комбинацией выходных символов 100.
На входе Т1 символ равен 0, так как согласно с табл.' 4.3
символ на выходе сумматора равен 0 Θ 0=0. С
поступлением на вход схемы очередного сдвигающего импульса
204 § 4.3
символы со входов триггеров «переходят» на их выходы.
Новое установившееся состояние регистра описывается
комбинацией выходных символов 010. На входе 7Ί
появляется 1, так как ;в соответствии ic табл. 4.3 выходной
символ сумматора равен 1θ0=1. Аналогично
определяются вое состояния регистра, приведенные в табл. 4.4.
Таблица 4.4
Номер такта
i
2
. 3
4
5
б
7
8
9
Вход Τι
О
1
1
1
0
0
1
0
1
Выход
Г,
i
0
1
1
1
0
0
1
0
τ,
ό
1
0
1
1
1
0
0
1
г,
ό
0
1
0
1
1
1
0
0
Из рассмотрения табл. 4.4 видно, что состояния
регистра (символы на выходе Т\, Гг, Тз) различны для
тактов 1—7, а для последующих тактов они повторяются.
Так как число разрядов регистра k=3, а основание
системы счисления (число используемых символов) ρ = 2,
то число возможных различных состояний регистра
равно р"='23=8.
В табл. 4.4 отсутствует нулевая .комбинация 000, так
как ее наличие согласно табл. 4.3 приводит к обращению
в нуль всех символов во всех остальных комбинациях.
Поэтому в табл. 4.4 приведены только возможные для
нормальной работы схемы (рис. 4.9) отстояния регистра,
число которых 23—1=7. После 7 тактов состояния
регистра повторяются. Если символы непрерывно считывать
§ 4.3 205
со входа 7Ί, то получим периодическую
последовательность
. 0 1 il il 0 0 1 0 1 1 1 0 0 1 0 1 1 1 0.
№
с периодом, равным М=7. Отметим, что символы можш
считывать с выхода любого триггера. В этом случае
получаются последовательности, сдвинутые во времени
(табл. 4.4).
Подчеркнем, что период последовательности (2)
является максимально возможным для данного числа
разрядов (триггеров) схемы рис. 4.9 и выбранного основа-
т Г, —р*| Тг —j· Г3 ——
ах*—Аи
Рис. 4.10.
ния системы счисления. Это следует из того, что в
регистре последовательно сменяются все возможные
состояния, кроме нулевого. (Период N = 7 для
последовательности (2) совпадает со значением, определяемым
формулой (1), при k=>3 и р = 2.
Необходимо отметить, что при заданных Лир период
последовательностей вида (2) определяется схемой
включения ' отводов сдвигающего регистра (выходов
триггеров) в цепь обратной связи. Следовательно, он
может быть получен меньше максимально возможного. Так,
для схемы рис. 4.10 N=4. Таким образом, выбор
соединений отводов сдвигающего регистра в цепи обратной
связи для получения максимального периода
последовательности при заданном числе разрядов регистра и
основания системы счисления является одной из
важных проблем при построении схем рассмотренного типа.
При рассмотрении работы схемы рис. 4.9 было
сделано допущение, что исходное состояние регистра
характеризуется комбинацией 100. Из табл. 4.4 видно, что
в качестве исходного можно взять любое состояние ре-
206
I 4.3
гистра. Это вызовет лишь сдвиг последовательности (2)
во времени.
Число единиц и нулей в периоде последовательности
(2) соответственно равно μι =4, μ0=3, причем μι + μ0=Μ
Отметим, что отличие между μι ,и μ0 на единицу в
последовательностях вида (2) имеет общий характер. В
общем случае при ρ = 2 число единиц в |последо.вателыности
равно 2ft_1, а число нулей — 2ft_1—1.
Сумма двух М-последовательностей, сдвинутых друг
относительно друга, является М-последовательностью.
В этом можно убедиться, суммируя согласно правилам
табл. 4.3 последовательность (2) и, например,
^-последовательность с выхода Т3 (рис. 4.9), т. е. ':
...01 1100101 1 100101 1 100101110...
...00101 1 100101 1 100101 1 1 0 0 1 0 1 ... (3)
...0 101 1 100101 1 100101 1 1 1 0 1 01 1 ...
Это является следствием того, что сдвинутые Λί-πο-
следовательности можно получить с помощью одной и
той же схемы.
Фазоманипулированный сигнал с помощью Λί-после-
довательностей формируется следующим образом.
Каждому символу последовательности ставится в
соответствие радиоимпульс со своей начальной фазой. В двоичной
системе счисления (р = 2) это соответствие можно
определить как
0ф=^е,0 = 1,
1<^е1я = -1, (4)
где двойная стрелка означает соотвегствие.
В соответствии с >(4) табл. 4.3 сложения символов 0
и 1 лрев'ращаегся в таблицу умножения символов 1 и
— 1 (табл. 4.5).
Таблица 4,5
X
1
— 1
1
1
— 1
— 1
— 1
1
§ 4*3
207
Согласно формуле (4.1.83) автокорреляционную
функцию периодического ФМн сигнала запишем как
N
1
°ш — -дГ у. Япйп-т, (5)
где а„=±<1. Обозначая символы Λί-последовательности
(2) через Ьп и сравнивая табл. 4.3 и 4.5, замечаем, что
апап _т <£==> Ьп θ bn_m (mod 2). (6)
Если πιφΙΝ для любого / = 0, 1, ..., то сумма двух
М-последовательностей является тоже Λί-последователь-
ностью. Но в ней число единиц >в периоде на единицу
больше числа !нулей. Поэтому сумма по всем bn®bn-m
при п=\, ..., N будет равиа единице, а в выражении
для автокорреляционной функции (5) сумма будет равна
согласно (4) — il/N. При m = lN для любого 1 = 0, 1, ...
временной сдвиг между двумя М-последовательностями
равен нулю. При этом из (5) получаем, что /?m='l·
Объединяя полученные результаты, формулу (5)
запишем в следующем виде:
Rm=,l-4N· если m^lN' (7)
I 1, если т = IN,
где/=0, 1, ...
Рассмотренный пример подтвердил основные
особенности ^-последовательности.
Теперь перейдем к анализу Λί-последовательностей
и способам построения сдвигающих регистров.
Матрица состояний. Общая схема сдвигающего
регистра, формирующего М-последовательность,
представлена на рис. 4.11. Триггерные ячейки Τι, Τ2, ..., Гц
осуществляют задержку входного символа на один такт
длительностью το. Допустим, что используются ρ различных
символов: 0, 1, 2 ρ—1, которые образуют конечное
множество символов
S=S{0, 1, ..., р-1). (8)
208
§ 4.3
Символы на выходах триггеров при /-м такте обозначим
через X\j, x2j Xkj, причем Xit 3fcS1.
Символ на входе первого триггера обозначим x0j.
Символ на выходе 1-го триггера на /+1 такте
Χι,}+ι—χι-ι,ϊ>
(9)
так как с каждым тактом символ со входа «переходит»
на выход.
Ч]
Τι
Χι
>
f
J
f
\
h
Ci
X
A
Рис. 4.11.
Символы с выходов триггеров поступают на
умножители, с выходов которых снимаются символы
"l^l.ji ^2-"-2,D' ·"·' "k^k.j·
(10)
Множители Ci£S. Поэтомчу, если операция умножения в
умножителе производится по модулю ρ (mod ρ), то
символы CiXij^S. Смысл умножения по модулю становится
понятным при рассмотрении сравнения двух чисел по
третьему числу (модулю) [85]. Два целых числа α и Ь
называются сравнимыми по модулю р, 1если при делении
обоих чисел на ρ их остатки равны. Сравнение двух чисел
обозначается как
a=b (mod p). (11)
Остаток от деления любого числа на ρ всегда меньше ρ
и лежит ,в пределах от 0 до ρ—1. Например, если р=5,
то 12з='2 (mod5), так как остатки от деления обоих
1 Запись Xij ζ 5 означает, что символ Χι,ι принадлежит
множеству S,
§ 4.3
209
чисел равны двум. Сравнение ι(11) означает, что
разность а—Ъ делится wa ρ без остатка, что иногда
записывается как р\а—Ь, или а—b=Q (modp). Сравнимость
двух чисел по модулю ρ позволяет записать их в
следующем виде:
α = ςφ+τ, b = q2p+r, (12)
тде qh q2 — любые целые числа; г — остаток, 0^/^р—1.
В приведенном .ранее примере 12 = 2X6 + 2; 2=0X5 + 2.
Таким образом, сравнение по модулю ρ означает
перевод произвольного целого числа >в конечное множество 5,
состоящее из ρ элементов.
Умножение двух чисел по модулю ρ производится
следующим образом. Два числа перемножаются
обычным образом, а !их произведение переводится в
конечное множество S (8) с помощью сравнения по модулю р.
Умножение двух чисел ло модулю ρ записывается как
ab = d == г (mod ρ) при 0<г<р— 1. (13)
Например, если а=2, 6 = 4, то d=8 и для р = Ъ 8з=3
(mod 5), т. е. число 8, которого нет (в множестве 5,
переводится в число 3. Правило умножения двух чисел по
модулю 5 определяется табл. 4.6.
Таблица 4.6
<8>
0
1
2
3
4
0
0
0
0
0
0
1
0
1
2
3
4
2
0
2
4
1
3
3
0
3
1
4
2
4
0
4
3
2
1
Отметим, что каждая строка и столбец таблицы
состоят из всех возможных символов множества 5 (8) и
ке содержат, за исключением нулевого столбца и
строки, одинаковых символов. Это является следствием того,
210
§ 4.3
что ιΒ качестве модуля ρ взято простое число 5. Если
ρ—составное число, то при умножении в одной строке
или столбце могут оказаться одинаковые числа, т. е.
операция умножения не будет однозначной. Чтобы
убедиться в этом, возьмем р = 4. Для данного ρ
произведения 2x1 = 2 и 2X3 = 6s2 (mod4) сводятся к одному и
тому же числу 2 по модулю 4. В общем случае при р =
= Р\Рг, где ρι,2 простые числа, всегда можно найти
такие О^а, Ь, с^р, что а—Ь = р\, с=р2. Тогда (а—Ь)с=
= р = 0 (modp), т. е. произведения ac=bc (modp)
сводятся друг к другу. Поэтому для сохранения
однозначности в качестве модуля берут простые числа.
Отметим, что умножение любого числа >на нуль
означает, что символ iHa выходе умножителя всегда равен
нулю. Это эквивалентно разрыву цепи между выходом
триггера и сумматором. Следовательно, умножитель
может быть опущен. Например, при р = 2 (символы 0 и 1)
множитель Ci может принимать значение или 0, или 1,
т. е. выходы триггеров или подсоединены к сумматорам,
или нет.
После умножения суммирование производится также
по модулю р. Сумма двух целых чисел переводится с
помощью сравнения β конечное множество S (8), т. е. а +
+ b = d=r (modp) для (Χ>«£Ξρ—1. Для примера
в табл. 4.7 приведено правило сложения по модулю 5.
Таблица 4,7
θ
0
1
2
3
4
0
0
1
2
3
4
1
1
2
3
4
0
2
2
3
4
0
1
3
3
4
0
1
2
4
4
0
1
2
3
Следовательно, в результате операций умножения и
сложения получаются только элементы множества 5 (8).
§ 4.4
δϋ
Возвращаясь к работе сдвигающего регистра (см.
рис. 4.11), можно записать, что .символ «а входе 7Ί в /-м
такте равен
(14)
Выражение (14) является линейным рекуррентным
уравнением. Оно позволяет по известным k символам «а
выходах триггеров найти символ Xo,i, который в
последующем такте согласно формуле (9) перейдет на
выход 7Y
Для /+1 такта состояние регистра характеризуется k
переменными, которые можно записать как
Xi.5+i =c,x,,3+CiX1,3+...+c,Xi,3+...+c1l-,x1l-t,}+c}lx}l,} \
Хг,5 + 1 = Χι,ί
Xt,5+i = Xi,i
Χι + ι. i+i —
xi.i
^hj+ι—
*fc- 1,3
(15)
Обозначим состояния регистра в / и / -(- 1 такте через
матрицы-столбцы
Xj =
Χι,ί
Хг,з
x*.i
Xj+i —
*l,3+l
*2,3+l
xhJ+l
(16)
Определим матрицу состояний регистра следующим
образом:
Т =
с2
О
I
ch - г
. О
. О
О
О
О О
О О
О О
0 0 0
1 0 0
0 I 0
(17)
212 § 4.3
Матрица Т — квадратная порядка к (число строк и
столбцов равно к). Первая строка -состоит ,из
коэффициентов первого уравнения в формуле (15), а остальные
строки — из коэффициентов последующих уравнений.
Отметим, что в каждой строке, кроме первой, только
одна единица, а остальные — нули, и единица во второй
строке расположена ттод первым элементом первой
строки, а затем циклически смещается вправо.
Следовательно, единицы расположены под .главной диагональю
матрицы, состоящей из нулей и элемента с\.
Используя правило перемножения матриц [65],
можно показать, что
Χί+ι = ΤΧ,. "(18)
Выражение (18) означает, что состояние регистра в /+1
такте определяется его предыдущим состоянием,
измененным в соответствии с матрицей Т. Матричная запись
(18) эквивалентна системе к уравнений (15).
Состояние регистра в /-f-2 такте определяется как
X:+2 = TXj+1 = T2Xj, а в j-\-n такте — как
Xj+, = T"X,. (19)
Как было сказано раньше, каждый символ Xi,,-e5,
т. е. может принимать одно из ρ возможных значений.
Каждое состояние регистра описывается одновременно k
символами. Поэтому общее число состояний регистра
равно ph. Если нулевую комбинацию символов (k нулей)
отбросить, то число возможных состояний регистра будет
определяться как
N = ph—l. (20)
При любых конечных ρ и k величина N конечна.
Поэтому в общем случае состояния регистра после
некоторого числа тактов начнут повторяться. В матричной
записи это означает, что Xj+l = Xj, или
ТЧС, = Х,-=ЕХ,, (21)
§ 4.3
213
где
10 0.
0 10.
0 0 1.
0 0 0.
. 0
. 0
. 0
. 1
— единичная матрица [65]; число L — период колебаний
в сдвигающем регистре (см. рис. 4.11), являющемся
системой с замкнутой обратной связью. Для Л1-,последр-
вательности период максимален, т. е. L = N, поэтому для
нее уравнение (21) записывается в виде T^X^EXj, или
(ΎΝ—E)Xj = 0. Так как матрица X,- — ненулевая, то
можно записать, что
ΊΝ—Ε = 0. (23)
Таким образом, матрица состояний Τ сдвигающего
регистра, который формирует ^-последовательность,
удовлетворяет матричному уравнению (23).
Если заданы числа N, p, k, связанные соотношением
(20), и необходимо найти структуру сдвигающего
регистра, то сначала надо найти матрицу состояний Τ (17),
а затем по коэффициентам ее первой строки с ι, .... сц
определить сдвигающий регистр (см. рис. 4.1ι1).
Согласно уравнению (23) матрица Τ является корнем
N-й степени из единичной матрицы, т. е. Т= у/ Ε .
Таких корней по меньшей мере должно быть N. Поэтому
задача нахождения матрицы Τ как корня уравнения (23)
при большом N является сложной. Для упрощения
решения этой задачи сведем решение уравнения (23)
степени N к уравнению меньшей степени (как будет
показано, к уравнению k-Ρί степени). Допустим, что двучлен
χΝ—1 непрерывного аргумента χ можно представить
в виде произведения двух многочленов f,(x) и g(x), т. е.
x»-l=f(x)g(x). (24)
Из (24) следует, что каждый многочлен делит
двучлен xN—1 без остатка. Подставляя в (24) вместо χ
матрицу Т, получаем представление матрицы ΎΝ—Ε в виде
4U
I 4.3
произведения двух многочленов от матрицы Т:
Tff-E = f(T)0(T). (25)
Левая часть равенства (25) согласно (23) равна
нулю. Поэтому в правой части (25) по меньшей мере один
из многочленов должен быть равен нулю. Допустим, что
/(Т) =0, a g(T) Ф0. Из равенства (25) следует, что
корни матричного уравнения f(T) будут входить в состав
корней матричного уравнения (23).
Чтобы найти матрицу Τ как решение уравнения f(T),
рассмотрим многочлен Р(х). Многочлены ft{x), которые
при замене χ ,на .квадратную матрицу Τ удовлетворяют
матричному уравнению f(T)=0, называются
аннулирующими многочленами матрицы Τ [Θ5]. Степень
аннулирующего многочлена матрицы Τ в данном случае
меньше или равна Ν, так как согласно (24) f(x) делит
двучлен степени N без остатка. Среди всех аннулирующих
многочленов, удовлетворяющих (24), есть многочлен
наименьшей степени с коэффициентом при старшем члене,
равным единице, Он называется минимальным
многочленом матрицы Τ ι[65]. Для матрицы Τ (17) можно найти
минимальный многочлен следующим образом. По своей
структуре матрица Τ является сопровождающей [65],
а для таких матриц минимальный многочлен совпадает
с характеристическим {65], степень которого равна
порядку k матрицы Т.
Из всего ранее сказанного следует, что для
определения структуры сдвигающего регистра, формирующего
М-последовательность с периодом N, необходимо
выбрать многочлен, который должен быть
характеристическим для матрицы Τ (17) порядка k, затем найти
матрицу Т, после чего по ее первой строке определить регистр
Однако, как будет показано, знание характеристического
многочлена позволяет сразу получить первую строку
матрицы Τ по коэффициентам этого многочлена, т. е.
позволяет определить структуру регистра, не решая
уравнения f(T)=0.
Перейдем к рассмотрению характеристического
многочлена, который является определителем
характеристической матрицы Τ—хЕ [65]. Характеристическая матрица
получается в соответствии с обычными правилами ело-
§ 4.3
215
женил матриц и согласна (17), (22) имеет вид
С ι —X С 2 С з *
1 —х 0 ..
0 1 —χ .
0 0 0.
0 0 0.
0 0 0.
• ch-a
. 0
.. 0
. —X
I
.. 0
Cfc-1
0
0
0
—X
1
с*
0
0
0
0
—X
Ί—χΕ
Характеристический многочлен записывается как
■хЕ\
(26)
1 — X Cj
1 -X
0 1
0 0
0 0
0 0
с, .
0 .
— X .
0 .
0 .
0 .
.. С„-2
.. 0
.. 0
. —X
1
.. 0
Сц-1
0
0
0
—X
1
С*
0
θ
0
0
—χ
(27)
Для вычисления определителя (27) разложим его по
элементам первого столбца:
-х 0 . . . о 0 о
ι —χ ... 0 0 о
| Τ—λ: Ε | = (с, —л-)
0
0
0
0 . .
0 . .
0 . .
. —X
1
0
0 0
— χ 0
I -X
1 -х .
0 0 .
0 0 .
0 0 ..
. . 0
. —X
1
. 0
0
0
—χ
1
с*.
0
0
0
—χ
Оба полученных определителя .имеют k—1 строку и
столбец. Так как первый определитель — треугольный, то он
равен произведению элементов главной диагонали, т. е,
216
§ 4.3
(—x)h~l. Разлагая второй ■определитель по элементам
первого 'столбца, находим, что
| Τ — хЕ | = (— x)h + c, (— χ)"-1 —
са. .
1 .
0 . .
0 . .
0 . .
• с„-2
. 0
. — χ
1
0
с*-ι
0
0
— χ
1
С*
0
0
0
— χ
Полученные определители имеют уже k —2 строк и
столбцов. Продолжая процесс разложения полученных
определителей по элементам столбцов методом
индукции, находим характеристический многочлен (27):
|Т — хЕ| = (— x)h + c,(— xf-1— c2(— x)ft-a + ...=
k
= (- x)h + Σ (- 1 )h~ *ι (- x)h~l =
1=1
= (—l)k(xh — clxh'l—c3xh-\—..,—ch_lx—ck). (28)
Сравнивая коэффициенты характеристического мно-
•гочлена (28) с элементами первой строки матрицы
состояний (17), видим, что ιπο заданному
характеристическому многочлену можно однозначно восстановить
первую строку и, следовательно, всю матрицу (17), т. е.
определить структуру регистра на рис. 4.11.
Действительно, пусть задан многочлен
f(x) = x* + rf1x*-, + rfaxft-2 + ---+rffc-i* + rffc. (29)
являющийся характеристическим многочленом матрицы
Τ порядка к. Сравнивая (29) € (28), получаем, что
С(=(—' l)ft+'4 (30)
Отметим, что отрицательные значения С; можно
свести € помощью сравнения по модулю ρ к
положительному числу множества 5 (8). Например, при р = 5, ct=—2
справедливо равенство —>2= (—Л) Х5+3, т. е.
—2=3(mod5). При р = 2 и f(x)=xs+x+i получаем,
что di = 0, d2=l, d3=i, Ci = 0, c2=l, с3=1 (схема рис. 4.9).
— χ . .
0 . .
0. .
0. .
0 0 0
— χ "0 0
1 —χ 0
0 1-х
+
§ 4.3
217
Таким образом, для определения структуры регистра,
состоящего из k триггеров, необходимо знать
характеристический многочлен f(x) степени k матрицы
состояний Т, который делит без остатка двучлен xN—1 и
является минимальным для матрицы Т.
Особенности характеристического многочлена. Во-
первых, М'ногочлен f(x) должен быть неприводимым, т.е.
его .нельзя представить в виде произведения
многочленов меньших степеней. Это означает его неразложимость
на простые множители. Для доказательства первого
свойства многочлена f(x) допустим обратное. Пусть
характеристический ή минимальный многочлен f(x)
степени k приводим, т. е. f{x) =/i (x)f?(x), где Ufi{x)
—неприводимые многочлены, степень которых меньше k. Из
равенства f(Τ) =/г(Т)f2(Τ) =0 следует, что по меньшей
мере один из многочленов fi(T) или f2(T) равен нулю.
Пусть, например, /|(Т)=0, а степень этого многочлена
равна k\<k. Многочлен f\{x) является аннулирующим
для матрицы Τ порядка k. Это противоречит тому, что
степень аннулирующего многочлена должна быть не
меньше степени минимального многочлена f(x).
Следовательно, характеристический многочлен должен быть
неприводимым. Таблицы неприводимых многочленов для
р = 2 приведены в работе (79].
Во-вторых, характеристический и неприводимый
многочлен f (χ) должен делить без остатка двучлен χΝ — 1 и не
должен делить двучлен χΝ'— 1 при любых Л^ < N. Для
доказательства второго свойства многочлена f(x) допустим
обратное. Пусть xN — 1 = / (jc) g (χ) и χΝ'—1 =f (χ) gi (x),
при этом ΛιΊ<Ν, Поскольку Xм'—1 делится на f{x), то
Νι является периодом Λί-последовательности. Точно так
же и N является периодом ^-последовательности. Так
как Νι<Ν, то последовательность должна повторяться
с периодом Νι, а N должно быть кратным Νγ.
Следовательно, периодом будет наименьшее значение степени
двучлена, при котором он делится на f{x). Отметим, что
обычно при данных ρ и k заданным считается период
последовательности N и надо найти неприводимый
характеристический многочлен f{x), который делит без остат-
218
§ 4.3
ка xN— 1, но не делит х''— 1 при любых NX<^N.
Неприводимые многочлены, обладающие
указанными свойствами, (Называются первообразными
(примитивными). В таблицах, приведенных в ![79], указано, какие
неприводимые многочлены являются первообразными
(примитивными). Последнее название неприводимых
многочленов обусловлено особыми 'свойствами .корней
этих многочленов. Рассмотрим двучлен xN—1. Он имеет
N корией, которые являются решениями уравнения
*да—1=0. (31)
Среди этих решений обязательно существует
первообразный (примитивный) корень а такой, что все степени
этого корня тоже являются корнями уравнения (31). Эти
степени а, а2 uN~l, aN=\. Таким образом, зная один
корень а, можно восстановить все остальные корни.
Именно поэтому корень а и получил название
первообразного корня. Действительно все степени корня а с
показателями, изменяющимися от 1 до N, являются
корнями уравнения (31), так как (aq)N= (aN)9= \q= 1.
Любая степень корня а, большая чем N, сводится к
степени, меньшей N. Действительно, пусть Q = pN + r, где Q,
р, г целые числа, 0<'Г<'#—1. Тогда aQ = apNar=aT.
Отметим, что решения уравнения в матричной форме
(23) соответствуют решениям уравнения (31). Можно
показать, что каждому состоянию регистра TnXj (19)
соответствует свой корень уравнения (31), т. е. своя
степень корня а. Так как структура регистра определяется
характеристическим многочленом, то для формирования
рэгистром М-последовательности периода >N необходимо,
чтобы среди корней характеристического многочлена был
первообразный корень а. Так как степень
характеристического многочлена равна k, то он имеет k корней. Из
равенства
x"-\=f(x)g(x)=0 (32)
следует, что уравнения xN—1 =0 и f(x) =0 имеют общие
корни. Пусть корень уравнения f(x) есть β, т. е. f (β) =0-
Корень β может быть равен одной из степеней корня а.
§ 4.3
219
Если корень β=«χ, то одним из состояний регистра,
построенного в соответствии с принятым
характеристическим многочленом f(x), будет «первообразная»
комбинация символов, соответствующая первообразному конрюа.
Все остальные комбинации символов соответствуют
остальным корням уравнения (31). Если корень ιβ^ια (не
совпадает с первообразным), то период Λί-тюследова-
тельности будет меньше, чем Ν, так .как часть корней
уравнения (31) не будет воспроизведена регистром.
Таким образом, чтобы при заданных N, k м ρ
определить структуру 'регистра для формирования М-последо-
вательности с периодом N=ph—1, необходимо в качестве
характеристического многочлена взять первообразный
многочлен степени k. Пусть, например, ρ=2, k = 3. Тогда
N=7. Из таблиц [79] для k = 3 первообразный многочлен
имеет вид χ3 + χ+ι\. Соответствующий этому многочлену
регистр представлен на рис. 4.9.
Число ΛΙ-последовательностей. Определим возможное
число таких ^-последовательностей одинакового
периода N, каждую из которых нельзя было бы представить
в виде циклического сдвига любой другой. Представим
двучлен xN—il в виде произведения неприводимых
многочленов. Сначала рассмотрим пример. Пусть р = 2, fe = 6,
N=63. Тогда [вО]
= (хв + х+1)(хв + х3 + 1)(л;в-т-л;4 + л;2 + ;с+1)Х
Х(*в + х4 + х3-т-х+1)(хв + *5+1)(л;в-т-л;5 +
+ ха+ х+1) (хв + хь + jc3+x2+1 ) (х* + х5+ *4 + х+1 )Х
X (^св + л:8Ч-х4 + ^" + !)(^3 + л:3^4- 1)(л;3-4-л: + !) X
Х(*» + *+1)(*+1).
Наивысшая степень неприводимых многочленов в
разложении двучлена я*''—1 равна 6 и совпадает с числом
разрядов регистра к. Отметим, что этот факт имеет общий
характер: степень неприводимого многочлена в
разложении двучлена xN—1 всегда меньше или раина к.
Поэтому при заданном N в качестве характеристических
многочленов надо выбирать те, степени которых равны k.
Среди этих многочленов есть некоторое число первооб-
220
§ 4.3
разных (примитивных), каждый из которых создает свою
Λί-последовательность. Число первообразных
многочленов определяется числом первообразных корней. Бели
а — первообразный корень уравнения (31), то а1 тоже
первообразный корень этого уравнения, если / взаимно
просто с N. Например, если УУ = 1б, то полная
последовательность корней
а, а", а3, а4, а5, а", а7, а», а", а1», а", а1а, а18, а14, а15 == 1.
При этом период М-последовательности будет
максимальным. Если выбрать в качестве исходного корня а2
(2 взаимно просто с 16) и найти все степени (α2)μ для
μ = 1, 2 15 три условии αΙΒ=Ί, το получим всю
последовательность корней. Если же выбрать и3
(показатель степени 3 делит без остатка Ν= 16), получим
неполную последовательность корней α3, α6, а9, а12, а15=1, т.е.
период последовательности не будет максимальным.
В соответствии со сказанным в последовательности
корней а, а2 aN=\ первообразными будут только те,
показатели степени которых взаимно просты с числом N.
Число чисел в ряду 1,2 N—1, взаимно простых с
числом N, есть функция Эйлера φ(Ν) (85]. R общем случае
[85], ©ели
N = p]'p\\..p\\
где все pi — простые числа, то
9 (Ν)=(ΡΪ ~ Р\ ~1)(ΡΪ ~ ΡΪ~1) ■ · · (Plh ~ Р^ )· (33)
Если N — простое число, то
ψ(Ν)=Ν—\. (34)
Каждый первообразный многочлен степени k имеет k
корней, при этом, если один из них первообразный, то и
все остальные также являются первообразными [78].
Поэтому число первообразных многочленов для данного N.
равно [76]
' § 4.3
221
Значения Q для различных ρ и k приведены
в табл. 4.8 (77].
Таблица 4.8
k
1
2
3
4
5
6
7
8
9
10
Q
р=2
1
1
2
2
6
6
18
16
48
60
р=3
1
2
4
8
22
48
156
320
1008
2640
р=Ь
2
4
20
48
304
720
/>=?
2
8
48
160
1120
/,= 11
4
16
176
960
Отметим, что общего метода нахождения
первообразных многочленов в настоящее время не существует [76].
Можно указать только два частных способа их
определения.
1. Для простых N все неприводимые многочлены
степени k будут первообразными. Допустим, что N простое
число и неприводимый многочлен / (х) делит без остатка
двучлены xN~ 1 и xNl — 1, т. е. χ —l = f(x)g(x),
xNl — 1 =f (x)g1(x). Тогда и Ν, и Nlt как уже
отмечалось, должны быть периодами М-последовательности.
Допустим, что Νι<Ν. Тогда Νι должно делить без
остатка N. Но N по условию простое и, следовательно, Νι не
может делить без остатка N. Поэтому остается
предположить, что Νι = Ν. Таким образом, при простом N
неприводимые многочлены f(x) степени к являются
первообразными.
2. Многочлен f(x) = хк-\-а1хк~1-\- ... -\-dk-iX-\-dk
является первообразным, если многочлен F(x) = xp~ -f-
+ rf1xp<ft~1)"14-^fc-i;c + ^fc неприводимый. Доказательство
этого свойства можно найти в [76].
Рассмотрим пример для /? = 2, k = 5. Известно [79],
что хъ -f- x" -f-1 является первообразным многочленом.
222
§ 4.3
Тогда χ'1-\-χ3-\-\ = χ2' '—χ22 '+1 будет
неприводимым многочленом. Многочлен х8'-}-х3 + 1 может быть
использован в качестве характеристического, поскольку он
тоже будет первообразным, так как из теории чисел
известно, что 2 — 1 является простым числом для
k<{\3. Поэтому (231—1) —простое число и,
следовательно, (х31+х3+\)—первообразный многочлен.
Таким образом, чтобы получить М-последователь-
ность периода N = ph—1, необходимо найти
первообразный многочлен степени йипо его виду определить
структуру цепи обратной связи сдвигающего регистра.
Первообразный многочлен можно найти указанными двумя
способами (или из таблиц [79].
Циклические свойства ^-последовательностей.
1. Сумма М-последовательности с циклически сдвинутой
М-последовательностью является М-последовательно-
стью. Для доказательства рассмотрим М-последователь-
ность, получаемую, например, при считывании символов
со входа Т\ схемы на рис. 4.11. Согласно ι(14)
k
bj = x0.j=Yiclxl,i. (36)
ι=ι
Для последовательности, сдвинутой относительно '(36) на
m тактов, получаем
k
Uj + m = -"-Oij + m == V ClXl,l + m· (о · )
1=1
Просуммируем по модулю ρ последовательности (36)
и (37):
k
b),m= £Ci(*i,3 + -*i,J + m)· (38)
1=1
Так как для суммы (38) коэффициенты ct
характеристического многочлена те же, что и для каждого
слагаемого, то последовательность символов Ь$т является М-по-
следавательностью. Указанное свойство М-последова-
телыности можно проиллюстрировать формулой (3).
§ 4.3
ИЗ
*
2. Последовательность {£>„}, сопряженная с Λί-последо-
вательностью {£>„}, является Λί-последовательностыо. Соп-
*
ряженная последовательность {&„} определяется
уравнением
&„ + £>„ = 0 (modp). (39)
Уравнение (39) означает, что каждому символу Ьп
последовательности {£>„} однозначно соответствует символ
* *
Ьп последовательности {Ьп}, который является дополнением
символа Ьп до величины модуля р. Например, для /7 = 5
соответствие между символами bn, bn,— ^устанавливается
табл. 4.9. Для /? = 5, k = 2 последовательности {Ьп},
*
{Ьп} имеют вид
{£>„} = ...01 1424022343044131033212,
{&„} = ...04413103321201 142402234 3.
Таблица 4.9
ьп
*
-ьп
0
0
0
1
4
-1
2
3
-2
3
2
-3
4
1
—4
Отметим, что уравнение (39) может быть записано также
в виде
Ьп = — bn (mod p),bn = — bn (mod p). (40)
Докажем, что {£>„} является Λί-последовательностью,
определяемой той же матрицей состояний Τ (17), что и исход-
#
ная Ж-последовательность {&„}, и, как следствие этого, {&„}
циклически сдвинута относительно {&„}. Состояние
регистра X} (16) характеризуется комбинацией символов Xt,j,...,
224
§ 4.3
Χι,ί, ..., Xh,3. Следующее состояние регистра
определяется через матрицу Τ (17) формулой X3+i = TXj (18).
Переход от {Ьп} к сопряженной последовательности
*
{Ьп} означает переход от Xj к сопряженному состоянию
» *
Χ,, которое характеризуется комбинацией символов xltj,
* *
..., xltj,..., xkj. Поскольку в регистре, формирующем
М-последовательность, невозможна ,нулевая комбинация
выходных символов, то всегда состоянию регистра Xj
*
будет соответствовать сопряженное Xj, так как элементы
обоих состояний регистра принадлежат множеству 5
*
(8). Но для того чтобы {&„} была действительно М-по-
следовательностью, циклически сдвинутой относительно
{Ьп}, необходимо выполнение следующего условия:
X; + i = TXi, (41)
означающего, что порядок (характер) чередования символов
*
в обоих последовательностях {£>„} и {Ьп} одинаков.
Докажем, что условие (41) выполняется. Рассмотрим
систему уравнений (15). Она состоит из уравнений двух
видов: (k—1) уравнений типа
Χι+ι,3+\=Χι,} при /=1, 2, ..., k—\, (42)
*
которые для Xj состояния регистра записываются как
Xi+»i+i = Xi.i. /=1,2,...,й—1, (43)
и уравнения
*ι.j+ι = CiXu} +. ·. + CiXi,} +... +ckxKi. (44)
Из уравнений (42) — (44) следует, что доказательство
справедливости условия (41) сводится к доказательству
следующего соотношения:
c1x1,j + ... + c^.j + ...+CftXft,j =*i.j+i. " (45)
§ 4.3
225
Отметим, что согласно определению сопряженной
последовательности (39)
*i.i+i + *i.i+i=0 (mod p). (46)
Тогда суммируя почленно суммы 1(44), (45) и учитывая,
что каждое слагаемое сравнимо по модулю ρ с .нулем
(46), получаем
# *
Οχ (*,. j + Xi.i) +...+C[ {XU + Xi.j) +
+ ...+cft(xft>j + xftJ)=0 (modρ). (47)
*
Следовательно, последовательность {bn} является
циклически сдвинутой Λί-последовательностью {Ьп}.
3. Обозначим
b] = bis. (48)
Пусть s взаимно просто с N=ph—il. Тогда
последовательность, образованная символами (48), где /=0, 1, ...,
является М-последовательностью [76]. Доказательство
этого свойства опускаем. Пусть, например, р = 2, k=3.
Тогда последовательность (2) запишется «ак
01 1 100101 1 100101 1 10010...
Для s = 2 согласно (48) последовательность {bs.}
запишется в виде
0101 1 100101... (49)
Сравнивая полученную последовательность ι(49) с
последовательностью (2), замечаем, что она является М-по-
следовательностью. Отметим, что если s не взаимно
просто с N, то последовательность Ь^ будет иметь период
меньше N.
4. Рассмотрим число символов вида 0, 1, ..., (р—1),
содержащихся в периоде N=pk—1 Λί-последовательно-
сти. Допустим, что ^-последовательность образуется
считыванием символов с выхода любого триггера
регистра. Число возможных различных ненулевых состояний
226
§ 4.3
регистра равно ph—1. С учетом нулевого состояния это
число равно ph. Поэтому каждый символ во 'всех ph
состояниях регистра встречается (pk/p) =ph~l раз.
Напомним, 'что нулевое состояние в формировании М-по-
следовательности не участвует, поэтому число нулей
в периоде М-последовательности будет равно (ph~l—1).
Корреляционные свойства ^последовательностей.
Допустим, что каждому символу Ьп вида 0, 1, ..., (р—1)
соответствует радиоимпульс с определенной начальной
фазой. В качестве элементарного фазового сдвига
примем величину 2л/р. При этом символу Ьп соответствует
символ ап:
&п4=»«,, = е ' . (50)
Согласно формуле (4.1.83) автокорреляционная функция
Λί-последовательности определяется выражением
Ν * Ν ι— Φ ~ь )
К"'=4г5] α"^«-™=ir5je' n n_m' (5ι)
где ап были заменены по формуле (50).
Так как — bn.m = bn_m(modp) (40), то выражение
(51) принимает вид
*«=irSe P ■ (52)
Согласно циклическим свойствам М-последовательностей
(свойства 1,2) сумма
*
bn,m = bn-\~bn_m (53)
ЯЕЛяется Λί-последовательностью. Поэтому подставляя
(53) в (52), запишем, что
л=1
§ 4.3
227
При m=qN, где q=0, ±1 сумма (53) согласно
(39) для всех η равна нулю. В этом случае согласно
(54)
RqN = \ для q = 0, ±\, ±2,... (55)
При ηιφηΝ, где ^=0, ±\, для вычисления Rm
воспользуемся 4-м циклическим свойством М-последо,вательно-
стей, согласно которому вое ненулевые элементы Ьп,т
встречаются в периоде последовательности ph~] раз,
а элемент 0 встречается (pft_1—1) раз. Объединим
слагаемые суммы (54) в группы таким образом, чтобы
в каждую группу по одному входили слагаемые со
значениями Ьп,т, равными 0, 1, ..., ρ— 1. Число таких
полных групп равно числу нулей в периоде М-последова-
тельности, т. е. pft_1— 1. Последняя неполная группа
будет содержать символы 1, 2, ..., ρ—1. Добавим в нее
символ 0, что эквивалентно прибавлению к сумме (54)
слагаемого вида е =1. В этом случае сумма (54) может
быть записана в виде
1 ι2-ι
р — 1
(56)
Так как в (56) слагаемое под знаком суммы равно [64]
то
р~\ ._2π_(
Je ' =0, (57)
Rm = — Τ для тФЯ^, q=0, ztl (58)
Пропорциональное уменьшение боковых пиков
автокорреляционной функции с ростом N для М-последова-
тельностей и обусловило их 'использование >в
радиолокационных станциях, так как при большом N уровень
боковых пиков мал (—1/N). Но чтобы получить такой
уровень, надо излучать периодическую М-последователь-
ность. На рис. 4.12 изображена автокорреляционная
функция М-последовательности для N=,15.
228
§ 4.3
Необходимо отметить, что в настоящее вр|емя еще не
■найдена оценка 'боковых пиков 1на плоскости (τ, Ω) для
корреляционной функции Μ-последовательности.
Приближенно оценку можно получить исходя из
статистического рассмотрения М-последовательности. В соответ-
W)
Рис. 4.12.
ствии с формулой (4.Ί.82), учитывая (50), (53),
получаем
где
Ω=— -£, при р. = 0, 1 N. (60)
Символы bn,m образуют М-последовательеость
согласно первому циклическому свойству. Согласно
циклическому свойству 4 среди всех N символов этой
последовательности каждый символ 0, 1 ρ—1 встречается
примерно одинаковое число раз. Это дает основание
говорить о квазислучайном расположении символов 0,
1, ..., ρ—1 в Μ-.последовательности, т. е. утверждать, что
2π&η,,η/ρ—случайная величина с равшмерным
распределением ;на отрезке [0, 2π].
§ 4.3
229
Положив для простоты рассмотрения г0 (μ)]= 1 для
всех μ и обозначив
Ъ = Ц-Ьп.т + ^{П-\)\>., (61)
запишем (59) в виде
Ν Ν
*«*=^Σ e'in =^r Σ(cos5n+j5ίηξη)· (62)
л=1 л=1
Так как величина ξη по предположению равномерно
распределена на отрезке [0, 2я], то среднее значение
экспоненты в (62) по определению, даиному в [40], равно
2π
m1{elin} = ^rjeli"^n=0. (63)
о
Поэтому и среднее значение т.! {/?т> μ} = 0. Среднеквадра-
тическое значение \Rm | найдем через центральный
момент случайной величины с нулевым средним, который
определяется выражением [40]
М9{С}=/я.{С}'. (64)
Согласно (62) квадрат модуля
N N
I *«. μ I · = -w Σ J}[&* {Хп ~h)+j sin (ξη ~ *k)] =
л=1 ft=l
Ν Ν
=-F+^S Σ icOS(Sn-Sft) + isin(5„-Eft)]. (65)
Усредняя (65) "по величине ξ и учитывая, что
m^cos^ — ξΛ)}=0 и m!{sin(Sn —ξΛ)}=0,
получаем
Λ4Ι*„,μ|} = «ι{|*„,μ|'}ΗΓ (66)
Из (66) следует, что среднеквадратическое значение
корреляционной функции TW-последовательности равно
IIVN.
230
§ 4.3
Усеченная Λί-последовательность. Под усеченной
Λί-последовательностью будем понимать отрезок М-по-
следо!вательности длиной в период, содержащий N
символов. Эти N символов можно вырезать из
периодической ^-последовательности различными способами.
Каждому способу соответствует циклически сдвинутая
М-поеледовательность. Например, для М-последователь-
ности € N=15 ι(ρ = 2, k = A)
J5
100011110101 lOOlOOOl 11101011 00100 0111101 (67)
1
13
можно получить 15 различных сигналов — усеченных
Λί-последовательностей. Первый сигнал, выделенный
фигурной скобкой 1, ,им>еет вид 1 il 1 Ί 0 1 0 1 10 0 10 0 0,
второй — 1 1 1 -0 1 0 1 1 0_0 1 0 0 0 1 и т. д.
Рис. 4.13.
Корреляционные и спектральные свойства усеченных
М-последовательностей зависят от способа выделения
периода N. Для примера рассмотрим усеченные
последовательности 1 и 13 для N=15, выделенные в (67)
фигурными скобками. На рис. 4.13 изображены
автокорреляционные функции, а на рис. 4.14 — амплитудные
спектры этих функций для 1-й (сплошная линия) и для
§ 4.3
23 i
Рис. 4.14.
боковой пик имеет минимальное значение, равное 3/15.
Сигналы, обладающие такими свойствами, получили
название минимаксных [6]. В табл. 4.11 приведены
минимаксные значения боковых пиков Ятмшшкс умноженные
на N, для различных N при р = 2 [6]. Как видно из
табл._4.11, значение М/?тМинмакс с ростом N близко
к YN, т. е. Ятмиимакс*=> \γΝ, что совпадает со
статистической оценкой корреляционной функции.
Найдем приближенную границу значения /?тМинмакс·
Аналогично (54) для автокорреляционной функции
усеченной М-последовательности согласно (4.1.65)
можно записать, что
йзй
§ 4.3
Номер
сигнала
Максимальный
боковой пик
1
3/15
2
4/15
3
4/15
4
4/15
5
4/15
6
4/15
Km —
Ν
п=т + \
(68)
где bn,m символы М-последовательности. Отметим, что
в сумме (68) N — т слагаемых, а не N, как в (54). Из-за
меньшего, чем N, числа слагаемых в (68) нарушается
четвертое циклическое свойство М-последовательностей.
Следовательно, часть символов 6n,m будет встречаться
в периоде последовательности реже, чем р<
й-1
раз.
Если отбросить ν одинаковых символов, то боковые пики
автокорреляционной функции усеченной
М-последовательности могут увеличиться сразу на ν единиц.
Максимальное число одинаковых символов равно числу
разрядов регистра k. Поскольку k и N связаны зависимостью
N=ph—.1, то приближенная граница минимаксного
значения бокового пика равна
k__ log(/V+l)
N Nlogp
(69)
Полученная оценка (69) приведена в табл. 4.11 в
последнем столбце. С ростом jV значения (69) становятся
меньше 1/ VN и RmwiK№S,KC, найденных с помощью метода
перебора [6].
Единственной оценкой уровня боковых пиков
корреляционной функции усеченной М-последовательности на
плоскости (τ, Ω) является величина ilVN, полученная
из статистического рассмотрения М-последовательности.
На рис. 4.15 приведено тело неопределенности М-после-
§ 4.3
233
Таблица 4.10
7
3/15
8
5/15
9
3/15
10
3/15
π
3/15
12
4/15
13
3/15
14
4/15
15
3/15
Рис. 4.15.
довательносги, выделенной в (67) фигурной скобкой 1.
Максимальный боковой пик равен 0,33 (т=\, μ=1).
При N=15 статистическая оценка l/j/N = 0,26.
Таблица 4.11
N
7
15
31
63"
127.
255 -
k
3
4 ,
5
6
7
8
^Rm миимакс
1
3
4
6
8
13
rw
2,6
3,9
5,6
7,9
11,3
16,0
ЧПГ
0,39
0,26
0,17
0,13
0,09
0,06
k/N
0,43
0,266
0,161
0,095
0,055
0,003
234
§ 4.4
4.4. ПОСЛЕДОВАТЕЛЬНОСТИ ЛЕЖАНДРА
И ЯКОБИ'
Свойства автокорреляционной функции
периодической кодовой последовательности. Пусть периодическая
кодовая последовательность, записываемая как {а„}=
ао, аи ..., а„, ..., α,Ν-ι, представлена набором
символов ±1, а ее период равен N символам. Нормированная
автокорреляционная функция периодической
последовательности определяется формулой (4.1.83), а
ненормированная автокорреляционная функция —
/V—I
Vm = NRm = V апап+т. (1)
л=0
Докажем, что N=Um (mod4), т. е. N сравнимо
с Vm по модулю 4 и, следовательно, разность N—Vm
делится на 4· без остатка. Обозначая
Ьп=±-(\-ап) (2)
и заменяя ап через Ьп в формуле (1), получаем
л=0 л=0
/V-l N-\
-2£bn-2£ £,n+m. (3)
га=0 га=0
Так как сумма 1 за период кодовой последовательности
■не зависит от величины сдвига т, то
JV—1 Ν—I
££>n+m = £&n. (4)
ra=0 ra=0
Учитывая (4), из формулы (3) находим, что
(Ν—Ι /V—1 \
£ Ьп - Σ W>n+« · (5)
л=0 л=0
1} § 4-4 изложены основные результату работы {86}.
§ 4.4
235
Разность сумм в формуле (5) является целым числом.
Следовательно, N—Vm делится на 4 без остатка, а это
означает, что
N = Vm (mod 4). (6)
Найдем нижнюю оценку максимального бокового
пика автокорреляционной функции кодовой
последовательности. Представляется очевидным, что
максимальное значение бокового пика VmMaKC не меньше среднего
значения боковых пиков, т. е.
/V-1
V,
тмакс
m*0(mod.jV)
Vm—N.
Υ,ν.
т
m = l
Прибавляя и вычитая из правой части суммы (7)
величину N и подставляя в (7) Vm согласно (1), получаем
V. У.апа„+т—N |. (8)
т=0 л=0
Меняя порядок суммирования в (8) и обозначая
N—\
κ = £ ап,
л=0
записываем (8) как
V,
тмакс =
Ν-
Τ(**-Ν)·
(9)
(10)
Таким образом, оценка VmmKC определяется величиной
κ2. Если N четное, то κΜΗΗ = 0, что соответствует случаю
равного числа символов -{-I и — 1 в периоде кодовой
последовательности. Если N нечетное, то κ
1. Найдем
оценки ν,η,ωκο для четных и нечетных значений N.
Пусть Ν — четное число. Тогда VmMaKC^
^с—N/(N—1)>1. Четное число N может быть
представлено как N = 41 или N = 41 + 2, где I — целое число.
Первому представлению соответствует N==0(mod4),
второму — yV = 2(mod4). Когда N = 41, подстановкой
в сравнение (6) различных значений Утманс, начиная
с Утма«с = 0, убеждаемся, что сравнение (6) выполняется,
236
§ 4.4
если Утмакс=0. Когда УУ = 4/ + 2, подставляя в (6)
значения Утмакс=0,1,2,..., убеждаемся, что
сравнение (6) ВЫПОЛНЯеТСЯ, если Утмакс = 2.
Пусть N — нечетное число. Тогда VmMaKc^ — 1.
Нечетное число N может быть представлено как
УУ = 4/+1 или УУ=4/ + 3, где / — целое число. Первому
представлению соответствует УУ=1(то<14), второму —
N=3(mod4). При N = 4/ + 3 сравнение (6)
выполняется при минимальном значении VmMaKc, равном —1.
Следовательно, максимальный боковой пик
принимает минимальное значение, равное Утмакс=1. только
при yV=i3i(mod4), т. е. при Ν = Ό{+3 или, что то же, при
Ν = Μ—1, где I, i— целые числа. Отметим, что М-по-
следовательности удовлетворяют сравнению N = 3
(mod4), так как 2й—l=4X2h_2—1. В дальнейшем
последовательности, у КОТОРЫХ 1/тмакс = —1 (#тмакс =
= — 1/N), будем называть минимаксными. Необходимым
условием существования минимаксных
последовательностей является следующее: число символов ,Ν в периоде
кодовой последовательности должно удовлетворять
сравнению
JV=3(mod4). (11)
Если для значений yV = 3(mod4) минимаксная
последовательность не существует, то можно показать, что
минимальное значение Утмакс = 3.
Объединяя сказанное ранее, можно записать, что
О для N = 0 (mod 4),
v ^ 1 Для N=\ (mod 4), ,„
ν м мм'Μ 2 для Ν Ξ 2 (mod 4), [ '
— 1 для Νξ3 (mod 4).
Найдем условие существования минимаксной
последовательности. Допустим, что величина боковых пиков
корреляционной функции кодовой последовательности
может принимать только два значения: Vi и V2=Vi—4.
Такие значения Vi и V2 удовлетворяют сравнению (6).
Пусть Vi встречается в периоде последовательности Νχ
раз. Тогда V2 встречается (Ν—Νι—\) раз. Поэтому
§ 4.4 237
в соответствии с (1), (9) для суммы всех Vm имеем
VVm = yV + iV1V1 + (yV-yV1-l)(l/1-4)=x2. (13)
m=0
Из (13) получаем, что
уу1= .'-*-(*-1)(г,-4). (14)
Так как A^S^O, то
κ'_Λ/>(Ν — 1)(V,— 4),
или
^<3+£^f (15)
Если 1^2 = — 1, то Vi = 3. Это возможно, если κ2=1.
Но тогда из (14) получаем, что Л^=0, т. е. бокового
пика со значением У4 = 3 при κ2= 1 нет. Следовательно,
чтобы минимаксная последовательность существовала
при yV = 3(mod4), необходимо, чтобы выполнялось
условие κ2=1, τ. е. чтобы число символов +1
отличалось на единицу от числа символов —1 в периоде
последовательности.
Параметры известных минимаксных
последовательностей приведены в табл. 4.12.
Следует отметить, что если данному периоду N
соответствуют различные по виду последовательности, то эти
Таблица 4.12
Период
Примечания
ериод
= 2*-1
= 4/+3
4<2 + 27
Примечания
k — целое число
N — простое число,
/ — целое число
N — простое число,
t — целое число
Вид последовательности
Μ-последовательности
Последовательности
Лежандра
Последовательности
Хопла
Последовательности
Як оби
N
N
Ν =
N=t(t + 2)
t, t + 2 — простые
числа
23Й § 4.4
последовательности могут совпадать.
Последовательности Холла с yV = 4i2+27 = 4(/2+6)+3 совпадают
с последовательностями Лежандра при / = ί2+6.
Последовательности Якоби в общем случае характеризуются
периодом t(t + l), где значение / может быть равно
2; 4; 6, но только при / = 2 эти последовательности
минимаксные (Vm= — 1). Последовательности Якоби с
периодом N = t(t + 2) называются также дважды простыми
последовательностями.
Таблица 4.13
N
3
7
11
15
19
23
31
Внд
Μ
Μ
L
Μ
L
L
Μ, L
Ν
35
43
47
59
63
67
71
Внд
У
L
L
L
Μ
L
L
Ν
79
83
J 03
107
127
131
139
Внд
L
L
L
L
M, L
L
L
N
143
151
163
167
179
191
199
Внд
/
L
L
L
L
L
L
Как видно из табл. 4.12, различным N могут
соответствовать различные последовательности. В табл. 4.13
указаны виды последовательностей для N,
изменяющегося от 3 до 200. Через L обозначены последовательности
Лежандра, через / — последовательности Якоби, Μ
соответствует М-последовательности.
Последовательности Лежандра. Если{-£Л есть
символ Лежандра (символ η по отношению к Ν), то символы
последовательности Лежандра определяются как
(1 при /г ξ 0 {modN),
(-J-) при /г ^ 0 (mod Λ/). (16>
Отметим, что в теории чисел [85] символы Лежандра
вводятся при рассмотрении сравнений второй степени:
x2=n(modN), (17)
§ 4.4
239
причем общий наибольший делитель (п, УУ) = 1. Решить
сравнение (17) означает найти такое х, при котором
(17) превращается в тождество. Сравнение (17) имеет
решения не при любых значениях п. Значения п, при
которых сравнение (17) имеет решения, называются
квадратичными вычетами, а значения п, при которых
(17) не имеет решений, называются квадратичными
невычетами. Символ Лежандра определяется как
W-U:
1, если η — квадратичный вычет,
если η — квадратичный невычет.
(18)
Он определен для в£ех п, не делящихся без остатка на
Ν, причем N — простое число, больше двух. Если символ
Лежандра найден, то становится известным, имеет ли
решение сравнение (17) при данном п. Из (17) следует,
что, если число η представляет собой квадрат какого-
то числа по модулю uV, то он является квадратичным
вычетом. Например, для сравнения хг= 17 (mod 19)
имеем решение 62= 36= 17 (mod 19), т. е. число 17 —
квадратичный вычет.
Без доказательства приведем основные свойства
символов Лежандра:
(*-) = " (тг)-<-'>
N-1
2
(*
=(-i)
8
(
nk . . . q \
N
(4)-<-)
л-1
2
(ν)(ν
(τ
■№
(19)
(20)
(21)
(22)
2
если η, k — простые
нечетные числа; (23)
если /г? = /г (taodN). (24)
240
§ 4.4
Отметим, что для « = 0(тос1УУ) символ Лежандра не
определен.
В качестве примера найдем символы Лежандра для
кодовой последовательности с периодом N=19.
Используя свойства (19) — (24), получаем что
(■ά)=·=(4)=--'··(*Ητ)<-^-
-(4)=-'=
(ΐΗ4)"-'> (4·)-(τ)<-·>·■'-
-w-w-1··
(i)-(i)(i) = t (^)-^)(-,r-
-(■f)-(-f)(-'r-(-f)=..
Аналогичным образом можно найти и все другие символы
Лежандра до Г —^—j включительно. Записывая их
последовательно друг за другом согласно (16) и учитывая,
что ао=1. получим последовательность Лежандра для
N = 19 в следующем виде:
1 1 — 1 —11111 — 1 1 — J 1 — 1 — 1 — 1 ^— 111 — 1.
" ' ,J /(25)
Рассмотрим корреляционные свойства
последовательностей Лежандра. В соответствии с выражением (9)
*=»+;в(тг)· (2б>
Из свойств решений сравнения (17) известно [85], что
если η меняется в пределах от 1 до \Ν —1, то половина
значений η является квадратичными вычетами, а поло1
вина — квадратичными невычетами. Поэтому половина
символов Лежандра принимает значения, равные 1,
а другая половина — значения, равные —I.
Следовательно, Ц-\.
§ 4.4
241
Автокорреляционная функция кодовой
последовательности Лежандра, учитывая, что а0 не выражается
через символ Лежандра, согласно (1), (16) запишется
в виде
ηφΝ—τη
Ν-\
Символ
N-l
= am(—\) 2 (28)
при TV ^ 4/ -f- 3 определяется как
aN_m = -am. (29)
Поэтому выражение (27) принимает вид
ν-= Σ (*■)("-*=)· <з°>
ηΦΝ—m
Для упрощения формулы (30) введем число п'
такое, что
пп'=\ (mod N). (31)
Например, при я—17, N=19 из (31) получаем п'=9,
так как 17-9=1 (mod 18).
Так как в соответствии с (31) п+пл'тза
==n+m(modN), то можно записать следующее
тождество:
fn+m\^fn+ пп'т\_( η \( 1 + п'т \ ,«„.
Ьг-Г[г-тг-)-[1г){-^г-)· (32)
Согласно (32) выражение (30) принимает вид
v»= J (-Чг*-)· (33)
fH#V —if)
242
§4.4
При вычислении суммы (33) следует убедиться, что
все символы Лежандра определены. Допустим обратное,
г. е. допустим, что 1+п'т = 0 (modN), или, что то же
самое, п'т=—1 (modN). Но такое же сравнение
получается, если в (31) подставить значение n = N— т. Так
как это значение η исключено из суммы (30), (33), то,
значит, в (33) определены все символы Лежандра,
число которых равно N—2. Можно показать, что, если η
принимает все значения от 1 до ·Ν—1, за исключением
η = Ν—т, то числа \+п'т принимают все значения от
2 до N— 1, приведенные по modN. Значения 1 среди них
нет, так как среди решений сравнения (31) нет решения
«' = 0. Следовательно, поскольку сумма всех символов
Лежандра при £=1,2 N—1 равна нулю, сумму (33)
можно представить как
ν-=Σ(τ)-ϋ'(*-) -'=-·■ (34>
Из (34) следует, что последовательности Лежандра
действительно являются минимаксными.
Последовательности Лежандра, как и Λί-последова-
тельнасти, являются линейными рекуррентными и
описываются линейным рекуррентным уравнением [6, 87]
вида
« = £>+(«-1), (35)
где Ь — целое число. Значение каждого символа
последовательности ап получается путем преобразования η
в символ Лежандра (-»т-)> если он определен.
Например, для сигнала (25) справедливо
уравнение «=1 + («—1). При 6 = 3 получаем следующий
закон чередования номеров и символов Лежандра:
О 3 69 12 15 18 2 5 8 11 14 17 1 4 7 10 13 16
1_1 1 1 —1 —1 —1 —1 1 —.1 1—1 1111 — 1 — 1 1.
При периодическом продолжении найденной
последовательности получим последовательность вида (25), но
с измененным на обратный порядком чередования
Импульсов.
§4.S
243
Последовательность Якоби. Если «Символ Якоби есть
(*Мт) (т> <36>
где общий наибольший делитель (п, р, q) = 1, а р, q —
простые числа, то последовательность Якоби для p>q
определяется как
ι (—J при η Φ 0 (mod/?), η ψ,0(mod q),
an=>\ 1 при я = 0 (mod/??), (37)
j 1 при « = 0 (mod/?), tιщO(vΆoάq),
i — l при η =£.0 (modρ), n = 0(modq).
Раньше было оговорено, что под последовательностями
Якоби будут подразумеваться такие, у которых
p = q + 2, период равен N, а п изменяется от 0 до N—1.
Так как символ Якоби определяется произведением
символов Лежандра, то вычисление его производится
согласно формулам (19) — (24).
Например, при ρ = 7, q => 5 период N = 35, а символы
последовательности ,Якоби за „период чередуются
следующим образом: 1 1 — 1 1 1 — 1 — 1 Ί -!■ 1'1 — 1 Ί
ϊ Ί f_'i iY-si^V-ri^i:±i^rxil-ii ι и
— 1 —1 —1 1 —1. Легко убедиться, что найденная
последовательность Якоби является минимаксной.
4.5. НЕЛИНЕЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Основные свойства. Период Λί-последовательности
(4.3.1) равен N = ph—1, где k — число разрядов
регистра, ρ — число различных используемых символов.
Напомним, что среди всевозможных кодовых комбинаций
символов в регистре комбинация из k нулей (000... 0)
является запрещенной. Если в регистре (см. рис. 4.11)
по каким-либо причинам такая комбинация возникнет,
то колебания в регистре сорвутся и регистр
установится в нулевое состояние.
244
§4.5
Используя дополнительные логические операции,
можно так построить схему регистра, что кодовая
комбинация символов из k нулей перестает быть запрещенной.
В этом случае период последовательности равен
N = ph, (1)
а получаемая в регистре последовательность символов
описывается нелинейным рекуррентным уравнением
Подобные последовательности называются нелинейными
[87, 88].
h h h
ι 1 1 χ, ι 1—ι ι 1 1
Χι
И
|Рис. 4.16.
Рассмотрим пример. На рис. 4.16 представлена схема
регистра (р = 2), отличающаяся от схемы, приведенной
на рис. 4.9, следующим.
Во-первых, каждый триггер на рис. 4.16 схематично
разделен вертикальной линией на две половины. С
выхода одной половины снимается прямой символ х,
с выхода другого — его инверсия х. Прямой и
инверсный символы удовлетворяют условию
je+'x=l(mod2). (2)
Если инверсный символ я=1, то это означает, что
прямой символ х = 0.
Во-вторых, на схему совпадения «И» поступают
инверсные символы со всех триггеров (7Ί, Т2), кроме
последнего. На выходе схемы «И» символ 1 появится
только тогда, когда инверсные символы триггеров 7Ί, Т2
принимают значение 1. При любых других комбинациях
инверсных символов Γι, Τ2 на выходе схемы «И» будет
символ 0.
§ 4.5
245
В-третьих, в схеме включен дополнительный
сумматор по mod 2, на входы которого поступают символы
со схемы «И» и сумма символов цепи обратной связи
регистра. Так как цепь обратной связи замкнута, то
в схеме возможны колебания. Последовательность
возможных кодовых комбинаций символов (состояний
регистра) при предположении, что первоначально в нем
была записана комбинация 100, приведена в табл. 4.14.
Таблица 4.14
Номер
такта
1
2
3
4
5
6
7
8
9
10
Вход Γι
0
1
1
1
0
0
0
1
0
1
Прямые выходы
Г,
1
0
1
1
1
0
0
0
1
0
т,
0
1
0
1
1
1
0
0
0
1
т,
0
0
1
0
1
1
1
0
0
0
Инверсные
выходы
г,
0
1
0
0
0
1
1
1
0
1
т.
1
0
1
0
0
0
1
1
1
0
Выход схе-
0
0
0
0
0
0
1
1
0
0
Как видно из табл. 4.14, после 8-го такта
комбинации в регистре начинают повторяться. Следовательно,
период повторения равен 23=8. Символ 1 на выходе
схемы «И» за период повторения появляется только
в двух тактах: в седьмом и восьмом тактах, когда
инверсная комбинация первых двух символов,
характеризующих состояние регистра, равна 11. Если
состояние регистра" описывается комбинацией символов 001,
то на выходе левого сумматора — символ 0. Поэтому
следующей кодовой комбинацией символов регистра
будет 000. Инверсия первых двух символов есть 11,
в результате чего на выходе схемы «И» появится символ
1, Который пройдет на вход регистра. И в следующем
такте кодовой комбинации в регистре будет 100.
246
Μ·ϋ
В последующих тактах комбинации символов следуют
друг за другом так же, как и в схеме на рис. 4.9. Таким
образом, введение в схему регистра нелинейного
элемента в виде схемы «И» приводит только к появлению
одной дополнительной комбинации символов 000.
Нелинейная последовательность символов может
быть получена при считывании символов со входа или
выхода любого триггера регистра. Например, считывая
символы со входа триггера 7\, получим периодическую
последовательность
• ••01110001011100010111··· (3)
Необходимо отметить, что в нелинейных
последовательностях вида (3) число символов 1 и 0 за период равно
друг другу.
В отличие от Λί-последовательностей сумма двух
сдвинутых нелинейных последовательностей не является
циклически сдвинутой относительно исходной
нелинейной последовательностью. Действительно, если
просуммировать последовательность (3) с
последовательностью, сдвинутой относительно нее, например, на три
такта, то получим
0 1110001011100010111
+ 0 01011 100О101 1100010
01011111010111110101" '4)
Малый уровень боковых пиков (—\/Ν)
периодической автокорреляционной функции М-последователь-
ностей (см. § 4.3) является следствием того, что сумма
двух М-последовательностей также
^-последовательность. Так как нелинейные последовательности этим
свойством не обладают, то можно предположить, что
уровень боковых пиков их автокорреляционных функций
будет больше уровня боковых пиков
автокорреляционных функций Λί-последовательностей.
Нелинейное рекуррентное уравнение. Когда число
различных используемых символов ρ является простым,
то одной из возможных схем регистра формирования
нелинейной последовательности будет схема,
приведенная на рис. 4.17. Она построена на том же принципе,
что <и схемы на рис. 4.11, 4.16. Схема «И» является схе-
§ 4.S
247
мой совпадения k—1 единиц, т. е. на выходе схемы «И»
символ 1 появляется тогда, когда на всех ее входах
единицы. При этом
х — Xjj-^- 1 (mod /7).
(5)
Схема «И», как было показано ранее, на работу
регистра не влияет, за тем лишь исключением, что
между кодовыми комбинациями 000...01 и 100...00 она
создает комбинацию символов из k нулей (000... 00).
Поэтому выбор характеристического многочлена
(определение коэффициентов сь ..., ch) для определения струк-
xo,j Tf *ij Тг XU Т3 X*J
τ>.,χ*-υ τ„ *kj
р71
ci X
XU
сг Χ
Cb
ΊίΤχ \X*J
гт
с$ X с*-2 X
Ш—<Ь
X c-t X с* Χ
■ιι. i \ m i—i J \ ■
Ш
Рис. 4.17.
туры регистра, приведенного на рис. 4.17, следует
делать так же, как и для Λί-последовательности (§ 4.3).
Прямой символ на выходе 1-го триггера на /+1
такте
xi,i+i = Xi-i.i, (6)
так как с каждым тактом символ со входа переходит на
выход. Символ на входе первого триггера в /-м такте
равен
k
1
■*·.*= 5Je***.i +Π *i.i·
Π
где
Π
_, I 0 при 5,ri
= 1,
(7)
(8)
248
§ 4.5
— операция символического умножения, выполняемая
схемой «И».
Используя (5), нелинейное рекуррентное уравнение
(7) можно записать как
k k—l
*..i=2c'*'.j+n(*i.i+1)· (g)
Нелинейность уравнений (7), (9) приводит к тому,
что непосредственный анализ состояний регистра сопря-
Рис. 4.18.
жен с большими математическими трудностями. Иногда
анализ состояний регистра не требуется, поскольку
выбор структуры регистра (рис. 4. 17) можно
производить на основе теории М-последовательностей.
В работе [87] приведена формула для числа
нелинейных последовательностей, возможных при данном
k: 2" . Например, если ^=13, то число возможных
нелинейных последовательностей равно 24083, в то время
как число М-последовательностей — 630. Такое большое
различие по числу последовательностей объясняется
тем, что введение нелинейных логических операций
значительно расширяет возможности при
проектировании формирующих схем,
§ 4.5
249
Автокорреляционная функция. На рис. 4.18
изображена автокорреляционная функция нелинейной
последовательности для N = 8, а на рис. 4.19,а —для N = 32*.
На этих рисунках для области τ^,Ο изображены перио-
Рис. 4.19.
дичеокие автокорреляционные функции, для области
τ:>0— непериодические. На рис. 4.18 изображены авто-
1 Автокорреляционные функции рассчитаны Л. Н. Волковым.
2S0
§4.6
корреляционные функции периодической
последовательности (3) и соответствующей ей непериодической
последовательности 01110001. Рис. 4.19,а соответствует
нелинейной последовательности с периодом 111110 1
00010010 10 1100000 11100110.
Как видно из рисунков, боковые пики периодических
автокорреляционных функций нелинейных
последовательностей значительно отличаются от величины —\/N.
Для сравнения на рис. 4.19,6 представлена
автокорреляционная функция М-последовательности, период
которой N = 31 имеет вид 11111010001001010
1 100001 1 1001 10. Несмотря на разницу в
периоде в один символ 0, автокорреляционные свойства
нелинейных периодических последовательностей, с
точки зрения уровня боковых пиков значительно хуже, чем
М-последовательностей, Это является следствием того,
что сумма двух нелинейных последовательностей не
является циклически сдвинутой нелинейной
последовательностью.
4.6. ДОПОЛНИТЕЛЬНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ
Последовательности {а„} и {αη} называются
дополнительными [89—93], если
did _ / 2 при т=0,
[ 0 при т = zL·
(1)
при от = гЬ 1, · ··, ±(N— 1),
где
Ν Ν
ra=m + l ra=m + l
Например, последовательности
111—1 1 1—1 1
1 1 1 _1 _1 _1 1 _l U
являются дополнительными. Значения их
автокорреляционных функций приведены в табл. 4.15.
§ 4.6
251
Таблица 4.15
т
NRm
NRm
N (Rm + Дт)
0
8
8
16
1
— 1
1
0
2
0
0
0
3
3
-3
0 '
4
0
0
0
5
1
— 1
0
6
0
0
0
7
1
-1
0
8
0
0
0
Отметим, что в дальнейшем рассматриваются
последовательности, у которых а„=1; —1. При заданном N
можно построить несколько различных пар
дополнительных последовательностей, комбинируя положения
символов.
Число одинаковых и различных пар символов. Из (2)
следует, что Rm и Rm состоят из N — т пар символов.
Каждая пара символов апап-т равна либо 1, либо —1.
Если оба символа в паре одного знака, то anan-m=l·
Назовем такую пару положительной. Если оба символа
разного знака, то апап-т = — 1, и пара будет
отрицательной. Допустим, что в Rm входит а положительных
и β отрицательных пар, т. е.
Ят = а—β, (4)
причем
α + β=Ν—т. (5)
В свою очередь в %т входит а положительных и β
отрицательных пар, которые связаны уравнениями
Ът= a — (Г, (6)
a-ff=N — т. (7)
Так как при т ф- 0 в соответствии с (1) Rm = —Rm, то
решая систему уравнений (4) — (7), получаем, что
252
§ 4.6
Следовательно, при любом сдвиге т, не равном
нулю, число положительных (отрицательных) пар
в последовательности {ап} равно числу отрицательных
(положительных) л ар в последовательности {а„}.
Число символов в последовательности. Необходимо
отметить, что в дополнительных последовательностях
число символов должно быть одинаково и равно N. При
этом число N является четным и равно сумме
квадратов двух целых чисел.
Докажем, что N— четное число. Рассмотрим Rm и
~Rm. Пусть m = N — 1. В этом случае суммы в формуле (2)
соответственно равны ataN и axaN. Согласно (8) одна из
этих пар символов положительная, другая отрицательная.
Поэтому их произведение равно —1, т. е.
axaNaxaN = —\. (9)
Пусть m = N — 2. В этом случае суммы в формуле (2
состоят из слагаемых a>\CLN__x , аган и ахац-\ , α2αΝ
соответственно. Пары axaN_x и asaN могут быть или обе
положительными, или обе отрицательными, или одна
положительной (отрицательной), а другая отрицательной
(положительной). В свою очередь согласно (8) пары аха^-\ и агак
будут или обе отрицательными, или обе
положительными, или одна отрицательной (положительной), а другая
положительной (отрицательной). Таким образом, среди
четырех пар всегда есть две положительные и две
отрицательные и, следовательно, произведение этих пар
будет равно 1, т. е.
αχαΝ_χ α,α^αΊα^, ataN =1. (10)
Разделив (10) на (9), получаем, что
агаы_х aJiN _, = — 1. (11)
§ 4.6
253
Пусть m = N — 3. В этом случае суммы в формуле (2)
состоят из слагаемых ataN_2, a2aN_r asaN и α,ιαΝ_2, a2aw_,,
a3aN соответственно. При различных комбинациях символов
три всегда будут положительные, а три — отрицательные.
Поэтому произведение
ataN_2 α2%_, α^α^α^α,Ν__2 ajx^ a,aN = — 1. (12)
Разделив (12) на (10), получаем, что
a3aN_2 a3aN_2 = — 1. (13)
При дальнейшем уменьшении т замечаем, что
всегда число положительных и отрицательных пар
символов в произведениях, аналогичных (9), (10), (12)
одинаково и равно α + β=Ν—т. С уменьшением т это
число последовательно принимает то четное, то
нечетное значение. Поэтому произведения всех пар
попеременно равны ±1.
Сравнивая (9), (II), (13), по методу индукции
записываем
αρΝ_,+&αΝ_]+1=—1. (14)
Допустим, что число символов N=2Ni + \, т. е.
является нечетным, a /=Ni + l. В этом случае выражение (14)
записывается как
К+1)гК1+1)г = -!.
что никогда не может выполняться. Следовательно,
число символов N может быть только четным.
Докажем теперь, что N равно сумме квадратов
целых чисел. Число всех пар символов (отрицательных
и положительных) при т= 1, ..., N— 1 равно
I+2+... + tf-I=^^. (15)
Допустим, что в последовательности {ап} число
символов — 1 равно р, а в последовательности {й„} — q. Тогда
число символов 1 равно соответственно N — ρ и N — q.
254
§ 4.6
Найдем, чему равно общее число положительных пар
символов в последовательности {ап}.
Положительные пары образуются при перемножении
символов одного знака. Поэтому последовательность
{ап} разобьем на две подпоследовательности, одна из
которых состоит только из символов 1, а другая — только
из символов —1. Так как число символов в первой
подпоследовательности равно N—р, то число положительных
пар символов, составленных из произведений вида 1X1,
равно
l+2 + ... + (fl-p-l) = W-'PW-P-V , (16)
Во второй подпоследовательности число символов
равно р. Поэтому число положительных символов,
составленных из произведений вида (—1)Х(—1), равно
1+2+...+(/7-1) = £<А=11. (17)
Суммируя (16) и (17), находим число положительных
пар символов в последовательности {ап}:
Si=/>(/>-!) | (N-P)(N-p-\) (18)
В последовательности {ап} число положительных пар
символов равно
0 _д(д-\) , (N-q)(N-q-\) ,.Q.
а число отрицательных пар символов равно
s =N(N-\) __q(q-\) _
2
(N-q)(N-q-\)
q{N-q). (20)
Согласно (8) при произвольном тфО число
положительных пар символов одной последовательности равно
числу отрицательных пар символов другой. Поэтому,
§4.6
255
приравнивая (18) и (20), получаем, что
p(p-l) + (N-p)(N-p-l) = 2q(N-q). (21)
После простых преобразований из (21) находим, что
N=(N-p-^+(p-g)2. (22)
Формула (22) означает, что число символов N может
быть только суммой квадратов двух целых чисел,
включая нуль. Например, при iV^lOO имеется ряд чисел S,
4, 8 10, 16, 18, 20, 26, 32, 36, 40, 50, 52, 58, 64, 68, 72, 74,
80, 82, 90, 98, 100, из которых можно найти N для
дополнительных последовательностей.
Необходимо отметить, что условие (22) является
необходимым, но не достаточным. Например, доказано,
что не существует дополнительных последовательностей
с N=18.
Композиции дополнительных последовательностей.
Если имеется пара дополнительных
последовательностей {ап} и {ап} длины N, то их композициями будем
называть дополнительные последовательности длины
2N, образованные по определенным правилам из
исходных последовательностей. Известны два правила
образования композиций: правила чередования и
присоединения.
Правило чередования означает следующее. Если заданы
две последовательности
\Яп/ = CL\, ... , 0>ηι ··· , dp/
И
\CLn} = Яц ··· > flljii ··· > (If/,
то последовательность
\fln'fln/ ^= <1ц Ац fla> ··· > fln> fljii ··· > fl^yi fl^y>
в которой символы одной исходной последовательности
чередуются с символами другой, называется составлен'
ной по правилу чередования.
256
§4.β
Докажем, что последовательности
{an:—'an}=a1, —ax,...,an, —an,...,aN,—aN (23)
являются дополнительными. Рассмотрим
автокорреляционные функции последовательностей (23), которые
определяются формулой (2). Пусть сдвиг т — четное число.
Тогда Rm и Rm состоят из слагаемых вида апак и апак.
Поэтому при четных т значения /?т = 0 и /?т = 0
вследствие дополнительности {ап} и {а„}. Пусть т — нечетное
число. Тогда Rm состоит из слагаемых вида апак, а
Rm состоит из слагаемых вида ап(—аь) = — #пЯи·
Следовательно, Rm-{- Rm = 0. Таким образом, последовательности
(23) являются дополнительными. ,
Используя правило чередования k раз, получим пару
дополнительных последовательностей длины
Nh = 2kN. (24)
Правило присоединения означает следующее. Если,
заданы две последовательности {ап} =аи ... , ап,... ,aN и
fan} =Яц ···.ап,..., αΝ, то последовательность {ап\ап} =
= а1У... ,ап, ... ,aN, atl... ,α„,... ,αΝ, в которой за
символами одной исходной последовательности следуют символы
другой, называется составленной [по правилу
присоединения.
Докажем, что последовательности
\CLn | UnJ = #ι> ... , йя) ··· > dfjt &ii ■■· > 1)ii ··· > ®ц> I
\CLn | — Лпу = flj, ... , Яп, ... , fl^y, — Л\, ... , — Яп> ··· > — ®ц )
(25)
являются дополнительными. Рассмотрим значения
автокорреляционных функций последовательностей (25) для
§4.7
257
сдвига m=l. Из (2) имеем суммы вида
NRm=i =\а&\ + · · · + апап _ ι + > · · + αΝαΝ-1 ~Ηια/ν +
+ «2«ι+··· + ««««-ι+ ···+«лЯу_| ·
NRm=1 = a^-}-... + ««««-ι + ··· + алгалг-1 — β»α/ν +
4-α,α14-...4-α„α„_14-...+α/ναΛ,_) . (26)
При суммировании обоих выражений формулы (26)
замечаем, что в сумме всегда есть две пары слагаемых вида
αηαη-ι и две пары слагаемых вида α„α„_ι. Сумма этих
слагаемых согласно (1), (2) при п, принимающем значения
от 2 до Ν, будет равна нулю. Слагаемые вида αχαΝ, —αχαΝ
входят в (26) с различными знаками и при
суммировании также дают нуль. Доказательство того, что
последовательности '(25) являются дополнительными при
произвольном т, можно провести аналогично случаю при
т = 2. Повторяя последовательно k раз правило
присоединения (25), получаем последовательность длины
2hN (24).
Частным случаем (24) является число 2*. В
качестве исходной последовательности при k=Q берется один
символ 1, при этом {αη} = {αη}=1. При &=1 согласно
(25) имеем
{а„}= 1, 1,
Я} = 1.-1. (27)
При k = 2
{ап}=\, 1, 1, —1,
{2»}=1, 1,-1, 1 (28)
и т. д.
4.7. ЧЕТВЕРИЧНЫЕ КОДЫ
D-код. Построение последовательностей,
составляющих D-код, основано на использовании правила
присоединения [94]. Обозначим ι'-ю последовательность D-кода
17—2366
258
§4.7
порядка k ,как
{dt} = dut, d2ti, ...,dn, {,..., dN}. (1)
Здесь длина последовательности N и ее порядок k сря-
заны соотношением N = 2h; номер символа изменяется
в пределах п=\, 2, ..., N; а номер последовательности
ί=0, 1, .... N-l. t
Число последовательностей по определению равно числу
символов в последовательности, т. е. N = 2". Введем
последовательность {с?*}, дополнительную для {dkt}. Тогда
правило образования D-кода с помощью правила
присоединения (4.6.25) записывается как
{d*} = {<-4^-'} при 1 = 0, 1 2*~» — 1, (2)
или как
{rff} = {<:2'ft-I|-2*i-} "Ρ" i = 2*-\...,2*-l. (3)
Последовательности {if*}, {d*} называются парными (а как
будет видно из дальнейшего, они являются
дополнительными), если |ϊ — j\=2h~l. Например, если k = 2,
1=1, то /=3.
Использование правил (2), (3) проиллюстрируем
на примерах. В качестве исходных возьмем
дополнительные последовательности для k=\. Полагая {d0}=l,
согласно (2), (3) имеем
Отметим, что последовательности (4) являются
дополнительными (4.6.27) и парными, т. е. можно записать, что
{2l0} = {d\}* {2\} = {dl).
§4.7
259
Введем обозначение символов α=1, β =—1. Для
этих символов правило умножения определяется
табл. 4.16.
Таблица 4.16
X
α
Ρ
α
1
— 1
Ρ
-л1
1
Используя указанные обозначения, из (4) получаем
(5)
Пусть k = 2. Согласно (2), (3) находим, что
Κ} = «|^} = {<μ;} = α, *,*, β;
{d]} = {d\\~d\} = {d\\d[} = *, β, α, α;
{^} = {rfj|-3'}={rfj|-rf!}=a, *, ρ. α;
Κ } = {<*! |-*ί } = (<*! !-<}=-«. Ρ. β. Ρ· (6)
При построении последних равенств в (6) знак минус
перед d\ и d\ определялся согласно табл. 4.16: —а =
= βα = β и —β==ββ = α, τ. е. операция умножения
символов α, β на — 1 эквивалентна умножению на β.
Аналогично, при k = 3 получаем, что
17*
260
§ 4.7
{<} = {< Κ2}=Κ|^} = α, α, α, β, *,«,$,*.
{d\} = {d)\d]}^{d)\dl) = *, β, α, α, α, β, β, β
{rf32 } = {d\ \d\} = {d] | rf* } = α, α, β, α, α, α, α, β
{dl} = {dl\dl}={dl\d]} = a, β, β, β, α, β, α, α;
{d\}={dl\-dl} = {d\\-d\} =
= «, «, «, β, β, β. «> β;
{dl) = {d\\-~d]}^{d]\-d\} =
= α, β, α, α, β, α, α, α;
{dl} = {d\\-d\}={d\\-di) =
= «> *, β, α, β> β, β> «;
= α, β, β, β, β, α, β, β.
(7)
Для других значений к метод построения D-кода
аналогичен рассмотренному в примерах. Общий метод
построения D-кода порядка к без 'Предварительного
построения кодов меньшего порядка можно найти в
работе [94].
Из рассмотрения кодов (5) — (7) следует, что парные
последовательности являются дополнительными. Например,
при k = 2 последовательности {d\ } и {d\} являются
парными. Но {d\} = {d]01 d J }, a {d\} = {d\\—d\}, т. е. они
соответствуют правилу присоединения (4.6.25).
Следовательно, они являются дополнительными. Из
рассмотренных примеров видно также, что 2й
последовательностей D-кода можно представить в виде 2h~i пар
дополнительных последовательностей. Обозначив через
{dh} и {Sh} произвольную пару дополнительных
последовательностей согласно правилу присоединения при
§ 4.7 261
опускании индекса i правило образования D-кода
можно записать как:
{dk\fi},
{rfk I - 34,
': (8)
{d*\d*},
{dh\ — d*}.
Если произвести операцию (8) для всех пар
дополнительных последовательностей порядка k, то получим
те же последовательности порядка k+l, что и при
использовании правил (2), (3). Однако чередование
последовательностей (по номеру ι) будет несколько
иным, чем при использовании правил (2), (3).
Поскольку каждая пара порождает четыре новые
последовательности, то общее число последовательностей будет
равно 2*+*.
Последовательности, образующие D-код, взаимноорто-
гональны. Условие ортогональности двух
последовательностей {if*}, {if*} записывается в виде
2*
£ dkn /*р., = 0 для I, 1=0, 1 2* — 1. (9)
Действительно, проверяя условие (9) для кодов (5)—
(7), убеждаемся, что все они ортогональны.
Следовательно, можно утверждать, что D-код порядка k+\
образуется на основе D-кода порядка k (8), все
последовательности которого попарно ортогональны.
Докажем это. Рассмотрим четыре кодовые
последовательности (8). Они попарно ортогональны, в чем
можно убедиться, находя сумму (9) для каждой пары
из формулы (8) и учитывая в соответствии с табл. 4.16,
что
dk dk ,'=α, dk /* =α,
η, ί η. д η,ί η,3
а последовательности {dк} и {d*} — ортогональные по по-
262
§ 4.7
строению. Последовательности, образованные другими
парами дополнительных последовательностей порядка k,
также будут попарно ортогональны с рассмотренными
благодаря взаимной ортогональности
последовательностей D-кода порядка к, из которых они образованы.
Следовательно, последовательности D-кода порядка k+\
попарно ортогональны.
Корреляционные свойства D-кода. Рассмотрим D-код
порядка k + \, каждая последовательность которого
представляет комбинацию двух дополнительных
последовательностей кода порядка k, т. е. имеет место
одна из комбинаций (8). Например, рассмотрим
последовательности {dh+l} = {dh\±Sh}, где знаки плюс и минус
относятся к разным комбинациям. Выпишем эти
последовательности:
{</*+»} = rff, dk2,dl,...,dkN_{,dkN,±~d\,±
±d\, ±dkz>...,±dkN_v + dkN. (10)
При исследовании корреляционных свойств D-кода
воспользуемся соотношениями, которые имеют место
между элементами (символами) дополнительных
последовательностей:
или
^ = -<-η + ,.^+1 = 4-η· (12)
Рассмотрим автокорреляционную функцию
последовательности (10). Докажем, что для
последовательности (10)
flm = 0 при /и = 2/ для /=1, 2,... (13)
В соответствии с (4.1.65) автокорреляционная
функция последовательности (10) записывается как
*™=4г Σ <+ι<-*'Ν=»· (14)
п= +1
§ 4.7
263
Подставляя в (14) символы последовательности (10)
получаем, что при m<N
Ят = 4г( V dkJkn +f] dkdk ±
/V V ^i η η - m ' / J η η - m
n=m + l n=m + l
m
^%ZkA+n-m} (15)
В справедливости (15) можно убедиться, подробно записав
Rm для фиксированного т. Например, для т = 2 значение
Rm получается перемножением согласно (14) символов
следующих строк с последующим сложением:
±~dk3 ±~dN
±rf|· · · ± rf/V-2' ±''/V-r ± 4v'
Втортя сумма
(16)
Первая и вторая суммы в (15) представляют
автокорреляционные функции пары дополнительных
последовательностей {dk} и {Sh}, поэтому в сумме они дают
нуль. Рассмотрим третью сумму в (15). При четном т
она всегда содержит четное число слагаемых, которые
можно объединить в пары. Так как для дополнительных
последовательностей справедливы соотношения (11)
или (12), то при четном т третья сумма равна нулю.
Например, в (16) третья сумма равна ± (d* dkN_x -J-
-\-dk2dN). Так как справедливы или соотношения
2hx=dkN, d\ = — £/*_,,
или соотношения
*УА jk ~jk ik
U\ — UN > а2 — aN—\'
". d*
1 2
dl <$■
"f 4-2
Первая сумма
±dr * d 2
d* d*
N-l' N
Третья суммт
то сумма равна нулю.
264
§4.7
Подставляя в (14) последовательности (10) при mt>N,
получаем
N
я=т, + I
где m1 = m — N.
Отметим, что для четных т значения /?„ = 0 по тем
же причинам, что и равенство нулю третьей суммы
в (15). Следовательно, при четных т всегда
справедливо равенство (13).
При нечетных т значение /?т<1/2, так как при
m<N оно определяется третьей суммой в (15), число
слагаемых которой равно т. Если все слагаемые
входят в сумму с одинаковым знаком, то Rm =m/2N при
0<m<N.
При т>N из (17) следует, что максимальное значение
Rm = {2N—rm)/2N при. /V<; т < 2Ν. Следовательно, макеи
мально возможное значение бокового пика
автокорреляционной функции последовательности (10) равно 0,5, при
этом m=\N. Расчеты показывают, что это значение
практически не достигается.
Значения автокорреляционной функции (14) при
нечетных т определяются произведениями символов вида
dndn-m, номера которых подчиняются следующему
условию: если га— четное (нечетное) число, то (га—т) —
нечетное (четное) число. Это означает, что dndn-m при
нечетном т всегда представляет произведение четного
символа на нечетный. Если для нечетного т выполняется
равенство
rf„rf„_Tn=0, (18)
то /?т = 0 и для нечетных т. Отметим, что условие (18)
является основным в определении четверичных или Е-
кодов [94J.
Ε-код. Если определен D-код, то Ε-код определяется
через него следующим образом: символ еп t
последовательности {ек\ связывается с символом dk „ последователь-
ности {if*} соотношением
§ 4.7
265
dk , если п — нечетное число,
η, i
γ, если п. — четное число, d „ = α,
ι ' η, t
δ, если η — четное число, dk . = Β.
' ' η, ι "
Таблица 4.17
Χ
α
Ρ
γ
3
α
1
—1
0
0
β
— 1
1
0
0
γ
0
0
1
—1
δ
α
0
—1
1
Правила умножения символов α, Β, γ, δ приведены в
табл. 4.17. Например, для последовательности
{<ί0} = α, α, α, β, α, α, Β, α,
согласно (19) получаем, что
{e03} = a, γ, α, δ, α, γ, β, γ.
Автокорреляционная функция каждой
последовательности Ε-кода при τ = mt0 равна
Rm = 0 для т = 1, 2, 3,..., 2\ (20)
При четном т соотношение (20) обусловлено
свойствами автокорреляционной функции D-кода (13), поскольку
произведения вида <?* ( е*_т>( определяются элементами
αβ и γδ в тех квадрантах табл. 4.17, в которых эти
элементы отличны от 'нуля. При нечетном т эти
произведения равны нулю аналогично (18), так как они
определяются элементами квадрантов, равными нулю.
Отметим без доказательства, что
взаимокорреляционная функция пары дополнительных последовательностей
266
§ 4.7
Е-кода равна нулю при всех значениях т,
удовлетворяющих условию — 2h^m^2h.
В некоторых случаях при перемножении четных и
нечетных символов Ε-кода получить полную
ортогональность нельзя. Тогда правило умножения будет
отлично от идеального, приведенного в табл. 4.17.
Неидеальное правило умножения приведено в табл. 4.18.
Таблица 4.18
X
а
Ρ
γ
s
а
1
'Ζ— ι
ν
—ν
Ρ
— 1
1
—ν
ν
γ
β
—β
1
—1
δ
—ε
β
— 1
1
Оценка для Rm [94] в этом случае определяется как
т+ 1
т + 1
при т=\, 3,... .г*"1— 1,
Ν
2 ; ■ ν 2
при m = 2"-1 + l 2h — 1.
(21)
Полное представление автокорреляционной функции.
Сказанное ранее относится к значениям
автокорреляционной функции в дискретные моменты времени, т. е.
соотношение (20) имеет место только при τ —mto,
причем предполагается, что четные и нечетные символы
удовлетворяют правилам умножения табл. 4.17. Однако
даже в случае идеального правила умножения вряд ли
можно получить нулевые боковые пики
автокорреляционной функции при произвольных значениях τ, так как
в промежутках между значениями т = х0
автокорреляционная функция каждой последовательности Ε-кода может
быть отличной от нуля.
§ 4.7
267
Действительно, пусть символам поставлены в
соответствие сигналы с комплексными огибающими:
α (=>£/, (/), β <=> — £Л (0. Ϊ <=> 17. (0. δ(=>-£Μ0· (22)
Допустим, что энергия сигналов равна Е0> а их
длительность— ν Комплексные огибающие Ui(t) и U2(t) согласно
нулевым квадрантам табл. 4.17 должны быть
ортогональны. Более того, предположим, что они ортогональны при
произвольном сдвиге τ, т. е.
00
Λι(Ό= -Щ Г «Л С) А С — *)Л=чО при —τ0<τ<τ0. (23)
—00
Отметим, что (23) справедливо, если спектры сигналов
отстоят друг от друга по оси частот на значительном
расстоянии.
Рассмотрим автокорреляционную функцию Е-кода.
Выделим в ней слагаемые, которые соответствуют
одному т. Пусть т — четное число. Тогда сумма Rm (τ)
содержит N — т слагаемых. Обозначим
автокорреляционные функции комплексных огибающих (22) как
оо
Яг (τ) = 5ΙΓ j tfi {t) ^ {t ~ Z) ^ (24)
—00
об
R,(*) = 2ET§U.(t)U,(t-x)dt. (25)
—00
Отметим, что /?, (0) = R3 (0) = 1, что соответствует
ненулевым квадрантам табл. 4.17. Автокорреляционная функция
Rm (τ) состоит из слагаемых вида Rt (τ) и /?„ (τ), число
которых одинаково, и поэтому равна нулю при τ = mt0,
т. е.
I Rm ЫI = N-^ I /?i (т — m\) - Λ. (τ - mx0) |. (26)
Необходимо отметить, что выполнение условия (20)
для т=тто не означает, что оно справедливо при любых
τ. Чтобы равенство (20) было справедливо при любом
τ, необходимо, чтобы /?, (τ)Ξ/?2(τ). Но равенство
автокорреляционных функций означает, что совпадают энер-
268
§ 4.7
гетические спектры сигналов, т. е. спектры сигналов не
могут быть разнесены по оси частот. Это противоречит
предположению и равенству (23). Следовательно,
/? (τ)ξ^Ο. Если же равенство (23) не выполняется, то
тогда /?m(t) =£0 по крайней мере при нечетных т.
глава б СИНТЕЗ СЛОЖНЫХ
СИГНАЛОВ
5.1. ОСОБЕННОСТИ СИНТЕЗА СЛОЖНЫХ
СИГНАЛОВ
В гл. 1,2 исследованы основные свойства сложных
сигналов, в гл. 3,4 рассмотрены
частотно-модулированные и фазоманипулированные сигналы.
Однако следует отметить, что среди известных не
всегда можно выбрать сигналы, полностью
удовлетворяющие требованиям, предъявляемым к проектируемой
системе. Нахождение сигнала (или сигналов),
соответствующего заданным требованиям, составляет задачу
синтеза.
Выходные характеристики радиотехнической системы
зависят от формы сигнала, т. е. определяются его
корреляционной функцией. Это значит, что вид требуемой
корреляционной функции /?! (su s3,...) в области S параметров
(sb sa,...) может быть определен (или задан) по этим
характеристикам. Синтез сводится к тому, чтобы найти
такой сигнал U(t), корреляционная функция которого
/?а (si, Sa....) наименее отклоняется от заданной /d (su sa,...)
по принятому критерию.
Перечислим возможные критерии. При критерии
равномерного приближения выполняется неравенство
8 = 1 Λ (si, *·....) — *·(*!. *·.-)!<«. (1)
где Si £ S; i ='l,*2,...; ε — наперед заданная величина.
Оно означает, что при любых значениях параметров s{,
принадлежащих области S, разность 6 не превышает
заданную величину ε.
Частным случаем критерия равномерного
приближения является минимаксный критерий. Пусть в некоторой
области слабой корреляции S', являющейся частью
области S, /?! (su s2, ...)=0. При минимаксном критерии
270
§ 5.1
находится такой сигнал, который минимизирует
максимальное значение модуля корреляционной функции
|#а($ь 52,...)|макс в области S', т. е. обеспечивает
мин{| /?а(<?!, s,,...)L„c} при S(£S', i=l, 2,... (2)
Примеры сигналов, определенных в соответствии с
минимаксным критерием, приведены в § 4.3, 4.4.
Необходимо отметить, что критерии (1), (2) редко
позволяют получить решение .с помощью
аналитических методов. Поэтому их используют в основном при
решении задач синтеза на ЦВМ.
Критерий минимума среднеквадратичного
отклонения, позволяющий решать некоторые задачи
аналитически, сводится к тому, что значение интеграла
oa = J ...f|/?i(si, s„ ...) —Λ(*ι. *·. ...)|arfsi<fca... (3)
s
должно быть минимальным, т. е. корреляционная функция
/?л должна стремиться к jfd в среднем по области S.
Однако минимум среднеквадратичного отклонения не
означает, что в каждой точке области S разница между /?ι и /?„
меньше требуемой величины. Возможно, что в некоторых
точках эта разница будет велика, даже если
среднеквадратичное отклонение мало. Это является недостатком
данного критерия.
Отметим, что иногда критерий равномерного
приближения и критерий минимума среднеквадратичного
отклонения приводит к одинаковому результату.
Рассмотрим характерные особенности синтеза
сложных сигналов.
Во-первых, хотя Ri(su sa,...) можно считать заданной,
ее следует задавать так, чтобы выполнялись условия
поставленной задачи, а вычисления были наиболее простыми.
Во-вторых, из множества сигналов U(t) следует
выбирать такой класс сигналов, который заранее обеспечивает
значения /?„, достаточно близкие к значениям /?ι, τ. е.
упрощает процесс нахождения искомого сигнала.
§ 5.1 271
В-третьих, следует учитывать не только требования
к корреляционным свойствам сигналов, но и
ограничения, накладываемые на сигнал как по времени, так и
по спектру. Например, желательно иметь сигнал с
постоянной огибающей (равномерный сигнал), т. е. не
модулированный по амплитуде, что при ограниченной
пиковой мощности передатчика позволяет увеличивать
энергию излучаемого сигнала. Также желательно
обеспечивать равномерный амплитудный спектр сигнала, так
как при этом лучше используется отведенная для
передачи сигнала полоса частот. Таким образом, до решения
задачи синтеза сигнала, некоторые особенности
будущей структуры сигнала должны быть заранее учтены,
что усложняет задачу синтеза, так как это сужает класс
синтезируемых сигналов.
В-четвертых, следует учитывать метод формирования
и обработки сложного сигнала. Очень часто требования
к системе предопределяют эти методы, что также
ограничивает класс синтезируемых сигналов.
Отметим, что в настоящее время существуют
различные направления-синтеза сигналов. Наиболее
развитыми являются следующие:
— синтез сигналов по автокорреляционным
функциям;
— синтез сигналов по телу неопределенности для
совместного измерения дальности и скорости и для
измерения дальности при неизвестной скорости;
— синтез систем ортогональных и
квазиортогональных сигналов.
Синтезу сложных сигналов посвящен ряд работ [1, 5,
7, 12, 24, 34, 84, 86, 95—105]. В [5] приведены
результаты многих опубликованных до 1965 г. работ по синтезу
сложных сигналов, в [7] сформулирована задача
синтеза в общем случае и произведен синтез фазоманипулиро-
ванных сигналов по автокорреляционной функции при
некратном распределении скачков фазы.
В § 5.2—5.10 будут рассмотрены такие задачи
синтеза, которые либо не нашли отражения в монографиях
[5, 7], либо поставлены и решены иным способом.
272
§ 5.2
5.2. СИНТЕЗ ЧАСТОТНО-МОДУЛИРОВАННЫХ
СИГНАЛОВ ПО АВТОКОРРЕЛЯЦИОННОЙ
ФУНКЦИИ
Постановка задачи. При синтезе сигналов по
автокорреляционной функции определяют сигнал, который
обеспечивает хорошее измерение дальности до
неподвижного объекта или объекта, движущегося с малой
скоростью (скоростью, при которой (максимальная
частота Допплера £2макс<£:2п/Т).
Рассмотрим требования, предъявляемые к сигналу
и его автокорреляционной функции. Согласно условию
обнаружения сигнала необходимо, чтобы его энергия
на входе приемника превышала пороговую. При
ограниченной пиковой мощности передатчика излучаемая
энергия может быть увеличена только за счет увеличения
длительности сигнала Т, если, конечно, это обеспечивают
выходные устройства передатчика. Будем считать, что
длительность сигнала Τ задана. Следует иметь в виду,
что большинство мощных импульсных генераторов СВЧ
работает в ключевом режиме, при котором
амплитудная модуляция невозможна. При непрерывном
излучении некоторые генераторы могут работать в режиме
амплитудной модуляции, но в этом случае уменьшается
к. п. д. передатчика. Поэтому наилучшим следует
считать сигнал, огибающая которого постоянна (в течение
длительности Т.
Требование к разрешающей способности по
дальности определяет ширину области сильной корреляции
автокорреляционной функции. Грубо говоря, можно
считать, что ширина области сильной корреляции должна
быть равна заданной разрешающей способности по
времени (по дальности). Поскольку ширина области
сильной корреляции примерно равна XfF, то и ширину
спектра сигнала F можно считать заданной.
Требование однозначного измерения дальности и
уменьшения вероятности ложной тревоги при передаче
информации позволяет определить максимальный
уровень боковых пиков автокорреляционной функции Rbu
в области слабой корреляции. Наилучшим является
сигнал, у которого /?sm—*-0.
§5.2
273
Таким образом, исходными данными для синтеза
являются длительность сигнала Т, ширина его спектра/7
и уровень боковых пиков /?sm· По этим исходным
данным можно синтезировать и частотно-модулированные
и фазоманипулированные сигналы. В данном параграфе
будут рассмотрены частотно-модулированные сигналы.
Определение энергетического спектра ЧМ сигнала.
Согласно формуле (2.3.22) автокорреляционная функция
сигнала определяется энергетическим спектром сигнала
|0(ω)|»:
00
*(*)=-а· ранге'"*». (1)
—00
В соответствии с обратным преобразованием Фурье
оо
|<7(в)|1 = 2£1 Γ/?(τ)ε-*ω\ίτ. (2)
—00
Формула (2) позволяет определить энергетический спектр
сигнала по известной автокорреляционной функции /?(τ).
Определение энергетического спектра составляет первую
часть задачи синтеза сигнала. Отметим, что энергетический
спектр |0(<в)|а или соответствующий ему амплитудный
спектр |О (ω)| не определяет полностью сигнала,
поскольку последний характеризуется также и фазовым
спектром φ(ω) (2.2.20). Поэтому даже при известном
О (ω) | необходимо определить фазовый спектр φ(ω),)
при котором комплексная огибающая сигнала 0(1
удовлетворяет предварительным требованиям
[постоянство огибающей U(t) в течение времени Т]. Определение
фазового спектра составляет вторую часть задачи
синтеза сигнала.
При решении первой части задачи синтеза возникает
вопрос о том, как задать /?(τ). Предположим, что боковые
пики автокорреляционной функции /?s = 0. Выразим
аналитически область сильной корреляции. Обратимся к
представлению |/?(τ)| в этой области (2.5.5), полагая Ω = 0.
Тогда
|/?(x)|~i+-L/?Va· (3)
274
§ 5.2
Дважды дифференцируя (1) по τ, можно записать
00
R" = ——L- ГдаЧ i7(m)|ai/<» = — W\ . (4)
" 4π£ Ι ι ν '' эфф ' '
—oo
Выражение (4) совпадает (с точностью до знака)
с определением квадрата эффективной ширины спектра
сигнала (1.5.3).
Представление (3) справедливо только при малых τ.
С ростом τ для реальных сигналов в разложении! R (т)|
надо учитывать слагаемые с более высокими
степенями τ, поскольку эти слагаемые замедляют спад \R (τ)|
(см. § 2.6). Следовательно, наиболее узким основной
пик будет тогда, когда он не содержит слагаемых с
высокими степенями τ и совпадает по форме с параболой
(3). Поэтому идеальная автокорреляционная функция
определяется как
Rx(*) = r-**KSw\*\<*» (б)
(θπί
(&)
ipn τ„<|τ|<7'
где
_ УТ
Автокорреляционная функция /?}(τ) реального сигнала
отличается от идеальной fd (τ). Β гачестве критерия
приближения воспользуемся критерием минимума
среднеквадратичного отклонения (5.1.3):
г
°a = J |/?1Ы-/?»Ы|а^· (7)
—г
Согласно (1), (2) на основании равенства Парсеваля
выражение (7) можно записать как
00
1
'8π£2
—00
JdtfiWr-IG.HI1)1*». (8)
Следовательно, чтобы уменьшить среднеквадратичное
δ 5.2
275
отклонение между двумя автокорреляционными
функциями, надо уменьшить разницу между энергетическими
спектрами соответствующих им сигналов.
В качестве исходной возьмем идеальную
автокорреляционную функцию (5), которой соответствует спектр
ЯИ = Яо^(^'-со80п0), (9)
где
Η0 = 8Ετ0. (10)
Спектр, рассчитанный по формуле (9), изображен на
рис. 5.1. Поскольку значения Н(<о) могут быть как поло-
Рис. 6.1.
жительными, так и отрицательными, то выражение (9)
нельзя считать определяющим энергетический спектр.
Следовательно, идеальная автокорреляционная функция
276
§ Б-2
(5) не реализуема. Однако возможно существование
сигналов, выражения для энергетических спектров
которых близки к (9).
Как видно из рис. 5.1, отличие Η (ω) от
энергетического спектра начинается при значениях <о><вь при
которых спектр Η (ω) становится отрицательным. Если
энергетический спектр искомого сигнала близок к Η (ω) при
0<ω<'(ι)ι, то можно ожидать, что его
автокорреляционная функция близка к идеальной (5). При этом можно
считать, что энергетический спектр искомого сигнала
совпадает с //(to) при ι0<ω<ιωι. Таким образом,
характер энергетического спектра искомого сигнала можно
считать определенным.
Определение сигнала. Чтобы полностью определить
искомый сигнал, кроме энергетического спектра
необходимо определить и его фазовый спектр. Для этого
можно использовать метод стационарной фазы, изложенный
в § 3.1 [5, 96, 99, 103].
В дальнейшем рассматривается сигнал с Постоянной
огибающей. Комплексная огибающая такого сигнала
U{t) = U/Ht) при \t\<T[2, (11)
а ее спектр согласно (2.2.17) определяется выражением
Г/2
0(m) = U9 J β1Ιί(,)-ω'ΙΛ. (12)
-Г/2
Допустим, что на отрезке [—Г/2, Т/2] имеется одна
точка стационарной фазы. При этом в соответствии
с формулами (3.1.38), (3.1.39) можно записать уравне-
нение точки стационарной фазы
ω = θ'(Μ (13)
и асимптотическое выражение для спектра комплексной
огибающей сигнала
О[о)г^ * е I *]. (14)
§ Б,2 277
Из (13) следует, что ω является функцией to, т. е.
ω = <ύ(ίο)- Дифференцируя (13) по t0, получаем
^=в"(д. (15)
Подставляя (15) в (14), запишем выражение для
энергетического спектра сигнала как
IGMI'^-gggp Об)
или, записывая ω(ί0) как ω, получаем
[\O(*)\,d* = 2*U20dt„. (17)
Интегрируя (17), получаем, что
О (ω) |а du = 2%Ult0. (18)
ί1
Левая часть равенства (18) является функцией
мгновенной частоты ω (13). Поэтому (18) можно записать
в вила
ин=-АгР(*). (19)
где
ω
/>(«)= ^\0{*)\Ч*. (20)
о
Зависимость (20) для случая, когда модуль | О (ω) |а
заменен на Η (ω) (9), приведена на рис. 5.1. Из рис. 5.1
видно, что для ω>(ι)ι функция Я (ω) имеет
колебательный характер.
Функция, обратная (19):
ω(ί) = Ρ"1(2<α (21)
согласно (13) характеризует закон изменения частоты
Q'(t). Отметим, что вследствие колебаний функции Я (ω)
278
§ 5.2
при ω><ιΐι мгновенная частота сигнала на его краях
является многозначной, т. е. не имеет физического
смысла. Поэтому при определении зависимости ω(ί) следует
отбросить часть функции Ρ (ω), соответствующую
Ci)>Ci)l.
Нормированная зависимость мгновенной частоты
сигнала от времени представлена на рис. 5.2. Поскольку
0.8
Οβ
α*
ο,ζ
&юг
yi(t)
0,2
О,*
Рис. Б.2.
0,6
Οβ
(ύ(ί)—нечетная функция времени из-за предположения
о единственности точки стационарной фазы, то график
построен только для O^t^T/2. На этом же рисунке
приведена зависимость нормированной фазы сигнала,
являющейся четной функцией времени и
определяющейся формулой
8.(0 =
В(0
9(7"/2)'
где
9(t)=^m{x)dx.
(22)
(23)
§ Б-2
279
Необходимо отметить, что л метод определения
энергетического спектра исходного сигнала, и метод
стационарной фазы, который использовался для определения
фазы искомого сигнала, являются приближенными. В
частности решение (21) не учитывает «краевых» эффектов,
возникающих тогда, когда точка стационарной фазы
приближается к краям отрезка интегрирования в (12),
поэтому оно является приближенным. Дальнейшее
уточнение решения целесообразно производить с помощью
ЦВМ.
На рис. 5.3 изображен график модуля
автокорреляционной функции | R (τ) | для сигнала, кривая изменения фазы
которого θο(0 приведена на рис. 5.2, причем заранее
положено, что 6(7/2) =2π. При этом сжатие сигнала
(его база) FT = 8, а максимальный боковой пик
автокорреляционной функции /?sm=1/12 (22 дб).
280
§5.3
5.3. СИНТЕЗ НЕРАВНОМЕРНЫХ
ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ
ПО АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ
(АСИМПТОТИЧЕСКИЙ МЕТОД)
Постановка задачи. Согласно формуле (4.1.65)
автокорреляционная функция в точках х=т%о определяется
как
N
1 «-ι *
Лт^~й~ J, 0"nfln-m< (1)
ra=m + l
где ап—n-ti символ кодовой последовательности {ап}·
С другой стороны, значения Rm можно найти, используя
выражение (4.1.80) для спектра кодовой
последовательности Η (χ):
π
Rm = ^Fr\j\H{x)\^mxdx. (2)
—π
Определим условия, при которых отсутствуют
боковые пики автокорреляционной функции. Предположим,
что амплитудный спектр кодовой последовательности
является постоянным:
\H(x)\ = fN. (3)
Подставляя (3) в (2), получаем
1 при /и = 0, .„,
(4)
ри тфО,
*т~{о!
т. е. автокорреляционная функция состоит из одного
основного пика и не имеет боковых пиков. Такая
автокорреляционная функция является идеальной с точки
зрения подавления боковых пиков.
Выясним, какие сигналы характеризуются
автокорреляционной функцией (4). Для .полного определения
сигнала кроме модуля амплитудного спектра (3)
необходимо знать (или определить) и фазовый спектр кодовой
§ 5-3
281
последовательности ψ (я). Из формул (4.1.30), (4.1.44),
(3) получаем
к
—π
= !™j> «+»»*</*. ' (5)
—π
Если экспонента εχρ[ΐψ(Λ;)] может быть разложена
на конечное число грамоник с периодами, кратными 2π,
то согласно (5) существует конечное число символов
апф0. Это означает, что боковые пики
автокорреляционной функции сигнала отличны от нуля, или? по
крайней мере, всегда
**_, = «*«££ О, (6)
так как α,ιφΟ и αΝ=φΟ. Поэтому автокорреляционная
функция (4) может быть только у сигналов, состоящих
из бесконечно большого числа импульсов. Следователь*
но, реализовать автокорреляционную функцию (4) н£Л*>«
эя. Однако из теории рядов Фурье известно, что
амплитуды гармоник при достаточно больших η начинают
уменьшаться и асимптотически стремятся к нулю.
Поэтому символы ап (5), соответствующие краям сигнала,
оказываются малыми и начиная с некоторых η (η<Νι,
η>Νζ) их можно отбросить. Но при этом из-за
конечного числа импульсов в сигнале нарушается свойство
(4), т. е. боковые пики не являются тождественно
равными нулю. Выбирая амплитуду отброшенных
импульсов, можно регулировать уровень боковых пиков
автокорреляционной функции: чем меньше по амплитуде
краевые импульсы в сигнале, тем меньше боковые пики.
Это означает, что для большего подавления боковых
пиков автокорреляционной функции необходимо
увеличивать длительность сигнала.,
Покажем, как преобразуются формулы (2), (5) при
бесконечном числе импульсов в сигнале. Предположим,
282
9 5-3
что сигнал состоит из бесконечного числа импульсов
с комплексными амплитудами Оп- Обозначим
М= £ \ϋη\3 (7)
и допустим, что Μ—конечно (это соответствует
конечной энергии сигнала). Тогда выражение (1) для
автокорреляционной функции запишется в виде
«о
1 V"i *
га=—оо
При т = 0 величина основного пика /?„= 1. Спектр
кодовой последовательности {Un} по аналогии с (4.1.43)
определяется как
»£,(*)= Σ One-lnx. (9)
я=—оо
Можно показать так же, как это сделано в § 4.1, что
π
Un=-^\tiu(x)ei"xdx, (10)
—π
π
—π
Из-сравнения формул (2), (5) с формулами (11), (10)
видно, что N пропорционально М. При конечном числе
импульсов в сигнале символ ап = UnlU0 определяется
однозначно, так как с помощью (4.1.11) можно вычислить
среднюю амплитуду ί/0.
Согласно (4.1.10), (4.1.11)
ЛГ=£|а„|а. (12)
Аналогично соотношению (Ί2) при бесконечном числе
импульсов в сигнале можно условно определить «число»
импульсов как
Л= £ |α.1·. (13)
П=—00
§ 5.3
283
При этом сумма (13), так же и сумма (7), должна быть
конечной. Из (2) при т = 0 имеем
π
Ы = -^^\Н(х)\Чх. (14)
Из сказанного следует, что при бесконечном числе
импульсов в сигнале надо использовать формулы (10),
(11) вместо формул (2) и (5). При этом формула (3)
заменяется на соотношение
\Ηυ(χ)\=\/'Μ. (15)
При синтезе сигнала будем использовать
минимаксный критерий. Предварительно необходимо оценить
максимальный боковой пик автокорреляционной функции
сигнала.
Оценка боковых пиков автокорреляционной функции.
Сигнал, которому соответствует идеальная
автокорреляционная функция (4), состоит из бесконечного числа
импульсов. Отсчет номеров импульсов будем вести от
середины сигнала, где п = 0. Реальный сигнал всегда состоит
из конечного числа импульсов Ν, которое для простоты
расчетов будем считать нечетным. Обозначим
JVi = 0,5 (JV—1). (16)
Тогда величины ±Νι представляют номера крайних
импульсов в сигнале.
Спектр последовательности {Un} реального сигнала
согласно (9) можно записать как
Подставляя (17) в (11), получаем -
где Μ определяется согласно формуле (7) с учетом
конечных пределов суммирования.
284
§Б.З
Обозначим через Wlia суммы амплитуд Оп отброшенных
импульсов с номерами | η | > Л^:
(19)
(20)
С учетом (19), (20) выражение (18) можно записать в
следующем виде:
π 00
w,
w,
= Σ D»e~
-(W. + l)
= ς tf"e~
Ira*
»
-In*
*-=ώ-ίΙϋ^"'"-«'.-
w,
2
—π ra=—oO
eimxcf*. (21)
Раскрывая квадрат модуля (21), получаем, что
π 00
1 ГΙ ^Ί »-. —in*
*"*=*ΗΙΣ и^
\inxdx-\-
—π /г=—Οο
1 r,.„ . ... .,βι«*ώ
2πΛί
j|W, + W,|2
—π л=—оо
■ω-Κ Σ ^'"О (w«+w»)e,m^· (22)
—π ra=—00
Первое слагаемое в (22) согласно (9), (11) при
выполнении условия (16) представляет идеальную
автокорреляционную функцию без боковых пиков. Вторым
слагаемым можно пренебречь .по сравнению с третьим или
четвертым, так как W\# намного меньше (9). Поэтому
можно считать, что боковые пики автокорреляционной
функции определяются в основном двумя последними
слагаемыми в (22).
§ Б.З
285
Меняя местами операции суммирования и
интегрирования в (22), для тФО получаем амплитуды боковых
пиков:
00 «
1 «-« 1 С » . * I (m—η) χ
га=—00 —*
+Ж I] Un i \ (W, + W.) е' ""-» V*. (23)
га=—оо —π
Подставляя (19), (20) в формулу (23) и вычисляя в ней
интегралы, находим
оо оо оо — (ΛΓ, + 1)
*-=τ(Σ Σ^+Σ.Σ «■*)+
га=—оо ft=wT+1 л=—оо ft=—oo
га—m—ft=0 n—m—k—O
oo oo oo —(Λ?ι +1)
+τ(Σ Σ α*+Σ Σ te)· (24)
ra=—ooft=s#i + l n=—oo ft=—oo
га + m—ft=0 η + m—ft=0,
где £/ft — комплексные амплитуды отброшенных импульсов
на краях сигнала. Под каждой двойной суммой записано
уравнение, которому должны удовлетворять п, т и k.
Поясним характер сумм в (24). На рис. ЪА,а
изображен модуль решетчатой функции 'произвольного
сигнала. Сплошная огибающая соответствует сигналу из N
импульсов, пунктирная — отброшенным краевым
импульсам. На рис. 5.4,6 изображены группы отброшенных
краевых импульсов, соответствующие суммам в
первой круглой скобке в (24), а на рис. 5.4,в — суммам
во второй круглой скобке. Относительно исходного
положения в сигнале на рис. ЪА,а эти группы сдвинуты
в обе стороны на т>6. Такое положение групп
обусловлено уравнениями под двойными суммами в (24).
Учитывая эти уравнения, двойные суммы (24) можно
286
§ Б.З
представить в более простом виде:
— (/ν, + U + m
Rm— ~ТТ ( J. UnUn-m~T~ /j UnUn~m~T
n=N1 + m+\ n=—oo
oo — (\, + l)—m
+ J] i/„i/n+m+ J] UnUn+my (25)
Из рис. 5.4 видно, что при тфЪ из четырех сумм,
рходящих в (25), две соответствуют группам отброшен-
\Ч i
ных краевых импульсов, совпадающим с сигналом, а две
суммы — группам краевых импульсов, совпадающих
с такими же группами. Последние суммы вносят малый
вклад в боковой пик автокорреляционной функции (17)
и их можно не учитывать.
Для нахождения оценки 'сверху величины Rm (25)
допустим, что характер изменения краевых импульсов
одинаков для n>Nl и «<—Νι, и положим, что в сигнале
\ип\<иы,
(26)
где £/м — максимальное значение комплексной
амплитуды импульса в сигнале.
§5.3
287
С учетом сделанных замечаний выражение (25)
можно преобразовать к следующему виду:
—№ + l) + m
— ~~М ( /1 ~т ' /1 UrAJn+i
η——оо η=Λί, + 1—m
<1^| Σ а«\<нг Σ Ι α·Ι- (27)
Обозначая
получаем
n=/V, + l
Wu= £ |£Г„|, (28)
AT"
(29)
Найдем U?M. Из теории рядов Фурье известно [54],
что асимптотическое поведение коэффициентов Фурье
определяется терпящей разрыв низшей производной
функции, разлагаемой в ряд. Если разрыв терпит /-я
производная, то
\Un\<-±r- (30)
Здесь L — постоянная, которую можно определить из
следующих соображений. Допустим, что изменение \ Un\ на
краях сигнала подчиняется закону (30). Амплитуду |£7П|,
соответствующую первому отброшенному импульсу (п =
= Ni + l) на рис. 5.4, обозначим через а. Беря в (30)
знак равенства для n = Nl + \, получаем
а= (#,+ΐ)ΐ+ι· ί31)
Из (31)
'1 = а(Л7, + 1)' + \ (32)
Подставляя (32) в (30), находим
|Ь.| = .(«Ш.)'". (33,
288
§ Б.З
Заменяя | Un | в (28) согласно (33), имеем
'■=■ Σ (^Г' (34)
η=~ΝΓ+1
Для вычисления суммы в (34) введем новую переменную
При изменении η от Ν, -|- 1 До оо величина je, меняется
от 1 до оо через интервалы
^• = ^ТТ' (36)
поскольку в (35) η — целые числа.
С учетом (35), (36) выражение (34) можно
переписать как
^ΗΣ^=~£τΣ>· (37)
Χι—Ι *,= 1
Для сложных сигналов Л^»1, поэтому Δχ4 является
малой величиной. Переходя в (37) в пределе от суммы
к интегралу, получаем
Wu = a(Nl+\)]^=a-^±^. (38)
J χ.
Интеграл в (38) имеет смысл, если 1Ф0. Случай / = 0
соответствует разрыву функции. Подставляя (38) в (29),
находим, что
Rm<ju^±lL. (39)
Поскольку Νι^'β,5Ν^> 1, a Μ W£/q N, где
U0—средняя амплитуда импульсов сигнала конечной
длительности, оценка сверху для бокового пика автокорреляцион-
§ 5.3
289
ной функции принимает вид
Согласно выражению (40) для уменьшения боковых
пиков следует, во-первых, уменьшать пик-фактор
сигнала (уменьшать UM/U0), т. е. делать сигнал более
постоянным по амплитуде (равномерным). Отметим, что
минимальное значение отношения UM[U0 равно единице.
Во-вторых, уменьшать α/ί/0 — относительную амплитуду
первого отброшенного импульса на краях сигнала, т. е.
использовать более мелкую структуру на краях сигнала.
При такой структуре сигнала увеличивается его
длительность (соответственно и сложность согласованного
фильтра) без существенного увеличения его энергии, что
является недостатком. В-третьих, следует увеличивать
номер / производной функции exp(ii|>(*)], терпящей
разрыв.
Первые два условия, обеспечивающие уменьшение
боковых пиков автокорреляционной функции сигнала,
очевидны. Остановимся более подробно на последнем.
Покажем, как связана разрывность функции exp[itp(*)]
с разрывностью фазового спектра ψ (я) кодовой
последовательности. Это необходимо знать для правильного
выбора ψ (я).
Обозначим
y(x) = exp[i<J>(*)]. (41)
Запишем первые три производные по χ выражения (41):
y'(x) = iy(x)Y(x), 1
'У"(х) = УШГ(х)-УЧ*)], \ (42)
у'" (х) = у (χ) Ιΐψ'" (χ) — 3ψ' (χ) ψ" {χ) — Ιψ' »(*)!· J
Определим характер функции у(х). Если эта
функция имеет разрыв, то этот разрыв соответствует /=0,
и \Un\ в (30) убывает медленно (как Lin). В
результате боковые пики становятся значительными. Поэтому
положим, что у(х) непрерывна. Однако это не означает,
что и ψ (χ) должна быть непрерывной.
290
§5.3
Как следует из соотношений (42), разрыв
производных функции у(х) определяется разрывом
соответствующей производной функции ψ (я). Например, если ψ'(я)
имеет разрыв, то и у'(х) разрывна, так как функция
у(х) фО, Это справедливо для всех у{п)(х), что можно
доказать с помощью формул для «-Й производной сложной
функции. Следовательно, в соответствии с (39) для
уменьшения боковых пиков автокорреляционной
функции надо увеличивать номер производной функции ψ (я),
которая терпит разрыв.
Выяснив требуемые свойства фазового спектра ψ (я),
перейдем к синтезу ФМн сигнала.
Синтез сигнала. Фазовый спектр ψ (я) ФМн сигнала,
у которого фазы импульсов равны 0 или π, является
нечетной функцией χ (рис. 4.2). Поэтому согласно
формулам (10), (15)
t/n = MRefe1[*w+nf;c (43)
о
— действительная величина.
Чтобы сигнал был сложным, т. е. состоял из
большого числа импульсов, пределы изменения (размах)
функции ·ψ(*) должны быть большими. Это означает, что
функция ψ (χ) должна содержать в неявном виде
большой параметр D. Поэтому применим метод
стационарной фазы. Предположим, что на отрезке [0, π]
существует одна точка стационарной фазы. Обозначим
фазовую функцию как
φι (χ) = ψ (χ) + пх. (44)
Точка стационарной фазы х0 определяется из уравнения
?Ί (*.) = *'(*.) + * = 0. (45)
Согласно (3.1.39) выражение (43) запишем в виде
υη^νΨγψ^^\ηΧα) + ηχ0±^\ (46)
где знак перед л/4 определяется знаком ty"(xo)·
§ 5.3
291
Формула (46) может служить основой для синтеза
ФМн сигнала. Автокорреляционная функция такого
сигнала близка к идеальной (4). Поэтому ψ(*) следует
выбирать так, чтобы огибающая сигнала была близка к
постоянной. Это означает, что желательно в результате
синтеза получить сигнал с |£/n|=const на большей
части значений п. При этом надо иметь в виду, что метод
стационарной фазы обеспечивает достаточную точность
только тогда, когда точка стационарной фазы не близка
к краям отрезка интегрирования 0 и π. Поэтому в
дальнейшем будем сначала определять характер сигнала на
основании асимптотической формулы (46), а затем
уточнять результаты, получая (если возможно) точное
решение.
При | Un | = const из (46) следует, что
cos [ψ(*.) + пх0 ± */4] = AYW'ixJ\. (47)
где А = const.
Заменяя в (47) η согласно (45) и возводя обе части
равенства в квадрат, получаем дифференциальное
уравнение
cos» [ψ (*,) _>,ψ' (χ0) ±[*/4] = А■ | ψ" (*,) |, (48)
которое, как можно показать, не имеет смысла, так как
его решение ψ (я) не может быть монотонной функцией,
а это противоречит условию единственности точки
стационарной фазы. Поэтому изменим постановку задачи.
Найдем условия, при которых в (46) и знаменатель, и
числитель в отдельности постоянны. Положим, что
знаменатель— постоянная величина. Тогда
ψ"(*ο)= const. (49)
Решением этого дифференциального уравнения
является парабола
Ц(х)в=Ьх* + ах-{-с при 0<jt<it, (50)
где а, Ь, с —· постоянные величины.
292
§ 5.3
Поскольку ψ (χ) — нечетная функция, то
ΨΜ
_( bx2-\-ax-\-c при 0<*<π, _
\—bx*-\-ax — с при —π<Λ<;0.
Фазовый спектр кодовой последовательности
целесообразно выбирать следующим образом:
Ι &Λ24"^π^ при —π <*</}.
Во-первых, при таком выборе устраняются разрывы
функций ψ(Λ) и ty'(x). Так как устранить разрыв
ty"(x) нельзя лри любых значениях коэффициентов а,
Ь, с, входящих в формулу (51), то согласно формулам
(30) и (42) значения |£/„| на краях сигнала
уменьшаются не быстрее, чем 1/«3.
Во-вторых, фазовый спектр, соответствующий (52),
обладает симметрией относительно точек х=±п/2. При
этом согласно формуле (4.1.45) имеем U_n=(—l)nUn,
т. е. вычисление сигнала упрощается.
Обратимся теперь к числителю правой части
асимптотического равенства (46). Подставляя (52) в (46) при
0=О^я и используя (45), получаем
В формуле (53) Un может быть постоянной величиной,
если аргумент косинуса удовлетворяет равенству
где q должно быть целым числом. Можно показать, что
равенство (54) возможно только тогда, когда, по
крайней мере, гс2=0 (modfrn). Но последнее сравнение имеет
решение только при п = 1Ья, где / — целое число, т. е.
только при п, кратном Ьп. Следовательно, косинус в
формуле (53) ни при каких Ьп, когда η не кратно Ьп (п=
—О, ±1, ±2, ...,) не может быть тождественно
постоянной величиной. Поэтому сигнал является неравномер·
§ 5-3
293
ным, так как его огибающая изменяется по косинусои-
дальному закону согласно (53). Очевидно, что проигрыш
в излучаемой энергии при ограниченной пиковой
мощности составляет не менее двух раз.
Таким образом, допуская неравномерность
огибающей, обусловленную косинусоидальным множителем
(пик-фактор порядка У2), получаем наилучший
неравномерный сигнал с квадратичным фазовым спектром
(52). Рассмотрим его подробно.
Сигнал с квадратичным фазовым спектром.
Обозначим
D = 2foO (55)
γη=£/η]/Α· (56)
Подставляя (52) в (10) с учетом (15), после
преобразований получаем
Τη = [С (г,) -С;(г,)] cos [-=-'HL±°*°L] +
+ [S(z2)-S(z,)lsin[-f fr+^rj; '(57)
где
_л-0,БР. _л+0,5Р. ,„
C(z),S(z) — интегралы Френеля [42].
Формула (57) определяет уп для η от —оо до +оо.
Исходя из заданного уровня боковых пиков (40) и
числа импульсов в сигнале Ν, определим величину D.
Основная часть сигнала, исключая края с импульсами
малой, амплитуда, сосредоточена, как показывают расчеты,
в пределах \n\^0,5D. Рассмотрим граничные значения
т.очки стационарной фазы. Заменяя ψ'(·*) в (45) на
·\-Ώχ/η + Ο,φ-D в соответствии с (52), получаем п.= —0.5D
при х = 0 и n=Q,5D при х=т. При |«|>0,51> точки
стационарной фазы нет в интервале (0, π). Поэтому при
\n\>Q$D значения Интеграла (43) меньше; чем.«при
|rt|<0,5D. Следовательно, можно считать, что краяецп·
нала> начинаются* с f«|5*0,5D.
294
§ 5.3
Перейдем к анализу γη на краях сигнала.
Рассмотрим левый край сигнала, соответствующий «<—0.5D.
Так как сигнал с квадратичным фазовым спектром
согласно (52) характеризуется свойством симметрии
γ_„=(— 1)"γη, то изменение |γ„| на его краях
одинаково. Обозначим
«o=n<+0,5D, (59)
откуда «о<0 при «<—0.5D. Подставляя (59) в (67) и
(58) и учитывая симметрию интегралов Френеля (3.1.14),
можно записать, что
πη.
b0 = \C(z\)-C(z'2)]cos^D ,
+ [S(z'.)-S(z'2)]sin-2£-, (60
где
Д^_;2'а = * (61
YD ' 3 YD
В зависимости от значений па в функции γ„ по
характеру ее изменения можно выделить две области. Назовем
областью А ту, в которой 0 <|/г01 < YD , а областью В—
в которой \n0\^>VD . Рассмотрим сначала область А,
полагая, что D > 1.
В области A z',»l, а 0<г'2<1. Заменяя в (60)
C(z'i) и S(z\) согласно асимптотическим формулам
(3.1.17) и (3.1.18), C(z'a) и S(z'z) - (3.1.15) и (3.1.16)
и удерживая в C(z'z), S(z'2) только первые слагаемые
благодаря малости z'%, после преобразований получаем
Wt+^)«":£+(4-+£)-'
π/1|
■sin ' — ' nnpl
πφ-/ι0)
/π£> A £»3/2 , JnD \
(62)
Четвертым слагаемым в (62)< можно пренебречь по
сравнению со вторым, так как отношение четвертого ко
второму слагаемому примерно равно 1/π'<1· При чет*
§ 5.3
295
ном D третье слагаемое равно нулю. В этом случае,
обозначая
YD YD
(63)
и разлагая косинус и синус в (62) в ряд Тейлора,
получаем зависимость
γ/ΐ^ΊΓ_ν+_ν.___ν4ι
(64)
а.*
0,3
0,2
ο,ι
1
s4
'
'
ι
а,*
0,8
1,2
f,6 о_Ш
Рис. 5.5.
показанную яа рис. 5.5 пунктирной линией при v>0,4 и
сплошной линией при v<0,4.
В области В ζ'ι»1 и z'2»l. Поэтому интеграл
Френеля в формуле (60) можно заменить согласно
.асимптотическим формулам (3.1.17), (3.1.18). В результате, пос-
296
§ 5.3
ле преобразований можно записать выражение
D3/2 , Dl>2' . fnD
Yr гч' Т--+- -^-7Т> Г Sin -н-
>В π>ηΙ ~ [π(£>- /ί0) I 2
о-
■COS ( -S π«0 ). (65)
пг(/>—л0)« ^^ 2
в котором третьим слагаемым можно пренебречь по
сравнению с первым, а второе равно нулю при четном D.
Поэтому с учетом обозначения (63) для области В
окончательно имеем зависимость
Тв^-^г. (66)
изображенную на рис. 5.5.
Зависимость функции γηο=γ от ν показана на рис. 5.5
сплошной линией, которая на участках А и В повторяет
ход кривых уА (ν) и Yri(v).
На участке 0,7<ν<1,3 функция γηο построена из
условия сохранения монотонности кривой β целом.
Следует заметить, что в действительности характер кривой
γ„ο не является монотонным. При учете малых
колебательных слагаемых в формулах (62) и (65) 1на «ривую
γ (ν), представленную |на рис. 5.5, накладывается
пульсирующая составляющая. Но для ориентировочных
расчетов, которые рассматриваются в данном 'параграфе,
эти пульсации не существенны.
По кривой γ можно определить уровень первого
отброшенного импульса на краю сигнала. Если номером
этого импульса является «о, то в формуле (40)
=у. При этом число импульсов ,в сигнале
N=D+2\n0\—l. (67)
Здесь D + 1 —число импульсов в основной части сигнала
(где есть точка стационарной фазы); 2|п0|—2 — число
испульсов на краях сигнала до первого, отброшенного
импульса.
Для оценки величины Ят в формуле (40) необходимо
«айти также UM и (ί/0- Для основной части сигнала
справедливо асимптотическое равенство (53). .Используя
§ 5.3
297
обозначения (55) и (56), это равенство можно записать
в виде
/сГ Г π (я + 0,5£>)2 π 1 /со.
Y„^/2cos l^— ^D· Г; (68)
Из (68) следует, что максимальное значение γΜ=^2,
а среднее γ0 ^ 1 - Производя замены в формуле (40)
согласно равенствам UM = V2 Ги^= 1,α= γ, получаем
η _ Υ _ тг(|я,1 /УЩ . (М
Rm-yr w— (69)
Обозначая через γ-1 функцию, обратную функции у,
иыражаем |«о| через Rm:
\nt\ = VWrl(V2~Rm). (70)
Подставляя (70) в (67), определяем число импульсов в
сигнале
N=>D+2VDvl(V2Rm)-\. (71)
Решая уравнение (71) относительно D, и принимая
во внимание, что D<N, получаем
D = N+l+2[ri(Vr2~Rm)]i-
-2rl(V2Rm)V'N+\+[rW2Rm)y . (72)
.Формула (72) позволяет по заданным N ;и Rm «айти
D — единственный параметр который входит β расчетную
формулу (57).
Рассмотрим пример расчета сигнала. Пусть N = 21,
/?т = 6-10-2. Из £рафика рис. 5.5 для ]/"27?т= 0,085
имеем у~1=\п0\/УВ = 0,8. Подставляя N=21 и γ-1 = 0,8
в формулу (72), получаем D = 15,68. Округляем
полученный результат до ближайшею четного числа: D = 16. Для
такого D по формулам (57), (58), был рассчитан сигнал,
который изображен на рис. 5.6,а. На рис. 5.6,6
представлена автокорреляционная функция рассчитанного
сигнала. Максимальный боковой пик автокорреляционной
функции равен 3· 10~2, т. е. меньше заданного. Непосред-
298
§ 5.3
ственныи расчет показывает, что по сравнению с энергией
сигнала, имеющего равномерную огибающую при огра,-
ниченной пиковой мощности и N = 21, энергия сигнала
с квадратичным фазовым спектром в 2,3 раза меньше,
т. е. пик-фактор сигнала равен 1,52, что нескольку
превышает пик-фактор косинусоиды (68), равный ]/2.
Недостатком таких сигналов является неравномерность их
а)
IUL
δ)
Рис. 5.6.
т г
огибающей. Однако в некоторых случаях с указанным
недостатком приходится мириться.
Необходимо отметить, что методика приведенного
синтеза основана, с одной стороны, на выборе
амплитудного спектра, близкого к амплитудному спектру
идеального сигнала (15). Такое приближение эквивалентно
среднеквадратичному приближению (5.1.3). С другой
стороны, фазовый спектр сигнала выбирался по
критерию минимизации максимального бокового пика (40)
§ 5.4
299
автокорреляционной функции. Следовательно,
рассмотренный пример показывает, что оба .критерия
совместимы IB мекоторых задачах.
5.4. СИНТЕЗ НЕРАВНОМЕРНЫХ
ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ
ПО АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ
(МЕТОД ХАФФМЕНА)
Постановка задачи. Если сигнал состоит из конечно-
ного числа импульсов, то его автокорреляционная
функция имеет по крайней мере два 'боковых пика,
расположенных ,на ее краях (5.3.6), поскольку эти пики
определяются произведением первого ih последнего 1Импульсов
и (ничем не компенсируются. В работах {98, 100] дано
решение задачи синтеза ФМн сигнала,
автокорреляционная функция которого имеет только эти два неизбежных
боковых лика. Решение этой задачи основано на
использовании оператора задержки и свойств многочленов.
Оператор задержки. Пусть сигнал состоит из N + 1
импульсов и определяется кодовой
последовательностью
{θη} = αα, аг а„ аы. (1)
Формально можно ввести оператор задержки D, который
задерживает импульс iHa время to, равное задержке
между соседними импульсами. Например, если взять
импульс u0(t), то
O[u0(t)] = ua(t—to). (2)
В таком случае, кодовую последовательность ,(1) можно
записать ,в виде многочлена
^(D)=a0 + a1D + ... + fl„D»' + ...+aNDA', (3)
каждое слагаемое которого действует на своем
временном интервале. Представление последовательности (1)
в виде многочлена (3) позволяет рассматривать D как
независимую переменную и использовать для решения
300
§ 5.4
задач синтеза сигналов свойства многочленов. В частно-
ст1И, если αΝφ®, то многочлен (3) имеет N корней du
где 1= 1, 2, ..., N, и может быть представлен в виде
произведения
Α{Ό)=αΝ{Ό-αλ)...φ-<ίΝ) = αΝ Пф-^у (4)
Если известны корни Ль то по формулам Виета 1106]
можно найти коэффициенты ап-
Аналогично (4) можмо записать многочлен,
соответствующий импульсной характеристике фильтра. При
этом следует учесть, что импульсная характеристика
фильтра определяется сопряженной кодовой
последовательностью, в которой нумерация импульсов обратна
рассмотренной:
* * * *
«Λ/. «л,_ «ι. «о·
Поэтому многочлен, описывающий импульсную
характеристику фильтра, имеет вид
i-'(D)=a;+aw_,D + ... + a„DA'-" + ...+
+ «1D"-,+«oD\ (5)
где индекс — 1 у А соответствует перемене номеров
символов.
Для того чтобы получить автокорреляционную функ-
нию сигнала при представлении ее многочленом в
симметричном виде, принятом в данной книге, многочлен
* — N
Α'ι(Ό) умножим на D :
B(O)=A-l(V)u-N^
= 4D~A' + - + ^D-" + ...+o1D->+a0. (6)
Такое умножение эквивалентно сдвигу импульсной
характеристики фильтра в сторону запаздывания на
длительность сигнала.
§ 5.4 301
Автокорреляционная функция и оператор задержки.
Умножая (3) иа (6), после приведения подобных членов
получаем
A(O)B(O) = u£llO-« + (utull_l + u1oll)O-<N-l> + ...
+ (а0а0 + «.«. + ...+θηάη + ···+«ν«/ν) + ···
+ («„_, α0 + αΝ α,) D*"1 + a^a.D^. (7)
Сопоставляя коэффициенты (7) при различных
степенях переменной D со значениями автокорреляционной
функции (5.3.1), замечаем, Что эти коэффициенты с
точностью до постоянной \/(N+\) совпадают с Rm. Поэтому
i4(D)Ji(D) = (tf+l) £ Λ„(Ι>». (8)
Ν
/?™=лг+т5]а"а"-то ПРИ/n=0,1 N' (9)
n-m
R-m=Rm. (1°)
Идеальной является такая автокорреляционная функция,
для которой /?т = 0 при всех т, кроме т — 0 (основной
пик) in m=±N (два крайних боковых пика) [98, 100].
Обозначая
[Е=У\ап\\ (11)
получаем произведение многочленов
i4(D)£(D) = a0awD-w + £ + awa0D\ (12)
соответствующее идеальной автокорреляционной фуик-
ции.
302
§ 5.4
В работах [98, 100] приведено .интересное
представление (12) ιΒ виде произведения двух многочленов1,
которое в принятых обозначениях записывается как
Α(Ό)Β(0)=>-(ΌΝ-ρΝ)(\ -Ό-%-% (13)
или
Α(Ό)*Β(0)=(ΌΝ + ΡΝ)(\+Ό-%-Ν). (14)
Перемножая двучлены в правых частях равенства
(13) 1И (14), можно убедиться в тождественности этих
равенств с представлением (12), 'если положить, что
|a0aw|=l, a
Ε=9Ν+ρ-Ν. (15)
В (13) и (14) каждый из двучленов содержит N
корней, а каждое из равенств — 2Ν корней. Половина этих
*
корней принадлежит многочлену A (D), а половина В (D).
Определим эти корни.
Рассмотрим сначала двучлен D^—pN, корни которого
являются решением уравнения D^—р^ = 0. Запишем 1-й
корань как
• Ηΐί.
rfl=(pw)l/w = pe " при /=1,2 Ν. (16)
Действительно, dt — ρ =0, τ. e. di является корнем
уравнен ия D* — pN = 0.
Рассмотрим теперь двучлен 1 — D~ p~ . Его корни
определяются из уравнения 1—Ό~Ν ρ~Ν=0, 1-й корень
которого
rfi = (T*r=-V=p"e ". (17)
1 Ν
ре
Корни (16) и (17) являются комплексносопряженны-
м,и. Графически их можно изобразить на комплексной
1 Единственность такого представления не доказана
§ 5.4
303
плоскости (рис. 5.7, N=13). Корни di расположены на
окружности радиуса р, а номер / определяет угловое
положение корня, поскольку окружность делится на N
одинаковых секторов.
В свою очередь корни di расположены на окружности
радиуса р-1. Из всех 2N корней, как было отмечено,
половина принадлежит многочлену А(Щ (черные точки на
рис. 5.7). Часть из них расположена на внешен окруж-
Рис. 5.7. Рис. 5.8.
ности, часть—на внутренней. Каждый сопряженный
корень расположен на другой окружности и 'принадлежит
многочлену В (D) (светлые точки на рис. 5.7).
Синтез сигнала сводится к нахождению радиуса ρ и
распределению всех 2Ν корней между многочленами A (D)
*
и Β(Ό). Как р, так и 2Ν определяют временною
структуру сигнала. Например, если р=1, то корни полиномов
*
.«4(D) и Β(Ό) совпадают, так как располагаются на одной
окружности. Поэтому'Л (D) = D*—1, т. е. сигнал будет
состоять из двух импульсов, расположенных на его
краях. При очень большом ρ вся энергия сигнала
сосредотачивается в одном импульсе [98, 100].
В настоящее время аналитический метод определения
ρ и распределения корней еще не найден. В работах
304
§ 5.4
(98, 100] была использована ЦВМ для решения этой
задачи при случайном распределении корней на
окружностях. На рис. 5,8 приведено распределение корней одного
из многочленов при Ν=Ί00. На рис. 5.9,α представлен
сигнал, которому соответствует полученное
распределена
а)
5)
т^
Рис. 5.9.
1ние корней (рис. 5.8), а на рис. 5.9,6 — его
автокорреляционная функция. Подавление бокового пика
автокорреляционной функции составляет 25,64.
К сожалению, рассмотренный метод не позволяет
заранее определить (неравномерность синтезируемого
сигнала, что является недостатком. Однако с помощью
этого метода можно получить большое число различных
неравномерных сигналов, поскольку принципиально воз-
§ 5.5
305
можно 2N способов размещения корней, отличающихся
расположением хотя бы одного корня.
5.5. СИНТЕЗ МНОГОФАЗНЫХ СИГНАЛОВ
Постановка задачи. Рассмотренные >в § 5.3, 5.4
методы синтеза сигнала позволяют находить
неравномерные ФМн сигналы. Синтез равномерных ΦΜιη сигналов
связан -с -решением ряда серьезных математических задач
и в настоящее время еще окончательно не решен.
ЧМ сигналы могут быть представлены аналитически
так, что задача их синтеза, решается, например, методом
стационарной -фазы. Поэтому оинтез ΦΜιη сигналов
целесообразно проводить, используя ;их аналогию с ЧМ
сигналами. Последние предварительно должны -быть
определены по требуемой автокорреляционной функции.
Затем непрерывный ЧМ -сигнал должен быть заменен
дискретным ФМн сигналом таким образом, чтобы их
автокорреляционные функции отличались
незначительно.
Поскольку ФМн сигнал состоит из последовательности
прямоугольных радиоимпульсов, то необходимо
определить амплитуду, длительность и начальную фазу
каждого .импульса. При -синтезе равномерных ФМн сигналов
в качестве исходного следует брать ЧМ сигнал с
равномерной (прямоугольной) огибающей. Это значит, что
амплитуды импульсов должны -быть одинаковыми.
Естественно, -что и длительности импульсов должны быть
равны. Если Τ — длительность сигнала, а То —
длительность импульса, то число импульсов равно Ν = Τ/χο·
Однако число импульсов N и начальные фазы всех
импульсов следует определять исходя из близости
автокорреляционных функций ЧМ и ФМн -сигналов.
Отметим, во-первых, что принципиальная
возможность замены сигнала с непрерывной частотной
модуляцией дискретным ФМн сигналом следует из теоремы
Котельникова {13]. Действительно, любой
-радиочастотный сигнал с ограниченным спектром может быть
представлен последовательностью импульсов вида sinx/x,
амплитуды и фазы которых определяются отсчетами
огибающей и фазой непрерывного сигнала, а несущая часто-
306
§ 5.5
та >равна средней частоте спектра. В отличие от теоремы
Котельникова в данном параграфе исследуются
прямоугольные импульсы (с практической точки зрения они
представляют большой интерес), а на непрерывный
сигнал не накладывается никаких ограничений, за
(исключением постоянства огибающей. Последнее также
обусловлено практическими соображениями.
Во-вторых, рассматриваемые ФМн сигналы являются
многофазными1. Согласно методу аинтеза, приведенному
в дальнейшем, число градаций 'фаз может быть равно
числу импульсов в сигнале. Но при малом увеличении
боковых лепестков автокорреляционной функции число
градаций фаз может быть значительно уменьшено, как
будет показано, округлением значений фаз до кратных
л/4.
Приближенное представление ЧМ сигнала. Для
простоты сравнения автокорреляционных функций ЧМ и
ФМн сигналов можно ЧМ сигнал приближенно
представить в виде последовательности радиоимпульсов с
мгновенной частотой, линейно меняющейся в течение
импульса.
На рис. 5.10 изображена зависимость фазы θ от ί
ЧМ сигнала, длительность которого равна Т. Согласно
рисунку, сигнал разбит 1на N импульсов длительностью
to = T/N. Принята следующая нумерация импульсов:
0, 1 N-J\.
Заменим непрерывную функцию Q(t)
линейно-ломаной, значения которой совпадают с Q(t) в точках,
кратных То. Обозначим
θ„=θ(/ζτ0) при /ζ = 0, Ι,.,.,Ν— 1, (1)
6'„ = 9"+'-9" . (2)
Введем единичный импульс
и0(0=1 при 0<ί<τ0. (3)
Тогда фаза ЧМ сигнала на п-ш интервале приближенно
запишется как
К (0 = [6„ + θ'„ (t — пх0)] «0 (t - пх0), (4)
1 Анализ некоторых многофазных сигналов приведен в работах
[107—109].
§ 5.5
307
а в течение длительности сигнала представится в виде
л/—ι л—ι
θ (0 ** £ βη (О = £ [θ„ + β'„ (* - «τ0)] «0 (t - ηχ0). (5)
га=0
га=0
Отметим, что погрешности, возникающие гори замене
непрерывной фазы линейно-ломаной (5), незначительны
при Л/>1.
Для сигналов с равномерной огибающей, т. е. с
(6)
комплексная огибающая автокорреляционной функции
согласно (2.3.21) определяется формулой
Л(т) = у-|е' '(,;-ί(|-τΛ.
(7)
Поскольку при дискретном представлении ЧМ
сигнала полную информацию об автокорреляционной функции
308
§ 5.5
дают <ае значения в точках, отстоящих друг от друга на
То, то комплексную огибающую автокорреляционной
функции будем о,П|ределять ib точках
(8)
Согласно (7) с использованием (5), (8) получаем
■· и n,m Lo
п=т
где индекс Ч обозначает, что комплексная огибающая
автокорреляционной функции соответствует ЧМ сигналу,
индекс т — значениям согласно (8);
"п,т ==3 "п — On-rr? 0n.tr, On 0 η-
Обозначая через θ„ среднее значение фазы, т. е.
(10)
9"+29"+' =6п+-^. (И)
vntm —υη νη _ т »
(12)
выражение (9) преобразуем к следующему виду:
... .0 n.tn^o
W-1 _ sin —s-
**.=1Σβ,Ί"·":*ώ:· (13)
2
Ι
2"
Представление ФМн (многофазного) сигнала.
Начальная фаза д-го импульса 6фга ФМн сигнала (см. рис. 5. 10)
принципиально может принимать любое значение в
пределах 0—2π. Поэтому фаза ФМн сигнала может быть
записана как
<КО = Х«ф„"о('-'»0). (14)
га=0
§ 5.5
309
Подставляя (14) в (7) и учитывая (8), получаем
*om=4Se,Wi. (15)
где индекс Φ указывает, что автокорреляционная
(функция соответствует ФМн сигналу;
Фп.т Фга νΦη —m"
(16)
Сравнение автокорреляционных функций ЧМ и ФМн
сигналов. Сравним формулы (13) и (15). Как
было.отмечено, .критерием замены одного сигнала другим
является близость их автокорреляционных функций. С точки
зрения критерия равномерного приближения (5.3.1) это
означает, что модуль разности между
автокорреляционными функциями
8гП = |ЛЧи-Лфт|<в, (17)
где ε — любая наперед заданная величина.
Отметим, что общий метод определения θφη w Ν,
соответствующий (17), при произвольной фазе ФМн
сигнала в настоящее время неизвестен.
Сравнивая (13) и (15), можно заметить, что их
структура одинакова, за исключением множителя вида
sin jc/jc (где jc = 0'„imTo/2) в формуле (13). Если положить,
что
"Фга'
(18)
то (13) от (15) будет отличаться только наличием
указанного множителя, который зависит от п, т и от
скорости изменения фазы. Согласно соотношению (18)
начальные фазы ФМн сигнала должны быть равны
значению фазы ЧМ сигнала ,в середине «-го импульса.
Выбор числа импульсов Л/ обусловлен^следующим. Чем
больше N, тем меньше разница между /?Чт и /?, так как
при этом το убывает и множитель вида sin χ/χ β формуле
(13) стремится к единице. Но чем (больше Ν, тем
сложнее линия задержки согласованного фильтра, число от-
310
§ 5.5
водов которой возрастает. Поэтому N следует выбирать
та:к, чтобы число отводов линии задержки было бы
порядка FT. При этом следует оценивать разницу между
(13) я.(15).
Допустим, что девиация частоты ЧМ сигнала равна
" == " макс — " мин· I'")
Тогда Q'n^W, a Q'n,m<W. Если положить
то 0/n,mW2<W7To/2 = n. В этом случае множитель вида
s'mx/x(x = Q'n,mXo/2) всегда больше нуля и не изменяет
знака слагаемых в сумме (13). Отметим, что при το>
>2nJW знаки некоторых слагаемых в сумме (13)
отличаются от знаков аналогичных слагаемых в сумме (15).
Это приводит к тому, что автокорреляционные функции
(13) и ι (15) сильно различаются. При выполнении
условия (20) все слагаемые в (13) и ,(15) имеют одинаковые
знаки, а разница обусловлена только наличием в (13)
множителя вида sin х/х, в этом (Случае не равного
единице. Для дальнейшего исследования различия между
автокорреляционными функциями ЧМ и ФМн сигналов
уточним характеристики рассматриваемых сигналов.
Допустим, что Q(t) —монотонная функция времени.
Тогда разница между двумя значениями θ'η с номерами
η и п + \ намного меньше W. Поэтому при малых т
величина e'n,mto/2<l и ЯЧт^ Яфт при m<W, т. е. при
малых т разница между автокорреляционными
функциями ЧМ и ФМн сигналов мала.
Пусть фаза сигнала является степенной функцией
времени:
Ht) = -^t* + x при 0<f<7\ (21)
где κ — постоянная фаза, при которой начальная фаза
первого импульса равна нулю. Нормирующий
коэффициент, стоящий перед tk, таков, что девиация частоты
равна W, поскольку
V(t)=w(-LY~lni>viO<t<T. (22)
§ 5.5
311
Можно показать, что если θφ0 = 0, то
κ = — w/jfe2k-Wk-·. (23)
В этом случае
9фп = 7тЪ(« + 0,5)"+х, β'„=7^τ(/ι+0,5)"-1, (24)
так как t = (n-\-0,5)z0. Соответственно
9.,.« = й£п К» + 0,5)· - (я + 0,5 -»»■] =
= 2«и[(^1)-' +Ц^^)- -+...+
+(-')'т (тг)""]· ί25»
•V·» = -д^гГ[(л + 0,5)»-1-(/1+0,5-и)»-,]=>
χ(^ + Μ.)'-(-.)-+..+(-1)»-(ί-)-]. (26,
При значениях m<^N в'7,,т определяется в основном
первым слагаемым в квадратных скобках выражения
(26), т. е.
■ W
(^(-Ч^Гх· (27)
Множитель {(« + 0,5)/AT|ft-2 в (27) при изменении «
меняется от значения 1/2N до значения, приблизительно
равного единице. Однако порядок величины б'п.т определяет
произведение W(k—\)т/М, поскольку оно намного
меньше множителя {(я + 0,5)/ЛП''-2. Поэтому, положив [(п +
+ 0,5)/Л/]й_2«1, можно записать
0 n.m «=* дг · (·*»)
312
§ 5.5
Подставляя (28) в ι(Ί3), получаем выражение,
связывающее автокорреляционные функции ЧМ ;и ФМн
сигналов:
π (k — 1) т
sin-
\о — ττ п /?* ппи т <έ Ν- ^
*4m π (fc — 1) от хФт
Ячт = ,/ь_мт Лфт при т < N.
N
Определим значения т, при которых R4m «* 0,64 Кф)п ,
т. е. при которых переход ικ дискретной структуре
сигнала приводит к увеличению уровня боковых пиков
автокорреляционной (функции меньше, чем в два раза. В этом
случае аргумент n(k—'\)mjN = nl2, т. е.
Таким образом, если m<N[2(k—1), то боковые пики
автокорреляционной функции ФМн сигнала увеличатся
не более чем в два раза по .сравнению с боковыми
пиками автокорреляционной функции ЧМ сигнала.
Допустим, что уровень боковых пиков у ЧМ сигнала
составляет 5%. Тогда для ФМн сигнала при m<lNJ2(k—1)
уровень боковых пиков не превысит 10%.
При больших значениях т резкое увеличение
боковых тиков автокорреляционной функции ФМн сигнала
ограничено. Во-первых, чем больше т, тем меньше
слагаемых β формулах (13), (15), т. е. с ростом т
максимально возможное значение боковых пиков
уменьшается.
Во-вторых, при пг ~ N согласно формуле (21) величина
φ η m*»2WV/fe. Векторные суммы (13) и (15) в этом случае
можно представить в виде групп, сдвиг фаз между
векторами в каждой из которых равен '2я. Число таких
групп равно Nfk. При большом N можно считать, что
результирующий эффект в основном определяется
ориентацией векторов в группах, а не изменением амплитуд
векторов, обусловленным множителями вида sin xfx.
Поэтому можно полагать, что боковые пики при т>
>N/2(k—1) увеличиваются незначительно.
§5.5
313
Таким образом, три замене 'непрерывного ЧМ
сигнала многофазным сигналом, фазы .которого определяются
формулой (18), а длительность импульса формулой (20)
при т, удовлетворяющих условию (30), боковые пики
автокорреляционной (функции такого сигнала <не более
чем в два раза превысят уровень боковых ликов
автокорреляционной функции ЧМ 'сигиала. При других
значениях т увеличение боковых пиков при переходе от
ЧМ к ФМн сигналу будет незначительным. Для
подтверждения этого рассмотрим примеры.
Сигнал с линейной частотной модуляцией. В этом
случае k = 2 в (21). Модуль комплексной огибающей
автокорреляционной функции ЛЧМ сигнала для τ^Ο
согласно точной формуле (3.1.52) имеетвид
|Λ(*)Ι =
sin-
(-Т-)
Jul
2
(31)
При τ = /ητο с учетом (20) соотношение (31)
преобразуется в следующее выражение:
I Кцт I
sin π/я ( 1 —
(32)
Начальные фазы многофазного сигнала согласно (18), (21)
равны
6ФП = -£-("' + "). (33)
Подставляя (33) в (15), (16) и производя суммирование,
находим
I °фт I дг
( т\
Sin. π/Я I 1 — -тг 1
кт
Сравнивая (32) и (34), получаем соотношение
пт
Υ
I ЯФт | = | R4m |
■кт
sin-дг
(34)
(35)
314 §5^5
При т <£.N различие между модулями комплексных
огибающих автокорреляционных функций ЧМ и ФМн сигналов
является незначительным. С ростом т второй множитель
в (35) увеличивается, но при этом функция R4n
уменьшается, и резулотирующее увеличение боковых пиков Цфт
остается малым.
\лт\ 1Г~Т
|Рис. 5.11.
На рис. 5.11 приведены графики" изменения модуля
комплексной огибающей автокорреляционной функции
от τ/Γ для Ν=3&, построенные по точной формуле (31)
для ЛЧМ сигнала (сплошная линия), и по дискретным
значениям (34) для многофазного сигнала (пунктир).
Как видно из рисунка, при τ<Τ/2 (m<N/2) различие
автокорреляционных функций ЧМ и ФМн сигналов
незначительно. Более того, многофазный сигнал имеет
даже лучшую автокорреляционную функцию, так как
§ 5.5
315
в ней нет первого большого бокового пика. Как
показывают расчеты, с ростом N отличие автокорреляционных
функций рассматриваемых сигналов будет небольшим
и при больших т.
Сигнал с квадратичной частотной модуляцией. Пусть
°(0=^(* —-£-)' при jp<t<T. (36)
Как показано ib гл. 3, модуль комплексной опибающей
автокорреляционной функции согласно (3.3.42) имеет вид
\^^)\ = yi^VC^z) + S^(z), (37)
где
С (z), S (ζ) — интегралы Френеля.
Отсчетные значения начальных фаз согласно (16), (18)
равны
»*.=х(тг-0'· (да)
На рис. 5.12 ' приведены графики зависимости модуля
автокорреляционной функции от τ/Γ при W=24,
рассчитанные .по 'формуле '(37) для КЧМ сигнала (.сплошная
линия) и для ΦΜιη сигнала по формулам ι(15), (39)
(пунктир). Как видно из рисунка, отличие между ними
незначительно.
Уменьшение градаций фаз. При расчете начальных
фаз ιπο формулам (1), (11), (18) может оказаться, что
все начальные фазы импульсов различны, т. е. число
градацией фаз равно N. Как показали многочисленные
расчеты, при округлении расчетных значений фаз до
я/4 боковые пики автокорреляционной функции ФМн
сигнала удваиваются ι(β худшем случае). Дальнейшее
округление фаз до я/2 значительно ухудшает структуру
автокорреляционной функции.
1 Графики рис. 6.11 и 6.12 рассчитаны И. А. Ястребцовым.
316
§ 5.5
Особенности спектра многофазного сигнала.
Рассмотрим, как взаимосвязаны спектр многофазного и спектр
исходного ЧМ сигналов. За исходный примем ЛЧМ
сигнал (§ 3.1), спектр комплексной огибающей которого,
соответствующий закону изменения фазы (21) пр,и k = 2,
приведен на рис. 5.13. Основная часть спектра ЛЧМ сиг-
\Ш)\
0,8
0,6
ОЛ
0,2
1
1
1
1
1
I
I
ι
\*
+ч—
0
г* -
^
2
\
0
Ρ
Л
\
\
ис. 5.
s\
1
0,
12.
L/j
В
V
ч
0
•
8
Г
Τ
нала согласно (22) сосредоточена ιβ области частот от О
до W. Графики ЛЧМ сигнала рассчитаны для N=18.
Можно показать, что 'если фазы многофазного
сигнала изменяются по закону (33), то спектр комплексной
огибающей сигнала
Λ-1 .Г-._._^1
G(v)=\S.
slniw _—1«»
Σ'
η—θ
i LL („·+η)_2
(4Θ)
§ 5.6
317
где
S0 = U0T; ν = ω/«7. (41)
Модуль комплексной огибающей спектра
многофазного ФМн сигнала, рассчитанного согласно формуле (40)
для ιΝ=Λ8, приведен на рис. 5.13. Как видно, из графика,
этот спектр имеет две спектральные полосы, что является
J
г
\
ι
А
л
ш
Г
ИЛ
П\фМи '
^
ЛЧМ
V
9
Рис. 5.13.
естественным для ФМн сигналов. Правая спектральная
полоса сохраняет чередование максимумов и минимумов
спектра ЛЧМ сигнала. Отличие спектров
рассматриваемых сигналов обусловлено множителем s'mnyjnv в
формуле (40). Так (как определяющей в спектре
многофазного сигнала является одна полоса, то некоторая
близость по форме спектров многофазного и ЧМ сигналов
при v>0 приводит к близости их автокорреляционных
функций.
5.6. СИНТЕЗ РАВНОМЕРНЫХ
ФАЗОМАНИПУЛИРОВАННЫХ
СИГНАЛОВ
Постановка задачи. В § 5.3—5.5 приведено решение
нескольких задач синтеза ФМн сигналов. Однако
наибольший практический интерес представляют равномер-
318
δ 5.6
ные ФМн сигналы с импульсами одинаковой
длительности in со значениями фаз 0 или и. Напомним, что для
малых значений числа импульсов в сигнале N известны
ΦΜιη сигналы ((Например, сигналы Баркера) с малым
уровнем боковых пиков автокорреляционных функций,
а для средних (/V<200) сигналы могут быть найдены с
помощью ЦВМ методом «перебора». Для jV>200 нахождение
ФМн сипналов с помощью ЦВМ методом «перебора»
требует значительного машинного времени. Поэтому
решать задачу синтеза равномерных ФМн сигналов имеет
смысл только для больших jV ι (порядка 200 и выше). При
таких больших N следует заранее предполагать, что
ФМн сигнал должен состоять из импульсов одинаковой
длительности. Назовем условно такой сигнал
дискретным. Формирование и обработка дискретных ФМн
сигналов несколько упрощается при использовании
элементов цифровой техники. Но из-за дискретности сипналов
точное аналитическое решение вряд ли возможно. Чтобы
довести решение задачи до конца, приходится разбивать
его !на два этапа — аналитический и машинный.
На .первом определяются характеристики
неравномерного ФМн сигнала с заданным N и .хорошими
корреляционными свойствами. Затем полученный сигнал
преобразуется в равномерный путем 'квантования по
амплитуде на два уровня и вычисляется его
автокорреляционная функция. Указанные операции можно производить
с помощью ЦВМ.
На втором этапе меняются знаки наиболее
характерных импульсов для уменьшения боковых пиков
автокорреляционной функции и каждый раз проверяется вся
автокорреляционная функция. Эта-операция может быть
выполнена только с помощью ЦВМ из-за большого
объема вычислений. В этом случае требуется меньшее
машинное время, чем при методе «перебора», так как надо
проверить гораздо меньшее число характерных
импульсов. Легко показать, что число таких импульсов, намного
меньше числа импульсов в сигнале.
Решение задачи 'синтеза в целом значительно зависит
от выбора исходного сигаала. В настоящее время синтез
может <быть осуществлен на основе сигналов, получен·
^ 5.6
319
ных либо с помощью метода стационарной фазы >(§ 5.3),
Л1ибо по аналогии с ЧМ сигналами >(§ 5.5).
Синтез дискретного ФМн сигнала с помощью метода
стационарной фазы. Как было показано в § 5.3,
неравномерный сигнал с квадратичным фазовым спектром
(5.3.52) при бесконечном числе импульсов обладает
идеальной автокорреляционной функцией (5.3.4) без
боковых пиков. Ограничивая по определенному правилу
число импульсов в таком сигнале, можно получить
любой заданный уровень боковых пиков.
Чтобы перейти от сигнала с квадратичным фазовым
спектром и неравномерной огибающей к сигналу с
равномерной огибающей, необходимо по исходному сигналу,
амплитуды импульсов которого равны Unu найти сигнал, у
которого | иП21 = const, а число импульсов ограничено. При
этом автокорреляционная функция искомого сигнала Rmt
должна минимально отклоняться от ^автокорреляционной
функции исходного сигнала #?т1 по выбранному критерию
аппроксимации.
Решение задачи аппроксимации непрерывного
вещественного (Сигнала равномерным ФМн сигналом с
сохранением положения нулей, т. е. при длительности
знакочередующихся участков, н«е кратных длительности
одиночного (импульса приведено в [7]. ιΒ качестве критерия
приближения использован критерий минимума
среднеквадратичного отклонения автокорреляционных функций.
В данном параграфе в отличие от метода,
использованного в работе [7], предложен метод синтеза дискретных
ФМн сигналов.
Пусть искомый дискретный ФМн сигнал состоит из
N импульсов. Дискретный аналог критерия минимума
среднеквадратичного отклонения (5.1.3) запишется как
Выражение (1) является суммарным квадратическим
320
δ 5.6
отклонением автокорреляционной функции исходного
сигнала от автокорреляционной функции искомого
сигнала. Заменяя /?mi,2 β (1) 'Согласно формуле (5.3.11) и
приписывая индексы 1 и 2 соответственно исходному и
искомому сигналам, получаем
— π / \ —π
π ν
\\»uSy)
2пМг
\*е-тиау\,
(2)
где Ми М2 определяются равенством (5.3.7), причем
значение Мъ равно сумме конечного числа слагаемых,
отличных от нуля.
Производя перемножение в (2) с учетом того, что
Η и\ = \Ни\, и меняя порядок суммирования и
интегрирования, находим, что
*-£\\
\"0,Ю\*\"и,Ш* \ffUt(.x)\*\HVtly)\*
Mi
МгМг
I^WPI^.WIl , 1*0, (χ) Ι*. 1*0, ΜI
MiAji
Χ
со
яг 2j
\m(x—y)
Mi
dxdy.
X
(3)
m=—oo
Из теории обобщенных функций известно равенство [22]
оо со
2~ Σ е'**= Σ 8<*-2"*>·
(4)
k =—00
§ 5.6
ψ
правая часть которого является суммой.дельта-функций,
смещенных друг относительно друга на 2π.
В интегралах правой части (3) интервал
интегрирования равен 2π. Такому интервалу соответствует только
одна дельта-функция. Подставляя (4) ιβ (3) и используя
фильтрующее свойство дельта-функции, получаем
°-ν л-
—π
π
= 2V j{
HVl Μ I
I Н„ (x) I
mv
Mi
!"£/,(*)! I ffv, (*) I
Ум,
Vm2
dx =
X
X
" 1 hUi (x)
!^(*)l
Км2
ifX.
(5)
В подынтегральном выражении (5) определяющей
является разность модулей как разность двух близких
функций. Сумма модулей приближенно равна двум по
следующим соображениям. Исходный сигнал с
квадратичным фазовым спектром удовлетворяет условию (5.3.15).
Поэтому | Ηυ (χ) | / VMi = 1.
Искомый сигнал должен мало отличаться от исходного.
Следовательно, можно полагать \Ηυ (х)|/|/Ж„ « 1. С
учетом отмеченного (5) можно преобразовать к виду
'я=8
1
2π VMiMi
\\Ηυι{Χ)\\Ηυ,(Χ)\άχ
(6)
Поскольку у ФМн амплитудный спектр Ни—четная
функция, а фазовый—нечетная функция, то интеграл от
произведения модулей (6) больше, или равен интегралу
от произведения комплексно-сопряженных величин, т. е.
:8
1 —
2nVM1Mt
π
^HUt{x)HUt{x)dx
(7)
Заменяя спектры Ни· входящие в формулу (7),
согласно (5.3.9) и производя 'при этом суммирование в
выражении для Ни2 в конечных пределах от —(N—1)/2 до
322
§ 5.6
(Ν—1)/2 (Ν — нечетное), получаем равенства
π
air \Ηυι{Χ)Ηυ+χ)άχ=
—к
π οο (Ν-1>/2
=4 ί Σ Σ «.^e-,^^=
—π η=-οθΑ=-(Μ-1)/2
οο (W-1J/2 π
= j Σ "«^ ρ«-^*=
—π
UmUm. (8)
η=-οοΑ=—(/V—1)/2
(Λ/—1)/2
= Σ
я=-(/V-1 )/2
Подставляя (8) в (7), можно записать, что
(jV-1)/2
;8
1~7ШГ Σ £/nl£/n2
(9)
-(/V-l)/2
Отметим интересную особенность соотношения (9):
суммарное квадратичное отклонение двух
автокорреляционных функций зависит от взаимокорреляционной
функции сигналов при нулевом временном сдвиге.
Оценим теперь величину σ2(9). Поскольку первый
сигнал — исходный, то М\ = const и определяется
формулой (5.3.7). Так как второй сигнал — равномерный, то
можно записать, что
Un2=anU0, (10)
где а„ = ±1; знак кодовых символов ап зависит от
метода аппроксимации; Uq — амплитуда импульса.
Согласно (5.3.7) для равномерного ФМн сигнала М„ =
= МУ~ . С учетом (10) неравенство (9) преобразуем к
следующему виду:
σ2<8(1— δ), (11)
где
(JV-IJ/2
*=w Σ anU- (12)
η^-(Ν—1)/2
§ 5.6
323
Как следует из формул (11) и (12), а2 зависит как
от метода аппроксимации (выбор знака а„), так и от
числа импульсов в сигнале N. В общем случае σ2
следует минимизировать одновременно как по а„, так и
по N. Но для простоты положим сначала, что N
фиксировано. Тогда σ2 минимальна, если максимальна 6.
Максимум последней при заданных £/ηι, Μί η Ν
возможен только тогда, когда
an = s\%nUm·
(13)
Докажем справедливость формулы (13) аналогично
доказательству второй теоремы, приведенной в [7].
Разобьем сумму (12) на последовательность частных сумм,
в каждой из которых есть слагаемые одного знака.
Рассмотрим частную сумму, в которой £/ηι>0. Так
как ап может принимать только два значения: =±=1, то
выбранная частная сумма максимальна, если ап = -f-1 ·
Рассмотрим другую частную сумму, в которой £/ni<C0.
Здесь след/ет выбрать ап = — 1. Если ап не совпадает
со знаком Um. то произведение αη£/η1 является
отрицательным и уменьшает величину суммы. Таким образом,
для выбора ап получаем правило (13). При этом из (11)
с учетом (12), (13) имеем
W-l)/2
г <8
мин
1
1
ϋη
ΫΜλΝ Li
п=— (/V-l)/2
Подставляя в (14) определение (5.3.56), получаем
(/V-l)/2
{~7Ш Σ ,Υη
cf <8
МИн
(14)
(15)
л=—(N—1)/2
Теперь необходимо найти значение N, минимизирующее
°мии· Предварительно необходимо вычислить сумму | γη|.
Представим
(JV-0/2 β/2 —(W—1)/2
Σ 1т«1= Σ Ιτ·ι+2 Σ им- <16>
л=—(/V—1)/2 л=—С/2 га=—(O/2 + l)
324
§ 5.6
Определим первую сумму в (16). Поскольку |γ„| при
«>0 и «<0 изменяется одинаково, будем
рассматривать только область гс^О. В области изменения η от
п = 0 до п, соответствующего крайнему максимуму в
левой части сигнала, функцию γη можно весьма точно
аппроксимировать косинусоидой (5.3:68) с нелинейной
фазой.
Крайнему максимуму сигнала соответствует п=—(D/2—
— \/"Щ2) = — пк. При п = — D/2 имеем γ_Β/2 =С(у7Г)*=»
«1/2. Аппроксимируя γη на участке от « = — пм до
η = — D/2 линейной зависимостью, можно найти первую
сумму в (16):
J |Т.|~Ц£в. 07)
л=— β/2
с точностью до малых высокого порядка эквивалентную
косинусоидальной аппроксимации (5.3.68) до n=±D/2.
Чтобы определить вторую сумму в (16), следует
воспользоваться асимптотическим представлением
интегралов Френеля в (5.3.57) при большом аргументе и рядом
Тейлора при малом. В результате можно записать
Y„^0,5+(« + D/2)(D)-1/2 при «« — D/2, (18)
что совпадает с выражением (5.3.64), если в нем
отброшены малые высокого порядка.
Используя линейное представление γη в окрестности
значений п = —D/2, можно вычислить и вторую сумму
в (16), а с учетом (17) и всю сумму (16). После этого,
дифференцируя (15) по Ν, в соответствии с (17), (18)
можно найти оптимальное значение N0m> при котором
получается а^иимин:
ЛГо„т»0+1, (19)
т. е. оптимальное число импульсов в сигнале
приближенно совпадает с числом импульсов, для которых точка
стационарной фазы лежит в пределах интегрирования от
О до π в (5.3.43).
§ БЯ
32Б
В качестве примера рассмотрим сигнал с
квадратичным фазовым спектром, рассчитанный по точным
формулам (5.3.57), (5.3.58) при D = 36. Фазовый спектр такого
сигнала описывается параболой (5.3.52) (рис. 5.14,
сплошная линия).
it· 9> гж w
г
Рис. Б.14.
Сигнал рассчитан для значений η от 0 до |я| = Р. В
соответствии с правилом (13) доставлен гдискретныйГФМн
сигнал (дп = ±1), а затем с помощью равенства в (15)
вычислена σ2 и /8 как функция числа импульсов 'JJ в сигна -
ле. Зависимость <з^Вн/8 от Ν, приведенная на рис. 5.15,
имеет минимум при N=.37, соответствующем точному
значению, рассчитанному по -формуле (19).
326
§Б.в
Наличие минимума а можно объяснить, если
рассмотреть слагаемое
(/V-l)/2
8-=шг Σ |γ«1· (20)
n=—(/V-l)/2
входящее в (15). При N<0,5D 'сумма в (20) растет
пропорционально JV, и с учетом У N в знаменателе (20) bt
растет пропорционально УЫ. Поскольку при |«|<0,5D
огибающая сигнала является косинусоидой, α2(, (ΛΓ) имеет
0,6 Ас;-
0,5 \
о,* V" 1—I—I—I—I—I—I
о,з Г^ —. . _
42 -S ___,.
0,1 ^= = =^
о\—I—I—I—I—I—I—I—I—LJ—I—I—
1 5 9 13 17 21 25 29 33 J7 <й Ϊ5 <* Η
Рис. Б.1Б.
несколько промежуточных минимумов. При N>0,5D
сумма в (20) растет очень медленно, так как
увеличение N соответствует добавлению малых импульсов на
краю сигнала. А изменение YN в знаменателе приводит
к уменьшению δι. Промежуточный случай (19) и
определяет максимум максиморум δι (20), при котором
σ (15) минимальна.
минν '
На рис. 5.16,а изображен неравномерный ФМн
сигнал с квадратичным фазовым спектром при N = 37,
рассчитанный по формулам (5.3.56) — (5.3.58).
Максимальный боковой пик его автокорреляционной функции ра-
§ Б.6
327
вен 1,5%. На рис. 5.16,6 представлен соответствующий
ему дискретный ФМн сигнал, определенный согласно
формуле (13), автокорреляционная функция которого
приведена на рис. 5.16,в. Максимальный боковой пик
им l
такой автокорреляционной_функции_ равен 5/37=^0,135,
что несколько меньше lf\/N=lf[ 37. Таким образом,
при переходе от неравномерного сигнала к равномерному
боковые пики автокорреляционной функции увеличились
примерно на порядок, но все же остались малыми.
На рис. 5.14 пунктиром изображен фазовый спектр
такого сигнала. На первый взгляд отличие фазового
спектра от параболы невелико. Но наличие нескольких
максимумов у фазового спектра приводит к появлению
328
§ 5.6
нескольких точек стационарной фазы, что не позволяет
определить сигнал непосредственно с помощью метода
стационарной фазы при предположении единственности
точки стационарной фазы (см. § 5.3). Именно поэтому
не имеет смысла уравнение (5.3.48). Отметим, что син-
тезириуемые дискретные ФМн сигналы и сигналы Бар-
кера характеризуются сходством фазовых спектров
(сравните рис. 5.14 и 4.6 для N=13).
' Τ
-
11
II
11
noon
ι
10
111
111
1
1v
* * *) i
:.:.:.:.:.:.l
I
Ι1Ι1Ι1ΙΪ
ΙΪΙΡΪ<
ПИ Π Π ΠΙ
ι Ι
1111111
... JSUUUllll
»)
Рис. Б.17.
Среднеквадратичная оценка боковых пиков. Если
в формуле (l)/?mi является идеальной автокорреляционной
функцией (5.3.4), то оа равна сумме квадратов боковых
пиков автокорреляционной функции /?„,„. Число^боковых
пиков Rml равно Ν— \**Ν, так как из-за симметрии
фазового спектра согласно (4.1.73) боковые пики при
нечетных т равны нулю. Поэтому среднеквадратичное
значение боковых пиков автокорреляционной функции /?т2
равно
§5.β
329
\
Полагая согласно (19) N = D + \**D, из формулы (15)
с учетом (17) находим выражение для σ2, подставляя
которое в (21), получаем
7?m=]/8(l — 2|/2"/ii)/W =0,№]'y~N~\f\/~N. (22)
Таким образом, рассмотренный метод синтеза дает
результат, который довольно часто встречается на
практике [5—7, 25, 34, 84, ПО]1.
Возможности уменьшения боковых пиков
автокорреляционной функции. Приведенный метод синтеза ФМн
сигналов позволяет найти равномерный сигнал, который
может быть использован в качестве исходного для
поиска минимаксного сигнала с помощью ЦВМ. При этом
значительно сокращается машинное время то
сравнению с методом «перебора», так как изменяются знаки
у меньшего числа импульсов. Изменять знаки следует
у импульсов, которые расположены около нулей
исходной косинусоиды (5.3.68). Чтобы дополнительно
уменьшить боковые пики, следует изменить число импульсов
в сигнале, добавляя или уменьшая импульсы на краях
сигнала, поскольку равенство (19) приближенное.
Синтезируемый сигнал обладает симметрией, что приводит
к пропаданию боковых пиков автокорреляционной
функции при нечетных т. Если нарушается это свойство
симметрии, то число боковых пиков становится равным
2(N—1)«2N, а их среднеквадратичное значение
уменьшается по сравнению со значением боковых пиков (22)
в 1/2 раз и составляет 0,63/l/Af,что совпадает с
результатами для равномерного, но не дискретного ФМн
сигнала, приведенными в [7].
На рис. 5.17,а приведен исходный равномерный
сигнал с N=109. Максимальные боковые пики
автокорреляционной функции такого сигнала составляют 13/109
и —15/109. Изменением знаков двух импульсов
(обозначены стрелками на рис. 5.17,6) боковые пики уменьшены
до 13/109 и —11/109. Измененные импульсы расположе-
1 В работе (110] синтез ФМн сигналов произведен на основе
теории разностных классов. Расчеты на ЦВМ показали, что при
Af<100 можно найти минимаксные сигналы с максимальными
боковыми пиками автокорреляционных функций порядка (0,6—0,8)/У"Л.
330
§ 5.6
ны симметрично относительно середины сигнала. Если
нарушить симметрию (рис. 5.17,в), то максимальные
боковые пики станут равными ±10/109. Отметим, что
измененные импульсы на рис. 5.17,в выбраны произвольно.
Были также проведены расчеты для сигналов с N=
= 1021».
Первоначально боковые пики составляли θ9/102Ι. После
изменения знаков нескольких характерных импульсов
боковые пики были уменьшены до 51/1021.
Синтез, основанный на аналогии с ЧМ сигналами.
Результаты, полученные в § 5.5 для многофазных
сигналов, можно обобщить на ФМн сигналы с фазами 0 и π.
В частности ФМн сигналы можно определять на основе
ЛЧМ сигнала или близкого к нему. Такое определение
основано на том, что фаза наилучших сигналов —
сигналов Баркера — меняется по закону, близкому к
параболическому.
На рис. 5.18 изображен закон Изменения фазы
сигнала Баркера при N=13 в виде ступенчатой линии. Из·
В(х)\
Рис. Б. 18.
ломы этой линии соответствуют смене знака в сигнале,
а высота каждой ступеньки равна π. Изменение фазы
1 Расчеты сигналов с Ы=Ъ7, 109 и 1021, их
автокорреляционных функций и фазового спектра (см. рис. 5.14) были проведены на
ЦВМ Г. Я. Гельманом.
§Б.в
331
сигнала за его длительность при условии, что импульсы
одного знака по фазе дают π, составляет θκ = 7π. В
течение каждого импульса фаза постоянна. На рис. 5.18
изображена также парабола
Ь(х) = 7п^у при x = -L, (23)
которая подчеркивает близость закона изменения фазы
сигнала Баркера к параболическому. Парабола (23)
построена в соответствии с условием, чтобы ее
максимальное значение равнялось θΜ = 7π.
Можно показать, что для всех сигналов Баркера
справедливо соотношение, связывающее максимальное
значение фазы ΘΜ и число импульсов Ν:
вм=^-. (24)
Покажем на примере, что метод, основанный на
аналогии с ЧМ сигналами, позволяет синтезировать ФМн
сигналы. Возьмем N=21. Тогда согласно (24) θΜ=Ππ и
Q(x) = 11π (jc/21)2. Последняя зависимость изображена
на рис. 5.19. -Однако следует определить, как в этом
случае выбирать фазы импульсов. Примем следующее
правило. Всю область изменения фазы разделим на ряд
областей горизонтальными штрих-пунктирными
линиями. Одни области соответствуют четным значениям,
кратным π, другие — нечетным. Если точка пересечения
кривой Θ(Χ) и вертикали, проведенной из конца
импульса сигнала, попадает в область четных фаз, то
начальная фаза принимается равной нулю, если в область
нечетных фаз —то равной π. На рис. 5.19 показана
вертикаль для импульса с номером «=12. Полученный
сигнал «ι изображен под графиком θ(χ) на рис. 5.19, а его
фаза показана ступенчатой линией. Максимальный
боковой пик автокорреляционной функции равен ±3/21,
т. е. сигнал «ι является минимаксным (при нечетном
числе слагаемых, образующих боковой пик, значение
суммы, равное 3, является минимальным, так как
сумма может быть равна единице только у сигналов типа
сигнала Баркера, которые при Ν>Ϊ3 не существуют).
332
§_Б.в
Может быть рассмотрен другой вариант метода
синтеза по аналогии с ЧМ сигналом, при котором не
требуется, чтобы импульсы имели одинаковую
длительность. Перемена знака в сигнале (рис. 5.19) происходит
Рис. Б. 19.
в те моменты времени, когда фаза достигает значений,
кратных π. Сигнал иг, форма которого показана на
рис. 5.19, получен таким методом. Длительности
импульсов одного знака сигнала «2 не кратны το, что
является недостатком. Подробно этот метод рассмотрен в
работе [71.
Грубая оценка боковых пиков автокорреляционной
функции. Все рассмотренные в данном параграфе
методы синтеза основаны на замене сигнала с огибающей,
изменяющейся по закону, близкому" к
«гармоническому», сигналом с равномерной огибающей.
Действительно, для сигнала с квадратичным фазовым спектром
закон изменения амплитуды импульсов на большей части
сигнала является косинусоидальным. Закон изменения
§ 5Л
333
частоты Q'(t) соответствует сигналу cos9(i) или sin9(i)«
квантуя который, получим искомый ФМн сигнал.
Пусть задан некоторый сигнал u(t) =sinQ(t)
(рис. 5.20,α, сплошная линия). Из этого сигнала
квантованием получен равномерный сигнал Ui{t) (рис. 5.20,а,
«)
и,и7 А)
\
ΙΛ
7
/
м
л
\
Л
ш
А \/1
/J 1У1 \
1 <"
Л
ю
тШ
Рис. Б.20.
пунктир). Разность между исходным и полученным
сигналами составляет &(t)=ui{t) — u{t) (рис. 5.20,6).
Согласно (2.1.19) при замене г на R автокорреляционная
функция исходного сигнала записывается в виде
/?(т)=-1 Г sin θ (t) sin θ (t — τ) dt.
(25)
Аналогично автокорреляционная функция
равномерного сигнала может быть представлена формулой
т
Ri (τ) = щ- Г [sin θ (t) + ε (t)] [sin θ (t — τ) + ε (t — τ)] dt =
τ
Τ Τ
= ^- Γ sin β (ί) Sin θ (ί— τ) Λ 4"^- [ε(ί)ε(ί—τ)Λ-|-
χ χ
Τ Τ
+^- Γ ε (ί) sin θ (ί — τ) Λ -f- J- f sin θ (t) ε (t — τ) dt. (26)
334
§ 5.6
Здесь Ei=\ ·Τ>Ε. Первые два слагаемых являются
автокорреляционными функциями, причем первая —
исходного сигнала, а вторая — разности ε(ί). Два
последних слагаемых определяют взаимокорреляционные
функции sin θ (ί) и ε(ί)· Оценим одно из двух последних
слагаемых. Обратим внимание на то, что максимумы
функции e(t) сдвинуты относительно максимумов sin θ (ί) и
что сдвиг зависит от ширины рассматриваемого
полупериода исходного сигнала (грубо говоря, сдвиг равен
половине этого полупериода). Поэтому у
взаимокорреляционных функций в (26) с изменением τ максимумы e(t)
и sin θ (ί) находятся в иных временных соотношениях,
чем у автокорреляционной функции для sin θ (ί).
Поэтому при совпадении первых максимумов sin θ (ί) и
ε(ί) (например, точки Л4 и Л2) другие максимумы не
совпадают и два последних интеграла в (26) будут
определяться той областью подынтегрального
выражения, которая близка к точкам Aii2, а от остальной
области вклады в указанные интегралы близки к нулю.
Следовательно, для грубой оценки боковых пиков
автокорреляционной функции исходного сигнала, обусловленных
взаимокорреляционными составляющими в (26),
достаточно учесть вклад в два последних интеграла (26)
только от знакопостоянного участка наибольшей
длительности. При этом sin9(f)«l и
τ tt
щ Г β (/) sin β (ί — z)dt**-^ Γ «(f) Λ, (27)
χ 0
где to — длительность выбранного знакопостоянного
участка функции ε(ί) наибольшей длительности.
Можно допустить, что в пределах этого участка
сигнала его фаза меняется линейно. Тогда интеграл (27)
равен
о
Найдем to — время, за которое фаза изменится иа
π/2. Допустим для простоты, что фаза меняется по
параболическому закону (аналог ЛЧМ). Тогда мгновен-
§ 5.7
335
ная частота сигнала Q'(t) =Wt/T. Если ширина спектра
№=2π/τ0, а Ν = Τ/τ0,το
Полагая t = ί0, а θ (ί0) = -g-, из (29) получаем, что
Согласно (28), (30) грубая оценка интеграла (27) равна
0,36/ \ίΝ. Так как в (26) суммируются два таких
интеграла и автокорреляционная функция разности ε(ί), то можно
считать, что боковые '^пики автокорреляционной функции
имеют величину порядка l/j/Ж
Оценка (30) получена на основе довольно грубых
рассуждений, но, тем не менее, совпадает со
среднеквадратичной оценкой (2), а следовательно и с оценкой,
приведенной в [7]. Конечно, можно получить в
некоторых случаях и меньшие величины боковых пиков, но
в большинстве случаев они близки к величине 1/|/4V.
Оценка (SO) получена при учете наибольших по
длительности участков сигнала, соответствующих его
началу. Поэтому возникающие из-за этих участков боковые
пики автокорреляционной функции должны быть
расположены близко от основного, что подтверждают расчеты.
Таким образом, на основании полученных
результатов можно полагать, что для больших N
детерминированные методы расчета равномерных ФМн сигналов
позволяют найти сигналы, боковые пики
автокорреляционных функций которых близки к ^IVN.
5.7. СИНТЕЗ ЧАСТОТНО-МОДУЛИРОВАННЫХ
СИГНАЛОВ ПО ТЕЛУ НЕОПРЕДЕЛЕННОСТИ
Постановка задачи. В § 5.3—5.6 были рассмотрены
вопросы синтеза сигналов, корреляционные свойства
которых зависят только от одной переменной —
времени. В тех случаях, когда требуется измерять и
336
§ 5.7
дальность (время), и скорость (частота Допплера),
корреляционные свойства сигналов зависят уже от двух
переменных. Поскольку фаза корреляционной функции
с точки зрения измерения параметров (дальности и
скорости) интереса не представляет, то синтез сигнала
следует производить по телу неопределенности. Основной
задачей является синтез сигнала с хорошими
разрешающими способностями по дальности и скорости. Тело
неопределенности такого сигнала близко к идеальному
(см. рис. 2.12).
Сначала рассмотрим синтез ЧМ сигналов. Положим,
что
U(t) = U0e,w при \t\<T(2. (1)
Тело неопределенности такого сигнала согласно § 2.4
определяется в соответствии с формулой (2.3.19), (1)
и может быть представлено в виде
|Λ(τ,Ω)| = 4-
Правая часть выражения (2) при τ = const представляет
амплитудный спектр импульса вида ехр 1[θ(0—Q(t—τ)].
В области слабой корреляции сечение тела
неопределенности ЧМ сигнала должно иметь как можно
меньшую высоту, чтобы боковые пики тела
неопределенности были малыми. Но, как было показано в § 2.9,
функция сечения тела неопределенности при T=const и
заданной огибающей сигнала постоянна. Поэтому, чтобы
боковые пики были наименьшими, указанное сечение
должно иметь наибольшую ширину. Это означает, что
энергетический спектр импульса ехр ΐ[θ(ί)—Q(t—τ)] должен
быть широким. Следовательно, импульс должен быть
частотно-модулированным, при котором для вычисления
интеграла (2) можно использовать метод стационарной
фазы.
Асимптотическое вычисление тела неопределенности
ЧМ сигнала в области слабой корреляции. Фазовая
функция в интеграле (2)
77 2
61[θ(ί)-θ(<-χ)] + Ι«^
-772+χ
(2)
φ(ί) *=θ(ί)—θ(ί—τ) +Ωί.
(3)
§5.7
337
Допустим, что существует одна точка стационарной
фазы to, определяемая уравнением
φ' (t0) = О ИЛИ Ь' (t0) - θ' (ί, - τ) + О = 0. (4)
Допущение о единственности точки стационарной
фазы является естественным, поскольку при нескольких
точках возможна интерференция их вкладов в тело
неопределенности, при которой уровень боковых пиков
в некоторых точках плоскости (τ, Ω) оказывается
больше, чем в других. При изменении Ω точка стационарной
фазы to передвигается в интервале (—Τ/2+τ, Г/2).
Асимптотическое значение тела неопределенности (2),
определенное в соответствии с (3.1.39), будет равно
|/?(τ,Ω)|^ /2π (5)
Формула (5) связывает сечение тела
неопределенности τ=const с фазой сигнала и справедлива для области
слабой корреляции. Поскольку функция сечения (2.9.2)
(интеграл от [R (τ, Ω)|2) не зависит от фазы сигнала"
и постоянна при τ = const (§ 2.9), то наилучшим в
смысле уменьшения боковых пиков является случай, при
котором
l^(x,Q)lx=const = const. (6)
При этом сечение тела неопределенности имеет
наибольшую ширину, а боковые пики в сечении одинаковы, и,
следовательно, минимальны. Следует заметить, что
такой подход к синтезу соответствует минимаксному
критерию (9.1.2).
-Соотношение (6) выполняется при условии, что
φ" (ίο) = const, (7)
причем <р"Ца)ф~0. Невыполнение условия <f>"(tn)=£0 может
привести к тому, что |/?(τ, Ω)| достигнет больших
значений, сравнимых'с |/?(0,0)| = 1. Естественно, если φ"(ί„)->
—»0, то это еще не означает, что | R (τ, Ω) {—»оо, так как
равенство (5) —асимптотическое и прн φ"(ίο) —»-0 в зна-
338
§ Б.7
менатель формулы (5) входят другие члены,
значительно превышающие φ"(ίο).
Примем за основу уравнение (7), которое должно
быть справедливым для всех t0, лежащих в интервале
(τ—Г/2, Г/2). Вычисляя вторую производную φ"(ίο) из
(3) и подставляя ее в (5), получаем
8" С.— τ) — 6"(i„) = const = c. (8)
Дважды интегрируя^выражение (8) по tn, находим
θ (t0 - τ) - 9 (ί0) = -f t] +\cfo + <y (9>
Допустим, что b(t) можно представить многочленом вида
в(0=5>к'к· (Ю)
k=0
Тогда I
ν«-τ)=να4«-τ)Κ (llj
k=o
Разность между (10) и (11) при t = t0 записывается как
8 (*.-*)-β С.) = Χ MC»-^-"?]·' (12>
*=о
Наивысшая степень переменной to в квадратных скобках
(12) равна k—1, что можно доказать, раскрывая
(t0—τ)\ С другой стороны, в выражении (9) наивысшая
степень to равна 2. Поэтому, чтобы дифференциально-
разностное уравнение (8) имело решение, необходимо
положить
aft==0 при &3э4. (13)
Следовательно, фаза сигнала, тело неопределенности
которого имеет равномерно распределенные боковые
пики при t = const, описывается уравнением
з
8(ο=Σ «***. (14)
ft=0
в котором ао—начальная фаза; a^t — постоянный сдвиг
§ 53
339
по частоте. Так как эти слагаемые не определяют
характер сигнала, то можно положить ao=«i = 0.
При заданной ширине спектра сигнала (или заданной
величине девиации мгновенной частоты сигнала)
наличие члена a2t2 приводит к уменьшению коэффициента аз-
Коэффициент а3 определяет значение φ"(ίο), так как
φ"(ί0)=6αΆτ. Следовательно, чем больше а3> тем
меньше |/? (τ, Ω)|. Поэтому сигнал следует выбирать так,
чтобы а2 = 0.
Окончательно закон изменения фазы ЧМ сигнала
запишем в виде
b(t)=-Lt' при \t\<T/2, ■(№)
где аг=Ь1Ъ.
Мгновенная частота ЧМ сигнала изменяется по
квадратичному закону:
Q'(t)=bt2 при \t\^T/2. (Т6)
Свойства сигнала с квадратичной частотной
модуляцией были подробно рассмотрены в § '3.4, где было
показано, что его тело неопределенности близко к
идеальному.
5.8. СИНТЕЗ ФАЗОМАНИПУЛИРОВАННЫХ
СИГНАЛОВ ПО ТЕЛУ
НЕОПРЕДЕЛЕННОСТИ
Постановка задачи. Для решения задачи синтеза ФМн
сигнала, тело неопределенности которого близко к
идеальному, воспользуемся формулой (4.1.79), согласно
которой можно записать
\R{m-za,ij)\ =
где
[Н(х — y)H(x)eimxdx
2πΝ
—π
(1)
У = й\1 (2)
го (у) —сечение вдоль оси частот тела неопределенности
340
§ 5.8
прямоугольного импульса длительностью to;
Я(х) = |Я(х)|е,фМ (3)
— спектр кодовой последовательности.
Формула (1) определяет сечение тела
неопределенности ФМн сигнала вдоль оси частот при постоянном
τ = mto-
Следует отметить, что в формуле (1) в отличие от
(5.7.2) интегрирование"] производится по частоте, а не по
времени, и, кроме того, имеется множитель га (у). Интеграл
*
в (1) представляет спектр „импульса" Н(х— у)Н(х),
причем т— дискретная величина. Так же, как и в § 5.7,
допустим, что в области слабой корреляции интеграл
должен вносить малый вклад в тело неопределенности
при различных т. Из-за ограниченности функции
сечения (2.9.2) наилучшим в смысле уменьшения боковых
пиков является случай, когда интеграл имеет одно и то
же значение на возможно большем интервале измене-
» *
ния т. При этом «импульс» Η (χ — у) Η (χ) должен
обладать «частотной» модуляцией; т. е. для нахождения
интеграла в (1) можно воспользоваться
асимптотическим методом.
Асимптотическое решение задачи синтеза. Допустим,
как и в § 5.7, что имеется одна точка стационарной
фазы. Используя формулу (3.1.39), с учетом (3) запишем
асимптотическое выражение для тела неопределенности
(1):
ιff(тт. ιοί-1 гЛу) '"(*'-у>""(*■"
1 *П | ΝΫΤπ νΠΨ"(*·-ΐΟ-Ψ"(*·)Ι
(4)
Точка стационарной фазы согласно (3.1.38)
определяется из уравнения
f(xa-y)'-f (x„)+m = 0 (5)
При изменении т функция г0(у) в 'формуле (4) остается
постоянной, а изменяются числитель и знаменатель. Чтобы
модуль | R(mz0, у) \ был постоянным, необходимо иметь
постоянное отношение числителя к знаменателю, что
§ 5.8-
341
приводит к дифференциально-разностному уравнению,
решение которого в настоящее время не найдено.
Поэтому для упрощения задачи положим, что |//(х)| =
= Ϋ"Ν, τ. е. | Н{х) | является постоянной величиной. Это
аналогично постоянству огибающей в задаче с ЧМ сиг-
Ни
JUL
J L
t
б)
Pi
к. 5.2
1.
налом (§ 5.7) и предопределяет в какой-то степени
поведение тела неопределенности вдоль оси времени, где
боковые пики будут малыми. При принятом допущении (4)
приобретает вид
'^"H»>rh-V^i I· (6)
Для того чтобы | R (тт„, у) | = const, надо положить
Ψ" (*. —У) —ψ (*.) = const. (7)
Уравнение (7) совпадает по форме с уравнением (5.7.8).
Следовательно, решением уравнения (7) является
(8)
342
§ 5.8
Таким образом, ФМн сигнал с кубичным законом
изменения фазового спектра должен иметь тело
неопределенности, близкое к идеальному (см. рис. 2.12). По
сравнению с КЧМ сигналом у сигнала с кубичным
изменением фазового спектра все спектральные
(временные) соотношения заменены на временные (спектраль-
Рис. 5.22.
ные). Поэтому можно считать, что тело
неопределенности ФМн сигнала с кубичным фазовым спектром
близко к телу неопределенности КЧМ сигнала.
Символы ап сигнала определяются согласно (4.1.44):
π
«n = -^ jexp^i-^+i/wjiix· (9)
§ Б.9
343
Из (9) следует, что значения символов совпадают со
значениями составляющих спектра КЧМ сигнала (3.4.6),
взятых в точках, кратных to. Огибающая сигнала (9)
неравномерна (рис. 3.12), а фазы импульсов принимают
два значения: 0 и π.
На рис. 5.21,α представлен ФМн сигнал для FT = 20,
а на рис. 5.21,6 — равномерный ФМн сигнал, полученный
из первого квантованием по амплитуде. Малые
импульсы на краях первого сигнала отброшены. Число
импульсов в равномерном сигнале jV=22. Тело
неопределенности равномерного ФМн сигнала1 (рис. 5.21,6)
представлено на рис. 5.22. Наибольший боковой пик равен
0,37.
5.9. ОДНОКАНАЛЬНЫЙ СИГНАЛ
Иногда нет необходимости измерять скорость
объекта. В таких случаях нецелесообразно использовать
сигналы с хорошими разрешающими способностями по
дальности и по скорости, поскольку для обработки этих
сигналов требуется многоканальная схема. Если тело
неопределенности имеет узкий основной пик, ширина
которого вдоль оси частот составляет 2π/7\ а диапазон
изменения частоты Допплера Ω = 2π/^, то необходимо
FgT каналов. Каждый канал должен быть настроен на
свою частоту. Следовательно, когда не требуется
измерять скорость, целесообразно использовать сигнал,
который можно обрабатывать одноканальной схемой.
Такой сигнал условно будем называть одноканальным.
Решение задачи синтеза одноканального ЧМ сигнала
приведено в работе [1].
Рассмотрим принципиальную возможность
нахождения одноканального сигнала. Допустим, что имеется
сигнал, комплексная огибающая которого
U(t) = Uaem при |/1<7/2. (1)
1 Сигнал, форма которого показана на рнс. 5.21, н его тело
неопределенности рассчитаны В. В. Рубель.
344 § Б.9
Его корреляционная функция согласно (2.3.19)
Г/2
R (,, Q) = JL j 6,[θ(<)-θ('-χ)+β" Л при τ > О- (2)
-Г/2 + Т
Определим, чему может быть равен максимум |/?(τ,Ω)|
при τφΟ, ΩφΟ. Так как модуль интеграла (2) меньше,
чем'интеграл от модуля, то имеем оценку
Т/2
|Λ(,.Ω)|<4- j |eW>-°«-^«<' |Л = 1—i при τ>0.
-Г/2 + х
(3)
Следовательно, максимальное значение
/?Μ(τ,Ω)=1-Μ, (4)
где знак модуля взят для —Г^гг^Г.
Таким образом, в произвольном сечении тела
неопределенности максимальное значение не может быть
больше, чем определяемое формулой (4). Поэтому однока-
нальный сигнал должен быть таким, чтобы при любом
значении Ω в допустимом диапазоне частот Допплера
сечение тела неопределенности имело максимальное
значение (4).
Согласно (2) выражение (4) справедливо, если
9(f) —в(/—τ)_|-Ωί = ί, (5)
где с = const.
Допустим, что фаза может быть представлена
многочленом:
e(f)=£ak7*. (6)
Подставляя (6) в (5), получаем
0/ + £ак[/ь-(*-т)*]=с. (7)
ft=2
§ Б.9
345
Раскрывая круглые скобки в (7) и группируя слагаемые,
получаем
&, + *!*+ *.*Ч \-bK_ltK-l=c, (S)
где
60 = -α2τ2 + α3τ3Η (—\faKxK;
61 = Ω + 2α1τ-3α,τ«Η (—lf~l Κακτκ~ι; .
bKi_t=KaKx.
Положим c — ba. Тогда имеем уравнение
b1t-j-b1tt+...+bK_ltK-l = 0, (10)
в котором все слагаемые линейно независимы. Поэтому (10)
справедливо, если
bl = 0,bt = 0 \_ι = °· <П)
Из уравнения 6 , = 0 получаем ак = 0, из Ьк_2 = О
получаем, что и α =0 и т. д. Наконец, уравнению
fr2 = 0 соответствует а3 = 0, и из уравнения ^ = О
следует, что Ω-|-2α2τ = 0. Следовательно,
aft = 0 при fe>2, (12)
аа = —Ω/2τ^=0. (13)
Таким образом, одноканальным является сигнал с фазой
β(/) = α,/\ (14)
т. е. ЛЧМ сигнал, подробно исследованный в § 3.1.
Тело неопределенности такого сигнала имеет вид хребта,
протянувшегося из одного угла плоскости (τ, Ω) в
другой (см. топографическую диаграмму, рис. 3.3). Этим
и объясняется свойство одноканальности ЛЧМ
сигнала— при любом значении Ω сечение тела
неопределенности имеет максимум (4).
346
§5.10
Для ФМн сигналов необходимо обратиться к
представлению корреляционной функции через спектр
сигнала^, е. к (5.8.1). Полагая для простоты | Η (χ) | =
= \Ζ~Ν , получаем
\R(mtvy)\ =
IjJM) Ρ е' 1Ψ(*-»)-ф(*)+тх] άχ
2π J
(15)
где у = 9л0;
Ψ'(λ:)—фазовый спектр кодовой последовательности
ФМн сигнала.
Сравнивая (15) и (2), замечаем, что их
подынтегральные выражения имеют одинаковый вид. Поэтому
одноканальный ФМн сигнал должен иметь обобщенный
фазовый спектр, изменяющийся по параболе,
аналогичной (14), т. е. быть четным. Но ФМн сигналы с
начальными фазами импульсов, равными 0 или π, обладают
нечетным фазовым спектром (§ 4.1). Следовательно,
среди ФМн сигналов не может быть одноканального.
5.10. СИСТЕМЫ ОРТОГОНАЛЬНЫХ
И КВАЗИОРТОГОНАЛЬНЫХ СИГНАЛОВ
Ортогональными называются сигналы Uh(t), которые
удовлетворяют соотношению
о
где Ε — энергия сигнала.
Полагаем, что все сигналы, обладают одинаковой
энергией. Сравнивая (1) с (2.1.7), можно показать, что
(1) является взаимокорреляционной функцией, когда
сдвиг во времени между сигналами uk(t) и Ui(t)
отсутствует. Последовательность {«&(/)} образует систему
ортогональных сигналов. Число сигналов в системе может
быть конечным или бесконечным. В обоих случаях оно
счетно.
Ортогональные сигналы применяются по следующим
причинам. Во-первых, эти сигналы разделяются при син-
§ Б.10
347
хронном приеме без взаимных помех. Это следует из
нижнего равенства в (1), которое является следствием
линейной независимости ортогональных сигналов [111].
Во-вторых, использование ортогональных сигналов
увеличивает помехоустойчивость системы передачи
информации при повышении основания кода [37, 112].
К ортогональным сигналам предъявляются
следующие основные требования.
1. Огибающая каждого сигнала должна быть близка
к постоянной в течение длительности сигнала. Т. При
этом будет излучен сигнал с наибольшей энергией при
ограниченной пиковой мощности передатчика. Отметим,
что большинство известных систем ортогональных
сигналов удовлетворяет этому требованию.
2. Система сигналов должна занимать наименьшую
допустимую полосу частот. Если ширина спектра
произвольного сигнала из системы равна F, то система
сигналов должна занимать такую же полосу частот.
Расчеты показывают, что это требование не выполняется
для большинства известных систем ортогональных
сигналов. Оказывается, что спектры сигналов либо
смещаются друг относительно друга, либо по-разному
концентрируются в отведенной для сигналов полосе частот.
3. Боковые пики взаимокорреляционных функций
сигналов должны быть малыми. Это означает, что
τ
r*i{x) = -jr\uh{t)ul(t — x)dt^l при— Τ<τ<Τ. (2)
τ
Такое требование является особо важным в
асинхронных системах связи, когда различные абоненты работают
независимо друг от друга [113, 114].
В данном параграфе исследуем спектральные и
корреляционные свойства некоторых систем ортогональных
сигналов. Сначала рассмотрим одну физическую задачу,
решениями которой являются ортогональные сигналы.
Краевая задача Штурма — Лиувилля. Если дано
линейное однородное дифференциальное уравнение
Pn{x)y™{x) + Pn-i{x)y"-l{x) + ...+pl{x)y,{x) +
+ w(x)y(x)=0, (3)
348
§ 5.10
то краевая задача [115] состоит в том, чтобы найти такое
решение у(х) уравнения (3), которое удовлетворяет
краевым (или граничным) условиям. Краевые условия
связывают значения у(х) и всех производных до ί/(η_1)(Χ)
включительно на краях заданного отрезка [а, в].
Краевая задача имеет решения только при определенных
значениях параметра μ = μϊ, которые называются
собственными значениями. Решение, соответствующее
определенному μι, называется собственной функцией.
Известно [115—117], что собственные функции
ортогональны. Изменяя μ,, можно получить систему
ортогональных функций. Наибольшее развитие, по-видимому,
получила краевая задача Штурма — Лиувилля, которую
и рассмотрим.
Система Штурма — Лиувилля есть дифференциальное
уравнение второго порядка
-$-+[V-Q(t)]u = 0 . (4)
совместно с краевыми условиями [115]
и'(0) — Аи(0) = 0, и'(*) + Яи(1!)=0. (5)
Согласно (5) отрезок, на котором ищется решение,
равен [0, π]. Величины h и Η — постоянные. Будем
полагать, что h-φΐ) и НФО.
Решения системы (4), (5) —собственные функции
Uk(t)—являются ортогональными. Пусть λ*,
λ;—собственные значения, a uh(t) и ui(t)—соответствующие им
собственные функции, причем lh¥=k- Тогда
т(-4?-)+(»:-о)—°-
Умножая первое равенство на ui, второе — на Uh,
вычитая из второго первое равенство и интегрируя
полученную разность по t, находим
["ft (■) и'ι (*) - и, («) и\ (*)] - [ик (0) и', (0) - и, (0) и\ (О)] +
+ {*]-%) $"и*И|Л = 0, (6)
о
§ 5.10
349
где согласно краевым условиям (5) слагаемые в
квадратных скобках равны нулю.
Так как Ккфк, то
π
[uk(i)ut(t)dt = 0 при кф1, (7)
о
т. е. собственные функции действительно ортогональны.
При исследовании спектральных свойств
ортогональных сигналов необходимо знать асимптотическое
представление собственных функций.
Асимптотическое представление собственных функций.
Уравнение (4) можно переписать как
-з£-+я««=<г(/)И. (8)
Методом вариации произвольных постоянных [115]
можно показать, что общее решение неоднородного
уравнения (8) имеет вид
t
и, (t) = с, cos Xt -f- ca sin U -f- -J- \Q (χ) и (χ) sin λ (t — χ) dx, (9)
о
где u(t) определено с точностью до постоянного
множителя. Положим и(0) = 1. Тогда с1=1. Учитывая первое
равенство в (5), получаем с2=АД. При этом уравнение
(9) преобразуется к следующему виду:
t
и (Ζ) == cos Xt + -γ sin λί -^—i- Cq (χ) и (χ) sin X(t — x) dx. (10)
о
В дальнейшем выбираем достаточно большие λ, при
которых собственную функцию (10) можно представить
как >
«(/)=costt + ?i^il, (11)
где α (λ, t) —ограниченная на интервале [0, я] функция.
350
§ Б. 10
Подставляя (11) в (10), шолучаем асимптотическое
представление k-Ά собственной функции, которую
записываем в нормированном виде:
4V^[±(A+4-j<3M<<*-a)+^]*n«.
о
(12)
где
Ек =
-к
о
J u\{t)dt\
с =
±(h + H + ±r\Q{x)dxy
При большом k — оо функция ψΐι(ή'-*- V2j^co&kt.
Смещение спектров собственных функций
системы Штурма—Лиувилля.4 Пусть спектром сигнала u(t)
является g(u>)· Допустим, что u(t) — действительная
функция времени. Тогда | g (ω) | — четная функция частоты.
Поэтому средняя частота спектра сигнала определяется
аналогично формуле (1.5.2):
"ср·
Ш J-lfMI'*·-0· (13)
а „эффективная* ширина спектра й^вфф — аналогично
эффективной длительности сигнала (1.5.3):
W. =■
2^ ^**\g{*)\*dm. (14)
эф φ. Ίτ.
Используя равенство Парсеваля, получаем
W2
βφ φ
оо
= 4 jKWl'di· (15)
§ Siie
351
Эффективная ширина спектра характеризует
местоположение ftp оси частот основной части спектра.
Действительно, если взять сигнал u(t) =cos(2nki/T)
длительностью Τ, то №Θφφ = 2π£/7\ т. е. й?Эфф совпадает с
несущей частотой, которой соответствует середина
спектра.
Для нормированных сигналов вида ^{t)=^u{t)jYE
соотношение (15) приобретает вид
К*= ί^ίΟΙ'Λ· (16)
—00
Вычислим согласно (16) эффективную ширину
спектра собственной функции (12). Дифференцируя (12) и
обозначая через $(t, k) ограниченную функцию,
получаем
+ rft + ^fQ(*)iix-^+p-^WA. (17)
о
Подставляя (17) в (16) и отбрасывая малые высокого
порядка, получаем
π
о
π t
о о
В пределе при k —» оо выражение (18) записывается как
π t
ft-00 J ч J J
Второе слагаемое в (19) от номера собственной
функции k не зависит и определяется только особенностями
системы Штурма — Лиувилля (4), (5): величинами А,
Η и функцией Q(t). Поэтому при различных k это
слагаемое неизменно, т. е. с ростом k эффективная ширина
Μ
§ 5.10
спектра 1Уэффл растет пропорционально k. Это
означает, что спектры собственных функций системы
Штурма— Лиувилля смещаются друг относительно друга по
частоте. Характер смещения Ψ3φφ такой же, как и для
косинусоиды в примере, приведенном после формулы
(15). Если в системе (4), (5) изменить масштаб
времени так, чтобы сигналы были ортогональны на
отрезке [О, Т], то масштаб по оси частот изменится в я/Т
раз. Поэтому смещение по частоте окажется
пропорциональным kitjT.
\9рМ\
Яо
0,75
0,5
0,25
Pi
fl·
А
у]
ι
kl
ДА;
^
•
Л&.
/у
&
Рго
fr
У
>С"^ч
X
\1
VC
к
Рис. Б.23.
№
го
24
Ψ
Были найдены спектры ряда классических
ортогональных функций [105, 118] (многочленов Лежандра,
Чебышева и др.), являющихся решениями различных
задач Штурма — Лиувилля. В качестве примера на
рис. 5.23 приведены модули спектров многочленов
Лежандра Pk(t) для k=\\ 2; 20; 21. Приведенные графики
построены по формулам1
gP„ П = ёо
0 /5F
τ γα
*,_>> = *.75F
2m +1
3,
3,2m+-Ly 2 J|'
-\ 2
2m +
(20)
(21)
где Sfn(x) — функции Бесселя первого рода; g0 = const.
Из сравнения спектров, представленных на рис. 5.23,
видно, что они смещены друг относительно друга по ча-
1 Спектры, представленные на рнс. 5.23, рассчитаны Л Η
Волковым
§ 5.10
533
стоте. Аналогичное смещение наблюдается и для
других известных классических ортогональных многочленов.
Следует отметить, что в общем случае вопрос о
сдвиге по частоте спектров ортогональных функций остается
открытым, так как рассмотренная задача Штурма —
Лиувилля является частной и, кроме того, решениями
задачи Штурма — Лиувилля могут быть только
непрерывные функции, т. е. дискретные функции
исключаются из рассмотрения.
Однако до настоящего времени не найдено полных
ортогональных систем непрерывных сигналов, спектры
которых не сдвинуты по частоте. Это в какой-то мере
говорит о том, что результат задачи Штурма —
Лиувилля (сдвиг по частоте) может иметь общий характер.
Косвенным подтверждением этого является
существование решения обратной задачи Штурма — Лиувилля.
Нахождение собственных функций по дифференциальному
уравнению и краевым условиям составляет прямую
задачу Штурма — Лиувилля. Если задана полная система
ортогональных собственных функций с
соответствующими собственными значениями (спектр собственных
значений), то определение дифференциального уравнения
составляет обратную задачу Штурма — Лиувилля. Для
регулярных условий (отрезок определения функций
конечен и сами собственные функции ограничены)
обратная задача имеет решение [119]. Следовательно, в
такой системе спектры ортогональных функций будут
сдвинуты по частоте друг относительно друга.
Система квазиортогональных сигналов со сдвигом
несущей частоты. В практических системах наиболее
часто применяются сигналы с постоянной огибающей, т. е.
такие, которые можно записать как
«k(/) = cos[fcD0£fek(0] при 0</«7\ (22)
Можно показать [105], что среди систем сигналов,
удовлетворяющих краевой задаче Штурма — Лиувилля, не
существует системы из сигналов вида (22). Однако
можно построить большое число квазиортогональных
систем из сигналов вида (22), для которых отличие от
ортогональности будет незначительном.
354
§5.10
Рассмотрим систему сигналов
uk(/) = cos [«,/ + (*-1)-^+9 (/) + ak-J-'
при 0</<7\ й=1,2 М. (23)
Здесь Μ — число пар сигналов в системе,
принципиально любое, в том числе Μ—>-оо. Величина аь равна либо
нулю, либо единице, что соответствует наличию двух
квадратурных сигналов — косинусоидального н
синусоидального. Следовательно, общее число сигналов равно
2М. Сдвиг по частоте между сигналами составляет
2л/Т.
Для сигналов (23) корреляционный интеграл (2) при
т = 0 записывается в виде
τ τ
о о
τ
+ (ek-*i)-i-]^ + -^Jcos[2»0/ + (* + *-2).^_|-
о
+ 26(/) + (ak + a,)-jj-]d/. (24)
Основной вклад в гы вносит первый интеграл в
выражении (24), который обозначим Ru. Поскольку 2Е = Т, то
τ
/?«=4-|εοβ[(*-0^+(α»-α,)-ί-]Λ. (25)
о
После вычисления интеграла (25) получаем
!1 при & = /, aft = a2,
0 при & = /, ацфаъ (26)
О при k=fcl.
Оценим второй интеграл в (24), пользуясь
асимптотическими методами {55]. В общем виде, отбросив
несущественный постоянный сдвиг фазы (α*+'αί)π/2, этот
§ 5.10
355
интеграл можно записать как
τ
5,«=4-fcos2Krf + e(0]rf'. (27)
где β|Μ = ω0+ (* + / —2) «/7\
Введем обозначения
_ t _ 2π Г
Χ— r , y0_—, /?_4πτ-;
Μ*) = 2^; ?(*) = * + Μ*)-
Тогда
^^Rey^^Refe"^*.
ί
(28)
(29)
Точки стационарной фазы нет внутри отрезка
интегрирования (29), так как ω0>θ'(ί) {55]. Поэтому
воспользуемся разложением ^(р) в асимптотический ряд
ff(p)
J_¥l /" 1 У fit(x) if<p(*)
«ρ
k=0
ipj f'{x)
1
0'
где
U*) = i; ЫдоНг^
(χ)
(30)
(31)
Оставляя только первый член ряда (30), можно
записать
3(Р)ъ
ijsf (х)
J/"fW
1 1 H"f U+t,(x)|
— г с
«^-«-[Ι+β',Ιχ)]
(J 'о
1
0
Поскольку согласно (28)
в'1(*)-±да-.
(33)
356
§5.10
TO
, 2 + -§-[θ'(0) + θ'(Γ)]
|-7(/>)|<——; f- гт f τ- (34)
4πΎΓ [, + ^-9'(0)J[a + -^-9'(r)J
Полагая для определенности d'{t)>0 и θ'(0) <6'(Г),
приближенно получаем
№)K-W7· (35)
Таким образом, если длительность сигнала
составляет более десяти периодов высокой частоты (Т/То>\0),
то модуль второго интеграла (27) согласно (35) не
превышает 2% от максимально возможного и им можно
пренебречь. При этом
r>a~Rhi (36)
и систему (23) можно считать ортогональной с
точностью до малых величин, порядок которых определяется
формулой (35).
Следовательно, построение системы
квазиортогональных сигналов (23) основано на использовании
частотного сдвига между сигналами. Этот сдвиг кратен 2л/Г.
Нелинейная часть фазы всех сигналов Q(t) одинакова
для всех сигналов. Ее следует выбирать исходя из
требуемых взаимокорреляционных свойств системы
сигналов в целом. Например, если необходимо, чтобы
взаимные помехи были малыми при асинхронном приеме, то
сигнал должен выбираться из следующих соображений.
При системе сигналов, образуемой из одного исходного
сигнала путем частотного сдвига,
взаимокорреляционная функция двух сигналов представляет собой сечение
тела неопределенности для значения частоты Допплера,
равной расстройке по частоте между этими сигналами.
Следовательно, чтобы обеспечить минимум взаимных
помех, надо в качестве исходного брать сигнал, тело
неопределенности которого близко к идеальному (см.
рис. 2.12). В этом случае можно использовать сигнал
с квадратичной ЧМ, М-последовательности и др.
§ 5.10
357
Если ширина спектра, определяемая диапазоном
изменения мгновенной частоты Θ'{ί), равна F, то полоса
частот, занимаемая каналом связи, использующим 2М
ортогональных сигналов, составляет
FKaVi = FV(M-l)/T. (37)
При Μ порядка FT полоса частот канала связи
/гкан~2/г, т. е. в два раза больше, чем ширина спектра
одиночного сигнала. Обычно используется Μ сигналов,
чтобы не разделять сигналы при приеме по различию
начальных фаз (при этом коэффициенты а*, в (23)
равны нулю).
Фазоманипулированные ортогональные сигналы.
Приведенный ранее анализ относится к ортогональным
сигналам со сдвигом по частоте. В случае точной
ортогональности (1) рассмотренные сигналы непрерывны, что
подтверждается решением дифференциального
уравнения в краевой задаче. Квазиортогональные сигналы
могут быть как непрерывными, так и дискретными.
Известны также системы дискретных ортогональных
ФМн сигналов, ортогональность которых определяется
выбором формы сигналов. Наиболее распространены
ортогональные ФМн сигналы, построенные на базе
последовательностей (функций) Уолша. Кодовые
последовательности Уолша можно получить с помощью матрицы
Адамара. Матрицей Адамара называется ортогональная
квадратная матрица порядка Ν, элементами которой
являются символы ап=±\[79]. Ортогональной
называется матрица, строки которой взаимно ортогональны,
т. е. каждая строка отображает ортогональную
последовательность. Общий метод построения матрицы Адамара
сводится к следующему: если Ну — матрица Адамара
порядка N, то матрица
(38)
Hj+.=
является матрицей Адамара порядка 2N.
358
§ δ. ίο
Докажем это утверждение на примере [79]. Пусть
сначала Н0=1. Тогда матрицы
Н,=
н2=
1 1
1 —1
— 1 —1
— 1 1
(39)
(40)
являются матрицами Адамара. В ортогональности строк
матриц (39), (40) можно убедиться, определив
взаимокорреляционную функцию ФМн сигналов, которая в
общем виде записывается аналогично (2.1.7) и (4.1.65):
Rki(m) =
N
,п- т·
(41)
п=т+ 1
В (41) первый индекс символа α^η обозначает номер
последовательности (в матрице Адамара номер строки),
второй — номер символа в последовательности. Число т
определяет временной сдвиг между сигналами, равный
mto, a to — длительность одиночного импульса. Если
т = 0, то Ды(0) =Rhi-
Для последовательностей Уолша, которые являются
строками матрицы Адамара с N=2i, Rhi = 0, т. е.
последовательности Уолша ортогональны. При произвольных
значениях т взаимокорреляционная функция Rhi(m)
принимает различные значения, некоторые из них
сравнимы с максимальным значением, равным единице.
Последовательности Уолша имеют много общего с
тригонометрическими ортогональными многочленами вида
cos(nst/T) и s'm(nst/T), где s — целое число. Кроме
того, они являются функциями вида sign cos(nst/T) или
sign sin (nst/T). Поэтому спектры последовательностей
Уолша так же, как и спектры тригонометрических
многочленов, сдвинуты друг относительно друга в общей
полосе 1/то [118].
§5.10
359
Последовательности Уолша можно использовать как
основу для ортогональных последовательностей с
хорошими взаимокорреляционными свойствами.
Предварительно рассмотрим некоторые свойства
взаимокорреляционных функций.
Интегральные свойства взаимокорреляционных
функций. Для ФМн сигналов длительностью Т, у которых
авто- и взаимокорреляционные функции—действительные
функции времени, согласно (2.3.68) можно записать
следующее равенство:
J/£(x)dx= J/?k(x)/?!(x)rfx, (42)
—τ -г
дискретным аналогом которого является соотношение
Σ КМ) = Σ Я*С")Я|(т). (43)
m=-(/V—I) m=—(W—1)
Левая часть (43) пропорциональна квадрату
эффективного значения взаимокорреляционной функции k-το и
/-го сигналов, которое обозначим Вы. Тогда, по опреде
лению,
к=-ш=г Σ *>>■ (44)
/и =—(Ν—1)
Если N ^> 1, то
Λ/-Ι
m=—[N—\)
Правая часть (43) пропорциональна среднему
значению произведения двух автокорреляционных функций
k-το и /-го сигналов, которое всегда положительно, так
как левая часть (43) неотрицательна. Поскольку
Rk(0) = Ri(0) = 1, то слагаемое с m=0 в правой части
(43) равно единице. Если Rh(tn) =—Ri(m) при т^О,
то сумма произведений Rh(m) Ri(m) при тфО
отрицательна, т. е. правая часть (43) минимальна. Таким свой-
360
§ 5.10
ством обладают дополнительные последовательности
(§ 4.6). Можно показать, что уровень боковых пиков
взаимокорреляционных функций у дополнительных
последовательностей, взятых попарно, меньше, чем у
последовательностей, взятых из разных пар.
Построить систему, в которой все сигналы попарно
дополнительны, вряд ли возможно. Однако можно
составить систему, в которой все сигналы характеризуются
хорошими автокорреляционными функциями (с малыми
боковыми пиками). Для идеальной автокорреляционной
функции Rh{m) =0 при тФ§, поэтому правая часть (43)
равна единице, а
Л'=тЬг· (46)
Когда боковые пики не равны нулю, то из (43)
можно получить неравенство
^«^ Σ \Rb(m)WRd>n)\. (47)
ш=-(Л/-1)
Если положить | Rk (т) | = Уа/N, где α — постоянная,
зависящая от выбранной системы сигналов, то получим
*«</т· <48>
Оценки (46) и (48) получены при дискретном
представлении корреляционных функций. В действительности
усреднение по времени в (42) дает несколько иной
результат. Допустим, что автокорреляционные функции
идеальны, т. е.
!1 — при |τ |<τ0,
*· (49)
0 при τ0<|τ|<7\
Тогда правая часть (42) будет равна 2t0/3, a
1
Вы
— V 3-2Г VW ' ( 1
где Ν = Τ/το.
8 5.10
361
Из соотношений (42), (43) следует, что для
уменьшения боковых пиков взаимокорреляционных функций
надо составлять систему из сигналов,
автокорреляционные функции которых имеют малые боковые пики.
Рассмотрим пути уменьшения боковых пиков.
Пусть даны двз сигнала, у которых комплексные
огибающие U(t) и V(t) являются действительными
функциями времени, причем
\V(t)\ = l. (51)
Образуем новый сигнал
S(t) = U(t)V(t). (52)
автокорреляционная функция которого запишется в виде
00
Q^) = i \S(t)S(t-z)dt =
—00
00
= Ж §UV)V(t)U(t-z)V(t-x)dt. (53)
—00
Рассмотрим особенности интеграла (53). Для этого
вычислим вспомогательный интеграл
00 00
г= ^Q,b)dz = j^r^U(x)V(x)U(x-T)V(x-T)X
—00 —00
XU (y)V (y)U (у - x)V(y - z)dxdy άτ. (54)
Меняя в (54) порядок интегрирования, выделяя
сомножители, зависящие от τ и интегрируя по τ, замечаем, что
00
—00
00
1
2£
—00 —00
00 00
\u(x)V(x) ^U(y)V(y)Q(x-y)dydx. (55)
362
§5.10
Переменные в правой части (55) не разделяются.
Чтобы выяснить зависимость ζ от свойств сигналов U
и V, можно предложить следующий качественный метод.
Выделяя интеграл по у в (55)
Р(х)= \u{y)V{y)Q{x-y)dy, (56)
-00
который является функцией х, и оценивая его с
помощью неравенства Буняковского — Шварца:
Р(х)<У ]\U(y)V(y)\*dy ]Q>(x-y)dy =
— 00 —00
= V2£V/ ^*(τ)άτ = ν^Εζ, (57)
—00
получаем, что оценка Р(х) от χ уже не зависит. Если
вместо интеграла по у в (55) подставить значение (57),
то в полученном выражении нельзя считать, что ζ
меньше или равно правой части, так как зависимость от χ
потеряна. Поэтому справедливым оказывается только
приближенное равенство, причем степень приближения
не определена:
°°
г~ГЖ \v{x)V{x)dx=\fjRuvVT, (58)
— оо
где Ruv — значение взаимокорреляционной функции
сигналов U и V при нулевом временном сдвиге, т. е. Ruv =
=Ruv(x) при т=0;УТ — нормирующий множитель,
обусловленный тем, что энергия сигнала V(t) равна Т.
Полагая в соответствии с (54), что
г=ф2Т, (59)
где Q — эффективное значение боковых пиков
автокорреляционной функции сигнала S (52), из (58) получаем
§5.10
363
Согласно (60) для уменьшения боковых пиков
автокорреляционной функции надо перемножить сигналы,
у которых Itvv мало. Предельным случаем является тот,
при котором <RUV = 0- Однако Q=^0. Поэтому полученный
результат обусловлен очень приближенной оценкой (55).
Отметим, что эмпирический метод уменьшения
боковых пиков взаимокорреляционных функций приведен
в работе [120]. При этом методе последовательности
Уолша посимвольно умножаются на специально
подобранный сигнал с хорошей автокорреляционной
функцией. В результате получаются новые последовательности
(модифицированный код Рида — Мюллера),
взаимокорреляционные функции которых лучше, чем у
последовательностей Уолша.
В заключение докажем, что если перемножить
ортогональные сигналы Uh(t) с сигналом V(t), который
удовлетворяет (51), то сигналы Sh(t)=Uh(t)V(t) будут
ортогональны.
Действительно,
J Sft (t) St (i) dt= J Uk (i) Ut (t) V2 (t) at =
—00 —00
= f Uh(t)U{{i)dt = 0 при кф1, (61)
—oo
поскольку согласно (51) V2(f) = l.
Сравнение ширины спектра системы ЧМ и ФМн
сигналов. Спектры ортогональных ФМн сигналов в явном
виде могут и не смещаться друг относительно друга в
отличие от спектров ЧМ сигналов. Примером может
служить система ортогональных сигналов, построенная на
основе модифицированного кода Рида — Мюллера [120].
Но для их передачи необходимо обеспечить полосу
канала, по крайней мере равную FKAB=2/xo, где το —
Длительность элементарного импульса. Отметим, что если
сигнал состоит ил N элементарных импульсов, то можно
построить N ортогональных сигналов (например, на
базе последовательностей Уолша). Сравним такую
систему с системой ЧМ сигналов (23). Пусть длительность
ЧМ сигналов равна Τ=Ντ0, а полоса частот — F=l/x0.
364
§5.10
Тогда N=FT и N ортогональных ЧМ сигналов займут
ту же полосу частот 2F, что и N ФМн сигналов.
Поэтому с точки зрения занимаемой полосы частот эти
системы эквивалентны.
ЛИТЕРАТУРА
1. Фалькович С. Ε Прием радиолокационных сигналов на
фоне флюктуациопных помех. Изд-во «Советское радио», 1961.
2. Ш и ρ м а и Я. Д, Голиков В. Н. Основы теории
обнаружения радиолокационных сигналов и измерения их параметров.
Изд-во «Советское радио», 1963
3. Гоноровский И С Радиотехнические цепи и сигналы.
Изд-во «Советское радио», 1963.
4 Л ё з и н Ю С Оптимальные фильтры и накопители
импульсных сигналов Изд-во «Советское радио», 1963.
5 Вакман Д. Е. Сложные сигналы и принцип
неопределенности в радиолокации Изд-во «Советское радио», 1965.
6 Тихонов В И. Статистическая радиотехника. Изд-во
«Советское радио», 1966
7 Вакман Д Ε Регулярный метод синтеза фазоманипули-
рованных сигналов. Изд-во «Советское радио», 1967.
8. Башарииов А. Е. Применение широкополосных
зондирующих сигналов при измерениях дальности и скорости (конспект
лекций). Изд МЭИ, 1965.
9. В а раки н Л. Е. Формирование и обработка сложных
сигналов в радиолокационных и радиосвязных системах. ВЗЭИС,
Министерство связи СССР, 1967
10. Гуревич М. С Спектры радиосигналов. Связьиздат, 1963.
11. Харкевич А А Спектры и анализ Гостехиздат, 1957.
12. Лернер Р. Μ Представление сигналов. Гл. 7 в кн.
«Лекции по теории систем связи». Пер с аигл , под ред. Б Р. Левина.
Изд-во «Мир», 1964
13 Гуткнн Л С Теория оптимальных методов радиоприема
при флуктуационных помехах. Госэнергоиздат, 1961
14 Харкевич А. А. Борьба с помехами. Физматгиз, 1963.
15. Вайнштейн Л. А, Зубаков В. Д. Выделение
сигналов на фоне случайных помех Изд-во «Советское радио», I960
16 Клюев Η И. Информационные основы передачи
сообщении. Изд во «Советское радио», 1966
17. ЭльсгольцЛ Э. Вариационное исчисление. Гостехиздат,
1958
18. Турин. Согласованные фильтры. «Зарубежная
радиоэлектроника», 1961, № 3, стр. 30
19. Варакин Л. Е. Действие помех на согласованный фильтр.
Труды научно-технической конференции
профессорско-преподавательского состава МЭИС, Министерство связи СССР, 1967, стр. 18.
20. Броуи В. М. Анализ линейных инвариантных во времени
366
Литература
систем Пер с англ , под ред В А Боднера Изд-во
«Машиностроение», 1966.
21 Мэзон С, Циммерман Г. Электронные цепи, сигналы
и системы. Пер. с англ, под ред П. А. Ионкина Изд-во
иностранной литературы, 1963
22. Виленкин Н. Я., Горин Е. А. и др. Функциональный
анализ. Под ред. С. Г. Крейна Изд-во «Наука», ]964.
23 Вудворт Φ Μ. Теория вероятностей и теория
информации с применением в радиолокации. Пер с англ, под ред. Г С Го
релика Изд-во «Советское радио», 1955.
24 Sussman S. Μ Least-square synthesis of radar ambiguity
functions. IRE Trans, on Inf Th , 1962, ν IT-8, № 3, ρ 367.
25. С т а л д е ρ, Кап. Граничные значения для пиков
корреляционных функций периодических дискретных последовательностей
ТИИЭР, 1964, т. 52, № 10, стр. 13Θ2.
26. S t u 11 С. A. A note on invariant relations for ambiguity
and distance functions. IRE Trans, on Inf. Th., 1959, ν ΙΤ-5, № 4,
p. 164.
27. R e i s F. B. A linear transformation of the ambiguity finction
plane. IRE Trans, on Inf. Th., 1962, v. IT-8, № 1, p. 59
28. S t u 11 С A. Some results of real-part /imaginary-part and
magnitude/ phase relations in ambiguity functions IEEE Trans, on
Inf Th., 1964, v. IT-10, № 4, p. 321.
29. Price R, Hofstetter Ε. Μ. Bounds on the volume and
height distributions of the ambiguity function. IEEE Trans, on Inf.
Th, 1965, v. IT-]], №2, p. 207.
30. Τ i 11 e b a u m E. L. A generalization of a two-dimensional
Fourier transform property for ambiguity functions. IEEE Trans, on
Inf. Th., 1966, ν IT-12, № 1, p. 80.
31. Τ i 11 e b a u m E. L., D e Claris N. Linear transformations
on the ambiguity functions. IEEE Trans, on Inf. Th., 1966, v. IT-12,
№ 2, p. 120.
32. В a κ μ a η Д. Е. Оптимальные сигналы, максимизирующие
частичный объем тела неопределенности «Радиотехника и
электроника», 1967, т. 12, № 8, стр 1352.
33. Rihaczek A. W. Delay-doppler ambiguity function for
wideband signals IEEE Trans on Aerosp. Elect. Syst., 1967, ν AES-3,
№ 4, ρ 705.
34. С о о к С. Ε., В е г η f e 1 d M. Radar signals. An introduction
to theory and application. Academic Press. New York — London, 1967.
35. D e В u d a R. An extension of Green's condition to cross-
ambiguity functions. IEEE Trans on Inf. Th., 1967, v. IT-13, № 1,
p. 75.
36. В a p а к и η Л. Е. Вопросы теории тела неопределенности
Труды II научно-технической конференции «Проблемы оптимальной
фильтрации», МЭИС, 1968, вып. 1, стр 14.
37. Котельников В. А. Теория потенциальной
помехоустойчивости. Госэнергоиздат, 1956
38. Μ и д д л τ о н Д. Введение в статическую теорию связи. Пер.
с англ., под ред Б. Р. Левина. Изд-во «Советское радио», т. 1, 1961,
т. 2, 1962.
Литература
367
39 Вудворт Φ. Μ, Дэвис И Статистическая теория
приема радиолокационных сигналов В сб «Теория передачи
электрических сигналов при наличии помех». Пер с аигл , под ред. Н. А. Же-
лезнова. Изд-во иностранной литературы, 1953.
40. Левин Б. Р. Теоретические основы статистической
радиотехники. Книга I Изд-во «Советское радио», 1966.
41. Саве лов А А. Плоские кривые Систематика, свойства,
применения Физматгиз, I960
42 «Таблицы интегралов Френеля». Изд-во АН СССР, ] 953.
43. К е 1 ] у Е. J„ Reed I. S., Root W L., The detection of
radar echoes in noise. Jour. Soc. Ind. Appl Math, I960, v. 8, № 7,
p. 309; № 9, p. 481.
44. В e 11 о P. Joint estimation of delay, doppler and doppler rate
IRE Trans, on Inf Th., I960, v. IT-6, № 3, ρ 330.
45. Келли Радиолокационное измерение дальности, скорости
и ускорения «Зарубежная радиоэлектроника», 1962, № 2, стр. 35.
46 Красногоров С. И Совместная оценка амплитуды,
фазы, расстояния и его производных радиолокационными методами
«Радиотехника и электроника», 1964, т. 9, № 1, стр. 78.
47. Келли, Вишне р. Теория согласованной фильтрации
целей, движущихся ускоренно с высокими скоростями. «Зарубежная
радиоэлектроника», 1965, № 10, стр 37.
48. Башаринов А. Е, Выделение радиолокационной
информации при приеме сигналов в шумах. Изд. МЭИ, 1966.
49 Рихачек Разрешение подвижных целей в радиолокации.
«Зарубежная радиоэлектроника», 1968, № 1, стр. 3
50. Л и η м а н. Полезное свойство обобщенной функции
неопределенности с линейной ЧМ. ТИИЭР, 1967, № 7, стр 188.
51. Кибблер. КЭВОРТ — устройство оптимальной обработки
пачечного радиолокационного сигнала с учетом ускорения целей
«Зарубежная радиоэлектроника», 1968, № 6, стр. 27.
52. Barker R Η. Group synchronizing of binary digital system.
In the book «Communication theory», ed. by W Jackson, London,
1953, ρ 273.
53. Кук. Повышение эффективности радиолокационных
устройств за счет сжатия импульсов. «Зарубежная
радиоэлектроника»,, I960, № 9, стр. 38
54 Смирнов В. И Курс высшей математики, τ II Гостехиз-
дат, 1954.
55. В а к м а н Д. Е. Асимптотические методы в линейной
радиотехнике. Изд-во «Советское радио», 1962.
56. Ε в г ρ а ф о в Μ А. Асимптотические оценки и целые
функции. Физматгиз, 1962.
57. D е В u d a R. Stationary phase approximations of FM
spectra. IEEE Trans, on Inf. Th., 1966, v. IT-12, № 3, ρ 305.
58. Кук, П а о л и л о. Предыскажение сжимаемых импульсов
мощной РЛС, обеспечивающее эффективное ослабление боковых
лепестков. ТИИЭР, 1964, т. 52, № 4, стр. 404.
59. Palmier! С. A, Cook С. Е., Bernfeld Μ, Paolil-
1 о J. Matched filtering, pulse compression and waveform design,
p. Π J. Microwave Journal, Ί964, v. 7, № 12, p. 70.
368
Литература
60. Φ о к В А Диффракция радиоволн вокруг земной
поверхности Изд-во АН СССР, 1946.
61 Пересада В. Π К вопросу о вычислении интегралов
в конечных пределах с быстропеременной фазой. «Радиотехника»,
1957, № 9.
62. ВаракинЛ Ε Спектр сигнала с кубичной угловой
модуляцией. Труды учебных институтов связи, 1966, вып 32, стр 47.
63. Эр д ей и А Асимптотические разложения, Физматгиз, 1962.
64. Град штейн И С, Рыжик И М. Таблицы интегралов,
сумм, рядов и произведений. Физматгиз, 1962
65 Г ант махе ρ Φ. Р. Теория матриц Изд-во «Наука», 1967.
66. S t о г е г J Ε., Τ и г у π R. Optimum finite code groups Proc.
IRE, 1958, v. 46, № 9, p. 1649.
67. Поляк Ю В, Мошетов Р. В. О существовании кодов
Баркера Научные труды радиотехн. ин-та АН СССР, 1959, т. I,
вып. I, стр. 124
68. Иванова И М.КетковЮ Л.ЯмпольскаяТ С.
О существовании кодов Баркера «Известия вузов», Радиофизика,
I960, т. 3, № 5, стр 911
69 Τ ury n R., St ore r S. On binary sequences. Proc. Am.
Math Soc, 19Θ1, v. 12, № 3, p. 394.
70. Τ ury η R. On Barker codes of even length. Proc. IEEE,
1963, v. 51, № 9, p. 1256.
71. LuenbergerD С On Barker codes of-jeven length. Proc.
IEEE, 1963, v. 51, № 1, ρ 230.
72. Мешковский К- А, Кириллов Η Ε. Кодирование
в технике связи Изд-во «Связь», 1966.
73 ЛёзииЮ СО вычислении амплитудных спектров
сигналов с известной автокорреляционной функцией. «Электросвязь»,
1966, № 9, стр 62
74. Zierler N. Several binary-sequences generators. Proc. Am.
Math. Soc, 1956, v. 7, № 8, p. 675.
75. X а ф ф м е н Д. А. Синтез линейных многотактных
кодирующих схем. В сб. «Теория передачи сообщений», под ред В И. Си-
форова. Изд-во иностранной литературы, 1957, стр. 52.
76. Ц и ρ л е ρ Η Линейные возвратные последовательности.
«Кибернетический сборник», под ред О. Б. Лупанова. Изд-во
иностранной литературы, 1963, № 6, стр 55.
77. Э л с π а с Б. Теория автономных линейных
последовательных сетей. «Кибернетический сборник», под ред. А. А. Ляпунова
и О. Б. Лупанова. Изд-во иностранной литературы, 1963, № 7,
стр 90.
78. Π и τ е ρ с о н У. Кодирование и исправление ошибок для
кодов Боуза—Чоудхури. «Кибернетический сборник», под ред.
О. Б Лупанова. Изд-во иностранной литературы, 1963, № 6, стр.25.
79. Питер сон У. Коды, исправляющие ошибки. Пер с англ,
под ред. Р. Л. Добрушина Изд-во «Мир», 1964
80. С у π ρ у н А. П., У д а л о в Б. А. Избыточное кодирование
при передаче информации двоичными кодами. Изд-во «Связь», 1964.
81. Μ а тс он X., Соломон Г Новая трактовка кодов Боу-
Литература
369
за — Чоудхури В сб «Теория кодирования» Пер с англ, под ред
Э. Л. Блоха. Изд-во «Мир*, 1964, стр. 7.
82. Пелехатый М. И, Потапов Н. А Принципы
формирования четверичных шумоподобных ФМ сигналов для систем
связи В сб «Фазовая и относительная фазовая телеграфия». Изд-во
«Связь», 1967, стр 68
83 Φ и ш б е й и, Риттенбэч. Корреляционная '
радиолокационная станция с псевдослучайной модуляцией. «Зарубежная
радиоэлектроника», 1962, № 5, стр 28
84. Golomb S. W, et al, Digital Communication with space
applications. Prentice — Hall, Englwood Cliffs New Jersey. 1964.
85 Виноградов И. М Основы теории чисел. Изд-во
«Наука», 1965
86 TitsworthR С Optimal and minimax sequences
International Telemetry Conference. London, 1963, ρ 381
87 Roberts Τ A Analysis and synthesis of linear and
nonlinear shift register generators International Telemetry Conference,
London, 1963, ρ 390.
88 Reed 1 S, Stewart R M, Note on the existence of
perfect maps. IRE Trans, on Inf. Th., 1962, v. 1T-8, № 1, p. 10.
89 G о 1 а у Μ J. Ε Complementary series. IRE Trans, on Inf.
Th, 1961, v. 1T-7, № 2, p. 82
90. G о 1 а у Μ. J С. Note on complementary series. Proc. IRE,
1962, ν 50, № 1, ρ 84.
91. Kruskal J В Golay's complementary series. IRE Trans, on
Inf. Th, 1961, v. 1T-7, № 4, p. 273.
92 Jauregui S Complementary series of length 26 IRE Trans,
on Inf. Th , 1962, ν 1Τ-8, № 4, p. 323
93 Turyn R. Ambiguity functions of complementary sequences,
IEEE Trans on Inf. Th , 1963, v. 1T-9, № 1, p. 46.
94. В е л τ и. Четверичные коды для импульсного
радиолокатора «Зарубежная радиотехника», 1961, № 4, стр 3.
95. Lerner R. Μ Signals with uniform ambiguity functions.
IRE National Conv. Record, 1958, pt. 4, p. 27.
96 Key E. L, F о w 1 e Ε. Ν Haggarty R. D. A method of
designing signals of large timebandwithd product IRE Intern. Conv.
Rec. H961, pt. 4, p. 146.
97. Клаудер. Радиолокационные сигналы с высокой
разрешающей способностью по дальности и по скорости. «Зарубежная
радиоэлектроника», 1961, № 1, стр. 15.
98 Η a i f πι е η D. A The generation of impulse-equivalent pulse
trains. IRE Trans, on Inf. Th., 1962, v. IT-8, № 5, p. 10.
99. Η a r g e r R. O. A note on realization of ambiguity functions.
IEEE Trans, on Sp El. Tel, 1963, SET-9, № 4, p. 127.
100. Хаффмеп Д А Исследование сигналов, эквивалентных
импульсу «Раднотехтча», 1964, Kz 8, стр. 3.
101. Кук. О некотором классе сжимаемых импульсных
сигналов с нелинейной ЧМ. ТИИЭР, 19G4, № 11, стр. 1477.
102. Рихачек Синтез радиолокационных сигналов и
улучшение разрешения целей ТИИЭР, 1965, т. 53, № 2, стр. 137.
370
Литература
103 Фоул Синтез ЧМ импульсных сигналов для систем со
сжатием «Зарубежная радиоэлектроника», 1965, № 6, стр. 49.
104. Бараки н Л Е. Синтез фазоманипулированных сигналов
по аналогии с частотно-модулированными сигналами. Труды
научно-технической конференции. Проблемы оптимальной фильтрации.
Изд-во «Советское радио», 1967, стр 48.
105. ВаракинЛ Ε К вопросу о построении системы
ортогональных сигналов Труды научно-технической конференции
Проблемы оптимальной фильтрации Изд-во «Советское радио», 1967,
стр. 72.
106 Мишина А П, Проскуряков И В Высшая алгебра.
Физматгиз, 1962
107 Η е i in i 1 ] е г R. С Phase shift pulse codes with good
periodic correlation properties IRE Trans, on Inf. Th., 1961, ν ΙΤ-7, № 4,
ρ 254
108. Frank R.ZadoffS. Phase shift codes with good
periodic correlation properties. IRE Trans on Inf. Th , 1962, ν ΙΤ-8, № 6,
p. 381.
109. Фрэнк. Многофазные коды с хорошими
непериодическими корреляционными свойствами. «Зарубежная радиоэлектроника»,
1963, № 12, стр. 39.
110. В о е h in e r A. Binary pulse compression codes. IEEE Trans,
on Inf. Th., 1967, v. IT-13, № 2, p. 156.
111. Харкевич А А. Очерки общей теории связи. Гостех-
издат, 1955.
112. Фиик Л. М. Теория передачи дискретных сообщений.
Изд-во «Советское радио», 1963.
113. Варакин Л. Е., Пышкин И М. К вопросу применения
сложных сигналов в адресных системах связи. «Электросвязь»,
1967, № 1, стр. 72.
114. Варакии Л. Е., Пышки и И. М. О помехоустойчивости
асинхронно-адресной системы связи со сложными сигналами и
частотно-временным кодированием. Труды учебных институтов связи,
1967, вып. 35, стр. 98.
115. Самсоне Д. Обыкновенные дифференциальные
уравнения, т. I, 2. Пер. с итал. Н. Я- Виленкина. Изд-во иностранной
литературы, 1953
116. Кампе де Ферье Ж-, Кемпбелл Р., Петьо Г.,
Фогель Т. Функции математической физики. Пер. с фр. Н. Я·
Виленкина, Физматгиз, 1963.
117. Левитан Б. Μ Разложение по собственным функциям.
Гостехиздат, 1950
118. ВаракинЛ Е, Волков Л. Н. Спектры классических
ортогональных сигналов Труды научно-технической конференции.
Проблемы оптимальной фильтрации. Изд-во «Советское радно»,
1967, стр. 84.
119. Левитан Б. М. Операторы обобщенного сдвига и
некоторые их применения Физматгиз, 1962.
120. Сандерс Р. В Система связи «Диджилок». В сб.
«Передача цифровой информации». Под ред С И. Самойленко. Изд-во
иностранной литературы, 1963
ПРЕДМЕТНЫЙ
Адамара матрица 357, 358
Автокорреляционная функция
47
идеальная 274
кодовой последователь
ности Баркера 197
Лежандра 24]
Мипаследовательности
226, 227, 228
усеченной 202
нелинейной последова
тельности 249
периодической кодовой
последовательности 234
· прямоугольного импульса
48
— —, свойство симметрии 194
сигнала с квадратичным
фазовым спектром 297, 298
с квадратичной
частотной модуляцией (КЧМ)
156
с линейной частотной
модуляцией |(ЛЧМ) 136
с симметричной
линейной частотной
модуляцией (СЛЧМ) 146
фаэомаиипулироваино-
го (ФМн) 19], 092, 291, 337
периодического 207
Аналитический сигнал 50
База сигнала 7, 26, 106
Баркера кодовая
последовательность 197
Белый шум 7
Вектор сигнальный 46, 47
Гамма-функция 163
Граница области сильной
корреляции 79, 87, 116
УКАЗАТЕЛЬ
Дельта-функция 62, ]]7, 320,
32]
Диаграмма топографическая
78, 80, 95, ] ]4
Дискрет 180, 185
D-код 257, 260, 261
—, корреляционные свойства
262
Допплера частота 60, 62, 72, 82
Дисперсия оценок 85
Е-код 264
—, автокорреляционная
функция 266, 267
Закон частотной модуляции 88,
90, 91, 114
квадратичный 91, 93
— симметричный
линейный 9], 93, 96
Намерение дальности 98, ] 12,
115
— скорости 98, 106, 107
— ускорения 98, 108, Ί12
Импульс тактовый 203
Интеграл Дюамеля 8, 42
— корреляционный 7, 8, 354
— Френеля .127, 128
Кодовая комбинация
запрещенная 243, 244
Комплексная огибающая
корреляционной функции 60, 64,
65, 69, 142, 154, 170, 171
сигнала 50, 52, 55, 69,
101, 126, 139, 148, 161, 167,
185, 188, 192
, спектр 53
Композиция дополнительных
последовательностей 255
, травило
присоединения 255, 25Θ, 257, 268, 260
—, — чередования 265
372
Предметный указатель
Корень первообразный 218
Коррелятор 8
Корреляционная функция 62,
73, 101, 102, 107
— 'комплексной огибающей 122
М-'Паследо®ательнО'СТи
228, 229
, усредненные
характеристики 72
широкополосного сигнала
122
Критерий равномерного
приближения 269
— минимаксный 270
Коэффициент передачи
линейного фильтра 10
— — согласованного фильтра
10, 11, 17
Лагранжа множитель 19
Леж,андра кодовая
последовательность 238
— символ 239, 240
Линия задержки 309, 310
— уровня 78, 79, 88
Матрица квадратная 193
— состояний регистра 211—213
— характеристическая 214, 215
Метод комплексной огибающей
49
— максимального
правдоподобия ®2
— перебора 318
— перевала 148
— стационарной фазы 131, 132,
135, 276, 290, 305, 318
Многочлен характеристический
214, 217
— неприводимый 217
— первообразный 218, 219, 220,
221
Модуляция степенная 90
М-последовательность,
автокорреляционная функция 226,
227
—, основные свойства 201
— усеченная 230
Напряжение на выходе
фильтра 8, 11, 72, 74'
Норма 46
Область сильной корреляции
— 79, 89 ,97,1113
—, размеры 172
— слабой корреляции 79
Обнаружение сигнала при
неизвестном ускорении 115
Оператор задержки 299
Отклик фильтра 8, 11, 16, 39
Оценка близости формы двух
сигналов 44, 45
Перемножитель 8
Помеха в виде белого шума
и узкополосных помех 20
—, изменение спектра 18
— импульсная 29
— и собственные шумы
приемника 27
— шумовая 25
, спектральная плотность
25
Последовательность
дополнительная 250
— минимаксная 236, 243
, параметры 237
— ортогональная 261
— парная 258
Поверхность неопределенности
76, 78
, боковые пики 78
Правило присоединения 257
Прием неоптимальный 22
Приемник оптимальный 7
Радиус влияния точки
стационарной фазы 133, 154
Разрешающая способность по
дальности 75, 79, 272
по скорости 76
Регистр сдвигающий 202, 207,
243, 244
Сжатие сигнала во времени 33,
39, 40, 79
по частоте 33, 41 '
Сигнал минимаксный 231
— ортогональный 46, 346, 347
— простой 7, 40, 79
— с квадратичным фазовым
спектром 293, 325
— сложный 7, 36, 37, 39
— широкополосный 122
Предметный указатель
373
Синтез сигналов 269
, исходные данные 273
, критерий максимального
бокового пика 289, 298
, — минимаксный 269, 283
, — минимума
среднеквадратичного отклонения
270, 274
, — равномерного
приближения 269, 309
, определение
амплитудного спектра 298
, — фазового спектра 273,
' 276, 290, 292, 293, 298
, — энергетического
спектра 273
, основанный на аналогии
с ЧМ сигналом 328, 331
, — на использовании
оператора задержки 299
с линейной ЧМ 312
с квадратичной ЧМ 315
с квадратичным фазовым
спектром 325
Спектр кодовой
последовательности 180, 198
— комплексной огибающей
сигнала с КЧМ 148
с ЛЧМ 127, 316,
317
с СЛЧМ 139, 140, 141
' с частотной
манипуляцией 168, 169
— сигнала амплитудный 14, 35,
38, 54
с КЧМ 150, 151, 153
с ЛЧМ Ί34, 142
с СЛЧМ 141
фазовый 14, 35, 38, 54,
273, 276, 335, 337
Схема совпадений 244, 245—
247
Тело неопределенности 76, 77,
80, 111
, влияние закона ЧМ 88,
89,91
идеальное 81
, основной пик 81
, сечение 77, 91, 96, 97,
158, 337
сигнала с КЧМ 97, 147
с СЛЧМ 96, 146
Точка стационарной фазы 132,
134, 140
порядка т 161, 164
Точность измерения дальности
108, 112
скорости 108
ускорения 108, 112
Ускорение объекта 99, 100
Фаза сигнала 50
Фильтр активный 8
— пассивный 8
— согласованный 9, 10
Функция взаимокорреляционная
43, 44, 46, 47
— решетчатая 180
— сечения 116
— собственная 348, 349
Характеристики сигнала 5
— корреляционные 42
— с точки зрения разрешающей
способности и точности 78
Частотная модуляция
нелинейная высшего порядка 160,
161, 165
Ширина спектра
прямоугольного импульса 6
Широкополосный сигнал 122
', объем тела
неопределенности 125
Штурма — Лиувилля краевая
задача 347
Эйри функция 149
Энергия сигнала 5, 6
Якоби символ 243
ОГЛАВЛЕНИЕ
Предисловие . . . . .3
Глава 1. Общие свойства сложных сигналов ... 5
1.1 Простые и сложные сигналы . . 5
1.2 Краткие сведения из теории оптимального
приема сигналов .... ... 7
1.3 Отношение сигнал/помеха на выходе согласо
ванного фильтра при произвольной помехе . 17
1.4. Выигрыш в помехоустойчивости при
использовании сложных сигналов 25
1.5. Сжатие сложных сигналов . ... 33
Глава 2. Корреляционная функция и тело неопределенности 42
2.1. Корреляционные свойства сигналов . . 42
2.2. Комплексная огибающая сигнала и ее спектр 49
2.3 Комплексная огибающая корреляционной
функции и ее основные свойства ... 58
2.4. Тело неопределенности 72
2 5 Совместное измерение дальности и скорости.
Поверхность второго порядка .... 82
2 6. Область сильной корреляции. Поверхность
четвертого порядка 89
2.7. Совместное измерение дальности, скорости и
ускорения 98
2.8. Область слабой корреляции 116
2.9. Влияние широкопрлосиости сигналов
иа уровень боковых пиков корреляционной
функции 122
Глава 3. Сигвалы с частотной модуляцией 126
3.1. Сигнал с линейной частотной модуляцией . 126
3.2. Сигнал с симметричной линейной частотной
модуляцией 139
3.3. Сигнал с квадратичной частотной модуляцией 147
3.4. Сигналы с нелинейной частотной модуляцией
высшего порядка 159
3.5. Сигналы с частотной манипуляцией . . . 166
Глава 4. Фазомаиипулироваииые сигналы 177
4.1 Общие свойства фазоманипулированных
сигналов 177
4.2. Сигналы Баркера . . 197
4.3. Λί-последовательности 201
4.4. Последовательности Лежандра и Якоби . 234
4.5. Нелинейные последовательности .... 243
4.6. Дополнительные последовательности . . 250
4.7. Четверичные коды 257
Глава' 5. Синтез сложных сигналов 269
5.1. Особенности синтеза сложных сигналов . 269
5.2. Синтез частотно-модулированных сигналов
по автокорреляционной функции .... 272
5.3. Синтез неравномерных фазоманипулирован-
ных сигналов по автокорреляционной
функции (асимптотический метод) .... 280
5.4. Синтез неравномерных фазоманипулирован-
ных сигналов по автокорреляционной функции
(метод Хаффмена) 299
5.5. Синтез многофазных сигналов .... 305
5.6 Синтез равномерных фазоманипулированиых
сигналов 317
5.7. Синтез частотно-модулироваиных сигналов по
телу неопределенности 335
5.8. Синтез фазоманипулированиых сигналов по
телу неопределенности ...... 339
5.9. Одноканальный сигнал 343
5.10 Системы ортогональных и
квазиортогональных сигналов 346
Литература ... ... . . ... 365
Предметный указатель 371
ЛЕОНИД ЕГОРОВИЧ ВАРАК.ИН
ТЕОРИЯ СЛОЖНЫХ СИГНАЛОВ
Редактор Ю. А. Рюжин
Художественный редактор 3. Е. Вендрова
Обложка художника Б. К. Шаповалова
Технический редактор 3. Н. Ратникова
Корректоры: Е. П. Озерецкая, И. Г. Багрова
Сдано в набор 10/VII 1989 г.
Подписано в печать 25/Ш 1970 г.
Т-05248
Формат 84Х Ю8'/э«
Бумага машниомеловлииая
Объем 19.74 усл. п. л. Уч.-изд. л. I7.3S9
Тираж 12 000 экз Зак. 23У>
Цена 1 р. 28 к.
Издательство .Советское радио".
Москва, Главпочтамт, п/я 693
Московская типография № 10 Главполнграфпрома
Комитета по печати
при Совете Министров СССР
Москва, Шлюзовая наб . д 10