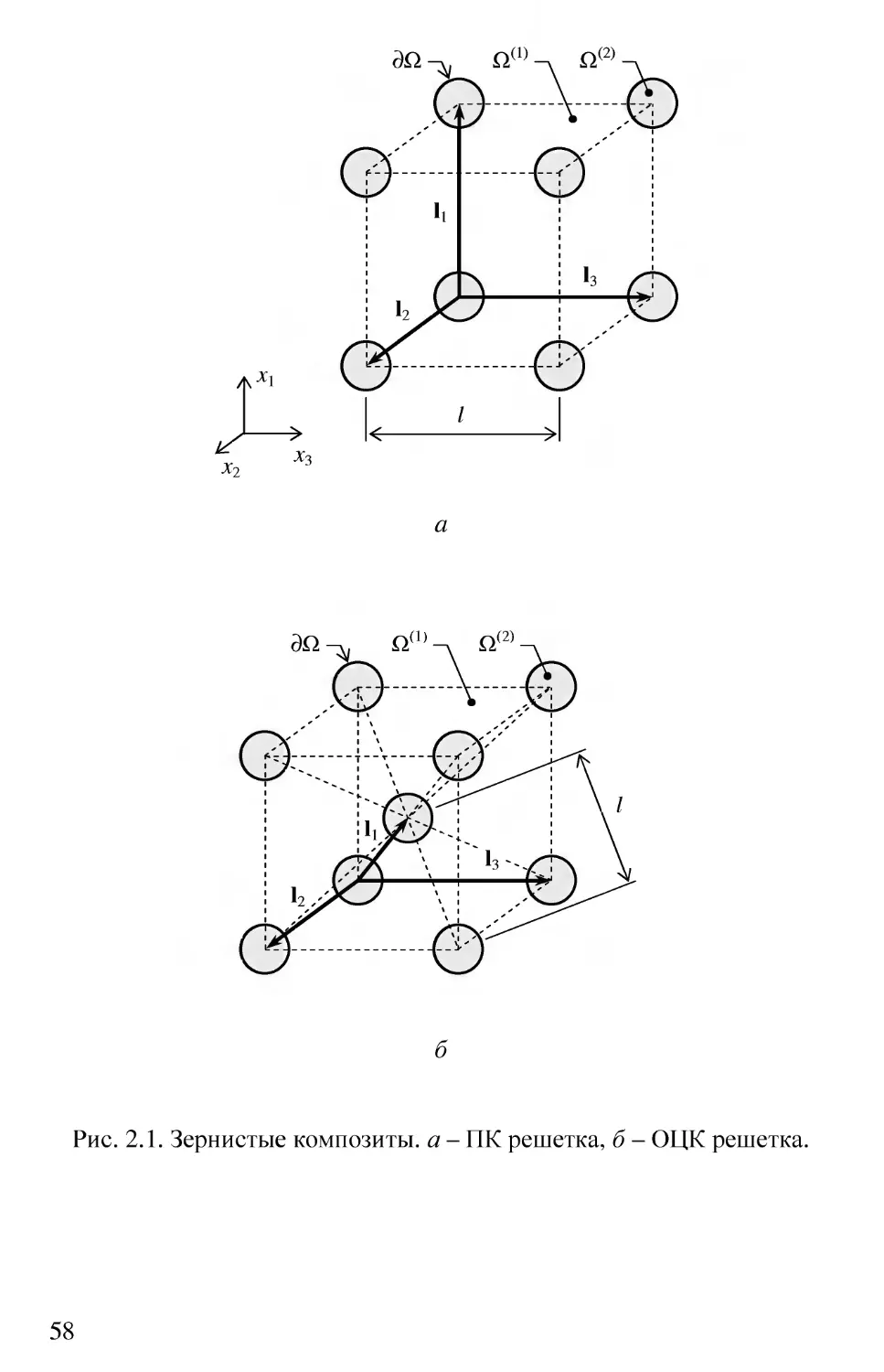
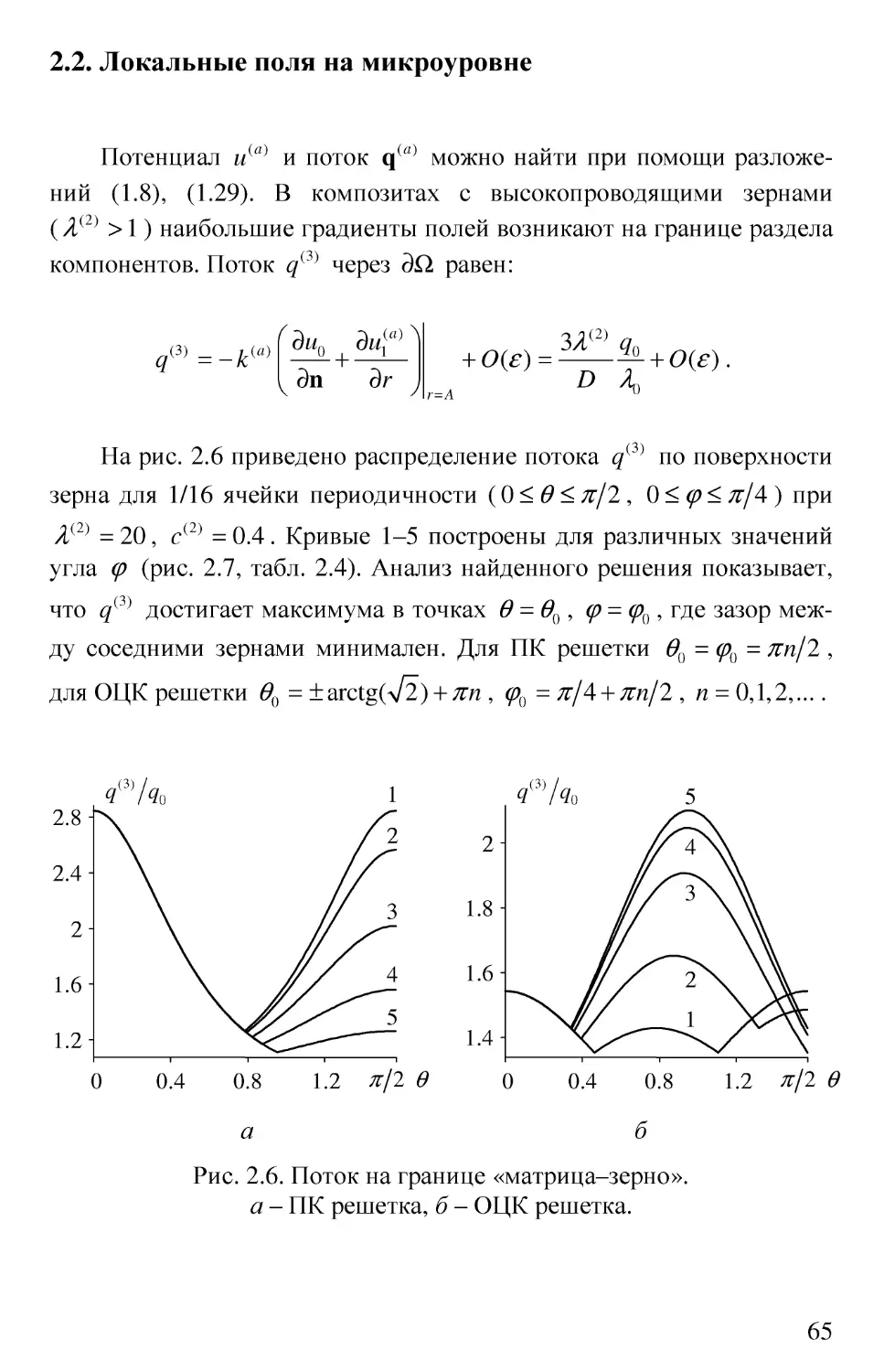
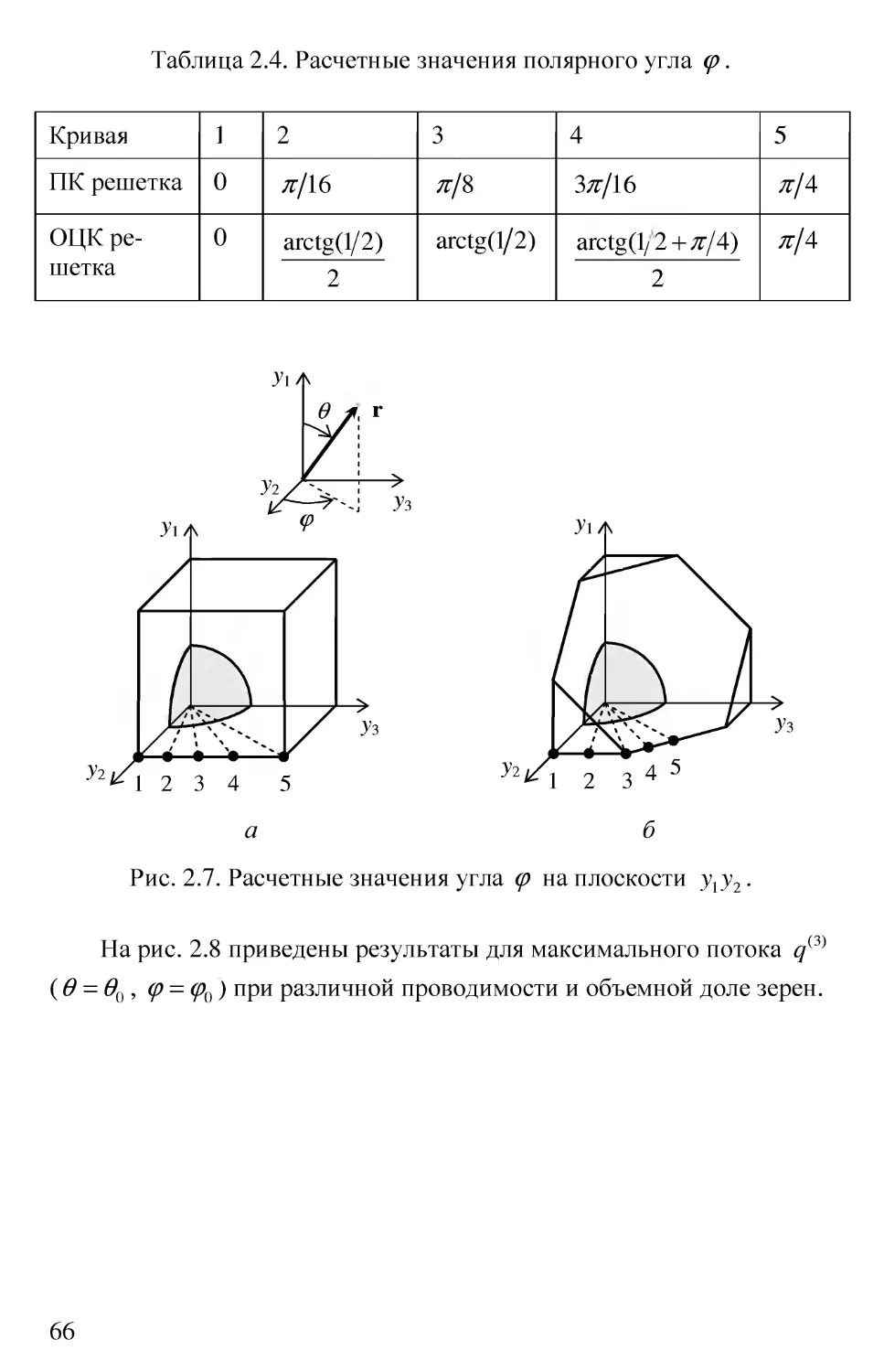
Автор: Большаков В.И. Андрианов И.В. Данишевский В.В.
Теги: механика деформируемых тел упругость деформация механика физика
ISBN: 978-966-525-935-0
Год: 2008
Текст
Министерство образования и науки Украины
Приднепровская государственная академия
строительства и архитектуры
В.И. Большаков, И.В. Андрианов, В.В. Данишевский
АСИМПТОТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА
КОМПОЗИТНЫХ МАТЕРИАЛОВ С УЧЕТОМ
ВНУТРЕННЕЙ СТРУКТУРЫ
Дншропетровськ
„Пороги"
2008
УДК 539.3 : 624.016
ББК 22.251+ 30.36
Б79
Большаков В.И., Андрианов И.В., Данишевский В.В.
Асимптотические методы расчета композитных материалов с учетом внутренней
структуры. - Днепропетровск: «Пороги», 2008. - 196 с.
В монографии рассматриваются асимптотические методы расчета
неоднородных композитных материалов с учетом микромеханических
эффектов, вызванных особенностями внутренней структуры.
Получены решения широкого круга задач, касающихся вычисления
эффективных характеристик композитов и определения концентраций полей
на микроуровне. Для научных работников, инженеров, студентов
старших курсов.
В монографИ' розглядаються асимптотичш методи розрахунку
неоднорщних композитних матер1ал1в i3 урахуванням мжромехашч-
них ефеютв, викликаних особливостями внутр1шньо1 структури.
Одержано розв'язки широкого кола задач, що стосуються обчислення
ефективних характеристик композит1в та визначення концентращй
пол1в на MiKpopiBHi. Для наукових пращвниюв, шженер1в, студен™
старших KypciB.
Рекомендовано до друку Вченою радою ПридншровськоУ
державноУ академй' буд1вництва та арх1тектури,
протокол № 9 вщ 22 кв1тня 2008 р.
Рецензенти:
доктор ф1зико-математичних наук, професор А.В. Павленко
доктор ф1зико-математичних наук, професор A.M. Пас1чник
© B.I. Большаков, I.B. Андр1анов, В.В. Данпиевський, 2008
© Придншровська державна академ1я
буд1вництва та арх1тектури, 2008
ISBN 978-966-525-935-0
ОГЛАВЛЕНИЕ
Предисловие 5
Список основных обозначений 9
Введение 12
Глава 1. Проводимость волокнистых композитов 26
1.1. Математическая модель задачи проводимости 26
1.2. Эффективный коэффициент проводимости 27
1.3. Локальные поля на микроуровне 37
1.4. Волокна с покрытиями 40
1.5. Неидеальный контакт между волокнами и матрицей 46
1.6. Композиты нерегулярной структуры 49
1.7. Кластерная проводимость волокнистых композитов 52
Глава 2. Проводимость зернистых композитов 57
2.1. Эффективный коэффициент проводимости 57
2.2. Локальные поля на микроуровне 65
2.3. Зерна с покрытиями 67
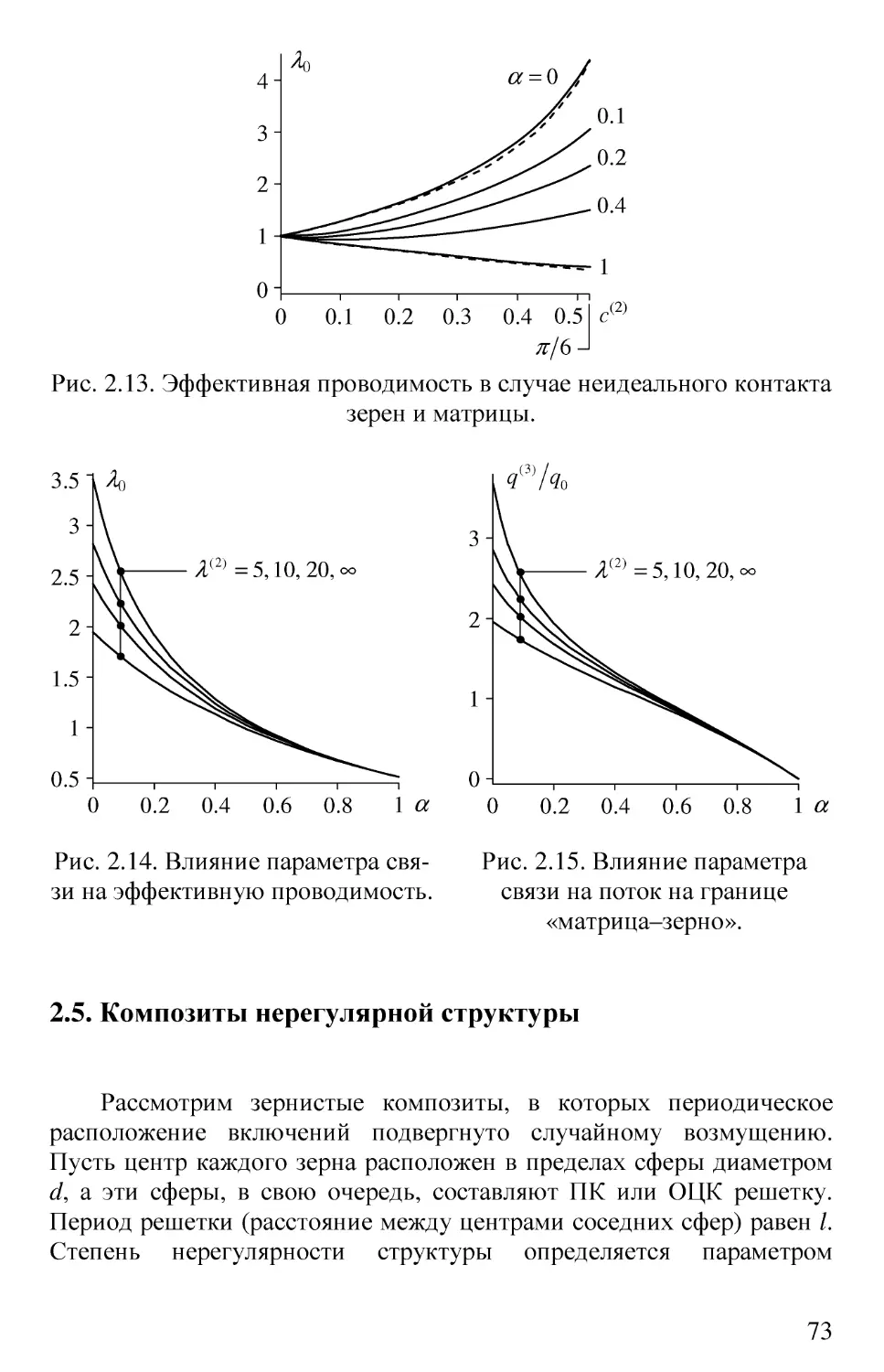
2.4. Неидеальный контакт между зернами и матрицей 71
2.5. Композиты нерегулярной структуры 73
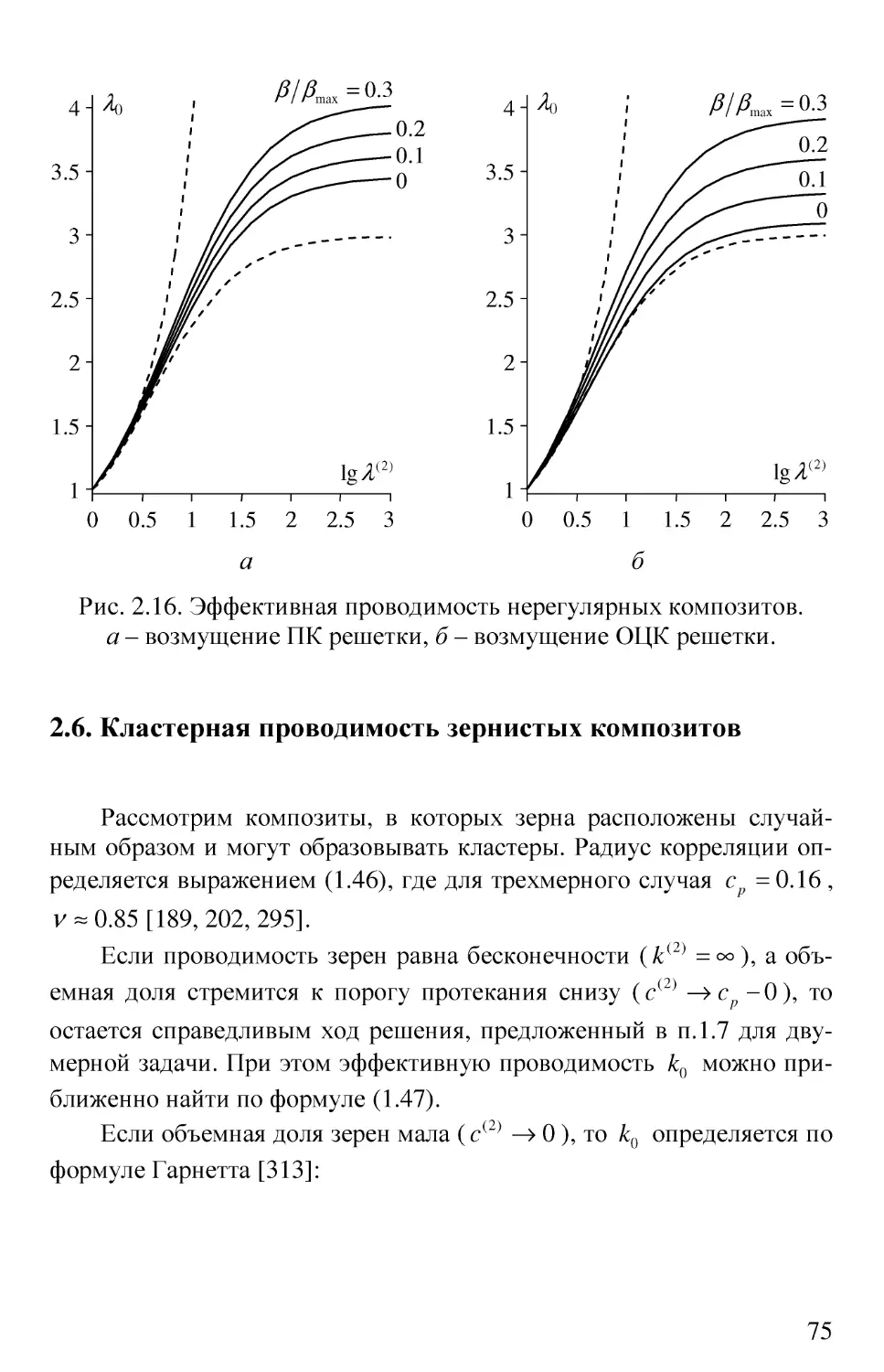
2.6. Кластерная проводимость зернистых композитов 75
Глава 3. Упругие свойства композитов 79
3.1. Основные соотношения теории упругости 79
3.2. Эффективные характеристики волокнистых композитов 82
3.3. Эффективные характеристики зернистых композитов 88
Глава 4. Вязкоупругие свойства композитов 92
4.1. Основные соотношения теории вязкоупругости 92
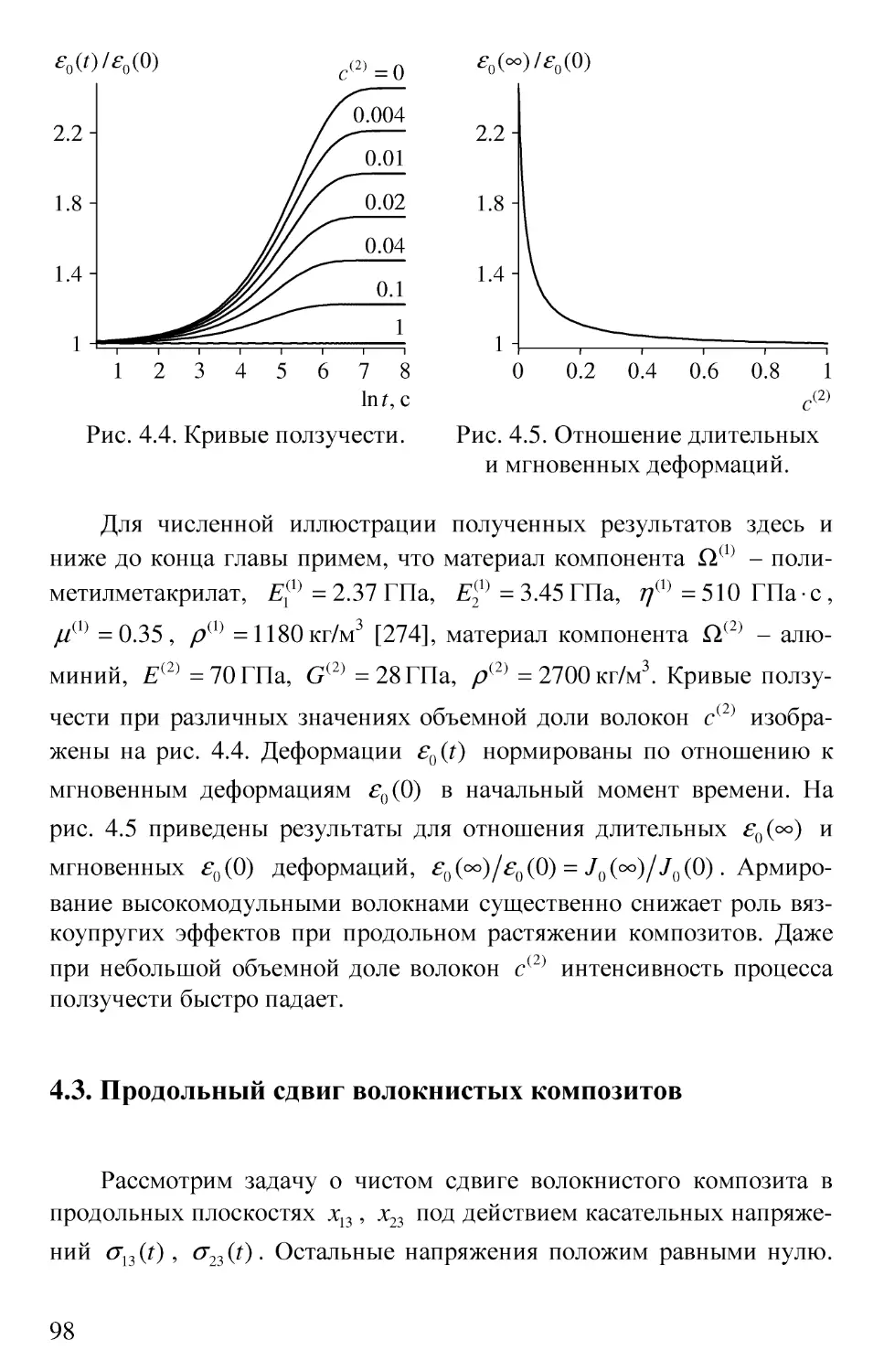
4.2. Продольное растяжение волокнистых композитов 95
4.3. Продольный сдвиг волокнистых композитов 98
4.4. Распространение длинных волн в слоистом композите 101
Глава 5. Холодное волочение биметаллических композитов 103
5.1. Основные гипотезы и пластическая краевая задача 103
5.2. Аналитическое решение 108
3
5.3. Асимптотический расчет 112
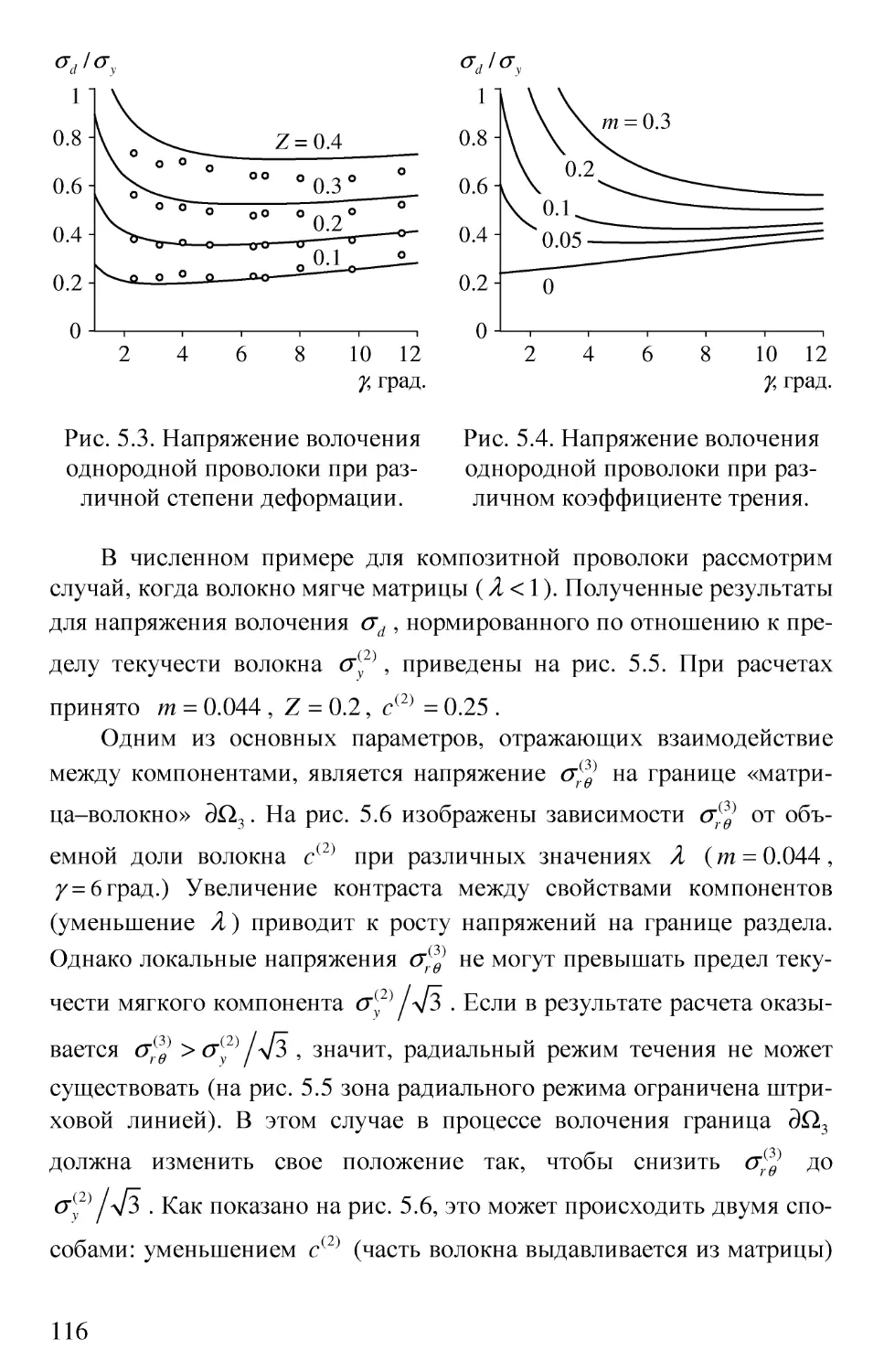
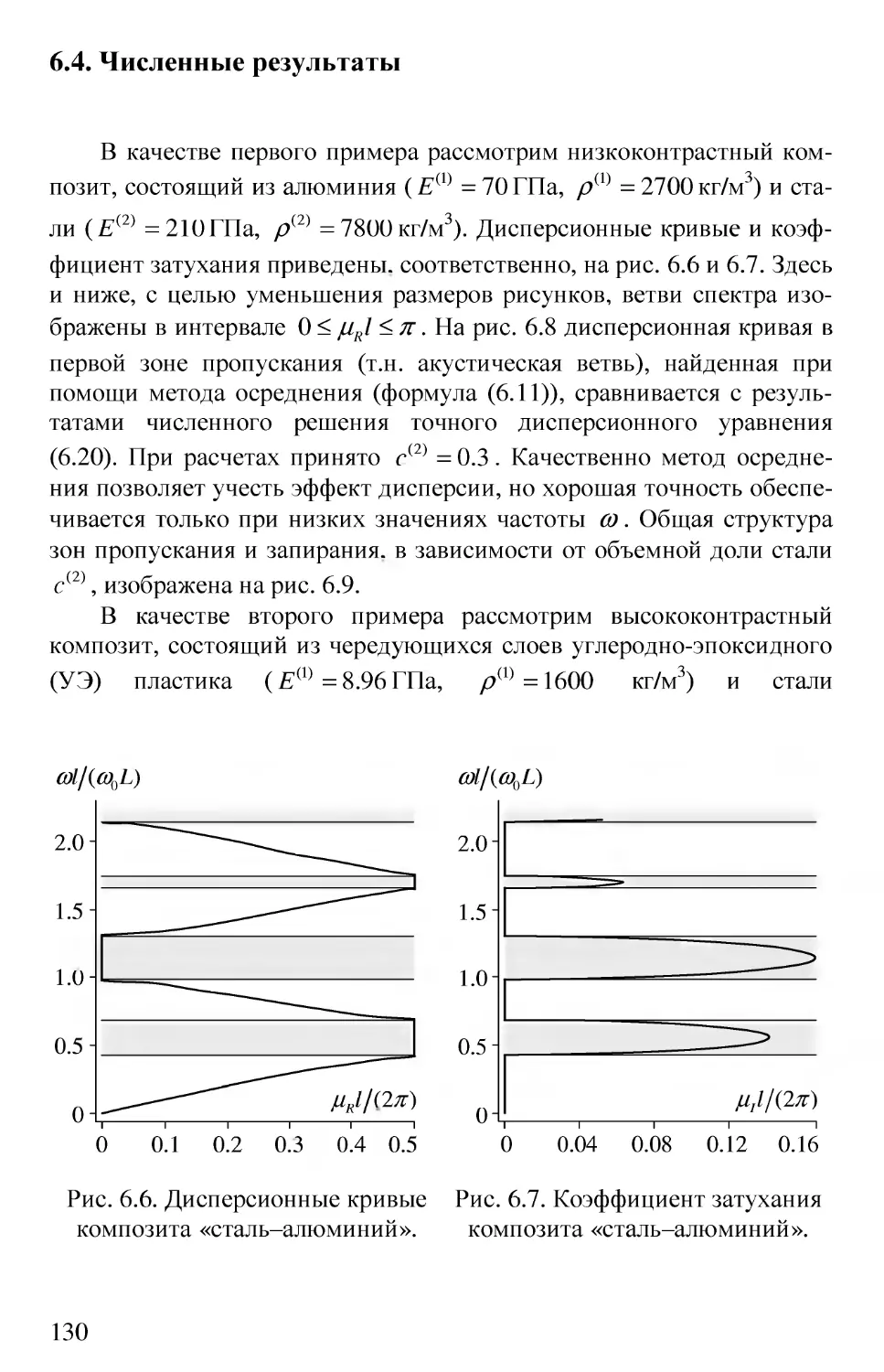
5.4. Численные результаты 115
Глава 6. Распространение волн в слоистых композитах 118
6.1. Одномерная динамическая задача 118
6.2. Метод осреднения высшего порядка 119
6.3. Метод Флоке-Блоха. Точное дисперсионное уравнение 125
6.4. Численные результаты 130
Глава 7. Распространение волн в волокнистых композитах 133
7.1. Двумерная динамическая задача 133
7.2. Метод осреднения высшего порядка 134
7.3. Метод Флоке-Блоха. Решение при помощи рядов Фурье 141
7.4. Численные результаты 143
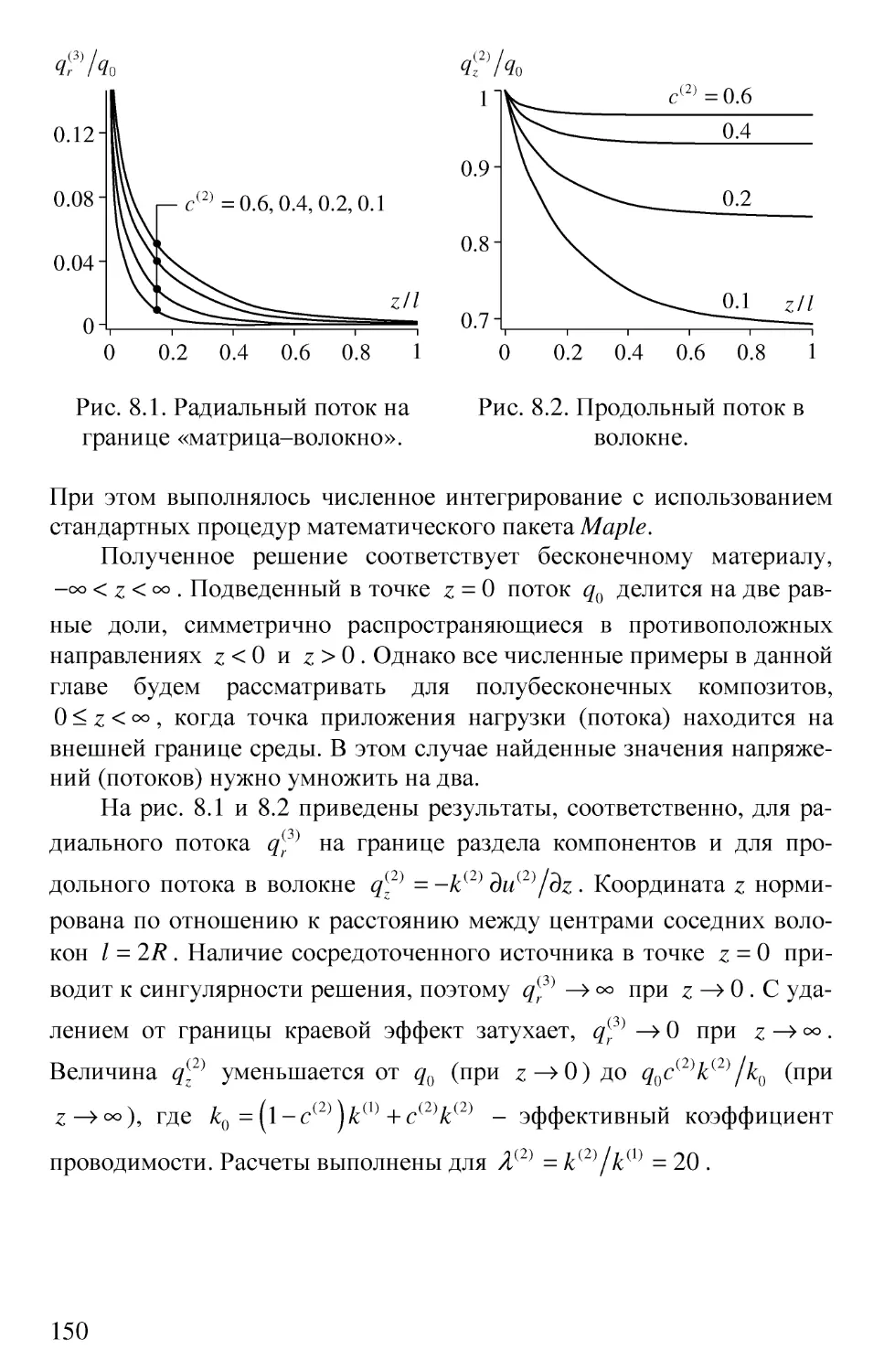
Глава 8. Краевые эффекты в композитных материалах 147
8.1. Проводимость волокнистых композитов 147
8.2. Учет неидеального контакта между компонентами 151
8.3. Продольная деформация волокнистых композитов 153
8.4. Продольная деформация в случае неидеального контакта 157
Литература 160
4
ПРЕДИСЛОВИЕ
Профессионалу, вроде меня, такая ерунда
представляется чрезвычайно увлекательной.
Надеюсь, что и читатель найдет ее
увлекательной и любопытной.
Р.Ф. Фейнман
Главная задача предисловия - убедить потенциального читателя,
что ему стоит хотя бы пролистать предлагаемую книгу. В нашем
случае это непросто. Задав в Интернете поиск по ключевым словам
«композитный материал», нетрудно убедиться, что каждый год
публикуются десятки книг и сотни статей, посвященных данной
тематике. В чем же отличие нашей монографии?
В названии книги фигурируют три основные понятия:
«композитный материал», «внутренняя структура», «асимптотические
методы». Композиты пронизывают нашу жизнь, поэтому говорить об их
важности и распространенности излишне. В то же время - попробуйте
точно определить, что такое композитный материал (трудности
подобного определения отмечал Б.Е. Победря [153])! Поэтому будем
считать этот термин интуитивно понятным.
Понятие «внутренняя структура» нам представляется также
интуитивно ясным. Имея дело с композитным материалом, мы можем
интересоваться как его глобальными характеристиками (например,
модулем упругости достаточно большого объема этого композита),
так и локальным распределением физических полей. Последние и
определяются реальной (внутренней) структурой композита. Остаются
«асимптотические методы». Их массированное применение и есть
главная особенность книги, поэтому остановимся на этом понятии
подробнее.
Термин «асимптота» (asymptotos по-гречески - не совпадающий)
связан с наглядным геометрическим представлением о линии, к
которой неограниченно приближается, никогда с ней не совпадая,
некоторая кривая. Идея асимптотического приближения - одна из наиболее
важных и глубоких в математике, особенно в той ее части, которая
тесно соприкасается с физикой, механикой и техникой. Дело в том,
что почти любая физическая теория, сформулированная в общем виде,
5
очень сложна с математической точки зрения. Поэтому и при
создании теории, и в дальнейшем ее развитии особое значение имеют
простейшие предельные случаи, допускающие аналитические решение. В
этих предельных случаях обычно уменьшается число уравнений,
понижается их порядок, становится возможным переход от дискретной
системы к сплошной среде или от неоднородной среды к однородной,
происходит локализация процессов вблизи границы рассматриваемой
области и т.п. Но за всеми этими упрощениями, сколь бы различными
они ни казались, стоит высокая степень симметрии, присущая
математической модели рассматриваемого явления в предельной
ситуации. Асимптотический подход к сложной задаче заключается в
трактовке исходной (недостаточно симметричной) системы как
близкой к некоторой симметричной. Принципиально важно, что
определение поправок, учитывающих отклонения от предельного
случая, гораздо проще, чем непосредственное исследование исходной
системы. На первый взгляд, возможности такого подхода ограничены
узким диапазоном изменения параметров системы. Однако опыт
исследования различных физических задач показывает, что при
значительном изменении параметров системы и удалении ее от
одного предельного симметричного случая, как правило, существует
другая предельная система, часто с менее очевидной симметрией, и
возмущенное решение можно строить уже для нее. Это позволяет
описать поведение системы во всем диапазоне изменения параметров,
опираясь на небольшое число предельных случаев.
Повышенный интерес к асимптотическим методам в последние
годы тем более примечателен, что успехи вычислительной
математики, казалось бы, должны были привести к противоположной
тенденции. Дело в том, что асимптотические методы всемерно развивают
нашу интуицию и поэтому играют важную роль в формировании
мышления современного ученого-естественника или инженера. Даже
в тех случаях, когда основной целью остается получение численных
результатов, предварительный асимптотический анализ позволяет
выбрать лучший вычислительный метод и разобраться в обширном,
но неупорядоченном числовом материале. Кроме того, такой анализ
особенно эффективен в тех областях значений параметров, где
прямые компьютерные вычисления встречают серьезные затруднения. Об
этом аспекте асимптотических методов хорошо сказал известный
английский механик Д. Крайтон [290]: «Расчеты или эксперименты без
определяющей роли асимптотической информации бесполезны в
лучшем случае и опасны в худшем из-за невозможности
идентифицировать области резкого (жесткого) изменения процесса и его локали-
6
зации в пространстве и во времени. Более того, весь накопленный
опыт показывает, что асимптотические решения полезны с точки
зрения численных результатов далеко за пределами их формальной
области применимости и часто могут быть использованы
непосредственно» (перевод наш - авт.)
Эффективность асимптотических методов, особенно метода
гомогенизации, в теории композитов - не новость [87]. Однако, как
правило, они используются только на определенном этапе расчета в
комбинации с численными подходами. Наше кредо таково: начав
применять асимптотические методы, имеет смысл довести решение до
максимально простых вычислительных формул. Здесь приходится
изощряться - искать дополнительные малые параметры, использовать
формулы суммирования и интерполяции, расширять область
применимости известных асимптотических подходов, и т.д. Именно
указанная идея и стала основной при написании данной книги.
Теперь попробуем очертить круг потенциальных читателей. Это,
в первую очередь, - механики, основные интересы которых лежат в
области исследования композитных материалов. Надеемся, что наша
работа будет небезынтересна физикам и математикам (хотя кланы
механиков, физиков и математиков общаются между собой,
переоткрытие одних и тех же методов и явлений в разных областях скорее
правило, чем исключение). Хочется также верить, что специалисты,
нацеленные больше на практическую сторону дела, сумеют
использовать многие из приведенных результатов, не вникая в кухню их
получения.
Для чтения книги достаточно знания стандартных курсов высшей
математики, сопротивления материалов и теории упругости
технического вуза.
Желающим ознакомиться с основами механики композитов мы
рекомендуем монографию P.M. Кристенсена [117]. Ответы на
вопросы по асимптотическим методам, если таковые возникнут, можно
найти в [17, 143, 144, 148]. Отметим также, что современные
электронные средства связи открывают возможность интерактивного
диалога с читателем. Авторы с удовольствием ответят на замечания,
которые можно присылать по адресам: bolshakov@pgasa.dp.ua,
igor_andrianov@hotmail.com, vdanish@ukr.net. Кроме того, мы будем
признательны за сообщения об опечатках; их список будет приведен
на сайте http://asymptotic.hmarka.net.
Многие изложенные в монографии идеи появились как результат
многолетнего сотрудничества с Я. Аврейцевичем, Д. Вайхертом,
А.Л. Каламкаровым, С.Г. Кобликом, Л.И. Маневичем, |В.Г.Ошмяном|,
7
А.В. Павленко, Г.А. Старушенко, С. Токажевским, |В.В. Шевченко |.
Всем им наша глубокая благодарность.
Мы признательны А.В. Павленко и А.Н. Пасечнику, взявшим на
себя труд по рецензированию книги.
Авторы
8
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
Латинский алфавит
а размер включения в медленных координатах
А размер включения в быстрых координатах
Ъ толщина покрытия в медленных координатах
В толщина покрытия в быстрых координатах
с объемная доля
ср порог протекания
d диаметр окружности или сферы, определяющей расположение
центров включений в композитах нерегулярной структуры
е базисные векторы декартовой системы координат
Е модуль Юнга
E(t) функция релаксации
Е* (со) комплексный модуль жесткости
Е скорость изменения энергии
/ плотность объемных источников (гл. 1, 2) или объемная сила (гл.
3,8)
F модулирующая функция в волновом представлении Блоха
G модуль сдвига
G(t) функция релаксации при сдвиге
h безразмерная толщина покрытия
H(t) функция Хевисайда
/ мнимая единица
10, 1Х модифицированные функции Бесселя первого рода
/ коэффициент податливости
J(t) функция ползучести
/* (со) комплексный коэффициент податливости
k коэффициент проводимости
К объемный модуль
К0, Кх модифицированные функции Бесселя второго рода
/ размер внутренней структуры композита
1 векторы трансляции периодической решетки
L макроскопический размер задачи (гл. 1, 2) или длина волны (гл. 4,
6,7)
9
т масса
Э/Эт производная по нормали к границе раздела компонентов в
быстрых координатах
Э/Эп производная по нормали к границе раздела компонентов в
медленных координатах
q поток
г полярная или сферическая координата
R расстояние от центра до внешней границы ячейки периодичности
Rc радиус корреляции бесконечного кластера
s параметр интегрального преобразования
S площадь
t время
и, [/потенциал (гл. 1, 2, 8.1, 8.2) или перемещение (гл. 3, 4, 6, 7, 8.3,
8.4)
v скорость
V объем
W упругий потенциал Лява
х медленные декартовы координаты
х радиус-вектор в медленных декартовых координатах
у быстрые декартовы координаты
у радиус-вектор в быстрых декартовых координатах
z координата (гл. 3, 5, 8) или волновой импеданс (гл. 6)
Z степень деформации
Греческий алфавит
а параметр, определяющий степень адгезии компонентов
Р параметр, определяющий степень нерегулярности композитной
структуры
у угол волочения
8 малый параметр в методе возмущения формы границы
S(t), S(z) дельта-функция Дирака
82t символ Кронекера
е малый параметр в методе осреднения, определяющий степень
неоднородности композита, или деформация
е интенсивность деформаций
£ скорость деформации
£ интенсивность скоростей деформаций
7] вязкость (гл. 4)
10
в полярная или сферическая координата
Я безразмерные свойства материалов
Л0 функция, определяющая безразмерную эффективную
проводимость регулярного композита в зависимости от объемной доли
включений
ju волновое число или коэффициент Пуассона
JLI волновой вектор
V индекс радиуса корреляции
Е, параметр сращивания в методе асимптотически эквивалентных
функций
р сопротивление (гл. 1, 2) или плотность (гл. 4, 6, 7)
а напряжение
(Ту предел текучести
т время релаксации или время ретардации
(р сферическая координата
ф угол, определяющий направление волнового вектора
X отношение радиуса включения к расстоянию от центра до
внешней границы ячейки периодичности
у/ фазовый угол запаздывания деформации относительно
напряжения в вязкоупругих материалах
со частота
£1 область
д£1 граница области
11
ВВЕДЕНИЕ
Композитными называют материалы, состоящие из нескольких
компонентов с различными физико-механическими
характеристиками. Путем оптимального выбора компонентов, их объемного
содержания и геометрической формы удается создавать новые
конструкционные материалы, обладающие ценными свойствами: высокие
прочность и жесткость могут сочетаться с малым объемным весом,
улучшенными тепло- и электропроводящими характеристиками,
стойкостью к действию агрессивных сред, пр.
Характерный масштаб / внутренней структуры композита (размер
армирующей частицы или зерна) мал по сравнению с размерами
изделия (конструкции). В то же время предполагается, что / значительно
больше межатомных расстояний. В этом случае физическое
поведение композитного материала может быть описано при помощи
уравнений механики сплошной среды. На практике степень
неоднородности композитов изменяется в широких пределах. Диапазон
возможных значений параметра / приведен в табл. 0.1, составленной на
основании данных работ [74, 75]. Для сравнения: расстояние между
атомными плоскостями в металлах имеет порядок 10"10 м.
Таблица 0.1. Характерный размер внутренней структуры композитов.
Материал
Бетоны, слоистые пластики и фанеры
Сплавы и керамика
Композиты, армированные частицами и волокнами
Дисперсно-упрочненные композиты
Нанокомпозиты
/, м
10-3-10"2
10"8-10-3
10"7-10-4
10"8-10-7
10"9
С точки зрения механики, общепринятым является разделение
композитных материалов на волокнистые, зернистые и слоистые.
Волокнистые и зернистые композиты состоят из матрицы и
армирующих включений (тонких волокон или частиц). Слоистые композиты
12
изготавливаются из чередующихся слоев различных материалов
(которые, в свою очередь, также могут быть композитными).
В качестве матрицы обычно применяются полимеры (эпоксидные
и полиэфирные смолы, термопласты), металлы (алюминий, медь),
керамика. Матрицы из кремнийорганических соединений
используются для создания жаростойких материалов, работающих в широком
диапазоне температур.
Армирующими включениями являются волокна из стекла,
углерода, бора, стали, титана, вольфрама, ниобия. Улучшение
прочностных характеристик композитов достигается применением в качестве
армирующих элементов специально выращенных нитевидных
монокристаллов (усов) из оксидов алюминия, циркония, титана, карбидов
бора и кремния, графита. Такие материалы обладают высоким
сопротивлением хрупкому разрушению и находят применение в
конструкциях и узлах, испытывающих большие термомеханические нагрузки
(лопасти турбин, сопла реактивных двигателей).
В большинстве случаев современные технологии позволяют
получать нитевидные монокристаллы с минимальным диаметром до
1 мкм [145, 173]. Поперечный размер сверхтонких базальтовых
волокон составляет 200...400 нм. Диаметр микрокристаллических волокон
из неорганического титаната (коммерческое название файбекс)
достигает 100 нм, волокон в виде паутинообразных усов сапфира
(коммерческое название кобвеб) - 18 нм. В дисперсно-упрочненных
композитах тонкие включения (характерный размер от 10 нм до 100 нм)
препятствуют развитию дислокаций в кристаллической структуре
матрицы, что приводит к существенному повышению прочности.
Последние примеры, очевидно, следует отнести уже к категории нанокомпо-
зитов.
Под нанокомпозитами обычно понимают [74, 75] композитные
материалы, армированные наночастицами с поперечными размерами
от 1 нм до 100 нм. К замечательной особенности многих наночастиц
относится то, что, в отличие от обычных веществ, большинство
атомов в них размещены на поверхности. Примерами могут служить
интенсивно изучаемые сегодня молекулы углерода - фуллерены
(диаметр фуллерена С60 0.71 нм), а также различные виды нанотрубок
(поперечный диаметр от 0.4 нм до 50 нм), которые образуются
свернутыми в кольца молекулярными сетками графита. Поверхностное
размещение атомов в молекулах-наночастицах обуславливает их
особые механические, оптические и магнитные свойства, которые
значительно превосходят свойства традиционных материалов. Так, модуль
Юнга стали составляет 210 ГПа, высокомодульных углеродных воло-
13
кон Торнел 300 - 228 Па, в то время как для углеродных нанотрубок
он может достигать значения 1240 ГПа [482].
Наночастицы представляют собой дискретные образования,
состоящие из отдельных элементов (атомов), связи между которыми
реализуются через силы межатомного взаимодействия. Поэтому
описание физических свойств наночастиц не может быть выполнено с
помощью одной только механики сплошной среды, а должно также
основываться на применении различного рода дискретных моделей, в
том числе и с учетом имеющих место квантовых эффектов. В то же
время при изучении нанокомпозитов каждую армирующую наноча-
стицу можно рассматривать как элемент, подчиняющийся законам
континуальной механики. Взаимодействие между наночастицами
происходит через материальную среду - матрицу. Следовательно,
существенная часть задач механики нанокомпозитов может быть
поставлена и решена с помощью методов теории композитных
материалов в рамках механики сплошной среды.
Необходимо отметить широкое применение теории композитных
материалов при решении задач биомеханики. Практически все ткани
организма представляют собой композиты со сложной внутренней
структурой и несколькими уровнями неоднородности. Так, мышцы
образуются набором волокон; волокно состоит из клеток; отдельная
клетка, в свою очередь, может быть представлена в виде упругой
оболочки, заполненной композитной суспензией с помещенным внутри
ядром. Кровеносные сосуды моделируются многослойными
оболочками. Спонгиозные кости представляют собой пористую среду,
образованную пересекающимися стержнями и пластинками. Подобные
механические модели являются в известной мере упрощенными, тем
не менее, они позволяют получить ряд важных результатов при
расчете физико-механических свойств тканей в хирургии и протезировании
[265].
Наконец, большинство материалов, используемых в
строительстве, также являются композитными. К ним следует отнести все виды
бетонов, кирпич, древесно-слоистые пластики и фанеры, пр.
В табл. 0.2 приведены приближенные данные о свойствах
некоторых распространенных компонентов композитных материалов [47,
75, 145, 173, 261, 447, 482]. Обозначено: р - плотность, ав - предел
прочности при растяжении, Е - модуль Юнга, jU - коэффициент
Пуассона, / - средний диаметр волокна (частицы). Модуль сдвига G
изотропных компонентов можно определить по формуле:
G = £/[2(1 + //)] . Упругие свойства анизотропных включении
14
Таблица 0.2. Свойства компонентов композитных материалов.
Материал
Стеклянные волокна
Углеродные волокна
Графитовые усы
Нанотрубки
зигзагообразные
хиральные
Борные волокна
Сталь (проволока)
Бериллий
Титан
Алюминий
Медь
Эпоксидные смолы
Полиэфирные смолы
р, кг/м3
2500
1750-
2000
2250
1330
1400
2600
7800
1850
4500
2700
8900
1000
1100
сгв, ГПа
2.4-3.5
2.5-4
2.5-3
0.4
0.25-
0.5
0.3-
0.45
0.07
0.25
0.04-
0.12
0.02-
0.1
£,ГПа
69-86
200-
350
1000
648
1240
400-
450
210
250-
450
ПО
70
125
3-5
1.5-
4.5
_М
0.25
0.3
0.3
0.33
0.3
0.1
0.3
0.32
0.32
0.32
0.3
0.3-
0.4
/, мкм
7-10
7-10
1
0.01
0.01
50-200
50-100
250
(волокна, усы, нанотрубки) приведены для случая продольной
деформации.
Одной из основных задач механики композитных материалов
является определение свойств композитов в зависимости от их
внутренней структуры. Простейшие модели основываются на информации
о свойствах и объемных долях компонентов. Более совершенные
методы расчета позволяют учитывать различные микромеханические
эффекты, такие как взаимодействие соседних включений,
неидеальный контакт между матрицей и включениями, рассеяние волн на не-
однородностях среды, пр. В наиболее строгой и общей постановке
механика композитов разработана сотрудниками Института механики
НАН Украины. Полученные результаты отражены в 12-томной
коллективной монографии [138] и обобщающих статьях А.Н. Гузя, И.Ю.
15
Бабича, В.Т. Головчана, Ю.В. Коханенко, Я.Я. Рущицкого, Л.П. Хо-
рошуна, В.Н. Чехова, Н.А. Шульги [18, 56, 67, 104, 160, 186, 193, 194,
318,319].
Широкое распространение в механике композитов получила
теория эффективного модуля. Если характерный размер / внутренней
структуры композита существенно меньше макроскопического
размера L задачи, то исходный неоднородный материал можно
приближенно заменить однородной средой с некоторыми осредненными (т.н.
эффективными) свойствами. При этом осцилляции физических полей
в композите на микроуровне сглаживаются и заменяются средними
значениями. Размер L может быть связан, например, с минимальной
длиной волны или минимальным удерживаемым периодом
разложения внешней нагрузки в ряд Фурье.
Осредненные модели используются в механике композитов уже
более 100 лет. В 1889 г. В. Фойгт [479] предложил вычислять
эффективные модули упругости путем простого арифметического
осреднения жесткостей компонентов. Такое приближение отвечает гипотезе
об однородности поля деформаций. В работе А. Рейсса [421]
предполагается однородным поле напряжений, и тогда эффективные модули
можно найти путем осреднения податливостей компонентов.
Аналогичные результаты были получены О. Винером [480].
На основе теорем о минимуме потенциальной и дополнительной
энергий Р. Хилл [334] показал, что метод Фойгта дает верхнюю, а
метод Рейсса - нижнюю оценку для эффективных упругих модулей.
Однако полученная таким образом вилка является слишком широкой и
почти не имеет практического значения. Значительно более точные
оценки были найдены 3. Хашином и С. Штрикманом [321, 330, 331] с
помощью вариационного метода. Оценки Хашина-Штрикмана
являются теоретически наилучшими, которые можно получить без учета
внутренней структуры материала. Они справедливы для любых
статистически-изотропных композитов и могут использоваться в случаях,
когда отсутствуют данные о форме и взаимном расположении
включений.
В работах [387, 390, 415, 449, 468, 481] предложены уточненные
оценки для эффективных характеристик, которые учитывают
информацию о микроструктуре композитов с помощью методов
статистической механики [253].
Невариационные оценки могут быть получены на основе дробно-
рационального преобразования Паде [27]. В некоторых случаях
искомые эффективные коэффициенты можно представить в виде
разложений в ряды Стильтьеса по отношению свойств компонентов. Пере-
16
страивая такие разложения в цепные дроби или аппроксимации Паде,
удается получить сходящиеся последовательности верхних и нижних
оценок для эффективных характеристик [256, 454, 457-467].
Интересной и практически важной задачей является нахождение
математических связей между различными физическими свойствами
материалов. Если известно решение для какого-либо из эффективных
коэффициентов, то оно содержит в себе определенную
морфологическую информацию о строении данного композита. Теоретически, эту
информацию можно использовать для определения других
эффективных характеристик. Так, в работах [259, 315, 388] получены строгие
оценки, связывающие между собой проводимость и упругие модули
неоднородных сред.
Подробные обзоры различных уточненных оценок и полученных
с их помощью результатов приведены в монографиях Дж. Мильтона
[389] и С. Торквато[469].
Кроме строгих оценок, существует много приближенных методов
определения эффективных характеристик. Одним из самых простых
является метод вириального разложения [115, 188]. Искомые
эффективные модули представляются в виде разложений в степенные ряды
по концентрации одного из компонентов. Как правило, в
практических задачах удается построить только первое приближение, которое
отвечает случаю одиночного включения в бесконечной матрице. При
этом учитывается возмущение упругого поля матрицы, вызванное
влиянием включения, но игнорируется взаимодействие между собой
соседних включений. Полученные таким образом результаты
применимы в случае малой объемной доли включений. Отметим, что данная
модель была впервые использована в классических работах Дж.
Максвелла [375], Дж. Гарнетта [313], А. Эйнштейна [302, 303], а формулы
для расчета энергии деформирования и упругих полей получены Дж.
Эшелби [203,305].
Очевидным недостатком первого приближения вириального
метода является то, что не только вблизи от включения, но и на больших
расстояниях от него свойства среды принимаются равными свойствам
матрицы. Более последовательным было бы принять, что на больших
расстояниях от включения свойства среды определяются
эффективными характеристиками композита. Эта идея лежит в основе
трехфазной модели, предложенной Э. Кернером [350] и К. Ван-дер-Полем
[476]. В рамках данной модели (известной также как обобщенный
метод самосогласования) исходный композитный материал
заменяется одиночным включением, окруженным слоем матрицы, за
пределами которого находится бесконечная однородная среда с искомыми
17
эффективными характеристиками. Такая расчетная схема позволяет
получить хорошие результаты при малых и средних значениях
объемной доли включений [117, 221, 277, 289, 322].
В случае, когда объемная доля включений близка к
максимальному предельному значению, могут быть найдены асимптотические
решения, где в качестве малого параметра используется ширина
зазора между соседними зернами. Дж. Келлер [347], Дж. Бэтчелор, Р.
О'Брайен [244] получили первые члены асимптотических разложений
для эффективной проводимости высококонтрастных композитов с
включениями, стремящимися к контакту. Построение высших
приближений рассмотрено в работе [477].
Если известны выражения для эффективных характеристик при
малой и большой объемной доле включений, сращивание позволяет
получить решения для любых объемных долей компонентов. Для
этого используются двухточечные аппроксимации Паде [454, 457, 464] и
метод асимптотически эквивалентных функций (т.н.
квазирациональные аппроксимации) [223, 225, 226].
Точные решения для композитов регулярной структуры могут
быть найдены путем представления упругих полей в виде
бесконечных рядов по периодическим функциям комплексного переменного.
Данный подход позволяет не только найти эффективные
характеристики, но и вычислить распределение напряжений и деформаций на
микроуровне. Увеличивая количество удерживаемых членов ряда,
можно учитывать взаимодействие соседних включений и исследовать
различные микромеханические эффекты. Основные результаты
получены в работах Э.И. Григолюка, Л.А. Филыитинского [62-64], Г.А.
Ванина [45-48], Б.Е. Победри [153], В.Т. Головчана, А.Н. Гузя [52, 54,
60], В.И. Куща [118-124]. Обширная библиография по применению
метода рядов в статических и динамических задачах для
многосвязных пластин и оболочек приведена в статье А.С. Космодамианского
[102]. Связанные задачи термо-, электро- и магнитоупругости
рассмотрены в [20-22, 89-92, 103, 155, 180-185]. Как правило,
практическая применимость найденных решений ограничена областью
сходимости вычисленных отрезков ряда.
К хорошим результатам приводит представление упругих
потенциалов в виде разложений по мультиполям. Идея данного метода
принадлежит Дж.У. Стретту (лорду Рэлею) [420], который в 1892 г.
получил первое приближение для задачи об эффективной
проводимости суспензии сферических частичек. Развитию метода Рэлея и
построению высших приближений посвящены работы [377-381, 384,
412,436,492].
18
В основе теории эффективного модуля лежит принцип осреднен-
ного описания неоднородных материалов. В 1970-х годах была
осознана асимптотическая природа метода осреднения и разработан
соответствующий математический аппарат. Физические процессы в
композитах моделируются уравнениями в частных производных с быстро
осциллирующими коэффициентами. Асимптотические решения таких
уравнений удобно искать с помощью двухмасштабных разложений.
Метод многих масштабов и метод усреднения были разработаны в
теории обыкновенных дифференциальных уравнений и успешно
применялись для задач нелинейных колебаний, включающих члены с
разной изменяемостью по времени [30, 139]. В.А. Марченко, Е.Я.
Хруслов [135-137] одними из первых предложили применять данные
методы к уравнениям в частных производных, когда компоненты
решения имеют разную изменяемость по пространственным
координатам. Математические основы метода осреднения в механике
композитов разработаны Н.С. Бахваловым, Г.П. Панасенко [23-26], О.А.
Олейник [149, 150], В.Л. Бердичевским [28, 29], Б.Е. Победрей, В.И.
Горбачевым [153, 154], Э. Санчес-Паленсия [168, 433-435], И.
Бабушкой [239-242], А. Бенсуссаном, Ж.-Л. Лионсом, Дж. Папаниколау
[250], Л. Тартаром [452, 453], Ж. Дюво [79, 300, 301]. Применение
метода осреднения для расчета неоднородных конструкций,
подкрепленных пластин и оболочек началось с работ И.В. Андрианова, В.А.
Лесничей, Л.И. Маневича и соавторов [2, 6-10, 12, 128, 129]. История
развития метода осреднения изложена в обзорах И.В. Андрианова,
Л.И. Маневича [11] и А.Л. Каламкарова, Б.А. Кудрявцева, В.З. Парто-
на [87]. Некоторые новые результаты получены в работах [3, 4, 5, 13,
34, 35, 77, 80, 215, 217, 219-222, 224, 227-230, 234, 235, 254, 255, 262,
263, 269, 291, 317, 341, 342, 372, 382, 385, 405, 408, 409, 411, 424, 430,
437].
Основная идея метода осреднения заключается в следующем.
Рассмотрим композит с регулярной структурой; пусть
микроскопический размер / равен размеру ячейки периодичности. Определим
малый параметр е - 1/L , характеризующий степень неоднородности
материала. Введем два масштаба пространственных координат.
Вместо исходных переменных х будем использовать т.н. «медленные»
х = х и «быстрые» у = £~1х координаты, при этом оператор
дифференцирования запишется в виде: д/дх = д/дх + £~х д/ду . Физическое
поле и в композите представим в виде асимптотического разложения
и = и0 (х) + €щ (х, у) + £2и2 (х, у) +...,
19
где первый член и0 не зависит от быстрых координат и представляет
собой осредненную (макроскопическую) часть решения, а члены
высших порядков иг , / = 1,2,3,... вносят поправки порядка е1 и
описывают локальные осцилляции решения на микроуровне. В силу
периодичности среды иг также удовлетворяют условию периодичности:
иг (х, у) = ut (x, y + L). Асимптотическое расщепление исходной
краевой задачи в многосвязной области по параметру е приводит к
рекуррентной последовательности краевых задач, рассматриваемых в
пределах выделенной ячейки периодичности. Решая задачи на ячейке,
находим члены иг . Затем осреднение по быстрым координатам
позволяет определить неизвестные эффективные коэффициенты.
Многие авторы, использующие метод осреднения,
ограничиваются построением первого приближения. Такое решение
соответствует гипотезе о квазиоднородном материале (е = 0). Учет высших
приближений позволяет исследовать масштабные эффекты, которые
определяются размером внутренней структуры композита и не могут
быть описаны в рамках теории эффективного модуля.
Метод осреднения высшего порядка применительно к задачам
статики развит в работах Б. Гамбин, Э. Кренера [312], К. Бутина [268],
В.П. Смышляева, К.Д. Чередниченко [283, 446]. Неоднородность
материала приводит к появлению градиентов упругих полей высшего
порядка. Полученные макроскопические уравнения равновесия
включают дополнительные члены со старшими производными по
координатам. Нелокальные эффекты, вызванные различным
асимптотическим порядком свойств компонентов, рассмотрены в работах [213,
284,488].
В задачах динамики одним из проявлений масштабного эффекта
является дисперсия волн в композитах, вызванная локальными
отражениями и преломлениями сигнала на неоднородностях среды. К.
Бутин [267, 270], Дж. Фиш, В. Чен [281, 309, 310], Н.С. Бахвалов, М.Э.
Эглит [243], И.В. Андрианов, В.И. Большаков, В.В. Данишевский, Д.
Вайхерт [216, 292, 293] при помощи метода осреднения высшего
порядка получили решения, пригодные для длинных волн (£ « 1).
Дисперсия в неоднородных средах может быть также описана на
основании теории эффективных жесткостей [207, 298, 299, 333, 448] и
теории смесей [146, 147, 158, 159, 163, 167, 237, 245, 247, 271, 272, 332,
426]. Подробные обзоры микроструктурных теорий высшего порядка
приведены в работах Т. Тинга [456], Я.Я. Рущицкого [160], Л.П. Хо-
рошуна [186]. Осреднение динамических задач с использованием
различных вариантов метода самосогласования предложено в [343-345,
20
429]. Я.А. Жук, И.А. Гузь [81-83] исследовали влияние начальных
напряжений на распространение волн в нанокомпозитных материалах.
Рассеяние волн на одиночных неоднородностях среды (трещинах,
отверстиях, включениях) рассмотрено в работах [44, 140, 141, 179,
266]. Задачи распространения и взаимодействия волн в нелинейных
композитах исследованы Я.Я. Рущицким и соавторами [99, 159, 161,
164-167,426].
Когда длина волны уменьшается и становится соизмеримой с
размером внутренней структуры, в композите обнаруживаются
частотные зоны пропускания и запирания. Если частота попадает в зону
запирания, в материале возникает стоячая волна, групповая скорость
которой равна нулю. При этом амплитуда сигнала на макроуровне
экспоненциально затухает. Таким образом, композит играет роль
избирательного волнового фильтра. Результаты экспериментальных
исследований зон запирания для акустических волн в неоднородных
средах приведены в монографии Дж. Вольфа [484] и в работах [369,
374,392,410,427,450,471].
Решение для коротких волн может быть получено при помощи
представления Блоха [260], которое является интерпретацией теоремы
Флоке [311] для дифференциальных уравнений с периодическими
коэффициентами. Согласно данному методу, решение ищется в виде
произведения осредненной гармонической волны ехр(///х) exp(icot) и
некоторой модулирующей функции F(x) , причем в силу
периодичности композитной структуры F(x) также удовлетворяет условию
периодичности: F(x) = F(x + l). Для определения F(x) получаем
систему линейных алгебраических уравнений. Приравняв нулю
определитель данной системы, найдем дисперсионные соотношения
между частотой со и волновым числом //. Подробно метод Блоха описан
в работах Л. Бриллюэна, М. Пароди [37], Л.М. Бреховских [36], Н.А.
Шульги [191-194], А. Бедфорда, Д. Драмхеллера [246], а также в
обзорных статьях А.Н. Гузя, Н.А. Шульги [319] и СЮ. Карпова, С.Н.
Столярова [98].
Для одномерно-периодичных материалов (например, слоистых
композитов) часто удается получить точные дисперсионные
уравнения [36-38, 98, 127, 190-201, 246, 319, 428, 444]. Для двумерных и
трехмерных периодических сред (волокнистых и зернистых
композитов) могут быть найдены приближенные дисперсионные соотношения
путем представления F(x) в виде разложений в ряды Фурье [264, 293,
355-359, 440-443, 478] или ряды Рэлея по мультиполям [316, 392-394,
403, 413, 414, 416, 487] и их модификации [340, 369, 417].
21
В.Т. Головчан [49, 53, 55-59] разработал строгий метод решения
краевых задач о распространении волн в волокнистых композитах
регулярной структуры. В основу метода положены разложения
внешних периодических решений двумерного уравнения колебаний по
системе внутренних частных решений, которые получены в
диссертации [51]. Данный подход также успешно применялся для
исследования дифракции упругих волн в многосвязных телах [50, 51, 68, 72].
Важную роль в механике композитов играет эффект
неидеального контакта между компонентами. Оптимальное использование жест-
костных и прочностных свойств материалов непосредственно зависит
от эффективности передачи нагрузки от матрицы к включениям.
Кроме того, наибольшие концентрации локальных напряжений
возникают, как правило, на границе раздела между компонентами. Поэтому
прочность границы является одним из ключевых факторов,
определяющих несущую способность композита в целом. Ослабление связи
между компонентами не только приводит к снижению эффективных
характеристик, но и является причиной развития дислокаций и
трещин на микроуровне, что в большинстве случаев влечет за собой
быстрое разрушение всего материала.
Для моделирования процессов разрушения межкомпонентной
границы А. Нидельман [400-402] предложил использовать функцию
когезии, связывающую напряжения аш и скачок перемещений Аиш
на границе. При ослаблении контакта между матрицей и
включениями (и с ростом Аиш) <7Ш возрастает, достигает некоторого
максимального значения, а затем падает до нуля, что отвечает полному
разрушению границы. В. Твергаард, X. Эспиноза и соавторы [306-308,
472^-75] рассмотрели несколько видов когезионных зависимостей,
описывающих различные сценарии микроскопического разрушения
композитов. Дальнейшее развитие данный метод получил в работах
[278, 279, 314, 336, 354, 406, 419, 431, 432, 486, 489, 490]. Границы с
нелинейными свойствами исследованы в [365-367].
Экспериментальному определению законов когезии посвящена работа [451].
Микромеханическое влияние границы можно также учесть путем
введения между компонентами тонкого промежуточного слоя
(покрытия). Задачи расчета композитов с покрытиями рассматривались
многими авторами [34, 46, 206, 208, 209, 215, 222, 227, 248, 251, 262, 263,
282, 323-326, 337, 360, 362, 364, 368, 371, 404, 407, 418, 485, 491].
Если жесткость покрытий меньше жесткости включений (т.н. мягкая
граница), то такая модель отвечает случаю неидеального контакта.
Наоборот, если жесткость покрытий больше жесткости включений
(жесткая граница), то покрытия являются дополнительным несущим
22
компонентом. Предельные случаи мягкой и жесткой границы
исследованы в работах И. Бенвенисте, Т. Милоха [252, 386], 3. Хашина
[327, 328], И.В. Андрианова, В.И. Большакова, В.В. Данишевского, Д.
Вайхерта [217].
Неоднородность композитных материалов приводит к появлению
краевых эффектов. Вдали от внешней границы осредненные свойства
композита могут быть описаны с помощью теории эффективного
модуля. Но вблизи границы существенное влияние на напряженно-
деформированное состояние среды оказывает краевой эффект,
связанный с перераспределением нагрузки между компонентами. Зона
затухания краевого эффекта определяется характерным размером
внутренней структуры композита.
Э. Мелан [383] одним из первых предложил решение контактной
задачи о передаче нагрузки от одиночного бесконечного волокна к
матрице и определил касательные напряжения <7Ш на границе раздела
компонентов. Когда на волокно действует внешняя сосредоточенная
сила, то в окрестности точки ее приложения аш неограниченно
возрастает. Данная сингулярность носит логарифмический характер.
Если же нагрузка прикладывается непосредственно к матрице, то
касательные напряжения стремятся к бесконечности по степенному
закону. Этот результат свидетельствует о преимуществе использования
жестких волокон и стрингеров для передачи сосредоточенной
нагрузки к матрице.
В дальнейшем задача Мелана рассматривалась в работах [1, 14,
16, 88, 142, 249, 273, 275, 276, 304, 352, 396], где были исследованы
полубесконечные волокна и волокна конечной длины в плоскости,
полуплоскости и полосе. Большое количество результатов обобщено в
монографии Э.И. Григолюка, В.М. Толкачева [61]. Трехмерная
постановка задачи Мелана (волокна в пространстве и полупространстве)
рассмотрена в [397-399]. Г.Т. Сулим, Д.В. Грилицкий [66, 175-178]
получили решения пространственно-периодических задач для сред с
тонкостенными включениями. Случай неидеального контакта и
различные микромеханические модели границы между волокном и
матрицей рассматривались в работах [15, 236, 297, 362-364, 376, 391,
395].
А.Н. Гузь, Ю.В. Коханенко, В.М. Быстров, B.C. Зеленский, И.М.
Царипа, В.В. Ясинский [39-42, 69, 105-108, 113, 114, 187]
исследовали краевые эффекты в слоистых композитах при различных видах
внешней нагрузки. Получены численные решения задач теории
упругости для кусочно-однородных тел с помощью метода сеток [60, 65].
А.Н. Гузь, Ю.В. Коханенко, Е.С. Яковлева, СВ. Фесенко [70, 71, 109,
23
ПО, 204] рассмотрели краевые эффекты в слоистых композитных
материалах при наличии внутренних разрывов, полостей и межслойных
трещин. Краевые эффекты в композитах, армированных волокнами
квадратного и прямоугольного поперечного сечения, изучались А.Н.
Гузем, Ю.В. Коханенко, В.Ю. Бойчуком, В.В. Ясинским [31-33, 76,
111,112].
Я.Я. Рущицкий [162] исследовал совместное влияние внешней
нагрузки и внутренней структуры на напряженное состояние
неоднородных материалов с помощью приближенных микроструктурных
теорий. Полученные результаты учитывают краевые эффекты и
локальные перераспределения напряжений между компонентами.
И.В. Андрианов, В.В. Данишевский, Д. Вайхерт [218, 231-233]
предложили асимптотический метод расчета волокнистых композитов
с учетом краевых эффектов. Исходная плоская задача асимптотически
упрощается с помощью метода Маневича-Павленко [131-134, 151,
152], где в качестве малого параметра используется отношение жест-
костей анизотропных материалов при деформациях в различных
направлениях. Аналитическое решение упрощенной задачи находится с
помощью метода интегральных преобразований. Определены
напряжения на микроуровне вблизи границы (краевой эффект) и в толще
материала (осредненное состояние). Исследовано влияние покрытий и
эффекта неидеального контакта между компонентами.
В данной монографии обобщены результаты, полученные
авторами в области расчета периодически-неоднородных композитных
материалов. Центральное место в книге занимает асимптотический
метод осреднения.
Как правило, основной трудностью в практических приложениях
метода осреднения является решение задач на ячейке.
Взаимодействие между соседними включениями может вызывать значительные
осцилляции физических полей на микроуровне. Увеличение
жесткости и объемной доли включений приводит к росту локальных
напряжений на границе раздела компонентов. В этом случае применение
многих известных методов расчета связано с трудностями
вычислительного характера. Так, аналитические подходы, основанные на
представлении полей в виде разложений в периодические ряды,
требуют увеличения количества удерживаемых членов ряда. Численные
методы требуют повышения плотности сетки дискретизации и,
соответственно, увеличения затрат машинного времени.
В этой книге приведены приближенные аналитические решения
задач на ячейке с помощью некоторых асимптотических упрощений.
Как показывает численное сравнение с данными других авторов, по-
24
лученные результаты пригодны для любых значений свойств и
объемных долей компонентов, включая случай идеально
жестких/проводящих включений, стремящихся к контакту.
Определены эффективные свойства композитов, найдены
распределения полей на микроуровне, исследовано влияние покрытий и
эффекта неидеального контакта между компонентами. Предложены
уточненные оценки для эффективных характеристик композитов с
нерегулярной структурой, в которых периодическое расположение
включений подвергнуто случайному возмущению (что может быть
вызвано, например, технологическими причинами). На примере
пластической задачи о холодном волочении биметаллической проволоки
рассмотрено, как еще на стадии производства взаимодействие между
компонентами может влиять на свойства получаемого материала. С
помощью метода осреднения высшего порядка получены
дисперсионные соотношения для задач о распространении длинных волн в
неоднородных средах. Решения для коротких волн найдены на
основании метода Флоке-Блоха. Рассмотрены краевые эффекты в
композитах, при этом учтено микромеханическое влияние покрытий.
В главах 1 и 2 рассмотрены задачи тепло-, электро- и массопере-
носа в волокнистых и зернистых композитах. Глава 3 посвящена
упругим свойствам композитов. В главе 4 полученные результаты
обобщены на вязкоупругие материалы. В главе 5 приведено решение
пластической задачи о холодном волочении биметаллической
проволоки. Распространение волн в неоднородных средах рассмотрено в
главах 6 и 7. В главе 8 исследуются краевые эффекты в композитных
материалах.
25
Глава 1
ПРОВОДИМОСТЬ ВОЛОКНИСТЫХ КОМПОЗИТОВ
1.1. Математическая модель задачи проводимости
Несмотря на различную физическую природу, стационарные
задачи тепло- и электропроводности, диффузии, диэлектрической и
магнитной проницаемости описываются математически аналогично с
помощью уравнения проводимости
и уравнения сохранения
-кУи
Vx-q = /s
(1.1)
(1.2)
где и - потенциал, q - вектор потока, к - коэффициент проводимости,
представляющий собой физическую характеристику среды, / -
плотность объемных источников, Vx = ^ es d/dxs , es - базисные
векторы декартовой системы координат, s = 1,2,3 , ^ (•) обозначает
суммирование по s. Возможные физические значения величин,
входящих в уравнения (1.1), (1.2), приведены в табл. 1.1
В общем случае для анизотропных материалов коэффициент к
можно представить в виде симметричной матрицы
к к к
л,п /v12 /v13
Для многих задач проводимости взаимное влияние направлений мало,
поэтому в дальнейшем будем рассматривать случай ки = кхъ -к1Ъ - 0.
26
Таблица 1.1. Физические значения величин в задаче проводимости.
Потенциал и
Температура
Концентрация
вещества
Электрическое
напряжение
Электрический
заряд
Магнитный
потенциал
Поток q
Тепловой поток
Массовый поток
Плотность тока
Электрическая
индукция
Магнитная
индукция
Коэффициент к
Теплопроводность
Коэффициент
диффузии
Электропроводность
Диэлектрическая
проницаемость
Магнитная
проницаемость
1.2. Эффективный коэффициент проводимости
В данной главе рассматриваются однонаправленные волокнистые
композиты, состоящие из бесконечной матрицы £2(1) и периодической
решетки цилиндрических включений £2(2). Геометрическая структура
материала определяется векторами трансляции \s, s = 1,2. В качестве
примера рассмотрим квадратную (рис. 1.1, а) и гексагональную (рис.
1.1, б) решетки.
Эффективный коэффициент проводимости к33 в продольном
направлении х3 можно вычислить по правилу смеси:
k}}=(l-c(2,)km+ci2)k<2),
где с(2) - объемная доля волокон, к{а) - проводимости компонентов,
верхние индексы а = 1,2 обозначают, соответственно, матрицу и
волокна.
Более сложной является задача определения эффективной
проводимости к0 = кп = к22 в поперечной плоскости ххх2. Запишем
исходные уравнения (1.1), (1.2) в виде
27
*2a
Х\
Рис. 1.1. Однонаправленные волокнистые композиты.
а - квадратная, б - гексагональная решетка.
k{a)Vzxxu(a) = -/"
(1.3)
где V2x = ^ Э2/Эх2 - оператор Лапласа. На границе раздела
компонентов д£1 примем условия идеального контакта, отвечающие
равенствам потенциалов и потоков:
К'=«<21
а,/1) а#/2)
Эп
Эп
(1.4)
где Э/Эп - производные по нормали к д£1.
Вьщелим в композите два пространственных масштаба:
микроуровень, связанный с расстоянием / между центрами соседних
включений, и макроуровень, связанный с размером L всего образца
материала. В практических задачах L может соответствовать минимально-
м) периоду, оставляемому в разложении внешнего потока в ряд
Фурье. Введем малый параметр
€ = l/L,
(1.5)
характеризующий степень неоднородности композита.
Изменим масштаб координат и вместо исходных переменных xs
введем т.н. «медленные» xs и «быстрые» ys координаты:
28
xs = xs, ys = £ lxs, (1.6)
Производные запишутся в виде
dxs dxs dys
Решение исходной краевой задачи (1.3), (1.4) представим в виде
разложения
и{а) = uQ(x) + £u[a\x,y) + £2u{f(x,y) + ..., (1.8)
где х = ^ xses , у = ^ yses . Первый член и0 представляет собой
осредненную часть решения, которая изменяется на макроуровне в
пределах всего образца материала и не зависит от быстрых координат
(du0/dys = 0). Последующие члены u{ta), / = 1,2,3,... вносят поправки
порядка £1 и описывают локальные осцилляции потенциала на
микроуровне. В силу периодичности среды иг(а) также удовлетворяют
условию периодичности:
«,<a)(x,y) = M,(a,(x,y + L;,), (1.9)
где Ъ,=е-\,\р =2>А . Р. =0,±1,±2,....
Подставим выражения (1.6)—(1.8) в краевую задачу (1.3), (1.4) и
выполним расщепление по £, полагая, что проводимости
компонентов имеют одинаковый асимптотический порядок: к{2)/к{1) = 0(£°). В
результате получим рекуррентную последовательность краевых задач
на ячейке, включающих микроскопические уравнения проводимости
k(a) (V>^ +2V>S + V^uf) = -S2fa) (1.10)
и микроскопические условия идеального контакта
29
п0(1Ч
дп0^
дО. -^
у2/\
/ N.
/ \у^
! /N,
\ /
/\ '
\
J&
/
1
/
A 'V
^^
У\
Рис. 1.2. Ячейка периодичности, я - квадратная,
б - гексагональная решетка.
,(i)
— + ?_
^ Эп Эт )
ГД2)
г 1 +
(2) Л
Эп Эт
(1.12)
где и^ = 0, Sf - символ Кронекера, Sf = 1 при i = 2, <Sf = О при
<*2' ^=Х,Э2/(аг,Эу,). V2,,=X.^7^2, Э/Эт -производные
по нормали к д£1, записанные в быстрых координатах.
В силу периодичности и\а) (1.9), достаточно рассмотреть
уравнения (1.10)-(1.12) в пределах одной выделенной ячейки периодичности
Ц^О^+О^ (рис. 1.2).
Решение краевой задачи (1.10)-(1.12) при / = 1 позволяет
определить член и[а). Введем в ячейке полярную систему координат
г2 =yl +yl, tg# = у21У\ • Уравнения (1.10)—(1.12) при i = 1
запишутся в виде:
Ъ2и\а) 1 Ъи\а) 1 Э2^
{"Г=«Г}|^
(1.13)
(1.14)
30
/с(1) 1 /с(2) 1 = (к{2) /с(1))
Эг Эг Эп
(1.15)
где А - радиус включения в быстрых координатах.
Согласно [26], для симметричной области £10 условия
периодичности (1.9) при i = 1 можно заменить нулевыми граничными
условиями в центре и на внешней границе Э£20 ячейки периодичности:
К2,=4
(i.i6)
(1.17)
В уравнении (1.17) форма границы Э£20 задается следующим
образом:
R(0):
R,
cos 8
(1.18)
где R0 = L/2 - радиус вписанной окружности, 8 - в-в0 < 1. Для
квадратной решетки: -ж/4 <8<ж/4, в0=жп/2, /2 = 0,1,2,..., для
гексагональной решетки: - ж/6 < 8 < ж/6 , в{) - жп/Ъ .
Будем искать решение краевой задачи (1.13)—(1.17) с помощью
метода возмущения формы границы [73]. Представим и[а) в виде раз-
= ща0} + 8 и$ + 8Х,4 + ••• •
(1.19)
Перенесем граничное условие (1.17) с контура Э£20 (г = R0/cos8) на
вписанную окружность (г = R0) при помощи ряда Тейлора
Щ #0
+ gi Ro <Ч
2 Эг
5Д0 du\l) R* d2u{]
24 Эг + ~8~~Э^
(1.20)
+ ....
r=Ro
31
Выполнив расщепление уравнений (1.13)—(1.17) по параметру д,
находим:
ц(«)=(С(«)г + С(«)г-1)^9 ./ = 0,2,4,...; С^=0; (1.21)
v ' Эп
^1,0
г^) -
4,2 ~~
(^-^о wl) (^<2)-l)A2
А
' ^2,0 '
Dn
, с:
(2) .
(*(2>-i)(i-*0)
А,
(A(2)f-1
D
О)
> *-"2,2 ~~
(^(2)-1)2^оА2 Ы2) 2{Я^-1)Хо
■>с:
D D
^1,4
[л<2>+1-3*0(Л<2>-1)] (Л<2>)2-1
%{)
2Д
^2,4
(1) _
[^24l-3Zo(^-l)](^-l)2ZoA2
2Д3
(2) .
^1,4
[^+1-3Z)(^-1)](^>-1)Z)
д
D()=A(2>+l-Zo(^-l);
где А(2) = к{2) /к{1) - безразмерная проводимость волокон,
Х{) - A2/Rq = c{2)IcmL ' cmax ~~ геометрически максимально возможная
объемная доля волокон, с{2) = kA2/S0 , S0 - площадь ячейки в
быстрых координатах, S0 = L2, с^ = я/4 = 0.7853... для квадратной
решетки, S0 = v3L2/2, c^x = Л"л/3/б = 0.9068... для гексагональной
решетки, Э/Эп = д/дх1 cos # + Э/Эх2 sin в .
Запишем полученное решение (1.21) в виде:
^>=(СГ>Г + С^г-1)^-,
(1.22)
где
С = С$ + дгС\% + <ГС$ +..., р = 1,2 .
(1.23)
32
Ряд (1.23) расходится при Л{2) —> °о , с(2) —> с^х, что отвечает случаю
идеально проводящих волокон предельно большого размера.
Рассмотрим два способа устранения данной сингулярности.
Первый способ заключается в улучшении сходимости степенного
разложения (1.23) при помощи дробно-рационального преобразования
Паде [27]. Диагональная аппроксимация Паде порядка [2/2] имеет
вид:
с{% + дЦс{а]-с{а1с{а\1с{а])
i-fc«/c% ■ (L24)
Второй способ состоит в приближенной оценке значений
коэффициентов C£fl) на основе следующих соображений. Первый член
С(р1 ряда (1.23) представляет собой точное решение краевой задачи
(1.13)—(1.17) в случае, когда внешняя граница Э£20 ячейки заменена
окружностью так, что R{9) = R0. Такое решение точно удовлетворяет
уравнению (1.13) и граничным условиям (1.14-1.16), но вносится
невязка в условие (1.17) на Э£20 . Эта невязка последовательно
компенсируется в высших приближениях метода возмущения формы
границы. С другой стороны, данную невязку можно устранить уже в
нулевом приближении, если в формулах для С^ принять зависимость
R0 —> R(0) = R0/cosS согласно выражению (1.18). В этом случае
граничные условия (1.14-1.17) удовлетворяются точно, а уравнение
(1.13) - приближенно. В результате получим:
(1.25)
^1 ~~
/~(2) _
^1 ~~
D ' 2 '
(л(2)-1)(1-;г)
D
С^А2
X
cf=o,
D = A(2)+l-x(Ai2>-l)
где Ж=А2/Щв)2 =(cm/cZ)[R0/Rmf ■
33
Для нахождения эффективного коэффициента к0 применим к
уравнению (1.10) при / = 2 оператор осреднения по области ячейки
периодичности S"1 \\ (-)dS , где dS = dyxdy2. Члены и(2а) можно ис-
JJQ,0
ключить при помощи теоремы Гаусса-Остроградского, что с учетом
условий (1.9), (1.12) дает:
*(1,JJ(v>«+v>«)ds+^JJ(vX>+v>S)dS=o.
Осредненное уравнение имеет вид:
Q(1) Q(2)
-\\fl)ds-\\rds.
(1.26)
^
Подставив в соотношение (1.26) выражения для и[а), найденные
выше, получим макроскопическое уравнение проводимости порядка
KK«o=-fo> (1-27)
где /0 = (1-с(2) )/(1) +с(2)/(2) - осредненная плотность объемных
источников. Эффективный коэффициент проводимости к0 может быть
определен после вычисления интегралов в уравнении (1.26). В
настоящей работе выполнялось численное интегрирование с
использованием стандартных процедур математического пакета Maple.
Численные результаты для безразмерной эффективной
проводимости Дз = к0/к(1) в случае идеально проводящих волокон (Я(2) = <х>)
приведены в табл. 1.2. Как показывает сравнение с теоретическими
данными работы [412], полученными при помощи метода Рэлея, оба
приближенных решения (1.24) и (1.25) позволяют определить
эффективную проводимость с приемлемой точностью при любых объемных
долях компонентов. Окончательно решение задачи на ячейке примем
в виде (1.22), (1.25).
34
Таблица 1.2. Эффективная проводимость композитов
с идеально проводящими волокнами.
с(2)
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.74
0.76
0.77
0.78
0.783
0.784
0.785
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.76
0.8
0.84
0.86
0.88
0.89
0.895
0.9
0.905
0.9055
(1.23)
1.210
1.470
1.811
2.306
3.270
7.106
73.93
1.220
1.496
1.849
2.323
2.997
4.058
6.207
9.702
17.12
Настоящее решение
(1.24)
(1.25)
Квадратная решетка
1.247
1.544
1.918
2.417
3.145
4.386
7.409
10.91
15.29
20.18
35.01
1.223
1.506
1.879
2.395
3.172
4.517
7.769
11.46
15.99
21.04
36.60
55.58
73.08
136.8
Гексагональная решетка
1.232
1.519
1.885
2.369
3.048
4.079
5.872
7.818
10.00
14.03
17.83
25.24
33.53
41.69
56.09
109.3
128.3
1.222
1.501
1.861
2.344
3.028
4.079
5.924
7.938
10.20
14.36
18.27
25.99
34.32
42.00
56.90
113.2
132.3
Данные
[412]
1.222
1.500
1.860
2.351
3.080
4.342
7.433
11.01
15.44
20.43
35.93
1.222
1.500
1.857
2.334
3.005
4.027
5.811
7.760
9.959
14.01
17.84
25.45
33.70
41.34
56.23
112.8
35
Таблица 1.3. Сравнение теоретических и экспериментальных данных.
с(2)
0.651
0.754
0.802
Настоящее
решение
4.871
7.681
10.35
Эксперимент [412]
4.93+0.15
7.58+0.23
10.34+0.31
с(2)
0.849
0.873
0.881
Настоящее
решение
15.86
22.51
26.59
Эксперимент [412]
16.12+0.48
22.79+0.68
27.39+0.82
Рис. 1.3. Эффективная проводимость в случае сильного
взаимодействия соседних волокон, а - квадратная, б - гексагональная решетка.
В табл. 1.3 найденное решение для Я^ при Я{2) =°о сравнивается
с результатами экспериментальных измерений [412]
электропроводности гексагональной решетки идеально проводящих цилиндров.
Асимптотика Я^ в случае сильного взаимодействия соседних
а(2)
,) рассмотрена на рис. 1.3. Найденное
решение (сплошные кривые) хорошо согласуется с асимптотической
формулой [412] (штриховые кривые), полученной для двух высоко-
проводящих цилиндров, стремящихся к контакту:
36
0"
8-
6-
4-
2-
1-
Л) о
i<2) = 20
О
/io
я °
А/ $
___^eaSBS^^=^ c(2)
0.2 0.4 0.6 я/4
12"
ю-
8-
6-
4-
2-
1-
i(2) = 20J
у 10
У/ 5
_^^^^^^ ,(2)
0 0.2 0.4 0.6 0.8 I
л-л/з/б-
Рис. 1.4. Эффективная проводимость при различных значениях
проводимости волокон, а - квадратная, б - гексагональная решетка.
К=м
2 1пЯ<2> 1
ж А<2) я\
г ст \1П
, с<2) ,
(1.28)
где М = 1 для квадратной и М = л/З для гексагональной решетки.
На рис. 1.4 (а - квадратная, б - гексагональная решетка)
приведено сравнение полученного решения для \ (сплошные кривые) с
результатами расчета методом Рэлея [412] (кружки) при различных
провод имостях волокон.
1.3. Локальные поля на микроуровне
На основании разложения (1.8) для потенциала и{а) можно
определить поток q(a) в материале на микроуровне:
q(«> = _£(«> Гул + vXfl) +^(vXa) + vy,a))+
п (1.29)
^2(v^fl)+v^)+...
где Vy =Х,е,Э/ЭЛ •
37
2-
1.5 •
1
0.5-
^V%
-^__c^ = 0.2
^\^^^^
я/4^^
1.6
1.4-
1.2-
1
0.8-
0.6
ч(У)/%
c{2)=0.2
^^^^^^04
\\^^^^>
\ \0.8
л-л/з/б4^
0.2 0.4 0.6 7ij\ в
0 0.1 0.2 0.3 0.4 я/6 в
б
Рис. 1.5. Поток на границе «матрица-волокно», а - квадратная
решетка (1/8 ячейки), б - гексагональная решетка (1/12 ячейки).
В композитах с высокопроводящими волокнами (Л{2) > 1)
наибольший поток возникает на границе раздела компонентов. Поток q(3)
по нормали к д£1 равен:
„(3)
диа ди
(а) Л
Эп дг
+ 0(8).
Um*>- + Oie)t
D Л
где q{) - -к0 ди0/дп - осредненный поток через д£1 на макроуровне.
На рис. 1.5 приведено распределение потока q{3) по поверхности
волокна (Я(2) = 20). Анализ найденного решения показывает, что q(3)
достигает максимума в точках в = в{), где зазор между соседними
волокнами минимален.
На рис. 1.6 полученные результаты для максимального потока
q{3) при в' = 0О (сплошные кривые) сравниваются с решением
Г.А. Ванина [47] третьего порядка (штриховые кривые).
Даже при малой объемной доле волокон с(2) на границе раздела
компонентов возникают локальные концентрации градиентов. С
увеличением с(2) вначале наблюдается некоторое снижение локальных
градиентов, объясняющееся равномерным перераспределением
38
2.4-
2.2-
2.0-
1.8-
1.6-
1.4-
ei%
^^^^
У •
c(2)
0.2 0.4 0.6 я/4
0 0.2 0.4 0.6 0.8 I
л-л/з/б-
Рис. 1.6. Максимальный поток на границе «матрица-волокно»,
Я{2) = 20. а - квадратная, б - гексагональная решетка.
<7(37<7о
8-
6-
4-
2-
<7<3,/<7о
.^w^.
0.6 я/4
0.2
0.4 0.6 я/4
Рис. 1.7. Максимальный поток на границе «матрица-волокно»
(квадратная решетка), а - Я{2) = 120, б - Я{2) = 400.
потока между компонентами. Дальнейшее увеличение с(2) приводит к
усилению взаимодействия между соседними волокнами и
сопровождается ростом потока на границе раздела. В этом случае решение
Г.А. Ванина может расходиться, что иллюстрируется различием в
результатах для квадратной решетки при ск'
.(2)
. При качественно
схожих эффективных свойствах квадратная упаковка волокон
характеризуется большей степенью структурной неоднородности, чем
гексагональная, и поэтому в ней сильнее проявляются эффекты,
связанные с неравномерностью распределения полей на микроуровне.
39
Поток на границе раздела значительно возрастает с увеличением
проводимости волокон. На рис. 1.7 приведены результаты для д(3)
(в = в{)) в квадратной решетке при различных значениях Я{2).
Сплошные кривые - настоящее решение, штриховые кривые -
решение Г.А. Ванина [47] третьего порядка, кружки - теоретические
данные работы [338].
1.4. Волокна с покрытиями
Рассмотрим композиты, в которых волокна и матрица разделены
слоем покрытия £2(3). Ячейки периодичности изображены на рис. 1.8.
Исходное уравнение проводимости имеет вид (1.3), где а = 1,2,3. На
границах раздела «матрица-покрытие» Э^11 и «включение-покрытие»
д£12 примем условия идеального контакта:
{«(1)=«<з))|
дм(1) Ди(3)
£(1> ™ = £(3)—
{И(2)=и(3>]| , \к(2) —
1 Jbo2 Эп
дп
Эи(2)
1.(3)
дп
Эи(3)
дп
(1.30)
Решение краевой задачи (1.3), (1.30) будем искать с помощью
метода осреднения, при этом остаются справедливыми выкладки
(1.5Н1.10).
Микроскопические условия контакта (1.11), (1.12) принимают
вид:
K^L. К4 =44
с-\ а) а„аЛ
1-Х
ди{
ди°
Эп Эт
<А^
Ъи?] ди
(2) Л
Эп Эт
= к(
д£12
(ди{3] ди{3))
—— +——
у Эп Эт J
(Ъи?\ Эц(3)Л
L± + —
Эп Эт
(1.31)
(1.32)
40
од
Q0{
О)
->
/
/
f
л1
<ч
' ->
\
J&
\
\ \
1В>
А *У
^^
Рис. 1.8. Ячейка периодичности, а - квадратная,
б - гексагональная решетка.
Краевая задача на ячейке (1.9), (1.10), (1.31), (1.32) при i-\ в
полярных координатах включает соотношения (1.13), (1.16), (1.17) и
граничные условия
п) дщ (3) <Ц _ (т (3) _ т а) \ °и0
к ~эГ к 1Г~[к к ]йГ
д.(2) <Ц__£(3) ОЩ _ /^(3) ^(2) \ "М0
Эг
Эп
(1.33)
(1.34)
где В - толщина покрытия в быстрых координатах.
Следуя асимптотической процедуре, предложенной в п. 1.2,
приближенное решение задачи на ячейке (1.13), (1.16), (1.17), (1.33).
(1.34) запишем в виде (1.22). Коэффициенты С^а) имеют следующие
значения:
ст = _^с(*> +c<3))[2/t(2U<3)c<2) +,t<2),t<3)c(3) +
(/1(3>)V3) - 2/t(3V2> - 1(3У3) - 1(2V
.(3)
D\
(1.35)
с:
(i).
-CaVj,
41
с:
(2) _
2/t(2)/t(3) (с<2)) + 31<3)хс{2)с{Ъ) + А&х{с{Ъ)) -
2А{3) (cmf+2A<3)z{ci2)f -3l(3,c<2,C<3) -(1<3))2 jc(2,c<3) +
Amzcl2)cl3)-2AmAmz(cmf -A(2)A(3)z{c<3)f +
(1(3) )2 с(2)с<3) + /L(2)c(2)c<3) + /t(2)/t(3,c<2,c<3) -
31<2U<3)zc(2)c<y> - (/t(3) )2 j(c(3) )2 +1(2)j(c<3) )21 D~
C<2)=0,
C,<3) = Г21<2Ы<3) (с<2))2 +3/l(V<2,c(3) +/l<3)z(c<3))2 -
21<2) (c(2) )2 + 2Д(3) j(c<2) )2 -l(3,C<2,c(3) -(1(3) )2 zc(2)c<y> +
A™zcl2)cm -2AmAl3)z(cmf -A(2)A(3)z{c(3)f +
(A(3)f c(2)c(3) -A(2)c(2)c<3) +A(2)A<3,c<2)c<3) -
3A(2)Ai3)zc(2)c<3) -{A<3)f z{c<3)f +A(2)z{c<3)f \D~
Cf =2А2с<2,(с<2,+с<3))(Д(2)-Д<3))о-1,
D = -2A(2)A(y> (c(2) f + 2A<2>A<y>z{c<2> f + A(2>A(y>z{c0> У +
\2
(A(3))2^(2)c(3) -A(2V2)c(3) -A(3)c(2)c(3) -(/i(3)) c-c
(2)c(3) .
2 / ,,лЧ2
^)zc(2)c(3) _ 3^0)^(2)^3) _2Я(3) (C(2)) +(A(3)) Z(C(3)) -
я(3)ж{с(3))2 -a(2)z(^(3))2+3A(2U(V(2)c(3) -
A(2U(3)c(2)c(3)-2/l(3)z(c(2))2,
где Я{3) = к(3)/к{1) - безразмерная проводимость, с(:
](2h + h
объемная доля, h = В/А - безразмерная толщина покрытий.
Вычислив интегралы в осредненном уравнении
кт Я(У»"о +V^1(1))dS + Jk(2) JJ (V>0 +V2vu™)dS +
*(3) jj Ku0+K<)dS = - JJ /(V5 - JJ /<»<« - JJ /^,
Q(3) Q(1) Q(2) Q(3)
определим эффективный коэффициент проводимости к0 .
Найдем локальные добавки и[Ъ), f/^ к осредненному
потенциалу щ на обеих сторонах Э^11, д£12 покрытия:
с/Г = (»(3)-"о)|-
= £и)
+ 0(е2)--
а
Эм0
А2(1 + /г)
—- + 0(е),
+ 0(е),
а
С(3)+- '■
V
Az
Эп
где а = 6*А - радиус волокна в медленных координатах.
Потоки q[3), q{3) на границах раздела Э^11, д£12 можно
вычислить по формулам:
:-£(3)
А)
диа Эм1(3) *
—- +—-
Эп Эг
+ 0(*) =
1 + С(;
с-
A2(l + /i)2
+ 0(*),
Эип ди,
(3)Л
Эп Эг
+ <9(£) = 40-
А
1 + С(:
с
(3)Л
+ 0(£).
Рис. 1.9, 1.10 иллюстрируют влияние проводимости покрытия
Л{3) на локальные потенциалы и[Ъ), f/^ (нормированы по
отношению к / ди0 /Эп) и локальные потоки qf], #£3) в точках в = в0 .
43
U(3)/(ldu0/dn)
0.1
-6-4-20246
lg(/l(3)//l(2))
а
U(3)/(ldu0/dn)
0.1
-6-4-20246
lg(/l(3)//l(2))
б
Рис. 1.9. Потенциал на границах «матрица-покрытие» и «включение-
покрытие», я - квадратная, б - гексагональная решетка.
-6-4-20246
lg(/l(3)//l(2))
а
-6-4-2 0 2 4 6
lg(/l(3)//l(2))
Рис. 1.10. Поток на границах «матрица-покрытие» и «включение-
покрытие», а - квадратная, б - гексагональная решетка.
44
5"
4-
з-
2-
1-
о-
4)
a
/^__ _ r-^
lg(/l(3)//l(2))
0
Рис. 1.11. Эффективная проводимость волокнистых композитов
с покрытиями.
Штриховыми линиями обозначены значения потенциала U{} и
потока q{3), которые достигаются на границе раздела «матрица-волокно»
(при h = 0) в случае идеально проводящих (Я{2) = °о ) и абсолютно
непроводящих (Л{2) = 0) волокон.
Для тонких покрытий (h —» 0) при Я(3) < Я(2) условия контакта
матрицы и волокна отвечают модели мягкой (низкопроводящей)
границы: непрерывность потока (q{3) = q^}) и скачок потенциала
(Uf} > U^ ). При Я{3) > Я{2) реализуется модель жесткой (высокопро-
водящей) границы: равенство потенциалов (U[3) = U^) и разрыв в
поле потока {q{3) >^3)). Имеют место следующие предельные
переходы:
при Я{3) -* 0 : U{x
при Я{3) —> оо :
U(2)=o 2
>U
(3)
«Г =<£'-><
[/
/1(2)=0
(3)1
U<2)=o
= 0.
(1.36)
Результаты для эффективной проводимости Я^ приведены на
рис. 1.11. Сплошные кривые а и б - настоящее решение, соответст-
45
венно, для квадратной и гексагональной решетки, штриховая кривая -
решение 3. Хашина [328], полученное при помощи трехфазной
модели. Трехфазная модель не учитывает геометрию пространственной
упаковки волокон и дает заниженное значение Л^ при Я(3) —> °о .
Все расчеты выполнены для Я{2) = 20, с{2) = 0.6 , h = 0.01.
1.5. Неидеальный контакт между волокнами и матрицей
Для моделирования эффекта неидеального контакта рассмотрим
случай, когда объемная доля с(3) и проводимость Л{3) покрытия
стремятся к нулю. Тогда в зависимости от отношения Я{3)/с{3) можно
учесть различные степени адгезии компонентов. Введем
безразмерный параметр связи а так, что
Л(3)=—с(3)? о<*<1, (1.37)
а
и положим h —> 0, с(3) = с{2) (lh + h2) —> 0 . Значение а = 0
соответствует идеальному контакту, от = 1 - полному отсутствию контакта
между волокнами и матрицей. Промежуточные значения 0 < а < 1
отвечают модели низкопроводящеи границы. При этом поток q{3) через
границу «матрица-волокно» Э£2 пропорционален скачку потенциала
Аи(3)=\и(1)-и(2)}\ :
4(3)=-—Л*/3), (1.38)
Ъ
где b = еВ - толщина покрытия в медленных координатах, параметр
к* описывает проводимость границы. В случае идеального контакта
(а = 0) Аи{3) = 0. В случае полного отсутствия контакта (а = 1)
q{3) = 0, что соответствует композиту с абсолютно непроводящими
волокнами (пустотами).
Поток на границе матрицы и волокна составляет:
46
дип Ъи{ла) Л
Эп дг
4Я<У2>(1-«)<?„
А. Л
+ 0{е) =
+ 0(h) + 0(e),
(1.39)
где Д_ =2c(2,(l-a)[Ai2)+l-(Ai2)-l)z] + aAi2)(l + z).
Рассмотрим связь между параметрами а, к* и к(У>,
характеризующими свойства границы. Подставив решение для потенциала и(а}
(1.8), (1.22), (1.35) в уравнение (1.38), получим
к*
Ч{У) =~[е{и? -и?) + 0{е2)\
2аА(2>
А
+ 0(h)
k'q0
(1.40)
к'Ч
+ 0(е).
Приравнивая выражения (1.39) и (1.40), в асимптотическом пределе
h —» 0 найдем:
\-а
а
+ 0(h) ^к{3)+0(h).
На рис. 1.12 приведены результаты для эффективной
проводимости Дз в случае неидеального контакта (Я{2) = 20). При а = 0 и а = 1
найденное решение (сплошные кривые) хорошо согласуется с
данными работы [412] (кружки), полученными для Я{2) = 20 и А(2) = 0. Рис.
1.13 и 1.14 иллюстрируют влияние параметра связи а ,
соответственно, на эффективный коэффициент Я0 и на поток q{3) (в = в0) на
границе раздела «матрица-волокно». Расчеты выполнены для Я{2) = 20,
п(2) _
0.6.
47
Рис. 1.12. Эффективная проводимость в случае неидеального контакта
волокон и матрицы, а - квадратная, б - гексагональная решетка.
/1(2)=5,10,20,оо
/1(2)=5,10,20,
О 0.2 0.4 0.6 0.8 1 а 0 0.2 0.4 0.6 0.8 1 а
а б
Рис. 1.13. Влияние параметра связи на эффективную проводимость.
а - квадратная, б - гексагональная решетка.
48
4(3)Ч
1.5 Ч
0.5 И
т г~
0 0.2 0.4 0.6 0.8 1 а 0 0.2 0.4 0.6 0.8 1 а
а б
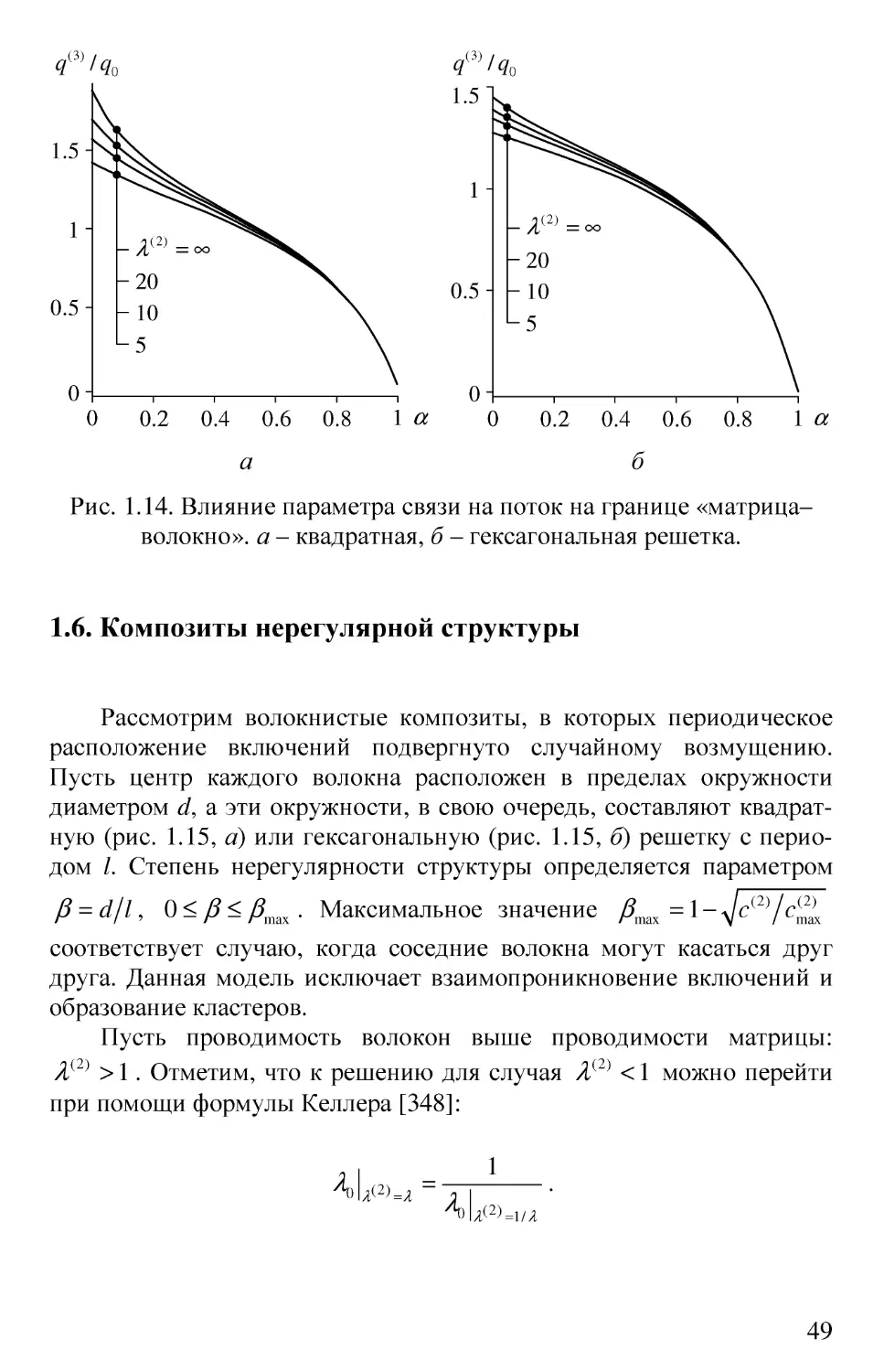
Рис. 1.14. Влияние параметра связи на поток на границе «матрица-
волокно», а - квадратная, б - гексагональная решетка.
1.6. Композиты нерегулярной структуры
Рассмотрим волокнистые композиты, в которых периодическое
расположение включений подвергнуто случайному возмущению.
Пусть центр каждого волокна расположен в пределах окружности
диаметром d, а эти окружности, в свою очередь, составляют
квадратную (рис. 1.15, а) или гексагональную (рис. 1.15, б) решетку с
периодом /. Степень нерегулярности структуры определяется параметром
J3 = d/l, 0 < J3 < Двах. Максимальное значение Дтх = 1 - ф(2)/с^х
соответствует случаю, когда соседние волокна могут касаться друг
друга. Данная модель исключает взаимопроникновение включений и
образование кластеров.
Пусть проводимость волокон выше проводимости матрицы:
Л{2) > 1 . Отметим, что к решению для случая Л{2) < 1 можно перейти
при помощи формулы Келлера [348]:
4,1.
1
х<Ъ=х
Мло-
2)=ш
49
к—
/'~ Г^х)
+^i
\ /
\ /
\ /
< >
d
>
I I
а б
Рис. 1.15. Волокнистые композиты нерегулярной структуры.
Введем нижнюю \ и верхнюю ^ оценки для эффективной
безразмерной проводимости Дз рассматриваемых нерегулярных
композитов:
4*4,^.
(1.41)
Обозначим эффективную проводимость в регулярном случае
(при /3 = 0) как функцию Л0(-) от объемной доли волокон, т.е.
Л0(с(2)) = Д)к_0 • Решение для Л0(с(2)) получено в п. 1.2.
СМ. Козлов [100], J1. Берлянд, В. Митюшев [257, 258] показали,
что строгую нижнюю оценку \ дает решение для соответствующей
регулярной структуры:
А=Ап(ст).
(1.42)
Верхнюю оценку ^ можно получить, если заменить случайно
расположенные волокна радиуса а периодической решеткой волокон
радиуса а + d/2. Данное приближение (т.н. «метод безопасных сфер»)
было предложено Дж. Келлером, Л. Рубенфельдом [349, 425] и
использовалось в работах [469, 470]. В результате найдем:
50
]Л)
г г
/?//Lx=o.3
/^ ^2
/у^ ^
' //s ^^—""""
' / / / /^
1 //// +'-'
' /ту '"
' /// '
1 и/А'
ч///'
ч//г
iff//1
1 1 1 1 1
/V/Lx=o.3
О 0.5 1 1.5 2 2.5 3
а
Рис. 1.16. Эффективная проводимость нерегулярных композитов.
а - возмущение квадратной решетки, б - возмущение
гексагональной решетки.
Я2=А0
(v^+a/^)2
(1.43)
Для сравнения рассмотрим также известные вариационные
оценки Хашина-Штрикмана [321]:
4=1 +
„<2)
л2=я(2> +
l/(A<2)-l) + (l-c<2,)/2'
1-с<2)
l/(l-A<2,) + c<2,/(2A<2))
(1.44)
(1.45)
Численные результаты приведены на рис. 1.16 для с{2) = 0.6 . При
высокой проводимости волокон (Л{2) —> оо ) полученные уточненные
оценки (1.42), (1.43) (сплошные кривые) оказываются значительно
лучше оценок Хашина-Штрикмана (штриховые кривые). Однако для
низкоконтрастных композитов (Я(2) —> 1) верхняя оценка Хашина-
Штрикмана (1.45) дает более точный результат. Поэтому в практиче-
51
ских расчетах из двух верхних оценок (1.43), (1.45) следует выбирать
наименьшую: Я, = min(^|(143) Д2|(145)).
1.7. Кластерная проводимость волокнистых композитов
В предыдущем параграфе рассмотрены композиты нерегулярной
структуры, в которых соседние волокна отделены друг от друга слоем
матрицы. Если расположение включений носит совершенно
случайный характер, то с увеличением их объемной доли с{2) в материале
образуются цепочки контактирующих включений (кластеры).
Критическое значение с{2) = с , при котором возникает кластер бесконечной
длины, называется порогом протекания.
Бесконечный кластер имеет фрактальную структуру. Согласно
модели Шкловского - Де Жена [189, 202, 295], его скелет
(проводящую часть) можно представить в виде сети с периодом Rc, который
называется радиусом корреляции:
Яс=: Цг ПРИ с{2)^ср> (L46)
где / - расстояние между центрами контактирующих включений, v -
индекс радиуса корреляции. Если с{2) < ср , то величина Rc
определяет максимальный размер конечных кластеров.
Эффективные характеристики к0 композита вблизи порога
протекания (с(2) —» ср ) определяются асимптотическими зависимостями
вида к0 ~ \с{2)-с\ , где t - критический индекс соответствующего
физического свойства. Для упругих модулей индекс t примерно в два
раза выше, чем для проводимости [295].
Различные модели перколяционных сред и соответствующие им
методы вычисления критических индексов рассмотрены в
монографии А.А. Снарского, И.В. Безсуднова, В.А. Севрюкова [170].
Отметим, что до настоящего времени имеют место расхождения между
результатами разных авторов (в основном это касается трехмерного
52
случая). Приведенные ниже выкладки (см. также п. 2.6) являются в
значительной степени упрощенными и носят оценочный характер.
Согласно общепринятым представлениям, критические индексы
зависят только от размерности пространства. Для двумерных задач
Ср =0.5, v-1.33.
Рассмотрим композит с идеально проводящими волокнами,
объемная доля которых стремится к порогу протекания снизу (к{2) = °о ,
с(2) —» с -0). Выделим область с характерным размером Rc+l, в
которую помещается один кластер максимальной длины Rc.
Удельное сопротивление такой области составляет
Ро=Р* 1
К+1
где р{1) = \/к{1) - удельное сопротивление матрицы, а эффективная
проводимость равна
1 к{1)
К= — ^ , (1.47)
А (ср-с^
Формула (1.47) получена из приближенных соображений и поэтому
не может претендовать на правильный учет численных множителей.
Однако она позволяет выявить характер сингулярности решения и
оценить его порядок.
В случае малой объемной доли волокон (с(2) —» 0 ) эффективная
проводимость определяется по формуле Гарнетта [313], которая для
двумерной задачи имеет вид:
к0/к{1) =1-2с
При к{2) = оо получим:
(2)
'l^A^y1
КД2> //Л1)
(1.48)
1 -и ^(2)
*оЛ(1,=^- (1-49)
53
Путем сращивания выражений (1.47), (1.49) можно найти
приближенное аналитическое решение, пригодное для любых значений
О < с(2) < с . Для этой цели используем метод асимптотически
эквивалентных функций [169, 214, 223, 225, 226, 373]. Искомую
эффективную проводимость представим в виде
kjk{l)=^ 1Ь * \ Ъ) , (1.50)
где £ = с{2) [ср -с(2)). Асимптотика функции (1.50) при ci2)—>cp
совпадает с выражением (1.47). Коэффициенты а0, ах, Ъх
определяются из условия совпадения разложения функции (1.50) в ряд по
степеням с(2) при с(2) —> 0 с соответствующим разложением формулы
(1.49) вплоть до порядка 0\ (с(2))2 включительно. В результате
находим: я0 =1, ai=l + cp+(l-cl)/(2cp), bl=l-cp+(l-cl)/(2cp).
Численные результаты приведены на рис. 1.17 (сплошная кривая
- функция (1.50), штриховая кривая 1 - формула (1.49), штриховая
кривая 2 - формула (1.47)). В принятом масштабе изображения
графики решений, полученных выше для регулярных решеток,
практически совпадают с результатами расчета по формуле Гарнетта (1.49).
Рассмотрим композит с абсолютно непроводящей матрицей, в
котором объемная доля волокон стремится к порогу протекания
сверху (к{1) =0, с{2) —>ср +0). Выделим прямоугольную область с
характерными размерами Ц , L2, причем Ц - L2» Rc. Сторону такого
прямоугольника пересекают п = Ц /Rc ветвей скелета бесконечного
кластера. Сопротивление одной ветви равно рх- p{2)L2/l, где
р{2) = 1/к{2) - удельное сопротивление материала волокна, L2 - длина
ветви в пределах выделенной области, / - поперечная ширина ветви.
Удельное сопротивление всей области составляет р0 = р^/(nL2) .
Тогда эффективная проводимость равна
*о= — = к™(с™-ср)\ (1.51)
Л)
54
2.5
2
1.5
1
0.5 i
0
lg(k0/k(l))
0"
0.5-
-1 -
1.5-
-2-
-2.5 -
lg(k0/k(2))
1 S -''''
/ **''' 2
//
ii
c<2)
0
0.1 0.2 0.3 0.4 0.5
0.5 0.6 0.7 0.:
0.9
1
Рис. 1.17. Эффективная проводи- Рис. 1.18. Эффективная
проводимость композита с идеально про- мость композита с абсолютно
неводящими волокнами. проводящей матрицей.
Если объемная доля матрицы мала (с(1) = 1 - с{2) —> 0 ), то к0
можно определить при помощи формулы Гарнетта (1.48), выполнив в
ней взаимную перестановку компонентов: к{1) <-> к{2), с(1) <-» с{2).
Тогда в случае к{1) = 0 получим:
к0/ к
г-(2)
2-е1
.(2) '
(1.52)
Срастив предельные решения (1.51), (1.52), найдем
асимптотически эквивалентную функцию, пригодную для любых значений
с. < с<2) < 1:
к0/к
2) _a0+a^ + f(l-cj
" i+ь^+е (i+#)"
(1.53)
где
1-с(-
1,
l + 2cp{l-cp)-{l~cj
2(1-,)
l + 2(l-cj(2-cj-(l-cj
2(1-J
55
Асимптотическое поведение функции (1.53) при с(2) —» с
определяется выражением (1.51), а разложение в ряд по степеням 1-с(2) при
с(2) —>1 совпадает с соответствующим разложением формулы (1.52)
до порядка 0[(1-с(2))2] включительно.
Численные результаты приведены на рис. 1.18 (сплошная кривая
- функция (1.53), штриховая кривая 1 - формула (1.52), штриховая
кривая 2 - формула (1.51)). Выражение (1.53) позволяет вычислить к0
вплоть до предела с(2) —> 1, когда материал включений полностью
заполняет весь объем композитной среды. Отметим, что если
включения имеют вид цилиндрических волокон, то максимально возможное
значение с^х = Ял/З/6 ~ 0.91 достигается при гексагональной
упаковке. Этот предел отмечен на рис. 1.18 вертикальной штриховой линией.
На пороге протекания с(2) = с эффективная проводимость
двумерного композита со статистически эквивалентным расположением
компонентов определяется по точной формуле Келлера-Дыхне [78,
348]:
N)L(2)=
:(к™к<
При Ас = с(2) -с U0 имеет место т.н. соотношение взаимности
[78], связывающее между собой значения эффективной проводимости
выше и ниже порога протекания:
JL|(2) a iU(2) A = к{1)к{2). (1.54)
Формулы (1.47), (1.51) удовлетворяют соотношению (1.54), что
подтверждает правильный асимптотический порядок полученных
решений.
56
Глава 2
ПРОВОДИМОСТЬ ЗЕРНИСТЫХ КОМПОЗИТОВ
2.1. Эффективный коэффициент проводимости
В данной главе рассматриваются зернистые композиты,
состоящие из бесконечной матрицы £2(1) и сферических включений £2(2),
составляющих простую кубическую (ПК) (рис. 2.1, а) и объемноцен-
трированную кубическую (ОЦК) (рис. 2.1, б) решетки. Ячейка
периодичности (1/8 часть) изображена на рис. 2.2. Для определения
эффективного коэффициента проводимости к0 =кп = к22 = к33 рассмотрим
уравнение (1.3), где 5 = 1,2,3, и граничные условия идеального
контакта (1.4). Используем асимптотический метод осреднения (п. 1.2),
при этом остаются справедливыми соотношения (1.5)—(1.12).
Краевая задача на ячейке (1.10)—(1.12) при i = \ в сферической
системе координат г2 = у2 + у\ + у\ , \%(р- у3/у2 , cos# = yxjr
запишется в виде:
д2и\а) 2ди\а) 1 ди\а)
1 - + —+ -; —+
дг2 г дг r2tgO дв
1 д2и\а) 1 д2и\а) Л
(2.1)
г2 дв2 г2 (sin0)2 Ъ(р2
{и?=и?\_ , (2.2)
;ь(1) 7)п{2) 7)i j
/с(1) 1 к{2) = (к{2) /с(1))
дг дг Эп
(2.3)
В силу пространственной симметрии задачи условия
периодичности (1.9) для и[а) можно заменить нулевыми граничными
условиями в центре и на внешней границе Э£20 ячейки периодичности [26]:
57
^(1) _ П(2) .
*1
0-A-,0
0;-I- 0 !
11 i i
(B^ 0
l< >l
X2
*3
dQ. -д, ^ "Д ^
(1) rV2)
Рис. 2.1. Зернистые композиты. я - ПК решетка, б - ОЦК решетка.
58
ЛА
И
У\
V3L/6 V3L/6
< >\< >\
а б
Рис. 2.2. Ячейка периодичности, а - ПК решетка, б - ОЦК решетка.
{<>=о}|
1 J\r=R(e,(p)
(2.4)
(2.5)
Форма поверхности Э£20 в уравнении (2.5) задается функцией
R(6, (р). Для 1/16 ячейки (0 < в < njl, 0 < (р < ж/4 ) выражения для
R{6,(p) приведены в табл. 2.1, где R0 = L/2 - радиус вписанной
сферы. При других шачениях углов в, (р функция R{6, (p) продолжается
периодически.
При помощи метода возмущения формы границы [73] заменим в
первом приближении поверхность Э£20 сферой постоянного радиуса
R(6, o) = Rq. С учетом данного упрощения решение задачи на ячейке
(2.1)-(2.5) можно записать в явном аналитическом виде:
k ди,
м(«)=(С(«)г + С(«)г-2\^
v ' Эп
(2.6)
59
Таблица 2.1. Функция R{6,<p) .
9
Я(в,<р)
ПК решетка
о..Д
4
0...arctg
( 1
^cos^?
arctg
1
coscp) 2
Л"
COS0
л
sin # cos (p
ОЦК решетка
0...
arctg
0... arctg
2[sin^ + cos^]
arctg
arctg
1
2[sin#? + cos#?]
2
cos#?-2sin#?
arctg
cos#?-2sin#?
л
*2~
2R»
V3cos#
7зя„
cos в + sin #(sin <p + cos #?)
2#n
v3sin#cos#?
arctg
71
■■■~4
0... arctg
2[sin#? + cos#?]
2#n
V3cos#
arctg
2[sin#? + cos#?]
л-
"~2
V3^n
cos # + sin #(sin #? + cos #?)
где Э/Эп = Э/Э^ cos в + Э/Эх2 sin 0cos<p + д/дх3 sin # sin <p, C1(a), Cf} -
некоторые коэффициенты. Такое решение точно удовлетворяет
уравнению (2.1) и граничным условиям (2.2)-(2.4), но вносит невязку в
условие (2.5) на внешней границе Э£20 ячейки. Эта невязка должна
компенсироваться в следующих приближениях метода возмущения
формы границы.
60
Полученное решение расходится в случае идеально проводящих
зерен, стремящихся к контакту. Данную сингулярность можно
устранить с помощью приближенной процедуры, предложенной в п. 1.2.
Определив коэффициенты С[а), С2а) из предположения R(0, <р) = R0,
восстановим затем исходную форму поверхности Э£20, приняв в
окончательном решении зависимость R(6,(p) согласно выражениям
табл. 2.1. В этом случае граничные условия (2.2)-(2.5)
удовлетворяются строго, а уравнение (2.1) - приближенно. Как показывают
приведенные ниже численные сравнения с результатами других авторов,
полученное таким образом решение позволяет определить к0 с
приемлемой точностью при любых значениях проводимостей и объемных
долей компонентов.
Окончательно находим:
(2.7)
^1 ~~
Г(2) _
^1 ~~
D ' 2 '
D
С?>АЪ
X
cf=o,
где Я{2) = к{2) /к{1) - безразмерная проводимость зерен,
Z = A3/R(0,<p)3 =(ci2)/c^x)[RjR(0,g))]\ c{2) = 4ttA3/(3V0)
-объемная доля зерен, 0 < с(2) < с^х, У0 - объем ячейки в быстрых
координатах, У0 =L3, cl2l =^/6 = 0.5235... для ПК решетки, У0 = W3L3/9,
с^1 = ял/з/8 = 0.6801... для ОЦК решетки.
Применим к уравнению (1.10) при / = 2 оператор осреднения по
области ячейки периодичности Vq_1 ГГГ (-)dV , где dV = dyldy2dy3.
JJJQ,0
Члены и{2а) можно исключить при помощи теоремы Гаусса-
Остроградского, что с учетом условий (1.9), (1.12) дает:
kmttk»W +KOdv+ki2)l\LAKu-2)+v>^)dv=°-
Осредненное уравнение имеет вид:
61
Таблица 2.2. Эффективная проводимость композитов
с идеально проводящими зернами.
ПК решетка
с(2)
0.1
0.2
0.3
0.36
0.4
0.44
Настоящее
решение
1.339
1.787
2.420
2.965
3.457
4.142
Данные
[379]
1.334
1.756
2.333
2.821
3.261
3.879
с(2)
0.46
0.48
0.5
0.51
0.515
0.52
Настоящее
решение
4.617
5.266
6.303
7.214
7.956
9.362
Данные
[379]
4.312
4.912
5.887
6.762
7.487
8.863
ОЦК решетка
с(2)
0.1
0.2
0.3
0.4
0.5
0.56
0.6
Настоящее
решение
1.335
1.760
2.319
3.100
4.304
5.453
6.621
Данные
[377]
1.333
1.751
2.292
3.035
4.166
5.243
6.341
с(2)
0.62
0.64
0.65
0.66
0.67
0.675
0.677
Настоящее
решение
7.450
8.617
9.437
10.58
12.51
14.38
15.72
Данные
[377]
7.127
8.238
9.026
10.13
11.99
13.81
15.03
Таблица 2.3. Сравнение теоретических и экспериментальных данных.
с(2)
0.0848
0.446
0.497
0.565
0.575
Настоящее
решение
1.279
3.581
4.257
5.575
5.836
Эксперимент [377]
1.31+0.04
3.52+0.11
4.15+0.12
5.24+0.16
5.56+0.17
с(2)
0.606
0.623
0.642
0.660
0.671
Настоящее
решение
6.846
7.599
8.763
10.58
12.80
Эксперимент [377]
6.41+0.19
7.16+0.22
8.42+0.25
9.59+0.29
11.8+0.35
62
1 f 1 1 1 1 l-l 1 I 1 1 1 1 1 1 1
0 0.1 0.2 0.3 0.4 0.51 0 0.1 0.2 0.3 0.4 0.5 0.6 I
Ф-* W3/sJ
а б
Рис. 2.3. Эффективная проводимость при различных значениях
проводимости зерен, а - ПК решетка, б - ОЦК решетка.
k(l1lk»Ku0+n«.(,))^+*w> ffi^K*+п»;2)к = 2 8
-ш^/^-Шср./^- (2'8)
Подставив в соотношение (2.8) выражения (2.6), (2.7) и выполнив
интегрирование, получим макроскопическое уравнение проводимости
(1.27) и определим эффективный коэффициент к0 .
Численные результаты для безразмерной эффективной
проводимости А^=к0/к(1) в случае идеально проводящих зерен (А(2)=оо)
приведены в табл. 2.2, 2.3. Найденное решение сравнивается с
теоретическими данными [377, 379], полученными при помощи метода Рэ-
лея (табл. 2.2), и с результатами экспериментальных измерений [377]
электропроводности ОЦК решетки, составленной из идеально
проводящих шаров (табл. 2.3).
На рис. 2.3 приведены зависимости \ от с(2) при различных
проводимостях зерен. Сплошные кривые - настоящее решение,
штриховые кривые - результаты расчета методом Рэлея [377, 379].
Асимптотика Я^ в случае сильного взаимодействия соседних
зерен рассмотрена на рис. 2.4, 2.5. Найденное решение (сплошные
кривые) хорошо согласуется с асимптотическими формулами [244]
(штриховые кривые), полученными для двух высокопроводящих
сфер, стремящихся к контакту:
63
л
л
1п<Г
6^
4-
2-
о-
1п<Г
1 2
Рис. 2.4. Эффективная проводимость в случае Я{2) = °о , с{2) —» с^ .
а - ПК решетка, б - ОЦК решетка.
8-
6-
4
2-
0 -
4, /
/у'
^у'
^у' ч^2)
юН
0 0.5 1 1.5 2 2.5
а б
Рис. 2.5. Эффективная проводимость в случае с{2) = с^ » ^(2)
я - ПК решетка, б - ОЦК решетка.
Ад=М1Ы£-М2 при Я(2) = оо , с(2) -> с^,
Дз = М! In /£(2) - М2 при с{2) = с^ , Я{2) -> оо ,
где С = [l-(c(2)/c^)1/3]_1, Мх =я/2, М2 = 0.7 для ПК и Мх = Ял/з/2 ,
М2 = 2.4 для ОЦК решетки.
64
2.2. Локальные поля на микроуровне
Потенциал и{а) и поток q(a) можно найти при помощи
разложений (1.8), (1.29). В композитах с высокопроводящими зернами
(Я{2) > 1) наибольшие градиенты полей возникают на границе раздела
компонентов. Поток q{3) через д£1 равен:
f Э^
,»
'и0 duY
v Эп дг у
+ 0(e) = Щ^^ +0(e).
D Л^
На рис. 2.6 приведено распределение потока q{3) по поверхности
зерна для 1/16 ячейки периодичности (0 < в < ж/2 , 0 < (р < ж/А ) при
А(2)=20,
Л2)
■ 0.4. Кривые 1-5 построены для различных значений
угла (р (рис. 2.7, табл. 2.4). Анализ найденного решения показывает,
что q{3) достигает максимума в точках в = 0О, <р = <р0, где зазор
между соседними зернами минимален. Для ПК решетки в0 = (pQ = жп/2 ,
для ОЦК решетки 0О = ±arctg(V2) + жп , % = ж/4 + жп/2 , п = 0,1,2,....
2.8-
2.4-
2-
1.6
1.2 \
*(3)/*о
1
/2
// 3
// 4
У^^^ 5
0.4
0.8 1.2 я/2 в
2-
.8-
.6
А-
е/%
5
//^\\
Г/3\\
^\ N\r-
1 y<2\S
0.4 0.5
Рис. 2.6. Поток на границе «матрица-зерно».
а - ПК решетка, б - ОЦК решетка.
1.2 л/2 в
65
Таблица 2.4. Расчетные значения полярного угла (р.
Кривая
ПК решетка
ОЦК
решетка
1
0
0
2
л/16
arctg(l/2)
2
3
л/8
arctg(l/2)
4
Зл/16
arctg(l/2 + ^/4)
2
5
л/4
л/4
Jl/N
^12 3 4 5 yz^ 1 2 3
я б
Рис. 2.7. Расчетные значения угла (р на плоскости 3^2.
На рис. 2.8 приведены результаты для максимального потока q(3)
(в = в0 , (p = (pQ) при различной проводимости и объемной доле зерен.
66
0"
8-
6-
4-
2-
ei%
Я{2) =00,50,20,10,5 -j
с{2)
еч%
О 0.1 0.2 0.3 0.4 0.5
я/6
О 0.1 0.2 0.3 0.4 0.5 0.6 I
Д2)
л-л/з/8-
Рис. 2.8. Максимальный поток на границе «матрица-зерно».
а - ПК решетка, б - ОЦК решетка.
2.3. Зерна с покрытиями
Рассмотрим ПК решетку сферических включений, отделенных от
матрицы слоем покрытия £2(3). Ячейка периодичности (1/8 часть)
изображена на рис. 2.9. Исходное уравнение проводимости имеет вид
(1.3), где 5 = 1,2,3, а = 1,2,3. На границах раздела «матрица-
покрытие» Э^11 и «включение-покрытие» д£12 примем условия
идеального контакта (1.30).
Решение краевой задачи (1.3), (1.30) будем искать с помощью
метода осреднения, при этом остаются справедливыми выкладки
(1.5)—(1.10). Микроскопические условия контакта запишутся в виде
(1.31), (1.32). Краевая задача на ячейке (1.9), (1.10), (1.31), (1.32) при
i = l в сферической системе координат включает уравнение (2.1) и
граничные условия (2.4), (2.5), (1.33), (1.34). Следуя
асимптотическому упрощению, предложенному в п. 2.1, найдем приближенное
решение задачи на ячейке в виде (2.6), где коэффициенты С(а) равны:
Cl(1) =-z{c{2) +c(3))[3A(2U(3)c(2) +A(2U(3V3) +
2(A(3))V3) -ЗЛ(3У2) -2A(3)c(3) -A(2)c(3)1d-
(2.9)
67
У1А
Г{2) _
4 ~~
Рис. 2.9. Ячейка периодичности.
С?=-С?>А3/х,
ЗД(2)Дт (c(2'f +5Л^жс(2,с0' +2^,z{c(J,f -
ЪЛ0) (с(2) f + ЗЛтх{с{2) f -5Л(3¥2У3' -2{Л0) f Zc{2V
Л^Хс(2)с(Ъ) -ЪЛтЛ^х{ст)2 -/t(2U(3)4c(3))2 +
2(Д<3))2 с(2)с(3) +2Л(2,c(2,c<3, +Д(2,Д(3)с(2)с(3) -
4Д(2)Д,3^с(2)с(3' -2(Я(3')2^(с(3))2 +ЛтХ{с&)2
D"
С<2)=0.
-(3)
'зЛ(2)Л(3) (с(2))2 +5Д<3,zc<2)c<3, +2Д(3)х(с(3))2 -
ЗД<2) (с(2) f + ЗД<3,^(с<2) )2 - 2Д(3,С<2)С<3) - 2(Л0) f zc(2\
Л^Хс^с(г> -3/l(2)/l(3)j(C(2))2 -l(2U(3)j(C<3))2 +
2(Лт)2 с<2¥31 -/t(2V2V31 + 1,2U(3¥2¥3) -
4l(2),L<3V2y3) -2(1<3))2 j(c<3))2 +/l(2)j(C<3))2lz)-1>
68
с^'&
лъ\
С?> = ЗА3с<2) (с<2) +с(3))(Д(2) -Xm)D~l,
D = -ЗЯ(2>Я(У> (с<2> f + ЗЛ<2>Л<у>ж(с<2> f + Л<2>Л<у>ж(с(У> f +
2(Д<3))2 zci2)c0) -21<2,с<2У3) -4Д(3)С<2,С<3) -2(1<3))2 -<2,-<3)
Л{2)Хс{2)с{Ъ) -5/t(3V2,c(3) -61<3) (c(2)f +2(1<3))2Х{<-
2/t(3)j(C<3))2 -Л(2)х(с(Ъ))2 +4Л(2)Л(Ъ)хс(2)с& -
Я<2'Я<3>с(2)с(3)-ЗЯ(3)^(с(2))2.
Здесь с(3)=с(2)(3/г + 3/г2+/г3) - объемная доля, Л(3)=к(3)/кт
-безразмерная проводимость, h = В/А - безразмерная толщина покрытий.
Вычислив интегралы в осредненном уравнении
JJJo... Kuo+Ku?')dv+k(2>\ll^ (vi«o + П«Г )dv+
]dV,
определим эффективный коэффициент проводимости к0 .
Локальные потенциалы и[Ъ), U^ и потоки q[3), q{3) на границах
раздела Э^11, д£12 равны:
и[Ъ)=иъ)-и A =£ul3)\ +0(£2) =
CJ3'(1 + A) + —
/-(3)
^2
—°- + 0(г),
Эп
А3(1 + /г)
t/f =(и(3)-и0)|ао =^(3)|г_а+0(^)
.^~
Ч3) ^ дм
W3) , ^2_ | "М0
^1 "*" i3
С(3:
-(3) , ^2
'• А3
Эп
69
(3)
q\]
П3>
—- +——
Эп дг
+ 0(е)-.
Я{Ъ)
А)
( диа ди?} *
—- +—L
^ Эп дг j
1 + С(;
2Q:
A3(l + /i)J
+ 0{е\
+ O(e) = q0
Я^
1 + С(:
1С
■О) Л
+ 0(е).
где а = еА - радиус зерна в медленных координатах.
Численные результаты для потенциалов и[Ъ), U^ и потоков
q{3), gf0 в точках 9 = #0, (р-% приведены на рис. 2.10, 2.11. Для
тонких покрытий (h —> 0) при А(3) < А(2) условия контакта матрицы и
зерна отвечают модели низкопроводящей границы: q{3) = q{3),
и[Ъ) > U^ . При Я{3) > Я{2) реализуется модель высокопроводящей
границы: U{ = U{2 \ q[' > q\ . Штриховыми линиями обозначены
значения потенциала U{3) и потока q{3) на границе раздела «матрица-
[/(3)/(/Эи0/Эп)
qV/q0
о-
-0.1-
-0.2-
-о.з-
-0.4-
иА
ufl
1
/l(2)=0
Л(2)=оо \^
-| 1 1 1 1
-4-20246
lg(/l(3)//l(2))
4]
3-
2-
1-
o-
1 /l(Z)=oo
_J /i(2)=o
1 1 1
/f>
u3)
—1 1 1
-4-20246
lg(/l(3)//l(2))
Рис. 2.10. Потенциал на границах
«матрица-покрытие» и
«включение-покрытие»
Рис. 2.11. Поток на границах
«матрица-покрытие» и
«включение-покрытие».
70
3.5
3
2.5
2
1.5
1
0.5
-6-4-20246
Рис. 2.12. Эффективная проводимость зернистого композита
с покрытиями.
зерно» (при h = 0) в случае идеально проводящих (Л{2) = °о ) и
абсолютно непроводящих (Я(2) = 0) зерен. Имеют место предельные
переходы (1.36).
Рис. 2.12 иллюстрирует влияние проводимости покрытия Л{3) на
эффективный коэффициент \. Сплошная кривая - настоящее
решение, штриховая кривая - результаты, полученные при помощи
трехфазной модели [327] без учета вида пространственной упаковки зерен.
При расчетах принято Я{2) = 20, с{2) = 0.4 , h = 0.01.
2.4. Неидеальный контакт между зернами и матрицей
Рассмотрим случай, когда объемная доля с(3) и проводимость
Я(3) покрытия стремятся к нулю. Введем безразмерный параметр
связи а (1.37) и положим /г->0, с(3) = с{2) (3h + 3h2 + /г3) -»0. Значение
а = 0 соответствует идеальному контакту, а = 1 - полному
отсутствию контакта между зернами и матрицей. Промежуточные значения
0 < а < 1 отвечают модели низкопроводящей границы, когда поток
q{3) через границу «матрица-зерно» д£1 пропорционален скачку
потенциала Аи{3) (1.38). В случае идеального контакта (а = 0)
Аи(3) = 0. В случае полного отсутствия контакта (а = 1) д(3)=0, что
соответствует композиту с абсолютно непроводящими зернами
(пустотами).
71
Поток на границе матрицы и зерна составляет:
„(3)
ди0 ди[а)
Эп дг
4l-a)q0
+ 0(е).
Д
А
+ 0(h) + 0(e),
(2.10)
где Д =3ci2)(l-a)[A(2} +2-(А(2} -l)z] + aA(2)(2 + z)-
Рассмотрим связь между параметрами а, к* и &(3),
характеризующими свойства границы. Подставив решение для потенциала и{а)
(1.8), (2.6), (2.9) в уравнение (1.38), найдем
qty>=~[e{u?-u?) + 0(e2)]l__
д
+ 0(й)
£'ffo
(2.11)
*°ч
+ 0(е).
Приравнивая выражения (2.10) и (2.11), в асимптотическом пределе
h —> 0 получим:
Г = 3k(l)c(2)h
\-а
а
+ 0(h) ^ к{Ъ) + 0(h),
На рис. 2.13 приведены результаты для эффективной
проводимости Дз ПК решетки в случае неидеального контакта (Л{2) =20). При
а = 0 и яг = 1 найденное решение (сплошные кривые) хорошо
согласуется с теоретическими данными работы [379] (штриховые кривые),
полученными для Я(2) = 20 и Я(2) = 0. Рис. 2.14 и 2.15 иллюстрируют
влияние параметра связи а, соответственно, на эффективный
коэффициент Д и на поток q(3) на границе матрицы и зерна (Я{2) = 20,
Л2)
= 0.4, 0 = 6>о,#> = %).
72
Рис. 2.13. Эффективная проводимость в случае неидеального контакта
зерен и матрицы.
^/%
/1(2)=5,10,20,с
/1(2)=5,10,20,оо
О 0.2 0.4 0.6 0
1 а
0 0.2 0.4 0.6 0,
1 а
Рис. 2.14. Влияние параметра
связи на эффективную проводимость.
Рис. 2.15. Влияние параметра
связи на поток на границе
«матрица-зерно».
2.5. Композиты нерегулярной структуры
Рассмотрим зернистые композиты, в которых периодическое
расположение включений подвергнуто случайному возмущению.
Пусть центр каждого зерна расположен в пределах сферы диаметром
d, а эти сферы, в свою очередь, составляют ПК или ОЦК решетку.
Период решетки (расстояние между центрами соседних сфер) равен /.
Степень нерегулярности структуры определяется параметром
73
P = d/l, 0 < P < Дтах. Максимальное значение Дшх = 1 - (с(2)/с^)
отвечает случаю, когда соседние зерна могут касаться друг друга. При
этом исключается взаимопроникновение включений и образование
кластеров.
Пусть проводимость зерен выше проводимости матрицы:
Л{2) > 1 . Введем нижнюю Л[ и верхнюю ^ оценки для эффективной
проводимости Дз (1.41).
Как показано в работах [100, 257, 258], нижняя оценка \
совпадает с решением для соответствующей регулярной структуры и может
быть записана в виде (1.42), где функция Л0(с(2)) = Л^\
определяется согласно результатам п. 2.1.
Чтобы получить верхнюю оценку Л1, заменим случайно
расположенные зерна радиуса а периодической решеткой зерен радиуса
а + d/2 . Тогда
Л2=А0
(c«T+fi№
(2.12)
Для сравнения рассмотрим вариационные оценки Хашина-
Штрикмана [330]:
Д =1 + — — —, (2.13)
4 1/(Я(2)-1) + (1-с(2))/з
1 - г(2)
Л2=Л{2)+—-/ —^ Г/ -. (2.14)
h l/(l-A(2)) + c(2)/(3A(2))
Численные результаты приведены на рис. 2.16 (с(2) =0.4). При
высокой проводимости зерен (Л{2) —> °о ) полученные уточненные
оценки (1.42), (2.12) (сплошные кривые) оказываются значительно
лучше оценок Хашина-Штрикмана (штриховые кривые). Если же
проводимость зерен близка к проводимости матрицы {Л{2) —>1), то
верхняя оценка Хашина-Штрикмана (2.14) дает более точный
результат. Поэтому из двух верхних оценок (2.12), (2.14) следует выбирать
наименьшую: Л, = min(^|(212) Л|(2.14)) •
74
/V/Lx=q3 4
3.5 H
3^
2.5
2
1.5
1
0 0.5 1 1.5 2 2.5 3
а б
Рис. 2.16. Эффективная проводимость нерегулярных композитов.
а - возмущение ПК решетки, б - возмущение ОЦК решетки.
J А,
/
А 1
/
11
II
1 /1
г 1
/?//L.=o.3
1 / У
1 / / ^.
1 / / s ^
'//А
—i 1 1
0.2
0.1
0
lg^(2)
~i 1
2.6. Кластерная проводимость зернистых композитов
Рассмотрим композиты, в которых зерна расположены
случайным образом и могут образовывать кластеры. Радиус корреляции
определяется выражением (1.46), где для трехмерного случая с = 0.16 ,
V-0.85 [189, 202, 295].
Если проводимость зерен равна бесконечности (к{2) = °о), а
объемная доля стремится к порогу протекания снизу (с
(2)
-0), то
остается справедливым ход решения, предложенный в п. 1.7 для
двумерной задачи. При этом эффективную проводимость к0 можно
приближенно найти по формуле (1.47).
Если объемная доля зерен мала (с(2) —> 0 ), то к0 определяется по
формуле Гарнетта [313]:
75
^A<1)=1-3c<1tSt^+c<2)J ' (2Л5)
которая при к{2) = °о дает:
К1кт=Ц^-. (2.16)
Асимптотически эквивалентная функция, полученная путем
сращивания предельных решений (1.47) и (2.16), имеет вид (1.50), где
а0 = 1, а, = l + 2cp +(l-cvp)/(3cp) , \ = 1 -ср + (1 -с\)/(Зср) .
На рис. 2.17 приведены результаты для эффективной
проводимости к0 в случае идеально проводящих зерен, объемная доля которых
не превышает порог протекания. Сплошная кривая - функция (1.50),
штриховая кривая 1 - формула (2.16), штриховая кривая 2 - формула
(1.47).
Рассмотрим композит, в котором матрица является изолятором, а
объемная доля зерен стремится к порогу протекания сверху (к{1) = 0,
с{2) —>ср+0). Выделим область в виде параллелепипеда с
характерными размерами сторон Ц , L2, Ц , причем Ц - 1^ - Ц » Rc. Число
ветвей скелета бесконечного кластера, проходящих через боковую
грань, равно п = Ц^/Я2 . Сопротивление каждой ветви составляет
рх = p^Lj/l2 , где р{2) = \/к{2) - удельное сопротивление зерен, Ц -
длина ветви в пределах выделенной области, I2 - площадь
поперечного сечения ветви. Удельное сопротивление всей области равно
р0 = р^ЦI\пЦ), где Ц - размер области в продольном
направлении, LJ-^- площадь боковой грани. Тогда для эффективной
проводимости к{) получим:
К= — ^к{2){с{2)-ср)2\ (2.17)
Л)
При малых значениях объемной доли матрицы (с(1) = 1 - с(2) —» 0 )
определим к0 при помощи формулы Гарнетта (2.15), выполнив в ней
76
2.5"
2-
1.5-
1 -
0.5-
о-
lg(V*
2
^(1)) 1
/I
"~'~ /
^^ 1
0
-0.5 i
-1
-1.5
-2
-2.5
\g{kQlk{2))
1 ^
0 0.04 0.08 0.12 0.16
0.2 0.4 0.6 O.i
1
Рис. 2.17. Эффективная проводи- Рис. 2.18. Эффективная
проводимость композита с идеально про- мость композита с абсолютно
неводящими зернами. проводящей матрицей.
взаимную перестановку компонентов: к{1) <-» к{2\ с(1) <-» с(2). В
случае к{1) = 0:
к{)/к
2^
3-е1
.(2) *
(2.18)
Срастив предельные решения (2.17), (2.18), найдем
асимптотически эквивалентную функцию, пригодную для любых значений
с < с(2) < 1:
к0/к
' 1 + ^ + f (1 + £)2"
(2.19)
где
2 + 3cp(l-cp)-2(l-cpf 4 + 3(l-c,)(3-c,)-4(l-c,)2'
3(!-s)
Ь=-
6(!-cJ
77
Численные результаты приведены на рис. 2.18. Сплошная кривая
- функция (2.19), штриховая кривая 1 - формула (2.18), штриховая
кривая 2 - формула (2.17). Кружками обозначены экспериментальные
данные [172], полученные путем измерения электрического
сопротивления композитной смеси проводник (графит) - диэлектрик
(парафин).
Выражение (2.19) позволяет вычислить к0 вплоть до предела
с(2) —> 1, когда материал включений полностью заполняет весь объем
композитной среды. Если включения имеют вид сферических зерен,
то при случайном расположении в пространстве их максимальная
объемная доля составляет с^х ~ 0.637 . Это значение отмечено на рис.
2.18 вертикальной штриховой линией.
В случае сильного различия свойств компонентов (к{2) » к{1))
эффективная проводимость трехмерного композита на пороге проте-
= с подчиняется зависимости [19, 346]:
S)L(2)=
(£(1))V
(2.20)
Запишем асимптотические формулы (1.47), (2.17) в виде:
к{1) - k0Acv, к{2) - k0Ac~2v, (2.21)
где Ас = с(2) -с I —> 0 . Выражения (2.21) удовлетворяют
соотношению (2.20).
78
Глава 3
УПРУГИЕ СВОЙСТВА КОМПОЗИТОВ
3.1. Основные соотношения теории упругости
Линейная теория упругости устанавливает следующие
зависимости между перемещениями иг , деформациями е и напряжениями а
в сплошной среде.
а) Уравнения Коши:
dut
—-
Эх
ди, ди
£ = —+ —^
Эх, Эх
i, j = 1,2,3. (3.1)
б) Уравнения совместности деформаций:
(3.2)
Ъх\
dxl
д2£2.
~~dxf
2 У- +
Эх2Эх3
ЭххЭх3
2 ^- +
ЭххЭх2
, О £22 О £п
Эх2 ЭххЭх
1 , ЭЧз ^^13
Эх2 ЭххЭх,
1+э^1__э^з
Эх2 Эх2Эх
ЭЧз__
Эх2
дх\
д2£и
Эх32
Э2£12
ЭххЭх3
Э2£12
Эх2Эх3
_Э^_
Эх2Эх3
- = о,
- = о,
S
- = о,
3
ЭЧз
ЭххЭх2
Э2£23
ЭххЭх2
ЭххЭх3
= 0.
Ниже рассматриваются решения упругих задач в перемещениях, при
этом соотношения (3.2) выполняются тождественно,
в) Уравнения равновесия:
79
д<7и Э(719 Э(Х
дхх
Э<т91
дх2 Эх
да,, д(70
^ + /,=0,
Эх Эх, Эх.
•+/2=о,
дет,. Э(Х0 д<7
Эх Эх.
Эх
^+/3=о,
(3.3)
г) Закон Гука для анизотропного тела:
*Лз J v
"*и"
^22
^зз
^23
^13
_£п_
=
'Л
24
^34
*М4
^25
^35
Л5
^55
Л
^
Л
^
Л
16
26
36
46
56
66.
"Oil"
сг22
^зз
сг23
<713
_сг12_
(3.4)
В приведенных выражениях /г - компоненты объемной силы, [Jmn] -
симметричная матрица коэффициентов податливости, Jmn = Jnm,
Gu =ал> £v =£»> U j = 12,3, m,n = l,...,6.
Для ортотропных материалов, свойства которых симметричны
относительно трех взаимно перпендикулярных плоскостей,
коэффициенты матрицы [Jmn] равны:
Jn = l/El , J22 = l/E2 , /33 = l/E3 , (3.5)
*M2 ~~ ftlll^l ' *ЧЗ -~№ъ\1^Ъ ' ^23 -~№ъ21^Ъ
J44 = VG23 > ^55 = VG13 > Лб = VG12 >
*44 = *M5 = *M6 = ^24 = ^25 = ^26 = ^34 = ^35 = ^36 = ** 45 = *M6 = ** 56 = " '
где Et - модули Юнга, Gt] - модули сдвига, juy - коэффициенты
Пуассона, jui]E] =MjA-
Однонаправленные волокнистые композиты (рис. 1.1) являются
трансверсально-ортотропными. Пусть ось х3 совпадает с
направлением волокон. Закон Гука (3.4), (3.5) можно записать в виде:
80
£,,=
p —
°22
^*33 —
a\\ ^22 °ЪЪ
Jjjrj-, iZj'Y -^7
/7 /7 /7
<Tn (T22 (T33
^ EL EL
(3.6)
p _ ^23 p _ ^VS_ p _ G\2
fc23 ^ ' fc13 ^ ' fc12 ^ •
UL UL UT
Свойства таких композитов описываются при помощи шести
независимых упругих констант: EL = Е3 , Ет = Ех - Е2, GL = G13 = G23 ,
GT = Gn , juL = //31 = //32, /^ = /^2 = //21, причем /^ = //23 = MlEt/El •
Гексагональная решетка цилиндрических волокон (рис. 1.1, б)
является трансверсально-изотропной. К соотношениям (3.6)
добавляется зависимость GT = Ет/[2(1 + jiiT)j , а число независимых упругих
констант сокращается до пяти.
В зернистых композитах (рис. 2.1) три плоскости симметрии
взаимно заменяемы. Закон Гука имеет вид:
(3.7)
Е =
Ег
= Е2
°\\ ^22
11 ЕЕ
22 ЕЕ
0\\ ^22
£^~^-^
С723 С713
Р — —— Р — ——
23 G ' 13 G '
= Е3, G = Gl2 — G13 = G23,
азз
Е
а33
*12" G
A = /V
ju = jug. Число независимых
упругих констант равно трем.
Наконец, в случае изотропной среды дополнительно к
уравнениям (3.7) выполняется соотношение G = £/[2(1 + //)] . При этом
независимыми остаются только две упругие постоянные.
81
В практических задачах для описания свойств материалов часто
используется объемный модуль К, устанавливающий связь между
объемной деформацией и суммой нормальных напряжений. При
плоской поперечной деформации волокнистых композитов (е33 = 0):
<7п + <722 — 2КТ у£п + 6*22 )
'2(1-/0 4//
где Кт
. При деформации зернистых
компози°\\ + ^22 + °ЪЪ ~ ЗК (€п + 6*22 + £33 )
где К ■
3(1-2//)
3.2. Эффективные характеристики волокнистых
композитов
Армирование волокнами значительно повышает жесткость и
прочность материалов в продольном направлении х3 (рис. 1.1).
Поэтому с практической точки зрения наиболее важным представляется
определение эффективных модулей, описывающих свойства
композитов в направлении ориентации волокон.
Если пренебречь взаимодействием компонентов в плоскости
хгх2, эффективный продольный модуль Юнга EL и эффективный
продольный коэффициент Пуассона jUL можно вычислить по правилу
смеси:
EL={\-cm)Em+cmE{2\
//,=(1-с<2,)//1)+с<2У2)-
(3.8)
(3.9)
82
^о(1Ч
<V2)^
X2/t
->
®^-
—\*-У
R
< >
X\
Рис. З.1. Модель волокнистого композита в задаче о продольном
растяжении (сжатии).
Чтобы уточнить формулы (3.8), (3.9), рассмотрим задачу об
однородном продольном растяжении (сжатии). Выделим ячейку
периодичности и в первом приближении заменим ее внешнюю границу
окружностью радиуса R (рис 3.1). В цилиндрической системе координат
х\ + х\, tg в = х2 jxx , z '-
исходные соотношения (3.1), (3.3),
(3.4) запишутся следующим образом.
Деформации:
Эй?
Ла)
дг
Р(«>-
€г =■
Г
duz
э7'
(3.10)
где иг , и7 - перемещения, соответственно, в радиальном и продоль-
направлениях
Напряжения:
ном направлениях, uz = uf* = u[2), ez = £„(1) = £(z2).
of = 2К(та) [(1 - ju(a)) 4а) + М£(га) + №z ] ,
(3.11)
83
где К
(а) __
2(1+^)(1-2//<">)-
Уравнения равновесия в перемещениях:
Эг2
дг
■"• f -»■
(3.12)
Осесимметричное равновесное состояние среды предполагает
нулевые радиальные перемещения в центре ячейки и нулевые
радиальные напряжения на внешней границе Э£20:
{М,<2) =0)1 , {<т(1) =о]| .
1 r Jlr=o l J lr=/e
Условия идеального контакта между компонентами:
1 Jlr=a *■ J\r=a
Решение краевой задачи (3.12)—(3.14) имеет вид:
--С\а)г + С{2а)г-\ и =£7,
С?
£z
D
V1}(l-c(2)) yV2) y1)"
Ar Ar Lr
„(2) _ (1)
C?=-£R2c(2)e £-,
2 z £>G(1)
C|2>=cl(1)+^T, Q(2)=0,
c#2
£>
l-c<2) c(2) 1
Kl2) + *<" + G(1) '
(3.13)
(3.14)
где с(2) =(a/R) .
Зная wja), можно определить искомые эффективные
характеристики следующим образом:
84
EL
Ml
£R
где (<Jz) = J \ra{za)drde - осредненное продольное напряжение.
Окончательно находим:
EL={l-
с(2) £(l)+c(2,£(2) +
4c(2)(l-c(2))(//(2>-//(1
D
//L=(i-c<2V1)+c<v2)+
c(2)(l-c(2))(/z(2)-//a
Z>
*<'> K<2:
(3.15)
(3.16)
Третьи слагаемые в выражениях (3.15), (3.16) учитывают
радиальное взаимодействие компонентов, вызванное различием
коэффициентов Пуассона матрицы и волокна. На рис. 3.2, 3.3 приведены
отношения численных результатов, получаемых по формулам (3.8), (3.9)
и (3.15), (3.16). При расчетах принято с{2) = 0.5 , //(1) = 0.3 . Для
высокомодульных композитов (Е{2) > Е{1)) влияние взаимодействия
компонентов мало. Особенно это касается эффективного модуля Юнга
EL, который с высокой точностью можно определить по простому
правилу смеси (3.8). В то же время решение (3.16) для эффективного
коэффициента Пуассона jUL значительно отличается от линейной
зависимости (3.9) при Е{2) / Е{1) —» 0 , //(2) —» 0 . Этот предельный случай
соответствует материалу с пустотелыми включениями (порами).
Чтобы найти эффективный продольный модуль сдвига GL,
рассмотрим деформацию чистого сдвига в плоскостях х13, х23 под
действием касательных напряжений охъ, о1Ъ. Остальные напряжения
положим равными нулю. Уравнение равновесия в перемещениях
запишется в виде:
^2„(«)
д2и[а) д2и
2„(«) ^
Эх2
Эх2
(3.17)
85
1 2
lg(£(2) / £(1))
Рис. 3.2. Влияние учета взаимодействия между компонентами на
точность определения эффективного модуля Юнга.
1 2
lg(£(2) / £(1))
Рис. 3.3. Влияние учета взаимодействия между компонентами на
точность определения эффективного коэффициента Пуассона.
Условия идеального контакта на границе раздела компонентов
д£1 отвечают равенствам продольных перемещений
{<=<}!.
(3.18)
86
и касательных напряжений по направлению нормали п к д£1:
->(1) ии3
->(2) OU3
Эп
Эп
(3.19)
Краевая задача (3.17)—(3.19) математически тождественна задаче
проводимости (1.3), (1.4). Таким образом, все результаты, полученные
в главе 1 для эффективного коэффициента проводимости к0, могут
быть перенесены на эффективный модуль сдвига GL .
Эффективный объемный модуль Кт и эффективный модуль
сдвига GT при деформации в поперечном направлении можно
приближенно определить по следующим формулам:
Кт=К?+с™
GT
1
1-е1
.(2)
Л"1
+ 2С
KL[)+G{i
(3.20)
(3.21)
где
С, =3ci2) (l-ci2)f (Л(2) -1)(Л(2) +g(2}) +
[л(2>д<1> + д(1>д<2> -(Л(2)д<1> -g<2>)(c<2>f
[c(2)gm (Л{2> -1)-(Л(2,д(1) +1)],
С2=-Зс(2)(1-с(2))2(Д<2,-1)(Д<2)+^2)) +
-[Xmgm + (Л(2> -l)c<2) + l][(<T(1) -1)(Д<2) +д(2>)-
2(/t<V,-?<2,)(c<2)) |+—(дт+1)(Л<2)-1)х
''л{2) +дс-> +(Л(2)дт -gi2))(cr->f
87
С3 = Зс(2) (1-с(2) )2 (Я(2) -1)(Я(2) + ^(2)) +
[я{2)д{1) + (Л(2) -1)с(2) +1]Ь2) + д{2) + {Л{2)д{1) -д{2)){с{2))Ъ
Я(2)=С{2)/с{1\ gia)=3-4juia).
Выражения (3.20), (3.21) получены, соответственно, при помощи
полидисперсной [329] и трехфазной [289] моделей. Они не учитывают
геометрическую структуру композита и дают заниженные значения
для эффективных модулей в случае высокой жесткости и большой
объемной доли волокон. Уточнить решение можно при помощи
асимптотических методов, предложенных в главе 1.
3.3. Эффективные характеристики зернистых композитов
Если не учитывать вид пространственной упаковки зерен и
предположить, что сферические включения равномерно распределены в
матрице (и не образуют кластеров), то эффективный объемный
модуль К и эффективный модуль сдвига G можно приближенно
определить на основании полидисперсной [320] и трехфазной [289] моделей.
Соответствующие выражения имеют вид:
K = Kw+c{'
3(1-с(2))
K{Z)-K{i
3^(1)+4G'
(i)
(3.22)
где АГ(в)=Е(в)/[з(1-2//(в))],
СЛ^ +2С2 ^1 + С=°'
(3.23)
где
С1=8?ДЛ<2>-1)(4-5^^
252^2 (,Р -1)(с(2))5/3 -50(Л(2) -1)[7-12//(1) + 8(//(1))2 W2) +
4(7-10//(1))^3,
C2=-2ft(^-l)(l-5/^^^
252^2 (А(2) -1)(с(2))5/3 +75(/l(2) -l)(3-//(1))//(1V2c(2) +
С3 = 4Й (X* -1)(5^ -7)(^)ШЗ -2[63(^ -1)й +2ftft](c^)7/3 +
252^2 (А(2) -1)(с(2))5/3 +25(А(2) -1)[(//(1))2 -7]^2с(2) -
^2ft(7 + 5//(1)),
ft =(49-50//(V2))(^(2) -1) + 35Я(2) (//(2) - 2//(1)) + 35(2//(2) -//(1)),
^2=5//(2)(Л(2)-8) + 7(Л(2)+4),
ft=A(2)(8-10//(1)) + 7-5//(1),
A(2)=G(2)/G(1).
Для макроскопически изотропных композитов эффективный
модуль Юнга Е выражается через упругие постоянные К и G следующим
образом:
9KG
3K + G
(3.24)
Формулы (3.22), (3.23) неприменимы в случае сильного
взаимодействия соседних включений (при Е{2)/'Е{1) » 1, G(2)/G(1) » 1,
с(2) —» с^х). Однако для средних значений жесткости и объемной
доли зерен численная точность таких решений является практически
достаточной. На рис. 3.4 приведены результаты для эффективного
модуля Юнга Е композитного материала, состоящего из полиэфирной
матрицы и стеклянных микросфер (Е{2)/Е{1) = 40.8 , //(2)=0.21,
89
12"
10-
8-
6-
4-
2-
о-
G/G(l
)
"3^
ij
2 7
У l
c<2)
0 0.1 0.2 0.3 0.4 0.5
Рис. 3.4. Эффективный модуль
Юнга зернистого композита.
Рис. 3.5. Эффективный модуль
сдвига зернистого композита.
jun =0.45). Теоретическое решение (3.22)-(3.24) (сплошная кривая)
сравнивается с данными экспериментальных измерений (кружки),
полученными при одноосном нагружении [422].
Область применимости аналитических решений может быть
расширена при помощи метода аппроксимаций Паде [27]. Рассмотрим
эффективный модуль сдвига G в случае, когда включения абсолютно
жесткие, а матрица несжимаема (G(2)/G(1) = °о, //(1)=0.5). Данная
модель математически аналогична задаче об эффективной вязкости
суспензии из твердых частичек, равномерно распределенных в
жидкости с вязкостью G(1) (предполагается, что скорость сдвига близка к
нулю). При малой объемной доле зерен (с(2) —» 0) разложение для G
имеет вид [280]:
G 1+5 (2) , (2))2
Gd) 2 V )
(3.25)
Перестраивая ряд (3.25) в диагональную аппроксимацию Паде
порядка [1/1], получаем простую формулу:
G _1 + с(2)/2
Gm ~ 1-2с(2) ■
(3.26)
Численные результаты приведены на рис. 3.5. Аппроксимация
Паде (3.26) (сплошная кривая) хорошо согласуется с эксперименталь-
90
ными данными [353] (кружки), в то время как исходное решение
(3.25) (штриховая кривая 1) пригодно только для малых значений с(2).
В случае, когда упругие свойства матрицы и включений
существенно отличаются, а объемная доля включений близка к
максимальному предельному значению, могут быть найдены асимптотические
решения, где в качестве малого параметра используется ширина
зазора между соседними зернами. Компоненты локальных напряжений в
направлениях вдоль и поперек зазора имеют разный порядок,
следовательно, в первом приближении одним из этих компонентов можно
пренебречь. В механике жидкости такое упрощение носит название
теории смазки [43].
Пусть абсолютно жесткие включения расположены в
несжимаемой матрице в виде ПК решетки. Асимптотика эффективного модуля
сдвига при с{2) —» с^ = я/6 имеет вид [117]:
Ъл
G = — -=. (3.27)
16[l-(^(2Ve) ]
Результаты расчета по формуле (3.27) показаны на рис. 3.5 штриховой
кривой 2.
91
Глава 4
ВЯЗКОУПРУГИЕ СВОЙСТВА КОМПОЗИТОВ
4.1. Основные соотношения теории вязкоупругости
Для многих композитных материалов, содержащих компоненты
на полимерной основе, характерна зависимость процессов
деформирования от скорости и времени. Свойства таких композитов
описываются в рамках теории вязкоупругости. Линейные изотермические
соотношения между напряжениями a(t) и деформациями e(t) имеют
вид [116]:
<T(t)=[E(t-T)^Q-dT9 (4.1)
о dt
e(t)JlJ(t-T)E£WdT9
о "т
где E(t) - функция релаксации, J(t) - функция ползучести.
Выбор функций E(t), J(t) и определение их параметров
производится на основании экспериментальных данных. В практических
задачах для моделирования процессов релаксации обычно используют
степенное ядро Дюффинга, экспоненциально-степенное ядро Ржани-
цина, дробно-экспоненциальное ядро Работнова и их суммы [93, 95,
101, 156, 157]. Отметим, что при описании объемных и сдвиговых
деформаций часто используют разные реологические модели. Так, во
многих случаях принимают, что объемные деформации - упругие, а
сдвиговые - вязкоупругие.
Применим к соотношениям (4.1) преобразование Лапласа
f(s) = jf(t)Qxip(-st)dt,
о
92
где s - комплексный параметр преобразования, f(s) обозначает
изображение функции f(t). Используя теорему о свертке, получим:
a(s) = sE(s)£(s), £(s) = sJ(s)a(s), (4.2)
где
s2E(s)J(s) = l. (4.3)
Выражения (4.2) математически аналогичны соотношениям (3.4)
теории упругости. Таким образом, решения статических вязкоупругих
задач можно получить на основании известных решений для упругой
среды, если вместо модулей жесткости и коэффициентов
податливости подставить, соответственно, величины sE(s) и sJ(s), а упругие
напряжения а и деформации е заменить изображениями a(s) и
e(s).
Данный принцип может быть использован при определении
эффективных функций релаксации E0(t) и ползучести J0(t)
композитных материалов. Решения для эффективных упругих характеристик,
полученные в главе 3, можно интерпретировать как решения для
изображений sE0(s) , sJ0(s) , при этом вместо упругих свойств
компонентов нужно подставить их вязкоупругие аналоги sE{a) (s), sJ{a) (s) .
Окончательное решение находится путем обратного преобразования
E0(s), J0(s), для чего могут использоваться различные методы [84-
86,94,96,97,438].
В динамических задачах вязкоупругие свойства материалов
удобно описывать при помощи комплексных модулей. Рассмотрим
режим стационарных колебаний, когда напряжения и деформации
являются гармоническими функциями времени:
a{t) = <j0 exp(iax), e(t) = £0 exp(iax), (4.4)
где <jQ, £Q - амплитуды, со - частота.
Подставив (4.4) в (4.1) и применив преобразование Лапласа,
получим:
а0 = Е* (со)£0, £0=J* (со)а0, (4.5)
93
<j{t) = E* (6))£(t), e{t) = J* {co)a{t),
где E*{co) - комплексный модуль жесткости, J* {со) - комплексный
коэффициент податливости,
E*((D) = i(DE(s), J*{co) = icoJ{s). (4.6)
Из выражений (4.3), (4.6) следует, что для данной задачи s = ico.
Тогда Е*{со) = icoE{ico), J* {со) = icol{ico).
Физический смысл соотношений (4.5) заключается в том, что при
постоянной амплитуде деформаций е0 = const амплитуда напряжений
в вязкоупругом материале зависит от частоты: сг0 = сг0 {со), и
наоборот.
Формулы (4.5) математически аналогичны закону Гука (3.4).
Следовательно, эффективные комплексные модули вязкоупругих
композитов можно определить при помощи решений для
эффективных упругих характеристик, если вместо вещественных упругих
свойств компонентов подставить их комплексные аналоги.
На основании соотношений (4.5) запишем:
a{t) = e0 Qxp{i[cot + ^(ю)]}, (4.7)
где ехр[г^(*у)] = Е*{со). Сравнивая (4.7) и (4.4), можно
интерпретировать параметр у/{со) как фазовый угол запаздывания деформации
относительно напряжения. В практических задачах часто оперируют
величиной, которая называется тангенсом потерь и представляет
собой отношение мнимой Е*{со) и действительной E*R{co) частей
комплексного модуля Е* {со) = ER {со) + 1Е\ {со):
tg[ys{co)] = E;{co)/E;{co),
где E'R{со) = со\ E{t)sin{cot)dt, Е*{со) = со\ E{t)cos{cot)dt. Тангенс
потерь - важная характеристика вязкоупругой среды, определяющая
интенсивность релаксационных процессов. Чем больше tg[ys{co)], тем
быстрее затухают динамические эффекты.
94
Рассмотрим гармоническую волну, распространяющуюся в
изотропном вязкоупругом материале. Уравнение движения имеет вид:
., ч Э и д и ,А ^
Е\а>)—Т = р—Т, (4.8)
дх dt
где и - перемещение, р - плотность среды. Решение уравнения (4.8)
можно записать следующим образом:
и = UQxip[i(cm-jUx)] = UQxip(-jUIx)Qxip[i(cm-jURx)], (4.9)
где U - амплитуда, ju = jUR- ijil - комплексное волновое число,
мнимая часть jUj которого представляет собой коэффициент затухания, а
действительная часть равна juR = Injh, L - длина волны.
Распространение волн в вязкоупругом материале носит
дисперсионный характер. При этом фазовая скорость vp = co/jUr зависит от
частоты со, а эффект затухания вызван превращением механической
энергии в тепло вследствие релаксационных процессов. Подставив
(4.9) в (4.8), путем несложных преобразований найдем:
Mi = Mr tg
\//(CQ)
\E\co)\
P {cos[iK<»)/2]}
(4.10)
4.2. Продольное растяжение волокнистых композитов
Рассмотрим задачу о продольном растяжении (сжатии)
однонаправленного волокнистого композита, состоящего из вязкоупругой
матрицы £2(1) и упругих волокон £2(2). Свойства матрицы можно
приближенно описать при помощи реологической модели стандартного
линейного тела [116], которая представляет собой систему из двух
упругих пружин с жесткостями Е^ , Е^ и демпфирующего элемента
с вязкостью 7]{1) (рис. 4.1).
Функция ползучести матрицы имеет вид:
95
Hi-
Рис. 4.1. Модель стандартного линейного тела.
/(1)(0 = /(1)(oo)-[/(1)(oo)-^(1)(0)]exp(-f/r(1)), (4.11)
где /(1)(оо) = (^+^1)|д£'1(1)^1)| - длительная податливость,
/(1)(0) -XJE^ - мгновенная податливость, т(1) = 7]{1)/'Е^ - время
ретардации (запаздывания). Коэффициент податливости волокон
равен /(2)=1/Е(2).
Эффективную функцию ползучести J0(t) будем искать на
основании решения (3.8) для соответствующего упругого модуля. Тогда
/wWw(j)
<2и
Ms) =
Г(1),^_^(1)(-) + ^(1)/(1)(0) у(2), . _ ,-! ,(2)
/w(*) =
(l-c(2))/(2)W + c(2)/(1)W
?r(1)7(1)rm ,.„ , ,.
(4.12)
(4.13)
s(l + ^(1))
Оригинал выражения (4.12) имеет вид:
J0(t) = J0(oo)-[j0(oo)-JQ(0)]QXp(-t/T0),
где /0(оо) - эффективная длительная податливость, /0(0) -
эффективная мгновенная податливость, т0 - эффективное время
ретардации,
ЛЮ =
J(l>(oo)J<'-
(l-C(2>)j(2>+C(2>J(l>(oo)
J0(0)--
7(1)(0)7(:
(l-c<2,)7(2)+c<2,7(1)(0)
96
1
0.8
0.6
0.4
0.2
0
/1=1
^—^^8
IX^4^^^^^^
\ \ ^\а4^^^
1 \ ^^о
V ^^-^^0075
V o.oi —
4i^
л л
1
0.9-
0.8-
0.7-
0.6-
=; 0.5-
\\>
\\\
1 0.075
\0Ш
\/(2)//(1)(оо) = 1
\о.4\
О 0.2 0.4 0.6 0.8 1
с(2)
Рис. 4.2. Эффективные
коэффициенты податливости.
О
0.2 0.4 0.6 О.!
.(2)
(1-
Рис. 4.3. Эффективное время
ретардации.
J/^+c^CO)
(1-
)^2>+ст^(оо)
Зависимость эффективных коэффициентов /0 (оо), jQ (0) от
объемной доли волокон с{2) приведена на рис. 4.2, где использованы
следующие безразмерные единицы: Я^ = /0(°о)//(1)(оо) соответствует
A = J{2)/j{l)(oo), AQ=J0(0)/J{1)(0) соответствует Я = J{2)/j{l)(0).
Результаты для т0 приведены на рис. 4.3; при расчете принято
/(1)(0)//(1)(°°) = 0.5.
Пусть композит подвержен действию мгновенно приложенной
постоянной нагрузки
a(t) = a0H(t),
(4.14)
где (Т0 - осредненное продольное напряжение, H(t) - функция Хеви-
сайда, H(t) = 0 при t<0, H(t) = \ при t>0, dH(t)/dt = S(t), S(t) -
дельта-функция Дирака, S{s) = 1. Подставив (4.14) в (4.1) и применив
преобразование Лапласа, определим продольную деформацию:
£0(t) = <r0J0(t).
97
О 0.2 0.4 0.6 0,
Рис. 4.4. Кривые ползучести. Рис. 4.5. Отношение длительных
и мгновенных деформаций.
Для численной иллюстрации полученных результатов здесь и
ниже до конца главы примем, что материал компонента £2(1) - поли-
метилметакрилат, Е® = 2.37 ГПа, £<1} =3.45 ГПа, т]{1) = 510 ГПа с ,
//(1) =0.35, р{1) =1180кг/м3 [274], материал компонента £2(2) -
алюминий, Е{2) = 70 ГПа, G(2) =28ГПа, р{2) = 2700кг/м3. Кривые
ползучести при различных значениях объемной доли волокон с(2)
изображены на рис. 4.4. Деформации £0(t) нормированы по отношению к
мгновенным деформациям £0(0) в начальный момент времени. На
рис. 4.5 приведены результаты для отношения длительных £0(°°) и
мгновенных £0(0) деформаций, £0 (оо)/£0 (0) = J0(°°)/J0(0).
Армирование высокомодульными волокнами существенно снижает роль вяз-
коупругих эффектов при продольном растяжении композитов. Даже
при небольшой объемной доле волокон с{2) интенсивность процесса
ползучести быстро падает.
4.3. Продольный сдвиг волокнистых композитов
Рассмотрим задачу о чистом сдвиге волокнистого композита в
продольных плоскостях х13, х23 под действием касательных
напряжений <т13(0 , 0"23(t). Остальные напряжения положим равными нулю.
98
Функция ползучести матрицы при одноосном растяжении
(сжатии) /(1)(0 имеет вид (4.11). В теории упругости модуль сдвига G
можно выразить через продольную податливость / = Е~1 по формуле:
G = [2/(1 + //)] . Применив данное соотношение к соответствующим
вязкоупругим характеристикам, найдем изображение функции
релаксации матрицы при сдвиге
2s2Jm(s)(l + M(l>)
где J(l)(s) определяется выражением (4.13). Для волокон имеем:
Gi2\s) = s-lG<2\
Эффективная функция ползучести J0(t) при продольном сдвиге
может быть определена на основании решения для эффективного
коэффициента проводимости к0 , полученного в п. 1.2. При этом вместо
проводимостей компонентов к{а) следует подставить величины
sG{a) (s), а результаты расчета для к0 интерпретировать как решение
для sG0(s), где G0(•$■)= s2J0(s) - эффективная функция
релаксации.
Окончательно функция J0(t) находится путем обращения
изображения /0 (s). В настоящей работе для этого использовался
численный алгоритм Гавера (Gaver) [205]:
f(t) =
Г2п^
\* п
inn;]/
\п + к)\п2
(4.15)
где
Kkj
—-—:—— - биноминальные коэффициенты, параметр п оп-
к\{п-к)\
ределяет точность аппроксимации, п = 1,2,3,....
В качестве тестового примера вычислим функцию ползучести
матрицы при сдвиге J^it) путем обращения изображения
^sh (5) ~ Г^2^(1) С?)] • Точное решение имеет вид:
99
^(0/^(0)
0.4 0.6 я/4
In г, с с(2)
Рис. 4.6. Функция ползучести мат- Рис. 4.7. Эффективные коэффи-
рицы. Численная аппроксимация и циенты податливости,
точное решения.
S0(t)/£0(0)
s0M/s0(0)
In г, с
Рис. 4.8. Кривые ползучести.
Рис. 4.9. Отношение длительных
и мгновенных деформаций.
J% (?) = 2(1 + jum)jm(t).
(4.16)
Результаты расчета приведены на рис. 4.6. Сплошные кривые -
численная аппроксимация (4.15), штриховая кривая - аналитический
результат (4.16). Увеличение п обеспечивает быструю сходимость
алгоритма Гавера. В дальнейших расчетах принято п = 6 .
Рассмотрим композит, в котором волокна расположены в виде
квадратной решетки (рис. 1.1а), с^х = я/А = 0.7853.... На рис. 4.7 при-
100
ведены зависимости эффективных коэффициентов J0(°°) и /0(0) от
объемной доли волокон с(2); кривая 1 соответствует значению
\ = J0 (°°)l Jfh (°°)' кривая 2 - \ = J0(0)/j^(0). Кривые ползучести
в случае мгновенно приложенной постоянной нагрузки вида (4.14)
изображены на рис. 4.8. Результаты для отношения длительных £0(°°)
и мгновенных £0(0) сдвиговых деформаций приведены на рис. 4.9.
Как следует из расчета, при продольном сдвиге волокнистых
композитов вязкоупругие эффекты проявляются значительно сильнее, чем
при продольном растяжении.
4.4. Распространение длинных волн в слоистом композите
Рассмотрим задачу о распространении гармонической волны в
слоистом композите, состоящем из периодически чередующихся вяз-
коупругого £2(1) и упругого £2(2) компонентов. Допустим, что длина
волны L намного больше характерного размера / внутренней
структуры материала, 1/L —» 0 . В этом случае можно пренебречь
масштабными эффектами, связанными с локальными отражениями сигнала на
границах раздела компонентов, и описать динамические свойства
композита при помощи эквивалентной однородной среды с осреднен-
ными характеристиками. Пусть продольная волна распространяется в
направлении х, перпендикулярном плоскости укладки слоев.
Исходное уравнение движения имеет вид (4.8), а его решение представлено
выражениями (4.9), (4.10).
Согласно модели стандартного линейного тела (рис. 4.1),
запишем функцию релаксации компонента £2(1) в виде:
Е{1) (t) = Е{1) (оо) - [£(1) (оо) - Е{1) (0)] ехр(-t/T{l)),
где Е(1) (<*>) = [е^ Е^)/(Е^+Е£)) - длительная жесткость,
Еа)(0) = Е™ - мгновенная жесткость, т(1) =7]{1) Ке[1) + Е^) -время
релаксации. Комплексные модули компонентов равны:
£(1)* (со) = ШЕ*> (ico) = \f* \!Щ \ , £(2)* (со) = iaE™ (ico) = £(2).
£4D + ЕЦ) + i0)7]W
101
v,(*»)/vrO)
Рис. 4.10. Фазовая скорость. Рис. 4.11. Коэффициент затухания.
Эффективный комплексный модуль Е*(со) находим на
основании известной формулы для упругого модуля Юнга слоистого
композита:
е:(со) =
Е{1)\со)Е{2)\со)
{\-с{2))е{2)\со) + с{2)Е{1)\с0)
Осредненная плотность материала равна р0 =\1-с(2))рт+с(2)р(2}.
Для эффективного тангенса потерь получим:
tg[pr0(fl»] = Im[£0*(«)]/Re [e'0(o))] =
щтЕ?Ет{\-ст)
(£«) +Е<»Е?>+со2(т]т) (l-c(2,) + c(2)£f (£<") +af(i7m)
Тангенс потерь tg[^0(#;)] и коэффициент затухания //7
обращаются в ноль как при со —»°о (когда релаксационные процессы
протекать не успевают), так и при со —» 0 (когда скорость деформирования
настолько мала, что упругие и вязкоупругие процессы протекают и
завершаются одновременно).
Зависимости фазовой скорости vp и коэффициента затухания //7
от частоты со приведены, соответственно, на рис. 4.10 и 4.11.
102
Глава 5
ХОЛОДНОЕ ВОЛОЧЕНИЕ БИМЕТАЛЛИЧЕСКИХ
КОМПОЗИТОВ
5.1. Основные гипотезы и пластическая краевая задача
Микромеханические эффекты, в частности, взаимодействие
между компонентами, могут оказывать значительное влияние на свойства
композитных материалов еще на стадии их изготовления. В качестве
примера рассмотрим задачу о холодном волочении биметаллической
проволоки.
Холодное волочение (выдавливание) является эффективным
способом пластического формирования и упрочнения металлов. Данная
технология позволяет также создавать волокнистые и нитевидные
композиты с высокой степенью структурной неоднородности. На рис.
5.1 приведена микрофотография композитной проволоки типа «медь-
графит» [219], полученной методом холодного волочения. При
внешнем диаметре 5.2 мм она включает два уровня неоднородности и
содержит 482 нитей графита.
В.В. Соколовский [171] одним из первых предложил модель
пластического течения металла через коническое отверстие (волок). В
дальнейшем эта задача рассматривалась многими авторами [238, 335,
339, 439, 455]. Применение метода конечных элементов позволило
рассчитать сложные режимы течения [285, 296]. Современные
исследования в данной области связаны с анализом влияния различных
критериев пластичности [211], моделированием нестационарных
процессов [423], оптимизацией геометрической формы волоков [286,
370].
Пластическому течению биметаллических композиций
посвящены работы [210, 212, 287, 288, 294, 445]. Взаимодействие между
компонентами приводит к концентрации локальных напряжений на
границе раздела. При этом свойства границы и ее несущая способность
становятся ключевыми факторами, определяющими режим течения и
характеристики получаемого композитного материала.
103
Рис. 5.1. Композитная проволока «медь-графит».
волок
матрица £2т
волокно £2(2)
Рис. 5.2. Течение композитной проволоки через конический волок.
Рассмотрим осесимметричное пластическое течение композитной
проволоки, состоящей из матрицы £2(1) и волокна £2(2), через
конический волок (рис. 5.2). В зависимости от угла волочения у, степени
деформации Z = l-(zl/z0) и величины трения на границе волока
пластическая деформация может принимать различные формы. Огра-
104
ничимся исследованием радиального режима течения, который
является устойчивым при небольших значениях у и представляет
наибольший интерес с практической точки зрения. В этом случае все
линии тока направлены в радиальном направлении сферической
системы координат г, в, (р с центром в точке О. Поперечные сечения
волокна и матрицы уменьшаются пропорционально так, что объемные
доли компонентов в процессе волочения не изменяются.
Зона пластической деформации ограничена границами Э£20 на
входе и Э^11 на выходе волока. В общем случае форма поверхностей
Э£20, Э^11 не может быть известна заранее, но для радиального
режима течения их можно аппроксимировать плоскостями [238, 296].
Предположим также, что изломы линий тока (разрывы в поле
скоростей) локализованы на границах Э£20, Э^11.
В процессе холодного волочения, благодаря использованию
соответствующей смазки и относительно небольшой скорости
деформирования, температура повышается незначительно, поэтому
термомеханические эффекты можно не учитывать. Поскольку
рассматривается стационарный режим течения, в уравнениях равновесия опустим
инерционные члены. Пластические деформации значительно
превышают упругие, поэтому последними можно пренебречь. Наконец
предположим, что волокно и матрица являются идеальными упруго-
пластическими материалами. На основании данных гипотез исходная
краевая задача может быть записана следующим образом.
Уравнения равновесия:
Эо?> 1до% 2(<-<)) + ^)ctg0
—?_ + rJ- + ^ :
дг г дв г
дг г дв г
где а{га), а(ва) = о{^ , а^ - компоненты напряжений, о^ = о{^ = О .
Условие пластичности Мизеса:
(o?>-o?>f+3{o}?f={o?>)\ (53)
где <7{уа) - предел текучести при растяжении, <7{уа) НЪ - предел
текучести при сдвиге.
105
(5.1)
(5.2)
Закон течения:
(5.4)
где £{га), £{ва), ё$ - скорости деформаций. Здесь и ниже точка вверху
обозначает производную по времени.
Условие несжимаемости:
£аг+2еав=0. (5.5)
К уравнениям (5.1)—(5.5) следует добавить следующие краевые
условия.
1) Граница Э£22. Распространенный способ моделирования
трения между матрицей и волоком заключается в том, что касательные
напряжения на Э£22 полагаются пропорциональными пределу
текучести матрицы при сдвиге:
У»=то?>Щ\ , (5.6)
1 ' ' }\в=у
где т - коэффициент трения.
2) Граница Э£23 • Условия идеального контакта между матрицей и
волокном отвечают равенству скоростей v(a)
{v(1)=v<2,]| (5.7)
И=^}Ц, (5.8)
3) Центральная ось. Из осевой симметрии задачи следует, что
касательные напряжения в центре волокна равны нулю:
106
4) Граница Э£20 . В случае отсутствия трения между матрицей и
волоком (т = О) продольная компонента скорости (по модулю)
равняется начальной скорости образца v0 до входа в пластическую зону:
{v(fl)cos0 = -vo}l _0 . (5.11)
'z=rcos0=zO
Линии тока на границе Э£20 испытывают излом в радиальном
направлении. Осредненное продольное напряжение а0 на Э£20
должно быть достаточным, чтобы обеспечить соответствующий разрыв в
поле скоростей. Определим сг0 из следующих соображений.
Скорость диссипации энергии на поверхности Э£20 равна:
^o=-^JJ|Avo|^o =
V3 ЭЦ) (5Л2)
^Ttzl v0[ of tg3y0 + of (tg3 y- tg3 y0)],
где dS0 = zl [tg 6/cos26 jdOdcp, |Av0| = v0tg# - величина разрыва в
поле скоростей в тангенциальном направлении (параллельно
плоскости Э£20).
Скорость изменения энергии волочения на входе в пластическую
зону:
Kd = <V<A = <г0я&0 tg2y, (5.13)
где S0 = кz\ tg2 у - площадь Э£20.
Приравнивая выражения (5.12) и (5.13), найдем:
ао =^3Сё^)(с(2)^+<7«[1-(сга)3/21 (5.14)
107
где с(2) = tg2 %Л§2 Y - объемная доля волокна.
С другой стороны, а0 можно вычислить непосредственным
осреднением продольной компоненты напряжения
т(а) _ _(*)
а:а) cos в - а:аа} sin в
(5.15)
по поверхности Э£20:
°b=-f JJ <<«<>•
(5.16)
J0 ЭЦ)
На основании выражений (5.14), (5.16) получим следующее
граничное условие на Э£20:
-Ijj(<cos6>-<,sin6>)<«0 =
2>/з
~9~
ЛЕв{а? (c^f\a?U-(c^f Ъ\
(5.17)
5.2. Аналитическое решение
Рассмотрим аналитическое решение исходной краевой задачи
(5.1)—(5.11), (5.17). Кинематически допустимое поле скоростей может
быть найдено из уравнения несжимаемости (5.5) и граничного
условия (5.11):
zl p{a\0)
V cos30 '
(5.18)
где функция р{а) (в) учитывает влияние трения на границе матрицы и
волока. В случае отсутствия трения (m = 0) получим р{а) (в) = 1. Из
осевой симметрии задачи также следует р{2) (0) = 1 при любых m .
Выражение (5.18) позволяет определить скорости деформаций:
108
?0)= — = 2v,
V3 cos30
*0
^ P(a)(^)
1 dv(l
r r3 cos3#
v0 zl р{а)(в)' + Ър{а)(в)1шв
гв 2r дв 2 r3 cos30
Интенсивность скоростей деформаций равна:
12
I l + -tg26> + -^v"./ tg<9 +
2 //e,(0)
Р{а)(в)''
Р{"\в)
(5.19)
(5.20)
Интенсивность деформаций £{а) можно определить путем
интегрирования £{а) по времени t вдоль линий тока. Принимая во внимание
соотношения dz = v{a) cos вdt и z = г cos в , найдем:
i<-=\¥-dt = \-
v{a) cos в
-dz '■
-2 In
fi+v^^4^tg.+-L
4 2 p<a)(#) 12
P(o)(0)
(5.21)
Решение (5.21) для £{a) позволяет на основании известных
эмпирических законов упрочнения реальных материалов вычислить предел
текучести биметаллического композита после процесса волочения.
Компоненты напряжений, удовлетворяющие условию
пластичности (5.3), можно записать в параметрическом виде:
а{га)/а{уа) = С[а) In г + f{a) {в) + sjl-g^ief
<7< =<7< =С1(в)1пг + /(в>(60,
(5.22)
109
где С[а) - константы интегрирования, функции g{a){6) учитывают
влияние трения на границе матрицы и волока. В случае отсутствия
трения (ro = 0): g(fl)(0) = O.
Подставив выражения (5.22) в уравнения равновесия (5.1), (5.2) и
граничные условия (5.6), (5.8)—(5.10), получим две краевые задачи:
g{a\6)' + 2jb^-g{a\0? +£(a4#)ctg0 + V3C1(a) =0, (5.23)
#(2)(0) = 0, §{1)(Го)/§{2)Ш = Л, (5.24)
8«ЧГ) = т, С?/С?=Л
/а)(Уо)//(2)(7Ь) = Я,
(5.25)
(5.26)
где Л = of/of.
Приближенное асимптотическое решение задачи (5.23), (5.24)
приведено в п. 5.3. Зная g{a){6) и С[а), можно определить функции
f{a){6) путем непосредственного интегрирования уравнения (5.25) с
учетом граничных условий (5.17) и (5.26).
Чтобы найти функции р{а) {в), подставим выражения для
скоростей деформаций (5.19) и напряжений (5.22) в уравнение течения
(5.4). Принимая во внимание граничное условие (5.7), получим
следующую краевую задачу:
р{а\в)' +
2Sga(0)
+ 3tg0
Р{а\0) = 0,
Vwe(0)
/>(2)(0) = i, р{1)ш1р{2)Ш = \.
Отсюда:
p(e)(^) = exp|-J
2y/3gia\0)
^-g{a\0)2
+ 3tg0
</0 + C<fl)
110
где
С9(2)=0,
^2
:ехр
2VV40) 2j3g{2\6>)
^-g{l\of
VwW
de\
в=т
Одним из важных параметров является требуемое напряжение
волочения od , которое представляет собой некоторую осредненную
характеристику процесса. В отличие от локальных напряжений и
скоростей в зоне пластической деформации, od несложно измерить
экспериментально, что может быть использовано для проверки
теоретических результатов.
Распределение напряжений oda) на выходе волока Э^11
определим следующим образом:
т(а) _ _(*)
<тГ+Д<тГ
где а[а) - продольная компонента напряжений на Э^11, вычисляемая
по формуле (5.15) при z = rco&0 = zx* Асг1(а) - добавка, вызванная
разрывом в поле скоростей.
Рассмотрим элемент поперечного сечения площадью dS1,
который пересекает границу Э^11. Разрыв в поле скоростей в
тангенциальном направлении составляет | Avx | = vx tg в , где vl - скорость образца
после выхода из пластической зоны. Скорость диссипации энергии на
поверхности dSl равна:
дЁл - —*=г Av, dS, .
л/3 ' '
(5.27)
Скорость изменения дополнительной энергии волочения,
необходимой для создания разрыва в поле скоростей:
dEld = AalvldSl.
(5.28)
Приравнивая выражения (5.27) и (5.28), получим:
111
Окончательно напряжение волочение od можно вычислить
осреднением ada) по поверхности Э^11:
где dS1 = z\ (tg&/cos2б}d6d(p , Sx = 7iz\ tg2 у - площадь Э^ .
5.3. Асимптотический расчет
Найдем приближенное асимптотическое решение краевой задачи
(5.23), (5.24). Представим неизвестные функции g{a)(0) в виде
разложений по степеням угла в:
g{2\e) = а^+а^в + а^в2 +... , (5.29)
Подставляя ряды (5.29) в уравнение (5.23) и приравнивая
коэффициенты при одинаковых степенях в и у-в , получим:
а%> = 0, / = 0,1,2,... ,
Д(2)=_Л/3_1Л/3С(2)
2
af As+—Sc™+-yl3{c™)\
3 3 24 l 16 v l J
<} =mctgy+ 2V3Vl-m2 + Sc® ,
112
af =Г(2л/3-4л/Зт2)^^-6тС1<1) -[Пт-Sc^ ctgy-2mctg2 y)x
yll-m2V(2yll-m2),
af> = -|1^л/5 + л/з(С1<1))2 - — Sm1 + 3л/3т4 +2m(2-m2)ctg jC*" -
л/3 л/3от2+2л/3от4 |ctg2^+
s
(ll-5m2)C,(1) +
1 1
-(43m-31m3)ctg^—^(l-m2)^ ctg2 ^+(m-m3)ctg3 у
6 2
л/1-т2}/Г(1-т2)л/1-т21,
a<X) =(Г53т-180т(С1(1))2-130т3+77т5-7з(85 + 10т2+25т4)х
C1(1)ctg^-(200m-256m3+116m5)ctg2^+
12V3(l-m2)2 Cx(1) ctg3 ^+24(m-2m3 + m5)ctg4 r\(l-mf -
|Г120т + 54т(С1(1))2 -78m3 -42m5lci(1) + {l4^3 +
24л/з(С^)2-30л/зГ5-(С^)21т2+132л/Зт4-56л/Зт6|с1§^+
(l 14m - 108m3 + 48m5) C^ ctg2 ^-(24^3 -110л/3т2 +
128V3m4-48V3m6)ctg3^}>/l-m2)/r24(l-m2^
Константы интегрирования С1(а) вычисляются из краевых условий
(5.24).
Область применимости решения (5.29) можно приближенно
оценить при помощи метода аппроксимаций Паде (АП) [27]. Во многих
задачах применение АП позволяет значительно улучшить сходимость
асимптотических разложений (АР). Таким образом, имеет место
следующее «практическое» правило: АР обеспечивает хорошую
численную точность в той области, где оно согласуется с соответствующей
диагональной АП. Перестраивая ряды (5.29) в АП порядка [2/2],
получим:
113
Таблица 5.1. Касательные напряжения на границе
«матрица-волокно».
У, град.
1
2
3
4
6
8
10
12
АР (5.29)
/2 = 1
0.2037
0.2608
0.3179
0.3750
0.4894
0.6041
0.7191
0.8345
/2 = 3
0.2096
0.2726
0.3359
0.3996
0.5281
0.6587
0.7920
0.9285
/2 = 5
0.2106
0.2748
0.3392
0.4040
0.5350
0.6686
0.8057
0.9474
АП (5.30)
0.2110
0.2755
0.3403
0.4054
0.5369
0.6706
0.8073
0.9476
(D/
(2) , (2)0 (2)^2
р(2)//ЭЧ _ С0 +С1 С/ + С2 °
* ^ ; d™+d™e+d™& '
^_с?+<#>(г-в) + с*>(Г-в)2
d^+df){y-e) + df{Y-ey
(5.30)
где
С = a^(a(ff-a^a(la>af>,
с<а) = а[а)«)2 -«> f а\а) - а{0а)а(?а\а) + а^а[а)а\а),
cf = а(0а> (af> f +(ai2") f + (a(f f af - lafafaf - a^a\a)a\a),
Для сравнения АР (5.29) и АП (5.30) рассмотрим численный
пример. В общем случае, точность полученного асимптотического
решения снижается при увеличении угла волочения у, коэффициента
трения т и разницы между свойствами компонентов (Я»1 или
Л «1). Примем т = 0.044 , Л = 0.15 , с{2) = 0.25 . В табл. 5.1 приве-
(3)
дены результаты для касательных напряжении а)в} на границе
раздела «матрица-волокно» Э£23» ofe = о\°в
нормированных по отно-
114
шению к пределу текучести при сдвиге более мягкого компонента
(волокна) <jf}/л/3 . Как следует из выражений (5.22),
a^J / 1а(2) / ^/3) = g(2)(y0). Отметим, что с физической точки зрения
о{^ не может превышать а{2)/v3 , т.е. g{2)(y0) < 1.
При расчетах в разложениях (5.29) удерживались члены вплоть
до порядка О(0п), О \(уо-0)п включительно. С увеличением п
точность найденного решения повышается. При этом численная
разница между АР (5.29) и АП (5.30) невелика. Окончательно решение
краевой задачи (5.23), (5.24) примем в виде (5.30).
5.4. Численные результаты
Рассмотрим вначале случай однородной проволоки (Я = 1). На
рис. 5.3 приведены результаты для напряжения волочения od ,
нормированного по отношению к пределу текучести материала о , при
различной степени деформации Z и фиксированном значении т = 0.044 .
Сплошные кривые - настоящее решение, кружки -
экспериментальные данные работы [483]. Рис. 5.4 иллюстрирует влияние
коэффициента трения т при Z = 0.2.
Поведение решения можно описать следующим образом. При
очень малых значениях угла волочения у для достижения заданной
степени деформации Z волок должен иметь достаточно большую
длину. В этом случае основная часть энергии тратится на преодоление
трения на границе «волок-проволока» д£12, что приводит к высоким
значениям напряжения волочения od . С увеличением у (при
постоянном Z) площадь границы д£12 уменьшается, соответственно,
уменьшается требуемое напряжение ad . Наименьшее достигнутое
значение ad соответствует технологически оптимальному значению
у, при котором энергоемкость процесса будет минимальной.
Дальнейшее увеличение у вызывает значительные пластические
деформации материала, что требует дополнительных затрат энергии. При
этом ad снова возрастает.
115
10 12
% град.
Рис. 5.3. Напряжение волочения
однородной проволоки при
различной степени деформации.
10 12
% град.
Рис. 5.4. Напряжение волочения
однородной проволоки при
различном коэффициенте трения.
В численном примере для композитной проволоки рассмотрим
случай, когда волокно мягче матрицы (Я < 1). Полученные результаты
для напряжения волочения <7d , нормированного по отношению к
пределу текучести волокна сг^2), приведены на рис. 5.5. При расчетах
принято т = 0.044 , Z = 0.2, с(2) = 0.25 .
Одним из основных параметров, отражающих взаимодействие
(3)
между компонентами, является напряжение cry на границе
«матрица-волокно» Э£23 • На рис. 5.6 изображены зависимости of^ от
объемной доли волокна с(2) при различных значениях Я (т = 0.044,
у=6град.) Увеличение контраста между свойствами компонентов
(уменьшение Л) приводит к росту напряжений на границе раздела.
Однако локальные напряжения of^ не могут превышать предел
текучести мягкого компонента а^ /v 3 . Если в результате расчета
оказывается ofe > af] /V3 , значит, радиальный режим течения не может
существовать (на рис. 5.5 зона радиального режима ограничена
штриховой линией). В этом случае в процессе волочения граница Э£23
должна изменить свое положение так, чтобы снизить of^ до
(7^ ЫЪ . Как показано на рис. 5.6, это может происходить двумя
способами: уменьшением с(2) (часть волокна выдавливается из матрицы)
116
или увеличением с(2) (часть матрицы срезается волоком). Таким
образом, анализ напряжений на границе раздела компонентов позволяет
определить, при каких значениях исходных параметров возможен
радиальный режим пластического течения.
оА1&:
^ms
|\\^л ч^_
1 NV>_o.i3
"1 ^ 0.2
JV^ 0.4
/1 = 1
Jln^--._
10 12
% град.
Рис. 5.5. Напряжение волочения композитной проволоки.
выдавливание
волокна —у
сг(3)
игв
(<}/>/3)
1.2"
1-
0.8-
0.6-
0.4-
0.2-
о-
\
\т /
-—^
0.13
0.2
0.4
/1 = 1
1
срезание
/— матрицы
/
0.1
■л
\0.08
1
А
Я
[ьныи ре.
4 к
о
0.2 0.4
0.6
0.8
1 с{
,(2)
Рис. 5.6. Напряжения на границе «матрица-волокно»
и различные режимы течения.
117
Глава 6
РАСПРОСТРАНЕНИЕ ВОЛН В СЛОИСТЫХ
КОМПОЗИТАХ
6.1. Одномерная динамическая задача
Процессы распространения волн в однородных и неоднородных
средах качественно различны. В композитных материалах локальные
отражения и преломления сигнала на границах раздела компонентов
приводят к дисперсии волны на макроуровне. Это явление можно
описать при помощи метода осреднения высшего порядка, который
позволяет получить решения, пригодные для длинных волн.
Когда длина волны уменьшается и становится соизмеримой с
размером внутренней структуры, в композите обнаруживаются
частотные зоны пропускания и запирания, так что материал играет роль
избирательного волнового фильтра. Такое поведение может быть
описано на основании кусочно-однородных моделей, в частности, с
использованием метода Флоке-Блоха.
Рассмотрим задачу о распространении упругих волн в слоистом
композите, состоящем из чередующихся компонентов £2(1) и £2(2)
(рис. 6.1). Пусть продольная волна распространяется в направлении,
перпендикулярном плоскости слоев, при этом перемещения и
напряжения зависят от одной координаты х. Исходное волновое уравнение
имеет вид:
д2и{а) {а) д2и<пЛ
дх dt
Условия идеального контакта на границе раздела компонентов д£1
отвечают равенству перемещений
{и(1)=и<2,]| (6.2)
и напряжений
118
эп-,п(1)-,п(2)-.
I
1
< >
1
h
h
I
< >
Рис. 6.1. Слоистый композит.
7(1)
ди(1)
дх
7(2)
Эх
(6.3)
Пространственно-одномерная задача (6.1)—(6.3) позволяет найти
точное дисперсионное уравнение (см. п. 6.3). Таким образом, ее
можно рассматривать как модельный пример для исследования области
применимости метода осреднения высшего порядка. Практическая
ценность метода осреднения заключается в том, что его можно
использовать в случаях, когда точные дисперсионные уравнения
неизвестны (двумерные и трехмерные задачи, нелинейные композиты, пр.)
6.2. Метод осреднения высшего порядка
Следуя процедуре, описанной в п. 1.2, определим малый
параметр е - 1/L , где / - размер ячейки периодичности, L - длина волны.
Изменим масштаб координаты х и введем «медленную» х = х и
«быструю» у = £~хх переменные, причем Э/Эх = Э/Эх + £~х д/ду .
Неизвестное решение для перемещений представим в виде разложения
и(а) = и0(х) + £и{а)(х.у) + £2и(2а)(х,у) + ..., где и\а\х,у) = и\а\х.у + Ц,
/ = 1,2,3,.... Полагая, что свойства компонентов имеют одинаковый
асимптотический порядок: Е(2) / Еа) = 0(£°), р(2)/р(1) = 0(£°),
выполним расщепление краевой задачи (6.1)—(6.3) по £. В результате
119
получим последовательность краевых задач на ячейке, включающих
микроскопические уравнения движения
(Э2и,-2 А-? эУв)>1
Эх2
дхду ду
,(«) Э2ц,(-2
Э?2
(6.4)
где z/f = 0, и микроскопические условия идеального контакта
w.n-n.
' du^l Эй
1-1. + ,
аЛ
Эх Э_у
( Эи(2) ди{2) ^
Эх Э_у
(6.5)
(6.6)
В случае пространственно-бесконечного композита условия
периодичности для u{ta) можно заменить нулевыми граничными
условиями в центре и на внешней границе ячейки периодичности (рис. 6.2)
[26]:
{«,m=0}| K^Ojb.
(6.7)
Алгоритм метода осреднения выглядит так. Решение /-ой краевой
задачи (6.4)-(6.7) позволяет определить член и[а). Зная и[а),
применим к (/ + 1)-му уравнению (6.4) оператор осреднения Г1 \ (-)ф по
JQ.Q
области ячейки периодичности £20 = £1® + £lf}. Члены и^
исключаются на основании граничного условия (6.6), которое с учетом
периодичности и%1 по переменной у дает следующее выражение:
Е{1) 1— + l-^dy + E{2) 1— + l-^-dy = 0.
L дхду ду J ЭхЭ^ ду
В результате получим осредненное уравнение движения порядка £1 :
120
о?Ч &
о?
-да
к->|
L/2
о у
Рис. 6.2. Ячейка периодичности (относительно координаты _у).
£,„ г Э2М« . ЭУ>
„(1)
^+^ib^,2,f ,.,
Эх дхд\
дх дхду
l—dy-
en Г Э V _ ,2) f Э2и2 _
(6.8)
Объединяя соотношения (6.8) при / = 1.../2, запишем
макроскопическое волновое уравнение порядка еп.
В настоящей работе выполнены расчеты вплоть до значения
/2 = 3. Точные аналитические решения задач на ячейке имеют вид:
при у > О :
dx
*ȣ
,/2) =
j_
_2
/
1 + 2А-
/>(2) ^о
Л Я'
(2)
/+-л^
Эх2
1 + 2Яг
о 1 1 о
;y2+-B2Ly + -C2L2
4 2 8 2
Э ип
Эх2
121
'/2> - <
2 + 3А+(Л-2)^--^
Ро &
'->"+5^£
о{1) Е
2 + ЗЦ+(Ц-2)£-^
/-
в,+а-а
Ро £(1)
Ly2+ — В3Ь2у + — СЪЬЛ , ^ _ ,
24 3 48 3 Эх3
при j < 0 :
■ #(2)
./2) _
2
, Эип m f „ 1 т^Эип
А?—Ч Mi = вхУ—C\L\—^->
Эх I 2 у Эх
/?(2) £
Л Я(2).
/--AL.y
d ип
dx
,#(i) _
, 1 1 ,
y2—B?Ly + -C?L2
4 2 8 2
Э2и0
lix7"
2 + ЗД+(Д-2)
Ро £(2)
у ,-A.Ly +-А,Ьу\-^
1
4
2 + 3Bi+(Bi-2)£-A.
Ро ^
г +
24 3 48 3 Эх3
Коэффициенты Д , В,, С, равны:
Д=-(1-с<2,)(£<2,-£(1))/^,
В1=с<2,(£<2,-£(1))Д>,
С1=-В,
D = (l-c(2))£<2,+c(2,£(1
122
А7=-
Ul-ci2)){[(l-ci2))pm+2ci2>p(2>]E0+p0Em}Ei2) +
{c<2>)2p<2>E"Eoy{p0E<2>D),
B2 = (c(2)Em [c(2) (p<2) - 2pm) E0 - 2p0Em ] +
£<2'{(1 + 2с(2>)А£т-[1-(с(2>)2]/>«£0}У(/>0£^),
C2=ci2)\p0(Emf + (l-c(2))pmEmE0-Em{p0Em +
[C<V2)+Pcl)(l-2c(2>)]£0}/(p0£(1>D),
Л=-{(cra)V<2)(^,)2^+(l-c<2,)(£<2,)2[/?<1Ч(l-c<2,)2-
р0Ет] + {зЕ0(1-с(2))[с(2)рт+(1-с(2))ртУр0Ет}х
c(2)EmE(2)}/(p0E(2)D2),
B3 = (j(c<2) )2 £0 [5c(2V<2) + 3p(1) (l-4c<2))] - 2cp0£<2) (l -3c<2))}x
(£(1,)2+£<1)£<2,{p0£(2)(l-c(2))(l + 3c<2,) + 3(c(2))2£0x
[/7<2,(l-c<2))-p(1)(4-5c<2,)]}-3(c<2))2A,(£<1))3 +
р(1)(£<2))2£0(1-с(2))Г1 + с(2)-5(с<2))2])/(/>0£(1)О2),
C3 = c(2) Г(£(1) )2 {/>0£<2> (l - 2c(2)) - c(2)£0 [2с<2,р<2) + 3p(1) (l - 2c<2))]} -
'(1) 17(2)
£l"£'
{Po£<2,(
1-е12' +//"£,
l-6c<2)+6
^<2))2]}
C<24(£(,))3+P(,,(£<2,)2£o(l-^(2))(l-2C<2,)J/U£<1)Z)2).
В приведенных формулах £0 = с(2)/Я(2)+(l-c(2))AE(1) -
эффективный модуль упругости слоистого композита в квазиоднородном
случае (при £ = 0), р0 = (l-c(2))/?(1) +c{2)p{2) - осредненная плот-
123
ность, с{2) = /2 // = 2A/L - объемная доля компонента £1{2),
А = 12/(2е).
Макроскопическое волновое уравнение порядка £2 имеет вид:
E°l^+£LE^+0{£)-p^> (6-9)
где коэффициент
т-З / W2) (2) 77(1) пО) \2
12v Po(£<1)£(2))
можно интерпретировать как эффективный упругий модуль порядка
£2 .
Второе слагаемое в левой части уравнения (6.9) описывает
эффект дисперсии, обусловленный рассеянием волны на микронеодно-
родностях среды. Коэффициент Е2 обращается в ноль и дисперсия
исчезает а) в случае однородного материала (с{2) = 0, с{2) = 1) и б)
при равенстве акустического импеданса компонентов
(Е{2)р{2) = Е{1)р{1)), когда отсутствуют локальные отражения сигнала
на границе раздела Э£2.
Рассмотрим гармоническую волну
и0 = U exp(ijux) exp(icot) (6.10)
с амплитудой U , частотой со и волновым числом ju = 2ж/Ь .
Подставив выражение (6.10) в уравнение (6.9), получим дисперсионное
соотношение:
со2 = со2
Х-АЖ2^£2+0(£А)
Ео
(6.11)
где е - l/L = juI/(2k) , со0 = jiiv0 - частота и v0 = ^Е0/р0 - скорость в
квазиоднородном случае.
Фазовая vp и групповая vg скорости равны:
124
— \ =vn
\-Ал2£2^+0(£А)
dco
dju
(l-87T2£2E2/E0f
1-4kz£zE2/E0
+ 0(£А).
(6.12)
(6.13)
Асимптотическое решение (6.11)—(6.13) представляет собой
длинноволновое приближение. С уменьшением длины волны L (и с
ростом частоты со) групповая скорость vg уменьшается. Условие
vg = О определяет границу первой зоны запирания. Достигаемый при
можно найти из выражений
этом верхний частотный предел 0)г
(6.11), (6.13):
со2
<*>:
«2Шр)
+ 0(£4).
Отметим, что предложенная процедура осреднения построена для
пространственно неограниченных сред. Это позволило определить
дисперсионные соотношения как собственную характеристику
композитного материала, не зависящую от вида краевой задачи на
макроуровне. Если же рассматривается композитная конструкция конечных
размеров, то при решении задач на ячейке высшего порядка нужно
учитывать влияние заданных макроскопических граничных условий.
Формальный перенос результатов, полученных для бесконечной
среды, на случай композита конечных размеров может привести к
ошибкам в граничных условиях на макроуровне.
6.3. Метод Флоке-Блоха. Точное дисперсионное уравнение
Решение, пригодное для коротких волн, можно получить на
основании представления Флоке-Блоха [260, 311]. Согласно данному
методу, запишем следующее выражение для гармонической волны,
распространяющейся в кусочно-неоднородной среде:
и{а) = F{a) (x) exp(ijux) exp(icot).
(6.14)
125
£2(1Ч &
dQ^
с h >
^А^
Рис. 6.3. Ячейка периодичности (относительно координаты х).
где F(a)(x) - некоторая периодическая функция, учитывающая
влияние микроструктуры материала, F(a) (х) = F(a) (х + /). Из
периодичности F(a\x) следует:
uw(x + l) = uw(x)exp(ijul).
(6.15)
Подставив выражение (6.14) в исходное волновое уравнение
(6.1), найдем:
F(a)(x) = F/fl) exp(/[//(a) -ju]x) + Ff exp(-/[//(a) + //]*), (6.16)
где ju(a) = co^jр(а) /Е(а) - волновые числа компонентов.
Чтобы определить коэффициенты F^a), F^a), следует
использовать условия контакта (6.2), (6.3). Рассмотрим ячейку периодичности,
изображенную на рис. 6.3. На границе х = 0 имеем:
{ит=и<%_о,
7(1)
ди(1) ,2л ди(
дх
дх
(6.17)
Перемещения и напряжения на границах х = —1[ и х = /2 можно
связать при помощи уравнения (6.15) следующим образом:
126
«<2)
Эм<2)
= uw Qxp(ijul),
x=l2 \x=—1\
(6.18)
Эх
, Э^
.a)
x=h
Эх
exp(ijul) .
x=-l\
Подставив анзац (6.14), (6.16) в краевые условия (6.17), (6.18),
получим систему из четырех линейных алгебраических уравнений:
F{l) + F^-
F?\
■F?\
-F2(2)=0,
(2).
F^z^F^z, = 0
Fx(1) exp [-/(//(1) - ju)h ] + F? exP [*G"(1) + M ] -
F/2) exp [z(//(2) - ju)l2 ] - F2(2) exp [-/(//(2) + //)/2 ] = 0,
F1(1)z1exp[-/(//(1) -//)/1]-F2(1)z1exp[/(//(1) +//)/х]
-F/2)z2 exp[/(//(2) -//)/2] + F2(2)z2 exp[-/(//(2) +//)/2] = 0,
(6.19)
где z{a) = yjE{a)p{a) - импеданс компонентов.
Система (6.19) имеет нетривиальное решение только в том
случае, когда определитель матрицы, составленной из ее коэффициентов,
равен нулю. Данное условие позволяет записать дисперсионное
уравнение в явном аналитическом виде [36, 191, 193]:
cos(jul) = cos(//( )/1)cos(//( }/2) -
^2Л
ji)
sin(//(1)^)sin(//(2)/2).
(6.20)
Точное решение (6.20) позволяет исследовать различные
упрощенные случаи. Предельный переход /2 —» 0 , р{2)12 —» m, /?(1) —» 0
F(1) Д ~~* С Дает известное дисперсионное соотношение для
колебаний цепочки масс т, соединенных пружинами жесткостью С :
cos(jul) = 1 ■
тсо
~1С
127
Положив /2 —» 0 , р{2)12 —» т, /?(1) = р , £(1) = Е, получим
дисперсионное уравнение продольных колебаний стержня с
присоединенными массами:
cos(jul) = cos
Ш4У
тсо .
-sin
2у[Ер^
"''I;
Для длинных волн можно представить частоту со в виде ряда по
степеням £ , где £ = 1/L = ////(2л") —» 0 . Коэффициенты такого ряда,
вычисленные из уравнения (6.20), совпадают с коэффициентами
асимптотического разложения (6.11), полученного при помощи
метода осреднения.
Перепишем выражение (6.14), разделив действительную jUR и
мнимую jUj части волнового числа ju = jUR+ ijut:
и(а) _ /7(а)(х)ехр(_^х)ехр(/^х)ехр(/^) > (6.21)
Значения //7 = 0 отвечают зонам пропускания, а //7 > 0 - зонам
запирания. Параметр //7 представляет собой коэффициент затухания. Как
следует из уравнения (6.20), границы зон пропускания и запирания
определяются условием cos(///) = ±1. Соответствующие длины волн
равны L = 21/п , п = 1,2,3,....
Общий вид решения приведен на рис. 6.4, 6.5, где зоны запирания
отмечены серым цветом. С математической точки зрения уравнение
(6.20) имеет бесконечное количество корней. Выбор однозначного
решения является одним из принципиальных вопросов теории
распространения волн в периодических структурах.
В работах по динамике кристаллических решеток [37, 126, 351,
361] часто рассматриваются многомодовые режимы, когда
одновременно реализуются несколько гармоник, отвечающих различным
ветвям дисперсионных кривых. Взаимодействие мод с нормальной
(dco/djU>0) и аномальной (dco/djU<0) дисперсией исследовано в
статье [125].
В механике материалов физически оправданным представляется
одномодовый режим, при котором для заданной гармоники (6.14)
сохраняется однозначная зависимость между со и // [191, 193, 246].
128
®А
О м£
2л-
Рис. 6.4. Дисперсионные кривые. Рис. 6.5. Коэффициент затухания.
Соответствующие ветви спектра изображены на рис. 6.4 сплошными
линиями, а все остальные ветви - штриховыми линиями.
Правомерность данного выбора подтверждается асимптотическим переходом от
решения для кусочно-однородной среды к решению для однородной
среды: при равенстве импеданса компонентов (z(2)/zw —> 1) ширина
зон запирания уменьшается и сплошные ветви сливаются в прямую
линию, со —» со0 = jUvQ.
Для коэффициента //7 получаются симметричные пары
положительных и отрицательных корней (рис. 6.5). Положительные значения
jUj (сплошные линии) описывают эффект затухания. Отрицательные
значения //7 (штриховые линии; должны соответствовать режиму
экспоненциального усиления сигнала, что не имеет физического
смысла в рассматриваемой консервативной системе.
Поведение решения можно описать следующим образом. При
низких значениях частоты со дисперсионная кривая близка к прямой
линии, со~щ, фазовая vp =0)//j и групповая vp -dcojdji скорости
примерно равны и не зависят от со, vp ~ vg ~ v0. Данный случай
принято называть квазиоднородным. С увеличением частоты угол
наклона дисперсионной кривой уменьшается. Фазовая и групповая
скорости уменьшаются, однако групповая скорость уменьшается быстрее,
vp > vg . На границе зоны запирания групповая скорость обращается в
ноль, vg = 0, при этом в композите возникает стоячая волна. В
следующих зонах пропускания групповая скорость изменяется от нуля на
границах до максимальных значений в центре.
129
6.4. Численные результаты
В качестве первого примера рассмотрим низкоконтрастный
композит, состоящий из алюминия (Е(1) = 70 ГПа, р(1) = 2700 кг/м3) и
стали (Е(2) =210 ГПа, р(2) =7800 кг/м3). Дисперсионные кривые и
коэффициент затухания приведены, соответственно, на рис. 6.6 и 6.7. Здесь
и ниже, с целью уменьшения размеров рисунков, ветви спектра
изображены в интервале 0 < juRl < п. На рис. 6.8 дисперсионная кривая в
первой зоне пропускания (т.н. акустическая ветвь), найденная при
помощи метода осреднения (формула (6.11)), сравнивается с
результатами численного решения точного дисперсионного уравнения
(6.20). При расчетах принято г(2) = 0.3. Качественно метод
осреднения позволяет учесть эффект дисперсии, но хорошая точность
обеспечивается только при низких значениях частоты со. Общая структура
зон пропускания и запирания, в зависимости от объемной доли стали
Д2)
, изображена на рис. 6.9.
В качестве второго примера рассмотрим высококонтрастный
композит, состоящий из чередующихся слоев углеродно-эпоксидного
(УЭ) пластика (Е(1) = 8.96 ГПа, р(1) =1600 кг/м3) и стали
0.1 0.2 0.3 0.4 0.5
0.04 0.08 0.12 0.16
Рис. 6.6. Дисперсионные кривые Рис. 6.7. Коэффициент затухания
композита «сталь-алюминий». композита «сталь-алюминий».
130
аЯ/(щЬ)
0.5
0.4
0.3
0.2
0.1
0^
квазиоднородныи
случай -
метод
осреднения -
точное решение -
0 0.1 0.2 0.3 0.4 0.5
Рис. 6.8. Акустическая ветвь
композита «сталь-алюминий».
Рис. 6.9. Зоны пропускания
и запирания композита
«сталь-алюминий».
0.1 0.2 0.3 0.4 0.5
Рис. 6.10. Дисперсионные кривые Рис. 6.11. Коэффициент затухания
композита «УЭ пластик-сталь». композита «УЭ пластик-сталь».
(Е(2) =210ГПа, р(2) =7800 кг/м3). Дисперсионные кривые
приведены на рис. 6.10, коэффициент затухания - на рис. 6.11. Результаты,
полученные для акустической ветви методом осреднения, хорошо
согласуются с точным решением (рис.6.12). При расчетах принято
с(2) = 0.5 . Структура зон пропускания и запирания изображена на рис.
6.13.
131
o)l/(o)nL)
метод
осреднения -
точное решение -
0.1 0.2 0.3 0.4 0.5
0)l/(o)nL)
2.0
1.5 Н
1.0
0.5
0
0
0.2 0.4 0.6 0.8
Рис. 6.12. Акустическая ветвь
композита «УЭ пластик-сталь».
Рис. 6.13. Зоны пропускания
и запирания композита
«УЭ пластик-сталь».
132
Глава 7
РАСПРОСТРАНЕНИЕ ВОЛН В ВОЛОКНИСТЫХ
КОМПОЗИТАХ
7.1. Двумерная динамическая задача
Если перемещения и напряжения в композитном материале
зависят от двух пространственных координат хх, х2, то задача о
распространении упругих волн распадается на две независимые задачи,
относящиеся к плоской и антиплоской деформации. Рассмотрим
антиплоскую задачу, которая описывает сдвиговую волну,
распространяющуюся в плоскости ххх2 в волокнистом композите с квадратной
решеткой цилиндрических включений (рис. 1.1, а). Исходное
волновое уравнение запишем в виде:
Vx.(GVxu) = p^, (7.1)
где и - перемещения в направлении х3, Vx = ех Э/Эхх + е2 д/дх2 .
Вследствие неоднородности среды модуль сдвига G и плотность р
являются разрывными функциями координат:
G(x) = G(a), р(х) = р{а) при хе£1(а).
Уравнение (7.1) можно представить в математически
эквивалентной форме:
G<«>V^ii<«> =/><«> ^£-. (7.2)
ot
где V2xx = d2/dxf +д/дх22 .
На границе раздела компонентов д£1 примем условия идеального
контакта:
133
{и(,)=и(2)]|
ди
(1)
>ди(
Эп
Эп
(7.3)
Отметим, что краевая задача (7.1)—(7.3) допускает различные
физические интерпретации. Кроме рассматриваемого здесь примера
упругой сдвиговой волны, она также описывает процессы
распространения электромагнитных волн в композитах с диэлектрическими
включениями.
7.2. Метод осреднения высшего порядка
Для построения длинноволнового приближения используем
асимптотический метод осреднения (п. 1.2), при этом остаются
справедливыми соотношения (1.5)—(1.9). Рекуррентная система краевых
задач на ячейке имеет вид:
G^(V>^+2V>S+V>:«>) = ^>
Э2м,°
dt2
K^L*
Эй™ ди?
-+-
Эп Эт
:G(2)| СЦ-i | СЦ
Эп Эт
(7.4)
(7.5)
(7.6)
где г = 1,2,3 и!? =0, Vx2y = Э2/(Э^Эу1) + Э2/(Э^Эу2),
у;=э2/э^2+э/э^.
Для пространственно-бесконечного композита заменим условия
периодичности (1.9) нулевыми граничными условиями в центре и на
внешней границе Э£20 ячейки [26]:
{м,<2, = о]| , К1'=о]| .
1 l j\x,y=0 l l *Ш0
(7.7)
Определив член и[а) из /-ой краевой задачи (7.4)-(7.7), применим
к (/ + 1)-му уравнению (7.4) оператор осреднения по области ячейки
134
периодичности S0l \\ (-)dS , где dS = dyxdy2 . Члены и%1 исключают-
JJQ,0
ся при помощи теоремы Гаусса-Остроградского, которая с учетом
условий (1.9), (7.6) дает:
Gm jj (V>,(,) + K^)dS + Gi2) Я (Ku?+Ku%)dS = 0.
Осредненное уравнение движения порядка е1 х имеет вид:
G(,) tf(«> + Vlu?>)dS + G™ Я K«!-l + K^)dS =
Q(1) Q(2)
"о "о
•"Я^^'Я^-
Объединяя соотношения (7.8) при i = l...n, получим
макроскопическое волновое уравнение порядка еп.
Для решения краевых задач на ячейке (7.4)-(7.7) могут
использоваться различные методы. Как правило, наибольшие вычислительные
трудности возникают в случае сильного взаимодействия соседних
включений, когда имеют место значительные осцилляции полей на
микроуровне. Рассмотрим асимптотическое решение, используя в
качестве малого параметра безразмерную ширину зазора между
соседними волокнами 7] =2(1-A/L) (рис. 7.1). Пусть 7] «1 и
нулевом приближении 0(т]°) для полос d£lx, d£l2
верны оценки [220, 229]:
ЭЧ(1) э2ц(1)
^ГГ»^ГГ ПРИ ye<KV (7.9)
дух ду2
эу1} эу(1)
-у- « \ при у g d£l2.
Физический смысл оценок (7.9) заключается в том, что для
полосы d£lx (в пределах узкого зазора между волокнами) изменяемость
локальных напряжений в направлении ух существенно больше, чем в
135
Рис. 7.1. Ячейка периодичности.
направлении у2. Таким образом, членом Э2ига) /ду% можно
пренебречь по сравнению с d2u^l) /dyf . Аналогично для полосы d£l2 можно
пренебречь членом Э2ига) /Э_у2 по сравнению с Э2ига) \Ъу\ . Данное
упрощение хорошо известно в механике жидкости, где получило
название теории смазки [43].
Соотношения (7.9) позволяют записать уравнение (7.4) в
приближенном виде:
Эх2
}2 аЛ
+ 2-
dxsdys Ъу\
2
s J
= РУ1
dt
^, s = l,2, (7.10)
r{2) (^2 (2) 9X72 (2) V2 (2) \ _ i
G ( Vxr Mi-2 + 2Vxv Ui-\ + Vvy M* J - />
,(2)
Эг2
Решая краевые задачи (7.5)-(7.7), (7.10) при / = 1,2,3 , найдем:
при ys > 0:
„(2)
.*,.£. «.-k,.+iv)£.
136
,(D
.,(2) =
2"
Л+-Л,Лл
1 + 2Я р{Ц G°
A ^
9 1 1 9
s 4 2'* 5 8 2's
d2u0
Э ип
Эх
„(2)
2 + ЗА,5+(А,5-2)^^
1
2 , 1 . Г2 I Э Hn
./, 4 2^ Js 24 3'* * Эх
nf
1
2 + 3A,,+(A.,-2)
/>(1) ^0
A ^(1)
B2,s +Cl,s _Cl,s
т 9 1 ~ ^9 1 ^ TJ ^Mn
Ly]+ — B3sL2ys+ — C3sL3\—-f
'J 24 3'* * 48 3'* Эх
при ys < 0 :
M(2)-A v <Ч ц^-Гй V --C Л^-
Щ ~А'ЛЭх ' Щ ЛиУ° 2^ )Ъх ■
(2)
1 + 2А -
s A ^(2)y
Л--Л,ЛЛ
Э ип
1 + 2Д
А С(1)
9 1 1 9
у2—В, Ly +-Q L2
-'.у л 2,s J s q 2,s
Эх? '
д2ип
Эх?
«f
2 + 3A,s+(A,s-2)^-^
A G<2)
з , 1
Э ип
yt+^A2.,Lyt+—\^y1\-f,
24
Эх?
2 + 3Bu+(B,,s-2)^--^
А ^
У>
^2,5 + CU ~ С1,5
A G(1)
Ly2+ — B,sL2ys C3,L3f ^ . .
Js 24 3'* s 48 3'* Эх
Здесь G0 - эффективный модуль сдвига в квазиоднородном случае
(вычисляется из уравнения (7.8) при / = 1), р0 =\1-с{2))р{1) +с{2)р{2)
- осредненная плотность, с(2) = ж А2 /L2 - объемная доля волокон,
137
0<c<2) <cZ
таковы:
■ л/4 = 0.7853.... Коэффициенты Als, Bls, ChS
au=-(i-z,){g(2>-g(V,)/ds,
Bu=Xs{Gm-Gm)/Ds,
A =(l-Zs)G(2)+zsG(l>;
A,=-[(l-Z!){[(l-zJp<1,+2Zy2»]G0+A)G(1>}G<2> +
Z>pmG*G0]/{p0G^Ds),
B2,s = {ZSG<* [Z, (pm - 2^)G0 - 2p0Gm ] +
G^[(l + 2zs)p0G^-{l-z>)pmG0]}/{p0G"Ds),
C,
[p0 (G«) + (1 - zs)PmG^>G0 - G<'> {p0G^ +
[zsPi2)+Pm(l-2zs)]G0}/{p0GmDs),
4.,=-{^P(2)(G(,))2Go+(l-^)(Gc2))2[p(1)G0(l-^)2-
A)G(1>] + {3G0(1-ZJ[Z!P<2,+(1-ZJ)P(1,]-^„G<1)}X
^G(1)G(2)}/(p0G(2)^),
*,, = [{z; G0 [5ZP<2> + 3p(1) (1 - 4 jj] - 2 js/j0G<2> (1 - 3Xs)} x
(G(1>)2+G<"G(2>{AG<2'(l-^)(l + 3^) + 3^G0x
[pra(l-Z!)-/1>(4-5zj]}-3z>„(G(1>)3 +
^(с^)2о0(1-^)(1+^-5^)]/(р0е(Ч2).
C3,=^[(G«)2{p0G^(l-2^)-^G0[2^y2)+3p(1>(l-2^)]}-
G(1>G<2>[AG^(l-jJ + p<1>G0(l-6j3+6j2)] +
^A)(G«)3+^(G«)2G0(l-^)(l-2jjl/(p„G«Z)2),
138
где X^^/cZ^l-yl/A2) , Z2=J{c™/cZ){l-y?/A2) .
Макроскопическое волновое уравнение порядка г2 имеет вид:
G0V>0 +£2L2G2V1\ +0(£4) = р0 —^, (7.11)
где V4 = Э4/Эх4 + Э/Эх4 , коэффициент G2 представляет собой
эффективный модуль порядка б*2 (вычисляется из уравнения (7.8) при
i = 3).
С целью проверки полученного решения рассмотрим численные
результаты для безразмерного эффективного модуля сдвига
Дз = G0/G(l) . На рис. 7.2 приведена асимптотика Л^ в случае
сильного взаимодействия соседних волокон (Я{2) = G(2)/G(1) -^оо ,
с(2) —» с^). Согласно математической аналогии между задачами
проводимости и продольного сдвига (п. 3.2), настоящее решение
(сплошные кривые) сравнивается с асимптотической формулой (1.28)
(штриховые кривые), полученной для двух высокопроводящих цилиндров,
стремящихся к контакту [412].
Оценки (7.9) справедливы только в случае высокой жесткости и
плотности упаковки включений. Тем не менее, найденное решение
обеспечивает хорошую точность при любых значениях параметров
1 < Я{2) < ©о и 0 < с(2) < с{^х. Это иллюстрируется на рис. 7.3, где
полученные результаты для \ (сплошные кривые) сравниваются с
данными работы [412] (кружки).
Рассмотрим гармоническую волну
и0 = U ехр(/ц • х) exp(icot), (7.12)
где U - амплитуда, со - частота, ц = //1е1 + //2е2 - волновой вектор,
/I = |ц| = 2ж/Ь - волновое число. Проекции вектора ц на оси
координат равны: fix- /Icosф, //2=//sin0, где ф - угол между осью хх и
направлением распространения волны, ф = (ех, ц). Подставив
выражение (7.12) в уравнение (7.11), получим дисперсионное соотношение:
139
801
60
40
20
Л
.
it
1 '/
i i/
Э 1 2
/у
i /
i /
11
11
3 4
Ч^
5 6
а
100
80
60
40
20
0^
Л
о
„(2)
г(2) _г(2>
Рис. 7.2. Эффективный модуль в случае сильного взаимодействия
соседних волокон, а - Я{2) -> оо , с(2) = 0.784, б - Я{2) = оо , с{2) -> с™ .
35-
зо-
25-
20-
15-
10-
5-
о-
Л
<ь
*^>-^ с(2)
12-
ю-
8"
6-
4-
2-
о-
Л
о
J
1:
Ж
^^^Jb^-P^'
^^Яе^^^^*^^^
с(2)
0 0.2 0.4 0.6 ж/А
а
0 0.2 0.4 0.6 ж/А
Рис. 7.3. Эффективный модуль при различных значениях жесткости
волокон, а- Л{2) =оо,б- Л{2) =5,10,20,50.
I-4л2 (sin4 cp + cos4 cp) — £2 +0(£4)
(7.13)
где £ = l/L = jul/(27t), щ - juv0 - частота и v0 = ^G0/p0 - скорость в
квазиоднородном случае. Фазовая v и групповая vg скорости равны:
140
v
l-4^2(sinV + cosV)^^2+^(^4)
dco
d/i
[l - 8;rV (sinV +cosV)G2/G0
1 -4л-2б*2 (sin4 ф + cos4 ф)G2 /G0
(7.14)
(7.15)
- + 0(£4).
Асимптотическое решение (7.13)—(7.15) получено для случая,
когда длина волны существенно больше размера внутренней
структуры композита. Верхний частотный предел бУтах, который
соответствует началу первой зоны запирания, определяется из условия vg = О :
GL
4l2G2p0 (sin4 ф + cos4 ф)
i^T+0(f4)-
(7.16)
В квазиоднородном случае рассматриваемый волокнистый
композит является трансверсально-изотропным, при этом решение для
G0, v0, й)0 не зависит от направления распространения волны в
плоскости ххх2. Высшие приближения позволяют выявить анизотропию
задачи. Начиная с членов порядка £2, выражения (7.13)—(7.15) зависят
от направления ф волнового вектора. Данный эффект можно также
наблюдать на численных примерах, приведенных в п. 7.4.
7.3. Метод Флоке-Блоха. Решение при помощи рядов Фурье
Согласно методу Флоке-Блоха, будем искать решение волнового
уравнения (7.1) в следующем виде:
и- F(x) ехр(/ц • х) exp(iax),
(7.17)
141
где F(x) - периодическая функция координат, F(x) = F(x + \p),
\р = рх\х + /?212, рх,р2 = 0,±1,±2,..., 1х, 12 - векторы трансляции
квадратной решетки (рис. 1.1, а).
Представим функцию F(x) и свойства компонентов G(x), р(х)
в виде разложений в бесконечные ряды Фурье:
' Ля,
I (/21Х1 +П2Х2
Ля
(пххх +п2х2)
щ =— оо п2 =—оо [
G(x)= I] Z^expl
/>(х)= £ £ с»1П2ехр
«1=-оои2=-°о L 1
Коэффициенты Впп , С вычисляются по формулам:
' Ля,
г — \пххх +п2х2
(7.18)
B»,»2=^||G(x)exP
о %
Ul^
ехр
"о q0
Ля ( х"
-г — (/21х1 + /г2х2 J
-г — (пххх +п2х2)
dS ,
где оператор [Г (•)£& означает интегрирование по площади выде-
ленной ячейки периодичности £20, dS = dxxdx2, S0 =l2 - площадь
ячейки.
Подставив выражения (7.17), (7.18) в уравнение (7.1) и приравняв
коэффициенты при членах вида &хр\ИяГ1(]1х1 + ]2х2)\,
Л'Л = 0,±1,±2,..., получим бесконечную систему линейных
алгебраических уравнений для Ап^ :
Zu Zu Щп2 | ]х-пу,
2я )(2я .
2л- У 2л- .
Tn2+M2\TJ2+M2
С, „ ОГ
(7.19)
:0.
142
Условием существования решения системы (7.19) является
равенство нулю определителя матрицы, составленной из ее
коэффициентов. Приравняв определитель нулю, получим дисперсионное
соотношение для со и ju . Следует отметить, что данный метод решения
не использует краевые условия (7.3) на границе раздела компонентов
в явном виде. При этом условия идеального контакта между
волокнами и матрицей «зашиты» в уравнении (7.1) и в разложении (7.18) для
F(x) , где поля перемещений и напряжений неявно предполагаются
непрерывными.
В численных примерах, приведенных ниже, дисперсионные
соотношения вычисляются путем усечения системы (7.19) полагая
_Лиах - Л'Л - Лиах • Количество удерживаемых уравнений равно
(2утах +1) . С физической точки зрения такое усечение означает
потерю решений в области высоких частот.
Чтобы проиллюстрировать эффект волнового фильтра, разделим
в выражении (7.17) действительную \iR и мнимую ц7 части вектора
и = F(x) ехр(-ц7 • х) exp(i\iR ■ х) exp(iax). (7.20)
Мнимая часть //7 = |ц7| волнового числа представляет собой
коэффициент затухания. Значения jut = 0 отвечают зонам пропускания, а
jiij Ф 0 - зонам запирания. Границы зон пропускания и запирания
определяются условием jul = 7Гп/^ sin4 ф-\-cos4 ф , п = 1,2,3,....
Соответствующие длины волн равны L = (2l/n)y]sin4 ф + cos4 ф .
7.4. Численные результаты
Для сравнения решения, полученного при помощи рядов Фурье, с
результатами других авторов рассмотрим неоднородный материал,
состоящий из матрицы с приведенными свойствами G(1) = 1, /?(1) = 1 и
пустотелых включений, G(2) = 0, р{2) = 0 , A/L = 0.4, с(2) « 0.503 .
143
1.0-
0.8-
0.6-
0.4-
0.2-
0-
cd
co0L ^^^
"Л*
ф = ж/4 N.
b<>Cj>
/ 0 = ° 2ж
1 1 1 1
л/2 0.6
2
0.4 0.2
0.2
0.4 0.5
Рис. 7.4. Дисперсионные кривые композита с пустотелыми
включениями.
Дисперсионные кривые изображены на рис. 7.4. Штриховые линии
результаты расчета при jm
■ 1, сплошные линии - при jm
= 2,
кружки - данные работы [416], полученные методом Рэлея.
Дисперсионная диаграмма состоит из двух частей, разделенных
вертикальной штриховой линией. Правая часть соответствует ортогональному
(ф = 0), а левая - диагональному (ф = л/4) направлению
распространения волны. В квазиоднородном случае (со^О) решение является
изотропным и не зависит от угла ф. Однако с ростом частоты со
композит проявляет анизотропные свойства. Серым цветом изображена
т.н. полная зона запирания, когда прохождение сигнала невозможно в
любом из направлений. Увеличение jmax повышает точность
численных результатов.
В качестве примера низкоконтрастного композита рассмотрим
материал, состоящий из алюминиевой матрицы (G(1) = 27.9 ГПа,
= 2700кг/м ) и никелевых волокон (G( } =75.4 ГПа, /г
= 8936
кг/м
Д2) .
: 0.35). Дисперсионные кривые приведены на рис. 7.5.
144
1.0-
0.8-
0.6-
0.4-
0.2-
о-
cd *^
co0L У^
^^H.
ф = я/4 \
1 1 1
\ 1
2n
Л 0.6 0.4 0.2 0 0.2 0.4 0.5
2
Рис. 7.5. Дисперсионные кривые композита «никель-алюминий».
аЯ/щЬ)
0.5
0.4
0.3
0.2
0.1
0
квазиоднородныи
случай -
метод
осреднения -
Фурье,утах=2-
1 1 1 1 1
0 0.1 0.2 0.3 0.4 0.5
Рис. 7.6. Акустическая ветвь композита «никель-алюминий», ф = 0.
Результаты, полученные при jmax = 1 (штриховые линии) и jmax = 2
(сплошные линии) очень близки, что свидетельствует о быстрой
сходимости решения. Как следует из расчета для акустической ветви
спектра (рис. 7.6), метод осреднения позволяет учесть эффект диспер-
145
сии, но хорошая точность обеспечивается только в диапазоне низких
частот.
В случае высококонтрастного композита (эпоксидная матрица
G(1) =1.53ГПа, р{1) =1250кг/м3 и углеродные волокна G(2) =86ГПа,
р{2) =1800кг/м3, с(2) =0.5) решение при помощи рядов Фурье
сходится гораздо медленнее (рис. 7.7). При этом метод осреднения дает
качественно верные результаты вплоть до границы первой зоны
запирания (при jURl = 7r/yjsm4 ф + cos4 ф получаем vg ~ 0).
а>1/(со0Ь)
0.5"
0.4-
0.3-
0.2-
0.1-
0 -
Фурье,
1 г% о _
Ушах- ^5 ^->Э
/ / у ;
' / / /,
/ ''S'
j7 квазиоднородный
г случай -
метод
г'
осреднения -*
jurI/(2tt)
0 0.1 0.2 0.3 0.4 0.5
Рис. 7.7. Акустическая ветвь углеродно-эпоксидного пластика,
146
Глава 8
КРАЕВЫЕ ЭФФЕКТЫ В КОМПОЗИТНЫХ
МАТЕРИАЛАХ
8.1. Проводимость волокнистых композитов
Краевые эффекты, связанные с перераспределением нагрузки
между компонентами, играют важную роль в микромеханике
неоднородных сред. Протяженность зоны краевого эффекта невелика и, как
правило, находится в пределах одного-двух характерных размеров
внутренней структуры композита. Однако именно здесь возникают
наибольшие локальные напряжения, которые могут приводить к
развитию дислокаций и трещин на микроуровне. Поэтому при анализе
процессов разрушения композитных материалов необходимо
учитывать не только их осредненные свойства, но и особенности
напряженно-деформированного состояния вблизи внешней границы.
В настоящей главе исследуются краевые эффекты, возникающие
в однонаправленных волокнистых композитах (рис. 1.1) при передаче
нагрузки (потока) от волокон к матрице. Предложенные методы могут
также использоваться для расчета свайных фундаментов и опор
платформ, установленных на морском шельфе.
Выделим ячейку периодичности и в первом приближении
заменим ее внешнюю границу окружностью радиуса R (рис 3.1). Такое
упрощение соответствует предположению о статистически-
равномерном распределении волокон и позволяет описать материалы,
для которых отсутствует информация о внутреннем геометрическом
строении. Используемая расчетная схема математически аналогична
полидисперсной модели, которая дает хорошие результаты для транс-
версально-изотропных композитов при малых и средних значениях
объемной доли волокон с{2) ={a/R) [111, 322]. Среди регулярных
моделей наиболее близкие свойства проявляет гексагональная
решетка.
Следующее упрощение заключается в том, что для
высокомодульных (высокопроводящих) волокон можно пренебречь
поперечными деформациями (потоками). Данная гипотеза используется во
147
многих работах [362, 364, 376] и позволяет рассматривать волокно как
одномерный объект.
Рассмотрим задачу о продольной проводимости, когда к
поперечному сечению волокна z = 0 подведен сосредоточенный внешний
поток плотностью q{). В области матрицы Q^>, при отсутствии
объемных источников, уравнение проводимости имеет вид:
VV1}=0, (8.1)
где V2 = д2/дг2 + r~ld/dr + d2/dz2 - осесимметричный оператор
Лапласа в цилиндрических координатах.
На внешней границе Э£20 ячейки радиальный поток равен нулю:
На границе раздела д£1, в случае идеального контакта между
компонентами, выполняется условие равенства потенциалов:
{м(1)=м<2,}[ . (8.3)
Поток через границу д£1 равен
(8.4)
Уравнение проводимости для волокна £l{2) запишем в виде:
?2и{2)
k{2)^-^ + f0(z) + Mz) = 0, (8.5)
oz
где f0(z) - объемная плотность внешнего источника, f0(z) = q0S(z) ,
fx(z) - объемная плотность потока, проходящего через границу д£1,
Mz) = S2Q*q™ade/(xa2) = -2q™/a .
Применим к соотношениям (8.1)—(8.5) преобразование Фурье
(8.2)
,ди°
148
f(s)= I f(z)exp(-isz)dz ■
(8.6)
В пространстве изображений получим:
— 2—(1)
V и = 0,
где V =Э2/Эг2 + г ld/dr-s2,
ом
дг
г-(1)
(3)
г
-(2)11
-и
\г=а
^~(1) 1
Эг
4Г
2;,(2)-<2> 2-0)
-s Л 'м
, +«о=0.
(8.7)
(8.8)
(8.9)
(8.10)
(8.11)
Решая уравнения (8.7), (8.11), найдем:
-(1)
и =Cl(s)I0(\s\r) + C2(s)K0<\rtr),
"(2)
1
2U2) ^0
s к
2-(3)
(8.12)
где 10, К0 - модифицированные функции Бесселя, соответственно,
первого и второго рода [174]. Функции C^s), C2(s) определяются из
граничных условий (8.8), (8.9) с учетом соотношения (8.10).
Окончательное решение строится путем обращения найденных
изображений по формуле
1 °°
/Cz) = —f f(z)Gxp(isz)ds .
2л
(8.13)
149
Рис. 8.1. Радиальный поток на
границе «матрица-волокно».
Рис. 8.2. Продольный поток в
волокне.
При этом выполнялось численное интегрирование с использованием
стандартных процедур математического пакета Maple.
Полученное решение соответствует бесконечному материалу,
-оо < z < °° . Подведенный в точке z = 0 поток q0 делится на две
равные доли, симметрично распространяющиеся в противоположных
направлениях z < 0 и z > 0 . Однако все численные примеры в данной
главе будем рассматривать для полу бесконечных композитов,
О < z < °°, когда точка приложения нагрузки (потока) находится на
внешней границе среды. В этом случае найденные значения
напряжений (потоков) нужно умножить на два.
На рис. 8.1 и 8.2 приведены результаты, соответственно, для
радиального потока qf] на границе раздела компонентов и для
продольного потока в волокне q{2) = -к{2) du(2)/dz . Координата z
нормирована по отношению к расстоянию между центрами соседних
волокон / = 2R . Наличие сосредоточенного источника в точке z = 0
приводит к сингулярности решения, поэтому qf} —> оо при z —> 0 . С
удалением от границы краевой эффект затухает, qf] —> 0 при z —> °° .
Величина qf} уменьшается от q0 (при г^0)до q0c(2)k(2)/к0 (при
z^°°), где к0 = \1-с{2))к{1) +с{2)к{2) - эффективный коэффициент
проводимости. Расчеты выполнены для Я{2) = к{2)/к{1) = 20 .
150
8.2. Учет неидеального контакта между компонентами
Для моделирования эффекта неидеального контакта примем, что
поток через границу раздела д£1 пропорционален скачку потенциала
Аи{3)={и{1)-и{2)}[а:
где к{3) - проводимость, Ъ - толщина границы. Введем параметр
связи а :
(8.14)
где Я(3) = к{3) /к{1) - безразмерная проводимость, h = b/a -
безразмерная толщина границы, и положим h —» 0 . В асимптотическом пределе
значение а = 0 соответствует идеальному контакту (Аи{3) = 0), а = 1
- полному отсутствию контакта между волокнами и матрицей
(q{3) =0). Промежуточные значения 0<df<l описывают случай
неидеального контакта.
При построении решения остаются справедливыми выкладки
п. 8.1, однако вместо условия идеального контакта (8.9) следует
использовать соотношение
(8.15)
Искомые потенциалы определяются выражениями (8.12), где функции
Cx{s), C2(s) находятся из граничных условий (8.8), (8.15).
Численные результаты для потоков q{3) и qf} приведены,
соответственно, на рис. 8.3 и 8.4. При расчетах принято Я{2) = 20,
с(2) = 0.4. В случае неидеального контакта увеличивается
протяженность зоны краевого эффекта. Кроме того, ослабление связи между
волокнами и матрицей устраняет сингулярность решения в точке
151
z = 0 , так что q\' (z) < q; (0) = q; ^ = const. При проектировании
композитных материалов это позволяет ограничить поток q\' на
границе раздела так, чтобы он не превышал заданной критической
величины. Зависимость максимального значения q\x
изображена на рис. 8.5 (Я{2) = 20).
от параметра а
а = 0,0.2,0.4, 0.6, 0.8
0 0.2 0.4 0.6 0
Рис. 8.3. Радиальный поток на
границе «матрица-волокно» в
случае неидеального контакта.
Рис. 8.4. Продольный поток в
волокне в случае неидеального
контакта.
с(2) =0.6,0.4,0.2,0.1
0 0.2 0.4 0.6 0
Рис. 8.5. Влияние параметра связи на максимальный поток
на границе «матрица-волокно».
152
8.3. Продольная деформация волокнистых композитов
Рассмотрим задачу о продольном растяжении (сжатии), когда к
поперечному сечению волокна z = 0 приложена нагрузка плотностью
(70. Для области матрицы £1^ исходные соотношения теории
упругости имеют следующий вид.
Деформации:
е^=^-9 4}= — > *f=^, (8.16)
дг г dz
dz дг гв ez
где и® , uf} - перемещения, соответственно, в радиальном и
продольном направлениях.
Напряжения:
of = 2К?> [(1 -мт)е? + jue? + М^ ] , (8-17)
<> = 2К?> [(l-ju(l>)e? +Jue'll> +М£?
of = IK? [(1-Мт)ег +М£?} +М$)
o%=Gmt%\ о%=о%=0,
где К? = G(1)/(l-2//(1>).
Уравнения равновесия:
^+££z£?+*£ = 0, Э^ + Эа£+^ = 0. (818)
dr r dz dz дг г
Напряжения на внешней границе Э£20 ячейки равны нулю:
{^=0}\r__R, №=0}[__r. (8.19)
153
На границе раздела д£1, в случае идеального контакта,
выполняется условие равенства продольных перемещений:
{Мщ=Мга]| . (8.20)
1 J\r=a
Гипотеза об отсутствии поперечной деформации волокна дает:
К1}=0}| . (8.21)
Уравнение равновесия для волокна £lf} запишем в виде:
(8.22)
где <7^2) = Е{2) duf}/dz - продольное напряжение, f0(z)
-приложенная к волокну объемная сила, f0(z) = &0S(z), ft(z) - объемная сила,
связанная с передачей нагрузки от волокна к матрице,
/1(z) = J g^adOКжа2^ = 2а^/а , где <т^3) - касательное
напряжение на границе д£1, <т^3) = а^
Компоненты перемещений и напряжений в матрице удобно
выразить через упругий потенциал Лява W [130, §188]:
(8.23)
154
Тогда уравнения равновесия (8.18) удовлетворяются тождественно, а
условия совместности деформаций (3.2) приводят к бигармоническо-
му уравнению
v2v2w = о.
(8.24)
Применим к соотношениям (8.19)-(8.24) преобразование Фурье
(8.6). В пространстве изображений получим следующие зависимости.
Перемещения:
(8.25)
Напряжения:
(8.26)
Граничные условия:
(8.27)
155
О 0.2 0.4 0.6 0.
Рис. 8.6. Касательные напряжения Рис. 8.7. Продольные напря-
на границе «матрица-волокно». жения в волокне.
Г-(1) -(2)11
\uz -uz [
(8.28)
Уравнение для упругого потенциала:
v2v2w = o.
Решение уравнения (8.29) имеет вид:
W = Q (лг)/0 (|лг| г) + С2 (лг) |лг| г/х (|лг| г) +
C,(s)K,(\s\r) + C,(s)\s\rKx^s\r\
(8.29)
(8.30)
где функции Сх (s), C2 (s), C3 (s) , C4 (s) находятся из граничных
условий (8.27), (8.28).
Зная W , можно определить перемещения и напряжения путем
обращения изображений (8.25), (8.26) по формуле (8.13).
Для численной иллюстрации полученного решения рассмотрим
композит, состоящий из эпоксидной матрицы (G(1) =1.53 ГПа,
//(1) =0.33) и стеклянных волокон (Е{2) =69 ГПа). На рис. 8.6, 8.7
изображены зависимости напряжений сг^3), af] от продольной
координаты z. Имеют место следующие пределы:
при z —» 0 :
<3)Uoo, W2)Ut70)
156
при z -> °° : \о^ | -> 0, |of} | -> сг0с(2)£(2) /ео ,
где ^ - эффективный модуль Юнга, ^ ~ (l-c(2))£(1) + с(2)£(2),
£(1)=2G(1)(l + //(1)).
8.4. Продольная деформация в случае неидеального
контакта
В рассматриваемой задаче касательные напряжения на границе
раздела д£1 значительно превышают нормальные, поэтому
нарушение связи между компонентами проявляется, прежде всего, в
проскальзывании волокна относительно матрицы. В то же время в
радиальном направлении условия контакта могут оставаться идеальными.
Особенно это верно в случае слабого поперечного взаимодействия
компонентов при //(1) - //(2)«1, что справедливо для большинства
волокнисто-армированных композитов.
Примем, что касательные напряжения на границе д£1
пропорциональны разнице продольных перемещений Auf} = {uf} - uf} j :
G(3)
b
где G(3) - сдвиговая жесткость границы, Я(3) = G(3)/G(1) . Введем
параметр связи а (8.14) и положим h = b/a —» 0 . Как и в задаче
проводимости, значение а = О соответствует идеальному контакту
(Auf} =0), а = 1 - полному отсутствию контакта (сг^3) = 0 ).
Промежуточные значения 0 < а < 1 описывают различные степени адгезии
между компонентами.
При построении решения остаются справедливыми выкладки
п. 8.3, но вместо граничного условия (8.28) следует использовать
соотношение
157
О 0.2 0.4 0.6 0.S
1
О 0.2 0.4 0.6 O.S
1
Рис. 8.8. Касательные напряжения Рис. 8.9. Продольные напряжения
на границе «матрица-волокно» в в волокне в случае неидеального
случае неидеального контакта. контакта.
Рис. 8.10. Влияние параметра связи на максимальные касательные
напряжения на границе «матрица-волокно».
—(3) Gy> l-orf-(i) -(2)i
GrZ \UZ ~UZ
a a I >\r=a
(8.31)
Выражение для упругого потенциала W имеет вид (8.30), где
функции Cx(s), C2(s), C3(s) , C4(s) определяются из уравнений (8.27),
(8.31).
Численные результаты для напряжений сг^3), crz(2) приведены на
рис. 8.8, 8.9. Свойства компонентов соответствуют принятым в п. 8.3,
158
с{ } = 0.4. Ослабление связи между волокнами и матрицей снимает
сингулярность решения и позволяет ограничить максимальные
напряжения <т^3)тах = <г^3) на границе раздела д£1. При этом также
обеспечивается более равномерное перераспределение нагрузки.
Зависимость сг^3)тах от параметра а изображена на рис. 8.10.
159
ЛИТЕРАТУРА
1. Александров В.М., Мхитарян СМ. Контактные задачи для тел с
тонкими покрытиями и прослойками. - М.: Наука, 1983. - 487 с.
2. Андрианов И.В. Расчет оболочек с периодическими шарнирами //
Известия вузов. Строительство и архитектура. - 1984. - №5. -
С.37-39.
3. Андрианов И.В., Данишевский В.В., Старушенко Г.А., Токажев-
ский С. Асимптотическое представление эффективной
теплопроводности композитного материала с волокнистыми включениями
ромбовидной формы // Изв. РАН. Механика твердого тела. - 2000.
-№4.-С.87-98.
4. Андрианов И.В., Данишевский В.В., Токажевский С.
Асимптотическое представление эффективных вязкоупругих сдвиговых
характеристик периодически микронеоднородного композитного
материала с волокнистыми включениями ромбовидной формы //
Теоретичш основи буд1вництва. - 1998. - Т.6. - С.386-392.
5. Андрианов И.В., Данишевский В.В., Токажевский С, Сеферов-
ский Ю.В. Эффективный коэффициент Пуассона композитного
материала с волокнистыми включениями квадратного
поперечного сечения // Теоретичш основи буд1вництва. - 1999. - Т.7. -
С. 16-20.
6. Андрианов И.В., Дисковский А.А. Исследование гофрированных
пластин методом усреднения // Сопротивление материалов и
теория сооружений. - 1982. - №40. - С.45-53.
7. Андрианов И.В., Коблик С.Г. Расчет ортотропной полосы с
периодически меняющимися граничными условиями // Докл. АН
УССР, сер. А. - 1984. - №7. - С.28-30.
8. Андрианов И.В., Лесничая В.А., Маневич Л.И. Метод усреднения
в статике и динамике ребристых оболочек. - М.: Наука, 1985. -
221с.
9. Андрианов И.В., Маневич Л.И. К расчету напряженно-
деформированного состояния ортотропной полосы,
подкрепленной ребрами жесткости // Изв. АН СССР. Механика твердого
тела. - 1975. - №4. - С. 135-140.
10. Андрианов И.В., Маневич Л.И. К расчету складчатых оболочек //
Сопротивление материалов и теория сооружений. - 1975. - №26.
-С.11-14.
160
11. Андрианов И.В., Маневич Л.И. Применение метода осреднения к
расчету оболочек // Успехи механики. - 1983. - Т.6, №3/4. - С.З-
29.
12. Андрианов И.В., Маневич Л.И., Наливайко Л.А. К расчету
круглых цилиндрических ортотропных пластин, подкрепленных
радиальными ребрами // Строительная механика и расчет сооружений.
-1975.-№5.-С.19-13.
13. Андрианов И.В., Старушенко Г.А., Данишевский В.В.
Асимптотическое определение эффективного коэффициента
теплопроводности свайного поля // Основания, фундаменты и механика
грунтов. - 1999. - №1. - С.26-29.
14. Антипов Ю.А. Эффективное решение интегро-
дифференциальных уравнений Прандтля и его приложение к
контактной задаче для полосы // ПММ. - 1993. - Т.57, №3. - С. 146-
155.
15. Антипов Ю.А., Арутюнян Н.Х. Контактная задача с трением и
адгезией для упругого слоя с подкреплениями // ПММ. - 1993. -
Т.57,№1.-С.137-147.
16. Арутюнян Н.Х. Контактная задача для полуплоскости с упругим
креплением // ПММ - 1968. - Т.32, №4. - С.632-646.
17. Асимптотические методы в механике твердого тела / СМ. Бауэр,
А.Л. Смирнов, П.Е. Товстик, СБ. Филиппов М. - Ижевск: НИЦ
«Регулярная и хаотическая динамика», Ин-т компьютерных иссл.,
2007. - 356 с.
18. Бабич И.Ю., Гузь А.Н., Чехов В.Н. Трехмерная теория
устойчивости волокнистых и слоистых материалов // Прикл. механика. -
2001.-Т.37,№9.-СЗ-43.
19. Балагуров Б.Я., Кашин В.А. Квадратичные эффективные
характеристики в задаче о проводимости двухкомпонентных сред.
Численный эксперимент на трехмерной неупорядоченной решетке //
ЖЭТФ. - 1996. - Т. ПО, Вып.З. - С. 1001-1017.
20. Бардзокас Д., Фильштинский М.Л. Дифракция сдвиговой волны
на цилиндрических включениях в пьезоэлектрическом
пространстве // Изв. РАН. Механика твердого тела. - 1997. - №3. - С. 77-
84.
21. Бардзокас Д., Фильштинский М.Л. Электроупругость кусочно-
однородных тел. Сумы: Университетская книга, 2000. - 309 с.
22. Бардзокас Д., Фильштинский М.Л., Фильштинский Л.А.
Усреднение электрических свойств анизотропных волокнистых металло-
композитов // Механика композитных материалов. - 1997. - Т.33,
№2. - С.263-268.
161
23. Бахвалов Н.С. Осредненные характеристики тел с периодической
структурой // Докл. АН СССР. - 1974. - Т.218, №5. - С. 1046-
1048.
24. Бахвалов Н.С. Осреднение дифференциальных уравнений с
частными производными с быстро осциллирующими
коэффициентами // Докл. АН СССР. - 1975. - Т.221, №3. - С.516-519.
25. Бахвалов Н.С. Осреднение нелинейных уравнений с частными
производными с быстро осциллирующими коэффициентами //
Докл. АН СССР. - 1975. - Т.225, №2. - С.249-252.
26. Бахвалов Н.С, Панасенко Г.П. Осреднение процессов в
периодических средах. - М.: Наука, 1984. - 352 с.
27. Бейкер Дж., Грейвс-Моррис П. Аппроксимации Паде. - М.: Мир,
1986. - 502 с.
28. Бердичевский В.Л. Вариационные принципы механики сплошной
среды. - М.: Наука, 1983. - 447 с.
29. Бердичевский В.Л. Пространственное осреднение периодических
структур // Докл. АН СССР. - 1975. - Т.222, №3. - С.565-567.
30. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы
в теории нелинейных колебаний. - М.: Наука, 1974. - 504 с.
31. Бойчук В.Ю. Исследование краевых эффектов в
слабоармированном прямоугольными волокнами композите //
Прикл. механика. - 2001. - Т.37, №5. - С.126-132.
32. Бойчук В.Ю. Краевые эффекты в композите, армированном
волокнами квадратного поперечного сечения при одноосном
нагружении // Доп. НАН Укра'ши. - 2003. - №2. - С.42-45.
33. Бойчук В.Ю., Коханенко Ю.В. Задача о краевом эффекте в
матричном композите регулярной структуры // Доп. НАН
Укра'ши. - 2006. - №4. - С.36-39.
34. Большаков В.И., Данишевский В.В. Асимптотическая методика
расчета волокнисто-армированных композитов при продольном
сдвиге с учетом микромеханического влияния покрытий // Мате-
р1алознавство та терм1чна обробка метал1в. Науков. та шформ.
бюл. - Дншропетровськ: ПДАБА. - 2006. - №2. - С.7-18.
35. Большаков В.И., Данишевский В.В. Асимптотическое
моделирование теплопроводности в зернисто-армированном композитном
материале // Строительство, материаловедение, машиностроение:
Сб. научн. трудов. - Днепропетровск: ПГАСиА. - 2007. - Вып.41,
ч.2. - С.33-39.
36. Бреховских Л.М. Волны в слоистых средах. - М.: Наука, 1973. -
343 с.
162
37. Бриллюэн Л., Парод и М. Распространение волн в периодических
структурах. - М.: Изд-во иностр. лит., 1959. - 457 с.
38. Булгаков А.А., Ольховский Е.А., Шрамкова О.В. Дисперсионные
свойства геликонов в периодической полупроводниковой среде //
Доп. НАН Укршни. - 2007. - №3. - С.83-88.
39. Быстров В.М. Анализ затухания краевых эффектов в материалах
слоистой структуры на основе представительного элемента //
Прикл. механика. - 2000. - Т.36, №6. - С. 135-144.
40. Быстров В.М. Влияние неоднородности материала на зону
краевого эффекта Сен-Венана при плоской деформации
полуограниченной трансверсально-изотропной матрицы с покрытием // Доп.
НАН Укршни. - 2004. - №1. - С.38^2.
41. Быстров В.М. Затухание краевого эффекта Сен-Венана в
слоистом композитном материале при наличии ненагруженных слоев
наполнителя // Теорет. и прикл. механика - 2005. - Вып.41. -
С.55-59.
42. Быстров В.М., Коханенко Ю.В. Анализ затухания краевых
эффектов Сен-Венана в трансверсально-изотропной матрице с
изотропным покрытием // Механика композитных материалов. - 2002. -
Т.38,№2.-С.147-160.
43. Бэтчелор Дж. Введение в динамику жидкости. - М.: Мир, 1973. -
758 с.
44. Вайсфельд Н.Д., Попов Г .Я. Нестационарные динамические
задачи концентрации упругих напряжений возле сферического
дефекта // Изв. РАН. Механика твердого тела. - 2002. - №3. - С.90-102.
45. Ван Фо Фы Г.А. Конструкции из армированных пластмасс. - К.:
Технжа, 1971.-220 с.
46. Ван Фо Фы Г.А. Теория армированных материалов с покрытиями.
- К.: Наукова думка, 1971. - 231 с.
47. Ванин Г.А. Микромеханика композиционных материалов. - К.:
Наукова думка, 1985. - 304 с.
48. Ванин Г.А., Семенюк Н.П., Емельянов Р.Ф. Устойчивость
оболочек из армированных материалов. - К.: Наукова думка, 1978. -
212 с.
49. Гиря М.Г., Головчан В.Т. Волны сдвига в твердой бесконечно
протяженной среде, пронизанной рядом цилиндрических
полостей // Акуст. журнал. - 1978. - Т.24, №4. - С.498-503.
50. Головчан В.Т. Дифракция продольной волны на бесконечном
ряде круговых отверстий в упругой пластинке // Прикл. механика. -
1971.-Т.7,№4.-С.74-81.
163
51. Головчан В.Т. Дифракция волн в многосвязных деформируемых
телах: Автореферат дис. д-ра физ.-мат. наук / Ин-т. механики АН
УССР.-К., 1972.
52. Головчан В.Т. Об эффективных коэффициентах
теплопроводности зернистой среды // Инж. физ. журнал. - 1981. - Т.40, №2. -
С.336-344.
53. Головчан В.Т. Волны сдвига в композиционных волокнистых
материалах // Докл. АН УССР. Сер. А. - 1983. - №7. - С.33-36.
54. Головчан В.Т. Анизотропия физико-механических свойств
композитных материалов. - К.: Наукова думка, 1987. - 304 с.
55. Головчан В.Т. Волны в однонаправленном волокнистом
композите регулярной структуры // Прикл. механика. - 1995. - Т.31, №12.
- С.29-34.
56. Головчан В.Т. Распространение гармонических волн в
волокнистых и пористых упругих материалах с регулярной
микроструктурой // Прикл. механика. - 2002. - Т.38, №10. - С.27-51.
57. Головчан В.Т., Гиря М.Г. Распространение упругих волн сдвига в
полупространстве с бесконечным рядом цилиндрических
полостей // Прикл. механика. - 1978. - Т. 14, №10. - С. 119-122.
58. Головчан В.Т., Гиря М.Г. Распространение упругих волн сдвига в
композитной волокнистой среде // Механика композитных
материалов. - 1979. -№1. - С. 146-149.
59. Головчан В.Т., Гузь А.Н. Распространение волн сдвига в упругом
слое, перфорированном рядом цилиндрических полостей //
Прикл. механика. - 1976. - Т.12, №9. - С.18-33.
60. Головчан В.Т., Гузь А.Н., Коханенко Ю.В., Кущ В.И. Статика
материалов. - К.: Наукова думка, 1993. - 455 с. (Механика
композитов: В 12 т. / Под общ. ред. А.Н. Гузя. - Т.1).
61. Григолюк Э.И., Толкачев В.М. Контактные задачи теории пластин
и оболочек. - М.: Машиностроение, 1980. - 411 с.
62. Григолюк Э.И., Филыитинский Л.А. Перфорированные пластины
и оболочки. - М.: Наука, 1970. - 556 с.
63. Григолюк Э.И., Филыитинский Л.А. Периодические кусочно-
однородные упругие структуры. М.: Наука, 1992. - 288 с.
64. Григолюк Э.И., Филыитинский Л.А. Регулярные кусочно-
однородные структуры с дефектами. М.: Физматлит, 1994. - 336 с.
65. Григоренко Я.М., Шевченко Ю.В, Василенко А.Т. и др.
Численные методы. - К.: «А.С.К.», 2002. - 448 с. (Механика композитов:
В 12 т. / Под общ. ред. А.Н. Гузя. - Т. 11).
164
66. Грилицкий Д.В., Сулим Г.Т. Периодическая задача для упругой
плоскости с тонкостенными включениями // ПММ. - 1975. - Т.39,
№3. - С.520-529.
67. Гузь А.Н. Об описании и исследовании некоторых
неклассических проблем механики разрушения и соответствующих
механизмов // Прикл. механика. - 2000. - Т.36, №12. - С.3-37.
68. Гузь А.Н., Головчан В.Т. Дифракция упругих волн в
многосвязных телах. - К.: Наукова думка, 1972. - 254 с.
69. Гузь А.Н., Коханенко Ю.В. Краевые эффекты в композитах //
Прикл. механика. - 1995. - Т.31, №3. - С.3-23.
70. Гузь А.Н., Коханенко Ю.В., Яковлева Е.С. Определение области
краевых эффектов при разрыве наполнителя в слабоармирован-
ных композитах // Докл. АН УССР. Сер. А. - 1991. - №7. - С.44-
47.
71. Гузь А.Н., Коханенко Ю.В., Яковлева Е.С. Определение областей
краевых эффектов в слоистых композитах при наличии разрывов
наполнителя // Прикл. механика. - 1992. - Т.28, №3. - С. 14-49.
72. Гузь А.Н., Кубенко В.Д., Черевко М.А. Дифракция упругих волн.
- К.: Наукова думка, 1978. - 308 с.
73. Гузь А.Н., Немиш Ю.Н. Метод возмущения формы границ в
механике сплошных сред. - К.: Вища школа, 1989. - 352 с.
74. Гузь А.Н., Рущицкий Я.Я. Наноматериалы. О механике наномате-
риалов // Прикл. механика. - 2003. - Т.39, № 11. - С.36-69.
75. Гузь А.Н., Рущицкий Я.Я., Гузь И.А. О построении основ
механики нанокомпозитов // Прикл. механика. - 2007. - Т.43, № 3. - С.З-
35.
76. Гузь А.Н., Ясинский В.В., Бойчук В.Ю. Плоская задача о краевых
эффектах в композите, слабоармированном прямоугольными
волокнами // Доп. НАН Укра'ши. - 2000. - №8. - С.52-55.
77. Данишевский В.В., Чесанов Л.Г. Асимптотическая методика
определения теплофизических характеристик композитных
материалов // В1сник ПридншровськоУ державноУ академй' буд1вництва
та архгтектури. - 2003. - № 7. - С.31-36.
78. Дыхне A.M. Проводимость двумерной двухфазной системы //
ЖЭТФ. - 1970. - Т.59, №7. - С. 110-115.
79. Дюво Ж. Функциональный анализ и механика сплошной среды.
Приложение к изучению композиционных упругих материалов с
периодической структурой - гомогенизация // Теоретическая и
прикладная механика. - М.: Мир, 1979. - С.323-346.
80. Жиков В.В., Козлов СМ., Олейник О.А. Усреднение
дифференциальных операторов. - М.: Физматлит, 1993. - 461 с.
165
81. Жук Я.А., Гузь И.А. Влияние предварительных напряжений на
скорости распространения плоских волн перпендикулярно слоям
в нанокомпозитных материалах // Прикл. механика. - 2006. - Т.42,
№7. - С.3-22.
82. Жук Я.А., Гузь И.А. Особенности распространения плоских волн
вдоль слоев предварительно напряженного нанокомпозитного
материала // Прикл. механика. - 2007. - Т.43, №4. - С.3-26.
83. Жук Я.О., Гузь I.O. Визначення швидкост1 поширення плоскоУ
поздовжньоУ хвил1 перпендикулярно шарам нанокомпозитного
матер1алу в присутност1 початкових напружень // Доп. НАН Укра-
1ни. - 2006. - №12. - С.36-43.
84. Кагадий Т.С. Метод возмущений в механике упругих (вязкоупру-
гих) анизотропных и композиционных материалов. -
Днепропетровск: Национальная горная академия Украины, 1998. - 260 с.
85. Кагадий Т.С., Моссаковская Л.В., Павленко А.В. Метод
возмущений в пространственной задаче линейной вязкоупругости
анизотропных тел // Изв. РАН. Механика твердого тела. - 1992. - Т.56,
№1.-С.147-151.
86. Кагадий Т.С, Павленко А.В. Осесимметричная задача о передаче
нагрузки к вязкоупругому ортотропному телу посредством
упругого стержня // Изв. РАН. Механика твердого тела. - 1989. - Т.53,
№ 5. - С.619-622.
87. Каламкаров А.Л., Кудрявцев Б.А., Партон В.З. Асимптотический
метод осреднения в механике композитов регулярной структуры
// Итоги науки и техники. Механика деформируемого твердого
тела. - 1987. - Т. 19. - С.78-147.
88. Каландия А.И. О напряженном состоянии в пластинках,
усиленных ребрами жесткости // ПММ. - 1969. - Т.ЗЗ, №3 - С.538-543.
89. Калоеров С.А., Антонов Ю.С. Термонапряженное состояние
анизотропной пластинки с отверстиями и трещинами // Прикл.
механика. - 2005. - Т.41, №9. - С. 127-136.
90. Калоеров С. А., Борон енко О.И. Задача магнитоупругости для тела
с периодическими упругими включениями // Прикл. механика. -
2006. - Т.42, №9. - С.32-40.
91. Калоеров С.А., Мироненко А.Б. Исследование вязкоупругого
состояния пластинки с упругими эллиптическими или линейными
включениями // Прикл. механика. - 2007. - Т.43, №2. - С.88-98.
92. Калоеров С.А., Хорошев К.Г. Термоэлектроупругое состояние
многосвязной анизотропной пластинки // Прикл. механика. -
2005.-Т.41, №11.-С.116-126.
166
93. Каминский А.А. Разрушение вязкоупругих тел с трещинами. - К.:
Наукова думка, 1990. - 310 с.
94. Каминский А.А. Исследование деформирования анизотропных
вязкоупругих тел // Прикл. механика. - 2000. - Т.36, № 11. - С.39-
63.
95. Каминский А.А., Гаврилов Д.А. Длительное разрушение
полимерных и композитных материалов с трещинами. - К.: Наукова
думка, 1992. - 248 с.
96. Каминский А.А., Селиванов М.Ф. Об одном методе решения
граничных задач линейной теории вязкоупругости для анизотропных
композитов // Прикл. механика. - 2003. - Т.39, № 11. - С.70-80.
97. Каминский А.А., Селиванов М.Ф. Об одном методе определения
характеристик вязкоупругого деформирования композитов //
Прикл. механика. - 2005. - Т.41, № 5. - С.9-21.
98. Карпов С.Ю., Столяров С.Н. Распространение и преобразование
волн в средах с одномерной периодичностью // УФН. - 1993. -
Т.163,№1.-С.63-89.
99. Каттани К., Рушицкий Я.Я., Синчило СВ. Физические
постоянные одного вида нелинейно-упругих волокнистых микро- и нано-
композитов волн при наличии жесткой или мягкой нелинейности
// Прикл. механика. - 2005. - Т.41, №12. - С.47-60.
100.Козлов СМ. Геометрические аспекты усреднения // УМН. - 1989.
- Т.44, №2. - С.79-120.
101.Колтунов М.А. Ползучесть и релаксация. - М.: Высшая школа,
1976. - 277 с.
102.Космодамианский А.С. Концентрация внутренней энергии в
многосвязных телах // Прикл. механика. - 2002. - Т.38, №4. - С.21-48.
10З.Космодамианский А.С, Калоеров С.А. Температурные
напряжения в многосвязных пластинках. - Киев-Донецк: Вища школа,
1983.-160 с.
104.Коханенко Ю.В. Численное исследование задач трехмерной
теории устойчивости композитов слоистой и ленточной структуры //
Прикл. механика. - 2001. - Т.37, №3. - С.35-64.
105.Коханенко Ю.В. Плоская задача о краевых эффектах для
трехслойной пластины // Прикл. механика. - 2004. - Т.40, №12. -
С.124-133.
106.Коханенко Ю.В. Плоская задача трехмерной устойчивости шар-
нирно закрепленной пластины с двумя симметричными
торцевыми трещинами // Прикл. механика. - 2005. Т.41, №4. - С.47-52.
167
107.Коханенко Ю.В., Быстров В.М. О краевом эффекте в слоистом
композитном материале при продольном сжатии слоев
наполнителя // Прикл. механика. - 2006. - Т.42, №8. - С.89-96.
108.Коханенко Ю.В., Быстров В.М., Зеленский B.C. Численное
исследование затухания краевых эффектов в металлических слоистых
материалах// Прикл. механика. - 1997. - Т.ЗЗ, №12. - С.50-59.
109.Коханенко Ю.В., Фесенко СВ. Влияние модулей Юнга
компонентов слоистого композита с периодической системой трещин на
характер краевых эффектов // Прикл. механика. - 2003. - Т.39,
№1.-С116-121.
110.Коханенко Ю.В., Фесенко СВ. Зависимость параметров краевых
эффектов от механических характеристик композита,
ослабленного трещиной на границе раздела слоев // Прикл. механика. - 2003.
-Т.39,№12.-С93-99.
111.Коханенко Ю.В., Ясинский В.В., Бойчук В.Ю. Краевые эффекты в
композите, слабоармированном волокнами квадратного
поперечного сечения и ослабленном контактной трещиной // Доп.
НАН Укра'ши. - 2001. - №4. - С. 48-51.
112.Коханенко Ю.В., Ясинский В.В., Бойчук В.Ю. Краевые эффекты в
композите, армированном волокнами квадратного поперечного
сечения, при наличии контактной трещины // Проблемы
прочности. - 2001. - №5. - С.76-86.
113.Коханенко Ю.В., Ясшський В.В., Царипа I.M. Плосю задач1
визначення крайового ефекту в шаруватих композитах з
трансверсально-1зотропним наповнювачем // Доп. НАН Укра'ши. -
2000.-№9.-С64-67.
114.Коханенко Ю.В., Ясшський В.В., Царипа I.M. Дослщження
залежност1 протяжност1 крайового ефекту в шаруватому
композит! з трансверсально-1зотропним наповнювачем вщ
мехашчних характеристик // Проблемы прочности. - 2001. - №4.
-С.127-137.
115.Кривоглаз М.А., Черевко А.С. Об упругих модулях твердой смеси
// ФММ. - 1959. - Т.8, №2. - С.161-164.
116.Кристенсен P.M. Введение в теорию вязкоупругости. - М.: Мир,
1974. - 338 с.
117.Кристенсен P.M. Введение в механику композитов. - М.: Мир,
1982. - 334 с.
118.Кущ В.И. Упругое равновесие среды, содержащей периодически
расположенные сферические включения // Прикл. механика. -
1985.-Т.21,№5.-С18-27.
168
119.Кущ В.И. О вычислении эффективных упругих модулей
зернистого композитного материала регулярной структуры // Прикл.
механика. - 1987. - Т.23, №4. - С.57-61.
120.Кущ В.И. Напряженное состояние и эффективные упругие
модули среды, армированной периодически расположенными
сфероидальными включениями // Прикл. механика. - 1995. - Т.31, №3. -
С.32-39.
121.Кущ В.И. Эффективные упругие модули изотропной среды,
ослабленной одинаково ориентированными дисковыми трещинами
// Прикл. механика. - 2000. - Т.36, №2. - С.91-98.
122.Кущ В.И. Коэффициенты интенсивности напряжений в
изотропном упругом теле, ослабленном одинаково ориентированными
дисковыми трещинами // Прикл. механика. - 2000. - Т.36, №5. -
С.74-80.
123.Кущ В.И. Концентрация напряжений на взаимодействующих
сферических включениях в трансверсально-изотропном теле //
Прикл. механика. - 2004. - Т.40, №8. - С.84-90.
124.Кущ В.И. Эффективные упругие модули зернистого композита
регулярной структуры с трансверсально-изотропными фазами //
Прикл. механика. - 2004. - Т.40, №9. - С.123-130.
125.Ланда П.С, Марченко В.Ф. К линейной теории волн в средах с
периодической структурой //УФН. - Т. 161, № 9. - 1991. - С.201-
209.
126.Ланда П.С. Нелинейные колебания и волны. - М.: Наука, Физмат-
гиз, 1997. - 495 с.
127.Левченко В.В. Магнитоупругие объемные волны сдвига в
периодически-слоистой среде // Прикл. механика. - 2001. - Т.37, №4. -
С.76-81.
128.Лесничая В.А., Маневич Л.И. Асимптотическое исследование
собственных колебаний цилиндрических оболочек,
подкрепленных продольными ребрами // Гидроаэромеханика и теория
упругости. - 1975. -№19. - С.115-125.
129.Лесничая В.А., Маневич Л.И. Асимптотическое исследование
колебаний пластин, подкрепленных ребрами жесткости // Прикл.
механика. - 1980. - Т. 16, №7. - С.67-72.
130.Ляв А. Математическая теория упругости. - М., Л.: ОНТИ, 1935. -
674 с.
131.Маневич Л.И., Павленко А.В. Передача продольной
динамической нагрузки, действующей на ребра жесткости, к упругой орто-
тропной пластине // Изв. АН СССР. Механика твердого тела. -
1975.-№2.-С. 117-124.
169
132.Маневич Л.И., Павленко А.В. Об учете структурной
неоднородности композита при оценке адгезионной прочности // ЖПМТФ. -
1982.-№3.-С.140-145.
133.Маневич Л.И., Павленко А.В. Асимптотический метод в
микромеханике композитных материалов. - К.: Вища школа, 1991. -
131с.
134.Маневич Л.И., Павленко А.В., Коблик С.Г. Асимптотические
методы в теории упругости ортотропного тела. - Киев-Донецк:
Вища школа, 1982. - 152 с.
135.Марченко В.А., Хруслов Е.Я. Краевые задачи с мелкозернистой
границей // Математический сборник. - 1964. - Т.65, №107. -
С.458-472.
136.Марченко В.А., Хруслов Е.Я. Краевые задачи в областях с
мелкозернистой границей. - Киев: Наукова думка, 1974. - 280 с.
137.Марченко В.А., Хруслов Е.Я. Усредненные модели
микронеоднородных сред. - Киев: Наукова думка, 2005. - 550 с.
138.Механика композитов: В 12 т. / Под общ. ред. А.Н. Гузя. - К.:
Наукова думка (Т.1-4), «А.С.К.» (Т.5-12), 1993-2003.
139.Митропольский Ю.А. Метод усреднения в нелинейной механике.
- К.: Наукова думка, 1971. - 440 с.
140.Михасьюв В.В., Бутрак I.O. Тривим1рш динам1чш задач1 для пру-
жного тша з пологою трщиною // Ф1з.-х1м. мехашка матер1ал1в. -
2003. - Т.39. - С.63-70.
141.Михаськив В.В., Бутрак И.О. Концентрация напряжений в
окрестности сфероидной трещины при произвольном направлении
падения на нее гармонической волны // Прикл. механика. - 2006. -
Т.42,№1.-С.70-77.
142.Морарь Г.А., Попов Г.Я. К контактной задаче для полуплоскости
с упругим конечным креплением // ПММ. - 1970. - Т.34, №3. -
С.412-421.
143.Найфэ А. Методы возмущений. - М.: Мир, 1976. - 456 с.
144.Найфэ А. Введение в методы возмущений. - М.: Мир, 1984. -
536 с.
145.Наполнители для полимерных композиционных материалов.
Справочное пособие / Под ред. Г.С. Каца, Д.В. Милевски. - М.:
Химия, 1981.-736 с.
146.Нигматулин Р.И. Динамика многофазных сред: В 2 ч. - М.: Наука,
1987.-464 с, 359 с.
147.Нигматулин Р.И. Основы механики гетерогенных сред. - М.:
Наука, 1978. - 336 с.
170
148.Образцов И.Ф., Нерубайло Б.В., Андрианов И.В.
Асимптотические методы в строительной механике тонкостенных
конструкций. - М.: Машиностроение, 1991. - 416 с.
149.0лейник О.А. О сходимости решений эллиптических и
параболических уравнений при слабой сходимости коэффициентов //
Успехи мат. наук. - 1975. - Т.ЗО, №4. - С.257-258.
150.Олейник О.А. О распространении тепла в многомерных
дисперсных средах // Задачи механики и математической физики. - М.:
Наука, 1976. - С.224-236.
151.Павленко А.В. Применение асимптотического метода к
пространственной задаче теории упругости для композитных материалов //
Изв. АН СССР. Механика твердого тела. - 1980. - №3. - С.50-61.
152.Павленко А.В. Передача нагрузки от стержня к упругому
анизотропному полупространству // Изв. АН СССР. Механика твердого
тела. - 1981. - №6. - С.103-111.
153.Победря Б.Е. Механика композиционных материалов. - М.: Изд-
во МГУ, 1984. - 336 с.
154.Победря Б.Е., Горбачев В.И. О статических задачах упругих
композитов // Вестник МГУ. Математика, механика. - 1977. - №5. -
С.101-110.
155.Подстригач Я.С., Ломакин В.А., Коляно Ю.М. Термоупругость
тел неоднородной структуры. - М.: Наука, 1984. - 368 с.
156.Потураев В.Н., Дырда В.И., Круш И.И. Прикладная механика
резины. - К.: Наукова думка, 1980. - 260 с.
157.Работнов Ю.Н. Элементы наследственной механики твердых тел.
-М.: Наука, 1977. - 384 с.
158.Рущицкий Я.Я. Элементы теории смеси. - К.: Наукова думка,
1991.-160 с.
159.Рущицкий Я.Я. Нелинейные волны в твердых смесях // Прикл.
механика. - 1997. - Т.ЗЗ, №1. - С.3-39.
160.Рущицкий Я.Я. Развитие микроструктурной теории двухфазных
смесей применительно к композитным материалам // Прикл.
механика. - 2000. - Т.36, №5. - С.33-65.
161.Рущицкий Я.Я. Об энергии распространения волн в нелинейно
деформирующихся композитных материалах // Прикл. механика.
-2001.-Т.37,№1.-С.113-119.
162.Рущицкий Я.Я. Характер совместного влияния микроструктуры и
нагрузки на статическое напряженное состояние в упругих телах
// Прикл. механика. - 2004. - Т.40, №4. - С. 13-34.
171
163.Рущицкий Я.Я. О чувствительности структурных моделей
композитного материала к масштабным параметрам структуры // Прикл.
механика. - 2006. - Т.42, №12. - С.58-66.
164.Рущицкий Я.Я., Каттани К. Сравнительный анализ нелинейных
гиперупругих волн с плоским или цилиндрическим фронтом в
материалах с внутренней структурой // Прикл. механика. - 2006. -
Т.42,№10.-С.21-46.
165.Рущицький Я.Я., Симчук Я.В. Теоретичний i числовий анал1з
квадратично-нелшшних цилшдричних хвиль, що поширюються в
композитах мжро- i наноструктури // Доп. НАН Укра'ши. - 2006. -
№2. - С.48-54.
166.Рущицкий Я.Я., Симчук Я.В. О моделировании цилиндрических
волн в нелинейно-деформируемых композитных материалах //
Прикл. механика. - 2007. - Т.43, №6. - С.63-72.
167.Рущицький Я.Я., Цурпал СБ. Хвил1 в матер1алах з мжрострукту-
рою. - К.: Гн-тут механки НАНУ, 1998. - 377 с.
168.Санчес-Паленсия Э. Неоднородные среды и теория колебаний. -
М.:Мир, 1984.-472 с.
169.Слепян Л.И., Яковлев Ю.С. Интегральные преобразования в
нестационарных задачах механики. - Л.: Судостроение, 1980. -
344 с.
170.Снарский А.А., Безсуднов И.В., Севрюков В.А. Процессы
переноса в макроскопически неупорядоченных средах: От теории
среднего поля до перколяции. - М.: Издательство ЛКИ, 2007. - 304 с.
171.Соколовский В.В. Теория пластичности. - М.: Гостехиздат, 1950.
- 396 с.
172.Соцков В.А., Карпенко СВ. Общие закономерности процессов
электропроводности в бинарных макросистемах // ЖТФ. - 2003. -
Т.73,Вып. 1.-С106-109.
173.Справочник по композиционным материалам: В 2 т. / Под ред.
Дж. Любина. - М.: Машиностроение, 1988. - 447 с, 580 с.
174.Справочник по специальным функциям / Под ред. М. Абрамович,
И. Стиган. - М.: Наука, 1979. - 832 с.
175.Сулим Г.Т. Концентрация напряжений возле тонкостенных
линейных включений // Прикл. механика. - 1981. - Т. 17, №11. -
С.82-89.
176. Сулим Г.Т. Упругое равновесие полуплоскости с системой
линейных включений // Прикл. механика. - 1983. - Т. 19, №2. -
С.96-100.
172
177.Сулим Г.Т. Основи математичноУ Teopii термопружноУ р1вноваги
деформ1вних твердих тш з тонкими включениями. - Льв1в: Досль
дно-видавничий центр НТШ, 2007. - 716 с.
178.Сулим Г.Т., Грилицкий Д.В. Напряженное состояние кусочно-
однородной плоскости с тонкостенным упругим включением
конечной длины // Прикл. механика. - 1972. - Т.8, №11. - С.58-65.
179.Филыитинский Л.А. Дифракция упругих волн на трещинах,
отверстиях, включениях в упругой среде // Изв. АН СССР.
Механика твердого тела. - 1991. -№4. - С. 119-127.
180.Филыитинский Л.А. Антиплоская деформация составного
пьезоэлектрического пространства, ослабленного туннельными
трещинами // Изв. РАН. Механика твердого тела. - 1998. - № 2. - С.59-
68.
181.Филыитинский Л.А., Бардзокас Д. Усреднение электрических
свойств волокнистых металлокомпозитов // Механика
композитных материалов. - 1995. - Т.31, №4. - С.533-539.
182.Филыитинский Л.А., Кравец Е.М. Плоская задача магнитоупруго-
сти для ферромагнитной среды, ослабленной отверстиями //
Физико-химическая механика материалов. - 1995. - № 6. - С.38-45.
183.Филыитинский Л.А., Шрамко Ю.В. Усреднение физических
свойств волокнистых пьезокомпозитов // Механика композитных
материалов. - 1998. - Т.34, №1. - С. 116-123.
184.Филыитинский М.Л. Дифракция акустоэлектрических волн на
туннельных полостях в неограниченной пьезокерамической среде
// Прикладная математика и механика. - 1998. - Т.62, Вып.4. -
С.699-706.
185.Филыитинский М.Л., Бардзокас Д. Концентрация напряжений в
составной пьезокерамической пластине с отверстиями // Прикл.
механика. - 1998. - Т.34, №1. - С.98-102.
186.Хорошун Л.П. Математические модели и методы механики
стохастических композитных материалов // Прикл. механика. - 2000.
-Т.36,№10.-С.30-62.
187.Царипа И.М. О краевом эффекте в слоистом композите с
трансверсально-изотропным наполнителем // Прикл. механика. -
2001. - Т.37, №4. - С.95-103.
188.Шермергор Т.Д. Теория упругости микронеоднородных сред. -
М.: Наука, 1977.-400 с.
189.Шкловский Б.Ш., Эфрос А.Л. Электронные свойства
легированных полупроводников. - М.: Наука, 1979. - 416 с.
173
190.Шульга Н.А. О формах объемных волн в периодически-
неоднородных средах // Прикл. механика. - 2005. - Т.41, №5. -
С.3-8.
191.Шульга Н.А. Основы механики слоистых сред периодической
структуры. - К.: Наукова думка, 1981. - 200 с.
192.Шульга Н.А. Распространение волн сдвига в
стратифицированных средах с периодическими свойствами // Прикл. механика. -
1984. - Т.20, №3. - С.116-119.
193.Шульга Н.А. Распространение упругих волн в периодически-
неоднородных средах // Прикл. механика. - 2003. - Т.39, №7. -
С. 15-56.
194.Шульга Н.А. Распространение связанных волн в периодически-
неоднородных средах при взаимодействии с электромагнитным
полем // Прикл. механика. - 2003. - Т.39, №10. - С.38-68.
195.Шульга Н.А., Зинчук Л.П. Дисперсия поверхностных волн в
слоисто-периодическом пьезоэлектрическом полупространстве с
жидким верхним слоем // Прикл. механика. - 2005. - Т.41, №3. -
С.55-61.
196.Шульга Н.А., Левченко В.В., Ратушняк Т.В. Поверхностные
магнитоупругие волны сдвига в периодических феррит-
диэлектрических регулярно-слоистых композитах // Прикл.
механика. - 2003. - Т.39, №11. - С.81-86.
197.Шульга Н.А., Левченко В.В., Ратушняк Т.В. Распространение
магнитоупругих волн сдвига поперек слоев в периодически-
слоистой среде // Прикл. механика. - 2006. - Т.42, №6. - С.54-60.
198.Шульга Н.А., Ратушняк Т.В. Формы объемных волн сдвига в
периодически-неоднородных средах // Прикл. механика. - 2005. -
Т.41,№8.-С.51-56.
199.Шульга Н.А., Ратушняк Т.В. Формы объемных магнитоупругих
волн сдвига на границах зон пропускания в периодически-
неоднородной магнитострикционной среде // Прикл. механика. -
2006. - Т.42, №2. - С.61-69.
200.Шульга Н.А., Ратушняк Т.В. О формах объемных волн в магнито-
стрикционных диэлектрических периодически-неоднородных
средах // Прикл. механика. - 2006. - Т.42, №7. - С.57-63.
201.Шульга Н.А., Ратушняк Т.В. Объемные магнитоупругие волны
сдвига в периодически-неоднородных средах // Прикл. механика.
- 2006. - Т.42, №10. - С. 13-20.
202. Эфрос А.Л. Физика и геометрия беспорядка. - М.: Наука, 1982. -
176 с.
174
203.Эшелби Дж. Континуальная теория дислокаций. - М.: Иностр.
лит., 1963. - 247 с.
204.Яковлева Е.С. Численное определение области краевых эффектов
в слабоармированном композите с полостью // Прикл. механика. -
1993. - Т.29, №7. - С. 19-22.
205.Abate J., Whitt W. A unified framework for numerically inverting
Laplace transforms // INFORMS J. Comput. - 2006. - V.18. - P.408-
421.
206. Aboudi J. Damage in composites - modelling of imperfect bonding //
Composites Science and Technology. - 1987. - V.28. - P.103-128.
207.Achenbach J.D., Herrmann G. Dispersion of free harmonic waves in
fiber-reinforced composites // AIAA J. - 1968. - V.6. - P. 1832-1836.
208.Achenbach J.D, Zhu H. Effect of interfacial zone on mechanical
behaviour and failure of fibre-reinforced composites // J. Mech. Phys.
Solids. - 1989. - V.37. - P.381-393.
209. Achenbach J.D., Zhu H. Effect of interphases on micro and macrome-
chanical behavior of hexagonal-array fiber composites // J. Appl.
Mech. - 1990. - V.57. - P.956-963.
210.Alcaraz J.L., Martinez-Esnaola J.M., Gil-Sevillano J. An analytical
approach to the stress field in the extrusion of bimetallic tubes // Int. J.
Solids Structures. - 1996. - V.33. - P.2075-2093.
211.Alexandrov S., Barlat F. Modelling axisymmetric flow through a
converging channel with an arbitrary yield condition // Acta Mechanica. -
1999. - V. 133.-P.57-68.
212.Alexandrov S., Mishuris G., Miszuris W. Planar flow of a three-layer
plastic material through a converging wedge-shaped channel. Part 1 -
Analytical solution // Eur. J. Mech. A/Solids. - 2000. - V.19. - P.811-
825.
213.Allaire G. Homogenization and two-scale convergence // SIAM J.
Math. Analysis. - 1992. - V.23. -P.1482-1518.
214.Andrianov I.V., Awrejcewicz J., Manevitch L.I. Asymptotical
Mechanics of Thin-Walled Structures: a Handbook. - Berlin, Heidelberg:
Springer-Verlag, 2004. - 535 p.
215.Andrianov I.V., Bolshakov V.I., Danishevs'kyy V.V., Weichert D.
Asymptotic simulation of imperfect bonding in periodic fibre-
reinforced composite materials under axial shear // Int. J. Mech. Sci. -
2007. -V.49. -P. 1344-1354.
216.Andrianov I.V., Bolshakov V.I., Danishevs'kyy V.V., Weichert D.
Higher order asymptotic homogenization and wave propagation in
periodic composite structures // Proc. R. Soc. Lond. A. - 2008. - V.464.
-P.1181-1201.
175
217.Andrianov I.V., Bolshakov V.I., Danishevs'kyy V.V., Weichert D.
Asymptotic study of low- and high-conducting interfaces in a granular
composite material // Theoretical Foundations of Civil Engineering. -
2008.-V.16.-P.49-60.
218.Andrianov I.V., Danishevs'kyy V.V. Load-transfer to an orthotropic
fibre-reinforced composite strip via an elastic element // Technische
Mechanik. - 2007. - V.27. - P.28-36.
219.Andrianov I.V., Danishevs'kyy V.V., Guillet A., Pareige P. Effective
properties and micro-mechanical response of filamentary composite
wires under longitudinal shear // Eur. J. Mech. A/Solids. - 2005. -
V.24. - P. 195-206.
220.Andrianov I.V., Danishevs'kyy V.V., Kalamkarov A.L. Asymptotic
analysis of effective conductivity of composite materials with large
rhombic fibers // Composite Structures. - 2002. - V.56, No.3. -
P.229-234.
221.Andrianov I.V., Danishevs'kyy V.V., Kalamkarov A.L. Asymptotic
justification of the three-phase composite model // Composite
Structures. - 2007. - V.77. - P.395-404.
222.Andrianov I.V., Danishevs'kyy V.V., Kalamkarov A.L., Microme-
chanical analysis of fiber-reinforced composites on account of
influence of fiber coatings // Composites: Part B. Engineering. - 2008. -
V.39. -P.874-881.
223.Andrianov I.V., Danishevs'kyy V.V., Tokarzewski S. Two-point
quasifractional approximants for effective conductivity of a simple
cubic lattice of spheres // Int. J. Heat Mass Transfer. -1996.-V.39.-
P.2349-2352.
224.Andrianov I.V., Danishevs'kyy V.V., Tokarzewski S. An asymptotic
method for effective properties of visco-elastic composite materials //
Z. angew. Math. Mech. - 2000. - V.80, Sup.2. - P.S371-S372.
225.Andrianov I.V., Danishevs'kyy V.V, Tokarzewski S. Quasifractional
approximants in the theory of composite materials // Acta Appl. Math.
-2000.-V.61.-P.29-35.
226.Andrianov I.V., Danishevs'kyy V.V., Tokarzewski S. The method of
quasifractional approximants in applications to mechanical problems //
Theoretical Foundations of Civil Engineering. - 2000. - V.8. - P.371-
376.
227.Andrianov I.V., Danishevs'kyy V.V., Tokarzewski S. Asymptotic
simulation of imperfect interfacial bonding in a fibre-reinforced
composite under longitudinal shear deformation // Theoretical Foundations
of Civil Engineering. -2003. -V. 11. -P. 19-26.
176
228.Andrianov I.V., Danishevs'kyy V.V., Tokarzewski S., Horseva L.,
Seferovskyy Yu. Effective plane shear modulus of a composite
material with fibrous square-shaped inclusions // Theoretical Foundations
of Civil Engineering. - 2002. - V.10. - P.535-542.
229.Andrianov I.V., Danishevs'kyy V.V., Weichert D. Asymptotic
determination of effective elastic properties of composite materials with
fibrous square-shaped inclusions // Eur. J. Mech. A/Solids. - 2002. -
V.21.-P.1019-1036.
230. Andrianov I.V., Danishevs'kyy V.V., Weichert D. Asymptotic
evaluation of effective complex moduli of fibre-reinforced visco-elastic
composite materials // Proc. Appl. Math. Mech. - 2003. - V.2. -
P.154-155.
231.Andrianov I.V., Danishevs'kyy V.V., Weichert D. Fibrous composite
with a weak interface // Строительство, материаловедение,
машиностроение: Сб. научн. трудов. - Днепропетровск: ПГАСиА. -
2007. -Вып.41, ч.1. -С.34-40.
232. Andrianov I.V., Danishevs'kyy V.V., Weichert D. Analytical study of
the load transfer in fibre-reinforced 2D composite materials // Int. J.
Solids Structures. - 2008. - V.45. - P. 1217-1243.
233.Andrianov I.V., Danishevs'kyy V.V., Weichert D. Load-transfer from
fibre to anisotropic half-space for dilute composites // Acta Mechanica.
- 2008. http://dx.doi.org/10.1007/s00707-007-0540-y
234.Andrianov I.V., Danishevs'kyy V.V., Weichert D. Simple estimation
on effective transport properties of a random composite material with
cylindrical fibres // Z. angew. Math. Phys. - 2008.
http://dx.doi.org/10.1007/s00033-007-6146-3
235.Andrianov I.V., Starushenko G.A., Danishevs'kyy V.V., Tokarzewski
S. Homogenization procedure and Pade approximants for effective
heat conductivity of composite materials with cylindrical inclusions
having square cross section // Proc. R. Soc. Lond. A. - 1999. - V.455.
-P.3401-3413.
236.Antipov Y.A., Movchan A.B., Movchan N.V. Frictional contact of
fibre and an elastic solid // J. Mech. Phys. Solids - 2000. - V.48. -
P.1413-1439.
237. Atkin R.J., Crain R.E. Continuum theory of mixtures: basic theory and
historical developments // Quart. J. Mech. Appl. Math. - 1976. - V.29.
- P.209-244.
238.Avitzur B. Metal Forming Processes and Analysis. - New York:
McGraw-Hill, 1968. - 486 p.
239.Babushka I. Solution of interface problems by homogenization. I. //
SIAM J. Math. Anal. - 1976. - V.7. - P.603-634.
177
240. Babushka I. Solution of interface problems by homogenization. II. //
SIAM J. Math. Anal. - 1976. - V.7. - P.635-645.
241. Babushka I. Solution of interface problems by homogenization. III. //
SIAM J. Math. Anal. - 1977. - V.8. - P.923-937.
242. Babushka I. The computational aspects of the homogenization problem
// Lect. Notes Math. - 1979. - V.704. - P.309-316.
243.Bakhvalov N.S., Eglit M.E. Equations of higher order of accuracy
describing the vibrations of thin plates // J. Appl. Math. Mech. - 2005. -
V.69.-P.593-610.
244.Batchelor G.K., O'Brien R.W. Thermal or electrical conduction
through a granular material // Proc. R. Soc. Lond. A. - 1977. - V.355.
-P.313-333.
245.Bedford A., Drumheller D.S. Theories of immiscible and structured
mixtures // Int. J. Eng. Sci. - 1983. - V.21. - P.863-960.
246.Bedford A., Drumheller D.S. Introduction to Elastic Wave
Propagation. - New York: Wiley, 1994. - 297 p.
247.Bedford A., Stern M. Toward a diffusing continuum theory of
composite materials // J. Appl. Mech. - 1971. - V.38. - P.8-14.
248.Benabou L., Nait Abdelaziz M., Benseddiq N. Effective properties of a
composite with imperfectly bonded interface // Theoretical and
Applied Fracture Mechanics. - 2004. - V.41. - P. 15-20.
249.Benscoter S. Analysis of a single stiffener on an infinite sheet // J.
Appl. Mech. - 1949. - V.16. - P.242-246.
250.Bensoussan A., Lions J.-L., Papanicolaou G. Asymptotic analysis for
periodic structures. - Amsterdam: North-Holland, 1978. - 700 p.
251.Benveniste Y. The effective mechanical behaviour of composite
materials with imperfect contact between constituents // Mech. Mater. -
1985. -V.4. - P. 197-208.
252.Benveniste Y., Mil oh T. Imperfect soft and stiff interfaces in two-
dimensional elasticity // Mech. Mater. - 2001. - V.33. - P.309-324.
253.Beran M.J. Statistical Continuum Theories. - New York: Wiley, 1968.
-424 p.
254.Berdichevsky V.L. Homogenization in micro-plasticity // J. Mech.
Phys. Solids. - 2005. - V.53. - P.2457-2469.
255.Berger H., Kari S., Gabbert U., Rodriguez-Ramos R., Guinovart R.,
Otero J.A., Bravo-Castillero J. An analytical and numerical approach
for calculating effective material coefficients of piezoelectric fiber
composites // Int. J. Solids Structures. - 2005. - V.42. - P.5692-5714.
256.Bergman D.J. Hierarchies of Stieltjes functions and their application to
the calculation of bounds for the dielectric constant of a two-
178
components composite medium // SIAM J. Appl. Math. - 1993. -
V.53. -P.915-930.
257.Berlyand L., Mityushev V. Generalized Clausius-Mossotti formula for
random composite with circular fibres // J. Stat. Phys. - 2001. - V.102.
-P.115-145.
258.Berlyand L., Mityushev V. Increase and decrease of the effective
conductivity of two phase composites due to polydispersity // J. Stat. Phys.
- 2005. - V. 118. - P.481-509.
259.Berryman J.G., Milton G.W. Microgeometry of random composites
and porous media // J. Phys. D: Appl. Phys. - 1988. - V.21. - P.87-94.
260.Bloch F. Uber die Quantenmechanik der Elektronen in Kristallgittern
// Z. Physik. - 1928. - V.52. - P.555-600.
261.Bogdanovich A.E., Pastore CM. Mechanics of Textile and Laminated
Composites. - London: Chapman & Hall, 1996. - 570 p.
262.Bolshakov V.I., Danishevs'kyy V.V. Asymptotic multiscale modelling
of heat conduction in fibre-reinforced composite materials with
imperfect bonding // Proc. AFES2006 Forum "Aims for Future of
Engineering Science". - Davos (Switzerland). - 2006. - P.97-107.
263.Bolshakov V.I., Danishevs'kyy V.V. Effective shear modulus and
microscopic stresses in a fibre-reinforced composite material with
interphases // Строительство, материаловедение, машиностроение: Сб.
научн. трудов. - Днепропетровск: ПГАСиА. - 2006. - Вып.36, ч.З.
-С.167-173.
264.Bolshakov V.I., Danishevs'kyy V.V., Weichert D. Propagation of
elastic waves in periodic composite structures // Строительство,
материаловедение, машиностроение: Сб. научн. трудов. -
Днепропетровск: ПГАСиА. - 2008. - Вып.45, ч.1. - С.31-39.
265.Bone Mechanics Handbook / ed. S.C. Cowin. - 2nd ed. - Boca Raton:
CRC Press, 2001.-980 p.
266.B6strom A., Olsson P. Scattering of elastic waves by nonplanar cracks
// Wave Motion. - 1987. - V.9. - P.61-76.
267.Boutin С Microstructural influence on heat conduction // Int. J. Heat
Mass Transfer. - 1995. - V.38. -P.3181-3195.
268.Boutin С Microstructural effects in elastic composites // Int. J. Solids
Structures. - 1996. - V.33. -P.1023-1051.
269.Boutin С Study of permeability by periodic and self-consistent ho-
mogenization // Eur. J. Mech. A/Solids. - 2000. - V.19. - P.603-632.
270.Boutin C, Auriault J.L. Rayleigh scattering in elastic composite
materials // Int. J. Eng. Sci. - 1993. - V.31. - P.1669-1689.
271.Bowen R.M. Toward a thermodynamics and mechanics of mixtures //
Arch. Rat. Mech. Anal. - 1967. - V.24. - P.370-403.
179
272.Bowen R.M. Theory of mixtures // Continuum Physics. - V.3:
Mixtures and EM Field Theories. - Ed. A.C. Eringen. - New York:
Academic Press, 1976. - P. 1-127.
273.Brown E.H. The diffusion of load from a stiffener into an infinite
elastic sheet // Proc. R. Soc. A: Mathematical and Physical Sciences. -
1957.-V.239.-P.296-310.
274.Briiller S.O., Piitz D. Einfache temperatur- und spannungsabhangige
Bestimmungsgleichungen fiir das Kriechen von Polymeren // Rheol.
Acta. - 1975. - V.15. -P.143-147.
275.Buell E.L. On the distribution of plane stress in a semi-infinite plate
with partially stiffened edge // J. Math. Phys. - 1948. - V.26. - P.223-
233.
276.Bufler H. Zur Krafteinleitung in Scheiben iiber geschweisste oder
geklebte Verbindungen // Osterreich Ingenieur-Archive - 1964. -
V.18,No.3-4.-P.284-292.
277.Buryachenko V.A. Multiparticle effective field and related methods in
micromechanics of composite materials // Appl. Mech. Rev. - 2001. -
V.54.-P.l-47.
278.Camacho G.T., Ortiz M. Computational modelling of impact damage
in brittle materials // Int. J. Solids Structures. - 1996. - V.33. -
P.2899-2938.
279.Chandra N., Li H., Shet C, Ghonem H. Some issues in the application
of cohesive zone models for metal-ceramic interfaces // Int. J. Solids
Structures. - 2002. - V.39. - P.2827-2855.
280.Chen H.-S., Acrivos A. The effective elastic moduli of composite
materials containing spherical inclusions at non-dilute concentrations //
Int. J. Solids Structures. - 1978. - V.14. - P.349-364.
281. Chen W., Fish J. A dispersive model for wave propagation in periodic
heterogeneous media based on homogenization with multiple spatial
and temporal scales // J. Appl. Mech. - 2001. - V.68. - V.153-161.
282. Chen X., Liu Y. Multiple-cell modelling of fiber-reinforced
composites with the presence of interphases using the boundary element
method // Comput. Mater. Science. - 2001. - V.21. - P.86-94.
283.Cherednichenko K.D., Smyshlyaev V.P. On full two-scale expansion
of the solutions of nonlinear periodic rapidly oscillating problems and
higher-order homogenised variational problems // Arch. Ration. Mech.
Analysis. - 2004. - V.174. - P.385^42.
284.Cherednichenko K.D., Smyshlyaev V.P., Zhikov V.V. Non-local
homogenized limits for composite media with highly anisotropic periodic
fibres // Proc. R. Soc. Edinburgh. - 2006. - V.136A. - P.87-114.
180
285.Chevalier L. Prediction of defects in metal forming: application to wire
drawing // J. Mat. Proc. Tech. - 1992. - V.32. - P. 145-153.
286.Chitkara N.R., Aleem A. Axi-symmetric tube extrusion/piercing using
die-mandrel combinations: some experiments and a generalised upper
bound analysis // Int. J. Mech. Sci. - 2001. - V.43. - P. 1685-1709.
287.Chitkara N.R., Aleem A. Extrusion of axi-symmetric bi-metallic tubes
from solid circular billets: application of a generalised upper bound
analysis and some experiments // Int. J. Mech. Sci. - 2001. - V.43. -
P.2833-2856.
288.Chitkara N.R., Aleem A. Extrusion of axi-symmetric bi-metallic tubes:
some experiments using hollow billets and the application of a
generalised slab method of analysis // Int. J. Mech. Sci. - 2001. - V.43. -
P.2857-2882.
289.Christensen R.M., Lo K.H. Solutions for effective shear properties in
three phase and cylinder models // J. Mech. Phys. Solids. - 1979. -
V.27.-P.315-330.
290.Crighton D.G. Asymptotics - an indispensible complement to thought,
computation and experiment in Applied Mathematical modelling //
Proc. 7th European Conference on Mathematics in Industry / Eds. A.
Fasano, M.B. Primicerio. - Stuttgart: Teubner, 1994. - P.3-19.
291.Danishevs'kyy V.V. Asymptotic microscale simulation of heat
conduction through the hexagonal array of cylindrical fibres // Theoretical
Foundations of Civil Engineering. - 2005. - V. 13. -P. 113-118.
292.Danishevs'kyy V.V. Higher-order homogenization of a dynamic
problem for a laminated composite material // Theoretical Foundations of
Civil Engineering. - 2006. - V.14. - P.543-550.
293.Danishevs'kyy V.V. Anti-plane shear waves in a square lattice of
cylinders: study of dispersion and phononic band gaps // Theoretical
Foundations of Civil Engineering. - 2007. - V. 15. -P. 103-110.
294.Danishevs'kyy V.V., Guillet A., Pareige P., Weichert D. An analytical
approach to the plastic flow of a bimetallic mono-filamentary wire
through a conical die // Mechanics of Materials. - 2008. - V.40. -
P.284-292.
295.De Gennes P.G. On a relation between percolation theory and
elasticity of gels // J. Phys. Lett. (Paris). - 1976. - V.37L. - P. 1-14.
296.Dixit U.S., Dixit P.M. An analysis of the steady-state wire drawing of
strain-hardening materials // J. Mat. Proc. Tech. - 1995. - V.47. -
P.201-229.
297.Dollar A., Steif P.S. Load transfer in composites with a Coulomb
friction interface // Int. J. Solids Structures. - 1988. - V.24. - P.789-803.
181
298.Drumheller D.S., Bedford A. Wave propagation in elastic laminates
using a second order microstructure theory // Int. J. Solids Structures. -
1974.-V.10.-P.61-76.
299.Drumheller D.S., Sutherland H.J. A lattice model for stress wave
propagation in composite materials // J. Appl. Mech. - 1973. - V.40. -
P.157-164.
300.Duvaut G. Comportement macroscopique d'une plaque perforee
periodiquement // Lect. Notes Math. - 1977. - V.594. - P.131-145.
301.Duvaut G. Homogeneisation des plaquse a structure periodique en
theorie nonlineaire de Von Karman // Lect. Notes Math. - 1978. -
V.665.-P.56-69.
302.Einstein A. Eine Neue Bestimmung der Molekiildimensionen //
Annalen der Physik. - 1906. - V.324. - P.289-306.
303.Einstein A. Berichtigung zu meiner Arbeit: „Eine neue Bestimmung
der Molekiildimensionen" // Annalen der Physik. - 1911. -V.339. -
P.591-592.
304.Erdogan F., Gupta G.D. The problem of an elastic stiffener bonded to
a half plane // J. Appl. Mech. - 1971. - V.38. - P.937-941.
305.Eshelby J.D. The determination of the elastic field of an ellipsoidal
inclusion and related problems // Proc. R. Soc. Lond. A. - 1957. -
V.241.-P.376-396.
306.Espinosa H.D., Dwivedi S.K., Lu H.-C. Modelling impact induced
delamination of woven fibre reinforced composites with
contact/cohesive laws // Computer Methods in Applied Mechanics and
Engineering. - 2000. - V. 183. - P.259-290.
307.Espinosa H.D., Zavattieri P.D., Dwivedi S.K. A finite deformation
continuum/discrete model for the description of fragmentation and
damage in brittle materials // J. Mech. Phys. Solids. - 1998. - V.46. -
P. 1909-1942.
308.Espinosa H.D., Zavattieri P.D., Emore G.L. Adaptive FEM
computation of geometric and material nonlinearities with application to brittle
failure // Mech. Mater. - 1998. - V.29. - P.275-305.
309.Fish J., Chen W. Higher-order homogenization of initial/boundary-
value problem//J. Eng. Mech. -2001. -V. 127. -P. 1223-1230.
310.Fish J., Chen W. Space-time multiscale model for wave propagation in
heterogeneous media // Comput. Methods Appl. Mech. Eng. - 2004. -
V.193.-P.4837-4856.
311.Floquet G. Sur les equations differentielles lineaires a coefficients
periodiques // Ann. Ecole Norm. - 1883. - Sup. 12. - P.47-88.
182
312.Gambin В., Kroner E. High order terms in the homogenized stress-
strain relation of periodic elastic media // Physica Status Solidi (b). -
1989.-V.151.-P.513-519.
313.Garnett J.CM. Colours in metal glasses and in metallic films // Phil.
Trans. R. Soc. bond. A. - 1904. - V.203. - P.385-420.
314.Geubelle P.H., Baylor J.S. Impact-induced delamination of
composites: a 2D simulation // Composites B. - 1998. - V.29. - P.589-602.
315.Gibiansky L., Torquato S. Connection between the conductivity and
elastic moduli of isotropic composite materials // Proc. R. Soc. Lond.
A. - 1996. - V.452. - P.253-283.
316.Guenneau S., Poulton C.G., Movchan A.B. Oblique propagation of
electromagnetic and elastic waves for an array of cylindrical fibres //
Proc. R. Soc. Lond. A. - 2003. - V.459. - P.2215-2263.
317.Guinovart-Diaz R., Rodriguez-Ramos R., Bravo-Castillero J., Sabina
F.J., Otero-Hernandez J.A., Maugin G.A. A recursive asymptotic ho-
mogenization scheme for multi-fibrous elastic composites // Mech.
Mater. - 2005.-V.37.-P.1119-1131.
318.Guz A.N. (Guest Editor), Akbarov S.D., Shulga N.A., Babich I.Yu.,
Chekhov V.N. Micromechanics of composite materials: Focus on
Ukrainian research // Appl. Mech. Rev. (Special Issue). - 1992. -
V.45,N.2.-P.13-101.
319.Guz A.N., Shulga N.A. Dynamics of laminated and fibrous composites
// Appl. Mech. Rev. - 1992. - V.45. - P.35-60.
320.Hashin Z. The elastic moduli of heterogeneous materials // J. Appl.
Mech. - 1962. - V.29. - P. 143-150.
321.Hashin Z. On elastic behaviour of fibre reinforced materials of
arbitrary transverse phase geometry // J. Mech. Phys. Solids. - 1965. -
V.13.-P.119-134.
322.Hashin Z. Analysis of composite materials - a survey // J. Appl. Mech.
-1983.-V.50.-P.481-505.
323.Hashin Z. Thermoelastic properties of fiber composites with imperfect
interface // Mech. Mater. - 1990. - V.8. - P.333-348.
324.Hashin Z. The spherical inclusion with imperfect interface // J. Appl.
Mech. - 1991. - V.58. - P.444-449.
325.Hashin Z. Thermoelastic properties of particulate composites with
imperfect interface // J. Mech. Phys. Solids. - 1991. - V.39. - P.745-
762.
326.Hashin Z. Extremum principles for elastic heterogeneous media with
imperfect interface and their application to bounding of effective
elastic moduli // J. Mech. Phys. Solids. - 1992. - V.40. - P.767-781.
183
327.Hashin Z. Thin interphase/imperfect interface in conduction // J. Appl.
Phys. - 2001. - V.89. - P.2261-2267.
328.Hashin Z. Thin interphase/imperfect interface in elasticity with
application to coated fiber composites // J. Mech. Phys. Solids. - 2002. -
V.50. - P.2509-2537.
329.Hashin Z., Rosen B.W. The elastic moduli of fiber-reinforced
materials // J. Appl. Mech. - 1964. - V.31. - P.223-232.
330.Hashin Z., Shtrikman S. A variational approach to the theory of the
effective magnetic permeability of multiphase materials // J. Appl.
Phys. - 1962. - V.33. -P.1514-1517.
331.Hashin Z., Shtrikman S. A variational approach to the theory of the
elastic behaviour of multiphase materials // J. Mech. Phys. Solids. -
1963. -V. 11.-P. 127-140.
332.Hegemier G., Gurtman G.A., Nayfeh A.H. A continuum mixture
theory of wave propagation in laminated and fiber reinforced composites
// Int. J. Solids Structures. - 1973. - V.9. - P.395-414.
333.Hermann G., Kaul R.K., Delph T.G. On continuum modelling of the
dynamic behaviour of layered composites // Archives of Mechanics. -
1978. - V.28, No.3. - 405-421.
334.Hill R. The elastic behaviour of a crystalline aggregate // Proc. Phys.
Soc. A. - 1952. - V.65. - P.349-354.
335.Hoffman O., Sachs G. Introduction to the Theory of Plasticity for
Engineers. - New York: McGraw-Hill, 1953. - 276 p.
336.Huang Y., Gao H. Intersonic crack propagation. Part I: The
fundamental solution // J. Appl. Mech. - 2001. - V.68. - P.169-175.
337. Jasiuk I., Kouider M.W. The effect of an inhomogeneous interphase on
the elastic constants of transversely isotropic composites // Mech.
Mater. - 1993. - V.15. - P.53-63.
338.Jiang СР., Xu Y.L., Cheung Y.K., Lo S.H. A rigorous analytical
method for doubly periodic cylindrical inclusions under longitudinal
shear and its application // Mech. Mater. - 2004 - V.36. - P.225-237.
339. Johnson W., Kudo H. The Mechanics of Metal Extrusion. -
Manchester: Manchester University Press, 1962. - 226 p.
340.Kafesaki M., Economou E.N. Multiple-scattering theory for three-
dimensional periodic acoustic composites // Phys. Rev. B. - 1999. -
V.60.-P.11993-12001.
341.Kalamkarov A.L, Kolpakov A.G. Analysis, Design and Optimization
of Composite Structures. - New York: Willey, 1997. - 356 p.
342.Kaminski M. Multiscale homogenization of n-component composites
with semi-elliptical random interface defects // Int. J. Solids Structures.
- 2005. - V.42. - P.3571-3590.
184
343.Kanaun S.K., Levin V.M. Self-consistent methods in the problem of
axial elastic shear wave propagation through fiber composites // Arch.
Appl. Mech. - 2003. - V.73. - P.105-130.
344.Kanaun S.K., Levin V.M. Propagation of shear elastic waves in
composites with a random set of spherical inclusions (effective field
approach) // Int. J. Solids Structures. - 2005. - V.42. - P.3971-3997.
345.Kanaun S.K., Levin V.M., Sabina F.J. Propagation of elastic waves in
composites with random set of spherical inclusions (effective medium
approach) // Wave Motion. - 2004. - V.40. - P.69-88.
346.Kazakov V.A., Satanin A.M. A renormalization group approach for
randomly distributed conductance // Phys. Stat. Sol. B. - 1981. -
V.108.-P.19-28.
347.Keller J.B. Conductivity of a medium containing a dense array of
perfectly conducting spheres or cylinders or nonconducting cylinders // J.
Appl. Phys. - 1963. - V.34. - P.991-993.
348.Keller J.B. A theorem on the conductivity of a composite medium // J.
Math. Phys. - 1964. - V.5. - P.548-549.
349.Keller J.B., Rubenfeld L.A., Molyneux L.A. Extremum principles for
slow viscous flows with applications to suspensions // J. Fluid Mech. -
1967.-30.-P.97-125.
350.Kerner E.H. The elastic and thermoelastic properties of composite
media // Proc. Phys. Soc. B. - 1956. - V.69. - P.808-813.
351.Kittel С Introduction to Solid State Physics. - 8th ed. - Hoboken,
New York: Wiley, 2005. - 680 p.
352.Koiter W.T. On the diffusion of load from a stiffener into a sheet // Q.
J. Mech. Appl. Math. - 1955. - V.8. - P. 164-178.
353.Krieger I.M. Rheology of monodisperse lattices // Adv. Colloid
Interface Sci. - 1972. - V.3. - P.ll 1-136.
354.Kubair D.V., Geubelle P.H., Huang Y. Analysis of a rate-dependent
cohesive model for dynamic crack propagation // Engineering Fracture
Mechanics. - 2003. - V.70. - P.685-704.
355.Kushwaha M.S. Stop-bands for periodic metallic rods: sculptures that
can filter the noise // Appl. Phys. Lett. - 1997. - V.70. - P.3218-3220.
356.Kushwaha M.S., Halevi P. Band-gap engineering in periodic elastic
composites // Appl. Phys. Lett. - 1994. - V.64. - P. 1085-1087.
357.Kushwaha M.S., Halevi P. Giant acoustic stop bands in two-
dimensional periodic arrays of liquid cylinders // Appl. Phys. Lett. -
1996.-V.69.-P.31-33.
358.Kushwaha M.S., Halevi P., Dobrzynski L., Djafari-Rouhani B.
Acoustic band structure of periodic elastic composites // Phys. Rev. Lett. -
1993. - V.71. - P.2022-2025.
185
359.Kushwaha M.S., Halevi P., Martinez G., Dobrzynski L., Djafari-
Rouhani B. Theory of acoustic band structure of periodic elastic
composites // Phys. Rev. B. - 1994. - V.49. - P.2313-2322.
360.Lagache M., Agbossou A., Pastor J., Muller D. Role of interphase on
the elastic behavior of composite materials: theoretical and
experimental analysis // J. Composite Mater. - 1994. - V.28. - P. 1140-1157.
361.Landa P.S. Regular and Chaotic Oscillations. - Berlin, New York:
Springer, 2001.-395 p.
362.Lend S. Melan's problems with weak interface // J. Appl. Mech. -
2000.-V.67.-P.22-28.
363.Lend S. Elastic and damage longitudinal shear behavior of highly
concentrated long fiber composites // Meccanica. - 2004. - V.39. -
P.415-439.
364.Lend S., Menditto G. Weak interface in long fibre composites // Int. J.
Solids Structures. - 2000. - V.37. - P.4239-4260.
365.Levy A.J. The effective dilatational response of fiber reinforced
composites with nonlinear interface // J. Appl. Mech. - 1996. - V.63. -
P.357-364.
366.Levy A.J. The fiber composite with nonlinear interface. Part I: Axial
tension // J. Appl. Mech. - 2000. - V.67. - P.727-732.
367.Levy A.J, Dong Z. Effective transverse response of fiber composites
with nonlinear interface // J. Mech. Phys. Solids. - 1998. - V.46. -
P. 1279-1300.
368.Lipton R., Vernescu B. Variational methods, size effects and extremal
microgeometries for elastic composites with imperfect interface //
Mathematical Models and Methods in Applied Sciences. - 1995. -
V.5.-P.1139-1173.
369.Liu Z., Chan СТ., Sheng P., Goertzen A.L., Page J.H. Elastic wave
scattering by periodic structures of spherical objects: theory and
experiment // Phys. Rev. B. - 2000. - V.62. - P.2446-2457.
370.Lo S.-W., Lu Y.-H. Wire drawing dies with prescribed variations of
strain rate // J. Mat. Proc. Tech. - 2002. - V.123. - P.212-218.
371.Mai A.K., Bose S.K. Dynamic elastic moduli of a suspension of
imperfectly bonded spheres // Proceedings of the Cambridge
Philosophical Society. - 1975. - V.76. - P.587-600.
372.Manevitch L.I., Andrianov I.V., Oshmyan V.G. Mechanics of
Periodically Heterogeneous Structures. - Berlin: Springer, 2002. - 264 p.
373.Martin P., Baker G.A. Jr. Two-point quasifractional approximant in
physics. Truncation error // J. Math. Phys. - 1991. - V.32. - P.1470-
1477.
186
374.Martinez-Sala R., Sancho J., Sanchez J.V., Gomez V., Llinares J., Me-
seguer F. Sound attenuation by sculpture // Nature. - 1995. - V.378. -
P.241.
375.Maxwell J.C. Treatise on Electricity and Magnetism. - Oxford:
Clarendon Press, 1873.
376.Mbanefo U., Westmann R.A. Axisymmetric stress analysis of a
broken, debonded fiber // J. Appl. Mech. - 1990. - V.57. - P.654-660.
377.McKenzie D.R., McPhedran R.C., Derrick G.H. The conductivity of
lattices of spheres. 2. The body-centered and face-centered lattices //
Proc. R. Soc. bond. A. - 1978. - V.362. - P.211-232.
378.McPhedran R.C. Transport properties of cylinder pairs and of the
square array of cylinders // Proc. R. Soc. Lond. A. - 1986. - V.408. -
P.31-43.
379.McPhedran R.C, McKenzie D.R. The conductivity of lattices of
spheres. 1. The simple cubic lattice // Proc. R. Soc. Lond. A. - 1978. -
V.359.-P.45-63.
380.McPhedran R.C, Milton G.W. Transport properties of touching
cylinder pairs and of the square array of touching cylinders // Proc. R. Soc.
Lond. A. - 1987. - V.411. - P.313-326.
381.McPhedran R.C, Poladian L., Milton G.W. Asymptotic studies of
closely spaced highly conducting cylinders // Proc. R. Soc. Lond. A. -
1988.-V.415.-P.185-196.
382.Meguid S.A., Kalamkarov A.L. Asymptotic homogenization of elastic
composite materials with a regular structure // Int. J. Solids Structures.
-1993. -V.31.-P.303-316.
383.Melan E. Ein Beitrag zur Theorie geschweisster Verbindungen //
Ingenieur-Archive. - 1932. - V.3. - P. 123-129.
384.Meredith R.E., Tobias C.W. Resistance to potential flow through a
cubic array of spheres // J. Appl. Phys. - 1960. - V.31.-P. 1270-1273.
385.Miehe C, Schroder J., Bayreuther С On the homogenization analysis
of composite materials based on discretized fluctuations on the micro-
structure // Acta Mechanica. - 2002. - V.155. - P.l-16.
386. Mil oh Т., Benveniste Y. On the effective conductivity of composites
with ellipsoidal inhomogeneities and highly conducting interfaces //
Proc. R. Soc. Lond. A. - 1999. - V.455. - P.2687-2706.
387.Milton G.W. Bounds on the elastic and transport properties of two-
component composites // J. Mech. Phys. Solids. - 1982. - V.30. -
P.177-191.
388.Milton G.W. Correlation of electromagnetic and elastic properties of
composites and microgeometries corresponding with effective medium
187
approximations // Physics and Chemistry of Porous Media / Eds. D.L.
Johnson, R.N. Sen. - New York: AIP, 1984. - P.66-77.
389.Milton G.W. The Theory of Composites. - Cambridge: Cambridge
University Press, 2002. - 719 p.
390. Milton G.W., Phan-Thien N. New bounds on the effective moduli of
two-component materials // Proc. R. Soc. Lond. A. - 1982. - V.380. -
P.305-331.
391.Mishuris G., Ochsner A. Edge effects connected with thin interfaces in
composite materials // Composite Structures. - 2005. - V.68. - P.409-
417.
392.Montero de Espinosa F.R., Jimenez E., Torres M. Ultrasonic band gap
in a periodic two-dimensional composite // Phys. Rev. Lett. - 1998. -
V.80.-P.1208-1211.
393.Movchan A.B., Movchan N.V., Poulton C.G. Asymptotic Models of
Fields in Dilute and Densely Packed Composites. - London: Imperial
College Press, 2002. - 190 p.
394.Movchan A.B., Nicorovici N.A., McPhedran R.C. Green's tensors and
lattice sums for elastostatics and elastodynamics // Proc. R. Soc. Lond.
A. - 1997. - V.453. - P.643-662.
395.Movchan A.B., Willis J.R. Asymptotic analysis of reinforcement by
frictional fibres // Proc. R. Soc. Lond. A. - 1997. - V.453. - P.757-
784.
396.Muki R., Sternberg E. Transfer of load from an edge stiffener to a
sheet - a reconsideration of Melan's problem // J. Appl. Mech. - 1967.
- V.34. - P.679-686.
397.Muki R., Sternberg E. On the diffusion of an axial load from an
infinite cylindrical bar embedded in an elastic medium // Int. J. Solids
Structures. - 1969. - V.5. - P.587-605.
398.Muki R., Sternberg E. Load-transfer to a half-space from a partially
embedded axially loaded rod // Int. J. Solids Structures. - 1970. - V.6.
-P.69-90.
399.Muki R., Sternberg E. Load-absorption by a discontinuous filament in
a fibre-reinforced composite // Z. angew. Math. Phys. - 1971. - V.22.
- P.809-824.
400.Needleman A. A continuum model for void nucleation by inclusion
debonding // J. Appl. Mech. - 1987. - V.54. - P.525-531.
401.Needleman A. An analysis of tensile decohesion along an interface // J.
Mech. Phys. Solids. - 1990. - V.38. - P.289-324.
402.Needleman A. Micromechanical modelling of interfacial decohesion //
Ultramicroscopy. - 1992. - V.40. - P.203-214.
188
403.Nicorovici N.A., McPhedran R.C., Botten L.C. Photonic band gaps for
arrays of perfectly conducting cylinders // Phys. Rev. E. - 1995. -
V.52.-P.1135-1145.
404.Nie S., Basaran C. A micromechanical model for effective elastic
properties of particulate composites with imperfect interfacial bonds //
Int. J. Solids Structures. - 2005. - V.42. - P.4179-4191.
405.Ohno N., Wu X., Matsuda T. Homogenized properties of elastic -
viscoplastic composites with periodic internal structures // Int. J.
Mech. Sci. - 2000. - V.42. - P.1519-1536.
406. Ortiz M., Pandolfi A. Finite-deformation irreversible cohesive element
for three-dimensional crack-propagation analysis // International
Journal for Numerical Methods in Engineering. - 1999. - V.44. - P. 1267-
1282.
407.Pagano N.J., Tandon G.P. Modelling of imperfect bonding in fiber
reinforced brittle matrix composites // Mech. Mater. - 1990. - V.9. -
P.49-64.
408.Parnell W.J., Abrahams I.D. Dynamic homogenization in periodic
fibre reinforced media. Quasi-static limit for SH waves // Wave
Motion. - 2006. - V.43. - P.474-498.
409.Parton V.Z., Kudryavtsev B.A. Engineering Mechanics of Composite
Structures. - Boca Raton: CRC Press, 1993. - 397 p.
410.Penciu R.S., Fytas G., Economou E.N., Steffen W., Yannopoulos S.N.
Acoustic excitations in suspensions of soft colloids // Phys. Rev. Lett.
- 2000. - V.85. - P.4622-4625.
411.Perin F. Bounds and asymptotic results for the effective
electromagnetic properties of a locally periodic distribution of conducting
inclusions in a conducting matrix // Eur. J. Mech. A/Solids. - 2004. - V.23.
-P.139-157.
412.Perrins W.T., McKenzie D.R., McPhedran R.C. Transport properties
of regular arrays of cylinders // Proc. R. Soc. Lond. A. - 1979. -
V.369.-P.207-225.
413.Platts S.B., Movchan N.V., McPhedran R.C, Movchan A.B. Two-
dimensional phononic crystals and scattering of elastic waves by an
array of voids // Proc. R. Soc. Lond. A. - 2002. - V.458. - P.2327-2347.
414.Platts S.B., Movchan N.V., McPhedran R.C, Movchan A.B. Band
gaps and elastic waves in disordered stacks: normal incidence // Proc.
R. Soc. Lond. A. - 2003. - V.459. - P.221-240.
415.Ponte Castaneda P., Suquet P. Nonlinear composites // Adv. Appl.
Mech. - 1998. - V.34. - P. 171-302.
416.Poulton C.G., Movchan A.B., McPhedran R.C, Nicorovici N.A., An-
tipov Y.A. Eigenvalue problems for doubly periodic structures and
189
phononic band gaps // Proc. R. Soc. Lond. A. - 2000. - V.456. -
P.2543-2559.
417.Psarobas I.E., Stefanou N., Modinos A. Scattering of elastic waves by
periodic arrays of spherical bodies // Phys. Rev. B. - 2000. - V.62. -
P.278-291.
418.Qu J. The effect of slightly weakened interfaces on the overall elastic
properties of composite materials // Mech. Mater. - 1993. - V.14. -
P.269-281.
419.Raghavan P., Ghosh S. A continuum damage mechanics model for
unidirectional composites undergoing interfacial debonding // Mech.
Mater. - 2005. - V.37. - P.955-979.
420.Rayleigh R.S. On the influence of obstacles arranged in rectangular
order upon the properties of medium // Philosophical Magazine. -
1892.-V.34.-P.481-502.
421.Reuss A. Berechnung der FlieBgrenze on Mischkristallen auf Grund
der Plastizitatsbedingungen fiir Einkristall // Z. angew. Math. Mech. -
1929.-V.9.-P.49-58.
422.Richard T.G. The mechanical behavior of a solid microsphere filled
composite // J. Сотр. Mater. - 1975. - V.9. - P. 108-113.
423.Richmond O., Alexandrov S. Nonsteady planar ideal plastic flow:
general and special analytical solutions // J. Mech. Phys. Solids. - 2000. -
V.48.-P.1735-1759.
424.Rodriguez-Ramos R., Sabina F.J., Guinovart-Diaz R., Bravo-Castillero
J. Closed-form expressions for the effective coefficients of fibre-
reinforced composite with transversely isotropic constituents. I. Elastic
and square symmetry // Mech. Mater. - 2001. - V.33. - P.223-235.
425.Rubenfeld L.A., Keller J.B. Bounds on the elastic moduli of composite
media // SIAM J. Appl. Math. - 1969. - V.17. - P.495-510.
426.Rushchitsky J.J. Interaction of waves in solid mixtures // Appl. Mech.
Rev. - 1999. - V.52. - P.35-74.
427.Russell P.St.J., Marin E., Diez A., Guenneau S., Movchan A.B. Sonic
band gaps in PCF preforms: enhancing the interaction of sound and
light // Optics express. - 2003. - V.ll. - P.2555-2560.
428.Ruzzene M., Baz A. Control of wave propagation in periodic
composite rods using shape memory inserts // J. Vibr. Acoustics. - 2000. -
V.122.-P.151-159.
429.Sabina F.J., Willis J.R. A simple self consistent analysis of wave
propagation in particulate composites // Wave Motion. - 1988. - V.10.
-P.127-142.
430.Saha G.C., Kalamkarov A.L., Georgiades A.V. Asymptotic homogeni-
zation modelling and analysis of effective properties of smart rein-
190
forced and sandwich shells // Int. J. Mech. Sci. - 2007. - V.49. -
P.138-150.
431.Samudrala O., Huang Y., Rosakis A.J. Subsonic and intersonic mode.
Part II: Crack propagation with a rate-dependent cohesive zone // J.
Mech. Phys. Solids. - 2002. - V.50. - P. 1231-1268.
432.Samudrala O., Rosakis A.J. Effect of loading and geometry on the
subsonic/inter sonic transition of a bimetallic interface crack //
Engineering Fracture Mechanics. - 2003. - V.70. - P.309-337.
433.Sanchez-Palencia E. Comportement local et macroscopique d'un type
de milieux physiques heterogenes // Int. J. Eng. Sci. - 1974. - V.12. -
P.331-351.
434.Sanchez-Palencia E. Solutions periodiques par rapport aux variables
d'espace et applications // Compt. Rend. Acad. Sci. Paris, serie A. -
1970.-V.271.-P.1129-1132.
435.Sanchez-Palencia E. Equations aux derivees partielles dans un type de
milieux heterogenes // Compt. Rend. Acad. Sci. Paris, serie A. - 1971.
-V.272.-P.1410-1413.
436.Sangani A.S., Acrivos A. The effective conductivity of a periodic
array of spheres // Proc. R. Soc. bond. A. - 1983. - V.386. - P.263-275.
437.Santos J.E., Ravazzoli C.L., Geiser J. On the static and dynamic
behavior of fluid saturated composite porous solids: A homogenization
approach // Int. J. Solids Structures. - 2006. - V.43. - P. 1224-1238.
438.Selivanov M.F., Chernoivan Yu.A. A combined approach of the
Laplace transform and Pade approximantion solving viscoelasticity
problems // Int. J. Solids Structures. - 2007. - V.44. - P.66-76.
439.Shield R.T. Plastic flow in a converging conical channel // J. Mech.
Phys. Solids. - 1955. - V.3. - P.246-258.
440.Sigalas M.M., Economou E.N. Elastic and acoustic wave band
structure // J. Sound Vibr. - 1992. - V.158. - P.377-382.
441.Sigalas M.M., Economou E.N. Band structure of elastic waves in two
dimensional systems // Solid State Communications. - 1993. - V.86. -
P.141-143.
442.Sigalas M.M., Economou E.N. Elastic waves in plates with
periodically place inclusions // J. Appl. Phys. - 1994. - V.75. - P.2845-2850.
443.Sigalas M.M., Economou E.N. Attenuation of multiple-scattered sound
// Europhys. Lett. - 1996. - V.36. - P.241-246.
444.Silva M.A.G. Study of pass and stop bands of some periodic
composites // Acustica - 1991. - V.75. - P.62-68.
445.Sliwa R., Mishuris G. A modified flow field in the extrusion of
bimetallic systems // Engng. Trans. - 1999. - V.47, No.2. - P.203-215.
191
446.Smyshlyaev V.P., Cherednichenko K.D. On rigorous derivation of
strain gradient effects in the overall behaviour of periodic
heterogeneous media // J. Mech. Phys. Solids. - 2000. - V.48. - P.1325-1357.
447.Starr T. Carbon and High Performance Fibers Directory and Databook.
- 6th ed. - London: Chapman & Hall, 1995. - 408 p.
448.Sun C.T., Achenbach J.D., Herrmann G. Continuum theory for a
laminated media // J. Appl. Mech. - 1968. - V.35. - P.467-475.
449.Talbot D.R.S. Improved bounds for the overall properties of a
nonlinear composite dielectric // Proc. R. Soc. Lond A. - 2001. - V.457. -
P.587-597.
450.Tamura S., Shields J.A., Wolfe J.P. Lattice dynamics and elastic pho-
non scattering in silicon // Phys. Rev. B. - 1991. - V.44. - V.3001-
3011.
451.Tan H., Liu C, Huang Y., Geubelle P.H. The cohesive law for the
particle/matrix interfaces in high explosives // J. Mech. Phys. Solids. -
2005.-V.53.-P.1892-1917.
452.Tartar L. Homogeneisation en hydrodynamique // Lect. Notes Math. -
1977.-V.594.-P.474-481.
453.Tartar L. Estimation de coefficientes homogeneises // Lect. Notes
Math. - 1979. - V.704. - P.364-373.
454.Telega J.J., Tokarzewski S., Galka A. Effective conductivity of
nonlinear two-phase media: homogenization and two-point Pade
approximants // Acta Appl. Math. - 2000. - V.61. - P.295-315.
455.Thomsen E.G., Yang СТ., Kobayashi S. Mechanics of Plastic
Deformation in Metal Processing. - New York: Macmillan, 1965. - 486 p.
456.Ting T.C.T. Dynamic response of composites // Appl. Mech. Rev. -
1980.-V.33.-P.1629-1635.
457.Tokarzewski S. Two-point Pade approximants for the expansion of
Stieltjes functions in real domain // J. Сотр. Appl. Math. - 1996. -
V.67. - P.59-72.
458.Tokarzewski S., Andrianov I. Effective coefficients for real non-linear
and fictitious linear temperature-dependent periodic composites // Int.
J. Non-linear Mech. - 2001. - V.36. - P.187-195.
459.Tokarzewski S., Andrianov I., Danishevs'kyy V. The investigation of
a complex conductivity of regular arrays of spheres // Theoretical
Foundations of Civil Engineering. - 1997. - V.5. - P.414-425.
460.Tokarzewski S., Andrianov I., Danishevs'kyy V. Dynamiczne moduly
skretne pretow sprezystych porami wypelnionymi ciecza lepka //
Theoretical Foundations of Civil Engineering. - 1998. - V.6. - P.393-
398.
192
461.Tokarzewski S., Andrianov L, Danishevs'kyy V. Parametric complex
bounds on effective transport coefficients of two-phase media //
Theoretical Foundations of Civil Engineering. - 2001. - V.9. - P.433^-40.
462.Tokarzewski S., Andrianov I., Danishevs'kyy V., Starushenko G.
Analytical continuation of asymptotic expansions of effective transport
coefficients by Pade approximants // Nonlinear Analysis. - 2001. - V.47.
- P.2283-2292.
463.Tokarzewski S., Blawzdziewicz J., Andrianov I. Effective conductivity
for densely packed highly conducting cylinders // Appl. Phys. A. -
1994.-V.59.-P.601-604.
464.Tokarzewski S., Blawzdziewicz J., Andrianov I. Two-point Pade
approximants for effective conductivity of a periodic array of cylinders //
Advances in Structured and Heterogeneous Continua. - New York:
Allerton Press, 1994. - P.263-267.
465.Tokarzewski S., Galka A., Andrianov I., Danishevs'kyy V. Pade
bounds on temperature-dependent conductivities of heterogeneous
materials // Theoretical Foundations of Civil Engineering. - 1999. - V.7.
-P.412-427.
466.Tokarzewski S., Galka A., Andrianov I., Danishevs'kyy V. Parametric
inclusion regions for transport coefficients of two-phase media //
Theoretical Foundations of Civil Engineering. - 2002. - V.10. -
P.465-470.
467.Tokarzewski S., Telega J.J. S-continued fraction method for the
investigation of a complex dielectric constant of two-component composite
// Acta Appl. Math. - 1997. - V.49. - P.55-83.
468.Torquato S. Random heterogeneous media: Microstructure and
improved bounds on the effective properties // Appl. Mech. Rev. - 1991.
-У.44.-Р.37-76.
469.Torquato S. Random Heterogeneous Materials. Microstructure and
Macroscopic Properties. - New York: Springer, 2002. - 701 p.
470.Torquato S., Rubinshtein J. Improved bounds on the effective
conductivity of high-contrast suspensions // J. Appl. Phys. - 1991. - V.69. -
P.7118-7125.
471.Torres M., Montero de Espinosa F.R., Garcia-Pablos D., Garcia N.
Sonic band gaps in finite elastic media: surface states and localization
phenomena in linear and point defects // Phys. Rev. Lett. - 1999. -
V.82.-P.3054-3057.
472.Tvergaard V. Effect of fibre debonding in a whisker-reinforced metal
// Materials Science and Engineering A. - 1990. - V.125. - P.203-213.
193
473.Tvergaard V. Fiber debonding and breakage in a whisker reinforced
metal // Materials Science and Engineering A. - 1995. - V.90. -
P.215-222.
474.Tvergaard V., Hutchinson J.W. The relation between crack growth
resistance and fracture process parameters in elastic-plastic solids // J.
Mech. Phys. Solids. - 1992. - V.40. - P. 1377-1397.
475.Tvergaard V., Hutchinson J.W. The influence of plasticity on mixed-
mode interface toughness // J. Mech. Phys. Solids. -1993. -V.41. -
P.1119-1135.
476. Van der Pol С On the rheology of concentrated dispersions // Rheol.
Acta. - 1958. - V.l. - P. 198-205.
477. Van Tuyl A.H. Asymptotic expansions with error bounds for the
coefficients of capacity and induction of two spheres // SIAM J. Math.
Anal. - 1996. - V.27. - P.782-804.
478.Vasseur J.O., Djafari-Rouhani В., Dobrzynski L., Kushwaha M.S.,
Halevi P. Complete acoustic band gaps in periodic fibre reinforced
composite materials: the carbon/epoxy composite and some metallic
systems // J. Phys. Condens. Matter. - 1994. - V.6. - P.8759-8770.
479.Voigt W. Uber die Beziehung zwischen den beiden
Elasticitatsconstanten isotroper Korper // Annalen der Physik und
Chemie. - 1889. - V.38. - P.573-587.
480. Wiener O. Die Theorie des Mischkorpers fiir das Feld der stationaren
Stromung. Erste Abhandlung die Mittelwertsatze fiir Kraft,
Polarisation und Energie // Abhandlungen der Mathematisch-
Physischen Klasse der Koniglich Sachsischen Gesellschaft der
Wissenschaften. - 1912. - V.32, N.6. - P.507-604.
481.Willis J.R. On methods to bound the overall properties of nonlinear
composites // J. Mech. Phys. Solids. - 1991. - V.39. - P.73-86.
482.Wilson N., Kannangara K., Smith G., Simmons M., Raguse B.
Nanotechnology: Basic Science and Emerging Technologies. - Boca
Raton: Chapman & Hall / CRC, 2002. - 271 p.
483.Wistreich J.G. Investigation of the mechanics of wire drawing // Proc.
Inst. Mech. Engrs. - 1955. - V.169. - P.654-665.
484.Wolfe J.P. Imaging Phonons: Acoustic Wave Propagation in Solids. -
Cambridge: Cambridge University Press, 1998. -411 p.
485.Wu Y., Ling Z., Dong Z. Stress-strain fields and the effectiveness
shear properties for three-phase composites with imperfect interface //
Int. J. Solids Structures. - 1999. - V.37. - P. 1275-1292.
486.Xu X.-P., Needleman A. Numerical simulations of fast crack growth in
brittle solids // J. Mech. Phys. Solids. - 1994. - V.42. - P. 1397-1434.
194
487.Zalipaev V.V., Movchan A.B., Poulton C.G., McPhedran R.C. Elastic
waves and homogenization in oblique periodic structures // Proc. R.
Soc. bond. A. - 2002. - V.458. - P.1887-1912.
488.Zhikov V.V. On an extension of the method of two-scale convergence
and its applications // Sb. Math. - 2000. - V.191. - P.973-1014.
489.Zhong X.A., Knauss W.G. Analysis of interfacial failure in particle-
filled elastomers // Journal of Engineering Materials and Technology.
- 1997. -V. 119. -P. 198-204.
490.Zhong X.A., Knauss W.G. Effects of particle interaction and size
variation on damage evolution in filled elastomers // Mechanics of
Composite Materials and Structures. - 2000. - V.7. - P.35-53.
491.Zhu H., Achenbach J.D. Effect of fiber-matrix interphase defects on
microlevel stress states at neighboring fibers // J. Composite Mater. -
1991.-V.25.-P.224-238.
492.Zuzovsky M., Brenner H. Effective conductivities of composite
materials composed of cubic arrangements of spherical particles embedded
in an isotropic matrix // Z. Angew. Math. Phys. - 1977. - V.28. -
P.979-992.
195
Наукове видання
Мшютерство освгти i науки Укра'ши
Придншровська державна акадеъпя буд1вництва та арх1тектури
БОЛЬШАКОВ Володимир 1ванович
АНДР1АНОВ Irop Васильович
ДАНШШВСЬКИИ Владислав Валентинович
АСИМПТОТИЧН1 МЕТОДИ РОЗРАХУНКУ
КОМПОЗИТНИХ МАТЕР1АЛ1В 3 УРАХУВ АННЯМ
ВНУТРШШЬО! СТРУКТУРИ
Вцщовщальна за випуск P.O. Лазарева
Художнш редактор В.В. Якименко
Техшчний редактор В.В. Якименко
Коректор В.М. Орищт
Здано на складання 14.05.08. Пщписано до друку 12.06.08. Формат 60x84 yi6
Пашр офсетний. Гарштура л1тературна. Друк офсетний. Умовн. друк.
арк. 11,39. Умовн. фарб.-вщб. 11,39. Обл.-видавн. Арк.. 11,2.
Тираж 300 прим. Зам. № 281
Видавництво „Пороги"
49000, м. Дншропетровськ, пр. К. Маркса, 60.
Свщоцтво про внесения до Державного реестру
сер1я ДК № 7 вщ 21.02.2000 р.
ТОВ ПКФ „Bi3ioH"
49050, м. Дншропетровськ, пл. Академ1ка Стародубова, 1.
Свщоцтво про внесения до Державного реестру
сер1я ДП № 60-Р вщ 20.03.2000 р.
ISBN 978-966-525-935-0
Владимир Иванович Большаков
Заслуженный деятель науки и техники
Украины, лауреат государственной премии Украины,
доктор технических наук, профессор, ректор
Приднепровской государственной академии
строительства и архитектуры. Научные
интересы: физическое материаловедение, разработка
новых конструкционных материалов в
строительстве. Подготовил 7 докторов и 15
кандидатов наук. Автор L300 научных работ, 60
монографий и учебников, 200 авторских
свидетельств и патентов.
Игорь Васильевич Андрианов
Доктор физико-математических наук,
профессор, научный сотрудник Технического
университета г. Ахен (Германия). Научные интересы:
асимптотические методы, теория пластин и
оболочек, механика композитов, нелинейная
динамика. Подготовил 1 доктора и 16
кандидатов наук. Автор 250 научных статей, 14
монографий.
Владислав Валентинович
Данишевский
Кандидат технических наук, доцент, докторант
Приднепровской государственной академии
строительства и архитектуры. Научные
интересы: асимптотические методы, механика
композитов, нелинейная динамика. Автор 50 научных
статей.
ISBN 978-966-525-935-0