BASIC OPTIMISA ION
METHODS
Brian D. Bunday.
B.Sc, Ph.D., F.S.S., F.I.M.A.
School of Mathematical Sciences,
University of Bradford
Edward Arnold
Б. Банди
М ТОДЫ
О ТИМИЗАЦИИ
вводный
КУРС
Перевод с английского О.В.Шихеевои
под редакцией В.А.Волынского
Москва «РАДИО И СВЯЗЬ»
1988

ББК 32.81
Б 23
УДК 517.977.5
Б 23
Редакция переводной литературы
Банди Б.
Методы оптимизации. Вводный курс: Пер. с англ.
связь, 1988. — 128 с: ил.
ISBN 5-256-00052-7.
М.: Радио и
В книге английского автора изложена теория и описаны алгоритмы оптими-
оптимизации непрерывных дифференцируемых функций при наличии ограничений и без
них. Приведены тексты программ, реализующих приведенные алгоритмы на
языке Бейсик. Предложено большое число примеров использования методов оп-
оптимизации при решении различных задач.
Для инженерно-технических работников, связанных с решением задач поиска
оптимальных решений.
1502000000^017
046 @1) -88
ISBN 5-256-00052-7 (рус.)
ISBN 0-7131-3506-9 (англ.)
ББК 32.81
©Bunday 1984.
This book was originally published in English language by
Edward Arnold (Publishers) Limited, 41 Bedford Square,
London WC1B 3DQ
©Перевод на русский язык, предисловие и примечания
редактора перевода, дополнительный список литера-
литературы. Издательство "Радио и связь", 1988
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В последние годы вышло несколько книг по нелинейному программиро-
программированию, однако книга Б. Банди "Методы оптимизации" занимает среди них
особое место.
Каждая книга имеет своего читателя. Книга Б. Банди ориентирована на
тех, кто хочет использовать методы оптимизации как инструмент решения
конкретных прикладных задач, но не имеет практически никаких знаний в
области нелинейного программирования. Все, что нужно для тех, кто хочет
воспользоваться книгой Б. Банди, — это иметь представление о функциях п
переменных и быть знакомыми с языком Бейсик. Для такого круга читате-
читателей книга дает четкое и лаконичное представление о подходе к решению за-
задач оптимизации с ограничениями и без ограничений. Кроме того, в ней мож-
можно найти подробное описание алгоритмов (и их математическое обоснова-
обоснование) небольшого числа ставших уже классическими методов нелинейного
программирования. Пожалуй, основной "изюминкой" книги является имен-
именно триада математический вывод — алгоритм — программа. Все описанные
методы проиллюстрированы большим числом примеров, что делает изложе-
изложение живым и легко усваиваемым.
В настоящее время, когда в нашей стране все шире распространяются пер-
персональные ЭВМ, на которых реализован язык Бейсик, к программам, напи-
написанным на этом языке, проявляется большой интерес. Поэтому приведенные
в книге программы станут существенным подспорьем как при решении прак-
практических задач, так и в учебном процессе.
В книгу Б. Банди вошли далеко не все алгоритмы оптимизации. Для тех,
кто стремится расширить число используемых алгоритмов, ниже приведен
дополнительный список литературы. В работах [Д1—Д2] можно найти более
детальное и математически полное описание теории оптимизации, в книге
[ДЗ] основное внимание уделено вопросам оптимизации при наличии ограни-
ограничений. В работах [Д4—Д6] изложены алгоритмы и приведены тексты про-
программ на Фортране, реализующие различные методы условной и безусловной
оптимизации. Кроме того, в работах [Д4—Д6] приведены сравнительные ха-
характеристики методов и результаты решения большого числа задач. В этих
работах можно также найти подробное обсуждение критериев завершения в
методах оптимизации, чему в книге Б. Банди не уделяется достаточного вни-
внимания.
Приведенные в книге тексты программ были проверены на 8-разрядной
ЭВМ ЮМ PC XT, работающей под управлением операционной системы MS DOS.
Полученные результаты несколько отличаются от приведенных автором в

книге, однако отличия незначительны и не влияют на логику изложения. Опе-
Операторы и их нумерация приведены в том же виде, в каком они даны автором.
Однако для вьюода на печать соответствующие операторы PRINT следует за-
заменить на операторы вывода на печать (в нашем случае на LPRINT). При ре-
решении примера 2 в разд. 4.1 в программе изменены константы: в строке
800 — 0.0005: в строке 1100 — 0.0001. В программе, реализующей комплекс-
комплексный метод, датчик случайных чисел, используемый автором, существенно от-
отличается от датчика случайных чисел, имеющегося в программном обеспече-
обеспечении IBM PC XT, поэтому значительное расхождение есть и в результатах реше-
решения. В примере 1 разд. 6.2 приведены для сравнения результаты, полученные
автором, и результаты, полученные на IBM PC XT.
Практическая направленность, лаконизм изложения и большое число удач-
удачно подобранных примеров, безусловно, сделают книгу полезной специалис-
специалистам различных областей, студентам старших курсов и аспирантам.
ДОПОЛНИТЕЛЬНЫЙ СПИСОК ЛИТЕРАТУРЫ
Д1. Сухарев А. Г., Тимохов А. В., Федоров В. В. Курс методов оптимизации. — М.: Нау-
Наука, 1986. -328 с.
Д2. Поляк Б. Т. Введение в оптимизацию. — М.: Наука, 1983. — 384 с.
ДЗ. Численные методы условий оптимизации. Пер. с англ./Под. ред. Ф. Гилла и У. Мюр-
рея. - М.: Мир, 1977. - 290 с.
Д4. БазараМ., Шетти К. Нелинейное программирование. Теория и алгоритмы: Пер. с
англ. - М.: Мир, 1982. - 583 с.
Д5. Химмельблау Д. Прикладное нелинейное программирование: Пер. с англ. — М.:
Мир, 1975. -534 с.
Д6. Гуснин С. Ю., Омельянов Г. А., Резников Г. А., Сироткин В. С. Минимизация в ин-
инженерных расчетах на ЭВМ. — М.: Машиностроение, 1981. — 121 с.
ПРЕДИСЛОВИЕ
Настоящая книга предназначена для тех, кто имеет представление о функ-
функциях п переменных и знаком с языком программирования Бейсик. Основной
упор сделан на осмысление того, как преобразовать теоретическую идею в
практическую вычислительную процедуру. Хотя все рассмотренные в книге
методы оптимизации пригодны для практического применения, основное
внимание было уделено не математической строгости доказательств, а глав-
главной цели — созданию алгоритмов, предназначенных для реализации на микро-
ЭВМ.
Мы надеемся, что читатель приложит серьезные усилия к тому, чтобы разо-
разобраться с приведенными программами. Не будем, однако, утверждать, что их
нельзя улучшить. Пытаясь это сделать, читатель получит более глубокое пред-
представление об идеях, лежащих в основе методов оптимизации практических
задач, которые должны быть решены в реальной ситуации.
Не все возможные методы оптимизации рассмотрены в этой книге, однако
мы думаем, что те, которые были нами выбраны, охватывают наиболее важ-
6
ные идеи, лежащие в основе оптимизации. Остается еще много нерешенных
вопросов, и мы надеемся, что некоторые читатели, прочтя эту книгу, захотят
внести собственный вклад в улучшение методологии изучения методов опти-
оптимизации.
Несколько замечаний по поводу языка Бейсик и его использования в этой
книге. Программы были написаны так, чтобы их выполнение на любой микро-
ЭВМ вызывало минимум затруднений.
В операторах присваивания слово LET было опущено. Для некоторых ма-
машин наличие этого слова обязательно, и тогда его необходимо вводить в про-
программы. В операторы IF ... THEN GOTO было включено ключевое слово
THEN, хотя для некоторых машин возможно отсутствие либо слова THEN,
либо оператора GOTO. Не использовались конструкции IF ... THEN . ..
... ELSE, а также возможности конструкции REPEAT ... UNTIL . .., по-
поскольку они не всегда доступны. Предполагалось, что массивы нумеруются
с нулевого элемента. Поэтому для машин, где нумерация массивов начина-
начинается с 1, необходимо внести некоторые изменения. Например, один из надеж-
надежных способов заключается в увеличении всех индексов, включая индексы в
операторе DIM, на 1. Таким образом, оператор DIM A(M) превращается в
оператор DIM А(М + 1), а оператор В(К, L) — в оператор В(К + 1, L + 1).
Однако в конкретных случаях читатель может найти более изящные способы
модификации. Приведенные в книге численные результаты получены на ЭВМ
PET. В случае использования других машин, в памяти которых числа пред-
представляются с иной точностью, полученные результаты не будут точно совпа-
совпадать с приведенными в книге, хотя отличие будет только в последних знача-
значащих цифрах.
В заключение хотелось бы поблагодарить миссис Валери Хантер, превра-
превратившую довольно беспорядочную рукопись в аккуратно перепечатанный текст.
Брайан Банди, 1984

ВВЕДЕНИЕ
В книге рассмотрены методы поиска оптимальных значений максимума
или минимума функции п действительных переменных / (хх, х2, ..., хп).
Если функция выражает прибыль, получаемую при производстве товаров xz-
в количестве Р/, то мы будем стремиться максимизировать функцию. Если, с
другой стороны, она выражает цену товара, участвующего в обороте, то мы
будем стремиться минимизировать функцию. С математической точки зре-
зрения не играет существенной роли, рассматривать максимизацию или миними-
минимизацию, поскольку максимизация / эквивалентна минимизации -/. Мы огра-
ограничимся рассмотрением минимизации.
Значения переменных могут подчиняться ограничениям или изменяться
без ограничений. Если, например, они действительно выражают количество
определенных производимых продуктов, то при этом будет существовать
ограничение на производственную мощность и ограничение на количество то-
товара, которое может поглотить рынок. Таким образом, любое решение опти-
оптимизационной задачи должно учитывать эти ограничения. Для удобства в ч. I
рассмотрены задачи, в которых на переменные не наложены ограничения,
а в ч. II рассмотрены задачи, в которых на переменные наложены ограниче-
ограничения.
В любой практической оптимизационной задаче существует много совпа-
совпадающих этапов. Наиболее важным этапом является моделирование рассмат-
рассматриваемой физической ситуации с целью получения математической функции,
которую необходимо минимизировать, а также определения ограничений,
если таковые существуют. Затем следует выбрать подходящую процедуру
для осуществления минимизации. Эта процедура должна быть реализована на
практике, что во многих реальных случаях вынуждает использовать ЭВМ для
выполнения большого объема вычислений. И наконец, математический ре-
результат должен быть интерпретирован опять же в терминах физического со-
содержания задачи.
Хотя ни одним из этих этапов нельзя пренебречь, основной упор в настоя-
настоящей книге сделан на изучение процедур, предназначенных для осуществления
минимизации, и возможностей их преобразования в такие вычислительные
процедуры, которые можно выполнить на ЭВМ.
Не случайно, что многие важные методы оптимизации были разработаны в
течение трех последних десятилетий, в период появления цифровых ЭВМ, и
эти методы являются машинными. Трудно считать их сколько-нибудь прак-
практически значимыми без большой скорости и эффективности вычислительных
машин, имеющихся в нашем распоряжении. На многих универсальных ЭВМ
имеются пакеты программ оптимизации, реализующие эти методы. Они мо-
8
гут оказаться весьма эффективными и позволят решить широкий круг задач.
При этом они могут быть достаточно самостоятельными и использоваться
без оценки того, что происходит в действительности. Для большинства мето-
методов, рассматриваемых в этой книге (причем не исчерпывающих список су-
существующих -методов), приведены программы на языке Бейсик. Дано под-
подробное объяснение процесса создания этих программ, что позволяет по-ново-
по-новому взглянуть на применимость методов оптимизации.
В течение многих лет программы опробовались в Университете г. Брадфорд.
Однако автор не утверждает, что они являются верхом изящества и эффек-
эффективности, По мере того как читатель будет становиться более эрудирован-
эрудированным, он сможет попробовать вносить улучшения в программы, и автору бы-
было бы интересно узнать точку зрения читателей по этому вопросу. Програм-
Программы могут выполняться на большинстве микроЭВМ, использующих язык
Бейсик или программное обеспечение фирмы Computer Microsoft. Все про-
программы были опробованы на ЭВМ PET и Tandy (TRS80). Несложно будет
"перевести" эти программы на другие языки, такие как Фортран или Алгол,
чтобы они могли выполняться и на универсальных машинах.

ЧАСТЬ I
ОПТИМИЗАЦИЯ БЕЗ ОГРАНИЧЕНИЙ
ГЛАВА 1. КЛАССИЧЕСКИЕ МЕТОДЫ
1.1. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Функция f(x) имеет локальный минимум в точке л:0, если существует не-
некоторая положительная величина 5, такая, что если \х - хо\ < 5, то f(x) >
^/(*о) > т- е- если существует окрестность точки х0, такая, что для всех зна-
значений х в этой окрестности f(x) больше f(x0). Функция f(x) имеет глобаль-
глобальный минимум в точке х*, если для всех х справедливо неравенство f(x) >
>/(**).
На рис. 1.1 дано графическое представление функции f(x), которая имеет
локальный минимум в точке х0 и глобальный минимум в точке х*.
Классический подход к задаче нахождения значений л:0 и х* состоит в поис-
поиске уравнений, которым они должны удовлетворять. Представленная на
рис. 1.1 функция и ее производные непрерывны, и видно, что в точках х0 и
х* производная f'(x) (градиент функции) равна нулю. Следовательно, Хо и
х* будут решениями уравнения
/'(*)= о. (l.i)
Точка хт, в которой достигается локальный максимум, и точка хС9 в ко-
которой имеется точка горизонтального перегиба функции, также удовлетворя-
удовлетворяют этому уравнению. Следовательно, уравнение A.1) является только необ-
X
ходимым условием минимума, но не является достаточным условием мини-
минимума.
Заметим, однако, что в точках х0 и х* производная f\x) меняет знак с
отрицательного на положительный. В точке хт знак меняется с положитель-
положительного на отрицательный, в то время как в точке хс он не меняется. Следова-
Следовательно, производная в минимуме является возрастающей функцией, а по-
поскольку степень возрастания f'(x) измеряется второй производной, можно
ожидать, что/"(*о) > 0, /"(**) >0, тогда как f"(xm) <0.
Если, однако, вторая производная равна нулю, ситуация остается неопре-
неопределенной.
Полученные выше результаты могут найти надежное обоснование, если
рассмотреть разложение функции f(x) в ряд Тейлора в окрестности точки
х0 (или х*, или хт), что, конечно, требует непрерывности функции f(x)
и ее производных:
h2
А*о + h) -А*о) = W(*o) + — /"(*о) + • • • A.2)
Если в точке х0 достигается минимум, то левая часть A.2) будет неотри-
неотрицательной для любого достаточно малого h (\h \ < 5). Следовательно, первая
производная /f(*o) должна быть равна нулю, и это является достаточным
условием (см. уравнение A.1)). Если бы она была положительной, то до-
достаточно малое отрицательное значение h делало бы правую часть A.2) от-
отрицательной, а если бы она была отрицательной, то достаточно малое поло-
положительное значение h делало бы правую часть отрицательной.
Так как в следующем члене A.2) всегда h2 > 0, то, если
А*о)>о, A.з)
в точке х0 достигается минимум. Если f\xm) = 0 и f"(xm) < 0, то из ана-
аналогичных соображений в точке хт достигается максимум. Для определения
различия между локальным и глобальным минимумами необходимо срав-
сравнить значения функций f(x0) и /(**).
Пример 1
Исследовать характер точек перегиба функции /(*) = х3 - 2х2 + х + 1:
fix) = 3x2 -
Рис. 1.1.
10
тогда (Зх - 1)(х - 1) = 0, т. е. х = 1/3 или х = 1.
При х = 1/3 производная f(x) меняет знак с положительного на отрицательный, а
при х = 1 — с отрицательного на положительный. Следовательно, в точке х = 1/3 дости-
достигается максимум, а в точке х = 1 — минимум.
Этот пример может быть решен более простым способом, если вычислить
вторую производную f"(x) = 6х — 4:
/ A/3) = —2, т. е. отрицательна, и при х = 1/3 достигается максимум;
/ A) = 2, т. е. положительна, и при х = 1 достигается минимум.
Неоднозначность, возникающую при f'\x) = 0, можно разрешить, увели-
увеличив количество членов в формуле разложения в ряд Тейлора:
11

2! 3! 4!
При этом можно сформулировать следующее правило:
Если функция f(x) и ее производные непрерывны, то точка х0 является
точкой экстремума (максимума или минимума) тогда, и только тогда,
когда п четное, где п — порядок первой необращающейся в нуль в точке
х0 производной. Если /"(хо) < 0, то в точке х0 достигается максимум,
если /" (х0) > 0, то в точке х0 достигается минимум.
Пример 2
Найти точку перегиба функции f(x) = (х - 1N:
= 6 (х - 1) 5 = 0 при х = 1.
Первой необращающейся в нуль в точке х = 1 производной будет /бA) = 6!. Следова-
Следовательно, функция f{x) имеет минимум в точке х — 1.
1.2. ФУНКЦИИ п ПЕРЕМЕННЫХ
Рассмотрим функцию п действительных переменных
f(xlPx2,x3t. --,xn) =/(х).
Точка в «-мерном евклидовом пространстве с координатами хи х2, х3, . • •
..., хп обозначается вектором-столбцом х. Градиент функции, т. е. вектор с
компонентами df/dxlf df/dx2, • . . , df/dxn, обозначается V/(x) или, иногда,
g(x). Матрица Гессе (гессиан) функции/(х) обозначается как G(x) и являет-
является симметрической матрицей п х п элементов вида
G -
Функция /(х) имеет локальный минимум в точке Хо, если существует окрест-
окрестность точки Хо, такая, что /(х) больше /(х0) во всех точках этой окрестно-
окрестности, т. е. существует положительная величина 5, такая, что для |х — Хо I <5
справедливо неравенство /(х) > /(х0).
В случае глобального минимума в точке х* для всех х справедливо нера-
неравенство /(х) > /(х*).
При таких определениях и очевидных предположениях относительно диф-
ференцируемости можно обобщить уравнение A.2) и получить.
п
df
и
и
d2f
2! i=i j=
(х
19
+ ••• A.4)
Тогда, если хо является точкой минимума функции /(х), то каждая пер-
первая частная производная df/dxf (i = 1, . . . , п) должна обращаться в нуль в
точке Хо. Если это не так, то соответствующим выбором hi можно добиться
того, что разность /(х0 + h) —/(х0) будет отрицательна.
12
Следовательно, необходимым условием минимума в точке х0 является
уравнение
V/(xo)=0, A-5)
т. е.
дх,
Тогда знак разности /(хо + h) —/(х0) определяется членом
#hTG(x0)h. A.7)
Если матрица G(xo) положительно определена, то этот член положителен
для всех h. Следовательно, необходимыми и достаточными условиями мини-
минимума являются
V/(Xo) =0, G(xo) положительно определена. A.8)
Необходимыми и достаточными условиями максимума являются
V/(xm) =0; G(xm) отрицательно определена. A.9)
Пример 1
Исследуйте экстремальную точку (точки) функции /(х) = х\ + х\ + х\ — 4хг —
- 12*з + 100:
.*!- 4
V/(x) =| 2х2 - 8 1= 0 при х, = 2,х2 = 4, х3 = 6.
положительно определена. Все соб-
собственные значения положительны
/2 0 0
0 2 0
\0 0 2
Следовательно, в точке B; 4; 6) функция /(х) достигает минимума.
1.3. МЕТОД НЬЮТОНА
Для функций одной переменной классический подход при поиске значе-
значений х в точках перегиба функции f(x) состоит в решении уравнения
f\x) = 0.
Решить такое уравнение не всегда просто. Поэтому кратко рассмотрим
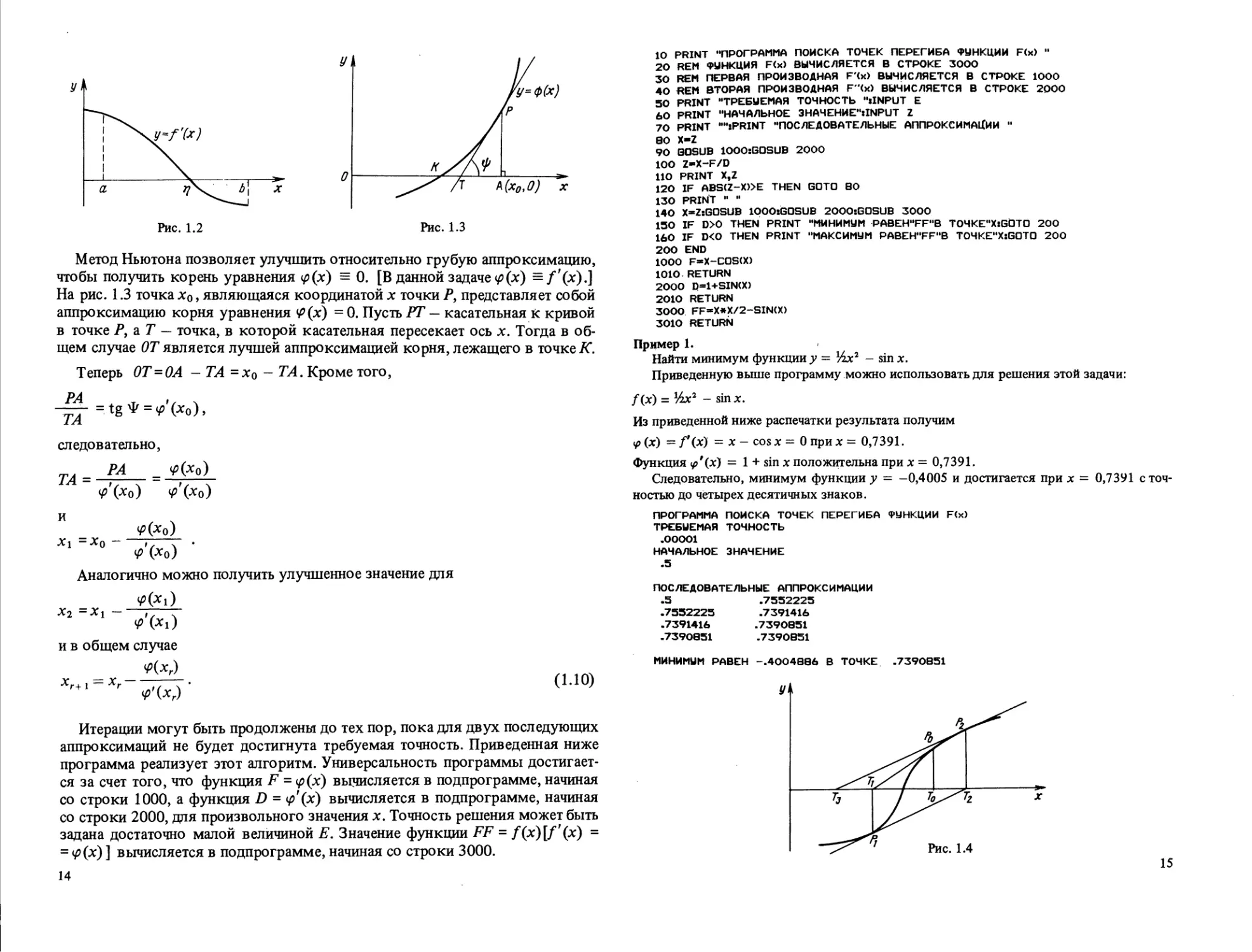
численный метод его решения. Приблизительный эскиз кривой^ =/'(*) поз-
позволит получить приближенное решение. Если можно найти два значения а и
by таких, что f\d) и f'(b) имеют противоположные знаки, то тогда, в силу
очевидных предположений о непрерывности, будет существовать корень т?
настоящего уравнения, причемa<r\<b (рис. 1.2).
13

/у=ф(х)
Рис. 1.2
Рис. 1.3
Метод Ньютона позволяет улучшить относительно грубую аппроксимацию,
чтобы получить корень уравнения $(х) = 0. [В данной задаче ip(x) =f'(x).]
На рис. 1.3 точка х0, являющаяся координатой х точки Р, представляет собой
аппроксимацию корня уравнения Ф(х) = 0. Пусть РТ — касательная к кривой
в точке Р, а Т — точка, в которой касательная пересекает ось х. Тогда в об-
общем случае ОТ является лучшей аппроксимацией корня, лежащего в точке А*.
Теперь 0Т=0А - ТА =хо - ТА. Кроме того,
—
следовательно,
РА
и
~х0 —
Аналогично можно получить улучшенное значение для
и в общем случае
Xr+ 1 ~ Xr
A.10)
Итерации могут быть продолжены до тех пор, пока для двух последующих
аппроксимаций не будет достигнута требуемая точность. Приведенная ниже
программа реализует этот алгоритм. Универсальность программы достигает-
достигается за счет того, что функция F = $(х) вычисляется в подпрограмме, начиная
со строки 1000, а функция D = $\х) вычисляется в подпрограмме, начиная
со строки 2000, для произвольного значения х. Точность решения может быть
задана достаточно малой величиной Е. Значение функции FF = f(x)[f'(x) =
= ф(х) ] вычисляется в подпрограмме, начиная со строки 3000.
14
10 PRINT "ПРОГРАММА ПОИСКА ТОЧЕК ПЕРЕГИБА ФУНКЦИИ F(x) "
20 REM ФУНКЦИЯ F(x> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 3000
30 REM ПЕРВАЯ ПРОИЗВОДНАЯ F'(x> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 1000
40 «ЕМ ВТОРАЯ ПРОИЗВОДНАЯ F"<x) ВЫЧИСЛЯЕТСЯ В СТРОКЕ 2000
50 PRINT 'ТРЕБУЕМАЯ ТОЧНОСТЬ "iINPUT E
60 PRINT "НАЧАЛЬНОЕ 3HA4EHHE":INPUT 2
70 PRINT ""SPRINT "ПОСЛЕДОВАТЕЛЬНЫЕ АППРОКСИМАЦИИ "
ВО X-Z
90 BOSUB 1OOO:GOSUB 2000
100 Z-X-F/D
110 PRINT X,Z
120 IF ABS<Z-X»E THEN GOTO BO
130 PRINT » "
140 X=Z:GOSUB IOOOiGOSUB 2000-.G0SUB 3000
150 IF D>0 THEN PRINT "МИНИМУМ PABEH"FF"B T04KE"X:G0T0 200
160 IF D<0 THEN PRINT "МАКСИМУМ PABEH"FF"B T04KE"X:G0T0 200
200 END
1OOO F*X-COS(X)
1010 RETURN
2000 P=1+SIN(X)
2010 RETURN
3OOO FF»X*X/2-SIN(X)
3010 RETURN
Пример 1.
Найти минимум функции у = Уис2 - sin x.
Приведенную выше программу можно использовать для решения этой задачи:
fix) = У2Х* - sin л:.
Из приведенной ниже распечатки результата получим
if> (х) = f{x) = х - cos x = 0 при х = 0,7391.
Функция if>'(x) = 1 + sin х положительна при х = 0,7391.
Следовательно, минимум функции у = -0,4005 и достигается при х = 0,7391 с точ-
точностью до четырех десятичных знаков.
ПРОГРАММА ПОИСКА ТОЧЕК ПЕРЕГИБА ФУНКЦИИ F(x)
ТРЕБУЕМАЯ ТОЧНОСТЬ
.ОООО1
НАЧАЛЬНОЕ ЗНАЧЕНИЕ
.5
ПОСЛЕДОВАТЕЛЬНЫЕ АППРОКСИМАЦИИ
.5 .7552225
.7552225 .7391416
.7391416 .7390851
.739О851 .7390851
МИНИМУМ РАВЕН -.4004886 В ТОЧКЕ .7390851
Рис. 1.4
15

Применение метода Ньютона будет неудачным, если первая аппроксима-
аппроксимация корня такова, что отношение ^(хо)/^\хо) недостаточно мало (рис. 1.4).
Для того чтобы итерации сходились, в общем случае необходимо улучшить
начальную аппроксимацию корня.
1.4. УПРАЖНЕНИЯ
1. Найдите значения максимума и минимума функции /(*) = х{х - 1) 2.
2. Найдите значения максимума и минимума функции f(x) — х/(х2 + 1).
3. Покажите, что минимальным значением функции a cos0 +b sin в является — \/a2 + b2 .
Можете ли вы получить этот результат, не используя производных?
4. Равнобедренный треугольник с вертикальным углом 20 вписан в окружность ради-
радиуса г. Найдите выражение для площади треугольника как функции от в и покажите,
что она максимальна, когда треугольник равносторонний.
5. Исследуйте функцию f(x) = х21Ъ - 1. Нарисуйте ее график. Покажите, что /(*) име-
имеет минимум при х = 0. Чему равно значение /'(*) ПРИ х = 0? Меняет ли знак /'(*)»
если х возрастает при прохождении через 0?
6. Исследуйте функцию /(*) = |jc|. Найдите ее минимум. Что можно сказать относи-
относительно поведения Р(х) в точке минимума?
7. Найдите минимум функции — e~~*sh(;c/2).
8. В процессе производства определенного количества некоторого товара его цена уста-
устанавливается равной ?/С. Товар хранится на складе до тех пор, пока не будет исполь-
использован, и стоимость хранения одной единицы товара составляет ?5 в единицу време-
времени. Норма потребления товара составляет R в единицу времени. Покажите, что если
товар производится регулярно в количестве х в течение времени x/R, то стоимость
функционирования такой системы в единицу времени
ч
С =
KR
х
Sx
Покажите, что стоимость С достигает минимума при х = \JlKRlS .
9. Исследуйте точки перегиба функции f(x) = х4 - 14х3 + вОх2 - Юх. [Этот кажу-
кажущийся простым пример иллюстрирует одну из классических задач. Требуется решить
уравнение /'(*) = 0. В данном случае оно является кубическим уравнением, кото-
которое не так просто раскладывается на множители. Необычным является способ реше-
решения, при котором используется один из численных методов, описанных в следующей
главе: он предназначается для минимизации функции <р(х) = [/'(*) ]2- Минимум
функции у(х) равен нулю, а это означает, что получено решение уравнения /'(*) =
= 0.]
10. Исследуйте точки перегиба функции /(х) = х\ + 4хгхг + 5х\.
11. Исследуйте точки перегиба функции /(х) = ~х\ - 6х\ - 2Ъх\ - 4ххх2 + 6хгхъ +
+ 20* х
12. Пусть /(х) есть квадратичная функция вида
/(х) = а + ЪТх + %xTGx,
где а — константа; b - вектор, не зависящий от х, a G - положительно определенная
симметрическая матрица, не зависящая от х. Покажите, что х* = -G"!b.
13. Покажите, что функция /(х) = (хх - аJ + (х2 - bJ + (х3 - с) 2 имеет минимум в
точке (а; Ь; с).
14. Функция /(х) = /(*!, х2) имеет минимум в точке (jq*; x2*). Покажите, что условия
A.8) будут иметь следующий вид:
16
J
*
dx\
f, x*) > 0,
dx]
>
d2f
дх1 дх2
, x*)
15. Фирма вьшускает два аналогичных товара 1 и 2. Прибыль от реализации товара со-
составляет Ctfj (i = 1, 2), где cz- — константа, &qj - объем реапиз лш' товара. Послед-
Последний зависит от цен (рх и р2) двух товаров. Анализ последних данных продажи дает
следующие эмпирические зависимости:
Яг =a2Pi ~
где ах, а2, Ъх, Ъ2 — положительные константы. Требуется определить цены рг и р2,
которые максимизируют общую прибыль.
Найдите уравнения для рх и р2, которые максимизируют прибыль, к решите их.
Покажите» что если решения этих уравнений положительныи4й162 > (fli +Д2J»ТО
эти уравнения дают оптимальные цены.
16. Найдите минимум функции е~* - cos x.
ГЛАВА 2. МЕТОДЫ ПОИСКА ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
2Л. ВВЕДЕНИЕ
Упражнение 9 разд. 1.4 иллюстрирует общую задачу, возникающую при
классическом подходе. Уравнение f (х) = 0 не решается простым способом,
и поэтому мы вынуждены прибегать к численным методам. В этой главе бу-
будут рассмотрены несколько простых численных процедур, непосредственно
локализирующих минимум функции f(x).
С помощью численных методов мы непосредственно ищем минимум функ-
функции f(x) в некотором интервале а < х < Ь, в котором, как предполагается,
лежит минимум, вычисляя значения функции в выбранных точках данного
интервала. Иногда это единственно возможная стратегия поиска. Например,
стоимость проведения химического процесса может зависеть от температуры
процесса. Инженер знает, что стоимость является функцией от Г, хотя может
и не знать явного вида функции. Однако он может поставить эксперимент и
провести процесс при различных температурах и, следовательно, найти стои-
стоимости для этих температур и надеяться определить минимальную стоимость
и температуру проведения процесса, при которой она достигается.
Можно попытаться найти положение минимума в точке, аппроксимирую-
аппроксимирующей его с нужной точностью, или определить малый интервал, в котором на-
находится минимум. Попытаемся достичь поставленной цели как можно более
эффективным способом, т. е. осуществляя наименьшее количество вычисле-
вычислений функции. В приведенном выше примере, вероятно, невозможно точно ре-
17

a
Рис. 2.1
гулировать температуру процесса,
поэтому точность в 1°С или даже в
10° С может быть вполне приемле-
приемлемой. Однако, поскольку проведе-
проведение эксперимента требует опреде-
определенных затрат, инженер захочет
добиться этой точности, проведя
как можно меньше экспериментов.
Предположим, что точки а и Ь
определяют (возможно, очень гру-
грубо) интервал, который содержит истинную точку минимума, и внутри этого
интервала функция унимодальна, т. е. имеет один минимум в точке х*. Сле-
Следовательно, данная функция имеет форму, близкую к той, что приведена на
рис. 2.1. Если известны значения функции такого вида в трех точках хlf х2,
х3, таких, что я <*! <х2 <х3 <b, a f(x2) </(*i) и f(x2) </(*з), то
Xi <х*<х3.
Тогда точка х* будет лежать внутри интервала (хг; х3), меньшего по раз-
размеру, чем интервал (а; Ь).
2.2. ПОИСК МЕТОДОМ ФИБОНАЧЧИ
Предположим, что нужно определить минимум как можно точнее, т. е. с
наименьшим возможным интервалом неопределенности, но при этом можно
выполнить только п вычислений функции. Как следует выбрать п точек, в
которых вычисляется функция? С первого взгляда кажется ясным, что не
следует искать решение для всех точек, получаемых в результате экспери-
эксперимента. Напротив, надо попытаться сделать так, чтобы значения функции, по-
полученные в предыдущих экспериментах, определяли положение последую-
последующих точек. Действительно, зная значения функции, мы тем самым имеем ин-
информацию о самой функции и положении ее минимума и используем эту ин-
информацию в дальнейшем поиске.
Предположим, что имеется интервал неопределенности (xi,x3) и известно
значение функции f(x2) внутри этого интервала (см. рис. 2.1). Если можно
вычислить функцию всего один раз в точке х4, то где следует поместить точ-
точку х4, для того чтобы получить наименьший возможный интервал неопреде-
неопределенности?
Положим х2 - хг - L ъ х3 - х2 = R, причем L > R, как показано на
рис. 2.1, и эти значения будут фиксированы, если известны xit x2 их3. Если
х4 находится в интервале (Xi; х2), то:
1) если f(x4) < f(x2), то новым интервалом неопределенности будет
(xi,x2) длинойх2 -хх -L\
2) если ffa) > f(x2), то новым интервалом неопределенности будет
(х*,х3) длиной х3 - х4.
Поскольку не известно, какая из этих ситуаций будет иметь место, выбе-
выберем х4 таким образом, чтобы минимизировать наибольшую из длин л: 3 -
18
и х _ Х\. Достигнуть этого можно, сделав длины х3 - х4 и х2 - Xi равны-
равными т. е. поместив х4 внутри интервала симметрично относительно точки х2,
уже лежащей внутри интервала. Любое другое положение точки х4 может
привести к тому, что полученный интервал будет больше L. Помещая д:4 сим-
симметрично относительно х2, мы ничем не рискуем в любом случае.
Если окажется, что можно выполнить еще одно вычисление функции, то
следует применить описанную процедуру к интервалу (хи х2), в котором
уже есть значение функции, вычисленное в точке х4, или к интервалу (х4,
х3), в котором уже есть значение функции, вычисленное в точке х2. Следова-
Следовательно, стратегия ясна с самого начала. Нужно поместить следующую точку
внутри интервала неопределенности симметрично относительно уже находя-
находящейся там точке. Парадоксально, но, чтобы понять, как следует начинать вы-
вычисления, необходимо разобраться в том, как его следует кончать.
На П'Ы вычислении и-ю точку следует поместить симметрично по отноше-
отношению к (п — 1) -й точке. Положение этой последней точки в принципе зависит
от нас. Для того чтобы получить наибольшее уменьшение интервала на дан-
данном этапе, следует разделить пополам предыдущий интервал. Тогда точка
х будет совпадать с точкой хп _ j. Однако при этом мы не получаем ника-
никакой новой информации. Обычно точки хп _ г и хп отстоят друг от друга на
достаточном расстоянии, чтобы определить, в какой половине, левой или пра-
правой, находится интервал неопределенности. Они помещаются на расстоянии
е/2 по обе стороны от середины отрезка Ln _ l; можно самим задать величи-
величину е или выбрать эту величину равной минимально возможному расстоянию
между двумя точками. (Предположим, что в нашем примере инженер может
регулировать температуру с интервалом в 1 ° С, поэтому е = 1.)
Интервал неопределенности будет иметь длину Ln, следовательно,
Ln _ j = 2Ln — е (рис. 2.2, нижняя часть).
На предыдущем этапе точки хп _ 1 и хп _ 2 должны быть помещены сим-
симметрично внутри интервала Ln _ 2 на расстоянии Ln _ l от концов этого ин-
интервала. Следовательно,
?и _ 2 =^л _ 1 + ^л (Рис- 2.2, средняя часть) .
Lrr-
к-з
ч^
1
Ln.z xn-3
\
—J*4 +-С-
1
i
i
»>
.;
^*
Рис. 2.2
19

Замечание. Из рисунка ясно, что на предпоследнем этапе хп
качестве внутренней точки.
Аналогично
Ln _3=Ln _ 2+Ln - i (Рис- 2-2, верхняя часть)
В общем случае
Lj_ l=Lj + LJ+ х при1</<и.
Таким образом,
Ln_l = 2Ln— eT
_ 2
остается ь
B.1)
Ln --=-
е,
и т.д.
Если определить последовательность чисел Фибоначчи следующим обра-
образом: FQ = \,Fl =lnFk=Fk_l+Fk_2 для к = 2, 3,..., то
Ln-] = Fn\Ln-F}-\*> У=1,2,...,л-1. B.2)
Если начальный интервал (я, Ь) имеет длину L { (= Ь - а), то
т. е.
B.3)
я
Следовательно, произведя п вычислений функции, мы уменьшим начальный
интервал неопределенности в l/Fn раз по сравнению с его начальной длиной
(пренебрегая е), и это — наилучший результат.
Если поиск начат, то его несложно продолжить, используя описанное выше
правило симметрии. Следовательно, необходимо найти положение первой
точки, которая помещается на расстоянии L2 от одного из концов начально-
начального интервала, причем не важно, от какого конца, поскольку вторая точка по-
помещается согяасно правилу симметрии на расстоянии L 2 от второго конца
интервала:
rp
' Л. „ a
L\ (Fn_lFrt_2-FnFn_3)
п
F
B.4)
П
п
После того как найдено положение первой точки, числа Фибоначчи больше
не нужны. Используемое значение е может определяться из практических со-
20
а)
Новый интервал, (хг, х2),
содержащий точку Хц.
Строка программы 330
б)
Новый интервал (хг,х3)
содержащий точку х%
Строка программы 350
А
Xi, Xj
в) Xif<X2
Новый интервал (х^, х3),
содержащий точку х2
Строка программы 420
А
г)
Новый интервал (хг,хь),
содержащий точку х2
Строка программы 460
\fz
и
Xq. Xj
Рис. 2.3
ображений. Оно должно быть меньше L г \Fn + х, в противном случае мы бу-
будем напрасно тратить время на вычисление функции (см. упр. 3 разд. 2.8).
Таким образом, поиск методом Фибоначчи, названный так ввиду появле-
появления при поиске чисел Фибоначчи, является итерационной процедурой. В про-
процессе поиска интервала (xit x2) с точкой х?, уже лежащей в этом интервале,
следующая точка х4 всегда выбирается такой, что хъ - х4 =х2 - ху или л:4 -
— Х\ — х$ — х2, т. е.
х4 =*! -х2 +х3. , B.5)
Если f(x2) = /2 и /(л:4) = Д, то можно рассмотреть четыре случая
(рис. 2.3).
В приведенной ниже программе реализованы указанные выше случаи.
В том виде, как она приведена здесь, эта программа позволяет производить
до 40 вычислений функции. В программе исследуется функция f(x) = х4 -
- 14х3 + 60х2 - 70х (см. строку 1000).
20 PRINT "ПОИСК МЕТОДОМ <PHBOHA44H":PRINT "":PRINT ""
30 REM В ПРОГРАММЕ ПРОИЗВОДИТСЯ ПОИСК ОТРЕЗКА <А,В>,
40 REM СОДЕРЖАЩЕГО ТОЧКУ МИНИМУМА УНИМОДАЛЬНОЙ
50 REM ФУНКЦИИ F<X), ЗА N ВЫЧИСЛЕНИЙ ФУНКЦИИ. ФУНКЦИЯ F(X)
60 REM ВЫЧИСЛЯЕТСЯ В СТРОКЕ 1000 В ВИДЕ Z=F(X).
70 REM НЕОБХОДИМЫЕ ЧИСЛА ФИБОНАЧЧИ
80 REM ВЫЧИСЛЯЮТСЯ ЗДЕСЬ ЖЕ.
90 REM
100 DIM FD0)
НО PRINT "ЗАДАЙТЕ N":INPUT N
120 F(O)*1:F<1)=1
130 FOR 1=2 TO N
140 F(I)=F_(I-l)+F(I-2)
21

150 NEXT I
160 PRINT "ЗАДАЙТЕ EPSILDNM:INPUT E
200 PRINT "ЗАДАЙТЕ ИНТЕРВАЛ <A,B>"
210 INPUT A,B
250 X1=A:X2=A+<<B-A>*RN-1>+E*<-1>'SN>/F<N>:X3=B
260 X=X2:G0SUB 1000:F2=Z
270 PRINT " ТЕКУЩИЙ ИНТЕРВАЛ11
280 K=1:PRINT X1,X3
290 X4=X1-X2+X3
300 X=X4:G0SUB 1000:F4=Z
310 IF F4>F2 THEN GOTO 400
320 IF X2<X4 THEN GOTO 360
330 X3=X2sX2=X4:F2=F4:PRINT X1,X3
340 GOTO 500
360 X1=X2:X2=X4:F2=F4:PRINT X1,X3
370 GOTO 500
400 IF X2<X4 THEN GOTO 460
420 X1=X4:PRINT X1,X3
430 GOTO 500
460 X3=X4:PRINT X1,X3
500 K=K+1
510 IF K<=N THEN GOTO 290
600 PRINT "КОНЕЧНЫЙ ИНТЕРВАЛ":РР:1МТ XI,ХЗ
610 PRINT "ЗНАЧЕНИЕ ФУНКЦИИ PABH0",F2
650 END
1000 Z=*X»X»X*X-14*X*X*X+60*X*X-70*X
10?0 RETURN
Пример 1
Использовать метод Фибоначчи для поиска минимума функции fix) = 2х2 - ех в ин-
интервале (О, 1) при 10-кратном вычислении функции.
Как видно из приведенной ниже распечатки, значение е выбрано равным нулю.
Окончательный интервал неопределенности имеет длину
0,359550563 - 0,348314606 = 0,01123957 * *
89
10
С точностью до шестого знака после запятой минимум достигается в точке **
= 0,357403, и в этой точке /(**) = -1,174138.
ПОИСК МЕТОДОМ ФИБОНАЧЧИ
ЗАДАЙТЕ N
10
ЗАДАЙТЕ EPSIL0N
0
ЗАДАЙТЕ ИНТЕРВАЛ (А,В)
0
1
ТЕКУЩИЙ ИНТЕРВАЛ
0
0
.235955
.235955
.3258425
.3258425
.325Э425
.348315
.348315
.35955
.35955
1
.6179775
.6179775
.47191
.47191
.41573
.3820225
.3820225
.3707875
.5707875
.370785
КОНЕЧНЫЙ ИНТЕРВАЛ
.35955 .370785
ЗНАЧЕНИЕ ФУНКЦИИ РАВНО
-1.174132
Пример 2
Найти минимум функции f(x) = х4 - 14*3 + 60л:2 - 70л: в интервале @, 2). Исполь-
Использовать 20 вычислений функции (см. упр. 9 разд. 1.4).
Функция z = f(x) вычисляется в строке 1000 при TV = 20 и е = 0. Распечатка резуль-
результата приведена ниже:
ПОИСК МЕТОДОМ ФИБОНАЧЧИ
ЗАДАЙТЕ N
20
ЗАДАЙТЕ EPSILON
О
ЗАДАЙТЕ ИНТЕРВАЛ (А,В)
О 2
ТЕКУЩИЙ ИНТЕРВАЛ
О
О
.472136
.472136
.6524761
.6524761
.7213602
.763932
.763932
.763932
.773985
.773985
.777Э313
.7778313
.7793176
.7801915
.7Э01915
.7804528
.7807141
.780804
2
1.236068
1.236068
.9442721
.9442721
.8328161
.8328161
.8328161
.8065038
.7902443
.7902443
.7840378
.7840378
.7816778
.7816778
.7816778
.7810653
.7810653
.7810653
.7810653
.7809753
.780804
КОНЕЧНЫЙ ИНТЕРВАЛ
.7В0В04 .7809753
ЗНАЧЕНИЕ ФУНКЦИИ РАВНО
-24.3696
2.3. ПОИСК МЕТОДОМ "ЗОЛОТОГО СЕЧЕНИЯ"
Не всегда можно заранее определить, сколько раз придется вычислять
функцию. В методе Фибоначчи это нужно знать для определения L2i т. е. по-
положения начальной точки (см. уравнение B.4)):
Метод "золотого сечения" почти столь же эффективен, как и метод Фибо-
Фибоначчи, однако при этом не требуется знать п — количество вычислений функ-
функции, определяемое вначале. После того как выполнено /вычислений, исходя
из тех же соображений, что и ранее (см. уравнение B.1)), записываем
4-i=Lj +^/+i- B-6)
Однако если п не известно, то мы не можем использовать условие Ln _ х =
%г п — е. Если отношение последующих интервалов будет постоянным, т. е.
""""" • • • """"" / j
B.7)
то
22
23

т. е. т = 1 +
Т
гда
ТаУи^образом, т> - г - 1 = 0, откуда г = A + >П)П « 1,618033989. То
J — т-3
= г3 и т. д.
Следовательно, —
т.е.
= Г
B.8)
В результате анализа двух рассмотренных значений функции будет опреде-
определен тот интервал, который должен исследоваться в дальнейшем. Этот интер-
интервал будет содержать одну из предыдущих точек и следующую точку, помеща-
помещаемую симметрично ей. Первая точка находится на расстоянии L j/t от одного
конца интервала, вторая — на таком же расстоянии от другого. Поскольку
lim Fn _ 1/Fn = \\п (см. упр. 2 разд. 2.8), то из уравнения B.4) видно, что
поиск методом "золотого сечения" является предельной формой поиска ме-
методом Фибоначчи. Название "золотое сечение" произошло от названия отно-
отношения в уравнении B.7) . Видно, что Lj _ 2 делится на две части так, что от-
отношение целого к большей части равно отношению большей части к меньшей,
т. е. равно так называемому "золотому отношению".
Таким образом, если ищется интервал (х0, х3) и имеются два значе-
значения функции /i и /г в точках JCj и Х2, то следует рассмотреть два случая
(рис. 2.4).
Следующая программа реализует поиск методом "золотого сечения". За-
Заданная точность может, конечно, меняться выбором значения в строке 300.
Ниже приведена распечатка результата использования метода "золотого се-
ft<fi , ,
Новый интервал (х0, хг)
Строка программы 190
6) fi>fz
Новый интервал(xj,x3)
Строка программы 250
•*>
чения" для функции f(x) = -е хЩх). Поиск производится в интервале
@, 2).
Истинный минимум находится в точке 1,76322211, где значение функции
равно -0,0972601313.
5 DEFDBL A-Z
10 PRINT и МЕТОД ЗОЛОТОГО CE4EHHR":PRINT "".-PRINT ""
20 REM ПРОГРАММА ПРОИЗВОДИТ ПОИСК ИНТЕРВАЛА
30 REM <А,В>, В КОТОРОМ ЛЕЖИТ ТОЧКА МИНИМУМА
40 REM УНИМОДАЛЬНОЙ ФУНКЦИИ F(X).
50 REM ОКОНЧАТЕЛЬНОЕ ЗНАЧЕНИЕ X ПОЛУЧЕНО С ТОЧНОСТЬЮ 4D
ЬО REM F(X) ОПРЕДЕЛЯЕТСЯ В СТРОКЕ 1000 В ВИДЕ Z=..
90 PRINT "ЗАДАЙТЕ ИНТЕРВАЛ (A,B)":INPUT A,B
100 Т1».3819660ПЗ#:Т2=1~Т1
110 Х0*А:Х1»А+Т1*<В-А):Х2=А+Т2*<В-А):ХЗ=В
120 X-X1:GOSUB 1OOO:F1=Z
140 X»X2:GC}SUB 1000:F2=Z
150 PRINT "ТЕКУЩИЙ ИНТЕРВАЛ"
170 PRINT X0,X3
180 IF F2<F1 THEN GOTO 250
190 I=X2-XO:X3=X2:X2=X1:X1»XO+T1*I
200 F2-F1:X=X1:GOSUB 1000
210 FleZ:GDTO 300
250 I»X3-X1:XO=X1:X1=X2:X2=XO+T2*I
260 Fl*F2;X=X2:G0SUB 1000:F2«Z
300 IF I>.00005 THEN GOTO 170
450 PRINT
470 PRINT "X»"X1,"F(X)="F1
SOO END
1000 Ze-EXP(-X)*LOG(X)
1010 RETURN
МЕТОД ЗОЛОТОГО СЕЧЕНИЯ
ЗАДАЙТЕ ИНТЕРВАЛ <А,В>
О 2
ТЕКУЩИЙ ИНТЕРВАЛ
О 2
.7639320226 2
1.2360679774
1.527864044976863
1.7О82О3932423137
1.708203932423137
1-708203932423137
1.708203932423137
1.73451516742761
1.750776404949797
1.750776404949797
1.756987644980199
1.76О8264О2424398
1.760826402424398
1.762292677297335
1.762292677297335
1.762292677297335
1.762638817842288
1.76263В817842288
1.762771031765554
1.762771031765554
1.762821532990448
1.762821532990448
Рис. 2.4
X" 1.762852744461857
2
2
2
1.88854381995464
1.819660112468496
1.777087639941836
1.777087639941836
1.777087639941836
1.76703764245955
1.76703764245955
1.76703764245955
1.764665159878096
1.764665159878096
1.763758952169844
1.763198885008787
1.763198885008787
1.7629Я4958387139
1.762984958387139
1.762903245688782
1.762903245688782
1.762872034215326
F(X)«-9.726013243198395D-02
24
25

2.4. АППРОКСИМАЦИЯ КРИВЫМИ
В двух предыдущих разделах была сделана попытка найти малый интер-
интервал, в котором находится минимум функции. В следующих двух разделах
применяется иной подход. Используется несколько значений функции в опре-
определенных точках для аппроксимации функции обычным полиномом по край-
крайней мере в небольшой области значений. Затем положение минимума функ-
функции аппроксимируется положением минимума полинома, поскольку послед-
последний вычислить проще.
2.5. КВАДРАТИЧНАЯ ИНТЕРПОЛЯЦИЯ
Если известны значения функции f(x) в трех различных точках ос, ]3, 7,
равные соответственно /а, fp,fy, то функция f(x) может быть аппроксими-
аппроксимирована квадратичной функцией
у(х) =Ах2 + Ях + С, B.9)
где А, В и С определяются из уравнений
Аа2 + Ва+ C=fQ>
B.10)
После преобразований этих уравнений получаем
А = [(у-р) fa + (а- у) /А + (р- a) fyVA,
В = [(Р - уг) /„ + (у2 - а2) /„ + (а2 - /?2) fr]/A,
С = Шу -P)fa + уа(а- у) /„ + фр- a) fy]/A,
B.11)
где А = (ос — ]3)(]3 - 7)G — а) • Ясно, что $(х) будет иметь минимум в точк!
х = —В/2А, если А > 0. Следовательно, можно аппроксимировать точку ми
нимума функции f(x) значением
-
2
-У') /tt+ (У2 ~
- /?2) /у
W-y)fa+ (У- <*)/>+ (<*- Р)А
А-Н
А+н А
Рис. 2.5
А+Н
A+ZH
Xj Xz
Рис. 2.6
B.121 <5=
ц одной переменной f(x), начальная аппроксимация положения минимума
и длина шага Я, являющаяся величиной того же порядка, что и расстояние
от точки А до точки истинного минимума х* (условие, которое не всегда
просто удовлетворить). Вычислительная процедура имеет следующие шаги:
1. Вычислить f(A) и f(A + Н).
2. Если f(A) < f(A + H), то взять в качестве третьей точки А - Н и вычис-
вычислить f(A — Н). В противном случае в качестве третьей точки взять А + 2#
и найти /(Л + 2Я) (рис. 2.5).
3. Используя эти три точки, найти 5 из уравнения B.12) и вычислить
/(S)-
4. Если разница между наименьшим значением функции и следующим наи-
наименьшим значением функции меньше заданной точности, то процедура за-
заканчивается.
5. Если процедура не завершалась на шаге 4, то точка с наибольшим зна-
значением обычно отбрасывается, и мы возвращаемся на шаг 3. Но еслл, оста-
оставив точку с наибольшим значением функции, мы определим конечные гра-
границы интервала, в котором лежит минимум, то следует действительно
оставить это значение и затем вернуться на шаг 3. Например, на рис. 2.6
оставлены точки Х\,х2 и л:4 , а не точки xlfx2 их3.
В программе, распечатка которой приведена ниже, реализована эта про-
процедура.
Заметим, что если точность Е задана слишком малой, то а, C, у, а также fa,
fp>fy будут очень близки друг к другу и значение 5 (см. уравнение B.12))
может стать вообще недостижимыми. Чтобы преодолеть эту трудность, пере-
перепишем уравнение B.12) для второй и последующих интерполяций:
'
Этот метод может непосредственно применяться к функциям одной пере
менной. Он может быть очень полезен для выполнения линейного поиска i
процедурах, описанных в гл. 4. В этих процедурах требуется найти миниму*
функции /(х) в точках прямой х0 + Ad, где х0 — заданная точка, a d опреде
ляет заданное направление. Значения функции /(х0 + Ad) на этой прямой яв
ляются значениями функции одной переменной А:
*(Х) =/(xo+Ad). B.1?
Идеи и результаты, изложенные выше, преобразуются в вычислительны1
процедуры, описанные далее. Предположим, что заданы унимодальная фК
26
10 PRINT "КВАДРАТИЧНАЯ ИНТЕРПОЛЯЦИЯ"
20 REM ПРОГРАММА РЕАЛИЗУЕТ ПРОЦЕДУРУ
25 REM КВАДРАТИЧНОЙ ИНТЕРПОЛЯЦИИ ПАУЭЛЛА ДЛЯ
30 REM ПОИСКА МИНИМУМА ФУНКЦИИ F<X),
40 REM ВЫЧИСЛЯЕМОЙ В ВИДЕ Z=F(X) В СТРОКЕ 1000
100 PRINTAAAHTE НАЧАЛЬНОЕ 3HA4EHHE":INPUT A
ПО PRINTAAAHTE ШАГ H":INPUT H
ISO PRINTAAAHTE ТОЧНОСТЬ E":INPUT E
1?0 REM НАЧАТЬ ПРОЦЕСС С ПЕРВЫХ ТРЕХ ТОЧЕК
200 DIM XD),F<4)
210 XA)*A:X=X<1):GOSUB 1OOO:FA)=Z
220 XB>»A+H:X»XB):G0SUB 1000:FB)=Z
230 IF FAXFB) THEN X<3)=A-H:X»XC):GDSUB 1000:FC)=Z:G0TQ 250
27

240 X<3)«A+2*HiX«X<3>:G0SUB 1000:FC)-Z
250 PRINT" ТЕКУЦИЕ ЗНАЧЕНИЯ"
260 PRINT" X(I) F(I)"
270 REM ВЫЧИСЛЕНИЕ ПЕРВОГО АППРОКСИМИРУЮЩЕГО МИНИМУМА
275 REM В СТРОКАХ 300-350
300 DN»<X<2)-XC»*F<1)
310 DN«DN+<XC)-X<l»*F<2)+<Xa>-X<2»*F<3>
320 NM-(XB)*XB)-XC)*XC»»FA)
330 NM*NM-HX<3)*X<3>-XU>#XU»*F<2)
340 NM*NM+(XA)*XA)-XB)*XB))*FC)
350 X<4>*NM/<2*DN):X*XD>:G0SUB 1000:FD)=Z
380 REM УПОРЯДОЧИТЬ ЗНАЧЕНИЯ ФУНКЦИИ В СТРОКАХ 400-460
400 FOR J*l TO 3
410 FOR K*J+1 TO 4
420 IF F(JX*F(K) THEN GOTO 460
430 X*X(J):X(J)=X(K)sX(K)-X
440 F-F<J)rfr(J)=F«<):F(K>*F
450 REM ПОМЕНЯТЬ МЕСТАМИ F(J) И F(K>, А ТАКЖЕ X(J) И Х(К>,
455 REM ЕСЛИ ОНИ НЕ УПОРЯДОЧЕНЫ
460 NEXT K:NEXT 3
470 FOR 1-1 TO 4:PRINT X.(I),F<I):NEXT I
480 PRINT IIM:PRINT ""
490 REM ЗАКОНЧИТЬ, ЕСЛИ ПОЛУЧЕНА ЗАДАННАЯ ТОЧНОСТЬ
500 IF ABS<X(l)-XB))<E THEN GOTO 800
510 REM ЗАПОМНИТЬ ТРИ ЛУЧШИХ ТОЧКИ
520 S1»SGN<XB)-XA)):S2=SGN(X<3)-X<1»
530 S3*SGN<XD)-X<1»
540 IF S1*S2 AND S1—S3 THEN XC)=XD):FC)»FD)
550 REM ВТОРАЯ ИНТЕРПОЛЯЦИЯ
560 DN»(XB)-XC))*FA)+<XC)-XA»*FB)-KXA)-X<2))*FC)
570 F*<FA)-FB))/B*DN)
580 F*F»<X<2)-XC»«(XC)-XA»
590 XD)*<X(l)+XB))/2+F
600 X-XD):G0SUB 10O0:FD)*Z
610 REM ПОВТОРИТЬ ВТОРУЮ ИНТЕРПОЛЯЦИЮ
620 GOTO 400
800 PRINT" "
810 PRINTltX-llX(l),ltF«"F(l)
850 END
1000 Z*2*X*X-EXP<X)
1010 RETURN
Пример 1
Используя квадратичную интерполяцию, найти минимум функции z
точностью 0,001. В качестве начальных значений положить А = 1 и Н— 0,5.
Ниже представлена распечатка результатов.
КВАДРАТИЧНАЯ ИНТЕРПОЛЯЦИЯ
ЗАДАЙТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ 1
ЗАДАЙТЕ ЫАГ Н .5
ЗАДАЙТЕ ТОЧНОСТЬ Е .0005
ТЕКУЫ.ИЕ ЗНАЧЕНИЯ
Х<1) FQ)
.5 -1.148721
.0470197 -1.043721
1 -.7182818
1.5 1.831102Е-02
е* с
.3615043
.3745917
.5
.0470197
.357937
.3615043
.3745917
.0470197
.3575219
.357937
.3615043
.0470197
-1.174117
-1.17376
-1.148721
-1.043721
-1.174138
-1.174117
-1.17376
-1.043721
-1.174138
-1.174138
-1.174117
-1.043721
X* .3575219 F—1.174138
2.6. КУБИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
Квадратичная интерполяция, рассмотренная в предыдущем разделе, часто
называется методом Пауэлла и аппроксимирует функцию квадратичным
трехчленом. Излагаемый в настоящем разделе метод Давидона обеспечивает
большую точность и аппроксимирует функцию кубическим полиномом. Для
кубической интерполяции в этом методе используются значения функции и
ее производной, вычисленные в двух точках. Этот метод широко использует-
используется в процедурах линейного поиска в гл. 4, и именно с этой точки зрения мы
и будем его изучать.
Рассмотрим задачу минимизации функции /(х) на прямой х0 + hd, т. е.
минимизацию функции
-t
Оп
hdn);
B.15)
Следовательно,
^ = V/(x0 +
дх
(х0 + hd) dn.
п
d - g(x0 + hdY d.
B.16)
Предполагаем, что известны следующие значения:
B.17)
.3745917
.5
.0470197
1
-1.17376
-1448721
-1.043721
-.7182818
28
Эту информацию можно использовать для построения кубического поли-
полинома
29

a + bh + cti1 + dh3,
который будет аппроксимировать функцию
определяющие a, b, cf d выглядят так:
B.18)
Если р = 0, то уравнения,
+ z +
а
а +
dq3 =
B.19)
Эти уравнения имеют следующее решение:
Gn+G,
, d =
B.20)
где
z =
Точки перегиба кубического полинома являются решением уравнения
Gp- 2(G
Следовательно, если г является точкой минимума кубического полинома, то
2z)\- ) = 0.
г
q
1/2
z ±
2z
2z
B.21)
где
w=(z2 -GpGqY'2. B.22)
Одно из значений B.21) соответствует минимуму. Вторая производная
равна
2с + 6dh.
Если мы выбираем положительный знак, то при
h Gp + z + w
B.23)
вторая производная будет
2(Gp + z)
2z) q(Gp + z + w)
2z)
= - (-2G - 2z + 2G
2w) =
2w
Ч Gp+Gq+^- ^
Лучшие численные результаты получаются при использовании следующей
эквивалентной формулы:
B.25)
G
Gp+2w
q Gq-Gp + 2w Gq
Доказательство эквивалентности уравнений B.24) и B.25) оставлено в
качестве упражнения.
Выбор точки q оставлен на наше усмотрение. Если Gp < 0, то следует выб-
выбрать значение q положительным, т. е. сделать шаг в направлении убывания
функции $(h)9 в противном случае значение q следует выбрать отрицатель-
отрицательным. Значение q должно быть таким, чтобы интервал @, q) содержал мини-
минимум. Это будет справедливо, если ^ > ^ (рис. 2.1,а) или если G > 0
(рис. 2.7, б).
Если ни одно из этих условий не выполнено, то мы удваиваем значение
q, повторяя это в случае необходимости до тех пор, пока указанный интер-
интервал не будет содержать минимум.
Остается задача определения начального значения д. Имеются реальные
трудности в определении такого значения, которое было бы приемлемо для
всех задач. Давидон, Флетчер и Пауэлл предложили выбирать q следующим
образом:
q = min {r?, -2(fy - *m)IGp } , B.26)
где ут — оценка наименьшего значения истинного минимума ^(/i), а ц —
константа, значение которой обычно выбирается равным 2 или 1.
Эта итерационная процедура имеет следующие шаги:
1. Найти *р =/(х0) и Gp = [g(xo)]Td.
2. Проверить, выполняется ли условие G < 0, и если оно не выполняется,
производить поиск вдоль направления —а. Выбрать q из выражения B.26).
При этом необходимо "угадать" фт.
3. Вычислить {pq =/(xo + qd) и Gq = [g(x0 + qd)]Td.
ф(И)
Рис. 2.7
30
31

4. Если Gq > 0 или $q > ippi то интервал, содержащий минимум, найден.
В противном случае заменить q на 2q и вернуться к шагу 3.
5. Использовать уравнение B.25) для аппроксимации точки минимума на
интервале @, q) значением г.
6. Если \d$/dh\ = | [g(x0 + /*d|]Td| = \Gr\ < e, где е — заданная точность,
то остановится.
7. Вернуться на шаг 5, используя интервал @, г), если Gr > 0, либо ис-
используя интервал (г, #), если Gr < 0.
На шаге 6 производится проверка значения производной. Предшествую-
Предшествующие проверки приводят к остановке тогда, когда положение минимума не
изменяется. Следует отметить, что в общем случае проще найти минимум
функции, чем положение точки минимума. Последнее определяется с мень-
меньшей точностью.
Описанный выше алгоритм реализуется следующей программой:
20 PRINT "КУБИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ"
30 REM В ПРОГРАММЕ ИЩЕТСЯ МИНИМУМ ФУНКЦИИ F<X+LAM*D)
40 REM ВДОЛЬ ПРЯМОЙ X+LAM*D. ЗНАЧЕНИЯ ФУНКЦИИ F(X1,X2,...>
ЗЪ REM ВЫЧИСЛЯЮТСЯ В СТРОКЕ 5000, ГДЕ Z=F(X1,X2,..XN)
60 REM ВЕКТОР-ГРАДИЕНТ ФУНКЦИИ F(X) ВЫЧИСЛЯЕТСЯ В СТРОКЕ
65 REM 6000 В ВИДЕ G<1>,GB),«.G(N>
100 PRINT "ЗАДАЙТЕ ЧИСЛО ПЕРЕМЕННЫХ "-.INPUT N
120 DIM X(N),P(N),Q(N),D(N),G(N)
130 СС~О:ТТ=О
150 PRINT "НАЧАЛЬНАЯ ТОЧКА "
160 FOR 1-1 TO N:INPUT X<I):NEXT I
200 PRINT "НАПРАВЛЕНИЕ D"
220 FOR 1=1 TO NrlNPUT D(I):NEXT I
300 PRINT "ЗАДАЙТЕ ТОЧНОСТЬ Е"
310 INPUT E
3
50 PRINT "ПРЕДПОЛАГАЕМОЕ ЗНАЧЕНИЕ MHHHMyMA":INPUT FM
400 PRINT " ТЕКУЩИЕ ЗНАЧЕНИЯ"
410 FOR 1=1 TO N:P(I)=X(I):PRINT "X";I,X(I):NEXT I
500 REM ПЕРВАЯ ТОЧКА Р
510 GOSUB 5000
520 PRINT "ИТЕРАЦИЯ ";СС;" ЗНАЧЕНИЕ ";Z
530 FP=Z:GQSUB 6000:Gl=G0
600 GP=O
610 FOR 1=1 TO N:GP=GP+G(I>*D(I):NEXT I
620 IF GP<=0 THEN GOTO 680
625 REM ОПРЕДЕЛИТЬ НАЧАЛЬНЫЙ ЫАГ И, ЕСЛИ НЕОБХОДИМО
626 REM ИЗМЕНИТЬ НАПРАВЛЕНИЕ СПУСКА НА ПРОТИВОПОЛОЖНОЕ
630 QX=ABSB*(FP-FM)/GP):IF QX>1 THEN QX=1
640 FOR 1=1 TO N
650 X(I)«P(IO-QX<HD(I):P(I)=X(I):NEXT I
660 GQSUB 5000:FP=Z:PRINT "ВОЗМОЖНА НЕСТАБИЛЬНОСТЬ?"
670 GOSUB 6000:Gl=G0:G0T0 600
680 QX=ABSB*(FP-FM)/GP):IF QX>1 THEN QX=1
690 HH=QX
700 REM НАЙТИ СЛЕДУЮЩУЮ ТОЧКУ Q
710 BB-HH
720 FOR 1=1 TO N
730 D(I)~P(I)+BB*D(I):X(I)=Q<I)
740 NEXT I
750 GOSUB 5000:FQ=Z
760 GOSUB 6000sG2=G0
770 GQ=O
780 FOR 1=1 TO N
790 GD=GQ+G<I)*D(I)
800 NEXT I
810 IF GQ>0 OR FQ>FP THEN GOTO 830
815 REM ВЫПОЛНИТЬ КУБИЧЕСКУЮ ИНТЕРПОЛЯЦИЮ ИЛИ УДВОИТЬ
816 REM ЫАГ ДЛЯ ТОГО, ЧТОБЫ ТОЧКА МИНИМУМА
817 REM ВХОДИЛА В ИНТЕРВАЛ НЕОПРЕДЕЛЕННОСТИ
820 HH=2*HH:G0T0 700
830 ZZ=3*<FP-FQ)/HH:ZZ=ZZ+GP+GQ
840 WW=ZZ*ZZ-GP*GQ:IF ИИ<0 THEN ИИ=О
850 W=SQR(UU)
860 DD=HH*U-(GQ+W-ZZ)/(GQ-GP+2*W»
870 FOR 1=1 TO N:X(I)=P(I)+DD*D(I):NEXT I
880 GOSUB 5000:FR=Z
890 GOSUB 6000:G3=G0
895 REM ВЫЧИСЛИТЬ ГРАДИЕНТ В НОВОЙ ТОЧКЕ
900 GR=O
910 FOR 1=1 ТО N:GR=GR+G(I>*D(I):NEXT I
920 IF GR>0 THEN GOTO 1000
925 REM НАЙТИ НОВЫЙ ИНТЕРВАЛ И ПРОИЗВЕСТИ ПРОВЕРКУ
927 REM УСЛОВИЯ ОКОНЧАНИЯ ПОИСКА МИНИМУМА
930 IF ABS(GRXE THEN GOTO 1300
940 HH=BB-DD
950 FOR 1=1 TO N:P(I)=X(I):PRINT "X";I,X(I):NEXT I
960 CC=CC+1:PRINT "ИТЕРАЦИЯ ";СС;" ЗНАЧЕНИЕ ";Z
970 FP=Z:GP=GR:Gl=GOsGOTO 830
1000 IF ABS<GRXE THEN GOTO 1300
1005 REM ПОВТОРИТЬ КУБИЧЕСКУЮ ИНТЕРПОЛЯЦИЮ. НОВЫЙ
1006 REM ИНТЕРВАЛ БУДЕТ BB--DD (СТРОКА 940) ИЛИ
1007 REM DD (СТРОКА 1010)
1010 HH=DD
1020 FOR 1=1 ТО N:Q(I)=X(I):PRINT "X";I,X<I):NEXT I
1030 CC=CC+1:PRINT '^ИТЕРАЦИЯ ";СС;" 3HA4EHME";Z
1040 FD=Z:GQ=GR:G2=G0:G0T0 830
1300 PRINT "МИНИМИЗАЦИЯ ЗАКОНЧЕНА"
1310 PRINT "КОЛИЧЕСТВО ИТЕРАЦИЙ="СС"ЗНАЧЕНИЕ МИНИМУМА*11*
1320 FOR 1=1 ТО N
1330 PRINT "X"iI,X(I>
1340 NEXT I
1350 END
5000 Z=0 ¦*
5010 Z=100*(XB)-X(l)*X(l))A2
5020 Z=Z+A-X<1))^2
5100 TT=TT+1
5200 RETURN
6000 G0=0
6100 G(l)=-400*X(l)*(XB)-X(l)*X(l»
6110 GA)=GA)-2*A-XA»
6200 G<2>=200»<XB).-X(l)*X(l»
7000 FOR 1=1 TO N:GO=GO+G(I>»G(I):NEX Г I
7010 GO=SQR(GO)
7500 RETURN
Пример 1
Найти минимум функции f(xx, x2) = 100(х2 - х\) 2 + A - х{) 2 на прямой, прохо-
проходящей через точку (-1; 0) в направлении E; 1).
Соответствующие подпрограммы начинаются в распечатке с операторов в строках
5000 и 6000. Выбраны значения Е = 0,0001 и ут = 0. Ниже приведена распечатка резуль-
результатов :
КУБИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
ЗАДАЙТЕ ЧИСЛО ПЕРЕМЕННЫХ 2
НАЧАЛЬНАЯ ТОЧКА
-1
О
32
НАПРАВЛЕНИЕ D
5
2 Зак. 768
33

ЗАДАЙТЕ ТОЧНОСТЬ Е
.0001
ПРЕДПОЛАГАЕМОЕ ЗНАЧЕНИЕ МИНИМУМА 0
ТЕКУЩИЕ ЗНАЧЕНИЯ
X 1
X 2
ИТЕРАЦИЯ
X 1
X 2
ИТЕРАЦИЯ
X 1
Х- 2
ИТЕРАЦИЯ
X 1
X 2
ИТЕРАЦИЯ
X 1
X 2
ИТЕРАЦИЯ
X 1
X 2
ИТЕРАЦИЯ
X 1
X 2
ИТЕРАЦИЯ
X 1
X 2
ИТЕРАЦИЯ
X 1
X 2
ИТЕРАЦИЯ
0
1
2
3
4
5
6
7
В
-1
0
ЗНАЧЕНИЕ 104
-.3994247
.1201151
ЗНАЧЕНИЕ 2.113823
-.3365114
.1326977
ЗНАЧЕНИЕ 1.В24123
-.3413863
.1317227
ЗНАЧЕНИЕ 1.822355
.2422956
.2484591
ЗНАЧЕНИЕ 4.174696
.5813206
.3162641
ЗНАЧЕНИЕ .2222494
.5611688
.3122338
ЗНАЧЕНИЕ .1932893
.9545786
.3909157
ЗНАЧЕНИЕ 27.07376
.5638282
.3127656
ЗНАЧЕНИЕ .1928843
МИНИМИЗАЦИЯ ЗАКОНЧЕНА
КОЛИЧЕСТВО ИТЕРАЦИЙ РАВНО 8 ЗНАЧЕНИЕ МИНИМУМА РАВНО .1928638
X 1
X 2
.5633697
.3126739
2.7. ЛИТЕРАТУРА
1 W. С. Davidon, 'Variable metric method for minimisation', AECR&DReport, ANL-5990,
Argonne National Laboratory, 1959.
2 R, Fletcher and M. J. D. Powell, 'A rapidly convergent descent method for minimisation',
The Comp Journal 6, 163-168, 1963.
3 J. Kiefer, 'Sequential minimax search for a maximum', Proc. Am. Math. Soc, 4, 502-506,
1953.
4 M. J. D. Powell, 'An efficient method of finding the minimum of a function of several
variables without calculating derivatives', The Сотр. Journal, 7, 155-162, 1964
1. ЕслиFo = 1 иFx — l,
2.8. УПРАЖНЕНИЯ
n_2 дляп > 2, то покажите, что
F =
л n
34
V*
где г =
y/S
1,618033989.
Используя это рекуррентное соотношение, покажите, что F2 = 2, F3 — 3,
i% = 8,F6 = 13, ...,F10= 89,...,F19=6765,F2O= 10946.
— 5,
2. Покажите, что
1) Fn _ lFn _ 2 - FnFn - 3
(см- уравнение B.4) ) ;
)
VЧ/Т для больших и;
n
3) Fn _xlFn^ IIт для больших п.
3. Если расстояние между точками равно по крайней мере е , то 26 будет наименьшим
интервалом неопределенности; следовательно, неравенство Ln > 2e устанавливает
границу для п - числа полезных экспериментов. Покажите, что это неравенство при-
приводит к соотношению е < L x \Fn + j.
4. Покажите, что для сокращения интервала неопределенности на 1 % от начальной ве-
величины необходимо сделать 11 вычислений функции при использовании методы Фи-
Фибоначчи. Если размещение точек задать в начале, каково будет минимальное число
необходимых точек? (Не рассчитывайте на получение удачных результатов.)
5. Примените метод Фибоначчи при наличии 10 вычислений функции для определения
минимума функции 2х2 + 3e"~* на интервале @; 1).
6. Воспользуйтесь методом Фибоначчи для нахождения минимума функции х4 - Ых3 +
+ вОх2 - 70* на интервале E; 7) с точностью 0,01. Сколько раз необходимо вычис-
вычислить функцию?
7. Используйте метод "золотого сечения" для определения минимума функции 2х2 +
+ 3e~* с точностью до двух десятичных знаков. В качестве начального интервала не-
неопределенности используйте интервал @; 1).' Сколько раз необходимо вычислить
функцию? Сравните с упр. 5.
8. При а=0, 0=f,7=2f покажите, что 5 в уравнении B.12) примет следующий вид:
и что при этом достигается минимум, если fa + f > 2f~.
9. Примените квадратичную интерполяцию для определения точки минимума функции
-e~~*ln(*) на интервале A, 3) с точностью 0,001. (Проверьте, не используете ли вы
отрицательных значений х, ибо в противном случае получите ошибку при работе про-
программы.)
10. Примените квадратичную интерполяцию для поиска минимума функции f{xx, х2) =
= х\ + Ъх\ + 2ххх2 на прямой а+ \d, где а = (-J") и d = (\), с точностью до двух
десятичных знаков.
11. Проверьте справедливость уравнений B.11), B.12) и B.14).
12. Проверьте справедливость уравнения B.20) .
13. Проверьте справедливость уравнений B.24) и B.25).
14. Для кривой у = ах2 покажите, что касательная в точке (х, у') пересекает ось х в
точке х'12. Подтверждает ли это правильность выбора q в уравнении B.26) ?
15. Решите уравнение е* sin л: = 1. Попытайтесь минимизировать функцию f(x) = A —
е* sin x)
35

ГЛАВА 3. МЕТОДЫ ПРЯМОГО ПОИСКА ДЛЯ ФУНКЦИЙ п ПЕРЕМЕННЫХ
3.1. ПРЕДВАРИТЕЛЬНОЕ ОБСУЖДЕНИЕ
На разработку методов прямого поиска для определения минимума функ-
функций п переменных было затрачено много усилий. Методы прямого поиска яв-
являются методами, в которых используются только значения функции. Мы
рассмотрим подробно лишь два
(х/ >xz) из них. Практика показала, что
эти два метода эффективны и
применимы для широкого числа
приложений.
Рассмотрим функцию двух
переменных. Ее линии постоян-
постоянного уровня1 представлены на
рис. 3.1, а минимум лежит в
точке Of, xf). Простейшим ме-
XJ
Рис. 3.1
тодом поиска является метод покоординатного спуска. Из точки А мы про-
производим поиск минимума вдоль направления оси хх и, таким образом, на-
находим точку В, в которой касательная к линии постоянного уровня парал-
параллельна оси Xj. Затем, производя поиск из точки В в направлении оси х2, по-
получаем точку С, производя поиск параллельно оси хх, получаем точку D, и
т. д. Таким образом, мы приходим к оптимальной точке. Любой из одномер-
одномерных методов, описанных в предыдущей главе, может быть использован здесь
для поиска вдоль оси. Очевидным образом эту идую можно применить для
функций п переменных.
Теоретически данный метод эффективен в случае единственного миниму-
минимума функции. Но на практике он оказьюается слишком медленным. Поэтому
были разработаны более сложные методы, использующие больше информа-
информации на основании уже полученных значений функции.
Было предложено несколько функций, которые из-за своих свойств яв-
являются тестовыми для таких методов. Ниже приведено несколько примеров
таких функций.
Функция Розенброка:
f(xltx2) =100(x2 -х\J
Функция Пауэлла:
/(х) = (*, + 10х2
х*=@; 0; 0; 0).
; х*=A; 1)
C.1)
-х4J + (х2 - 2х3)
C.2)
1 Линией постоянного уровня называется кривая в двумерном сечении пространства
параметров (в данном случае - в плоскости (xlf x2)), значение функции на которой -
константа. - Прим. ред.
* Имеется в виду ряд значений от ОД до 1 с шагом ОД. - Прим. ред.
36
Двумерная экспоненциальная функция:
v х2) =
= О, 1 @,1I*; х*=A; 10). C.3)
Любая серьезная оптимизационная процедура должна эффективно решать
задачи C.1), C.2), C.3) и другие тестовые задачи.
3.2. МЕТОД ХУКА - ДЖИВСА
Этот метод был разработан в 1961 году, но до сих пор является весьма эф-
эффективным и оригинальным. Поиск состоит из последовательности шагов
исследующего поиска вокруг базисной точки, за которой в случае успеха
следует поиск по образцу.
Описание этой процедуры представлено ниже:
А. Выбрать начальную базисную точку Ъх и шаг длиной hj для каждой пе-
переменной Xj , / = 1, 2, . . . , п. В приведенной ниже программе для каждой
переменной используется шаг Л, однако указанная выше модификация тоже
может оказаться полезной.
Б. Вычислить f{x) в базисной точке Ь2 с целью получения сведений о ло-
локальном поведении функции f(x). Эти сведения будут использоваться для
нахождения подходящего направления поиска по образцу, с помощью которо-
которого можно надеяться достичь большего убывания значения функции. Функция
f(x) в базисной точке Ъх находится следующим образом:
1. Вычисляется значение функции /(bi) в базисной точке Ъх.
2. Каждая переменная по очереди изменяется прибавлением длины шага.
Таким образом, мы вычисляем значение функции /(Ъ2 + h1e1), где ej -
единичный вектор в направлении оси хх. Если это приводит к уменьшению
значения функции, то bj заменяется на bj + h1e1. В противном случае вы-
вычисляется значение функции f(b1 - /чеО, и если ее значение уменьши-
уменьшилось, то Ь2 заменяем на Ьх — h ^. Если ни один из проделанных шагов не
приводит к уменьшению значения функции, то точка bi остается неизмен-
неизменной и рассматриваются изменения в направлении оси х2, т. е. находится
значение функции f(h1 + h2e2) и т. д. Когда будут рассмотрены все п пе-
переменные, мы будем иметь новую базисную точку Ъ2.
3. Если b2 = bj, т. е. уменьшение функции не было достигнуто, то исследо-
исследование повторяется вокруг той же базисной точки b!, но с уменьшенной
длиной шага. На практике удовлетворительным является уменьшение ша-
шага (шагов) в десять раз от начальной длины.
4. Если Ь2 Ф bi, то производится поиск по образцу.
В. При поиске по образцу используется информация, полученная в про-
процессе исследования, и минимизация функции завершается поиском в направ-
направлении, заданном образцом. Эта процедура производится следующим обр азом:
37

1. Разумно двигаться из базисной точки Ь2 в направлении Ъг - Ь1? по-
поскольку поиск в этом направлении уже привел к уменьшению значения
функции. Поэтому вычислим функцию в точке образца
P1=b1+2(b2-b1). C.4)
В общем случае
C.5)
2. Затем исследование следует продолжать вокруг точки Pi (Р,-).
3. Если наименьшее значение на шаге В, 2 меньше значения в базисной точ-
точке Ь2 (в общем случае Ьг+1), то получают новую базисную точку Ь3
(bi+ 2), после чего следует повторить шаг В, 1. В противном случае не про-
производить поиск по образцу из точки Ъ2 (hi+ г)9 а продолжить исследова-
исследования в точке Ь2 (Ьг- + j).
Г. Завершить этот процесс, когда длина шага (длины шагов) будет умень-
уменьшена до заданного малого зйачения.
Ниже приведена блок-схема данного метода.
Вычислить значение функ-
функции 8 базисной
точке
Выполнить исследование
екущее значе-
значение меньше значения в ба2
иеной точке ?
шаг достаточно
мал ?
Взять новую
базисную точку
Сделать шаг
поиска по образцу
Выполнить исследование
Уменьшить
длину шага
д ^^ /екущее
значение меньше
значения в базис
ной точке.?
Рис. 3.2
Вход
i
Первая координата
1
Увеличить координату
на шаг
Функция
уменьшилась р
Нет
Уменьшить координату
на шаг
Функция
уменьшилась
Нет
Оставить начальное
значение
координаты
Рассмотреть следую-
следующую координату
Нет ^^ все коорди-
координаты были рас-
рассмотрены 2
Запомнить
новое значение
координаты
и новое
значение
функции
3
Выход
Рис. 3.3
10 PRINT "МЕТОД ХУКА-ДЖИВСА"
20 REM ФУНКЦИЯ ВЫЧИСЛЯЕТСЯ В ВИДЕ Z»RX1,X2,...,XN> В СТРОКЕ 2000
30 PRINT "ВВЕДИТЕ ЧИСЛО nEPEMEHHblX":INPUT N
40 DIM X(N),B(N),Y<N),P(N)
SO PRINT "ВВЕДИТЕ НАЧАЛЬНЫМ ТОЧКУ X1,X2,..-XN"
60 FOR I»l TO NiINPUT X(I)»NEXT I
70 PRINT "ВВЕДИТЕ ДЛИНУ UArA"iINPUT H
BO K-HsFE-0
90 FOR I»l TO N
1OO Y(I)*X(I)sP(I)»X(I>iB(I)*X<I)sNEXT I
110 60SUB 2000:FI-Z
120 PRINT "НАЧАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ"!
130 FOR 1*1 TO NsPRINT X(I)j" "jiNEXT IiPRINT ""
140 PS-OiBS*l
150 REM ИССЛЕДОВАНИЕ ВОКРУГ БАЗИСНОЙ ТОЧКИ
180 J«1:FB«FI
200 X(J)*Y<J)+K
210 GOSUB 2000
220 IF Z<FI THEN GOTO 280
230 X<J)«Y(J)-K
38
39

240 GOSUB 2000
250 IF Z<FI THEN GOTO 2Э0
260 X(J)«=Y(J>
270 GOTO 290
280 Y<J)=X<J)
290 GOSUB 2000
300 FI»Z
310 PRINT "ИССЛЕДУЮЩИЙ ПОИСКА
320 FDR 1*1 TO NsPRINT X(I>;" ";:NEXT IsPRINT ""
330 IF J=N THEN GOTO 360
340 J=J+1
350 GOTO 200
360 IF FKFB-1E-0B THEN GOTO 540
370 REM ПОСЛЕ ОПЕРАТОРА 360, ЕСЛИ ФУНКЦИЯ УМЕНЬШИЛАСЬ,
ПРОИЗВЕСТИ ПОИСК ПО ОБРАЗЦУ
ЗВО IF PS-1 AND BS«O THEN GOTO 420
390 REM НО ЕСЛИ ИССЛЕДОВАНИЕ ПРОИЗВОДИЛОСЬ ВОКРУГ ТОЧКИ ШАБЛОНА РТ,
395 REM И УМЕНЬШЕНИЕ ФУНКЦИИ НЕ БЫЛО ДОСТИГНУТО, ТО ИЗМЕНИТЬ БАЗИСНУЮ
ТОЧКУ В ОПЕРАТОРЕ 420
400 REM В ПРОТИВНОМ СЛУЧАЕ УМЕНЬШИТЬ ДЛИНУ ШАГА В ОПЕРАТОРЕ 490
410 GOTO 490
420 FOR I»l TO NsP<I)»B(I)sY<I)*B<I):X(I>«»B(I)»NEXT I
430 GOSUB 2000sBS=liPS«0
440 FI«ZiFB-Z
450 PRINT "ЗАМЕНА БАЗИСНОЙ T04KH"Z
460 FOR I=»l TO NiPRINT X(I);" "jiNEXT IiPRINT ""
470 REM (СЛЕДУЕТ ЗА КОММЕНТАРИЕМ В СТРОКЕ 395)
И ПРОВЕСТИ ИССЛЕДОВАНИЕ ВОКРУГ НОВОЙ БАЗИСНОЙ ТОЧКИ
480 J-IjGOTO 200
490 К=К/10
500 PRINT "УМЕНЬШИТЬ ДЛИНУ ШАГА"
510 IF K< 1E-08 THEN GOTO 700
520 REM ЕСЛИ ПОИСК НЕ ЗАКОНЧЕН, ТО ПРОИЗВЕСТИ НОВОЕ
525 REM ИССЛЕДОВАНИЕ ВОКРУГ НОВОЙ БАЗИСНОЙ ТОЧКИ
530 J-lsGOTO 200
535 REM ПОИСК ПО ОБРАЗЦУ
540 FOR 1=1 ТО N8P(I)-2#Y(I)-B(I)
550 Ba>-Y<I)sX<I)-P<I)iY(I)-X<I)
560 NEXT I
570 GOSUB 2000:FB«FIiPS»1jBS=0»FI»Z
580 PRINT "ПОИСК ПО ОБРАЗЦУ'г
590 FOR 1*1 TO NsPRINT X(I)|" ";iNEXT I:PRINT ""
600 REM ПОСЛЕ ЭТОГО ПРОИЗВЕСТИ ИССЛЕДОВАНИЕ ВОКРУГ
ПОСЛЕДНЕЙ ТОЧКИ ОБРАЗЦА
610 J-lxGOTO 2OO
700 PRINT " МИНИМУМ НАЙДЕН"
710 FOR I-l TO NjPRINT "XiTi»mP<I)iNEXT IiPRINT ""
750 PRINT "МИНИМУМ ФУНКЦИИ РАВЕН "FB
760 PRINT "КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО "FE
790 END
2000 г»<Х<1)-2>л2+Ш2)-5>л2+ШЗ)+2)л4
2010 FE»FE+1
2020 REM СЧЕТЧИК КОЛИЧЕСТВА ВЫЧИСЛЕНИЙ ФУНКЦИИ
2030 RETURN
Приведенная выше программа реализует описанную процедуру. Одной или
двух точек бывает недостаточно для определения начальной точки. Первая
точка всегда должна выбираться осмотрительно. ЭВМ работает только с огра-
ограниченной точностью, и ошибки могут накапливаться в процессе сложных вы-
вычислений, особенно если шаг имеет "неудобную" длину. (Обычно мы будем
избегать "неудобной" длины, но программа должна быть работоспособна и в
таких ситуациях.) Поэтому в строке 360, где выясняется вопрос об измене-
40
нии базисной точки, мы избегаем уменьшения длины шага из-за накаплива-
накапливания ошибки введением длины шага, равной 10~8. Мы отслеживаем, где про-
производится исследование — в базисной точке (BS = 1, PS = 0) или в точке об-
образца (BS = О, PS = 1). Как можно убедиться на практике, если не принима-
принимаются такие меры предосторожности даже программа с удовлетворительной
логикой будет неработоспособна.
В приведенной программе минимальная длина шага равна 10~8, но она мо-
может быть изменена (например, в строке 510). Для контроля за выполнением
процедуры в программу введена печать промежуточных результатов. Для
увеличения скорости счета могут быть удалены строки с номерами 120, 130,
310, 320, 450, 460, 500, 580, 590.
Подпрограмма, начинающаяся со строки 2000, вычисляет значение мини-
минимизируемой функции
f{xux2, *з) = (*i -2J + (*2 -5J + (х3 + 2L.
Минимум, очевидно, находится в точке B ; 5 ; —2). Для начальной точки
D ; —2 ; 3) и начального шага длиной 1 приведены некоторые промежуточ-
промежуточные результаты. По ним можно легко проследить за изменениями в ходе ис-
исследований и поиска по образцу. Заметим, что значение 97,0000001 (О2 +
+ 42 + З4 = 97) является значением функции в точке, полученной ранее. Ко-
Количество выполненных вычислений функции запоминается в счетчике. Это ча-
часто используется как средство сравнения эффективности различных методов
поиска. Чем лучше метод, тем меньше в общем случае требуется вычислений
значений функции.
МЕТОД ХУКА-ДЖИВСА
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ 3
ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ X1,X2,...,XN 4-2 3
ВВЕДИТЕ ДЛИНУ ШАГА 1
НАЧАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ 678
4-2 3
ИССЛЕДУЮЦИЙ ПОИСК 675
3-2 3
ИССЛЕДУЮЩИЙ ПОИСК 662
3-13
ИССЛЕДУЮЩИЙ ПОИСК 293
3-12
ПОИСК ПО ОБРАЗЦУ 106
2 О 1
ИССЛЕДУЮЩИЙ ПОИСК 106
2 О 1
ИССЛЕДУЮЦИЙ ПОИСК 97
2 1 1
ИССЛЕДУЮЩИЙ ПОИСК 32
2 1 О
ПОИСК ПО ОБРАЗЦУ 5
1 3 -2
ИССЛЕДУЮЩИЙ ПОИСК 4
2 3-2
ИССЛЕДУЮЩИЙ ПОИСК 1
2 4-2
ИССЛЕДУЮЦИЙ ПОИСК 1
2 4-2
ПОИСК ПО ОБРАЗЦУ 20
2 7-4
41

ИССЛЕДУЮЦИЙ ПОИСК 20
2 7-4
ИССЛЕДУЮЦИЙ ПОИСК 17
2 6-4
ИССЛЕДУЮЦИЙ ПОИСК 2
2 6-3
ЗАМЕНА БАЗИСНОЙ ТОЧКИ 1
2 4-2
ИССЛЕДУЮЦИЙ ПОИСК 1
2 4-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
ПОИСК ПО ОБРАЗЦУ 1
2 6-2
ИССЛЕДУЮЦИЙ ПОИСК 1
2 6-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
ИССЛЕДУЮЦИЙ. ПОИСК О
2 5-2
ЗАМЕНА БАЗИСНОЙ ТОЧКИ О
2 5-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
УМЕНЬШИТЬ ДЛИНУ ШАГА
ИССЛЕДУЮЦИЙ ПОИСК О
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
ИССЛЕДУЮЦИЙ ПОИСК О
2 5-2
УМЕНЬШИТЬ ДЛИНУ ШАГА
МИНИМУМ НАЙДЕН
XI «2
X 2 - 5
X 3 —2
МИНИМУМ ФУНКЦИИ РАВЕН О
КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО
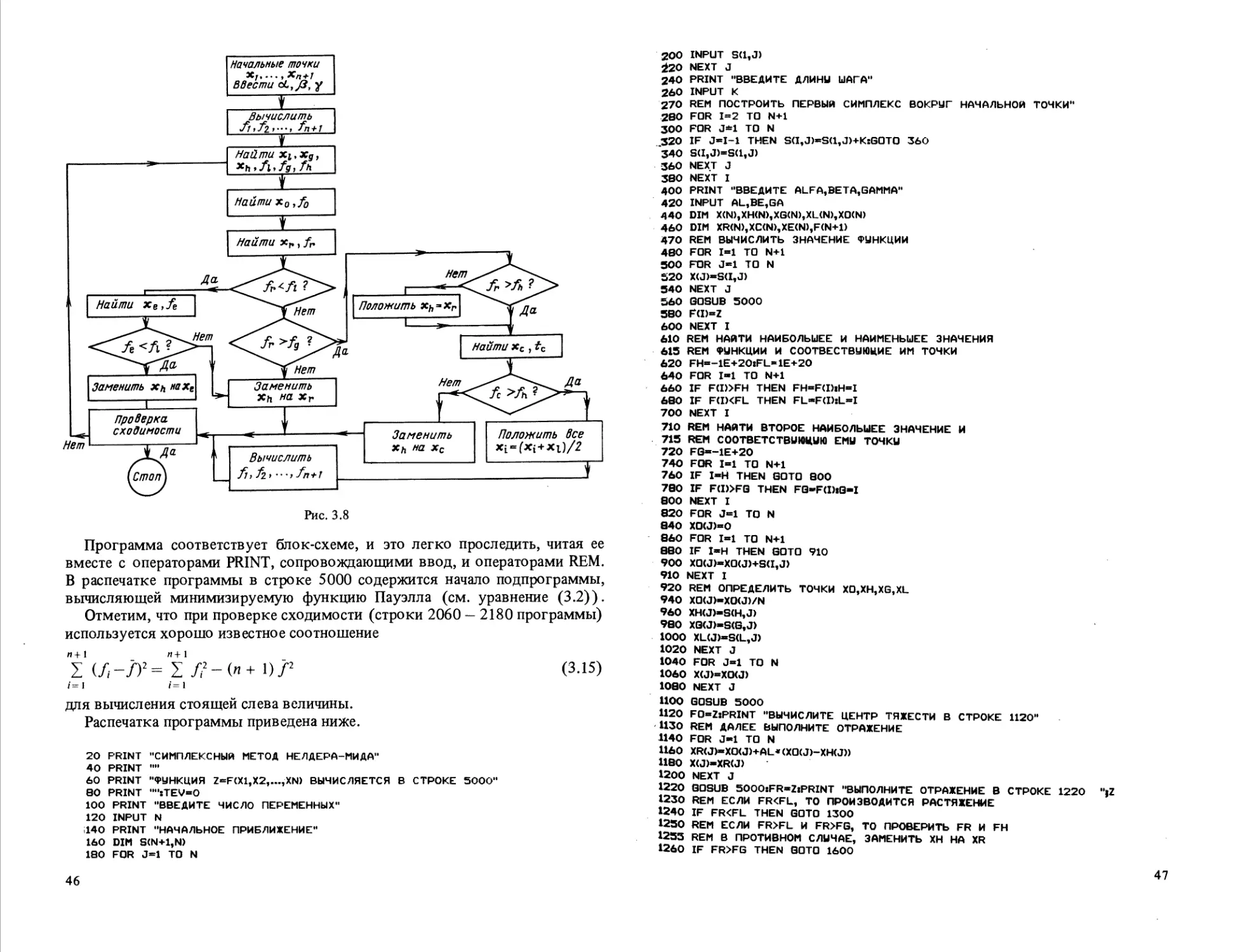
127
3.3. МЕТОД НЕЛДЕРА - МИДА
Метод Нелдера — Мида1 является развитием симплексного метода Спенд-
ли, Хекста и Химсворта. Множество (п + 1)-й равноудаленной точки в «-мер-
«-мерном пространстве называется регулярным симплексом. Эта конфигурация
рассматривается в методе Спендли, Хекста и Химсворта. Следовательно, в
двумерном пространстве симплексом является равносторонний треугольник,
а в трехмерном пространстве — правильный тетраэдр. Идея метода состоит в
сравнении значений функции в (п + 1) вершинах симплекса и перемеще-
перемеще42
1 Называется также поиском по деформируемому многограннику. - Прим. ред
нии симплекса в направлении оптимальной точки с помощью итерационной
процедуры. В симплексном методе, предложенном первоначально, регуляр-
регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили не-
несколько модификаций этого метода, допускающих, чтобы симплексы были
неправильными. В результате получился очень надежный метод прямого по-
поиска, являющийся одним из самых эффективных, если п < 6.
В методе Спендли, Хекста и Химсворта симплекс перемещается с помо-
помощью трех основных операций: отражения, растяжения и сжатия. Смысл этих
операций станет понятным при рассмотрении шагов процедуры.
A. Найдем значения функции
/i =/(xi), /2 =/(x2) .../„ + 1=/(х„+1)
в вершинах симплекса.
Б. Найдем наибольшее значение функции Д, следующее за наибольшим
значением функции fg9 наименьшее значение функции f\ и соответствующие
им точки щ , Xg и X/.
B. Найдем центр тяжести всех точек, за исключением точки х^ . Пусть цент-
центром тяжести будет
1
х/
C.6)
и вычислим /(х0) = /о.
Г. Удобнее всего начать перемещение от точки xh . Отразив точку xh отно-
относительно точки х0, получим точку хг и найдем f(xr) = /,. .
Операция отражения иллюстрируется рис. 3.4. Если а > 0 — коэффициент
отражения, то положение точки хг определяется следующим образом:
-х0 =а(х0 -
C.7)
т. е.
= A +а)х0 ~ocxh .
Замечание, а = \хг - х01/|х0 - xh \.
Д. Сравним значения функций fr и
1. Если /,. < //, то мы получили наименьшее значение функции. Направле-
Направление из точки х0 в точку Ху наиболее удобно для перемещения. Таким об-
образом, мы производим растяжение в этом направлении и находим точку
хе и значение функции fe - f(xe). Рисунок 3.5 иллюстрирует операцию
растяжения симплекса. Коэффициент растяжения у > 1 можно найти из
следующих соотношений:
Рис. 3.4
Рис. 3.5
43

r -x0),
т. e.
-7)x0. C.8)
Замечание, y=\xe—x0\l\xr—x0\.
а) Если fe < fj, то заменяем точку xh на точку хе и проверяем (п +
+ 1)-ую точку симплекса на сходимость к минимуму (см. шаг 3). Если
сходимость достигнута, то процесс останавливается; в противном слу
чае возвращаемся на шаг Б.
б) Если fe > //, то отбрасываем точку хе. Очевидно, мы переместились
слишком далеко от точки х0 к точке х,.. Поэтому следует заменить точ-
точку xh на точку хг , в которой было получено улучшение (шаг Д, 1),
проверить сходимость и, если она не достигнута, вернуться на шаг В.
2. Если /,. > // > но fr < fg, то хг является лучшей точкой по сравнению с
другими двумя точками симплекса и мы заменяем точку xh на точку хг и,
если сходимость не достигнута, возвращаемся на шаг Б, т. е. выполняем
пункт 1,6, описанный выше.
3. Если /,. >// nfr >fgiTO перейдем на шаг Е.
Е. Сравним значения функций /,. и fh .
1. Если fr > fh , то переходим непосредственно к шагу сжатия Е, 2.
Если /,. < fh , то заменяем точку xh на точку хг и значение функции fh
на значение функции /г Запоминаем значение fr > fg из шага Д, 2, приве-
приведенного выше. Затем переходим на шаг Е, 2.
2. В этом случае /,. > Д , поэтому ясно, что мы переместились слишком
далеко от точки х^ к точке х0. Попытаемся исправить это, найдя точку хс
(а затем /с) с помощью шага сжатия, показанного на рис. 3.6.
Если fr > fh , то сразу переходим к шагу сжатия и находим точку хс из
соотношения
где j3 @ < j3 < 1) — коэффициент сжатия. Тогда
. C.9)
Если fr <Д, то сначала заменим точку х^ на точку х,., а затем произве-
произведем сжатие. Тогда точку хс найдем из соотношения
т. е.
(рис. 3.7).
C.10)
Рис. 3.6
Рис. 3.7
Ж. Сравним значения функций fc и
1. Если fc<fh> то заменяем точку xh на точку х^ и если сходимость не
достигнута, то возвращаемся на шаг Б.
2. Если fc > Д , то очевидно, что все наши попытки найти значение мень-
меньшее fh закончились неудачей, поэтому мы переходим на шаг 3.
3. На этом шаге мы уменьшаем размерность симплекса делением пополам
расстояния от каждой точки симплекса до X/ — точки, определяющей наи-
наименьшее значение функции.
Таким образом, точка xt заменяется на точку xt + ^(xz- — xf), т. е. заменя-
заменяем ТОЧКУ Xf ТОЧКОЙ
Й(х* +х/). C.11)
Затем вычисляем /} для / =1,2,..., (п + 1), проверяем сходимость и,
если она не достигнута, возвращаемся на шаг В.
И. Проверка сходимости основана на том, чтобы стандартное отклонение
(п + 1)-го значения функции было меньше некоторого заданного малого
значения е. В этом случае вычисляется
п+Л
= 1 (/,-/O(и+1)
1=1
C.12)
Если а < б, то все значения функции очень близки друг к другу, и поэтому
они, возможно, лежат вблизи точки минимума функции Xj. Исходя из этого
такой критерий сходимости является разумным, хотя Бокс, Дэвис и Свенн
[1] предлагают то, что они считают более "безопасной" проверкой.
Шаги этой процедуры представлены в виде блок-схемы на рис. 3.8.
Коэффициенты а, 0, у в вышеприведенной процедуре являются соответ-
соответственно коэффициентами отражения, сжатия и растяжения. Нел дери Мид ре-
рекомендуют брать а = 1, р = 0,5 и у = 2. Рекомендация основана на результатах
экспериментов с различными комбинациями значений. Эти значения пара-
параметров позволяют методу быть эффективным, но работать в различных
сложных ситуациях.
Начальный симплекс выбирается на наше усмотрение. В данной программе
точка Xi является начальной точкой, затем в программе формируются точки
2 — Aj i I •
C.13)
1 ¦ = xi +
44
где к - произвольная длина шага, a tj - единичный вектор.
Обозначения, используемые в программе, в целом соответствуют обозначе-
обозначениям, приведенным в тексте, за исключением того, что используются пропис-
прописные буквы FE = fe, ХС = хс и т. д. Вершины симплекса обозначаются S. При
этом S(I, J) является J-й компонентой 1-й вершины, т. е.
) if. C.14)
45
=x

Начальные точки
Ввести oL,j3,y
1
Вычислить
jiflf'i fn + 1
Найти xi,xg,
xh ff f
l
Найти xOifo
i
Найти Xj,, fn
Да.
Найти xe,fe
Заменить х^ naxt
нет
Полошить xh=*xr
L
//5/77
Проверка
сходимости
Заменить
хг
Вычислить
JU fl> -"t fn +
Заменить
на хс
Полоти/ль все
/
Рис. 3.8
Программа соответствует блок-схеме, и это легко проследить, читая ее
вместе с операторами PRINT, сопровождающими ввод, и операторами REM.
В распечатке программы в строке 5000 содержится начало подпрограммы,
вычисляющей минимизируемую функцию Пауэлла (см. уравнение C.2)).
Отметим, что при проверке сходимости (строки 2060 — 2180 программы)
используется хорошо известное соотношение
л+1
i= I
l)/:
C.15)
i=
для вычисления стоящей слева величины.
Распечатка программы приведена ниже.
20 PRINT "СИМПЛЕКСНЫЙ МЕТОД НЕЛДЕРА-МИДА"
40 PRINT ""
60 PRINT "ФУНКЦИЯ Z«F(X1,X2,...,-XN) ВЫЧИСЛЯЕТСЯ В СТРОКЕ 5000"
80 PRINT imiTEV«O
100 PRINT "ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ"
120 INPUT N
140 PRINT "НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ"
160 DIM S(N+1,N)
180 FOR J=l TO N
200 INPUT SA,J)
220 NEXT J
240 PRINT "ВВЕДИТЕ ДЛИНЫ ЫАГА"
260 INPUT К
270 REM ПОСТРОИТЬ ПЕРВЫЙ СИМПЛЕКС ВОКРУГ НАЧАЛЬНОЙ ТОЧКИ"
280 FOR 1=2 ТО N+1
300 FOR J=l TO N
320 IF J«I-1 THEN S(I,J)«SA,J)+K:GOTO 360
340 S(I,J)-SA,J)
360 NEXT J
380 NEXT I
400 PRINT "ВВЕДИТЕ ALFA,BETA,GAMMA"
420 INPUT AL,BE,GA
440 DIM X(N),XH(N),XG(N),XL(N),XO(N)
460 DIM XR(N),XC(N),XE(N),F(N+1)
470 REM ВЫЧИСЛИТЬ ЗНАЧЕНИЕ ФУНКЦИИ
480 FOR 1=1 TO N+1
500 FOR J«l TO N
520 X(J)*S(I,J)
540 NEXT J
560 60SUB 5000
580 F(I)=Z
600 NEXT I
610 REM НАЙТИ НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
615 REM ФУНКЦИИ И СООТВЕСТВУЮЦИЕ ИМ ТОЧКИ
620 FH=-lE+20sFL»lE+20
640 FOR I-l TO N+1
660 IF F(I»FH THEN FH=F(I)iH=I
680 IF FdXFL THEN FL*F(I):L»I
700 NEXT I
710 REM НАЙТИ ВТОРОЕ НАИБОЛЬШЕЕ ЗНАЧЕНИЕ И
715 REM СООТВЕТСТВУЮЩУЮ EMU ТОЧКУ
720 FG—1E+20
740 FOR 1=1 ТО N+1
760 IF I*H THEN GOTO 800
780 IF F(I»FB THEN FG»F(I)iG-I
800 NEXT I
820 FOR J=l TO N
840 XO(J)=O
860 FOR 1=1 TO N+1
880 IF I*H THEN GOTO 910
900 XO<J)*XO(J)+S<I,J>
910 NEXT I
920 REM ОПРЕДЕЛИТЬ ТОЧКИ XO,XH,XG,XL
940 XO(J)«XO(J)/N
960 XH<J)«S(H,J)
980 XG(J)«S<G,J>
1000 XL(J)*S(L,J)
1020 NEXT J
1040 FOR J=l TO N
1060 X(J)=XO(J)
1080 NEXT J
1100 GOSUB 5000
1120 FO=Z:PRINT "ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120"
ИЗО REM ДАЛЕЕ ВЫПОЛНИТЕ ОТРАЖЕНИЕ
1140 FOR J«l TO N
1160 XR<J>*XO<J>+AL*<XO<J)-XH<J»
ПВО X(J)«XR(J)
1200 NEXT J
1220 80SUB 5000sFR*ZiPRINT "ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220
1230 REM ЕСЛИ FR<FL, TO ПРОИЗВОДИТСЯ РАСТЯЖЕНИЕ
1240 IF FR<FL THEN GOTO 1300
1250 REM ЕСЛИ FR>FL И FR>FG, TO ПРОВЕРИТЬ FR И FH
1253 REM В ПРОТИВНОМ СЛУЧАЕ, ЗАМЕНИТЬ ХН НА XR
1260 IF FR>FG THEN GOTO 1600
46
47

1280
1290
1300
1320
1340
1360
1380
1400
1420
1440
1460
1480
1490
1500
1520
1540
1560
1580
1600
1620
1640
1660
1680
1690
1700
1720
1740
1760
1780
1800
1820
1840
1860
1880
1900
1910
1920
1940
1960
1980
2000
2020
2040
2050
2060
2080
2100
2120
2140
2160
2180
2200
2220
2240
2260
2280
2300
2320
2340
5000
5020
5040
5060
5100
GOTO 1520
REM ДАЛЕЕ ВЫПОЛНЯЕТСЯ РАСТЯЖЕНИЕ
FOR J=l TO N
XE<J>=GA»XR<J)+<1-GA)*XO(J)
X(J)«XE(J)
NEXT J
GOSUB 5000:FE*Z
IF FE<FL THEN GOTO 1440
GOTO 1520
FOR J*l TO N
S(H,J)=XE(J)
NEXT J:F(H)=FE:PRINT "ВЫПОЛНИТЕ РАСТЯЖЕНИЕ В СТРОКЕ 1480
REM ПРОВЕРИТЬ СХОДИМОСТЬ В СТРОКЕ 2060
GOTO 2060
FOR J«l TO N
S(H,J)=-XR(J)
NEXT J:F(H)*FRsPRINT "ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1560"
GOTO 2060
IF FR>FH THEN GOTO 1700
FOR J*l TO N
XH(J)*XR(J)
NEXT J
F(H)=FR
REM ДАЛЕЕ СЛЕДУЕТ СЖАТИЕ
FOR J=l TO N
XC(J)*BE»XH(J)+A-BE)*XO(J)
X(J)«XC(J>
NEXT J
GOSUB 5000:FOZ
IF FOFH THEN GOTO 1920
FOR J=l TO N
S(H,J)=XC(J)
NEXT J
F(H)*FC:PRINT "ВЫПОЛНИТЕ СЖАТИЕ В СТРОКЕ 1880 ";Z
GOTO 2060
REM ДАЛЕЕ СЛЕДУЕТ РЕДУКЦИЯ СИМПЛЕКСА
FOR 1=1 ТО N+1
FOR J«l TO N
S<I,J)=<SU,J)+XL<J»/2
X(J)=S(I,J)
NEXT J
GOSUB 5000:F(I)=Z
NEXT I:PRINT "ВЫПОЛНИТЕ РЕДУКЦИЮ В СТРОКЕ 2040"
REM ДАЛЕЕ СЛЕДУЕТ ПРОВЕРКА СХОДИМОСТИ
Sl*0:S2«0
FOR 1=1 ТО N+1
S2*S2+F(I)»F(I)
NEXT I
SIG=S2-S1*S1/<N+1):SIG = SIGAN+1)
IF SIG<1E-1O THEN GOTO 2220
GOTO 620
PRINT "МИНИМУМ НАЙДЕН В ТОЧКЕ ¦•'
FOR J=l TO N
PRINT "X";J;" =";XL(J)
NEXT JrPRINT ""
PRINT "ЗНАЧЕНИЕ МИНИМУМА ФУНКЦИИ="Р<1_>
PRINT "КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ="ТЕУ
END
Z=(X(l)+10*XB))'42+5*<XC)-XD))^2
Z=Z+(X<2)-2*X<3»~4
Z=Z+10»(X(l)-XD))^4
TEV=TEV+1
RETURN
пример 1
Использовать метод Нелдера - Мида для минимизации функции Розенброка / {хг,
Х2) = 100(х2 - х\J + A - ххJ. Положив к = 0,5 и выбрав в качестве начального
приближения точку A,5; 2), и для коэффициента сжатия использовать значения а = 1, •
0 = 0,5 и у = 2.
При правильном изменении строки 5000 в подпрограмме начало и конец распечатки
результатов выглядят так, как это представлено ниже. При этом достаточно просто мож-
можно проследить за работой процедуры. Вывод на печать в строках 1120, 1220, 1480, 1560,
2040 можно "подавить", и это повысит скорость выполнения программы.
Истинный минимум имеет значение 0 в точке A; 1) .
СИМПЛЕКСНЫЙ МЕТОД НЕЛДЕРА-МИДА
ФУНКЦИЯ Z=F(Xl,X2f...?XM> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 5000
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ 2
НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ 1.5 2
ВВЕДИТЕ ДЛИНУ УАГА .5
ВВЕДИТЕ ALFA,BETAfGAMMA 1 .5 2
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 225
ВЫПОЛНИТЕ СЖАТИЕ В СТРОКЕ 1880 66.07813
ВЫЧИСЛИТЕ ЦЕНТР ТЯГЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 88.45312
ВЫПОЛНИТЕ СЖАТИЕ В СТРОКЕ 1880 17.93848
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 20.92285
ВЫПОЛНИТЕ СЖАТИЕ В СТРОКЕ 1880 4.80719
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 51.29157
ВЫПОЛНИТЕ С 'АТИЕ В СТРОКЕ 1880 .2411101
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 .3819754
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1560
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 7.327366
ВЫПОЛНИТЕ С АТИЕ В СТРОКЕ 1880 1.094459
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 6.В77291Е-05
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1560
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 1.433001Е-04
ВЫПОЛНИТЕ СЖАТИЕ В СТРОКЕ 1880 2.7В7633Е-05
ВЫЧИСЛИТЕ ЦЕНТР ТЯЖЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 3.54833Е-05
ВЫПОЛНИТЕ СЖАТИЕ В СТРОКЕ 1880 8.852308Е-06
ВЫЧИСЛИТЕ ЦЕНТР ТЯ/.ЕСТИ В СТРОКЕ 1120
ВЫПОЛНИТЕ ОТРАЖЕНИЕ В СТРОКЕ 1220 2.155905Е-05
ВЫПОЛНИТЕ СЖАТИЕ В СТРОКЕ 1880 5.518512Е-06
МИНИМУМ НАЙДЕН В ТОЧКЕ
X 1 - 1.000634
X 2 - 1.001357
ЗНАЧЕНИЕ МИНИМУМА ФУНКЦИИ РАВНО 1.194424Е-06
КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО 108
3.4. ЛИТЕРАТУРА
48
М. J. Box, D. Davies and W. H. Swann, Non-linear Optimisation Techniques, 1С I LtcL
Monograph No. 5, Oliver and Boyd, 1969.
R. Hooke and T. A. Jeeves, 'Direct search solution of numerical and statistical probierns\
J.Assn. Сотр. Mack*, 8, 212-229, 1961.
49

3 J. A. Nelder and R. Mead, 'A simplex method for function minimisation', The Comp
Journal, 7, 308-313, 1965.
4 M. J. D. Powell, 'An iterative method for finding stationary values of a function of several
variables', The Сотр. Journal, 5, 147-151, 1962.
5 H. H. Rosenbrock, 'An automatic method for finding the greatest or least value of a
function', The Сотр. Journal 3, 175-184, 1960.
6 W. Spendley, G. R. Hext and F. R. Himsworth, 'Sequential applications of simplex designs
in optimisation and evolutionary operation', Technometrics, 4, 441-461, 1962.
3.5. УПРАЖНЕНИЯ
1. Попробуйте написать программу на языке Бейсик, реализующую метод покоорди-
покоординатного спуска. Можете применить в качестве подпрограммы для этого метода лю-
любой из алгоритмов одномерного поиска для функции одной переменной, приведен-
приведенных в гл. 2.
2. Используйте программу, написанную вами в п. 1 упражнений для поиска минимума
функции (хг - 1J + (х2 - 2) 2 + (х3 - 3) 2 и функции Розенброка 100 (х2 - х\J +
3. Воспользуйтесь программой, реализующей метод Хука - Дживса для минимизаций
функций. Сравните количество вычислений функции, потребовавшихся в этом слу-
случае и в случае метода покоординатного спуска.
4. Повторите упр. 2 и упр. 3 с разными начальными точками.
5. Модифицируйте метод Нелдера - Мида, заменив коэффициент, уменьшающий дли-
длину шага, т. е. вместо 10 используйте (а) 2, (б) 4, (в) 8, (г) 100. Выполните повтор-
повторно упр. 2 и упр. 3. Сравните количество вычислений функции, необходимых для до-
достижения конечного результата.
6. Используя программу Нелдера - Мида, минимизируйте функцию Розенброка, функ-
функцию Пауэлла, двумерную экспоненциальную функцию (уравнения C.1) - C.3)).
Используйте различные начальные значения и сравните количество вычислений функ-
функции. Особенно неудобными для минимизации являются точки (-1,2; 1) для функ-
функции Розенброка и C; -1; 0; 1) для функции Пауэлла.
7. Ознакомьтесь с работой Бокса, Дэвиса и Свена, используйте предложенную ими про-
проверку сходимости в программе Нелдера - Мида и примените результаты к функци-
функциям, упомянутым в упр. 6.
8. Модифицируйте программу Нелдера — Мида, используя различные значения для
а, /3 и у. Проведите оценку получающихся результатов. Ознакомьтесь со статьей
[3] и с замечаниями по этому вопросу.
9. Ознакомьтесь с работой [б]. Напишите программу на языке Бейсик, реализующую
метод Спендли, Хекста и Химсворта, и примените ее на практике. Чем она отличается
от программы Нелдера - Мида в отношении требуемого количества вычислений
функции?
10. Минимизируйте функцию
Лх х } = х4 + х4 + 2х2х* — 4* + Я
11. Минимизируйте функцию
v(xlfx2) = (х\ +х2 -ИJ + (xj +х22 - 7J.
12. Решите уравнения
х\ +х2 = 11,
Как можно использовать упр. 11, чтобы помочь в решении этих уравнений?
13. Решите систему уравнений
x + y + z = 6,
Х2 +у2 +Z2 _ 14)
х3 + у3 +z3 ¦= 36.
14. Переменные F и С связаны соотношением F = а + ЬС, но при измерении величины F
появляется ошибка.
Определите значения а и Ъ по следующим данным:
F 51 68 84 103 121 141
С 10 20 30 40 50 60
Используйте принцип наименьших квадратов и найдите а и Ъ по результатам мини-
минимизации функции
S=i(F,-a- ЬС,)г.
Это - простая задача линейной регрессии. Данный вопрос рассматривается во мно-
многих книгах по элементарной статистике, существуют формулы, по которым легко
вычислить а и Ъ. Проверьте полученный вами ответ, используя эти результаты.
15. Известно, что переменные Q и h связаны соотношением (обусловленным ошибкой
в измерении Q) Q = ahn, гдеаип — постоянные.
Используя приведенные ниже данные, покажите, что это соотношение имеет смысл,
и получите значения аип:
h 4 6 8 10 12
Q 650 1740 3640 6360 9790
Замечание. Если Q — ahn, то h\(Q) = In (a) + n In (Л). Таким образом, можно привести
настоящую задачу к задаче линейной регрессии с преобразованными переменными
1п@ и In (Л). Решите ее с помощью преобразования и без него, основываясь на прин-
принципе наименьших квадратов, т. е. минимизируйте функции
1) Sx = 2 [In(?/) - In(e) - п 1п(Лг0]2,
n
изменяя значения а ил. Получились ли ответы одинаковыми?
х\ = 7.
50
ГЛАВА 4. ГРАДИЕНТНЫЕ МЕТОДЫ
4.1. МЕТОД НАИСКОРЕЙШЕГО СПУСКА
В этой главе рассматриваются методы поиска, в которых наряду со значе-
значениями функции используется и ее градиент. С помощью упомянутого в
разд. 3.1 метода покоординатного спуска осуществляется поиск из заданной
точки в направлении, параллельном одной из осей, до точки минимума в дан-
данном направлении. Затем поиск производится в направлении, параллельном
другой оси, и т. д. Направления, конечно, фиксированы. Кажется разумным
попытаться модифицировать этот метод таким образом, чтобы на каждом
этапе поиск точки минимума производился вдоль "наилучшего" направле-
направления. Не ясно, какое направление является "наилучшим", но известно, что на-
51

правление градиента является направлением наискорейшего возрастания
функции. Следовательно, противоположное направление является направле
нием наискорейшего убывания функции.
Это свойство может быть обосновано следующим образом. Предположим,
что осуществляется перемещение из точки х в следующую точку х + hd, где
d — некоторое направление, a h — шаг некоторой длины. Следовательно, не
ремещение производится из точки (xif х2, . . . , хп) в точку (xi + 8xlfx2 +
+ 8х2,.. ., хп + дхп), где
8x; = hdi9 D.1)
a dj — косинусы направления d, такие, что
п
D
2
Изменение значений функции определяется соотношениями
„ х2 + &с29..., хп + 6xn)-f{xv х29..., хя) =
8х
+ ... + — 5дгл D.3)
х 8х2 dxn
с точностью до первого порядка Ъх^ причем частные производные вычисли
ются в точке х (в соответствии с уравнением A.4)). Как следует выбрать
направления dh удовлетворяющие уравнению D.2), чтобы получить наиболь-
наибольшее значение изменения функции d/?
Здесь возникает задача максимизации с ограничением, и для ее решения
предвосхитим здесь результаты следующей главы, используя метод множите
лей Лагранжа, с помощью которого определим функцию
*(dl9d29.:.9dn)=&f+\{*Ld] -1).
Величина d/, удовлетворяющая ограничению D.2), достигает максимума,
когда функция
дх2
достигает максимума. Ее производная
df
+ 2kd:, при /=12 n
'n
8dj
Если
D.4)
= 0, то
Следовательно,
52
h_ df
2Л
D.5)
dxl
8x
D.6)
П
Тогда di ~ df/dxi и направление d параллельно направлению V/(x) в точке х.
Таким образом, наибольшее локальное возрастание функции для заданно-
заданного малого шага h имеет место, когда d есть направление V/(x) или g (х). По-
Поэтому направлением наискорейшего спуска является направление
-V/(x) или -g(x). D.7)
В более простом виде уравнение D.3) можно записать так:
d/=|V/(x)||dx|cos0,
где В - угол между векторами V/(x) и dx. Для заданной величины dx мы ми-
минимизируем d/, выбирая в = 180°, чтобы направление dx совпадало с направ-
направлением —V/(x).
Замечание. Направление градиента перпендикулярно в любой точке линии
постоянного уровня, поскольку вдоль этой линии функция постоянна. Та-
Таким образом, если (<2Ь d2i . . . , dn) — малый шаг вдоль линии уровня, то
f(xi +dux2 +d2f. .. ,хп +dn) = f(xux2,. ..,xn)
и, следовательно,
df
0.
(рис. 4.1).
В методе наискорейшего спуска же-
желательно использовать рассмотренное
свойство направления градиента. Поэто-
Поэтому, если мы находимся в точке xz- на
некотором шаге процесса оптимизации,
то поиск минимума функции осуще-
осуществляется вдоль направления —Vf(xj).
Данный метод является итерацион-
итерационным. На шаге / точка минимума аппрок-
аппроксимируется точкой xz-. Следующей ап-
аппроксимацией является точка
¦
Рис. 4.1
где X,- — значение X, минимизирующее функцию
D.9)
D.10)
Значение Х7- может быть найдено с помощью одного из методов одномер-
одномерного поиска, описанных в гл. 2. Блок-схема метода наискорейшего спуска
приведена на рис. 4.2.
53

-98»
начать из точки
Найти значение Х\,
минимизирующее функцию
f(x\+Xdi)
Полошить 1=1
мет ^ x-l+J
/почка оптимума?
да
Положить «*=3c*l+j
Рис. 4.2
2О PRINT "МЕТОД НАИСКОРЕЙШЕГО СПУСКА"
40 PRINT "ФУНКЦИЯ Z=F(X1,X2,...,XN) ВЫЧИСЛЯЕТСЯ В СТРОКЕ 2ООО"
60 PRINT "ЧАСТНЫЕ ПРОИЗВОДНЫЕ GU),G<2>f...,G<N> ВЫЧИСЛЯЮТСЯ В СТРОКЕ 3000"
80 PRINT "ОДНОМЕРНЫЙ ПОИСК ПРОИЗВОДИТСЯ МЕТОДОМ КВАДРАТИЧНОЙ ИНТЕРПОЛЯЦИИ11
100 PRINT "ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ":INPUT N
120 DIM X(N)fY<N)fG<N),D<N),L<4),FF<4)
140 REM МАССИВЫ LD) И FFD) ИСПОЛЬЗУЮТСЯ ПРИ КВАДРАТИЧНОЙ ИНТЕРПОЛЯЦИИ
160 PRINT "ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ
1В0 FOR 1=1 ТО NiINPUT X(I):NEXT I
200 PRINT "ВВЕДИТЕ НАЧАЛЬНЫЙ UAr":INPUT L
250 PRINT " ТЕКУ ИЕ ЗНАЧЕНИЯ"
260 REM ЗАГОЛОВОК ДЛЯ ПРОМЕЖУТОЧНОГО ВЫВОДА
300 FOR 1*1 ТО N:Y(I)=X(I):NEXT I
320 GOSUB 2000:G0SUB 3000:IF G0<.000001 THEN GOTO 1200
340 FOR 1=1 TO N:D<I>=-G<I)/GOsNEXT I
360 REM ЗАДАТЬ НАПРАВЛЕНИЕ НАИСКОРЕЙШЕГО СПУСКА ИЗ ТОЧКИ Yd)
370 REM СРАВНОЙ В НАЧАЛЕ ХШ:
ЗВО L<1)=O:FF<1)=Z:ZZ=Z
400 L<3>*L
410 FOR I=*l TO N:X<I)=Y<I>+L<3>*DCI)sNEXT I
430 GOSUB 2000:FFC>=Z
440 GOSUB 3000
450 G2=0
460 FOR 1=1 TO N:G2=G2+G(I>*D(I):NEXT I
470 IF FF<3)>=FFQ> OR G2>=0 THEN GOTO 500
480 L=2*L:G0T0 400
500 REM В СТРОКЕ 480 УДВОИТЬ ДЛИНУ ШАГА,
510 REM ЧТОБЫ "НАКРЫТЬ" МИНИМУМ
520 LB)=L/2
540 FOR 1*1 ТО NiX(I)=Y(I>+LB>*D<I):NEXT I
560 GOSUB 2000:FF<2)=Z
580 REM ВЫПОЛНИТЬ ПЕРВУЮ КВАДРАТИЧНУЮ ИНТЕРПОЛЯЦИЮ
54
600 LD)-L*(FF<2)-.75*FFA)-.25*FF<3))/<2*FFB)-FFA)-FF<3))
620 IF LC4K0 THEN PRINT "ВНИМАНИЕ"
640 FOR 1=1 TO N:X<I)=Y<I>+L<4)*D<I>:NEXT I
660 GOSUB 2000:FFD)=Z
6B0 REM ИМЕЕМ 4 ЗНАЧЕНИЯ LAMBDA И 4 ЗНАЧЕНИЯ ФУНКЦИИ,
690 REM УПОРЯДОЧИТЬ ИХ В ПОРЯДКЕ УБЫВАНИЯ
700 FOR J=l TO 3
710 FOR K=J+1 TO 4
720 IF FF(JX=FF(K> THEN GOTO 760
730 LL=L<J):L(J)-L<K):L(K)=LL
740 FO-FF<J)«FF<J)=FF<K):FF(K)=FO
750 REM ПОМЕНЯТЬ МЕСТАМИ FF<J> И FF(K), ЕСЛИ ОНИ НЕ УПОРЯДОЧЕНЫ
760 NEXT KsNEXT J
790 REM ЗАКОНЧИТЬ ПОИСК В ДАННОМ НАПРАВЛЕНИИ,
795 REM ЕСЛИ ТОЧНОСТЬ ДОСТИГНУТА В СТРОКЕ 800
800 IF ABS<L(l)-LB)X.00005 THEN GOTO 1000
810 REM ЗАПОМНИТЬ ТРИ ЛУЧШИХ ТОЧКИ
820 S1*SGN<L<2)-L<1)):S2=SGN<LC)-L<D)
830 S3-SGN<L<4)-L<1»
840 IF S1=S2 AND Sl=-S3 THEN L<3)=LD):FFC)=FFD)
850 REM ВТОРАЯ И ПОСЛЕДНЯЯ ИНТЕРПОЛЯЦИЯ
860 D№=<L<2)-LC»*FF<1)+(LC)-LA))*FFB)+(L<1)-LB))*FFC)
870 F=<FFU>-FF<2))/<2*DN>
880 F=F#(L<2)-LC»*<L<3)-L<1)>
890 ~L<4>-<LU)+L<2»/2+F
900 FOR 1-1 TO N:X<I>*Y<I)-H_<4)*D<I):NEXT I
910 GOSUB 2000iFFD)=Z
920 REM ПОВТОРИТЬ ВТОРУЮ ИНТЕРПОЛЯЦИЮ
930 GOTO 700
1000 FOR 1=1 TO N:X<I)=Y<I)+LA)*D(I)
1002 Y<I)=X(I):PRINT "Xn;l5"="sXa)
1005 NEXT I
1010 PRINT ""
1020 GOSUB 2000:G0SUB 3000
1040 PRINT "F="Z:PRINT ""
1080 L=L/2
1100 IF G0>.00001 THEN GOTO 340
1150 REM ПЕРЕХОД НА НАЧАЛО СЛЕДУЮЩЕЙ ИТЕРАЦИИ ПОИСКА ИЗ ТЕКУУ.ЕЙ ТОЧКИ
1200 PRINT "":PRINT
1220 FOR 1=1 ТО N:PRINT "X";I;"»";X(I):NEXT I
1240 PRINT "МИНИМУМ ФУНКЦИИ F<X1,X2,...,XN)="Z
1300 END
2000 2
2090 FE-FE+1
2100 RETURN
3000 GO-0
3100 G<1>-2*<X<1)-1>
3200 G<2>«2»<X<2>-3)
3300 G<3>»8#<X<3>+5>
3800 FOR 1=1 TO N:GO-GO+GU)*G<I>:NEXT I
3810 GO=SQR(GO)
4000 RETURN
Выше приведена программа, реализующая метод наискорейшего спуска.
В ней использованы те же обозначения, что и на блок-схеме, только записан-
записанные прописными буквами, а множитель Лагранжа X обозначен через L. Век-
Вектор в строке 340 является единичным.
Для поиска минимума функции
V>(\) = Дх,- + Ч) D.11)
в направлении dz- из точки хг- используется метод квадратичной интерполяции.
55

м
о
Рис. 4.3
В точке X/ Л = 0, и мы выбираем длину шага Л такой, чтобы шаг "пере-
"перекрыл" минимум функции <р (Л). Производная
па
Ad,)Td/.
D.12)
В строке 460 программы вычисляется выражение B.16), которое обознача-
обозначается G2. В строке 470 проверяется условие "перекрытия" минимума, кото-
которое выполняется, если либо <р(Х) > </>@), либо d</?(X)/dX(= G2) > 0.
Замечание. d^(O)/dX = -g(x/)Tg(x/) <0 (рис. 4.3,а) и
Если минимум не попал в отрезок @, X), то X удваивается, и это повторя-
повторяется столько раз, сколько необходимо для выполнения условия "перекры-
"перекрытия .
Удостоверившись, что отрезок @, X) содержит минимум, в качестве тре-
третьей точки возьмем точку Х/2. Минимальную точку сглаживающего квадра-
квадратичного полинома находим в соответствии с соотношением B.12) (см.
упр. 8 разд. 2.8) при t = Х/2, что отражено в строке 600 программы.
Теперь квадратичная интерполяция повторяет программу, приведенную в
разд. 2.4, за исключением того, что номера строк увеличены на 300. Точность,
заданная в строке 800, конечно, может быть изменена.
В строке 1000 производится присваивание хг+ х = щ, и если lg(xz- + г) | до-
достаточно мало, то процесс заканчивается (эта проверка производится в стро-
строке 1100 программы). Длину шага уменьшают в строке 1080. В процессе по-
поиска предполагается сходимость к экстремуму, поэтому для эффективности
процедуры разумно уменьшить длину шага. При этом деление шага именно
на 2 выбрано произвольно.
Пример 1
Используя приведенную выше программу, найти минимум функции
f(xlfx2)x3) = (хг -1J + (х2 -3J+4(г3+5J.
Для решения данной задачи подходит приведенная выше программа. Минимум, оче-
очевидно, равен нулю при хх = 1, х2= 3, хъ = -5. Из начальной точки D; -1; 2) и с на-
начальным шагом длиной 4 с помощью данной программы можно найти минимум за 11
итераций. Ниже приведена распечатка результата работы программы.
56
МЕТОД НАИСКОРЕЙШЕГО СПУСКА
ФУНКЦИЯ Z=F<X1,X2,...,XN> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 2000
ЧАСТНЫЕ ПРОИЗВОДНЫЕ G<D,G<2>,...,G<N) ВЫЧИСЛЯЮТСЯ В СТРОКЕ 3000
ОДНОМЕРНЫЙ ПОИСК ПРОИЗВОДИТСЯ МЕТОДОМ КВАДРАТИЧНОЙ ИНТЕРПОЛЯЦИИ
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
3
^ВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ
4
ВВЕДИТЕ НАЧАЛЬНЫЙ ШАГ
4
ТЕКУЩИЕ ЗНАЧЕНИЯ
X 1 = 3.232205
X 2 = .0237267
X 3 =-5.166087
F= 13.95128
X 1 = 1.189384
X 2 = 2.747488
X 3 =-4.558105
F= .880715
X 1 = 1.140915
Х2 = 2.812114
X 3 =-5.010485
F= .0555979
X 1 = 1.011955
X 2 = 2.98406
X 3 =-4.972104
F= 3.50976E-03
X 1 = 1.008896
X 2 = 2.988139
X 3 =-5.000662
F= 2.215617E-04
X 1 - 1.000754
X 2 = 2.998995
X 3 —4.99824
F= 1.396853E-05
X 1 = 1.000561
X 2 = 2.999252
X 3 =-5.000042
F- 8.804964E-07
X 1 * 1.000047
X 2 = 2.999937
X 3 —4.99989
F= 5.51017E-08
X 1 * 1.000035
X 2 = 2.999954
X 3 —5.00Q003
F= 3.422542E-09
57

X 1 - 1.000004
X2 = 2.999995
X 3 =-4.999993
F= 2.683578E-10
X 1 - 1.000003
X 2 * 2.999997
X 3 =-5
F« 1.966782E-U
X 1 - 1.000003
X 2 = 2.999997
X 3 =-5
МИНИМУМ ФУНКЦИИ F(X1,X2,...,XN)=
1.966782E-11
Критерий завершения каждой итерации приведен в строке 800. Как пока-
показывает опыт, не обязательно проводить одномерный поиск тщательно. Необ-
Необходимо добиться лишь уменьшения значения функции по сравнению со зна-
значением /(х,-). Поэтому, вероятно, лучше заменить оператор в строке 800 на
оператор
800 IF FFA) <ZZ THEN GOTO 1000
На первый взгляд это может показаться довольно грубым приемом. Однако
объем вычислений .при точном поиске минимума может оказаться весьма зна-
значительным. Практический опыт решения подобного рода задач показывает,
что это неоправданно. То, что теряется на этом этапе в "погоне за точностью",
компенсируется "продвижением к минимуму по изменяющимся обходным
направлениям". Это продемонстрировано в решении следующего примера 2.
Пример 2
Найти минимум функции
f(xlfx2,x3) = (х, - IL + (х2 -ЗJ +4(х3 +5L.
Очевидно, что минимум функции равен нулю в точке A; 3; -5) . Распечатка результа-
результата работы программы приведена ниже. Для поиска решения потребовалось девять ите-
итераций.
МЕТОД НАИСКОРЕЙШЕГО СПУСКА
ФУНКЦИЯ Z=F<Xl,X2f...,XN> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 2000
ЧАСТНЫЕ ПРОИЗВОДНЫЕ GA),GB),...,G(N) ВЫЧИСЛЯЮТСЯ В СТРОКЕ 3000
ОДНОМЕРНЫЙ ПОИСК ПРОИЗВОДИТСЯ МЕТОДОМ КВАДРАТИЧНОЙ ИНТЕРПОЛЯЦИИ
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
3
ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ
4
2
-1
ВВЕДИТЕ НАЧАЛЬНЫЙ ШАГ
4
ТЕКУЩИЕ ЗНАЧЕНИЯ
X 1 =-.1757255
X 2 - 2.077328
X 3 =-2.237252
F= 33.29327
58
X 1 = .6431065
X 2 * 2.30976
X 3 =-5.021118
F= .4944399
iX 1 = .7308417
X 2 = 2.975843
X 3 =-4.939602
F= 2.042376E-02
X 1 = .7408926
X 2 = 2.982069
X 3 =-5.001866
F= 4.842788E-03
X 1 = .8003951
X 2 = 3.012736
X 3 =-4.989102
F= 2.224726E-03
X 1 = .8051051
X 2 = 3.008965
X 3 =-5.002012
F= 1.539329E-03
Теперь все внимание должно быть сосредоточено на программах. Каза-
Казалось бы, достаточно заменить подпрограммы вычисления функции и аргу-
аргумента. Если бы все было так просто! На сегодняшний день не существует
"универсального оптимизатора", который всегда гарантирует удачный ре-
результат. Приведенные программы вполне ясны, однако при их использовании
требуется осторожность. Их работа может неожиданно завершиться неуда-
неудачей из-за слабого изменения критерия завершения (например, от значений
< 0,00001 до значений < 0,0001). Если требуется точность большая, чем мо-
может обеспечить ЭВМ, то программа может "зациклиться". Это справедливо
для всех программ, поэтому будьте готовы в отдельных случаях проявить
настойчивость.
Следует сказать, что метод наискорейшего спуска не рекомендуется в ка-
качестве "серьезной" оптимизационной процедуры. На первый взгляд он при-
привлекателен, но для практического применения "работает" слишком медлен-
медленно. Дело в том, что свойство наискорейшего спуска является лишь локаль-
локальным свойством, и поэтому необходимо частое изменение направления, что и
приводит в итоге к неэффективной вычислительной процедуре. Метод ока-
оказывается непригодным для использования вторых производных целевой
функции.
Наилучший способ применения вторых производных состоит в разработ-
разработке метода, основанного на свойствах квадратичных функций, которые явля-
являются одними из простейших. Если использовать разложение в ряд Тейлора
A.4), то можно заметить, что в окрестности минимума любая функция мо-
может быть аппроксимирована квадратичной функцией, если ее вторые произ-
59

водные не равны нулю. Поэтому методы поиска для квадратичных функций
могут успешно применяться и для других функций.
В следующем разделе будут получены некоторые важные свойства квадра-
квадратичной функции п переменных.
Квадратичная функция
4.2. КВАДРАТИЧНЫЕ ФУНКЦИИ
D.13)
где а — константа; Ъ — постоянный вектор и G — положительно определенная
симметрическая матрица — имеет минимум в точке х*, причем х* определяет-
определяется следующим образом:
VF(x*) =b + Gx* = 0, D.14)
откуда х* = —G"l b. Из уравнения A.4) следует, что при выполнении условий
непрерывности любую функцию можно аппроксимировать в окрестности
точки х0 функцией
D.15)
(ж - *о)т YAx0) + }(х - *о)
где G(xo) — матрица Гессе, вычисленная в точке х0.
Разумной аппроксимацией минимума функции /(х) может быть минимум
функции </>(х). Если последний находится в точке хт, то
откуда
хт = х0 - G-Чжо) V/(x0),
или
xw = х0 - Gxo) g(x0). D.16)
Таким образом следует модифицировать итерационное уравнение D.9), и
точкой xz- следующей аппроксимации минимума будет
x^^.-G-'O^gCx,) . D.17)
или, в более удобном виде,
x/+1 = x/-A/G-1(x/)g(x/), D.18)
где длина шага Хг- определяется одномерным поиском в направлении
Метод Ньютона — Рафсона основан на последнем уравнении. Не будем рас-
рассматривать его во всех подробностях, упомянем лишь некоторые его особен-
особенности. Уравнения D.17) и D.18) в том виде, как они записаны, требуют вы-
вычисления и обращения матрицы Гессе на каждом шаге, что часто является ос-
основной частью вычислений. Если точка Xj близко расположена к точке х*, то
сходимость будет быстрой, поскольку в общем случае функция </>(х) будет
хорошо аппроксимировать функцию /(х) в этой окрестности. Как норму
l ) |
градиента lg(x,-+ г) |, так и расстояние между точками |х,- + г
60
х,-| следует
проверить на выполнение критерия завершения. Интересно отметить, что по
сравнению с простым методом наискорейшего спуска направлением спуска
в данном случае будет не — g(Xj-), а —G"* (xy) g(xI), где учитываются и вторые
производные. Методом Давидона — Флетчера — Пауэлла можно получить
наилучший результат, производя поиск на i-м этапе в направлении -Hzg(xz),
где нг- — положительно определенная симметрическая матрица, которая в ко-
конечном счете становится равной — G~* (х*) *. Таким образом, этот метод об-
обходит как вычисление, так и обращение матрицы G(Xj) при каждой итерации.
Следовательно, направление поиска при каждой итерации является решаю-
решающим фактором, если говорить об эффективности итерационных методов
поиска. При каждой итерации желательно произвести одномерный поиск в
наилучшем направлении. Для квадратичной функции п переменных вида
D.13) наилучшим направлением является направление, сопряженное с пре-
предыдущим направлением поиска. Сначала дадим ему определение, а затем по-
поясним, чем оно полезно.
Говорят, что два направления р и q сопряжены относительно симметри-
симметрической положительно определенной матрицы G, если
TGq =
D.19)
Можно показать, что если р0, Pi, . . ., ри _ г есть п взаимно сопряженных
направлений в и-мерном пространстве, то они линейно независимы. Если это
не так, то существуют постоянные а0, <*i, . . . , ап _ г, не все равные нулю и
такие, что
_ !?„ _ ! = 0.
<*оРо
Тогда для любого кп._ } @ < к < п - 1) справедливо равенство
и-1
У=о
т
откуда оскрkGpk = 0, так как из-за сопряженности все другие члены исчезают
(| G0?)
g
Поскольку р# Ф 0 и матрица G положительно определена, оск = 0. Отсюда
следует, что векторы р0, pi,..., ри _ 1 линейно независимы.
Перед дальнейшими вычислениями удобно переписать функцию D.13) в
виде
причем ее минимум находится в точке
1 Этот предельный переход возможен при выполнении определенных условий (см.
работу [Д1]). - Прим. ред.
61

и
F(x) = F(x*) + (x - x*)T VF(x*) + i(x - x*)T G(x - x*) =
= F(x*) + i(x - x*)T G(x - х*)(так как VF(x*) = 0) =
= a + x*T b + ?x*T Gx* + i(x - x*)T G(x - x*) =
= fl _ ^bT G1 b + i(x - x*) G(x - x*)
или F(x) = с + i(x - x*)T = G(x - x*), D.20)
: = a- ^bTGb - константа.
Предположим, что для поиска минимума функции D.20) используется
итерационная процедура.
Ясно, что не следует сразу принимать решение о направлениях поиска
(как, например, при поиске методом покоординатного спуска), а лучше на-
накапливать информацию, полученную на предыдущих этапах поиска, для того
чтобы определять дальнейшие направления поиска.
Начнем из точки х0 и проведем поиск в направлении р0 с целью нахожде-
нахождения минимума в точке
Xi =х0 + АоРо, D-21)
где х0 _ некоторая скалярная величина.
Отметим, что в точке xi направление g(xi) = VF(xO ортогонально на-
направлению ро и
g(x1)Tpo=0 D-22>
(см. уравнения B.16) и D.12)).
В общем случае на шаге i производится поиск из точки х,- в направлении
Pl с целью нахождения минимума в точке
х- =х- + Х-р-, D-23)
где для F(x) справедливы соотношения
g(x/+1)TP/ = 0; <4-24)
g(x/)+ = G(xf -х*). . D-25>
Повторным применением уравнения D.23) после п шагов получим
П-1
Хя=хя-1 + К-\Рп-\ =
= Х
п_2
D.26)
п-1
для всех / в интервале 0 < / < п — 1.
Таким образом, согласно уравнению D.25)
G(xn-x-)-G(x/+1-x*) +
D.27)
Следовательно,
л-1
V Ру = g(xy
y+
X. рт Gp/
D.28)
и из уравнения D.28) получаем:
я/РтсРу.
п-1
D.29)
Теперь, если все векторы р0, pi, р2, . .., р„ _ х взаимно сопряжены так, что
при
то из соотношения D.24) следует
g(xw)Tp/ = 0 при/ = 0, 1,... ,w- 1.
Но поскольку в этом случае векторы р0, pi >:.., р„ _
мы и, таким образом, образуют базис, то
g(*,) =0»
откуда
Gfe-x*) =0
и
D.31)
линейно независи-
независиD.32)
D.33)
Следовательно, если поиск производится по взаимно сопряженным на-
направлениям, то минимум квадратичной функции п переменных будет найден
не более чем за п шагов. Метод Флетчера — Ривса, изложенный в разд. 4.4,
основан на этой идее.
4.3. МЕТОД ДАВИДОНА - ФЛЕТЧЕРА - ПАУЭЛЛА
Метод Давидона — Флетчера — Пауэлла (ДФП) основан на использовании
соотношений D.16) и D.18), но в нем не требуется на каждом шаге вычис-
вычислять обратный гессиан GT1 (х^), так как направление поиска на шаге /явля-
/является направлением —H^g(x^), где Нг- — положительно определенная симметри-
симметрическая матрица, которая обновляется на каждом шаге, как это будет описано
ниже. В пределе матрица Н становится равной обратному гессиану.
Начнем поиск из начальной точки х0, взяв в качестве начальной матрицу
Но (обычно единичную матрицу, хотя в этом случае может подойти любая
симметрическая положительно определенная матрица). Итерационная про-*
цедура может быть представлена следующим образом (вместо g(xz) удобнее
писать )
62
1. На шаге / имеются точка хг- и положительно определенная симметри-
симметрическая матрица Нг-.
63

2. В качестве направления поиска взять направление
d. = -H.g..
g
D.34)
3. Чтобы найти функцию X/, минимизирующую функцию /(xf +
произвести одномерный поиск вдоль прямой хг- + й
4. Положить
D.35)
5. Положить
6. Найти f(xi+ г) и gf + r Завершить процедуру, если величины |g/+
или | v^l достаточно малы. В противном случае продолжить.
Замечание. Из соотношения D.24) следует, что
gJ+1** = O. D.37)
7. Положить
8. Обновить матрицу Н следующим образом:
D-38)
D.39)
где
А/ = vi vj/ (VJU,-); D.40)
B, =-H/u/u4i//(uJH.u/). D.41)
9. Увеличить / на единицу и вернуться на шаг 2.
Поясним процедуру, следуя аргументации Флетчера и Пауэлла.
а) Процесс будет устойчив, если функция v^- убывает и величина Хг- положи-
положительна. Поскольку gz- есть направление наискорейшего возрастания, функция
Vj будет убывать тогда, когда произведение
-v7 g/
= -g7v/ =
D.42)
положительно.
Это справедливо, если Нг- — симметрическая положительно определенная
матрица для любого L Начальная матрица Но обладает этими свойствами по
определению. Процесс обновления в соответствии с соотношениями D.39) —
D.41) сохраняет симметричность гессиана. Методом индукции докажем, что
после обновления матрица Нг- остается положительно определенной. Если это
условие справедливо, то
D.43)
=C,CT=H,,
Положим
где 1? — произвольный вектор.
64
D.44)
Тогда
цт у, vT т\ цт Н, u, uT H, ц
yTu, uTH/U/
TqJ
=Р2-
(pTq)
vTU/
TqJ
/>V-(pTq)
(Лт vt
D.45)
поскольку p2 q2 > (pTqJ согласно неравенству Шварца.
Знаменатель в соотношении D.45) положителен, так как
поскольку vTgj-+ г = 0 из уравнения D.37).
'Следовательно,
g7H/g/ >D, D.46)
так как Х^- > 0 и матрица Hz- положительно определена.
Таким образом, 1?тНг+ хг\ > 0, что и доказывает положительную опреде-
определенность матрицы Н,- + !.
б) Теперь покажем, что если метод ДФП применяется к квадратичной
функции (см. D.13)) с симметрической положительно определенной матри-
матрицей G, то Нп = GT1 и поиск минимума закончится через п шагов. Для доказа-
доказательства достаточно показать, что v0, \\,..., v^ — линейно независимые соб-
собственные векторы матрицы Н^+ XG с собственными значениями, равными
единице. Тогда матрица HWG должна быть единичной.
Отметим, что из соотношения D.38) следует, что
и = в. — В- =
D.47)
= Gv-.
Кроме того,
Н,ч 1 Gv, = Н/+ j и, = Нг и; + А, и, + В, и, =
что следует из соотношений D.39) - D.41) и из того, что vju,- и ujHz-uf-
можно сократить.
3 Зак. 768 65

Таким образом,
Н* ¦!<*/=¦Ў,•
Далее методом индукции по к покажем, что для к = 2, 3,
вы соотношения
vjGv;. = 0 при 0</<
HA:Gv/ = v/ приО</<*.
Для доказательства в соотношении D.48) положим / = Ои получим Hj
= v0, т. е. соотношение D.50) при к-\. При к = 2 соотношение D.50) будет
иметь вид
Н2Gv0 =Vc и Н2GVi = ух.
Второе равенство следует из соотношения D,48) при / = 1.
Для первого равенства имеем
D.48)
п справедли-
справедлиD.49)
D.50)
H2 Gv0 = H, Gv0 + Vl
[ Gv0
j Gv0
Два последних члена в правой части равны нулю, поскольку
vl Gv0 = vj Gv, - voT
что следует из соотношения D.48) при / = 0 и из соотношения D.37) при
i = 0. Кроме того, n2 = Gvi, так что u^Hi Gv0 = v|Gv0. Таким образом, пока-
показано, что соотношение D.50) справедливо при к = 2. После переноса в дру-
другую часть уравнения получим требуемый результат:
VqGvj = 0,
что является соотношением D.39) при к = 2.
Теперь по индукции покажем, что если соотношения D.49) и D.50)
справедливы при к, то они справедливы и при к + 1.
Имеем
v/+2+
D-51)
Из соотношения D.49) при i<k — 1 получим
и из соотношения D.37) непосредственно следует, что
Тогда
vTg, =0 приО< i <k9
и из соотношения D.50) следует, что
vTGRg =0 приО</<?,
* К К
причем
D.52)
И
= 0, поскольку v^ =
Следовательно,
т. е.
= 0 при 0 < i < к,
JGv. = 0 при0<1</<*+1.
Из соотношений D.47) и D.50) также имеем
D.53)
D.54)
D.55)
J , 0 при 0 </<*(<*+ 1).
Тогда из соотношений D.39) - D.50) следует
vT Gv, Н. ик иГ Нк Gv,
** *
Нк+, Gv( = НА Gv, +
v*4
u, H, и
= Н, Gv,
кык
так как
и
< Нк Gv,- = u[ v,. = vj Gv,- = 0 при 0 < / <к.
Таким образом, показано, что
Н# + l G\j = H^Gv/ = vz- при 0 < i < к.
При г = к имеем
D.56)
+
= И
поскольку
vj Gv, = vj
и
H*uA
67
66

Следовательно, Щ + xGvk = v^ и из соотношения D.56) получаем
H* + iGvi' = vf Щ>иО</<^+1. D.57)
Соотношения D.54) и D.57) так же справедливы для следующего к, как
и соотношения D.49) и D.50). Следовательно, доказательство по индукции
закончено.
Из соотношения D.49) следует, что векторы v0, V! ..., vn _ х линейно не-
независимы. Они являются взаимно сопряженными по отношению к матрице
G. Из соотношения D.50) следует, что v0, Vi,..., уп _ х являются собствен-
собственными векторами матрицы H^G с собственным значением, равным единице.
Тогда матрица HWG должна быть единичной. Следовательно,
HW=G-1. D.58)
Из соотношения D.52) следует, что минимум найден за п итераций. Век-
Вектор gn должен быть ортогонален каждому из п независимых векторов v0,
,..., vn _ х. Следовательно,
=0- D.59)
в) Способ обновления матрицы Н описывается в соотношении D.39):
Н„ = Н„ +
A,
/=0
и-1
Покажем, что G = ? А;. Из условий ортогональности D,49) следует
VTGV = D, /=°
где V — матрица, состоящая из векторов v,-, a D — диагональная матрица с
элементами v!Gvz-.
Следовательно,
G=(VT)-1DV~1.
Тогда
G" =VD~1VT,
а поскольку D — диагональная матрица, то можно произвести инверсию и пе-
перемножить матрицы для получения выражения
и—1
* V/V7
и—1
(см. соотношение D.47)).
Таким образом,
и-1
G = ? А,.
/=0
Поскольку соотношение D.48) должно выполняться, то Н/+ .Gv,
означает, что vz- = H^-Gv,. + AfGv,. + B^Gv^. Так как
68
D.60)
• V;, а это
= A,. U/ =
V/
vTU/
= v.
А,
то
BjGt^-HjGv^-HjU,.
Отсюда просто найти Bf (хотя и неоднозначно)
D.61)
В,=
zT Gv,
где z — произвольный вектор. Поскольку мы хотим, чтобы матрица Bz- была
симметрической, то выберем в качестве вектора z = Нгц- , такой, чтобы
-Н, u, uT И,
В, = ^—^ . D.62)
Этим завершается теоретическое изложение метода ДФП, который исполь-
использует как идеи метода Ньютона — Рафсона, так и свойство сопряженных на-
направлений, и при применении для минимизации квадратичной функции п пе-
переменных он сходится не более чем за п итераций. Это весьма мощная опти-
оптимизационная процедура, очень эффективная при оптимизации большинства
функций независимо от того, квадратичны они или нет.
Начать из точки х-19
Hi A-0)
1
Положить
Найти значение
минимизирующее
Полошить i-1+l
Использовать H\,V\ и,
формирования
Рис. 4.4
69

Ниже приведены блок-схема процедуры (рис. 4.4) и текст программы, ре-
реализующий данный метод. В дополнении к программе должны быть написа-
написаны подпрограммы вычисления рассматриваемой функции и ее производных.
Логическое построение метода отражено в программе. Одномерный поиск
осуществляется кубической интерполяцией, но поиск заканчивается не при
достижении предельной сходимости, а после того, как будет получено улуч-
улучшение значения функции. Теоретически это означает, что метод утрачивает
свойство сходимости для квадратичных функций, но практически является
эффективным и быстрым. К тому же дополнительная работа, выполняемая
в случае полного завершения одномерного поиска, скорее всего, не будет
оправданной,
В тексте программы использованы обозначения, приведенные в алгоритме
и имеются комментарии. Для одномерного поиска в строках 600 — 1010 ис-
использована процедура кубической интерполяции из разд. 2.6, отличающаяся
в данном случае тем, что она завершается прежде, чем достигается сходи-
сходимость. Таким образом, строка 920 реализует выход из процедуры одномер-
одномерного поиска, если интерполированное значение функции меньше, чем оба зна-
значения функции, используемые в этой процедуре. Последующий интервал
поиска, если таковой существует, определяется в строке 930.
Пример 1
Ирпользуя точку с координатами C; —1; 0; 1) в качестве начальной точки, миними-
минимизировать функцию Пауэлла
f(xvx2,x39x4)
1Ох2J + 5(х3 -
- х4)\
Приведенная ниже подпрограмма справедлива для данной функции. Предложенная
начальная точка является одной из неудачных для данной функции. Минимум равен ну-
нулю в точке @; 0; 0; 0).
1ОО PRINT "МИНИМИЗАЦИЯ МЕТОДОМ ДФП"
120 REM ОДНОМЕРНЫЙ ПОИСК ПРОИЗВОДИТСЯ КУБИЧЕСКОЙ ИНТЕРПОЛЯЦИЕЙ
150 REM ФУНКЦИЯ F<X1,X2,...XN) ВЫЧИСЛЯЕТСЯ В СТРОКЕ 5000
155 REM ЗНАЧЕНИЯ GA),GB>,...G(N> ВЫЧИСЛЯЮТСЯ В СТРОКЕ 6000
200 PRINT "ВВЕДИТЕ ЧИСЛО nEPEMEHHblX":INPUT N
220 DIM X(N),P(N>,Q(N>,R(N),D(N),G(N),U(N>,V(N),Y(N>,M(N>
240 DIM H(N,N)
300 REM ПЕРВОНАЧАЛЬНО ЗАДАТЬ Н ЕДИНИЧНОЙ МАТРИЦЕЙ
320 CC=O:FOR 1=1 ТО NsFOR J=l TO N:H(I,J)=O:NEXT J:H(I,I)=1:NEXT I:TT=O
330 PRINT "ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ"
340 FOR 1=1 ТО N:PRINT "X";I;sINPUT X<I):NEXT IsPRINT ""
360 REM ПРОМЕЖУТОЧНЫЙ ВЫВОД
380 PRINT " ТЕКУЦИЕ ЗНАЧЕНИЯ"
400 FOR 1=1 ТО NsP(I)=X(I):Y(I)=X(I):PRINT "X";I,X(I):NEXT I
410 GOSUB 5000
420 PRINT "ИТЕРАЦИЯ";СС;" ЗНАЧЕНИЕ ";Z
430 FP=Z:GOSUB 6000:Gl=G0
440 REM ГРАДИЕНТ ЗАПОМНИТЬ В U И ВЫБРАТЬ НАЧАЛЬНОЕ НАПРАВЛЕНИЕ D
450 FOR 1=1 ТО N
460 U(I)=G(I):D(I>=0
470 FOR J=l TO N
480 D(I)=D(I)-H(I,J)*G(J)
490 NEXT J
500 NEXT I
600 GP=O
610 FOR 1=1 TO N:GP=GP+G<I)*D(I):NEXT I
620 IF GP < О THEN GOTO 680
70
25 REM НАЙТИ НАЧАЛЬНЫЙ УАГ И, ЕСЛИ НЕОБХОДИМО,
,627 REM ИЗМЕНИТЬ НАПРАВЛЕНИЕ СПУСКА НА ПРОТИВОПОЛОЖНОЕ
?30 QX=ABSB*FP/GP):IF QX>1 THEN QX-1
MO FOR I«l TO N
650 X(I)=Pa)-QX»D(I)sP(I)=X(I):NEXT I
i&60 GOSUB 5000:FP=Z:PRINT "НЕСТАБИЛЬНОСТЬ?"
70 GOSUB 6000:Gl=G0:G0T0 ,600
&80 QX=ABS<2»FP/GP):IF QX>1 THEN QX=1
90 HH-QX
- 00 REM НАЙТИ СЛЕДУЮЩУЮ ТОЧКУ Q
710 BB=HH
JJ20 FOR 1=1 TO N
§730 Q<I)=P(I)+BB*D<I):Xa>=GKI>
740 NEXT I
750 GOSUB 5000:FQ«Z
760 GOSUB 6000:G2=G0
770 GQ=O
710 BB=HH
720 FOR 1=1 TO N
730 GKI>=Pa)+BB*D(I>:X<I>=Qa)
740 NEXT I
750 GOSUB 5000iFQ=Z
760 GOSUB 6000:G2=G0
770 GQ=O
780 FOR 1=1 TO N
790 6Q«GQ+G(I)*Da)
BOO NEXT I
810 IF GQ>0 OR FO>FP THEN GOTO 830
B15 REM ВЫПОЛНИТЬ КУБИЧЕСКУЮ ИНТЕРПОЛЯЦИЮ
817 REM ИЛИ УДВОИТЬ ШАГ, ЧТОБЫ "НАКРЫТЬ" МИНИМУМ
820 HH=2*HH:G0T0 700
830 ZZ=3*(FP-FQ)/HH:ZZ=ZZ+GP+GQ
840 WW=ZZ*ZZ-GP*6Q:IF WW<0 THEN WW=O
S50 W=SQR<WW)
860 DD=HH*<1-<GQ+W^ZZ)/(GQ-GP+2*W»
870 FOR 1=1 TO N*X<I)=P<I)+DD*D<I>:NEXT I
880 GOSUB 5000:FR=Z
890 GOSUB 6000:G3=G0
895 REM НАЙТИ ГРАДИЕНТ В НОВОЙ ТОЧКЕ
900 GR=O
910 FOR 1=1 ТО N:GR=GR+G(I)*D<I):NEXT I
920 IF Z<=FP AND Z<=FQ THEN GOTO 1100
930 IF GR>0 THEN GOTO 990
960 HH=HH-DD
970 FOR 1=1 TO N:P<I)=X<I):NEXT I
980 FP=Z:GP=GR:61=G0s60T0 830
990 HH=DD
1OOO FOR 1=1 TO N:Q(I>=X(I):NEXT I
1050 REM ОБНОВИТЬ МАТРИЦУ Н
1100 KK»O:WK=O:DK=O
1110 FOR 1=1 TO N
1120 U<I)=G(I)-U(I);V(I)=X(I)-Y(I)
1130 NEXT I
U40 FOR 1=1 TO N:M(I)=0
U50 FOR J=l TO N
1160 M<I)«Ma>+H<I,J>*U<J>
1170 NEXT J
1180 KK«KK+M<I>«U<I):WH>WK+VQ)»U<I)
U90 DK«DK+V<I)»V<I)
1200 NEXT I
12О5 IF KK=O OR WK=O THEN GOTO 1260
1210 FOR 1=1 TO N
1220 FOR J=l TO N
1230 H(I,J)=H(I1J)-M<I)*M<J)/KK+V<I)*V<J)/WK
1240 NEXT J
1250 NEXT I
71

1260 COCO1
1265 REM ПРОВЕРКА КРИТЕРИЯ ЗАВЕРШЕНИЯ
1270 IF SQR(DKX.OOOO5 OR БЗ<.ОООО1 THEN GOTO 1300
1275 REM НАЧАТЬ НОВУЮ ИТЕРАЦИЮ ПОИСКА
1280 GOTO 400
1300 PRINT "МИНИМУМ НАЙДЕН"
1310 PRINT "КОЛИЧЕСТВО ИТЕРАЦИЙ=";СС;" ЗНАЧЕНИЕ МИНИМУМА= ";Z
1320 FOR I«l TO N
1330 PRINT "X";I,X(I)
1340 NEXT I
1350 END
50OO Z=0
5010 Z=(X<l)-H0*XB)K2+5*<XC)-XD))'2
5020 Z=Z+(X<2)-2*X<3» х4+10*Ш1>-ХD))л4
5100 TT«TT+1
5200 RETURN
6000 G0=0
61ОО G(l>«2*<Xa)+10*X<2»+40*<X<l>-X<4»'3.
6200 G<2)«2O*<Xa>+lO»X<2»+4*<X<2>-2*X<3))^3
6300 G<3)=1O*(X<3)-XD))-8*(X<2)-2*XC))'3
6400 Б<4)~-10*ШЗ>-Х<4»-40*<ХШ-Х<4»'3
7000 FOR I«l TO N:GO=GO+G(I)*G<I):NEXT I
7О1О GO=SQR<GO>
75ОО RETURN
МИНИМИЗАЦИЯ МЕТОДОМ ДФП
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
4
ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ
X 1 3
X 2 -1
X 3 О
X 4 1
X 1
X 2
X 3
X 4
ИТЕРАЦИЯ
X 1
X 2
X 3
X 4
ИТЕРАЦИЯ
X 1
X 2
X 3
X 4
ИТЕРАЦИЯ
X 1
X 2
X 3
X 4
ИТЕРАЦИЯ
X 1
X 2
X 3
X 4
ИТЕРАЦИЯ
X 1
X 2
X 3
X 4
ТЕКУЦИЕ ЗНАЧЕНИЯ
3
-1
о
1
215
ЗНАЧЕНИЕ
1.949874
-.5058231
6.863568Е-03
2.063853
ЗНАЧЕНИЕ 30.89246
1.952094
-.1460427
.1139128
1.983205
ЗНАЧЕНИЕ 17.73255
1.672088
-.1326144
.6173387
•1.740239
ЗНАЧЕНИЕ 9.919396
.1212769
-9.13И93Е-03
.2314347
.2154706
ЗНАЧЕНИЕ 5.25922ВЕ-02
.1124414
-1.592427Е-02
.1754911
.2051923
ИТЕРАЦИЯ 5
X 1
X 2
X 3
X 4
X 1
X 2
53
ИТЕРАЦИЯ 23
X 1
X 2
X 3
X 4
ЗНАЧЕНИЕ 2.U46394E-02
1.728326Е-02
-1.335926Е-04
.1186576
.1068345
1.669752Е-03
-1.67310ВЕ-04
1.655202Е-03
1.653915Е-03
ЗНАЧЕНИЕ 1.65В259Е-10
5-41309Е-04
-5.39442Е-05
9-644107Е-04
9.6542ОЗЕ-04
ЗНАЧЕНИЕ 2.436223Е-11
ЗНАЧЕНИЕ МИНИМУМА РАВНО 7.528931Е-12
ИТЕРАЦИЯ 24
МИНИМИЗАЦИЯ ЗАКОНЧЕНА
КОЛИЧЕСТВО ИТЕРАЦИЙ РАВНО 25
X 1 1.960656Е-04
X 2 -1.9А4616Е-05
X 3 7.700225Е-04
X 4 7-697501Е-04
4.4. МЕТОД ФЛЕТЧЕРА - РИВСА
Метод Флетчера - Ривса основан на том, что для квадратичной функции п
переменных п одномерных поисков вдоль взаимно сопряженных направле-
направлений позволяют найти минимум.
Рассмотрим функцию, описанную выражением D.13), т. е.
Лх\ — п + Ьт х + ixT Gx
Одномерный, поиск будем вести вдоль направлений, взаимно сопряжен-
сопряженных по отношению к матрице G.
В качестве Аервого направления поиска из первой точки Xi возьмем на-
направление наискорейшего спуска
d, = -g, D.63)
и найдем значение Xi, минимизирующее функцию
Положим
x2=x1+\1d1 D.64)
и произведем поиск в направлении d2, сопряженном направлению dj (выбе-
(выберем вектор d2 как линейную комбинацию векторов их и — g2), и найдем
x3=x2+X2d2 D.65)
минимизацией функции /(х2 + Xd2). Направление поиска d3 из точки х3 вы-
выбирается сопряженным направлениям di и d2. На (к + 1)-м шаге выбираем
d йй бна g dj, d2, . . . , dk, сопряженной
+ j в виде линейной комбинации —
всем направлениям d1, d2 s..., d^.
Таким образом, dk + г = —gk + l +
+ х
г=1
аг равны нулю, за исключением а^, так что
= 1,2,... Оказывается, все
73
72

dk
и
akdk
D.66)
Прежде чем перейти к индуктивным рассуждениям, докажем справедли-
справедливость соотношений D.66) и D.67) при к = 1. Поскольку /(х2) = /(Xj +
+ Xidj) является минимумом функции /(xi + Xdj) на прямой, то
eldi =—glgi =0. D.68)
Много раз мы уже получали этот результат раньше (соотношения D.37),
D.22), D.24)). Он, конечно, справедлив и для квадратичных функций
g2 =b + Gx2, gj =b + Gxj.
Тогда, если di и d2 = -g2 + a1dl сопряжены, то
т. е.
следовательно,
(— ст — a aT) G(x — х
- = и,
откуда
Таким образом,
-gl+aigi =0.
Остальные члены исчезают из соотношения D.68), и, следовательно,
что и требовалось доказать. Это как раз и есть соотношение D.67) при If =
= 1.
Теперь перейдем к доказательству соотношений D.66) и D.67) по индук-
индукции, полагая, что векторы di, d2, . . . , dk получены описанным выше спосо-
способом и являются взаимно сопряженными.
>cdk является минимумом функции f(xk + Xd^) на
Точка Х? + 1 = хк +
прямой хк + Хд-dfc.
Тогда
Имеем
— х
D.69)
Таким образом,
+1 = Х/+1+ I Я,с1,; при 1 <./<*-1,
следовательно,
D.70)
тогда
e*+i =
откуда
при
X
т
В результате преобразований имеем g;- + ^ =0 (в соответствии с соотноше-
соотношениями D.68) и D.69)) и из-за взаимной сопряженности dTGd;. = Опри /</.
Таким образом, каждое слагаемое в правой части равно нулю.
Следовательно,
? 2,...,/;-1 D.71)
D.72)
и из соотношения D.69) окончательно имеем
о7. d. = 0 при /=1,2, ...А:.
к • 1 /
Таким образом, было доказано, что вектор gk + г ортогонален каждому из
векторов dj, d2,..., d^.
Можно также показать, что вектор gk + г ортогонален векторам gi, g2,...
Из соотношения D.72) имеем
/=Ь2,. . . Д.
Так как из предположения в начале доказательства по индукции
d. = -g. + ос. d.
7 7 7-17-1
то nptrnеденное выше соотношение принимает вид
следовательно, -gfc+ig/ = 0» поскольку g]c+1dJ-_1 = 0 из соотношения
D.72).
Таким образом,
и т. д.
g[ + j% = 0 при /=1,2,..., к. D.73)
Доказательство по индукции будет закончено, если показать, что вектор
d# + l, определенный в соотношении D.66), сопряжен с векторами dj, d2,...
74
75

Для / = 1, 2,... ,к - 1 имеем
j+1 Gd, = -gj+, Gd7 + ak dj Gdj =
в силу взаимной сопряженности.
Тогда
-_„т
= 0
Л/
с учетом соотношения D.73).
Таким образом, d? + хСй, = 0 при / = 1, 2, . . . , к - 1, и это справедливо
для любого ак. Для завершения доказательства необходимо определить %
так, чтобы выполнялось равенство
+ iGdA:=0:
= ~gj+1 Gd, + ak dj Gd, =
a
k_
Следовательно,
поскольку все другие члены из правой части исчезают в силу соотношений
D.72) и D.73).
Следовательно, направление dk + 1 будет сопряжено с направлением dk, ес-
если ак = gk + 1/g^, что и требовалось доказать.
Таким образом, направление поиска в методе Флетчера - Ривса являются
взаимно сопряженными и в данном методе минимум квадратичной функции
п переменных можно найти не более чем за п шагов. Это означает, что одно-
одномерный поиск производится с нужной точностью и устраняются любые ошиб-
ошибки округления, которые могут возникнуть.
Вышеописанный метод будет применим и к неквадратичным функциям,
так как если поиск осуществляется вблизи минимума, то можно надеяться
на достижение квадратичной сходимости, когда имеет место квадратичная
аппроксимация. Флетчер и Ривс полагают, что в этой ситуации каждое л-е
76
Начать из точки
J)
Положить
Найти значение Ai,
минимизирующее функцию
f(bd)
Точка
- точка минимума 1
Рис. 4.5
направление поиска должно быть направлением наискорейшего спуска и при
построении сопряженных направлений должен быть произведен рестарт.
Приведенные ниже блок-схема (рис. 4.5) и текст программы реализуют
эту идею. В общем случае данный метод не столь эффективен, как метод
ДФП, но тем не менее бывает весьма полезен.
100 PRINT "МИНИМИЗАЦИЯ МЕТОДОМ ФЛЕТЧЕРА-РИВСА"
120 REM ОДНОМЕРНЫЙ ПОИСК ПРОИЗВОДИТСЯ КУБИЧЕСКОЙ ИНТЕРПОЛЯЦИЕЙ
150 REM ФУНКЦИЯ F<X1,X2,...,XN> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 5000
155 REM ЗНАЧЕНИЯ GA),GB),...,G(N) ВЫЧИСЛЯЮТСЯ В СТРОКЕ 6000
200 PRINT "ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫX"sINPUT N
22О DIM X(N),Y<N),P<N),Q(N),D(N),G(N)
300 PRINT "ВВЕДИТЕ НАЧАЛЬНЫЕ ЗНАЧЕНИЯ"
320 FOR I-l TO N:PRINT "X"$I$sINPUT X(I):NEXT IjPRINT ""
340 REM ЗАДАТЬ НАЧАЛЬНЫЕ ЗНАЧЕНИЯ СЧЕТЧИКОВ
350 SV«liTV«O
360 REM ПРОМЕЖУТОЧНЫЙ ВЫВОД
380 PRINT " ТЕКУЩИЕ ЗНАЧЕНИЯ"
550 FOR I«l TO N:P<I)*X(I)sPRINT "Х"}1;"-";ХAМЕХТ I
560 GOSUB 5000jFP«Z:PRINT "Z-"Z
570 GOSUB 6000iGl"G0tGK«*G0
575 REM В КАЧЕСТВЕ ПЕРВОГО НАПРАВЛЕНИЯ ВЗЯТЬ
577 REM НАПРАВЛЕНИЕ НАИСКОРЕЙШЕГО СПУСКА
580 FOR I«l TO NiD<I)*-G<I)jNEXT I
585 REM К - СЧЕТЧИК ИТЕРАЦИЙ
77

590 K-i
600 GP-0
610 FOR I«l TO NiGP-GP+G(I)*D<I):NEXT I
620 IF GP<«0 THEN GOTO 680
625 REM ОПРЕДЕЛИТЬ НАЧАЛЬНЫЙ ШАГ И,
627 REM ЕСЛИ НЕОБХОДИМО^ ЗМЕНИТЬ НАПРАВЛЕНИЕ СПУСКА НА ПРОТИВОПОЛОЖНОЕ
630 QX*ABSB»FP/GP):IF QX>1 THEN QX-1
640 FOR I-l TO N
650 X(I)«P(I)-QX*D<I):P(I>-X(I)8NEXT I
660 60SUB 5OOO8FP-Z8PRINT "НЕСТАБИЛЬНОСТЬ"
670 60SUB 6000iG1«G0jG0T0 600
680 QX«ABSB«FP/GP)iIF QX>1 THEN QX-1
690 HH«QX
700 REM НАЙТИ СЛЕДУЮЩУЮ ТОЧКУ
710 BB-HH
720 FOR I-l TO N
730 a<I)»P(I)+BB*D<I)iX<I)-Q<I)
740 NEXT I
750 GOSUB 5000:FQ«Z
760 GOSUB 6000iG2«G0
770 GQ«O
780 FOR I-l TO N
790 GQ-GQ+G(I>*D(I)
800 NEXT I
810 IF BQ>0 OR FQ>FP THEN GOTO 860
815 REM ВЫПОЛНИТЬ ИНТЕРПОЛЯЦИЮ,
817 REM УДВОИТЬ УАГ И ПЕРЕЙТИ К ТОЧКЕ D,
818 REM ИЛИ УДВОИТЬ ШАГ, ЧТОБЫ "НАКРЫТЬ" МИНИМУМ
820 НН=2»НН
830 FOR I«l TO NiP(I)«Q(I):NEXT I
840 FP»FQ8GP«6QiGl*G2
850 GOTO 710
860 ZZ«3«(FP-FQ)/HH:ZZ*ZZ+GP+GQ
870 WW«ZZ«ZZ-6P«GQ:IF WW<0 THEN WW-0
880 W«SQR<WW>
890 DD-HH-*<1-<GQ+W-ZZ)/(GQ-GP+2«W»
900 FOR I«l TO N:X<I)*P(I)+DD»D<I)iNEXT I
910 GOSUB bOOOiFR*Z
920 GOSUB 6000:G3-G0
925 REM НАЙТИ ГРАДИЕНТ В НОВОЙ ТОЧКЕ
930 GR-0
940 FOR 1*1 ТО NiGR*GR+G<I)»D<I)»NEXT I
950 IF Z<«FP AND Z<«FQ THEN GOTO 1100
960 IF GR>0 THEN GOTO 1020
990 HH-HH-DD
1000 FOR I«l TO N:P<I)*X(I)iNEXT I
1010 FP-ZsGP-GRsGOTO 860
1020 HH-DD
1030 FOR 1*1 TO NiQ<I)*X(I)xNEXT I
1040 FQ=Z:GQ«GRiGQTO 860
1100 REM ПРОВЕРКА КРИТЕРИЯ ЗАВЕРШЕНИЯ
1110 IF G3<.000001 THEN GOTO 1300
1120 IF K*N THEN GOTO 1250
1130 REM УВЕЛИЧИТЬ СОДЕРЖИМОЕ СЧЕТЧИКА ИТЕРАЦИЙ
1140 К*К+1
1150 REM НАЙТИ СОПРЯЖЕННОЕ НАПРАВЛЕНИЕ
1160 AK-G3*G3/(GK»GK)
1170 FOR 1*1 ТО NiD<I)«-GU>+AK«D(I):P(I)«X(I):NEXT I
1200 PRINT "НОВОЕ НАПРАВЛЕНИЕ";:0У=0У+1:РР1ЫТ "
1210 FP=Z:G1*GO:GK=GO
1220 FOR 1=1 TO N:PRINT "X";I;"-";X(I>iNEXT I:PRINT "Z«";Z
1230 GOTO 600
1250 PRINT "PECTAPT";:SV«SV + 1:DV«DV+1
1260 PRINT " MTEPAUHP'^SV;" nOHCK";DV
1270 PRINT ^
1280 GOTO 550
78
1300 PRINT "МИНИМУМ НАЙДЕН"
132О FOR I«1 TO NjPRINT "XmjI;ii-"}X(I)iNEXT I
1340 PRINT "МИНИМУМ ФУНКЦИИ РАВЕН "Z
1350 PRINT "КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО ";TV
1400 END
5ООО Z«100*(XB>-X<l)«X(l))/42
5010 Z»Z-Kl-X<l))/42
502Q, TV-TV+1
5200 RETURN
6000 G0«0
6100 G<D—400*X<l)»<X<2)-X<l)«X(l»
6110 GA)«GA)-2»A-X<1»
6200 B<2)-2OO*<XB>-XA)»X<1»
7000 FOR I»l TO NiGO«GO+S<I)«G(I)»NEXT I
7010 GO-SQR(GO)
7500 RETURN
Пример 1
Используя метод Флетчера — Ривса с начальной точкой (—1,2; 1), минимизировать
функцию Розенброка
/(*,,*,) = 100(х2 -xlJ + A-х,J.
Начальная точка (-1,2; 1) особенно неудобна для данной функции, да и функция
сама по себе весьма сложна для оптимизации. Минимум ее находится в точке A; 1). Ни-
Ниже приведены начало и конец распечатки результата работы программы:
МИНИМИЗАЦИЯ МЕТОДОМ ФЛЕТЧЕРА-РИВСА
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
2
ВВЕДИТЕ НАЧАЛЬНЫЕ ЗНАЧЕНИЯ
X 1 -1-2
X 2 1
ТЕКУЦИЕ ЗНАЧЕНИЯ
X 1 =-1.2
X 2: - 1
Z» 24.20001
НОВОЕ НАПРАВЛЕНИЕ ПОИСКА 1
X 1 —1.0302
X 2 - 1.069306
Z<* 4.128102
РЕСТАРТ ИТЕРАЦИЯ 2 ПОИСК 2
X 1 =-.7342701
Х2» .4632753
Z- 3.583429
НОВОЕ НАПРАВЛЕНИЕ
X 1 «-.6921596
X 2 = .4880884
Z- 2.871511
РЕСТАРТ ИТЕРАЦИЯ 3
ПОИСКА 3
ПОИСК 4
X 1 —.5967852
X 2 - .3241929
Z- 2.651865
НОВОЕ НАПРАВЛЕНИЕ
X 1 —.5726343
X 2 - .3384563
Z- 2.484301
ПОИСКА 5
79

РЕСТАРТ
ИТЕРАЦИЯ 45 ПОИСК 8S
X 1 « .9999818
X 2 - .9999634
Z- 3.34083E-10
НОВОЕ НАПРАВЛЕНИЕ
X 1 ¦ .9999818
X 2 - .9999634
Z« 3.330172E-10
РЕСТАРТ ИТЕРАЦИЯ 46
X 1 ¦ .9999821
Х2- .9999643
Z« 3.2S0769E-10
НОВОЕ НАПРАВЛЕНИЕ
X 1 - .9999822
X 2 - .9999642
Z« 3.190373E-10
РЕСТАРТ ИТЕРАЦИЯ 47
ПОИСКА 89
ПОИСК 90
ПОИСКА 91
ПОИСК 92
ПОИСКА 93
X 1 - .9999822
X 2 « .9999643
Z« 3.179714E-10
НОВОЕ НАПРАВЛЕНИЕ
X 1 - .9999823
X 2 » .9999644
Z« 3.165788E-10
МИНИМУМ НАЙДЕН
X 1 » 1
X 2 - 1
МИНИМУМ ФУНКЦИИ РАВЕН О
КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО
250
Пример 2
Найти минимум функции
t - IJ +2(х2 -2J + (*э -ЗJ.
По сравнению с примером 1 это тривиальная задача. В качестве начальной точки выб-
выбрана точка (9; -7; 11). Приведенная ниже распечатка результатов работы программы
иллюстрирует (в соответствии с теорией) тот факт, что с помощью метода Флетчера —
Ривса можно найти минимум за три итерации.
МИНИМИЗАЦИЯ МЕТОДОМ ФЛЕТЧЕРА-РИВСА
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
3
ВВЕДИТЕ НАЧАЛЬНЫЕ ЗНАЧЕНИЯ
X 1 9
X 2 -7
X 3 XI
ТЕКУЩИЕ ЗНАЧЕНИЯ
X 1 - 9
X 2 «-7
X 3 - 11
Z- 418
НОВОЕ НАПРАВЛЕНИЕ
X 1 —.481967
X 2 - .1114755
X 3 - 7.839344
Z- 37.14098
НОВОЕ НАПРАВЛЕНИЕ
X 1 - 1.206897
X 2 - 2.827586
Х3« 4.862069
Z» 4.965516
80
ПОИСКА 1
ПОИСКА 2
МИНИМУМ НАЙДЕН
X 1 - .9999999
X 2 - 2
X 3 - 3
МИНИМУМ ФУНКЦИИ РАВЕН 4.263257Е-14
КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО
4.5. ЛИТЕРАТУРА
За последние двадцать лет проводились активные исследования градиентных мето-
методов. Было опубликовано много статей, и достигнуты значительные успехи. В данной гла-
главе рассмотрено всего лишь три из множества методов, которые были предложены за
этот период. Фундаментальными являются идеи сопряженных направлений и свойство
квадратичных функций, описанное соотношением D.17). В разд. 4.3 было упомянуто,
что обновление матрицы Н в методе ДФП не является единственно возможным. Суще-
Существует целое семейство методов, основанных на этих идеях, среди которых методы
Давидона — Флетчера — Пауэлла и Флетчера — Ривса являются лишь двумя частными
случаями. Приведенная ниже литература представляет собой всего лишь часть из того
множества публикаций, которое следовало бы упомянуть.
1 С. G. Broyden, 'Quasi-Newton methods and their application to function minimisation',
Maths, of Сотр., 21, 368-381, 1967.
2 С. G; Broyden, The convergence of single-rank quasi-Newton methods', Maths, of Сотр.,
24,376-382, 4970.
3 R. Fletcher, JA new approach to variable metric algorithms', The Сотр. Journal, 13,
317-322, 19^0.
4 R. Fletcher ^nd M. J. D. Powell, 'A rapidly convergent descent method for minimisation',
The Comp./Journal, 6, 163-168, 1963.
[Имеется перевод: Р. Флетчер, М. Пауэлл. Быстросходящийся метод спуска. ГПНТБ,
" перевод П-5 9 064. ]
5 R. Fletcher and С. М. Reeves, 'Function minimisation by conjugate gradients' The Conip
Journal, 7, 149-154, 1964.
6 H. Y. Huang, 'Unified, approach to quadratically convergent algorithms for function
minimisation', J. Opt. Theory App., 5, 405-423, 1970.
7 H. Y. Huang and A. V. Levy, 'Numerical experiments on quadratically convergent
algorithms for function minimisation',/. Opt. Theory App., 6, 269-282, 1970.
8 M. J. D. Powell, 'On the convergence of the variable metric algorithm', J. Inst. Maths
App., 7,21-36, 1971.
9 M. J. D. Powell, 'Quadratic termination properties of minimisation algorithms. I. State-
Statement and discussion of results', J.Inst. Maths. App., 10, 333-342, 1972.
10 M. J. D. Powell, 'Quadratic termination properties of minimisation algorithms. II. Proofs
of theorems', J. Inst. Maths. App., 10, 343-357, 1972.
4.6. УПРАЖНЕНИЯ
1. Измените программу метода наискорейшего спуска, приведенную в разд. 4.1, так,
чтобы она могла выполнять линейный поиск методом Фибоначчи, методом "золото-
"золотого сечения", методом кубической интерполяции. Примените полученную программу
в решении задач, приведенных в примерах. Обратите внимание на любые возникаю-
возникающие трудности.
2. Попробуйте решить примеры 1 и 2 разд. 4.1, используя различные начальные точки.
Появились ли какие-нибудь трудности?
3. Пусть Ро, Pj и Р2 - следующие друг за другом точки, полученные методом наиско-
наискорейшего спуска. Предполагается, что расчеты будут проводиться быстрее, если сле-
следующий поиск произвести в направлении Ро Р2. Нарисуйте линии постоянного уров-
81

ня вблизи минимума для иллюстрации приведенных выше соображений. Отразите
эту идею в программе, приведенной в разд. 4.1.
4. Если /(х) — положительно определенная квадратичная функция двух переменных,
минимум которой находится в точке @; 0), а х0, х, и х2 — три точки, полученные
последовательно методом наискорейшего спуска, то покажите, что прямая, проходя-
проходящая через точки х0 и х2, проходит через точку минимума функции. (См. метод
ускорения расчетов, описанный в упр. 3.)
5. Рассмотрите квадратичную функцию f(x, у) = х2 /а2 +у2/Ь2, где аиЬ — константы.
Линиями постоянного уровня функции являются эллипсы
X* у*
1 —- С2
2 1.7 '
а2 Ъ2
где с2 - значение функции. Минимум функции равен нулю и находится в начале ко-
координат. Покажите, что прямая
у = тх ± с\/(а2т2 + Ь2)
направлена по касательной к этому эллипсу и касается его в точке Р с координатами
сЬ2
та2 с
т
а2т2 + Ъ2)
Следовательно, поиск из точки на этой прямой вдоль нее завершится в точке мини-
минимума функции Р. Градиент прямой, соединяющей точку Р с началом координат
(точкой минимума), равен т*. Покажите, что mm' = -b2/a2.
Покажите, что это эквивалентно соотношению
\/а2 0
0 \1Ъ2
где рт = (cos a, sin а); qT = (cos /3, sin /3) ит = tga,m' = tg /3. Следовательно, р и q -
сопряженные векторы и поиск вдоль вектора р, а затем вдоль вектора q позволяет
найти минимум за две итерации.
6. Минимизируйте функцию
/(х)
, -4J+5(х2 +3J +7Bх
используя: метод ДФП; метод Флетчера — Ривса. Покажите, что независимо от на-
начальной точки для нахождения минимума в первом случае потребовалось три итера-
итерации, а во втором — три поиска.
7. Минимизируйте функцию
/(*!, х2) = 1 - 2хх - 2х2 - 4х,х2 + 10x2
8. Минимизируйте функцию
2л:2
9. Минимизируйте функцию
{х\+х2-ПJ + {хх +х
10. Минимизируйте функцию
-7J.
У \
— "^1 ^2
• L,
ЧАСТЬ II
ОПТИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
ГЛАВА 5. ОБЩАЯ ТЕОРИЯ
5.1. ОГРАНИЧЕНИЯ В ВИДЕ РАВЕНСТВ
Рассмотрим задачу минимизации функции двух переменных
z =f(x,y),
где на х и у наложено ограничение, задаваемое уравнением
g(x,y) =0. E.1)
Вообще, уравнение g(x, у) = 0 можно разрешить относительно у как функ-
функцию от х9 т. е. у = h (x). Конечно, на практике может оказаться трудным или
даже невозможным найти явный вид функции h (x). При выполнении опреде-
определенных условий дифференцируемости производная функции h (x)
dx dx dxl ду
Тогда функцию
z=f(x,y)=f[x,h(x)] E.3)
можно записать как функцию одной независимой переменной х. Необходи-
Необходимым условием минимума функции z будет соотношение
dz df df dy
— -г ; — \J}
dx дх ду dx
т. е.
ду
дх + I dg
Ту
дх
E.4)
Соотношения E.1) и E.2) могут быть решены с целью получения значений
х*9 у* в точке минимума.
83

Этот результат может быть представлен в иной форме. Если положить
~df/ Idg
= — ix9y)—ix,y) E.5)
ду I ду
при х = х*, у = у*, то в точке минимума выполняются соотношения
g(x, у) = О,
ох
df
—
ду
ох
dg
—
ду
причем последнее следует непосредственно из соотношения E.5).
Получить эти три необходимых условия можно, используя функцию
Лагранжа
F(x, у, X) = /Ос, у) + Х^(дг, у), E.6)
которая представляет собой сумму целевой функции и произведения множи-
множителя Лагранжа X на функции ограничения. Тогда необходимые условия мини-
минимума функции f(x, у) при наличии ограничений могут быть записаны в сле-
следующем виде:
^ df dg >
:>У, А) = — (*, y\+k — U, у) = О,
дх
dF df dg
— (x, д;, Я) = — U ^) + Я — (х, .у) = 0,
dy dy dy
dF
E.7)
Это система трех уравнений, решениями которой являются значения х*, у*
и X* — в точке минимума.
Пример 1
Найти минимум функции f(x, у) = х2 + у2 при ограничении х + у = 4.
Функция Лагранжа имеет вид
F(x, у, \) = х2 +у2 + К D - х - у) .
Соответствующие условия минимума можно записать следующим образом:
dF
Or _ 2 — П
дх i
dF
~oj =
dF
84
Решением этой системы уравнений являются х = у = 2, Л = 4. Минимум функции ра-
равен 8. Читателю в качестве упражнения предлагается проверить этот результат, рассмо-
рассмотрев функцию одной переменной х, которая получена исключением у го функции Ла-
Лагранжа:
z = x2 + D -хJ.
Необходимые условия минимума E.7) могут быть обобщены для функ-
функций п переменных при наличии т ограничений в виде равенств.
Рассмотрим задачу минимизации функции
Z =/(х) - f{X\f X2, • . • , *л)»
где на переменную х наложены ограничения
*i (х) -0, *2(х) =0,... 9gm (x) = 0. E.8)
Ограничения можно использовать для того, чтобы выразить т переменных
(без ограничения общности их можно обозначить xif X2, . . . , хт) через
остальные '$п - т) переменных, которые можно рассматривать как незави-
независимые переменные. В точке минимума при наличии ограничений /(х + h) —
— /(х) > 0 для всех h, удовлетворяющих условию g,-(x + h) -ft(x) = 0 при
Тогда/fc точностью до первого порядка hi будем иметь
n
У=1
где
п
hj = 0 при /= 1, 2,..., т.
Это условие можно записать иначе:
п I df m
E.9)
где Xi, Х2,..., Xw - множители Лагранжа.
Поскольку hm + j, hm + 2,..., /zw являются независимыми приращениями,
коэффициенты при них должны быть равны нулю, т. е.
при y =
i=i
Приращения /zb /г2, •. ., hm не являются независимыми, и их можно поло-
положить равными нулю выбором множителей Лагранжа в уравнении E.9).
Таким образом, мы выбираем множители \\, Х2, . . . , Хт такими, чтобы
df_
dXs
85
m dgt
+ Z А/ —— = 0 при j = 1,2,..., т.

Тогда окончательно будем иметь
dz
&С, 1= 1
= 0 при y=l,2,...,/i.
Следовательно, если определить функцию Лагранжа в виде
т
Fix, X) =/(х) + ? А,&(ж),
E.10)
E.11)
1=1
то необходимые условия минимума функции /(х) при наличии ограничений
можно записать следующим образом:
dF df
dz,
Я,—= 0 при у= 1,2 я,
Яде
i=\
Яде,-
3F
= 0 при i =
E.13)
Отметим, что для допустимых значений х (таких, которые удовлетворяют
ограничениям) справедливо соотношение
т
F(x,X) =/(*) + 2 А/А(х)=Дх).
1=1
В точке минимума при наличии ограничений на значение х* можно запи-
записать, что /(х* + h) - /(х*) > О, где h удовлетворяет уравнению gf(x* + h) ¦=
= 0 для всех /.
Таким образом,
h)
« 3F
5;
п п
d2F
I J
где производные вычислены в точке х* при X = X*.
С учетом уравнения E.12) получим для всех h, удовлетворяющих ограни-
ограничениям, что
п п
\
J
Достаточными условиями минимума при наличии ограничений являются
уравнения E.12) и E.13), а также положительная определенность квадра-
квадратичной формы
п п
к I I К
Л/
E.14)
для значений h, удовлетворяющих ограничениям.
Замечание. Не всегда просто привести квадратичную форму к виду при-
пригодному для использования. '
86
Пример 2
Проверьте, что точка B; 2) является минимумом функции /(х) = х\ + х\ при огра-
огра+ 4
ничении х1 +#2 = 4.
Для F(x, X) = х\ + *2 + А D - х, - х2) были получены решения
dF
= и, * == и,
dx{ дх2
8F
~дХ
= 0 при Xj = jc2 = 2 и X = 4.
Матрица Гессе функции F имеет вид ( ) и, следовательно, положительно определе-
определена, а это доказывает, что точка B; 2) является точкой минимума.
5.2. ОГРАНИЧЕНИЯ В ВИДЕ НЕРАВЕНСТВ
В этом разделе метод множителей Лагранжа будет распространен на огра-
ограничения в виде неравенств. Рассмотрим общую задачу математического про-
программирования :
минимизировать функцию /(х)
при наличии т ограничений gf (х) < bj (/ = 1, 2,..., т), Причем такие огра-
Причем такие ограничения не ограничивают общности. (Ограничение
) >с можно записать в виде — <^(х) <-с.)
В настоящее время нет метода, гарантирующего существование решения
любой подобной задачи. Возможно, читатель предложит такой метод.
Ограничения в виде неравенств могут быть преобразованы в ограничения
в виде равенств добавления к каждому из них неотрицательной ослабляющей
переменной и2 (отметим, что переменная и2 всегда положительна):
g.(x)+uf=b.
ИЛИ
+w2-Z>. = Q. E.15)
Таким образом, задача сводится к минимизации функции /(х) при нали-
наличии т ограничений в виде равенства gy(x) + и2. — b^Q. Следуя изложенному
в предыдущем разделе методу, сформируем функцию Лагранжа
т
F(x, к, и) = Дх) + I АД&(х) + «? - *,].
E.16)
Необходимыми условиями, которые должны выполняться в стационар-
стационарной точке, являются следующие:
dF df
~ " ~' - ¦ ¦ - E 17)
dgt .
I Я, —- при ,/=l,2,...,/r,
дх. ы i ox i
dF
u}-b{ при /=.1,2, ...,m,
ди;
= 0 = 2Я, ut при / = 1,2,..., т.
E.18)
E.19)
87

Умножив последнее уравнение на мг-/2, получим
т. е.
X/[Ъг gj(x)] = О при / = 1, 2,..., т. E.20)
Уравнения E.17), E.18) и E.20) являются необходимыми условиями
минимума в точке х* при наличии ограничений. Уравнения E.18) являются
повторной записью ограничений gj(x) < 0. Уравнение E.20) означает, что ли-
либо \- = 0, либо b;- g;(x*) = 0. Если \j Ф 0, то g;(x*) = bj и ограничение явля-
является активным и представляет собой ограничение в виде равенства. С другой
стороны, если ограничение является ограничением в виде строгого неравен-
неравенства #/(х*) < Ь;9 то соответствующий множитель Лагранжа Хг- = 0. В самом
деле, если g/(x*) < bif то рассматривается минимум, удовлетворяющий огра-
ограничению, которое является неактивным, и которым можно пренебречь, а со-
соответствующие множители Х; = 0. Конечно, предварительно не известно, ка-
какими ограничениями можно пренебречь.
Есть также дополнительное условие, которое должно быть выполнено в
точке минимума при наличии ограничений, а «именно Х^ > 0.
Предположим, что уравнения E.17), E.18) и E.20) справедливы в точке
(х*; X*; и*). Если фактический минимум функции при наличии ограничений
z = /(х*), то можно рассматривать z как функцию от bi и изменения Ъ^ будут
изменять ограничения и, таким образом, изменять саму функцию z. Пока-
Покажем, что
82 —х*
1Г "
dz " 8f дх,
вь, jtidxj дЬ{
где частные производные вычисляются в точке х*.
Поскольку gk (x) + w? = bk, то
dbt
Тогда
О, если гфк,
1} . если | = к.
dbt
db{
dz
+ Af=I.
т dgk
+ 1 AJ —
dXi
y=i \dxj k^\ " dxjj dbt
Но это выражение равно нулю в соответствии с уравнением E.17). Таким
образом,
— — X*
С возрастанием Z>7- область ограничений расширяется, что не может приве-
привести к увеличению значения z — минимума функции /(х), находящегося вну-
внутри области ограничений^ а может лишь уменьшить его. Таким образом,
dz
т. е.
°- E.22)
Необходимые условия минимума функции /(х) при наличии ограничений
gt (х) < Ьг (i = 1, 2,..., m) имеют такой вид, что можно найти х и X, для ко-
которых
3X;
'=
при
О при
О при
i'= 1, 2,...,m;
/=l,2,...,wi,
E.23)
(Знак Хг- меняется на противоположный, если рассматривается максимум.)
Эти условия известны как условия Куна — Такера.
Пример 1
Написать условия Куна — Такера для минимума функции /(х) = Ъх\ +Аххх2 + 5х\
при ограничениях хх > 0, х2 > 0 и хг + хг > 4.
Эту задачу можно представить следующим образом:
минимизировать функцию
fix) = Зх \ + 4дгх х2 +
при ограничениях — хх < 0, — х2 < 0, —хх - х2 <—4. Функция Лагранжа F(x, u,Л) будет
иметь вид
F = Ъх\ +4ххх2 +5x1 +*i («? ~хх) +\2 (и\ - х2)
Необходимым условием минимума являются
4х2 -
- Х2 - Л3 — О,
! < О, -д:2 < О, -хх - х2 < -4,
с, = О, \2х2 = 0, ^D-jc, - jc2)
А2, Л3 > 0.
= 0,
Нетрудно проверить, что эти условия
выполняются при хх — 3, х2 = 1, \х — 0,
Л 2 = 0, \^ — 22 и функция имеет мини-
минимум, равный 44 в точке А с координатами
C; 1).
Рис. 5.1
89

Линиями постоянного уровня функции /(х) являются эллипсы
Ъх\ + Аххх2 +5x1 = с.
Минимум функции /(х) при отсутствии ограничений равен нулю и находится в нача-
начале координат. Область ограничений показана теневым контуром на рис. 5.1, иллюстри-
иллюстрирующем настоящую задачу.
5.3. ВЫПУКЛОСТЬ И ВОГНУТОСТЬ
Общая задача математического программирования, сформулированная в
начале предьщущего раздела, является очень сложной и до ?их пор не имеет
полного решения. Некоторые трудности встречаются в задачах, графически
проиллюстрированных рис. 5.2. На рисунке изображены линии постоянного
уровня функции. По мере перемещения от точки х* - точки минимума функ-
функции при отсутствии ограничений - значения функции будут расти. На рис. 5.2
показаны также границы области ограничений gf(x) = Ъь а сама область
заштрихована.
На рис. 5.2, а минимум функции при наличии ограничений совпадает с ми-
минимумом функции без ограничений. Все ограничения имеют вид строгих не-
неравенств, и, зная это, можно было бы пренебречь ограничениями и решить за-
9j =4j
а)
Рис. 5.2
Рис. 5.3
дачу методами, изложенными в ч. I этой книги. На рис. 5.2, Сточка миниму-
минимума при наличии ограничений лежит на кривой g2(x) = b2, а два других огра-
ограничения неактивны. Зная это, можно было бы пренебречь ограничениями gi
и g3 и решить эту задачу как задачу с ограничениями в виде равенств, учиты-
учитывая тольдсо ограничение g2 (х) = Ь2. Из этого следует, что в точке минимума
х при наличии ограничений справедливо соотношение V/(x) =XVg2(x), по-
поскольку направление V/(x) перпендикулярно линии постоянного уровня и
границе области ограничений в данной точке. (Сравните с уравнением E.17).)
Возможно, что наличие ограничений будет приводить к появлению локаль-
локального минимума. Это может произойти даже в том случае, когда функция
имеет только одну точку минимума при отсутствии ограничений. Такая ситу-
ситуация иллюстрируется рис. 5.3.
Функция имеет только одну точку минимума при отсутствии ограничений.
Однако Для задачи с ограничениями обе точки А и В являются локальными
минимумами, поскольку ни в одной из допустимых точек в ближайших
окрестностях А или В функция не принимает меньших значений.
Некоторые из рассмотренных трудностей устраняются, если ограничиться
случаем, когда область ограничений выпукла, а минимизируемая (максими-
(максимизируемая) функция выпукла (вогнута).
Определим эти термины. Область является выпуклой, если отрезок пря-
прямой, соединяющей любые две точки области, принадлежит этой области.
Следовательно, если Xi и х2 находятся в этой области, то любая точка вида
вх2 + A — в) Xi, где 0 < в < 1, находится в этой же области. На рис. 5.4, а
изображена выпуклая область, а на рис. 5.4, б — невыпуклая.
а)
Рис. 5.4
Рис. 5.5
91
90

Функция /(х) является выпуклой на выпуклой области X, если для лю-
любых двух точек Xi, х2 ? X выполняется соотношение
Двх2 + A - в) xj < 0/(х2) + A - в) f(xx) при 0 < в < 1. E.24)
Для функции одной переменной это означает, что она лежит ниже хорды,
соединяющей любые две точки ее графика (рис. 5.5).
Для вогнутой функции, определенной на выпуклом множестве, следует
изменить знак неравенства, в результате чего получим соотношение
Двх2 + A -0)xj > 0/(Х2) + A - в)Дх1). E.25)
Такая функция лежит выше хорды, соединяющей любые две точки ее гра-
графика.
Если в соотношениях E.24) и E.25) неравенства заменить на строгие не-
неравенства, то функция /(х) будет строго выпуклой или строго вогнутой.
Есть еще два важных свойства выпуклых (вогнутых) функций, которые
можно вьюести из соотношений E.24) и E.25).
Если функция /(х) выпукла на выпуклой области 1ихьХ2 ? Х9 то
/(х2) >/0О + («2 - *i)T V/W. E.26)
Для вогнутых функций знак неравенства меняется на противоположный,
что устанавливается следующим образом. Поскольку /(х) выпукла, то для
О < в < 1 справедливо соотношение
Двх2 + A - 0)х,К 0f(x2) + A - в)
0[/(х2) -
следовательно,
f\xx + 0(х2 - х
и
ft*
в
Но по теореме о среднем
хх + 0(х2 - Xl)] =/(Xl) + в(х2 - Xl)T V/[Xl + Л0(х2 - x,)],
где 0 < X < 1, т. е. производная вычисляется в некоторой точке, лежащей
между точками хг ихг + в (х2 — хО -
Следовательно,
/(х2) >f(xx) + (х2 - Xl)T V/[Xl + вХ(х2 - х{)]
и при в -* 0 получаем соотношение E.26).
Из соотношения E.26) следует, что выпуклые функции одной перемен-
переменной (двух переменных) лежат выше любой касательной (плоскости) к дан-
данной функции (см. рис. 5.5).
Функция выпукла, если гессиан
И
92
положительно определен. По теореме Тейлора можно записать
/(ж) =/(Xl) + (х - Xl)T V/(Xl) + i(x - Xl)T H(x - . x\
где Н вычисляется в точке Xi + Х(х -Xi)hO<X<1.
Т б
( )
Таким образом, достаточно показать, что положительно определенная
квадратичная функция ?хтНх является выпуклой. Это сделать несложно.
Пусть Xi и х2 — произвольные значения х и пусть х" = 0х2 + A - в)хг, где
0
Тогда
хт Нх -
Хак как 0 < в < 1, то A — в) > 0, и если матрица Н положительно определе-
определенна, то —0 A — в) < 0. Следовательно,
E.27)
{0х2 + A - в)х1ГН[вх
Для выпуклых функций одной переменной это означает, что вторая про-
производная неотрицательна, поэтому первая производная является возрастаю-
возрастающей функцией, которая может быть равна нулю только в одной точке. Сле-
Следовательно, такая функция может иметь только одну точку минимума.
Пример 1
Показать, что если gi (х) при i. = 1, 2, ..., m - выпуклые функции на выпуклой об-
обрасти X, то 2 \jgj(x), где Xj > 0, также выпукла.
Пусть
m
Тогда если хх, х2 ^ X, то
Н[вх
т
I
/=1
m
- в)
m
что # Показывает вьшуклость функции h (x).
Пример 2
Если область ограничений задана неравенствами ?/(х) <
) - выпуклые функции, то показать, что она выпукла.
j при i = 1, . . . , w, где
93

Предположим, что х, и х2 - допустимые точки внутри области ограничений. Тогда
f при /=1, ...,аи,
&/ ПРИ 1=1,...,/и.
Если 0 < 0 < 1, то при / = 1, 2,.. ., т
Следовательно, отрезок вх2 + A -0)х1 принадлежит множеству допустимых точек,
что справедливо для выпуклого множества.
Полученные выше результаты дают возможность доказать следующую теорему: если
/(х) - выпуклая функция на области ограничений, заданной неравенствами gj (х) < Ър
где gj (x) - выпуклые функции, то локальный минимум функции /(х) в этой области
является и глобальным минимумом в этой же области.
Предположим, что в точке х* достигается глобальный минимум, а ь точке х0 дости-
достигается локальный минимум, причем /(х*) < /(х0). Обе эти точки являются допустимы-
допустимыми, и поскольку допустимая область и функция /(х) являются выпуклыми, то
f[0x* + A _ в) х0] < Of(x*) + A - в) /(х0) <
для 0 < в < 1.
Но если в достаточно мало, то отрезок 0х* + A — 0) х0 лежит внутри 5-окрестности
точки х0. Тогда, поскольку в точке х0 достигается локальный минимум, /(х*) > /(х0).
Следовательно, мы приходим к противоречию и х* и х0 должны совпадать.
Пример 3
Записать условия Куна—Такера для следующей задачи:
минимизировать функцию f(x, у) = -х2 - у2 при ограничениях х, у > 0, х + 2у < 3.
Функция Лагранжа имеет вид
F(x,y, Х,и) = —х2 — у2 + Лх(—х + и\) + А2(—у + и\) + Л3(х + 2у + и\ — 3).
Необходимые условия минимума выражаются уравнениями
-2х - \ + \3 = 0;
-2у - \2 + 2\3 = 0;
Хгх = 0, \j = 0, \3 (х + 2у - 3) = 0;
х+2у <3;
Попытаемся найти решения этих уравнений,
а). Если х > 0, у > 0, то \t = Х2 = 0.
б). Если Х3 = 0, то а: = у = 0 и функция достигает максимума.
в). Если X, = Х2 = 0» ^з > 0, то 2д: = Х3 = j и х + 2у - 3 = 0, следовательно, х = 3/s,
Х3 = 6/5, j = 6/5, все условия минимума выполняются и / = —
94
г). Если Л, > 0, \2 = 0, \ъ > 0, то х = 0,
д? > 0, jc + 2^ = 3, следовательно, .у = 3/2,
^з = /2> \ — h> все условия минимума
выполняются и / = -9/4-
д). Если ^ = 0, \2 > 0, Х3 > 0» то ^ > 0»
V = 0, х + 2.у = 3, следовательно, х — 3, Л, =
55 6, \2 = 12, все условия минимума вы-
выполняются и / = -9.
Значит, есть несколько точек, удовлетво-
»яющих необходимым условиям. Глобаль-
ный минимум достигается в точке C; 0) и
равен — 9. Задача иллюстрируется рис. 5.6.
J
ГЖ 6/5]
х+2у = J
Рис. 5.6
Сложности, возникающие при ре-
ении примера 3, устраняются, если
^пункция /(х) и область ограничения выпуклы. Для задачи минимизации
(х) при ограничениях ?/(х) < bi9 где /(х) и ^/(х) — выпуклые функции,
необходимые условия Куна—Такера (см. соотношение E.23)) являются так-
также и достаточными.
Для данного случая функция Лагранжа (см. соотношение E.16))
т
и) =/(х) •
• —— я.
есть сумма выпуклых функций, поэтому сама также выпукла, а множители
X/ > 0. Следовательно, функция F имеет глобальный минимум в точке, где
ее производные исчезающе малы, и такая точка является единственной. По-
Поэтому необходимые условия являются также и достаточными.
Пример 3 не противоречит данному результату. Функции gj (x) — выпук-
выпуклые, но функция f(x, у) = — (х2 + у2 ) не выпукла, а вогнута.
5.4. ЛИТЕРАТУРА
1 В. Bernholtz, 'A new derivation of the Kuhn-Tucker conditions', Operations Research, 12,
No. 2, 295-299, 1964.
2 H. W. Kuhn and A. W. Tucker, 'Non Linear Programming', in Proc. of 2nd Berkeley
Symposium on Mathematical Statistics and Probability (Editor J. Neyman), Berkeley,
University of California Press, 481-492, 1951.
5 G. R. Walsh, Methods of Optimisation, John Wiley, 1975.
4 D. J. Wilde, 'Differential Calculus in Non Linear Programming', Operations Research 10,
No. 6, 764-773, 1962.
5 P. Wolfe, 'Methods of Non Linear Programming' in Recent Advances in Mathematical
Programming (Editors R. L. Graves and P. Wolfe), McGraw-Hill, New York, 67-86,
1963.
fe P. Wolfe, 'Methods of Non Linear Programming' in Non Linear Programming (Editor
J. Abadie), Nato Summer School, Menton, 1964, North Holland Publishing Co., Amster-
Amsterdam, 1967.
5.5. УПРАЖНЕНИЯ
.1. Покажите, что функция f{xx, x2) = х\ + х\, где хх, х2 = 4 имеет минимум, равный
. 8 при (х1гх2) = (±2; ±2).
2. Покажите, что функция f(x, у) = х2 + у2 при ограничении х - у = 5 достигает мини-
минимума при х = 2,5, у = -2,5.
95

3. Если константы а, Ъ, с, к — положительны, то найдите положительные х, у, z, такие,
что функции к — x+y + z hw = ax2 + by2 + cz2 минимальны.
4. Если а, Ъ,с- отрицательны и f(xv х2,хэ) - ах2хэ +bx3x1+cx1x2,mex1 +*2 +*3 = 1,
то покажите, что f(xt, х2,хъ) имеет минимальное значение, равное abc/ [2 (ab + Ьс +
+ са) — (а2 + Ъ% + са) ] при условии положительности знаменателя.
5. Найдите стационарное значение (значения) функции fix, у, z) = xy2z* при ограни-
ограничении х + у + z = 6.
6. Открытая коробка, изготовляемая из тонкого листа железа, имеет высоту z и пря-
прямоугольное основание с размерами х иу. Основание и стороны длиной х имеют тол-
толщину, равную d (малая величина), а стороны длиной у имеют толщину 2d. Если ко-
количество материала фиксировано, покажите, что объем коробки максимален при
х= 2у~ 4z.
7. Найдите условия Куна—Такера и таким образом решите задачу
минимизировать функцию f(x,y) = х2 +у2
при ограничениях х > 0, у > 0, х +у > 5.
8. Найдите условия Куна—Такера и таким образом решите задачу
минимизировать функцию f(x, у) = х2 + вху -4х-2у
при ограничениях х2 - 2у < 1, 2х - 2у < 1.
9. Если /(х) - выпуклая функция на области ЛГ, то покажите, что g(x) = -д/(х), где
а > 0, - вогнутая функция на области X.
10. Функции gj(x) при 1 = 1, 2, . . . , т выпуклы. Покажите, что множество точек
{х:?/(х) <к] , щек - константа, выпукло.
11. Пусть h(x) — положительная вогнутая функция и а <х <Ь. Покажите, что функция
g(x) = 1/Л (х) выпуклая на отрезке а < х < Ъ.
Обобщите этот результат на случай, когда h (x) — положительная вогнутая функция,
определенная на множестве X. Покажите, что гессиан функции g (х) = 1/Л (х) поло-
положительно определен.
12. Рассмотрите задачу минимизации выпуклой функции /(х) при ограничениях ^-(х) <
< 0, где i = 1, 2,..., т. Предположите, что минимум /(х) при отсутствии ограниче-
ограничений достигается в точке х* и что gt(x*) > 0, ?2(х*) > 0, ?3(х*) > 0. Если мини-
минимум при ограничениях достигается в точке х0, покажите, что по крайней мере одно
из значений функций gx (х0), g2 (х0), g3 (x0) равно нулю. Дайте геометрическую ин-
интерпретацию результата.
13. Найдите минимальное и максимальное значения функции
/(х, у) = х2 + у2
при ограничении Зх2 + 4ху + ву2 = 140. Дайте геометрическую интерпретацию ре-
результата.
14. Задача минимизации объема выпуска товара может быть сформулирована как зада-
задача минимизации функции
*!» *г) =— + — + УС*1 + х2),
хх х2
где хх, х2 > 0. Константы аиK связаны со стоимостями производства двух товаров,
а у - константа, связанная со стоимостью хранения товаров на складе (см. упр. 8
разд. 1.4).
Покажите, что вышеприведенная функция минимальна, если хх = \ГЩу, х2 =
96
В связи с тем что товары хранятся на складе, хг и х2 должны удовлетворять, кроме
того, условию хх +х2 <S, где S - некоторая константа.
Напишите условие Куна—Такера для сформулированной задачи и таким образом
получите решение.
15. Посылка, которую должны отправить по почте, имеет форму прямоугольника с раз-
размерами хх, х2, хг. При отправлении посылки накладываются следующие ограниче-
ограничения: хх < 20, х2 < 11, jc3 <42 и ху + 2х2 + 2хг < 72. Найдите размеры, при которых
объем будет максимальным. (Это модифицированная Розенброком задача о почто-'
вой посылке.,См. также следующую главу.)
16. Стандартная задача о почтовой посылке аналогична приведенной выше задаче, за ис-
исключением того, что ограничения имеют вид
xj < 42 при / = 1, 2, 3, Jtj + 2х2 + 2х3 < 72.
Напишите условия Куна-Такера для этой задачи и таким образом получите решение.
ГЛАВА 6. МЕТОДЫ ПОИСКА
6.1. МОДИФИЦИРОВАННЫЙ МЕТОД ХУКА-ДЖИВСА
В первую очередь рассмотрим методы решения задач нелинейного про-
программирования, в которых используются только значения функции. С этой
целью успешно применяются методы прямого поиска, изложенные в гл. 3,
где они были использованы для решения задач оптимизации без ограничений.
Эти методы нетрудно модифицировать и для учета ограничений. Было выдви-
выдвинуто предположение, что для этого будет вполне достаточно при решении за-
задачи минимизации присвоить целевой функции очень большое значение там,
где ограничения нарушаются. К тому же такую идею просто реализовать с
помощью программирования.
Нужно проверить, каждая ли точка, полученная в процессе поиска, при-
принадлежит области ограничений. Если каждая, то целевая функция вычисляет-
вычисляется обычным путем. Если нет, то целевой функции присваивается очень боль-
большое значение. Таким образом, поиск будет осуществляться снова в допусти-
допустимой области в направлении к минимальной точке внутри этой области.
В тексте программы модифицированного метода прямого поиска Хука—
Дживса сделана попытка реализовать такую процедуру. Рассматриваемая за-
задача формулируется следующим образом:
минимизировать f(xlfx2) =Ъх\ + Аххх2 +5x1
р
при ограничениях хг >0, х2 >0, хх +х2
(см. пример 1 из разд. 5.2).
Программа аналогична приведенной в разд. 3.2 программе Хука—Дживса,
за исключением того, что подпрограмма, начинающаяся со строки 2000, была
изменена с целью учета ограничений так, как об этом говорилось выше. Ми-
Минимум, равный 44, достигается в точке C; 1) при ограничении хх + х2 =4.
10 PRINT "МЕТОД ХУКА-Д ИВСА ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ"
20 REM ФУНКЦИЯ Z*F(X1,X2,...,XN) ВЫЧИСЛЯЕТСЯ В СТРОКЕ 2000
30 PRINT "ВВЕДИТЕ ЧИСЛО nEPEMEHHblX":INPUT N
40 DIM X(N),B(N),Y(NIP(N)
4 Зак. 768 97

50 PRINT "ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ X1,X2,...,XN"
60 FOR I«l TO N:INPUT X(I):NEXT I
70 PRINT "ВВЕДИТЕ ДЛИНУ UArA":INPUT H
80 K*HsFE*O
90 FOR I«l TO N
100 Y(I)«X<I):P(I)*X(I):B<I)«X(I):NEXT I
110 GOSUB 2000:FI=Z
120 PRINT "НАЧАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ^
130 FOR 1=1 TO N:PRINT X(I);11 ";:NEXT I:PRINT ""
140 PS«O:BS*1
150 REM ИССЛЕДОВАНИЕ ВОКРУГ БАЗИСНОЙ ТОЧКИ
180 J=*1:FB*FI
200 X(J)=Y(J)+K
210 GOSUB 2000
220 IF Z<FI THEN GOTO 2B0
230 X<J)=Y(J)-K
240 GOSUB 2000
250 IF Z<FI THEN GOTO 280
260 X(J)*Y(J)
270 GOTO 290
280 YCJ)-X(J>
290 GOSUB 2000
300 FI*Z
310 PRINT "ПРОБНЫЙ UAP'Z
320 FOR I«l TO N:PRINT X(D;" ";:NEXT IrPRINT im
330 IF J»N THEN GOTO ЗАО
340 J=J+1
350 GOTO 200
Для начальной точки D; 3) и при длине шага, равной единице, програм-
программой успешно решена задача минимизации. Ниже приведена распечатка резуль-
результата работы программы.
МЕТОД ХУКА-ДЖИВСА ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
2
ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ X1,X2,/..,XN
4
3
ВВЕДИТЕ ДЛИНУ ШАГА
1
НАЧАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ 141
4 3
ПРОБНЫЙ ШАГ 108
3 3
ПРОБНЫЙ ШАГ 71
3 2
ПОИСК ПО ОБРАЗЦУ 1Е+30
2 1
ПРОБНЫЙ ШАГ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
ПОИСК ПО ОБРАЗЦУ 1Е+30
3 О
ПРОБНЫЙ ЫАГ 48
4 О
ПРОБНЫЙ ШАГ 48
4 О
ЗАМЕНА БАЗИСНОЙ ТОЧКИ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
ПРОБНЫЙ ЫАГ 44
3 1
УМЕНЬШИТЕ ДЛИНУ ШАГА
98
ПРОБНЫЙ ЫАГ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
УМЕНЬШИТЕ ДЛИНУ ЫАГА
ПРОБНЫЙ ЫАГ 44
3 1 "'
ПРОБНЫЙ ШАГ 44
3 1
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ЫАГ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
УМЕНЬШИТЕ АЛИНУ ШАГА
ПРОБНЫЙ ШАГ 44
3 1
ПРОБНЫЙ ШАГ 44
3 1
УМЕНЬШИТЕ ДЛИНУ ЫАГА
МИНИМУМ НАЙДЕН
X 1 * 3
X 2 - 1
МИНИМУМ ФУНКЦИИ РАВЕН 44
КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО
Для начальной точки C; 4) и длины шага, равной единице, программой
также успешно решена задача минимизации.
Для начальной точки E; 6) и длины шага, равной единице, задача не реше-
решена, так как программа остановилась в точке A; 3), т. е. на активном ограни-
ограничении, и выдала неверный результат. Распечатка результата работы програм-
программы приведена ниже.
МЕТОД ХУКА-ДЖИВСА ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
2
ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ X1,X2,...,XN
5
6
ВВЕДИТЕ ДЛИНУ ШАГА
1
НАЧАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ 375
5 6
ПРОБНЫЙ ШАГ 324
4 6
ПРОБНЫЙ ЫАГ 253
4 5
d* 99

ПОИСК ПО ОБРАЗЦУ 155
3 4
ПРОБНЫЙ ШАГ 124
2 4
ПРОБНЫЙ ЫАГ 81
2 3
ПОИСК ПО ОБРАЗЦУ IE+30
О 1
ПРОБНЫЙ ШАГ 1Е+30
О 1
ПРОБНЫЙ ЫАГ 1Е+30
0 1
ЗАМЕНА БАЗИСНОЙ ТОЧКИ 81
2 3
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
ПОИСК ПО ОБРАЗЦУ 1Е+30
0 3
ПРОБНЫЙ ЫАГ 60
1 3
ПРОБНЫЙ УАГ 60
1 3
ЗАМЕНА БАЗИСНОЙ ТОЧКИ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 60
1 3
ПРОБНЫЙ ШАГ 60
1 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
ПРОБНЫЙ ШАГ 60
.9999999 3
ПРОБНЫЙ ШАГ 60
.9999999 3
ПОИСК ПО ОБРАЗЦУ IE+30
.9999998 3
ПРОБНЫЙ ШАГ 60
.9999999 3
ПРОБНЫЙ ЫАГ 60
.9999999 3
ЗАМЕНА БАЗИСНОЙ ТОЧКИ 60
.9999999- 3
ПРОБНЫЙ ШАГ 60
.9999999 3
ПРОБНЫЙ ШАГ 60
.9999999 3
УМЕНЬШИТЕ ДЛИНУ ШАГА
МИНИМУМ НАЙДЕН
X 1 » .9999999
X 2 - 3
МИНИМУМ ФУНКЦИИ РАВЕН 60
КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО
96
100
Аналогичные неутешительные результаты были получены для начальной
точки E; 6) и длины шага, равной 0,5. Неверное решение было найдено в
точке A,5; 2,5). Для начальной точки D; 3) и длины шага, равной ,0,5,
программа работала нормально, но было получено неверное решение в точке
B,5; 1,5).
Проблема понятна. С помощью данного метода невозможно двигаться
вдоль границы области ограничений и сходимость достигается в первой же
точке границы, где и находится решение. Как подчеркивалось в гл. 5, общая
задача оптимизации при наличии ограничений очень сложна и для получения
практического метода решения требуются более изощренные процедуры, чем
приведенная выше.
6.2. КОМПЛЕКСНЫЙ МЕТОД
Трудности, встречающиеся при попытке использовать существовавшие ра-
ранее методы поиска, подтолкнули Бокса в 1964 году к созданию своего мето-
метода. По существу, он является модификацией симплексного метода Нелдера—
Мида, однако позволяет учитывать ограничения. Бокс назвал его комплекс-
комплексным методом.
Решаемая задача состоит в минимизации функции /(х) = /(xi, х2, - . .
... > хп), где х определяется явными ограничениями
/.<*.< и. при/= 1,2,...,«, F.1)
а также неявными ограничениями
g.(x) <Z>. при /= 1, 2,... ,m. F.2)
Если целевая функция /(х) выпукла и функции ?;(х) тоже выпуклы, то
задача будет иметь единственное решение. Значения /у и Uj являются нижней
и верхней границами переменных. Если в конкретной задаче заданные пере-
переменные теоретически не имеют ограничений, то предположение о наличии у
них "безопасных" границ, т. е. границ, включающих оптимум, позволит при-
применить комплексный метод.
101

Данный метод является итерационным. В нем предполагается, что извест-
известны значения «и/и, lj и uf и начальная точка Xj, удовлетворяющая всем огра-
ограничениям (см. неравенства F.1) и F.2)). В первую очередь необходимо
выбрать к точек, которые удовлетворяют ограничениям, а также вычислить
целевую функцию во всех к точках. Множество этих точек называется комп-
комплексом. Бокс обнаружил, что к должно быть больше (п + 1) - числа точек,
используемых в симплексном методе Нелдера-Мида и положил к = In.
Как упоминалось выше, предполагается, что точка хх, удовлетворяющая
всем ограничениям, задана. Остальные точки, удовлетворяющие неравенству
F.1), могут быть выбраны следующим образом:
для / - 1,2,. %., п и / - 2, 3,... ,к9 где г — псевдослучайная равномерно рас-
распределенная переменная в интервале @; 1). Такая переменная в языке Бей-
Бейсик может быть задана с помощью оператора Y-RND(X).
Точки, выбираемые в соответствии с уравнением F.3) для данного /
будут автоматически удовлетворять неравенству F.1). Если эти точки удов-
удовлетворяют также неравенству F.2), то они принимаются в качестве началь-
начальных точек комплекса. Если точка, выбранная в соответствии с уравнением
F.3), не удовлетворяет неравенству F.2), то она смещается на половину
расстояния до центра тяжести множества уже принятых точек, т. е. формиру-
формируется точка
*с)
F-4)
где
хс =
1 '-1
е=1
F.5)
Если точка в соотношении F.4) все еще не является допустимой, то опи-
описанная соотношением F.3) процедура повторяется вновь до тех пор, пока
точка не станет допустимой. Если функция g (x) выпукла, то в конце кон-
концов ограничения будут выполняться. Конечно', поскольку точка Xi находит-
находится внутри области ограничений, то комплекс будет состоять из допустимых
точек.
Удобно упорядочить точки комплекса в соответствии со значениями функ-
функции. Процедуру инициализации комплекса можно описать с помощью блок-
схемы (рис. 6.1). Она реализуется в программе операторами в строках с но-
номерами до 1000.
Теперь мы подошли к итерационной процедуре комплексного метода, в
которой производится поиск минимума перемещением по направлению к
минимуму внутри области ограничений. Для этой процедуры необходимы
следующие шаги:
1. Найти точку с наибольшим значением функции Хи и найти центр
остальных (к - 1) точек.
102
Ввести т, п
1
Ввести
, / = /
I
Ввести lj, Uj, j-UZy ...,n
Положить хс =*/
Запустить еенератор случайных чисел
I
1
Полошить Xij =lj + r(uj- Ц
i - допустимая точка ?
'да
Обновить
Найти j
точку центра
Упорядочить F1,..., Fk
Пометить наименьшее значение
функции
Рис. 6.1
2. Попытаемся сместиться от точки х^ и получить при этом точку х,. отра-
отражением точки Xfr относительно точки Хо,используя коэффициент отражения
ос > 1, что можно записать как
= A+<к)хо ~ахн- F*6)
3. Проверить, является ли точка х^. допустимой.
а). Если точка хг не является допустимой и не выполняется ограниче-
ограничение пдя /;-, то полагаем xrj- = /у + 10~ 6; если не выполняется ограниче-
ограничение для Up то полагаем xr/- = Uj — 10~6
103

б). Если не выполняются ограничения, то точку х, перемещают на по-
половину расстояния между хг и центром Хо, т. е.
(новое) = (х, +Хо)/2. F.7)
Затем производится повторная проверка на допустимость и шаг 3 повторяет-
повторяется до тех пор, пока не будет получена допустимая точка.
4. Если точка хг является допустимой, то вычисляется значение функции
f(xr) и сравнивается с /(х^) — наибольшим значением функции.
Если /(х,) > f(xk), т. е. "хуже", чем наибольшее значение, полученное ра-
ранее, то точка хг смещается к центру Хо на половину расстояния между ни-
ними, т. е.
х^ (новое) = (х, +Хо)/2
и процесс возвращается на шаг 3.
5. Если /(Ху.) < /(хд.), то точка х заменяется на точку х,., затем точки и
значения функции комплекса снова упорядочиваются.
6. Вычисляются две величины, использующиеся при проверке сходимости
метода: среднее квадратическое отклонение о для к значений функции и
максимальное расстояние dm между двумя точками комплекса. Первая ве-
величина вычисляется как
а =
X [/(ж,)-/]2/*
^ 1/2
F.8)
где
. 1 *
f=jl
но для вычисления о2 лучше использовать формулу
' к И/Ш2)
F.9)
е=1
F,10)
7. Величины о2 и dm проверяются на сходимость. Если обе эти величины
достаточно малы, то процедура поиска минимума заканчивается. В против-
противном случае необходимо вернуться на шаг 1 и повторить процедуру.
В тексте программы промежуточные результаты печатаются в строке
3500, но только в том случае, если наименьшее значение функции было улуч-
улучшено.
На блок-схеме (рис. 6.2) приведены шаги 1 - 7, которые реализованы в
программе до оператора в строке 3800. Когда сходимость достигнута, с по-
помощью операторов в строках 4000-4100 находится решение.
Целевая функция вычисляется в подпрограмме, начинающейся с операто-
оператора 5000. Ограничения проверяются в подпрограмме, начинающейся с опера-
оператора 6000. Переменная 1С = 1 указывает на то, что были нарушены неявные
ограничения, а переменная ЕС = 1 - на то, что были нарушены явные ограни-
ограничения. Массивы ЕС (J), J = 1, 2,..., 2N, и 1С (L), L = 1,..., М, указывают на
конкретные ограничения, которые были нарушены.
104
Определить х0-
центр лучших (к-1) точек
1
1
Получить хг с помощью операции отражения
допустимая ?
Если нарушены границы
I) или uj
„
Да
нет
Если не выполняется
ограничение на функцию
Заменить точку х(к) на точку хг
Обновить Fr,...fFk и
точки комплекса
Найти стандартное отклонение
значений функции и максималь-
максимальное расстояние между точками
комплекса
Нет
Сходимость достиг
нута!
Рис. 6.2
Данные подпрограммы подходят для решения модифицированной задачи
о почтовых посылках (см. упр. 15 разд. 5.5)
минимизировать функцию /(х) =—Х\ХгХг
при ограничениях 0<Х!<20, 0<х2<11, 0<х3 <42и^ +2х2 +2х3<72.
В этой задаче есть только одно неявное ограничение, однако необходимо
выяснить, как следует модифицировать подпрограмму для других ограниче-
ограничений. Заметим, что если IM = 1 при входе в подпрограмму, то проверяются
только неявные ограничения. В этом смысл оператора в строке 640.
Процедура сходится, когда комплекс "стягивается" до такого размера,
при котором он помещается в небольшой окрестности точки минимума. Про-
105

верка сходимости будет успешно заканчиваться на этом шаге, поскольку раз-
,ница в значениях функции будет также мала.
Bbi6op к = 2п и а= 1,3 (см. строку 1120) является эмпирическим прави-
правилом, предложенным Боксом. Первое значение частично предотвращает преж-
преждевременное сжатие комплекса. Коэффициент отражения а > 1 позволяет
комплексу расширяться и перемещаться в нужном направлении. Перемеще-
Перемещения на половину расстояния от начальной точки к центру сжимают комплекс.
Поэтому комплекс может перемещаться внутри допустимой области вдоль
границ и огибать углы в местах пересечения ограничений.
Способ выбора начального комплекса означает, что легко может быть сде-
сделано несколько перемещений. Очевидно, что будет сделано более одного пе-
перемещения даже в том случае, когда метод преждевременно сходится по при-
причине какой-нибудь особенности используемых точек. Конечно, разумно полу-
получить некоторую информацию о значении минимума функции, а затем вклю-
включить эту информацию в подпрограмму, начинающуюся со строки 5000, чтобы
для реально минимизируемой функции минимум был бы близок к нулю. Это
позволит избежать любых осложнений в процессе вычисления погрешности
при проверке на сходимость. Если из девяти цифр значения функции восемь
первых цифр совпадают, то можно столкнуться с большими сложностями
при определении точности и даже получить отрицательную разность при опре-
определении погрешности (это как раз будет машинная точность, но все равно в
процессе вычисления появятся погрешности). Эти сложности были учтены в
подпрограмме, начинающейся со строки 5000. Итак, установлено, что мини-
минимум функции действительно равен нулю.
Пример 1*
Решить модифицированную задачу о почтовой посылке. В качестве начальной точки
взять точку B0; 10; 10). Датчик случайных чисел бы инициализирован значением 7199,
однако это не так важно. Приведена первая и последняя части распечатки программы.
Истинный минимум достигается в точке B0; 11; 15), так что этим методом получена
хорошая точность. Число вычислений функции равно 231, что довольно много (по срав-
сравнению со многими другими запусками), однако вполне согласуется с результатами, по-
полученными Боксом.
20 PRINT "КОМПЛЕКСНЫЙ METOA":PRINT '•"
40 REM ФУНКЦИЯ Z«F(X1,X2,...,XN> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 5000
60 REM ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ G1,62,...,GM И ПРОВЕРКА
65 REM ОГРАНИЧЕНИЙ ПРОИЗВОДИТСЯ В СТРОКЕ 6000
ВО PRINT "ВВЕДИТЕ КОЛИЧЕСТВО ОГРАНИЧЕНИЙ":ШРиТ М
100 PRINT "ВВЕДИТЕ КОЛИЧЕСТВО ПЕРЕМЕННЫX":INPUT N
120 DIM X(N),Y(N),L(N),U(N),XC(N),XCKN),XR(N),XH(N)
160 K*2»NsPP-0
180 DIM C<K,N),F<K),G<M>,IC<M),EC<2*N)
200 PRINT "ВВЕДИТЕ НАЧАЛЬНЫЕ ЗНАЧЕНИЯ"
220 FOR J*l TO N:INPUT X(J>:CA,J)=X<J):XC(J)*X(J):NEXT J
240 REM ПРОЧИТАТЬ ЗНАЧЕНИЯ НИЖНИХ И ВЕРХНИХ ГРАНИЦ
260 FOR J=l TO N:READ L<J),LKJ>:NEXT J
280 REM ВКЛЮЧИТЬ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ
290 PRINT "ВВЕДИТЕ X"sINPUT X
* В этом примере приведены результаты, полученные автором, и результаты, полу-
полученные на IBM PC XT (см. предисловие редактора перевода). - Прим. ред.
106
500 1-1
520 GOSUB 5000:F(l)-Z
600 I—1+1
620 FOR J«*l TO N:C(I,J)=L(J)+RND(X>*(U(J)-L(J»:X(J)=C(I,J):NEXT J
640 IM-lsGOSUB 6000
660 IF IC=1 THEN GOTO 720
670 REM ОБНОВИТЬ ЗНАЧЕНИЕ "ЦЕНТРА ТЯЖЕСТИ"
6В0 FOR J-1*TO N:XC(J>=«I-1>*XC<J)+C<I,J»/I:NEXT J
700 GOTO 760
720 FOR J*l TO N:C(I,J)=(C(I,J)+XC(J))/2:X(J)=C(I,J):NEXT J
740 GOTO 640
760 GOSUB 5000:F(I)«Z
780 IF KK THEN GOTO 600
790 REM УПОРЯДОЧИТЬ ЗНАЧЕНИЯ ФУНКЦИИ И ТОЧКИ,
795 REM В КОТОРЫХ ОНА ВЫЧИСЛЕНА
800 FOR J-l TO K-1
820 FOR I-J+l TO К
840 IF F(JK-F(I) THEN GOTO 900
860 F»F<J)#:(J)-F<I):F<I)*F
860 FOR L*l TO N:Y(L>-C(J,L)iC(J,L)=C(I,L>:C(I,L)*Y(L):NEXT L
900 NEXT I:NEXT J
910 REM ЗАПОМНИТЬ НАИМЕНЬШЕЕ ЗНАЧЕНИЕ*ФУНКЦИИ
920 FM*FA)
1000 PRINT "ПЕРВАЯ ТОЧКА"
1020 PRINT "МИНИМАЛЬНОЕ 3HA4EHHE-"FA)
1040 PRINT "МИНИМАЛЬНАЯ ТОЧКА"
1060 FOR L«l TO N:PRINT "X";L,CA,L)?NEXT L
1080 PRINT и"
1100 REM ЗАДАТЬ КОЭФФИЦИЕНТ ОТРАЖЕНИЯ
1120 A-1.3
1190 REM ОПРЕДЕЛИТЬ "ЦЕНТР ТЯЖЕСТИ" НАИЛУЧШИХ <К-1) ТОЧЕК
1195 REM И ЗАПОМНИТЬ НАИХУДШУЮ ТОЧКУ
1200 FOR L«l TO N:XH(L)=C(K,L>:XO(L>=(K*XC(L>-XH(L»/(K-1):NEXT L
1390 REM ПОЛУЧИТЬ ОТРАЖЕННУЮ ТОЧКУ
1400 FOR L*l TO N:XR(L)=A+A)*XO(L)-A»XH(L):X(L)=XR(L):NEXT L
1490 REM ПРОВЕРИТЬ, ДОПУСТИМА ЛИ НОВАЯ ТОЧКА
1500 IM-0
1520 GOSUB 6000
1540 IF EOO AND IC=O THEN GOTO 2000
1550 REM ЕСЛИ ТОЧКА ЯВЛЯЕТСЯ ДОПУСТИМОЙ, ТО ПЕРЕЙТИ К СТРОКЕ 2000
1555 REM И ВЫЧИСЛИТЬ ЗНАЧЕНИЕ ФУНКЦИИ
1600 IF EOO THEN GOTO 1800
1610 REM ЕСЛИ ЯВНЫЕ ОГРАНИЧЕНИЯ НАРУШЕНЫ, ТО
1615 REM ПОМЕСТИТЬ ТОЧКУ ВНУТРЬ ГРАНИЦ
1620 FOR J*l TO N
1640 IF EC(J)=1 THEN XR(J)=L(JH.00001:X(J)=XR(J)
1660 IF EC(J+N)=1 THEN XR(J)=U(J)-.00001:X(J)=XR(J)
1680 NEXT J
1800 IF IC-0 THEN GOTO 2000
1810 REM ЕСЛИ НЕЯВНЫЕ ОГРАНИЧЕНИЯ НАРУШЕНЫ, ТО
1815 REM ПЕРЕМЕСТИТЬСЯ НА ПОЛОВИНУ РАССТОЯНИЯ К "ЦЕНТРУ ТЯЖЕСТИ"
1820 FOR L«l TO N:XR<L)=(XR(L)+X0(L))/2:X(L)=XR(L):NEXT L
1840 GOTO 1490
2000 GOSUB 5000:FR«Z
2010 REM ЕСЛИ НОВОЕ ЗНАЧЕНИЕ - НАИХУДШЕЕ,
201Ь REM ТО ПЕРЕМЕСТИТЬСЯ НА ПОЛОВИНУ РАССТОЯНИЯ К ТОЧКЕ ХО
2018 REM И ВЫЧИСЛИТЬ НОВОЕ ЗНАЧЕНИЕ ФУНКЦИИ
2020 IF FR<F(K) THEN GOTO 2400
2040 FOR L*l TO N:XR(L)=(XR(L)+X0(L))/2sX(L>=XR(L);NEXT L
2060 GOTO 1490
2400 REM ОБНОВИТЬ ХС И ЗАМЕНИТЬ НАИХУДШУЮ ТОЧКУ НОВОЙ ТОЧКОЙ
2410 F(K)«FR
2420 FOR L-l TO N
2440 XC(L)*K»XC(L)-C(K,L)+XR(L)
2460 XC(L>=XC(L>/K:C(K,L)=XR(L)
2480 NEXT L
107

2490 REM УПОРЯДОЧИТЬ ЗНАЧЕНИЯ ФУНКЦИИ И ТОЧКИ,
2495 REM В КОТОРЫХ ОНА ВЫЧИСЛЕНА
2S00 FOR J-l TO K-1
2S20 FOR I-J+l TO К
2S40 IF F(JK-F(I) THEN GOTO 2600
2560 F«F<J)jF(J)-F(I):F(I)-F
2580 FOR L*l TO N:Y(L)*C<J,L):C(J,L)=C(I,L):C(I,L)=Y(L):NEXT L
2600 NEXT IiNEXT J
2610 REN ЕСЛИ НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ УМЕНЬШЕНО,
261S REM ВЫСТАВИТЬ ПРИЗНАК ПЕЧАТИ
2620 IF FdKFM THEN PP*1
2630 REM ЕСЛИ УМЕНЬШЕНИЕ ФУНКЦИИ НЕ ОБНАРУЖЕНО,
2635 REM ТО ПРОВЕРКА КРИТЕРИЯ ЗАВЕРШЕНИЯ ПОИСКА МИНИМУА НЕ ПРОИЗВОДИТСЯ
2640 IF PP-0 THEN GOTO 1190
2990 REM НАЙТИ ОТКЛОНЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ
3000 Sl=0:S2=0
3020 FOR 1*1 ТО K:S1=S1+F(I):S2=S2+F(I)»F(I):NEXT I
3040 SD-S2-S1*S1/K:SD«SD/K
3090 REM НАЙТИ МАКСИМАЛЬНОЕ РАССТОЯНИЕ МЕЖДУ
3095 REM ТОЧКАМИ КОМПЛЕКСА
3100 DM*O
3120 FOR 1*1 ТО K-1:FOR J=I+1 TO К
3140 D-0
3160 FOR L=l TO N:D«D+<C(I,L)-C(J,L))^2sNEXT L
3180 D=SQR(D)
3200 IF D>DM THEN DM=O
3220 NEXT J:NEXT I
3400 IF PP-0 THEN GOTO 3790
3500 PRINT "НОВАЯ ТОЧКА В СТРОКЕ 3500"
3520 PRINT "МИНИМАЛЬНОЕ 3HA4EHHE=MF<1>
3540 PRINT "ТОЧКА МИНИМУМА"
3560 FOR L«l TO NrPRINT "XL,CA,1_):NEXT L
3580 PRINT ""
3600 FM«FQ):PP=O
3790 REM ПРОВЕРКА СХОДИМОСТИ
3800 IF SD>.000001 AND DM>.0001 THEN GOTO 1190
4000 PRINT "МИНИМУМ НАЙДЕН"
4020 PRINT "ТОЧКА МИНИМУМА"
4040 FOR L*l TO NsPRINT "X"L,CA,L):NEXT L
4060 PRINT "МИНИМУМ ФУНКЦИИ='ТA)
4080 PRINT "КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ-''FE
4100 END
5000 Z=-XQ)*XB)»X<3>+3300
5050 FE-FE+1
5100 RETURN
6000 FOR 11*1 TO 2*N:EC(II)«0:NEXT IIsEOO
6020 FOR 11*1 TO M:IC<II)=O:NEXT II:IO0
6050 IF IM-1 THEN GOTO 7100
6090 REM ПРЕДЫДУЩАЯ СТРОКА .ПРЕДНАЗНАЧЕНА ДЛЯ ПРОВЕРКИ
6095 REM НЕРАВЕНСТВА GI(XX=BI
6100 FOR II-l TO N
6120 IF XCIIXLdI) THEN ECCID-lsEOl
6140 IF X(II»U(II) THEN EC(N+II)=1jEC-1
6160 NEXT II
7100 BU>«X<1>+2*X<2>+2»X<3>
7110 IF 6A»72 THEN ICA)-1:IC=1
8000 RETURN
9000 DATA 0,20,0,11,0,42
ВВЕДИТЕ НАЧАЛЬНЫЕ ЗНАЧЕНИЯ
20
10
10
ВВЕДИТЕ X
-71
ПЕРВАЯ,ТОЧКА
МИНИМАЛЬНОЕ ЗНАЧЕНИЕ» 243.2185
МИНИМАЛЬНАЯ ТОЧКА
X 1 19.03517
X 2 9.735619
X 3 16.49469
НОВАЯ ТОЧКА В СТРОКЕ 3500
МИНИМАЛЬНОЕ ЗНАЧЕНИЕ РАВНО 238.7466
ТОЧКА МИНИМУМА
X 1 19.0307
X 2 9.734394
X 3 16.52478
МИНИМУМ НАЙДЕН
ТОЧКА МИНИМУМА
X 1 19.0307
X 2 9.734394
X 3 16.52478
МИНИМУМ ФУНКЦИИ РАВЕН 238.7466
КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО
FIRST POIHT
MIN.
HIM.
X 1
X 2
X У
NEW
MIN.
MIN.
X 1
X 2
X 3
NEW
MIN.
MIN.
X 1
X 2
X 3
, VALUE -
, POINT
POINT AT
, VALUE -
, POINT
POINT AT
. VALUE =
, POINT
MINIMUM FOUND
MINIMUM POINT
X 1
X 2
X 3
FUNl
180.908875
19.21317268
9.87028714
16.4475982
3500
159.33961
19.3693315
10.0923334
16.0662587
3500
8.96072388E-03
19.9999048
10.9999616
15.000083
19.9999048
10.9999616
15.000063
:TION MINIMUM- в.96в723ввЕ-03
FUNCTION EVALUATIONS-231
Комплексный метод применим к широкому кругу задач с ограничениями.
Его, конечно, не следует рассматривать в качестве панацеи в этой области. Ес-
Если целевая функция выпукла и, кроме того, выпукла область ограничений,
то применение метода будет успешным, хотя определенные особенности за-
задачи могут потребовать некоторой модификации критерия завершения. Если
целевая функция вогнута или область ограничений не выпукла, нетрудно ви-
видеть, как поиск этим методом может закончиться неудачей. Действительно, в
случае, если область ограничений не выпукла, не очевидно, что центр допусти-
допустимых точек будет допустимой точкой. Таким образом, перемещение
(новое) = (Xj. *+ хо)/2
не гарантирует получения нужного результата.
Необходимо также обратить внимание на проверку того, что найден был
не локальный, а глобальный минимум. Бокс полагает, что, произведя более
одного запуска программы при различных начальных точках, можно решить
эту проблему с помощью вышеописанного метода. Случайный характер фор-
формирования начального комплекса означает, что первоначально формируется
хорошее покрытие области ограничений и поэтому существует тенденция
сходимости к глобальному минимуму. Сходимость к одному и тому же зна-
значению при нескольких запусках программы подтверждает это.
КОМПЛЕКСНЫЙ МЕТОД
ВВЕДИТЕ КОЛИЧЕСТВО ОГРАНИЧЕНИЙ
1
ВВЕДИТЕ КОЛИЧЕСТВО ПЕРЕМЕННЫХ
3
COMPLEX METHOD
NO. OF CONSTRAINTS 1
NO. OF VARIABLES 3
INITIAL VALUE 20,10,10
INPUT X 7199
6.3. ЛИТЕРАТУРА
M. J. Box, 4A new method of constrained optimisation and a comparison with other methods',
The Сотр. Journal, 8, 42-52, 1965.
108
109

6.4. УПРАЖНЕНИЯ
1. Используйте комплексный метод для минимизации функции f(x, у) = х2 + у2 при
ограничениях х > 0,у > 0, х +у > 5.
2. Минимизируйте функцию /(*, у) = х2 + бху - Ах - 2у при ограничениях х2+2у<
<1,2х-2у <1.
3. Минимизируйте функцию f(x, у) = Ъх\ + 4х,х2 + 5х2 при ограничениях хх > О,
*2 > 0их, +jc2 > 4. '
4. Проэкспериментируйте с программой, реализующей комплексный метод, заменив
к - число точек в комплексе (строка 160); а - коэффициент отражения (строка
1120). Решите задачи, приведенные ниже и рассмотренные в тексте данной главы, с
новыми значениями.
5. Решите задачу минимизации функции
4
p х2) = —
+ v
при ограничениях дс, > 0, *2 > 0, дс, + *2 <? Рассмотрите два случая- S= 6' S= 4
(см. упр. 14 разд. 5.5).
6. Минимюируйте функцию /(х) = -Д9 - (я, - 3)»]*!/27>/3 при ограничениях
1 , Vx,6.
7. Минимизируйте функцию /(х) = < + х\ при ограничениях *, > 0, х2 > 0, *,*, > 8.
8. Минимизируйте функцию /(х) = *» + х \ + ^ при ограничениях ^ + ^2 +«* > Ч
*1*2*з > 3. (В качестве начальной точки возьмите точку A* 2- 3) )
9. Минимизируйте функцию /(*„ х2) = (х, - 3J + (*а - 4) при ограничениях 2х? +
+ xj <342л, +3х2 <18,jc, > 0,jc2 > 0.
, 2 ,, 0,jc2 > 0.
10. Минимизируйте функцию /<*,.*,.*,) = -Xlx2x3 при ограничениях jct > 0, х2 > 0
*3 > 0,2^ +j:2 +3x1 < 51.
ГЛАВА 7. ПОСЛЕДОВАТЕЛЬНАЯ ОПТИМИЗАЦИЯ БЕЗ ОГРАНИЧЕНИЙ
7.1. ШТРАФНЫЕ ФУНКЦИИ
Основная идея метода штрафной функции состоит в преобразовании зада-
задачи минимизации функции
z = f(x)
с соответствующими ограничениями, наложенными на х, в задачу поиска ми-
минимума без ограничений функции
Функция Р(х) является штрафной. Необходимо, чтобы при нарушении огра-
ограничений она "штрафовала" функцию Z, т. е. увеличивала ее значение. В этом
случае минимум Z будет находиться внутри области ограничений. Функция
Р(х), удовлетворяющая этому условию, может быть не единственной.
Задачу минимизации можно сформулировать следующим образом:
минимизировать функцию z = /(x) G.1)
при ограничениях с;- (х) > 0, / = 1, 2,..., т. G.2)
НО
Замечание. Ограничение вида "меньше или равно", h (х) < 0, всегда может
быть записано как —h(x) > 0, поэтому в приведенной выше формулировке
нет потери общности.
Функцию Р(х) удобно записать следующим образом:
i^. G.3)
где г - положительная величина. Тогда функция Z = <р(х, г) принимает вид
Z = <р(х, г) =/(х) + г X -— • G.4)
7=1 C(x)
Если х принимает допустимые значения, т. е. значения, для которых Су (х) >
> 0, то Z принимает значения, которые больше соответствующих значений
/(х) (истинной целевой функции данной задачи), и разность можно умень-
уменьшить за счет того, что г может быть очень малой величиной. Но если х прини-
принимает значения, которые хотя и являются допустимыми, но близки к границе
области ограничений, и по крайней мере одна из функций с;. (х) близка к ну-
нулю, тогда значения функции Р(х) и, следовательно, значения функции Z ста-
станут очень велики. Таким образом, влияние функции Р(х) состоит в созда-
создании "гребня с крутыми краями" вдоль каждой границы области ограниче-
ограничений. Следовательно, если поиск начинается из допустимой точки и осущест-
осуществляется поиск минимума функции <р(х, г) без ограничений, то минимум, ко-
конечно, будет достигаться внутри допустимой области для задачи с ограниче-
ограничениями. Полагая г достаточно малой величиной, для того чтобы влияние
Р(х) было малым в точке минимума, мы можем сделать точку минимума
функции <р(х, г) без ограничений совпадающей с точкой минимума функции
/(х) с ограничениями.
Рассмотрим очень простой пример, который позволит понять, "что, соб-
собственно, происходит".
Пример 1
Используя штрафную функцию, заданную уравнением G.4), минимизировать функ-
функцию f(x) — х при ограничениях х > 2, т. е. х — 2 > 0. Минимальным значением функции
является 2 при х = 2. Как с помощью штрафной функции можно найти решение? Рас-
Рассмотрим функцию
г
х +.
х — 2
На рис. 7.1 изображен график функции #(х, г) и показано положение точек ее миниму-
минимума для различных значений г A; 0,25 и 0,01).
Область ограничений лежит справа от вертикальной прямой х = 2. Нетрудно видеть,
что последовательность точек Ql9 Q2, Q3 стремится к точке Q - минимуму функции
при наличии ограничений. Действительно, найдем минимум функции у(х, г) методом,
приведенным в гл. 1:
dx~
(х-2J
111

Рис. 7.1
Следовательно; если
d<p/djc =0, (jc — 2J
то
х= 2±
Тогда
2г
= r.
= (jc-2K
и минимум достигается при jc = 2 + \/F внутри области ограничений.
Следовательно, функция <р(х, г) имеет минимум, равный 2 + 2>/7"при х = 2 + v
Тогда ^, есть точка с координатами C; 4), Q2 - точка с координатами B,5; 3), Q3
точка с координатами B,1; 2,2). Ясно, что при г -> О минимум без ограничений функции
ф{х, г) приближается к значению 2 и минимальной точкой является точка х = 2.
В общем случае невозможно аналитически определить положение миниму-
минимума функции *р(рс, г), рассматривая ее как обычную функцию от г. Для его
определения необходимо обратиться к численным методам.
Следует отметить, что если целевая функция /(х) выпукла, а функция
с/ (х) вогнута, то функция <р(х, г), заданная уравнением G.4), также являет-
является выпуклой функцией в области ограничений, которая сама является вы-
выпуклой. Следовательно, <р(х, г) имеет для данного значения г единственный
минимум.
Если Xi и х2 - точки, принадлежащие допустимой области, т. е. су (хО > О
и Cj (х2) > О для / - 1, 2, . . . , га, то при 0 < в < 1 справедливо неравенство
CjFx2 +A - в)х1) > 0с/х2) + A - 0)cy(Xl) > 0,
так как функция с;(х) выпукла. Следовательно, допустимая область являет-
является выпуклой.
112
Таким образом, точка х2 + A - 0)xi при О<0 < 1 также является допу-
допустимой. (Сравните с упр. 2 разд. 5.3.)
Кроме TorOj функция 1/с/(х) является выпуклой для всех х, которые
удовлетворяют неравенству Cj (х) > 0. Если h (х) = 1/су (х), то
Следовательно, гессиан функции h (x) имеет вид
С(х) 2Ус(х) Ус(х)т
где С (х) ik = д2с^ (x)ldXjdxk есть гессиан функции су (х). Тогда, если р - про-
произвольный вектор, то справедливо равенство
ртС(х)р 2[pTVc(x)P
ртН(х)р = ....,+ /
где всегда рТН(х)р > 0, так как С(х) - отрицательно определенная матрица
ввиду того, что с^ (х) - выпуклая функция и ^ (х) > 0. Тогда матрица Н(х)
положительно определена и 1/с;-(х) выпукла во воей области. (Вернитесь к
упр. 11 р разд. 5.5.) Из результата, приведенного в упр. 1 разд. 5.3,следует,
что если г > 0, то функция Р(х), заданная уравнением G.3), и функция
х, г), заданная уравнением G.4), также выпуклы.
Теперь можно обобщить результат, полученный в примере 1 настоящего
раздела на случай общей задачи с ограничениями (см. уравнения G.1) и
G.2)).
Предположим, что xf, х?,. . . , х| - минимальные точки функции
для убывающей последовательности значений rlt r2,..., г%,..., стремящей-
стремящейся к нулю/Тогда последовательность точек xf, х*,..., х|,. • • сходится к оп-
оптимальному решению задачи с ограничениями (см. уравнения G.1) и G.2))
при гк -* 0.
Следовательно,
lim х* = х*
и
lim
r*->0
G.5)
G.6)
где х* - минимальная точка функции /(х) при наличии ограничений.
Полученный результат можно доказать следующим образом. Поскольку
/(х) непрерывная функция и /(х*) </(х) для всех допустимых точек, то,
задав произвольное достаточно малое значение е, можно найти допустимую
точку х', такую, что
/(х ) </(х*) + е/2. G.7)
Поскольку гк — убывающая последовательность, стремящаяся к нулю,
можно найти такое значение К,что для к> К справедливо неравенство
113

e
min
2m j
G.8)
Поскольку jP(x) > 0 из определения функции </>(х, г), имеем
Дх*) < min <р(х, гк) = <р(х*, гД G.9)
где х| - минимальная точка функции <р(х, г^) для задачи без ограничений.
Кроме того, если к >К, то г^ О^. и справедливо неравенство
<Р(х*,гЛ)<<Р(х*,гД. G.10)
Это следует из того, что, поскольку х? минимизирует функцию <р(х, г%) й
в любой другой точке области х, в частности в точке х?, функция будет при-
принимать значение, большее чем ^ (х?, /\ ).
Поэтому
ГК) = Дх*)
т
r=l Cj(x*)
1
7=1 C
m
поскольку г. <^
Следовательно,
Тогда
Дх*)<<р(х*, rk)^ip(x*9rk)
Но так как значение xt. минимизирует функцию
\rK)=f(x')
* О , TO
т
1
Следовательно, из уравнений G.11) и G.12) получим
т \
/(X*) <^(Х*, Г,) < ДХ') + ГК
Из уравнения G.8) следует, что
т 1 F
А*') + rK I —- < Дх') + - .
y=i с/ж') 2
Тогда из уравнения G.7) следует, что
И
G.11)
G.12)
G.13)
G.14)
G.15)
Поскольку е может быть выбрано произвольно малым, всегда можно найти
такое значение к, при котором
Таким образом, при к-*°° (гк -*¦ 0)
G.16)
Из приведенного выше доказательства следует, что при г. "* О
1
/(х*) -/(х*) и г
0.
G.17)
В качестве упражнения оставлено доказательство того, что /(х*), /(х?), ...
..., /(з^) образуют убывающую последовательность, такую, что
/(***+>)</«)• G-18)
Очевидно, что если функция /(х) выпукла, а функция & (х) при / = 1,...
. . . , п вогнута, то функция /(х) при наличии ограничении имеет единствен-
единственный минимум. (Сравните с результатами, полученными в разд. 5.3.)
Пример 2
Рассмотрим следующую задачу:
минимизировать функцию f(xlt х2) = у (х1 + 1) 3 + х2
при ограничениях jc, - 1 > 0, дг2 > 0.
По аналогии с уравнением G.4) запишем
Необходимые условия минимума функции </? записьшаются в виде уравнений
г г
= 0, 1 = О,
которые имеют следующее решение:
'\ хг{г)=ф-
Тогда минимальным значением функции </?(х, г) будет
+
+
0
Таким образом, при г -> 0
114
115

и
; 0) = 7з.
7.2. МЕТОД SUMT ФИАККО И МАККОРМИКА
Результаты предыдущего раздела показывают, что можно решить задачу
минимизации с ограничениями (минимизировать функцию /(х) при ограни-
ограничениях Cj(x) > 0), решая для последовательности значений г, стремящейся
к нулю, задач без ограничений следующего вида:
т
минимизировать функцию *Р(х, г) =/(х) + г
7=1 /
Метод SUMT (sequential unconstrained minimisation technique) был впервые
предложен Кэрролом в 1961 году. Его идеи были исследованы Фиакко и
Маккормиком, которые не только рассмотрели теоретические вопросы и
сходимость метода, но создали практическую систему для его реализации.
Редко можно будет использовать данный метод так, как это делалось в
двух примерах из предыдущего раздела, поскольку далеко не всегда можно
найти оптимальную точку для функций \р (х, г) в виде функции х* (г), предел
которой при г -> 0 можно исследовать.
Поэтому для того, чтобы можно было применить настоящий метод на
практике, необходимо построить вычислительный метод, использующий тео-
теоретическое свойство сходимости, рассмотренное в предыдущем разделе. Тео-
Теоретически здесь не возникает трудностей. Для заданных функцией /(х) огра-
ограничениях су (х) > 0, / = 1,..., п, необходимо выбрать начальное значение г -
- г0, чтобы сформировать функцию <р(х, г0), которая минимизируется без
ограничений методом ДФП, изложенным в гл. 4. Найдя минимум функ-
функции <р(х, г0), необходимо уменьшить значение г. Это можно сделать эффек-
эффективно и просто, если найти rx = ro/c, где константа с > 1. В приведенной ни-
ниже программе с = 10, однако этот выбор произволен. Удачными могут быть
также значения с = 12, с = 16 и т. д. Затем необходимо минимизировать
функцию <^>(х, гг), снова используя метод ДФП. Таким образом, будет
разработана итерационная процедура. На к-ы шаге минимизируется функция
<р(х, гк), минимум которой находится в точке х|\ Важно, что ее можно ис-
использовать в дальнейшем в качестве первой точки в итерационной процедуре
минимизации функции <р(х, гк _ г), гдеrk +1 = гк/с. Теперь ясно, что последо-
последовательность гк убывает и стремится к нулю, следовательно, последователь-
последовательность точек минимумов будет сходиться к решению задачи с ограничениями.
Ниже приведена блок-схема (рис. 7.2) метода SUMT. Остается уточнить
некоторые детали.
Предполагается, что в начале процедуры имеется допустимая точка. Важ-
Важно, чтобы в процессе последующих вычислений получаемые точки принадле-
принадлежали допустимой области. Метод ДФП является градиентным методом
минимизации, использующим при одномерном поиске кубическую интерпо-
интерполяцию. Тогда, по мере приближения точки х к границе внутри допустимой
области <р(х, г) -><», а по мере приближения точки х к границе снаружи допу-
допустимой области <р(х, г) -> — <». Таким образом, если поиск осуществляется
116
Начать из допусти-
допустимой точки х0
I
Поломить
Найти минимум функции
Ф(х,г\) В точке х#
Полошить к=к+1
Точка jf
является точкой on-
тумума?
Закончить
В качестве новой началь-
начальной точки взять точку
Рис. 7.2
вдоль прямой, соединяющей две точки, одна из которых лежит внутри, а
другая вне области ограничений, то кубическая интерполяция оказывается
неприемлемой, поскольку функция разрывна вдоль данной прямой. Дей-
Действительно, если минимум будет найден вне допустимой области, то метод
ДФП не позволит вновь войти в область ограничений. Необходимо тщатель-
тщательно исследовать такие вопросы при использовании метода ДФП в данной
задаче.
Выбор начального значения г может оказаться важным с точки зрения со-
сокращения числа итераций при минимизации функции <р(х, г). Если сначала
г выбрано очень малым, для того чтобы функция <р(х, г) мало отличалась от
функции fix), то метод будет сходиться очень быстро. Однако такой выбор
может привести к серьезным осложнениям при вычислениях. Как видно из
рис. 7.1, для малых г функция <р(х, г ) будет быстро меняться в окрестности
минимума, что может вызвать затруднения при использовании градиентного
метода. Слишком же большое значение г может привести к тому, что штраф-
штрафная функция Р(х) в уравнении G.4) станет доминирующей. Поэтому "ра-
"разумный" выбор начальной точки очень важен.
Для многих задач "разумным" значением для начальной точки является
значение г0 = 1. Более рациональный подход состоит в том, чтобы понять, что
если начальная точка х будет лежать вблизи минимума функции
т \
1Р(ж, г) =/(х) + г 2 —— =/(х) + гР(х),
7=1
G.19)
117
то градиент функции <р(х, г) будет мал:
W>(X, г) = V/(x) + rVP(x).

Квадрат нормы этого вектора
V/(x)T V/(x) 4- 2rV/(x)T VP(x) + r2 VP(x)T VP(x)
и минимум будет достигнут при
G.20)
VP(x)T VP(x)
Это начальное значение г, как предполагает Фиакко и Маккормик, должно
давать хорошие результаты в общем случае. Уменьшить значение г очень про-
ст0: гк + 1 = гк/с>где с = ^
Для минимизации функции v>(x, rk + х) используется метод ДФП. В ка-
качестве начальной точки используется оптимальная точка функции <р(х, rk), и
это оказывается очень эффективным. Программа аналогична программе,
приведенной в гл. 4, однако необходимо обратить внимание на то, чтобы в
процессе одномерного поиска не выйти за область ограничений. Грубым, но
вполне эффективным является следующий метод. Пусть имеются точка р и
направление поиска d = -Hg (см. соотношение D.34)). Следующая точка
q = р + Xd необходима для осуществления кубической интерполяции. Начнем
со значения X = 2 (удвоенный шаг в методе Ньютона) и проверим, является
ли точка q допустимой, т. е. выполняется ли неравенство с;- (q) > 0 для всех
/. Если оно выполняется, то X не меняется, но если неравенство не выполняет-
выполняется, то X заменяется на X/at находится новая точка ц и вновь производится
проверка. В конце концов допустимая точка q будет найдена, и тогда можно
осуществить интерполяцию. Выбор Значения а не вполне очевиден. Выбор а =
= 2 был успешным, при а = 1,05 длина шага становится близкой к расстоянию
до ближайшей границы области ограничений и поэтому является "безопас-
"безопасной" для интерполяционной процедуры. (Эти шаги выполняются в програм-
программе в строках 630 - 750.)
Важно не дать точкам выйти за область ограничений в процессе минимиза-
минимизации. Для этого в строках 1100 — 1220 были приняты меры предосторожно-
предосторожности, позволяющие убедиться в том, что минимум найден между двумя до-
допустимыми точками. Хотя изменение Н в строке 1110 является полуэвристи-
полуэвристическим, он кажется вполне удачным.
Функция \р(х, г) минимизируется до тех пор, пока два последовательных
значения Fx и F2 не станут такими, что | (Ft - F2)/F11 < 0,000001. Это усло-
условие, конечно, может быть изменено (строка 1570). В соответствии с соотно-
соотношением G.17) программа заканчивает работу, когда (строка 1600)
т
1
Ml
< 0,000 001.
Значение минимума /(х) при этом определяется с точностью до пяти деся-
десятичных цифр. Конечно, точность можно изменить. Критерий завершения осу-
осуществляет остановку программы при rk < 1СГ12.
Ниже приведен текст программы. Подпрограммы, в том виде как они на-
написаны, предназначены для решения следующей задачи:
118
минимизировать функцию /(х) = (*! - 1H*! -2)(xt -3) +х3 при ограни-
ограничениях *! > 0,х2 > 0,х3 > 0,х| -х\-х\ >09х\ +xl +xl -4>0,х3 <5.
Таким образом, чтобы
, г) =/(х) + г
1
1
Y2_Y2_ V2
f + х\ + х] — 4 5 — хъ
1 111
+ + 4- —
X
Итак, мы имеем задачу с тремя переменными и шестью ограничениями. Це-
Целевая функция не выпукла. Область ограничений тоже не является выпук-
выпуклой, однако данный метод применяется успешно. При начальной точке @,1;
2; 2,1) решение было найдено за 48 итераций. Истинный минимум достига-
достигается в точке @; \[~1, >/Т), значение функции в которой равно -6 + \fT.
Приведены первая и последняя страницы распечатки результатов работы про-
программы. Предыдущее значение г, при котором была достигнута оптимальная
точка, используется для определения следующего значения г, и оно выводит-
выводится на печать через небольшое число итераций, необходимое для поиска по-
последнего минимума.
20 PRINT " МЕТОД ФИАККО И МАККОРМИКА"
40 REM ФУНКЦИЯ Z*F(X1,X2,...,XN) ВЫЧИСЛЯЕТСЯ В СТРОКЕ 5ООО
60 REM ГРАДИЕНТ G<1),GB>,...,G(N> ВЫЧИСЛЯЕТСЯ В СТРОКЕ 6000
ВО REM ОГРАНИЧЕНИЯ СA),СB),...,С(М) ВЫЧИСЛЯЮТСЯ В СТРОКЕ 8000
100 PRINT "ВВЕДИТЕ ЧИСЛО nEPEMEHHblX":INPUT N
120 PRINT "ВВЕДИТЕ ЧИСЛО OrPAHH4EHHft"iINPUT M
140 DIM X(N),P(N),Y(N),U(N),G(N),CG(N),D(N)
145 DIM V(N),R(N),Q(N),M(N>
150 DIM H(N,N)
i60 DIM C(M),IC(M)
180 PRINT "ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ X1,X2,...,XN"
190 FOR 1*1 TO N:INPUT X(I):NEXT I
200 REM ПРОВЕРКА ВЫПОЛНЕНИЯ ОГРАНИЧЕНИЙ
205 REM IC(J)*O - ОГРАНИЧЕНИЕ J ВЫПОЛНЕНО
207 REM IC(J)«1 - ОГРАНИЧЕНИЕ J НАРУШЕНО
210 S=O
220 FOR II«1 TO MiGOSUB 8000
230 IF CdlXO THEN S=S+1:IC(II)*1
240 NEXT II
250 IF S>0 THEN PRINT "ПЕРВАЯ ТОЧКА НЕ ЯВЛЯЕТСЯ ДОПУСТИМОЙМ:БТОР
270 REM НАЙТИ НАЧАЛЬНОЕ ЗНАЧЕНИЕ R
290 T«0sB~0sR»0iCO0
300 BOSUB 6000
310 FOR 1=1 TO N
320 T*T-G(I)»CG(I):B*B+CG(I)»CG(I)sNEXT I
350 R~T/B
360 IF R<0 THEN R=l
410 PRINT "R«"R
420 REM В НАЧАЛЕ НОВОГО ЭТАПА МИНИМИЗАЦИИ
425 REM ЗАДАТЬ МАТРИЦУ Н РАВНОЙ ЕДИНИЧНОЙ МАТРИЦЕ
430 FOR I-l TO NrFOR J*l TO N
440 H(I,J)*OsNEXT J
450 H(I,I)=1:NEXT I
460 REM ПРОМЕЖУТОЧНЫЙ ВЫВОД
480 PRINT " ТЕКУЦИЕ ЗНАЧЕНИЯ"
500 FOR 1-1 TO N:P(I)*X(I):Y(I)*X(I)ePRINT "X";I,X(I):NEXT I
510 FOR *II*1 TO MsGOSUB 8000tNEXT IIsGOSUB 5000
520 PRINT "ИТЕРАЦИЯСС;" ЗНАЧЕНИЕ";!
530 FP=Z:GOSUB 6000sGl=G0iFF*Z
540 REM ЗАПОМНИТЬ ГРАДИЕНТ В МАССИВЕ U И ПЕРЕЙТИ К СЛЕДУЮЩЕМУ НАПРАВЛЕНИЮ
119

550 FOR 1-1 TO N
560 Ua>=GU>:D<I>«0
570 FOR J-l TO N
580 D(I)«D(I)-H(I,J>*G(J>
590 NEXT JsNEXT I
595 REM НАЙТИ ГРАДИЕНТ В ПЕРВОЙ ТОЧКЕ ОДНОМЕРНОГО ПОИСКА
600 GP~O
610 FOR I-l TO N:GP-GP+G(D»D(I>sNEXT I
620 IF GP>0 THEN PRINT "ФУНКЦИЯ ВОЗРАСТАЕТ (СТРОКА 620)"
625 REM НАЙТИ ЗНАЧЕНИЕ LAMBDA,TAKOE,
627 REM ЧТОБЫ ОГРАНИЧЕНИЯ НЕ БЫЛИ НАРУШЕНЫ
630 L-2
640 FOR 1*1 ТО NiX(I)-P(I)+L*D<I)iNEXT I
650 S*0
660 FOR II-l TO M
670 IC(II>«OiGOSUB 8000
680 IF C(II»«O THEN GOTO 730
690 IC(II)«liS«S+l
700 L-L/1.05
710 FOR I-l TO NiX(I>«P(I>+L»D(I>iNEXT I
720 GOTO 670
730 NEXT II
750 IF 8>0 THEN GOTO 650
1000 REM НАЙТИ СЛЕДУЮЩУЮ ТОЧКУ Q
1010 HH-L
1020 FOR I-l TO N
1030 Q(I)«P(I)+HH#D(I):X(I)-Q(I)
1040 NEXT I
1050 FOR II-l TO MiGOSUB 8OOO1NEXT IIiGOSUB 5000iFQ~Z
1060 GOSUB 6000iG2~G0
1080 GQ-0
1090 FOR 1*1 TO NsGQ=GQ+G(I)#D(I)»NEXT I
1095 REM ЕСЛИ МИНИМУМ НЕ ЛЕЖИТ МЕЖДУ ТОЧКАМИ Р И Q,
1096 REM ЗАМЕНИТЬ Р НА Q
1097 REM МОДИФИЦИРОВАТЬ Н И НАЙТИ НОВОЕ НАПРАВЛЕНИЕ
1100 IF GQ<0 AND FGKFP THEN GOTO 1110
1105 GOTO 1125
1110 FOR I-l TO NsFOR J*l TO NsH(I,J>«H(I,J>-D(I>»D(J>/GP:NEXT J
1115 P(I)-Q(I)sX(I)=P(I)iY(I)=X(I>iNEXT I
1120 FF-ZsFP-ZiGl-GOiGOTO 540
1125 REM ДАЛЕЕ ПРОИЗВОДИТСЯ КУБИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
ИЗО ZZ«3#(FP-FQ>/HH:ZZ*ZZ+GP+GQ
1140 WW-ZZ«ZZ-GP«GQ:IF WW<0 THEN ЫЫ-0
1150 W=SQR(WW)
1160 DD~HH»A-(GQ+W-ZZ>/(GQ-GP+2»W»
1170 FOR I-l TO NiX(I)-P(I)+DD»D(I)iNEXT I
1180 FOR II* 1 TO M:GOSUB 8OOO1NEXT IIsGOSUB 5000»FR=Z:G0SUB 6000
1195 REM НАЙТИ ГРАДИЕНТ В НОВОЙ ТОЧКЕ •
1200 GR-0
1210 FOR I 1 ТО NsGR«GR+G(I>«D(DiNEXT I
1215 REM ПОВТОРИТЬ ИНТЕРПОЛЯЦИЮ В НОВОМ ИНТЕРВАЛЕ
1216 REM (СТРОКИ 1260 ИЛИ 1290), ЛИБО ПРОДОЛЖИТЬ
1220 IF Z<-FP AND Z<-FQ THEN GOTO 1400
1230 IF GR>0 THEN GOTO 1290
1260 HH-HH-DD
1270 FOR I-l TO NiP(I)-X(I)iNEXT I
1280 FP-ZiGP-GRiGl-GOsGOTO ИЗО
1290 HH«DD
1300 FOR I-l TO NiQ(I)-X(I)iNEXT I
1310 FQ«ZjGQ=GRiG2=G0iG0T0 ИЗО
1350 REM ОБНОВИТЬ МАТРИЦУ Н
1400 KK-OiWK-OiDK-0
1410 FOR I-l TO N
1420 U(I>-G(I>
1430 NEXT I
120
1440 FOR I-l TO NsM<I>«0
1450 FOR J«l TO N
1460 M(I)-M(I)+H(I,J)#U(J)
1470 NEXT J
1480 KK-KK+M(I)#U(I):WK=WK+V(I)#U(I)
1500 NEXT I
1505 IF KK*O OR WK*O THEN GOTO 1560
1510 FdR I-l TO N
1520 FOR J~l TO N
1530 H(I,J)-H(I,J)-M(I)*M(J)/KK+V(I)*V(J)/WK
1540 NEXT J
1550 NEXT I
1560 CC-CC+1
1565 REM ПРОВЕРКА ДОСТИЖЕНИЯ МИНИМУМА ФУНКЦИИ PHI(X,R)
1570 IF ABS((FF-Z)/FFK.OOOO1 THEN GOTO 1600
1575 REM ЕСЛИ СХОДИМОСТЬ НЕ ДОСТИГНУТА,
1577 REM TO НАЧАТЬ НОВЫЙ ОДНОМЕРНЫЙ ПОИСК ИЗ ПОСЛЕДНЕЙ ТОЧКИ
1580 FF-ZsGOTO 500
1590 REM ОКОНЧАТЕЛЬНАЯ ПРОВЕРКА СХОДИМОСТИ;
1595 REM ЕСЛИ СХОДИМОСТЬ НЕ ДОСТИГНУТА,
1597 REM ТО УМЕНЬШИТЬ R И' СФОРМИРОВАТЬ НОВУЮ ФУНКЦИЮ PHI(X,R)
1600 IF R»Z2<.00001 THEN GOTO 1800
1610 R-R/10
1620 GOTO 410
1800 PRINT " "
1820 FOR 1=1 TO N
1830 PRINT "X"jIj"«"jX(I>
1840 NEXT I
1850 PRINT "F(X)-";Z1
2000 END
5000 REM ФУНКЦИЯ F(X) ВЫЧИСЛЯЕТСЯ КАК ФУНКЦИЯ ОТ Zl,
А Р(Х) КАК ФУНКЦИЯ ОТ Z2
5010 Zl«(X(l)-l>#(X(i)-2>*(X(l>-3>+XC>
5100 Z2-0
5110 FOR JJ-1 TO MiZ2«Z2+1/C(JJ)iNEXT JJ
5200 Z*Z1+R«Z2
5500 RETURN
6000 REM РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЯ ГРАДИЕНТА ФУНКЦИИ F(X> ХРАНЯТСЯ
В МАССИВЕ GA)..G(N)
6005 REM РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЯ ГРАДИЕНТА ФУНКЦИИ Р(Х) ХРАНЯТСЯ
В МАССИВЕ CGA)..CG(N)
6010 REM ЗАТЕМ ОНИ СУММИРУЮТСЯ В МАССИВЕ GA)»G(N)
6050 КА«ХA>-1sKB«XA)-2iKOXA>-3
6100 GA>-KA«KB+KB*KC+KC*KA
6150
6190 GA)-GA)+R»CGA)
6200 G<2>~0
6250 CGB)—(-2»XB)/(CA)»CA»+2«XB>/(CB>*CB»+
6290 GB)-GB)+R#CGB)
6300 GC)«l
6350 CGC)—
6360
6390
6900
6910
6920
6990
8000
8005
8010
8020
8030
CGC>«CGC>-1/(CF)»CF»
GC)**GC>+R*CGC)
GO-0
FOR JJ-1 TO NsGO«GO+G(JJ)#G(JJ)iNEXT JJ
GO-SQR(GO)
RETURN
REM РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ ОГРАНИЧЕНИЙ ХРАНЯТСЯ
В МАССИВЕ СA),СB)...С(М)
ON II GOTO 8010,8020,8030,8040,8050,8060
C(l>«XC>»XC)-X(l)»X(l>-XB>»XB>sGQTa 8500
CB)-X(l)»X(l)+XB)#XB)+XC)»XC)-4iG0T0 8500
CC)«5-XC)sGQTQ 8500
121

8040 CD)«X(l)sQ0T0 8S00
SOSO C(S)«XB>iQ0TQ 8S00
8060 СF)«ХCIВ0Т0 8S00
8500 RETURN
МЕТОД ФИАККО И МАККОРМИКА
ВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ
3
ВВЕДИТЕ ЧИСЛО ОГРАНИЧЕНИЙ
6
ВВЕДИТЕ НАЧАЛЬНУЮ ТОЧКУ X1,X2,...,XN
.1
2
2.1
R. .0901618
ТЕКУЩИЕ ЗНАЧЕНИЯ
X 1 .1
X 2 2
X 3 2.1
ИТЕРАЦИЯ О ЗНАЧЕНИЕ-1.592473
X 1 7.556441Е-02
X 2 1.941576
X 3 2.13685
ИТЕРАЦИЯ 1 ЗНАЧЕНИЕ-4.617675
X 1 .0953003
X 2 1.893447
X 3 2.162587
ИТЕРАЦИЯ 2 ЗНАЧЕНИЕ-1.671175
X 1 9.550905Е-02
X 2 1.502009
X 3 1.773026
ИТЕРАЦИЯ 3 ЗНАЧЕНИЕ-1.980767
X 1 9.55В208Е-02
X 2 1.360921
X 3 1.633317
ИТЕРАЦИЯ 4 ЗНАЧЕНИЕ-1.9954ЭЗ
X 1 9.520754Е-02
X 2 1.420405
X 3 1.686592
ИТЕРАЦИЯ 5 ЗНАЧЕНИЕ-2.014785
R- 9.016181E-03
ТЕКУЩИЕ ЗНАЧЕНИЯ
X 1 9.552066Е-02
X 2 1.418278
X 3 1.66902
ИТЕРАЦИЯ 6 ЗНАЧЕНИЕ-3.202302
X 1 3.626825Е-02
X 2 1.418279
X 3 1.663025
ИТЕРАЦИЯ 7 ЗНАЧЕНИЕ-3.659234
X 1 .0286065
X 2 1.418742
X 3 1.502301
ИТЕРАЦИЯ 8 ЗНАЧЕНИЕ-3.787412
X 1 2.960457Е-02
X 2 1.4090?
X 3 1.492017
ИТЕРАЦИЯ 9 ЗНАЧЕНИЕ-3.78796
X 1 2.97255ВЕ-02
X 2 1.41197
X 3 1.490826
ИТЕРАЦИЯ 10 ЗНАЧЕНИЕ-3.788081
X 1 2.В96714Е-02
X 2 1.4137
X 3 1.49338
ИТЕРАЦИЯ И ЗНАЧЕНИЕ-3.7&841
R« 9.01618E-04
ТЕКУЦИЕ ЗНАЧЕНИЯ
X 1 2.909472Е-02
X 2 1.413903
X 3 1.494199
ИТЕРАЦИЯ 12 ЗНАЧЕНИЕ-4.150575
R. 9.016181E-09
ТЕКУЩИЕ
X 1
X 2
X 3
ИТЕРАЦИЯ 35
X 1
X 2
X 3
ИТЕРАЦИЯ 36
X 1
X 2
X 3
ИТЕРАЦИЯ 37
R= 9.016181E-10
ТЕКУЧИЕ
X 1
X 2
X 3
ИТЕРАЦИЯ 38
X 1
X 2
X 3
ИТЕРАЦИЯ 39
R= 9.016181E-11
ТЕКУЧИЕ
X 1
X 2
X 3
ИТЕРАЦИЯ 40
X 1
X 2
X 3
ИТЕРАЦИЯ 41
ЗНАЧЕНИЯ
1.084033Е-04
1.414218
1.414491
ЗНАЧЕНИЕ-4.58421
3.620311Е-05
1.414218
1.414484
ЗНАЧЕНИЕ-4.584845
3.630842Е-05
1.414217
1.414308
ЗНАЧЕНИЕ-4.584977
ЗНАЧЕНИЯ
3.63019Е-05
.414206
.414307
ЗНАЧЕНИЕ-4.585262
.29642ВЕ-05
.414206
.414305
ЗНАЧЕНИЕ-4.585476
ЗНАЧЕНИЯ
1.30049Е-05
1.414207
1.41425
ЗНАЧЕНИЕ-4.5В559В
4.401657Е-06
1.414207
1.414249
ЗНАЧЕНИЕ-4.58568
122
R= 9.016181E-12
ТЕКУЧИЕ ЗНАЧЕНИЯ
X 1 4.414079Е-06
X 2 1.414208
X 3 1.41423
ИТЕРАЦИЯ 42 ЗНАЧЕНИЕ-4.585719
МИНИМУМ НАЙДЕН
X 1 - 1.619098Е-06
X 2 » 1.414208
Х3« 1.41423
F<X>—4.585752
7.3. ЛИТЕРАТУРА
Замечание, сделанное в разд. 4.5, справедливо и здесь. За последний три десятилетия
в этой области был выполнен большой объем исследований, которые продолжаются и
в настоящее время. В двух последних главах были подробно рассмотрены два важных
метода оптимизации при наличии ограничений. Но это лишь два метода среди множества
других методов. Мы надеемся, что читатель заинтересуется изучением приведенного ни-
ниже списка литературы, поскольку еще многое можно сделать для развития теории и вы-
вычислительных методов решения задач оптимизации с ограничениями.
123

1 M. J. Box, *A comparison of several current optimisation methods and the use of transforma-
transformations in constrained problems', Сотр. Journal, 9, 67-77,1966.
2 C. W. Carroll, 'The created response surface technique for optimising nonlinear restrained
systems*. Operations Research, 9,169-184, 1961.
3 A. R. Colville, 'A comparative study on nonlinear programming codes', IBM Report No.
320-2949, 1968.
4 A. V. Fiacco and G. P. McCormick, 'The Sequential Unconstrained Minimisation Technique
for nonlinear programming, a primal-dual method', Мал. 5с, 10, 360-366, 1964.
5 A. V. Fiacco and G. P. McCormick, 'Computational algorithm for the Sequential Uncon-
Unconstrained Minimisation Technique for nonlinear programming', Man. Sc, 10, 601-617,
1964.
6 A. V. Fiacco and G. P. McCormick, 'Extensions of SUMT for nonlinear programming:
equality constraints and extrapolation', Man. Sc, 12, 816-828,1966.
7 D. Goldfarb, 'Extensions of Davidon's variable metric method to maximisation under linear
inequality and equality constraints', SIAMJ. Appl. Math., 17, 739-764, 1969.
7.4. УПРАЖНЕНИЯ
1. Используя метод SUMT, минимизируйте функцию f(xt, х2) = Зх\ + 4ххх2 + 5jc*
при ограничениях хх > 0, х2 > 0, хх + x2 > 4.
2. Минимизируйте функцию /(*,, х2) = -х\ - х\ при ограничениях хх > 0, х2 > 0 и
хх + 2х2 <3.
3. Используя метод SUMT, решите задачу о почтовых посылках: минимизируйте функ-
функцию V = -ххх2хъ при ограничениях 0 <лу <42, где i = 1, 2, 3 и х, + 2х2 + 2хг < 72.
4. Используя метод SUMT, минимизируйте функцию
4 9
f(x19 х2) = — + — +
\ 2
при ограничениях хх > 0, х2 > 0, хх +х2 <S, где a) S = 6, б) S = 4.
5. Минимизируйте функцию /(х) = х\ + х\ + х\ при ограничениях хх + х2 + хг > 3,
ХХХ2Х$ ^ 3, ХХр Х2, Хд.*^ 0.
6. Поэкспериментируйте с программой SUMT, изменив начальный выбор г (строка
360), определение Л. (строка 700), уменьшение г (строка 1610).
7. Поэкспериментируйте с программой метода SUMT, изменив критерий сходимости в
строке 1570, в строке 1600. В последнем случае попробуйте условие IF R < IE - 12.
8. Покажите, что соотношение G.18) истинно, т. е. /(х? ) < /(х*).
9. Минимизируйте функцию (хх - IL + (х2 - ЗJ, если хх, х2 > 0 и Зх^ + 2х* <21,
4хх +5х2 <20.
10. Минимизируйте функцию f(xx, х2) = х\ + х\ при ограничениях хх > 2, х\ - х\ < 1.
РЕКОМЕНДАЦИИ ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Исследования в области оптимизации продолжают интенсивно проводиться. Мы наде-
надеемся, что читатели уже заинтересованы настолько, что готовы к изучению последних до-
достижений в этой области. Приведенный список является лишь малой частью из большого
числа книг и журнальных статей по данному вопросу.
P. R. Adby and M. A. H. Dempster, Introduction to Optimisation Methods, Chapman and
Hall, 1974.
D. P. Bertsekas, 'Combined primal-dual and penalty function methods,' SIAM Journal on
Control, 13, 521-545,1975.
D. P. Bertsekas, Constrained Optimisation and Lagrange Multiplier Methods, Academic Press,
1982. [Имеется перевод: Д. Бертсекас. Условная оптимизация и методы множителей
• ¦->«: Пер. с англ. - М.: ' ¦¦ о и связь, 1987. - 000 с. j
124
В. D. Craven, Mathematical Programming and Control Theory, Chapman and Hall, 1978.
J. E. Dennis and J. J. More, 'Quasi-Newton methods, motivation and theory', SIAM Review,
19,46-89,1977.
R. Fletcher, 'An ideal penalty function for constrained optimisation', /. Inst. Maths. App., 15,
319-342,1975.
P. E. Gill, W. Murray and M. H. Wainwrisht. Practical Ootimization* Academic Press, 1982.
[Имеется перевод:ф. Гилл, У. Мюррен, М. Райт. Практическая оптимизация: Пер. с англ. -
М.: Мир, 1985..-509 с]
S-P. Han, *A globally convergent method for nonlinear programming', J. Opt. Theory App.,
22, 297-309,1977.
M. R. Hestenes, Conjugate Direction Methods in Optimization, Springer-Verlag, 1980.
D. Q. Mayne and N. Maratos, 'A first order exact penalty function algorithm for equality
constrained optimisation problems', Math. Prog., 16, 303-324, 1979.
M. J. D. Powell, *Some convergence properties of the conjugate gradient method', Math.
Prog., 11,42-49,1976.
M. J. D. Powell, 'Algorithms for nonlinear constraints that use Lagrangian functions', Math.
Prog., 14,224-248,1978.
M. J. D. Powell, 'A fast algorithm for nonlinearly constrained optimisation calculations', (in
Numerical Analysis, Edited by G. A. Watson), 144-157, Springer-Verlag, 1978.
M. J. D. Powell (Editor), Nonlinear Optimization, Academic Press, 1982.
D. Shanno, 'Conjugate gradient methods with inexact searches', Maths, of Op. Res., 3, 244-256,
1978.
ОТВЕТЫ К УПРАЖНЕНИЯМ
1.4. УПРАЖНЕНИЯ
1. Локальный максимум равен 4/27 при х = 1/13; локальный минимум равен нулю
при х—1.
2. Максимум равен 1/2 при х = 1, минимум равен -1/2 при х = -1.
3. Отметим, что a cos в + Ъ sin в = V {а2 + Ъ2) cos@ - а) ', где tg a = Ь/а.
4. А = г2 sin 20 A + cos 20).
5. Хотя / (jc) изменяет свой знак с "-" на "+", но производная /' @) не определена.
6. Минимум равен нулю при х = 0. Хотя f (jc) изменяет свой знак с "-" на "+", но про-
производная / (jc) не определена.
7. Минимум функции равен -1/3 \рЪ .
9. Глобальный минимум равен -24,3696 в точке 0,7808; локальный максимум равен
40,7245 в точке 3,7619; локальный минимум равен 11,9676 в точке 5,9572.
10. Минимум равен 0 в точке @; 0).
11. Максимум равен 0 в точке @; 0; 0).
15. Уравнения для рхир2 имеют следующий вид:
-2blpl + (а1 + а2)р2 + Clbl- c2a2 = 0,
(«! + а2)рх - 2b2p2 + c2b2-сха{ = 0.
16. Минимум равен -0,2766 при х = 0,5885.
2.8. УПРАЖНЕНИЯ
4. Минимальное число необходимых точек равно 198.
5. Минимум функции лежит в точке х = 0,47.
6. Минимум равен 5,96 и найден за 12 итераций.
7. Минимум функции равен 2,32 в точке х = 0,47 и найден за 11 итераций.
9. Минимум функции равен -0,973 в точке х = 1,763.
10. Минимум функции равен 0,0465 в точке @,2558; -0,1163).
15. Решением уравнения является х = 0,5885.
125

3.5. УПРАЖНЕНИЯ
2. 1) Минимум функции равен 0 в точке A; 2; 3). 2) Минимум функции равен 0 в
точке A; 1).
6. 1) Минимум функции равен 0 в точке A; 1). 2) Минимум функции равен 0 в точке
@; 0; 0). 3) Минимум функции равен 0 в точке A; 10).
10. Минимум функции равен 0 в точке A; 0).
11. Минимум функции равен 0 в точке C; 2).
12. Система имеет следующие решения для xv x2: C; 2), C,5844; -1,8481), (-3,7793;
-3,2832), (-2,8011; 3,1313).
131 Система имеет следующие решения: х = 1, j> = 2, z = 3 или любая их перестановка.
14. д= 31,87, Ъ= 1,79.
15. 1) 1п(д) = 3,0296, а= 20,68, л = 2,48. 2) а = 22,3, л = 2,45.
4.6. УПРАЖНЕНИЯ
6. Минимум равен 0 в точке D; -3; -05).
7. Минимум равен 0 в точке @,25; 0,75).
8. Минимум равен 0 в точке A; 0).
9. Минимум равен 0 в точке C; 2). (См. также упр. 12).
10. Минимум равен -1 в точке A; 1) .
5.5. УПРАЖНЕНИЯ
kbc кас kab
3# х — ——, у = ——, z = —— , где А = аЪ + be + са.
А А А
5. Максимум равен 108 в точке A; 2; 3).
7. Минимум равен 12,5 при х = у = 2,5.
8. Минимум функции равен -371/196 в точке х = 9/14, у = 1/17.
13. Максимум равен 70, минимум равен 20.
14. Если Va + \//3 < Sx/7, то xt_= Vo/0 , x2 = \#7~. В противном случае jc, =
= Ss/al( у/1Г + v?"), x2 = SJ01( v?~ + y/jf) • Посылка имеет размеры*, = 20 см,
х2 - 11 см, хг = 15 см, и ее объем равен 3300 см3.
16. Посылка имеет размеры хх = 24 см, х2 = 12 см, хг = 12 см, и ее объем равен
3456 см3.
6.4. УПРАЖНЕНИЯ
1. Минимум равен 12,5 при х = у = 2,5.
2. Минимум равен -371/196 при я: = 9/14, у = 111.
3. Минимум равен 44 при х , = 3, х2 = 1.
5. Минимум достигается при хх = 2, х2 = 3; хх = 8/5, х2 - 12/5.
6. Минимум равен 1 при х = 3, х2 = \/Т .
7. Минимум равен 30, 24 при х, = 1,7818, х2 = 4,4898.
8. Минимум равен 6,2403 при xt = х2 = х3 = 1,4422.
9. Минимум равен 0 при л^ = 3, х2 = 4.
10. Минимум равен -28,6153 при х% = 2,9155, х2 = 4,1231, ха = 2,3805.
1. Минимум равен 44 при хг^3,х2 = 1. 7А' УПРАЖНЕНИЯ
2. Минимум равен -9 при хх = 3, х2 = 0.
3. Минимум равен -3456 при xt = 24, х2 = 12, jc3 = 12.
4. а) Минимум равен 10 при jc, = 2, jc2 = 3; б) минимум равен 41/4 при Xj = 8/5,
х2 = 12/5.
5. Минимум равен 6,2403 при х% = х2 = х3 = 1,4422.
9. Минимум равен 0 при jc, = 1, х2 = 3.
10. Минимум равен 7 при jc, = 2, jc2 =
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Дополнительный список литературы 6
Предисловие 6
Введение 7
ЧАСТЬ I. ОПТИМИЗАЦИЯ БЕЗ ОГРАНИЧЕНИЙ 10
Глава 1. Классические методы 10
1.1. Функции одной переменной 10
1.2. Функции л переменных 12
1.3. Метод Ньютона. . 13
1.4. Упражнения 16
Глава 2. Методы поиска для функций одной переменной 17
2.1. Введение 17
2.2. Поиск методом Фибоначчи 18
2.3. Поиск методом "золотого сечения" 23
2.4. Аппроксимация кривыми 26
2.5. Квадратичная интерполяция 26
2.6. Кубическая интерполяция 29
2.7. Литература 34
2.8. Упражнения 34
Глава 3. Методы прямого поиска для функций п переменных 36
3.1. Предварительное обсуждение 36
3.2. Метод Хука-Дживса 37
3.3. Метод Нелдера-Мида 42
3.4. Литература ¦. 49
3.5. Упражнения 50
Глава 4. Градиентные методы 51
4.1. Метод наискорейшего спуска 51
4.2. Квадратичные функции 60
4.3. Метод Давидона-Флетчера-Пауэлла 63
4.4. Метод Флетчера-Ривса. 73
4.5. Литература 81
4.6. Упражнения 81
ЧАСТЬ II. ОПТИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ 83
Глава 5. Общая теория ^ 83
5.1. Ограничения в виде равенств , 83
5.2. Ограничения в виде неравенств 87
5.3\ Выпуклость и вогнутость 90
127

5.4.. Литература 95
5.5. Упражнения 95
Глава 6. Методы поиска 97
6.1. Модифицированный метод Хука-Дживса 97
6.2. Комплексный метод < 101
6.3. Литература 109
6.4. Упражнения ПО
Глава 7. Последовательная оптимизация без ограничений ПО
7.1. Штрафные функции 110
7.2. Метод SUMTOHaKKO и Маккормика 116
7.3. Литература . 123
7.4. Упражнения . 124
Рекомендации для дальнейшего чтения. 124
Ответы к упражнениям 125
Производственное издание
БРАЙАН БАНДИ
МЕТОДЫ ОПТИМИЗАЦИИ. ВВОДНЫЙ КУРС
Заведующая редакцией О. В. Толкачева
Редактор М. Г. Коробочкина
Художественный редактор Т. В. Бусарова
Обложка художника В. В. Третьякова
Технический редактор Т. Н. Зыкина
Корректор Т. Л. Кускова
ИБ № 1644
Подписано в печать 5.10.87 Формат 60x88/16 Бумага офс. № 2 Гарнитура
"Пресс-роман" Печать офсетная Усл. печ. л. 7,84 Усл. кр.-отт. 8.21 Уч.-изд. л. 8,67
Тираж 50 000 экз. Изд. №22182 Зак. N°76fc Цена 60 к.
Издательство "Радио и связь". 101000, Москва, Почтамт, а/я 693
Московская типография № 4 Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли.
129041, Москва, Б. Переяславская ул., д. 46