Теги: математика химия аналитическая химия информатика компьютерные науки компьютерные технологии переводная литература издательство мир
ISBN: 5-03-001176-5
Год: 1988
Текст
К. Эберт Х.Эдерер
КОМПЬЮТЕРЫ
Применение в химии
Перевод с немецкого
канд. хим. наук А. Е. Гехмана
под редакцией
академика Н. С. Зефирова
Scan Pirat
Москва «Мир» 1988
Klaus Ebert/Hanns Ederer
Computeranwendungen
in der Chemie
Eine Einfuhrung in das
Arbeiten mit Kleinrechnern
Zweite, erweiterte Auflage
VCH Verlagsgesellschaft mbH, Weinheim, 1985
ББК24
Э13
УДК 518.12+541
Эберт К., Эдерер X.
Э13 Компьютеры. Применение в химии: Пер. с нем. — М.:
Мир, 1988. — 416 с., ил.
Книга специалистов из ФРГ посвящена'применению вычислительных машин для решения задач нз
самых различных разделов химии. Приводятся программы решения как типичных расчетных задач нз
области физической химии, так н нечисленных задач органической химии, в основном на языке
БЕЙСИК.
Для специалистов в области вычислительной техники и химиков широкого профиля.
ISBN 5-03-001176-5
2405000000 — 184
Э 201 — 88, ч. 1
041(01) — 88
ББК24
Редакция литературы по химии
ISBN 5-03-001176-5 (русск.)
ISBN 3-527-26189-3 (нем.)
© VCH Verlagsgesellschaft. Weinheim, 1985
© перевод на русский язык, «Мир», 1988
Предисловие редактора перевода
В настоящее время компьютеры все больше становятся составной час-
тью стандартного оборудования химических лабораторий. И все же вне-
дрение персональных ЭВМ в химию, и особенно в органическую химию,
происходит недостаточными темпами. Для этого есть веские причины. Од-
на из них — трудность формализации процессов синтеза. Не случайно по-
лучение сложных органических молекул до сих пор рассматривается как
«искусство органического синтеза». Далее, это трудности, связанные как с
недостаточной информацией о существующих программах и их возможно-
стях, так и с проблемой тиражирования и распространения программ.
Поэтому любые книги, содержащие описание и тексты программ, которые
могут быть использованы в повседневной работе химика, неоценимы на
данном уровне компьютеризации в нашей стране.
Предлагаемая читателю книга относится именно к такому типу: она ох-
ватывает самые разные области химии и содержит не только разнообраз-
ные примеры вычислительной практики в химии, но дает понятие и о не-
вычислительных задачах, а также содержит большое число конкретных
программ. Более того, все программы легко, с минимальными изменения-
ми могут быть адаптированы для производимого в СССР персонального
компьютера «Искра-226», снабженного графическим дисплеем.
При переводе книги мы отказались от попыток усовершенствовать про-
граммы, хотя в ряде случаев это можно было сделать; оставляем эту воз-
можность заинтересованному читателю. Мы надеемся, что книга будет
стимулировать интерес широкого круга химиков к использованию персо-
нального компьютера в их повседневной практике.
Н. С. Зефиров
Предисловие ко второму изданию
Прием, который встретила наша книга, обусловил необходимость вто-
рого ее издания спустя немногим более года. Многочисленные письма с по-
желаниями и критическими замечаниями (а также с положительными от-
зывами, за что мы особенно благодарны) показали, что книга нашла ши-
рокий круг заинтересованных читателей. Это побудило нас существенно пе-
реработать для нового издания некоторые разделы книги. Расширена и до-
полнена глава, посвященная системам нелинейных уравнений. В главе «Пе-
ременные с индексами» в качестве примера мы добавили расчет числа изо-
меров. Кроме того, читатель теперь может получить сведения по основам
машинной графики, автоматизации эксперимента и обработки эксперимен-
тальных данных. В последней главе мы решили на примере жестких систем
дифференциальных уравнений познакомить химиков с современными чис-
ленными методами. В это издание не включено приложение, в котором
рассматриваются вопросы адаптации приведенных в книге программ к
ЭВМ других систем. Необходимую информацию можно найти в обзорах,
публикуемых в специальных журналах [см., например, Nachr. Chem. Techn.
Lab., 32 (2), 1—23 (1984)].
Как и в первом издании, особое внимание уделено тому, чтобы исполь-
зуемые математические методы были представлены в наиболее понятной
для читателей форме. Это учитывалось при подборе примеров, и поэтому
применялись наиболее эффективные, надежные и быстрые методы, не-
смотря на то, что некоторые из них незаслуженно считаются устаревшими.
При работе на персональном компьютере время счета часто не имеет боль-
шого значения, следовательно, нет необходимости привлекать какой-
нибудь «быстрый», но более сложный алгоритм. Мы считаем, что химик
скорее овладеет элементами вычислительной математики, если математи-
ческие основы методов рассматриваются на наглядных примерах.
Сфера применения персональных ЭВМ в химии в последние годы стре-
мительно расширяется, и эта тенденция, по-видимому, сохранится еще не-
которое время. Если предлагаемая книга поможет читателю интенсивнее
использовать его персональную ЭВМ и даже, может быть, писать соб-
ственные программы, то наша главная цель будет достигнута.
Мы приносим глубокую благодарность У. Шредеру за тщательную под-
готовку рукописи к печати.
Гейдельберг, июль 1984 г.
Клаус Эберт
Ханс Эдерео
Предисловие к первому изданию
Развитие вычислительной техники привело к широкому использованию
ЭВМ и в химии. Проблемы и задачи в области химических наук, которые
можно решать с помощью компьютеров, можно разделить на две группы.
К первой группе относятся задачи, решение которых связано с очень боль-
шим объемом вычислительной работы, которую обычными средствами
выполнить невозможно. Программы для решения таких задач, как прави-
ло, сложны, а значительный объем вычислений требует применения боль-
ших ЭВМ. В этих случаях химик хотел бы использовать ЭВМ и программу
как «черный йщик» (“black box”). К задачам такого типа относятся кванто-
вохимические расчеты, обработка результатов рентгеноструктурного ана-
лиза, кинетическое описание сложных химических реакций, а также
компьютерное планирование синтеза.
Ко второй группе относятся небольшие, не требующие значительного
объема вычислений задачи, такие, как отображение экспериментальных
данных с их последующей обработкой для определения параметров или по-
строение диаграмм. Для решения подобных задач достаточно мини- и
микро-ЭВМ, называемых персональными компьютерами. Примером явля-
ется линейный регрессионный анализ, который часто используется в хи-
мии. Если раньше для получения параметров регрессии экспериментальные
данные изображали на миллиметровой бумаге и через полученные точки
«на глаз» проводили прямую, то сейчас можно просто ввести числовой ма-
териал в ЭВМ и получить через несколько секунд график, а также объек-
тивные значения параметров регрессии вместе с их стандартными отклоне-
ниями в виде распечатки или непосредственно на экране.
Персональная ЭВМ с соответствующими периферийными устройствами
(дисковым накопителем, быстродействующим печатным устройством и
графопостроителем) сегодня по цене сопоставима с обычными для хими-
ческой лаборатории приборами. Преимущество персонального компьютера
перед большой ЭВМ заключается в том, что он доступен в любой момент.
Это позволяет использовать вычислительную технику для решения даже
небольших задач. В области химии пока еще не созданы библиотеки про-
грамм. Пользователю не остается ничего другого, как писать свои про-
граммы самому. Однако это невозможно без определенных сведений о са-
мой ЭВМ и о языке программирования, который она «понимает». Усвоить
такие сведения довольно просто. БЕЙСИК среди других языков програм-
мирования наиболее подходит для персональных ЭВМ.
В этой книге мы хотим показать, как можно усвоить сведения, необхо-
8
Предисловие к первому изданию
димые для работы на мини- и микро-ЭВМ, для решения таких задач, кото-
рые часто встают перед химиками. При этом разбираются постановка за-
дачи, используемые операторы языка программирования, а также элемен-
ты математических методов, лежащих в основе алгоритма. Последующие
программы используют рассмотренные ранее и постепенно усложняются.
Поэтому советуем читателю прорабатывать все главы в том порядке, в ка-
ком они расположены в книге. Кто интересуется только отдельными зада-
чами, рассмотренными в этой книге, и, кроме отдельных команд, не хочет
знать, какие операции выполняет ЭВМ при решении задачи, может ограни-
читься описанием порядка ввода программ и данных, адаптацией программ
к данной ЭВМ и манипуляциями с программами. После обсуждения каж-
дой задачи, которая решается с помощью приведенной в тексте програм-
мы, читателю предлагается самостоятельно выполнить несколько заданий,
используя при необходимости дополнительную литературу.
Эту книгу не следует рассматривать ни как введение в изучение БЕЙ-
СИКа, ни как элементарный курс вычислительной математики. При напи-
сании программ полезно иметь под руками какое-нибудь руководство но
БЕЙСИКу (точно так же, как при переводе бывает очень полезен словарь).
Такие руководства, которые содержат и используемые в данной ЭВМ ма-
шинные команды, издают фирмы-изготовители ЭВМ. Тем, кто проявляет
интерес к математическим методам, можно порекомендовать обратиться к
систематическому курсу вычислительной математики.
Книга адресуется как студентам-химикам старших курсов, так и сотруд-
никам научно-исследовательских институтов и промышленных предприя-
тий.
Занятия со студентами Гейдельбергского университета показали, что ос-
воение языка программирования и приобретение навыков работы на ЭВМ
происходит гораздо быстрее, чем поначалу кажется. В полезности исполь-
зования вычислительной техники в повседневной работе начинающие убеж-
даются очень скоро — как только будут преодолены начальные трудности.
Мы приносим сердечную благодарность г-же Марианне Трой, г-ну Мат-
тиасу Фрею и г-ну Ульриху Шредеру за подготовку рукописи к печати и по-
мощь в правке корректуры.
Гейдельберг, ноябрь 1982 г. Клаус Эберт
Ханс Эдерер
1. Введение
1.1. Замечания общего характера
Мы не рекомендуем читателю слишком долго задерживаться на
этом введении. Как только появится возможность, приступайте к
работе на ЭВМ. Программы, операторы и примеры, приведенные
в данной книге, составлены и опробованы на ЭВМ “Commodore”,
иначе говоря, рассчитаны на этот компьютер; однако они носят до-
вольно общий характер и пригодны (возможно, с небольшими из-
менениями) для ЭВМ других типов, понимающих БЕЙСИК. Спи-
сок таких малых ЭВМ приводится в приложении.
Почти все персональные компьютеры «понимают» алгоритми-
ческий язык БЕЙСИК (BASIC — от англ. Beginners All Purpose
Symbolic Instruction Code). В книге рассмотрены только основы
этого языка, хотя программы для решения поставленных задач бу-
дут постепенно усложняться. Наш опыт подсказывает, что самое
главное — открыть перед начинающим перспективу просто и быст-
ро приобщиться к работе над интересующей его проблемой. Успех
в составлении сложных и эффективных программ с использованием
всех программных средств обязательно придет, как только исследо-
ватель увлечется решением своих проблем с помощью ЭВМ. Если
проблема решена и составлена работоспособная программа, то
имеет смысл заняться программой ради нее самой, сделать ее бо-
лее эффективной и удобной. Составить оптимальную программу,
реализующую все возможности ЭВМ и алгоритмического языка,
помогут многочисленные справочники по вычислительной технике,
программированию и языку БЕЙСИК.
1.2. Анализ задачи
Многие, особенно те, кто еще не работал на ЭВМ, думают, что
стоит только поставить перед компьютером задачу, как он ее тут
же решит. В принципе это так, однако не все знают, что исходную
задачу необходимо представить в виде последовательности элемен-
тарных шагов, а диалог с машиной должен проходить в виде про-
стых, коротких, строго установленных команд. Расчленение задачи
на мелкие, понятные ЭВМ шаги называют анализом задачи. Таким
10
Глава 1
образом, ЭВМ решает не исходную задачу, а нашу переработку
этой задачи. Каждый из этих элементарных шагов прост и легко
может быть выполнен вручную. Преимущество машины состоит в
том, что
*****************************************
*** ЭВМ БЫСТРА. ТЕРПЕЛИВА И ОЧЕНЬ НАДЕЖНА ***
****************************************
Программа — это развернутый план решения задачи, лежащей в
основе проблемы. Программа должна быть написана так, чтобы ее
«поняла» ЭВМ. Перед выполнением программы ее надо ввести в
ЭВМ.
Давайте начнем с решения простой задачи из механики:
Каково время падения тела, если известны высота, ускорение и начальная ско-
рость?
Физика дает решение этой задачи в виде формулы, которая связывает пять
величии — высоту Л, ускорение g, время t, начальную скорость д0 и начальную вы-
соту Л 0:
g
h =----— t2 + vrf + Ло (физический ответ)
Однако эта формула еще не дает ответа на поставленный вопрос. Поскольку мы хо-
тим знать время падения тела, необходимо математически преобразовать приведен-
ную выше формулу:
/2-----+ 20 - = 0
g g
Если принятья = -2v0/g и b = 20 - hj/g, то получится
, а ю-а
t2 + at + b = 0 и Zj 2=-----± Г-------Ь
Последняя формула — математический ответ на задачу. Эту формулу н необходимо
написать в виде программы.
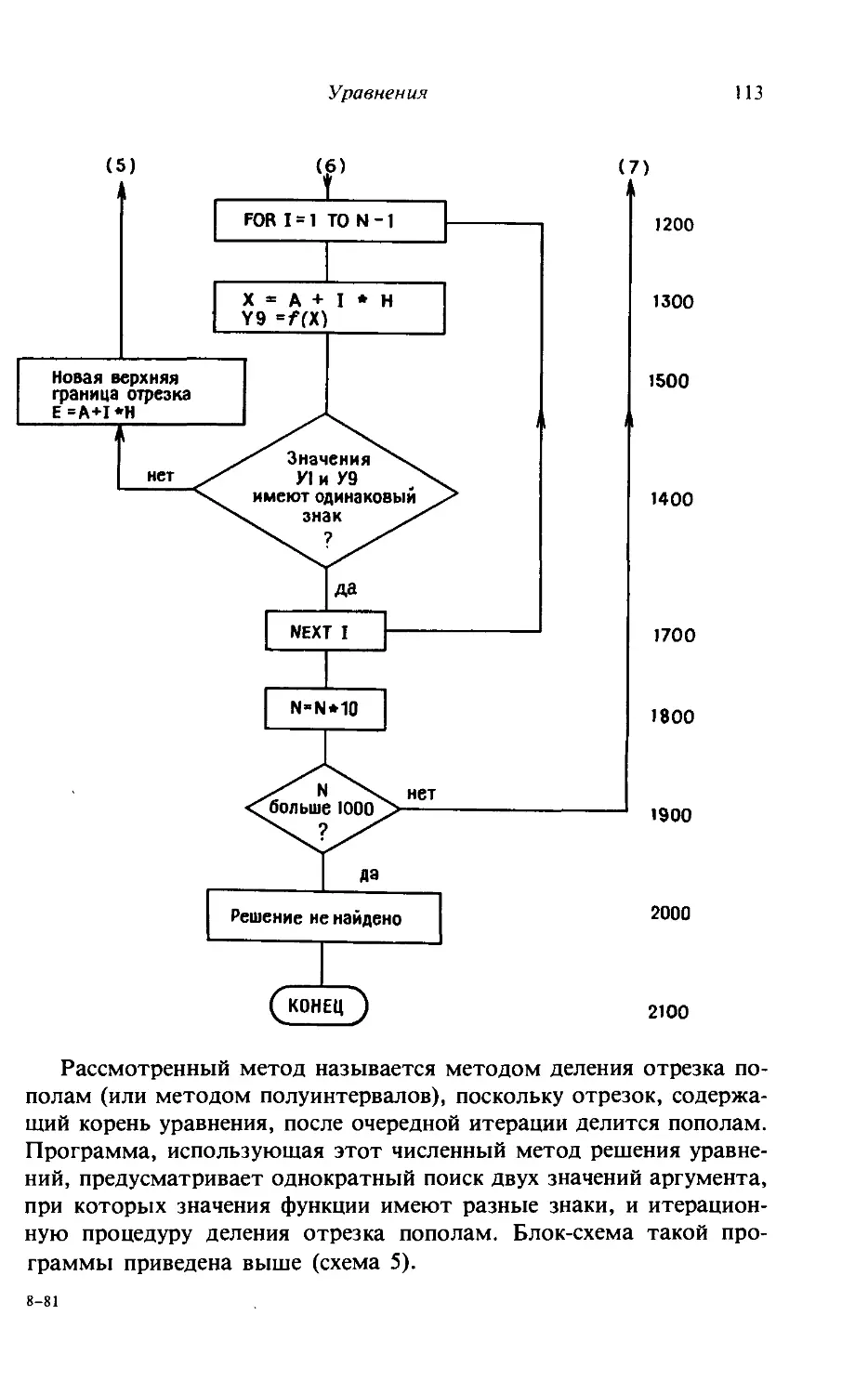
Представленные ниже блок-схема и программа для решения на-
шей задачи понятны практически без комментариев. Звездочка
(*) — это знак умножения. В отличие от традиций алгебры при на-
писании программ для обозначения умножения следует всегда поль-
зоваться этим знаком. Для сложных задач сначала составляют наи-
более рациональную блок-схему (схема 1), которая определяет
стратегию решения. Обычный порядок выполнения операций, ука-
занных в блок-схеме, — сверху вниз. Если порядок выполнения опе-
раций в каком-либо месте изменяется, то это указывают стрел-
ками.
Введение
11
Схема 1
Программа на БЕЙСИКе
10 INPUT VO, G, НО, Н
20 А = -2.V0/G
30 В = 2»(Н - H0)/G
40 D = А«А/4 - В
50 IF D < О THEN GOTO 90
60 Т1 = - А/2 + SQR(D)
65 Т2 = -А/2 - SQR(D)
70 PRINT Tl, Т2
80 STOP
90 PRINT «РЕШЕНИЙ НЕТ»
100 STOP
12
Глава 1
На следующем примере рассмотрим метод составления блок-схем. Пусть необ-
ходимо вычислить сумму квадратов первых ста чисел натурального ряда
S = I2 + 22 + З2 + 42 + ... + 99* + 1002
Блок-схема программы для решения этой задачи выглядит следующим образом (схе-
ма 2):
Схема 2
Овал — это символ начала, конца программы или
остановки.
В прямоугольниках записывают операции вычисле-
ния, присвоения и др. Целочисленный индекс I прини-
мает значения от 1 до 100 (почему две переменные
сначала приравнены нулю, будет объяснено ниже).
Знак ( = ) означает присвоить, т. е. при выполнении
этого оператора 1 увеличивается на 1.
Текущее значение суммы S увеличивается при выпо-
лнении этого оператора на член ряда 1 • I.
Ромб означает, что появилось несколько вариантов
продолжения (разветвление программы) и предстоит
сделать выбор; при любом ответе на поставленный
здесь вопрос должно иметься соответствующее про-
должение.
Параллелограмм означает, что на этом месте в про-
грамму вводятся исходные данные или выводятся ре-
зультаты
Соответствующую программу на БЕЙСИКе вы найдете в разд. 4.1.
Введение
13
1.3. Важнейшие команды
В этом разделе речь пойдет о машинных командах, которые с
самого начала важны при работе на ЭВМ. Если в дальнейшем по-
надобятся дополнительные команды, то они будут описаны в соот-
ветствующем разделе. Следует напомнить, что команды и операто-
ры даны в соответствии с синтаксисом языка БЕЙСИК ЭВМ
“Commodore CBM 8032”. В большинстве случаев их можно непо-
средственно переносить на ЭВМ других типов. Это можно прове-
рить по руководству к ЭВМ и, если необходимо, немного изменить
отдельные команды.
Сначала несколько замечаний о прописных и строчных буквах,
диагностике ошибок и курсоре.
В этой книге все программы и команды написаны прописными
буквами. Большинство ЭВМ могут воспринимать информацию, на-
бранную только прописными буквами. “СВМ 8032” в обычном
режиме использует только строчные буквы, но по команде
РОКЕ 59468,12 переключается на прописные. Если вы не знаете, ка-
кой шрифт используется в вашей ЭВМ, то попробуйте набрать ка-
кое-нибудь слово или загляните в руководство к ЭВМ.
На экране (пустом или с записью) хорошо виден мерцающий
знак, так называемый курсор, который указывает место на экране,
где будет записан очередной символ.
В случае ошибок при вводе команд и программ на экране
компьютера появляется сообщение ERROR. При этом обычно ис-
пользуется сокращенная запись вида ошибки. Список сокращений с
подробными комментариями приводится в руководстве к ЭВМ.
Диагностика ошибок очень помогает при их поиске и устранении.
СТЕРЕТЬ С ЭКРАНА! < SHIFT) <CLR/HOME>
Для этого следует нажать две клавиши: сначала SHIFT, затем
дополнительно CLR/HOME (так же, как при написании прописных
букв на обычной пишущей машинке). При этом программы, храня-
щиеся в памяти, а также находившиеся до сих пор на экране, не
стираются из памяти ЭВМ.
СТЕРЕТЬ ПРОГРАММУ! NEW (RETURN)
Сначала на клавиатуре набирают слово NEW, а потом нажима-
ют клавишу RETURN. Клавишей RETURN пользуются в тех случа-
ях, когда хотят ввести в ЭВМ какую-нибудь информацию (данные,
команды, операторы, программы). Клавишу RETURN следует на-
жимать также в конце каждой строки.
По команде NEW программа стирается из памяти ЭВМ; хотя
программа еще остается на экране, из памяти она уже стерта.
ВЫВЕСТИ ПРОГРАММУ НА ЭКРАН! LIST (RETURN)
14
Гаава 1
Чтобы вывести на экран хранящуюся в памяти ЭВМ програм-
му, набирают на клавиатуре команду LIST и нажимают клавишу
RETURN. У команды LIST есть много модификаций, которые по-
зволяют выводить только часть программы или выводить про-
грамму построчно в замедленном темпе, как бы считывая ее
(scrolling). Посмотрите в руководстве к вашей ЭВМ модификации
команды LIST.
ВЫПОЛНИТЬ ПРОГРАММУ! RUN (RETURN)
Чтобы запустить программу на выполнение, набирают команду
RUN и нажимают клавишу RETURN.
ПРЕРВАТЬ ВЫПОЛНЕНИЕ ПРОГРАММЫ! (RUN/STOP)
Чтобы приостановить выполнение программы, нажмите клави-
шу RUN/STOP.
ВВЕСТИ ПРОГРАММУ! LOAD (RETURN)
Для того чтобы программа, записанная на магнитной ленте,
была введена в память ЭВМ, наберите команду LOAD и нажмите
клавишу RETURN.
ЗАПИСАТЬ ПРОГРАММУ! SAVE (RETURN)
Для вывода на магнитную ленту программы, находящейся в па-
мяти ЭВМ, наберите команду SAVE и нажмите клавишу RETURN.
(Осторожно, не сотрите случайно соседнюю запись на магнитной
ленте!)
По команде LOAD очередная программа из внешнего запомина-
ющего устройства — магнитофонной панели — вводится в память
ЭВМ. По команде SAVE программа, находящаяся в памяти ЭВМ,
записывается на магнитную ленту, начиная с того места, на кото-
ром эта лента была остановлена. Обе эти команды, LOAD и
SAVE, можно дополнить именами программ, что обычно и дела-
ют. Тогда ЭВМ будет сама искать программу с заданным именем
и введет в память только эту программу. Соответствующие ко-
манды:
ВВЕСТИ ПРОГРАММУ! LOAD «Имя» (RETURN)
ЗАПИСАТЬ ПРОГРАММУ! SAVE «Имя» (RETURN)
Если в качестве носителя во внешнем запоминающем устройстве
используется не медленно действующая магнитофонная кассета, а
более удобный и оперативный носитель — магнитный диск (Floppy
Disk), достаточно для начала следующих трех команд:
ВЫВЕСТИ НА ЭКРАН КАТАЛОГ! CATALOG ( RETURN)
После того как на клавиатуре набрана команда CATALOG и на-
жата клавиша RETURN, на экран выводятся имена программ, за-
писанных на магнитном диске.
ВВЕСТИ ПРОГРАММУ! DLOAD «Имя» (RETURN)
Введение
15
Чтобы ввести определенную программу с магнитного диска, на-
бирают команду DLOAD и имя программы (можно указать только
несколько первых знаков имени программы), потом нажимают кла-
вишу RETURN. (Буква D — сокращение слова Disk.)
ЗАПИСАТЬ ПРОГРАММУ! DSAVE «Имя» (RETURN)
Чтобы вывести находящуюся в памяти ЭВМ программу на маг-
нитный диск и ее имя внести в каталог, набирают команду DSAVE
«Имя» и нажимают клавишу RETURN. Если на диске уже есть
программа с таким именем или на нем не хватает места, на экране
появится соответствующее сообщение.
С имеющимся теперь у вас запасом команд можно начинать ра-
боту на ЭВМ*. Однако после некоторого адаптационного периода
необходимо ознакомиться с дополнительными командами, приве-
денными в руководстве к ЭВМ, например, такими, которые позво-
ляют стирать часть программы Или копировать ее, копировать
диски целиком, а также переименовывать программы.
• Начинающему программисту прежде всего надо хорошо освоить клавиатуру.
Вы сэкономите впоследствии много времени, если сразу усвоите принципиальные
различия между близкими по написанию символами, например, буквой 1 и цифрой 1,
русскими буквами Н, Р, С, X и латинскими Н, Р, С, X. Чтобы отличать букву О от
цифры 0, последняя часто изображается в виде перечеркнутого овала, ио это не обя-
зательно. В книге встречаются два варианта изображения цифры 0: в виде обычного
и перечеркнутого овалов. — Прим, перев.
2. Формулы
2.1. Введение в алгоритмические языки
Научные и инженерно-технические работники часто используют
в расчетах более или менее сложные математические формулы. Ес-
ли расчеты проводят по одной и той же формуле, но с изменяющи-
мися значениями параметров, есть смысл написать для этого про-
грамму. В случае простых формул вычисления можно сделать с по-
мощью так называемых программируемых микрокалькуляторов.
Однако с помощью микро-ЭВМ эта задача решается гораздо про-
ще, и, что очень удобно, можно хранить программу, записав ее на
магнитофонную кассету или на магнитный диск.
Пусть требуется составить программу для расчета по следующей простой фор-
муле:
у = е~ь'/(1 + о
На машинно-ориентированном языке программируемого микрокалькулятора
SR56 Texas Instruments эта программа выглядит так:
; ввод значения b
х ; умножить на
R/S ; стоп, ввод I
STO ; поместить / в регистр 1
1
= ; вычислить Ы
+ /— ; вычислить — Ы
ЕХР(Х) ; вычислить exp(-Z>0 и
STO ; поместить в регистр О
О ; запомнить
RCL ; извлечь из памяти I
1
+
1
= ; вычислить / + 1
1/Х ; вычислить 1/(1 + 1)
х ; умножить на
RCL ; ехр( —Ь/), извлеченный из
О ; регистра О
= ; результат
R/S ; стоп
Если есть некоторый опыт работы с микрокалькулятором, составить такую
программу не так уж трудно, но все же довольно сложно сделать это без ошибок.
Формулы
17
Более крупные ЭВМ «понимают» так называемые алгоритмиче-
ские языки высокого уровня, в которых часто встречающиеся по-
следовательности нескольких простейших команд объединены в од-
ну сложную команду (слово). Это сокращает программу и делает
ее легкочитаемой. Чем длиннее комбинации простейших команд и
чем больше сложных команд, тем выше уровень языка. Имеется
целый ряд алгоритмических языков; многие из них разработаны
специально для решения определенного круга задач. В области
естественных наук используют главным образом ФОРТРАН, ПЛ/1
или БЕЙСИК. Большие ЭВМ, как правило, хорошо «понимают»
три языка. Программы для расчета по приведенной выше формуле
на трех языках выглядят так:
ФОРТРАН REAL*4 B,T,Y
READ(5,100) В,Т
100 FORMAT(El 2.5,Е12.5)
Y=EXP(-B*T)/(1+T)
WRITE(6,200) Y
200 FORMAT(El 2.5)
STOP
END
БЕЙСИК Ю INPUT B,T
20 Y » EXP(-B*T)/(1+T)
30 PRINT B,T,Y
ПЛ/1 FORMEL1s PROCEDURE OPTIONS(MAIN) ;
DECLARE (B,T,Y) DECIMAL FLOAT(10) ;
GET LIST(B,T) ;
Y=EXP(-B*T)/(1+T) ;
PUT LIST(Y) ;
END FORMEL1 ;
Если посмотреть на программы внимательно, то видно, что ис-
ходная математическая формула занимает только одну строчку; в
остальных строках находятся операторы описания типа перемен-
ных, ввода и вывода.
Эти примеры показывают, что прежде чем приступить к про-
граммированию, необходимы некоторые специальные знания. Для
больших ЭВМ потребуются дополнительные сведения об операци-
онной системе, чтобы запустить программу на выполнение и полу-
чить результаты в желаемом виде.
Из всех алгоритмических языков БЕЙСИК, безусловно, наибо-
лее доступен для начинающих. Командами в нем служат сокраще-
ния английских слов, строение программы наглядно, что удобно
2-81
18
Глава 2
при написании программ. Кроме того, этот язык наиболее приго-
ден для решения относительно простых задач научно-технического
характера. ФОРТРАН и ПЛ/1 имеют преимущество только при ре-
шении сложных фундаментальных проблем, связанных с обработ-
кой большого количества данных. Поэтому принято, что БЕЙСИК
используют для микро-ЭВМ (персональных компьютеров), в то
время как для больших ^ВМ наиболее подходящими считаются
ФОРТРАН, ПЛ/1 или какой-либо другой алгоритмический язык
высокого уровня.
Если вы освоите БЕЙСИК, то это в дальнейшем упростит пере-
ход к другим алгоритмическим языкам, поскольку сущность про-
граммирования вам уже известна и надо только выучить некото-
рые служебные слова и немного дополнительной «грамматики».
Если приведенную выше программу на БЕЙСИКе написать на
экране ЭВМ (не забывайте нажимать клавишу RETURN в конце
каждой строки), то с помощью команд RUN, SAVE и LOAD, рас-
смотренных в предыдущей главе, ее можно запустить на счет, вы-
вести из памяти и снова ввести в ЭВМ.
Данные также можно вводить непосредственно, не используя
оператор INPUT. Тогда ту же программу надо записать в следую-
щем виде:
5 В - -7
10 Т » 11.1
20 Y - ЕХР(-В*Т)/(1+Т)
30 PRINT B,T,Y
В и Т могут принимать произвольные значения. Эта программа
менее универсальна, чем программа с оператором ввода INPUT,
так как ее необходимо каждый раз изменять для других значений В
и Т.
2.2. Номер строки в БЕЙСИКе
Из приведенных примеров можно выяснить важную особен-
ность БЕЙ£ИКа:
**************************************************
*** КАЖДАЯ СТРОКА ПРОГРАММЫ ДОЛЖНА НАЧИНАТЬСЯ С ЧИСЛА, ***
*** ТАК НАЗЫВАЕМОГО НОМЕРА СТРОКИ ***
**************************************************
Программа всегда обрабатывается по порядку номеров строк
независимо от предусмотренных в ней переходов с одной строки на
Формулы
19
другую*. Однако совсем не обязательно при записи сохранять та-
кую последовательность строк. ЭВМ сама разместит строки в пра-
вильной последовательности.
При написании программ советуем оставлять достаточно боль-
шие интервалы между номерами соседних строк (как правило, 100),
чтобы при необходимости можно было их передвинуть и вставить
дополнительные. Так как максимальное число строк обычно доста-
точно велико, проблем, связанных с емкостью памяти, не возника-
ет. Впрочем, многие ЭВМ по команде RENUMBER перенумеровы-
вают программу, если ей становится «тесно». Наибольший номер
строки можно узнать из руководства к ЭВМ.
2.3, Изменения в программе
Возможность изменять программу, не стирая полностью, осво-
бождает от необходимости набирать ее заново. Значение этой воз-
можности для рационального программирования трудно переоце-
нить. Для внесения изменений в текст программы необходимо все
стереть с экрана и заново вывести программу на экран, после чего
ее строки становятся в правильной последовательности. Чтобы
стереть одну строку, набирают ее номер и нажимают клавишу
RETURN. Чтобы переписать одну строку, ее просто заново наби-
рают на клавиатуре. При этом старая строка будет автоматически
стерта, как только вы нажмете клавишу RETURN.
Исправление отдельных символов осуществляется в строке про-
граммы, выведенной на экран. Для этого курсор с помощью соот-
ветствующих клавишей, обозначенных стрелками, перемещают под
символ, подлежащий замене, и набирают нужный символ. Не за-
бывайте сообщать ЭВМ об исправлениях нажатием клавиши
RETURN. Если необходимо сместить (INSERT) или изъять отдель-
ные символы (DELETE), следует установить курсор на соответст-
вующее место и нажать клавишу < INST/DEL) (для INSERT с кла-
вишей SHIFT). Подробнее можно посмотреть в руководстве к
ЭВМ.
2.4. Обозначение переменных
В вышеприведенных программах мы использовали числовые пе-
ременные В, Т и Y. Практически все версии БЕЙСИКа допускают
* В некоторых версиях БЕЙСИКа нумерацию строк нельзя начинать с нуля. —
Прим, перев.
2*
20
Глава 2
для обозначения переменных любые буквы, а также комбинации
буква — цифра. Комбинации могут быть только двухпозиционны-
ми, причем буква должна стоять первой:
А, АО, Al, А2, ..., А9, В, ВО, ..., Z9
Для большинства ЭВМ возможна также комбинация двух букв. Не-
которые ЭВМ, «понимающие» БЕЙСИК, могут воспринимать име-
на переменных с 40 и более знаками. Нельзя только использовать в
качестве имен служебные слова алгоритмического языка, такие, как
IF, TI, ON, ... и др.
Пробел в БЕЙСИКе обладает приятным свойством:
********************************************
*** ПРОБЕЛ НЕ ИМЕЕТ В БЕЙСИКЕ (КАК ПРАВИЛО) ***
*** НИКАКОГО ЗНАЧЕНИЯ ***
********************************************
Это обстоятельство, позволяющее упростить структуру програм-
мы и придать ей хорошо читаемую форму, будет в дальнейшем ис-
пользовано в полной мере. Для персональных ЭВМ, где допускают-
ся переменные с большим числом символов, пробел необходим как
разделительный знак между оператором и переменными.
2.5. Первые элементы языка БЕЙСИК, используемые
для расчетов по формулам
2.5.1. Ввод данных
Ввод данных осуществляется оператором *************
*** INPUT ***
*************
*******************************
*** z INPUT v1,v2,v3,.•.,vn ***
*******************************
z — иомер строки; vl, v2, v3.vn — любые переменные.
Примеры:
ПРАВИЛЬНО: НЕПРАВИЛЬНО:
20 INPUT В,С
30 INPUT Е.Е0.Е1
50 INPUT Z
15 INPUT B*B
25 INPUT 3
55 INPUT
Формулы
21
Если необходимо ввести несколько переменных в одной строке,
то они должны быть разделены запятыми. Если при выполнении
программы встретится оператор INPUT, то на экране появится
знак вопроса (?) и выполнение программы будет приостановлено.
ЭВМ теперь ожидает ввода данных, количество и последователь-
ность ввода которых должны соответствовать переменным, стоя-
щим в операторе INPUT. В качестве ответа набирают данные, раз-
деленные запятыми, например:
3, 99.05, 4, 77.5
и после окончания ввода нажимают клавишу RETURN.
2.5.2. Вывод данных
_ *************
Вывод данных осуществляется оператором
*** PRINT ***
*************
* ******************************
*** z PRINT v1,v2,v3,...,vn ***
***★**★★**★★*★*★★★*★*★★★★★**★★★
z — номер строки; vl, v2, v3.vn — переменная или выражение.
Примеры:
ПРАВИЛЬНО: НЕПРАВИЛЬНО:
20 PRINT I 15 PRINT 1=3
30 PRINT A,2*A,A*A 25 PRINT SQR(-2)
50 PRINT 3.14,A*3.14 55 PRINT 1/0
70 PRINT J;J+1;J+2
312 PRINT SIN(4*A/K+2)
313 PRINT
4300 PRINT X,Y,X-Y,X*Y
Оператор PRINT выводит значения переменных на экран. Если
переменные в операторе PRINT разделены запятой (,), то резуль-
тат будет получен в форматированном виде, т. е. в виде наглядно-
го выражения. Если же переменные разделены точкой с запятой (;),
то данные будут записаны непосредственно друг за другом без про-
белов. «Пустой» оператор PRINT — без переменных — выводит на
экран одну строчку пробелов.
22
Глава 2
2.5.3. Оператор присваивания
Обозначение оператора присваивания: *************
*************** *************
★★★ z v=a
***************
z — номер строки; v — переменная; а — переменная, константа или выражение,
v = а означает, что переменной v придается значение а.
Слева от знака равенства (=) может стоять только переменная,
справа — любое разумное выражение, например формула. С обеих
сторон от знака равенства могут стоять одни и те же переменные.
Переменная, стоящая справа от знака равенства, получает свое зна-
чение в результате выполнения участка программы, предшествую-
щей оператору (=), а в дальнейшем используется заново вычислен-
ное значение переменной.
Примеры:
ПРАВИЛЬНО: 20 I = 9
33 I = 1+1
50 V9 = V*V
70 X = (А+Х)/(B+SIN(X))
312 J = О
НЕПРАВИЛЬНО: 15 9 = I
25 1+1 = 1+2
55 1.23 = .123Е1
75 Х*Х*Х = 19.2
95 0.5 = 1/2
Во всех ошибочных примерах слева от знака (=) стоит число или
выражение, а не переменная.
2.6. Запись чисел
Запись чисел для ЭВМ отличается от обычной, во-первых, тем,
что
**************************************************
*** ВМЕСТО ПРИВЫЧНОЙ ДЕСЯТИЧНОЙ ЗАПЯТОЙ. ОТДЕЛЯЮЩЕЙ ***
*** ДРОБНУЮ ЧАСТЬ ОТ ЦЕЛОГО ЧИСЛА, НАДО СТАВИТЬ ТОЧКУ (.) ♦♦♦
Формулы
23
Во-вторых, упрощено написание чисел в показательной форме. В
БЕЙСИКе используется прописная буква Е в качестве указателя ос-
нования 10, знак умножения опускается, а показатель степени запи-
сывается справа от Е.
Пример:
Обычное написание Написание на БЕЙСИКе
23 6,022-10 10 2,99-10 -34 6,626-10 6.022Е23 2.99Е+10 6.626Е-34
Число 0,08 можно записать для ЭВМ в виде
0.08 .08 .08Е0 0.00008Е+3
0.8Е - 1 .008Е1 8Е - 2 800.0Е - 4
но не так:
8/100 или 8*10(1—2) или 8*Е - 2,
поскольку эти выражения представляют собой совокупность математических опера-
ций.
2.7. Арифметические выражения
При написании арифметических выражений необходимо пом-
нить о двух важных правилах:
********************************************
*** НЕОБХОДИМО ВСЕГДА ПИСАТЬ ЗНАК УМНОЖЕНИЯ (•) ***
********************************************
*** в НЕЯСНЫХ СИТУАЦИЯХ ИСПОЛЬЗУЙТЕ СКОБКИ ***
♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦
Арифметические операции в БЕЙСИКе имеют те же приорите-
ты, что и в алгебре. Возведение в степень выполняется раньше ум-
ножения (или деления), а умножение — раньше сложения (или вы-
читания).
24
Глава 2
Знаки арифметических операций в БЕЙСИКе:
Сложение +
Вычитание —
Умножение ♦
Деление /
Возведение в степень t или (♦♦)
Ниже приведены примеры арифметических выражений и их за-
пись на БЕЙСИКе:
Формула Выражение на БЕИСИКе
А-В АВ 2В 2 2С+ЗВ -*=*- . 7 C-D а=в (’С—D ) . 7 X2 /Г [(а+в)2+ С]2 Е RT А-В А*В 2*В 2*С+3*В+2 или 2*С+3*В*В (А-В)/(C-D)*7 ИЛИ 7*(А-В)/(С-D) ИЛИ 7/(С-D)*(А-В) (А-В) / (С-D)/7 ИЛИ .(А-В) / ( (С-D)*7 ) ИЛИ 1/7/(С-D)*(А-В) Х+2 или Х*Х SQR(X) или Х+(1/2) или Х+ (0.5) ((А+В)+2+С)+2 E/(R*T) ИЛИ E/R/T E/T/R или 1/(T*R)*E
2.8. Стандартные функции
Для решения научных и инженерно-технических задач часто ис-
пользуются математические функции; некоторые из них у боль-
шинства ЭВМ постоянно занесены в память машины. Благодаря
этому устраняется необходимость составления программы для вы-
числения таких функций (что для большинства элементарных функ-
ций не составило бы слишком серьезной проблемы) и появляется
возможность вызывать эти функции набором соответствующего
сокращения.
Формулы
25
Ниже приведены важнейшие стандартные функции и соответст-
вующие сокращения:
SIN (X) Синус х (х выражен в радианах)
COS (X) Косинус х (х выражен в радианах)
TAN (X) Тангенс х (х выражен в радианах)
ATN (X) Арктангенс х (функция, обратная тангенсу)
SQR (X) Квадратный корень изх
EXP (X) Показательная функция х
LOG (X) Натуральный логарифм х (часто пишут 1пх)
ABS (X) Абсолютная величина; функция меняет знак у отрицательных чи-
сел
INT (X) Целая часть числа (все цифры после десятичной запятой отбрасы-
ваются)
SGN (X) Знак числа, принимает значения; + 1, если х > 0; 0, если х = 0;
- 1, если х < 0
RND (X) Датчик псевдослучайных чисел, генерирует псевдослучайные чис-
ла, равномерно распределенные на замкнутом интервале [0, 1]
тг Число ir (как правило, занесено в память ЭВМ); его можно также
задать выражением 4 ♦ ATN (1)
Аргумент стандартных функций должен стоять в скобках.
2.9. Оператор безусловного перехода
Недостаток программы, приведенной на с. 17, заключается в
том, что при многократном ее использовании с различными значе-
ниями В и Т необходимо всякий раз заново запускать программу
командой RUN и клавишей RETURN. Этот недостаток можно уст-
ранить, если после оператора PRINT в текст программы ввести
оператор, который передаст управление оператору, стоящему в на-
чальной строке программы. Оператор GOTO может передавать
управление оператору, стоящему в любой строке, надо только ука-
зать ее номер.
Оператор безусловного перехода ************
*** GOTO ***
************
******************
*** z1 GOTO z2 ***
******************
zl, z2 — номера строк.
Оператор GOTO называется оператором безусловного перехода
потому, что при его выполнении всякий раз прерывается обыч-
ный порядок выполнения программы по порядку номеров строк, и
управление передается оператору, стоящему в строке z2, номер ко-
торой указан в операторе GOTO. Переход может осуществляться
26
Глава 2
как вперед, так и назад. Если отсутствует или пропущен номер
строки, указанный в операторе GOTO, то на экране появится сооб-
щение об ошибке.
Задание 1. Ответьте, что произойдет, если в программе встретится оператор
100 GOTO 100
Если вы не можете ответить на этот вопрос, то воспользуйтесь
методом многих пользователей:
ПРОВЕРЬТЕ НА ЭВМ!!!
Напоминаем, что выполнение программы прерывается нажатием
клавиши RUN/STOP.
Примеры операторов:
ПРАВИЛЬНО: НЕПРАВИЛЬНО:
20 GOTO 3000 15 GOTO А
90 GOTO 10 100 GOTO 20,200
Дополненная оператором GOTO программа для решения ука-
занной выше задачи (с. 17) выглядит теперь следующим образом:
10 INPUT В,Т
20 Y = ЕХР(-В*Т)/(1+Т)
30 PRINT B,T,Y
40 GOTO 10
После вычисления значения переменной Y (строка 20) и вывода зна-
чений переменных В, Т, Y управление передается оператору ввода
INPUT, на экране появится знак вопроса (?) и ЭВМ будет ждать
очередных числовых значений В и Т. Если вы полностью закончили
вычисления по этой программе, то на запрос оператора INPUT на-
берите пробел или, не набирая никаких символов, нажмите клави-
шу RETURN. Выход из такой бесконечной программы часто зави-
сит от типа ЭВМ. Поэтому загляните в руководство к вашему
компьютеру.
Задание 2. Составьте программу для расчета константы скорости реакции по
уравнению Аррениуса, полагая известными энергию активации Е'а и предэкспоненци-
альный множитель kQ:
Задание 3. Проверьте функционирование следующих двух программ. Сначала
проанализируйте программы, не прибегая к помощи ЭВМ, н сравните результаты
ваших рассуждений с результатом, полученным на ЭВМ.
Формулы
27
10 1=1+1
20 PRINT 1,1*1
30 GOTO 10
10 INPUT X
20 X = SQR(ABS(SIN(X)))
30 PRINT X
40 GOTO 20
Правильно интерпретировать вторую программу довольно
трудно; впоследствии мы к ней еще вернемся. Анализ второй про-
граммы упростится, если вместо строки 20 подставить
20 X = SQR (X)
Сделайте при работе на ЭВМ умышленную ошибку! Разделите
на 0! Попытайтесь вычислить значение какой-нибудь стандартной
функции вне области допустимых значений аргумента, например
извлечь квадратный корень из отрицательного числа и т. п. Попы-
тайтесь выяснить с помощью программы или, работая в непос-
редственном режиме, какое наибольшее и наименьшее число допу-
скает ваша ЭВМ.
2.10. Непосредственный режим
Почти все персональные ЭВМ имеют очень удобный режим ра-
боты, так называемый непосредственный режим? в котором можно
проводить вычисления, не составляя программ, как и на обычном
микрокалькуляторе. Если набрать оператор, не указывая номера
строки, то после нажатия клавиши RETURN он будет выполнен.
Однако текст, содержащийся в этой строке, не запоминается; ре-
зультат выполнения оператора сразу появляется на экране, как это
показано на следующих примерах:
PRINT LOG(5.1)*SIN(3) <RETURN>
.229918438
I = 217 <RETURN>
PRINT 1*1 <RETURN>
47089
2.11. Расчет площади треугольника
по длинам трех сторон
Расчет можно провести, не используя тригонометрических функ-
ций. Исходя из длин сторон треугольника а, Ь, с, необходимо сна-
28
Глава 2
чала вычислить полупериметр:
S = (а + b + с)/2
Для площади треугольника справедливо
F = VS(S - <z)(S - b)(S - с)
Программа для решения этой задачи выглядит следующим об-
разом (приведены также два числовых примера):
0 КЕМ "ТРЕУГ" EBERTZEDERER 010504
1 КЕМ****************************************
2 REM** ВЫЧИСЛЕНИЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА •*
5 REM** ЗАДАНЫ ДЛИНЫ СТОРОН А, В. С **
9 КЕМ*****************************************
100 INPUT "СТОРОНА А В СМ"; А
200 INPUT "СТОРОНА В В СМ"; В
300 INPUT "СТОРОНА С В СМ"; С
400 S-.5*<R+B+C>
500 F»SQR<S«<S-R>*(S-B>*<S-C>>
1000 PRINT
1100 PRINT "ПЛОЩАДЬ ТРЕУГОЛЬНИКА ="; F; "CMt2"
2000 END
RUN
СТОРОНА A В CM? 5
СТОРОНА В В СМ? 6
СТОРОНА С В СМ? 7
ПЛОЩАДЬ ТРЕУГОЛЬНИКА = 14.6969385 СмЪ
RERDV.
RUN
СТОРОНА А В СМ? 3
СТОРОНА В В СМ? 4
СТОРОНА С В СМ? 5
ПЛОЩАДЬ ТРЕУГОЛЬНИКА = 6CMt2
RERDV.
Эта программа отличается по виду от составленных ранее и ка-
жется несколько избыточной. Ведь для решения задачи было бы
достаточно программы из четырех строк:
100 INPUT А,В,С
400 S=.5*(A+B+C)
500 F=SQR(S*(S-А)*(S-В)*(S-C))
1100 PRINT F
Менее сложная программа похожа на предыдущую, более объе-
мистую. В строках 400 и 500 производится расчет по формулам. В
строках 100—300 вводятся длины сторон, в строке 1100 выводится
на экран значение площади. Различие сразу обнаружится, если по-
Формулы
29
работать с обеими программами на ЭВМ. Работать с первой, бо-
лее объемистой программой гораздо проще и приятней, она содер-
жит полезные для пользователей сведения: как следует действо-
вать, что означает результат. Короткой программой, по содержа-
нию идентичной предыдущей, сможет пользоваться, по-видимому,
только ее составитель, потому что лишь он знает, какая информа-
ция вводится в ЭВМ, какая выводится и для чего вообще предна-
значена эта программа. Однако со временем и составитель забыва-
ет, для чего написана программа, и при повторном использовании
вынужден заново анализировать свою собственную программу.
Что нового в более удобной программе?
Комментарий ***********
*** rem ***
*** z REM ЫаЫа ***
********************
z — номер строки, ЫаЫа — любой текст (только без двоеточия (:))
Текст после оператора REM (от англ, remark — примечание,
комментарий) не оказывает никакого влияния на выполнение про-
граммы. При обработке программы в ЭВМ этот текст отбрасыва-
ется. Поэтому можно использовать оператор REM для написания
пояснений к программам. Это может оказаться очень полезным,
поскольку хорошо составленный комментарий впоследствии позво-
лит избежать повторного анализа собственной программы. Неко-
торые, пытаясь сэкономить на комментарии, пишут мало примеча-
ний или не пишут их вообще, однако через некоторое время они,
как правило, сожалеют об этой «экономии». Поэтому советуем
**************************************************
*** ЧЕМ БОЛЬШЕ КОММЕНТАРИЕВ И ПРИМЕЧАНИЙ, ТЕМ ЛУЧШЕ1 ***
*************************************************
В комментариях к программе «ТРЕУГ» записаны имя программы,
составитель, дата написания (это может оказаться полезным, если
впоследствии вы будете вносить изменения в программу) и крат-
кое, в общих чертах, описание содержания программы.
Другим новым элементом языка является расширение операто-
ров INPUT и PRINT, позволяющее вводить и выводить текст.
Текст в этих операторах напоминает, значение какой переменной
необходимо ввести, или обозначает на экране, какая величина вы-
числена.
30
Глава 2
Вывод данных
*************************
РАСШИРЕННЫЙ
ОПЕРАТОР
PRINT ***
*************************
*******************************
*** z PRINT v1,v2,v3,...,vn ***
*******************************
z — номер строки; vl, v2, v3, vn — переменные, выражения или текст (текст обя-
зательно в кавычках). Вместо текста можно написать выражение, состоящее из лю-
бых символов.
Примеры: print "результат=";r*r*r; liter"
PRINT “PI = "г 3.14159
Ввод данных: *******************************
*** РАСШИРЕННЫЙ ОПЕРАТОР INPUT ***
************************* ********
**************************************
*** z INPUT "ТЕКСТ”; v1 , v2 , v3.vn ***
**♦♦*♦*♦**♦♦♦*♦♦♦*♦♦♦★♦♦♦♦*♦♦♦********
z — номер строки; vl, v2, v3, ..., vn — переменные.
He все версии БЕЙСИК^ имеют такую конструкцию расширен-
ного оператора INPUT. Поэтому загляните в руководство к вашей
ЭВМ, чтобы найти правильную конструкцию расширенного опера-
тора INPUT для ввода текста. В рассматриваемом случае точка с
запятой (;) после текста имеет принципиальное значение и ее нельзя
заменить, например, запятой (,).
Примеры:
правильно: неправильно:
20 INPUT "ДЛИНА"; L 20 INPUT "ДЛИНА", L
30 INPUT "x,y";X,Y 30 INPUT X,Y,-“x,y“
Еще одно замечание общего характера о грамотном оформле-
нии программ. В задачах научного и инженерно-технического ха-
рактера исходные данные и результаты имеют, как правило, раз-
мерность (в нашем примере см и см2). Поскольку ЭВМ выполняет
операции не с величинами, а только с их числовыми значениями,
необходимо учитывать размерность исходных параметров и конеч-
ных результатов. Пользователю надо напоминать, в каких едини-
цах измерения должны быть выражены входные данные. Квалифи-
Формулы
31
цированный программист никогда не потребует, чтобы длина вол-
ны монохроматического света измерялась в морских милях (даже
если необходимо узнать число волн в миле), а использует для дли-
ны волны обычные единицы измерения — ангстремы или наномет-
ры. В программе следует предусмотреть перевод одних единиц из-
мерения в другие.
Конец программы ***********
*** END »»»
***********
*** z END ***
>»»***r*****«
z — номер строки.
В строке 2000 программы «ТРЕУГ» стоит оператор END. Он
указывает ЭВМ, что следует закончить выполнение программы,
даже если далее записаны еще другие операторы. Поскольку в дру-
гих алгоритмических языках и в некоторых версиях БЕЙСИКа ис-
пользование оператора END обязательно, полезно привыкнуть пи-
сать все программы с оператором END.
Задание 4. Напишите программу для расчета объема шара, площади поверхно-
сти шара н отношения этих величин. Радиус шара известен. Напоминаем формулы:
S = 4-2,; V = 4г3тг/3
Задание 5. Составьте программу для расчетов по интересующей вас формуле.
Попытайтесь составить такую программу, работать с которой было бы удобно и
другим пользователям.
2.12. Расчет средней длины свободного пробега
молекул газа
В учебниках по физической химии для средней длины свободно-
го пробега молекул газа приводится следующая формула:
I — средняя длина свободного пробега; N — число частиц; а — диаметр молекулы.
Молекулы рассматриваются как твердые частицы диаметром а.
Число частиц в заданном объеме находят по уравнению состояния
идеального газа.
Средняя длина свободного пробега молекул газа рассчитывается
в зависимости от давления, температуры и диаметра молекулы.
Эта величина используется при конструировании вакуумной аппара-
32
Глава 2
туры, для учета каталитического влияния стенки на скорость гомо-
генных газофазных реакций. Программа для расчета:
0 REM "СВО-БЕГ" EBERT/EDERER 810504
1 REM**********************************4HH**4
2 REM** РАСЧЕТ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО **
3 REM** ПРОБЕГА МОЛЕКУЛ В ГАЗЕ **
9 REM***************************************
10 PI-4*RTN<1>
100 INPUT "ДАВЛЕНИЕ В ATM"; Р
200 INPUT "ТЕМПЕРАТУРА В К"; T
400 INPUT "ДИАМЕТР МОЛЕКУЛЫ В М"; S
1000 REM*********************************
1010 REM** РАСЧЕТ ЧИСЛА ЧАСТИЦ В Mt 3 **
1040 REM*********************************
1100 N»6.022E23*P/<T*S.2IE-5>
1150 REM R»S.2056E-5 MT3* ATM/(МОЛЬ-К)
2000 REM****************************************
2010 REM** РАСЧЕТ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ••
2020 REM** ПРОБЕГА *«
2040 REM****************************************
2500 L»1/<PI*SQR<2:>*S#N*S>
2600 PRINT
3000 PRINT "СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА = "
3100 PRINT L;" M"
63999 END
RUN
ДАВЛЕНИЕ В ATM? J
ТЕМПЕРАТУРА В К? 283
ДИАМЕТР МОЛЕКУЛЫ В М? 3.64Е-10
СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
6.78562062Е-08 М
RERDV.
В этой програме вычисления выполняются по двум формулам.
По первой вычисляется число молекул в 1 м3 газа (строка 1100), по
другой формуле, приведенной на с. 31, — средняя длина свободного
пробега (строка 2500). При написании формул и составлении про-
граммы следует обратить особое внимание на размерность вели-
чин, входящих в формулы. Например, один из возможных вариан-
тов строки 3100:
3100 PRINT L*100; « см»
Большая часть строк этой программы отведена под коммента-
рий. Кроме того, три строки занимают операторы ввода и еще три
строки — операторы вывода, из которых в строке 2600 стоит пу-
стой оператор PRINT. В качестве числового примера приведен рас-
чет средней длины свободного пробега молекул аргона (диаметр
молекулы 3,64 А).
Задание 6. Измените программу «СВО-БЕГ» так, чтобы можно было вводить
входные данные в миллибарах, градусах Цельсия, ангстремах. Результат также дол-
жен выражаться в ангстремах.
Формулы
33
Задание 7. Используйте программу «СВО-БЕГ» (или ее модификацию) для рас-
чета давления в вакуумной аппаратуре, если длина свободного пробега молекул азо-
та (aN = 3,77 А) равна 20 см.
2.13. Распределение молекул идеального газа
по скоростям (распределение Максвелла)
GN , > / т \3/1 " \ти17(кТ)
---- = 4ttuz- I------ ) -е
du \2кТъ )
Для 1 моль газа
= L = 6.022Е23 = 1 моль
и — скорость; к — константа Больцмана; Т — температура, К; m — масса молеку-
лы; dN/du — плотность распределения частиц, т. е. доля частиц, скорость которых
лежит в интервале от и до и + du.
Прежде чем составлять программу, надо твердо установить для
себя, в каких единицах измерения будут выражены величины, вхо-
дящие в уравнение, и в какой системе единиц предполагается вво-
дить исходные данные и выводить результат вычислений. В про-
грамме есть «подсказчик», который напоминает, в каких единицах
следует вводить исходные параметры (строки 200, 400, 500), и ука-
зывает размерность выходных данных (строки 4600—5500). Для
ввода и вывода параметров используют общепринятые или удоб-
ные единицы измерения, а для вычислений все величины непо-
средственно в программе переводят в систему СГС. Так, скорость в
м/с (переменная U) вводится оператором INPUT в строке 500 и в
первой части строки 3000 переводится в см/с (переменная UH). Во
второй части строки 3000 размерность универсальной газовой по-
стоянной пересчитывается из Дж/(К*моль) (переменная R) в
эрг/(К * моль) (переменная RH). Кроме того, приведенное выше вы-
ражение разделено на число Авогадро (Z-), чтобы получить ответ в
мольных долях. Поскольку М = mL (М — молекулярная масса) и
R = kL, отношение m /к в приведенной выше формуле заменено
равным ему отношением M/R.
0 REM "МАКСВЕЛЛ" EBERTZEDERER 810504
1 REM****************************************
2 REM** РАСЧЕТ РАСПРЕДЕЛЕНИЯ МОЛЕКУЛ ПО **
3 REM** СКОРОСТЯМ ПО МАКСВЕЛЛУ **
9 REM****************************************
100 PI-4*ATN<1>
200 INPUT "ТЕМПЕРАТУРА В К"; T
400 INPUT "МОЛЕКУЛЯРНАЯ МАССА"; М
500 INPUT "СКОРОСТЬ В М/С"; U
3-81
34
Глава 2
2000 RgM******************************
2010 REM** R - В. 31441 ДЖ/(К «МОЛЬ) **
2020 REM** 1ДЖ = 1Е7 ЭРГ **
2030 REM** 1 ЭРГ = СМ12*Г/(С12) **
2040 REM** L - 6.022Е23 /МОЛЬ **
2500 REM******************************
2600 R»B.31441
3000 UH-U*100|RH-R*1E7
4000 0H-4*PI*UH*UH*< М/< 2*PI*RH*T > > T <3/2 >
4100 ON-ON*EXP<-M*UH/RH*UH/T/2>
4200 OH-DH*100> REM ПОСКОЛЬКУ РАЗМЕРНОСТЬ DN - МОЛЬ/(М/С)
4600 PRINT "ТЕМПЕРАТУРА =";T; "К"
4700 PRINT "МОЛЕКУЛЯРНАЯ МАССА = "; M
4000 PRINT "СКОРОСТЬ =-; U; 5000 PRINT 5200 PRINT "ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ = "; 5300 PRINT DN;"МОЛЬ/(М/С)" 5500 PRINT(PRINT 6000 GOTO 500 63999 END "М/С"
RUN
ТЕМПЕРАТУРА В К? 300
МОЛЕКУЛЯРНАЯ МАССА? 28
СКОРОСТЬ В М/С? 200
ТЕМПЕРАТУРА = 300 К
МОЛЕКУЛЯРНАЯ МАССА = 28
СКОРОСТЬ = 200 М/С
ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ = 9.58969264Е-04 МОЛЬ/ (М/С)
СКОРОСТЬ В М/С? 400
ТЕМПЕРАТУРА? 300
МОЛЕКУЛЯРНАЯ МАССА? 28
ТЕМПЕРАТУРА = 300 К
МОЛЕКУЛЯРНАЯ МАССА = 28
СКОРОСТЬ = 400 М/С
ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ = 1.95593562Е-03 МОЛЬ/ (М/С)
СКОРОСТЬ В М/С?
Вывод текста программы по частям. Программа «МАКС-
ВЕЛЛ» занимает довольно много места и целиком не помещается
на экране. Для работы с программой на экране ее вызывают по ча-
стям, дополнив команду LIST номерами соответствующих строк.
Для тех же целей можно использовать замедленный построчный
вывод программы на экран.
****************
* LIST z1 - z2 *
****************
zl, z2 — номера строк.
Например: LIST 9—500
LIST -999
LIST 500
LIST 2500-
Формулы
35
Следует обратить внимание на прием, встречающийся впервые в
программе «МАКСВЕЛЛ». В строке 3000 записано
3000 UH = U*100:RH = R*1E7
Эта конструкция эквивалентна двум операторам:
3000 UH = U *100
ЗОЮ RH = R*1E7
БЕЙСИК позволяет записывать в одной строке друг за другом
несколько операторов, разделяя их двоеточиями (:) (см.
разд. 5.3.1). Однако следует иметь в виду, что при выполнении опе-
ратора GOTO имеет значение только номер той строки, первому
оператору которой передается управление, и нет никакой возмож-
ности передать управление оператору, стоящему во второй полови-
не строки.
Для вычисления по довольно длинной формуле в программе
«МАКСВЕЛЛ» используется новый, ранее не встречавшийся при-
ем. В строке 4000 вычисляется первая часть формулы и промежу-
точный результат присваивается переменной DN; в строке 4100 вы-
числяется вторая часть формулы, умножается на DN, и произведе-
ние запоминается как новое значение переменной DN. В строке 4200
результат, вычисленный в предыдущей строке, для получения отве-
та в метрах умножается на 100.
Чтобы программа была наглядной, советуем
***************************************
*** ВЫЧИСЛЯТЬ ГРОМОЗДКИЕ ФОРМУЛЫ ***
*** ПО ЧАСТЯМ И ЗАТЕМ СОЕДИНЯТЬ ЧАСТИ ***
*** ******************************** ***
Задание 8. Используйте программу «МАКСВЕЛЛ» для расчета распределения
частиц по скоростям для аргона при 1000 °C для различных значений скорости, по-
стройте график функции распределения.
Задание 9. Используя программу «МАКСВЕЛЛ», найдите при заданной скоро-
сти н молекулярной массе такую скорость, для которой функция распределения мак-
симальна. Решите задачу методом проб и ошибок, не составляя новой программы
(программа для нахождения максимума функций будет рассмотрена ниже). Как сме-
щается максимум при изменении температуры? Ответы на эти вопросы можно по-
лучить в аналитической форме, однако очень простые численные методы в некото-
рых случаях дают ответ более коротким путем н позволяют избежать ошибок.
2.14. Расчет объемной плотности энергии излучения
абсолютно черного тела по формуле Планка
Формула, по которой проводятся вычисления, в программе
«ПЛАНК» записана в строке 2000. При написании этой программы
36
Глава 2
необходим анализ размерностей, чтобы твердо установить, каковы
размерности констант и в каких единицах измерения предполагает-
ся вводить исходные данные и получать результаты вычислений.
В этой программе нет новых конструкций алгоритмического
языка. Основной задачей является выбор соответствующей систе-
мы единиц.
0 КЕМ "ПЛАНК" EBERT/EDERER 610504
1 КЕМ****************************************
2 КЕМ#* РАСЧЕТ ОБЪЕМНОЙ ПЛОТНОСТИ ЭНЕРГИИ*#
3 КЕМ** ИЗЛУЧЕНИЯ ПО ПЛАНКУ ##
9 REM****************************************
100 INPUT "ЧАСТОТА В 1/С"; U
200 INPUT "ТЕМПЕРАТУРА В К"; Т
300 Н-6.6262В24Е-34
400 К=1.3B054E-23
500 С-2.9979245612Е10
600 Р1-4*АТН<1>
1000 КЕМ*********************************
1100 REM** ПОСТОЯННАЯ ПЛАНКА ##
1200 REM** Н - 6.6262624 Е-34 ДЖ* С ««
1300 REM** КОНСТАНТА БОЛЬЦМАНА **
1400 REM*# К - 1.38054 Е-23 ДЖ/К ««
1500 REM** СКОРОСТЬ СВЕТА **
1600 REM*# С = 2.9979245812 ЕЮ СМ/С ••
1700 REM*********************************
2000 U-8*PI*<V/C’>t3*H/<EXP<H*V/<K*T>>-1 >
2900 PRINTiPRINT
3000 PRINT "ОБЪЕМНАЯ ПЛОТНОСТЬ";
3100 PRINT "ЭНЕРГИИ ИЗЛУЧЕНИЯ"
3200 PRINT "НА ЧАСТОТЕ": U;"1/C"
3300 PRINT "ПРИ ТЕМПЕРАТУРЕ"; Т; "К”
3400 PRINT "=": U; "ДЖ’С/(СМ*СМ*СМ) "
3500 ЕНО
RUN
ЧАСТОТА В1/С7 1Е13
ТЕМПЕРАТУРА В К? 1000
ОБЪЕМНАЯ ПЛОТНОСТЬ ЭНЕРГИИ ИЗЛУЧЕНИЯ
НА ЧАСТОТЕ 1Е + 13 1 /С
ПРИ ТЕМПЕРАТУРЕ 1000 К
- 1.00332141Е-24 ДЖ*С/(СМ«СМ*СМ)
READY.
RUN
ЧАСТОТА В 1/C? 5Е13
ТЕМПЕРАТУРА В К? 273
ОБЪЕМНАЯ ПЛОТНОСТЬ ЭНЕРГИИ ИЗЛУЧЕНИЯ
НА ЧАСТОТЕ 5Е +13 1/С
ПРИ ТЕМПЕРАТУРЕ 273 К
- 1. 17551641Е-26 ДЖ * С/(СМ*СМ*СМ)
READY.
Задание 10. Измените программу «ПЛАНК» так, чтобы в результате была вы-
числена не объемная плотность энергии, а объемная плотность световых квантов.
Формулы
37
2.15. Перевод градусов Цельсия в градусы Фаренгейта
Формула для пересчета стоит в строке 400 программы «Ц-Ф».
Несмотря на тривиальность программы, она может оказаться по-
лезной, если химик будет иметь дело с литературой, в которой
температурные данные выражены в непривычных единицах измере-
ний (°F).
0 REM "Ц—ф" EBERT/EDERER В10504
1 REM********************************* •••••
2 REM** ПЕРЕСЧЕТ ТЕМПЕРАТУРЫ ИЗ ГРАДУСОВ **
3 REM** ЦЕЛЬСИЯ В ГРАДУСЫ ФАРЕНГЕЙТА «*
9 REM**************************************
150 PRINT
200 INPUT "ТЕМПЕРАТУРА В ГРАДУСАХ ЦЕЛЬСИЯ" ; С
400 F-C*9/5+32
500 PRINT Cf "С СООТВЕТСТВУЕТ"; F ; "F"
550 PRINT
600 GOTO 200
1000 ЕНО
RUN
ТЕМПЕРАТУРА В ГРАДУСАХ ЦЕЛЬСИЯ? О
О С СООТВЕТСТВУЕТ 32 F
ТЕМПЕРАТУРА В ГРАДУСАХ ЦЕЛЬСИЯ ? 37
37 С СООТВЕТСТВУЕТ 98.6 F
ТЕМПЕРАТУРА В ГРАДУСАХ ЦЕЛЬСИЯ? 100
100 С СООТВЕТСТВУЕТ 212 F
ТЕМПЕРАТУРА В ГРАДУСАХ ЦЕЛЬСИЯ?-40
-40 С СООТВЕТСТВУЕТ -40 F
ТЕМПЕРАТУРА В ГРАДУСАХ ЦЕЛЬСИЯ? -273
-273 С СООТВЕТСТВУЕТ -459.4 F
ТЕМПЕРАТУРА В ГРАДУСАХ ЦЕЛЬСИЯ?
Задание 11. Напишите программу, которая переводит градусы Фаренгейта в
градусы Цельсия.
Напишите программу, которая переводит американские единицы измерения в
общепринятые (например, фунт/кв.дюйм в бар).
2.16. Диффузионный потенциал
в растворах электролитов
Следующий пример касается расчета диффузионных потенциа-
лов. Приведенная ниже программа рассчитывает потенциал между
двумя водными растворами электролитов различной концентрации
при комнатной температуре. Нетрудно расширить программу для
расчетов диффузионных потенциалов при любых температурах. В
программе «ДИФ-ПОТ» в качестве исходных данных вводят кон-
38
Глава 2
центрации растворов, выраженные в моль/л, и числа переноса.
Напоминаем: если обозначить подвижность аннона и катиона и _ и и +, то число
переноса Я = и_/(и + и ). Число переноса— безразмерная величина.
0 REM "ДИФ-ПОТ" EBERT/EDERER 610504
1 REM**********************************
2 REM** ДИФФУЗИОННЫЙ ПОТЕНЦИАЛ НА **
3 REM** ГРАНИЦЕ ДВУХ ВОДНЫХ РАСТВО- **
4 REM** РОВ ПРИ КОМНАТНОЙ ТЕМПЕРАТУРЕ*
9 REM**********************************
200 INPUT "ЧИСЛО ПЕРЕНОСА"; Н
300 INPUT "ЗАРЯД ИОНА"; N
400 INPUT "КОНЦЕНТРАЦИЯ!"; С1
500 INPUT "КОНЦЕНТРАЦИЯ 2"; С2
600 E-<2*H-1>*.056/N*LOG<C1/C2)
800 PRINT "ДИФ. ПОТ. -". Е; "ВОЛЬТ"
63999 END
RUN
ЧИСЛО ПЕРЕНОСА? 0.4
ЗАРЯД ИОНА? 2
КОНЦЕНТРАЦИЯ 1? .1
КОНЦЕНТРАЦИЯ 2? .01
ДИФ. ПОТ. =-.0133549935 ВОЛЬТ
REAOY.
RUN
ЧИСЛО ПЕРЕНОСА? .3
ЗАРЯД ИОНА? 1
КОНЦЕНТРАЦИЯ 1?1.0
КОНЦЕНТРАЦИЯ 2? 1Е-3
ДИФ. ПОТ. = -.160259922 ВОЛЬТ
READY.
2.17. Скорость истечения газа
В качестве последнего примера расчета по формулам рассмот-
рим программу для вычисления скорости истечения идеального га-
за из сосуда под давлением. Скорость истечения зависит от давле-
ния внутри и вне сосуда, от молекулярной массы газа, от темпера-
туры и (из-за адиабатического расширения) от отношения моляр-
ных теплоемкостей к = Cp/Cv. Формула имеет вид
\2RT /, р V»
w = /----- ( 1 - — 1
У к9М \ р0/
w — скорость истечения; R — универсальная газовая постоянная; Т — температура
в сосуде; р — внешнее давление; р0 — давление в сосуде; М — молекулярная масса
газа; к9 — вспомогательная величина, которую рассчитывают, исходя из Ср и Cv:
к9= (к - \)/к
Как и в предыдущих примерах, сначала необходимо проанализи-
Формулы
39
ровать размерность входящих в формулу величин, чтобы не оши-
биться при выборе единиц измерения исходных параметров и ре-
зультата вычислений.
Рекомендуем:
**********************************************************
*** ВЫЧИСЛЕНИЯ В ЯДРЕ ПРОГРАММЫ ПРОВОДИТЬ В ОДНОЙ И ТОЙ ЖЕ ***
*** СИСТЕМЕ ЕДИНИЦ (НАПРИМЕР, СГС ИЛИ СИ) ***
*** ххх ***
*** ДЛЯ ВХОДНЫХ И ВЫХОДНЫХ ДАННЫХ ИСПОЛЬЗОВАТЬ ***
*** ПЕРЕСЧЕТНЫЕ КОЭФФИЦИЕНТЫ' ***
**********************************************************
0 REM "ИСТЕЧЕНИЕ" EBERT/EDERER 810504
1 REM#######################*####*#**###***
2 REM** РАСЧЕТ СКОРОСТИ ИСТЕЧЕНИЯ ГАЗА ИЗ **
3 REM** СОСУДА ПО ОБОБЩЕННОМУ £
4 REM** УРАВНЕНИЮ БЕРНУЛЛИ. WITTENBERGER /FRITZ**
5 REM** SPRINGER 1981 S. 19 ««
9 REM**************************************
200 INPUT "ТЕМПЕРАТУРА в К"; T
400 INPUT "МОЛЕКУЛЯРНАЯ МАССА"; M
500 INPUT "CP/CV "/K
510 REM*******************************
515 REM** CP/CV - ОТНОШЕНИЕ МОЛЬНЫХ ТЕП-*#
518 REM#* ЛОЕМКОСТЕЙ ПРИ ПОСТОЯННЫХ ##
521 REM## Р ИЛИУ СООТВЕТСТВЕННО ##
530 REM*#**#*#*#############****######
600 INPUT "ВНЕШНЕЕ ДАВЛЕНИЕ" ; Р2
620 INPUT "ДАВЛЕНИЕ ВНУТРИ"; Р1
2000 REM******************************
2010 REM** R - 8.31441 ДЖ/(К*МОЛЬ) **
2020 REM** 1 ДЖ= 1Е7 ЭРГ **
2030 REM** 1 ЭРГ = СМТ2*Г/ (С12) **
2040 REM** L - 6.022Е23 /МОЛЬ **
2500 REM******************************
2600 R-0.31441*1E7
4000 К9-<К-1>/К
4050 Р9-Р2/Р1
4100 R9-R*T/M
4200 U-SQR<2/K9*R9*<1-P9TK9>>/100
5000 PRINT "СКОРОСТЬ ИСТЕЧЕНИЯ В М/С"
5200 PRINT ",U
63999 END
RUN
ТЕМПЕРАТУРА В К? 293
МОЛЕКУЛЯРНАЯ МАССА? 2В.96
CP/CV ? 1.402
ВНЕШНЕЕ ДАВЛЕНИЕ? 1.2
ДАВЛЕНИЕ ВНУТРИ? 2.4
СКОРОСТЬ ИСТЕЧЕНИЯ В М/С
- 325.204413
REfiDY.
3. Ряды
В этой главе речь пойдет о задачах из области физики и химии,
которые можно решать с помощью последовательностей. Сумму
бесконечного числа элементов этих последовательностей будем на-
зывать рядами. Способы быстрого и удобного решения таких за-
дач с помощью персонального компьютера во многом зависят оТ
возможностей имеющейся ЭВМ. Программу составляют таким об-
разом, чтобы ЭВМ вычисляла неограниченное количество членов
ряда. Промежуточное значение вычисленной суммы выводят на
экран и через некоторое время счет приостанавливают вручную.
Если промежуточные результаты сменяют друг друга слишком
быстро и в процессе выполнения программы необходимо контроли-
ровать промежуточное значение вычисляемой суммы, то применя-
ют так называемый «тормоз», который имеется в каждой ЭВМ и
замедляет процесс вывода информации на экран. В ЭВМ
“Commodore 8032” для этого пользуются клавишей со стрелкой, на-
правленной влево. Этой клавишей можно замедлить также вывод
программы на экран по команде LIST.
"ТОРМОЗ"
Как только в результате вычислений будет достигнута желае-
мая сходимость, счет можно приостановить вручную. Хотя такой
прием нельзя считать математически корректным, для некоторых
задач он удобен и эффективен. Можно использовать автоматиче-
ское прекращение счета по заданным критериям.- Тогда в програм-
ме необходимо предусмотреть сравнение вычисляемых величин с
заранее заданными параметрами. Однако этот метод не всегда яв-
ляется более строгим и удобным по сравнению с ручной останов-
кой счета. В ЭВМ “Commodore” выполнение программы прерыва-
ется клавишей RUN/STOP. (Эта клавиша не действует, если ЭВМ
остановилась на операторе INPUT.)
Выполнение программы будет продолжено, если вторично на-
Ряды
41
жать клавишу RUN/STOP или отменить действие встретившегося в
программе оператора STOP. Для этого набирают CONT и нажима-
ют клавишу RETURN. (После оператора END продолжить выпол-
нение программы нельзя.)
ПРОДОЛЖИТЬ ВЫПОЛНЕНИЕ
ПРОГРАММЫ! CONT (RETURN)
Кроме этой команды, в этом разделе нет других новых элемен-
тов БЕЙСИКа.
Следующая задача очень проста, и ее решение можно проверить
с помощью школьной математики.
3.1. Геометрическая прогрессия
Геометрическая прогрессия задается первым членом а и знаме-
нателем прогрессии q. Суммой членов геометрической прогрессии
называется сумма бесконечной последовательности слагаемых
S = а + aq + aq1 + aq^ + aq* + aq5 + ...
Если I <71 < 1, то сумма конечна и для нее существует выражение в
аналйтической форме:
S = а/(1 - q)
Сумма п последовательных членов, начиная с первого, равна
с _ «(?" - О
s" -
Программа для вычисления суммы членов убывающей геометри-
ческой прогрессии выглядит следующим образом:
0 REM ’ТЕОПРОГ" EBERT/EDERER 810509
1 REM**********************************
2 REM*» ВЫЧИСЛЕНИЕ СУММЫ ГЕОМЕТРИЧЕ ••
3 REM** СКОЙ ПРОГРЕССИИ **
6 REM** S=R+R*Q+R*QT2+R*QT3+R*QT4+. . **
9 REM**********************************
100 INPUT "ПЕРВЫЙ ЧЛЕН ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ А
200 INPUT "ЗНАМЕНАТЕЛЬ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ"; О
300 S-0
400 Н-А
500 8«8+Н
600 H-H*Q
700 PRINT I;H>S
800 I-I+l
900 GOTO 500
2000 END
RUN
ПЕРВЫЙ ЧЛЕН ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ? 2
ЗНАМЕНАТЕЛЬ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ? .35
42
Глава 3
0.7 2
1 .245 2.7
2 .08575 2.945
3 .0300125 3.83875
4 . 018504 375 3.0607625
5 3.67653125Е-03 3.07126688
6 1.28678594Е-03 3.07494341
7 4.50375078Е-04 3.07623019
8 1.57631277Е-04 3.07668057
9 5.51709471Е-05 3.0768382
10 1.93098315Е-05 3.07689337
11 6.75844102Е-06 3.07691268
12 2.36545436Е-06 3.07691944
13 8.27909024Е-07 3.0769218
BRERK IN 700
Переменной А соответствует первый член прогрессии, перемен-
ной Q — знаменатель прогрессии. Переменная S принимает теку-
щее (промежуточное) значение вычисляемой суммы, переменной Н
присваивается текущее значение слагаемого, которое на следующем
шаге прибавляется к текущему значению суммы:
Н = aqn-, п = i + 1
После считывания входных данных а и q в строках 100 и 200 пере-
менная S обнуляется:
S = 0
и вычисляется первое слагаемое
Н = А
Первое промежуточное значение суммы вычисляется в строке 500
при первом прохождении этого участка программы:
S = S + H = 0+ A= A
В строке 600 при первом прохождении вычисляется второе слагае-
мое:
Н = H*Q- = A*Q
Оператор вывода PRINT в строке 700 выводит на экран число
итераций I, следующий член ряда и текущее значение суммы. В
строке 800 число итераций увеличивается на 1. Оператор GOTO в
строке 900 возвращает управление строке 500, в которой вычисля-
ется второе промежуточное значение суммы:
S = S + H = A + A*Q
В строке 600 теперь вычисляется третье слагаемое:
Н = H*Q = A*Q*Q
и так далее...
Ряды
43
Легко убедиться в том, что с помощью организованного цикла
слагаемые последовательно вычисляются и складываются и теку-
щее значение суммы выводится на экран.
Участок программы между строками 500 и 900 называют беско-
нечным или неограниченным циклом.
В приведенном примере сходимость достигается довольно быст-
ро и счет можно прервать после нескольких итераций. Следя за те-
кущим значением суммы на экране, продолжают выполнение про-
граммы. до тех пор, пока не перестанет изменяться результат вы-
числений.
Выполнение программы прерывается клавишей RUN/STOP, при
этом на экране появляется сообщение BREAK IN Z. Продолжить
выполнение программы можно, набрав команду CONTINUE и на-
жав клавишу RETURN.
Внимательный читатель обнаружит, что в программе «ГЕО-
ПРОГ » переменной I нигде не присвоено начальное значение. Лишь
в строке 800 записано, что I каждый раз увеличивается на 1. Вооб-
ще говоря, зто ошибка, которую мы умышленно оставили в про-
грамме, и такие ошибки надо устранять. Однако если программа
предназначена для персонального компьютера, то зта ошибка не
будет иметь никаких последствий, так как почти во всех ЭВМ этого
класса по команде RUN перед запуском программы все переменные
обнуляются.
Задание 12. Внесите изменения в программу «ГЕО-ПРОГ», чтобы вычислить
следующий ряд:
aq 4
S — а + aq + —
4
aq*2
N2
Q
aq
9
aq16
16
Вычислите другие суммы, найдите такие ряды (например, в справочнике по ма-
тематике), которые можно рассчитать аналитическими методами, и сравните ре-
зультаты численного и аналитического метода.
3.2. Ряды Фурье
Ряды Фурье используются во многих областях науки и техники
для решения дифференциальных уравнений (один из следующих
примеров) и для описания периодических функций (например, пило-
образных колебаний в электронике). Ряды Фурье — зто бесконеч-
ные ряды, они представляют собой сумму тригонометрических
функций, период которых монотонно убывает.
Ряд Фурье по синусам в общем виде выглядит следующим об-
разом:
/(г) = ffjsinflx) + ff2sin(2r) + ff3sin(3x) + ... + ff„sin(nx) + ...
44
Глава 3
Коэффициенты ап часто являются функцией п. В качестве первого
примера рассмотрим аппроксимацию симметричной зигзагообраз-
ной ломаной линии рядом Фурье. Формула, аппроксимирующая
эту линию рядом Фурье, имеет вид
90
V* ( 2 \2
/<Х) = 1 + / ( -- I [COS(«7r)-
\Л7Г /
л = 1
l]-cos
(Л7ГХ
Т
Программа, составленная для расчета по этой сложной форму-
ле, коротка и проста:
0 REM "ФУР-РЯД" EBERT/EDERER 810509
1 КЕМ***********************************
2 REM** РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ ПО **
3 REM** КОСИНУСАМ СИММЕТРИЧНОЙ **
5 REM** ЗИГЗАГООБРАЗНОЙ ЛИНИИ ««
9 КЕМ***********************************
10 PI-4*ATN<1>
100 INPUT "КООРДИНАТАХ"; X
200 F-1
300 N-0
400 N-N+1
500 H-4/N/N/PI/PI*<C0S<N*PI)-1>
550 H-H*C0S<N*PI*X/2>
600 F-F+H
700 PRINT N/X1F1H
800 GOTO 400
2000 END
RUN
КООРДИНАТАХ? 1.85
1 1.85 1.78817337 .78817337
2 1.85 1.78817337 0
3 1.85 1.85665802 .0684846512
4 1.85 1.85665802 0
5 1.85 1.86906568 .0124076603
б 1.85 1.86906568 0
7 1.85 1.86776779 - 1.29788875Е-03
8 1.85 1.86776779 0
9 1.85 1.86253913 - -5.22865909Е-03
18 1.85 1.86253913 0
И 1.85 1.85682736 -5.71176932Е-03
12 1.85 1.85682736 9.97158511Е-12
13 1.85 1.85204588 -4.78148375Е-03
14 1.85 1.85204588 0
15 1.85 1.84871758 -3.32830465Е-03
16 1.85 1.84871758 0
17 1»85 1.84689604 -1.82153205Е-03
BREAK IN 500
READS'.
Бесконечный цикл реализован в строках 400—800. Текущее зна-
чение суммы присваивается переменной F в строке 600. В строках
500 и 550 вычисляется текущее значение слагаемого, соответствую-
щее очередному значению переменной N.
Ряды
45
Из приведенного числового примера видно, что при некоторых
значениях х сходимость достигается быстро, при других — медлен-
но; медленнее всего сходимость достигается для значений х вблизи
излома.
Эта программа иллюстрирует аппроксимацию сложной перио-
дической функции суммой тригонометрических функций с различ-
ными периодами. Речь идет об известном фурье-преобразовании,
которое широко используется для обработки данных, полученных
импульсными методами, в ИК- и ЯМР-спектроскопии.
Задание 13. Составьте программу для описания рядом Фурье периодических пря-
моугольных импульсов:
4
ЛО = -
1Г
2
/W = -
к
00
п — 1
00
п — 1
Встречающийся в обеих формулах параметр L — это полупериод данных перио-
дических функций. Если вы хотите составить программы, полностью аналогичные
программе «ФУР-РЯД», то следует принять L = 1.
3.3. Вычисление теплопроводности
по второму закону Фурье
Явления переноса (диффузия, теплопроводность, вязкость и
многие другие) в стационарных условиях подчиняются так называе-
мому первому закону Фурье. Второй закон Фурье, который описы-
вает теплопроводность в нестационарных условиях, когда темпера-
тура в данной точке зависит от времени, представляет собой систе-
му дифференциальных уравнений в частных производных*.
Физическая проблема. В однородном стержне длиной 3 см на левом торце
(L = 0) поддерживается температура — 5 °C и на правом (L = 3 см)-h 25 °C. Ес-
ли стержень однороден, то через достаточно большой промежуток времени вдоль
стержня установится постоянный градиент температуры. При / < 0 температура
вдоль стержня описывается уравнением
Т = 10L - 5
В момент времени / = 0 температура торцов скачкообразно повышается до 10 °C
• Bird R. В., Stewart W. Е., Lightfoot Е. N., Transport phenomena. New
York/London, Wiley & Sons Inc., 1960; Carslow H. S., Jager J. C., Conduction of heat
in solids. Oxford University Press, 1959.
46
Глава 3
для левого торца и до 40 °C — для правого, и эти значения температуры в дальней-
шем не меняются:
Т(/, L = 0) = 10 °C для всех t > 0
T(l, L = 3) = 40 °C для всех t 0
t<0: -5°С +25°С
0 СМ
3 см
ТЕМПЕРАТУРА ВДОЛЬ СТЕРЖНЯ МЕНЯЕТСЯ ЛИНЕЙНО
t*0: +10°С +40°С
3 СМ
Определим, как будет изменяться температура вдоль стержня в зависимости от
времени. Процесс описывается дифференциальным уравнением
ЭТ(Г, L) d2T(t, L)
------ = к-----—
dt dL2
и приведенными выше граничными условиями. Эта задача рассматри-
вается практически во всех курсах физики. Решением является ряд
Фурье, который сам по себе, как и исходное дифференциальное
уравнение, еще не дает ответа на поставленный вопрос. Зависи-
мость температуры поперечного сечения стержня от времени t и
расстояния от торца L описывается следующим рядом Фурье:
Т = 10 + 10Z + У"* — [со5(лтг) — 1]-е3' 3к -sin (г^^-
птг \ 3
Л = 1
Расчет температуры по этой формуле без использования вычисли-
тельной техники связан с очень большим объемом утомительной
счетной работы.
Программу для расчетов можно составить по той же схеме, по
которой составлена программа «ФУР-РЯД».
0 REM "ТЕП—ПРОВ" EBERT/EDERER 810516
1 REM**********************************************
2 REM** РАСЧЕТ ТЕМПЕРАТУРЫ В ПОПЕРЕЧНОМ СЕЧЕНИИ **
3 REM** (СТЕРЖНЯ В ЗАВИСИМОСТИ ОТ ВРЕМЕНИ И РАС- **
4 REM** СТОЯНИЯ ОТ ТОРЦА ПО УРАВНЕНИЮ ФУРЬЕ. **
5 REM** ЛЕВЫЙ ТОРЕЦ (О СМ) 10 ГРАД. С **
6 REM** ПРАВЫЙ ТОРЕЦ (3 СМ) 40 ГРАД. С **
7 REM** В НАЧАЛЬНЫЙ МОМЕНТ ТЕМПЕРАТУРА ЛЕВОГО **
8 REM** ТОРЦА- -5. С; ПРАВОГО- + 25 ГРАД. С **
9 REM**********************************************
10 PI-4*RTN<1)
Ряды
41
100 PRINT "РАСЧЕТ ТЕМПЕРАТУРЫ"
200 INPUT "РАССТОЯНИЕ ОТ ЛЕВОГО ТОРЦА X”' X
300 INPUT "ВРЕМЯ Z
400 Т-10*Х+10
500 N>0
£00 N-N+1
700 Н-30/N/PHtKCOSCNitiPI>-1>
800 Н-НЖЕХР <-2«N«N«PI*РI«Z/Э/100>
900 H.H«SIN<N«PI«X/3>
1000 Т-Т+Н
1100 PRINT N;T;H
1200 GOTO 600
2000 END
RUN
РАСЧЕТ ТЕМПЕРАТУРЫ
РАССТОЯНИЕ ОТ ЛЕВОГО ТОРЦАХ? 2
ВРЕМЯ ? 4
1 2 3 4 5 6 7 8 9 18 11 12 13 14 15 14.8493441 -15.1586559 14.8493441 8 14.8493441 -8.4571678Е-89 14.8493441 8 15.2183622 .36981886 15.2183622 8 15.1862621 -.8321888549 15.1862621 8 15.1862621 1.81833873Е-11 15.1862621 8 15.186299 3.6895186Е-85 15.186299 -1.1318281Е-22 15.1862986 -4.63811117Е-87 15.1862986 8 15.1862986 8
BREAK IN 1100
READY.
Бесконечный цикл занимает строки 600—1200. Очередной член
ряда Фурье вычисляется в трех строках — 700, 800 и 900 (формула
довольно длинная и занимает три строки). Коэффициент теплопро-
водности принят равным 100.
Задание 14. Используйте программу «ТЕП-ПРОВ» для расчета температурного
профиля к моменту времени t = 5 и / = 50. Вычислите зависимость температуры от
времени в поперечном сечении на расстоянии L = 1,5 см и I = 0,2 см от левого
торца стержня.
3.4. Суммы по состояниям
При изложении статистической термодинамики в учебниках по
физической химии в качестве примера часто вычисляют суммы по
состояниям для гармонических осцилляторов, из которых рассчи-
тывают соответствующие термодинамические величины. На этом
примере будет показано, что такую на первый взгляд сложную за-
дачу можно легко решить с помощью простых численных методов.
48
Глава 3
Напомним, что сумма по состояниям определяется как
V -е</кт
е — энергетические уровни молекулы.
Для различных вращательных уровней двухатомной молекулы
й2
eBp(J) = J(J +1)^
J = 0, 1, 2, 3, 4, ... — вращательное квантовое число; I — момент инерции (для
двухатомных молекул I = цг2); г — межатомное расстояние; ц = +
+ m2) — приведенная масса; ml — масса атома 1; т2 — масса атома 2. Степень вы-
рождения («статистический вес») равна U + 1.
Формула для вращательной суммы по состояниям:
" _ JU + 1)/|2
<7вр = £ (2J + D-е 8’2ЛГ
J = о
к — константа Больцмана; h — константа Планка.
Вращательная сумма по состояниям зависит от температуры,
массы атомов и межъядерного расстояния. В случае идеального
жесткого ротатора можно пренебречь увеличением межъядерного
расстояния с увеличением квантового числа. Если необходимо
учесть увеличение длины связи, то программу надо расширить все-
го на одну строку, в которой вычисляется межъядерное расстояние
в зависимости от квантового числа J.
0 REM "ВРАЩ" EBERT/EDERER 810509
1 REM************************************
2 REM** РАСЧЕТ ВРАЩАТЕЛЬНЫХ СУММ ПО **
3 REM** СОСТОЯНИЯМ • ««
4 REM** E.ROT - J<J+1>*H*H/<8*PIT2*I> ««
5 REM** Н - е.б26176Е-34 ДЖ.С ««
6 REM** I - МОМЕНТ ИНЕРЦИИ - M*RT2 ««
7 REM** М - ПРИВЕДЕННАЯ МАССА ««
8 REM** ДЛЯ ДВУХАТОМНОЙ МОЛЕКУЛЫ **
9 REM** СТАТИСТИЧЕСКИЙ ВЕС = 2 * J + 1 **
10 REM***********************************
100 PI-4*RTN<1>
1000 Н-6.626176Е-34
1050 L-6.022E23
1100 К-1.380евЕ-231REM IN J/KELVIN
1200 INPUT "ТЕМПЕРАТУРА В К"; Т
1300 INPUT "АТОМНАЯ МАССА 1"; М1
1400 INPUT "АТОМНАЯ МАССА 2"- М2
1500 INPUT "РАССТОЯНИЕ В АНГСТРЕМАХ"; А
2000 REM ВЫЧИСЛЕНИЕ МОМЕНТА ИНЕРЦИИ ’
2100 М-М1#М2/<М1+М2>
2200 1-М/1000*<Я#1Е-10>Т2
3000 S-0
3100 J-0
3200 Е-J* < J+1 :> *H*LZ < 8*Р I *Р I«I > *Н
Ряды
49
3300 Q-< 2* J+1>«ЕХР <-E/K/T >
3400 S-S+Q
3500 PRINT
3510 PRINT "НОМЕР СОСТОЯНИЯ -",J
3520 PRINT "ЭНЕРГИЯ «";E; "ДЖ”
3530 PRINT "ОЧЕРЕДНОЕ СЛАГАЕМОЕ = Q
3540 PRINT "СУММА ПО СОСТОЯНИЯМ = S
3800 J-J+l
3900 GOTO 3200
20800 END
RUN
ТЕМПЕРАТУРА В К ? 1000
АТОМНАЯ МАССА 1 ? 14
АТОМНАЯ МАССА 2? 16
РАССТОЯНИЕ В АНГСТРЕМАХ ? 1.146
НОМЕР СОСТОЯНИЯ - 0
ЭНЕРГИЯ - 0 ДЖ
ОЧЕРЕДНОЕ СЛАГАЕМОЕ - 1
СУММА ПО СОСТОЯНИЯМ- 1
НОМЕР СОСТОЯНИЯ - 1
ЭНЕРГИЯ . 6.82984663Е-23 ДЖ
ОЧЕРЕДНОЕ СЛАГАЕМОЕ > 2.98519625
СУММА ПО СОСТОЯНИЯМ- 3.98519625
НОМЕР СОСТОЯНИЯ - 96
ЭНЕРГИЯ . 3. 17997659Е-19 ДЖ
ОЧЕРЕДНОЕ СЛАГАЕМОЕ - 1 • 9176064Е-08
СУММА ПО СОСТОЯНИЯМ" 404- 6Э540Э
НОМЕР СОСТОЯНИЯ . 97
ЭНЕРГИЯ . 3.24622611Е-19 ДЖ
ОЧЕРЕДНОЕ СЛАГАЕМОЕ > 1.19907169Е-08
СУММА ПО СОСТОЯНИЯМ > 404. 6Э5403
Бесконечный цикл реализуется в строках 3200—3900. В строке
2100 вычисляется приведенная масса и в строке 2200 — момент
инерции. Расчеты проводятся в системе СИ, чтобы уровни энергии
были выражены в джоулях. (Зачем в строке 2200 произведено деле-
ние на 1000?) В строке 3200 вычисляется энергия, соответствующая
очередному значению квантового числа. В строке 3300 слагаемые
суммы по состояниям умножаются на степень вырождения. Теку-
щее значение суммы вычисляется в следующей строке (3400). После
вывода на экран промежуточных результатов квантовое число уве-
личивается на 1 и управление возвращается строке 3200.
Для заданных значений исходных параметров вычисления в цик-
ле продолжают до тех пор, пока текущее значение вращательной
суммы по состояниям не перестанет существенно изменяться.
Задание 15. Исходя из суммы по состояниям #вр, можно рассчитать вклад вра-
4-81
50
Глава 3
шательиой составляющей во внутреннюю энергию 6/ по следующей формуле:
вр
(dlnWgoA
----вр' j
дТ /
Найдите, как зависит от температуры вклад вращательной составляющей внут-
ренней энергии для молекулы Н — D (длина связи 0,74136 А). Изобразите эту зави-
симость в виде графика. (При высоких температурах значение t/Bp, как известно,
стремится к RT.)
Для вычисления производной рассчитайте два значения суммы по состояниям
при двух близких значениях температуры (пусть разность температур составляет
1 градус) и воспользуйтесь приближенной формулой
din to) ln<7(T,) - \nq(T2)
dT Tj - Т2
Для выполнения этого задания вы можете использовать программу «ВРАЩ».
По-видимому, не имеет смысла тратить время на составление дополнительной про-
граммы, если в дальнейшем вы не будете ею пользоваться, поскольку расчеты по
формулам нескольких значений I/ и производной можно легко и быстро выпол-
нить с помощью микрокалькулятора. Для массовых расчетов целесообразно внести
в программу некоторые изменения, чтобы все вычисления выполнялись компьюте-
ром. (В этом случае затраты времени на составление и запись программы будут
оправданны.)
Задание 16. Напишите программу для расчета вращательной суммы по состоя-
ниям для гармонического и ангармонического осциллятора и сравните их значения.
Задание 17. Вычислите вращательную сумму по состояниям для двухатомной
молекулы и определите вращательную составляющую термодинамических функций
(например, S, U, Ср; соответствующие формулы приведены в учебниках по физичес-
кой химии). Для вычисления значения производной рассчитайте два значения суммы
по состояниям при двух близких по величине температурах и воспользуйтесь приве-
денной выше приближенной формулой (см. задание 15).
Задание 18. При вычислении вращательной суммы по состояниям для двухатом-
ной молекулы замена суммирования интегрированием приводит к приближенному
соотношению
q = ZiTlkT/h1
вр
Дополните программу «ВРАЩ», чтобы в строке 3540 выводилось не только
промежуточное значение суммы по состояниям, но и ее приближенное значение, рас-
считанное по этой формуле.
Сравните оба этих значения при разных температурах и постройте графики тем-
пературной зависимости точного и приближенного значений.
3.5. Вычисление числа тг методом Монте-Карло
Метод Монте-Карло служит еще одним примером эффективного
использования бесконечных циклов. В программе «ПИ» вам встре-
тится новый элемент БЕЙСИКа — оператор IF, который подробно
будет рассмотрен ниже (с. 69). Название метода подсказывает, что
метод Монте-Карло как-то связан с вероятностью. Рассмотрим ри-
Ряды
51
сунок. Мишень — единичный квадрат — «обстреливается» точка-
ми, равновероятно попадающими в любую часть квадрата. Коор-
динаты этих точек, равномерно распределенных на замкнутом ин-
тервале [0, 1], задаются датчиком псевдослучайных чисел RND в
строках 300 и 400. Вероятность, с которой точки попадают в за-
штрихованный сектор, равна отношению площади этого сектора к
площади квадрата:
w = гЧс/Ьг1 — тг/4
0 КЕМ "ПИ" EBERT/EDERER 810511
1 REM******************************
2 REM»* ВЫЧИСЛЕНИЕ ЧИСЛА ПИ **
3 REMW* МЕТОДОМ МОНТЕ-КАРЛО **
9 REM******************************
100 S«0
200 N-0
300 X.RND<X>
400 Y«RND<Y)
£00 N»N+1
700 IF X*X+Y*Y>1 THEN GOTO 300
000 S»S+1
1100 PRINT N,S,S/N*4
1200 GOTO 300
1300 END
Бесконечный цикл реализован в строках 300—1200. Переменной
N присваивается число выстрелов по мишени, переменной S — чис-
ло удачных выстрелов, т. е. таких, которые попали внутрь заштри-
хованного сектора. В строке 700 принимается решение, попала ли
точка внутрь сектора или нет. Если
х2 + у2 > 1
то точка находится вне сектора и управление передается строке
300, минуя строку 800, в которой подсчитывается число попаданий.
4*
52 Гпава 3
Число попыток присваивается переменной N. Чтобы получить
приближенное значение числа тг, согласно приведенной выше фор-
муле, надо разделить число попаданий на число попыток и умно-
жить на 4.
Ниже мы познакомимся еще с некоторыми областями примене-
ния метода Монте-Карло. Программы для решения задач методом
Монте-Карло, как правило, очень просты. Их можно написать не-
посредственно из физической модели, часто даже не прибегая к
сложному математическому анализу. Недостаток метода виден уже
на этом примере: точность результата в ходе вычисления возраста-
ет очень медленно. Причиной этого являются отклонения, которые
обусловлены стохастическим характером метода. Для N попыток
точность результата пропорциональна квадратному корню из ЛЛ
4. Циклы
В этой главе речь пойдет о различных задачах из области физи-
ки, химии и математики, которые можно решить с помощью ите-
рационных процедур (циклов).
4.1. Расчет сумм
Рассмотрим в качестве примера вычисление суммы квадратов
натуральных чисел, задачу, которая уже встречалась во введении:
S = I2 + 22 + З2 + 42 + ... + (N - I)2 + N2
Способ решения задачи на ЭВМ изображен ниже в виде блок-
схемы (схема 3). Левая блок-схема соответствует блок-схеме во вве-
дении (с. 12). TV-кратное повторение определенного участка про-
граммы контролируется счетчиком I, значение которого увеличива-
ется на 1 после каждого выполнения повторяемой группы операто-
ров, и оператором IF, который каждый раз сравнивает число по-
вторений I с числом N. До тех пор пока I не больше N, управление
возвращается на начало программы. Как только I станет больше
N, циклический процесс прекращается и выводится окончательный
результат вычислений.
В правой блок-схеме цикл организован с помощью оператора
цикла. Он состоит из двух частей с ключевыми словами FOR и
NEXT. Поэтому циклы такого типа в БЕЙСИКе называют цикла-
ми FOR — NEXT. В ФОРТРАНе или ПЛ/1 им соответствуют ци-
клы DO (в этих алгоритмических языках для организации циклов
используется служебное слово DO).
После служебного слова FOR указывается имя (идентификатор)
переменной, которая выполняет функцию счетчика (в примере I), ее
начальное и — после слова ТО — конечное значение, а также шаг
(служебное слово STEP) — приращение переменной I после каждо-
го выполнения повторяемой группы операторов. По окончании
цикла выполняется оператор, стоящий после оператора NEXT.
54
Глава 4
блок-схема.
Блок-схема
Схема 3
с оператором IF
с оператором цикла
Циклы
55
Циклы FOR — NEXT позволяют сократить объем программы и
сделать ее наглядной. Поэтому рекомендуем:
**********************************************
* * ПО ВОЗМОЖНОСТИ ЧАЩЕ ИСПОЛЬЗУЙТЕ ЦИКЛЫ FOR—NEXT ***
* ** ВМЕСТО ЦИКЛОВ С ОПЕРАТОРОМ IF ***
**********************************************
****************
Цикл FOR — NEXT *** for-next ***
****************
***********************************
* ** z1 FOR v = a1 TO a2 STEP a3 ***
* ** . ... ***
* ** . ЛЮБЫЕ ОПЕРАТОРЫ ***
* ** . ... ***
* ** z2 NEXT v ***
***********************************
zl, z2 — номера строк; v — переменная, так называемый параметр цикла; al, а2,
аЗ — значения арифметических выражений, переменные или константы (al — на-
чальное значение переменной; а2 — наибольшее значение, которое может принимать
переменная v; аЗ — шаг параметра цикла, приращение переменной v после каждого
выполнения повторяемой группы операторов*).
Между строками zl и z2 может стоять любое количество других
строк.
Примеры: ю for 1=1 то 15
20 PRINT I,SQR(I)
30 NEXT I
40 END
100 FOR T5=10 TO -10 STEP -2.5
110 FOR A=0 TO 20 STEP 3
120 PRINT T5 A
130 NEXT A
140 NEXT T5
150 END
Во втором примере один цикл вложен в другой. Допустимое
число вложенных друг в друга циклов зависит от операционной си-
стемы и вполне достаточно для решения не слишком сложных за-
дач. Нетрудно придумать такой пример, который позволил бы
• Если шаг не указан (отсутствует служебное слово STEP), то шаг полагается
равным 1. — Прим, перев.
56
Глава 4
найти наибольшее число вложенных циклов. Читатели могут рас-
сматривать это как очередное задание.
По строению вложенные циклы похожи на матрешки. Их мож-
но или расставлять друг за другом, или вкладывать один в другой,
но они никогда не должны пересекаться*.
ft*************-*'*'**'*'**'*'*'*'*'**'**'*'**' *******
* ** ЦИКЛЫ FOR-NEXT НИКОГДА ***
* ** НЕ ПЕРЕСЕКАЮТСЯ ***
***************************************
* ** В СОМНИТЕЛЬНЫХ СЛУЧАЯХ ИСПОЛЬЗУЙТЕ ***
* ** ДРУГИЕ ПРОГРАММНЫЕ СРЕДСТВА ***
***************************************
Циклы — эффективный инструмент программиста, применяйте
их как можно чаще.
Программа для вычисления суммы квадратов натуральных чи-
сел выглядит следующим образом:
0 REM "СУММА" EBERT/EDERER 810514
1 REM*********************************
2 РЕМ**ВЫЧИСЛЕНИЕ СУММЫ КВАДРАТОВ **
3 REM** N ЧИСЕЛ НАТУРАЛЬНОГО РЯДА, **
5 REM** НАЧИНАЯ С 1 **
9 REM*********************************
100 PRINT "ВЫЧИСЛЕНИЕ СУММЫ КВАДРАТОВ"
200 PRINT "N ЧИСЕЛ НАТУРАЛЬНОГО РЯДА"
300 INPUT ’’ N ";N
400 PRINTi PRINT "ПРОДОЛЖИТЕЛЬНОСТЬ ВЫЧИСЛЕНИЯ"
410 PRINT "ПРИМЕРНО"; N/1000#6.52; " С"
1000 S=0.
1100 FOR 1=1 TO N
1200 S=S+I*I
1300 NEXT I
2000 PRINT "СУММА = ";S
2100 END
RUN
ВЫЧИСЛЕНИЕ СУММЫ КВАДРАТОВ
N ЧИСЕЛ НАТУРАЛЬНОГО РЯДА
N ? 120
ПРОДОЛЖИТЕЛЬНОСТЬ ВЫЧИСЛЕНИЯ
ПРИМЕРНО .7В24С
СУММА = 583220
RUN
ВЫЧИСЛЕНИЕ СУММЫ КВАДРАТОВ
N ЧИСЕЛ НАТУРАЛЬНОГО РЯДА
ПРОДОЛЖИТЕЛЬНОСТЬ ВЫЧИСЛЕНИЯ
ПРИМЕРНО 5.7В976 С
СУММА = 233803444
• Кроме того, не разрешается передача управления в область действия цикла, ми-
нуя заголовок цикла. — Прим, перев.
Циклы
57
Цикл, в котором вычисляется сумма, занимает три строки
(1100—1300). В строке 2000 выводится результат. Непосредственно
перед началом цикла переменная S, которой присваивается текущее
значение суммы, приравнивается нулю.
Так как в процессе вычисления суммы переменная I принимает
значения от 1 до N, число N должно быть задано заранее. Это сде-
лано в строке 300. Операторы PRINT в строках 100 и 200 информи-
руют пользователя во время выполнения программы. Операторы в
строке 400 предоставляют программисту дополнительную инфор-
мацию. В этой строке оценивается время выполнения программы.
Когда время выполнения программы велико, оператор начинает
беспокоиться, сидя перед пустым экраном, на котором ничего не
происходит. Во избежание этого можно вывести на экран текущие
значения вычисляемых величин или параметра цикла, время счета,
предоставляя тем самым пользователю полезную информацию.
Задание 19. Напишите программу или переделайте программу «СУММА» для
вычисления следующих сумм:
зо
log( I sinfx2) I + 1)
х = -10
и др., например
е-(х + 0,5)/100
-100
S = О,50’5 + 1‘ + 1.51’5 + 22 + 2,52-5 + ... + 99
Вычислению абсолютной величины в БЕЙСИКе соответствует стандартная функция
ABS.
Задание 20. Напишите программу для вычисления факториала:
9! = 1-2-3-4-5-6-7-8-9 или в общем случае
/V! = 1-2-3-4 ... (N - l)-N
4.2. Составление таблиц
При выполнении расчетов по формулам часто получают не от-
дельные значения переменных, а большие массивы выходных дан-
ных. Для большей наглядности и удобства дальнейшей работы с
полученным числовым материалом эти данные целесообразно
представить в виде таблицы. В качестве примера составим табли-
цу, которая содержит значения средних скоростей молекул некото-
рых газообразных веществ с различной молекулярной массой в за-
висимости от температуры. Формула расчета средней скорости мо-
58
Глава 4
лекул выглядят следующим образом:
v = 'J'iRT/M
R = 8,314—Д- = 8,314—— м'м = 8314—Г‘-М——
К-моль К-моль-с-с К-моль-с-с
Т — абсолютная температура; М — молекулярная масса.
Если подставить величины Т и М в приведенной размерности
то скорость v будет выражена в м/с.
0 REM "СКОР-МОЛ" EBERT/EDERER 810509
1 REM*********************************
2 REM** СОСТАВЛЕНИЕ ТАБЛИЦЫ ♦*
3 REM#* СРЕДНИХ СКОРОСТЕЙ **
5 REM** МОЛЕКУЛ РАЗЛИЧНЫХ **
6 REM** ГАЗООБРАЗНЫХ ВЕЩЕСТВ ПО **
7 REM** ФОРМУЛЕ U = (3#R#T/M) t 0.5 **
9 REM*********************************
100 DATA "ВОДОРОД", 2
200 DATA "БЕНЗОЛ", 7B
300 N=2
350 PRINT
400 PRINT "СРЕДНЯЯ СКОРОСТЬ МОЛЕКУЛ В М/С"
450 PRINT
500 PRINT "ТЕМПЕРАТУРА
600 R=8314.34
1000 FDR 1=1 ТО N
1100 READ A»,X
1200 PRINT A»;"
1300 NEXT I
1400 PRINT
3000 FOR T=150 TO 600 STEF’ 50
3050 PRINT T:" ":
3100 RESTORE
3200 FOR 1=1 TO N
3300 READ A».X
3400 V= < 3«R*T/X’10.5
3500 PRINT V;
3600 NEXT t
3700 PRINT
3800 HEXT T
4000 END
RUN
СРЕДНЯЯ СКОРОСТЬ МОЛЕКУЛ в м/с
ТЕМПЕРАТУРА ВОДОРОД БЕНЗОЛ
150 1367.74504 219.014489
200 1579.33594 252.896148
250 1765.75126 282.746489
300 1934.28359 309.73326
350 2089.26506 334.550158
400 2233.5183 357.649162
450 2369.00391 379.344222
500 2497.14938 399.86392
550 2619.03236 419.380817
600 2735.49009 438.028977
Циклы
59
Проанализируем программу «СКОР-МОЛ», не обращая пока
внимания на новые элементы языка. Расчет средней скорости моле-
кул происходит в строке 3400. Эта строка находится внутри двух
вложенных друг в друга циклов. Внешний цикл по параметру Т за-
нимает 10 строк (с 3000 по 3800). В этом цикле при каждом про-
хождении значение температуры увеличивается на 50 К. В строке
3050 текущее значение температуры выводится на экран вместе с 7
пробелами. Точка с запятой в конце этой строки означает, что на
экране следующее значение будет записано в той же строке вслед за
первым. Внутренний цикл по параметру I занимает 5 строк (с 3200
по 3600). Переменная I соответствует z-му веществу. Оператор в
строке 3300 (действие этого оператора будет рассмотрено ниже)
считывает значение молекулярной массы z-ro вещества и присваива-
ет это значение переменной X. В строке 3500 выводится вычислен-
ное значение средней скорости, причем строка на экране не перево-
дится, так что следующее значение будет выведено на экран в той
же строчке вслед за первым. Если при некоторой температуре вы-
числены средние скорости молекул N веществ и эти значения выве-
дены на экран, т. е. если цикл по I завершен, то пустой оператор
PRINT начинает вывод на экран очередных данных с новой строки.
***************
Ввод данных, записанных в программе *** data ***
*** READ ***
*** RESTORE ***
********************
* ** z1 DATA c1,c2,c3
* ** z2 READ v1,v1,v3
* ** z3 RESTORE
*******************************
zl, z2, z3 — номера строк; cl, cn — константы; vl.vn — переменные.
С помощью оператора DATA можно записывать данные, т. е.
константы (числа или слова), в любом месте программы. В ЭВМ
имеется «метка»*, которая помечает одну из констант оператора
DATA. Оператор READ считывает эту меченную константу и при-
сваивает ее значение переменной V, метка продвигается на одну по-
зицию вперед и помечает следующую константу, которая будет
считана при очередном выполнении оператора READ.
* Разумеется, никакого физического устройства, называемого «меткой», в ЭВМ
нет. — Прим, перев.
60
Глава 4
Оператор RESTORE возвращает «метку» на первую константу
оператора DATA.
Пример:
10 DATA 3,5,2.5,7,8.1
15 8 = 0
20 FOR I = 1 ТО 5
30 READ X
40 S = S + X
50 NEXT I
60 P=1
70 RESTORE
80 FOR I = 1 TO 5
90 READ X
100 P = P * * X
110 NEXT I
120 PRINT S,P
В этой программе вы-
числяется сумма (S) пя-
ти чисел, стоящих в
операторе DATA
и
вычисляется произведе-
ние (Р) этих чисел.
В программе «СКОР-МОЛ» есть два оператора DATA (в стро-
ках 100 и 200), каждый с двумя константами. Первая константа —
название вещества, вторая — его молекулярная масса. Текстовые
константы следует писать в кавычках, числовые константы в опе-
раторе DATA разделяют запятыми.
Числовым переменным нельзя присваивать текстовые констан-
ты, для этого существует другой тип переменных, так называемые
текстовые, символьные или литерно-строчные, или $-переменные.
**************************************
*** ТЕКСТОВАЯ ПЕРЕМЕННАЯ $ ***
**************************************
Если за любым допустимым идентификатором (именем) пере-
менной поставить символ доллара ($)* (например, В$, R4$, КО$),
то такое сочетание символов является идентификатором перемен-
ной, которой можно присваивать произвольный текст. Это можно
сделать с помощью операторов INPUT и READ. Для вывода тек-
ста на экран используется оператор PRINT.
В программе «СКОР-МОЛ» в строках 1000—1300 размещен еще
один цикл. В этом цикле переменная I принимает значения от 1 до
N с шагом 1; в действительности она принимает значения 1 и 2.
При первом прохождении текстовой переменной присваивается
текст «ВОДОРОД», и в строке 1200 он сразу выводится на экран. В
том же цикле число 2 — молекулярная масса водорода — присваи-
вается переменной X. «Метка» в операторе DATA указывает те-
перь на текстовую константу «БЕНЗОЛ». При втором прохожде-
* В отечественных ЭВМ с идентификатором текстовых переменных используется
знак Ы. — Прим, перев.
Циклы
61
нии переменной А$ присваивается текст «БЕНЗОЛ», а переменной
X — число 78, и в строке 1200 выводится на экран значение тексто-
вой переменной А$ без перехода на следующую строку, т. е. вслед
за словом «ВОДОРОД». Этот цикл вместе со строкой 500 и стро-
кой 1400, которая переводит курсор на следующую строчку экрана,
используют для того, чтобы набрать головку таблицы. Оператор
RESTORE в строке 3100 возвращает «метку» на первую константу
оператора DATA, т. е. на «ВОДОРОД». После этого начинаются
вычисления, результаты которых выводятся на экран в виде табли-
цы. Если предстоит выполнить расчеты для большего количества
веществ, то необходимо лишь внести соответствующие изменения
в операторы DATA в строках 100 и 200 и задать количество ве-
ществ в строке 300.
Задание 21. Измените программу «СКОР-МОЛ» так, чтобы получилась таблица
для трех веществ (выбор веществ оставляем на ваше усмотрение) в интервале темпе-
ратур 750—150 К с шагом по температуре 25 К.
Задание 22. Напишите программу для составления таблицы констант скорости
реакции к, которые вычисляются по уравнению Аррениуса. Таблица должна содер-
жать константы скорости реакции при десяти различных температурах и для трех
различных значений энергии активации Е . Уравнение Аррениуса:
к = k0-e~E°/RT
Используйте к0 = 1013 с-1 в качестве предэкспонента константы скорости реак-
ции первого порядка.
4.3. Среднее значение и стандартное отклонение
Очередным примером использования циклов является расчет
статистических величин — средних значений и стандартных откло-
нений. Исходные данные лучше вводить операторами DATA и
READ. Преимущество этого способа ввода данных состоит в том,
что весь числовой материал записан в программе, и, поскольку
программа хранится в памяти ЭВМ, его можно в любое время вы-
вести на экран для проверки или внесения изменений.
Если в результате измерений некоторого постоянного парамет-
ра получено А значений этого параметрах,, то среднее арифметиче-
ское х составляет
п
и стандартное отклонение
П -*)2
I = 1
S = -----------
п - 1
62
Глава 4
Программа для вычисления этих величин называется «СРЕД-
НЕЕ».
0 REM "СРЕДНЕЕ" EBERT/EDERER 810514
1 REM********************************* ♦**
2 REM** ВЫЧИСЛЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ **
3 REM** И СТАНДАРТНОГО ОТКЛОНЕНИЯ. **
5 REM** ЧИСЛОВОЙ МАТЕРИАЛ ВВОДИТСЯ **
6 REM** С ПОМОЩЬЮ ОПЕРАТОРОВ ••
7 REM** "DATA" СО СТРОКИ 10000 ••
8 REM** ы = ЧИСЛО1 ДАННЫХ ••
9 REM************************************
100 N-9
200 М-0
300 FOR 1-1 ТО N
400 READ X
500 М-М+Х
600 NEXT I
700 M-M/N
900 RESTORE
1000 S—0
1100 FOR 1-1 TO N
1200 READ X
1300 S-S+<M-X>T2
1400 NEXT I
2000 S-SQR<S/<N-1>>
2500 PRINT "СРЕДНЕЕ ЗНАЧЕНИЕ -
3000 PRINT "СТАНДАРТНОЕ ОТКЛОНЕНИЕ = "; S
10000 DATA 5,5.5,3,7.2,8.1,5.95
10100 DATA 4.7,4,6.05
200O0 END
RUN
СРЕДНЕЕ ЗНАЧЕНИЕ =5.5
СТАНДАРТНОЕ ОТКЛОНЕНИЕ =1.5630499
READY.
Число проведенных измерений задано в строке 100. Результаты
измерений записаны в операторах DATA в строках 10000 и 10100. В
цикле (строки 300—600) вычисляется сумма всех значений, задан-
ных оператором DATA. Для этого оператор READ считывает зна-
чения в том порядке, в каком они стоят в операторах DATA, и
присваивает их значения переменной X, а в переменной М накапли-
вается результат сложения. После деления полученной суммы на N
частное присваивается все той же переменной М (строка 700). Все
предыдущие значения переменной утрачиваются, и, начиная со
строки 700, М принимает значение средней величины, которое вы-
водится на экран оператором PRINT.
Сумма квадратов отклонений (М—X)2 вычисляется в цикле, за-
писанном в строках 1100—1400. Для этого оператором RESTORE
переводят оператор READ на считывание первой константы опера-
тора DATA, и переменная S, которой после выхода из цикла будет
присвоено значение суммы квадратов отклонений, приравнивается
Циклы
63
О (строка 1000). После окончания цикла в строке 2000 сумма ква-
дратов отклонений делится на (N — 1), из частного извлекается
квадратный корень и полученное значение присваивается той же пе-
ременной S. Выполнение программы завершается выводом на
экран среднего значения и стандартного отклонения.
Примечание. Рассчитанное среднее значение и стандартное отклонение следует
всегда указывать вместе с числом проведенных измерений. Лишь тогда можно оце-
нить достоверность обеих статистических величин.
Задание 23. С помощью программы «СРЕДНЕЕ» вычислите среднее значение и
стандартное отклонение следующих результатов измерений:
а) 17,1; 23,2; 21,1; 19,8; 19,3; 20,0; 20,3;
б) 456, 444, 455, 411, 456, 438, 476, 423, 435, 455, 444, 429.
Дополните программу, чтобы выходные данные, как это указано в примечании,
включали в себя также и число экспериментальных значений.
Задание 24. Дополните программу «СРЕДНЕЕ» (или напишите новую), чтобы
можно было вычислять взвешенное среднее значение и стандартное отклонение.
«Взвешенное» означает, что каждое значениех(. имеет свой весовой коэффициент wjt
который пропорционален достоверности этого значения.
х(. — результат (-го измерения; w. — весовой коэффициент, соответствующий
значению х..
Задание 25. Напишите программу для вычисления среднего значения и стандарт-
ного отклонения и проверьте измеренные значения на случайный выброс. Нет необ-
ходимости использовать для этого какой-нибудь изощренный статистический тест,
достаточно, например, найти измеренное значение с наибольшим по абсолютной ве-
личине отклонением от среднего и использовать это отклонение в качестве стан-
дартного. Для выполнения задания вам придется использовать оператор IF, кото-
рый подробно рассмотрен на с. 69.
4.4. Интегрирование методом Монте-Карло
При вычислении кратных интегралов метод Монте-Карло часто
дает лучшие результаты, чем другие численные методы (например,
метод Эйлера, Симпсона и др.), которые будут обсуждены ниже.
Рассмотрим сначала одномерную задачу, т. е. вычисление опре-
деленного интеграла функции /(г) по отрезку на оси х (см. рис.).
Площадь криволинейной трапеции, ограниченной графиком этой
функции, осью х, прямыми х = а и х = е, равна площади прямо-
угольника, одна сторона которого равна среднему значению функ-
ции /(г) на отрезке fa, е], а другая — длине этого отрезка.
64
Глава 4
Вычисление среднего значения функции методом Монте-Карло
заключается в следующем. На отрезке [», е] выбирают случайные
точки, вычисляют значения функции в этих точках и находят их
сумму. После деления суммы на число точек получают среднее зна-
чение, которое тем ближе к истинному среднему значению функции
на заданном отрезке, чем больше выбрано случайных чисел на от-
резке [аг, е].
Если имеется функция двух независимых переменных и необхо-
димо вычислить двойной интеграл по некоторой области в плоско-
сти ху, то выбирают точки со случайными координатами внутри
области интегрирования, вычисляют значения функции в этих точ-
ках, определяют среднее значение, которое умножают на площадь
области интегрирования. Рассмотрим, например, интегрирование
функции/(г, 7), которая описывает плотность маргариток на газо-
не. Двойной интеграл функции плотности по определенному участ-
ку этого газона равен числу маргариток на этом участке.
Программа «МК-ИНТ» интегрирует функцию трех переменных
fly, у, z) по объему прямоугольного параллелепипеда. Для нагляд-
ности рассмотрим/(г, у, z) как функцию, которая описывает рас-
пределение плотности в трехмерном пространстве. Интегрируя по
параллелепипеду (трехмерному интервалу), мы получим массу па-
раллелепипеда.
Вычислим интеграл следующей функции трех переменных:
f(y, У, z) = х1 + у1 + z1
Эта функция выбрана потому, что ее интеграл можно вычислить
аналитическими методами и сравнить результат численного инте-
грирования с точным значением интеграла
хе Уе ze хе уе ze
j j j (г2 + 72 + z2)dxdydz - ~ (у2 + у2 + z2) | | |
Уа za уа za
Циклы
65
В выражении, стоящем справа от знака равенства, надо подста-
вить верхние и нижние пределы интегрирования со знаками плюс и
минус соответственно, т. е. как при вычислении определенного ин-
теграла функции одной переменной.
Программа «МК-ИНТ» для интегрирования этой функции мето-
дом Монте-Карло выглядит следующим образом:
0 REM "МК-ИНТ" EBERT/EDERER 810518
1 REM***********************************
2 REM** ИНТЕГРИРОВАНИЕ МЕТОДОМ МОН-**
3 РЕМ** ГЕ-КАРЛО ФУНКЦИИ НЕСКОЛЬКИХ ••
Л REM** ПЕРЕМЕННЫХ, НАПРИМЕР: ••
5 REM** F (X.Y, Z) = X*X+Y»Y+ Z* Z ••
6 REM** ПОДЫНТЕГРАЛЬНАЯ ФУНКЦИЯ ••
7 REM** ЗАДАНА В СТРОКЕ 1000 **
9 REM***********************************
100 INPUT "Х-ИНТЕРВАЛ ' ,Х0,Х9
120 Х5-Х9-Х0
200 INPUT "У-ИНТЕРВАЛ “,70,79
220 75-79-70
300 INPUT "Z-ИНТЕРВАЛ ",20,29
320 25-29-20
350 V—Х5#75#25
400 1-0
500 S-0
900 I-I + 1
910 X-RND<5>*X5+X0
920 7—RND<5>*75+70
930 2-RND<5>*25+20
1000 F-X*X+7*7+2*2
1100 S-S+F
1200 PRINT "ИНТЕГРАЛ- CR",S/I*V,I
1300 GOTO 900
RUN
X-ИНТЕРВАЛ? 0,1
7—ИНТЕРВАЛ? 0,1
2—ИНТЕРВАЛ? 0,1
ИНТЕ ГРАП - СЯ .938433441 1
ИНТЕГРАЛ - СЯ .859941069 2
ИНТЕГРАЛ — СЯ 1.18102896 3
ИНТЕГРАЛ"- СЯ 1.19240771 4
ИНТЕГРАЛ" СЯ 1.13013745 5
ИНТЕГРАЛ- СЯ 1.07356582 б
ИНТЕГРАЛ" СЯ 1.13409796 7
ИНТЕГРАЛ- СЯ 1.04119802 8
ИНТЕГРАЛ" СЯ 1.14876462 9
ИНТЕГРАЛ" СЯ 1.04111189 18
ИНТЕГРАЛ - СЯ 1.06223131 11
ИНТЕГРАЛ" СЯ 1.06166532 12
ИНТЕГРАЛ- СЯ 1.12556377 13
ИНТЕГРАЛ. СЯ 1.11550885 14
ИНТЕГРАЛ- СЯ 1.08873942 15
ИНТЕГРАЛ. СЯ 1.02554543 16
BREAK IN 1200
RERD7.
5-81
66
Гпава 4
RUN
X-ИНТЕРВАЛ? -1,1
Y-ИНТЕРВАЛ? 0,1
Z-ИНТЕРВАЛ? -1,0
ИНТЕГРАЛ - CR 2.40566398 1
ИНТЕГРАЛ - CR 2.75361864 2
ИНТЕГРАЛ- CR 2.76630911 3
ИНТЕГРАЛ- CR 2.18017523 4-
ИНТЕГРАЛ- CR 2.28138592 5
ИНТЕГРАЛ- CR 1.95830158 6
ИНТЕГРАЛ- CR 1.92935718 7
ИНТЕГРАЛ- CR 1.89570621 8
ИНТЕГРАЛ - CR 1.83326666 9
ИНТЕГРАЛ - CR 2.00552452 382
ИНТЕГРАЛ - CR 2.00291665 383
ИНТЕГРАЛ - CR 2.00197998 384
ИНТЕГРАЛ - CR 2.00203044 385
ИНТЕГРАЛ - CR 2.0037388 386
ИНТЕГРАЛ - CR 2.00059549 387
В строках 100, 200 и 300 вводятся верхние и нижние пределы неза-
висимых переменных х, у, z соответственно. В строках 120, 220 и
320, вычисляются длины интервалов по осям х, у и? соответствен-
но. В строке 350 все значения интервалов перемножаются. Чтобы
вычислить приближенное значение интеграла, полученное произве-
дение, соответствующее объему параллелепипеда, потом умножа-
ют на среднее значение функции.
Число вычисленных значений функции присваивается перемен-
ной I, сумма всех значений функции — переменной S. Среднее зна-
чение равно отношению S/I; интеграл приближенно равен (S/I)*V.
После того как начальные значения переменных S и I обнуляются,
в строках 910, 920 и 930 вычисляются координаты случайной точки
внутри заданного интервала. Датчик RND(5)*X5 генерирует слу-
чайные числа между 0 и Х5 (это длина отрезка на оси х). Если еще
прибавить Х0 — нижний предел интегрирования, получится набор
случайных чисел в замкнутом интервале [Х0, Х9], т. е. на заданном
отрезке. После вычисления трех координат случайной точки в стро-
ке 1000 вычисляется значение функции F = /(г, у, z) для тройки
случайных чисел. Сумма значений функции присваивается перемен-
ной S. В строке 1200 приближенное значение интеграла выводится
на экран. Бесконечный цикл задан в строках 900—1300.
Из приведенного решения контрольной задачи видно, что сходи-
мость достигается довольно медленно. Однако в сложных ситуаци-
ях, когда функцию невозможно проинтегрировать аналитическими
методами, вполне оправдывает себя применение метода Монте-
Карло. (Тем более что персональный компьютер можно оставлять
работающим на ночь.)
Задание 26. Используйте программу «МК-ИНТ» для интегрирования других
функций трех переменных, например sin(x + у + z) или ехр(— Ixyzl).
Циклы
67
Задание 27. Дополните программу «МК-ИНТ» для интегрирования функций
двух или четырех переменных.
Задание 28. Напишите программу для интегрирования методом Монте-Карло,
так чтобы можно было интегрировать функцию нескольких переменных не только
по объему TV-мерного параллелепипеда, но и по объему TV-мерного шара. В про-
странстве двух измерений шар вырождается в круг; для многомерного пространства
случайные числа надо выбирать так, чтобы выполнялось неравенство
х2 + х2 + х2 + х2 + ... + х2 < г2
Этот довольно абстрактный интеграл можно использовать для
вычисления средней скорости реакции в грануле катализатора.
Пусть имеются сферические гранулы катализатора диаметром
1 мм. Из-за выделения тепла в экзотермической реакции, подчиня-
ющейся кинетическому уравнению первого порядка, внутри грану-
лы устанавливается градиент температуры, например:
Т = 700 - 200г2
Т — температура, К; г — расстояние от центра, мм.
Это означает, что температура в центре гранулы составляет 700 К, на поверхно-
сти — 500 К и зависимость температуры от расстояния до центра гранулы описыва-
ется параболой. Константа скорости реакции первого порядка задается уравнением
Аррениуса:
к = 1О13е-2оооо/г c-i
Число 20000 — это энергия активации, поделенная на универсальную газовую посто-
янную. Концентрация реагента 0,01 моль/л. Это задание иллюстрирует применение
кратных интегралов по объему шара.
4.5. Вычисление брутто-формулы химического
соединения по данным элементного анализа
Наш пример ограничивается следующими элементами: углерод
С, водород Н, азот N и кислород О. Однако его можно легко рас-
пространить на другие элементы. Эта программа является еще од-
ним примером использования циклов и табличной формы вывода
результатов.
0 REM •C-H-N-O" EBERT/EDERER 810518
1 REM******»**»*»*»»»»»»**»********»*»***
2 КЕМ»» ВЫВОД БРУТТО-ФОРМУЛЫ С, Н, N, ••
3 КЕМ»» О—СОДЕРЖАЩЕГО СОЕДИНЕНИЯ ПО ••
4 КЕМ»» ДАННЫМ ЭЛЕМЕНТНОГО АНАЛИЗА ••
5 REM*» ««« ВНИМАНИЕ ««« ••
в REM»» СТЕХИОМЕТРИЧЕСКИЕ ИНДЕКСЫ В *•
7 REM»» ИСТИННОЙ БРУТО-ФОРМУЛЕ **
8 REM»» ДОЛЖНЫ БЫТЬ БЛИЗКИ К ЦЕЛЫМ ••
9 REM»»»»»»»*»»»*»*»»»»*********»*»***»»*
200 INPUT "МАСС. % С": С
5*
68
Глава 4
300 INPUT "МАСС. % Н"; Н
400 INPUT "МАСС. % N"; N
S08 0-100-С-Н—N
680 PRINT "МАСС. % О"; О
1200 С1-С/12.011
1300 Н1-Н/1.008
1400 N1-N/14.007
1500 01-0/15.999
1708 PRINT
1800 PRINT "CH N О"
2000 FOR 1-1 TO 15
2100 X-I/Cl
2200 C2-C1.X
2300 H2-INT<H1*X*100>/100
2400 N2-INT<N1*X*100?/100
2500 O2-INT<O1*X*100V100
3000 PRINT C2jTRB<5> 1H2j
3100 PRINT TRB<14>jN2jTRB<21>;02
4080 NEXT I
5000 END
RUN RUN
МАСС. % С? 77.7 МАСС. % Н? 7.46 МАСС. % N? 0 МАСС. % О? 1434 С н N о МАСС % С? 36.4 МАСС. % Н? 6.1 МАСС. % N 7 21.2 МАСС. % О 36.3 С Н N о
1 1.14 3 . 14 1 1.99 .49 .74
2 2.28 0 .28 2 3.99 .99 1.49
Э 3.43 0 .43 Э 5.99 1.49 2.24
4 4.57 0 .57 4 7.98 1.99 2.99
5 5.72 0 .71 5 9.98 2.49 3.74
б 6.86 0 .86 б 11.98 2.99 4.49
7 8 0 1 7 13.97 3.49 5.24
е 9.15 0 1.14 е 15.97 3.99 5.98
9 10.29 0 1.29 9 17.97 4.49 6.73
18 11.44 0 1.43 10 19.96 4.99 7.48
11 12.58 0 1.57 11 21.96 5.49 8.23
12 13.72 0 1.72 12 23.96 5.99 8.98
13 14.87 0 1.86 13 25.95 6.49 9.73
14 16.01 0 2 14 27.95 6.99 10.48
15 17.16 0 2. 15 15 29.95 7.49 11.23
RERDV RERDV
Для расчетов используются проценты по массе. Ввод процент-
ного содержания первых трех элементов происходит в строках
200—400, процентное содержание кислорода вычисляется по разно-
сти в строке 500.
Если разделить процентное содержание элемента в соединении
на его атомную массу, то получится мольная доля этого элемента
(в единицах моль/100 г вещества). Мольная доля вычисляется в
строках 1200—1500. Остается только привести ее к общему числу
атомов углерода. (Результат можно рассматривать как число ато-
мов данного элемента в молекуле или число молей этого элемента
Циклы
69
в 1 моль вещества.) Эта нормировка на 1, 2, ..., 15 атомов углеро-
да происходит в цикле в строках 1800—4000. В строке 2100 вычис-
ляется нормировочный коэффициент и присваивается переменной
X. В строках 2300—2500 доля элементов Н, N и О умножается на
нормировочный коэффициент.
В предыдущих примерах результаты вычислений выводились в
виде десятичных дробей с девятью значащими цифрами. Таблица
таких чисел была бы весьма громоздка, кроме того, для расчета
брутто-формулы вполне достаточно двух десятичных знаков. По-
этому в программе “С—Н—N—О” предусмотрено округление вы-
ходных данных до двух десятичных знаков. Сначала число, которое
необходимо округлить, умножается на 100, потом стандартная
функция INT выделяет целую часть полученного произведения и
это целое число делится на 100. Вывод данных происходит в стро-
ках 3000—3100. Здесь впервые встречается оператор TAB. Он
выполняет те же функции, что и табулятор на обычной пишущей
машинке. “ТАВ(21);И означает, что курсор передвинется на столбец
21 и вывод данных будет продолжен с этого места; точка с запятой
после ТАВ(21) блокирует переход курсора на следующую строчку
экрана после вывода очередных символов. Отсутствие точки с запя-
той в конце строки 3100 вызывает переход на следующую строчку
экрана.
После того как вся таблица выведена на экран, необходимо про-
анализировать комбинации приведенных в ней чисел. Целочислен-
ная комбинация с минимальными значениями индексов или близкая
к ней отвечает простейшей брутто-формуле. (Истинная брутто-
формула кратна простейшей.)
Задание 29. Дополните программу “С—Н —N—О” для обработки данных эле-
ментного анализа серу- и хлорсодержащих веществ. Кроме того, целесообразно сде-
лать изменяемым количество строк в таблице. Попытайтесь реализовать это в про-
грамме.
4.6. Оператор условного перехода
В этом разделе вводится новый оператор БЕЙСИКа — опера-
тор IF. Он уже использовался в предыдущих примерах
Оператор условного перехода *******************
*** IF ... THEN ***
*******************
*****************************
*** z1 IF а1 □ a2 THEN z2 ***
*****************************
70
Глава 4
ИЛИ
**********************************
*** z1 IF а1 □ a2 THEN GOTO z2 ***
**********************************
zl, z2 — номера строк; al, a2 — арифметические выражения, константы или пере-
менные; □ — операция отношения.
Операции отношения:
□ Значение
= Равно
< > Не равно
> Больше
< Меньше
> - Больше или равно
< = Меньше или равно
При выполнении этого оператора сравниваются оба арифмети-
ческих выражения al и а2, которые могут быть постоянными или
простыми переменными. Если выражение al □ а2 истинно, управ-
ление передается оператору в строке z2, в противном случае выпол-
няется очередной оператор, следующий за оператором условного
перехода.
Примеры:
200 INPUT Z
2 20 IF Z=1 THEN 200: REM ЗНАЧЕНИЕ ФУНКЦИИ РАССЧИТАТЬ НЕЛЬЗЯ
240 IF Z<1 THEN 300: REM РЕШЕНИЕ МНИМОЕ
260 E=SQR(1/(Z—1))
280 PRINT E
290 STOP
300 E=SQR(-1/(Z-1))
320 PRINT E;"*I"
10 INPUT I
20 IF I<=0 THEN GOTO 100
30 PRINT LOG(I)
40 STOP
100 PRINT "ОШИБКА ПРИ ВВОДЕ''
10 INPUT А,В,С
20 IF A*A < 4*B THEN 50
30 PRINT C+SQR(A*A-4*B)
40 GOTO 10
50 PRINT "ПОВТОРНЫЙ ВВОД"
60 GOTO 10
В БЕЙСИКе используется ряд конструкций с оператором IF.
После THEN может стоять номер строки, оператор GOTO, номер
строки или любой другой оператор.
Циклы
71
*******************************
*** z IF а1 ° a2 THEN xxxx ***
*******************************
z — номер строки; al, a2 — арифметические выражения, константы или перемен-
ные; □ — оператор отношения; хххх — любой оператор.
Пример:
5 DATA 4
10 INPUT А
20 IF А-1=0 THEN PRINT"EIUE РАЗ":GOTO 10
30 IF A=2 THEN INPUT В
40 IF A=3 THEN READ X
60 PRINT X
80 IF A=B THEN STOP
90 GOTO 10
Несмотря на дополнительные возможности, которые предостав-
ляет оператор IF, мы все же советуем при написании сложных про-
грамм пользоваться им как можно реже, тогда программы будут
более наглядными и легкопрослеживаемыми.
4.7. Определение брутто-формулы по пику
молекулярного иона в масс-спектрах высокого
разрешения
Идея, на которой основывается решение задачи определения
брутто-формулы, довольно проста. Пусть масса молекулы измере-
на достаточно точно и можно указать довольно узкий интервал
масс, в котором лежит молекулярная масса соединения. Тогда в
принципе можно рассчитать молекулярные массы всех существую-
щих и несуществующих соединений и проверить, попадает ли их
масса в заданный интервал. Если да, то брутто-формула этой ком-
бинации атомов и ее масса будут выведены на экран. Располагая
набором брутто-формул, химик должен знать, какие формулы во-
обще имеют смысл, какая из них соответствует данному соедине-
нию или наиболее вероятна.
0 REM "БРУТ—ФОРМ" EBERT/EDERER 810514
1 REM***************************************
2 REM** ПРОГРАММА ДЛЯ ОБРАБОТКИ **
3 REM** МАСС- СПЕКТРОВ ВЫСОКОГО ••
4 REM** РАЗРЕШЕНИЯ; РАСЧЕТ ВСЕХ ••
5 REM** КОМБИНАЦИЙ АТОМОВ. МАССА ••
6 REM** КОТОРЫХ ЛЕЖИТ В ЗАДАННОЙ ••
7 REM** ОБЛАСТИ МОЛЕКУЛЯРНЫХ МАСС; **
8 REM** В ДАННОМ ПРИМЕРЕ РАССМАТРИВАЮТСЯ ••
9 REM** н. С, N, О, S—СОДЕРЖАЩИЕ СОЕДИНЕНИЯ ••
18 REN**************************************
188 М1-1.0078iREM Н
200 М2-31.9721iREM S
300 МЗ-15.9949iREM О
400 М4-14.00Э1iREM N
508 N5-12.0800iREM С
1008 INPUT "ОБЛАСТЬ МАСС"; А, В
2000 N-B
72
Глава 4
3000 FOR 12-0 ТО М STEP М2
3100 FOR 13-12 ТО М STEP М3
3200 FOR 14-13 ТО М STEP М4
3300 FOR 15-14 ТО М STEP М5
4000 J1-INT<<R-I5>/M1+1>
4100 J2-INT<<B-I5>/M1>
4200 IF J1>J2 THEN 6100
5000 FOR II-JI TO J2
5100 IF I1<0 THEN 6000
5200 IF Il>M/4+2 THEN 6100
5300 S—15+11*M1
5310 P2-INTCI2/M2+. 1>
5320 P3-INT<<I3-I2>/M3+.1>
5330 P4—INT<<I4-I35/M4+.1>
5340 P5—INTC<I5-I45/M5+. 1>
5500 PRINT "S"iP2j" O"jP3,
5600 PRINT “ N",P4j" C“,P5j
5700 PRINT “ H'',I1j“-"jS
6000 NEXT 11
6100 NEXT 15
6200 NEXT 14
6300 NEXT 13
6400 NEXT 12
9999 END
RUN
ОБЛАСТЬ МАСС? 27.5,23.5
S 0 00 N0 C 2 H4- 28.0312
S0 00 N 1 Cl H2- 28.0187
S0 00 N2 C 0 H0- 28.0062
S0 01 N0 Cl H0 - 27.9949
RUN
ОБЛАСТЬ МАСС?
S 0 0 0 N 0 C
S 0 0 0 N 1 C
S 0 0 1 N 4 C
S 0 0 1 N 5 C
S 0 0 2 N 1 C
S 0 0 2 N 2 C
S 0 0 2 N 3 C
S 0 0 3 N 0 C
S 0 0 5 N 0 C
SI 0 0 N 0 C
SI 0 0 N 1 C
SI 0 3 N 0 C
S 2 0 0 N 0 C
S 2 0 0 N 1 C
88.01,00.04
7 H 4 - 88.0312
6 H 2 - 88.0187
1 H 4 - 80.0385
0 H 2 - 88.026
3 H 6 - 88.0397
2 H 4 - 88.0272
1 H 2 - 88.0147
3 H 4 - 88.0159
0 H 8 - 88.0369
4 H 8 - 88.0345001
3 H 6 - 88.022
0 H 8 - 88.0192
1 H 12 - 88.0378
0 H 10 - 88.0253
RUN
ОБЛАСТЬ МАСС?
S 0 0 3 N 6
SI 0 0 N 0
SI 01 N 12
SI 0 5 N 8
SI 0 6 N 5
S 2 0 2 N 2
S 3 0 0 N 0
S 3 0 5 N 1
3 5 0 0 N 1
234
C 8
C 16
C 1
C 0
C 2
C 8
C 1
C 2
C 3
049,234.051
H 6 - 234.0501
H 10 - 234.0501
H 6 - 234.051
H 10 - 234.0494
H 12 - 234.0506
H 14 - 234.0494
H 14 - 234.0503
H 20 - 234.0499
H 24 - 234.0508
Циклы
73
Программа «БРУТ-ФОРМ» применима для расчета брутто-
формул всех соединений, состоящих из пяти химических
элементов — С, Н, N, О и S. Чем больше элементов входит в со-
став соединения, тем больше появляется возможных комбинаций и
тем больше время, необходимое для выполнения программы. (Ре-
комендуется в качестве упражнения приспособить эту программу
для какой-нибудь конкретной задачи.) В начале программы (строки
100-500) задаются точные значения атомной массы пяти элементов
(наиболее распространенных изотопов). Затем оператором INPUT
задается область значений массы. Наименьшее значение молекуляр-
ной массы присваивается переменной А, наибольшее — перемен-
ной В.
Центральную часть программы занимают пять вложенных друг
в друга циклов, поскольку рассматривается задача для пяти элемен-
тов. Для большей наглядности можно выделить некоторые циклы,
обозначая левую границу соприкасающихся циклов скобкой. Значе-
ние параметра цикла по II, лежащего внутри всех остальных, соот-
ветствует числу атомов водорода в комбинации атомов. Значения
параметров внешних циклов 12, 13, 14 и 15 равны массам комбина-
ций атомов, являющихся «заготовками» для подбора допустимых
по массе комбинаций.
Текущее значение 12 равно массе атомов S в формируемой комбинации
Текущее значение 13 равно массе атомов (S + О) в формируемой комбинации
Текущее значение 14 равно массе атомов (S + О + N) в формируемой комбинации
Текущее значение 15 равно массе атомов (S + О + N + С) в формируемой комбина-
ции
Поэтому параметр внешнего цикла 12 принимает значения от 0
до М с шагом М2 (атомная масса S, см. строку 200). Наибольшее
значение массы М задано в строке 2000. Поскольку внешний цикл
по 12 задает массу атомов серы в комбинации, начальному значе-
нию параметра внутреннего цикла 13 присваивается текущее значе-
ние 12. Цикл по 13, увеличивая за каждое прохождение массу, за-
данную циклом по 12, на М3, формирует «заготовку» для следую-
щего цикла по 14 и т. д.*
* Аналогичный итерационный прием используется при взвешивании на обычных
равноплечных весах. Сначала массу пытаются уравновесить разновесами самой
большой массы. Найдя максимально допустимое число таких гирь, продолжают на-
гружать второе плечо гирями меньшей массы, и так до тех пор, пока ие будет до-
стигнут результат, ие превосходящий по точности погрешности весов. Отличие этого
алгоритма от алгоритма, реализованного в программе «БРУТ-ФОРМ», состоит в
том, что в этой программе подсчитываются все варианты взвешивания с заданной
точностью. — Прим, перев.
74
Глава 4
Текущее значение 15 равно массе элементов S, О, N и С в неко-
торой комбинации атомов, содержащей только эти элементы. К
этой комбинации атомов необходимо добавить некоторое число
атомов водорода так, чтобы масса новой комбинации входила в за-
данный интервал масс. В строке 4000 вычисляется число атомов во-
дорода, которое необходимо, чтобы по крайней мере перейти ниж-
нюю границу заданной области масс. Это число присваивается пе-
ременной Л. В строке 4100 определяется максимальное Число ато-
мов водорода в комбинации атомов, масса которой не превосходит
верхнюю границу интервала масс, и это значение присваивается пе-
ременной J2.
Если наибольшее число атомов водорода J2 меньше, чем мини-
мально необходимое число атомов водорода J1, то эта комбинация
атомов не соответствует заданному интервалу масс и необходимо
рассмотреть новую комбинацию элементов. Сравнение и возмож-
ный переход назад к внешним циклам происходит в строке 4200.
Если наибольшее число атомов водорода J2 больше, чем число
минимально необходимых атомов водорода J1, то эти комбинации
атомов попадают в интересующую нас область масс. Тогда сраба-
тывает самый внутренний цикл (строки 5000—6000). Параметр цик-
ла— переменная II, значения которой соответствуют количеству
атомов водорода, принимает значения от Л до J2. В строках 5100
и 5200 выполняется элементарная проверка, имеет ли результат фи-
зический смысл. Если число атомов водорода отрицательно (строка
5100), то оператор IF передает управление последнему исполняемо-
му оператору цикла по II. Значение II увеличивается на единицу, не
имеющая смысла формула не выводится на экран. Строка 5200 не-
обходима, чтобы исключить комбинации, в которых число атомов
водорода слишком велико. Число атомов водорода не должно пре-
вышать четвертой части молекулярной массы + 2. Если атомов во-
дорода слишком много, то снова начинаются вычисления во внеш-
них циклах.
В строке 5300 вычисляется молекулярная масса всех полученных
комбинаций атомов. Затем переменным Р2, РЗ, Р4 и Р5 присваива-
ется рассчитанное число атомов S, О, N и С. Чтобы рассчитать
массовую долю элемента, вычисляется масса каждого элемента в
комбинации атомов (разность 14—13, например, равна массе азота).
Если разделить массу элемента в комбинации атомов на его атом-
ную массу, то получится число атомов этого элемента. Так как в
ЭВМ арифметические операции выполняются с конечной точнос-
тью, можно получить дробное (но близкое к целому) число атомов,
например 2.9999997 для атомов азота. Чтобы индексы в брутто-
Циклы
75
формулах были целочисленными, необходимо округлить результа-
ты расчета до целого числа. Для этого к округляемому значению
прибавляется 0,1 и дробная часть полученной суммы отбрасывает-
ся, для чего используется стандартная функция INT (строки
5310—5340).
Вывод брутто-формулы происходит в строках 5500, 5600 и 5700.
Из-за отсутствия точки с запятой в строке 5700 происходит переход
на новую строчку при записи информации на экране. Какие из по-
лученных формул истинны, должен решать пользователь. В приве-
денном примере встречается комбинация О5Н8. Конечно, это хими-
ческая бессмыслица, но откуда это может знать ЭВМ?
Задание 30. Модифицируйте программу «БРУТ-ФОРМ» для подбора брутто-
формул соединений, состоящих из С, Н, О, F и Р. (4f(F) = 18,9984, ЛГ(Р) =
= 30,9738).
Задание 31. Измените программу «БРУТ-ФОРМ» для подбора брутто-формул
-фторорганических соединений, содержащих кроме F элементы С, Н, N, О и S
(4f(F) = 18,9984). (Вам понадобится еще один дополнительный цикл.)
Задание 32. В выходных данных программы «БРУТ-ФОРМ» надо обозначить
звездочкой (•) формулы, отвечающие свободным радикалам (группам атомов с не-
спарениым электроном). Это даст возможность уменьшить количество выводимых
на экран брутто-формул.
5. Интегрирование
При решении задач научного и инженерно-технического характе-
ра математическими методами часто возникает необходимость
проинтегрировать какую-либо функцию. Есть функции, которые не-
возможно интегрировать аналитически, т. е. только в некоторых
случаях по заданной функции можно найти первообразную. Общим
способом интегрирования любых функций является численное инте-
грирование, методы которого в большинстве своем просты и легко
переводятся на алгоритмические языки. В этой книге мы не будем
подробно изучать численные методы, а познакомимся лишь с их
основами. Геометрически интеграл функции/(х) в пределах от А до
Е представляет собой площадь криволинейной трапеции, ограни-
ченной графиком этой функции, осью х и прямыми х = А, х Е.
Приведенный рисунок иллюстрирует приближенные методы чис-
ленного интегрирования.
5.1. Интегрирование методом Эйлера
Пусть функцию, изображенную на рисунке, необходимо проин-
тегрировать численным методом на отрезке [А, Е]. Разделим отре-
зок [А, Е] на п интервалов* (на рисунке п = 4) и построим две ло-
маные линии, между которыми лежит график функции/(г), как это
показано на рисунке. Приближенным значением интеграла функции
/(г) в пределах от А до Е можно считать полусумму площадей под
верхней и нижней ломаной линиями на этом отрезке.
Рассмотрим на первом интервале [х0, xj прямоугольники, соот-
ветствующие верхней и нижней ломаным линиям. Высота меньше-
го из них равна значению функции на левой границе интервала
|У(г0)], а ширина — длине этого интервала (Г] — х0). Высота боль-
шего прямоугольника равна значению функции на первой границе
интервала /(*])], а ширина — длине того же интервала. Аналогич-
но для z-го интервала высота прямоугольника, соответствующего
нижней ломаной, равна/(*,_]) и верхней ломаной — /(*,). Если от-
* Здесь и далее под интервалами подразумеваются замкнутые (закрытые) интер-
валы. — Прим, перев,
Интегрирование
77
резок АЕ разбить на равные интервалы
й = х,- - х, _,
то площадь под нижней ломаной (5Н) и под верхней (5В) записыва-
ется в виде двух сумм
SH = №0)-h + fpCi)-h + fkj-h +
+ f^2)'h + f^3>'h +
Тогда площадь под графиком функции /(г) на отрезке АЕ можно
оценить по следующей приближенной формуле:
Площадь = 5 = (SH + 5в)/2
5= Ж +/(Г1) +/(v2) +/(Гз) +-ф].А
Эта формула называется также правилом трапеций, потому что
величину 5 можно представить как сумму площадей трапеций (в
данном случае четырех):
Т, = X «-< С «-< G <-*
1 о
t2=x1-g-I-
т3 = х2 - I ~ м ~
Т. = х, ♦* м <-< о <-<
4 3
Х1 -<-> XQ = h-[f(xQ) +
<-* x1 = h-[f(x.j) + f(x2)]/2
х3 <-* х2 = h-[f(x2) + f(x3)]/2
х4 ♦* х3 = h-[f(x3) + f(x4)]/2
5 = Г, + Т2 + Т3 + Т4
78
Глава 5
Схема 4
Интегрирование
79
В результате получается такая же, как и приведенная выше, фор-
мула.
Как правило, чем меньше длина каждого интервала, т. е. чем
больше число этих интервалов, тем меньше различаются прибли-
женное и точное значения интеграла. Это справедливо для боль-
шинства часто встречающихся функций. В методе трапеций обычно
считают, что ошибка приблизительно пропорциональна h2 Э 4 5 * 7 8:
F = Л2
Таким образом, для вычисления интеграла некоторой функции в
пределах от А до Е необходимо разделить отрезок [А, Е] на п ин-
тервалов и найти сумму площадей трапеций. Затем нужно увели-
чить число интервалов, опять вычислить сумму площадей трапеций
и сравнить полученное значение с предыдущим результатом. Это
следует повторять до тех пор, пока не будет достигнута заданная
точность результата. Выбор критерия, по которому прекращается
итерационная процедура, представляет собой наиболее сложную
проблему при составлении программы.
В приведенной ниже программе для интегрирования методом
Эйлера с помощью бесконечного цикла число интервалов удваива-
ется после каждой итерации. Каждое из вычисленных приближен-
ных значений интеграла вы можете увидеть на экране и, сравнивая
их, решить, удовлетворяет ли вас полученный результат. В соот-
ветствии с этим клавишей RUN/STOP можно прервать выполнение
программы.
Блок-схема (схема 4) в своем ядре содержит цикл FOR-NEXT, в
котором для N интервалов вычисляется интегральная сумма. Во
внешнем бесконечном цикле число интервалов удваивается после
каждого прохождения внутреннего цикла и текущее значение сум-
мы (приближенное значение интеграла) выводится на экран.
Ниже приведена распечатка соответствующей этой блок-схеме
программы для вычисления определенных интегралов методом Эй-
лера.
0 REM "ЭЙЛЕР" EBERT/EDERER 810518
1 REM*********************************
2 REM** ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ **
Э REM** ПРОИЗВОЛЬНОЙ ФУНКЦИИ **
4 REtl** МЕТОДОМ ЭЙЛЕРА **
5 REtl** в######################## **
8 REM** ФУНКЦИЯ ОПИСАНА **
7 REtl** В СТРОКАХ **
8 REtl** 2100, 3100 и 4000 •«
9 REM*********************************
80
Глава 5
50 INPUT "НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ"; А
60 INPUT "ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ"; Е
Э00 N-20
1000 S-0
1100 H-<E-fl>/N
2000 Х-Я
2100 V-EXP<-X*X>
2200 S-S+V/2
Э000 FOR X-fl+H ТО Е-Н STEP Н
Э100 V-EXP<-X*X>
Э200 S-S+V
ЭЭ00 NEXT X
Э900 X-E
4000 V-EXP<-X*X>
4100 SeS+V/2
4200 S-S*H
5000 PRINT i PR I NT "ИНТЕГРАЛ ОТ "; А; "ДО"; E
6000 PRINT "ПРИ"; N; "ЧАСТИЧНЫХ ИНТЕРВАЛАХ ="; S
7000 N-N*2
8000 GOTO 1000
10000 END
RUN
НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? 0
ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? 3
ИНТЕГРАЛ ОТ 0 ДОЗ
ПРИ 20 ЧАСТИЧНЫХ ИНТЕРВАЛАХ = 386161458
ИНТЕГРАЛ ОТ О ДОЗ
ПРИ 40 ЧАСТИЧНЫХ ИНТЕРВАЛАХ = . 886192567
ИНТЕГРАЛ ОТ О ДОЗ
ПРИ ВО ЧАСТИЧНЫХ ИНТЕРВАЛАХ = 386207261
ИНТЕГРАЛ ОТО ДОЗ
ПРИ 160 ЧАСТИЧНЫХ ИНТЕРВАЛАХ = 3B6207327
ИНТЕГРАЛ ОТ О ДОЗ
ПРИ 320 ЧАСТИЧНЫХ ИНТЕРВАЛАХ = .886206121
BREAK IN 3100
RERDV.
В этой программе интегрируется функция
/W = е“р
Интегрирование такой функции является непростой задачей. Если
умножить первообразную этой функции на постоянный множитель,
то получится функция, которая широко используется в статистике
и получила собственное название — функция ошибок:
/ = X
. 2
erf(x) = •
V7T
t = о
Эта функция, имеющая большое значение для статистической
обработки данных, обычно приводится в справочниках по стати-
стике в виде таблицы.
е '2d/
Интегрирование
81
В тексте программы подынтегральная функция записана в трех
различных местах (в строках 2100, 3100 и 4000). Ввод пределов ин-
тегрирования происходит в строках 50 и 60. Затем число интерва-
лов N приравнивается 20 (число 20 взято произвольно и может
быть заменено любым целым числом), и начальное значение сум-
мы S приравнивается 0. В строке 1100 делением разности (Е — Н)
на число интервалов N вычисляется длина интервала. В строке 2000
независимой переменной X присваивается значение нижнего преде-
ла интегрирования А. В следующей строке вычисляется значение
функции /(А), которое после деления на 2 присваивается перемен-
ной S. В строках 3000—3300 организован цикл по параметру X с
шагом, равным длине интервала Н. Первое и последнее значения X
сохраняются, поэтому начальное значение параметра цикла X рав-
но (А + Н), а наибольшее — (Е — Н). Для каждого значения X в
строке 3100 вычисляется значение функции/(г), которое в следую-
щей строке прибавляется к S. После окончания цикла в строках
3900—4100 к полученной сумме S прибавляется половина значения
функции на конце отрезка |/~(Е)/2]. В строке 4200 эта сумма умно-
жается на длину интервала Н и полученное значение присваивается
все той же переменной S. Значение S, равное приближенному значе-
нию определенного интеграла для N интервалов, выводится на
экран в строках 5000 и 6000. Потом число интервалов удваивается
и управление передается строке 1000.
В приведенном примере вычислен интеграл в пределах от 0 до 3.
Видно, что уже при N = 80 приближенное значение интеграла име-
ет 6 точных значащих цифр.
Существенный недостаток этой программы заключается в том,
что функция/(г) встречается в трех различных строках и поэтому
должна быть трижды описана. Для длинных формул это по мень-
шей мере нежелательно. Устранить этот недостаток можно с по-
мощью нового элемента языка, который позволяет вызывать функ-
ции, ранее описанные в программе. Название нового оператора —
определяемая функция*. Этот оператор называют еще подпрограм-
мой-функцией.
Функция, определяемая
пользователем
* **★*★★★★★★★★★
*** DEF FN ***
**************
• Этот оператор называется «функция, определяемая пользователем». В дальней-
шем для краткости оператор DEF FN мы будем называть определяемой функцией.
— Прим, перев.
6-81
82
Глава 5
Вызов определяемой функции
★★★★★★★★★★★★★★★★★★★★★★★★★
*** z1 DEF FNa(x) = b ***
*************************
************
*** FN ***
************
zl — номер строки; a — любая буква; FNa — имя определяемой функции; х — фор-
мальный параметр; b — арифметическое выражение, в котором фактический пара-
метр заменен на формальный параметр х‘.
В большинстве персональных компьютеров описание функции
оператором DEF FN возможно в любом месте программы, но
раньше той строки, в которой эта функция вызывается первый раз.
Некоторые ЭВМ не имеют этого ограничения. Кроме того, некото-
рые ЭВМ позволяют без ограничения использовать наряду с пере-
менной х идентификатор другой переменной так, что эти перемен-
ные не влияют друг на друга.
**********************
*** z2 XX FNa(b) ***
**********************
z2 — иомер строки; XX — любой допустимый оператор БЕЙСИКа, если FNa(b)
рассматривается как действительное число (например, PRINT, Y =); а — любая
буква; FNa — идентификатор функции; b — любое арифметическое выражение.
Разумеется, можно определять несколько функций, они должны
только иметь различные идентификаторы (т. е. различные буквы
после DEF FN). Эти функции можно вызывать потом в любой по-
следовательности.
Примеры:
5 GOTO 120
10 DEF FNY(X)=X+2+1/X
20 INPUT I
30 11 = FNY(I)
40 12 = FNY(I*I)
50 13 = FNY(SQR(I))
60 PRINT 1,11,12,13
100 PRINT FNC(7.34)
110 PRINT FNC(13.23*FNY( 1/I))
1 15 STOP
120 DEF FNC(D) = EXP(-SIN(D*D))
130 GOTO 10
• Функции, определяемые пользователем, могут занимать только одну строку. —
Прим, перев.
Интегрирование
83
10 DEF FNA(X) = X*X
20 X = 111
30 FOR 1=1 TO 10
40 PRINT FNA(I),FNA(FNA(1-1)),X
50 NEXT I
Если использовать оператор DEF FN вместе в вызовом функции
в программе «ЭЙЛЕР», то получится программа «ЭЙЛЕР2», рас-
печатка которой приведена ниже.
0 REM "ЭЙЛЕР2" EBERT/EDERER 810518
1 КЕМ*********************************
2 REM** ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ **
3 REM** ПРОИЗВОЛЬНОЙ ФУНКЦИИ **
♦ ♦
**
♦ ♦
♦♦
4 REM** МЕТОДОМ ЭЙЛЕРА
5 REM** ###########»######»####»#
6 REM** ФУНКЦИЯ ОПИСАНА В СТРОКЕ
7 REM** 100
9 REM*»»*****»*****»**»»*»********»*»*
50 INPUT "НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ";А
60 INPUT "ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ"; Е
100 DEF FNF<X>-EXP<-X*X>
300 N-20
1000 S-0
1100 Н-<Е-А>/Н
2000 S-FNF<R>/2
3000 FOR 1-1 ТО N-l|X-R+I*H
3200 S-S+FNF<X>
3300 NEXT I
4000 S-S+FNF<E>/2
4200 S-S*H
5000 PRINT iPRINT "ИНТЕГРАЛ ОТ"; А; "ДО"; E
6000 PRINT "ПРИ"; N; "ЧАСТИЧНЫХ ИНТЕРВАЛАХ = ";S
7000 N-N*2
8000 GOTO 1000
20000 END
RUN
НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? О
ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? 3
ИНТЕГРАЛ ОТ О ДО 3
ПРИ 20 ЧАСТИЧНЫХ ИНТЕРВАЛАХ ЗВ6205976
ИНТЕГРАЛ ОТ О ДО 3
ПРИ 40 ЧАСТИЧНЫХ ИНТЕРВАЛАХ 386207002
ИНТЕГРАЛ ОТ О ДО 3
ПРИ 80 ЧАСТИЧНЫХ ИНТЕРВАЛАХ .886207262
ИНТЕГРАЛ ОТ О ДОЗ
ПРИ 160 ЧАСТИЧНЫХ ИНТЕРВАЛАХ .886207327
BREAK IN 3200
READV.
В этой программе новой является строка 100. В ней описана
подынтегральная функция. Такая форма ввода подынтегральной
Функции очень удобна, поскольку для интегрирования какой-либо
6»
84
Глава 5
другой функции необходимо изменить содержание только одной
строки. Строки 2000, 2100 и 2200 программы «ЭЙЛЕР» заменены
одной строкой 2000, содержащей вызов определяемой функции.
Это же относится к строкам 3900, 4000 и 4100, которые в новой
программе заменены строкой 4000. Кроме того, отсутствует стро-
ка 3100 программы «ЭЙЛЕР», а в строке 3200 переменная Y заме-
нена вызовом функции FNF(X). Вывод данных и бесконечный цикл
в обеих программах одинаковы.
Задание 33. Вычислите определенные интегралы каких-либо функций по вашему
выбору, например:
sin(x)dy или Jl/[log(x) + x]d¥
Задание 34. Проинтегрируйте функции, интеграл которых можно вычислить
аналитически, и сравните результаты численного и аналитического метода, напри-
мер /(у) = = х2,/(х) = sin(x).
Задание 35. Зависимость мольной теплоемкости Ср некоторого гипотетического
вещества от температуры задана формулой
С = 3 10ё(Г + °
р 1 + log(7 + 1)
Размерность Ср совпадает с размерностью универсальной газовой постоянной.
В соответствии с приведенной выше формулой при Т, стремящейся к бесконечности,
Ср приближается к значению 3R. Рассчитайте по этой формуле энтальпию //. Пусть
Н = 0 при Г = 0.
Напоминаем:
н = j с (Ddr
Г
Составьте таблицу значений Ср н Н при разных температурах. При вычислении
Н нижиий предел интегрирования приравняйте нулю,- Постройте на миллиметровой
бумаге графики обеих функций,
5.2. Вычисление длины эллипса
Применением численного интегрирования является вычисление
длины эллипса. Площадь эллипса с полуосями а и b можно выра-
зить в аналитическом виде как
Площадь = аЬтг
В то же время длину эллипса можно рассчитать только с помощью
интегрирования или вычисления бесконечного ряда. Вспомним не-
которые математические соотношения. Окружность можно задать
в параметрической форме:
Zrcosm 0^/<2,
V / V'Sin(0 /
Интегрирование
85
г — длина радиуса-вектора г, равная радиусу окружности, t — угол между осью х и
радиусом-вектором.
За один оборот радиуса-вектора угол изменяется от 0 до 2тг (ес-
ли угол выражен в радианах), или от 0 до 360 (если он выражен в
градусах). Если вам понятна эта форма представления функций*,
то вычислите х и у для нескольких значений t и нанесите точки с
координатами х и у на миллиметровую бумагу.
Эллипс можно представить в параметрической форме как
□ /g • cos (/) \
= (а )> где 0 < 2тг
\6 • sin (О /
g и Ь — полуоси эллипса.
В качестве упражнения подставьте различные числовые значения g и b для неко-
торых значений параметра t, рассчитайте значения х и у и полученные данные пред-
ставьте графически.
В учебниках по математике приводится формула для вычисле-
ния длины линий, заданных параметрическими уравнениями, в за-
висимости от начального и конечного значения параметра. Если
принять /1 = 0и/2=2тг, то в данном случае кривая замыкается в
эллипс. Формула для расчета длины этой кривой становится фор-
мулой для расчета длины эллипса:
Если в эту формулу подставить уравнение эллипса, то полу-
чится
/ = 2т
L = j Vg2sin2f + 62cos2/d/
t = о
Для вычисления этого интеграла внесем небольшие изменения в
программу «ЭЙЛЕР2». Величины g и b (полуоси эллипса) можно
вводить любым способом.
0 КЕМ "ЭЛЛИПС” EBERT/EDERER 810601
1 REM*********************************
2 REM** РАСЧЕТ ДЛИНЫ ЭЛЛИПСА ПО **
3 REM** ПРОГРАММЕ ЭЙЛЕР2 ••
9 REM*********************************
50 INPUT "ДЛИНА ПЕРВОЙ ПОЛУОСИ"; G
60 INPUT "ДЛИНА ВТОРОЙ ПОЛУОСИ"; В
100 DEF FNF<X>-SaR<G*G*SIN<X>*SIN<X>+B*B*CDS<X>*COS<X>>
150 PI-4*RTN<1>
200 R-0sE-2*PI
300 N-10
Zachmann H. G., Mathematik fur Chemiker. Verlag Chemie, Weinheim, 1974.
86
Глава 5
1000 S-0
1100 H-<E-R>/|4
2000 S-FNF<R>/2
3000 FOR 1-1 TO N-l
3100 X-R+I*H
3200 S«S+FNF<X>
3300 NEXT I
4000 S«S+FNF<E>/2
4200 S-S*H
5000 PRINTiPRINT "ДЛИНА ЭЛЛИПСА" „
6000 PRINT "ПРИ"; N; "ЧАСТИЧНЫХ ИНТЕРВАЛАХ = ; S
7000 N-N*2
8000 GOTO 1008
20000 END
ДЛИНА ПЕРВОЙ ПОЛУОСИ? 1
ДЛИНА ВТОРОЙ ПОЛУОСИ? 1
ДЛИНА ЭЛЛИПСА
ПРИ 10 ЧАСТИЧНЫХ ИНТЕРВАЛАХ=6.2В31В531
ДЛИНА ЭЛЛИПСА
ПРИ 20 ЧАСТИЧНЫХ ИНТЕРВАЛАХ-6.2В31В531
RUN
ДЛИНА ПЕРВОЙ ПОЛУОСИ? 1
ДЛИНА ВТОРОЙ ПОЛУОСИ? 3
ДЛИНА ЭЛЛИПСА
ПРИ 10 ЧАСТИЧНЫХ ИНТЕРВАЛАХ =13.3840469
ДЛИНА ЭЛЛИПСА
ПРИ 20 ЧАСТИЧНЫХ ИНТЕРВАЛАХ =13.3646916
ДЛИНА ЭЛЛИПСА
ПРИ 40 ЧАСТИЧНЫХ ИНТЕРВАЛАХ»! 3.3648931
По сравнению с программой «ЭЙЛЕР2» в строке 100 заменена
подынтегральная функция. Нижний и верхний пределы интегриро-
вания 0 и 2тг вводятся не оператором INPUT, а заданы непосредст-
венно в программе в строке 200. Из входных данных запрашивают-
ся только длины обеих полуосей. В операторе вывода текст «ИН-
ТЕГРАЛ...» заменен на «ДЛИНА ЭЛЛИПСА». Приведенные чис-
ловые примеры показывают, что для длины окружности (первый
пример, полуоси равны) и для не слишком сплюснутого эллипса ре-
зультаты вычислений относительно быстро сходятся.
Задание 36. Модифицируйте программу «ЭЛЛИПС» и рассчитайте длину следу-
ющих кривых:
2 cos (/) — cos (2/)
2sin(/) — sin(2z)
Интегрирование
87
Представьте себе, как выглядят эти кривые, или постройте их графики на мил-
лиметровой бумаге.
5.3. Моделирование строения сополимеров
В этом разделе будет рассмотрена проблема из области химии
высокомолекулярных соединений. Речь пойдет о моделировании
строения сополимеров. Для этого будет использован метод Монте-
Карло.
Для образования сополимера можно взять оба мономера А и В
в одинаковых концентрациях или один из них в избытке. Полимер-
ная цепь, которая оканчивается активной концевой группой А (на-
пример, радикалом или ионом), обладает различной реакционной
способностью по отношению к мономерам А и В. То же самое от-
носится и к полимерной цепи, которая оканчивается активной груп-
пой В. Очевидно, что строго регулярный полимер с чередующими-
ся фрагментами образуется в том случае, если концевая группа А
реагирует только с мономером В, а концевая группа В реагирует
только с мономером А. Как будет выглядеть полимер, если нет
столь большого различия в реакционной способности концевых
групп? Строение сополимера в этом случае можно смоделировать
методом Монте-Карло.
Сначала надо задать, с какого мономера начинается полимерная
цепь. Потом необходимо знать вероятность Р1; с которой концевая
группа А реагирует с мономером А, и вероятность Р3, с которой
концевая группа В реагирует с мономером В. Тогда вероятность
(1 — Pj) будет соответствовать реакционной способности концевой
группы А по отношению к мономеру В, а (1 — Р3) — реакционной
способности концевой группы В по отношению к мономеру А.
ЭВМ должна запомнить, какой активной группой (А или В)
оканчивается полимерная цепь, потом выбрать, какой из мономе-
ров будет следующим в цепи, учитывая при этом как статистиче-
ский характер реакции, так и реакционную способность различных
концевых групп по отношению к мономерам А и В. Символ этого
мономера выводится на экран, и теперь это звено считается новой
активной группой. Потом в цикле продолжается выбор очередной
реагирующей молекулы мономера.
0 КЕМ "СОПОЛ" EBERT/EDERER 810511
1 КЕМ****************************************************
2 КЕМ** МОДЕЛИРОВАНИЕ СТРОЕНИЯ СОПОЛИМЕРОВ МЕТОДОМ
3 КЕМ** МОНТЕ-КАРЛО. ЗАДАНЫ ВЕРОЯТНОСТИ РЕАКЦИИ ««
4 КЕМ** КОНЦЕВОЙ ГРУППЫ А С МОНОМЕРОМ А И «*
5 КЕМ** КОНЦЕВОЙ ГРУППЫ В С МОНОМЕРОМ В. **
6 КЕМ** КОНЦЕНТРАЦИИ СА И СВ **
9 КЕМ***************************************************«
100 PRINT "С КАКОЙ ВЕРОЯТНОСТЬЮ"
200 PRINT "РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА А”
300 PRINT "ПОЛИМЕРА С МОНОМЕРОМ А"
4001 INPUT Pl
550 PRINT
600 PRINT
700 PRINT
800 PRINT
900 INPUT
"С КАКОЙ ВЕРОЯТНОСТЬЮ"
"РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА В"
"ПОЛИМЕРА С МОНОМЕРОМ В "
РЗ
1100 PRINT
2000 INPUT "НАЧАТЬ С КОНЦЕВОЙ ГРУППЫ А ИЛИ В"; Е$
2100 PRINT Е«,
2200 X-RND<X>
2300 IF Е«-"В" THEN GOTO 3000
2400 IF X<P1 THEN GOTO 2180
2500 E*-"B":GOTO 2100
3000 IF X<P3 THEN GOTO 2100
3100 E«-“A"tGOTO 2100
4000 END
RUN
С КАКОЙ ВЕРОЯТНОСТЬЮ
РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА А
ПОЛИМЕРА С МОНОМЕРОМ А
? .9
С КАКОЙ ВЕРОЯТНОСТЬЮ
РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА В
ПОЛИМЕРА С МОНОМЕРОМ В
? .9
НАЧАТЬ С КОНЦЕВОЙ ГРУППЫ А ИЛИ В? А
RRBBBBBBBBBBRRRRRRRRRRBBBBBBBBBBBBBBBBBB
BBBBRRBBRRRRRRBRRBBBBBBBBBBBBBBBBBBBBBBB
BRRRRBBRRRRRRBRRRRRRRRRRRRRRRBBBBBBBBBBB
RUN
С КАКОЙ ВЕРОЯТНОСТЬЮ
РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА А
ПОЛИМЕРА С МОНОМЕРОМ А
? .1
С КАКОЙ ВЕРОЯТНОСТЬЮ
РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА В
ПОЛИМЕРА С МОНОМЕРОМ В
? . 1
НАЧАТЬ С КОНЦЕВОЙ ГРУППЫ А ИЛИ В? А
RBRBRBRBRBRBRBRBRBRBRBRBRBRRBRRBBRBRBRBR
BRBBRBRBRBRRBRBRBRBRBBRRBRBRBRBRBRBRBBRB
RBRBRBRBRBRBRBRBRBRBRBRBRBRRBRBRBRBRBRRB
RUN
С КАКОЙ ВЕРОЯТНОСТЬЮ
РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА А
ПОЛИМЕРА С МОНОМЕРОМ А
? .2
С КАКОЙ ВЕРОЯТНОСТЬЮ
РЕАГИРУЕТ КОНЦЕВАЯ ГРУППА В
ПОЛИМЕРА С МОНОМЕРОМ В
? .8
НАЧАТЬ С КОНЦЕВОЙ ГРУППЫ А ИЛИ В? А
RBBBBBBRBRBBBBBBRRBBBBBBBBRBRRBRRBBBRBRB
BBBBRRBBBBBBBBBRBBRBBBBBBBBBBBBBBBBBBBBB
RBBBBBBRBRBRBBBBBBBBRBBBBBBBBRRBBBRBRRBB
Интегрирование
89
Ввод значений вероятности (Р1 и/3,) осуществляется оператором
INPUT в строках 400 и 900. Символ мономера, с которого начина-
ется полимерная цепь, вводится в строке 2000 и присваивается пере-
менной Е$. Символ концевой группы всегда присваивается перемен-
ной Е$. Потом, в строке 2100, символ активной концевой группы
выводится на экран. Этот участок программы можно рассматри-
вать как еще один пример ввода и вывода значений текстовых пере-
менных. В строке 2200 генерируется псевдослучайное число в зам-
кнутом интервале [0, 1]. Если полимерная цепь оканчивается актив-
ной группой А, то выполняются операторы в строках 2400 и 2500;
в противном случае выполняются операторы в строках 3000 и 3100.
Этот выбор между двумя вариантами продолжения программы
происходит в строке 2300. Если текстовая переменная имеет значе-
ние А, т. е. А является активной концевой группой, то управление
переходит к строке 2400. В этой строке сравниваются случайное
число X и вероятность Р1 (Р1 — вероятность взаимодействия конце-
вой группы А с мономером А). Если X < Рр то концевая группа
реагирует с мономером А и полимерная цепь опять оканчивается
группой А, т. е. концевая группа не меняется. Переменная Е$ со-
храняет свое значение, управление передается в строке 2100 опера-
тору PRINT, который выводит на экран букву А, и цикл начинает-
ся сначала. Если случайное числоX не меньше, чем вероятность Р1г
то оператор условного перехода IF в строке 2400 передает управле-
ние строке 2500, в которой меняется значение переменной Е$ (меня-
ется концевая группа); в данном случае Е$ присваивается значение
В. После двоеточия, которое позволяет в той же строке написать
еще один оператор, управление передается оператору вывода и на-
ращивание полимерной цепи возобновляется. В тех случаях, когда
полимерная цепь заканчивается группой В, выбор реагирующего с
этой группой мономера происходит по аналогичной схеме в стро-
ках 3000 и 3100. Разумеется, изменение концевой группы означает,
что переменной Е$ присваивается значение А. Как показывает ана-
лиз на ЭВМ, если вероятности, с которыми мономеры реагируют с
одноименными концевыми группами, очень велики, то образуется
соответствующий блок-полимер, и если эти вероятности очень ма-
лы, то образуется сополимер с чередующимися звеньями. Если од-
на из вероятностей велика, а другая мала, то образуется сополи-
мер, состоящий из блоков одного вида звеньев, с включениями от-
дельных звеньев другого мономера.
90
Глава 5
5.3.1. Двоеточие в БЕЙСИКе
Новый оператор:
***********
*** : *♦*
***********
Двоеточие, вообще говоря, не является оператором стандартно-
го БЕЙСИКа. Обычно в программах на БЕЙСИКе каждый опера-
тор пишут с новой строки, имеющей свой собственный номер.
Можно сэкономить одну или несколько строк, если после операто-
ра поставить двоеточие (:) и непосредственно за ним написать сле-
дующий оператор*. Поэтому двоеточие можно успешно использо-
вать для уменьшения количества строк.
Пример: 10 F0R 1=1 т0 50
20 PRINT LOG(I+1/l)
30 NEXT I
Его можно записать в сокращенной форме:
10 FORI=1T050sPRINTLOG(1+1/1)sNEXTI
10 FOR 1-1 TO 10
20 FOR J=1 TO 10
30 PRINT I*J;
40 NEXT J
50 PRINT
60 NEXT I
Или еще более коротко:
10 FORI = 1T010:FORJ = 1T010:PRINTI • J;:NEXTJ:PRINT:NEXTI
Насколько часто используется сокращенная форма, зависит от
привычек программиста. Используя двоеточие, программу можно
сделать более наглядной и компактной. Сокращенная программа
занимает меньше места в памяти ЭВМ и быстрее выполняется. Од-
нако при этом накладывается существенное ограничение на дейст-
вие операторов перехода, поскольку управление можно передать
только всей строке, начиная с первого оператора, а не ее части.
Задание 37. Измените программу «СОПОЛ» так, чтобы на экран выводилась
полимерная цепь, состоящая из 100 звеньев, по 25 звеньев в четырех строках.
Задание 38. Перепишите программу «СОПОЛ» или программу нз предыдущего
задания так, чтобы учитывалась различная начальная концентрация мономеров А
и В.
Некоторую помощь может оказать таблица:
В ряде версий БЕЙСИКа для этого используется символ «\». —Прим, перев.
Интегрирование
91
Группа Мономер Вероятность
А А Р1
А В (1-р3)
В В рз
В А (1-р3)
Эта таблица справедлива, если концентрации мономеров А и В равны (сд = св).
В общем случае:
Группа Мономер Вероятность
А А P1*CA/N1
А В (1-Р1)*cB/N1
В В Рз*сВ/Ы2
В А (1-p3)*сд/Ы2
Нормировочный делитель Л/, выбран так, чтобы сумма первых
двух вероятностей всегда была равна единице. То же относится и
к N2:
N, = Р, сА + (1 - Р,)св
N2 = Р3св + (1 - Р3)сА
Задание 39. Напишите программу, моделирующую сополимеризацию, не прибе-
гая к предположению об избытке мономеров.
Указание: Используйте две переменные, соответствующие концентрациям сд и
св. После присоединения каждой молекулы мономера его концентрация немного
уменьшается, и присоединение следующей молекулы мономера к полимерной цепи
будет протекать при другой концентрации мономера.
Задание 40. Напишите программу для моделирования сополимеризации, если
имеются в избытке не два, а три различных мономера.
5.4. Интегрирование методом Симпсона
После экскурса в область кинетики полимеризации вернемся к
методам численного интегрирования. По методу Эйлера в каждом
интервале вычисляется площадь криволинейной трапеции. Если со-
единить два интервала, то площадь под графиком функции/(г) на
двух интервалах можно аппроксимировать не площадью двух тра-
пеций, а площадью под параболой на сдвоенном интервале (см.
рис.) Этот прием называется методом Симпсона (правилом Симп-
сона). Примем это правило без строгого доказательства. Более
92
Глава 5
подробно это и другие правила изложены в учебниках по числен-
ным методам (некоторые из них указаны в списке литературы).
В примере, изображенном на рисунке, отрезок [А, Е] разделен
на 10 интервалов. Длина h одного интервала составляет
Л = (Е - А)/л = (х„ - х0)/п
п — число интервалов.
Если считать кривую на отрезке [х0, х2] параболой, то площадь
S под ней можно точно вычислить по формуле
S = j [Г(Го) + 4/(х,) + Ж)1
Если объединить все интервалы, то получится следующая фор-
мула:
5 = | Ж) + #(*,) + У(г2) + 4/-(х3) + У(г4) + 4/(х5) +
+ У(х6) + 4f(r7) + У(х8) + 4/(г9) + Жо)1
Задана произвольная функция /(г); надо вычислить определен-
ный интеграл этой функции в пределах от А до Е. При интегриро-
вании по методу Симпсона отрезок [А, Е] необходимо разделить на
2л интервалов:
п д
= Е~— |Ж) + + 4 £ Ж-1) + 2 £ Ж)
Ошибка этого приближенного метода уменьшается пропорцио-
нально длине интервала в четвертой степени, т. е. при увеличении
числа интервалов вдвое ошибка уменьшается в 16 раз.
Интегрирование
93
Ниже приведена распечатка программы для интегрирования
функции/(г) = х2-е~*2 методом Симпсона:
0 REM "СИМЛ1" EBERT/EDERER 810518
1 REM*********************************
2 REM** ИНТЕГРИРОВАНИЕ **
3 REM** ПРОИЗВОЛЬНОЙ ФУНКЦИИ »♦
4 REM** ПО СИМПСОНУ **
5 REM** I»######################*# *♦
б REM** ФУНКЦИЯ ОПИСАНА **
7 REM** В СТРОКЕ 100 **
9 REM*********************************
50 INPUT "НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ" ; А
60 INPUT "ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ"; Е
100 DEF FNFCX?—Х*Х*ЕХ₽<-Х*Х>
300 N-4
1000 S—0
1100 Н—<E-R>/N
2000 S-FNF<R>
3000 FOR 1-1 TO N-l STEP 2
3100 X—R+I*N
3200 S-S+4*FNF<X>
3300 NEXT I
3500 FOR 1-2 TD N-2 STEP 2
3600 X-R+IPH
3700 S-S+2*FNF<X>
3600 NEXT I
4000 S-S+FNF<E>
4200 S-SPH/3
5000 PRINT iPRINT "ИНТЕГРАЛ ОТ"; А; "ДО"; E
6000 PRINT "ПРИ"; N .''ЧАСТИЧНЫХ ИНТЕРВАЛАХ = "• S
7000 N-N*2
8000 GOTO 1000
RUN
НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? О
ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? 1
ИНТЕГРАЛ ОТО ДО 1
ПРИ 4 ЧАСТИЧНЫХ ИНТЕРВАЛАХ - • 189512038
ИНТЕГРАЛ ОТ О ДО 1
ПРИ В ЧАСТИЧНЫХ ИНТЕРВАЛАХ - . 189474449
ИНТЕГРАЛ ОТ О ДО1
ПРИ 16 ЧАСТИЧНЫХ ИНТЕРВАЛАХ - . 189472472
ИНТЕГРАЛ ОТ О ДО 1
ПРИ 32 ЧАСТИЧНЫХ ИНТЕРВАЛАХ - -189472354
ИНТЕГРАЛ ОТ О ДО 1
ПРИ 64 ЧАСТИЧНЫХ ИНТЕРВАЛАХ - - 189472346
ИНТЕГРАЛ ОТ О ДО 1
ПРИ 128 ЧАСТИЧНЫХ ИНТЕРВАЛАХ- • 189472346
BREAK IN 3200
RERDV.
Программа «СИМП1» похожа на программу «ЭЙЛЕР2»; в этих
программах имеется бесконечный внешний цикл, в котором число
94
Глава 5
интервалов при каждом прохождении удваивается. Выполнение
программы так же прерывается вручную. До строки 1100 програм-
мы в принципе одинаковы. Лишь определяемая функция в програм-
ме «СИМП1» другая и начальное число интервалов значительно
меньше (всего четыре). В строке 2000 с вычисления функции /(А)
начинается расчет интегральной суммы. Переменная N в тексте
программы соответствует числу 2п в формуле. В цикле, занимаю-
щем строки 3000—3300, вычисляется первая сумма формулы, в дру-
гом цикле (строки 3500—3800) вычисляется вторая сумма. В обоих
циклах выполняются два оператора: первый вычисляет значение х,
соответствующее параметру I, второй оператор умножает значение
функции на 4 (во втором цикле — на 2), вычисляет сумму этих про-
изведений, которая присваивается переменной S. В строке 4000 зна-
чение функции /(Е)— последнее слагаемое— прибавляется к S.
Умножением этой суммы на треть длины интервала вычисляется
приближенное значение интеграла. Вывод результата, увеличение
числа шагов и возвращение на начало цикла идентичны программе
«ЭЙЛЕР2».
Задание 41. Проинтегрируйте с помощью программы «СИМП1» функцию рас-
пределения Максвелла. Поскольку эта функция довольно длинная и не помещается в
одной строке, лучше всего использовать несколько вложенных друг в друга операто-
ров DEF FN. Так поступают всегда, когда имеют дело с длинными формулами.
Задание 42. Проинтегрируйте одну и ту же функцию с помощью программы
«ЭЙЛЕР2» и «СИМП1» и сравните время выполнения каждой из программ и число
итераций, необходимое для достижения одинаковой точности. Вы увидите, что
очень важно выбрать из множества численных методов наиболее эффективный для
данной конкретной задачи. Программа «СИМП1» несколько сложнее, чем
«ЭЙЛЕР2», но ее эффективность значительно выше. При интегральных преобразо-
ваниях, например фурье-преобразовании, необходимо вычислять довольно много ин-
тегралов. В таких случаях высокая эффективность программы позволяет решить за-
дачу с помощью персонального компьютера в разумный срок.
5.5. Численное интегрирование с ограничением числа
итераций по критерию сходимости
Если программа предусматривает вычисление большого числа
интегралов итерационными методами, то невозможно вручную
прерывать вычисление каждого интеграла. В такой программе надо
организовать выход из бесконечных итерационных циклов по до-
стижении необходимой точности результата. Однако следует иметь
в виду, что
Интегрирование
95
********♦*♦♦♦*♦♦***♦**♦♦***♦****♦♦**♦♦****♦*
* ** НЕТ ПРОСТЫХ И УНИВЕРСАЛЬНЫХ 'КРИТЕРИЕВ ***
* ** СХОДИМОСТИ. ДЛЯ КАЖДОГО КОНКРЕТНОГО ***
* ** 'ПРИМЕРА НЕОБХОДИМО ПРОВЕРЯТЬ АДЕКВАТНОСТЬ ***
*** ИСПОЛЬЗУЕМОГО КРИТЕРИЯ ***
********************************************
В следующем примере мы использовали очень простой прием,
легко реализуемый программными средствами. После каждой ите-
рации будем сравнивать полученное значение интегральной суммы
с ее значением S1, полученным в предыдущей итерации. Если раз-
ность этих интегральных сумм меньше заданной величины, то ци-
клическая процедура прерывается и значение S выводится на экран
в качестве окончательного приближенного значения интеграла.
0 REM "СИМП2" EBERT/EDERER 810602
1 REM*»»»»»»»»»»»»»*»»»»»»»»»*»»**»*»»
2 REM** ИНТЕГРИРОВАНИЕ **
3 REM** ПРОИЗВОЛЬНОЙ ФУНКЦИИ «*
4 REM** МЕТОДОМ СИМПСОНА **
5 REM** С ЗАДАННОЙ ТОЧНОСТЬЮ **
6 REM** ########################### **
7 REM*» ФУНКЦИЯ ОПИСАНА В **
0 REM** СТРОКЕ 100 **
9 REM*********************************
50 INPUT "НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ": А
60 INPUT "ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ"; Е
70 INPUT " ТОЧНОСТЬ В % "; G
100 DEF FNF<X>-X»X»EXP<-X»X>
300 N-4
500 S1-0
1000 S-0
1100 H-<E-R>/N
2000 S—FNF<R>
3000 FOR 1-1 TO N-l STEP 2
3100 X-R+IPH
3200 S-S+4*FNF<X>
3300 NEXT I
3500 FOR 1-2 TO N-2 STEP 2
3600 X-R+I»H
3700 S=S+2»FNF<X>
3B00 NEXT I
4000 S-S+FNF<E>
4200 S-SPH/3
4500 IF RBS<S-S1XRBS<S>»G/100 THEN 9000
4600 IF N>2500 THEN 8000
5000 SI-SiN-N*2iGOTO1000
8000 PRINT "ТРЕБУЕМАЯ ТОЧНОСТЬ HE МОЖЕТ БЫТЬ ДОСТИГНУТА"
0050 PRINT "ПОСЛЕДНИЙ ИНТЕГРАЛ": S1; S
8100 GOTO 70
9000 PRINT 1PRINT "ИНТЕГРАЛ ОТ"; А; "ДО"; E
9100 PRINT "ПРИ"; N; "ЧАСТИЧНЫХ ИНТЕРВАЛАХ = "; S
9200 PRINT SPRINT "ТРЕБУЕМАЯ ТОЧНОСТЬ"; ABS (GlPS/100
9300 PRINT "ДОСТИГНУТАЯ ТОЧНОСТЬ"; ABS (S-S1)
10000 END
96
Глава 5
RUN
НИЖНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? О
ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ? 1
ТОЧНОСТЬ В %? .1
ИНТЕГРАЛ ОТ О ДО 1
ПРИ 8 ЧАСТИЧНЫХ ИНТЕРВАЛАХ = .189474449
ТРЕБУЕМАЯ ТОЧНОСТЬ 1 .В9474449Е-04
ДОСТИГНУТАЯ ТОЧНОСТЬ 3.75883537Е-05
В программе «СИМП2» предусмотрен автоматический выход из
бесконечного цикла. Новой по сравнению с программой «СИМП1»
является строка 70, в которой задается желаемая точность резуль-
тата (в процентах). Ее значение присваивается переменной G. По-
скольку необходимо сравнивать значения интегральных сумм, вво-
дится еще одна переменная S1, которая сначала обнуляется (строка
500). Основной участок программы до строки 4200 совпадает с про-
граммой «СИМП1». В строке 4500 записано условие выхода из бес-
конечного цикла: если относительное изменение интегральной сум-
мы в смежных итерациях меньше, чем заданная точность, то чис-
ленное интегрирование прекращается и оператор IF передает управ-
ление строке 9000 для вывода на экран результата вычислений.
Если требуемая точность не достигнута, то в строке 4600 прове-
ряется, не превышает ли число выполненных итераций некоторого
максимально допустимого числа, которое в данной программе рав-
но 2500. Если превышает, то в строке 8000 на экран выводится со-
общение, что требуемая точность не может быть достигнута.
Если требуемая точность еще не достигнута и число итераций
не превысило допустимого значения, то в строке 5000 выполняются
три оператора, разделенные двоеточиями. Сначала переменной S1
присваивается текущее значение переменной S, поскольку сразу пос-
ле этого начнется вычисление нового значения S, потом удваивает-
ся число интервалов и управление передается строке 1000, в кото-
рой переменная S обнуляется, и опять начинается вычисление инте-
гральной суммы.
Задание 43. Модифицируйте программу «СИМП2» для вычисления значения
функции F(x), являющейся первообразной функции f(jc). Результаты представьте в
виде таблицы.
Указание-. Пусть нижний предел интегрирования равен А. Организуйте внешний
цикл, в котором параметром цикла будет верхний предел интегрирования. Шаг и
максимальное значение параметра цикла можете выбрать сами. Потом выведите на
экран значение верхнего предела вместе с вычисленным значением интеграла.
= j/(Od?
Интегрирование
97
откуда следует
dF(x)/dx = /(т)
Fix) — искомая первообразная.
Задание 44. Программу «СИМП2» можно легко приспособить для фурье-преоб-
разоваиия некоторых функций. Общие сведения о фурье-преобразовании можно най-
ти в литературе*. Если рассматривать только симметричные функции (симметрич-
ными называются такие функции, для которых fiy) = /(—х)), то фурье-образом
функции f (х) является действительная функция (для несимметричных функций все го-
раздо сложнее) и можно вывести формулу для такого преобразования:
+ ас
1 f
Tty) = I /(x)cos(xy)dx
\<2т J
— 00
T(y) — фурье-образ функции/(x).
Вычислите фурье-образы симметричных функций /(х) по вашему выбору, ре-
зультат представьте в виде таблицы. Возьмите такие функции, которые с увеличени-
ем х неограниченно уменьшаются. Тогда в формуле несобственный интеграл можно
заменить интегралом с конечными пределами интегрирования.
Опробуйте программу для фурье-преобразования сначала на следующей функ-
ции:
/(х) = 1, если Ixl 1, иначе/(х) = О
Формула для фурье-преобразования этой функции имеет вид
1
1 f
Т(у) = I 1 cos(xy)dx
/2тг J
-1
Фурье-образ этой функции можно выразить также и в элементарных функциях:
Сравните аналитическое решение с численным.
Фурье-преобразование используется в фурье-ИК-спектрометре,
который имеет лучшее по сравнению с обычным отношение сиг-
нал/шум и поэтому более предпочтителен. Для практических целей
обычно используется не рассмотренный выше метод, а так называ-
емый «быстрый алгоритм» (“Fast Fourier Transform”, FFT)**. Для
фурье-преобразования функции по п точкам обычным методом не-
обходимо выполнить п (п — 1) арифметических операций, тогда как
по методу FFT число операций составляет wlog2(«), т. е. для 4096
точек выполняется не 16700000 операций, а только 50000.
* Zachmann Н. G., Mathematik fur Chemiker. Verlag Chemie, Weinheim, 1974.
'* Cooley J. W., Tukey J. W., Math. Comput., 19, 297 (1965), Brigham E. D., The
fast Fourier transform. Prentice Hall, Englewood Cliffs, N.Y., 1974.
7-81
98
Глава 5
Ниже будут подробно обсуждены еще два примера из области
физической химии, в которых используются рассмотренные в пре-
дыдущих разделах методы численного интегрирования.
5.6. Мольная теплоемкость металлов по Дебаю
Значительный вклад в развитие общей теории теплоемкости ме-
таллов внесли работы Дебая. Согласно формуле, выведенной на ос-
новании этой теории, мольная теплоемкость металлов зависит от
температуры Т и так называемой температуры Дебая в, которая
является характеристическим свойством каждого металла. Эта
формула содержит интеграл, который невозможно вычислить ана-
литическими методами. Поэтому для расчета теплоемкости надо
привлечь численные методы интегрирования, реализованные в од-
ной из программ предыдущих разделов. Строго говоря, теплоем-
кость (Су) зависит не от абсолютных значений Т и в, а от отноше-
ния 0/Т. Если обозначить 0/Т = z, то формула Дебая принимает
вид
С =
v z3
О
0х
(е* - I)2
dr
Ниже приведена распечатка программы «ДЕБАЙ» для расчета
теплоемкости по формуле Дебая:
0 REM "ДЕБАИ'' EBERT/EDERER 810601
1 REM*********************************
2 REM»» РАСЧЕТ CV ПО ТЕОРИИ ДЕБАЯ **
3 REM** С ИСПОЛЬЗОВАНИЕМ **
4 REM** ИНТЕГРИРОВАНИЯ МЕТОДОМ *•
5 REM** СИМПСОНА CV - 9R/<0/T>T3* •*
б REM** *1<ХТ4*ЕХР<Х>/<ЕХР<Х>-1>Т2>**
7 REM** Ф ТЕМПЕРАТУРА ДЕБАЯ **
8 REM** !<...> ИНТЕГРАЛ **
9 REM*********************************
50 Я».80881
60 INPUT "Ф/Т ”1Е
70 G-.01
100 DEF FNF<X>-XT4*EXP<X>/<EXP<X>-1>T2
300 N-4
500 81-0
1000 S-0
1100 Н-<Е-Я>/Ы
2000 S-FNF<R>
3000 FOR 1-1 ТО N-l STEP 2
3100 X-R+I*H
3200 S-S+4»FNF<X>
3300 NEXT I
3500 FOR 1-2 TO N-2 STEP 2
3600 X-R+I*H
3700 S-S+2»FNF<X>
3800 NEXT I
Интегрирование
99
4000 S-S+FNF<E>
4200 S-S»H/3
4300 S«S*9/E/E/E
4500 IF RBS<S-S1><A8S<S>*6/100 THEN 9000
4600 IF N/2500 THEN 8000
5000 Sl«SsN»N*2sGOTO1000
8000 PRINT "ТРЕБУЕМАЯ ТОЧНОСТЬ HE МОЖЕТ БЫТЬ ДОСТИГНУТА"
8050 PRINT "ПОСЛЕДНИЙ ИНТЕГРАЛ"; SI; S
8100 STOP
9000 PRINT SPRINT " МОЛЬНАЯ ТЕПЛОЕМКОСТЬ МЕТАЛЛА"
9100 PRINT "ПРИ в/Т РАВНОМ'; Е;’=" 1S,"* R"
9999 END
RUN
0/Т ? 1
МОЛЬНАЯ ТЕПЛОЕМКОСТЬ МЕТАЛЛА
ПРИ 0/Т РАВНОМ 1 = 235519523 » R
RUN
0/Т ?
МОЛЬНАЯ ТЕПЛОЕМКОСТЬ МЕТАЛЛА
ПРИ 0/Т РАВНОМ .1 2.99850031 * R
RERDV.
RUN
0/т ? 3
МОЛЬНАЯ ТЕПЛОЕМКОСТЬ МЕТАЛЛА
ПРИ 0/Т РАВНОМ 3» 1.98826751 * R
RERDV.
В основе программы «ДЕБАЙ» лежит программа для численно-
го интегрирования «СИМП2». Подынтегральная функция задана в
строке 100. Ввод пределов интегрирования изменен. В формуле
нижний предел интегрирования равен нулю. Так как нахождение
значения функции/(г) при х = 0 численными методами связано со
значительными трудностями, в качестве нижнего предела интегри-
рования принято достаточно малое число А = 0.00001. Верхний
предел интегрирования задается отношением в/Т, значение которо-
го присваивается переменной Е. Требуемая точность интегрирова-
ния составляет 0,01%. Центральная часть программы такая же, как
в программе «СИМП2». В дополнительной по сравнению с про-
граммой «СИМП2» строке 4300 полученное приближенное значение
интеграла умножается в соответствии с приведенной выше форму-
лой Дебая на коэффициент (9/Е/Е/Е). Обратите внимание, что ре-
зультат вычислений представлен в виде произведения некоторого
множителя на универсальную газовую постоянную. Расчет несколь-
7*
10(1
Глава 5
ких примеров показывает, что с увеличением температуры мольная
теплоемкость Cv приближается к классическому значению 3R.
Вот другой наглядный пример, в котором возникают трудно-
сти, когда пытаются определить значение функции в сингулярных
точках*:
х х2 - 100
/(г) = ------— = х + 10
х — 10
Значение этой функции можно вычислить для любых значений х
(эта функция определена на всем множестве действительных чисел).
Однако если функцию подставить в программу, не сокращая числи-
тель и знаменатель на (х — 10), то при х = 10 на экране появится
сообщение об ошибке. В таких ситуациях проводить вычисления
можно или с помощью оператора условного перехода IF, рассчиты-
вая значения функции в сингулярных точках каким-либо другим
способом, или вообще отбрасывая их, как это сделано в программе
«ДЕБАЙ».
Задание 45. Используйте программу «ДЕБАЙ» для выяснения зависимости Су
от Т/в. Постройте график этой зависимости.
5.7. Расчет второго вириального коэффициента
на основе межмолекулярного потенциала
Для описания состояния реального газа часто пользуются урав-
нением состояния идеального газа, к правой части которого добав-
лены слагаемые в виде степенного ряда по давлению. Коэффициен-
ты этого степенного ряда называются вириальными коэффициента-
ми. Если ряд оборвать на втором члене, то получится следующая
формула:
pV = RT + В(Т)р
В (Г) можно определить из экспериментальных данных по уравне-
нию
В(Т) = д(рУ)/др
Размерность второго вириального коэффициента В (Г) —
ед. объема/моль. Отклонение поведения реального газа от идеаль-
ного обусловлено межмолекулярным взаимодействием. Второй ви-
риальный коэффициент можно рассчитать, исходя из межмолеку-
• В данном случае речь идет о разрыве функции в точке, в которой эта функция
не определена. — Прим, перев.
Интегрирование
лярного потенциала 21^ (г). Ради простоты атомы или молекулы бу-
дем считать шарообразными. Тогда на потенциал Ер будет оказы-
вать влияние только расстояние между частицами, а не их взаим-
ная ориентация. Пусть межмолекулярный потенциал имеет вид по-
тенциала Леннарда-Джонса:
г — расстояние между атомами; а — расстояние, на котором силы притяжения и
отталкивания равны; е — глубина потенциальной ямы; п соответствует члену, опи-
сывающему притяжение (обычно равно 6); т соответствует члену, описывающему
отталкивание (обычно равно 12).
Сила межмолекулярного взаимодействия К (г) в общем виде вы-
ражается как
К (г) = -d£p(r)/dr
Второй вириальный коэффициент В (Г) можно рассчитать по следу-
ющей формуле:
В (Г) = 2ttNl j(l - е Ep(r)/kT)-r2dr
о
Программа для расчета второго вириального коэффициента приве-
дена ниже (программа «ВИРИАЛ»).
0 REM "ВИРИАЛ" EBERT/EDERER 820318
1 REM*********************************
2 REM** ИНТЕГРИРОВАНИЕ **
3 REM** ПРОИЗВОЛЬНОЙ ФУНКЦИИ **
4 REM** МЕТОДОМ СИМПСОНА С **
5 REM** ЗАДАННОЙ ТОЧНОСТЬЮ, **
в REM** ВЫЧИСЛЕНИЕ ВТОРОГО **
7 REM** ВИРИАЛЬНОГО КОЭФФИЦИЕНТА **
8 REM*********************************
15 PRINT "ПЕРВЫЙ ПАРАМЕТР ПОТЕНЦИАЛА ЛЕННАРДА-ДЖОНСА"
20 INPUT "СИГМА"; S9
25 PRINT "ВТОРОЙ ПАРАМЕТР ПОТЕНЦИАЛА ЛЕННАРДА-ДЖОНСА"
30 INPUT "ЭПСИЛОН/К БОЛЬЦМАНА": Е9
40 INPUT "ТЕМПЕРАТУРА В К "; T9
50 R-S9/1000
60 Е—89*10
70 INPUT "ТОЧНОСТЬ В % G
100 DEF FNF<X>-<1-EXPC-4*E9/T9*<<S9/X>T12-<S9/X>T6>>>*Х*Х
300 N-4
500 81=0
1000 8*0
1100 H*<E-R>/N
2000 S-FNF<fl>
3000 FOR 1-1 ТО N-l STEP 2
3100 X-R+I*H
3200 S*S+4*FNF<X>
3300 NEXT I
3500 FOR 1-2 TO N-2 STEP 2
3600 X*R+I*H
102
Глава 5
3700 S-S+2*FNF<X>
3800 NEXT I
4000 S-S+FNF<E>
4200 S-S*H/3
4300 S-S*2*3.14159*6.022E23*1E-24
4500 IF RBS<S-S1><ABS<S>*G/180 THEN 9000
4608 IF N>2500 THEN 8800
5008 S1»SsN-N*2iGOTO 1000
8008 PRINT "ТРЕБУЕМАЯ ТОЧНОСТЬ HE МОЖЕТ БЫТЬ ДОСТИГНУТА"
8050 PRINT "ПОСЛЕДНИЙ ИНТЕГРАЛ"; S1; S
8100 STOP
9000 PRINT SPRINT "ИНТЕГРАЛ ОТ "; А; "ДО"; Е" АНГСТРЕМ"
9180 PRINT "ПРИ"; N; "ЧАСТИЧНЫХ ИНТЕРВАЛАХ = "; S
9200 PRINT SPRINT "ТРЕБУЕМАЯ ТОЧНОСТЬ"; ABS (G) * S /100
9300 PRINT "ДОСТИГНУТАЯ ТОЧНОСТЬABS (S-S1) :PRINT
9400 PRINT "СИГМА - "; S9 >'"АНГСТРЕМ"
9588 PRINT "ЭПСИЛОН/К (БОЛЬЦ.) = ";Е9;"К"
9600 PRINT "ТЕМПЕРАТУРА = ";Т9:"К"
9780 PRINT "ВТОРОЙ ВИРИАЛЬНЫЙ КОЭФФИЦИЕНТ = "; S ; ”Ьм13/МОЛЬ"
9999 END
RUN
ПЕРВЫЙ ПАРАМЕТР ПОТЕНЦИАЛА ЛЕННАРДА-ДЖОНСА
СИГМА? 3.698
ВТОРОЙ ПАРАМЕТР ПОТЕНЦИАЛА ЛЕННАРДА-ДЖОНСА
ЭПСИЛОН/К БОЛЬЦМАНА? 95.05
ТЕМПЕРАТУРА В К? 773
ТОЧНОСТЬ В %? .1
ИНТЕГРАЛ ОТ 3.698Е-03 ДО 36.9В АНГСТРЕМ
ПРИ 512 ЧАСТИЧНЫХ ИНТЕРВАЛАХ = 26.6624513
ТРЕБУЕМАЯ ТОЧНОСТЬ .0266624ЫЗ
ДОСТИГНУТАЯ ТОЧНОСТЬ В.2500279Е-05
СИГМА —3.69В АНГСТРЕМ
ЭПСИЛОН/К (БОЛЬЦ.) = 95.05 К
ТЕМПЕРАТУРА = 773 К
ВТОРОЙ ВИРИАЛЬНЫЙ КОЭФФИЦИЕНТ =26.6624513 СМТЗ/МОЛЬ
Числовые значения второго вириального коэффициента можно
найти в учебниках по физической химии*. Строки 70—9300 про-
граммы «ВИРИАЛ» совпадают с программой «СИМП2». Только в
строке 8100 оператор условного перехода заменен на оператор
STOP и в строке 9400 в операторе вывода добавлено слово
«АНГСТРЕМ». Новой является строка 4300, в которой проводится
нормировка. Подынтегральная функция определена в строке 100
так, чтобы входной параметр а измерялся в ангстремах, параметр
£ — в градусах Кельвина (т. е. энергию е надо разделить на кон-
станту Больцмана к, см. табл.) и температура — также в градусах
Кельвина. Ввод исходных данных происходит в строках 15—40.
Нормировка в строке 4300 служит для пересчета вириального коэф-
фициента В (Г) в единицы СГС (см3/моль). Кроме того, в той же
строке значение интеграла умножается на имеющийся в формуле
* Berry R. S., Rice S. A., Ross J., Physical chemistry. John Wiley & Sons, 1980, ISBN 0-
471-04829-1, p. 761, 784.
Интегрирование
103
Вещество б, А Б/к,К
Не 2,556 10,22
Н2 2,928 37,00
Ne 2,749 35,60
Аг 3,405 119,8
Кг 3,60 171
Хе 4,100 221
°2 3,58 117,5
СО 3,763 100,2
N2 3,698 95,05
СН4 3,817 148,2
множитель. Вывод данных занимают четыре строки; на экран вы-
водятся значения трех входных параметров и вычисленного второ-
го вириального коэффициента. Несобственный интеграл в приве-
денной выше формуле с пределами интегрирования от 0 до оо не-
возможно вычислить приближенными методами. Пределы инте-
грирования в численных методах должны иметь конечные значе-
ния. Для этого надо выбрать такую область интегрирования, вне
которой слагаемые интегральной суммы пренебрежимо малы. В
строке 60 для верхнего предела интегрирования принято значение
10а. Если вспомнить форму потенциальной кривой, то это пред-
ставляется разумным. (Можно, конечно, увеличить верхний предел
интегрирования и посмотреть, как изменится при этом результат;
время вычисления интеграла тем больше, чем больше интервал.)
Нуль в качестве нижнего предела интегрирования, как уже указыва-
лось, вызывает автоматическую остановку программы, поэтому
для нижнего предела интегрирования выбрано значение а/1000.
Вместе с программой приведен пример вычисления второго вири-
ального коэффициента при 773 К с параметрами потенциала Лен-
нарда-Джонса для азота. (Примечание для нетерпеливых: при вы-
полнении этой программы результат появляется на экране пример-
но через несколько минут. Однако можно дополнить программу со-
ответствующими операторами и выводить на экран промежуточ-
ные результаты.)
По программе «ВИРИАЛ» вычисляют вторые вириальные ко-
эффициенты, исходя из межмолекулярного потенциала. Однако ча-
104
1 лава 5
ще бывает наоборот: экспериментально определяют вторые вири-
альные коэффициенты и по ним рассчитывают межмолекулярные
силы. Эта задача называется обратной. С помощью программы
«ВИРИАЛ» мы можем попытаться решить обратную задачу мето-
дом проб и ошибок.
Задание 46. С помощью программы «ВИРИАЛ» составьте таблицу, которая пе-
редавала бы зависимость вторых вириальных коэффициентов различных веществ от
температуры. Представьте результаты графически, постройте графики зависимости
вторых вириальных коэффициентов от Т и от 1/Т.
Задание 47. Вычислите Су металлов по формуле Дебая и заполните таблицу по
следующей форме:
е/т' 0,01 0,1 0,5 1 3 5 10
С V
Постройте график зависимости Су никеля (температура Дебая 375 К) от темпера-
туры.
Задание 48. Исходя из значений Су, рассчитайте разность значений внутренней
энергии при двух различных температурах по следующей формуле:
Г1
U(Tt) - U(T2) = j Cy(T)dT
?2
Значения Cy вычислите по формуле Дебая. Для расчета Д1/ вам необходимо со-
ставить программу для двойного интегрирования.
Задание 49. Зависимость Ср (Г) от температуры описывается следующей форму-
лой:
I _ е-Г2/10000
С(Т) = ЗЯ-----------------
₽ 1 + 100/Г
Вычислите ДЯ и AS при двух произвольных температурах (например, при 78 К
и 532 К). Для выполнения этого задания используйте одну из имеющихся программ
для интегрирования функций.
Задание 50. Важной задачей аналитической химии высокомолекулярных соедине-
ний является определение средней молекулярной массы полимера, исходя из функции
молекулярно-массового распределения. Пусть молекулярно-массовое распределение
некоторого полимера описывается так называемым нормальным логарифмическим
распределением :
.... л^-i ( l10^) ~ И (АЛ,)]2 \
w (Л/) = М exp I — ------------------— I
\ Ь2 /
w (М) — функция молекулярно-массового распределения; М — молекулярная масса;
Л/о — медиана распределения w (Л/), т. е. половина пробы полимера состоит из мо-
лекул, имеющих массу меньше чем Л/о; b — параметр, характеризующий ширину
распределения.
Исходя из нормального логарифмического распределения, вычислите среднечис-
ленную Мп, среднемассовуюMw иZ-среднююMz молекулярные массы полимера по
Интегрирование
105
следующим формулам:
j w(A/)dM
о
О
о
оо
j w(M)dM
о
j M2 w (M)dM
о
Mz ~ --------------
ОО
j М • w (М) дМ
о
Попытайтесь выяснить взаимосвязь параметров Л/о, b и средних значений моле-
кулярных масс (или их отношений).
Задание 51. Вычислите следующие определенные интегралы и сравните резуль-
таты численного интегрирования с точными значениями интегралов:
х = в х = в
j sin(x)dr j re-x dr
х = А х = А
Задание 52. Пусть дана химическая реакция
к
А —-------продукты
скорость которой подчиняется кинетическому уравнению первого порядка:
t — время; к — константа скорости реакции.
Зависимость к от температуры описывается уравнением Аррениуса:
к(Г) = k0-e~E°'RT
Пусть температура в реакторе (начальное значение 300 К) меняется со временем
106
Глава 5
в соответствии с уравнением
Г(0 = 300 + (ТЕ - 300)(1 -
ТЕ — конечное значение температуры; q — постоянная времени, которая определяет
скорость изменения температуры.
Тогда константа скорости реакции будет зависеть также и от времени г.
k[T(t)] = к (/) = k0<TE°'R™
Концентрацию А при постоянной температуре можно рассчитать по формуле
[А] = [А]0-е-*<г> '
Для неизотермических условий справедливо
t
- I *(П01Л
[А] = [А]ое 0
Составьте программу, позволяющую выяснить зависимость концентрации А
от [А]о, Еа,к0, TE,q at.
Задание 53. Составьте программу для расчета летучести f в зависимости от дав-
ления р и температуры Г, полагая, что для реальных газов выполняется соотноше-
ние Ван-дер-Ваальса:
р
G) Гт J (к- - т)*
о
Уравнение Ван-дер-Ваальса имеет вид
RT а
Р =------------z
V - b V2
Вычислите несколько примеров по вашему выбору; исходные параметры можно вы-
брать из приведенной таблицы.
а/(лаатм-моль2) 100Ь/(лмоль')
Бензол 18,00 1,154
хе 4,194 5,105
Н2° 5,464 3,049
С02 3,592 4,261
Задание 54. В квантовой химии часто возникает необходимость вычислять инте-
гралы перекрывания. Ниже рассмотрен гипотетический пример, на котором объяс-
няется принцип вычисления интегралов перекрывания. Пусть дана одномерная вол-
новая функция и’бс):
и'(х) = N-e~1x1
Интегрирование 107
Сначала рассчитывают нормировочный коэффициент N, который выбирают
так, чтобы выполнялось следующее условие:
+ 00
j W (г)-И'(т)<Ьг = 1
— 00
Для нормированной волновой функции интеграл перекрывания рассчитывают по
формуле
+ 00
S = /V2 j w(?c — A)w^c — B)dx
— ec
А и В — расстояния от произвольной нулевой точки до атомов А н В соот-
ветственно; IA — BI — расстояние между атомами. Вычислите интегралы перекры-
вания при различных расстояниях между атомами.
6. Уравнения
В этой главе речь пойдет об уравнениях с одним неизвестным и
о некоторых процессах и явлениях в химии и физике, которые мож-
но описать этими уравнениями. Простые линейные или квадратные
уравнения можно легко решить с помощью ЭВМ по программам
для расчетов по формулам. Хотя алгебраические уравнения третьей
и четвертой степени еще можно решить аналитическими методами,
соответствующие формулы настолько сложны, что численные ме-
тоды имеют неоспоримые преимущества. Неразрешимы в элемен-
тарных функциях, например, следующие уравнения:
хб + 4х5 — 5х4 + х3 + Зх2 — Str + 11 - О
х2 = sin(x)
С последним уравнением мы уже сталкивались в задании 3.
В этой главе будут рассмотрены следующие типы уравнений:
алгебраические уравнения, например
х7 + Зх4 - 8х2 - 17х + 1 = О
трансцендентные уравнения, например
10г2 = е*2
неявные функции, например
e-(r2 + z2) _ хг^
Неявные функции относятся к более сложным типам уравнений,
поскольку включают два неизвестных. Решением уравнения этого
типа является таблица, содержащая все пары чисел х, z, которые
удовлетворяют данному уравнению. Функцию, которую нельзя
представить в виде комбинации элементарных функций, изобража-
ют графически, откладывая значениях, z на диаграмме.
Для поиска общих методов решения уравнений трех типов при-
ведем их к единому виду:
/W = о
Алгебраическое уравнение в исходной форме уже имеет этот вид.
Уравнения 109
Трансцендентное уравнение в этой «нормальной форме» выглядит
следующим образом:
/(г) = 10г2 - е*2 = 0
и неявная функция имеет вид
/(х) = е-^2 + г2) — xh — z^x3 — 0
Это выражение следует рассматривать как функцию переменной
х; z считается параметром, которому присвоено определенное зна-
чение. Тогда выражение, заданное неявной функцией, будет функци-
ей только одной переменной х. Эта функция на заданном отрезке
может обращаться в нуль один или несколько раз или же вообще
не иметь нулевых значений. Таким образом, в результате простых
преобразований рассматриваемая общая задача свелась к поиску та-
ких значений аргумента, при которых функция /(г) обращается в
нуль.
6.1. Метод деления отрезка пополам
При изложении этого материала мы не будем касаться таких
важных для математиков «тонкостей», как непрерывность, диффе-
ренцируемость и т. д. Будем просто считать, что функции «хоро-
шие»*.
Как бы мы искали корни, например трансцендентного уравне-
ния, если бы располагали достаточным временем, терпением и (на-
стольной) ЭВМ? Сначала мы попытались бы выяснить, существу-
ют ли вообще такие значения аргумента, при которых функция f (х)
обращалась бы в нуль. Уравнение имеет действительные корни в
том случае, если найдутся два значения аргументах! их2, для кото-
рых и/(х2) имеют различные знаки.
В нашем примере для трансцендентного уравнения
/(0) = - 1 < 0
/(1) = 10 - е > 0
Таким образом, корень этого уравнения лежит между 0 и 1.
Это, конечно, не значит, что на данном отрезке имеется только
* Непрерывность и дифференцируемость являются не математическими «тонко-
стями», а основными свойствами функций. И только в том случае, если функции не-
прерывны и дифференцируемы на отрезке, на котором ищутся корни уравнения,
применимы методы решения уравнений, рассматриваемые в этом разделе. — Прим,
перев.
но
Глава 6
один корень. Кроме того, другие корни могут лежать вне отрезка
[О, 1]. Чтобы найти корень данного уравнения на отрезке [0, 1],
есть смысл вычислить значение функции на середине отрезка, т. е.
при х = 0,5:
/(0,5) = 1,2156 > 0
Следовательно, корень уравнения лежит между 0 и 0,5. Следующая
попытка предпринимается при х = 0,25:
/(0,25) = -0,43949 < 0
т. е. корень должен лежать между 0,25 и 0,5. С каждым новым ша-
гом этой процедуры отрезок, на котором лежит корень уравнения,
уменьшается в два раза. Если отрезок становится достаточно ма-
лым (это определяет пользователь), то деление пополам можно
прекратить. В рассмотренном примере корень уравнения с точнос-
тью до четырех значащих цифр на отрезке [0, 1] равен 0,3344.
Остальные корни, найденные тем же методом, равны -0,3344,
+ 1,8913 и — 1,8913. Приведенный рисунок поясняет принцип дейст-
вия метода.
/(/о) >
т. е. /
/<Л> >
т. е. /2
/(/г) >
т. е. /3
fd3) >
т. е. /4
0 > /(го)
= /0 и
0 > /(Г1)
= (/1 + г,)/2 и
0 > /(Гг)
= /2 и
0 > /(г3)
= (/3 + г3)/2 и
/[(/0 + rJ/2] < 0
г 1 = (!о + г о)/2
/КЛ + rJ/2] > 0
г2 = г,
/[(/2 + rJ/2] < 0
г3 = (/2 + Г2)/2
/[(/3 + г3)/2] > 0
г4 = г3
Схема 5
о
100
200
зоо
500
600
800
5000
5500
5600
5800
6000
6100
И2
Глава 6
(1) (2) (3) (4)
(5)
(6)
Уравнения
113
Рассмотренный метод называется методом деления отрезка по-
полам (или методом полуинтервалов), поскольку отрезок, содержа-
щий корень уравнения, после очередной итерации делится пополам.
Программа, использующая этот численный метод решения уравне-
ний, предусматривает однократный поиск двух значений аргумента,
при которых значения функции имеют разные знаки, и итерацион-
ную процедуру деления отрезка пополам. Блок-схема такой про-
граммы приведена выше (схема 5).
8-81
114
Глава 6
Блок-схема составлена таким образом, что если значения функ-
ции в начале и конце отрезка имеют один и тот же знак, то выпол-
няется вторая часть программы (строка 1000). Отрезок [А, Е] де-
лится не более чем на 1000 частичных отрезков и на каждом прове-
ряется, не меняет ли функция знак на одном из них. Если на грани-
цах всех частичных отрезков функция имеет один и тот же знак, то
делается вывод, что на заданном отрезке решений нет. Если обна-
ружен частичный отрезок, на котором функция меняет знак, то его
верхняя граница считается концом нового отрезка, и на нем дол-
жно быть по крайней мере одно решение. Затем управление возвра-
щается первой части программы, в которой и реализован, соб-
ственно говоря, метод деления отрезка пополам. Если верхнюю
границу частичного отрезка взять как начальную точку нового от-
резка, то можно найти другой корень уравнения. Если значения
функции на обеих границах отрезка имеют один и тот же знак, то
на этом отрезке или вообще нет решений, или число их четное.
Ниже приведена распечатка программы «ПОЛ-ДЕЛ», соот-
ветствующая этой блок-схеме. Стоящие справа числа в блок-схеме
совпадают с номерами строк программы «ПОЛ-ДЕЛ».
0 REM "ПОЛ-ДЕЛ" EBERT/EDERER 81060Э
1 REM***********************************
2 REM** ПОИСК КОРНЕЙ УРАВНЕНИЯ »*
3 REM#* ВИДА F (Х)= 0 **
4 REM** МЕТОДОМ ДЕЛЕНИЯ ОТРЕЗКА **
5 REM** ПОПОЛАМ **
б REM** ФУНКЦИЯ F (X) ОПИСАНА **
7 REM** В СТРОКЕ 100 **
9 REM*****#*********************#***^^**
100 DEF FNF<X>»23+X*<-17*X*<2*X*<-3*X*<1*. 1»Х> > •> >
200 INPUT "ГРАНИЦЫ ПОИСКА" ; А, Е
300 INPUT "АБСОЛЮТНАЯ ТОЧНОСТЬ РЕШЕНИЯ "; ЕР
500 yi«fnf<r:> «print »яг’> - ";Vi
600 72«FNF<E)SPRINT “VC'/E;") « ";V2
900 IF SGN<V1)»-SGN<V2) THEN 5000
10GG N-10
1100 H«<E-RVN
12G0 FOR I«1 TO N-l
1300 V9»FNF<A+I#H>
1400 IF SGN<V9)«SGN<V1) THEN 1700
1500 E«A+I*H
1600 GOTO 5000
1700 NEXT I
1900 N»N*18
1900 IF N<«1000 THEN 1100
2000 PRINT "РЕШЕНИЯ HE НАЙДЕНО"
2100 STOP
5000 НАЧАЛО ПРОЦЕДУРЫ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
5500 V1«FNF<A> «PRINT ” V< " /А; '• > s "/VI
5600 V2»FNF<E> SPRINT "V<*‘.sE/"> = ",sV2
5800 IF ABS<R-E:><ABS<EP.) THEN 9000
6000 Ms<A+E>/2
6108 V3»FNF<r-n
6200 IF SGN<V3>»SGN<VI> THEN 6600
Уравнения
115
6400 E=M:GOTO 5000
6600 A.MlGOTO 5000
9000 PRINT «PRINT ’’КОРЕНЬ = " ;
9100 PR I NT <E+R>/211ABSC (E-AV
9999 END
RUN
ГРАНИЦЫ ПОИСКА? О, 2
АБСОЛЮТНАЯ ТОЧНОСТЬ РЕШЕНИЯ? .1
Y< 0 > = 23
Y< 2 > » -7.8
Y< 0 > » 23
Y< 2 > = -7.8
V< 1 > = 6.1
V< 2 > » -7.8
Y< 1 > = 6.1
V< 1.5 > = -2.303125
V< 1.25 > = 1.76220703
V< 1.5 > = -2.303125
V< 1.25 > = 1.76220703
V< 1.375 > » -.326626587
V< 1.3125 > » .706888294
V< 1.375 > » -.326626587
КОРЕНЬ = 1.34375+/-.03125
RERDV.
Функция, входящая в уравнение, задана в строке 100 как опреде-
ляемая функция. В качестве примера решено алгебраическое уравне-
ние пятой степени:
/(г) = 0,1г5 + х4 - Зх3 + 2х2 - 17х + 23 = 0
Если переписать этот полином в порядке увеличения показателя
степени при аргументе и провести элементарные преобразования,
то получится
/(х) = 23 — 17х + 2х2 — Зх3 + х4 + 0,1х5 = 0 или
/(х) = 23 + х(-17 + х[2 + х(-3 + х(1 + 0,1х))])
При этом не совсем обычном способе написания полинома вместо
возведения в степень используются только умножение и сложение.
При записи полинома в такой форме, которая называется схемой
Горнера, соответствующее уравнение решается с помощью ЭВМ
значительно быстрее.
Деление отрезка пополам начинается со строки 5000. Значения
функции на границах отрезка вычисляются в строке 5500 и выво-
дятся на экран в строке 5600. Это дает информацию о промежуточ-
ных результатах. Закончить ли вычисления или продолжать расчет
дальше, решается в строке 5800. В ней сравниваются длина отрезка
на данной итерации и требуемая точность результата, которая за-
дана в строке 300. Критерий устойчивости решения, используемый
8*
116
Глава 6
в программе «ПОЛ-ДЕЛ», для некоторых уравнений не дает удов-
летворительных результатов, поскольку требуемую точность ре-
зультата надо задать, не приступая к расчетам. Конечно, можно
использовать другие критерии. Например, потребовать, чтобы точ-
ность вычисления корней уравнения составляла одну миллионную
от исходного отрезка. Кроме того, можно задать число итераций,
например ограничивая наибольшее значение параметра цикла FOR-
NEXT. Пожалуй, единственное, что невозможно выполнить, так
это продолжать расчеты до тех пор, пока не совпадут нижняя и
верхние границы частичного отрезка. Попробуйте это сами, заме-
ните строку 5800 на
5800 IF А = Е THEN 9000
и понаблюдайте, что произойдет. Скорее всего, вы обнаружите,
что при такой конструкции оператора условного перехода вычисле-
ния в цикле будут продолжаться бесконечно долго.
Поиск середины отрезка и вычисление значения функции на сере-
дине отрезка происходят в строках 6000 и 6100. В строках 6200,
6400 и 6600 выясняется, является ли новый половинный отрезок ле-
вой или правой частью старого отрезка. Промежуточное значение
корня, соответствующее середине частичного отрезка, вместе со
средним отклонением, равным полуширине частичного отрезка,
выводится на экран в строках 9000 и 9100. Таким образом, получа-
ется более или менее удовлетворительное приближенное значение
корня уравнения, которое учитывает значения функции на обоих
концах отрезка. В приведенном примере функция f (х) обращается в
нуль при х ~ 1,35508, однако это не единственный корень уравне-
ния.
Происходит ли переход к поиску корней делением отрезка попо-
лам сразу или сначала надо найти отрезок, на концах которого зна-
чения функции имеют разные знаки, решается в строке 800. Для
этого используется стандартная функция SGN (сокращ. от signum),
называемая также знаком числа. Если Y1 и Y2 разного знака, то
оператор условного перехода в строке 800 передает управление
строке 5000. Этот фрагмент программы функционирует следую-
щим образом. Функция SGN(x) принимает значение + 1, если х —
положительное число, — 1, если х — отрицательное число, и 0, если
х равен нулю. В строке 800 сравнивается число + 1 или — 1 с чис-
лом +1 или - 1. Функция SGN используется также в строках 1400
и 6200. Если знаки значений функции на выбранном отрезке одина-
ковы, то для поиска частичного отрезка, на котором функция меня-
Уравнения
1 i
ет знак, исходный отрезок разбивается на частичные (не более чем
на 1000).
Задание 55. Сравните время выполнения программы «ПОЛ-ДЕЛ», когда поли-
ном задан в соответствии со схемой Горнера и в обычной форме.
Задание 56. По программе «ПОЛ-ДЕЛ» можно считать в два раза быстрее, если
после каждой итерации вычислять значение функции только на новом конце отрезка.
Составьте соответствующую программу. Прн этом в программе «ПОЛ-ДЕЛ» надо
заменить всего две строки.
6.2. Метод Ньютона (метод касательных)
Для большей наглядности рассмотрим рисунок.
Пусть при поиске корня получено значение х, (это значение мож-
но считать начальным приближением). Сначала рассчитывают зна-
чение функции при х = х.. Затем проводят касательную к графику
функции fix) в точке с координатами х,, f QCj) и находят точку пере-
сечения этой касательной с осьюх. Точка пересечения рассматрива-
ется теперь как новое приближенное значение корня, и описанная
процедура повторяется с новым значением х. Как видно из рисунка,
точки пересечения касательных с осью х быстро сходятся к точке
пересечения графика функции/(х) с осьюх. Конечно, можно подо-
брать такие функции, для которых метод касательных неэффекти-
вен.
Касательную в точке х можно построить с помощью производ-
ной d/(x,)/dx. Из рассмотрения треугольника, образованного f(х,),
х; их/+1, следует
W,)
dx
= Г (*,)
/(*,)
Xi ~ Xi+i
118
Глава 6
После простых преобразований получается итерационная фор-
мула метода Ньютона:
Из этой рекурентной формулы видно, что на каждом итерацион-
ном шаге используется как значение функции/(г,), так и значение
производной f (х,)- Кроме того, необходимо задать начальное зна-
чение х, от которого зависят достоверность результата и время, не-
обходимое для его получения.
Блок-схема алгоритма решения уравнений по методу Ньютона
выглядит следующим образом (схема 6):
Схема 6
Уравнения
119
Блок-схема не содержит всех деталей программы; она передает
липп> основные черты алгоритма. Так, например, в блок-схеме пе-
ред итерационной процедурой пропущен оператор условного пере-
хода, который проверяет условие: f (г) = 0? Если f (г) = 0, то
произойдет деление на 0 и выполнение программы будет прервано.
Геометрически это означает, что касательная параллельна оси х и
нигде ее не пересекает. Аналогично функционирует оператор услов-
ного перехода при выяснении того, достигнута ли желаемая точ-
ность. О том, что существуют различные критерии сходимости, из-
вестно из обсуждения программы «ПОЛ-ДЕЛ». Ниже приведена
распечатка программы «НЬЮТОН».
0 REM "НЬЮТОН” EBERT/EDERER 810609
1 REM********************************** *******
2 REM** РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ НЬЮТОНА**
9 REM********************************** ****** *
100 DEF FNF<X>-10*XT5-EXP<X*X>
200 DEF FND<X>-50*XT4-2*X*EXP<X»X>
1100 INPUT "НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ"; T
1200 Y-FNF<T>
1300 V1-FND<T>
1400 IF ABS<Y1 XIE-20 THEN 1100
1900 Tl-T-V/Vl
1000 IF RBS<T-TlXRBS<T*lE-7> THEN 3000
1700 T»T1(GOTO 1200
300© PRINT "KOPEHb = "; (T + TD/2
3100 PRINT "ЗНАЧЕНИЕ ФУНКЦИИ = "; Y
9999 END
RUN
НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ? 1
КОРЕНЬ = .694940033
ЗНАЧЕНИЕ ФУНКЦИИ = 2.1769652Е-07
RUN
НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ?5
КОРЕНЬ = 2.69402396
ЗНАЧЕНИЕ ФУНКЦИЙ = -4.17957083Е-04
«НЬЮТОН» — очень короткая программа. В строке 100 описа-
на входящая в уравнение функция f (х), в строке 200 — ее производ-
ная f (х). Необходимость вводить производную в аналитическом
виде является существенным недостатком метода Ньютона; для
сложных и громоздких выражений это вызывает серьезные затруд-
нения. Кроме того, ручное дифференцирование может стать источ-
ником ошибок, о которых часто даже и не подозревают.
В строке 1100 пользователем задается начальное приближение.
В строке 1200 переменной Y присваивается значение функции в этой
начальной точке и в строке 1300 переменной Y1 присваивается зна-
чение производной f (х) в этой точке. Затем выясняется, не сли-
шком ли малб значение производной. Геометрически это равно-
120
Глава 6
сильно вопросу, не очень ли полого расположена касательная. Если
значение производной слишком мало, то последует повторный за-
прос на ввод более приемлемого начального приближения, для чего
предусмотрен переход на строку 1100. Потому следует проверка
сходимости результата; проверяется, совпадают ли в значениях х,
полученных в последних двух итерациях, первые 7 знаков. Если со-
впадают, то управление передается оператору вывода (строки 3000
и 3100). Если требуемая точность еще не достигнута, то новое зна-
чение х присваивается переменной Т и оператор GOTO передает
управление строке 1200, с которой начинается очередной шаг итера-
ции.
Если вы опробуете эту программу, то увидите, что время счета
в значительной степени зависит от начального приближения. Мо-
жет также случиться, что выполнение программы будет приоста-
новлено из-за переполнения (Overflow-Error). Выяснить возможно-
сти и недостатки программы «НЬЮТОН» вам помогут задания 57
и 58.
Задание 57. Расширьте программу «НЬЮТОН» так, чтобы на экран выводились
промежуточные результаты, т. е. результаты отдельных итераций.
Задание 58. Так как программа «НЬЮТОН» при неудачно выбранных началь-
ных приближениях выполняется очень долго, это задание направлено на ее дальней-
шее улучшение. Ограничьте максимальное число итераций. Если это значение будет
превышено, то выполнение программы должно заканчиваться выводом на экран со-
ответствующего сообщения.
6.3. Метод хорд (правило пропорциональных частей)
Другим часто используемым приближенным методом вычисле-
ния корней уравнений является метод хорд (правило секущих, пра-
вило ложного положения, regula falsi. — Прим, перев.); он очень
Уравнения
12i
похож на метод Ньютона. Главное его преимущество состоит в
том, что не надо вводить в программу аналитическое выражение
для производной. При рассмотрении метода будем руководство-
ваться рисунком.
Поиск точки, в которой функция обращается в нуль, начинается
с того, что через две точки, лежащие на графике функции/(х), про-
водят прямую. Точку пересечения этой прямой с осьюх принимают
за новое значение х. Как показано на рисунке, такие построения да-
ют набор лучей:
/(у,) - 0 _ Ду,-1) - о
х,-х/+1 х,_, - х/+1
Эта формула отличается от итерационной формулы метода
Ньютона только тем, что производная в формуле Ньютона замене-
на отношением конечных приращений функции и аргумента. К со-
жалению, эта замена связана с двумя недостатками. При решении
уравнений методом хорд необходимо задавать два начальных зна-
чения независимой переменной, и, кроме того, сходимость резуль-
татов в большинстве случаев достигается медленнее по сравнению
с методом Ньютона.
Ниже приведены блок-схема алгоритма решения уравнений ме-
тодом хорд (схема 7) и программа.
0 REM "ХОРДА" EBERT/EDERER 810609
1 REM»*»»»»»*»»»»»»»»»»»»***»*»»»*»»»»
2 REM** РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ »*
3 REM»» ХОРД **
9 REM*********************************
100 DEF FNF<X>-<X-4:>»<X-2.3>*<X+2.1>*<Х+3.34>
1000 INPUT "ИНТЕРВАЛ [ А, Е] А, Е
1100 INPUT "ВЫВОДИТЬ ПРОМЕЖУТОЧНЫЕ РЕЗУЛЬТАТЫ"; А$
1200 X0=AiXl=E
1300 Y0»FNF<X0>
1400 Y1=FNF<X1>
1500 IF ABS<X0-X1><RBS<X0»lE-7> THEN 3000
1600 IF RBS<Y0-Y1><ABS<Y041E-25? THEN 1000
1700 X»X1-<X1-X0>/<Y1-Y0>*Y1
1800 IF Я»О"ДА" THEN 2000
1900 PRINT X0;Y0,X1;Y1
2000 X0=X1sXl=X>GOTO 1300
3000 PRINT "КОРЕНЬ = (XO + XD/2
3100 PRINT "ЗНАЧЕНИЕ ФУНКЦИИ = ',’ (Y 0+Y1)/2
9999 END
ИНТЕРВАЛ [A,E] ? 3,5
ВЫВОДИТЬ ПРОМЕЖУТОЧНЫЕ РЕЗУЛЬТАТЫ? N
КОРЕНЬ = 3.99999995
ЗНАЧЕНИЕ ФУНКЦИИ = -3.79252708Е-06
READY.
RUN
ИНТЕРВАЛ [A, Ej ? 2,3
ВЫВОДИТЬ ПРОМЕЖУТОЧНЫЕ РЕЗУЛЬТАТЫ? N
122
Глава 6
КОРЕНЬ = 2.3
ЗНАЧЕНИЕ ФУНКЦИИ = О
RERDV.
RUN
ИНТЕРВАЛ [А. Е] ? 1.8,1.9
ВЫВОДИТЬ ПРОМЕЖУТОЧНЫЕ РЕЗУЛЬТАТЫ? N
КОРЕНЬ = 2.299999995
ЗНАЧЕНИЕ ФУНКЦИИ = 2.3377486Е-06
RERDV.
Схема 7
Уравнения
123
Программа «ХОРДА» также очень короткая; функция, входя-
щая в уравнение, задана в строке 100. Для большей наглядности
она задана в виде произведения линейных двучленов. Все корни
этого уравнения очевидны. В отличие от программы «НЬЮТОН»
отсутствует строка 200, зато в строке 1000 необходимо ввести два
начальных значения неизвестной величины, которые присваиваются
переменным А и Е. С помощью конструкции в строке 1000 у поль-
зователя запрашиваются два числа. Совершенно не обязательно,
чтобы корень уравнения лежал между этими числами. Лучше вы-
брать близкие, но обязательно различающиеся значения х.
Для обоих выбранных значений х в строке 1300 и 1400 рассчиты-
ваются соответствующие значения функции. Участок программы
от строки 1300 до строки 2000 занимает итерационная процедура. В
строке 1500 происходит проверка результата на сходимость. Если
оба последних значения х достаточно близки, то управление перехо-
дит к оператору вывода данных в строке 3000. В строке 1600 выяс-
няется, не слишком ли мала разность между обоими значениями
функции. Если эти значения близки (хорда близка к горизонтали),
то происходит передача управления оператору INPUT (строка 1000)
и ЭВМ запрашивает новые начальные значения х. Новое текущее
значение х рассчитывается в строке 1700. В строке 2000 переменная
X высвобождается для следующей итерации. Для этого значение
переменной X присваивается переменной XI после того, как ее зна-
чение было присвоено переменной Х0 (предыдущее значение Х0 при
этом утрачивается). Переменная XI имеет теперь значение корня
уравнения, вычисленного в этой итерации, и управление передается
строке 1300.
Программа «ХОРДА» содержит три строки, которые еще не
обсуждались. Первая — это строка 1100 с оператором INPUT. В
ней содержится вопрос, на который пользователь должен ответить
«ДА» или «НЕТ». Ответ присваивается текстовой переменной А$.
В строке 1800 с помощью оператора IF проверяется, отличается ли
значение переменной А$ от текста «ДА». Если А$ имеет значение
«НЕТ», то управление передается строке 2000, минуя оператор
PRINT в строке 1900, в котором выводятся на экран промежуточ-
ные результаты. Если условие, проверяемое оператором IF, не вы-
полняется, т. е. переменная А$ имеет значение «ДА», то после каж-
дой итерации на экран будет выводиться промежуточный резуль-
тат.
Оператор условного перехода с текстовыми константами и тек-
стовыми переменными начинается с ключевого слова IF:
124
Глава 6
tttttttttttt Оператор с текстовыми
*** if *** константами и текстовы-
************ ми переменными
Конструкция оператора условного перехода с текстовыми кон-
стантами и переменными функционирует точно так же, как и рас-
смотренные ранее конструкции оператора IF. Надо только знать,
по каким признакам сравниваются текстовые постоянные и пере-
менные.
Сравнение текстов с помощью операций РАВНО (=) и НЕ РАВ-
НО (< >), по-видимому, не требут объяснений. Операции отноше-
ния МЕНЬШЕ (<) или БОЛЬШЕ (>) учитывают только лексико-
графическую конструкцию текста: «КОЛБА», например в этом
смысле меньше, чем «ХИМИЯ», а «УГОЛ» меньше, чем «УГОЛЬ-
НИК».
Задание 59. С помощью программ «НЬЮТОН», «ХОРДА» и «ПОЛ-ДЕЛ» по-
стройте график следующей неявной функции:
е-^2 + '2> =
предварительно заполнив следующую таблицу
X 4 2 1 0,9 0,8 0,6 0,5 0,4 0,2 0,1 0,05
У
Задание 60. Составьте таблицу значений неявной функции
(х + у \
--------------- I
10 /
и постройте ее график.
Теперь рассмотрим использование численных методов решения
уравнений применительно к некоторым конкретным задачам науч-
ного и инженерно-технического содержания.
6.4. Термо-э.д.с. термопары Ni — Cr/Ni
Обычно измерение термо-э.д.с. проводят двумя соединенными
навстречу друг другу термопарами, например термопарами
Ni — Cr/Ni. При этом один спай термостатируют при О °C, в то
время как другой имеет температуру объекта. Экспериментально
полученную зависимость термо-э.д.с. от температуры в определен-
ном температурном интервале обычно описывают полиномом. Это
делают с помощью так называемой линейной регрессии (см. с. 185).
Уравнения
125
Пусть разность э.д.с. холодного и горячего спаев термопары и
температура горячего спая связаны следующей зависимостью:
С = 25,4498 И - 0,559195К2 + 0,10452439V3 -
- 8,776153-10-3К4 + 3,76041 10-4К5 - 8,64943-Ю 6V6 +
+ 1,021005-10-7 К7 - 4,891009-10-9 10 К8
V — термо-э.д.с., мВ; С — температура, °C.
Необходимо указывать размерность при представлении резуль-
татов измерений в виде полинома. Зная, в каких единицах измеря-
ются температура и э.д.с., можно легко найти размерности отдель-
ных коэффициентов полинома.
Если поставлена обратная задача, т. е. спрашивается, каково
значение термо-э.д.с. при данной температуре, то ответ можно
дать в виде таблицы или программы. Для этого мы используем
уже рассмотренную программу «ПОЛ-ДЕЛ».
е REtl'TEPMO—ЭДС-’EBERT/EDERER 010610
1 REM*********************************
2 REM** ЭДС ТЕРМОПАРЫ NI-CRNI **
3 REM** ПРИ ЗАДАННОЙ ТЕМПЕРАТУРЕ, **
4 REM** ВЫРАЖЕННОЙ В ГРАД. С **
3 REM** ЭДС - В МВ, **
€ REM** ПРИ ТЕМПЕРАТУРЕ **
7 REM** ХОЛОДНОГО СПАЯ О ГРАД. С **
9 REM*********************************
51 К1-23.4497
32 К2—.339193
53 КЗ».19432439
54 К4—8.776153Е-3
35 КЗ-З.76041Е-4
36 Кб—8.64943Е-6
37 К7-1.021003Е-7
38 К8—4.891009Е-10
100 DEF FNF<X)«K1*X+K2*X*X+K3*X*X*X+K4*XT4
+K3*Xt3+K6*Xt6+K7*Xt7+K8*Xt8-TE
150 INPUT "ТЕМПЕРАТУРА В ГРАД. С": ТЕ
200 Я—б iE-35
300 ЕР-.001
300 V1«FNF<A)tREM PRINT "7<"лАГ‘> « "jYl
600 V2«FNF<E) iREM PRINT ,,V<,,jEj,‘) = “jV2
800 IF SGN<71 >— SGNCY2) THEN 3000
1000 N-10
1100 H«<E-A>/N
1200 FOR 1-1 TO N-l
1380 V9«FNF<A+I*H)
1400 IF SGN<Y9)-SGN<V1) THEN 1700
1500 E«A+I*H
1600 GOTO 3000
1700 NEXT I
1800 N-N*10
1900 IF N<«1000 THEN 1100
2880 PRINT "РЕШЕНИЯ HE НАЙДЕНО"
2100 STOP
126
Глава 6
5000 REM НАЧАЛО ПРОЦЕДУРЫ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
5500 V1-FNF<R>iREM PRINT = "1V1
5600 V2-FNFCE)iREM PRINT "V<")E)"> - "1V2
5800 IF RBS<R-EXRBS<EP> THEN 9000
6000 M«<R+E>/2
6100 V3-FNFCM>
6200 IF SGN<V3>-SGN<V1> THEN 6600
6400 E-MiGOTO 5000
6600 R-M i GOTO 5000
9000 PRINT "ЭДС ТЕРМОПАРЫ NI—«CRNI "
9100 PRINT "ПРИ"; ТЕ; "ГРАД. С"
9200 PRINT INT(50*(A+E)+ .51/100; "MB"
9999 END
RUN
ТЕМПЕРАТУРА В ГРАД. С ? 200
ЭДС ТЕРМОПАРЫ NI-CRNI
ПРИ 200 ГРАД. С
8.18 МВ
RERDV.
Программа «ТЕРМО-ЭДС» от строки 1000 до строки 6600 со-
впадает с программой «ПОЛ-ДЕЛ», за исключением участка выво-
да промежуточных результатов.
Указанный выше полином надо представить в виде функции, ко-
торая обращается в нуль при искомом значении термо-э.д.с. В дан-
ном случае надо просто перенести С (температуру) в правую часть.
Этот полином задан в строке 100 в виде определяемой функции.
Значения восьми коэффициентов полинома заданы в тексте про-
граммы (строки 51—58) перед определяемой функцией. Значение
температуры запрашивается с помощью оператора INPUT. Если
ввести значение температуры (переменная ТЕ), то задача сводится
к решению уравнения, заданного в строке 100. Для этого в строке
200 задаются границы отрезка, внутри которого находится корень
уравнения. Физический смысл имеют значения термо-э.д.с. в интер-
вале -б-;- + 55 мВ, поэтому эти значения выбраны в качестве гра-
ниц отрезка. (По формуле можно было бы вычислить термо-э.д.с.
и при 5000 °C, но какая термопара выдержит такую температуру?)
Требуемая точность также связана с физическим содержанием зада-
чи. Точность измерения термо-э.д.с. обычно не превышает 1 мкВ.
Поэтому переменной ЕР в строке 300 присвоено значение 0,001.
В этой прикладной программе необходим вывод данных в обще-
принятых единицах измерения и с разумным числом значащих
цифр. В строке 9200 вычисленное значение (А + Е)/2 округляется
до двух значащих цифр после запятой с помощью стандартной
функции INT. Напоминаем, что эта функция у любого действитель-
ного положительного числа отбрасывает все цифры, стоящие после
Уравнения
127
десятичной запятой. Если число отрицательное, то к нему, кроме
того, прибавляется — 1. В строке 9200 результат сначала умножает-
ся на 100, произведение увеличивается на 0,5 (тем самым происхо-
дит округление до ближайшего целого числа), потом отбрасывают-
ся цифры после запятой и, наконец, полученное целое число делит-
ся на 100.
Задание 61. Модифицируйте программу «ТЕРМО-ЭДС» так, чтобы можно было
рассчитывать по выбору или термо-э.д.с., исходя из значения температуры, или
температуру, исходя из значения термо-э.д.с.
Задание 62. Напишите программу, аналогичную программе «ТЕРМО-ЭДС», в
которой для решения уравнения использовался бы метод Ньютона или метод хорд.
6.5. Персистентная длина молекулы полимера
Если в растворе молекула полимера не имеет определенной фик-
сированной третичной структуры, например, в гелях, то ее можно
рассматривать как «статистический* клубок». Для описания пове-
дения таких макромолекул в качестве модели обычно используют
так называемый «эрзац-клубок Куна»**. В то время как в реальной
полимерной цепи отдельные связи и углы между ними достаточно
жесткие и имеет место лишь более или менее заторможенное вра-
щение, свободно сочлененная цепь состоит из небольших, одинако-
вых, соединенных друг с другом участков***, статистически ориен-
тированных по отношению друг к другу. Длину этих участков на-
зывают персистентной длиной. Спрашивается, какова персистент-
ная длина свободно сочлененной цепи, обладающей такими же фи-
зическими свойствами, как и реальная цепочечная макромолекула?
По персистентной длине можно судить о жесткости молекулы по-
лимера. Среднеквадратичное расстояние между концами свободно
сочлененной цепи / и ее радиус инерции г связаны с персистентной
длиной а соотношением * * * *
г а " т ~ ( е
Перенесем г2 в правую часть и будем рассматривать ее как
функцию/(а) с параметрами г nl. Радиус инерции г можно опреде-
лить экспериментально, исходя из угловой зависимости рассеяния
света в видимой части спектра. Среднеквадратичное расстояние
между концами персистентной цепи можно определить непосредст-
• Гауссов. — Прим, перев.
** Имеется в виду свободно сочлененная цепь. — Прим, перев.
’"Их называют сегментами Куна. — Прим, перев.
Garg S. К., Stivala S. S., J. Pol. Sci. Pplym. Phys., 16, 1419—1434 (1978).
128
Глава 6
венно из рассеивания рентгеновского излучения при малых углах.
Это расстояние можно также оценить, исходя из молекулярной
массы и длины одного звена полимерной цепи. Для решения напи-
санного выше уравнения мы опять используем метод деления
отрезка пополам. Ниже приведена программа для расчета перси-
стентной длины молекулы полимера с конкретными примерами.
0 REM "ПЕРСИСТ" EBERT/EDERER 820325
1 REM*********************************
2 REM** РАСЧЕТ ПЕРСИСТЕНТНОЙ ДЛИНЫ **
3 REM** ПОЛИМЕРА ПРИ ЗАДАННОМ **
4 REM** РАДИУСЕ ИНЕРЦИИ R И- **
5 REM** КОНТУРНОЙ ДЛИНЕ L *•
6 REM** (В АНГСТРЕМАХ). **
? REM** в ЭТОЙ ПРОГРАММЕ ИСПОЛЬЗО- **
8 REM** ВАНА ПРОГРАММА "ПОЛ-ДЕЛ" **
9 REM*********************************
50 INPUT "РАДИУС ИНЕРЦИИ В АНГСТРЕМАХ R
68 INPUT "КОНТУРНАЯ ДЛИНА В АНГСТРЕМАХ"; L
100 DEF FNF<R>-R*R*<L/3/R-l+2*R/L-2*<1-EXP<-L/R>>*R/L*R/L>-R*R
200 R-.0001iE-100000
300 EP-.0001
500 Y1«FNF<R>
600 Y2-FNF<E>
880 IF SGN<Y1> — SGN<Y2> THEN 5000
1000 N>10
1100 H-<E-R>/N
1200 FOR 1-1 TO N-l
1300 Y9-FNFCR+I*H>
1400 IF SGN<Y9>-SGN<Y1 > THEN 1700
1500 E-R+I*H
1600 GOTO 5000
1700 NEXT I
1000 N-N*10
1900 IF NC-1000 THEN 1100
2000 PRINT "РЕШЕНИЯ HE НАЙДЕНО "
2100 STOP
5000 REM НАЧАЛО ПРОЦЕДУРЫ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
5800 IF RBS<R-EXRBS<EP> THEN 9000
6000 M-<R+E>/2
6100 Y3-FNF<M>
6200 IF SGN<Y3>-SGN<Y1> THEN 6600
6400 E-MiY2-Y3iG0T0 5000
6600 R-MiYl-Y3iG0T0 5000
9000 PRINT iPRINT "ПЕРСИСТЕНТНАЯ ДЛИНА В АНГСТРЕМАХ = "
9100 PRINT <E+R>/2j"+/-'• ;RBS<<E-R>/2>
9999 END
RUN
РАДИУС ИНЕРЦИИ В АНГСТРЕМАХ? 8940
КОНТУРНАЯ ДЛИНА В АНГСТРЕМАХ? 8900000
ПЕРСИСТЕНТНАЯ ДЛИНА В АНГСТРЕМАХ =
26.9407941 +/- 4.65661287Е-05
RERDY.
RUN
РАДИУС ИНЕРЦИИ В АНГСТРЕМАХ? 20
КОНТУРНАЯ ДЛИНА В АНГСТРЕМАХ? 200
ПЕРСИСТЕНТНАЯ ДЛИНА В АНГСТРЕМАХ =
6.61421322 +/- 4.65661287Е-05
RERDY.
Уравнения
129
Программа «ПЕРСИСТ» представляет собой несколько изме-
ненную программу «ПОЛ-ДЕЛ». Левая часть уравнения задана в
строке 100 в виде определяемой функции /(а). В строках 50 и 60
пользователь должен ввести числовые значения радиуса инерции г и
среднеквадратичного расстояния между концами свободно сочле-
ненной цепи /, выраженные в ангстремах. Отрезок, на котором
ищется решение уравнения, выбирается (строка 200) таким, чтобы
он включал все имеющие физический смысл значения персистент-
ной длины. Параметр, входящий в критерий сходимости решения,
задан в строке 300. Вывод данных (строки 9000 и 9100), как и в
предыдущем примере, учитывает содержание конкретной физико-
химической задачи.
Задание 63. Выясните, как зависит персистентная длина молекул полимера от
радиуса инерции г при постоянном среднеквадратичном расстоянии между концами
персистентной цепи /. Отобразите эту зависимость графически.
6.6. Расчет эффективности разделения при ректификации
Рассмотрим сначала проблему для идеальных смесей (т. е. для
таких растворов, давление пара над которыми описывается уравне-
нием Августа) при бесконечном флегмовом числе, полагая, что эф-
фективность тарелок близка к теоретической.
Зависимость давления пара компонентов бинарной смеси от
температуры можно описать следующими уравнениями:
Вещество 1: log(p^) = у +
Вещество 2: log(p^) = ~ + b2
Константы ар а2, Ьх иЬ2 зависят от природы веществ; их число-
вые значения можно найти в соответствующих справочниках. Зна-
чение констант зависит от того, в какой системе единиц измеряется
давление. Согласно закону Рауля, для давлений пара вещества над
смесью справедливы соотношения
Pi = х*-Р° пр2 = xf-p°2
х*— мольная доля вещества i в жидкой фазе; р°— парциальное давление вещества /
в газовой фазе.
Соответственно общее давление над газовой фазой ргаз будет
равно
/’газ = Pl + Рг = Х\Р° + ХтР2 = Х1Р° + (1 - *1)Р2
9-81
130
Глава 6
Если теперь учесть зависимость давления пара компонентов от
температуры и перенести все члены этого уравнения в его левую
часть, то получится функция
, U + *1 “г + Ь2
7(*1) = /’газ “ х1^ - (1 - ^1)еГ
которая обращается в нуль при интересующих нас значениях х, и Г.
Чтобы найти корни этого уравнения, необходимо знать значения
констант в], а2, Ьх иЬ2. Пусть общее давление равно атмосферному
(760 мм рт.ст.). Если теперь еще задать значение мольной доли
первого вещества в жидкой фазеХ] на первой теоретической тарел-
ке, то из полученного уравнения можно найти температуру кипения
раствора. Тогда по формуле для давления пара и из закона Рауля
можно рассчитать состав газовой фазы х( газ. Состав жидкой фазы
на второй тарелке ректификационной колонны такой же, как состав
газовой фазы на первой тарелке. Если продолжить расчет по этой
методике, то можно вычислить состав и температуру вдоль всей
ректификационной колонны. Ниже приведены блок-схема (схема 8)
и соответствующая ей программа для решения этой задачи («РЕКТИФ»),
Правая часть уравнения, по которому вычисляется температура
кипения, задается в виде определяемой функции в строке 100. Об-
щее давление составляет 760 мм. рт.ст. Затем вводятся физические
параметры др а2, Ьх и Ь2. В строках 500 и 600 вычисляются темпе-
ратуры кипения индивидуальных компонентов при 760 мм. рт.ст. В
строке 700 выясняется, у какого вещества наименьшая температура
кипения. Если вещество 1 имеет более низкую температуру кипе-
ния, то управление передается строке 1000. Если более легкокипя-
щим является вещество 2, то в строках 800, 900 и 920 вещество 1
переименовывается в вещество 2, а их термодинамические парамет-
ры обмениваются. Переменная А9 имеет теперь значение, которое
меньше или равно температуре кипения низкокипящей жидкости, а
переменная Е9 имеет значение, которое больше или равно темпера-
туре кипения высококипящего компонента. В следующих трех стро-
ках (1000—1200) у пользователя запрашивается мольная доля легко-
кипящего компонента на первой тарелке, значение которой присва-
ивается переменной XI. В строке 1300 вводится число теоретиче-
ских тарелок, для которого будет выполняться расчет. В строке
2000 счетчику тарелок присваивается начальное значение 1. Нижней
границей температурного интервала, внутри которого ищется тем-
пература кипения смеси, служит значение переменной А9, которое
не больше, чем температура кипения легколетучего вещества; верх-
Уравнения
131
Схема 8
9’
132
Глава 6
0 REM "РЕКТИФ" EBERT/EDERER 810610
1 REM*********************************
2 REM** РЕКТИФИКАЦИЯ ИДЕАЛЬНОЙ **
3 REM** СМЕСИ LOG(P) = A/T + B **
4 REM** НЕОБХОДИМО ЗАДАТЬ ЗНАЧЕНИЯ *
5 REM** АИВ КАЖДОГО КОМПОНЕНТА **
9 REM*********************************
100 DEF FNF<T>«X1*EXP<A1/T+B1> + <1-Х1>*ЕХР<А2/Т+В2>-760
200 INPUT "Al,Bl ";A1,B1
300 INPUT "A2,B2 ">A2,B2
500 A9»A1/<LOG<760>-B1>
600 E9=A2/<LOG<760>-B2>
700 IF A9CE9 THEN 1000
800 H-E9iE9-A9+lsA9=H-l
900 H-Al;Al-A2iA2«H
920 H-B1iВ1»B2 > B2-H
1000 PRINT "МОЛЬНАЯ ДОЛЯ ЛЕГКОКИПЯЩЕГО"
1100 PRINT "КОМПОНЕНТА";
1200 INPUT XI
1300 INPUT "ЧИСЛО ТАРЕЛОК"; 16
1500 PRINT iPRINT "ТАРЕЛ Х-ЖИДК Х-ГАЗ T КИП В C"
2000 15=1
2100 A=A9iE«E9
5000 REM НАЧАЛО ПРОЦЕДУРЫ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
5500 V1=FNF<A>
5600 V2-FNF<E>
5800 IF ABS<A-EXABS<A>/1E7 THEN 9000
6000 M-<A+E>/2
6100 Y3=FNF<M>
6200 IF SGN<V3>=SGN<VI> THEN 6600
6400 E=M|GOTO 5000
6600 A=MiGOTO 5000
9000 X3-X1*EXP < A1/А+В1>/760
9100 PRINT 151" "1
9110 PRINT INT<X1*10000>/10000J" " J
9125 PRINT INT<X3*10000>/10000;" ">
9130 PRINT INT<<A-273.15>*1000>/1000
9200 IF 16=15 THEN 9999
9300 15=15+1iXl=X3sG0T0 2100
9999 END
RUN
Al,Bl ? -3609.9,17.785
A2,B2 ? -3330.0,17.403
МОЛЬНАЯ ДОЛЯ ЛЕГКОКИПЯЩЕГО
КОМПОНЕНТА?.!
ЧИСЛО ТАРЕЛОК? 8
ТАРЕЛ Х-ЖИДК Х-ГАЗ ткип в
1 . 1 .2398 63.395
2 .2398 .4792 57.285
3 .4792 .736 48.877
4 .736 .8972 41.844
5 .8972 .9653 38.165
6 .9653 .9889 36.746
7 .9889 .9965 36.271
8 .9965 .9989 36. 12
ней границей этого интервала является значение переменной Е9, ко-
торое не меньше, чем температура кипения высококипящего ве-
щества. В строках 5000—6600 размещается ядро программы «ПОЛ-
ДЕЛ». Здесь происходит вычисление температуры кипения смеси.
Уравнения
133
После окончания итерационной процедуры управление передается
строке 9000, в которой вычисляется мольная доля легкокипящего
вещества в газовой фазе. В строках 9100 и 9130 на экран выводятся
следующие величины: мольная доля легкокипящего вещества в га-
зовой фазе и жидкости, соответствующая температура кипения и
порядковый номер тарелки. В строке 9200 проверяется, для всех ли
тарелок выполнен расчет. Если больше тарелок не осталось, то вы-
полнение программы заканчивается строкой 9999. Если рассмотре-
ны еще не все тарелки и условие, записанное в операторе IF, не вы-
полняется, то в строке 9300 состав жидкой фазы на следующей та-
релке приравнивается составу газовой фазы на предыдущей тарел-
ке. Одновременно счетчик тарелок 15 увеличивается на единицу и
управление передается строке 2100, с которой начинается очередная
процедура вычисления температуры кипения смеси на соответству-
ющей тарелке.
В приведенном здесь примере использованы данные для н-гекса-
на и н-пентана.
Задание 64. Расширьте программу «РЕКТИФ» так, чтобы можно было прово-
дить расчеты не только для одного фиксированного значения давления, но и для лю-
бых значений давления.
Задание 65. Модифицируйте расширенную программу «РЕКТИФ», чтобы эта
программа рассчитывала процесс ректификации также и при конечной величине
флегмового числа. Для этого необходимо учитывать рабочую линию процесса. До-
полнительно вводятся: флегмовое число v и мольная доля легкокипящего компонен-
та в отводимом дистилляте xd. Формула в строке 9300 заменяется на следующую:
(’ X. \ V + 1
„газ а 1 ,
*/ I
V + 1 / V
Теперь строка 9300 имеет вид
9300 15 = 15 + 1:Х1 = (ХЗ - XD/(V + I))*(V + 1)/И: GOTO 2100
Выполнение программы заканчивается, когда значение XI превысит значение XD.
Задание 66. Расширьте программу «РЕКТИФ» для расчета процесса ректифика-
ции тройных смесей.
6.7. pH растворов слабых кислот
Пусть имеются некоторая кислота и вода, которые диссоцииру-
ют по следующему уравнению:
НА Н+ + А” (1)
Н2О Н+ + ОН- (2)
Соответствующие константы равновесия имеют вид
„ [Н+][А“]
Ка = -------— константа диссоциации кислоты (3)
134
Глава 6
Kw = [Н+][ОН ] ионное произведение воды (4)
Поскольку анион А- образуется только из кислоты НА, уравне-
ние материального баланса по кислоте выглядит следующим обра-
зом:
[НА]0 = [НА] + [А-] материальный баланс по кислоте (5)
Раствор электролита в целом электронейтрален, поэтому коли-
чество положительных и отрицательных ионов должно быть оди-
наково:
[Н+] = [А-] + [ОН-] баланс по заряду (6)
Если выражение для концентрации недиссоциированной кислоты
[НА], найденное из уравнения (3), подставить в уравнение (5), то
получится
[НА]0 = [Н+-рА ] + [А-] (7)
Если выражение для концентрации ионов ОН-, полученное из
уравнения (4), подставить в уравнение (6), то выражение для А-
примет вид
[А-] = [Н+] - (8)
Если выражение (8) подставить в уравнение (7), то получится
формула, в которую входят только константы равновесия, кон-
центрация кислоты и концентрация ионов водорода:
[НА]0 = [Н+]^ + [Н+] -
[Н+]
Ниже приведена программа на БЕЙСИКе для расчета pH раство-
ров:
0 REM "КИСЛ" EBERT/EDERER 810610
1 REM*********************************
2 REM»» РАСЧЕТ PH РАСТВОРА СЛАБОЙ «*
3 REM»» кислоты **
4 REM»» ЭТА ПРОГРАММА ПРЕДСТАВЛЯЕТ СОБОЙ »»
5 REM»» НЕСКОЛЬКО МОДИФИЦИРОВАННУЮ »»
6 REM»» ПРОГРАММУ "ПОЛ-ДЕЛ"
9 REM»»»»»»»»»»»»»»»#»#»»»»»»»»»»»»»»»
100 DEF FNF<X>«X»<X-KW/X>/KR+X-KW/X-EW
200 R-lE-lOiE-l
Уравнения
135
320 INPUT "КОНЦЕНТРАЦИЯ КИСЛОТЫ В МОЛЬ/Л"; EW
340 INPUT "КОНСТАНТА ДИССОЦИАЦИИ КА"; КА
360 INPUT "ИОННОЕ ПРОИЗВЕДЕНИЕ ВОДЫ"; KW
500 Y1-FNF<A>
600 Y2-FNF<E>
800 IF SGN<Y1>—SGN<Y2> THEN 5000
1000 N-10
1100 H-CE-A5/N
1200 FOR 1-1 TO N-l
1300 Y9-FNF<A+I*H>
1400 IF SGN<Y9>-SGN<VI> THEN 1700
1500 E-A+I4H
1600 GOTO 5000
1700 NEXT I
1800 N-N410
1900 IF N<-1000 THEN 1100
2000 PRINT "РЕШЕНИЕ HE НАЙДЕНО"
2100 STOP
5000 REM НАЧАЛО ПРОЦЕДУРЫ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
5500 Y1-FNFCA?
5600 Y2-FNF<E>
5700 ЕР-<А+Е>/10000
5000 IF ABSCA-EXABSCEP) THEN 9000
6000 M—<R+E>/2
6100 Y3-FNF<M>
6200 IF SGN<Y3>-SGN<Y1 > THEN 6600
6400 E-MiGOTO 5000
6600 A-MiGOTO 5000
9000 PRINT«PRINT "PH J-LOG<<E+A>/2>/LOO<10>
9999 END
RUN
КОНЦЕНТРАЦИЯ КИСЛОТЫ В МОЛЬ/Л? .1
КОНСТАНТА ДИССОЦИАЦИИ КА? 1.85Е-5
ИОННОЕ ПРОИЗВЕДЕНИЕ ВОДЫ? 1Е-14
PH - 2.86934498
READY.
Формула для расчета задана в строке 100 программы в виде
определяемой функции. Так как для расчета концентрации ионов
водорода используется метод деления отрезка пополам, заданные в
строке 200 граничные значения концентраций 1Е—10 и 1 безуслов-
но достаточны для слабой кислоты. Далее необходимо ввести зна-
чения трех входящих в формулу параметров, а именно: концентра-
цию кислоты, выраженную в моль/л, константу диссоциации кис-
лоты и ионное произведение воды. До строки 6600 программа
«КИСЛ» идентична программе «ПОЛ-ДЕЛ». Добавлена только
строка 5700 для автоматического выхода из итерационной процеду-
ры. Для данной задачи достаточно достоверности четвертого знака
после запятой. pH, как известно, это отрицательный десятичный
логарифм концентрации ионов водорода. Поскольку многие ЭВМ
имеют в наборе стандартных функций только натуральный лога-
рифм, при выводе данных на экран для пересчета использована еле-
136
Глава 6
дующая формула:
logj0 (х) = ln(x)/ln(10)
Задание 67. С помощью программы «КИСЛ» составьте две таблицы или по-
стройте два графика, которые отражали бы зависимость pH от концентрации кисло-
ты при заданной и постоянной константе диссоциации, а также от константы диссо-
циации кислоты при постоянной концентрации.
Задание 68. Заново перепишите программу «КИСЛ», используя в качестве ите-
рационной процедуры программу «НЬЮТОН». Поскольку для программы «НЬЮ-
ТОН» необходимо задать только одно начальное значение, уравнения (5) и (6) заме-
ните приближенными соотношениями:
[НА] = [НА]о и [Н+] « [А-] (5а), (6а)
Если подставить эти формулы в формулу (3), то получится вполне разумное вы-
ражение для начального приближения:
[Н+] = V/Ce-[HA]o
Задание 69. Напишите программу для расчета pH буферного раствора и проана-
лизируйте, что произойдет, если к нему добавить сильную кислоту.
Буферный раствор — это раствор, содержащий слабую кислоту й соль этой кис-
лоты. При добавлении не очень большого количества сильной кислоты значение pH
раствора меняется в относительно небольших пределах. Количественно это можно
описать следующим образом:
НА г* Н+ + А- (1)
Н2О г* Н+ + ОН- (2)
КА К* + А- (диссоциирует полностью) (3)
В качестве сильной кислоты возьмите НС1, которая полностью диссоциирует:
НС1 Н+ + СГ (4)
[Н+][А~]
К = ----------константа диссоциации слабой кислоты (5)
° [НА]
Л’д, + [Н+][ОН~] ионное произведение воды (6)
Анион А- образуется из слабой кислоты и из соли этой кислоты, что отражено
в уравнении материального баланса:
[НА]о + [КА]о = [НА] + [А-] материальный баланс по аниону (7)
Вследствие полной диссоциации КА
[КА]о = [К+] (8)
Уравнение баланса по заряду имеет вид
[Н+] + [К+] = [А’] + [ОН’] + [СГ] (9)
Если концентрацию недиссоциированной кислоты выразить из уравнения (5) и
полученную формулу подставить в уравнение (7), то
[НА]о = + [А-] - [КА]о (Ю)
К
Уравнения
137
Выражение для концентрации иоиов ОН", найденное из уравнения (6), подста-
вим в уравнение (9). Полагая, что сильная кислота и ее соль полностью диссоцииро-
ваны, после соответствующих преобразований получим
[А-] = [Н+] - + [КА]о - [НС1]о (11)
Совместное решение уравнений (10) и (11) дает окончательную формулу, в кото-
рую входят константы равновесия, концентрации слабой кислоты, соли н сильной
кислоты, а также концентрация ионов водорода:
([Н+] \ / \
—1 + 1 ) (1н+1 + 1КА]О - [НС1]о - )
Лв / \ IH J /
Используйте в вашей программе следующие входные данные: концентрации сла-
бой кислоты и ее соли равны 1 моль/л, константа диссоциации слабой кислоты рав-
на 1,85-10“5, ионное произведение воды равно 1-10“14. Введите разные концентра-
ции сильной кислоты и посмотрите, как при этом изменится pH раствора. Отобра-
зите изменение pH в зависимости от концентрации сильной кислоты в виде графика.
Задание 70. Напишите программу для расчета pH буферного раствора при до-
бавлении к нему сильного основания.
Задание 71. Напишите программу для расчета pH смеси растворов двух слабых
кислот.
Задание 72. Пусть имеется раствор слабого электролита К2А, который непо-
средственно диссоциирует на три иона:
К2А s 2К+ + А2~
Согласно закону разбавления Оствальда, это равновесие можно описать следую-
щей формулой:
4“’с0
Рассчитайте степень диссоциации этого электролита при заданных значениях Кс и с0
(например, Кс = 0,01 и с0 = 0,001).
Задание 73. Дана обратимая реакция первого порядка:
ki
А В
кг
Если проинтегрировать соответствующее кинетическое уравнение, то получится
^,[А] - Лг2[В] \ =
Л.1А]О - *2[В]О/
+
[А]о, [В]о — начальные (ие равновесные) концентрации веществ; / — время; х — из-
менение концентрации веществ А и В: [А] = [А]о —хи [В] = [В]о + х.
Даиы начальные концентрации веществ А и В и коистаита скорости к{. Кроме
того, известно одно значение х в момент времени /. Напишите программу для расче-
та константы скорости реакции к2.
Задание 74. Зависимость константы скорости реакции по теории Эйринга описы-
138
Глава 6
вается следующей формулой:
к Т гГ -
к - В R RT
Л — --- V С
Л
кв — константа Больцмана; Л — постоянная Планка.
Выберите какие-нибудь значения для энтропии активации AS* (например,
— 11,8 кал/(моль- К)) и энтальпии активации А//* (например, 25 000 кал/моль). Кро-
ме того, следует задать значение константы скорости (например, 0,001 1/с). Найди-
те температуру Т, которая соответствует выбранному значению к. Сравните резуль-
тат численного метода решения уравнения Эйринга с результатом аналитического
расчета по приближенной формуле, которая не учитывает зависимость от темпера-
туры предэкспоненциального множителя. Для этого можно воспользоваться форму-
лой Аррениуса:
к = k0-e~E“'RT
Чтобы привести формулу Эйрннга к виду уравнения Аррениуса, можно исполь-
зовать среднюю температуру Т .
к Т »
кп = _в_сЕ.е-Д5 /R иЕ = ДЯ* + RT
° Л а ср
6.8. Метод итераций
В этом последнем разделе главы, посвященной решению уравне-
ний, рассмотрим задачу, обсуждение которой было начато во вве-
дении:
10 INPUT X
20 X = SQR(ABS(SIN(X)))
30 PRINT X
40 GOTO 20
Если написать эту программу немного подробнее, то станет яс-
но, что вычисление корней уравнения
х2 = sin (г)
проводится итерационным методом.
10 INPUT X
20 Y = SQR(ABS(SIN(X)))
22 IF X=Y THEN STOP
24 X=Y
30 PRINT X
40 GOTO 20
Если будет найдено значение*, которое равно значению у, вы-
численному в строке 20, то это значение х и является решением
приведенного выше уравнения. Если в первом квадранте построить
Уравнения
139
график функции, описанной в строке 20, и биссектрису прямого
угла (биссектриса прямого угла является графиком функции, опи-
санной в строке 24), то станет понято, почему результат итераци-
онной процедуры сходится к этому значению.
При графическом выполнении итерационной процедуры, как это
показано на рисунке, видно, что приближенное решение сходится к
значению х = 0,876726216, нулевое решение при этом выпадает.
7. Переменные с индексами
В математике при решении задач научно-технического характера
очень часто используются так называемые переменные с индекса-
ми, например, при составлении таблиц экспериментальных данных,
при вычислении сумм, при описании энергетических уровней в ато-
ме или молекуле и т. д.
Такие переменные являются также элементами различных язы-
ков программирования. Они называются индексированными пере-
менными, массивами*, векторами, матрицами. При описании мас-
сива необходимо указать количество индексов и их наибольшие зна-
чения, т. е. сколько надо зарезервировать ячеек памяти ЭВМ. По-
этому в программе, прежде чем начнутся какие-либо операции с
массивами, их надо описать, т. е. указать размерность** и
размер***. Для идентификаторов переменных с индексами действу-
ют те же правила, что и для простых (скалярных) переменных. Ин-
дексы указываются не подстрочными знаками, как в алгебре, а за-
писываются в скобках после идентификатора и разделяются запя-
тыми.
Описание массивов *******
* DIM *
*******
*******************
* z1 DIM v(n) *
* z2 DIM y(n,m) *
* z3 DIM z(n,m,l) *
*******************
zl, z2, z3 номера строк; v, у, z — идентификаторы; n, m, 1 — положительные це-
лые числа.
Обычно для персональных компьютеров максимальная размер-
ность массивов не превышает трех. Допускает ли ваша ЭВМ ис-
* Точнее, переменными типа массив. — Прим, перев.
** Размерность массива — это количество индексов. — Прим, перев.
*** Верхние границы изменения индексов. — Прим, перев.
Переменные с индексами
141
пользование массивов большей или меньшей размерности, можно
узнать из руководства к ней.
Примеры программ с использованием индексированных пере-
менных:
10 DIM X(10),Y(10)
20 FOR 1=1 ТО 10
30 X(I)=I*I
40 Y(I)=ЕХР(—X(I))
50 PRINT I,X(I),Y(I)*X(I)
60 NEXT I
10 DIM F(3,3,3)
20 FOR I = 0 TO 3
30 FOR J = 0 TO 3
40 FOR К = 0 TO 3
50 F(I,J,K) = SQR(I*I+J*J+K*K)
60 NEXT К
70 NEXT J
80 NEXT I
Приведенная ниже программа вычисляет среднее арифметиче-
ское результатов измерений и отклонения каждого эксперименталь-
ного значения от среднего. Эта программа с использованием масси-
вов значительно проще и нагляднее, чем описанная ранее програм-
ма для вычисления среднего значения (с. 62). В этой программе вве-
денные экспериментальные значения можно вызвать непосред-
ственно, тогда как раньше для этого использовались операторы
RESTORE и READ.
О REM СРЕДНЕЕ ЗНАЧЕНИЕ
10 DIM X (100),Y(100)
20 INPUT "СРЕДНЕЕ ЗНАЧЕНИЕ" ;N
30 FOR I = 1 ТО N
40 INPUT X(I)
50 NEXT I
60 S = 0
70 FOR I = 1 TO N
80 S = S + X(I)
90 NEXT I
100 PRINT "СРЕДНЕЕ ЗНАЧЕНИЕ = ” ;S/N
200 FOR I = 1 TO N
210 PRINT I,X(I),X(I)-S/N
220 NEXT I
Существуют задачи, для решения которых необходимо вычис-
лять факториалы. Целесообразно рассчитать значения факториалов
и ввести их в память ЭВМ в виде элементов массива. Как только
142
Глава 7
эти значения понадобятся, их можно извлечь из памяти. Напом-
ним, что
О! =1; 1! = 1; N! = N-(N - 1)!
Программа для вычисления факториалов:
10 DIM G(60)
20 G(0) = 1
30 G(1) = 1
40 FOR I = 2 TO 33
50 G(I) = G(I-1)*I
60 NEXT I
Другим примером служит вычисление чисел Фибоначчи, кото-
рые играют важную роль при решении проблем оптимизации.
Числа Фибоначчи рассчитывают по следующим формулам:
Fi = 1 и F2 = 1
Fi = Ft_2 + Fi-i
Программа для вычисления этих чисел:
1000 DIM F(100)
1100 F(1) = 1 : F(2) = 1
1200 FOR I = 3 TO 100
1300 F(I) =F(I-2) + F(I-1)
1400 NEXT I
1500 FOR I = 1 TO 100
1600 PRINT I,F(I)
1700 NEXT I
С помощью оператора DIM F(100) в памяти ЭВМ резервируется
место для размещения чисел, соответствующих переменным F с ин-
дексами от 0 до 100. Наибольшее значение индекса ограничено пра-
вилами синтаксиса данной версии языка или объемом памяти ЭВМ.
Каково максимально допустимое число элементов массива, можно
узнать из руководства к ЭВМ или, что часто проще, опробовав
программу на ЭВМ.
Задание 75. Организуйте вывод таблицы в программе «БРУТ-ФОРМ» с по-
мощью индексированных переменных.
Задание 76. Перепишите программу «СРЕДНЕЕ» так, чтобы в ней использова-
лись индексированные переменные.
7.1. Сортировка чисел и слов
Одна из задач, часто встречающихся при обработке эксперимен-
тальных данных, заключается в их сортировке. Программа, рас-
сматриваемая в этом разделе, реализует метод, который использу-
ется при сортировке игральных карт.
Переменные с индексами
143
Блок-схема (схема 9) иллюстрирует методику сортировки экспе-
риментальных данных.
Схема 9
(1) (2) (з) (4)
144
Глава 7
(1) (2) (3) (4)
Используемый в этой программе метод можно проиллюстриро-
вать на примере сортировки игральных карт. Просматривая по по-
рядку исходную последовательность карт, ищут карту, достоин-
ство которой больше, чем первой. Если такая карта существует, то
ее ставят на место первой карты, а бывшую первую карту ставят
на ее место. Теперь из оставшихся п — 1 карт ищут старшую карту
(вторую по старшинству) и обменивают ее со второй картой. Эту
процедуру продолжают до тех пор, пока не доходят до предпослед-
ней карты.
Программа для сортировки чисел в порядке их убывания приве-
дена ниже.
В строке 1000 описаны используемые в программе массивы.
Размеры массивов — 100 — выбраны произвольно. Если предпола-
Переменные с индексами
145
0 REM "СОРТ—ЧИСЛ" EBERT/EDERER 810620
1 REM*****##**#*****#*#*##***####*#***
2 REM** УПОРЯДОЧИВАНИЕ ЧИСЕЛ ПО ИХ **
3 REM** ВОЗРАСТАНИЮ. ЧИСЛА **
4 REM** ВВОДЯТСЯ В ПРОИЗВОЛЬНОЙ **
5 REM** ПОСЛЕДОВАТЕЛЬНОСТИ **
9 REM*********i*i**i*****i****************
1000 DIM X<100>,V<100>
1100 INPUT "ЧИСЛО ДАННЫХ"; N
1200 FOR 1 = 1 TON
1300 INPUT X<I>sY<I>=X<I>
1400 NEXT I
2000 FOR 1=1 TO N-l
2100 H=V<I>sHl = I
3000 FOR J-I+l TO N
3100 IF THEN 3400
3200 H=Y<J>sHl=J
3400 NEXT J
4000 ?<H1>=?<!>s?<I>=H
4100 NEXT I
5000 PRINT SPRINT "ИСХОДНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5100 FOR 1=1 TO NsPRINT X<I>ssNEXT I SPRINT
5200 PRINT SPRINT "ОТСОРТИРОВАННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5300 FOR 1 = 1 TO NsPRINT Y<I>;sNEXT I SPRINT
9999 END
RUN
ЧИСЛО ДАННЫХ? 6
? 4
? 2
? -6
? 6
? 3
? 0
ИСХОДНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
4 2 -6 6 3 0
ОТСОРТИРОВАННАЯ ПОСЛЕДОВАТЕЛ ЬНОСТЬ
6 4 3 2 0 -6
READY.
гается сортировать большее количество чисел, то необходимо соот-
ветственно увеличить размеры массивов.
Ввод исходной последовательности чисел происходит в строках
1100—1400. Входные данные присваиваются элементам одномер-
ных массивов Y( ) и одновременно Х( ). Массив X предназначен
для хранения исходной последовательности чисел.
Внешний цикл по параметру I (порядковый номер числа в после-
довательности) занимает строки 2000—4100. Внутренний цикл
(цикл по J), в котором проводится поиск наибольшего значения, ре-
ализован в строках 3000—3400. Перед входом в этот цикл вспомо-
гательной переменной Н присваивается значение Y(I). После этого
во внутреннем цикле начинается поиск числа, большего чем значе-
ние переменной Н. Если таковое найдено и поэтому на вопрос, за-
данный в операторе IF, дается ответ «нет», то это новое наиболь-
шее значение теперь присваивается переменной Н, а индекс пере-
менной с наибольшим значением присваивается переменной Н1. Ес-
10-81
146
Глава 7
ли поиск наибольшего значения среди оставшихся чисел продолжа-
ется, то в конце цикла по параметру J переменная Н имеет значе-
ние наибольшего числа, а переменная Н1 имеет значение индекса
элемента массива, соответствующего этому числу. В строке 4000,
следующей непосредственно после окончания внутреннего цикла, 1-й
элемент массива обменивается местами с найденным наибольшим
элементом.
Вывод отсортированных и несортированных чисел происходит в
строках 5000—5300.
Задание 77. Напишите программу для сортировки чисел в порядке их убывания
и возрастания так, чтобы можно было выбрать тип последовательности.
С помощью следующей программы можно выстраивать слова в
определенном порядке. Она во многом похожа на программу
«СОРТ-ЧИСЛ», однако для записи слов в ней использованы тек-
стовые переменные, на что указывает знак $ после идентифи-
катора.
В REM "СОРТ-СЛОВ" EBERT/EDERER 810620
1 REM*********************************
2 REMHUK УПОРЯДОЧИВАНИЕ ПОСЛЕДОВА- •*
Э REM** ТЕЛЬНОСТИ' СЛОВ. СЛОВА ВВО- •*
4 REM** ДЯТСЯ В ПРОИЗВОЛЬНОМ ПОРЯД-**
5 REM** КЕ, ВЫВОДЯТСЯ ПО АЛФАВИТУ ••
9 REM*********************************
1000 DIM Х»<100>,V»<1003
1100 INPUT "КОЛИЧЕСТВО СЛОВ"; N
1200 FDR 1-1 ТО N
1300 INPUT Х»<1>sV»<I>-X»<I>
1400 NEXT I
2000 FOR 1-1 ТО N-l
2100 H»-V»<I>sHl-I
3000 FOR J-I + l TO N
3100 IF H»>V»<J> THEN 3400
3200 H»-V»<J>sHl-J
3400 NEXT J
4000 V*CH1>-V*CI>|V*<I>-H*
4100 NEXT I
5000 PRINT SPRINT "ИСХОДНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ СЛОВ"
5100 FOR 1-1 TO NSPRINT X»CI>," "> sNEXT I SPRINT
5200 PRINT SPRINT "ОТСОРТИРОВАННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ СЛОВ"
5300 FOR 1-1 TO N SPRINT ?»<1>Г‘ "> sNEXT I SPRINT
9999 END
RUN
КОЛИЧЕСТВО СЛОВ? 4
? SORTIEREN
? KANN
? UNSINN
? SEIN
ИСХОДНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ СЛОВ
SORTIEREN KANN UNSINN SEIN
ОТСОРТИРОВАННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ СЛОВ
UNSINN SORTIEREN SEIN KANN
READV.
Переменные с индексами
147
Задание 78. Предположим, что имеется некоторое количество пар данных (на-
пример, температура/скорость реакции, среднее значение pH воды в водоеме/год
или номер телефона/фамилня) и необходимо упорядочить эти пары по первой вели-
чине (например, по номеру телефона) или по второй величине (например, по фами-
лии). Напишите для этого программу так, чтобы можно было выбрать один нз ва-
риантов, соответствующий характеру данных.
7.2. Интегрирование кинетического уравнения
первого порядка методом Монте-Карло
Для реакции первого порядка (например, реакции распада или
изомеризации) число реагирующих частиц в единицу времени про-
порционально числу оставшихся частиц. Это дает в итоге (для
очень большого числа частиц) следующее кинетическое уравнение:
N, = Noe~kl
Nt — число частиц в момент времени t;N0 — число частиц в момент времени 0-, к —
константа скорости распада.
Принцип моделирования процессов с помощью стохастического
метода можно популярно объяснить на следующем примере:
Пусть у нас есть N ящиков и в каждом ящике находится одна
частица, которая может реагировать. Выберем наугад один ящик.
Если в нем еще оставалась непрореагировавшая частица, то теперь
она прореагирует. Если частица ранее уже прореагировала, то ниче-
го не произойдет. Таким образом, вероятность того, что реакция
произойдет, пропорциональна числу имеющихся непрореагировав-
ших частиц. Этот метод лежит в основе следующей программы:
В REM "КИН-МК" EBERT/EDERER 810511
1 REM**********************************************
2 REM** ИНТЕГРИРОВАНИЕ КИНЕТИЧЕСКОГО УРАВНЕНИЯ «•
3 REM** ПЕРВОГО ПОРЯДКА МЕТОДОМ МОНТЕ-КАРЛО ••
9 REM**************************f*****************••
100 DIM ХС100>
200 FOR 1-1 ТО 100»Х<I>«1«NEXT I
220 Т-0
250 N—100
260 PRINT T,N,EXP<-.01*Т>
300 FOR 1-1 TO 10
350 T-T+l
400 J-INT<RND<5>*100+1>
500 IF X<J>-0 THEN 00T0 1000
600 XCJ3-0
?00 N-N-l
1000 NEXT I
1200 GOTO 260
9999 END
В строке 100 число «ящиков» принято равным 100. В строке 200
всем элементам массива Х( ) присваивается значение 1. Число 1
ю»
148
Глава 7
означает, что частица, соответствующая данному элементу мас-
сива, еще не участвовала в реакции. Число попыток пропорцио-
нально времени (переменная Т, которой в строке 220 присваивается
начальное значение 0). Переменная N имеет значения числа еще не-
распавшихся частиц. Поэтому в начале к моменту времени 0 эта пе-
ременная имеет значение 100. В строках 300—1000 проводится 10
стохастических экспериментов без вывода результатов на экран.
Кроме того, счетчик времени увеличивается на 1. В строке 400 гене-
рируется случайное число в интервале [1, 100], которое присваива-
ется переменной J. Если J-й элемент массива (X(J)) равен нулю
(т. е. в J-м «ящике» находится распавшаяся частица), то ничего не
происходит, управление передается следующему оператору — опе-
ратору цикла (строка 1000) и тем самым начинается новая серия
попыток. Если же переменная X с индексом J (X(J)) имеет значение
1, то соответствующая частица распадается, этому элементу мас-
сива присваивается нулевое значение и число нераспавшихся частиц
уменьшается на 1 (строка 700). После 10 стохастических экспери-
ментов управление передается строке 260. В этой строке на экран
выводится число попыток (время), число нераспавшихся частиц и
результат, полученный аналитически (для сравнения). При каждом
прохождении внутренней области бесконечного цикла проводится
очередная серия из 10 стохастических экспериментов.
Задание 79. Используйте метод Моите-Карло для моделирования последова-
тельной реакции первого порядка
А:
А - В -b С
и напишите соответствующую программу.
Задание 80. Напишите программу, реализующую метод Монте-Карло, для мо-
делирования реакции второго порядка:
А + В - С + D
Задание 81. Имеется А ящиков (например, 100) н М шариков разложены случай-
ным образом по этим ящикам. Как изменяется вероятность обнаружения шарика в
данном ящике в зависимости от значений W и Напишите для этой задачи про-
грамму, реализующую метод Монте-Карло.
7.3. Умножение квадратных матриц
Из операций сложения, вычитания и умножения матриц послед-
няя самая сложная и наиболее часто используемая. В дальнейшем
матрицы будем обозначать прописными буквами.
Сложение: С = А + В соответствующие матричные элементы
складываются
С/,7 = a>,J + bi,J
Переменные с индексами
149
Вычитание: С = А - В соответствующие матричные элементы
вычитаются
Умножение: С = А- В
Ci,7 = Е ai,k'bk,j
k = I
При умножении матриц подг-й строкой матрицы А записывают
у’-й столбец матрицы В, стоящие друг против друга матричные эле-
менты перемножают и эти п произведений складывают. Получен-
ная сумма является с, • матричным элементом искомой матрицы С.
Число п — это число строк в матрице А и число столбцов в матри-
це В.
Ниже приведена программа «УМН-МАТР» для умножения двух
матриц.
0 REM "УМН-МАТР" EBERT/EDERER 810620
1 REM*********************************
2 REtl** УМНОЖЕНИЕ ДВУХ **
3 REM** КВАДРАТНЫХ МАТРИЦ *•
9 REM*********************************
200 DIM Я<15,15>,В<15,15>,С<15,15>
300 INPUT "ПОРЯДОК МАТРИЦ"; N
400 PRINT
300 PRINT "ВВОД ЭЛЕМЕНТОВ МАТРИЦ"
550 PRINT "А И В"
600 FOR 1-1 ТО NiFOR J-l TD N
?00 PRINT I ; "-Я СТРОКА"; J ;"—Й СТОЛБЕЦ";
800 INPUT Я<I,J>,ВСI,J>
900 NEXT J«NEXT I
1000 FOR 1-1 TO N
1100 FOR J-l TO N
1200
1300 FOR K-l TO N
1400 C<I,J>-C<I,J>+A<I,K>*B<K,J>
1508 NEXT К
1608 NEXT J
1Z00 NEXT I
2000 FOR 1-1 TO NiPRINTiFOR J-l TO N
2100 PRINT A<I,J>I«NEXT J«NEXT I
2200 PRINT«FOR 1-1 TO N«PRINT«FOR J-l TO N
2300 PRINT B<I,J>> «NEXT J«NEXT I
2400 PRINT«FOR 1-1 TO N«PRINT«FOR J-l TO N
2500 PRINT C<I,J>««NEXT J«NEXT I
9999 END
RUN
ПОРЯДОК МАТРИЦ? 2
ВВОД ЭЛЕМЕНТОВ МАТРИЦ
АИ В
1-Я СТРОКА 1-й СТОЛБЕЦ? 1,2
1 -Я СТРОКА 2 “А СТОЛБЕЦ? 3, 4
2-Я СТРОКА 1-Й СТОЛБЕЦ? В,7
2 -Я СТРОКА 2-Й СТОЛБЕЦ? 2,6
150
Глава 7
1 з
8 2
2 4
? 6
23 22
30 44
RERDV.
Для вычисления матричного элемента произведения организован
цикл по переменной К (строки 1300—1500). Предварительно (в
строке 1200) элементы двумерного массива С( ), которым будут
потом присвоены значения соответствующих матричных элемен-
тов, обнуляются. Поскольку необходимо вычислить все элементы
матрицы С, цикл по К расположен внутри двух других циклов. Те-
кущие значения параметров I и J равны номеру строки и номеру
столбца матрицы С соответственно. Непосредственно умножение
матриц выполняется в строках 1000—1700. Следующие далее стро-
ки служат для вывода на экран трех матриц: А, В и С. В строке
200 описаны три массива. С помощью оператора INPUT в строке
300 у пользователя запрашивается ранг матриц (N). Если число
столбцов или строк матриц больше, то необходимо изменить раз-
мер массивов в строке 200. В строках 500 и 550 на экран выводится
информация о порядке ввода данных. Соответствующие элементы
матриц А и В вводятся в одной строке друг за другом.
Задание 82. Перепишите программу «УМН-МАТР» так, чтобы элементы мат-
риц А и В вводились не оператором INPUT, а с помощью оператора DATA.
Задание 83. Напншнте программу, которая позволяла бы по выбору пользовате-
ля складывать, вычитать и умножать матрицы. Обобщите ее для выполнения этих
операций с прямоугольными матрицами.
Задание 84. Напишите программу для возведения в степень квадратной матрицы
А. Показатель степени — положительное целое число, например:
А7 = А-АААААА
Задание 85. В этом задании рассматривается пример практического использова-
ния умножения прямоугольных матриц. Даны нормированные масс-спектры (фик-
тивные) четырех углеводородов.
1 2 13 14 15 16 24 25 26 27 28 29 30
СН4 1 3 12 100 35
С2Н6 2 80 3 4 13 37 24 100 70
С2Н4 4 7 48 13 2 7 21 18 100
С2Н2 5 23 57 2 40 45 100
Переменные с индексами
151
Напишите программу для определения состава смеси по ее масс-спектру. Мето-
дика определения состава смеси основывается на аддитивности масс-спектров инди-
видуальных компонентов. Используя приведенные выше данные, рассчитайте масс-
спектры смесей с соотношением компонентов 1:1:1:1, 1:2:3:4 и 4:5:2:8.
Расширьте программу так, чтобы можно было также учитывать различия в се-
чениях ионизации компонентов. Например, /(СН4) = 1, /(С2Н6) = 0,8, /(С2Н4) =
= 1,8 и /(С2Н2) = 0,9.
7.4. Алгебра комплексных чисел
Комплексное число состоит из действительной части х и мни-
мой части у. Комплексные числа обычно записывают в виде
z = х + iy
Однако для ЭВМ используется векторная форма записи ком-
плексного числа:
z = (г, у)
Для этого вводится одномерный массив Z. Z(l) соответствует
значению х, т. е. действительной части, и Z(2) — значению у, т. е.
мнимой части. Напоминаем правила сложения, вычитания, умно-
жения и деления комплексных чисел:
Zj = х, + 1У1 и z2 = х2 + iy2
Z1 + Z2 = (Xj + х2) + i(y, + у2)
Z1 - z2 = (Xj - х2) + /(у, - у2)
ZfZ2 = (х,х2 - у{у2) + i^c{y2 4- х2ух)
£1 = ft 1*2 + Л-Уг) + - Х\У1)
z2 Х^с2 + У1у2
Следующая программа выполняет все четыре действия с ком-
плексными числами.
0 REM "КОМПЛЕКС" EBERT/EDERER 810620
1 REM*************************************
2 REM** АЛГЕБРА КОМПЛЕКСНЫХ ЧИСЕЛ **
3 REM** МАТЕМАТИЧЕСКИЕ ДЕЙСТВИЯ* -* / **
4 REM** ПОРЯДОК ВВОДА ЧИСЕЛ : ДЕЙСТВИ- **
5 REM** ТЕЛЬНАЯ ЧАСТЬ, МНИМАЯ ЧАСТЬ ••
9 REM*************************************
200 DIM А<2>,В<2>,С<2>
300 PRINT "ВВОД КОМПЛЕКСНОГО ЧИСЛА"
400 PRINT "А + В*1 КАК А, В"
500 INPUT "ПЕРВОЕ КОМПЛЕКСНОЕ ЧИСЛО"; А (1), А (2)
600 INPUT "ВТОРОЕ КОМПЛЕКСНОЕ ЧИСЛО": В (1),В (2)
?00 INPUT "МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ (+- */)'; А$
1000 IF А»-"+" THEN 2000
1100 IF A»-"-" THEN 3000
1200 IF A»-"*“ THEN 4000
1300 IF A»-"/" THEN 5000
152
Глава 7
1400 GOTO 700
2000 FOR 1-1 TO 2:C<I>«R<I>+B<I>sNEXT I
2100 GOTO 6000
3000 FOR 1-1 TO 2 sC< I >«R< I I > sNEXT I
3100 GOTO 6000
4000 C<1).R<1>*B<1>-R<2>*B<2>
4100 C<2>«R<1>*B<2>+R<2>*B<1>sGOTO 6000
5000 H-B<1>*B<1>+B<2>*B<2>
5100 C<1>.<R<1>*B<1>+R<2>*B<2>>,'H
5200 C<2>.<R<2>*B< 1>-R<1 >*B<2>>/H
6000 PRINT
6100 PRINT ,R<1,R<2>;"*I> ";R«;
6200 PRINT " <";B<1>,"+",B<2>>"*I> - "
6300 PRINT SPRINT "<",С<1>," + ",С<2>,"#1>"
9999 END
RUN
ВВОД КОМПЛЕКСНОГО ЧИСЛА
A + В* I КАК А, В
ПЕРВОЕ КОМПЛЕКСНОЕ ЧИСЛО? 2,3
ВТОРОЕ КОМПЛЕКСНОЕ ЧИСЛО? 1, 1
МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ <+ — */)? +
< 2 + 3 *I> + < 1 + 1 »1> .
< 3 + 4 *1>
RUN
ВВОД КОМПЛЕКСНОГО ЧИСЛА
А + В*1 КАК А. В
ПЕРВОЕ КОМПЛЕКСНОЕ ЧИСЛО? 2, 3
ВТОРОЕ КОМПЛЕКСНОЕ ЧИСЛО? 1,1
МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ (+-*/)? /
<2+3*1>/<1+1#1>-
< 2.5 + .5 *1>
В самом начале программы (строка 200) описаны одномерные
массивы размера 2, элементы которых равны компонентам ком-
плексных чисел. Переменные с индексом 1 соответствуют действи-
тельным частям, переменные с индексом 2 — мнимой. После опи-
сания массивов с помощью оператора INPUT вводятся четыре чис-
ла, которые отвечают действительной и мнимой частям двух ком-
плексных чисел и присваиваются индексированным переменным А
и В соответственно. В строке 700 после того, как выбрано, какое
действие будет производиться с комплексными числами, знак этой
операции присваивается текстовой переменной А$. В следующих че-
тырех строках значение переменной А$ сравнивается со знаками
сложения, вычитания, умножения и деления. Если значение пере-
менной А$ не совпадает ни с одним из этих знаков, то управление
передается оператору ввода знака операции. В этом случае пользо-
ватель должен ввести новый, соответствующий содержанию про-
граммы знак операции. Фактически программа состоит из четырех
частей, що одной для каждой операции с комплексными числами. В
Переменные с индексами
153
конце каждой из этих частей, в которых вычисляется комплексное
число С, происходит переход на строку 6000. В этой строке выво-
дятся на экран комплексные числа А и В в обычном виде вместе со
знаком операции и результатом. Первая, арифметическая часть
программы, которая выполняется, если знаком операции является
«+», занимает строки 2000—2100. Здесь вычисляются суммы дей-
ствительных и мнимых частей комплексных чисел и эти два значе-
ния присваиваются элементам массива С. Разумеется, эту часть
программы можно было бы сделать проще. Однако в учебных це-
лях в рассматриваемой программе использован оператор цикла.
Участок программы со строки 3000 по строку 3100 предназначен
для вычисления разности комплексных чисел. В строках 4000—4100
происходит умножение двух комплексных чисел по приведенной вы-
ше формуле. Частное рассчитывается в строках 5000—5200. В ка-
честве примера рассчитаны разность и частное двух комплексных
чисел.
Задание 86. Пусть z — комплексное число. Напишите программу для вычисле-
ния
/(Z) = Z5 = Z-Z-Z-Z-Z
/(Z)
z2 + z3 " Ч (5 + 3/)z5
--------- И /(Z) = ---------------
1 + z z - 3
Постарайтесь составить достаточно универсальную программу в таком виде, чтобы
ввод вида функции комплексного переменного (отношение полиномов) мог легко вы-
полнить пользователь, который заранее не знаком с программой.
Задание 87. Напишите программу для вычисления/(z) = z1/л (га — целое число).
Задание 88. Напишите программу для вычисления ег, sinz, cosz, Inz.
ег = ех + iy = е*е‘у
е'у = cosy + / sin у (формула Эйлера)
cosz = - (ек + е_,г)
Задание 89. (Для читателей, которые уже перестали бояться математики.) Напи-
шите программу для интегрирования функции комплексного переменного. Начните с
интегрирования вдоль действительной оси. С этой целью можно переписать уже го-
товую программу для интегрирования. Затем попытайтесь вычислить интеграл
вдоль произвольной кривой на комплексной плоскости.
Интегрирование в плоскости комплексных чисел проводится аналогично инте-
грированию в плоскости действительных чисел. Выберите ряд точек zk и вычислите
следующую сумму:
п
J/(z)dz =nlimQo £ f(zk^Zk ~ Zk-J
с п ~ °° к « 1
154
Глава 7
Точки zk лежат на кривой С, вдоль которой проводится интегрирование. Эти
точки надо выбирать как можно ближе друг другу, чтобы вычисляемая сумма как
можно меньше отличалась от значения интеграла.
7.5. Угол рассеяния Брэгга при дифракции
рентгеновского излучения*
Для упрощения задачи мы будем рассматривать элементарную
кристаллографическую ячейку с идентичными центрами рассеяния.
Такая элементарная ячейка полностью характеризуется
тремя линейными размерами а, Ь, с
и тремя углами а, 0, у
Через кристаллическую решетку, которая состоит из повторяю-
щихся элементарных ячеек, можно провести сколь угодно много
плоскостей, проходящих через определенные центры рассеяния.
Эти плоскости полностью определяются так называемыми индек-
сами Миллера й, к и /. Расчет расстояния между двумя плоскостя-
ми с индексами Миллера й, к, I элементарной ячейки с линейными
параметрами а, Ь, с и углами а, 0 и у проводится по следующим
формулам (а, /3 и 7 в формулах обозначены прописными буквами
А, В и С; А р 5р С\, Ьх,сх — вспомогательные величины):
„ cosfi-cosC — cos Л
cos Л = -----------------
sin5- sin С
„ совС-совЛ — cos5
cos# । = ------------------
sin C-sin Л
„ совЛ-совВ — cos С
cos С, = ------------------
япЛ • sinB
О] = (o-sinfi-sinCj)-1
й, = ф-япС-втЛ j)-1
с, = (с-sinЛ -sinfi])-4
Вспомогательную величину Q можно вычислить по формуле
Q = + k^b\ + + 2klbtc lcosAl +
+ 2hlc{a lcosBl + Ihkafi lcosCl
Из этих соотношений получают расстояние d между обеими пло-
• См. например: Berry R. S., Rice S. A., Ross J., Physical chemistry. John Wiley &
Sons, 1980, p. 427.
Переменные с индексами
155
скостями:
d = <\7Q
Условие Брэгга для угла рассеяния 0 рентгеновского излучения с
длиной волны X, при котором не наблюдается тушения, имеет вид
d-sin0 = Х/2
Это условие можно записать по-другому:
в = arcsin(X/2d)
0 REM "БРЭГГ" EBERT/EDERER 810620
1 REM********************************** **
2 REM** РАСЧЕТ УГЛОВ БРЭГГА В ЗАВИ- **
3 REM** СИМОСТИ ОТ ИНДЕКСОВ МИЛЛЕРА. **
4 REM** НЕОБХОДИМО ВВЕСТИ ДЛИНУ ВОЛНЫ**
5 REM** РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ И **
6 REM** ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ **
7 REM** ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ •*
9 REM******************************* *****
100 Р1»4*АТН<1>
20В DIM 0<3>,01<3>,ЖЗ>
300 DIM C<3>,C1<3>,S<3>,S1<3>
400 PRINT "ВСЕ ЛИНЕЙНЫЕ РАЗМЕРЫ В АНГСТРЕМАХ"
500 PRINT "ДЛИНА ВОЛНЫ РЕНТГЕН. ИЗЛ."
520 INPUT L9
600 PRINT "ЛИНЕЙНЫЕ ПАРАМЕТРЫ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ"
620 INPUTD<1>,*D<2>,D<3>
700 PRINT "УГЛОВЫЕ ПАРАМЕТРЫ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ В ГРАД."
720 INPUT Я<1>,Я<2>,Я<3>
1000 FOR I - 1 ТО 3
1100 S<I>-SIN<R<I>/180*PI>
1200 C<I>-COS<R<I>/180*PI>
1300 NEXT I
2000 Cl<1>-<С<2>*С<3>-С<1>>/<S<2>*S<3>>
2100 Cl <2>-<C<3>*C< 1 >-C<2> >/<S<3>*S< 1 > >
2200 Cl<3>-<C<1>*C<2>—C<3>>/<S<1>*S<2>>
2500 FOR I-1TO 3
2600 Sl<I).SQR<l-Cl(I)t2)
2700 NEXTI
3000 Dld>-1/<O<1>*S<2>*S1<3>>
3100 D1<2>-1/<O<2>*S<3>*S1<1>>
3200 DI<3>-l/<D<3>*S<1>*S1<2>>
5000 J-llJl-0
5100 FOR L - 0 TO J
5200 FOR К - 0 TO J-L
5300 H - J - L - К
6000 Q-H*H*O1<1>T2+K*K*D1< 2 >t2+L*L*D1< 3 > T2
6100 Q-Q+2»K*L*D1<2>*D1<3>*C1<1>+2*L*H*Dl<3>*D1<1>*C1<2>
6200 Q“Q+2*H*K*D1<1>*D1<2>*C1<3)
6300 D-SQR<1/Q>
7000 IF J1/12OINTCJl/12> THEN 7800
7500 PRINT"***"
7520 .....GETR*1IFR*«""THEN7520
7600 PRINT" H К L УГОЛ БРЭГГА"
7800 IF L9/2/D>l THEN 8500
7900 S-L9/2/D>S-S/SQR<1-S*S >1S-RTN < S > *180/PI
8000 PRINTH,K.>L;TRB<15>,S
8100 Jl-Jl+1IGOTO9000
8500 Jl-Jl+1 1PRIN7H,-K,L, " УСЛОВИЕ БРЭГГА HE ВЫПОЛНЯЕТСЯ"
9000 NEXT К
9200 NEXT L
156
Глава 7
9500 J-J+i
9700 GOTO 5100
9999 END
RUN
ВСЕ ЛИНЕЙНЫЕ РАЗМЕРЫ В АНГСТРЕМАХ
ДЛИНА ВОЛНЫ РЕНТГЕН. ИЗЛ.
? 1.537
ЛИНЕЙНЫЕ ПАРАМЕТРЫ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ
? 5.64,5.64,5.64
УГЛОВЫЕ ПАРАМЕТРЫ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ В ГРАД.
? 90,90,90
***
Н К L УГОЛ БРЭГГА
1 0 0 7.83142025
0 1 0 7.83142025
0 0 1 7.83142025
2 0 0 15.0141416
1 1 0 11.1103447
0 2 0 15.8141416
1 0 1 11.1103447
0 1 1 11.1103447
0 0 2 15.0141416
3 0 0 24.1280056
2 1 0 17.7391587
1 2 0 17.7391587
***
RUN
ВСЕ ЛИНЕЙНЫЕ РАЗМЕРЫ В АНГСТРЕМАХ
ДЛИНА ВОЛНЫ РЕНТГЕН. ИЭЛ.
? 1.537
ЛИНЕЙНЫЕ ПАРАМЕТРЫ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ
? 3.962,13.858,3.697
УГЛОВЫЕ ПАРАМЕТРЫ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ В ГРАД.
? 90,90,90
***
Н К L УГОЛ БРЭГГА
1 0 0 11.1844254
0 1 0 3.17890732
0 0 1 11.997631
2 0 0 22.826094
1 1 0 11.6386892
0 2 0 6.36781408
1 0 1 16.5177918
0 1 1 12.4238131
0 0 2 24.5660836
3 0 0 35.5045067
2 1 0 23.0714674
1 2 0 12.9110573
***
В программе «БРЭГГ» приведенные выше формулы заменены
соответствующими арифметическими выражениями. Чтобы облег-
чить чтение и анализ программы, есть смысл составить таблицу, в
которой дано соответствие между символами формул и переменны-
ми программы.
Все массивы, которые используются в этой программе, описаны
в строках 200 и 300. Ввод исходных параметров происходит в стро-
Переменные с индексами
157
Символы в формулах Переменные 6 программе
h к 1 Н К L
Л L9
а Ь с D(1) D(2) D(3)
а В Y A(1) A(2) A(3)
sina sinB sin> S(1) S(2) S(3)
cosa cos В cosy C(1) C(2) C(3)
sin«1 sinB1 siny1 S1(1) Si(2) S1(3)
cosa^ cos B^ cosY1 C1(1) C1(2) C1(3)
a1 b1 C1 Did) D1(2) D1(3)
Q d Q D
ках 400—720. Вводятся длина волны рентгеновского излучения, ли-
нейные и угловые параметры элементарной ячейки. Поскольку в
формулах часто используются значения синуса и косинуса опреде-
ленных углов, эти значения вычисляются отдельно — в цикле
(строки Н00—1200). Так как угловые параметры вводятся в граду-
сах, а аргументы стандартных тригонометрических функций выра-
жаются в радианах, необходимо перевести входные данные в радиа-
ны. В строках 2000, 2100 и 2200 вычисляется косинус вспомогатель-
ных углов а,, /3] и 7Г Далее в цикле, исходя из известных значений
косинуса вспомогательных углов, по известной формуле вычисля-
ются значения синуса вспомогательных углов. Вспомогательные ве-
личины о,, Ь1 и с, рассчитываются в строках 3000, 3100 и 3200 по
приведенным выше формулам.
Чтобы понять, что происходит в заключительном цикле, надо
обратиться к физическому содержанию задачи. Дело в том, что
наибольший вклад в рассеяние рентгеновского излучения вносят те
плоскости, у которых меньше сумма индексов Миллера. В програм-
ме сумма индексов Миллера присваивается переменной J. Началь-
ное значение J равно 1 (строка 5000). Переменная J1 используется в
качестве счетчика строк выходных данных. После вывода 12 строк
выполнение программы приостанавливается. Поэтому в строке
7000 стоит конструкция оператора IF. Число Л/12 больше или рав-
но числу INT(J1/12) лишь в том случае, если Л кратно 12. Если Л
кратно 12, то управление строке 7800 не передается, а выполняются
операторы, стоящие в следующих трех строках. Эти три строки
158
Глава 7
предназначены для вывода на экран трех звездочек (***) (в строке
7500), для организации «ждущего цикла» (строка 7520) и для выво-
да заголовка таблицы для 12 углов Брэгга. «Ждущий цикл» — но-
вое программное средство — будет подробно рассмотрен после об-
суждения программы. Следующие 12 строк будут выведены на
экран лишь в том случае, если пользователь нажмет какую-нибудь
клавишу.
Если длина волны монохроматического излучения больше, чем
удвоенное расстояние между рассматриваемыми плоскостями, то
никакой дифракционной картины не наблюдается. Это можно уста-
новить чисто формально из приведенной выше формулы. Значение
функции arcsin числа больше, чем единица, не определено. В этом
случае условие Брэгга не выполняется. Оператор условного перехо-
да с соответствующим разветвлением стоит в строке 7800. В стро-
ке 7900 находятся три отделенных двоеточиями оператора, кото-
рые вычисляют углы Брэгга в градусах. Первый оператор рассчи-
Переменные с индексами
159
Схема 11
тывает значение синуса этого угла. Так как некоторые ЭВМ не име-
ют в наборе стандартных функций функции arcsin, второй оператор
160
Глава 7
по значению синуса угла рассчитывает тангенс этого угла. Третий
оператор с помощью функции arctg вычисляет угол, который здесь
же пересчитывается из радиан в градусы. Затем значение этого
угла вместе с соответствующими ему индексами Миллера выводит-
ся на экран. В следующей строке счетчик строк J1 увеличивается на
1 и управление передается оператору NEXT К (строка 9000). Бе-
сконечный цикл по J, который подсчитывает сумму индексов
Миллера, размещен в строках 5100—9700. Непосредственно перед
входом в этот цикл переменная J увеличивается на единицу. Пара-
метр цикла L принимает значения от нуля до J. Это указано в опе-
раторе (строка 5100). Начальное значение параметра цикла К также
равно 0. Однако наибольшее значение К составляет J—L, так как
сумма всех индексов Миллера не может быть больше J. Цикл, рас-
положенный внутри всех остальных, т. е. цикл по параметру К,
размещен в строках 5200—9000. Третий индекс Миллера принимает
значение J — (К + L), поскольку Н + К + L = J (строка 5300).
Для большей наглядности ниже приведены две блок-схемы алго-
ритма, реализованного в программе «БРЭГГ» (схемы 10 и 11).
Циклы в этой общей блок-схеме подробно рассмотрены в схеме 11.
Теперь обсудим, для чего же нужен «ждущий цикл», который
реализован в строке 7520. Сначала текстовая переменная А$ лиша-
ется какого бы то ни было значения с помощью оператора А$ =
” ”. Третий оператор в этой строке выясняет, имеет ли перемен-
ная в данный момент какое-нибудь значение. Если переменной А$
не присвоено никакого значения, то управление возвращается на на-
чало строки. Все это выглядит как бесконечный цикл, из которого
выйти невозможно. Возможность выхода из этого цикла предо-
ставляет оператор GET.
Ввод знака
* ★ ★ ★ ★ ★ *
* GET *
★★★★★★★
************
* Z GET z$ *
z — номер строки; z$ — текстовая переменная.
Оператор GET позволяет вводить любой знак в ходе выполне-
ния программы, не прерывая ее выполнения. При выполнении это-
го оператора ЭВМ запрашивает, есть ли в буферной памяти дис-
плея какой-нибудь знак. Затем этот знак присваивается переменной,
Переменные с индексами
161
указанной оператором GET. Знак, набранный на клавиатуре, попа-
дает в буферную память, даже если в это время выполняется про-
грамма. Если в списке операторов вашей ЭВМ нет оператора
GET*, то «ждущий цикл» можно организовать с помощью опера-
тора INPUT AS.
Задание 90. Рассчитайте набор углов Брэгга кристалла КС1 для рентгеновского
излучения с длиной волны 0,708 А (анод из Mo). КС1 имеет кубическую решетку, по-
стоянная решетки равна 3,1 А.
7.6. Моделирование колонки в газовой хроматографии
В этом разделе рассматриваются не сами реальные процессы,
которые протекают в хроматографической колонке, а их Идеализи-
рованная модель. Эта модель позволяет получить описание процес-
са разделения смеси веществ в хроматографической колонке в ана-
литической форме. Однако с помощью используемых здесь числен-
ных методов легко преодолеть те небольшие трудности, которые
встречаются при описании процесса аналитическими методами.
В рамках этой модели колонку мысленно разбивают на ряд по-
следовательных одинаковых элементарных участков, так называе-
мых теоретических тарелок. На каждой из этих тарелок устанавли-
вается равновесное распределение определенного вещества между
жидкой и газовой фазой в соответствии с коэффициентом распреде-
ления, значение которого постоянно для всех тарелок. Поток газа-
носителя через колонку также считается идеальным. Газ-носитель
подается порциями и последовательно проходит через весь ряд та-
релок. Время нахождения порции газа-носителя в объеме элемен-
тарного участка (тарелки) является единицей шкалы времени.
Для лучшего понимания приведем небольшой числовой пример. Пусть коэффи-
циент распределения между жидкой и газовой фазой равен 1. Определенное количе-
ство вещества (в данном примере 2048 единиц) впрыскивается на первую тарелку.
Эта проба распределяется между обеими фазами. Так как коэффициент распределе-
ния равен 1, мы можем в этом примере записывать концентрации вещества лишь в
одной фазе. В момент времени t = 1 газовая фаза каждой тарелки скачкообразно пе-
реходит на следующую тарелку. Первая тарелка заполняется порцией чистого газа-
носителя, и на каждой тарелке устанавливается новое равновесное распределение.
Данные, приведенные в таблице, показывают, как изменяется со временем концент-
рация вещества в газовой и жидкой фазах на каждой из тарелок.
* В версии языка БЕЙСИК для ЭВМ «Искра 226» функции оператора GET вы-
полняет оператор KEYIN. Строка 7520 в этом случае выглядит так:
7520 KEYIN Z$, (номер строки), (номер строки): GOTO 7520
К исполнению первого номера программа переходит после ввода какого-либо знака,
а к исполнению второго — после ввода номера помеченной подпрограммы. —
Прим. ред.
11-81
162
Глава 7
1 2 3 4 5 6 7 8 9 10 11 Время
1024 0 0 0 0 0 0 0 0 0 0 t=0
512 512 0 0 0 0 0 0 0 0 0 t=1
256 512 256 0 0 0 0 0 0 0 0 t=2
128 384 384 128 0 0 0 0 0 0 0 t=3
64 256 384 256 64 0 0 0 0 0 0 t=4
32 160 320 320 160 32 0 0 0 0 0 t=5
16 96 240 320 240 96 16 0 0 0 0 t=6
8 56 168 280 280 168 56 8 0 0 0 t = 7
4 32 112 224 280 224 112 32 4 0 0 t=8
2 18 72 168 252 252 168 72 18 2 0 t=9
1 10 45 120 210 252 210 120 45 10 1 t=10
По программе «ГХ» вычисляются время удерживания и полу-
ширина хроматографического сигнала.
в REM "ГХ" EBERT.'EOEREP 810524
1 REM*********************************** *»
2 REM** МОДЕЛИРОВАНИЕ ГАЗОХРОМАТОГРА- ♦»
3 REM** ФИЧЕСКОЙ КОЛОНКИ С N ТЕОРЕТИ- **
4 REM»» ЧЕСКИМИ ТАРЕЛКАМИ. N ВЫБИРАЕТ- **
5 REM»# СЯ ПРОИЗВОЛЬНО, НО МЕНЬШЕ 100 *»
9 РЕМ»***»»#»»*»»*****»»»*»***»****»***»**
100 DIM G<250>,F<250>
200 INPUT "ЧИСЛО ТЕОРЕТИЧЕСКИХ ТАРЕЛОК"; N
300 INPUT "КОЭФФИЦИЕНТ РАСПРЕДЕЛЕНИЯ"; А
400 Р1«Я/<1+Я> >Р2«1/<1+Я>
420 REM Р1/Р2-Я UND Р1+Р2=1
600 G<l>«liREM ВВОД ПРОБЫ
1000 T>0:T5>0ltj5>0
1200 M«0tREM МАКСИМУМ
1300 REM Т5-ВРЕМЯ УДЕРЖИВАНИЯ
2000 ТжТ+1
3000 REM1PRINT T,G<N>
3050 IF Т5>0 THEN GOTO 4000
3100 IF G<NX-G<N-1> THEN GOTO 5000
3200 T5-T+1|M«G<N>
3300 GOTO 5000
4000 IF D5>0 THEN GOTO 9000
4100 IF 0<N»M/2 THEN GOTO 5000
4200 D5-T-T5
5000 REM РАВНОВЕСНОЕ РАСПРЕДЕЛЕНИЕ
5100 FOR 1-1 TO N
5200 S-G<I>+F<I>
5300 G<I>*S»P1
5400 F<I>-S*P2
5500 NEXT I
6000 REM ПРОДУВКА ГАЗОМ-НОСИТЕЛЕМ
6100 FOR I-N TO 2 STEP -1
6200 G<I>-G<I-1>
6300 NEXT I
6400 G<1>«0
7000 GOTO 2000
9000 PRINT "ВРЕМЯ УДЕРЖИВАНИЯ = "; T5-N
9100 PRINT "ПОЛУШИРИНА ="; D5
9999 END
RUN
ЧИСЛО ТЕОРЕТИЧЕСКИХ ТАРЕЛОК? 20
КОЭФФИЦИЕНТ РАСПРЕДЕЛЕНИЯ? .2
ВРЕМЯ УДЕРЖИВАНИЯ = 90
ПОЛУШИРИНА = 30
READS'
Переменные с индексами
163
Число элементов двух массивов G( ) и F( ), соответствующих
количеству вещества на тарелках в газовой и жидкой фазе, не дол-
жно превышать по 250 в каждом. Это число равно максимально
возможному количеству теоретических тарелок. (Чем больше таре-
лок, тем больше требуется времени для выполнения программы.)
Число тарелок N вводится с помощью оператора INPUT так же,
как и коэффициент распределения, значение которого присваивается
переменной А. Величина А по определению равна отношению кон-
центраций вещества в газовой и жидкой фазах. Из коэффициента
распределения в строке 400 вычисляют «доли» Р1 и Р2 обеих фаз
(Р1/Р2 = А и Pl + Р2 = 1).
Если после каждого скачкообразного продвижения газа через ко-
лонку жидкая и газовая фазы оказываются в неравновесном состоя-
нии, то для всех тарелок рассчитывается равновесное распределе-
ние. Это происходит на участке программы со строки 5000 по стро-
ку 5500. В цикле по параметру I выполняется расчет для всех таре-
лок. В строке 5200 вычисляется суммарное содержание вещества в
обеих фазах и в строках 5300 и 5400 рассчитывается новое равновес-
ное распределение.
Скачкообразное продвижение газовой фазы имитируется в стро-
ках 6000—6400. (I — 1)-я порция газовой фазы становится I-й пор-
цией (строка 6200); содержание вещества в газовой фазе на первой
тарелке становится равным нулю (строка 6400). Почему в данном
случае шаг параметра цикла отрицателен?
После расчета равновесного распределения и «продувки» хрома-
тографической колонки одной порцией газа, объем которой равен
объему тарелки, управление передается строке 2000. В этой строке
счетчик времени Т увеличивается на единицу и его значение вместе
с составом газовой фазы на последней тарелке выводится на экран.
(В данном конкретном примере вывод этих значений опущен.) Пока
не достигнута максимальная концентрация вещества G(N) на по-
следней тарелке, оператор условного перехода в строке 3100 будет
передавать управление строке 5000, в которой в цикле моделирует-
ся распределение вещества вдоль хроматографической колонки. Ес-
ли на последней тарелке достигнута максимальная концентрация,
то переменной Т5 присваивается значение времени удерживания, а
переменной М — значение максимальной концентрации. Далее
управление передается строке 4000. В строке 4100 происходит вы-
числение половины высоты хроматографического сигнала. Если по-
ловина высоты найдена, то вычисляется ширина хроматографиче-
ского пика на половине высоты, которая после еще одного прохож-
дения внутренней области цикла по I выводится на экран.
и»
164
Глава 7
Задание 91. Число тарелок, время удерживания и полуширина хроматографиче-
ского пика связаны простым математическим соотношением. Постарайтесь иайти
это соотношение. (Вычислительный эксперимент с помощью ЭВМ гораздо проще
теоретического рассмотрения проблемы. Теоретический вывод упомянутого выше
соотношения можно найти, например, в практикуме по физической химии*.)
Задание 92. Напишите программу для моделирования анионной полимеризации,
использующую метод Монте-Карло. Представьте себе, что имеется некоторое на-
чальное число анионов. Аниону соответствует элемент массива, равный 1. Индекс
единичного элемента массива выбирается случайным так, что единицы распределе-
ны в этом массиве стохастически. На каждом шаге полимеризации мономер присое-
диняется к одному случайно выбранному аниону. Всякий раз, когда средняя степень
полимеризации увеличивается на 1, надо рассчитывать среднее значение распределе-
ния. Как зависит это среднее значение от времени? Промоделируйте анионную поли-
меризацию в присутствии примеси, которая может реагировать с анионами (в том
числе и с полимерами, имеющими на конце анион) и тем самым уменьшать количе-
ство активных центров. Это уменьшение также можно имитировать с помощью ге-
нератора случайных чисел.
7.7. Линейная регрессия
При обработке экспериментальных данных для расчета пара-
метров, таких, как, например, энергия активации и энтальпия реак-
ции, часто используют линейные соотношения между измеряемыми
величинами или их функциями (например, между логарифмом кон-
станты равновесия или логарифмом константы скорости и обрат-
ной температурой), откладывая попарно значения измеренных ве-
личин или их функций и проводя через полученные точки прямую.
По отрезкам, отсекаемым этой прямой на осях координат, и тан-
генсу угла наклона прямой рассчитывают значения физических па-
раметров. Для того чтобы провести прямую через множество то-
чек с помощью ЭВМ наилучшим образом, необходимо сначала вы-
яснить, каким критериям должна удовлетворять эта прямая.
В большинстве случаев прямую стараются провести так, чтобы
сумма квадратов отклонений экспериментальных значений величи-
ны у от прямой была минимальна (см. рис.).
Пусть даны п пар экспериментальных значений (г,, у,); по теоре-
тическим соображениям, величины х и у связаны линейной зависи-
мостью
у = а + Ьх
Сумму квадратов разностей экспериментальных значений у и
ординат соответствующих точек на аппроксимирующей прямой
* Forsterling Н. D., Kuhn Н., Physikalische Chemie in Experimented Verlag Chemie,
1971, S. 206.
Переменные с индексами
165
можно записать следующим образом:
Е О^сп - Леор)2 = £ [У, - (Я + Ч)]2 = S
i = 1
Надо подобрать такие значения параметров а и b, чтобы сумма
квадратов отклонений S была минимальна. Для этого надо прирав-
нять нулю частные производные от S по а и Ь:
п
i = 1
п
55 = ~2 £ - ° “ = 0
<• = 1
Деление обоих уравнений на (—2), раскрытие скобок и приведе-
ние подобных при параметрах а и b дает
Е у. = а'п + *• Е xi
i = 1 i = 1
f УГХ, = a- £ x,. + &• £ x?
i = 1 i = 1 / == 1
Введем обозначения
Sj = л; S2 = £ xz; S3 = £
i = 1 i = 1
166
Глава 7
s4= f $; s5 = E угх,
i=i i=i
Тогда получится следующая простая система уравнений относи-
тельно параметров а и Ь:
S3 = Sj' и + S2* b
S5 = $2.'4- S4-b
По экспериментальным данным можно вычислить суммы Sp S2, S3,
S4 и S5 и решить систему уравнений относительно а и Ь:
а = ^з'^4 ~ Ss'S2
5j-S4 - S2 S2
b = ~ $2"?з
5j-S4 - S2 S2
Итак, задача решена. Блок-схема алгоритма линейной регрессии
по описанному выше методу выглядит следующим образом (схе-
ма 12):
Схема 12
Переменные с индексами
167
Соответствующая этой блок-схеме программа называется
«ЛИН-РЕГР»:
0 REM "ЛИНРЕГР" EBERT/EDERER 810628
1 REM*********************************
2 REM** АППРОКСИМАЦИЯ ЛИНЕЙНОЙ **
3 REM** ФУНКЦИЕЙ Y=A + B*X »*
9 REM*********************************
1000 DIM X<100>,100>
1100 INPUT "ЧИСЛО ПАР ЗНАЧЕНИЙ"; N
1208 FOR 1-1 TO N
1300 PRINT "У<"л!л”> , Х<"л1л"> "1
1400 INPUT ?<I>,X<I>
1700 NEXT I
1800 PRINT
2000 Sl-N
2100 S2-0IS3-0184-0iS5-0
2280 FOR 1-1 TO N
2308 S2-S2+X<I>
2488 S3-S3+V<I>
2500 S4-S4+XCI>*X<I>
2600 S5-S5+Y<I>*X<I>
2700 NEXT I
3080 01-81*84-82*82
3100 02-83*84-85*82
3200 03-81*85-82*83
4000 fl-D2/D1
4108 B-D3/D1
5000 PRINT "УРАВНЕНИЕ РЕГРЕССИИ"
5100 PRINT •' V - "лАл" + "лВл"* X"
6000 8—0
6100 FOR 1-1 TO N
6200 S-S+<I>-<fl+B*X<I>>>T2
6300 NEXT I
6500 PRINT nPRINT "СУММА КВАДРАТОВ ОТКЛОНЕНИЙ ="; S
9999 END
RUN
ЧИСЛО ПАР ЗНАЧЕНИЙ? 7
Y< 1 > X< 1 > ? 1,0
Y< 2 > X< 2 > ? 3. 1,.9
Y< 3 > x< 3 > ? 4.8,1.98
Y< 4 > x< 4 > ? 7.2,3.05
Y< 5 > x< 5 > ? 8.9,4.2
Y< 6 > x< 6 > ? 11,5.02
Y< 7 ) x< 7 > ? 12.7,6.3
УРАВНЕНИЕ РЕГРЕССИИ
У - 1.22961069 + 1.86912472 * X
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ-=.453344113
READY.
В строке 1000 описаны используемые в программе массивы
Х( ) и Y( ). В следующей строке вводится число эксперименталь-
ных точек N. Это число является наибольшим значением парамет-
ра цикла FOR—NEXT, с помощью которого вводятся эксперимен-
тальные данные (строки 1200—1700). Со строки 2000 начинается
расчет сумм. Сначала SI = N. В цикле FOR—NEXT (строки
168
Глава 7
2200—2700) вычисляются суммы, входящие в формулы. Перед на-
чалом цикла соответствующие этим суммам переменные обнуля-
ются. Из рассчитанных теперь значений сумм в строке 3000 вычис-
ляется знаменатель и в строках 3100—3200 — числители в приве-
денных выше формулах. Потом вычисляются и выводятся на экран
значения параметров а и Ь. В заключительной части программы
(строки 6100—6300) вычисляется сумма квадратов отклонений, зна-
чение которой выводится на экран в предпоследней строке про-
граммы.
Задание 93. Расширьте программу «ЛИН-РЕГР» так, чтобы а) по желанию
можно было вывести иа экран таблицу входных данных вместе с теоретическими
значениями у, рассчитанными по уравнению регрессии; б) для значений %, для кото-
рых нет экспериментально полученных значений у, можно было вычислить по урав-
нению регрессии соответствующее значение у и вывести его на экран; в) можно бы-
ло определить параметры регрессии, используя взвешенные значения эксперимен-
тальных данных.
Задание 94. Исследована кинетика следующей реакции при 190 °C:
,, к
трицикло-[5,3,0^' ]-декадиен-3,9 — 2-циклопентадиен
Измерены концентрации исходного вещества в различные моменты времени. Ре-
акция подчиняется кинетическому уравнению первого порядка:
Из этого следует: —In[с] = — ln[c]0 + kt
Полученные экспериментальные данные (концентрации в моль/л, время в секундах)
приведены в таблице.
1 / [С ] 1,85 2,04 2,34 2,70 3,83 5,28
t 524 620 752 876 1188 1452
С помощью регрессионного анализа найдите по этим экспериментальным дан-
ным значения [с]0 и к.
Задание 95. Измерена константа скорости реакции первого порядка:
CH3CHF2 - СН2 = CHF + HF
при различных температурах. Зависимость константы скорости реакции от темпера-
туры описывается уравнением Аррениуса:
Полученные экспериментальные данные сведены в таблицу.
к•107/с 7,9 26 52 58 69 230 250 620 1400
Т/град. С 429 447 460 462 463 483 487 507 521
Переменные с индексами
169
Определите с помощью линейной регрессии предэкспонеициальный множитель
к0 и энергию активации Е°. (Примечание: найдите параметры линейной регрессии
In (к) от 1/Т.)
7.8. Линейная регрессия с оценкой
отклонения параметров
Ниже будет рассмотрена более удобная программа для расчета
параметров линейной регрессии, которая позволяет использовать
взвешенные входные данные. Кроме того, эта программа рассчи-
тывает ошибку определения параметров регрессии и предусматри-
вает различные варианты вывода информации. Необходимые для
этого математические формулы можно найти в книгах по
статистике*. Соответствующие формулы имеют вид (D и Т —
вспомогательные функции)
п / л \ 2
D = п- Y, Xj ~ ( £ xi) = N'S* ~
/ = 1 ' / = 1 '
T=y/L^-a - bx^n - 2> = SQR(S/(tf - 2))
Ошибка определения a: T*SQR(S4/D),
Ошибка определения b: T*SQR(N/D)
Ниже дана распечатка программы «ЛИН-РЕГР 4»:
0 REM "ЛИН—РЕГР4" EBERT/EDERER 820506
1 REM************************************************
2 REM** ЛИНЕЙНАЯ РЕГРЕССИЯ С РАСЧЕТОМ **
3 REM** СТАНДАРТНОГО ОТКЛОНЕНИЯ **
4 REM** ПАРАМЕТРОВ А И В. **
5 REM** ОБЯЗАТЕЛЬНО НАДО УКАЗЫВАТЬ **
6 REM** ЧИСЛО ЭКСПЕРИМЕНТАЛЬНЫХ *•
7 REM** ТОЧЕК **
8 REM** ########################################## **
9 REM** РЕГРЕССИЯ С УЧЕТОМ ВЕСОВЫХ КОЭФФИЦИЕНТОВ **
10 REM***********************************************
1000 DIM Х<100>,?<100>,|4<100>
1010 Я*-'1
1020 E«»CHR«<145>
1100 INPUT "ЧИСЛО ПАР ЗНАЧЕНИЙ"; N
1120 FOR 1-1 ТО N«W<I>-1iNEXT I
1140 PRINTiPRINT "ХОТИТЕ ВВЕСТИ ВЕСОВЫЕ КОЭФФИЦИЕНТЫ" ;> INPUT В*
1200 FOR 1-1 TO N
1300 PRINT " ?<"|I|"> - "л INPUT I>iPRINT E*l
1330 PRINT fl*iPRINT E«l
1350 PRINT " «",!,>
1400 PRINT " X<";I|"> - "л INPUT X< I > iPRINT E«;
* См., например: Ludwig R., Methoden der Fehler- und Ausgleichsrechnung. Vieweg,
Braunschweig, 1969.
170
Глава 7
1450 IF В«О "ДА" THEN GOTO 1615
1490 PRINT R*SPRINT E*>
1500 PRINT ” Y<",I,"> -",?<!>,
1600 PRINT “ X<",!,"> -";X<I>1
1610 PRINT " WC“,I,“> - ",sINPUT Ы<I>:PRINT E« >
1615 PRINT R«SPRINT E«;
1620 PRINT " Y<”,I,"> »”,Y<I>,
1630 PRINT " X<",!,"> -",X<I>,
1640 PRINT ' W<",!,"> -",Ы<1>
1700 NEXT I
2000 31-0
2100 32-0s33-0s34-0s35-0
2200 FOR 1-1 TO N
2250 S1-S1+I4<!>
2300 S2-S2+X<I>*Ы<I>
2400 S3-S3+Y<I>*H<I>
2500 S4-S4+XCI>*X<I>*Ы<I>
2600 S5-S5+V<I> *X <I> *Ы <I>
2700 NEXT I
3000 DI-SI*34-32*32
3100 02-33*34-35*32
3200 D3-81*S5-82*33
4000 R-D2/D1
4100 B—03/01
5000 PRINT "УРАВНЕНИЕ РЕГРЕССИИ"
5100 PRINT " V - ">R>" + ">B,"* X"
6000 S—0
6100 FOR 1-1 TO N
6200 S-S+WCI>*<¥<I>-<R+B*X<I> > >T2
6300 NEXT I
6500 PRINT SPRINT "СУММА КВАДРАТОВ ОТКЛОНЕНИЙ = "; S
6600 D-SQR<S/<N-2>> _ ,
6605 PRINT SPRINT "СТАНДАРТНОЕ ОТКЛОНЕНИЕ = ;D
6610 DR-D»SQR<S4/D1> sDB-D*SQR<Sl/Dl>
6620 PRINT SPRINT "ЧИСЛО ПАР ЗНАЧЕНИЙ =";N: PH1NT
6630 PRINT "R - ",R," +/- ",DRSPRINT
6640 PRINT "B - ",B," +/- ",OB SPRINT
7000 PRINT SPRINT" ХОТИТЕ СРАВНИТЬ ИСХОДНЫЕ ЗНАЧЕНИЯ"
7100 PRINT "С РАССЧИТАННЫМИ" >
7200 INPUT R«
7300 IF R*-"ДА" THEN GOTO 8000
7500 GOTO 8400
B000 PRINT
8050 PRINT " X Y (ИЗМЕР) Y (TEOPET)"
8100 FOR I —1 TO N
8200 PRINT X<I>,Y<I>,R+B*X<I>
8300 NEXT I
8400 PRINT SPRINT "ХОТИТЕ РАССЧИТАТЬ ПО УРАВНЕНИЮ РЕГРЕССИИ"
В500 PRINT "ЗНАЧЕНИЯ Y ДЛЯ КАКИХ-НИБУДЬ ЗНАЧЕНИЙ X";
8600 INPUT R«
8700 IF R«-"ДА" THEN GOTO 9000
8800 GOTO 9999
9000 PRINT "ЗНАЧЕНИЕ X"; sINPUT XsPRINT £♦,
9050 PRINT" "SPRINT E«,
9100 PRINT "7<",X,"> « ",R+B*X
9200 GOTO 9000
9999 END
RUN
ЧИСЛО ПАР ЗНАЧЕНИЙ? 4
ХОТИТЕ ВВЕСТИ ВЕСОВЫЕ КОЭФФИЦИЕНТЫ? ДА
V< 1 >- 4.1
У< 2 >-8.1
У< 3 > — 9.9
У< 4 >- 12.1
Х< 1 >-2.1
Х< 2 >- 3.9
Х< 3 >а 5.1
Х< 4 >-5.8
Ы< 1 >» .5
Ы< 2 >« 3
3 >- 10
4 >а 1
Переменные с индексами
171
УРАВНЕНИЕ РЕГРЕССИИ
У - .536199933 + 1.86448743 *Х
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ -1.09079431
СТАНДАРТНОЕ ОТКЛОНЕНИЕ = .738510093
ЧИСЛО ПАР ЗНАЧЕНИЙ= 4
R - .536199933 +/- 1.26927237
В - 1.8644В743 +/- .261514508
ХОТИТЕ СРАВНИТЬ ИСХОДНЫЕ ЗНАЧЕНИЯ
С РАССЧИТАННЫМИ ? ДА
X V (ИЗМЕР)
2.1 4.1
3.9 8.1
5.1 9.9
5.8. 12.1
V (ТЕОРЕТ)
4.45162355
7.80770093
10.0450858
11.3502271
ХОТИТЕ РАССЧИТАТЬ ПО УРАВНЕНИЮ РЕГРЕССИИ ЗНАЧЕНИЕ Y
ДЛЯ КАКИХ-НИБУДЬ ЗНАЧЕНИЙ X ?
? ДА
У<-1 > . -1.3282875
V< 2 > - 4.2651748
У< 17 > - 32.2324863
55 > - 103.0В3009
0 > - .536199933
у< 7.23 > » 14.0164441
ЗНАЧЕНИЕ X?
Эта программа предоставляет возможность учитывать досто-
верность каждой пары экспериментальных значений. Переменным,
соответствующим весовым коэффициентам, перед вводом данных
присваивается значение 1. Если весовые коэффициенты не вводятся,
то эти переменные сохраняют значение 1. По сравнению с предыду-
щей программой в каждой строке главного цикла (строки
2200—2700) происходит умножение на весовой коэффициент. Кроме
того, добавлена строка 2250, в которой вычисляется сумма весовых
коэффициентов, входящая вместо»числа экспериментальных точек в
формулы для расчета параметров регрессии. Следующий участок
программы до строки 6500 отличается от предыдущей программы
«ЛИН-РЕГР» тем, что при вычислении суммы квадратов отклоне-
ний квадрат каждого отклонения умножается на соответствующий
весовой коэффициент. Далее по приведенным выше формулам вы-
числяются и выводятся на экран стандартное отклонение зависи-
мой переменной (строка 6600) и стандартные отклонения парамет-
ров а и b (строка 6610). В строке 7200 вводится ответ на вопрос,
надо ли выводить на экран таблицу исходных данных и рассчитан-
ных по полученному уравнению регрессии соответствующих значе-
ний у. Если ввести слово ДА, то происходит ввод на экран этой
172
Глава 7
таблицы (строки 8000—8400). И наконец, программа предоставляет
пользователю возможность рассчитать для любого значения х со-
ответствующее значение у, вычисленное по уравнению регрессии
(строки 8400—9200). Дополнительно операторы в строках 1330,
1490, 1615 и 9100 вызывают движение курсора, что улучшает на-
глядность выходных данных.
Задание 96. Программу «ЛИН-РЕГР4» можно успешно использовать для реше-
ния ряда задач, связанных с обработкой экспериментальных данных. Однако эта
программа содержит один существенный для практики недостаток. Если при вводе
исходных данных будет сделана опечатка, то не остается ничего другого, как заново
запустить программу. Поскольку опечатки встречаются довольно часто и их едва ли
можно избежать при вводе большого количества данных, этот недостаток очень
раздражает.
Модифицируйте программу «ЛИН-РЕГР4», чтобы у пользователя была воз-
можность исправить допущенные при вводе ошибки. Простейший способ заключает-
ся в замене ввода данных с помощью оператора INPUT на ввод с помощью опера-
тора DATA и READ. Удобный для пользователей, но более трудно программируе-
мый способ исправления опечаток заключается в следующем. Между строками 1700
и 2000 размещают дополнительный участок программы, который повторно выво-
дит на экран входные данные. Пользователь может остановить правильно набран-
ные значения или заменить ошибочные.
8. Линейные системы
Линейные зависимости между величинами широко распростра-
нены и часто используются при решении задач научно-технического
характера. Эти зависимости описывают аддитивные свойства объ-
ектов. В математическом смысле линейные соотношения обычно
моделируют идеальное поведение. Приведем некоторые конкрет-
ные примеры:
— зависимость свойств идеальных смесей от концентрации компо-
нентов;
— интенсивности линий в (масс-)спектрах смесей;
— анализ смесей методом газовой хроматографии;
— зависимость скорости реакции первого порядка от концентрации
исходных веществ (зависимость скорости реакции от температу-
ры, разумеется, нелинейная);
— зависимость тепло- и массообмена в стационарных условиях от
разности концентраций или температур;
— зависимость «потоков» и «сил» в неравновесной термодинамике
(уравнение Онзагера);
— зависимость силы электрического тока от напряжения и сопро-
тивления;
— зависимость состава пара и парциального давления компонентов
над идеальными растворами от состава раствора;
— зависимость стоимости химических реактивов от их используе-
мого количества (это справедливо только в идеальном случае и
не выполняется, когда поставщик, пользуясь возросшим спро-
сом, делает свой «бизнес» и повышает цены);
— методы ЛКАО-МО в квантовой химии и т. д.
Очень часто нелинейные соотношения заменяют линейными,
разбивая интересующую область на интервалы, внутри которых за-
висимость можно рассматривать как линейную. При значительных
отклонениях от линейности (например, для зависимости скорости
реакции от температуры) интервалы надо выбирать достаточно
малыми. В термодинамике реальные соотношения между величина-
ми можно приближенно считать линейными, если ограничить с од-
ной стороны область применения приближенных соотношений.
174
Глава 8
Примером служат законы Рауля и Генри для малых концентраций
компонентов. Сведение нелинейной задачи к линейной путем выде-
ления областей, в которых выполняются линейные соотношения
между параметрами, является общим приемом, который использу-
ется не только в инженерных расчетах, но и в математике.
8.1. Подпрограммы
Поскольку программы и примеры становятся все более длинны-
ми (но совсем не обязательно более сложными), в этом разделе
будет введен очень важный элемент языка БЕЙСИК — подпро-
грамма. Подпрограммы позволяют улучшить структуру программ.
Практически во. всех языках программирования используется ан-
глийский язык, поэтому принято английское название подпрограм-
мы — subroutines.
В программе для интегрирования «ЭЙЛЕР» мы должны были
три раза писать одну и ту же подынтегральную функцию в трех
различных местах программы. Вместо этого в программе
«ЭЙЛЕР2» была использована так называемая подпрограмма-
функция*. Математическое выражение, описываемое в подпрограм-
ме-функции, может занимать только одну строку. В принципе под-
программы используются в аналогичных случаях; они являются со-
ставными частями программы и могут сколько угодно вызываться
на различных участках основной программой или другими подпро-
граммами. Подпрограммами могут быть и завершенные програм-
мы. Объем подпрограмм не ограничен одной строкой или одной
математической формулой, как оператор DEF FN. Подпрограмма
вызывается оператором:
***************
* z1 GOSUB z2 *
***************
zl, z2 — номера строк; z2 — номер строки, с которой начинается подпрограмма.
Начало подпрограммы в БЕЙСИКе никак дополнительно не
обозначается, а заканчиваться подпрограмма должна оператором
RETURN.
************
* z RETURN *
************
z — номер строки.
* Оператор DEF FN, используемый в программе «ЭЙЛЕР2», соответствует
оператору-функции. — Прим, перев.
Линейные системы
175
Подпрограмма в БЕЙСИКе не имеет явно выраженного начала.
Оператор GOSUB очень похож на оператор GOTO. Оба оператора
прерывают нормальный порядок выполнения операторов програм-
мы и передают управление заданной строке. Основное различие со-
стоит в том, что оператор безусловного перехода GOTO «забыва-
ет», с какой строки произошел переход, в то время как оператор
GOSUB «помнит» это, т. е. «помнит» номер строкиzl, и операто-
ром RETURN управление передается строке, следующей за стро-
кой, из которой вызывалась подпрограмма.
Чтобы после выполнения подпрограммы вернуться в основную
программу или вызывающую подпрограмму, подпрограмма до-
лжна заканчиваться оператором RETURN.
Пример:
10 DIM Х(100)
20 FOR 1=1 ТО 100
30 Х(I) = 1*1
40 NEXT I
50 GOSUB 1000
60 GOSUB 2000
70 FOR 1=1 TO 100
80 X(I) = 1*1*1
90 NEXT I
100 GOSUB 1000
110 GOSUB 2000
120 STOP
1000 S=0
1010 FOR 1=1 TO 100
1020 S = S + X(l)
1030 NEXT I
1040 S = S/100
1050 RETURN
2000 PRINT "СРЕДНЕЕ = ";S
2010 RETURN
2020 END
В этом примере сначала возводятся в квадрат 100 чисел нату-
рального ряда, начиная с 1 (строки 20—40). В строке 50 вызывается
подпрограмма, которая вычисляет среднее арифметическое этих
ста квадратов. В строке 60 вызывается другая подпрограмма для
вывода данных на экран. Далее в основной программе возводятся в
куб сто первых чисел натурального ряда (строки 70—90) и происхо-
дит обращение к подпрограммам для вычисления среднего арифме-
тического и вывода данных. Программа построена таким образом,
что в основной ее части по заданным формулам вычисляются зна-
чения индексированной переменной Х(1). Обращение к подпрограм-
176
Глава 8
ме GOSUB 1000 используется для вычисления среднего арифметиче-
ского элементов массива Х( ).
В следующем примере вычисляется число т уже знакомым нам
методом Монте-Карло. Эта программа выглядит иначе, чем рас-
смотренная выше (с. 51).
10 N1 = О
20 N2 = О
30 GOSUB 1000: REM ВЫЧИСЛЕНИЕ КОМПОНЕНТОВ СЛУЧАЙНОГО ВЕКТОРА
40 GOSUB 1200: REM ПРОВЕРКА ПОПАДАНИЯ В ЕДИНИЧНЫЙ КРУГ
50 GOSUB 1400: REM ВЫВОД ДАННЫХ
60 GOTO 30
1000 Х1 = RND(5)
1010 Х2 = RND(5)
1020 RETURN
1200 Н = Х1*Х1 + Х2*Х2
1210 IF Н>1 THEN GOTO 1230
1220 N1 = N1 + 1
1230 N2 = N2 + 1
1240 RETURN
1400 PRINT N1,N2,N1/N2*4
1500 RETURN
2000 END
В этом примере программа разделена на подпрограммы не в си-
лу какой-то необходимости, а для того, чтобы сделать ее в целом
более наглядной. Основная программа (строки 10—60) короткая и
состоит из обращений к подпрограммам. В подпрограммах произ-
водятся различные вычисления и организован вывод выходных дан-
ных.
Следующая короткая демонстрационная программа предназна-
чена для сглаживания результатов измерений. Этот метод часто
используется при обработке экспериментальных данных.
0 REM 1 3 7 3 1 СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
100 DIM X (100),Y(100)
200 GOSUB 2000 : REM ВВОД ДАННЫХ
3 00 GOSUB 3000 : REM СГЛАЖИВАНИЕ И ВЫВОД ДАННЫХ
500 INPUT "НАДО ЛИ ПРОВОДИТЬ СГЛАЖИВАНИЕ ЕЩЕ РАЗ";
600 IF А$="ДА" THEN GOTO 300
700 STOP
2000 N = 10
2010 DATA 1,1.8,2.8,4.3,5,6,6.9,7.8,9.2,10
2020 FOR 1=1 TO N: READ X(I):Y(I)=X(I):NEXT I
2040 RETURN
3000 Y(1) = X(1):Y(N) = X(N)
3010 Y(2) = (X(1)+3*X(2)+X(3))/5
3O2OY(N-1) = (X(N-2)+3*X(N-1)+X(N))/5
Линейные системы
177
3100 FOR 1=3 ТО (N-2)
3110 Y(I)=(X(1-2)+3*Х(1-1)+7*X(I)+3*x(1+1)+X(I+2))/15
3120 NEXT I
3200 GOSUB 4000:REM ВЫВОД СГЛАЖЕННЫХ ДАННЫХ
3900 RETURN
4000 FOR 1=1 TO NsPRINT I,X(I),Y(I):X(I)=Y(I)sNEXT I
4100 RETURN
Метод сглаживания получил широкое распространение. Предва-
рительно надо решить, в большей или меньшей степени будет про-
водиться сглаживание, т. е. сколько соседних точек и с какими ве-
совыми коэффициентами необходимо учитывать при выполнении
процедуры сглаживания. В приведенном выше примере учитывает-
ся по два соседних значения с каждой стороны с весовыми коэффи-
циентами 1, 3, 7, 3, 1. Однако и количество учитываемых соседних
точек, и весовые коэффициенты можно легко изменить. Подпро-
граммы служат прежде всего для улучшения структуры программ.
В рассмотренном примере продемонстрирована возможность вызо-
ва подпрограммы из другой подпрограммы. Количество таких по-
следовательных обращений к подпрограмме из других подпро-
грамм зависит от типа компьютера и указано в руководстве к не-
му. Однако вы можете это выяснить самостоятельно, попробовав
непосредственно на ЭВМ.
**************************************
* ЗАПОМНИТЕ: НЕЛЬЗЯ ВЫЗЫВАТЬ *
* ПОДПРОГРАММУ ИЗ ТОЙ ЖЕ ПОДПРОГРАММЫ! *
**************************************
За простоту, с которой части программы на БЕЙСИКе можно
превратить в подпрограммы, и за легкость вызова подпрограммы
(по сравнению с другими алгоритмическими языками высокого
уровня) приходится расплачиваться наличием некоторых недостат-
ков. Программа на БЕЙСИКе, включая все подпрограммы, пред-
ставляет собой единое целое, и переменные, в какой бы части они
ни встречались, сохраняют свои значения во всех частях програм-
мы. В стандартном БЕЙСИКе нет возможности Йспользовать
идентификаторы переменных одной подпрограммы независимо от
других подпрограмм или основной программы (т. е. так, как ис-
пользуются формальные параметры в операторе DEFFN). Для
больших программ, части которых написаны независимо друг от
друга (возможно, даже различными авторами) и затем объединены
в одну программу, это является большим недостатком. Если, не-
12-81
178
Глава 8
смотря на это, необходимо все же составить большую программу
из нескольких подпрограмм, то предварительно надо четко устано-
вить порядок использования идентификаторов переменных в раз-
личных частях программы.
8.2. Системы линейных уравнений
В этом разделе будет рассмотрено решение системы линейных
уравнений методом Гаусса — Жордана. Для лучшего понимания
метода решим сначала систему линейных уравнений вручную.
Пусть даны три уравнения с тремя неизвестными:
4х + Зу + z = 13
2х - у - z = -3
7х + у - 3z = О
Если написать эту систему уравнений, отбросив символы «х»,
«у», «г» и «=», то получится так называемая расширенная матри-
ца системы:
4 +3 +1 13 \
2 -1 -1 -3 )
7+1-3 0 /
Решение системы линейных уравнений не изменится, если умно-
жить правую и левую части каждого уравнения на любое число*.
Чтобы первый коэффициент первого уравнения стал равен 1, разде-
лим первое уравнение на 4:
1 +3/4 +1/4 13/4 \
2-1 -1 -3 I [2]- 2-[1]
7+1 -3 0 / [3] - 7 [1]
Поскольку уравнения системы можно умножать иа любые чис-
ла, а также складывать и вычитать, коэффициенты, стоящие в пер-
вом столбце, кроме первого, можно обратить в 0. Для этого умно-
жим строку [1] на 2 и произведение вычтем из второй строки. Пер-
вую строку умножим на 7 и произведение вычтем из третьей стро-
ки:
+ 3/4 +1/4 13/4 \
-5/2 -3/2 -19/2 I /(-5/2)
-17/4 -19/4 — 91/4/
* Кроме нуля. — Прим, перев.
Линейные системы
179
Теперь надо обратить в 1 диагональный элемент второй строки.
Для этого разделим второе уравнение на этот диагональный эле-
мент (—5/2) и получим
(1 +3/4 +1/4 13/4 \ [1] - 3/4- [2]
О 1 3/5 19/5 I
О -17/4 -19/4 -91/4 / [3] + 17/4-[2]
Теперь попытаемся исключить элементы, расположенные над и
под диагональным элементом второго столбца. Для этого вычтем
из первого уравнения умноженное на 3/4 второе уравнение, а
третье уравнение сложим со вторым, умноженным на 17/4:
10 -1/5 2/5 \
0 1 3/5 19/5 )
0 0 - 11/5 -33/5 //(-11/5)
Для того чтобы диагональный элемент третьей строки стал ра-
вен 1, разделим третье уравнение на диагональный элемент третьей
строки:
1 0 -1/5 2/5\[1] + 1/5-[3]
0 1 3/5 19/5 1[2] — 3/5 -[3]
0 0 13/
Прибавляя умноженную на соответствующие коэффициенты
третью строку к первой и второй, можно исключить недиагональ-
ные элементы третьего столбца:
/ 1 0 0 1 \
(0102 1
\ 0 0 1 3 /
Если теперь дописать «забытые» символы, то получится следу-
ющая система уравнений:
lx + 0у + 0z = 1
Ох + ly + 0z = 2
Ох + Оу + lz = 3
Из этой системы уравнений непосредственно получается иско-
мое решение:
х = 1; у = 2; z = 3
Прежде чем привести блок-схему этого алгоритма, дадим неко-
торые определения и прокомментируем их. Расширенной матрицей
системы называется совокупность ее элементов A (i, j). Размер-
12*
180
Глава 8
Схема 13
ность системы уравнений, т. е. число уравнений, будем обозначать
буквой п. Деление/-го уравнения на/-й диагональный элемент (А (/,
/)) назовем нормировкой z-й строки*. Если этот диагональный эле-
В отечественной литературе такого термина нет. — Прим, перев.
Линейные системы
181
мент равен нулю, то z-e уравнение меняют местами со следующими
за ним уравнениями до тех пор, пока не будет найден ненулевой г'-й
диагональный элемент. Если такой элемент найти не удастся, то
система уравнений не имеет единственного решения. Уравнения си-
стемы можно произвольным образом менять местами, корни при
этом не меняются. Блок-схема алгоритма решения системы линей-
ных уравнений методом Гаусса — Жордана приведена на схеме 13.
Ниже приведена распечатка программы «Г—Ж», в которой ис-
пользован метод Гаусса — Жордана.
0 REM "Г-Ж" EBERT/EDERER 810628
1 REM***********************************
2 REM** РЕШЕНИЕ СИСТЕМЫ ИЗ N ЛИНЕЙ- **
3 REM** НЫХ УРАВНЕНИЙ С N НЕИЗВЕСТНЫ-**
4 REM** МИ МЕТОДОМ ГАУССА-ЖОРДАНА **
9 REM***********************************
50000 DIM R<20,18>
50100 INPUT "ЧИСЛО НЕИЗВЕСТНЫХ"; N
50200 PRINT "ВВОД РАСШИРЕННОЙ МАТРИЦЫ КОЭФФИЦИЕНТОВ"
50300 FOR 1-1 ТО N
50400 FOR J-l ТО N
50500 PRINT "Ж" Ji lINPUT R<I,J>
50600 NEXT J
50700 PRINT "B<"1•INPUT R<I,N+1>
50800 NEXT I1PRINT
50900 FOR S-l TO N
51000 FOR T-S TO N
51100 IF R<T,S><>0 THEN 51300
51200 NEXT TiPRINT "ЕДИНСТВЕННОГО РЕШЕНИЯ HET": GOTO 63999
51300 GOSUB 53000
51400 C-1/R<S,S>
51500 GOSUB 54000
51600 FOR T-l TO N
51700 IF T-S THEN 52000
51800 C—R<T,S>
51900 GOSUB 55000
52000 NEXT T
52100 NEXT S
52200 GOSUB 560001G0T063999
53000 REM*****************************
53002 REM** ПОДПРОГРАММА **
53004 REM** ДЛЯ ОБМЕНА **
53006 REM** УРАВНЕНИЙ ••
53010 REM*****************************
5Э100 FOR J-l TO N+l
53200 B-R<S,J>iR<S,J>-fl<T,J>1R<T,J>-B
53300 NEXT J
53400 RETURN
54000 REM*****************************
54002 REM** ПОДПРОГРАММА ДЛЯ **
54004 REM** ДЕЛЕНИЯ СТРОКИ НА **
54006 REM** ДИАГОНАЛЬНЫЙ ЭЛЕМЕНТ**
54010 REM*****************************
54100 FOR J-l TO N+l
54200 R<S,J>-C*fl<S,J>iNEXT J
54400 RETURN
182
Глава 8
55000 REM*****************************
55002 REM** ПОДПРОГРАММА ДЛЯ ««
55004 REM** ВЫЧИТАНИЯ *«
55005 REM** УМНОЖЕННОЙ НАС **
55006 REM** S-Й СТРОКИ ИЗ ««
55007 REM** Т-Й СТРОКИ **
55010 REM*****************************
55100 FOR J-l ТО N+1
55200 R<T,J>-R<T,J>+C*R<S,J>
55300 NEXT J
55400 RETURN
56000 REM*****************************
56001 REM** ПОДПРОГРАММА ДЛЯ ВЫ- ««
56002 REM** ВОДА РЕШЕНИЯ НА ЭКРАН ««
56010 REM*****************************
56100 FOR Т-1 ТО Н
56200 PRINT "Х<",Т,“>-"»R<T,N+1>
56300 NEXT Т
56400 RETURN
63999 END
RUN
ЧИСЛО НЕИЗВЕСТНЫХРЗ
ВВОД РАСШИРЕННОЙ МАТРИЦЫ КОЭФФИЦИЕНТОВ
R< 1 , 1 >.? 4
R< 1 , 2 >-? 7
R< 1 , 3 >-? 2
В< 1 >-? 38
R< 2 , 1 >-? 6
R< 2 , 2 >-? 3
R< 2 , 3 >-? 2
B< 2 >-? 26
R< 3 , 1 >-? 5
R< 3 , 2 >', -2
RC 3 , 3 >-? -3
B< 3 >-? -1
X< 1 >- 2
X< 2 >- 4
X< 3 >- .999999996
RERDV.
Программа «Г—Ж» содержит четыре подпрограммы. Первая
подпрограмма, которая начинается со строки 53000, меняет места-
ми две строки матрицы, а именно S-ю строку с Т-й. Следующая
подпрограмма умножает всю строку матрицы на константу С
(строки 54000—54400). Подпрограмма, которая начинается со стро-
ки 55000, вычитает из Т-й строки умноженную на С S-ю строку
расширенной матрицы системы. Подпрограмма в строках 56000—
56400 выводит на экран N значений X.
Ввод исходных данных происходит в основной программе в
строках 50000—50800. В строке 50000 описан двухмерный массив
А( ), соответствующий расширенной матрице системы. Размер
массива А( ) позволяет решать системы уравнений с 18 (наиболь-
шее число) неизвестными. Число неизвестных вводится в строке
50100. Потом с помощью конструкции из двух циклов вводятся эле-
Линейные системы
183
менты матрицы коэффициентов и вектора правой части системы
уравнений.
Основные вычисления происходят в цикле, расположенном в
строках 50900—52100. В цикле по параметру S диагональные эле-
менты матрицы приводятся к единице, а элементы, стоящие над и
под диагональю, исключаются. Но прежде чем приступить к этой
процедуре, необходимо убедиться в том, что соответствующий
диагональный элемент не равен нулю. Это выполняется в цикле по
параметру Т в строках 51000—51200. В этом цикле происходит по-
иск ненулевого элемента матрицы, стоящего в S-м столбце S-й
строки. Если такого элемента не найдено, то цикл по Т заканчива-
ется и на экран выводится сообщение о том, что система уравнений
не имеет решений и выполнение программы заканчивается. Если
все же в Т-й строке S-ro столбца найден ненулевой элемент, то опе-
ратор условного перехода IF в строке 51100 передает управление
строке 51300. В данном случае этот цикл по Т не заканчивается как
обычно. В строке 51300 вызывается подпрограмма для обмена ме-
стами Т-й строки матрицы с S-й. После обмена матричный эле-
мент A(S, S) теперь уже не равен нулю. В следующей строке (51400)
вычисляется нормировочный коэффициент 1/A(S, S), потом вызы-
вается подпрограмма, начинающаяся со строки 54000, в которой
S-я строка матрицы умножается на нормировочный коэффициент,
после чего S-й диагональный элемент становится равным 1.
Затем следует цикл, который исключает недиагональные эле-
менты S-ro столбца. Так как параметром этого цикла опять явля-
ется переменная Т, «чрезвычайный»* выход из предыдущего цикла
по Т «забывается». В этом цикле по Т из каждой строки матрицы,
кроме S-й, начиная с Т-й, вычитается произведение А(Т, S) на S-ю
строку. После этого матричный элемент А(Т, S) становится равен
нулю. Если цикл по параметру Т завершил свою работу, то можно
продолжить поиск следующего ненулевого диагонального элемен-
та, т. е. параметр цикла S увеличивается на 1. После окончания ци-
кла по S все диагональные элементы матрицы равны 1, в (N + 1)-м
столбце стоят найденные значения неизвестных, остальные элемен-
ты матрицы равны 0. В следующей строке программы (52200) вы-
зывается подпрограмма для вывода результата на экран, и после
этого выполнение программы заканчивается (строка 63999).
В приведенном числовом примере найдены корни системы трех
уравнений с тремя неизвестными. Затраты машинного времени для
• «Обычный» выход нз цикла происходит после того, как параметр цикла прини-
мает наибольшее значение. «Чрезвычайный» выход из цикла происходит, если вы-
полняется условие, записанное в операторе IF (строка 51100). — Прим, перев.
184
Глава 8
решения системы линейных уравнений возрастают приблизительно
пропорционально квадрату числа уравнений.
Задание 97. Даны масс-спектры (фиктивные), такие же, как в задании 85. Даны
также интенсивности четырех различных пиков, четырех различных смесей четырех
веществ. Исходя из приведенных в таблице данных, рассчитайте состав каждой сме-
си. (В этом задании калибровочные коэффициенты, связывающие интенсивности пи-
ков с концентрациями соответствующих компонентов, также равны 1, и их можно
вообще не учитывать.)
Высота пика Смесь! Смесь 2 Смесь 3 Смесь 4
Масса 14 119 169 326 60
Масса 15 1 95 284 501 113
Масса 26 134 168 433 21
Масса 28 124 148 124 100
Задание 98. Как вы уже, наверное, заметили при выполнении предыдущего зада-
ния, к недостаткам программы «Г—Ж» относится прежде всего форма ввода исход-
ных данных в виде расширенной матрицы системы. Невозможно ни проверить вве-
денный числовой материал, ни исправить допущенные опечатки.
Сделайте ввод данных удобным для пользователей! Предусмотрите возмож-
ность исправления входных данных; кроме того, желательно, чтобы система уравне-
ний сохранялась в памяти ЭВМ и после решения задачи ее можно было бы вывести
на экран. Написанная один раз удобная для пользователя входная часть программы
в принципе может применяться также и в других программах. Такая входная часть
программы предусматривает: первоначальный ввод данных, возможность вывода
исходных данных на экран (целиком и по отдельности), возможность исправлять от-
дельные значения, вставлять пропущенные знаки, зачеркивать ошибочные и добав-
лять новые данные.
Задание 99. Даны четыре емкости с растворами кислоты различной концентра-
ции. Если смешать растворы в определенном соотношении, то получится кислота
заданной процентной концентрации:
Соотношение Концентрация
кислоты, %
1:1:1:1 25
4:3:2:1 20
4:1:1:4 25
4:1:4:1 22
Определите, какова концентрация кислоты в каждом нз четырех сосудов.
Задание 100. Пусть имеется система уравнений
х + wy =1
WX + у = 1
где w много меньше единицы.
Нетрудно найти решение этой системы. Значениях ну близки к единице, а точ-
нее:
1 1
X = ------ и у = ---------
1 + W 1 + W
Линейные системы
185
Если решить эту систему на ЭВМ, которая выполняет арифме-
тические операции с точностью до 8 значащих цифр, и подставить
в приведенную выше систему уравнений w = IE — 10, то в резуль-
тате получится х = 1, у = 1. Этот результат не вызывает никаких
возражений. Если же уравнения поменять местами, то по програм-
ме «Г—Ж» получится: х = 0, у = 1. Ясно, что этот результат
ошибочный. Если в исходной системе уравнения поменять местами
и разделить оба уравнения на w, то при решении полученной систе-
мы по программе «Г—Ж» получится: х = 4,671875, у = 1. Таким
образом, операции, которые не должны были бы отражаться на
решении системы уравнений, приводят к различным и, следова-
тельно, ошибочным результатам. Появление ложных корней связа-
но с тем, что ЭВМ производит арифметические действия с конеч-
ной точностью и в процессе вычисления накапливаются ошибки
округления. Системы уравнений, которые ведут себя так же, как
рассмотренная в этом примере, называют плохо обусловленными.
Для систем уравнений с числом неизвестных больше двух, как пра-
вило, невозможно сразу установить, является ли эта система плохо
обусловленной. Поэтому надо обязательно проверять, удовлетво-
ряют ли в действительности найденные значения неизвестных ис-
ходной системе уравнений.
Дополните программу «Г—Ж» подпрограммой, которая подставляла бы най-
денные значения неизвестных в систему уравнений, сравнивала бы результат этой
подстановки с правой частью исходных уравнений н вычисляла бы их разность.
8.3. Линейная регрессия общего вида
В разд. 7.7 мы уже познакомились с линейным регрессионным
анализом, когда уравнение регрессии линейное. Часто функция не-
зависимой переменной и подгоночных параметров не является ли-
нейной, а представляет собой линейную комбинацию функций той
же независимой переменной. В качестве примера можно привести
зависимость высоты свободного падения тела.? от времени t. В об-
щем виде связь между величинами выражается в форме полинома:
у = at2 + bt + с
В этом случае у линейно зависит от трех функций переменной t:
/1(0 = t2, f2(t) = t, /3(0 = 1
Параметрами, которые определяются в регрессионном анализе,
являются а, b и с. Рассмотренная в предыдущем разделе линейная
регрессия представляет собой частный случай линейной регрессии
186
Глава 8
общего вида. Это становится наглядным, если в приведенном выше
примере отбросить первую функцию. Тогда получится
у = bt + с
Другим примером описания процессов с помощью линейной ре-
грессии общего вида служит следующая простая система реакций
первого порядка:
В —2 Р
Уравнение относительно концентрации продукта Р, полученное,
исходя из этой кинетической схемы, при заданных константах ско-
рости кх и к2 имеет вид
[Р] = [Р]о + [А]о (1 - е"*1') + [В]о-(1 - е“*2')
Если в различные моменты времени t измерены концентрации
вещества Р и известны константы скорости реакции кх и к2, то за-
дача сводится к поиску параметров линейной регрессии общего ви-
да, в которой концентрация вещества Р линейна относительно трех
функций независимой переменной t. Определяемыми параметрами
являются начальные концентрации трех веществ: [Р]о, [А]о и [В]о.
При выводе формул для вычисления параметров регрессии огра-
ничимся пока уравнением регрессии, включающим две функции об-
щего вида. Потом по аналогии мы обобщим полученные формулы
для уравнений регрессии с произвольным количеством функций.
Пусть даны и значений величин х и у и, кроме того, известен
вид математического выражения, связывающего х и у.
У = а- /](*•) + b-f2fy)
Линейные системы
187
Необходимо найти такие значения параметров а и b, чтобы сум-
ма квадратов разностей заданных и вычисленных по уравнению ре-
грессии значений у была минимальна.
Математически проблема формулируется так:
S = £ [у. - - b-f2(Xi)]2
i = 1
Поскольку сумма квадратов отклонений S должна быть мини-
мальна, ее частные производные по параметрам регрессии а и b
должны равняться нулю:
= -2 У [у, - a-f^) - = 0
да ,Т,
Й = “2 Е ~ = 0
дЬ < = i
Если преобразовать эти два уравнения и сгруппировать коэффи-
циенты при параметрах а и Ь, то получится следующая линейная
система уравнений относительно а и Ь:
« Е W-W + b £ W-W = i
i = I / = 1 / = 1
а Е -W’-W + b Е -W’-W = Е
i=i i=i /=1
Таким образом, задача свелась к решению системы из двух
уравнений с двумя неизвестными. Решение систем линейных урав-
нений рассмотрено в предыдущей главе и не представляет трудно-
стей.
Если этот подход применить к уравнению регрессии, в которое
входят т различных функций переменной х, то возникает следую-
щая задача.
Пусть для п пар полученных экспериментально значений х(, у,
существует теоретическое уравнение, описывающее зависимость у
от Х‘.
У = Е kj‘fjW = *i‘-W + + - + km-fm(x)
j = 1
188
Глава 8
Анализ регрессии статистических величин yt и х, позволяет опре-
делить параметры ку. Как и в предыдущем случае, минимизируется
сумма квадратов отклонений:
п |“ т nJ
s = L л - Е V-W
i = 1 L j = i J
Продифференцируем S no kj и потом все частные производные
приравняем нулю. Раскрывая скобки и снова группируя коэффици-
енты при параметрах регрессии, получаем систему линейных урав-
нений. Если ввести обозначения
Л* = Е и bj = i W-y,
< = 1 i = 1
то систему можно написать в следующем виде:
АЛ1 + АЛг + АЛз
АЛ1 + + ААз
АЛ> + + АЛз
+ ••• + f \ткт = Ь\
+ ••• + f-2mkm ~ Ь2
+ •" + flmkm = Ь3
+ ••• + fmmkm =
•s mi i * J mz 2 J ms 3 J mm m m
Эту систему уравнений можно решить методом Гаусса — Жор-
дана (см. программу «Г — Ж»). Программа для вычисления пара-
метров линейной регрессии общего вида вместе с числовым приме-
ром приведена ниже.
0 REM "ОБЩ—РЕ ГР" EBERT/EDERER 810628
1 REM************************************
2 REM** ЛИНЕЙНАЯ РЕГРЕССИЯ ОБЩЕГО ««
3 REM** ВИДА. В ПОДПРОГРАММЕ 40000 ОПИ- «*
4 REM** САНЫ N ФУНКЦИЙ, ВХОДЯЩИХ *«
5 REM** В УРАВНЕНИЕ РЕГРЕССИИ ««
9 REM************************************
600 DIM Х<100>,У<108>,Я<19,20>
788 DIM K<20>,F<20>
1008 GOSUB 10000! REM ВВОД ДАННЫХ
2808 GOSUB 28080iREM РЕГРЕССИЯ
3808 GOSUB 388081 REM ВЫВОД ДАННЫХ
4088 END
10808 REM A************************************
10058 REM «« ПОДПРОГРАММА ДЛЯ ВВОДА ДАННЫХ •«
10180 REM *************************************
18280 INPUT "ЧИСЛО ФУНКЦИЙ"; N
10400 INPUT "ЧИСЛО ПАР ЗНАЧЕНИЙ"; N1
’.0600 FOR 1-1 ТО N1
10708 PRINT ”ХС,л1|"> "Л INPUT Х<1>
10880 PRINT "Y<"»!»"> ";«INPUT V<I>
10900 NEXT I:RETURN
20000 REM **********************************
28050 REM ** РАСЧЕТ ПАРАМЕТРОВ РЕГРЕССИИ *•
20100 REM к*********************************
Линейные системы
189
20200 FOR 1-1 ТО NiFOR J-l TO N+l
20300 RCI,J>-0«NEXT JoNEXT I
20400 FOR 1-1 TO N1оGOSUB 40000
20700 FOR 11-1 TO N
гевее for 12-1 to 11
20900 RC11,12>-R<11,I25+FCX1>*FCI2>
21000 RC12,11>-AC 11,I2>«NEXT 12
21200 R< 11 ,N+1 >-RC11,N+1>+YCI>*FC11>
21300 NEXT Il«NEXT I
2isee gosub 509001return
30000 REM ************** »*♦♦♦♦
30050 REM ** ВЫВОД ДАННЫХ ««
30100 REM ********************
30400 PRINT «PRINT "ПАРАМЕТРЫ РЕГРЕССИИ"
30500 FOR 1-1 TO N
30600 PRINT "KC”;I,”> - ",RCI,N+1>
30700 NEXT I
30900 S—01FOR 1-1 TO N1
31000 008UB 40000«S1—0
31100 FOR 11-1 TO NiSl-Sl+RCI 1,N+l>*FCU> «NEXT II
31200 S-S+CVCI>-SI>T2
31300 NEXT 11PRINT
31500 PRINT "СУММА КВАДРАТОВ ОТКЛОНЕНИЙ = "; S
31000 RETURN
40000 REM******************************* *♦**
40002 REM** ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ **
40010 REM******************************* ***•
40400 FС 1>—XCI>*XCI>
40500 FC2>—EXPCXCI>>
40600 FC3>—1/XCI1
42000 RETURN
50000 REM**********************************
500O1 REM** НАЧАЛО ПОДПРОГРАММЫ Г-Ж **
50002 REM**********************************
50100 INPUT "ЧИСЛО НЕИЗВЕСТНЫХ"; N
50200 PRINT "ВВОД РАСШИРЕННОЙ МАТРИЦЫ КОЭФФИЦИНТОВ"
50300 FOR 1-1 ТО N
50400 FOR J-l TO N
50500 PRINT “RC",I>",“>J>“> - ">«INPUT RCI,J>
50700 PRINT "ВС",1Г'> - ”, «INPUT RCI,N+1>
50B00 NEXT I«PRINT
50900 FOR S-l TO N
51000 FOR T-S TO N
51100 IF RCT,S>O0 THEN 51300
51200 NEXT T «PRINT "ЕДИНСТВЕННОГО РЕШЕНИЯ HET": GOTO 63999
51300 OOSUB 53000
51400 C-1/RCS,S>
51500 OOSUB 54000
51600 FOR T-l TO N
51700 IF T-S THEN 52000
51000 C—RCT,S>
51900 OOSUB 55000
52000 NEXT T
52100 NEXT SiGOTO 63999
52200 GOSUB 56000«00Т063999
53000 REM*****************************
53002 REM*» ПОДПРОГРАММА ДЛЯ **
53004 REM*» ОБМЕНА УРАВНЕНИЙ **
53010 REM*****************************
53100 FOR J-l TO N+l
53200 B-RCS,J>|RCS,J>-RCT,J> «RCT,J>-B
53300 NEXT J
53400 RETURN
54000 REM****************************************
54002 REM** ПОДПРОГРАММА ДЛЯ ДЕЛЕНИЯ СТРОКИ **
54006 REM** НА ДИАГОНАЛЬНЫЙ ЭЛЕМЕНТ **
54010 REM****************************************
190
Глава 8
54100 FOR J-l TO N+l
54200 RCS,J>-C*R<S,J>«NEXT J
54400 RETURN
55000 REMlIlMllIlKlDllIlKllIlKlllHllMlltllllMllIlMlltlMllIllIlMllIlMlltllllMllIlMl
55002 REM** ПОДПРОГРАММА ДЛЯ «Hi
55004 REM** ВЫЧИТАНИЯ УМНОЖЕННОЙ ««
55005 REM** HA C S-Й СТРОКИ ИЗ •*
55006 REM** Т-Й СТРОКИ **
55010 REM*****************************
55100 FOR J-l TO N+l
55200 R<T,J>-R<T,J>+C*R<S,J>
55300 NEXT J
55400 RETURN
56000 REM*****************************
56001 REM** ПОДПРОГРАММА ДЛЯ ВЫ- *•
56002 REM** ВОДА РЕШЕНИЯ НА ЭКРАН **
56010 REM*****************************
56100 FOR Т-1 ТО N
56200 PRINT "Х<"«Т,"> -",R<T,N+1>
56300 NEXT Т
56400 RETURN
63999 RETURN
RUN
ЧИСЛО ФУНКЦИЙ? 3
ЧИСЛО ПАР ЗНАЧЕНИЙ? 5
Х< 1 > ? 1
V< 1 > ? 2
Х< 2 > ? 2
V< 2 > ? 4.5
Х< 3 > ? 3
V< 3 > ? 9.33333333
Х< 4 > ? 4
V< 4 > ? 16.25
Х< 5 > ? .5
V< 5 > ? 2.25
ПАРАМЕТРЫ РЕГРЕССИИ
К< 1 > - 1
К< 2 > - —6.49379217Е-10
К< 3 > - 1
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ = 1 3964524Е-16
RERDV.
RUN
ЧИСЛО ФУНКЦИЙ? 3
ЧИСЛО ПАР ЗНАЧЕНИЙ? 5
Х< 1 > ? 1
v< 1 :> ? 4.73
Х< 2 > ? 2
YC 2 > ? 14.5
Х< 3 > ? -.5
V< 3 > ? -1.15
Х< 4 > ? -10
VC 4 > ? 100
Х< 5 > ? -1
V( 5 > ? .368
ПАРАМЕТРЫ РЕГРЕССИИ
КС 1 > - 1.00100031
КС 2 > - 1.31078527
КС 3 ? — .«72358746
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ = .838752564
Линейные системы
191
Вторая часть программы (строки 50000—63999) представляет со-
бой программу «Г—Ж» для решения системы линейных уравнений
произвольного порядка. Программа «Г—Ж» оформлена как под-
программа. Для этого в ней надо лишь заменить последний опера-
тор программы END на оператор RETURN. Программа «ОБЩ-
РЕГР» иллюстрирует блочный* принцип построения больших про-
грамм. Эта программа включает в себя всю программу «Г—Ж»,
даже те ее части, которые не используются в регрессионном анали-
зе. Небольшое отличие от программы «Г—Ж» состоит в том, что
в начале соответствующей подпрограммы в строке 50000 стоит
оператор REM. Описание массива, соответствующего расширенной
матрице системы, вынесено из подпрограммы в основную програм-
му.
Три функции, которые используются в этом примере, заданы в
подпрограмме в строках 40000—42000. В этой подпрограмме для
каждого значения Х(1) вычисляются значения N функций, которые
присваиваются переменным F(l), F(2) и F(3).
Основная программа очень короткая; она состоит из коммента-
рия (краткого изложения содержания программы), описания масси-
вов: X и У (одномерные, соответствуют исходным данным), F и К
(соответствуют значениям функций и параметрам регрессии), А
(двумерный, соответствует расширенной матрице системы) и обра-
щений к трем подпрограммам. Сначала вызывается подпрограмма
для ввода данных, потом подпрограмма для расчета параметров
регрессии и, наконец, подпрограмма для вывода выходной инфор-
мации. Основная программа заканчивается оператором END. По-
сле выполнения этого оператора записанные ниже подпрограммы
не транслируются и поэтому не выполняются.
Подпрограмма для ввода данных со строки 10000 до строки
10900 запрашивает у пользователя число функций в уравнении ре-
грессии и присваивает это число переменной N. Потом запрашива-
ется число пар значений измеряемых величина иу, которое присва-
ивается переменной N1. Далее с помощью цикла вводится N1 пар
значений х и у.
Подпрограмма, в которой вычисляются параметры регрессии,
занимает строки 20000—21500. Эта подпрограмма в свою очередь
обращается к другим подпрограммам, и поэтому она сравнительно
коротка, наглядна и состоит в основном из трех вложенных друг в
* Программы на БЕЙСИКе представляют собой единый блок. Подпрограммы
создают лишь дополнительные удобства при написании программ и не являются
элементами структуры. — Прим, перев.
192
Глава 8
друга циклов, в которых по приведенным выше формулам вычис-
ляются элементы расширенной матрицы системы (вложенные ци-
клы со строки 20200 по строку 20300). Сначала элементы этой мат-
рицы обнуляются. Во внешнем цикле по параметру I (строки
20400—21300) поочередно считываются все N1 пар значений х и у.
Второй оператор строки 20400 вызывает подпрограмму, которая
вычисляет значения N функций для каждого значения Х(1). Далее в
циклах по II и 12 вычисляются все двойные произведения значений
функций, произведения F(I1) *F(I2) суммируются и значение суммы
присваивается элементу двумерного массива А(П, 12). Поскольку
полученная таким образом матрица симметрична относительно
главной диагонали, матричный элемент A(I2, II) можно и не вы-
числять, если известно значение А(И, 12). Аналогичным способом
рассчитывается значение величины Ь, входящей в приведенные вы-
ше формулы, и заполняется (N + 1)-й столбец матрицы А. Для
этого значения всех функций F(I1) умножаются на соответствую-
щие значения Y(I).
После окончания этих трех циклов в подпрограмме остаются не-
выполненными еще два оператора. Это оператор вызова подпро-
граммы «Г—Ж» для решения системы линейных уравнений, кото-
рая записана в виде матрицы А (оператор GOSUB 50900 передает
управление строке, с которой непосредственно начинается решение
системы уравнений), и оператор RETURN для возвращения в ос-
новную программу.
В строке 3000 основной программы оператор GOSUB 30000 вы-
зывает подпрограмму для формирования и вывода выходных дан-
ных. Поскольку корни системы линейных уравнений при использо-
вании метода Гаусса — Жордана стоят в (N + 1)-м столбце преоб-
разованной матрицы, в подпрограмме вывода данных элементы
этого столбца выводятся на экран в качестве параметров регрессии.
Это происходит в строках 30000—30700.
Во второй части подпрограммы для формирования и вывода
выходных данных вычисляется сумма квадратов отклонений экспе-
риментальных значений у от рассчитанных по уравнению регрес-
сии. Для этого опять используется цикл (строки 30900—31300). Для
каждого значения х с помощью соответствующей подпрограммы
рассчитываются значения N функций. Далее каждое из этих значе-
ний умножается на соответствующий параметр регрессии и произ-
ведения складываются. Полученное таким образом теоретическое
значение у присваивается переменной 51. Затем вычисляется раз-
ность между теоретическим и экспериментально полученным значе-
ниями у и эта разность возводится в квадрат. Квадраты всех раз-
Линейные системы
193
ностей суммируются и значение суммы присваивается переменной
S. После окончания этих вычислений для всех экспериментальных
точек в строке 31500 на экран выводится сумма квадратов отклоне-
ний. После возвращения в основную программу оператором END
завершается выполнение всей программы.
В приведенных числовых примерах отклонения эксперименталь-
ных значений от теоретических малы* **. Об этом свидетельствует
очень малое значение суммы квадратов отклонений.
Задание 101. Что надо изменить в программе «ОБЩ-РЕГР», чтобы можно бы-
ло рассчитать параметры прямой регрессии?
Задание 102. Организуйте ввод данных в программу «ОБЩ-РЕГР» так, чтобы
была возможность корректировать введенные данные. Дополните участок ввода
данных и подпрограмму, рассчитывающую параметры регрессии, для обработки
экспериментальных данных с учетом весовых коэффициентов.
Задание 103. Возьмите в качестве входных данных координаты 20 точек, лежа-
щих на синусоиде, и попытайтесь аппроксимировать эту зависимость (по 20 точкам)
различными полиномами (начиная с полинома третьей степени). Для этой задачи на-
пишите подпрограмму, формирующую выходные данные в виде таблицы, в которой
сопоставлялись бы «экспериментальные» и «теоретические» значения у.
Задание 104. Если в законе разбавления Оствальда выразить степень диссоциа-
ции через отношение эквивалентной электропроводности прн концентрации с (Л.) и
эквивалентной электропроводности при бесконечном разбавлении (Л^, то получится
следующая формула:
с = л2 ^-(1/Лс)2 - Л0-^с-(1/Лс)
с — концентрация; Кс — константа равновесия; Лс — эквивалентная электропро-
водность при концентрации с; Ло — эквивалентная электропроводность при концент-
рации 0.
c, 10“’моль/л Ac, 0м*'см"'/ОКВ-л'1)
0,028014 210,38
0,15321 112,05
1 ,02831 48,146
2,41400 32,217
5,91153 20,962
12,829 14,375
50,000 7,358
52,303 7,202
Для уксусной кислоты при 25 °C получены следующие экспериментальные
данные* * (см. табл.). По этим данным с помощью программы «ОБЩ-РЕГР» рассчи-
тайте константу равновесия Кс и эквивалентную электропроводность при бесконеч-
ном разбавлении Ло.
Сравните результаты регрессионного анализа при единичном взвешивании, с ре-
зультатами, полученными для взвешенных исходных значений, полагая, что весовой
* По крайней мере в первом примере. — Прим, перев.
** Kortiim G., Lehrbuch der Elektrochemie. Verlag Chemie, Weinheim, 1972, S. 149.
13-81
194
Глава 8
коэффициент равен (Лс/с)2. Истинные значения Ло и Кс равны 390,71 и
1,8-10“ 5 моль/л соответственно.
Задание 105. Внесите изменения в программу «ОБЩ-РЕГР» для обработки экс-
периментальных данных с помощью так называемой многофакторной регрессии.
Многофакторную регрессию используют тогда, когда величина у зависит не от од-
ной переменнойх, а от нескольких переменныххр х2, Измеряемые величины
(Xj р х2 р ..., хт t, у*) и неизвестные параметры Arp к2 и т. д. описываются следую-
щим уравнением:
т
у = S ~ + ••• +
j = i
Уравнениями такого типа часто аппроксимируют в ограниченной области слож-
ные зависимости или их используют для чисто эмпирического описания сложных
процессов. Следующий пример иллюстрирует использование таких соотношений.
Выход т,°с рн
66,8 38,6 4,36
47,1 23,6 5,31
64,8 30,6 3,15
50,0 22,4 4,68
63,8 31 ,0 3,44
44,3 25,3 6,21
33,6 11,2 5,51
56,2 38,3 6,43
Выход U некоторой химической реакции зависит от температуры и pH. Реакция
исследована в интервале pH 3—7 и при температуре от 10—40 °C, получены следую-
щие результаты (см. табл.). Выход линейно зависит от температуры и pH:
U = а + b-с + dpH
Рассчитайте по приведенным выше данным с помощью программы для много-
факторного регрессионного анализа коэффициенты а, b яд.
Задание 106. Даны три набора экспериментальных точек, через которые необхо-
димо провести три параллельные прямые. Надо рассчитать длину трех отрезков,
отсекаемых этими прямыми на оси ординат, и тангенс угла наклона так, чтобы сум-
ма квадратов отклонений была минимальна. Для решения этой задачи напишите
аналитическое выражение для суммы квадратов отклонений н минимизируйте эту
сумму по четырем параметрам. Задачу можно рассматривать также как частный
случай многофакторной регрессии, которая была рассмотрена в предыдущем зада-
нии.
Задание 107. Даны калибровочные масс-спектры (см. задание 85). Дополнитель-
но даны еще два спектра двух смесей (см. табл.). Поскольку интенсивности пиков в
спектрах индивидуальных веществ измерены с некоторой погрешностью, интенсив-
ности пиков в масс-спектрах не являются линейными комбинациями интенсивностей
соответствующих пиков в масс-спектрах индивидуальных веществ (см. задание 85).
Нет ни одной комбинации концентраций четырех индивидуальных веществ, которая
точно соответствовала бы спектрам смесей. Разработайте метод определения кон-
Линейные системы
195
12 13 14 15 16 24 25 26 27 28 29 30
СН4 1 3 12 100 35
С2Н6 2 80 3 4 13 37 24 100 70
С2Н4 4 7 48 13 2 7 21 18 100
С2Н2 5 23 57 2 40 45 100
Смесь 1 11 32 120 193 37 44 57 136 53 124 102 68
Смесь 2 10 33 110 104 17 44 52 117 35 113 52 33
центраций веществ, в котором сумма квадратов отклонений интенсивностей экспе-
риментального спектра от аддитивного была бы минимальна.
Мы здесь только наметим путь решения этого задания. Ваша задача — реализо-
вать его в виде программы.
М — вектор спектра смеси (12 строк, 1 столбец)
Е — матрица спектров четырех индивидуальных веществ (калибровочная
матрица) (12 строк, 4 столбца)
Ет — транспонированная калибровочная матрица (4 строки, 12 столбцов)
(при транспонировании матрица зеркально отражается относительно
главной диагонали)
С — вектор концентраций (4 строки, 1 столбец)
Если бы экспериментальный спектр смеси был линейной комбинацией спектров
индивидуальных веществ, то состав смеси можно было бы найти из следующего
матричного уравнения:
(•) М = ЕС
Из-за обычных погрешностей эксперимента точно решить это уравнение нельзя.
Однако можно найти такое решение относительно С, при котором разность
IM - Е-Cl минимальна. Для этого правую и левую части приведенного выше урав-
нения умножим слева на транспонированную калибровочную матрицу Ет:
ЕТМ = ЕТЕС
Ет-М — матрица, состоящая из 4 строк и одного столбца (четырехмерный век-
тор), которую можно легко вычислить, исходя из транспонированной калибровоч-
ной матрицы и вектора спектра смеси. Исходя из матрицы Е, можно вычислить
также матрицу Ет-Е размера 4x4. В результате получается простая система урав-
нений, которую можно решить с помощью программы «Г—Ж».
Рассмотренный простой способ решения довольно сложной
проблемы, связанной с обработкой экспериментальных данных, да-
ется без строгого доказательства. Впрочем, для доказательства
можно использовать подход, который применен при выводе урав-
нений для линейной регрессии. Выражение для минимизируемого
13»
196
Глава 8
параметра имеет вид
S = i (Л/.ИЗМ - Л,- рас,)2
/ = 1
Л. изм — измеренная высота пика i; — рассчитанная высота пика /.
Если в это уравнение подставить линейное уравнение (*), полу-
ченное выражение продифференцировать по искомым концентраци-
ям компонентов и составить соответствующую систему уравнений,
то станет ясно, что эта система уравнений совпадает с полученной
по рассмотренному выше методу.
Для этой и аналогичных задач целесообразно присвоить интен-
сивностям отдельных пиков определенные весовые коэффициенты.
Попытайтесь написать программу так, чтобы была возможность
обрабатывать взвешенные значения интенсивностей пиков.
8.4. Обращение квадратной матрицы
Хотя для линейных задач в предыдущем разделе был выбран
путь решения, основанный на составлении системы линейных урав-
нений, часто бывает необходимо или просто удобно найти матри-
цу, обратную данной. Метод обращения матрицы, который мы
рассмотрим в этом разделе, также называется методом Гаусса —
Жордана. Программа, реализующая этот метод, очень похожа на
программу «Г—Ж». Расширенная матрица системы, которая в
программе «Г—Ж» имела размер Nx(N + 1), при вычислении об-
ратной матрицы расширяется до матрицы размера Nx2N.
К исходной квадратной матрице добавляют л-мерную единич-
ную матрицу, т. е. необходимо решить систему уравнений одновре-
менно для л правых частей. Для этого рассмотрим ту же самую си-
стему уравнений, которую мы решали ранее, исключая недиаго-
нальные элементы методом Гаусса — Жордана:
4х + Зу + z = 1 О О
2х - у - z = 0 1 О
1х + у - 3z = 0 0 1
Эту систему можно написать в матричной форме как расширенную
матрицу системы:
( 4 3 1 1 0 0 4/4
2 -1 -1 0 1 0 I [2] - [1]/2
7 1 -3 0 0 1 / [3] - [!]• 7/4
Линейные системы
197
Разделим первую строку на 4 и исключим недиагональные эле-
менты первого столбца, вычитая из второй и третьей строки умно-
женную на соответствующие коэффициенты первую строку:
1 3/4 1/4 1/4 О
О —5/2 -3/2 -1/2 1
О -17/4 -19/4 -7/4 О
О \ [1] + [2] -3/10
0 1 /(-5/2)
1 / [3] - [2]-17/10
Второй диагональный элемент становится равным 1 после деле-
ния второй строки на (—5/2). Складывая и вычитая умноженную
на соответствующий коэффициент вторую строку с первой и треть-
ей, можно исключить недиагональные элементы второго столбца:
1 0 -1/5 1/10 3/10 0 > \ [1] - [3]-1/11
0 1 3/5 1/5 -2/5 0 1 [2] + [3]- 3/11
0 0 -11/5 -9/10 -17/10 1 , f /(-11/5)
Третий диагональный элемент третьей строки становится рав-
ным единице после деления на (— 11/5). Остальные недиагональные
элементы обращаются в нуль после соответствующих преобразова-
ний первой и второй строк матрицы:
/ 1 0 0 2/11
(010- 1/22
\ 0 0 1 9/22
5/11 -1/11 \
-19/22 3/11 )
17/22 -5/11/
Три последних столбца полученной матрицы образуют матрицу,
обратную исходной. Предлагаем читателю самостоятельно прове-
рить это утверждение.
Программа «ИНВ-ГЖ» для обращения матриц выглядит следу-
ющим образом:
В REN "ИНВ-ГЖ" EBERT/EDERER 810628
1 REM*»*»»»»*»»»****»»»»****»»*»****»*
2 REM** ОБРАЩЕНИЕ МАТРИЦЫ МЕТОДОМ**
4 REM** ГАУССА-ЖОРДАНА **
9 REN*********************************
50000 DIN R<20,40>
50100 READ NiREN ПОРЯДОК МАТРИЦЫ
50300 FOR I«1 ТО N
50400 FOR J-l ТО N
50500 READ A<I,J>
50550 R<I,N+J>-0
50600 NEXT J
50700 R<I,N+I>«1
50800 NEXT I
50900 FOR S«1 TO N
51000 FOR T«S TO N
51100 IF A<T,S><>0 THEN 51300
51200 NEXT T «PRINT "ЕДИНСТВЕННОГО РЕШЕНИЯ HET": GOTO 63999
51300 OOSUB 53000
51400 C-1/R<S,S>
51500 OOSUB 54000
198
Глава 8
51600 FOR Т«1 ТО N
51700 IF T«S THEN 52000
51800 C«-A<T,S>
51900 GOSUB 55000
52000 NEXT T
52100 NEXT S
52200 GOSUB 56000I00T063999
53000 REN*****************************
53002 REN** ПОДПРОГРАММА **
53004 REN** ДЛЯ ОБМЕНА **
53006 REN** УРАВНЕНИЙ **
53010 REN*****************************
53100 FOR J«1 TO 2*N
53200 B=A<S,J> iA<S,J>«A<T,J> :A<T,J>«8
53300 NEXT J
53400 RETURN
54000 REN*****************************
54002 REN** ПОДПРОГРАММА ДЛЯ **
54004 REN** ДЕЛЕНИЯ СТРОКИ НА **
54006 REN** ДИАГОНАЛЬНЫЙ ЭЛЕМЕНТ **
54010 REN*****************************
54100 FOR J-ITO 2*N
54200 ACS,J>«C*A<S,J>iNEXT J
54400 RETURN
55000 REN*****************************
55002 REN** ПОДПРОГРАММА **
55004 REN** ДЛЯ ВЫЧИТАНИЯ **
55005 REN** УМНОЖЕННОЙ НА С **
55006 REN** S-Й СТРОКИ ИЗ **
55007 REN** Т-Й СТРОКИ **
55010 REN*****************************
55100 FOR J«1 ТО 2*N
55200 ACT,J>«ACT,J>+C*ACS,J>
55300 NEXT J
55400 RETURN
56000 REN*****************************
56001 REN** ПОДПРОГРАММА **
56002 REN** ДЛЯ ВЫВОДА МАТРИЦ **
56003 REN»* и ПРОВЕРКИ **
56010 REN*****************************
56030 RESTORE:READ N
56100 FOR I«1 TO N
56200 FOR J«1 TO N
56220 READ ACI,J>
56300 PRINT ACI,J>|" "t
56400 NEXT JiPRINT
56500 NEXT IiPRINT
57100 FOR 1-1 TO N
57200 FOR J«N+1 TO 2*N
57300 PRINT ACI,J>1"
57400 NEXT JiPRINT
57500 NEXT IiPRINT
5B100 FOR I«1 TO N
58200 FOR J«1 TO N
58210 C-0
58220 FOR K«1 TO N
58230 C-C+ACI,K>*ACK,J+N>
58240 NEXT К
58300 PRINT С?" "l
58400 NEXT JiPRINT
58500 NEXT IiPRINT
59400 RETURN
60000 DATA 4
60100 DATA 7,5,3,1
Линейные системы
199
60208 data 0,1,1,1
60300 DRTA 4,2,1,3
60400 DATA 8,1,9,5
63999 END
RUN
? 5 3 1
0 1 1 1
4 2 1 3
8 1 9 5
.0526315787 -.5 .105263158 .0263157895
.140350878 .5 -.0526315781 -.096491228
.0350877183 .25 -.263157896 .100877193
-.175438596 .25 .315789474 -4.38596492Е-03
1 0 0 -5.4569682IE-12
0 1 -1.16415322E-10 -5.45696821E-12
0 0 1 1.27329258E-11
-9.54605639E-09 0 -8.84756447E-09 1
READV.
Отличие всех подпрограмм для обмена строк, деления на диаго-
нальный элемент и вычитания строк матрицы от программы
«Г — Ж» заключается лишь в том, что наибольшее значение пара-
метра цикла равно 2N, а не (N + 1).
Упрощен участок ввода данных. Для ввода размера и элементов
матрицы вместо оператора INPUT используется оператор READ
(строки 50100—50800). Там же элементы столбцов с (N + 1)-го до
2N-ro обнуляются, а элементам A(I, N + I) присваивается значение
1. В конце программы в операторе DATA записаны соответствую-
щие числовые данные (размер матрицы и ее элементы
(построчно)). А в остальном основная программа совпадает с про-
граммой «Г — Ж».
Новой является подпрограмма формирования и вывода выход-
ных данных. В этой подпрограмме сначала с помощью операторов
RESTORE н READ еще раз считывается исходная матрица, т. е.. ле-
вая половина матрицы А, которая затем выводится на экран. По-
сле выполнения программ правая половина матрицы А представля-
ет собой матрицу, обратную исходной; обратная матрица выводи-
тся на экран в строках 57100—57500. В следующих за ними строках
обе половины матрицы А перемножаются в соответствии с прави-
лом умножения матриц. Если обращение проведено корректно, то
полученная в результате проверки матрица должна быть единичной
матрицей соответствующего размера. Из приведенного примера
видно, что малые ошибки округления приводят к незначительным
отклонениям от этой единичной матрицы.
200
Глава 8
Ниже приведена распечатка более совершенной программы для
обращения матриц, в которой реализован известный из лите-
ратуры* алгоритм, основанный также на методе Гаусса — Жор-
дана. Пусть читатель с помощью указанного литературного ис-
точника самостоятельно проанализирует этот алгоритм и про-
грамму.
0 REM "ОБРАЩ" EBERT/EDERER 810613
1 REM*********************************
г REM** ОБРАЩЕНИЕ МАТРИЦЫ **
3 REM** МЕТОДОМ **
4 REN** ГАУССА-ЖОРДАНА **
5 REM** ########################### **
6 REN** ИСХОДНАЯ МАТРИЦА **
7 REM** ВВОДИТСЯ С ПОМОЩЬЮ ••
8 REN** ОПЕРАТОРОВ DATA **
9 REN*********************************
100 DIN R<20,20>,В<20,20>,U<20,20>
110 DIM V<20.20>,W<20,20>
300 READ Hl REM ПОРЯДОК МАТРИЦЫ
400 FOR I«1 TO N
420 FOR J«1 TO N
440 RERD R<I,J>
460 B<I,J>-0
400 V<I,J>-0
500 IF IO J THEN GOTO 600
520 B<I,J>-1
540 V<I,J>«1
600 NEXT J
620 NEXT I
1000 FOR Z«1 TO N
1050 S>0
1100 REN*********************************
1105 REN** ПОИСК ВЕДУЩЕГО ЭЛЕМЕНТА **
1110 REN*********************************
1120 FOR I-Z TO N
1150 IF S>RBS<R< I ,Z> > THEN GOTO 1300
1200 S-RBS<R<I,Z>>iT-I
1300 NEXT I
2000 REN********************************
2001 REN** ОБМЕН СТРОК Z И T **
2005 REN********************************
2050 FOR 1-1 TO N
2100 S-R<Z,I>1R<Z,I>.R<T,I>|R<T,I>-S
2200 NEXT I
2300 IF RBS<R<Z,Z>»lE-30 THEN GOTO 2400
2350 PRINT "МАТРИЦУ ОБРАТИТЬ НЕЛЬЗЯ": END
2400 V<Z,Z>«01VCT,T>«0
2450 V<Z,T>-11V<T,Z>-1
3000 REN**************************************
3010 REN** ИСКЛЮЧЕНИЕ НЕДИАГОНАЛЬНЫХ ЭЛЕ-4*
3020 REN** МЕНТОВ МЕТОДОМ ГАУССА-ЖОРДАНА **
3040 REN**************************************
3100 FOR 1-1 TO N
3200 FOR J«1 TO N
3300 IF I«Z THEN GOTO 4000
3350 IF J«Z THEN GOTO 4500
* Torning W., Numerische Mathematik fur Ingenieure. Band 1, 2. Springer-Verlag, Hei-
delberg, 1979.
Линейные системы
201
3400 U<I ,J>-A<I ,J>-A<Z,J>*A<I ,Z>/A<Z,Z>
3500 GOTO 5000
4000 IF I-J THEN GOTO 4350
4050 U<I,J>—ACI,J>/ACZ,Z>
4100 GOTO 5000
4350 UCZ,Z>-1/ACZ,Z>
4400 GOTO 5000
4500 U<I,Z>-A<I,Z>/ACZ,Z>
5000 NEXT JNEXT I
5100 REN******************************
5102 REN** УМНОЖЕНИЕ В - V*B •*
5110 REN******************************
5200 FOR 1-1 TO N
5250 FOR J-l TO N
5300 WCI,J>-0
5350 FOR K-l TO N
5400 wci,j>-h<i,j>+vci,k:>*b<k,j>
5450 NEXT КiNEXT JiNEXT I
5500 FOR 1-1 TO NiFOR J-l TO N
5550 BCI,J>-WCI,J>
5600 NEXT Ji NEXT I
6000 FOR 1-1 TO N
6050 FOR J-l TO N
6100 AC I,J>«U<I,J>:V<I,J>-6
6250 IF I-J THEN VCI,J>-1
6300 NEXT JiNEXT I
6500 NEXT Z
7000 REN******************
7005 REN** УМНОЖЕНИЕ **
7010 REN** МАТРИЦЫ A. **
7020 REN** НА МАТРИЦУ В **
7030 REN******************
7100 FOR 1-1 TO N
7200 FOR J-l TO N
7300 U<I,J)-0
7400 FOR K-l TO N
7500 wci,j>-wci,j>+aci,k>*bck,j>
7600 NEXT К iNEXT J«NEXT I
6000 REN****************
8010 REN** ПРОВЕРКА **
8020 REN****************
8040 RESTORE(READ N
8050 FOR 1-1 TO N
8060 FOR J-l TO N
8070 READ ACI,J>
8088 NEXT JiNEXT I
8100 FOR 1-1 TO N
8200 FOR J-l TO N
8300 BCI,J>-0
8400 FOR K-l TO N
8500 BCI,J>-BCI,J>+ACI,К>*ЫСК,J>
8600 NEXT КiNEXT JiNEXT I
9000 REN********************************
9050 REN** ВЫВОД ИСХОДНОЙ МАТРИЦЫ A, **
9100 REN** МАТРИЦЫ W, ОБРАТНОЙ A, **
9200 REN** и ПРОИЗВЕДЕНИЯ A* W **
9250 REN********************************
9300 FOR 1-1 TO NiPRINTiFOR J-l TO N
9310 PRINT AC I,J>?iNEXT JiNEXT IiPRINTiPRINT
9400 FOR 1-1 TO NiPRINTiFOR J-l TO N
9410 PRINT WCI,J>/iNEXT JiNEXT IiPRINTiPRINT
9500 FOR 1-1 TO NiPRINTiFOR J-l TO N
9510 PRINT ВС I,J>jiNEXT JiNEXT IiPRINTiPRINT
50000 DATA 4
50100 DATA 7,5,3,1
202
Глава 8
50200 DATA 0,1,1,1
50300 DATA 4,2,1,3
50400 DATA 8,1,9,5
60000 END
RUN
7 5 3 1
0 111
4 2 13
8 19 5
.0526315789 -.5 .105263158 .0263157894
.140350877 .5 -.052631579 -.0964912281
.0350877193 .25 -.263157895 .100877193
-.175438597 .25 .315789474 -4.3859649E-03
1 0 5.82076609E-10 —4.82032192E—10
5.82076609E-11 1 0 -1.63709046E-11
0 0 1 -2.23735697E-10
-3.49245965E-10 0 9.31322575E-10 1
READV.
Задание 108. Пусть в некоторой системе одновременно протекают две химиче-
ские реакции. Они характеризуются выходами Uх и Ur Зависимость выхода, выра-
женного в процентах, в достаточно узкой области описывается двумя линейными
относительно четырех параметров уравнениями:
Ux = 10 + 1с, - 2-с2 + 2,0-рН + 0,5(7 - 300)
U2 = 15 - 1с, - 1-с2 + 1,2-рН + 0,9-(7 - 300)
Т — температура в градусах Кельвина; с, — концентрация вещества 1, моль/л;
с2 — концентрация вещества 2, моль/л.
При с, = с2 = 2 моль/л, 340 К и pH 4 выходы С/, и U2 составляют 36 и 51,8%
соответственно.
Задача состоит в том, чтобы иайти такие условия, при которых указанные вы-
ше выходы увеличились бы на 1%. Сумма квадратов изменений значений парамет-
ров, которые характеризуют условия реакции, должна быть минимальна. Вообще
говоря, приращению каждого параметра следует присвоить свой весовой коэффици-
ент. Проблемы такого типа возникают, когда число параметров, влияющих на ре-
зультат, больше, чем число интересующих величии (переопределенные системы). В
качестве примера можно привести механизмы сложных реакций с участием несколь-
ких различных веществ, которые могут также взаимодействовать друг с другом.
Кинетика каждой из этих элементарных стадий определяется более чем двумя кине-
тическими параметрами, и все оии влияют на динамику концентрации веществ.
Изложенный ниже подход к решению таких задач дается без
строгого доказательства. Соответствующие математические фор-
мулы можно вывести самостоятельно по аналогии (см. выше) или
используя метод Лагранжа для нахождения экстремума функции не-
скольких переменных с дополнительным условием*. Впрочем, стро-
Метод множителей Лагранжа. — Прим, перев.
Линейные системы
203
гое доказательство можно найти в справочнике по прикладной
математике*.
Если для приращений выходов и параметрон оставить те же
буквы, что и для обозначения выходов и параметров, то получится
Ux = 1-С! - 2-с2 + 2,0-рН + 0,5-Г
U2 = - 1-с, - 1-с2 + 1,2-рН + 0,9-Г
Та же самая система уравнений, записанная в матричной форме,
имеет вид
( 1 -2 2,0 0,5\ (с2 А
\и2/ У-1 -1 1,2 0,9/ Vr/
или, в краткой форме, U = S-k.
S — матрица чувствительности.
Вектор приращения параметров должен быть минимальным.
Вектор приращения выхода U и матрица чувствительности S зада-
ны. В матричной форме решение выглядит следующим образом:
к = S^CS-S1)-1-^
Чтобы найти искомый вектор к, надо умножить матрицу S на
транспонированную матрицу ST и найти матрицу, обратную мат-
рице этого произведения. Далее эту обратную матрицу следует ум-
ножить слева на транспонированную матрицу чувствительности и
это произведение умножить на вектор U. В результате получается
искомый вектор приращения параметров к.
При выполнении этого задания используйте одну из программ для обращения
матриц.
Задание 109. Известно, что обращение обратной матрицы приводит к исходной
матрице. Напишите программу для проверки этого утверждения.
8.5. Определение собственных значений матрицы
Вычисление собственных значений используется в химии, напри-
мер, при решении задач из области химической кинетики и теории
реакторов, при анализе нормальных колебаний в молекулярной
спектроскопии и, по-видимому, наиболее часто в приближенных
квантово-химических расчетах. Прежде чем перейти к составлению
программы, поясним математический смысл этой операции.
Надо найти собственные значения X, и собственные векторы evt
квадратной матрицы А. Нас будут интересовать лишь действитель-
* Handbook of applied mathematics (ed. С. E. Pearson). Reinhold, New York, 1974,
p. 931.
204
Глава 8
ные собственные значения, и поэтому мы будем рассматривать
только симметричные* матрицы, так как лишь они имеют действи-
тельные собственные значения. Собственное значение матрицы X, и
соответствующий ему собственный вектор ev, удовлетворяют сле-
дующему уравнению:
A-eVj = \-eVj
Это означает: если умножить матрицу А на собственный вектор,
то получится тот же собственный вектор evt, но умноженный на
некоторое число Х(, которое является собственным значением мат-
рицы А.
Для определения собственных значений мы воспользуемся мето-
дом, который носит название метода Якоби и подробно рассмот-
рен в учебниках по математике (в разделах, посвященных теории
чисел). Согласно этому методу, исходная матрица преобразуется
Зеркально-симметричные относительно главной диагонали. — Прим, перев.
Линейные системы
205
(1) (2)
....-.... I.______________________________
Вычисление угла р:
если оба диагональных элемента
a(m1,ml) и а(т2,т2) равны,то
p=arct0(l)- sgn[a(ml,m2)].
Если оба диагональных элемента различны,
то р рассчитывается по формуле
р = 0,5 -arctg f 2 a(ml,m2)-------1
L a(m2,m2)-a(m1,ml)J
Преобразование недиагональных и незначащих
элементов матрицы А. Преобразуются только ml-e и
л12-е столбцы и строки.t-й элемент ml-го столбца
преобразуется следующим образом:(4<>т1,1 <>т2):
ml)cos(p)-a(i,m2)sln (р).
i-Й элемент т 2-го столбца преобразуется следую-
щим образом: (г от 1, io m2): a(i,m2)=afi,ml)-sin(p)+
+а(б,т2)-со5(р).Поскольку матрица симметрична,
соответствующие строки получаются при переписы-
вании столбцов
Преобразование остальных элементов:
a(ml,ml) =a(ml,ml) cos2(p)-a(m1,m2)sln(2p) +
+ a(m2,m2) sin2(p)
e(m2,m2)=a(ml,m1) sin2(p)+a(ml,m2) sln( 2p) +
+afm2,m2) cos2(p)
a(m1Lm2)=0
a(m2,m1) =0
по определенным правилам до тех прр, пока недиагональные эле-
менты не станут пренебрежимо малыми (или вообще обратятся
в 0). Диагональные элементы этой преобразованной матрицы и яв-
ляются собственными значениями исходной матрицы. Алгоритм
метода показан на блок-схеме (схема 14).
Ниже приведена соответствующая этому алгоритму программа
на БЕЙСИКе:
0 REM "СОБСТВ" EBERT/EDERER 820511
1 REM»»»»»»»»»»»»»»»»»»»»*************
2 REM»» ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ »»
3 REM»» ЗНАЧЕНИЙ । СИММЕТРИЧНОЙ **
4 REM»» МАТРИЦЫ МЕТОДОМ ЯКОБИ **
9 REM*********************************
10 DIM R<20,20>
20 E9»1E-8:REM ТОЧНОСТЬ EPS
206
Глава 8
30 READ NiREM ПОРЯДОК СИММЕТРИЧНОЙ МАТРИЦЫ
35 REM ВВОД МАТРИЦЫ А
40 FOR 1=1 ТО N
50 FOR J=1 ТО N
60 READ R<I,J>
80 NEXT J
90 NEXT I
100 FOR Z9-1 TO 400
200 REM ПОИСК НАИБОЛЬШЕГО ЭЛЕМЕНТА
210 М-0
220 FOR 1=1 ТО N-l
230 FOR 7=1 + 1 TO N
240 IF M>RBS<R<I,J>> THEN GOTO 280
250 M-ABS<A<I,J>>
260 M1-I|M2«J
280 NEXT J
290 NEXT I
300 IF M<E9 THEN GOTO 9000
400 REM ВЫЧИСЛЕНИЕ УГЛА
410 IF R<M1,M1><>A<M2,M2> THEN GOTO 500
420 P-RTN<1>*SGN<ЖМ1,M2>>
430 GOTO 600
500 P-2»R<M1,M2>/<R<M2,M2>-R<M1,M1X>
520 P-0.5*RTN<P>
600 REM ПРЕОБРАЗОВАНИЕ МАТРИЦЫ
620 FOR 1-1 TO N
630 IF I-Ml THEN GOTO 700
635 IF I=M2 THEN GOTO 700
640 R5-Rd,Ml>
660 Rd,Mi:>-Rd,Ml >«COS<P>-R< I,M2>»SIN<P>
670 R<M1, I >=Rd ,M1 >
680 R< I ,M2>=R5*SIN<P:>+R< I ,М2>«COS<P>
690 R<M2,I>=R<I,M2>
700 NEXT I
720 R6-R<M1,M1>
730 R7=A<M2,M2>
740 R8-R<M1,M2>
750 R<Ml,M2>-0
760 R<M2,Ml>-0
770 R<M1,M1>-R6«C0S<P>t2-Re«SIN<2«F>+A7«SIN<P>T2
780 A < М2 , М2 > -R6«S IN < P > T2+A8«S IN < 2«P > + A7«C0S < P > 12
8000 NEXT 29
9000 REM ВЫВОД СОБСТВЕННЫХ ЗНАЧЕНИЙ
9100 FOR 1-1 TO N
9200 PRINT "СОБСТВЕННОЕ ЗНАЧЕНИЕ ="; A (I , I )
9210 NEXT I
10000 DRTA 61REM ПОРЯДОК МАТРИЦЫ
10100 DATA 0.1,0,0.1.0
10200 DRTA 1,0,1,0,0,0
10300 DRTR 0,1,0,1,0,0
10400 DRTA 0,0,1,0,1,0
10500 DRTA 1,0,0,1,0,1
10600 DRTA 0,0,0,0,1,0
63999 END
RUN
СОБСТВЕННОЕ ЗНАЧЕНИЕ - -1.61803399
СОБСТВЕННОЕ ЗНАЧЕНИЕ = .61803399
СОБСТВЕННОЕ ЗНАЧЕНИЕ « -1.86080571
СОБСТВЕННОЕ ЗНАЧЕНИЕ = 2.11490737
СОБСТВЕННОЕ ЗНАЧЕНИЕ “ - .254101691
СОБСТВЕННОЕ ЗНАЧЕНИЕ = 1
RERDV.
Линейные системы
207
В строке 10 описан двухмерный массив, соответствующий мат-
рице А, собственное значение которой необходимо найти. В строке
20 задано число «eps», равное в данном случае 1Е—8, и это значе-
ние присваивается переменной Е9. Число «eps» выбирают для каж-
дой конкретной задачи, исходя из требуемой точности. В строке 30
с помощью оператора READ считывается размер матрицы Айв
следующих строках 40—90 считываются ее элементы.
Участок программы от строки 100 до строки 8000 предназначен
для преобразования матрицы. Если даже 400 преобразований не
обеспечивают заданной точности, то эта процедура все равно за-
канчивается и полученные данные выводятся на экран.
На участке программы от строки 200 до строки 290 происходит
поиск наибольшего недиагонального элемента. Поскольку матрица
симметрична, достаточно рассмотреть элементы, расположенные
над диагональю. Значение наибольшего недиагонального элемента
присваивается переменной М. Переменной Ml присваивается номер
строки, а переменной М2 — номер столбца, на пересечении кото-
рых расположен этот элемент.
В строке 300 абсолютная величина найболыпего недиагонально-
го элемента сравнивается с числом «eps». Если этот элемент уже
достаточно мал, то управление передается строке 9000, где диаго-
нальные элементы преобразованной матрицы выводятся на экран в
качестве искомых собственных значений. В строках 400—780 проис-
ходит преобразование матрицы А в соответствии с приведенной
выше блок-схемой.
Матрица, которая приведена в качестве числового примера, со-
стоит только из нулей и единиц. Это секулярная матрица для фуль-
вена в приближении метода Хюккеля (МОХ). Каждое собственное
значение этой матрицы пропорционально энергии соответствующей
молекулярной орбитали.
Задание ПО. Вычислите с помощью программы «СОБСТ» собственные значения
следующих матриц:
Задание 111. Определите собственные векторы, соответствующие собственным
значениям секулярной матрицы для фульвена в приближении МОХ. Каждый соб-
ственный вектор этой матрицы можно рассматривать как молекулярную орбиталь,
являющуюся линейной комбинацией атомных орбиталей. Энергия каждой такой ор-
битали равна соответствующему собственному значению секулярной матрицы.
Для определения собственных векторов в принципе можно использовать про-
грамму «Г—Ж» для решения систем линейных уравнений. Надо решить следующую
208
Глава 8
систему линейных уравнений:
(А - \.Е)х. = 0
Е — единичная матрица: Х;—/-е собственное значение; — z-й собственный
вектор; 0 — нулевой вектор.
Системы уравнений такого вида ие имеют единственного решения. Используя
модифицированную программу «Г—Ж», приведите соответствующую этой системе
матрицу к диагональному виду как можно более точно. (Для этого в программе
«Г—Ж» надо заменить операторы в строке 51200 на операторы
NEXT T:S9 = S:GOTO 52100.) Необходимо также в конструкции оператора IF в
строке 51100 нуль заменить на малое число: IF ABS(A(T, S)) > IE—6 THEN 51300.
Таким образом находят значение переменной X(S9), которой после исключения ие-
диагональных элементов по обычному методу Гаусса — Жордана можно присвоить
любое значение. (В S9-M столбце на диагонали и под ней могут находиться только
нули.) Целесообразно выбрать X(S9) = —1. Если дополнить S9-H столбец в S9-H
строке элементом, равным — 1, то элементы этого столбца станут компонентами
искомого собственного вектора. Этот собственный вектор обычно нормируют на
единичную длину. Для этого находят длину вектора (квадратный корень из суммы
квадратов компонентов) и каждый компонент вектора делят на эту длину.
Трудности появляются в тех случаях, когда матрица имеет несколько одинако-
вых собственных значений. Тогда при вычислении собственного вектора с помощью
программы «Г—Ж» получают две строки матрицы, которые состоят из нулей. Это
означает, что для компонентов соответствующих векторов можно выбрать произ-
вольные значения и с помощью оставшейся системы найти два линейно независи-
мых вектора.
Задание 112. Вычислите собственное значение секулярной матрицы в приближе-
нии МОХ для катиона пентадиеиила, для бензола, гексатриена, циклооктатетраеиа,
бутадиена и антрацена. В методе МОХ секулярная матрица для х-системы состоит
только из нулей и единиц. Если между атомом 1 и атомом j имеется химическая
связь, то матричные элементы A(z, j) и А(/, /) равны 1. Более подробно о расчетах
по методу МОХ можно прочитать в литературе*.
8.6. Определение числа изомеров
Проблема расчета числа возможных структурных изомеров хи-
мических соединений по тематике относится скорее к гл. 7 (пере-
менные с индексами). Однако, поскольку при построении соот-
ветствующей программы широко используется блочный принцип,
эта проблема будет рассмотрена в данном разделе.
Расчет числа изомеров основывается на теории графов. Чита-
тель, который захочет более подробно познакомиться с применени-
ем теории графов в химии, найдет нужные сведения в
литературе**. В этом разделе мы обсудим программу, по которой
• Heilbronner Е., Воск Н., Das HMO-Modell und seine Anwendung. Verlag Chemie,
Weinheim, 1968.
** См., например, Balaban A. T., Chemical application of graph theory. Academic
Press, London, 1976.
Линейные системы
209
можно рассчитать число изомерных алкильных радикалов, алканов
и, как пример сложных соединений, алкенонов (ациклических кето-
нов или альдегидов с одной двойной связью).
Расчет числа изомеров различных алкильных групп или алкиль-
ных радикалов, которые содержат определенное число атомов С,
является основой для определения числа изомеров более сложных
химических соединений. Теория графов в применении к этой проб-
леме рассматривает только углеродный остов молекулы. Соот-
ветствующий граф состоит из точек*, обозначающих атомы С, и
линий связи**, обозначающих связи между атомами. Вершина, со-
ответствующая атому С со свободной валентностью, выделяется
среди остальных и называется корневой вершиной. Математически
проблема сводится к подсчету всех деревьев*** с максимальным
числом разветвлений в вершине, равным четырем (почему?). Тео-
рия графов дает решение этой задачи в виде полинома А (х) с беско-
нечным числом членов:
А(х) = Ао + АуХ + А2х2 + А3х3 + ...
Коэффициенты этого полинома соответствуют числу изомерных
алкильных радикалов с i атомами углерода. А 0 равен 1, поскольку
атом Н рассматривается как алкильная группа без атомов углеро-
да. Расчет остальных коэффициентов происходит по следующей
формуле****, которую можно считать неявной функцией величины
Л(х):
Л(х) = 1 + (х/6)-[А3(х) + ЗЛ (х)Л (г2) +2Л(х3)]
Эту формулу можно использовать как рекуррентную. Если из-
вестны, например, четыре первых коэффициента (число изомеров
алкильных радикалов до пропильного), то с помощью приведенной
выше формулы можно вычислить пятый коэффициент. Таким же
* Вершин. — Прим, перев.
** Ребер. — Прим, перев.
*** Дерево — это связный граф, не имеющий циклов. — Прим, перев.
Вывод этой формулы базируется на фундаментальной теореме перечисли-
тельного анализа, доказанной в 1936 г. венгерским математиком Д. Пойа. Исполь-
зование ее для подсчета структурных и стереоизомеров органических соединений об-
суждается в работах: Пойа Д. Комбинаторные вычисления для групп, графов и хи-
мических соединений. В ки.: Перечислительные задачи комбинаторного анализа.
Пер. с англ. — М.: Мир, 1979, с. 36—138; Balaban А. Т., Chemical application of
graph theory. Academic Press, London, 1976, p. 176; Зефиров H. С., Трач С. С., Чи-
жов О. С. Каркасные и полициклические соединения. Молекулярный дизайн на осно-
ве принципа изоморфного замещения. — ИНТ, сер. орг. хим., 1979, т. 3,
с. 38—46. — Прим. ред.
14-81
210
Глава 8
способом рассчитывают полином А (х) вплоть до заданного числа
атомов С.
Исходя из этого полинома, справедливого для алкильных ради-
калов, и принимая во внимание перестановки и соображения сим-
метрии, получают полиномы для других классов органических сое-
динений.
Полином для алкенонов:
ЕЦх) = х3Л4(х)- £ (1/2[Л2(х) + Л(х2)]К
р = о
Из него получают полином для соответствующих альдегидов:
ALIQc) = х3Л3(х)- £ { 1/2[Л 2(х) + Л (х2)])р
р = о
Полином для кетонов ХЕ 1(х) вычисляют по формуле
ХЕ1(х) = ЛЕ1(х)-|Л£) - 1]
Если не учитывать транс-цис-изомеры, то формулы для алкено-
нов имеют вид
Е2(х) = х3Л2(х)- £ (1/2[Л2(х) + Л(х2)])₽-[Л2(х) + Л(х2)]/2
р = о
ЛЕ2(х) = х3Л(х)- £ [ 1/2[Л2(х) + Л(х2)]^-[Л2(х) + Л(х2)]
р = о
КЕ2(х) = ЛЕ2(х)-[Л(х) - 1]
Вывод полинома АК (х) для алканов из полинома Л (г) для ал-
кильных радикалов несколько сложнее. Сначала рассчитывают два
вспомогательных полинома Р (х) и Q (х), которые входят в выраже-
ние для АК (х):
Р(х) = хИ4Ю + 6Л2(х)Л^2) + ЗЛ2(х2) + 8Л(х)Л(х3) + 6Л(х4)]/24
Q(r) = |И W - I]2 + Л (х2) - 1) /2
ЛХ(х) = Р(х) - Q(x) + Л (х2) - 1
Программа, которая рассчитывает эти полиномы, носит назва-
ние «ИЗОМЕРЫ»; ее распечатка приведена ниже:
Линейные системы
211
0 REM "ИЗОМЕРЫ" EBERT/EDERER 840105
1 REM*********************************
2 REM** РАСЧЕТ ЧИСЛА ИЗОМЕРОВ **
3 REM** АЛКИЛЬНЫХ РАДИКАЛОВ, **
4 REM** АЛКАНОВ И АЛКЕНОНОВ **
5 REM** BA LABAN ««
б REM** СНЕМ. APPL. GRAPH THEORY**
7 REM** ACADEMIC PRESS 1976 **
9 REM*********************************
100 DIM R<50>ZR2<50>,R3<50>,R4<50>,R9<50>,RK<50>
105 DIM B2<50>,B3<50>,B4<50>,C<50>,C2<50>
110 DIM E<50>,E2<50>,F<50>,H2<50>
120 DIM HV<50>,K2<50>,KE<50>,P<50>,Q<50>
130 DIM X<50>,V<50>,Z<50>
206 REM********************************
210 REM** РЕКУРЕНТНАЯ ФОРМУЛА ДЛЯ **
220 REM** АЛКИЛЬНЫХ РАДИКАЛОВ ««
230 REM** R<X>-1+X/6*':RCX>T3+ **
240 REM** 3*R<X>*R<XT2>+2*R';XT3> **
300 REM********************************
350 INPUT "МАКСИМАЛЬНОЕ ЧИСЛО АТОМОВ С N
400 R<0>-1|R<1>-1|R<2>-1iR<3>-2
500 FOR 1-3 TO N-l
520 S-0
550 FOR J-I TO 0 STEP -1
see for к-e to i-j
620 L-I-J-K
?ee s-s+r<j>*r<k>*R';l>
720 NEXT К
740 NEXT J
800 FOR J—0 ТО I STEP 2
820 K-I-J
B50 S-S+3*R<J/2>*R<K>
870 NEXT J
900 IF INT<I/37-I/3 THEN S-S+2*R<I/3>
910 S-S/6
920 RCI+17-S
960 NEXT I
1000 REM ВЫЧИСЛЕНИЕ At 2
1020 M-N1FOR 1-0 TO M1X<I>«R<I>1V<I>-R<I>1NEXT I
1066 GOSUB 9000iFOR 1—0 TO M1R2<I>-F<17iNEXT I
1200 REM ВЫЧИСЛЕНИЕ At 4
1220 M-NtFOR 1-0 TO M|X<I>-R2<I>I>-R2<I>iNEXT I
1240 GOSUB 90001FOR 1-0 TO M|R4<I>-F<17iNEXT I
1360 REM ВЫЧИСЛЕНИЕ At3
1362 M-NlFOR 1=0 TO M:X<I>-R2<I>I>=R' 17sNEXT I
1364 GOSUB 9000:FOR 1-0 TO M |R3<I7=F<I 7iNEXT I
1400 REM ВЫЧИСЛЕНИЕ (1/2*X»|A (X)t2 + A (Xt 2)) (МАССИВ AK ( '))
1420 FOR 1-0 TO N:RK<I 7=0sNEXT I
1440 FOR 1-0 TO N/2:RK<2*I7=R<I 7:NEXT I
1460 FOR 1-0 TO N:RK<I7-RK<I7+R2<I 7sNEXT I
1480 FOR I-N+l TO 1 STEP -1|RK<I>-RK<1-17/2iNEXT IsRK(07=R
2880 REM ВЫЧИСЛЕНИЕ СУММЫ AK (X) t M
2001 REM ПО ВСЕМ MOT О ДО N (МАССИВ Z( ))
2002 REM E И P - ВСПОМОГАТЕЛЬНЫЕ ВЕКТОРЫ
2010 FOR 1-0 TO NiZ<I7-0sNEXT I:Z<0>=1
2020 FOR 1-0 TO N:Z<I7-Z<I7+RK<17:P<I>=RK<17sNEXT I
2100 FOR M-2 TO N
2120 FOR 1-0 TO N|E<I 7=0sNEXT I
2200 FOR J-0 TO N
2220 FOR K-0 TO J
2240 L-J-K:E<J7-ECJ7+RK<K7*P<L7
2260 NEXT К : NEXT J
2300 FOR 1=0 TO NiP<I7-E<I7iZ<I7-Z<I7+P<I 7sNEXT I
2400 NEXT M
14*
212
Глава 8
3000 REM ВЫЧИСЛЕНИЕ ПОЛИНОМОВ ДЛЯ АЛКЕНОНОВ (МАССИВ Е ( ))
3100 FOR 1-0 ТО N+3iE<I>-0iNEXT I
3200 FOR J—0 ТО N
3220 FOR К-0 ТО J
3240 L-J-KlE<J+3>-E<J+3>+ZOO*A4<L>
3260 NEXT КiNEXT J
3300 REM ВЫЧИСЛЕНИЕ ПОЛИНОМОВ ДЛЯ АЛЬДЕГИДОВ (МАССИВ HY ( ))
3310 M-N+31FOR 1-0 ТО NlXd>—А3<1>tY<I>-Z<I>iNEXT I
3320 GOSUB 9000iFOR 1-0 TO NiHY<I+3>-F<I>iNEXT I
3400 REM ВЫЧИСЛЕНИЕ ПОЛИНОМОВ ДЛЯ КЕТОНОВ (МАССИВ KE ( ))
3410 M-N+3lFOR 1-0 ТО NlXd>-HY< I > |Y< 1>-А< I> iNEXT I :Х<0>-0
3420 GOSUB 90001FOR 1-0 ТО МiKE<I>-F<I>iNEXT I
4000 REM АЛКЕНОНЫ БЕЗ УЧЕТА ЦИС-ТРАНС ИЗОМЕРИИ
4030 FOR 1-0 ТО N iXd >-AKd + l > lYd >-A2d > iNEXT I
4040 GOSUB 9000IFOR 1-0 TO N|X<I>-F<I>:Y<I>-Z<I>iNEXT I
4050 GOSUB 9000iFOR 1-0 TO N|E2<I+3>-F<I>iNEXT I
4100 REM АЛЬДЕГИДЫ БЕЗ УЧЕТА ЦИС-ТРАНС ИЗОМЕРИИ
4130 М—N+3lFOR 1-0 ТО М «ХС I >-АК< I + 1 > lY< I >- Ad>lNEXT I
4140 GOSUB 9000iFOR 1-0 TO M:X<I>-F<I>iY<I>-Z<I>iNEXT I
4150 GOSUB 9000IFOR 1-0 TO M iH2d+3>-Fd > iNEXT I
4200 REM КЕТОНЫ БЕЗ УЧЕТА ЦИС-ТРАНС ИЗОМЕРИИ
4230 M-N+3|FOR 1-0 ТО М |Х<I>-Н2<I>:Y<I>- Ad > iNEXT IiY<0>-0
4240 GOSUB 9000iFOR 1-0 TO M|K2<I>-F<I>iNEXT I
5000 REM ВЫЧИСЛЕНИЕ A (Xt 2) (МАССИВ B2 ( ))
5010 FOR 1-0 TO NlB2<I>-0iNEXT I
5020 FOR 1-0 TO N/2 |B2<2*I >-Ad >iNEXT I
5100 REM ВЫЧИСЛЕНИЕ A (Xt3) (МАССИВрЗ! ))
5110 FOR 1-0 TO N|B3<I>-0iNEXT I
5120 FOR 1-0 TO N/3iB3<3*I>-Ad> iNEXT I
5200 REM ВЫЧИСЛЕНИЕ A (Xt 4) (МАССИВ B4 ( ))
5210 FOR 1-0 TO N|B4<I>-0iNEXT I
5220 FOR 1-0 TO N/4|B4<4*I>-Ad>iNEXT I
5300 REM ВЫЧИСЛЕНИЕ A (Xt2)t2 (МАССИВ C2 ( ))
5310 M-NiFOR 1-0 TO M iXd >-B2d > lYd >-B2d > iNEXT I
5320 GOSUB 9000IFOR 1-0 TO M iC2d >-Fd > iNEXT I
5500 REM ВЫЧИСЛЕНИЕ P (X) (МАССИВ P ( ))
5510 REM P<X>-X*<A4+6*A2*B2+3*C2+8*A*B3+6*B4>/24
5580 M-NiFOR 1-0 TO M|X<I>-A2<I>iY<I>-B2<J> iNEXT I
5620 G08UB 9000iFOR 1-0 TO M|P<I>-A4<I>+F<I>*6iNEXT I
5640 FOR 1-0 TO N iPd >-Pd >+3*C2d >«NEXT I
5660 M-NiFOR 1-0 TO MiXd>-Ad>iYd>-B3d>iNEXT I
56B0 GOSUB 9000iFOR 1-0 TO M1P<I>-<P<I>+F<I>*8+6*B4<I>>/24iNEXT I
5700 FOR I-N TO 0 STEP -11P<1+1>-P<I>iNEXT IiP<0>-0
5800 REM ВЫЧИСЛЕНИЕ Q (X) (МАССИВ Q ( ))
5810 REM Q<X> - <<A<X>-1>T2+A<XT2>-1>/2
5840 M-NiFOR 1-0 TO M|X<I>-A<I>iY<I>-A<I>iNEXT IiX<0>-0iY<0>-0
5860 GOSUB 9000iFOR 1-0 TO M iQd >-<Fd >+B2d > >/2 INEXT I
5880 Q<0>-Q<0>-.5
6000 REM ВЫЧИСЛЕНИЕ ПОЛИНОМОВ ДЛЯ АЛКАНОВ С (X) (МАССИВ С ( ))
6040 FOR 1-0 ТО N :Cd >-Pd >-Qd >+B2d >iNEXT I|С<0>-С<0>-1
8500 PRINT
8505 PRINT" АТОМОВ С АЛКИЛ.РАД. АЛКЕНОНЫ АЛЬДЕГИДЫ КЕТОНЫ"'
0510 PRINT" АЛКАНЫ" iPRINT iFOR 1-0 ТО N
8520 PRINT ТАВ<3> I ,TABd1 > Ad >)TAB<19>E(I > ;TAB<32>HY< I > ,ТАВ<47ЖЕ< I > ;
8530 PRINT TAB<61 >Cd > iPRINT TABC21 >E2d > >TAB<34>H2d > ,TAB<49>K2d >
8540 NEXT I
8999 STOP
9000 REM**********************
9001 REM** ВЫЧИСЛЕНИЕ X* Y **
9002 REM**********************
9010 FOR 19-0 TO MiFd9>-0
9020 FOR J9-0 TO I9:K9-I9-J9iF< I9>-Fd9>+X< J9>*Y<K9> iNEXT J9INEXT 19
9040 RETURN
63999 ENO
Линейные системы
213
RUN
МАКСИМАЛЬНОЕ ЧИСЛО АТОМОВ С? 10
АТОМОВ С АЛКИЛ. РАД. АЛКЕНОНЫ АЛЬДЕГИДЫ КЕТОНЫ АЛКАНЫ
0 1 0 0 0 0
0 0 0
1 1 0 0 0 1
0 0 0
2 1 0 0 0 1
0 0 0
3 2 1 1 0 1
1 1 0
4 4 5 4 1 2
4 3 1
5 8 16 11 5 3
12 0 4
б 17 47 30 17 5
34 21 13
7 39 135 02 53 9
95 56 39
0 09 300 222 150 10
262 149 113
9 211 1056 599 457 35
716 390 320
10 507 2921 1621 1300 75
1965 1060 697
Программа начинается с описания одномерных массивов (строки
100—130), элементы которых соответствуют вспомогательным ве-
личинам и конечным результатам. Часть исходных данных вводит-
ся в строке 350. Здесь задается максимальное число атомов С в сое-
динениях, для которых вычисляется число возможных изомеров.
На участке программы в строках 400—960 рассчитывается число
изомеров алкильных радикалов, которое присваивается соответст-
вующему элементу массива А( ). В строке 400 задаются четыре
первых значения А(1). Во внешнем цикле по I рассчитываются ко-
эффициенты Ai+1 при х'+1. Внутри цикла по параметру I два вло-
женных цикла вычисляют коэффициенты при х' (строки 550—740).
При этом используется рекуррентный вид формулы. Результат
суммирования присваивается переменной S. В следующем цикле,
вложенном в цикл по I (строки 800—870), вычисляется следующее
слагаемое, входящее в общий коэффициент и имеющее вид
34 (х)Л (г2). В следующей строке учитывается вклад еще одного
слагаемого — А (г3), и расчет завершается делением суммы S на 6.
В качестве промежуточного результата в строке 940* выводится
число изомерных алкильных радикалов, содержащих i атомов угле-
рода.
* Строка 940 в тексте программы отсутствует. Вывод числа изомерных алкиль-
ных радикалов (переменная А(1)) происходит в строке 8520. — Прим, перев.
214
Глава 8
Прежде чем продолжить обсуждение основной программы, рас-
смотрим важную и часто вызываемую подпрограмму, которая на-
чинается со строки 9000. Эта подпрограмма рассчитывает М пер-
вых коэффициентов полинома F(r), который представляет собой
произведение двух заданных полиномов X (г) и У (г):
F(r) = Х(г)*У(г)
Для определения F(I9) (19-го коэффициента полинома F (г)) рассмат-
риваются все возможные комбинации индексов К9 и J9, которые в
сумме дают 19, и вычисляется сумма соответствующих произведе-
ний X(J9)*Y(K9). Когда мы говорим о «вычислении полиномов»,
то подразумеваем под этим расчет коэффициентов этих полиномов.
В строках от 1000 до 1364 с помощью программы 9000 вычисля-
ются полиномы Л2(г), Л4(х) и Л3(х), и их коэффициенты присваи-
ваются элементам одномерных массивов А2( ), А4( ) и А3( ).
В строках 1400—1480 рассчитывается полином Х\А2(х) +
+ А (х2)]/2, стоящий в приведенных выше формулах под знаком
суммы, и его коэффициенты присваиваются элементам одномерно-
го массива АК( ). При возведении в степень используются вспомо-
гательные переменные Р(1) и Е(1).
После вычисления основного полинома по приведенным выше
формулам можно легко рассчитать число изомеров алкенонов, аль-
дегидов и кетонов, учитывая или не учитывая при этом цис —
/пране-изомерию. Это происходит на участке программы от строки
3000 до строки 4240. Нет необходимости подробно анализировать
этот участок программы, поскольку выполняемые здесь операции
ограничиваются главным образом умножением различных полино-
мов. Какие полиномы перемножаются, можно узнать из формул.
Для умножения полиномов каждый раз вызывается подпрограмма
9000.
Расчет числа изомерных алканов начинается со строки 5000.
Здесь сначала вычисляются вспомогательные полиномы, а именно
А (г2), А (г3), А (г4) и А 2(х2), коэффициенты которых присваиваются
элементам одномерных массивов В2( ), В3( ), В4( ) и С2( ) со-
ответственно (строки 5000—5320). Коэффициенты вспомогательно-
го полинома Р (г) для подсчета числа изомерных алканов определя-
ются в строках 5500—5700. На этом участке программы так же,
как и для других классов соединений, например алкенонов, арифме-
тические операции ограничиваются сложением и умножением поли-
номов, для чего вызывается подпрограмма 9000. В строках
5800—5880 рассчитывается вспомогательный полином Q (г). В стро-
Линейные системы
215
ках 6000—6040 суммированием найденных ранее вспомогательных
полиномов вычисляется полином, соответствующий алканам.
Начиная со строки 8500, происходит вывод на экран рассчитан-
ного числа изомеров. Для алкенонов, кетонов и альдегидов на
экран выводится по два числа: верхнее равно числу изомеров с уче-
том цис — транс-изомеров, нижнее равно соответствующему числу
изомеров без учета этого вида изомерии.
Задание 113. Напишите программы или внесите изменения в программу «ИЗОМЕ-
РЫ» для расчета числа изомеров других классов соединений. Соответствующие фор-
мулы, в которые входит полином A fy) для алкильных радикалов, приведены ниже:
Первичные спирты: РА (х) = х-А (х)
Вторичные спирты — SA (х):
SA (х) = х-И2to ~ 2Л (х) + А (х2)]/2
Третичные спирты — ТА (х):
Г4(х) = х[43(г) - 342(х) + 34(х)Л(х2) - 34 (х)2 + 2Л (х3)]/6
Кетоны и альдегиды вместе — КА (х):
КА (х) = х-И 2(х) + А (х2)]/2
Для альдегидов (без кетонов) пригодна та же формула, что и для первичных
спиртов. Для кетоиов можно получить соответствующую формулу, если из выраже-
ния для КА (х) вычесть выражение для РА (х).
Олефины — AY (х):
ЛУ(х) = И4(г) + 2Л2(х)Л(х2) + 342(х2) + 2А (х4)]/8
Ацетилены —АС(х):
АС(х) = х2-И2« + А(х2)]/2
Эфиры: £5(х) = х-А (х)- И (х) - 1]
9. Дифференциальные уравнения
При решении научных и инженерно-технических задач часто бы-
вает необходимо математически описать какую-либо динамическую
систему. Лучше всего это делать в наиболее «естественной»
форме — в виде дифференциальных уравнений или систем диффе-
ренциальных уравнений. Приведем несколько примеров:
а) Кинетика химических реакций: с' — f(c, t) (с может означать
как концентрацию вещества, так и вектор концентраций).
б) Явления переноса (перенос тепла, массы и импульса)*. В ста-
ционарных условиях для описания этих процессов можно использо-
вать обыкновенные дифференциальные уравнения; в нестационар-
ных условиях эти явления описываются уравнениями в частных
производных. В технике такие процессы, как перенос тепла и мас-
сы, описываются соответствующими уравнениями, которые носят
часто эмпирический характер (например, в случае теплоообмена,
перемешивания, высушивания, экстракции, адсорбции и многих
других).
в) Динамика популяций. Изменения численности популяций
хищников и их жертв можно описать, например, двумя сравнитель-
но простыми дифференциальными уравнениями, предполагая, что
известна зависимость рождаемости и гибели отдельных видов жи-
вотных от их «концентрации».
д) Распространение «нового». Распространение эпидемий, слу-
хов, опыта и мнений в определенных условиях также можно опи-
сать дифференциальными уравнениями. Для эпидемий следует учи-
тывать также различия между «здоровыми», «инфицированными»,
«резистентными» и «изолированными» популяциями. Кинетические
закономерности для каждой из этих популяций в соответствии с
выбранной моделью могут различаться.
’ Т. е. явления теплопроводности, диффузии и динамической вязкости соответст-
венно. — Прим, перев.
Дифференциальные уравнения
217
При решении дифференциальных уравнений могут встретиться
три типа задач*:
а) Дифференциальные уравнения с заданными начальными усло-
виями. Эта задача встречается при решении дифференциальных
уравнений, которые описывают кинетику химических реакций.
Обычно известны концентрации веществ в начальный момент вре-
мени (t = 0), и необходимо найти концентрации веществ через не-
который промежуток времени t.
б) Краевая задача. В этом случае известны значение функции
или ее производных в определенных точках, и необходимо найти
решение между этими точками. В качестве примера можно приве-
сти расчет прогиба балки под нагрузкой. Если концы балки закреп-
лены, то прогиб обоих концов балки равен нулю. Другой пример:
стационарное распределение температуры в кубе, температура трех
граней которого равна 20 °C, а трех других граней 80 °C.
в) Задачи на собственные значения. Задачи этого типа очень по-
хожи на краевую задачу. Поясним это на следующем примере. В
уравнение Шредингера для гармонического осциллятора полная
энергия системы входит как параметр. Нас интересует, при каких
значениях энергии уравнение Шредингера имеет «разумные» в отно-
шении физического содержания задачи решения. (Эти решения дол-
жны соответствовать таким волновым функциям, которые с увели-
чением расстояния уменьшаются до нуля.) Значения энергии, кото-
рые удовлетворяют этому условию, называются собственными
значениями, а соответствующие этим значениям энергии волновые
функции — собственными функциями. Другой, более простой при-
мер — дифференциальное уравнение, описывающее колебания стру-
ны. Краевые условия в этом случае определены, поскольку струна
закреплена с обеих сторон. В дифференциальное уравнение, описы-
вающее колебания струны, входит параметр, который по смыслу
задачи соответствует «длине волны». Нужно найти, какие значения
может принимать этот параметр, т. е. при каких значениях пара-
метра решение дифференциального уравнения удовлетворяет крае-
вым условиям.
Сначала рассмотрим два метода, которые позволяют решать
задачи с заданными начальными условиями. Эти методы общеиз-
вестны, и мы их обсуждали выше, когда рассматривали методы
численного интегрирования. Если возникнет необходимость исполь-
• Под «задачей» в этой книге понимается задача Коши, т. е. интегрирование
дифференциальных уравнений вида/' = F(x, у). — Прим, перев.
218
Глава 9
зовать какой-нибудь более сложный, изощренный алгоритм, то
следует обратиться к учебникам и справочникам по вычислитель-
ной математике.
9.1. Метод Эйлера
Даны дифференциальное уравнение у' = ffy,y) и начальное ус-
ловие у (о) = уа. Надо найти такую функцию у = g (х), которая
удовлетворяла бы как дифференциальному уравнению, так и на-
чальному условию.
Пример: у' = х-у, начальное условие у (0) = 1
Решение: у = g(x) = е*2/2
Чтобы иайти решение при х = 1, в формулу для g (х) вместо аргумента х под-
ставляют его числовое зиачеиие и получают у = 1,648721. Однако получить функ-
цию, удовлетворяющую заданному уравнению и начальному условию, в аналитиче-
ском виде удается лишь в очень редких случаях. В общем случае надо иайти значе-
ние функции g(x) в точке х = 1 (и, разумеется, при всех других интересующих нас
значениях х). Таким образом, численные методы дают решение дифференциальных
уравнений ие в виде аналитических функций, а в виде набора заданных значений х и
соответствующих нм приближенных значений у. Откладывая значения х и у на диа-
грамме, по этим данным можно построить график искомой функции.
Рассмотрим такой численный метод на простых и наглядных
примерах, не привлекая строгих математических доказательств.
Для этого заменим производную в левой части дифференциального
уравнения на близкое ей по величине отношение конечных прираще-
ний зависимой и независимой переменной:
Вместо у' ~ dy/dx = ffy,y), стало Ду/Дх = /(х, у)
Если теперь преобразовать полученное уравнение, то получится
формула, по которой можно вычислить Ду:
Ду = /(х, _у)-Дх
При заданных начальных значениях _у0 и х0 можно вычислить
У1 = Jo + /(v0> Jo)-Av Xi = х0 + Дх
У2 = У1 + /(УР Ji)Av х2 = X! + Дх
Уз = У2 + /(*2> х3 = х2 + Дх
У4 = Уз + /(«’з» Уз)** Х4 = х3 + Дх
Таким способом можно продолжить вычисления с достаточно
малым шагом по х вплоть до заданного значения х. Ошибка в
определении значения у при этом будет тем меньше, чем меньше
выбрана длина шага Дх. В курсах вычислительной математики вы
Дифференциальные уравнения
219
можете найти строгое доказательство того, что ошибка прямо про-
порциональна длине шага.
Ошибка ~ h
Если программа не предусматривает автоматического выхода из
бесконечного цикла и прекращения вычислений по достижении за-
данной точности результата (так же, как, например, для интегри-
рования по методу Эйлера), то блок-схема алгоритма решения диф-
ференциальных уравнений методом Эйлера имеет следующий вид
(схема 15):
Схема 15
220
Глава 9
Блох-схема состоит из трех частей. Первая часть соответствует
основной программе. В ней вызывается подпрограмма (ей соот-
ветствует вторая часть блок-схемы), реализующая алгоритм Эйле-
ра. Эта подпрограмма в свою очередь при каждом обращении к
ней вызывает подпрограмму «ДУ» (третья часть блок-схемы), в ко-
торой вычисляется правая часть дифференциального уравнения
Дифференциальные уравнения
221
fQc, у). Ниже приведена распечатка программы «ДУ-ЭЙЛЕР1», со-
ответствующей этой блок-схеме:
0 REM "ДУ—ЭЙЛЕР1" EBERT/EDERER 810706
1 REM********************************************
2 REM** РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ **
3 REM** МЕТОДОМ ЭЙЛЕРА ..ПРАВАЯ ЧАСТЬ ДИФФЕ- ♦♦
4 REM** РЕНЦИАЛЬНОГО УРАВНЕНИЯ DY/DX= FIX, Y ) **
5 REM** ОПИСАНА В ПОДПРОГРАММЕ 10000 **
9 REM******************************* *********** **
500 INPUT "НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y "; Y 1
600 INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ '; А, Е
1000 N1-2
1050 PRINT
1100 H-<E-A>/N1
1200 GOSUB 5000
1300 PRINT N1,TAB<7>, "ЧАСТИЧНЫХ ИНТЕРВАЛОВ”;
1400 PRINT •’ Y-";Y
1500 N1-N1*2
1600 GOTO 1100
5000 REM************************************ ********
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ **
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
5010 REM********************************************
5100 Y-Y1
5200 FOR Х-А ТО Е-Н STEP Н
5300 GOSUB 10000
5400 Y-Y+D*H
5500 NEXT X
5600 RETURN
10000 REM*************************************
10002 REM** ЗДЕСЬ ЗАДАЕТСЯ ПРАВАЯ ЧАСТЬ **
10004 REM** ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
10010 REM*************************************
11000 D-X*Y
12000 RETURN
63999 END
RUN
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y? 1
ЗНАЧЕНИЯ’X НАЧАЛЬНОЕ, КОНЕЧНОЕ? 0,1
2 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V» 1.25
4 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V- 1.41943359
8 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V» 1.52400597
16 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V» 1.50338613
32 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V- 1.61523952
64 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V. 1.63176718
128 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V» 1.64018964
256 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V- 1.64444164
512 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V» 1.64657799
1824 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V» 1.64764877
2848 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V- 1.64818479
BREAK IN 5300
READY.
PRINT EXPC.5?
1.64872127
READY.
Как уже упоминалось, для наглядности и сокращения объема
программы в ней не использовались критерии сходимости для ав-
222
Глава 9
тематического прекращения вычислений. В программе имеется бес-
конечный цикл, в котором непрерывно вычисляется решение диф-
ференциального уравнения в заданной точке, причем точность ре-
зультата после каждой итерации удваивается. Пользователь может
вручную прервать выполнение программы, как только два последо-
вательных значения у будут отличаться друг от друга на достаточ-
но малую величину. Поскольку время счета каждой последующей
итерации в два раза больше, чем предыдущей, счет прекращается
почти «естественным» образом, когда число шагов достигнет не-
скольких тысяч.
Из исходных данных сначала вводится начальное условие, т. е.
надо указать начальное значение х и соответствующее ему началь-
ное значение у. Отсюда и появилось название этого типа задач —
задачи с заданными начальными условиями. Кроме того, необходи-
мо ввести значением, для которого надо найти значение у.
Если хотят рассчитать значение у не в одной, а в нескольких
точках, то необходимо запустить программу «ДУ-ЭЙЛЕР1» соот-
ветствующее число раз (разумеется, с тем же начальным
условием). Затем полученные точки вместе с начальным условием
можно нанести на диаграммную бумагу и построить график иско-
мой функции.
В качестве примера приведено решение дифференциального
уравнения:
dy/dx = х-у
Решение этого уравнения в аналитической форме выглядит следую-
щим образом:
у = А • &г,г
что геометрически соответствует семейству кривых.
Правильность решения можно легко проверить, подставив эту
функцию в исходное уравнение. Константу А можно определить из
начального условия. Если подставить в выражение для у начальное
условие х = 0, у = 1, то получится А = 1. Начальное условие по-
зволяет из семейства функций выбрать одну, и, следовательно, за-
дача решена. Для данного конкретного примера можно использо-
вать аналитическое решение для проверки численного решения, по-
лученного с помощью программы «ДУ-ЭЙЛЕР1».
В принципе программа «ДУ-ЭЙЛЕР1» позволяет решать любые
дифференциальные уравнения. Для этого в строке 11000 переменной
D надо присвоить арифметическое выражение в соответствии с пра-
вой частью дифференциального уравнения.
Дифференциальные уравнения
223
Задание 114. Решите в численном виде приведенные ниже дифференциальные
уравнения; найдите решения при нескольких значениях независимой переменной и на-
несите найденные точки на диаграмму. Сравните результаты численного и аналити-
ческого метода (в тех случаях, когда уравнение можно решить аналитически),
dy/dx = -у; dy/dx = к - у2
dy/dx = —к-у2 + sin2(xy); dy/dx = ху + ух
Начните с начального условия у = 1 при х = 0. Решите затем эти дифферен-
циальные уравнения с другими начальными условиями.
Задание 115. Пусть скорость радиолиза вещества А пропорциональна заданной
безразмерной величине — плотности излучения D.
d[A]/dZ = -k0 D- [А]
Уменьшение величины D приближенно описывается экспоненциальной функцией
времени:
D = Doe-k‘
Параметры имеют следующие значения:
к = 0,001 1/с
Doko = 0,001 1/с
Если подставить эти значения в приведенные выше уравнения, то получится сле-
дующее дифференциальное уравнение:
d[A]/dr = — 0,001-е-0-001'-[А]
С помощью программы «ДУ-ЭЙЛЕР1» найдите зависимость [Aj/IAJ от време-
ни и вычислите, какой станет [А] через бесконечно большой промежуток времени.
Решение этой задачи в аналитическом виде выглядит следующим образом:
£Jo 3 = J. O. (1 _ е-*<)
[А] / к
Сравните результат численного решения с аналитическим.
Задание 116. Пусть порядок реакции термического разложения вещества А равен
2, а порядок разложения А под действием УФ-излучения равен 0 (квантовый выход
равен 1). Скорость расходования вещества А описывается следующим уравнением:
d[A] ,
— = [А]2 - «(/)
dr z
Если u(r) пропорциональна интенсивности УФ-нзлучения солнца, то ее можно
аппроксимировать синусоидой.
Реакция начинается с восходом солнца. Вычислите концентрацию вещества А в
момент захода солнца, если параметры имеют следующие значения:
Восход солнца 6.00, т. е. / = 0 с
Заход солнца 18.00, т. е. / = 43200 с
[А]о 1 моль/л
к2 0,00002 л/(моль-с)
и(1) = 0,00001 sin (//43200) моль/(л-с)
224
Глава 9
Задание 117. Выполните предыдущее задание при условии, что имеются два раз-
личных источника излучения и реакция разложения подчиняется кинетическому урав-
нению произвольного порядка. Зависимость интенсивности излучения обоих источ-
ников от времени описывается различными уравнениями. Порядок фотохимического
разложения по концентрации А не обязательно равен 1 или 0, н его можно выбрать
произвольно.
9.2. Улучшенный метод Эйлера*
При решении дифференциальных уравнений по методу Эйлера
производная аппроксимируется отношением конечных приращений,
что приводит к следующей итерационной формуле:
Л+1 = У, + Л-/(г, , у,)
Правую часть дифференциального уравнения вычисляют, исходя
из известных уже значений х, и у,. Поскольку метод решения диф-
ференциальных уравнений такого типа работает как при положи-
тельных приращениях Дх, так и при отрицательных, было бы го-
раздо лучше, если бы можно было оценивать правую часть диффе-
ренциального уравнения между (г,, у,) и (х|+1, у, + 1). К сожалению,
непосредственно сделать это нельзя, поскольку еще не вычислено
значение у( + 1. Однако с помощью так называемого прогноза можно
найти вспомогательную величину у *+1. В качестве прогноза примем
приведенную выше рекуррентную формулу Эйлера:
У *+1 = Л + О)
За прогнозом следует коррекция, которая позволяет оценить
правую часть дифференциального уравнения между обеими точ-
ками:
Л + 1 = Л + 3 + Лч+1>Л*ц)1
Если применить этот простой метод прогноза и коррекции, то
ошибка уменьшается пропорционально А в кубе:
Ошибка — А3
Рассмотренную последовательность операций можно записать в
виде
Y 2 = Y 4- Н */(Х, Y)
Y 3 = Y 4- Н*/(Х 4- Н, Y2)
Y H = (Y2 4- Y3)/2
Если два первых выражения подставить в третью формулу, то
станет ясно, что этот участок программы соответствует уравнению
(1).
Метод прогноза и коррекции. — Прим, перев.
Дифференциальные уравнения
225
Ниже приведена распечатка программы «ДУ-ЭЙЛЕР2», в кото-
рой использован метод прогноза и коррекции.
0 REM "ДУ—ЭЙЛЕР2" EBERT/EDERER 810706
1 REM****************************************
2 REM** РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕ- »*
3 REM** НИЙ МЕТОДОМ ПРОГНОЗА И КОРРЕКЦИИ **
4 REM»* (УЛУЧШЕННЫЙ МЕТОД ЭЙЛЕРА) **
5 REM** ПРАВАЯ ЧАСТЬ ДИФФЕРЕНЦИАЛЬНОГО **
6 REM** УРАВНЕНИЯ DY/DX = F (X.Y) **
7 REM** ОПИСАНА В ПОДПРОГРАММЕ 10000 **
8 REM** В ВИДЕ D = F (Х9. Y9) **
9 REM****************************************
500 INPUT "НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y"; Y 1
600 INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ"; А, Е
1000 Nl«2
1050 PRINT
1100 H-<E-A>/N1
1200 GOSUB 5000
1300 PRINT NI,TAB<7>, "ЧАСТИЧНЫХ ИНТЕРВАЛОВ”;
1400 PRINT" V-";V
1500 N1-N1*2
1600 GOTO 1100
5000 REM****************************** *************
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ**
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
5010 REM******************************************
5100 V-V1
5200 FOR Х=А ТО Е-Н STEP Н
5250 X9-X1V9-V
5300 GOSUB 10000
5320 V2-V+D*H
5340 X9-X+HtV9-V2
5123 GOSUB 10000
5360 V3-V+D*H
5400 V-<V2+V3>/2
$500 NEXT X
5600 RETURN
10000 REM*************************************
10002 REM** ЗДЕСЬ ЗАДАЕТСЯ ПРАВАЯ ЧАСТЬ **
10004 REM** ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
10010 REM*************************************
11000 D-X9*Y9
12000 RETURN
63999 END
RUN
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y? 1
ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ? О, 1
2 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Y- 1.6171875
4 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Ya 1.64228563
8 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Ya 1."4735461
16 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Ya 1.64841453
32 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Ya 1.64864928
64 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Y- 1.64870389
128 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Ya 1.64871702
256 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Ya 1.64872025
512 ЧАСТИЧНЫХ ИНТЕРВАЛОВ Y« 1.6487211
BREAK READV. IN 5340
PRINT ЕХР(.5>
1.64872127
RERDV.
226
Глава 9
Основная программа здесь такая же, как в программе «ДУ-
ЭЙЛЕР1». Сохранена также и структура программы «ДУ-
ЭЙЛЕР1». В подпрограмме 10000, в которой вычисляется правая
часть дифференциального уравнения, теперь нельзя использовать
переменные X и Y, так как они уже применяются в подпрограмме
5000. Поэтому они заменены на переменные Х9 и Y9. Подпрограм-
ма 5000 расширена. До строки 5320 она совпадает с соответствую-
щей подпрограммой программы «ДУ-ЭЙЛЕР1». Однако получен-
ный результат рассматривается не как окончательное новое значе-
ние у, а как прогноз значения у, и это значение присваивается пере-
менной Y2. В четырех строках (5340—5400) происходит коррекция
нового значения.
Поскольку в качестве примера использовано то же самое уравне-
ние, что и в программе «ДУ-ЭЙЛЕР1», видно, что по улучшенной
программе результаты сходятся к точному решению значительно
быстрее, чем по программе «ДУ-ЭЙЛЕР1». Небольшое дополнение
привело к значительному ускорению вычислительного процесса, к
повышению точности результата.
Задание 118. Решите следующие дифференциальные уравнения и в соответствии
с выбранными начальными условиями постройте один или несколько графиков.
у' = 2у + е*; у' = х3 + 2ху
у’ = log(r) + х/у; у' = (1 + у)-х-у/у'
Задание 119. Сравните решения, полученные при использовании программ
«ДУ-ЭЙЛЕР1», и «ДУ-ЭЙЛЕР2».
Задание 120. Составьте программу для расчета динамики популяции, в основе
которой лежит следующая простая, но в то же время и фундаментальная модель
(модель Ферхюльта). Эта модель предполагает, что рождаемость пропорциональна
численности популяции, а смертность пропорциональна квадрату численности (пере-
население, недостаток ресурсов). Данной модели соответствует следующее диффе-
ренциальное уравнение:
dp/dt = а-р — Ь-р2
Рассчитайте, как меняется численность популяции со временем, если а = 1,
b = 0,0001. Пусть начальная численность равна 10. Какова численность популяции
через очень большой промежуток времени (стабильная популяция)?
Задание 121. Многим видам животных и растений для воспроизводства необхо-
дим партнер. С другой стороны, смертность пропорциональна численности популя-
ции. Развитие такой популяции описывается дифференциальным уравнением:
dp/dl = -а-р + b -р2
При а = 1 и b = 0,001 в рамках этой модели существует такая предельная чис-
ленность популяции, ниже которой популяция вымирает.
Выберите различные начальные численности популяции н установите, начиная с
какой численности популяция склонна к вымиранию.
Задание 122. В этом задании рассматривается распространение информации сре-
ди населения. Пусть Р — общая численность населения, р — количество лиц, кото-
Дифференциальные уравнения
227
рые в момент времени t = 0 знают какую-то новость. Тогда для распространения
этой новости справедливо следующее дифференциальное уравнение:
ф/d/ = а-р-(Р - р) + Ь(Р - р)с
Первое слагаемое соответствует распространению информации при контактах
«незнающих» (Р — р) со «знающими» (р). Второе слагаемое описывает вклад
средств массовой информации, которые действуют только на «незнающих» лиц.
Опишите математически распространение новости со временем; в качестве на-
чального условия возьмите р - 1 в момент времени t = 0. Через какой промежуток
времени новость узнает 1000 человек, если а = 0,00001, Ь - 0,001 нс = 0,9?. Как бу-
дет распространяться информация, если b = 0 (т. е. средства массовой информации
не участвуют в распространении). В каких случаях средства массовой информации
играют наибольшую роль в распространении новостей?
9.3. Метод Рунге — Кутта
Численный метод Рунге — Кутта, который часто используется
для решения задач научного и инженерно-технического характера,
приводится здесь без строгих доказательств. Метод эффективен,
надежен и легко реализуется программными средствами. (Еще одно
преимущество заключается в том, что в отличие от других мето-
дов, впрочем не рассматриваемых в этой книге, процедура Рунге —
Кутта не требует для ее запуска других программ.) Метод Рунге —
Кутта аналогичен методу Эйлера, однако
Ошибка ~ А4
Это означает, что при уменьшении шага ошибка уменьшается зна-
чительно быстрее по сравнению с методом Эйлера.
В методе Рунге — Кутта вводятся четыре вспомогательные ве-
личины К{, К2, К3 иА4 (это различные значения у). Дифференциаль-
ное уравнение, как обычно, задано в виде
У'
Вычисление координат очередной точки (к( + 1, у( + j), исходя из
уже известных координат предыдущей точки, происходит по следу-
ющей схеме:
Ki = h-ft^yj
К2 = h-ffy, 4- А/2, у, + К /2)
кз = Л -/(г, + А/2, у,- + К2/1)
к4 = h-fk, + h,yt + KJ
xi+i = xi + h
Л+i = У, + + 2K2 + 2K3 + KJ/6
15*
228
Глава 9
Эта последовательность уравнений использована в программе
«Р-К-Н».
0 REM "Р-К-Н" EBERT/EDERER 810706
1 REM********************************* ************
2 REM** РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ **
3 REM** МЕТОДОМ РУНГЕ-КУТТА-НИСТРЕМА ПРАВАЯ **
5 REM** ЧАСТЬ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
6 REM** DY/DX= FIX, Y ) ОПИСАНА В ПОДПРОГРАММЕ **
7 REM** 10000 В ВИДЕ D= FIX9, Y9) **
8 REM** ОШИБКА ПРОПОРЦИОНАЛЬНА Ht5 **
9 REM*********************************************
500 INPUT "НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y"; Y 1
600 INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ"; А Е
1000 N1-2
1050 PRINT
1100 H=<E-A>/N1
1200 GOSUB 5000
1300 PRINT Nl;TpB<7>; "ЧАСТИЧНЫХ ИНТЕРВАЛОВ";
1400 PRINT" V=",V
1500 N1-N1*2
1600 GOTO 1100
5000 REM********************************************
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ **
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
5010 REM********************************************
5100 V-V1
5200 FOR Х-Я ТО Е-Н STEP Н
5300 ХЭ-Х>79-71GOSUB 10000>K1-H*D
5400 Х9-Х+Н/2179-7+K1/2lGOSUB 10000>K2-H*D
5500 X9-X+H/2I79-7+K2/21G0SUB 10000>K3-H*0
5600 X9-X+H179-7+K31G0SUB 10000>K4-H*D
5700 7=7+<Kl+2*K2+2*K3+K4>/6
5800 NEXT X
5900 RETURN
10000 REM******************************** *****
10002 REM** ЗДЕСЬ ЗАДАЕТСЯ ПРАВАЯ ЧАСТЬ **
10004 REM** ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
10010 REM*************************************
11000 D-X9*79
12000 RETURN
63999 END
RUN
НАЧАЛЬНОЕ ЗНАЧЕНИЕY? 1
ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ? О, 1
2 ЧАСТИЧНЫХ ИНТЕРВАЛОВ У- 1.6485277
4 ЧАСТИЧНЫХ ИНТЕРВАЛОВ 7- 1.64870974
8 ЧАСТИЧНЫХ ИНТЕРВАЛОВ 7- 1.64872061
16 ЧАСТИЧНЫХ ИНТЕРВАЛОВ 7- 1.64872123
32 ЧАСТИЧНЫХ ИНТЕРВАЛОВ V- 1.64872127
64 ЧАСТИЧНЫХ ИНТЕРВАЛОВ 7- 1.64872127
BREAK IN 5700
READV.
PRINT EXP(.5>
1.64872127
Приведенный пример показывает, что программа «Р-К-Н» на-
ходит верное решение значительно быстрее, чем программы для
Дифференциальные уравнения
229
решения дифференциальных уравнений «ДУ-ЭЙЛЕР1» и «ДУ-
ЭЙЛЕР2».
Основная программа и подпрограмма для вычисления правой
части дифференциального'уравнения совпадают с соответствующи-
ми частями программ «ДУ-ЭЙЛЕР1» и «ДУ-ЭЙЛЕР2»; в основной
программе также организован бесконечный цикл, и после каждой
итерации шаг по независимой переменной уменьшается в два раза.
Несколько изменен цикл FOR—NEXT внутри подпрограммы
5000. Там в пяти строках (5300—5700) стоят арифметические выра-
жения, соответствующие пяти приведенным выше формулам. (Вы-
зов определяемой функции ffy, у) заменен на GOSUB 10000*, после
чего переменным Х9 и Y9 присваиваются исходные значения.)
Задание 123. Сравните три метода решения дифференциальных уравнений с по-
мощью следующих контрольных уравнений:
У' = —ху; у' = у; у' = -у
у' = х + у; у' = sin (у); у' = log (у)
Задание 124. Используйте в основной программе, общей для программ «ДУ-
ЭЙЛ ЕР 1», «ДУ-ЭЙЛЕР2» н «Р-К-Н» критерий сходимости решения, с помощью
которого сравнивались бы результаты трех последовательных итераций. Выходные
данные в этом случае можно ограничить одним результатом трех последовательных
итераций, удовлетворяющим критерию сходимости.
Задание 125. Модифицируйте программу «Р-К-Н» так, чтобы в результате полу-
чалось не одно значение у при данном значении х, а 20 значений у, соответствующих
20 значениям х на заданном отрезке. С помощью этой программы вы сможете про-
следить ход кривой на отрезке, ограниченном начальным и конечным значениями х.
Задание 126. Решите одно или несколько из следующих дифференциальных урав-
нений н сравните численное и аналитическое решение (в том случае, если последнее
вообще существует):
у' = -0,1у - О,5у2; у' = 1 - у - е~х
у' = sin(xy) + cos(x/y); у' = y-log(x) - у
У' = ху3 - у; у' = е*-у2 - 2у
Задание 127. Химическая реакция протекает в термически изолированном сосуде.
Дифференциальное уравнение, описывающее изменение концентрации исходного ве-
щества, имеет вид
с’ = -к-с
Для константы скорости к выполняется уравнение Аррениуса:
• В программах «ДУ-ЭЙЛЕР1» и «ДУ-ЭЙЛЕР2» значения функции/(х, у) рас-
считываются подпрограммой 10000 так же, как н в программе «Р-К-Н». — Прим,
перев.
230
Глава 9
Температура в реакторе изменяется в зависимости от степени превращения:
Т = То + (со " с)я
Н — величина, пропорциональная энталышн реакции.
Постройте график зависимости концентрации с от времени для эндотермической
и экзотермической реакций. Соответствующее дифференциальное уравнение можно
легко вывести из приведенных выше уравнений. Решите аналогичную задачу для ре-
акции второго порядка.
Задание 128. Рост опухоли, которая обычно увеличивается экспоненциально,
часто можно описать простым дифференциальным уравнением. Однако со временем
константа роста опухоли уменьшается. Пример соответствующего дифференциаль-
ного уравнения:
dV/dt = a-Ve~b,c
V — размер опухоли; с = 1 (как правило); а, Ь — характеристические константы.
Найдите зависимость размера опухоли от времени, если рост опухоли описыва-
ется приведенным уравнением. При некоторых значениях параметра с существует
предельный размер опухоли (например, при с = 1); при других значениях параметра
такого ограничения на размер опухоли нет (например, при с = 0). Выясните с по-
мощью ЭВМ, начиная с какого значения с размеры опухоли при достаточно продол-
жительном времени ее роста не превосходят некоторой конечной величины (пара-
метры а н b можно выбрать произвольно).
Задание 129. Рассмотрим реактор идеального смешения объемом И литров.
Пусть в этом реакторе протекает реакция а-го порядка. Концентрация вещества С в
начальный момент времени (/ = 0) равна с0. В реактор непрерывно подводится ве-
щество С и из реактора непрерывно отводится смесь исходных и конечных продук-
тов реакции. Поскольку объем реакционной смеси остается постоянным, то оба по-
тока (г) одинаковы и не меняются со временем. В реактор попадает раствор вещест-
ва С с концентрацией сг, а на выходе из реактора концентрация этого вещества рав-
на с.
Кинетическое уравнение для реакции первого порядка, протекающей в проточ-
ном реакторе идеального смешения, имеет вид
de/Л = —к-с° + czz/V — cz/V
Рассчитайте кинетическую кривую этой реакции в начальный период, а также
стационарную концентрацию, которая устанавливается через достаточно большой
промежуток времени. Скорость реакции зависит от значений параметров с0, сг, к, а,
z и V. (Для расчетов возьмите следующие значения параметров: сд = 3 моль/л, сг =
= 2 моль/л, а = 1, к = 0,001 1/с, z = 1 л/с и V = 1000 л.)
9.4. Метод Эйлера для систем дифференциальных
уравнений
Рассмотрим простейший механизм ферментативной реакции
к\
Е + S ES
к2
кз
ES - Р + Е
Е — фермент; S — субстрат; ES — фермент-субстратный комплекс; Р — продукт.
Дифференциальные уравнения
231
Если обозначить концентрации веществ символами этих веществ
и скорости их расходования или накопления соответствующими
символами со штрихами, то кинетику реакции можно описать сле-
дующей системой дифференциальных уравнений:
[Е]' = -kt- [Е] • [S] + A2-[ES] 4- A3-[ES]
[ES]' = +kt- [E]- [S] - A2-[ES] - Jt3 [ES]
[S]' = -fcf[EHS] + A2[ES]
[P]' = +A3-[ES]
Аналитическое решение этой системы по методу стационарных
концентраций дает известное уравнение Михаэлиса — Ментен. Ерли
же решать эту систему уравнений, не привлекая гипотезу о стацио-
нарности концентрации фермент-субстратного комплекса, то необ-
ходимо воспользоваться одним из численных методов. Для нагляд-
ности обсудим сначала метод Эйлера. Чтобы не усложнять задачу,
ограничимся пока системой из двух дифференциальных уравнений.
(Для сравнения справа приведено решение одного дифференциаль-
ного уравнения методом Эйлера.)
У1 =/i(r,j„j2)
У2 = /2&’У1> Уг)
у’ =fb,y)
Если в дифференциальных уравнениях производные заменить
отношениями малых конечных приращений и обозначить прираще-
ние независимой переменной через h, то получатся следующие ите-
рационные формулы:
У& + h) = у^) + /ifr, Ji(r), J2(r)]-A
у (г + А) = у (г) + /fr, j(r)]-A
j2(r + А) = j2(r) + /2fr, j,(r), y2fr)]h
Видно, что итерационные формулы для одного дифференциаль-
ного уравнения и системы дифференциальных уравнений аналогич-
ны. Однако вторые слагаемые в формулах для системы уравнений
(/j и/2) зависят как отх, так и OTjj и у2 (впрочем, могут и не зави-
сеть).
Программа «СИСТ-ЭЙЛЕР» составлена аналогично программе
«ДУ-ЭЙЛЕР1».
0 REM "СИСТ—ЭЙЛЕР" EBERT/EDERER В10711
1 REM*****************************************
2 REM** РЕШЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ ♦*
3 REM** УРАВНЕНИЙ МЕТОДОМ ЭЙЛЕРА **
4 REM** DY/DX=F(X. Y) **
5 REM** ВЕКТОРЫ F ИУ ОПИСАНЫ В *♦
6 REM** ПОДПРОГРАММЕ 1000 ♦♦
9 REM*********************************** ******
100 DIМ V '20 ' .VI' 20 .' . D' 20 *
200 Н=2 :РЕМ ЧИСЛО ДИФ. УРАВНЕНИЙ В СИСТЕМЕ
232
Глава 9
300 FOR I-l то N
400 PRINT "НАЧАЛЬНОЕ ЗНАЧЕНИЕУ ("• I ;') ="
500 INPUT V1<I>
600 NEXT I
700 INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ,КОНЕЧНОЕ"-A E
1000 Nl-4
1050 PRINT
1100 H-<E-R>/N1
1200 OOSUB 5000
1300 PRINT N1,TRB<7>,"ЧАСТИЧНЫХ ИНТЕРВАЛОВ"
1400 FOR I-l TO N
1420 PRINT "Y<"1I,"> - "1Y<I>
1440 NEXT I
1500 Nl—Nl*2
1600 OOTO 1100
5000 REM********************************************
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ ••
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ••
5010 REM********************************************
5100 FOR I-l ТО N1V<I>—V1<I>(NEXT I
5200 FOR Х-Я ТО Е-Н STEP Н
5300 OOSUB 10000
5400 FOR I-l ТО NiV<I>-V<I>+D<I>*HINEXT I
5500 NEXT X
5600 RETURN
10000 REM********************************************* ««
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ПРАВЫЕ ЧАСТИ ДИФФЕРЕНЦИ- **
10003 REM** АЛЬНЫХ УРАВНЕНИЙОУ! / DX = F1(X,Y1 ...YN) **
10004 REM** D(I)=F(X,Y (1)..Y (NH **
10010 REM***********************************************
10100 D< 1 >—3*V< 1 >*V< 1 >+2*V< 2>+EXP<-X>
10200 0<2>-3*V<1>*V<1>-l2*Y<2>+EXP<-X>
12000 RETURN
63999 END
RUN
НАЧАЛЬНОЕ ЗНАЧЕНИЕУ (1) = ? 1
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y (2) = ? 1
ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ? О 1
4 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
V< 1 > - -3.171875
V< 2 У - 14.046875
8 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
V< 1 > — .68511351
Y< 2 > - .216641239
16 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
Y< 1 > - .693142272
YC 2 > - .204709107
32 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
V< 1 > — .695695918
V< 2 > - .205934681
64 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
Y< 1 > - .697023049
V< 2 > - .206576611
128 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
V< 1 > - .697697541
V< 2 > - .206904498
256 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
V< 1 > - .698037313
V< 2 > - .207070129
Начальные значения у, текущие значения у и производных явля-
ются элементами одномерных массивов Y( ),Y1( ) и D( ), кото-
Дифференциальные уравнения
233
рые описаны в строке 100. Главное отличие от программы «ДУ-
ЭЙЛЕР1», которая решает одно дифференциальное уравнение, со-
стоит в том, что простые переменные (Y, Y1 и D) стали перемен-
ными с индексами.
В подпрограмме 10000, вычисляющей правые части дифференци-
альных уравнений, используются индексированные переменные D(I)
и Y(I). В этой подпрограмме для данной конкретной задачи вычис-
ляются две правые части двух дифференциальных уравнений и по-
лученные значения присваиваются переменным D(l) и D(2) соот-
ветственно.
В основной программе после описания массивов переменной N
присваивается значение 2 и тем самым задается размерность систе-
мы дифференциальных уравнений. Вместо одного начального усло-
вия теперь вводится N начальных условий, по одному для каждого
дифференциального уравнения системы. Это осуществляется в
строках 300—600. Еще одно отличие в основной программе касает-
ся вывода данных, поскольку для системы уравнений надо выво-
дить не одно, a N значений (строки 1400—1440).
В подпрограмме 5000, реализующей алгоритм Эйлера, в отли-
чие от аналогичной подпрограммы в программе «ДУ-ЭЙЛЕР1»
операторы присваивания значений и арифметических выражений
простым переменным (строки 5100 и 5400) заменены циклами
FOR—NEXT, в которых значения и арифметические выражения
присваиваются индексированным переменным; так, в строке 5100
вместо
«ДУ-ЭЙЛЕР1» 5100 Y = Y1
стоит
«СИСТ-ЭЙЛЕР» 5100 FOR I = 1 ТО N:Y(I) = Y1(I):NEXT I
и в строке 5400 вместо
«ДУ-ЭЙЛЕР1» 5400 Y = Y + D*H
стоит
«СИСТ-ЭЙЛЕР» 5400 FOR I = 1 ТО N:Y(I) =
Y(I) + D(I)*H:NEXT I
Чтобы решить систему дифференциальных уравнений, отличаю-
щуюся от системы, решенной в приведенном вместе с программой
примере, надо в строке 200 задать другое значение N и в подпро-
грамме 10000 элементам массива D( ) присвоить арифметические
выражения, соответствующие правым частям дифференциальных
уравнений.
234
Глава 9
Задание 130. В программе «СИСТ-ЭЙЛЕР», так же как и в программе «ДУ-
ЭЙЛЕР1», не предусмотрено прекращения итерационной процедуры по критерию
сходимости решения. Дополните программу «СИСТ-ЭЙЛЕР» проверкой результата
на устойчивость и измените вывод данных так, чтобы промежуточные результаты
выводились на экран только по желанию пользователя.
Задание 131. Дан следующий механизм сложной реакции (буквами обозначены
различные химические соединения, числа над стрелками — это константы скорости):
1
А - М + М
10
А + М - В + С
4
С - М + D
20
М + М - Е
Кинетика этой реакции описывается системой дифференциальных уравнений:
[А]' = -[А] - 10-[А] -[М]
[М]' = 2-[А] - 10- [А]-[М] + 4-[С] - 40 [М] [М]
[В]- = 10-[А] -[М]
[С]' = 10-[А] [М] - 4- [С]
[D]' = 4- [С]
[Е]' = 20 [М]- [М]
Заменим в этой системе дифференциальных уравнений буквы индексированными
переменными:
[А]' - D(l), [A] - Y(l)
[М]' - D(2), [M] - Y(2)
[В]' - D(3), [B] - Y(3)
[СГ - D(4), [C] - Y(4)
[D]- - D(5), [D] - Y(5)
[Е]'' - D(6), [E] - Y(6)
Тогда система дифференциальных уравнений получится в том виде, в каком она за-
писывается в подпрограмме 10000 программы «СИСТ-ЭЙЛЕР»:
D(l) = — Y(l) - 10 Y(l) Y(2)
D(2) = 2-Y(l) - 10-Y(l)-Y(2) + 4 Y(4) - 40-Y(2) Y(2)
D(3) = 10Y(l)-Y(2)
D(4) = 10Y(l)Y(2) - 4-Y(4)
D(5) = 4Y(4)
D(6) = 20-Y(2)-Y(2)
Попытайтесь самостоятельно составить систему дифференциальных уравнений,
исходя из механизма реакции, и с помощью программы «СИСТ-ЭЙЛЕР» рассчитай-
те кинетические кривые расходования вещества А и накопления продуктов реакции
В, D и Е. (Эта система решается значительно точнее и быстрее с помощью програм-
мы «СИСТ-РКН», которая будет рассмотрена ниже.)
Задание 132. Дана уже знакомая по предыдущим примерам реакция разложения
а-го порядка:
. ... , -Ea/RT -
dc/dz = — kg-e -с
Дифференциальные уравнения
235
Тепловой эффект реакции равен Н. Реактор помещен в термостат с температу-
рой Ть. Количество тепла, передаваемое от реактора к термостату, пропорциональ-
но (Т — Ть). Зависимость температуры в реакторе от времени можно описать следу-
ющим дифференциальным уравнением:
dT/dZ = H (k0-e~Ea'RT ca) + D-(Tb - Т)
Величина Н пропорциональна энтальпии реакции; D — коэффициент теплопередачи
через стенку реактора.
Составьте программу для решения соответствующей системы дифференциаль-
ных уравнений и найдите зависимость с от времени при заданных значениях пара-
метров Tb,k0,Ea,H,D на при начальном условии (t = 0)с = сд, Т = TQ. (Обрати-
те внимание, что в случае сильноэкзотермической реакции и малого отвода тепла
при выполнении программы могут встретиться трудности, связанные с приближен-
ным характером численного метода, например отрицательные концентрации в про-
межуточных результатах, неустойчивость решения, неправдоподобно большие зна-
чения температуры и многое другое.) При достаточно малом шаге интегрирования,
т. е. если отрезок, ограниченный начальным и конечным значениями аргумента, раз-
делить на очень большое число частичных отрезков, эти трудности устраняются и
ЭВМ выдает вполне разумные результаты.
9.5. Метод Рунге — Кутта для систем
дифференциальных уравнений
Программа «СИСТ-РКН» точно так же представляет собой рас-
ширенную программу «Р-К-Н» как программа «СИСТ-ЭЙЛЕР» яв-
ляется модификацией программы «ДУ-ЭЙЛЕР1». Ниже приводят-
ся распечатка программы «СИСТ-РКН» и решения той же самой
системы из двух дифференциальных уравнений, которая была реше-
на с помощью программы «СИСТ-ЭЙЛЕР».
В КЕМ "СИСТ-РКН" EBERT/EDERER 610620
1 КЕМ*************************************** **
2 КЕМ** РЕШЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ **
3 КЕМ** УРАВНЕНИЙ МЕТОДОМ РУНГЕ-КУТТА- ♦♦
4 КЕМ** НИСТРЕМА DY /DX=F (X, У ) **
5 КЕМ** ВЕКТОРЫ F ИУ ОПИСАНЫ В **
6 КЕМ** ПОДПРОГРАММЕ 10000 **
9 КЕМ******************************************
100 DIM Y<20>,Y1<20>,D<20>,Y9<20>
120 DIM К1<20>,К2<20>,КЗ<20>,К4<20>
260 N-2|REM ЧИСЛО ДИФ. УРАВНЕНИЙ В СИСТЕМЕ
300 FOR I-l ТО N
400 PRINT "НАЧАЛЬНОЕ ЗНАЧЕНИЕ У I ; = ";
500 INPUT Y1<I>
600 NEXT I
700 INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ"; А, Е
1000 N1-4
1100 H-<E-A>/N1
1200 OOSUB 5000
1300 PRINT N11TAB<7>> "ЧАСТИЧНЫХ ИНТЕРВАЛОВ"
1400 FOR I-l TO N
1420 PRINT "VC"ill”> » "»YCI>
1440 NEXT I
1500 N1-N1*2
1600 GOTO 1100
236
Глава 9
5000 REM****************************** *************
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ **
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ••
5010 REM*******************************************
5100 FOR 1-1 ТО NsYCI>-yiCI>iNEXT I
5200 FOR 19=0 TO Nl-1sX-R+I9*H
5300 X9-XsF0R 1-1 TO N sY9< Г.>=У< I > sNEXT I
5320 GOSUB 10000
5340 FOR 1=1 TO NsK1CI>=H*D<I>«NEXT I
5400 X9=X+H/2sF0R 1-1 TO NsY9CI>-YCI>+К1CI>/2sNEXT I
5420 GOSUB 10000
5440 FOR 1=1 TO NsK2<I>=H#DCI>sNEXT I
5500 X9=X+H/2:F0R 1-1 TO NsY9CI>-YCI>+K2CI>/2sNEXT I
5520 GOSUB 10000
5540 FOR 1=1 TO NsK3CI>=H*D<I>sNEXT I
5600 X9=X+HsF0R 1 = 1 TO NsY9<I>=У<I>+K3<I>sNEXT I
5620 GOSUB 10000
5640 FOR 1=1 TO NsK4<I>=H#DCI>sNEXT I
5700 FOR 1=1 TO N
5720 YCI>=YCI>+CKl<I>+2*K2<I>+2*K3<I>+K4CI>>/6
5740 NEXT I
5800 NEXT I9SRETURN
10000 REM*************************************•«*••«••*
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ПРАВЫЕ ЧАСТИ ДИФФЕРЕНЦИ-**
10003 REM** АЛЬНЫХ УРАВНЕНИЙ DYI/D X =F1 (X.Y 1 YN) **
10004 REM** D (I) = F (X9.Y9 (1).Y9(N>) **
10010 REM**********************************************
10100 O< 1 >=-3*Y9<1>*V9C 1 :>+2*V9<2>+EXP'"-X9>
10200 DC2>—3*V9C1>*Y9<1>-12»V9<2>+EXP<-X9>
12000 RETURN
63999 ENO
RUN
НАЧАЛЬНОЕ ЗНАЧЕНИЕY (1) = ? 1
НАЧАЛЬНОЕ ЗНАЧЕНИЕУ (2) = ? 1
ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ? 0,1
4 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
УС 1 > = —1.66567203
УС 2 > = 5.69006504
8 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
VC 1 > - .528465604
УС 2 > - .109645126
16 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
УС 1 > = .528515129
УС 2 > .109563509
32 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
УС 1 > = .528515861
УС 2 > = .109560677
64 ЧАСТИЧНЫХ ИНТЕРВАЛОВ
УС 1 ) - .528515883
УС 2 > = .109560527
Если сравнить обе программы, реализующие метод Рунге —
Кутта, то станет видно, что в программе ссСИСТ-РКН» операторы
присваивания значений и арифметических выражений переменным
Y, Yl, Y9, D, KI, К2, КЗ и К4 заменены циклами FOR—NEXT, в
которых значения и арифметические выражения присваиваются со-
ответствующим индексированным переменным. Можно легко убе-
Дифференциальные уравнения
237
диться в том, что программа «СИСТ-РКН» считает значительно
точнее и быстрее, чем программа «СИСТ-ЭЙЛЕР». Уже после 8
итераций достигается более высокая точность, чем при использова-
нии программы «СИСТ-ЭЙЛЕР» после 128 операций.
Если эта программа используется для решения другой системы
дифференциальных уравнений, то надо указать количество уравне-
ний в системе, присвоив переменной N соответствующее значение
(строка 200), и в подпрограмме 10000 с помощью переменной Х9 и
индексированных переменных D( ) и Y9( ) описать правые части
дифференциальных уравнений.
Задание 133. Сравните точность и быстродействие программ «СИСТ-РКН» и
«СИСТ-ЭЙЛЕР», решая одни и те же системы уравнений как по первой, так и по
второй программе.
Задание 134. Для того чтобы расширить область применения программы
«СИСТ-РКН» надо внести в программу два дополнения:
1) Надо использовать критерий сходимости решения для выхода из итерацион-
ной процедуры по достижении заданной точности результата. Промежуточные ре-
зультаты должны выводиться на экран только по указанию пользователя.
2) Надо предусмотреть возможность вычисления и вывода на экран 20 значений
у, соответствующих 20 равно отстоящим друг от друга значениямх. (Указание: нач-
ните итерационную процедуру сразу для 20 частичных интервалов, для чего в строке
1000 напишите N1 = 20. Кроме того, в строке 100 зарезервируйте место для разме-
щения элементов массива Е( ) размера 20 x 20, которым будут присваиваться ре-
зультаты вычислений (в действительности, понадобится массив размера N х 20, где
N — число уравнений в системе)). После первой итерации с 20 частичными интерва-
лами значения у, соответствующие значениям х на левой границе каждого интерва-
ла, присваиваются элементам массива Е( ). Для этого целесообразно вставить до-
полнительную строку 5760:
5760 FOR I = 1 ТО N: Е(1, 19 + 1) = Y(I): NEXT I
в которой элементам массива Е в цикле присваиваются вычисленные значения у. В
следующей итерации элементам массива Е( ) будут присваиваться значения у, соот-
ветствующие каждому второму частичному интервалу, в следующей — каждому
четвертому и т. д. Этот отбор значений у можно организовать в дополнительной
строке после строки 5740 с помощью оператора IF.
Задание 135. С помощью программ «СИСТ-РКН» можно решать не только си-
стемы дифференциальных уравнений первого порядка, но и системы дифференциаль-
ных уравнений высших порядков. Возьмем в качестве простого примера дифферен-
циальное уравнение второго порядка, решением которого является функция синус
или косинус:
У" = -У
Если ввести новые переменные Y1 и Y2 так, что Y1 = у' и Y2 = у, то это урав-
нение второго порядка можно представить в виде системы дифференциальных урав-
нений:
Yl' = -Y2
Y2' = Y1
238
Глава 9
Систему можно решить с помощью программы «СИСТ-РКН». Ее решением яв-
ляются значения у и у'.
Решите этим методом приведенное выше дифференциальное уравнение второго
порядка, а также следующее дифференциальное уравнение:
У" = -У
Сравните результаты численного и аналитического методов.
Решите дифференциальное уравнение, описывающее вынужденные колебания
(г — отклонение от положения равновесия):
т-х" + к-х' + D-x = K-cos(a-t)
Найдите для заданных значений параметровm,k,D и К такое значение частоты
а, при котором амплитуда колебаний максимальна.
Задание 136. Рассмотрим простую модель распространения эпидемий. Пусть
N — число жителей (прирост населения за счет рождаемости не учитывается), G —
число лиц, которые здоровы, но могут заболеть, I — число заболевших, Е — число
«выбывших», т. е. умерших, изолированных от остальных, а также выздоровевших,
здоровых и обладающих иммунитетом. Заболеваемость пропорциональна числу кон-
тактов между людьми групп G и/. Скорость, с которой лица «выбывают» из груп-
пы I, пропорциональна численности этой группы. Отсюда получается следующая си-
стема дифференциальных уравнений:
dG/dt = -a-GI
dl/dt = +a-G-I — b-I
dE/di = +b-I
Задайте значения параметров а и b, начальные значения G и I и рассчитайте динами-
ку заболеваемости. Проиллюстрируйте примерами известную в эпидемиологии тео-
рему о пороговом характере распространения эпидемий, т. е. покажите, что инфек-
ционное заболевание не перерастает в эпидемию, если выполняется условие
G < Ь/а
Задание 137. Есть несколько очень наглядных примеров из области динамики
популяций хищников и их жертв (например, песцы и лемминги, щуки и караси). Обо-
значим число (концентрацию) хищников и жертв буквами R и В соответственно.
Предположим, что жертвы располагают достаточным количеством корма.. Тогда,
если бы не было хищников, то прирост травоядных был бы пропорционален числен-
ности имеющейся на данный момент популяции:
dB/dt = кВ
При наличии хищников число съедаемых ими травоядных пропорционально числу
контактов между обоими видами животных. Из этих соображений можно составить
дифференциальное уравнение для изменения численности травоядных:
dB/dt = кВ - r-B-R
Если смертность среди хищников носит естественный характер, то она пропор-
циональна числу хищников: -S-R. Увеличение популяции хищников пропорцио-
нально их числу и количеству пищи (т. е. численности травоядных): 1-B-R. Отсюда
дифференциальное уравнение, описывающее динамику популяции хищников, имеет
вид
dR/dt = —s-R + l-B-R
Дифференциальные уравнения
239
Покажите, что при определенных значениях параметров к, г, s и / численности
обеих популяций колеблются.
Если использовать эту модель для описания динамики популяций хищных и рас-
тительноядных рыб, предположив, одиако, что численность обоих видов рыб допол-
нительно уменьшается в результате промысла, то получится следующая система
дифференциальных уравнений:
dB/dZ = кВ - r-B-R - f -B
AR/At = -s-R + l-B R - f-R
Покажите, что уловы (квоты), которые меньше, чем параметр прироста к рас-
тительноядных рыб В, увеличивают среднюю долю растительноядных и уменьшают
долю хищных рыб. Таким образом, если бы рыбу вообще не ловили, то относитель-
ная численность растительноядных рыб, большинство видов которых относятся к
промысловым, уменьшилась бы, а хищных — возросла (принцип Вольтерра).
Задание 138. Дан реактор идеального смешения с непрерывной подпиткой реа-
гентами и отбором продуктов, в котором протекает химическая реакция А — В. Из-
вестны порядок этой реакции и ее тепловой эффект. Тогда изменение концентрации
вещества А и температуры в реакторе описывается следующей системой дифферен-
циальных уравнений:
d[A]/dz = -k0-e~E°/RT- [А]" + ([А]е - [А])<7
dT/dZ = H-k0-e~E°/RT [A]n + ([А1е - [А])-и + w-(Tw - Т)
В обоих дифференциальных уравнениях первые слагаемые аналогичны, они об-
условлены химической реакцией. Вторые слагаемые учитывают материальные пото-
ки, входящие и выходящие из реактора. Третье слагаемое во втором уравнении со-
ответствует теплопередаче через стенку реактора.
Найдите зависимость выхода реакции и температуры от времени. Рассчитайте
стационарную концентрацию вещества А и стационарную температуру при различ-
ных начальных значениях параметров.
При каких условиях имеется только одно стационарное состояние и при каких
условиях существует несколько различных стационарных состояний (multipe steady
states)?
Задание 139. Рассмотрим кинетическую схему OREGONATOR, предложенную
Филдом и Нойесом* для описания кинетики колебательных реакций:
А + Y - X (1)
X + Y - Р (2)
В + X - 2Х + Z (3)
X + X - Q (4)
Z-/Y (0,5 </< 2,4) (5)
Вещества А и В расходуются, Р и Q накапливаются. В определенных условиях,
зависящих от кинетических параметров, концентрации веществ X, Y и Z могут коле-
баться.
Составьте дифференциальные уравнения для концентраций всех веществ, участ-
вующих в этой реакции, и, выбрав определенные значения констант скорости и сте-
хиометрического коэффициента /, рассчитайте ход кинетических кривых. Попытай-
тесь найти такие значения параметров, при которых в системе начнутся колебания
Field R. J., Noyes R. М., Асе. Chem. Res., 10, 221 (1977).
240
Глава 9
концентрации веществ X, Y и Z. (Если вы столкнетесь с трудностями, то обратитесь
к указанной в этом разделе литературе.)
Напишите систему дифференциальных уравнений для приведенной выше схемы,
если реакция протекает не в статическом, а в проточном реакторе идеального сме-
щения; рассчитайте кинетические кривые и сопоставьте их с кинетическими кривы-
ми, полученными для статического реактора.
Остановимся вкратце на одной из трудностей, которая часто встречается при
кинетическом описании сложных реакций. В принципе, исходя из механизма реак-
ции, который представляет собой последовательность элементарных стадий, не
трудно написать систему дифференциальных уравнений. Если механизм реакции
очень сложен, эту работу можно поручить ЭВМ (гл. 12).
Если попытаться решить такую систему дифференциальных уравнений с по-
мощью обычной программы для решения системы дифференциальных уравнений, то
может оказаться, что либо концентрации веществ практически не изменяются (т. е.
реакция не идет), либо результаты вообще не имеют физического смысла (например,
отрицательные концентрации). Стандартные программы приводят к ложным ре-
зультатам главным образом потому, что константы скорости реакций, входящих в
кинетическую схему, различаются по величине на несколько порядков. Такие систе-
мы дифференциальных уравнений называют «жесткими». Для их решения надо ис-
пользовать специальные программы (“Solver”)*. Элементарное введение в моделиро-
вание кинетики сложных химических реакций можно найти в литературе**.
Задание 140. При описании кинетики процессов растворения лекарственного пре-
парата в определенном объеме жидкости различают твердое, еще не растворившееся
вещество F и уже растворенное вещество L. При этом исходят из следующих упро-
щений: 1) Скорость, с которой расходуется растворенное вещество, пропорциональ-
на количеству растворенного вещества. (Это соответствует кинетическому уравне-
нию первого порядка, однако порядок может иметь и другие значения.) 2) Скорость
растворения вещества F пропорциональна величине F". (Если препарат вводится в
виде таблетки сферической формы, то разумно принять а = 2/3.) 3) Кроме того,
скорость растворения пропорциональна разности (Emax — L), где Етах — раствори-
мость препарата в данной жидкости.
Этой модели соответствует система дифференциальных уравнений
dF/d/ = -^•F“-(Emax - L)
dL/di = +Ar,-F“-(Emax - L) - ka-L"
Рассчитайте кинетику расходования лекарственного препарата при следующих
значениях параметров: а = 2/3, к{ = 1, Етах = 0,8, п = 1, ка = 0,1. Начальные ус-
* Рекомендуем читателям лучшие на сегодняшний день программы, которые
можно использовать и для моделирования кинетики химических реакций: Deuflhard
Р„ Bader G., Novak U., LARKIN — A software package for the numerical simulation of
LARge systems arising in chemical reaction KI-Netics, Proceedings of the Workshop on
Modelling of Chemical Reaction Systems, Springer Series in Chemical Physics (ed:
К. H. Ebert, P. Deuflhard, W. Jager), 18, 38 (1981); Deuflhard P., Bader G., Novak U.,
An advanced simulation package for large chemical reaction systems, in: Stiff computation
(ed. Aiken). Oxford University Press, 1983; Gear C. W., Numerical initial value problems
in ordinary differential equations. Prentice Hall, New Jersey, 1971; Gear C. W., Shampine
L. E, SIAM Rev., 21, 1 (1979).
** См., например, Ebert К. H., Ederer H. J., Isbarn G., Angew. Chem. Int. Ed.
Eng., 19, 333 (1980).
Дифференциальные уравнения
241
ловия (I = 0): F = 1 и L = 0. В рамках этой простой модели при больших значени-
ях t концентрация F может оказаться отрицательной величиной. Эти значения F
надо просто отбросить, используя для этого оператор IF, н заменить нх на нулевые.
9.6. Краевая задача
До сих пор в этой главе рассматривались только такие задачи, в
которых известны начальные значения величин yt (Xq). Если извест-
ны не все начальные значения у, но зато известны значения у при
одном или нескольких значениях х, то этот тип задач относится к
краевым задачам.
В качестве математического примера приведем следующее диф-
ференциальное уравнение:
у" = х — у
с двумя краевыми условиями: у(0) = 0 и у(1) = 2.
В качестве примера из химической кинетики рассмотрим меха-
низм химической реакции. Даны кинетическая схема и значения
констант скорости:
А - В к{ = 0,1
А + В — Продукты к 2 = 0,1
Дифференциальные уравнения для концентраций веществ А и В
имеют вид
d[A]/df = —0,1- [А] - 0,1-[А]-[В]
d[B]/dr = 0,1-[А] - 0,1-[А]-[В]
Будем рассматривать все концентрации и константы скорости
как безразмерные величины, тогда вопрос можно сформулировать
следующим образом: как выглядят кинетические кривые для ве-
ществ А и В, если выполняются условия [А] = 0 при t = 0 и
[А] = 0,75 при t = 1? Чтобы выполнялось второе краевое условие
(первым краевым условием является начальное значение концентра-
ции вещества А), начальная концентрация вещества В должна
иметь строго определенное значение.
Если рассматривать эту систему как задачу с полностью извест-
ными начальными условиями и решать ее с помощью программы
«СИСТ-РКН», то при различных начальных значениях концентра-
ции вещества В получатся следующие результаты:
[А](Г = 0) [B](Z = 0) [A](Z = 1) [B](Z = 1)
1,0 0,0 0,90061 0,09064
1,0 5,0 0,55774 4,70887
16-81
242
Гпава 9
Следовательно, начальное значение концентрации В, которое
удовлетворяет заданному при постановке задачи условию
[А](Г = 1) = 0,75, должно лежать между 0 и 5: [А](Г = 0) [В](/ = 0) [А](Г = 1) [В](/ = 1) 1,0 2,5 0,70929 2,37839 1,0 1,25 0,79941 1,22858 и т. д. Таким образом, чтобы полностью найти начальные условия,
надо задать (хотя бы произвольно) значение концентрации вещест-
ва В, найти решение системы дифференциальных уравнений, срав-
нить полученное значение концентрации вещества А в момент вре-
мени t = 1 и выбрать новое, «улучшенное» начальное значение кон-
центрации вещества В. Поскольку этот алгоритм похож на стрель-
бу по мишени, то его еще называют «методом стрельбы» (англ,
shooting).
Этот метод проб и ошибок (англ, per trial and error) можно ис-
пользовать вместе с обычными программами для решения систем
дифференциальных уравнений (см. выше). Однако его надо сначала
«перевести» на алгоритмический язык, как это сделано для данного
примера в программе «КРА-КИН».
0 REM "КРА-КИН" EBERT.'EDERER 810620
1 REM*********************************
2 REM** КИНЕТИКА СЛОЖНОЙ ХИМИНЕС- *#
3 REM** КОЙ РЕАКЦИИ РЕШЕНИЕ КРАЕВОЙ**
4 REM** ЗАДАЧИ С ПОМОЩЬЮ ПРОГРАММ **
5 REM** "СИСТ-РКН" И "ПОП-ДЕЛ” **
9 REM*********************************
100 DIM V<20>,V1<20>,D<20>
120 DIM Kl<20>,K2<20>,K3<20>,K4<20>
200 N=2:REM ЧИСЛО ДИФ. УРАВНЕНИЙ В СИСТЕМЕ
300 Vl < 1 > = 1 |R«0|E=1
400 VR=0:VE=5
500 VS=0.75:REM ПУСТЬ В ТОЧКЕ E У ИМЕЕТ ЗНАЧЕНИЕ Y (1)
1000 Nl = 16
1100 H=<E-R>/N1
1200 Vl <2>=VR :GOSUB 5000 sFl=V< 1 > :GOSUB 6000
1300 Vl<2j=VEsGOSUB 5000|F9=V<1>«GOSUB 6000
1350 IF SGN<F1-VS>=SGN<F9-VS> THEN GOTO 7000
1400 VM=<VR+VE>/2IV1<2>=VM(GOSUB 5000iFM=V<1>:GOSUB 6000
1420 IF SGN<F1-VS>OSGN<FM-VS> THEN GOTO 1460
1440 VR=VMiFl=FMsGOTO 1400
1460 VE=VM:F2=FM:GOTO 1400
1600 GOTO 1100
5000 REM********************************************
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ **
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ *«
5010 REM********************************************
5100 FOR 1=1 ТО NsV<I>=V1<I>iNEXT I
5200 FOR 19=0 TO Nl-1:X=R+I9*N
5300 X9=X:FOR 1=1 TO N>V9<I>=V<I>:NEXT I
5320 GOSUB 10000
5340 FOR 1=1 TO NiKl<I>=H*D<I>(NEXT I
5400 X9=X+H/2iF0R 1=1 TO NiV9<I>=V<I>+К1<I>/2:NEXT I
Дифференциальные уравнения
243
5420 GOSUB 10000
5440 FOR I-l TO N|K2<I>-H*D<I>INEXT I
5500 ХЭ-X+H/2iF0R 1=1 TO Ni?9<I>=?<I>+K2<I>/2iNEXT I
5520 OOSUB 10000
5540 FOR I-l TO NiK3<I>-H*D<I>iNEXT I
5600 X9-X+HiFOR 1 = 1 TO N |V9< I >-?.< I >+K3< I > iNEXT I
5620 GOSUB 10000
5640 FOR I-l TO NiK4<I>=H«0<I>iNEXT I
5700 FOR I-l TO N
5720 V<I>-V<I>+<Kl<I>+2«K2<I>+2*K3<I>+K4<I> >/6
5740 NEXT I
5000 NEXT I9lRETURN
6000 REM**************************************
6001 REM**ВЫВОД ПРОМЕЖУТОЧНЫХ РЕЗУЛЬТАТОВ*»
6602 REM**************************************
6100 PRINT "T -","V<1> - ’•fVlCOr' V<2> - ",Y1<2>
6200 PRINT "T -">E>"1 ","V<1> = “> V<1>,” V<2> - " > V<2>
6300 PRINT IRETURN
7000 PRINT “НАЧАЛЬНЫЙ ИНТЕРВАЛ ВЫБРАН НЕВЕРНО” iSTOP
10000 REM****M*****************************************
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ПРАВЫЕ ЧАСТИ ДИФФЕРЕНЦИ- ♦*
10003 REM** АЛЬНЫХ УРАВНЕНИЙ DY I / DX = F1 (Х,У 1, ...У N) **
10004 REM** D (l)= F (Х9,У9 (1).У9 (N)) ««
10010 REM***********************************************
10100 0<1>— 0. 1*У9<1>-0. 1*79<1>*79<2>
10200 О<2>-+0.1*У9<1>-0.1*79<1>*У9<2>
12000 RETURN
63999 ENO
RUN
Т т I е । 1 । 7(1) ¥( 1) 1 У<2> - .900610129 0 7(2) » .0906411878
т 0 I 7(1) 1 У<2> - 5
т 1 1 7(1) .557744932 7(2) « 4.70887595
т 0 1 7(1) 1 У<2> = 2.5
т 1 1 7(1) .709292888 7(2) 2.37839033
т 0 1 7(1) 1 У<2> = 1.25
т 1 1 7(1) .799416623 7(2) - 1.22857В56
т 0 1 7(1) 1 У<2> - 1.875
т 1 1 7<1) .753045894 7(2) - 1.80207913
т I 0 1 7(1) 1 У<2> - 2.1875
т 1 1 7(1) .730851136 7(2) - 2.08989286
т 0 1 7(1) 1 У<2> - 2.03125
т 1 1 V(l> о .741867848 7(2) « 1.94589936
т 0 1 VC1) 1 У<2> = 1.953125
т 1 1 7(1) .747436566 7(2) - 1.87396744
т 0 1 7(1) 1 У<2> - 1.9140625
т 1 1 V(l) .750236136 7(2) « 1.83801782
т 0 1 7(1) 1 У<2> - 1.93359375
т 1 1 7(1) .74883508 У<2> - 1.85599126
т 0 1 7(1) 1 У<2> - 1.92382813
т 1 1 7(1) .74953529 У<2> - 1.8470042
16«
244
Гпава 9
т ж 0 : 7<1> а 1 72) = 1.91894531
т - 1 : V < 1 > .749885633 7<2> » 1.84251092
т * G : Y< 1 > 1 7<2> - 1.91650391
т = 1 : = .750060865 Y<2> = 1.84026435
т Ж 0 : 1 > = 1 7<2> = 1.91772461
т = 1 1 Y-: 1 > = .749973244 7<2> « 1.84138763
т = О : Y < 1 .> к 1 7<2.> » 1.91711426
т = 1 : 1 > = .750017053 7<2> = 1.84082599
т 0 : ?< 1 1 - 1 7<2> = 1.91741943
т = 1 : 7-: 1 / — .749995149 7<2> = 1.84110681
Программа «КРА-КИН» представляет собой модифицирован-
ную программу «СИСТ-РКН». Изменена лишь основная програм-
ма и в подпрограмме 10000 записаны соответствующие дифферен-
циальные уравнения.
Начальное значение концентрации вещества A[Y1](1)], которое
равно 1, начальное и конечное значение времени (переменные А и
Е) заданы непосредственно в программе (строка 300). В строке 400
вводятся граничные значения YA и YE, между которыми проводит-
ся поиск начального значения концентрации вещества B[Y1(2)]. Гра-
ницы поиска устанавливают или подбором, или исходя из каких-ли-
бо соображений. В строке 500 задано второе краевое условие
YS = 0,75; это значение должна иметь переменная Y(l) в момент
времени t = 1. Число частичных интервалов (N1), как и область
поиска второго начального условия, устанавливается подбором. В
данном случае оказывается, что при N1 = 16 решение имеет семь
верных значащих цифр, поэтому в строке 1000 переменной N1 при-
сваивается значение 16.
В строках 1200—1600 выполняется процедура, которая построе-
на аналогично рассмотренной выше программе «ПОЛ-ДЕЛ». В
строках 1200 и 1300 рассчитываются значения В в момент времени
t = 1 для обоих граничных значений YA и YE. Результаты присва-
иваются переменным F1 и F2 соответственно и выводятся на экран.
Для этого переменной Yl(2) присваивается начальное значение ин-
тервала и оператор GOSUB 5000 вызывает процедуру Рунге — Кут-
та. Оператор GOSUB 6000 вызывает подпрограмму для вывода на
экран результата данной итерации. Подпрограмма 6000 для вывода
промежуточных результатов является также модификацией исход-
ной программы «СИСТ-РКН».
Если в основной программе замкнутый интервал [YA, YE] выб-
ран неправильно, т. е. искомое начальное значение концентрации
вещества B[Y(2)] не принадлежит этому интервалу, то обе разности
между рассчитанными краевыми значениями Y(l) и заданным крае-
вым значением Y имеют одинаковые знаки. Это проверяется в
Дифференциальные уравнения
245
строке 1350, и если знаки одинаковы, то управление передается
строке 7000 и на экран выводится соответствующее сообщение.
В строке 1400 вычисляется середина интервала, потом для оче-
редной попытки («выстрела») вызывается подпрограмма 5000. По-
лученный результат присваивается переменной FM и подпрограм-
мой 6000 выводится на экран.
В строке 1420 проверяется, меняется ли в двух последователь-
ных попытках знак разности между рассчитанным и заданным кра-
евыми значениями. Если обе разности имеют одинаковый знак, то
середина интервала принимается за начало нового интервала [YM,
YE], на котором будет продолжен поиск второго начального значе-
ния. Если разности имеют противоположные знаки, то середину
интервала будем считать концом нового интервала [YA, YE], В со-
ответствии с этим принимается YA = YM или YE = YM. В любом
случае новый интервал, на котором продолжается поиск, уменьша-
ется в два раза. В зависимости от того, какая половина интервала
оставлена для продолжения итерационной процедуры, рассчитан-
ное значение FM присваивается переменной F1 или F2. Затем управ-
ление передается строке 1400, с которой начинается очередная ите-
рация.
Поскольку процедура поиска начального значения представляет
собой бесконечный цикл, пользователь, анализируя выводимую на
экран информацию, должен решить, когда будет достигнута требу-
емая точность результата. Как организовать выход из бесконечной
итерационной процедуры программными средствами, не раз рас-
сматривалось в предыдущих программах и заданиях.
В нашем примере уже после 10 итераций результат имеет четы-
ре верные значащие цифры. Начальное значение концентрации ве-
щества В, которое удовлетворяет указанным выше краевым усло-
виям, составляет 1,916.
Задание 141. Усовершенствуйте программу «КРА-КИН», предусмотрев в ней:
а) автоматический поиск подходящего начального интервала [YA, YE]; б) автомати-
ческое определение числа частичных интервалов N1 для подпрограммы Рунге —
Кутта и в) автоматический выход из итерационной процедуры, когда достигнутая
точность соответствует вашим требованиям.
Задание 142. Даны приведенная в начале этого раздела схема реакции и соот-
ветствующая ей система дифференциальных уравнений. Изменим только постановку
задачи. Спрашивается, каковы начальные значения концентраций веществ А и В в
момент времени 1 = 0, если в момент времени t = 2 А = 1,1 ив момент времени
t = 4 А = 0,7. В форме таблицы задание выглядит следующим образом:
t = 0 t = 2 t = 4
А В ? 1,1 0,7 2 г3 '4
246
Глава 9
Указание: вычислите сначала, как и в программе «КРА-КИН», значения В при
t = 2 и t = 4, рассматривая t = 2 как начальный момент времени и принимая в ка-
честве второго краевого условия t = 4, А = 0,7. Таким образом, с помощью про-
граммы «КРА-КИН» вы получите значения ?3 и ?4.
Значения ?, и ?2 можно рассчитать по программе «СИСТ-РКН», если в качестве
начального условия использовать I = 2, А = 1,1 и вычисленное значение ?3 и прове-
сти интегрирование системы дифференциальных уравнений с отрицательным шагом.
Это произойдет автоматически, если на запрос оператора INPUT ответить так:
ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ? 2,0
Таким образом, вы найдете концентрации вещества А и В в момент времени t = 0.
Задание 143. Решите следующую краевую задачу. Дано дифференциальное урав-
нение второго порядка:
у" - (у')2 + х2 - у = О
Напоминаем, что это дифференциальное уравнение второго порядка можно пре-
образовать в систему двух дифференциальных уравнений первого порядка. Если обо-
значить у' = z, то получится
У' = Z
Z' = z2 - х2 + у
Постройте график функции у = /(х) от х = 0 до х = 1, если Ух=0 = 1 и
Ух=1 = 0,5. Для решения этой задачи надо найти неизвестное пока значение Ух=0
(или в полученной системе уравнений значение zx=0; для поиска возьмите интервал
(—3, 0]). Если вы определите начальное значение?, то, зная начальные значения у и
Z, с помощью программы «СИСТ-РКН» вы сможете рассчитать значения у и? при
различных значениях х на отрезке [0, 1] и построить график функции у = fix).
Задание 144. Балка обеими концами опирается на неподвижные основания. Кон-
цы балки соответствуют координатам* = 0 их = 1. Прогиб балки обозначим у.
Прогиб нагруженной посередине балки в рамках теории упругой деформации можно
описать следующим дифференциальным уравнением с безразмерными переменными
и параметрами:
d^y/dx2 = —а-(1 - 2-lx — 0,51) + b-y
Полагая a = 0,1 и b = 5,0, рассчитайте прогибу как функцию* между точками
х = 0 и х = 1.
9.7. Гармонический осциллятор —
задача на собственные значения
Одномерное стационарное уравнение Шредингера является диф-
ференциальным уравнением второго порядка не в частных, а в пол-
ных производных. Применительно к двухатомной молекуле оно
имеет вид
= -[Е -
й2
W — волновая функция (неизвестная); Е — полная энергия (неизвестная), собствен-
ное значение; h — постоянная Планка; д — приведенная масса двухатомной молеку-
лы; х — расстояние между атомами; И(х) — потенциальная энергия, зависящая от
расстояния между атомами.
Дифференциальные уравнения
247
Необходимо найти также значения полной энергии Е (собствен-
ные значения), при которых решением дифференциального уравне-
ния будет волновая функция, удовлетворяющая определенным тре-
бованиям, вытекающим из физического содержания задачи. По-
скольку квадрат волновой функции пропорционален вероятности
реализации данного состояния системы, разумно потребовать, что-
бы волновая функция при очень больших значениях х стремилась к
нулю.
Чтобы решить эту задачу с помощью программы
«СИСТ-РКН», надо, как и в предыдущем примере, преобразовать
это дифференциальное уравнение второго порядка в систему из
двух уравнений первого порядка. По уже опробованной схеме вве-
дем вспомогательную переменную U, которая является произво-
дной от W. Тогда система дифференциальных уравнений имеет вид
W' = U
U' = -[£ -
Коэффициент f тот же, что и в исходном уравнении. В прибли-
жении гармонического осциллятора уравнение для К(г) можно за-
писать как
к
V (*) = « • (v - х)2
2 s
к = р- (2ят)2
v — частота колебаний осциллятора.
Найти ответ на задание можно с помощью программы
«ГАРМ», в которой для решения системы дифференциальных урав-
нений использована процедура Рунге — Кутта.
0 REM "ГАРМ" EBERT/EDERER 810620
1 RE1M******!******************************
2 REM** РЕШЕНИЕ ЗАДАЧИ НА СОБСТВЕННЫЕ **
3 REM** ЗНАЧЕНИЯ МЕТОДОМ РУНГЕ-КУТТА-**
4 REM** НИСТРЕМА. РЕШЕНИЕ ОДНОМЕРНОГО «*
5 REM** УРАВНЕНИЯ ШРЕДИНГЕРА ДЛЯ ГАР- **
6 REM** МОНИЧЕСКОГО ОСЦИЛЛЯТОРА.ИЩЕТ-**
7 REM** СЯ ЗНАЧЕНИЕ ЭНЕРГИИ И СООТВЕТ- **
8 REM*# СТВУЮЩАЯ ЕМУ ВОЛНОВАЯ ФУНКЦИЯ**
9 REM************************************
100 DIM V<20>,V1<20>,D<20>
120 DIM К1<20>,К2<20>,КЗ<20>,К4<20>
123 NL-6.022E23
125 DG-7. 6064Е-12 sREM ГЛУБИНА ПОТЕНЦИАЛЬНОЙ ЯМЫ ДЛЯ Н2, В ЭРГ
130 MV-0. 504/NL :REM ПРИВЕДЕННАЯ МАССА Н2
135 RG-0.7412Е-8 iREM РАВНОВЕСНОЕ МЕЖЪЯДЕРНОЕ РАССТОЯНИЕ, В СМ
140 ЯЯ-<2« 3.1415>Т2«1.3192Е+14*МУ*1.31Э2Е14/2
145 НН—6.626176Е-27sREM ПОСТОЯННАЯ ПЛАНКА, В ЭРГ/ГЦ
195 DEF FNV<R>=AR«<R-RG>*<R-RG>
200 N=2iREM ЧИСЛО ДИФ. УРАВНЕНИЙ В СИСТЕМЕ
300 PRINT "ЗНАЧЕНИЕ ВОЛНОВОЙ ФУНКЦИИ НА РАВНОВЕСНОМ РАССТОЯНИИ";
310 INPUT V1<1>
248
Гпава 9
400 PRINT "ПРОИЗВОДНАЯ ВОЛНОВОЙ ФУНКЦИИ НА РАВНОВЕСНОМ РАССТОЯНИИ";
410 INPUT Vl<2>
500 INPUT "ПОЛНАЯ ЭНЕРГИЯ В ЭРГАХ"; EG :REM ДЕЛЬТА (ЕОДЛЯ Н2 ОКОЛО 1Е-12
600 R-RG(REM НАЧАЛЬНОЕ ЗНАЧЕНИЕ X
650 E=RG*5(REM КОНЕЧНОЕ ЗНАЧЕНИЕ X
1000 Н1=100
1100 H=<E-R>/H1
1200 GOSUB 5000
1600 STOP
5000 REM********************************************
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ **
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
5010 REM********************************************
5100 FOR I-l ТО NiV<I>-V1<I>(NEXT I
5200 FOR 19-0 TO Nl-1(X-R+I9«H
5300 X9-X1F0R I-l TO N:V9<I>=?<!>(NEXT I
5320 GOSUB 10000
5340 FOR I-l TO NiK1<I>=H*O<I>:NEXT I
5400 X9-X+H/2(F0R I-l TO NIV9<I>=V<I>+K1<I>/2(NEXT I
5420 GOSUB 10000
5440 FOR 1=1 TO N(K2<I>=H*D<I>(NEXT I
5500 X9-X+H/2IF0R 1=1 TO NiV9<I>=V<I>+K2<I>/2(NEXT I
5520 GOSUB 10000
5540 FOR 1=1 TO N(K3<I>=H#D<I>(NEXT I
5600 X9=X+H(F0R I-l TO N|V9<I>-V<I>+K3<I>(NEXT I
5620 GOSUB 10000
5640 FOR I-l TO NlK4<I>=H«D<I>(NEXT I
5700 FOR 1=1 TO N
5720 I>-V<I>+<К1<I>+2*K2<I>+2«K3<I>+K4<I>>/6
5740 NEXT I
5770 GOSUB 6000 iREM ВЫВОД ПРОМЕЖУТОЧНЫХ РЕЗУЛЬТАТОВ
5800 NEXT 19(RETURN
6000 REM****************************************
6050 REM»# ВЫВОД ЗНАЧЕНИЯ ВОЛНОВОЙ ФУНКЦИИ •
6100 REM***********************************««««*
6200 PRINT "PSI<”>X,"> - " ,(V< 1 '> ,EG,V<2>
6300 RETURN
10000 REM*********************************************
10002 REM«« ЗДЕСЬ ЗАДАЮТСЯ ПРАВЫЕ ЧАСТИ ДИФФЕРЕН- ♦♦
10003 REM*« ЦИАЛЬНЫХ УРАВНЕНИЙ DYI/DX= F1(X, Y1....YN)**
10004 REM«« D (l)= F (X9.Y9 (1).Y9 (N)) **
10010 REM*********************************************
10100 D<1>=Y9<2>
10200 D < 2 > =- < EG-FNV ' X9 > > *78. 952*MY/HH*Y9 < 1 > /НН
12000 RETURN
6399Э END
Два дифференциальных уравнения, полученные при преобразова-
нии уравнения Шредингера, заданы в подпрограмме 10000. Пере-
менная EG соответствует полной энергии системы, потенциальной
энергии соответствует определяемая функция FNV(X9) в строке
195.
В этой программе в качестве примера приведен расчет колеба-
ний молекулы водорода. Физические постоянные заданы в строках
123—145 в единицах системы СГС. Из них только для молекулы
водорода характерны параметры: приведенная масса (строка 130),
равновесное расстояние (строка 135) и частота в формуле для снло-
Дифференциальные уравнения
249
вой постоянной (строка 140). Для расчета колебаний других моле-
кул значения этих параметров надо каждый раз менять.
Поскольку для гармонического осциллятора потенциал V (г)
симметричен относительно положения равновесия, волновые функ-
ции могут быть только двух типов: симметричные, т. е. W' — 0 в
точке равновесия, и антисимметричные волновые функции, т. е.
W = 0 при равновесном расстоянии между ядрами.
Решение системы дифференциальных уравнений начинается при
равновесном расстоянии. Поэтому в строке 600 принимается
А = RG. Вполне достаточно, если наибольшее значение х будет в
пять раз больше равновесного расстояния (Е = RG*5). В строке
1000 задано число частичных интервалов для процедуры Рунге —
Кутта.
Чтобы решить эту систему дифференциальных уравнений, необ-
ходимо еще знать начальные значения — Yl(l) и Yl(2). Начальные
значения запрашиваются у пользователя в строках 300 и 400 с по-
мощью оператора INPUT. Введите 1 и 0, если вы хотите получить
симметричную волновую функцию, или 0 и 1, если — антисиммет-
ричную. (В данной задаче можно не учитывать постоянную норми-
ровки!) В строке 500 запрашивается значение полной энергии EG.
Затем подпрограмма 5000 рассчитывает значение волновой функции
при этом значении полной энергии, причем решение ищется в ин-
тервале межъядерных расстояний от RG до 5*RG с шагом инте-
грирования, равным 1/100 этого интервала. В строке 5770 подпро-
граммы 5000 вызывается подпрограмма для вывода на экран всех
промежуточных результатов.
Правильное значение полной энергии (собственное значение
уравнения Шредингера) определяется методом проб и ошибок. Сле-
дует отметить, что полная энергия молекул имеет величину поряд-
ка 10_ 12 эрг.
В качестве примера рассмотрим поиск нулевой энергии осциллятора. Если пред-
положить, что EG = 0,3-10-12, то волновая функция стремится к +«; при EG =
= 0,5-10“12 волновая функция стремится к — Процесс поиска можно представить
в виде следующей таблицы:
Y1(1 ) Y1 (2) Е.10'12 эрг Перепол- нение Расстояние, Ю‘*см
1 0 0,3 + гуу 1,90
1 0 0,5 “* СО 1,90
1 0 0,4 + ОО 1,93
1 0 0,45 “• ОО 1,93
1 0 0,43 ♦ ОО 1.93
1 0 0,44 — со 1,96
1 0 0,436 + ОО 1,96
1 0 0,438 “ *УУ 1,96
1 0 0,437 + ОО 1,99
250
Гпава 9
Нулевая энергия, таким образом, вычислена с точностью до трех значащих
цифр; если вы хотите узнать это значение точнее, то поиск можно продолжить.
Кроме того, для повышения точности можно увеличить число частичных интерва-
лов (строка 1000).
С помощью программы «ГАРМ» рассчитаны четыре первых собственных зна-
чения (см. табл.). Полученные результаты иллюстрируют известные положения, что
разность энергий соседних уровней постоянна и что нулевая энергия осциллятора со-
ставляет половину этой разности.
Симмет- рия Y1 (1) Y1(2) Полная энергия, 10‘“эрг
Симм. 1 0 0,43708
Антисимм. 0 1 1,31140
Симм. 1 0 2,18620
Антисимм. 0 1 3,06176
Поскольку программа «ГАРМ» позволяет рассчитать также за-
висимость значения волновой функции от смещения атомов от рав-
новесного положения, можно изобразить эту зависимость в виде
графика на миллиметровой бумаге. Однако следует иметь в виду,
что отклонение волновой функции от нуля при больших межъядер-
ных расстояниях связано с приближенным характером численного
метода решения уравнения Шредингера. При большой амплитуде
колебаний даже небольшое изменение энергии вызывает уход вол-
новой функции в +оо или —оо. При построении графиков эти зна-
чения лучше всего не учитывать и считать, что в этих точках вол-
новая функция имеет нулевое значение.
Задание 145. Найдите с помощью программы «ГАРМ» другие собственные зна-
чения полной энергии гармонического осциллятора. Определите энергию колебатель-
ных уровней в двухатомных молекулах по данным, приведенным в таблице.
Молекула Частота, 10'3 с"’ Равновесное расстояние, 10’3см Приведенная масса, а.ем.
Н2 1,31920 0,7412 0,5039
HD 1,14290 0,7412 0,6717
D2 0,93445 0,7412 1,00705
N2 0,70693 1,0940 7,00154
F2 0,27551 1,4090 9,49910
Задание 146. Попытайтесь автоматизировать поиск собственных значений, кото-
рый в программе «ГАРМ» проводится вручную (метод деления отрезка пополам).
Задание 147. Замените функцию, соответствующую гармоническому осциллято-
ру (строка 195), на потенциал ангармонического осциллятора. Используйте для это-
Дифференциальные уравнения
251
го потенциал Морзе
И(х) = De(l - е“~х*’2
De — глубина потенциальной ямы (для молекулы водорода De = 7,6064-10“12 эрг).
Параметр а в потенциале Морзе можно рассчитать по следующей формуле:
а = x-(2^/De)1/2
Поскольку потенциал в случае ангармонических колебаний больше не является
симметричным, волновые функции также нельзя больше рассматривать как точно
симметричные или антисимметричные.
Следовательно, надо найти не только подходящее значение полной энергии, но
и правильное начальное значение производной волновой функции, соответствующее
начальному значению волновой функции при равновесном расстоянии между ядра-
ми. Это влечет за собой значительное увеличение объема вычислений. Кроме того,
рекомендуем с самого начала проводить вычисления с более высокой точностью.
При поиске собственных значений энергии ангармонического осциллятора исполь-
зуйте в качестве начального приближения результаты, полученные для гармониче-
ского осциллятора.
9.8. Уравнения в частных производных
В качестве примера рассмотрим задачу о распределении темпе-
ратуры вдоль стержня (см рис.), которая решается с помощью вто-
рого закона Фурье:
dT/dt = с-д2Т/дх2
т=о°с
I
т=о°с
Т=100°С
I i I Н М I i П
Х1 х2 Х3 Х4 Х5 Х6 Х7 Хв' Х9 Х10 Х11
Пусть однородный стержень имеет длину 100 см. В момент вре-
мени t = 0 температура левого конца 0 °C, правого 100 °C и рас-
пределение температуры вдоль стержня описывается формулой
Tz=0(r) = х
Начиная с момента времени t = 0 на обоих торцах стержня под-
держивается температура Т = 0 °C.
Если стержень разделить на п равных интервалов длиной h, то
первую частную производную от Т по х в точке х, приближенно
можно представить в виде
9х xi+l-xi_l
252
Глава 9
Вторую частную производную можно приближенно выразить
как
а2Т , ч дТ' ч
Зх2 Ы Ы =
Т' fr,+ 1) - Г ft,-,)
х/+1 - *, -1
Подставим в эту формулу приближенное выражение для Т'.
Тогда
= Г^-2) - 2 Т(У,) +
Зх2 4-й2
Если каждый интервал разделить пополам и провести диффе-
ренцирование тем же способом, то получится окончательная фор-
мула, с которой мы будем работать (2й заменяется на й):
Г^-1) ~ + T^i+i)
ax2 й2
Подстановка этого приближенного выражения в приведенное
выше уравнение второго закона Фурье дает
_ СЛ^-.) - 2-Т^) + TQcj+l)
at й2
Если стержень разделить на 10 частей, как показано на рисунке,
то получится 11 точек: хрх2, •••»хю ихп- Для краткости будем пи-
сать Т- вместо T(r,), Т- вместо dT^/dt иЬ вместо с/й2. Учитывая,
что на торцах стержня температура равна 0 °C, можно написать
следующую систему дифференциальных уравнений:
т; = 0
Т’ 1 2 = Ь-(Г1 - 2Т2 + Т3)
т; = Ь-(Г2 - 2-Т3 + Тд)
г; = Ь-(Г3 - 2-Т\ + Т5)
ц = Ь (Г4 - 2 Т5 + TJ
Т'ь = Ь-(Г5 - 2-Т6 + Т7)
т; = Ь-(Т6- 2-Т7 + Т8)
T't = Ь-(Г7 - 2-Т8 + Т9)
Т'9 = b-(Ts - 2-Т9 + Т10)
Т» = Ь-(Т9 - 2-Т10 + Тн)
Т’п = 0
Таким образом, в этом приближении задача свелась к системе
обыкновенных дифференциальных уравнений. Чем больше взято
интервалов, тем больше эта система и тем точнее результаты.
Дифференциальные уравнения
253
Полученную систему уравнений можно теперь решить с по-
мощью программы «СИСТ-РКН». Она использована в качестве
подпрограммы в программе «ЧАСТ-ПРО»:
0 REM "ЧАСТ-ПРО" EBERT/EDERER 8 Г
1 РЕГТ**************1*1******|»ч*ч*и»ч»ч»ч*и*и»ч»ч*чр
2 REM** РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИ Й **
3 REM** В ЧАСТНЫХ ПРОИЗВОДНЫХ С ПО- **
4 REM** МОЩЬЮ ПРОГРАММЫ"СИСТ-РКН" •*
5 REM** ПРИМЕР: ВТОРОЙ ЗАКОН ФУРЬЕ. ♦♦
6 REM** РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ♦ ♦
7 REM** В СТЕРЖНЕ ДЛИНОЙ 100 СМ ••
9 REM*********************************
100 DIM V<20>,V1<20>,D<20>,V9<20>
120 DIM K1<20>,K2<20>,K3<20>,K4<20>
200 N-lliREM ЧИСЛО ДИФ. УРАВНЕНИЙ В СИСТЕМЕ
250 V1<1>-0|REM ТЕМПЕРАТУРА НА ЛЕВОМ ТОРЦЕ
260 VI <N>-0 iREM ТЕМПЕРАТУРА НА ПРАВОМ ТОРЦЕ
300 FOR 1-2 ТО N-1
400 VI < I >-< 1-1 >*10 IREM РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В НАЧАЛЕ
600 NEXT I
650 R-0IREM В МОМЕНТ ВРЕМЕНИ Т= О НАЧАЛЬНОЕ ЗНАЧЕНИЕ А = 0
6В0 PRINT "ДЛЯ КАКОГО МОМЕНТА ВРЕМЕНИ РАССЧИТЫВАТЬ"
690 PRINT "РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ";
700 INPUT Е
1000 N1-4
1100 Н—<E-A>/N1
1200 GOSUB 5000
1210 PRINT!PRINT "РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В МОМЕНТ ВРЕМЕНИ"; Е
1220 PRINT "В ГРАД. ЦЕЛЬСИЯ""ПРИ"; N1; "ИНТЕРВАЛОВ"
1230 FOR 1-1 ТО NiPRINT ТАВ< 1*6-6> > < 1-1 >*10,"СМ" , 1NEXT I
1Э00 PRINT
1400 FOR 1-1 ТО NiPRINT ТЯВ<I*6-6>,<INT<V<I>*10+.5>>/10,1NEXT I1PRINT
1500 N1-N1»2
1600 GOTO 1100
5000 REM*********************************************
5002 REM** ПОДПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ПРАВОЙ **
5004 REM** ЧАСТИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ **
5010 REM*********************************************
5100 FOR 1-1 ТО NiV<I>-Vl<I>iNEXT I
5200 FOR 19-0 ТО Nl-1|Х-А+19*Н
5300 Х9-X1F0R 1-1 ТО N|V9<I>-V<I>iNEXT I
5320 GOSUB 10000
5340 FOR 1-1 TO N:K1<I>—H*D<I>iNEXT I
5400 X9-X+H/21F0R 1-1 TO NiV9<I>-V<I>+К1<I>/2iNEXT I
5420 GOSUB 10000
5440 FOR 1-1 TO N|K2<I>-H*D<I>iNEXT I
5500 X9—X+H/2:F0R 1-1 TO NIV9<I>-V<I>+K2<I>/2iNEXT I
5520 GOSUB 10000
5540 FOR 1-1 TO N:K3<I>—H*D<I>iNEXT I
5600 X9-X+H1F0R 1-1 TO N I V9<I>-V<I>+K3<I>iNEXT I
5620 GOSUB 10000
5640 FOR 1-1 TO N|K4<I>-H*D<I>iNEXT I
5700 FOR 1-1 TO N
5720 V<I>-V<I>+<К1<I>+2*K2<I>+2*K3<I>+K4<I>>/6
5740 NEXT I
5800 NEXT I9IRETURN
10000 REM**********************************
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ПРАВЫЕ ЧАСТИ **
10003 REM** ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ**
10004 REM** DY I / D X = F1 (X,Y1, ... YN) **
10005 REM** D (I) =F (X9.Y9 (1), ...,Y9 (ND **
10010 REM**********************************
254
Глава 9
10100 FOR 09-2 ТО 10
10200 0<D9>—<V9<09+1>-2* V9<09>+V9<09-1 > >*.0023
10300 NEXT 09
10400 D<l>-0
10500 O<ll>-0
12000 RETURN
63999 ENO
RUN
ДЛЯ КАКОГО МОМЕНТА ВРЕМЕНИ РАССЧИТЫВАТЬ
РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ? 1000
РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В МОМЕНТ ВРЕМЕНИ 1000 В ГРАД. ЦЕЛЬСИЯ
ПРИ 4 ИНТЕРВАЛАХ
0 СМ 10 СМ 20 СМ 30 СМ 40 СМ 50 СМ 60 СМ 70 СМ 80 СМ 90 СМ 100 СМ
0 10 19.9 29.8 39.2 47.6 53.1 53.5 44.8 26.3 0
РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В МОМЕНТ ВРЕМЕНИ 1000 В ГРАД. ЦЕЛЬСИЯ
ПРИ В ИНТЕРВАЛАХ
0 СМ 10 СМ 20 СМ 30 СМ 40 СМ 50 СМ 60 СМ 70 СМ 80 СМ 90 СМ 100 СМ
0 10 19.9 29.8 39.2 47.6 53.2 53.4 44.9 26.1 0
Система уравнений задана в подпрограмме 10000. Первая и по-
следняя производные в соответствии с приведенной выше системой
дифференциальных уравнений приравниваются нулю. Значения про-
изводных начиная с Т'2 до T'lQ вычисляются в цикле, поскольку эти 9
дифференциальных уравнений по форме близки (индексы соответст-
вующих переменных увеличиваются каждый раз на 1).
Число уравнений (всего 11) задается в строке 200, температура
на торцах стержня, равная О °C, — в строках 250 и 260. В цикле со
строки 300 до строки 600 рассчитывается начальное распределение
температуры вдоль стержня до момента времени t = 0. В строке
650 начальное время приравнивается нулю. Распределение темпера-
туры рассчитывается на момент времени t = Е, значение Е вводит-
ся с помощью оператора INPUT в строке 700.
Остальная часть программы до вывода данных идентична про-
грамме «СИСТ-РКН». Вывод данных организован таким образом,
что выходные данные дают наглядное представление о физической
картине процесса. В числовом примере рассчитано распределение
температуры вдоль стержня в момент времени t = 500.
Задание 148. Измените программу «ЧАСТ-ПРО» так, чтобы расчет проводился
для 20 интервалов. Сравните результаты, полученные для 10 и 20 интервалов. Для
этого надо изменить размерность системы дифференциальных уравнений, участок
программы для расчета нормального распределения температуры, участок вывода
данных, наибольшие значения параметров цикла в подпрограммах 5000 и 10000, а
также значение коэффициента, входящего в каждое уравнение системы. Этот коэф-
фициент зависит от величины шага А вдоль осих (см. приведенные выше формулы).
Задание 149. Диффузия описывается уравнением такого же вида, как и теплопро-
водность (уравнение Фика). Для одномерной задачи это уравнение выглядит следую-
Дифференциальные уравнения
255
шим образом:
dc/dt = а-д^с/дх2
Рассмотрим следующий пример. Пусть имеется конструкция из стеклянных тру-
бок в виде буквы Н (см. рис.). Концентрации некоторого вещества в газе, протекаю-
щем по двум параллельным трубкам, равны с, ис2 соответственно. Концентрация
С,-------
С2
этого вещества в соединительной трубке в момент времени t = 0 равна 0. Как вы-
глядит распределение концентрации вдоль соединительной трубки в определенный
момент времени?
С точки зрения математики эта задача ничем не отличается от задачи, решен-
ной в качестве иллюстрации с помощью программы «ЧАСТ-ПРО». Если время,
концентрацию и длину соединительной трубки рассматривать как безразмерные ве-
личины, то, выбрав числовое значение для коэффициента а, можно получить иско-
мое распределение вещества в соединительной трубке в определенный момент вре-
мени.
Как выглядит стационарное распределение концентраций? Чтобы ответить на
этот вопрос, надо рассчитать распределение при нескольких значениях / и выбрать
такое, которое не меняется с увеличением I.
Задание 150. Дана трубка, диаметр которой много меньше ее длины. Трубка за-
паяна с обеих сторон, и посередине имеется закрытый кран. Левая половина трубки
заполнена газом А, правая — газом В. Давление в обеих частях трубки одинаково. В
момент времени t = 0 кран открывают. Как выглядит распределение газов А и В
вдоль трубки в определенный момент времени? В каждом поперечном сечении кон-
центрации газов постоянны.
Поскольку давление в обеих частях трубки одинаково и при открытом кране
давление вдоль всей трубки тоже будет постоянным, можно ограничиться расчетом
распределения вещества А. Парциальное давление вещества В равно разности обще-
го давления и парциального давления вещества А.
Разделите трубку нал равных частей. Тогда система дифференциальных уравне-
ний для внутренних интервалов аналогична системе из предыдущего задания. Лишь
дифференциальные уравнения для первой точки Xj и последней хп + f в этой задаче
другие, так как концентрации в этих точках так же, как и в остальных, изменяются.
Система дифференциальных уравнений при л = 10 имеет вид
[А,]' = Ь- ([А2] - [А,])
[А2]' = d-([Aj] - 2- [А2] + [А3])
[А5Г = * -([А4] - 2- [As] + [AJ)
[А10]' = й-([А9] - 2 [А10] + [А,,])
[А,,]' = й ([А10] - [А,,])
256
Глава 9
Дифференциальные уравнения для Aj и Ап можно получить из уравнения Фика.
В крайних точках х} и хп диффузия происходит только в одном направлении. Эти
уравнения можно вывести гораздо проще, исходя из уравнения материального ба-
ланса. Общая масса веществ А и В в трубке постоянна. Поэтому сумма всех измене-
ний концентраций вещества А должна равняться нулю:
[А,]' + [Aj]' + [Aj]' + [AJ' + [А,]' + [AJ' + [AJ' +
+ [Ag]' + [А,]' + [AI0]' + [Ан]' =0
Задание 151. Имеется длинная трубка, заполненная чистым растворителем. С
двух сторон в момент времени t = 0 вводится твердое вещество А. Это вещество
сравнительно малорастворимо в данном растворителе, так что на концах трубки все
время поддерживается концентрация cs, равная растворимости вещества А при дан-
ной температуре.
Если надо рассчитать просто распределение вещества А вдоль трубки в опреде-
ленный момент времени, то эту задачу можно легко решить с помощью программ
«ЧАСТ-ПРО». Однако допустим, что вещество А вступает в химическую реакцию,
скорость которой подчиняется кинетическому уравнению порядка п по концентрации
этого вещества. Таким образом, мы имеем дело не с чисто диффузионным процес-
сом, а с совмещенным реакционно-диффузионным. Соответствующее дифференци-
альное уравнение выглядит теперь следующим образом (к уравнению Фика добавлен
еще один член, соответствующий химической реакции):
Эс д2с
— = а-—- — к-с”
dt дх2
Рассчитайте распределение вещества вдоль трубки, учитывая протекающую в
системе химическую реакцию. Вам надо к правой части каждого из дифференциаль-
ных уравнений (пусть их всего будет опять 11) добавить член, соответствующий
скорости расходования вещества А на данном интервале, например:
С5 = *<С4 “ 2 с5 + С6> “ к с5
Задание 152. Рассмотрим модель другого реакционно-диффузионного процесса,
связанную с проблемой загрязнения атмосферы. В этой очень упрошенной модели
предполагается, что концентрации двух веществ А и В у поверхности Земли постоян-
ны. Кроме того, концентрации обоих веществ на определенной высоте he очень
быстро уменьшаются до нуля (например, в результате фотохимических реакций).
Пока задача выглядит как простая задача о диффузии двух различных веществ, и по-
этому число дифференциальных уравнений удваивается. Однако предположим, что
вещества А и В вступают в химическую реакцию, которая описывается кинетиче-
ским уравнением и = к- [А]- [В].
Как выглядит распределение веществ А и В по высоте? (Распределение веществ
вдоль поверхности в рамках этой модели считается постоянным.) Система уравне-
ний составляется так же, как и в предыдущем задании. Для пятого интервала, на-
пример, дифференциальные уравнения имеют вид
[Aj]' = d([AJ - 2 [А5] + [AJ) - A: [Aj]-[B5]
[В5]' = Z>([BJ - 2- [В5] + [В6]) - A: [Aj] [Bs]
Аналогично составляются дифференциальные уравнения для других интервалов.
Задание 153. Распад радиоактивного элемента сопровождается выделением теп-
ла. Из сплава этого элемента изготовлены шарики. Начальная температура шарика
в момент изготовления t = 0 равна 600 °C. Затем шарики помещают в среду с тем-
Дифференциальные уравнения
257
пературой 40 °C. Это означает, что на поверхности шариков поддерживается посто-
янная температура, равная 40 °C.
Для расчета распределения температуры уравнение Фурье надо дополнить чле-
ном, отвечающим тепловыделению. Трехмерную задачу для шара можно свести к
одномерной, если рассматривать радиальное распределение температуры. Для этого
радиус делят на п равных частей и для каждого отрезка составляют дифференциаль-
ное уравнение.
Рассчитайте радиальное распределение в различные моменты времени. Как вы-
глядит распределение температуры через очень большой промежуток времени?
9.9. Стационарные решения уравнений
в частных производных
Рассмотрим однородную квадратную пластину, стороны кото-
рой имеют разную температуру. Обе верхние грани пластины тер-
мически изолированы, и теплообмен со средой происходит только
через боковые стороны. Уравнение, которое описывает распределе-
ние температуры в пластине, представляют собой двухмерное урав-
нение Фурье:
ЭТ(/, X, у) _ d2i\t, X, у) д2тц, X, у)
dt дх2 ду2 (4
Распределение называется стационарным, если со временем оно
больше не изменяется. Это означает, что производная от темпера-
туры по времени становится равной нулю:
+ с.^) = 0
дх2 ду2
Если разделить каждую сторону пластины на (л — 1) равных
частей длиной h (на рисунке стороны разделены на три части), то
вторые производные можно аппроксимировать отношением конеч-
ных приращений, как это не раз делалось в предыдущем разделе:
д2Т(х,у) _ Т(х + й,у) - 2-Т(х,у) + Т(х - h,y)
дх2 h2
&T(x,y) = Т(х,у + й) - 2"Т(х,у) + Т(х,у - h)
ду2 й2
Подстановка этих приближенных соотношений в уравнение (2)
дает
Т(х + й, у) - 4-Т(х, у) + Т(х - й, у) + Т(х, у + й) +
+ Т(х, у - й) = 0 (5)
17-81
258
Глава 9
Или при использовании индексированных переменных:
T(xi+l,yj) - 4-Т(хру^ + Г^.рК) +
+ Т{х(, j,+ l) + T(xit = 0 (6)
Это уравнение справедливо для всех точек внутри указанного
квадрата. На границах квадрата поддерживается заданная темпера-
тура, на каждой стороне различная. В углах квадрата температура
равна среднему арифметическому температур соседних сторон.
Если каждая сторона квадрата разделена на (л — 1) частей, то по-
лучится система (п ~ Z)2 линейных уравнений, которую и необхо-
димо решить.
Учитывая особенности этой системы и ее размеры, для решения
вместо метода Гаусса — Жордана лучше применить более эффек-
тивный итерационный метод. Использованный здесь метод, кото-
рый в математической литературе известен как метод Гаусса —
Зайделя, дается без строгого доказательства. Он применяется, как
правило, в тех случаях, когда матрица коэффициентов имеет диаго-
нальное преобладание. Решим уравнение (5) относительно Т(х, _у):
Т(х, у) = [Т(х + й, у) + Т(х - й, у) + Т(х, у + й) +
+ Г(х, у - й)]/4 (7)
или, используя переменные с индексами:
J,)H = [Г(х,.+ 1, jy.) + Т(х-._р +
+ Г(хр jy+1) + Т(х,., ^_,)]/4 (8)
Дифференциальные уравнения
259
В качестве начального приближения выбирают какое-нибудь
распределение, например, всем внутренним точкам квадрата при-
сваивается температура, равная средней арифметической темпера-
туре его сторон. Затем по итерационной формуле (8) для всех точек
рассчитывают новые значения _у^)н. Итерационную процедуру
можно закончить, если новые значения почти не отличаются от по-
лученных в предыдущей итерации. Если же они существенно разли-
чаются, то проводится следующая итерация, в которой использу-
ются эти новые значения Т. Итерационная процедура продолжает-
ся до тех пор, пока значения температуры в одних и тех же точках,
полученные в двух последовательных итерациях, не будут разли-
чаться на незначительную величину. Этот метод использован в
программе «СТАЦИОНАР», распечатка которой приведена ниже:
0 КЕМ "СТАЦИОНАР" EBERT/EDERER 810624
1 REM**********************************
2 REM** СТАЦИОНАРНОЕ РЕШЕНИЕ СИСТЕ- **
3 REM** МЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕ-**
4 REM** НИЙ.ПРИМЕР:РАСЧЕТ РАСПРЕДЕЛЕ-**
S REM** НИЯ ТЕМПЕРАТУРЫ В ДВУМЕРНОЙ **
6 КЕМ** КВАДРАТНОЙ ПЛАСТИНЕ, 4 СТОРО-**
7 REM** НЫ ИМЕЮТ РАЗЛИЧНУЮ ТЕМПЕРАТ.**
9 REM**********************************
180 OIM Т<30,30>,Т0<30,30:>,8<4>
200 PRINT "НА СКОЛЬКО ИНТЕРВАЛОВ РАЗДЕЛИТЬ"
250 PRINT "КАЖДУЮ СТОРОНУ"; : INPUT N
300 Н-Н+1
400 FOR 1=1 ТО 4
500 FRIHT "ТЕМПЕРАТУРА";! ; "СТОРОНЫ";: INPUT S (I)
600 HEXT I
650 T5=<S<1)+8<2)+S<3>+S<4>>/4
700 FOR 1=2 TO <N-1>:T<I,1>=S<1>sNEXT I
720 FOR 1=2 TO <N-1>:T<N,I>=S<2>1NEX.T I
730 FOR 1=2 TO <N-1>:TCI,N>=SC3>:NEXT I
740 FOR 1=2 TO <N-1>:T<1,I>=S<4>sNEXT I
800 T<1,1>=<S<1>+S<4>>/2
810 T<N,1>=<S<11+SC2)>/2
820 T<H.H>=<S<2>+S<3>>/2
830 T<1 .H>=(S<3)+S<4»^2
980 FOR 1=2 TO H-l:FOR J=2 TO N-l:T<I,J>=T5:NEXTJiNEXTI:GOSUB 10000
1800 REM НАЧАЛО ИТЕРАЦИОННОЙ ПРОЦЕДУРЫ РЕШЕНИЯ СИСТ. ДИФ. УР.
1050 Е9-. 1 1REM ТОЧНОСТЬ РЕШЕНИЯ
1060 Е5-0
1100 FOR 1-2 ТО N-1
1200 FOR J-2 ТО N-1
1300 Т<I,J>-<Т0<1+1,J>+T0<1-1,J>+T0<I,J+l>+T0<I,J-l>>*.25
1400 IF ABS<T<I,J>-T0<I,J>»E9 THEN E5-1
1600 NEXT J
1700 NEXT I
1750 REM OOSUB 5000 iREM ПРОМЕЖУТОЧНЫЕ РЕЗУЛЬТАТЫ
1800 IF E5-0 THEN GOTO 2000 iREM ВЫВОД
1900 OOSUB 100001GOTO 1000
2000 OOSUB 50001END
17»
260
Глава 9
5000 REM******************************
5004 REM** ВЫВОД РАСПРЕДЕЛЕНИЯ **
5006 REM** ТЕМПЕРАТУРЫ **
5010 REM******************************
5100 PRINT
5200 FOR J-N TO 1 STEP -1
5300 PRINT
5400 FOR I-l TO N
5500 PRINT ТЯВ<2+<I-1>»5>,INT<T<I,J>+.5>>
5600 NEXT IiPRINTI NEXT J
5700 RETURN
10000 REM******************************************
10002 REM** ЗДЕСЬ ЭЛЕМЕНТЫ МАССИВА TO ( ) ПРИ- **
10003 REM** СВАИВАЮТСЯ ЭЛЕМЕНТАМ МАССИВА Т ( ) ♦*
10010 REM******************************************
10100 FOR I-l ТО NiFOR J-l ТО N
10200 T0<I,J>-T<I,J>
10300 NEXT JiNEXT I
12000 RETURN
63999 ENO
RUN
НА СКОЛЬКО ИНТЕРВАЛОВ РАЗДЕЛИТЬ
КАЖДУЮ СТОРОНУ? 4
ТЕМПЕРАТУРА 1 СТОРОНЫ? О
ТЕМПЕРАТУРА 2 СТОРОНЫ? 100
ТЕМПЕРАТУРА 3 СТОРОНЫ? О
ТЕМПЕРАТУРА 4 СТОРОНЫ? О
0 0 0 0 50
0 7 19 43 100
0 10 25 53 100
0 7 19 43 100
0 0 0 0 50
READY.
RUN
НА СКОЛЬКО ИНТЕРВАЛОВ РАЗДЕЛИТЬ
КАЖДУЮ СТОРОНУ? 12
ТЕМПЕРАТУРА 1 СТОРОНЫ? О
ТЕМПЕРАТУРА 2 СТОРОНЫ? 100
ТЕМПЕРАТУРА 3 СТОРОНЫ? 200
ТЕМПЕРАТУРА 4 СТОРОНЫ? 300
250 200 200 200 200 200 200 200 200 200 200 200 150
300 247 224 212 204 198 194 190 185 180 170 150 100
300 263 23? 219 206 196 187 180 172 Ь63 150 130 100
300 269 243 222 205 191 180 170 161 150 137 120 100
300 270 243 220 201 185 172 161 150 139 128 115 100
300 269 241 215 194 177 162 150 139 130 120 110 100
300 266 235 207 184 165 150 138 128 120 ИЗ 106 100
Дифференциальные уравнения
261
зее 261 225 194 170 150 135 123 115 109 104 102 100
300 252 210 176 150 130 116 106 99 95 94 96 100
зее 237 187 150 124 106 93 85 80 78 81 8В 100
300 209 150 ИЗ 90 75 65 59 57 57 63 76 100
300 150 91 63 48 39 34 31 30 31 37 53 100
150 0 0 0 0 0 0 0 0 0 0 0 50
В строке 100 описаны два двумерных массива, которые исполь-
зуются для запоминания нового (Т( )) и старого (Т0( )) распреде-
ления. Число интервалов, на которые делился каждая из сторон
квадрата, запрашивается и вводится в строках 200 и 250. В следую-
щей строке N увеличивается на 1, и тем самым определяется число
точек, ограничивающих интервалы на каждой стороне квадрата.
Значения температуры сторон вводятся пользователем в цикле
(строки 400—600) с помощью оператора INPUT. В строке 650 вы-
числяется среднее арифметическое значений температур четырех
сторон, которое присваивается переменной Т5.
В четырех циклах (строки 700, 720, 730 и 740) точкам, лежащим
на сторонах, присваивается температура соответствующей сторо-
ны. В следующих четырех строках рассчитываются значения темпе-
ратуры в угловых точках, и эти значения присваиваются перемен-
ным Т(1, 1), T(N, 1), T(N, N) и T(l, N). Конструкция из двух вло-
женных циклов (строка 900) присваивает внутренним точкам ква-
драта среднюю температуру Т5. При обращении к подпрограмме
10000 (GOSUB 10000) элементам массива Т0( ) присваиваются
значения соответствующих элементов массива Т( ). Этим заканчи-
вается начальная стадия расчетов и начинается итерационная про-
цедура.
В строке 1050 задается требуемая точность, с которой надо вы-
числить значения температуры во всех выбранных точках квадрата;
в данном случае Е9 = 0,J. В строке 1060 вспомогательной перемен-
ной Е5 присваивается нулевое значение. Эта переменная входит в
конструкцию оператора условного перехода, в которой проверяет-
ся, достигнута ли на данной итерации требуемая точность и можно
ли выводить на экран окончательный результат.
Собственно сама итерационная процедура выполняется в кон-
струкции из двух циклов со строки 1100 до строки 1700. На этом
участке программы по формуле (8) вычисляются элементы массива
Т( ), исходя из соответствующих элементов массива Т0( ). Здесь
же сравниваются соответствующие элементы этих массивов [T(I, J)
с T0(I, J)]. Если эти элементы различаются на величину, большую,
262
Глава 9
чем требуемая точность Е9, то вспомогательной переменной Е5
присваивается значение 1. Это означает, что при выходе из цикла
переменная Е5 получит значение 0 только в том случае, если соот-
ветствующие элементы массивов Т( ) и Т0( ) различаются мень-
ше чем на Е9. Строка 1750 в том виде, в каком она стоит в тексте
программы «СТАЦИОНАР», при трансляции отбрасывается (из-за
оператора REM в начале строки) и записанные в ней операторы не
выполняются. Однако если удалить первый оператор REM, то на
экран будут выводиться промежуточные результаты. В строке 1800
проверяется точность полученных в данной итерации результатов,
т. е. выясняется, какое значение имеет переменная Е5. Если
Е5 = 0, то управление передается строке 2000, в которой вызыва-
ется подпрограмма для формирования и вывода данных, после чего
выполнение программы заканчивается. Если требуемая точность
еще не достигнута, то оператор условного перехода передает
управление строке 1900. В этой строке вызывается подпрограмма
10000, которая переписывает новое распределение из массива Т( )
в массив Т0( ). После этого оператор GOTO 1000 передает управ-
ление строке 1000, с которой начинается очередная итерация.
Подпрограмма для формирования и вывода данных (строки
5000—5700) выводит на экран распределение температуры в виде
прямоугольной таблицы. При этом используется функция TAB.
Чтобы числовые данные не занимали слишком много места и вся
таблица была наглядной и компактной, значения температуры
округляются до целых чисел.
Задание 154. Напишите программу, аналогичную программе «СТАЦИОНАР»,
для расчета стационарного распределения температуры в образце кубической фор-
мы. Количество интервалов можно ограничить семью.
Постарайтесь составить более общую программу так, чтобы можно было рас-
считывать распределение температуры в прямоугольнике и параллелепипеде.
Задание 155. Рассчитайте стационарное распределение температуры в грануле
катализатора, имеющей форму прямоугольного параллелепипеда. Температура ше-
сти граней задана (обычно все грани имеют одинаковую температуру). В результате
химической реакции в грануле катализатора непрерывно выделяется тепло. Чтобы
учесть это, надо лишь добавить к правой части итерационной формулы (8) постоян-
ный член, соответствующий количеству тепла, выделяющегося в единицу времени.
Например, для гипотетической двухмерной гранулы небольшое изменение про-
граммы «СТАЦИОНАР» касается только строки 1300:
1300 T(I, J) = (Т0(1 + 1, J) + Т0(1 - 1, J) + T0(I, J + 1) +
+ T0(I, J - 1))*25 + 10
10. Интерполяция
Иногда расчет значений функции у = f(x) связан с большим
объемом вычислений, например, когда значения у вычисляются
итерационными методами или когда у является решением диффе-
ренциального уравнения. В таких случаях в распоряжении имеется
лишь ограниченное число пар значений х, у, тогда как для дальней-
шей математической обработки требуется большее число точек.
Следовательно, надо найти способ просто и быстро определять
значения в промежутке между известными. Такая сравнительно
простая задача возникает, когда хотят построить какую-нибудь
кривую с помощью ЭВМ. Для этого, как правило, необходимо
очень много точек.
Эти же проблемы появляются в том случае, если числовые зна-
чения получены экспериментально. Поскольку на каждый экспери-
мент расходуются время и деньги, исследователь, как правило,
ограничивается таким числом экспериментальных точек, которые
передают основные черты зависимости. Поэтому для математичес-
кой обработки экспериментальных данных или построения графи-
ков с помощью ЭВМ часто используют точки, лежащие между экс-
периментальными или вычисленными.
Проблемы подобного рода решаются с помощью интерполяции.
В этой главе рассматриваются два метода: очень простой и нагляд-
ный метод Лагранжа и получившая широкое распространение
сплайн-интерполяция. Слово «сплайн» (англ, spline) происходит от
названия гибких лекальных линеек, которыми издавна пользова-
лись английские корабелы. Само название метода очень точно от-
ражает принцип построения искомых точек.
10.1. Метод Лагранжа
Принцип метода состоит в том, что через п точек с координата-
ми х;, проводят полином. Если все значения х различны, то, как
следует из курса математического анализа, это можно сделать с
помощью полинома (и — 1)-й степени.
264
Глава 10
В данном случае полином лучше написать в виде формулы Ла-
гранжа:
™ = i (п Нт) 'Ук
к = I ' , = 1 Xi '
I # *
Нетрудно показать, что перед нами действительно полином:
формула Лагранжа является просто несколько непривычной фор-
мой записи полинома (п — 1)-й степени. Произведение, являющееся
коэффициентом при ук, состоит из (л — 1) сомножителей. Если в
выражение для Р(х) вместо х подставить хт, то получится сумма п
произведений вида
Д хт - Xj _ Cl, если т = к
И, — X; to, если т Ф к
/ = 1 * »
Индекс / пробегает все целочисленные значения от 1 до л, кроме к.
В том случае, если т Ф к, в произведение входит сомножитель
(хт - хт), и поэтому все произведение равно нулю.
При подсчете произведения отбрасывается только сомножитель,
у которого индекс i = к. Следовательно, если т = к, то все сомно-
жители в произведении имеют вид
Хм — Xi
т i
Для х с индексом т все сомножители и произведение в целом
равны единице. Р(хт) можно написать в следующем виде:
Р(хт) = 0-yt + 0-j2 + ... + 1-ут + 0-ym+1 + ... + 0у„ = ут
Таким образом, показано, что Р(хт) = ут, и, следовательно,
доказана истинность формулы Лагранжа. Остается только пере-
вести ее на алгоритмический язык, что и сделано в программе
«ЛАГРАНЖ».
0 REM "ЛАГРАНЖ" EBERT/EDERER 010711
1 REM*********************************
2 REM** ИНТЕРПОЛЯЦИЯ ««
Э REM** МЕТОДОМ ««
4 REM** ЛАГРАНЖА ««
9 REM*********************************
1000 DIM Х<70>,¥<70>
1100 INPUT "ЧИСЛО ПАР ЗНАЧЕНИЙ"; N
1200 FOR I-l ТО N
1300 PRINT ''Х<",1,“> , ¥<",1>"> ",
1400 INPUT Х<!>,¥<!>
Интерполяция
265
1500 NEXT I
2000 PRINT1PRINT "ДЛЯ КАКОГО ЗНАЧЕНИЯ X ВЫЧИСЛИТЬ"
2005 PRINT "ИНТЕРПОЛИРОВАННОЕ ЗНАЧЕНИЕY";
2100 INPUT X
5000 Y-0
6000 FOR К-1 ТО NiP-1
6400 FOR 1-1 ТО N
'6600 IF I-К THEN 7000
6000 P-P*<X-X<I>>/<X<K>-X<I>>
7000 NEXT I
7200 V - Y+P*Y<K>
7400 NEXT К
8000 PRINT " X - "jX
8100 PRINT “ V - ",Y
9088 GOTO 2808
9999 END
RUN
ЧИСЛО ПАР ЗНАЧЕНИЙ? 5
X< 1 > , Y< 1 > ? 0,0
X< 2 > , Y< 2 > ? 1,1
X< 3 > , Y< 3 > ? 2,4
X< 4 > , Y< 4 > ? 3,9
X< 5 > , Y< 5 >’ ? 4,16
ДЛЯ КАКОГО ЗНАЧЕНИЯ X ВЫЧИСЛИТЬ
ИНТЕРПОЛИРОВАННОЕ ЗНАЧЕНИЕ Y ? 2, 5
X - 2.5
Y - 6.25
ДЛЯ КАКОГО ЗНАЧЕНИЯ X ВЫЧИСЛИТЬ
ИНТЕРПОЛИРОВАННОЕ ЗНАЧЕНИЕ Y? .5
X - .5
Y - .25
ДЛЯ КАКОГО ЗНАЧЕНИЯ X ВЫЧИСЛИТЬ
ИНТЕРПОЛИРОВАННОЕ ЗНАЧЕНИЕ Y? 1.1
X - 1.1
Y - 1.21
ДЛЯ КАКОГО ЗНАЧЕНИЯ X ВЫЧИСЛИТЬ
ИНТЕРПОЛИРОВАННОЕ ЗНАЧЕНИЕ Y?
В строке 1000 описаны два одномерных массива Х( ) и Y( ),
элементам которых присваиваются значения х и у. В следующей
строке с помощью оператора INPUT вводится число пар значений.
Ввод значений х и у происходит в цикле FOR—NEXT в строках
1200—1500. Значение х, для которого необходимо вычислить интер-
полированное значение у, вводится с помощью оператора INPUT в
строке 2100.
В строках 5000—7400 выполняются вычисления по формуле Ла-
гранжа. В цикле по К (строки 6000—7400) вычисляется сумма про-
изведений. В него вложен цикл по параметру I, в котором рассчи-
тываются произведения. Перед началом этого цикла переменная Р,
которая при выходе из цикла имеет значение произведения, прирав-
нивается единице. В строке 6800 уже вычисленные произведения ум-
ножаются на следующий сомножитель и полученное произведение
присваивается этой же переменной Р. Согласно формуле Лагранжа,
сомножители с индексами i = к пропускаются. В программе это
выполняется с помощью оператора IF в строке 6600.
266
Глава 10
Перед началом суммирования (цикл по К) переменная У, кото-
рая после выхода из цикла имеет значения суммы, обнуляется
(строка 5000). Вычисленные во внутреннем цикле произведения в
строке 7200 суммируются и значение суммы присваивается пере-
менной Y. В строках 8000 и 8100 выводятся на экран заданное зна-
чение х и вычисленное значение интерполяционного полинома.
В приведенном примере вводятся пять пар значений х и у, кото-
рые соответствуют полиному второй степени. Вы можете убедить-
ся, что интерполированные значения точно лежат на этой пара-
боле.
Задание 156. Выберите пять значений х в интервале [0, 2] и пять значений у, со-
ответствующих функции у = ехр(х). Вычислите интерполированные значения и срав-
ните их с точными значениями функции у = ехр(х).
Интерполируйте точки, лежащие на логарифмической кривой.
Задание 157. Проведите интерполяцию по «экспериментальным» данным, кото-
рые описываются какой-нибудь функцией. Для моделирования «экспериментальных»
данных рассчитайте сначала по соответствующему уравнению точные значения, а
потом с помощью генератора случайных чисел превратите их в статистические, на-
пример:
Y(I) = X(I).EXP(-X(I).X(I))*(O,95 + 0.1»RND(5))
Используйте программу для интерполяции: один раз для «экспериментальных»
данных с очень малыми отклонениями, а другой раз — с довольно большими.
Задание 158. Если заданных точек очень много, ио, несмотря на это, необходи-
мо найти точки между ними, то совсем не обязательно при интерполяции учитывать
все заданные точки. Как правило, целесообразно брать лишь несколько (например,
четыре) соседних точек (по две с каждой стороны от искомой точки).
Напишите программу, использующую для интерполяции только часть заданных
точек, число которых вводится оператором INPUT. Эти точки целесообразно вы-
брать так, чтобы искомая точка лежала между известными. Приходится мириться с
отсутствием на концах соседних точек справа или слева.
Главное в этом задании — выбрать подходящие соседние точки, а саму интер-
поляционную процедуру можно переписать из программы «ЛАГРАНЖ».
На практике четырех соседних точек, как правило, достаточно; одиако в зависи-
мости от поставленной задачи может оказаться целесообразным взять большее чис-
ло точек.
Задание 159. Чтобы использовать программу предыдущего задания для обра-
ботки экспериментальных данных, полученных с большими случайными отклонения-
ми, необходимо к этой программе добавить процедуру сглаживания. Методы и сте-
пень сглаживания должны быть адекватны каждой конкретной задаче. Бывают та-
кие экспериментальные данные, которые вообще не надо сглаживать, н такие, кото-
рые требуют сильного сглаживания. Степень сглаживания зависит от числа соседних
точек, которые учитываются в процедуре. Кроме того, для достижения лучшего
сглаживания процедуру можно повторить несколько раз, вызывая каждый раз соот-
ветствующую подпрограмму.
Задание 160. Одна из самых неприятных проблем, возникающих при оораоотке
экспериментальных данных, — это дифференцирование экспериментально найден-
ных зависимостей, поскольку даже маленький разброс в результатах измерений при-
водит к очень большому разбросу значений производной. Поэтому часто поступают
Интерполяция
267
следующим образом: результаты измерений сначала сглаживают, потом по сгла-
женным значениям строят интерполяционный полином, по которому рассчитывают
небольшие приращения переменных, и вычисляют приближенное значение произво-
дной.
Напишите программу, которая рассчитывала бы производные непосредственно
из экспериментально полученных данных. Используя интерполяционный полином
Лагранжа, рассчитайте координаты двух точек, расположенных близко к заданной,
и вычислите отношение соответствующих приращений.
Опробуйте эту программу на модельных «экспериментальных» данных, кото-
рые можно получить, накладывая с помощью генератора случайных чисел шум на
точные значения выбранной функции.
10.2. Интерполяция с помощью сплайн-функции
Интерполяция с помощью сплайн-функции особенно эффективна
для построения гладких интерполяционных кривых. Поэтому она
часто используется в машинной графике. Возьмем опять п экспери-
ментальных точек или точек, удовлетворяющих некоторой функ-
ции. При сплайн-интерполяции через каждые две соседние (сгла-
женные) точки проводят полином третьей степени. Разумеется, что
по двум заданным точкам невозможно однозначно определить ко-
эффициенты этого полинома, поскольку две точки однозначно
определяют только полином первой степени (т. е. прямую).
Для /-го полинома Р(-, проходящего через точки с координатами
х(., у,- и х(+1, у(+1, справедливо
Р,(х,) = у,. и Р.(х,+ 1) = у/+1 (1),(2)
Переход от полинома Р,_р который соединяет точки (х,_Р .У,-])
и (хр у(), к полиному Р( , проходящему через точки (хр у(.) и (х/+Р
_у(+1), должен быть плавным (без излома). Чтобы выполнялось это
условие, значения первой и второй производных соседних полино-
мов Р(_] и Р(. в их общей точке (хр _у() должны быть равны. Это ус-
ловие выглядит как
= W И Р"_ ^Х,.) = Р/Ц) (3), (4)
Таким образом, для всех внутренних полиномов сформулирова-
ны и формализованы четыре условия, которые достаточны для по-
строения этих полиномов. Если объединить эти условия, то полу-
чится система уравнений.
Обе концевые точки имеют только по одной соседней, и поэто-
му для концевых полиномов требуются дополнительные условия.
Если принять, что точки, лежащие вне рассматриваемого интерва-
ла значений х, можно аппроксимировать прямыми, то последнее
268
Гпава 10
недостающее условие можно записать в следующем виде:
Pf(x1) = O и р;_1(хл) = о (5)
Введем следующие обозначения:
А, = (х,+1 - х), d, = (yi+i - y)/hit t = (х - x^/hi
Тогда для z-го полинома получается выражение
Р,(х) = t-yi+i + (1 - t)yj + - ОЧ(А, ~
- d^ (I - 0 - (ki+i - di)-t] (6)
Видно, что это полином третьей степени относительно t и, сле-
довательно, относительно х, поскольку t является линейной функ-
цией х. Если t = 0, т. е. х = х(, то из (6) следует
t = 0: => х = х,.: => Р,.(х(.) = (ба)
Это совпадает с нашим первым условием (1). Если t = 1, т. е.
х = х(+1, то из (ба) получается
t = 1: => х = х,+я: =» Р,(х;+1) = л,+ 1 (66)
Следовательно, полином (6) удовлетворяет условию (2). Неиз-
вестные величины — параметры Л(. — можно определить из уравне-
ний (4) и (5). В том, что полином (6) удовлетворяет условию (3),
можно убедиться, если продифференцировать уравнение (6) по х:
Р,’(х) = di + (1 - 21)[(к{ - di)(l - t) - (Arf+1 - d?)t] +
+ (Z - fl)(2di - ki - ki+x) (7)
Подставим в (7) t = 0 и t = 1. Тогда
t = 0: * P!(x) = kt и при t = 1: => P-(xi+l) = ki+x
Это в точности соответствует условию (3), если в правой части
формулы вместо i подставить i — 1. Если полином (6) дважды про-
дифференцировать по х, то получится
Р1х) -2[(А,- - ^)(1 - Z) - - d.)z] + 2(1 - 2t)Qdj - kf - ki+i)
hi (8)
Если, исходя из этого уравнения, выразить вторые производные
Р”_ 1 и РДх,) и, согласно условию (4), приравнять их, то после не-
больших математических преобразований получим
h-ki_x + 2(hi_x + h^-ki + hi_x-ki+x = 3hi_x-di + 3hi-di_x (9)
Это уравнение справедливо для всех i от i = 2 до i = (н — 1),
т. е. для п неизвестных параметров к имеется теперь (л — 2) линей-
Интерполяция
269
ных уравнений. Недостающие два линейных уравнения можно по-
лучить из условия (5) для крайних точек:
2-кх + к2 = 3d] и кп_г + 2-Лл = 3dn_l (10)
Эти п линейных уравнений с п неизвестными параметрами мож-
но решить с помощью программы для решения систем линейных
уравнений. Если параметры к найдены, то сплайн-полиномы пол-
ностью заданы, и теперь для любого значения х можно рассчитать
соответствующее интерполяционное значение у. Сначала надо най-
ти для данного значения соответствующий полином, т. е. опреде-
лить, между какими узловыми точками лежит это значение х. По-
том переходят от переменной х к переменной t и вычисляют значе-
ние полинома Р(х). Рассмотренный алгоритм реализован в. про-
грамме «СПЛАЙН», распечатка которой приведена ниже.
0 REM "’’СПЛАЙН" EBERT/EDERER 010711
1 REM***********************************
2 REM»» АППРОКСИМАЦИЯ ФУНКЦИИ С N »»
3 REM»» ТОЧКАМИ ПЕРЕГИБА КУБИЧЕСКИМ »*
4 REM»» СПЛАЙНОМ. НАИБОЛЬШЕЕ ЧИСЛО ••
5 REM»» ТОЧЕК ПЕРЕГИБА 2S. »»
б REM*» ЕСЛИ ТАКИХ ТОЧЕК БОЛЬШЕ, ТО ••
7 REM»» ИЗМЕНИТЕ ОПИСАНИЕ МАССИВОВ ••
9 REM»»»»»»»»»»»»»»»»»»»»»»»»»»»»»*»»»»*
1000 DIM R<25,26>,Н<25>,D<25>,К<25>,Х<25>,V<25>
1100 INPUT "ЧИСЛО ПАР ЗНАЧЕНИЙ"; N
1200 FOR I-l ТО N
1300 PRINT "Х<, ¥<",!,"> ",
1400 INPUT X<I>,Y<I>iNEXT I
1500 REM СОРТИРОВКА ВХОДНЫХ ДАННЫХ ПО ВОЗРАСТАНИЮ X
1550 FOR I-l ТО N-11Н-Х<1>1H1-I
1570 FOR J-I+l ТО N
1600 IF HCX<J> THEN 1700
1650 H-X<J>1H1-J
1700 NEXT J
1750 X<H1>-X<I>1X<I>-H
1760 H-V<H1>iVCHl>-¥<!>1V<I>-H
1000 NEXT I
2000 FOR I-l TO N-l
2100 H<I>-X<I+1>-X<I>
2200 D<I)-(Y(! + 1)-V(!»/H<I)
2300 NEXT I
5000 R<1,1>-2iR<N,N>-2
5100 R<1,2>-1|R<N,N-1>-1
5200 R< 1 ,N+1 >-D< 1 >»3 |R<N,N+15-DCN-l >»3
6000 FOR 1-2 TO N-l
6500 R<I,N+1>-<D<I>»H<I-1>+D<I-1>»H<I>>»3
7000 R<IлI-l>—H<I>1R<I,I+1>-H<I-1>
7200 R<I,I>-2»<H<I>+H<I-l>>
7500 NEXT I
0000 GOSUB 50000
10000 INPUT "ЗНАЧЕНИЕ X"; X
11000 GOSUB 20000
12000 T-<X-X<J>>/H<J>
12200 Y-T»V<J+l> + <1-T>»V<J>
12400 V-V+HCJ>»<1-T>»T»<<R<J,N+l>-D<J>>•<1-T>-<R<J+l,N+1>-D<J>>»T>
270
Гпава 10
13000 print "сплайн-интерполяция в точке"
13100 PRINT “ X -;Xj" - "iViPRINT
14000 GOTO 10000
20000 IF Х>ХС1> THEN 20050
20010 J-l i'GOTO 22000
20050 IF X<XCN> THEN 20100
20060 J-N-l i GOTO 22000
20100 FOR 1-1 TO N
20200 IF XCIXX THEN 21000
20500 J—I—III—N
21000 NEXT I
22000 RETURN
50000 GOTO 50900:FOR 1-1 TO NiFOR J-l TO N
50005 FOR 1-1 TO NiFOR J-l TO N+l
50010 PRINT ACI,J>>" ",iNEXT Ji^RINTiNEXT I
50100 INPUT "ЧИСЛО НЕИЗВЕСТНЫХ"; N
50200 PRINT "ВВОД РАСШИРЕННОЙ МАТРИЦЫ КОЭФФИЦИЕНТОВ"
50300 FOR 1-1 TO N
50400 FOR J-l TO N
50500 PRINT "AC"jIj","jJj " > - ",:INPUTACI,J>
50600 NEXT J
50700 PRINT “BC",I,") - ",: INPUTAC I ,N+1 >
50000 NEXT I : PR I NT
50900 FOR S-l TO N
51000 FOR T-S TO N
51100 IF ACT,S><>0 THEN 51300
51200 NEXT TtPRINT "ЕДИНСТВЕННОГО РЕШЕНИЯ HET": GOTO 63000
51300 GOSUB 53000
51400 C-1/ACS,S>
51500 GOSUB 54000
51600 FOR T-l TO N
51700 IF T-S THEN 52000
51B00 C—ACT'S)
51900 GOSUB 55000
52000 NEXT T
52100 NEXT S
52200 GOSUB 56000:GOTO63000
53000 REM*****************************
53002 REM** ПОДПРОГРАММА »»
53004 REM** ДЛЯ ОБМЕНА **
5Э0В6 REM»» УРАВНЕНИЙ **
53010 REM*»»*»»***»»»»»»»»*»»»»»»»»»»»
53100 FOR J-l TO N+l
53200 B-ACS,J):ACS,J>-ACT,J>:ACT,J>-B
53300 NEXT J
53400 RETURN
54000 REM***»*»»**»*»*****»»»»»»»**»**
54002 REM»» ПОДПРОГРАММА ДЛЯ »»
54004 REM»» ДЕЛЕНИЯ СТРОКИ НА ДИА-**
54006 REM»» ТОНАЛЬНЫЙ ЭЛЕМЕНТ **
54010 REM****»*»»»»»*»»»»»»»»»»»»»»»»»
54100 FOR J-l TO N+l
54200 ACS,J)-C»ACS,J)iNEXT J
54400 RETURN
55000 REM**»»*»»*»»»*»»»»»»»*»»»»»»»»»
55002 REM»» ПОДПРОГРАММА ДЛЯ »«
55004 REM»» ВЫЧИТАНИЯ »»
55005 REM»» УМНОЖЕННОЙ НА С »»
55006 REM«« S-Й СТРОКИ ИЗ »»
55007 REM»» Т-Й СТРОКИ »»
55010 REM»»*»»*»»»»»»»»»»»»»*»»»»»»»»»
55100 FOR J-l TO N+l
55200 ACT,J>-ACT,J)+C»ACS,J)
55300 NEXT J
55400 RETURN
Интерполяция
271
S6000 REM*****************************
56001 REM** ПОДПРОГРАММА ДЛЯ ВЫ- **
56002 REM** ВОДА РЕШЕНИЯ НА ЭКРАН **
56010 REM*****************************
56100 REM FOR Т-1 ТО N
56200 REM PRINT"X<",T,”>-“,A<T,N+1>
56300 REM NEXT T
56400 RETURN
6Э000 RETURN
63999 END
RUN
ЧИСЛО ПАР ЗНАЧЕНИЙ? 5
X< 1 > , Y< 1 > ? 0,.l
X< 2 > , V< 2 > ? 1,.9
X< 3 > , V< 3 > ? 2,3.8
X< 4 > , V< 4 > ? 3,9.2
X< 5 > , Y< 5 > ? 4,16
ЗНАЧЕНИЕ X? 3
СПЛАЙН-ИНТЕРПОЛЯЦИЯ В ТОЧКЕ
X - 3 - 9.2
ЗНАЧЕНИЕ X? 2.5
СПЛАЙН-ИНТЕРПОЛЯЦИЯ В ТОЧКЕ
X - 2.5 - 6.23816964
ЗНАЧЕНИЕ X? 7
СПЛАЙН-ИНТЕРПОЛЯЦИЯ В ТОЧКЕ
X - 7 - 30.7857144
ЗНАЧЕНИЕ X? .25
СПЛАЙН-ИНТЕРПОЛЯЦИЯ В ТОЧКЕ
X - .25 - .204157366
ЗНАЧЕНИЕ X? О
СПЛАЙН-ИНТЕРПОЛЯЦИЯ В ТОЧКЕ
X - 0 - .1
ЗНАЧЕНИЕ X? 4.2
СПЛАЙН-ИНТЕРПОЛЯЦИЯ В ТОЧКЕ
X - 4.2 - 17.4049143
ЗНАЧЕНИЕ X?
READY.
В этой программе число заданных точек, по которым вычисля-
ются коэффициенты интерполяционных полиномов, не должно пре-
вышать 25. Поэтому максимальное число элементов одномерных
массивов Х( ) и Y( ), элементы которых равны координатам за-
данных точек, и одномерных массивов Н( ), D( ) и К( ), исполь-
зуемых в программе для запоминания вспомогательных величин,
равно 25. Максимальный порядок системы линейных уравнений ра-
вен, таким образом, 25, и двухмерный массив А( ), соответствую-
щий расширенной матрице системы, имеет наибольший размер
25 x 26.
Вторая часть программы «СПЛАЙН», начинающаяся со строки
50000, представляет собой программу «Г—Ж» для решения системы
линейных уравнений. Вообще говоря, метод Гаусса — Жордана не
272
Глава 10
самый удачный для решения данной системы линейных уравнений.
Он требует слишком много машинного времени н большого объе-
ма памяти. Особенность данной системы уравнений состоит в том,
что в матрице системы только элементы главной диагонали и двух
соседних диагоналей имеют ненулевые элементы. Однако пока нет
смысла вводить новый метод решения системы линейных уравне-
ний прежде всего потому, что при составлении сложных программ
очень удобно использовать уже готовые программы в виде целых
блоков и, кроме того, метод Гаусса — Жордана вполне работоспо-
собен применительно к данной конкретной задаче. Однако если при
интерполяции необходимо учитывать большое число точек, то луч-
ше поискать в справочниках по вычислительной математике какой-
нибудь метод решения для так называемых трехдиагональных мат-
риц.
В строках 1100—1400 вводятся координаты п точек, которые
присваиваются элементам массивов Х( ) и У( ). На участке про-
граммы от строки 1500 до строки 1800 входные данные сортируют-
ся в порядке возрастания значений х в соответствии с рассмотрен-
ной выше процедурой сортировки данных. Это особенно удобно
для экспериментальных данных, поскольку их не всегда получают
уже упорядоченными.
В цикле, занимающем строки 2000—2300, рассчитывается п
вспомогательных величин D(I) и Н(1), соответствующих величинам
dj и Л; в уравнении (6). В следующих строках (5000—7500) в соот-
ветствии с линейными уравнениями (9) и (10) вычисляются элемен-
ты расширенной матрицы системы. В строках 5000, 5100 и 5200 по
уравнению (10) рассчитываются элементы первой и л-й строк мат-
рицы. С помощью цикла в строках 6000—7200 по уравнению (9) вы-
числяются элементы (л — 2) строк матрицы.
После того как вычислены все элементы расширенной матрицы
системы, в строке 8000 вызывается подпрограмма для решения си-
стемы линейных уравнений. После преобразования расширенной
матрицы системы решение — значения параметров к — находится
в ее (л + 1)-м столбце.
Поскольку теперь все параметры вычислены, можно вводить
значения х, для которых рассчитываются интерполированные зна-
чения у. Это происходит в строке 10000.
После ввода значения х вызывается подпрограмма 20000. Она
определяет число J, по которому подбирается интервал [X(J),
X(J + 1)], внутри которого лежит это значение х. Число J опреде-
ляет также, какой из полиномов привлекается для интерполяции.
Если значение х лежит за пределами области заданных точек, то в
Интерполяция
2ТЗ
зависимости от того, справа или слева от границы области оно на-
ходится, для экстраполяции используется первый или последний
полином. Это устанавливается с помощью двух операторов IF в
строках 20000—20050. Если известно число J, то можно вычислить
значение вспомогательной переменной Т (строка 12000). В строках
12200 и 12400 по формуле (6) рассчитывается интерполированное
значение у. Поскольку эта формула довольно длинна, она занимает
две строки. Значение х вместе с вычисленным значением у выводит-
ся на экран в строках 13000 и 13100. Затем управление передается
строке 10000 и у пользователя запрашивается следующее значение х.
В приведенном примере заданы 5 точек, лежащих достаточно
близко к параболе. Значения сплайн-функции в узлах интерполяции
совпадают с заданным, и интерполированные точки вполне досто-
верны. Лишь для одного значения х, лежащего за пределами задан-
ной области, программа дает экстраполированное значение у, кото-
рое явно отклоняется от параболы. Поэтому для экстраполяции
этой программой лучше не пользоваться.
Задание 161. Модифицируйте участок ввода программы «СПЛАЙН». Исполь-
зуйте для ввода данных операторы READ и DATA. Расширьте возможности про-
граммы, для чего напишите подпрограмму для сглаживания экспериментальных
данных, которая вызывалась бы по указанию пользователя.
Задание 162. Примените алгоритм «сплайн» и «сглаживающий сплайн» при со-
ставлении программы для численного дифференцирования.
Задание 163. Перепишите подпрограмму 50000, в которой использован метод
Гаусса — Жордана, для решения системы линейных уравнений. Поскольку в данной
задаче ненулевые элементы расширенной матрицы системы находятся только на
главной диагонали и на двух соседних диагоналях, вместо этой матрицы размера
Nx(N +• 1) можно использовать матрицу А размера Nx4, три столбца для элемен-
тов трех диагоналей и один для правых частей системы уравнений.
18-81
11. Нелинейные системы
В предыдущих разделах этой книги было приведено множество
примеров использования систем линейных уравнений и линейных
регрессий в химии и инженерных дисциплинах. Однако для решения
ряда задач и описания многих процессов используются также систе-
мы нелинейных уравнений и нелинейные регрессии. Вообще говоря,
линейные задачи являются частным случаем более сложных и об-
щих нелинейных задач. Разумеется, линейную задачу можно ре-
шать также методами, предназначенными для решения нелинейных
задач, что, однако, в большинстве случаев менее удобно.
11.1. Системы нелинейных уравнений
Рассмотрим следующую систему нелинейных уравнений:
Надо найти такие значения хр х2 и х3, при которых все три
функции одновременно обращаются в нуль:
/ДХр х2, х3) = /2(хр х2, х3) = /3(Хр х2, х3) = О
На примере нелинейного уравнения с одним неизвестным было
показано, что решение алгебраических, трансцендентных уравнений
можно свести к поиску точек пересечения графика соответствующей
функции с осью х. Аналогичным приемом пользуются и при реше-
нии системы нелинейных уравнений. Решим в качестве примера
следующую систему уравнений:
х| + х2 — 2
sin(XjX2) = 0,5
/](Хр х2) = xj + х> - 2 = 0
/2(Хр х2) = sin(X] X2) - 0,5 = 0
Нелинейные системы
275
Эту систему уравнений еще можно решить аналитическими метода-
ми:
х} = V1 + V1 - х2/36 = 1,3608692
х, = = 0,3847532
2 бХ]
Аналитически решить систему, приведенную в самом начале разде-
ла, уже нельзя, однако подбором удается найти все же три числа,
которые, как нетрудно убедиться, являются решением данной си-
стемы:
х} = 3, х2 = 2, х3 = 1
Как же найти общий целенаправленный путь решения систем не-
линейных уравнений? Для этого рассмотрим снова один из методов
решения уравнения с одним неизвестным, а именно метод Ньюто-
на, относящийся к группе итерационных методов. Чтобы найти
приближенное решение уравнения вида Дх) = 0, выбирается на-
чальное приближение х = х0, которое потом уточняется по следую-
щей итерационной формуле:
Xj = х0 - f(x0)/f' (х0)
или для точек общего положения:
х< +1 = х, ~ fWf’W
Предполагается, что для системы уравнений вид итерационной
формулы сохраняется:
Xi+,= Xt- \F’(X^ F(X) (1)
/Х1\
X = I х2 I — вектор трех переменных
хз / /1(Хр х2, х3)\ =| /2(ХР Х2> Хз) ) “ \ /3(ХР Х2> Х3> / ' ЭХ] дх2 дх3 \ F' (X) = ^2 1 — ЭХ] дх2 дх3 | \ Э/з / ' ЭХ] дх2 дх3 ' вектор трех значений функций матрица Якоби
18*
276
Глава 11
Показатель степени — 1 для уравнения с одним неизвестным оз-
начает просто деление на f (х(); в многомерной задаче [F' (Х()]~1 —
это обращенная матрица Якоби. Умножение в формуле (1) означа-
ет умножение матрицы, обратной матрице Якоби, на вектор значе-
ний функций. Их произведение также является вектором. Этот век-
тор вычитается из вектора начального приближения Xjt ив резуль-
тате получается улучшенный вектор решения Xj+,. Такой метод не
всегда приводит к улучшенным значениям х, т. е. итерационная
процедура не всегда сходится к искомому вектору решения. Одна-
ко, чем лучше выбран начальный вектор Хо, т. е. чем ближе этот
вектор к вектору решения, тем больше вероятность успешного за-
вершения итерационной процедуры.
Основная проблема, возникающая при использовании этого ме-
тода, заключается в катастрофическом возрастании объема вычис-
лений с увеличением числа уравнений в системе. Для решения си-
стемы из п уравнений на каждой итерации необходимо рассчиты-
вать п2 частных производных — элементов матрицы Якоби и про-
водить обращение этой матрицы.
Примечание. С точки зрения оптимального программирования в данном случае
лучше не пользоваться обращением матрицы, на которое затрачивается довольно
много машинного времени. Тем более что если обе части итерационной формулы (1)
умножить слева на матрицу Якоби, то получится
(Xj - X+t) = \F'(X)]-' F(X)
F'(Xi) (Xi - X.+ i) = F'lXJFlF'tXfl-' FtXJ
F'iX) ^- Xi+l) = F(Xi) (2)
Это сокращенная форма записи системы линейных уравнений с матрицей коэффици-
ентов F' (X?) и вектором правых частей F(Xj. Вектором решения является разность
векторов старого и нового решения системы нелинейных уравнений — вектор (X —
- X. (). Отсюда можно легко рассчитать Л\+р так как вектор Xf известен.
Расчет элементов матрицы Якоби занимает очень мало машин-
ного времени, если в программе заданы п2 аналитических выраже-
ний для частных производных. Однако для сложных задач это по-
требовало-бы от пользователя большого объема кропотливой ра-
боты, которая, кроме того, служит потенциальным источником
ошибок. Поэтому все же лучше дифференцировать численным ме-
тодом, аппроксимируя производную отношением конечных прира-
щений. Это делает программу удобной в работе. Ниже дана распе-
чатка программы «НЕЛИН-НЫОТЗ» для решения систем нелиней-
ных уравнений, в которой используется рассмотренный метод.
Нелинейные системы
277
0 ВЕМ"НЕЛИН-НЬЮТОНЗ" EBERT/EDERER 840225
1 REM**********************************
2 REM** РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ ««
3 REM** МЕТОДОМ НЬЮТОНА.»» 12000»»-**
4 REM** ПОДПРОГРАММА ДЛЯ ОПИСАНИЯ •«
5 REM** ФУНКЦИИ. РАЗМЕРНОСТЬ **
£ REM** СИСТЕМЫ ЗАДАЕТСЯ В •«
7 REM** СТРОКЕ •• 20100»# **
9 REM**********************************
100 DIM Я<20,20>,В<20,20>,1К20,20>
110 DIM V<20,20>,N<20,20>
200 DIM Х<20>,Х9<20>,F<20>,F9<20>
210 DIM F0<20>,H<20>
2S0 00T0 20000
300 REM*******************************
305 REM** ОБРАЩЕНИЕ МАТРИЦЫ ••
310 REM** ИСХОДНАЯ МАТРИЦА A ««
320 REM** ОБРАЩЕННАЯ МАТРИЦА W «•
350 REM*******************************
400 FOR 1-1 TO N
420 FOR J-l TO N
460 B<I,J>-0
480 V<I,J>-0
500 IF IOJ THEN GOTO 600
520 B<I,J>-1
540 V<I,J>-1
600 NEXT J
620 NEXT I
1000 FOR Z-l TO N
1050 S-0
1100 REM ПОИСК ВЕДУЩЕГО ЭЛЕМЕНТА
1120 FOR I-Z TO N
1150 IF S>ABS<A<I,Z>> THEN GOTO 1300
1200 S-ABS<A<I,Z>>
1250 T-I
1300 NEXT I
2000 REM ОБМЕН Z-Й СТРОКИ С Т-Й
2050 FOR I«1 TO N
2100 S-A<Z,I> iR<Z,I>-A<T,I>tA<T, I >«S
2200 NEXT I
2300 IF ABS<A<Z,Z> >>1Е-Э0 THEN GOTO 2400
2350 PRINT "МАТРИЦУ ОБРАТИТЬ НЕВОЗМОЖНО": END
2400 V<Z,Z>-0iV<T,T>-0
2450 V<Z,T>-1|VCT,Z>-1
3000 REM ИСКЛЮЧЕНИЕ НЕДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ
3002 REM МЕТОДОМ ГАУССА-ЖОРДАНА
3100 FOR 1-1 TO N
3200 FOR J-l TO N
3300 IF I-Z THEN GOTO 4000
3350 IF J-Z THEN GOTO 4500
3400 U<I,j:>-Aa,J>-A<Z,J>*Ad,Z.>/A<Z,Z>
3500 GOTO 5000
4000 IF I-J THEN GOTO 4350
4050 IKI,J> —A<I,J>/A<Z,Z>
4100 GOTO 5000
4350 IKZ,Z>-1/A<Z,Z>
4400 GOTO 5000
4500 IK I,Z>-A<I,Z>/A<Z,Z>
5000 NEXT J
5050 NEXT I
5100 REM УМНОЖЕНИЕ МАТРИЦ
5110 REM В - V*B
5200 FOR 1-1 TO N
5250 FOR J-l TO N
5300 N<I,J>-0
278
Глава 11
5350 FOR K-l TO N
5400 W<I,J>-W<I,J>+V<I,K>*B<K,J>
5450 HEXT К«NEXT J«NEXT I
5500 FOR I-l TO NiFOR J-l TO N
5550
5600 NEXT J «HEXT I
6000 FOR I-l TO N
6050 FOR J-l TO N
6100 fi<I,J>-U<I,J>
6200 V<I,J>-0
6250 IF I-J THEN V<I,J>-1
6300 NEXT J «NEXT I
6500 NEXT Z
7000 REN РЕЗУЛЬТАТ УМНОЖЕНИЯ МАТРИЦЫ А НА МАТРИЦУ В
7100 FOR 1-1 ТО' N
7200 FOR J-l ТО N
7300 N<I,J>-0
7400 FOR K-l TO N
7500 W<I,J>-NCI,J>+RCI,K>*B<K,J>
7600 NEXT К«NEXT J«NEXT I
7700 RETURN
12000 REM*****************************
12010 REN** «« ФУНКЦИЯ «« **
12020 REN** ЗДЕСЬ ОПИСЫВАЮТСЯ **
12030 REN** ФУНКЦИИ, ВХОДЯЩИЕ «*
12040 REN** В УРАВНЕНИЯ СИСТЕМЫ **
12060 REM*****************************
12100 F<1>-Х<1>#Х<1>—Х<2>#Х<1>-3
12200 F<2>-X<3>*X<2>*X<1>-Х<2>*Х<2>«1.5
12300 F<3>-X<1>T3+X<2>T3+X<3>T3-36
12999 RETURN
15000 REM*********************************
15010 REN** ВЫЧИСЛЕНИЕ ЧАСТНЫХ ПРОИЗ- **
1502О REM** ВОДНЫХ (ЭЛЕМЕНТЫ МАССИВА **
15030 REM«« А( )) В ТОЧКАХ Х9( ) **
15040 REM*********************************
15100 FOR I-l ТО N«X<I>«Х9<I>«NEXT I
15200 FOR I-l ТО N «01 -RE«S<X< I1/1E5J+ IE-9
15210 X<I>-X<I>+DI«OOSUB 12000
15240 FOR J-l TO N«R<J,i:>-F<J:>
15260 NEXT J«ХСI>«X9<I>«NEXT I
15300 FOR I-l TO N«DI-RBSCXCI>/1Е5>+1Е-9
15310 X<I>«X<I>-DI«GOSUB 12000
15340 FOR J-l TO N«R<J,I>-<R<J,I>-F<J>>/2/0I
15360 NEXT J«X<I>-X9<I>«NEXT I
15999 RETURN
19000 REN********************
19010 REN** ВЫВОД ДАННЫХ ••
19020 REN********************
19100 PRINT
19120 FOR I-l TO N
19140 PRINT "X<"«I«">-"«X9<i:>«
19160 PRINT " F< " « I «*’>-" «F9< I >
19180 NEXT I«RETURN
20000 REM****************************
20010 REM** ОСНОВНАЯ ПРОГРАММА ••
20020 REN****************************
20100 N-3
20200 PRINT "ВВОД ПРИБЛИЖЕННЫХ";
20220 PRINT "ЗНАЧЕНИЙ X": PRINT
20300 FOR I-l TO N«PRINT “X<"«I«">-";
20320 IHPUT X<I>«X9<I>-X<I>«NEXT I
20400 OOSUB 15000 «REN ВЫЧИСЛ. ЧАСТИ. ПРОИЗВОДН.
20410 FOR I-l TO N«Х<I>-X9<I>«NEXT I«GOSUB 120001REM ФУНКЦИИ
20420 FOR I-l TO N1F9<I>-F<I>«NEXT I
20450 GOSUB 19000 «REN ВЫВОД ДАННЫХ
Нелинейные системы
279
20500 GOSUB 300 lREM УМНОЖЕНИЕ МАТРИЦ
20600 FOR 1-1 TO NiH<I>-0
20700 FOR J«1 TO N|H<I>«H<I>+Ы<I,J>*F9<J>
20720 NEXT Ji NEXT I
20900 OOSUB 25000 lREM ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА ОПТИМИЗАЦИИ OF
21000 FOR I«1 TO NiX9<I>«X9<I>-OF*H<I>iNEXT I
21100 GOTO 20400
25000 REM*************************************************
25001 REM** ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА ОПТИМИЗАЦИИ OF **
25002 REM*************************************************
25010 0F-.6lOF~lIFF-OF
25020 FOR I«1 TO NiX<I>«X9<I>-FF*H<I>«NEXT I
25040 S5«0iGOSUB 120001FOR I«1 TO N:S5«S5+F<I>*F<I>iNEXT I
25100 FOR J-0 TO 3iDF«DF*<~.5>TJ
25120 FF«0F+DFlS7»S5
25140 FOR 1-1 TO NiX<I>«X9<I>-FF*H<I>iNEXT I
25160 S6-0IGOSUB 12000iFOR 1-1 TO N|S6«S6+F<I>*F<I>iNEXT I
25180 IF S6<S5 THEN S5-S610F-FF
25200 IF S6<.9*S7 THEN GOTO 25120
25300 NEXT J
26990 RETURN
60000 END
RUN
ВВОД ПРИБЛИЖЕННЫХ ЗНАЧЕНИЯХ
X< 1
X< 2
X< 3
1
1
1
>«?
X< 1 >« 1 F< 1
X< 2 >- 1 F< 2
X< 3 >- 1 F< 3
X< 1 >- 3.11247993
X< 2 >- 2.1374B066
X< 3 >- 1.32498126
X< 1 >- 2.998B0293
X< 2 >- 2.00048114
X< 3 >- 1.00097311
X< 1 >- 3.00000064
X< 2 >- 2.00000014
X< 3 >- .99999955
X< 1 >- 2.99999999
X< 2 >« 2.00000002
X< 3 >- 1.00000003
X< 1 >- 3 F< 1
X< 2 >- 2.00000001
X< 3 >- 1.00000001
> —3
> — .5
>—33
F< 1 >- .0346656665
F< 2 >- 1.96168698
F< 3 >- 6.24412319
F< 1 >—6.22966606E-03
F< 2 >- 1.999301B4E-03
F< 3 > —. 0236106664
F< 1 >- 2.11596489E-06
F< 2 > —1.05798854E-06
F< 3 >- 1.67191029E-05
F< 1 >—9. 77888703E-08
F< 2 >- 8.7544322E-08
F< 3 >—2.90023224E-08
>—2.98023224E-0B
F< 2 >- 2.6077032IE-08
F< 3 >- 2.98023224E-08
BREAK IN 4000
RERDV.
RUN
ВВОД ПРИБЛИЖЕННЫХ ЗНАЧЕНИЙ X
X< 1 >«? 4
X< 2 >-? 5
X< 3 >-? 6
X< 1 >- 1.73205081
XC 2 > — 1.2080337E-13
X< 3 >- 3.13474093
F< 1 >- 1.49011612E-08
F< 2 >—6.55905588E-13
F< 3 >« 0
280
Глава 11
BREAK IN 3400
RERDV.
RUN
ВВОД ПРИБЛИЖЕННЫХ ЗНАЧЕНИЙ X
X< 1 >«? -5
X< 2 >-? 4
X< 3 >«? -2
X< 1 > — 1.7320500
X< 2 > —1.48B52505E-12
X< 3 >« 3.45370749
F< 1 > — 1.39698386E-88
F< 2 >- 8.90435214E-12
F< 3 >« 2.98023224E-0B
BREAK IN 5400
RERDV.
После описания массивов, которым соответствуют матрицы и
векторы в формулах (строки 100—210), управление передается стро-
ке 20000, с которой начинается основная программа. Участок со
строки 300 до строки 7700 занимает рассмотренная выше подпро-
грамма для обращения матриц. Исходной матрице соответствует
двумерный массив А( ), обратной — массив W( ).
После операторов REM со строки 20100, в которой задается
число уравнений в системе, начинается основная программа. Это
одна из строк, которые пользователю приходится постоянно ме-
нять, если необходимо решать какие-нибудь другие системы урав-
нений. В строках 20200—20320 у пользователя запрашивается на-
чальное приближение — N начальных значений неизвестных вели-
чин х. Эти значения присваиваются элементам массивов Х( ) и
Х9( ). Массив Х9( ) используется для 'запоминания лучших до
определенного шага итерационной процедуры значений х. В следу-
ющей строке (20400) оператором GOSUB 15000 вызывается подпро-
грамма для расчета элементов матрицы Якоби. Затем в строках
20410 и 20420 рассчитываются значения функций лучших текущих
значений индексированной переменной Х9(1), которой соответству-
ет вектор решения на данной итерации. Значения функций присваи-
ваются элементам массива F9( ). В следующей строке (20450) вы-
зывается подпрограмма для формирования и вывода данных. Эта
подпрограмма выводит на экран лучшие текущие значения х, кото-
рым соответствует одномерный массив Х9( ) вместе с N значения-
ми функций (массив F9( )), которые, вообще говоря, должны бы-
ли бы равняться нулю. Если продолжить дальше анализ основной
программы, то можно обнаружить, что в строке 20500 вызывается
подпрограмма для обращения матриц; обратной матрице соот-
Нелинейные системы
281
ветствует массив W( ). Теперь в нашем распоряжении имеются все
данные для расчета по итерационной формуле (1). Умножение мат-
рицы W, обратной матрице Якоби, на вектор значений функций F9
происходит в двух сдвоенных циклах (строки 20600—20700). Резуль-
татом является вектор Н. Значения Н(1), согласно формуле (1), ис-
пользуются для коррекции текущего вектора решения, в результате
которой рассчитываются новые улучшенные значения Х9(1). Это
происходит в цикле по параметру I (строка 21000). В отличие от
формулы (1) вычитаемое предварительно умножается на коэффици-
ент оптимизации. Этот коэффициент определяется в подпрограмме
25000, которая вызывается в строке 20900. Хотя коэффициент опти-
мизации обычно имеет значение, близкое к единице, однако при
плохом начальном приближении он может значительно отклонять-
ся от этой величины и даже может становиться отрицательным.
Таким образом, строкой 21100 итерационный цикл заканчивается и
управление передается строке 20400, с которой начинается новый
цикл.
В основной программе не предусмотрен критерий сходимости
решения, и, следовательно, пользователю надо вручную приоста-
навливать выполнение программы, как только решение станет с
его точки зрения достаточно точным. За сходимостью итерацион-
ной процедуры можно следить по значениям функций, которые
должны быть близки нулю. Если это достигнуто, то значения х в
последующих итерациях изменяются обычно незначительно.
Подпрограмма для вычисления значений функций начинается со
строки 12000 и заканчивается оператором RETURN в строке 12999.
В строках 12100, 12200 и 12300 записаны арифметические выраже-
ния, соответствующие трем функциям из первого раздела этой гла-
вы. Разумеется, эти строки надо переписывать заново и при необ-
ходимости вводить дополнительные, если предстоит решать дру-
гую систему уравнений. Однако форма записи сохраняется; функци-
ям соответствует индексированная переменная F(I), и в программе
они записываются как функции индексированной переменной Х(1).
Подпрограмма для расчета элементов матрицы Якоби занимает
участок со строки 15000 по строку 15999. Сначала в строке 15100
элементам массива Х( ) присваиваются лучшие на данный момент
значения х. В строке 15200 начинается цикл по параметру I, в кото-
ром значения Х(1) увеличиваются на одну стотысячную своей вели-
чины. Это выполняется с помощью второго оператора строки
15200 и первого оператора строки 15210. Увеличение Х(1) на очень
малую величину 1Е - 9 необходимая перестраховка на случай, если
одно или несколько из значений Х(1) равны нулю. После того как
282
Глава 11
Х(1) уже увеличено на DI, оператор GOSUB 12000 вызывает под-
программу для вычисления значений функций. Найденные значения
в следующих строках присваиваются элементам массива А( ). По-
сле оператора NEXT J индексированной переменной Х(1) возвраща-
ются ее прежние значения — Х9(1) и цикл по параметру I заверша-
ется. В следующих четырех строках (15300—15360) выполняются
точно такие же вычисления, но с уменьшенными значениями Х(1).
Частные производные dfj/dxi вычисляются в строке 15340 по при-
ближенной формуле:
х,- + DI, ...) - /(..., х,-» )
DI
Там же значения частных производных dfj/dXj присваиваются эле-
ментам массива A(J, I). При выходе из цикла по I оператор
Х(1) = Х9(1) возвращает Х(1) первоначальные оптимальные значе-
ния.
В подпрограмме для вычисления коэффициента оптимизации
значение этого коэффициента принимается равным 1 и, исходя из
значений Х9(1), рассчитываются значения Х(1) (строка 25020). По-
том рассчитываются значения функций и сумма их квадратов, зна-
чение которой присваивается переменной S5 (строка 25040). Далее в
цикле по параметру J (строки 25100—25300) коэффициент коррек-
ции после каждой итерации изменяется на величину 0,6 •(—0,5)J.
После коррекции с использованием нового значения коэффициента
коррекции опять вычисляются значения функций и сумма их ква-
дратов (строки 25140 и 25160). Если эта сумма уменьшилась по
сравнению с ее предыдущим значением, то данный коэффициент
коррекции становится коэффициентом оптимизации (строка 25180).
Если уменьшение суммы квадратов значений функций превышает
10%, то делается еще одна попытка уменьшить эту сумму путем
аналогичного изменения. Однако теперь на каждом шаге итераци-
онной процедуры изменение коэффициента коррекции в два раза
меньше, чем раньше (цикл по параметру J).
Из приведенного контрольного примера, точное решение кото-
рого известно, видно, что, хотя при плохом начальном приближе-
нии сначала получаются явно неудовлетворительные решения, в по-
следующих итерациях результаты довольно быстро сходятся к точ-
ному решению. При очень уж неудачном начальном приближении
результаты могут расходиться. Значения функций после каждой
итерации тогда не уменьшаются, а увеличиваются до тех пор, пока
выполнение программы не будет автоматически приостановлено
из-за переполнения (слишком большие числа). После таких (или
Нелинейные системы
283
аналогичных) неудачных попыток программу надо запустить зано-
во, но уже с другим начальным приближением.
Задание 164. Решите следующую систему уравнений:
х2 + у2 = х3 + у3
х-у + log(xy) + log(2) = log(x + у) + 1
Если при решении этой системы вы зададите в качестве начального приближе-
ния одинаковые значения х и у, то ЭВМ выдаст явно неудовлетворительные резуль-
таты, даже если начальное приближение близко к истинному решению. Однако если
начальные значения х и у хоть немного различаются, то таких трудностей не возни-
кает.
Задание 165. Решите следующую систему уравнений:
х + у + z = yz
x-yz - z2 - z
X2 + у2 + z2 = 1-y
Задание 166. Дана следующая система химических реакций:
ki
А — продукт 1 (термическая реакция)
к2
А — продукт 2 (фотохимическая реакция)
Из этой схемы следует кинетическое уравнение:
^ = -(*, + *2) [А] = - (к0 , e"£,/RT + к2у [А]
Примем k()i = 1 • 1012 1/с.
При Т = 300 К время полупревращения вещества А составляет 0,5985 с, при
Т = 350 К — 0,14 с. Рассчитайте с помощью программы «НЕЛИН-НЫОТЗ» энер-
гию активации и константу скорости фотохимической реакции к2.
Указание: г1/2 = Iog2/(A, + к2)
Задание 167. Уравнение Ван-дер-Ваальса имеет вид
(р + а/У2)-(У - b) = nRT
Надо определить константы Ван-дер-Ваальса для этана с помощью программы
«НЕЛИН-НЫОТЗ», исходя из определенных экспериментально значений молярных
объемов при двух значениях давления.
Если входящие в уравнение величины имеют размерность литр, атмосфера,
моль и градус Кельвина, то универсальная газовая постоянная будет равна
0,08206 л-атм/(моль- К).
Экспериментальные данные для 1 моль этана при 400 К:
р = 3,2486 атм при V = 10 л
р = 29,577 атм при V = 1 л
Если известны более чем две пары значений давления и объема, то система
уравнений будет переопределенной. Для определения параметров таких систем ис-
пользуется нелинейная регрессия, которая будет рассмотрена ниже.
284
Гаава II
Задание 168. Дана последовательная реакция
Скорость расходования и накопления вещества В описывается формулой
d(B] , l. mi . -E,/RT гд, , -Ег/НТ
г = —— = fc,• [А] - Лг2-[В] = fc0I-e -[А] - Аг02-е 2 -[В]
<и
Скорость реакции измерена при четырех различных концентрациях и температу-
рах (см. табл.). Рассчитайте с помощью программы «НЕЛИН-НЫОТЗ» четыре па-
раметра уравнения Аррениуса kQ р Е{, kQ2, Е2. Правильное решение этого задания:
fc01 = 2-1012 Е,/Л = 9500
fc0’2 = 1- Ю13 E2/R = 10000
Зная решение, вы можете опытным путем установить, насколько грубым может
быть начальное приближение.
[A J [В] Т Г
1 1 300 +1,966• 10*3
1 2 310 -0,0975
2 1 320 +0,2435
1 1 330 -0,06219
Задание 169. Напишите программу для решения системы нелинейных уравнений
методом Ньютона, в которой использовался бы рассмотренный в примечании на
с. 276 алгоритм, исключающий обращение матриц.
Замените подпрограмму для обращения матриц на подпрограмму, решающую
системы линейных уравнений методом Гаусса — Жордана. Остальные подпрограм-
мы оставьте без изменений. Кроме того, потребуется внести изменения в основную
программу в соответствии с итерационной формулой (2) (с. 276).
Введите в основную программу критерий сходимости для автоматического вы-
хода из итерационной процедуры.
11.2. Нелинейная регрессия
Пусть по некоторым теоретическим соображениям дано уравне-
ние, связывающее определяемые экспериментально величины х и у,
а также физические параметры кх, к2, .... кп:
у = f(x, kv к2, ..., к„)
Кроме того, известно ш пар экспериментальных значений (xt, у).
Исходя из заданного уравнения и экспериментальных данных, необ-
ходимо определить значения параметров kt, к2, ..., кп таким обра-
Нелинейные системы
285
зом, чтобы сумма квадратов отклонений экспериментальных значе-
ний у от теоретических была минимальна.
Пример. Дано уравнение изотермы адсорбции для двух различных центров ад-
сорбции:
Л, -р к, -р
9 = -----(1 - к,)
1 + к{-р 1 + к^р
9 — степень заполнения поверхности; р — давление газа над поверхностью.
Из экспериментально полученного ряда значений (9jt р,) необходимо определить
параметры изотермы kt, к2, ку
Задача состоит в том, чтобы найти такие значения параметров, при которых
сумма S будет иметь наименьшее зиачеиие:
т
S = У (у. — у. I2
те°Р Л, эксп'
i = 1
s = £ [/(%;, kv к2.кп) - yf
i = I
В точке минимума суммы квадратов отклонений все п частных производных от
S по параметрам к^ равны нулю:
9S 9S 9S
— = ---- = ... = - = 0
Эк, дк, дк
1 L И
После дифференцирования по параметрам kj получаем п уравнений, причем J-e
уравнение выглядит следующим образом:
3S Л д/(х,, ..., к )
........-'.1—»
Для определения неизвестных параметров Jt(, к2, ..., кп надо решить систему из
п нелинейных уравнений.
Для решения этой задачи можно привлечь уже имеющуюся про-
грамму «НЕЛИН-НЫОТЗ» в качестве основы для нелинейного ре-
грессионного анализа.
Для удобства пользователей частные производные dS/dkj рас-
считывают численным способом. Это избавляет пользователей от
необходимости вносить в программу большое количество громозд-
ких арифметических выражений. Численное дифференцирование
происходит точно так же, как и в программе «НЕЛИН-НЫОТЗ».
Рассмотренный метод использован в программе «НЕЛИН-
РЕГРЗ»:
286
Гпава 11
0 REM "НЕЛИН—РЕГРЗ" EBERT/EDERER 831212
1 REM********************************************
2 REM** НЕЛИНЕЙНАЯ РЕГРЕССИЯ.В ЭТОЙ ПРОГРАММЕ **
3 REM** ИСПОЛЬЗОВАНА ПРОГРАММА"НЕЛИН-НЬЮ- **
4 REM** ТОНЗ" ДЛЯ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ **
5 REM** #######«#################«#############»»
6 REM** УРАВНЕНИЕ РЕГРЕССИИ ЗАДАНО В СТРОКЕ **
7 REM** ##50000## ЧИСЛО ПАРАМЕТРОВ В СТРОКЕ **
8 REM** ## 20100«« ДАННЫЕ ВВОДЯТСЯ **
9 REM** ПОПАРНО СО СТРОКИ **
10 REM* ## 60000 ## **
19 REM********************************** *********
100 DIM А<20,20>,В<20,20>,U<20,20>
110 DIM V<20,20>,Ы<20,20>
200 DIM Х<20>,Х9<20>,F<20>,F9<20>
210 DIM F0<20>,HC20>.K<20>
220 DIM XX<100>,VY<100>
250 GOTO 20000
300 REM*******************************
305 REM** ОБРАЩЕНИЕ МАТРИЦЫ **
310 REM** ИСХОДНАЯ МАТРИЦА A **
320 REM** ОБРАЩЕННАЯ МАТРИЦА W **
350 REM*******************************
400 FOR I-l TO N
420 FOR J-l TO N
460 8<I,J>«0
480 V<I,J>-0
500 IF 1OJ THEN GOTO 600
520 8<I,J>-1
540 V<I,J>-1
600 NEXT J
620 NEXT I
1000 FOR Z-l TO N
1050 S-0
1100 REM ПОИСК ВЕДУЩЕГО ЭЛЕМЕНТА
1120 FOR I-Z TO N
1150 IF S>ABS<A<I,Z>> THEN GOTO 1300
1200 S-ABS<A<I,Z>>
1250 T-I
1300 NEXT I
2000 REM ОБМЕН Z-Й СТРОКИ С Т-Й
2050 FOR I-l TO N
2100 S-A<Z,I> sA<Z,I>-A<T,i:> :A<T,I>-S
2200 NEXT I
2300 IF ABS<A<Z,Z>>>lE-30 THEN GOTO 2400
2350 PRINT "МАТРИЦУ ОБРАТИТЬ НЕВОЗМОЖНО". END
2400 V<Z,Z>«0|VCT,T>«0
2450 V<Z,T>-1sV<T,Z>-l
3000 REM ИСКЛЮЧЕНИЕ НЕДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ
3002 REM МЕТОДОМ ГАУССА-ЖОРДАНА
3100 FOR I-l TO N
3200 FOR J-l TO N
3300 IF I-Z THEN GOTO 4000
3350 IF J-Z THEN GOTO 4500
3400 U<I,J>-A<I,J>-ACZ,J>*A<I,Z>/A<Z,Z>
3500 GOTO 5000
4000 IF I-J THEN GOTO 4350
4050 U<I,J>— A<I,J>/A<Z,Z>
4100 GOTO 5000
4350 U<Z,Z>-1/A<Z,Z>
^400 GOTO 5000
4500 U<I,Z>-A<I,Z>/A<Z,Z>
5000 NEXT J
5050 NEXT I
5100 REM УМНОЖЕНИЕ МАТРИЦ
5110 REM В - V*B
Нелинейные системы
287
5200 FOR 1-1 ТО N
5250 FOR J-l TO N
5300 W<I,J>-0
5350 FOR K-l TO N
5400 W<I,J>-H<I,J>+V<I,K>*B<K,J>
5450 NEXT КsNEXT JiNEXT I
5500 FOR 1-1 TO NiFOR J-l TO N
5550 B<1,J>=H<1,J>
5600 NEXT JsNEXT I
6000 FOR 1-1 TO N
6050 FOR J=1 TO N
6100 A<I,J>-U<I..J>
6200 V<l,J>-0
6250 IF I-J THEN V<I,J>=1
6300 NEXT JsNEXT I
6500 NEXT Z
7000 REN РЕЗУЛЬТАТ УМНОЖЕНИЯ МАТРИЦЫ А НА МАТРИЦУ В
7100 FOR 1-1 ТО N
7200 FOR J-l TO N
7300 U<I,J>-0
7400 FOR K-l TO N
7500 W<I,J>-UI<I,J>+R<I,K>*B<K,J>
7600 NEXT КsNEXT JsNEXT I
7700 RETURN
12000 REN*****************************
12010 REN** «4 ФУНКЦИЯ «4 **
12020 REN** ЗДЕСЬ ОПИСЫВАЮТСЯ **
12030 REN** ФУНКЦИИ, ВХОДЯЩИЕ **
12040 REN** В УРАВНЕНИЯ СИСТЕМЫ **
12050 REN** (DS/DK(J>) **
12060 REN*****************************
12100 FOR J-l TO NsK<J>-X<J>sNEXT J
12200 GOSUB 30000sF0-SS
12300 FOR J-l TO NsDJ-ABS<X<J>/lE4>+lE-8
12400 K<J>-K<J>+DJsGOSUB 30000
12410 F<J>-SSsK<J>-K<J>-2*DJsGOSUB 30000
12500 F<J>—<F<J>—SS>/2/DJ
12600 K<J>-X<J>sNEXT J
12999 RETURN
15000 REN*********************************
15010 REN** ВЫЧИСЛЕНИЕ ЧАСТНЫХ ПРОИЗ- **
15020 REN** ВОДНЫХ (ЭЛЕМЕНТЫ МАССИВА **
15030 REN** А ( ) ) В ТОЧКАХ Х9 ( ) **
15040 REN** (DIDS/DK (J ) ) /DK (I ) ) **
15050 REN*********************************
15100 FOR 1-1 ТО NsX<I>-Х9<I>sNEXTI
15120 GOSUB 12000 sREN ФУНКЦИИ
15160 FOR 1-1 TO NsF9<I>-F<I>sNEXT I
15200 FOR 13-1 TO NsDI-ABS<X<I3>/lE4>+lE-8
15210 X<I3>-X<I3>+DIsGOSUB 12000
15240 FOR J3-1 TO NsA<J3,I3>-F<J3>
15260 NEXT J3sX<I3>—X9<I3>sNEXT 13
15300 FOR 13-1 TO NsDI-ABS<X<I3>/lE4>+lE-8
15310 X<I3>-X<I3>-DIsGOSUB 12000
15340 FDR J3-1 TO NsA<J3,I3>-<R<J3,I3>-F<J3>>/2/DI
15360 NEXT J3sX<I3>-X9<I3>sNEXT 13
15999 RETURN
19000 REN*********************
19010 REN** ВЫВОД ДАННЫХ **
19020 REN*********************
19100 PRINT
19120 FOR 1-1 TO N
19140 PRINT"K< " л I » " > -" ,X9< I > > ,SQR<ABS<U< I , I >*SS/<NP-N> > >
19160 REN PRINT" F<"sIs">«";F9<I>
19180 NEXTI
19185 PRINT "СУММА' КВАДРАТОВ ОТКЛОНЕНИЙ ="; SS
288
Глава 11
19190 RETURN
20000 REN***************************
20010 REN** ОСНОВНАЯ ПРОГРАММА **
20020 REM***************************
20100 N-2
20130 FF=1:SM=1E30
20150 GOSUB 25000
202О0 PRINT "ВВОД НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ"
20220 PRINT
20300 FOR 1=1 TO N:PRINT"K<";Is"> = ">
20320 INPUT X< I > :X9< IX< I > «NEXT I
20400 GOSUB 15000 sREM ВЫЧИСЛ. ЧАСТИ. ПРОИЗВОДНЫХ
20450 REM GOSUB 19000 sREM ВЫВОД ДАННЫХ
20500 GOSUB 300: REM ОБРАЩЕНИЕ МАТРИЦЫ
20600 FOR 1 = 1 TO N:H<i:>«0
20700 FOR J«1 TO N sH< I >«H< I :>+W< I , J>*F9< J>
20720 NEXT J:NEXT I
20750 GOSUB 19000 sREM ВЫВОД ДАННЫХ
20800 GOSUB 35000 iREM КОЭФФИЦИЕНТ ОПТИМИЗАЦИИ
21000 FOR 1=1 TO N:X9<I>=X9<I>-FF*H<I>sNEXT I
21100 GOTO 20400
25000 REM**************************
25010 REM** СЧИТЫВАНИЕ ДАННЫХ**
25015 REM** В XXO И WO **
25080 REM**************************
25100 READ NP
25200 FOR 1=1 TO NPsREAD XX<I>,YV<I>
25300 NEXT I
25400 RETURN
30000 REM*******************************
30010 REM** ВЫЧИСЛЕНИЕ СУММЫ **
30020 REM** КВАДРАТОВ ОТКЛОНЕНИЙ **
30100 REM*******************************
30200 SS=0
30300 FOR 1=1 TO NP
30350 X»XX<I> :GOSUB 50000 sV=V-W< I >
30400 SS«SS+V*ViNEXT I
30500 RETURN
35000 REM******************************
35010 REM** ВЫЧИСЛЕНИЕ КОЭФФИ- «*
35020 REM** ЦИЕНТА ОПТИМИЗАЦИИ FF **
35100 REM******************************
35200 FF«.60iFM=0 »DF«.5
35310 GOSUB 35600
35320 IF SS<SM THEN SM-SSsFM-FFsFF=FF+DFsGOTO 35310
35330 FF-FM-DF
35335 GOSUB 35600
35340 IF SS<SM THEN SM-SSsFM-FFsFF-FF-DFiGOTO 35335
35360 FOR J=1 TO 7
35380 DF-DF/2
35390 FF-FM+DFsGOSUB 35600
35400 IF SS<SM THEN SM=SSsFM-FFsGOTO 35430
35410 FF-FM-DF:GOSUB 35600
35420 IF SS<SM THEN SM-SSsFM-FF
35430 NEXT J
35450 FF-FM
35500 RETURN
35600 FOR 1-1 TO NsK<I>-X9<I>-FF*H<I>sNEXT I
35620 GOSUB 30000
35630 REM PRINT SS,FF
35650 RETURN
50000 REM************************
50010 REM** УРАВНЕНИЕ **
50020 REM** РЕГРЕССИИ **
50100 REM************************
Нелинейные системы
289
50200 V- КС1>*ЕХРС-КС2>*Х>+КС1>*КС2>
50999 RETURN
60000 REN*****************************
60010 REN** ЧИСЛО ПАР ДАННЫХ **
60020 REN** ДАННЫЕ **
60030 REN** ПОПАРНО X.Y **
60100 REN*****************************
61000 DATA
62010 DATA
62020 DATA
62030 DATA
62040 DATA
62050 DATA
62060 DATA
63999 END
6
0,2
1,1.368
2,1.1353
3,1.04979
0.5,1.6065
1.5,1.2231
RUN
ВВОД НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
K< 1 > - ? 2
КС 2 > - ? 3
КС 1 >« .95522558 +/- 1.05701092Е-03
КС 2 >- 1.08858183 +/- 1.7068308Е-03
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - 1.09920664Е-03
КС 1 >« .997126581 +/- 2.05415639Е-03
КС 2 >- 1.0033201 +/- 4.03904685Е-03
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ -1.72847357Е-05
КС 1 >- .999976509 +/- 7.02568177Е-05
КС 2 >- 1.00006179 +/- 1.30844947Е-04
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ- 1.97393405Е-08
КС 1 >- 1.00004353 +/- 6.59745293Е-05
КС 2 >- .999923981 +/- 1.2243266Е-04
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ-1 . 66993773Е-08
КС 1 >- 1.00004354 +/- 6.59757223Е-05
КС 2 >- .999923961 +/- 1.22425229Е-04
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ -1.669937436-08
BREAK IN 30300
READV.
По сравнению с программой «НЕЛИН-НЫОТЗ» в данной про-
грамме имеется дополнительно подпрограмма (строки 30000—
30500), вычисляющая сумму квадратов отклонений, значение кото-
рой присваивается переменной SS. Величины x(. и yt соответствуют
переменным ХХ(1) и YY(I). Для расчета теоретического значения у
по уравнению регрессии в строке 30350 вызывается подпрограмма
50000. В данной программе уравнение регрессии имеет вид
у = к^-е~к^ + к^кг
Это же уравнение в виде строки программы выглядит так:
50200 Y = К(1)*ЕХР(—К(2)*Х) + К(1)*К(2)
19-81
290
Гпава II
Частные производные суммы квадратов отклонений dS/dkj рас-
считываются приближенно как отношения конечных приращений
соответствующих величин. Для этого вычисляется сумма квадра-
тов отклонений для текущего значения параметра kjt значение ко-
торой присваивается переменной F0 (строка 12200). Затем параметр
kj увеличивается на малую величину DJ и снова вычисляется сумма
квадратов отклонений (строки 12300 и 12400). После того как значе-
ние суммы присвоено переменной F(J), рассчитывается другое зна-
чение суммы с новым, уменьшенным на DJ значением параметра ку
(строка 12410). Разность сумм, деленная на 2*DJ, является прибли-
женным значением частной производной dS/dkj, которое присваи-
вается переменной F(J) (строка 12500).
В первой строке этой подпрограммы (строка 12100) вводится
новая переменная K(J), для которой K(J) = X(J). Это делается по-
тому, что в программе «НЕЛИН-НЫОТЗ», без изменений исполь-
зуемой в программе «НЕЛИН-РЕГРЗ», в роли известной величины
выступает переменная X(J), в то время как в этой программе неиз-
вестной является переменная K(J).
Основная программа, начинающаяся со строки 20000, в целом
совпадает с основной программой программы «НЕЛИН-НЫОТЗ».
Изменены только идентификаторы переменных, соответствующих
неизвестным величинам — K(J) вместо X(J). Подпрограмма 19000
для формирования и вывода выходных данных в первый раз вызы-
вается в строке 20150. При этом выводятся на экран текущие значе-
ния параметров K(J), их стандартные отклонения и сумма квадра-
тов отклонений.
В строке 20800 вызывается подпрограмма 35000 для определе-
ния оптимального значения коэффициента коррекции FF. Расчет
происходит практически так же, как и в программе «НЕЛИН-
НЫОТЗ». Ищется такое значение коэффициента FF, при котором
сумма квадратов отклонений имеет наименьшее значение. Поиск
осуществляется в цикле по переменной J (строки 35360—35430),
причем после каждой итерации интервал поиска уменьшается в два
раза. В данной программе коэффициент FF вычисляется довольно
точно благодаря тому, что проводится семь итераций. Однако за
это приходится расплачиваться увеличением времени счета.
В начале основной программы в строке 20150 вызывается под-
программа 25000 для ввода данных. Значения х(. и у( присваиваются
переменным ХХ(1) и YY(I). Числовой материал вводится с по-
мощью оператора DATA. Первым считывается число пар значений
х и у, потом — значения xjt уг
Нелинейные системы
291
В заключение повторим, чтб именно пользователю надо изме-
нить в программе «НЕЛИН-РЕГРЗ» для решения его собственной
регрессионной задачи: а) во всех операторах DATA, начиная со
строки 60000, надо задать соответствующее число пар значений х, у
и сами значения х и у; б) в строке 20100 с помощью оператора при-
сваивания задать число определяемых параметров регрессии; в) в
строке 50200 надо записать арифметическое выражение, соответст-
вующее уравнению регрессии; г) кроме того, для экономии машин-
ного времени, если позволяет содержание задачи, можно изменить
подпрограмму 35000, рассчитывающую коэффициент оптимизации
FF.
Из примера, приведенного вместе с текстом программы, видно,
что сумма квадратов отклонений после каждого итерационного ци-
кла уменьшается почти на порядок. При решении реальных задач
так бывает не всегда. Рассмотренный числовой пример является де-
монстрационным, входные данные смоделированы и исходные точ-
ки точно лежат на теоретической кривой. Из-за обычных погреш-
ностей эксперимента сумма квадратов отклонений часто не обра-
щается в нуль. Однако частные производные dS/dkj должны стре-
миться к нулю при условии, что уравнение регрессии адекватно
описывает эксперимент.
Задание 170. Температурная зависимость константы скорости реакции первого
порядка описывается уравнением Аррениуса. Кроме того, получены значения кон-
станты скорости при различных температурах (см. табл.). Определите
предэкспоненциальный множитель и энергию активации Еа как с помощью линейной
регрессии, используя линейную зависимость log (А:) от 1/Г, так и с помощью нели-
нейной регрессии по программе «НЕЛИН-РЕГРЗ». Для нелинейной регрессии лучше
-1 -8 -7 л . -б -5 _ .^-4 . -3 -2
к,с 4-10 7-1O 8*10 7-1O 5’10 3-10 2*10
Т.К 3 20 340 360 3 80 400 4 20 440
пользоваться хорошим начальным приближением, которое в данном случае можно
легко получить из линейной регрессии. На контрольном примере, в котором вход-
ные данные рассчитаны по уравнению Аррениуса, вы можете убедиться, что резуль-
таты обоих вариантов анализа экспериментальных данных совпадают тем лучше,
чем точнее экспериментальные значения соответствуют уравнению Аррениуса, т. е.
чем меньше погрешности измерений. Не совпадающие результаты линейного и нели-
нейного регрессионного анализа можно объяснить тем, что в этих алгоритмах мини-
мизируются разные функционалы.
Задание 171. Получены 10 пар экспериментальных значений, которые описыва-
ются изотермой адсорбции, приведенной на с. 285 (см. табл.). С помощью програм-
е 0,05 0,09 0,15 0,23 0,34 0,48 0,64 0,77 0,В6 0,93
р 2 4 8 15 30 60 130 250 500 1000
19»
292
Глава 11
мы «НЕЛИН-РЕГРЗ» определите параметры Агр к2 ик,. При решении этой задачи
используйте коэффициент оптимизации, существенно меньший чем единица.
Если все значения у измерены с одинаковой относительной точностью, то, по-
скольку программа минимизирует сумму квадратов отклонений, надо учитывать
также и абсолютные значения у. Поэтому при обработке экспериментальных дан-
ных целесообразно учитывать весовые коэффициенты значений. Тогда вместо двух
чисел, соответствующих одной экспериментальной точке, вводятся три числа, при-
чем третье число — это весовой коэффициент. Значения этого коэффициента присва-
иваются элементам массива WW( ) (не забудьте в начале программы описать этот
массив). При вычислении суммы квадратов отклонений в строке 30400 каждое слага-
емое надо умножить на соответствующий весовой коэффициент WW(I).
Введем другой коэффициент оптимизации FG. Добавьте строку 15900 со следую-
щими операторами:
15900 FOR 13 = 1 ТО N: А(13, 13) = А(13, 13) + FG: NEXT 13
Новый коэффициент оптимизации должен быть больше нуля. Можно также для
каждого значения 13 в данной точке использовать свой собственный коэффициент
оптимизации FG(I3). Этот метод известен в литературе как метод Гаусса — Ньюто-
на. Если новый коэффициент оптимизации равен нулю, то метод Гаусса — Ньютона
превращается в наш старый метод Ньютона. Хотя метод Гаусса — Ньютона надеж-
нее, сходимость достигается обычно медленнее.
Бывает, что математический минимум суммы квадратов отклонений соответ-
ствует таким значениям параметров, которые не имеют физического смысла. Появ-
ление отрицательных значений параметров можно предотвратить, если в формулах
использовать ие К( J), a ABS (К( J)). Другие, не имеющие физического смысла значе-
ния можно устранить с помощью так называемых штрафных функций. Так, напри-
мер, в последнем задании параметр к2 задает долю различных поверхностей. Его
значение должно лежать в интервале от нуля до единицы. Чтобы добиться этого,
подпрограмма, рассчитывающая сумму квадратов отклонений, запрашивает значе-
ние к2. Если значение к2 больше допустимого, то к сумме квадратов отклонений
прибавляется, например, увеличенное в 104 раз значение к2. Этот прием возвращает
значение к2 в заданную область.
Задание 172. Если вообще нет никаких разумных соображений о порядке величи-
ны неизвестного параметра, то упомянутые выше методы обычно ие приводят к ис-
комому решению. Надо использовать другие приемы. Довольно медленный, ио лег-
ко реализуемый программными средствами метод заключается в том, что задается
некоторая область значений параметра, в этой области произвольно выбирается его
значение и рассчитывается сумма квадратов отклонений, которая сравнивается с
аналогичной суммой, соответствующей лучшей комбинации параметров. Если новая
сумма меньше, то новая комбинация параметров считается теперь лучшей. Этим
так называемым методом Монте-Карло имеет смысл пользоваться лишь в тех слу-
чаях, когда все другие методы неэффективны.
Есть еще один очень хороший метод. Все параметры, кроме первого, полагают
известными и, варьируя этот первый параметр, ищут минимум суммы квадратов
отклонений. Для функции с одной независимой переменной можно использовать ме-
тод Ньютона или метод деления отрезка пополам. Если найден минимум функцио-
нала для первого параметра, то значение этого параметра на данном этапе считает-
ся наилучшнм и минимизируется сумма квадратов отклонений по второму парамет-
ру. Эта процедура повторяется по всем параметрам, входящим в уравнение регрес-
сии. Если получены неудовлетворительные результаты, то процедуру повторяют,
начиная опять с первого параметра. Напишите и опробуйте программу, использую-
щую этот метод.
Нелинейные системы
293
Если в процессе решения задачи встретятся серьезные трудности, например, та-
кие, как слишком большое время счета, или возникнут проблемы, связанные со схо-
димостью метода (иногда вообще невозможно однозначно определить значение па-
раметра, что при постановке задачи может быть и неочевидным), то обратитесь к
специалистам по вычислительной математике.
Задание 173. Расширьте программу «НЕЛИН-НЫОТЗ» так, чтобы уравнение ре-
грессии получалось в результате решения дифференциального уравнения.
Для этого подпрограмму 50000, описывающую уравнение регрессии, надо заме-
нить на программу для решения дифференциальных уравнений.
Задание 174. Взяв за основу программу для нелинейного регрессионного анали-
за, напишите программу для решения многомерной регрессионной задачи. В уравне-
ние многофакторной регрессии входит не одна независимая переменная х и парамет-
ры кр
у = F(x, kvk2.....к„)
а несколько независимых переменных и параметры к с.
у = F(xl, х2..хт, kv к2, .... кп)
Дан набор экспериментальных значений (у;, xlt, х2., ..., хт.). Надо найти значе-
ния параметров Агр к2, ..., кп.
Задание 175. Напишите программу для решения нелинейной регрессионной зада-
чи, с помощью которой можно было бы определять параметры не одной кривой, а
набора (пучка) кривых. В уравнение регрессии, соответствующее этим кривым, мо-
жет входить один или в общем случае несколько параметров.
Если по одному и тому же уравнению регрессии обсчитывается
обширный экспериментальный материал, то для экономии машин-
ного времени можно посоветовать задать частные производные
суммы квадратов отклонений по параметрам в аналитическом
виде:
т
s= £ {/, - Ж, х,)р (1)
i = 1
Первые частные производные, которые приравниваются нулю,
имеют вид
U- - /(Г, х,)}
ЭЖ х,.)
(2)
Если сократить на 2 и найти вторые частные производные, то по-
лучится
d2S
dkjdkt '
т
-2. £ U.-/(r,xf)|.2Wi)
dkfikj
. V УУ. *,). УУ. (3,
' дк, dkj
294
Глава 11
Приведенная ниже программа «НЕЛИН-РЕГР» использует
частные производные в аналитическом виде. Однако математиче-
ский алгоритм остался таким же, как и в программе «НЕЛИН-
РЕГРЗ».
0 REM "НЕЛИН-РЕГР" EBERT/EDERER 840102
1 REM*****************************************
2 REM** НЕЛИНЕЙНАЯ РЕГРЕССИЯ.В ПРОГРАММЕ **
3 REM** ИСПОЛЬЗУЕТСЯ МЕТОД НЬЮТОНА ДЛЯ **
4 REM** РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ.ПЕРВЫЕ **
5 REM** И ВТОРЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ,ВХО- **
6 REM** ДЯЩЕЙ В УРАВНЕНИЕ РЕГРЕССИИ, ЗАДА- **
7 REM** НЫ АНАЛИТИЧЕСКИ В ПОДПРОГРАММАХ **
В REM** 44 50000 44 И 44510 00:4#ДАННЫЕ ВВОДЯТСЯ **
9 REM** ПОПАРНО СО СТРОКИ 446000044, ЧИСЛО **
10 REM* ПАРАМЕТРОВ ЗАДАНО В СТРОКЕ 442010044 **
19 REM*********************************** *****
100 DIM Я<20,20> ,В<20,20> ,U<20,20>
110 DIM V<20,20>,Ы<20,20>
200 DIM Х<20>,Х9<20>,F<20>,F9<20>
205 DIM Fl<20>,F2<20,20>
210 DIM F0<20>,H<20>,K<20>
220 DIM XX<100>,YY<100>
250 GOTO 20000
300 REM*******************************
305 REM** ОБРАЩЕНИЕ МАТРИЦЫ **
310 REM»» ИСХОДНАЯ МАТРИЦА A **
320 REM»» ОБРАЩЕННАЯ МАТРИЦА W **
350 REM*******************************
400 FOR 1-1 TO N
420 FOR J-l TO N
460 B(I,J>.0
480 V<I,J>-0
500 IF IOJ THEN GOTO 600
520 B<I,J>-1
540 V<I,J>-1
600 NEXT J
620 NEXT I
1000 FOR Z-l TO N
1050 S—0
1100 REM ПОИСК ВЕДУЩЕГО ЭЛЕМЕНТА
1120 FOR I-Z TO N
1150 IF S>RBS<fi<I,Z>> THEN GOTO 1300
1200 S-ABS<A<I,Z>>
1250 T-I
1300 NEXT I
2000 REM ОБМЕН Z-Й СТРОКИ С Т-Й
2050 FOR 1-1 TO N
2100 S-A<Z,I>|R<Z,I>-A<T,I>|A<T,I>-S
2200 NEXT I
2300 IF ABS<fi<Z,Z>>>lE-30 THEN GOTO 2400
2350 PRINT "МАТРИЦУ ОБРАТИТЬ НЕВОЗМОЖНО": END
2400 V<Z,Z>-0iV<T,T>-0
2450 V<Z,T>-1|V<T,Z>-1
3000 REM ИСКЛЮЧЕНИЕ НЕДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ
3002 REM МЕТОДОМ ГАУССА-ЖОРДАНА
3100 FOR 1-1 TO N
3200 FOR J-l TO N
3300 IF I-Z THEN GOTO 4000
3350 IF J-Z THEN GOTO 4500
3400 U<I,J>-R<I,J>-A<Z,J>*A<I,Z>/A<Z,Z>
3500 GOTO 5000
Нелинейные системы
295
4000 IF I-J THEN GOTO 4350
4050 U<I,J>—A<I,J>/A<Z,Z>
4100 GOTO 5000
4350 U<Z,Z>-1/A<Z,Z>
4400 GOTO 5000
4500 U<I,Z>-A<I,Z>/A<Z,Z>
5000 NEXT J
5050 NEXT I
5100 REM УМНОЖЕНИЕ МАТРИЦ
5110 REM В - V*B
5200 FOR I-l TO N
5250 FOR J-l TO N
5300 H<I,J>-0
5350 FOR K-l TO N
5400 H<I,J>-H<I,J>+V<I,K>*B<K,J>
5450 NEXT KtNEXT J iNEXT I
5500 FOR I-l TO NiFOR J-l TO N
5550 B<I,J>—Ы<I,J>
5600 NEXT JiNEXT I
6000 FOR I-l TO N
6050 FOR J-l TO N
6100 A< I,J)-U<I,J)
6200 V<I,J>-0
6250 IF I-J THEN V<I,J>-1
6300 NEXT JiNFXT I
6500 NEXT Z
7000 REM РЕЗУЛЬТАТ УМНОЖЕНИЯ МАТРИЦЫ А НА МАТРИЦУ В
7100 FOR I-l ТО N
7200 FOR J-l TO N
7300 H<I,J>-0
7400 FOR K-l TO N
7500 U<I,J>-U<I,J>+fl'I,K>*B<K,J:<
7600 NEXT КiNEXT J:NEXT I
7700 RETURN
16000 REM*******************************
16010 REM** ВЫЧИСЛЕНИЕ ЧАСТНЫХ ПРО- **
16020 REM** ИЗВОДНЫХ13ЛЕМЕНТЫ MAC- **
16030 REM** СИВА A ( )) В ТОЧКАХ X9 ( ) **
16040 REM*******************************
16100 SS-OtFORI-tTONiF9<I>-0tK<I>-X9<I> »FORJ-tTONs«<I ,J)-0-.NEXTJ iNEXTI
16150 FOR IP-1 TO NP
16160 X-XX<IP>iGOSUB 50000
16180 DI-VV< IP>-V sSS-SS+DI*DI
16200 FOR 13-1 TO N
16220 F9<I3>-F9<I3>-DI*F1<I3>
16240 FOR J3-I3 TO N
16260 A<13,J3>-fi<13,J3>-DI*F2<13,J3J+F1<I3>*F1<J3>
16280 NEXT J3
16300 NEXT 13
16350 NEXT IP
16400 FOR 13-1 TO NiFOR J3-I3 TO N|A<J3,I3>-A<13,J3>iNEXT JSiNEXT 13
16999 RETURN
19000 REM********************
19010 REM** ВЫВОД ДАННЫХ **
19020 REM********************
19100 PRINT
19120 FOR I-l TO N
19140 PRINT"K<">I>"> -"jX9<IJSQR<ABS<H< I,I>*SS/<NP-N>>>
19160 REM PRINT" F<»>I>"jF9<I>
19180 NEXT I
19185 PRINT "СУММА КВАДРАТОВ ОТКЛОНЕНИЙ = "; SS
19190 RETURN
20000 REM**************************
20010 REM** ОСНОВНАЯ ПРОГРАММА **
20020 REM**************************
28100 N-3
296
Гпава 11
20138 FF-1BSM-1E30
20150 GOSUB 25000
20200 PRINT "ВВОД НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ"
20220 PRINT
20300 FOR 1-1 TO NiPRINT"K<">I>"> - ",
20320 INPUT X<I>sX9<I>-X<I>sNEXT I
20400 GOSUB 16000sREM ВЫЧИСЛ. ЧАСТИ. ПРОИЗВОДНЫХ
20450 REM GOSUB 19000 sREM ВЫВОД ДАННЫХ
20500 GOSUB 300IREM ОБРАЩЕНИЕ МАТРИЦЫ
20600 FOR 1-1 TO NsH<I>—0
20700 FOR J-l TO NsH<I>-H<I>+H<I,•J>*F9<J>
20720 NEXT J вNEXT I
20750 GOSUB 19000 iREM ВЫВОД ДАННЫХ
20800 GOSUB 35000 sREM КОЭФФИЦИЕНТ ОПТИМИЗАЦИИ
21000 FOR 1-1 TO NsX9<l>-X9<I>-FF*H<I>bNEXT I
21100 GOTO 20400
25000 REM************************
25010 REM** СЧИТЫВАНИЕ ДАННЫХ **
25015 REM** В XXO И WO **
25080 REM************************
25100 READ NP
25200 FOR I —1 TO NPsREAD XX<I>,VV<I>
25300 HEXT I
25400 RETURN
30000 REM*******************************
30010 REM** ВЫЧИСЛЕНИЕ СУММЫ **
30020 REM** КВАДРАТОВ ОТКЛОНЕНИЙ **
30100 REM*******************************
30200 SS-0
30300 FOR 1-1 TO NP
30358 x»xx<i:> bgosub 51000 sv=v-w< 1 >
30400 SS-SS+V*?SNEXT I
30500 RETURN
35000 REM******************************
35010 REM** ВЫЧИСЛЕНИЕ КОЭФФИЦИ- **
35020 REM** ЕНТА ОПТИМИЗАЦИИ FF ♦*
35100 REM*********************«********
35200 FF=.60sFM=8 sOF=.5
35310 GOSUB 35600
35320 IF SS<SM THEN SM-SSsFM-FFsFF-FF+OFsGOTO 35310
35330 FF-FM-OF
35335 GOSUB 35600
35340 IF SS<SM THEN SM-SSsFM-FFsFF-FF-DFsGOTO 35335
35360 FOR J-l TO 7
35380 DF-DF/2
35390 FF-FM+DFsGOSUB 35600
35400 IF SS<SM THEN SM-SSsFM-FFsGOTO 35430
35410 FF-FM-OFsGOSUB 35600
35420 IF SS<SM THEN SM-SSsFM-FF
35430 NEXT J
35450 FF-FM
35500 RETURN
35600 FOR 1-1 TO NsK<. I >—X9< I >—FF*H< I > sNEXT I
35620 GOSUB 30000
35630 REM PRINT SS.-FF
35650 RETURN
50000 REM******************************
50010 REM** Y-ФУНКЦИЯ, ВХОДЯЩАЯ **
50020 REM** В УРАВНЕНИЕ РЕГРЕССИИ, **
50030 REM** Fl ( ) И F2 ( ) - ЕЕ **
50040 REM** ПЕРВЫЕ И ВТОРЫЕ **
50050 REM** ПРОИЗВОДНЫЕ ПО **
50060 REM** ПАРАМЕТРАМ К **
50100 REM******************************
50200 REM Y-K<1:>+ К<2>*ЕХР<-К<3>*Х>
50210 F1<1>»1 sF2< 1, i:>»0sF2< 1 ,.2>,0 sF2< 1,3>»0
50220 F1<2>»EXP<-K<3>*X> sF2<2,2>=0sF2<2,3>=-X*Fl<2>
Нелинейные системы
297
50230 F1<3>»K<2>*F2<2,3>:F2<3,3>=-X*F1<3>
50240 V»K<1>+K<2>*F1<2:>
50999 RETURN
51000 REM************************
51010 REM** УРАВНЕНИЕ **
54020 REM** РЕГРЕССИИ **
51100 REM************************
51200 V-K<1>+K<2>*EXP<-K<3>*X>
51999 RETURN
60000 REM*****************************
60010 REM** ЧИСЛО ПАР ДАННЫХ **
60020 REM** ДАННЫЕ **
60030 REM** ПОПАРНО X.Y **
60100 REM*****************************
61000 DATR 64
62010 DRTA .000 , 1.000000
62020 DRTR .005 , .854415
62030 DATA .010 , .734266
62040 DATA .015 , .627988
62050 DATA .020 , .535742
62060 DATA .025 , .459174
62070 DATA .030 , .395416
62080 DRTR .035 , .337545
62090 DATA .040 , .288678
62100 DATA .045 , . 249475
62110 DATA .050 , .213886
62120 DATA .055 , .185657
62130 DRTA .060 , .157447
62140 DRTR .065 , . 135157
62150 DRTR .070 , •11B451
62160 DATA .075 , .099275
62170 DATA .080 , .0B5432
62180 DATA .085 , .074251
62190 DATA .090 , .063035
62200 DATA .095 , .054768
62210 DATA . 100 , .047787
62220 DATA . 105 , .039426
62230 DATA . 110 , .0345IB
62240 DATA . 115 , .030223
62250 DATA . 120 , .026509
62260 DATR .125 , •823732
62270 DRTA . 130 , .019B86
62280 DRTR . 135 , .814693
62290 DRTR .140 , .011B94
62388 DRTR .145 , .889542
62318 DRTR . 150 , .886593
62328 DRTR .155 , .885535
62338 DRTR . 160 , .085548
62348 DRTR .165 , .087713
62358 DRTR .170 , .883393
62368 DRTR .175 , .884965
62378 DRTR .180 , .8819B1
62388 DATR .IBS , .883614
62398 DATR .190 , .008934
62488 DRTR .195 , .8888215
62418 DRTA .200 , .8882637
62428 DRTR .205 , .8813678
62438 DRTR .210 , .8811571
62448 DATR .215 , -.8886458
62458 DRTR .220 , .8819994
62468 DRTA .225 r -.8835763
62478 DATA .230 , -.8826426
624В8 DATA .235 , -.0023520
62490 DATR .240 , -.0026480
62588 DRTR .245 , -.0054493
298
Глава II
62510 DATA
62520 DATA
62530 DATA
62540 DATA
62550 DATA
62560 DATA
62570 DATA
62580 DATA
62590 DATA
62600 DATA
62610 DATA
62620 DATA
62630 DATA
62640 DATA
63999 END
250 ,
255 ,
260 ,
265 ,
270 ,
275 ,
600 , -
605 , -
610 ,
615 , -
620 , -
625 , -
630 , -
635 , -
0026830
0028068
8018326
000B719
0006889
0008531
0052879
0058611
0047900
0052341
0022847
0024500
0030974
0
RUN
ВВОД НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
КС 1 > - ? 1
КС 2 > - ? 1
КС 3 > - ? 10
КС 1 ). 1 +/- .156036987
КС 2 >- 1 +/- .40080606
КС 3 >- 10 +/- 1.68152014
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ-92.1335121
КС 1 > — .19584303 +/- .0427455014
КС 2 >- 1.08797207 +/- .0794971779
КС 3 >- 10.9090293 +/- 2.06749773
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - 1.16786672
КС 1 > — .0318751033 +/- .0152241204
КС 2 >- .962819373 +/- .0549799238
КС 3 >- 16.5313358 +/- 1.27672154
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - .463788389
КС 1 > — .0372730558 +/- 7. 11891972Е-03
КС 2 >- .872616841 +/- .0236781374
КС 3 >- 21.634655 +/- 1.06515773
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - .091367313
КС 1 >- 1.2085240ВЕ-03 +/- 1.43394994Е-03
КС 2 >- .970039673 +/- 5.95231473Е-03
КС 3 >- 29.024518 +/- .293961415
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - 4. 81591002Е-03
КС 1 >—2.42522659Е-03 +/- 3.48782441Е-04
КС 2 >- .996269793 +/- 1.45417862Е-03
КС 3 >- 30.50В1712 +/- .0786752015
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - 2.7987233Е-04
КС 1 > — 1.75022635Е-03 +/- 3.36111893Е-04
КС 2 >- .998132961 +/- 1.403В1228Е-03
КС 3 >- 30.6227869 +/- .0762313919
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - 2.60479391Е-04
КС 1 > —1.7521792Е-03 +/- 3. 36113469Е-04
КС 2 >- .99813384 -г/- 1.40381214Е-03
КС 3 >- 38.622887 +7- .0762327937
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ- 2. 60479094Е-04
BREAK IN 51200
READY.
Нелинейные системы
299
Уравнение регрессии вместе с его первыми и вторыми производ-
ными по параметрам kj описано в подпрограмме 50000. Подпро-
граммы 12000 и 15000 из программы «НЕЛИН-РЕГРЗ» не нужны,
их заменяет подпрограмма 16000. Эта подпрограмма рассчитывает
первые производные суммы квадратов отклонений согласно уравне-
нию (2), и их значения присваиваются элементам массива F9( ).
Вторые производные рассчитываются по формуле (3), и их значе-
ния присваиваются элементам массива А( ). Остальные части про-
граммы — основная программа, подпрограмма для обращения
матриц и коэффициента оптимизации — остаются без изменений.
Использованные в этой программе числовые данные получены в
эксперименте по рассеянию света раствором полимера. При обра-
ботке этих данных по уравнению, записанному в строке 51200,
определяется значение параметра К(3). Если умножить зто значение
на калибровочный коэффициент, то получается константа диффу-
зии исследуемого полимера.
Задание 176. Используйте числовые данные и уравнение регрессии из программы
«НЕЛИН-РЕГР» в программе «НЕЛИН-РЕГРЗ». Сравните результаты и время
счета.
Метод, реализованный в программе «НЕЛИН-РЕГР», можно
упростить, если пренебречь в уравнении (3) слагаемыми, содержа-
щими вторые производные.
8 REM "НЕЛИН—РЕГР1" EBERT/EDERER 831231
1 REM***********************************
2 REM** НЕЛИНЕЙНАЯ РЕГРЕССИЯ **
3 REM*» В ПРОГРАММЕ ИСПОЛЬЗУЕТСЯ **
4 REM** МЕТОД НЬЮТОНА ДЛЯ РЕШЕНИЯ **
5 REM** СИСТЕМЫ УРАВНЕНИЙ **
6 REM*» ############################# **
7 REM** ФУНКЦИЯ,ВХОДЯЩАЯ В УРАВНЕНИЕ**
В REM** РЕ ГРЕССИИ,ЗАДАНА В ПОДПРОГРАММ*
9 REM** ME#» 50000 •• ЧАСТНЫЕ ПРОИЗВОЛ-**
18 REM# НЫЕ ВЫЧИСЛЯЮТСЯ В ПОДПРОГРАМ-**
И REM* МЕ»»15000»»ПО СООТВЕТСТВУЮЩИМ**
12 REM* ФОРМУЛАМ ИЛИ ЧИСЛЕННЫМ МЕТО-**
13 REM* ДОМ, ДЛЯ ЧЕГО НАДО УДАЛИТЬ **
14 REM* ОПЕРАТОР REM В СТРОКЕ »»15105»#**
19 REM**********************************
188 DIM Я<28,28>,В<28,28>,U<28,28>
118 DIM V<28,28>,Ы<28,28>
288 DIM Х<28>,Х9<28>,F<28>,F9<28>
218 DIM F8<2e>,H<2e>,K<28>
228 dim xx<iee>,YY<iee>
258 GOTO 28888
388 REM*******************************
385 REM** ОБРАЩЕНИЕ МАТРИЦЫ **
318 REM** ИСХОДНАЯ МАТРИЦА A **
328 REM** ОБРАЩЕННАЯ МАТРИЦА W **
358 REM*******************************
488 FOR 1-1 TO N
428 FOR J-l TO N
300
Глава 11
460 BCI,J>-0
480 VCI,J>-0
500 IF IOJ THEN GOTO 600
520 BCI,J>-1
540 V<I,J>-1
600 NEXT J
620 NEXT I
1000 FOR Z-l TO N
1050 S-0
1100 REM ПОИСК ВЕДУЩЕГО ЭЛЕМЕНТА
1120 FOR I-Z TO N
1150 IF S>ABSCA<I,Z>> THEN GOTO 1300
1200 S-ABSCAC I,Z>>
1250 T-I
1300 NEXT I
2000 REM ОБМЕН Z-Й СТРОКИ С Т-Й
2050 FOR I-l TO N
2100 S-ACZ,I>iACZ,I>-ACT,I>|ACT,I>-S
2200 NEXT I
2300 IF ABSCACZ,Z>>>1E-30 THEN GOTO 2400
2350 PRINT "МАТРИЦУ ОБРАТИТЬ НЕВОЗМОЖНО": END
2400 VCZ,Z>-01VCT,T>-0
2450 VCZ,T>-1|VCT,Z>-1
3000 REM ИСКЛЮЧЕНИЕ НЕДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ
3002 REM МЕТОДОМ ГАУССА-ЖОРДАНА
3100 FOR I-l TO N
3200 FOR J-l TO N
3300 IF I-Z THEN GOTO 4000
3350 IF J-Z THEN GOTO 4500
3400 UCI,J>-ACI,J>-ACZ,J>#ACI,Z>/RCZ,Z>
3500 GOTO 5000
4000 IF I-J THEN GOTO 4350
4050 UCI,J> — RCI,J>/RCZ,Z>
4100 GOTO 5000
4350 UCZ,Z>-1/RCZ,Z>
4400 GOTO 5000
4500 UCI,Z>-RCI,Z>/RCZ,Z>
5000 NEXT J
5050 NEXT I
5100 REM УМНОЖЕНИЕ МАТРИЦ
5110 REM В - V*B
5200 FOR I-l TO N
5250 FOR J-l TO N
5300 HCI,J>-0
5350 FOR K-l TO N
5400 WCI,J>-WCI,J>+VCI,K>*BCK,J>
5450 NEXT КiNEXT JiNEXT I
5500 FOR I-l TO NiFOR J-l TO N
5550 BCI,J>-W<I,J>
5600 NEXT JiNEXT I
6000 FOR I-l TO N
6050 FOR J-l TO N
6100 AC I,J>-UCI,J>
6200 VCI,J>-0
6250 IF I-J THEN VCI,J>-1
6300 NEXT JiNEXT I
6500 NEXT Z
7000 REM РЕЗУЛЬТАТ УМНОЖЕНИЯ МАТРИЦЫ А НА МАТРИЦУ В
7100 FOR I-l ТО N
7200 FOR J-l TO N
7300 WCl,J>-0
7400 FOR K-l TO N
7500 WCI,J>-WCI,J>+RCI,K>*BCK,J>
7600 NEXT КiNEXT JiNEXT I
7700 RETURN
Нелинейные системы
301
12000 REM*****************************
12010 REM** ВЫЧИСЛЕНИЕ **
12020 REM** ЭЛЕМЕНТОВ **
12030 REM** МАТРИЦЫ A **
12060 REM*****************************
12100 FOR 1-1 TO NiFOR J-l TO NiA<I,J>-0iNEXT J
12150 K<I>-X9<I>1F9<I>-0iNEXT I
12200 FOR IP-1 TO NPiX-XX<IP>1GOSUB 50000IYI-Y
12300 OOSUB 15000 iREM ПРОИЗВОДНЫЕ
12400 FOR 13-1 TO N
12410 FOR J3-I3 TO N
12440 A<13,J3>-A<13,J3>+F<I3>*F<J3>
12460 NEXT J3
12500 F9<I3>-F9<I3>-<YY<IPJ-VI>*F<I3>
12550 NEXT 13
12600 NEXT IP
12700 FOR 1-1 TO NiFOR J-I TO N|A<J,I>-A<I,J>iNEXT JiNEXT I
12999 RETURN
15000 REM*********************************
15010 REM»* ВЫЧИСЛЕНИЕ *»
15020 REM** ЧАСТНЫХ **
15030 REM»* ПРОИЗВОДНЫХ ПО **
15040 REM** К (J ) В ТОЧКЕ X **
15050 REM*********************************
15100 FOR 1-1 TO NiK<I>-X9<I>(NEXT I
15105 REM GOTO 15300
15110 F<1>-1
15120 F<2>-EXP<-K<3>*X>
15160 F<3>—K<2>*X*F<2>
15200 RETURN
15300 FOR 1-1 TO N
15310 DI-ABS<X9<I>Z1E4>+1E-8
15340 K<I>-X9<I>+DIlOOSUB 500001F<I>- Y
15360 K<I>-X9<I>-DIlGOSUB 50000iF<I>-<F<I>-Y>/2/DI
15400 K<I>-X9<I>iNEXT I
15999 RETURN
19000 REM********************
19010 REM** ВЫВОД ДАННЫХ **
19020 REM********************
19100 PRINT
19120 FOR 1-1 TO N
19140 PRINT"K<">I>"> -",X9< I> >ISQR<ABS<H< I,I>*SS/<NP-N> >>
19160 REM PRINT" F<"iI)"jF9<I>
19180 NEXTI
19185 PRINT "СУММА КВАДРАТОВ ОТКЛОНЕНИЙ =": SS
19190 RETURN
20000 REM**************************
20010 REM** ОСНОВНАЯ ПРОГРАММА **
20020 REM**************************
20100 N—3
20130 FF-1ISM-1E30
20150 GOSUB 25000
20200 PRINT "ВВОД НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ"
20220 PRINT
20300 FOR 1-1 TO NiPRINT"K<"}I:"> - “>
20320 INPUT X<I>iX9<I>-X<I>iNEXT I
20400 GOSUB 120001REM ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ МАТРИЦЫ A
20410 FOR 1-1 TO N :F0< I :>-A< I , I > iNEXT I
20420 FOR 1-1 TO NiK<I>-X9<I>iNEXT IiGOSUB 30000:SM-SS
20450 GOSUB 190001 REM ВЫВОД ДАННЫХ
20500 GOSUB 3001REM ОБРАЩЕНИЕ МАТРИЦЫ
20600 FOR 1-1 TO NiH<I>—0
20700 FOR J-l TO NiH<I>—H<I>+W<I,J>*F9<J>
20720 NEXT JiNEXT I
20750 OOSUB 19000 iREM ВЫВОД ДАННЫХ
20000 GOSUB 35000 iREM КОЭФФИЦИЕНТ ОПТИМИЗАЦИИ
302
21000
21100
25000
2S010
25015
25080
25100
25200
25300
25400
30000
30010
30020
30100
30200
30300
30350
30400
30500
35000
35010
35020
35100
35200
35310
35320
35330
35335
35340
35360
35380
35390
35400
35410
35420
35430
35450
35500
35600
35620
35630
35650
50000
50010
50020
50100
50120
50200
50999
60000
60010
60020
60030
60100
61000
62010
62020
62030
62040
62050
62060
62070
62080
62090
62100
62110
Глава 11
FOR 1-1 TO NiX9<I>-X9<I>-FF*H<I>iNEXT I
GOTO 20400
REM** СЧИТЫВАНИЕ ДАННЫХ**
REM** В XXО и VYO **
REM************************
READ NP
FOR 1-1 TO NPiREAD XX<I>,YY<I>
NEXT I
RETURN
REM*******************************
REM** ВЫЧИСЛЕНИЕ СУММЫ ««
REM** КВАДРАТОВ ОТКЛОНЕНИЙ *4
REM*******************************
SS-0
FOR 1-1 TO NP
X-XX<I> IGOSUB 50000|Y-Y-YY<I>
SS-SS+Y*?iNEXT I
RETURN
REM******************************
REM** ВЫЧИСЛЕНИЕ КОЭФФИЦИ- ««
REM»* ЕНТА ОПТИМИЗАЦИИ FF **
REM******************************
FF-.60IFM-0 IDF-.5
GOSUB 35600
IF SS<SM THEN SM-SSiFM-FFiFF-FF+DFsGOTO 35310
FF-FM-DF
GOSUB 35600
IF SS<SM THEN SM-SSiFM-FFiFF-FF-DFiGOTO 35335
FOR J-l TO 7
DF-DF/2
FF-FM+DFiGOSUB 35600
IF SS<SM THEN SM-SSiFM-FFIGOTO 35430
FF-FM-DFIGOSUB 35600
IF SS<SM THEN SM-SSiFM-FF
NEXT J
FF-FM
RETURN
FOR 1-1 TO N|K<I>-X9<I>-FF*H<I>iNEXT I
GOSUB 30000
REM PRINT SS,FF
RETURN
REM************************
REM** УРАВНЕНИЕ **
REM** РЕГРЕССИИ ««
REM************************
REM V-K< 1 >*EXP<-K<2>*X>+K< 1 >*K<2>
Y-K < 1 >+K < 2 > *EXP <-K < 3 > *X >
RETURN
REM*****************************
REM** ЧИСЛО ПАР ДАННЫХ **
REM** ДАННЫЕ ««
REM** ПОПАРНО X.Y **
REM*****************************
DRTR 64
DRTR .000 , 1.000000
DRTR .005 , .854415
DRTR .010 , .734266
DRTR .015 , .627986
DRTR .020 , .535742
DRTR .025 , .459174
DRTR .030 , .395416
DRTR .035 , .337545
DRTA .840 , .288678
DRTA .045 , .249475
DATA .050 , .213886
Нелинейные системы
303
62120 DATA .655 -185657
62130 DATA • 068 .157447
62140 DATA .065 .135157
62150 DATA .070 .11S451
62160 DATA .075 .099275
62170 DATA .080 .085432
62180 DATA .085 r .074251
62190 DATA .090 . 063035'
62200 DATA .095 .054768
62210 DATA . 100 .047787
62220 DATA . 105 .839426
62230 DATA . 110 .034518
62240 DATA . 115 .830223
62250 DATA .120 .026589
62260 DATA . 125 .623732
62270 DATA . 130 .019806
62280 DATA . 135 .014693
62290 DATA . 140 .011894
62300 DATA . 145 .009542
62310 DATA . 15G .0O6593
62320 DATA . 155 .Й05535
62330 DATA . 160 .0O5540
62340 DATA . 165 .007713
62350 DATA . 170 .O03393
62360 DATA . 175 .804965
62370 DATA . ISO .801981
62380 DATA . 1S5 .003614
62390 DATA . 190 .000934
62400 DATA . 195 .0O00215
62410 DATA . 200 .0002637
62420 DATA . 285 .0013670
62430 DATA .210 .0011571
62440 DATA .215 -.0006458
62450 DATA .220 .0019994
62460 DATA .225 -.8035763
62470 DATA . 230 -.0026426
62480 DATA .235 -.0023520
62490 DATA . 240 -.0026488
62500 DATA .245 -.0054493
62510 DATA . 250 -.0026830
62520 DATA . 255 -.0028068
62530 DATA .268 -.0018326
62540 DATA .265 -.0008719
62550 DATA .270 -.0006889
62560 DATA • 275 -.0008531
62570 DATA .600 -.0052879
62580 DATA .605 -.0050611
62590 DATA .610 -.00479O0
62600 DATA .615 -.0052341
62610 DATA .620 -.0022847
62620 DATA .625 -.0024500
62630 DATA .630 -.0030974
6264^ DATA . 635 -.0
63999 END
RUN
ВВОД НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
1 > -= ? 1
К< 2 » ? 1
К 3 > = ? 10
К< 1 >- 1 +/- 0
К< 2 >- 1 +/- 0
К< 3 >- 10 +/- 0
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - 92.133512
304
Глава 11
КС 1 > — .0189503164 +/- .0186654604
КС 2 >- .73170541 +/- .0283672004
КС 3 >- 10.0536549 +/- .655741013
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - .22592,5567
КС 1 >- .0114060054 +/- 2.36877814Е-03
КС 2 >- 1.01437729 +/- 6.27315116Е-03
КС 3 ) 32.5029937 +/- .3093526
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ- 7.82629643Е-03
КС 1 > — 1.7950В506Е-03 +/- 3.30628460Е-04
КС 2 >. .997260961 +/- 1.439936В5Е-03
КС 3 >- 30.5693072 +/- .0000914430
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ - 2.63044007Е-04
КС 1 > —1.75309261Е-03 +/- 3.35771594Е-04
КС 2 ) .998135625 +/- 1.40047067Е-03
КС 3 ) 30.6227474 +/- .0756619617
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ- 2. 60479144Е-04
BREAK IN 2100
READY.
В подпрограмме 15000 записаны аналитические выражения для
первых производных. Вторая часть этой программы является
«дремлющим» участком для расчета значений производных числен-
ным методом. Этот участок можно задействовать, если удалить
оператор REM в строке 15105. Подпрограмма вычисляет элементы
массивов А( ) и F9( ).
В программе «НЕЛИН-РЕГР1» применен еще один прием для
уменьшения суммы квадратов отклонений. В строках 20800 и 21000
происходит расчет коэффициента оптимизации и обычная в методе
Ньютона попытка улучшить решение. В следующих трех строках
(21010—21030) производится еще одна попытка уменьшить сумму
квадратов отклонений методом крутого спуска. В качестве вектора
коррекции используется вектор первых производных (в программе
ему соответствует индексированная переменная F9( )). Сам по се-
бе метод крутого спуска лишь в редких случаях приводит к успеху,
однако комбинация различных процедур может существенно уско-
рить сходимость.
Задание 177. Сравните результаты и время счета, когда вы используете методы
Ньютона и крутого спуска по отдельности и в комбинации друг с другом в програм-
ме «НЕЛИН-РЕГР1».
Задание 178. Организуйте расчет и вывод на экран матрицы ковариаций*. Эта
матрица получается, если матрицу W (матрица, обратная матрице А) справа и слева
• Матрица парных коэффициентов корреляции или корреляционная матрица. —
Прим, перев.
Нелинейные системы
305
умножить на диагональную матрицу, диагональные элементы которой имеют вид
D(I, I) = 1/VW(I, I)
Матрица ковариаций = D • W • D
По недиагональным элементам матрицы ковариаций можно судить, как зависят
друг от друга соответствующие параметры. Если матричный элемент KO(I. J) = 0,
то параметры К(1) и K(J) взаимно независимы, если KO(I, J) = 1, то имеется одно-
значное соответствие между обоими параметрами.
12. Нечисленные методы обработки данных
Едва ли можно четко разграничить численные и нечисленные
методы обработки данных. Можно лишь отметить, что при чис-
ленной обработке данных основное внимание уделяется расчетам и
вычислениям. К нечисленным методам относятся такие операции,
как упорядочивание, поиск, перезапись, стирание, регистрация, ото-
бражение данных и т. д. В качестве примеров использования нечис-
ленных методов можно привести резервирование авиабилетов, ав-
томатизированный абонемент в крупных библиотеках, идентифика-
цию личности и поиск преступников в криминалистике, составление
расписаний школьных уроков и компьютерные игры.
В этой книге рассматриваются два примера нечисленной обра-
ботки информации. Сначала мы составим систему дифференциаль-
ных уравнений, описывающую кинетику сложной химической реак-
ции, включающей несколько элементарных стадий. В качестве вто-
рого примера будут рассмотрены компьютерные игры. На этих
примерах мы познакомим читателей с операторами БЕЙСИКа,
еще не встречавшимися в этой книге, но широко использующимися
в программировании. Эти операторы (например, LEN, VAL, STR,
ASC, CHRS, LEFTS, MID$, RIGHTS) упрощают многие операции с
текстовыми переменными. Однако в обоих примерах эти операто-
ры будут использоваться как можно реже, только в тех случаях,
когда они незаменимы.
12.1. Вывод системы дифференциальных уравнений
из кинетической схемы реакции
Когда перед химиком встает задача получить из кинетической
схемы сложной реакции, включающей довольно большое число эле-
ментарных стадий, кинетическое описание, т. е. составить систему
дифференциальных уравнений, это рассматривается как утомитель-
ная техническая работа. Если механизм реакции сложен, то задача,
хотя она и не трудна, связана с преобразованием и записью доволь-
но громоздких математических выражений, в ходе которых воз-
Нечисленные методы обработки данных
307
можны ошибки. Поэтому есть смысл возложить эти однотипные
операции иа ЭВМ. Но сначала надо систематизировать составление
дифференциальных уравнений. Как это сделать, показано на следу-
ющем простом примере.
Дан механизм термического разложения этана, который вклю-
чает 9 элементарных стадий:
С2Н6 - СН3 + СН3 (1)
С2Н6 + СН3 - С2н5 + СН4 (2)
С2Н5 - С2Н4 + Н (3)
С2Н6 + Н С2Н5 + н2 (4)
СН3 + С2н5 - С3Н8 (5)
снз + Н - СН4 (6)
С2Н5 + Н - н2 + С2н4 (7)
С2н5 + С2н5 - С2н4 + С2Н6 (8)
Н + Н - н2 (9)
Скорость каждой элементарной стадии равна произведению кон-
центраций исходных веществ на соответствующую константу ско-
рости:
г, = Л,-[ад
г2 = л2чадчсн31
r3 =
г4 = л4-[адчн]
r5 = к5 • [сн3] • [ад
г6 = к6 • [СН3] • [Н]
г7 = *7 - [С2Н5] - [Н]
г8 = л,-[ад-[ад
Г9 = *9[Н][Н]
Так как кинетическая схема включает только моно- и бимолеку-
лярные реакции, в выражениях для скорости элементарных стадий
встречаются произведения не более двух концентраций. Так называ-
емое тройное соударение рассматривается как последовательная ре-
акция, что более корректно:
вместо А + А + А — продукты
лучше А + А — В
В — А + А — быстрая реакция
В + А — продукты
Если вторая реакция — распад промежуточного соединения, со-
стоящего из двух молекул А, протекает быстро, то легко показать,
что суммарная реакция подчиняется кинетическому уравнению
третьего порядка по концентрации вещества А.
20*
308
Глава 12
Интегрируя в аналитическом виде кинетические уравнения, опи-
сывающие тримолекулярную реакцию, также можно показать, что
оба подхода кинетически неразличимы. Между прочим, для инте-
грирования кинетического уравнения, соответствующего стадийно-
му механизму тримолекулярной реакции, можно использовать про-
грамму «СИСТ-РКН».
Чтобы составить дифференциальное уравнение, описывающее
скорость накопления и расходования одного вещества, надо ото-
брать те элементарные стадии, в которых оно образуется или рас-
ходуется. Если это вещество стоит в левой части уравнения реак-
ции (исходный продукт), то скорость этой элементарной стадии (г(.)
входит в кинетическое уравнение для данного вещества со знаком
«минус»; и наоборот, если вещество стоит в правой части уравне-
ния реакции (конечный продукт), то скорость этой элементарной
стадии входит в кинетическое уравнение со знаком «плюс». При
этом надо учитывать стехиометрические коэффициенты. В нашем
примере в реакции (9) на образование одной молекулы водорода
расходуется два атома Н, поэтому в дифференциальном уравнении,
описывающем изменение [Н], скорость элементарной стадии (9) (г9)
должна встречаться два раза, разумеется, со знаком «минус». Си-
стема уравнений для нашего примера имеет вид
d[C2H6]/dr = -fj - r2 - r4 + r8
d[CH3]/d/ = -r2 - r5 — r6 + Г] + f]
d[C2H5]/d/ = -r3 - r5 - r7 - r8 - r8 + r2 + r4
d[CH4]/dZ = +r2 + r6
d[C2H4]/d/ = + r3 + r7 + r8
d[H]/dZ = -r4 ~ r6 - r7 - r9 - r9 + r3
d[H2]/d/ = +r4 + r7 + r9
d[C3H8]/dz = +r5
Ниже приведена распечатка программы «ЭС-КИН», использую-
щая рассмотренный подход.
в REM "ЭС-КИН" EBERT/EDERER 811111
1 REM***** *«♦ «♦*♦ **** «*«♦«*«*♦ ♦*»(***♦****
2 REM** ВЫВОД СИСТЕМЫ **
3 REM#* ДИФФЕРЕНЦИАЛЬНЫХ **
4 REM»* УРАВНЕНИЙ ИЗ КИНЕТИЧЕСКОЙ **
5 REM** СХЕМЫ РЕАКЦИИ **
9 REM************************************
200 DIM ER«<40> ,N«<20> ,L«<40,2> ,U40> ,R*<40,4> ,R<40>
1000 DRTR "C2Hi5 ««> CH3 4- CHS”
1010 DRTR "C2Hi5 4- CHS ««> C2H5 4 CH4”
1020 DRTR "C2H5 Я? C2H4 4 H"
1030 DRTR “С2Нв 4- H C2H5 4- HZ"
1040 DRTR "CH3 4- C2H5 ==j> C3H8 '
1050 DRTR "CHS 4 H =s»> CH4"
Нечисленные методы обработки данных
309
1069 DATA "C2H5 4 H ««> H2 ч- C2H4"
1970 DATA "C2H5 4 C2H5 яж> C2H4 4- C2H6”
1989 DATA "H 4- H —> H2 ”
1999 DATA "КОНЕЦ"
2999 N-lIRESTORE
2929 READ ER«<N>
2039 IF ER*<N>—"КОНЕЦ" THEN GOTO 2199
2959 GOSUB 10990iREM РАЗДЕЛЕНИЕ
2999 N-N+liGOTO 2929
2190 N-N-l
2209 GOSUB 119901 REM ВЕЩЕСТВА
2399 OOSUB 129901 REM СКОРОСТИ РЕАКЦИИ
2409 GOSUB 139001REM ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
9999 END
10009 REM******************************************
10991 REM** РАЗДЕЛЕНИЕ УРАВНЕНИЯ РЕАКЦИИ ЭЛЕМЕН-»*
19902 АЕМ**ТАРНОЙ СТАДИИ НА ПРАВУЮ И ЛЕВУЮ ЧАСТЬ**
10993 REM******************************************
10929 Н«-""
19930 b-len<er*':n>>
10033 PRINT N,ER«<N>
10949 FOR I-l TO В
19960 IF MID*<ER*<N>,I,1" THEN GOTO 19990
10989 H*-H*+MIO»<ER»<N>,I,1>
10999 NEXT I
10199 B-LEN<H»>
19139 Zl-1iBl-1iI-l
19169 IF MID«<H»,I,!>-"+" THEN GOTO 19229
10179 IF MID»<H»,I,1THEN GOTO 10250
19189 I-1+1iGOTO 16160
19229 L«<N,Z1>-MID»<H*,B1,I-B1>
19239 I-I+l1Z1-21B1-IiGOTO 10169
19250 L»<N,Z1>-MID»<H»,Bl,I-Bl>
10269 L<N>-Z1
19280 I-I+3iZl-liBl-I
10299 IF I-B THEN 10409
10399 IF Г110«<Н», I, !> = " + " THEN GOTO 10329
19319 I—I+liGOTO 19299
19329 R*<N,Z1>-MID*<H*,B1,I-B1>
19339 I-I+lsZl-Zl+1iBl-IiGOTO 19290
10409 r»<n.zi:>-mim<h»,bi,i-bi+i:>
19410 r<n:>-zi
10599 RETURN
11090 REM***»»*»******»****
11091 REM** ВЕЩЕСТВА **
11092 REM******************
11019 PRINT
11029 S-l|N«<1>-L»<1,1>
11039 FOR I-l TO N
11040 FOR J-l TO L<I>
11979 Sl-0
11980 FOR K-l TO S
11199 IF LKI,J)ON»<K> THEN GOTO 11149
11129 Sl-1
11149 NEXT К
11150 IF Sl-1 THEN GOTO 11170
11160 s-s+i in»<s:>-l»<i,j:>
11179 NEXT J
11240 FOR J-l TO R<l>
11279 Sl-0
11280 FOR K-l TO S
11390 IF R«<I,J)ON»(K> THEN GOTO 11340
11329 Sl-1
11340 NEXT К
11359 IF Sl-1 THEN GOTO 11370
11369 S-S+l |N»':S>-R»<I, J>
310
Глава 12
11370 NEXT J
11400 NEXT I
11500 FOR 1-1 TO SiPRINT "V<",N»<I>iNEXT I
11510 PRINT
11900 RETURN
12000 REM*****Ж********Ж*Ж***Ж***
12001 REN** СКОРОСТИ РЕАКЦИЙ **
12002 REN***W*****IMI*4**«****«***
12030 FOR 1-1 TO N
12040 PRINT "R<- KC",I,"> * "i
12050 FOR J-l TO L<I>
12060 FOR K-l TO S
12070 IF N»<K>OL»<I,J> THEN GOTO 12100
12080 PRINT "V<",K,">",
12090 IF JOL(I> THEN PRINT " * ",
12100 NEXT К
12120 NEXT J«PRINTiNEXT I
12200 PRINT IRETURN
13000 REM************************************
13001 REM** ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ **
13002 REM************************************
13040 FOR 1-1 TO S
13050 PRINT "DV<">I>">/DT - ",
13080 FOR J-l TO N
13098 FOR K-l TO L<J>
13100 IF N»<I>-L»<J,K> THEN PRINT "-R<",J,">",
13120 NEXT КiNEXT J
13180 FOR J-l TO N
13190 FOR K-l TO R<J>
13200 IF N»<I>-R»<J,K> THEN PRINT "+R<",J,">",
13220 NEXT КiNEXT J
13240 PRINTiNEXT I
13300 PRINT IRETURN
63999 END
RUN
1 C2H6 CH3 + CH3
2 C2H6 + CH3 C2H5 + CH4
3 C2H5 C2H4 + H
4 C2H6 + H C2H5 + H2
5 CH3 + C2H5 C3H8
6 CH3 + H CH4
7 C2H5 4- H H2 •t- C2H4
8 C2H5 + C2H5 C2H4 + C2H6
9 H + H H2
V< 1 :>
V< 2 >
V< 3 >
v< 4 :>
V< 5 >
V< 6 >
V< 7 >
v< e ;>
- C2H6
- CH3
- C2H5
- CH4
- C2H4
- H
- H2
» C3H8
R< 1 > ж к< 1 ) * V< 1 )
R< 2 > ж к< 2 > * v< 1 > * Y< 2 >
R< 3 > я к< 3 > * v< 3 >
R< 4 > ж к< 4 ) * v< 1 ) * Y< 6 )
R< 5 > ж к< 5 > v< 2 ) * V< 3 >
R< 6 > = к< б > * Y< 2 > * Y< 6 >
R( > ж к< 7 ) * V< 3 > * V( 6 )
R< e > ж к< 0 ) V< 3 > * Y< 3 >
RC 9 > = к< 9 ) * V< 6 ) * Y< 6 )
Нечисленные методы обработки данных
311
□V< 1 >/DT - -R< 1 >-R< 2 >-R< 4 >+R< 8 >
DV< 2 >/DT - -R< 2 >-R< 5 >-R< 6 >+R< 1 >+R< 1 >
DV< 3 >/DT - -R< 3 >-R< 5 >-R< 7 >-R< 8 >-R< 8 >+R< 2 >+R< 4 >
DY< 4 >/DT =. +R< 2 >+R< 6 >
DV< 5 >/DT - +R< 3 >+R< 7 >+R< 8 :>
DV< 6 >/DT - -R< 4 >-R< 6 >-R< 7 >-R< 9 >-R< 9 >+R< 3 >
DY< 7 >/DT - +R< 4 >+R< 7 >+R< 9 >
DY< 8 >/DT - +R< 5 >
RERDV.
Программа «ЭС-КИН» предназначена для обработки кинетиче-
ских схем, включающих не более 40 элементарных стадий, в кото-
рых участвует не более 20 веществ. Если необходимо обрабатывать
более сложные кинетические схемы, то следует увеличить размеры
массивов, описанных в строке 200.
Участок программы от строки 1000 до строки 1999 отводится
для записи механизма реакции. Кинетическая схема вводится с по-
мощью оператора DATA. Каждая элементарная стадия заключена
в кавычки. Правая часть уравнения отделена от левой стрелкой. Ес-
ли в одной элементарной стадии участвует несколько одинаковых
исходных веществ или образуется несколько одинаковых продуктов
реакции, то их надо записывать отдельно друг от друга, а не с по-
мощью привычных стехиометрических коэффициентов. Раздели-
тельным знаком между веществами является знак « + », поэтому
знак «+ » не может входить в формулы веществ, даже если в реак-
циях участвуют катионы. Каждое вещество должно иметь только
одно определенное название; например, нельзя внутри одной кине-
тической схемы использовать в качестве названий и СН4, и
METHAN, иначе компьютер будет считать, что это названия раз-
ных веществ. Пробелы при записи элементарных стадий не играют
никакой роли, поэтому, чтобы кинетическая схема была более на-
глядной, ими можно пользоваться без всяких ограничений. Запись
схемы реакции должна заканчиваться оператором с ключевым сло-
вом КОНЕЦ (строка 1999). Эти довольно строгие правила позволя-
ют сделать программу простой и короткой. Вообще говоря, чем
меньше программа накладывает ограничений на форму записи
входных данных, тем больше объем программы и больше трудно-
стей при ее написании.
В строках 2000—2100 происходит ввод данных. Число элемен-
тарных стадий присваивается переменной N. Для запоминания
уравнений реакций использован текстовой массив ER$( ). Считы-
вание данных заканчивается, когда оператор условного перехода
обнаружит слово КОНЕЦ. Поскольку слово КОНЕЦ не является
элементарной стадией, N уменьшается на единицу.
312
Гаава 12
После считывания каждого уравнения элементарной стадии вы-
зывается подпрограмма 10000, которая делит это уравнение на пра-
вую и левую часть. В первой части этой подпрограммы со строки
10020 до 10100 из уравнения удаляются пробелы и оно выводится
на экран. Для записи уравнения реакции без пробелов используется
текстовая переменная Н$, которая перед этим обнуляется. В строке
10030 с помощью нового оператора В = LEN (ER$(N)) определяет-
ся число знаков в тексте, записанном в переменной ER$(N), и это
число присваивается переменной В.
Длина текста ***********
*** LEN ***
* **********
***************
*** LEN(BS) ***
***************
В$ может быть текстовой переменной или «текстовым выражением». LEN(B$)
равно числу знаков в тексте, записанном в текстовой переменной В$.
В строках 10040—10090 организован цикл по I с наибольшим
значением параметра цикла, равным В. В этом цикле знак за зна-
ком переписывается текст из переменной ER$(N) в переменную Н$,
причем пробелы отбрасываются. I-й знак значения текстовой пере-
менной ER$(N) можно определить с помощью оператора MIDS
(ER$(N), I, 1).
Часть текста ************
*** мю$ * * *
************
********************
**♦ MID$(A$,P,L) ♦**
********************
А$ — текстовая переменная, из которой вырезается «часть»; Р — позиция, с кото-
рой начинается эта «часть текста»; L — длина этой «части текста».
Если I-й знак является пробелом (это проверяется с помощью
оператора IF в строке 10060), то управление передается оператору
NEXT I (строка 10090), и, следовательно, пробел не вносится в
текст, который присваивается переменной Н$. В противном случае
символ, стоящий на I-й позиции, с помощью оператора в строке
10080 добавляется к уже имеющемуся тексту. Знак « + » также пере-
Нечисленные методы обработки данных
313
носится в текстовую переменную Н$. Если удаление пробелов за-
кончено, то далее в строке 10100 определяется число символов в
уравнении элементарной стадии, которое присваивается перемен-
ной В.
Во второй половине этой подпрограммы определяется число ве-
ществ в левой и правой части N-ro уравнения элементарной стадии,
которое присваивается переменным L(N) и R(N) соответственно.
Определяются также и названия веществ, которые присваиваются
элементам двумерных массивов L$(N, I) и R$(N, I) соответственно.
В строках 10160—10180 последовательно просматриваются все
знаки текста, присвоенного текстовой переменной Н$, пока не
встретится знак « + » или « = » (начало стрелки, отделяющей пра-
вую часть уравнения от левой). Если обнаружен знак « + », то
управление переходит к строке 10220 и часть текста, записанного в
переменной Н$, начиная с первого символа и до знака « + »,
присваивается соответствующему элементу массива L$(N, 1) как
первое вещество левой части N-й элементарной стадии.
После того как отмечено положение знака « + », управление воз-
вращается строке 10160. Надо еще найти символ « = » от стрелки,
которая означает конец левой части уравнения реакции. Если обна-
ружен символ « = », то в строке 10250 часть текста, стоящего после
знака «+ » и перед знаком «= », присваивается соответствующему
элементу массива L$(N, 2) или L$(N, 1) в качестве названия вещест-
ва в зависимости от того, является ли это вещество первым или
вторым исходным веществом в уравнении элементарной стадии.
Здесь же определяется число исходных веществ в N-й элементарной
стадии, которое присваивается элементу массива L(N). В стро-
ках 10280—10410 аналогичным образом проводится анализ пра-
вых частей элементарных стадий. Элементы массива R$(N, 1),
R$(N, 2), ... имеют значения названий веществ, входящих в правую
часть N-ro уравнения элементарной стадии, а значение переменной
R(N) равно числу этих веществ. На этом заканчивается подпро-
грамма, которая устанавливает названия исходных и конечных ве-
ществ. В строке 10033 уравнения реакций вместе с их порядковыми
номерами N выводятся на экран в том виде, в каком они записаны
в операторах DATA.
После того как установлены названия исходных и конечных ве-
ществ во всех элементарных стадиях, в строке 2200 основной про-
граммы вызывается подпрограмма 11000. Эта подпрограмма отыс-
кивает различающиеся между собой вещества, зашифровывает их
названия и выводит новые обозначения на экран. Для этого в стро-
ке 11020 первое вещество в первой элементарной стадии считается
314
Гаава 12
первым веществом и число найденных соединений (переменная S)
приравнивается единице. В цикле по I (строки 11030—11400) про-
сматриваются все N элементарных стадий. Во внутренней области
этого цикла размещены два следующих друг за другом цикла по
параметру J (строки 11040—11170 и 11240—11370). Наибольшее зна-
чение параметра этих циклов равно числу исходных веществ (L(I)) и
соответственно продуктов (Р(1)) I-й элементарной стадии. Внутри
каждого цикла по J организован цикл по параметру К. Перед вхо-
дом в каждый из этих циклов по К вспомогательная переменная S1
обнуляется. В циклах по параметру К все S найденных до сих пор
различающихся веществ сравниваются с J-м исходным и соответст-
венно с J-м конечным веществом элементарной стадии I. Если оди-
наковых веществ не найдено, то переменная S1 сохраняет свое зна-
чение. Если обнаружены одинаковые вещества (т. е. название ве-
щества уже встречалось ранее), то переменной S1 присваивается
значение 1. Если S1 = 0, то это значит, что название вещества еще
не встречалось; тогда число веществ S увеличивается на 1 и назва-
ние этого вещества присваивается элементу массива N$(S).
В конце этой подпрограммы (строка 11500) названия веществ
вместе с их порядковыми номерами выводятся на экран в виде
Y(I) = название вещества
Использование индексированной переменной У(1) вместо названий
веществ при выводе на экран системы дифференциальных уравне-
ний делает выходные данные компактными и наглядными. Кроме
того, записанную в таком виде систему дифференциальных уравне-
ний можно без изменений вводить в программу для решения си-
стем дифференциальных уравнений (см. гл. 9).
Далее из основной программы вызывается подпрограмма 12000,
которая выводит кинетическое уравнение каждой элементарной
стадии. Подпрограмма состоит из цикла по I, в котором поочеред-
но анализируются все элементарные стадии. В него вложен цикл по
J, где поочередно рассматриваются исходные вещества I-й элемен-
тарной стадии. В цикл по J вложен цикл по К, в котором определя-
ется, какой порядковый номер (из предыдущей подпрограммы) со-
ответствует исходному веществу L$(I, J). Этот номер К выводится
на экран в виде «Y(K)» (строка 12080). Если в данной элементарной
стадии имеется еще одно исходное вещество (строка 12090), то до-
бавляется знак «»». Строка 12040 обеспечивает вывод данных в ви-
де произведения константы скорости и концентраций исходных ве-
ществ:
Rd) = K(D*
Нечисленные методы обработки данных
315
Если все выражения для скорости элементарных стадий выведе-
ны на экран, то основная программа вызывает подпрограмму
13000, которая составляет дифференциальные уравнения. Эта под-
программа состоит из цикла по I, в котором поочередно рассмат-
ривается каждое из S веществ (строки 13040—13240). В него вложе-
ны два последовательных цикла по J (строки 13080—13120 и
13180—13220) для поиска всех исходных веществ (первый цикл) и
продуктов (второй цикл). Если найдено исходное вещество, которое
совпадает с I-м веществом, то на экран выводится — R(J) (строка
13100) и соответственно для продукта +R(J) (строка 13200). После
окончания этой подпрограммы заканчивается также и основная
программа. В качестве примера рассмотрена кинетическая схема,
которую мы проанализировали вручную.
Задание 179. Измените программу «ЭС-КИН» так, чтобы константы скорости и
концентрации веществ фигурировали непосредственно в дифференциальных уравне-
ниях. В отношении удобства обработки этой системы уравнений с помощью вычис-
лительной техники такая форма записи неудачна, однако для химиков она привычна
и наглядна.
Задание 180. Проанализируйте с помощью программы «ЭС-КИН» механизм ре-
акции между водородом и кислородом*:
ОН + н2 Н2О + Н
Н + О2 ОН + О
О + Н2 ОН + Н
ОН + ОН Н2О + О
Н + Н - н2
Н + ОН - Н2О
н + о2 - но2
н + но2 - но + он
н + но2 - н2 + о2
он + но2 - н2о + о2
о + но2 - он + о2
Задание 181. Расширьте программу «ЭС-КИН» так, чтобы оиа проверяла, пра-
вильно ли расставлены стехиометрические коэффициенты в уравнениях реакции эле-
ментарных стадий. Для этого вместо названий веществ надо пользоваться их брут-
то-формулами. Во всех уравнениях реакций число атомов каждого элемента с обеих
сторон от стрелки должно быть одинаково.
12.2. Компьютерные игры
В последнее время широкое распространение получили компью-
терные игры. В большой группе этих игр игровая ситуация возни-
кает при движении по экрану различных «объектов» (как правило,
* Warnatz J., Chemistry of stationary and non-stationary combustion, in: Ebert К. H.,
Deuflhard P., Jager W., Modelling of chemical reaction systems. Springer Series in
CHEMICAL PHYSICS 18. Springer, Berlin/Heidelberg/New York, 1981, p. 177.
316
Гпава 12
имитируется стрельба). Другая большая группа игр относится к
так называемым интеллектуальным играм, например шахматы, го,
реверси и т. д. Для игр первой группы используется главным об-
разом графический дисплей, на котором можно изображать более
или менее непрерывное движение объектов. При составлении про-
грамм для интеллектуальных игр привлекаются некоторые сведе-
ния из теории данной игры и из новой области информатики —
«искусственного интеллекта». В еще одной небольшой группе игр
ЭВМ используется как вспомогательное устройство для игры без
партнера (например, солитер и кубик Рубика).
Общим для всех компьютерных игр является то, что играющие
довольно быстро теряют к ним интерес, потому что обычные про-
граммы не способны к самообучению, а главное, потому, что в иг-
ре с ЭВМ отсутствуют специфика и динамизм живого партнера.
Исключение, пожалуй, составляет игра, программу которой мы
рассмотрим в этом разделе. В эту игру даже приятней играть с
ЭВМ, чем с человеком. Причина довольно проста: хотя игра и
предполагает наличие двух партнеров, однако в игре фактически
участвует только один из них. Второй партнер является храните-
лем информации, которой он делится по запросу первого. Для пер-
вого партнера игра представляет какой-то интерес, а вот у второго
довольно скучная задача — поставлять информацию первому. С та-
ким заданием может справиться и так называемый «болван». ЭВМ
и соответствующая программа прекрасно подходят, чтобы возло-
жить на них такую довольно скучную обязанность.
Игра, для которой мы будем составлять программу (точнее для
части игры за того партнера, который только отвечает на вопросы
играющего), по-немецки называется не совсем удачно — “Su-
perhirn” (английское название “Mastermind”)*.
Вкратце о правилах нашей версии игры. Из десяти первых букв
алфавита выбирают комбинацию из 5 букв, которая неизвестна
первому партнеру. Буквы могут повторяться. Первый игрок дол-
жен отгадать эту комбинацию за наименьшее число попыток. По-
сле каждой попытки второй игрок сообщает, сколько угадано букв,
занимающих ту же позицию, что и в заданной комбинации, и
сколько, кроме того, угадано букв, стоящих на других местах. Наи-
большее число попыток равно 15.
Ниже приведена программа «УГАДАЙ-КОД» с игровым приме-
ром.
* Разные версии этой игры у иас называются «Угадай код», «Мыслитель», и так-
же не очень удачно — «Быки и коровы». — Прим, перев.
Нечисленные методы обработки данных
317
0 REM "УГАДАЙ KOfl"EBERT/EDERER 820504
1 REM*********************************
2 REM** ИГРА "УГАДАЙ КОД" ••
3 REM** ("SUPERHIRN" ИЛИ 'MASTERMIND") ••
9 REM*********************************
10 DIM А*<10>,2*<10>,В*<10>,Н»<10>,К*<10>
100 PRINT "УГАДАЙ КОД"
200 PRINTiPRINT "ЦЕЛЬ ИГРЫ - УГАДАТЬ' ПЯТИБУКВЕННУЮ"
300 PRINT "КОМБИНАЦИЮ, СОСТАВЛЕННУЮ ИЗ СЛЕДУЮЩИХ"
400 PRINT "БУКВ: А В С D Е F G Н J". ЭВМ УКАЗЫВАЕТ"
500 PRINT "ЧИСЛО БУКВ В ВАШЕЙ КОМБИНАЦИИ, СТОЯЩИХ"
600 PRINT "НА ВЕРНЫХ ПОЗИЦИЯХ, И ДОПОЛНИТЕЛЬНО ЧИСЛО"
700 PRINT iPRINT "БУКВ, ВСТРЕЧАЮЩИХСЯ В ИСКОМОЙ КОМБИНАЦИИ"
000 PRINT "В ВАШЕМ РАСПОРЯЖЕНИИ 15 ПОПЫТОК) ” iPRINT
900 PRINT "НАБЕРИТЕ НА КЛАВИАТУРЕ 5 ВЫБРАННЫХ ВАМИ БУКВ"
1000 PRINT"M НАЖМИТЕ КЛАВИШУ RETURN PRINT
1100 PRINT" ПРИ ВВОДЕ КАКОЙ-НИБУДЬ ДРУГОЙ БУКВЫ (К—Z) "
1150 PRINT "ВСЯ ДАННАЯ КОМБИНАЦИЯ СТИРАЕТСЯ И ВЫ МОЖЕТЕ"
1200 PRINT "ВЫБРАТЬ НОВУЮ КОМБИНАЦИЮ"
2000 REM ЗДЕСЬ ЭВМ ВЫБИРАЕТ ЦЕЛЕВУЮ КОМБИНАЦИЮ
2010 2*<1>-"Я"|2*<2>-"В"|2*<3>-"С"|2*<4>-"0"|2*<5>-"Е"
2015 2*<6>-"F"|2*<7>-"G"|2*<S>-"H“iZ*<9>-“I”iZ*<10>-"J"
2020 FOR 1-1 TO 5iX-INT<RND<5>*10+1>
2040 fl*CI>-Z*<X>iNEXT I
2900 PRINT
2930 PRINTiPRINT " ВВЕДИТЕ ТЕПЕРЬ КОМБИНАЦИЮ "iPRINT
3000 REM ЗДЕСЬ ИГРАЮЩИЙ ВВОДИТ СВОЮ КОМБИНАЦИЮ
3005 FOR М-1 ТО 15
3010 FOR 1-1 ТО 5|B*<I>-Я*<I>iNEXT I
3020 PRINT М,ТЯВ<5>,
3030 FOR 1-1 ТО 5
3040 GET О»I IF G»-"" THEN GOTO 3040
3070 IF G*>"J" THEN GOTO 3200
3072 IF 0*<"Я“ THEN GOTO 3200
3080 K*<I>-O*iPRINT K*<I>," ”)iH»(I>.K»<I>
3100 NEXT I
3110 GET 0*1 IF G*-"" THEN GOTO 3110
3112 IF ASC<0*>-13 THEN GOTO 4000
3114 IF 0*>"J" THEN GOTO 3200
3118 IF 0*<"Я" THEN GOTO 3200
3120 GOTO 3110
3150 GOTO 4000
3200 PRINT CHR»<145>,
3210 PRINT IMPRINT "
3220 PRINT CHR*<145>,
3240 PRINTiGOTO 3020
4000 REM АНАЛИЗ КОМБИНАЦИИ ИГРАЮЩЕГО
4100 P-0IREM АНАЛИЗ ПОЗИЦИЙ
4120 FOR 1-1 ТО 51 IFfl*< I >OK»< I > THEN GOTO 4180
4140 P-P+1iВ*<I>-"0"IH* <I>-“1"
4160 NEXT I
4200 PRINT " ПОЗ - ",P,
4500 REM ВЫЯВЛЕНИЕ ДОПОЛНИТЕЛЬНО УГАДАННЫХ БУКВ
4540 В-0
4560 FOR 1-1 ТО 5iF0R J-l TO 5
4580 IF H»<IX>BI<J) THEN GOTO 4700
4600 B-B+l|H*<I>-"1"iB*<J>-"0"
4700 NEXT JiNEXT I
4800 PRINT " БУКВ - ",B
5000 IF P-5 THEN GOTO 9000
8000 NEXT M
8100 PRINT iPRINT "К СОЖАЛЕНИЮ. ВАМ HE УДАЛОСЬ УГАДАТЬ"
8120 PRINT "ЦЕЛЕВУЮ КОМБИНАЦИЮ"
8140 PRINT ТЯВ<5>> iFOR 1-1 TO 5iPRINT Я*<1>," ",iNEXT I
8999 ENO
9000 PRINTiPRINT "ПОЗДРАВЛЯЮ"
318
Гаава 12
RUN
УГАДАЙ КОД
ЦЕЛЬ ИГРЫ - УГАДАТЬ ПЯТИБУКВЕННУЮ КОМБИНАЦИЮ, СОСТАВЛЕННУЮ
ИЗ СЛЕДУЮЩИХ БУКВ*"А В С D. Е F G Н J ". ЭВМ УКАЗЫВАЕТ
ЧИСЛО БУКВ В ВАШЕЙ КОМБИНАЦИИ, СТОЯЩИХ НА ВЕРНЫХ
ПОЗИЦИЯХ, И ДОПОЛНИТЕЛЬНО ЧИСЛО БУКВ,
ВСТРЕЧАЮЩИХСЯ В ИСКОМОЙ КОМБИНАЦИИ
В ВАШЕМ РАСПОРЯЖЕНИИ 15 ПОПЫТОК!
НАБЕРИТЕ НА КЛАВИАТУРЕ 5 ВЫБРАННЫХ ВАМИ БУКВ
И НАЖМИТЕ КЛАВИШУ RETURN
ПРИ ВВОДЕ КАКОЙ-НИБУДЬ ДРУГОЙ БУКВЫ (К-Z)
ВСЯ ДАННАЯ КОМБИНАЦИЯ СТИРАЕТСЯ И ВЫ МОЖЕТЕ
ВЫБРАТЬ НОВУЮ КОМБИНАЦИЮ
ВВЕДИТЕ ТЕПЕРЬ СВОЮ КОМБИНАЦИЮ
1 А А В в С поз м в БУКВ - В
2 D D Е Е F поз м в БУКВ - 1
3 F 0 0 н Н поз м в БУКВ - 2
4 I I I J J поз м 0 БУКВ - 2
5 0 Н J D I поз м 1 БУКВ - 1
б J Е J 0 0 поз м 1 БУКВ - В
7 н Е н 1 I поз м 5 БУКВ - В
ПОЗДРАВЛЯЮ
Операторы PRINT в начале программы (строки 100—1200) вы-
водят на экран правила и краткое описание игры. На участке от
строки 2000 до строки 2040 ЭВМ выбирает случайную комбинацию
букв, так называемую искомую комбинацию, которую должен уга-
дать сидящий перед компьютером игрок. (Подсматривать с по-
мощью разного рода уловок искомую комбинацию неспортивно.)
Поскольку генератор случайных чисел может задавать только чис-
ловые комбинации, для нашей задачи надо перевести числовую
комбинацию в буквенную. Правила такого перевода даиы в виде
таблицы (строки 2010 и 2015). С помощью операторов присваива-
ния Z$(l) = “А”, ..., Z$(10) = “J” числам от 1 до 10 ставятся в со-
ответствие буквы от А до J. В следующем далее цикле по I с по-
мощью стандартной функции RND отбираются пять случайных чи-
сел между 0 и 10. Буква, соответствующая случайному числу X, с
помощью оператора
A$(I) = Z$(X)
присваивается индексированной текстовой переменной А$(1). После
окончания этого цикла значения переменных А$(1), А$(2), А$(3),
А$(4) и А$(5) задают последовательность букв искомой комбина-
ции.
Нечисленные методы обработки данных
319
В строках 3005—8000 организован цикл по параметру М, теку-
щее значение которого равно номеру попытки. Текущее значение
переменной М выводится на экран в строке 3020. На участке про-
граммы (строки 3020—3240) в цикле по I пользователь вводит свою
комбинацию букв. Эти буквы присваиваются элементам массивов
К$( ) и Н$( ). Поскольку по правилам игры количество букв в
комбинациях равно 5, начальное и наибольшее значение параметра
цикла I равны 1 и 5 соответственно. Ввод организован с помощью
рассмотренного выше оператора GET, который вводит буквы, на-
бранные на клавиатуре и хранящиеся в буферной памяти (операто-
ром GET можно вводить данные в процессе выполнения програм-
мы). Оператор GET является первым оператором строки 3040
(GET G$). Если ни одна клавиша не нажата, то буферная память
пуста и второй оператор этой строки — оператор условного
перехода — возвращает управление оператору GET, стоящему в
той же строке. Этот своеобразный бесконечный цикл продолжается
до тех пор, пока буферная память остается пустой, т. е. до тех
пор, пока не нажата какая-нибудь клавиша.
В строках 3070 и 3072 проверяется, является ли буква, хранящая-
ся в буферной памяти, одной из 10 первых букв латинского алфави-
та (А—J), и если эта буква входит в число допустимых, то она при-
сваивается соответствующим элементам массивов К$( ) и Н$( ) и
одновременно выводится на экран. Если буква, находящаяся в бу-
фере, больше чем J (т. е. К, L, ...) или меньше чем А (т. е. знак или
число), то управление передается строке 3200. Эта строка стирает с
экрана всю строчку, в которой встретился ошибочный знак, и
управление передается строке 3020, с которой возобновляется М-я
попытка играющего. Таким образом, можно умышленно ввести не-
допустимый знак, чтобы данная попытка не учитывалась. Это
может пригодиться, если при наборе комбинации обнаружена
ошибка или внезапно в голову пришла новая идея. Ерли введены
все пять допустимых букв, то цикл по I заканчивается (строка
3100).
Однако набранную комбинацию можно еще исправить, посколь-
ку в строке 3110 для продолжения выполнения программы требует-
ся дополнительное нажатие клавиши. Если набрать одну из так на-
зываемых допустимых букв (А—J), то ровным счетом ничего не
произойдет и с помощью операторов IF (строки 3114, 3118 и 3120)
управление возвращается строке 3110. При наборе какой-либо дру-
гой буквы или знака управление передается строке 3200, которая
стирает уже набранную комбинацию, и пользователь получает воз-
можность заново набрать комбинацию букв.
320
Гаава 12
Только когда пользователь нажмет клавишу RETURN, ввод
комбинации будет полностью завершен и управление перейдет к
строке 4000, с которой начинается анализ введенной комбинации
букв. Как проверяется, нажата ли клавиша <RETURN)? С по-
мощью оператора ASC(G$) определяется некоторое целое число,
соответствующее значению текстовой переменной GS и являющееся
характеристикой каждого знака. Таблица кодов всех знаков имеется
в руководстве к вашей ЭВМ.
Код знака* ***********
*** ASC ***
***********
***************
*** ASC(B$) ***
***************
В$ может быть текстовой переменной или «текстовым выражением».
Оператор ASC можно рассматривать как функцию, которая
простой переменной присваивает по первому знаку текста в тексто-
вой переменной В$ определенное число в соответствии с таблицей
кодов.
В нашей ЭВМ клавише (RETURN) соответствует число 13. По-
этому в строке 3112 записано:
3112 IF ASC(G$) = 13 THEN GOTO 4000
С помощью оператора условного перехода проверяется, была ли
нажата клавиша (RETURN), и если она была нажата, то управле-
ние передается строке 4000, с которой начинается анализ введенной
комбинации букв.
Прежде чем приступить к анализу введенной комбинации, целе-
вая комбинация дублируется, ее буквы присваиваются элементам
массивов А$( ) и В$( ). Это делается потому, что в ходе сопо-
ставления обеих комбинаций в искомую комбинацию будут вно-
ситься изменения.
В строках 4100—4200 определяется число букв, стоящих на вер-
ных позициях. Для этого счетчик верных позиций Р сначала обну-
ляется, и в цикле по параметру I каждая буква искомой комбина-
ции А$(1) сравнивается с соответствующей буквой выбранной игра-
ющим комбинации К$(1). Если эти буквы одинаковые, то счетчик
Код символа, или код литеры. — Прим, перев.
Нечисленные методы обработки данных
321
числа угаданных позиций Р увеличивается на 1. Буквы, стоящие на
верных позициях в искомой комбинации, с помощью оператора
В$(1) = 0 заменяются на «О» и в предложенной пользователем ком-
бинации с помощью оператора Н$(1) = ”1” заменяются на 1. Эти
изменения вносят в сравниваемые комбинации для того, чтобы бук-
вы, стоящие на верных позициях, не учитывались при последую-
щем подсчете угаданных букв, имеющихся в целевой комбинации,
но стоящих не на нужном месте.
Если сравнены все пять букв, то в строке 4200 на экран
выводится число верных позиций. Определение числа дополнитель-
но угаданных букв происходит на участке программы от строки
4540 до строки 4800. С помощью конструкции из двух циклов, один
из которых вложенный, сравнивается каждая буква искомой комби-
нации с каждой буквой предложенной пользователем комбинации*.
При совпадении букв счетчик угаданных букв, который перед нача-
лом процедуры обнуляется, в строке 4600 увеличивается на едини-
цу, и буквы в обеих комбинациях заменяются нулями и соответст-
венно единицами (как это было при определении числа верных по-
зиций), чтобы уже угаданные буквы повторно не подсчитывались.
После окончания этих циклов в строке 4700 число дополнительно
угаданных букв выводится на экран.
В строке 5000 выясняется, угаданы ли все пять позиций искомой
комбинации. Если это так, т. е. искомая комбинация найдена, то
управление передается строке 9000, в которой на экран выводятся
поздравления. В противном случае цикл по М продолжается. В на-
чале этого цикла с помощью оператора В$(1) = А$(1) восстанавли-
вается исходная искомая комбинация, в которую при анализе вно-
сились некоторые изменения. Если цикл по М после 15 шагов за-
канчивается обычным образом, т. е. после 15 попыток искомая
комбинация еще не найдена, то пользователю сообщается, что на
этот раз ему не удалось установить загаданную комбинацию. На
экран выводится ответ (строка 8140), и программа заканчивается
оператором END (строка 8999).
Задание 182. Напишите программу для игры «Угадай код», в которой для вво-
да комбинации букв вместо оператора GET использовался бы оператор INPUT.
Задание 183. Напишите модифицированную программу «УГАДАЙ-КОД», кото-
рая при анализе первых пяти попыток могла бы (но не обязательно) один раз вы-
* На данном этапе сравниваются не искомая и введенная пользователем комбина-
ции, а уже измененные. В искомой комбинации на месте угаданных позиций стоят
нули, а во введенной пользователем — единицы. — Прим, перев.
21-81
322
Глава 12
дать играющему ложные данные. При этом играющий не должен знать, в какой из
этих пяти попыток ЭВМ его «обманывает».
Задание 184. Напишите программу для так называемого программированного
обучения по следующей довольно простой теме: «брутто-формулы алканов, алкенов
и алкинов» (необходимо рассмотреть также соединения с несколькими кратными
связями и циклические соединения).
Программированное обучение состоит в следующем: пользователю (обучаемо-
му) задаются различные вопросы по некоторой теме. При правильных ответах он
получает положительную оценку. Если обучаемый ошибается, то этот раздел еще
раз объясняется и по этой же тематике опять задаются вопросы, но уже другие, и
т. д.
Задание 185. Напишите программу имитации игры в так называемый волшеб-
ный (заколдованный) кубик. Для этого вам надо составить таблицу отдельных вра-
щений. Другой проблемой является наглядное и понятное представление результа-
тов. Вы можете закодировать цвета всех шести граней буквами и выводить на экран
только изменения, происходящие при вращениях.
Напишите также программы для имитации игры с кубиками размером 4x4x4
и 5x5x5.
12.3. Игра «Жизнь» (Game of Life)
Имитационная модель развития популяций была популярно из-
ложена в журнале Scientific American*. Игра происходит на поверх-
ности, разделенной на квадратные ячейки. Поверхность считается
бесконечной. События, происходящие на этой поверхности, можно
изобразить на экране, если мы будем рассматривать его как моди-
фикацию конечной прямоугольной плоскости, верхняя граница ко-
торой соединяется с нижней, а левая граница — с правой. Таким
образом, события развертываются на поверхности тора.
Игра начинается с задания начальной популяции, т. е. числа за-
нятых ячеек. Занятые поля на экране обозначаются звездочками, в
то время как незанятые поля остаются темными. Из начальной по-
пуляции развивается следующее поколение в соответствии с прави-
лами:
а) Обитатель ячейки выживает, если рядом есть две или три за-
нятые соседние ячейки. Соседними считаются ячейки, которые име-
ют общую сторону или общую вершину.
б) Обитатель ячейки погибает и ячейка становится незанятой,
если она окружена четырьмя и более занятыми ячейками (перенасе-
ление), а также если около нее имеется только одна соседняя оби-
таемая ячейка или вообще нет соседей (изоляция).
в) Рождение в незанятой ячейке происходит только в том слу-
чае, если около этой ячейки имеются ровно три соседние обитае-
мые ячейки.
Gardner М., Mathematical games. — Scientific American, Oct. 1970, p. 120.
Нечисленные методы обработки данных
323
По этим простым правилам развиваются геометрические струк-
туры, обладающие удивительной подвижностью и изменчивостью.
Есть популяции, которые сначала процветают, однако впоследст-
вии полностью вымирают. Другие в своем развитии образуют от-
дельные островки стабильности с постоянной численностью обита-
телей. Некоторые популяции образуют устойчивые и пульсирую-
щие фигуры, которые могут двигаться по экрану самым причудли-
вым образом.
Имитационные игры такого рода имеют не только учебное и
развлекательное значение, их можно использовать для решения го-
раздо более серьезных научных проблем (разумеется, с другими
правилами), например для моделирования процессов фазовых прев-
ращений или распространения злокачественной опухоли печени.
По программе «ЖИЗНЬ» игра происходит на игровом поле раз-
мером 20 x 20 ячеек. Игровое поле представляет собой развертку
тора, т. е. первая строка экрана является соседней с двадцатой
строкой и первый столбец является соседним с двадцатым.
0 REM "ЖИЗНЬ" EBERT/EDERER 840211
1 REM*******************************************
2 REM** ИГРА "ЖИЗНЬ" (GAME OF LIFE) **
3 REM** SCIENTIFIC RMERICRN OCT 1970 И **
4 REM** SCIENTIFIC RMERICRN OCT 1983 **
5 REM** ИМИТАЦИЯ РАЗВИТИЯ ПОПУЛЯЦИИ **
6 REM** НА ПОВЕРХНОСТИ ТОРА, Т Е. ВЕРХНЯЯ **
7 REM** ГРАНИЦА ЭКРАНА ПЕРЕХОДИТ В НИЖНЮЮ, **
8 REM** ПРАВАЯ - В ЛЕВУЮ **
9 REM*******************************************
50 DIM Х<21,21>,У<21,21>,L<17>,М»<20>
60 PRINT "ВЫ МОЖЕТЕ ВЫБРАТЬ ОДИН ИЗ ТРЕХ ВАРИАНТОВ";
62 PRINT "НАЧАЛЬНОЙ ПОПУЛЯЦИИ"
65 PRINT " 1 - ЗАДАННАЯ В ПРОГРАММЕ НАЧАЛЬНАЯ ПОПУЛЯЦИЯ"
70 PRINT "2 - НАЧАЛЬНАЯ ПОПУЛЯЦИЯ В ЗАДАННЫХ ГРАНИЦАХ"
75 PRINT " 3 - СЛУЧАЙНАЯ НАЧАЛЬНАЯ ПОПУЛЯЦИЯ"
80 INPUT "КАКУЮ ПОПУЛЯЦИЮ ВЫ ВЫБИРАЕТЕ"; Q
100 IF Q=1 THEN GOSUB 1000
105 IF 0=2 THEN GOSUB 5008
110 IF 0=3 THEN GOSUB 2508
120 GOSUB 2000 iREM ТАБЛИЦА ВЫЖИВАНИЯ И ГИБЕЛИ
130 PRINT CHR»<147> jiREM ОЧИСТКА ЭКРАНА
140 GOSUB 3000 sREM ВЫВОД ИНФОРМАЦИИ
160 GOSUB 4000 iREM НОВОЕ ПОКОЛЕНИЕ
200 GOTO 148
999 STOP
1000 REM*******************************
1001 REM** НАЧАЛЬНАЯ ЗАСЕЛЕННОСТЬ **
1002 REM*******************************
1020 FOR 1 = 1 TO 20
1030 FOR J=1 TO 20
1040 X<I,J>=0
1068 NEXT J
1088 NEXT I
1100 X<8,10>=1sX<8,11>=1
1128 X<9,9>=1iX<9,10>»1
1140 X<10,10>.1
21*
324
Глава 12
1890
1900
2000
2001
2002
2020
2040
2060
2080
2200
2500
2501
2502
2510
2520
2540
2620
2630
2640
2650
2660
2680
2940
2960
3000
3001
3002
3020
3040
3060
3080
3100
3120
3140
3160
3200
3250
3300
4000
4001
4002
4020
4040
4060
4100
4120
4140
4160
4200
4300
4990
5000
5001
5002
5101
5102
5103
5104
5105
5106
5107
5108
5109
5110
5111
5112
G-l
RETURN
REN**************************************
REN** ТАБЛИЦА ВЫЖИВАНИЯ И ГИБЕЛИ ♦*
REN**************************************
FOR 1=1 TO 17:L<I>-0iNEXT I
L<3>=1
L<11>=1
L<12>=1
RETURN
REN**************************************
REN** СЛУЧАЙНАЯ НАЧАЛЬНАЯ ПОПУЛЯЦИЯ **
REN**************************************
PRINT "КАКОВА ПЛОТНОСТЬ ПОПУЛЯЦИИ"
PRINT "ЕЕ ВЕЛИЧИНА ДОЛЖНА ЛЕЖАТЬ МЕЖДУ О И 1";
INPUT Р
FOR 1=1 ТО 20
FOR J-l ТО 20
X<I,J>-0
IF RND<5XP THEN X<I,J>-1
NEXT J
NEXT I
0-1
RETURN
REN**************************
REN** ВЫВОД! ИНФОРМАЦИИ **
REN**************************
PRINT CHR<<19>лiREN СМЕЩЕНИЕ КУРСОРА В УГОЛ
FOR I-l TO 20
PRINTiPRINT" "л
FOR J-l TO 20
IF X<I,J>-0 THEN PRINT " "t
IF X<I,J>-1 THEN PRINT " *“л
NEXT J
NEXT I
PRINTiPRINT "
PRINT CHR*<145>лiPRINT " "лОл" - E ПОКОЛЕНИЕ
RETURN
REN***********************
REN** НОВОЕ ПОКОЛЕНИЕ **
REN***********************
FOR I-l TO 20IFGR J-l TO 20|V<I,J>-X<I,J>iNEXT JiNEXT I
FOR I-l TO 20lYCI,0>-V<I,20>|Y<I,21?-V<I,1>iNEXT I
FOR J-0 TO 21|Y<0,J>-Y<20,J>|Y<21,J>-V<1,J>iNEXT J
FOR I-l TO 20IFOR J-l TO 20
H-9*Y<I,J>+Y<I-1,J-l>+Y<I-1,J>+Y<I-1,J+l>+Y<I,J-1>+V<I,J+l>
H-H+V<I+1,J-1>+V<I+1,J>+V<I+1,J+1>
X<I,J>-L<H>
NEXT JiNEXT I
G-G+l
RETURN
REN*************************************************
REN** НАЧАЛЬНАЯ ПОПУЛЯЦИЯ В ЗАДАННЫХ ГРАНИЦАХ **
REN*************************************************
N*<1> -“
N«<2> -" “
N*<3>
N*<4> = " "
N*<5> =" **
N*<6> =“ **
N*<7> -"
N«<8> ****
N*<9> ** * *
N*<10) =" ** ** *
N*<11> =" * * * **
N*<12> =" * * * ** "
Нечисленные методы обработки данных
325
5113 М»<13> -" **** "
5114 М»<14>
5115 М»<15> **
5116 М»<16> -" *•
5117 М»<17>
5110 М»<18>
5119 М»<19> -°
5120 М»<20>
5200 FOR 1-1 ТО 201FOR J-l ТО 20
5220 X<I,J>-0
5240 IF MID»<M»<I>,J,1THEN X<I,J>-1
5260 NEXT JiNEXT I
5200 0-1
5300 RETURN
RUN
ВЫ МОЖЕТЕ выбрать один из трех вариантов начальной популяции
1 - заданная в программе начальная популяция
2 - начальная популяция в заданных границах
3 - случайная начальная популяция
КАКУЮ ПОПУЛЯЦИЮ ВЫ ВЫБИРАЕТЕ? 2
* *
* *
* * * *
* * * ♦
* * * * *
* * * * *
* * * * *
* * * *
* *
* *
1 —Е ПОКОЛЕНИЕ
* *
* *
* * * *
* * * * *
* * * * *
* * * * *
* ♦ * ♦
* * ♦ »
* *
* *
2 —Е ПОКОЛЕНИЕ
* *
* *
* * * *
* * * • ♦
* * * * *
* * ♦ * *
* * * *
* * * *
* *
* *
3 —Е ПОКОЛЕНИЕ
* *
* *
* * * *
* ♦ ♦ *
* * * * *
* * * * *
* * ♦ ♦ »
* ♦ ♦ »
* *
* *
S —Е ПОКОЛЕНИЕ
* ♦
* *
* * * *
* * * *
♦ * * * *
* ♦ * ♦ *
♦ ♦ * ♦ ♦
* * * *
* *
* *
4 —Е ПОКОЛЕНИЕ
326
Глава 12
RUN
ВЫ МОЖЕТЕ ВЫБРАТЬ ОДИН ИЗ ТРЕХ ВАРИАНТОВ НАЧАЛЬНОЙ ПОПУЛЯЦИИ
1 - ЗАДАННАЯ В ПРОГРАММЕ НАЧАЛЬНАЯ ПОПУЛЯЦИЯ
2 - НАЧАЛЬНАЯ ПОПУЛЯЦИЯ В ЗАДАННЫХ ГРАНИЦАХ
3 - СЛУЧАЙНАЯ НАЧАЛЬНАЯ ПОПУЛЯЦИЯ
КАКУЮ ПОПУЛЯЦИЮ ВЫ ВЫБИРАЕТЕ? 1
* *
* *
*
* * ♦
*
* *
1 —Е ПОКОЛЕНИЕ
2 —Е ПОКОЛЕНИЕ
* *
* * » * ♦
* *
* ♦ ♦ * * *
* * * ♦ *
♦ * *
*
* * * ♦
* ♦
• ♦
* *
♦
♦
♦
* *
26 —Е ПОКОЛЕНИЕ
♦ * * *
♦ * * * * * *
♦ * * * *
* * * * * ♦ *
♦ * * * * *
***** *
* * *
* * *
* * * *
27 —Е ПОКОЛЕНИЕ
*
* *
* *
* *
*
*
*
*
60 —Е ПОКОЛЕНИЕ
Нечисленные методы обработки данных
327
61 —Е ПОКОЛЕНИЕ
*
*
62 —Е ПОКОЛЕНИЕ
Программа начинается с описания двух двумерных массивов
Х( ) и Y( ) размером 21x21. Для упрощения расчетов можно
приравнять элементы двадцать первой строки элементам первой
строки и элементы двадцать первого столбца элементам первого
ртолбца. Двумерный массив Y( ) соответствует текущей популя-
ции, а двумерный массив Х( ) — новой популяции. Одномерный
массив используется для размещения так называемой таблицы вы-
живания и гибели; одномерный массив М$( ) предназначен для за-
дания границ начальной популяции.
В следующей строке запрашивается тип начальной популяции, с
которой начинается эволюция. Если хотят выбрать вариант игры с
жестко заданной в программе начальной популяцией, то в строке
80 вводят число 1; тем самым вызывается подпрограмма 1000. В
этой подпрограмме сначала обнуляются все элементы массива
Х( ), а затем с помощью оператора X(I, J) = 1 заселяются опре-
деленные ячейки. До строки 1900, пока выполняется эта подпро-
грамма, счетчик поколений G равен 1. Если хотят, чтобы эволюция
системы протекала в определенных рамках, в строке 80 вводят чис-
ло 2; тем самым вызывается подпрограмма 5000, в которой с по-
мощью 20 операций присваивания формируется текстовой массив
М$( ), задающий границы, в которых будет развиваться популя-
328
Глава 12
ция. Поскольку все 20 элементов массива М$( ) имеют длину 20
знаков (текст между кавычками), рамка в программе и на экране
имеет один и тот же размер. Со строки 5200 по строку 5260 эле-
ментам массива Х( ) присваивается значение 1 или 0 в зависимо-
сти от того, стоит ли в соответствующем месте звездочка или нет
(конструкция оператора IF в строке 5240).
Если хотят, чтобы начальная популяция задавалась стохастиче-
ски, то в строке 80 вводят число 3 и тем самым вызывается под-
программа 2500. Сначала эта подпрограмма запрашивает плот-
ность начальной популяции. Затем с помощью двух вложенных
циклов (строки 2620—2680) для каждой из 400 ячеек генерируется
случайное число. Если случайное число, соответствующее данной
ячейке, меньше заданной плотности популяции, то элементу мас-
сива X(I, J), соответствующему этой ячейке, присваивается значе-
ние 1, в противном случае — 0. В конце обеих последних подпро-
грамм счетчику поколений присваивается значение 1.
После того как в соответствии со сделанным выбором сформи-
рована начальная популяция, в строке 120 вызывается подпрограм-
ма 2000, в которой по заданным правилам составляется таблица
выживания и гибели. Это происходит следующим образом. Для
каждой ячейки рассчитывается число соседей, и если ячейка заселе-
на, то к числу соседей прибавляется число 9. Таким образом, каж-
дое из возможных состояний ячейки можно однозначно охаракте-
ризовать некоторым числом между 0 и 17. В таблице выживания и
гибели каждому из этих чисел (статусу ячейки) соответствует число
1, если в следующем поколении ячейка будет заселена. По прави-
лам игры значение 1 имеют только переменные L(3) (рождение),
L(ll) и L(12) (выживание). Обитатели тех ячеек, которым соот-
ветствуют другие значения индекса I переменной L(I), вымирают, а
если эти ячейки не заселены, то они остаются пустыми. Правила
игры можно легко изменить, если соответствующим образом изме-
нить или дополнить строки 2020—2200.
После возвращения в основную программу с экрана все стирает-
ся (строка 130) и вызывается подпрограмма 3000 для отображения
нового шага эволюции. Курсор смещается в левый верхний угол, и
на экран выводится изображение, содержащее 20 строк по 20 зна-
ков в каждой строке. Если элемент массива X(I, J) равен 0, то J-я
позиция в I-й строке останется на экране пустой (строка 3100); если
элемент X(I, J) равен 1, то в J-й позиции I-й строки экрана появит-
ся звездочка (строка 3120). Чтобы изображение было наглядным и
занимало весь экран, звездочки отодвигают друг от друга на один
пробел. Для этого перед выводом на экран каждой строки сначала
Нечисленные методы обработки данных 329
выводится одна строка пробелов (строка 3060)*. В строке 3200 на
экран выводится порядковый номер поколения.
На заключительном этапе из основной программы вызывается
подпрограмма 4000, которая рассчитывает очередной шаг эволю-
ции. Для этого элементы массива Y( ) приравниваются элементам
массива Х( ) (строка 4020), нулевой столбец приравнивается двад-
цатому и двадцать первый — первому (строка 4040). В строке 4060
последняя строка матрицы Y приравнивается первой. Далее кон-
струкция из двух циклов определяет статус Н каждой ячейки. Для
этого подсчитывается число соседних обитаемых ячеек, и если сама
ячейка обитаема, то к числу соседей прибавляется число 9. Соглас-
но таблице выживания и гибели, с помощью оператора X(I, J) =
= L(H) элементу массива X(I, J) присваивается значение 0 или 1 в
соответствии со статусом Н данной ячейки. После того как опреде-
лена зависимость ячеек на этом шаге эволюции, перед возвращени-
ем в основную программу счетчик поколений G увеличивается на
единицу.
Затем управление переходит к строке 140 основной программы,
и после вывода на экран полученной популяции начинается расчет
нового шага эволюции. Программа «ЖИЗНЬ» представляет собой
бесконечный цикл.
Задание 186. Проследите за эволюцией популяции, выбирая разные типы исход-
ных популяций.
Задание 187. Измените в программе «ЖИЗНЬ» правила игры или замените
строго детерминированные правила стохастическими, приписывая каждому статусу
ячейки определенную вероятность, с которой заселяется эта ячейка.
Задание 188. С помощью имитационной модели, заложенной в программе
«ЖИЗНЬ», можно моделировать такие реальные процессы, как экстракция (завари-
вание кофе), полимеризация, электропроводность расплавов, работа телефонных се-
тей, распространение лесных пожаров или инфекционных заболеваний.
Постройте двухмерную имитационную модель ферромагнетизма. Каждая ячейка
может находиться в двух спиновых состояниях. В рамках этой модели считается,
что около каждой ячейки имеются только четыре соседние, которые располагаются
по сторонам квадрата. Если сумма спинов соседних ячеек равна нулю, то спин цент-
ральной ячейки с равной вероятностью может принять одно из двух значений. Если
в окружении преобладают ячейки с одним из значений спина, то вероятность того,
что спин этой ячейки примет доминирующее значение, возрастает. Кроме того, ве-
роятность обратно пропорциональна абсолютной температуре. Пусть для трех со-
седних ячеек с одинаковыми спинами вероятность параллельной ориентации спина
равна 0,5 + 0,25/(1 + а *Т); для четырех одинаковых ячеек эта вероятность состав-
ляет 0,5 + 0,5/(1 + а* 7). Коэффициент пропорциональности а зависит от точки
Кюри рассматриваемого материала.
* Так изображение растягивается по вертикали. Чтобы раздвинуть изображение
по горизонтали, звездочки выводятся на экран с одним пробелом. — Прим, перев.
330
Глава 12
Не следует ожидать, что такая простая двухмерная модель хорошо описывает
резкое падение намагниченности в точке Кюри, как это наблюдается в действитель-
ности. Однако эта модель хорошо передает статистическое распределение спинов
при высоких температурах и наличие больших областей с одинаковыми спинами при
низких температурах. Можно обнаружить, что при 0 К антиферромагнитное состоя-
ние так же стабильно, как и ферромагнитное.
Задание 189. Напишите программу для моделирования самоорганизации ДНК в
качестве примера самоорганизующихся систем. Используйте для этого следующую
простую модель. Пусть имеется 100 молекул ДНК, состоящих из 12 нуклеотидов че-
тырех видов (их обозначим буквами А, Т, С и G). Последовательность нуклеотидов
в этих 100 молекулах ДНК случайная. Назовем одну из последовательностей «иде-
альной»; она имеет некоторые преимущества перед остальными. Из 100 молекул
ДНК в результате репликации получается еще 100 молекул. Однако при репликации
встречаются ошибки (мутации), например в количестве 1%. Теперь из 200 молекул
100 погибает. При этом имеет значение преимущество, которым обладают молеку-
лы с последовательностью нуклеотидов, похожей на «идеальную». (Например, при
каждом совпадении нуклеотида и его положения в цепи с идеальной последователь-
ностью вероятность гибели уменьшается в два раза.) Процессы репликации и гибели
протекают очень быстро. В конце концов все молекулы ДНК должны получить
«идеальную» последовательность нуклеотидов, хотя вероятность ее образования в
результате случайного процесса составляет 1:16777216. Что будет, если мутации бу-
дут возникать чаше или реже?
13. Машинное построение графиков
Результаты измерений или расчетов, представленные в виде
таблицы, не всегда могут дать полную и наглядную информацию
об исследуемом процессе. Чтобы пояснить это, проведем следую-
щий мысленный эксперимент. Пусть имеется длинная таблица, ко-
торая содержит в каждой строке значения синуса и косинуса неко-
торого угла. Установить взаимосвязь между двумя столбцами чи-
сел довольно трудно. Однако если отложить эти значения попарно
на осях координат и построить график, то станет ясно, что эти
данные описывают окружность.
Практически всегда целесообразно представлять результаты в
виде рисунка или графика. В некоторых заданиях мы рекомендова-
ли построить соответствующие графики вручную. В этой главе бу-
дут рассмотрены некоторые методы машинного построения гра-
фиков.
Чтобы строить графики с помощью ЭВМ, надо соответствую-
щим образом описать методику их построения. Конечно, для выво-
да графической информации лучше использовать специально пред-
назначенные для этого устройства: графический дисплей или графо-
построитель. Несколько огрубленный график можно получить и на
обычном алфавитно-цифровом дисплее; разрешающую способность
в этом случае можно оценить произведением числа строк на число
знаков в строке.
Поскольку команды и операторы для построения графиков зави-
сят от версии языка, использующегося в данной ЭВМ, и от ее типа,
возможно, вам придется заменить некоторые операторы в приве-
денных здесь программах. В этой книге рассматриваются только
такие операторы и команды вывода графической информации, ко-
торые пригодны для большинства ЭВМ, имеющих машинную гра-
фику, в крайнем случае эти операторы можно легко заменить ком-
бинацией других ключевых слов. (В этой главе вводятся и исполь-
зуются операторы машинной графики высокого разрешения ЭВМ
Commodore CBM 8032.)
332
Глава 13
Для облегчения адаптации приведенных программ к ЭВМ дру-
гих типов, использующих другие версии БЕЙСИКа, будут рассмот-
рены довольно подробно синтаксис и семантика операторов и ко-
манд вывода на экран графической информации.
*****************
*** SYS 40960 ***
*****************
Вызов графического интерпретатора
По этой команде вызывается записанная на магнитном диске
служебная программа — графический интерпретатор, после чего
можно пользоваться командами и операторами для вывода на
экран графической информации.
************
*** INIT ***
************
Инициализация
По этой команде с экрана стираются все графики, а параметры
других операторов, использующихся при выводе графической ин-
формации, возвращаются в исходное состояние.
******************
*** DISPLAY(I) *** Режим дисплея
******************
Эта команда задает режим работы дисплея:
1=1 — вывод графической информации;
1 = 0 — вывод алфавитно-цифровой информации (обычный режим работы дис-
плея).
************************
*** мар(хо, хэ, yo, Y9) *** Математическая система координат
************************
ХО — наименьшее значение координаты X изображаемого графика;
Х9 — наибольшее значение координаты X изображаемого графика;
Y0 — наименьшее значение координаты Y изображаемого графика;
Y9 — наибольшее значение координаты Y изображаемого графика.
При каждом обращении к графопостроителю для определения
координат соответствующей точки на экране используется заданная
Машинное построение графиков
333
здесь система координат. По команде INIT задается следующая си-
стема координат МАР (0, 1, 0, 1).
***************************
*** PSPACE(X1,X2,Y1,Y2) ***
***************************
Границы графика («окно»)
XI — левая граница; Х2 — правая граница; Y1 — нижняя граница; Y2 — верхняя
граница.
С помощью этой команды выбирается часть экрана («окно»),
внутри которой будет построен график. Параметры XI, Х2, Yl, Y2
могут иметь значения от 0 до 1. PSPACE (0, 1,0, 1) означает, что
график будет занимать весь экран. Эти значения параметры прини-
мают по команде INIT.
*******************
*** PLOT(X,Y,I) ***
*******************
Команда на построение графика
в заданной ранее системе координат
X — новое значение координаты X; Y — новое значение координаты Y; I — пара-
метр, контролирующий изменение позиции:
1 = 0 — линия, по которой движется перо, не обозначается (перо поднято);
1=1 — линия обозначается (перо опущено);
1 = 2 — линия стирается;
1 = 3 — линия инвертируется.
По этой команде перо* передвигается по прямой из своей преж-
ней позиции в новую, с координатами X, Y.
**********************
*** DPLOT(DX,DY,I) ***
* * * DPLOT(О ,0 ,1) * * *
**********************
То же, что и PLOT (см. в тексте)
Построение одной точки
В целом DPLOT используется так же, как и команда PLOT.
Только параметры DX и DY относятся не к новой позиции пера, а
к последней текущей позиции. Задавая нулевые значения DX и DY,
можно изобразить на экране отдельно одну точку.
*** LINTYP(T) ***
★★★★*★★**★*★★★★**
Выбор типа линии
• Перо — это луч в ЭЛТ дисплея или перо двухкоординатного самописца. —
Прим, перев.
334
Глава 13
Т = 0 — сплошная линия (Т = 0 устанавливается по команде INIT); Т = 1 —
пунктир; Т = 2 — штриховая линия; Т = 3 — штрихпунктирная линия.
По этой команде выбирается тип линии, которая используется
для построения графика оператором PLOT. По команде INIT пара-
метр Т принимает нулевое значение.
********************
*** CHPLOT(A$,I) ***
Вывод на экран знака
********************
По этой команде на экран можно вывести знак на то место, на
котором в данный момент стоит перо. Для этого используется пер-
вый знак значения текстовой переменной А$. Параметр I в этой
команде имеет те же функции, что и в команде PLOT.
13.1. Узор
Сначала составим небольшую программу, чтобы просто потре-
нироваться в построении графиков на экране дисплея. Эта програм-
ма рисует абстрактные, но довольно красивые узоры. Ниже приве-
дена распечатка этой программы, носящей название «УЗОРЫ».
в REM ''УЗОРЫ” EBERT/EDERER 840104
1 REM **i*i*i*i*i*i*i*i*i*i*iki*i*i*i*i*i*i*i*i*i«i*i*i*i*i*i*i*i*i*i*i*i«iki*i*i*i*i*i*i«i*i*i*i*i*i*i*i*i*i*
2 REM ** ЭТА ПРОГРАММА ИЗОБРАЖАЕТ НА ЭКРАНЕ СЕМЕЙСТВО **
Э REM ** ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ **
4 REM ** СО СЛУЧАЙНЫМИ ЗНАЧЕНИЯМИ ПАРАМЕТРОВ **
9 REM **1*1*1«1*1*»1*»»*1*1|11**1*1*1*1*1**1*1*1*1|11*1*1*1*1к1*1*1*1*1*|*|*1*|*|«|*|*|*|*|*|*|*И11*|*1Н1
50 SYS 40960
100 INIT
200 MRF<3,-3,3,-3>
250 DISFLRY<1>
260 R4-RND < 5 > sA3-RND< 5 >
270 B4-RND<5>|B3-RND<5>
280 C1-RND<5>*2
300 FOR 7.0 TO 12.6 STEF .05
310 D-T+Cl
400 X-2*C0S<R4«T>-C0S<R3*2#T;.
410 X2-2*C0S<R4*D>-C0S<R3*2*D>
500 V.2*SIN<B4*T>-SIN<B3«2*T>
510 V2-2*SIN<B4«D>-SIN<B3*2i*D>
590 FLOT<X2,V2,0>
600 FLOT<X,V,1>
700 NEXT T
800 INPUT Ft»
900 DISPLRY<0>
999 END
Машинное построение графиков
335
На четырех рисунках изображены графики, полученные для раз-
личных случайных значений параметров уравнений. После неболь-
шого комментария и вызова графического интерпретатора про-
грамма начинается с команды INIT (строка 100). При этом очища-
ется экран, и параметры графических операторов принимают ис-
ходные значения. Оператор МАР в строке 200 определяет коорди-
наты системы, в которой на экране будут изображаться фигуры.
Обе координаты точек наших графиков лежат между —3 и +3.
Программа строит график функции, заданной в параметричес-
кой форме. Координата X является функцией косинуса параметра Т
(строки 400 и 410), а координата У — функцией синуса параметра Т
(строки 500 и 510). Четыре различных коэффициента, входящие в
параметрическое уравнение (от них зависит период тригонометри-
ческих функций), выбираются с помощью датчика случайных чисел
(строки 260 и 270).
При каждом прохождении внутренней области цикла по пара-
метру Т вычисляются координаты двух точек (два значения X и Y).
Для получения координат второй точки параметр Т увеличивается
на С1. Случайное число С1, которое генерируется в строке 280, ле-
жит между 0 и 2. В строке 590 с помощью оператора PLOT (Х2,
Y2, 0) перо устанавливается в точке с координатами Х2, Y2; пере-
мещение пера в эту точку не оставляет на экране никаких следов.
Это достигается с помощью третьего параметра, входящего в one-
336
Глава 13
ратор PLOT, который имеет нулевое значение. Следующий опера-
тор PLOT (X, Y, 1) (строка 600) перемещает перо по прямой в точ-
ку с координатами X, Y. Теперь это перемещение оставляет на
экране след в виде сплошной линии.
После окончания цикла график остается на экране до тех пор,
пока на запрос оператора INPUT пользователь не выберет на кла-
виатуре какой-нибудь знак. Тогда оператор DISPLAY (0) переведет
дисплей в алфавитно-цифровой (обычный) режим. Однако график
при этом не утрачивается, его можно в любой момент вернуть на
экран с помощью оператора DISPLAY (1).
Задание 190. Постройте с помощью ЭВМ график параметрических функций из
задания 36. Постройте аналогичные кривые.
Задание 191. Добавьте к программе «ПОЛ-ДЕЛ» процедуру для построения гра-
фика, отображающую на экране график функции, точки пересечения которого с осью
х ищутся в основной программе, и саму ось х. Таким образом, прежде чем задать
гранипы поиска решения, вы можете оценить, имеется ли на этом отрезке решение н
где оно приблизительно находится.
Задание 192. Расширьте программу «ТЕП-ПРОВ», введя в нее подпрограмму
для построения графика, и организуйте автоматический выход из бесконечного цик-
ла по критерию сходимости.
Введите подпрограмму для построения графиков к другим программам, если по-
лучаемые в них результаты в виде графиков более информативны, чем числовые
данные.
13.2. Линейная регрессия с графиком
Приведенная ниже программа представляет собой программу
«ЛИН-РЕГР4», дополненную подпрограммой для построения гра-
фика-
0 REM 'РЕ ГР-ГРАФ" EBERT/EDERER 840217
1 REM***********************************
2 REM*# ЛИНЕЙНАЯ РЕГРЕССИЯ С РАСЧЕТОМ**
4 REM** СТАНДАРТНОГО ОТКЛОНЕНИЯ **
5 REM** ПАРАМЕТРОВ А И В. ОБЯЗАТЕЛЬНО**
6 REM** НАДО УКАЗЫВАТЬ ЧИСЛО **
7 REM** ЭКСПЕРИМЕНТАЛЬНЫХ ТОЧЕК **
8 REM** ###########»;################# **
9 REM** РЕГРЕССИЯ С УЧЕТОМ ВЕСОВЫХ ♦*
10 REM* КОЭФФИЦИЕНТОВ **
19 REM**********************************
1000 DIM Х<100Э,7<100ЪЫ<100>
1010 А$=в
1020 E$=CHR$<145)
1100 INPUT "ЧИСЛО ПАР ЗНАЧЕНИЙ"; N
1120 FOR I»1 ТО N:W<I>®1sNEXT I
1140 PRINT SPRINT "ХОТИТЕ ВВЕСТИ ВЕСОВЫЕ КОЭФФИЦИЕНТЫ";:1НРиТ В$
1200 FOR Г«1 ТО N
1300 PRINT ” Y(H;I :•••) « ” .st INPUT V<I>:PRINT Е»;
1330 PRINT AtxPRINT E$;
1350 PRINT " V-. ”;I
1400 PRINT M X<" И:11' = “st INPUT X-'I) sPRINT Et.s
1450 IF "ДА" THEN GOTO 1615
Машинное построение графиков
337
1490 PRINT Rt«PRINT Et«
1500 PRINT " V<"= V<I);
1600 PRINT " X<"«I«"> =";X<I>;
1610 PRINT " NC",I,"> - "««INPUT N<I>:PRINT E»«
1615 PRINT Rt«PRINT E«;
1620 PRINT “ V<";I;"> = ";V<I>>
1630 PRINT X(";I«"> ="«X<I>;
1640 PRINT " N<",I,"> ="«Ы<1>
1700 NEXT I
2000 S1=0
2100 S2=0:S3=0:S4=0:S5=0
2200 FOR 1=1 TO N
2250 S1=S1+IKI>
2Э00 S2=S2+X<1)*W<I>
2400 S3=S3+V<I>*H<I>
2500 S4=S4+X<I>*X<I>*Ы<I>
2600 S5=S5+V<I>*X<I>«Ы<I>
2700 NEXT 1
3000 D1=S1*S4-S2*S2
3100 D2=S3*S4-S5*S2
3200 D3=S1*S5-S2*S3
4000 R-D2/D1
4100 B-D3/D1
5000 PRINT «PRINT "УРАВНЕНИЕ РЕГРЕССИИ "
5100 PRINT " V - "«R«" + X”
6000 S-0
6100 FOR 1-1 TO N
6200 S-S+UK I >♦< Y< I >-<R+B*X<I > > >T2
6300 NEXT I
6500 PRINT «PRINT "СУММА КВАДРАТОВ ОТКЛОНЕНИЙ ="; S
6600 D=SQR<S/<N-2>>
6605 PRINT «PRINT "СТАНДАРТНОЕ ОТКЛОНЕНИЕ = "; D
6610 DR=O*SQR< S4/D1):OB=D*SQR< S1/01>
6620 PRINT «PRINT "ЧИСЛО ПАР ЗНАЧЕНИЙ «NiPRINT
6630 PRINT "R - ">»>'• "«DR «PRINT
6640 PRINT ”B - ">B«“ +/- "«DB«PRINT
6690 GOSUB 20000
7000 PRINT iPRINT "ХОТИТЕ СРАВНИТЬ ИСХОДНЫЕ ЗНАЧЕНИЯ"
7100 PRINT "С РАССЧИТАННЫМИ";
7200 INPUT R»
7300 IF R*. "ДА" THEN GOTO 8000
7500 GOTO 8400
0000 PRINT „
0050 PRINT " X Y (ИЗМЕР) Y (TEOPET)
0100 FOR 1-1 TO N
0200 PRINT X<I>,V<I)««PRINT TRB<20> R+B*X<I>
0300 NEXT I
0400 PRINT «PRINT "ХОТИТЕ РАССЧИТАТЬ ПО УРАВНЕНИЮ РЕГРЕССИИ"
0500 PRINT "ЗНАЧЕНИЯ У ДЛЯ КАКИХ-НИБУДЬ ЗНАЧЕНИЙ X"
0600 INPUT Я*
0700 IF А»="ДА" THEN GOTO 9000
В000 GOTO 9800
9000 PRINT "ЗНАЧЕНИЕ X"; «INPUT XiPRINT Е»?
9050 PRINT •' "«PRINT E»«
9100 PRINT "?<"«X«"> ="«R+B*X
9200 GOTO B400
9000 1=1
9020 ......GET GtiIF G»-"" GOTO 9820
9040 DISPLRVCI)1I=RBS<I-1>«GOTO 9820
9999 END
20000 REM*********************************************
20001 REM** ПОДПРОГРАММА ДЛЯ ПОСТРОЕНИЯ ГРАФИКА **
29002 REM*********************************************
20010 Х1=Х<1>«Х9=Х<1>
20020 Y1-V<1>«V9=V<1>
22-81
338
Глава 13
20100 FOR 1-1 то N
20110 if xaxxi THEN X1-X<I>
20120 IF X<I»X9 THEN X9-X<I>
20130 IF VtIXVl THEN V1-V<I>
20140 IF V<I>>V9 THEN V9-V<I>
20150 NEXT I
20160 DX-<X9-X1>*.1iDV-<V9-V1>*.1
20170 X1-X1-DXIX9-X9+DX
20180 V1-V1-DVIV9-V9+DV
20200 INIT
20210 PSPRCEt.01,.99,.01,.99>
20220 MAP<X1,X9,V1,V9>
20230 PLOTtXl,V1,0>
20240 PLOT < X1,Y9,1>iPLOT < X9,V9,1>
20250 PLOT<X9,V1,1> iPLOTCXl ,S>1,1 >
20300 FOR 1-1 TO N
20310 PLOT<X<I>,V<I>,0>
20320 R»-"*"
20330 CHPLOT < R»,1>
20340 NEXT I
20500 V2-R+B*X1 |V8-A+B*X9
20503 M-N+l
20505 IF 8-0 THENIX2-1E30:X8-1E30:OOTO 20520
20510 X2-<Vl-A>/81X8-<V9-A>/B
20520 IF V2>-V1 AND V2C-V9 THEN>X<M>-X11Y<M>-V2tM-M+1
20530 IF V8>-V1 AND V8C-Y9 THENtX<M>-X9sV<M>-V81M-M+1
20540 IF X2>-X1 AND X2C-X9 THENtX<M>-X2:V<M>-V1tM-M+1
20550 IF X8>-X1 AND X8C-X9 THENtX<M>-X8iV<M>-V9tM-M+1
20600 PLOT<X<N+1>,V<N+1>,0>
20610 PL0T<X<N+2>,V<N+2>,1>
20900 RETURN
RUN
ЧИСЛО ПАР ЗНАЧЕНИЙ? 10
ХОТИТЕ ВВЕСТИ ВЕСОВЫЕ
1 > 18
v< 2 >» 12
3 >» 13
v< 4 )» 15
v< 5 >» 14
VC 6 >» 17
VC 7 >- 18
VC 8 >» 19
VC 9 >» 28
Х< 1 >-
Х< 2 >-
Х< 3 >-
Х< 4 >-
Х< 5 >-
Х< 6 >-
Х< 7 >-
Х< 8 >-
Х< 9 >-
КОЭФФИЦИЕНТЫ? ДА
9 Ы< 1 >- 1
8 Ы< 2 >- 2
7 Ы< 3 >- 1
5 Ы< 4 >- 1
6 И< 5 >- 1
3 Ы< 6 >- 2
1 Ы< 7 >- 1
2 Ы< 8 >- 1
0 И< 9 )- 2
V< 10 >- 22 Х< 10 >— 2 И< 10 >- 1
УРАВНЕНИЕ РЕГРЕССИИ
V - 20.027027 + -1.02702703 *Х
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ = 231081081
СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ = .592748979
ЧИСЛО ПАР ЗНАЧЕНИЙ = 10
А - 20.027027 +/- .24666704
В - -1.02702703 +/- .0478128629
CBM GRAPHIC REV.1 ON - FORMAT 512 * 256
ХОТИТЕ СРАВНИТЬ ИСХОДНЫЕ ЗНАЧЕНИЯ
С РАССЧИТАННЫМИ ? ДА
Машинное построение графиков
339
X Y (ИЗМЕР) Y (ТЕОРЕТ)
9 10 10.7837838
е 12 11.8108108
7 13 12.8378378
5 15 14.8918919
6 14 13.8648649
3 17 16.9459459
1 18 19
2 19 17.972973
0 20 20.027027
-2 22 22.0819811
ХОТИТЕ РАССЧИТАТЬ ПО УРАВНЕНИЮ РЕГРЕССИИ
ЗНАЧЕНИЯ Y ДЛЯ КАКИХ-НИБУДЬ ЗНАЧЕНИЙ X
? НЕТ
К исходной программе «ЛИН-РЕГР4» добавлена всего одна
строка 6690. В этой строке после расчета параметров регрессии вы-
зывается подпрограмма 20000 для построения графика. График по-
является на экране не сразу, а в самом конце основной программы.
В строках 9800—9840 организован «переключатель». (Здесь пара-
метру I присваивается значение 1.) В строке 9820 проверяется, на-
бран ли на клавиатуре какой-нибудь знак. Если нажать одну из кла-
виш, то в следующей строке оператор DISPLAY (I) изменяет
режим работы дисплея. При выполнении следующего оператора
I = ABS(I — 1) первоначальное значение I, равное единице, изменя-
ется, I становится равным 0 и управление передается предыдущей
строке. Таким образом, при следующем нажатии клавиши дисплей
опять будет работать в обычном режиме.
Подпрограмма для построения графика начинается с поиска ми-
нимальных и максимальных значений X и У. Найденные экстре-
мальные значения присваиваются переменным XI, Х9 и Yl, Y9.
Сначала переменным XI, Х9 и Yl, Y9 присваиваются значения Х(1)
и Y(l) соответственно. Затем в цикле (строки 20100—20150) каждое
значение X и Y сравнивается с найденными ранее экстремальными
значениями и таким образом все время корректируется. Следующие
три строки программы настолько расширяют определенную ранее
22’
340
Глава 13
область в координатной плоскости, чтобы крайние заданные точки
не лежали на границах окна. Для этого протяженность окна вдоль
оси х и вдоль оси у умножается на 0,1 и эти произведения вычита-
ются из соответствующих наименьших значений X и Y и прибавля-
ются к наибольшим.
В строке 20200 экран очищается. Следующий оператор
PSPACE(.01, .99, .01, .99) уменьшает «окно», в котором строится
график, на два процента. В строке 20220 оператором МАР задают-
ся математические координаты «окна», и в следующих трех стро-
ках это «окно» обводится рамкой. В цикле (строки 20300—20340)
заданные точки изображаются на экране в виде звездочек.
Оставшаяся часть подпрограммы для построения графика выво-
дит на экран отрезок прямой, соответствующий уравнению регрес-
сии. Главная проблема заключается в таком построении этого от-
резка, чтобы он начинался на одной границе «окна», а заканчивался
на другой. Для этого по уравнению регрессии вычисляются два зна-
чения Y (Y2 и Y8), которые соответствуют минимальному (XI) и
максимальному (Х9) значению X. Из уравнения регрессии рассчи-
тываются также два значения X (Х2 и Х8), при которых Y имеет
наименьшее и наибольшее значения соответственно. Если угловой
коэффициент в уравнении регрессии равен нулю, то переменным Х2
и Х8 присваивается очень большая величина (1Е30). Итак, мы полу-
чили четыре точки пересечения графика линейной регрессии с про-
должениями границ «окна». Надо еще установить, какие из них ле-
жат на границах «окна». Это выясняется в следующих четырех
строках (20520—20550) с помощью еще не встречавшейся конструк-
ции оператора IF. В каждой из этих строк проверяется выполнение
двух условий, связанных логической операцией AND. Наряду с ло-
гическим умножением AND существуют также логические операции
OR и NOT. Чтобы пользоваться этими логическими операциями,
надо знать, как они функционируют. Если условие, стоящее в опе-
раторе IF, выполняется, то оно называется «истинным» и обозна-
чается цифрой 1. Если это условие не выполняется, то оно называ-
ется «ложным» и обозначается цифрой 0. Соответствующие опре-
деления логических операций называют таблицами истинности.
AND 1 0 OR 1 о
1 1 0 1 1 1
0 0 0 0 1 0
NOT 1 дает 0 NOTO дает!
Машинное построение графиков
341
Принята следующая иерархия операций: сначала выполняются
арифметические операции, потом операции отношения и, наконец,
логические операции. Повторим рекомендацию: если порядок
выполнения операций не очевиден или если надо выполнить опера-
ции в ином порядке, чем это диктуется правилами, используйте
скобки.
Координаты точек, определенные с помощью указанных кон-
струкций оператора IF, присваиваются (N + 1)-м и (N + 2)-м эле-
ментам одномерных массивов Х( ) и Y( ) соответственно. Поэто-
му в строке 20503 М приравнивается N + 1. В строке 20520 рас-
сматривается левая граница «окна» для построения графика. Если
точка (XI, Y2) графика регрессии лежит на левой границе, т. е. ес-
ли Y2 меньше чем Y9 и больше чем Y1, то точка с координатами
XI, Y2 — искомая точка. Ее координаты присваиваются элементам
массивов Х( ) и Y( ) и М увеличивается на 1. Таким же способом
проверяются остальные три границы «окна» и на одной из них
определяется вторая точка пересечения. В строке 20600 поднятое
перо перемещается в первую точку пересечения графика с рамкой,
не оставляя, разумеется, следа на экране. В следующей строке две
точки пересечения графика с рамкой соединяются отрезком пря-
мой.
В приведенном примере дана распечатка результатов регресси-
онного анализа и изображен график полученной регрессии. График
значительно облегчит исследователю оценку достоверности и ка-
чества регрессии.
Задание 193. Для большей наглядности наложите на график сетку, состоящую
из пунктирных прямых, параллельных осям координат. С помощью дополнительно-
го участка программы надпишите оси и оцифруйте их.
Задание 194. Дополните программу нелинейного регрессионного анализа под-
программой для построения графика. Составьте эту подпрограмму так, чтобы после
каждой итерации на экране изображались улучшенный график регрессии и экспери-
ментальные точки.
13.3. График решения дифференциального уравнения
Пусть необходимо изобразить кинетические кривые четырех ве-
ществ, участвующих в сложной химической реакции, описываемой
следующей кинетической схемой:
А + В — С (1)
С - D (2)
Для численного решения системы дифференциальных уравнений,
описывающей кинетику этой последовательной реакции, мы вое-
342
Глава 13
пользуемся методом Рунге — Кутта, реализованным в программе
«СИСТ-РКН». Чтобы упростить систему дифференциальных урав-
нений, надо преобразовать все физические параметры и переменные
в безразмерные величины. Система дифференциальных уравнений,
соответствующая приведенной выше кинетической схеме, записыва-
ется в подпрограмме 10000 программы «СИСТ-РКН». Эта про-
грамма является ядром программы «КИНЕТИКА», распечатка ко-
торой дается ниже.
0 REM "КИНЕТИКА" EBERT/EDERER 840206
1 REM*********************************
2 REM** ИМИТАЦИЯ КИНЕТИКИ РЕАКЦИИ **
3 REM** А + В C <<3D ««
4 REM** С --> D (G2) **
9 REM*********************************
100 DIM V<20>,V1<20>,D<20>,V9<20>,VA<20>
120 DIM KI<20>,K2<20>,K3<20>,K4<20>
200 N-4«REM ЧИСЛО ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В СИСТЕМЕ
310 01-1 IREM КОНСТАНТА СКОРОСТИ РЕАКЦИИ 1
320 02-1 1REM КОНСТАНТА СКОРОСТИ РЕАКЦИИ 2
410 V1<1>-1.5 «REM КОНЦЕНТРАЦИЯ ВЕЩЕСТВА А
420 Vl<2>—1 «REM КОНЦЕНТРАЦИЯ ВЕЩЕСТВА В
430 Vl<3>-0 1REM КОНЦЕНТРАЦИЯ ВЕЩЕСТВА С
440 Vl<4>-0 «REM КОНЦЕНТРАЦИЯ ВЕЩЕСТВА D
600 СМ-1.5 1REM НАИБОЛЬШАЯ КОНЦЕНТРАЦИЯ
700 REM INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ. ШАГ ХА. ХЕ XD
710 ХЯ—0«ХЕ—5«XD—1
715 OOSUB 20001REM ПОДГОТОВКА К ВЫВОДУ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
720 FOR I-l ТО N1V<I>—VI<I>«VA<I>—VI<I>«NEXT I
740 Nl-1
1000 FOR А-ХЯ TO XE STEP XD
1020 E-A+XD
1040 H-<E-A>/N1iOOSUB 5000
1050 FOR I-l TO N1VA<I>-V<I>iNEXT I
1060 N1-N1*21H-<E-A>/N1lOOSUB 5000
1080 FOR I-l TO N
1090 IF ABS<V<I>>*ABS<VA<I>XlE-6 THEN 1120
1100 IF ABS<VA<I>-V<I>>/<ABS<VA<I>>*ABS<V<I>>».01 THEN 1050
1120 NEXT I
1200 OOSUB 15000 iREM ВЫВОД ИНФОРМАЦИИ
1220 FOR 1-1 TO N«VI<I>-V<I>«NEXT I
1240 N1-INTCN1/4)«IF Nl-0 THEN Hl-1
1260 NEXT A
1899 STOP
2000 REM******************* ****«********«********iMiMft*iMil',l',
2001 REM** ПОДГОТОВКА К ВЫВОДУ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ **
2002 REM***************************************************
2010 INIT
2020 PSPАСЕ<.01,.99,.01,.99>
2030 PJ-0
2040 DISPLAVCPJ)
2060 MAP<XA,XE,0,CM>1PLOT<XA,0,0>
2100 PLOT<XA,CM,1>1PLOT<XE,CM,1>1PLOT<XE,0,1>1PLOT<XA,0,1>
2200 RETURN
5000 REM************************************
5002 REM** ПОДПРОГРАММА ДЛЯ РЕШЕНИЯ **
5004 REM** ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ **
5010 REM************************************
5100 FOR I-l TO N 1V< I >-Vl < I > «NEXT I;
Машинное построение графиков
343
5200 FOR 19-0 ТО Nf-1sX-R+I9*H
Й300 Х9—XsFOR 1-1 ТО N|Y9<I>-VCI>«NEXT I
5320 GOSUB 10000
5340 FOR 1-1 TO NsKlС I>«H*D<I>sNEXT I
5400 X9-X+H/2sF0R 1-1 TO N:Y9CI>-V<I>+Kl<I>/2sNEXT I
5420 GOSUB 10000
5440 FOR 1-1 TO NsK2<I>«H*D<I>sNEXT I
5500 X9-X+H/2sF0R 1.1 TO NsY9CI>-Y<I>+K2<I>/2iNEXT I
5520 GOSUB 10000
5540 FOR 1-1 TO NsK3CI>-H*DCI>sNEXT I
5600 X9=X+H:F0R 1-1 TO NsY9CI>=Y<I>+K3CI>sNEXT I
5620 GOSUB 10000
5640 FOR 1-1 TO N sK4< I >«H*DC-I > sNEXT I
5700 FOR 1-1 TO N
5720 VC I >-VC I > + CK 1 < I >+2*K2C I >+2*K3C I >+K4C I > >/6
5740 NEXT IsX-E
5800 NEXT’ ISsRETURN
10000 REMsR*******»»**sR**SH****l«lR*****sR*IK *st<st<44t<
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ДИФ. УРАВНЕНИЯ **
10003 REM** DYI/DX=FI (X,Y 1 YNI **
10004 REM** D (I) =F (X9,Y9 (1) Y (9» **
10010 REM*************************************
10100 DC 1>--Gl*Y9<1>*Y9C2>
10200 DC2>-DC1>
10300 DC3>«G1*V9C 1 >*V9<2>-G2*Y9C3>
10400 DC4>-G2*V9C3>
12000 RETURN
15000 REM*************************
15001 REM** ВЫВОД ИНФОРМАЦИИ «*
15002 REM********************* **«*
15020 PRINT X,sFOR 1-1 TO NsPRINT VCI>,sNEXT IsPRINT NI
15040 FOR 1-1 TO N
15050 PLOTCR,Y1<I>„0>sPLOTCE,VCI>,1>sNEXT I
15080 R*-'’" sGET R*
15100 IF R*-"" THEN 15500
15120 PJ-RfeSCPJ—1>sDISPLRVCPJ>
15500 RETURN
63999 END
В приведенном примере на экран выведены только кинетические
кривые. Они показывают, что в ходе реакции концентрации ве-
ществ А и В монотонно уменьшаются, концентрация конечного
продукта D монотонно увеличивается, а концентрация промежуточ-
ного соединения С описывается кривой с максимумом. Часть про-
344
Глава 13
граммы, в которой решается система дифференциальных уравнений
(строки 5000—12000), совпадает с программой «СИСТ-РКН». Но-
выми являются несколько строк в основной программе, подпро-
грамма для формирования и вывода данных и подпрограмма для
построения графиков.
В строке 100 дополнительно описан одномерный массив YA( )
(DIM YA(20)). Система дифференциальных уравнений имеет раз-
мерность N = 4 (строка 200). Константы скорости реакций приня-
ты равными 1, поэтому в следующих двух строках переменным G1
и G2 присвоено значение 1. Переменной Yl(l), соответствующей
начальной концентрации вещества А, присвоено значение 1,5. На-
чальная концентрация вещества В (переменная Yl(2)) равна 1. На-
чальные концентрации веществ С и D равны 0. Время отсчитывает-
ся от момента начала реакции и изменяется в пределах 0—5. Кон-
центрации веществ рассчитываются через промежуток времени 0,1.
Начальному, конечному моментам времени и интервалу между дву-
мя расчетами концентраций соответствуют переменные ХА, ХЕ и
XD (строка 710). Переменной СМ присваивается значение найболь-
шей концентрации одного из веществ. Это значение определяет раз-
меры «окна» на экране, в котором изображаются кинетические кри-
вые. Далее вызывается подпрограмма 2000 для подготовки вывода
на экран графической информации. Сначала все стирается с экрана,
потом определяются границы «окна» для построения графиков, ко-
торые затем изображаются на экране. В строке 720 начальные кон-
центрации веществ присваиваются элементам массивов Y( ) и
А( ). Чтобы понять, что происходит в цикле по параметру А
(строки 1000—1260), надо вспомнить, что подпрограмма 5000 реша-
ет систему дифференциальных уравнений при начальных условиях,
которым соответствуют элементы массива Yl( ), т. е. подпро-
грамма рассчитывает новые значения Y с шагом N1, при условии,
что значения переменных А и Е задают интервал значений незави-
симой переменной X, по которой производится интегрирование.
Весь интервал от ХА до ХЕ, в котором лежат интересующие
нас кинетические кривые, делится на частичные интервалы длиной
XD (в нашем случае на 50 частичных интервалов). Точно эти интер-
валы определяются в цикле по А. В строке 1020 вычисляется теку-
щее значение верхней границы частичного интервала. После того
как найдена длина частичного интервала Н, оператором GOSUB
5000 вызывается подпрограмма для решения системы дифференци-
альных уравнений. Результаты этого шага итерационной процеду-
ры присваиваются элементам массивов Y( ) и YA( ). Потом ите-
рационная процедура повторяется, но с удвоенным числом шагов
Машинное построение графиков
345
(Nl = Nl*2). Проверка результата на сходимость производится в
цикле (строки 1080—1120). В данном примере результаты считают-
ся достаточно точными, если разность значений, полученных в
двух последовательных итерациях, по абсолютной величине мень-
ше, чем 1Е—6, или если отношение этой разности к сумме значений
по абсолютной величине меньше, чем 0,01. Если требуемая точ-
ность не достигнута, то управление передается строке 1050, в кото-
рой результаты последней итерации присваиваются элементам мас-
сива YA( ) и потом рассчитывается новое приближение с удвоен-
ным числом шагов.
Если результаты удовлетворяют критерию точности, то вызы-
вается подпрограмма 15000 для формирования и вывода алфавит-
но-цифровой и графической информации. Рассчитанные подпро-
граммой 5000 значения У( ) для верхней границы интервала Е рас-
сматриваются как начальные значения для следующего интервала.
Число шагов интегрирования N1 уменьшается в 4 раза (но остается
все же не меньше 1); цикл по параметру А заканчивается и управле-
ние передается строке 1000 для расчета концентраций веществ через
промежуток времени XD. После того как концентрации всех ве-
ществ рассчитаны для всех временных интервалов, выполнение
программы заканчивается.
В первой строке подпрограммы для формирования и вывода вы-
ходных данных (строка 15020) на экран выводятся значения кон-
центраций для каждого временного интервала. Потом в цикле по
параметру I на экране строятся кинетические кривые всех четырех
веществ. Для этого оператор PLOT(A, Y1(I), 0) перемещает подня-
тое перо в точку, которая для данного временного интервала слу-
жит начальной, и следующий оператор PLOT соединяет начальную
точку с конечной отрезком прямой. Если внимательно присмот-
реться к полученным графикам, то станет видно, что они состоят
из коротких отрезков. Если хотят получить более гладкие кривые,
то надо уменьшить длину частичных интервалов, т. е. уменьшить
XD (строка 710). Следующие три строки подпрограммы позволяют
по желанию пользователя изменить режим работы дисплея. Если в
процессе выполнения программы набрать на клавиатуре какой-ни-
будь знак, то произойдет переключение режима дисплея, например,
из алфавитно-цифрового в графический.
Задание 195. Рассчитайте динамику популяций хищников и их жертв (см. зада-
ние 137). Изобразите зависимость плотности обеих популяций от времени. Эти ре-
зультаты можно представить в другой форме, если построить график в координатах
концентрация жертв — концентрация хищников. Колебаниям плотности популяций
в таком представлении соответствует спираль, а незатухающие колебания изобража-
ются в виде замкнутой кривой.
346
Гпава 13
Задание 196. Используйте для имитации колебательной химической реакции ки-
нетическую модель OREGONATOR (см. задание 139) и результаты представьте в
графической форме.
Теперь рассчитаем и изобразим траектории двух частиц при со-
ударении, полагая, что потенциал И(г), обусловленный взаимо-
действием частиц, на расстояниях, превышающих удвоенный ради-
ус частицы, зависит только от расстояния между ними*. Чтобы
уменьшить число дифференциальных уравнений, мы будем рас-
сматривать соударение частиц как соударение материальных точек
и для описания использовать полярную систему координат. В соот-
ветствии с этими упрощениями уравнение Гамильтона имеет вид
Н = |д(г2 + г2ф2) + V (г)
Запишем выражение для кинетической энергии Т-.
Т = (г2 + г2ф2)
Компоненты импульса рг и рф можно записать как
дТ . дТ
» Я, = = Л
Учитывая эти соотношения, уравнение Гамильтона можно перепи-
сать в виде
Н = (W + (цг2фУ-~Л + У(г)
2д \ г2 /
Н = (ргг + + к(г)
2/л \ v г2 /
Дифференцируя это уравнение по компонентам импульса ргп рф, а
также по координатам г и ф, получаем четыре дифференциальных
уравнения, которые описывают динамику соударения:
дН/дф = -рф = О
дН/дг = —рг = —рф/^г3 + дУ(г)/дг
дН/дрф = ф = рф/цг2
дН/дрг = г = рг/ц
Ф = Y9(l), г = Y9(2), pr = Y9(3)
• Smith I. W. M., Kinetics and dynamics of elementary gas reactions. Butterworths,
London/Boston, 1980, p. 61.
Машинное построение графиков
347
Правая часть первого дифференциального уравнения равна ну-
лю, поскольку равна нулю производная момента количества движе-
ния по времени, т. е. момент количества движения системы посто-
янный:
РФ = p-b-w
д — приведенная масса; w — относительная скорость в начальный момент времени;
Ь — так называемый параметр соударения, зависящий от минимального расстояния,
на которое сблизились бы частицы, если бы оии двигались относительно друг друга
прямолинейно.
Если использовать потенциал Леннарда-Джонса для аргона,
то потенциал И(г) и его производную можно записать в виде
=4£ [(;)" - (’)“]
ЭИ(г) _ 4с
дг а
— 12
Значения параметров а и е/к можно найти в таблице в разд. 5.7.
Если теперь подставить в эти выражения константу Больцмана,
выраженную в молекулярной системе единиц:
к = 1,3807 (г-А2)/((?-К)
то получится формула, которая записана в строке 160 программы
«СОУДАР».
0 REM "СОУДАР" EBERT/EDERER 831228
1 REM*********************************
2 REM** МОДЕЛИРОВАНИЕ СОУДАРЕНИЯ *♦
3 REM** ДВУХ ЧАСТИЦ. ПО КНИГЕ I.W.M. ♦*
4 REM** SMITH KINETICS AND DYNAMICS... **
5 REM** BUTTERWORTH 1980.P.62 **
a rem*********************************
100 DIM Y<20>,V1-,20>,D<20> .Y9<20>
120 DIM KI<20>,K2<20>,K3<20>.K4<20>
150 REM DV/DR ПОТЕНЦИАЛА АРГОНА
160 DEF FNV<R>-<-12*<3.405/R>T13+6*<3.405/R>T7>*194.3
200 N-3iREM ЧИСЛО ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В СИСТЕМЕ
210 MY-20/6.022E23
220 Ы-1.245Е12 iREM НАЧАЛЬНАЯ СКОРОСТЬ В A/C
250 B-8.0IREM ПАРАМЕТР СТОЛКНОВЕНИЯ В АНГСТРЕМАХ
400 Yl<2>-16iREM НАЧАЛЬНЫЙ РАДИУС В АНГСТРЕМАХ
450 Y1<1>-RTN<B/SQR<Y1<2>T2-BT2>> iREM НАЧАЛЬНЫЙ УГОЛ
470 Vl<3>-MY*W*COS<Y1 < 1 >> iREM НАЧАЛЬНЫЙ ИМПУЛЬС (R)
700 REM INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ "; А, Е
710 R-0IE-1E-10
1000 N1-1000
1100 H-<E-R>/N1
2000 REM ПОДГОТОВКА К ВЫВОДУ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
2010 INIT
2020 PSPRCEC.05,.95,.05,.95>
2030 PJ-1
348
Гпава 13
2040 DISPLRY<PJ>
2050 РР-20
2060 МЯР<-РР,РР,-РР,РР>
20В0 PLOT<-PP,-PP,0>
2100 PLOT<-PP,PP,1> tPLOT<PP,PP,l>1PLOT<PP,-PP,1>
2120 PLOT<-PP,-PP,1>iPLOT<0,0,0>
2140 ICRCL<10,1>
4200 OOSUB 5000
4300 STOP
5000 КЕН***********************************
5002 REM** ПОДПРОГРАММА ДЛЯ РЕШЕНИЯ **
5004 REM«« ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ **
5010 REM***********************************
5100 FOR I-l TO NIY<I>-Yl<I>iNEXT I
5110 PI-0IOOSUB 15000
5200 FOR 19-0 TO Nl-1iX-R+I9*H
5300 X9—XlFOR I-l TO NIV9<I>—V<I>lHEXT I
5320 OOSUB 10000
5340 FOR I-l TO NiKl<I>—H*D<I>iNEXT I
5400 X9—X+H/2iF0R I-l TO Ni¥9<I>-V<I>+К1<I>/2iNEXT I
5420 OOSUB 10000
5440 FOR I-l TO NiK2<I>-H*D<IJiNEXT I
5500 X9—X+H/2iFOR I-l TO NiY9<I>-Y<I>+K2<I>/2iNEXT I
5520 OOSUB 10000
5540 FOR I-l TO NiK3<I>—H*D<I>iNEXT I
5600 X9—X+HiFOR I-l TO NiY9<I>-Y<I>+K3<I>iNEXT I
5620 OOSUB 10000
5640 FOR I-l TO N|K4<I>—H*D<I>INEXT I
5700 FOR I-l TO N
5720 Y<I>-Y<I> + <Kl<I>+2*K2<I>+2*K3<I>+K4<I> >/6
5740 NEXT I
5760 OOSUB 15000iREM ВЫВОД ИНФОРМАЦИИ
5800 NEXT I9IRETURN
10000 REM************************************** ***
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ДИФФЕРЕНЦИАЛЬНЫЕ ««
10003 REM** УРАВНЕНИЯ DYI/ DX =FI (X.Y 1 YN) **
10004 REM** D (I) =F (X9.Y9 (1) Y (9)) **
10010 REM*****************************************
10100 DC 1>-B*W/Y9<2>/Y9<2>
10200 0<2>-У9<3>гМУ
10300 D < 3 >-MY*B*B*WZ< Y9 < 2 > T3 > *W-FNY < 79 < 2> >
12000 RETURN
15000 REM*************** **********
15001 REM** ВЫВОД ИНФОРМАЦИИ «*
15002 REM*************************
15020 PRINT X,Y<1>,Y<2>,Y<3>
15030 PX-Y<2>*SIN<Y<1>>iPY-Y<2>*C0S<Y<1>>
15040 PLOT<PX,PY,PI>
15060 PI-1
15080 ......OET R«
15100 IF R*-"" THEN 15580
15120 PJ-RBStPJ—1>iDISPLRY<PJ>
15500 RETURN
63999 END
Здесь также используется программа «СИСТ-РКН» для решения
полученных дифференциальных уравнений. Они заданы в строках
10100—10300. Число уравнений в системе, приведенная масса, на-
чальная скорость, параметр столкновения, начальный угол и на-
чальный импульс задаются или рассчитываются в строках
200—470. Начальное и конечное значения независимой переменной
Машинное построение графиков
349
X принимаются равными 0 и 1Е—10 соответственно (строка 710).
Переменная X соответствует временной координате в реальном фи-
зическом процессе.
Для расчета параметров, используемых при выводе на экран
изображения траекторий, выбран несколько другой, чем в програм-
ме «КИНЕТИКА», путь. Сначала вызывается подпрограмма 5000
для решения системы дифференциальных уравнений, причем исход-
ный интервал делится на 1000 частичных интервалов (N1 = 1000).
Заранее установлено, что такого количества частичных интервалов
достаточно, чтобы решение имело 3 верные значащие цифры. По-
сле окончания вычислений на каждом частичном интервале в стро-
ке 5760 вызывается подпрограмма для вывода графической инфор-
мации. Значения переменных А, Е й N1 выбраны такими потому,
что решение системы дифференциальных уравнений требует значи-
тельно больше времени, чем вывод соответствующего графика на
экран.
В строках 2000—2120 выполняются операторы и команды, под-
готавливающие вывод графической информации: установление раз-
мера «окна», обозначение его границ и переключение дисплея в гра-
фический режим. В строке 2140 использована команда для построе-
ния графика, которая раньше не встречалась. По команде
ICRCL(10, 1) на экране сплошной линией изображается окружность
радиусом 10. (Мы будем считать, что в центре этой окружности
находится центр массы частицы.)
Для вывода на экран траектории полярные координаты частицы
переводятся в декартовы (строка 15030) и с помощью следующего
оператора (строка 15040) траектория изображается на экране. В
этом операторе параметром типа линии является переменная PI.
При первом обращении к подпрограмме 15000 переменной PI при-
сваивается значение 0 (строка 5110). При следующих обращениях к
подпрограмме 15000 этот параметр равен 1. Это делается для того,
чтобы перемещение пера к точке, с которой начинается траектория
частицы, не оставляло следа на экране. Операторы в строках
15080—15120, как и в предыдущей программе, позволяют пользова-
телю переключать дисплей с одного режима на другой.
Примеры, в которых меняется только параметр соударения Ь,
приведены на рисунках. Как видно на левом рисунке, если частицы
пролетают на большом расстоянии (Ь = 14), то наблюдаются
лишь небольшие отклонения траектории от прямолинейной. Если
соударение частиц близко к центральному (b = 1), то проявляется
сильное отталкивание. На правом рисунке изображены траектории
частиц, когда параметр столкновения b выбран в интервале 7—8,5.
350
Глава 13
В этом случае наблюдается сильное искривление траекторий ча-
стиц; они могут даже совершать два или три оборота друг относи-
тельно друга. (В этом случае говорят о молекулах Ван-дер-
Ваальса.)
Задание 197. Используйте программу «СОУДАР» для изображения на экране
траекторий частиц при фиксированном значении параметра Ь и различных началь-
ных скоростях w. Расширьте графическую часть программы так, чтобы по изобра-
жению траектории можно было оценить относительную скорость частицы. Для это-
го можно, например, отмечать траекторию точками, которые выводятся на экран
на каждом I-м частичном интервале интегрирования. Чем плотнее располагаются
точки, тем меньше относительная скорость частицы.
Задание 198. Подставьте в выражение для потенциала К(г) параметры для гелия
и сравните траектории атомов гелия с траекториями атомов аргона.
В следующем примере мы не будем стремиться во что бы то ни
стало уменьшить число дифференциальных уравнений в системе.
Теперь время счета несколько увеличится, но зато мы получим бо-
лее полную модель процесса без всяких приближений.
Рассмотрим опять столкновение двух атомов аргона, энергия
взаимодействия между которыми описывается формулой Леннар-
да-Джонса:
И(г2) = 4с
= Г(хр х2, J2)
Воспользуемся на этот раз декартовой системой координат.
При этом достаточно рассмотреть задачу на плоскости, поскольку
при двойном столкновении траектории частиц лежат в одной пло-
скости. Это обстоятельство позволяет уменьшить число дифферен-
циальных уравнений в системе с 12 до 8. Уравнение Гамильтона
для выбранной физической модели имеет вид
н = Т + У(Хр х2, Ур у2) = Т + K(V(X! - х2)2 + О'! - у2)2)
Выражение для кинетической энергии выглядит следующим обра-
зом:
Машинное построение графиков
351
Т = A ml (х2 + yl) + А т2(х22 + j>|)
Отсюда можно получить выражения для компонентов импульса ча-
стиц:
дТ . дТ .
= = т>х> р^=1^ =
дТ . дТ .
рг = = m7xJ Р« = ----- =
Х2 дх2 * 2 О2 2-^2
Теперь уравнение Гамильтона можно переписать так, что в него
будут входить лишь пространственные переменные и соответству-
ющие компоненты импульсов:
н = + p2J + щ + р21} + К(х” *2’71 ’у*}
Дифференцируя правую часть уравнения Гамильтона по про-
странственным и динамическим переменным, получаем восемь
уравнений в частных производных, которые описывают эту физиче-
скую систему (см. табл.). В правом столбце приведены индексиро-
Рх.
ЭН = X. - Д1 0(1)
’Рх, т,
ЭН = У1 = т. 0(2)
ЭН а₽х *2 = *2 = 1 "° э * » 1» 0(3)
ЭН эру '2 = У2 = pv “2 т2 D(4)
ЭН = Л av 'К' D(5)
ЭН = Л av = «У. D(6)
ЭН **2 = Л ЭУ Эх2 D(7)
ЭН = Л av - Эх2 D(8)
352
Гпава 13
ванные переменные, которые используются в программе
«СОУДАР2» (строки 10000—12000), соответствующие частным
производным в левом столбце.
0 REM "СОУДАР2" EBERT/EDERER 840202
1 REM*********************************
2 REM** МОДЕЛИРОВАНИЕ СОУДАРЕНИЯ **
3 REM** ДВУХ ЧАСТИЦ. ПО КНИГЕ I.W.M. **
4 REM»» SMITH KINETICS RND DYNAMICS.-**
5 REM** BUTTERWORTH 1980, $.62 FF **
6 REM»* МЕТОД 'BRUTE FORCE' **
9 REM************************)*********
100 DIM V<20>,Vl<20>,D<20>,V9<20>,VR<20>
120 DIM Kl<20>,K2<20>,K3<20>,K4C20>
150 REM FNVCR> ПОТЕНЦИАЛ ДЛЯ АРГОНА
160 REM FNVCRJ-C<3.405/R>T12-C3.405/R>T6>*479.2
200
210
400
410
420
430
440
450
460
470
480
700
710
715
720
NwSiREM ЧИСЛО ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В СИСТЕМЕ
MI-40/6.022Е23:М2-М1
REM НАЧАЛЬНЫЕ ЗНАЧЕНИЯ В А. Г. С
V1<1> —15
Vl<2> —3
Vl<3>-15
Vl<4>-3
VlC5>-1.6Е12ФМ1
V1<6>-0»M1
Vl<7> — 1.6Е12ФМ2
V1<8>«0»M2 ____ ___________________________________
REM INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ, ШАГ ХА, ХЕ, XD
XR-0 :ХЕ=» IE-18 i XD-ЗЕ-13
GOSUB 2000 iREM ПОДГОТОВКА К ВЫВОДУ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
FOR 1-1 ТО NiV<I>-Vl<I>iVR<I>-Vl<I>iNEXT IiGOSUB 15000
iREM
iREM
REM
iREM
iREM
REM
iREM
iREM
КООРДИНАТА X ПЕРВОЙ ЧАСТИЦЫ
КООРДИНАТАY ПЕРВОЙ ЧАСТИЦЫ
КООРДИНАТА X ВТОРОЙ ЧАСТИЦЫ
КООРДИНАТА Y ВТОРОЙ ЧАСТИЦЫ
ИМПУЛЬС ПЕРВОЙ ЧАСТИЦЫ ВДОЛЬ ОСИ X
ИМПУЛЬС ПЕРВОЙ ЧАСТИЦЫ ВДОЛЬ ОСИ Y
ИМПУЛЬС ВТОРОЙ ЧАСТИЦЫ ВДОЛЬ ОСИ X
ИМПУЛЬС ВТОРОЙ ЧАСТИЦЫ ВДОЛЬ ОСИ Y
740 Nl-1
1000 FOR R-XR TO XE STEP XO
1020 E-R+XD
1040 H»<E-R>/N1iGOSUB 5000
1050 FOR 1-1 TO NiVR<I>—V<I>iNEXT I
1060 Nl-Nl*2iH-<E-R>/NliGOSUB 5000
1080 FOR 1-1 TO N
1090 if rbs<v<i>>+rbs<vr<i:>:xie-6 THEN 1120
1100 IF RBS<YR<I>-V<I>>/<RBS<YR<I>>+RBS<V<I>>;:>.01 THEN 1050
1120 NEXT I
1200 GOSUB 15000 iREM ВЫВОД ИНФОРМАЦИИ
1220 FOR 1-1 TO N1Vl<I>-V<I>iNEXT I
1240 Nl-INT<Nl/4>iIF Nl-0 THEN Nl-1
1260 NEXT R
1899 STOP
2000 REM**********************************************
2001 REM** ПОДПРОГРАММА ДЛЯ ПОСТРОЕНИЯ ГРАФИКА **
2002 REM**********************************************
2010 INIT
2020 PSPRCEt.05,.95,.05,.95>
2030 PJ-0
2040 DISPLRVCPJJ
2050 PP-16
2060 mrp<-pp,pp,-pp,pp:>
2080 PLOT<-PP,-PP,0>
2100 PL0T<-PP,PP,1>1PLOT<PP,PP,1> iPLOT<PP,-PP,1>
2120 PLOT<-PP,-PP,1>iPLOT<0,0,0>
2200 RETURN
5000 REM************************************
5002 REM»» ПОДПРОГРАММА ДЛЯ РЕШЕНИЯ **
5004 REM** ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ **
5018 REM************************************
5100 FOR 1-1 TO NiV<I>»V1<I>iNEXT I
Машинное построение графиков
353
5200 FOR 19-0 ТО Nl-1вХ-А+19*Н
3300 X9=.X:F0R I-l ТО N : V9< I > .V< I > sNEXT I
5320 GOSUB 10000
5340 FOR I-l TO NsKl<I>—H*O<I>sNEXT I
5400 X9-X+H/2sF0R I-l TO NsV9CI)»V<I>+К1<I>/2iNEXT I
5420 GOSUB 10000
5440 FOR I-l TO NiK2CI>-H*D<I>sNEXT I
5500 X9»X+H/2sFOR 1-1 TO NsV9CI>-Y<I>+K2<I>/2sNEXT I
5520 GOSUB 10000
5540 FOR I-l TO NsK3CI>-H*D<I>sNEXT I
5600 X9-X+HsFOR I-l TO NsV9<I>-V<I>+K3<I>sNEXT I
5620 GOSUB 10000
5640 FOR I-l TO NsK4<I>-H*D<I>sNEXT I
5700 FOR I-l TO N
5720 V<I>-VCI>+CKl<I>+2*K2CI>+2*K3<I>+K4CI> >/6
5740 NEXT IsX-E
5760 REM GOSUB 15000 iREM ВЫВОД ИНФОРМАЦИИ
5800 NEXT I9sRETURN
10000 REM***************************************************
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ **
10003 REM** DYI/DX=FI (X.Y1....YN) **
10004 REM** D (I) =F (X9,Y9 (1), ...Y (9)) *«
10010 REM******************************** *******************
10100 D<1>-V9<5>/M1
10200 DC2>-V9C6>/M1
10300 DC3>-V9C7>/M2
10400 DC4>-Y9<8>/M2
10500 RX»V9<1>-V9<3>sRV»V9<2>-V9<4>
10560 R2»RX*RX+RV*RV
10600 VR--342.4* < <11.6/R2 >T4-2* <11.6/R2 > t7 >
11500 D<5>»RX*VR
11600 D<6>»RY*VR
11700 DC7> — DC5>
11000 DC8> —DC6>
12000 RETURN
15000 REM************************
15001 REM** ВЫВОД ИНФОРМАЦИИ **
15002 REM************************
15020 PRINT X,sFOR I-l TO NSPRINT V<I>,sNEXT I SPRINT NI
15030 PLOTCV<1>,Y<2>,0>iDPLOTC0,0,1>
15040 PLOT<Y<3>,Y<4>,0>|DPLOTC0,0,1>
15080 A«-""sGET A*
15100 IF A*-"" THEN 15500
15120 PJ-ABS<PJ-1>sDISPLAV<PJ>
15500 RETURN
63999 END
Чтобы найти частные производные потенциальной энергии по про-
странственным переменным, продифференцируем сначала V по г2:
дУ(г2)
3 (г2)
12с
Для аргона получается
дУ(г2)
Если выразить г2 и его производные по пространственным пере-
23-81
354
Глава 13
менным через координаты частиц, то получится
г2 = (Х, - xj2 + О] - У2)2
*£> = 2^)
дх ] ду ।
= -2U, - х2) ’ = -20., - у2)
дх 2 ду2
откуда производные V по пространственным переменным можно
записать как
ЭИ _ dV dr2 dV _ dV dr2
dxt dr2 Эх, ’ dyj dr2 dyt
Значения физических параметров и восемь начальных условий
{координаты и компоненты импульса частиц в начальный момент)
заданы в тексте программы (строки 400—480). Остальная часть ос-
новной программы и цикл в строках 1000—1260 практически совпа-
дают с соответствующим участком программы «КИНЕТИКА».
Лишь в строке 710 заданы другие числовые значения временных ин-
тервалов в соответствии с физическим содержанием задачи. В стро-
ке 715 вызывается подпрограмма 2000, подготавливающая вывод
графической информации.
В подпрограмме 15000, предназначенной для вывода на экран
графических данных, первые операторы строк 15030 и 15040 пере-
мещают поднятое перо в точки экрана, соответствующие рассчи-
танным координатам обеих частиц. Операторы DPLOT(0, 0, 1)
опускают перо и ставят на экране светящуюся точку в том месте,
где в данный момент находится перо. Так на экране появляется
изображение траекторий, плотность точек на которых служит ме-
рой скорости частиц.
На рисунках приведены примеры траекторий при различных на-
чальных условиях (см. табл.).
Хотя в данной задаче использованы числовые параметры потен-
циала Леннарда-Джонса для аргона, в учебных целях проведен
также расчет траекторий частиц различной массы. Результаты в
целом верно описывают изменение поведения частиц, связанное с
существенным изменением скорости их движения. На следующих
рисунках сопоставлено поведение частиц при столкновении в зави-
симости от их массы.
Машинное построение графиков
355
Пример 1 2 3 4 5 6
Y1 (1 ) -15 -15 -15 -1 5 -15 -15
Y1 (2 ) - 3 -3 -3 -3 -3 -3
Y1 (3) 15 1 5 15 15 15 15
Y1 (4) 3 3 3 3 3 3
Y1 (5) 1.7Е12 2Е12 1.97Е12 1.7Е12 1.71Е12 1.5Е12
Y1 (6) 0 0 0 0 0 0
Y1 (7) -1.7Е12 -2Е1 2 -1.97Е12 -2.7Е12 -2.71Е12 -2.5Е12
Y1 (8) 0 0 0 0 0 0
М1 20 40 20 40 40 40
М2 20 10 20 10 10 10
23»
356
Глава 13
Задание 199. Постройте имитационную модель для эксперимента с молекуляр-
ным пучком, считая соударения атомов абсолютно упругими. Задайте постоянное
значение начального импульса вдоль оси х. Начальный импульс вдоль оси у равен 0.
Зафиксируйте координату у одной частицы и постройте иа экране дисплея траекто-
рии второй частицы, меняя иа небольшую величину ее у-коордииату. Как меняется
угол рассеивания с изменением начального положения частицы?
13.4. Изображение поверхностей и тел (3-D-график)
Существует много задач, в которых результат зависит не от од-
ной, а от двух переменных. Наглядным изображением величины z,
которая зависит от переменных х и у, будет трехмерная модель.
Если спроецировать эту модель на плоскость, то получится так на-
зываемый З-В-график. Такой график изображен на рисунке. Эта не-
сколько гротескная ковбойская шляпа является З-В-графиком функ-
ции
z = 3cos(Vx2 + у2)
Проекция характеризуется двумя углами: углом поворота р си-
стемы координат X—Y вокруг оси Z и углом наклона т оси Z к оси
X. Нулевой угол наклона соответствует виду сверху. В этом случае
видна только прямоугольная сетка в плоскости XY. Объемность
такому изображению придает сетка, которая соединяет соседние
точки поверхности, имеющие одинаковые координаты X и Y соот-
ветственно. Кроме того, заслоненные участки поверхности не изо-
Машинное построение графиков
357
бражаются, а на тех частях поверхности, которые видны с обрат-
ной стороны, сетка проводится линиями другого типа (лучше бы
другого цвета). Как получается такое изображение, показано в про-
грамме «З-Д-ГРАФИК».
0 REM "З-Д-ГРАФИК" EBERT/EDERER 840115
1 REM #ЖИ1Й1***И1И1*******И1********************
2 REM mm ПОСТРОЕНИЕ З-Д-ГРАФИКА **
9 REM 1Й»И»И>Й*4(|«*«К>Й«К**«К«К>Й*********************
20 DIM Т<3>,1М<20>,12<20>
30 DIM D<3,3>,D1<3,3>,D2<3,3>
40 DIM X<50>,Y<50>,Z<50,50>
50 DIM Ml<251>,M9<251>
60 PI-RTN<1>*4
200 DEF FNV<X>-<VR+SL*<X-XR>>
1006 REM МАТРИЦЫ ВРАЩЕНИЯ И МАТРИЦА ПРЕОБРАЗОВАНИЯ
1020 RH-30 sTA-30 sREM В ГРАДУСАХ, МЕЖДУ О И 90
1040 Dl(l,l>-COSCRH/180*Pi:> sDl(2,2>=Dl<l,l >
1060 D1 <2,1 >-SIN(RH/180*Pl > t01< 1 ,2>—DI <2,1 >
1080 Dl<3,3)-1 sDl<1,3>=0sDl<2,3)=0:D1<3,1)=0:0К3,2>=0
1088 FOR 1=1 ТО 3sPRINTsF0R J-l TO 3sPRINT Dl<I,:sNEXT JsNEXT I
1140 О2С2.2)жйО8СГА/1:20*Р1> s02<3,3>-D2<2,2>
1166 D2<3,2>=-SIN<TA/180*FT> sCi2(2,3-)—D2<3,2>
1180 D2C1 . 1>«1 :D2( 1 ,2>-8 $D2< 1,3>-0 sD2C2, 1 >-0 sD2<3,1')-0
1188 FOR 1 = 1 TO 3 iPRINTsFOR J=1 TO 3 SPRINT D2CI,J>;sNEXT JsNEXT I
1200 FOR 1=1 TO 3;F0R J-l TO 3
1210 DCI,J>-0sFOR K-l TO 3
1220 D< I,J>»D(I,J5+D2CI,K>*D1<K,J)sNEXT К
1230 NEXT JsNEXT I
1288 FOR 1-1 TO SsPRINTsFOR J-l TO 3sPRINT D<I,J>;sNEXT JiNEXT I
1400 REM ВЫЧИСЛЕНИЕ X ( ) ,Y ( ),И Z( )
1418 NX-0sZ5-lE30sZ6—1E30
1430 FOR X0—10 TO 10 STEP . 5 sNX-NX+1 sNY-0
1458 FOR Y0—10 TO 10 STEP .5sNV-NV+l
1460 X<NX>-X0:VCNV.)wV0
1470 Z < NX,NV >-3*C0S(SQR < X0*X0+V0*V0 >)
I486 IF Z<NX,NV><Z5 THEN Z5-Z<NX,NV>
1490 IF Z<NX,NV>:>Z6 THEN Z6-Z<NX,NV>
1500 NEXT V0sNEXT X0
1600 REM ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ XMIN И XMAX. ПОСЛЕ
1602 REM ПРЕОБРАЗОВАНИЯ ИМ СООТВЕТСТВУЮТ ПЕРЕМЕННЫЕ XI И X9
1605 К1>-ХС1> sT<2>-Y(l>sT(3>-25sGOSUB 8000sXl-XNSX9-XNsV5-VN
1610 T<1)«X<1) :T<2>«V,'NV) sGOSUB 8000
1620 IF XN<X1 THEN Xl-XN
1625 IF XN>X9 THEN X9-XN
1630 T<1>-X(NX>:TC2>-V(NV>:T<3>-Z6sGOSUB 8000IV6-VN
1640 IF XNCX1 THEN XI-XN
1650 IF XN>X9 THEN X9-XN
1660 T(1>-XCNX>sT(2>-V<1>sGOSUB 8000
1678 IF XN<X1 THEN XI-XN
1680 IF XN>X9 THEN X9-XN
1690 DX-250/<X9-X1>
1700 FOR 1-1 TO 251 :M1<I )®1E30sM9<I5--1E30 iNEXT I
2000 REM ПОДГОТОВКА К ВЫВОДУ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
2010 INIT
2020 3M-ABS<V6-V5)/250*0.2
210G MAPC0.252/t’5,V6?
2150 T<1>»XC1> sTC2>-V<l > sT<3>-Z( 1, 1.)
2188 GOSUB 8200 sREM Л P&O БРА30 BA НИЯ
2200 DISPLAV(1>
358
Гпава 13
2226 FLOT'XN,VN,0>:XR—XN|YR-YN
2246 FOR 1-2 TO NY
2260 Td >-Xd > iT<2>-Vd > iT<3>-Zd , I > iGOSUB 8200
2280 GOSUB 9000:NEXT 1
2310 Td>-X(l>iT<2>—Y<1 > :T<3>-Zdd>
2320 GOSUB 8200 iREM ПРЕОБРАЗОВАНИЯ
2340 FLOT<XN,YN,0> : XR-X.N: VR-VN
2360 FOR 1-2 TO NX
2380 T<1>-X<I>iT<2>-Y<1>:T<3>-Z<I,1>iGOSUB 8200
2400 GOSUB 9000:NEXT I
2500 FOR 1-2 TO NY
2510 J-IiK-2
2520 Td>-Xd>|T<2>-Y<I>|T(3>-Z(1,I>:GOSUB 8200:FLOT<XN,YN,0>
2530 XR-XN:YR-VN
2550 T<1>.X<K>:T<2>-V<J>:T<3>=Z<K,J>iGOSUB 8200iGOSUB 9000
2580 J-J-liIF J<1 THEN GOTO 2700
2600 T<1>-X<K>iT<2>-Y<J>iT<3>-Z<K,J>:GOSUB 8200:GOSUB 9000
2620 K-K+llIF K>NX THEN GOTO 2700
2640 GOTO 2550
2700 NEXT I
2800 FOR 1-2 TO NX-1
2810 J-NY:K-I+1
2820 T<1).X(I>iT<2>-V<J>iT<3>-Z<I,NV>:GOSUB 8200iPLOTCXN,VN,0>
2830 XR=XN:VR=YN
2850 T<1>-X<K>:T<2>-V<J>:T<3>-Z<K,J>:GOSUB 8200:GOSUB 9000
2880 J-J-liIF J<1 THEN GOTO 3000
2900 Td).X(K):T<2>-V<J>:T<3>-Z<K,J>iGOSUB 8200iGOSUB 9000
2920 K-K+liIF K>NX THEN GOTO 3000
2940 GOTO 2050
3000 NEXT I
3100 Td>-Xd>:T<2>-V<NY>iT<3>»Z6iGOSUB 8200:FLOT<XN,YN,0>
3120 Td>-Xd> :T<2>-V<NV> |T<3>-Z5iGOSUB 8200 :PLOT<XN.,VN, 1 >
3160 T<2>-Vd> iGOSUB 8200:PLOT<XN,VN,1>
3180 T<1>-X<NX>rGOSUB 8200|PLOT<XN,YN,1>
3190 XR-XNrVR-VN
3200 T<2>-V<NV>rGOSUB 8200iGOSUB 9000
3220 Td>-Xd>iGOSUB 8200iGOSUB 9000
7990 INPUT R«
7995 OISPLRV<0>
7999 STOP
B000 REM********************************************************
8001 REM** ПРЕОБРАЗОВАНИЯ В СООТВЕТСТВИИ С МАТРИЦЕЙ ВРАЩЕНИЯ**
8002 REM********************************************************
8060 XN-0IFOR J9-1 ТО 3:XN-XN+D<1,J9>*T<J9>iNEXT J9
8080 VN-0IFOR J9-1 TO 3:VN»VN+D<2,J9>*T<J9>iNEXT J9
8100 RETURN
8200 REM************************
8201 REM*- ПРЕОБРАЗОВАНИЯ **
8202 REM**>*********************
8220 XN-01FOR J9»l TO 3 :XN-XN+Dd ,J9 >*T<J9> iNEXT J9
8240 VN-0IFOR J9-1 TO 3iVN-VN+D<2,J9>*T<J9>iNEXT J9
8260 XN-INT<<XN-X1>*DX+1.5:>
8280 REM PRINT Td>,T<2>,T<3>,XN,VN
8300 RETURN
9000 REM*********************************************
9001 REM** ПОДПРОГРАММА ДЛЯ ПОСТРОЕНИЯ ГРАФИКА **
9002 REM*********************************************
9030 IF XR-XN THEN GOTO 9800
9040 SL-<YN-VR>/<XN-XR>
9060 IM <1>-XR:S1-SGN <XN-XR >11L—2:VK-YR
9100 IZd>-0iIF YK>M1<XR> THEN GOTO 9140
9120 1Z<1> — 1 |M1<XR>=YK
9140 IF VK<M9<XR> THEN GOTO 0
9160 IZd>-l |M9<XR>-VK
9200 FOR R-XR+S1 TO XN STEP SI
9220 VK»FNY<R>:IZ<IL>»0
Машинное построение графиков
359
9240 IF R-XN THEN VK-VN
9260 IF VK>ril<R> THEN GOTO 9300
9200 IZ<IL> — 1 iVL-MlCR> |M1<R>»YK
9300 IF VK<M9<R> THEN GOTO 9340
9320 IZ<IL>-1iVL-M9<R>1M9<R>-VK
9340 IF IZ<IL>=IZCIL-1> THEN GOTO 9380
9350 IM< IL>-R iKO»Sl*<FNY<R-Sl >-VL>/<FNY<R-Sl >-VK>
9360 IF RBSCSL>>SM RND RBS<KO><1 THEN IM<IL5-R-S1+KG
9370 IL-IL+1
9380 NEXT R:IM<IL)=XN
9500 IF IL>2 THEN GOTO 9600
9520 IF IZ<2> — 1 THEN 1LINTYF< 1 >
9540 FLOT<XN,YN,RBS<IZ<2>>>sXR«XN:VR-YN
9560 LINTVF<0>sGOTO 9990
9600 FOR «.1 TO IL-2
9620 IF IZCR> — 1 THENsLINTVPt1>
9640 PLOT<IMCR+1>,FNY<IM<R+1>>,RBS<IZ<R> >>iLINTVF<0>
9660 NEXT R
9680 IF IZ<IL-1>«-1 THEN:LINTVF<1>
9700 PLOT<XN,YN,RBS<IZ<IL-1>>>sLINTVP<0> jXR-XN:VR»YN
9720 GOTO 9990
9800 REM XR=XN
9820 IZ<l>«0lIF YR>M1<XR> THEN GOTO 9860
9840 IZ<1 >«- 1 :M1 <XR>-VR
9860 IF VR<M9<XR> THEN GOTO 9900
9880 IZ<1>=1iM9<XR>-VR
9900 IZ<2>-0sIF YN>M1<XR> THEN GOTO 9920
9910 IZ<2> —1 :VK-M1<XR> :M1<XR>=VN
9920 IF YN<M9<XR> THEN GOTO 9940
9930 IZ<2> = 1 :W-M9<XR> :M9<XR>=VN
9940 IF IZ<1>-IZ<2> THEN GOTO 9970
9945 IF IZ<1> — 1 THEN:LINTYP<1)
9950 PLOT < XR , VK , RBS < IZ •' 1 > > : : LINTVP < 01
9955 IF IZ<2> —1 THEN lLINTVP< 1 >
9960 PLOT<XR,YN,RBS<IZ<2>>> :LINTVP<0>iVR-VN
9965 GOTO 9990
9970 IF IZ<1> —1 THEN|LINTYF<1>
9980 PLOT<XN,YN,RBS<IZ<1>>>:VR»YNiLINTYP<0>
9990 RETURN
Каждая из сторон прямоугольника, на котором строится по-
верхность функции Z = F(x, у), делится не более чем на 50 отрез-
ков. Во всех узлах сетки рассчитываются значения Z (не больше
чем 2500). Координатам точек поверхности соответствуют одно-
мерные массивы Х( ), Y( ) и двухмерный массив Z( ), которые
описаны в строке 40. Расчет выполняется на участке программы от
строки 1400 до строки 1500. Координаты точек присваиваются эле-
ментам массивов Х( ), Y( ),' Z( ) и одновременно определяется
наименьший (Z5) и наибольший (Z6) элемент массива Z( ). Значе-
нию X, равному Х(1), и значению Y, равному Y(J), соответствует
значение функции Z(I, J).
Проецирование каждой точки поверхности с координатами Х(1),
Y(J), Z(I, J) на плоскость можно представить как простое перемно-
жение матриц. Матрица вращения D может быть представлена в
виде произведения двух матриц D1 и D2 (D = D2*D1):
360
Гпава 13
cosp
sinp
0
-sinp
cosp
О
О
COST
sin 7
0 \
— sin 7 I
COST /
(cosp
sinp
0
— sinp ’COS 7
COS p • COS 7
sin 7
sinp sint
— cos p • sin 7
COST
Матрица преобразования D рассчитывается в начале программы
до строки 1288. Для вычисления двух координат точки на плоско-
сти проекции (им соответствуют переменные XN и YN) вызывается
подпрограмма 8000. В этой подпрограмме вспомогательный вектор
Т, компонентами которого являются исходные значения X, Y и Z,
умножается на матрицу D. Координата Z после преобразования нас
не интересует и поэтому не рассчитывается.
Участок программы со строки 1600 до строки 1690 предназначен
для вычисления наименьшего и наибольшего значения X на проек-
ции (XI и Х9). В следующей строке делением отрезка XI, Х9 на 250
частей рассчитывается значение переменной DX. Одномерные мас-
сивы М1( ) и М9( ), элементам которых сначала присваиваются
очень малые и очень большие числовые значения соответственно,
используются для того, чтобы запомнить для каждой из 251 точек
экрана, какие точки на изображаемой поверхности лежат ближе к
плоскости проекции (экрану), а какие дальше. Это делается для то-
го, чтобы на экране не изображались те части поверхности, кото-
рые в данной проекции закрыты другими ее частями.
За ходом построения изображения лучше всего наблюдать непо-
средственно на экране. Сначала строятся линии пересечения поверх-
ности с плоскостями, перпендикулярными оси X (X = const) (стро-
ки 2220—2280), потом линии пересечения с плоскостями, перпенди-
кулярными оси Y (Y = const) (строки 2310—2400). Для отображе-
ния этих линий на экране каждый раз вызывается подпрограмма
9000. Сетка линий как бы покрывает изображаемую поверхность от
ближнего к наблюдателю края к дальнему благодаря тому, что
расчет и отображение точек на экране происходят ступенчато. Это
можно лучше себе представить, если проследить за работой цикла
по параметру I (строки 2500—2700), например при I = 10, и выяс-
нить, какие значения X, Y и Z преобразуются и потом выводятся
на экран. Переменные ХА и YA, которые встречаются на этом
участке программы, необходимы для запоминания текущих коорди-
нат пера; получающиеся при преобразовании координаты XN и YN
соответствуют новой позиции пера, и обе позиции соединяются от-
резком прямой.
Машинное построение графиков
361
Х(1) Y(10) Z(l, 10) перо поднято
Х(2) Y(10) Z(2, 10) перо опущено
Х(2) Y(9) Z(2, 9) п
Х(3) Y(9) Z(3, 9) »
Х(3) Y(8) Z(3, 8)
Х(4) Y(8) Z(4, 8) W
Х(8) Y(4) Z(8, 4) »
Х(8) Y(3) Z(8, 3) »
Х(9) Y(3) Z(9, 3) »
Х(9) Y(2) Z(9, 2)
Х(10) Y(2) Z(10, 2) п
Х(Ю) Y(l) Z(10, 1)
Подпрограмму вывода на экран графической информации остав-
ляем читателям для самостоятельного анализа.
На рисунке, помещенном перед текстом программы «З-Д-ГРА-
ФИК» дано изображение поверхности z = 3 cos (Vx2 + у2) при углах
проекции RH = 90 и ТА = 45. На приведенных здесь двух рисунках
эти углы составляют RH = 30, ТА = 30 и RH = 45, ТА = 70 со-
ответственно. На следующих двух рисунках изображена поверх-
362
Гпава 13
ность функции z = cos(x) • cos(y/2). Углы проекции составляют:
RH = 45, ТА = 60 и RH = 45, ТА = 80.
13.5. Контурный график
Для наглядного изображения поверхности трехмерного тела на
плоскости можно использовать ее проекцию, на которую нанесены
линии уровня*. Такое изображение называют контурным графи-
ком. Ниже приведена распечатка программы «КОНТУР», с по-
мощью которой можно построить такой график.
0 REM "КОНТУР" EBERT/EDERER 840117
1 REM **i*i*i*i*i*itli*i*i*i*i*i*i*itliln*i*i*i*i*i*i*i*i*i*i*i*itli*i*i*i*i*i*i*
2 REM ** НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ ГРАФИКА **
3 REM ««ФУНКЦИИ Z=F(X,Y) ««
4 REM ««С ПОМОЩЬЮ ЛИНИЙ УРОВНЯ ««
9 REM *************************************
40 DIM H<20>,XC50>,XPC4>,YC50>,YPC4>,Z<50,50>
100 NH-0IREM ЧИСЛО ЛИНИЙ УРОВНЯ
1400 REM ВЫЧИСЛЕНИЕ X I ),Y I ) И Z | )
1410 NX-0lZ5-lE30lZ6—1Е30
1430 FOR Х0—10 ТО. 10 STEP . 5 iNX-NX+1 tNY-0
1450 FOR Y0—18 TO 10 STEP .5iNY-NY+l
1460 XCNX>-X0iYCNY>-Y0
1470 Z < NX,NV >-3*C0SC SQRC X0*X0+Y0*Y0> >
1480 IF Z<NX,NYXZ5 THEN Z5-Z<NX,NY>
1490 IF ZCNX,NY»Z6 THEN Z6-Z<NX,NY>
1500 NEXT Y0«NEXT X0
1600 FOR I-l TO NHiHCI>-Z5+CI-.75>*.95*<Z6-Z5>/<NH-1>«NEXT I
2000 REM НАЧАЛО ПРОЦЕДУРЫ ВЫВОДА ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
2010 INIT
2100 МЯР<Х<1>,X<NX>,YC1>,Y(NY>>
2200 DISPLAYED
2220 PLOTCX<1>,YC1>,0>iPLOTCXC1>,YCNY>,1> tPLOTCXCNX>,YCNY>,1>
2240 PLOTCXCNX>,YC1>,1>iPLOTCXC1>,Y<1>,1>
2500 FOR IH—1 TO NHiHY«H<IH>
2510 LINTYPCIH-INTCIH/4>*4>
2520 FOR IX—2 TO NXiFOR IY-2 TO NY
2540 IP-8
2550 Z1-HV-Z<IX-1,IY-l>IZ2-HY-ZCIX-1,IY>
2560 Z3-HV-Z<IX,IY>1Z4-HV-Z<IX,IY-1>
2700 IF S0NCZ1>-S0N<Z2> THEN 2800
2720 IP-IP+1iXPCIPJ-XCIX-1>
2740 YPCIP>-YCIY-1>+CYCIY>-Y<IY-1>>*Z1/<:Z1-Z2>
2800 IF SGH<Z2>-S0N(Z3> THEN 2900
2820 IP-IP+1iYPCIP>-YCIY>
2840 XP<IPJ-XCIX-1>+<XC1ХЭ-ХСIX-1 >>*Z2/<Z2-Z3>
2900 IF SGN<Z3>-S0N<Z4> THEN 3000
2920 IP-IP+1 iXPC IP>-X< IX>
2940 YP<IP5-YCIY-1> + CYC I Y>-Y<IY-1>>*Z4/CZ4-Z3>
3000 IF SGNCZ4>-SGH<Z1> THEN 3100
3020 IP-IP+1|YPCIP>-YCIY-1>
* Линия уровня — это линия или линии пересечения поверхности с плоскостью
параллельной плоскости XY. — Прим, перев.
Машинное построение графиков
363
3040 ХР<IP>-X<IX-1> + <Х(IX>-X<IX-1>>*21/(21-24>
3100 IF IPO2 THEN GOTO 3200
3120 PLOT(XP(1>,VP(1>,0>iPL0T(XP(2>,VP(2>,1>
3200 NEXT IViNEXT IXtNEXT IH
7990 INPUT fi»
7995 DISPLfiV(0>
7999 STOP
Первый выполняемый оператор этой программы задает число
линий уровня (строка 100). В данной программе оно равно 8. На
плоскость XY опять налагается сетка, рассчитываются значения
Z = F(X, Y) в узлах, и координаты точек изображаемой поверхно-
сти присваиваются элементам массивов Х( ), Y( ) и Z( ). Потом
определяются наименьшее (Z5) и наибольшее (Z6) значения коорди-
наты Z. Исходя из этих значений, в строке 1600 вычисляются коор-
динаты Z линий уровня, которые затем присваиваются элементам
массива Н( ). Часто целесообразно задать эти значения вручную,
например с помощью оператора INPUT, и совсем не обязательно,
чтобы они были равноудаленными друг от друга.
Далее до строки 2240 дисплей подготавливается для вывода гра-
фических данных и строится рамка «окна». Координатная сетка не
изображается, хотя во многих случаях ее лучше все же нанести.
Оставшаяся часть программы состоит из цикла по параметру IH
(переменная IH определяет тип линии). Для каждой ячейки коорди-
натной сетки проверяется, проходит ли горизонталь через данную
ячейку. Для этого в строках 2520—3200 организованы циклы по па-
раметру IX и по параметру IY. В четырех углах ячейки вычисляют-
ся разности между высотой HV данной линии уровня и значениями
функции F(X, Y). Разности присваиваются переменным Zl, Z2, Z3
и Z4 (строки 2550 и 2560). Если значения этих переменных имеют
одинаковые знаки, то данная линия уровня вообще не пересекает
эту ячейку и исследуется следующая ячейка. Если же знаки различа-
ются, то в зависимости от того, какая из сторон ячейки рассматри-
вается, значение координаты X или Y присваивается переменной
ХР(1Р) или YP(IP) соответственно и линейной интерполяцией опре-
деляется и запоминается координата Y или X. Если ячейка доста-
точно мала, то линия уровня или вообще не проходит через нее,
или пересекает ячейку только один раз. Последний оператор кон-
струкции из трех вложенных циклов соединяет две точки пересече-
ния отрезком прямой. Тип линии определяется в строке 2510. По-
скольку невозможно изобразить каждую линию уровня своим ти-
пом линии (рассматриваемая версия графического интерпретатора
предусматривает использование не более четырех типов линий), че-
рез каждые четыре линии уровня тип линии повторяется. Для это-
364
Глава 13
го способа изображения поверхностей трехмерных тел также жела-
тельно использование цветного дисплея.
В качестве примера приведены контурные графики тех же функ-
ций, которые рассматривались в программе «З-Д-ГРАФИК» (см.
рис.):
z = 3cos(Vx2 + у2)
z — cos (х) cos (у/2)
В качестве примера использования контурных графиков изобра-
зим поверхность потенциальной энергии линейной трехатомной ча-
стицы (Н—С—Н). Необходимо построить поверхность потенци-
альной энергии, заданной несколько модифицированной формулой
Морзе*. Программа и изображение поверхности потенциальной
энергии приведены ниже.
0 REM "МОРЗЕ" EBERT,'EDEREF' 840283
i REM 4444444444444444444444444444444444444
2 REM 44 ИЗОБРАЖЕНИЕ ПОВЕРХНОСТИ **
3 REM 44 ПОЛНОЙ ЭНЕРГИИ Н-С-Н **
4 REM 44 С ПОМОЩЬЮ КОНТУРНОГО **
5 REM 44 ГРАФИКА СОГЛАСНО **
6 REM 44 R.F.NRLEWRJSKI •*
7 REM 44 R.E.WVRTT **
8 REM 44 CHEM. PHVS. 81,357<1983> **
9 REM 4444444444444444444444444444444444444
40 DIM H<40>,X<50>,XP<4-zY<50>,VP<4>.Z<50,50>
100 NH-30IREM ЧИСЛО ЛИНИЙ УРОВНЯ
1400 REM ВЫЧИСЛЕНИЕ X ( ),У ( ) И Z ( )
1410 NX-0iZ5-lE30iZ6=-1Е30
14Э0 FOR Х0-1 ТО 5 STEP .1iNX-NX+1:NV-0
1450 FOR-70-1 TO 5 STEP .1sNY-NV+1
1460 X<NX>-X0lV<NY>-70
1470 ZX-EXP<-2.072264<X0-2.1163>>-24ЕХР<-1.036134CX0-2.1163>>
Nalewajski R. F., Wyatt R. E„ Chem. Phys., 81, 357 (1983).
Машинное построение графиков
365
1472 ZY-EXP<-2.07226*<Y0-2.1163>5-2*ЕХР<-1.03613*<Y0-2.1163>>
1475 Z<NX,NV>-<ZX+ZV>*0. 1339
1480 IF Z<NX,NYXZ5 THEN Z5-Z<NX,NY>
1490 IF Z<NX,NY»Z6 THEN Z6-Z<NX,NY>
1500 NEXT Y0iNEXT X0
1600 FOR I-l TO NH1H<I>-Z5+<I-.75>*.95*<Z6-Z5>/<NH-1>iNEXT I
2000 REM НАЧАЛО ПРОЦЕДУРЫ ВЫВОДА ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
2010 INIT
2020 Р8РАСЕ<0, . 99,0, . 99>
2100 MfiP<X<l>,X<NX>,Y<1>,Y<NY>>
2200 DISPLfiVd)
2220 PLOT<X< 1 >,Y< 1 >,0> iPLOT<X<l>,Y<NY:>,i:> |PLOT<X<NX>,V<NY>,1>
2240 PLOT <X<NX> ,Y< 1 > , 1 > :PLOT<Xd > , Yd > , 1 >
2500 FOR IH-1 TO NH:HV-H<IH>
2510 LINTVPCIH-INTCIH/4>*4>
2520 FOR IX-2 TO NX:FOR IY-2 TO NY
2540 IP-0
2550 Zl-HV-ZdX-1, I V-l >:Z2-HV-Z<IX-1,IV>
2560 Z3-HV-ZCIX,IY>:Z4—HV-Z<IX,IY-l>
2700 IF SGNCZl>-SGN<Z2> THEN 2800
2720 IP-IP+1sXP<IP>-X<IX-1>
2740 VP< IP>-Y< IV-1>+<V< IV>—VdV—1 >>*Z1/<Z1-Z2>
2800 IF SGN<Z2>-SGN<Z3> THEN 2900
2820 IP-IP+1:YP<IP>-Y<IY>
2840 XP< IP>=X< IX-1 > + <X< IX>-X< IX-1 > >*Z2/<Z2-Z3>
2900 IF SGN<Z3>-SGN<Z4> THEN 3000
2920 IP-IP+1 :XPdP>=XdX>
2940 YP< IP>-Vd V-l > + < V< IV>—V< IY-l > >*Z4/<Z4-Z3>
3000 IF SGN<Z4>-SGN<Z1> THEN 3100
3020 IP-IP+1 :YPdP>-V< IV-1 >
3040 XPdP>-X< IX-1 > + <X< IX>-X< IX-1 >>*Z1/<Z1-Z4>
3100 IF IPO2 THEN GOTO 3200
3120 PLOT<XPd>,YPd>,0> lPLOT<XP< 2> , VP< 2> , 1 >
3200 NEXT IY:NEXT IXsNEXT IH
7990 INPUT Я»
7995 DISPLRY<0>
7999 STOP
В качестве координат выбраны оба расстояния С—Н. Поэтому
график симметричен относительно диагонали квадранта. При ма-
лых межъядерных расстояниях скаты поверхности очень круты,
при больших расстояниях поверхность переходит в плоскость, что
соответствует полной диссоциации частицы. Между крутыми скло-
нами и плоскостью диссоциации находится самая глубокая впадина
366
Глава 13
(внутри замкнутых кривых). Перпендикулярное сечение этой по-
верхности при очень большом одном из расстояний С—Н пред-
ставляет собой график потенциала Морзе для двухатомной моле-
кулы.
В программе «ТРИ АТОМА» эта поверхность потенциальной
энергии использована для расчета траекторий.
0 REM "ТРИ АТОМА" EBERT/EDERER 840206
1 REM*********************************
2 REM** ДВИЖЕНИЕ АТОМОВ Н ♦*
3 REM** ВДОЛЬ СВЯЗЕЙ **
4 REM*» С-Н В Н-С-Н **
5 REM** R.F. NRLEURJSKI **
6 REM** R.E. WVRTT *»
7 REM** CHEM. PHVS. 81,357<1983> ♦»
9 РЕМ*********************************
400 DIM Y<20> , Vl <20> ,D<20>,. V9<20> , VR<20>
128 DIM Kl<20> ,K2<20> ,.K3<20> ,K4<20>
150 DEF FNV<R> —4*<EXP<—4*<R-2. 1 > >-EXP<-2*<R-2. 1>>>
200 N-6 sREM ЧИСЛО ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В СИСТЕМЕ
210 MR—1sMB—12s MC—1
410 Vid > — 1.8 sREM КООРДИНАТА X ЧАСТИЦЫ A
420 Vl<2>- 0 sREM КООРДИНАТАХ ЧАСТИЦЫ В
430 Vl<3>-5.0 sREM КООРДИНАТА X ЧАСТИЦЫ C
440 Vl<4>—0 sREM ИМПУЛЬС ЧАСТИЦЫ А ВДОЛЬ ОСИ X
450 Vl<5>-0 sREM ИМПУЛЬС ЧАСТИЦЫ В ВДОЛЬ ОСИ X
460 VI С6> —. 05 sREM ИМПУЛЬС ЧАСТИЦЫ С ВДОЛЬ ОСИ X
700 REM INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ, ШАГ";ХА, ХЕ, XD
710 ХЯ-0sXE-10000sXD-.1
715 OOSUB 2000 sREM ПОДГОТОВКА К ВЫВОДУ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
720 FOR 1-1 ТО HsVd>-Vld>sVfl<I>-Vld> SNEXT I sGOSUB 15000
740 Nl-1
1000 FOR fl-Xfl ТО ХЕ STEP XD
1020 E-fl+XD
1040 H-<E-R>/N1sGOSUB 5000
1050 FOR 1-1 TO NiVR<I>—V<I>sNEXT I
1060 Nl-Nl*2sH=<E-R>,'Nl sGOSUB 5000
1080 FOR 1-1 TO N
1090 IF flBS<V< I > >+RBS<VR< I > XIE-6 THEN 1120
1100 IF RBS<VR<I>-V<I>>/<RBS<Vfl<I>>+RBS<V<I>>>>.01 THEN 1050
1120 NEXT I
1200 GOSUB 15000 sREM ВЫВОД ИНФОРМАЦИИ
1220 FOR 1-1 TO NsVl<I>-V<I>sNEXTI
1240 N1-INT<N1X4> sIF Nl-0 THEN Nl-1
1260 NEXT R
1899 STOP
2000 REM*********************************************
2001 REM** ПОДПРОГРАММА ДЛЯ ПОСТРОЕНИЯ ГРАФИКА •*
2002 REM******************* **************************
2010 INIT
2020 PSPRCE<.01,.99,.01.. 99>
2030 PJ-0
2040 DISPLRV<PJ>
2060 MflPd,5,l,5>lPLOTd,l,0>
2100 PLOTC1,5,1>sPL0T<5,5,1> SPLOTC5,1,1>sPLOT<1,1,1>
2200 Peturn
5000 REM************************************
5002 REM** ПОДПРОГРАММА ДЛЯ РЕШЕНИЯ **
5004 REM** ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ **
5010 REM************************************
5100 FDR 1-1 TO N sVd >-Vl d > sNEXT I
5200 FOR 19-0 TO Nl-1iX-fl+I9*H
Машинное построение графиков
367
5300 ХЭ-XiFOR I-l ТО N|79<I>-7<I>iNEXT I
5320 GOSUB 10000
5340 FOR I-l TO N1K1<I>-H*D<I>iNEXT I
5400 X9-X+H/2iFOR I-l TO Ni79<I>-7<I>+К1<I>/2iNEXT I
5420 GOSUB 10000
5440 FOR I-l TO NiK2CI>-H*DCI>iNEXT I
5500 X9-X+H/21F0R I-l TO N |79CI>-7CI>+K2CI>/2iNEXT I
5520 GOSUB 10000
5540 FOR I-l TO N1K3<I>-H*D<I>«NEXT I
5600 X9-X+H1F0R I-l TO N:Y9<I>-7<I>+K3<I>iNEXT I
5620 GOSUB 10000
5640 FOR I-l TO N:K4<I>-H»DCI>«NEXT I
5700 FOR I-l TO N
5720 7<I>-7CI> + <К1<I>+2*K2<I>+2*K3<I>+K4<I> >/6
5740 NEXT IiX-E
5760 REM GOSUB 15000IREM ВЫВОД ИНФОРМАЦИИ
5800 NEXT I91RETURN
10000 REM****************************************
10002 REM** ЗДЕСЬ ЗАДАЮТСЯ ДИФФЕРЕНЦИАЛЬНЫЕ**
10003 REM** УРАВНЕНИЯ DYI/DX= Fl(X,Y1....Y N) **
10004 REM** D(I)=F (X9, Y9(1)..Y (9)1 ♦♦
10010 REM******************************** ********
10100 D<1>-79<4>/Mfl
10200 DC2>-79<5>/MB
10300 DC3>-79<6>/MC
10500 RX-ABS<79C1>-79C2>>iR7-flBSCY9<2>-79<3>>
10560 V1-FNV<RX>iV2-FNV<R7>
10600 D<4> — <79<1>-Y9<2>>*V1/RX
10800 D<6>-<79<2>-79<3>>*V2/R7
11500 D<5> — DC4>-DC6>
12000 RETURN
15000 REM*************************
15001 REM** ВЫВОД ИНФОРМАЦИИ **
15002 REM*************************
15020 PRINT X,iFOR I-l TO NtPRINT 7CI>,iNEXT IiPRINT N1
15030 RX-flBS < 79 <1>-79 C 2 > > IR7-ABS < 79 < 2 >-79 C 3 > >
15040 PL0T<RX,R7,FJ>iFJ-1
15080 fl»-..GET fl»
15100 IF fl»-"" THEN 15500
15120 PJ-flBS<PJ-l>iDISPLAYCPJ)
15500 RETURN
63999 END
368
Глава 13
В данной программе рассчитываются лишь валентные колеба-
ния в молекуле. Поэтому для описания достаточно рассматривать
только координаты х трех атомов. Шесть дифференциальных урав-
нений аналогичны дифференциальным уравнениям из программы
«СОУДАР2» и решаются тем же методом. Чтобы импульс и время
имели «нормальные» числовые значения, за единицу временной
шкалы принят интервал 10_|3с, а за единицу массы— атомная
единица массы.
Для траекторий, изображенных на рисунках, были выбраны на-
чальные условия, приведенные в таблице.
Tp.1 Tp.2 Tp.3 Tp.4
Y1 (1 ) -1,8 -2 -3 -3
Y1 (2) 0 0 0 2
Y1 (3) 5 5 5 5
Y1 (4) 0 0 0 0,2
Y1(5) 0 0 0 0
Y1(6) -0,05 -0,2 -0,2 -0,2
В программах «МОРЗЕ» и «ТРИ АТОМА» поверхность потен-
циальной энергии описывается следующими формулами:
у (г.) = Т>-(е-2с'<г' ~ gi) - ' ft))
— = -2-c-D-(e"2c'(r' " «'> - e~c,(r' ~ *->)
dr.
K(ABC) = K(AB) + K(BC) = K(rAB) + K(rBC)
14. Автоматизированная обработка данных
В этой главе будет рассмотрено сопряжение ЭВМ с измеритель-
ными приборами. Основные этапы на пути от измерения физиче-
ского параметра до его числового значения, хранящегося в памяти
ЭВМ, схематически можно представить следующим образом (в
скобках — примеры):
Физическая величина — электрический сигнал —
(концентрация) (электродный потенциал)
сигнал в цифровой форме — число в памяти ЭВМ
(универсальный цифровой вольтметр)
Мы остановимся лишь на последней стадии процесса, которая
осуществляется с помощью специального устройства, так называе-
мого интерфейса. Наиболее часто употребляется как в ЭВМ, так и
в измерительных приборах IEEC-интерфейс или IEEC-шина. Если
конструкция ЭВМ и универсального цифрового вольтметра преду-
сматривает доступ к IEEC-шине, то надо просто соединить оба
прибора с помощью стандартного разъема. IEEC-шина использует-
ся также в некоторых приборах для соединения ЭВМ с печатаю-
щим устройством и дисководом. К ЭВМ можно подключить сразу
несколько приборов, только они должны иметь различные адреса.
Коммутация приборов осуществляется обычно с помощью внут-
реннего переключателя. IEEC-шину применяют как для ввода дан-
ных; так и для их вывода; это позволяет не только обрабатывать
экспериментальные данные, но и управлять приборами. Техниче-
ские детали автоматизации эксперимента в этой книге не обсужда-
ются. Более подробную информацию можно найти в руководстве к
ЭВМ или в соответствующей литературе по вычислительной техни-
ке.
Рассмотрим несколько программ для обработки данных, непо-
средственно считываемых с измерительных приборов; к ним отно-
сятся программы для ускоренной сортировки данных и программы
для сглаживания экспериментальных данных (сплайн-регрессия).
24-81
370
Глава 14
14.1. Отображение экспериментальных данных
Проиллюстрировать отображение данных лучше всего на ка-
ком-нибудь простом эксперименте. Возьмем реакцию Белоусова —
Жаботинского — наиболее известную колебательную реакцию, ко-
торую можно осуществить в обычном химическом стакане. Окис-
лительно-восстановительный потенциал измеряют платиновым и
каломельным электродами, результаты измерений поступают в
ЭВМ и отображаются в виде графика на дисплее. Для эксперимен-
та потребуются следующие реактивы: 50 мл 1,2 М раствора мало-
новой кислоты, 50 мл 0,004 М раствора сульфата церия(Ш), 50 мл
0,35 М раствора бромата калия, 50 мл 15%-ного раствора серной
кислоты. Раствор серной кислоты добавляют через 20 с после за-
пуска программы для сбора и отображения данных, поступающих
непосредственно от измерительного прибора. Результаты представ-
лены на рисунках.
Размах графиков по оси х составляет 600 с. Наибольшее значе-
ние ординаты равно 1,95 В, наименьшее — 1,65 В. На левом рисун-
ке изображен начальный период реакции. В течение довольно боль-
шого промежутка времени разность потенциалов монотонно убы-
вает и затем начинает колебаться. На правом рисунке изображены
колебания разности потенциалов спустя некоторое время; посколь-
ку исходные реагенты расходуются, амплитуда колебаний посте-
пенно уменьшается.
Приведенная ниже программа «ОТОБР-ДАН» позволяет считы-
вать и изображать в виде графика результаты измерений.
в REM "ОТОБР-ДАН" EBERT/EDERER 840211
1 REM*******************************************
2 REM** СЧИТЫВАНИЕ ПОКАЗАНИЙ С 1ЕЕС-ШИНЫ •*
3 REM** УНИВЕРСАЛЬНОГО ЦИФРОВОГО **
Автоматизированная обработка данных
371
4 REM** ВОЛЬТМЕТРАМ **
5 REM** ВЫВОД НА ЭКРАН ГРАФИКА **
9 REM*******************************************
100 PRINT "ПРОДОЛЖИТЕЛЬНОСТЬ СЧИТЫВАНИЯ"
110 PRINT "ОДНОГО ПОКАЗАНИЯ"
115 PRINT ' УКАЖИТЕ ВРЕМЯ В СЕКУНДАХ';
120 INPUT DTiIF DT<.5 THEN GOTO 120
1Э0 PRINT "ПРОДОЛЖИТЕЛЬНОСТЬ ЭКСПЕРИМЕНТА";
1Э5 INPUT TM
140 DT-INTCDT*60>
150 TM-INTCTM*60>
200 INIT
210 V1-165001V9-19500
220 MAP<0,TM,V1 ,V9>
2Э0 PLOTC0,Y1,0>|PLOT<0,V9,1>iPL0TCTM,V9,1>
240 PLOTCTM,V1,1>1PLOTC0,V1,1>
300 T0-TI+60IIT-0
400 TV-T0+DT*IT
500 IF TKTV THEN 500
550 T-TIIGOSUB 50000
570 PRINT CT-T0>/60,R
500 PLOT<T-T0,fl,0>|DPLOT<0,0,1>
600 IT-IT+1iIF <T-T0>< TM THEN 400
999 STOP
50000 REM********************************************************
50001 REM** ПОДПРОГРАММА ДЛЯ СЧИТЫВАНИЯ ДАННЫХ С УНИВЕРСАЛЕ**
50002 REM** НО ГО ЦИФРОВОГО ВОЛЬТМЕТРА KEITHLEV 177 *♦
50003 REM********************************************************
50010 OPEN 5,25
50020 INPUT«5,R« I IF 2 AND ST THEN 50020
50040 A-VAL<A«>
50050 CLOSE 5«OPEN 5,24«GET45,I*«CLOSE 5
50060 RETURN
Сначала у пользователя запрашивается временной интервал
между двумя измерениями (DT) (строка 120). Поскольку используе-
мый в данном случае универсальный цифровой вольтметр имеет
время преобразования 0,5 с, более короткие интервалы времени от-
брасываются. Затем запрашивается максимальная продолжитель-
ность эксперимента (ТМ) (строка 135). Обе переменные, DT и ТМ,
умножаются на 60 и у произведений отбрасываются десятичные
знаки. Это делается потому, что за единицу отсчета счетчика вре-
мени ЭВМ (TI) принята 1/60 с. Показание этих внутренних часов
можно запросить в любой момент. (Если в ЭВМ нет счетчика вре-
мени, то вместо него можно использовать циклы. Внутренняя об-
ласть этих циклов не содержит никаких операторов, и они только
расходуют время. Наибольшее значение параметра каждого цикла
определяет время, затрачиваемое на его выполнение. Таким обра-
зом можно имитировать счетчик времени.) Переменные Y1 и Y9
имеют значения минимального и максимального напряжения вход-
ного сигнала соответственно (строка 210). Следовательно, извест-
ны размеры «окна» для вывода графических данных и можно обо-
значить его границы, что и происходит в строках 220—240. В стро-
ке 300 начинается считывание показаний измерительного прибора,
24*
372
Глава 14
причем здесь предусмотрена односекундная задержка. Для этого к
текущему машинному времени Т1 прибавляется число 60 и получен-
ное значение присваивается переменной ТО времени начала считы-
вания данных. Счетчику считанных значений IT присваивается зна-
чение 0. В строке 400 рассчитывается момент времени TV, в кото-
рый необходимо ввести очередное значение. Для этого к начально-
му моменту времени прибавляется интервал времени DT*IT.
Управление сохраняется за строкой 500 до тех пор, пока внут-
реннее время ЭВМ Т1 не достигнет времени считывания очередного
показания TV. Текущее время присваивается переменной Т и для
считывания очередного показания универсального цифрового
вольтметра оператором GOSUB вызывается подпрограмма 50000.
В строке 570 на экран выводится время в секундах, прошедшее с
момента запуска программы вместе со значением измеряемого па-
раметра. В следующей строке считанное значение отображается в
виде точки на графике. Затем счетчик точек IT увеличивается на
единицу, и управление передается строке 400 в том случае, если еще
не достигнуто время окончания данного эксперимента.
Непосредственно считывание показания цифрового прибора на-
чинается с оператора
OPEN 5, 25
Этот оператор открывает для ввода данных канал, обозначен-
ный первым числом. В приведенном примере это число 5. Второе
число указывает, с каким прибором соединен этот канал. Для уни-
версального цифрового вольтметра предусмотрен «физический»
адрес 25.
Следующий оператор INPUT # 5,А$ считывает символы из ка-
нала 5, которые присваиваются текстовой переменной А$. Кон-
струкция оператора IF в той же строке, вообще говоря, не обяза-
тельна. Она используется для того, чтобы ЭВМ ждала до тех пор,
пока не установится устойчивое показание цифрового вольтметра.
Оператор в строке 50040 превращает последовательность знаков,
стоящих в переменной А$, в число, которое присваивается простой
переменной А.
Первый оператор следующей строки:
CLOSE 5
закрывает канал 5, и считывание показания измерительного прибо-
ра заканчивается. Следующие после двоеточия операторы являются
особенностью используемого в данном случае универсального ци-
фрового вольтметра Keithley 177. Они позволяют продолжить счи-
тывание данных, даже если ЭВМ не затребовала следующих.
Автоматизированная обработка данных
373
В следующем примере рассматривается случай соединения ЭВМ
с жидкостным хроматографом. Программа, распечатка которой
приведена ниже, позволяет отображать на экране хроматограммы
и одновременно рассчитывать, исходя из них, молекулярно-массо-
вое распределение полимеров.
в КЕМ "ОТОБР-ДАНЗ" EBERT,‘EDERER 840211
1 REM*******************************************
2 КЕМ** СЧИТЫВАНИЕ ПОКАЗАНИЙ С IEEC—ШИНЫ **
3 КЕМ** УНИВЕРСАЛЬНОГО ЦИФРОВОГО **
4 КЕМ** ВОЛЬТМЕТРА. ВЫВОД НА ЭКРАН **
5 КЕМ** ХРОМАТОГРАММЫ, РАСЧЕТ МОЛЕКУЛЯРНО-**
6 КЕМ** МАССОВОГО РАСПРЕДЕЛЕНИЯ **
7 КЕМ** И ПОСТРОЕНИЕ ЕГО ГРАФИКА **
9 REM*******************************************
50 DIM Х<250>,М<250>,DM<250>,ХР<250>
100 PRINT "ПРОДОЛЖИТЕЛЬНОСТЬ СЧИТЫВАНИЯ”
110 PRINT "ОДНОГО ПОКАЗАНИЯ”
115 PRINT "УКАЖИТЕ ВРЕМЯ В СЕКУНДАХ";
120 REM INPUT DTsIF DTC.5 THEN GOTO 120
130 PRINT "ПРОДОЛЖИТЕЛЬНОСТЬ ЭКСПЕРИМЕНТ A";
135 REM INPUT TM
138 DT-5 sTM-1250
140 OT-INT':DT*60>
150 TM-INT<TM*60>
200 INIT
210 Vl —1000SV9-10000
220 MAP<0,TM,V1,V9>
230 PLOT<0,V1,0> sPLOT<0,V9zl> sPL0T<TM,V9,1>
240 PLOT<TM,V1,1>sPLOT<0,Vl,1>
300 T0-TI+60sIT-0
400 TV-T0+DT*IT
500 IF TKTV THEN 500
550 T-TIsGOSUB 50000
570 PRINT <T-T0>/60,A
580 PLOT<T-T0,A,0>sDPLOT<0,0,l>
590 X<IT>-A
600 IT-IT+lsIF (T-T0XTM THEN 400
650 GOSUB 12000IREM КОРРЕКЦИЯ НУЛЕВОЙ ЛИНИИ
700 GOSUB 10000 sREM РАСЧЕТ МОЛЕКУЛЯРНО-МАССОВОГО
701 REM РАСПРЕДЕЛЕНИЯ И ПОСТРОЕНИЕ ЕГО ГРАФИКА
999 STOP
10000 REM******************************************
10001 REM## РАСЧЕТ МОЛЕКУЛЯРНО—МАССОВОГО *«
10002 КЕМ#* РАСПРЕДЕЛЕНИЯ И ПОСТРОЕНИЯ ГРАФИКА**
10002 REM******************************************
10100 DEF FNM< Т>-ЕХР< 13-. 005*Т>
10200 ММ-0
10240 FOR 1—0 ТО 250
10260 М<I>-FNM<I*5>sNEXT I
10300 FOR 1-1 ТО 250
10320 D-М< 1-1 >-М< I >
10340 DM< I :>-<X< I >+X< 1-1 > >/<2#D>
10360 IF DM<n>MM THEN MM-DM<I>
10380 NEXT I
10580 MAP<M<250>,M<0>,0,MM*1.01>
10510 Xl-0sX2-0sX3-0:X4-0
10520 IP-0sFOR 1-1 TO 250
10540 XP< I >»<M< I >+M< I-1 > >/2
10560 S1-S1+DM<I>/XP<I>
10580 S2—S2+DMCI)
10600 S3-S3+DM<i:>#XP<I>
10620 S4-S4+DM<I .J#XP';i>*XP<I >
314
Глава 14
10680 PLOT<XP<I>,DM<I>,IP>iip»l
10690 PRINT I,XP<I>,DM<I>
10700 NEXT I
10740 PRINT "СРЕДНЕЧИСЛЕННАЯ - ”;S2/S1
10760 PRINT "СРЕДНЕМАССОВАЯ - ";S3/S2
10780 PRINT "Z—СРЕДНЯЯ - ";S4/S3
10800 FOR I-l TO 250
10020 II-IiIF DM<I>>MM/50 THEN GOTO 10900
10840 NEXT I
10900 FOR 1-250 TO 1 STEP -1
10920 I9-IiIF DM<I>>MM/50 THEN GOTO 10980
10940 NEXT I
10980 MAP<M<I9>,M<I1>,0,MM*1.01')
11000 IP-0IFOR I—Il TO 19
11020 PLOT<XP<I>,DM<I>,IP>I IP-1
11040 NEXT I
11990 RETURN
12000 REM********************************
12001 REM** КОРРЕКЦИЯ НУЛЕВОЙ ЛИНИИ **
12002 REM********************************
12020 X0-X < 0 >IX9-X <250 >
12040 FOR 1-0 TO 250
12060 PRINT I,X<!>,"
12100 X<I>-X<I>-<X0+<X9-X0>/250*I>
12120 IF X<I><0 THEN X<I>-0
12130 PRINT XCI)
12140 NEXT I
12300 RETURN
50000 REM********************************************************
50001 REM** ПОДПРОГРАММА ДЛЯ СЧИТЫВАНИЯ ДАННЫХ С УНИВЕРСАЛЬ'**
50002 REM** НОГО ЦИФРОВОГО ВОЛЬТМЕТРА KEITHLEV 177 **
50003 REM********************************************************
50010 OPEN 5,25
50020 INPUT45,А*:IF 2 AND ST THEN 50020
50040 A-VAL<A»>
50050 CLOSE 5:0PEN 5,24:GET#5,I»1CLOSE 5
50060 RETURN
Подпрограмма 50000, считывающая показания датчика, такая
же, как и в предыдущем примере. В основную программу внесены
незначительные изменения. Так, в строке 210 расширена область
допустимых напряжений до -1-5- +10 В. Кроме того, значения
измеряемого параметра не только отображаются на экране, но и
запоминаются, для чего в строке 590 значения А присваиваются ин-
дексированной переменной Х(1Т). Основная программа заканчива-
ется вызовом двух подпрограмм. Первая подпрограмма корректи-
рует нулевую линию, вторая рассчитывает по хроматографическо-
му пику молекулярно-массовое распределение. Расчет проводится
по 251 точке хроматограммы. Поскольку за 5 с считывается одно
значение, на регистрацию всей хроматограммы отводится 1250 с.
При коррекции нулевой линии (подпрограмма 12000) предпола-
гается, что первая (Х(0)) и последняя точки (Х(250)) хроматограм-
мы лежат точно на нулевой линии. Через эти две точки проводится
прямая, которая и принимается за нулевую линию, и из сигнала де-
тектора вычитается значение, равное дрейфу нулевой линии в дан-
Автоматизированная обработка данных
375
ной точке хроматограммы (строка 12100). Значения, лежащие ниже
нулевой линии, обнуляются. Этот метод коррекции очень прост, но
его можно использовать лишь в том случае, если шумы малы.
Подпрограмма для пересчета хроматографических данных в мо-
лекулярно-массовое распределение начинается с описания калибро-
вочной кривой. Эта формула связывает молекулярную массу М с
временем удерживания Т, которое прошло с момента ввода пробы
в хроматограф. В цикле (строки 10240—10260) для каждой точки
хроматограммы определяется соответствующая молекулярная мас-
са, в следующем цикле (строки 10300—10380) рассчитывается плот-
ность молекулярно-массового распределения. Площадь хромато-
графического пика пропорциональна количеству вещества. Поэтому
при преобразовании хроматограммы в функцию молекулярно-мас-
сового распределения площади под обеими кривыми должны быть
равны. Поскольку зависимость молекулярной массы от времени
удерживания описывается экспоненциальной функцией, равноуда-
ленным друг от друга точкам хроматограммы на кривой молеку-
лярно-массового распределения соответствуют точки, сходящиеся к
области малых масс. Однако площади под обеими кривыми между
двумя соответствующими точками равны. Одновременно определя-
ется и запоминается максимум молекулярно-массового распределе-
ния. Каждому значению DM(I) функции распределения соответству-
ет молекулярная масса (М(1) + М(1 + 1))/2. По этим точкам в цик-
ле по I (строки 10520—10700) строится график. Одновременно рас-
считываются моменты распределения SI, S2, S3, S4 и из них вычис-
ляются различные средние молекулярные массы. Оставшаяся часть
подпрограммы сжимает график функции молекулярно-массового
распределения вдоль оси масс, причем отбрасываются участки
очень малых и очень больших масс, на которых функция распреде-
ления имеет значения меньше, чем 1/50 от максимального.
На рисунке изображены хроматограмма (пунктирная кривая) и
функция молекулярно-массового распределения, общий вид кривой
и растянутый вдоль оси масс график.
Задание 200. Расширьте участок вывода графической информации программ для
отображения экспериментальных данных так, чтобы обозначались и оцифровыва-
лись координатные осн.
Задание 201. Напишите программу для отображения данных, которая считыва-
ла бы как окислительно-восстановительный потенциал химической реакции, так и
температуру в реакторе. Напишите программы таким образом, чтобы можно было
считывать показания через различные промежутки времени. Разумеется, для прове-
дения эксперимента понадобятся еще один цифровой вольтметр (или один многока-
нальный прибор) с другим адресом и датчик температуры (например, термометр со-
противления или термопара).
376
Глава 14
14.2. Быстрая сортировка
В качестве подпрограммы при обработке экспериментальных
данных, считываемых с измерительных приборов, часто использу-
ется процедура быстрой сортировки данных, которая позволяет от-
сортировать большой объем данных за сравнительно короткое вре-
мя. Время выполнения рассмотренных выше программ «СОРТ-
ЧИСЛ» и «COPT-БУКВ» увеличивается пропорционально квадрату
числа сортируемых данных.
В этом разделе будут рассмотрены три процедуры быстрой сор-
тировки, известные в литературе под названиями Shell-Sort, Quick-
Sort и Address-Sort, время выполнения которых приблизительно
пропорционально числу сортируемых данных.
Сначала рассмотрим алгоритм Shell-Sort. Соответствующая
программа приведена ниже:
0 REM "О-СОРТ" EBERT/EDERER 830510
1 REM*********************************
2 REM** СОРТИРОВКА ДАННЫХ-ВВОД в **
3 REM** ПРОИЗВОЛЬНОЙ ПОСЛЕДОВАВ »»
4 REM** ТЕЛЬНОСТИ , ВЫВОД »»
5 REM** ПО ВОЗРАСТАНИЮ ЗНАЧЕНИЙ **
6 REM** УСКОРЕННЫЙ АЛГОРИТМ ##
9 REM*********************************
1000 DIM Х<256>,V<256>
1100 INPUT "ЧИСЛО ДАННЫХ"; N
1200 FOR I .1 TO H
1300 X<I>-RND<5>1V<I>-X<I>
1400 NEXT I
1410 T-TI
1500 D-INT<L0G<N>/L0G<2>>;D-2TD-1
2000 FOR I-l TO N-D
3000 FOR J-I TO 1 STEP -D
3100 IF V<JX.V<J+D) THEN 4100
Автоматизированная обработка данных
377
3200 iV<J>-V<J+D>1VCJ+D5-H
3400 NEXT J
4100 NEXT I
4200 De I NT < D/2 >
4300 IF D>0 THEN GOTO 2000
4400 T-<TI-T>/60
5000 (PRINT iPRINT "ИСХОДНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5100 FOR I-l TO NiPRINT X<I>JiNEXT IiPRINT
5200 PRINT SPRINT "ОТСОРТИРОВАННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5300 FOR I-l TO NiPRINT Y<I>JiNEXT IiPRINT
6000 PRINT iPRINT "ВРЕМЯ СЧЕТА:"; T; "С ДЛЯ N; "ЧИСЕЛ"
9999 END
Идея, лежащая в основе этого метода сортировки, заключается
в том, что данные предварительно сортируются в блоках и затем
число блоков уменьшается до тех пор, пока все данные не окажутся
в одном блоке. Тем самым значительно уменьшается число обме-
нов (строка 3200). На операции обмена в программе для сортиров-
ки данных затрачивается довольно много машинного времени.
В строках 1200—1400 генерируются случайные числа, которые
присваиваются элементам одномерных массивов Х( ) и У( ). От-
сортированные данные присваиваются элементам массива У( ) и в
строках 5000—5300 выводятся на экран. В строке 1410 рассчитыва-
ется время выполнения процедуры, которое в строке 6000 выводит-
ся на экран. Сама процедура сортировки занимает участок про-
граммы от строки 1500 до строки 4300. Число блоков (переменная
D), с которого начинается процесс сортировки, рассчитывается в
строке 1500; оно, во всяком случае, меньше, чем число сортируе-
мых данных.
В двух вложенных циклах по параметрам I и J (строки
2000—4100) сравниваются друг с другом и потом обмениваются
только такие элементы массива У, индексы которых различаются
на величину D. В строке 4200 D делится пополам и у частного от-
брасывается дробная часть. Полученное число является новым зна-
чением D. Затем опять начинается сортировка, но уже с меньшим
числом блоков. Процедура повторяется до тех пор, пока D не ста-
нет равным 1. При D = 1 сортировка происходит так же, как и по
программе «СОРТ-ЧИСЛ», только теперь значительная часть дан-
ных уже отсортирована и для окончания процедуры остается про-
вести лишь очень небольшое число перестановок. (Например, если
число данных N = 100, то в процессе сортировки D принимает зна-
чения 63, 31, 15, 7, 3 и 1.)
Ниже приведена распечатка программы «QQ-СОРТ» в которой
использован один из наиболее быстрых методов сортировки, так
378
Глава 14
называемый метод Quick-Sort:
0 REM "QQ—СОРТ" EBERT/EDERER 840121
1 REM*********************************
2 REM** СОРТИРОВКА ДАННЫХ **
3 REM## ВВОД В ПРОИЗВОЛЬНОЙ ПОСЛЕ- **
4 REM## ДОВАТЕЛЬНОСТИ.ВЫВОД ПО **
5 REM## ВОЗРАСТАНИЮ ЗНАЧЕНИЙ.ОЧЕНЬ**
6 REM*# БЫСТРЫЙ АЛГОРИТЦДФФЕКТИВЕН*
7 REM** ДЛЯ БОЛЬШОГО ЧИСЛА ДАННЫХ **
9 REM###****#*************************
1000 DIM X<2000>,Y<2000>
1010 DIM L<50>,R<50>
1100 INPUT "ЧИСЛО ДАННЫХ"; N
1200 FOR 1-1 TO N
1300 X<I>-RND<5>iY<I>-X<I>
1400 NEXT I
1410 T-TI
2000 L<1>-liR<1>-NtSZ-1
3000 L1-L<SZ>1R1-R<SZ>iD-Y<Rl>
3020 IF R1-L1< 5 THEN 3400
3040 M1-INT<<L1+R1>/2>
3060 IF D>-Y<L1> THEN 3200
3080 IF D>-«Ml) THEN 3400
3100 IF YfLDWMl) THEN 3160
3120 D-V<M1>|V<M1>-Y<R1>iV<Rl>-DiGOTO 3400
3160 D-V<L1>|Y<L1>-V<R1>|V<R1>—DiGOTO 3480
3200 IF D<-V<M1> THEN 3400
3220 IF Y<L1>>Y<M1> THEN 3260
3240 D-V<M1>iV<Ml>-V<Rl>|Y<R1>-0iGOTO 3400
3260 D-V<L1>iV<Ll>-Y<Rl>sY<Rl>-D:GOTO 3400
3400 REM ОПРЕДЕЛЕНИЕ СРЕДНЕГО ЧИСЛА
3500 Ll-Ll-1
3520 Ll-Ll + lilF RK.L1 THEN 4000
3540 IF V<L1XD THEN 3520
3560 Rl—Rl-liIF RK.Ll THEN 4000
3600 IF D<-Y<R1> THEN 3560
3700 VH-V<R1>|V<R1>-V<L1>|V<L1>-VHiGOTO 3520
4000 R1-R<SZ>1VH-V<L1>|Y<L1>-V<R1>|V<R1>-YH
4060 IF <L1-L<SZ> >«R<SZ>-L1 > THEN 4100
4080 L<SZ+l>-L<SZ>iR<SZ+l>-Ll-liL<SZ>-Ll+liGOTO 4200
4100 LCSZ+D-Ll + l :R<SZ+1 >-R<SZ> 1R<SZ>«L1-1
4200 SZ-SZ+1
4300 IF L<SZXR<SZ> THEN 3000
4340 SZ-SZ-1
4360 IF SZ>0 THEN 4300
4500 T-<TI-T>/60
5008 PRINTiPRINT "ИСХОДНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5100 FOR 1-1 TO NiPRINT X<I>>iNEXT IiPRINT
5200 PRINTiPRINT "ОТСОРТИРОВАННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5300 FOR 1-1 TO NiPRINT V<I>nNEXT I iPRINT
6888 PRINTiPRINT "ВРЕМЯ СЧЕТА:"; T: "С ДЛЯ"; N; "ЧИСЕЛ"
9999 END
В этой программе, как и в предыдущей, исходная последова-
тельность моделируется в самой программе с помощью датчика
случайных чисел RND (строки 1200—1400). Исходные и отсортиро-
ванные данные выводятся на экран на участке программы начиная
со строки 5000. Исходная последовательность чисел отсортировы-
вается сначала на две группы; каждая из этих групп в свою очередь
делится на две группы. Это продолжается до тех пор, пока во всех
Автоматизированная обработка данных
379
группах не останется по одному числу. Для предварительной сорти-
ровки на две группы используется любое число исходной последо-
вательности. Если сортируется более четырех чисел, то выбирают
три числа и среднее число* присваивают переменной D (строки
3000—3260). Группа разделяется на подгруппу с числами, меньши-
ми чем D, и подгруппу с числами, не меньшими чем D (строки
3520—4000).
Рассмотрим этот процесс на следующем примере. Дана некото-
рая последовательность чисел:
437891025
Выберем первое (4), последнее (5) и стоящее посередине (9) число.
Средним числом D является 5, и по нему исходная последователь-
ность делится на две подгруппы. Для этого число D переставляется
на правое крайнее место. (В этом примере оно там уже и стоит.)
Теперь, начиная с крайнего левого числа, ищется число больше пя-
ти, а с правого края — число меньше пяти, и эти числа обменива-
ются местами. В данном примере это числа 7 и 2.
432891075
Поиск продолжается до тех пор, пока не остановится на числе, ко-
торое не удастся обменять ни с каким другим числом. Таким об-
разом, получается последовательность
432019875
Потом это число (в данном случае 9) обменивается со стоящим в
правом конце числом 5. Это дает
432015879
Теперь число 5 стоит на том месте, на котором оно будет стоять
после окончания сортировки. Этим же способом сортируются обе
подгруппы (4 3 2 0 1) и (8 7 9), пока в каждой подгруппе не оста-
нется по одному числу.
Задание 202. Дополните программу «QQ-СОРТ» выводом на экран промежуточ-
ных результатов, а также размеров групп (LI, Rl, L( ), R( )), чтобы можно было
проследить за процессом сортировки.
Если сортируются положительные целые числа, то можно ис-
пользовать специальный очень быстрый метод. Программа
Это число больше наименьшего, но меньше наибольшего. — Прим, перев.
380
Глава 14
«АДРЕС-СОРТ»* сортирует до 1000 таких частиц. Этот специаль-
ный метод называют адресной сортировкой.
в REM "АДРЕС—СОРТ" EBERT/EDERER 840125
1 КЕМ»и1«1*11КЖ»и1н1«**********»1***Н1**********
3 REM** АДРЕСНАЯ СОРТИРОВКА **
4 REM** ЦЕЛЫХ ЧИСЕЛ ОТ 1 ДО М **
5 REM** НАИБОЛЬШИЕ ЗНАЧЕНИЯ **
6 REM** М - 1000, N - 1000 **
? REM** ввод В ПРОИЗВОЛЬНОЙ **
8 REM** ПОСЛЕДОВАТЕЛЬНОСТИ **
9 REM** ВЫВОД ПО ВОЗРАСТАНИЮ **
1( 1 REM* ЗНАЧЕНИЙ **
19 REM********************************
1000 DIM X<1001>,R<1001>,V<1001>
1050 м.1000
1100 INPUT "ЧИСЛО ДАННЫХ"; N
1120 К.0
1140 FOR 1.1 ТО М|R<I>-0iNEXT I
1200 FOR 1.1 ТО N
1300 Х<I>-INT<M*RND<5>>+1
1400 NEXT I
1410 T-TI
2000 FOR I-l ТО N|R<X<I>>-R<X<I>>+1iNEXT I
3000 FOR I-l TO Mi IF R<I>-0 THEN NEXT IiGOTO 4500
3200 FOR J-l TO R<!>iK-K+1iV<K>-tiNEXT J
4000 NEXT I
4500 T-<TI-T>/60
5000 PRINT iPRINT "ИСХОДНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5100 FOR I-l TO NiPRINT X<I> JiNEXT IiPRINT
5200 PRINT iPRINT "ОТСОРТИРОВАННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ"
5300 FOR I-l TO NiPRINT V< I>jiNEXT IiPRINT
6000 PRINTiPRINT "ВРЕМЯ СЧЕТА:";T;"C ДЛЯ ”; N; "ЧИСЕЛ-
9999 END
В строках 1200—1400 генерируются случайные целые числа в
интервале [1, 1000]. Участок программы, начиная со строки 5000,
выводит на экран исходную и отсортированную последователь-
ность чисел. В строке 2000 рассчитываются компоненты вектора
адресов (массив А( )). Ранее, в строке 1140, все элементы этого
массива обнуляются. Если в исходной последовательности встреча-
ются одинаковые числа, то соответствующие элементы массива
А( ) каждый раз увеличиваются на 1 (строка 2000). Таким обра-
зом, вектор адресов А представляет собой распределение частоты
чисел в заданной последовательности в порядке их возрастания.
Теперь, чтобы получить отсортированную последовательность
чисел, индексированной переменной Y(K) присваивается текущее
значение параметра внешнего цикла по I (строки 3000—4000) столь-
* В оригинале, по-видимому, в строке 3000 опечатка. Вместо THEN NEXT I:
GOTO 4500 следует записать THEN GOTO 4000. — Прим, перев.
Автоматизированная обработка данных
381
ко раз, сколько раз число I встречается в исходной последователь-
ности (внутренний цикл по J, строка 3200).
В таблице приведено время сортировки чисел различными мето-
дами.
N 'COPT- ЧИСЛ" "O-COPT" 'OOCOPT' "АДРЕС- СОРТ"
10 1 1 1 7
20 3 2 2 7
40 8 5 5 8
80 29 13 1 3 9
1 25 69 23 22 10
250 262 57 49 13
500 1042 144 1 10 20
1000 3765 355 238 32
2000 16645 810 530 55
4000 1080 99
Сортировка 1000 чисел по обычной методике продолжается око-
ло 1 ч, а процедура Quick-Sort длится только 4 мин. Адресную сор-
тировку по сравнению с другими алгоритмами можно считать наи-
лучшей, однако если надо сортировать большие массивы не только
целых, но и дробных чисел, то приходится использовать другие ме-
тоды, хотя они требуют весьма большого объема памяти и больше
машинного времени.
14.3. Сплайн-регрессия
В этом разделе, посвященном обработке экспериментальных
данных, рассматриваются два метода, которые реализованы в про-
граммах для сглаживания данных, дифференцирования эксперимен-
тальных зависимостей, интерполяции и наглядного представления
данных. Идея, лежащая в основе этих методов, заключается в том,
что экспериментальные точки аппроксимируются сплайн-функцией,
причем степень сглаживания задается пользователем (см. также
раздел 10.2, посвященный сплайн-интерполяции).
Первый метод подробно рассмотрен в книге Лоусона и
Хансона*. При сплайн-интерполяции сплайн-функция проходит че-
рез каждую экспериментальную точку, причем эти точки совпада-
ют с точками перегиба сплайн-функции. Если уменьшить число то-
* Lawson С. L., Hanson R. J., Solving least square problems. Prentice-Hall, Eng-
lewood Cliffs, New Jersey, 1974, p. 222.
382
Глава 14
чек перегиба, то сплайн-функция не будет больше проходить точно
через заданные точки. Дополнительное условие для построения та-
кой сплайн-функции очевидно и естественно: необходимо, чтобы
сумма квадратов отклонений заданных точек от аппроксимирую-
щей функции была минимальной (сплайн-регрессия). В этом методе
точки перегиба находятся на одинаковом расстоянии друг от друга
вдоль осих. Ниже приведена распечатка программы, в которой ис-
пользуется этот метод.
О REM "СПЛАЙН—РЕП " EBERT/EDERER 831207
1 REM****************************************** Ии**
2 REM** АППРОКСИМАЦИЯ ДАННЫХ КУБИЧЕСКОЙ **
3 REM** СПЛАЙН—ФУНКЦИЕЙ. ТОЧКИ ПЕРЕГИБА **
4 REM** СПЛАЙН-ФУНКЦИИ ЛЕЖАТ НА ОДИНАКОВОМ **
5 REM** РАССТОЯНИИ ДРУГ ОТ ДРУГА ВДОЛЬ ОСИ X. ♦*
6 REM** ПО КНИГЕ LRUSON/HRNSON SOLVING LEAST '**
7 REM** SQUARE PROBLEMS PRENTICE HRLL 1974 **
Э REM*********************************************
100 DIM ХС250Э,V<250>,Z<250>
110 DIM R<252,5>,D<252,7>
120 DIM B<250>,C<250>
130 INIT
200 DEF FNP<T>-.25*T*T*T
210 DEF FNQ<T>«1-.75*<1+T>*<1-T>*<1-T>
300 INPUT "ЧИСЛО ТОЧЕК ПЕРЕГИБА"; N
310 IF N<2 THEN H-2
320 GOSUB 10000 iREM СЧИТЫВАНИЕ ДАННЫХ (X ( > ИУ( >>
330 GOSUB 11000SREM СОРТИРОВКА ДАННЫХ ПО ВОЗРАСТАНИЮ ЗНАЧЕНИЙ X
360 IF N>-M-2 THEN N-M-2
400 В<1>—Х<1>:BCN>—ХСМ>
410 Н-СВСЮ-ВС1>>/<Н-1>
420 FOR 1-2 ТО N-1
430 В<1>-ВС1>+Н*<1-1>
440 NEXT I
460 OOSUB 12000:REM ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ МАТРИЦЫ А
4В0 GOSUB 1300B:REM ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ЛЕНТОЧНОЙ
481 REM МАТРИЦЫ D= АТ* А И Z-RT*V
500 GOSUB 14000IREM РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ D*C = Z
550 GOSUB 20000iREM ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ СПЛАЙН-ФУНКЦИИ
650 OOSUB 16000 :REM ИЗОБРАЖЕНИЕ ИСХОДНЫХ ДАННЫХ В ВИДЕ ТОЧЕК
9900 ......GET R*iIF R»-"" THEN 9900
9910 IZ-RBS<IZ-1>:DISPLRY<IZ>:GOTO 9900
9999 STOP
10000 REM*************************************
10001 REM** СЧИТЫВАНИЕ ДАННЫХ (X ( ) И Y( ) )**
10002 REM*************************************
10010 RERD MiREM ЧИСЛО ПАР ЗНАЧЕНИЙ
10020 FOR I-l TO MsRERD X<I>,УСI>:HEXT I
10030 RETURN
11000 REM*************************************************** ****
11001 REM** СОРТИРОВКА ДАННЫХ ПО ВОЗРАСТАНИЮ ЗНАЧЕНИЙ. ОПРЕ- **
11002 РЕМ**ДЕЛЕНИЕ НАИБОЛЬШИХ И НАИМЕНЬШИХ ЗНАЧЕНИЙ ХИТ**
11003 REM*************************************************** ****
11020 X0-X <1>:У0-У <1>•XM-X0:УМ-У0
11040 FOR 1-2 ТО М
11060 IF Х0>Х<1> THEN X0-XCI)
110В0 IF ХМ<Х<1> THEN ХМ-ХСП
11100 IF У0>У<1> THEN У0«У<1>
11120 IF УМ<У<1> THEN УМ-УС1>
11140 NEXT I
Автоматизированная обработка данных
383
11200 0-INT<L0G<M>/L0G<2>>10-2Т0-1
11220 FOR I-l ТО М-0
11240 FOR J-I TO 1 STEP -0
11260 IF X(JX.X(J*D> THEN 11300
11270 HV-V<J>iV<J>-Y<J+O>IY<J+D>-HV
112B0 HX-X<J>iX<J>«X<J+0>iX<J+O>«HX
11290 NEXT J
11300 NEXT I
11320 D-INT<0/2>iIF O>0 THEN OOTO 11220
11900 RETURN
12000 REM***************************************
12001 REM** ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ МАТРИЦЫ A **
12002 REM***************************************
12010 IB-1iREM ИНДЕКС ТОЧКИ ПЕРЕГИБА
12020 IX-1 :REM ИНДЕКС ЗАДАННОЙ ТОЧКИ
12030 IF X<IX)>BCIB+1> THEN GOTO 12150
12060 T-<X<IX>-BCIB>>/H
12070 АС IX,1>-FNP<1-T>
12080 RC IX,2>-FNG1C 1-T>
12090 ACIX,3>-FNQCT>
12100 RCIX,4>-FNPCT>
12110 ACIX,5>«IB
12120 IF IX-M THEN GOTO 12200
12130 IX-IX+1(GOTO 12050
12150 IB-IB+1sGOTO 12050
12200 RETURN
13000 REM************************************************
13001 REM** ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ЛЕНТОЧНОЙ МАТРИЦЫ *«
13002 REM** 0= АТ*А И Z=AT»Y **
13003 REM************************************************
13060 FOR I-l TO N+2
13080 FOR J-l TO 7iDCI,J>—0
13100 NEXT JiZCI>«0iNEXT I
13140 FOR K-l TO M
13160 FOR I-l TO 4:F0R J-l TO I
13200 I0«I+RCK,5>-1:J0-J+ACK,5>-1
13220 DC 10,J0-I0+4)—DC 10,J0-I0+4>+RCK,I)*ACK,J>
13240 NEXT J :ZC I0>-Z< I0>+RCK, I >*VCK>
13260 NEXT IiNEXT К
13300 FOR I-l TO N+2IF0R J-l TO 3
13320 IF DCI,J>-0 THEN GOTO 13400
13340 DCJ+I-4,B-J>-DCI,J>
13400 NEXT JiNEXT I
13900 RETURN
14000 REM******************************************
14001 REM** РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ D*C =2*»
14002 REM******************************************
14040 FOR I-l TO N+2|D4—DC I,4>iFOR J-l TO 7
14060 0<I,J>-OCI,J>/04iNEXTJiZCI>-ZCI>/04
14000 J-1+31 IF JXN+2) THEN J-N+2
14100 IF I-N+2 THEN OOTO 14400
14140 FOR K-I+l TO J
14150 L3-DCK,4 -CK-I>>
14160 FOR L»1 TO 4
14180 Ll-L+3iL2-L+3-CK-I>
14200 DCK,L2>-DCK,L2>-L3*DCI,L1>
14220 NEXT LiZCK>»ZCK>-L3*ZCI>
14240 NEXT К
14400 NEXT I
14500 FOR I-l TO N+5|CCI>- 0iNEXT I
14520 FOR I-N+2 TO 1 STEP -1
14540 CCI>-ZCI>-0<I,5>*C<I+1>-DCI,6>*CCI+2J-DCI,7>*CCI+3>
14560 NEXT I
14900 RETURN
384
Глава 14
16008 REM************************ **************************
16001 REM** ИЗОБРАЖЕНИЕ ИСХОДНЫХ ДАННЫХ В ВИДЕ ТОЧЕК **
16002 REM************************ **************************
16020 DISPLAV<1>
16030 PSPRCEC.05,.95,.05,.95>
16040 ОI - <XM-X0 >/20X0-X0-DItXM-XM+OI
16060 Ol«<VM-V0>/20iV0«V0-OIiVM-VM+DI
16000 MAP<X0,XM,V0,VM>
16100 A»-"*"
16120 FOR 1-1 TO M
16140 PLOTCXCI>,V<I>,0>
16160 REM CHPLOT<A»,1>
16170 CURSOR
16100 HEXT I
16200 PLOTCX0,V0,0>
16220 PLOT<X0,VM,1>iPLOTCXM,VM,1>
16240 PLOTCXM,V0,1>IPLOTCX0,V0,1>
16260 LIHTVP<1>
16270 FOR I«1 TO H
16200 PLOTCBCI>,V0,0>:PLOT<B< t > , VM,1>
16300 HEXT I
16320 LIHTVP<0>
16400 X-X<l>iGOSUB 22000iPLOT<X,V,0>
16420 FOR X-X<1> TO X<M> STEP <X<M>-X<1>>/100
16440 .GOSUB 220001PLOT <X,V, 1 >
16460 HEXT X
16880 IZ-1
16900 RETURH
20000 REM*********************************************
20001 REM** ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ СПЛАЙН—ФУНКЦИИ **
20002 REM*********************************************
20020 FDR 1-1 TO M
20030 X-X<I>
20040 GOSUB 21000 iREM ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА J
20060 T-<X-B<J>>/H
20080 V-C<J>*FHP<1-T>+C<J+l>*FNO<l-Tl+CCJ+2>*FN0<T>+C<J+3>*FHP<T>
20100 PRIHT I,X<I>,V<I>,V
20200 HEXT I
20990 RETURH
21000 REM***********************************
21001 REM** ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА J **
21002 REM***********************************
21010 J-0
21020 IF X<-B<1> THEM I J-l IRETURH
21040 IF X>-B<H> THEHiJ-N-1IRETURN
21060 J-J+l
21080 IF X>B<J> THEN GOTO 21060
21100 J-J-l
21200 RETURH
22000 REM**********************************************************
22001 REM** ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ СПЛАЙН-ФУНКЦИИ В ДАННОЙ ТОЧКЕ**
22002 REM**********************************************************
22040 GOSUB 21000 iREM ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА J
22060 T-<X-B<J>>/H
22060 V-C<J>*FNP<l-Tl+CCJ+l>*FHQ<l-Tl+CCJ+2>»FNQ<T>+C<J+3>*FHP<T>
22980 RETURH
60000 DATA 20
60010 DATA 0, 0.5
60020 DATA b 1
60030 DATA 2, 3.5
60040 ORTA 3, 4.2
60050 DATA 4, 5.5
60060 DATA 5, 8.2
60070 DATA 6/ 8.5
60080 DATA 7, 18.2
Автоматизированная обработка данных
385
£0065 DATA 8, 10.9
£0696 DATA 9, 11.5
60100 DATA 10, 11.6
60110 DATA 11, 11.5
60120 DATA 12, 10.6
60130 DATA 13, 9.5
60140 DATA 14, 7.2
60150 DATA 15, 5.5
60160 ORTA 16, Э.2
60170 DATA 17, 2. 1
601B0 DATA IB, 0.9
60190 DATR 19, 0.0
63999 ENO
RUN
CBM GRAPHIC REV.1 ON - FORMAT 512 * 256
ЧИСЛО ТОЧЕК ПЕРЕГИБА? 7
1 0 .5 .380808711
2 1 1 1.47392224
3 2 3.5 2.84734222
4 3 4.2 4.38751442
5 4 5.5 5.98212207
6 5 B.2 7.5270749
7 6 8.5 8.9216386
8 7 10.2 10.0691437
9 8 10.9 10.9200592
18 9 11.5 11.4552662
11 10 11.6 11.6540103
12 11 11.5 11.4462651
13 12 10.6 10.712732
14 13 9.5 9.33527211
15 14 7.2 7.39384742
16 15 5.5 5.27547683
17 16 3.2 3.39311057
18 17 2.1 1.99626079
19 18 .9 .933799354
20 19 0 -5.66667793E-03
BRERK IN RERDV. 9980
25-81
386
Глава 14
В качестве примера взяты 20 точек, которые аппроксимируются
сплайн-функцией с 12, 7, 5 и 3 точками перегиба. Чем меньше вы-
брано точек перегиба, тем более гладкой получается сплайн-функ-
ция, но зато тем дальше она может проходить от заданных точек.
Математическая основа метода заключается в том, что любой
сплайн с N точками перегиба можно представить как линейную
комбинацию N + 2 независимых базисных сплайн-функций. В ка-
честве базисных сплайн-функций выбраны два кубических полинома
Р(Т) и Q(T), которые описаны в строках 200 и 210. Коэффициенты
этой линейной комбинации определяются с помощью линейной ре-
грессии.
В первой части программы после описания полиномов третьей
степени Р(Т) и Q(T) считываются исходные данные и с помощью
процедуры для быстрой сортировки упорядочиваются по возраста-
нию значений X. Число точек перегиба вводится с помощью опера-
тора INPUT. Координаты X в точке перегиба присваиваются эле-
ментам одномерного массива В( ). Размер матрицы А, элементы
которой рассчитываются подпрограммой 12000, довольно боль-
шой; Однако, поскольку ненулевые элементы расположены только
на главной диагонали и на четырех соседних с ней диагоналях, для
экономии памяти матрица рассматривается как ленточная матрица
размера 252 х 5. Подпрограмма 13000 рассчитывает из матрицы А
матрицу D и вектор Z (D = АТА и Z = ATY). В матрице D семь
диагоналей содержат ненулевые элементы. Эти математические
операции соответствуют составлению системы линейных уравнений
для линейной регрессии общего вида (см. разд. 8.3).
Для решения полученной системы линейных уравнений вызыва-
ется подпрограмма 14000, т. е. рассчитываются коэффициенты ли-
нейной комбинации базисных сплайн-функций. Для этого использу-
Автоматизированная обработка данных
387
ется рассмотренный ранее метод Гаусса — Жордана (см. разд. 8.2).
Однако следует учитывать, что в памяти ЭВМ хранятся не все эле-
менты расширенной матрицы коэффициентов, а только ее ненуле-
вые элементы. После того как вычислены коэффициенты С(1),
можно считать, что сплайн-функция найдена. Затем вызывается
подпрограмма 20000, которая рассчитывает значения сплайн-функ-
ции при тех значениях X, для которых известны значения Y, и срав-
нивает рассчитанные и известные значения Y. Подпрограмма для
отображения графической информации строит на экране заданные
точки, пунктирные прямые, на которых лежат точки перегиба
сплайн-функции, и саму сплайн-функцию.
Задание 203. Взяв за основу программу «СПЛАЙН-РЕГ1», составьте програм-
му, которая может дифференцировать сглаживающую сплайн-функцию. Для этого
надо продифференцировать полиномы Р(Т) н Q(T) по X н ввести выражения для
производных в программу, например:
201 DEFFN Р1(Т) = 0.75»Т-Т/Н
211 DEFFN Q1(T) = (1.5 -Т + 0.75 - 2.25»Т.Т)/Н
Точно так же, как в строке 20080 вычисляются значения сплайн-функции, можно рас-
считать значения производной:
20081 Yl = -C(J)-FNP1(1 - Т) - C(J + 1)-FNQ1(1 - Т) + C(J + 2)»FNQ1(T)
20082 Yl = Yl + C(J + 3).FNP1(T)
В программе необходимо предусмотреть вывод значений производной н ее графика.
Можно также рассчитать и вторую производную сплайн-
функции. Следует напомнить, что, хотя по определению значения
второй производной сплайн-функции невелики по абсолютной вели-
чине, зависимость второй производной от X не является гладкой;
между каждыми двумя точками перегиба сплайн-функция описыва-
ется соответствующим полиномом. Если необходимо вычислить
гладкие вторые производные, то лучше найти по исходным дан-
ным с помощью сплайн-регрессии первые производные и по ним
построить аппроксимирующий сплайн; производная этой сплайн-
функции и будет сглаженной второй производной исходной зависи-
мости. Эту процедуру можно продолжить дальше, однако следует
учитывать, что полученные таким способом производные высоких
порядков становятся весьма ненадежными. (Напомним давно из-
вестное экспериментаторам правило, что экспериментально найден-
ные зависимости легко интегрировать, но, как правило, гораздо
труднее дифференцировать.)
Задание 204. Используйте метод сглаживающего сплайна для интегрирования
полученных экспериментально зависимостей.
Задание 205. Расширьте программу «СПЛАЙН-РЕГ1», чтобы можно было учи-
тывать весовые коэффициенты отдельных значений.
25*
388
Глава 14
Второй метод, реализованный в программе «СПЛАЙН-РЕГЗ»,
также аппроксимирует и сглаживает экспериментальные данные
сплайн-функциями. В качестве меры гладкости используется кри-
визна аппроксимирующей функции, т. е. ее вторые производные.
Каждое значение X считается точкой перегиба сплайна. Без допол-
нительных условий сплайн-функция проходила бы точно через каж-
дую точку X(I), Y(I). Однако надо найти такую сплайн-функцию,
для которой линейная комбинация суммы квадратов отклонений
значений Y и интеграла квадрата вторых производных была бы
минимальна. Если в этой линейной комбинации учитывать только
сумму квадратов отклонений (параметр РР равен 1, строка 200), то
получится сплайн-интерполяция. Если же учитывать только инте-
грал квадрата вторых производных (РР = 0, строка 200), то полу-
чится прямая, т. е. линейная регрессия (максимальное сглажи-
вание).
0 КЕМ "СПЛАЙН-РЕГЗ'' EBERT/EDERER В40327
1 КЕМ****************************************************
2 REM** АППРОКСИМАЦИЯ КУБИЧЕСКОЙ СПЛАЙН-ФУНКЦИЕЙ **
3 КЕМ** МИНИМИЗИРУЕТСЯ ЛИНЕЙНАЯ КОМБИНАЦИЯ ИЗ **
4 REM** СУММЫ КВАДРАТОВ ОТКЛОНЕНИЙ И ИНТЕГРАЛА **
5 REM** КВАДРАТОВ ВТОРЫХ ПРОИЗВОДНЫХ **
6 КЕМ** КОЭФФИЦИЕНТ ПРИ СУММЕ КВАДРАТОВ **
7 REM** ОТКЛОНЕНИЙ ЗАДАЕТСЯ В СТРОКЕ 200 **
9 КЕМ****************************************************
100 DIM X(100>,V(100>,Z<300>
110 DIM 0(300,10>,АС100>,В(100>,С<100>
120 DIM Н(100>,IH(100>,RC300>
200 PP-.500IQO-1-PP
220 PP—2*PPiQQ-QQ/3
320 GOSUB 10000 iREM СЧИТЫВАНИЕ ДАННЫХ (X ( ),Y ( ))
330 GOSUB 11000rREM СОРТИРОВКА ПО ВОЗРАСТАНИЮ X
350 GOSUB 115001 REM ВЫЧИСЛЕНИЕ H (I)
480 GOSUB 13000 iREM ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ЛЕНТОЧНОЙ МАТРИЦЫ
500 GOSUB 14000 iREM РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ D * Z = R
520 GOSUB 12000 iREM ВЫЧИСЛЕНИЕМ, L А, А. В, C
550 GOSUB 20000 iREM ВЫЧИСЛЕНИЕ СПЛАЙНА
560 GOSUB 17000 iREM ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
650 GOSUB 16000IREM ИЗОБРАЖЕНИЕ ЗАДАННЫХ ТОЧЕК
9900 А»-”“iGET Я»lIF Я»-"" THEN 9900
9910 IZ-ABSCIZ-i>iDISPLAVCIZ>1GOTO 9900
9999 STOP
10000 REM*************************************
10001 REM** СЧИТЫВАНИЕ ДАННЫХ X( ) ,Y ( )**
10002 REM*************************************
10010 READ NlN-N-liREM ЧИСЛО ТОЧЕК
10020 FOR 1-0 TO NiREAD X(I>,Y(I>«NEXT I
10030 RETURN
11000 REM***************************************************
11001 REM** СОРТИРОВКА ДАННЫХ ПО ВОЗРАСТАНИЮ X **
11002 REM** ОПРЕДЕЛЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО **
11003 КЕМ** ЗНАЧЕНИЯ ХИ Y **
11004 REM***************************************************
11020 Х0«Х < 0 >IV0-V < 0 >1XM«X01УМ-V0
11040 FOR I-l ТО N
11060 IF Х0>Х<1> THEN Х0-Х<1>
Автоматизированная обработка данных
389
11080 IF XM<XCI> THEN XM-XCI)
11100 IF V8>V<I> THEN Y0-Y<I>
11128 IF VM<YCI> THEN YM-YCI)
11148 NEXT I
11200 D-INT<LOOCN+1>/LOG<2>> iD-2TD-l
11220 FOR 1-0 TO N-D
11240 FOR J-I TO 8 STEP -0
11280 IF X<JX-XCJ+D> THEN 11300
11270 HY-YCJ>lYCJ>«V<J+D>iV<J+Ol-HY
11280 HX-XCJ)iXCJ>-X<J+0>iXCJ+D>-HX
11290 NEXT J
11308 NEXT I
11320 D-INT<0/2>I IF 0>8 THEN GOTO 11220
11400 RETURN
11500 REN***************************
11501 REM** ВЫЧИСЛЕНИЕ H (I) **
11502 REM***************************
11510 FOR I-l TO NiNCI>-X<I>-X<I-l>IIHCI>-l/H<I>iNEXT I
11548 RETURN
12000 REM*************************************
12801 REM** ВЫЧИСЛЕНИЕМ, LA, А, В, C **
12002 REM*************************************
12010 R<0>-0|R<N>-0
12028 FOR I-l TO N-l1R<I>-Z<3*I-l>iNEXT I
12048 REM ПЕРЕПИСАТЬ MBH
12060 IH<0>«Z<0>|IHCN>-ZCM>
12080 FOR I-l TO N-lIIHCI>»ZC3*I-2>iNEXT I
12108 REM ПЕРЕПИСАТЬ LA В D<*,0>
12128 FOR I-l TO N-llOCI,0>-ZC3*I>iNEXT I
12200 SI-01FOR 1-0 TO NiSl-Sl+<VCI>-IHCI>1T21NEXT I
12228 PRINTiPRINT .“СУММА КВАДРАТОВ ОТКЛОНЕНИЙ -“,S1
12246 S2-0IFOR 1-0 TO N-l
12258 S2-S2+HC1 + 1>*<AC I>*A<I>+A<I>*R<I+ 1>+A<1 + 1>*A<I+ 1>>
12260 NEXT I tS2»S2/3
12280 PRINT "ИНТЕГРАЛ КВАДРАТОВ ВТОРЫХ ПРОИЗВОДНЫХ-" >S2 iPRINT
12300 FOR 1-0 TO N-l
12328 CCI>-IHCI>-RCI>*HC1+1>*HC1+1>/6
12340 BCI>-CIHC1+1>-IHCI>>/HC1+1>-H<1+1>/6*CRC1+1>-R<I>>
12368 NEXT I
12900 RETURN
13000 REM**************************************************
13001 REM** ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ЛЕНТОЧНОЙ МАТРИЦЫ D **
13002 REM**************************************************
13028 M»3*N-2
13030 FOR 1-0 TO MlFOR J-0 TO 10
13048 DC I,J>-0iNEXT J1RCI1-0
13058 NEXT I
13060 REM ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПО M И ПРАВЫХ СТОРОН
13080 D<0,5>-PPiO<0,8> — IHC1> |RC0>-PP*VC8>
13180 ОС 1,5>-PPlOC 1,7>-IHC 1 >+IHC2> |DC1,10> —IHC2> iRC 1 >-PP*YC 1 >
13120 DCM-3,4> — IHCN-l) iDCM-3,5>-PP
13130 DCM-3,?>-IHCN>+IHCN-l>|RCM-3>«PP*YCN-1>
13148 DCM,4> — IHCN> |DCM,5>-PP|RCM>-PP*YCN>
13168 FOR 1-2 TO N-2iJ-3*I-2
13100 DCJ,5>-PPiRCJ>-PP*YCI>
13208 DCJ,4> —IHCI> |DCJ,Z>-IHCI> + IHCI + 1> |DCJ,10> —IHCI+1)
13228 NEXT I
13240 REM ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПО A
13268 DC2,5>-2*QQ*CHC1>+HC2>>|DC2,6>-CHC1>+НС2>>/3
13200 0C2,8>-00*HC2>iOC2,9>-HC2>/6
13300 DCM-2,2>-QQ*HCN-l>iDCM-2,3>-HCN-l>/6
13328 DCM-2,5>-2*QQ*CHCN-l>+HCN>> iDCM-2,6>-CHCN-l l+HCND/3
13348 FOR 1-2 TO N-2iJ«3#I-l
13368 0<J,2>-QQ*HCI>lOCJ,3>-HCI>/61DCJ,5>-2*QQ*CHCI>+HC1 + 1> >
13380 DCJ,6>-CHCI>+H<1+1>>/3lOCJ,8>-QQ*HC1+1>lOCJ,9>-H<1+1>/6
13400 NEXT I
390
Глава 14
13500 REM ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ OOLA
13540 0СЗ,2> —IHC1> iOC3,3>«IHCl> + IH<2> sDC3,4>-<H<1)+H<2>>/3
13560 DC3,6> —INC2>iDC3,7>-H<2>/6
13500 OCM-1,0> — IHCN—1> |OCM-1,1>-HCN-1>/6:DCM-1,6> — IHCN>
13600 DCM-1,3>-IHCN> + IHCN-l> sDCM-1,4>«<HCN-1>+H(N>>/3
13640 FOR 1-2 TO N-2iJ-3*I
13660 DCJ,0>--IN<I>iDCJ,1>-HCI>/6iDCJ,3>-IHCI>+IH<1+1>
13600 DCJ,4>-CHCt>+HCI + l>)/3iDCJ,6> — IH(I+1> :D(J,7>-H(I+l>/6
13700 NEXT I
13900 RETURN
14000 REM******************************************
14001 REM*» РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ D*C-Z **
14002 REM******************************************
14040 FOR 1-0 TO M|D4-DCI,5>iFOR J-5 TO 10
14060 DC I,J>-0<I,J>/04iNEXT J|R<I>.R<I>/D4
14000 J-I+SiIF J>M THEN J-M
14100 IF I-M THEN GOTO 14400
14140 FOR K-I + l TO J
14150 L3—DCK,5-K+I>
14155 IF L3-0 THEN GOTO 14240
14160 FOR L-0 TO 5
14100 Ll-L+51L2-L+5-CK-I>
14200 DCK,L2>-DCK,L2>+L3*0CI,L1>
14220 NEXT L1R<K>-RCK>+L3*R<t>
14240 NEXT К
14400 NEXT I
14480 FOR 1-0 TO MiZCI>- 0iNEXT I
14500 ZCM>-RCM>1ZCM-1>-R<M-l>-DCM-i,6>*ZCM>
14510 ZCM-2>«RCM-2>-DCM-2,6>*ZCM-l>-DCM-2,7>*ZCM>
14520 ZCM-3>-RCM-3>-DCM-3,6>»ZCM-2>-DCM-3,7>*ZCM-l>-DCM-3,B>*ZCM>
14530 ZCM-4>-RCM-4>-DCM-4,6>»ZCM-3>-0CM-4,7>»ZCM-2>-DCM-4,8>»ZCM-l>
14540 ZCM-4>«ZCM-4>-DCM-4,9>*ZCM>
14560 FOR I-M-5 TO 0 STEP -1
14500 Z<I>-R<I>-DCI,6>*ZC1+1>-DCI,7>*ZCI+2>-DCI,8>*ZCt+3>
14600 ZC I >-ZC I >-O< I ,9>*ZC I+4>-DC I , 10>*ZC I+5>
14620 NEXT I
14900 RETURN
16000 REM************************************
16001 REM** ИЗОБРАЖЕНИЕ ЗАДАННЫХ ТОЧЕК **
16002 REM************************ ************
16010 INIT
16020 OISPLRVCl)
16030 PSPRCEC.05,.95,.05,.95>
16040 OI-CXM-X0>/20iX0-X0-OI1XM-XM+DI
16060 DI-CVM-Y0>/20IV0-V0-OI (VM-VM+0I
16080 MRP<X0,XM,V0,VM>
16100 R*-"*"
16120 FOR 1-0 TO N
16140 PLOTCXCI>,VCI>,0>
16160 REM CHPLOTCR»,1>
16170 CURSOR
16180 NEXT I
16280 PLOTCX0,V0,0>
16220 PLOTCX0,VM,1>1PL0TCXM,VM,1>
16240 PLOTCXM,V0,1>1PLOTCX0,V0,1>
16400 X—XC0> iGOSUB 22000|PLOTCX,V,0>
16420 FOR X-XC0> TO XCN> STEP CXCN>-X<0>>/100
16440 GOSUB 220001PLOTCX,V,1>
16460 NEXT X
16800 IZ-1
16900 RETURN
20000 REM***************************
20001 REM** ПОСТРОЕНИЕ СПЛАЙНА **
20002 REM***************************
20020 FOR 1-0 TO N
Автоматизированная обработка данных
391
20030 Х-Х<1>
20040 GOSUB 22000 iREM ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ СПЛАЙН-ФУНКЦИИ
20100 PRINT 1,Х<1>,У<1>,У
20200 NEXT I
20990 RETURN
21000 REN***********************************
21001 REM** ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА J **
21002 REN***********************************
21010 J1-0IJ2-N
21020 IF X<-X<J1> THEN|J-01RETURN
21040 IF X>-X<J2> THEN|J«N-1iRETURN
21060 J-INTC<JI+J2>/2>
21000 IF X>X<J> THENiJ1»JiGOTO 21120
21100 J2«J
21120 IF J2-J1M THEN GOTO 21060.
21140 J-JI
21200 RETURN
22000 REM****!*****************************************
22001 REM** ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ СПЛАЙН-ФУНКЦИИ **
22002 REM*********************************************
22040 GOSUB 21000«REM ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА J
22060 Tl-X<J+l>-XiT2-X-X<J>
22000 V-R < J> *T1*T1*T1Z6/H< J+1>+R < J+1>*T2«T2*T2/6/H < J+1>
22100 V-V+B<J>*<X-X<J>>+C<J>
22900 RETURN
60000 DRTR 27
60010 ORTR 0, 0.5
60020 ORTR 1, 1
60030 DRTR 2, 3.5-
60040 DRTR 3, 4.2
60050 DRTR 4, 5.5
60060 ORTR 5, В. 2
60070 DRTR 6, 0.5
60000 DRTR 7, 10.2
60005 ORTR B, 10.9
60090 DRTR 9, 11.5
60100 DRTR 10, 11.6
60110 DATR 11, 11.5
60120 DRTR 12, 10.6
60130 DRTR 13, 9.5
60140 DRTR 14, 7.2
60150 DATR 15, 5.5
60160 DATA 16, 3.2
6017B DATA 17, 2.1
60100 DATA 10, 0.9
60190 DATA 19, 0.0
60200 DATA 0.3 , 0.6
60210 DATA 4.0 , 0.6
60220 DATA B.5 , 11.6
60230 DATA 12.1 , 10.5
60240 DATA 12. В , 10.0
60260 DATA 16.7 , 2.5
60270 DATA 10.2 , 0.5
63999 END
RUN
СУММА КВАДРАТОВ ОТКЛОНЕНИЙ = 3.33725266
ИНТЕГРАЛ КВАДРАТОВ ВТОРЫХ ПРОИЗВОДНЫХ = 1.99108033
0 0 .5 .232598733
1 .3 .6 .610520046
2 1 1 1.53229091
3 2 3.5 3.00325783
4 3 4.2 4.54164265
392
Глава 14
5 4 5.5 6.22904708
6 4.8 8.6 7.5842014
7 5 8.2 7.88194794
8 б 8.5 9.11399131
9 7 10.2 10.1676486
10 8 10.9 11.0211456
И 8.5 11.6 11.3379299
12 9 11.5 11.5572129
13 10 11.6 11.699249
14 11 11.5 11.4213532
15 12 10.6 10.640491
16 12.1 10.5 10.5327035
17 12.8 10 9.61603011
18 13 9.5 9.29930751
19 14 7.2 7.44705428
20 15 5.5 5.45377771
21 16 3.2 3.59073376
22 16.7 2.5 2.5031921
23 17 2.1 2.00434759
24 18 .9 .056422009
25 18.2 .5 .635326911
26 19 0 -.201426402
CBM GRAPHIC REV.1 ON - FORMAT 512 * 256
BREAK IN 9900
READV.
Участок программы «СПЛАЙН-РЕГЗ» co строки 60000
отводится для записи исходных данных. Параметр РР — весовой
коэффициент суммы квадратов отклонений — вводится в строке
200. В числовом примере, который соответствует приведенной вы-
ше распечатке, весовой коэффициент обеих частей линейной комби-
нации равен 0,5.
Алгоритм построения сплайна описан здесь лишь в общих чер-
тах. Полагают, что координаты Y точек, через которые проходит
сглаживающий сплайн, при заданных значениях X уже известны, и
с этими значениями составляют систему линейных уравнений для
расчета параметров сплайна. Эта система уравнений является
дополнительным условием для минимизации указанной линейной
комбинации. Поиск минимума функционала с учетом дополнитель-
ного условия проводится методом множителей Лагранжа. Таким
образом, получают опять систему линейных уравнений ленточной
структуры. Решение этой системы уравнений дает значения пара-
метров сплайна, значения Y в точках перегиба и множителей Ла-
гранжа.
На рисунках приведены различные варианты аппроксимации
экспериментальных данных сглаживающей сплайн-функцией при
различных значениях весового коэффициента.
Автоматизированная обработка данных
393
394
Глава 14
Если вы хотите учитывать весовые коэффициенты исходных
данных, то в программе нужно описать дополнительно еще один
одномерный массив W( ) и в операторах DATA задать значения
весовых коэффициентов. Весовые коэффициенты считываются под-
программой 10000 и сортируются по возрастанию значений X. Из-
менения в расчетной части программы касаются только начала
подпрограммы 13000. Начало этой подпрограммы выглядит теперь
так:
13800 REM ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ЛЕНТОЧНОЙ МАТРИЦЫ D
13020 М-3*Н-2
13030 FOR 1-0 ТО MlFOR J-0 ТО 10
13040 D<I,J>-0 NEXT J R<I>-0
13050 NEXT I
13060 REM ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПО M И ПРАВЫХ СТОРОН
13080 D<0,5>-PP*W<0>|D<0,8>—IH<1>|R<0>-PP*Y<0>*W<0>|D<1,5>-РР#Ы<1
13100 D< 1,7>-IH< 1 >+IH<2> |D<1,10> — tH<2> IRC 1 >«=PP#Y< 1 >#Ы< 1 >
13120 0<M-3,4> — IH<N-1> iD<M-3,7>-IH<N>+IH<N-1>
13130 0<M-3,5>-PP#W<N-1> iR<M-3>-PP»Y<N-l >i»HCN-l >
13140 D<M ,4> —IH<N >iD<M ,5>-PP#W<N> |R<M >-PP#Y<N >#N<N>
13160 FOR 1-2 TO N-2 J-3H4-2
13180 D<J,5>-PP#W<I> R<J>-PP*Y<I>*N<I>
13200 0<J,4> — IH<I> 1 D<J,7>-IHCI> + IH<I + l>iDCJ,10> — IH<I + 1>
13220 NEXT I
14.4. Жесткие системы дифференциальных уравнений
В экскурсе в область жестких систем дифференциальных уравне-
ний мы обсудим программу, которая позволяет решать такие си-
стемы. Рассмотрим сначала принципиальную сторону проблемы,
которая связана с описанием кинетики сложных химических реак-
ций, константы скорости которых различаются на несколько по-
рядков. В рассмотренных выше программах для решения систем
дифференциальных уравнений длина шага интегрирования задается
довольно жестко, нет возможности также и оптимизировать саму
процедуру интегрирования. Поэтому необходимо разработать об-
щие принципы решения жестких систем дифференциальных уравне-
ний. В некоторых работах* предложены весьма совершенные алго-
ритмы численного решения жестких систем.
* Bader G., Nowak U., Deuflhard P., An advanced simulation package for large
chemical reaction systems, in: Stiff computation (ed. Aiken). Oxford University Press,
1983; Bader G., Deuflhard P., Semi-implicit midpoint rule for stiff systems of ordinary
differential equations. Numer. Math., 1983; Chance E. M., Curtis A. R., Jones I. P.,
Kirby C. R., FACSIMILE: A computer program for flow and chemistry similation, and
general initial value problems. Harwell, AERE Tech. Rep. R. 8775, Dec. 1977; Kee R. J.,
Milter J. A., Jefferson T. H., CHEMK1N: A General-purpose, problem-independent,
transportable, Fortran chemical kinetics code package. Sandia National Laboratories,
Livermore: Techn. Rep. SAND80—8003, 1980.
Автоматизированная обработка данных
395
Если попытаться решить жесткую систему дифференциальных
уравнений, описывающую вполне реальную химическую реакцию,
обычными численными методами, например широко распростра-
ненным в естественных науках методом Рунге — Кутта, то, как
правило, получаются ложные результаты. Если интегрировать
дифференциальные уравнения с очень малым шагом, то даже при
больших затратах машинного времени решение соответствует не-
значительным изменениям в системе, т. е. очень малой степени
превращения.
Такое поведение, типичное для жестких систем*, мы рассмот-
рим на примере системы дифференциальных уравнений, описываю-
щей кинетику химической реакции, причем эту систему можно ре-
шить также и аналитическими методами. Как поведет себя числен-
ный алгоритм, например алгоритм Эйлера, при решении такой си-
стемы? (На данном примере будет показано, как решить эту проб-
лему с помощью неявного метода Эйлера.)
Пусть дана система из двух дифференциальных уравнений, кото-
рая описывает скорость последовательной реакции:
А - R (ki = 1)
R - Р (k2 = 106)
d[A]/d/=—[А] [А],=о = 1
d[R]/dZ = + [А] — lO^R] [R]z=0 = О
R — неустойчивый промежуточный продукт (к2 ► к}).
С учетом указанных выше начальных условий решение этой систе-
мы относительно концентраций вещества А и R имеет вид
[А] = е-'
[R1 = - е-'«)
Если обозначить [А] через х и [R] через у, а правые части диф
ференциальных уравнений через/] и/2 соответственно, то по мето-
ду Эйлера для решения будут использоваться следующие итераци-
онные формулы (см. также разд. 9.1):
х/+1 = xi + f&i, У №
Л+1 = Л +/2(г,.,у,.)-Д/
* См. также Curtiss С. F., HirschJelder J. О., Proc. Nat. Acad. Sci. USA, 38, 235
(1952).
396
Глава 14
Если заменить индексы i в правых частях системы на i + 1, то
формулы
*(+1 = xi + f&i+v У,+ 1)-^
л+1 = л + Ш.я+1)^
описывают итерационную процедуру неявного метода Эйлера. Та-
ким образом, для простой последовательной реакции имеем
[А(Г + А/)] = [А(0] - [А(/ + Д/)]-Д7
[R(/ + А/)] = [R(OJ + {[А(Т + А/)] - Ю6^ + А/)]) • Д/
Если решить эту простую систему линейных уравнений относитель-
но А(Т + Д/) и R(? + Д/), то получатся следующие итерационные
формулы неявного метода Эйлера:
[А(Г + ДО = —А (/)1
1 + Д/
[R(/ + А/)] = f[R(/)] + tA(01 -Д----------------?—
С 1 + Д/ J 1 + 106
В таблицах сопоставлены результаты неявного метода Эйлера
(в графе «жесткий») с результатами аналитического решения (в гра-
фе «точный») и явного метода Эйлера в графе «Эйлер».
Время Эйлер А Эйлер R ТОЧНЫЙ Жесткий it
Точный Жесткий
ОЕ-7 1.0000 1.0000 1.0000 0.00Е+00 0.00Е+0 0.00Е+0 1Е-7
1Е-7 0.9999 0.9999 1.0000 9.99Е-08 9.51Е-8 9.09Е-8 1Е-7
2Е-7 0.9999 0.9999 1.0000 1.89Е-07 1.81Е-7 1.73Е-7 1Е-7
ЗЕ-7 0.9999 0.9999 1.0000 2.7ОЕ-О7 2.59Е-7 2.48Е-7 1Е-7
4Е-7 0.9999 0.9999 1.0000 3.43Е-07 3.29Е-7 3.16Е-7 1Е-7
5Е-7 0.9999 0.9999 1.0000 4.09Е-07 3.93Е-7 3.79Е-7 1Е-7
6Е-7 0.9999 0.9999 1.0000 4.68Е-07 4.51Е-7 4.35Е-7 1Е-7
7Е-7 0.9999 0.9999 1.0000 5.21Е-О7 5.ОЗЕ-7 4.86Е-7 IE-7
8Е-7 0.9999 0.9999 1.0000 5.69Е-07 5.5ОЕ-7 5.33Е-7 IE-7
9Е-7 0.9999 0.9999 1.0000 6.12Е-07 5.93Е-7 5.75Е-7 IE-7
10Е-7 0.9999 0.9999 1.0000 6.51Е-07 6.32Е-7 6.14Е-7 IE-7
** *** *** *** *** *** *** **
91Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
92Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
93Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
94Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
95Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
96Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 1 E-7
97Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
98Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
99Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
100Е-7 0.9999 0.9999 1.0000 9.99Е-07 9.99Е-7 9.99Е-7 IE-7
Автоматизированная обработка данных
397
Время Эйлер А Точный Жесткий Эйлер R Точный Жесткий it
1Е-3 0.9989 0.9989 0.9990 3.05Е-08 9.98Е-7 9.98Е-7 IE-3
2Е-3 0.9979 0.9979 0.9980 9.67Е-04 9.97Е-7 9.97Е-7 IE-3
ЗЕ-З 0.9969 0.9969 0.9970 -9.65Е-01 9.96Е-7 9.96Е-7 IE-3
4Е-3 0.9959 0.9959 0.9960 9.64Е+02 9.95Е-7 9.95Е-7 IE-3
5Е-3 0.9949 0.9950 0.9950 -9.63Е+О5 9.95Е-7 9.94Е-7 IE-3
6Е-3 0.9940 0.9940 0.9940 9.62Е+08 9.94Е-7 9.93Е-7 IE-3
7Е-3 0.9930 0.9930 0.9930 -9.61Е+11 9. 93Е-7 9.92Е-7 IE-3
8Е-3 0.9920 0.9920 0.9920 9.60Е+14 9.92Е-7 9.91Е-7 1E-3
9Е-3 0.9910 0.9910 0.9910 -9.59Е+17 9.91Е-7 9.90Е-7 1E-3
10Е-3 0.9900 0.9900 0.9900 9.58Е+20 9.9ОЕ-7 9.89Е-7 IE-3
** *** ♦ *** *** **
91Е-3 0.9129 0.9130 0.9131 оо 9.13Е-7 9.12Е-7 1E-3
92Е-3 0.9120 0.9120 0.9121 оо 9.12Е-7 9.11Е-7 IE-3
93Е-3 0.91 1 1 0.9111 0.91 12 оо 9.11Е-7 9.10Е-7 IE-3
94Е-3 0.9102 0.9102 0.9103 оо 9.10Е-7 9.09Е-7 1E-3
95Е-3 0.9093 0.9О93 0.9094 оо 9.09Е-7 9.08Е-7 1E-3
96Е-3 0.9084 0.9084 0.9085 оо 9.08Е-7 9.07Е-7 IE-3
97Е-3 ' 0.9074 0.9075 0.9076 оо 9.О7Е-7 9.06Е-7 IE-3
98Е-3 0.9065 0.9066 0.9067 оо 9.06Е-7 9.05Е-7 1E-3
99Е-3 0.9056 0.9057 0.9058 оо 9.05Е-7 9.04Е-7 IE-3
100Е-3 0.9047 0.9048 0.9049 оо 9.04Е-7 9.04Е-7 IE-3
Если начать с шага Д/ = 1Е — 7, то оба численных метода вер-
но описывают накопление и расходование промежуточного продук-
та R. После 100 шагов достигается стационарное состояние по ве-
ществу R. Поскольку при таком шаге концентрация вещества А
практически не меняется, т. е. еще очень мала степень превраще-
ния, шаг интегрирования увеличивают с 1Е — 7 до 1Е — 3. При ис-
пользовании метода Эйлера решение относительно концентрации
вещества R становится неустойчивым и [R] может принимать очень
большие значения, ограниченные только допустимой величиной
констант данной ЭВМ. Неявный метод дает верные значения [R] и
при таком шаге.
Если рассматривать систему линейных дифференциальных урав-
нений общего вида, то ее лучше записывать в матричной форме:
d?/dZ = AY
Y — вектор, А — матрица.
Алгоритм Эйлера можно представить как
Y(Z + Д/) = Y(Z) + А-У(/)-Д/
В неявном алгоритме Эйлера эта итерационная процедура выгля-
дит следующим образом:
Y(t + Д/) = Y(Z) + A-Y(Z + Д/)-Д/
398
Глава 14
Решим это уравнение относительно Y(/ + Аг):
Y(r + А?) = (I - A-A/)-*-Y(O
I — единичная матрица.
В неявном методе решения системы линейных дифференциаль-
ных уравнений надо на каждом шаге итерации обращать матрицу.
Матрица А соответствует матрице Якоби для нелинейных систем.
Систему нелинейных дифференциальных уравнений, записывае-
мую в общем виде как
dY/dZ = /(Y)
решить нельзя. Однако если разложить функцию/(у) в ряд Тейло-
ра, то получится следующая итерационная формула:
Y(r + Д/) = (I - A-A/)-‘-Y(O
где
А = — = df&>
dY 3Y
В этом случае А — матрица Якоби правых частей системы дифференциальных
уравнений.
Для расчета матрицы Якоби системы дифференциальных урав-
нений, описывающей механизм сложной химической реакции, мож-
но расширить программу «ЭС-КИН» так, чтобы наряду с диффе-
ренциальными уравнениями получалась и матрица Якоби.
В качестве примера рассмотрим довольно простую кинетиче-
скую схему:
Аг,
А —1 М + М
Аг,
А + М - В + R
Аг,
R —3 М + D
Аг
М + М -4 Е
Из нее можно вывести следующие дифференциальные уравнения
и ненулевые элементы матрицы Якоби:
= -Аг,[А] - Аг2[А]-[М]
Автоматизированная обработка данных
399
= 2*,[А] - *2[А]-[М] + *3[Kj - 2£ДМ]2
= *2[А]-[М]
® = *2[А]-[М] - *3[R]
т=
d[E] dZ = *4[М]2
а [А] а [А] = -kl - *2[М] а [6] д[М] = Аг2[А1
а [А] Э[М] = -Лг2[А] d[R] d[R] = -к3
Э[М] Э[М] = -*2[А] - 4&ДМ] d[R] а [А] = *2[М]
Э[М] а [А] = 2кг- Лг2[М] Э[Р] d[R] = к3
Э[М] d[R] = к3 ЭЙ Э[М] = 2£4[М]
Э[В] а [А] = Аг2[М]
Ниже приводится распечатка программы для имитации кинети- ческих зависимостей в соответствии с предложенным механизмом
реакции.
0 REM "ЖЕСТ—КИН" EBERT/EDERER 840506
1 REMM*******************************
2 REM** НЕЯВНЫЙ МЕТОД ЭЙЛЕРА ДЛЯ *«
4 REM** РЕШЕНИЯ ЖЕСТКОЙ СИСТЕМЫ ««
5 РЕМ**ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ**
9 REM*********************************
20 REM А -> KI -> М ♦ М
30 REM А + М -> К2 -> В ♦ R
40 REM R -> КЗ -> М ♦ D
400
Глава 14
50 REM М + М -> К4 -> Е
100 DIM R<20,40>,Y<20>,Y1<20>,O<20>,YR<20>
200 N-6tREM ЧИСЛО УРАВНЕНИЙ В СИСТЕМЕ
300 FOR I-l ТО N
400 PRINT "НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y ("; I *) =
300 INPUT Yl<I>IY<I>-VI<I>|УЯ<I>-Y<I>INEXT I
600 INPUT "ЗНАЧЕНИЯ X НАЧАЛЬНОЕ.KOHE4HOE";XA, XE:X=XA:DV =(XE-XA) /50
700 INPUT "ДЕЛЬТАХ": DO
710 K1-.01
720 K2-1000
730 КЗ-100
740 K4-1E8
800 INIT
805 DISPLRY<1>
810 PSPRCE<.01,.99,.01,.99>
820 MRP<XR,XE,0,Y<1>>
830 PLOT<XR,0,0>iPLOT<XE,0,1>1PLOT<XE,V<1>,1>
840 PLOT<XR,Y<1>,1>iPLOT<XR,0,l>
999 GOTO 5000
1000 OOSUB 20000 iREM ВЫВОД ДАННЫХ
1100 OOSUB 10000 lOOSUB 11000 iREM ПРОИЗВОДНЫЕ И МАТРИЦА ЯКОБИ
1200 GOSUB 500001REM ОБРАЩЕНИЕ МАТРИЦЫ ЯКОБИ
1300 X-X+DX
1400 FOR I-l ТО N
1420 DY—0
1440 FOR J-l TO NiDY-DY+R<I,N+J>*D<J>iNEXT J
1460 Y<I>-Y<I>+DY*DX
1480 NEXT I
1600 RETURN
5000 REM***************************
5010 REM** ОСНОВНАЯ ПРОГРАММА «*
5020 REM***************************
5030 NI—1
5100 OOSUB 20000
5140 DX-DD/N11X-XR1FOR ID-1 TO NIiGOSUB 1100iNEXT ID
5160 IF Nl>50 THENlDD-DD/1000lNl-11GOTO 5140
5170 FOR I-l TO NIYA<I>—Y<I>|Y<I>—Y1<I>iNEXT I INI-Nl*2
5180 DX-DD/N11X-XR1FOR ID-1 TO NIlOOSUB 1100INEXT ID
5200 FOR I-l TO NlYS—RBS<Y<I>>+RBS<YR<I>>+lE-6
5210 REM PRINT X,I,Y<I>,YR<I>,N1
5240 IF RBS<Y<I>-YR<I>>/YS>.05 THEN 5160
5300 NEXT I
5320 GOSUB 15000
5340 XR-XR+DD
5360 FOR I-l TO NlYl<I>—Y<I>iNEXT I
5400 IF NI—2 THEN DD-DD42
5420 N1-INT<N1X5>+1
5430 IF DD>DY THEN DD-DY
5440 IF DDXXE-XR> THEN DD-<XE-XR>
6200 IF XR<XE THEN 5100
6400 GOSUB 20000
9900 STOP
10000 REM*******************
10001 REM** ПРОИЗВОДНЫЕ ««
10002 REM*******************
10100 D<1>—K1*Y< 1 >-K2*Y< 1 >*Y<2>
10200 D<2>—2*K1*V<1>-K2*Y<1>*Y<2>+K3*Y<4>-2*K4*Y<2>#Y<2>
10300 D<3>—K2*Y<1>*Y<2>
10400 D<4>-K2*Y<1>*Y<2>-K3«Y<4>
10500 D<5>—K3#Y<4>
10600 D<6>-K4*Y<2>«Y<2>
10999 RETURN
11000 REM********************
11081 REM** МАТРИЦА ЯКОБИ**
11002 REM********************
11010 FOR I-l TO 2*NiF0R J-l TO N1R<J,I>-0iNEXT JiNEXT I
Автоматизированная обработка данных
401
11020 FOR 1*1 ТО NiACI,I>-11А<I,N*I>-1iNEXT I
11100 R<1,1>-A<1,1>-DX*<-Kl~K2*Y<2> >
11120 A<1,2>-DX#K2#V<1>
11200 A<2,2>-A<2,2>-DX#<-K2*V< 1 >-4#K4#V<2> >
11210 A<2,1>—DX*<2*K1-K2*V<2>>
11220 A<2,4>—DX#K3
11300 A<3,1> — DX*K2*V<2>
11301 A<3,2>—DX#K2#V<1>
11400 A<4,4>-A<4,4>+DX#K3
11410 A<4,1>*-DX#K2#Y<2>
11420 A<4,2>—DX#K2#Y< 1 >
11520 A<5,4>«=-DX#K3
11620 R < 6,2 > *-DX#K4*2*V < 2 >
14900 RETURN
15000 REM############ »»**»*»»***»»»
15001 REM** ПОСТРОЕНИЕ ГРАФИКА **
15002 REM#####*#**#*********»***##*
15020 FOR 1-1 TO N
15040 PLOT<XA,Vl<I>,0>1PLOT<X,V<I>,1>
15080 NEXT I
15990 RETURN
20000 REM**************************
20001 REM** ВЫВОД ДАННЫХ ••
20002 REM******######*************»
20010 PRINT
20100 FOR 1-1 TO N
20120 PRINT X,I,YCI>
20140 NEXT I
20200 RETURN
50000 REM************************************
50001 REM## ОБРАЩЕНИЕ МАТРИЦЫ ЯКОБИ **
50002 REM************************************
50900 FOR S«=l TO N
51000 FOR T-S TO N
51100 IF R<T,S><>0 THEN 51300
51200 NEXT T iPRINT "ЕДИНСТВЕННОГО РЕШЕНИЯ HET": GOTO 63999
51300 FOR J-l TO 2*N|B—A<S,J> 1A<S,J>-A<T,J> |A<T,J>«=BiNEXT J
51400 C«=1/A<S,S>
51500 FOR J-l TO 2*N1R<S,J>-C#R<S,J>iNEXT J
51600 FOR T-l TO N
51700 IF T-S THEN 52000
51800 C—R<T,S>
51900 FOR J-l TO 2*N|A<T,J>-A<T,J>*C#A<S,J>«NEXT J
52000 NEXT T
52100 NEXT S
52200 RETURN
63999 END
RUN
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y (1) - ? 1
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y (2) “ ? О
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y (3) - ? О
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y (4) - ? О
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y (5) “ ? О
НАЧАЛЬНОЕ ЗНАЧЕНИЕ Y (6) - ? О
ЗНАЧЕНИЯ X НАЧАЛЬНОЕ, КОНЕЧНОЕ? О, 100
ДЕЛЬТАХ? 1Е-7
CBM GRAPHIC REV.1 ON - FORMAT 512 « 256
0 1 1
0 2В
0 3 0
0 4 0
0 5 0
0 6 0
26-81
402
Гаава 14
1Е-0? 1 .999999999
1Е-07 2 1.Э9984998Е-09
1Е-0? 3 1.49989999Е-13
1Е-0? 4 1.49988999Е-13
1Е-07 5 9.99931247Е-19
1Е-0? б 1.49979999Е-17
ЭЕ-0? 1 .99999999?
ЭЕ-0? 2 5.99884928Е-09
ЭЕ-0? 3 1.1498199Е-12
ЭЕ-0? 4 1.14980191Е-12
ЭЕ-0? 5 1.79972351Е-1?
ЭЕ-0? б 4.54855937Е-16
• • • • • •
35.3554431 1 .52343398
35.3554431 2 ?.23550142Е-06
35.3554431 3 ,.220601294
35.3554431 4 3.78773061Е-05
35.3554431 5 .22056341?
35.3554431 б .255942169
3?.3554431 1 .505938875
3?.3554431 2 7.1135437Е-86
37.3554431 3 .227891043
37.3554431 4 3.59942141Е-05
37.3554431 5 .227855049
37.3554431 б .266148528
• * • • » •
99.3554431 1 .193895023
99.3554431 2 4.4035877Е-06
99.3554431 3 .342476128
99.3554431 4 8.53930642Е-06
99.3554431 5 .342467589
99.3554431 б .463622378
108 1 . 1921092?
100 2 4.38316058Е-06
100 3 . 343820758
100 4 8.42218606Е-06
108 5 .343012335
100 б .4648635?
На рисунке изображены кривые расходования вещества А и на-
копления веществ В, D и Е. Размах по оси х составляет 100 с, кон-
центрации реакционноспособных веществ М и R настолько малы,
Автоматизированная обработка данных
403
что в этом масштабе и в линейных координатах их кинетические
кривые совпадают с осью х.
В подпрограмме 10000, исходя из кинетической схемы, рассчи-
тываются значения производных, т. е. правых частей дифференци-
альных уравнений. Подпрограмма 11000 рассчитывает элементы
матрицы I — А-Л/, а подпрограмма 50900 обращает эту матрицу.
Для построения на экране кинетических кривых после расчета коор-
динат соответствующих точек вызывается подпрограмма 15000.
Подпрограмма 20000 выводит результаты расчета в числовой фор-
ме. Участок программы до строки 999 служит для ввода исходных
данных и подготовки вывода графической информации. Единичный
шаг итерации реализован в подпрограмме 1100. Эта подпрограмма
вызывается из основной программы, которая начинается со строки
5000. Интервалу времени соответствует переменная DD. Итераци-
онная процедура проводится N1 раз с шагом DD/N1. Если при уд-
воении числа шагов N1 решение удовлетворяет требованиям точно-
сти, то итерационная процедура заканчивается (строка 5240). В
противном случае N1 опять удваивается. Если N1 станет больше
50, то интервал времени DD делится на 1000 и итерационная про-
цедура начинается заново (строка 5160). Если требуемая точность
достигается при N1 = 2, то интервал времени DD увеличивается в
два раза. После каждого итерационного шага N1 уменьшается при-
мерно в два раза (строка 5420). Переменный шаг интегрирования,
организованный довольно простыми программными средствами,
необходим здесь потому, что на начальном этапе выполнения про-
граммы (т. е. при очень малых степенях превращения) за очень ма-
лые промежутки времени концентрации промежуточных продуктов
существенно меняются, тогда как изменение концентраций других
веществ в начальной стадии реакции происходит гораздо медлен-
нее. В строках 5430 и 5440 ограничивается длина шага интегрирова-
ния, поскольку кинетические кривые, построенные при слишком
большой длине шага, будут выглядеть на экране слишком грубы-
ми. Кроме того, эти строки позволяют приостановить выполнение
программы, когда достигается заданная граница временного интер-
вала.
26*
ЛИТЕРАТУРА
Техническая литература
1. Appel U., Mikrocomputer — Minicomputer, eine Einfiihrung in Aufbau und Funktions-
weise von Kleincomputern. Miinchen/Wien, Oldenbourg, 1981.
2. Dworatschek S., Einfiihrung in die Datenverarbeitung. De Gruyter, 1970.
3. Koch G., Rembold U., Einfiihrung in die Informatik fur Ingenieure und Naturwissen-
schaftler. Miinchen/Wien, Carl Hanser Verlag, 1977.
4. Leonhardt E., Grundlagen der Digitaltechnik. Eine systematische Einfiihrung.
Miinchen/Wien, Carl Hanser Verlag, 1976.
5. Schaaf B., Schroder W., Digitale Datenverarbeitung. Hanser, 1980.
6. Schmitt G., Grundlagen der Mikrocomputertechnik. Miinchen/Wien, Oldenbourg, 1981.
7. Tafel H. J., Einfiihrung in die digitale Datenverarbeitung. Miinchen/Wien, Carl Hanser
Verlag, 1976.
8. Ullmans Enzyklopadie der technischen Chemie. Band 4. Digitalrechner, Aufbau und Ar-
beitsweise. Weinheim, Verlag Chemie, 1974, S. 235.
Программирование на языке БЕЙСИК
9. Brauch W., Programmierung mit BASIC. Stuttgart, Teubner, 1981.
10. Gateley W. Y., Bitter G. G., BASIC-Fibel. Hamburg, R.v. Decker’s Verlag, 1973.
11. Gottfried B. S., Theory and problems of programming with BASIC. Schaum’s Outline
Series. New York, McGraw-Hill, 1975.
12. Haase V., Stucky W., BASIC Programmieren fiir Anfanger. Mannheim/Wien/Ziirich,
Bibliographisches Institut, 1977. (B.I. Hochschultaschenbiicher, Bd. 744).
13. Hamann G. O., Datenverarbeitung mit BASIC, Programmierte Unterweisung. Gerns-
bach, Deutscher Betriebswirte-Verlag, 1980.
14. Kaucher E., KlatteR., Ullrich Ch., Programmiersprachen im Griff, Band 3: BASIC.
Mannheim/Wien/Ziirich, Bibliographisches Institut, 1981.
15. Magerle E., Einfiihrung in das Programmieren in BASIC. Berlin/New York, Walter de
Gruyter, 1974.
16. Menzel K., BASIC in 100 Beispielen. Stuttgart, B.G. Teubner, 1981.
17. Rehbein H., BASIC leicht gemacht — eine BASIC-Einfiihrung— 50 vollstandige
Ubungsaufgaben mit Lbsungen. Dusseldorf, VDI-Verlag, 1972.
18. Sack J., Meadows J., BASIC eine Einfiihrung. Stuttgart, SRA Arbeitstexte, 1975.
19. Scharf J., BASIC fiir Anfanger. Munchen, Oldenbourg, 1975.
20. Schneider W., Programmieren von Heimcomputern 1. Einfiihrung in BASIC.
Braunschweig/Wiesbaden, Vieweg, 1979.
21. Schneider W., BASIC — Einfiihrung fiir Techniker. Braunschweig, Vieweg, 1978.
22. Schwill W.-D., Weibezahn R., Einfiihrung in die Programmiersprache BASIC. Braun-
schweig, Vieweg, 1976.
Литература
405
23. StiefS., BASIC Systematische Darstellung fur den Anwender. Miinchen/Wien, Olden-
bourg, 1980.
24. Weber K., Tiirschmann С. V., BASIC 1 und BASIC 2. Bern/Stuttgart, UTB 588 und
589, Verlag Paul Haupt, 1977.
25. Wilkins C. L., Klopfenstein С. E., Isenhour T. L., Jurs P. C., Introduction to com-
puter programming for chemists — BASIC version. Boston/London/Sydney, Allyn and
Bacon, 1974.
Литература по численным методам
26. Acton F. S. ..Numerical method that work. New York, Harper and Row, 1970.
27. Bajpai A. C., Calus I. M.,Fairley J. A., Numerical methods for engineers and scientists.
London/New York/Sydney/Toronto, John Wiley & Sons, 1977.
28. Bjorck A., Dahlquist G., Numerische Methoden. Munchen, Oldenbourg, 1979.
29. Gronitz J., Praktische Mathematik. VEB Volk und Wissen, 1975.
30. Hamming R. W., Numerical methods for scientists and engineers. New York, McGraw
Hill, 1973.
31. Jordan-Engeln G., Reutter F., Band 1: Numerische Mathematik fur Ingenieure, Band 2:
Formelsammlung zur Numerischen Mathematik mit Fortran IV — Programmen.
Mannheim/Wien/Ziirich, B.I. Wissenschaftsverlag, 1973.
32. Mennicken R., Wagerifiihren E., Numerische Mathematik. Rororo-Vieweg, 1977.
33. Pollard J. H., A handbook of numerical and statistical techniques. Cambridge/Lon-
don/New York/Melbourne, Cambridge University Press, 1977.
34. Scheid F., Theory and problems of numerical analysis. Schaum’s Outline Series. New
York, McGraw Hill, 1968.
35. Stoer J., Einfiihrung in die numerische Mathematik I, II. Berlin, Springer, 1976, 1978
(Band II gemeinsam mit R. Burlisch).
36. Stummel F., Hainer K., Praktische Mathematik. Stuttgart, Teubner, 1982.
37. Tbmig W., Numerische Mathematik fur Ingenieure und Physiker. Band 1: Numerische
Methoden der Algebra. Band 2: Eigenwertprobleme und numerische Methoden der Ana-
lysis. Berlin, Springer, 1979.
38. Werner H., Praktische Mathematik I, II. Berlin, Springer, 1975, 1979 (Band II gemein-
sam mit R. Schaback).
39. Zurmiihl.R., Praktische Mathematik fur Ingenieure und Physiker. Berlin, Springer, 1965.
Предметный указатель
Автоматизированная обработка
данных 369
Адресная сортировка 380
Алгебра комплексных чисел 151
Алгоритмический язык 16
Анализ проблемы 9
Арифметические выражения 23
Аппроксимация
полиномом 185
произвольной функцией 284
прямой 164
сплайн-функцией 381
Безусловного перехода оператор 25
Блок-схема 11
Брутто-формула
по данным масс-спектрометрии
71
---элементного анализа 67
Брэгга угол 154
Ван-дер-Ваальса
константы 283
уравнение 106
Ввода данных операторы
GET 160
INPUT 20
— расширенный 30
READ 59
Вириальные коэффициенты 100
Волыперра принцип 239
Вращательные суммы по состо-
яниям 47
Вывода данных операторы
PRINT 21
— пустой 21
— расширенный 30
TAB 69
; 21
Вызов функции, определяемой
пользователем 82
Вынужденные колебания 238
Выход из бесконечной итерацион-
ной процедуры 94
Газожидкостная хроматография,
моделирование 161
Гармонический осциллятор 246
Гаусса — Жордана метод
обращения квадратной матри-
цы 196
решения системы линейных
уравнений 178
Гаусса — Зайделя итерационная
процедура 258
Гаусса — Ньютона оптимизация
292
Горнера схема 115
Графика машинная 331
Графики 334
3-D 356
трехмерные 356
Графов теория 208
Двоеточие, оператор 90
Деление отрезка пополам 109
Динамика популяций 216, 226
хищников и их жертв 238
Дифференциальные уравнения см.
Уравнения дифференциальные
Дифференциальных уравнений си-
стемы 306
Предметный указатель
жесткие 238, 394
метод решения Рунге — Кут-
та 235
----Эйлера 230
решение стационарное 257
Дифференцирование численное 266
экспериментальных зависимо-
стей 387
Диффузионный потенциал 37
Диффузия 45
Длина
кривых 84, 85
эллипса 84
«Жизнь», игра 322
Задача краевая 241
Знак числа (сигнум), функция 116
Идентификатор 19
Изомеры 208
Интеграл перекрывания 106
Интегрирование 76
метод Монте-Карло 63
— Симпсона 91
— Эйлера 76
с критерием сходимости 94
функции комплексного пере-
менного 153
— нескольких переменных 66
численное 76
Интерполяция 263
методом Лагранжа 263
сплайн-функцией 267
Интерфейс IEC 369
Искусственный интеллект 316
Итерационная процедура бесконеч-
ная 38
Катализатор, реакция в грануле 67
Квантовая химия 106
Кинетика химическая 105, 216
407
моделирование с графиком 341
Колебания
пилообразные 45
прямоугольные 45
Команды основные 13
Комментарии 29
Комплексные числа 151
Компьютерные игры 315
Контурный график 362
Критерий сходимости 94
Курсор 13
Лекарственный препарат, модели-
рование всасывания 240
Леннарда-Джонса потенциал 101
Летучесть 106
Линии уровня 362
Логические операции 340
Ложного положения (regula falsi)
метод решения уравнений 120
Максвелла распределение частиц по
скоростям 33
Масс-спектрометрия высокого раз-
решения 71
Масс-спектры смесей 150
Матрица системы 196
расширенная 178
Матрицы
квадратные 149
обращение 196
операции 148
собственные значения 203
умножение 149
Механизм химической реакции 239,
240
OREGONATOR 239
Михаэлиса — Ментен уравнение
231
Молекулярно-массовое распределе-
ние 104
Монте-Карло метод
вычисления числа тг 50
интегрирования 63
408
Предметный указатель
— кинетического уравнения
147, 148
моделирования строения поли-
мера 87
Морзе потенциал 368
Наименьших квадратов метод 164,
187
Непосредственный режим 27
Нечисленные методы обработки
данных 306
Неявные функции 108, 109
Номер строки в БЕЙСИКе 18
Ньютона метод решения уравне-
ний 109, 117
Обращение квадратной матрицы
196
Округление 126
Описание
массивов 140
определяемых функций 81
Оствальда закон разбавления 137
Отклонение стандартное 61
взвешенное 63
Первообразная 96
Переменные
идентификатор 19
простые (скалярные) 19
с индексами 140
текстовые (литерные, строч-
ные) 60
Планка формула излучения черного
тела 35
Площадь треугольника 27
Поверхность потенциальной энер-
гии 364
Подпрограммы 174
Полимеры
моделирование строения 87
молекулярная масса 105
персистентная длина молекулы
127
распределение молекулярно-
массовое 104
Представление чисел 22
Присваивания оператор 22
Программа
запуск на выполнение 14
прерывание выполнения 14
продолжение выполнения 38
Прогрессия геометрическая 41
Распространение
«нового» 216
новостей 226
эпидемий 236
— теорема о пороговом харак-
тере 238
Рассеивание рентгеновского излуче-
ния 154
Растворы, вычисление pH
буферные 136
слабой кислоты 133
Реакционно-диффузионная задача
256
Регрессия
линейная 164
— общего вида 185
— с графиком 336
— с оценкой ошибок 169
нелинейная 284
сплайн-регрессия 381
Ректификация
с бесконечным флегмовым чис-
лом 129
с конечным флегмовым числом
133
тройных смесей 133
Рост опухоли 230
Рунге — Кутта метод 227, 235
Ряды 40
Фурье 43
Сглаживание экспериментальных
данных 176, 266
Сигнум (знак числа), функция 116
Системы уравнений
Предметный указатель
409
линейных 178
нелинейных 274
Скорость истечения газа 38
Собственные значения матрицы
203
Сортировка
адресная 380
быстрая 376
слов, чисел 142
Среднее значение 62, 141
взвешенное 63
Средняя
длина свободного пробега 31
скорость молекул 57
Сплайн-интерполяция 267
СпЛайн-регрессия 381
Сплайн-функция 267
Статистическая термодинамика 50
Статистический
клубок 127
тест 63
Суммы
бесконечные 45
вычисление 52
конечные 52
по состояниям 47
Счетчик времени 371
Таблицы 57
истинности 340
Температура, пересчет 37
Теплоемкость по Дебаю 98
Теплопроводность 45
Термопара Ni — Cr/Ni, градуиров-
ка 124
Траектории 366
«Тормоз» 38
Угол рассеяния рентгеновского из-
лучения 154
Уравнения
алгебраические 108
дифференциальные 216
— в частных производных 251
— высших порядков 237
— задача краевая 241
— на собственные значения 246
-с начальными условиями
216, 218
— линейные 176
— методы решения 109, 138,
218, 224, 227
— нелинейные 117, 274
— обыкновенные 216
трансцендентные 108
Условного перехода оператор 69,
124, 340
Факториал 141
Ферромагнетизм 328
Фибоначчи числа 142
Фика уравнение 254
Формулы, написание 16
Функции стандартные (встроенные)
25
Фурье
второй закон 45, 251
преобразование 97
Циклы
бесконечные 43
ограниченные 54
FOR — NEXT 55
Эйлера метод решения уравнений
218, 224
Языки программирования 16
Указатель ключевых слов и символов
LIST 13
ABS 25 модификации 34
AND 340 LOAD 14
ASC 320 LOG 25
ATN 25 MAP 332
BREAK IN 41 MID$ 312
CATALOG 14 NEW 13
CHPLOT 334 NOT 340
CLOSE 372 OPEN 372
CONT 38 OR 340
CONTINUE 43 PLOT 333
COS 25 PRINT 21
DATA 59 расширенный 30
DEF FN 81 PSPACE 333
DELETE 19 READ 59
DISPLAY 332 REM 29
DLOAD 14 RENUMBER 19
DPLOT 333 RESTORE 59
DSAVE 15 RETURN 13, 174
END 31 RND 25
EXP 25 RUN 14
FN 82 RUN/STOP клавиша 14. 38
FOR — NEXT 55
GET 160 SAVE 14
GOSUB 174 SIN 25
GOTO 25 SGN 25
ICRCL 349 STEP 55
IF 69 STOP 31
общего вида 69 SQR 25
с текстовыми переменными 124 TAB 69
логический 340 TAN 25
INIT 332 THEN 69
INPUT 20 VAL 306
расширенный 30 $ 60
INSERT 19 22
INT 25 21
LEN 312 90
LINTYP 333 Пробел 20
Указатель программ
«АДРЕС-СОРТ» 380 «МК-ИНТ» 65 «Q-СОРТ» 376
«БРУТ-ФОРМ» 71 «МОРЗЕ» 364 «QQ-СОРТ» 378
«БРЭГГ» 155 «НЕЛИН-НЬЮТОНЗ» 276 «СОУДАР» 347
«ВИРИАЛ» 101 «НЕЛИН-РЕГР» 294 «СОУДАР 2» 352
«ВРАЩ» 48 «НЕЛИН-РЕГР1» 299 «СРЕДНЕЕ» 62
«ГАРМ» 247 «НЕЛИН-РЕГРЗ» 283 «СРЕДНЕЕ ЗНАЧЕНИЕ
«ГЕОПРОГ» 41 «НЬЮТОН» 119 141
«Г-Ж» 181 «ОБРАЩ» 200 «СПЛАЙН» 263
«ГХ» 162 «ОБЩ-РЕГР» 188 «СПЛАЙН-РЕГ1» 382
«ДЕБАЙ» 98 «ОТОБР-ДАН» 370 «СПЛАЙН-РЕГЗ» 388
«ДИФ-ПОТ» 38 «ОТОБР-ДАНЗ» 373 «СТАЦИОНАР» 259
«ДУ-ЭЙЛЕР1» 221 «ПЕРСИСТ» 128 «СУММА» 56
«ДУ-ЭЙЛЕР2» 225 «ПИ» 51 «ТЕП-ПРОВ» 46
«З-О-ГРАФИК» 357 «ПЛАНК» 36 «ТЕРМО-ЭДС» 125
«ЖЕСТ-КИН» 399 «ПОЛ-ДЕЛ» 114 «ТРЕУГ» 28
«ЖИЗНЬ» 323 «РЕГР-ГРАФ» 336 «ТРИ АТОМА» 366
«ИЗОМЕРЫ» 211 «РЕКТИФ» 132 «УГАДАЙ КОД» 317
«ИНВ-ГЖ» 197 «Р-К-Н» 228 «УЗОРЫ» 334
«ИСТЕЧЕНИЕ» 39 «СОБСТВ» 205 «УМН-МАТР» 149
«КИНЕТИКА» 342 «СВО-БЕГ» 32 «ФУР-РЯД» 44
«КИН-МК» 147 «СГЛАЖИВАНИЕ» 176 «ХОРДА» 121
«КИСЛ» 134 «СИМП 1» 93 «Ц-Ф» 37
«КОМПЛЕКС» 151 «СИМП 2» 95 «ЧАСТ-ПРО» 253
«КОНТУР» 362 «СИСТ-РКН» 235 «ЭЙЛЕР» 79
«КРА-КИН» 242 «СИСТ-ЭЙЛЕР» 231 «ЭЙЛЕР 2» 33
«ЛАГРАНЖ» 264 «СКОР-МОЛ» 58 «ЭЛЛИПС» 85
«ЛИН-РЕГР» 167 «СОПОЛ» 87 «ЭС-КИН» 308
«ЛИН-РЕГР4» 169 «СОРТ-СЛОВ» 146 «С—Н —N—О» 67
«МАКСВЕЛЛ» 33 «СОРТ-ЧИСЛ» 145
Оглавление
Предисловие редактора перевода............................. 5
Предисловие ко второму изданию............................. 6
Предисловие к первому изданию.............................. 7
1. Введение................................................ 9
1.1. Замечания общего характера ...................... 9
1.2. Анализ задачи ................................... 9
1.3. Важнейшие команды .............................. 13
2. Формулы ............................................... 16
2.1. Введение в алгоритмические языки................ 16
2.2. Номер строки в БЕЙСИКе.......................... 18
2.3. Изменения в программе........................... 19
2.4. Обозначение переменных ....................... 19
2.5. Первые элементы языка БЕЙСИК, используемые
для расчетов по формулам........................... 20
2.5.1. Ввод данных.................................. 20
2.5.2. Вывод данных ................................ 21
2.5.3. Оператор присваивания ....................... 22
2.6. Запись чисел ................................... 22
2.7. Арифметические выражения........................ 23
2.8. Стандартные функции ............................ 24
2.9. Оператор безусловного перехода.................. 25
2.10. Непосредственный режим ......................... 27
2.11. Расчет площади треугольника по длинам трех сто-
рон ................................................ 27
2.12. Расчет средней длины свободного пробега молекул
газа ............................................... 31
2.13. Распределение молекул идеального газа по скоро-
стям (распределение Максвелла) ..................... 33
2.14. Расчет объемной плотности энергии излучения аб-
солютно черного тела по формуле Планка............. 35
2.15. Перевод градусов Цельсия в градусы Фаренгейта .. 37
2.16. Диффузионный потенциал в растворах электроли-
тов ................................................ 37
2.17. Скорость истечения газа ........................ 38
Оглавление 413
3. Ряды .............................................. 40
3.1. Геометрическая прогрессия ................... 41
3.2. Ряды Фурье................................... 43
3.3. Вычисление теплопроводности по второму закону
Фурье ............................................ 45
3.4. Суммы по состояниям.......................... 47
3.5. Вычисление числа ж методом Монте-Карло...... 50
4. Циклы .............................................. 53
4.1. Расчет сумм ................................. 53
4.2. Составление таблиц .......................... 57
4.3. Среднее значение и стандартное отклонение... 61
4.4. Интегрирование методом Монте-Карло........... 63
4.5. Вычисление брутто-формулы химического соедине-
ния по данным элементного анализа................. 67
4.6. Оператор условного перехода.................. 69
4.7. Определение брутто-формулы по пику молекуляр-
ного иона в масс-спектрах высокого разрешения .... 71
5. Интегрирование ..................................... 76
5.1. Интегрирование методом Эйлера................ 76
5.2. Вычисление длины эллипса .................... 84
5.3. Моделирование строения сополимеров........... 87
5.3.1. Двоеточие в БЕЙСИКе....................... 90
5.4. Интегрирование методом Симпсона.............. 91
5.5. Численное интегрирование с ограничением числа
итераций по критерию сходимости................... 94
5.6. Мольная теплоемкость металлов по Дебаю...... 98
5.7. Расчет второго вириального коэффициента на осно-
ве межмолекулярного потенциала................... 100
6. Уравнения ......................................... 108
6.1. Метод деления отрезка пополам............... 109
6.2. Метод Ньютона (метод касательных)........... 117
6.3. Метод хорд (правило пропорциональных частей) ... 120
6.4. Термо-э.д.с. термопары Ni — Cr/Ni........... 124
6.5. Персистентная длина молекулы полимера....... 127
6.6. Расчет эффективности разделения при ректифика-
ции ............................................. 129
6.7. pH растворов слабых кислот.................. 133
6.8. Метод итераций.............................. 138
7. Переменные с индексами............................. 140
7.1. Сортировка чисел и слов..................... 142
7.2. Интегрирование кинетического уравнения первого
порядка методом Монте-Карло ..................... 147
414
Оглавление
7.3. Умножение квадратных матриц................ 148
7.4. Алгебра комплексных чисел ................. 151
7.5. Угол рассеяния Брэгга при дифракции рентгенов-
ского излучения ................................. 154
7.6. Моделирование колонки в газовой хроматографии . 161
7.7. Линейная регрессия ........................ 164
7.8. Линейная регрессия с оценкой отклонения парамет-
ров ............................................. 169
8. Линейные системы ................................. 173
8.1. Подпрограммы .............................. 174
8.2. Системы линейных уравнений ................ 178
8.3. Линейная регрессия общего вида............. 185
8.4. Обращение квадратной матрицы .............. 196
8.5. Определение собственных значений матрицы .. 203
8.6. Определение числа изомеров................. 208
9. Дифференциальные уравнения ....................... 216
9.1. Метод Эйлера............................... 218
9.2. Улучшенный метод Эйлера.................... 224
9.3. Метод Рунге — Кутта ....................... 227
9.4. Метод Эйлера для систем дифференциальных урав-
нений ........................................... 230
9.5. Метод Рунге — Кутта для систем дифференциаль-
ных уравнений ................................. 235
9.6. Краевая задача ............................ 241
9.7. Гармонический осциллятор — задача на собствен-
ные значения ................................... 246
9.8. Уравнения в частных производных............ 251
9.9. Стационарные решения уравнений в частных про-
изводных ........................................ 257
10. Интерполяция .................................... 263
10.1. Метод Лагранжа............................. 263
10.2. Интерполяция с помощью сплайн-функции...... 267
11. Нелинейные системы .............................. 274
11.1. Системы нелинейных уравнений .............. 274
11.2. Нелинейная регрессия....................... 284
12. Нечисленные методы обработки данных.............. 306
12.1. Вывод системы дифференциальных уравнений из
кинетической схемы реакции....................... 306
12.2. Компьютерные игры ......................... 315
12.3. Игра «Жизнь» (Game of Life) .......••...... 322
13. Машинное построение графиков..................... 331
Оглавление 415
13.1. Узор ........................................ 334
13.2. Линейная регрессия с графиком ............... 336
13.3. График решения дифференциального уравнения... 341
13.4. Изображение поверхностей и тел (3-D-график).. 356
13.5. Контурный график ............................ 362
14. Автоматизированная обработка данных................ 369
14.1. Отображение экспериментальных данных ........ 370
14.2. Быстрая сортировка........................... 376
14.3. Сплайн-регрессия ............................ 381
14.4. Жесткие системы дифференциальных уравнений .... 394
Литература ......................................... 404
Предметный указатель ............................... 406
Указатель ключевых слов и символов.................. 410
Указатель программ ................................. 411
МОНОГРАФИЯ
Клаус Эберт, Ханс Эдерер
КОМПЬЮТЕРЫ. ПРИМЕНЕНИЕ В ХИМИИ
Заведующий редакцией академик О. А. Реутов
Зам. зав. редакцией 3. Ф. Ходецкая
Научный редактор Н. А. Козырева
Младший редактор Н. П. Власова
Художник В. С. Потапов
Художественный редактор М. Н. Кузьмина
Технические редакторы Л. А. Тихомирова, Т. К. Такташова
Корректор Н. А. Вавилова
ИБМ6293
Подписано к печати 29.12.87.
Формат 60 х 9O'/i6. Бумага офсетная № 1.
Гарнитура тайме. Печать офсетная.
Объем 13,00 бум.л. Усл. печ.л. 26,00.
Усл. кр.-отт. 52,00. Уч.-изд.л. 25,56.
Изд. № 3/5152. ТЬраж 16000 экз. Зак 81.
Цена 4 р. 90 к.
Издательство «Мир»
129820, ГСП Москва, 1-й Рижский пер., 2.
Набрано в Межиздательском фотонаборном центре
издательства «Мир»
Можайский полиграфкомбинат
Союзполиграфпрома при Государственном
комитете СССР по делам издательств,
полиграфии и книжной торговли.
143200, Можайск, ул. Мира, 93.