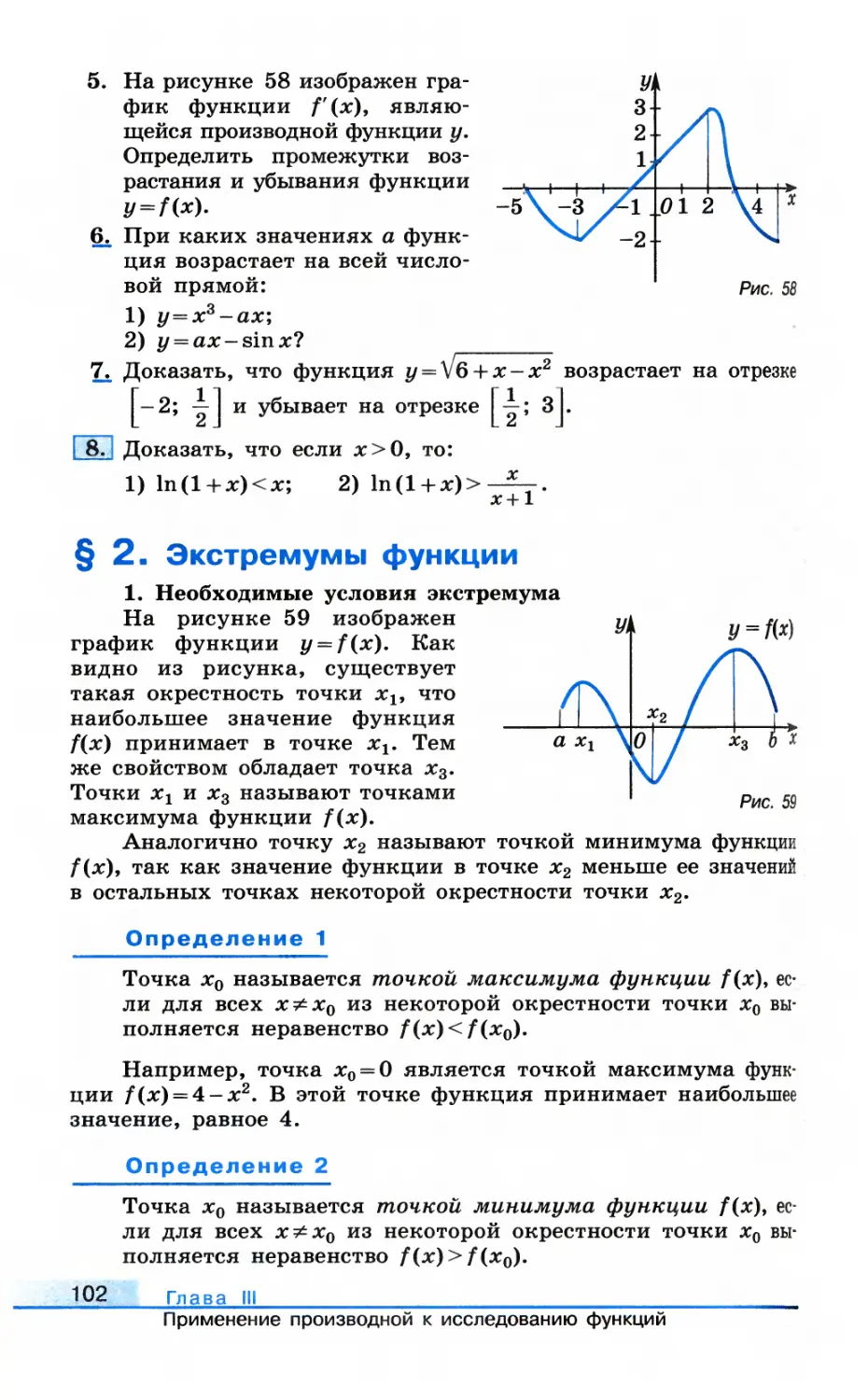
Автор: Колягин Ю.М.
Теги: общее школьное образование общеобразовательная школа алгебра математический анализ
ISBN: 978-5-09-022250-1
Год: 2010
Текст
L
И НАЧАЛА
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
ПРОСВЕЩЕНИЕ
ИЗДАТЕЛЬСТВО
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
= l,5sin(2(*-f))
у = sin2x
у = sin(2(* - \))
ПРОИЗВОДНАЯ
и . .. /(*+/*)-/(*)
'(ж) = Jim — ■£—L-L-
Г (*) = (/'(*))'
(е*У = е>
(In*)' =
(sin*)' =
(tg*)' =
cos*
1
COS2*
(ax)' = axlna
(cosjc)' = - sinjc
(ctgx)' = - -
v б ' si
sin2*
(/(*) + ^))' = fix) + g'(x) (cf(x))' = cf'(x)
(fix) • g(x)Y = /'(*) • g(x) + f(x) • g'(x)
(fix) у f'(x)-g(x)-f(x)-g'(x)
\g(x)l
g4x)
(f(g(x)Y= f'(g(x)) • g'(x)
ИНТЕГРАЛ
x = F(b)-F(a)
a
Функция
F'(x) = f(x)
Первообразная
X
p+1
e*
sin*
cos*
0, *<0
P +1
In* +C
e*+ С
- cos* + С
sin* + С
i|lttt|l!ll|lil
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
Учебник
для общеобразовательных
учреждений
Базовый и профильный
уровни
Под редакцией
А. Б. Жижченко
2-е издание
Москва
Рекомендовано
Министерством
образования и науки
Российской
Федерации
» Просвещение
2010
УДК 373.167.1:[512 + 517]
ББК 22.14я72
А45
На учебник получены положительные заключения
Российской академии наук (№ 10106-5215/519 от 24.10.08)
и Российской академии образования (№ 01-206/5/7д
от 11.10.07)
Авторы:
Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова,
М. И. Шабунин
Условные обозначения
C3I материал для изучения на профильном уровне
ИИ материал для интересующихся математикой
t> ^ решение задачи
О • обоснование утверждения или вывод формулы
25 упражнения для базового уровня
26 упражнения для профильного уровня
|27l упражнения для интересующихся математикой
Алгебра и начала математического анализа. 11 класс :
А45 учеб. для общеобразоват. учреждений : базовый и
профил. уровни / [Ю. М. Колягин, М. В.
Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред.
А. Б. Жижченко. — 2-е изд. — М. : Просвещение,
2010.— 336 с. : ил.— ISBN 978-5-09-022250-1.
УДК 373.167.1:[512 + 517]
ББК 22.14я72+22.161я72
ISBN 978-5-09-022250-1 © Издательство «Просвещение», 2009
© Художественное оформление.
Издательство «Просвещение», 2009
Все права защищены
Тригонометрические
функции
Я не мог понять содержание вашей
статьи, так как она не оживлена иксами
и игреками,
У. Томсон
§ 1. Область определения
и множество значений
тригонометрических
функций
Известно, что каждому действительному
числу х соответствует единственная точка
единичной окружности, получаемая поворотом
точки (1; 0) на угол х радиан; sinx — ордината
этой точки, cos л: — ее абсцисса. Тем самым
каждому действительному числу х поставлены в
соответствие числа sin л: и cos л:, т. е. на
множестве R всех действительных чисел определены
функции y = sinx и y = cosx.
Областью определения каждой из
функций y = sinx и y = cosx является
множество R всех действительных чисел.
Напомним, что множество всех значений,
которые функция принимает на области
определения, называют множеством значений функции.
Таким образом, чтобы найти множество
значений функции y=sinx, нужно выяснить,
какие значения может принимать у при
различных значениях х из области определения,
т. е. установить, для каких значений у
существуют такие значения х, при которых sinx = y.
Известно, что уравнение sinx = a, так же как и
уравнение cosx = a, имеет корни, если |а|<1, и
не имеет корней, если |а|>1.
Множеством значений каждой из функций
y = sinx и y = cosx является отрезок
-Ку<1. Функции y = sinx и y = cosx
ограничены сверху и снизу (по
определению ограниченной функции).
§ 1 3
Область определения и множество значений
тригонометрических функций
Задача 1. Найти область определения функции
* sinjc + cosa:
t> Найдем значения х, при которых выражение — не
имеет смысла, т. е. такие значения х, при которых знаменатель
равен нулю. Решая уравнение sinx + cosx = 0, находим tgx = -l,
x = --j+nn, n€Z. Следовательно, областью определения данной
функции являются все значения л:^ —— н-я/г, n€Z. M
Задача 2. Найти множество значений функции
t> Нужно выяснить, какие значения может принимать у при
различных значениях х9 т. е. установить, для каких значений а
уравнение 3 + sin x cos x = а имеет корни. Применяя формулу
синуса двойного угла, запишем уравнение так: 3 + — sin 2л: = а,
CU
откуда sin2л: = 2а-6. Для всех значений а, таких, что |2а-6|<1,
т.е. 2,5<а<3,5, это уравнение имеет корни. Таким образом,
множеством значений данной функции является отрезок
2,5<i/<3,5.
Ответ. [2,5; 3,5]. ^
Замечание. Задачу 2 можно решить иначе. Так как
у = 3 + — sin2л:, где -Кsin2л:< 1, то - — < — sin2л: < —, откуда
CU CU CU CU
2,5<3 + — sin 2л:< 3,5. Следовательно, множество значений функ-
CU
ции — отрезок [2,5; 3,5].
Функция у = tg х определяется формулой tg х = .
COS X
Значит, она определена при тех значениях х, для которых
, т. е. при х^ — -\-пп9 n€Z.
Областью определения функции y = tgx является
множество чисел л^у+ятг, n€Z.
Множеством значений функции y = tgx является
множество R всех действительных чисел, так как уравнение
tgл: = a имеет корни при любом действительном значении а.
Функция у = ctg л:, где ctg х = ——, определена при тех зна-
sin х
чениях х, для которых этл^О, т. е. при х^пп, n€Z.
Следовательно, областью определения функции y — ctgx является
множество R с выброшенными из него точками х = пп, n€Z.
Так как уравнение ctgл: = a имеет корни при любом
действительном значении а, то множеством значений функции
у = ctg х является множество R всех действительных чисел.
Функции y = tgx и y = ctgx не являются ограниченными.
_4 Гл а в а I
Тригонометрические функции
Функции у = sin x, y = cosx, y = tgx и y = ctgx называются
тригонометрическими функциями.
Задача 3. Найти область определения функции
t> Нужно выяснить, при каких значениях х выражение
sin Зх + tg 2x имеет смысл. Выражение sin3x имеет смысл при
7С
любом значении х, а выражение tg2x — при 2х^ — +пп, n€Z,
т.е. при х^ — + —, /i€Z. Следовательно, областью определе-
4 dt
ния данной функции является множество действительных
чисел, таких, что jc^-^-H-^-, n€Z.
4 Ci
Ответ. x^^r + ^r-, neZ.M
4 Z
E^l Задача 4. Найти множество значений функции
у = 3 sin х 4- 4 cos л;.
t> Преобразуем функцию, используя метод вспомогательного
угла («Алгебра и начала анализа, 10», гл. IX, § 4). Умножим
и разделим у на V32 + 42 = 5. Получим у = 5[ — sinxH- — cos л:).
(3\2/4\2 «
— I +(-^-1 =1» то существует угол а такой, что
Q Л Q
cosa= —, sina=—. В качестве а можно взять arccos — . Тогда
о о о
у = 5 (sin х cos a + cos x sin a) = 5 sin (x + а), где -К sin (х + а) < 1.
Поэтому —5<i/<5, т. е. множество значений данной функции —
отрезок [-5; 5].^
Задача 5. Найти множество значений функции
у = 3 sin2 х + 4 sin л: cos л: + cos2 л:.
[> Используя формулы двойного аргумента, получаем
у = 3 • + 2 sin 2х + ~ = 2 + (2 sin 2x - cos 2x).
Преобразовав выражение в скобках и применив метод
вспомогательного угла, получим
2 sin 2х - cos 2х = \Гь[ —= sin 2х —— cos 2х) = VE^sin (2x - а),
VV5 V5 /
2
2
где а = arccos -=.
V5
Тоща i/ = 2 + V5^sin(2x-a). Так как -V5"<V5"sin(2x-a)<V5,
то 2-v5 <i/<2 +v5. Следовательно, множество значений данной
функции — отрезок [2 — V^ V^
^Д Задача 6. Доказать, что функция у = 3 cos 2x + 5 sin 2x
ограничена.
> Для того чтобы доказать, что функция у = 3 cos 2x + 5 sin 2л;
эграничена, нужно найти такое положительное число С, чтобы
§ 1 5
Область определения и множество значений
тригонометрических функций
для любого значения х из области определения функции, т. е.
для jcG/2, выполнялось неравенство |3cos2xH-5sin2x|<C.
Так как -Kcos2x<l, -Ksin2x<l, то для любого
значения х из области определения выполняются неравенства
-3<3cos2x<3, -5<5sin2x<5, следовательно, -8<i/<8 и
функция ограничена на множестве R. 4|
х
Задача 7. Доказать, что функция y=—z sin2x ограни-
дГ + 1
чена.
> Данная функция определена на множестве R. Воспользуемся
неравенством х2 + 1>2\х\, которое равносильно неравенству
|х| I |х| 1
(\х\-1)2>0. Тогда \у\=—о |sin2x|<-, так как —^ <^, а
яг + 1 ^ дг + 1 ^
|sin2x|<l. Следовательно, функция ограничена на
множестве R. <4
Задача 8. Доказать, что функция y = xsinx не является
ограниченной на множестве R.
> Пусть С — произвольное положительное число. Тогда
найдется натуральное число /г, такое, что хп=^г + 2пп>С.
Так как \y(xn)\ = xnsinxn = xn>C, то функция не является
ограниченной на множестве R. 4| Ml
Упражнения
1. Найти область определения функции:
2) i/ = cos^; 3) i/ = cos—;
2
4) i/ = sin—; 5) i/ = sinV^; 6)
2. Найти множество значений функции:
1) i/=l + sinjc; 2) i/ = l-cosx;
3) i/ = 2sinxH-3; 4) i/= 1 -4cos2x;
5) i/ = sin2jccos2xH-2; 6) y= — sinxcosx-l.
3. Найти область определения функции:
4. Найти область определения функции f(x) и вычислить ее
значение в заданных точках:
-I \ л/ \ cos2jc п 7п
Найти область определения функции (5—6).
5± 1) г/ = Vsin х н-1; 2) г/ = Vcos х -1; 3) i/ = lgsinx;
4) i/ = V2cosjc-1; 5) i/ = Vl-2simc; 6) i/ =
Глава 1
Тригонометрические функции
i) у 1 ; 2) у-
2 sin x — sin x
3)
о 9
cos x — sin j
sinjc-
Найти множество значений функции (7—9).
Т. 1) # = 2sin2л:-cos2х; 2) # = 1 -8cos2xsin2x;
" 8) J/=l+8W£; 4) у = 10-9 sin2 3*;
5) «/ = 1-2|cosx|; 6) i/ = sinxH-sin(xH-
_8. 1) у = sin л: -5 cos x\ 2) i/ = sin2 x -2 sin л:;
3) у = 10 cos2 л: - 6 sin x cos x + 2 sin2 л:;
с; 2)
Доказать ограниченность функции:
-ч COSJC оч 1
*) у ; 2) у
'У 1 к
1,О —
fllj Доказать, что функция /(л:) не является ограниченной в
области ее определения, если:
1)/(ж)_~££; 2)/(x)=±sin±.
§ 2. Четность, нечетность, периодичность
тригонометрических функций
Каждая из функций i/ = sinx и i/ = cosx определена на
множестве /2, и для любого jcGiJ верны равенства
sin(-x) = —sinx, cos(—x) = cosx.
Следовательно, i/ = sinx — нечетная функция, a i/ = cosx —
четная функция.
Для любого значения х из области определения функции
y = tgx верно равенство tg(-x) = - tg(x) и область определения
функции y = tgx симметрична относительно начала координат.
Поэтому y = tgx и y = ctgx— нечетные функции.
ИЗ Можно доказать следующие свойства четных и нечетных
функций:
1) сумма, разность, произведение и частное двух четных
функций являются функциями четными;
2) сумма и разность двух нечетных функций являются
функциями нечетными;
3) произведение и частное двух нечетных функций
являются четными функциями;
4) произведение и частное четной и нечетной функций
являются нечетными функциями. Wmm%
§2 7
Четность, нечетность, периодичность
тригонометрических функций
Задача 1. Выяснить, является ли функция
у = 2 + sin х cos f -~ + дп
четной или нечетной.
[> Функция определена на множестве R. Используя формулу
приведения, запишем данную функцию в виде у = 2 + sin2 x. Так
как sin(-x) = -sinx, то (sin (- х))2 = sin2 x, и поэтому у(-х) = у(х),
т. е. данная функция является четной. М
Известно, что для любого значения х верны равенства
sin(xH-27c) = sinx, cos(jc + 27c) = cosx. Из этих равенств следует,
что значения синуса и косинуса периодически повторяются при
изменении аргумента на 2п. Такие функции называются
периодическими с периодом 2я.
Определение
Функция f(x) называется периодической, если существует
такое число 7V0, что для любого х из области
определения этой функции значения х + Т и х — Т также
принадлежат области определения и выполняются равенства
f(x-T) = f(x) = f(x + T). Число Т называется периодом
функции f(x).
Из этого определения следует, что если число х
принадлежит области определения функции f(x), то числа х + пТ, n€Z,
также принадлежат области определения этой функции и
Задача 2. Доказать, что число 2я является наименьшим
положительным периодом функции y = cosx.
t> Пусть Т>0 — период косинуса, т. е. для любого х
выполняется равенство cos(xh-T') = cosx. Положив х = 0, получим
cosT=l. Отсюда T = 2nk, keZ. Так как Т>0, то Т может
принимать значения 2я, 4я, 6я, ..., и поэтому период не может
быть меньше 2я. <Щ
Аналогично можно доказать, что наименьший
положительный период функции y = sinx также равен 2п.
Задача 3. Доказать, что f(x) = sinSx — периодическая функ-
2я
ция с периодом —.
о
t> Функция f(x) = sinSx определена на R. Поэтому достаточно
показать, что для всех x€R справедливы равенства
/(х) и f(x~)=f(x). Имеем
Аналогично fix—^-1 =sin(3x-27c) =
_§ Глава I
Тригонометрические функции
Задача 4. Доказать, что функция y=tgx является
периодической, и найти наименьший положительный период.
> Если х принадлежит области определения этой функции,
т. е. х^-^+пп, neZ, то по формулам приведения получаем
Таким образом, tg(x-n) = tgx = tg(x + n). Следовательно, п —
период функции y = tgx. Покажем, что п — наименьший
положительный период функции y=tgx.
Пусть Т — период тангенса, тогда tg (х + Т) = tg x, откуда
при х = 0 получаем tgT = O, T = kn, k€Z.
Так как наименьшее целое положительное k равно 1, то
п — наименьший положительный период функции y = tgx. M
1^1 Задача 5. Доказать, что y = tg— —периодическая функ-
о
ция с периодом Зя.
[> Область определения функции — множество x€R таких, что
х^ — +3пп, n€Z, отсюда следует, что если х принадлежит
области определения, то х + Зк и х-Зк также принадлежат ее
области определения.
m х + Зп (х \ х х-Зп (х \
Так как tg-g- = tg(- +n) = tg-, tg-g-=tg(--*) =
= tg —, то tg— — периодическая функция с периодом Зл. М
о о
Задача 6. Доказать, что функция г/= — :— является пе-
А ~т~ Sill X
риодической с периодом 2л.
[> Областью определения D функции являются все
действительные числа х, кроме тех, при которых sinx = -l, т. е.
кроме чисел х = - — + 2пп, n€Z. Таким образом, если x€D, то
числа х + 2п и х-2п также принадлежат множеству D. Так как
COS(JC±27C) COSJC / ч t ч
==У(Х) то У(*) - периадичес-
кая функция с периодом 2я. М f^
Ш5Ш Задача 7. Найти наименьший положительный период
функции i/ = 3sinx + sin2x.
[> Функция определена на множестве R. Пусть Т — период
данной функции, т. е. для всех xeR верно равенство
3sin(xH-Tr) + sin2(x + 7T) = 3sinx + sin2x. (1)
Если х = 0, то из равенства (1) следует, что 3sinTr + sin2T' = 0
или 3sinT + 2sinT'cosT = 0, откуда получаем sin7r(3 + 2cosT') = 0.
Так как 3 + 2cos7V0, то sinT^0, и поэтому наименьший
положительный период нужно искать среди чисел Т = пп, n€Z.
Покажем, что число п не является периодом данной
функции, т. е. равенство (1) для Т = п не выполняется хотя бы при
одном значении x€R.
§_2 9_
Четность, нечетность, периодичность
тригонометрических функций
Пусть *=77- Вычислим у(^+п) и #(f")- Имеем у(^+п\ =
= 3sin(-|+7c)+sin2(-|+7c)=-3f i/(|) = 3sin-|+sin2|- = 3.
Таким образом, для Т = п равенство (1) не является верным при
При Т = 2я равенство (1) является верным для любого x€R,
так как y(x + 2n) = 3sm(x + 2n) + sm2(x + 2n) = 3sinx + sin2x = y(x).
Следовательно, х = 2п — наименьший период функции. Щ
Задача 8. Доказать, что функция i/ = sin — не является
периодической. х
t> Областью определения данной функции являются все
действительные числа, кроме числа 0. Пусть Т — произвольное
положительное число, тогда из того, что — TV0, следует, что
точка хо = — Т принадлежит области определения. Но точка
хо + Т = -Т+Т = О не принадлежит области определения.
Пришли к тому, что для любого Т>0 существует такое
число х = х0 (из области определения функции у), что точка
х + Т не принадлежит области определения. Следовательно,
функция y = sin— не является периодической. «4
Задача 9. Доказать, что функция y = sinx2 не является
периодической.
t> Достаточно доказать, что функция не имеет положительного
периода, так как если бы число Т<0 было периодом, то число
— Т было бы положительным периодом. Доказательство
проведем методом от противного.
Допустим, что число Т>0 — период функции, т. е. для
любого x€R справедливо равенство sin(xH-T')2 = sinx2. При х = 0
отсюда следует, что sinT2 = 0, т. е. Т2 = пп, а Т = \/пп при
некотором n€N. Если 0<х<у/п, то sinx2^0, а поскольку \[тт —
период, то и sin(xH-\/7m)2^0. Если же х = ^п, то sin(V7t + \/7m)2 =
= sin(V7t)2 = 0. Значит, число у/п + \/пп является ближайшим
справа к у/пп числом, при котором sinx2 = 0. Отсюда \/я
Глава I
Тригонометрические функции
), так как \/п(п+1) >у/пп и sin(\fn(/гн-1))2 = 0. Но
неравенство V7c+V7in<Vrc(/H-l), равносильное неравенству К\/п+1-\[п ,
неверно для любого n€N, так как \1п+1-\[п= <1. Зна-
\/п+1+\[п
чит, неверно и допущение о периодичности функции sinx2. М ВЯ
Периодическими функциями описываются многие
физические процессы (колебания маятника, вращение планет,
переменный ток и т. д.). На рисунке 1 изображены графики
некоторых периодических функций.
Упражнения
Выяснить, является ли данная функция четной или
нечетной (12—13).
12. 1) i/ = cos3x; 2) у = 2sin4x; 3) y=^tg2x;
4) у = хъоъ^-\ 5) у = хsinx; 6) y = 2sin2x.
13. 1) y = sinx + x; 2) y = cos(x- — )-x2;
3) у = 3-cos(^ + x) sin(n-x);
4) z/=|cos2xsin(f-2jc)+3; 5) y = x2+
14. Доказать, что функция y = f(x) является периодической с
периодом 2тг, если:
1) y = cosx-l; 2) y = sinx+l; 3) i/ =
6) y-8i
15. Доказать, что функция y = f(x) является периодической с
периодом Т, если:
1) i/ = sin2jc, Т = тс; 2) i/ = cosf, Т = 4тс;
с*
3) y = tg2x, Г-|; 4) j/ = sin^, Т=|я.
16. Определить, является ли данная функция четной или
нечетной:
U у= l-cosx 2) Узш2д:
з) y=
l+cos2*' ' * sins;
4) y=x + sin2x; 5) у = л:Isinx|sin3x; 6)
COS Jt
17. Доказать, что:
1) произведение и частное двух нечетных функций
являются четными функциями;
2) произведение и частное четной и нечетной функций
являются нечетными функциями.
§2 11
Четность, нечетность, периодичность
тригонометрических функций
Найти наименьший положительный период функции (18—
19).
18. 1) y = cos-f *; 2) j/ = sinf x; 3) j/ = tgf; 4) y = \sinx\.
О Ci Ci
19. 1) у = sin x + cos л:; 2) i/ = sinxH-tgx;
3) «/ = sinx.sin3x; 4) i/ = 2tg|-3tg|.
20. Выяснить, является ли периодической функция:
1) y = yjsinx; 2) y = sin*\[x; 3) y = |sin|x||.
[21.[Доказать, что функция не является периодической:
1) у = sin\/\x]; 2) i/ = sin:x; + sinV2x.
22. Доказать, что функция i/ = sin4 л: + cos4 x периодическая, и
найти ее наименьший положительный период.
23. Доказать, что функция периодическая, и найти ее
наименьший положительный период:
2) i/ = cos(sinx).
эик функции y = f(x), x€R, симметричен относительно
каждой из прямых х = а9 х = Ь9 где а^Ъ. Доказать, что
f(x) является периодической, и найти ее период.
[>ик функции y = f(x), x€R, симметричен относительно
точки А (а; Ь) и прямой х = с (с^а). Доказать, что функция
y = f(x) является периодической, и найти ее период.
оказать, что функция y = f(x) является периодической,
если существует 7V0 такое, что для любых трех
значений х, х + Т и х — Т из области определения функции
выполнено условие f(x+T) = -f(x). Найти период функции /.
[27^1 Пусть функция f(x) определена на всей числовой прямой.
Доказать, что:
1) f(x) + f(-x) — четная функция;
2) f(x)-f(-x) — нечетная функция.
§ 3. Свойства функции y=cosx и ее график
Напомним, что функция y = cosx определена на всей
числовой прямой и множеством ее значений является отрезок [— 1; 1].
Следовательно, функция ограничена и график ее расположен в
полосе между прямыми i/ = -l и у=1.
Так как функция y = cosx периодическая с периодом 2я, то
достаточно построить ее график на каком-нибудь промежутке
длиной 2я, например на отрезке — 7с<л:<7г. Тогда на
промежутках, получаемых сдвигами выбранного отрезка на 2пп, n€Z,
график будет таким же.
Функция y = cosx является четной. Поэтому ее график
симметричен относительно оси Оу. Для построения графика на
отрезке —7с<л:<7г достаточно построить его для 0<л:<7с, а затем
симметрично отразить его относительно оси Оу.
12 г л а в а I
Тригонометрические функции
1
т
0
1
2
-1
\ 1
n
6 Я w
X
Рис. 2
Рис. 3
-n /
Vi
1
Уо
^/-XoO
-1
\ n
Рис.
X
4
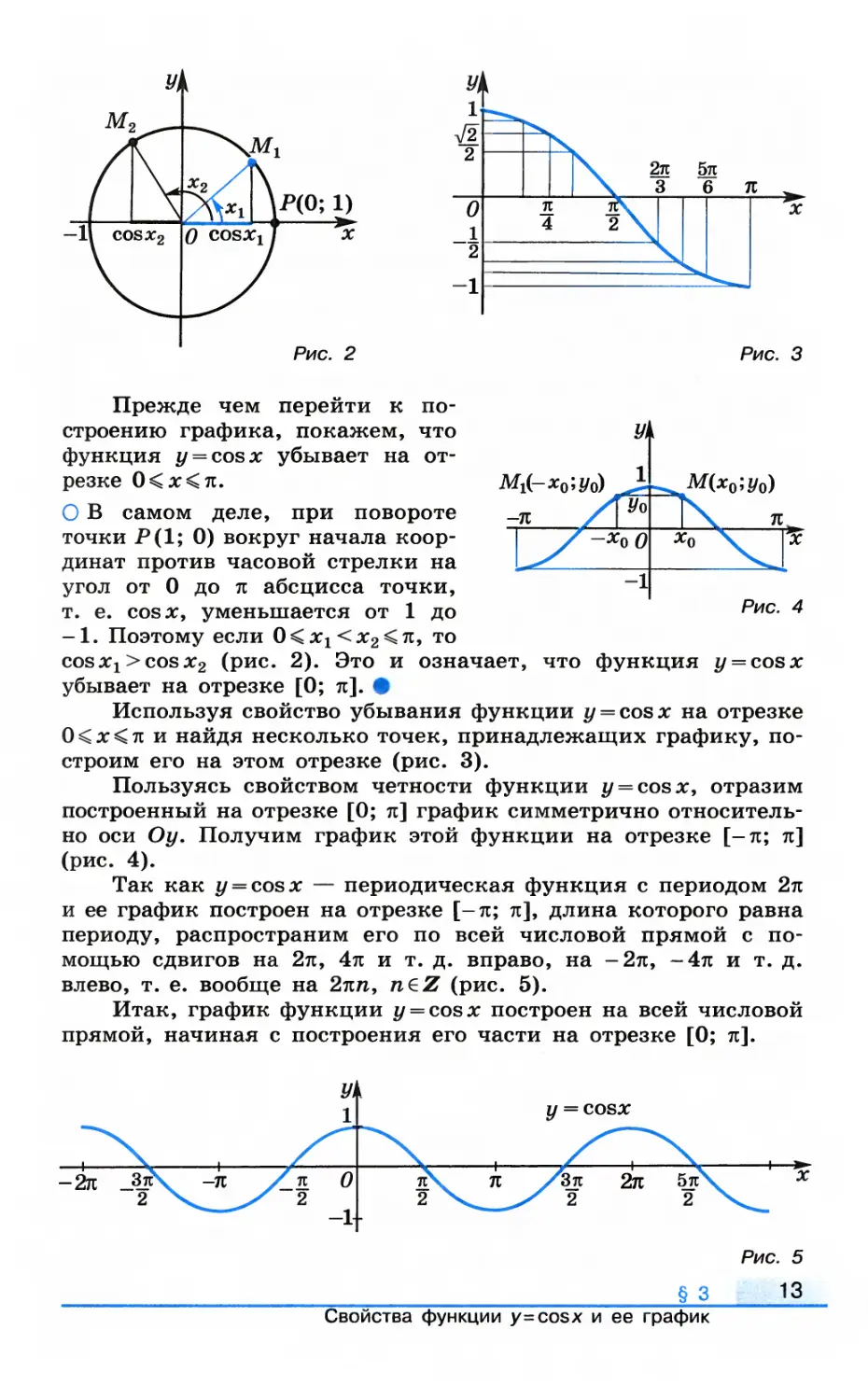
Прежде чем перейти к
построению графика, покажем, что
функция y = cosx убывает на
отрезке 0<х<п.
О В самом деле, при повороте
точки Р(1; 0) вокруг начала
координат против часовой стрелки на
угол от 0 до я абсцисса точки,
т. е. cos л:, уменьшается от 1 до
-1. Поэтому если 0<х1<х2<п, то
cosxx > cos x2 (рис. 2). Это и означает, что функция y = cosx
убывает на отрезке [0; я]. •
Используя свойство убывания функции y = cosx на отрезке
0<л;<71 и найдя несколько точек, принадлежащих графику,
построим его на этом отрезке (рис. 3).
Пользуясь свойством четности функции y = cosx, отразим
построенный на отрезке [0; я] график симметрично
относительно оси Оу. Получим график этой функции на отрезке [—я; я]
(рис. 4).
Так как y = cosx — периодическая функция с периодом 2я
и ее график построен на отрезке [—я; я], длина которого равна
периоду, распространим его по всей числовой прямой с
помощью сдвигов на 2я, 4я и т. д. вправо, на -2я, -4л и т. д.
влево, т. е. вообще на 2я/г, n€Z (рис. 5).
Итак, график функции y = cosx построен на всей числовой
прямой, начиная с построения его части на отрезке [0; я].
у = cos*
0
-1-1-
2я
§ 3
Рис. 5
13
Свойства функции y=cosx и ее график
Поэтому свойства функции y = cosx можно получить,
опираясь на свойства этой функции на отрезке [0; я]. Например,
функция y = cosx возрастает на отрезке [-п; 0], так как она
убывает на отрезке [0; я] и является четной.
Основные свойства функции y = cosx
1) Область определения — множество R всех
действительных чисел.
2) Множество значений — отрезок [—1; 1].
3) Периодическая, Т = 2п.
4) Четная.
5) Функция принимает:
— значение, равное 0, при x=^z+nn, n€Z\
— наибольшее значение, равное 1, при х = 2пп, n€Z;
— наименьшее значение, равное —1, при х = п + 2пп, n€Z;
— положительные значения на интервале (--^1 ^ ) и на
интервалах, получаемых сдвигами этого интервала на 2пп,
— отрицательные значения на интервале (^; -£-) и на
интервалах, получаемых сдвигами этого интервала на 2пп,
neZ.
6) Возрастающая на отрезке [п; 2я] и на отрезках,
получаемых сдвигами этого отрезка на 2пп, n€Z;
убывающая на отрезке [0; я] и на отрезках, получаемых
сдвигами этого отрезка на 2пп, n€Z.
Задача 1. Найти все корни уравнения cos х = — —,
принадлежащие отрезку -7c<jc<27c.
t> Построим графики функций у = cos х и у = - — на данном
отрезке (рис. 6). Эти графики пересекаются в трех точках,
абсциссы которых х19 х2, х3 являются корнями уравнения
cosx = -—. На отрезке [0; п] корнем уравнения cosx = - —
/ 1 \ 2л
является число Jc1 = arccos(- — )=—-. Из рисунка 6 видно, что
V 2 / о
точки х2 и хх симметричны относительно оси Оу, т. е.
= -х =-— а х =л
3
~ 2л 2л 4л ^
V/ 1 DUX t яЛ/ J q 9 *п/2 Q ' "^3 Q ^^
Рис. 6
14
Глава I
Тригонометрические функции
Задача 2. Найти все решения неравенства cos x>-—9
принадлежащие отрезку — 7
£> Из рисунка 6 видно, что график функции y = cosx лежит вы-
ше графика функции у = - — на промежутках ( ; — ) и
Ответ. -^у ^
ЕЛ Задача 3. Решить неравенство 4cos2x-8cosxH-3<0.
О Пусть cosx = ^, тогда получаем квадратное неравенство
4£2-8£ + 3<0, равносильное неравенству (t- — j(t- — j<0.
Поэтому исходное неравенство равносильно каждому из
неравенств:
— )(cosx- — ) <0, ( —-cosx)(cosx- —)>0, cosx>—.
Построим график функции i/ = cosx (рис. 7). На отрезке
[-п; п] уравнение cosx=— имеет корни -^ и ^, а решениями
неравенства cos л: > — на этом отрезке являются все числа из
интервала (-—; -J). Множество решений неравенства cosx> —
\ о о / 2
и равносильного ему исходного неравенства представляет собой
n€Z.
cos2x.
объединение интервалов (-^-
Ответ. -?- + 2тт<х<^- ^
3 о
Задача 4. Построить график функции
[> Область определения данной функции — множество R,
множество значений — отрезок [0; 1], функция четная с периодом %
у = cos*
Рис. 8
15
Свойства функции y=cosx и ее график
и cos2x= + c°s x. Следовательно, график функции y=—+cos x
можно получить из графика функции y = cosx сжатием вдвое
вдоль оси Ох, сдвигом на — вверх по оси Оу и сжатием вдвое
вдоль оси Оу (рис. 8). ^ 1"Н1
И^Д Задача 5. Построить график функции y = xcosx.
> Функция определена на множестве R и является нечетной.
Поэтому можно построить ее график при х>0, а затем с
помощью симметрии относительно начала координат изобразить
его для отрицательных значений х.
у = jccosjc
Рис. 9
Так как -Kcosx<l при x€R, то при х>0 справедливо
неравенство - х < х cos х < х или -хКуКх. Отсюда следует, что
при лгХ) график данной функции расположен между лучами
у = -х и у = х (х>0). При этом точки графика функции
y = xcosx лежат на луче у = х(х>0), если cosx=l, т. е. х = 2пп,
n€Z, n>0. Аналогично при х = п(2п-1), n€N, точки графика
этой функции лежат на луче у = — х(х>0). График функции
у = х cos х изображен на рисунке 9. ^ ВЯ
Упражнения
Упражнения 28, 32—35 выполнить с помощью графика
функции y = cosx.
28. (Устно.) Выяснить, при каких значениях х,
принадлежащих отрезку [0; Зя], функция y = cosx принимает: 1) значе-
16 Глава I
Тригонометрические функции
ние, равное 0, 1, -1; 2) положительные значения; 3)
отрицательные значения.
29. Найти значения функции y = cos(x+^-j при х = а, если:
30. Найти значения функции y = cos2x при:
1) ж=|; 2) ж-f; 3) x=f; 4) ж-i*.
31. Выяснить, принадлежит ли графику функции y = cosx
точка с координатами:
32. (Устно.) Выяснить, возрастает или убывает функция
i/ = cosx на отрезке:
1) [Зтг; 4тг]; 2) [-2я; -тс]; 3) [2тг; Щ;
4) [-|; О]; 5) [1; 3]; 6) [-2; -1].
33. Разбить данный отрезок на два отрезка так, чтобы на
одном из них функция y = cosx возрастала, а на другом
убывала:
1Ч Гя. Зя~|. ох I я . я~|. оч Гп. ЗяТ ^ч Г <тг# я 1
1} Li; "tJ; 2) г г- 2J'3) L0' ~rJ'4) гп; 2i-
34. С помощью свойства возрастания или убывания функции
y = cosx сравнить числа:
3) cos(--5*) и cos(-f); 4) cos(--^) и cos(--^);
5) cosl и cos3; 6) cos 4 и cos 5.
35. Найти все принадлежащие отрезку [0; Зтг] корни
уравнения:
1 \fz \f2 I
1) cosx=—; 2) cos л; =-У—; 3) cosx = --^—; 4) cosx = -—.
2 2 Z ^
36. Найти все принадлежащие отрезку [0; Зя] решения
неравенства:
i; 2) cosx>-^; 3) cosx<-^; 4) ^
Li Li Li Ci
37. Построив график функции y = f(x), найти: а) область
определения функции; б) множество значений; в) промежутки
возрастания:
Г cos л:, если 0<л:<2т1,
1} Пх)=[х2, если х<0;
2)
cos л:, если -
— +1, если
я
§ 3 17
Свойства функции y=cosx и ее график
38. Выразив синус через косинус по формулам приведения,
сравнить числа:
1) cos^- и sin^-;
5 5
3) cos^ и sin-^;
~6 ~Ы '
39. Найти все принадлежащие промежутку - ^ < х < -£- корни
уравнения:
2)
4)
6)
sin
sin
cos
п_
7
Sn
5
п
8
и cos
И СО!
и sin
7'
3!;
Sn
10'
V3
40. Найти все корни уравнения cos х = — -—, принадлежащие
множеству реп1ений неравенства Iog2(x—1)<3.
41. Найти все принадлежащие промежутку — — < х < — penie-
ния неравенства:
42. Найти множество значений функции y = cosx, если х
принадлежит промежутку:
1) Г|; я1; 2) (-f; ^).
Lo J \ 4 4 /
43. Найти промежутки возрастания функции у = cos 2x + sin2 л:
на отрезке [0; 2я].
44. Решить графически уравнение:
1) cosx=l-—; 2)
3) cosx=l-\-y/x-2n;
45. С помощью графиков выяснить, имеет ли решение система
уравнений:
с-1, 2)
г = cos л:;
= cosx.
46. Сколько решений имеет система уравнений:
47. Построить график и установить свойства функции:
1) y=l+cosx; 2) i/ = cos2x; 3) i/
4) i/ = 2cosf; 5) у=™Щ±*-1; 6) i/ = 2-
48. Построить график функции:
1) y = \cosx\; 2) i/ = 3-2cos(x-l);
3) y = sinxctgx; 4) г/ = 2СО8ДС.
J_8 г л а в а I
Тригонометрические функции
jQ В одной системе координат построить графики функций
у = cos х и у = - .
Vl+tg2*
3 Решить неравенство:
4 '
2) 2cos2x-3cosx-2>0;
Г - cos 4x
>-2cosx.
§ 4. Свойства функции y=sinx и ее график
Функция y = sinx определена на всей числовой прямой,
является нечетной и периодической с периодом 2я. Ее график
можно построить таким же способом, как и график функции
у — cosх, начиная с построения, например, на отрезке [0; я].
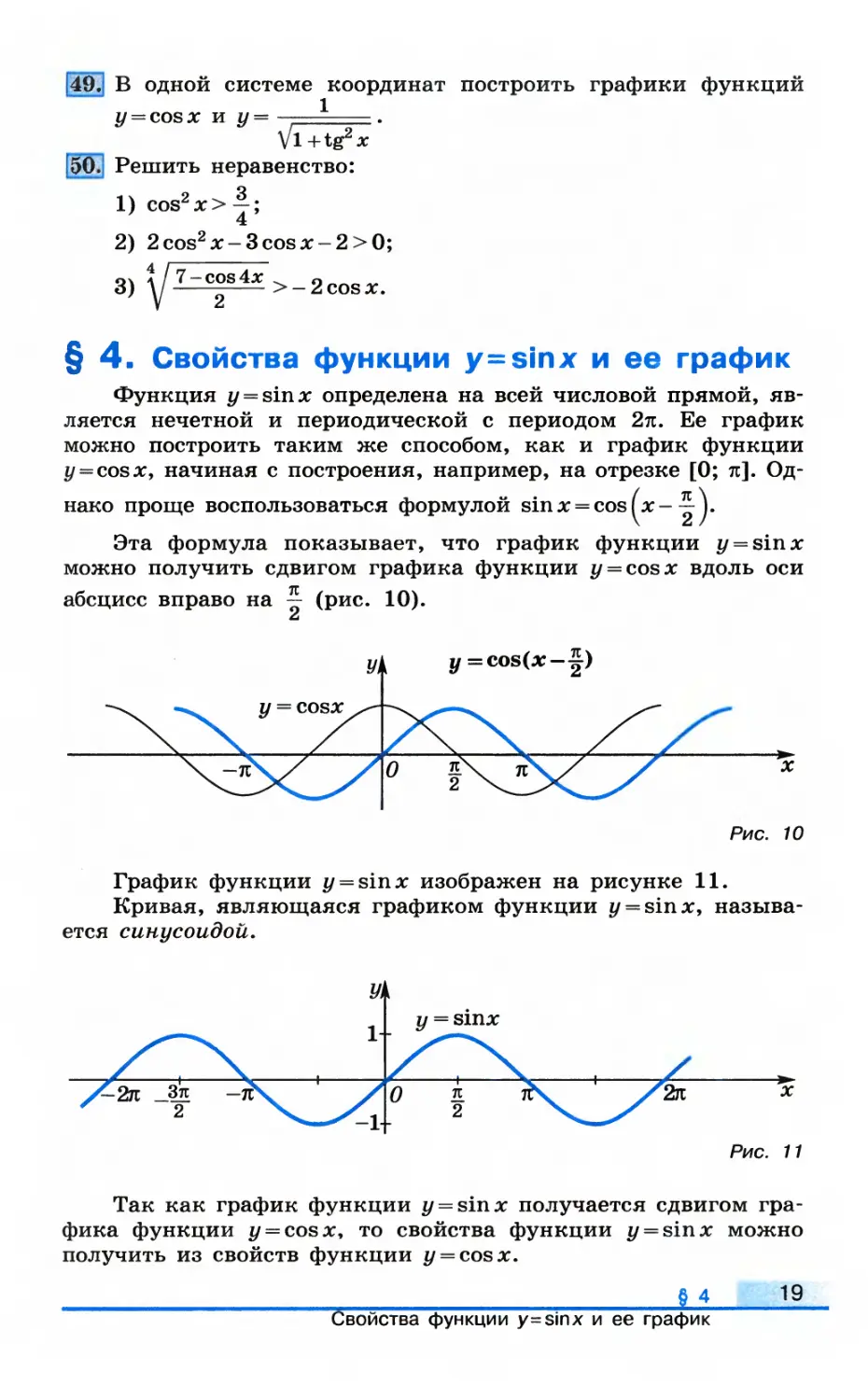
Однако проще воспользоваться формулой sin д: = cos мс - ^ J.
Эта формула показывает, что график функции y = sinx
можно получить сдвигом графика функции y = cosx вдоль оси
абсцисс вправо на ^ (рис. 10).
X
Рис. 10
График функции y = sinx изображен на рисунке 11.
Кривая, являющаяся графиком функции y = sinx,
называется синусоидой.
X
Рис. 11
Так как график функции y = sinx получается сдвигом
графика функции y = cosx9 то свойства функции y = sinx можно
получить из свойств функции y = cosx.
§ 4
19
Свойства функции y=sinx и ее график
Основные свойства функции y = sinx
1) Область определения — множество R всех
действительных чисел.
2) Множество значений — отрезок [-1; 1].
3) Периодическая, Т=2п.
4) Нечетная.
5) Функция принимает:
— значение, равное 0, при х = пп, n€Z;
— наибольшее значение, равное 1, при х= ^-+2пп9 n€Z;
— наименьшее значение, равное —1, при х = — ~ + 2пп,
2
— положительные значения на интервале (0; п) и на
интервалах, получаемых сдвигами этого интервала на 2пп,
neZ;
— отрицательные значения на интервале (п; 2п) и на
интервалах, получаемых сдвигами этого интервала на 2пп,
neZ.
6) Возрастающая на отрезке --; | ина отрезках, полу-
L 2 2i J
чаемых сдвигами этого отрезка на 27m, /i€Z;
убывающая на отрезке —; —— и на отрезках, получаемых
сдвигами этого отрезка на 27с/г, n€Z.
Задача 1. Найти все принадлежащие отрезку -n<tx<t2n
корни уравнения sinx = —.
t> Построим графики функций у = sin х и у = — на данном
отрезке (рис. 12). Эти графики пересекаются в двух точках,
абсциссы которых являются корнями уравнения sin х = —. На
отрезке - ~; 77 Уравнение имеет корень хх = arcsin — = ^. Вто-
L 2 2 J At)
рой корень х2 = п-^: = -тг, так как sin (я - ^ ) = sin ^.
6 6 V 6 / 6
Ответ. *! = |, лг2=-у-^
Рис. 12
Задача 2. Найти все решения неравенства sinx<—,
принадлежащие отрезку -п<х<2п.
20 Глава I
Тригонометрические функции
Из рисунка 12 видно, что график функции y = sinx лежит
ниже графика функции у= — на промежутках \-п; -М и
(Ч
(т;
Задача 3. Исследовать функцию y = f(x) и построить ее
график:
1) y = \og2sinx;
1
2) у =
sin I j
[> 1) Областью определения функции являются все значения х,
при которых sinх>О, т. е. 2nn<x<n-t-2nn, n€Z.
Так как 0<sinx<l, то по свойствам логарифмической
функции с основанием а>1 получаем log2sinx<0, т. е.
множество значений функции — промежуток (— оо; 0].
Функция у = log2 sin x — периодическая с наименьшим
положительным периодом 2я, как и функция y = sinx. Поэтому
достаточно исследовать эту функцию на интервале (0; я).
Функции f(x) = sinх и y(t) = log2t являются
возрастающими на промежутках (0; ^ и (0; 1], откуда следует, что
функция у = log2 sin x также является возрастающей на промежутке
(0; —) и принимает все значения из промежутка (— оо; 0]. Так
как значения функции y = sinx в точках промежутка (0; я),
симметричных относительно точки х=—, равны, то график функции
у = log2 sin л; на промежутке —; п\ симметричен графику этой
0; -^ , а функция i/ = log2sinjc
является убывающей при х€\^; п).
Прямые х = 0 и х = п — вертикальные асимптоты графика
функции i/ = log2sinjc на промежутке (0; я). Теперь можно
строить график функции (рис. 13).
Свойства функции y=sinx и ее график
2) Функция у-
Рис. 14
является четной и периодической с
возрастает,
sin|x|
периодом 2тг и областью определения хт^пп, n€Z.
На промежутке fO; -^ функция f(x) = sinx
множество ее значений — промежуток (0; 1], а функция y(t)= —
на промежутке (0; 1] убывает. Поэтому у= . , , = —— — убы-
sin | х | sin х
вающая функция на промежутке К); ^ , принимает все
значения, большие или равные 1.
Как и в задаче 2, график функции у= . на проме-
[7С \ S111'Х'
—; п) симметричен графику этой функции на
промежутке (0; ^ относительно прямой х=^- Прямые л: = 0 и х = п —
вертикальные асимптоты графика функции на интервале (0; я).
Пусть х € (п; 2п). Так как sin(xH-7c) = -sinx, то в точке
х = хо + п, где хов(О; ^), функция sinx принимает значение
- sin xQ. Поэтому для построения графика функции у =
sin | х |
на
промежутке (я; 2я) достаточно перенести построенный на (0; п)
график этой функции на промежуток (я; 2я), а затем заменить
его на симметричный с ним относительно оси Ох (рис. 14).
Множество значений функции у= . — все значения у, та-
sin | ос I
кие, что \у\>\. ^ 1^3
Ml Задача 4. Построить график функции y =
Гл а в а 1
Тригонометрические функции
Рис. 15
[> Функции У\ = х и у2 — sin л: определены на множестве R. Для
построения графика сложим ординаты точек графиков у1 = х и
i/2 = sin л; с одинаковыми абсциссами (рис. 15). <^ ИИ
Упражнения
Упражнения 51, 55—59 выполнить с помощью графика
функции y = sinx.
51. (Устно.) Выяснить, при каких значениях х,
принадлежащих отрезку [0; Зя], функция y = sinx принимает: 1)
значение, равное 0, 1, — 1; 2) положительные значения; 3)
отрицательные значения.
52. Найти значения функции i/ = sin2x при:
53. Найти значения функции i/
sin2*
при:
1) х—-; Z) х-—, 6) *---£-> 4) х——.
54. Выяснить, принадлежат ли графику функции ^ = sinx
точки с координатами:
'Зтг. V2\. лл /2я. У/3\
§ 4 23
Свойства функции y=sinx и ее график
55. (Устно.) Выяснить, возрастает или убывает функция y = sinx
на промежутке:
5) [2; 4]; 6) (6; 7).
56. Разбить данный отрезок на два отрезка так, чтобы на
одном из них функция y = sinx возрастала, а на другом
убывала:
1) [0; тс]; 2) [|; 2тс]; 3) [-тс; 0]; 4) [-2тс; -тс].
57. С помощью свойств возрастания или убывания функции
y = sinx сравнить числа:
1) sin-^ и sin^; 2) sin^f* и sin^;
3) sin(-^) и sin(--^); 4) sin7 и sin6.
58. Найти все принадлежащие отрезку [0; Зтс] корни
уравнения:
^fs 2) sinx=^; 3) sinx = -^; 4) ^
2 2 2 2
59. Найти все принадлежащие отрезку [0; Зтс] решения
неравенства:
1) sinjo^-; 2) sinx<^;
£t 2
3) sinx>-—; 4)
2
60. Построив график функции y = f(x), найти: а) область
определения функции; б) множество значений; в) промежутки
убывания:
[sinл:, если 0<л:<Зтс,
J-x, если х<0;
2) /(*)=
sin л:, если —
4
cos л:, если -2тс<д:<-^.
4
. п
61. Выразив косинус через синус по формулам приведения,
сравнить числа:
1) sin£ и cos£; 2) sin^ и cos^;
9 9 о о
3)sin|H cos|j; 4) sin | и cos |J.
62. Найти все принадлежащие промежутку — < х < тс корни
уравнения:
1) sin2x = -i; 2) sin3x=^.
2 2
24 Глава I
Тригонометрические функции
63. Найти все принадлежащие множеству решений
неравенства \1х — 1 < 2 корни уравнения sinx = ——.
64. Найти все принадлежащие промежутку —~ < х < п
решения неравенства:
--^; 2) ^
65. Найти множество значений функции i/ = sinx, если х
принадлежит промежутку:
1} Le; Я1'2) 1т- tJ-
66. Найти промежутки убывания функции на заданном отрезке:
2) y = -sinx, [-n; 2тг].
67. Реп1ить графически уравнение:
1) sinx=-^-x-|; 2) sinx = 2--x;
О7Г о К
3) -sinx = Vx; 4) sin x = cos л:.
68. С помощью графиков функций выяснить, имеет ли
решение система уравнений:
sin л:,
1)
69. Сколько решений имеет система уравнений:
1) у = 2 sin х, 2) Г у + 1 = - sin x,
y = logix; [y=Vx?
з
70. Построить график и выяснить свойства функции:
1) y=l-sinx; 2) y = 2 + sinx; 3) i/ = sin3x;
4) i/ = 2sinx; 5) i/ = 3sin|s 6) i/ = 2-sin2x.
71. Построить график функции:
1) y = sin\x\; 2) y = \sinx\;
3) i/ = sin x -x; 4) y = log! sinx.
|72.j Сила переменного электрического тока является
функцией, зависящей от времени, и выражается формулой
J=Asin(co£ + (p), где А — амплитуда колебания, ю —
частота, ф — начальная фаза. Построить график функции, если:
1) А = 2, ш = 1, Ф=|; 2) А=1, ш = 2, Ф=|.
f7371 Решить неравенство:
[X — 2 cos2 л:<0.
§ 4 25
1) sin2x>v; 2) 3 sin л:-2 cos2 л: <0.
4
Свойства функции y=sinx и ее график
§ 5. Свойства и графики функций y=tgx
и y=ctgx
Функция y = tgx определена при х^^+пп, n€Zy является
нечетной и периодической с периодом п; поэтому достаточно
построить ее график на промежутке 0; ^-J. Затем, отразив его
симметрично относительно начала координат, получить график
на интервале (—•?■; ^-)» Наконец, используя периодичность, по-
строить график функции y = tgx на всей области определения.
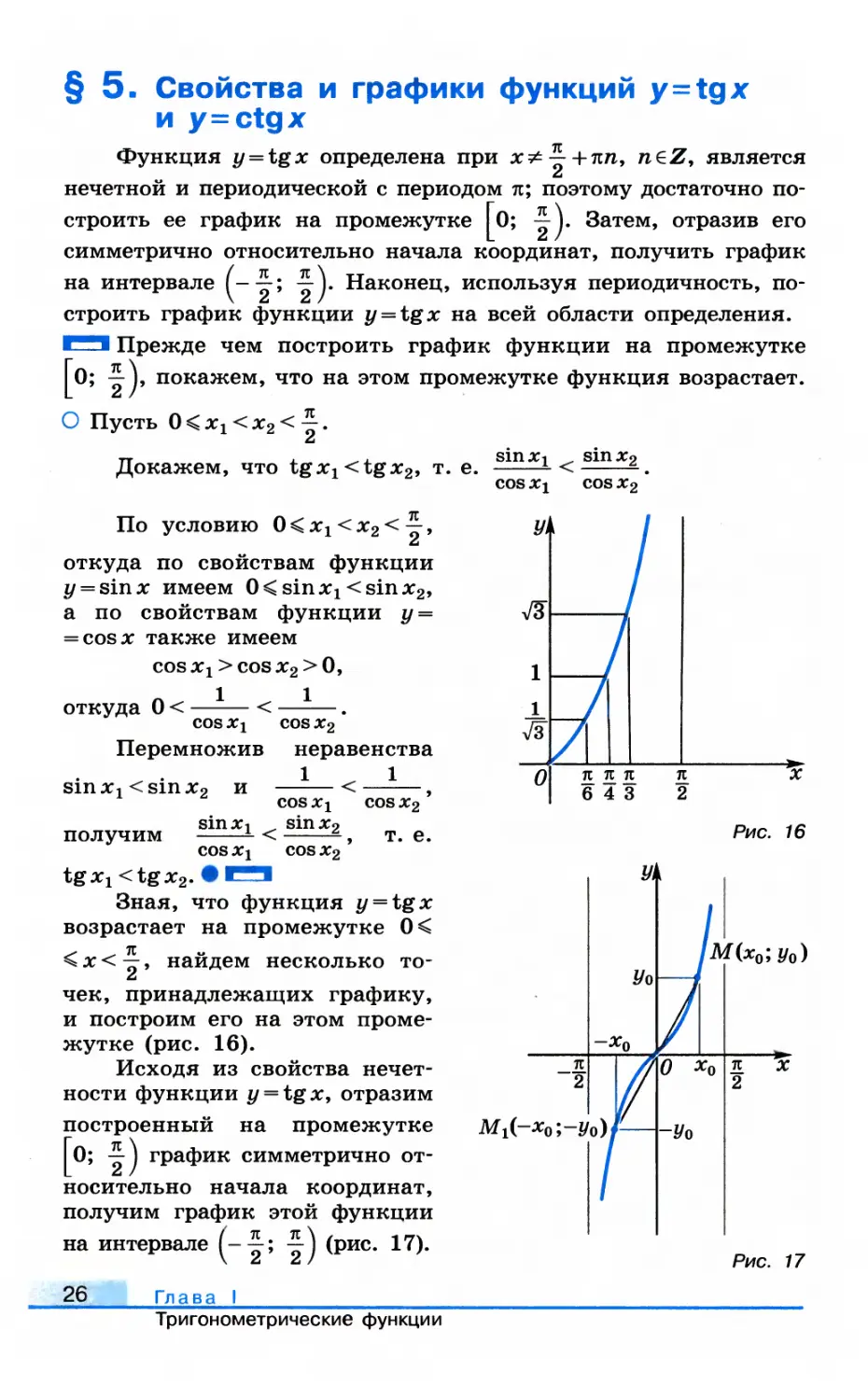
Прежде чем построить график функции на промежутке
0; -М, покажем, что на этом промежутке функция возрастает.
О Пусть 0<хг<х2<%-
Докажем, что tgxr<tgx2, т. е. smxi < smx2 ^
cos xi cos x2
По условию 0<x1<x2<^r,
откуда по свойствам функции
i/ = sinx имеем 0<sinx1<sinx2»
а по свойствам функции у =
= cosx также имеем
cos х1 > cos х2 > 0,
откуда 0 < < .
cos xi cos х2
Перемножив неравенства
sinx1<sinjc2 и <
1 z
получим
COS Xi COS X2
Зная, что функция y = tgx
возрастает на промежутке 0<
< х < ~, найдем несколько
точек, принадлежащих графику,
и построим его на этом
промежутке (рис. 16).
Исходя из свойства
нечетности функции y = tgx, отразим
построенный на промежутке
0; — j график симметрично
относительно начала координат,
получим график этой функции
на интервале (-^; ^) (рис. 17).
26
Уо
-хп
Рис. 16
М(хо;уо)
-Уо
Рис. 17
Гл а в а I
Тригонометрические функции
Зл
"2
1
-1
Рис. 78
Напомним, что при х = ±— функция y = tgx не определена.
Если х<^- и х приближается к ^, то sinx приближается к 1,
a cosjc, оставаясь положительным, стремится к нулю. При этом
дробь smx =tgx неограниченно возрастает, и прямые х=^- и
COS X ли
х = -^г являются вертикальными асимптотами.
Перейдем к построению графика функции y = tgx на всей
области определения. Функция y = tgx — периодическая с
периодом я. Следовательно, график этой функции получается из ее
графика на интервале (-^; ^) (см. рис. 17) сдвигами вдоль оси
абсцисс на яп, neZ (рис. 18).
Итак, весь график функции y = tgx строится с помощью
геометрических преобразований его части, построенной на
промежутке [0; |-).
Свойства функции y = tgx можно получить, опираясь на
свойства этой функции на промежутке 0; ^-1. Например,
функция y = tgx возрастает на интервале (-—; ^), так как эта функ-
ция возрастает на промежутке 0; — J и является нечетной.
Основные свойства функции y = tgx
1) Область определения — множество всех действительных
чисел jc^-^+тш, neZ.
2) Множество значений — множество R всех
действительных чисел.
3) Прямые х=^+пп, n€Z, являются вертикальными
асимптотами.
4) Периодическая, Т = п.
§ 5
27
Свойства и графики функций y=tgx и y=ctgx
5) Нечетная.
6) Функция принимает:
— значение, равное 0, при х = пп, n€Z;
— положительные значения на интервалах (пп; ^
neZ; V г
— отрицательные значения на интервалах ( — -^г
V 2
пп),
7) Возрастающая на интервалах (—^+пп; ~
Задача 1. Найти все корни уравнения tgx = 2,
принадлежащие отрезку - п < х < -£-.
t> Построим графики функций y = tgx и у = 2 на данном отрезке
(рис. 19, а). Эти графики пересекаются в трех точках,
абсциссы которых Xi9 х2, х3 являются корнями уравнения tgx = 2. На
интервале (-—1 ^) уравнение имеет корень Xj=arctg2. Так как
функция y = tgx периодическая с периодом п, то x2 = arctg2 + n,
Ответ. x1 = arctg2, x2 = arctg2 + n, xs = arctg2-n. M
Задача 2. Найти все решения неравенства tgx<2,
принадлежащие отрезку - п < х < -^-.
—п
а)
Зтс
2
Рис. 79
28
Гл а в а I
Тригонометрические функции
[> Из рисунка 19, а видно, что график функции y = tgx лежит
не выше прямой у = 2 на промежутках [—п; xs], (~^» xi\ и
(■|; х2], т. е. -7c<x<-7cH-arctg2, -|-<x<arctg2, -|<:x;<7i+arctg2. <4
СЗ Задача 3. Реп1ить неравенство tgx>l.
t> Построим графики функций y = tgx и у=1 (рис. 19, б).
Рисунок показывает, что график функции y = tgx лежит выше
прямой i/=l на промежутке f-j; —l, а также на промежутках,
полученных сдвигами его на п, 2тг, Зя, —я, — 2п и т. д.
Ответ. ^+пп<х<^-+пп, n€Z. 4^3
По формулам приведения функция у = ctgx может быть
представлена как у = — tg(x+ — J. Свойства функции у = ctgx
можно получить, исследуя функцию у = — tg(x+^J.
E^l Основные свойства функции у = ctgx
1) Область определения — все действительные числа,
кроме х = пп, n€Z.
2) Множество значений — множество R всех
действительных чисел.
3) Прямые х = пп, n€Z, являются вертикальными
асимптотами.
4) Периодическая, Т = п.
5) Нечетная.
6) Убывающая на интервалах (пп; к + пп), n€Z.
График функции у = ctgx можно построить сдвигом
графика функции y = tgx на ^ единиц влево, затем осуществить
симметрию относительно оси Ох (рис. 20).
\у =tgx
Свойства и графики функций y=tgx и у = ctgx
Задача 4. Построить график функции y = ctg(2x + ^ J.
[> График функции y = ctg(2x + -jM =ctg2fx-h -^V Функция
периодическая с периодом ^, ее график можно построить с
помощью преобразований графика функции y = ctgx так:
1) выполнить сдвиг на -^ единиц влево;
2) выполнить сжатие графика функции y = ctg(x+^?J
вдоль оси абсцисс к прямой х = -^ в 2 раза.
о
Полученный график изображен на рисунке 21. ^
i/ = ctgx
Рис. 21
30
Глава I
Тригонометрические функции
"Ж"
"2"
-п -
2
Рис. 22
Задача 5. Построить график функции y = yigx.
[> Функция определена при условии, что функция tgx
принимает неотрицательные значения, т. е. при 7m<x< ~ +7m, n€Z.
Функция периодическая с периодом я, так как если х
принадлежит области определения, то х — п и х + п принадлежат
области определения и при этом y/tg(x±n) = y/tgx.
Функция возрастает при 0 < х < — (по свойству сложной
функции) и принимает только неотрицательные значения.
График функции изображен на рисунке 22. М ^3
Тригонометрические функции широко применяются в
математике, физике и технике. Например, многие процессы,
такие, как колебания струны, маятника, напряжение в цепи
переменного тока и т. д., описываются функциями, которые
задаются формулами вида i/=Asin(co:x; + (p). Такие процессы
называют гармоническими колебаниями, а описывающие их
функции — гармониками (от греческого слова harmonikos —
соразмерный). График функции y=Asin((dx + (p) получается из
синусоиды y = sinx сжатием или растяжением ее вдоль
координатных осей и сдвигом вдоль оси Ох. Обычно гармоническое
колебание является функцией времени t, т. е. i/=Asin(co£ + (p),
где А — амплитуда колебания, со — частота, ср — начальная
фаза, а — — период колебания,
со
Упражнения
74. (Устно.) Выяснить, при каких значениях х из
промежутка -п<х<2п функция y = tgx принимает: 1) значение,
равное 0; 2) положительные значения; 3) отрицательные
значения.
§ 5
31
Свойства и графики функций y=tgx и y=ctgx
75. (Устно.) Выяснить, является ли функция y = tgx
возрастающей на промежутке:
76. Найти значение функции при заданном значении
аргумента:
1) y = tgx, x=^; 2) y = tg3x, x=^;
3) y = ctgx, х=^-; 4) i/ = ctg|, х=|.
77. Найти значение функции i/=- при:
78. Выяснить, принадлежит ли графику функции i/ = tg 2л:
точка с координатами:
„ (&, _!), 2) (Ш, f):
«(•41, VI).
79. С помощью свойств функций i/ = tga: и y = ctgx сравнить
числа:
1) tg| и tgi; 2) ctg^ и ctg^;
3)tg(-f)ntg(-f); 4)tg(-f)ntg(-f);
5) ctg2 и ctg3; 6) tgl и tgl,5.
80. Найти все принадлежащие промежутку (-п; 2п) корни
уравнения:
1) ctgx=l; 2) tgx = V3; 3) ctgx = -V3; 4) tgx = -l.
81. Найти все принадлежащие промежутку (-п; 2п) решения
неравенства:
1) tgx>l; 2) tgx<^§-; 3) ctgx<-l; 4) V
82. Построив график функции y = f(x), найти: а) область
определения; б) множество значений; в) промежутки
возрастания:
[sinл:, если — п<:Х<п;
2) ft.
cosx, если -~к^х<-^-
2 2
83. Решить неравенство:
1) ctgjc<l
32 г л а в а I
ctgjc<l; 2) tgx>V3; 3)tgx<-^; 4)
о
Тригонометрические функции
84. Найти все принадлежащие промежутку [0; Зтг] корни
уравнения:
1) tgx = 3; 2) ctgx = -2.
85. Найти все принадлежащие промежутку [0; Зя] решения
неравенства:
1) tgx>3; 2) tgx<4; 3) tgx<-4; 4) tgx>-3.
86. Решить неравенство:
1) ctgx>4; 2) tgx<5; 3) ctgx<-4; 4) tgx>-5.
87. Найти все принадлежащие промежутку (-~; тс) корни
уравнения:
1) tg2* = V3; 2) tg| —1; 3) ctg|=-^L; 4) ctg3x=l.
88. Найти все принадлежащие промежутку (- -^; я) решения
неравенства:
1) tg2*<l; 2) tg3*<-V3; 3) ctgf < ^-; 4) ctgf >1.
89. Построить график и выяснить свойства функции:
() 2) i/ = tg|;
3) y = ctg(x-|); 4) ye
90. Найти множество значений функции y = tgx, если л:
принадлежит промежутку:
1} Г 4; "з J; 2) 1Х; Т> 3) (0; п); 4) [т;
Построить график функции (91—93).
91. 1) y = tg\x\; 2) y = \tgx\; 3) y = ctgx; 4) ^
92; 1) ^-tgxctgx; 2) y = sinxctgx; 3) i/ = 2tg;>£:; 4) i/ =
93. 1) y = tg(Bx-j); 2) z/ = ctg(2x-|).
|94j Решить неравенство:
1) tg2jc<l; 2) tg2x>3; 3) 3sin2xH-sinxcosx>2.
§ 6. Обратные тригонометрические функции
И1. Функция y = arcsinx
По определению арксинуса числа (см. учебник 10 класса)
для каждого х€[-1; 1] определено одно число у = arcsinx. Тем
самым на отрезке [-1; 1] задана функция
у = arcsin х.
Покажем, что функция у = arcsin x является обратной к
функции y = sinx, рассматриваемой на отрезке - —
§ 6 33
Обратные тригонометрические функции
I -1
у = arcsinocу
у = sin*
-1
1 п х
2
-1
-I
Рис. 23
1 х
у = агсэтл;
т
2
Рис. 24
— 9 относи-
О Рассмотрим уравнение sinx = y, где у — заданное число из
отрезка -1<у<1, а л: — неизвестное. На отрезке --^<х<— это
уравнение по определению арксинуса числа имеет
единственный корень х = arcsin у.
Поменяв в этой формуле местами х и у, получим у = arcsin x. •
Таким образом, свойства функции у = arcsin x можно
получить из свойств функции y = sinx. График функции у = arcsin x
симметричен графику функции y = sinx, - —
тельно прямой у = х (рис. 23, 24).
Основные свойства функции у = arcsin x
1) Область определения — отрезок [-1; 1].
2) Множество значений — от-
резок [--; -J. ук
3) Нечетная, так как
arcsin (- х) = — arcsin x. ■ —
4) Возрастающая. d5i
ИИ Для функции у = sin x
обратную можно найти, например, на
отрезке ^ ; -£ . На нем
функция y = sinx убывает от 1 до
— 1, т. е. на этом промежутке
функция имеет обратную. Для
ее нахождения возьмем
произвольное значение у0 из
множества [-1; 1] и найдем соответству-
34 Глава I
Тригонометрические функции
-1
Рис 26
Рис. 27
Г л Зтс ]
ющее значение х0, исходя из того, что yo = smxo, хо€ —; — .
Очевидно, что х0 = п — arcsin Уо> Поменяв местами х и у,
получим функцию у = п- arcsin x. Таким образом, для функции
у = sin а; на отрезке ^ ; -^ обратной будет функция у = п - arcsin x
с областью определения [—1; 1] и множеством значений —; —
(рис. 25). ВЯ
■^12. Функция у = arccos л:
По определению арккосинуса числа для каждого х€[— 1; 1]
определено одно число у = arccos x. Тем самым на отрезке [—1; 1]
определена функция у = arccos x. Эта функция является
обратной к функции i/ = cosx, рассматриваемой на отрезке 0<л:<7с.
График функции у = arccos x симметричен графику функции
у = cosх, 0<х<п, относительно прямой у = х (рис. 26, 27).
Основные свойства функции у = arccos x
II) Область определения — отрезок [-1; 1].
2) Множество значений — отрезок [0; я].
3) Убывающая.
3. Функции y = sirctgx и y = Sircctgx
По определению арктангенса числа для каждого
действительного х определено одно число y = arctgx. Тем самым на
всей числовой прямой определена функция y = arctgx. Эта
функция является обратной к функции y = tgx, рассматриваемой
на интервале -^ <х<^. График функции y = arctgx (рис. 28)
tgx, - — <x<— (см. рис. 17),
получается из графика функции y
симметрией относительно прямой у = х.
§ 6
35
Обратные тригонометрические функции
Рис. 28
Основные свойства функции y = arctgx
1) Область определения — множество R всех
действительных чисел.
2) Множество значений — интервал (-тг ; 1>\
3) Возрастающая.
4) Нечетная, arctg(-x) = -arctgx.
По определению арккотангенса числа для каждого
действительного х определено одно число y = arcctgx. Тем самым на
всей числовой прямой определена функция y = arcctgx. Эта
функция является обратной к функции y = ctgx9
рассматриваемой на интервале (0; я). График функции y = arcctgx
получается из графика функции y = ctgx, x€(0; я), симметрией
относительно прямой у = х.
Основные свойства функции i/ = arcctgx
1) Область определения — множество JR.
2) Множество значений — интервал (0; я).
3) Убывающая.
4) Нечетная, arcctg(-x) = -arcctgx.
<\
Задача 1. Решить уравнение arccos(3xH-l)= —.
D> Так как -^€[0; я], то по определению арккосинуса числа
данное уравнение равносильно уравнению Зх +1 = cos —,
откуда Зх+1 = -|, х = -±. <4
Задача 2. Найти область определения функции
. х-2
у = arcsin .
о
t> Так как функция у = arcsint определена при -КК1, то
х-2
функция у = arcsin определена для тех значений х, для ко-
х — 2
торых выполняются неравенства -К < 1. Отсюда -3<л:-2<3,
36
Гл а в а I
Тригонометрические функции
\
п
2
У,
п
2
/
п
2
/
0
п
2
У
\
\
= arcsin (sinjc)
\
"\ Чу
/
/2л
Т
\,
Рис. 29
Задача 3. Найти значение функции у = tg х при х = arcsin —.
2 п п 2
[> Так как х = arcsin—, то — — <л:< —, sinx=—, т. е. х — угол
о Z Z о
первой четверти.
Найдем cos л:: по формуле | cos х\ = Vl - sin2 х = у1-( —) =
= -^-. Так как х—угол I четверти, то cosx=-^- и tgx =
о о
_ 2tV5_ 2V5 ^ и
"3: 3 " 5 # ^
^Д Задача 4. Построить график функции у = arcsin (sin x).
t> Функция определена на всем множестве действительных
чисел, ее период равен 2тг. Построим график функции на от-
~~2; ~2У ЛИ ~~2 ¥' Т° ^ = ЛГ# ЕсЛИ 2^ X Y'
^^ из определения арксинуса следует,
что arcsin(sin(x-7c)) = x-7c. Так как sin (х - п) = - sin x, то
arcsin (sin (x — п)) = arcsin (— sin x) = — arcsin (sin x).
Таким образом, если jc€ — ; -5-» то х —п — — arcsin (sin x) и
arcsin (sin х) = п — х. Следовательно, на отрезке — — ; —
то --^
у = arcsin (sin x) =
\х9 если --<х< -,
: — х, если —
Зя
—.
График изображен на рисунке 29. М ВЯ
Упражнения
Сравнить числа (95—97).
95. 1) arcsin^ и arcsin-== ; 2) arcsinf- —) и arcsinf- —);
— УЗ V10 v 3/ V 4/
оч 3 . V5 А ч . / V2 \ . / 3 \
3) arcsin— и arcsin — ; 4) arcsin (——I и arcsin (- — I.
§ 6
37
Обратные тригонометрические функции
96. 1) arccos-т= и arccos-т=; 2) arccosf-—] и arccosf- —);
3) arccos-V и arccosf-; 4) arccosf—=) и arccosf- — ).
4 7 ^ v 5 ' V 7 /
97. 1) arctg2\/3 и arctg3\/2; 2) arctg (--p) и arctgf--iA-
3) arcctgV5 и arcctgV^; 4) arcctgf-— ) и arcctg(-V2).
Решить уравнение (98—100).
98. 1) arcsin(2-3x)=^; 2) arcsin(3-2x)= ^;
О 4
оч x-2 n AX . jc + 3 n
3) arcsin = - —; 4) arcsin —— = - —.
99. 1) arccos(2x + 3)=^; 2) arccos(3x+l)= ^;
O4 jc+1 2л А. 2x-\
3) arccos —-— = -r-; 4) arccos —-— = я.
О О О
100,1) arctg -^ - f; 2) arctg ^±^ = J;
3) arctg(2x+l) = -|; 4) arctg(2-3x) = - |.
101. Найти область определения функции:
х— 3
1) у = arcsin ; 2) z/ = arccos(2-3x);
^ 2^*i
3) i/ = arccos(2V^-3); 4) y = arcsin—о—;
5) у = arccos—^—; 6) у = arcsin(Z^fx — 2);
7) i/ = arcsin (x2 -2); 8) i/ = arccos (x2-x).
102. Доказать, что график функции у = arccos x симметричен
относительно точки (О; ^J.
103. Построить график функции:
1) у = arcsin (2x + 3); 2) у = 2 arccos (х-1);
3) i/ = arcctgx; 4) i/ = arcctg(jc+l).
104. Доказать, что arcsin х + arccos х = ■£.
&.O57IДоказать, что arccos(-л:) = я-arccosx.
[10бТ]Построить график функции:
1) у = arccos (cos x);
2) у = arcsin (cos x).
107. Найти функцию, обратную к функции y = cosx на
отрезке [-я; 0].
38 Глава I
Тригонометрические функции
Упражнения к главе К
108. Найти область определения функции:
1) w = sinx + cosjc; 2) у = sinx + tgx; 3) y = \Jsinx;
I 2х cos x
4) y=\cosx; 5) у=-^—. г-; 6)
7 v v 2sinjc-l
* 2sin2*-sin*'
109. Найти множество значений функции:
1) i/ = l-2sin2x; 2) i/=2cos2x-l;
3) i/ = 3-2sin2x; 4) i/ = 2cos2xH-5;
5) i/ = cos Sx sin х- sin Sx cos л: + 4;
6) у = cos 2л: cos x + sin 2x sin л: — 3.
110. Выяснить, является ли четной или нечетной функция:
1) y = x2 + cosx; 2) y = xs-sinx;
3) i/ = (1-х2)cosx; 4) i/ = (lH-sinx)sinx.
111. Доказать, что наименьший положительный период
функции y = f(x) равен Т:
T=^; 2) i/ = sin|, Т
112. Сравнить числа:
1) sinl и cos2; 2) sin(-l) и cosl;
3) sin3,5 и tg3,5; 4) cos3 и tg4.
113. Выяснить, какая из функций y = sinx или y = cosx
является убывающей на промежутке:
1) [«;?]; 2) [О; |]; 8) [-Я;-|]; 4) [|;Я].
114. Найти множество значений функции y = f(x) на промелсут-
I я я 1
ке|-6; ^>если:
1) f(x) = sinx; 2) f(x) = cosx; 3) /(x) = tgx.
115. С помощью графика функции y = cosx найти такие
значения х из заданного промежутка, при которых
справедливо равенство:
14 1 Г Я 1 оч V2 Г ЗТГ Л1
1) cosx = --, [--; TiJ; 2) cosx=—, [--у; 0J.
116. С помощью графиков функции y = tgx и y = ctgx найти все
такие значения х из заданного промежутка, при которых
справедливо неравенство:
1) tgx<V3, [-тс; тс]; 2) ctgx<l, (-тс; -^];
3) ctgx>-l, [-|; 2тс); 4) tgx>-V3, (-^; тс].
117. Найти принадлежащие промежутку [0; Зтс] корни
уравнения:
0; 2) V3
3) 3tgx = V3; 4) cosjch-1 = 0.
39_
Упражнения к главе I
118. Найти все принадлежащие промежутку [-2п; —п] решения
неравенства:
1) l + 2cosx>0; 2) l-2sinx<0;
3) 2 + tgx>0; 4) l-2tgx<0.
119. С помощью графиков функций найти число корней
уравнения:
1) cosх = х2; 2) sinx=—.
120. Построить график функции:
1) y= — sinx; 2) y = cosx-—.
121. Расположить в порядке убывания числа:
2) tg3, tgl,8, tg2, tg4,5.
122. Найти область определения функции:
l)y-tg(2*+£); 2) y-Vtg^.
123. Найти наиболыпее и наименыпее значения функции:
1) у = cos4 л; — sin4 x; 2) i/ = sinfxH- —I sinlx-— J;
3) i/=l-2|sin3jc|; 4) i/ = sin2x-2cos2x.
124. Выяснить, является ли четной или нечетной функция:
1) y = sinx + tgx; 2) y = sinxtgx; 3) у = sinx|cosx|.
125. Найти наименьший положительный период функции:
1) y = 2sin(2x+l); 2) i/ = 3tg|(x+l).
126. Решить графически уравнение:
1) cosx = |x|; 2) sinx = -|x+l|.
127. Найти нули функции:
1) г/ = cos2 л: - cos x;
2) г/ = cosх-cos2дг-sinЗл:.
128. Решить уравнение:
1) arccos(x-3)=-^-; 2) arcsinl—— 1=-—.
1129. i Найти все значения х, при которых функция
принимает положительные значения.
ft.30.1 Построить график функции:
1) i/ = 2sin^H-|-j-2; 2)
3) y = cos\x\; 4) y = -sinx;
5) i/ = sinx + |sinx|; 6) y = 2sinx.
40 Глава 1
Тригонометрические функции
1j Найти множество значений функции:
1) I/= 12 sin л:-5 cos jc; 2) i/ = cos2x-sinx.
[I32j Решить неравенство:
2) tgx>sinx.
Вопросы к главе I
1. Назвать множество значений каждой из функций
y = sinx, y = cosx.
2. Назвать область определения каждой из функций
y = tgx, y = ctgx.
3. Какая из функций
y = sinx, y = cosx, y = tgx, y = ctgx
является четной?
4. Какая функция называется периодической?
5. Привести пример функции, у которой наименьший
положительный период равен: 2п; к; —; Зтг.
6. Назвать промежутки возрастания каждой из функций
7. При каких значениях х каждая из функций
y = tgx, y = ctgx
принимает положительные значения?
8. При каких значениях х каждая из функций
y = sinx, y = cosx
принимает наибольшее и наименьшее значения?
Назвать область определения каждой из функций
у = arcsin xf i/ = arccosx.
Ж1 Назвать множество значений каждой из функций
y = arctgx, y = arcctgx.
Проверь себя!
1. Найти область определения функции y = tg2x. Является ли
эта функция четной?
2. Построить графики функций y = sinx, y = cosx на отрезке
[-2тг; я]. Для каждой из этих функций найти значения х
из данного отрезка, при которых:
1) у(х)=1; 2) у(х) = -1; 3) у(х) = О;
4)у(х)>0; 5) у(х)<0.
3. Найти все значения х из промежутка —; 2тг , для которых
1 L2
выполняется неравенство cos л: < - —.
4. Расположить в порядке возрастания числа:
.71 . 4% 57С . п
ctg-; ctg —; ctg —; ctg2.
41
Вопросы к главе I
Построить график функции y = -cosx и найти значения х,
при которых функция: а) принимает отрицательные
значения; б) убывает.
2. Построить график функции y = sin(^ -x) и найти значения х,
при которых функция принимает положительные
значения.
3. С помощью графиков функций выяснить, сколько корней
имеет уравнение cos x = \g x.
4. Найти множество значений функции у = sin2 x 4- 2 cos 2x.
Исследовать функцию y = —sin(2x——) + l и построить ее
график.
I ^А I Историческая справка
Тригонометрические функции (получившие название от
греч. trigonon — треугольник и metreo — измеряю) играют
большую роль в математике и ее приложениях.
Исследованием тригонометрических функций практически
занимались еще древнегреческие математики, изучая взаимное
изменение величин в геометрии и астрономии. Отношения
сторон в прямоугольных треугольниках, по своей сути
являющиеся тригонометрическими функциями, рассматривались уже в
IV — III в. до н. э. в работах Евклида, Архимеда, Аполлония
и других ученых.
Учение о тригонометрических величинах получило
развитие в VIII — IX вв. в странах Среднего и Ближнего Востока.
Так, в IX в. в Багдаде аль-Хорезми составил первые таблицы
синусов. Аль-Бузджани в X в. сформулировал теорему синусов
и с ее помощью построил таблицу синусов с интервалом 15', в
которой значения синусов приведены с точностью до восьмого
десятичного знака. Ахмад-аль-Беруни в XI в. вместо деления
радиуса на части при определении значений синуса и
косинуса, сделанного до него Птолемеем, начал использовать
окружность единичного радиуса. В первой половине XV в. аль-Каши
создал тригонометрические таблицы с шагом 1', которые в
последующие 250 лет были непревзойденными по точности.
Самым крупным европейским представителем той эпохи,
внесшим вклад в развитие исследования тригонометрических
функций, считается Региомонтан.
В начале XVII в. в развитии тригонометрии наметилось
новое направление — аналитическое. Если до этого учения о
тригонометрических функциях строились на геометрической
основе, то в XVII — XIX вв. тригонометрия постепенно вошла в
состав математического анализа и стала широко использоваться
в механике и технике, особенно при рассмотрении
колебательных процессов и иных периодических явлений.
42 Глава I
Тригонометрические функции
О свойствах периодичности тригонометрических функций
знал еще Ф. Виет. Швейцарский математик И. Бернулли в
своих работах начал применять символы тригонометрических
функций. Однако близкую к принятой теперь символику ввел
Л. Эйлер в 1748 г. в своей работе «Введение в анализ
бесконечных». В ней он рассмотрел вопрос о знаках всех
тригонометрических функций любого аргумента.
Тригонометрические функции Эйлер рассматривал как
особые числа, называя их общим термином трансцендентные
количества, получающиеся из круга. Для вычисления
приближенных значений sin л: и cos л: он получил их разложения в
ряды:
х2 х4 х6
1- — + — - — + • m
2! 4! 6! » l *
xs х5 х7
у I |_ (О\
3! 5! 7! ### # '
Можно показать, что графики функций, образованных
разным числом членов ряда (1) или (2), постепенно приближаются
к графику функции y = cosx или i/ = sinx.
В XIX в. дальнейшее развитие теории тригонометрических
функций было продолжено в работах русского математика
Н.И.Лобачевского (1792—1856), а также в трудах других
ученых, например в работах профессоров МГУ Д. Е. Меньшова,
Н. К. Бари, А. Н. Колмогорова.
Глава
Производная
и ее геометрический
смысл
Все большие этапы развития
математики всегда были связаны
с воздействием тех или иных видов
практической деятельности.
А. Н. Тихонов
§ 1. Предел последовательности
1. Числовые последовательности
Обратимся к понятию числовой
последовательности, рассмотренному в курсе алгебры
9—10 классов.
Если каждому натуральному числу п
поставлено в соответствие некоторое
действительное число хп, то говорят, что задана числовая
последовательность (или просто
последовательность)
Кратко последовательность обозначают
символом {хп} или (хп), при этом хп называют
членом или элементом этой
последовательности, п — номером члена хп.
Числовая последовательность — это
функция, область определения которой есть
множество N всех натуральных чисел. Множество
значений этой функции, т. е. совокупность
чисел хп9 n€N, называют множеством значений
последовательности.
Множество значений последовательности
может быть как конечным, так и
бесконечным, в то время как множество ее элементов
всегда является бесконечным: любые два
разных элемента последовательности отличаются
своими номерами.
Например, множество значений
последовательности {(-1)"} состоит из двух чисел 1 и -1,
а множества значений последовательностей
{п2} и I— бесконечны.
I п J
Глава II
Производная и ее геометрический смысл
Последовательность может быть задана с помощью
формулы, позволяющей вычислить каждый член последовательности
„ (- 1)п +1
по его номеру. Например, если хп = -6 , то каждый не-
четный член последовательности равен 0, а каждый четный
член равен 1.
Иногда последовательность задается рекуррентной
формулой, позволяющей находить каждый член последовательности
по известному предыдущему. При таком способе задания
последовательности обычно указывают:
а) первый член последовательности хх (или несколько
членов, например хх, х2);
б) формулу, связывающую n-й член с предыдущими членами.
Так, арифметическая прогрессия с разностью d и
геометрическая прогрессия со знаменателем q^O задаются
соответственно рекуррентными формулами
n+i nq
Зная первый член каждой прогрессии аг и Ь19 можно
получить формулу (тг+1)-го члена соответствующей прогрессии:
Рекуррентной формулой хп = хп_х +хп_2, neN, п>3, и
условиями х1 = 1у х2 = 1 задается последовательность Фибоначчи.
В некоторых случаях последовательность может быть
задана описанием ее членов. Например, если хп — простое число
с номером п, то хг = 2, х2 = 3, xs = 5, х4 = 7, дг5 = 11 и т. д.
Отметим, наконец, что последовательность {хп} можно
изобразить:
а) точками с координатами (/г; хп), neN, на плоскости;
б) точками хп, neN, на числовой оси.
2. Определение предела последовательности
Понятие предела последовательности было введено в
учебнике алгебры и начал математического анализа для 10 класса
(глава IV, § 1) и использовалось при вычислении суммы
бесконечно убывающей геометрической прогрессии.
Предваряя введение строгого определения предела
последовательности, рассмотрим примеры числовых
последовательностей {хп} и \уп}, где
.ИГ 1
1 +
\хп). и>2'3'4'5'6'7'8'9' ##"
(„1.1 I i i 1 1
Wnh 2' 4' 8' 16' 32' 64' "" "
Изобразим члены этих последовательностей точками на
числовой прямой (рис. 30, 31).
§ 1 45
Предел последовательности
0 1 0 1
—• • ♦ I •—• ► • ♦# # 1 ►
xx x3 x5 x4 x2 x УъУ2Ух У
Рис. 30 Рис. 31
Заметим, что члены последовательности {хп} как бы
«сгущаются» около точки 1 (см. рис. 30), располагаясь правее
точки 1 при четных п и левее точки 1 при нечетных п. С
увеличением п расстояние от точки хп до точки 1 уменьшается
(стремится к нулю). Поэтому число 1 называют пределом
последовательности {хп} при п->оо и пишут lim xn = l.
п —► оо
Аналогично члены последовательности {уп} с ростом п
«приближаются» к точке 0 (см. рис. 31), и поэтому lim yn = 0.
п —*■ оо
^^Я Введем определение предела последовательности.
Определение
Число а называется пределом последовательности {хп},
если для каждого е>0 существует такой номер iVe, что для
всех n>NE выполняется неравенство \хп — а|<е. Г^Ч
Если а — предел последовательности, то пишут lim xn = a
п —► оо
или хп-+а при /г—►оо.
Последовательность, у которой существует предел,
называют сходящейся. Последовательность, не являющуюся
сходящейся, называют расходящейся; иначе говоря,
последовательность называют расходящейся, если никакое число не
является ее пределом.
СЭЗаметим, что если хп = а для всех n€N (такую
последовательность называют стационарной), то lim xn = a.
п —► оо
Из определения предела последовательности следует, что
последовательность {хп} имеет предел, равный а, тогда и
только тогда, когда последовательность {хп-а} имеет предел,
равный нулю.
Задача 1. Доказать, что предел последовательности {хп}
равен а:
1) **=^, а = 1; 2) xn=-U a = 0;
1 1 1
Г> 1) Докажем, что lim хп = 1. Так как хп = 1 — —, то \х„ —1|=—.
п — оо п п
Возьмем произвольное число е>0. Неравенство \хп-\\<г будет
выполняться, если ^<8» т# е# ПРИ n>Y' ^ы^ерем в качестве
NE какое-нибудь натуральное число, удовлетворяющее условию
46 Глава 11
Производная и ее геометрический смысл
ЛГе>у, например число ЛГе= у +1, где \ — \ — целая часть
числа —, т. е. наибольшее целое число, не превосходящее —.
Ь о
Тогда для всех n>N£ будет выполняться неравенство
|#л-1|= — <
<е. По определению предела это означает, что
e
lim х„=1, т. е. lim -^1 = 1.
П-+ оо п —► оо 71
2) Воспользуемся тем, что
-о
= —— И ПРИ 8 > О
1 1 9
неравенство —=-<8 равносильно каждому из неравенств — <8 ,
п>—. Пусть ЛГе= — +1, тогда <82, -у=<г и при всех
выполняются неравенства
-О
е.
Поэтому lim —j=- = 0.
Аналогично можно доказать, что lim — = 0, если а>0.
3) Умножив и разделив хп на V/M^+V/i+T, получим
откуда \хп\<
:. Неравенство
2Ул
<8 будет выполняться,
если у/п>—, т. е. при тг>—j. Пусть iVe= —^ +1, тогда для
всех тг >АГе выполняются неравенства |л:п|<
^^т=
<8. ЭТО
означает, что lim хп = 0, т. е. lim (\jn+l-y
71 —► ОО П —► ОО
4>Так как *(*ттг i~ *тт'TO *--1-i+W+-+
Обратимся еще раз к определению предела. Согласно
определению число а является пределом последовательности {хп},
если при всех n^Ne выполняется неравенство \хп — а|<8,
которое можно записать в виде а-г<хп<а + г.
Другими словами, для каждого 8>0 найдется номер АГе,
начиная с которого все члены последовательности {хп}
принадлежат интервалу (а-г; а + г). Этот интервал называют г-окрест-
ностъю точки а (рис. 32).
Итак, число а — предел (iiiiiiimii»iiiiiiiiiiiq >-
последовательности {хп}9 если а—е а а+г х
для каждой 8-окрестности Рис 32
§ 1
47
Предел последовательности
точки а найдется номер, начиная с которого все члены
последовательности принадлежат этой окрестности, так что вне этой
окрестности либо нет ни одного члена последовательности,
либо содержится лишь конечное число членов.
3. Свойства сходящихся последовательностей
Перечислим основные свойства сходящихся
последовательностей.
Свойство 1. Если последовательность {хп} имеет предел,
то она ограничена, т. е. существуют числа сг и с2, такие,
что Ci<:Xn^c2 для всех n€N.
Замечание. Из ограниченности последовательности не
следует ее сходимость. Например, последовательность {(-1)п}
ограничена, но не является сходящейся.
Свойство 2. Если последовательности {хп}, {уп}, {zn}
таковы, что xn<tyn<iZn для всех n€N и lim xn= lim zn = a,
п —► оо п —► оо
то последовательность {уп} сходится и lim yn = a.
п —► оо
Доказательство свойства 2 основано на том, что в любой
окрестности точки а содержатся все члены последовательностей
{хп} и {zn}, за исключением, быть может, конечного числа.
Этим же свойством обладает и последовательность {уп}9 так как
все ее члены заключены между соответствующими членами
последовательностей {хп} и {zn}.
Задача 2. Пусть ап>—1 при всех n€N и lim ап = 0. Дока-
п —► оо
зать, что
lim Vl+ocn=l, keN. (1)
п —► оо
[> Докажем сначала, что
, keN. (2)
В самом деле, если an>0, то
если -1<а„<0, то
1 > Vl+an>( Vl+an)fe = l+an = 1—|an|,
откуда следуют неравенства (2). Применяя свойство 2,
получаем утверждение (1). ^
Замечание. Если хп = \1а+ап, где а>0, ан-ап>0,
^/— ^ / ос
lim an = 0, то хп = \а- \/1ч—- и из (1) следует, что
п —► оо V Л
fty kj—
lim \a + an=\a.
п —*■ оо
48 Глава II
Производная и ее геометрический смысл
Свойство 3. Если хп>уп для всех п и lim хп = а,
lim yn = b, то а>Ъ. Г^
п -* оо
4. Предел монотонной последовательности
Определение 1
Последовательность {хп} называется возрастающей, если
каждый ее последующий член больше предыдущего, т. е.
если хп<хп + 1 для всех п.
Если хп<хп + 1 для всех п, то последовательность {хп}
называют неубывающей.
Определение 2
Последовательность {дгп} называется убывающей, если
каждый предыдущий ее член больше последующего, т. е.
Хп>хп+1 ДЛЯ всеХ п-
Если хп>хп + 1 для всех /г, то последовательность {хп}
называют невозрастающей.
Возрастающие, неубывающие, убывающие и невозрастаю-
щие последовательности называют монотонными.
Теорема 1
Если последовательность {хп} является возрастающей
(или неубывающей) и ограничена сверху, т. е. jcn<M
для всех п, то она имеет предел.
Теорема 2
Если последовательность {хп} является убывающей (или
невозрастающей) и ограничена снизу, т. е. хп>т для
всех /г, то она имеет предел.
Доказательство теорем 1 и 2 обычно дается в курсе
высшей математики. Эти теоремы широко применяются в
математике и, в частности, в геометрии. Рассмотрим квадрат ABCD,
вписанный в круг радиуса R (рис. 33). Соединив отрезками
вершины этого квадрата с серединами
дуг АВ, ВС, CD и DA, получим
правильный 8-угольник,
вписанный в тот же круг.
Продолжая аналогичные
построения, образуем
последовательность правильных 2п-угольников
(п>2), каждый из которых вписан
в тот же круг и получен из
предыдущего удвоением числа его
сторон.
Последовательность площадей
этих правильных многоугольников
является возрастающей, так как
Предел последовательности
каждый последующий многоугольник содержит предыдущий.
Кроме того, эта последовательность ограничена сверху:
площадь каждого из этих многоугольников меньше площади
квадрата, описанного около круга радиуса R. По теореме 1 данная
последовательность имеет предел. Этот предел равен nR2.
И5. Число е
Рассмотрим последовательность {хп}, где xn = (l + — ).
Можно доказать, что {хп} — возрастающая и ограниченная
сверху последовательность. По теореме 1 она имеет предел,
который обозначается е, т. е.
Число е играет важную роль в математике и ее
приложениях. Оно является иррациональным, причем
е^ 2,718281828459045.
6. Вычисление пределов последовательностей
При вычислении пределов последовательностей
используются определение предела, свойство 2 (п. 3), теорема о
пределе монотонной последовательности, а также теорема 3,
связанная с арифметическими действиями над последовательностями
и сформулированная ниже.
Теорема 3
Пусть lim xn = af lim уп = Ъ. Тогда:
Л —♦ ОО Л —• ОО
1) lim (xn + z/n) = a + b;
Л —• ОО
2) lim (xnyn) = ab> в частности если уп = С для всех л, то
Л —- ОО
lim (Cjcn) = Clim xn = Ca9 т. е. постоянный множитель
Л —• ОО Л —» ОО
можно вынести за знак предела;
lim ~
— оо У л
3) lim ~- = £ при условии, что уп*0 для всех пи
л оо У л О
Задача 3. Найти предел последовательности {хп}9 если:
1) Разделив числитель и знаменатель дроби на /г3, получим
2+-?—5-
2 3
= ^ ^—. Так как — —►() при /г-^-оо (AjGiV), то предел
3+
числителя равен 2, а предел знаменателя равен 3. Поэтому по
теореме 3 получим lim хп = —.
Л —» оо о
50 Глава И
Производная и ее геометрический смысл
2) Так как
IS
где -тг-Н т-^ 0 при /г—►оо, то, используя результат задачи 2,
2л 22
получаем lim х„ = lim V^T А / 1 - -^т— н т = \[2.
п-+оо п-юо \' £71 2п
3) Пользуясь тем, что
зг з/ 4 5
Зп Зп3
п
и снова используя результат задачи 2, находим lim хп = у/3. ^ С
1 Задача 4. Найти предел последовательности {хп}9 если:
I; 2) *„-■§£.
[> 1) Умножив и разделив xn на выражение V2/i2+ 4/1 + 5 +
+V2n2-2n + 3, которое называют сопряженным с хп, получим
2
" 2п2 V " 2п2/
откуда следует (задача 2 и теорема 3), что
,. 6 3V2
lim дсп=—^—= —^—.
п-+оо п 2V2 2
2) Так как
а —=—<1, то при всех п выполняется неравенство хп+1<хп, т. е.
{хп} — невозрастающая последовательность. Кроме того, хп > О
при всех п, т. е. последовательность {хп} ограничена снизу.
По теореме 2 эта последовательность имеет предел.
Обозначим его а. Чтобы найти число а, перейдем к пределу в
равенстве (1), учитывая, что lim 2 =0. Отсюда, используя теоре-
п — оо П+1
му 3, получаем а = 0а, т. е. а = 0.
Итак, lim хп = 0. ^ ШШШ
§ 1 51
Предел последовательности
Упражнения
1. Изобразить на числовой прямой несколько членов
последовательности {хп} и выяснить, к какому числу они
приближаются:
х -(1). ЗЪ х - n+1- 4\ х -
2. Исходя из определения предела последовательности,
доказать, что lim xn = 0:
П-+ ОО
1)Ж»"7^Т; 2) *a~Jj=; 3) Хп = ~Ь'
6) хп =
3. Найти предел последовательности {хп}9 если:
х - Sn + 4 - А) X = П~3
Хп- п , 4)Хп
4. Доказать, что последовательность {хп} является
ограниченной, если:
1Ч n\fn оч п + 2 оч 1 1 1
1) ^„ = Sin^-; 2) х.- —; 3) „^-^-ь-^+ ... + _.
Найти Итл:„ (5—6).
Л>CXD
3) xn = V3/i2H-4/n-l-V3/i2-2/iH-5; 4) xn = V/*3 + 2/г - /г.
Найти lim 1 I-...H , где {аЛ — арифметиче-
n-+ooaia2 a2as anan + 1
екая прогрессия, все члены и разность d которой отличны
от нуля.
52 Глава 11
Производная и ее геометрический смысл
§ 2. Предел функции
Ell. Определение предела функции
Важную роль в математике играет понятие предела,
связанное с поведением функции в окрестности данной точки,
т. е. на некотором интервале, содержащем эту точку.
Предваряя определение предела функции, рассмотрим две
задачи.
Задача 1. Исследовать функцию f(x)=—^т- в окрестности
точки х=1.
0 Эта функция определена при хч*1, и f(x) = x+l при х^1.
х2-1
Графиком функции у =——у- (рис. 34) является прямая у = х+1
с «выколотой» точкой (1; 2). Из рисунка видно, что если
значения х близки к 1, то соответствующие значения функции
близки к 2. Число 2 называют пределом функции f(x) в точке
х=1 (при х, стремящемся к 1) и пишут
lim/(x) = 2 или f(x)-+2 при х-*1. М
Задача 2. Исследовать функцию
1х2 + 1 при х>0,
О при дс = О,
х + 1 при х<0
в окрестности точки х = 0.
[> Функция f(x) определена при всех xeR, ее график
изображен на рисунке 35. Из рисунка видно, что при значениях х,
близких кх = О, значения функции близки к I. В этом случае
limf(x)=l. <4
*—О
Замечание. В задаче 1 функция f(x) не определена
в точке х=1, a lim/(x) = 2. В задаче 2 функция f(x) определе-
X—»1
на в точке х = 0, lim/(x)=l, а значение функции в точке х = 0
х-*0
равняется 0.
Рис 34
Предел функции
В задаче 1 абсолютную величину разности f(x)-2 можно
сделать сколь угодно малой (меньше любого положительного
числа е), если значения аргумента х будут достаточно близки
к точке х = 19 причем с уменьшением величины \f(x)-2\ будет
уменьшаться окрестность точки а, в которой выполняется
неравенство |/(л:)-2|<8 (сама точка х=1 из рассмотрения
исключается). Придадим этому утверждению точную формулировку.
Пусть задано число е>0. Найдем такое число 6>0, чтобы
для всех х, таких, что |л;-1|<6, х^1, выполнялось неравенство
|/(л:)-2|<8. Иначе говоря, найдем такое 6>0, чтобы для всех
х, удовлетворяющих условию 0<|л: —1|<6, соответствующие
точки графика функции y = f(x) лежали в горизонтальной
полосе, ограниченной прямыми у = 2-г и у = 2 + 8 (см. рис. 34).
В качестве 6 в задаче 1 можно взять число 6 = 8.
Обратимся к задаче 2, в которой lim/(x)=l. Пусть б>0.
Проведем прямые у=1 — б и у = 1 + г. Тогда в горизонтальной
полосе, ограниченной этими прямыми, лежат все точки графика
функции y = f(x), если 0<|л;|<6, где в качестве 6 выбрано
наименьшее из чисел 8 и Ve (см. рис. 35).
Определение
Число А называется пределом функции f(x) в точке а (при
х, стремящемся к а), если для любого 8>0 найдется
число 6>0, такое, что для всех jc, удовлетворяющих условию
0<|л;-а|<6, выполняется неравенство |/(л:)-Л|<б.
Множество точек х, таких, что |л:-а|<6, х^а9 или
0<|л: —а|<6, называют проколотой Ъ-окрестностью точки а.
Заметим, что число 6, вообще говоря, зависит от 8
(задачи 1, 2). Если А — предел функции f(x) в точке а, то пишут
\imf(x)=A или f(x)-+A при х-+а.
х-+а
Задача 3. Показать, что функция f(x) = (x-3)2 + 5 имеет в
точке х = 3 предел, равный 5.
[> Пусть задано число 8>0. Покажем, что найдется число 6>0,
такое, что для всех х, удовлетворяющих условию \х — 3|<6,
выполняется неравенство |/(д:)-5|<8. Так как \f(x)-5\ = (x-3)2, то
неравенство | / (х) - 51 < 8 равносильно неравенству | х - 31 < Ve".
Возьмем 6 = \/б, тогда из неравенства |л:-3|<6 следует
неравенство \f(x) — 5|<8. По определению предела это означает, что
3
М 2. Различные типы пределов
Односторонние конечные пределы
г> тх ^ *, ч \х2 при х<1,
Задача 4. Исследовать функцию f(x) = \
[дг+1 при х>1
в окрестности точки х=1.
54 Глава II
Производная и ее геометрический смысл
[> График функции y = f(x)
изображен на рисунке 36. Видно, что если
значения х близки к 1, но меньше
1, то значения функции f(x) близки
к 1; если же значения х близки к
1, но больше 1, то значения
функции f(x) близки к 2. В этом случае
говорят, что функция f(x) имеет в
точке х=1 предел слева, равный 1,
и предел справа, равный 2, и пишут
Ит/(л:)= 1, limf(x) = 2. Эти пределы
X—1
1
ЛГ—1
называют односторонними.
Определение 1
-2
Рис. 36
Число Аг называется пределом слева функции f(x) в
точке а, если для любого е>0 существует число 6>0, такое,
что для всех х, удовлетворяющих условию а — &<х<а,
выполняется неравенство \f(x)—A1\<z.
В этом случае пишут lim f(x)=A1 или lim f(x)=A1.
х-+а jc—а-0
х<а
Определение 2
Число А2 называется пределом справа функции f(x) в
точке а, если для любого е>0 существует число 6>0, такое,
что для всех х, удовлетворяющих условию а<х<а + &,
выполняется неравенство |/(лг)-А2|<8.
В этом случае пишут limf(x)=A2 или lim f(x)=A2.
х—>а х—*а + О
х>а
Из определений предела функции f(x) в точке а и
односторонних пределов следует, что функция f(x) имеет в точке а
предел, равный А, тогда и только тогда, когда существуют
пределы этой функции слева и справа и эти пределы совпадают
Бесконечный предел в
конечной точке
Задача 5. Исследовать функцию
f(x)=— в окрестности точки х = 0.
\> Функция у=—, график которой
изображен на рисунке 37,
определена при jc^O. При приближении
к точке jc = 0 слева и справа
значения этой функции по абсолютной
величине неограниченно возраста-
Vi
1
0
\
I
1
_1
X
Рис.
X
37
§ 2
55
Предел функции
Рис. 38
ют, причем знак у совпадает со
знаком х.
В этом случае говорят, что
функция f(x)=— имеет в
точке х = О бесконечный предел
(является бесконечно большой), и пишут
lim f(x) = oo. Если х<0 и х стре-
jc — О
мится к нулю, то \f(x)\
неограниченно возрастает и f(x)<0. В этом
случае пишут lim/(x) = -oo или
Рис. 40
lim f(x) = -oo и говорят, что функция f(x) имеет предел слева
jc —-О
в точке х = 0, равный минус бесконечности. Если х>0 vl x
стремится к нулю, то функция f(x)=— имеет предел справа в
точке х = 0, равный плюс бесконечности:
Ит/(л:) = + оо или lim
jc —О jc —+0
В общем случае запись lim f(x) = oo означает, что для лю-
jc — a
бого 8>0 существует число 6>0, такое, что для всех х,
удовлетворяющих условию 0<|лг —а|<6, выполняется неравенство
1/(*)|>е. (1)
Если неравенство (1) можно заменить неравенством f(x)>z,
то lim f(x) = + oo. Например, если /(x)=—-, то lim/(д:) = + оо
jc — а х jc —О
(рис. 38).
Аналогично рассматриваются записи вида lim f(x) = -oo,
jc —a
lim f(x) = + oo и т. д. Например, если f(x) = \ogsx, то Ит/(л:) =
О
= -оо (рис. 39), а если f(x) = log1 х, то li
3 jc>0
56 Глава 11
jc
jc>0
(рис. 40).
Производная и ее геометрический смысл
У
1
0
\
\у
\
1
*- —
Рис
*х
42
Рис 41
■ Прямую х = 0 (ось Оу) называют вертикальной асимптотой
графиков функций
у=—, у=—2> y = logsx, y = logx х (см. рис. 37—40).
х "з
Предел в бесконечности
Рассмотрим функцию f(x)=l-\—, график которой
изображен на рисунке 41. При больших по абсолютной величине
значениях х значения этой функции близки к 1.
Поэтому говорят, что существует предел функции f(x) при
х, стремящемся к бесконечности, и пишут lim/(x)=l.
Прямую у = 1 называют горизонтальной асимптотой
графика функции у = 1 н— при х —* оо.
Аналогично прямая у = 0 — асимптота графиков функций
у=— и y=—z при лг-^оо (см. рис. 37, 38).
х хг
В общем случае запись lim f(x)=A означает, что для
любого 8>0 существует число 6>0, такое, что для всех х,
удовлетворяющих условию |л:|>6, выполняется неравенство
|/(jc)-A|<6. (2)
Если неравенство (2)
справедливо при всех х>Ь, то пишут
lim f(x)=A,
а если при всех дг>-6, то пишут
lim f(x)=A.
х—►-оо
Например, если f(x) = — (рис. 42),
то lim f(x) = 0, а если f(x)=-
то lim f(x) = 0 (рис. 43). Т^.
*^-°° Рис. 43
§2 57
Предел функции
3. Бесконечно малые функции
Функцию а(х) называют бесконечно малой при х-+а, если
a(x) = O.
Бесконечно малые функции обладают следующим свойством:
Если а(х) и Р(х) — бесконечно малые функции при х-+ а,
а сх и с2 — некоторые постоянные, то с1а(х)-\-с2Р(х) также
является бесконечно малой функцией при х-*а.
В частности, сумма и разность бесконечно малых
функций — бесконечно малые функции. Кроме того,
произведение a(x)fi(x) бесконечно малых функций а(х) и р(лг)
также является бесконечно малой функцией.
Например, функции Зх, 4х3 являются бесконечно малыми
при х-+0. Если х-+0 и х>0, то Vx—►(), т. е. \[х — бесконечно
малая функция при дс—► + (). Аналогично >0 при лг-^ + оо,
т. е. — — бесконечно малая функция при л;—►н-оо.
& 12 12
Если лг-^оо, то ► (), — —►(), т. е. —, —^ — бесконечно
х X Х X
малые функции при л;—►оо.
Замечание. Из определений предела функции и
бесконечно малой функции следует, что число А является пределом
функции f(x) при х-^а тогда и только тогда, когда f(x) =
=А + а(х), где а(л:)—>-0 при дс—»а, т. е. а(х) — бесконечно
малая функция при х-+а.
4. Свойства пределов функций
Свойство 1. Если \imf(x)=A, limg(x) = B9 то
Xhm(f(x)g(x))=AB,
х-*а
lim = — при условии, что
х-+а g{X) В
Свойство 2. Если в некоторой проколотой
окрестности точки а справедливы неравенства f (х) < ф (х) < g (x) и
\imf(x)=A, limg(x)=A, то Итф(^) существует и равен А.
х-+а х-+а х-*а
Для доказательства свойства 1 можно воспользоваться
свойствами бесконечно малых функций и замечанием п. 3; а
свойства 1 и 2 следуют из определения предела функции.
Задача 6. Пусть 6>0 и lima(x) = 0. Доказать, что
дс—а
t> Обозначим ф (х) =Vb + a (x)—Vb. Нужно доказать, что ф(лг) —
бесконечно малая функция при х-+а9 т. е. Итф(л;) = 0. Умножив
х—*а
58 г л а в а II
Производная и ее геометрический смысл
и разделив ф(дс) на Vb + а (х) + V&, получим ф(г)= — aW——,
\1Ъ + а(х)+\[Ъ
где & + а(д:)>0 в некоторой окрестности точки а, так как
lima(*) = O и Ь>0. Тогда \^(х)\=-=^Ш—=<^Щ, и поэто-
*-a V& ()Vb Vb
му Ишф (#) = 0. ^
х-* а
Задача 7. Вычислить:
1) hm г; 2) hm
о l2 33 2
m
-+2 x-2
3) lim3^2-4^5; 4) lim V*2+2*+3 .
2 1 л:
[> 1) Так как Сдг*, где С — постоянная, k€N, является
бесконечно малой функцией при лг-^О, то предел числителя
равен 3, а предел знаменателя равен 1. Поэтому искомый предел
равен 3 (свойство 1).
2) Умножив числитель и знаменатель дроби на \1х — 1 +1,
л/у_ I _ 1 у—2 1
получим ——-—= , = # —— при
а^2 (2)(Vl + (2)+l) Vl + (2)+l
где \/1 + (л;-2)-^1 при л:-*2 (задача 6). Используя свойство 1
пределов, находим, что искомый предел равен —.
3) Разделив числитель и знаменатель дроби на х2, запи-
s 4 5
шем ее в виде . Так как —г -* 0 при л: -* оо (С — посто-
х з
янная, k€N), то искомый предел равен —.
4) Последовательно преобразуем данную функцию (л:>0):
V*2 + 2* + 3 \ I x2 + 2x + Z Г 2 3" ^
= у —2 =yi+ — + -£. Отсюда следует
(задача 6), что искомый предел равен 1. М ШШШ
Упражнения
8. Построить график функции y = f(x) и найти lim/(jc), если:
дс—а
1) А*)=щ, а = 0; 2) /(х)^| 3;
V3
4)
^ 6
JC — ^
9Г| Найти пределы слева и справа функции /(л:) в точке а,
если:
§2 59
Предел функции
при х>-1,
10. Используя определение предела, доказать, что:
(
2) iim(
JC—1
11. Найти вертикальные асимптоты графика функции:
1 х+1
1} ^"^I^ 2)/W=2FT3;
8)Пх)-—± ; 4) /(ж)-——.
*2 + х-2 лг2 —|jc|
12. Найти горизонтальную асимптоту графика функции:
1) ,(*)-*££; 2)
113.1 Вычислить:
1) hm
3) hm
5) lii
x—»- + oo
§ 3. Непрерывность функции
1. Понятие непрерывности
Обратимся к графику функции, изображенному на
рисунке 36 (§ 2, задача 4). Он состоит из двух «кусков»: у = х2, х<1,
и у = х+1, х>1. Каждый из них может быть нарисован
непрерывным движением карандаша без отрыва от бумаги. Однако
эти «куски» не соединены непрерывно: в точке х=1
происходит скачкообразное изменение функции.
Поэтому все значения х, кроме х=1, называют точками
непрерывности функции y = f(x), а точку х=1 — точкой
разрыва этой функции.
Аналогично функция, график которой изображен на
рисунке 34 (§ 2, задача 1), непрерывна в каждой точке х, кроме
точки 1, хотя функция имеет предел в этой точке, равный 2.
Функция не является непрерывной при х=19 так как она не
определена в точке х = 1.
Функция у=— (§2, задача 5, рис. 37) непрерывна при
х<0 и при х>0, точка х = 0 — точка разрыва этой функции.
60 Глава II
Производная и ее геометрический смысл
I Дадим определение непрерывности.
Определение 1.
Функция f(x) называется непрерывной в точке а, если
Например, функция f(x) = (x-3)2 + 2 (§ 2, задача 3)
непрерывна в точке х = 3, так как lim/(x) = /(3) = 2.
х->3
Функция f(x) непрерывна в точке а, если выполнены
следующие условия:
а) функция f(x) определена в некоторой окрестности
точки а (включая точку а);
б) существует limf(x)=A;
B)A = f(a).
Если хотя бы одно из этих условий не выполняется, то
говорят, что а — точка разрыва функции f(x).
Задача 1. Выяснить, является ли функция
f(x) =
при x^ — 2,
непрерывной в точке х = -2.
10 при х = -2
> Если х^-2, то f(x) = x2-2x + £, и поэтому lim f(x)=12. Так
как f(-2) =10, то lim f(x)^f(-2). Следовательно, функция f(x)
jc —-2
не является непрерывной в точке х = — 2, т. е. х = — 2 — точка
разрыва функции f(x). М !^штт^
вИ Заметим, что функция f(x) непрерывна в точке а тогда и
только тогда, когда lim/(x) = limf(x) = f (a).
х <а х>а
Если lim/(x) = /(a), то функцию f(x) называют
непрерывной слева в< точке а, если же lim/(x) = /(a), то функцию назы-
дс — а
вают непрерывной справа в хточке а. Отсюда следует, что
функция f(x) непрерывна в точке а тогда и только тогда, когда
она непрерывна как слева, так и справа в точке а.
Обозначим x — a = h и назовем h приращением аргумента.
Разность f(x)-f(a) = f(a + h)-f(a) назовем приращением
функции и обозначим А/. В этих обозначениях равенство limf(x) =
= f(a) примет вид limA/=0.
Л—»0
Таким образом, непрерывность функции f(x) в точке а
означает, что бесконечно малому приращению аргумента
соответствует бесконечно малое приращение функции, т. е. Д/-*0
при h-»0. ШШШ
СЗЗадача 2. Функция f(x)= не определена в точке
лг = 1. Определить ее в точке х=1 так, чтобы получившаяся
функция была непрерывна при х = 1.
§ 3 61
Непрерывность функции
[> В задаче 1 из § 2 было показано, что lim f(x) существует и
равен 2. Если положить f(x) = 2, т. е. рассмотреть функцию
I* ч \f(x) при х^\, ,
f(x) = \ у ' * то эта функция непрерывна в точке
[2 при х=1,
х=1. В таком случае говорят, что функция f(x) доопределена
по непрерывности в точке а. М Т^Ч
вН В задаче 4, § 2, была рассмотрена функция
[х+1прих>1.
Она не является непрерывной в точке х=1, но lim/(x) = /?(l) = l.
jc—1
Поэтому данная функция непрерывна слева в точке 1, но не
является непрерывной справа в этой точке: lim/(x) = 2. ВЯ
Х-— 1
х>1
Отметим, что все основные элементарные функции
(степенная, показательная, логарифмическая, тригонометрические)
непрерывны в каждой точке своей области определения. В
частности, любой многочлен — функция, непрерывная в каждой
точке x€R; рациональная функция (отношение многочленов) —
функция, непрерывная во всех точках, где знаменатель этой
рациональной функции не равен нулю.
■^"■Определение 2
Функцию f(x) называют непрерывной на интервале (а; Ь),
если она непрерывна в каждой точке х из этого
интервала. И
'Определение 3
Если функция y = f(x) непрерывна на интервале (a; b), a
также непрерывна справа в точке а и слева в точке Ь, то
ее называют непрерывной на отрезке [а; Ь].
Задача 3. Найти числа бис, такие, при которых функция
х2 при х<2,
f(x) = < Ь при х = 2, непрерывна в точке х = 2.
х + с при х>2
\> Так как lim/(x) = 4, Ит/(л;) = 2 + с, f(2) = b, to непрерывность
jc —2 дс —2
х<2 х>2
в точке 2 будет только при условиях 4 = 2 + с и 2 + с = Ь,
которые выполняются при Ь = 4, с = 2. М
2. Свойства функций, непрерывных на отрезке
Теорема 1
Если функция f(x) непрерывна на отрезке [а; Ь], то она
принимает на этом отрезке свое наибольшее и свое наи-
62 Глава II
Производная и ее геометрический смысл
меньшее значения, т.е. существуют точки хге[а; Ь],
х2е[а', Ь], такие, что для всех хе[а; Ь] выполняются
неравенства f(x)>f(xl), f(x)<f(x2).
Теорема 2 (о промежуточных значениях)
Если функция f(x) непрерывна на отрезке [a; Ь] и
/(а)*/(Ь), то она принимает на этом отрезке любое
значение С, заключенное между f(a) и /(&), т. е.
существует точка дс0, такая, что а<хо<Ь и /(дсо) = С.
В частности, если функция f(x)
непрерывна на отрезке [а; Ь] и
принимает на концах этого отрезка
значения разных знаков, т. е.
f(a)f(b)<0,
то существует точка с€(а; Ь),
такая, что f(c) = O (рис. 44).
Задача 4. Доказать, что
уравнение л:3-4л:2н-3 = 0 имеет корень на рис 44
отрезке [-1; 0].
> Функция f(x) = xs-4x2 + 3 непрерывна на отрезке [-1; 0],
/?(-1) = ~2, /(0) = 3. По теореме 2 на интервале (-1; 0)
существует точка с, такая, что /(с) = 0, т. е. данное уравнение имеет
корень на отрезке [-1; 0]. М
Теорема 3 (об обратной функции)
Если функция f(x) непрерывна и возрастает на отрезке
[а; Ь], то на отрезке [/(a); f(b)] определена обратная к
f(x) функция, которая является непрерывной и
возрастающей.
Например, функция y = sinx, где -^-<#<^-, непрерывна и
возрастает. Обратная функция i/ = arcsinx определена на отрезке
[-1; 1], является непрерывной и возрастающей. ВЯ
Упражнения
14. Принадлежит ли графику функции y = f(x) точка А, если:
*2-4
1) у = 2х+2 , А(2; 1); 2) */ = tg(f + j), a(^; о);
3) */ = 3*2"2, A(-V2; 1);
§ 3 63
Непрерывность функции
б)
Рис. 45
15. Функция y = f(x) задана графиком (рис. 45). Найти
область определения и множество значений функции.
16. Найти область определения и множество значений
функции:
1) у = х2-Зх-4; 2) у = 3-2х-х2;
3)У=-Ч; 4)i/ =
1)
р
{х
4
17. Построить график функции:
-2 при
при л: = 3;
64
г-Ах при
:-3 при х>3;
2) */ =
4) i/ =
1-л:2 при хч£2,
3 при л: = 2;
2-\х2 при л:<
л:2-4 при л:>2.
Гл а в а II
Производная и ее геометрический смысл
18. На рисунке 45 (а — г) изображены графики функций. Для
каждой из этих функций выяснить:
1) какие из функций являются непрерывными на своей
области определения;
2) какие точки являются точками разрыва на отрезке
[-2; 2];
3) какие из функций являются непрерывными на
интервале (-2; 1).
19. Построить график функции:
2х при х<2,
4 + \1х-2 при х>2;
\og2x при дс<2,
при х>2;
!)/(*) =
;-4|при*>2; [,_1 при
Выяснить:
а) имеет ли эта функция предел при х-*2; б) является ли
эта функция непрерывной на всей числовой прямой; в) на
каких промежутках функция непрерывна.
20. Выяснить, является ли непрерывной в точке х0 функция:
при
13 при х = -2,
3) //^-f*2-1"4 ПРИ
при
fsinx при д:<7с,
t -*| при
У Доказать, что функция f(x) непрерывна в точке а, если:
1-х2 при х<2, _9#
Здг-9 при дс>2,
f|cosx| при х<п,
1(х — п) +1 при л:>7с,
У Найти число Ь, чтобы функция f(x) была непрерывна в
точке а, если:
l) при х<19
jl при х>1,
§ 3 65
Непрерывность функции
IX
sin— при x<n,
2
bx при x>n,
3) f(x)=
4)
a = -l;
b при х = — 1,
cos я: при л;<0,
-l) при x>0 a =
§ 4. Определение производной
Пусть материальная точка движется вдоль оси Os, где О
(начало отсчета) определяет положение материальной точки в
момент времени t = 0.
Если в момент времени t координата движущейся точки
равна s(t), то говорят, что функция s(t) задает закон движения.
Пусть рассматриваемое движение не является
равномерным, тогда за равные промежутки времени материальная
точка может совершать перемещения, разные как по величине, так
и по направлению.
Средняя скорость движения за промежуток времени от X
до t + h определяется формулой vCD = s^ + / s^ '.
Определение
Скоростью точки в момент t (мгновенной скоростью)
называют предел, к которому стремится средняя скорость,
когда h-+0, т. е. скорость v(t) в момент t определяется
равенством v(t) = lim
Л О
Л —О П
Таким образом, скорость в момент времени t — предел
отношения приращения координаты движущейся точки за
промежуток времени от t до t + h, т. е. разности s(t + h)-s(t), к
приращению времени /г, когда h-^0*
Например, если материальная точка движется по закону
,2
s=2— (закон свободного падения), то
Vcp=s(t+h)-s(t)= _g_{(t + h)2_t2h или Vef=gt+£h, откуда
hm vcp = gt, т. е. v(t) = gt.
Л —►О
Мгновенную скорость v(t) называют производной функции
s(t) и обозначают s'(t) (читается: «эс штрих от тэ»), т. е.
1. Производная
Перейдем теперь к общему определению производной.
Пусть функция f(x) определена в окрестности точки х0, т. е.
66 Глава II
Производная и ее геометрический смысл
на некотором интервале, содержащем точку х0, и пусть точка
xo + h также принадлежит этому интервалу. Рассмотрим
приращение функции f(xo + h) — f(xo) и составим дробь
/(*o + ft)-/(xo)
h
Дробь (1) есть отношение приращения функции f(xo + h) —
-f(x0) к приращению аргумента Л, эту дробь будем называть
разностным отношением. Если существует предел дроби (1)
при Л->0, то этот предел называют производной функции f(x)
в точке х0 и обозначают f'(x0).
Определение
Производной функции f(x) в точке х0 называется предел
разностного отношения при h-+0, т. е.
f'(x0) = lim Н*о + *)-/(*о) (2)
Из определения предела следует, что
(3)
где a(h)-+O при h-+0.
Запишем равенство (3) в виде
Если h-*0, то правая часть равенства (4) стремится к
нулю, поэтому А/—► 0 при h-+0. Это означает, что функция /(л:)
непрерывна в точке х0. ШШШ
Итак, если функция имеет производную в точке х0, то она
непрерывна в этой точке.
Если существует f'(xo)9 то говорят, что функция f(x)
дифференцируема в точке х0, а если функция f(x) имеет
производную в каждой точке некоторого промежутка, то говорят,
что функция f(x) дифференцируема на этом промежутке.
Заметим, что из непрерывности функции f(x) в точке х0
не следует ее дифференцируемость в этой точке. Например,
функция f(x) = \x\ непрерывна в точке х = 0, но не имеет
производной в этой точке. Действительно,
№)-№) _ \h\ Г1» если h>0>
h h 1-1, если h<(
если h<0,
откуда следует, что разностное отношение '^ ~. не имеет
предела при h—>0. Шшттй
ШШ Если функция f(x) непрерывна слева в точке х0 и
существует lim ^*)-Д*о) ^ то этот предел называется левой
производило х-х0
ной функции f(x) в точке х0 и обозначается /1 (х0).
§4 67
Определение производной
Если функция f(x) непрерывна справа в точке х0, то
правая производная fi (x0) определяется равенством
-14*6)
ix)f(XG) или /;(xo) lim
х>% х~х° *>8 h
Например, если f(x) = \x\, то /1(0) = -1, /;(0)=1. ИЯ
2. Нахождение производной функций kx + b* x2, Xs
Задача 1. Найти производную постоянной, т. е. функции
f(x) = C, принимающей при всех х одно и то же значение.
t> Составим разностное отношение:
f(x + h)-f(x) C-C Q
h h
Следовательно, f'(x) = 0. M
Таким образом, производная постоянной равна нулю:
С'=0.
Задача 2. Найти производную линейной функции
\> Составим разностное отношение:
f(x + h)-f(x) _ k(x + h) + b-{kx + b) _ kh _ ь
h h ~ h ~П'
Следовательно, (kx + b)' = k. M
Например, (2х + 5)' = 2, (-3xH-4y = -3, (7хУ=7, (х)'=1.
Задача З. Найти производную функции f(x) = x2.
t> Составим разностное отноп1ение:
f(x + h)-f(x) = (x + hf-x2 = 2xh + h2
Если &—►(), то 2x + h-+2x. Отсюда получаем
)-flx) =
lim \im
—о h л—о
Следовательно, (х2)' = 2х. М
Задача 4. Найти f'(x), если f(x) = xs.
\> f(x + h)-f(x) = (x + h)s-x3. По формуле разности кубов
(х + hf - х3 = ((х + К) - х) ((х + К)2 + (х + h) х + х2) = h (Зх2 + Зх/г + Л2).
Составим теперь разностное отношение:
2
Если /г -^ 0, то h2 -» 0 и Зхй —0, поэтому Зх2 + Sxh + /г2 -^ 3jc2,
откуда
л-»о Л
Следовательно, (л:3)' = Зл:2. М
68 Гл а в а II
Производная и ее геометрический смысл
Упражнения
23. Составить разностное отношение, если:
1) f(x) = 4x; 2) f(x) = x-l; 3) f(x) = 4x2;
4) f(x) = x2 + 2; 5) f(x) = xs-x2; 6) f(x) = 2x* + x.
24. Используя определение производной, найти производную
функции:
1) /(*) = 2х + 3; 2) f(x) = 5x-6;
3) f(x) = -3x2 + 2; 4) /(x) = 3x2H-5x.
25. С помощью формулы (kx + b)' = k (задача 2) найти
производную функции:
1) f(x) = 3x; 2) f(x) = -4x;
3) /(*) = -5х+7; 4) f(x) = -7x + 8.
26. Тело движется по закону s(t)=l + 5t. Найти среднюю
скорость движения за промежуток времени:
1) от *! = 2 до t2 = 5; 2) от t1 = 0,9 до £2 = 1.
27. Закон движения задан формулой:
1) s(t) = 2t + l; 2) s(t) = 0,3t-l.
Найти среднюю скорость движения от t1 = 2 до t2 = S и
скорость движения в момент tx = 2 и в момент t2 = 8.
28. Найти мгновенную скорость движения точки в каждый
момент времени t, если закон ее движения s(t) задан
формулой:
1)«№ = §*2; 2) s(t) = 5t2.
29. Дана функция f(x) = \ х3 - ^ х2 + Зл;.
1) Используя определение производной, найти f'(x).
2) Найти значение f(x) в точке дг = О,1.
§ 5. Правила дифференцирования
1. Дифференцирование суммы, произведения, частного
Производная суммы равна сумме производных:
(Г(х)+Ш(х)У = Г(х) + &(х). (1)
Это правило означает, что если функции f(x) и g(x)
дифференцируемы в точке х, то их сумма также дифференцируема
в точке х и справедлива формула (1).
О Пусть F(x) = f(x) + g(x). Тогда
Поэтому разностное отношение равно
-F(x) f(x + h)-f(x) g(x + h)-g(h)
h
h h
§ 5 69
Правила дифференцирования
При h-+ О первая дробь в правой части имеет предел,
равный f'(x), а вторая дробь имеет предел, равный g'(x). Поэтому
по свойствам пределов функций левая часть имеет предел,
равный Fr(x) = f'(x) + gr(x), т. е. справедливо равенство (1). •
Например, (х3 + х)' = (х3)' + (х)г = Зх2 +1.
I Постоянный множитель можно вынести за знак
производной:
(cf(x))'=cf'(x). (2)
О Пусть F(x) = cf(x). Тогда
Fjx + h)-Fjx) _ Cf{x + h)-cf{x) _ f{x+ h)-f{x)
h h h
Переходя в этом равенстве к пределу при /*—►(), получаем
F'(x) = cf'(x). •
Например, (4х2)' = 4 • (х2)' = 4 • 2х = 8х.
Задача 1. Найти производную функции f(x) = bx2 + lx.
> Так как (х2)' = 2х, (х)'=1, то по формулам (1) и (2)
получаем (5л:2 + 7х)' = (5х2У + (7х)' = 5(х2У + 7(*)' =5-2лгн-71 = 1Ол: + 7. ^
Формула (1) справедлива не только для суммы двух
функций, но и для суммы трех, четырех и более функций.
Задача 2. Найти производную функции
> (2х3 - 5х2 + Зх + 8)' = (2х3)' + (- Ъх2)' + (Зх)' + (8)' = 2 (х3)' - 5 (*2)Ч
Пусть функции f(x) и £(*:) дифференцируемы в точке х.
Тогда в этой точке функция f(x)-g(x) имеет производную,
которая выражается формулой
*(x). (3)
Задача 3. Пользуясь формулой (3), найти производную
функции
Ф (х) = (х2 + х - 6) ix2 - х - 2).
>По формуле (3) находим у'(х) = (2х+1)(х2-х-2) + (х2 + х-6)Х
Задача 4. Пусть k и Ь — постоянные,
f(x) = (kx + h)2, gix)=(k
Доказать, что
/'(*) = ((*х + Ь)2)' = 2/г (*х + &), (4)
^' (х) = ((AjX h- ft)3y = 3Aj (kx + &)2. (5)
t> Так как /(x) = (AjxH-b)(AjxH-b), то, применяя формулу (3),
получаем f'(x) = k(kx + b) + (kx + b)k = 2k(kx + b). Аналогично, ис-
70 Глава II
Производная и ее геометрический смысл
пользуя равенство g(x) = f(x) (kx + b), формулы (3) и (4) ,
находим g'(x) = 2k(kx + b)(k f 2
Задача 5. Пусть
Найти корни уравнения f'(x) = O.
> Применяя правило дифференцирования произведения и
формулы (4) и (5), получаем f'(x) = 2(x-2)(x+lf + (x-2)23(x+l)2 =
= (jt:-2)(jc+l)2(2xH-2H-3x-6), т. е.
Г(х) = (х-2)(х+1)2(бх-4),
откуда следует, что корнями уравнения f'(x) = O являются
числа-1, |, 2.М
о
ИЯ Задача 6. Доказать формулу (3).
> Обозначим <p{x) = f{x)g(x), Af=f(x + h)-f(x), Ag=g(x + h)-g(x),
Дф = ф(х + Л)-ф(х). Тогда f(x + h) = f(x) + Af, g(x + h) = g(x) + Ag,
А£ e f(x + h)g(x + h)-f(x)g(x) = (f(x) + Af)(g(x) + Ag)-f(x)g(x)
h h h
f-fwf+ewf + f**. (6)
По определению производной — —>gr(x), — —*/'(x) при
h h
h-+Q. Кроме того, А^-^0 при Л~*0, так как дифференцируемая
в точке х функция непрерывна в этой точке (§ 4).
Следовательно, правая часть (6) имеет при h—>0 предел, равный правой
части формулы (3). Поэтому существует предел в левой части (3),
который равен производной функции f(x)g(x). M вЯ
Пусть функции f(x) и g(x) дифференцируемы в точке х
и g(x)^O. Тогда функция ~-^ имеет производную в точ-
g\X)
ке х, которая выражается формулой
Формулу производной частного можно доказать тем же
способом, что и формулу (3).
(х-1)3
Задача 7. Найти f'(x), если f(x) = -—-—, и решить урав-
х
нение /г'(х) = 0.
t> Применяя формулы (7) и (5), получаем
f(x\ = ((х-1)8/х2-(х-1)8(х2)У = S(x-l)2x2-(x-lf2x =
откуда следует, что корнями уравнения f'(x) = O являются
числа 1 и -2. ^
§5 71
Правила дифференцирования
Задача 8. Решить неравенство / (х)>0, если
х
Найдем f'{x), используя формулы (7) и (5):
.,, л Зх2(2x-lf-х3■ 4(2*-1) *2(6*-
Г l ' (2*-l)4 (2*
(2jc-1)3
1 о
откуда следует, что f'(x)>0, если х< — (х^О) и х>—, т. е. при
2. Производная сложной функции
|Если имеется функция f(kx + b), где k и Ь — постоянные
и Aj^O, to
(/(fe* + b))' = fe/'(fe* + b). (8)
Докажем эту формулу.
О Обозначим F(x) = f(kx + b), t = kx + b, тогда
AF F(x + h)-F(x) f{k{x + h) + b)-f{kx + b) f(t + kh)-f(t) (q,
T= h = h = h ' (9)
AF
=k
Если Л-0, то Л1 = М-0 и /vf«">- / w = и* т»y / w _»f(t]
kh hi
при кг-*0. Следовательно, правая часть в формуле (10) имеет
при Л-*0 предел, равный kf'(t) = kf'(kx + b).
Но тогда существует предел в левой части этой формулы,
который равен (f (kx + b))'. •
СЗ Напомним понятие сложной функции. Пусть задана
функция f(y), где у, в свою очередь, является функцией от х, т. е.
y = g(x). Тогда функцию F(x) = f(g(x)) называют сложной
функцией (или суперпозицией) функций y = g(x) и f(y). При этом
предполагается, что множество значений функции g(x)
содержится в области определения функции f(y).
Например, если f(y) = ey, y = g(x) = 2x3, то F(x) = f(g(x)) = e2x .
Пусть функция g(x) имеет производную в точке х, а
функция f(t) имеет производную в точке t = g(x). Тогда
сложная функция f(g(x)) имеет производную в точке х,
которая выражается формулой
»•£'(*)• (И)
Задача 9. Найти производную функции (Зл;2 + 4)3.
> Здесь y = g(x) = Zx2 + ±, f(y) = y3. Так как f'(y) = 3y2, a g'{x)
= 6лг, то по формуле (11) находим
((Зх2 + 4)3)' = 3 (Зх2 + 4)2 • 6х = 18* (Зх2 + 4)2. А
72 Гл а в а И
Производная и ее геометрический смысл
3. Производная обратной функции
Пусть y = f(x) и х = у(у) — взаимно обратные функции.
Тогда для всех y€Y, где Y — область определения функции ср,
справедливо равенство
/(Ф(*/)) = *Л (12)
Предположив, что функции / и ф дифференцируемы, из
равенства (12) по правилу дифференцирования сложной
функции получим Г(ф0/))-ф'0/)=1* откуда ф'(*/) = ,,, \ „, если
/ (ф(«/))
. Заменив у на х, получим формулу производной
обратной функции
С помощью формулы (13) в § 7 будут найдены формулы
производных обратных тригонометрических функций.
Упражнения
30. Найти производную функции:
1) х2 + х\ 2) х2-х; 3) 8л:2; 4) -27л:2;
5) -4л:3; 6) 0,6л:3; 7) 13л:2+ 26; 8) 8л:2-16.
31. Продифференцировать функцию:
1) Зл;2-6л: + 6; 2) 6л:2 + 5л:-7;
3) *+12л:2; 4) х -8л:2;
5) л:3 + 6л:; 6) - 12л:3 + 18л:;
7) 2л:3-8л:2 + 6л:+1; 8) -Зл:3 + 2л:2-л:-5.
32. Найти /'(О) и Г(2), если:
1) f(x) = x2-2x+l; 2) /(л:) = л:3-2л:;
3) Дл:) = -л:3 + 2л:2; 4) f(x) = 3x2 + x+l.
33. Найти значения х, при которых значение производной
функции f(x) равно 0 (решить уравнение /'(л:) = 0), если:
1) /Чл;) = л:3-2л:; 2) 2
3) /?(л:) = 2л:3 + Зл:2-12л:-3; 4)
5) f(x) = (x-2)2(x+l); 6)
34. Найти производную функции:
1) (х-3)2л:3; 2) (л:2 -2л:) (л:3 + л:); 3) (л:н-3)л:3; 4) (л:-4)3л:2.
Найти /41) (35 — 36).
35. 1) /(х) = (2л:-3)2(л:-1); 2) /(л:) = (л:+ 1)3(л:н-2).
37. Найти производную функции:
х ол 2jc3 + 3jc2 + 1
; 1) х~^1 *
§ 5 73
Правила дифференцирования
38. Записать формулой функцию f(g(x)); найти ее область
определения и множество значений, если:
1) ПУ)=У2, y=g(x) = x+l; 2)
3) /(«/) = Е~,
у -z
4) V
39. С помощью формулы (8) найти производную функции:
1) (2х- I)3; 2) (лгН-3)2; 3) (Зх2-2х)2; 4) (xs-x2f.
40. Выяснить, при каких значениях х производная функции
f(x) принимает отрицательные значения, если:
1) f(x) = х2-7x4-10; 2) f(x) = -x2 + 4x;
3) /(x) = -3x3 + 3x2 + 4; 4) f(x) = (l-3xf.
41. Выяснить, при каких значениях х производная функции
f(x) принимает положительные значения, если:
1) f(x) = (x + 2)2xs; 2) f(x) = (x-S)Sx2.
42. Выяснить, при каких значениях х производная функции
f(x) принимает отрицательные значения, если:
1 о „3
43. Записать формулой функцию f(g(x)) и найти ее
производную, если:
2)
44. Найти производную функции ^(л:), обратной к функции f(x)t
если:
Найти производную функции:
32l)2; 2)
§ 6. Производная степенной функции
Рассмотрим степенную функцию у = хр. При р = 1, 2, 3 эта
функция дифференцируема и ее производная равна
соответственно 1, 2х, Зх2 (§ 4), т. е.
(х)'=1, (лг2У = 2лг, (л:3У = Зл:2.
I Производная степенной функции при любом
действительном показателе р находится по формуле
(хРу=рхР-К (1)
Эта формула справедлива при тех значениях х, при
которых имеют смысл обе части равенства (1). Она будет доказана
в § 7.
74 Глава II
Производная и ее геометрический смысл
I Задача 1. Доказать справедливость формулы (1) при р = -1,
т. е. доказать, что
л \х) х*-
> Пусть f(x)=—, лг^О. Тогда
~ v = _J_ _ 1 в х-(х + Ц
" ' * + Л * (* + Л)*
Составим разностное отношение:
f (x + h)-f(x) _ 1
Л (# + /*)**
При /г-*0 знаменатель дроби стремится к х2, поэтому
limf )= -. Таким образом, f'(x) = -, т. е. (—)= т.
ft-o\ ix + h)x/ х х \х ' х
Полученное равенство можно записать так:
Это и означает, что формула (1) верна при р = -1. ^
Задача 2. Доказать формулу (1) при р=—.
t> Пусть f(x) = Vx* л:>0. Составим разностное отношение:
fjx + h)-fjx) = \/x + h-\[x
h h
Умножим числитель и знаменатель на сумму \]x + h + \[x.
Получим
)-fjx) _ (Ул: + h-Vx) jyjx + h + Vx) _ jx + h)-x
h
Если h-+0, то \lx + h-*\[x (§ 2, задача 6), поэтому
знаменатель последней дроби стремится к 2\[х. Следовательно,
Полученное равенство можно записать так:
т. е. формула (1) справедлива при р=—. М Г^
Задача 3. Найти /'(1), если f(x) = \fx~+ -j=.
1 _1
[> Так как f(x) = x2 +х 2 , то по формуле (1) получаем
1 _i 1 _i 1 3
Следовательно, /'(!)= — - — = 0.
2\[х 2хУх'
§ 6 75
Производная степенной функции
Задача 4. Вычислить f'(-3), если f(x) = \/4-7x.
j.
D> Так как f(x) = (-7x + 4)2 , то, используя формулу (1) и
формулу (9) из § 5, получаем / (х) = — (- 7х + 4) 2 -(-7), откуда
находим /'(-3) = -|(-7(-3) + 4)"2=-|.25"2 =-0,7. Л
Задача 5. Найти /'(*), если
1 I
> Так как f(x) = xs (х + 3) 3 , то
f'(x) = x 3
3/— 1
Задача 6. Доказать, что (V#)' = —^— при
Если х>0, то ул'^^ и по формуле (1) получаем
^
V?
з з
Если х<0, то Vjc = — V— л: = — (— л:)3 . Используя формулу (1)
и правила дифференцирования, находим
2
--Z 1 1
) 3(1)< ^^
Упражнения
Найти производную функции (46—47).
46. 1) х6; 2) х12; 3) Зх4 + 2х13;
4) 7*3-3х7; 5) 4; 6) **+\-
х* х*
47. 1) Ух; 2) V^; 3) 2Ух-Ух; 4)
7) ——-; 8)
х
6) р;
х\х
48. Найти /'(3) и f'(l), если:
76 Гл а в а И
Производная и ее геометрический смысл
о
3) /(*)=- ~;
1— х
5) Д*) = (*-1)2(*-3);
7)/<*)-<*«-1)<* + 8);
4) /(л:
6) /(ж
8) /(ж
3
v 2
) = <*-
) = (*2
3
-ж"1
О\3 /.
~ О) у.
-9)(
49. Найти значения х, при которых значение производной
функции f(x) равно 0:
1) f(x) = 3x4-4xs-12x2; 2) f(x) = х4 + 4х3-8л:2-5;
4) А
6)
50.
5L
52.
—
53.
3)
5)
Найти /'(!)> если:
1J Т\Х) — уХ—L) \6 — X) ,
3) /(jc)=\^T-(2-3x)6;
А
2)
4) f(x) = (6х-4)6.V3jc-2.
При каких значениях х значение производной функции
y=(x-Zf(2 + bxf равно О?
Найти производную функции (52—56).
1)
2)
2
1) —-;
jc4
4)
2) 4*
6
2;
5) 6V^-g—
3)
6)
+6х
6;
xV?
54.
4)
2)
5)
/4 1 \/4- 1 \
3)
6)
55.
1) (2jc-3)5(3x2h-2xh-1);
3) yj3x + 2(3x-l)4;
14 2jc2-3jc+1 o. 3jc
) ; 2)
2) (x-l)4(:x:+l)7;
4) /
2-*
57.
1 —л:"2 * Yjc 4-х
Найти точки, в которых значение производной функции
f(x) равно 1:
-3; 2)
§6
77
Производная степенной функции
58. Решить неравенство f'(x)>0, если:
1) f(x) = x4-4x2 + l; 2) f(x) = 3x4-4xs-12x2 + 3;
3) /(*) = (*+A)2; 4)^
5) /(x) = (x + 2)2v£; 6)
59. Угол поворота тела вокруг оси изменяется в зависимости
от времени t по закону ф(£) = 0,1£2 — 0,5£ + 0,2. Найти
угловую скорость (рад/с) вращения тела в момент времени
t = 20 с.
60. Тело, масса которого т = 5 кг, движется прямолинейно по
закону s(t)=l-t + t2 (где s выражается в метрах, t — в
секундах). Найти кинетическую энергию тела —г— через 10 с
после начала движения.
61. В тонком неоднородном стер лене длиной 25 см его масса
(в граммах) распределена по закону m(Z) = 2Z2 + 3Z, где I —
длина стержня, отсчитываемая от его начала. Найти
линейную плотность: 1) в точке, отстоящей от начала
стержня на 3 см; 2) в конце стержня.
62. Найти производную функции f(x) = \/x2-5x + 6 при х<2 и
"" при х>3.
§ 7. Производные элементарных функций
Показательная, логарифмическая и тригонометрические
функции дифференцируемы в каждой точке, где они
определены. Приведем некоторые формулы производных этих функций:
1. (sinх)' = cosх. 3. (1пл:)'=—, л:>0.
2. (cos х)' = - sin х. 4. (ех)'=ех.
СЭ Доказательство формул 1 и 2 основано на использовании
равенства
lim^ = l, (1)
а при выводе формул 3 и 4 используется равенство
lim(l+*)*=€?. (2)
t-*o
Соотношения (1) и (2) называют замечательными
пределами, их доказательство дается в курсе высшей математики.
Докажем формулу 1, используя предел (1).
О Если f(x) = sin x, то
f(x + h)-f(x) _ sin (x + h) - sin x
h ~
78 Глава
2 sin—cos(jc + — ) sin —
2^2/ 2
h h h h_ cos
2
Производная и ее геометрический смысл
sin —
2 ( h\
Так как h -»1 при /*—►() (равенство (1)), a cos(xH- — ) —►cos*
2
, v ,. sin (x + Л) - sin x
(непрерывность косинуса), то существует lim т1 =
л—о п
=cosjc, т. е. справедлива формула 1. • И
Применяя формулы 1, 3, 4 и правила дифференцирования,
выведем формулу 2 и докажем равенства:
5. (tgx)f * х*^ + ы, kez.
6. (ctgjc)' 1—9 x*kn,
sirrx
7. (ln|jc|)'=-, x*0.
X
8. (a*)'=a*lna, a>0,
9. (logax)'
10. (xPY=pxp~19 p€R, x>0.
СЯ02. Так как cosjc = sinfxH- ^-J, то, применив формулу 1,
получим (cos л:)'= cos (х+ ~п)\х+-к) =cos(xH- — J = — sin л:.
5. Применив правило дифференцирования частного и
формулы 1 и 2, получим
w /sinjc\' (
(tgx) = I =
V cos* /
6. Аналогично
cos2 х cos2 х
-sinjcsinjc-cosjccosjc
7. Пусть л:<0, тогда \х\ = -х и ln|x| = ln(-x), откуда,
применяя формулу 3 и правило дифференцирования сложной
функции, получаем (\п\х\У = (\п(-х)У= -—(-1)=—. Отсюда и из
формулы 3 следует, что
(ln|*D'-i, ^^0.
8. Возводя обе части равенства а = е1па в степень х,
получаем ах = ех1па. Применяя формулу 4 и правило
дифференцирования сложной функции, находим
(ax)f = exlna In a = ax\na.
9. Так как logax=-—, то, применяя формулу 3, получаем
79
Производные элементарных функций
10. Воспользуемся равенством хр = е1пхР = ер1пх. Тогда
XX
Применяя формулы 1—5, 7—10 и правила дифференциро
вания, решить задачи 1—3.
Задача 1. Найти f'(x), если f(x) = cos3x.
> (cos Зх)' = (- sin Зх) • (Зх)' = - 3 sin Зх. <4
Задача 2. Найти f'(x)9 если:
1) f(x) = e~x; 2) f(x) = tg2x;
3) f(x) = 2~xsin2x; 4) /(д:) = 1п
5) f(x) = logs(x2 + 4); 6) f(x)= =
2)
1 (2xy-_£-
2x
3) (2~x sin 2л:У = 2"ж In 2 • (- x)' • si
= 2~x (2 cos 2x - In 2 • sin 2x);
ccos2x(2:*:)' =
2
*2-l
5, (,oga(»+4))
6) ((л:3 + 2л:)2 e3x)' =2(x3 + 2x)(x3 + 2x)'e3x + (x3 + 2л:)2 е3х • 3 =
Задача 3. Найти /"(^), если:
1) /W =
2)
3) f(x) = 3x ctg2x;
4) 2
5)
-2х2
(л;3+1)2
2) (1п(л: + \/!
80 Глава II
1+дс3\ (l-xz\ з _ 2jc2 л /l-лг3 .
1-JC3/\1+JC3/ JC6- 1 V 1 + X3
х + \1х2 + 1 V
Л-
2VJc2TT/ Vl + л:2
Производная и ее геометрический смысл
{
\ztg2x+z (|
\ jc2/ V sin2 2*
2
sin2 2*
4) (122
/'
(*d + l)lnl0 \ cosz3* (*d + l)lnl0
Задача 4. Доказать формулы
1
(arcsinx)' =—=, |л:|<1, (З)
yjl-x2
(arctg x)r = ——2 , x e R. (4)
[> а) Если i/= ф(дс) = arcsin л;, где |х|<1, то обратная функция
x=f(y) = siny, где \у\<—. По формуле (13) из § 5 находим
. v 1 1
(arcsin х) = ——- = ,
(sini/) cosy
где sin^ = jc, cosi/ = Vl-^2, так как \у\<—. Формула (3) доказана.
б) Если i/ = arctg х, где дг€Д, то обратная функция x = tgy,
где |^|<^. По формуле (13) из § 5 получаем
(arctg х)' = ^^7 = cos21/,
где cos2^= £~~ = ^. Формула (4) доказана.
l + tgzi/ 1 + 2
Упражнения
Найти производную функции (63—75).
63. 1) lnjc + sinx; 2) e^-sinx; 3) \fx-
4) —+ех\ 5) tgx + lnx; 6) ex-ctgx.
x2
64. 1) 2cos3jc; 2) -5е2дс; 3) -41n2x;
4) -3 sin 2x; 5) j- e~2x; 6) 2^-4e"2;>£:.
65. 1) 6x*-9eSx; 2) 1 x8 + 3sinSx; 3) 3V^-4cos4x;
4
1 1 3^
—^ + j- In Ax; 6) 3tg2a:-2VJc.
§7 81
Производные элементарных функций
66. 1)
3)
з
67. 1) 3x2-4\[x + 2
3) v£+-J-
3 *,
2)
4)
A sin 4*;
4
2)
4)
5) 8л;4 + 7л;7 -cos4x;
5)
6) i
5
68. 1) (лг + 3)8; 2) (*-4)7;
1 . 1 .
6)
чЗ'
3)
7)
\/x + 3
4)
8)
69. 1) (Зх + 1)5; 2) (5л;-4)6; 3) (1-Зх)7;
4)
70. 1)
4)
71. 1)
' 5)
72. 1)
5)
/2-8jc;
5)
2)
(2-Зх)4'
(4-3jc)5
sin2 л:;
e2*2;
tg|;
V3-8x
2) cos2 x;
6) е-4;
2) е"*;
6) cos 4л:;
6)
3)
6)
V2-9jc
3) cos3 л:; 4) sin4 л:;
7) 1пЗх4; 8) 1п(-2х).
5
3) 1п(2л:-1);
7)
4) 1пЗлг;
8) si
73. 1) cos(l-|);
2) Sin(2-^);
1-х
5)
7)
9)
cos
2 '
4-5*
3
sin3 2x;
ctg2 4x;
74.
4) cos
6) sin
8) cos43x;
10) tg4|.
2) ln(3-4x2); 3) e
ж+1;
4)
>2jc+3 .
5) In
3 -
5» '
6) In
2x2 + 7x
4) 7X~S;
8) lg(x + 3).
75. 1) 5X; 2) 4*; 3) 9*+2;
5) loggx; 6) iog4x; 7) Ig(x-l);
82 Глава II
Производная и ее геометрический смысл
76. Найти значения х, при которых значение производной
функции f(x) равно 0, если:
1) f(x) = х-cosx; 2) f(x)=^x-sinx;
3) f(x) = ln(x+l)-2x; 4) f(x) = 2\n(x + 3)-x;
5) f(x) = 2x + 2~x; 6) f(x) = 32x-2xln3;
Найти производную функции (77—81).
77. 1) \Z2^"1 | in 2* + 3 . o\ л /l-«* oi~ 2-5*
-™"1 V 3 о
1-х
3) 2e 3 +3cos
2-х
78.1) log2(*
3)tg22*;
79. 1) V^2 + lctg4x; 2)
" 3) V^sin4jc; 4)
3) «-+4Х+Г
fti 1\ *?-e. o\ 2 - Iog2 ^. q\ sinjc-cosjc . ^ч 1 - sin 2x
oi. i; , Zj - - , o) , <±) — .
— X X\n2 X SIIIJC-COSJC
82. Найти значения х, при которых значение производной
функции f(x) равно 0, если:
1) f(x) = x2-6x-S\nx; 2) /(x) = 2VJc-31n(xH-2);
3) f(x) = yJx+l-ln(x-2); 4) /(x) = ln(x-1) + 21п(л:Н-2).
83. Решить неравенство f'(x)>0, если:
1) f(x) = ex-x; 2) f(x) = 6x + cos3x;
3) /?(jc) = lnx-x; 4) f(x) = x-21nx;
5) Ал:) = 6л:-л:^; 6) f{x) = (x+l)Vx + T-3x.
84. Выяснить, при каких значениях х значение производной
функции f(x) равно 0, если:
1) f(x) = 5(sinx — cos л:) H-V^cos 5л:;
2)
85. Найти значения производной функции f(x) в точках, в
которых значение этой функции равно 0, если:
) = e2xln(2x-l); 2) f(x) =
sin х — cos x
sinjc
86. Вычислить f'(x) + f(x) + 2, если f(x) = xsin2x, x = n.
§7 83
Производные элементарных функций
87. Найти значения х, при которых значение производной
функции f(x) равно 0; положительно; отрицательно, если:
1) f(x) = х-Inx; 2) f(x) = хInx;
3) f(x) = х2 In x; 4) /(x) = x3-31nx.
88. Найти производную функции f (x) = ln(x2-5x + 6) при х<2
и при дг>3.
§ 8. Геометрический смысл производной
1. Угловой коэффициент прямой
Напомним, что графиком линейной функции y = kx + b
является прямая. Число & = tga называют угловым коэффициен
том прямой, а угол a — углом между этой прямой и осью Ох
(рис. 46).
Если Aj>0, то 0<сс<^ (см. рис. 46, а), в этом случае функ-
ция y = kx + b возрастает. Если &<0, то -—<а<0 (см. рис. 46, б),
в этом случае функция y = kx + b убывает.
а)
0
б)
Рис. 46
84
Гл а в а II
Рис. 47
Производная и ее геометрический смысл
Выведем уравнение прямой с заданным угловым
коэффициентом, проходящей через заданную точку М0(х0; у0).
Пусть прямая не параллельна оси Оу и М(х; у) —
произвольная точка этой прямой (рис. 47).
Из ААММ0 находим у~Уо =tgcc. Обозначив tga = k,
получаем y-yo = k(x-xo), откуда
y = yo + k(x-xo). (1)
Уравнение (1) называют уравнением прямой с угловым
коэффициентом Aj, проходящей через точку (х0; у0).
Задача 1. Записать уравнение прямой, проходящей через
точку (-2; 3) и образующей с осью Ох угол — —.
4
t> Находим угловой коэффициент прямой k = tg(—^-)= — l. Так
как лг0 = — 2, уо = 3, то по формуле (1) получаем
-(-2)), т. е. y = -
2. Геометрический смысл производной
Выясним геометрический смысл производной
дифференцируемой функции y = f(x).
Пусть функция y = f(x) определена в некоторой
окрестности точки х0 и существует ее производная f'(x0).
Если А и М — точки графика этой функции с абсциссами
х0 и xo + h (рис. 48), то угловой коэффициент k = k(h) прямой,
проходящей через точки А и М (эту прямую называют
секущей), выражается формулой
y£nx + h}fix)(2)
где С — точка с координатами xo + h, f(x0), а уравнение
секущей AM можно записать в виде
y-yo = k(h)(x-xo). (3)
Пусть h-+ 0, тогда М, двигаясь по графику, приближается
к точке А, а секущая поворачивается вокруг точки А. Если
существует lim k (k) = k0, т. е. существует предельное положение се-
л—о
кущей, то прямая
У- У о = ko(x-xo), (4)
f(xo+h)
85
Геометрический смысл производной
уравнение которой получается из
уравнения (3) заменой k(h) на k0,
называется касательной к
графику функции y = f(x) в точке с
координатами (х0; f(x0)). Таким
образом, касательная к графику
функции y = f(x) в точке (х0; f(x0))
есть предельное положение
секущей МА при &—►().
Если существует f'(x0), то
= limk(h) =
Л—>0
Рис. 49
=lim
л —о
h
Так как k0 — угловой коэффициент касательной, то
ko = f'(xo) = tga, где а — угол, образуемый касательной с
положительным направлением оси Ох (рис. 49). Таким образом,
f'(xo) = tga. (5)
Геометрический смысл производной состоит в том, что
значение производной функции f(x) в точке х0 равно
угловому коэффициенту касательной к графику функции
y = f(x) в точке (х0; f(x0)).
Задача 2. Найти угол между касательной к графику
функции y = sinx в точке (0; 0) и осью Ох.
£> Найдем угловой коэффициент касательной к кривой y = sinx
в точке (0; 0), т. е. значение производной этой функции при
Производная функции f(x) = sinx равна /' (х) = cos x. По
формуле (5) находим tgct = /'(0) = cosO = l, откуда ct = arctgl = |
(рис. 50).
Замечание. Это свойство полезно для построения
графика y = sinx: в точке (0; 0) синусоида касается прямой у = х. 4
Задача 3. Найти угол между касательной к параболе у=х2
в точке (1; 1) и осью Ох.
И1 \У = *2
Рис. 50
86
Гл а в а И
Производная и ее геометрический смысл
arctgi
Рис. 53
> Производная функции f(x) = x2 равна f'(x) = 2x. По формуле
(5) находим tga = f'(l) = 2-1 = 2, откуда a = arctg2 (рис. 51). ^
3. Уравнение касательной к графику функции
Заменяя в формуле (4) k0 на f'(x0), получаем уравнение
касательной (рис. 52) к графику функции y = f(x) в точке
(х0; f(x0)):
У = Нхо) + Пхо){х-хо). (6)
Задача 4. Найти уравнение касательной к графику
функции у = cos х в точке с абсциссой х0 = ^.
о
t> Найдем значения функции f(x) = cosx и ее производной в
точке *о="|:
Используя формулу (6), найдем искомое уравнение
касательной
Касательная к графику функции y = cosx в точке (^; ^—
изображена на рисунке 53. ^
ЕЯ Задача 5. Найти уравнение касательной к графику
функции у = х2 — 2х + 3, если эта касательная:
1) проходит через точку пересечения графика с осью Оу;
2) параллельна прямой у = 4х — 3.
[> Пусть f(x) = x2-2x + 3, тогда /'(х0) = 2х0-2 — угловой
коэффициент касательной к графику функции y = f(x) в точке
(дс0; /(#о))> и уравнение касательной в этой точке можно
записать так:
У = f(x0) + 2 (х0 -1) (х - х0).
1) Точка пересечения графика с осью Оу имеет
координаты х0 = 0, f(xo) = 3, a f'(xo) = -2. Поэтому прямая у = 3-2х
является касательной к графику в точке (0; 3).
§ 8 87
Геометрический смысл производной
пересекает ось Ох в точке —.
2) Из равенства угловых коэффициентов прямой у = 4х-$
и касательной в точке (х0; f(x0)) следует, что f (хо) = 2хо-2 = 4,
откуда хо = 3, f(xo) = 6, а уравнение касательной в точке (3; 6)
имеет вид у = 6 + 4(х-3) = 4х-6.
Ответ. 1) у = 3-2х; 2) у = 4х-6. <4
Задача 6. Показать, что касательная к параболе у = х2 в
точке с абсциссой
> Пусть f(x) = x2, тогда f'(x) = 2x, f(xo) = x% и f'(xo) = 2xo. По
формуле (6) находим уравнение касательной:
у = х% + 2х0 (х - х0) = 2хох - х%.
Найдем точку пересечения этой касательной с осью
абсцисс из равенства 2х0х-х% = 0, откуда х=-£-. ^
Из задачи 6 следует простой
геометрический способ построения
касательной к параболе у = х2 в точке
А с абсциссой х0: прямая,
проходящая через точку А и точку -^ оси
абсцисс, касается параболы в точке А
(рис. 54).
Построив касательную к
параболе, можно найти ее фокус.
Напомним, что фокусом F является точка,
в которую нужно поместить
источник света так, чтобы все лучи,
отраженные от параболического зеркала,
были параллельны оси симметрии
параболы. Для построения фокуса F надо построить прямую АВ,
параллельную оси Оу, и прямую AF, образующую с
касательной такой же угол, как и прямая АВ. ^—1
М 4. Дифференциал функции
Пусть функция f(x) имеет производную в точке х0, а
Af=f(xo + Ax)-f(xo) — приращение функции f(x) в точке х0,
соответствующее приращению аргумента Ах. Тогда
Af=f'(xo)Ax + a(Ax)Ax, (7)
где а(Ал;)—►() при Адг—►().
Первое слагаемое в формуле (7), т. е. произведение f'(xo)Ax,
называется дифференциалом функции f(x) в точке х0 и
обозначается df(x0), т. е. df(xo) = f'(xo)Ax.
Пусть f'(xo)^O9 тогда отношение второго слагаемого а(Алг)Адс
в формуле (7) к первому слагаемому стремится к нулю при
Ал:—►(). Поэтому при малых Ах можно заменить А/ на (i/(jc0),
т. е. записать приближенное равенство Af~df(x0) или равенство
Рис 54
88
Глава И
Производная и ее геометрический смысл
по которому можно находить значения функции f(x) в точке
хо+Ах с помощью значений этой функции и ее производной в
точке х0.
Если функция f(x) дифференцируема в каждой точке
интервала (а; Ь), то
df(x) = f'(x)Ax,
где Ал: — произвольное приращение аргумента.
Заметив, что dx = (x)'Ax = Ax, определим дифференциал
независимого переменного как его приращение. Тогда df(x) = f'(x)dx,
откуда
т. е. производную можно рассматривать как отношение
дифференциала функции к дифференциалу аргумента. Понятие
дифференциала будет использовано в главе IV.
Выясним геометрический и физический смысл
дифференциала.
Пусть функция y = f(x) дифференцируема в точке х0, тогда
в точке A(jc0; f(x0)) существует касательная (см. рис. 48),
пересекающая прямую x = xo + h в точке Б. Из треугольника ABC
находим ВС =ACtga = hf (x0). Полагая h = Ax, получаем
BC = f'(xo)Ax = df(xo). (8)
Равенство (8) позволяет дать геометрическое истолкование
дифференциала.
Если функция f(x) имеет производную в точке х0, то
дифференциал этой функции при х = х0 равен приращению
ординаты касательной в точке (х0; f(x0)) при изменении аргумента от х0
до xQ + h = x0 + Ax.
Обратимся к физическому смыслу дифференциала. Пусть
s(t) — путь, пройденный материальной точкой за время t от
начала движения. Тогда s'(£) = lim +— — мгновенная
At^O At
скорость и точки в момент времени t, т. е. v = s'(t). По
определению дифференциала ds=v-At. Поэтому дифференциал
функции s(t) равен расстоянию, которое прошла бы точка за
промежуток времени от t до t + At, если бы она двигалась со
скоростью, равной мгновенной скорости точки в момент
времени t. ей
Упражнения
89. Написать уравнение прямой с угловым коэффициентом k,
проходящей через точку (х0; у0), если:
1) k = 2, xo=l, уо = -1; 2) /г = 3, хо = -29 уо=1;
3) * —2, хо = 3, 1/0 = -4; 4) Aj=|, хо=1, Уо = О;
5) fc=|, хо=|, 1/0=|; 6) * = -|, хо = О, (/0 = 0.
§8 89
Геометрический смысл производной
90. Написать уравнение прямой, проходящей через точку (х0; у0)
и образующей с осью Ох угол а, если:
l) а——, х0 — — о, i/0 —z,
3) а=|, жо = 6, у0— 5;
О\ г* — ОЯ -v _ 1 »# _ 1 .
91. Найти угловой коэффициент касательной к графику функ
ции y = f(x) в точке с абсциссой х0, если:
1) f(x) = x\ хо=1; 2) f(x) = sinx, xo=^;
3) f(x) = lnx, xo = l; 4) f(x) = ex, л:о = 1п3;
°/ /ix; = ox — 4х, xo = z; о; /^х;=ух—=, Xq=l.
92. Найти угол между осью Ох и касательной к графику
функции y = f(x) в точке с абсциссой х0, если:
1 ^ ■f('v\ — -v*2 .у. I . o\ -f i<г\ -уЗ ^. -I .
3)
3jc+1
4)
5) /(х) = е 2 , хо = 1; 6) /(х) = 1п(2х + 1), хо=|.
93. На рисунке 55 изображен график функции y = f(x) и
касательные к графику в точках А, Б, С, D. Определить знак
производной этой функции в точках А, Б, С, D.
94. Написать уравнение касательной к графику функции
y = f(x) в точке с абсциссой х0, если:
L, хо=1; 2>
3)
±, жо-1;
5) /(л:) = cos л:, жо=-|;
7)
жо
4)
6)
8)
жо =
А
/
/
Л
'^—
\
\
6
Гл а в а И
Рис. 55
Производная и ее геометрический смысл
95. Написать уравнение касательной к графику функции
= f(x) в точке с абсциссой х = 0, если:
2) f() f
96. Найти угол между осью Оу и касательной к графику
функции y = f(x) в точке с абсциссой х = 0, если:
2) f(x) = cosxm
2
4)
6)
97. Под каким углом пересекаются графики функций (углом
между кривыми в точке их пересечения называют угол
между касательными к этим кривым в этой точке):
2) у= — (lH-x)" и
2
3) у = \п(1+х) и
4) у = ех и у = е~х?
98. Показать, что графики двух данных функций имеют одну
общую точку и в этой точке — общую касательную;
написать уравнение этой касательной:
1) У = х4, у = х6 + 2х2; 2)
3) i/ = (* + 2)2, y = 2-x2; 4)
5) y = Vx+l, у = х2 + ±х + 1; 6)
99. Найти точки графика функции y = f(x), в которых
касательная к этому графику параллельна прямой y = kx, если:
2)
3) f(x)=±x3 + x2-2x, ft-1; 4)
jc + 2
-
х — Z
6> /(^)
100. В каких точках касательная к графику функции i/
——
образует с осью Ох угол, равный — — ?
101.1 Найти точки, в которых касательные к кривым
f(x) = xs-x-l и g(x) = 3x2-4x+l
параллельны. Написать уравнения этих касательных.
102.1 Написать уравнение касательной к графику функции
y = f(x) в точке с абсциссой х0, если:
i2l 2) f(x)=±sin^-, xo = l.
§8
91
Геометрический смысл производной
Упражнения к главе II
103. Построить график функции y = f(x) и выяснить, является
ли эта функция непрерывной на всей числовой прямой:
1) нх)=\1х-4 п?и/*3' 2) /(*)-(5;2* при
' к ' \2 при х = 3; [-1 при х=1;
3) /(x)-f^ при *>0' 4) /(х) = (|х2-11 при х<
[л: при х<0; [х2 при #>-1.
Найти производную функции (104—108).
104. 1) 2л:4-л:3 + Зл: + 4; 2) - х5 + 2л:3 - Зх2 -1;
/1-4*
9) sin 0,5л:; 10) cos(-3x).
105. 1) e^-sin л:; 2) cos x-tg x; 3) ctg x-Vx;
4) 6х4-9^; 5) ^+4е*; 6) J_ + I
106. 1) sin 5л: + cos(2л:-3); 2) е2х-\п Зх;
3) эт(л:-3)-1п(1-2л:); 4) 6 sin^-e1"3*.
107. 1) х2 cos x; 2) л:3 In х; 3) 5л: ctg л:;
4) sin 2xtgx; 5) ^"^sin л:; 6) e^cos x.
i\ *3 + l. o\ jc2 . ox sin*. 4ч In
109. Найти значения х9 при которых значение производной
функции f(x) равно 0; положительно; отрицательно, если:
1) /(л:) = -Зл:3 + 2л:2 + 4; 2) /(л:) = (л: + 3)3(л:-4)2;
3) /(х)=-^,; 4) |
110. Найти значение производной функции f(x) в точке дг0,
если:
1) fix) = cos x sin л:, ^o=f; 2) /(x) = e*lnx, л:0=1;
111. Написать уравнение касательной к графику функции в
точке с абсциссой х0, если:
1) у = х2-2х, хо = 3; 2) 1/ = л:3 + Зл:, л:0 = 3;
3) y = slnx, *о = -|; 4> y
112. Закон движения тела задан формулой s(t) = O,5t2 + 3t+2
(s — в метрах, t — в секундах). Какой путь пройдет тело
за 4 с? Какова скорость движения в этот момент времени?
92 Глава II
Производная и ее геометрический смысл
Найти производную функции (113—115).
113. 1) sin л: cos хл-х\ 2) (д:3 + 1) cos 2x;
3) (х + 2)V?; 4) fyx-1 (л:4- 1).
Ш* ** l + cos2*' 2)
3)
4х '
^ч sin jc + cos х
sin л:-cos
115. 1) \
5
lnx-cos x;
2) ±x2-
sinx;
3) 15\/Gc + e*-6tg:x:; 4) 6 V^-ln x+-i-cos л:;
5) #2(#-l) + 3 sin лгн-4 ctg x;
6) #(:x; + 2)2 + 2 In x-3 cos л:;
7) (л:-]
8)
Построить график и указать промежутки непрерывности
функции:
Iog2(x-1) при
2)
/х+3 при х>3,
лгн-3 при -3<л:<3,
(лгн-3)2 при х<-3.
117. Найти вертикальные асимптоты графика функции
y = f(x), если:
1) fix)-
2)
118. Вычислить предел функции:
2 + x-xs
1) lim
2) lim
*-°° 14jc3-jc2-5 "
119. Найти производную функции:
1) In2 x; 2) Vln x; 3) sin \[x; 4) cos4 x; 5) Vtg х; 6) ctg Зх.
120. 1) i/ = cos2 Зх; 2) y = tg2^;
о) sin (^!лг —oX)i 4^ cos (дс н~ ^дс ^; о^ в ;
6) cos(^); 7) З*2; 8) 2COSX.
121. Найти значения х, при которых значение производной
функции f(x) равно нулю; положительно; отрицательно,
если:
3) f(x) = х + In 2x; 4)
5) f(x) = 6x-xVx; 6)
93
Упражнения к главе II
122. Найти все значения а, при которых f'(x)>0 для всех
действительных значений х, если
123. Найти все значения а, при которых f'(x)<0 для всех
действительных значений х, если
) = axs-6x2-x.
124. Найти все значения а, при которых уравнение f(x) = O не
имеет действительных корней, если:
1) f(x) = ax2-±; 2) \
3) f(x) = axs + 3x2 + 6x; 4)
125. Найти все значения а, при которых неравенство f(x)<Q
не имеет действительных решений, если:
3) f(x) = (x + a) Vx; 4)
126. Под каким углом пересекаются графики функций:
1) у = 2\[х и у = 2V6 — х; 2) у = у]2х+1 и i/ = l?
127. Написать уравнение касательной к графику функции в
точке с абсциссой х0, если:
1) z/ = 2sin|, xo=^; 2) */ = 2-*-2"2*, хо = 2;
3) У=^-, хо = 2; 4) y-x + ln x, хо = е;
£t — ОС
5) у = ех2~\ хо = 1; 6) i/ = sin(7ix2), xo=l.
112В7| Написать уравнение касательной к графику функции
y = f(x), параллельной оси Ох, если:
1) f(x) = x2-4x; 2) f(x) = (
3) /(x) = x4 + 32x-3; 4) f(x) =
[1297] Найти уравнения касательных к графику функции
г/ = i л:3 - 4 ^2> параллельных прямой у = бл:.
о ^
1130.1 Прямая касается гиперболы i/=— в точке (1; 4). Найти
площадь треугольника, ограниченного этой касательной и
осями координат.
*мая касается гиперболы у= — , где &>0, в точке с
абсциссой х0. Доказать, что:
1) площадь треугольника, ограниченного этой
касательной и осями координат, не зависит от положения точки
касания; найти эту площадь;
2) эта касательная проходит через точки (х0; —^ и(2л:0; 0).
94 Глава II
Производная и ее геометрический смысл
Вопросы к главе
1. Перечислить способы задания числовой
последовательности.
2. Какая последовательность называется сходящейся?
3. Какая последовательность называется монотонной?
4. Привести пример функции, имеющей вертикальную
(горизонтальную) асимптоту.
5. Привести пример непрерывной функции и построить ее
график.
6. Что называется мгновенной скоростью?
7. Что называется производной функции f(x) в точке х0?
8. В чем состоит физический смысл производной?
9. Сформулировать правила дифференцирования суммы,
произведения, частного.
10. Чему равна производная функции у = хр (p€R), y = sinx,
y = cosx, у = ех?
11. Что называется угловым коэффициентом прямой?
12. Записать уравнение прямой с угловым коэффициентом k,
проходящей через точку (х0; i/0).
13. В чем состоит геометрический смысл производной?
14. Что называется пределом последовательности?
15. Что называется пределом функции?
16. Какая функция называется непрерывной в точке а?
YL Как найти производную сложной функции? обратной
функции?
18. Вывести формулу для нахождения производной функции
y = tgx; y = ctgx.
19. Какую прямую называют касательной к графику функции
в данной точке?
J Что называется пределом слева (справа) функции f(x) в
точке а?
Какую функцию называют бесконечно малой?
Lj Сформулировать свойства предела функции.
У Сформулировать свойства функций, непрерывных на
отрезке.
]. Чему равна производная функции у = arcsin x? y = arctgx?
2 Что называется дифференциалом функции в точке?
L В чем состоит геометрический и физический смысл
дифференциала?
9^
Вопросы к главе II
Проверь себя!
1. Найти значение производной функции f(x) = 2xs + 3x2-x
в точке х = -2.
2. Найти производную функции:
1) A+4vGc-e*; 2) (3*-5)3;
3) 3 sin 2x cos х; 4) -£—.
3. Найти угол между касательной к графику функции
у = х4 — 2xs + 3 в точке с абсциссой х0 = — и осью Ох.
4. Найти значения х, при которых значения производной
функции
отрицательны.
5. Написать уравнение касательной к графику функции
f(x) = sin 2x в точке с абсциссой хо = -^.
1. Найти предел функции:
4 оч v V*-3-2
-; 2) lim .
Л^°° бх~-х~ + 2 х^7 х-7
2. Выяснить, является ли непрерывной в точке а = 3 функция
[2 при л: = 3.
3. Найти значения л:, при которых значения производной
функции
равны 0.
4. Написать уравнение той касательной к графику функции
у= -i- xs — x2 + 5, которая параллельна прямой у = Зх-2.
о
I ^J I Историческая справка
Основными понятиями математического анализа яляются
понятия функции, предела, производной и интеграла.
Термин «функция» впервые был употреблен в 1692 г.
немецким математиком Г. Лейбницем (1646—1716). Первое
определение понятия функции, основанное на геометрических
представлениях, сформулировал в 1718 г. Л. Эйлер (1707—1783).
Ему принадлежит и введение символа f(x). Эйлер фактически
отождествлял функцию с ее аналитической формулой, хотя
уже современники Эйлера понимали, что функцию можно
задавать не только аналитически.
96 г л а в а II
Производная и ее геометрический смысл
В 1834 г. великий русский математик Н. И. Лобачевский
(1792—1856) дал определение понятия функции на основе идеи
соответствия элементов двух числовых множеств. В 1837 г.
немецкий математик П. Дирихле (1805—1859) сформулировал
обобщенное определение понятия функции: «у является
функцией переменной х на отрезке а<л;<Ь, если каждому значению
х соответствует вполне определенное значение i/, причем не
имеет значения, каким образом установлено это
соответствие — формулой, графиком, таблицей или словесным
описанием».
После создания теории множеств во второй половине XIX в.
определение понятия функции было дано на множественной
основе. В XX в. в связи с развитием естественных наук
происходило дальнейшее расширение понятия функции. Так, в 1936 г.
российский математик академик С. Л. Соболев (1908—1990)
дал наиболее обобщенное определение понятия функции.
Понятие производной определяется через понятие предела,
история появления которого уходит в глубокую древность. Еще
в IV в. до н. э. знаменитый древнегреческий математик Евдокс
Книдский в неявном виде использовал предельные переходы
для обоснования методов вычисления площадей
криволинейных фигур. В явном виде предельные переходы
встречаются в работе фламандского математика А. Такке (1612—1660)
«Начала плоской и телесной геометрии», опубликованной
в 1654 г. Первое определение предела дал английский
математик Д. Валлис (1616—1703). Метод пределов получил свое
развитие в работах знаменитого английского ученого И. Ньютона
(1643—1727). Ему же принадлежит введение символа lim.
Существенный вклад в развитие основ дифференциального
исчисления внесли французские ученые П. Ферма (1601—1665)
и Р. Декарт (1596—1650). В середине 60-х гг. XVII в. Ньютон
пришел к понятию производной, решая задачи механики,
связанные с нахождением мгновенной скорости. Результаты своей
работы он в 1671 г. изложил в трактате «Метод флюкций и
бесконечных рядов». Однако этот трактат был опубликован
лишь в 1736 г., и поэтому первой работой по
дифференциальному исчислению считается статья Лейбница, опубликованная
в 1684 г., в которой рассматривается геометрическая задача о
проведении касательной к кривой.
Приращение абсциссы — бесконечно малую разность х2 —
-х1 — Лейбниц обозначал dx (d — первая буква лат. слова
differentia — разность), а приращение ординаты у^ — Ух он
обозначал dy. В середине XVIII в. Эйлер для обозначения
приращений стал пользоваться греческой буквой А. Термин
«производная» (по-франц. derivee) впервые появился в 1800 г.
в книге французского математика Л. Арбогаста (1759—1803)
«Вычисление производных». Обозначение производной у' и
/ (х) ввел французский математик Ж. Лагранж (1736—1813).
97_
Историческая справка
Глава
Применение производной
к исследованию
функций
Рано или поздно всякая правильная
математическая идея находит
применение в том или ином деле.
А. Н. Крылов
i
§ 1. Возрастание
и убывание функции
С помощью производной можно находить
промежутки монотонности функции.
Условимся термин «промежуток»
использовать для обозначения таких числовых
множеств, как отрезок [а; Ь], интервал (а; Ь),
полуинтервалы [а; Ъ) и (а; Ь].
При этом точки а и Ъ называют
граничными точками, а все остальные точки
интервала (а; Ь) — внутренними точками
промежутка.
Напомним, что функция f(x) называется
возрастающей на некотором промежутке, если
большему значению аргумента соответствует
большее значение функции, т. е. для любых
точек хг и х2 из этого промежутка, таких, что
х2>х19 выполняется неравенство
Если для любых точек хх и х2 из данного
промежутка, таких, что х2>хи выполняется
неравенство
f(x2)<f(x1),
то функция f(x) называется убывающей на
этом промежутке.
При доказательстве теорем о достаточных
условиях возрастания или убывания функции
используется следующая теорема, которая
называется теоремой Лагранжа.
Глава III
Применение производной к исследованию функций
Теорема 1
Пусть функция f{x) непрерывна на отрезке [а; Ь] и
дифференцируема на интервале (а; Ь). Тогда существует
точка с€(а;Ь), такая, что
a). (1)
■ Эта теорема доказывается в
курсе высшей математики.
Поясним геометрический смысл
формулы (1). Проведем прямую I
(рис. 56) через точки
А(а; f(a)) и В(Ъ; f(b))
графика функции y = f(x) и
назовем эту прямую секущей.
Угловой коэффициент k секущей
I равен
Ь-а • (г)
Равенство (1) можно записать в виде
f'(c)=fib)~fia)
Ь-а
У,
0
»■
а/
/ /
а
2
с
1
/
j X
Рис 56
(3)
Из равенств (2) и (3) следует, что угловой коэффициент
f (с) касательной к графику функции y = f(x) в точке С с
абсциссой с равен угловому коэффициенту k секущей Z.
Таким образом, на интервале (а; Ь) найдется такая точка с,
что касательная к графику функции y = f(x) в точке С (с; /(с))
параллельна секущей L C3I
Теорема 2
Пусть функция f(x) непрерывна на отрезке [а; Ь] и
дифференцируема на интервале (а; Ь). Тогда если f'(x)>0
для всех х€(а;Ь)> то функция f(x) возрастает на
отрезке [a; b]9 a если /'(jc)<0, то она убывает на этом
отрезке.
Докажем эту теорему (достаточные условия возрастания
и убывания функции) с помощью теоремы 1.
О Пусть хх и х2 — произвольные точки отрезка [а; Ь], такие,
что х1<х2. Применяя к отрезку [хг; х2] формулу (1), получаем
f(x2)-f(x1) = f'(c)(x2-x1), ce(Xl; x2). (4)
Так как х2-хг>09 то из равенства (4) следует, что при
f'(x)>0 выполняется неравенство f(x2)>f(x1), а при f'(x)<0 —
неравенство f(x2)<f(x1). Это означает, что если f'(x)>0, то
функция f(x) возрастает на отрезке [а; Ь], а если /'(л;)<0, то
она убывает на этом отрезке. •
Промежутки возрастания и убывания функции называют
промежутками монотонности этой функции.
§ 1 99
Возрастание и убывание функции
Задача 1. Найти промежутки
возрастания и убывания функции
данной функции
у = (х — 1)2(х - 4)
[> Производная
равна
откуда следует, что /'(л;)>0 при
х<1 и х>3. Следовательно,
функция f(x) возрастает на
промежутках х< 1 и х> 3.
На интервале 1 < х < 3
выполняется неравенство /'(л;)<0. По
теореме 2 функция f(x) убывает на
этом интервале и на отрезке [1; 3].
График функции у = (х — 1)2(х — 4)
ке 57. 4
Задача 2. Доказать, что функция
возрастает на всей числовой прямой.
9 // 1 \2 Я \
Р> Так как / (х) = бдг -6xH-6 = 6[[x-—1 -Ь ^ ) > О
W 2) 4)
то функция /(л:) возрастает на всей числовой прямой.
Рис- 57
изображен на
рисунвсех
Задача 3. Найти промежутки монотонности функции:
2)
Если х<Ъ или л:>15, то /'(л;)>0. По теореме 2 функция
f(x) возрастает на промежутках л:<5 и л:>15.
На интервале 5<л:<15 выполняется неравенство f'(x)<0,
и поэтому функция f(x) убывает на отрезке 5<л:<15.
2) f'(x) = e-x-xe-x = (l-x)e-x.
Если х<19 то f'(x)>0, а если д:>1, то /'(л;)<0. По
теореме 2 функция f(x) возрастает на промежутке л:<1 и убывает
на промежутке х > 1. ^
FfH Задача 4. Пусть функция f(x) непрерывна на отрезке [а; Ь],
дифференцируема на интервале (а; Ь) и для всех х€(а; Ъ)
справедливо равенство f'(x) = O. Доказать, что f(x) = C, x€[a; b], т.е.
функция f(x) постоянна на отрезке [а; Ь].
1> Пусть х0 — некоторая точка отрезка [а; Ь], х —
произвольная точка этого отрезка. По теореме Лагранжа f(x)-f(xo)=
= f'(c)(x-x0). Так как с€(а;Ь), то f'(c) = O, и поэтому f(x)=
= f(xo) = C. Ч ТП
1ЯЗадача 5. Доказать, что если 0<х<^, то справедливы
неравенства
400 Глава 111
Применение производной к исследованию функций
tg x>x, sinjc> — х.
D> 1) Рассмотрим функцию <p(x) = tg х-х. Эта функция
дифференцируема на интервале (0; ^Л, причем ф'(л;) = 1, от-
V г ) cos2 х
куда следует, что ф'(л;)>0, так как 0<cos2x<l при xe(0; ^-j.
Кроме того, функция <р(х) непрерывна при х = 0. По теореме 2
эта функция возрастает на промежутке 0; ^-j. Так как ф(0) =
=0, то при 0<х<^ справедливо неравенство ф(л;)>ф(0), т. е.
tgjc-JC>0, откуда следует неравенство tg x>x.
2) Рассмотрим функцию /4*)=^^, х*0; /(0)=1. Эта
функция дифференцируема на интервале (0; ^-J и непрерывна
во всех точках отрезка 0; ^ I, включая точку д; = 0, так как
Найдем f'(x). По правилу дифференцирования произведе-
1 1 cos х /Л п\
ния / (х) = sin х + — cos х =—— (x-tg х). Если х€ О; — ,
хг х хг \ г /
TOJt-tgx<O (из п. 1). Кроме того, cos х>0 при х^(0; ^-J и
х2>0. Следовательно, f'(x)>0 и по теореме 2 функция f(x)
убывает на интервале (0; -^ ). Поэтому f(x)>f(-^ J при л:^(0; -^ J,
■ /<тг\ /тг\ 9
т. е. >f( -J )» где /( — ) = —, откуда следует неравенство
Упражнения
Найти интервалы возрастания и убывания функции (1—2).
1. 1) у = 5х2-Зх-1; 2) у = х2-\
3) i/ = 2jc^4-3jc2 — 4" 4) и = *
2, 1) # = *2-3:jc + 4; 2) у
Z)y = x*-3x; 4) у
Найти промежутки монотонности функции (3—4).
X
4) i/ = 3V#-5 + l; 5) i/ = jc-sin2x; 6) i/ = 2л:н- — cosЗл:.
о
4. 1) j^-i—; 2) !/ = (л:-1
4) у = хе-*х.
§ 1 101
Возрастание и убывание функции
5. На рисунке 58 изображен
график функции Г(х),
являющейся производной функции у.
Определить промежутки
возрастания и убывания функции
у=/(*)•
6^ При каких значениях а
функция возрастает на всей
числовой прямой:
1) у=х3-ах;
2) y = ax-sinx?
3
2
,,, >
Л
/
.01 2 \4
Рис
X
58
± Доказать, что функция у = V6 + х - х2 возрастает на отрезке
— 2; — и убывает на отрезке —; 3 .
.1 Доказать, что если х>0, то:
2) Л
' х+1
§ 2. Экстремумы функции
1. Необходимые условия экстремума
На рисунке 59 изображен
график функции y = f(x). Как
видно из рисунка, существует
такая окрестность точки х19 что
наибольшее значение функция
f(x) принимает в точке хх. Тем
же свойством обладает точка xs.
Точки х1 и jc3 называют точками
максимума функции f(x).
Аналогично точку х2 называют точкой минимума функции
f(x), так как значение функции в точке х2 меньше ее значений
в остальных точках некоторой окрестности точки х2.
Определение 1
Рис. 59
Точка х0 называется точкой максимума функции f(x),
если для всех х^х0 из некоторой окрестности точки х0
выполняется неравенство f(x)<f(x0).
Например, точка хо = О является точкой максимума
функции f(x) = 4 -х2. В этой точке функция принимает наибольшее
значение, равное 4.
Определение 2
Точка х0 называется точкой минимума функции f(x),
если для всех хч*х0 из некоторой окрестности точки х0
выполняется неравенство f(x)>f{x0).
102 Глава 111
Применение производной к исследованию функций
Например, точка х0 = 1 является точкой минимума
функции /(д:) = 2ч-(л:— I)2- В этой точке функция принимает
наименьшее значение, равное 2.
Точки минимума и точки максимума называются точками
экстремума.
Теорема 1 (теорема Ферма)
Пусть функция f{x) определена в некоторой
окрестности точки х0 и дифференцируема в этой точке. Если х0 —
точка экстремума функции f(x)y то f'(xo) = O.
Строгое доказательство этой теоремы выходит за рамки
школьного курса математики. Теорема имеет наглядный
геометрический смысл: в точке экстремума касательная к графику
функции параллельна оси абсцисс, и поэтому ее угловой
коэффициент f'(x) равен нулю (рис. 60).
Например, функция f(x) = 2x-x2 (рис. 61) имеет в точке
#о=1 максимум, и ее производная f'(x) = 2 — 2х, /'(1) = 0.
Функция f(x) = (x+1)2 — 4 (рис. 62) имеет минимум в
точке *0 = -1, и f(*) = 2(*+l), f(-l) = 0.
2х-х2
Рис 61
Рис 62
103
Экстремумы функции
Условие f'(x) = O является необходимым условием
экстремума дифференцируемой функции f(x). Это означает, что если
х = х0 — точка экстремума дифференцируемой функции, то
Г(хо) = О.
Поэтому точки экстремума дифференцируемой функции
f(x) следует искать среди корней уравнений f(x) = O. Однако
уравнение f(x) = O может иметь корни, которые не являются
точками экстремума функции f(x).
Например, если f(x) = xs, то Г(0) = 0, но точка х = 0 не
является точкой экстремума функции, так как эта функция
возрастает на всей числовой оси (рис. 63).
Точки, в которых производная функции обращается в
нуль, называются стационарными точками этой функции.
Задача 1. Найти стационарные точки функции:
1) f(x) = 2xs-3x2-12x + 4; 2) f(x) = xex.
> Так как f'(x) = 6x2-6x-12 = 6(x2-x-2) = 6(x + l)(x-2), то
уравнение f'(x) = O имеет корни х1 = -19 х2 = 2. Следовательно,
-1 и 2 — стационарные точки данной функции.
2) В этом случае f(x) = ex + xex = ex(x+l). Поэтому х = -1 -
стационарная точка функции f(x). M
^^1 Заметим, что функция может
иметь экстремум и в точке, в
которой она не имеет производной.
Например, функция f(x) = \x\-2 не
имеет производной в точке х = 0,
однако эта точка является для нее
точкой минимума (рис. 64). ^^1
Внутренняя точка области
определения непрерывной функции
f(x), в которой эта функция не
имеет производной или имеет производную, равную 0, называется
критической точкой функции f(x).
Таким образом, для того чтобы точка х0 была точкой
экстремума непрерывной функции f(x)9 необходимо, чтобы эта точка
была критической для данной функции.
2. Достаточные условия экстремума
Теорема 2
Пусть функция f(x) дифференцируема в некоторой
окрестности точки хОУ кроме, быть может, самой точки х0
и непрерывна в точке х0. Тогда:
1) если f(x) меняет знак с«-»на« + » при переходе
через точку х0, т. е. в некотором интервале (a; х0)
производная отрицательна и в некотором интервале (х0; Ь)
положительна, то х0 — точка минимума функции f{x)
(рис. 65);
104 Глава III
Применение производной к исследованию функций
/'(*)< о
f'(x)>0
О х0
x
Рис. 65
/'(*)> о
0
x0
Рис. 66
2) если f С*) меняет знак с « + » на «-» при переходе
через точку jc0, то х0 — точка максимума функции f{x)
(рис. 66).
^Ё О Пусть f'(x) меняет знак с «-» на «+» при переходе
через точку х0. Тогда f'(x)<0 при а<х<хо и f'(x)>0 при
хо<х<Ь. По теореме 2 из § 1 функция f(x) убывает на
промежутке (а; х0] и возрастает на промежутке [х0; Ъ). Тогда f(x0) —
наименьшее значение функции на интервале (а; 6), и поэтому
х0 — точка минимума функции f(x).
Аналогично рассматривается случай максимума. # СЗ
Задача 2. Найти точки экстремума функции:
1) f(x) = x*-x; 2) ff
t> 1) Найдем производную
Приравнивая ее к нулю, находим две стационарные точки:
JCi=—7= и Хо=-т=. При переходе через точку хл =—р= произ-
водная меняет знак с «+» на «—». Поэтому #! =—j= — точка
максимума. При переходе через точку х2 = -= производная ме-
•j V3
няет знак с «-» на «+», поэтому x2 = -F= — точка минимума.
V3
2) Функция f(x) дифференцируема на R, поэтому все ее
точки экстремума содержатся среди стационарных точек,
являющихся корнями уравнения f'(x) = O, т. е. уравнения
—
откуда (л:-2)(л:н-1)2(5л:-4) = О.
Полученное уравнение имеет корни л:1 = -1,
При переходе через точку х1 функция f'(x) сохраняет знак, и
поэтому (теорема 2 из § 1) хх не является точкой экстремума.
При переходе через точку х2 функция f'(x) меняет знак с
«+» на «-», а при переходе через точку xs меняет знак с «-»
на «+». Поэтому х2 — точка максимума, a jc3 — точка
минимума функции f(x) (по теореме 2). М
§ 2
105
Экстремумы функции
I Задача 3. Найти экстремумы функции f(x)
1-х'
\> Область определения данной функции х ^ 1. Найдем
производную:
/'(*) =
(1-х)2 (1-х)2
Ъх2-2хъ = х2(3-2х)
=
(1-х)2 (1-х)2 (1-х)2
Найдем стационарные точки функции, решив уравнение
х2 (S — 2х) 3
— =0, которое имеет корни х1 = 0, х2 = —.
(1-*) 2
При переходе через точку л: = 0 ни одно из выражений: #2,
3-2д:, (1-л:)2 — не меняет знак, поэтому точка # = 0 не
является точкой экстремума.
Q
При переходе через точку х=— выражения х2 и (1 — jc)2 не
2
2>
меняют знак, выражение 3-2л:, а с ним и f'(x) меняют знак с
о
с «+» на «-»; это означает, что х=— — точка максимума. ^ ^П1
Ш^ Задача 4. Найти экстремумы функции
f(x) = 5xs-x\x+l\.
\> Если л:<-1, то f(x) = f1(x) = 5xs + x2 + x, а если х>-1, то
5xs-x2-x. Тогда f[(x)=15x2 + 2x+ l>0 при всех х,
р
а уравнение f2=l^x2 — 2x—l=0 имеет корни х1 — — —, х2 = —>
11 5 3
При этом f2(x)>0 при х< — — и х> —, f2(x)<0 при х1<х<х2.
5 3
Функция f(x) не имеет производной в точке хо = — 1, и
f(x) = 0 при х = хх и х = лг2. Следовательно, хо = — 1, jc1? x2 —
критические точки функции f(x).
Так как /' (х) > 0 при х < -1 и при -1 < # < - —, то х0 не яв-
о
ляется точкой экстремума. Производная меняет знак с «+» на
«—» при переходе через точку х1 и с «—» на «+» при переходе
через точку х2. Следовательно, х1 = —- —точка максимума,
1
а х2 = — — точка минимума функции. ^ ВЯ
3
Упражнения
9. Найти стационарные точки функции:
2) у = х2-Ых+1Ь\
4) 1/=- + —;
7) i/ = sin x -cos x; 8) i/ = cos 2x + 2 cos л:.
106 Глава HI
Применение производной к исследованию функций
10. Найти критические точки функции:
■П а 1*1 • 9} it— v3 Iv II-
L) у— 2' ' У— ""I*""1!»
3) у = 2х2-\х2-1\; 4) у = 3х + |3х-х2|.
Найти точки экстремума функции (11 —12).
11. 1) у = 2х2-20х+1; 2) у = 3*2 + 36х-1;
5) y =
7) j/ =
6) у = х4-8х2 + 5;
8) i/= 6 sin л:-cos 2л:.
2) i/ = (x-l)7;
4) у = со&3х-£х\
6) i/=l-(x+l)6;
8) у = (х-б)в*.
13. На рисунке 67 дан график функции, являющейся
производной функцией y = f(x). Определить промежутки
возрастания и убывания функции, ее точки экстремума.
14. Найти экстремумы функции:
1) */ =
2 + *'
!/ = |*-5|(*-3)3;
4) у=-
JC+1
X
Рис. 67
§ 3. Наибольшее и наименьшее значения
функции
Если функция f(x) непрерывна на отрезке [а; 6], то
существует точка этого отрезка, в которой функция f(x)
принимает наибольшее значение, и точка, в которой эта функция
принимает наименьшее значение.
Чтобы найти наибольшее и наименьшее значения
непрерывной на отрезке [а; Ь] функции f(x), имеющей на
интервале (а; Ь) несколько критических точек, достаточно
вычислить значения функции f(x) во всех этих точках, а
также значения f(a) и f(b) и из всех полученных чисел
выбрать наибольшее и наименьшее.
В прикладных задачах при нахождении наибольшего
(наименьшего) значения функции f(x) на отрезке [а; Ь] или на
интервале (а; Ъ) часто встречается случай, когда функция f(x)
дифференцируема на интервале (а; Ъ) и непрерывна на отрезке
§ 3
107
Наибольшее и наименьшее значения функции
[а; 6], а уравнение f'(x) = O имеет единственный корень хо€(а; &),
такой, что на одном из интервалов (а; хо)9 (х0; Ъ) выполняется
неравенство f'(x)>0, а на другом — неравенство /'(jc)<0.
В этом случае число f(x0) является наибольшим или
наименьшим значением функции f(x) на отрезке [а; Ь] или на
интервале (а; Ь).
Замечание. Пусть g(x)>0 на некотором промежутке,
f(х) = (g(х))п, где nGiV, л>2. Тогда, если одна из функций f(x)
и £Т(д;) принимает в точке х0 из этого промежутка наибольшее
(наименьшее) значение, то и другая функция принимает в
точке х0 наибольшее (наименьшее) значение.
Задача 1. Найти наибольшее и наименьшее значения
функции f(x) = xs-\— на отрезке —; 2 .
X L 2t J
куда Х1
б|, /(2) = 9|; П*) = 3*2-^ = ^^, 3*4-3=0,
отОтрезку —; 2 принадлежит одна стационарная точка
11 1
хг = 1, /(1) = 4. Из чисел 6—, 9— и 4 наибольшее — число 9-,
о 2 2
наименьшее — число 4, т. е. наибольшее значение функции
равно 9—, а наименьшее равно 4. ^
Задача 2. Найти наибольшее значение функции g(x) =
= х\6 — х2 на интервале 0<jc<V6.
[> Так как £(л;)>0 для всех #€(0; V6), то точка х0 является
точкой наибольшего значения функции g(x) тогда и только
тогда, когда эта точка является точкой наибольшего значения
функции f(x) = (g(x))4 = x4(6-x2) = 6x4-x6.
Найдем производную /' (x) = 24xs-6x5 = 6xs(2 + x)(2-x). На
интервале 0<л:<2 функция f(x) возрастает, так как на этом
интервале f'(x)>0. На интервале 2<jc<V6 функция f(x)
убывает, так как на этом интервале f'(x)<0. Следовательно,
точка х = 2 является точкой максимума функции f(x) и в этой
точке функция f(x) принимает наибольшее из ее значений на
интервале 0<л:<\/б.
Функция g(x) также принимает наибольшее значение на
интервале 0<л:<\/б^ в точке х = 29 и это значение равно
j 4
Задача 3. Найти наибольшее и наименьшее значения
функции f(x) на множестве Е, если:
1) /(л:) = 2л:3-Зл:2-36л:-8, Е = [-3; 6];
2) f(x) = (x-2)2(x+lf, E = [0; 3].
[> Пусть М — наибольшее, am — наименьшее значение
функции f(x) на множестве Е.
108 Глава III
Применение производной к исследованию функций
1) Так как /' (х) = 6х2 -6х -36 = 6 (х + 2) (х -3), то функция
f(x) имеет две стационарные точки хг=-2, х2 = 3, каждая из
которых принадлежит отрезку [-3; 6]. Вычислим значения
функции f(x) в точках х19 х2 и в концах отрезка [—3; 6]:
/(-3)=19, /Ч-2) = 36, /(3) = -89, /(6)=100.
Следовательно, М=100, т = —89.
2) Функция f(x) имеет три стационарные точки л:1 = -1,
jc2 = —, хг = 2 (§ 2, задача 2), из которых множеству Е
принадлежат только точки х2 и хг. Так как /(0) = 4, /(— ) = плпг, ,
\ 5 / о125
= 0. Ч
Д
) = 64, то М = 64,
Задача 4. Из всех
прямоугольников, вписанных в окружность
радиуса R, найти прямоугольник
наибольшей площади.
[> Найти прямоугольник — это
значит найти его размеры, т. е. длины
его сторон. Пусть прямоугольник
ABCD вписан в окружность радиуса jR
(рис. 68). Обозначим АВ = х. Из
треугольника ABC по теореме Пифагора
находим BC = V4R2-x2.
Площадь прямоугольника равна
-^2, (1)
где 0<jc<2jR. Задача свелась к нахождению такого значения х,
при котором функция S(x) принимает наибольшее значение на
интервале 0<jc<2jR.
Так как S(x)>0 на интервале 0<x<2R, то функции S(x)
и f(x) = (S(x))2 принимают наибольшее значение на этом
интервале в одной и той же точке.
Таким образом, задача свелась к нахождению такого
значения х9 при котором функция f(x) = x2(4R2-x2) = 4R2x2-x4
принимает наибольшее значение на интервале 0<jc<2jR.
Имеем
На интервале 0 < х < 2R есть только одна стационарная
точка x = R\[2 — точка максимума. Следовательно, наибольшее
значение функция f(x) (а значит, и функция S(x)) принимает
при jc = jR\/2.
Итак, одна сторона искомого прямоугольника равна R}[2,
другая равна V4R2-(R\[2)2 = R\[2\ т. е. искомый
прямоугольник — квадрат со стороной R\[2, его площадь равна 2jR2. ^
TSt Задача 5. Найти высоту конуса, имеющего наибольший
объем среди всех конусов, вписанных в сферу радиуса jR.
§ 3 109
Наибольшее и наименьшее значения функции
[> В сечении сферы плоскостью,
проходящей через ось конуса, образуется
окружность радиуса jR, а в сечении
конуса той же плоскостью —
равнобедренный треугольник ABC (AB = BC),
вписанный в эту окружность с
центром О (рис. 69).
Пусть D — центр основания
конуса, х — его высота, г — радиус
основания. Тогда BD — x, AD = r.
Продолжим BD до пересечения с
окружностью в точке Е. Так как угол ВАЕ
прямой, то по свойству перпендику- ^
ляра, опущенного из вершины прямо- гии- оу
го угла треугольника ABE на гипотенузу, AD2 = EDDB, где
> = BE-BD = 2R-x. Следовательно, r2 = (2R-x)x.
Пусть V— объем конуса, тогда V(x)= — пг^х = — n(2Rx2 - х\
3 о
откуда
V'(x) = \ п (4Rx - Зх2) = ± nx (4R- Зх).
о о
Так как 0<x<2R, а на интервале (0; 2R) уравнение
V'(x) = 0 имеет единственный корень х=——, причем V'(x)>0
при 0 < х < — и V (х) < 0 при — < х <2jR, to значение функции
3 3
V(x) при х=—■ является наибольшим значением этой функ-
3
ции. Ответ. —-. ^ П
3
ИИ Задача 6. На координатной плоскости Оху дана точка
М(2; 4). Рассматриваются треугольники, у которых две
вершины, симметричные относительно оси Оу, лежат на параболе
у = 3х2, — 1<х<1, а точка М является серединой одной из
сторон каждого треугольника. Среди этих треугольников
выбран тот, который имеет наибольшую площадь. Найти эту
площадь.
О Пусть 0<х<1, А(—х; Зх2), В(х; Зх2) — вершины одного из
рассматриваемых треугольников (рис. 70).
Третья вершина С определяется неоднозначно, так как
точка М может быть либо серединой стороны ВС, либо
серединой стороны АС (на рисунке это точки С1 и С2).
Площади треугольников АСХВ и АС2В равны, так как у
них общее основание АВ и равные высоты h1 и Л2, где
h1 = h2 = h, причем h равняется удвоенной разности ординат
точек М и А, т. е. /* = 2(4-Зл;2).
Пусть S = S(x) — площадь треугольника ABC, тогда
s. Так как уравнение S'(*) = 0, т. е.
110
Глава III
Применение производной к исследованию функции
уравнение 8 - 18л:2 = 0 имеет на
отрезке [0; 1] единственный
о
корень х0 = —, причем S' (х) > 0
при 0<л:<-| и S'(*)<0 при
2 3
-<#<1, то значение
о
является наибольшим
значением функции S(x) на
отрезке [0; I].
Ответ. 3 —. "4
0
х
Рис. 70
Задача 7. Найти наибольшее и наименьшее значения функ-
/(л:) = 5л:3-л:|л:+1|
на отрезке [-2; 0].
> Данная функция непрерывна на отрезке [-2; 0] и
дифференцируема во всех точках интервала (-2; 0), кроме точки хо = -1.
В § 2 (задача 4) было установлено, что функция f(x) имеет на
интервале (-2; 0) единственную точку экстремума х1 = -—9
которая является точкой максимума этой функции. Находим
значения функции в точке х1 и в концах отрезка [—2; 0]. Получа-
(1 \ 3
- — ) = —, /(0) = 0. Наибольшее из этих чисел —
число —, а наименьшее — число -38. <
Упражнения
Найти наибольшее и наименьшее значения функции (15—17).
15. 1) f(x) = xs-6x2 + 9 на отрезке [-1; 2];
2) f(x) = x4-8x2 + 3 на отрезке [-1; 2];
3) f(x) = 2хг + 3х2-36х на отрезке [-2; 1];
4) f(x) = xs + 9х2 + 15х на отрезке [-3; -2].
л;2-- на отрезке [1; 2];
16. 1) /
2) f(x) = x-Vx на отрезке [0; 4].
17. 1) f(x) = 2 sin л: + cos 2л: на отрезке [0; 2я];
2) /Ч*) = 2cosх-cos2л: на отрезке [0; я].
18. Найти наибольшее значение функции:
1) jc5 - 5л:4 + 5л:3 + 1 на отрезке [-1; 2];
2) 1-х4-х6 на интервале (-3; 3);
3) л:2 на промежутке х<0;
4) — н— на промежутке л:<0.
111
__
Наибольшее и наименьшее значения функции
19. Найти наименьшее значение функции:
1) х2 + — при х>0; 2) л:+— при х>0.
х2 х
20. Число 50 записать в виде суммы двух чисел, сумма кубов
которых наименьшая.
21. Записать число 625 в виде произведения двух
положительных чисел так, чтобы сумма их квадратов была
наименьшей.
22. Из всех прямоугольников с периметром р найти
прямоугольник наибольшей площади.
23. Из всех прямоугольников, площадь которых равна 9 см2,
найти прямоугольник с наименьшим периметром.
Найти наибольшее и наименьшее значения функции (24—25).
24. 1) f(x) = x-2\nx на отрезке —; е ;
2) f(x) = x + e~x на отрезке [-1; 2].
25. 1) f (х) = sin х + cos x на отрезке я; -£- ;
2) f {х) = sin х + cos х на отрезке 0; — .
26. Найти наибольшее значение функции:
1) 3\[х-х\[х на промежутке х>0;
2) Зх-2х\[х на промежутке х>0;
3) \пх — х на промежутке х>0;
4) 2х-е2х на интервале (-1; 1).
27. Найти наименьшее значение функции:
1) eSx-Sx на интервале (-1; 1);
2) —i-lnx на интервале (0; 2).
28. Найти наибольшее значение функции:
о ____________
1) \1х2(1-х) на интервале (0; 1);
2) V*(2-x) на интервале (0; 2).
29. Найти наибольшее и наименьшее значения функции:
*4 + 1
1) f(x)= на отрезке [— 1; 1];
2 1
2) /(х) = |х2 + 2л;-3|+!1пхна отрезке [|; 2].
30. Найти наибольшее и наименьшее значения функции:
1) f(x) = \ , ' на отрезке [-1; 2];
IVх— 1 при х> 1
при х> 1
-2*2-12л;-17 при х<-2,
при х>-2 На 0ТреЗКе ["5; "
112
Глава III
Применение производной к исследованию функций
3L Найти наибольшую площадь прямоугольника, одна из
вершин которого лежит на оси Ох, вторая — на
положительной полуоси Оу, третья — в точке (0; 0), а четвертая — на
параболе у = 3-х2.
32. Из всех прямоугольников с периметром р найти
прямоугольник с наименьшей диагональю.
ЩЗ Из всех прямоугольных параллелепипедов, вписанных в
сферу радиуса jR и имеющих в основании квадрат, найти
параллелепипед наибольшего объема.
§Щ Найти угловой коэффициент прямой, проходящей через
точку А(1; 2) и отсекающей от первого координатного
угла треугольник наименьшей площади.
^SilHa координатной плоскости даны точки Б(3; 1) и С(5; 1).
Рассматриваются трапеции, для которых отрезок ВС
является одним из оснований, а вершины другого основания
лежат на дуге параболы у = (х — I)2, выделяемой условием
0<лс<2. Среди этих трапеций выбрана та, которая имеет
наибольшую площадь. Найти эту площадь.
[Ж] Рассматриваются всевозможные параболы, касающиеся
х
оси Ох и прямой у = — — 3 и такие, что их ветви
направлены вниз. Найти уравнение той параболы, для которой
сумма расстояний от начала координат до точек пересечения
параболы с осями координат является наименьшей.
§ 4. Производная второго порядка,
выпуклость и точки перегиба
1. Производная второго порядка
Пусть функция f(x) дифференцируема на интервале (а; Ь).
Производную этой функции f(x) называют первой производной
или производной первого порядка функции f(x).
Если функция f(x) дифференцируема на интервале (а; 6),
то ее производную называют второй производной или
производной второго порядка функции f(x) и обозначают f"(x), т. е.
Задача 1. Найти f"(x), если:
+5; 2) f(x) = sinSx;
4) f(x) 2
, f"(x) = 12x2-6;
2) /"(*) = 3cos3x, r(*) = -9sin3x;
3) f'(x) = 2xex\ f"(x) = 2ex2 + 4x2ex2;
4) Г(x)--?*-, Г(х) ^
*2 + 4 (*2 + 4)2 (л:2 + 4)2
§4 113
Производная второго порядка, выпуклость и точки перегиба
О
f(x)
а
х0 Ь х
а)
б)
в)
Рис. Л
Выясним физический смысл второй производной. Пусть
закон движения задается формулой y = s(t), где s — путь,
пройденный материальной точкой, t — время. Тогда мгновенная
скорость движения v(t) = s'(t) характеризует быстроту
изменения пути, а быстроту (скорость) изменения самой скорости
определяет ускорение a(t) = v'(t), т. е. a(t) = s"(t).
Я 12. Выпуклость функции
На рисунке 71 (а—в) изображены графики функций,
имеющих на интервале (а; Ь) первую и вторую производные.
Выясним, в чем состоит различие в поведении этих функций и
какими общими свойствами они обладают.
На рисунке 71, б изображен график убывающей функции,
а на рисунке 71, а — график возрастающей функции;
функция, график которой представлен на рисунке 71, в, не
является монотонной.
Однако все кривые, изображенные на рисунке 71,
обладают общим свойством: с возрастанием х от а до Ъ угловой
коэффициент касательной каждой из этих кривых уменьшается,
т. е. производная каждой из соответствующих функций —
убывающая функция на интервале (а; 6), откуда следует, что
Г(х)<0.
Из рисунка видно, что для любой точки хое(а; Ъ) график
функции y = f(x) лежит ниже касательной к этому графику
в точке {х0; f(x0)) при всех хе(а; Ь) и хч*х0. Поэтому функции,
графики которых представлены на этом рисунке, называют
выпуклыми вверх.
Определение
Функция y = f(x)9 дифференцируемая на интервале (a; ft),
называется выпуклой вверх (см. рис. 71) на этом
интервале, если функция f'(x) убывает на интервале (а; 6), и
выпуклой вниз (рис. 72), если функция f'(x) возрастает на
интервале (а; Ь).
Глава 111
Применение производной к исследованию функций
У-fix)
fix)
У = f(x) A
a
x0
a)
6)
Рис. 72
Отметим, что если функция y = f(x) выпукла вверх на
интервале (а; Ь), а Мх и М2 — точки графика этой функции с
абсциссами хг и х2, где а<х1<х2<Ь (рис. 73), то на интервале
(хл1; х2) этот график лежит выше прямой, проведенной через
точки М1 и М2.
Интервалы, на которых функция выпукла вверх или вниз,
называют интервалами выпуклости этой функции.
С помощью второй производной f"(x) можно находить
интервалы выпуклости функции f(x).
Пусть функция f(x) имеет на интервале (а; Ъ) вторую
производную. Тогда если f"(x)<0 для всех хе(а; Ь), то f'(x) —
убывающая функция (§ 1, теорема 2), и поэтому функция f(x)
выпукла вверх на интервале (а; 6). Если f"(x)>0 при всех
*€(а; Ь), то функция f'(x) возрастает на интервале (а; Ь), и
поэтому функция f(x) выпукла вниз на интервале (а; Ь).
Задача 2. Найти интервалы выпуклости вверх и
выпуклости вниз функции f(x)9 если:
= xs; 2)
-n<x<n; 3) f(x) = tgx, -f
I> 1) f"(x) = 6x. Если х<0, то f"(x)<0, и поэтому функция f(x)
выпукла вверх; если х>0, то f"(x)>0, и поэтому функция f(x)
выпукла вниз (рис. 74).
М9
а х
х2Ъ х Рис 73
1
■ 1
Г
J
^
Рис 74
§4
Производная второго порядка, выпуклость и точки перегиба
у = sinjc
0 I
X
Рис. 75
Рис. 76
2) f"(x) = -sinx. На интервале (-л; 0) справедливо
неравенство f"(x)>0, и поэтому функция выпукла вниз (рис. 75),
а на интервале (0; л) она выпукла вверх.
3) П*Н-Л-, Г (*) = (-2)
cos2 л:
q
COS *
cos3*
х€\-^'> о\ то sinх<0, cosjc>0, f"(x)<0, и поэтому функция /(*)=
= tgx выпукла вверх на интервале (-^-; 0J. На интервале fO; ||
эта функция выпукла вниз (рис. 76). ^
Задача 3. Доказать, что если 0<л:<—, то sina;> — x.
z %
[> Прямая у= — х проходит через точки (0; 0) и (^; 1). Функ-
ция y = sinx выпукла вверх (задача 2) на интервале (0; |
и поэтому ее график на этом интервале лежит выше прямой
2
у= — х (см. рис. 75), т.е. неравенство справедливо. Заметим,
тс
что это же неравенство в задаче 5 из § 1 доказано иначе. 4
3. Точки перегиба
Для функций f(x) = xs9 f(x) = sinx при -n<x<iz, f(x)=tgx
при -^ <х<^9 рассмотренных в задаче 2, точка х = 0 являет-
ся одновременно концом интервала выпуклости вверх и концом
интервала выпуклости вниз.
Определение
Пусть функция дифференцируема на интервале (а; Ь),
хо€(а; Ъ) и пусть функция f(x) выпукла вверх на одном из
интервалов (а; х0), (х0; Ъ) и выпукла вниз на другом
интервале. Тогда точка х0 называется точкой перегиба этой
функции, а точка (х0; f(x0)) — точкой перегиба
функции y = f(x).
Глава
Применение производной к исследованию функций
Иначе говоря, в точке перегиба дифференцируемая
функция меняет направление выпуклости.
Пусть функция f(x) имеет вторую производную на
интервале (а; Ь) и хое(а; Ъ). Тогда если f"(x) меняет знак при
переходе через точку х0, то х0 — точка перегиба функции f(x).
Задача 4. Найти точки перегиба функции:
1/ / \Л) — ЛС , £t) I \Jb) — Jt — UX ~t" I .
> 1) /'(x) = ex + xex = ex (1 + x), f" (x) = ex (1 + x) + ex = ex (x + 2).
Так как f"(x)<0 при х<-2 и f"(x)>0 при х>-2, то # = -2 —
точка перегиба функции хех. Других точек перегиба у этой
функции нет.
2) Г(х) = 4хг-12х, Г (х) = 12л:2 -12 = 12 (х2 -1).
Функция f"(x) меняет знак при переходе через точки
д?1=-1 и JC2 = 1, которые являются точками перегиба функции
Отметим, что график дифференцируемой функции f(x) при
переходе через точку перегиба этого графика М0(х0; f(x0))
переходит с одной стороны касательной к этому графику в точке
Мо на другую сторону.
Задача 5. Найти точки перегиба функции:
2
х-3'
2) /(*)
4х
(1 + л:2)4
л/3" л/3"
Рис 77
Так как Зл*2-1>0 при х<
V3
тх>—, а Злс2-1<0 при <х< —, то точки х= и х=— —
уз V3 V3 V3 V3
точки перегиба (рис. 77).
2) Найдем первую производную:
(л:-1)2 (л:-3)2 \(л:-1)2 (*-3)2/
Из этой формулы видно, что f'(x)<0 при х^1 и х^З.
Следовательно, функция убывает на промежутках х<1, 1<л:<3,
х>3. Найдем вторую производную:
fix)-
(x-lf (*-3)3
§ 4
117
Производная второго порядка, выпуклость и точки перегиба
Решим неравенство f"(x)>0, т. е. неравенство
1 1
(х-if (x-Sf'
Извлекая корень кубический, получаем равносильное не-
1 1 2(*-2) Л
равенство _>-_, откуда (дс.1)(дс.8) >0-
Полученное неравенство верно при 1<л:<2, л:>3, а
неравенство /"(л:)<0 справедливо при х<1, 2<л:<3. Следовательно,
данная функция выпукла вверх на промежутках х<1, 2<лс<3
и выпукла вниз на промежутках 1<л:<2, л:>3.
Так как в точках л:=1 и х = 3 функция не определена, то
х = 2 — единственная точка перегиба. ^ ^^Ч
Упражнения
37. Найти вторую производную функции:
" 1) f(x) = sin2 x; 2) f(x) = хг sin x;
3) f(x) = x4 + 3x2-x+l; 4) /(л:) = л:4-Зл:3 + 5л: + 6;
5) f(x) = esinx; 6) /r(x) = ln(jc2 + l).
38. Найти интервалы выпуклости вверх и интервалы
выпуклости вниз функции:
1) /(х) = л:5-10л;2 + Зл;+1; 2) 42
39. Найти точки перегиба функции:
) f()
2) /(л:) = х5 -80л:2;
3) 3
4) f(x) = sinx— — sin2л:, — 7г<л:<71.
4
40. Найти интервалы выпуклости вверх и интервалы выпук-
~ лости вниз функции:
1) /(л:) = (л:2-Зл: + 2)^; 2) f(x) = xs -6x In x.
41. Найти точки перегиба функции:
" 1) f(x) = 12л:3 - 24л:2 + х + 5; 2) Дл:) = л:4-12х3 + 48л:2 + 3;
3) /(x) = xV4x; 4) f(x) = л:2Inx.
§ 5. Построение графиков функций
^^Ч 1. Асимптоты
В главе II (§ 2) было введено понятие асимптоты
(вертикальной и горизонтальной). Рассмотрим понятие наклонной
асимптоты.
Назовем прямую y = kx + b асимптотой (невертикальной
асимптотой) графика функции y = f(x) при л:-> + оо, если
разность ординат графиков функции f(x) и прямой стремится к
нулю при х—> + оо, т. е.
lim (f(x)-(kx + b)) = O. (1)
118
Глава III
Применение производной к исследованию функций
Если k^O, то асимптоту называют наклонной, а если £ = 0,
то асимптоту у = Ь называют горизонтальной.
Теорема
Для того чтобы прямая y=*kx + b была асимптотой
графика функции y = f(x) при х—► + оо, необходимо и
достаточно, чтобы существовали конечные пределы
lim H?l = k, (2)
*—> +0О #
lim (f(x)-kx) = b. и (3)
НО 1) Пусть прямая y=kx+b — асимптота графика
функции y = f(x) при х—* + оо. Тогда выполняется условие (1) или
равносильное ему условие
f(x) = kx + b + a(x), a(jc) — O при х-^ + оо. (4)
Разделив обе части равенства (4) на х, получим
дс дс дс
откуда следует, что существует предел (2). Из равенства (4)
получаем
/(л:)-Л;л: = 6Н-а(л:), а(л:)-^0 при х—► + оо,
откуда следует, что существует предел (3).
2) Пусть существуют пределы (2) и (3), тогда
где а(лс)—►О при д;-> + оо, т. е. выполняется условие (4) и
равносильное ему условие (1).
Это означает, что прямая y = hx + b — асимптота графика
функции i/ = /(x). • ШШ
ЕЯ Аналогично вводится понятие асимптоты при х—> — оо. В этом
случае должно выполняться условие
lim (f{x)-(kx + b)) = O. (5)
х->-оо
Задача 1. Найти асимптоту графика функции y = f(x) при
я-* + оо и х—»>-оо, если:
2) f{x)-
3) /Ч*)=-^Ц;; 4) f(x)=\lx2-2x-Z.
(x+lf
>1)Так как
д;-*оо, то прямая i/ = —2 — горизонтальная асимптота графика
§ 5 119
Построение графиков функций
3-2*
функции у= — при х—►Н-оо и х—> — оо.
2) Из равенства = = х , где ——
х
►О при х—»оо, следует, что прямая у = х — асимптота
л:
графика функции у = при д;-» + оо и д;-*-оо.
*2 + 1
3) Для нахождения уравнения асимптоты вычислим пре
делы (2) и (3):
fix) х 1
lim -^—*■ = lim = lim =1, т. е. k=l. Далее,
X (2 ('
Таким образом, прямая у = х-2 — асимптота графика функ-
х
ции у= при х
(х+1)2
Заметим, что уравнение этой же асимптоты можно
получить, разделив хг на (jc+1)2 по правилам деления многочленов.
При этом можно воспользоваться равенством
х3 = (л: + 1 - I)3 = (л: 4-1)3 - 3 (л: н-1)2 + 3 (jc + 1) -1.
Тогда получим
3 I Ъх + 2 -х 2 I
2
}2 ' vv;
откуда следует, что прямая у = х — 2 — асимптота графика
функции y — f(x) при х—* + оо и х—* — оо.
4) Найдем асимптоту графика этой функции при х-
Пусть х>0, тогда ух2=х, и поэтому
т. е. & = 1 (условие (2)).
Далее, У2
>1 прих» + оо, т. е. Ь = -1.
420 Глава
Применение производной к исследованию функций
Следовательно, прямая у = х— 1 — асимптота графика
функции y = \jx2-2x-Z при д;-> + оо.
Аналогично можно показать, что прямая i/=l — x —
асимптота графика этой функции при л;—►-оо. *4 Т^Ш
2. Графики функций
Задача 2. Построить график функции
у = х*-2х* + х.
1) Область определения функции JR.
2) График функции имеет с осью Ох две общие точки: (0; 0)
и (1; 0).
3) Так как у' = 3х2-4х+ 1 = 3( х- — )(х-1), то уравнение
у'=0 имеет корни хх — — , х2 — 1»
1
Производная положительна на промежутках х<— и х>1,
о
следовательно, на этих промежутках функция возрастает.
При — <х<1 производная отрицательна, следовательно, на
1
этом интервале функция убывает. Точка х1 = — является точ-
о
кой максимума, так как слева от этой точки функция
возрастает, а справа убывает. Значение функции в этой точке равно
'1\ /1'
/i\2 !_ 4
" КЗ) +^~27*
Точка jc2 = 1 является точкой минимума, так как слева от
этой точки функция убывает, а справа возрастает; ее значение
в точке минимума равно /(1) = 0.
Результаты представим в таблице.
X
Г(х)
f(x)
*<!
3
+
/
1
3
0
4
27
-<х<1
3
-
\
1
0
0
х>1
+
Символ «/» означает, что
функция возрастает, а символ «\»
означает, что функция убывает.
Для более точного построения
графика найдем значения функции
еще в двух точках
/I--^ J = - ^,
Используя результаты
исследования, строим график функции
y=xs-2x2 + x (рис. 78).
§ 5
Рис. 78
121
Построение графиков функций
I При построении графика функции y = f(x) можно
придерживаться следующего плана:
1) найти область определения функции; выяснить,
является ли функция четной (нечетной), периодической;
2) найти точки пересечения графика с осями координат и
промежутки, на которых f(x)>0 и f(x)<0;
3) найти асимптоты графика функции;
4) вычислить f(x), найти промежутки возрастания
(убывания) функции и ее экстремумы;
5) вычислить f"(x)9 определить направление выпуклости и
найти точки перегиба;
6) изобразить график функции.
Задача 3. Построить график функции у = хг — 4х2 + 4х.
[> 1) Область определения функции R.
2) График функции у —Xs — 4х2л-4х = х(х—2)2 имеет с осью Ох
две общие точки (0; 0) и (2; 0).
3) График не имеет асимптот.
4) Так как у' = Зх2-8х + 4 = {х-2)(Зх-2)9 то уравнение
2
у =0 имеет корни хх = —, лг2 = 2. Производная положительна, т. е.
2
функция возрастает на промежутках х<— и х>2. Если
2 /2 \
— <х<2, то i/'<0, и функция убывает на интервале (—; 21.
Стационарные точки хх = — и х2 = 2 — точки экстремума
о
функции. При этом хг — точка максимума, так как при пере-
2
ходе через точку хх = — производная у меняет знак с «+» на «-»;
о
х2 — точка минимума, так как при переходе через точку х2 = 2
(2 \ 32
~о}~ "от"»
(4 \ 4
х- — ). Если х<—, то i/"<0, и по-
4 4
этому функция выпукла вверх на интервале х<—; если х>—,
о О
4
то i/">0, и поэтому функция выпукла вниз при х> — . Следова-
4 * ^ /4\ 16
тельно, х=— — точка перегиба функции, причем у\-^ )= -^=.
Результаты исследования представим с помощью таблицы.
X
/'(*)
rw
/(*)
3
+
-
2
3
0
-
32
27
max
-
-
4
3
-
0
16
27
перегиб
-<*<2
3
-
+
2
0
+
0
min
х>2
+
+
122
Глава III
Применение производной к исследованию функций
Символ «^» означает, что
функция выпукла вверх, а символ «^»
означает, что функция выпукла
вниз.
6) Отметим еще, что f(x)<0
при *<0 и f(x)>0 при х>0, х*2.
Используя результаты
исследования, строим график функции
i/=JC3-4*2 + 4:x: (рис. 79). <
Задача 4. Построить график
х3-4х2+4х
Рис. 79
функции у = х-\—.
1>1) Область определения хч*О. Данная функция нечетная, так
4
-х
2) График не пересекает координатные оси.
3) Исследуем эту функцию и построим ее график при х>0.
Прямая у = х — асимптота графика функции при х —* + оо и
£->-оо. При х>0 график лежит выше асимптоты (так как
4 \
->01, а при х<0 — ниже асимптоты.
На промежутке х>0 функция
имеет одну стационарную точку
*=2.
Производная положительна на
промежутке х> 2, следовательно,
на этом промежутке функция
возрастает. На интервале 0 < х < 2
производная отрицательна,
следовательно, на этом интервале функция
убывает.
Точка х = 2 является точкой
минимума, так как при переходе
через эту точку производная
меняет знак с «-» на «+»; /г(2) = 4.
Составим таблицу:
Рис. 80
X
Пх)
Пх)
Пх)
0<*<2
-
+
2
0
+
4
min
х>2
+
+
§ 5
123
Построение графиков функций
5) Так как i/"=(l )= — , то при х<0 функция вы-
V х2) хъ
пукла вверх, а при х>0 выпукла вниз.
6) График функции у = х-\— изображен на рисунке 80. ^
* Xs
Задача 5. Построить график функции у =
t> 1) Функция определена при
2) Функция принимает положительные значения при #>0
и отрицательные при х<0.
3) Прямая х = — 1 — вертикальная асимптота графика
функции, причем у—* — оо при х—> — 1 + 0 и х—* — 1— 0.
Прямая г/ = д;-2 — наклонная асимптота графика функции
при х-^ + оо и лг-^-оо (задача 1 (3)). При этом из равенства (6)
2
следует, что при х> — — график лежит выше асимптоты, а при
2 3
х<— — — ниже асимптоты.
о
4) Находим производную:
У'=
х2(х + 3)
У
(x + lf
(7)
Рис. 81
Из формулы (7) следует,
что у'>0 при л:<-3 и х>-1,
а если -3<л:<-1, то у'<0.
Следовательно, функция
возрастает на промежутках
л:<-3 и х>-1 и убывает на
интервале (-3; -1).
Согласно формуле (7) функция имеет две стационарные
точки х = 0 и х — — 3. Точка jc = O не является точкой
экстремума, так как у' не меняет знак при переходе через эту точку,
ajc = -3 — точка максимума функции у(х), так как у' меняет
знак с «+» на «-» при переходе через точку х = -3, причем
4
5) Найдем у'\ используя формулу (7), которую запишем
в виде у'= л ^°**з . Тогда у"= {
(x+lf
6х
124
(х+1)4
Глава III
(х+1)4'
Применение производной к исследованию функций
Из формулы (8) следует, что у"<0 при х<Ои х^ — 1, у">0
при #>0. Поэтому функция г/(л:) выпукла вверх на интервалах
дг<-1 и -1<jc<0 и выпукла вниз на интервале х>0. Точка
х = 0 является точкой перегиба функции, причем i/'(0) = 0, и
поэтому касательной к графику функции в точке (0; 0)
является прямая у = 0.
6) График функции изображен на рисунке 81.
Упражнения
Построить график функции (42—43).
42. 1) у = хг-Зх2 + 4; 2) у =
3) y = -xs + 4x2-4x; 4) у = хг
43. 1) у = х4-2х2 + 2; 2) i/=|
3) i/=|x3(8-3jc); 4)
о
44. Найти асимптоты графика функции:
Г2
2)/() ^
3) /W-*"^"8; 4) /(*)?!
45. Найти асимптоты графика функции:
£; 2) V2
Построить график функции (46—51).
46. 1) у = 2 + 5х3-3х5; 2) г/ = З*5-5х3;
~3 55x4; 4) j/ = (jc-13
47.1) j/ = 3x+^-; 2)j/ = x-^; 3)j/=^-x; 4) y-x--p.
48. 1) y = -je3 + 4x2-3; 2) y = x3
Й D^; 2)У-
Й: D^~;
4; )J/^
л:2-2л:+1 (л:-2)2
6) у=
\ 6) у
(дг-2)2 х2-1
3
50. 1) у = (х + 3)\/х; 2) y= K + ' ; 3) y = x2lnx; 4) */= — .
x2 (* + 2)3
5L 1) y = xs-x2-x+l;
"" 2) u = x^ — x2 + x— 1
52. Сколько действительных корней имеет уравнение
§ 5 125
Построение графиков функций
Упражнения к главе III
53. Найти интервалы возрастания и убывания функции:
2; 2) i/= ?-хг-х2-
о
3)г/=^-1; 4)у=-^-.
X X — О
54. Найти стационарные точки функции:
1) у = х4-4х*-8х2 + 1; 2) у = 4х
3) 1/=^- + —; 4) i/ = cos 2x + 2 cos л:.
о X
55. Найти точки экстремума функции:
1) у = х*-4х2; 2) i/ = 3jc4-4jc3.
56. Найти точки экстремума и значения функции в этих
точках:
1) г/ = л:5-2,5л;2 + 3; 2) i/ = 0,2x5
57. Построить график функции:
16; 2) У=^4
3) у^ + Зх2; 4) у«-^
58. Построить график функции:
1) г/ = Злг2-6хн-5 на отрезке [0; 3];
1 2
2) у= — х4- — хг на отрезке [-1; 3].
59. Найти наибольшее и наименьшее значения функции:
1) f(x) = x*-6x2 + 9 на отрезке [-2; 2];
2) /(л;) = л;3 + 6л;2 + 9л; на отрезке [-4; 0];
3) f(x) = x4-2x2 + 3 на отрезке [-4; 3];
4) f(x) = х4 -8х2 + 5 на отрезке [-3; 2].
60. Доказать, что из всех равнобедренных треугольников,
вписанных в данный круг, наибольший периметр имеет
равносторонний треугольник.
61. Из всех равнобедренных треугольников с периметром р
найти треугольник с наибольшей площадью.
62. Из всех прямоугольных параллелепипедов, у которых в
основании лежит квадрат и площадь полной поверхности
равна 600 см2, найти параллелепипед наибольшего объема.
63. Найти асимптоты графика функции:
(х— "И3 г4
1) Пх) =&-?-; 2) /(*)£
2
х2 х3-1
64. Доказать, что функция у=1,8хь-2 — jc3h-7jch- 12,5
возрастает на всей области определения.
65. Доказать, что функция у^х(1л-2^[х) возрастает на всей
области определения.
126 Глава III
Применение производной к исследованию функций
66. Найти точки экстремума функции:
3) 4 16 4 25* 9
х-3 х-79 7-х 3-х
67. Построить график функции:
'1)у_ 2 , 2) 2
3) г/ = (л:-1)2(л: + 2); 4) у
68. Найти наибольшее и наименьшее значения функции:
1) f(x) = 2sinx + sin2л: на отрезке 0; — 7г I;
2) /(л:) = 2 cos х + sin 2x на отрезке [0; я];
3) /(л:) = 3 sin х + 4 cos 2л: на отрезке 0; ^ ;
4) /(л:) = sin л:+ 2 У2созл: на отрезке 0; — .
69. Найти наибольшее значение функции:
1) хуб-Заг на интервале (0; \ — ;
2) л:У1-л:2 на интервале (0; 1).
70. Тело движется по закону s(£) = 6£2-£3. Какова наибольшая
скорость тела?
71. Из всех прямоугольных треугольников, у которых сумма
одного катета и гипотенузы равна I, найти треугольник с
наибольшей площадью.
72. Найти точку касания графика функции и данной прямой,
если:
2) у = Зх2-2х + 5, у=10х-7;
3) 1/ = л:3-5л: + 8, г/=7л:+24;
4) y = xs-5x2-3x+l, y = -13x-6.
ШУ При каком значении а график функции у = л:2 + а касается
прямой г/ = -4л:+5?
74. Сечение тоннеля имеет форму
прямоугольника, сверху
завершенного полукругом.
Определить радиус полукруга, при
котором площадь сечения
будет наибольшей, если
периметр сечения равен р.
ИЗ Равнобедренный треугольник
описан около квадрата со
стороной а так, что одна сторона
квадрата лежит на основании
треугольника (рис. 82). Обо-
а
С
Рис. 82
127
Упражнения к главе III
Рис. 83
Рис. 84
значая ВК = х, найти такое значение х, при котором
площадь треугольника наименьшая.
[76.1 Из квадратного листа картона со стороной а (рис. 83)
надо сделать открытую сверху коробку прямоугольной
формы, вырезав по углам квадраты и загнув образовавшиеся
края. Какой должна быть высота коробки, чтобы ее объем
был наибольшим?
177.1 Найти наибольший объем цилиндра, площадь полной
поверхности которого равна S.
178.1 Найти наибольшую площадь полной поверхности
цилиндра, вписанного в сферу радиуса jR.
айти точки экстремума функции у =
Построить график функции:
2) f(x) = x-Vx2-2x;
о-Х.
Груз, лежащий на горизонтальной плоскости, нужно
сдвинуть с места силой, приложенной к этому грузу (рис. 84).
Определить угол, образуемый этой силой с плоскостью,
при котором сила будет наименьшей, если коэффициент
трения груза k.
Bonpoci
1. Какая функция называется возрастающей (убывающей)?
2. Сформулировать достаточное условие возрастания
(убывания) функции.
3. Что называется точкой максимума (минимума) функции?
4. Сформулировать теорему Ферма.
5. Что является необходимым условием экстремума
дифференцируемой функции?
128
Глава III
Применение производной к исследованию функций
6. Какие точки называются стационарными?
7. Какие точки называются критическими?
8. Сформулировать достаточные условия экстремума.
9. Каков алгоритм нахождения наибольшего и наименьшего
значений непрерывной на заданном отрезке функции?
10. Сформулировать теорему Лагранжа.
П. Доказать достаточное условие возрастания (убывания)
функции.
12. Доказать достаточные условия экстремума.
13. Что называется производной второго порядка?
14. Сформулировать определение выпуклости вверх (вниз)
функции.
15. Что называется точкой перегиба функции?
16. Как с помощью второй производной выяснить, является ли
функция выпуклой вверх (вниз); имеет ли точку перегиба?
Шц Пояснить геометрический смысл теоремы Лагранжа.
ВО При каком условии прямая у=кх+Ъ является асимптотой
графика функции y = f(x) при x
1. Найти интервалы монотонности функции:
1) у = 2х2-Ьх\ 2) y = -yJx + 4.
2. Найти точки экстремума функции у = х4 - 4х3 + 20 и
значения функции в этих точках.
3. Построить график функции у = х'6 + Зх2-4.
4. Найти наибольшее и наименьшее значения функции
g
f(x) = x-\— на отрезке [1; 4].
5. Отливка объемом 72 дм3 имеет форму прямоугольного
параллелепипеда с отношением сторон основания 1:2. При
каких размерах отливки площадь ее полной поверхности
будет наименьшей?
1. При каких значениях а функция г/ = д;3 + 3ал; возрастает на
всей числовой прямой?
2. Построить график функции
у = х+-.
3. Найти наибольшее и наименьшее значения функции
х2
f(x) = — на отрезке [-1; 3].
ех
4. Найти высоту конуса наименьшего объема, описанного
около сферы радиуса jR.
129
Проверь себя!
Историческая справка
Как и многие разделы математики, дифференциальное
исчисление возникло из необходимости решения практических
задач. В основном источником дифференциального исчисления
явились задачи двух видов: а) на нахождение наибольших
и наименьших значений величин, т. е. задачи на нахождение
экстремумов (от лат. extremum — крайнее); б) на вычисление
скоростей. В древности и в Средние века задачи этих видов
решались геометрическими и механическими методами и не
были связаны общими идеями.
Задачи на нахождение максимума и минимума можно
найти еще в «Началах» Евклида. Так, в VI книге «Начал»
доказывается, что из всех параллелограммов, вписанных в данный
треугольник, наибольшую площадь имеют те, основание
которых равно половине основания треугольника.
В 1615 г. в опубликованной работе «Стереометрия винных
бочек» немецкий ученый И. Кеплер (1571 —1630) высказал
идею о том, что вблизи максимума величины ее изменения
незаметны, предугадав тот факт, что в точке максимума
производная функции равна нулю. Известно, что в 1629 г.
французский математик П. Ферма уже владел методом определения
максимумов и минимумов. Но только в середине XVII в.
И. Ньютон и Г. Лейбниц исследовали проблему максимумов
и минимумов функций с позиций идеи бесконечно малой
величины. Так, Лейбницем была сформулирована теорема о
достаточном условии возрастания и убывания функции на отрезке.
Огромный вклад в развитие дифференциального исчисления
при решении прикладных задач внесли швейцарские
математики Я. Вернул л и и И. Бернулли. Голландский ученый X. Гюй*
гене (1629—1695) после решения задачи о форме подвешенной
за концы массивной цепи написал известному французскому
математику Г. Лопиталю (1661—1704) о широте применимости
методов дифференциального исчисления: «Я вижу с
удивлением и восхищением обширность и плодовитость нового метода.
Куда бы я ни обратил взор, я замечаю для него новые
приложения, я предвижу его бесконечное развитие и прогресс».
В 1755 г. Л. Эйлер в своей работе «Дифференциальное
исчисление» развил понятия «абсолютных экстремумов» и
«относительных экстремумов», называемых им экстремумами
«местного характера». В этой работе он подчеркивал, что
значение функции в точке максимума, вообще говоря, не
совпадает с ее наибольшим значением. Для исследования функций
Эйлер пользовался не только первой и второй производными,
но и производными более высоких порядков.
Отметим, что теория экстремумов функций и сегодня
находит многочисленные практические применения в решении
задач производства и экономики, связанных с оптимальным
использованием сырья и времени.
430 Глава III
Применение производной к исследованию функций
Первообразная
и интеграл
Одно можно сказать наверняка:
завтра математика станет
еще могущественней и нужнее людям,
чем сегодня.
И. Я. Депман
§ 1. Первообразная
В главе II была рассмотрена задача о
нахождении мгновенной скорости точки по
заданному закону движения. Пусть закон движения
точки задан функцией s = s(t), где s(t) —
координата движущейся точки в момент времени t.
Тогда мгновенная скорость движения тела в
момент времени t равна v — s'(t). В этой задаче по
заданной функции s(t) вычисляется ее
пронзят2
водная. Например, если s=^—, то v = s'(t) = gt.
В физике встречается обратная задача: по
заданной скорости v — v(t) найти закон
движения, т. е. найти s = s(t). Так как s'(t) = v = v(t),
то в этой задаче требуется найти такую
функцию s(t), производная которой равна v(t). В
этом случае функцию s(t) называют
первообразной для функции v(t).
Определение
Функция F(x) называется первообразной
для функции f(x) на некотором интервале,
если для всех х из этого интервала
выполняется равенство
F'(x) = f(x). (1)
Например, функция хг является
первообразной для функции Зх29 так как (xs)' = 3x2;
функция sin х — первообразная для функции
cos х, так как (sin a;)' = cos x.
Задача 1. Показать, что функция
F(x)=^sin Зх
о
является первообразной для функции f(x)=cos Зх.
§ 1
131
Первообразная
[> Так как F'(х) = ( -§-sin Зх) = -^ • 3cosЗх = cosЗл;, то — sin3jc —
\ о / о о
первообразная для функции cos3a\ M
Замечание. Если функция F(x) дифференцируема на
интервале (а; 6), непрерывна на отрезке [а;Ь] и для всех х€(а; Ь)
выполняется равенство (1), то функцию F(x) называют
первообразной для функции f(x) на отрезке [а; 6].
Задача 2. Доказать, что для любого действительного р*
р + 1
^ — 1 функция F(jc)=- является первообразной для функции
Р + 1
f(x) = xp на промежутке д;>0.
>Так как (x" + 1)' = (P+l)*p, то
В частности, при р = 0, 3, -2, -g получаем:
1) ^(л:) = л: — первообразная для функции f(x)=l при x€R;
2) .Р(л:)=^- — первообразная для функции f(x) = xs при
x€R;
промежутках jc<0 и л:>0;
4) F(
при х>0.
Замет
же являются первообразными, так как
3) F(x)=-— — первообразная для функции f(x) = —- на
х2
4) F{x)=^x\fx — первообразная для функции f(x)=\x
о
4 4
Заметим, что для функции f(x) = x6 функции — +2, — -3 так-
^.4
Вообще любая функция —+С9 где С — постоянная, явля-
4
ется первообразной для функции хг. Это следует из того, что
производная постоянной равна нулю.
Этот пример показывает, что для заданной функции ее
первообразная определяется неоднозначно.
Если F(x) — первообразная для f(x) на некотором
промежутке, то и функция F(x) + C, где С — любая постоянная,
также является первообразной для функции f(x) на этом
промежутке.
Оказывается, что функциями вида F(x) + C исчерпываются
все первообразные для заданной функции f(x).
В главе III (§ 1, задача 4) было доказано, что если F'(x)=Q
на интервале (а; Ь) и функция F(x) непрерывна на отрезке [а;Ь],
то F(x) = C на отрезке [а; 6]. Используя это утверждение,
докажем теорему.
132 Глава IV
Первообразная и интеграл
Теорема
Пусть Fx(x) и F2(x) — две первообразные для одной и
той же функции f(x). Тогда F2 (х) = Fx (х) + С, где С —
некоторая постоянная.
О Обозначим F(x) = F2(x)-Fl(x). Тогда F'(x) = F2(x)-F1'(x) =
=/(*)-/(*) = О, откуда F(x) = C, т. е. F2(x)-F1(x) = C, откуда
Итак, если F(x) — некоторая первообразная для f(x)9 то
все первообразные для функции f(x) находятся по формуле
F(x)-\-C9 где С — любая постоянная.
Задача 3. Найти все первообразные для функции -^=, х>0.
Ух
t> Из задачи 2 при р = — — следует, что 2 \[х — первообразная
для функции —= при х>0. Ответ. 2\[х + С. М
УХ
Приведем таблицу первообразных для некоторых функций.
Функция
ХРу Р*-1
i, x>0, х<0
ех
sin*
cos*
Первообразные
*Р+\с
Р+1
1п|х| + С
ех + С
- cos дс + С
sinoc + C
Эта таблица проверяется дифференцированием
первообразных. Например, так как (1п|лг|н-С)'= — (гл. II, § 7), то 1п|х| +
+С — первообразная для функции — при х>0 и при х<0.
Рассмотрим графики всех
первообразных заданной функции f(x).
Если F(x) — одна из первообразных
f(x), то все первообразные
получаются прибавлением к F(x) любой
постоянной: F(x) + C. Следовательно,
графики функций y = F(x) + C
получаются из графика y = F(x) сдвигом вдоль
оси Оу (рис. 85). Выбором постоянной
С можно добиться того, чтобы график
первообразной проходил через
заданную точку.
§ 1
Рис. 85
133
Первообразная
Задача 4. Для функции — найти такую первообразную на
х2
промежутке х>09 график которой проходит через точку (1; 3).
[> Все первообразные для функции — находятся по формуле
х
F(x) = -— + C. Найдем такое значение С, чтобы график
функции y = F(x) проходил через точку (1; 3), т. е. воспользуемся
условием F(l) — 3, Отсюда — 1+С = 3, С = 4. Следовательно,
F(x) = 4-±.M
Упражнения
1. Показать, что функция F(x) является первообразной для
функции f(x) на всей числовой прямой:
1) F(x) = x\ f(x) = 4x*; 2) F(x)=l-e~\ f(x) = e~x;
5 £ £
3) F(*)=^- + l, f(x) s s
5
5) F(x)
6) F(x)
2. Показать, что функция F(x) является первообразной для
функции f(x) при л:>0:
) = - ±; 2) F(x)=-L
2л:2
3) F(x) = 2-x\ /(х)—|V^; 4) F(x) = V2^, /(x
2
3. Найти все первообразные для функции:
1 _ 1
1) х6; 2) х5; 3) ^-; 4) tfc 5) xs; 6) х"1.
V^
4. Для функции f(x) найти первообразную, график которой
проходит через точку М:
1) f(x) = x2, M(l; 2); 2) /(х) = х, М(-1; 3);
3) /(x)=if M(l; -1); 4) /(x) = V^, M(9; 10).
§ 2. Правила нахождения первообразных
Из главы II известно, что операцию нахождения
производной для заданной функции называют дифференцированием.
Обратную операцию нахождения первообразной для данной
функции называют интегрированием.
Правила интегрирования можно получить с помощью
правил дифференцирования. Напомним правила
дифференцирования.
134 Глава IV
Первообразная и интеграл
Пусть функции F(x) и G(x) имеют производные на
некотором промежутке; a, b, k — постоянные. Тогда:
2) (aF(x))r = aF'(x);
3) (F(kx + b))' = kF' (kx + Ъ).
Из этих правил дифференцирования следуют правила
нахождения первообразных.
Пусть F(x)9 G(x) — первообразные соответственно для
функций f(x) и g(x) на некотором промежутке, т. е.
F'(x) = f(x), G'(x) = g(x), a, b9 k — постоянные, k^O. Тогда:
1) F(x)-\-G(x) — первообразная для функции f(x) + g(x);
2) aF(x) — первообразная для функции af(x);
3) — F(kx + b) — первообразная для функции f(kx + b).
k
Приведем примеры применения этих правил.
Задача. Найти первообразные F(x) для функции f(x):
1) f{x) = 2ex + sinx;
2) f{x) = x5-3cos2x;
I> 1) Так как ех — первообразная для ех, а — cosjc —
первообразная для sin л:, то 2e*-cosa; — одна из первообразных для
функции 2
2) Первообразная для хь равна —, первообразная для
6
cos2л: равна —sin2л:, следовательно, одна из первообразных
для хъ-3cos2х равна -—- — sin2x.
О А
3) Обозначим
Тогда Ft (x) = , F2 (х) = — е2х — первообразные
соответственно для fi(x) и /гС^)»
F(x) = F1(x) + F2(x) + C = -^ + ±
все первообразные для функции f(x).
Ответ. 1) F(x) = 2ex-cos х + С;
2) ^^
х + 1 2
§ 2 135
Правила нахождения первообразных
П Третье правило нахождения первообразных позволяет
дополнить таблицу первообразных, приведенную в предыдущем
параграфе.
Функция
(kx + bf, pit 1, k*0
1 , k*o
kx + Ъ
sin(kx + b), k^O
cos(kx + b), k*0
Первообразные
(kx + b)P+1
k(p+l)
— ln\kx + b\ + C
k
-ekx + b + C
k
- — cos(kx + b) + C
к
— s\n{kx + b) + C
к
Упражнения
Найти первообразные для функции (5—12).
5. 1) 2*5-3x2; 2) 5*4 + 2х3; 3)
4) 6л:2-4л:+3; 5) -| + 4> 6>
х 2
7) \[х + 2\[х\
8)
X* *'
6.
7.
—
136
1)
3)
1)
5)
1)
4)
7)
4)
5 sin x + 2 cos x;
(x+1)3; 2)
i A paq(у А
V3^2l;
cos(3* + 4);
Гл а в а IV
(X
-2);
2)
5)
8)
2)
5)
2) 3e* — sin л
\fx x
-2)4; 3) -
\
6) 3
Ь) x-3
(Ь + 2)5;
3 .
8, '
3/
sin(3jc-4);
x+l
e " ;
2 • 1)
/ 9 ' ;
2
3) (2*-3)5;
6) 4 •
3) cos^|--
6) e3*"5.
3
3^ '
* + 3
•>
Первообразная и интеграл
10. 1) e3*-cos2x;
2:
3)
2;
5) ]p£- 5 cos (6л: -1);
7)
11.1)
4)
7)'
6) ^/| +4 sin (4*+ 2);
2л;3 -3*
6) 2л;(1-
8) (2*-3)(2 + 3jc).
12. 1) (2x+l)Vx; 2) (3x-2)\[x;
3)
x + 4,
zr- '
4)
13. Для функции f(x) найти первообразную, график которой
проходит через точку М:
1) f(x) = 2x+3, M(l; 2); 2) f(x) = 4x-l, M(-l; 3);
3) f(x) = \/x~+2, M(2; -3); 4) f(x)=^L=, M(-2; -1);
5) /(ж).
7) /(*) =
f^5>
, М(-2; 4);
6)
8)
, М(0; 0);
г, М(-2; 2).
§
3. Площадь криволинейной трапеции.
Интеграл и его вычисление
УД
1. Площадь криволинейной трапеции
Рассмотрим фигуру G (рис. 86), ограниченную отрезками
прямых х = а9 х = Ь, у = 0 и графиком непрерывной функции
У-fix), такой, что f(x)>0 на отрезке [а; Ь] и f(x)>0 при х€(а; Ъ).
Такую фигуру называют
криволинейной трапецией, а отрезок [а; 6] —
ее основанием.
Поясним, как вводится
понятие площади криволинейной
трапеции и как можно вычислить эту
площадь. Для этого введем
понятие определенного интеграла.
Разобьем отрезок [а; Ь] на п
(необязательно равных) частей
точками хи х2, ..., хп_г и проведем
через эти точки вертикальные пря-
0
'-Лж)
G
а
§ з
Рис. S6
137
Площадь криволинейной трапеции. Интеграл и его вычисление
мые до пересечения с
графиком функции y = f(x). При
этом криволинейная трапеция
разобьется на п частей,
каждая из которых также
является криволинейной трапецией
(рис. 87). Обозначим хо = а,
x
Рассмотрим криволиней- " а *о *i X2
ную трапецию с основанием рис qj
[xk_1; xk] (рис. 88). Если
длина отрезка [xk_1; xk] мала, то эта трапеция мало отличается от
прямоугольника с основанием Axk = xk-xk_1 и высотой f(ck),
где ck — какая-нибудь точка отрезка [xk_1; xk], а площадь
криволинейной трапеции с основанием [xk_1; xk] приближенно
равна площади этого прямоугольника, т. е. приближенно равна
f(ck)Axk.
Вся криволинейная трапеция с основанием [а; Ь] мало
отличается от многоугольника, состоящего из прямоугольников,
построенных указанным способом на отрезках [х0; х{\9 [хг; х2],
[х2; хг], ..., [хп_1; хп] (рис. 89), а площадь криволинейной тра-
О
а
88
У-fix)
х2
Рис. 89
138
Гл а в а IV
Первообразная и интеграл
пеции приближенно равна площади этого многоугольника, т. е.
приближенно равна
f(cl)Ax1+f(c2)Ax2 + ... + f(ck)Axk + ...+f(cn)Axn. (1)
Сумму (1) называют интегральной суммой функции f(x)
на отрезке [а; Ь]. Будем увеличивать число точек разбиения
так, чтобы наибольшая из длин отрезков [хк_г; xk] стремилась
к нулю. Тогда длина Л xk каждого отрезка также будет
стремиться к нулю. Можно доказать, что при этом интегральные
суммы будут стремиться к некоторому числу S, т. е. имеют
предел, равный S. Это число S называется площадью
рассматриваемой криволинейной трапеции (см. рис. 86).
2. Интеграл
Рассмотрим теперь любую непрерывную на отрезке [а; Ь]
функцию f(x) (необязательно неотрицательную). Составим для
нее интегральную сумму (1) и затем будем увеличивать число
точек разбиения отрезка [а; Ь] так, чтобы длина наибольшего
из отрезков [xk_x\ xk] стремилась к нулю. Можно доказать (это
доказывается в курсе высшей математики), что и в этом
случае интегральные суммы стремятся к некоторому числу, т. е.
имеют предел, не зависящий от выбора точек с19 с2, ..., сп. Этот
предел называют определенным интегралом от функции f(x)
ъ
на отрезке [а; 6] и обозначают так: \f(x)dx (читается: интег-
а
рал от а до Ъ эф от икс дэ икс); функцию f(x) называют
подынтегральной функцией.
В частности, если функция
f(x) положительна на отрезке [а; 6],
получаем формулу для площади
криволинейной трапеции:
ь
\f
= \f(x)dx.
(2)
Площадь закрашенной фигуры
з
на рисунке 90 равна \ x2dx.
1
Формула (2) справедлива и
для случая, когда функция f(x)
положительна внутри отрезка [а; 6], a
на одном из концов отрезка или на
обоих концах равна нулю.
Например, площадь
закрашенной фигуры на рисунке 91 равна
Площадь криволинейной трапеции. Интеграл и его вычисление
Таким образом, задача о нахождении площади
криволинейной трапеции сводится к вычислению интеграла.
Аналогично с помощью интеграла решаются и многие другие
геометрические и физические задачи. Примеры физических задач будут
рассмотрены в § 5. В курсе геометрии часто рассматриваются
примеры вычисления с помощью интегралов объемов тел
(пирамиды, конуса, шара и т. д.).
3. Вычисление интегралов
Приближенное значение интеграла можно получить,
составив интегральную сумму. Однако непосредственное нахождение
предела интегральных сумм часто оказывается трудоемким.
Для вычисления определенного интеграла обычно
используется следующая формула:
ь
dx=F(b)-F(a), (3)
где F(x) — любая первообразная для функции f(x) на
отрезке [а; 6].
Формула (3) справедлива для любой функции f(x),
непрерывной на отрезке [а; Ь]. В частности, эта формула
справедлива для всех ранее изученных функций (степенной,
показательной, тригонометрических и др.) на каждом отрезке [а; Ь], где
эти функции определены.
Формулу (3) называют формулой Ньютона — Лейбница в
честь создателей дифференциального и интегрального
исчислений.
Г^П Поясним геометрически, как получается формула (3).
Обозначим S(x) площадь криволинейной трапеции с
основанием [а; х], где х — любая точка отрезка [а; Ь] (рис. 92). При
л: = а отрезок [а; х] вырождается в точку, и поэтому
естественно считать, что S(a) = O.
Покажем, что S(x) является первообразной для функции
f(x), т. е. S'(x) = f(x).
Рассмотрим разность AS = S(x + h)-S(x), где Л>0 (случай
h<0 рассматривается аналогично). Эта разность равна
площади закрашенной на рисунке 93 фигуры, которая представляет
собой криволинейную трапецию с основанием [х; х + Щ.
S(x)
140
х
Гл a s a IV
Ъ х
Рис. 92
0
х x+h Ъ х
Рис. 93
Первообразная и интеграл
Заметим, что площадь этой фигуры равна площади
прямоугольника с основанием [х; x + h] и высотой /(с), где х<с<х +
+ Л, т. е.
AS = S(x + &)-S(x) = /(c)&, (4)
откуда
Строгое доказательство формулы (4) (это «теорема о
среднем» для интеграла) рассматривается в курсе высшей
математики.
Пусть h—>0, тогда с—>д\ Так как f(x) — непрерывная
функция, то f(c)-*f(x) при Л—►(). Переходя к пределу в
равенстве (5), получаем lim S(* + h)~S(x) =S'(x) = f(x). Итак, S'(x) =
Л —0 fi
=/(#), т. е. S(x) — первообразная для функции f(x).
Пусть теперь F(x) — произвольная первообразная для
функции f(x). Так как любые две первообразные для одной и
той же функции отличаются на постоянную (теорема из § 1),
то
F(x) = S(x) + C. (6)
Так как S(a) = O, то при х = а из равенства (6) получаем
F(a)=C, откуда S(x) = F{x)-F(a). Из этого равенства при х = Ь
имеем
S(b) = F(b)-F(a). (7)
Напомним, что S(x) — площадь криволинейной трапеции
с основанием [а; х\ (см. рис. 92), и поэтому
ъ
S(b)=^f(x)dx. (8)
а
Из равенств (7) и (8) следует формула Ньютона—Лейбница:
ъ
Заметим, что формула (3) справедлива для любой
непрерывной на отрезке [а; 6] функции f(x). ^^Ч
Задача 1. Вычислить интеграл j x2dx.
i
[> Функция F(x)=— является первообразной для функции
о
3
{(х) = х2. По формуле (3) получаем \ x2dx = = 9 — -|- = 8 -=-.
i 3 3 3 3
Замечание. Этот интеграл равен площади S фигуры,
л
представленной на рисунке 90, т. е. S = S— кв. ед. <4
о
§ 3 141
лощадь криволинейной трапеции. Интеграл и его вычисление
2
Задача 2. Вычислить интеграл J si
о
[> Функция F (х) = — cos л: является первообразной для функции
_я
2
/(a;) = sin:x;. По формуле (3) получаем ^sinxdx = F(^) -
= -(cos|--cosO) =1. °
Замечание. Площадь фигуры, изображенной на
рисунке 91, равна 2 кв. ед. ^ х
Задача 3. Вычислить интеграл \(x-l)dx.
о
[> Одной из первообразных функции х-1 является функция
1
— -х. Поэтому \(x-l)dx = (— -1) -(—-0) = —-1 = -—. ^
2 0 V 2 / V 2 / 2 <г
При вычислении интегралов удобно ввести следующее
обозначение:
F(6)-Ji(a) = F(x)|*.
Тогда формулу Ньютона — Лейбница можно записать так:
ь
\\
Например, с помощью этой формулы запишем решение
задачи 3:
j
а
13адача 4. Вычислить интеграл }sin3xdx.
С* л i
[> з sin Sxdx = — (- cos Sx) a_ = — (- cos 3a + cos (- 3a)) = 0, так
-a
cos(-3a) = cos 3a. ^
-l
Задача 5. Вычислить интеграл j ——.
x
e
[> Так как In \x\ — первообразная для функции — на
промежутке х<0, то §— =l
~е п
ИИ Задача 6. Вычислить интеграл 3Cos2(2jch- -j ) dx.
2
[> Преобразуем подынтегральную функцию f(x), используя
формулы cos2f= +c^s t, cos(^- + Л =-sin/. Получим
142 Глава IV
Первообразная и интеграл
1 sin4x
2222'
Так как первообразной для функции f(x) является функция
5x+|cos4xf To5cosf2x+^)dx fjc+^cos4x)|iL = -. ^
2 8 п \ 4/ \2 8 /24
2" 3
Задача 7. Вычислить интеграл Ja;V#+ I dx.
о
Упражнения
14. Найти площадь криволинейной трапеции, ограниченной
прямыми х = а, х = Ь, осью Ол: и графиком функции y = f(x),
если:
1) а = 3, 6 = 4, f(x) = x2; 2) а = 0, 6 = 2,
3) а = 1, 6 = 8, Пх) = \[х; 4) а = 4, 6 = 9,
5) a=f, 6=^, /(x) = sinx; 6) a = -f, 6 = 0,
о о о
15. Найти площадь фигуры, ограниченной прямой л: = 6, осью Ох
и графиком функции y = f(x), если:
1) Ь = 3, f(x) = x2; 2) 6 = 2,
3) Ь = 4, /(x)-Vx; 4) 6 = 8,
5) Ь = 2, /(л:) = 5х-л:2; 6) 6 = 3,
7) Ь=1, f(x) = ex-l; 8) 6 = 2,
Вычислить интеграл (16—18).
ш.
д.
is.
1)
4)
3
\x2dx;
0
е
2
\ \CiX—О)'
-3
1
-1
-1
2)
2)
dx;
ix;
3
5 2xdx;
-2
In 2
0
-1
2) § (5
-2
2
5) §(2д
l
3)
3)
— 4лг)
, н~ ox
2
2
я
J sinxc
dx;
2)dX''
'■'-
3)
6)
9
4) \^=dx.
4 V«^
0
4) з cos3xdj
-371
2
-1
0
5 (9x2-4x)d:x;;
-2
7) § (6*2 + 2x -10) dx; 8) § (3x2 - 4* + 5) dx.
-2 0
§ 3 143
Площадь криволинейной трапеции. Интеграл и его вычисление
19. Изобразить фигуру, площадь которой равна данному
интегралу, и вычислить эту площадь:
з
1) ) (-2-3x)dx;
-2
4
3) §(12 + x-x2)dx;
о
371
5) з sinxdx;
2я
2) J (6-2x)dx;
-2
0
4) ^ (x2-3x)dx;
-2
_я
2
6) з cosxdx;
7) з cosxdx;
я
8) з sin лг^л:.
Вычислить интеграл (20—24).
2)
-2
О
3)
-1
4
4)
о \/Зл:+1
2
dx;
2x-\
dx;
144
Гл а в а IV
-1
4) $ A(i_A
-2 * V X
9
2)H2*-tJ
4
5)
1
7
3)
6)
Ц
yfx
2) \2e2xdx\
x 3*-f 5
71
2) з cos(3x — — J dx;
з
3) \cos24xdx; 4) \sin2(x-^-j dx.
о о v 3/
Первообразная и интеграл
§ 4. Вычисление площадей фигур
с помощью интегралов
СЗ Задача 1. Вычислить площадь S криволинейной
трапеции, ограниченной осью Ох, прямыми х = — 1, х = 2 и
параболой у = 9-х2 (рис. 94).
Р> Так как на отрезке [—1; 2] функция i/ = 9—x2 принимает
положительные значения, то искомая площадь S равна интегралу:
S = ) (9-x2)dx.
По формуле Ньютона—Лейбница находим
2
Задача 2. Найти площадь
фигуры, ограниченной
параболами у = х2, у = 2х-х2 и осью Ох.
> Построим графики функций
у = х2, у = 2х-х2 и найдем
абсциссы точек пересечения этих
графиков из уравнения х2 = 2х—х2,
корни которого х1 = 09 х2 = 1-
Данная фигура изображена на
рисунке 95, из которого видно,
что она состоит из двух
криволинейных трапеций.
Следовательно, искомая площадь равна
сумме площадей этих трапеций:
] 2
S = ^ x2dx + § (2х - х2) dx =
о 1
Задача 3. Найти площадь
фигуры, ограниченной отрезком
оси Ох и графиком
1*1 3*1
1.2' 2J
функции y = cosx на этом отрезке.
Р> Заметим, что искомая
площадь равна площади фигуры,
симметричной данной
относительно оси Ох (рис. 96), т. е.
Рис. 94
А/У
•Xе
2\ х
у = 2х - х2
Рис. 95
-COSJC
Вычисление площадей фигур с помощью интегралов
равна площади фигуры,
ограниченной отрезком ^-; -£-\ оси
Ох и графиком функции
— cos л:
на отрезке \^; -^-1. На этом
отрезке -cosjOO, и поэтому
2
3 (-cos л:) dx = (-sin л:)
= (-Sinf)-(-Sinf)=2.«
Замечание. Если /г(л:)<0
на отрезке [а; Ь] (рис. 97), то
площадь S криволинейной
трапеции равна
ь
S = $(-/<*))<**.
Задача 4. Найти площадь
фигуры, ограниченной
параболой
и прямой
0
fix)
Рис. 97
Рис. Sfl
[> Построим графики функций г/ = д;2-+-1 и г/ = лг+3. Найдем
абсциссы точек пересечения этих графиков из уравнения #2 + l=
= л; + 3. Это уравнение имеет корни х1 = —19 х2 — 2. Фигура,
ограниченная графиками данных функций, изображена на
рисунке 98. Из рисунка видно, что искомую площадь можно найти
как разность площадей S1 и S2 двух трапеций, опирающихся
на отрезок [-1; 2], первая из которых ограничена сверху
отрезком прямой г/ = д; + 3, а вторая — дугой параболы i/ = jc2 + 1. Так
2 2
как
= 5 (x + 3)dx, S2 =
l)dx, то
-l -l
Используя свойство первообразных, можно записать S
виде одного интеграла:
2 2 2 3
-1
-1
146
Глава IV
Первообразная и интеграл
0
<
2
У =
S
—~*у
**> -v
= fi(x)
Ъ
в2
X
Рис. 99
Рассмотрим фигуру,
ограниченную отрезками прямых х = а, х = Ъ
и графиками непрерывных функ-
ций y = fx(x) и y = f2(x), где f2(x)>
>fx(x)>0 (рис. 99). Площадь S
этой фигуры равна разности
площадей криволинейных трапеций aA2B2b
и аАфф. Площади S2 и Sx этих
трапеций соответственно равны:
ъ ъ
()d и S1
Следовательно,
ъ ъ
S = \f2(x)dx-\fl(x)dx. Отсюда
а а
Ъ
S = iS(f2(x)-f1(x))dx. (1)
а
Эта формула справедлива для
любых непрерывных функций fx (x)
и /г (*) (принимающих значения
любых знаков), удовлетворяющих
условию f2(x)>f1(x).
Задача 5. Найти площадь фи-
гуры, ограниченной параболами
у=х2 и у = 2х2-1.
[> Построим данную фигуру (рис. 100) и найдем абсциссы точек
пересечения парабол из уравнения х2 = 2х2-1, корни которого х12 =
= ±1. По формуле (1), где fx(х) = 2х2- 1, f2(x) = x2, находим
1 1
-1
-1
Упражнения
25. Найти площадь фигуры, ограниченной осью Ох и
параболой:
1) у=1-х2; 2) у = -х2 + 4х-3;
3) */ = -х(* + 3); 4) у = (1-х)(х + 2);
5) у = (х + 2)(3-х).
26. Найти площадь фигуры, ограниченной:
1) параболой у = (х+1)2, прямой у=1-х и осью Ох;
2) параболой у = 4-х2, прямой у = х + 2 и осью Ох;
3) параболой у = 4х-х2, осью Ох и прямой, проходящей
через точки (4; 0) и (1; 3);
4) параболой у = 3х2, осью Ох и прямой, проходящей через
точки (-3; 0) и (-1; 3);
§ 4
147
Вычисление площадей фигур с помощью интегралов
5) параболами у = 6х2, у = (х-3)(х-4) и осью Ох;
6) параболами у = 4 — х2, у = (х — 2)2 и осью Ох.
27. Найти площадь фигуры, ограниченной:
1) графиком функции y = sinx, отрезком [0; л] оси Ох и
прямой, проходящей через точки (0; 0) и f-^-; 1J;
2) графиками функций i/ = sinx, y = cosx и отрезком 0; |
оси Ox; L 2J
3) графиками функций y = Vx, у = (х-2)2 и осью Ох;
4) графиками функций у = хг, у = 2х-х2 и осью Ох.
28. Найти площадь фигуры, ограниченной:
1) параболой у = 9-х2, прямой у = 7-х и осью Ох;
2) параболой у = х(4-х), прямой у = 3 и осью Ол:;
3) параболами у = (х — 2)2, г/ = (д; + 2)2, прямой у—1 и осью
Ох;
4) параболами г/ = (д; + 2)2, г/ = (л:-3)2, осью Ojc и прямой,
проходящей через точки (-1; 1) и (1; 4); г-
5) графиком функции j/ = sinjc, прямой У=^~ и отрезком
[0; 7i] оси Ох; 2
6) графиком функции у = cos л:, прямой у—-^ и отрезком
Г *. JLl
Г¥' 2J
оси Од;.
29. Найти площадь фигуры, ограниченной:
1) параболой у — х2 — Ах + 3 и осью Ол:;
2) графиком функции j/ = cosjc, прямыми х=-^-, х = п и
осью Ол:.
30. Найти площадь фигуры, ограниченной:
1) параболой у = 6х-х2 и прямой г/ = д; + 4;
2) параболой 1/ = 4-л:2 и прямой г/ = л:н-2.
31. Найти площадь фигуры, ограниченной:
1) параболой г/ = (д; + 2)2 и прямой у^хл-2;
2) графиком функции у=ух и параболой г/ = д;2;
3) графиком функции y = Vx и прямой у — х;
4) параболой г/ = (д;-1)2 и прямой у^Ъл-х;
5) прямой у=19 осью Оу и графиком функции j/ =
32. Найти площадь фигуры, ограниченной:
1) параболой 1/ = -л:2 + 4л:-3 и прямой, проходящей через
точки (1; 0) и (0; -3);
2) параболой у = — х2 и прямой i/ = —2;
3) параболами i/=l— л:2 и у — х2 — 1;
4) графиком функции г/ = л:3 и прямыми i/=l и д; = -2;
5) прямой у = х и графиком функции у —Xs, — 1 < л:< 0;
6) параболами г/ = л:2 —2л: и i/ = —л:2.
148 глава IV
Первообразная и интеграл
§ 5. Применение интегралов для решения
физических задач
1. Нахождение пути по заданной скорости
Пусть точка движется со скоростью v(t). Нужно найти путь
s, пройденный точкой от момента t = a до момента t — b.
Обозначим через s(t) путь, пройденный точкой за время t от
момента а. Тогда s'(t) = v(t), т. е. s(t) — первообразная для
функции v(t). Поэтому по формуле Ньютона — Лейбница найдем
ь
s(b)-s(a) = \v(t)dt. Так как s(a) = O, то искомый путь равен
ь
(1)
Например, если точка движется со скоростью v(t) —
= 2£+1 (м/с), то путь, пройденный точкой за первые 10 с, по
ю
Г 110
формуле (1) равен s = J (2f+ l)df = (*2 + *)|о =110 (м)-
о
2. Вычисление работы переменной силы
Пусть тело, рассматриваемое как материальная точка,
движется по оси Ох под действием силы F(x), направленной вдоль
оси Ох. Вычислим работу силы при перемещении тела из
точки а в точку Ъ.
Пусть А(х) — работа данной силы при перемещении тела
из точки а в точку х, где х€[а; 6]. При малом h силу F на
отрезке [х; x + h\ можно считать постоянной и равной F(x).
Поэтому А (лен- h)- A (x) ~F (x) h, т. е.
h
При h9 стремящемся к нулю, получаем, что A'{x) = F{x),
т. е. А(х) — первообразная для функции F(x). По формуле Нью-
ь
тона — Лейбница получаем A(b) = \F(x)dx, так как А(а) = 0.
а
Итак, работа силы F(x) при перемещении тела из точки а
в точку Ъ равна
ъ
(2)
Заметим, что если F выражается в ньютонах (Н), а путь —
в метрах, то работа А — в джоулях (Дж).
Задача. Вычислить работу силы F при сжатии пружины на
0,08 м, если для ее сжатия на 0,01 м требуется сила ЮН.
t> По закону Гука сила F пропорциональна сжатию пружины,
т. е. F=kx, где х — сжатие (в м), k — постоянная. Из условия
находим k. Так как при д; = 0,1 м сила F=10 H, то &=— =1000.
§ 5 149
Применение интегралов для решения физических задач
Следовательно, F = kx=1000x, и по формуле (2), где F(x)*
= 1000л:, получаем
0,08
Г х2 0,08
А = \ 1000л;<*л;==1000^- 0 =3,2 (Дж). ^
о
Упражнения
33. Тело движется прямолинейно со скоростью v(t) (м/с).
Вычислить путь, пройденный телом за промежуток времени
от £ = *! до t = t2, если:
2)
3)
4)
34. Скорость прямолинейно движущегося тела v(t) = 4t-t2.
Вычислить путь, пройденный телом от начала движения
до остановки.
§ 6. Простейшие дифференциальные
уравнения
J,o сих пор мы рассматривали уравнения, в которых
неизвестными являлись числа. Однако в математике и ее
приложениях приходится рассматривать уравнения, в которых
неизвестными являются функции.
Задача о нахождении пути s(t) по заданной скорости v(t)
сводится к решению уравнения s (t) = v(t), где v(t) — заданная
функция, a s(t) — искомая функция.
Это уравнение содержит производную неизвестной
функции s(t). Такие уравнения называют дифференциальными.
Задача 1. Решить дифференциальное уравнение
> Требуется найти функцию у(х), производная которой равна
л:н-1, т. е. найти первообразную функции х+l. По правилам
х2
нахождения первообразных получаем i/= -g- +x + C9 где С —
произвольная постоянная. ^
Решение дифференциального уравнения вида y' = f(x)
находится неоднозначно (с точностью до постоянной С). Обычно к
дифференциальному уравнению добавляется условие, из
которого постоянная С однозначно определяется.
Задача 2. Найти решение у(х) дифференциального
уравнения j/' = cosjc, удовлетворяющее условию г/(0)= 1.
> Все решения этого уравнения записываются формулой у(х)=
= sina; + C. Из условия г/(0)= 1 находим sinO + C=l, откуда
С=1.
Ответ. y = l + sinx. ^
150 Глава IV
Первообразная и интеграл
Рассмотрим задачу о размножении бактерий.
Экспериментально установлено, что при определенных
условиях скорость размножения бактерий пропорциональна их
количеству.
Пусть m{t) — масса всех бактерий в момент времени t,
тогда т'(t) — скорость их размножения. По условию
m'(t) = km(t), (1)
где k — заданная постоянная, зависящая от вида бактерий и
внешних условий. Уравнение (1) является дифференциальным
уравнением, описывающим закон размножения бактерий.
Покажем, что функции
m(t) = Cekt, (2)
где С — постоянная, являются решениями уравнения (1). В
самом деле, (Cekt)r = Ckekt = k(Cekt). Можно показать, что формула
(2) содержит все решения уравнения (1).
Пусть известна масса т0 бактерий в момент времени t0, т. е.
mo. (3)
Тогда из равенств (2) и (3) получаем mo = Cekto, откуда
C = moe~kto и
т(г) = тоек«-'о)
дает искомое решение дифференциального уравнения (1) при
начальном условии (3).
К решению дифференциального уравнения сводится
задача о радиоактивном распаде.
Эксперименты показывают, что скорость распада
радиоактивного вещества пропорциональна имеющемуся количеству
этого вещества.
Следовательно, если m(t) — масса вещества в момент
времени t, то
m'(t) = -km(t), (4)
где k — положительная постоянная.
Знак «—» в уравнении (4) обусловлен тем, что m(t)>0, a
m'(t)<0, так как с течением времени количество вещества
уменьшается.
Как и для уравнения (1), проверяется, что функции
m(t) = Ce~kt (5)
являются решениями уравнения (4). Если задано начальное
условие
m(to) = mo, (6)
то из равенств (5) и (6) имеем C = moekto. Следовательно,
функция
тЮ = тое-**-'о> (7)
является решением дифференциального уравнения (4) при
начальном условии (6).
§ 6 151
Простейшие дифференциальные уравнения
Заметим, что на практике скорость распада
радиоактивного вещества характеризуется периодом полураспада, т. е.
промежутком времени, в течение которого распадается половина
исходного вещества.
Пусть Т — период полураспада, тогда из равенства (7) при
t = to + T находим ^ = moe-kT, откуда e~kT=^, kT = ln29 k = ^~.
Подставляя найденное значение k в формулу (7), получаем
или
-t
T
В частности, если to = O, то m(t)=^mo2
В практике часто встречаются процессы, которые
периодически повторяются, например колебательные движения
маятника, струны, пружины и т. д.; процессы, связанные с
переменным электрическим током, магнитным полем и т. п.
Решение многих таких задач сводится к решению
дифференциального уравнения
i/" + co2i/ = O, (8)
где со — заданное положительное число.
Уравнение (8) называют уравнением гармонических
колебаний.
Решениями уравнения (8) являются функции cos соя и
sincox, а любое решение этого уравнения можно записать в
виде
y = C1cos(ox-hC2sin(ox. (9)
Если заданы значения функции у(х) и ее производной
у'(х) в точке х = х0, то этими условиями определяется
единственное решение уравнения (8).
Задача 3. Найти решения уравнения
у" + 4у = 0, если i/(0) = 0, у'(0)=1.
[> Решения данного уравнения согласно формуле (9) имеют вид
у = С1 cos 2х + С2 sin 2x.
Используя условия задачи, получаем O = C1cosO + C2sin0,
откуда С1 = 09 l = C22cos0, т. е. С2 = —. Следовательно,
Упражнения
Решить дифференциальное уравнение (35—36).
[35Л 1) у' = 3-4х; 2) у' = 6х2-8х+1;
3) у' = 3е2х; 4) i/' = 4cos2x.
[ЗбТ] 1) y' = 3sinx; 2) у' = cos х - sin x;
3) у' = 4л:3 -2 cos х; 4) у' = Зх2 - 4е2х.
152 Глава IV
Первообразная и интеграл
7JНайти решение дифференциального уравнения,
удовлетворяющее данному условию:
1) y' = sinx, i/(0) = 0;
2) y' = 2cosx, г/(тг) = 1;
3) y' =
4) у' =
5) у' = е\
6) */' = *"*, i/(0) = 2.
|] Показать, что функция j/ = C1<?(0XH-C2e~(0X при любых
значениях Сх и С2 является решением уравнения у" — co2i/ = O.
Упражнения к главе IV
39. Для функции /(л:) найти первообразную, график которой
проходит через точку М, если:
1) f(x) = cosx, М(0; -2); 2) /(jc) = sinjc, М(-тг; 0);
3) /(x)=-J=, М(4; 5); 4) f(x) = ex, M(0; 2);
Ух
5) /(jc) = 3x2 + 1, M(l; -2); 6) f(x) = 2-2x, M(2; 3).
40. Найти площадь фигуры, ограниченной линиями:
1) y = Vx, *=1, л: = 4, i/ = 0; 2) i/ = |
3) 1/ = л:2, г/ = 2-
4) у = 2х2, i/ = 0,
5) i/ = V^, л: = -8, x = -lf i/ = 0;
6) i/=-\, л: = -3, x = -lf i/ = 0.
4L Вычислить интеграл (41—43).
-1
1
4) $ (2x- Sx2) dx;
-l
2)
5)
2
^(S-x)d
-2
8
j yfxdx;
l
*; 3)
6)
3
§(x2-
l
2
S^f;
1 -^
7) Jsinjcdjc; 8) jcosjcdx.
0 _£
2
1 14
42. 1) J(5jc4-8x3)dx; 2) J (6xs - 5x) dx; 3)
о -l
8 3 6
4) J4V^Yl jdx; 5) jV^H- ldx; 6)
x \ x / 0
153
Упражнения к главе IV
2 3
43. 1) $iCos(*+ J)d*; 2) $l
3 3
3) §3sin(3x-6)dx; 4) §
1 0
Найти площадь фигуры, ограниченной данными линиями
(44—45).
44. 1) 1/=-, у = 4х, х=1, у = 0; 2) у=\, у = х, * = 2, у=0\
х х
3) г/ = л;2 + 1, у = х+1\ 4) у = 2
45. 1) 1/ = л;2-6л; + 9, г/ = л2
" 2) z/ = jc2H-1, y = 3-x2;
3) */ = *2, i/ = 2\/2x; 4)
|46.| Найти площадь фигуры, ограниченной:
1) параболой у = х2-2х + 2, касательной к ней, проходящей
через точку пересечения параболы с осью Оу, и прямой
* = 1;
2) гиперболой у— —, касательной к ней, проходящей через
точку с абсциссой х = 2, и прямыми i/ = 0, x = 6.
^1 Найти площадь фигуры, ограниченной линиями:
2) 1/ = л:4
[48] При каком значении k площадь фигуры, ограниченной
параболой у = х2+рх, где р — заданное число, и прямой
у — kx+l, наименьшая?
Вопросы к главе IV
1. Что называется первообразной для функции y = f(x) на
некотором интервале?
2. Как задать все первообразные функции y = f(x), если ^(л:) —
одна из них?
3. Записать формулы первообразных для функций
у = хр(р*-1), y=-(x>0, x<0), y = ex, y = sinx, y = cosx.
4. Перечислить правила нахождения первообразных.
5. Привести пример криволинейной трапеции.
6. Какую фигуру называют криволинейной трапецией?
7. Записать формулу Ньютона — Лейбница.
8. Привести пример фигуры, площадь которой можно вычис-
ъ
лить
по формуле S = \(-f(x))dx.
а
154 Глава IV
Первообразная и интеграл
2. Привести пример фигуры, площадь которой можно вычис-
ь
лить по формуле S = \(f2(x)-f1(x))dx.
а
1Q. Как с помощью интеграла найти путь по заданной
скорости, вычислить работу переменной силы?
В Какую сумму называют интегральной суммой функции
y = f(x) на отрезке [а; Ь]?
И Что называют определенным интегралом от функции
y = f(x) на отрезке [а; Ь]?
£| Какое уравнение называют уравнением гармонического
колебания? Как записывается его решение?
Проверь себя!
1. Показать, что F (х) = е2х + Xs — cos x является первообразной
для функции f(x) — 2e2x + 3x2 + sinx на всей числовой
прямой.
2. Для функции f(x) = 3x2 + 2x-3 найти первообразную,
график которой проходит через точку М(1; -2).
3. Вычислить:
2)3^ S))cos2xdx; 4)
1 2*0 £
2
4. Найти площадь фигуры, ограниченной параболой у = :
+ х-6 и осью Од\
1. Для функции f(x) = ex — 3sinjc найти первообразную,
график которой проходит через точку А(0; 2).
2. Вычислить:
4 1
3. Изобразить фигуру, площадь которой равна }(2х — x2)dx9 и
вычислить эту площадь. i
4. Найти площадь фигуры, ограниченной линиями
у = 2 + 4;Х-х2 и у = х2-2х + 2.
5. Найти площадь фигуры, ограниченной параболой г/ = д;2 + 1
и касательными к ней, проведенными из точки (0; -3).
| УД | Историческая справка
Несмотря на то что интегральное исчисление появилось
в XVII в., его истоки можно обнаружить в глубокой древности.
Так, в Московском папирусе, возраст которого около 4000 лет,
155
Историческая справка
описывается алгоритм вычисления объема усеченной
пирамиды с квадратными основаниями и ставятся проблемы
нахождения общих приемов вычисления площадей криволинейных
фигур и объемов различных тел.
Метод древнегреческого ученого Евдокса Книдского,
названный впоследствии методом исчерпывания, позволял
достаточно точно вычислять площади любых фигур на основе
неявного использования предельных переходов. Суть этого метода,
например для вычисления площадей плоских фигур,
заключается в следующем. В фигуру вписываются и вокруг нее
описываются многоугольники, число сторон которых увеличивается.
Находится предел, к которому стремятся площади этих
многоугольников; его и принимают за площадь рассматриваемой
фигуры. Сложность применения этого метода в том, что для
каждой фигуры надо было искать свой способ вычисления
предела. В древности этим методом пользовались Архимед и Евклид.
В дальнейшем развитие методов, которые применяли
древнегреческие ученые при вычислении площадей и объемов,
привело к понятию интеграла.
В XVII в. немецкий математик и астроном И. Кеплер,
открывший законы движения планет, одним из первых
попытался возродить метод вычисления площадей и объемов, идущий
от Евдокса и развитый Архимедом. Кеплер вычислял площади
плоских фигур и объемы тел, основываясь на идее разбиения
фигур и тел на большое число малых частей, которые он
называл «тончайшими кружочками» или «частями крайне малой
ширины». Затем суммировал площади (или объемы)
полученных при разбиении фигур (тел).
В отличие от Кеплера итальянский математик Б.
Кавальери (1598 —1647) в книге «Геометрия неделимых», деля
фигуру (тело) параллельными прямыми (плоскостями), считал эти
линии (плоскости) лишенными всякой толщины, однако
«складывал» их для нахождения площади фигуры (объема тела).
Под понятием «все линии» Кавальери понимал то же, что мы
ь
сегодня понимаем под
Труды Кеплера, Кавальери и других ученых послужили
основой, на которой Ньютон и Лейбниц выстроили теорию
интегрального исчисления. Развитие этой теории продолжили
Эйлер и П. Л. Чебышев (1821 —1894). В частности, Чебышев
разработал способы интегрирования отдельных классов
иррациональных функций.
Определение интеграла как предела интегральных сумм
принадлежит О. Коши. Символ \f(x)dx ввел Лейбниц. Термин
«интеграл» (от лат. integer — целый) впервые был предложен
И. Бернулли.
156 Глава IV
Первообразная и интеграл
о
Комбинаторика
Математическая истина независимо от
того, в Париже или в Тулузе,
одна и та же.
Б. Паскаль
§ 1. Математическая индукция
ИЯ Рассмотрим значения квадратного
трехчлена п2 + п + 41 при /г=1, 2, 3, 4, 5, 6, 7, ...,
14. Они соответственно равны 43, 47, 53, 61,
71, 83, 97, ..., 251. Все полученные числа
простые. Напрашивается вывод, что при любом
натуральном п число
ЛГ = п2 + п + 41 (1)
является простым.
Вывод, сделанный на основании проверки
большого числа примеров, называют
доказательством методом неполной
математической индукции1. Однако при таком
доказательстве нельзя быть абсолютно уверенным, что
утверждение справедливо при других,
непроверенных значениях п. Так, например, значение
рассмотренного квадратного трехчлена (1) при
п = 41 равно 412 + 41+41=41(41 + 1 + 1) = 4143,
т. е. не является простым числом.
Для строгого доказательства утверждений
на множестве натуральных чисел используют
метод полной математической индукции
(кратко метод индукции). Поясним его на
примерах.
Задача 1. Доказать, что неравенство
2п>п
справедливо для любого натурального п.
[> Заметим, что 2*>1, т.е. неравенство
справедливо при п — 1.
(2)
(2)
1 Индукция (от лат. inductio — наведение) —
умозаключение от фактов к общему утверждению.
1
157
Математическая индукция
Предположим, что неравенство (2) справедливо для
некоторого натурального л. Докажем, что тогда из этого
предположения следует справедливость аналогичного неравенства для
следующего натурального числа л+1, т. е., что 2п+1>л + 1.
Умножив обе части верного неравенства (2) на положительное
число 2, получим верное неравенство 2-2n>2n, т. е.
2" + 1>2п. (3)
Но 2л = л + л>л+1, так как л>1. Поэтому из верного
неравенства (3) следует верное неравенство 2Л + 1>л + 1.
Итак, при л = 1 формула (2) верна. По доказанному она
верна и для следующего натурального числа п = 2. А так как
формула (2) верна при л = 2, то по доказанному она верна и при
л = 3, поэтому она верна и при л = 4 и т. д., т. е. при всех
натуральных л. М
Таким образом, способ доказательства методом полной
математической индукции состоит в следующем:
Пусть требуется доказать, что некоторое утверждение
справедливо для любого натурального числа л. Для этого:
1) проверяется справедливость утверждения при л = 1;
2) доказывается, что если это утверждение верно для
некоторого натурального числа л, то оно верно и для
следующего за ним натурального числа л + 1.
Тогда данное утверждение верно для л = 2, л = 3, л = 4 и
вообще для любого натурального л.
Задача 2. Доказать, что для любого натурального п
справедливо равенство
п2(п + 1)2 (4)
4
\> Воспользуемся методом математической индукции.
1) При л=1 равенство (4) верно: 13=—к .
4
2) Докажем, что если равенство (4) верно для некоторого
натурального числа п, то оно верно и для п+1, т. е. верно
равенство
13 + 23 + 33 + ... + п3 + (п + 1)3=(п + 1>2^ + 2)2. (5)
4
Прибавляя к обеим частям верного по предположению
равенства (4) число (пн-1)3, получаем верное равенство
)3. (6)
)^
4
Преобразуем правую часть этого равенства:
158 Глава V
Комбинаторика
Поэтому из справедливости равенства (6) следует
справедливость равенства (5). Следовательно, равенство (4)
справедливо при любых натуральных л. ^ В9
Упражнения
(Методом математической индукции доказать, что для
любого натурального п справедливо равенство:
1) 1 + 3 + 5 + .. . + (2п-1) = п2;
2) 3 + 5 + 7 + ...+(2n+l) =
3) 1 + 2 + 4 + ... + 2""1 = 2/l-l;
4) 3 + 9 + 27 + ... + 3"=!(3"-l).
оказать, что для любого натурального л справедливо
равенство:
3 Методом математической индукции доказать:
1) формулу суммы Sn первых п членов арифметической
о 2ai+(n-l)d „ ,
прогрессии Sn= —-— — • п, где а1 — первый член, а —
разность арифметической прогрессии;
2) формулу суммы Sn первых п членов геометрической
прогрессии Sn= l^q ~ , где Ь1 — первый член, q — знаме-
q-1
натель геометрической прогрессии,
•казать, что при любом натуральном п число:
1) б2""^! делится на 7; 2) 4п + 15п-1 делится на 9.
§ 2. Правило произведения.
Размещения с повторениями
В основной школе решались элементарные
комбинаторные задачи, связанные с составлением различных соединений
(комбинаций) из имеющихся элементов. Было сформулировано
правило произведения, упрощающее подсчет числа
определенных соединений.
Правило произведения
Если существует п вариантов выбора первого элемента и
для каждого из них имеется т вариантов выбора второго
элемента, то существует п • т различных пар с
выбранными первым и вторым элементами.
§ 2 159
Правило произведения. Размещения с повторениями
Задача 1. Сколько различных двузначных чисел можно
записать с помощью цифр 0, 2, 4, 6, 8?
t> В качестве первой цифры числа может быть выбрана любая
из цифр 2, 4, 6, 8 (л = 4). Второй цифрой может служить
любая из данных цифр 0, 2, 4, 6, 8 (т = 5).
Согласно правилу произведения число всевозможных
двузначных чисел, составленных из предложенных цифр, равно
n-m = 4-5 = 20. <4
Задача 2. В школьной олимпиаде по математике
победителями оказались 3 человека, в олимпиаде по физике — 2
человека, в олимпиаде по химии — 4 человека. На районные
олимпиады по математике, физике и химии школа должна
направить по одному учащемуся из числа победителей школьных
туров по трем предметам. Сколькими способами можно это
сделать?
\> Согласно правилу произведения одного участника на
олимпиаду по математике и одного участника на олимпиаду по
физике можно выбрать 3-2 = 6 способами. К каждой из
полученных 6 пар можно присоединить любого из четырех
победителей олимпиады по химии. Таким образом, троих человек для
участия в названных трех олимпиадах согласно правилу
произведения можно выбрать 6-4 = 24 способами. ^
Решение задачи 2 показало, что правило произведения
может быть применено неоднократно для подсчета соединений из
трех, четырех и т. д. элементов, выбираемых из определенных
множеств с конечным числом элементов.
Задача 3. Сколько различных четырехбуквенных слов
можно записать с помощью букв «м» и «а»? (Словом в
комбинаторике называют любую последовательность букв.)
t> Каждая из четырех букв составляемого слова
последовательно выбирается из имеющихся двух букв. Применив трижды
правило произведения, найдем число составляемых
четырехбуквенных слов:
2-2-2.2 = 24 = 16. Л
d5i Заметим, что среди образуемых в задаче 3 слов были,
например, слова «мммм» и «ммма», отличающиеся друг от
друга наборами (составом) букв. Были, например, и слова
«ааам» и «аама», отличающиеся друг от друга порядком
расположения в них букв.
Определение
Соединения, содержащие п элементов, выбираемых из
элементов т различных видов, и отличающиеся одно от
другого либо составом, либо порядком следования в них
элементов, называют размещениями с повторениями из т
по л.
160 Глава V
Комбинаторика
Число всевозможных размещений с повторениями из т
элементов по п обозначают А^ (А — первая буква
французского слова Arrangement — размещение, приведение в порядок) и
читают: «Число размещений с повторениями из эм по эн» или
«А с чертой из эм по эн».
Так, в задаче 3 было найдено
А! = 16.
Можно доказать, что для любых натуральных тип верно
равенство
Апт=т\ Ж^Ш (1)
ШШ Доказательство формулы (1) проведем с помощью
математической индукции поп — числу элементов в размещении при
фиксированном т.
1) При п=1 очевидно, что
так как каждое размещение состоит из одного элемента и
различные размещения получаются только из разных элементов,
число видов которых равно т.
2) Предположим, что формула (1) верна для некоторого п.
Докажем, что она верна и для п + 1, т. е. справедлива формула
Рассмотрим любое размещение (с повторениями),
состоящее из п элементов, и присоединим (припишем) к нему
элемент одного из имеющихся т видов. Получится размещение из
(/1+1) элементов. При этом очевидно, что из каждого
размещения, состоящего из п элементов, получается столько
размещений по (п + 1) элементам, сколько имеется различных видов
элементов, т. е. т размещений. Действуя таким способом, мы
не упустим ни одного возможного размещения по (п+1)
элементам и ни одного не получим дважды. Поэтому число
размещений с повторениями из т видов элементов по (п+1)
элементам в каждом выборе будет в т раз больше, чем число
размещений с повторениями из т по п, т. е.
А%+ г = тАпт= т • тп = тп+\
Тем самым формула (1) доказана. ШШШ
Pfl Задача 4. В двоичной системе счисления, применяемой
в ЭВМ, используют два символа: 0 и 1. В некоторой ЭВМ
каждое машинное слово записывается в памяти с помощью этих
символов в 16 пронумерованных разрядах. Сколько различных
машинных слов можно записать в этих разрядах?
[> В каждом из 16 разрядов может стоять один из двух
символов. Очевидно, число различных машинных слов равно A|6 =
= 216 = 65536. ^С31
§ 2 161
Правило произведения. Размещения с повторениями
Упражнения
5. Сколько разных трехзначных чисел, не имеющих
одинаковых цифр, можно записать с помощью цифр:
1) 1, 2 и 3; 2) 1, 2, 3 и 4?
6. Сколько разных трехзначных чисел можно записать с
помощью цифр:
1) 6, 7 и 8; 2) 6, 7, 8 и 9?
7. Сколько разных двузначных чисел можно записать,
используя цифры 1, 2, 3 и 4?
8. Путешественник может попасть из пункта А в пункт С,
проехав через пункт Б. Между пунктами Aw. В имеются
три автодороги, а между пунктами В и С —
железнодорожное и речное сообщения. Сколько существует
различных маршрутов между пунктами А и С?
9. Сколькими способами могут быть распределены золотая
и серебряная медали по итогам первенства страны по
футболу, если число участвующих в первенстве команд равно 16?
10. Сколькими способами можно составить расписание уроков
на один день из шести разных учебных предметов?
11. В классе 20 учащихся. Необходимо выбрать из их числа
старосту, физорга и культорга. Сколькими способами
можно осуществить этот выбор, если один ученик может
занимать только одну должность?
12. В одной из стран автомобильные номера из четырех цифр
(нуль может стоять и на первом месте) записываются на
пластинках пяти различных цветов (каждый из пяти
штатов этой страны имеет номера своего цвета). Сколько
разных пластин с номерами может быть выдано
автовладельцам в этой стране?
13. Десять участников конференции обменялись визитными
карточками (каждый вручил свою карточку другим
участникам). Сколько всего карточек было роздано?
14. Десять участников конференции обменялись
рукопожатиями, пожав руку каждому. Сколько всего рукопожатий
было сделано?
15. Сколько различных шифров можно набрать в
автоматической камере хранения, если шифр составляется с помощью
любой из тридцати букв русского алфавита с последующим
трехзначным числовым кодом?
16. Сколько имеется семизначных натуральных чисел, в
которых все цифры, стоящие на нечетных местах, различны?
17. Сколько нечетных четырехзначных чисел можно записать
с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, если любую из них
можно использовать в числе не более одного раза?
162 Глава V
Комбинаторика
§ 3. Перестановки
Задача 1. Сколькими способами можно поставить рядом
на полке четыре различные книги?
D> На первое место можно поставить любую из четырех книг,
на второе — любую из трех оставшихся, на третье — любую из
двух оставшихся и на четвертое место — последнюю
оставшуюся книгу. Применяя последовательно правило произведения,
получим 4-3-2-1 = 24, т. е. книги можно поставить 24
способами. ^
В этой задаче фактически было найдено число
всевозможных соединений из четырех элементов, которые отличались
одно от другого порядком расположения этих элементов. Такие
соединения называют перестановками.
Определение
Перестановками из п элементов называются соединения,
которые состоят из п элементов и отличаются одно от
другого только порядком их расположения.
Число перестановок из п элементов обозначают Рп (Р —
первая буква французского слова Permutation — перестановка)
и читают «пэ энное».
В задаче 1 было найдено Р4 = 24.
Последовательно применяя правило произведения, можно
получить формулу числа перестановок Рп из п различных
элементов:
Рп = п(п- 1)(п- 2) .... 3-2-1 = 1- 2- 3-...(n-2)(n-l)n.
Произведение первых п натуральных чисел обозначают л!
(читается «эн факториал»), т.е. п! = 1 • 2 • 3 •... -(л — 1)- л,
причем по определению 1! = 1. Таким образом,
Рп = п\ (1)
Задача 2. Сколькими способами можно положить 10
различных открыток в 10 имеющихся конвертов (по одной
открытке в конверт)?
[> По формуле (1) находим
Р10 = Ю!=1-2-3 •...•910 = 3 628800. А
ВИВ рассмотренных задачах мы занимались перестановками
различных элементов. Если же некоторые переставляемые
элементы будут одинаковыми, то всевозможных различных
перестановок из них будет меньше — некоторые перестановки
совпадут одна с другой. Например, переставляя буквы в слове
«парк», получим 24 различных «слова» — перестановок из
четырех различных букв. Если же записать всевозможные
перестановки из букв слова «папа» (среди которых две пары
одинаковых букв), то их получится всего шесть:
папа, паап, ппаа, апап, аапп, аппа.
§ з 163
Перестановки
Обобщенно аналогичные задачи формируются следующим
образом. Пусть имеются элементы т различных видов.
Требуется найти число перестановок, образованных из пх
элементов первого вида, п2 элементов второго вида, ..., пт элементов
т-го вида.
_ Число таких перестановок с повторениями обозначают
Рпх* п2> •••» пт- Количество элементов в каждой из них равно
п = пх + п2 + ... + пт. Очевидно, что если бы все элементы в
перестановках были различны, то их число равнялось бы п\. При
наличии же совпадающих элементов число перестановок будет
меньшим числом. Выведем формулу для подсчета числа
перестановок с повторениями.
О Рассмотрим перестановку элементов
аа...а ЪЪ...Ъ ... zz...z, (2)
пх п2 пт
в которой последовательно записаны все элементы первого вида
(их число равно пх), элементы второго вида (их число равно
л2), ..., элементы т-го вида (их число равно лт).
Элементы &-го вида можно переставить друг с другом nk\
способами. Но в связи с тем что эти элементы одинаковы, то
перестановки из них ничем не отличаются одна от другой.
Например, в перестановке «ппаа» ничего не изменится, если
поменять местами первый со вторым и (или) третий с
четвертым элементами.
Перестановки элементов первого, второго, ..., т-го видов
можно осуществлять независимо друг от друга. Поэтому
согласно правилу произведения элементы перестановки (2), не
меняя ее вида, можно переставлять друг с другом пх\- п2\- ...X
X пт\ способами. Значит, число перестановок с повторениями
будет в пх\ • п2\ •... • пт1 раз меньше, чем л!. Таким образом,
Р"1' П2 Пт= П\П\П\'
где п =
Заметим, что задача о подсчете числа перестановок из букв
слова «папа» сводилась к нахождению числа перестановок с
повторениями Р2у2:
р (2 + 2)! 24 ~
Задача 3. Слова и фразы с переставленными буквами
называют анаграммами. Сколько анаграмм можно составить из
слова «макака»?
[> В слове из 6 букв «макака» буква «а» используется 3 раза,
буква «к» — 2 раза, а буква «м» — 1 раз. Согласно формуле
(3) число всевозможных анаграмм равно
ъ (3 + 2 + 1)1 6! 4-5-6
3'2Д 3I-2M! 3!-2! 2
164 Глава V
Комбинаторика
Упражнения
18. Найти значение:
1) Р6; 2) Р8; 3) Р7; 4) Р9.
19. Сколькими способами можно рассадить четверых детей на
четырех стульях в столовой детского сада?
20. Сколькими способами можно установить дежурство по
одному человеку в день среди семи учащихся группы в
течение 7 дней (каждый должен отдежурить один раз)?
21. Сколько пятизначных чисел, не содержащих одинаковых
цифр, можно записать с помощью цифр 1, 2, 3, 4, 5 так,
чтобы:
1) последней была цифра 4;
2) первой была цифра 2, а второй — цифра 3;
3) первыми были цифры 2 и 3, расположенные в любом
порядке.
22. Упростить форму записи выражений (k — натуральное
число, k>6):
1) 7!-8; 2) 16 15!; 3) 12! 13 14;
4) Аг!*(Л + 1); 5) (k — 1)! •/z; 6) {k—.
7) (k — 2)! • (k — 1) k' 8) (k — 5)! • (k2 — 7k -f-12)
23. Упростить:
П Ш. o\ 22[. o\ 6!• 4! . 4v 10! .
' 18!' ' 20!' ' 8! ' ' 8!-3!'
; 8)
№+6)!
если буквами k, m, n обозначены натуральные числа.
24. Решить уравнение относительно п:
D -/=- = ■?; 2)^^ = 0,1; 3)^--1 = 0.
25. Сколько различных слов можно составить, переставляя
местами буквы в слове «треугольник» (считая и само это
слово)?
26. Сколько различных пятизначных чисел (не содержащих
одинаковых цифр), не кратных пяти, можно составить из
цифр 1, 2, 3, 4, 5?
27. Имеется 10 книг, среди которых:
1) 8 книг различных авторов и двухтомник одного автора,
которого не было среди предыдущих восьми;
2) 7 книг разных авторов и трехтомник восьмого автора.
Сколькими способами можно расставить эти книги на
полке так, чтобы книги одного автора стояли рядом?
|§3 Сколько анаграмм можно составить из слова:
1) клок; 2) окно; 3) драма; 4) банан; 5) шарабан;
6) кукушка; 7) математика; 8) тетраэдр?
§ 3 165
Перестановки
£9. На Новый год троим братьям родители купили в подарок
6 различных книг и решили каждому подарить по 2
книги. Сколькими способами можно сделать эти подарки?
|30.1 Когда X. Гюйгенс (1629—1695) открыл кольцо Сатурна, он
составил следующую анаграмму:
ааааааа ссссс d eeeee g h iiiiiii llll mm
nnnnnnnnn oooo pp q rr s ttttt uuuuu.
Этими буквами записывается фраза «Annulo cingitur tenui,
piano, nusquam cohaerente, ad eclipticam inclinato»
(«Окружен кольцом тонким, плоским, нигде не подвешенным*
наклонным к эклиптике»). Сколько различных анаграмм
можно составить из букв зашифрованной Гюйгенсом фразы?
§ 4. Размещения без повторений
Задача 1. Сколько различных двузначных чисел можно
записать с помощью цифр 1, 2, 3, 4 при условии, что в
каждой записи нет одинаковых цифр?
t> Перебором убедимся в том, что из четырех цифр 1, 2, 3,4
можно составить 12 двузначных чисел, удовлетворяющих
условию:
12, 13, 14,
21, 23, 24,
31, 32, 34,
41, 42, 43.
В записи двузначного числа на первом месте может стоять
любая из данных четырех цифр, а на втором — любая из трех
оставшихся. По правилу произведения таких двузначных
чисел 4-3 = 12. <4
При решении задачи 1 из четырех данных элементов
(цифр 1, 2, 3, 4) были образованы всевозможные соединения
по два элемента в каждом, причем любые два соединения
отличались друг от друга либо составом элементов (например, 12
и 24), либо порядком их расположения (например, 12 и 21).
Такие соединения называют размещениями.
Определение
Размещениями из т элементов по п элементов (n<m)
называются такие соединения, каждое из которых содержит
п элементов, взятых из данных т разных элементов, и
которые отличаются одно от другого либо самими
элементами, либо порядком их расположения.
Иногда такие размещения называют размещениями без
повторений.
Число всевозможных размещений без повторений из m
элементов по п элементов обозначают А^ и читают «А из эм по
166 Гл а в а V
Комбинаторика
эн». Так, например, при решении задачи 1 было установлено,
чтоА|=12.
Выведем формулу для вычисления А^ — числа
размещений из т элементов по п элементов.
О Пусть имеется т различных элементов. Тогда число
размещений, состоящих из одного элемента, выбранного из
имеющихся т элементов, равно т, т. е. А^^т.
Чтобы составить все размещения из т элементов по 2,
к каждому из ранее образованных размещений из т элементов
по 1 будем последовательно присоединять по одному из
оставшихся т-1 элементов. По правилу произведения число таких
соединений равно m(m-l). Таким образом, A^ = m(m-1).
Для составления всех размещений из т по 3 к каждому
из ранее полученных размещений из т элементов по 2
присоединим по очереди по одному из оставшихся (т-2) элементов.
По правилу произведения число таких соединений равно
m(m-l)(m-2), т.е. A^ = m(m-l)(w-2).
Последовательно применяя правило произведения, для
любого п<т получаем
А?п = т(т-1)(т-2)...(т-(п-1)).* (1)
Например, А| = 4-3 = 12; А| = 4-3-2 = 24; А| = 5-4-3 = 60.
Отметим, что правая часть формулы (1) содержит
произведение п последовательных натуральных чисел, наибольшее из
которых равно т. Пусть в формуле (1) т = п. Тогда
т. е. число размещений из п элементов по п равно числу
перестановок из этих элементов:
Апп=Рп. (2)
Задача 2. Сколькими способами можно обозначить
вершины данного треугольника, используя буквы А, Б, С, £>, Е, F?
t> Задача сводится к нахождению числа размещений из 6
элементов по 3 элемента в каждом. По формуле (1) находим
А| = 6* 5*4 = 120, т. е. вершины можно обозначить 120
способами. ^
Задача 3. Решить уравнение А% = 42 относительно п.
\> Заметим, что п>2, по формуле (1) имеем А„ = п(п- 1). По
условию А^ = 42, поэтому п(п-1) = 42, откуда п2-п-42 = 0, п1 = 7,
п2 = -6.
Так как корнем уравнения должно быть натуральное
число п>2, то п2 — — 6 — посторонний корень.
Ответ. П — 7.М
Преобразуем формулу (1) для нахождения числа
размещений Апт.
О Запишем формулу (1) так:
§ 4 167
Размещения без повторений
Умножим обе части этого равенства на
(т - п)! = 1 • 2 • 3 •... • (т - п),
получим
(m-n)!-A£==l-2-3-...-(m-n)(m-n+l)(m- n + 2)-... -(m-l)m,
т. е. (m-n)!-A£ = m!, откуда
Для того чтобы формула (3) была справедлива не только
для т>п, но и для т = п, полагают 0! = 1.
Задача 4. Вычислить
а\2+а\
\> По формуле (3) находим
121 | 12!
А\2
Упражнения
31. Вычислить:
1) А\; 2) А\\
8!
3)Af;
7) А210;
2
' 6!
4)
8)
Q _4_
— о -г
Л,-
64.
32. В классе изучают 9 предметов. Сколькими способами
можно составить расписание на понедельник, если в этот день
должно быть 6 разных предметов?
33. Сколько существует способов для обозначения вершин
данного четырехугольника с помощью букв А, Б, С, Z), E, F?
34. В классе 30 человек. Сколькими способами могут быть
выбраны из их состава староста и казначей?
35. В чемпионате по футболу участвуют 10 команд. Сколько
существует различных возможностей занять командам
первые три места?
36. Найти значение выражения:
n Afx-Afp m А412-А77
37. Решить относительно т уравнение:
1)^ = 90; 2)А3т
38. Найти значение выражения
168 Гл а в а V
Комбинаторика
39. В шахматном турнире участвуют пять юношей и три де-
" вушки. Сколькими способами могут распределиться места
среди девуп1ек, если все участники набрали разные
количества очков?
40. Доказать, что А* +1 = (л - к) А„, где k<n, k€N9 n€N.
§ 5. Сочетания без повторений
и бином Ньютона
Задача 1. Из пяти шахматистов для участия в турнире
нужно выбрать двоих. Сколькими способами это можно
сделать?
> Из пяти шахматистов можно составить А\ пар. Но из этих
пар надо выбрать только те, которые различаются лишь
составом участников. Таких пар в 2 раза меньше, поэтому -^- =
= ^— = 10, т. е. двоих можно выбрать 10 способами. -^
При решении этой задачи из 5 человек были образованы
пары — соединения по 2 человека, которые отличались друг от
друга составом. Такие соединения называют сочетаниями.
Определение
Сочетаниями из т элементов по п в каждом (n<m)
называются такие соединения, каждое из которых содержит п
элементов, взятых из данных т элементов, и которые
отличаются одно от другого по крайней мере одним
элементом.
Иногда такие сочетания называют сочетаниями без
повторений.
Число всевозможных сочетаний из т различных
элементов по п элементов обозначают С£ (С — первая буква
французского слова Combinaison — сочетание) и читают «це из эм по
эн». При решении задачи 1 было установлено, что С§ = 10.
Выведем формулу для подсчета числа сочетаний из т
различных элементов по п элементов в каждом.
0 Образуем все соединения, содержащие п элементов,
выбранных из данных т разных элементов, без учета порядка их
расположения. Число таких соединений равно С^.
Из каждого полученного соединения перестановками его
элементов можно образовать Рп = п\ соединений, отличающихся
одно от другого только порядком расположения элементов. Тем
самым получаются размещения из т элементов по л, число
которых равно А^. По правилу произведения число таких
соединений равно С^-Рп. Итак, С^-Рп=А^9 откуда
<Ъ=4=.« (1)
§ 5 169
Сочетания без повторений и бином Ньютона
Например, Cf-^-i^f-4.
Заметим, что если т = п, то
Учитывая, что А^= при и m>n и Рп = л!, формулу
(1) можно представить в виде
где т>п.
Например, Cl =
Задача 2. Сколько существует способов выбора трех карт
из колоды в 36 карт?
[> Изъятые из колоды 3 карты без учета порядка их
расположения в наборе являются сочетаниями из 36 по 3. По
формуле (2) находим
гз 361 _ 361 _ 34-35-36 q
Сзб~ (36-3)131 - We"" 6 ~34 Зб 6-7140'
т. е. существует 7140 способов. ^
Замечание. В учебнике 10 класса при разложении
степени бинома (а + Ъ)п было введено понятие биномиальных
коэффициентов, которые в общем виде обозначались С£. Была без
доказательства принята формула (2) для вычисления этих
коэффициентов. Теперь стало очевидным, что ранее
рассмотренные биномиальные коэффициенты — это числа сочетаний из т
по п.
С помощью формулы (2) в курсе 10 класса доказывались
свойства сочетаний:
т — ^т 9 [О)
т + Ст =Ст + 1. (4)
Докажем свойство (4), так называемое рекуррентное
свойство числа сочетаний, пользуясь соотношением (1):
лП Лп+1
-l)- ...-(m-(n-l)) m(m-l)-... {т-(п-1)){т-п)
m(m-l)-... -(т-(п-1))(п +1) + m(m-l)•... • (т-(п-1))(т-п)
170 Глава V
Комбинаторика
На основе свойства (4) и с учетом того, что С^ = С™ = 1,
составляется так называемый треугольник Паскаля — таблица
значений С%. (Ниже приведен фрагмент таблицы.)
\ п
1
2
3
4
5
6
7
8
9
10
0
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
2
1
3
6
10
15
21
28
36
45
3
1
4
10
20
35
56
84
120
4
1
5
15
35
70
126
210
5
1
6
21
56
126
252
6
1
7
28
84
210
7
1
8
36
120
8
1
9
45
9
1
10
10
1
Эта таблица наглядно иллюстрирует и свойство (3) —
равны числа, одинаково удаленные от концов строки
треугольника Паскаля (CJJj=C™~n).
Треугольником Паскаля пользуются при возведении
бинома а + b в натуральные степени по знакомой вам из курса
10 класса формуле бинома Ньютона:
(а + Ь)т = С®тат + С1тат~1Ъ + С^а™~2Ь2 +... + С%~ 1abm~х + С™Ьт. (5)
/ 1 \5
Задача 3. Записать разложение бинома \2х-—\ .
> По формуле (5) находим:
(2x-l)5 = Cl(2xf + Cl(2x)4(-\)^CU2xf(-l)\cl(2x
о 32
Задача 4. Доказать свойство элементов строки
треугольника Паскаля
cUcUc^ + ...+cr1+c- = 2"1. (6)
> Равенство (6) получается из равенства (5) при а = 6 = 1. М
ШШ Проведем доказательство справедливости формулы бинома
Ньютона (5), используя теорию соединений с повторениями.
§ 5 171
Сочетания без повторений и бином Ньютона
Проследим процесс возведения в натуральную степень
бинома а + Ь, не выполняя приведения подобных слагаемых:
(а + b)2 = (a + b)(a + b) = aa + ab + ba + bb, (7)
= ааа + aab + aba + аЬЬ + baa + баб + bba + 666. (8)
Заметим, что в результат возведения бинома во вторую
степень (7) входят все размещения с повторениями,
составленные из букв а и b по две буквы в каждом размещении. В
результат возведения бинома в третью степень (8) входят все
размещения с повторениями, составленные из тех же букв а и b
по три буквы в каждом.
После раскрытия скобок при возведении двучлена а + b в
степень т, т. е. в равенстве
(9)
т множителей
будут получены всевозможные размещения с повторениями из
букв а и 6, состоящие из т элементов.
Подобными членами после раскрытия скобок в равенстве
(9) будут слагаемые, содержащие одинаковое число букв а
(очевидно, букв Ъ в них тоже будет одинаковое число). Выясним,
сколько будет подобных членов, содержащих k раз букву b
(букву а соответственно (m — k) раз).
Эти члены являются перестановками с повторениями,
составленными из k букв b и m-k букв а. Согласно формуле (3)
§ 3 имеем
Но выражение, стоящее в правой части этой формулы,
есть не что иное, как Ckm. Следовательно, Pky m-^ = C^, а значит,
после приведения подобных слагаемых в равенстве (9) одно*
член с буквенной частью bkam~k (или am~kbk) будет иметь
коэффициент Ckm. Это доказывает формулу (5). • Hi
Упражнения
41. Найти:
1) С26; 2) Cl; 3) С|; 4) С|; 5) С*; 6) С|;
7) С}§; 8) С%; 9) С\о; 10) С\о; И) C?g0; 12) С270.
42. Сколькими способами можно делегировать троих
студентов на межвузовскую конференцию из 9 членов научного
общества?
43. Сколько различных аккордов, содержащих 3 звука,
можно взять на 13 клавишах одной октавы?
44. В помещении 20 ламп. Сколько существует разных
вариантов освещения, при котором должны светиться только
18 ламп?
172 Глава V
Комбинаторика
45. Имеется 15 точек на плоскости, причем никакие 3 из них
не лежат на одной прямой. Сколько различных отрезков
можно построить, соединяя эти точки попарно?
46. На окружности отмечено 12 точек. Сколько существует
треугольников с вершинами в этих точках?
47. Сколькими способами можно составить из партии,
содержащей п деталей, комплект из р деталей (р < л) для
контроля за качеством продукции?
48. Записать разложение бинома:
1) (1+х)7; 2) (*-2)4; 3) (2*
4) (3*-2)4; 5) (2а-|)5; 6) (|
49. В школьном хоре 6 девочек и 4 мальчика. Сколькими
способами можно выбрать из состава школьного хора двух
девочек и одного мальчика для участия в выступлении
окружного хора?
50. Решить уравнение относительно т:
A2; 2) i
l)Cm=Cm+2;
3) 5C3m=C4m+2; 4) С3";} = 120.
51. Найти значение выражения, предварительно упростив его:
l)C\l + C\l; 2)Cf1+Cfi;
52. С помощью свойств числа сочетаний найти сумму:
1) C°5 + Cl + C25 + Cl + Ci + Cl; 2)
53. Решить уравнение:
" 1) С2х + Сгх=15(х-1); 2)
54. Доказать свойство числа сочетаний
Сп g~*ni — n
т — ^т
55. В вазе лежат 5 разных яблок и 6 различных апельсинов.
Сколькими способами из них можно выбрать 2 яблока и
2 апельсина?
56. Колода карт содержит по 13 карт каждой из четырех
мастей. Сколькими способами можно выбрать из колоды
следующий набор: 3 карты пиковой, 4 карты трефовой,
5 карт червовой, 2 карты бубновой масти?
57. Найти член разложения [Vx+ —=) , содержащий х2.
\ \х)
58. Найти член разложения (Vx+-—\ , содержащий х3.
(
v
На плоскости проведены k прямых, причем никакие две из
них не параллельны и никакие три не пересекаются в
одной точке. Определить число точек пересечения этих
прямых.
§ 5 173
Сочетания без повторений и бином Ньютона
Сколькими способами можно расставить 12 белых и 12
черных шашек на 32 черных клетках шахматной доски?
J6JL] С помощью математической индукции доказать
справедливость формул (6) и (7).
§ 6. Сочетания с повторениями
■ВЯ Определение
Сочетаниями с повторениями из т по п называют
соединения, состоящие из п элементов, выбранных из
элементов т разных видов, и отличающиеся одно от другого
хотя бы одним элементом.
Число сочетаний с повторениями из т по п обозначают Спп.
Задача 1. В киоске продаются карандаши трех цветов:
красные, синие и черные (карандашей каждого цвета в киоске
больше четырех). Сколькими способами можно купить 4 карандаша?
[> В задаче требуется найти число соединений, состоящих из
4 элементов, выбранных из элементов 3 видов, порядок
расположения _которых в соединениях не имеет значения, т. е. нужно
найти С\. Обозначим карандаш красного цвета буквой к,
синего — буквой с, черного — буквой ч. Выпишем всевозможные
наборы из 4 карандашей:
к, к, к, к к, к, к, ч к, к, ч, ч к, ч, ч, ч ч, ч, ч, ч
к, к, к, с к, к, с, ч к, с, ч, ч с, ч, ч, ч
к, к, с, с к, с, с, ч с, с, ч, ч (1)
к, с, с, с с, с, с, ч
с, с, с, с
Число полученных соединений Сз = 15. М
Для вывода формулы числа сочетаний с повторениями
будем использовать искусственный прием, который поясним на
сочетаниях, составленных в задаче 1.
Так как в сочетаниях (1) порядок расположения элементов
не имеет значения, то при перечислении сочетаний все
элементы одного вида будем записывать рядом, а между наборами
элементов разных видов будем ставить знак границы видов П.
В задаче 1 различных видов элементов было 3, значит, границ
СИ должно быть 2. Например: кПч,чПс; кПчСПс,с. При
«расширении» в наборе числа элементов некоторого вида граница
видов будет «перемещаться». С использованием знака П
перечень соединений (1) может быть записан следующим образом:
k,k,k,kDD к,к,к,ПСПч к,кПСПч,ч кППч,ч,ч ППч,ч,ч,ч
k,k,kDc СП к,к,СПс СПч кПс Пч,ч СПсПч,ч,ч
k,kDc, с СП кПс, с СИч Пс,с СИч,ч (2)
кПс,с, с П Пс,с, с Пч
Пс,с,с,с □
174 Глава V
Комбинаторика
В общем виде любой набор из п элементов, выбранных из
элементов т видов, можно представить в виде
а, а, ..., аП 6, 6, ..., b\3 ... П z> z, ..., 2, (3)
nx n2 ... nm
где число разделительных знаков СИ равно т—1, хотя бы одно
из чисел /ij, n2, ..., пт отлично от нуля и n1-hn2-^ ... + nm = n.
Так, например, в каждом из соединений (2) число знаков
П равно т-1 = 3-1 = 2, а число букв п = 4.
Легко заметить, что как соединения (2) в наборе, так и
соединения (3) отличаются друг от друга, по существу, лишь
месторасположением в них разделителей. Заменим все
элементы-буквы знаком П. Тогда соединения (3) можно представить
в виде
П П ... П □ П П ... П П ... П □ □ ... П, (4)
пх п2 ... пт
где nl + n2 + ... + nm = n.
^Учитывая принцип составления соединений (4), видим,
что С^ равно числу перестановок с повторениями из (т— 1)
элементов Пип элементов СИ, т. е.
Таким образом, в задаче 1 подсчитанное число С\ можно
найти с помощью формулы (5):
Т;4 (3 + 4-1)1 6! _ 5-6 лк
U3~ (3-1)!4! ~2!4!~ 2 ~
Задача 2. В продажу поступили мячи 7 различных цветов.
Сколькими способами можно купить 3 мяча?
t> He имеет значения, в каком порядке будут находиться
мячи в приобретенном наборе из 3 мячей. Поэтому решение
задачи сводится к подсчету числа сочетаний с повторениями из 7
по 3:
^з (7 + 3-1)1 91 789
^7~ (7-1)131 "6131" 1.2-3 f
т. е. покупку можно совершить 84 способами. ^ шь*ш
Упражнения
Вычислить:
1) С64; 2) С46; 3) С29; 4) С%.
В кафе подавали мороженое четырех видов. Сколькими
способами трое друзей могут сделать заказ официанту на
3 порции мороженого?
Семь детских игрушек выбираются из игрушек четырех
видов. Сколькими способами это можно сделать, если
игрушек каждого вида больше семи?
§6 175
Сочетания с повторениями
Сколько существует различных прямоугольных
параллелепипедов, если длина каждого его ребра может
выражаться любым целым числом от 1 до 8?
Упражнения к главе V
66. Вычислить:
л\ 5!~4! о* 7!~6! 54[ 7Ш ^ 60! 501
1) 2! ; Zj 5! ; *' 53! + 69!; 4j 58! 48!'
67. Упростить:
1); 2
68. Найти значение выражения:
69. Решить относительно п уравнение:
12; 2)-±- = -^-; 3)
4) А5п.1=2А5п_2; 5)^- = |; 6) С3„=4С2„_2-
70. Сколькими способами можно составить график
очередности ухода в отпуск восьми сотрудников лаборатории?
71. Сколько существует способов делегирования на
конференцию двоих человек из восьми сотрудников лаборатории?
72. Восемь сотрудников лаборатории участвовали в научном
конкурсе, по результатам которого были присуждены
одна первая и одна вторая премии. Сколькими способами
могли быть присуждены рассматриваемые премии?
73. Сколькими разными способами можно рассадить троих
учащихся, пришедших на факультативные занятия, на
сорока имеющихся в классе стульях?
74. Сколькими способами можно назначить патруль из двух
солдат и одного офицера, если в роте 80 солдат и 5
офицеров?
75. Сколько диагоналей имеет выпуклый пятиугольник?
семиугольник? л-угольник?
76. Найти значение выражения, предварительно упростив его:
77. Используя свойства числа сочетаний, найти:
1) С2 + С4 + С4 + С4 + С4; 2) С% + С\ + С$ + С$.
78. Найти разложение бинома:
1) (*+1)6; 2) (x-lf; 3) (2-а)4; 4) (а + 3)4.
79. Доказать, что число перестановок при любом п > 1
является четным числом.
176 Глава V
Комбинаторика
80. Имеются отличающиеся друг от друга 7 роз и 5 веток
зелени. Нужно составить букет из трех роз и двух веток
зелени. Сколькими способами это можно сделать?
81. В двоичной системе счисления, используемой в ЭВМ,
информация записывается с помощью цифр 0 и 1. В
некоторой ЭВМ каждое «машинное слово» записывается в
ячейке памяти, содержащей 32 пронумерованных двоичных
разряда. Сколько различных «слов» может быть записано
в такой ячейке?
82. В одной стране номера автомобилей составляются из двух
неодинаковых букв алфавита, содержащего 20 букв, и
четырех цифр (с возможными повторами). Скольким
машинам можно присвоить полученные таким образом номера?
83. Сколько различных экзаменационных комиссий,
состоящих из 5 членов, можно образовать из 10 преподавателей?
84. С помощью свойств числа сочетаний найти:
1) ^12 + ^12 + ^13» 2) Сд + Сд + С10; 3) С8 —С7; 4) С9 — С%;
5) С| + С| + С? + С|; 6) S S
85. Найти разложение бинома:
1)5; 2) (i+2b)6; 3)(з*+|); 4)
86. В чемпионате страны по футболу участвуют 18 команд,
каждые 2 команды встречаются на футбольных полях 2
раза. Сколько матчей играется в сезоне?
WH Сколькими способами 2л разных элементов можно разбить
на пары?
[Ж] Сколькими способами можно разделить колоду из 36 карт
пополам так, чтобы в каждой из двух стопок было
по 2 туза?
89. В классе 28 учеников. Каждый день двое из них
назначаются дежурными. Можно ли составить на весь год
ежедневное расписание дежурства таким образом, чтобы
никакие 2 ученика не дежурили вместе в течение года дважды?
90. Найти член разложения бинома (\[х+ —р= ) , содержащий х4.
\ ух /
(3 l \i2 1
\х+ —= ) , содержащий —.
\х / х
Щ] Даны числа от 1 до 20. Сколькими способами можно
выбрать из них 3 числа, сумма которых будет числом
четным?
Щ] Доказать, что число круговых перестановок (важен
порядок следования расположенных на окружности элементов,
а начальный элемент безразличен) из п элементов равно
(в-1)!.
Щ] Найти значение выражения:
177
Упражнения к главе V
В цветочном магазине продают цветы 7 видов (каждый вид
представлен более чем 3 цветками). Сколькими способами
можно составить букет из 3 цветков?
Вопросы к главе V
1. Решением каких задач занимается комбинаторика?
2. Сформулировать правило произведения.
3. Какие соединения называют размещениями с
повторениями? Чему равно число размещений с повторениями из т
элементов по п?
4. Какие соединения называют перестановками? Чему равно
число перестановок из п элементов?
5. Какие соединения называют размещениями без
повторений? Чему равно число размещений без повторений из т
элементов по п?
6. Какие соединения называют сочетаниями без повторений?
Чему равно число сочетаний без повторений из т
элементов по п?
7. Перечислить свойства сочетаний без повторений.
8. Что такое треугольник Паскаля?
9. Записать формулу бинома Ньютона.
Рв
1. Найти:
1) Р7; 2) Ah 3) Cl;
2. Упростить:
9
1} (п-1)!' ' (п-2)Г
3. Сколькими способами можно выбрать для подарка 3
предмета из девяти различных предметов?
4. В одном классе изучается 10 разных предметов. В
пятницу завуч должен поставить в расписание этого класса 4
различных предмета. Сколькими способами он может это
сделать?
5. Сколькими разными способами можно разместить 6 групп
школьников в шести классных комнатах (по одной группе
в комнате)?
6. Сколько существует трехзначных цифровых кодов, в
которых нет одинаковых цифр?
7. Записать разложение бинома: 1) (х + у)6; 2) (1-а)5.
1. Решить относительно п уравнение:
1) Рп+4 = 20Рл+2; 2) З 2
2. Решить неравенство
178 Глава V
Комбинаторика
3. Шифр некоторого сейфа образуется из двух чисел. Первое,
трехзначное число, составляется из цифр 1, 2, 3, 4, 5
(каждая цифра встречается не более одного раза); второе,
пятизначное число, записывается с помощью цифр 6, 7, 8.
Сколько различных шифров можно использовать в этом
сейфе?
4. Сколькими способами можно разложить 6 монет по двум
карманам?
5. Используя свойство числа сочетаний, найти:
1) Clo-Cg; 2) С| + С| + С5 + С| + С|.
в. Найти член разложения бинома / \[х \ , содержащий хь.
|
Историческая справка
Задачи, связанные с возможным выбором и
упорядочением определенных объектов, приходилось решать во многих
сферах человеческой деятельности. С такими задачами,
получившими название «комбинаторные», люди сталкивались еще
в древности. Так, в Древнем Китае не только математики,
но и простые люди увлекались составлением магических
квадратов (в них заданные числа надо было расположить так,
чтобы их суммы по горизонталям, вертикалям и главным
диагоналям были одинаковые). В Древней Греции занимались
теорией фигурных чисел, а также составлением различных фигур
из частей специальным способом разрезанного квадрата. В
разных странах решались комбинаторные задачи, связанные с
такими играми, как шахматы, шашки, карты, кости и т. п.
Первые научные исследования по комбинаторике
принадлежат итальянским ученым Дж. Кардано (1501—1576),
Н.Тарталье (ок. 1499—1557), Г. Галилею (1564—1642) и
французским ученым Б. Паскалю (1623—1662) и П. Ферма (1601—
1665). Комбинаторика как наука стала развиваться в XVIII в.
параллельно с возникновением теории вероятностей, так как
для решения вероятностных задач необходимо было
подсчитывать число разных комбинаций элементов.
Комбинаторику как самостоятельный раздел математики
первым стал рассматривать немецкий ученый Г. Лейбниц в
своей работе «Об искусстве комбинаторики». Ему также
принадлежит и введение самого термина «комбинаторика».
Значительный вклад в развитие комбинаторики внес Л. Эйлер.
В современном обществе с развитием вычислительной
техники комбинаторика добилась новых успехов. Так, с помощью
ЭВМ была решена комбинаторная задача, известная под
названием проблема четырех красок. Удалось доказать, что любую
карту можно раскрасить в 4 цвета таким образом, что никакие
две страны, имеющие общую границу, не будут окрашены
в один и тот же цвет.
179
Историческая справка
Глава ЕЛ
ы
Элементы теории
вероятностей
Без учета влияния случайных явлении
человек становится бессильным
управлять развитием интересующих его
процессов в желательном для неге
направлении,
Б. В. Гнеденко
§ 1. Вероятность события
Практикой установлено, что в часто
происходящих случайных явлениях (событиях)
существуют определенные закономерности.
Задача теории вероятностей — установление и
математическое исследование закономерностей
массовых случайных явлений.
1. Случайные, достоверные и
невозможные события
Определение
Некоторое событие называют случайным
по отношению к данному опыту
(испытанию), если при осуществлении этого опыта
оно либо происходит, либо не происходит
Примеры случайных событий:
1) выпадение орла при подбрасывании
монеты;
2) выпадение шестерки при бросании
игральной кости;
3) выигрыш по данному лотерейному
билету;
4) выход из строя электролампы в течение
определенного отрезка времени.
Случайные события обычно обозначают
буквами Л, Б, С и т. д.
Событие U называется достоверным, если
оно обязательно наступает в результате
данного опыта.
Событие V называется невозможным, если
оно заведомо не может произойти в результате
данного опыта.
Гл а в а VI
Элементы теории вероятностей
Пусть, например, в урне находятся только черные шары,
а опыт заключается в извлечении шара из урны. Тогда
событие «извлечен черный шар» является достоверным, а событие
«извлечен белый шар» — невозможным.
При одном бросании игральной кости возможны
следующие события (исходы испытания): на верхней грани может
оказаться одно из чисел 1, 2, 3, 4, 5, 6. Каждое из этих событий
является случайным, так как оно может произойти, а может
не произойти. Тот факт, что выпадет одно из чисел 1, 2, 3, 4,
5, 6,— достоверное событие, так как при бросании игральной
кости оно обязательно произойдет, а выпадение, например,
числа 7, является невозможным событием.
Рассмотренные возможные при бросании игральной кости
события несовместны (появление одного из них исключает
появление другого), единственно возможны (обязательно
появится одно число) и равновозможны (у всех чисел шансы
появиться одинаковы).
2. Комбинации событий. Противоположные события
Предположим, что в результате некоторого опыта
обязательно происходит одно из взаимно исключающих друг друга
событий, причем каждое из них не разделяется на более
простые (элементарные). Такие события называют
элементарными событиями (или элементарными исходами испытания).
Пусть с некоторым опытом связаны события А и Б.
Определение
Суммой (объединением) событий А и Б называется
событие, которое состоит в том, что происходит хотя бы одно
из данных событий. Сумму событий А и Б обозначают
А+В (или A U Б).
На рисунке 101 с помощью кругов Эйлера
проиллюстрировано понятие суммы событий
А и В: большой круг изображает
все элементарные события, свя- / ^—-^*- ^
занные с рассматриваемым опытом; [ [А [) В )
левый круг изображает событие А, \ \^ J
правый круг — событие Б, а
закрашенная область — событие А Л-В.
Определение рис Ю1
Произведением (пересечением) событий А и Б называется
событие, которое считается наступившим тогда и только
тогда, когда наступают оба события А и Б. Произведение
событий А и Б обозначают АВ (или А П Б).
Рисунок 102 иллюстрирует с помощью кругов Эйлера
произведение событий А и Б: общая часть кругов (закрашенная
область) изображает событие АВ.
§ 1 181
Вероятность события
Рис 102 Рис. 103
Рассмотрим примеры с конкретными событиями А и Б.
1) Пусть в опыте с бросанием игральной кости события А
и В определяются так: А — выпало число очков, кратное 2, Б —
выпало число очков, кратное 3. Тогда событие А + В означает,
что выпало хотя бы одно из чисел 2, 3, 4, 6; событие АВ -
выпало число 6.
2) Пусть опыт заключается в том, что из колоды
вынимается наудачу одна карта, и пусть рассматриваются следующие
события: А — вынут король, В — вынута карта пиковой
масти. Тогда событие А-{-В — вынут король или карта пиковой
масти, АВ — из колоды вынут король пик.
События А и В называют равносильными (равными) и
пишут А = £, если событие А происходит тогда и только тогда,
когда происходит событие В. Например, в опыте с бросанием
игральной кости событие А — выпала шестерка и событие Б -
выпало наибольшее число очков являются равносильными.
Для каждого события А можно рассматривать противопо
ложное для него событие А, которое считается наступившим
тогда и только тогда, когда А не наступает. Например, если А —
выпадение нечетного числа очков при бросании игральной
кости, то А — выпадение четного числа очков; если А —
попадание в цель при выстреле, то А — промах.
На рисунке 103 проиллюстрирована взаимосвязь событий
А и А на множестве всех элементарных событий
рассматриваемого опыта (событие А изображено закрашенной областью).
Задача 1. А, В, С — три произвольных события. Записать
с помощью введенных символов следующие события:
1) А1 — все три события произошли;
2) А2 — ни одно событие не произошло;
3) А3 — произошло только событие А;
4) А4 — произошло по крайней мере одно из событий А, Б, С;
5) А5 — произошло одно и только одно из этих событий;
6) А6 — произошло по крайней мере два из этих событий.
> 1) Ах =АВС; 2) А2 =АВС; 3) А3 =АВС;
4) А4 = А + В + С; 5) А5 = ABC+ABC+ABC;
6) А6=АВС+АСВ + ВСА+АВС, или А6=АВ+АС + ВС. 4
182 Глава VI
Элементы теории вероятностей
3. Опыт с равновозможными исходами. Классическое
определение вероятности события
Пусть событие А, связанное с опытом с п
равновозможными исходами, наступает тогда, когда осуществляется один из
каких-то т исходов, и не наступает, когда осуществляется
любой из оставшихся п — т исходов. Тогда говорят, что исходы,
приводящие к наступлению события А, благоприятствуют
событию А.
Определение
Вероятностью Р(А) события А в опыте с
равновозможными элементарными исходами называется отношение числа
исходов, благоприятствующих событию А, к числу всех
исходов.
Если п — число всех исходов, т — число исходов,
благоприятствующих событию А, то вероятность Р(А) события А
определяется формулой
f. (1)
Приведенное определение вероятности называется
классическим определением вероятности.
Заметим, что вероятность каждого элементарного события
в опыте с п равновозможными исходами равна —.
п
Из формулы (1) следует, что
где V— невозможное, a U — достоверное события.
Задача 2. Бросается игральная кость. Найти вероятности
событий А1 и А2, если Ах — число выпавших очков кратно 3,
А2 — число выпавших очков четное.
t> Так как событию Ах благоприятствуют два исхода (3 и 6),
событию А2 — три исхода (2, 4, 6), а число всех исходов
равно 6, то PIAJ-1-1, Р(А2)=| = |.
, Р(А2)|
Задача 3. Монета бросается дважды. Найти вероятность
события А — хотя бы один раз выпадет орел.
> Пусть О — появление орла, Р — появление решки. Тогда
результат двух бросаний — появление одной из четырех равно-
возможных комбинаций ОО, OP, PO, PP. Событию А
благоприятствуют первые три комбинации. Поэтому искомая
вероятность Р(А)=-. <4
4
Задача 4. Брошены две игральные кости. Найти
вероятность события А — произведение выпавших очков есть
нечетное число.
§ 1 183
Вероятность события
[> Результат бросаний двух игральных костей — появление
равновозможных упорядоченных пар чисел. Согласно правилу
произведения число таких пар равно 6-6 = 36. Событию А
благоприятствуют 9 пар:
1 и 1, 1 и 3, 1 и 5, 3 и 1, 3 и 3, 3 и 5, 5 и 1, 5 и 3, 5 и 5,
9 1
а искомая вероятность Р (А) = —— = —. ^
36 4
Задача 5. В ящике лежат десять одинаковых на ощупь
шаров, из них четыре белых и шесть черных. Наугад
вынимаются два. Найти вероятности событий А и В, если А — оба
вынутых шара белого цвета, В — вынутые шары имеют разный
цвет.
> 1) Общее число возможных исходов опыта — число сочета-
^2 _
-10"
ний из 10 элементов по 2, т. е. С\о = ^^- =—-1— =45, а число
■^2 2
А 4 Ч
благоприятствующих событию А исходов равно С\=—±- = -~-=б.
„9 Р2 2
Поэтому P(A)=|UJL = A.
2) Так как любой из четырех белых шаров может
комбинироваться с любым из шести черных шаров, то по правилу
произведения имеется 4 • 6 = 24 исхода, благоприятствующие
событию В. Искомая вероятность Р (В) = —у = —— = ——. ^
Упражнения
1. Каким событием (достоверным, невозможным или
случайным) является следующее событие:
1) при комнатной температуре и нормальном атмосферном
давлении сталь находится в жидком состоянии;
2) наугад вынутая из кошелька монета оказалась
пятирублевой;
3) наугад названное натуральное число больше нуля?
2. Выяснить, являются ли события А и В несовместными, если:
1) А — появление туза, В — появление дамы при взятии
одной карты из колоды карт;
2) А — появление туза, В — появление карты пиковой
масти при взятии одной карты из колоды карт;
3) А — выпадение четырех очков, В — выпадение четного
числа очков при одном бросании игральной кости;
4) А — выпадение четырех очков, В — выпадение
нечетного числа очков при одном бросании игральной кости.
3. Установить, что является событием, противоположным
событию:
1) сегодня первый урок — физика;
2) экзамен сдан на «отлично»;
184 Глава VI
Элементы теории вероятностей
3) на игральной кости выпало меньше пяти очков;
4) хотя бы одна пуля при трех выстрелах попала в цель.
4. Пусть А и В — произвольные события. Записать
следующие события: 1) произошли оба данных события; 2)
произошло по крайней мере одно из событий; 3) произошло
только одно из двух данных событий; 4) ни одно из
событий не произошло; 5) произошло только событие В.
5. Какова вероятность выпадения числа, кратного 3, в
результате подбрасывания игральной кости?
6. Какова вероятность того, что на открытом наугад листе
нового отрывного календаря на високосный год окажется
пятое число?
7. В коробке находится 3 черных, 4 белых и 5 красных
шаров. Наугад вынимается один шар. Какова вероятность
того, что вынутый шар: 1) черный; 2) белый; 3) красный;
4) черный или белый; 5) черный или красный; 6)
красный или белый; 7) или черный, или белый, или красный;
8) зеленый?
8. Среди 100 электроламп 5 испорченных. Какова
вероятность того, что выбранные наудачу 3 лампы окажутся
исправными?
9. Брошены три игральные кости. Какова вероятность того,
что:
1) на всех трех костях выпало одинаковое количество
очков; 2) сумма очков на всех костях равна 4; 3) сумма
очков на всех костях равна 5?
10. Брошены две игральные кости. Какова вероятность того,
что:
1) сумма очков, выпавших на обеих костях, есть число
нечетное; 2) произведение очков, выпавших на обеих
костях, есть число четное; 3) сумма выпавших очков
больше 6?
11. В лотерее участвует 15 билетов, среди которых 3
выигрышных. Наугад вынуты 2 билета. Какова вероятность
того, что:
1) оба вынутых билета выигрышные; 2) только один билет
выигрышный; 3) выигрышного билета не оказалось?
12. Бросаются две игральные кости. Какова вероятность того,
что на первой игральной кости число очков будет больше,
чем на второй?
13. Имеются две урны: первая содержит 1 белый, 3 черных и
4 красных шара, вторая — 3 белых, 2 черных и 3 красных
шара. Из каждой урны наудачу извлекают по одному
шару. Найти вероятность того, что цвета вынутых шаров
совпадут.
§J_ 185
Вероятность события
§ 2. Сложение вероятностей
Напомним, что сумма событий А и В — это событие А+В,
состоящее в наступлении либо только события А9 либо только
события В, либо и события А и события В одновременно.
Например, если стрелок сделал два выстрела по мишени и
А — попадание в мишень при первом выстреле, В — попадание
при втором выстреле, то событие Ал-В — это попадание
стрелком по мишени хотя бы при одном из выстрелов.
Теорема 1
Вероятность суммы двух несовместных событий равна
сумме вероятностей этих событий, т. е.
Р(А + В) = Р(Д) + Р(В). (1)
0 Пусть событиям А и В благоприятствуют соответственно k и
1 исходов, а всего имеется п равновозможных исходов. Так как
события А и В несовместны, то среди п исходов нет таких,
которые одновременно благоприятствовали бы как событию А, так
и событию В. Поэтому событию Ал-В будут благоприятствовать
k I
исходов. По определению вероятности Р(А)=—, Р(В) = —,
п п
— л—, откуда следует равенство (1). •
п п
п п п
I Следствие. Сумма вероятностей противоположных
событий равна единице, т. е.
Р(А) + Р(А) = 1. (2)
О События А и А ^несовместны, поэтому по теореме 1 имеем
Р(А+А) = Р(А)_+Р(А). Но A+A=U—^достоверное ^обытие, и
поэтому Р(А+А) = Р(£/)=1, т. е. Р(А+А) = Р(А) + Р(А)=1.#
Замечание. Теорема 1 верна для любого конечного числа
событий, т.е. Р(А1н-А2н-...н-Лп) = Р(А1)н-Р(А2) + ...н-Р(Ап),
если Al9 А2, ..., Ап — попарно несовместные события.
Задача 1. В ящике лежат 10 шаров: 3 красных, 2 синих и
5 белых. Наугад вынимается один шар. Какова вероятность
того, что этот шар цветной (не белый)?
[> I способ. Пусть событие А — появление красного шара, В —
появление синего шара, тогда А Л-В — появление цветного ша-
о 2 1
ра. Очевидно, что Р(А)=—-, Р(В)= — = —. Так как события А
10 10 о
и В совместны, к ним применима теорема сложения вероят-
ностей: ^ | ^ |
II способ. Пусть событие С — появление белого шара,
тогда событие С — появление не белого (т. е. цветного) шара. Оче-
видно, Р(С)=^ = |, аР(С)=1-Р(С)=1-| = |.^
186 Глава VI
Элементы теории вероятностей
Задача 2. Вероятность попадания в мишень стрелком
равна 0,6. Какова вероятность того, что он, выстрелив по
мишени, промахнется?
[> Если событие А — попадание в мишень, то по условию
Р(А) = 0,6. Промах^— противоположное попаданию событие, и
его вероятность Р(А) = 1-Р(А) = 1-0,6 = 0,4. Ч
Задача 3. В роте из 100 солдат двое имеют высшее
образование. Какова вероятность того, что в случайным образом
сформированном взводе из 30 солдат будет хотя бы один
человек с высшим образованием?
t> Пусть событие А — во взводе хотя бы один человек имеет
высшее образование, тогда событие А — ни один человек во
взводе не имеет высшего образования. В данной ситуации
проще вычислить Р(А), чем Р(А). Найдем Р(А).
Число способов составления взвода в количестве 30
человек из 100 солдат роты равно Cfoo- Число солдат, не имеющих
высшего образования, равно 100 — 2 = 98. Из 98 человек
составить взвод в количестве 30 человек можно С|в способами.
Найдем вероятность того, что среди отобранных 30 человек нет ни
одного с высшим образованием:
981
С^8 301-68! в 98!- 70! = 69-70 = 161
C?g0 ЮР! 68!-100! 99 100 330
30! -70!
Отсюда находим Р(А) = 1-РСА)«1-||£« Щ «0,612.
Теорема 2
Вероятность суммы двух произвольных событий равна
сумме вероятностей этих событий без вероятности их
произведения, т. е.
Р(А+В)=Р(А)+Р(В)-Р(АВ). (3)
0 Пусть событиям А и В благоприятствуют соответственно k и
/ равновозможных исходов, а совместному осуществлению
событий А и В благоприятствует г исходов. Если число всех равно-
возможных исходов равно л, то Р(А)——, Р(В)=—, Р(АВ)=—.
п п п
Так как событию Ал-В благоприятствует (k — r) + (l — r) + r=
= k + l-r исходов, то Р(А + В)= + ~г = —I —, откуда следу-
п п п п
ет равенство (3). •
Задача 4. Из колоды в 36 карт наудачу вынимается одна
карта. Какова вероятность того, что будет вынута карта
бубновой масти или туз?
§ 2 187
Сложение вероятностей
О Введем обозначения событий: А — вынута карта бубновой
масти, В — появился туз. Нужно найти вероятность события А+В.
Воспользуемся формулой (3). Так как
36
то
Упражнения
14. В колоде 36 карт. Наугад вынимается одна карта. Какова
вероятность того, что эта карта либо туз, либо дама?
15. В пачке находится 12 билетов денежно-вещевой лотереи,
16 билетов спортивной лотереи и 20 билетов
художественной лотереи. Какова вероятность того, что наудачу
вынутый один билет будет билетом либо денежно-вещевой,
либо художественной лотереи?
16. В ящике лежат 5 белых, 10 черных и 15 красных шаров.
Какова вероятность того, что наугад вынутый шар не
будет белым? (Решить задачу двумя способами.)
17. Вероятность выигрыша главного приза равна 10~8. Какова
вероятность не выиграть главный приз?
18. Найти вероятность того, что наугад вынутая из полного
набора домино (28 костей) одна кость домино не будет
«дублем».
19. В вазе стоят 4 белых и 7 красных астр. Какова
вероятность того, что среди случайным образом вынутых из
вазы трех цветков окажется по крайней мере одна белая
астра?
20. В студенческой группе 22 человека, среди которых 4
девушки. Какова вероятность того, что среди троих
случайным образом выбранных из этой группы студентов для
участия в конференции окажется по крайней мере одна
девушка?
21. Вероятность поражения мишени при первом выстреле
равна 0,7. Вероятность поражения мишени при втором
выстреле равна 0,8. Вероятность поражения мишени и при
первом, и при втором выстрелах равна 0,56. Найти
вероятность того, что:
1) мишень будет поражена хотя бы одним выстрелом;
2) мишень не будет поражена ни одним из выстрелов.
22. Известно, что Р(А) = 0,3, Р(Б) = 0,8, Р(АВ) = 0,1. Доказать,
что A + B = U.
188 Глава VI
Элементы теории вероятностей
§ 3. Условная вероятность. Независимость
событий
ШШ1. Условная вероятность
В теории вероятностей для характеристики зависимости
одних событий от других вводится понятие условной
вероятности.
Определение
Если А и В — два события, связанные с некоторым
опытом, причем Р(Б)т^О, то число „/рч называют веро-
ятностъю события А при условии, что наступило событие
Б, или просто условной вероятностью события А и
обозначают Р(А/В).
Таким образом, по определению
*^ (1)
Задача 1. Какова вероятность того, что наугад вынутая из
полного набора домино кость окажется «дублем», если
известно, что сумма очков на этой кости меньше, чем 5?
> В наборе домино 28 костей, из них 7 «дублей». На девяти
костях сумма очков меньше, чем 5:
О — 0, 0 — 1, 0 — 2, 0 — 3, 0 — 4, 1 — 1, 1 — 2, 1 — 3, 2 — 2.
Пусть событие В — сумма очков на вынутой кости меньше
пяти, а событие А — вынутая кость есть «дубль». Тогда событие
АВ — на вынутой кости, являющейся «дублем», сумма очков
меньше пяти (таких костей три: 0 — 0, 1 — 1, 2 — 2). Вычис-
28
Значение Р(А/В) в задаче 1 можно было найти, рассуждая
следующим образом: из тех 9 случаев, к которым сводится
событие Б, событию А благоприятствуют 3 случая:
Пусть в некотором опыте с числом п равновозможных
элементарных исходов событию Б благоприятствуют I
элементарных исходов (/у*0), а событию АВ благоприятствуют
г исходов. Тогда Р(В) = —9 а Р(АВ)=—. Согласно формуле (1)
п п
имеем
189
Условная вероятность. Независимость событий
Равенство Р (А/В) = у определяет фактически вероятность
события А в условиях, которые возникают при наступлении
события В.
Так как формула (1) верна для любых событий, то,
поменяв местами А и Б, а также полагая Р(А) 5*0, получаем
(2)
Задача 2. В ящике лежат 3 белых и 2 черных шара. Из
ящика дважды вынимают по одному шару, не возвращая их
обратно. Найти вероятность того, что: 1) первым был извлечен
белый шар, а вторым — черный; 2) вторым был вынут черный
шар при условии, что первым уже был извлечен белый.
[> При решении задачи рассмотрим события:
А — первым вынут белый шар;
В — вторым вынут черный шар;
АВ — последовательно извлечены белый, затем черный
шары;
В/А — вторым вынут черный шар при условии, что
первым был извлечен белый.
1) Число всех возможных вариантов извлечения двух
шаров из ящика с пятью шарами (с учетом порядка их
появления) равно А§ = 5 -4 = 20, т. е. л = 20. Благоприятствующими
событию АВ будут все возможные упорядоченные пары «белый
шар, черный шар», составленные из имеющихся трех белых и
двух черных шаров. Таких соединений согласно правилу умно-
жения будет 3-2 = 6 (т = 6). Таким образом, Р(АВ)= — = —.
^0 10
2) После извлечения из ящика первым белого шара
(произошло событие А) там останутся 2 белых и 2 черных шара.
Появлению черного шара вторым из четырех оставшихся (я=4)
О 1
благоприятствуют два исхода (т = 2), поэтому Р(В/А)= — = -.
4 2
о
Имеем Р (А) = —, так как п = 5 (в ящике первоначально на-
5
ходилось 5 шаров) и т = 3 (белых было 3). Подставив в
формулу (2) значения Р(АВ)=-^- и P(A)=f-, получим Р(В/А) =
10 5
(3)
(4)
Элементы теории вероятностей
3
10
190
. з
' 5
Из
Из
3-5 1
10-3 2
равенства
равенства
Глава VI
(1)
(2)
1
]
следует, что
Р(АВ) = Р(Б).
получаем
Р(АВ) = Р(А).
Р(А/В).
Р(В/А).
Равенства (3) и (4) можно записать в виде следующих
равенств:
Р (АВ) = Р(А)Р (В/А) =Р(В)Р (А/В). (5)
Задача 3. В лаборатории работают 7 женщин и 3
мужчины. Случайным образом из числа этих сотрудников для
научной конференции выбираются один докладчик и один
содокладчик. Какова вероятность того, что докладчиком будет
выбрана женщина, а содокладчиком — мужчина?
t> Пусть событие А — докладчиком выбрана женщина, событие
В — содокладчик — мужчина.
1-й способ. Вероятность того, что сначала выбирался
основной докладчик и им оказалась женщина (наступило
событие А), равна Р(А)=-^.
Вероятность того, что вторым выбирался содокладчик и им
оказался мужчина (произошло событие Б), вычисляется при
условии, что первой уже была выбрана женщина, т. е.
По формуле (2) имеем Р(АВ) = Р(А)Р(В/А)=-^ ■ | = ^-
2-й способ. Вероятность того, что первым выбирался
содокладчик и им оказался мужчина (произошло событие Б),
равна Р(В)= А.
Вероятность того, что вторым выбирался докладчик и им
оказалась женщина (событие А), вычисляется при условии, что
п
первым уже выбран мужчина, т. е. Р(А/В) = —. По формуле (2)
у
получаем Р(ВА) = Р(В)Р(А/В)=-^ . J--^. <
2. Независимость событий
Определение
События А и Б называют независимыми, если
Р(АВ) = Р(А)Р(В). (6)
Если равенство (6) не выполняется, то события А и Б
называют зависимыми.
Определение независимости событий согласуется с
введенным понятием условной вероятности. Действительно, событие
А является независимым от события В тогда и только тогда,
когда наступление события В не влияет на вероятность
наступления события А, т. е. когда Р(А/В) = Р(А). В самом деле,
соотношение Р (А/В) = —-—- = Р (А) имеет место тогда и только тог-
Р(В)
да, когда выполняется равенство (6).
§ 3 191
Условная вероятность. Независимость событий
Задача 4. Из колоды в 36 карт наудачу вынимается одна
карта. Выяснить, являются ли независимыми события А и Б,
если А — появился король, Б — вынута карта червовой или
пиковой масти.
[> Общее число элементарных исходов равно 36, событию А
благоприятствуют 4 исхода, поэтому Р (А) = — = —. Если про-
36 9
изошло событие Б, то осуществилось одно из 18 элементарных
событий, среди которых событию А благоприятствуют 2, и
поэтому Р(А/Б)=^- = —. Итак, Р(А/В) = Р(А), т. е. события А и Б
независимы. ^
Определение независимости обобщается на случай п > 2
событий. События А19 А2, ..., Ап называются независимыми в
совокупности, если независимы всевозможные пары из этих
событий, а также если каждое из этих событий и событие,
являющееся произведением любого числа остальных событий,
независимы.
Например, независимость трех событий А, Б и С означает,
что независимыми должны быть 6 пар событий: А и Б, В и С,
С и А, А и ВС, В и СА, С и АВ. Из определений независимости
и формулы (6) следует, что если А, В, С — независимые в
совокупности события, то Р(АВС) = Р(А)Р(В)Р(С).
Задача 5. Из колоды, содержащей 36 карт,
последовательно вынимаются 2 карты. Рассмотрим события А и Б, где А —
вторым вынут туз, Б — первым вынут туз. Зависимы ли
события А и Б?
[> Запишем событие А в виде А=^АВл-АВ. Эта запись означает,
что вторая карта может быть тузом либо в случае, когда
первая карта — туз, либо в случае, когда первая карта — не туз.
Предположим, что события А и Б независимы, тогда
Но Р(А/В)=-§-, и поэтому Р(А)*Р(А/В), т. е. события А и В
Зо
зависимы. М вЯ
Упражнения
!23Т] На столе лежат 4 синих и 3 красных карандаша.
Редактор дважды наугад берет по одному карандашу и обратно
их не кладет. Найти вероятность того, что:
1) вторым был взят красный карандаш при условии, что
первым был синий;
2) вторым взят синий карандаш при условии, что первым
оказался синий;
3) вторым взят синий карандаш при условии, что первым
был красный;
192 Глава VI
Элементы теории вероятностей
4) вторым взят красный карандаш при условии, что
первым также оказался красный карандаш.
В барабане находится 10 лотерейных билетов, из них 2
выигрышных. Из барабана 2 раза вынимают по одному
билету, не возвращая их обратно. Какова вероятность того,
что:
1) во второй раз был извлечен билет без выигрыша при
условии, что первым оказался выигрышный билет;
2) в первый раз был вынут выигрышный билет, а во
второй раз — билет без выигрыша?
Из ящика, содержащего 4 белых и 5 красных шаров, 2
раза наугад извлекают по одному шару, не возвращая их
обратно. Найти вероятность того, что:
1) вторым извлечен красный шар при условии, что первым
также оказался красный шар;
2) оба раза извлекались красные шары.
Из колоды в 36 карт последовательно наугад вынимаются
и не возвращаются 2 карты. Какова вероятность того, что:
1) оба раза извлекались карты красной масти;
2) первой была вынута карта красной масти, а второй —
черной масти;
3) второй вынута карта черной масти при условии, что
первой была карта красной масти?
Выяснить, являются ли независимыми события А и В, если:
1) игральная кость бросается дважды; событие А — при
первом бросании выпало 2 очка, событие В — при втором
бросании выпало 5 очков;
2) брошены две игральные кости; А — на первой кости
появилось 6 очков, В — на второй кости также 6 очков;
3) из колоды карт вынимают по одной карте, возвращая
вынутую карту в колоду; А — первой вынута дама пик, В —
второй также вынута дама пик;
4) из колоды карт дважды вынимают по одной карте, не
возвращая их в колоду; событие А — первой вынута
шестерка треф, событие В — вторым вынут король пик.
В букете 10 гвоздик и 5 нарциссов. Оля и Таня случайным
образом вынимают из букета по одному цветку. Какова
вероятность того, что Оля вынула гвоздику, а Таня —
нарцисс? (Решить задачу разными способами.)
В партии из 100 деталей 2 детали бракованные. Два
контролера вынимают случайным образом по одной детали.
Какова вероятность того, что первому контролеру досталась
бракованная, а второму — небракованная деталь? (Решить
задачу разными способами.)
§ 3 193
Условная вероятность. Независимость событий
Студент, которому предстояло сдать зачет, знал ответы на
70 вопросов из 90. Какова вероятность того, что он:
1) верно ответит на два вопроса;
2) ответит на второй вопрос при условии, что он не знал
ответа на первый вопрос?
§ 4. Вероятность произведения
независимых событий
Допустим, что из колоды с 36 картами случайным образом
дважды извлекают по одной карте и вычисляют вероятность
события А — второй извлечена дама треф. Если первая карта
в колоду не возвращается, то или Р(А) = 0 (если первой была
извлечена именно дама треф), или Р(А)=— (если первой бы-
оо
л а извлечена отличная от дамы треф карта). Таким образом,
вероятность события А зависит от того, наступило ли событие,
связанное с извлечением из колоды первой карты. Если же
первая извлеченная карта возвращается обратно в колоду, то
Р(А)=— независимо от того, какова была первая карта.
36
Существует немало испытаний (называемых
независимыми), в которых вероятности рассматриваемых событий не
зависят от того, произошли или нет другие события, связанные с
этим испытанием.
События А и В называют независимыми, если
выполняется равенство
Р(АВ) = Р(А)Р(В). (1)
Рассмотрим опыт с бросанием двух игральных костей и
исследуем два события: А — на первой кости выпало 5 очков, В -
на второй кости выпало 5 очков. Выясним, будут ли события
А и В независимыми.
О Появление любого числа очков на первой кости (в частности,
наступление события А) не влияет на событие В и его
вероятность. И наоборот, наступление события В не влияет на
вероятность события А. Таким образом, события А и В
независимые, причем Р(А)=^ и Р(Б)=^-.
о о
Событие АВ состоит в совместном наступлении событий А
и В. Элементарные исходы события АВ — это пары чисел, в
которых на первом месте стоит число очков первой кости, на
втором — число очков второй кости. Всего элементарных
исходов испытания п = 36. Среди них присутствует лишь одна пара
(5 и 5 очков), благоприятствующая событию АВ, т. е. т = 1.
Таким образом, P(AB)=^ = i- ^=Р(А)Р(В)9 т.е. события Л
и В независимые. •
Наверняка можно говорить о независимости событий, если
они появляются в независимых испытаниях.
194 Глава VI
Элементы теории вероятностей
Когда же независимость испытаний неочевидна, то
независимость событий А и В проверяют с помощью формулы (1).
Задача 1. Из чисел 1, 2, 3, ..., 11, 12 случайным образом
выбирают одно число и рассматривают два события: А —
выбрано четное число, В — выбрано число, кратное трем.
Выяснить, являются ли события А и В независимыми.
(л 1
> Среди данных чисел четных чисел 6, поэтому Р(А)= —= —.
4 1
Кратных трем в данном наборе чисел 4, т. е. Р(В) =—— = —. Со-
1Z о
бытие АВ состоит в выборе числа, кратного как числу 2, так
и числу 3, т. е. кратного числу 6. Таких чисел в наборе 2,
поэтому Р (АВ) = А = i. Так как Р (А). Р (В) - \ -± = \ = Р (АВ), то
1Z о <s о о
события А и Б независимые. «^
Задача 2. Выяснить, являются ли события А и В
независимыми, если:
1) Р(А) = 0,8, Р(Б) = 0,6, Р(АВ) = 0,48;
2) Р(А)=|, Р(Б)=|, Р(АВ)=±.
>1) Так как Р(Л)Р(Б) = 0,8 0,6 = 0,48 = Р(АВ), то события А
и В независимые.
2) Так как Р(А)Р(Б)= - • -| = ^^ Лг=^(^В)> то события
4 3 о 12
А и В не являются независимыми. -^
Задача 3. В изготовленной партии детских мячей
вероятность появления бракованного мяча равна 0,004. Произволь-
ным образом в красный цвет окрашены — всех мячей, а ос-
4
тальные мячи окрашены в синий. Какова вероятность того, что
наугад вынутый мяч будет небракованным и красным?
> Пусть событие А — появление бракованного мяча. По
условию Р(А) = 0,004. Появление небракованного мяча — событие А,
и Р(А) = 1-Р(А) = 1-0,004 = 0,996. Пусть событие Б — появле-
о
ние красного мяча, тогда согласно условию Р (Б) = —.
4
Задача сводится к нахождению вероятности совместного
появления независимых событий А и Б, т. е. к нахождению
вероятности события АВ. Согласно формуле (1) имеем
Р (АБ) = Р (А) Р (Б) = 0,996 • j=0,747. ^
ЕЭ Более двух событий называют независимыми в
совокупности, если независимы всевозможные пары из этих событий и
если каждое из этих событий и событие, являющееся
произведением любого числа остальных событий, независимы.
Вероятность совместного появления независимых в совокупности
событий равна произведению вероятностей этих событий.
§ 4 195
Вероятность произведения независимых событий
Задача 4. Три стрелка независимо друг от друга стреляют
по мишени по одному разу. Вероятности попадания в мишень
для них равны соответственно 0,2; 0,5 и 0,4. Найти
вероятность того, что все три стрелка попадут в мишень.
[> Введем обозначения: Ах — попадание в мишень первым
стрелком, А2 — попадание в мишень вторым стрелком, Аз-
попадание в мишень третьим стрелком. Тогда А1А2А3 —
попадание в мишень всеми стрелками. Так как события Alt А2, Л3
независимые, то
Р (АхА2Аг) = Р(АХ)Р (А2) • Р (А3) = 0,20,50,4 = 0,04. 4 И
Упражнения
31. Вероятность попадания в мишень стрелком равна 0,6.
Какова вероятность того, что стрелок попадает в мишень в
каждом из двух последовательных выстрелов?
32. Вероятность поражения цели первым орудием равна 0,7, а
вторым — 0,6. Найти вероятность поражения цели обоими
орудиями, стрелявшими независимо друг от друга.
33. В урне 2 белых, 3 красных и 5 черных шаров. Дважды
вынимают по одному шару и возвращают их обратно в урну,
Какова вероятность того, что:
1) первым вынут красный шар, а вторым — черный;
2) первым вынут черный шар, а вторым — белый?
34. Бросают три игральные кости. Найти вероятность
выпадения четного числа очков на каждой кости.
35. Дважды бросают игральную кость. Событие А — при
первом бросании выпало 6 очков, событие В — в результате
второго бросания появилось число очков, кратное трем.
Найти вероятность события АВ.
36. Дважды бросают игральную кость. Событие А — первый
раз выпало четное число, событие В — второй раз выпало
число, меньшее трех. Найти вероятность события АВ.
37. Вероятность попадания в мишень стрелком равна 0,7.
Какова вероятность хотя бы одного попадания в мишень этим
стрелком в результате двух выстрелов?
38. Вероятность попадания в мишень первым стрелком равна
0,2, а вторым — 0,3. Какова вероятность того, что мишень
будет поражена хотя бы одним выстрелом, если стрелки
выстрелили независимо друг от друга?
39. В выпущенной заводом партии деталей 2% брака, и
произвольным образом выбранные 0,3 от числа всех деталей
окрашены в зеленый цвет. Какова вероятность того, что
случайным образом вынутая из партии деталь окажется
неокрашенной и небракованной?
196 Глава VI
Элементы теории вероятностей
40. Вероятность попадания по мишени первым стрелком
равна 0,6, вторым — 0,7, третьим — 0,8. Каждый из них
стреляет по мишени один раз. Какова вероятность того,
что мишень поразят только первый и третий стрелки?
41. На предприятии 120 человек, среди которых 40 женщин.
Каждый сотрудник покупает один билет денежно-вещевой
лотереи (20% выигрышных билетов) и один билет
спортивной лотереи (10% выигрышных билетов). Какова
вероятность того, что выбранный случайным образом из списка
сотрудников предприятия один человек окажется
мужчиной, выигравшим в обеих лотереях?
§ 5. Формула Бернулли
в Задача 1. Стрелок поражает мишень при каждом выстреле
с вероятностью 0,8. Какова вероятность того, что мишень
будет поражена лишь при первом и третьем выстрелах, если
стрелок выстрелил по мишени 3 раза?
t> Пусть событие А — попадание стрелком по мишени при
одном выстреле, тогда событие А — промах. По условию задачи
Р(А) = 0,8, тогда Р(А) = 1-Р(А) = 1-0,8 = 0,2. Рассматриваемое
в задаче событие В состоит в том, что стрелок при первом
выстреле поразил мишень, при втором промахнулся, при третьем
снова попал, т. е. В=ААА.
Попадание и непопадание по мишени в рассматриваемой
серии независимых испытаний — независимые события, поэтому
Р(В) = Р(ААА) = Р(А)Р(А)Р(А) = 098'0,2 0,8 = 0,128. <
Задача 2. Стрелок поражает мишень при одном выстреле
с вероятностью 0,8. Найти вероятность поражения мишени
шнь двумя выстрелами, если всего стрелок стрелял 3 раза.
t> Пусть событие А — попадание по мишени при одном
выстреле, а событие В состоит в попадании по мишени при любых
двух из трех сделанных выстрелов. Иначе событие В
произойдет, когда_ произойдет одно из_ несовместных событий ААА,
ААА или ААА, т. е. В = ААА+ААА + ААА.
Согласно теореме о вероятности суммы несовместных
событий (см. § 2) имеем
Р(В) = Р(ААА) + Р(ААА) + Р(ААА). (1)
Используя рассуждения задачи 1, заметим, что каждое
слагаемое в правой части равенства (1) равно 0,128. Таким
образом, искомая вероятность Р(В) = 3 • 0,128 = 0,384. М
Допустим, производятся п независимых друг от друга
испытаний, в каждом из которых событие А может произойти,
а может не произойти (т. е. произойдет событие А). Условимся
считать, что в каждом из испытаний вероятность события А
одна и та же и равна р. Тогда вероятность противоположного ему
события А будет равна 1 —р.
§ 5 197
Формула Бернулли
Поставим задачу:
Вычислить вероятность события Б, заключающегося в том,
что при п испытаниях событие А произойдет ровно k раз. И
Ш^ШРассмотрим событие Bl9 состоящее в том, что в первых k
испытаниях наступило событие А, а в следующих (n-k)
испытаниях — событие А9 т. е.
Вг=А'А- ...-А-А-А- ...-А.
k множителей n-k множителей
События А и А, одно из которых наступило в каждом из
п испытаний,— независимые в совокупности события.
Согласно утверждению о вероятности произведения независимых
событий (см. предыдущий параграф)
= Р(А)Р(А)-...Р(А)Р(А)Р(А)...Р(А) =
k множителей n-k множителей
...-р(1-р)(1-р)....(1-р)=рк(1-РГ-к. (1)
k n-k
Рассмотрим события Bi9 в которых событие А повторяется
k раз в различных последовательностях. Тем не менее
вероятность любого события Bi9 являющегося произведением k
событий А и (n-k) событий А9 будет равна pk(l-p)n~k.
Число способов записи произведений из k событий А
и (n-k) событий А9 отличающихся друг от друга порядком
расположения в них множителей А и А9 равно числу
перестановок с повторениями Pk n_k.
По доказанному в § 5 предыдущей главы
Pu-rC*. (2)
Событие Б, состоящее в том, что в п испытаниях событие
А наступит k раз и не наступит (n — k) раз, очевидно, равно
сумме несовместных событий Bi9 отличающихся друг от друга
лишь порядком расположения в них k множителей А и (n-k)
множителей А. Число таких событий согласно равенству (2)
равно Скп:
Сп слагаемых
По теореме 1 из § 2 о вероятности суммы несовместных
событий имеем
Р (В) =
Сп слагаемых
С„ слагаемых
198 Глава VI
Элементы теории вероятностей
Вероятность события В принято обозначать Pn(k),
подчеркивая тем самым, что рассматривается вероятность события,
наступившего ровно k раз в серии из п однотипных испытаний.
По доказанному выше
Pn(k) = Cknpk(l-p)n-k, (3)
Формулу (3) называют формулой Бернулли в честь
швейцарского математика Якоба Бернулли, изучавшего в начале
XVIII в. испытания с двумя возможными исходами.
Задача 3. Игральный кубик бросается 4 раза. Какова
вероятность того, что в этой серии испытаний 5 очков появятся
ровно 3 раза?
\> Пусть А — появление 5 очков в одном испытании. Событие
А в каждом из четырех независимых испытаний может
произойти, а может и не произойти. Известно, что р = Р(А)=—.
о
Тогда согласно формуле (3)
Задача 4. Вероятность того, что лампа определенного
вида не перегорит в течение 1000 ч, равна 0,3. Какова
вероятность того, что из пяти ламп данного вида не менее четырех
останутся исправными после 1000 ч горения?
Р> Рассмотрим горение каждой из 5 ламп в течение 1000 ч как
независимые испытания, в которых вероятность неперегорания
лампы равна 0,3. В серии из 5 подобных испытаний
фактически требуется найти вероятность суммы следующих
несовместных событий: А — исправными остались 4 лампы и Б —
исправными остались 5 ламп. Вероятность этого события равна
сумме вероятностей событий А и В:
= 50,0081 0,7 + 1 0,00243-1 = 0,03078^0,03. А
Упражнения
42. Монету бросают 10 раз. Какова вероятность того, что орел
появится при этом ровно: 1) 4 раза; 2) 5 раз?
43. Игральный кубик бросают 5 раз. Какова вероятность того,
что 6 очков появятся ровно: 1) 2 раза; 2) 4 раза?
44. Игральный кубик бросают 4 раза. Какова вероятность
того, что 6 очков в этой серии испытаний появятся не менее
трех раз?
45. Вероятность попадания по кольцу у некоторого
баскетболиста при каждом броске равна 0,7. Какова вероятность
у этого баскетболиста попасть по кольцу хотя бы один раз
в серии из трех бросков?
§ 5 199
Формула Бернулли
Упражнения к главе VI
46. Какова вероятность того, что при одном бросании
игральной кости выпадет либо 5, либо 6 очков?
47. Из урны, содержащей 15 белых, 10 красных и 5 синих
шаров, наугад извлекается один шар. Какова вероятность
появления белого шара?
48. Одновременно бросают две игральные кости. Найти
вероятность того, что сумма выпавших очков равна 8.
49. Набирая номер телефона, абонент забыл две последние
цифры и, помня лишь, что эти цифры различны, набрал их
наугад. Какова вероятность того, что номер набран
правильно?
50. Брошена игральная кость. Какова вероятность того, что не
выпадут 3 очка?
51. Брошена монета и игральная кость. Какова вероятность
того, что выпадут орел и 6 очков?
52. По мишени стреляют 2 раза. Вероятность попадания в
мишень при первом выстреле равна 0,8, при втором
выстреле — 0,9. Какова вероятность того, что мишень не будет
поражена ни одним выстрелом?
53. Игральная кость брошена 2 раза. Найти вероятность того,
что оба раза появится одинаковое число очков.
54. Из урны, содержащей 3 черных, 4 белых и 5 красных
шаров, наудачу вынимают один. Какова вероятность того, что
вынутый шар окажется: 1) черным; 2) черным или белым?
55. Брошены две игральные кости. Найти вероятность того,
что 3 очка появятся хотя бы на одной из костей.
56. Из колоды в 36 карт последовательно наугад вынимают
две карты и не возвращают обратно. Найти вероятность
того, что:
1) вынуты два туза;
2) сначала извлечен туз, а затем дама;
3) вынуты 2 карты бубновой масти;
4) вторым извлечен туз, если известно, что первой была
вынута дама.
57. В урне находится 10 белых и 10 черных шаров. Из нее
последовательно вынимают 2 шара и не возвращают
обратно. Какова вероятность того, что:
1) оба раза извлекались шары черного цвета;
2) первым вынут белый шар, а вторым — черный;
3) вторым извлечен черный шар, если известно, что
первым был вынут белый шар?
58. Брошены три монеты. Найти вероятность того, что
выпало не более двух орлов.
200 Глава VI
Элементы теории вероятностей
59. Из полного набора костей домино берутся наугад две
кости. Определить вероятность того, что вторую кость можно
приставить к первой.
60. В лотерее из 100 билетов 10 выигрышных. Какова
вероятность того, что ни на один из трех купленных билетов не
выпадет выигрыш?
6L В лотерее п билетов, из которых т выигрышные. Найти
вероятность выигрыша (наличия хотя бы одного
выигрышного билета) у того, кто имеет k билетов (k<n-m).
Щ] В партии из т деталей п бракованных. Выбирают наугад
k деталей. Определить вероятность того, что среди этих k
деталей будет р бракованных (р < k < п < т).
Щ] Полная колода карт (52 листа) делится наугад на две
пачки по 26 листов в каждой. Найти вероятность того, что в
каждой пачке окажется по два туза.
Щ] В розыгрыше первенства страны по волейболу участвуют
18 команд, из которых случайным образом формируются
две группы по 9 команд в каждой. Среди участников
первенства имеются 5 команд из одной республики. Найти
вероятность того, что все 5 команд этой республики попадут
в одну и ту же группу.
Ш] Монету бросают 8 раз. Какова вероятность того, что орел
появится:
1) ровно 2 раза; 2) ровно 6 раз;
3) не менее 6 раз; 4) не более 2 раз?
Ш] Игральный кубик бросают 5 раз. Какова вероятность того,
что одно очко появится:
1) ровно 2 раза; 2) ровно 3 раза;
3) не более 2 раз; 4) не менее 4 раз?
ШП Вероятность того, что насекомое определенного вида будет
жить более 100 дней, равна 0,5. Какова вероятность того,
что среди выбранных для наблюдения 10 насекомых этого
вида не менее 8 экземпляров будут жить более 100 дней?
Вопросы к главе VI
1. Какие события называют случайными? достоверными?
невозможными?
2. Что называют суммой событий?
3. Что называют произведением событий?
4. Какое событие называют противоположным данному
событию?
5. Какие события называют равновозможными?
6. Что называют вероятностью (в классическом понимании)
события А?
7. Какие события называют несовместными?
201
Вопросы к главе VI
8. Чему равна вероятность суммы двух несовместных
событий?
9. Какие события называют независимыми?
10. Чему равна вероятность произведения двух независимых
событий?
11. Чему равна вероятность суммы двух произвольных
событий?
12. Записать формулу Бернулли и пояснить ее смысл.
1. Бросают 2 монеты. Какова вероятность того, что на обеих
монетах выпадет орел?
2. Вероятность извлечения из партии бракованной детали
равна 0,05. Какова вероятность того, что наугад
извлеченная деталь окажется небракованной?
3. В ящике лежат 2 черных, 3 белых и 10 красных шаров.
Какова вероятность того, что наугад вынутый один шар
окажется или черного, или белого цвета?
4. В вазе лежат 3 апельсина и 5 яблок. Мальчик не глядя
берет из вазы один плод, затем, не возвращая его, берет
другой. Найти вероятность того, что первым был взят
апельсин, а вторым — яблоко.
5. Вероятность попадания в мишень стрелком равна 0,8.
Какова вероятность попадания в мишень в каждом из двух
произведенных выстрелов?
6. Ученик знал ответы на 15 вопросов из 20, которые
предлагались к зачету. Ответа на первый попавшийся на
зачете вопрос он не знал. Какова вероятность того, что ученик
ответит на второй из предложенных ему вопросов?
1. Вероятность попадания в мишень стрелком равна 0,9.
Какова вероятность того, что после двух выстрелов в
мишени окажется одна пуля?
2. Вероятность попадания стрелком по мишени равна 0,8.
Какова вероятность того, что мишень после трех
выстрелов будет поражена хотя бы одним выстрелом?
3. В коробке лежат 20 одинаковых по форме шаров, причем
8 из них легче остальных. Известно, что произвольные
5 шаров из 20 окрашены в красный цвет. Какова
вероятность того, что случайным образом вынутый один шар
окажется не красным, но легким шаром?
4. В первой коробке находятся 2 белых, 3 черных и 4 красных
шара, а во второй коробке — 1 белый, 2 черных и 3
красных шара. Какова вероятность того, что вынутые по
одному из каждой коробки шары окажутся разных цветов?
202 Глава У»
Элементы теории вероятностей
Я fJ I Историческая справка
Возникновение теории вероятностей как науки было
обусловлено развитием в XVII в. страхового дела, демографии,
а также широким распространением в Европе азартных игр.
В таких играх (картах, домино, костях и пр.) выигрыш в
основном зависел не от искусства игрока, а от случайности.
Слово «азарт» и произошло от французского слова hasard,
означающего «случай», «риск». Богатые люди, увлеченные
азартными играми, порой прибегали к помощи математиков для
решения проблем, возникающих во время игры. Годом
рождения теории вероятностей многие ученые считают 1654 г., к
которому относится переписка двух великих французских ученых
Б. Паскаля и П. Ферма по поводу решения задачи, возникшей
при игре в кости.
В XVII в. ученые начали использовать азартные игры как
удобные и наглядные модели для исследования понятий теории
вероятностей. Первая книга по теории вероятностей
называлась «О расчетах в азартной игре» и была опубликована
в 1657 г. Ее автор, голландский ученый X. Гюйгенс, писал:
«...при внимательном изучении предмета читатель заметит, что
он занимается не только игрой, а что здесь даются основы
теории вероятностей, глубокой и весьма интересной».
В 1713 г. была опубликована книга известного
швейцарского математика Я. Бернулли «Искусство предположений»,
в которой автор изложил основы комбинаторики и аппарата
вычисления вероятностей, а также доказал одну из
замечательных теорем теории вероятностей, названную впоследствии
теоремой Бернулли. На доказательство этой теоремы ученый
потратил 20 лет жизни, а само оно заняло 12 страниц. Эта
теорема — важный частный случай одного из основных законов
теории вероятностей — закона больших чисел, открытого в
середине XIX в. русским ученым П. Л. Чебышевым. Закон
больших чисел имеет широкое практическое применение в
вопросах, связанных с определением вероятностей событий, для
которых рассчитать точное значение вероятности (в ее
классическом понимании) невозможно.
Дальнейшее развитие теории вероятностей связано с
работами французского математика и астронома П. Лапласа (1749—
1827), немецкого математика К. Гаусса, российских
математиков А. А. Маркова (1856—1922), А. М. Ляпунова (1857—1918)
и др. Значительный вклад в теорию вероятностей внесли
отечественные ученые А. Н. Колмогоров (1903—1987), А. Я. Хинчин
(1894—1959), Б. В. Гнеденко и др.
В настоящее время теория вероятностей продолжает
развиваться и находит широкое применение в естествознании,
экономике, производстве и гуманитарных науках.
203
Историческая справка
Глава
Комплексные числа
Мнимые числа — это прекрасное
и чудесное убежище божественного
духа, почти что сочетание бытия
с небытием.
Г. Лейбниц
§ 1. Определение
комплексных чисел.
Сложение и умножение
комплексных чисел
^^1. Введение
Наше представление о числе изменялось
по мере расширения круга задач, которые
необходимо было решать. Если для счета
отдельных предметов достаточно было натуральных
чисел, то для решения уравнений вида х+а=Ъ
натуральных чисел недостаточно, нужно было
вводить отрицательные числа и нуль.
Для того чтобы решать уравнения вида
ах+Ь=О, где a€N nb€N, понадобились
рациональные числа. Но уже решение таких, например,
уравнений, как х2 = 3, х2 — 2 = 0, потребовало
введения иррациональных чисел. Однако
оказалось, что рациональных и иррациональных
чисел (образующих множество действительных
чисел) также недостаточно даже для решения
простейших квадратных уравнений с
натуральными коэффициентами, таких, например, как
Потребовалось введение новых чисел,
названных комплексными.
Таким образом, стремление сделать
уравнения разрешимыми явилось одной из
главных причин расширения понятия числа.
Прежде чем давать определение
комплексных чисел, необходимо понять, какими
свойствами должны обладать новые числа, какие
операции желательно ввести для них и каким
законам должны подчиняться эти операции.
Глава VII
Комплексные числа
Прежде всего для новых чисел введем понятие равенства,
определим операции сложения и умножения новых чисел так,
чтобы для них имели место переместительный, сочетательный
и распределительный законы.
В случае, когда комплексные числа совпадают с
действительными, новые операции сложения и умножения должны
превращаться в известные: сложение и умножение
действительных чисел.
Для того чтобы на множестве комплексных чисел
уравнение х2 +1 = 0 имело решение, было введено некоторое новое
число — корень этого уравнения, которое было обозначено
буквой i. Таким образом, i — комплексное число, такое, что
?—1.
2. Понятие комплексного числа
Определение
Комплексными числами называют выражения вида а + Ы,
где а и Ъ — действительные числа, a i — некоторый
символ, для которого по определению выполняется равенство
i1—1.
Название «комплексные» происходит от слова
«составные» — по виду выражения а + Ы. Число а называется
действительной частью комплексного числа а + Ы, а число Ь — его
тимой частью. Число i называется мнимой единицей.
Например, действительная часть комплексного числа 2-Si
равна 2, мнимая часть равна -3. Запись комплексного числа
в виде а + Ы называют алгебраической формой комплексного
числа.
3. Равенство комплексных чисел
Определение
Два комплексных числа а + Ы и c + di называются
равными тогда и только тогда, когда а = с и Ь = <2, т. е. когда
равны их действительные и мнимые части.
Например, 1,5 + \/Ш= ^ + 3i, так как 1,5 = ^, V9 = 3.
Задача 1. Найти действительные числа х и у из равенства
[> По определению равенства комплексных чисел запишем
систему уравнений
решая которую находим х=19 у = — 3. ^
4. Сложение и умножение комплексных чисел
Операции сложения и умножения двух комплексных
чисел определяются следующим образом:
§ 1 205
Определение комплексных чисел.
Сложение и умножение комплексных чисел
Определения
Суммой двух комплексных чисел а + Ы и c + di называется
комплексное число (a + c) + (b + d)i, т. е.
(a + bi) + (c + di) = (a + c) + (b + d)L (11
Произведением двух комплексных чисел а + Ы и c + di
называется комплексное число (ac — bd) + (ad + bc)i, т. е.
(а + Ы) (с + di) = (ас - bd ) + (ad + be) i. (2)
Из формул (1) и (2) следует, что сложение и умножение
комплексных чисел можно выполнять по правилам действий с
многочленами.
Поэтому нет необходимости запоминать формулы (1) и (2),
их можно получить по обычным правилам алгебры, считая, что
*2 = -1.
Задача 2. Найти произведение
Принято считать, что a + O-i = a, т. е. комплексное число
a + Oi — это действительное число а.
Число вида 0 + Ы обозначают Ы, т. е. О + Ы = Ы; его
называют чисто мнимым числом.
Комплексное число 0 + 0/ = О является единственным
числом, которое одновременно и действительное, и чисто мнимое.
Комплексное число принято обозначать одной буквой,
чаще всего буквой z. Запись z = a + bi означает, что комплексное
число а + Ы обозначено буквой z.
Операции сложения и умножения комплексных чисел
обладают такими же свойствами, как и операции для
действительных чисел.
Основные свойства сложения и умножения
комплексных чисел
1. Переместительное свойство
2. Сочетательное свойство
(zx + z2) + z3 = zx + (z2 + z3), (zxz2) z3 = zx (z2z3).
3. Распределительное свойство
Докажем, например, свойство 3.
О Пусть 21=а1н-Ь1/, z2 = a2 + b2i и zs = a3 + b3i. Доказать, что
zl(z2 + z3) = zlz2 + zlz3. (3)
Преобразуем левую часть равенства (3):
*i (*2 + *з) = (ах + bxi) (a2 + a3 + (b2 + b3) i) =
= ах (а2 + а3) - Ъх (Ъ2 + Ъ3) + (Ъх (а2 + а3) + ах (Ъ2 + Ъ3)) i =
= аха2 + аха3 — ЪХЪ2 — ЬХЪ3 + (Ъха2 + bxa3 + axb2 + axb3) i.
206 Глава VII _
Комплексные числа
Преобразуем правую часть равенства (3):
(ах + bxi) (а2 + 620 + («i + &iO (a3
Следовательно, равенство (3) выполняется. #
Аналогично доказываются свойства 1 и 2.
Заметим, что числа 0 = 0 + 0i и 1 = 1+0i на множестве
комплексных чисел обладают теми же свойствами, что и на
множестве действительных чисел:
2 + 0 = 2, 2-1 = 2.
Задача 3. Выполнить действия:
БЯ Определение комплексного числа как числа вида а + Ы
несет в себе определенную неясность, которая связана с
применением знаков сложения и умножения до того момента, когда эти
операции вводятся явно.
Устранению этой неясности способствует иное определение
комплексного числа.
Определение
Комплексным числом z называют пару (а; Ь)
действительных чисел а и 6, взятых в определенном порядке.
Пары (а; Ъ) и (с; d) задают одно и то же комплексное
число тогда и только тогда, когда они совпадают, т. е. тогда,
когда а = с, b = d.
Сложение и умножение комплексных чисел определяются
в этом случае равенствами
(а; 6) + (с; d) = (a + c; b + d),
(а; b)(c; d) = (ac-bd; ad + bc).
Далее доказываются основные свойства арифметических
действий. Затем особо выделяют числа вида (а; 0), a€R, и (0; 1)
и устанавливают, что сложение и умножение комплексных
чисел полностью согласуются со сложением и умножением
действительных чисел, если пару (а; 0) считать действительным
числом а.
Число а называют действительной частью комплексного
числа и обозначают a = Rez, число b называют мнимой частью
комплексного числа и обозначают b = Imz (от французских слов
reele — действительный и imaginaire — мнимый).
Комплексные числа (а; Ь) при Ь^0 называют мнимыми
числами, а числа вида (0; Ь) называют чисто мнимыми чис-
§ 1 207
Определение комплексных чисел.
Сложение и умножение комплексных чисел
Упражнения
1^ (Устно.) Назвать действительную и мнимую части
комплексного числа:
1) 3+4*; 2) ! + !*; 3) V2-V5*;
4) -y/4 + i; 5) 12; 6) 3,5*.
2. Записать комплексное число, у которого действительная и
мнимая части соответственно равны:
1) 2 и 5; 2) 2,3 и -1,7;
3) 0 и -6; 4) -6 и 0.
3. (Устно.) При каком значении х равна нулю
действительная часть комплексного числа:
1) (x-5) + 2i; 2) ()
3) (2x+l)-3i; 4) (Зх-5)
4. (Устно.) При каком значении х равна единице мнимая
часть комплексного числа:
-ЗН; 2) -
3) V2 + (2x-l)i; 4) --t-(3x-
о
5. Указать, какие из данных комплексных чисел равны:
i£; 5-6i; Ve + i; -0,5 + 3*; 2 + i; -5-V36i; ■у-
6. Найти сумму комплексных чисел:
" 1) (5 + 4*) + (-2 + 30; 2) (1
3) (0,5-3,2i) + (l,5-0,8i); 4) (-l-2i
5) (3 + V5i) + (3-V50; 6) (I-l
7. Найти произведение комплексных чисел:
" 1) (2 + 30(4 + 50; 2) (1-20(5-0;
3) (-3-20(2 + 30; 4) (3-0(3 + 0;
5) (-| + 1,5Л(2-40; 6) (V2 + 30(V2 + 30.
8. Выполнить действия:
1) 2(1 + 0 + 3-7*; 2) (2 + 0(-3-20+
3) 2*(1 + 0 + 4^2--|Л; 4) (-3 + 4O2i + (-2
5) (V3 + 20(V3-0+l-4V3i;
6) 1^(6-120+^(4 + 80.
9. Какое число можно прибавить к числу 7,5-2V5i, чтобы
оно стало:
1) действительным; 2) чисто мнимым?
208 Глава VII
Комплексные числа
10. Найти действительные числа х и у, если:
2) x-2yi = - l-
3) 2*-(3 + i/H = -4 + 5,3*; 4) -3x + (y- f
5) (Jc + i/) + (x-i/)i = 3 + i; 6) (5
1L Упростить выражение (a, b — действительные числа):
" 1) (a + Sbi) + (a - 5bi); 2) (3a + 2bi) + (- Ча - 2bi);
3) (a + Sbi)(a-Sbi); 4) (2a + bi)(2a-bi);
5) (2b + 3ai)(3a + 260; 6) (3a + 4to)(4b + 3aO.
12. Найти действительные значения х, при которых число z
будет действительным:
1)2 = 6*2£ + 2xi-Ьх2\ 2) z = (х-Sxi) + (5 + х2/).
13. При каких действительных значениях х и у комплексные
числа Z1 = x2 — 7x + 9yi и z2 = y2i + 2Oi —12 равны?
14. Найти действительные значения х и i/, если:
" 1) (* + 2i/0 + (Sy- 2xi) = 2 + 4i; 2) (2x + 5z/i) + («/ + **) = 2 + i\
3) y-M + 7*-| +yi-2; 4) I + I + JL.f-l
||] Доказать равенство:
1) г1 + г2 = г2 + г1; 2) zxz2 = z2zx\ 3)
4) (2?i + 2?2) + ^3 = 2, +(22 + z3); 5) 2 + 0 = 2; 6) 2-1 = 2.
§ 2. Комплексно сопряженные числа.
Модуль комплексного числа.
Операции вычитания и деления
П1. Комплексно сопряженные числа
Определение
Сопряженным с числом z = a + bi называется комплексное
число a — bi, которое обозначается г, т. е.
i = a — bi.
Например, 3 + 4£ = 3-4£, -2-5i = -
Отметим, что а — Ы = а + Ы, поэтому для любого
комплексного числа z имеет место равенство
(Т) = 2.
Равенство ~z=z справедливо тогда и только тогда, когда
г — действительное число.
О Пусть z = a + bi. Тогда г= а-Ы9 и равенство а + Ы = а — Ы по
определению равенства комплексных чисел справедливо тогда и
только тогда, когда 6 = —Ь, т. е. 6 = 0, а это и означает, что
z=a + bi = a + 0i = a — действительное число. •
Из определения следует, что
§ 2 209
Комплексно сопряженные числа. Модуль комплексного числа.
Операции вычитания и деления
2. Модуль комплексного числа
Определение
Модулем комплексного числа z = a + bi называется число
Vа2 + Ъ2, т. е.
V2 2 (2)
Например, |3 + 4i| = V32+42 = 5, |l + i| = Vl2 + 12 = V2, |i|=
=Vo2 + i2=i.
Из формулы (2) следует, что |2|>0 для любого
комплексного числа 2, причем | аг | = 0 тогда и только тогда, когда 2=0,
т. е. когда а = О и 6 = 0.
Докажем, что для любого комплексного числа z
справедливы формулы
|*| = |г|, 2г=|2|2.
О Пусть z = a + bi. Тогда z=a-bi, и по определению модуля
|2| = |a-6i| = V
Найдем произведение:
3. Вычитание комплексных чисел
Определение
Комплексное число (-1)2 называется противоположным
комплексному числу z и обозначается —z.
Если z = a + bi, то —z = — a-bi. Например, — (3 — 5£) = — 3+5i.
Для любого комплексного числа z выполняется равенство
Вычитание комплексных чисел вводится как операция,
обратная сложению: для любых комплексных чисел zx и z2
существует, и притом только одно, число 2, такое, что
2 + 02=2!, (3)
т. е. уравнение (3) имеет только один корень.
Прибавим к обеим частям равенства (3) число (-22),
противоположное числу 22:
2 + 22 + (-22)==21+(-22), ОТКуда Z = Z1+(-Z2).
Число z = zx+(-z2) обычно обозначают z = z1-z2 и
называют разностью чисел гг и 22.
Если zi = a1+b1i, z2 = a2 + b2i, то разность zx—z2 имеет
следующий вид:
(аг + bti) - (а2 + b2i) = (а, - а2) + (b, -b2)i. (4)
Формула (4) показывает, что разность комплексных чисел
можно находить по правилам действий с многочленами.
210 Глава VII
Комплексные числа
Задача 1. Найти разность (1 + 30 - (-4 + 50-
4. Деление комплексных чисел
Деление комплексных чисел вводится как операция,
обратная умножению: для любых комплексных чисел zl и z2^0
существует, и притом только одно, число z9 такое, что zz2 = zi9
т. е. это уравнение относительно z имеет только один корень,
который называется частным чисел zx и z2 и обозначается
гх\гъ или |±, т. е. z = zx :z2 = ^.
Комплексное число нельзя делить на нуль.
Докажем, что уравнение z2z = zt для любых комплексных
чисел zx и z2^0 имеет только один корень, и найдем этот
корень.
О Умножив обе части уравнения на г2, получим zz2'z2 = zi'z29 т. е.
Полученное уравнение равносильно данному, так как
0, и потому 22^0. Умножим обе его части на
действительное число -—- (заметим, что \z2\2^09 так как z2j^0)9 получим
1*2 f
так
найти по формуле
Z\Zo
2=—г. Итак, частное комплексных чисел zx и z2^0 можно
1*2 Г
Каждое комплексное число z, не равное нулю, имеет
обратное ему число w, такое, что z-w = l. Если z = a + bi и
w=x+yi9 то это равенство принимает вид
(а + Ы) (х + yi) = 1 или (ах — by) + (6л: + ai/) i = 1.
Из последнего равенства получаем систему
[ах-Ьу=1,
\
а -Ъ
решая которую находим х = , у =
2 ъ2 2 Ъ
Заметим, что а2 + Ь2^0, так как
Таким образом, если z = a + bi, то число, ему обратное,
принимает вид
Если
ставить в
г\
zx = a
виде
аг + ЬХ
а2 + Ь2
w =
i («1 + <
i
1
z
a
a2 + b2
i2 + b2i9
b\
a
TO
a
b
формулу
la2 + b1b2
2 2
(5)
a2b]
МОЖНО
§ 2
пред-
211
Комплексно сопряженные числа. Модуль комплексного числа.
Операции вычитания и деления
Эту формулу можно не запоминать, достаточно помнить,
что она получается умножением числителя и знаменателя дро-
би — на число, сопряженное со знаменателем.
a2 + b2i
Например,
l-2i ~ (1-20(1 + 20 ~ 1+4 5 5
По определению умножения комплексных чисел
8 2
Вообще
Например, i23 = i45+3 = i3
Задача 2. Вычислить (1 ^
. (1-20(1 + 0 1 l + i-2i-2i2 1 (3-0(3-0 (-Q
3 + i i 3 + i + i (3 + 0(3-0 H-i)
9-3i-3i + i2 . 8-6i . 4 3 . . 4 8 . ^
Задача 3. Вычислить
Задача 4. Доказать, что для любых двух комплексных
чисел 2i и г2 справедливо равенство
|> Используя свойство комплексно сопряженных чисел,
получаем
Упражнения
16. Записать комплексное число, сопряженное с числом:
1) 1 + £; 2) 3 + 4*; 3) -2 + 5*;
4) -6-Si; 5) -0,7-1,3*; 6) |- - | *.
17. Найти модуль комплексного числа:
1) 6 + 8*; 2) 8-6i; 3) -V3 + i; 4) V2-V3i;
5) 5i; 6) -2i; 7) {-|«; 8) "|-|^
Глава VII
Комплексные числа
18. Записать число, противоположное числу:
~ 1)5 + 3*; 2) 4-2*; 3) -3 + *; 4) -\[2-li.
19. Найти разность комплексных чисел:
~ 1) (3 + 4Q-(l + 30; 2) (2-70-
3) (1 + 0-(1-0; 4) (5-2Q-(3-2Q;
5) (2 + 5i)-(-i + 6i); 6) (-i-4i)-(-i-30;
7) (V2 + 2V30-(3\^-V30; 8) (3V
20. Вычислить:
~ 1) (5-3i)-(l + 2i) + (2-0; 2) (4-
3) (8+ 2i)-(3-70-(5+ 6i); 4)
21. Найти частное комплексных чисел:
" Ь-£. 3 + 3£. _2*_. Ь-£.
1} Z) 1-3»' d) 1-i' 4) 2l '
6) ПГ27' 7> Т34Г' 8) 32^57
22. Вычислить:
(4-30(2-0. (1 + 0(2 + 0.
-0(1 + 30'
s~4i к\ 2~3i
"' 2-5i ' 4 + 3i' "' 1 + 4/ 1-4Г
23. Найти модуль комплексного числа z, если:
\i; 2) 2 = -9; 3) z = -i; 4) 2 = cos^
24. При каких действительных значениях х и у комплексные
числа 21 = 9y2-4-10xi и z2 = 8y2 + 20i7 являются
сопряженными?
25. При каком значении х комплексные числа z1 = x-8-6i и
г2 = 2х2 + Ы-2 являются противоположными?
Решить уравнение (26—27).
26. 1) (l-60 + * = -4-7i; 2)
" 3) (5-40-2? = 3-5i; 4)
27.1) 2(3-20 = l + 2i; 2) 2(-
"3) 2(l-30-6 = 2i; 4) 2(-
28. Вычислить:
l) (3-202; 2) (1 + 203; 3) (l + O4;
4) (l-o6; 5) (
29. Выполнить действия:
(1 + 2Q2. (1 + 2Q2-(1-Q3
. 5 + Ш (1 + 2Q.
' 8-6i 2 + i ' j
§ 2 213
Комплексно сопряженные числа. Модуль комплексного числа.
Операции вычитания и деления
Решить уравнение:
1) \z\-iz = l-2i; 2)
Вычислить:
2) -L + -L + -L.
lo Ca So
i32j Доказать, что \z1 + z2\2 + \z1-z2\2 = 4:C29 если
33.1 Вычислить:
1) (1 + 08; 2) (1-012.
34.1 С помощью равенства (т + ni)(m- ni) = т2 + п2 доказать, что
произведение двух чисел, каждое из которых есть сумма
квадратов двух целых чисел, является также суммой
квадратов двух целых чисел.
35. Доказать, что комплексное число является чисто
1+2
мнимым тогда и только тогда, когда | z | = 1.
§ 3. Геометрическая интерпретация
комплексного числа
1. Комплексная плоскость
Действительные числа геометрически изображаются
точками числовой прямой. Комплексное число а + Ы можно
рассматривать как пару действительных чисел (а; Ъ). Поэтому
естественно комплексные числа изображать точками плоскости.
Пусть на плоскости задана прямоугольная система
координат. Комплексное число z = a + bi изображается точкой
плоскости с координатами (а; 6), и эта точка обозначается той же
буквой г (рис. 104).
Такое соответствие между комплексными числами и
точками плоскости взаимно однозначно: каждому комплексному
числу а + Ы соответствует одна точка плоскости с
координатами (а; Ь) и, наоборот, каждой точке плоскости с координатами
(а; Ъ) соответствует одно комплексное число а + Ы. Поэтому
слова «комплексное число» и «точка плоскости» часто
употребляются как синонимы. Так, вместо слов «точка, изображающая
число 1 + i» говорят «точка 1 + £». Можно, например, сказать
«треугольник с вершинами в точках £, 1 + i, —i».
При такой интерпретации
действительные числа а, т. е. комплексные
числа а + Oi, изображаются точками
с координатами (а; 0), т.е. точками fr z-a-tm
оси абсцисс. Поэтому ось абсцисс
называют действительной осью. Чисто
мнимые числа Ы = 0 + Ы изображаются
точками с координатами (0; 6), т. е.
точками оси ординат, поэтому ось ор- рис
214 Глава VII
Комплексные числа
-2 4
-3
-2
-3-2i
Vi
2i
i
-i
2-
H
\*
1
2-
Ь3£
2 5:
-Si
— z —
—a
a + bi
/
—z =—a — bi
7
0
-b z =
a + bi
a x
= a-bi
Рис. 105
Рис. 106
динат называют мнимой осью. При этом точка с координатами
(0; Ь) обозначается Ы. Например, точка (0; 1) обозначается i9
точка (0; -1) — это -i9 точка (0; 2) — это точка 2i (рис. 105).
Начало координат — это точка О. Плоскость, на которой
изображаются комплексные числа, называют комплексной плоскостью.
Отметим, что точки z и -z симметричны относительно
точки 0 (начала координат), а точки г и г симметричны
относительно действительной оси (рис. 106).
0 Пусть г = а-\-Ы. Тогда -z = — a-bi9 ~z = a — bi. Точки z и —z
имеют координаты соответственно (а; Ь) и (-а; -6), следовательно,
они симметричны относительно начала координат. Точка ~z
имеет координаты (а; -Ь), следовательно, она симметрична
точке z относительно действительной оси (см. рис. 106). •
Комплексное число z = a-\-bi можно изображать вектором
с началом в точке О и концом в точке z. Этот вектор будем
обозначать той же буквой 2, длина этого вектора равна \z\.
Число Zi + z2 изображается вектором, построенным по
правилу сложения векторов zx и 22» а вектор zx — z2 можно
построить как сумму векторов zx и — z2 (рис. 107).
zx-z2
Рис. 107
Рис. 108
§ 3 215
Геометрическая интерпретация комплексного числа
2. Геометрический смысл модуля комплексного числа
Выясним геометрический смысл \г\.
Пусть г = а + Ы. Тогда по определению модуля |2|=Va2+b2,
Это означает, что \z\ — расстояние от точки 0 до точки г.
Например, равенство |г| = 4 означает, что расстояние от
точки 0 до точки z равно 4 (рис. 108). Поэтому множество всех
точек 2, удовлетворяющих равенству |г| = 4, является
окружностью с центром в точке 0 радиуса 4. Уравнение \z\ = R
является уравнением окружности с центром в точке 0 радиуса R, где
R — заданное положительное число.
3. Геометрический смысл модуля разности комплексных
чисел
Выясним геометрический смысл модуля разности двух
комплексных чисел, т. е. \zx — z2\. Пусть zl = ai + b\i, z2=a2+b2i.
Тогда \z1-z2\ = \(a1-a2)-t(bl-b2)i\=^/(al-a2)2-^(bl-b2)2.
Из курса геометрии известно, что это число равно
расстоянию между точками с координатами (ах\ Ъг) и (a2; b2).
Итак, \z1-z2\ — расстояние между точками zx и z2.
Например, расстояние между точками 1 и -3 + 3£ равно
11-(-3 + 301 = 14- 3i| = V42 + (-3)2 = 5.
Покажем, что \z-zo\ = R — уравнение окружности с
центром в точке zQ радиуса R, где z0 — заданное комплексное
число, R — заданное положительное число.
О Так как |2-20| — расстояние между точками z и zo> то
множество всех точек z, удовлетворяющих уравнению \z-zo\=R, -
это множество всех точек, расстояние от которых до точки 20
равно R. %
Например, | z + i \ = 2 — уравнение окружности с центром в
точке —i радиуса 2, так как данное уравнение можно записать
в виде |z-(-0l = 2.
Задача 1. Пусть zl9 z2 — разные точки комплексной
плоскости. Доказать, что \z-z1\ = \z-z2\ — уравнение прямой,
перпендикулярной отрезку, соединяющему точки zx, z2, и
проходящей через его середину.
[> Так как \z-zt\ — расстояние от
точки z до точки zl9 а \z-z2\ —
расстояние от точки z до точки z2, то
множество всех точек,
удовлетворяющих уравнению \z-zl\ = \z-z2\,—
это множество всех точек,
равноудаленных от двух точек zx и z2. M
Например, \z-2i\ = \z-l\ —
уравнение прямой,
перпендикулярной отрезку, соединяющему точки —
zt = 2i и z2 = l, и проходящей через
его середину (рис. 109).
Ук
1
Рис. 109
216
Глава VII
Комплексные числа
Задача 2. Найти множество
точек комплексной плоскости,
удовлетворяющих условию 1 < | z + 211 < 2.
\> Условию \z + 2i\<2
удовлетворяют все точки, лежащие внутри
круга радиуса 2 с центром в точке
20=-2i, а условию \z + 2i\>l — все
точки, лежащие вне круга радиуса
1 с центром в точке z0 (рис. 110).
Искомое множество точек —
кольцо между окружностями радиусов
1 и 2 с общим центром в точке
20=-2i. ^ Ш^Л
Упражнения
*
1
1
1
I
\
\
4
V\
0
Jf -" ~"
\
\
-4
ч
\
/
4
\
\
\
1
/
•
Рис
X
110
36. На комплексной плоскости построить точки:
1) 3; 2) 4; 3) -2; 4) 6i; 5) 4i; 6) -2i; 7) 1 + 3£; 8)
9) -3 + i; 10) -1 + £; 11) -1 -3f; 12) -4-i; 13) l-4i; 14) SSL
37. Построить окружность:
~ l)|z| = 3; 2)|2?| = б; 3)|2?-2Ё| = 1; 4) |ar + 3£| —2.
38.
40.
41.
Решить уравнение:
1) z + 3z=8 + 12i; 2) 4г-г=-9 + Ш.
Найти расстояние между точками:
1) 6 и Si; 2) li и -2i; 3) 1 + i и 2 + 3i; 4) S-2i и l-4i.
Найти множество точек комплексной плоскости,
удовлетворяющих условию:
1) 1*1 = 5; 2) |*-1| = 3;
3) |* + Зё|=1; 4) |* + 2£-1| = 2;
5) |*-2Н* + *|; 6) |*-1-Ё| = |*+1 + Ё|.
Найти множество точек комплексной плоскости, которое
задается условием:
1) |*-il<3; 2) |г + 3£|>4; 3) l<\z + 2\<2; 4)
Решить систему уравнений:
2)
|*z + 51i|=l.
| Доказать, что система уравнений
не имеет решений.
Решить систему уравнений
*-4
*-8
г-12
*-8i
-1=0,
_5
3'
§ 3
217
Геометрическая интерпретация комплексного числа
§ 4. Тригонометрическая форма
комплексного числа
1. Аргумент комплексного числа
Определение
Аргумент комплексного числа 2^0 — это угол ф между
положительным направлением действительной оси и
вектором О2 (рис. 111). Этот угол считается положительным,
если отсчет ведется против часовой стрелки, и
отрицательным при отсчете по часовой стрелке.
Связь между действительной и мнимой частями
комплексного числа 2 = а + Ы9 его модулем г=\г\ и аргументом ф
выражается следующими формулами:
rcoscp,
(1)
(2)
Рис. т
Аргумент комплексного числа z — аЛ-Ы (г^О) можно
найти, решив систему (2). Эта система имеет бесконечно много
решений вида ф = фо + 2/ея, где keZ, ф0 — одно из решений
системы (1), т. е. аргумент комплексного числа определяется
неоднозначно.
Для нахождения аргумента комплексного числа г = а+Ы
можно воспользоваться формулой
I (3)
При решении уравнения (3) нужно учитывать, в какой
четверти находится точка г = а + Ы.
Задача 1. Найти все аргументы комплексного числа z:
1) z = -2i; 2) 2 = -l + iV3.
t> 1) Число 2 лежит на отрицательной части мнимой оси, т. е.
п
один из аргументов этого числа равен - —, а множество всех
аргументов имеет вид ф==—— н-2/гя, keZ.
2) По формуле (3) находим tg(p = -V3\ Учитывая, что числом
лежит во второй четверти, получаем ф= —+2/ея, keZ. ^
о
218
Гл а в а VII
Комплексные числа
2. Запись комплексного числа в тригонометрической форме
Из равенства (1) следует, что любое комплексное число
z=a + bi, где 2^0, представляется в виде
2 = r(coscp +isincp), (4)
где r=\z\ = ya2 + b2 — модуль комплексного числа z, ф — его
аргумент. Запись комплексного числа в виде (4), где г>0,
называют тригонометрической формой комплексного числа 2.
Задача 2. Записать в тригонометрической форме
комплексное число:
1) 21 = -l-i; 2) г2 = - cos -=■ + i sin -=■.
t> 1) Применяя формулу (3), получаем tgcp=l, откуда <р=—,
так как точка —1 — i лежит в третьей четверти. Учитывая, что
\гх\=у/29 имеем 21=у/2[cos-^- + isin-^ J.
2) Так как точка г2 лежит во второй четверти, то,
используя формулы приведения, получаем - cos — = cos —, sin -=■ =
6ti бтс . . бтс ^
=sin —, и поэтому z2 = cos — +1 sin —. ^
Пусть комплексные числа гх и z2 записаны в
тригонометрической форме:
z1 = r1 (cos фх + i sin фх), z2 = r2 (cos ф2 + i sin ф2).
Тогда равенство zx = z2 имеет место в том и только в том
случае, когда rt = r2, ф1=ф2 + 2Ля, keZ.
Обратим внимание на то, что выражения
- ( 7Г . . ТС \ о/ ТС . . ТС \
- 5 (cos — + г sin — 1, 31 cos — -1 sin — 1,
t/o7 . Зтс . 3tc\ tc . . 3tc
V2 sin -— +1 cos —- , cos — +1 sin -7-
\ 4 4 / 4 4
не являются тригонометрическими формами записи
каких-либо комплексных чисел. ^^31
Упражнения
45. Найти все аргументы комплексного числа:
""l)z = 7; 2) г = -4; 3) z = i;
4) z = -3i; 5)2 = -l-hi; 6) 2=V3+i;
7) z = 2-2£; 8) 2 = -l-V^i.
46. Записать в тригонометрической форме комплексное число:
1) z = 3; 2) z = -l; 3) г =
4) z = -2 + 2\/3i; 5) 2 = -l-V3i; 6) 2 = 5-
7) 2 = V57cos^--£sin^-j; 8) z = -cos у -hisin у .
§4 219
Тригонометрическая форма комплексного числа
47. Записать в алгебраической форме комплексное число:
1) cos —+isin-^; 2) 3 (cos 2л+ i sin 2л);
оч ^fcl 3ТС 37Г\ А. .( 9ТС . . 9тЛ
3) V2(cos — + *sin — 1; 4) 4( cos — +*sin— I;
t4 7тс . . 77Г „4 13тс . . 13я
5) cos -^- +1 sin -r-; 6) cos —— +1 sin —^-
DO О о
48. Записать в тригонометрической форме комплексное число:
1) cos — - isin —;
9 9
2)
3)
4)
49. Число 2 = ■£■ - -^ i можно выразить через тригонометричес-
кие функции следующим образом:
,ч 1 V3 , 5тс , ,^' 5тс.
оч 1 V3 . / 5тЛ . . 5я
2) 2--2-'cos+'sin
ОЧ1 V3 .
3) ^-^rl
А. 1 V3 . 5тс
4) 2--^l = COS
D) 2 2 i-COS3 ISlIlg.
Какая из этих записей является тригонометрической
формой комплексного числа?
50. Представить в тригонометрической форме комплексное
число:
2"31 (1 + 0 i3 3-i1
Доказать, что если |г| = 1, то г= —.
I52J Записать в тригонометрической форме комплексное
число:
1) _^(i + i); 2) -5(cos40° + isin40°);
1 Pit 1 9чг
3) l + cosa + £sina, 0<a<—; 4) 1 + cos——+£sin—.
220 Глава VII
Комплексные числа
§ 5. Умножение и деление комплексных чисел,
записанных в тригонометрической форме.
Формула Муавра
C3IC помощью тригонометрической формы удобно находить
произведение и частное комплексных чисел zx и z2.
Вычислим произведение:
zxz2 = rx (cos фх + i sin фх) • r2 (cos ф2 + i sin ф2) =
= rxr2 (cos фх cos ф2 - sin фх sin ф2 + i (sin фх cos ф2 + cos фх sin ф2)) =
= rxr2 (cos (фх + ф2) + i sin (фх + ф2)).
Итак,
zxz2 = rtr2 (cos (Ф1 + Ф2) + * sin (фх+Фг)). (1)
Из формулы (1) следует, что при перемножении комплексных
чисел их модули перемножаются, а аргументы складываются.
Вычислим частное (z2^0):
2х Гх (cos фх + i sin фх) гх (совфх +£8И
г2 ~ r2 (cos ф2 + i sin ф2) ~ r2 cos2 ф2 + sin2 ф2
= — (cos фх cos ф2 + sin фх sin ф2 + i (sin фх cos ф2 - cos фх sin ф2)) =
= —(со8(фх-ф2) + 18т(фх-ф2)), т. е.
Г2
71 = 7" (cos Фх - Ф2) + i sin (фх - ф2)). (2)
Из формулы (2) следует, что модуль частного двух
комплексных чисел равен частному модулей делимого и делителя,
а разность аргументов делимого и делителя является
аргументом частного.
Задача 1. Найти произведение
V2(cos^+iSin
t> По формуле (1) имеем
о
Задача 2. Выполнить деление
+ tsin
6(cos— + tsin—)
3(COS12+lSini2)
§ 5 221
Умножение и деление комплексных чисел, записанных
в тригонометрической форме. Формула Муавра
> По формуле (2) имеем
T+Isin-6-) е
efcoe^r + iein^
\ О
БЯИз формулы (1) следует, что
(cos ф + i sin ф)2 = cos 2ф + i sin 2ф,
(cos ф + i sin ф)3 = cos Зф + i sin Зф.
Вообще для любого n€N (и для всех n€Z) справедлива
формула
(cos ф + i sin ф)п = cos /1ф + i sin гсф, (3)
которую называют формулой Муавра.
Для n-й степени комплексного числа, записанного в
тригонометрической форме 2 = г(со8ф + £8Шф), справедлива формула
zn = rn (cos пф + i sin шр). (4)
Задача 3. Возвести в степень ^2fcos -^- + i sin ^г)) •
[> По формуле (4) имеем
Задача 4. Вычислить ^ +t^ ' .
(1-I)4
t> Так как
то, применяя формулу (4), находим
(1 + i V3)6 = 26 (cos 2п + £ sin 2л) = 2б,
Следовательно, <1 + ^>6 = ^i = _ 16. ^
(1-04 "4
Задача 5. Решить уравнение z2 = i.
t> Представим число i в тригонометрической форме: i = cos|^ +
+ isin^-. Пусть z = r(cos<p + isin<p). Тогда уравнение z2 = i примет
вид г2 (cos 2ф + i sin 2ф) = cos —■ + i sin —•. Отсюда находим г=1,
2<p=^ + 2nk, т. е. ф= j+я/г, где
222 Глава VII
Комплексные числа
Таким образом, все решения уравнения z2 = i
представляются в виде 2 = cos(^-+kn)+isin(-j + kn), где k€Z.
Заметим, что для всех четных k эта формула дает
комплексное число
а для всех нечетных k — комплексное число
^cosf + isinf-f-if.
Итак, уравнение z2 = i имеет два корня: zli2 = ±(^ + i-
Задача 6. Записать формулы для сов4ф и вт4ф.
t> По формуле Муавра
(cos ф + i sin ф)4 = cos 4ф + i sin 4ф. (5)
С другой стороны, используя формулу
(а + б)4 = а4 + 4asb + 6a2b2 + 4abs + б4,
получаем
(cos ф + i sin ф)4 = cos4 ф + 4 cos3 ф (i sin ф) Н- 6 cos2 ф (i sin ф)2 4-
Н-4С08ф(181Пф)3Н-(181пф)4. (6)
Сопоставляя правые части равенств (5) и (6), имеем
сов4ф = cos4 ф - 6 cos2 ф sin2 ф + sin4 ф = cos4 ф - 6 cos2 ф (1 - cos2 ф) +
+ (1 - cos2 ф)2 = 8 cos4 ф - 8 cos2 ф +1;
sin4(p = 4 cos3 ф sin ф - 4 cos ф sin3 ф = 4 cos ф ((1 - sin2 ф) sin ф - sin3 ф) =
Упражнения
53. Найти произведение комплексных чисел:
(cos
2) 2(c
3)
4)3(cos|+/sin|).4(cos(-|)+fsin(-|));
5) V2 (cos 55° + i sin 55°) • V2 (cos 35° + i sin 35°);
6) (cos7 + isin7)(cos3 + £sin3).
j>4. Найти частное:
cos—+isin— 8(cos——hisin——)
1) * £.. 2) Ч 4 1_L;
§ 5 223
Умножение и деление комплексных чисел, записанных
в тригонометрической форме. Формула Муавра
Cos30°-Hsin30°
cos(--|)+*sin(-|) '
gv Vl2(cos20o + isin20o) cos7 + isin7
V3(cos50° + isin50°) ' cos2 + 1мп2'
155.1 Возвести в степень комплексное число:
1) (2(cos-~+£sin-^-)) ; 2) (cos^- + jsin
3)(l(cos|+isin|))4; 4)(cos(-f)+*sin(-f))9.
3. Выполнить действия и записать результат в
алгебраической форме:
./ 5л,.. 5п
2)
)
+isin cos__lsin
cos 6 б cos_lsin_
4)
; 4)
. fi. (2Q7
4
J57.1 Записать в тригонометрической форме результат действий:
1) 2 =
2) Z'—3(cos|+isin|)(cos^-isin^)4;
8) ,.(^tl)-; 4) '*-(!*££)-.
С помощью тригонометрической формы комплексного
числа решить уравнение:
1) 22 = Ш; 2) 22 = -4i;
3) 22 = 2-2iV3; 4) 22 = -l-V3i.
Представить в тригонометрической форме число:
^ ^-; 2) sina + i(l-cosa), |
3) (tgl-*)4; 4) (1 + 02n , neN.
(l-i)2""1
Применяя формулу Муавра, доказать равенство:
1) cos 2a = cos2 a -sin2 a; 2) sin 2a = 2 sin a cos a;
3) cos3a = 4cos3a-3cosa; 4) sin 3a = 3 sin a - 4 sin3 a.
[61.1 Доказать равенство (п — натуральное число):
y== 1 + itgmx
=
V 1-itga/ = 1-itgna
224 Глава VII
Комплексные числа
у Найти сумму:
2)
Ц] Доказать равенство (x^nk, keZ):
nx . (n + l)x
sin—--sin-^——'—
1) sin^: + sin2jc4-...4-sin/i^:= ;
sinf
nx . (n+l)x
cos—-sin-^——'—
2) l + cosjc + cos2a: + ...+costta:= .
sin-
§ 6. Квадратное уравнение с комплексным
неизвестным
ЕЯ Рассмотрим уравнение z2 = a9 где а — заданное
действительное число, z — неизвестное.
Это уравнение:
1) имеет один корень 2 = 0, если а = 0;
2) имеет два действительных корня zx 2 = ±Va, если а>0;
3) не имеет действительных корней, если а<0.
Например, уравнение
*2 = -1 (1)
не имеет действительных корней.
Покажем, что уравнение (1) имеет два комплексных
корня, и найдем их. Подставляя в уравнение вместо -1 число i2,
получаем z2 = i29 откуда z2-i2 = 0.
Применяя формулу разности квадратов, разложим левую
часть последнего уравнения на множители: (z-i)(z + i) = 0.
Произведение равно нулю, когда хотя бы один из множителей
равен нулю. Следовательно, zl = i, z2 = — i, т. е. уравнение (1)
имеет два корня 2X 2 = ±i-
Аналогично можно показать, что уравнение
z2 = a (2)
при а<0 также имеет два комплексных корня zlf2 = ^i/\/\a\-
Например, уравнение
22 = -25 (3)
имеет два корня 012 = ±iVl-25|=±5i.
По аналогии со случаем а > 0 корни уравнения (3)
записывают в виде 21>2 = ±V-25 . При этом считается, что
V-25 =i}/\-25\=5i.
Вообще если а<0, то Va определяется формулой Va = i
Например,
§ 6 225
Квадратное уравнение с комплексным неизвестным
Такое соглашение удобно тем, что для любого
действительного а корни уравнения
22 = а (4)
можно находить по формуле
*lt2 = ±V£. (5)
Если а Ф 0 (а > 0 или а < 0), то уравнение (4) имеет два
различных корня. При а = 0 уравнение (4) имеет один корень г=0;
в этом случае говорят также, что уравнение имеет два равных
корня 2Х 2 = 0 или один корень кратности два. Это часто
удобно, например, для того, чтобы во всех случаях была
справедлива теорема Виета.
Отметим, что теперь для любого действительного а
справедливо равенство
(\/^)2 = а. (6)
Введенное понятие корня из отрицательного числа
позволяет записать корни любого квадратного уравнения с
действительными коэффициентами
az2 + hz + c = 0 (7)
по известной общей формуле
Задача 1. Решить уравнение
г2-162 + 65
[> По формуле (8) находим
= 16±У256-260 = 16±£][ = 16 + iVi = 16±2i
2 2 2 2'
т. е. z1 = 8 + i, z2 = S-i. M
Итак, при любых действительных а, 6, с, а^О, корни
уравнения (7) можно находить по формуле (8). При этом если
дискриминант D = b2-4ac, т. е. подкоренное выражение в формуле
(8), положителен, то уравнение (7) имеет два действительных
различных корня. Если D = 0, то уравнение (7) имеет один
корень (два равных). Если D<0, то уравнение (7) имеет два
различных комплексных корня.
Отметим, что в задаче 1 корни квадратного уравнения
являются сопряженными.
Замечание. Корни квадратного уравнения с
действительными коэффициентами и отрицательным дискриминантом
являются сопряженными.
Комплексные корни квадратного уравнения обладают
свойствами, аналогичными известным вам свойствам
действительных корней.
Задача 2. Составить приведенное квадратное уравнение с
действительными коэффициентами, имеющее корень z1 = -l-8i.
226 Глава VII
Комплексные числа
!> Второй корень z2 = -l+8j.
По формулам Виета находим
p = -(z1 + z2) = 2, q
откуда искомое уравнение z2 + 2z + 65 = 0. ^
Задача 3. Разложить на множители квадратный трехчлен
z2- 182 + 82.
t> Корнями квадратного уравнения z2-18z + 82 = 0 являются
числа z1 = 9 + i, z2 = 9-i. Следовательно,
ШШ Задача 4. Решить уравнение z2
\> Пусть z = x + iy9 где х и у — неизвестные действительные
числа. Тогда z2 = (х + iy)2 = х2 - у2 + 2xyi и данное уравнение
можно записать так:
Отсюда по определению равенства комплексных чисел
получаем систему
[*2-V=3,
[2ху = 4.
Найдем действительные решения этой системы. Из второ-
2
го уравнения находим у = — и, подставляя это выражение для у
в первое уравнение системы, получаем х2 = 3, откуда
*4-3*2-4 = 0. *
Решая это биквадратное уравнение, получим х2 = =
= -^—, т. е. х2 = 4 или х2 = -1. Уравнение х2 = -1 не имеет дей-
ствительных корней, а из уравнения х2 = 4 находим х1 = 2,
о
лс2=—2. По формуле у=— находим г/х = 1, г/2 = -1. Следовательно,
Ответ. 212 ( 0 ^
Задача 5. Решить уравнение 23=1.
[> Перенесем единицу в левую часть со знаком «-»: г3-1 = 0 —
и разложим левую часть на множители по формуле разности
кубов:
23-13 =
Отсюда 2x = l, а из уравнения 22 + 2 + l = 0 находим
^ 1 , . V3
Ответ.
§ 6 227
Квадратное уравнение с комплексным неизвестным
Упражнения
64. Решить уравнение:
1)г2 = -16; 2) 22 = -7; 3) z2 + 0,36 = 0;
4) 25г2 + 9 = 0; 5) z4-16 = 0; 6) 24-81=0.
65. Вычислить:
1) V-100; 2) V-0,25; 3) V-12; 4) V-27.
Решить уравнение (66—67).
66. 1) 22-2г+10 = 0; 2)
3) 22-6г+13 = 0; 4)
67. 1) 4г2-4г + 5 = 0; 2) 9г2 +182+10 = 0; 3)
4) 22 + 2г + 6 = 0; 5) z3 + 27 = 0; 6) z3 = 8.
68. Составить приведенное квадратное уравнение с
действительными коэффициентами, имеющее данный корень,
и проверить ответ, решив полученное уравнение:
1) zx = 2 + \u 2) 21==-1-±*;
3) z1=\f2-]/6i; 4) 0! = -V6 + V3i.
69. Решить уравнение:
1) 24-Зг2-4 = 0; 2) z4 + 15z2- 16 = 0.
Разложить квадратный трехчлен на множители (70—71).
70. 1) 22-4г+5; 2) 22 + 4г+ 13; 3) 22 + 2z + 4; 4) z2-62 + 11.
71. 1) 4г2 + 4г + 5; 2) 16-г2-32^+17;
3) 25z2 + 502 + 26; 4) - z2 + 10z - 26.
|72.] Составить квадратное уравнение с действительными
коэффициентами, имеющее данный корень:
U 2 -3-2*. о. 4-г
1} Z Z) 2
173.! Решить уравнение:
1) z2 = -5+12i; 2) z2 = -3-4i; 3) гв = 1;
4) 26 = -1; 5) 26-7г3-8 = 0.
§ 7. Извлечение корня из комплексного
числа. Алгебраические уравнения
ВЯ Перейдем к операции извлечения корня данной степени из
комплексного числа.
Число г называется корнем степени п из числа w (обозна-
п i—
чается Vw), если zn = w.
Из данного определения вытекает, что каждое решение
уравнения zn = w является корнем степени п из числа w.
Другими словами, для того чтобы извлечь корень степени п из
числа w9 достаточно решить уравнение zn = w.
228 глава VII
Комплексные числа
Если w = 0, то при любом п уравнение zn = w имеет одно и
только одно решение 2 = 0. Если и;^0, тоиг^О, а
следовательно, и г и w можно представить в тригонометрической форме:
2 = r(cos ф н- i sin ф), w =p (cos 9 н- i sin 9).
Уравнение 2n = w примет вид
rn (cos шр + £ sin шр) =р (cos 9 + i sin 9).
Два комплексных числа равны тогда и только тогда, когда
равны их модули, а аргументы отличаются слагаемым, кратным 2я.
Следовательно,
гп=р и шр
или
Итак, все решения уравнения 2n = w могут быть записаны
следующим образом:
^(^±2k^±2k\ (1)
п п
k = 0, 1, 2, ..., /i-l.
В самом деле, придавая в полученной формуле числу k целые
значения, отличные от выписанных (k = 0, 1, 2, ..., п-1), мы
не получим других комплексных чисел. Например, при k = n
получаем
|- + 2л) + £ sin (-5- + 2л)) = Vp (cos |- + £ sin - ) = г0.
Таким образом, если w;^0, то существует ровно п корней
степени п из числа w; все они содержатся в формуле (1). Все кор-
ни степени п из числа w имеют один и тот же модуль \р, но
разные аргументы, отличающиеся слагаемым, кратным числу —.
п
Отсюда следует, что комплексные числа, являющиеся корнями
степени п из комплексного числа w, соответствуют точкам
комплексной плоскости, расположенным в вершинах правильного
/i-угольника, вписанного в окружность радиуса Vp с центром в
точке 2 = 0.
Сделаем еще одно замечание относительно обозначения
п— п I—
\w. Символ yw не имеет однозначного смысла. Поэтому,
употребляя его, следует четко представлять себе, что под этим
символом подразумевается. Например, используя запись V^T,
следует позаботиться о том, чтобы было ясно, понимается ли
под этим символом пара комплексных чисел i и —i или одно
число, и если одно, то какое именно.
4,
Задача 1. Найти все значения V-16.
[> Запишем число м; = -16 в тригонометрической форме:
м; = -16 = 16 (cos я + i sin я).
§ 7 229
Извлечение корня из комплексного числа.
Алгебраические уравнения
Формула (1) в нашем случае дает уи
где /г = 0, 1, 2, 3.
Следовательно,
z0 = 2 (cos ^ + * sin ^ ) = V2 + i V2,
V 4 4 /
Рис. 112
На рисунке 112 изображены все четыре значения V—16.
Точки, соответствующие числам z0, zl9 z2, z3, находятся в
вершинах квадрата, вписанного в окружность радиуса 2, с
центром в точке z = 0. M
Задача 2. Решить уравнение z6 = - 1.
> Применяя формулу (1), гдер=1, п = 6, 9 = л (с. 218), получаем
гъ = cos
6
+ isin
6
, где
, 1, 2, 3, 4, 5 (рис. 113).
Следовательно,
Рис. 773
Если приведенное квадратное уравнение z2+pz + q = 0 имеет
р
комплексные коэффициенты, то заменой z = y—— его можно
о р2 2
привести к виду у = ^ — q, где в правой части равенства
некоторое комплексное число.
Извлекая квадратный корень из этого числа (который
всегда имеет два значения, кроме случая, когда дискриминант
равен нулю), получаем затем два комплексных корня этого
уравнения (или один двукратный корень).
230
Г л а в а VII
Комплексные числа
Вообще существует так называемая «основная теорема
алгебры» (ее доказательство в курсе школьной математики не
рассматривается), которая гласит:
Уравнение л-й степени вида zn + cxzn~l + с22л~2 + ...+
+ cn_1z + cn = O, где сг, с2, ..., cn_lf cn — комплексные
числа, имеет хотя бы один комплексный корень.
Эта теорема имеет важное следствие:
Любое уравнение n-й степени (/г>1) с комплексными
коэффициентами имеет п комплексных корней; при
этом каждый корень считается столько раз, какова его
кратность.
Например, уравнение zs-5z2 + 82-6 = 0 имеет три
комплексных корня: 2Х = 3, z2 = l + i, гг = 1 — 1.ШШЛ
Упражнения
р Найти все значения корня:
1) Уг; 2) y^J; 3) vT; 4) )Jy/a+i.
Решить уравнение (75—76).
2) 823-27 = 0; 3) z* = i;
4) z3 = -2i; 5) zs = -2 + 2i; 6) z4-i = l.
2) Зб28-13г4 + 1 = 0;
3) z4-203 + 202-22+l = O; 4) 23+ -z2 + -2 + 1 = 0.
Решить квадратное уравнение с комплексными
коэффициентами:
2) 22-2(1
Упражнения к главе VII
78. Найти значения х, при которых действительная часть
комплексного числа равна 1:
1) (* + 3) + 2i; 2) (х+1)-4£;
3) (4x-l)-7i; 4) (-Зх-8) + £.
79. Найти значения х9 при которых действительная часть
комплексного числа равна его мнимой части:
1) (х + 3) + £; 2) Sx-8i;
3) 0,4-(х-2Н; 4) -l + 2xi.
Выполнить действия (80—81).
80. 1) (2 + 30(3-2i) + (2-30(3 + 20; 2)
3) (8-V3 0(8 + V3i); 4) (_
231
Упражнения к главе VII
5-4i
4)
82. Выполнить действия над комплексными числами в
тригонометрической форме:
1) 3 (cos 130° + i sin 130°) (cos 140° + i sin 140°);
(ff)()(
cos50°-Msin50
' 2 (cos 20° + i sin 20°)'
2 (cos 20° + i sin 20°)' ,/^/ / я \ , . . / n \\
83. Найти модуль комплексного числа:
1) 15i; 2) -2П; 3) -5 + 2i; 4) V3-i; 5) -l-4i; 6)
84. Записать в алгебраической форме комплексное число:
^ + rsin^-); 2) 4(cos^ + isin-^Y
6 6/ \4 4/
85. Отметить на плоскости точки, изображающие
комплексные числа:
1) 1 + i; 2) 2i; 3) -5; 4) -2£-3.
86. Решить уравнение:
) ( 0 ;
2) (-2 + 0 + 2 = 3-2*;
3) 5 + £ = 2
4) (i-z)(l
87. Записать в тригонометрической форме число:
1) -4 + 4*; 2) -V3-*.
88. Решить уравнение:
1) 22-2г + 5 = 0; 2) г2 + 10г + 26 = 0;
3) 502 + 60 + 5 = O; 4) 2г2 + Зг + 3 = 0.
89. Найти действительные числа х и у из равенства:
2) xy + xyi-2i-yi-3 =
90. Выполнить действия:
(1-04 2-i7
о I f 19
91. Сравнить модули чисел и
2 + i13
92. Найти мнимую часть числа 2, если:
3-4iu
232 Глава VII
Комплексные числа
93. Определить, при каких действительных значениях х и у
х-1 и-\
сумма ——г + -—т равна i.
94. Составить приведенное квадратное уравнение с
действительными коэффициентами, если один из его корней
равен:
1 \ л/О \/fC i• О\
А.) \ tJ— \*Jl9 с*}
[95] Вычислить:
:~т+|-»т)Г'
2) (cos20o + isin20°)12;
3) (2(cos(-20°) + isin(-20°)))3;
1
(cos- + * sin-)
[у Записать в тригонометрической и алгебраической формах
комплексное число:
2) 2 = (V3-
(cosl2o + isinl2°)5 '
4) 2 =
] Решить систему уравнений:
1) |<г1 + 2г2=1 + 1, 2) jz2 + |2|=O,
| З^х + i22 = 2 - Зг, | ~z= - Az.
I Найти все значения:
1) t/4; 2) \/i; 3) vT; 4) V1^
] Решить уравнение:
1) 22 = - 16£; 2) 22
3) 23 = -125; 4) г4
5) 03-l = i; 6) г5
| Записать в тригонометрической форме комплексное число:
1) 2 = (tg2-04; 2) 2 = (si:
I Найти корни уравнения
действительные части которых отрицательны.
На комплексной плоскости даны точки zl9 z2, 23, являю"
щиеся вершинами треугольника. Найти точку
пересечения его медиан.
233
Упражнения к главе VII
103. Найти множество точек z комплексной плоскости,
заданное условием:
1) один из аргументов числа z равен нулю;
2) один из аргументов числа г равен -^;
3) один из аргументов числа z удовлетворяет
неравенствам 2я<ф<3я;
4) один из аргументов числа г удовлетворяет
неравенствам 0<(р<2л.
[164J1 Доказать, что для любых комплексных чисел zx и z2
справедливо равенство:
; 2) ^- = ^,
ясь записью комплексных чисел в
тригонометрической форме, найти cos 15° и sin 15°.
Вопросы к главе VII
1. Как определяется равенство комплексных чисел,
записанных в алгебраической форме?
2. Как производится сложение, вычитание, умножение и
деление комплексных чисел, записанных в алгебраической
форме?
3. Какими свойствами обладают сложение и умножение
комплексных чисел?
4. Всегда ли выполнима операция умножения комплексных
чисел? Всегда ли одно комплексное число можно
разделить на другое?
5. Какие числа называют чисто мнимыми?
6. Какое число называют сопряженным комплексному числу
а + Ы?
7. Какое число называют противоположным комплексному
числу z?
8. Как геометрически интерпретируются комплексные числа?
9. Каково взаимное расположение на комплексной плоскости
чисел: а) г и г; б) г и (-z)?
10. Что называется модулем комплексного числа?
11. В чем состоит геометрический смысл модуля разности
двух комплексных чисел?
12. Что называется аргументом комплексного числа?
13. Как записываются комплексные числа в
тригонометрической форме?
14. Как перейти от алгебраической формы записи
комплексного числа к тригонометрической форме?
234 Глава УН
Комплексные числа
Что называется корнем степени п(п>19 n€N) из
комплексного числа?
Как производится умножение, деление, возведение в
степень, извлечение корня для комплексных чисел,
записанных в тригонометрической форме?
Сформулировать основную теорему алгебры и следствие из
нее об алгебраическом уравнении п-й степени
Проверь себя!
1. Выполнить действия:
1) (3 + i) + (5-2i); 2) (6-0-
к о:
3) (7 + 0(10-0; 4)
2. Вычислить:
2-5i.
3. Записать в тригонометрической форме комплексное число:
1) -l+iV3; 2) sinf -icosf.
5 5
4. Решить уравнение:
1) z2 + 5 = 0; 2) 22-10г + 34 = 0.
5. Найти множество точек комплексной плоскости,
удовлетворяющих условию |аг| = 3.
6. Записать в алгебраической форме комплексное число:
7. Выполнить действия:
1) (cos 18° + i sin 18°) (cos 42° + i sin 42°);
2)
8. На множестве комплексных чисел решить уравнение:
1) 24 = 16; 2) 23=64.
-LO I COS ~ТГ I *• Sill ~ТГ
| Историческая справка
История развития числа уходит корнями в древние
времена. Древнегреческие математики только натуральные числа
считали «настоящими». В Древнем Египте и Древнем
Вавилоне во втором тысячелетии до н. э. при решении практических
задач использовались дроби. В III в. до н. э. китайские
математики ввели понятие отрицательного числа, а в III в. н. э.
Диофант уже пользовался правилами действий с отрицательными
числами. В VII в. н. э. индийские математики придавали на-
235
Историческая справка
глядный образ отрицательным числам, сравнивая их с
долгами. В VIII в. ученые знали, что у положительного числа
существует два квадратных корня: один — положительное число,
другой — отрицательное, но считали, что из отрицательных
чисел нельзя извлекать квадратный корень.
Потребность в извлечении квадратного корня из
отрицательного числа возникла в XVI в. в связи с решениями
уравнений. Итальянский математик Дж. Кардано (1501—1576) в
1545 г. ввел числа новой природы. Он предложил считать
решением системы уравнений
не имеющей решений на множестве действительных чисел,
пару чисел х = 5 + V— 15 иу = 5-V— 15. При этом Кардано
предлагал выполнять действия с числами новой природы аналогично
тому, как выполнялись действия с действительными числами.
в частности считать, что V— 15 -V— 15 = - 15.
Числа новой природы Кардано называл «чисто
отрицательными» и «софистически отрицательными».
В 1572 г. итальянский математик Р. Бомбелли
установил правила арифметических действий с новыми числами.
Термин «мнимые числа» ввел в 1637 г. Р. Декарт, а в 1777г.
великий отечественный математик Л. Эйлер (1707—1783)
предложил обозначать число V^T первой буквой французского
слова imaginaire (мнимый). Символ i = V— 1 стал широко
использоваться математиками после употребления его в своих
работах К. Гауссом (1777—1855).
Гаусс заменил название «мнимые числа» на «комплексные
числа» и окончательно закрепил для науки геометрическую
интерпретацию комплексного числа а + Ы как точки
координатной плоскости с координатами (а; Ь). Позднее комплексные
числа также стали изображать с помощью векторов на
координатной плоскости с началом в начале координат и концом
в точке М(а; Ъ).
Понятия «модуль» и «аргумент» комплексного числа ввел
французский математик Д'Аламбер (1717—1783), а сами
термины были введены в обиход после широкого их
использования в своих работах швейцарским математиком Ж. Арга-
ном (1768—1822) и французским математиком О. Коши
(1789—1857).
В начале XVIII в. была построена теория корней л-й
степени из отрицательных и комплексных чисел, основанная на
выведенной в 1707 г. английским математиком А. Муавром
(1667—1754) формуле
(cos ф + i sin ф)п = cos п ф + i sin n ф.
236 Глава VII
Комплексные числа
шт
Уравнения
и неравенства
с двумя переменными
Строго говоря, задача решена,
если составлено для нее уравнение,
так как это значит, что установлена
точно зависимость нескольких
величин от данных.
Д. Попа
§ 1. Линейные уравнения
и неравенства
с двумя переменными
1. Линейные уравнения
Пусть на плоскости задана прямоугольная
система координат Оху. Тогда уравнение
y = kx + b (1)
определяет прямую I (рис. 114), пересекающую
ось Оу в точке D(0; Ь) и образующую угол а с
положительным направлением оси Ох, где
tga = k. Число k называют угловым
коэффициентом прямой I.
Для построения прямой Z, заданной
уравнением (1), достаточно найти две точки этой
прямой. В качестве таких двух точек можно
0
1 &
X
Рис. 114
\
2
0
/
/
-i \w
Рис 115
§ 1 237
Линейные уравнения и неравенства
с двумя переменными
-.
взять точки пересечения прямой I с каждой из осей координат
(при /г*О, Ь*0).
На рисунке 115 изображены две прямые, заданные
уравнениями у = х-1 и у = -2х + 2.
Рассмотрим уравнение
Ах + Вг/ + С = О, (2)
где хотя бы одно из чисел А, В не равно нулю. Если Б*0, то
уравнение (2) можно записать в виде
У~ ВХ В'
т. е. в виде (1), где k = -^-, Ь = -^.
Следовательно, если В^О, то уравнение (2) представляет
собой уравнение прямой.
Если В = 0, то уравнение (2) можно записать в виде
Это уравнение прямой, параллельной оси Оу.
Таким образом, если А, В, С — заданные числа, такие, что
А и Б одновременно не равны нулю, то уравнение (2)
является уравнением некоторой прямой.
2. Линейные неравенства с двумя переменными
Задача 1. Найти множество точек координатной плоскости,
удовлетворяющих неравенству 2у-Зх-6<0.
[>Уравнение 2у-Зх-6 = 0 является уравнением прямой (рис. 116),
проходящей через точки (-2; 0) и (0; 3).
Пусть М1(х1; ух) — точка, лежащая ниже прямой / (в
заштрихованной на рисунке 116 полуплоскости), а М2— точка
с абсциссой хх и ординатой у2, лежащая на прямой I. Тогда
2у2-Зх1-6 = 0, а 2ух -Зхх-6<0,
так как ух <у2.
Таким образом, в любой точке М(х; у), лежащей ниже
прямой /, выполняется неравенство 2у-Зх-6<0. ^
Точно так же можно решить
неравенство общего вида
Ax + £z/ + C<0, (3)
где по крайней мере одно из чисел
А и Б не равно нулю.
Если В>0, то неравенство (3)
выполняется во всех точках,
лежащих ниже прямой, заданной
уравнением Ах + Ву + С = 0.
Если £<0, то неравенство (3)
справедливо в точках, лежащих
выше этой прямой.
Если £ = 0, то неравенство (3)
примет вид Ал; + С<0.
Рис. 116
238
Глава VIII
Уравнения и неравенства с двумя переменными
Рис 117
Рис. 118
Полученное неравенство равносильно неравенству х <
А
Q
при А>0 и неравенству х> — — при А<0.
Например, неравенство 2л; + 3<0 равносильно неравенству
о
jc<- —, которому удовлетворяют точки, лежащие слева от пря-
мойд: = - — (рис. 117).
В общем случае прямая Ах + Ву + С = О разделяет плоскость
на две полуплоскости, в одной из которых выполняется
неравенство (3), а в другой — неравенство
Ах + Ву + С>0. (4)
Чтобы решить неравенство (3) или (4), достаточно взять
какую-нибудь точку М1(х1; уг)9 не лежащую на прямой
Ах+Ву + С = О, и определить знак числа Ахt+ Вух+ С.
Например, неравенство Зл: — 4i/-12<0 верно в
полуплоскости, расположенной выше прямой Зх — 4у— 12 = 0, так как при
х=у = О выражение Ъх-4у-\2 отрицательно (рис. 118). Эта
прямая проходит через точки (4; 0) и (0; -3).
3. Система линейных неравенств с двумя переменными
Рассмотрим систему неравенств
(5)
предполагая, что А\ + В\>09 А|н-В|>0. Тогда первому
неравенству системы (5) удовлетворяют точки множества Ml9 лежащие
по одну сторону от прямой 1и заданной уравнением Ахх +
Аналогично второе неравенство системы (5) является
верным на множестве М2 — одной из полуплоскостей, на которые
разбивается координатная плоскость прямой 129 заданной
уравнением А2х + В2х + С2 = 0.
1
239
Линейные уравнения и неравенства с двумя переменными
Множество решений системы представляет собой
пересечение множеств Мх и М2.
Задача 2. Решить систему неравенств
[> Построим прямые 1Х и 12 (рис. 119), заданные
соответственно уравнениями х-у = 2 и jc + 3i/ = 6.
Решив систему
Г2
получим хо = 3, 1/0=1. Следовательно, прямые /2 и Z2
пересекаются в точке А(3; 1).
Так как координаты точки О(0; О) не удовлетворяют ни
одному из неравенств данной системы, то системе
удовлетворяют координаты тех и только тех точек координатной плоскости,
которые лежат ниже прямой 1Х и выше прямой 12, т. е. точки
внутри угла Мх с вершиной А (см. рис. 119). ^
Аналогично решаются системы неравенств, получаемые из
системы (5) заменой одного или двух знаков неравенств на
противоположные.
Если пересекающиеся в точке А прямые 1Х и 12 задаются
соответственно уравнениями
= 0 и
то множеством решений неравенства
(Ахх + Вху + Сх) (А2х + В2у + С2) > 0 (6)
является либо объединение одной пары Мх и М2 вертикальных
углов с вершиной А (рис. 120), либо объединение другой пары
Nx и N2 вертикальных углов с той же вершиной.
В самом деле, во всех точках каждого из множеств Мг, Nb
М2, N2 левая часть неравенства (6) принимает либо
положительные, либо отрицательные значения, а при переходе от одного из
этих множеств к соседним (через одну из прямых ll9 l2) знак
левой части этого неравенства меняется на противоположный.
240
Рис. 119
Глава VIII
Рис 120
Уравнения и неравенства с двумя переменными
Если, например, на множестве М1 левая часть
неравенства (6) положительна, то на множествах Nt и N2 она будет
отрицательной, а на М2 — положительной.
Чтобы определить, на каком из двух множеств Мг U М2
или N1l)N2 справедливо неравенство (6), достаточно
определить знак левой части этого неравенства в какой-либо точке
одного из множеств Ml9 М2, Nl9 N2.
Задача 3. Решить неравенство
{х-у-2)(х + Зу-6)>0.
> Прямые х-у-2 = 0 и х +
+ 3z/-6 = 0 пересекаются (за-
дача 2) в точке А(3; 1). В
точке ОеМ2 (рис. 121) левая
часть неравенства
положительна, и поэтому множество
его решений — объединение
множеств М2 и Мх (эти
множества заштрихованы на
рисунке 121). <4
Задача 4. Решить систему неравенств
(2х-у>49
[Зу-6х>-5.
[> Второе неравенство этой системы равносильно неравенству
2х-у<—, и поэтому исходная система равносильна системе
о
(2х-у>4,
Рис. 121
Если бы пара чисел (х0; у0) была решением полученной
системы, то число 20 = 2х0-у0 удовлетворяло бы двум условиям zo>4
5
и zo<—, что невозможно.
о
Следовательно, исходная система неравенств не имеет
решений. М
Задача 5. Найти множество точек координатной
плоскости, удовлетворяющих системе неравенств
х>09
У>0,
2|/-дг-К0.
[> Первым двум неравенствам системы удовлетворяют все
точки, у которых обе координаты неотрицательны, т. е. точки,
лежащие в I квадранте (включая точки положительных полуосей
Ох и Оу).
§ 1 241
Линейные уравнения и неравенства с двумя переменными
Чтобы решить неравенство x + i/-2<0, рассмотрим прямую
х+у-2=0 (рис. 122). Эта прямая проходит через точки (2; 0)
и (0; 2). При х = 0, у = 0 неравенство л; + 1/-2<0 является
верным. Следовательно, неравенству jc + i/-2<0 удовлетворяют все
точки, лежащие ниже прямой х+у-2=0 и на самой
прямой. В результате получаем, что первым трем неравенствам
исходной системы удовлетворяют точки, расположенные
внутри и на границе треугольника с вершинами О(0; 0), А(2; 0),
Б(0; 2).
Решим, наконец, последнее неравенство системы, т. е.
неравенство 2у-х-1<:0. Рассмотрим прямую 2у-х-1=0.
Полагая х = 0, находим у = 0,5. Таким образом, прямая проходит
через точку С(0; 0,5).
Найдем точку D пересечения пря- ч у
мой 2у-х-1=0 с прямой х + у-2 = 0.
Для этого решим систему уравнений
[2у-х-1 = 0.
Складывая уравнения этой
системы, получаем Зу-3 = 0, откуда у=1.
Подставляя у=1 в первое уравнение
системы, находим х=1. Значит,
точка D имеет координаты х = у=1 (см.
рис. 122).
Так как неравенству 2у-х-К0
удовлетворяют точки, лежащие ниже
прямой 2у — х-1 = 0 (точка О(0; 0) удовлетворяет этому
неравенству), то исходной системе неравенств удовлетворяют все
точки, лежащие внутри и на границе четырехугольника OADC
(см. рис. 122). <4
Рис. 122
Задача 6. Пусть М — множество точек плоскости с коор*
динатами (х; у), таких, что числа Зх9 2у и 9-у являются
длинами сторон некоторого треугольника. Найти площадь фигуры М.
[> По свойству длин сторон треугольника справедливы
неравенства, образующие систему
0<Зх<2у + 9-у,
0<2у<Зх + 9-у,
0<9-у<Зх + 2у.
Эта система равносильна
системе неравенств
у-Зх + 9>0,
у-х-3<09
242
х>0, у>09 у<9.
Глава VIM
Рис. 123
Уравнения и неравенства с двумя переменными
Условиям полученной системы удовлетворяют точки
треугольника ABC (рис. 123), где А(0; 3), Б(6; 9), С(3; 0). Площадь S
фигуры М равна S1-S2-S3, где IS1 — площадь трапеции OABD,
D(6; 0), S2 — площадь треугольника ОАС, Ss — площадь
тре^ ^ ^
угольника BCD. Так как
97
= f, toS=18. *
-^(3 + 9)6 = 36, S2 = ^, £3 = ^ -3-9 =
Задача 7. Найти все пары целых чисел х9 у, для которых
верны неравенства
Зу-х<Ъ, x + i/>26, Зх-2у<46.
> Умножая первое неравенство на 3 и складывая с третьим,
получаем 7у<619 откуда у<8—. Умножая второе неравенство
на -3 и складывая с третьим, находим -5i/<-32, откуда
2
у>6 —. Итак, 6<у<9. Исходной системе удовлетворяет только
о
значение i/ = 8, и тогда х = 20.
Ответ. х = 20, у = 8. <4 СП
Упражнения
1. Записать уравнение прямой, проходящей через точки А и В:
1) А(1; 0), В(0; 2); 2) А(-3; 0), В(0; 4);
3) А(-2; 0), В(0; -1); 4) А(5; 0), В(0; -6).
2. Найти множество точек координатной плоскости,
удовлетворяющих неравенству:
1) Зу-2х + 4<0; 2) х-4у>0.
3. Изобразить на плоскости множество точек (х; у)9
координаты которых удовлетворяют системе неравенств:
D J
3)
\x-2y<
.y-2x>
x + y>2
x-y<2
x-3y>
1,
l;
,
9
-2;
2) 1
4)
x-3y<3,
_3x-2y<6;
y>0,
2y-x<6,
^2x-y<-2.
4. Найти все пары (х; у) натуральных чисел х и у, которые
являются решениями системы неравенств:
1)
2)
x-y-2<0,
x + 2i/-9>0,
-2i/ + 3>0; [x-2y + 4>0.
5. Изобразить на координатной плоскости Оху множество
точек, координаты которых удовлетворяют неравенству:
1) (х-у + 3)(х + у-1)>0; 2) (2х-у-4)(2х + у + 2)<0;
3) х2-ху-2у2>0.
§ 1 243
Линейные уравнения и неравенства с двумя переменными
6. Пусть М — множество точек плоскости с координатами
(х; у)у таких, что числа 2х, у и 3-х являются длинами
сторон некоторого треугольника. Найти площадь фигуры М.
7. Пусть М — множество точек плоскости с координатами
(х; у), таких, что числа Зх9 у и 18 — 2у являются длинами
сторон некоторого треугольника. Найти площадь фигуры М.
8. Найти все пары целых чисел х9 у, для которых верны
неравенства:
1) Зу-5х>16, Зу-х<44, Зх-у>1;
2) Зу-2х<45, х + у>24, Зх-у<3.
§ 2. Нелинейные уравнения и неравенства
с двумя переменными
f^l 1. Нелинейные уравнения
Задача 1. Найти множество точек координатной
плоскости, удовлетворяющих уравнению:
2)
3)
[> 1) Уравнение можно записать в виде (х-у)(х + у) = О, откуда
следует, что либо х-у = О, либо х + у = О. Заметим, что данное
уравнение равносильно уравнению |jc| = |i/|. Поэтому множество
точек, удовлетворяющих уравнению х2-у2 = 0,— пара
пересекающихся прямых х = у и у = -х.
2) Разложим левую часть уравнения на множители:
2х2 + Ъху - Зу2 - 2х + у = 2х2 - ху + Зу (2х - у) - (2х - у) =
Искомое множество — пара пересекающихся прямых
2х-1/ = 0 и лг + Зг/-1 = 0.
3) Преобразуем левую часть уравнения, используя метод
выделения полного квадрата:
Это уравнение имеет единственное решение х = 29 i/=-3,
т. е. множество решений уравнения — точка (2; -3). ^
Пусть на координатной плоскости Оху выбрана точка
А(а; 6), М(х; у) — произвольная точка этой же плоскости, R —
расстояние от точки М до точки А. Тогда
Если задано число R>0, то данное уравнение — это
уравнение окружности С радиуса R с центром в точке А(а; Ь).
244 Глава VIII
Уравнения и неравенства с двумя переменными
Задача 2. Найти множество точек координатной
плоскости, удовлетворяющих уравнению:
2)
t> 1) Применяя метод выделения полного квадрата, получаем
3)2-16 = 09 откуда
+ (i/-3)2=16.
Следовательно, множество решений данного уравнения —
окружность радиуса 4 с центром (-2; 3).
2) Преобразуем уравнение:
у(2х-у)(4х2
у(2х-у)«х
Так как равенство (х + у)2 + Зл:2 = 0 выполняется только при
х = 0 и у = 0у то множество решений исходного уравнения —
совокупность прямых у = 0 и 2х — у = 0. ^
Рассмотрим примеры уравнений с двумя переменными,
содержащих знак модуля.
Задача 3. Найти множество точек координатной
плоскости, удовлетворяющих уравнению:
2) \х\ + \у\~2;
3) \х\ + 2\у\ + \2у-3х\=12.
[> 1) Уравнение равносильно совокупности двух систем:
|
1У>0, [у<0.
Первой системе удовлетворяют точки, принадлежащие
биссектрисе II координатного угла, второй системе — точки,
принадлежащие биссектрисе III координатного угла (рис. 124).
Рис 124
Рис. 125
§ 2 245
Нелинейные уравнения и неравенства с двумя переменными
2) Если х>0, у>0, то
уравнение можно записать в виде х + у =
= 2. Множество решений этого
уравнения — отрезок АВ, где А(2; 0),
Б(0; 2).
Так как |-х| = |х|, \-у\ = \у\, то
множество решений исходного
уравнения — граница квадрата
ABCD (рис. 125), где С(-2, 0),
D(0; -2).
Замечание. Для
нахождения координат вершин квадрата
нужно в уравнении |x| + |i/| = 0 взять
х = 0 (и тогда \у\ = 2, т.е. у = ±2), а
затем у = 0 (тогда х = ±2).
3) Множество решений уравнения — граница
многоугольника с вершинами в точках, лежащих на прямых х = 0, у=0,
i/= —jc. Найдем эти вершины. Если х = 0, то из данного
уравнения следует, что |i/| = 3, т. е. у = ±3.
3 9
Если у = 0, то |х| = 3; если у=-^х, то |х| = 3, \у\=-^. Лома-
ная — граница многоугольника АХСХВХА2С2В2У где Ах(-3; 0),
А2(3; 0), Бх(0; -3), В2(0; 3), С^-3; -|j, C2^3; |),
изображена на рисунке 126. ^ ^^31
ИИ1 Задача 4. Найти все пары действительных чисел (jc; i/),
для которых справедливо равенство
\ ./ _ г-
(1)
-3
с
А
0
-3
fin ^^
1
J
/
/3
Рис.
х
126
[> Равенство (1) имеет смысл, если выполнены условия
у>0, y-x>0, xVy-l>0,
Пусть
Тогда равенство (1) можно записать в виде
). (2)
(3)
(4)
(5)
Так как 6>0, с>1 (условия (5)), то равенство (6)
является верным тогда и только тогда, когда 6 = 0, с=1. Из равенст-
■
где
при выполнении условий (2).
Из равенства (4) и условий (5) следует, что
Ь = ас>а9 и поэтому
246
Глава VIII
Уравнения и неравенства с двумя переменными
/о* » (xVy-l = 09
ва (3) получаем систему уравнении \ ,— откуда на-
ходим \x + y-2\ft=0,
J х32х+1 = 0, (х-1)(х2 + х-1) = 0.
х2 *'
Если х=1, то у=1 и условие у-х>0 не выполняется. Ес-
9 Л V5-1 Л Г-
ли х^н-х- 1 = 0, то х=—-—, так как х>0 (х\у = 1).
m 14 2 3 + V5 „ „
Тогда у = — = = = —-—. Наиденная пара чи-
х2 (V5-1)2 3-V5 2
сел х, у удовлетворяет условиям (2) и является решением
данного уравнения.
Ответ. (-^; ^Y^j- < «"
В 2. Нелинейные неравенства
Если А (а; Ь) — точка координатной плоскости, i?>0, то
неравенству
(x-a)2 + (y-b)2<R2
удовлетворяют все те точки, которые находятся от точки А на
расстоянии, меньшем R, т. е. все точки (и только они),
расположенные внутри окружности С радиуса R с центром в точке
А(а; Ь).
Аналогично множество решений неравенства
(x-a)2 + (y-b)2>R2
есть множество точек, лежащих вне окружности С.
Задача 5. Найти множество точек координатной
плоскости, удовлетворяющих неравенству:
2) 9х2 + 9у2 + 6х-12у-76>0.
1) Преобразуем неравенство, выделяя полный квадрат:
Множество решений этого неравенства — множество точек,
лежащих внутри окружности радиуса 3 с центром ( — ; --о г
Искомое множество решений неравенства — множество
точек, лежащих на окружности радиуса 3 с центром (--«; ■« )
и вне этой окружности. ^
§ 2 247
Нелинейные уравнения и неравенства с двумя переменными
Задача 6. Найти множество
точек координатной плоскости,
удовлетворяющих неравенству:
1) |*| + М>2;
2) х2 + у2<4\х\;
х-2Ъ 1
х2+у2-62Ь 2«'
[> 1) Пусть х^О, у>0, тогда
неравенство примет вид х + у>2.
Этому неравенству
удовлетворяют точки первого квадранта,
лежащие выше прямой х + у = 2 (рис. 127)
и на этой прямой (вне треугольника
АОВ, гдеА(2; 0), В(0; 2)).
Так как |-jc| = jc, \-y\ = y, то множество решений
исходного неравенства — множество точек, лежащих на сторонах
квадрата ABCD и вне этого квадрата.
2) Если х^09 то неравенство можно записать в виде
Рис. 127
Полученному неравенству удовлетворяют точки множества Ег,
лежащие на окружности радиуса 2 с центром (2; 0) и внутри
этой окружности.
Аналогично если х<0, то исходное неравенство можно
записать в виде
а множество Е2 решений этого неравенства — множество точек,
лежащих на окружности радиуса 2 с центром (-2; 0) и
внутри этой окружности. Следовательно, множество Е решений
исходного неравенства — объединение множеств Е1 и Е2, т. е.
3) Данное неравенство, равносильное неравенству
является верным в тех и только в тех точках плоскости Оху,
которые лежат вне круга радиуса 12 с центром (13; 0) и
внутри круга радиуса 25 с центром в точке О. ^
3. Системы нелинейных уравнений
Решение системы уравнений с двумя неизвестными
р(х; у)-0, (1)
[G(x; y) = 0 (2)
геометрически можно истолковать как отыскание координат
точек пересечения линий Г1 и Г2, заданных уравнениями (1) и (2).
Построив эти линии на клетчатой бумаге и найдя
координаты точек пересечения линий 1\ и Г2, можно найти
приближенные решения системы.
248
Глава VIII
Уравнения и неравенства с двумя переменными
Ук
Рис. 128
Задача 7. Решить систему уравнений
Гл:2-ьу2-4л:н-б1/=13,
[
[> 1) Первое уравнение системы, записанное в виде
задает окружность радиуса V26 с центром (2; -3) (рис. 128).
Второе уравнение системы, записанное в виде
11-Зх 3(х-2)-5
= -3 +
х-2 ~ х-2 " ' х-2'
задает гиперболу. Окружность и гипербола, изображенные на
рисунке 128, имеют четыре общие точки А(1; -8), Б(-3; -4),
С(3; 2), £>(7; -2).
Следовательно, данная система уравнений имеет четыре
решения (1; -8), (-3; -4), (3; 2), (7; -2). <4
Замечание. Для аналитического решения системы
прибавим к первому уравнению удвоенное второе, получив
уравнение (х + у)2 + 2(х + у)-35 = 09 откуда следует, что либо х + у = Ь,
либо # + !/ = -7. Исключив из системы одно из неизвестных,
получим квадратное уравнение относительно другого неизвестного.
Задача 8. Решить систему уравнений
[х2 + у2 + 2х- 6у + 5 = 0.
t> Первое уравнение системы, записанное в виде у = (х-1)29
задает параболу. Второе уравнение системы, записанное в виде
(jc+1)2 + (i/-3)2 = 5, задает окружность радиуса V^ с центром
(-1; 3).
Окружность и парабола, изображенные на рисунке 129,
имеют две общие точки А(0; 1) и В(х2; у^ где лг2~-1,3,
1/2*5,3.
Ответ. Xx = 0, i/i = l; х2~-1,3, у2^5,3. <4
§ 2
249
Нелинейные уравнения и неравенства с двумя переменными
4. Системы нелинейных неравенств
Задача 9. Решить систему неравенств
(х2 + 9у2-18у<0,
D> Складывая первое неравенство со вторым, умноженным на 3,
находим
*2-6jq/ + 9i/2 + 6(:x;-3i/) + 9<0, или ((х-Зу) + З)2<О,
откуда х-Зу + 3 = 0. Подставляя х = 3у — 3 в исходную систему,
получаем систему неравенств
которую можно записать в виде
2у2-4у+1>0,
откуда следует, что 2у2 — £у + 1 = 0. Решив систему уравнений
найдем два ее решения, которые являются решениями
исходной системы неравенств.
VV2 V2/ V V2 V2/
Задача 10. Найти все такие пары целых чисел х9 у,
которые удовлетворяют системе неравенств
[> Запишем данную систему так:
Ь + |>|х2-2х| (1)
[у<2-\х-1\. (2)
Так как \х2-2х\>09 |х-1|>0, то из неравенств полученной
системы следует, что
\ (3)
Целыми числами, удовлетворяющими неравенству (3),
являются лишь 0 и 1, поэтому система (1), (2) может иметь
целые решения только при у = 0 и у=1.
1) Если у = 0, то система (1), (2) примет вид
Второму из этих неравенств удовлетворяют целые числа О,
1 и 2. Проверка показывает, что первому неравенству удовле-
250 Глава VIH
Уравнения и неравенства с двумя переменными
творяют лишь 0 и 2. Следовательно, пары чисел xl = 0, г/х = 0 и
дг2 = 2, у2 = 0 образуют решения исходной системы неравенств.
2) Если у=19 то система (1), (2) приводится к виду
Второму неравенству этой системы удовлетворяет
единственное целое число х = 1, которое является также и решением
первого неравенства.
Задача 11. Изобразить на координатной плоскости Оху
фигуру Ф, заданную системой неравенств, и найти площадь S
этой фигуры:
2) [х2 + у2<4,
\(х-1)2 + у2>1.
[> 1) Неравенство х2-\-у2<4 задает множество точек, лежащих
внутри окружности с центром в начале координат и радиусом 2,
а неравенство х + у>2 — множество точек, расположенных
выше прямой х + у = 2. Эта прямая пересекает окружность в
точках А(— 2; 0) и В(0; 2), а фигура Ф представляет собой сегмент
(рис. 130). Искомая площадь S равна разности площадей
четверти круга (jSx) и треугольника АОВ (S2).
Так как S1 = n, S2 = 29 то S = rc-2.
2) Фигура Ф — это множество точек, лежащих внутри
окружности с центром в точке О(0; 0) и радиусом 2, но вне
окружности с центром в точке (1; 0) и радиусом 1 (рис. 131).
Значит, площадь фигуры Ф равна £ = 4я-я = 3я.
Ответ. 1) 5 = л-2; 2) 5 = 3я. <4
/
А
-я
\
в
7
/
0
У
2*\
J
2 х
-^*+у2=4
Рис 130
Нелинейные уравнения и неравенства с двумя переменными
Задача 12. Дана система
неравенств
{(у-Зх-2)(Зу-
Найти площадь фигуры,
координаты точек которой
удовлетворяют:
а) первому неравенству
системы;
б) первым двум
неравенствам системы; Рис 132
в) всем трем неравенствам системы.
[> а) Первому неравенству (см. задачу 6) удовлетворяют точки,
лежащие в квадрате (рис. 132) с вершинами А(— 2; 0), В(0; 2),
С(2; 0), D(0; -2). Площадь этого квадрата Sl = 8.
б) Второму неравенству, которое можно записать в виде
А/
-2\
^*
2
4
Ф
/ "2s
В
D
/
Е
С
\ х
удовлетворяют точки, лежащие вне круга радиуса 2 с центром
в точке Е(2; 2).
Площадь закрашенного на рисунке 132 сегмента равна
я-2, а площадь фигуры, координаты точек которой
удовлетворяют первым двум неравенствам, равна S2 = 8 — (я — 2) = 10-71.
в) Прямые у-Зх-2 = 0 и Зу-х + 2 = 0 пересекаются в
точке F(-l; -1) и проходят соответственно через точки Б и С.
Третьему неравенству удовлетворяют точки двух
вертикальных углов с вершиной F, один из этих углов — угол,
образуемый лучами FB и FC и содержащий точку О (см. рис. 132).
Пусть jS3 — площадь фигуры, координаты точек которой
удовлетворяют всем трем неравенствам системы, S4 — сумма
площадей треугольников ABF и CDF. Тогда S4 = — S1=4,
Ответ, а) 8; б) 10-я; в) 6-я. 4 Г"Ч
вИ Задача 13. Дана система неравенств
\я*+у*<4\х\,
\х\ + \у\>2,
Найти площадь фигуры, координаты точек которой
удовлетворяют:
а) первому неравенству системы;
б) первым двум неравенствам системы;
в) всем трем неравенствам системы.
[> а) Первому неравенству, равносильному совокупности двух
неравенств (jc-2)2 + i/2<4, (jc + 2)2 + i/2<4, удовлетворяют
координаты точек, находящихся внутри и на границах двух кругов
252
Глава VIII
Уравнения и неравенства с двумя переменными
Рис. 133
радиуса 2 с центрами (-2; 0) и (2; 0) (рис. 133). Площадь этой
фигуры Sx = 2 • я • 22 = 8л.
б) Второму неравенству удовлетворяют координаты точек
(см. задачу 6), расположенных вне и на границе квадрата с
вершинами (-2; 0), (0; 2), (2; 0), (0; -2). Площадь S2 фигуры Ф2,
координаты точек которой удовлетворяют первым двум
неравенствам системы, равна S1-S09 где So — половина площади
круга радиуса 2, т. е. 52 = 8я-2я = 6я.
в) Третье неравенство можно записать в виде
(х-4)2-у2>0, или {х + у-4)(х-у-4)>0.
Этому неравенству удовлетворяют координаты точек,
лежащих внутри и на границе одной из двух пар вертикальных
углов, образующихся при пересечении прямых х + у — 4 = 0 и
x-i/-4 = 0. Так как (0; 0) — решение третьего неравенства
системы, то этому неравенству и первым двум неравенствам
удовлетворяют координаты точек фигуры Ф3, лежащих внутри
прямого угла с вершиной (4; 0), таких, что х<4. Площадь Ss фи-
2
гуры Ф3 равна — S2 + ст0, где а0 — площадь прямоугольного тре-
3
угольника с вершинами (2; 2), (4; 0), (2; -2), т. е. ао = 4.
Следовательно, £3 = 4я + 4.
Ответ, а) 8я; б) 6я; в) 4я + 4. М
Задача 14. Найти площадь фигуры Ф, которая задается на
координатной плоскости системой неравенств
2 + у2>109
(Зх-2у)(Зу-х+10)>0.
§ 2 253
Нелинейные уравнения и неравенства с двумя переменными
D> Первое неравенство системы определяет множество точек,
лежащих вне и на границе круга с центром в точке О(0; 0) и
радиусом Vl() (рис. 134).
о
Решив второе неравенство, получим <х<4. Поэтому
3
второе неравенство системы задает вертикальную полосу,
лежащую между прямыми х = - — и х = 4 (включая и точки этих
прямых).
Наконец, третьему неравенству системы удовлетворяют
точки множества М, которое состоит из двух острых
вертикальных углов, образованных прямыми Зх-2у = 0 и Зу-х+
+ 10 = 0 (включая и точки этих прямых), так как в точке (4; 0),
принадлежащей множеству М, левая часть этого неравенства
положительна. Множество М можно увидеть на рисунке 134,
где указанные прямые обозначены 1Х и 12.
о
Прямая 1Х пересекается с прямыми х = -— их = 4в точках
-—; -41 и Б(4; 6), а прямая 12 пересекается с теми же пря-
(о go \
-—; -~5") и С (4; -2). Далее, прямая 12
касается окружности л:2н-г/2 = 10, так как система уравнений
имеет единственное решение (1; -3); наконец, прямая 1Х
проходит через центр этой окружности.
Рис. 134
254
Глава VIII
Уравнения и неравенства с двумя переменными
Итак, фигура Ф — это трапеция ABCD, из которой удален
полукруг радиуса \flO с центром в точке О. Искомая площадь
2
Ответ.
740
27
-5л.
Задача 15. На координатной плоскости рассматривается
фигура М, состоящая из всех точек, координаты которых
удовлетворяют системе неравенств
26
х-25
х2+у2-625
Изобразить фигуру М и найти ее площадь.
t> Второму неравенству системы удовлетворяют координаты
точек (задача 6), лежащих внутри круга радиуса 25 с центром в
точке О и вне круга радиуса 12 с центром (13; 0).
Нелинейные уравнения и неравенства с двумя переменными
Рис. 135
255
Первое неравенство системы имеет смысл, если ху>0, т. е.
для точек I и III квадрантов. Считая условие ху>0
выполненным, рассмотрим два возможных случая: у<2х, у>2х.
1) Если у<2х и JO/X), то первое неравенство является вер-
\у<2х9
ным. Система неравенств |л:1/>о задает множество точек I и
III квадрантов, лежащих ниже прямой у = 2х (рис. 135).
2) Если у>2х и ху>0, то первое неравенство системы
равносильно каждому из неравенств
XD
Полученное неравенство при условии у>09 ху>0
определяет множество тех точек I квадранта, которые заключены
12
между прямыми у=2х и у= — х, и точек III квадранта, кото-
5
рые заключены между прямыми у = 2х и у= — х.
3
12
Заметим, что прямая у = — х имеет единственную общую
5
точку с окружностью (х-13)2 + у2 = 144 и, следовательно,
касается этой окружности. Площадь S фигуры Ф равна 'S1-S2 = S3,
где jSx — сумма площадей двух секторов (им соответствуют
12 " 3 \
центральные углы arctg— и arctg — j, a S2 — площадь
полукруга радиуса 12.
Ответ. ^ (arctg ^ + arctg |Л-72я.
2 \ о о /
Упражнения
,9. Найти множество точек координатной плоскости,
удовлетворяющих уравнению:
1) 4х2-9у2 = 0;
2) 2j2 2
3) 2
4) 3x2 + 3i/2-6:x;+12i/+10 = 0;
5) х2-2ху + 2у2-4у + 4 = 0;
6) ху + х-у-1 = 0; 7) у + \у\ = х; 8) у = х\у\.
10. Найти множество точек координатной плоскости,
удовлетворяющих уравнению:
1) 2* + Ы = 0; 2) |х-1| + |у + 2|-1; 3) 2|х| + |у| + |2х-3у| = 12.
|11.] Найти все пары действительных чисел, для которых
справедливо равенство:
256 Глава VIII
Уравнения и неравенства с двумя переменными
12. Найти множество точек координатной плоскости,
удовлетворяющих неравенству:
1) 2х2 + 2у2 + 2х-6у-13>0; 2) х2+у2<4\у\;
3) \х+1\ + \у-2\>2; 4) ^lZ^x+4^+1 <Q
х2+у2-169
13. Найти площадь фигуры, заданной на координатной
плоскости неравенством:
1) (х2 + У2 + 2х + 2у)(4-х2-у2)>0;
2) (х2
3) 2|
14. Решить графически систему уравнений:
1)
3)
2)
15. Решить систему неравенств:
0, 2) f
9jc2-12jc-8i/<0; [л:z/+ z/ч- К 0.
16. Найти площадь фигуры, заданной на координатной
плоскости системой неравенств:
4у-6, 2)
3) Г|х + 1| + |у|<2, 4)
[
5)
17. Найти все пары целых чисел х, у, удовлетворяющих
системе неравенств
Г 2 х2 + 2 г/2 - 12 jc + 2 0 г/ + 6 5 < 0,
[
18. Дана система неравенств
Г1*1+Ы<з,
1х2 + у2>3(2у-2х-3),
Найти площадь фигуры, координаты точек которой
удовлетворяют:
а) первому неравенству системы;
б) первым двум неравенствам системы;
в) всем трем неравенствам системы.
§ 2 257
Нелинейные уравнения и неравенства с двумя переменными
19. Дана система неравенств
\х\ + \у\<4,
Найти площадь фигуры, координаты точек которой
удовлетворяют:
а) первому неравенству системы;
б) первым двум неравенствам системы;
в) всем трем неравенствам системы.
[20J Дана система неравенств
\\х\ + \у\>2,
[х2-у2
Найти площадь фигуры, координаты точек которой
удовлетворяют:
а) первому неравенству системы;
б) первым двум неравенствам системы;
в) всем трем неравенствам системы.
|2lT] Дана система неравенств
\\х\ + \у\>2,
[
Найти площадь фигуры, координаты точек которой
удовлетворяют:
а) первому неравенству системы;
б) первым двум неравенствам системы;
в) всем трем неравенствам системы.
J22.1 Найти площадь фигуры, заданной на координатной
плоскости системой неравенств:
1)
3) f4
[
2) [4г/2-25<0,
4)
<25,
16*4-И
>ху,
>2х-у,
5)
258 Глава VIII
6)
Уравнения и неравенства с двумя переменными
§ 3. Уравнения и неравенства с двумя
переменными, содержащие параметры
IH 1. Уравнения с параметрами
Задача 1. Найти все значения а, при которых существует
ровно одна пара действительных чисел (х; у)9 удовлетворяющая
уравнению
[> Запишем уравнение в виде 2(х+ 1)2 + 2(у-2)2 = а, откуда
следует, что исходное уравнение имеет единственное решение (-1; 2)
при а = 0. М
Задача 2. Найти все значения а, при которых найдется
хотя бы одна пара действительных чисел (х; у),
удовлетворяющая уравнению
2 ^^ 0. (1)
[> Будем рассматривать уравнение (1) как квадратное
относительно х. Найдем дискриминант этого уравнения:
D(y; а) = (2-Ьу)2-4(Ьау2 + 2ау-Ц-у + 2) =
= 5(5-4a)i/2 + 2(5-4a)i/-4.
Хотя бы одна пара действительных чисел (х; у),
удовлетворяющая уравнению (1), существует тогда и только тогда,
когда неравенство D(y; a)>0, т. е. неравенство
5(5-4a)i/2 + 2(5-4a)i/-4>0 (2)
имеет решения.
Возможны три случая:
В первом случае неравенство (2) не является верным. Во
втором случае это неравенство имеет решения, так как у
параболы z = ay2 + $y + y, где а>0, имеются точки, расположенные
выше оси Оу (ветви параболы направлены вверх). Наконец,
в третьем случае, т. е. при а> —, неравенство (2) имеет реше-
4
ния тогда и только тогда, когда дискриминант Dx квадратного
трехчлена, стоящего в левой части этого неравенства,
неотрицателен:
JD1(a) = 4(5-4a)2-h80(5-4a) =
-|-)(a--^)>0, откуда
64(a-f)(a-f)>0. (3)
Действительно, если а<0, то ветви параболы z = ay2 + Ру + у
направлены вниз и хотя бы одна точка параболы лежит выше
оси Оу (или на этой оси) тогда и только тогда, когда Dx = р2 —
§ 3 259
Уравнения и неравенства с двумя переменными,
содержащие параметры
-4ау>0. При а> — решениями неравенства (3) являются
значения а, такие, что а>—.
4
Ответ, а < —, а > —г-. Щ
4 4
2. Система уравнений с параметрами
Задача 3. Найти значения а, при которых система
уравнений
(4)
имеет действительные решения при любом значении 6.
[> Подставляя у=ах+Ъ в уравнение х2 — у2 = 19 получаем
х2 (1 - а2) - 2аЪх - (1 + б2) = 0. (5)
Система (4) имеет действительные решения при любом
значении 6 тогда и только тогда, когда уравнение (5) имеет
действительные корни, так как уравнение (5) вместе со вторым
уравнением системы (4) образует систему, равносильную
системе (4).
Если |а|^1, то уравнение (5) является квадратным, а его
дискриминант D = 4(l + 62-a2).
Пусть |а|<1, т. е. —1<а<1, тогда 1—а2>0, откуда
следует, что Z>>462>0, и поэтому уравнение (5) имеет
действительные корни при любом значении 6. Пусть |а|=1, тогда при 6 = 0
уравнение (5) не имеет корней. Пусть, наконец, |а|>1, тогда
D<0 при 6 = 0. Итак, если |а|>1, то найдется такое значение Ь
(именно 6 = 0), для которого система (4) не имеет
действительных решений.
Ответ. -1<а<1. ^
Задача 4. Найти все значения а, при которых система
уравнений
Г log2 (3 - х + у) + 3 = log2 (25 - 6х + 7у),
[ 2 (2)2 2
имеет ровно два решения.
[> Первое уравнение системы равносильно уравнению
8(3-jch-i/) = 25-6jch-7i/, или уравнению у = 2х+1, если у + 3-
— х>0, откуда следует, что х> — 4. Тогда второе уравнение
принимает вид 2jcH-3 = (jc-2a)2H-aH-2x, или
и задача сводится к нахождению тех значений а, при которых
полученное уравнение имеет ровно два корня хх и х2, такие,
что х1>-4 и х2>-4.
Обозначим f(x) = x2-4ax + 4a2 + a-3, D=16a2-4(4a2 + a-3)=
= 4(3-а) и воспользуемся тем, что указанные условия
выполняются тогда и только тогда, когда 2)>0, /(-4)>0, хо>-4, где
260 Глава VIII
Уравнения и неравенства с двумя переменными
хо = 2а — абсцисса вершины параболы y = f(x). Итак, D =
= 4(3-а)>0, /(-4) = 4а2 + 17а+13 = 4^а+^)(а + 1)>0, 2а>-4,
откуда -1<а<3.
Ответ. -1<а<3. А
Задача 5. Найти все значения а, при которых система
уравнений
\1х2+у2 + 64- 16x + V*2 + i/2 + 36 + 12i/ = 10,
имеет единственное решение.
|> Первому уравнению системы удовлетворяют координаты
точки М(х; у), такой, что сумма расстояний от точки М до точек
Мх(8; 0) и М2(0; -6) равна 10. Так как расстояние МХМ2
равно 10, то точка М должна принадлежать отрезку МХМ2 (в
противном случае сумма указанных расстояний была бы больше
10 согласно свойству сторон треугольника).
Итак, первому уравнению системы удовлетворяют
координаты точек отрезка М1М2> и только они.
Второму уравнению системы удовлетворяют координаты
точек окружности радиуса \а\ с центром О(0; 0). Эта
окружность имеет с отрезком МХМ2 единственную общую точку
в следующих случаях:
1) окружность касается отрезка М1М2; в этом случае \а\ =
-ft, где /* = — = —;
2) окружность пересекает отрезок МХМ2 в одной точке;
в этом случае ее радиус должен быть больше катета ОМ2> но не
превышать катета ОМХ прямоугольного треугольника ОМгМ2,
т.е. 6<|а|<8.
Ответ. -8<а<-6, а — Щ-, а=Щ-, 6<а<8. А
О О
Задача 6. Найти все значения а, при которых система
уравнений
имеет ровно два действительных решения.
t> Множество решений первого уравнения данной системы,
полученное при решении задачи 3 (3) из § 2,— граница
шестиугольника, изображенного на рисунке 126. Множество решений
второго уравнения системы — окружность радиуса \[а с
центром (0; 0).
Данная система имеет ровно два решения в следующих
случаях:
1) окружность касается отрезков А1В2 и А2В19 тогда Va= -т=,
§ 3 261
Уравнения и неравенства с двумя переменными,
содержащие параметры
2) радиус окружности равен расстоянию от точки О до
точек Сх и С2, тогда а==з2 + (^) =~Т~-
Ответ. f, -Ц^. А
Задача 7. Найти все значения а, при которых система
уравнений
имеет хотя бы одно решение.
t> Из первого уравнения системы находим
i/=i(*2 + 4x + 3). (6)
Так как х2 + 4х + 3 = (х + 2)2 -1 > -1, то из равенства (6)
следует, что y>~jj-
Поэтому задача сводится к нахождению тех значений а,
при которых второе уравнение системы имеет хотя бы один
корень, удовлетворяющий условию у>——»
3
Рассмотрим квадратный трехчлен
а2 -2а. (7)
Его дискриминант D = (5-2а)2-4(а2-2а) = 25- 12а>О при
25
а < —. Чтобы второе уравнение имело хотя бы один корень, не-
25
обходимо выполнение условия а < —.
Пусть у0 — абсцисса вершины А
параболы (7), изображенной на
рисунке 136. Тогда у0 = g~ = а — —, и если
выполняется условие а < —, то
12
12
1
3'
т. е. вершина А параболы расположена
левее прямой у = —— (см. рис. 136).
3
Квадратный трехчлен (7) имеет
корень у2, такой, что у2 > — — тогда и толь-
3
T* е-
ко тогда, когда ^f""^
Рис. 136
откуда
9a2-12a-14<0.
Ответ. ■§• -V2<a<f +V2.
3 3
262
Глава VIII
Уравнения и неравенства с двумя переменными
Задача 8. Найти все значения а, при которых система
уравнений
имеет хотя бы одно решение.
> Данная система равносильна системе
х>0,
откуда
x2 + 2(a-l)x + a2-9a-6 = 0. (8)
Уравнение (8) имеет действительные корни хх и х2 тогда и
только тогда, когда D = 4((a-l)2-(a2-9a-6)) = 28(a + l)>0, т. е.
при а > - 1, причем
Данная система и равносильная ей имеют хотя бы одно
решение, если уравнение (8) имеет хотя бы один положительный
корень, а это условие равносильно тому, что наибольший из
корней этого уравнения х2>0.
Таким образом, задача
свелась к решению
неравенства V7(a+l)>a-l, для
решения которого построим
графики функций i/ = V7(a+l) и
у=а~1 (рис. 137). Из
рисунка видно, что решения этого
неравенства образуют
промежуток [-1; а0), где а0 —
положительный корень уравнения
V7(a+l) = a-l. Отсюда
получаем
(а-1)2, а2-9а-6 = 0, ао =
Ответ. -
Рис. 137
3. Неравенства и системы неравенств с параметрами
Задача 9. Найти все значения параметра а, при которых
существует хотя бы одна пара действительных чисел (х; у),
удовлетворяющая неравенству х2-6х + у2 + 4у<:а.
[> Исходное неравенство, равносильное неравенству
имеет хотя бы одно решение тогда и только тогда, когда
а+13>0, т. е. при а>-13. <4
§ 3
263
Уравнения и неравенства с двумя переменными,
содержащие параметры
Задача 10. Вершины А, В, С параллелограмма ABCD
имеют соответственно координаты (-2; -3), (1; 3), (6; 1). Найти
все значения а, для которых координаты вершины D
являются решением системы неравенств
[бх-2у + 7а>0.
О Пусть х0, у0 — координаты вершины D. Тогда из равенства
АВ=Т>С, гдеАБ = (3; 6), ~DC = (6-x0; 1-у0), следует, что хо = 3,
у0 = -5. Подставляя х = 3, i/ = -5 в систему неравенств,
получаем - 4 < а < —. М
Задача 11. Найти все значения а, при которых множество
решений системы неравенств
(х2-(а-2)х-2-у<0,
[2х+у-а<0
содержит отрезок [—1; О] оси Ох.
[> Подставив в данную систему i/ = 0, получим
\х2-(а-2)х-2<0, (9)
[2х-а<0. (10)
Множество решений неравенства (10) — луч х<—, а отре-
зок Д = [-1; 0] принадлежит этому лучу тогда и только тогда,
когда -^>0, т. е. при а>0.
Множество решений неравенства (9) — отрезок А1 = [л:1; я2],
где хх и х2 — абсциссы точек пересечения параболы y = f(x) =
= х2-(а-2)х-2 с осью Ох. Если AczAl9 то
/Ч-1Х0, /(0)<0, (11)
так как /(jc)<0 для всех хеАг. Обратно, если выполняются
условия (11), то -1GA! и OgA!, откуда следует, что A<=A1# Таким
образом, условиям задачи удовлетворяют те и только те
значения а>0, для которых выполняются неравенства (11), т. е.
/(-1)=1+(а-2)-2<0, /(0) = -2<0, откуда находим 0<а<3. 4
Задача 12. Найти все значения а, при которых система
неравенств
х2-2ху-7у2>
1+а
1-а'
[Зх2-10ху-5у2<-2
имеет решение.
[> Пусть а0 — значение параметра а, при котором данная
система имеет решение (х0; у0). Тогда верны неравенства
- х% + 2хоуо + 1у% < 1 - ——,
1~ао (12)
3x%-10x0y0-5y2)<-2.
264 Глава VIII
Уравнения и неравенства с двумя переменными
Сложив второе неравенство системы (12) с первым,
умноженным на 2, получим верное неравенство (хо — 3уо)2<:- ,
4 х~ао
откуда следует, что >0, т. е. ао>1.
1-а0
Итак, искомые значения параметра удовлетворяют
условию а> 1.
Докажем, что для каждого а>1 данная система имеет ре-
2
шение. Если а> 1, то 1-- > 1. Поэтому достаточно показать,
1 — а
что система уравнений
fx2-2xy-7y2 = -l9
[Зх2-10ху-Ьу2 = -2
имеет решение. Любое ее решение является решением
исходной системы неравенств.
При решении системы (13), как и при преобразовании
системы неравенств (12), сложим второе уравнение системы (13)
с первым уравнением, умноженным на -2. Получим уравнение
(x-3i/)2 = 0, (14)
которое вместе с любым из уравнений системы (13) образует
систему, равносильную системе (13). Из уравнения (14)
следует, что х = 3у9 и тогда из первого уравнения системы (13)
найдем У1 = -^9 У2==~-^- Проверка показывает, что обе пары чисел
3 1\ / 3 1\ /1ОЧ
-; — I, l--^; ~~o) являются решениями системы (13),
а зна-
чит, и решениями исходной системы неравенств.
Ответ. а> 1. <4
Задача 13. Найти все значения параметра а, при которых
множество решений системы неравенств
содержит отрезок I с концами в точках А(1; 0) и В(1; 1).
[> Пусть точка М(х; у) принадлежит отрезку Z, тогда х=19
0<z/<l. Поэтому задача сводится к нахождению значений а,
при которых система неравенств
\(у-а)2<99
полученная из данной системы при х = 1, имеет решения при
любом у€[0; 1]. Система (15) равносильна системе
<-V-l.
Если 0<i/<l, то из системы (16) следует, что
Условия (17) выполняются только при а = -2. ^ БЯ
§ 3 265
Уравнения и неравенства с двумя переменными,
содержащие параметры
Упражнения
7| Найти все значения а, при которых нет ни одной пары
действительных чисел (х; у), удовлетворяющей уравнению
J24J Найти все значения а, при которых найдется хотя бы
одна пара действительных чисел (х; у), удовлетворяющая
уравнению Ъх2 + аху + у2 + 8ах + 8у + 20 = 0.
7] Дана система уравнений
Найти все значения а, при которых система уравнений:
а) имеет единственное решение;
б) не имеет решений;
в) имеет бесконечное множество решений.
ЗЗ Найти все значения а, при которых система уравнений
_. , имеет два решения.
2 Найти все значения а, при которых система уравнений
( x + yfy = 1,
I о г~ 1 / \2 имеет единственное решение.
I 2
7) Найти все значения а, при которых система уравнений
= log3(17-8x-10y),
имеет ровно два решения.
)j Найти все значения а, при которых система уравнений
\х2+у2 = а
имеет ровно два действительных решения.
Найти все значения а, при которых система уравнений
имеет хотя бы одно решение.
Найти все значения а, при которых система уравнений
flog2(i/-3)-21og4x = 0,
((x + a)2_ 2у-5а = 0 ИМееТ ХОТЯ ОДН° Решение-
Найти все значения а, при которых нет ни одной пары
действительных чисел (х; у), удовлетворяющей неравенству
.] Вершины Ву Су D параллелограмма ABCD имеют
соответственно координаты (-3; 2), (2; 3), (3; —4). Найти все
значения а, для которых координаты вершины А являются
[2х-у-2а<0,
решением системы неравенств i n "1
l2x + 6i/ + 5a<0.
266 Глава VIII
Уравнения и неравенства с двумя переменными
4. Найти все значения а, при которых множество решений
системы неравенств
содержит отрезок АВ9 где А(-2; О), £(-1; 0).
5. Найти все значения параметра а, при которых система нера-
{
венств
а + 2 имеет хотя бы одно решение.
главе VIII
36. Найти множество точек координатной плоскости,
удовлетворяющих неравенству:
1) 2х-у + 5>0; 2) х-Зу + 4<0.
37. Найти множество точек координатной плоскости,
удовлетворяющих системе неравенств:
1)
х-у+1>0,
2)
Зх-2у + 6>0,
Зх + 4у-12<0,
38. Решить неравенство:
1) (х-у+1)(х + 2у-2)<0;
2)
39. Пусть М — множество точек плоскости с координатами
(х; у)9 таких, что числа х9 у и 6-2х являются длинами
сторон некоторого треугольника. Найти площадь фигуры М.
40. Найти все пары целых чисел х, у, для которых верны
неравенства у-3х<1, 2у-3х>19, 4у-х<78.
41. Найти множество точек координатной плоскости,
удовлетворяющих уравнению:
) /
2) 6х2-ху-у2
3) |х+1| + |у-2| = 1.
[42.1 Найти все пары действительных чисел, для которых
справедливо равенство
43. Найти множество точек координатной плоскости,
удовлетворяющих неравенству:
1) Зх2 + Зу2-6х+12у-11>0; 2) \х-\
3) х2 + у2<6\у\.
'\х\ + \у\<б,
44. Дана система неравенств
х2 + у2>5(2х-2у-5),
267
Упражнения к главе VIII
Найти площадь фигуры, координаты точек которой
удовлетворяют:
а) первому неравенству системы; б) первым двум
неравенствам системы; в) всем трем неравенствам системы.
45. Дана система неравенств < \х\ + \у\^2,
1у2-х2 + 16-8у>0.
Найти площадь фигуры, координаты точек которой
удовлетворяют:
а) первому неравенству системы; б) первым двум
неравенствам системы; в) всем трем неравенствам системы.
46. Найти площадь фигуры, заданной на координатной
плоскости системой неравенств:
, 2) [ х2 + у2<ь4х,
1; \\у\>\2-х\.
7] Найти все значения а, при которых имеет единственное
решение система уравнений:
1) fx2 + i/2 = a, 2) \х-у=1+ху,
3
3) \2х + 2(а-1)у = а-2, 4) аху + х-ул— = 0,
2
Г] Найти все значения а, при которых система уравнений
имеет ровно два решения.
Найти все значения а, при которых система неравенств
имеет единственное решение.
Вершины А, Б, С треугольника имеют соответственно
координаты (-2; -1), (0; 9), (8; 1). Найти:
а) все значения а, для которых координаты точки
пересечения медиан треугольника ABC являются решением сие-
темы неравенств
б) все значения а, для которых координаты хотя бы одной
точки отрезка ВС являются решением этой системы.
Найти все значения параметра а, при которых множество
решений системы неравенств
содержит отрезок с концами в точках (1; 0) и (1; 1).
268 Глава VIII .
Уравнения и неравенства с двумя переменными
Вопросы к главе VIII
1. Привести пример уравнения прямой.
2. В каких точках координатной плоскости выполняется
неравенство Ах + Ву + С<0, если В>0 (В<0)?
3. Найти множество точек координатной плоскости,
удовлетворяющих уравнению 4х2-у2 = 0.
4. Записать уравнение окружности с центром в точке А(а; Ъ)
и радиусом R.
5. Найти множество точек координатной плоскости,
являющихся решением неравенства (х-а)2+ (у-Ъ)2 <R2.
6. Что представляет собой множество решений системы нера-
венств
7. Что представляет собой множество решений неравенства
(Ахх + Вгу + Сх) (А2х + В2у + С2) > О,
где А1х + В1у + С1 = О и А2х + В2у + С2 = О — уравнения
пересекающихся прямых?
8. Привести пример нелинейного уравнения с двумя
неизвестными, решением которого является единственная пара
чисел.
Проверь себя!
1. Найти множество точек координатной плоскости,
удовлетворяющих уравнению:
1) 2x + 3i/-l = 0; 2) х2 + г/2-6х + 21/ = 6.
2. Найти множество точек координатной плоскости,
удовлетворяющих неравенству:
1) 2х-8у<0; 2) (x + 2)2 + (i/-5)2<4.
3. Изобразить на координатной плоскости множество точек,
координаты которых удовлетворяют системе неравенств
х + 2у>-2.
1. Решить неравенство (л: — 2i/ -h 3) (л: +1/ — 6) < 0.
2. Изобразить на координатной плоскости фигуру Ф, задан-
ную системой неравенств \ % 9 rt n Л
^ [х2 + у2-2х-3<0,
и найти площадь этой фигуры.
3. Найти множество точек координатной плоскости,
удовлетворяющих:
1) уравнению |jc| + |i/| = 3; 2) неравенству |jc| + |i/|<3.
269
Проверь себя!
I f A I Историческая справка
Французские математики XX в. А. Гротендик и Ж. Дьедо-
не в одной из своих статей справедливо отметили: «Можно
утверждать, что решение полиноминальных уравнений
послужило исторически источником алгебры и что со времен
вавилонян, индусов и Диофанта и до наших дней оно остается одной
из ее основных целей».
Добавим от себя, что решение уравнений, неравенств и их
систем является одной из основных содержательных линий
школьного курса алгебры. И это неудивительно: уравнение
наиболее привычный вид математической модели.
Математические же модели — один из основных инструментов познания
человеком явлений окружающего мира.
Уравнения и их системы (линейные и нелинейные) имеют
давнюю историю. Так, в древневавилонских текстах,
написанных в IV—III вв. до н. э., содержатся задачи, решаемые с
помощью системы уравнений, одно из которых является
уравнением второй степени. Вот одна из таких задач: «Площади двух
своих квадратов я сложил и получил 25—. Сторона второго
2
квадрата равна — стороны первого и еще 5. Каковы стороны
о
этих квадратов?» Современная запись условий этой задачи
имеет вид
Для решения этой системы вавилонский автор возводит во
втором уравнении у в квадрат, получая у2 = — х2 + — х + 25. Под-
У о
ставив это значение у2 в первое уравнение системы, автор
получает уравнение с одним неизвестным
1|*2 + 6§* = 25А,
решив которое находит х, а затем и у.
В этой главе вы познакомились с решением различных
систем нелинейных уравнений. В технологии современных
вычислений такие уравнения и их системы встречаются часто,
так как модели реальных процессов во многих случаях
являются нелинейными.
Упражнения
для итогового повторения
курса алгебры и начал
математического анализа
Умение решать задачи — практическое
искусство, подобное плаванию,
или катанию на лыжах, или игре на
фортепьяно: научиться этому можно,
лишь подражая избранным образцам
и постоянно тренируясь.
Д. Попа
1. Вычисления и преобразования
1. Найти число, если 42% его равны 12,6.
2. Какой процент составляет 1,3 от 39?
3. Какой процент составляет 46,6 от 11,65?
4. Найти 180% от 7,5.
5. Цена товара была снижена сначала на
24%, а затем на 50% от новой цены.
Найти общий процент снижения цены товара.
6. В сплаве содержится 18 кг цинка, 6 кг
олова и 36 кг меди. Каково процентное
содержание составных частей сплава?
7. Стоимость товара и перевозки составляет
3942 р., причем расходы по перевозке
товара составляют 8% стоимости самого
товара. Какова стоимость товара без учета
стоимости его перевозки?
8. Высота пирамиды равна 5 см, а площадь
ее основания равна 4 см2. На сколько
процентов увеличится объем этой пирамиды,
если и площадь ее основания, и высоту
увеличить на 10%?
9. При делении некоторого числа на 72
получится остаток, равный 68. Каким будет
остаток, если это же число разделить на 12?
10. Сумма двух чисел равна 1100. Найти
наибольшее из них, если 6% одного числа
равны 5% другого.
271
Упражнения для итогового повторения курса
алгебры и начал математического анализа
11. По вкладу, вносимому на срок не менее года, Сбербанк
выплачивает 3% годовых. Вкладчик внес в Сбербанк вклад
в размере 6000 р. Какую сумму денег он получит в конце
второго года со дня вклада? в конце третьего года со дня
вклада?
12. По обычному вкладу Сбербанк выплачивает 2% годовых.
Вкладчик внес 5000 р., а через месяц снял со счета 1000 р.
Какая сумма денег будет на его счету по истечении года
со дня выдачи ему 1000 р.?
13. Выработка продукции за первый год работы предприятия
возросла на р%, а за следующий год по сравнению с
первоначальной она возросла на 10% больше, чем за первый
год. Определить, на сколько процентов увеличилась
выработка продукции за первый год, если известно, что за два
года она увеличилась в общей сложности на 48,59%.
14. Доказать, что при любом простом р > 3 число р2 — 1
делится на 24.
15. Доказать, что при любом натуральном п>1 число я4+ 4
является составным.
16. Доказать, что при любом натуральном п:
1) 6п5-11п делится на 5;
2) п7 — п делится на 7.
17. Доказать, что З6"-26" делится на 35 при n€N.
18. Доказать, что /i5-5/i3 + 4n делится на 120 при n€N.
19. Найти последнюю цифру числа:
1) 999; 2) 23\
20. Найти две последние цифры числа:
1) 2999; 2) З999.
21. Делится ли на 7 число сочетаний из 1000 элементов по 500?
22. Доказать, что произведение любых п последовательных
натуральных чисел делится на п\.
23. Найти неизвестный член пропорции:
l)10:l-*:lI; 2) *:0,75 = 9 £ : 14 I; 3)^ = ^f.
Вычислить (24—28).
25. 1) Iog27729; 2) Iog9729; 3) log г 729.
26. 1) log^Vei; 2) log8log4log216.
Тб
272
Упражнения для итогового повторения курса
алгебры и начал математического анализа
J_\V8
27. 1) \2^) ; 2)
28. 1) log3 —+ log6\/36; 2)
5
29. Найти значение выражения V36log65-5log59.
30. Сравнить числа:
А 1 Л
1) 2,5 7 и 2,50-5; 2) 0,2 3 и 0,2 4;
3) log3,iVl0 и Iog3,i3; 4) Iog0,3f и Iog0,3f.
3L Какому из промежутков 0 < а < 1 или а > 1 принадлежит
число а, если:
1) а°'2>1; 2) а-1-8>1; 3) а"зд<1;
4) а27<1; 5) loga0,2>0; 6) logal,3>0?
32. Какое из чисел больше:
1""1 ^"
1) V18 или 4--' + ^П; 2) Vl8 или (I
33. Между какими целыми заключено число:
1) lg50; 2) Iog210?
34. Сравнить без таблиц и калькулятора числа Iog34 и у/2.
35. Доказать тождество logfea-logc6
Упростить (36—37).
36. ) \
13
2)
V6-V5 V5 + V2 V6-V2"
37. 1) Va4(9a2-6a+l); 2) V*
38. Освободиться от иррациональности в знаменателе дроби:
1) 5 . 2) 3 . 3) 12 4) 8
V3-V2' V6+V5' VT0-V7' VTi+V3#
39. Освободиться от иррациональности в числителе дроби:
1) УЕ; 2) ^; 3) ^-^.
10 6 2
40. Записать в виде обыкновенной дроби число:
1) 0,(4); 2) 2,(7); 3) 0,(21);
4) 1,(36); 5) 0,3(5); 6) 0,21(3).
41. Записать в виде десятичной периодической дроби число:
|; 2)21; з)1;
273
Упражнения для итогового повторения курса
алгебры и начал математического анализа
42. Может ли быть рациональным числом:
1) сумма двух положительных иррациональных чисел;
2) произведение двух иррациональных чисел;
3) частное от деления суммы двух неравных
иррациональных положительных чисел на их произведение?
43. Доказать, что если а и Ъ — натуральные числа и \[ab —
рациональное число, то v-j~ также рациональное число,
а если \[ab — иррациональное число, то и \ %- — ир-
V о
рациональное число.
44. Пусть а — рациональное число, Ъ — иррациональное
число, а^О, Ьу^О. Доказать, что а + b, а-Ь, —-, — —
иррациональные числа.
45. Имеют ли общие точки промежутки:
1) [1; 3V2 + 2V7] и [3V3 + 4; 15];
2) (0; V27+V6) и (Vi8-1; 10);
3) [2; 2V5 + 2\/6] и (3V2 + V2^; 11);
46. Пусть 0<а<6. Доказать, что на числовой оси:
1) точка а* — середина отрезка [а; Ь];
2) точка ** + с , где с>0, лежит внутри отрезка [а; Ь].
1 + с
47. Выполнить действия:
2) (-
3) (l + i)(-l + 2i)+l-3i; 4) (3-
кч (3-0(1 + 30 Лч i
2-3i
48. Вычислить:
1) (2-О3; 2)
3) (2 + 302-(2-3i)2; 4)
49. На комплексной плоскости построить точки:
1) 5; 2) 2i; 3) -Si; 4) 3 + 2i; 5) -2 + £; 6) -
50. Доказать равенство
51. Доказать, что для любых комплексных чисел zx и z2
справедливо равенство zx +z2 =z~l + z~2>
274
Упражнения для итогового повторения курса
алгебры и начал математического анализа
Рис. 138
Рис. 139
Рис. 140
Рис. 141
52. Вычислить:
53. Найти значение выражения:
1} "~^~; 2) ~^~; 3) ^Г +й^; 4) VТо""157 ^Г
54. 1) Вычислить диаметр х круга, вписанного в
равносторонний треугольник (рис. 138), если а = 6 см.
2) Вычислить угол а заготовки, изображенной на
рисунке 139, если а = 4 см.
55. Вычислить ширину / ущелья по данным, указанным на
рисунке 140.
56. Вычислить длину моста по данным, указанным на
рисунке 141.
57. Найти числовые значения всех остальных
тригонометрических функций по данному значению одной из них, если
1) cosa = 0,8; 2) sina=y^; 3) tga = 2,4; 4)
58. Вычислить:
1) cos(arcsin-|); 2) sinfarccosf - —^ )).
275
Упражнения для итогового повторения курса
алгебры и начал математического анализа
59. Разложить на множители многочлен:
1) 4x4 + 4x3-25x2-x + 6; 2) х4-2х3-Ых2-6х + 6.
60. Сократить дробь:
3
л:3-2л:2 + 4л:-3
л:4-2л:3 + л:-2 .
4
2л:4-Зл:3-7л:2-5л:-3
2л:4-3л:3-л:-б' ' 2л:3 - 5л:2 - 2л: - 3
61. Найти разложение бинома:
1) (х-1)5; 2) (а + 3)4.
Упростить выражение (62—64).
( 2а2-а-3 . 2а-3 V
63.
а2-1
а2-а-1
а3-а2
2а3
а4-1
64.
2)
4-4Va' a\/2-2-\/2 + 2a
65. Упростить выражение и найти его значение:
при а = 5, х = 4;
при а = 3, х = \[Б.
Упростить выражение (66—72).
66. 1)
2)
1
1+л:2
I
1-л:2
Г2 — 1
I
2т2
_2т2_
ш2-1
_1
4т2
т-1
Упражнения для итогового повторения курса
алгебры и начал математического анализа
_j 2 2 ! I I
69. a b ~a b
ч-2
а + У^Ь Vafr + Ь2 \ yasb+yab3
\f^Tb )
71
7O
73.
74.
/ _
1
\ 3a2-5a~
/ sVb
Доказать,
если a>0
Доказать,
1 a + 7 + 10a
что
, 6>0, a2 + b2
что
lncr 2a
-2
= 7ab, c>0, c^l
,3b logca+log,b
если a>0, 6>0, 13a6 = 4a2 + 962, c>0, c^l.
75. Выразить Iog89,8 через а и 6, если Ig2 = a и Ig7 = 6.
76. Выразить log^8 через a, если Iog123 = a.
77. Упростить:
1) 1 + tg9a ; 2) (l + tga)(l+ctga)--^—^ .
1 + ctg a sinacosa
„o тт 1 - (sin a + cos a)2 o, 2
78. Доказать тождество — = 2 tg^ a.
sin a cos a-ctg a
Упростить выражение (79—80).
79. 1) sin2 (a + 8л) + cos2 (a + Юл);
2) cos2 (a + 6л) + cos2 (a -4л).
~~ sin 2a sin a cos {n - a)
2(l-2cos2a) l-2sin2a
81. Доказать тождество
cos2 x sin2 x
= - sm x - cos x.
1 + sinjt 1-cosjc
277
Упражнения для итогового повторения курса
алгебры и начал математического анализа
82. Разложить на множители:
1) 1 + cosa + sina; 2) 1-cos a-sin a;
3) 3-4sin2a; 4) l-4cos2a.
83. Доказать, что если а + Р + у = я, то:
3 у
1) sina + sinp-siny = 4sin^ sin — cos —;
£ £ £
2) sin 2a + sin 2p + sin2y = 4 sin a sin P siny.
84. Известно, что tga = 2. Найти значение выражения:
-. sin2 a + sin a cos a # ~. 2-sin2 a
cos a + 3 cos a sin a 3 + cos2 a
85. Известно, что tga + ctga = 3. Найти tg2a + ctg2a.
Упростить выражение (86—90).
о*э i\ cosa + sina /тс \ m . 2/j[ \ 1-sin2a
оо. 1) : tgl — +a ; z) tg — -a
cosa-sina \4 / \2 / l + sin2a
. /71 \ /71 \ . o . / 7t \
sin (—ha - cos (—ha) sin a + 2 sin ( a 1
37 J4 ^4 / ^4 / . 2) ^3 / .
sin(—ha) +cos(—ha) 2cos( a) -V3cosa
\4 / \4 / \6 /
3) ———iJ—; 4) (sin a + cos a)2 + (sin a -cos a)2,
ctg a + ctg p
88. 1) tg2" ; 2)
ctg^a
3) tga-tgp . 4 (tga +
ctg a + ctg p
1v l + cos2a , 2v tga-sina
1 2
2cosa ' tga + sina'
. sin a + sin 3a + sin 5a # 2 sin 2a + sin 4a
cos a + cos 3a + cos 5a '
cos a + cos 3a + cos 5a ' 2 sin 2a - sin 4a
sin 2a + cos 2a + 2 sin2 a O4 cos 2a - sin 2a - 2 cos2 a
sin (- a) — sin (2,5л + a) cos (- a) — cos (2,5тг + a)
91. Доказать тождество:
92.
l-cos(2K-2a) sh.v Q a_
l-cos2(a + 7r) l + sin(-a)
Упростить выражение (92—97).
5cosjc-3sinjc sin 2x -8 sin2 x
sin (—-x\+ sin (- x)
"o. sin ix
COS 2x
278
Упражнения для итогового повторения курса
алгебры и начал математического анализа
94. 1) cos2(a + 2P) + sin2(a-2P)-l;
2) sin2(a + 2P) + sin2(a-2P)-l.
cos4a -cos 2a # p. 1 + cos a + cos 2a + cos 3a
sin3asina ' cosa + 2cos2a-l
4 sin2 a-sin2 2a tg22atg2a-l
b. l) ; zj —
4-4 sin2 a - sin2 2a tg2 a - tg2 2a
Q- 14 V2-cosjc-sinjc
sinx-cosjc sinjt + cosjt
Лл „ sin a cos a 3
98. Вычислить —- — , если ctga = ^.
sura-cos a 4
99. Упростить выражение
2-3sin2a _ sina + 2cosa
cos 2a sin a + cos a
и найти его числовое значение при a = - -^-.
о
Доказать тождество (100—106).
шо tg(a-p)+tgp _ cos(a + P)
tg(a + P)-tgP cos(a-P)
101.1) 1 +sina = 2cos2f -?-- -^ ); 2) 1-si
102.1) f^f
2) cos(^+aWcos/^
V 6 / \ 6
in* -.4 -. . 9 cos2a O4 . ,2 cos2a
103.1) l-tg2a= ; 2) l-ctg2a = -
cos a sin a
104.
105, 1) l-2sin^ = lztga.
l+sin2a 1 + tga
1+
l+sin2a 1 + tga 4sin2acos2a 4tg2a
3) tgfi +a) = i±^a5 4)
V4 / cos2a
106.1) 4sinxsinf|--jcN)sinf|-H-jc>j=sin3jc;
2) cos Sx cos 6x cos 12x = **in ^x .
8sin3x
107. Записать в тригонометрической форме число:
1) 2; 2) -3; 3) Si; 4) -2£; 5) у/3-i; 6) 2-2£.
108. Записать в алгебраической форме комплексное число:
1) 4f cos — +*sm — j; 2) 6( cos — +isin — 1.
279
Упражнения для итогового повторения курса
алгебры и начал математического анализа
109. Выполнить действия и записать результат в
алгебраической форме:
2) (1 + 0 (cos — +1 sin — 11 cos - +1 sin - 1;
; 4)
cos-|+isin^ cos—+i sin —
5 5 4 4
2. Уравнения
110. Решить уравнение:
1Ч 3jc-16 , i _ jc + 6 х + 3 .
12 +1" 4 6 '
111. При каком значении а уравнение а(л;-3) + 8 = 13(л:+ 2)
имеет корень, равный О?
112. При каком значении Ь уравнение 1 -Ь(х + 4) = 2(х — 8)
имеет корень, равный 1?
Решить уравнение (113—122).
3 2 4 5 2 11
ц«5. 1) — — - ; Z) — н — — -
114.1) (а-6)х = а2 + (а + 6)д:; 2) а2
115.1) (х-3)(х-2) = 6(х-3); 2) х2-^ + | = 0.
116.1) + 0; 2) 2 |f
jc + 1 лг1 Злг1 Злг+1
JC+1
лг+1
2
лг-1
7
2 + х
12
7*
2-
3-
2)
2-28
2х-1
Злг-1
1 18 •
1 2-х'
2)
2х2 Зх ^ 2(4*-1)
120.1) jc4-11x2 + 30 = 0; 2)
121.1) 2х~2 + 4л:-1 + 3 = 0; 2)
122. 1) *2 + ax-62 + ^ = 0; 2)
7 4
2л:-а
280
Упражнения для итогового повторения курса
алгебры и начал математического анализа
123. Решить относительно п уравнение:
-V ^"» И _ 1 - ~V . О
3) С1= ±С4п + 2; 4)
124. При каком условии трехчлен ах2 + Ъх + с является
квадратом двучлена?
125. Доказать, что корни уравнения ах2 + Ъх + а = О есть
взаимно обратные числа, если а^О.
Решить уравнение (126—127).
126.1) |2х-3| = 7; 2) |x + 6| = 2x; 3) 2х-7 = |х-4|.
127.1) |6-2x| = 3x + l; 2) 2\х-2\ = \х\-1.
128. Найти наименьший корень уравнения
\х2-3х-6\ = 2х.
129. Найти наибольший рациональный корень уравнения
130. Найти действительные корни уравнения:
1) x3-3x2 + x = 3; 2) x3-
3) *3-5л;2 + 8л;-6 = 0; 4) x4-
5)
6)
Найти действительные корни уравнения (131—136).
131. 1)
2)
132.1)
2)
133.1)
2)
134. 1)
2)
2)
—-^; 2) (|)(4
12 V x V л:2
137. Пересекает ли график функции y = xs-6x2 + llx-6 ось Ojc
в точках, абсциссы которых являются целыми числами?
138. Уравнение 2xs + mx2 + nx+12 = 0 имеет корни хг = 1,
х2 = — 2. Найти третий корень этого уравнения.
_ 281
Упражнения для итогового повторения курса
алгебры и начал математического анализа
139. Могут ли корни уравнения (х - т) (х — п) = k2 быть чисто
мнимыми, если т, п и k — действительные числа?
Решить уравнение (z — комплексное число) (140—144).
140. 1) 22 + 42 + 19 = (
141. 1) 2(2 + 0-7 = 3
142. 1) |г| + *2 = 2-*;
143. 1) 22 + 3 = 0;
3) z2-
144. 1) z2
3) z*
2) 22-
2) 5i-z(3-2i) = -l.
2) \z\-iz = 3 + 2L
2) 9г2 = -125;
4) 22-
2) 22 = -
4) 24-1 = 0.
145. Найти все целые числа, равные сумме квадратов своих
цифр.
[146J Решить в целых числах уравнение:
2)
.1 Найти все пары целых чисел, сумма которых равна их
произведению.
Решить уравнение (148—151).
148. 1) V2x + 7 = x + 2; 2) x = 2-
149. 1) 2Vx + 4-Vl-x = V^+5; 2)
-Зх-1 =х2-1.
152. Найти все числа а, для которых выполняется условие
4-23а = 0,25 2 .
Решить уравнение (153—172).
153. 1) 3*"7 = 81; 2) 2*2-5*+65=V2;
3) (j
= 22дс+6.
154. 1)
3)
5)
155. 1)
156. 1)
282
= 35
3jc-2.
2) 2*+4-2*=120;
4) 32х-2 32х-1-2\
6) Здс+2 + Злс=10.
2)
\3/ \5/ V8V16/
Упражнения для итогового повторения курса
алгебры и начал математического анализа
157. 1) (l)-.(^)*-1-!; 2)
158. 1) 32*-3*=72; 2) 4*-2*+1=48.
159. 1) 0,5* = 2x+l; 2) 2* = 3-x2; 3) log3x = 4-x;
4) log! x = 4x2; 5)2* = Iog0,5 *; 6) ( ± Y = log3 *.
1) (log2x)2-31og2x + 2 = 0; 2) (log3 x)2 + 5 = 2 log3 x3.
160.
161.
162.
163.
1) In
X ~\~ X
ln(x + 2);
2) log3V3x-6-log3Vx-3=l.
2) ^
3) ^ log3 (x +1) = log
1 I i
169. 1) 9-4*+5-6*=4-9*;
" 2) log2(x2-3)-log2(6x-10)+l = 0;
3) 21og2x
4) logx(2x2-3x-4)
170.
2)
2)
2) log27 (sin 2x- j cos Xs) = i + log3 (- cosx).
1 Решить уравнение:
1) log3 (sin Sx - sin x) = 2 log9 (17 sin 2x) -1;
2) logv^(sin jc - cos x) + 1 = log7 (7 + 3 cos 4x).
283
Упражнения для итогового повторения курса
алгебры и начал математического анализа
J174.] Найти все решения уравнения, удовлетворяющие данному
неравенству:
*2-8:x;), sinx<tg2*;
2) Wlogi(x2+|x).log36jc2+6jc6 = l, sinx>tg6*.
V 6
175. Решить уравнение cos(3x- т)= "о и Указать любой его
положительный корень.
176. С помощью графика синуса или косинуса найти все
корни уравнения, принадлежащие промежутку [-я; Зя]:
1) cosx = -|; 2) sinx = -^.
Решить уравнение (177—192).
177. 1) sin2x=-t; 2) cos3x = -^fs 3)
178. 1) 3cos2x-5cosx-12 = 0; 2) 3tg2x-4tgx + 5 = 0.
179. 1) (3-4sinx)(3 + 4cosjt:) = 0; 2)
180. 1) sin2jc = 3sinjccos2jc; 2) si
3) cos2jch-cos2jc = 0; 4) si
181. 1) sin2jc = 3cosjc; 2) si
3) 2cos2jc=l+4sin2x; 4)
182. 1) cosjc + cos2jc = 0; 2) cosjc-cos5jc
3) sin3jc + sinjc = 2sin2jc; 4) si
183. 1) 2cosjc + sinjc = 0; 2) si
184. 1) 4sin4jc + sin22x = 2; 2) sin4 - + cos4 § = -|.
3 3 8
185. 1) sin3x + cos3jc = 0; 2)
3) 8 sin x cos 2x cos x = V3; 4) 4 sin x cos x cos 2x = cos 4x
186. 1) sin4jc-cos4jc + 2cos2jc = cos2x;
2) 2 sin2 jc - cos4 jc = l-sin4jc.
187. 1) sinjc + sin5jc = sin3jc; 2) cos 7x - cos Sx = 3 sin 6x.
188. 1) cosjcsin9jc = cos3jcsin7jc; 2)
189. 1) 5 + sin2jc = 5(sinjc + cosjc);
2) 2H-2cosjc = 3sinjccosjcH-2sinj
190. 1) sinjcH-sin2jcH-sin3jcH-sin4jc =
2) cosjc + cos2jc + cos3jc + cos4jc =
3) cosjccos3jc = -0,5.
191. 1) tg23x-4sin23jc = 0; 2)
3) ctgx(ctgx+-A-) = l; 4)
smjc
192. 1) tg2x = 3tgjc; 2) ctg2x = 2ctgx;
3) tg(x+|)+tg(x-|) = 2; 4) tg(2x+l)ctg(*+l)=l.
284
Упражнения для итогового повторения курса
алгебры и начал математического анализа
193. Решить графически уравнение:
3) cosx = V#; 4)
Решить уравнение (194—197).
Ш1Л poqV?- г2= -!?_• 9Л Gin — г = г2-
2) V5 sin 2jc - 2 = sin x — cos jc.
2sin*!
4sin(W
cos jc - cos 3x 3 V 4
.Найти все корни уравнения cosx + (l + cosx)tg2jc- 1 = 0,
удовлетворяющие неравенству tgx>0.
.Найти все корни уравнения sin4х + sin4(х + — ) = sin2——,
V 4 / 6
удовлетворяющие неравенству lg (х - \/2х + 23) > 0.
.Найти наибольший на интервале (-^; ^) корень
уравнения
1.1 Найти все значения а, при которых уравнение
sin8 х + cos8 x = а
имеет корни, и решить это уравнение.
3. Неравенства
202. При каких значениях х положительна дробь:
1\ 5лс-4 . 9Л Злс+10. о\ х + 2. л\ 8-jc
203. При каких значениях х отрицательна дробь:
1\ 3-2*. п\ Ю-4х. о\ 18-7л: о
х) *) ^)
Решить неравенство (204—211).
204. 1) ^<4; 2) ^<1; 3)
205. 1) 8х2-2х-1<0; 2)
206. 1) 4^<0' 2>
х -4
207. 1) 3*-15 >0; 2)
2
x2-\-4x-\-2
3) * + 2*-8>0. 4)
л:2-2л:-3
285
Упражнения для итогового повторения курса
алгебры и начал математического анализа
208. 1) |2х-5|<3; 2) |5*-9|>4;
209. 1) \x-l\(x4-2x2-3)>0; 2) \x2-9\(x4-2x2-8)<0.
210. 1) \2x-3\<x; 2) \4-x\>x;
" 3) |jc2-7jc + 12|<6; 4)
5) \2x2-x-l\>b\ 6)
211.
[2127J Найти все значения а, для которых является верным при
всех значениях х неравенство:
1} <a; 2)
1х2-2х+\ 9х2 - 12* +16
213. При каких значениях х выражение
не имеет смысла?
214. При каком наименьшем целом значении т уравнение
(т-1)х2 - 2 (m + l)x +m-3 = 0
имеет два различных действительных корня?
215. При каких целых значениях т уравнение
(771- 7)Х2 + 2(771- 7)Х + 3 = 0
не имеет действительных корней?
216. При каком наибольшем целом значении х выражение
Jt2-9x+14
принимает отрицательное значение?
217. При каком наименьшем целом значении х выражение
х2-х-6
-1-х2
принимает положительное значение?
218. Найти все пары целых чисел х и у, для которых верны
три неравенства:
1) Зу-х<5, х + у>26, Зх-2у<46;
2) Зу-5х>16, Зу-х<44, Зх-у>1.
Решить неравенство (219—233).
219. 1) 2,51-дс>2,5~3дс; 2) 0,13*"4>0,132-*;
3) (^'^(т)""1; 4> 3~4*>V3.
220.1)2^<1; 2,V3/
221. 1) 5*2 + 3*+1-5<5\/5; 2) 092х2~6х+7>1.
222. 1) 3*+1-9* 2 >3\/3; 2) Зх + 1 + Зх1< 1С
286
Упражнения для итогового повторения курса
алгебры и начал математического анализа
223.
224.
225.
226.
227.
228.
•2"4>52;
1) Зх2+6х<1;
4) 22дс+1-21
х-З
2) (I)*"**>!
!;
5)
3) 4
**+вх+11
<1;
х+ 6>0.
9
2)
i; 3)
5
log6(2-x)<log6(2x
|; 2) lo
2) log
1
2 2
2) Iog3(l-2x)<-l.
229. 1) log0,5(^2-5jt: + 6)>-l; 2) log8(x2-4* + 3)< 1.
230.
230. 1) logi(log1 3*±
2 Ч 2 ^ A
2) log x (Iog4(x2-5))>0.
3
231.
232.
1) log1(l+x-Vx2-4)<0;
1 1
2)
<0'
Iog5(3-2x) 4-log5(3-2jc)
!) log,2x+1,x2>2; 2)
Найти все значения а, при которых неравенство
выполняется для всех х из промежутка
Решить неравенство (235—241).
1) xlg2*~31g*+1>1000; 2) &**+2<31**+*-2.
237. 1) (x2-4)log0,5^>0; 2) (3x-l)log2x>0.
ВЗ&11) x1 +
3) 3-
2) x2lgx<10x;
. 1) Iog6x+1(25x)-21og25x(6x+l)>l;
2) ^
2)
287
Упражнения для итогового повторения курса
алгебры и начал математического анализа
242. Решить неравенство 9|д:|-8 • 3х > 9 и указать наименьшее
натуральное число, удовлетворяющее неравенству.
Решить неравенство (243—246).
243. 1) V9jc-20<jc; 2) /
S44.ll)
5-л:
х-3
лг-4
2)
246.
^fs 2)
2
х-6
~2'
>2х-10.
247. Решить графически неравенство:
1) sinjc<—; 2) sinjc>-—; 3) tgjc-3<0; 4) cosx>—.
4 4 3
248. С помощью графиков тригонометрических функций найти
все решения неравенства, заключенные в промежутке
[-Зл; тс]:
1) 2cosx-V3<0; 2) V2sinjt+ I >0;
3) V3 + tgx<0; 4) 3tgjt-2>0.
Решить неравенство (249—250).
7 - cos 4jc
>-2cosjc.
У
7-cos 4л:
Доказать неравенство (251—253).
251.
2)
3, если а>0, b>0, a*b.
252. 1) (а + 6)(а6+1)>4а6, если а>0, 6>0;
" 2) а4 + 6а2&2 + 64>4а6(а2 + Ь2), если
253. 1) f + -
ос
2)
>3, если а>0, 6>0, с>0;
4. Системы уравнений и неравенств
Решить систему уравнений (254—255).
254. 1) ( 5х-7у = 3, 2)
255. 1)
288
-*±1U1O, 2)
5 2
f+f=10'
=6,
х + г/
Упражнения для итогового повторения курса
алгебры и начал математического анализа
Найти действительные решения системы уравнений
(256—260).
256. 1) [i/ + 5 = x2, 2) [*!/=16, 3)
[
257. 1)
х-у=1;
258. 1, fi-i-f
f"*
1*-2».
2)
4)
2)
— +3*1/ = 25,
2
3)
259. 1)
260. 1)
Решить систему уравнений (261—264).
* ш *? О * '
xy2
[3-2^ = 7;
3) [3Л. 2^ = 576,
4)
262. 1) [\og4x-\og2y = 0, 2)
263.
1)
2)
ху
6
^ =0.
289
Упражнения для итогового повторения курса
алгебры и начал математического анализа
265. При каких значениях а система уравнений
flog3(i/-3)-21og9Jt: = 0,
[ (х + а)2 - 2у - 5а = О
имеет хотя бы одно решение?
Решить систему уравнений (266—272).
266. 1) [Vx + Vi7=16, 2)
267. 1)
268. 1)
269. 1)
2)
270.
271. 1)
2 log! (x + 2i/)
J2x + y2 = x + y.
! (x + 2y)log1 (x-y) + log2s(x-y),
2
\x2-xy-2y2 = 4.
2 '
sin x + cos y=l,
Q
sin2 x + 2 sin x cos у =—;
2)
2'
[ cos2 x + 2 sin jc sin i/ H- 4 cos21/ = 4.
272. 1) I sin x cos i/ = — —, 2) sin jc sin у = —,
i 2 4
[tgxctgi/ = l; [3tgx = ctgi/.
273. Найти наименьшее и наибольшее целые решения системы
неравенств
3 2
274. Решить систему неравенств
5 4
х-2 ^ . ,
<xzA+x-4
2 '
15
290
Упражнения для итогового повторения курса
алгебры и начал математического анализа
275. Найти все значения параметра а, при которых система
уравнений
имеет решение; решить эту систему.
76. Для всех значений параметра а решить систему уравнений
х2 + у2 - 2 у - cos (ху) +И-6а + а2 = 0.
Решить систему уравнений (277—279).
2)
U 1)
4)
Xs = у2;
cos2 ял: - sin2 пу = —;
у, з) (V
х4; [V2cosjc = V3cosi/;
5) I cosxsini/ = —,
[ sin 2jc ч- sin 2i/ = 0.
[ 6 sin jc cos у + 2 cos x sin i/ = - 3,
[ 5 sin jc cos i/ - 3 cos x sin i/ = 1.
280. Изобразить на плоскости фигуру, задаваемую множеством
решений системы неравенств, и найти ее площадь:
1)
3)
x + 3i/-3>0,
2)
4)
JC-1/+K0,
5x-3i/+15>0,
5. Текстовые задачи
281. Пассажир поднимается по неподвижному эскалатору за
3 мин, а по движущемуся за 45 с. Определить, за какое
время поднимает эскалатор неподвижно стоящего на нем
пассажира.
282. Теплоход прошел расстояние между двумя пристанями по
течению реки за 7 ч, а против течения за 9 ч. Определить
расстояние между пристанями, если скорость течения
реки 2 км/ч.
291
Упражнения для итогового повторения курса
алгебры и начал математического анализа
283. Теплоход должен был пройти некоторое расстояние за
2,25 суток, но оказалось, что он проходил за каждый час
на 2,5 км больше, чем предполагалось, а потому прошел
намеченный путь за 2 суток. Какое расстояние должен
был пройти теплоход?
284. Один рабочий выполняет некоторую работу за 24 дня,
другой рабочий ту же работу может выполнить за 48 дней.
За сколько дней будет выполнена эта работа, если
рабочие будут работать вместе?
285. При уборке урожая было собрано 4556 ц яровой
пшеницы с общей площади 174 га, причем на целинных землях
собрано по 30 ц с 1 га, а на остальной площади — по 22 ц.
Сколько гектаров целинных земель было освоено?
286. Разность двух чисел относится к их произведению как
1:24, а сумма этих чисел в 5 раз больше их разности.
Найти эти числа.
287. Две организации приобрели театральные билеты. Первая
организация израсходовала на билеты 7500 р., а вторая,
купившая на 5 билетов меньше и заплатившая за каждый
билет на 50 р. меньше первой организации, уплатила за
билеты 5000 р. Сколько театральных билетов купила
каждая организация?
288. Три дроби имеют числители, равные единице. Сумма этих
дробей равна 1. Разность между первой и второй дробями
равна третьей дроби. Сумма первых двух дробей в 5 раз
больше третьей дроби. Найти эти дроби.
289. Бригада рабочих должна была к определенному сроку
изготовить 360 деталей. Перевыполняя дневную норму на
9 деталей, бригада за день до срока перевыполнила
плановое задание на 5%. Сколько деталей изготовит бригада
к сроку, если будет продолжать работать с той же
производительностью труда?
290. Катер отправился от речного причала вниз по реке и,
пройдя 36 км, догнал плот, отправленный от того же
причала за 10 ч до начала движения катера. Если бы катер
отправился одновременно с плотом, то, пройдя 30 км и
повернув обратно, встретил бы плот на расстоянии 10 км
от речного причала. Найти собственную скорость катера.
291. От пристани отправился по течению реки плот. Через 5 ч
"20 мин вслед за плотом с той же пристани отправилась
моторная лодка, которая догнала плот, пройдя 17 км.
Какова скорость плота, если известно, что скорость
моторной лодки по течению больше скорости плота на 48 км/ч?
292. При уборке урожая с каждого из двух участков собрано
по 210 ц пшеницы. Площадь первого участка была на 0,5 га
меньше площади второго участка. Сколько центнеров
пшеницы собрано с 1 га на каждом участке, если урожай
292
Упражнения для итогового повторения курса
алгебры и начал математического анализа
пшеницы с 1 га на первом участке был на 1 ц больше,
чем на втором?
293. Расстояние от дома до школы 700 м. Сколько шагов
делает ученик от дома до школы, если его брат, шаг
которого на 20 см длиннее, делает на 400 шагов меньше?
294. Найти четыре числа, являющиеся последовательными
членами геометрической прогрессии, если третье число
больше первого на 9, а второе больше четвертого на 18.
295. Найти сумму первых двенадцати членов арифметической
прогрессии, если сумма первых трех ее членов равна
нулю, а сумма четырех первых членов равна 1.
296. Найти четыре числа, зная, что первые три из них
являются тремя последовательными членами геометрической
прогрессии, а последние три — арифметической
прогрессии. Сумма первого и четвертого чисел равна 16, а сумма
второго и третьего равна 12.
297. Сумма первых пяти членов геометрической прогрессии
равна 62. Известно, что пятый, восьмой и одиннадцатый
ее члены являются соответственно первым, вторым и
десятым членами арифметической прогрессии. Найти
первый член геометрической прогрессии.
298. Произведение пятого и шестого членов арифметической
прогрессии в 33 раза больше произведения ее первого и
второго членов. Во сколько раз пятый член прогрессии
больше второго, если известно, что все члены прогрессии
положительны?
299. В треугольнике, площадь которого равна 12 см2,
середины сторон соединены отрезками. Во вновь полученном
треугольнике точно так же образован новый треугольник
и т. д. Найти сумму площадей всех получающихся таким
построением треугольников.
300. В цветочный магазин поставили 50 красных, 100 белых и
150 желтых гвоздик.
1) Сколько различных букетов по 3 гвоздики в каждом
можно составить из имеющихся цветов?
2) Сколько различных букетов, состоящих из одной
красной, одной белой и одной желтой гвоздик, можно собрать
из имеющихся цветов?
3) Сколько различных букетов, содержащих 2 красные,
2 белые и одну желтую гвоздики, можно составить из
имеющихся цветов?
4) Сколько различных букетов, содержащих 3 красные,
одну белую и 5 желтых гвоздик, можно составить из
имеющихся цветов?
301. Состав нужно скомплектовать из 7 плацкартных, 6
купейных вагонов и одного вагона-ресторана. Сколькими
способами можно скомплектовать вагоны в состав?
293
Упражнения для итогового повторения курса
алгебры и начал математического анализа
302. Состав нужно скомплектовать из 7 плацкартных, 6
купейных вагонов и одного вагона-ресторана. Сколько
существует последовательностей расположения имеющихся
вагонов трех типов?
303. Для проверки на всхожесть было посеяно 300 семян,
из которых 255 семян проросли. Какова вероятность
прорастания отдельного семени в этой партии? Сколько
семян в среднем взойдет из 1000 посеянных?
304. Вероятность того, что размеры детали, выпускаемой
станком-автоматом, окажутся в пределах заданных допусков,
равна 0,96. Какое количество годных деталей в среднем
будет содержаться в каждой партии объемом 400 штук?
305. Отдел технического контроля проверяет половину изделий
некоторой партии и признает годной всю партию, если
среди проверенных изделий не более одного
бракованного. Какова вероятность того, что партия из 20 изделий, в
которой 2 бракованных, будет признана годной?
306. В ящике 10 деталей, 4 из которых окрашены. Сборщик
наугад взял 3 детали. Найти вероятность того, что хотя
бы одна из взятых деталей окрашена.
307. Отдел технического контроля проверяет изделия на
стандартность. Вероятность того, что изделие стандартно,
равна 0,9. Найти вероятность того, что из двух проверенных
изделий только одно стандартное.
308. Завод в среднем дает 27% продукции высшего сорта и
70% первого сорта. Найти вероятность того, что наугад
взятое изделие будет или высшего, или первого сорта.
309. При каждом включении двигатель начнет работать с
вероятностью 0,8. Какова вероятность того, что для его
запуска потребуется не более двух включений?
310. С первого станка на сборку поступает 40% всех изделий,
со второго — 30%, с третьего — 30%. Вероятности
изготовления бракованной детали для каждого станка
соответственно равны 0,01; 0,03 и 0,05. Найти вероятность того,
что наугад поступившая на сборку деталь бракованная.
6. Функции и графики
311. Найти коэффициенты k и Ь линейной функции y = kx + b,
если ее график проходит через точки А и В:
1) А(-1; -2), Б(3; 2); 2) А(2; 1), В(1; 2);
3) А(4; 2), Б(-4; -3); 4) А(-2; -2), Б(3; -2).
312. Через точку А(-3; 2) проходит прямая, параллельная
прямой, проходящей через точки В(-2; 2) и С(3; 0).
Записать формулы, задающие линейные функции,
графиками которых являются данные прямые.
294
Упражнения для итогового повторения курса
алгебры и начал математического анализа
313. Выяснить, принадлежит ли прямой х + Цг = 1 точка А:
1)А(-1;4); 2) А(0; 3); 3) А(1; 0); 4)
О
314. Линейная функция задана формулой У = --т х + 2. Найти:
1) точки А и В пересечения графика этой функции с
осями координат;
2) длину отрезка АВ;
3) расстояние от начала координат до прямой у = — — х + 2.
315. Найти значения х, при которых график функции у = 2х-1
лежит ниже графика функции у = Зх-2.
316. Найти значения х, при которых график функции
у = {\[3—2)х — у/3 лежит выше графика функции
317. Доказать, что функция у = 2х-3 возрастает.
318. Доказать, что функция у = — У[Зх — 3 убывает.
319. Выяснить, пересекаются ли графики функций:
1) у = Зх-2 и у = Зх+1; 2) у=Зх-2 и у = 5х+1.
320. Построить график функции:
1) у = 2-\х\; 2) у = \2-х\; 3) у = \2-х\ + \х-3\.
Выяснить, пересекает ли график каждой из данных
функций прямую у = 3. В случае утвердительного ответа найти
координаты точек пересечения.
321. Дана функция у = х2-2х-3.
1) Построить ее график и найти значения х, при которых
у(х)<0.
2) Доказать, что функция возрастает на промежутке [1; 4].
3) Найти значение х, при котором функция принимает
наименьшее значение.
4) Найти значения х, при которых график функции
у = х2-2х-3 лежит выше графика функции у = -2х-{-1.
5) Записать уравнение касательной к параболе
у = х2-2х-3
в точке с абсциссой, равной 2.
322. Дана функция у = -2х2-\-Зх-\-2.
1) Построить ее график и найти значения х, при которых
У(х)<0.
2) Доказать, что функция убывает на промежутке [1; 2].
3) Найти значение х, при котором функция принимает
наибольшее значение.
4) Найти значения х9 при которых график данной
функции лежит ниже графика функции у = Зх + 2.
5) Записать уравнения касательных к параболе
у = — 2х2 + Зх + 2 в точках с ординатой, равной 3.
295
Упражнения для итогового повторения курса
алгебры и начал математического анализа
200
100
Рис 142
1005
1000 20 30
Рис. 143
323. Совершая воскресную прогулку, автомобилист дважды
останавливался для осмотра достопримечательностей. После
второй остановки он вернулся домой. На рисунке 142
изображен график движения автомобилиста (по оси абсцисс
откладывалось время в часах, по оси ординат —
расстояние в километрах). С помощью графика ответить
на вопросы:
1) С какой скоростью автомобилист ехал до первой
остановки?
2) Сколько времени он потратил на осмотр
достопримечательностей?
3) Какова средняя скорость движения автомобилиста (без
учета остановок)?
324. На рисунке 143 представлено изменение курса акций
некоторой компании в течение октября (по оси абсцисс
отложены числа месяца, по оси ординат — стоимость
одной акции в рублях). Два брокера 4 октября купили по
90 акций каждый, 12 октября первый из них продал
30 акций, второй — 35 акций. Оставшиеся акции оба
брокера продали 30 октября. Которому из брокеров сделка
принесла меньшую прибыль? На сколько рублей он
получил меньше, чем другой брокер?
325. Сигнал с корабля можно различить в море на расстоянии
одной мили. Корабль А идет на юг, делая 3 мили в час,
и в настоящее время находится в 5 милях к западу от
корабля В, который идет на запад со скоростью 4 мили в
час. Будут ли корабли на расстоянии, достаточном для
приема сигнала?
326. Выяснить, пересекаются ли графики функций:
и у =
2) У-I
X
и */ = 4(х+1);
3) У=-^
и !/=-;
-1 и i/=i.
296
Упражнения для итогового повторения курса
алгебры и начал математического анализа
327. Построить график и выяснить, является ли ограниченной
функция:
2х- х2 при х<1, ЛЧ \х2 + 2х + 2 при
2) у
I — х при х > 1; [ ух при
328. Построить график и выяснить, является ли непрерывной
функция:
Iog2{x-1) при х<1,
у ~
3) ^Л*"1! ПРИ х<1> 4) г/ = 1|З11 при *<0>
[|log2x| при х>1; [Vx-1 при х>0.
329. Выяснить, является ли четной или нечетной функция:
1) у = 2х + 2~х; 2) у = Зх-3-х;
330. Исследовать на четность и нечетность функцию:
1)у = 2х2-1; 2) у = х-х3; 3)у = х5-±; 4)у-^
331. Выяснить, является ли четной или нечетной функция:
1) i/ = jcsinjc; 2) i/ =
3) y = x + sinx; 4) i/ =
332. Выяснить, при каких значениях х возрастает функция:
1) у = Ух2-9х-10; 2) у = ^/7-6х-х2;
5) i/=i
х2-4
333. Выяснить, является ли периодической функция:
1) 2/ = 25x"1; 2) i/ = 2Vcos2;j:-1.
Найти наименьший положительный период функции
(334—335):
334. 1) i/ = cos^; 2) t/ =
335. 1) t/ = cos3jc; 2) i/ = sin^;
о
3) y = tgbx\ 4) i/ = si
336. Исследовать на четность и нечетность и построить график
функции:
1) у = -х4 + 4х2-5; 2) y = xs-4x.
337. Найти наибольшее или наименьшее значение функции
у = ах2 + Ъх-4, если i/(l) = 0 и i/(4) = 0.
338. Найти наибольшее и наименьшее значения функции:
V3cos2jc; 2) i/ = 2cos2jc + sin2jc.
297
Упражнения для итогового повторения курса
алгебры и начал математического анализа
339. Дана функция f(x). Найти корни уравнения f(x) = a9 а
также наибольшее и наименьшее значения функции, если:
i\ *< ч _ sin4 л: + cos4 л: _ 10 оч -. ч _ 2 sin4 х + 3 cos2 x _ 15
ч Т\Х)— — —, а— —; б) Т\Х)— — , а——.
6 х +cos6* ' 2cos4jc + sin^jc '
sin6 х +cos6*
340. Найти коэффициенты а, 6, с квадратичной функции
" i/ = ajc2 + 6x + c, если i/(-2)=15, y(3) = 0, г/(0) = -3.
341. Построить график функции i/ = V25— x2. Найти по
графику промежутки монотонности функции. Доказать, что
график данной функции симметричен относительно оси Оу.
342. Построить график функции у = . Показать, что функ-
х — £
ция убывает на промежутках х<2 и х>2. В какой точке
график функции пересекает ось ординат?
343. Выяснить основные свойства и построить график
функции:
1) i/ = 3*+l; 2) У=(!)*-3;
4) y = logL(x-l); 5) i/ = Vx+T-2;
з
344. Построить график функции:
" 1) i/ = 2--1-3; 2) # =
3) y = 2sin{x-j); 4) у» Т~^+1-
345. При каких значениях а графики функций
имеют общие точки?
Найти область определения функции (346—349).
346. 1) y = 2x + lg(6-3x); 2) у = г~х-\
2-6*-16
348. 1) y = \/\ogs±±-^-; 2) y = y/logi(x-3)- 1.
2
349. 1) i/ =
2) у =
3) у
4) i/
298
Упражнения для итогового повторения курса
алгебры и начал математического анализа
Найти множество значений функции (350—353).
О\ л 9v2 I fiv 1 •
Ct) у — СлЛ, ТОЛ — Xj
4) 1/ = 2 + |.
2) j/ = 0,5cosx + sinjc.
2) i/ = V*2-
353. 1) i/= sin*-cosx; 2) z/ = log2(
354. Найти все значения х9 при которых функция
у = 6 cos2 jc + 6 sin jc - 2
принимает наибольшее значение.
все значения а, при каждом из которых
наименьшее значение функции
на отрезке [0; 2] равно -4.
все значения а, при каждом из которых
наименьшее значение квадратичной функции
у = 4л;2 - 4ах + а2 - 2а + 2
на отрезке [0; 2] равно 3.
357. Найти все значения параметра а, при каждом из которых
вершины двух парабол
у = 4х2 + 8ах-а и у = 4ах2-8х + а-2
лежат по одну сторону от прямой i/ = -5.
[358.1 Найти наибольшее и наименьшее значения функции
_ 2 cos4 х + sin2 x
2 sin4 л:+ 3 cos2 л:'
359. Найти угловой коэффициент касательной к графику
функции y = f(x) в точке с абсциссой х0, если:
*o=^; 2) ^
360. Найти угол между осью Ох и касательной к графику
функции y = f(x) в точке с абсциссой х0, если:
JV7, хо = 1; 2)
V*, хо 1;
4л:2
361. Написать уравнение касательной к графику функции
y = f(x) в точке с абсциссой х0, если:
1) f(x)^ *o=T' 2) 42
4
362. Найти угловой коэффициент касательной к графику
функции y = xs-x+l в точке пересечения его с осью Оу.
363. Найти угловой коэффициент касательной к графику
функции y = 3xs-l в точке с ординатой у = 2.
364. Прямая у = 4х+а является касательной к параболе
у = 6-2х + х2. Найти а и координаты точки касания.
299
Упражнения для итогового повторения курса
алгебры и начал математического анализа
365. Найти точки, в которых касательные к графику функции
параллельны оси абсцисс.
366. На параболе у = Зх2 + 7х + 1 найти такую точку, в которой
касательная к параболе образует с осью абсцисс угол —.
4
х_
367. Найти все точки графика функции f(x) = es, в которых
касательная к этому графику проходит через начало
координат.
368. Написать уравнение касательной к графику функции
y = f(x) в точке с абсциссой х0, если:
2)
369. Найти угол между осью Ох и касательной к графику
функции y = xs-x2-7x + 6 в точке М(2; -4).
370. Найти тангенс угла, который касательная к графику
функции у = х2е~х в точке с абсциссой х=1 образует с осью Ох.
371. Найти угол между осью Ох и касательной к графику
функции у = — cos (Зх - -^ ] в точке с абсциссой х = -^.
372. Записать уравнение касательной к графику функции
в точке его пересечения с осью Ох.
373. Записать уравнение касательной к графику функции
f(x)=\[x1+l
в точке с абсциссой х = 4.
374. Найти тангенс угла между касательными, проведенными
к параболе у = х2 из точки (0; 9).
375. Найти промежутки монотонности функции:
2) у
Х2-1
2) у
х -1 х
Найти точки экстремума функции (376—377).
376. 1) у = (х-1)3(х-2)2; 2) j/ =
Найти наибольшее и наименьшее значения функции
(378—380).
378. 1) I/= 2 sin х + sin 2л; на отрезке 0; -£- ;
2) i/ = 2sinx + cos2jc на отрезке 0; ^ .
300
Упражнения для итогового повторения курса
алгебры и начал математического анализа
379. 1) у = Ух + 5 на отрезке [-1; 4];
2) z/ = sinx + 2\/2^cosx на отрезке О; ^ \.
380. 1) у = \пх-х на отрезке [0,5; 4];
2) i/ = :x;Vl-*2 на отрезке [0; 1].
381. Найти наибольшее и наименьшее значения функции
о о • Г 4я 2я1
z/ = 2-3sinxH-4cosjt: на отрезке ——; — I.
382. При каком значении а наибольшее значение функции
г/ = х3-3л:ч-а на отрезке [-2; 0] равно 5?
383. При каких значениях а функция у = х3- Sax2 + 2 7х -5
имеет единственную стационарную точку?
. Найти эстремумы функции:
2)
385. Исследовать с помощью производной функцию
у = х3-Зх + 2
и построить ее график. Найти точки, в которых
касательные к графику параллельны оси Ох.
386. Исследовать с помощью производной функцию
у = х3 - Ъх2 - х + 5
и построить ее график. Записать уравнение касательной к
графику этой функции в точке с абсциссой, равной 4.
Исследовать функцию y = f(x) и построить ее график
(387—389).
387. 1) f(x) = 4x3 + 6x2; 2) f(x) = 3x2-2x3;
3) f(x)=±x3-x; 4) f(x) = x4-±x2.
388. 1) y = -^+x2; 2) i/ = x4-2x2-3.
ооУ. ij г/= — x —x — dx + y, zjz/ = -,x
9 9
O4 jcz + 1 .4 jc^ + 2
3) y= ; 4) w=—-—.
' u x ' u 2x
390. Периметр осевого сечения цилиндра 6 дм. При каком
радиусе основания цилиндра его объем будет наибольшим?
391. Найти наибольший возможный объем цилиндра, площадь
полной поверхности которого равна 54л см2, если известно,
что радиус основания не меньше 2 см и не больше 4 см.
392. В правильной пирамиде SABC из вершины S проведена
высота SO. Найти сторону основания пирамиды, если
объем пирамиды является наибольшим при условии, что
SO+AC = 9 и 1<ЛС<8.
301
Упражнения для итогового повторения курса
алгебры и начал математического анализа
393. В правильной четырехугольной призме диагональ равна 2V3.
При какой высоте призмы ее объем наибольший?
394. Для функции f(x) = х~2 + cos x найти первообразную,
график которой проходит через точку М(о,5л; J.
395. Найти наибольшее и наименьшее значения функции
f(x) = х2 (2х - 3) -12 (Зх - 2)
на отрезке — 3<л:<6.
|396.| Найти наибольшее и наименьшее значения функции
f(x) = 2\nsx-9\n2x+12\nx
_3
на отрезке e4<x<es.
;397. На параболе у = х2 найти точку, расстояние от которой до
точки А(2; — J является наименьшим.
3987] На координатной плоскости даны точки Л(3; -1) и JD(4; —1).
Рассматриваются трапеции, у которых отрезок AD
является одним из оснований, а вершины другого
основания лежат на параболе у = 1 — х2, заданной на отрезке
[-1; 1]. Среди этих трапеций выбрана та, которая имеет
наибольшую площадь. Найти эту площадь.
399.] На координатной плоскости дана точка К(3; 6).
Рассматриваются треугольники, у которых две вершины
симметричны относительно оси Оу и лежат на параболе
г/ = 4х2, заданной на отрезке [— 1; 1], а точка К —
середина одной из сторон. Из этих треугольников выбран тот,
который имеет наибольшую площадь. Найти эту площадь.
400. Каковы должны быть коэффициенты р и q квадратичной
функции y = x2+px + q, чтобы при х = 5 она имела
минимум, равный 1?
401. Какой должна быть высота конуса с образующей 20 дм,
чтобы его объем был наибольшим?
402. Какую наименьшую площадь полной поверхности имеет
цилиндр, если его объем равен VI
403. Найти радиус основания цилиндра, вписанного в шар
радиуса R и имеющего наибольшую площадь боковой
поверхности.
404. Найти высоту цилиндра наибольшего объема, вписанного
в шар радиуса R.
405. Найти высоту конуса наибольшего объема, вписанного в
шар радиуса R.
406. В конус с заданным объемом V вписана пирамида, в
основании которой лежит равнобедренный треугольник с
углом при вершине, равным а. При каком значении а
объем пирамиды будет наибольшим?
302
Упражнения для итогового повторения курса
алгебры и начал математического анализа
407. Из всех цилиндров, у которых периметр осевого сечения
равен р, выбран цилиндр наибольшего объема. Найти этот
объем.
408. Из всех цилиндров, которые можно поместить внутри
сферы радиуса Я, найти цилиндр наибольшего объема.
409. Консервная жестяная банка заданного объема должна
иметь форму цилиндра. При каком соотношении между
диаметром основания D и высотой Н цилиндра расход
жести будет наименьшим?
410. Из всех правильных треугольных призм, которые
вписаны в сферу радиуса R, выбрана призма наибольшего
объема. Найти высоту этой призмы.
411. Из всех цилиндров, вписанных в конус с радиусом
основания R и высотой Н, найти цилиндр наибольшего объема.
412.
413.
414.
415.
416.
417.
Найти площадь
(412—416).
1) у
2) у
2) у
3) у
4) у
1) У
1) У
1)У
3) у
= Vx-l, г/ =
1 _
х '
= 4х —х2, у =
= х2-2х + 8,
= sinx, i/ = C
= cosx, y = i
= \^, У = 2,
= 9-х2, i/ =
= cosx, х = -
1
фигуры, ограниченной
3-х, г/ = 0;
2, ^=-.
| 2тг
' 3 ' Х %у
), х = -^9 х=|.
Jt === 1/ , CijU === Jt "Т" О, ы —
(х-1)2-4; 2) i/ = x2,
-, г/ = 0; 2) г/ = 3*,
= 2cos3x-5sin2x+10, г/ = 0, х = --
Найти площадь
фигуры, ограниченной
данными линиями
х + 5.
з
ж —1, ж-1, г/ = 0;
графиком функции
y = 9x — xs и касательной к этому графику в его точке с
абсциссой 3.
18. Доказать, что при -1 <х< 1 сумма arcsinх + arccosx равна С,
где С — постоянная. Найти С.
19. Найти все значения Ь, при каждом из которых
производная функции
f(x) = sin 2x - 8 [Ъ + 2) cos х - (4&2 +166 + 6) х
отрицательна на всей числовой прямой.
20. Найти все значения х9 при которых касательные к
графикам функций
z/ = 3cos5x и z/ = 5cos3x + 2
в точках с абсциссой х параллельны.
303
Упражнения для итогового повторения курса
алгебры и начал математического анализа
421. Графику функции y = — x3 + ax2 + bx + c принадлежат точки
Аи В, симметричные относительно прямой х = 2.
Касательные к этому графику в точках А и В параллельны
между собой. Одна из этих касательных проходит через
точку (О; 2), а другая — через точку (О; 6). Найти а, Ь, с.
422, Графику функции у = х3 + ах2 + Ьх + с принадлежат точки А
и Б, симметричные относительно прямой х = — 2.
Касательные к этому графику в точках А и В параллельны между
собой. Одна из этих касательных проходит через точку
(О; 1), а другая — через точку (О; 5). Найти а, Ь, с.
4237J График функции у = х3+ ах2+ Ъх + с, с<0, пересекает ось
ординат в точке А и имеет ровно две общие точки М и N
с осью абсцисс. Прямая, касающаяся этого графика в
точке М, проходит через точку А. Найти а, &, с, если
площадь треугольника AMN равна 1.
424.1 График функции у = — х3 + ах2 + Ьх + с9 о О, пересекает ось
ординат в точке D и имеет ровно две общие точки А и В
с осью абсцисс. Прямая, касающаяся этого графика в
точке Б, проходит через точку D. Найти а, Ъ, с, если
площадь треугольника ABD равна 1.
1425J В какой точке графика функции у = (х-1)2, 0<д;<1,
нужно провести касательную к графику, чтобы площадь
треугольника, ограниченного этой касательной и осями
координат, была наименьшей?
] На параболе у = 2х2-Зх + 8 найти точки, касательные в
которых проходят через начало координат.
] Парабола у = х2 +рх + q пересекает прямую у = 2х - 3 в
точке с абсциссой 1. При каких значениях р и q расстояние
от вершины параболы до оси Ох является наименьшим?
Найти это расстояние.
|428Т! Найти площадь фигуры, ограниченной параболой
у = 4х-х2 и касательными к ней, проходящими через
точку м(|; б).
429.] При каком значении k площадь фигуры, заключенной
между параболой у = х2 н- 2х — 3 и прямой y = kx + l,
наименьшая?
1430J Найти площадь фигуры, ограниченной параболой
у = 0,5х2-2х + 2 и касательными к ней, проведенными
через точки Al 1; — J и Б(4; 2).
1431.1 Через точку графика функции y = Vx с абсциссой а, где
— <а<2, проведена касательная к этому графику. Найти
значение а, при котором площадь треугольника,
ограниченного этой касательной, осью Ох и прямой х = 3, будет
наименьшей, и вычислить эту площадь.
304
Упражнения для итогового повторения курса
алгебры и начал математического анализа
1432.1 Дана фигура, ограниченная кривой у = sin x и прямыми
г/ = 0, х=— (0<л:< —J. Под каким углом к оси Ох нужно
провести прямую через точку (О; О), чтобы эта прямая
разбивала данную фигуру на две фигуры равной площади?
7. Производная и интеграл
433. Найти значение производной функции f(x) в точке х0, если:
1) f(x) = xs-^-+x, *„=!; 2) /(*)«i5£, жо = 1;
3) f(x) = x-*-^+3x, *0 = 3; 4) /(ж)
434. Найти значения дг, при которых равно нулю значение
производной функции:
1) f(x) = sin2x-x; 2) f(x) = cos2x + 2x;
3) f(x) = (2x-lf; 4) f(x) = (l-3xf.
435. Показать, что f (l) = f (0), если f(x) = (2x-3)(3x2 + 1).
436. Найти значения л:, при которых значения производной
функции
отрицательны.
437. Пуля вылетает из пистолета вверх со скоростью 360 м/с.
Найти скорость пули в момент £=10 с и определить,
сколько времени пуля поднимается вверх. Уравнение
движения пули h = vot-4:,9t2.
438. Колесо вращается так, что угол поворота прямо
пропорционален кубу времени вращения. Первый оборот был
сделан колесом за 2 с. Определить угловую скорость
колеса через 4 с после начала вращения.
439. Трудоемкость (объем) комплекса работ Q измеряется в
человеко-часах (чел./ч). Бригада осваивает объект так, что
выполненный объем работ как функция времени
описывается формулой Q = 160t чел./ч (где t — время в сутках).
Какова скорость освоения объема работ (интенсивность)
q чел./ч в сутки? Сколько человек в бригаде, если
суточная норма рабочего 8 чел./ч в сутки?
440. Дневная производительность труда (за 7 рабочих часов)
рабочего машиностроительного завода описывается
функцией у = -0,09£2 + 0,28^+10,06, где t — время в часах, у —
количество продукции. Сколько продукции производит
рабочий за один год (260 рабочих дней)?
Найти производную функции (441—443).
305
Упражнения для итогового повторения курса
алгебры и начал математического анализа
х+1 '
)2V^I; 2) i/ = x2
3) у = sin 2дг cos Sx; 4) г/ = х cos 2л;.
444. Найти производную функции y = \ogSx + 4(7x-4:) в точке
х = 2.
Найти значения х, для которых производная функции
равна — 1.
446. Определить знак числа Г(2), если:
~2
el~x
Дана функция /(*)- ^^2« ' Найти f(0)' ^(j)'
448. Найти значения х, при которых f'(x)^g'(x)9 если
449. Для функции /(x) = cos4x найти первообразную F(x), ее-
ли
450. Найти первообразную функции:
4jc-1 "
Вычислить интеграл (451—452).
9 1
11) J Vx^ldx; 2)
2 £
6
6
4)
3 0
п ~3
1) ^sinxdx; 2) \
Я. £
2 6
1 2
3) \ (x2 + 2x + 3)dx; 4)
-2 1
3 1
5) [(x~2 + l)dx; 6)
i -i
306
Упражнения для итогового повторения курса
алгебры и начал математического анализа
Предметный указатель
Алгебраическая форма
комплексного числа 205
Асимптота вертикальная 57
— невертикальная 114, 115
Бином Ньютона 171
Вероятность события 183
— произведения независимых
событий 194
произвольных событий 190
— суммы несовместных событий
186
произвольных событий 187
противоположных событий
186
Выпуклость вверх (вниз) 114
Вычитание комплексных чисел
210
Гармонические колебания 31, 152
Геометрический смысл модуля 216
производной 85
Действительная ось 214
— часть комплексного числа 205
Деление комплексных чисел 211
Дифференциал функции 88
Дифференциальные уравнения 150
Индукция 157
Интегральная сумма 139
Интегрирование функций 134
Касательная к графику функции
86
Комплексная плоскость 214
Комплексные числа 205
равные 205
чисто мнимые 206
сопряженные 209
противоположные 210
обратные 211
Криволинейная трапеция 137
Математическая индукция 157
Мнимая ось 214
— часть комплексного числа 205
Модуль комплексного числа 210
Основная теорема алгебры 231
Первообразная функции 132
Перестановки 163
— с повторениями 164
Период функции 8
Площадь криволинейной
трапеции 139
Последовательность
возрастающая 49
— монотонная 49
— расходящаяся 46
— сходящаяся 46
— убывающая 49
Правило произведения 159
Предел последовательности 46
монотонной 49
— функции 53
бесконечный 55
в бесконечности 55
слева 55
справа 55
Приращение аргумента 61
— функции 61
Произведение комплексных
чисел 206
— событий 181
Производная функции 67
логарифмической 78
обратной 73
обратной
тригонометрической 81
показательной 79
сложной 72
степенной 74
тригонометрической 78
Размещения 166
— с повторениями 160
Синусоида 19
События достоверные 180
— зависимые 191
— невозможные 180
— независимые 191
— несовместные 181
— противоположные 181
— равновозможные 181
— равносильные 182
307
предметный указатель
— случайные 181
— элементарные 181
Сочетания 168
— с повторениями 174
Сумма комплексных чисел 206
— событий 181
Теорема Лагранжа 99
— об обратной функции 63
— о промежуточных значениях
63
— Ферма 103
Треугольник Паскаля 171
Тригонометрическая форма
комплексного числа 219
Точка критическая 104
— максимума функции 102
— минимума функции 102
— перегиба 116
— разрыва функции 60
— стационарная 104
— экстремума функции 103
Уравнение касательной к
графику функции 87
Условная вероятность 189
Формула Бернулли 199
— Муавра 222
— Ньютона—Лейбница 140
Функция бесконечно малая 58
— дифференцируемая в точке 67
на интервале 67
— непрерывная в точке 61
на интервале 62
на отрезке 62
— нечетная 7
— обратная тригонометрическая
36
— периодическая 8
— тригонометрическая 5
— четная 5
Ответы
Глава I
1. 2) xeR; 4) х*0; 6) х<-1, х>1. 2. 2) 0<i/<2; 6) -l,25<i/<-0,75.
3. 2) **тсп, /i€Z; 4) ** JL+™ /i6Z. 4. 1) x*nn, n^Zy f(
10 5 \4
100. 5.
; 4) --^- +27t/i<jc< -^- + 2nn, neZ; 6) - ^- + 2nn<x< ^- + 2nn9 neZ.
3 3 2 2
6. 2) **^ + ^, ^€Z; 4) jc^^+tt/i, neZ. 7. 2) -Ki/<1; 4)
6)-V3<i/<\/3. 8. 1)-V26<i/<V26; 2)-l<i/<3;4)-2<i/<4. 9. 1) ^
2) —<i/<l- 12. 2) Нечетная; 4) нечетная; 6) четная. 13. 2) He является
4
четной и нечетной; 4) четная; 5) четная. 16. 2) Четная; 4) нечетная; 6) чет-
4тг
ная; 8) нечетная. 18. 2) —; 4) тт. 19. 2) 2тг; 3) тг; 4) бтг. 20. 1) Является, Т=2п;
о
2) не является; 3) является, Т = %. 22. ^-. 23. 1) 2тг; 2) тт. 24. Т = 2\Ь-а\.
25. Г = 4|а-с|. 26. 2Г. 29. 1) 0; 2) -1; 3) -Щ-; 4) 0. 30. 1) ^; 2) 0;
3) —; 4) —. 31. 1) Принадлежит; 2) не принадлежит; 3) не принадле-
4 4
жит; 4) принадлежит. 33. 2) [--|; о], [о; |]; 4) [-тг; 0], [о; -|].
34. 2) cos — <cos^^; 4) Cos(-—)<cos(--y-); 6) cos4<cos5. 35. 2) ^-,
f • f; 4' f • f • f • »■ 2io<«f • f ««f! 4> t "-^
J^<jc<37t. 37. 1) a) (-oo; 2тг]; б) [-1; oo); в) [п; 2n]; 2) а) [-Зтг; оо);
6
6) [-1; oo); в) [-Зтг; -2тс], [-тс; оо). 38. 2) sin^<cos|-; 4) sin -^>cos^;
7 7 5 5
43. [|; я], [■?£; 2тс]. 44. 1) x1=0,
4) x = - —. 45. 1) Имеет; 2) не имеет. 46. 1) 2 решения; 2) 3 ре-
шения. 50. 1) - — + %k<x< — +%k, keZ\ 2) — + 2%n<x< — + 2nn,
6 6 3 3
3) -Z± + 2nk<x<^ + 2nk, ktZ. 52. 1) 1; 2) ^; 3) ^; 4) ^.
4 4 La La £i
53. 1) 1; 2) 2; 3) —; 4) 2. 54. 1), 3) не принадлежит; 2), 4) принад-
лежи*. « „ [|; f ], [f, 2,]; 4, [-2, -f ], [-&, -,].
309
Ответы
57. 2) Sin-^>sin-i^; 3) sin(--^)>sin(--^-); 4) sin7>sin6.
7 7 \ 7 / \о/
«а 9ч я Зтс 9я Il7t . ^ч 4л 5л ко о\{\^„^п
5о- ^) —» —» —» ——; 4) —, —. 59. 2) О<#<—, — <*< — » ~~7
4444 о о 44 44
; 4) -^ <*<"|L- 60. 1) а) (-оо; 37t]; б) [-1; оо); в) (-оо; 0), [|; ^],
-|^; Зя]; 2) а) [-2я; 2я]; б) [-1; 1]; в) [-2тс; -л],
л
9'
2п
9 '
7л
9 '
8л а
9
Q 7л
6 '
11л
6
i 2)- — f - - ll7r 1Ол 57t
[тг; 2тг]; 2) [-|; |], [^; 2тг]. 67.
jc5 = -y; 2)xl = ^9 x2 = n,xs = ^-; 3) * = 0; 4)jc = -+tt/i, neZ. 68. 1)
Имеет; 2) не имеет. 69. 1) Три; 2) три. 73. 1) — +%п<х< — + тг/г, /i€Z;
6 6
2) 27Г/1- — <х< — +2пп, ntZ. 76. 1) -1; 2) 0; 3) -V3; 4) 1. 77. 1) у= —;
6 6 W3 ^
2) i/ = 0; 3) i/ = V3; 4) у=-—. 78. 1) Принадлежит; 2) не принадлежит;
3) принадлежит; 4) принадлежит. 79. 2) tg — <tg —; 4) ctg(- — )>ctg(- —);
о 9 \o/ \7/
6) tgl<tgl,5. 80. 2) -Щ-, ±, ^; 4) -i, i" ^. 81. 2) -^L
о о о 4 4 4
82.
n; |); 2) а) (-тс; 2тс); б) Д;
. 1) а) [-я; ^]; 6) [-1; оо); в) [-1; -|],
в) Г~Т; °1' \п; ^г\ 83' 2) -|+яп<ж<-|+яге, пе^; 4) -^-
L ct \ L ^ J о ct 4
neZ. 84. 2) -arcctg2 + ?r, -arcctg2 + 2?r, -arcctg2 + 3?r. 85. 2) 0<*<arctg4,
— <jc<arctg4 + 7r, — <jc<arctg4 + 2?r, — <x<Sn; 4) 0<jc<—,-arctg3+7t<
Ct Ct Ct Ct
<х<Щ-у -arctg3 + 2?r<jc<-^, - arctg 3 + 3тг<л:<37г. 86. 2) - —+tt/i<
2л 2л 2t
<jc<arctg5 + 7r/i, nzZ; 4) - arctg5 + я/г < jc < — +7r/i, nzZ. 87. 2) Нет кор-
2л
ней на промежутке; 4) * ±-, |f, ^. 88. 2) -|<ж<^, -f <*<-^.
4 1^ \2t 4 «i У о У
|^ |-|L, ^<х<^. 90. 2) «/>!; 4) «/>!, j/<-1. 94. 2)-| +
- — +7Ш, — +7t/i<jc<— + 7г/г, /16^.95. 1) arcsiii — <arcsin ;
332 V3 vio
/ 2 \ / 3 \ 3 yfb I \/2 \
2) arcsin I ) > arcsin ( ); 3) arcsin — > arcsin -^—; 4) arcsin ( - — ) >
V 3 / V 4 / Y5 3 V 3 /
> arcsin (— — ). 96. 1) arccos — < arccos — ; 2) arccos ( ) > arccos ( ).
V 4/ д/з ^5 V 5/ V 3/
310
Ответы
97. 1) arctg2\/3<arctg3V2; 2) arctgf- —) <arctgf-—); 3) arcctg V5>
^ V2' V \lb'
>arcctgV7; 4) arcctg(- — )<arcctg(-V2). 98. 2) * = 6~^; 4) x = -3-V3.
* д/З ' 4
99. 2)x = --; 4)jc = -1. 100. 2)jc=1; 4)jc = 1. 101. 1) 1<*<5; 2) -
3 3
3) 1<jc<4; 4) -2<jc<-1, 1<jc<2; 5) 0<jc<25; 6)—
У
8) Г^=г^; -ЦД1- 108- 2) x*%+nn, neZ; 4) -£ + 2тш<x< £ + 2nn,
; 6) x*%n, хФ(-1)п — +7t/i, /i€Z. 109. 2) -Ki/<1; 4) 5<i/<7;
6
6) -4<i/<-2. 110. 2) Нечетная; 4) не является четной и нечетной.
112. 2) sin(-l)<cosl; 4) cos3<tg4. 113. 2) i/ = cosjc; 4) обе.
114. 2) [1; l]. 115. 1) Ц-% 2) -|. 116. 2) [-^; о); [|; тг),
Г5я. Зя1. .v Г 4тс. я\ Г я. я\ Г 2я 1 117 9. я 2тг 7тг 8я .
LT' TJ; 4) ГУ "¥> Г¥' ^> LT; "J-117' 2) ^' Tf Tf Т;
4) тс, Зтг. 118. 2) -H^<jc<- —; 4) arctg- -2tt<jc<- —. 119. 1) Два;
О О £ £
2) три. 121. 2) tg4,5, tg3, tg2, tgl,8. 122. 2) tt/i<jc< —+ tch, neZ.
123. 2) - и --; 4) 1 и -2. 124. 2) Четная; 3) нечетная. 125. 2) 4тг.
127. 1) jc^-1+яп, х = 2пп, neZ; 2)x= — , x = --+2nn, neZ. 128. 1) х =
2 3 2
= -1?-+3; 2)jc=-3,5. 129.- —+2tt/i<jc< —+2тг/г, neZ. 131. 2)-l<i/<-.
2 3 3 4
132. 1) — +2nn<x< — +2nn, neZ; 2) nn<x< — +nn, neZ.
4 4 2
Глава II
3. 1) 1; 2) 2; 3) 3; 4) 1. 5. 1) |; 2) I; 3) |; 4) 1; 5) y|; 6) -|.
6. 1) ^; 2) 2; 3) V3; 4) 0. 7. —. 8. 1) 0; 2) -6; 3) 3; 4) 7.
2 <2ах
9. 1) 1 и 2; 2) 2 и 1; 3) 0 и 1; 4) -1 и 2. 11. 1) х = 2, х = -2; 2) х = --;
3) * = -2, jc = 1; 4) * = -1, jc = O, д:=1. 12. 1) у = 3; 2) i/ = 5; 3) у—1
о
13. 1) |; 2) |; 3) |; 4) |; 5) V3; 6) |. 14. 2) Нет; 4) да. 15. 1) [-2; 4],
[-3; 3]; 2) [-2; 5], [-3; 0]U[2; 6]; 3) [-3; -1)U(-1; 3), (0; 4]; 4) [-6; 3],
(-3; 1]. 16. 1) Л, [~~; +°°); 2) Л, (-оо; 4]; 3) хф\у у*0; 4) jc^-1,
18. 1) а) и в); 2) jc = — 1 в случаях в) и г); 3) а), б).
19. а) 1) и 4) — да; 2) и 3) — нет; б) все — нет; в) 1) при х^2; 2) при
0<jc<2 и при х>2; 3) при х*2; 4) при jc^I. 20. 1) Нет; 2) нет; 3) да;
4) нет. 22. 1)1; 2) —; 3) -; 4) -1. 23. 2) (* + /г~1)~(*~1) ;
п 3 Л
311
Ответы
4) ((* + fr) + 2)-(* + 2). (2(* + fr) + (* + fr))-(2* + *) 24 2) g;
h h
4) 6* + 5. 25. 2) -4; 4) -7. 26. 2) 5. 27. 2) i;(2) = 0,3, i;(8) = 0,3.
28. 2) 10*. 29. 2) 2,91. 30. 2) 2*-l; 4) -54*; 6) 1,8л:2;
8) 16*. 31. 2) 12*+5; 4) 1-16*; 6) -36*2+18; 8) -9*2 + 4*-l.
32. 2) f (0) = -2, f (2)= 10; 4) f (0)=l, f (2) = 13. 33. 2) *=1,5; 4) *=-0,5;
6) x = -l. 34. 2) 5*4-8*3 + 3*2-4*; 4) 9*2-24*. 35. 2) 44.
36. 2) 1; 4) - —. 37. 2) 4*3-3*2-6*-l 3g 2) ^(^(jc)) = lgV^^T;
18 (*-l)2
4) f(g(x)) = \/^±1. 39. 4) 3(*3-*2)2(3*2-2*) = 3*5(*-l)2(3*-2).
у * —3
40. 2) *>2; 4) **-. 41. 2) *<0, *>2. 42. 2) *>0,5. 43. 2)
3
44.1) g(x)=i^±3.; g'(x) 4-—; 2)
Дг-2 (*-2)2
45. 2) 3(x3-2x2 + 3jc + 2)2(3jc2-4jc + 3). 46. 2) 12jcu; 4) 21jc2-21x6;
6) 3*2-4-- 47. 2) -^— ; 4) _J_ + _-i ; 6) ^— ; 8)
> • • g 9 2'
6) f(3) = 0, f(l) = -8; 8) f(3) = 24, f(l) = -4. 49. 2) ^=-4, *2=0,
лг3 = 1; 4) л:х — 1, *2 = 1; 6) x=l. 50. 2) 192; 4) 31,5. 51. xx = -^,
5
х^М, Хз = 3. 52. 2) Зд:4-4д:3+д:2-2д:-1 53 2) _6xl. 4) 4ж"?+
11 (л:-1)2 7
+ |Д 6)f ,t-7,-". 54.2) ЦД
_1 _1
6) 1-Ajc 6-fljc з 55 2) (*-l)3(*+l)6(ll*-3); 4) -
X(2*-3)2(10* + 3). 56. 2) 2(3*2 + 3* + 2); 4) (* + 2)(5*-*2-4)
(2*+1)2 2*Vi"(2-*)2
57. 2) *! = 0, x2 = -U 4) * = 3. 58. 2) -l<*<0, *>2; 4) *>2; 6)
59. 3,5 рад/с. 60. 902,5 Дж. 61. 2) 103 г/см. 62. 2*~5
2V(*-2)(*-3)
63. 2) e*-cos*; 4) -A+^; 6) ex + ——. 64. 2) -10e2*; 4) -6cos2x;
xs sin2* ж 2
6) 2ex + 8e~2x. 65. 2) 2*7 + 9cos3*; 4) --1°+Л; 6) 5 -x1.
4 5 *3 cos2 2* 3
66. 2) -3* 3-cos4*; 4) -^* ^-sin-. 67. 2) 6*2 + -^= + 2sin2x;
2 5 x 2V*
4) 16*7 ? cos3*; 6) 4* ^ - — e2x. 68. 2) 7(*-4)6;
cos2 3* 5 sin2 * 2
4) —-i ; 6) ^—-; 8) -(*-4) 3 . 69. 2) 30(5*-4)5; 4) -24(3*-1)"3;
2V*T5 (*-l)4
312
Ответы
_2_ _3 _4_
6) 15(4-3*)~6. 70. 2) -(4*+1) 3 ; 4) -2(4*+1) 2 ; 6) 15(2-9*) 3 .
3 _ 1
71. 2) -sin2*; 4) 4sin3*cos*; 6) -4*V*4; 8) -. 72. 2) А «Г * ;
* 2
4) ~^-^\ 6) -4sin(4* + 3); 8) | cosf-^-+ l). 73. 2) -1 cos(-?£-2);
о* + ^ 6 \ 6 / 4 V 4 /
4) -Isin^^; 6) —cos 2* + 3 ; 8) - 12cos33*-sin3*; 10) 2tg3 —x
3 3 5 5 2
2 sin3— l
xJ=2 74 2) 8*__.2e2,+3. 6) 4*+7
423
=74 2) e 6)
21 cos51 4*2-3 (2* + 3)2 2*2 + 7*
1 1
75. 2) 4*ln4; 4) 7*-3ln7; 6) —Ц-; 8) ^-—. 76. 2) * = ±^-
*ln4 (* + 3)lnlO 3
ntZ; 4) * = -l; 6) jc = O; 8) корней нет. 77. 2) --1 + 10
2V6(1)
_з ь з-5£ 2V6(1-*) 2-5*
4) A CoS 2* + 3 +2(jc-1) 2;6) 4(2-jc) 3-10e 2 .78. 2) 2^2+3x(2jc + 3)ln2;
2 4 x x
4) -JL-. 79. 2) -e2 sin33* + e2 • 9sin23*• cosSx; 4) -2e3~2a:cos(3-2jc)-
^^ 80. 2) №±I) _ Vto3Mn3 . 4)
2 V" (3^l)2
81. 2) —-—f*2^1n2-^—-2^ + log2^); 4) sin* + cos*. 82. 2) x1 = l,
*2ln2 v In2 /
*2 = 4; 4) корней нет. 83. 2) *6Л; 4) *>2; 6) *>3. 84. 2) *= —+2тг/г,
г, neZ. 85. 2) 2. 86. 2(тг+1). 87. 2) f(*) = 0 при х = е~1, f'(x)>0
при х>е"1, Г(*)<0 при 0<х<е~х; 4) f(*) = 0 при *=1, f(*)>0 при
при 0<*<l. 88. 2x~6 . 89. 2) i/ = 3*+7; 4) i/=--
25 6 3
-1; 6) i/ = -f. 90. 2) i/ = -*-2; 4) i/ = -V3*+4\/3-3. 91. 2) ^; 4) 3;
6) 1. 92. 2) -5-; 4) -; 6) -. 93. f(*)>0 в точках А и D, f'(x) = 0 в точ-
4 6 4
ке В и f (*)<0 в точке С. 94. 2) i/ = -6*+12; 4) у= — + —; 6) i/ = *+l;
4 4
8) i/=| + |. 95. 2) г/=| + 1; 4) i/=l; 6) i/ = *. 96. 2) |; 4) i; 6) |.
97. 2) —; 4) -. 98. 2) у = 0; 4) у = 2х; 6) i/=-*+l. 99. 2) (1; 2);
о о о
La La La
4) (ln2; -); 6) (тг + 2тт; тг + 2тт), /i€Z. 100. (0; -1), (4; 3). 101. (1; -1),
V 2 /
i/ = 2*-3; (0; 1), y = 2x-2. 102. 1) i/ = tt + 1-*; 2) y = S-2x. 103. 2) Нет;
_з_
4) нет. 104. 2) -5*4 + 6*2-6*; 4) -A_2* 4; 6) -21(4-3*)6;
_I л:4
8) 2(1-4*) 2; 10) -3sin3*. 105. 2) -sin* —; 4) 24*3-9ex;
cos2*
6) - —+ —. 106. 2) 2e2x- —; 4) 4cos — +3el~3x. 107. 2) *2(31n*+l);
д.4 2* * 3
313
Ответы
4) 2sin2*; 6) e* (cos*-sin*). 108. 2) x(2~x ); 4) .
(*3 + l)2 *(1-*)2
109. 2) f(*) = 0 при * = -3, при *= — , при * = 4; f(x)>0 при *<-3,
5
при -3<*<—, при x>4; f'(x)<0 при — <х<4; 4) f(*) = 0 при *=1;
5 5
f (*)>0 при х>1; f (*)<0 при *<0 и при 0<*<l. 110. 2) e; 4) —.
111. 2) i/ = 30*-54; 4) y = -^- * + - + ^L 112. s(4) = 22 м, и(4) = 7 м/с.
2 2 6
4 1 \ - — 3
113. 2) 3*2cos2*-2(*3 + l)sin2*; 4) (* -1) (l) 343\/
114. 2) - * + 8 : 4) -— . 115. 2) —-e*+2cos*; 4) * 6 -х~1--^пх\
sin Ах—X 2t о
6) 3*2 + 8* + 4+ — + 3sin*; 8)
*
118. 2) -. 119. 2) - \ ;4) - 4 sin * • cos3 *; 6) -
2л
2) **3.
3
sin2 3*"
117.
120.
2)
2)
О
. *
sm2
3*'
cos 2
4) -(l + 6*2)sin(* + 2*3); 6) -ехъшех\ 8) -sin*. 2cos*ln2. 121. 2) f(*) =
при * = 0; f(*)>0 при *>0; f(*)<0 при *<0; 4) f(*)>0 при *>-—;
6) f(jc) = O при * = 3; /'(^)>0 при *>1; f(*)<0 при -
122. a>3. 123. a<-12. 124. 2) a<0; 4) a>12. 125. 2) a>0; 4) a<0.
126. 2) 1. 127. 2) i/ = -|.ln2 + ^ + 4ln2; 4) y = (l + e-1)x; 6) г/ = 2тг(1-л:).
4 о lb 4
128. 2) i/ = --; 4) y = -7. 129. i/ = 6*+—, i/ = 6*-54. 130. 8 кв. ед.
4 6
131. 2 кв. ед.
Глава III
1. 2) Возрастает при *>5, убывает при *<5; 4) возрастает при *<-3
и при *>2, убывает при -3<*<2. 2. 2) Возрастает при *<1, убывает
при *>1; 4) возрастает при -1<*<0 и при *>1, убывает при *<-1
и при 0<*<1. 3. 2) *<0 и *>0 — промежутки убывания; 4) возрас-
Q
тает при *>5; 6) возрастает на Л. 4. 2) Возрастает при *< и при
х> —, убывает при <*<—; 4) возрастает при *<—, убывает при
о 2 о 3
*> —. 5. Возрастает при -1<*<3, убывает при -5<*<-1 и при
3
3<*<5. 6. 1) а<0; 2) а>1. 9. 2) *=7; 4) *1 = -6, *2 = 6; 6) * = 0; 8) *=
* ±
* ± +2тш, /16Z. 10. 2) *=1; 4) *х = 0, *2 = 3. 11. 2) * = -6 —
3
точка минимума; 4) * = -8 — точка максимума, * = 8 — точка
минимума; 6) *1 = -2, *2 = 2 — точки минимума, * = 0 — точка максимума;
8) *= — +27Г/1, /16Z,— точки максимума, * = - — + 2ъп9 n^Z,— точ-
ки минимума. 12. 2) Экстремумов нет; 4) экстремумов нет; 6) * = -1 —
точка максимума; 8) * = 4 — точка минимума. 13. Функция возрастает
на промежутках -6<*<-4 и 0<*<3, убывает на промежутках
314
Ответы
-7<jc<-6 и -4<jc<0; jc = -6 и х = 0 — точки минимума, х = -4 — точ-
25
ка максимума. 14. 1) х = -3 — точка минимума; 2) х=— — точка мак-
4
9
симума; 3) х=— — точка максимума, jc = 5 — точка минимума; 4) х =
= —3 — точка максимума, х = 1 — точка минимума. 15. 2) 3 и —13; 4) 9
и -2. 16. 1) 2 и --. 17. 2) — и -3. 18. 2) 1; 4) -2. 19. 2) 4. 20. 50 =
= 25 + 25. 21. 625 = 25-25. 22. Квадрат со стороной —. 23. Квадрат со
стороной 3 см. 24. 2) 2 + е~2 и 1. 25. 2) у/2 и 1. 26. 2) 1; 4) -1. 27. 2) 1.
28. 2) 1. 29. 2) 5+ — 1п2 и 0. 30. 2) 1 и -7. 31. 2. 32. Квадрат со сто-
роной ?-. 33. Куб со стороной —. 34. -2. 35. —. 36. у = - -±- (х-8)2.
4 Y3 27 16
37. 2) jc(6-jc2)sinjc + 6x2cosjc; 4) 12jc2-18jc; 6) 2^~х >. 38. 2) Выпук-
2 2
ла вверх на интервале -1<jc<1 и выпукла вниз на интервалах х<-1
и х>1. 39. 2) хг = 0, х2 = -—, х3 = — . 40. 2) Выпукла вверх на интер-
3 3
2
вале 0<jc<1, выпукла вниз на интервале х>1. 41. 1) х= —; 2) #1=2,
о
о
х2 = 4; 3) ^=0, х2= 3~^* , jc = 3 + V3 ; 4) JC = e"¥ 42. 2) i/ = -(jc+1)2x
4 4
x(jc-2), i/' = 3(1-jc2), y" = -6x; точки пересечения графика с осями
координат: (— 1; 0), (2; 0), (0; 2); минимум у = 0 при х =—1, максимум i/ = 4
при jc = 1; jc = O — точка перегиба; 4) у' = 3(х + 1)(х-\-3), у" = 6(х + 2);
точки пересечения графика с осями координат: (-3; 0), (0; 0); максимум
у = 0 при х = — 3, минимум у = — 4 при jc = —I; jc = —2 — точка перегиба.
4 9 4
43. 2) у'= — х (jc + 3), y"=— jc(jc + 2); точки пересечения графика с осями
координат: (0; 0), (—4; 0); у>0 при х< — 4 и jc>0, y<0 при — 4<jc<0;
минимум i/ = —3 при х = — 3; jc = —2 и jc = O — точки перегиба; 4) функция
четная, точки пересечения графика с осями координат: (0; 0), (-у — » 0J,
[\/—; 0); у>0 при |лг|<А/— и i/<0 при |jc|
\ V 2 / V 2
точка максимума, у(0) = 0; х = ±1 — точки минимума, у(±1) = 2;
у" = 24х2(3-5х2); х=±\ — — точки перегиба. 44. 2) х = 4; 4) х = -3, у=х-6.
V 5
45. 1) х=1, у = х + 11; 2) i/ = jc + 2 при дг-^ + оо, i/ = —jc —2 при jc-»-oo.
46. 2) Функция нечетная; точки пересечения графика с осями координат:
(0; 0), (^/|; О), (-^/|; о); у>0 при jc>^ и -^<;с<0, у<0 при
х'<-\— и O<jc<y—; i/' = 15jc2(jc2-1), jc = -1 — точка минимума,
V 3 V 3
у(-1) = -2; х=1 —точка минимума, у(1) = -2; i/" = 30jc(2jc2-1), jc = O,
х = ±— —точки перегиба; 4) у' = (х-1)2(х+ 1)(5jc2 + 6jc+1); точки пе-
V2
ресечения графика с осями координат: (—1; 0), (1; 0), (0; —1); х = — 1 —
315
Ответы
точка максимума, у(—1) = 0; х = —точка минимума, у[ ) =
о \ о /
= ; точки перегиба: х1 = 1, х2 з = -—=^~ • 47. 2) у' = 1 н — экс-
3125 5 х
тремумов нет, у = х — асимптота при х—юо, л; = 0 — асимптота;
функция нечетная, (—3; 0) и (3; 0) — точки пересечения графика с
координатными осями; 4) (1; 0) — точка пересечения графика с осью Ох, х = 0
и у = х — асимптоты. 48. 2) i/ = (jc + 1)(jc-1)(jc-3); (-1; 0), (1; 0), (3; 0),
(0; 3) — точки пересечения графика функции с координатными осями;
i/=Sx2-6x-l; хх = 1 —точка максимума; у(х{) = —, jc2 = 1h —
V3 9 V3
точка минимума; у" = 6(х— 1), х = 1 — точка перегиба. 49. 2) у = — jc + З ,
/3-V5 л\ /3 + V5 л\
асимптоты jc = O и у = — jc + 3; ( —; 0) и -—; 0) — точки пересе-
\ 2 / V 2 /
чения графика с осью Ох; у'= — 1н , х=—1 — точка минимума; у(—1) = 5,
х2
х = 1 — точка максимума, у(1) = 1; 4) асимптоты х = 2 и у = -2; точки
(1+V33 \
~ —; 0) и (0; 1);
У'=7*-10, «-1» _ Точка максимума, «/( ™)=-^; (I; »!) - точка
<*-2)3 7 W7 8 W 9^
перегиба; 6) функция нечетная; х=±1 и у=х — асимптоты, у'= —^- -,
. 3\1з ^ ~
jc=V3 — точка минимума, у(\3)=—-—, jc = -V3 —точка максимума,
о * /о
у(— \[3) = —; jc = O — точка перегиба. 50. 2) Асимптоты jc = O и у = х + 3;
у'=- — -, х = 2 — точка минимума, у (2)=—, х = -1 — точка
х3 4
перегиба; 4) асимптоты х = — 2 и у = 0; у'=— -, х = 0 — точка ми-
/л. _ 2 „ 2(jcz
нимума, i/(0) = 0, х = 4 — точка максимума; у (4)= —, у = — ,
27 (jc + 2)5
jc = 4±2v3 — точка перегиба. 51. 2) (1; 0) и (0; —1) — точки
пересечения графика с координатными осями; /' (х) = 3х2 - 2х +1 > 0 при x€R,
функция возрастает на R; f"(x) = 6x-2, x=— —точка перегиба.
о
52. Один. 53. 2) Возрастает при х<— 1 и х>2, убывает при — 1<jc<2;
4) убывает при х<3 и х>3. 54. 2) jcx = O, х2 = , xs = —; 4) х = пп,
х = ± — +2тт> n€Z. 55. 2) jc=1 — точка минимума. 56. 2) jc = O — точ-
3
ка максимума, у(0) = -3; х = 2 — точка минимума, у (2) = -12,6. 57. 2)
Точки пересечения графика с осями координат: (0; 0), (±V6; 0); функция
четная; у'= — (4 — х2), х = 0 — точка минимума, х = ±2 — точки макси-
4
мума; у(±2)=—, у"= — (12-5jc2), х = ±\ — — точки перегиба; 4) точки
3 4 V 5
пересечения с осями координат: (0; 0), (±2; 0); функция четная; у'—
= х(2-х2), х = 0 — точка минимума, х = ±у/2 —точки максимума;
316
Ответы
y(±y/2) = l, y" = -3x2 + 2, x = ±\ — — точки перегиба. 58. 2) Точки пе-
V 3
(О \ 11 Q
—; 01; у(-1)=—, 1/(3)=—;
3 / 12 4
у' = х2(х-2), х = 2 — точки минимума, у (2) = ; у" = х(Зх-4), х = 0
л / 4 \ в4
и х=— — точки перегиба, у( — ) = - —. 59. 2) 0 и -4; 4) 14 и -11.
3 \о / 31
61. Равносторонний треугольник со стороной —. 62. Куб с ребром 10 см.
3
63. 1) х = 0, у = х-3; 2) х=1, у = х. 66. 2) х = -1 — точка минимума;
о
4) х = — 3 — точка максимума, х=— — точка минимума. 67. 2) у = 0 —
асимптота; х = 0 — точка максимума, у(0)=—; функция четная; 4) у'=
зУз
= (jc-1)2(4jc-1), x=— —точка минимума, у( — ) = --^-. 68. 2)
4 V 4/ 256
и ; 4) 3 и 1. 69. 2) -. 70. 12. 71. Катеты -и-, гипотену-
2 2t о уЗ
за —. 72. 2) (2; 13); 4) (-1; 8). 73. 9. 74. —£—. 75. * = а. 76. -.
3 7Г + 4 6
77. ——. 78. 7r(V5 + l)i?2. 79. jc = -V2 — точка максимума, х = у[2 — точ-
3Vfo
ка минимума. 80. 2) Область определения: jc<0 и х>2; (0; 0) — точка
пересечения с осями координат; асимптоты у=1 при jc—* + оо и i/ = 2jc-1
при jc-»-oo; функция возрастает при jc<0 и убывает при х>2;
выпукла вниз; 4) асимптота у = 0 при jc-* + oo; (0; 0) — точка пересечения
с осями координат; х = 3 — точка максимума, y(3) = 27e~s^l93; хг =
= 3-V3 и jc2 = 3 + V3 — точки перегиба; 6) (0; 0) — точка пересечения
с осями координат; асимптоты х = -1 и у = х-3; минимум у = 0
при jc = O, максимум у = при дг = -4. 81. arctgA;.
3. 2)
**_
2
6. 1)
+ 3h
Глава IV
^-+C; 4) — x
6 ^ 5
+ C; 4) 2jc3-,
5 1
4+C; 6) 4jc4
2*2 + 3* + C;
2 sin jc - 5 cos jc + C; 2) 3ex +
\\x\-2ex + C. 7,
+ 2cos(#-l) + C. 8.
+ C;
4)-<
oj (Z —o#J
4
/ V \
Icos —h5) + C
\4 /
i
г ~* +С; 6) -
. 2) -(jc-2
о
Q\ 1 v _i_ О
4 2 V3
3+C. 9. 1)
;6)I,--4
LO ( x\2
— — - coj
3 V 5/
+ C. 4.
6)
COi
)6
1
3
3(4
3jc
SJC + i
ЬС;
+ C;
2)
4
3 _
C;
4)
4)
*2
2
4*
3)
9
2
"21
+ 2'
3
2+C;
x + 3eJ
(jc + 3
(3jc-
sin(3jc + 4) + C;
л:
10.
2)i
C;
4«
00
cojoo
4)
8) -
с
)3
1)
2)
OS
з
2-8. 5. 2)jc5 +
— -31n|jc| + C.
4sinjc + C; 4) 8Vjc+
+ C;
7
4 +^
1
3
3* +
6) 31n|jc-3|+
- 6) 2V4^ + 1 +
cos(3x-4) + C;
C; 4) 21 sin — +
L--ln|2*-5| +
317
Ответы
+С. 11. 2) A *4- A jc2+fjc+C; 4) -|*2 + 51п|:х:|+С; 6) jc2--jc3+C; 8) 2xs-
10 10 5 2 3
]_ ± 11
-Ь-Х2-6Х + С. 12. 2) ^jc3--^Jt3+C; 4) A * 2 - 6* 2 + C. 13. 2) 2*2-x;
2 7 2 3
4) 2V* + 3-3; 6) -sin3jc; 8) 1 —. 14. 1) 12-; 2) 4; 4) 12-; 6) -.
3 jc + 1 3 3 2
15. 2) 4; 4) 12; 6) 18; 8) l-ln2. 16. 1) 9; 2) 5; 3) -; 4) 2. 17. 2) 1; 3) 2;
4) 0. 18. 2) 11; 4) -; 6) 32; 8) 10. 19. 2) 25; 4) 8-; 6) 2; 8) 1 + ^?-.
3 3 2
20. 2) -—; 4) 5. 21. 2) 68; 4) 4у/3; 6) -3. 22. 2) 8. 23. 2) e3-e; 4) -In4.
12 3
24. 2) 0; 4) 4я~^ . 25. 1) 11; 2) 11; 3) 4 А; 4) 4 1. 26. 2) 6 I; 4) 4;
z4 о о Z Z о
6)8. 27. 2) 2-V2; 4) —. 28. 2) 9-; 4) 8; 6) 2+^-V3. 29. 1) 1-; 2) ^.
12 3 6 3 2
30. 2) 4,5. 31. 1) —; 3) -; 4) 20-; 5) --1. 32. 2) ^^-; 4) 6-; 6) б1.
6 6 6 2 3 4 3
33. 2) 21- m; 4) 44- м. 34. 10- м. 35. 2) y = 2x3-4x2+ x + C; 4) y =
3 6 3
= 2sin2jt + C. 36. 2) i/ = sinjc + cosJC + C; 4) y = xs-2e2x + C. 37. 2) z/ =
= 2sinjc+l; 4) i/ = 2jc + jc2-jc3 + 2; 6) y = S-e~x. 39. 2) -cosjt-1; 4) ex+ l\
6) 2*-*2 + 3. 40. 2) ^; 4) 1 151; 6) ±. 41. 2) 12; 4) -2; 6) |; 8) 2.
42. 2) 0; 4) -3; 6) 8-. 43. 2) -1; 4) 2sinl2. 44. 2) 1; 4) ll. 45. 2) 2-;
3 6 3 3
4) -. 46. 1) 1; 2) 41n3-2. 47. 1) 10 1; 2) 3-. 48. k=p.
9 о 4 lo
Глава V
5. 1) 6; 2) 24. 6. 1) 27; 2) 64. 7. 16. 8. 6. 9. 240. 10. 720. 11. 6840.
12. 50000. 13. 90. 14. 45. 15. 30000. 16. 4536000. 17. 720. 18. 1) 720;
2) 40320; 3) 5040; 4) 362880. 19. 24. 20. 5040. 21. 1) 24; 2) 6; 3) 12.
22. 1) 8!; 2) 16!; 3) 14!; 4) (fc + 1)!; 5) kl; 6) (fc+1)!; 7) k\; 8) (fe-3)!.
23. 1) 19; 2) 462; 3) —; 4) 15; 5) /i2 + 3/i + 2; 6) X ; 7) ;
7 2
8) —1—. 24. 1) /i = 2; 2) /i = ll; 3) корней нет. 25. Pn. 26. 96.
Дг + 6
27. 1) 725760; 2) 241920. 28. 1) 12; 2) 12; 3) 60; 4) 30; 5) 840; 6) 420;
7) 151200; 8) 10080. 29. 90. 30. ~1060. 31. 1) 3; 2) 6; 3) 42; 4) 5040;
5) 336; 6) 1680; 7) 90; 8) 5040. 32. 60480. 33. 360. 34. 870. 35. 720.
36. 1) 100; 2) 3. 37. 1) m = 10; 2) m = 9; 3) m = 12; 4) m1 = 9, m2 = 10.
38. 10(11-/1). 39. 336. 41. 1) 15; 2) 56; 3) 28; 4) 56; 5) 9; 6) 9; 7) 1;
8) 1; 9) 120; 10) 120; 11) 4950; 12) 2415. 42. 84. 43. 286. 44. 190.
45. 105. 46. 220. 47. Cpn. 48. 1) 1 + 7jc + 21jc2 + 35jc3 + 35jc4 + 21jc5 + 7jc6 + jc7;
2) jc4-8jc3 + 24jc2-32jc+16; 3) 16jc4 + 96jc3 + 216jc2 + 216jc + 81; 4) 81*4-
-216jc3 + 216jc2-96jc+16; 5) 32a5-40a4 + 20a3-5a2 + - a- —; 6) — +
+ la5 + — a4 + 20a3 + 60a2 + 96a+ 64. 49. 60. 50. 1) mx=49 m2 = 8;
2) m = S; 3) m = S; 4) m = 5. 51. 1) 560; 2) 220; 3) 1140; 4) 4950.
318
Ответы
52. 1) 32; 2) 62. 53. 1) х = 9; 2) *=10. 55. 150. 56. Cf3 • C43 • Cf3 • Cf3.
57. C?0.jc2. 58. C?6oc3. 59. C|. 60. С^.С^. 62. 1) 84; 2) 126; 3) 45;
4) 10. 63. 20 способами. 64. 120 способами. 65. 120. 66. 1) 48; 2) 36;
3) 124; 4) 1090. 67. 1) n2 + 3/1 + 2; 2) —^—. 68. 1) 47; 2) 10. 69. 1) n = 2;
/i+l
2) /i = 7; 3) /i = 4; 4) /i = ll; 5) /i = 7; 6) /ix = 4, /i2 = 9. 70. 40320. 71. 28.
72. 56. 73. 59280. 74. 15800. 75. 5; 14; n(n~3\ 76. 1) 364; 2) 455.
77. 1) 16; 2) 64. 78. 1) jc6 + 6jc5 + 15jc4 + 2Ojc3 + 15jc2 + 6jc+1; 2) jc5-5jc4 +
+ 10jc3-10jc2 + 5jc-1; 3) 16-32a + 24a2-8a3 + a4; 4) a4 +12a3 + 54a2 +
+ 108a + 81. 80. 350. 81. 232. 82. 3800000. 83. 252. 84. 1) 1001; 2) 462;
3) 35; 4) 56; 5) 64; 6) 262. 85. 1) 32a5 - 80a4 + 80a3-40a2 + 10a-1;
2) -L+Z-b+ — b2 + 20bs + 60b4 + 96bb + 64b6; 3) 81jc4 + 36jc3 + 6jc2 + -± * +
64 8 4 9
т- 306-87-
C2 C16 1
88. 4* 32 . 89. Можно. 90. 364*4. 91. C?2 • —. 92. 570 способами.
2 *
94. 1) 20; 2) 26. 95. 84 способами.
Глава VI
1. 1) Невозможное; 2) случайное; 3) достоверное. 2. 1) Являются; 2) не
являются; 3) не являются; 4) являются. 3. 1) Сегодня первый урок —
не физика; 2) экзамен сдан не на «отлично»; 3) на игральной кости
выпало не меньше пяти очков; 4) ни одна пуля не попала в цель.
4. 1) АВ; 2) А + В; 3) АВ+АВ; 4) АВ; 5) АВ. 5. -. 6. —. 7. 1) -;
3 61 4
2> l; 3> i; 4> 1^; 5> 1; 6> Т; 7> 1; 8> °- 8- -^-«0,86.
3 12 12 3 4 СЗоо
9-Х) ^: 2) w; 3) w10-1} 1; 2)!: 3) п-u-1} ^; 2) 1;
3) —. 12. А. 13. 11. 14. ^. 15. -. 16. -. 17. 0,99999999. 18. -.
35 12 64 9 3 6 4
19. ||. 20. i|l. 21. 1) 0,94; 2) 0,06. 23. 1) I; 2) I; 3) |; 4) I.
ОО дОЭ Z Z О О
24. 1) |; 2) А. 25. 1) I; 2) А. 26. 1) II; 2) 1|; 3) ||. 27. 1) Яв-
ляются; 2) являются; 3) являются; 4) не являются. 28. —. 29. 1
21 2475
30. 1) ^i; 2) ^. 31. 0,36. 32. 0,42. 33. 1) 0,15; 2) 0,1. 34. I.
267 89 8
35. -. 36. —. 37. 0,91. 38. 0,44. 39. 68,6%. 40. 0,144. 41. —.
9 6 7о
42. 1) 1^-; 2) -^-. 43. 1) -^-; 2) -^_. 44. -^-. 45. 0,973. 46. 1.
512 256 3888 7776 432 3
47-1-48- -k-49- ^-50- i 51- п-52- °'02-53- т 54-1} i;
2) -й- 55- i-56-1) ж; 2) if»; 3) i>4) ж-57-Х) h2) ^:
Ответы
3)
66.
10 5 7
ср-с*Г-рп
Cm
о\ 125 г
"} 3888 '
Глава
8
.63.
; 4)
VTT
59.
С52
13 gy
3888
7
18
325
833
V
128
60.
.64. 2
•
Cioo
cfc
«0,729.
13 1
34 "а
61. 1
64
Сп-т
4) 37
1} 256'
2. 1) 2 + 5*; 2) 2,3-1,7i; 3) -6i; 4) -6. 5. 1 и 4, 2 и 7, 3 и 5. 6. 1) 3 + 7i;
2) 7-2*; 3) 2-4*; 4) -1 + i; 5) 6; 6) -*. 7. 1) -7 + 22*; 2) 3-Ш;
3) -13*; 4) 10; 5) 5 + 5*; 6) -7 + 6V2*. 8. 1) 5-5*; 2) -3 + 4*; 3) Ш;
4) -29; 5) 6-3V3*; 6) 2 + 3*. 9. 2) Например, -7,5. 10. 1) *=-, y=-;
\fit 3 ^
2) x = -l; y=^f> 3) jc = -2, i/ = -8,3; 4) x = -0,5y = 1; 5) * = 2, i/=l;
6) x=l> y = -2. 11. 1) 2a-2&*; 2) -4a; 3) a2 + 9&2; 4) 4a2 + &2;
5) (4&2 + 9a2)*; 6) (9a2 + 16&2)*. 12. 1) 0; --; 2) 0; 3. 13. (3; 4), (3; 5),
(4; 4), (4; 5). 14. 1) * = -l, i/=l; 2) *=1, i/ = 0; 3) jc = 2, y = 3; 4) jc=1,
i/=-. 16. 1) 1-i; 2) 3-4i; 3) -2-5i; 4) -6 + 3i; 5) -0,7 + l,3i; 6) - + -*.
17. 1) 10; 2) 10; 3) 2; 4) V5; 5) 5; 6) 2; 7) ^-; 8) -5-. is. 1) -5-3i;
r- 4 7
2) -4 + 2i; 3) 3-i; 4) V2 + 7L 19. 1) 2 + i; 2) -3-9i; 3) 2i; 4) 2; 5) S-i;
6) -i; 7) -2V2 + 3\/3i; 8) 2V5-5\/3i. 20. 1) 6-6i; 2) -l-4i; 3) 3i; 4) -1.
21. 1) -*; 2) -| + |«; 3) -1 + /; 4) -}-}«; 5) ||-|y; 6) -
22. l)-|-M,; 2)/; 3)A_^/; 4)^-li«; 5)0; 6) -1| I.
23. 1) 7; 2) 9; 3) 1; 4) 1. 24. *1 = -2, У1 = -2; х2 = -2, y2 = 2. 25. -2,5; 2.
V V
26. 1) z^—5-i; 2) z = V5-4\/3i; 3) z = 2 + i; 4) z =
27. 1) z = --^- + ^i; 2) z = -|| + ^i; 3) z = 2i; 4) z = 4-3L 28. 1) 5-Ш;
13 13 13 13 1Q 1 7Q 99
2) -ll-2i; 3) -4; 4) 8i; 5) 41; 6) -1. 29. 1) - -±f + ±£ i; 2) -£--
к q ^O 5U 159
—i. 30. 1) z = 2- — i; 2)г1 = 0, z2 = -3i, zs = 3i. 31. 1) -1; 2) -i.
33. 1) 16; 2) -64. 38. 1) z = 2-6i; 2) z = -3 + 2i. 39. 1) 10; 2) 9; 3) V5;
4) 2V^. 40. 1) Окружность радиуса R=5 с центром в точке z = 0; 2)
окружность радиуса R = 3 с центром в точке 2 = 1; 3) окружность
радиуса i?=l с центром в точке z = -3i; 4) окружность радиуса i? = 2
с центром в точке z=l-2i; 5) прямая, перпендикулярная отрезку,
соединяющему точки 2 и — i, и проходящая через его середину; 6)
прямая, перпендикулярная отрезку, соединяющему точки 1 + / и —1-i,
и проходящая через его середину. 41. 1) Множество точек, лежащих
внутри круга радиуса R=3 с центром в точке z = i; 2) множество точек,
лежащих вне круга радиуса Я = 4 с центром в точке z = — 3i; 3) кольцо
между двумя окружностями радиусов 1 и 2 с общим центром в точке
— 2 (исключая точки окружности); 4) кольцо между двумя
окружностями радиусов 2 и 3 с общим центром в точке Ы (включая точки ок-
3 17 3
ружности). 42. 1) z1= i, z2 = 2i; 2) zl = 5-5i, z2 =
'A 4 'Л
320
Ответы
*. 44. zl = 6 + 17i, z2 = 6 + 8i. 45. 1) 2nk, keZ;
2) n+2nk, keZ; 3) -5- + 2ti&, keZ; 4) -^ +2ti&, fc€Z; 5) — +2nk, keZ; 6) - +2nk,
2 2 4 6
; 7) --* +2тгДг, fceZ; 8) i?L+27rfc, keZ. 46.
(
2) z = cos7r + isin7r; 3) z = 3\/2(cos- + isin -); 4) z = 4(cos — + *sin — );
V 4 4/ V 3 3/
5) z = 2^cos — + *sin — ); 6) z = 5 V2(cos(--)+*sin(--));
7) z = V5(cos(-|) + isin(-|)); 8) * = cos-^ +£sin^. 47. 1) *-}-^ft
2)z = 3; 3)z — 1+*; 4) z = 4i; 6) z = -^--±i; 6)2=-^ + ^/.
La La La La
48. 1) (cos(-^)+*sin(-^)); 2) 12 (cos ^- +isin -^-); 3) V2 (cos -^ +
\ \ У / \ У / / \ о о/ V i
+ /sin^lV 4) 3(cos —+isin—). 49. 1) и 3). 50. 1) Vlfcos — +isin -);
7 / V 10 10/ \4 4/
2) -(cosO + isinO); 3) 2(cos — +isin — ); 4) — (cos — +isin -).
2 V 6 6 / 10 V 2 2 /
52. 1) cos — + г sin -^; 2) 5 (cos 220° + i sin 220°); 3) 2 cos - (cos - + i sin -^ );
4 4 La \ La La
4) _2cos-^(cos-i|^+£sin-i|^). 53. 1) cos|+£sin|; 2) 2(cos|+£sin|);
3) 2V3(cos-+isin^V 4) 12(cos - +isin -); 5) 2(cos90° +/sin90°);
\3 3/ \6 6/
6) coslO+isinlO. 54. 1) cos — +isin—; 2) 4(cos-+isin—); 3) V3(cos(--) +
6 6 V 2 2/ V V 6/
+ isin(--)); 4) - (cos45° + isin45°); 5) 2(cos(-30°) + *sin(-30°));
V 6 // 2
6) cos5 + isin5. 55. 1) 8; 2) -1; 3) — i; 4) i. 56. 1) 1; 2) ---^i;
16 2 2
3) -1281; 4) \ + \i; 5) JL - ^ i; 6) -2. 57. 1) f (cos | +isin i);
2) 3(cos-^+isin-^); 3) gfcos-^+isin-|i); 4) cos(- Ц- )
58. 1) 21?2 = ±(2\/2 + 2V2i); 2) «1>2 = ±(V2-\/2i); 3) 2l>2 =
4) 2l>2 = ±(-^2 +^.|). 59. 1) ^(coei+ieln-5-); 2)
\ ^ / ^V4 4/
fcos —+isin —); 3) (cos4 + isin4); 4) 2(cos0 + isin0), если п —
^2 2 / cog41
cog41
sin nx; 2) Sln2/l:x:
64. 1) ;
66. 1)
67. 1)
2i; 6) г
i; 2) zlt2 = z
t3i; 2) z
±i; 2) zu.
t,4 = ±3i. 65. 1) lOi;
1 + /• Ч^ у
, = -l±-*, 3)г1>2 =
4)
2)
= 2d
sinjc
г12 = ± — i9 о) ,
0,5i; 3) 2V3i;
3±2i; 4) zWi
bVSi; 4) zlt2 =
2sinjc
4) 3y3i.
i = — 4±i.
-l±V5l;
321
Ответы
5) *!=-3, *2>3=3±^; 6) z1 = 2, z2t3 = -l±iVs. 68. 1) z24z+
1
2) z2 + z+-=0; 3) z2-2V22 + 7 = 0; 4) г2 + 2#г + 9 = 0. 69. 1) z1)2 =
г3)4 = ±£; 2) z12 = ±l, z3)4 = ±4*. 70. 1) (z-2-*)(z-2 + i); 2)
x(z+2+30; 3) (z+l-iV3)(z+l+iV3); 4) (z-3-*V2)(z-3+*V2). 71. 1)
x(z+-|+*); 2) 16(z-l--|i)(z-l + -|i); 3) 25(z+l-0,20(z +1 + 0,20;
4) _(z_5 + j)(z_5_j). 72. 1) 5z2 + 8z + 13 = 0; 2) 2z2 + 10z + 17 = 0. 73. 1) ^ 2
= ±(2 + 30; 2) г1)2 = ±(1-20; 3) *1)2 = ±1, 2Гз>4= ^
4) zh2=±i, ^4=^-, 25,6=^1^; 5) ъ—h 22>3= 1±M, z4=2, а^в—1±
. 74. 1) l, i, -l, -i; 2) | + ^fi; -|; | - ^- i; 3) i; cos^ +
6 6 3 6 6 5
in^; cos^+isin^; cos-^+isin^; cos^+isin^; 4) \/2x
f-{.> 5)
76. 1) 21>2 = ±2(VV5-2 + VV5+2i); 2) 21 = ^, гг = -Щ-
±i; 4) «! —1, -, 1 + l^t г,- ^^ ?? 1} г 3 + 3i) г
4 4
i; 2) Z! = l + 4i, z2 = l-2i. 78. 1) jc = -2; 2) * = 0; 3) jc=-; 4) x = -S.
Li
79. 1) jc = -2; 2) * = - —; 3) jc=1,6; 4) jc = -0,5. 80. 1) 24; 2) -5 + 3i;
3
3)67; 4)8. 81. D-f-lf»; 2) 2*; 3)-§ + f,; 4) if + ± i.
82. 1) 3(cos270° + isin270°); 2) V3"fcos — +isin — ); 3) -(cos30° +
V 4 4 / 2
+ isin30°); 4) VlYcos^- —) +isin(- — )\ 83. 1) 15; 2) 21; 3) V29; 4) 2;
5) \IVJ-9 6) 4. 84. 1) - + ^ i; 2) -2V2-2V2*. 86. 1) z = -9-4i; 2) г =
322
Ответы
= 5-3*; 3) z = 8 + (l-V2)i; 4) z = -l-i. 87. 1) 4V2fcos — + *sin —
V 4 4
2) 2fcos —+isin—V 88. 1) l±2i; 2) - — ± - i; 3) -5±i; 4) - —±
V 6 6 / 5 5 4
±^5j[j. 89. 1) jc = 6, i/ = 4; 2) * = 3, i/ = l. 90. 1) Si; 2) - - — i. 91. Mo-
4 5 5
дуль первого числа больше модуля второго числа. 92. 1) -9; 2) 1.
93. * = -4, i/ = 6. 94. 1) z2-2V3z + 8 = 0; 2) z2 + l = 0. 95. 1) -81i;
2) -i-^fi; 3) 4-4V3*; 4) ^-i^. 96. 1) 8(сов(-*) +
2 2 2л 2 \ \ 4 /
i; 2) 64 (cos тс + i sin ti)— 64; 3)cos(--) +
-^)=i-^i; 4) 27(cos-^+isin-^)=-27i. 97.
& 2 2 \ 2 2 t
z2=i; 2) z=0. 98. 1) V2; -V2; iV2; -iV2; 2) ^ + — i; -^ + — i; -i; 3) 1;
L-uVJL,-. L^-Vi,-. i. I V3.. i V3 .. 4. Ve VI. V2.V6.
-Щ--Щ-1- Щ--Щ-1- 99. 1) г1>2 = ±(2VI-
2 2 2 2
— 3-1; 3)-5; |
2
5) z1 =
^+Jsin^L£); z^Wcos J^L +isin i^
15 15 / V 15 15
x(cos — +isin— ). 100. 1) —-—(cos8 + isin8); 2) -32cos5 —x
V 3 3 / cos4 2 ^
+isinJL). 101. Zl=2(cosi^+isini^
2 2/ \5 5
-j\o 5
102. — (г1+г2 + 23). 103. 1) Действительная положительная полуось
3
z = x>0; 2) мнимая полуось z = iy, y>0; 3) верхняя полуплоскость
z = x + iy, y>0; 4) вся комплексная плоскость за исключением точки
г-0. 105. cosl5°=^±^, sinl5°=
4
Глава VIII
-2 = 0; 2) 4jc-3i/ + 12 = 0; 3) * + 2i/ + 2 = 0; 4) 6jc-5i/-30 = 0.
2. 1) Множество точек, лежащих ниже прямой 3i/-2jc + 4 = 0; 2)
множество точек, лежащих ниже прямой х — 4у = 0. 3. 1) См. рис. 144;
2) см. рис. 145; 3) см. рис. 146; 4) см. рис. 147. 4. 1) (4; 3); 2) (4; 3).
5. 1) См. рис. 148; 2) см. рис. 149; 3) см. рис. 150. 6. 6. 7. 18.
323
Ответы
-3
Рис 145
О
х
Рис 147
-I1
Рис 149
Рис. 150
324
Ответы
8. 1) jc = 6, у =16; 2) jc = 7, i/=19. 9. 1) Пара прямых 2# + 3i/ = 0,
2jc-3i/ = 0; 2) пара прямых 2jc-i/ + 1 = 0, jc + 3i/ = 0; 3) точка (-1; 2);
4) окружность радиуса у — с центром (1; -2); 5) точка (2; 2); 6) пря-
мые х=\ и i/ = —1; 7) лучи у =—, i/>0 и jc = O, i/<0; 8) ось Ох, лучи
*=1, i/>0 и jc = -1, i/<0. 10. 1) Лучи 2# + 1/ = 0, i/>0 и 2#-i/ = 0, i/<0;
2) граница квадрата с вершинами (0; —2), (2; —2), (1; —1), (1; —3);
3) граница шестиугольника с вершинами (0; —3), (0; 3), (—3; 0), (3; 0),
12. 1) Точки вне круга радиуса 3 с центром ( ; —1; 2) объединение
\ 2 Л /
кругов радиуса 2 (включая их границы) с центрами (0; 2) и (0; —2);
3) точки вне квадрата (включая его границу) с вершинами (—3; 2),
(-1; 4), (1; 2), (— 1; 0); 4) множество точек, расположенных внутри
круга радиуса 13 с центром (0; 0) и вне круга радиуса 2 с центром
(1; -2). 13. 1) 2тг + 4; 2) 1 + |; 3) 25. 14. 1) (3; 4), (-1; 8), (-7; 2),
«/2«1,4. 15. 1) (1^; 1-Vl), (--^, 1 + Vl); 2) (-1 + -JL; -V2"),
-1--==; V2). 16. 1) 1 + —; 2) 3\/3 + 107с; 3) 1 + —; 4) — - — n; 5) 27Г.
17. (3; -4), (4; -5). 18. a) 18; б) — (10-тг); в) ^-(6-п). 19. а) 32;
б) 4(10-7г); в) 4(6-тг). 20. а) 8тг; б) бтг; в) 4тг + 4. 21. а) 8тг; б) бтг;
в) 4тг + 4. 22. 1) 9V5-2-57r + 5arctg-; 2) 12,5-2,бтг; 3) 12,5(5-тс);
4) 25arctgV2 + 20+-^^; 5) 32farctg -+arctg3)-- тс; 6) -^
3 V 4 /2 о
23. a<0. 24. a<-2, a>2. 25. а) аФ-\, аФ—\ б) а = -1; в) a=—.
4 4
26. a = -V2, -Ka<l. 27. a = --, -Ka<5. 28. -5<a<2-
4
9^ПП 1 7
29. a = 2, a=^^. 30. -2<a<-. 31. -6<a< —. 32. a<13.
33. — <a<—. 34. - —<a<l. 35. a>-2. 36. 1) Множество точек, ле-
жащих ниже прямой 3i/-2jc+5 = 0; 2) множество точек, лежащих
выше прямой jc-3i/ + 4 = 0. 37. 1) Множество точек, лежащих внутри
треугольника с вершинами (—2; -1), (0; 1), (2; —1); 2) множество точек,
лежащих внутри треугольника с вершинами (—2; 0), (0; 3), (12; —9).
38. 1) Два вертикальных угла, образованные прямыми х — i/+l = 0,
х + 2у-2 = 0 и содержащие точку (0; 0); 2) два вертикальных угла,
образованные прямыми 3jc + 4i/-12 = 0, jc + 2i/ + 2 = 0 и не содержащие
точку (0; 0). 39. 6. 40. х=7, у = 21. 41. 1) Окружность с центром (-1; 3)
радиуса у—; 2) пара пересекающихся прямых у — 2х = 0 и 3jc + i/+1 = 0;
3) граница квадрата с вершинами (-2; 2), (-1; 3), (0; 2), (-1; 1).
42. (———; —1. 43. 1) Множество точек, лежащих на окружно-
325
Ответы
о
сти радиуса -= с центром (1; -2) и вне этой окружности; 2) множество
V3
точек, лежащих внутри квадрата с вершинами (-1; -2), (1; 0), (3; -2),
(1; -4); 3) объединение множества точек, лежащих внутри кругов
радиуса 3 с центрами (0; 3) и (0; -3). 44. а) 50; б) — (10-тг);
4
в) ^-(6-тг). 45. а) 8тг; б) бтг; в) 4тг + 4. 46. 1) 1 + -|; 2) 2тг. 47. 1) а=-;
2) 1; 2; w; "W; 3) I<а<2; 4) 1; 4; f1
48. 1<а<5. 49. а=\. 50. a) --?1<а<-1; б) -9<а<9. 51. а = 2.
8 5
Упражнения для итогового повторения курса алгебры
и начал математического анализа
1. 30. 2. 3-%. 3. 400%. 4. 13,5. 5. 62%. 6. 30%, 10%, 60%. 7. 3650 р.
8. На 21%. 9. 8. 10. 600. 11. 6365 р. 40 к., 6556 р. 36 к. 12. 4088 р. 50 к.
13. На 17%. 19. 1) 9; 2) 2. 20. 1) 88; 2) 47. 21. Нет. 22. Указание.
Сравнить степени, в которых входит какое-нибудь простое число в
произведение а! и в произведение (t + l)(t + 2)...(t + а). 23. 2) 0,5; 3) 20,8.
_2
24. 1083. 25. 2) 3. 26. 2) 0. 27. 2) 64. 28. 2) 160. 29. 2. 30. 2) (0,2)3 >
>(0,2)4; 4) 1о£0з4<1оеоз4- 31' 2> °<а<1> 4) 0<а<1; 6) а>1.
5 ' 4 4_
32. 2) Первое. 33. 2) 3<log210<4. 34. log34>V2. 36. 2) 0. 37. 2) |Ь|х
х(2&2 + 1). 38. 2) 3(V6-V5); 4) VTI-V3. 39. 1) -i-; 2) А; 3) * .
2V5 V6 V7 + V5
40. 2) 2^; 4) 1-^-; 6) 1|. 41. 2) 2,(1); 4) 5,(18). 42. 2) Да. 45. 2) Име-
ют; 4) не имеют. 47. 1) — i; 2) 36 + 9V2*; 3) -2-2i; 4) 14 + 5i; 5) -+
6 5
+ -^*; 6) 0,7-0,4i; 7) 4|; 8) f. 48. 1) 2-1П; 2) 1; 3) 24*; 4) -14.
5 13 5
52. 1) -i; 2) 1. 53. 1) 100; 2) 3; 3) 47; 4) 64. 54. 2) 2arctg —«58,7°.
16
55. 120tg36°^87 м. 56. 130(tg22° + tg44°)^ 178 м. 57. 2) cosa= —,
13
tga= A. 4) tga--^, sina=|i, cosa=-^. 58. 2) -J|. 59. 1) (ж-2)х
1Z 7 ZD ^O lo
у I Q
); 2) (jc-5)(jc+1)(jc+1+V2)(jc+1-V2). 60. 1) ~—r;
л — j.
X -X+l . 4) Л+1 61 X) jc55j
2) a4 + 12a3 + 54a2 + 108a + 81. 62. 2) ^1. 63. 2) 0. 64. 2) -L. 65. 2) 4,8.
2*> ^ 2^ V2
66. 2) 1+V^T. 67. 2) Va~-1. 68. 2) 1-Vfe. 69. a3 +fe3. 70. 2) —. 71. 16a2.
ab
72. -6V&. 75. 2& + a~1 . 76. 3(1~a). 77. 2) 2. 79. 2) 2cos2a. 80. -tg2a.
3a a
326
Ответы
82. 2) 2V2sin-sin(^--); 4) 4sin(<x+ |Л sinfa- -). 84. 2) -. 85. 7.
2 \ 2 4 / \ 3 / \ 3 / 8
86. 2) 0. 87. 2) V3ctga; 4) 2. 88. 2) ——; 4) 4. 89. 2) tg2 ^; 4) ctg2a.
cos2 a 2
90. 2) -sin a-cos a. 92. —-—. 93. cos2*. 94. 2) -cos 2a cos 4p. 95. 2) 2 cos a.
cos 2a
96. 2) ctgactg3a. 97. 2) 1 + -J—. 98. 1-. 99. --. 107. 1) z =
cos x 7 2
= 2(cosO + isinO); 2) z = 3(cos7r + isin7r); 3) z = 3(cos — + Jsin — \; 4) z =
s^+isin-|b); 5) z = 2(cos^+isini|*); 6) *
xfcos — + isin — Y 108. 1) 2 + 2V3i; 2) 3V2 + 3V2*. 109. 1) - + -^ i;
\ 4 4 / 2 2
)£;4) ^ + ^i. 110. 2)jc = 8. 111. a = -6. 112. ft = 3. 113. 2) * = 5.
114. 2) jc=-^-. 115. 2) *! = -, jc2=— . 116. 2) jc = 3. 117. 2) Корней
a —ft 3 2
нет. 118. 1) jc = 2; 2) 1. 119. 1) jc1 = -1, jc2 = -0,4; 2) jc1>2= ~1I: -
2 2
120. 1)jc1)2 = ±V5, ^3,4 = ±V6; 2)jc1)2 = ±V2, xSt4 = ±^. 121. 2) jc1>2 = ±2,
jc3 = -1, jc4 = 3. 122. l)xlt2 = -^r±b; 2) xx = a, x2 = -2,5a. 123. 1) Нет кор-
ней; 2) 12; 3) 4; 8; 4) 8. 124. a>0, b? = 4ac. 126. 2) *=6; 3) *=3 —. 127. 2) jc1 =
3
=3, x2 = —. 128. jc = 3. 129. jc = 5. 130.
133. 2) xU2=
136.
. 137. x1 = l,
= 3. 138. л:3 = 3. 139. Нет. 140. 2)
= ^-|i; 2) 2=--L + lIi. 142.
5 5 l l
-1-1*; 2) z—2+|i. 143.
4 b
); 3) z1=-2,
= ±1, z3 4 = ±i. 145. 1. 146. 1) (5; 0), (-5; 0), (3; 2), (-3; 2), (3; -2),
(_3; _2); 2) (-5; 1), (5; -1). 147. 2; 2 и 0; 0. 148. 2) Корней нет. 149. 1) x =
= ~12+V44 . 2) корней нет 150 X) x = ±y/s; 2) jc = -1. 151. 1) -5<jc<3;
5
5 3^ 3
2) jc>3; 3) xx = 0, jc2 = -19. Указание. Пусть у = у/8-х, z = y/27+x,
тогда y2-yz + z2 = 7, 1/3 + г3 = 35, откуда 1/ + г = 5, 1/г = 6. 4) jcx = -73,
jc2 = -8. 152. a!=-l, a2 = -2. 153. 2) jcx = 3, jc2 = 2; 3) xl = 3, x2 = -l.
154. 2) jc = 3; 4) jc=1; 6) x = 0. 155. 2) jcx=4, *2 = -2. 156. 2) jc1 =
327
Ответы
= 1; 3) х = ~ —. 157. 2) х = 9. 158. 2) * = 3. 160. 2) jc1 = 3, *2 = 243. 161. 2) х=
о
= 3,5. 162. 2) jc = V3. 163. 2) jc1 = 1, x2 = 9. 164. 2) * = 9. 165. 2) jc1 = -,
3
*2 = 9; 4) хг = 1, *2 = 4. 166. 2) * = -3. 167. 2) jc1 = -1, *2 = 3; 3) * = 0.
168. 2) ^ = 100, jc2 = 0,1; 4) x = 0. 169. 2) jc = 2; 4) x = 4. 170. 2) * = -9.
171. 1) xx = \, x2 = ^-; 2) *! = ^, JC2 = f. 172. 1) x = ± \ arccosf +тт,
/i6Z; 2) # = arcsin —+(2/i + 1)tt, neZ. 173. 1) * = тг + arccos — + 2яп, /i€Z;
3 6
2) #= — + —arcsin —+27m; jc = 7c- — arcsin — + 2nn, /i6Z. 174. 1) jc =
--., 2» x.I. i76. -f, -|, f, f. OT. „ x.±i ^
/i6Z; 3) jc = -arctg2,5 + 7m, /i6Z. 178. 1) Корней нет; 2) корней нет.
179. 2) х = - — +7Ш, jc = -arctg3 + 7c/i, /i6Z. 180. 2) # = тт, jc = ±^- +
4 6
+ ^L, n6Z; 4) х = -| + тг/г, jc = arctg- + ^/i, /i€Z. 181. 2) jc = ^ + ^-, jc =
о ^ 2 4 ij
= (-l)n JL + ^EZL, reeZ; 4)jc=-+tt/i, /i6Z. 182. 2)x= —, jc=- + tc/i, /i€Z;
12 2 4 3 2
4) *=—, jc = ± —+27Г/1, /i6Z. 183. 2) jc = --+7m, /i€Z. 184. 2) jc =
2 3 3
= 21+™ n6Z. 185. 2) *=£+тт, ^=iL + ^, n6Z; 4) X=JL + ^,
4 2 2 4 2 16 4
/i6Z. 186. 2) jc= —+ —, /i6Z. 187. 2) jc= —, /i6Z. 188. 2) *= —, jc =
4 ct о о
eiL + 2E5.f /jeZ. 189. 2) х = 7г + 2тт, jc=-+2tt/i, jc= — +(-l)narcsin
8 4 2 4
+ f /jeZ. 189. 2) х 7г + 2тт, jc+2tt/i, jc +(l)arcsin
8 4 2 4 3^/2
. 190. 2) *=^-+тт, jc=^ + -^, /i€Z. 191. 2) jc = (-1)" + 1^ +
2 5 5 6
+ 7Г/1, /i€Z; 4) x = (-l)n + 1 arcsin — +tt/i, /i6Z. 192. 2) Корней нет; 4) x =
3
= 7г/г, /i€Z. 194. 1) x12 = ±\ 2-—; 2) 2. 195. 1) x= —+тг/г, jc = tt/i, neZ;
V b ^
2) *=-+7ш, /i€Z. 196. 2) jc= — +2тш, jc=-^-+(2/i + 1)7t, /i6Z. 197. jc=
■!((-!>"
arcsin —+7г/г), /i6Z. 198. x= — +(2/г + 1)тг, /i6Z. 199. jc = t
3 / 3
х = --+тш, /гбЛГ, /г>3. 200. jc=—. 201. JC = ±-arccos(4V2(l+a)-7)+ —,
4 3 4 2
/i6Z, при -<a<l. 202. 2) -3 —<jc<40; 4) -2<jc<8. 203. 1) *<-,
8 3 3
x>—; 2) *<-—, jc>-; 3) x<2-. 204. 1) -16<jc<3; 2) x<4, x>6;
3) jc<-3, jc>-2,5. 205. 2) -l,4<*<0. 206. 2) jc>-4. 207. 1) -7<*<2,
; 2) jc<-2-V2, -2 + V2<jc<1; 3) jc<-4, -1<jc<2, jc>3. 208. 1) 1<
; 2) jc<1, jc>2,6; 3) 0,25<jc<1,5; 4) *<-4, x>-. 209. 1) *<-V3,
о
jc=1, jc>V3; 2) jc = -3, -2<jc<2. 210. 2) jc<-2; 4) jc<2, 1<jc<2, jc>5;
328
Ответы
6) 1-V73 <JC<_1> _1<л:<1> i<JC<i+Vlle 211. x<-4, -3<x<-2,
-1<jc<1, jc>2. 212. 1) a>—; 2) a<-. 213. -5<*<-3. 214. m = 2.
215. 7; 8; 9. 216. x = 6. 217. * = -l. 218. 1) * = 20, i/ = 8; 2) jc = 6,
i/=16. 219. 2) jc<3; 4) *<--. 220. 2) -1<*<5. 221. 2) 3-V2<*<3 + V2.
222. 2) *<1. 223. 2) Решений нет. 224. 2) xeR; 3) *<3; 5)
--Iog35. 225. 2)
3
228.
<x<
233.
235.
238.
2
7
x>7;
x=5,
2) !<*<-
3 2
3. 231. x<-
!)-!<*<
3
2) *>0,01.
9\ <r у <^
ia) <^д: «^
cjc<0, jc>0;
, x = S. 243.
2)jc<-4, Ь
, 6<jc<7,5.
x<l, jc>3.
. 229. 2) -
4, -|<*<-
0; 2) -1<
236. -£<
2
10. 239. 1) .
9
Cjc<3, jc>5.
246. 2) £ч
226. 2)
1<X<1
0. 232.
^<log32
,2)1<
3
7'
I, jc>5;
245. 1)
-nn<x<
-V5<jc<
Л/9 Л/9 ^«^ ■*• ^ \/^ 99*7 9^ -у >n» Q
, 3<jc<5. 230. 2) -3<jc<-V6, V6<
1) x>2;
, <^
2
3
2)-7<j
g
^*^ —
- —
6
2)-311<х<-11, 1<х<1,5.
зс<0, 0<jc<1. 234. a<yj2.
cO. 237. 2) 0<jc< —, x>l.
3
, л>1; 2) log3-^-<x<l.
0
16
c<2. 244. 1) jc<-2, 3<jc<5,
, x=—, 4<jc<5; 2) 0<jc<4,
3
, /i6Z. 247. 2) -arcsin — +
4
+ 27стг < x < arcsin—\-n + 2nn, neZ; 4) -arccos—\- 2nn <x < arccos—\-2nn,
4 3 3
neZ. 248. 2) -37c<jc<-ii^, - — <*<- —, - —<jc<tc; 4) arctg —-Зтс<
4 4 4 4 3
-—, arctg--2tt<jc<--^, arctg- -tt<jc<- -, arctg- <jc<-.
^ 3 «и 3 2.32
249. - — +2nn<x< — + 2nn, neZ. 250. - — +2nn<x< — +2nn9 neZ.
4 4 4 4
254. 1) (2; 1); 2) (5; -3). 255. 1) (-1200; 500); 2) (7; 1). 256. 2) (-8; -2),
(8; 2); 3) (8; 4), (-8; -4). 257. 1) (7; 6); 2) (2; 3), (-9; 281). 258. 2) (3; 1),
(-3; -1); 4) (3; -5), (3; 5), (4; 2V2), (4; -2V2). 259. 1) (4; 2), (-4; -2);
2) (2; 4), (-2; -4). 260. 1) x—2, i/=i-; 2) * = -2, i/=i. 261. 2) (4; 1);
4 4
4) (10; 1000), (1000; 10). 262. 2) (V8; \s). 263. (1; 0), (-; 1-).
\ 9 9 /
264. 1) (2; -3), (-6; 1); 2) (1; -6), (-3; 2). 265. - —<a<6. 266. 2) (100; 81).
3
3
267. 2) (0; 1). 268. 1) (log3 ||; log3 |), (o; log3 ||); 2) (o; log2 Щ-),
(21og27-6; 4-log27). 269. 1) (3; 0), (^-i ~^) 2> (2? <»• (^-; ^).
329
Ответы
270.
((-If+1 |+7ш; --|L+(-lf |-7m), /i€Z. 271. 1) ((-If |
; 2) (nn; (~l)m — +nm\ meZ, neZ; ((-l)narcsin — +nn;
^+m), m€Z, /i€Z. 272. 1) (-
; 2) ( —+ 7г(Дг + /м); —+7г(/м-Дг)),
V 6 6 /
_&)V m6z, fceZ. 273. 2; 12. 274. *>5. 275. 1) (a; a2), (a2; a),
/
6
если a>0 и a?*l; (-a-1; (a + 1)2), ((a + 1)2; -a-1), если a<-l и a;*-2.
276. При a7*3 нет решений, при a = 3 — (0; 1). Указание. Записать
второе уравнение системы в виде х2 + (у-1) +(a — 3)2 + 1 — cos(xy) = 0.
277. 2) (1; 1), (2; 4); 4) (--+/*; -+А /i€Z; 5) ((-1)Л-+тт;
\ 6 6 / \ 4
278. (-1 +(-l)fc JL + ^
Указание. Реш:ить систему как линейную относительно и и и, где
u = sinjtcosi/, i; = cosjcsini/. 279. (81; 16). 280. 1) 7,5; 2) 5,125; 3) 2; 4) 7.
281. 1 мин. 282. 126 км. 283. 1080 км. 284. 16 дней. 285. 91 га.
286. 8, 12. 287. 25 и 20 билетов или 30 и 25 билетов. 288. —, —, -.
289. 432 детали. 290. 18 км/ч. 291. 3 км/ч. 292. 21 ц, 20 ц. 293. 1400
шагов. 294. 3, -6, 12, -24. 295. 27. 296. 1, 3, 9, 15 или 16, 8, 4, 0.
297. 2 или 12 -. 298. В 3 раза. 299. 16 см2. 300. 1) Cl00; 2) 50-100-150;
о
3) Cl0Cf00.150; 4) Cio-lOO-Cfgo- 301. Ры. 302. Ры . 303. 0,85; 850.
304. 480. 305. —. 306. -. 307. 0,18. 308. 0,97. 309. 0,96. 310. 0,028.
38 6
311. 2) k = -l, Ь = 3; 4) k = 0, Ь = -2. 312. i/ = -A *+А, у = -1х+^.
5 5 5 5
313. 2) Нет; 4) да. 314. 2) 3-. 315. х>1. 316. *<-#. 319. 2) Да.
320. 2) (-1; 3), (5; 3). 321. 4) *<-2, х>2. 322. 4) х*0. 323. 1) 75 км/ч;
2) 5 ч; 3) ^71,4 км/ч. 324. Второму; на 40 р. 325. Нет, так как
наименьшее расстояние между кораблями будет равно 3 милям через 48 мин.
327. 1), 2) не является. 328. 1) Является; 2) не является; 3)
является; 4) не является. 329. 2) Нечетная; 4) четная. 330. 2) Нечетная;
4) четная. 331. 2) Четная; 4) не является четной и не является
нечетной. 333. 1) Нет; 2) да. 334. 2) —. 335. 2) Ютг; 4) 2я. 337. 2,25.
3
338. 2) 2 и -1. 339. 1) jc = ±| + ^, ntZ, /max = 2, /min = l; 2) * = ±|
к= —; /min = -. 340. а = 2, fe = -5, c = -3. 345. а>1. 346. 2) х>-2;
к 7 тш 2
4) **27г + 47т, /i€Z. 347. 2) #<-1, jc>3. 348. 1) *<-7, ;
2) 3<jc<3-. 349. 2) -VT0<Jt<-3, 3<*<VlO; 3) -!<*<--, х>0;
2 7 8
330
Ответы
4) -A<jc<--, x>0. 350. 2) i/<7; 4) уФ2. 351. 2) -VlT25<i/<V
7 4
352. l)y<_l|; 2)i/>0. 353. l)-i<i/<i; 2)i/>l. 354. x = (-l)n^
neZ. 355. a = -3,5. 356. a=l-V2, a = 5 + VTo. 357. a<-4, --
4
358. 1; JL. 359. 2) -3. 360. 2) £. 361. 2) г/ = -6*-1. 362. -1. 363. 9.
3 15 3
364. (3; 9), a = -3. 365. (1; 2), (0,5; 2,25). 366. (-1; -3). 367. (3; e).
368. 2) i/ = 0,5(l + ln2-Jcln2). 369. -. 370. e"1. 371. --. 372. г/=*+1.
12 4 4
373. i/ = 3jc-3. 374. —. 375. 2) Возрастает на промежутках jc<0 и
35
jc>0. 376. 2) jc = 6 — точка минимума. 377. 2) jc = 2 — точка
минимума, х = 0 — точка максимума. 378. 2) 1,5 и 1. 379. 2) 3 и 1. 380. 2) 0,5
и 0. 381. 7, -3. 382. а = 3. 383. а = ±3. 384. 2) # = 0 — точка минимума,
* = 0,4 — точка максимума. 385. (1; 0), (-1; 4). 386. у=7х-43. 390. 1 дм.
391. 54тг см3. 392. 6. 393. 2. 394. sin*- — -1. 395. 132, -57. 396. 9 и 4.
Х
397. (1; 1). 398. —. 399. 4V2. 400. р = -10, ? = 26. 401. -^-^ дм.
27 3
^Л 404 405 406 ^
402. 3^2тиЛ 403. —. 404. —. 405. —. 406. -. 407. -^-. 408. r=R\J^,
V2 V3 3 3 216 V3
H = R — . 409. D=H. 410. —. 411. г= —, h=—. 412. 2) In2. 413. 2) 9-;
V3 #33 3
4) 1. 414. 2) 4,5. 415. 2) —. 416. 2) —^—. 417. 546—. 418. С=-.
419. &>V3-1, &<-3-V3. 420. * = тш, jc= —+ —, /i€Z. 421. a = 6, fe =
= -11, c = 6. Указание. Так как точки Аи В симметричны
относительно прямой х=2, то А(хг; у0), В(х2; Уо), где xx = 2-t, x2 = 2 + t, t>0. Из
условия ff(x1) = f'(x2) следует, что а = 6 и f'(x{) = f (x2) = - 3^2 +12 + ft, а
равенство f(xi) = f(x2) можно записать в виде b = t —12 (так как ^>0), откуда
-2^2<0. 422. a = 6, fe=ll, c = 5. 423. a = -4, fe = 5, c = -2.
424. a = 4, fe = -5, c = 2. 425. (-; -). 426. (-2; 22), (2; 10). 427. р = -2,
\ 3 9 /
g = 0, d=l. 428. 2,25. 429. k = 2. 430. 1-. 431. а = 1, s = 4. 432. arctg —.
8 7Г2
433. 3) 3—; 4) -2. 434. 2) *= — +тш, /i€Z; 4) jc=—. 436. -2<jc<3.
9 4 3
437. u(10) = 262 м/с, ^«37 с 438. 12тг. 439. 160 чел.-ч/сут.; 20 чел.
440. 17417 ед. продукции. 441. 2) 5x~6. 442. 2) 4* +4дс-5^
9r^4rj.4^ 9 (2#+1)
443. 2) ZXiffcXi"^ ; 4) cos2jc-2jcsin2jc. 444. —-—. 445. х = 2.
SyfxTT 51nl°
SyfxTT
446. 2) f(2)>0. 447. f(0) = 4, f(^) = 8(7 + 4V3). 448. --
\ 6 / 3
449. -(2sin4*-9). 450. - ln|4jc-l| + C. 451. 1) 11,25; 2) 2-V^;
8 4 4
3) 5,5+71n2; 4) 72. 452. 2) ^~Х ; 4) 1-; 5) -; 6) In3.
2 3 3
331
Ответы
Ответы к заданиям «Проверь себя!»
Глава I
1. хф — + —, /i€Z; функция нечетная. 2. i/ = sinjc: 1) хг= -,
х2 = +^; 2) х = -^> 3) х1 = -2п9 х2 = л, х3 = 0, х4 = п; 4) -2п<х<-п,
; 5) -7t<jc<0; y=cosx: 1) xl = -2n, x2 = 0; 2) xl=-n, x2=n; 3) x1= —,
f.
3.
-f: 4) -
^- 4. ct
f; 5) -f
, l
, ctg2. ctg|.
1. Рис. 151, a) - — + 2nn<x< — +2nn, neZ; б) -п + 2пп<х<2пп.2. Рис. 152,
i/>0 при - — +2nn<x< — + 2%n, n€Z. 3. 3 решения. 4. [-1; 2]. 5. Рис. 153.
3 3
Рис. 151
X/
IN
i/ = sin
\
-n\
/—^
у
У
. 3
\
0
f — sinjc
\/^
N
;in(-
^—v,
у
У
V ^.
X/
/ зЧ
Рис.
752
2
j,=isin(2*-f) + l
= Isin(2jc-|)
\ X
Рис. 153
332
Ответы
Глава II
1. 11. 2. 1) --^+ -jL -е*; 2) 9(3*-5)2; 3) 6 cos 2* cos *-3 sin 2* sin*;
4)
4- 4.
4
-!. 5. у = х- ** + *.
3*26
1. 1) 2_; 2) -. 2. Нет. 3. jc1 = 1, jc2 = 4. 4. i/ = 3jc-4, i/ = 3jc + 6-.
3 4 3
Глава III
1. Возрастает при х>1—, убывает при jc<1— ; 2) убывает при х>-4.
4 4
2. Минимум у = -7 при jc = 3. 3. См. рис. 154. 4. Наибольшее 10,
наименьшее 6. 5. 3 дм, 6 дм, 4 дм.
1. а>0. 2. 1) См. рис. 155. 3. Наибольшее е, наименьшее 0. 4. 4R.
Глава IV
2.
-3jc-1. 3. 1) 4-; 2) —; 3) 0; 4) 1. 4. 20 -| кв. ед.
3 16 6
1. F(x) = ex + 3cosx-2. 2. 1) М; 2) -?-1п2. 3. S=- кв. ед. (рис. 156).
3 3 3
4. 5 = 9 кв. ед. 5. S =
16
кв. ед.
TV
\
I
1
Рис
X
154
Ук
?-*+#
Рис 155
333
Ответы
Рис. 157
Рис. 158
Глава V
-. 3. 84 спосо-
1. 1) 5040; 2) 336; 3) 56; 4) ^. 2. 1) п2 + п; 2)
7 n2-5#i + 6
бами. 4. 5040 способами. 5. 720 способами. 6. 720. 7. 1) /
+ 15х4у2 + 20xsys + 15х2у4 + 6ху5 + у6; 2) 1-5а+ 10а2 - 10а3 + 5а4-а5.
1. 1) /г = 1; 2) /г = 2. 2. /*i = 0, п2 = 1, /13 = 2, /14 = 3. 3. 14580.
4. 64 способами. 5. 1) с£ = 36; 2) 29:2 = 256. 6. -15504 х5.
Глава VI
1. I. 2. 0,95. 3. I. 4. |§. 5. 0,64. 6. 1|.
1. 0,18. 2. 0,992. 3. 0,3. 4. —.
27
Глава VII
1. 1) 8-/; 2) 4-4*; 3) 71 + 31; 4) | -1 i. 2. 1) -l||; 2) -^-^ *•
3. 1) 2(^^) (
2) 2rlt 2 = 5 ру
6. \ + \1- 7. 1) "| + -у-*; 2> -|'
г3 = -2г, 2) zo = 4, z1 = -2 + 2V3i, z
Глава VIII
1. 1) Прямая, проходящая через точки (0; — 1 и ( —; 0); 2) окружность
радиуса 4 с центром в точке (3; -1). 2. 2) круг радиуса 2 с центром в
точке (-2; 5). 3. Внутренняя область треугольника с вершинами (1; 0),
(0; -1), (4; -3).
4тг-3\/3
^+isin^); 2) cos(- |i) + «ein(- |^). 4. 1) zU2
. 5. Окружность с центром в точке (0; 0) и радиусом Я=3.
1. См. рис. 157. 2. См. рис. 158; S =
-. 3. 1) Квадрат с
вершинами в точках А(-3; 0), В(0; -3), С(0; 3), D(3; 0); 2) все точки,
лежащие внутри квадрата ABCD.
334
Ответы
Оглавление
Глава I. Тригонометрические функции
§ 1. Область определения и множество значений
тригонометрических функций 3
§ 2. Четность, нечетность, периодичность
тригонометрических функций 7
§ 3. Свойства функции y = cosx и ее график 12
§ 4. Свойства функции y = sinx и ее график 19
§ 5. Свойства и графики функций y = tgx и y = ctgx .... 26
§ 6. Обратные тригонометрические функции 33
Глава II. Производная и ее геометрический
смысл
§ 1. Предел последовательности 44
§ 2. Предел функции 53
§ 3. Непрерывность функции 60
§ 4. Определение производной 66
§ 5. Правила дифференцирования 69
§ 6. Производная степенной функции 74
§ 7. Производные элементарных функций 78
§ 8. Геометрический смысл производной 84
Глава III. Применение производной
к исследованию функций
§ 1. Возрастание и убывание функции 98
§ 2. Экстремумы функции 102
§ 3. Наибольшее и наименьшее значения функции .... 107
§ 4. Производная второго порядка, выпуклость и точки
перегиба 113
§ 5. Построение графиков функций 118
Глава IV. Первообразная и интеграл
§ 1. Первообразная 131
§ 2. Правила нахождения первообразных 134
§ 3. Площадь криволинейной трапеции. Интеграл и его
вычисление 137
§ 4. Вычисление площадей фигур с помощью
интегралов 145
§ 5. Применение интегралов для решения физических
задач 149
§ 6. Простейшие дифференциальные уравнения 150
335
Глава V. Комбинаторика
§ 1. Математическая индукция 157
§ 2. Правило произведения. Размещения с повторениями 159
§ 3. Перестановки 163
§ 4. Размещения без повторений 166
§ 5. Сочетания без повторений и бином Ньютона 169
§ 6. Сочетания с повторениями 174
Глава VI. Элементы теории вероятностей
§ 1. Вероятность события 180
§ 2. Сложение вероятностей 186
§ 3. Условная вероятность. Независимость событий .... 189
§ 4. Вероятность произведения независимых событий ... 194
§ 5. Формула Бернулли 197
Глава VII. Комплексные числа
§ 1. Определение комплексных чисел. Сложение и
умножение комплексных чисел 204
§ 2. Комплексно сопряженные числа. Модуль комплексного
числа. Операции вычитания и деления 209
§ 3. Геометрическая интерпретация комплексного числа . 214
§ 4. Тригонометрическая форма комплексного числа ... 218
§ 5. Умножение и деление комплексных чисел, записанных
в тригонометрической форме. Формула Муавра 221
§ 6. Квадратное уравнение с комплексным неизвестным 225
§ 7. Извлечение корня из комплексного числа.
Алгебраические уравнения 228
Глава VIII. Уравнения и неравенства с двумя
переменными
§ 1. Линейные уравнения и неравенства с двумя
переменными 237
§ 2. Нелинейные уравнения и неравенства с двумя
переменными 244
§ 3. Уравнения и неравенства с двумя переменными,
содержащие параметры 259
Упражнения для итогового повторения
курса алгебры и начал математического
анализа 271
Предметный указатель 307
Ответы 309
Учебное издание
Колягин Юрий Михайлович
Ткачева Мария Владимировна
Федорова Надежда Евгеньевна
Шабунин Михаил Иванович
Алгебра и начала
математического анализа
11 класс
Учебник для
общеобразовательных учреждений
Базовый и профильный уровни
Зав. редакцией Т. А. Бурмистрова
Редактор Л. Н. Белоновская
Младший редактор Е. А. Андреенкова
Художник В. А. Андрианов
Художественный редактор О. П. Богомолова
Компьютерная графика: Г. М. Дмитриев
Технический редактор С. Н. Терехова
Корректоры Л. А. Ермолина, Н. И. Новикова, А. В. Рудакова,
И. В. Чернова
Налоговая льгота — Общероссийский классификатор продукции
ОК 005-93—953000. Изд. лиц. Серия ИД № 05824 от 12.09.01. Сдано
в набор 19.04.06. Подписано в печать 21.04.10. Формат 60x90Vi6-
Бумага офсетная. Гарнитура Школьная. Печать офсетная. Уч.-изд. л. 20,6+
форз. 0,43. Доп. тираж 20 000 экз. Заказ № 30062.
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано в ОАО «Саратовский полиграфкомбинат».
410004, г. Саратов, ул. Чернышевского, 59. www.sarpk.ru
КОМПЛЕКСНЫЕ ЧИСЛА
(а + Ы) + (с + di) = (a + c) + (b + d)i
(а + Ы) (с + di) = (ас - bd) + (ad + be) i
bi = a-bi
* i
0
i
1
a
-«
b
+ bi
cosqp =
a
p4F
2 = r (cos ф + i sin cp)
-J- = ZL (cos (ф - ф2) + £ sin (ф - ф2))
z 2 r2
Формула Муавра
+ i sfrup)л = cos ny + i sin
КОМБИНАТОРИКА
л! = 1 • 2 • 3 • ... • (л-1) • л О!
1п~п' Лт~(то-л)! "
Бином Ньютона
Г л + Ъ\ == С«, £1 "г* CL. £1 Ь + ... "+" С«, tt Ь "Т" . .
= J
[ XI OT-"~J
л! (m-n)!
[аЬт~г+СтЪт
Треугольник Паскаля
1 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
ВЕРОЯТНОСТЬ
Р(А) =
т
п
Р(А) =1-Р(А)
Р (А+В) = Р(А) + Р(В)-Р (АВ)
Р (АВ) = Р(А)Р (В/А) = Р(В)Р (А/В)
БАЗОВЫЙ • ПРОФИЛЬНЫЙ
УРОВНИ
Учебник соответствует Федеральным
компонентам государственного
стандарта общего образования
В учебно-методический комплект
по алгебре и началам математического
анализа для 10-11 классов
под редакцией А. Б. Жижченко входят:
• Учебники для 10 и 11 классов
(авторы Ю. М. Колягин, М. В. Ткачева,
Я. Е. Федорова, М. И. Шабунин)
Дидактические материалы
для 10 и 11 классов
(авторы М. И. Шабунин, М. В. Ткачева,
Я. Е. Федорова, О. Н.Доброва)
• Изучение алгебры и начал
математического анализа
в 10 и 11 классах. Книги для учителя
(авторы Я. Е. Федорова, М. В. Ткачева)
ISBN 978-5-09-022250-1
9 785090 222501
ПРОСВЕЩЕНИЕ
ИЗДАТЕЛЬСТВО