Автор: Пратусевич М.Я. Столбов К.М. Головин А.Н.
Теги: общее школьное образование общеобразовательная школа анализ алгебра
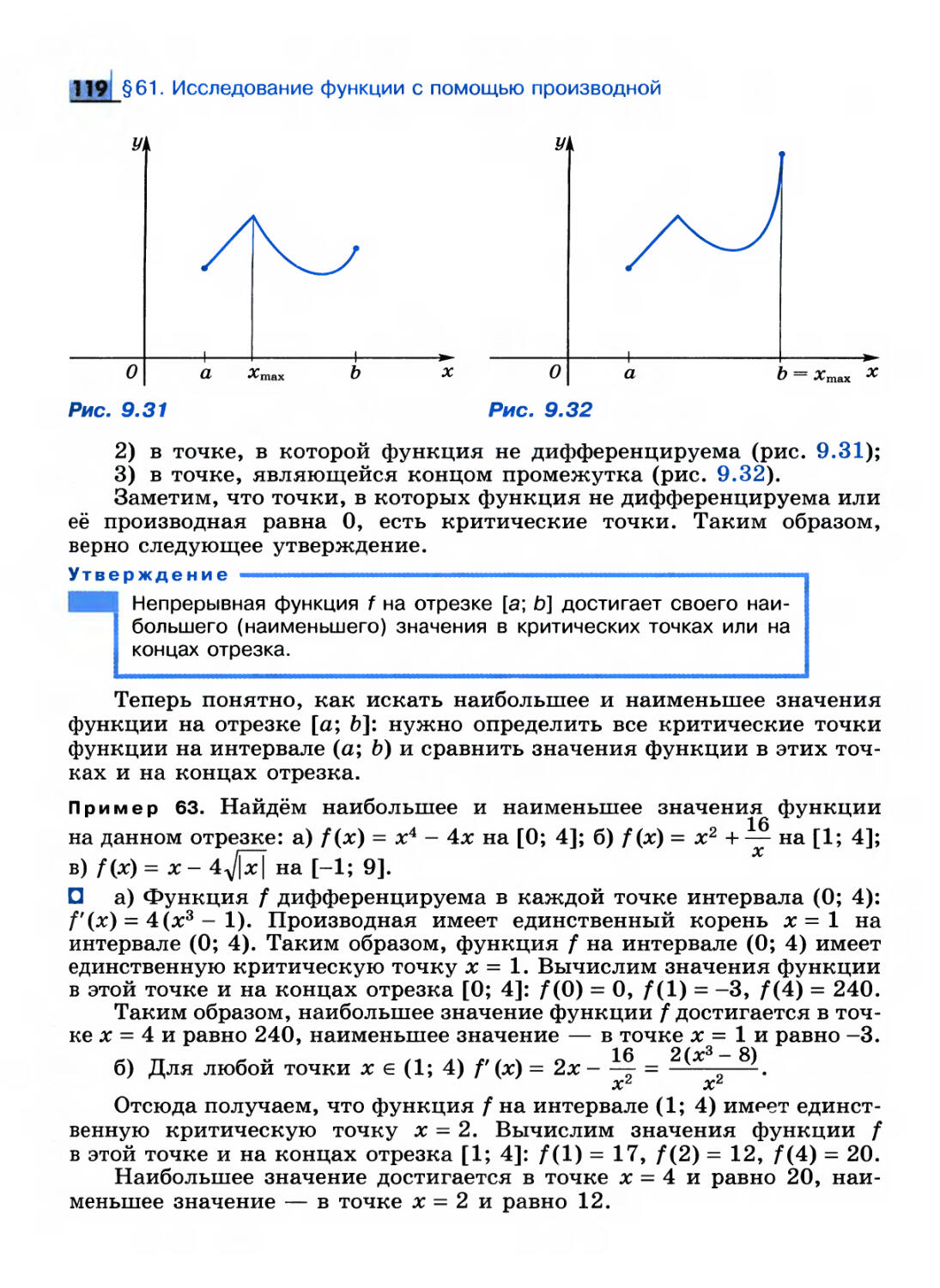
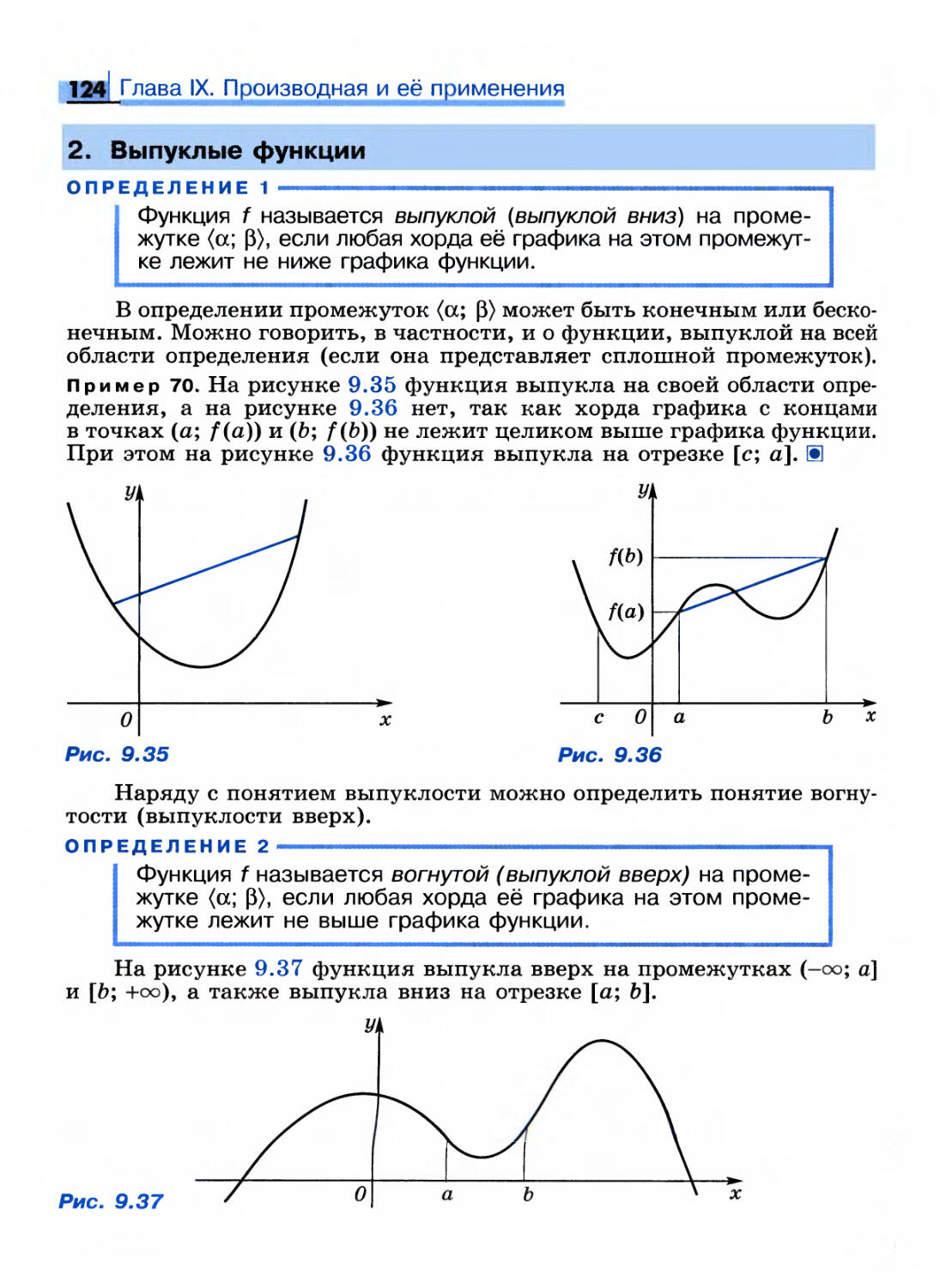
ISBN: 978-5-09-017190-8
Год: 2010
Текст
М. Я. Пратусевич
К. М. Столбов
А. Н. Головин
АЛГЕБРА
И НАЧАЛА
МАТЕМАТИЧЕСКОГО
"^ НАЛИЗА
ПРОСВЕЩЕНИЕ
ИЗДАТЕЛЬСТВО
Б.ПАСКАЛЬ
(1623 - 1662)
К. ВЕИЕРШТРАСС
(1815-1897)
О. КОШИ
(1789-1857)
П. ФЕРМА
(1601 - 1665)
W
ДЖ. КАРДАНО
(1501 - 1576)
Ж. ЛАГРАНЖ
(1736-1813)
ТАБЛИЦА ПРОИЗВОДНЫХ
f(x) = с
f(x) = ха
f(x) = ах (а ф 1)
f(x) = е*
/(х) = lnx
f(x) = sinx
f(x) = cosx
/(x) = tgx
/(x) = ctgx
f(x) = arcsinx
fix)
f'(x) = 0
f'(x)=axa-1
f\x) = lna-g»
(x>0)
X
= cosx
/'(*) =
= - smx
1
COS2X
1
sin2x
f'(x) =
Дх) = arccosx /'(x) = -
/(x) = arctgx
Vl -x2
f(x) = arcctgx
f'(x) = -
М. Я. Пратусевич
К. М. Столбов
А. Н. Головин
АЛГЕБРА
И НАЧАЛА
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
11
класс
Учебник для
общеобразовательных
учреждений
Профильный уровень
Рекомендовано Министерством
образования и науки
Российской Федерации
Москва
«Просвещение»
2010
УДК 373.167.1:[512+517] Ш
ББК 22.14я72
П70
На учебник получены положительные заключения
Российской академии наук (№ 10106-5215/82 от 22.10.09)
и Российской академии образования (№ 01-5/7д-72 от 10.07.09)
Условные обозначения:
D — начало обоснования, доказательства или вывода
Ш — окончание обоснования, доказательства или вывода
* — задача повышенной трудности
О — обратите внимание
— необязательный материал
— теоремы, определения, свойства, утверждения, правила
Группа А — задачи и упражнения на непосредственное
применение понятий и теорем, аналогичные разобранным в тексте
Группа В — задачи и упражнения, требующие привлечения
знания пройденного материала, но не требующие неизвестных идей
для решения
Группа С — задачи, требующие для своего решения новых, не
разобранных в тексте идей, методов, приёмов
Пратусевич М. Я.
П70 Алгебра и начала математического анализа. 11 класс :
учеб. для общеобразоват. учреждений : профил. уровень /
М. Я. Пратусевич, К. М. Столбов, А. Н. Головин. — М. :
Просвещение, 2010. — 463 с. : ил. — ISBN 978-5-09-017190-8.
УДК 373.167.1:[512+517]
ББК 22.14я72+22.161я72
ISBN 978-5-09-017190-8 © Издательство «Просвещение», 2010
© Художественное оформление.
Издательство «Просвещение», 2010
Все права защищены
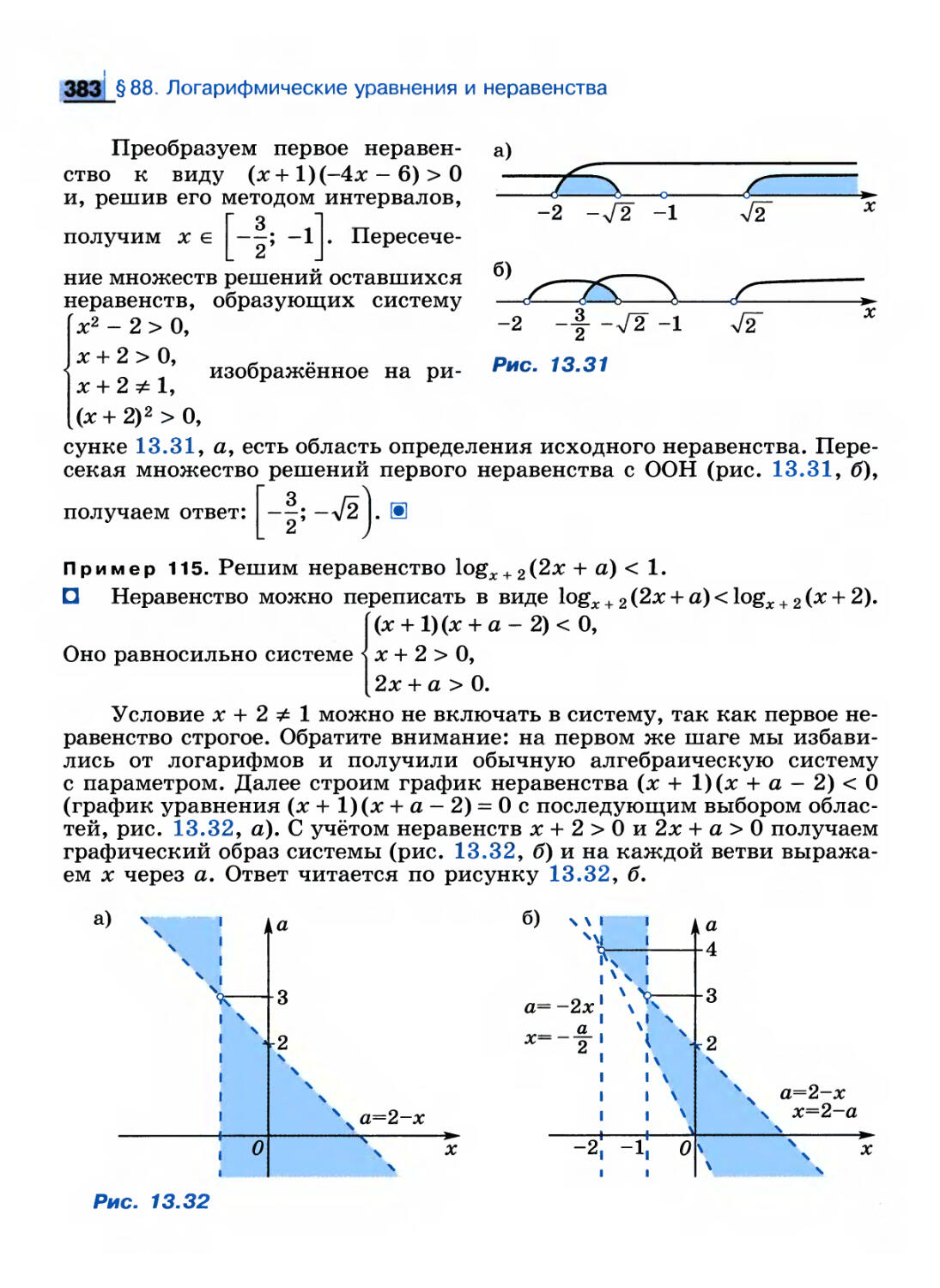
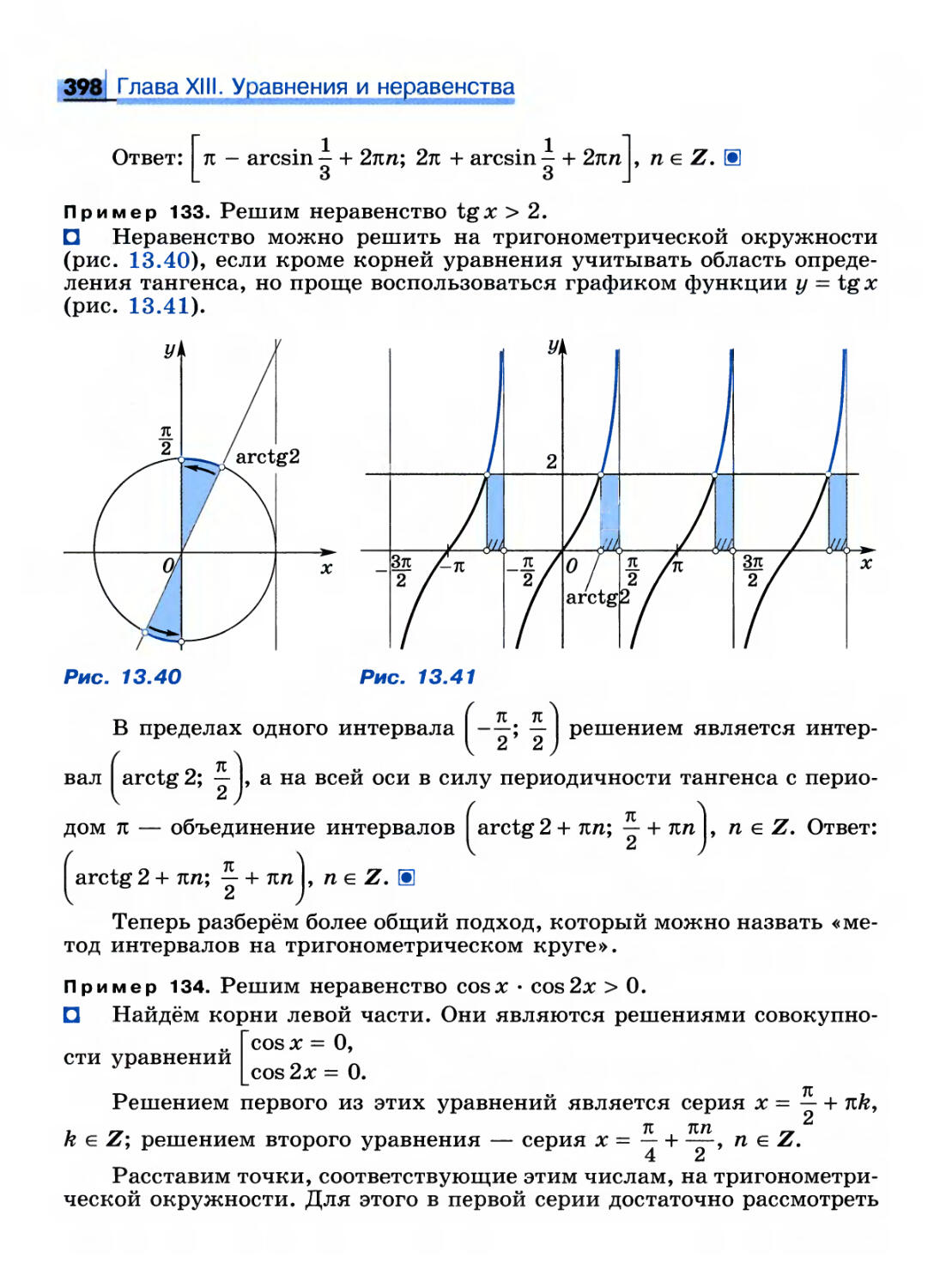
Предел и непрерывность
функции
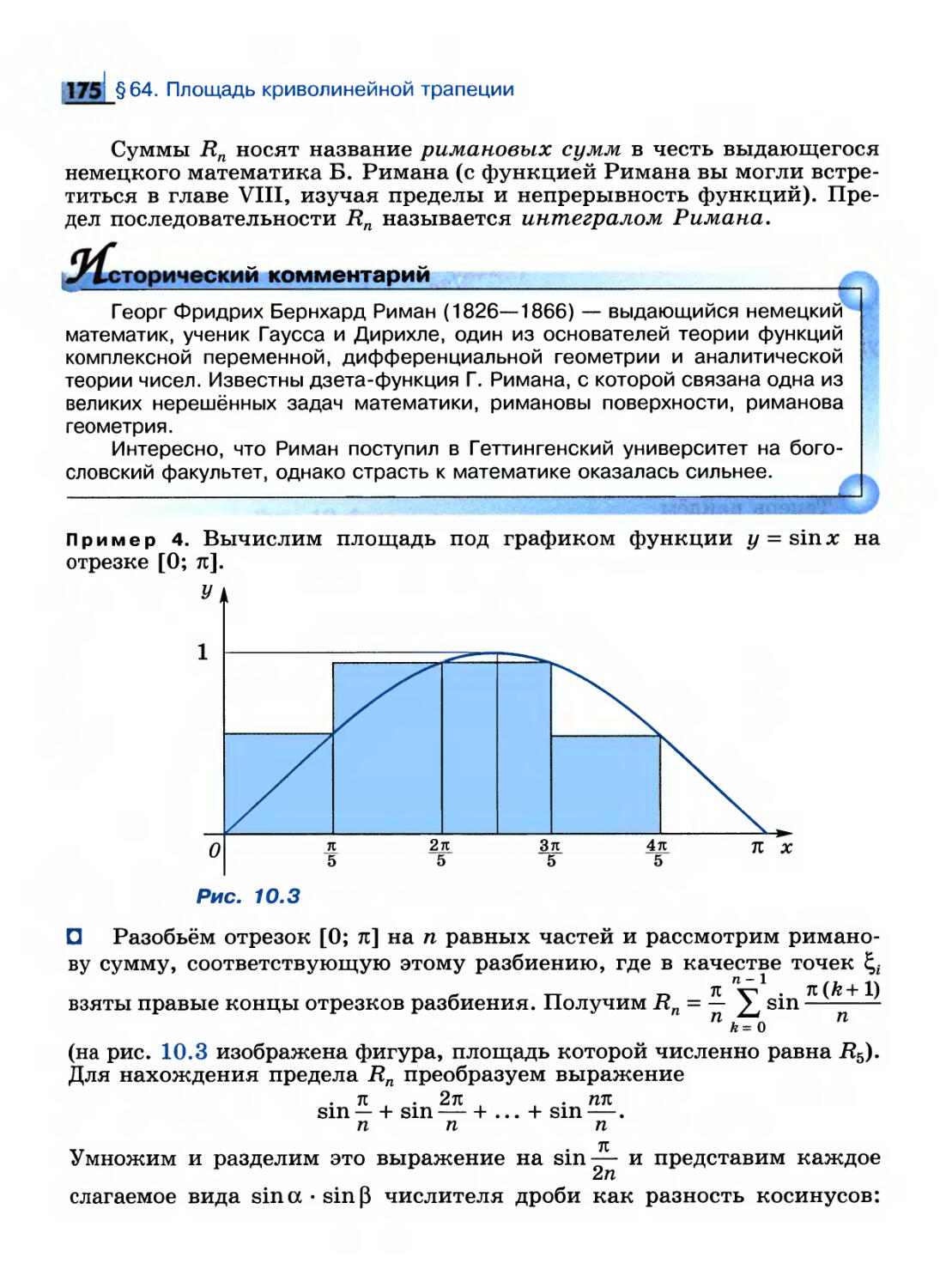
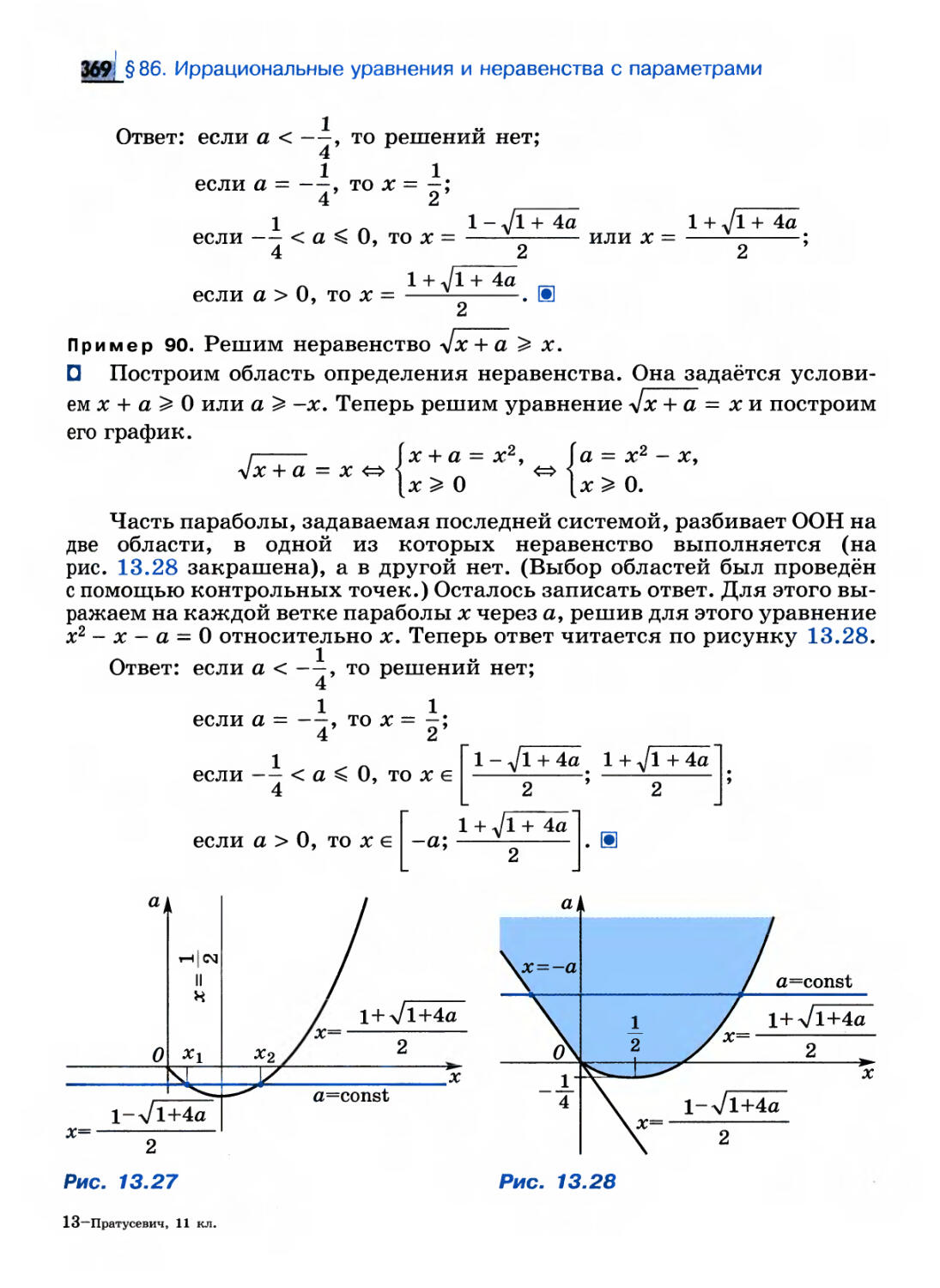
044, Понятие предела функции
1. Два определения предела функции и их эквивалентность
В 10 классе было изучено понятие предела последовательности.
Поскольку последовательность является частным случаем функции
(заданной на множестве натуральных чисел), понятие предела
последовательности является частным случаем понятия предела функции.
Понятие предела функции иллюстрирует поведение функции при
неограниченном «приближении» аргумента к некоторому значению.
Натуральный аргумент не может неограниченно «приближаться»
никуда, кроме +оо. В то же время произвольный вещественный аргумент
может приближаться к произвольному вещественному числу, а также
к +оо или -оо.
Определение предела функции выражает ту же мысль, что и в
случае предела последовательности: значение функции неограниченно
приближается к числу или бесконечности по мере неограниченного
приближения её аргумента к заданному числу или бесконечности.
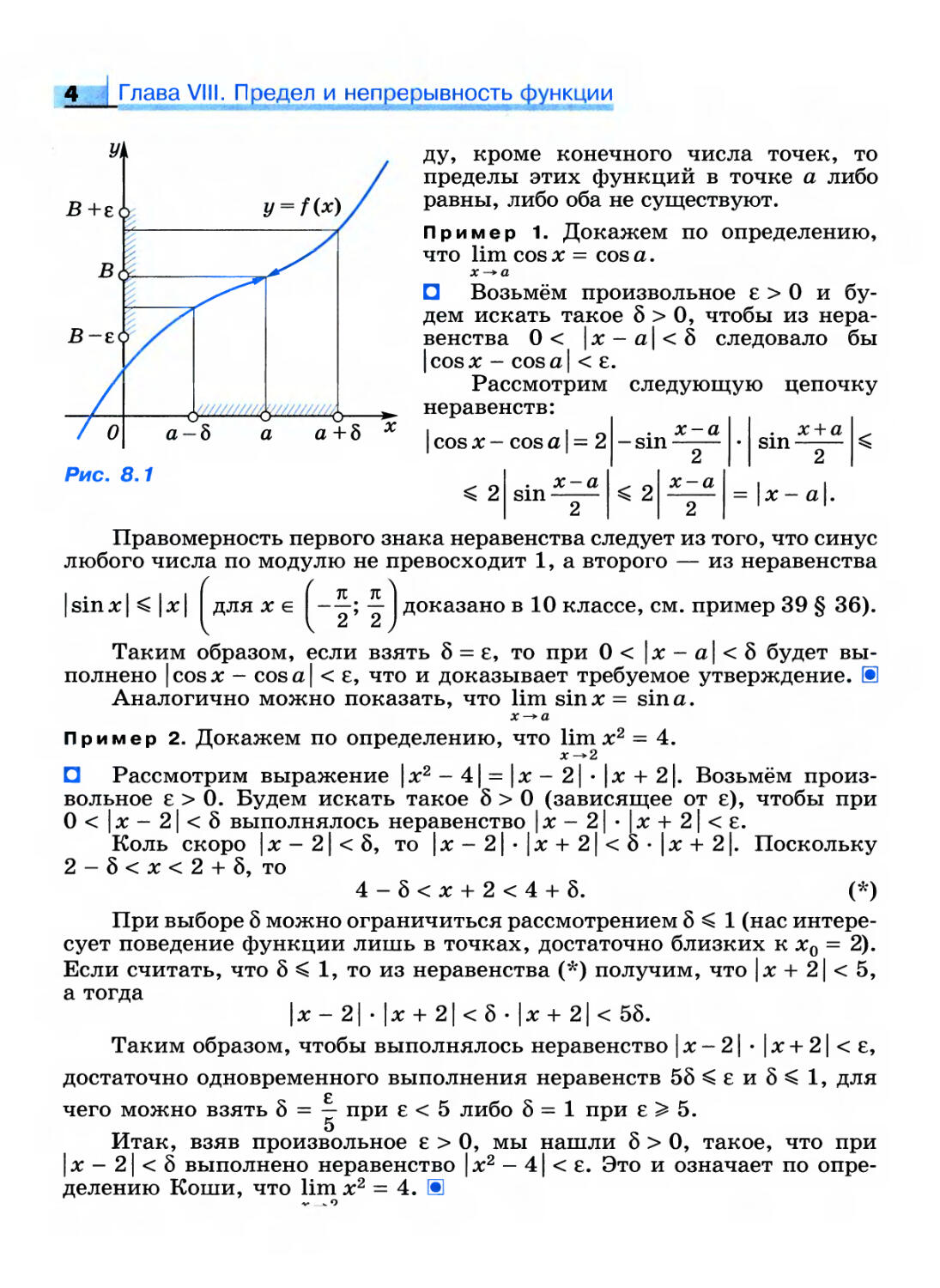
ОПРЕДЕЛЕНИЕ (по Коши)
Число В называется пределом функции f в точке а, если
для любого е>0 найдётся 8>0, такое, что из неравенства
0< |х-а|<8 следует | f(x) - В | <е, т. е.
B= limf(x)» Ve>0 36
x-+a
Vxe()8(a) f(x)eU£(B).
Замечания. 1) Здесь и всюду в дальнейшем изложении мы
подразумеваем, что значения функции берутся лишь в тех точках, где она
определена. Сама точка а может и не принадлежать области
определения D(f) (на это указывает неравенство 0 < | х - а |) (рис. 8.1).
2) Определение предела показывает, что для нахождения предела
функции в точке а необходимо знать её значения в некоторой
проколотой окрестности этой точки. В частности, изменение значения функции
в точке а не изменяет предела функции. Отметим также, что если две
функции совпадают в некоторой проколотой окрестности точки а всю-
4 [_Глава VIII. Предел и непрерывность функции
В-г<
/ 0
Рис. 8.1
/////////А
а+8
ду, кроме конечного числа точек, то
пределы этих функций в точке а либо
равны, либо оба не существуют.
Пример 1. Докажем по определению,
что lim cos x = cos a.
х-+а
П Возьмём произвольное е > 0 и
будем искать такое 8 > 0, чтобы из
неравенства 0 < | х — а | < 8 следовало бы
\cosx - cosa| < e.
Рассмотрим следующую цепочку
неравенств:
I cos х - cos a I = 2 - sin -
х-а
sin-
х-а
х-а
sin-
= \х-
х + а
Правомерность первого знака неравенства следует из того, что синус
любого числа по модулю не превосходит 1, а второго — из неравенства
|sinx| ^ \х\ \ для х е -—; — доказано в 10 классе, см. пример 39 § 36).
V V 2 2У
Таким образом, если взять 8 = е, то при 0 < \х — а\ < 8 будет
выполнено \cosx - cosa| < e, что и доказывает требуемое утверждение. В
Аналогично можно показать, что lim sin л: = sin a.
х—>а
Пример 2. Докажем по определению, что lim л:2 = 4.
*—2
D Рассмотрим выражение |х2-4| = |л:- 2| • |л: + 2|. Возьмём
произвольное е > 0. Будем искать такое 8 > 0 (зависящее от е), чтобы при
0 < | х — 21 < 8 выполнялось неравенство |л: — 2|-|jc + 2|<e.
Коль скоро \х — 21 < 8, то |л: — 2|-|jch-2|<o-|jch-2|. Поскольку
2-8<x<2 + 8, то
4-8<х + 2<4 + 8. (*)
При выборе 8 можно ограничиться рассмотрением 8^1 (нас
интересует поведение функции лишь в точках, достаточно близких к х0 = 2).
Если считать, что 8 ^ 1, то из неравенства (*) получим, что \х + 2\ < 5,
а тогда
\х-2\ • |х + 2|<8.|* + 2|<58.
Таким образом, чтобы выполнялось неравенство |л:-2|-|хн-2|<е,
достаточно одновременного выполнения неравенств 58 ^ е и 8 ^ 1, для
с
чего можно взять 8 = — при е < 5 либо 8=1 при е > 5.
Итак, взяв произвольное 8 > 0, мы нашли 8 > 0, такое, что при
| jc - 2| < 8 выполнено неравенство \х2 - 4| < е. Это и означает по
определению Коши, что lim х2 = 4. IS
5 | §44. Понятие предела функции
Отметим, что нахождение далее такого несложного предела
функции по определению весьма непросто. Как и в случае предела
последовательности, нахождение предела облегчается посредством
применения теорем об арифметических действиях с пределами функции,
а также аналогов теоремы Вейерштрасса (о пределе монотонной
ограниченной последовательности) для функции.
Доказательству этих теорем служит другое определение предела.
ОПРЕДЕЛЕНИЕ (по Гейне)
Число В называется пределом функции f в точке а, если
для любой последовательности {хп} с D(f), такой, что:
1> xnnzT^
2) начиная с некоторого номера хпфа;
последовательность значений функции f (xn) имеет своим
пределом В.
Замечание. Можно дать определение предела в точке а и для
функций, не определённых в точках сколь угодно близких к а
(например, / определена только на множестве Q рациональных чисел и
принимает при любом рациональном х значение, равное 0). В этом случае,
как мы уже отмечали выше, в обоих определениях следует брать лишь
те значения аргумента из малой окрестности точки а, при которых
функция определена.
ТЕОРЕМА
Определения по Коши и по Гейне предела функции в точке
равносильны.
D доказательство. Докажем сначала, что из определения по Коши
следует определение по Гейне.
Пусть определение по Коши выполнено и В = lim f(x).
х-+а
Возьмём произвольную последовательность {xn} d D(f), такую, что
1) хп -> а и 2) начиная с некоторого номера хпФ а. Возьмём произ-
п —*■ оо м
вольное е > 0 и по этому е найдём 8 > 0, такое, что \/х е £/§(а)
выполняется неравенство \f(x) - В\ < е.
По найденному 8 > 0 найдётся номер &, начиная с которого для всех
членов последовательности {хп} выполняется неравенство 0 < | хп — а \ < 8,
влекущее за собой неравенство \f(xn) — В\ < е. Таким образом, взяв
произвольное е > 0, мы нашли номер fe, начиная с которого выполняется
неравенство \f(xn) - В\ < е. Тем самым по определению предела
последовательности f(xn) -> В и число В является пределом функции /
п —>• оо
согласно определению по Гейне.
Теперь докажем, что из определения по Гейне следует определение
по Коши. Доказывать будем от противного. Для этого предположим,
что определение по Гейне выполнено, а определение по Коши — нет.
6 ^Глава VIII. Предел и непрерывность функции
Это означает, что найдётся (хотя бы одно) е0 > 0, такое, что для
любого 8 > 0 мы сможем указать такое значение аргумента лг§, что
О < \хь - а\ < 8, но при этом |/(х§) - В\ > е0. Итак,
для 8=1 Зхг: 0 < \хг - а\ < 1 и \f(xx) -B\> е0;
для 8 = - Зх2: 0 < | х2 - а | < - и | f(x2) - В \ > е0;
для 8 = - Зхп: 0<|хл-а|<-и \f(xn)-B\>eo и т. д.
Таким образом мы получили последовательность {хп}, такую, что
хп Ф а и хп —> а\ поскольку \/п е N \ хп — а \ < — . Согласно
определению по Гейне, последовательность {f(xn)} должна стремиться к Б. В то
же время \/п е N \ f(xn) - В \ > е0 (по построению {хп}) и, следовательно,
lim f(xn)^ В. Полученное противоречие доказывает, что предположе-
П —*■ оо
ние о том, что определение по Коши не выполняется, было неверно. ®
Заметим, что при решении задач удобно использовать определение
по Гейне для доказательства того, что функция не имеет предела.
ПримерЗ. Докажем, что функция f(x) = sign х не имеет предела при х -> 0.
D Рассмотрим последовательности хп = — и уп = —, пределы
которых равны нулю. Тогда при всех натуральных п выполнены равенства:
f(xn) = -1 и f(yn) = 1. Таким образом, lim f(xn) = -1, a lim f(yn) = 1,
п —»-+оо п -»-+оо
что противоречит определению предела функции в точке по Гейне,
поэтому предела функции / при х -» 0 нет. Ш
На основании определения по Гейне для пределов функций можно
доказать теоремы, аналогичные теоремам о пределах последовательностей:
• теорему о единственности предела функции в точке;
• теоремы об арифметических действиях с пределами функций
в одной и той же точке;
• теорему о предельном переходе в неравенстве;
• теорему о сжатой функции (аналог теоремы «о двух милиционерах»).
Например, докажем теорему о пределе суммы функций, используя
определение по Гейне.
ТЕОРЕМА
Пусть функции f \л д определены в некоторой проколотой
окрестности точки а и существуют пределы: lim f(x) = A, lim g(x) = В.
х -*а х-+а
Тогда существует lim (f(x)+ д(х)), причём
= A+B.
7 1 §44. Понятие предела функции
□ доказательство. Рассмотрим произвольную последовательность
{хп} — такую, чтохл ^ аи ни один член которой не равен а, начиная с
некоторого номера. Тогда по определению предела по Гейне lim f(xn) = A,
П —*■ оо
lim g(xn) = В. По теореме о пределе суммы сходящихся последователь-
п —*■ оо
ностей получаем, что существует lim (f(xn) + g(xn)) = А + В.
П —>оо
Итак, взяв произвольную последовательность хп—> а, ни один член
которой не равен а, начиная с некоторого номера, мы показали, что
\im(f(xn) + g(xn)) = А + В. Согласно определению предела функции в
П —>оо
точке по Гейне это и означает, что lim(f(x) + g(x)) = А + В. Ш
х-^а
Аналогично формулируются и доказываются и остальные теоремы
об арифметических действиях с пределами.
ТЕОРЕМА (о предельном переходе в неравенстве)
I Пусть в некоторой проколотой окрестности точки а определе-
I ны две функции f и д, имеющие предел в точке а. Пусть для всех
точек х из этой окрестности выполнено неравенство f(x)>g (x).
Тогда lim f(x) > lim g(x).
П доказательство. Пусть \imf(x)= A, limg(x)=B. Нужно дока-
х—>а х-+а
зать, что А > В. Рассмотрим произвольную последовательность хп-^ а,
ни один член которой не равен а, начиная с некоторого номера. Тогда
согласно определению предела по Гейне lim f(xn) = A, lim g(xn) = В.
n —► оо n —»■ оо
Начиная с некоторого номера ai0, все члены последовательности хп
попадают в ту проколотую окрестность точки а, где выполнено
неравенство f(x) ^ g(x). Поэтому, начиная с некоторого номера а*0,
выполняется неравенство f(xn) ^ g(xn). По теореме о предельном переходе
в неравенствах для последовательностей имеем lim f(xn) ^ lim g(xn).
П —*■ оо n —*■ оо
Итак, поскольку lim f(xn) = A, lim g(xn) = В, получаем А ^ Б, что
П -»-оо п —>оо
и требовалось доказать. Ш
Аналогично доказывается теорема о сжатой функции,
сформулированная ниже:
ТЕОРЕМА (о сжатой функции) ———-—---—■-——--——-———-——.
I Пусть в некоторой проколотой окрестности точки а определены две
■ функции fv\ g, имеющие одинаковый предел в точке а. Пусть в этой
же окрестности определена функция h и для всех точек х этой
окрестности выполнено неравенство f(x)>h (x) > д(х). Тогда существует
lim h(x), равный общему пределу функций f (x) и д (х) в точке а.
8 _Глава VIII. Предел и непрерывность функции
2. Различные типы пределов
Односторонние пределы
ОПРЕДЕЛЕНИЕ
Число ВА называется левосторонним пределом функции f
в точке а (пределом f при х, стремящемся к а слева),
если Ve > 0 35 > 0: Vx е (а - 5, а) | f(x) - В, \ < е.
Vi
Обозначение: f(a -0) = Вг = lim f(x).
Аналогично можно дать
определение правостороннего предела функции.
Обозначение: f(a + 0) = В2 = lim fix)
(см. рис. 8.2).
Замечание. Нетрудно доказать,
что функция / имеет предел в точке а
тогда и только тогда, когда существуют
и равны между собой односторонние
пределы функции / в точке а.
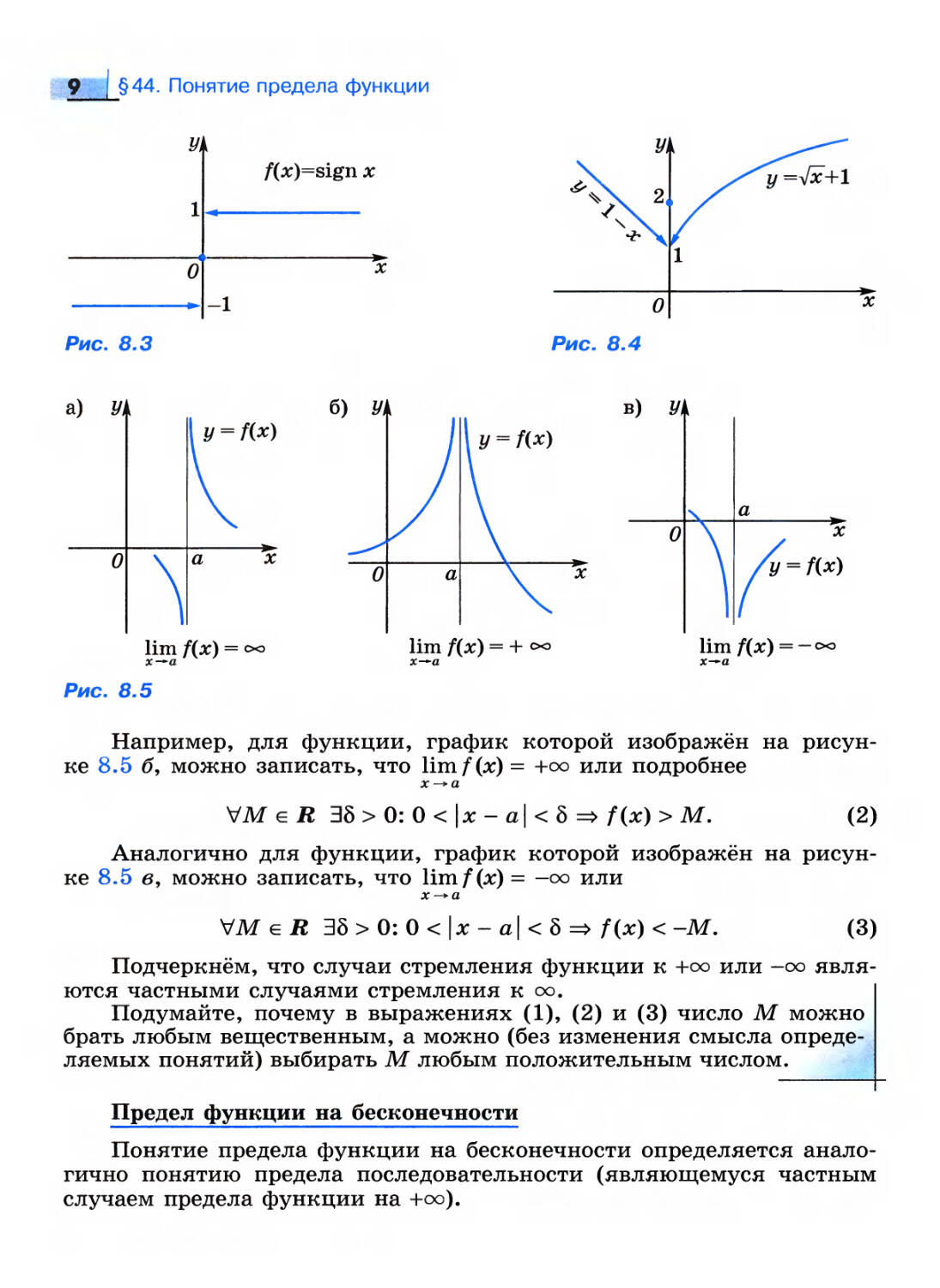
Пример 4. Функция fix) = sign* (рис. 8.3) имеет односторонние
пределы в точке 0, но эти пределы различны. Поэтому предела в точке 0
эта функция не имеет. Ш
11 - х9 при х < 0,
Пример 5. Функция fix) = < 2, при х = 0, (рис. 8.4) имеет равные
[\х +1, при х > 0
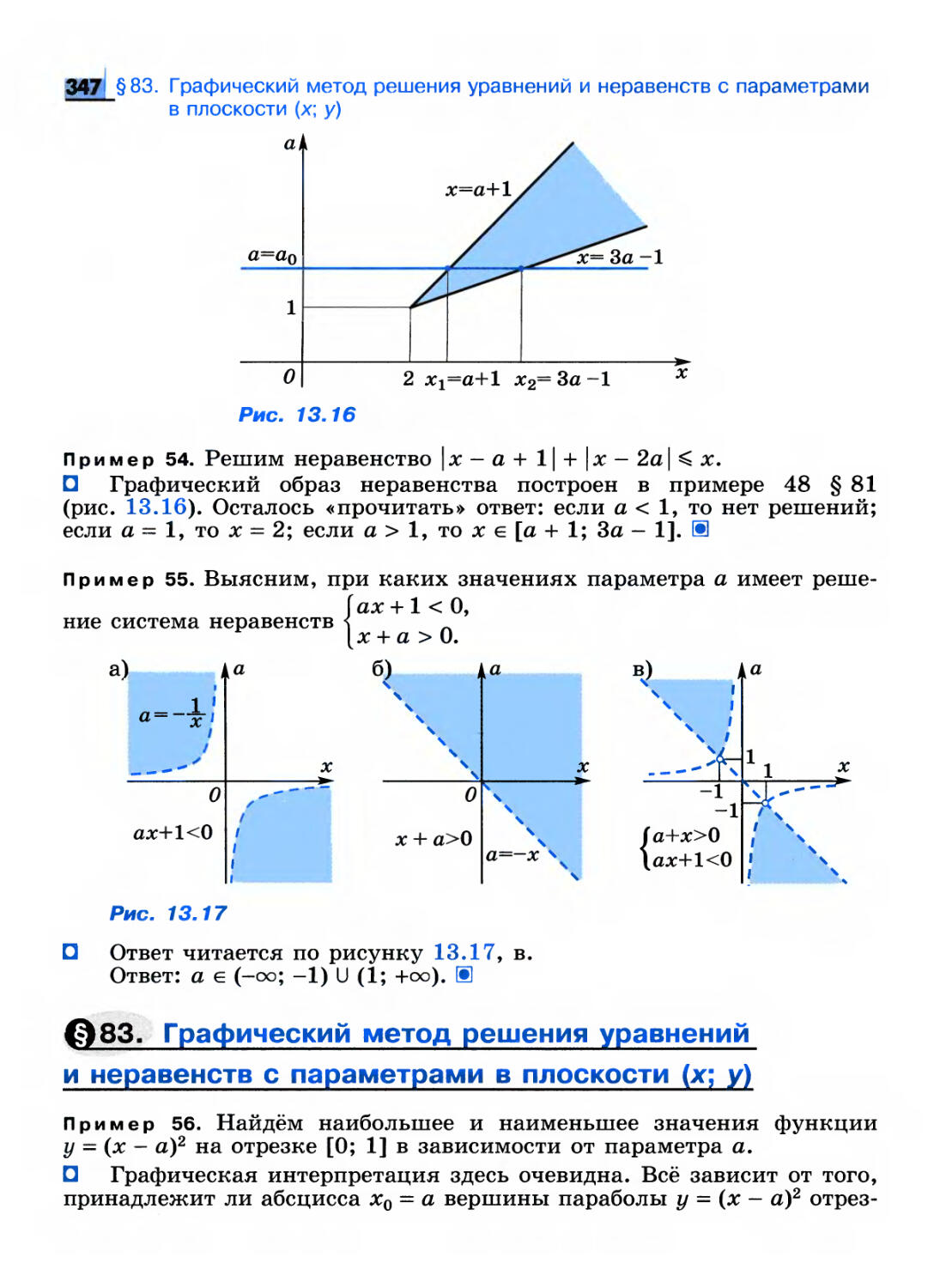
односторонние пределы при х -» 0. Поэтому lim/(x) = 1. Обратите вни-
х-* 0
мание на то, что lim/(jc) Ф fid). В
х —0
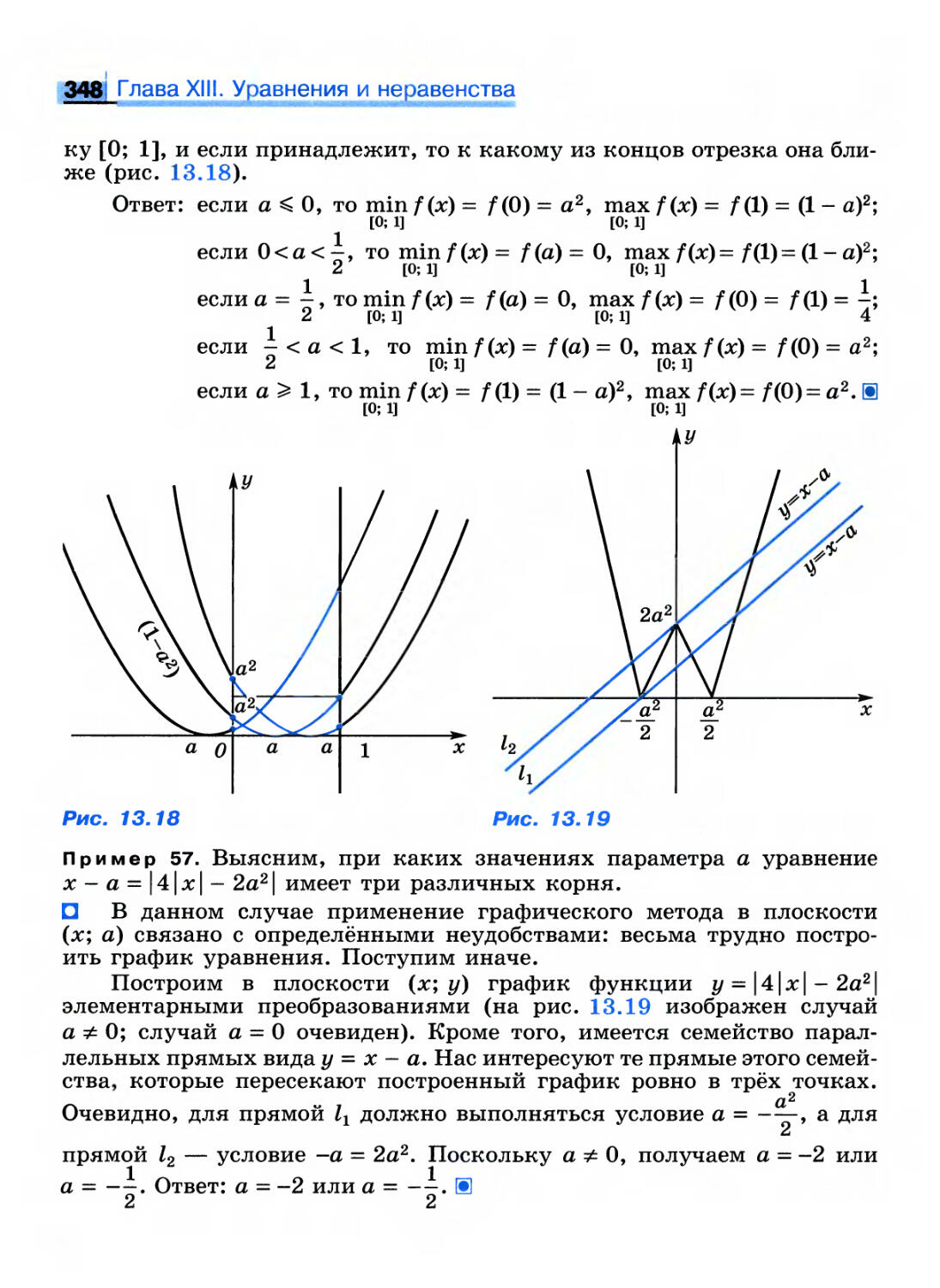
Бесконечные пределы в точке
ОПРЕДЕЛЕНИЕ
Функция f имеет бесконечный предел в точке а, если при
приближении аргумента к точке а значения функции
становятся сколь угодно большими по модулю, т. е.
VMeR 35>0: 0 < | х- а | < 5 => | f (х) \ > М. (1)
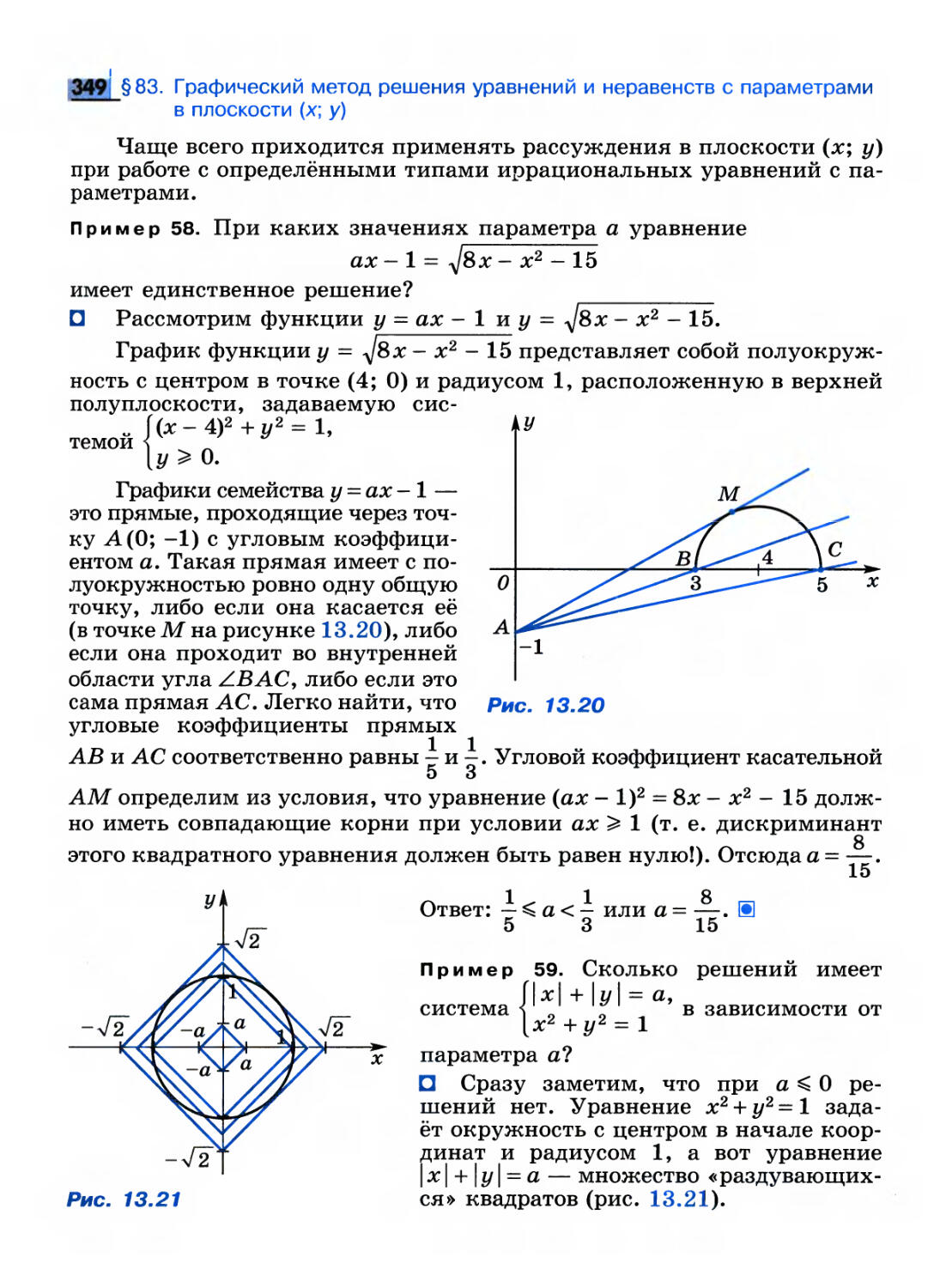
Обозначение: limf(x)= oo.
Примеры графиков функций с бесконечными пределами
представлены на рисунке 8.5. При этом для функций, графики которых
изображены на рисунках 8.5 б, в, можно уточнить «знак бесконечности»,
к которой указанная функция стремится.
9 I §44. Понятие предела функции
У,
1
0
f(x)=signx
X
1
Рис. 8.3
а) У,
0
\
с
а х
lim
х—а
б) г/А
lim f(x) = +
Рис. 8.5
Например, для функции, график которой изображён на
рисунке 8.5 б, можно записать, что \imf(x) = +оо или подробнее
VM eR 38 > 0: 0 < \х - а\ < 5 => /(*) > М.
(2)
Аналогично для функции, график которой изображён на
рисунке 8.5 в, можно записать, что lim/(jc) = —оо или
VM ей 35>0:0<|jc-a|<5=> f(x) < -М.
(3)
Подчеркнём, что случаи стремления функции к +оо или -оо
являются частными случаями стремления к оо.
Подумайте, почему в выражениях (1), (2) и (3) число М можно
брать любым вещественным, а можно (без изменения смысла
определяемых понятий) выбирать М любым положительным числом.
Предел функции на бесконечности
Понятие предела функции на бесконечности определяется
аналогично понятию предела последовательности (являющемуся частным
случаем предела функции на +оо).
10 Глава VIII. Предел и непрерывность функции
а) Ук
7
О
б)
В
lim f(x) = В
ЛГ—+ОО
X
lim f(x) = С
jc—»-oo
Рис. 8.6
ОПРЕДЕЛЕНИЕ
Число В называется пределом функции f при х -> +оо, если
Ve>0 Зх0: Vx>xo | f(x)-B | < е.
Обозначение: В = lim f(x).
Х-+ +ОО
Замечание. Как и в других определениях, мы подразумеваем,
что среди х > х0 выбираются лишь те, в которых функция определена.
Например, если функция / определена на множестве Q рациональных
чисел и в каждом из них принимает значение 0, то lim f(x) = 0.
х —*■ +00
Итак, предел последовательности есть частный случай предела
функции при х —> +оо, если функция определена на множестве N.
Аналогично определяется lim f(x).
ОПРЕДЕЛЕНИЕ *~* °°
Число С называется пределом функции f при х -> -оо, если
Ve>0 3x0: Vx<xo | f(x)-C\ <e.
Наконец, если пределы функции при х —> +оо их^ -оо равны, то
можно говорить о пределе функции при х —> оо:
ОПРЕДЕЛЕНИЕ ттттятттттяттттттт^^
Число А называется пределом функции f при х -> оо, если
Ve > 0 Зх0: | х | > х0 => | f (х) - А \ < е.
Примеры графиков функций с конечными пределами при х —> +оо,
х —> -оо и х —> оо представлены на рисунке 8.6.
О 45. Некоторые свойства пределов функции
Докажем некоторые свойства функции, имеющей предел в точке.
1. Локальные свойства функции, имеющей предел
Локальными свойствами называются свойства, которые
выполняются в некоторой окрестности точки.
11 , §45. Некоторые свойства пределов функции
ОПРЕДЕЛЕНИЕ
Функция f называется локально ограниченной в точке а,
если существует 8-окрестность точки а, такая, что функция
ограничена на D(f) П Ub(a).
Заметим, что в самой точке а функция может быть не определена.
Пример 6. а) Функция f(x) = , которая равна х + 1 при х Ф — 1
X I А
и не определена при # = -1, является локально ограниченной в
точке -1 (можно взять е = 1, и в этой окрестности функция будет
ограничена, например, числами —1 и 3).
б) Функция f(x) = — не является ограниченной в 0 (какую бы ма-
х
лую е-окрестность точки 0 мы бы ни взяли, в этой окрестности
функция будет принимать сколь угодно большие по модулю значения). 11
ТЕОРЕМА
Если функция имеет в точке а конечный предел, то функция
локально ограничена в этой точке.
□ доказательство. Рассмотрим функцию /, имеющую в точке а
конечный предел. Докажем, что существует окрестность точки а, в
которой функция ограничена.
Возьмём в определении предела по Коши е = 1. Тогда из
определения следует существование 8 > 0, такого, что \/х е D(f) П £/§(а)
выполняется неравенство В — 1 < f(x) < В + 1, где В = lim/(x), что и означает
х—*а
ограниченность / в D(f) П иъ(а) (см. рис. 8.1). IS
Пример 7. Функция / локально ограничена в точке х = 5. Докажем,
что функция g (х) = (х — 5)f(x) имеет предел в точке х = 5, равный 0.
□ В самом деле, раз функция / локально ограничена в точке х = 5,
то существуют 8-окрестность точки х = 5 и число М > 0, такие, что
\/х е D(f) П С/§(5) выполняется неравенство |/(л:)| ^ М, тогда Vx e D(f) П
П Ub (5) выполняется неравенство 0^\f(x)(x-5)\^M\x-5\. По теоремам
о пределе суммы и произведения lim(M|x- 5|)= 0, а значит, по теоре-
ме о сжатой функции, lim| f(x)(х- 5)| = 0, откуда lim(f(x)(& - 5)) = 0. Ш
5 5
ТЕОРЕМА (о сохранении знака функции) ——--—■-—--«---—-——-—------
Если функция f имеет в точке а конечный предел В ф О, то в
некоторой проколотой окрестности точки а все значения f имеют тот
же знак, что и число В.
Точнее, если, например, lim/(x) = В и В > 0, то 38 > 0: \/х е U§(a)
х—*■ а
выполняется неравенство f(x) > 0.
12 Глава VIII. Предел и непрерывность функции
\в\
П доказательство. Пусть limf(x) = В Ф 0. Возьмём 8 = -—- > 0. Для
х-*а # 2
этого 8 найдётся такое 8 > 0, что \/х е Е/§(а) выполняется
| f(x) — В\< -—- или, что то же самое, В- —- < f(x) < В + ■—-.
Если В > 0, то из левой части неравенства следует, что \fx e Ub(a)
f(x)> — >0; если же В < 0, то из правой части неравенства следует,
что Ух е й&(а) f(x) < — < 0. ®
Пример 8. Функция / имеет в точке а конечный и отличный от нуля
предел. Докажем, что функция g = — локально ограничена в точке а,
т. е. если lim f(x) = В, где В Ф 0, то 38 > 0 такое, что g ограничена в Щ(а).
х-+а
П Из доказательства теоремы о сохранении знака функции мы
знаем, что
• В
если В > 0, то 3 8 > 0: \/х е иъ(а) выполняется неравенство f(x) > — > 0;
• В
если В < 0, то 3 8 >0: \/х е Ub(a) выполняется неравенство f(x) < — < 0.
Отсюда следует, что при В Ф 0 существует 8-окрестность точки а,
• I в\
такая, что \/х е Ub(a) выполняется неравенство | f(x)\ > -—- > 0. А тогда
12
\/х е иъ(а) |#Сх:)|= г- г < г—г, откуда и следует локальная ограничен-
1/(^)1 1^1
ность функции g в точке а. Ш
2. Предел монотонной функции
ТЕОРЕМА
Если функция f определена и монотонна на отрезке [a; to], то
в каждой внутренней точке х е (a; to) эта функция имеет конечные
односторонние пределы, а в точках а и to соответственно
конечные правосторонний и левосторонний пределы lim f(x)
и lim f(x). x^a+
x-*b-
D доказательство. Пусть функция / возрастает (может быть,
нестрого) на отрезке [а; 6]. Возьмём точку х0 е (а; 6]. В силу возрастания
функции / при всех х < х0 выполнено неравенство f(x) < f(x0), т. е.
множество значений функции / на полуинтервале [а; х0) ограничено
сверху, а тогда по аксиоме супремума существует точная верхняя
граница: sup / (х) = М.
х € [a; xq)
13 §46. Вычисление предела функции в точке
М
М-г
Докажем, что число М будет
левосторонним пределом функции / в точке х0>
т. е. М= lim f(x).
Возьмём е > 0. Тогда найдётся такая
точка хг е [а; х0), что f(xx) > М - е (по
свойству точной верхней границы). В силу
возрастания функции / для всех х е (хг; х0) будет
верно неравенство f(x) > М - е. Ясно также,
что Vx e [а; х0) выполняется неравенство 0
f(x) ^ М <М + е. Пусть 8 = х0 - хг. Мы
получим, что \/х е (х0 - 8; х0) выполняются нера- РиСт 8т 7
венства М — е < f(x) < М + е, т. е. lim f(x)= M по определению (в силу
произвольности выбора е > 0) (рис. 8.7).
Доказательство существования правостороннего предела
аналогично приведённому выше. IS
О46. Вычисление предела функции в точке
1. Вычисление предела с помощью теорем
об арифметических действиях с пределами
Рассмотрим несколько примеров на вычисление пределов
функции в точке.
х3 — 8
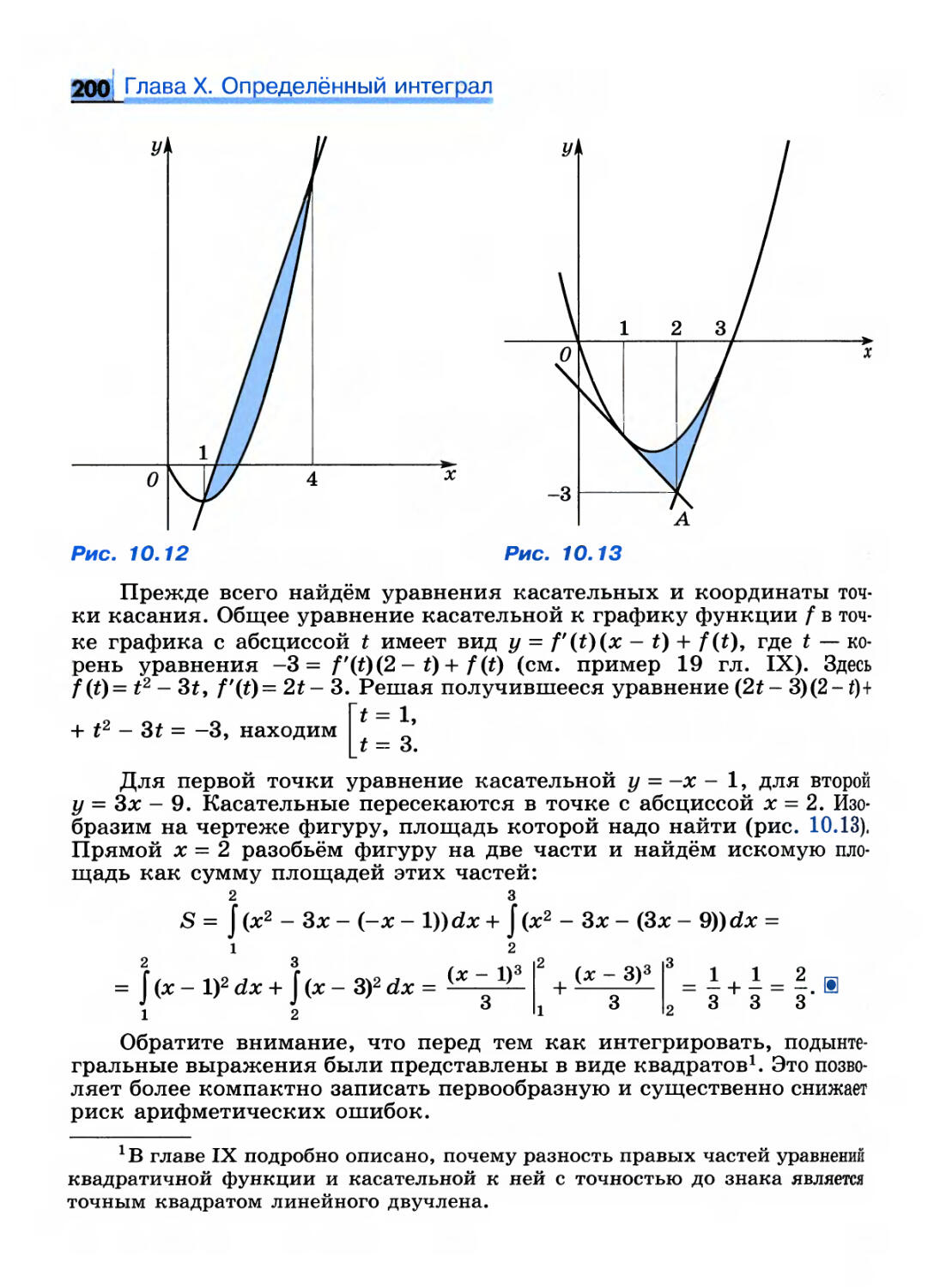
Пример 9. Вычислим: a) lim (х3 + 2л:2 + 1); б) lim .
*—2 х—2 2Х - 4
D а) На основании теорем об арифметических действиях с
пределами можно записать: lim (х3 + 2л:2 +1) = 23 + 2 • 22 + 1 = 17.
*~"2 х3-8
б) При х = 2 функция f(x) = не определена, но в остальных
АХ 4
точках области определения х — 2 Ф 0, и мы можем сократить дробь;
при этом получится новая функция g, совпадающая с функцией /
везде, кроме точки х = 2:
х3-8 (х - 2)(х2 + 2х + 4)
/(*) =
2х-4 2(х-2)
= ^х2 +х + 2.
Рассмотрим функцию g(x) = -х2 +
А
+ х + 2 при х Ф 2. Согласно замечанию
на с. 3 lim f(x) = lim g(x) = 6, посколь-
дг-»2 #-»2
ку функции fug совпадают в
некоторой проколотой окрестности точки
х = 2 (рис. 8.8). 11
14 Глава VIII. Предел и непрерывность функции
fj 4jc \х\
Пример 10. Вычислим: a) lim -— ■—■—-; б) lim-
x^l Х3-4Х + 3 х-+4 X - 4
П а) Заметим, что в некоторой 8-окрестности точки х = 1 при 5< —
I 4 J
выполняется равенство
|5 - 4х\ - \х\ 5 - 4х - х 5 - Ъх
х3 - 4х + 3 х3 - 4х + 3 х3 - 4х + 3"
Тогда
,. 15-4x1-1*1 ,. 5-5х ,. 5(1-х) ,. -5 -
lim j— !—!—L = lim —г = lim ^— = lim — = 5.
34 3 34 3 (l)(2 3) 2 3
Последнее равенство верно в силу теорем об арифметических
действиях с пределами. Обратим внимание на то, что мы опять (как и в
примере 9, б) заменили одну функцию на другую, совпадающую с данной
в некоторой проколотой окрестности точки х0 = 1.
yjx 7 3 *2-16 ,. х + 4 4
б) lim = lim . = lim
4 х4 4(/2 7 3Н 4) 4
lim . lim . .
х-4 *^4(л/*2- 7 + 3Н*- 4) *-"4V*2- 7 + 3 3
В этом примере мы воспользовались тем, что lim 4х = 4а, а также
теоремой о замене переменной, доказанной в следующем пункте. IS
2. Теорема о замене переменной
При вычислении пределов часто помогает следующая теорема
о замене переменной, она же теорема о пределе композиции.
ТЕОРЕМА ^^^^—^^^~^-^^^—^^^^—
Если существуют lim д(х) = bv\ lim f(y) = с, причём в некоторой
проколотой окрестности точки а выполнено условие д(х) фЬ, то
существует предел композиции lim f(g(x)) = lim f(y) = с.
x —> a y—> b
D доказательство. Возьмём произвольную последовательность {хп},
такую, что хп —> аи, начиная с некоторого номера, ни один член
П —>• оо
которой не равен а.
Пусть yn = g(xn). Тогда по определению предела функции по
Гейне lim yn = b, причём, начиная с некоторого номера, уп^Ъ. По-
п—»- оо
скольку lim f(y)=c, то согласно определению по Гейне lim f(g(xn)) =
у —*b n —><х>
= lim f(yn) = с. Итак, взяв произвольную последовательность хп—> а,
П —»-оо
получили, что lim f(g(xn)) = с, а значит, в силу определения по Гей-
П —»-оо
не lim/(£(x))= с. Ш
15 1 §46. Вычисление предела функции в точке
Замечание. От условия существования 5-окрестности точки х = а,
такой, что \/xeUb(a) g(x)*b отказаться нельзя. В самом деле,
рассмотрим функцию g(x) = 1 при всех вещественных значениях х
и f(y) = \ л л Тогда lim g(x) = 1, lim f(y) = 0, но предел
[1 При у = 1. лг-^1 у—1
lim /(£(:*:)) = lim f(l) = 1.
Пример 11. Вычислим:
a) lim l-ctg»x . б) Ит
П а) Пусть t = ctgx. На основании теоремы о замене переменной
1 - ctg3 х 1 - t3
верно следующее равенство: lim — = lim -. При этом
х_^п_ 2-ctgx-ctgsx t-+i2-t-t3
4
l+t+t2 3
б) Сделаем замену переменной £ = л/л?. Тогда
3 2 ^ r f 3
2t =1
~ 2
+ 0(1 +t + t2) 2
3. Замечательные пределы
Вычислим несколько пределов, которые по традиции носят
название «замечательных пределов».
О X
_ о sinx sin(-x)
D Заметим, что = — , поэтому достаточно доказать, что
sin х х —х
lim = 1. Для этого воспользуемся доказанным в 10 классе нера-
х—0+ X
венством (пример 39, § 36) sinx < х < tgx при х е 0; — . Из этого не-
V 2)
Sin X л I /ч ТС I тт
равенства следует, что cosx < < 1 при х е 0; — . Из теоремы
х \ 2)
о сжатой функции (учитывая, что limcosx= cosO= 1, см. пример 1,
§ 44) следует, что lim = 1. SI
х-+ 0+ X
16 Глава VIII. Предел и непрерывность функции
л^ т» ч ,. sin ах -ч ,. 2cosx
Пример 12. Вычислим: a) lim-:—т^—\ б) lim —
П а) lim *»« = lim (*Е«. _J*. «fl = « в последнем равенст-
* — osinpx * — о^ ах sinpx рху p
,. sin ах ,. sinPx
ве для вычисления lim и hm ——*— мы воспользовались первым
*—о ах л: —о рх
замечательным пределом, теоремой о пределе композиции и теоремой
о произведении функции.
б) Сделаем замену переменной t = х .
3
2 f cos ft + —
i- 2cos*+l .. I I 3
hm = hm
2 З
0,5
sin-
= lim-
* —о
sini('+¥)
= hm
«I 271 | К
21 cos I t + — + cos —
3 у 3
-Sin|*
= lim
* — о
4cos|- + -
sin —
sin— t
2
2V3
. m
2. lim (1+ x)x = e
0
D Заметим, что функция f(x) = (1 + x)x определена на промежутке
(-1; +оо), кроме точки х = 0. Используем для доказательства
определение предела функции по Гейне. х
1. Докажем сначала, что lim (1 + х)х = е. Выберем
последовательность {хп} так, что хп -> 0 и хп > 0. Можно при этом считать, что,
начиная с некоторого п, хп< 1.
ПОЛОЖИМ =/1.1
Ы Ч
как обычно, — обозначает целую часть чис-
ла — . В силу того что хп < 1, выполнено неравенство nk> 1. Тогда
Х
откуда
1 ^1
(*)
Поскольку л^з^О и jcft > 0, то очевидно, что nk —^^ +оо.
17 §46. Вычисление предела функции в точке
Из неравенств (*) и (**) с учётом свойств степеней получаем:
+
Легко видеть, что в последнем двойном неравенстве оба крайних
выражения при k —> н-оо имеют своим пределом число е, например1,
N Hff +1 / Ч Hff /
lim I 1 + — = lim 1 + — • lim 1 + — I = e • 1 = e.
Значит, по теореме о сжатой последовательности, существует
предел lim (l + xk)Xk = e. В силу произвольности выбора
последовательности {хп} мы доказали, что существует lim (1 + х)х = е.
2. Пусть теперь хп -> 0 и хп < 0 (можно считать, что при этом
п П —» оо "
\/п е N хп> -1). Положим yk - -xk. Тогда 0 < yk < 1 и yk -► 0.
Заметим, что lim -^—= Ои Vfee ЛГ -^—>0 и lim 1 + -*— Ук =е
k^+ool-yk l-yk yk^o{ l-yk)
(это следует из пункта 1), а последовательность s 1 + ^ стремит-
ся к 1, следовательно, lim (1 + xk)*k = e. Как и в предыдущем случае,
отсюда lim (1 + х)х= е. А значит, lim (1 + х)х= е. Ш
х-+0- х — 0
1 Здесь мы воспользовались утверждением, которое не доказывали: если
последовательность натуральных чисел {nk} стремится к бесконечности, то
( lYh ( lV
lim 1 н = е9 так как е = lim 1 + — (определение числа е). Пусть за-
k—► оо I Пу I п —*■ оо I П I
дано е > 0, тогда существует га такое, что 1+ — sUe(e) для любого п е N,
( \п
гс > га в силу того, что lim 1н— = е . При этом, так как lim nk = +oo, то
N: \/k е N k > К выполняется пк > т, а значит, 1 + — б[/£(е) для лю-
( ,Г l "fcJ
бого k > К. Таким образом, lim 1 + — = в по определению предела.
л1 я )
18 Глава VIII. Предел и непрерывность функции
Следствия 1. lim 1 + — = е.
х-^оо^ X J
2. Если lim а (х) - О и а(л:)>-1, а(х)фО в некоторой проколотой окрест-
х —а 1
ности точки а, то lim (1 + а (х))а(х) = е.
х-^а
Оба утверждения прямо следуют из только что доказанной
формулы и теоремы о замене переменной.
3. lim
х —О
х)
- =
= 1
D lim
X)
X
o\x
Поскольку li
lim ln(l +
x —0
= lne = 1, т. e. lim
0
= e, то, по теореме о пределе композиции,
= 1.
Заметим, что здесь мы воспользовались тем, что lim \пх = In а. Ш
iogea+*) 1
Следствие, lim
о х
г, ю т loge(l+*) .. ln(l+x) 1
D В самом деле, lim = lim —-1 = -—.
х-о х х^о lna-л: lna
4. lim
= 1
= 1. Щ
D Сделаем замену переменной: у = ех — 1. Тогда у -> 0 (в силу того,
что lim ех = еа). Значит, lim = lim
х-^а х-+0 X у-+ 0
Следствие, lim = lna.
х —О X
D Из формулы 4 и соотношения ах = ех ln a следует, что
— — 1
X
5.
lim ^
x —0
xlna
1 + x)a
X
-1
- a
Этот предел носит название биномиального.
19 J §46. Вычисление предела функции в точке
□ Положим (1 + х)а - 1 = у. Тогда у -> О и (1 + х)а = 1 + у. Логариф-
X —* О
мируя последнее равенство, получим 1п((1 + х)а) = 1п(1 + у), откуда
aln(l + х) = 1п(1 + у), тогда
(1 + хГ - 1 = у а
а
х ln(l+z/) х
Окончательно, переходя в последнем равенстве к пределу при х —> О
(1 + х)а — 1
(а значит, у —► 0), получаем lim = a. IS
х-»о х
Итак, мы получили следующие «замечательные пределы»:
r sin* л r log(l + x) 1
lim = 1 lim
m1 lim
о * . х — о я lna
lim (I + х)х = е lim = 1
х-+0 х-+0 X
lim | 1 + — = е lim = In a
х) х-+о х
,. ln(l + jc) 1 ,. (l + x)-l
lim — = 1 lim = a
x^o x x-+o x
л t» ,. In cos x
Пример 13. Вычислим lim
o
m.
olncos2x
-- ,. In COS X ,. ln(l + COSX-l)
D lim = lim
о Incos2x x-+o ln(l + cos2x - 1)
,. (In (1 + cos x - 1) cos 2x - 1 cos x - 1 ^
* — o^ cosx-1 ln(l + cos2x - 1) cos2x-lj"
Вычислим отдельно
-2sin2-
,. cos x - 1 ,. 2 ,.
lim = lim — = lim
x —о cos2x — 1 x — о — 2 sin2 x * —о
х ( . ху
sin —
Li.
sin x J
Таким образом,
,. In cos л: ,. fln(l + cosx - 1) cos2x-l cos x- 1 ^ _. 1
x — olncos2x x —ol cosx-1 ln(l + cos2x - 1) cos2x-lj 4'
,. ln(l + cosx - 1) ^ i. / 1X л
поскольку lim — = 1, так как lim (cos* - 1) = 0 и
x — 0 COS X — 1 x — 0
lim = 1, так как lim (cos 2x — 1) = 0. IS
x — oln(l+ cos2x - 1) x —о
20 1 Глава VIII. Предел и непрерывность функции
Пример 14. Найдём предел lim
cos-
кх
D Убедимся, что под знаком предела неопределённость вида -
Выполним замену, чтобы иметь возможность воспользоваться замеча
тельными пределами: положим t = х — 3. Тогда t -> 0. Получим:
X —*■ О
cos-
кх
t = х- 3
х= t + 3
= lim
= 2 lim
= 2 lim
8
sinf
lt + if- l H 8
8 J 2 8
sinT T
Так как lim
з
8
• = — и lim = 1, то в результате мы
3 t —>о •_ к*
о 1 3 2 1 ш
получим, что искомый предел равен 2 •-•-• — = —. Ш
3 8 к 2к
О47, Классификация бесконечно малых функций
Определим понятия бесконечно малой и бесконечно большой
функций в окрестности точки а:
ОПРЕДЕЛЕНИЕ
1. Функция а называется бесконечно малой в окрестности
точки а (или при х-» а), если lim ос(х) = 0.
2. Функция ф называется бесконечно большой в
окрестности точки а (или при х-» а), если lim ср(х) = оо.
ха
Например, f(x) =
х-1
является бесконечно малой в окрестности
х-2
точки a = 1 и бесконечно большой в окрестности точки a = 2.
Отметим, что функция, бесконечно малая в окрестности одной
точки, может не быть бесконечно малой в окрестности другой точки.
21, §47. Классификация бесконечно малых функций
Одним из самых важных вопросов является сравнение бесконечно
малых (бесконечно больших) функций между собой.
Например, ясно, что в окрестности точки х = О обе функции
f(x) = х и g(x) = х2 будут бесконечно малыми, но при этом функция g
«гораздо меныпе» функции / (не столько в смысле неравенства,
сколько в смысле скорости стремления к 0).
В то же время при х —> +оо обе функции будут бесконечно
большими, но теперь уже g «гораздо больше», чем / (опять же в смысле
скорости стремления этих функций к +оо).
Введём следующее определение:
ОПРЕДЕЛЕНИЕ
Пусть аир— бесконечно малые (бесконечно большие)
функции при х-> а, причём р(х) ф 0 в некоторой проколотой
окрестности точки а. Если lim ^—- = 1, то функции аир на-
х->а Р(Х)
зываются эквивалентными в окрестности точки а.
Обозначение: a(x) ~ $(х) при х -> а.
Замечание. Вообще говоря, понятие эквивалентных функций
вводится для произвольных функций / и g, но чаще всего используется,
когда обе функции либо бесконечно малые, либо бесконечно большие.
«Замечательные пределы» могут быть записаны теперь
следующим образом:
(1 +х)а- 1 ~осх при х-* 0;
sin х~х при х—► 0;
In (1 + х) ~ х при х -> 0;
loga(1 + х) ~ — при х -► 0;
In a
6х- 1 ~х при х—► 0;
ах - 1 ~ х In а при х -> 0.
Эту таблицу можно несколько расширить. Например, очевидно
tg х ~ х при х
tfif X
0 поскольку lim —— = 1.
л: —О X
Соотноп1ения в таблице удобно формулировать словесно.
Например: «В окрестности нуля синус эквивалентен своему аргументу».
Таким образом, при х -> 0 выполнены, например, такие соотношения:
sin (л:3) ~ Xs, sin(tgx) ~ tgx ~ х и т. п.
х2
Пример 15. Покажем, что 1 - cosх при х —> 0.
х
П Действительно, поскольку 1 - cos л: = 2 sin2 —, имеем
2
sin* —
,. 1 - cos x ,. 2 i.
lim = lim — = lim
x — о x^_ x —о x^_ x —о
~2~ 1Г
sin —
2
= 1,
откуда и получаем требуемое соотношение эквивалентности. Щ
22 Глава VIII. Предел и непрерывность функции
Можно сказать, что эквивалентные бесконечно малые функции
стремятся к нулю с «одинаковой скоростью». Часто приходится
различать бесконечно малые по характеру их стремления к 0: одни
бесконечно малые стремятся к 0 «быстрее», а другие — «медленнее».
ОПРЕДЕЛЕНИЯ
1. Если аир —функции, бесконечно малые (беско-
нечно большие) при х-»а, причем lim = К, где
х^а Р(Х)
— число, то ос и р называются бесконечно
малыми одного порядка малости (бесконечно большими
одного порядка роста) при х -> а.
2. Если аир —функции, бесконечно малые при х->а,
причём lim ^—- = 0, то а называется бесконечно ма-
хар(х)
лой высшего порядка по отношению к Р при х—> а.
Обозначение бесконечно малой высшего порядка: а(х) = оф(х))
при х -» а или, короче, а = о(р), я —► а.
Эта запись читается так: «а есть о малое от Р при х9
стремящемся к а».
В частности, запись «/(х) = о(1), х -> а» означает, что функция
f(x) есть бесконечно малая в окрестности точки а.
Следует отметить, что запись а(х) = о($(х)) при х —> а не
информирует нас ни о чём, кроме того, что а стремится к нулю «быстрее»,
чем р при х -* а!
Например, обратим внимание, что при х -> 0 выполнены
равенства sin л: — х = о(х) и tga: - х = о(х). Однако нельзя на основании
одинакового вида правых частей этих равенств сделать вывод о равенстве их
левых частей!
Утверждение (критерий эквивалентности бесконечно малых)
Бесконечно малые функции аир эквивалентны тогда и только
тогда, когда их разность есть бесконечно малая высшего порядка по
отношению к каждой из них:
/ ч о/ ч Г(Х(Х)-Р(Х) = О((Х(Х)),
ос х - р х , х -> а <=> \ £ ; ; ;;' х -> а.
[а х -р х =о р х ,
доказательство. Пусть а(х) ~ Р(л:), при х —> а. Тогда поскольку
1 при х -+ а, то lim v ' ИУ ' = lim I - zm = 0. Это и озна-
а(х))
чает, что а (л:) - $(х) = о (а (л:)), при х -> а.
Аналогично можно доказать, что ос (л:) — р(л:) = о(р(л:)), при л: -^ а.
23 §47. Классификация бесконечно малых функций
Пусть теперь а(х)-$(х) = о (а), при х-> а, т. е. lim
x-^a a(x)
Отсюда lim 1 - = 0, откуда lim - = 1. Последнее означает,
*—ay a(x)J ' x-^aa(x)
$ Щ
a(x)
что $(х) ~ а(х), х -> а.Ш
Следствие. а(х) ~ р(л:), х -» а <=> а(х) = $(х) + о(р), х -» а.
Утверждение -——------------------«-«----------------^^
Пусть f и д — функции, бесконечно малые в точке a, h — функция,
ограниченная в некоторой окрестности точки а.
Тогда (все равенства следует читать только слева направо):
1. 0(0 + 0(0 = 0(0- 2. 0(^0 = 0(0. 3. /7-0(0 = 0(0-
4. o(f)-o(g) = o(fg). 5. o(f+o(0) = o(0- 6. g-o(0 =
7. о (о(0) = о(0.
Для доказательства свойств полезно хорошо понять, что означают
их формулировки. Рассмотрим, например, первое свойство. Оно может
быть прочитано так: «Сумма двух бесконечно малых функций, каждая
из которых является бесконечно малой высшего порядка по
отношению к /, есть также бесконечно малая функция высшего порядка по
отношению к /».
О Ни в коем случае нельзя «уничтожать равные слагаемые» по
обе части знака равенства! Каждая из записей о(/) в этом равенстве
означает свою функцию!
П доказательство. Докажем 1. Нужно показать, что левая часть
есть бесконечно малая высшего порядка малости по отношению к /,
т. е. что предел отношения левой части равенства к / равен 0.
Действительно, имеем:
х —> a
f x^a f x^a f
Последнее равенство верно, так как lim —^ = 0 по определению
симх—>а f
вола о.
Аналогично доказываются остальные равенства. Ш
ТЕОРЕМА (о замене бесконечно малых функций эквивалентными)
Пусть имеется две пары бесконечно малых функций: а, Р и а^
таких, что а ~ а, и р ~ р^ при х -► а. Тогда lim ^iL = |jm _J
при условии существования хотя бы одного из этих пределов.
— л. а(х) ,. (а(х)
П доказательство, lim -f^ = lim —Y-
$(х) х^а^а^Х)
х-+а
,. а(х) 1 ,. Р(х) 1
поскольку lim —^- = 1 и lim „ = 1.
а^х) ^(х)
24 j Глава VIII. Предел и непрерывность функции
Замечание. Нельзя производить замену на эквивалентные
бесконечно малые отдельных слагаемых в сумме. Если же выражение в
числителе или знаменателе дроби есть произведение бесконечно малых,
то множители (все или некоторые) при отыскании предела можно
заменять на эквивалентные.
Продемонстрируем, как можно использовать сравнение
бесконечно малых при вычислении пределов.
тт „ .. ч .. l-cos5x -,. ,. 1 - cos x • cos 2х
Пример 16. Найдем: a) hm —; б) hm .
*-*о 2sinx2 x^o 2х2
П а) Так как 1 - cos 5х ~ , х-> О (см. пример 15), a sin(x2)~x2,
по теореме о замене бесконечно малых функций эквивалентными
получаем:
,. 1 - cos5x ,. 2 25
lim 1Г~- V = lim о 2 = Т-
л: —О 2siUXz * —О 2хг 4
X2
б) Так как 1 - cosx , х —> 0, то согласно критерию эквивалент-
X2 ( X2 Л
ности бесконечно малых 1 - cos х = — + о\ — , * -» 0, а тогда (по свой-
х2 ^ '
ствам символа о) cos л: =1 но (л:2), х—> 0. Получим:
( х2 \
1 - 1 - — + о(х2) • (1 - 2х2 + о(х2))
,. 1 -cosx • cos2x ,. v 2 )
lim -— = hm
х-
► о 2х2 х^о 2х2
-х2 - х4- о(х2) - о(х2) + 2jc2o(x2) + —о(х2) + о(л;2)о(л:2)
А теперь, заметив, что л:4 = о (л:2), а также использовав свойства
символа о (например, 2л:2 о (л*2) = о (л:2), получим
^48, Непрерывность функций
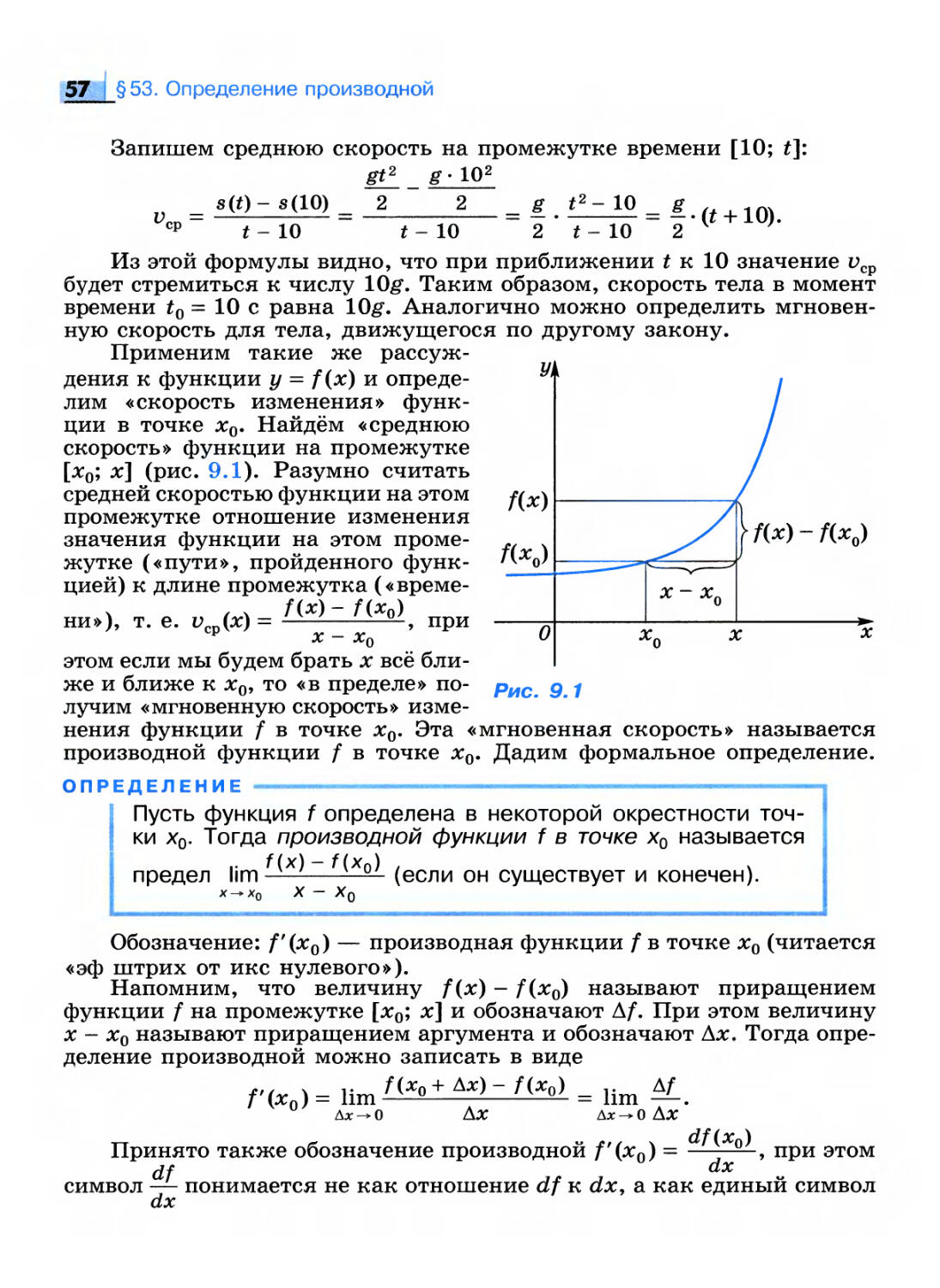
1. Понятие непрерывности функции в точке
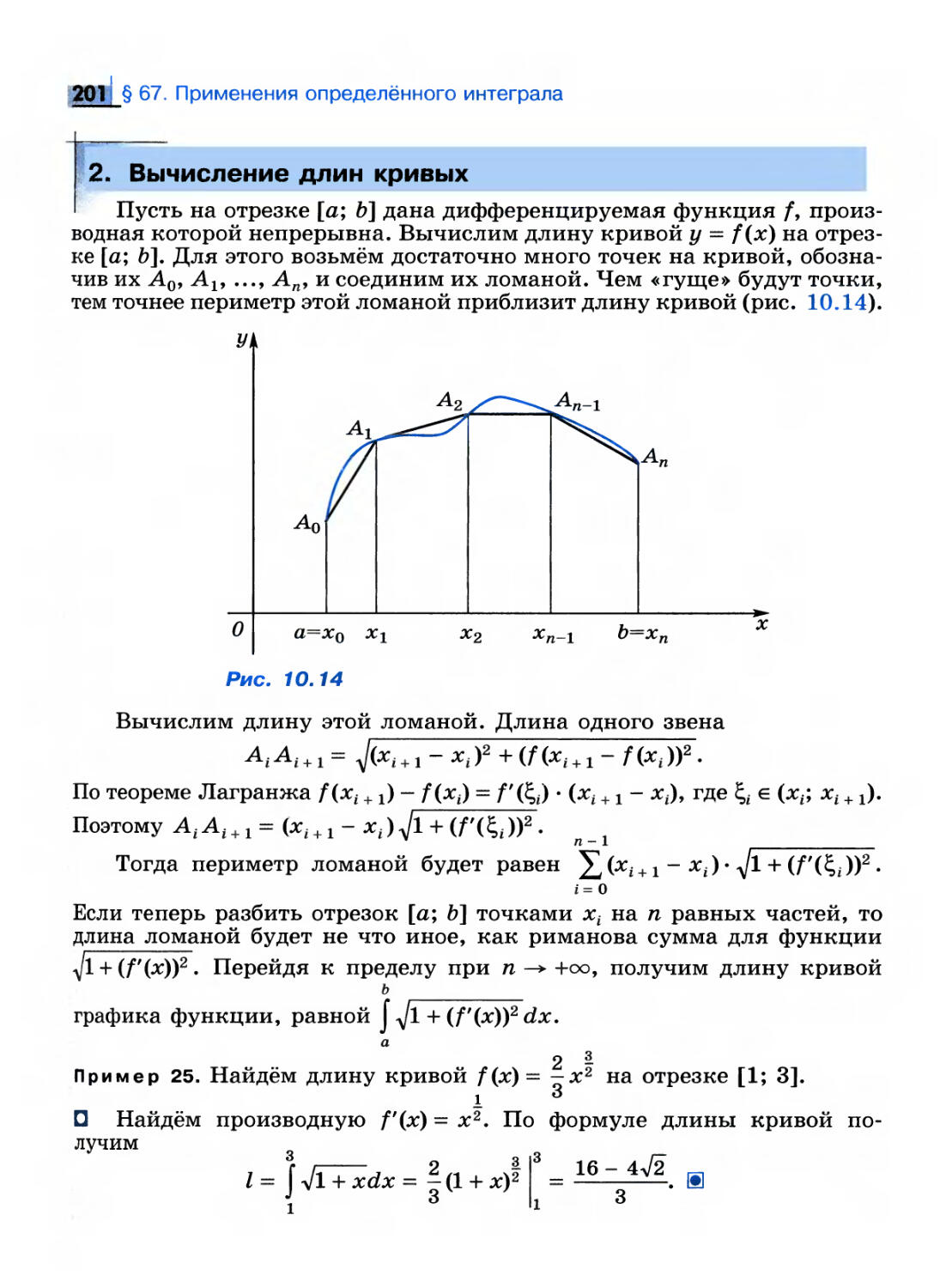
ОПРЕДЕЛЕНИЕ 1 ________________«__.
Функция f называется непрерывной в точке х0, если
выполняются два условия:
1) функция f определена в некоторой окрестности точки х0;
2) lim f(x) = f(x0).
25 1 §48. Непрерывность функций
Из этого определения прежде всего следует, что о непрерывности
функции можно говорить лишь по отношению к тем точкам х0, в
которых функция определена, т. е. х0 е D(f).
Можно предложить ещё несколько эквивалентных вариантов
определения непрерывной функции в точке. Первое условие, которое
требуется во всех последующих определениях: функция / определена
в точке х0 и в некоторой её окрестности, второе условие можно
заменить на равносильные.
2') Ve > 0 35 > 0: \/х е Ub(x0) \ f(x) - f(xo)\ < e.
2") Еслихпп^оох09 то f{xn)n-*J(xQ).
2'") Существуют односторонние пределы функции / в точке х0,
равные f(x0).
Для следующего определения введём ещё несколько важных
понятий. Назовём разность х - х0 = Ах приращением аргумента, & разность
f(x) — f(x0) = Af — приращением функции, соответствующим данному
приращению аргумента (А читается «дельта»).
Таким образом, А/ = f(x) - f(x0) = f(x0 + Ах) - f(x0).
Обратим внимание, что приращение функции в данной точке х0
есть функция от приращения аргумента.
ОПРЕДЕЛЕНИЕ 1
Функция f непрерывна в точке х0, если выполняются два
условия:
1) функция f определена в некоторой окрестности
точки х0;
2) Af -> 0.
' Ах —0
(Последнее условие читается: приращение функции стремится к 0
при условии, что приращение аргумента стремится к 0.)
Последнее определение, пожалуй, более всего соответствует
нашим интуитивным представлениям, связанным с графиками.
Действительно, согласно этому определению, малое изменение аргумента Ал:
вызывает лишь малое изменение функции Аг/, значения которой в
результате не могут меняться скачками, т. е. график функции нигде
«не рвется».
Равносильность данных определений очевидна.
По аналогии с понятием одностороннего предела введём
понятие непрерывности слева или справа: если функция /
определена на полуинтервале (х0 - 8; х0] и lim f(x) - f(x0), то функция
называется непрерывной слева в точке х0. Аналогично, если
функция / определена на полуинтервале [х0; х0 + 8) и lim f(x)= f(x0),
X -»• Х()+
26 Глава VIII. Предел и непрерывность функции
функция называется непрерывной справа
в точке х0.
Ясно, что для непрерывности функции
в точке необходимо и достаточно её
непрерывности в этой точке слева и справа.
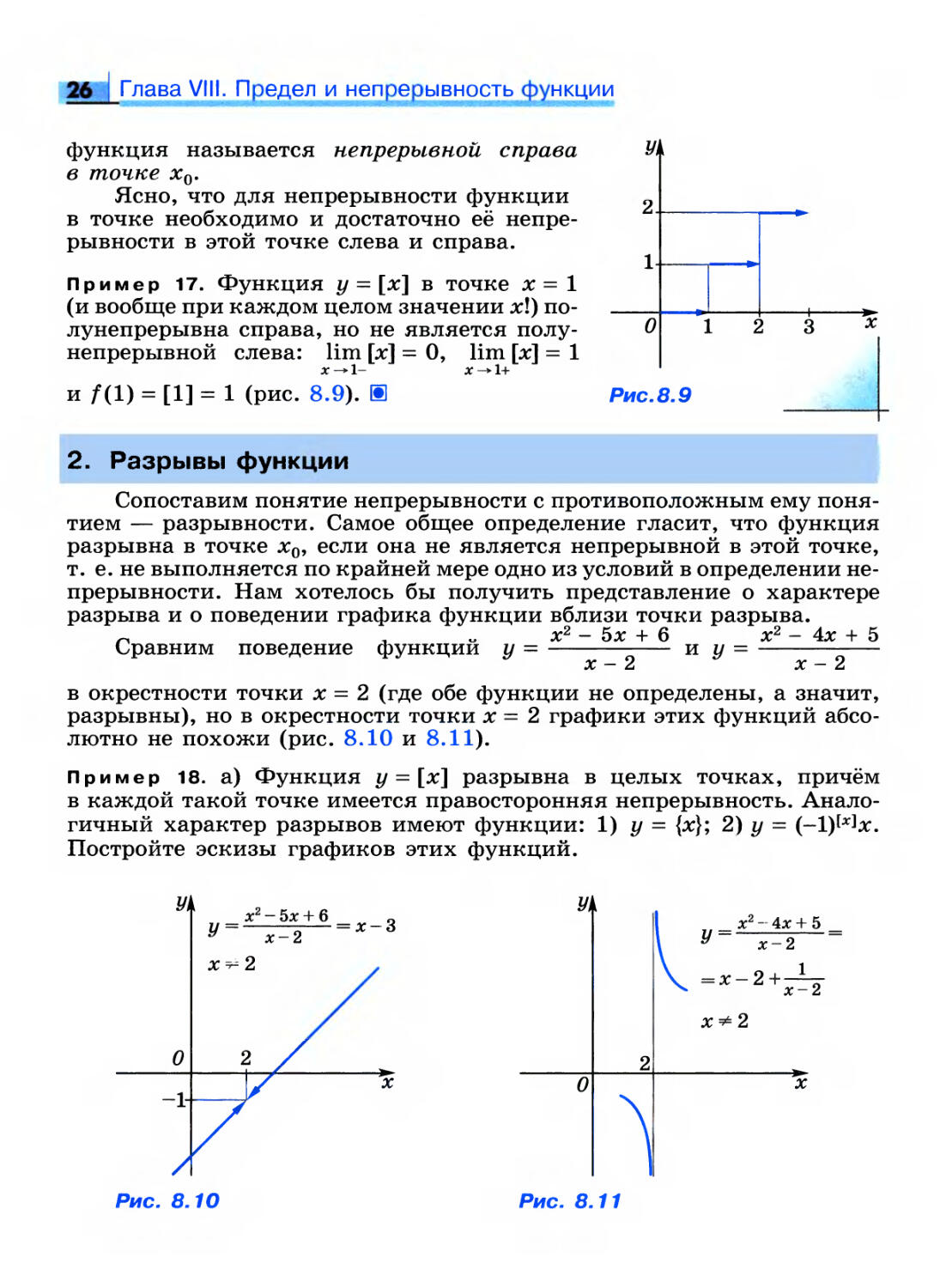
Пример 17. Функция у = [х] в точке х = 1
(и вообще при каждом целом значении х\)
полунепрерывна справа, но не является
полунепрерывной слева: lim [x] = 0, lim [x] = 1
х -»- 1- х -* 1+
и /(1) = [1] = 1 (рис. 8.9). II
О
Рис.8.9
2 3*
Л
2. Разрывы функции
Сопоставим понятие непрерывности с противоположным ему
понятием — разрывности. Самое общее определение гласит, что функция
разрывна в точке х0, если она не является непрерывной в этой точке,
т. е. не выполняется по крайней мере одно из условий в определении
непрерывности. Нам хотелось бы получить представление о характере
разрыва и о поведении графика функции вблизи точки разрыва.
~ ^ „ х2 - Ъх + 6 х2 - 4х + 5
Сравним поведение функции у = и у =
X — А X ^
в окрестности точки х = 2 (где обе функции не определены, а значит,
разрывны), но в окрестности точки х = 2 графики этих функций
абсолютно не похожи (рис. 8.10 и 8.11).
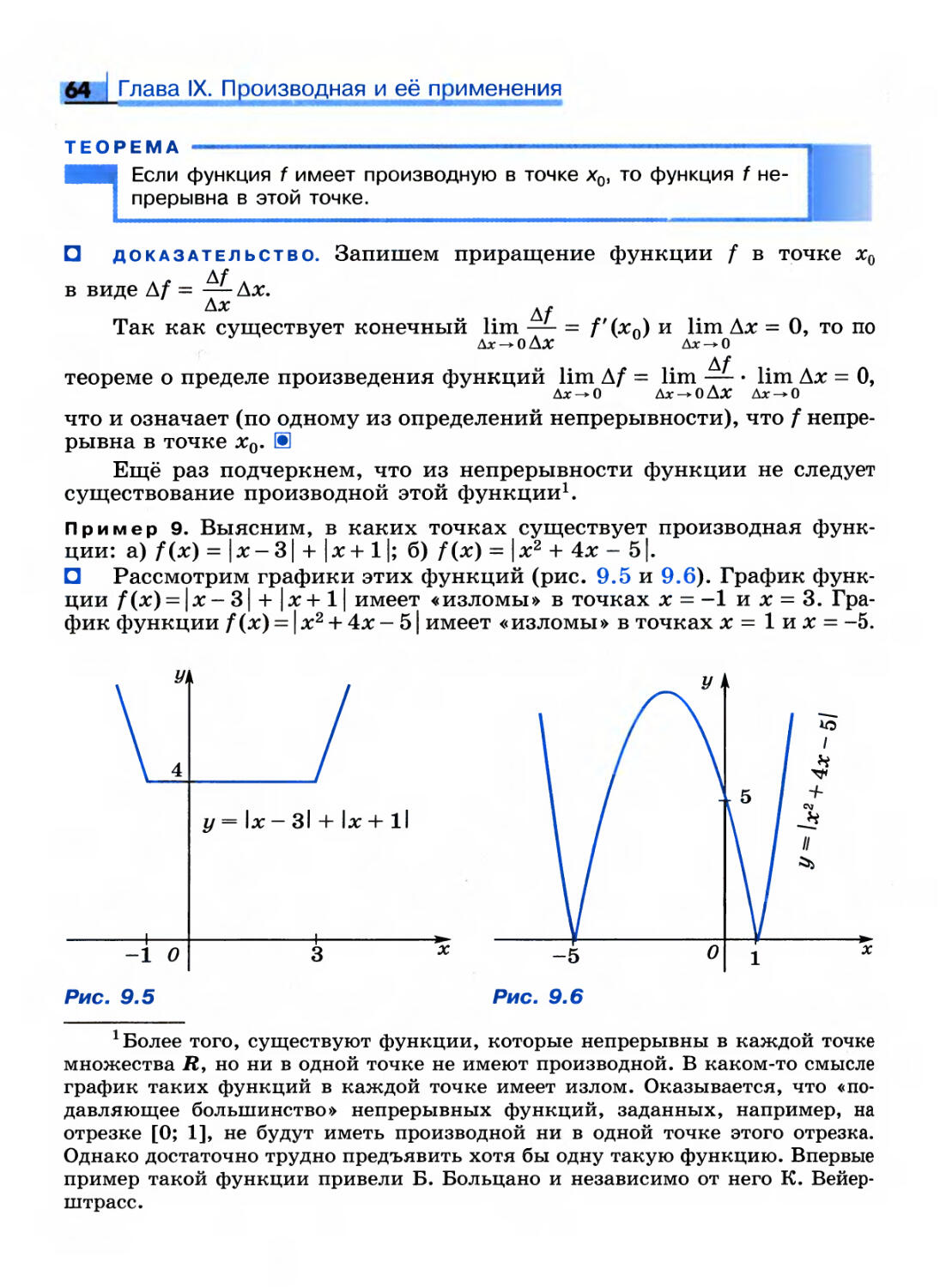
Пример 18. а) Функция у = [х] разрывна в целых точках, причём
в каждой такой точке имеется правосторонняя непрерывность.
Аналогичный характер разрывов имеют функции: 1) у = {х}; 2) у = (-1)мх.
Постройте эскизы графиков этих функций.
У1
0
У
X
/
х2 - Ъх + 6
х-2
2 /
/
у
/
X
У)
0
2
V х
х2-
X
о
4^ + 5
-2
1
х-2
Рис. 8.10
Рис. 8.11
27 §48. Непрерывность функций
Рис. 8.12
б) Функция у = sin — определена везде, кроме точки х = 0, и
принимает все значения между -1 и 1, когда число — пробегает значения
от \ п— — \п до I аи— I я, п е Z. В точках вида х =
V *)
функция принимает значение 1, а в точках вида х =
(4п +
2
-, п е Z
, П €: Z
(4п- 1)71
значение —1. Отсюда видно, что по мере приближения к точке х = О
функция «всё быстрее и быстрее колеблется» между значениями 1 и -1.
Таким образом, предела функции sin— при л:-> Оне существует. По-
X
этому, даже если доопределить эту функцию в точке х = 0
произвольным числом, разрыв в этой точке сохранится (рис. 8.12).
Напротив, функцию у = arsin— можно доопределить до
непрерывной в 0, если положить /(0) = 0, так как lim х• sin— = 0(как предел
х-+о{ х)
произведения ограниченной функции sin— на бесконечно малую х).
в) Функция Дирихле D (х) =
каждой точке имеет разрыв! Ш
1, при х е Q,
0, при х € Q
везде определена и в
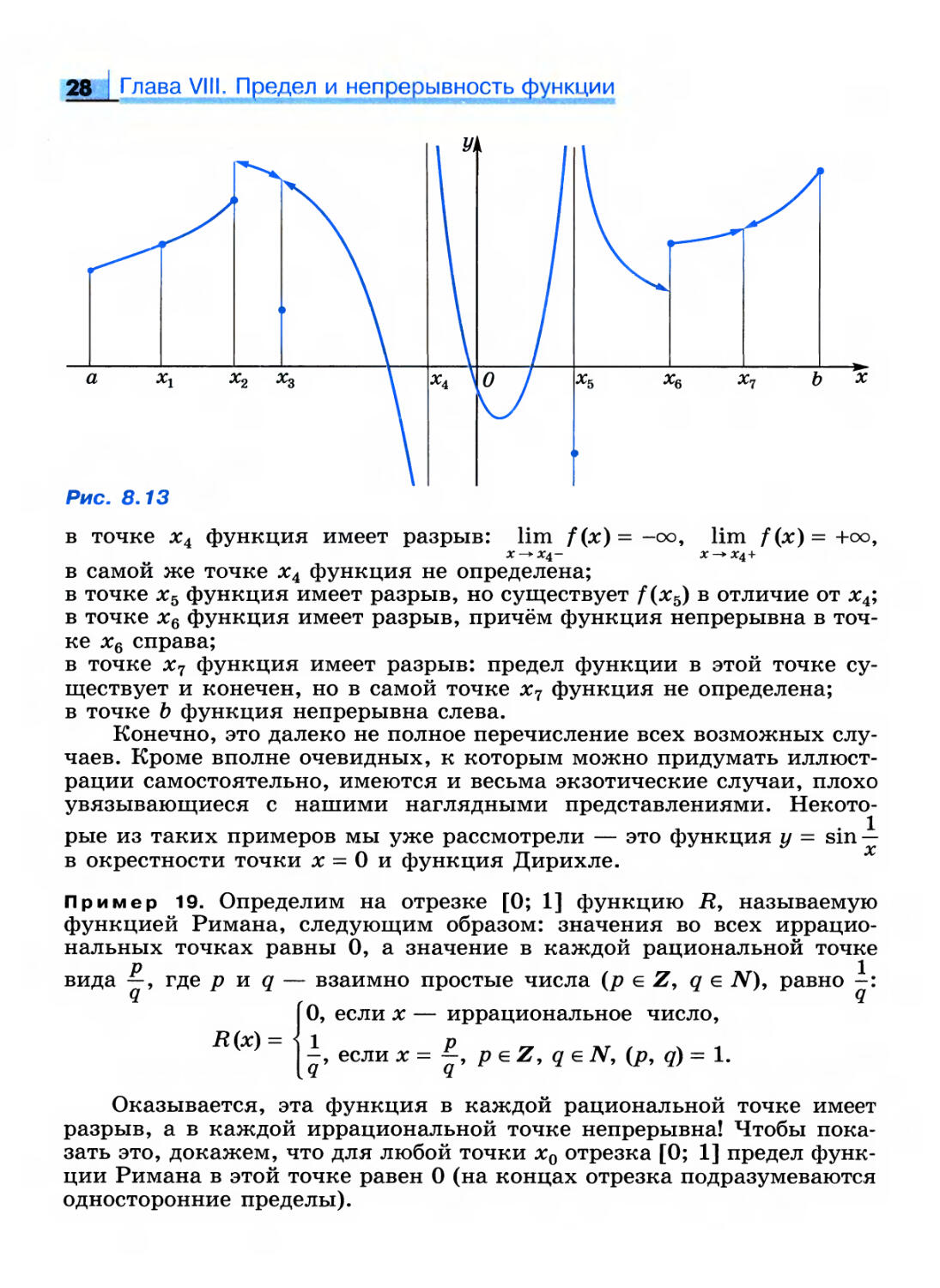
Изобразим различные простейшие случаи разрывов на
рисунке 8.13.
В точке а функция непрерывна справа: f(a + 0) = f(a);
в точке хг функция непрерывна: lim f(x) = /(лгх);
в точке х2 функция имеет разрыв, но при этом она непрерывна слева;
в точке xs существует предел функции, не равный f(xs);
Глава VIII. Предел и непрерывность функции
Рис. 8.13
в точке х4 функция имеет разрыв: lim f(x)=-oo, lim f(x)=+oo,
x-+x±— x—> x^+
в самой же точке х4 функция не определена;
в точке хь функция имеет разрыв, но существует f(x5) в отличие от х4;
в точке хе функция имеет разрыв, причём функция непрерывна в
точке х6 справа;
в точке х7 функция имеет разрыв: предел функции в этой точке
существует и конечен, но в самой точке х7 функция не определена;
в точке Ь функция непрерывна слева.
Конечно, это далеко не полное перечисление всех возможных
случаев. Кроме вполне очевидных, к которым можно придумать
иллюстрации самостоятельно, имеются и весьма экзотические случаи, плохо
увязывающиеся с нашими наглядными представлениями.
Некоторые из таких примеров мы уже рассмотрели — это функция у — sin —
в окрестности точки х = Ои функция Дирихле.
Пример 19. Определим на отрезке [0; 1] функцию i?, называемую
функцией Римана, следующим образом: значения во всех
иррациональных точках равны 0, а значение в каждой рациональной точке
вида —, где рид — взаимно простые числа (peZ, q e N), равно -:
!0
0, если х — иррациональное число,
-, если х = ^-, р е Z, q е ЛГ, (/?, q) = 1.
Оказывается, эта функция в каждой рациональной точке имеет
разрыв, а в каждой иррациональной точке непрерывна! Чтобы
показать это, докажем, что для любой точки х0 отрезка [0; 1] предел
функции Римана в этой точке равен 0 (на концах отрезка подразумеваются
односторонние пределы).
29 1 §48. Непрерывность функций
Q Действительно, пусть х0 — произвольная точка отрезка [0; 1].
Возьмём е > 0. Выясним, в каких точках выполнено неравенство
R(x) > 8. Для выполнения этого неравенства необходимо и достаточно,
чтобы х было рациональным числом — несократимой дробью —, зна-
^ 1
менатель q которой удовлетворяет неравенству q ^ —.
Таких натуральных чисел q существует лишь конечное
количество и для каждого такого q на отрезке [0; 1] имеется не более q
несократимых дробей со знаменателем д, а значит, на отрезке [0; 1] имеется
лишь конечное число точек х, для которых R(x) ^ е. Можно теперь
окружить точку х0 такой 8-окрестностью, чтобы в неё не попала ни
одна из этих точек (кроме, может быть, самой точки х0). Тогда для
всех х е Ub(x0) выполнено неравенство |i?(#)| < £ (независимо от того,
будет ли число х0 рационально или нет).
Тем самым мы доказали по определению предела функции, что
limi?(x)= 0.
Если теперь х0 — иррациональное число, то f(x0) = 0 и функция
непрерывна в этой точке, а если xoeQ, то f(xo)^O и в этой точке
имеется разрыв. IS
3. Свойства функции, непрерывной в точке
Рассмотрим свойства функции, вытекающие из её непрерывности
в одной точке.
СВОЙСТВа ——---—---•-—-■-■-—•--•-—---■■--—--—-^^
1. Если функция f непрерывна в точке х0, то она ограничена в
некоторой окрестности этой точки Ub (х0), т. е. 35 > 0 и 3/. > 0:
Vx g L/6 (x0) выполняется неравенство \ f(x) \ < L.
2. Если функция f непрерывна в точке х0 и f (x0) ^0, то в некоторой
окрестности точки х0 знак функции f совпадает со знаком числа
f(xo)\ 35 > 0: Vx g 1/§(х0) sign f(x) = sign f(x0).
3. (Непрерывность суммы, произведения и частного.) Если
функции f и g непрерывны в точке х0, то функции f + g, f • g и — (по-
следняя при условии g (х0) ф 0) также непрерывны в точке х0.
4. (Непрерывность композиции.) Если функция f непрерывна в
точке х0, а функция g непрерывна в точке у0 (где yo = f(xo)), то
функция h = g о f непрерывна в точке х0.
П доказательство. Свойства 1—3 прямо следуют из определения
непрерывности функции и соответствующих свойств пределов функций.
Докажем свойство 4. Воспользуемся определением
непрерывности (с. 25, 2'). Пусть z0 = g(y0). Возьмём е > 0. В силу непрерывности
30 ; Глава VIII. Предел и непрерывность функции
функции g в точке у0 найдётся такая
о-окрестность точки у0, что
выполняются 2 условия: 1) Uc(y0) с D(g)
2)VU((U(
h(x0)
h(xn)
В силу непрерывности функции /
в точке х0 найдётся такая 8-окрест-
ность точки х0, что выполняются
2 условия: 1) Щ(х0) с!)(/)и 2) \/х е
Рис. 8.14 е иъ(х0) f(x) e Ua(y0).
Таким образом, на множестве
U8(x0) определена композиция h(x) = g(f(x))9 причём для всех х из
С/§(х0) выполняется h(x) e Ue(z0). А это по определению (в силу
произвольности выбора е, это верно для всех е > 0) и означает, что функция
h = g(f) непрерывна в точке х0 (рис. 8.14). Ш
О49. Непрерывность функций на промежутке
ОПРЕДЕЛЕНИЯ
1. Функция f называется непрерывной на интервале (a; to),
если она непрерывна в каждой точке этого интервала.
2. Функция f называется непрерывной на отрезке [a; to],
если она непрерывна на интервале (a; to), непрерывна
справа в точке а и непрерывна слева в точке to.
3. Функция f называется непрерывной на полуинтервале
[a; to), если она непрерывна в каждой точке интервала
(a; to) и непрерывна справа в точке а.
Аналогично определяется функция, непрерывная на
полуинтервале (а; 6].
1. Непрерывность монотонной функции
Утверждение (достаточное условие непрерывности монотонной функции)
■■ Если функция f монотонна на промежутке <а; Ь) и её множество
] значений на этом промежутке есть некоторый промежуток (с; d),
I т. е. f((a\b)) = (с; с/>, то f непрерывна на промежутке (а; Ь).
D доказательство. Пусть для определённости функция /
возрастает (может быть, нестрого) на (а; Ъ).
Предположим, что функция / разрывна в некоторой точке х0
промежутка (а; Ъ). Не умаляя общности, можно считать, что f(x0) Ф lim f(x),
а тогда f(x0) < lim f(x). Из возрастания функции / следует, что
\/х < х0 f(x) ^ f(x0) и \/х > х0 f(x) > lim f(x) (рис. 8.15).
X-+XQ +
31 I §49. Непрерывность функций на промежутке
/(*b-0)
0
х0
x
Таким образом, функция / не мо- ^
жет иметь значений между f(x0) и
f(x0 + 0), а это противоречит тому, что
множество значений промежутка (с; d)
есть сплошной промежуток. Ш
2. Непрерывность некоторых
элементарных функций
1. Функция f(x) = const непрерывна Рис. 8.15
на R.
2. Функция f(x) = х непрерывна на R.
3. Функция f(x) = 4х непрерывна на [0; +оо).
Утверждения 1—3 легко доказать по определению.
4. Функция f(x) = х2 непрерывна на R как произведение
непрерывных функций.
5. Многочлен Р(х) = аохп + ... + ап непрерывен на R как сумма
непрерывных функций.
6. Дробно-рациональная функция f(x) = , где Р(х) и Q(x) много-
Q(x)
члены, непрерывна везде на R за исключением тех точек, где Q(x) = 0,
т. е. корней знаменателя, — как частное непрерывных функций.
7. Функции sin л; и cos л: непрерывны на Л, что следует из
утверждения примера 1 § 44.
8. Функции tgx и ctgx непрерывны на своих областях определения
как частные непрерывных функций.
9. Функция у = ах при а Ф 1, а > 0 непрерывна на R.
П Докажем сначала, что lima* =1 (т. е. непрерывность функции
у = ах в точке х = 0). Возьмём любое е > 0. Нужно найти такое 8 > 0,
что из \х\ < 8 следует \ах - 11 < е.
Решая неравенство \ах - 11 < е, получаем loga(l - е) < х < loga(l + е)
при е < 1. Теперь можно выбрать 8 = min {|loga(l - е)|, |loga(l + е)|}.
Непрерывность функции у = ах в произвольной точке следует из
доказанного. А именно, рассмотрим приращение функции в
произвольной точке х0, вызванное приращением аргумента Ах:
При стремлении Ах к 0 выражение в скобках стремится к 0 по
ранее доказанному, а потому и всё выражение также стремится к 0.
Непрерывность функции у = ах при 0 < а < 1 следует из
непрерывности функции f(x)= ах и теоремы о непрерывности частного
непрерывных функций при а > 1, поскольку ах = -——г. Ш
1
32 Глава VIII. Предел и непрерывность функции
Замечание. Непрерывными на своих областях определения
оказываются и другие элементарные функции, а именно степенная
функция с произвольным показателем у = ха, логарифмическая функция
у = logax и обратные тригонометрические функции, но эти факты
будут доказаны позднее и другими методами, а сейчас мы будем просто
пользоваться ими без доказательства.
Замечания об использовании непрерывности при вычислении
пределов были сделаны выше (см. § 46, п. 2).
О50, Свойства функций, непрерывных на отрезке
1. Корни непрерывной функции. Промежуточные значения
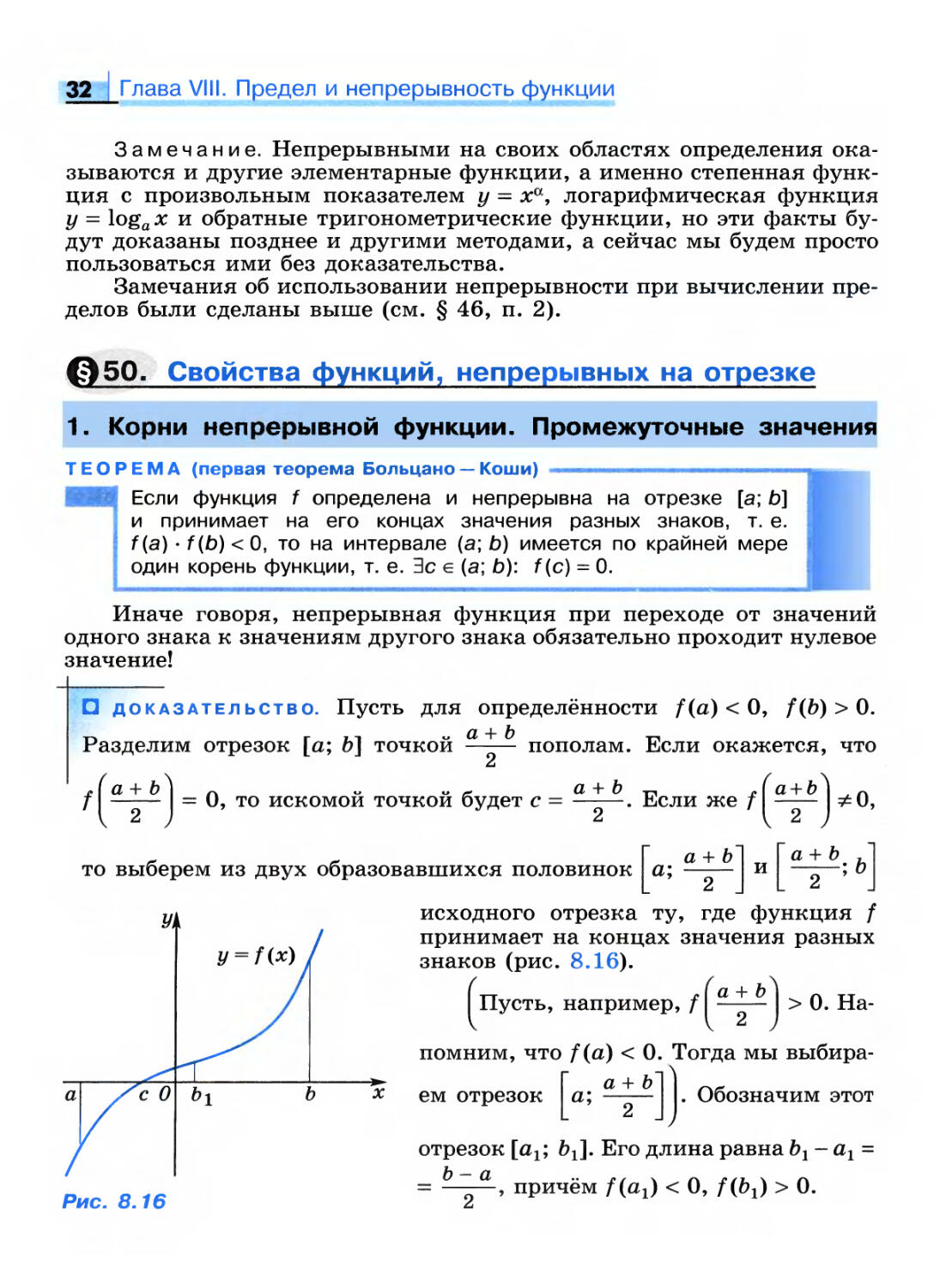
ТЕОРЕМА (первая теорема Больцано — Коши) . ■ ■
Если функция f определена и непрерывна на отрезке [а; Ь]
и принимает на его концах значения разных знаков, т. е.
f(a) • f(b)<0, то на интервале (а; Ь) имеется по крайней мере
один корень функции, т. е. Зс е (a; b): f(c) = 0.
Иначе говоря, непрерывная функция при переходе от значений
одного знака к значениям другого знака обязательно проходит нулевое
значение!
D доказательство. Пусть для определённости f(a) < 0, f(b) > 0.
Р
/Ч
Разделим отрезок [а; 6] точкой пополам. Если окажется, что
= 0, то искомой точкой будет с =
. Если же Л
у 2 )
то выберем из двух образовавшихся половинок а; и ; Ъ
I
Vi
с О
Рис. 8.16
исходного отрезка ту, где функция /
принимает на концах значения разных
знаков (рис. 8.16).
Пусть, например,
помним, что f(a) < 0. Тогда мы
выбираем отрезок | а; гЧг— I I. Обозначим этот
отрезок [аг; Ьг]. Его длина равна Ьг - аг =
= —^-, причём /(«!> < 0, /(bj) > 0.
§50. Свойства функций, непрерывных на отрезке
Поступим аналогичным образом с отрезком [аг; Ьг]: поделим его
„ ai + ь\
пополам точкой .
Если / —-— = 0, то — искомая точка; если / —-— Ф О,
V 2 ) 2 V 2 )
то снова выбираем ту из двух частей, где / принимает на концах
значения разных знаков, и обозначаем её [а2; 62]«
Далее повторяем ту же процедуру. Может оказаться, что на
каком-то шаге при очередном половинном делении поставленная точка
окажется корнем функции. Тогда требуемое будет доказано.
Если же нет, то выделится бесконечная последовательность
вложенных отрезков [а; Ь] з [аг; Ьг] з ... z> [an; Ьп] з ..., причём Vn e N
f(an) < О, f(bn) > 0 и длина ai-го отрезка Ъп — ап — —— -> 0. Тогда
по теореме о вложенных отрезках существует единственная точка с,
принадлежащая одновременно всем отрезкам, и с = lim ап = lim Ьп.
п —*■ сю п —► оо
Функция / непрерывна в точке с, поскольку с е [а; 6], поэтому
f(an) —> /(с). В силу выбора точек ап при всех л е N f(an) < 0, а тогда
по теореме о предельном переходе в неравенстве f(c)= lim f(an)^ 0.
П —»>оо
Аналогично можно доказать, что f(c)= lim f(bn)> 0. Отсюда f(c) = 0. SI
n —► oo
Обратим внимание, что приведённый алгоритм позволяет
реализовать процедуру поиска корня функции на компьютере. Поскольку на
* (
практике требуется не точная запись корня например, х—
например, х
I 123
а его значение, подсчитанное с требуемой точностью, процесс поиска
можно завершить, когда Ьп — ап < е, где е — требуемая точность.
Таким образом, количество циклов, гарантирующих нахождение корня
с точностью е методом половинного деления, можно оценить сверху
числом п =
Следующее утверждение — теорема о промежуточных
значениях функции.
ТЕОРЕМА (вторая теорема Больцано — Коши) ---—-—-------—■
-1
Если функция f определена и непрерывна на отрезке [а; Ь] и
принимает на его концах различные значения (f(a) = Л, f(b) = Б,
А ф В), то для любого числа С, лежащего между Л и Б, на
интервале (а; Ь) найдётся такая точка с, что f(c) = С.
34 ! Глава VIII. Предел и непрерывность функции
О
а
Ь х
Рис. 8.17
П доказательство. Пусть для
определённости А < В. Возьмём
произвольное число С е (А; В). Рассмотрим
вспомогательную функцию <р(х) = f(x) - С.
Она непрерывна на отрезке [а; Ь] как
разность непрерывных функций и
принимает на его концах значения
разных знаков: ф(а) = f(a) — С — А — С < О,
ф(6) = f(b) -С = В-С>0. Тогда по
первой теореме Больцано — Коши Зс е (а; Ь):
(р(с) = 0, т. е. f(c) - С = О, или f(c) = С
(рис. 8.17). 11
Замечание. Первая теорема
Больцано — Коши является частным
случаем второй теоремы (достаточно во второй теореме положить А < О, В > О
и С = 0).
Следствие. Если функция, отличная от константы, определена
и непрерывна на промежутке (а; 6), то её множество значений также
представляет собой промежуток.
П Пусть М = sup f(x), если функция / ограничена сверху на (а; Ь);
х<=(а;Ь)
в противном случае положим М = +оо. Аналогично т = inf f(x), если
лге (а; Ь)
функция /ограничена снизу на (а; Ь), в противном случае т = -оо.
Возьмём произвольное у0 е (т; М) и выберем пару значений
функции уг и у2 так, что т < ух < у0 < у2 < М. Это заведомо возможно
сделать по определению точных границ. Пусть yi = f(x1) и у2 = f(x2).
(Для определённости пусть хг < х2.) Согласно второй теореме
Больцано — Коши для функции / на отрезке [хг; х2] с (а; Ъ) Зх0 е (хг; х2):
f(xo) — У о» т. е. число у0 действительно есть значение функции / в
некоторой точке промежутка (а; Ъ). Таким образом, множеством значений
непрерывной функции на промежутке (а; Ъ) является промежуток
(т; М). Ш
Утверждения теорем Больцано — Коши часто используются для
доказательства существования корней уравнений.
Пример 20. Докажем, что уравнение (х - а)(х - Ъ) + (х - с)(х - Ь) +
+ (х - а) (х - с) = 0 имеет два различных корня, если числа а, 6 и с
различны.
D Действительно, рассмотрим f(x) = (х - а) (х - Ъ) + (х - с)(х - Ъ) +
+ (х - а) (х - с). Пусть, не умаляя общности, а <Ь < с. Тогда f(a) > 0,
f(b) < 0, f(c) > 0. Значит, по первой теореме Больцано — Коши f(x)
имеет по крайней мере один корень на интервале (а; 6) и по крайней
мере один корень на интервале (6; с). Поскольку / — многочлен
второй степени, то более двух корней он иметь не может. IS
35 1 §50. Свойства функций, непрерывных на отрезке
2. Ограниченность непрерывной функции
ТЕОРЕМА (первая теорема Вейерштрасса)
Если функция f(x) непрерывна на отрезке [a; to], то она ограни
чена на этом отрезке.
доказательство. Нужно доказать: существуют такие числа т
и М, что \/х е [а; 6] выполнено неравенство т < f(x) ^ М.
Докажем ограниченность сверху (ограниченность снизу
доказывается аналогично). Доказательство будем вести от противного: пусть
функция / не ограничена сверху на отрезке [а; 6]. Это значит, что
никакое число М не является верхней границей / на отрезке [а; 6],
т. е. VM е R Зхм e [a; b]: f(xM) > М. Полагая М равным 1, 2, 3,
..., л, ..., получим
при М = 1 Зхг е [a; b]: f(xx) > 1;
при М = 2 Зх2 е [а; 6]: /(л:2) > 2;
при М = п Зхп е [а; 6]: f(xn) > п.
В результате получилась последовательность {хп}, являющаяся
ограниченной, так как а ^ хп^ Ь. Сама эта последовательность не
обязательно сходится, но по теореме Больцано — Вейерштрасса из
неё можно выделить сходящуюся подпоследовательность {хп },
такую, что ^n^fci^o0' причём с е [а; Ь] (по теореме о предельном
переходе в неравенстве). Тогда, с одной стороны, в силу непрерывности
функции / в точке с имеем f(xn.).-+ f(c). С другой стороны, в силу
К К —► ОО
выбора точек хп выполняется f(xnk)>nk, и, значит, f(xnk)k~* +°°«
Получили противоречие.
Значит, наше предположение было неверным, и на самом деле
функция / ограничена сверху. 11 ______
Замечание. Теорема будет неверна, если отрезок заменить,
например, полуинтервалом. Пример: функция f(x)= — непрерывна на
полуинтервале (0; 1], но не ограничена на нём!
3. Достижимость точных границ
ТЕОРЕМА (вторая теорема Вейерштрасса)
Если функция f непрерывна на отрезке [a; to], то она достигает
на этом отрезке своего наибольшего и наименьшего значений
36 ! Глава VIII. Предел и непрерывность функции
] доказательство. Поскольку функция / непрерывна на отрезке
[а; 6], то по первой теореме Вейерштрасса она ограничена на этом
отрезке, т. е. множество её значений ограничено сверху и снизу.
Следовательно, существуют точная верхняя и точная нижняя границы
функции на этом отрезке sup f(x) = М и inf f(x) = т. Покажем,
хе[а;Ь] хе[а;Ь]
что число М есть значение функции / в некоторой точке х0 отрезка
[а; Ь] (тогда М и будет наибольшим значением / на [а; &]).
Рассуждаем от противного: пусть такой точки х0 на отрезке [а; Ь]
нет. Тогда \/х е [а; 6] f(x) < М. Рассмотрим вспомогательную
функцию <р(х)= ——. Она непрерывна на отрезке [а; Ь] как частное
JVL / \Х)
двух непрерывных функций (объясните, почему знаменатель отличен
от 0) и принимает на [а; Ь] положительные значения. Тогда, по первой
теореме Вейерштрасса, она ограничена. Пусть её верхняя граница —
число [I > 0, тогда
Отсюда f(x)^ М , и, следовательно, число М , меньшее М,
является верхней границей для множества значений функции / на
отрезке [а; 6]. Но это противоречит тому, что sup f(x) = М. Значит,
предке [а;Ь]
положение было неверно, и, следовательно, Зх0 е [а; Ь\: f(x0) = М.
Аналогично доказывается, что функция f(x) достигает и своего
наименьшего значения inf f(x)= т. Щ
х<=[а;Ь]
Следствие. Если функция / непрерывна на отрезке [а; 6], то её
множеством значений на нём будет отрезок [т; М], где т и М —
наибольшее и наименьшее значения функции / на отрезке [а; 6].
D Действительно, как показано ранее, множеством значений
непрерывной функции на отрезке [а; 6] является промежуток между инфи-
мумом и супремумом функции. Поскольку супремум и инфимум
непрерывной функции на отрезке достигаются, то этот промежуток является
отрезком. IS
Теоремы Вейерштрасса являются одними из важнейших теорем
о непрерывных функциях. Их применение является необходимым
элементом при решении многих задач.
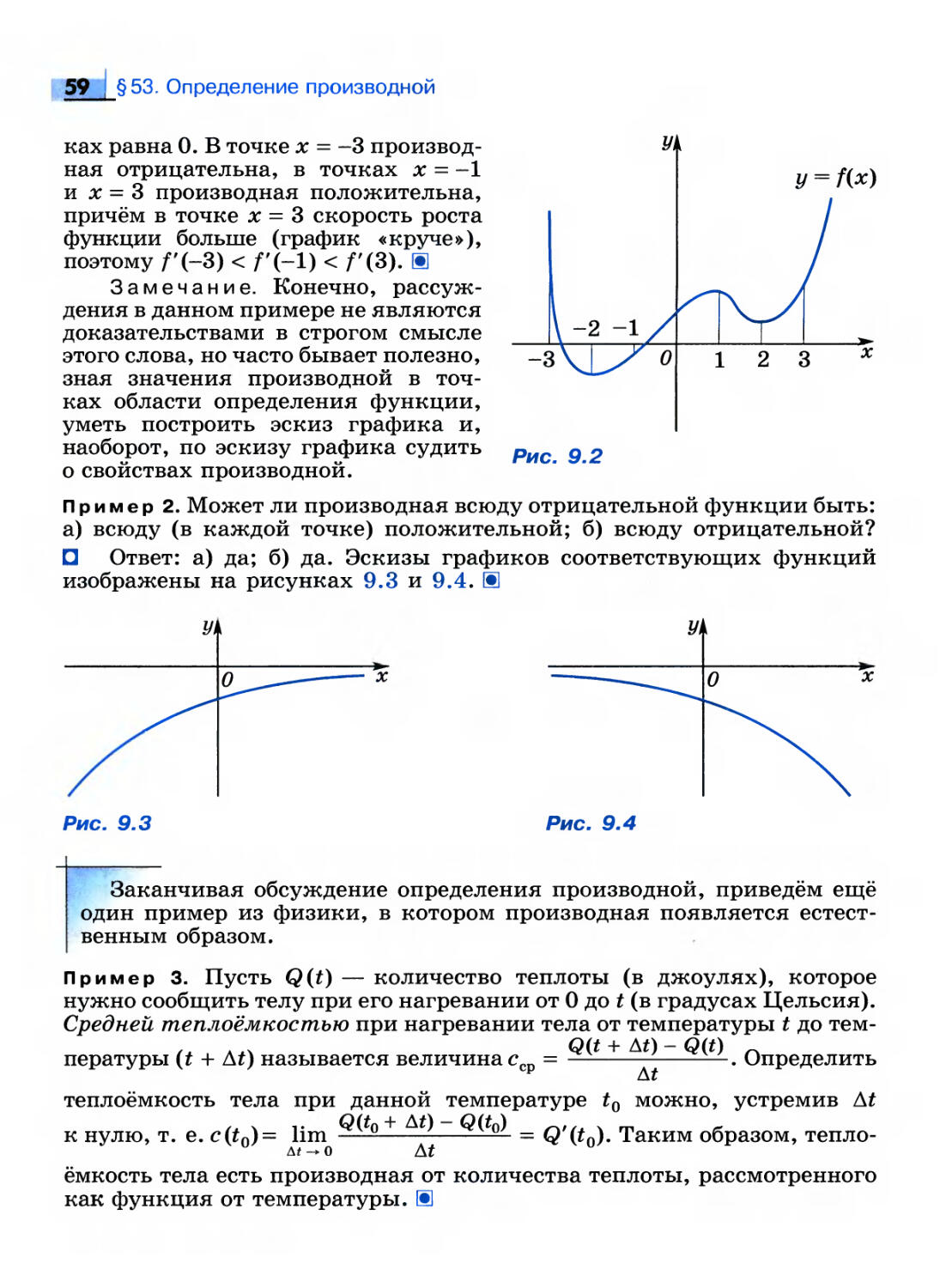
Пример 21. Пусть / — многочлен чётной степени с положительным
старшим коэффициентом. Докажите, что / достигает наименьшего
значения на R.
D Утверждение очевидно, если / — многочлен нулевой степени.
Поэтому далее будем считать, что deg f> 2. Действительно, f(x) -> +oo при
х —* оо. Пусть М = f(x0) — значение многочлена в какой-либо точке.
Найдётся А > 0, такое, что из неравенства \х\ > А следует f(x) > М.
37 | §51. Существование и непрерывность обратной функции
Рассмотрим отрезок [-А; А]. В этом отрезке содержится точка х0
(поскольку за его пределами f(x) > М). По второй теореме Вейер-
штрасса функция достигает на нём наименьшего значения. Это
значение будет наименьшим на всей вещественной оси, так как оно не
превосходит М = f(x0), а за пределами этого отрезка все значения
функции больше М. Ш
ф51- Существование и непрерывность
обратной функции
Свойства непрерывных функций дают возможность доказать
следующую теорему:
ТЕОРЕМА (о непрерывности обратной функции) —"■-■———
Пусть на некотором промежутке (а; Ь) определена непрерывная
строго монотонная функция с множеством значений У. Тогда
на множестве У существует обратная функция д, непрерывная
и имеющая тот же характер монотонности, что и функция f.
□ доказательство. В 10 классе было доказано, что монотонная
функция обратима и обратная к монотонной функция имеет тот же
характер монотонности. Пусть g — функция, обратная к /. Множество
Y = /((а; Ь)) является промежутком.
Монотонная функция g определена на промежутке Y и имеет
множеством значений промежуток (а; 6), а тогда в силу утверждения
п. 1 § 49 функция g непрерывна на Y. Ш
Из этой теоремы следует непрерывность функций f(x) = vjc, n e N,
а также логарифмической и обратных тригонометрических функций.
Необходимость условия существования непрерывной строго
монотонной функции именно на промежутке в теореме о непрерывности
обратной функции иллюстрирует пример VIII.61.
О52. Асимптоты графика функции
Вернёмся к разговору об асимптотах графика функции, начатому
в 10 классе (глава IV). Напомним определение вертикальной
асимптоты: если какой-либо из односторонних пределов функции / в точке х0
является бесконечным (т. е. f(x) -> оо или f(x) _-^> _оо), то прямая
х = х0 называется вертикальной асимптотой графика функции Гг.
Заметим ещё, что для наличия вертикальной асимптоты нам
достаточно выполнения хотя бы одного из условий lim f(x)= оо или
lim f(x)= оо, причём справа и слева от точки разрыва функция мо-
жет вести себя по-разному!
38 Глава VIII. Предел и непрерывность функции
Пример 22. Найдём вертикальные асимптоты графика функции у = е*.
D lim ex — lim ег = О, lim £* = +оо, следовательно, прямая х = О
# -* О- * -* -оо jc -»> 0+
является вертикальной асимптотой графика этой функции (рис. 8.18).
В остальных точках вертикальных асимптот нет, поскольку функция
в этих точках непрерывна. Щ
Напомним также определение
наклонной асимптоты (и в
качестве частного случая
горизонтальной асимптоты): если функция /
представима в виде f(x) = kx + b +
+ ос (л:), где а(х) -> 0, то прямая
X —>+сх>
у = kx + b называется асимптотой
графика функции f при х —> +оо.
Аналогично определяется
асимптота графика функции / при х —> -оо;
если k ^ 0, то асимптота у = kx + Ъ
называется наклонной^ если k = 0,
то асимптота у = Ь называется
горизонтальной.
Очевидно, что при наличии
наклонной асимптоты расстояние от
точек графика функции / до этой
асимптоты (т. е. длина
перпендикуляра, опущенного из точки
графика на асимптоту) стремится к
нулю при стремлении х к
соответствующей бесконечности (рис. 8.19).
В 10 классе мы занимались
поиском невертикальных асимптот,
пытаясь вручную выделить
«главную линейную часть» функции.
Теперь у нас появилась возможность
указать универсальный способ
нахождения таких асимптот.
Рис. 8.18
//
Рис. 8.19
р(М,1)=\МР\
ТЕОРЕМА
Для того чтобы прямая у = кх+b была асимптотой графика
функции у = f(x) при х—► +оо, необходимо и достаточно, чтобы
существовали конечные пределы lim
X—*+оо
и lim (f(x)-kx) =
X—*+оо
□ ДОКАЗАТЕЛЬСТВО.
необходимость. Пусть у = kx + Ъ — асимптота графика функции
у = f(x) при х -> +оо. По определению это означает, что f(x) = kx + Ъ +
39 I §52. Асимптоты графика функции
0. Тогда —— = k + — + и существует предел
о # XX
fix)
lim :L^ = fe. Так как /(х) - /ел: = Ъ + а(х), то существует предел
х—>+оо X
+ а(х), где а(х)
х
fix)
lim (/•(#)-£*)= 6.
fix)
oo
достаточность. Пусть существуют конечные пределы lim
X ->- +оо X
= k
x-+ +00 X
и lim (fix)- kx)- b. Отсюда f(x) - kx = b + a(x), где oc(x) -> 0 и f(x) =
X -*■ +00 X -*■ +OO
= kx + b + a(x), где ос(л:) -> 0, т. е. прямая у = kx + b по определению
л:-»-+оо
является асимптотой графика функции у = f(x) при х -> +оо. Ш
Для случая л: —> —оо все формулировки и рассуждения аналогичны.
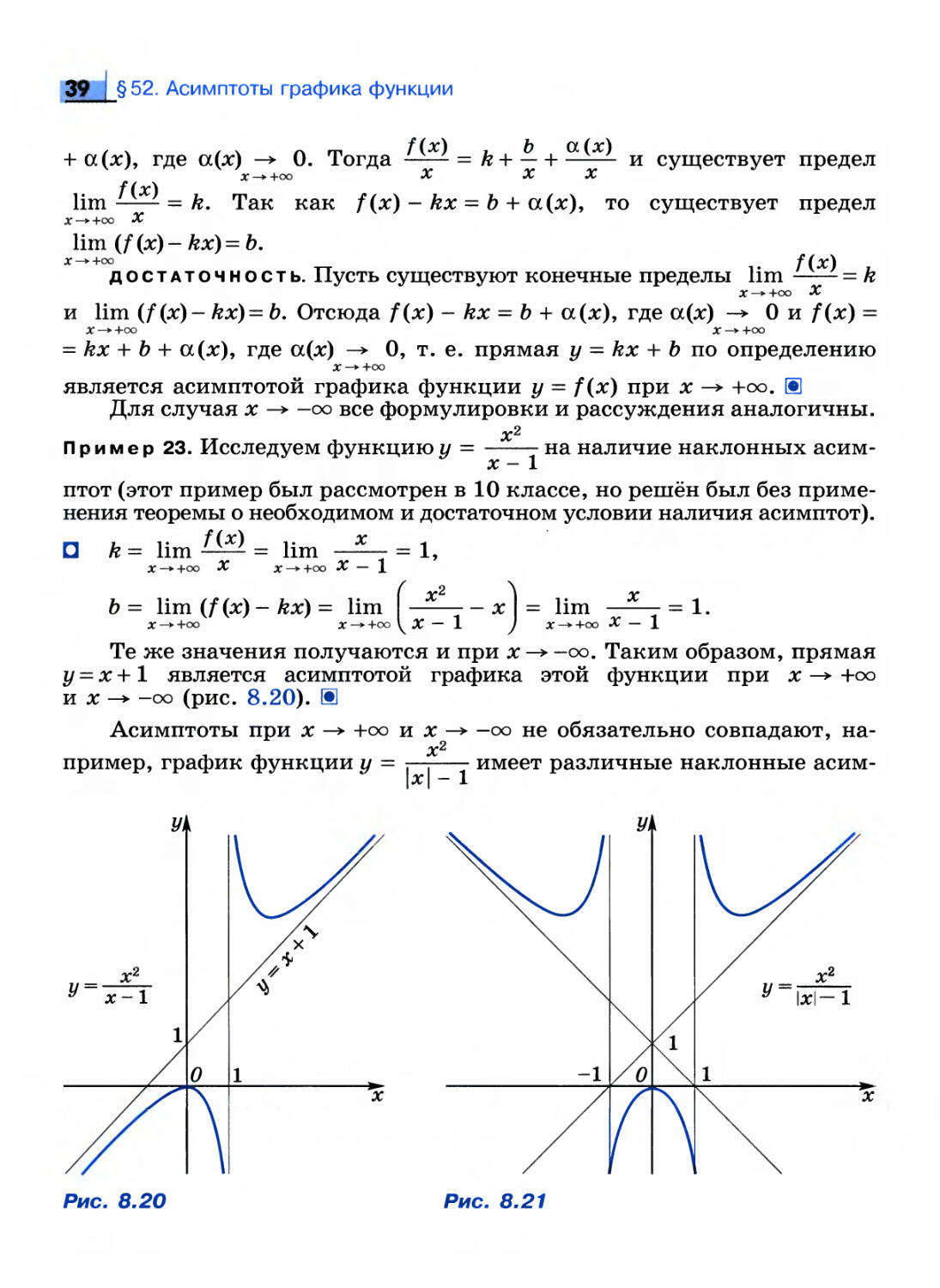
Пример 23. Исследуем функцию у = на наличие наклонных
асимптот (этот пример был рассмотрен в 10 классе, но решён был без
применения теоремы о необходимом и достаточном условии наличия асимптот).
X
П k = lim ^^ = lim
х-* +00 X х—*-+сх> X — 1
Ъ = lim (f(x) - kx) = lim
= 1,
- x | = lim —£
у x -* +oo X —
= 1.
Те же значения получаются и при х -> -оо. Таким образом, прямая
= х+1 является асимптотой графика этой функции при х —> +оо
jc^-oo (рис. 8.20). 11
Асимптоты при х -> +оо и х -> -оо не обязательно совпадают,
например, график функции у =
\x\-l
имеет различные наклонные асим-
о
-1
Рис. 8.20
Рис. 8.21
40 ; Глава VIII. Предел и непрерывность функции
п
"2
у = arctgх/
к
"2
1 >
0 i л:
Рис. 8.22
Рис. 8.23
птоты при х —> +оо и х —> — оо. Асимптотой графика этой функции при
х —> +оо является прямая г/ = jc + 1, а при л: —> —оо наклонной
асимптотой будет прямая у = —х+1 (рис. 8.21). Проверьте это самостоятельно.
Пример 24. Классический пример функции с разными
горизонтальными асимптотами при х —> +оо и х —> -оо представляет собой функция
(рис. 8.22). Действительно, lim
л:-»>±оо
= 0, lim arctg x= —,
л:-»-+оо 2
a lim arctg x =— (убедитесь в этом самостоятельно). И
Пример 25. Ещё один пример функции с разными наклонными
асимптотами при х -> +ОО и х -» -оо — функция f(x) - х - arctg л:. Нетрудно
видеть, что асимптотой при х —> +оо будет прямая у = х , а при
х -> -оо — прямая у = х + — (рис. 8.23). Ш
Не нужно думать, что два предела, о которых идёт речь в теореме,
всегда существуют одновременно! Может случиться так, что
существует только один из них. Тогда асимптоты в соответствующей
бесконечности не будет.
Пример 26. Исследуем на наличие асимптот функцию f(x)=x + y[x.
D Поскольку D (/) = [0; +оо), имеет смысл говорить только об
асимптоте ПРИ X —> +ОО.
1 +
lim
= lim -
X—»-+оо
= 1,
т. е. k = 1, но при этом
lim (f(x)-kx) = lim uc + yfx - x) = lim 4x = +00.
Таким образом, асимптоты при х —> +оо не существует. IS
41 Задачи и упражнения
и упражнения
Понятие предела функции
Группа А
VIII. 1. Найдите предел А функции / в данной точке а и укажите
какую-либо проколотую окрестность точки а, при значениях
аргумента из которой выполняются неравенства | / (х) — А | < е при
е = 1, е = -, е = —:
a) f(x) = 2х- 1, а = 1;
в) f(x) = sin л:, а = 0;
б)
= х*, а =
г) /(*) = -?-, а
= 0.
VHI.2. Верно ли, что:
а) если /(л:2) -> 0 при х -> 0, то и /*(*) -» 0 при я -» 0;
б) если f(xs) —> 0 при jc ~» 0, то и /(х) —> 0 при х —> 0?
VIH.3. Постройте график функции, обладающей свойствами:
a) D(f) = [-3; +оо], lim /(x) = -оо, /(2) = 3, lim f(x) = 4, /(3) = 6,
*—2 лг—3
1
б) lim f(x) = +oo, /(4) = 1, lim f(x) = 2, lim f(x) = -3;
x—*4 x—►ч-оо л:—»■—оо
в) lim/(x)=-oo, lim
JC — O+ * —0-
= 1, /(0) = 2, lim f(x) = +oo, /(3) = 0.
3
Группа В
Vlii.4. Докажите существование бесконечного предела, пользуясь
определением предела функции в точке по Коши:
a) lim х2; б) lim (2л:2 - х);
v т х2+ 7х
в) hm ———;
х—»-+оо X + Z
г) lim Qx4 + 1 - х).
VIII.5. Докажите, что функция / не имеет предела в точке а, если:
при х g Q, _ Л
jc + 3 при
VHI.6. Приведите пример или докажите, что не существует такой
функции /, что lim f(x) = 1 и выполняется:
a) Ve>0 38 > 0: \/х е йъ(1) \f(x)- 1|<е;
- 1|>е.
в) Зе>0: 36 >0: Vjc €
42 | Глава VIII. Предел и непрерывность функции
Пользуясь определением по Коши, докажите существование
предела функции (конечного или бесконечного), подобрав его значение
(VIII.7—VIII.10).
Vlii.7. a) lim —f ; б) lim '
#-►+00 2хг — 1 #-*+ос
в) lim
Х2+ 2Х + 6'
г) lim(Jx2+l-x).
. a) lim (2л:
viii.9. a) lim (-х2 - х + 1);
л:—*-оо
в) lim
б) lim
в)
б) lim
о
г) lim (2xJx2 + 1 - х + sin л:) .
Vlll.10. Имеет ли предел при х —> 0 функция:
a)f(x)=[x]-±; 6)g(x)=\±\-x?
Свойства пределов функций
Группа А
vin.ll. Верно ли, что если не существует lim f(x), то для любой
функции g не существует: х^а
a) lim (/(х) + g (х)); б) lim (/(x) • g (*))?
х—>а х-^а
VIII. 12. Укажите функцию /, такую, что в некоторой точке а не
существует lim f(x), но существует предел:
х—>а
a) lim| f(x)\; б) lim f2(x); в) ]im(f*(x) + 2f(x)- 3).
л: —>a x-^a x—>a
Vlll.13. Докажите, что если limf(x) = Л, то Ve > 0 38 > 0: 0<\х'-а\<Ь9
х^*а
0 < \х" - а\ < 8 => \f(x') - f(x")\ < е (т. е. если функция имеет
предел в точке а, то в двух достаточно близких к а
значениях аргумента значения функции будут близки между собой.
Утверждение очевидно, если неформально понимать, что такое
предел функции в точке).
VIII.14. Докажите, что если lim/(я) = А и lim/(я) = Б, причём А > В,
х-^а х-^-а
то существует проколотая окрестность точки а, для всех
значений х из которой выполняется неравенство f(x) > g(x).
viii.15. Можно ли определить, чему равен предел (конечный или
бесконечный) lim \f(x)- g (х))9 если известно, что:
43 I Задачи и упражнения
ничена и g(x) > 0.
Докажите это в случаях, если определить предел можно,
а в других случаях приведите примеры, показывающие, что
возможны различные пределы.
VHI.16. Можно ли определить, чему равен предел (конечный или
бесконечный) lim —7—(, если известно, что:
ничена и g(x) > 0.
Докажите это в случаях, если определить предел можно, и
приведите примеры, показывающие, что возможны различные
пределы, в других случаях.
Группа В / \
VIII.17. а) Пусть при всех а е R выполнено lim / — = 0. Верно ли,
П -»оо I 2п )
что Ит/(х)= 0?
б) Пусть при всех а е R выполнено lim / — = 0. Верно ли,
/I—оо уП J
что lim f(x) = 0?
В случае утвердительного ответа приведите доказательство, а в
случае отрицательного — контрпример.
VIII.18. Пусть lim f(x) = 0. Докажите, что
a) lim lf(x) + f(2x)) = 0; б) lim (f(x) + fix*)) = 0.
Приведите примеры, показывающие, что обратные
утверждения неверны.
Группа С
VIII. 19. Пусть lim f(x)=Ott lim —-— ^ = 0. Докажите, что lim
л: —0 * —0 X л: —0 X
VIII.20. Пусть функция /, определённая на /2, является периодической,
причём существует lim f(x). Докажите, что / — константа.
Предел отношения двух функций на бесконечности
Группа А
Найдите предел (viii.21, vni.22).
VTTTn< ч ,. (х+1)2 -v т ЮООх ч ,. х2-Ьх
VIII.21. a) lim ^——'—; б) lim ——-; в) lim
———; 6) lim ——-; в) lim — -
X2+l лг^ооХ2-! х^оо SX + 7
44 I Глава VIII. Предел и непрерывность функции
ч ,. (2х + З)3 • (Зх - 2)2 ч .. 2х2 - Ъ^
г) hm ^-^ —; д) hm , —; е) hm
Х2+5
ж) lim
г; з) lim
; д) liin
х2+ 1
viii.22. a) lim
в) lim
х5+ 55
:-1)6 .
; и) lim
_ ,. (х + I)2 • (7х - З)2
б) lim —-— —;
7 ^-оо (2Х- I)4
X)3
Г)
VIII.23. Пусть Рп(х) = алл:л + ... + а0, ап Ф 0 и
Р (х)
Ъкф0 — многочлены. Найдите lim — .
*^оо Qk(x)
viii.24. Найдите предел:
a) lim
. (1+ хп+ 7х13)3
= boxk + ... + 6fe,
2х
в) lim
б) lim
г) lim
5х6-
Предел отношения двух многочленов в точке
Группа А
Найдите предел (vni.25, vill.26).
vin.25. a) lim
xs
б) lim
10
9 r»t '
x2-25
ч r x2- 2x ч r x3- 3x + 2
r) lim — ; д) lim—; .
' x^2 x2- 4x+ 4 ' x-+i x4 - 4x + 3
в) lim
vni.26. a) lim
o
6) li
X3 - X2 - X + 1
. x101- 101л; + 100
Предел иррациональных выражений
Группа А
VIII.27. Найдите предел функции, применив метод замены переменной:
ч1. Vx-1 ^ ,. л/х-8 ч1. Чх-l ч1.
a) hm -; б) lim -= ; в) lim -==—; г) lim
l Х1 643/^2 lVl 1
45 Задачи и упражнения
VIH.28. Найдите предел функции, «переводя иррациональность» из
числителя в знаменатель (или наоборот):
...
a) lim
i
—;
x2 - 49
б) lim
v i. Vx - 1
в) hm
д) lim
0
m ;
->i vx- 1
l+ X - Jl- X
г) lim
3 - д/5 + х
1-J5^T:
ч
e)
. Jx2 - 2x + 6 - J*2 + 2x - 6
im-i г— ^ ;
х2- 4х + 3
ж) lim (д/х2 - 5х + 6 - х); з) lim (jx2 + 1 - х);
и) lim (x
Биномиальный предел
Группа А
VIH.29. Найдите предел:
a) lim , где m, n e N; б) lim
-, где m, n e N;
в) lim
л: —-8
5/9+ x + x + 7
r) lim
о
+ Юх + 1 - 7Jx2 + Юх + 1
;
x
Д) hm
3/1 + 4x -
- 5/1 - 5x
-; е) lim
, где /г, k e N.
Предел выражений, содержащих тригонометрические функции
Группа А
Найдите предел (vill.30—viii.33).
ч ,. sin3x -ч т sin5x ч ,. sin7ix ч ,. [ 7С ■
Vill.30. a) hm—-—; б) hm — ; в) hm-——; г) hm Jnsin—|;
ч т. 1 - cos х ч т. sin х - sin а ч л. cos x - cos a
д) lim ; е) lim ; ж) lim
О Хг X п
О Хг
X — п
з) lim ——; и) hm
х-+а X - п
sin х - cos x
; к) lim
к 1-tgx '
4
л) lim xsin— ; м) lim xsin— ; н) lim (l-x)tg^ ;
jc — 0\ XJ x-+ oo ^ XJ x-+l\ 2 )
X
1 - sin —
ч .. 2 ч ,. l-2cosx ч ,. cosmx - cosnx
o) hm ; n) hm ; p) hm;
П X n n SX 0
П - X
- SX
46 j Глава VIII. Предел и непрерывность функции
с) lirrl
tgx-sinx
hm
x-sin2x
х —о х + sin3x
; у) lim
1-Vcosx
1X111 л
x —О Хг
,ч .. д/1 + sin х - Jl- sin л:
ф) lim -
х-0 X
vin.31. a) lim —
х — О Sin X
cos3x - cos7x
в) lim
► о
б) lim
O
г) lim —
sin л:
vih.32. a) li
6) lim
о sin6x - sin7x
sinx
х-»л 7t" —
COS
, ■ At-)
b) lim x sin — ; r) lim —=^—
ЛГ^оо^ X J * —— Л/3 -
viii.33. a) lim
x-+O X
6) lim
x —0
arcsin 2x
ч ,. arctgx ч ,. arccos(l-x)
з) lim *—; r) lim p= -.
Раскрытие неопределённостей вида (1 )
Группа А
Viii.34. Найдите предел:
2 +х |
a) lim
o
г) hm
б) lim
i
, r (л IV
; д) lim 1 - - .
в) lim
Предел выражений, содержащих логарифмическую функцию
Группа А
Найдите предел (Vin.35, viii.36)
vin.35. a) lim (ln(2x + l)-ln(x + 2)); 6) lim
x —+oo x —0 X
в) lim (x(In (x + 1) - In x));
г) lim
In (cos x)
О X2
viii.36. a) lim
в) lim
lgx-1
"io x - 10 '
lntgf 4 +
_ ,. ln(l+3x+x2) + ln(l-3x+x2)
o) lim ;
г) lim
Incos5x
х — о In cos 4х
47 I Задачи и упражнения
Предел выражений, содержащих показательную функцию
Группа А
VIH.37. Найдите предел:
a) lim
г) lim
о х
10*- 1т
-о 2х- 1 '
б) lim х 3* -1
в) lim \х2 4х -4*+1
Д) И
е7х _ е2х
е) lim
X —*■ оо I
е5х_ (
2хУ
ж) lim ■
л: —О
>*2-
COS X
Вычисление пределов
Группа А
В задачах, предлагаемых ниже, используются различные приёмы
и, как правило, несколько «замечательных» пределов внутри одной задачи.
Найдите предел (viii.38—viii.39).
tg2x
viii.38. a) lim
^ъ 42 -
+ cos x
б) lim
2 sin Sx - д/l - 4sin5x
Группа В
VIII.39. lim
в) lim (sinд/л:2 + 1 - sin^x2 - l).
ex2- 1
sinx2 - 1
Группа С
Vlll.40*. Докажите, что не существует многочленов Р и Q, таких, что
при всех х > 0 выполнено равенство
Р(х)
Q(x)
= 2х.
Vlll.41*. Пусть Р — многочлен. Докажите, что функция f(x) = sinP(x)
периодическая тогда и только тогда, когда deg P ^ 1 (где
deg Р — степень многочлена Р).
Односторонние пределы
Группа А
VIH.42. Найдите предел:
a) lim
1 + ех
б) lim
* —о+
г) lim
ж) lim
х
х- 1
i-\x- 11
д) lim
0
1 + ех
I sin х I
х —0- X
в) lim
#—»--оо
е) lim
о
X
sinxl
; з) lim
х-1
; и) lim
х
-; к) lim .
!' ' х^2+ х-2
48 ! Глава VIII. Предел и непрерывность функции
VHI.43. Найдите односторонние пределы функции в нуле, если:
^-^i; б) f(x)=e~*2; в) f(x) =
Ах
Сравнение бесконечно малых и бесконечно больших.
Эквивалентность функций
Группа А
VHI.44. Выясните, является ли функция бесконечно малой:
\ л, \ х2 - 2х -\- 1 Л
a) f(x) = г при х -* 1;
б) f(x) = Jx2 +1 — х при х —> +оо; при х —> -оо;
1 - COS yfx
г) f(x) = при х -> +oo; при х -» -оо;
д) f(x) = sin In (л:2 + 1) - sin In (х2 - 1) при х -» оо.
viii.45. Выясните, является ли функция бесконечно большой:
а) f(x) = ———-— -— при х -+ 2;
Xs - 4х2 + 4х х2 - Зх + 2
б) f(x) = л: (д/л:2 +1 - л:) при л: -> Н-оо; при х -> -оо;
Г х+ 1 V
в) /(л:) = при х -^ -оо; при х -» -оо;
у2х - \)
г) /(л:) = (1 - х)*2 при л: -^ 0+; при х -» 0-.
VIII.46. Выясните, верно ли утверждение:
а) х2 = о(х) при х —* 0; при л: —> оо;
б) л: = о (л:2) при л: —> 0; при л: -> оо.
VIII.47. Определите порядок малости относительно х при л:-»0 функции:
a) f(x)=-^-; б)
X I X
г) /(л:)= 1 - cosx; д) f(x) =
Группа В
VIII.48. Докажите свойство бесконечно малых (здесь х->а, CeR —
произвольная константа, равенство читается только слева направо):
а) о (Cf) = о (/); б) С • о (/) = о (/); в) о (о (/)) = о (/);
г) о (fn) • о (fm) = о (fm + л), т, пе N; д) fn ~ х • о (/) = о (/л), п е N;
е) (о(/))л = о(/л); ж) = o(fn~1).
Задачи и упражнения
VIH.49. Докажите, что сумма двух бесконечно малых различных
порядков (при х -» а) эквивалентна тому из слагаемых, порядок
которого ниже.
VHL50. Докажите эквивалентность следующих функций:
a) arcsinx ~ х при х —> 0; б) arctga: ~ х при х —> 0;
в) cos л: ~ 1 при х
0;
+оо.
0;
vni.51. Найдите предел, пользуясь теоремой об отношении
эквивалентных функций:
a) lim —; б) lim
л:— 0 Sin3x х ~
х - l) • (2х - 1)'
arcsin -
х
в) lim
С
Д)
sin Sx • sin Ъх
о (х- х3)2 '
In а;
;
г) lim
* —с
е) lim
о ln(l-x)
cosx - cos2x
1 - cos х
Viii.52. Докажите или опровергните следующее утверждение. Пусть
/ ~ fl9 g - gx при х —> а. Тогда если существует предел
Ит(}г(х) - gilxfihix), то существует и предел lim(f(x) - g(x))h(x),
хю ха
причём они равны.
VIH.53. Витя дал на зачёте такое определение того, что f=o(g) при
х —> 0 (если известно, что \/х g(x) ^ 0):
f = o(g), если 35 > 0: Ve > 0 \/х е (-8, 5)\{0} => |/(х)| < е|^(х)|.
Рита же дала другое определение:
f=o(g), если Ve>0, 38>0: \/х е (-5, 5)\{0} => |/(х)| < е|*(х)|.
Что они определили на самом деле? Дал ли кто-нибудь из них
правильное определение?
Определение непрерывной функции.
Свойства функции, непрерывной в точке
Группа А
VIH.54. При каких значениях параметра а функция
3 ~ х2 ПРИ х е Q>
[ах - 1 при х е R\Q
непрерывна ровно в 2 точках?
viii.55. В каких точках непрерывна функция f(x)
-{
Ъх-2 при xeQ,
50 Глава VIII. Предел и непрерывность функции
VIH.56. Известно, что функция / непрерывна в точке а, а функция g
в точке а разрывна. Верно ли, что обязательно разрывна в
точке а функция: а) / • g; б) / + g?
Vlll.57. Известно, что функции f + g и f — g непрерывны в точке а.
Докажите, что функция / непрерывна в точке а.
Группа В
VIII.58. Известно, что функция / непрерывна в точке а и V8 > 0
Зхг е С/§(а) и х2 е £/§(а), такие, что выполняется неравенство
f(xx) • f(x2) < 0. Докажите, что /(0) = 0.
VIII.59. Верно ли, что если функция / непрерывна в точке х0, то и |/|
непрерывна в этой точке? Верно ли обратное?
VIII.60. Функция / задана найи такова, что для любых х и у
выполнено равенство f(x + у) = f(x) + f(y).
а) Найдите /40).
б) Докажите, что при любом натуральном п и любом
вещественном х выполнено равенство f(nx) = nf(x).
в) Докажите, что при любом целом т и любом вещественном
х выполнено равенство f(mx) = mf(x).
г) Докажите, что при любом натуральном л и любом вещест-
венном х выполнено равенство f\ — \ = —f(x).
д) Пусть с = /(1). Докажите, что при всех рациональных х
выполнено f(x) = ex.
е) Пусть / непрерывна на R. Докажите, что при всех
вещественных х выполнено f(x) = ex.
ж*) Пусть / непрерывна в точке х = 0. Докажите, что при
всех вещественных х выполнено f(x) = ex.
з*) Пусть / ограничена на R. Докажите, что при всех
вещественных х выполнено f(x) — ex.
и*) Пусть / ограничена в некоторой окрестности точки х = 0.
Докажите, что при всех вещественных х выполнено f(x) = ex.
VIIL61*. Приведите пример обратимой функции Д непрерывной в
точке х0, обратная к которой имеет разрыв в точке у0 = f(x0).
Разрывы функции
Группа А
VIII.62. Функция / определена в окрестности точки х0, кроме самой
точки х0. Доопределите функцию, задав f(x0) так, чтобы
функция стала непрерывной в точке х0.
a) fix) = ^—\, х0 = -1; б) f(x) = 4^> х0 = 1;
X I X. X JL
51 1 Задачи и упражнения
\ л/ \ Jl+ х - 1 sinx ~
в) fix) = - , х0 = 0; г) fix) = , х0 = 0;
X X
д) fix) = xctgx, х0 = 0; е) fix) = ~ c^s х, х0 = 0.
х
VIII.63. Докажите, что функция / не является непрерывной в
точке х0. Постройте её график:
_ /х + 1при*>0, _ _^
б)
[О при х = О,
в) /(х) = sign (л: + 1), хо = -1;
—? ПРИ х ф О,
г) j
[1 при х = О,
Д) /(*) = М, х0 = 2.
Найдите точки разрыва функции, доопределите функцию до
непрерывной в точках, где это можно сделать (viii.64, viii.65).
4a) ^ б>У^; )
2л; - 1 ч 1 -
cos —
ini; в) у = -j_^; г) у =
Группа В
VIII.66. Выясните, существует ли значение а, при котором функция /
непрерывна в точке х0, если:
ч .. ч ре sin — при х Ф О, Л
а) /(*)= j * '^о = О;
[а при х = О,
[а при л: = — 1,
Г ал:2 + 1 при л: > 0, _
= S Л л:0 = 0;
\-х при л:^ 0, °
ч /cosл: при д: ^ О,
г) /(л:)= ^ . ^ _ хо = 0.
[а(л:- 1) при л:> 0, °
52 Глава VIII. Предел и непрерывность функции
VIH.67. Выясните, можно ли доопределить функцию / в точке разрыва
х0 так, чтобы она стала непрерывной в этой точке, если:
1
a) f(x) = 1 + ±9 х0 = 0; б) f(x) = 2^~\ х0 = 1;
1 [1
в) /(х) = ±е *2 , *0 = 0; г) f(x) =2lx\x0 = 0.
VIH.68. Исследуйте на непрерывность функции f(g) и g(f) в точках, где
определены эти композиции.
а) f(x) = sign л:, g(x) = 1 + х2;
б) f(x) = sign л:, g(x) = xs - х;
в) f(x) = sign (л: - 1), g(x) = sign(x + 1);
г) f(x) = sign*, g(x) = 1 + {x}.
viii.69. Исследуйте на непрерывность и постройте график функции /:
a) f(x)= lim —— ; б)
в) f(x)= lim cos"*; г) f(x)= lim
П —*■ oo n —*■ oo
д) /0*0= lim ; e) f(x)= lim
ж) f(x)= lim ^/1 + x2- ; з) /(x)= lim
и) /(х)= lim (l +
t
Свойства функции, непрерывной на отрезке
Группа А
VIII.70. Функции fug непрерывны на отрезке [1; 3], причём
и /(3) > g(3). Докажите, что существует точка х = с на отрезке
[1; 3], такая, что /(с) = g(c).
viii.71. а) Функция / непрерывна на отрезке [0; 1], причём E(f) с [0; 1].
Докажите, что существует точка с на отрезке [0; 1], такая, что
f(c) = с
б*) Существует ли непрерывная на отрезке [0; 1] функция
/(х), принимающая значения также из [0; 1] и такая, что
образом рационального числа является число иррациональное, а
образом иррационального числа — число рациональное?
VIH.72. Докажите, что многочлен нечётной степени имеет хотя бы один
вещественный корень.
VUI.73. Докажите, что: а) уравнение cosx = x имеет корень; б*) этот
корень единственный.
53 , Задачи и упражнения
VHI.74. Функции /, g и h непрерывны на отрезке [а; 6], причём
\/х е [a; b] f(x) ^ g(x) ^ h(x), f(a) = h(b) = 0. Докажите, что
существует точка с на отрезке [а; 6], такая, что g(c) = 0.
viii.75. Докажите, что уравнение Xs — 20л: — 30 = 0 имеет более одного
корня.
Группа В
VIII.76. Функции / непрерывна на отрезке [1; 5] и принимает только
иррациональные значения. Известно, что /(я) = е. Чему может
равняться f(e)?
VIII.77. Существует ли такая непрерывная на вещественной оси
функция /, что для любого х число f(x) рационально тогда и только
тогда, когда иррационально число f(x + 1)?
VIII.78. Докажите, что если уравнение f(x) = x не имеет корней для
некоторой непрерывной на R функции /, то и уравнение
/(/0*0) = х также не имеет корней.
VIH.79. Функция / непрерывна и положительна на отрезке [а; Ь].
Докажите, что найдётся положительное число М, такое, что \/х е [а; Ь]
f(x) > М.
VIII.80. Функция / непрерывна и ограничена на вещественной оси.
Докажите, что уравнение f(x) = x имеет решение.
VIII.81. Функция / непрерывна на вещественной оси. Известно, что
последовательность, заданная следующим образом: хг = 0,
xn + i = f(xn)> имеет предел. Докажите, что уравнение f(x) = х
имеет решение.
VIH.82. Известно, что для непрерывной на вещественной оси функции /
для любого х выполняется равенство f(x)= f — I. Докажите,
что f константа.
Vin.83. Функция /непрерывна на луче [0; +оо), lim f(x) = 3. Докажите,
что / ограничена на [0; +оо).
VIH.84. Докажите, что непрерывная на R периодическая функция
ограничена и достигает своих максимума и минимума.
VIH.85. Пусть fug — функции, непрерывные на отрезке [а; 6].
Докажите, что функции
hx(x) = max{f(x); g(x)} и h2(x) = min{f(x); g(x)}
непрерывны на отрезке [a; b].
Группа С
Vin.86. Функция / — непрерывна на отрезке [а; Ь] и f(a) • f(b) < 0.
Докажите, что существуют три числа, составляющих
арифметическую прогрессию, таких, что сумма значений функции в этих
точках (соответствующих этим числам) равна 0.
54 j Глава VIII. Предел и непрерывность функции
VIH.87. а) Приведите пример (можно графически) непрерывной на R
функции, принимающей каждое свое значение ровно три раза,
б) Существует ли ограниченная непрерывная функция,
принимающая каждое своё значение ровно три раза?
в)* Докажите, что не существует непрерывной на R
функции, принимающей каждое своё значение ровно два раза.
VIII.88. Пусть / — непрерывная на отрезке [0; 1] функция и /(0) =
а) Докажите, что существует отрезок длины 0,5,
параллельный оси абсцисс, концы которого лежат на графике функции,
б*) Докажите, что для любого натурального п существует
отрезок длины —, параллельный оси абсцисс, концы которого
лежат на графике функции.
в*) Докажите, что если число а не является обратным
натуральному, то существует функция /, непрерывная на отрезке
[0; 1] и такая, что /(0) = /(1) = 0, для которой нет отрезка
длины а, параллельного оси абсцисс, концы которого лежат
на графике функции /.
VIH.89*. Непрерывная на R функция такова, что при всех
вещественных х выполнено равенство f(x) • /(/(#)) = 1, причём /(2007) =
= 2005.
а) Найдите /(2006). б) Приведите пример такой функции.
VIH.90*. Пусть / непрерывная на R периодическая функция, отличная
от константы. Докажите, что она имеет главный (наименьший
положительный) период.
VIH.91*. Найдите все функции /, определённые на й, для которых
выполнено следующее условие: если последовательность {хп} такова,
х1+х2+...+ хп f{x1)+f(x2)+...+ f(xn)
что hm = х0, то lim = f(x0).
П—*оо Jl /l—*оо П
Асимптоты графика функции
Группа А
Найдите асимптоты графика функции (viii.92—-viii.95).
VHI.92. а) у = , ^-j-|;
в) у = Jx2 + 3x-l; г) у = *Jxs - 6х.
VIIL93. а) у = - • cosx; б) у = х + ^^; в) у = *sin-;
2 1 1
г) у = 2 + cos—; д) у = arctg—; е) у = arcsin —.
XX х*
55 Задачи и упражнения
VIII.94. а) у = е х; б) у = 2 х ; в) у = —; г) у = х2 • е*.
х
VIII.95. а) у = Iog3(4 - х2); б) у = log!(2л:2 - Зх + 1).
2
Найдите асимптоты графика функции и постройте эскиз этого
графика, пользуясь соображениями монотонности (vill.96—Vlll.lOO).
VIII.96. а) у = д/*2 + 1; б) у =
VIH.97. а) у =
В) У = 1 -
1
VIII.98. а) у = ех+
в) г/ = ——
+ 1;
+ 2х; в) у = ^х2 + 2х + 3.
б) у = In (4-х2);
r) y =
д) у =
ж) у = In sin x + In cos я;
и) у = esinx.
viii.99. а) у = х • arctg x;
в) у = (х + 1) • arctg л:;
д) г/ = arctg — - x;
ж*) У = —
и*) г/ = (х + 1)2 • sin-|.
. а) у = {^\; б) у = -^-;
[х] х2 - х
е) у = lncosx;
з) у = In arctg x;
б) у = х + arctg л:;
г) у = х- arccos—;
7 * х9
е) г/ = х- arctg-;
3*) у = х -\ sin л:;
в) у =
Х2+ Г
VIII.101. а) График чётной функции имеет одну и ту же асимптоту при
х —► +оо и при л: —> -оо. Докажите, что эта асимптота
горизонтальна.
б) График нечётной функции имеет одну и ту же асимптоту
при х -> +оо и при х —> -оо. Докажите, что эта асимптота
проходит через начало координат,
тальна.
б) График нечётной функции имеет одну и ту же асимптоту
при х —> +оо и при х —> -оо. Докажите, что эта асимптота
проходит через начало координат.
J
Производная
и её применения
О53. Определение производной
1. Понятие производной. Производная как скорость
Рассмотрим задачу. Пусть тело падает с большой высоты, причём
расстояние, пройденное телом за время £, выражается формулой
st2
s(t)= -—, где g= 9,8 м/с2 — ускорение свободного падения. Найдём
скорость тела в момент времени 10 = 10 с.
Для того чтобы решить задачу, вспомним, как определяется
скорость тела в момент времени t0 = 10 с. Найдём среднюю скорость тела
на промежутке от 10 с до 20 с (напомним, что средней скоростью тела
за время от 10 до t секунд называется величина
8(0-я (10)
cpl' t - 10 '
равная отношению пройденного телом пути к времени, за которое этот
путь пройден), потом от 10 с до 15 с, от 10 с до 12 с, от 10 с до 11 с,
на промежутке длиной 0,5 с, 0,25 с и т. д.
Запишем полученные средние скорости в таблицу
Время от 10
до t, с
Средняя
скорость за это
время, в м/с
10
150
5
12.50
2
110
1
Ю,5о
0,5
10,250
0,25
10,125д
0,1
10,059
0,01
Ю.ООбд
Мы получили последовательность скоростей, члены которой (как
это видно из таблицы) с уменьшением интервала времени, на котором
мы подсчитываем среднюю скорость, всё ближе и ближе к некоторому
числу.
Это число и называется мгновенной скоростью тела в момент
времени t0 = 10 с. Найдём это число.
57 §53. Определение производной
Запишем среднюю скорость на промежутке времени [10; t]:
gt2 g-102
v _s(t)-s(10)= 2 2 = g t2-10 = g | 1Q
Cp i i л i 1 л о i 1 л О
t — 1U t — 1U Z t — 1U Z
Из этой формулы видно, что при приближении t к 10 значение vcp
будет стремиться к числу 10g. Таким образом, скорость тела в момент
времени t0 = 10 с равна 10g. Аналогично можно определить
мгновенную скорость для тела, движущегося по другому закону.
Применим такие же
рассуждения к функции у = f(x) и
определим «скорость изменения»
функции в точке х0. Найдём «среднюю
скорость» функции на промежутке
[х0; х] (рис. 9.1). Разумно считать
средней скоростью функции на этом
промежутке отношение изменения
значения функции на этом
промежутке («пути», пройденного
функцией) к длине промежутка («време-
ч , ч /(*)- f(XQ)
ни»), т. е. vCXi(x) = —L-1 ^-у-, при
ср х - х0
этом если мы будем брать х всё
ближе и ближе к х0, то «в пределе» по- рис д j
лучим «мгновенную скорость»
изменения функции / в точке х0. Эта «мгновенная скорость» называется
производной функции / в точке х0. Дадим формальное определение.
ОПРЕДЕЛЕНИЕ
Пусть функция f определена в некоторой окрестности
точки х0. Тогда производной функции f в точке х0 называется
предел lim
f(x)-f(x0)
х - х«
(если он существует и конечен).
Обозначение: f'(x0) — производная функции / в точке х0 (читается
«эф штрих от икс нулевого»).
Напомним, что величину f(x) — f(x0) называют приращением
функции / на промежутке [х0; х] и обозначают А/. При этом величину
х - х0 называют приращением аргумента и обозначают Дл\ Тогда
определение производной можно записать в виде
f>(xo)= limA*o+A*>-/(*o>= lim A/..
Ал: —0 АХ Дх — 0 Ах
Принято также обозначение производной f'(x0) - —^-^, при этом
df dx
символ — понимается не как отношение df к dx, а как единый символ
dx
58 1 Глава IX. Производная и её применения
(эти обозначения ввёл ещё Лейбниц, при этом символы df и dx
подчёркивают, что мы рассматриваем «бесконечно малое приращение
функции», соответствующее «бесконечно малому приращению
аргумента»).
В дальнейшем мы будем пользоваться той формой записи
определения производной, которая нам будет удобнее.
Заметим, что для того, чтобы производная функции в точке суще-
ствовала, должен существовать конечный предел lim—^ ^-^.
х-+х0 Х-Хо
Ещё раз подчеркнём, что, по сути, производная функции в точке —
это «мгновенная скорость изменения функции»1. Это соображение
в дальнейшем позволит нам увидеть, что многие теоремы о
производных «очевидны» и наглядны. Например, верны следующие
утверждения, которые мы докажем ниже:
1. Если производная функции в каждой точке положительна, то
функция возрастает (если скорость положительна, то «едем вперёд»,
т. е. функция возрастает).
2. Если в точке х0 значения функций f ы g равны, а производная /
в каждой точке больше производной g (т. е. для любого х
выполнено f'(x) > g'(x)), то при х, большем х0, и значения f(x) будут больше
значений g(x). В самом деле, если в некоторой точке графики двух
функций «повстречались», а в дальнейшем одна функция растёт
быстрее другой, то и значения первой функции будут больше, чем
значения второй.
В решении следующего примера мы будем опираться не на
формальное определение производной, а на приведённые выше
соображения о производной как о скорости изменения функции.
Пример 1. По графику функции / (рис. 9.2) определим, в каких
точках производная функции / больше 0, меньше 0, равна 0. Сравним
значения производной в точках х = — 3, х = —1, х = 3.
D На промежутках (-оо; -2) и (1; 2) функция убывает, поэтому её
производная в точках этих промежутков отрицательна. На
промежутках (-2; 1) и (2; +оо) функция возрастает, поэтому её производная в
точках этих промежутков положительна. В точках х = -2, х = I и х = 2
функция имеет нулевую скорость, поэтому её производная в этих точ-
1 Во второй половине XIX века курс математической физики в
Кембриджском университете читал знаменитый учёный-физик В. Томсон, лорд Кельвин
(1824—1907), а курс математического анализа — профессор И. Тодгентер.
Рассказывают, что однажды, войдя в аудиторию, Томсон внезапно обратился
к студентам с вопросом: «Что такое —?» В ответ он получил все мыслимые
dx
строго логические определения. Все они были отвергнуты: «Ах, бросьте вы
этого Тодгентера, — — это скорость!»
dx
§53. Определение производной
-f ~\
ках равна 0. В точке х = -3
производная отрицательна, в точках х = -1
и jc = 3 производная положительна,
причём в точке х = 3 скорость роста
функции больше (график «круче»),
поэтому /'(-3) < /'(-1) < /'(3). 11
Замечание. Конечно,
рассуждения в данном примере не являются
доказательствами в строгом смысле
этого слова, но часто бывает полезно,
зная значения производной в
точках области определения функции,
уметь построить эскиз графика и,
наоборот, по эскизу графика судить
о свойствах производной.
Пример 2. Может ли производная всюду отрицательной функции быть:
а) всюду (в каждой точке) положительной; б) всюду отрицательной?
П Ответ: а) да; б) да. Эскизы графиков соответствующих функций
изображены на рисунках 9.3 и 9.4. И
12 3
Рис. 9.2
Рис. 9.3
Рис. 9.4
Заканчивая обсуждение определения производной, приведём ещё
один пример из физики, в котором производная появляется
естественным образом.
Пример 3. Пусть Q(t) — количество теплоты (в джоулях), которое
нужно сообщить телу при его нагревании от 0 до t (в градусах Цельсия).
Средней теплоёмкостью при нагревании тела от температуры t до
температуры (t + At) называется величина сср = — —5lLL# Определить
теплоёмкость тела при данной температуре t0 можно, устремив At
к нулю, т. е. с(£0)= lim —— ^ = Q'(t0). Таким образом, тепло-
емкость тела есть производная от количества теплоты, рассмотренного
как функция от температуры. IS
60 1 Глава IX. Производная и её применения
Аналогично можно показать, что сила тока есть производная
количества протекшего заряда, рассмотренного как функция от
времени, линейная плотность неоднородного стержня есть производная
массы стержня, рассмотренной как функция от длины и т. д. Таким
образом, с помощью производной можно изучать различные
неоднородные процессы и объекты.
2. Вычисление производных некоторых функций
Пример 4. Пользуясь определением производной, найдём
производную функции / в точке х0 = 2, если: a) f(x) = х; б) f(x) = х2.
□ а) Г(2) = limA2+A*W(2) Um 2+Д*-2
0 АХ Ах — 0 Ах
б) Г(2) = um /(2 + Д*>-/(2) = lim (2 + Д">-2 = lim
А0 АХ А 0 Ах А
um lim lim
Ал:-*0 АХ Ах — 0 Ах Ах — 0 Ах
= lim (4 + Ах) = 4. 11
Дл:-*О
Заметим, что если функция имеет производную в каждой точке
её области определения, то мы можем определить новую функцию,
значение которой в каждой точке х0 равно производной функции /
в точке х0. Эта функция также называется производной функции /
(без указания точки) и обозначается /'.
П р и м е р 5. Найдём производную функции /, если: a) f(x) = х; б) f(x) = х2.
П а) По определению в любой точке х0 производная функции / равна
л ч ,. f(x0 + Ах) - f(x0) ,. хо+ Ах - х0
f (х0) = lim ^-^ — ° = lim -g = 1.
Ал: —0 АХ Ах — 0 Ах
б) /'<*о> = lim Пх° + Ах) ~ ПХо) = lim
АО АХ AO
lim
АХ Ajc-^O АХ
= lim — = lim (2xn + Ах) = 2хп. Таким образом, мы полу-
Дл: —0 АХ Ал: —0
чили (х)'= 1, (х2у=2х. Ш
Обратим внимание на то, что производная функции f(x) = x
получилась равной константе. Это означает, что скорость изменения этой
функции постоянна. В то же время производная f(x) = х2 равна 2х9
т. е. «скорость роста» функции f(x) = х2 увеличивается с
увеличением х (можно сказать, что график квадратичной функции на луче
[0; +оо) становится всё «круче и круче» с ростом х).
Если мы рассматриваем функцию / на отрезке [а; 6], то на его
концах можно говорить об односторонних производных: правосторонней
производной fl(a) и левосторонней производной fl(b). Они
соответственно определяются как правосторонний и левосторонний пределы:
f;(a)= Цщ'<*>-'<«>, f'(b)= Цт
х — а+ Х- а х — Ь- Х-Ь
61 §53. Определение производной
Заметим, что если функция / в точке х0 имеет производную, равную
f'(x0), то по замечанию из главы VIII (с. 8) в точке х0 существуют также
левосторонняя и правосторонняя производные, которые равны f'(x0).
Пример 6. Докажем, что функция f(x)= ых не имеет правосторонней
производной в нуле, а в остальных точках её производная равна —=.
2л/х
Q Преобразуем отношение:
f(xo+ Ax)- f(x0) = Vxo+ Ax-
Ах Ах
+ Ах - Т^о) • (л/^о + Ах +
Ах
Ах • (д/xq + А* + Jx^) Ах • (т]х0 + А*
<у]х0 + Ах +
Видно, что при х0 = О
lim -== рг = lim = н-оо.
Дл:-О+ ^0 + АХ + л/0 Л*-0+ yj АХ
Таким образом, искомый предел не является конечным и,
следовательно, правосторонней производной функция f(x) = 4x в нуле не
имеет, а для всех положительных х0
lim г — = —£=. И
Ах-^°^х0 + Ал: V 2y
3. Производная линейной комбинации функций
ТЕОРЕМА
Пусть функции f и д имеют производную в точке х0, а с —
произвольное вещественное число. Тогда:
1. Существует производная функции cf в точке х0, причём
2. Существует производная суммы функций f и д в точке х0,
причём (f+g)'(xo) = f'(xo) + g'(xo).
П доказательство. 1. Найдём приращение функции с/ на
промежутке [х0; х0 + Ах]:
А (с ■ /) = (с • f)(x0 + Ах) - (с • f)(x0) = с • f(x0 + Ax)-c- f(x0) =
= с . (f(x0 + Ах) - f(x0)) = с • А/.
По определению производной получим
62 ! Глава IX. Производная и её применения
Известно, что существует предел
lim^= f'(x0),
Ал: ОАх
поэтому существует и предел
lim ^- = с- lim £L = с- f'(xQ)9
длг-о Ах ал--+оАх °
что и требовалось доказать.
2. (/ + вУ(Хо) = lim (
Ал: -► О АХ
/(х0 + Ах) + g(x0 + Ах) - (f(x0)
= lim =
А* —О АХ
_ j /Ч*о + Ах) - /(х0) + g(x0 + А*) - g(x0) _ Af + Ag
Ал: —О АХ Ал: —О Ах
Известно, что существуют пределы
lim -^ = f'(x0) и lim ^ = g'(x0),
д^оАх 7 v 0/ алгоАх 6 v o;
поэтому по теореме о пределе суммы существует предел
А
Ах ал-^оАх
что и требовалось доказать. IS
Таким образом, мы доказали, что производная суммы функций
равна сумме производных, а постоянный множитель можно выносить
за знак производной. Если воспринимать производную как скорость,
то доказанная теорема становится очевидной: если одна функция
растёт со скоростью vl9 а вторая функция — со скоростью у2» то их сумма
растёт со скоростью иг + v2; если же функцию умножить на
константу с, то её скорость изменится в с раз.
Следствие (о производной линейной комбинации функций). Пусть
в точке х0 существуют производные функций fl9 f2, ..., /„, равные
соответственно f{(x0), %(хо)9 ..., /„(*())> и ai> a2» •••» ап —
вещественные числа. Тогда в точке х0 существует производная функции
8 — aifi "•" a2f2 + ... + ocn/n (называемой линейной комбинацией
функций fl9 f29 ..., fn)9 причём g'(xo)= a1/1'(x0) + a2/2'(x0) + ... +anf^{xQ).
Доказательство следствия проведите самостоятельно, применив
метод математической индукции.
Воспользуемся доказанной теоремой, а также выведенными выше
формулами производных функций vx, x9 х2 для вычисления
следующей производной.
63 j §53. Определение производной
Пример 7. Вычислим производную функции у = 4vx - Ъх + 0,5л:2.
П у'= (4у[х-5х + 0,5х2)'= (4л/х)'- (5х)' + (0,5х2)' = ±(4х)'- 5(х)'
0,5(х2)' = 4-^=- 5 + 0,5- (2х) = -JL - Ь + х. Ш
2/ 1
4. Производная и непрерывность.
Производная и гладкость функции
Не каждая функция имеет производную во всех точках её области
определения. Например, мы доказали, что функция f(x) = 4х не имеет
производной в нуле. Рассмотрим ещё один пример функции, не
имеющей производной в нуле.
Пример 8. Докажем, что f(x) = \x\ не имеет производной в нуле.
D По определению производная функции f(x) = \x\ в нуле, если она
существует, должна быть равна пределу
,. |*| - 0 ,. \х\
hm —■ = hm —-.
jc —0 X - 0 х^О X
\х\ /1, х> 0, \х\ 1 .. \х\ 1
Однако поскольку -—L = < н Л то lim ■—L = 1, hm ■—L = -1, т. е. ле-
х [-1, х<0, х^о+х х-+о- х
\х
восторонний и правосторонний пределы функции g (х) = ■—-в нуле раз-
X
\х\
ные, значит, lim — , а вместе с ним и производная функции f(x) = \х\
^—►0 X
в нуле не существуют.
Это же рассуждение можно было бы оформить по-другому, заметив,
что /ДО) = 1, а /_'(0) = -1 [по определению /ДО) = lim !^1 и /_'(0) = lim ^ |,
^ ЛГ — О+ X лг — О- X J
а значит, производной в нуле не существует (см. с. 61). IS
Если рассмотреть пример 8 менее формально, то можно заметить,
что на любом промежутке [t; 0] при отрицательном t средняя скорость
функции у = \х\ равна -1, а на любом промежутке [0; t] при
положительном t средняя скорость функции равна 1. В точке х = 0 график
функции «ломается», модуль меняет свою скорость «скачком», поэтому
говорить о скорости изменения этой функции в точке х = 0 бессмысленно.
Аналогично складывается ситуация для любой другой функции
в тех точках, где её график имеет «излом». Поэтому функции,
имеющие производную в каждой точке области определения, называют
гладкими функциями.
Из примера 8 видно, что непрерывные функции не обязательно
имеют производную в каждой точке области определения (функция
у = \х\ непрерывна в точке х = 0), однако обратное утверждение
оказывается верным.
64 I Глава IX. Производная и её применения
ТЕОРЕМА
Если функция f имеет производную в точке х0, то функция f
непрерывна в этой точке.
D доказательство. Запишем приращение функции / в точке х0
в виде А/ = — Ах.
Ах Af
Af
Так как существует конечный lim —- = f
Д ОД*
и lim Ax = О, то по
Ал: —О
теореме о пределе произведения функций lim A/ = lim — • lim Ax = О,
д* —о д* —оАх д*—о
что и означает (по одному из определений непрерывности), что /
непрерывна в точке х0. Ш
Ещё раз подчеркнем, что из непрерывности функции не следует
существование производной этой функции1.
Пример 9. Выясним, в каких точках существует производная
функции: а) /(х) = |х-3| + |х+1|; б) f(x) = \х2 + 4х - 5|.
D Рассмотрим графики этих функций (рис. 9.5 и 9.6). График
функции f(x) = |jc — 3| + |jc+1| имеет «изломы» в точках х = —1 и х = 3.
График функции f(x) = |х2 + 4х - 51 имеет «изломы» в точках х = 1 и х = -5.
-1 О
Рис. 9.5
1 Более того, существуют функции, которые непрерывны в каждой точке
множества R9 но ни в одной точке не имеют производной. В каком-то смысле
график таких функций в каждой точке имеет излом. Оказывается, что
«подавляющее большинство» непрерывных функций, заданных, например, на
отрезке [О; 1], не будут иметь производной ни в одной точке этого отрезка.
Однако достаточно трудно предъявить хотя бы одну такую функцию. Впервые
пример такой функции привели Б. Больцано и независимо от него К. Вейер-
штрасс.
65 I §53. Определение производной
В этих точках производных данные
функции не имеют, в остальных
точках функции «гладкие» и производ- у = \xs\
ные там существуют. Формальное
рассуждение с использованием
левосторонней и правосторонней
производных мы приведём в пункте 5. IS
Из рассмотренных примеров
может показаться, что если функция /,
заданная на /2, в каждой точке
имеет производную, то функция |/| не Рис д у
имеет производной в точках —
корнях функции /. Однако это не так! Например, функция | Xs \ имеет
производную в нуле и «излома» в нуле график функции г/ = | jc3 | не имеет
(рис. 9.7).
Заметим, что существование производной функции f(x) = | х2 + 4х — 51
во всех остальных точках, кроме точек х = 1 и х = —5, следует из
очевидного, но весьма полезного утверждения.
Утверждение ■
Если две функции в некоторой окрестности точки х0 совпадают
и одна из них имеет производную в этой точке, то другая также
имеет производную в точке х0 и эти производные равны.
Доказать это утверждение можно, используя замечание о
равенстве пределов функций в точке, совпадающих в некоторой окрестности
этой точки (с. 3).
+ 4х — 5, если х > 1 или х < — 5,
В примере 9,6 /(*)= \х2 +4х- б| = {
[-л:2-4х + 5, если -
т. е. при х > 1 или х < -5 функция / совпадает в некоторой
окрестности точки х с функцией у = х2 + 4х - 5 (которая по теореме о
производной линейной комбинации функций имеет производную в каждой
точке), а при — 5 < х < 1 — с функцией f(x) = —х2 — 4х + 5 (которая
также имеет производную в каждой точке).
Пример 10. Приведём пример функции, которая определена на R и:
а) имеет производную всюду, кроме точек х = 1 и л: = 2; б) имеет
производную только в точках х = 1 vl x = 2.
П а) Нетрудно видеть, что график функции f(x) = \(x-l)(x-2)\
имеет «изломы» в корнях функции (рис. 9.8), т. е. в точках х = 1
и х = 2 и производной в этих точках не существует. Как показано в
примере 9, в остальных точках производная данной функции существует,
б) Рассмотрим функцию f(x) = D(x) • (х - I)2 • (х - 2)2, где D(x) —
функция Дирихле напомним, что D(x) = \ ' ' .
I 0, х £ Q )
66 1 Глава IX. Производная и её применения
Докажем, что эта функция
имеет производную в точке х=1. Для
этого рассмотрим
lim-
x^l X - 1
D(x)(x-1)2
(x - 2)2 _
0
Рис. 9.8
x
х- 1
= lim£>(:x:).(*-l)-(*-2)2 = 0.
Последний предел существует и
равен 0 как предел произведения
функции у = х - 1 бесконечно малой
в точке х = 1 на ограниченную в
некоторой окрестности этой точки
функцию у = D (х) • (х — 2)2.
Таким образом, мы доказали
по определению, что производная
функции / в точке х = 1 существует и равна 0. Аналогично можно
доказать, что производная функции / в точке х = 2 равна 0.
Заметим, что во всех остальных точках функция / разрывна.
Действительно, для произвольной точки х0 можно выбрать
последовательность {хЛ рациональных чисел, сходящуюся к х0, и
последовательность {yj иррациональных чисел, сходящуюся к х0; при этом
lim f(xn) = (х0 - 1)Чх0 ~ 2)2, a lim f(yn) = 0.
П —*■ оо п —*■ оо
Эти пределы различны при х0 Ф 1 и х0 Ф 2, а значит (согласно
определению по Гейне предела функции), функция / не имеет предела
в точке х0, т. е. разрывна в этой точке. Ранее мы доказали, что если
функция имеет производную в точке, то она непрерывна в этой
точке. Поэтому разрывная в некоторой точке функция производной
в этой точке не имеет и, таким образом, функция / не имеет
производной в точках, отличных от точек х=1их = 2.1
5. Односторонние производные
Напомним, что правосторонняя и левосторонняя производные
функции / в точке х0 определяются как соответственно правосторонний
и левосторонний пределы
f; (x0) = hm
х - хп
Г- (х0) = hm
fix)-f(x0)
х -
В главе VIII было отмечено, что предел функции в точке
существует тогда и только тогда, когда левосторонний и правосторонний
пределы этой функции в данной точке существуют и равны. Таким образом,
67 j §53. Определение производной
для того чтобы функция имела производную в точке х0, необходимо
и достаточно, чтобы левосторонняя и правосторонняя производные
в данной точке существовали и были равны.
□ Вернёмся к примеру 9 и докажем, например, что функция
f(x) = \х - 3\ + \х + 1\ не имеет производной в точке х = 3. В самом
деле,
Г 2х- 2, если х > 3,
f(x)= |x-3| + |x + l| = <J4, если -1 ^ х ^ 3,
[2 - 2х, если х < -1.
Найдём правостороннюю и левостороннюю производные в точке
ft (3) = lim '<«> ~ /(3) = lim (2Х ~ 2) - 4 = lim 2 = 2;
х—3+ X - 3 х—3+ X - 3 л:—3+
/'(3) = Пт '<*> - /(3) = lim ±^± = lim 0=0.
л:-3- Х-3 лг^З-Х-3 *-+3-
Односторонние производные не равны, а значит, и производной в
точке х = 3 не существует. И
Пример 11. Вычислим /'(0), /'(2), /Ч~2) для функции /(х) = х
2, если х > 0,
П Рассмотрим функцию /(я) = я • Ш = ,
[-л:2, если х < 0.
Таким образом, при jc > 0 функция / в некоторой окрестности
совпадает с функцией у = х2, поэтому её производная равна 2х,
аналогично при х < 0 производная равна -2х. Итак, f'(2) = 4 и f'(-2) = 4.
Найдём левостороннюю и правостороннюю производные
функции / в нуле:
/+'(0) = lim Пх) ~ fi0) =lim^= lim x = 0,
аналогично /_'(0) = 0. Значит, в точке х = 0 функция / имеет
производную, и она равна нулю. И
тт ^ ^/ ч (*» если х ^ !» ^»
Пример 12. Пусть дана функция гт = < „ Выясним,
[ах2 + Ьх, если х < 1.
при каких значениях параметров а и 6 функция /: а) непрерывна
в точке х0 = 1; б) имеет производную в точке х0 = 1.
□ а) Для того чтобы функция / была непрерывной в точке х0 = 1,
необходимо и достаточно, чтобы lim f(x) = lim f(x) = /(1) = 1. Так как
X -»> 1+ X -► 1-
lim f(x) = lim x = 1 = /(1), a lim f(x) = lim (ax2 + 6x) = a + 6, то необ-
jc—*• 1+ а; —► 1+ x-*l— х—>1—
ходимым и достаточным условием непрерывности функции / в точке
х0 = 1 является a + Ь - 1.
68 j Глава IX. Производная и её применения
б) Приведём неправильное, но часто встречающееся «решение».
Найдём левостороннюю и правостороннюю производные в точке х0 = 1:
/+()/()() ;
X -»> 1+ X -► 1+
fl (1) = lim f (x) = lim (ax2 + bx)' = lim 2ax + b=2a + b.
x—> 1- x—► 1+ x—► 1+
Тогда необходимое и достаточное условие существования
производной / в точке х0 = 1 (равенство левосторонней и правосторонней
производных в точке х0 = 1) задаётся условием 2а + Ь = 1.
Итак, мы получили, что при условии 2а + Ъ = 1 функция имеет
конечную производную в точке х0 = 1. Но из существования конечной
производной следует непрерывность функции в этой точке, а это
означает согласно пункту а), что а + Ъ = 1. То есть из равенства 2а + Ъ = 1
следует равенство а + Ъ = 1, что неверно для большинства значений
а и Ь. В чём же дело?
Оказывается, что в неверном решении пункта б) мы вычислили
не левостороннюю и правостороннюю производные в точке х0 = 1,
a lim/'(x) и lim f'(x). В самом деле, по определению левосторонняя
*—1- х—1+
производная в точке х0 будет равна
1- X - 1 x^l- X - 1
Чтобы данный предел был конечным, необходимо, чтобы
числитель в точке х0 = 1 был равен нулю (иначе предел будет бесконечным),
т. е. чтобы а + Ъ — 1, а тогда
ах2 + Ьх - 1 = ах2 + (1 - а)х - 1 = (х - 1)(ах + 1)
и
х,/1Ч ,. ах+6х-1 т (я 1)(ах + 1) л. , -.ч 1
/_' (1) = lim = lim = lim (ax + 1) = a + 1.
x-+l- X - 1 x^l- X - 1 *-+l-
Таким образом, равенство а + Ь = 1 есть необходимое и
достаточное условие существования левосторонней производной функции /
в точке х0 = 1. При этом левосторонняя производная будет равна а + 1,
Вычислим правостороннюю производную функции / в точке х0 = 1
= Ит /(*>-/0> = Ит
1
т Ит х.
1+ X— 1 х—1+Х— 1
Для существования производной / в точке х0 = 1 должна выпол-
а + Ь = 1,,
няться система < л л (первое равенство — необходимое и
достала +1 = 1
точное условие существования левосторонней производной, а второе
равенство — левосторонней и правосторонней производных). Отсюда
получим а - О, Ь = 1. Ш
69 I §54. Производные некоторых элементарных функций
С)54. Производные некоторых элементарных функций
В этом параграфе мы вычислим производные некоторых
элементарных функций.
Утверждение
Функция f(x) = с, где сей, имеет производную в каждой точке
вещественной оси, причём с' = 0.
D доказательство. В самом деле, для произвольной точки х0
существует предел
f(xo+Ax)-f(xo) с-с п
lim = lim = 0.
д*— о Ах д*— о Ал:
Это означает, что в каждой точке вещественной оси функция /
имеет производную, равную нулю. Ш
Позже мы докажем, что константа — это единственная функция,
определённая на промежутке, производная которой тождественно (т. е.
в каждой точке промежутка) равна нулю.
Утверждение <
Функция f(x) = хп, где п е N, имеет производную в каждой точке
вещественной оси, причём (xn)' = nxn~1.
□ доказательство. Возьмём произвольную точку х0 и рассмотрим
предел
lim
(х + Ах)п - хп
~ Ах
— lim
хп + С\хп-хАх + С%хп-2(Ах)2+ ...
(Ах)п - хп
Дл:-»>0
Ах
= С1пхп~1=
(в первом равенстве мы воспользовались формулой бинома Ньютона,
а третье равенство верно в силу теоремы о пределе суммы). Поскольку
этот предел существует и конечен, то существует и производная
Утверждение
Функция
anxn + an_1xn"1 + ... + a1x + a0, где ao,a1f ...,апеЯ,
п е N имеет производную в каждой точке вещественной оси,
причём Г(х) = ап • пхп"1 + ал_ -, • (п - 1)хп~2 + ... + av
70 1 Глава IX. Производная и её применения
D доказательство. Справедливость формулы следует из только что
доказанной формулы для производной функции хп, а. также теоремы
о производной линейной комбинации функций:
f'(x) = (anxn + an_1xn~1 + ... + a1x + a0)' = (anxn)' + (an_1xn-1)'+ ... +
+ (агх)' + (аоу = аппхп~х + ап_г(п - 1)хп~2 + ... + аг. Ш
Пример 13. Вычислим производную функции f(x) = х11 + Зх* — х2 — 4х - 5.
□ f'(x)=
Утверждение <
Функция f(x) =xa, а е /?, имеет производную в каждой точке
полуинтервала (0;+оо), причём (ха)' = ссха~1.
D доказательство. Возьмём произвольную точку х0 > О и
рассмотрим предел
(х0 + АхГ - xg
hm
Ах-+ 0 АХ
= lim
х0
^1 -1
Дл:
= lim
д*—о
-а
с0
-1
= xj~x- lim
Ах
( Ах (1 + £)а — 1 ^
так как ^ Ои lim = а . Поскольку этот предел сущест-
^ ХД0 t0 t )
^ 0
вует и конечен, то f'(x0) = ouCq "\ Й1
Пример 14. Найдём производную функции a) f(x)=— при * > 0;
б) f(x) = 4x при х > 0.
D Поскольку — = х"1, то в силу последнего утверждения
ij=<*->■=-*-=-^.
б)
Аналогично, поскольку 4х = х2, то (V^)' = I *2 I = - х 2 = —=. Ш
Утверждение
ШШЩ
Функция f (x) = sinx имеет производную в каждой точке
вещественной оси, причём (sinx)' = cosx.
71 j §54. Производные некоторых элементарных функций
Q доказательство. Возьмём произвольную точку х0 и рассмотрим
Ах 2х0 + Ах
. , А ч . 2 sin cos
sin(x0 + Ах) - sin x0 2 2
lim = lim =
Д*-»0 АХ Д* —0 AX
2x0 + Ax
= lim
Ах
sin cos
2 2
Ax_
2
= cosx0.
sin*
Последнее равенство выполняется в силу того, что lim = 1 (пер-
*— о t
выи замечательный предел — см. с. 15) и lim cos
А*—*•()
= cos x0 (в силу
непрерывности функции косинус, доказанной в примере 1 главы VIII).
Поскольку этот предел существует и конечен, то существует
производная синуса в любой точке х0 вещественной оси, причём f'(x0) = cosjc0. Ill
(cos*; sin*)
Отметим, что результат этого и
следующего утверждений следует из
физического смысла производной.
Действительно, пусть точка движется по
тригонометрической окружности в
положительном направлении с линейной
скоростью, модуль которой равен 1,
стартовав из точки Ро. Тогда
координаты точки в момент времени t будут
(cos*; sin*). Так как вектор скорости
точки, отложенный от самой точки,
является касательным к траектории,
т. е. к окружности, то он будет
перпендикулярен радиус-вектору точки,
а потому координаты вектора
скорости, очевидно, будут (-sin*; cos*). Это и есть производные
горизонтальной и вертикальной координат движущейся точки (рис. 9.9).
Рис. 9.9
Утверждение
Функция f(x) = cosx имеет производную в каждой точке
вещественной оси, причём (cosx)' = -sinx.
Доказательство аналогично доказательству предыдущего
утверждения.
Пример 15. При каких значениях параметра а производная функции
f(x) = a cosx + 2х по модулю больше 1 при любом вещественном xl
П Найдём f'(x) =—asinx + 2. Нетрудно заметить, что поскольку
sin л: g [-1; 1], причём принимает все значения из этого отрезка, то
72 ! Глава IX. Производная и её применения
—a sin л: принимает все значения из отрезка [—|а|; |#|]. Таким образом,
множество значений производной — отрезок [2 - \а\; 2 + |а|]. Для
того чтобы все значения производной по модулю были больше 1,
необходимо и достаточно, чтобы выполнялось неравенство 2 — | а \ > 1
(поскольку 2 + \а\ > 1 при любом а), т. е. \а\ < 1, откуда получаем
ответ: а е (-1; 1). Ш
Утверждение
"I
Пусть а > 0, а * 1. Функция f(x) = ax имеет производную в каждой
точке вещественной оси, причём (ах)' = In a • ах.
D доказательство. Возьмём произвольную точку х0 и рассмотрим
предел
Д (л1)
ао -ао ао.(а-1) _ ,
lim = lim = а*° • 1па.
Ах —О АХ Ах —О АХ
Мы воспользовались «замечательным пределом» lim = In a
(см. с. 18). И &х~° АХ
Следствие. При а = е получим (ех)' = ех.
Пример 16. Вычислим производную функции f(x)= xn +пх.
П Воспользуемся формулами (ха)' = аха~г и (ах)' = ах • \пх, получим
(хп +пху = их*-1 + к х - In п. Ш
Утверждение
Функция f(x) = lnx имеет производную в каждой точке
полуинтервала (0; +оо), причём (Inx)' = —.
D доказательство. Возьмём произвольную точку хо>Ои
рассмотрим предел
1д х0 + Ах 1
П
1д 1п1+
ln(xo+Ax)-lnx0 П х0 [ х0
lim = lim = lim
А А
= lim= lim т=
АХ Ах —О АХ Ах —О &Х_ х0
х0
, л, 1п(1 + t) л -i г>\ тт
(последнее равенство верно, так как lim = 1, см. с. 18). По-
* —о t
скольку этот предел существует и конечен, то (1плг0)' = —.Ш
х0
Следствие. Пусть а > 0, а Ф 1. Функция f(x) = loga:x:имеет
производную в каждой точке полуинтервала (0; +оо), причём (loga х)' = .
1П CL X
Доказательство очевидно, поскольку loga x и lnjc отличаются лишь
постоянным множителем: log,, х = 1пл\
In a
73 ! §55. Задача о касательной. Уравнение касательной
Пример 17. При каких значениях параметра а производная функции
f(x) = ах отрицательна при любом вещественном х?
П Заметим, что функция ах определена только при положительных а.
При а = 1 функция равна константе, и её производная равна 0 при
любом вещественном х.
При а > О, а Ф 1 выполняется равенство (ах)' = In a • ах. При этом
для любого вещественного х выполняется ах > О, поэтому знак
производной функции / постоянен найи совпадает со знаком In а. Таким
образом, производная отрицательна тогда и только тогда, когда
отрицателен In а, т. е. при О < а < 1.
Можно было бы рассуждать «менее формально» (пока у нас не
доказаны признак и свойство возрастающей функции): мы знаем, что
функция ах убывает при 0 < а < 1, и, значит, скорость её изменения
(производная) отрицательна при этих а, если же а > 1, то ах возрастает
и её производная положительна. Ш
О55. Задача о касательной. Уравнение касательной
1. Определение касательной
Вы уже встречались с понятием касательной в геометрии, когда
определяли касательную к окружности. Попробуем определить смысл
выражения: «Прямая является касательной к графику функции / в
точке графика с абсциссой х0 (в дальнейшем будем говорить «в точке лг0»)».
Проведём прямую через точки с координатами А(х0; f(x0)) и В(х0 + Ах;
f(x0 + Ах)) (рис. 9.10), такая прямая обычно называется секущей (Ах Ф 0,
значение Ах может быть и отрицательным). Будем устремлять Ах к
нулю, и пусть точка В «стремится» к точке А по кривой. Если при этом
секущая АВ будет «стремиться» к некоторой прямой, т. е. будет
стремиться занять некоторое предельное положение, то эта прямая
называется касательной к графику функции / в точке х0. Можно сказать, что
касательная — это предельное положение секущей.
Рис. 9.10
= f(xo+Ax)-f(xo)
74 1 Глава IX. Производная и её применения
Что плохо в этом «определении»? Главным образом то, что
определение неформально — непонятно, что значит «точка стремится к
точке» и «прямая (секущая) „стремится" к прямой». Тем не менее
попробуем на основании интуитивного представления о касательной как
о «предельном положении секущей» вывести уравнение касательной.
Ясно, что касательная будет проходить через точку (х0; f(x0))
(через эту точку проходят все секущие).
Найдём угловой коэффициент касательной. Пусть секущая АВ
проходит через точки А(х0; f(x0)) и В(х0 + Ах; f(x0 + Ах)). Угловой
коэффициент секущей АВ, равный тангенсу угла наклона прямой АВ
к положительному направлению оси абсцисс (в дальнейшем мы будем
просто говорить «тангенс угла наклона прямой»), равен
д/ = /4*0+ Ах)- f(x0)
Ах ~ Ах
(см. рис. 9.10). Разумно предположить, что угловой коэффициент
касательной k (к которой «стремится» секущая) будет равен пределу
углового коэффициента секущей (или, что то же самое, тангенс угла наклона
касательной равен пределу тангенса угла наклона секущей) при Ах -> 0:
f(xo+ Ax)-f(x0)
&кас = ЛИтЛек
Ал: —► 0
Ал: —► 0
Ах
Заметим, что последний предел есть не что иное, как производная
функции / в точке х0, т. е. k = f'(x0).
ОПРЕДЕЛЕНИЕ
Пусть функция /"имеет производную в точкех0. Касательной
к графику функции f в точке х0 называется прямая с угловым
коэффициентом к = Г (х0), проходящая через точку (х0; f(x0))
(рис. 9.11).
Заметим, что из этого
определения следует геометрический смысл
производной: производная функции
в точке — это угловой коэффициент1
касательной к графику функции,
проведённой в этой точке. Если
производная положительна, то чем она
больше, тем «быстрее растёт»
функция в данной точке, тем больше
угловой коэффициент касательной и тем
«круче» сама касательная.
1 Напомним, что угловой
коэффициент прямой равен тангенсу угла,
образованного этой прямой и
положительным направлением оси Ох.
75 I §55. Задача о касательной. Уравнение касательной
Вы встречались и с другими подходами к определению
касательной: касательной к окружности называлась прямая, которая имеет
ровно одну общую точку с окружностью, однако ясно, что это
определение не годится в общем случае: прямая х = О не является
касательной к графику у = х2, хотя имеет с ним ровно одну общую точку.
Другое и на первый взгляд разумное определение касательной
как такой прямой, что график функции лежит по одну сторону от
неё (иногда добавляют «хотя бы в некоторой окрестности»), тоже
«работает» не всегда. Например, касательной к графику функции
у = Xs в нуле является прямая у = О, а график функции у = Xs
лежит по разные стороны от этой прямой.
Отметим, что касательной к графику линейной функции (в
любой точке) является сам этот график. Таким образом, касательная
к графику функции может иметь даже бесконечно много общих
точек с этим графиком.
2. Уравнение касательной
Выведем уравнение касательной. Будем искать его в виде у — кхл-Ъ.
По определению k = f'(x0). Найдём 6. Касательная проходит через
точку (х0; f(x0)), поэтому верно равенство f(x0) = f'(x0) • х0 + 6, откуда
b = f(x0)- f'(xo)xo.
Отсюда получим уравнение касательной:
у = f'(xo)x + f(x0) - f'(xQ) • х0.
Часто его записывают в виде
y = f'(xo)(x-xo) + f(xo) (1)
или
y-f(xo) = f'(xoHx-xo). (2)
Уравнение (2) можно получить, если воспользоваться уравнением
прямой, с угловым коэффициентом &, проходящей через точку (х0; у0),
записанным в виде Ау = kAx или у — у0 = k(x — х0), где k — угловой
коэффициент этой прямой.
По введённому определению касательной, график функции не
может иметь вертикальной касательной (вертикальная прямая х = а
не является графиком линейной функции). Однако будем говорить,
что график функции имеет вертикальную касательную в точке,
если существует бесконечный предел
hm kceK = lim = оо
д*-+о сек д*-+о Ах
(угловой коэффициент секущей стремится к бесконечности). Так,
например, обстоит дело с функцией J\x\ в нуле.
76 1 Глава IX. Производная и её применения
Пример 18. Найдём уравнение касательной к графику функции f(x) = Xs
в нуле.
D Воспользуемся формулой (1) и запишем уравнение касательной
к графику функции / в точке х0 = 0. Получим у = f'(O)(x - 0) + /(0).
Поскольку f'(x) = Зх2 и /(0) = 0, то получим уравнение касательной:
у = 0. Ш
Ещё раз обратим внимание на то, что запись f'(0) — это значение
производной в нуле, т. е. сначала нужно найти производную функции /
как функцию, а затем найти значение полученной функции в нуле.
Пример 19. Найдём уравнения всех касательных к графику функции
у = х2 — Зх + 1, проходящих через точку А (2; -2).
D Точка А не принадлежит графику, поэтому нам неизвестна
точка графика, через которую проводится касательная. Запишем
уравнение касательной в произвольной точке графика с абсциссой t:
y = f'(t)(x-t) + nt). (*)
Так как искомая касательная проходит через точку А (2; -2), то
подставив координаты точки А в уравнение, мы получим уравнение
с одной неизвестной t.
Поскольку f(t) = t2 - 3t + 1, f'(t) = 2t - 3, уравнение (*)
приобретёт вид
y = (2t - 3)(х - t) + t2 - 3t + 1.
Подставляя в него х = 2 и у = -2, получим
-2 = (2t - 3)(2 -t) + t2-3t + l.
Решив это уравнение, находим, что t = 1 или t = 3. Подставив эти
значения в уравнение (*), мы получим уравнения касательных в этих
точках. Ответ: у = -х, у = Зх - 8.Ш
Утверждение•
Уравнения всех касательных, проведённых к графику функции
у = f(x) через произвольную точку /W0(x0; y0) (не важно,
принадлежит ли точка Мо графику функции), могут быть записаны
в виде у = f'(t)(x -1) + f(t), где t является корнем уравнения
При мер 20. Существуют ли значения параметра а, при которых
касательная к графику функции f(x) = ах в точке с абсциссой х0 = 0
параллельна прямой у = х + 12?
D Уравнение касательной к графику функции f(x) = ax в точке с
абсциссой х0 = 0 имеет вид у = In а • х + 1. Для того чтобы прямая
у = In а • х + 1 была параллельна прямой у = х + 12, необходимо, чтобы
их угловые коэффициенты были равны, т. е. In а = 1, откуда а = е.
Очевидно, что найденное значение а подходит: действительно,
уравнение касательной к графику у = ех в точке х0 = 0 имеет вид
у = х + 1 и касательная параллельна прямой у = х + 12 (такая проверка
77 I §55. Задача о касательной. Уравнение касательной
была нужна, так как могло оказаться, что при найденном значении а
полученная касательная совпала бы с данной прямой, а не была бы
параллельна ей). Ответ: а = е. Ш
Пример 21. Докажем, что к графику многочлена степени л > 1 можно
провести не более л — 1 касательных, параллельных друг другу.
□ Если касательные параллельны, то их угловые коэффициенты
равны. В то же время угловые коэффициенты касательных равны
производной многочлена в абсциссах точек касания. Таким образом, чтобы
найти т параллельных касательных, нужно найти как минимум т
точек на графике многочлена, в которых производные равны. Но
производная многочлена степени л — это многочлен степени л - 1, который
никакое значение не принимает больше л — 1 раз. Таким образом, и
точек, в которых производные равны, не может быть более л — 1, а
значит, нельзя провести и более л - 1 касательных, параллельных друг
другу. 11
Пример 22. Найдём уравнения общих касательных к графикам
функций f(x) = х2 + 1 и f(x) = 4х2 - 2.
□ Пусть общая касательная к графикам функций касается первого
графика в точке с абсциссой хЛ и второго графика в точке с абсциссой х2.
Уравнение касательной к графику функции f(x) = х2 + 1 в точке хг
имеет вид у = 2хгх - х\ + 1, уравнение касательной к графику функции
f(x) = 4х2 - 2 в точке х2 имеет вид у = 8х2х — 4х2 — 2.
Так как это уравнение одной и той же (общей!) касательной, то
одновременно должны выполняться равенства 2хг = 8х2 (равенство
угловых коэффициентов) и -х\ + 1 = -4л| - 2 (равенство свободных
членов). Из этих равенств получаем хг = 2, х2 = 0,5 или хх — -2, х2 = -0,5.
Таким образом, существуют две общие касательные к графикам
данных функций: у = 4х — Злу = —Ах — 3. Ш
3. Угол между графиками функций
Напомним как искать угол между прямыми, заданными
уравнениями у = кхх + Ъх и у = kx2 + Ь2.
Угловой коэффициент прямой равен
тангенсу угла наклона этой прямой. На ри- у>
сунке 9.12 отмечены углы наклона данных
прямых аир. Таким образом, кх -
2 p
Искомый угол ф равен разности углов
аир. Тогда
tgcp = tg(a - Р) = tga "
1+ tga tgP 1+ kxk2
При этом если kxk2 = tga • tg(3 = -1, то
формула тангенса разности неприменима
Рис. 9.12
78 1 Глава IX. Производная и её применения
и, как мы знаем, прямые взаимно перпендикулярны: ф = 90°. Если бы
мы обозначили углы «наоборот» (т. е. больший из углов за (3), то полу-
k — k
чили бы формулу tgcp = —. Таким образом, при k1k2 Ф -1 верна
1 + k1k2
, не зависящая от способа обозначения углов.
формула tg ф =
ОПРЕДЕЛЕНИЕ
k2 —
Углом между графиками функций в точке их пересечения
называется угол между касательными (если они существуют)
к графикам этих функций, проведёнными в указанной точке.
Пример 23. Найдём углы между графиками функций f(x) = х2 - 9х + 26
/ ч 24
и g(x) = — в точках их пересечения.
□ Для того чтобы найти абсциссы точек пересечения графиков, ре-
24
шим уравнение х2 — 9х + 26 = —. Решив это уравнение, найдём корни:
х
хг = 2, х2 = 3 и л:3 = 4. Вычислим производные данных функций в этих
точках:
f{x) = 2* - 9, /'(2) = -5, Г(3) = -3, /'(4) = -1;
g'(x) = -Ц, g'(2) = -6, ^'(3) = -|, ^'(4) = -|.
X о ^
Угловые коэффициенты касательных в точках графиков с
абсциссой х0 равны производным соответствующих функций в точках с
абсциссой х0. Найдём тангенс угла между графиками данных функций в
точке их пересечения с абсциссой 2 (он же угол между касательными к
графикам функций в этой точке), воспользовавшись полученной
формулой. Получим
-5 - (-6) =±_
L + (-6)(-5) 31'
Аналогично вычислим тангенс угла между графиками в точках
с абсциссами х2 = 3 и х3 = 4:
tgcp2 =
-Ч-f)
J_
27'
.,.,.=
1
5'
Итак, углы между графиками функций / и g в точках их
пересечения равны arctg—, arctg—, arctg-. 11
31 21 о
79 j §55. Задача о касательной. Уравнение касательной
Разобранный пример показывает, что угол между кривыми может
быть различным для различных точек пересечения.
ОПРЕДЕЛЕНИЕ
Два графика касаются друг друга в их общей точке, если
в этой точке они имеют одну и ту же касательную.
Заметим, что для того, чтобы графики функций касались друг
друга, необходимо и достаточно, чтобы в точке пересечения графиков были
равны производные этих функций. Это следует из того, что производная
равна угловому коэффициенту касательной, а прямая однозначно
определяется угловым коэффициентом и точкой, через которую она
проходит (в данном случае эта точка — точка пересечения графиков).
Пример 24. Найдём общие точки графиков функций f(x) = xs + 2x2
и g(x) = х2 + 5х — 3 и установим, в каких из них графики касаются
друг друга.
D Для того чтобы найти абсциссы точек пересечения графиков
функций, решим уравнение Xs + 2х2 = х2 + 5х - 3, его корни: хг = 1,
х2 = -3. Вычислим производные данных функций в этих точках:
/'(*) = З*2 + 4х, Г(1) = 7, Г(-3) = 15,
= 2*+ 5, £'(1)=7, g'(-3)=-l.
Производные равны только в точке хг = 1.
Таким образом, графики касаются в точке с абсциссой хг = 1 и
пересекаются в точке с абсциссой х2 = -3. Ответ: общие точки графиков
А(1; 3), В(—3; -9); в точке А(1; 3) графики касаются друг друга. IS
Замечение. Если бы в условии примера 24 требовалось найти
только точки касания, разумно было бы решить уравнение f'(x) = g'(x)
и при найденных значениях х проверить, выполняется ли равенство
= g(x).
Пример 25. Найдём множество точек на координатной плоскости,
через каждую из которых можно провести две касательные к параболе
у = х2, угол между которыми равнялся бы —.
□ Пусть через точку (а; Ь) проходят две касательные к графику
у = х2, которые касаются графика в точках с абсциссами хх и х2-
Запишем уравнение касательной в точке графика с абсциссой хг:
у = 2хг(х - хг) + xf.
Уравнение касательной в точке графика с абсциссой х2 выглядит так:
у = 2х2 (х — х2) + х\.
80 ! Глава IX. Производная и её применения
Точка (а; Ь) принадлежит обеим касательным, поэтому
выполняются равенства Ъ = 2хг(а - хг) + х\ и Ъ = 2х2(а - х2) + х2, тем самым
числа хг и х2 являются корнями квадратного уравнения
Ъ = 2х(а - х) + х2 <=> х2 - 2ах + 6 = 0.
Значит, по теореме Виета хгх2 = Ь. Для того чтобы касательные были
перпендикулярны, необходимо, чтобы произведение их угловых
коэффициентов равнялось -1, т. е. 2хх2х2--\^ откуда хгх2 = --. Таким
образом, Ъ = — есть необходимое условие того, чтобы через точку с ко-
4
ординатами (а; Ъ) проходили две перпендикулярные касательные.
Кроме того, при любом а уравнение х2 - 2ах = 0 имеет два ре-
4
шения (дискриминант этого уравнения равен 4а2 + 1) хх и х2, и
нетрудно видеть, что касательные в этих точках пройдут через точку с
координатами а; -- и будут перпендикулярны.
Таким образом, искомым множеством точек является множество
точек с координатами (а; 6), где а — любое число, Ь = —, т. е. пря-
I I 4
мая у = —. Ответ: прямая у = --. Ш
О56. Приближение функции линейной функцией.
Дифференциал
1. Дифференцируемые функции
Для решения многих практических задач оказывается достаточно
знать лишь приближённое значение данной функции. Поэтому
полезно уметь находить функцию более простого вида, нежели данная,
достаточно точно приближающую данную. Одной из самых простых (и
самых важных в математическом анализе) функций является линейная
функция, график которой есть прямая. Многие функции в
окрестности каждой точки своей области определения «похожи на линейную».
Рассмотрим некоторую функцию / в малой окрестности точки х0 и
зададим линейную функцию следующим образом: g(x) = f(x0) + k(x- x0).
При этом приращению функции А/ = f(x) - f(x0) в точке х0
соответствует приращение линейной функции Ag = k (x - х0) = k Ax в этой точке.
Нам хотелось бы, чтобы приращение линейной функции Ag мало
отличалось от соответствующего приращения А/ (точнее, чтобы малое
приращение Ag было «почти равно» малому приращению А/). Каждому
значению k соответствует своя прямая. Оказывается (что
неудивительно), что «теснее всего прилегает» к графику функции в окрестности точ-
81 §56. Приближение функции линейной функцией. Дифференциал
ки х0 касательная, проведённая через точку графика с абсциссой х0.
Тем самым линейная функция, графиком которой является эта
касательная, будет лучше всего приближать функцию /в малой окрестности
точки х0.
Уточним сказанное. Погрешность от замены функции / на
функцию g равна r(Ax) = Af - kAx. Угловой коэффициент касательной по
определению равен f'(x0), и соответствующая линейная функция
имеет вид g(x) = f(x0) + f'(xQ)(x — х0). Покажем, что в этом случае
погрешность, рассмотренная как функция от Ах, есть бесконечно малая
более высокого порядка по отношению к Ах, т. е. г (Ах) = о (Ах) при
Ах -► 0. Действительно,
,. r(Ax) v Af-ff(x0)Ax
lim ——- = lim
о Ах
Дл; —0
Ах
^-- Г(хо)) =
Заметим, что если бы мы взяли другую линейную функцию вида
У = /(*о) + k(x - х0), для которой k Ф f'(x0), то погрешность г (Ах) =
= Af - kAx была бы величиной того же порядка малости, что и Ах, а не
о (Ал:). Именно в этом смысле линейная функция, графиком которой
является касательная, даёт наилучшее приближение данной функции
в малой окрестности точки х0.
Фактически при такой замене функции на линейную маленький
участок кривой в окрестности точки х0 заменяется маленьким
отрезком прямой (рис. 9.13).
Однако всё сказанное оказывается верным не для всех функций,
а для некоторого ограниченного (хотя и достаточно широкого) класса
функций. Функции, которые ведут себя «почти как линейная
функция» в окрестности точки х0, называются дифференцируемыми в
точке х0. Такой функцией будет, например, функция синус в точке х = 0.
На рисунках 9.14—9.16 изображён график функции синус в
окрестности нуля в разных масштабах. Мы видим, что при большом увеличе-
У
погрешность от замены
функции f(x) на линейную
у — кхЛ-Ъ в окрестности
точки х0
y=kx+b
Рис. 9.13
Рис. 9.14
82 , Глава IX. Производная и её применения
1"
Рис. 9.15
Рис. 9.16
нии график синуса почти неотличим в окрестности нуля от графика
прямой у = х (касательной к графику функции у = sin х в точке х = 0).
Конечно, все вышесказанное является пока не определением,
а описанием понятия «дифференцируемая функция».
Дадим формальное определение функции, дифференцируемой в точке.
ОПРЕДЕЛЕНИЕ
Функция f называется дифференцируемой в точке х0, если
существуют вещественное число А и функция а, такие, что
Af = А • Ах + ос (Ах), причём а (Ах) = о (Ах) при Ах -» 0.
Иногда представление дифференцируемой в точке х0 функции /
записывают в виде А/ = ААх + р (Ал:) • Ал:, где Р (Ал:) — бесконечно малая
функции при Ах -> 0. Ясно, что это равносильные определения (в
качестве Р(Ах) можно взять —-—19 которая будет бесконечно малой в нуле
в силу того, что а (Ах) = о (Ах) при Ах -> О)1.
Какие же функции являются дифференцируемыми в точке? Какие
функции «ведут себя как линейная» в окрестности данной точки?
Оказывается, что это те и только те функции, у которых существует
производная в данной точке.
ТЕОРЕМА
Функция 1 имеет производную в точке тогда и только тогда, когда
она дифференцируема в этой точке
1 Заметим, что в отличие от функции а, значение функции Р при Ах —> 0
можно доопределить произвольно, однако удобно считать, что Р (О) = О. При этом
все формулы остаются верными.
83 ! §56. Приближение функции линейной функцией. Дифференциал
□ доказательство. 1. Докажем, что если / имеет производную
в точке, то она дифференцируема в этой точке. Пусть в точке х0
функция имеет производную f'(x0), т. е. существует конечный предел
lim ^. Пусть р (А*) = jL- f'(x0).
Д#-»>0 АХ АХ
Тогда р — бесконечно малая функция при Ах —> О по теореме
о пределе разности. Из определения Р получим (домножив на Ах)
р(Ах)Ах = Af - f'(xo)Ax, откуда Af = f'(xo)Ax + p(Ax)Ax. Таким
образом функция / дифференцируема в точке х0 по определению.
2. Докажем обратное утверждение. Пусть / дифференцируема
в точке х0, тогда существуют число А и функция а, такие, что
Af=AAx + a(Ax), где а (Ах) — бесконечно малая более высокого поряд-
л л л гл А/ , <х (Ах)
ка, нежели Ах при Ах —* О. Отсюда получим — = А н .
Ах Ах
Переходя к пределу при Ах -> 0, в этом равенстве получим
lim ^L = lim I A + ^™ I = A,
Дл; — О АХ Д* —0^ Ax J
т. е. функция / имеет производную в точке х0, и эта производная
равна А. Ш
Итак, мы доказали, что если функция имеет производную в
точке х0, то она дифференцируема в этой точке, т. е. представима в виде
Af = ААх + а (Ах), где а (Ах) = о (Ах) при Ах —> 0; при этом А = /'(х0).
В дальнейшем в формулировках теорем и задач выражения
«функция / имеет производную в точке х» и «функция / дифференцируема
в точке х» мы будем употреблять как синонимы.
2. Дифференциал функции
Величину /'(хо)Ах, рассматриваемую как функцию от Ах,
называют дифференциалом функции f в точке х0. Обозначают его обычно
df(x0). Таким образом, df(x0) = fr(x)Ax.
При этом часто величину Ах обозначают dx (если рассмотреть
функцию у = х, то можно написать dx = (х)'Ах = Ах), и мы получим
формулу df(x0) = f'(xo)dx.
Геометрический смысл дифференциала становится ясен при
рассмотрении рисунка 9.17, на нём ВС = df(x0), AC = Af, т. е. Af есть
приращение функции, a df(x0) — соответствующее приращение линейной
функции. Значение приращения А/ = /(х0 + Ах) - /(х0) приближённо
равно значению дифференциала в точке х0, т. е. А/ ~ df(x0) (заметим,
что в этом приближённом равенстве и справа и слева стоит функция
от аргумента Ах: слева приращение функции при приращении
аргумента, равном Ах, справа дифференциал, который является линейной
функцией от аргумента Ах). Теперь равенство /(х) = /(х0) + А/ можно
84 I Глава IX. Производная и её применения
переписать в виде f(x) ~ f(x0) + df(x0).
Эту формулу можно использовать для
приближённого вычисления значения
функции вблизи точки х0. При этом
погрешность, возникающая в результате
замены А/ на df(x0), будет равна о (Ах)
при Ах —► 0 и равна длине отрезка АВ на
рисунке 9.17.
Пример 26. Сравним значения
приращения и дифференциала функции
f(x) = Зх2 + 2 в точке хо = 2 при
приращениях аргумента, равных: а) Ах = 0,1;
б) Ах = 0,01; в) Ах = 0,001.
D Дифференциал функции f(x) = Зх2 + 2 в точке хо = 2 равен
df(2) = f'(2)Ax = 12Ах, а приращение функции А/ = /(2 + Ах) - f(2) =
= 3 (2 + Ах)2 + 2-3-22-2 = 12Ах + 3 (Ах)2. Их разность А/ - d/(2) равна
З(Ах)2. При Ах = 0,1 эта разность равна 0,03, при Ах = 0,01 она равна
0,0003, при Ах = 0,001 она равна 0,000003. Ш
Пример 27. Найдём дифференциал функции у = vx в точке х0 = 64 и
с его помощью вычислим приближённо значение функции при х = 65.
□ df(64) = f'(64)Ax = —^=Ах = — Ах. Ах = 65 - 64 = 1. Из форму-
2V64 16
Рис. 9.17
лы А/
получим /(65) ~ /(64) + — Ах = 8 + — = 8,0625.
16 16
Вычислите на калькуляторе значение V65 и посмотрите, на
сколько мы «ошиблись», заменяя приращение функции значением
дифференциала. Ш
О57, Производная произведения, частного,
композиции функций
1. Производная произведения и частного
ТЕОРЕМА (о производной произведения функций)1 -
Пусть функции f и д имеют производные в точке х0, тогда их про
изведение имеет производную в точке х0, причём
№' (*о) = Г (*о) Я (*о) + Я' (*о) f (*o)-
1 Интересно, что один из основателей дифференциального исчисления
Г. В. Лейбниц вначале считал, что справедлива неверная формула
дифференцирования произведения функций: (fg)'(x0) = f'(xo)g'(xo).
85 ! §57. Производная произведения, частного, композиции функций
□ доказательство. Рассмотрим предел
,. fg(x0 + Ах0) - fg(x) f(x0 + Ax)g(x0 + Ах) - f(xo)g(xo)
lim = lim . (*)
Д* —О АХ А* —О Ах
Представим f(x0 + Ал:) и g(x0 + Ал:) в виде f(x0 + Ал:) = f(x0) + A/
п g(xo + Ал:) = g(x0) + Ag. Тогда выражение (*) приобретёт вид
(f(x0) + А/) • (#(х0) + Д*) - f(x0) - я(х0)
lim =
А* —О АХ
/(х0) - Д£ + #(х0) -Af+Af-Ag
— \1т т
Дл; — О АХ
Разделив каждое слагаемое в числителе на Ал:, получим
4
—
^АХ
Предел каждого из слагаемых существует — -► /'(^о)> -^ 5'(^о)»
^АХД О Ах Длг — О
а в последнем слагаемом Д# -> 0 в силу непрерывности функции g
Дл; — О
в точке л:0). Значит, существует предел
,. (fg){xo+Ax)-(fg)(xo)
lim = f'(x0) • g(x0) + g'(x0) • /(x0),
Дл: -► 0 AX
а вместе с ним и производная функции /g в точке х0:
(fgY(x0) = Пх0)■ g(x0) + g'(x0)■ f(x0). Ш
Для доказательства формулы производной частного сначала
докажем лемму.
ЛЕММА ———-——————---——
Пусть функция f имеет производную в точке х0 и f(x0) ф О, тогда
существует производная функции - в точке х0, причём
доказательство. Рассмотрим предел
11
Ах) /(х0) = Ит /(хо)-/(хо
0 АХ Ал: —О Ах • f (Хо + Ах) • f (XQ)
/(хо+Ах)-/(хо) # 1 # )
^ Ах /(хо+Ах) /(xo)
Функция / дифференцируема в точке х, поэтому
lim = Г(ж )
Ал: —О АХ
86 I Глава IX. Производная и её применения
В силу непрерывности функции / в точке х0 (напомним, что
непрерывность / в точке следует из её дифференцируемое™ в этой точке)
существует предел lim f(x0 + Ах) — f(x0). Таким образом, существует предел
Ал:—>0
f(xo+Ax)-f(xo) ^ 1 О
^ Ах f(xo+Ax) f(xo)y
fix )
ТЕОРЕМА (о производной частного функций)
fix )
и он равен - * ° , что и требовалось доказать. И
/ (*o)
Пусть функции f и д имеют производные в точке х0 и д (х0) ф О,
тогда существует производная функции — в точке х0, причём
- g'(xo)'f(xo)
D доказательство. Представим отношение функций fug как
произведение функций /и—, т. е. —=/•—. По доказанной лемме функ-
ция — дифференцируема в точке л:0 и её производная в этой точке
равна —2 ° . Воспользуемся формулой производной произведения,
1
применённой к функциям / и — в точке х0. Получим
= П*о)
что и требовалось доказать. HI
Следствие. Для любого вещественного х Ф — + nk, k e Z, справед-
лива формула (tgx)'= —-—; для любого вещественного х Ф nk, k e Z,
cos2x
справедлива формула (ctgx)'= ———.
sin х
О доказательство. Воспользуемся доказанной формулой
производной частного и выведенными ранее формулами производных синуса
и косинуса.
/+ у — I s*nx | — (sinx)'; cosx - sinx • (cosx)' _ cos2x + sin2x _ 1
^ cos x J cos2 x cos2 x cos2 x'
Аналогично доказывается формула для производной котангенса. Ш
87 §57. Производная произведения, частного, композиции функций
Пример 28. Вычислим производную функции: а) (х2 + In х) • (х + 1); б) —.
П а) ((х2 + In х) - (х + 1))' = (х2 + 1пхУ ■ (х + 1) + (х2 + lnx) • (х + 1)' =
= I 2х + ^ 1 - (л: + 1) + (х2 + lnx);
Г £1V - И;'^-^'ИУ _ <?*- х2-е*-2х = е*-(*~ 2)
' \х*) = х4 х4 х3
Пример 29. Выведем формулу производной произведения трёх
функций (fgh)'.
п (fghy = (fgyh + fgh' = (fg + fg')h + fgh' = fgh + fg'h + fgh'. m
2. Производная композиции
ТЕОРЕМА (о производной композиции функций) ■■'
Если функции д и f дифференцируемы соответственно в
точках х0 и у0 = д (х0) и Е(д) с D (О, то функция h = f(g)
дифференцируема в точке х0, причём h' (х0) = V (у0) • д' (х0).
D доказательство. Пусть Ах — произвольное приращение
аргумента. Приращение Ах определяет приращение Ag, зависящее от Ах>
которое, в свою очередь, определяет приращение Ah функции h в
точке х0, причём:
АЛ = f(g(x0 + Ах)) - f(g(x0)) = f(y0 + Ag) - f(y0) = f'(y0) -Ag + Ag. a(Ag),
где a(Ag) -> 0.
Последнее равенство верно в силу дифференцируемости функции /
в точке у0.
Таким образом,
Ah AS Aff
— ~ff(u ) • — -\- — • (х (As) где ос (As) ^ 0.
Ах Ах Ах д# —о
Из непрерывности функции g в точке х0 получаем, что Ag —► 0, а
тогда а (А^) --> 0. Кроме того, — -► g'(x0), поскольку функция g диффе-
Ajc — O АХ Дл; —0
ренцируема в точке х0. Таким образом, существует lim — = h'(x0),
Дл:-»>0 АХ
причём h'(x0) = f'(y0) • g'(x0). Ш
Смысл доказанной теоремы простой: функция / похожа на
линейную функцию с коэффициентом f'(y0), функция g похожа на
линейную функцию с коэффициентом g(x0). Если подставить о,гну
линейную функцию в другую, получится линейная функция, коэффициент
которой равен произведению коэффициентов исходных функций. На
полученную линейную функцию похожа композиция функций fug,
поэтому её угловой коэффициент и есть производная этой композиции.
88 Глава IX. Производная и её применения
Пример 30. Вычислим производную функции: a) f(x) = \n(5x2+l);
б) (х2+ I)100; в) tg3x2.
D При вычислении производной композиции функции удобно
использовать обозначение, введённое в 10 классе (§ 26). Напомним, что
f(t)\t = g(X) обозначает значение функции f(t) при t = g(x), т. е. в точке
g(x). Тогда формулу производной композиции можно записать в виде
)' = f'(t)\t=eM-
t = б** + 1
б) (( \t = x + 1
= 100(х2 + 1)" • 2х = 200х(х2 +1)99;
в) (tg3x2)'=(f3)'|^t
^ 2*.
cos2 хг
Пример 31. Найдём производную функции f(x)= Чх.
П Пусть х > 0. Тогда %]х = х^, и производная находится по формуле
Пусть теперь х < 0. Тогда (-л:) > 0, и мы можем представить >/^
в виде степени с рациональным показателем: %[х = -(-л:)3, тогда
производная равна
В нуле данная функция производной не имеет.
Итак, мы получили, что для всех ненулевых вещественных х:
Замечание. Аналогичный результат верен для всех корней
нечётной степени: (л/х) = — , л е N.
Пример 32. Вычислим производную функции Л(х) = хх.
D Заметим, что функция h определена лишь при х > 0 (напомним,
что при определённых условиях о виде функции g любая функция вида
f8 определена только при / > 0) и принимает лишь положительные
значения. Для любого положительного числа а верно равенство а = е1п а,
поэтому данную функцию можно представить в виде h(x) = eln(**> = exlnx.
89 | §57. Производная произведения, частного, композиции функций
Вычислим теперь производную функции h как производную
композиции функций f(x) = е* и g(x) = х • \пх:
1) = хх - (1пх+ 1). И
Пример 33. Вычислим производную функции
f(x) = log^ + г(х4 + 3 + sinx).
Q Воспользуемся формулой перехода к другому основанию логарифма.
ч/ I 1п(х4 + 3 + sinx) |
_ (ln(x4 + 3 + sin х)У • ln(x2 + 1) - (ln(x2 + 1))/ - ln(x4 + 3 + sin x) _
In2 (x2 + 1)
4x3+cosx u ^ + 2x_ 1п(л.4 + 3 + sin x)
x4 + 3 + sin x x2 + 1 i^.
In2 (x2 + 1) "
3. Производная обратной функции.
Производные обратных тригонометрических функций
ТЕОРЕМА (о производной обратной функции)
Пусть f— непрерывная и строго монотонная функция на проме
жутке (а; Ь), д — обратная к ней функция. Если функция f диффе
ренцируема в точке х0 g (а; Ь) и f'(x0) ф 0, то функция д диффе
ренцируема в точке у0 = f(x0), причём д'(у0) =
Заметим, что существование обратной функции g (к непрерывной
и строго монотонной функции /), а также её монотонность и
непрерывность мы уже доказывали в главе VIII (с. 37).
□ доказательство. По определению
ч ч т 8{у)-8Ш ,. g(f(x))-g(f(x0)) x-x0 1
Во втором равенстве мы сделали замену у = f(x), x = g(y),
воспользовавшись однозначностью функций fug, после чего по свойствам
взаимно обратных функций заменили g(f(x)) на * и g(f(x0)) на х0. Кроме
этого, тот факт, что у стремится к у0 тогда и только тогда, когда х
стремится к х0, следует из непрерывности функции / в точке х0 и
непрерывности функции g в точке у0. Наконец, тот факт, что f(x) Ф f(x0) при
х Ф х0, следует из монотонности функции /. Ш
Замечание. Данная теорема имеет наглядный геометрический
смысл. Нам известно, что графики взаимно обратных функций
симметричны относительно прямой у = х. Поэтому если функция /имеет
касательную в точке (х0; у0), то функция g также имеет касательную в точке
90 i Глава IX. Производная и её применения
(y0; xo)j причём касательные
будут симметричны относительно
прямой у — х (рис. 9.18), а
значит, их угловые коэффициенты,
равные f'(x0) и g'(y0), будут
удовлетворять соотношению
8'(Уо) = 777ГТ-
Утверждение
Для любого хе(-1; 1)
справедливы формулы
(arcsin х)'= —
(arccosx)' = -
1-х2
1
/1-х2
X
f'(xo)'g'(x)=l
Рис. 9.18
П доказательство. Как мы знаем, функции арксинус и синус,
рассматриваемый на отрезке —; — , взаимно обратные.
( Л
Пусть у0 е (-1; 1) и х0 = arcsin*/0. При этом х0 е --|; £ . Функ-
V z z J
ция синус дифференцируема в любой точке х0 интервала —; —
причём её производная в этой точке равна cosx0 Ф 0. Тогда по теореме
о производной обратной функции функция арксинус имеет
производную в точке г/0, причём она равна
(arcsmx)
1
х - у о cos x0 cos (arcsin y0)
1 1
- sin2 (arcsinу0)
Заметим, что cos (arcsin y0) = Jl— sin2(arcsin y0) в силу того, что
{ Л
{ * Л
у0 g ; — , а косинус на этом интервале положителен.
V 2 2)
Можно было бы аналогично вывести формулу производной
функции арккосинус, однако есть путь проще.
Вспомним, что для любого х е [-1; 1] выполняется тождество
arcsin л: + arccosx = —, откуда
П . , v_(rc «Г
arccosx = arcsin л: и (arccosx) = arcsin л: =
2 2 J
:. В
91 i §58. Таблица производных. Первообразная
Утверждение
Для любого вещественного х справедливы формулы
(arctg х)'= —!—, (arcctgx)' =-_!_.
Q доказательство. Функции арктангенс и тангенс,
рассматриваемый на интервале -■^-; ;j L взаимно обратные.
Пусть i/0 е Д и л:0 = arctg г/0. При этом хое ; — . Функция
V 2 2У
тангенс дифференцируема в любой точке х0 интервала -—; ^- , при-
V 2 2)
чём её производная в этой точке равна —-— Ф 0. Тогда функция арк-
cosz х0
тангенс имеет производную в точке у0, причём она равна
(arctg х)> \х=уо= —|— = cos^arctg у0) = ^^ ^
cos2 х0
Формула производной функции f(x) = arcctgx следует из
формулы производной арктангенса и тождества arctg х + arcctg х = —,
справедливого для любого х е R. Ш
- Таблица производных- Первообразная
1. Таблица производных
Напомним, что понятие производной изначально было определено
для данной функции в данной точке как некоторое число. Если же
функция в каждой точке области определения имеет производную, то
мы можем говорить и о функции, ставящей в соответствие значению
аргумента число, являющееся производной данной функции.
Все элементарные функции имеют производные почти на всей
области определения. Сведём известные нам производные
элементарных функций в таблицу (см. с. 92).
С помощью этой таблицы посредством ранее доказанных теорем
можно получать производные многих функций, заданных формулами.
Однако таблицу производных можно читать и «справа налево».
Например, из формулы 7 таблицы видно, что функция, производной
которой является cos л:, — это sin л:. А из формулы 6 таблицы можно
выяснить, что это производная функции In л: при х > 0.
92 Глава IX. Производная и её применения
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Функция
f(x) = c
f(x)=xa
f(x) = ax (а ф 1)
f(x) = ex
f(x)-logax
f(x) = lnx
f(x) = slnx
f(x) = cosx
f (x) = tg x
f (x) - ctg x
f(x) = arcsinx
f(x) -arccosx
f (x) = arctg x
f(x) -arcctgx
Производная
V (x) = 0
Г(х) = оха"1
f (x) = In a • ax
f (x) = e*
f'(x) = -(x>0)
X
V (x) = cos x
f' (x) = -sin x
f'(x)- 1
cos2x
f (X) — ^
sin^x
1
/■j _ X2
f'(y\ ]
Пример 34. Выясним, производной какой функции является f(x) = х2.
П В правом столбце таблицы производных нет функции х2. Однако
во второй формуле таблицы при а = 3 имеется функция Зх2,
являющаяся производной функции Xs. Для того чтобы «избавиться» от
множителя 3, достаточно разделить Xs на 3 (ведь константа выносится за знак
х3
производной). Таким образом, х2 является производной функции —. Ш
3
П р и м е р 35. Выясним, производной какой функции является — при х < 0.
X
П Запишем при х < 0 выражение — в виде — = -—• Чтобы по-
X X X
лучить в качестве производной функцию —, можно брать как ис-
93 | §58. Таблица производных. Первообразная
ходную функцию 1п(-х), подбирая необходимый множитель. Тогда
(In (-*))'= (-1) = —. Итак, при х < 0 функция — является производ-
X X X
ной функции In {—х). Ш
Отметим, что полученный результат вместе с шестой формулой
таблицы можно записать в виде (1п(|л:|))'= —.
2. Первообразная
Удобно иметь название для функции, чьей производной является
данная функция.
ОПРЕДЕЛЕНИЕ
Функция F называется первообразной функции f на
множестве А если при всех х е А выполнено равенство Р (х) = f(x).
Если задача отыскания производной имеет физический смысл,
например отыскание скорости, то физическим смыслом первообразной
может считаться, например, отыскание координаты как функции
времени по скорости, заданной как функция времени.
Так функция синус на всей вещественной оси является
первообразной для функции косинус. В примере 34 мы выяснили, что на всей
вещественной оси первообразной для функции х2 является функция —Xs.
3
В примере 35 показано, что 1п(|л:|) является первообразной для
функции — на множестве /2\{0}.
X
Чтобы проверить, что функция F является первообразной
функции / на множестве А, достаточно найти производную функции F
и проверить, что в каждой точке множества А она равна значению
функции / в этой точке.
Всюду далее множество А мы будем считать промежутком или
объединением промежутков.
х \ х\
Пример 36. Покажем, что функция G(x)= —■—- является первообраз-
ной функции g(x) = \x\ на всей вещественной оси.
□ Рассмотрим х > 0. В некоторой окрестности точки х функция G
X2
совпадает с функцией —, поэтому согласно утверждению со с. 65 § 53
£)'=*.
Осталось отметить, что при х > 0 выполнено равенство |я| = я.
Итак, при х > 0 функция G является первообразной функции g.
94 | Глава IX. Производная и её применения
Аналогично в некоторой окрестности точки х9 при х < О функ-
X2
ция G совпадает с функцией , производная которой равна -х.
Отметим, что при х < О, g(x) = \х\ = -х.
Таким образом, остаётся проверить, что G'(x)\x = 0 = |0| = 0.
Вычислим эту производную по определению:
х\х\
Итак, при всех вещественных jc выполнено равенство (
что и доказывает требуемое. Ш
Замечания. 1) Из теоремы о дифференцировании суммы
следует, что если F — первообразная функции / на множестве А> то для
любого вещественного С функция F(x) + С также является первообразной
функции /. Таким образом, если функция имеет одну первообразную,
то она имеет бесконечно много первообразных.
2) В § 60 будет доказано, что если А является промежутком, то
любые две первообразные одной и той же функции различаются на
константу. Таким образом, чтобы найти все первообразные данной
функции на промежутке, достаточно найти одну первообразную, а
затем прибавлять к ней всевозможные постоянные.
3) В главе X будет пояснено, почему любая непрерывная на
промежутке функция имеет первообразную.
4) В отличие от производной, являющейся локальным понятием
(т. е. для рассмотрения производной в точке достаточно знать
функцию лишь в некоторой окрестности этой точки), первообразная —
понятие глобальное, т. е. можно говорить о первообразной на
промежутке, но не представляет интереса изучение первообразной функции /
в точке х0 (т. е. того, что у некоторой функции в одной точке
производная совпала со значением другой функции в этой точке).
5) Существуют функции, не имеющие первообразной ни на каком
промежутке. Ниже (с. 112) будет приведён пример такой функции.
3. Элементарные свойства первообразных
Свойства первообразных фактически являются иной
формулировкой соответствующих свойств производных. Объединим их в теорему.
ТЕОРЕМА (об элементарных свойствах первообразных) ————————
Пусть функции f и д на множестве А имеют первообразные F и G
соответственно, тогда:
1. Функция f+д имеет на множестве А первообразные, одна из
которых равна F+ G.
2. Для любого к g R функция kf имеет на множестве А
первообразные, одна из которых равна kF.
95 §58 Таблица производных. Первообразная
П доказательство. Докажем, например, свойство 1. Запишем
производную функции (F + G)(x):
((F + G)(x)Y = (F(x) + G(x)Y = F'(x) + G'(x) = f(x) + g(x) = (/ + *)(*).
Аналогично доказывается утверждение 2 теоремы. 11
Пример 37. Найдём какую-либо первообразную функции f(x) = 2x2 + x.
□ В примере 34 показано, что первообразной функции х2 являет-
х3
ся —. Аналогично можно проверить по определению, что первообраз-
х2
ной функции х является —. Используя утверждения теоремы, получим,
2 хз Х2
что одной из первообразных функции / является F(x) = 2 — + —. Ш
3 2
4. Таблица первообразных
Для отыскания первообразных удобно использовать следующую
таблицу, получаемую из таблицы производных.
№
1
2
3
4
5
6
7
8
9
Функция
f{x)=xa (сс*-1)
X
f(x) = sinx
f(x) = cosx
cos2x
fM = sin12x
f (x) = a"
w=—*—
1 + X2
fix) - 1 1- 1)
Первообразная
F(x)-—Цх« + 1
a + 1
F(x) = lnx
F(x) = -cosx
F(x) = slnx
F(x) = tgx
F(x) = -ctgx
In а
F(x) = arctgx
F(x) = arcsinx
Пример 38. Найдём какую-либо первообразную функции f(x) =
2x2-Z
П Такой функции нет в таблице. Однако, если преобразовать
выражение, поделив числитель почленно на знаменатель дроби, получим
jL 2хЛ 4 J {
96 ! Глава IX. Производная и её применения
- 2 -
Первообразной функции х2 может служить -х2, первообразной
_I I 5
функции х 2 может служить 2х2. Согласно теореме об элементарных
свойствах первообразных ответом в задаче может служить функция
4 ~ 1
-х2 -6х2.
Отметим, что ответами также являются функции
^х2 - 6х2 + 239, ^х2 - 6х2 + 566
5 5
и множество других функций, отличающихся от данных на константу. Ш
Рассмотрим более сложный пример.
Пример 39. Найдём какую-либо первообразную функции f(x) = \х — 1|
на R. г 1 >. *
\х- 1, если х ^ 1,
□ По определению модуля f(x)=<.
[1-х, если л: ^ 1.
Первообразной данной функции при х ^ 1 согласно таблице и
теореме об элементарных свойствах первообразных может служить лю-
х2
бая функция вида х + С, где С — произвольная постоянная. Ана-
логично, первообразной данной функции при х ^ 1 может служить
х2
любая функция вида х \- Cv
Функция, являющаяся первообразной на й, должна быть
непрерывной в любой точке, так как если нет непрерывности в точке, то тем
более нет и производной в этой точке. Для непрерывности функции
в точке х = 1 необходимо и достаточно равенства односторонних
пределов значению функции в данной точке. Таким образом, необходимо
выполнение равенства --1 + С=1-- + С1, откуда С = Сг + 1.
Положим, например, Сг = 0, тогда С = 1 и «кандидатом в
первообразные» для функции f(x) = \x- l| может служить функция
х2
х + 1, если х > 1,
2 *2
я , если х ^ 1
(точку л: = 1 можно включить в оба промежутка, так как значения
обеих квадратичных функций в этой точке равны).
Во всех точках, кроме точки х = 1, функция F дифференцируема,
поскольку совпадает в некоторой окрестности с дифференцируемой
функцией (квадратным трёхчленом) и её производная в точке х равна /.
Осталось проверить дифференцируемость функции F в точке х = 1.
97 j § 59. Неопределённый интеграл
Найдём левостороннюю производную функции F в точке х = 1:
х-— --
ъ,, ч| т F(x)-F(l) ,. 2 2 1,. (х-1)2 Л
^'(х) = hm —— — = lim = — lim — = 0.
Найдём правостороннюю производную функции F в точке х= 1:
„f/ vi r F(x)-F(l) ,. 2 *Ч 2 1 ,. (х-1)2 п
F'0*0 1 = lim ———г-^ = lim = - lim — = 0.
Таким образом, и в точке х = 1 функция F дифференцируема, и её
производная в этой точке равна нулю, т. е. /(1). Ответ: одна из искомых
первообразных равна
{х2
х + 19 если х > 1,
х ——, если х ^ 1.
2
О59. Неопределённый интеграл
1. Определение неопределённого интеграла
В предыдущем параграфе мы заметили, что если функция имеет
первообразную, то она имеет бесконечно много первообразных,
получаемых из данной добавлением константы. В следующем параграфе
будет доказано, что любые две первообразные одной и той же
функции, заданной на промежутке, различаются на константу и тем
самым, чтобы найти все первообразные данной функции на промежутке,
достаточно найти одну из этих первообразных, а затем прибавлять
всевозможные вещественные константы.
ОПРЕДЕЛЕНИЕ
Пусть на множестве А задана функция f, имеющая
первообразную. Совокупность всех первообразных функции f
называется неопределённым интегралом функции f.
Обозначение: \f(x)dx (читается: «интеграл эф от икс дэ икс»).
Если множество А является промежутком1, то множество
первообразных данной функции можно записать в виде {F(x) + С : С е R}
(здесь F — одна (любая!) из первообразных данной функции).
Такая запись чересчур громоздка, поэтому традиционно неопределённый
интеграл записывают так2: \f(x)dx = F(x) + С, С е R.
1По умолчанию в качестве множества А мы будем рассматривать
естественную область определения функции /.
2Сравните с записью корней тригонометрического уравнения. Вместо
{n + 2nk: k g Z) пишем просто к + 2nk, k e Z.
98 Глава IX. Производная и её применения
Например: | sinxdx = -cos* + С, \x2dx = — + С и т. д.
Вместе с тем не следует забывать о том, что такая запись верна
лишь для функций, заданных на промежутке!
Пример 40. Запись | — dx = \n\x\ + С достаточно часто встречается
в литературе, но не является верной. Как показано в примере 35,
функция 1п|л:| действительно является первообразной функции — на
X
всей области определения. Однако эта область определения
представляет собой объединение двух лучей, на каждом из которых любые две
первообразные различаются на константу. Но константы эти могут
быть разными!
Таким образом, правильная запись в данном случае такова:
г 1 Jinx + С19 если х > 0, Сг е Л,
J х " \\п(-х) + С2, если х < О, С2 е R.
Выясним, что понимать под записью J f(x)dx + J g(x)dx. Ведь
каждое слагаемое — это множество, состоящее из функций. Будем
понимать (аналогично, например, задаче 1.167 из учебника 10 класса) под
суммой множеств множество сумм их элементов. Иначе говоря,
jf(x)dx + jg(x)dx = {F +G:Fe \f(x)dx, G e jg(x)dx}.
Аналогичным образом понимается запись k\f(x)dx, где k —
некоторое число. А именно, k\f(x)dx = $kF(x): F e JT
ТЕОРЕМА (об элементарных свойствах неопределённого интеграла)
Пусть f и д — функции, имеющие первообразные на
множестве Л, тогда:
2. )kf{x)dx = k\f{x)dx.
доказательство. Докажем утверждение 1 теоремы. В обеих
частях равенства стоят множества. Таким образом, требуется доказать
равенство двух множеств.
Рассмотрим элемент множества \f(x)dx + \g(x)dx. По
определению он равен сумме некоторых первообразных F и G функций fug
соответственно. По теореме об элементарных свойствах первообразных
функция F + G является первообразной функции / + g, & потому
является элементом множества \(f(x) + g(x))dx. Тем самым
\f(x)dx + jg(x)dx с j(f(x) + g(x))dx.
99 ! § 59. Неопределённый интеграл
Для доказательства включения J (/ (х) + g (х)) dx с [ / (х) dx + f g (x) dx
возьмём элемент множества J (f(x) + g(x))dx, т. е. Н — первообразную
функции f + g, и докажем, что Н является элементом множества
\f(x)dx + \g(x)dx, т. е. представима в виде суммы F + G, где F и G —
первообразные функций / и g соответственно.
Пусть F — произвольная первообразная функции /. Рассмотрим
функцию G = Н - F. Докажем, что G — первообразная функции g.
Для этого возьмём производную:
G'(x) = Н'{х) - F'(x) = (f(x) + g(x)) - f(x) = g(x).
Это равенство доказывает, что G — первообразная функции g,
а тогда Н = F + G — искомое представление функции Н как суммы
первообразных функций fug.
Аналогично доказывается утверждение 2 теоремы. IS
Пример 41. Найдём J (х2 - 2х + 5)dx.
□ Согласно теореме об элементарных свойствах неопределённого
интеграла имеем \(х2 - 2х + 5)dx = \x2dx - 2Jxdx + b\dx = — + Сг -
- x2 + C2 + Ъх + C3; Cl9 C2, С3ей. 3
Из этой записи видно, что функция х2 + Ъх является одной из
3
первообразных функции х2 — 2х + 5. Поскольку функция и её
первообразная заданы на всей вещественной оси, то любая другая первообразная
данной функции получается из найденной прибавлением произволь-
г х^
ной постоянной. Поэтому I (х2 - 2х + 5)dx = х2 + 5х + С, С е Н.Ш
В дальнейшем мы не будем писать столь подробных рассуждений,
ограничиваясь краткой записью, как продемонстрировано в
следующем примере.
Пример 42. Найдем J dx при х < 0.
dx= jix + 2 + ±}dx= \xdx + 2\dx + \^dx= — + 2x
x) + C, С eR. Ш
2. Интегрирование методом подстановки.
Интегрирование рациональных функций
Мы знаем формулу производной композиции функций:
(здесь эта формула записана «справа налево» по сравнению с её
записью в § 57). Будем далее считать, что указанная композиция
определена на некотором промежутке.
ТОО Глава IX. Производная и её применения
Из этой формулы следует то, что если первообразная функции /
равна F, то первообразной функции f(g(x)) • g'(x) будет функция
F(g(x)), т. е. по определению интеграла верна формула
JF'(g(x)) - g'(x)dx = F(g(x)) + C, С tR.
Пример 43. Найдём jvsinx • cosxdx при х е [0; я].
D Обозначим g(x) = sinx. Получим
Таким образом, в роли F'(t) выступает функция <Jt9 а. тогда в роли
Г 2 -
F(t) — первообразная функции \t9 т. е. — t2. Таким образом,
3
2 -
cosxdx = -(sinx)2 + С, С е R.
3
Обычно такие подробности опускают и оформляют решение так:
[Vsinx -cosxdx = \Jtdt= -t* +C= -(sinx)2" + С, С sR.M
J t = sin xJ 3 3
Обратим внимание на то, что в приведённой краткой записи
вместо t'(x)dx используется обозначение dt, что согласуется с ранее
введёнными обозначениями. В дальнейшем мы будем использовать
подобное обозначение.
Пример 44. Найдём \sin2xdx.
П способ 1. [sin 2x dx = 2 [sin x • cosxdx = 2\tdt = t2 + C =
J J t = sin x J
= sin2x + С, С e R.
способ 2. [sin2xdx = 2 [sinx • cosxdx = -2 [cos* • (-sinx)dx =
* J J J t = COS X
= -2jtdt = -t2 = -cos2л: + С, С е R.
способ з. [sin2xdx = - [sin2x- 2dx = - \ sintdt = —cos£ + C =
, J 2J t = 2x2J 2
= --cos2x + C, Сей.
La
Обратите внимание на то, что, применяя тригонометрические
формулы, можно показать, что три полученных ответа определяют одно
и то же множество функций. IS
Заметим, что в разобранном примере при решении первым
способом подстановка была очевидной, а при решении двумя другими
способами пришлось «подогнать» выражение к нужному виду. Умение
видеть нужную подстановку достигается лишь практикой.
Часто встречающейся подстановкой является подстановка
линейной функции.
lOij § 59. Неопределённый интеграл
Пример 45. Найдём U3x + 5dx.
П При замене t = Зх + 5 имеем t'(x) = (Зх + 5)' = 3, а тогда dt = 3<2д\
Имеем [J3x + bdx = - \yfidt = -t2+C = -(Зх + Sf + C, Сей. S
J v *=з*+5 3J 9 9
Аналогично можно получить общую формулу:
jf(ax + b)dx= ±F(ax + b) + C,
где F — одна из первообразных функции /.
Иногда до подстановки линейной функции выражение ещё нужно
преобразовать.
Пример 46. Найдём [—^—.
J 9 + х2
П Мы знаем из таблицы \ -, поэтому попытаемся привести
данный интеграл к виду известного интеграла. Чтобы получить
слагаемое 1 в знаменателе, нужно знаменатель подынтегральной функции
разделить на 9, а тогда, чтобы интеграл не изменился, нужно домно-
жить интеграл на -.
dx I f dx
_ 1 Г dx 1 f 3dt
x^~9J /^y f=x9 J 1+ t2
^
Для обоснования третьего знака равенства использовалась замена
*=|, откуда *Ч*)=(|J =|. Ш
Пример 47. Найдём f —г dx при х > 1.
J х2- 1
□ Запишем подынтегральную функцию в виде
1 1 Г 1 1
х2-1
Рассмотрим
f—^— dx = f—=
Аналогично
|^ 1) + С2, C2eiJ.
I Глава IX. Производная и её применения
Таким образом, при х > 1
^dxUln(xl)ln(x + l)) + CUn(
x2- 1 2 2 {x+l
:, с eR.m
Отметим, что интеграл данной функции на всей её области
определения может быть записан так:
-lnf 2—± \+С19 еслил:>1,
2 ух+ 1)
±ln(j-^J + C2, если-1<*<1,
1 (х-Л
- In + С3, если х < -1.
2 I х + 1)
Остановимся на использованном выше приёме подробнее. Пусть
нужно проинтегрировать рациональную функцию, знаменатель
которой разложен на множители, а степень числителя меньше степени
знаменателя (такого соотношения между степенями всегда можно
добиться, разделив с остатком числитель на знаменатель, т. е.
выделив «целую часть»). Тогда можно разложить эту функцию в сумму
так называемых «простейших дробей» и интегрировать каждую
дробь по отдельности.
Пример 48. Найдём [ — dx при 1 < х < 2.
J (х - 1)(х - 2)(х - 3)
П Попробуем представить подынтегральную функцию в виде
суммы простейших дробей:
4х - 6 а Ь с
(х - 1)(х - 2)(х - 3) " х - 1 х-2 х-3'
Приведя к общему знаменателю и приравняв числители, получим
равенство, которое должно выполняться при всех значениях х, кроме
х = 1, х = 2, х = 3:
4х-6 = а(х- 2)(х - 3) + Ь(х - 1)(х - 3) + с(х - 1)(х - 2). (*)
Равенство (*) — это равенство двух многочленов, поэтому, если оно
выполнено при всех х, кроме х = 1, х = 2, х = 3, то эти многочлены
совпадают, а потому и при jc=1,jc = 2,jc = 3 это равенство тоже выполнено.
Подставив в равенство (*) х = 1, получим —2 = 2а, откуда а = -1.
Аналогично, подставив в равенство (*) х = 2, получим 2 = -Ь, откуда
Ъ = -2. Наконец, подставив в равенство (*) х = 3, получим 6 = 2с,
откуда с = 3.
Таким образом, получаем равенство
4х - 6 -1-2.3
- 1)(х - 2)(х -3) х-1 х-2 х-3
103, § 59. Неопределённый интеграл
Осталось найти интеграл с учётом ограничений на х:
Г
J (х -
dx[2[ + 3f
1)(х - 2)(х - 3) J х-1 * х-2 * х-3
= -\п(х- 1)- 21п(2-л;) + 31п(3-*) + С, С е Н.Ш
Вопрос об интегрировании рациональных функций может быть
рассмотрен существенно глубже, но здесь мы этого делать не будем.
Для нахождения интегралов бывает также полезно осуществлять
подстановку в форме х = g(t)9 где g — обратимая функция.
Пример 49. Найдём jvl - x2dx, при х е (-1; 1).
□ Сделаем подстановку х = sint. Чтобы sint принимал все значения
между -1 и 1, достаточно положить t е ; — . Тогда л]1 — х2 = cost,
V 2 2)
так как при выбранных t функция cos t принимает неотрицательные
значения. Из равенства х = sint, t e -—; — , получим t = arcsinjc, откуда
V 2 2у
*'(*) =
/1- х2 cos(t(x))
Итак, t'(x) - cos(t (x)) = 1, откуда исходный интеграл равен
j cos2 (t (х)) -Г (х) dx.
Получаем
Г ?ij, Г1 + cos2t .. г 1 .. If o^ .. t sin2t ~
J cos2 tdt = J dt = J -dt + -J cos2t dt = - + + C.
Подставив t = arcsin x в формулу интеграла, получим
, СеК.Ш
Отметим, что если подынтегральная функция имеет в своей записи
выражение вида д/а2 - х2, то можно пробовать подстановку х = а sin t
при t е -—; — , так как при этом корень извлекается. Если же
подынтегральная функция имеет в своей записи выражение вида у/а2 + х2 , то
бывает полезным использ<
Пример 50. Найдём [ Х
одстановку :
х2 = А + tg21 = -!— и dx = d(tgt) = -\-dt.
бывает полезным использовать подстановку х = а tg t, где t e I ; — |.
dx
□ Сделаем подстановку х = tgf, где £ е | ; — |. Тогда
Ct Ct
COS t COS2 t
104: Глава IX. Производная и её применения
Таким образом, имеем [ х = \
J Jl+ х2 x=tgt J cost
cost
С полученным интегралом можно поступить двумя способами.
способ 1. Выразим cos* через тангенс половинного аргумента:
l-tg*|
cos t = . Получим
1+tg2- 1+tg-
Ut = f^ ^
(здесь мы использовали найденное в примере 47 значение с учё-
J х2 - 1
том того, что и = tg— при выбранном промежутке изменения t нахо-
дится в интервале (—1; 1)). Осталось выразить tg —через tg£ = ;c (это
выражение получается, например, решением относительно t уравнения
х = -, с выбором того из корней, который лежит в промежутке
i-tg*f
(-1; 1)), а затем подставить полученные выражения в формулу (*).
В результате получим
f . dx =\n(x + Jx2+l)+C, CgR.
J Vl+ x2 v y
способ 2. Умножим числитель и знаменатель дроби на cos t.
т-г COS*
Получаем
f dt Ccostdt _ г costdt с du .^^.
J COS f J COS2 f J 1 - Sin2 £ w = sin * J 1 - M2
in + cin+c.
2 1-w 2 1-sin^
При получении данной формулы мы вновь, как и в предыдущем
Г dx
способе, использовали значение при х е (—1; 1). Теперь нужно
( Л
выразить sin* через x = tgt с учётом того, что £ е -—; — , т.е.
tgt х V 2 2У
sint = —===== = , и после преобразований получить
Vi + tg2* Vi+^
J yjl+ X2 V У j_
105 § 59. Неопределённый интеграл
3. Интегрирование по частям
Рассмотрим формулу производной произведения:
(f-gy=f-g+g'- f.
Выразив из неё одно из слагаемых правой части и взяв интеграл
от обеих частей, получим
\f'(x) ■ g(x)dx = f(x) . g(x) - jg'(x) • f(x)dx.
Эта формула называется формулой интегрирования по частям.
Она бывает полезной при интегрировании произведений функций, один
сомножитель которых при дифференцировании упрощается, а другой
не слишком усложняется при интегрировании.
Если воспользоваться ранее введёнными обозначениями dv = v'dx,
du = u'du, то формула приобретёт компактный и легко запоминаемый
вид: judv = uv - jvdu.
Пример 51. Найдём \х sinxdx.
П Воспользуемся формулой интегрирования по частям, приняв
и = х, du- dx,
dv = sinxdXy v = -cos л:.
Имеем
[л;sin*da; = \xd(-cosx) = -cos* • x - \(-cosx)dx =
= -arcosjc + sin* + С, С e R. Ш
Рассмотрим более интересный пример.
Пример 52. Найдём \ех • sinxdx.
П Воспользуемся формулой интегрирования по частям, где
и = ех9 du = exdx,
dv = sinxdx, v = -cos л:.
\ex • sin x dx = \exd (-cos x) = -cos x • e* - J-cos xdex =
= -cos л: • e* + \ex • cos x dx. (*)
Для отыскания \ех • cos x dx вновь воспользуемся формулой
интегрирования по частям, где
и = ех9 du = exdx,
dv = cosxdx, v = sin л:.
\ex • cos#da; = j^dsinjc = sina; • ex - \sinxdex = sina; • ex — \ex • sinxdx.
Казалось бы, мы в тупике, ведь пришли к тому же интегралу,
с которого начали. Но... Подставим найденное выражение \ех • cosxdx
в формулу (*):
\ех • sinxdx = -е* • cos* + ех • sin* - \ех • sinxdx.
откуда
106; Глава IX. Производная и её применения
Осталось перенести слагаемое из правой части в левую, получив
2 \е* • sinxdx = -ех • cosx + ех • sin* + С, С е R,
jex • sinarda; = -ех • (sinar- cos;c) + С, С е R.
Самостоятельно продумайте вопрос о том, откуда взялась
константа после перенесения в другую часть интеграла, почему
\ех • sinxdx + je* • sinxdx = 2 \ех • sin#dx и почему после деления
на 2 всей формулы константа на 2 не поделена, й
. «Французские» теоремы
В этом параграфе будут доказаны теоремы, позволяющие
использовать производную как мощное средство исследования свойств
функции, с помощью которого легко определять экстремумы функции,
промежутки возрастания и убывания функции, находить множество
значений функции, доказывать неравенства и тождества.
ТЕОРЕМА ФЕРМА
Пусть в точке х0 функция f имеет производную. Если точка х0
является точкой экстремума (максимума или минимума), то
f'(xo) = O.
Физический смысл: скорость изменения функции в точке
экстремума равна нулю.
Геометрический смысл: касательная в точке экстремума
параллельна оси абсцисс (рис. 9.19).
П доказательство. Докажем утверждение теоремы в
предположении, что х0 — точка максимума.
Пусть g (х) =
f(x)-f(x0)
X - Хп
\
0
Рис. 9.19
X
хо
. По определению /'(*о)= lim^(jc).
Так как точка л:0 является точкой
локального максимума, то существует
окрестность Ub(x0), такая, что Ух е Ub(x0)
выполняется неравенство f(x0) ^ f(x).
Тогда при х е (х0; х0 + 8) будет
выполняться неравенство g(x) ^ 0 (так как
при этих х выполняются неравенства
f(x) ^ f(x0) и х > х0). Отсюда следует
(см. с. 7), что lim g(x) ^ 0. Аналогич-
х-*хо+
но можно показать, что lim g(x)^0.
§60. «Французские» теоремы
Мы знаем, что существует предел limg(x) = f'(x0), а значит,
левосторонний и правосторонний пределы равны между собой и равны
f'(x0). Тогда
f'(xo)= lim
X-*Xq +
и одновременно
Ук
Л
откуда f'(x0) = 0. Ш х^х°-
Таким образом, если функция везде дифференцируема, то её
экстремумы стоит искать лишь в тех точках, где производная равна 0.
Как показывает пример функции f(x) = х3, имеющей в точке х = 0
производную, равную 0, но не имеющей в этой точке экстремума,
утверждение, обратное теореме Ферма, неверно.
ТЕОРЕМА РОЛЛЯ -—-~--———■——
Пусть функция f определена и непрерывна на отрезке [a; to],
а также дифференцируема на интервале (a; to) и при этом
f (a) = f (to). Тогда существует точка с е (a; to), такая, что V (с) = 0
Геометрический смысл: если
значения дифференцируемой функции на
концах отрезка [а; 6] равны, то на
интервале (а; Ь) существует точка, в которой
касательная к графику функции будет
параллельна оси абсцисс (рис. 9.20).
D доказательство. Поскольку
функция / непрерывна на [а; Ь], то по
теореме Вейерштрасса она достигает на этом
отрезке своих наибольшего и
наименьшего значений, т. е. существуют
точки хх е [a; b] и х2 е [а; Ь], такие, что
f{xx) = т — наименьшее значение
функции / на отрезке [а; Ь] и f(x2) = М — наибольшее значение функции /
на отрезке [а; Ь].
Если хотя бы одна из точек хг и х2 находится внутри отрезка
[а; Ь], то по теореме Ферма (так как тогда эта точка является точкой
экстремума, возможно нестрогого) производная функции / в этой
точке равна 0 и искомая точка с найдена. Если же обе точки являются
концами отрезка [а; Ь], то т = М в силу того, что f(a) = f(b), sl значит,
функция является константой на [а; Ь]. В этом случае в качестве
точки с можно взять любую точку интервала (а; Ь), поскольку
производная константы равна нулю в любой точке. Ш
Замечание. Конечно, из дифференцируемости функции на (а; Ъ)
следует её непрерывность на (а; 6), поэтому требование непрерывности
функции / на [а; Ь] фактически добавляет нам требование
непрерывности функции / в точках а и 6. В то же время отказаться от этого уело-
а
Рис. 9.20
1081 Глава IX. Производная и её применения
О
а
х
вия нельзя: на рисунке 9.21 приведён
пример функции, для которой
выполняются все условия теоремы Ролля, кроме
непрерывности функции в точке а. При
этом не существует точки с е (а; 6),
такой, что f'{c) = 0.
Рис. 9.21
Пример 53. Докажем, что производная
многочлена р(х) = (х2 - 4)(х - 5)(х - 7)
имеет ровно три вещественных корня.
О Нетрудно проверить, что по теореме Ролля, применённой к
функции р и отрезкам [-2; 2], [2; 5] и [5; 7] (так как р(-2) = р(2) = р(5) =
=Р(7) = 0), существуют точки сг е (-2; 2), с2е (2; 5), с3е (5; 7), такие, что
/?'(ci) =Р'(С2) =Р'(сз) - 0« Производная данного многочлена — многочлен
третьей степени, поэтому больше трёх корней у него быть не может. В
ТЕОРЕМА ЛАГРАНЖА
Пусть функция f определена и непрерывна на отрезке [a; to],
а также дифференцируема на интервале (a; to). Тогда существует
ЦЬ) - f(a)
точка с е (а; Ь), такая, что Г (с) =
b- a
Геометрический смысл: правая часть формулы представляет
угловой коэффициент прямой, проходящей через точки А (а; f(a))
b — а
и В (b; f(b)) (рис. 9.22). Таким образом, теорема Лагранжа утверждает,
что на интервале (а; Ъ) найдётся точка, в которой касательная к
графику функции параллельна секущей АВ.
Q доказательство. Нетрудно проверить, что для функции
g(x)= f(x)-
f(b)-f(a)
b- a
(x-a)
выполняются все условия теоремы Ролля на промежутке [а; Ь].
Действительно, во-первых, она
непрерывна как разность непрерывных
функций. Во-вторых, она имеет произ-
f(b) - f(a)
У
водную на (a; b): g'(x) = f'(x)-
b-a
и, в-третьих, g(b) = g(a).
По теореме Ролля существует
точка с е (а; Ь), такая, что g'(c) = 0, т. е.
Г (с)-
f(b)- f(a)
b-a
= 0, что и требовалось до-
Рис. 9.22
казать. IS
109'§60. «Французские» теоремы
Заключение теоремы Лагранжа может быть сформулировано
иначе: при Ал: > 0 существует точка с е (а; а + Ах), такая, что
Af = f'(c)Ax. (1)
Интересно сравнить эту формулу с определением дифференцируе-
мости функции в точке: функция / называется дифференцируемой
в точке а, если она представима в виде
Д/=/'(а)Дх + <х(Дх), (2)
причём ос (Ал;) = о (Ал:) при Ал: -> 0.
И формула (1), и формула (2) позволяют записать приращение
функции в точке а, при этом формула (2) говорит, что остаток будет
о (Ах) при Ал: —> 0, но не позволяет его оценить, зато производная
берётся в известной точке. Формула (1) позволяет записать приращение
функции без использования остатка (что бывает полезно, если нам
известны границы значений производной), но при этом неизвестна точка,
в которой следует брать производную.
Пример 54. Докажем, что если функция дифференцируема на
интервале (а; Ь) и не ограничена на нём, то и её производная не ограничена
на интервале (а; 6).
П Предположим, что производная ограничена на интервале (а; 6),
т. е. существует число М, такое, что Ух е (а; Ь) выполняется
неравенство \f'(x)\^M. Зафиксируем некоторое х0 е (а; Ь). Теперь возьмём
ещё одно произвольное хг е (а; Ь). По теореме Лагранжа существует
точка с е (х0, хг) (или с е (х19 х0), если хг <хо)9 такая, что
Пс)-
Х1 ~ х0
Отсюда получаем f(xx) = ff(c)(x1 - х0) + f(x0), откуда
|/(*i)l = \f'(c)(xx - х0) + /(хо)| < \Г(с)\ • \хг - хо\
||
т. е. (в силу произвольности выбора точки хг) функция /
ограничена на (а; Ъ) сверху числом М{Ъ - а) + |/(хо)|, а снизу — числом
-(М(Ь - а) + \f(xo)\)9 что противоречит условию. Ш
Докажем как следствие теоремы Лагранжа следующее,
неоднократно упоминавшееся нами, важное утверждение.
Следствие. Если производная непрерывной на промежутке [а; Ъ)
функции равна 0 в каждой точке интервала (а; Ь), то эта функция
постоянна на промежутке (а; Ъ).
U доказательство. Возьмём произвольную точку х0 Ф а из [а; Ь).
Применяя теорему Лагранжа к функции /, заданной на отрезке [а; х0],
получим, что существует точка с е (а; х0), такая, что
f(xo)-f(a) = f'(c)(xo-a) = O.
1101 Глава IX. Производная и её применения
Таким образом, f(x0) = /(а), а значит, в силу произвольности
выбора х0, функция / постоянна на [а; Ь), т. е. \/х е [а; Ъ) f(x) = f(a). Ш
Самостоятельно докажите, что утверждение следствия верно и для
интервала (а; 6), в том числе если а = —оо или Ъ = +оо.
Пример 55. Докажем тождество arctg х + arctg = — при х > -1.
1-х
П Вычислим производную функции f(x)= arctg x + arctg .
1 + X
Для любого х из области определения функции / (т. е. при х Ф -1)
( 1-х\ 1 1 (l-x
fix) = (arctg x)'+ arctg ±—=- = —1— +
1+
+ (1.+х); -^^г=о.
1+х2 2(1+х2) (1+х)2
По следствию (с. 109) функция / постоянна на промежутке
(-1; +оо), т.е. f(x) = с при любом х>—1. Для того чтобы найти
константу с, вычислим какое-либо значение функции /; например,
/(0) = — при х = 0. Таким образом, при любом х > -1 верно равенство
4
1
arctg х + arctg = —, что и требовалось доказать. Н
1 + х 4
Замечание. Из этого примера видно, что даже если производная
функции / равна 0 на всей области определения функции /, нельзя
утверждать, что функция / принимает постоянное значение на всей
области определения. Проверьте, например, что при х < -1
значение функции не равно —. Таким образом, существенным для постоян-
4
ства функции является условие равенства 0 производной именно на
интервале!
Теперь можно доказать теорему о строении класса первообразных.
ТЕОРЕМА
Пусть на промежутке (а; Ь) задана функция f, имеющая
первообразную на этом промежутке. Тогда любые две первообразные
функции f на (а; Ь) различаются на константу.
Тем самым любая первообразная функции / на промежутке (а; Ь)
может быть получена прибавлением какой-либо константы к
некоторой фиксированной первообразной.
П доказательство. Пусть Fx и F2 — две первообразные функции /
на (а; Ь). Тогда рассмотрим функцию G = Fl — F2. Получим
G'(x) = F{(x) - Fi(x) = f(x) - f(x) = 0.
111 §60. «Французские» теоремы
Итак, при х е (а; Ъ) G'(x) = 0, а тогда по следствию из теоремы
Лагранжа G — константа, что и требовалось доказать. IS
В заключение этого параграфа докажем ещё одну теорему.
ТЕОРЕМА ДАРБУ (теорема о промежуточных значениях производной)
I Пусть f дифференцируема на (а; Ь) и точки х^ х2 е (а; Ь). Тогда
производная на отрезке [x^Xg] принимает все значения между
f (х,) и Г(х2).
i сиг
1
D доказательство. Не умаляя общности, будем считать, что
Г(х1)<Г(х2).
Сначала разберём случай, когда ff(x{) < 0, a f'(x2) > 0. Докажем,
что существует точка 6 на интервале (хг; х2)> такая, что f'(Q) = 0. По
теореме Вейерштрасса функция / достигает наименьшего и
наибольшего значений на отрезке [хг; х2].
Если хотя бы одно из этих значений достигается не на границе
промежутка [хг; х2], то соответствующая точка будет точкой
экстремума, производная в которой равна 0 по теореме Ферма.
Пусть теперь наибольшее и наименьшее значения функции
достигаются только на границах промежутка [хг; х2] (в частности, это
означает, что функция отлична от константы). Если f(x±) — наименьшее
значение функции, то
х-*хх+ X - Х1
(поскольку числитель и знаменатель указанной дроби положительны
при х > хг)9 что противоречит предположению. Значит, в точке хг
достигается наибольшее значение функции. Тогда наименьшее значение
функции достигается в точке х2. Но теперь
f (х2) = hm ^ 0
*-»*2" X — Х2
(так как числитель дроби положителен, а знаменатель отрицателен
при х < х2)9 что противоречит предположению о том, что f'(x2) > 0.
Полученные противоречия показывают, что хотя бы одно из
максимального и минимального значений должно достигаться во
внутренней точке G е (хг; х2)9 и f'(Q) = 0, как уже было показано.
Рассмотрим теперь общий случай. Пусть с — произвольное число,
такое, что /4^i) < с < f'(x2). Докажем, что существует точка G на
интервале (хг; х2), такая, что f'(Q) = с.
Рассмотрим вспомогательную функцию g(x) = f(x) — ex. Она
удовлетворяет условиям теоремы Дарбу и g'(*i) < 0 < #4*2)- По
доказанному выше существует точка G на интервале (хг; х2)9 такая, что g'(Q) = 0,
но g'(Q) = f'(Q) - с, т. е. /'(6) = с, что и требовалось доказать. Ш
112 Глава IX. Производная и её применения
Заметим, что описанное в теореме Дарбу свойство промежуточных
значений (т. е. тот факт, что для любых хг и х2 из области определения
функции g функция принимает все значения между g(x^) и g(x2)) ВЬ1~
полняется для непрерывных функций (см. главу VIII). Производная
произвольной дифференцируемой функции / не обязательно
является непрерывной, однако любая производная (в том числе разрывная)
обладает свойством промежуточных значений согласно доказанной:
теореме. Так, например, функция Дирихле D не имеет первообразной |
ни на каком промежутке уже потому, что ни на каком промежутке не
обладает свойством промежуточного значения.
^/хст
орический комментарий
Ж. Г. Дарбу (1842—1917) — выдающийся французский математик,
профессор College de France. Его многочисленные исследования относятся
практически ко всем современным ему областям математики. Наибольший вклад
внёс в теорию дифференциальных уравнений и дифференциальную геометрию.
С его именем связаны вектор Дарбу, тензор Дарбу, поверхность Дарбу и т. д.
Интересно, что, когда Дарбу умер, немецкие математики во главе с
Гильбертом выразили соболезнование в связи с его кончиной, за что были
обвинены чуть ли не в измене Германии. Шла Первая мировая война, и Германия
с Францией были по разные стороны фронта. Однако признание
математических заслуг оказалось выше политической вражды.
. Исследование функции с помощью производной
В 10 классе (IV глава) мы видели, как непросто подчас находить
промежутки возрастания и убывания функции, экстремумы функции.
Применение производной позволяет превратить эти задачи в чисто
технические (и, как правило, несложные).
1. Возрастание и убывание функции
ТЕОРЕМА (критерий нестрогой монотонности функции)
П Пусть функция f непрерывна на промежутке (а; Ь) и
дифференцируема на интервале (а; Ь), тогда:
1. Функция f возрастает на {а\Ь) (возможно, нестрого) тогда
и только тогда, когда Vx е (а; Ь) V (х) > 0.
2. Функция f убывает на (а; Ь) (возможно, нестрого) тогда
и только тогда, когда Vx e (а; Ь) V (х) < 0.
D доказательство. Докажем 1. Пусть функция / нестрого
возрастает на (а; Ъ).
1) Докажем необходимость условия, а именно, что \/х0 е (а; Ъ)
Г(х0)>0.
VI3|_§61. Исследование функции с помощью производной
Заметим, что если Ах > О, то f(x0 + Ах) - f(x0) > О, а если Ах < О,
то f(x0 + Ал:) - f(x0) ^ 0 в силу возрастания /.
Рассмотрим функцию g(Ax) = —— ^-^, тогда
Ах
ё(Ах)=Г(х°+Ах)-Пх°) > О при Д** 0.
laX
По определению f (х0) = lim g(Ax). По теореме о предельном Пере-
Дл:-► О
ходе в неравенстве f'(x0) ^ 0.
2) Докажем достаточность. Пусть \/х е (а; Ъ) f'(x) > 0, возьмём
xl9 x2 e (a; b) (пусть хг < х2). По теореме Лагранжа существует такая
точка с е (хг; х2)> что f(xx) - f(x2) = ff(c)(x1 - х2) < 0. Таким образом,
f(X\) ^ /(^2)» что и означает, в силу произвольности выбора точек хх
и х29 возрастание функции / на (а; Ь). Ш
Заметим, что мы доказали критерий нестрогой монотонности
функции. По аналогии, казалось бы, можно сказать, что функция /
строго возрастает на (а; Ь) тогда и только тогда, когда f'(x) > 0 на
(а; 6). Но это неверно. Если производная строго положительна на
интервале, то функция действительно будет строго возрастающей,
однако функция будет строго возрастающей и в том случае, если
производная равна нулю лишь в конечном числе точек.
ТЕОРЕМА (достаточное условие строгого возрастания функции) —
П Пусть функция f непрерывна на промежутке (а; Ь) и
дифференцируема на интервале (а; Ь), причём Vxe (a; b) f'(x)>0 и
производная равна нулю лишь в конечном числе точек, тогда f строго
возрастает на промежутке (а; Ь).
□ доказательство. Пусть функция / удовлетворяет всем
перечисленным условиям. Согласно предыдущей теореме / нестрого возрастает
на (а; Ь). Осталось доказать строгое возрастание, т. е. что \/х2 > х1
f(x2) > f(xi) (фактически f(x2) ^ fix^). Предположим, что Зх\, х2 е (а; Ь),
такие, что fixx) = f(x2), но тогда функция постоянна на промежутке
[хг; х2] (так как функция нестрого возрастает на [х^ х2]), а тогда её
производная на [х\\ х2] тождественно равна 0, что противоречит условию
о конечности множества точек, в которых производная равна 0. Ш
Замечание. Сформулированное в теореме условие не является
необходимым для строгого возрастания дифференцируемой функции, но
соответствующий пример достаточно сложен.
Следствие. Если функция / непрерывна на (а; Ъ) и f'(x) > 0 на
(а; 6), то / строго возрастает на (а; Ъ).
Аналогично можно сформулировать и доказать достаточное
условие строгого убывания функции на промежутке.
Пример 56. Найдём промежутки возрастания и убывания функции:
a) f(x) = xs- Зх; б) f(x) = х + -.
114 Глава IX. Производная и её применения
X
Рис. 9.23
Рис. 9.24
х
П а) Так как/'(*) = 3*2-3 = 3(л;-1)х
х (х + 1), то /'(*) > 0 при х > 1 и при
х<-1 и /'(*)< О при х е (-1; 1),
а значит, функция / возрастает на
лучах (-оо; -1] и [1; +оо) и убывает на
отрезке [-1; 1].
Схематичную запись знаков
производной и промежутков
возрастания и убывания функции мы видим
на рисунке 9.23.
Обратим внимание на то, что
точки -1 и 1 включены в оба промежутка
монотонности, общей границей
которых они являются. В формулировке
теоремы говорилось про знак
производной на интервале, а вывод о
монотонности делался для промежутка
(в том числе замкнутого).
б) Функция / дифференцируема
в каждой точке области определения
Рис. 9.25
(при х Ф 0) и /' (х) = 1 - -^ = ^-^.
X X
Получим, что f'(x) > 0 при х > 1
или х < -1 и f'(x) < 0 при х е (-1; 0)
или х е (0; 1), а значит, / возрастает
на [1; +со) и (-со; -1] и убывает на
[-1; 0) и (0; 1] (рис. 9.24).
Заметим, что доказанные теоремы о монотонности функции
применимы лишь к функции, заданной на промежутке, поэтому
неправильно было бы утверждать, например, что функция / убывает на
[-1; 0) U (0; 1] (рис. 9.25). Ш
Пример 57. Решим уравнение Зх + 1 + 2 sin х = 1.
П Рассмотрим функцию f(x) = Зх + 1 + 2 sin*. Её производная
f'(x) = 3 + 2 cos х. Ясно, что для любого х производная f'(x) > 0. Таким
образом, / строго возрастает на К и каждое своё значение (в частности,
значение, равное 1) принимает не более одного раза. Отсюда следует,
что уравнение f(x) = 1 имеет не более одного корня. Проверка
показывает, что х = 0 является корнем уравнения. Ответ: х = 0. В
Пример 58. Сколько корней имеет уравнение х4 - 4х + 2 = 0?
П Рассмотрим функцию f(x) = х4 - 4х + 2. Её производная f'(x) -
= 4л:3 - 4 = 4(х - 1)(х2 + х + 1).
Ясно, что f'(x) > 0 при х > 1 и f'(x) < 0 при х < 1, а значит,
функция / возрастает на луче [1; +со) и убывает на луче (-со; 1].
Заметим, что /(1) = -1, lim f(x) = lim f(x) = +co. Эскиз графика
X —*■ +oo x —> —оо
функции / изображён на рисунке 9.26. В силу убывания функции на
115 §61. Исследование функции с помощью производной
луче (-оо; 1] функция / имеет не более одного корня
на этом луче, по теореме Больцано — Коши о
промежуточных значениях непрерывной функции (а
функция / непрерывна) хотя бы один корень на этом луче
существует. Таким образом, на луче (-оо; 1]
функция / имеет ровно один корень. Аналогично
нетрудно показать, что на луче [1; +со) функция / также
имеет ровно один корень. Поскольку х = 1 не
является корнем уравнения, делаем вывод, что уравнение
х4 - 4х + 2 = 0 имеет два различных корня, й
х
-1-
Рис. 9.26
Пример 59. При каких значениях параметра а
функция f(x) = -xs + 4л:2 - ах - 8 строго
возрастает на промежутке (1; 2)?
□ f'(x) = -Зх2 + 8л: - а. Для того чтобы / возрастала на (1; 2),
необходимо и достаточно, чтобы на этом промежутке f'(x) > О (точек, в
которых производная может быть равна нулю, конечное число, поэтому
можно воспользоваться достаточным условием возрастания функции).
Неравенство —Зх2 + 8х — а ^ 0 выполняется на интервале (1; 2),
если точки х = 1 и х = 2 располагаются между корнями
квадратичной функции g(x) = -Зх2 -\- 8х - а (ветви графика которой направлены
вниз) или совпадают с ними, а для этого необходимо и достаточно
выполнение двух неравенств: g(l) ^ 0 и g(2) ^ 0:
igQ)>0, l5-a>0,
\g(2)>0 <>\4-a>0
Ответ: а ^ 4. й
Пример 60. Что больше: еп или
<=> а ^ 4.
D Рассмотрим функцию f(x)=
.
Её производная f'(x)=
Отсюда получим f'(x) < 0 при х > е9 т. е. функция / убывает на
промежутке [е; +оо), а значит, f(e) > f(n). Таким образом, > ,
откуда nine > elnrc, что даёт \пек > \ппе, и окончательно ек > пе.
Ответ: ек > п€. Ш —
2. Точки экстремума. Критические точки
Теорема Ферма даёт нам необходимое условие экстремума и сильно
сокращает количество «кандидатов на точки экстремума». В самом деле,
экстремумы нужно искать лишь в тех точках, в которых производная
отсутствует (а сама функция определена), или в точках, в которых
производная равна нулю. Заметим, что равенство нулю производной —
необходимое, но не достаточное условие экстремума (контрпримером
является точка х0 = 0 для функции у = Xs. Производная этой функции
в нуле равна нулю, но х0 = 0 не является точкой экстремума).
1161 Глава IX. Производная и её применения
Пример 61. Найдём точки экстремума функции f(x) = х4 + Xs.
П Функция / дифференцируема в каждой точке вещественной оси,
поэтому необходимым условием экстремума (по теореме Ферма)
является равенство нулю её производной.
f'(x)=
3х2 = 4х2
X
f'(x) = О при х = О и х = —.
4
Рис. 9.27
Эти точки и являются
«подозрительными на экстремум». Исследуем
«знак производной» (рис. 9.27). Из
рисунка видно, что точка х = О не является точкой экстремума
(функция / возрастает на отрезке [-0,75; 0], в нуле «замедляет» своё
возрастание, а потом продолжает возрастать). Точка # = -0,75 является
точкой минимума, так как на луче (-оо; -0,75] функция / убывает, на
отрезке [-0,75; 0] возрастает, и, следовательно, существует 8-окрест-
ность точки х0 = -0,75 (например, при 5 = 0,75), такая, что для любого
хФ— 0,75 из этой окрестности
выполняется неравенство f(x) > /(-0,75).
Таким образом, точка х = -0,75 является
точкой локального минимума по
определению.
Эскиз графика функции /
изображён на рисунке 9.28. Ш
Этот пример не только показывает,
что условия равенства нулю
производной недостаточно для того, чтобы точка
была точкой экстремума, но и помогает
понять, какие дополнительные условия
нужны для того, чтобы точка,
производная в которой равняется нулю (или в которой сама функция
определена, а производная не существует), оказалась точкой экстремума.
Сформулируем эти условия в следующей теореме.
0,5
Рис. 9.28
ТЕОРЕМА (достаточное условие экстремума)
Пусть функция f дифференцируема в окрестности точки х0 и
непрерывна в точке х0. Если в точке х0 производная функции f
меняет знак, т. е. существует 8 > 0, такое, что на интервалах
(х0 - 8; х0) и (х0; х0 + 8) производная принимает значения разных
знаков, то х0 является точкой строгого экстремума. При этом:
1. Если производная меняет знак с «+» на «-», то это точка
максимума.
2. Если производная меняет знак с «-» на «+», то это точка
минимума.
117I §61. Исследование функции с помощью производной
D доказательство. 1. Пусть / дифференцируема в 8-окрестности
/ g \
точки х0. По условию на интервале х0 ; х0 производная положи-
Г 8 1
тельна, а на отрезке \х0 ; хо\ функция / непрерывна. По критерию
|_ 2 J
возрастания функции на промежутке функция / строго возрастает на
отрезке \х0 ; хо\ и, следовательно, Ух е \х0 ; х0 \ выполняется
L 2 J V 2 )
неравенство f(x0) > f(x).
Аналогично функция / убывает на отрезке мс0; х0 + - и
\/х е х0; х0 + - выполняется неравенство f(x0) > f(x).
\ 2 J
_8 8]
С° 2; Х° 2]
Таким образом, \/хфх0 из отрезка х0 ; лго + — выполняется не-
[ 2 2J
равенство f(x0) > f(x), а значит, точка х = х0 является точкой максимума.
Доказательство утверждения 2 теоремы проводится аналогично, й
Используя рассуждение, аналогичное приведённому в доказательстве
теоремы, можно показать, что если f'(x0) = 0, но производная «не меняет
знак»1 при прохождении через точку х0 (т. е. существует 8-окрестность
точки, такая, что на интервалах (х0 - 8; х0) и (х0; х0 + 8) производная
имеет один и тот же знак), то точка х0 не является точкой экстремума.
Ещё раз подчеркнём, что точками экстремума для функции могут
являться только точки, в которых производной не существует, или
точки, в которых она равна нулю.
ОПРЕДЕЛЕНИЕ ■—-—■——"——-----———---^^
Точки, в которых производная функции f существует и равна
нулю, а также точки, в которых функция f определена, а
производная не существует, называются критическими точками
функции f.
Замечание. Часто критические точки называют также точками,
«подозрительными на экстремум». В большинстве случаев это точки, в
которых может меняться характер монотонности функции (хотя правилом
это считать нельзя: соответствующие примеры приводились в 10 классе).
Пример 62. Найдём критические точки и экстремумы функции:
a) f(x) = (х- 2)2 • (х + З)3; б) f(x) = \x\.
П а) Функция / дифференцируема в каждой точке, поэтому
критические точки функции есть корни производной.
1 Слова «не меняет знак» поставлены в кавычки, поскольку
соответствующее свойство не является отрицанием свойства «меняет знак».
118 Глава IX. Производная и её применения
f\x) = ((х - 2)2(х + З)3)' = 2(х- 2)(х + З)3 + 3(х - 2)2(х + З)2 =
= (х - 2)(х + 3)2(2* + 6 + Зх - 6) = 5х(х - 2)(х + З)2.
Корни производной (и, соответственно, критические точки): х - О,
х = 2, х — —3. Из рисунка 9.29 видно, что производная меняет знак
в точках х = О и jc = 2. Согласно
теореме о достаточном условии
экстремума точка х = О является
точкой максимума (производная
меняет знак с «+» на «-»), точка
х = 2 — точкой минимума
(производная меняет знак с «-» на «+»).
В то же время точка х = -3 не является точкой экстремума. Ответ:
критические точки х = О, х = 2, х = -3, точка максимума х = 0, точка
минимума х = 2.
б) Функция дифференцируема во всех точках, кроме х = 0, при этом
1 при*>0,
-I при х< О,
т. е. во всех точках, где производная существует, она не равна 0.
Таким образом, функция имеет одну критическую точку х = 0,
которая является точкой минимума (это видно на графике, формально это
следует, например, из теоремы о критерии монотонности функции:
/ убывает на промежутке (-оо; 0] и возрастает на луче [0; +оо)). Ответ:
критическая точка х = 0, она же точка минимума. Ш
уем
= J
3. Наибольшее и наименьшее значения функции на отрезке
Пусть непрерывная функция / задана на промежутке [а; Ь]. По
теореме Вейерштрасса функция достигает на [а; Ь] своего наибольшего
и наименьшего значений. В каких точках эти значения могут
достигаться? Оказывается, есть всего два варианта.
а) Если наибольшее (наименьшее) значение достигается во
внутренних точках, то это точка
экстремума, а значит (см. пункт 2),
либо производная в этой точке
равна 0, либо функция не
дифференцируема в этой точке.
б) Наибольшее (наименьшее)
значение достигается на одном из
концов отрезка.
Приведём соответствующие
примеры.
Наибольшее значение
достигается:
1) в точке, в которой произ-
Рис. 9.30 водная равна 0 (рис. 9.30);
х
119| §61. Исследование функции с помощью производной
X
Рис. 9.31
2) в точке, в которой функция не дифференцируема (рис. 9.31);
3) в точке, являющейся концом промежутка (рис. 9.32).
Заметим, что точки, в которых функция не дифференцируема или
её производная равна 0, есть критические точки. Таким образом,
верно следующее утверждение.
Утверждение ~~~~-»--—~-~~m—~--~—m^^
Непрерывная функция f на отрезке [а; Ь] достигает своего
наибольшего (наименьшего) значения в критических точках или на
концах отрезка.
Теперь понятно, как искать наибольшее и наименьшее значения
функции на отрезке [а; Ь]: нужно определить все критические точки
функции на интервале (а; Ъ) и сравнить значения функции в этих
точках и на концах отрезка.
Пример 63. Найдём наибольшее и наименьшее значения функции
на данном отрезке: a) f(x) = х4 - 4х на [0; 4]; б) f(x) = х2 + — на [1; 4];
Д[19]
D а) Функция / дифференцируема в каждой точке интервала (0; 4):
f'(x) = 4 (xs - 1). Производная имеет единственный корень х = 1 на
интервале (0; 4). Таким образом, функция / на интервале (0; 4) имеет
единственную критическую точку х = 1. Вычислим значения функции
в этой точке и на концах отрезка [0; 4]: /(0) = 0, /(1) = -3, /(4) = 240.
Таким образом, наибольшее значение функции /достигается в
точке х = 4 и равно 240, наименьшее значение — в точке х = 1 и равно -3.
б) Для любой точки х е (1; 4) /' (х) = 2х - Щ = 2^3~8\
X2 X2
Отсюда получаем, что функция / на интервале (1; 4) имеет
единственную критическую точку х = 2. Вычислим значения функции /
в этой точке и на концах отрезка [1; 4]: /(1) = 17, /(2) = 12, /(4) = 20.
Наибольшее значение достигается в точке х = 4 и равно 20,
наименьшее значение — в точке х = 2 и равно 12.
120! Глава IX. Производная и её применения
, .м . /j—г \х- 4у[х9 если 0 ^ х ^ 9,
в) f(x)=x-4j\x\ = \ г—
[х - 4V-X, если -1 ^ х < 0.
1--I-, 0<х<9,
При этом f'(x) = \ *"*
В нуле функция / не имеет производной. Производная равна нулю
только в точке х = 4. Таким образом, функция / на промежутке [-1; 9]
имеет две критические точки: х = 0 и х = 4. Сравним значения
функции / в этих точках и её значения на концах отрезка: /(-1) = -5,
/(0) = 0, /(4) = -4, /(9) = -3.
Наибольшее значение функции достигается в точке х = 0 и
равно 0 (обратим внимание на то, что производной в этой точке функция /
не имеет), наименьшее значение — в точке х = — 1 и равно -5. Ш
Полезно понимать, что, например, наибольшее значение функции
(отличной от константы) не может достигаться в точке минимума.
Это соображение уменьшает перебор значений, если требуется найти
только наибольшее значение функции. Также ясно, что левый конец
отрезка, лежащий на промежутке возрастания, не может быть точкой,
в которой достигается наибольшее значение функции.
Пример 64. Найдём множество значений функции f(x) = cos х • е1 ~cos2x.
П Можно было бы сразу вычислить производную функции для
нахождения наибольшего и наименьшего значений, но мы сначала преобразуем
функцию f(x)= cosx- e1~cos2x = cosx - e2~2cos2x и сделаем замену
переменной t = cos л:. Получим функцию g(t)=t • е2~2*2, где t е [—1; 1].
Найдём множество значений функции g на промежутке [—1; 1]
(и тем самым множество значений исходной функции).
g'(t)=e2-2t2(l-4t2).
Корни производной (они же критические точки) t = ±—.
Сравним значения функции g в критических точках и на концах
отрезка [—1; 1]:
4
Т
1 е2
Наибольшее значение достигается в точке t = — и равно —, наи-
з 2 2
1 е2
меньшее значение — в точке t = — и равно . Функция / непрерыв-
на, поэтому принимает все свои значения от наименьшего до наиболь-
3 3
niero. Ответ: E(f) =
е2 е2
. й
121j §61. Исследование функции с помощью производной
1ример 65. При каких значениях параметра а наибольшее значение
функции f(x)=x-\— на отрезке [1; 2] достигается в точке х = 2?
D Функция / дифференцируема в каждой точке интервала (1; 2)
при любом а, при этом /' (х) = 1 -.
X
Если а ^ О, то производная положительна на области определения
функции /, функция строго возрастает на отрезке [1; 2] и наибольшее
значение функции / достигается в правом конце отрезка.
Если а > О, то производная равна 0 в точках х = ±Va, причём
точка х = \а (единственный положительный корень производной) — это
точка минимума (в ней производная меняет знак с «-» на «+»). Таким
образом, наибольшее значение функции / на промежутке [1; 2] может
достигаться только на одном из концов промежутка: в точке х = 1 или
в точке х = 2. Для того чтобы наибольшее значение достигалось в
точке х = 2, необходимо и достаточно, чтобы выполнялось неравенство
/(2) > /(1), т. е. 2 + ->l + a»a<2.
Таким образом, из положительных а нас устраивают а е (0; 2].
Объединяя ответы обоих случаев, получаем ответ: а ^ 2. Ш
4. Решение задач с использованием производной
Пример 66. Из всех равнобедренных треугольников с площадью 1
найдём тот, у которого периметр наименьший.
D Обозначим основание треугольника 2Ь. Тогда высота,
проведённая к основанию, равна -, а боковая сторона J— + Ь2 (рис. 9.33).
о V &
Периметр треугольника равен р(Ь) = 2Ъ + 2J— + Ъ2 . Положим
Ъ = х и рассмотрим функцию р(х) = 2х + 2J— + х2 , определённую на
(0; +оо). Её производная равна
2*-2- 4
р\х)= 2 + 2 == 2 + 2-
Найдём корни производной:
р'(х)= 0<=> 2 + 2—х*~ Х = 0 <=> х2 • Vl + х4 = 1-х4<=>
<=>
122! Глава IX. Производная и её применения
Рис. 9.33
Рис. 9.34
т. е. производная на промежутке (0; +оо) имеет единственный корень
х = —=. Нетрудно проверить, что при х е 0; -= производная мень-
VS \ VSJ
ше 0, при х е —; +оо производная больпге 0, таким образом, при
W3 )
х = — функция р достигает наименьшего значения. При этом длина
V3 2
основания равна 2Ь = —, длина боковой стороны равна
л/3
т. е. наименьпгий периметр будет у равностороннего треугольника. В
Пример 67. Дан квадратный лист жести со стороной 1. В четырёх углах
квадрата вырезают маленькие квадраты, после чего загибают боковые
стороны по штриховым линиям и составляют коробку (рис. 9.34). При
какой длине стороны маленьких квадратов объём получившейся
коробки будет наибольшим?
П Пусть длина стороны маленьких квадратов равна х. Тогда объём
получившейся коробки будет равен V(x) = (1 — 2л:)2 • х, при этом по
смыслу задачи х е | 0; - |. Найдём наибольшее значение функции V на
интервале 0; — :
V'(x) = (1 - 2л:)2 - 4х • (1 - 2х) = (1 - 2х) • (1 - 6х).
Производная функции V имеет единственный корень х = - (и, сле-
6
довательно, единственную критическую точку) на интервале | 0; - ,
123) § 62. Вторая производная. Выпуклые функции
причём это точка максимума. Значит, в этой точке достигается наи-
(\\ 2
большее значение функции, и оно равно V - = —.
2
Ответ: наибольший объём коробки будет равен — при стороне вы-
1 27
резаемого квадрата, равной -. Ш
6
Q62. Вторая производная, Выпуклые функции
1. Вторая производная. Производные высших порядке
Пусть функция / имеет производную в каждой точке области
определения. Тем самым определена функция /' с той же областью
определения, что и функция /. Функция /' тоже может иметь производную
в каждой точке области определения, тем самым будет определена
производная производной (/')'. Эта функция называется второй
производной функции / и обозначается /".
Пример 68. Пусть f(x) = х3 + Зх2 + х. Вычислим /".
D Производная функции / равна f'(x) = Зх2 + 6х + 1. Вторая
производная функции / равна /"(*) = (/')'(*) = (3*2 + 6х + 1)' = 6х + 6. IS
Вторая производная имеет ясный физический смысл: она
определяет скорость изменения первой производной, т. е. скорость
изменения скорости, тем самым являясь ускорением. Аналогично можно
определить третью, четвёртую и последующие производные —
производные высших порядков. Производная п-то порядка обозначается /(л).
Пример 69. Вычислим четвёртую производную функции f(x)= —
X
X —
П Можно было бы вычислять производные по формуле
производной частного, но тогда вычисления получились бы громоздкими
(проверьте). Преобразуем функцию:
f(x)- 1 1 *L
2) х-2 :
Теперь вычисления будут проще:
f'(x) = — - — — - = — —г- +
ГМ=-т-^ +
х-2 х-1) ' (х-2)2 (х-1)2'
1 1 V 2 2
(х - 2)2 (х - I)2 ) (х- 2)3 (х - I)3 *
Г(х)=-^1 2_Y 6_ 6
(х - 2)3 (х - I)3 ) ' (х- 2)4 (х - I)4 *
6 i 6 У= 24 24 Щ
( I)4 J ( 2)5 ( I)5 "
i
(х - 2)4 (х - I)4 J (х- 2)5 (х - I)5
124J Глава IX. Производная и её применения
2. Выпуклые функции
ОПРЕДЕЛЕНИЕ 1 ———
Функция f называется выпуклой {выпуклой вниз) на
промежутке (а; (3), если любая хорда её графика на этом
промежутке лежит не ниже графика функции.
В определении промежуток (а; (3) может быть конечным или
бесконечным. Можно говорить, в частности, и о функции, выпуклой на всей
области определения (если она представляет сплошной промежуток).
Пример 70. На рисунке 9.35 функция выпукла на своей области
определения, а на рисунке 9.36 нет, так как хорда графика с концами
в точках (а; /(а)) и (6; f(b)) не лежит целиком выше графика функции.
При этом на рисунке 9.36 функция выпукла на отрезке [с; а]. Щ
№
f(a)
о
Рис. 9.35
х
с 0 а
Рис. 9.36
7
Наряду с понятием выпуклости можно определить понятие
вогнутости (выпуклости вверх).
ОПРЕДЕЛЕНИЕ 2
Функция f называется вогнутой (выпуклой вверх) на
промежутке (а; (3), если любая хорда её графика на этом
промежутке лежит не выше графика функции
На рисунке 9.37 функция выпукла вверх на промежутках (-оо; а]
и [Ь; +оо), а также выпукла вниз на отрезке [а; Ь].
Рис. 9.37
х
125; § 62. Вторая производная. Выпуклые функции
Важными примерами выпуклых и вогнутых функций являются
функции у = ах (при а > 1) и у = loga;c (также при а > 1)
соответственно. Свойства выпуклости этих функций мы докажем ниже.
Геометрически выпуклость функции означает, что множество
точек координатной плоскости, лежащих над графиком функции на
промежутке (а; (3) (т. е. множество точек, координаты которых
удовлетворяют неравенству y^f(x) при х е (ос; (3)), является выпуклым.
Аналогично вогнутость функции означает, что множество точек
координатной плоскости, лежащих под графиком функции на
промежутке (а; (3) (т. е. множество точек, координаты которых
удовлетворяют неравенству у ^ f(x) при х е (ос; (3)), является выпуклым.
Заметим, что согласно этому определению линейная функция
является одновременно выпуклой и вогнутой на R.
Запишем геометрический факт «хорда лежит не ниже графика
функции» аналитически. Тот факт, что хорда графика с концами
в точках (a; f(a)) и (6; f(b)) лежит не ниже графика, означает, что для
любого х е (а; 6) значение функции в точке х не больше, чем
«значение хорды» в этой точке (т. е. чем значение линейной функции,
частью графика которой является хорда) (рис. 9.38).
х = Qa + (1 - 0)6,
0<9<1
Рис. 9.38
Любое число х е [а; Ь] представимо в виде х = ва + (1 - 6)6 при
некотором G е [0; 1] (при 6 = 0 это будет точка Ь; при 6 = 1 это будет
точка а; при 6, пробегающем значения от 0 до 1, точка х будет пробегать
отрезок [а; Ь] от Ъ до а), при этом нетрудно показать, что 6 = .
о — а
Пусть прямая, задаваемая уравнением у = kx + Z, проходит через
точки (a; f(a)) и (6; f(b)) (что означает выполнение равенств ka + I = f(a)
nkb + 1 = f(b)). Тогда в точке х = да + (1 - 6)Ь соответствующая
линейная функция принимает значение у (6а + (1 - 6)6) = k(Qa + (l-6)6) + Z =
126' Глава IX. Производная и её применения
Таким образом, тот факт, что значение функции в этой точке не
больше, чем «значение хорды» в этой точке, равносилен выполнению
неравенства
(1 _ 0)Ь) ^ ef(a) + (1 _ в)/(Ь).
Итак, определение 1 можно сформулировать иначе.
ОПРЕДЕЛЕНИЕ 1'
Функция f выпукла на (а; (3), если V6 е [0; 1] Va,fo e (а;
выполняется неравенство
f (ва + (1 - в) Ь) < 9f (а) + (1 - в) f(b).
Можно доказать (но здесь мы это делать не будем), что для
непрерывных функций определение выпуклости можно заменить на
следующее (равносильное данному).
ОПРЕДЕЛЕНИЕ 1"
Непрерывная функция f выпукла на (а; (3), если Va, b e (а; (3)
выполняется неравенство
ta+b)^ f(a) + f(b)
Замечания. 1) Неравенство из определения 1" означает, что
середина любой хорды лежит не ниже графика функции.
2) Если в определениях 1' и 1" неравенство является строгим
(в определении V для G е (0; 1) и а * 6, а в определении 1" для а * Ь),
то говорят о строгой выпуклости функции / на (а; (3).
3) Аналогичные определения можно сформулировать и для
вогнутых (выпуклых вверх) функций. При этом знак неравенства
заменяется на противоположный.
Таким образом, для непрерывной функции выведенное выше
неравенство /(6а + (1 - 6)Ь) ^ 6/(а) + (1 - 6)/(Ь) можно проверять только
для середины любой хорды т. е. для G = — , а тогда оно будет выпол-
2
няться (если функция / непрерывна) и для любого G е [0; 1].
В дальнейшем изложении мы будем пользоваться последним
определением. Далее, говоря о выпуклости функций в этом параграфе, мы
будем говорить только о выпуклости непрерывных функций, не всегда
упоминая об этом1.
Пример 71. Докажем, что функция f(x) = х2 выпукла.
П Пусть а, Ъ — любые вещественные числа. Тогда неравенство
1 Можно доказать, что любая выпуклая на интервале функция является
непрерывной.
127j § 62. Вторая производная. Выпуклые функции
для функции / записывается в виде
а + b
Ъ2
-, которое равносиль-
\2
но верному неравенству
а-Ь
х
и, значит, функция / выпукла по
определению 1". й Рис- 9'39
Пример 72. Верно ли, что если непрерывная функция / выпукла на
промежутках [а; Ь] и [Ь; с], то она выпукла на их объединении?
D Неверно. Контрпример можно увидеть на рисунке 9.39. Ш
3. Признак выпуклости функции
Для функции f(x) = х2 мы легко доказали, что она выпукла,
однако для произвольной функции проверять неравенство
2 ) 2
может быть весьма непросто. В то же время существует простой
признак выпуклости.
ТЕОРЕМА (достаточный признак выпуклости) —————————
1
Пусть функция f дифференцируема на интервале (а; Р),
непрерывна на промежутке (а; Р) и её производная f возрастает
(может быть, нестрого) на интервале (а; Р), тогда функция f выпукла
на промежутке (а; Р).
□ доказательство. Докажем, что \/a,b e (а; (3) выполняется
неравенство
На) + f(b)
Зафиксируем а, Ъ е (а; (3).
Рассмотрим отрезок а; (от левого конца до середины отрезка
L 2 J
[а; &]). Для функции / на этом отрезке выполняются все условия
теоремы Лагранжа, поэтому существует точка Gx е а; , такая, что
Ъ-а
128 Глава IX. Производная и её применения
Аналогично можно показать, что существует точка G2 е ; Ъ ,
{
такая, что f'(Q2) = jr^ • Так как G2 > в1э то в силу нестрогого
и а
2
возрастания функции f'(x) выполняется неравенство
f(b)-f(a+b
Ъ-а Ь-а
2 2
Ла + Ь\ . f(a)+ f(b)
эквивалентное неравенству f\ ^ —— , которое и требова-
)
\ )
лось доказать. Щ
Аналогично можно сформулировать и доказать теорему для
функции, дифференцируемой на интервале, производная которой убывает
на нём.
Следствие. Пусть функция / непрерывная на промежутке (а; (3)
и дважды дифференцируема на интервале (а; (3). Тогда
1. Если f"(x) > 0 при всех х е (а; (3), то функция / выпукла на
промежутке (а; Р);
2. Если f"{x) ^ 0 при всех х е (а; (3), то функция / вогнута на
промежутке (а; (3).
Утверждения следуют из доказанной теоремы и достаточного
условия возрастания дифференцируемой функции.
Замечание. Верно и обратное утверждение, т.е. если дважды
дифференцируемая на промежутке (а; (3) функция / выпукла на
промежутке (а; (3), то для любого х е (а; (3) выполняется неравенство f"(x) ^ 0.
Идею доказательства этого утверждения можно увидеть в серии
задач (IX.250). В дальнейшем мы будем пользоваться этим утверждением.
Пример 73. Исследуем на выпуклость функцию: а) у = ех; б) у = \пх;
в) у = sin л:.
П Вычислим вторую производную функции:
а) Ух е R (ех)" — ех > 0, поэтому функция у = ех выпукла на R;
б) Ух > 0 (In*)" = —-9 поэтому функция у = \пх вогнута на интер-
X
вале (0; +оо);
в) Ух е R (sin;c)" = -sin*. Вторая производная не является
функцией постоянного знака, и функция синус не является выпуклой на
всей области определения. Однако она выпукла на промежутках вида
[п + 2nk; 2л + 2nk], k e Z и вогнута на промежутках [2nk; к + 2nk],
k G Z. Ш
§ 62. Вторая производная. Выпуклые функции
Пример 74. Докажем, используя вогнутость функции f(x) = у[ху
неравенство л/2005 + л/2007 ^ 2л/2006.
D Функция / вогнута на [0; +оо), поэтому Va, b> 0 выполняется
неравенство
2 J 2
Подставив a = 2005 и 6 = 2007, получим верное неравенство
2005 + V2007
/2006, эквивалентное доказываемому.
Пример 75. Докажем, что sin— > 0,1.
30
□ Функция синус является строго
вогнутой на отрезке 0; — , поэтому
хорда графика синуса с концами в
точках (0; 0) и —; - лежит ниже графи-
ка (рис. 9.40). В частности, значение
функции sin х в точке х = — больше
30
ординаты соответствующей точки
прямой, проходящей через точки (0; 0) и
Зх
Уравнение этой прямой у = —,
71
и при х= — получаем у = 0,1. Таким образом, sin— > 0,1, что и требо-
30 30
валось доказать. Ш
Пример 76. Докажем, что \/х9 у > 0 выполняется неравенство
х + У *
мои, пр<
й
1
2
од
0
п
"30
f(x) = sin*
/
X X
Рис. 9.40
arctg -
2 x + y
D Исследуем на выпуклость функцию f(x) = л: arctg л::
/'(*)= aretg * + —*_■;
1 V~' 1+X* (1+X2)2 (1+X2)2 ' ^'
поэтому функция / выпукла на R, а тогда и для любых чисел х и у
выполняется неравенство
f(x) + f(y)
записываемое в
виу
arctg
х + у xarctgx + i/arctg i/
. Из последнего неравенства
Де 2 —- 2 2
легко получается (учитывая, что х> у > 0) требуемое неравенство. II
1301 Глава IX. Производная и её применения
4. Касательная к выпуклой функции. Точки перегиба
ТЕОРЕМА
1
Пусть функция f задана и выпукла на промежутке (ос; Р), и
дифференцируема на интервале (ос; Р), тогда все точки графика
функции f лежат над любой касательной к этому графику
(проведённой в точке х0 е (а; Р)) или на ней.
П доказательство. Возьмём точку х0 е (ос; (3). Уравнение
касательной к графику функции / в этой точке имеет вид:
y = f'(xo)(x-xo) + f(xo).
Рассмотрим функцию g(x) = f(x) - f'(xo)(x - х0) - f(x0). Покажем,
что производная функции g нестрого возрастает на [а; Ь]:
g'(x) = f'(x)-f'(x0).
Функция / выпукла на промежутке (а; (3), следовательно, /' нестрого
возрастает на (ос; (3), а следовательно, и g' возрастает на интервале (а; Р).
При этом g'(x0) = 0, а значит, g'(x) ^ 0 при х < х0 и g'(x) > О при х > х0.
Таким образом, функция g нестрого убывает на промежутке (а; х0]
и нестрого возрастает на промежутке [х0; (3), и для всех х е (а; р)
g(x)> g(xo)= 0. Итак, для всех ж е (а; Р> выполняется неравенство
g(x) ^ 0, а это и означает, что все точки графика функции / лежат выше
касательной в точке х0 (или на этой касательной) (рис. 9.41). Ш
ОПРЕДЕЛЕНИЕ
Пусть функция f непрерывна в некоторой окрестности
точки х0. Точка х0 называется точкой перегиба функции f
(точкой смены характера выпуклости функции), если
существует 8 > 0, такое, что функция f имеет разный
характер выпуклости на промежутках (х0 - 8; х0] и [х0; х0 + 8).
Точка (х0; f(x0)) называется точкой перегиба кривой (графика
функции f).
1(х) — касательная
к f(x) в точке xQ
f(x)
Рис. 9.42
1311 § 62 Вторая производная. Выпуклые функции
Замечания. 1) График функции в точке перегиба (если функция
дифференцируема) переходит с одной стороны касательной к нему
в данной точке на другую её сторону (рис. 9.42).
2) Каждая точка линейной функции является точкой перегиба.
Утверждение (необходимое условие точки перегиба)
Пусть функция f дважды дифференцируема в некоторой
окрестности точки х0 и её вторая производная непрерывна в точке х0.
Если х0 — точка перегиба, то f"(x0) = 0.
D доказательство. В самом деле, вторая производная принимает
значения разных знаков на интервалах (х0 - 8; Хп) и (х0; х0 + 8). Пусть,
для определенности, f"(x) ^ 0 на интервале (х0 — о; х0) и f (x) ^ 0 на
интервале (х0; х0 + 8), тогда lim f"(x) ^ Ои, одновременно, lim f"(x) ^ 0.
X-»XQ- X-*XQ +
В силу непрерывности второй производной в точке х0 lim / "(х) =
{f "(X ) ^ 0 x-*xq-
*»i °\ Zr! откуда f"(xo) = O.\S
Утверждение (достаточное условие точки перегиба) ■■<
Пусть функция f дважды дифференцируема в окрестности
точки х0, Г'(х0) = 0 и f" меняет знак при переходе через точку х0.
Тогда х0 —- точка перегиба функции f.
Доказательство следует из теоремы о достаточном условии
выпуклости и определения точки перегиба.
Пример 77. Найдём точки перегиба функции f(x) = Зх5 - 5х4 + 2х — 1.
I \JL) — Л. О Л — £j\JJL Т^ &у I v*^/ — WA? — \J\JA' — \J\JJL \Л? — -'-/•
Знаки второй производной
показаны на рисунке 9.43. /" меняет f'(x)
знак в точке х = 1, и, значит, эта точ- характер ^Л 0~Г\ IV
ка является точкой перегиба, а в точ- выпуклости
ке х = 0 знак второй производной ~ v
не меняется и, значит, точкой
перегиба она не является. Ответ: х— 1. й Рис. 9.43
5. Неравенства Йенсена и Коши
В этом пункте мы докажем два полезных неравенства.
ТЕОРЕМА (неравенство Йенсена) --------------------------—-——
Для выпуклой на промежутке функции f и любых чисел
хп из этого промежутка выполняется неравенство
. f(x,)+ ...+ f(xn)
132J Глава IX. Производная и её применения
П доказательство. Воспользуемся методом математической индукции.
база индукции. При п = 2 неравенство Йенсена превращается
в неравенство, верное по определению выпуклой функции:
f(xx) + f(x2)
< I •
По индукционному предположению
...+ f(xn_x)
'{"*:-г""Уп")ф:!;
индукционный переход. Если в определении выпуклой функ-
Х1+...+ Хп_1 п-1
ции положить а = , о = хп и 6 = , то получим
п — \ и
I п ) In п-1 п
^
п-1 (х1+ ...+ хлА+1
п у п-1 ) п
Воспользовавпгись индукционным предположением, получим
п
I tt ч
п
п п-1 п
что и требовалось доказать. IS
Замечание. Аналогично, для вогнутой на промежутке функции/
можно доказать неравенство
...+ Пхп)
(хх+ ...+ хЛ > ПХ0+...+
( п У п
ТЕОРЕМА (неравенство Коши)
Для любых положительных чисел хА хп выполняется
неравенство ~ ^ ^lx^ ' ••• * хп •
П доказательство. Прологарифмируем обе части неравенства:
Хл + ... + Х„ I ( Хл + ... + Х„
( хх + ... + хп Л In хх + In х2 + ... + In хп
<=> In ^
I
133| §63. Построение эскизов графиков с помощью производной.
Решение задач с помощью производной
Последнее неравенство есть неравенство Йенсена для выпуклой
вверх функции f(x) = \nx, справедливость которого доказана выше.
Другое доказательство приведено в учебнике 10 класса (см. с. 37). В
Пример 78. Докажем, что для любых положительных чисел х19 х2,
..., хп выполняется неравенство
(хг + х2 + ... + хп) А — + — + ...+ — \> п2.
\ У У У I
V Х1 Х2 Хп )
П Функция f(x)= — выпукла на промежутке (0; +оо), поэтому по
неравенству Йенсена для любых чисел х19 х2, ..., хп е (0; +со)
выполняется неравенство
.(xi+...+ xn\ /(х1)+...+ f(xn)
т. е.
что и требовалось доказать. Щ
063. Построение эскизов графиков
с помощью производной.
Решение задач с помощью производной
1. Построение эскизов графиков функции
Обычно при построении графика нас интересуют промежутки
возрастания и убывания, экстремумы функции, промежутки
выпуклости, точки перегиба, пределы функции на бесконечности и асимптоты.
Часто графики используются как вспомогательное средство при
решении задач (см., в частности, пункт 4).
Пример 79. Построим график функции: а) у = Xs — Зх2; б) у =
D а) */' = Зх2 - 6х = Зх(х - 2). Производная положительна на
промежутках (-оо; 0) и (2; +со) и отрицательна на интервале (0; 2).
Функция у возрастает на лучах (-со; 0] и [2; +со) и убывает на отрезке [0; 2].
Функция дифференцируема в любой точке х е R, поэтому
критические точки функции — точки, в которых производная равна 0, т. е.
точки х = 0 и х = 2. Производная меняет знак в этих точках, поэтому
они являются точками экстремума: х = 0 — точка максимума, х = 2 —
точка минимума.
Далее, у" = (Зх2 - 6х)' = 6х — 6 = 6(х - 1), откуда получаем, что на
луче (-со; 1] функция у вогнута, на луче [1; +со] функция у выпукла,
при этом точка х = 1 является точкой перегиба.
134' Глава IX. Производная и её применения
- -4
Так как lim
л:-*>оо
fix)
не является ко-
х
нечным, график функции не имеет
наклонных и горизонтальных асимптот.
В силу непрерывности функции / на R
её график не имеет и вертикальных
асимптот.
Эскиз графика функции приведён
на рисунке 9.44.
( V 2 2
Рис. 9.44
Найдём промежутки знакопостоян-
ства функции у':
,, ч 2(х + 1)(х2-х + 1)
Рис. 9.45
X
Таким образом, у возрастает на
промежутках (-со; -1] и (0; +со) и убывает
на промежутке [-1; 0) (рис. 9.45).
Функция дифференцируема при любом х е R, х Ф 0 (в нуле
функция не определена), поэтому критические точки функции — точки,
в которых производная равна 0, такая точка единственная: х = -1.
Производная в этой точке меняет знак с «+» на «-», поэтому х = -1 — точка
максимума.
2 V 2
—- = —-, откуда получаем, что у" < 0 при л ю-
OX J X
Далее, у" = |-
бом х g R, х Ф 0, и, следовательно, на промежутке (-оо; 0) функция у
вогнута, на промежутке (0; +со) функция у вогнута.
Поскольку у(х)=— х -, график функции имеет наклонную
3 Зх
2
+со, так и при х -> -со.
асимптоту у = —х как при х
3
Поскольку
асимптотой графика.
У,
lim y(x) = со,
о
Рис. 9.46
прямая х = 0 является вертикальной
О Несмотря на то что вторая
производная функции всюду отрицательна
на области определения, нельзя сделать
вывод о том, что функция выпукла вверх
на всей области определения, а можно
утверждать только, что она выпукла
вверх на промежутках (-со; 0) и (0; +оо)
по отдельности!
Эскиз графика изображён на
рисунке 9.46. Ж
135) §63. Построение эскизов графиков с помощью производной.
Решение задач с помощью производной
2. Доказательство неравенств с помощью производной
С помощью производной можно доказывать неравенства. Часто
при этом мы будем опираться на следующее утверждение.
Утверждение •■•-•--•••■--■-■■---■■--•-——■--------■—-^^
Если две непрерывные на промежутке [а; Ь) и
дифференцируемые на интервале (а; Ь) функции f и д удовлетворяют условиям:
2) Vx e (a; b) выполняется неравенство V (х) > д' (х), то Vxe (a; b)
выполняется неравенство f (х) > д (х).
D доказательство. Это утверждение следует из достаточного
условия возрастания функции, применённого к функции (р(х) = f(x)-g(x).
В самом деле, (р(а) = 0, Ух е (а; Ъ) выполняется неравенство ф'(*) > О,
следовательно, функция ф возрастает на [а; 6), т. е. Ух е (а; Ь)
выполняется неравенство <р(х) > (р(а) <=> f(x) - g(x) > О <=> f(x) > g(x). Ш
Пример 80. Докажем неравенство: 3
а) 1п(1 + х) < х при х > 0; б) tgx > х + — при 0 < х < —.
3 2
D а) Применим утверждение к функциям 1п(1 + х) и #,
рассматриваемым на промежутке [0; +оо).
При х = 0 значения функций равны: 1п(1 + 0) = lnl = 0.
Вычислим производные функций 1п(1 + х) и х:
4
4
л. I X -
При х > 0 выполняется неравенство < 1, и таким образом, из
1 + х
утверждения следует неравенство 1п(1 + х) < х при х > 0.
Xs
б) Рассмотрим функции tga; и х + —. При х = 0 значения функций
3
равны: tgO = 0. Докажем, что при 0 < х < -- выполняется неравенство
<=> —\ 1 > х2 <=> tg2 х > х2.
COS2 X
COS2 X COS2 X
Последнее неравенство следует из доказанного в 10 классе
неравенства х < tg х для х е 0; — .
V 2) п
Итак, мы доказали, что при 0 < х < — выполняется неравенство
( X3 V X3
(tg х)' > \ х ч , при х = 0 значения функций tga; и х ч- — равны, отку-
^ 3 ^ х3 3 я
да следует справедливость неравенства tga; > л: ч- — при 0 < х < —. Ш
3 2
136 Глава IX. Производная и её применения
3. Касательная к графику многочлена.
Кратные корни многочленов
ТЕОРЕМА (о кратных корнях многочлена) ———————
Пусть число а является корнем кратности п (п е N, п > 2) много
члена р. Тогда число а является корнем его производной кратно
сти п - 1.
П доказательство. По определению корня кратности п многочлену
представим в виде р(х) = (х — а)п q(x), причём q(a) Ф 0. Тогда
р'(х) = ((х - а)п q(x)Y = п(х - a)"-1 q(x) + (х - а)п q'(x) =
= (х - a)n~l(nq(x) + (х - a)q'(x)) = (х - а)71"1 г (л:),
причём г (а) = nq(a) Ф 0, т. е. число а является корнем кратности п - 1
многочлена рг по определению. IS
ТЕОРЕМА (о касательной к графику многочлена)
Если прямая, заданная уравнением у = кх + Ь, касается графика
многочлена р в точке с абсциссой а, то число а является корнем
многочлена q (х) = р (х) - kx - b кратности 2 или более.
П доказательство. Уравнение касательной к графику функции р
в точке с абсциссой а имеет вид у = р'(а)(х - а) + р(а). Отсюда следует,
что q (a) = q'(a) = 0 (так как q'(x) = р'(х) — k = р'(х) - р'(а)). Докажем, что
q делится на (х - а)2 (что и будет означать, что число а является корнем
кратности 2 или более многочлена q).
В самом деле, раз q(a) = 0, то q(x) = (х - а) г(х).
Продифференцируем это равенство:
q'(x) = (х- а)г'(х) + г(х).
Мы знаем, что q' (а) = 0, поэтому 0 = q' (а) = (а — а) г' (а) + г (а) = г (а),
откуда г (л:) • (х-а), т. е. r(x) = (x- a)s(x), и, значит, q(x) = (x-a)r(x) =
= (х - a)2s(x)j что и требовалось доказать. Ш
Пример 81. К графику функции у = Xs + Юх2 + 13л: + 19 в точке с
абсциссой 5 проведена касательная. Найдём абсциссы всех точек её
пересечения с графиком.
□ Пусть уравнение касательной y = kx + b. Тогда нам нужно решить
уравнение Xs + Юл;2 + 13л: + 19 = kx + b. Но по предыдущей теореме
х = 5 должно быть корнем кратности 2 (или более) многочлена р (х) = хг +
+ Юл;2 + 13л: + 19 - kx - b. Это многочлен 3-й степени, который имеет
три корня (с учётом кратности), причём хг = х2 = 5. По теореме Виета
их сумма хг + х2 + х3 = -10, откуда х3 = -20. Ответ: 5, -20. й
4. Решение задач с помощью производной
Часто построение эскизов графиков является не целью, а
средством решения задачи. При этом при построении эскиза графика мы
исследуем те свойства функций (промежутки возрастания и убывания,
137| §63. Построение эскизов графиков с помощью производной.
Решение задач с помощью производной
выпуклость, асимптоты), которые нам нужны для решения
конкретной задачи.
Пример 82. На графике функции у = х — х0'25 + 1 найдём точку, сумма
расстояний от которой до осей координат будет наименьшей.
□ Функция у определена при х > 0. Для любой точки графика с
координатами (х; у(х)) сумма расстояний до осей равна
S(x) = х + \у\ = х + \х - х°>25 + 1|.
Докажем, что при любом х > 0 функция у(х) ^ 0. В самом деле,
при 0 < х ^ 1 выполняется неравенство
х - *0-25 + 1 > 1 - я0-25 = 1 - ilx > 0,
при х > 1 выполняется неравенство
х - х°>25 + 1 > х - х°>25 = V* (V*5" - l) > 0.
Это позволяет нам раскрыть модуль:
S(x) = x + \x- *°>25 + 11 = х + х - *0>25 + 1 = 2х - *0>25 + 1.
Нам нужно найти наименьшее значение функции S. Для этого
вычислим производную S'(x) =2
Знаки производной показаны на рисунке 9.47. Видно, что S
убывает на отрезке 0; —- и возрастает на луче —; +оо . Таким образом,
L 16J L16 )
наименьшее значение функции S достигается в точке с абсциссой
±;±\*
S\x)
S(x) не определено
Рис. 9.47
Пример 83. На графике функции у = 4х найдём точку, ближайшую
к точке (3; 6).
D способ 1. Квадрат расстояния от точки графика функции у = \[х
с координатами (х; 4х) до точки (3; 6) равен
S(x) = (х- З)2 + (у[х - б)2 = х2 - 5х - 12л/х + 45.
Нам требуется найти наименьшее значение этой функции. Чтобы
удобнее было вычислять производную, сделаем замену переменной t = 4х
(t > 0). Тогда
S(t) = t4- Ы2- 12* + 45.
S'(t) = 4ts - 10t - 12 = 2(2*3 - Ы - 6) = 2(t - 2)(2t2 + At + 3).
1381 Глава IX. Производная и её применения
S'(t)
S(t)
не определено q
Рис. 9.48
Знак производной S' и промежутки возрастания и убывания S
показаны на рисунке 9.48. Наименьшее значение функции S на
промежутке [0; +оо) достигается при t = 2. Таким образом, наименьшее
расстояние от точки графика функции у = 4х с координатами (х; у[х)
до точки (3; 6) достигается при х = 4. Ответ: (4; 2).
способ 2. Нетрудно доказать, что для того, чтобы точка А ух;у[х)
была ближайшей к точке В (3; 6), необходимо и достаточно, чтобы
касательная к графику функции у = vx, проведённая в точке А, была
перпендикулярна прямой АВ (рис. 9.49).
Докажите это самостоятельно, используя
вогнутость функции у = 4х и теорему
о касательной к графику выпуклой
функции. Прямые перпендикулярны тогда и
только тогда, когда произведение их
угловых коэффициентов равно -1.
Касательная к графику в точке А ух; \xj имеет
угловой коэффициент к- у'(х)=
6
Прямая АВ имеет угловой
коэффициент k = . Отсюда получаем
х-3
Рис. 9.49
уравнение
Решив это уравнение (например, с помощью замены переменной t-4x\
получим х = 4. Ответ: (4; 2). Ш
Пример 84. Определите, сколько существует касательных к
графику функции у = Xs + 1, проходящих через точки, лежащие на: а) оси
абсцисс; б) оси ординат.
Перед тем как читать решение примера, попробуйте «прикинуть»
ответ, исходя из интуитивных соображений, нарисовав график
функции у = Xs + 1.
П Запишем уравнение касательной к графику функции у = Xs + 1
в точке х0:
y = 3xl'(xx) + x*
139[ §63. Построение эскизов графиков с помощью производной.
Решение задач с помощью производной
а) Точка оси абсцисс с координатами (а; 0) принадлежит
касательной к графику данной функции в точке х0 тогда и только тогда, когда
2х3 — 1
0 = 3x1 • (а - х0) + xl + 1 <=> 3x1'а = 2хо - 1 <=> а = —^—
Зх0
(в последнем переходе мы поделили на Зх\, заметив, что х0 = 0 не
является корнем предыдущего уравнения). Таким образом, через точку
оси абсцисс с координатами (а; 0) проходит столько касательных,
сколько решений (относительно х0) имеет уравнение а =
3x1 '
Для того чтобы определить количество решений данного
уравнения в зависимости от а, проще всего построить эскиз графика функ-
ции у = —, что мы уже делали в примере 79, б) (см. рис. 9.46).
Таким образом, на рисунке 9.46 видно, что при а < -1 через точку
(а; 0) можно провести три касательные, через точку (-1; 0) можно
провести две касательные и при а > -1 через точку (а; 0) можно провести
одну касательную.
б) Для того чтобы понять, когда
точка оси ординат с координатами (0; а)
принадлежит касательной к графику
данной функции в точке х0, подставим
в уравнение касательной х = 0 и у = а.
Получим а = 1 - 2xq . Данное уравнение
(относительно х0) имеет единственное
решение при любом а (эскиз графика
функции у = 1 - 2х3, который можно
построить элементарными
преобразованиями из графика функции у = х3,
приведён на рисунке 9.50). Поэтому через
любую точку на оси ординат проходит
единственная касательная к графику
данной функции, й
Рис. 9.50
Пример 85. Найдём все значения параметра а, для каждого из
которых существует только одно значение 6, такое, что Ь2 • (Ь + а) = 1.
□ Преобразуем равенство:
Ь2 • (Ь + а) = 1 <=> ab2 = 1 - Ъ3 <=> а = -Ц^-
(при делении на Ъ2 мы учли, что при 6 = 0 равенство аЪ2 = 1 - Ъ3 не
может быть верным).
Таким образом, в задаче требуется найти, при каких значениях
параметра а функция f(b) = —-— принимает значение, равное а, ров-
но один раз.
140! Глава IX. Производная и её применения
Построим эскиз графика функции /.
го»-1'1 "
Значение f'{b) положительно при 6е(-л/2;0) и отрицательно на
-оо; -д/2) и (0; +оо), поэтому / возрастает на промежутке
[-л/2; 0) и / убывает на промежутках (-оо; -л/2] и (0; +со).
Исходя из того, что lim f(b) = -со, lim f(b) = +оо, нарисуем эскиз
Ь —*■ +оо b —*■ —оо
графика функции / (рис. 9.51).
По графику видно, что уравнение f(b) = а имеет единственное
решение при а < /(-л/2), т. е. а < —=. Ш
4 у л/4
Пример 86. При каких значениях х наибольшее значение функции
f(t) = t3 - 3t2 на отрезке [х - 1; х] будет больше, чем -4?
П Построим эскиз графика функции f(t) = t3 - St2; f'(t) = St2 - 6t =
= 3t(t - 2). Производная /' положительна при t e (-co; 0) и t e (2; +oo)
и отрицательна на интервале (0; 2), поэтому / возрастает на
промежутках (-со; 0] и [2; +со) и / убывает на промежутке [0; 2].
Эскиз графика функции / изображён на рисунке 9.52.
Заметим, что функция / принимает значение, равное —4, при t = 2
и t = -1.
1) Если л: < 0, то на отрезке [л:-1;л:] функция / возрастает,
наибольшее значение на этом отрезке достигается на правом конце
и равно f(x). Для того чтобы оно было больше (-4), необходимо и
достаточно, чтобы было верным неравенство f(x)>—4, которое
выполняется при -1<л:<0 (см. рис. 9.52).
2) Если х ^ 0, то значение в точке х больше (-4) (кроме точки х = 2,
но тогда значение в точке х — 1 больше (-4)), поэтому наибольшее значение
функции на отрезке [х-1; х] и подавно больше (-4). Ответ: при х > -1. В
f(b),
\ 1
1
0
\
\ .
-1 х
х-1
1
\
-4
Рис. 9.51
Рис. 9.52
§63. Построение эскизов графиков с помощью производной.
Решение задач с помощью производной
Пример 87. При каких значениях параметра а уравнение
ах3 + (За - 1)х2 + (За + 2)х + а - 1 = О
имеет два корня на отрезке -; 3 ?
L2 J
D Преобразуем данное уравнение, выразив а через х:
ах3 + (За - 1)х2 + (За + 2)х + а - 1 = 0 »
= (г - П2
I)2
а =
(х - I)2
(х + I)3
(обе части уравнения можно разделить на (х + I)3 с учётом того, что
равенство а(х + I)3 = (х - I)2 не может быть верным при х = -1).
Итак, требуется найти, при каких значениях параметра а уравне-
(х - I)2
ние а = имеет два корня на отрезке
(х + I)3
(х — I)2
функцию fix) = — и построим её график.
(х + I)6
Н-д
ля этого исследуем
(х + I)6
А 1 ;
= Г(*-1)2У =
{
I)3
I)6
I)4
Знаки производной и
промежутки возрастания и убывания функции / 'f (x)
изображены на рисунке 9.53. Эскиз
графика функции / на отрезке
представлен на рисунке 9.54. Видно,
что уравнение f(x) = а имеет два кор-
-1
-; 3
при 0 < а ^ /(3).
ня на отрезке
Ответ: при а е 0; — . й
Пример 88. Найдём наибольший член
последовательности хп = Ц[п. х
D Заметим, что xn = f(n), где f(x)=xx,
и найдём промежутки возрастания и
убывания функции /.
= \е
0,5 1 1,5 2 2,5 3
Рис. 9.54
142 Глава IX. Производная и её применения
Рис. 9.55
Знаки производной и промежутки возрастания и убывания функции /
(при х > 0) показаны на рисунке 9.55.
Функция / возрастает на промежутке (0; е], поэтому /(1) < /(2),
т. е. хг < х2.
Функция / убывает на промежутке [е; +оо), поэтому /(3) > /(4) >
> /(5) > ..., т. е. х3 > хп при любом п > 3.
Отсюда можно сделать вывод, что наибольшим членом
последовательности является либо х2, либо х3. Сравним их. Так как 8 < 9, то
л/8 < л/9, откуда л/2 < л/3. Таким образом, наибольший член последо- j
вательности xs = л/3. IS
И Задачи и упражнения
Определение производной.
Производная суммы и линейной комбинации функций
Группа А
Пользуясь определением производной, найдите производную
функции / в точке х0 (ix.i—IX.3).
б) fix) = 5х - 2, х0 = 0;
г) f(x) = 2х2 - х, х0 = 2.
ix.l. a) fix) = 2х + 3, х0 = 1;
в) fix) = х2 + 5х9 х0 = 1;
ix.2. a) fix) = у/х- 3, х0 = 4;
в) fix) = 12х + 11, х0 = 1;
IX.3. а)
в)
= Ух, хо= 1;
1
б) f(x)=
г) f(x) = \3x-2\, xo = -l.
б) ifc
Пользуясь определением производной, найдите производную данной
функции в каждой точке области определения (ix.4—ix.6).
IX.4. а) у = Ъх + 2;
т) у = х2 + х;
IX.5. а) у = у/х- 1;
1Х.6. а) у = 1
б) у = -Зл: - 1; в) у = 2х2;
д) у = л:3; е) у = х4.
б) у = V2- Зл:; в) у = л/л:- 1; г) у =
б) у = __§_; В) у = е*;
б) у __§_;
г) y = sinx; д) у = cos ix + 2); е) у = \пх.
IX.7. Приведите пример функций fug (можно построить их графики),
заданных на (а; 6), таких, что для всех х из этого интервала
выполнялось бы неравенство / > g и: а) /' = g'\ б) /' < gr.
143] Задачи и упражнения
IX.8. Может ли производная всюду положительной функции быть:
а) всюду положительной; б) всюду отрицательной?
Вычислите производные следующих функций, пользуясь известными
производными и формулами (например, производной суммы) (IX.9, IX.10).
IX.9. а) у = 7х + 11; б) у = -5х + 2; в) у = 2;
г) у = 5х2; д) у = 4х2 + 5х; е) у = 2х2 + 6х - 7.
1Х.Ю. а) у = 2у[х + х - 0,5л;2; б) у = -yfx + Зх - 7;
в) у = 2х2 - у[х; г) у = Зх - 1 + 4<Jx - Зх2.
ix.ll. Известно, что в точке х0 функция имеет производную. Найдите:
а) lim п \f *о + - " f(xo) Ь б) lim n / хо + - -/(х0) , где Л—
некоторое фиксированное число, п е N.
Группа В
IX.12. Докажите, что существует f'(x0), и найдите её, если
f(x) = (х- х0) • g(x),
причём функция g непрерывна в точке х0 и g(x0) = 2.
IX.13. Известно, что функция / принимает только неотрицательные
значения и в точке х0 равна 0. Найдите производную в точке х0,
если известно, что она существует.
IX.14. Функции f и g имеют производную в точке х0, f(x0) = g(x0),
и для любого х выполняется неравенство f(x) ^ g(x). Докажите,
что f'(xo) = g'(xo).
IX.15. а) Докажите, что производная чётной функции есть нечётная
функция.
б) Докажите, что производная нечётной функции есть чётная
функция.
IX.16. Приведите пример функции, которая не является нечётной, но
её производная есть чётная функция.
IX.17. Может ли производная всюду определённой функции, не
являющейся ни чётной, ни нечётной, быть: а) чётной функцией; б)
нечётной функцией?
IX.18. Докажите, что производная периодической функции будет
периодической.
IX.19. Известно, что производная некоторой функции периодическая.
Верно ли, что сама функция периодическая?
IX.20. Докажите или опровергните утверждение:
а) Если функция / имеет, а функция g не имеет производной
в некоторой точке, то функция / + g не имеет производной в этой
точке (обе функции определены в данной точке).
144 Глава IX. Производная и её применения
б) Если функции f и g не имеют производной в некоторой точке,
то и функция / + g не имеет производной в этой точке (обе
функции определены в данной точке).
IX.21. Функция / имеет производную в точке а, равную Ъ. Найдите
следующие пределы:
где k — фиксированное натуральное число, п е N.
a + ^] + ... + /fa + ^-]-/i/(a)||, где/геЛГ.
Производная и непрерывность
Группа А
В каких точках существует производная данной функции (IX.22—IX.27)?
IX.22. а) у = \х + 2\; б) у = \2х-1\; в) у = \1-4х\; г) у = \5х + 1\.
ix.23.
19
IX.24. а) i/ = |x+2| + |x|;
в) у = ||х-1|-1|;
IX.25. а) у = х • | х |;
в) # = |л:2 + 2л-- 3|;
19х>19
б) у = |2х- 1|-|х
г) у = ||х|-|д:-1|
б) у = 1x2-11;
г) у = \х2 + х-6|.
IX.26. а) у =
л: при дс е Q,
_ i х при х е Q,
У ' \-х при х е R\Q;
г) у =
х2 при х е Q,
х2 при х е Q,
[-х2 при хе R\Q.
ix.27. а) f(x)= -Vx; б) f(x)= y/x - 3; в) f(x)= л/б-дг;
г) f(x) = yfx; д) f(x) = у/3х+ 7; е) f(x) = Vl - 2х.
- при jc > О,
IX.28. Вычислите /'(0), /'(2), /'(-2), если f(x) =
х4 при jc ^ 0.
IX.29. Вычислите /'(0), /'(I), /'(2), если f(x)= l** ПрИ ^Д1'
[х при л: ^ 1.
IX.30. Приведите пример определённой на R функции, имеющей
производную: а) везде, кроме точки 5; б) везде, кроме точек 0; 1; 2.
IX.31. Найдите необходимое и достаточное условие, связывающее
параметры а, Ъ и с (а Ф 0), при котором функция у — \ах2 + Ъх + с\
имеет точки, в которых не существует производная.
IX.32. Приведите пример функции, которая имеет производную только
в точке: а) х = 0; б) х = 1.
1451 Задачи и упражнения
Группа В
IX.33. Приведите пример функции, определённой на Л, которая не
имеет производной во всех целых точках, и только в них.
IX.34. При каких значениях положительного параметра а имеет
производную в нуле функция f(x) = xa • |х|?
IX.35. Покажите, что функция g(x) = х2 • D(x), где D(x) — функция
Дирихле, непрерывна только в нуле, причём в нуле существует
производная.
IX.36. Приведите пример функции, не имеющей производной ни в одной
вещественной точке, квадрат которой есть всюду
дифференцируемая функция.
IX.37. Постройте график производной функции: a) f(x) = {x}; б) f(x) = [x];
в) f(x) = х + |х|; г) f(x) = ||х - 1| - 1|; д) f(x) = {2х}.
IX.38. При каких значениях параметров а и Ъ функция является: 1)
непрерывной; 2) дифференцируемой в точке х0 = 1:
_ Г х при х>19 _ [х при х > 1,
aj У ~~~ [ах + Ъ при х < 1; } У "= [х2 + ал: при х < 1?
IX.39. Найдите /_'(^о) и f+(xo) Для функции /(х) = |х - хо| ф(х), где
ф(х) — функция, непрерывная в точке х0.
, , ч f/(*) ПРИ Х ^ ^0»
IX.40. Функция h (х) = \ . ч где / и g имеют производные и
[Я(^) при х<х09
lim /'(^) = lim ^'(^)- Верно ли, что функция h имеет производ-
х-*хо+ х-*х0-
ную в точке хо1
IX.41. Функция / имеет производную на R. Найдите необходимое и
достаточное условие того, что функция |/| имеет производную на R.
Группа С
IX.42. Пусть функция / имеет производную в каждой точке отрезка [а; Ь]
и бесконечно много корней на [а; Ь]. Докажите, что существует
корень функции /, являющийся также корнем её производной.
Вычисление производных некоторых элементарных функций
Группа А
Вычислите производную функции по определению (IX.43, IX.44).
ix.43. a) f(x) = eSx; б) f(x) = 3х.
IX.44. a) f(x) = ln2x; б) f(x) = Iog5(6*).
Вычислите производную функции (IX.45—IX.47).
IX.45. a) f(x) = х3 + Зх2 -7х + 5; б) f(x) = х4 - Зх2 + 2;
в) f(x) = х10 - 9х7 + Xs - х - 1; г) f(x) = (х - I)3.
1461 Глава IX. Производная и её применения
ix.46. a) fix) = sinx + cosх; б) f(x) = 2sin;c + х11 - log2jc;
в) f(x) = cos л: - x4 + 2х + 2у[х; г) fix) = 2х + log2^:;
д) f(x) = 5л:4 - Inх + 4 sinx - (0,5)*;
е) fix) = ех - х + ecosa; - Зл/л*.
ix.47. a) f(x) = lnx- х2; б) f(x) = xs - 5х;
в) f(x) = \пх2 - \пх; г) f(x) = 2х • 3*.
IX.48. При каких значениях параметра а производная функции /
всегда положительна:
a) f(x) = ах + 5; б) f(x) = ах2 + Зх - 4;
в) f(x) = xs + х2 + ах + 5; г) f(x) = х3 + Зал:2 + 3* - 7?
Решите уравнение /'(*) = 0 (IX.49—IX.51).
IX.49. a) f(x) = 2sinx + х; б) /(*) = 2cosa; - yfSx.
IX.50. a) f(x) = 3 sin x + 4 cos л: - 5x; б) /(л:) = sin x + cos л: - х.
IX.51. а) /(х) = 2 Inх - л:2; б) /(х) = -е* - 0,5л:2 + х;
в) f(x) = lnx + yfx; г) /(х) = 0,25*4 + 5л:2 + 11л: + 2.
х3
IX.52. Постройте график производной функции: a) f(x)= \-x2+x;
б) f(x) = sinx-l; в) f(x) = \x-l\; г) f(x) = \х\ - \х - 1|.
IX.53. При каких значениях параметра а производная функции /
принимает значения одного знака на всей области определения:
a) f(x) = 3x + acosx; б) f(x) = — - х2 + (а - 1)х + 1?
3
Решите неравенство f'(x) > 0 (IX.54, IX.55).
л/2 л/3
IX.54. а) /(л:) = cos л: х; б) f(x)=sinx + —х.
ix.55. a) f(x) = ех - х; б) f(x) = ex-e\nx.
Укажите как минимум две функции, производные которых равны
данной функции (IX.56, IX.57).
IX.56. а) х; б) л:5; в) Зх11; г) 2л:3 + Зл:2 + 1; д) 0,5л:2 + х - 2.
IX.57. а) ех; б) 2Х\ в) —, х > 0; г) —, jc g й\{0}; д) sinx; e) cosjc.
Л X
IX.58. Вычислите /'(0), если f(x) = х(х - 1)(х - 2) • ... • (х - п)> п е N.
Касательная и её уравнение
Группа А
Напишите уравнение касательной к графику функции / в точке с
абсциссой Хо (IX.59—IX.61).
ix.59. a) f(x) = х2, х0 = 2; б) fix) = х\ х0 = -2.
147j Задачи и упражнения
IX.60. a) f(x) = хъ - Зх + 2, *0 = 1; б) f(x) = х2 - х - 1, х0 = -1;
в) f(x) = Vx, *0 = 1; г) /(х) = *б - |, х0 = 1.
IX.61. a) /(#) = cos л:, х0 = п; б) f(x) = sin л:, дг0 = 0;
в) f(x) = 2х, х0 = 1; г) /(*) = In л:, л:0 = е.
IX.62. Напишите уравнения всех касательных к графику функции
у = х2 - 4х, проходящих через точку (-2; 11).
IX.63. Напишите уравнения всех касательных к графику функции
у = х2 + Зх + 2, проходящих через точку (2; 8).
IX.64. Найдите все касательные к графику функции f(x) = -Xs - Зх:
а) в точке графика с абсциссой -4; 4
б) проходящие через точку графика с абсциссой —4.
1Х.65. Докажите, что касательные к графику функции у = х3 — х в
точках с абсциссами -1 и 1 параллельны.
IX.66. В каких точках графика функции у = х3 + х - 2 касательная к её
графику параллельна прямой у = 4х - 1?
ТХ.67. Найдите точки на графике функции у = х3 - Зх + 5, касательные
в которых параллельны прямой у = —2х.
IX.68. Найдите расстояние между касательными к графику функции
у — —х3 — х2 — Зх +1, которые параллельны оси абсцисс.
3
IX.69. При каких значениях х0 касательные к графикам функций
у = х2 и у = х3 в точках с абсциссой х0 параллельны?
Группа В
х
IX.70. Число х = 1 не является корнем уравнения х2 — х = 2х , но
является корнем уравнения, полученного приравниванием
производных его левой и правой частей. Объясните геометрический
смысл этого факта.
IX.71. Касается ли прямая х + 4у - 4 = 0 гиперболы у = — ?
IX.72. При каком значении параметра а прямая у = х + а касается
графика функции у = 2*Jx?
IX.73. При каком соотношении коэффициентов а, 6, с (аФ 0) парабола
у = ах2 + Ъх + с касается оси абсцисс?
IX.74. Найдите все точки на графике функции у = \пху касательные
ос
в каждой из которых перпендикулярны прямой у = .
IX.75. Напишите уравнения всех общих касательных к графику
функции:
а) у = х2 + х и у = х2 — Зх; б) у = х2 + 2х и у = х2 — 4х;
в) у = х2-6х + 5иу = -х2; г) у = х2 - 5х + 6 и у = х2 + х + 1;
д) У = -х2 + 6х - 2 и у = 4х2; е) у = е* и у = е2х.
148 Глава IX. Производная и её применения
IX.76. В каких точках тангенс угла наклона касательной к графику
функции у = sin л:— л/3 cos x наибольший?
IX.77. Напишите уравнение касательной (хотя бы одной) к графику
функции у = х2 — 2х — 4 \х\9 которая касается графика ровно
в двух точках.
IX.78. Напишите уравнение прямой, касающейся графика функции
у = х2 — 2\х— 11 в двух точках.
IX.79. Изобразите множество точек на плоскости, таких, что через них
к графику функции у = х2: а) можно провести одну касательную;
б) можно провести две касательные; в) нельзя провести ни одной
касательной.
IX.80. Касательная к кривой у = ех в точке с абсциссой а пересекает ось
абсцисс в точке (Ь; 0). Найдите Ъ - а.
IX.81. а) Докажите, что если провести две касательные к графику
х2
функции у — — через точку прямой у = -1, то они будут взаимно
4
перпендикулярны.
б) Найдите все точки плоскости, из которых можно провести
две взаимно перпендикулярные касательные к графику
функции у = Щ-.
4
Группа С
IX.82. Найти геометрическое место вершин всех парабол вида у — х2 +
+ ах + by касающихся прямой у = 4х - 1.
IX.83. При каких р через точку В(р; -1) можно провести три
различные касательные к графику функции у = х3 — Зх2 + 3?
IX.84. а) На прямой у = 2х — 1 найдите все точки, через каждую из
которых проходит две касательные к графику функции у = х2,
л
а угол между ними равен —.
4
б) На прямой у = 6х - 9 найдите все точки, через каждую из
которых проходит две касательные к графику функции у = х2,
а угол между ними равен —.
4
IX.85. а) Найдите все значения а, при каждом из которых касатель-
х +11
ная к графику функции у= sin—-—+ 1,5а-а2 в точке графика
с абсциссой а не имеет точек пересечения с графиками функций
*/ = 0,5а + 2 и у = .
х
б) Найдите все а, при которых касательная к графику функции
у = cos 2х + а2 - а + 1 в точке графика с абсциссой а не имеет
точек пересечения с графиками функций у = 3 - 2х и у = х + —.
4#
149; Задачи и упражнения
IX.86. Окружность радиуса 1 с центром на положительной полуоси Оу
касается параболы у = х2. Найдите точку касания и координаты
центра окружности.
Угол между графиками функции
Группа В
IX.87. Найдите общие точки графиков функций f(x) = 1 — х2 и g(x) =
yfej и выясните, в каких из них графики касаются друг
друга.
IX.88. Под каким углом пересекаются графики функций:
а) у = sin л: и у = cosar; б) у = Xs - х и у = х + 4;
в) у = Xs - х и у = х2 - 10; г) у = ех и e2xl
IX.89. При каких значениях параметра а кривые пересекаются под
углом —: а) у = ах2 - 1 и у = ах2 +1; б) у = ах2 и у = —;
2 х
в) у = a sin л: и у = acosx?
IX.90. При каких значениях параметра Ъ график функции у — пе-
4
ресекает ось Ох под углом 45° с её положительным направлением?
Приближение функции линейной функцией. Дифференциал
Группа В
IX.91. Сравните значение приращения и дифференциала функции
f(x) = х2 в точке х0 = 1, если приращение аргумента равно:
а) Ах = 0,1; б) Ах = 0,01; в) Ах = 0,001.
Af-df(x0)
Покажите, что lim = 0.
Длг — О АХ
IX.92. Сравните значение приращения и дифференциала функции
f(x) = Xs + 2л:2 в точке хо = 1и приращений аргумента, равных:
а) Ах = 0,1; б) Ах = 0,01; в) Ах = 0,001.
Af-df(x0)
Покажите, что lim = 0.
Длг —0 АХ
Группа С
IX.93. Найдите дифференциал функции у = Xs + 5л:2 в точке х0 = 1 и
с его помощью вычислите приближённо значение функции при
х =1,01.
IX.94. Найдите дифференциал функции у = 4х в точке х0 = 25 и с его
помощью вычислите приближённо значение функции при х = 26.
IX.95. Найдите дифференциал функции i/ = л/х в точке х0 = 64 и с его
помощью вычислите приближённо значение функции при х = 65.
150] Глава IX. Производная и её применения
Производная произведения и частного
Группа А
Найдите производную функции в точках, в которых она
дифференцируема (IX.96—IX.100).
IX.96. a) fix) = х • sin л:;
в) f(x)= y[x-tgx;
б) f(x) = х2 - cosar;
г) f(x) = ctgx -ex.
IX.97. a) f(x) = Xs • пх; б) f(x) = *°>2 • tgx;
в) fix) = хп • cos л:; г) f(x) = х^2 • ctgar.
IX.98. a) f(x) = х2 • 2х + Iog2;c - tgx; б) f(x) = cos* • 3* + ctgx • log3x.
ix.99. a) f{x) =
ctgx
6)
ix.100. a)
= ^; в)
I
6)
r) f(x) =
cos х-
Группа В
Найдите производную функции в точках, в которых она
дифференцируема (IX.101—IX.105).
ix.lOl. a) f(x) = хп + л;х; б) f(x) = хп • я*.
ix.102. a) f(x) = х2 • sin л: • 2*; б) f(x) = sinx
ix.103. a) fix) = x4 • ifx + log2 x + log2 x2;
6) /(x) = 2^ • 3^ • x2 + tgx • cos* • yfx.
cos*-sin*; 6) /(x) tgx"ctgx
yfx.
ix.104. a) f{x) =
cosx + sinx
6)
tgx + ctgx
IX.105. a) /(x) = arcsinx2 + arccosjc2;
6) fix) = 2* • 3* • 4* • (log24 x + log24 x2 + log24 x3).
IX. 106. Выведите формулу производной произведения:
а) четырёх функций; б) п функций.
IX.107. Найдите производную функции ix - a) • /(jc), если известно, что
функция / имеет производную в точке а и /(а) = 2.
IX. 108. Докажите или опровергните утверждение:
а) если функция / имеет производную, а функция g не
имеет производной в некоторой точке, то функция fg не имеет
производной в этой точке (обе функции определены в данной
точке);
б) если функции / и g не имеют производной в некоторой
точке, то и функция fg не имеет производной в этой точке (обе
функции определены в данной точке).
Задачи и упражнения
Производная композиции функций
Группа А
Найдите производную функции в точках, в которых она
дифференцируема (IX.109—IX.111).
1Х.Ю9. a) f(x) = jx - I)100; б) f(x) = (2х - I)10;
в) /(*)= л/Зх-7; г) f(x)= л/4- 5х.
IX.110. a) f(x) = (х+ I)4 • (х - 2)3; б) /(л:) = (х + 7)11 • (2* - I)4;
в) /(л:) = (х2 + I)10 • Xs; г) /(*) = (л: + 5)10 • (х - 5)10.
IX.111. a) f{x) = ех2+х; б) f(x) = 2соа2х; в) f(x) = 3**^.
тт « л • v #2 sin —, л: Ф О,
IX.112. Найдите производную функции f(x)= I x в точке:
а) х = 2; 6)^ = 0. l°'X=°
IX.113. При каких значениях параметров а и b функция
Г ал:2 + Ьх + с, х ^ О,
х, х<0
дифференцируема в каждой точке своей области определения?
IX.114. Выясните, является ли функция: 1) непрерывной; 2)
дифференцируемой в нуле:
ч ., ч sin—, хфО, _ £/ ч
а) /(*)= i х' б) /(л:)=
О,
[О, х=0; [0, х=0.
Если функция дифференцируема в нуле, выясните, является ли
производная непрерывной в нуле функцией.
Группа В
Найдите производную функции в точках, в которых функция
дифференцируема (IX.115, IX.116).
IX.115. a) f(x) = log3jc - i (5* + 2); б) fix) = log2jc + г (10 - 2х);
в) fix)= ( )
IX.116. a) fix) = J1"sin"; 6) fix) = In(x + Jx2 + l) + 3.
\ 1 + sin x \ v /
IX.117. Вычислите производную функции в указанных точках.
ч 1 + X - X2 ~ 1*ч otg- 1
а) у = 1 _ х2 , х = 0, х = 1; б) у = 2 *, х = —;
в) у=
г) г/ =
д) у = 3cos2o:- д/l - sin2;c • (sinл: + cos л:), х = —;
152[ Глава IX. Производная и её применения
Группа С
IX.118. Рассмотрев производную функции f(x) = х + х2 + Xs + ... + хп,
найдите формулу для суммы: а) 1 + 2х + Зх2 + ... + пхп~г;
б) I2 + 22х + 32х2 + ... + п2хп'г.
IX. 119. Пользуясь формулой бинома Ньютона, найдите суммы:
а) С\ + 2С2п+ЗС*+... + пС2;
б) ЗС\ + 2-32-С2п + 3-3s-Csn + ... + 71-3я-С».
IX. 120. Существуют ли такие функции /и^, что:
а) / дифференцируема в g(jco), g не дифференцируема в дс0,
а функция /(^) дифференцируема в х0 (функции определены
в соответствующих точках);
б) / не дифференцируема в g(x0), g не дифференцируема в х0,
а. функция f(g) дифференцируема в х0 (функции определены
в соответствующих точках)?
Производная обратной функции.
Производные обратных тригонометрических функций
Группа А
Найдите производную функции (IX.121, IX.122).
IX.121. a) g(x) = 2х • arccoso: + arcsina; • (1 + х2) - х;
б) g(x) = ex • arcsino: + arccosa; • 1пл:.
IX.122. a) h(x) = arccosx2; б) h(x) = arccos2^:;
в) h(x) = arcsinx2; г) h(x) = a.rcsm2x.
Группа В
IX.123. Вычислите производную функции в указанных точках:
а) у = ln(l + sin2л:) - 2sin* • arctg(sinx), x = —;
2х ^
б) у = arcsin -у х = 0, х = 2;
1 + х2
1-х2
в) у = arcsin -у х = —1, х = 1, х = 0;
г) у = ^arctg ^/cos In3 л: , x = 1.
Найдите производную функ
в точках, в которых функция дифференцируема.
^лТТ„ , л/ч arcsin х sin (2 arcsin x)
IX.124. Найдите производную функции f(x) = +
Таблица производных
Группа А
IX.125. Пользуясь таблицей производных, определите, производной
какой функции является: а) Xs; б) 2х; в) — при х>0; г) cosx; д) 1.
Зх
.128. a> /(x) = |2: J;;; 1;
Задачи и упражнения
Первообразная
Группа А
IX.126. Докажите, что функция F является первообразной функции /,
если:
а) F(x) = (х- I)3 • х2, f(x) = (х - I)2 • х • (5* - 2);
r2 i 1 у2 _ 1
б) FM=^,fW=y;
в) F(x) = cosx • cos3x, f(x) = -sin2л: • (8cos2* - 3);
г) F(x) = \n(x + yll + x2), f(x)= * .
Найдите какую-либо первообразную функции (ix.127, IX.128).
IX.127. a) f{x) = (x + 1) • (*2 + 2); 6) f(x) = *'~"^~"1;
ч-/ч X4- X2+ 1 \ s/ \ X3- X2+ X - 1
Д) /(x)= ( )
6) /(x) = |* +\;^ 2;
в) /(л:) = max{l - x; 2 + x}; r) f(x) = min{o:2 - 3; x - 1};
[1-х, x^ 0,
Д) f(x) = s2cosx- 1, 0 < x < n9
[ 2 sin x - 3, x > n.
IX. 129. Пусть функция / задана на отрезке [а; [3] и имеет первообразную на
нём. Что можно сказать про число а, если через точку А (а; 2а - 1)
не проходит график ни одной первообразной функции ft
Группа В
IX.130. Найдите какую-либо первообразную функции:
а) Зх-1*1 + 1; б) |х-1| + 1; в*) *2,+ 1 ; г) |х + 2|-(х-1).
& I х I ~~ х
IX.131. а) Докажите, что первообразная нечётной, непрерывной на R
функции обязательно является чётной функцией.
б) Верно ли, что первообразная чётной, непрерывной на R
функции обязательно будет нечётной функцией?
в) Верно ли, что среди первообразных периодической,
непрерывной на R функции обязательно найдётся периодическая функция?
IX.132. Пусть / имеет производную второго порядка на интервале (а; Ь),
причём нашлось такое число со Ф 0, что при всех х е (а; Ь)
выполнено равенство f"(x) + (of(x) = 0. Докажите, что функция
g(x)= f'(x) является первообразной функции / на (а; Ь).
154J Глава IX. Производная и её применения
Определение неопределённого интеграла.
Теорема об элементарных свойствах неопределённого интеграла
Группа А
Найдите интеграл (IX. 133—IX. 140).
ix.133. a) Jmin(2;c; х2); б) j\x - 2\dx; в) \\{2х + |x|)dx;
г) ]f(x)dx, где f(x)= \х2_2Ху х> О; Д)
IX.134.
ix.135. a) J
IX
); 6)J
x, x > 0;
x3 + x2 - 1
; b*)J
4x2-3x + 5
dx.
(2x - 1) ■ (Зх2 + Зх + 2) ^ # f(4x + l)(2x2- 1) ^
dx; o) I .— ax.
2
X3
3cosx-
COS2 X
.136. a)J
IX. 137. а) у °° dx; 6) [
J Jl - x4 J
1+ х2
' x3 + x + 1
x2+ 1
dx.
ix.138. Найдите |2sin4xdx + Jsin22xdx + [2cos4xdx.
ix.139. a) ]-^^-dx; 6) j * х*г * dx; в) J— -dx.
ix. 140. a) \e2x (ex + l)dx; 6)
в)
Группа В
IX. 141. Найдите интеграл: а) [—-—-—-—; б) \tg2xdx.
J sin^ х • cos"2 x J
— при x ^ — 1,
IX. 142. Найдите ту первообразную функции f(x)= I x
график которой касается прямой у = 2х - 5.
[х при х > -1,
Интегрирование методом подстановки
Группа А
Найдите интеграл (ix.143, IX.144).
IX.143. а) \ . dx; б) \JSx- 5dx; в) [з/бх + 3dx.
JA/x4-2 J J
IX.144. a) J ~ + 2 dx; 6) j(2x- l)100dx; в) j(6x- l)sdx.
IX. 145. Объясните, в чём ошибка в следующем рассуждении: «Рассмот-
Г х3
рим I (х2 - 2х + l)dx = х2 + х + С. С другой стороны,
Задачи и упражнения
x = j(x-l)2dx = jt2dt =
Приравняв эти выражения и уничтожив одинаковые слагаемые
в обеих частях равенства, получим — = О»,
3
Найдите интеграл (IX.146—IX.150).
IX.146. a) J32*-!<**; б) jeSx-*dx.
2 3
j
х2+х+1, -. г х3 + х2 - 1 , 4.4 Г4*2 - Зх + 5
dx; б) jdx; в*) J
г„~ чгх2+х+1, -. г х3 + х2 - 1 , 4.4 Г4* - Зх + 5 ,
IX.147. a) J——— dx; б) j-^—^-dx; в*) J ^ dx.
ix.148. a) f . о *——; б) [—^—; в) f sinxo dx; г) fsin2x- cosxdx.
J sin2 (Зх + 5) J cos2 4x J 1 - sin2 x J
IX.149. a) |cos2xdx; 6) |sin3xdx; в) Jsin3x
r) Jcos6x-cos2xdx; д) Jsin8x • cos2xdx.
TV^^ _ч f dx ^ г dx . _ч Г dx . _ч г dx
IX.151. Найдите интегралы, обратив особое внимание на запись ответа:
а) \tgxdx; б) Г ~cosxdx; в) [tg3xdx; г) \tg4xdx.
J J sin x J J
Найдите интегралы (ix.152—ix.154).
IX.152. a) \-^—dx; 6) \
J 1 + ex J 1 + ex
IX.153. a) JWl - x2 dx; 6) \x2 • Vl - x2 dx; в) Jx3 • Vl - л:2 dx.
IX.l54. a) J^; )J^
J sin2 x J sin4 x
8x — 3
IX.155. Найдите первообразную функции f(x)= — , график кото-
X i АО
рой проходит через точку А(0; 2).
IX.156. Найдите первообразную функции у = -, график которой
1 CiOC — 1
касается прямой у = —х + 3.
3
Группа В
IX.157. Найдите интеграл Jsinx - cos2x • sin3xdx.
IX.158. Найдите наименьшее натуральное значение а, при котором
существует целое by такое, что функция (ах + б)238 имеет
первообразную, являющуюся многочленом с целыми коэффициентами. Для
найденного а найдите хотя бы одно соответствующее значение Ь.
156! Глава IX. Производная и её применения
IX.159. Предложите метод интегрирования выражения вида
Jsinm;c- cosnxdx,
если хотя бы одно из натуральных чисел тип нечётно.
Проверьте этот метод при небольших значениях тип.
IX.160. Найдите: a) \cos4xdx; б) [sin6 x dx.
IX.161. Найдите:
dx ^ч г 2х - 4 , . г 2xdx
*4х + з'' б) dX' B)
- 6)dx , г х3 - х2 + 2х - 2
; Д) J
. f (4л; - 6)dx , г
Г) Ь-4* + 3; Д) J
Обобщите решённые задачи, сформулировав алгоритм
нахождения интеграла рациональной функции, знаменателем которой
является квадратный трёхчлен, имеющий два различных
вещественных корня.
IX.162. Найдите:
d 22 2х ,
dX;
v Г 4х-6 . ч f х3- х2+ 2х - 2
Г) Jx»2x+l<fa; Д) 1
х>-2х+1 ^
Обобщите решённые задачи, сформулировав алгоритм
нахождения интеграла рациональной функции, знаменателем которой
является квадратный трёхчлен, имеющий ровно один
вещественный корень.
IX. 163. Найдите:
d -, г 2х-2 , ч 2
б) h*2x + 2dX> B)
г) JХ2 *2х + 2 dx; Д^ \°° х2*- 2х + 2—dXm
Обобщите реп1ённые задачи, сформулировав алгоритм нахождения
интеграла рациональной функции, знаменателем которой
является квадратный трёхчлен, не имеющий вещественных корней.
IX. 164. Найдите: a) |Vl + x2 dx; б) jx2 • Vl + x2dx.
IX.165. Постройте множество точек плоскости, через каждую из
которых не проходит график ни одной из первообразных функции
., ч 1- 2х
хг - 6х + 5
Интегрирование по частям и комбинированные методы
Группа А
Найдите интеграл (IX.166—IX.171).
ix.166. a) \x- cos 2x dx; б) \х2 -sinxdx.
157| Задачи и упражнения
IX.167. a) jx-exdx; б) jx2-exdx.
IX.168. а) }(5 + 2х) • 2хdx; б) J(5 + 2х) • 2хdx.
IX.169. a)\x-lnxdx; 6)\\nxdx; в) f(3a; + 4) • \og7xdx; г*) fin ^-^ dx.
IX.170. a) I arcsinarda;; 6) Jarctgarda;; в) I arccos(2x)dx.
Группа В
ix.171. a) \ex-cosxdx; 6) \e2x -sin3xdx;
в) \sin(\nx)dx; r) fcos2(21nx)da:.
Теоремы Ролля, Ферма, Лагранжа, Дарбу
Группа А
IX.172. Применима ли теорема Ролля к функции f(x) = 1- лрс2 на
отрезке [-1; 1]? Поясните ответ графически.
IX.173. Применима ли теорема Лагранжа к функции /, заданной на
отрезке [-1; 1]: 2
a) f(x) = %Jx; б) f(x) = х~*;
ч „, ч f I — х2 при х ^ 0, ч ^. ч f 1 + х при л: ^ О,
j^ j^«> ui3jj j^ > Q* i X (>эс jj^jj JC ^ 0 •
В тех случаях, когда теорема Лагранжа применима, найдите
число с из теоремы Лагранжа.
Группа В
IX.174. Вычислите значение с в теореме Лагранжа для функции /
на отрезке: a) f(x) = \пх на [1; е]; б) f(x) = arctgjc на [0; 1];
в) f(x) = ^с на [1; 4]; г) fix) = х* на [1; 3].
IX.175. Приведите примеры функций, для которых выполняются два
условия теоремы Ролля из трёх: 1) функция непрерывна на
промежутке [а; &]; 2) функция дифференцируема на интервале
(а; Ь); 3) /(а) = /(Ь), но при этом не верно заключение.
IX.176. Докажите, что -^-^—-^- > 0 при любых а, Ь > 1; афЪу если
f(x)=±x*-x.
IX. 177. Используя теорему Лагранжа, докажите справедливость
неравенства: a) |sina - sinfe| ^ \а - Ъ\ для любых чисел а и Ь;
б) |lna - 1пЬ| ^ \а - Ь\9 если а, Ъ е [1; +оо).
IX.178. На графике функции f(x) = х2 + Зх + 1 найдите точку, в которой
касательная параллельна хорде, соединяющей точки (—1; 1) и (1; 5).
IX.179. Докажите, что производная многочлена
Пх) = (х2 - 1) . (х2 - 4) • (х + 3)
имеет ровно четыре корня.
158| Глава IX. Производная и её применения
Группа С
IX. 180. Пусть функция / определена и непрерывна на промежутке
[0; а], а также дифференцируема на интервале (0; а), причём
/(0) = 0. Докажите, что существует точка с е (0; а), такая, что
IX.181. Пусть функция / определена и непрерывна на промежутке
[а; &], а также дифференцируема на интервале (а; Ъ) и при этом
f(a) = f(b). Докажите, что существует точка с е (а; &), такая,
что f(a)-f (с) = cf'(с).
IX. 182. Функция, заданная на множестве всех вещественных чисел,
дважды дифференцируема, и её вторая производная не равна
нулю ни в какой точке. Докажите, что график функции / имеет
единственную общую точку с любой своей касательной.
IX. 183. Пусть функция / дифференцируема на отрезке [0; 1], причём
/(0) = /(1) = 0 и Л - = 1. Докажите, что существует с е (0; 1),
такое, что |/'(с)| > 2.
IX.184. Пусть функция / определена и непрерывна на промежутке [0; 1],
а также дважды дифференцируема на интервале (0; 1), причём
/(0) = /(1) = 1 и min f(x) = -1. Докажите, что max |/"(*)l > 8.
[01] [01]
IX.185. Функция / непрерывна на [а; Ь] и дифференцируема на (а; 6).
Докажите, что при любом значении параметра а уравнение
ос/(х) + f'(x) = 0 имеет хотя бы один корень на (а; 6), если
f(a) = f{b) = 0.
ix.186. a) Пусть / — функция, дифференцируемая на R. Докажите,
что если \/х е R f(x) • f'(x) = 0, то / — константа,
б*) Пусть / — функция, имеющая п производных на R, причём
f(n) — непрерывная на R функция. Докажите, что если \/х е R
f (х) • /' (х) •... • /(л) (х) = 0, то / — многочлен степени не выше п — 1.
в**) Пусть / — функция, имеющая п производных на R.
Докажите, что если \/х е R f(x) • f'(x) • ... • f^n)(x) = 0, то / —
многочлен степени не выше п - 1.
IX.187. Функция g дифференцируема на [а; 6], где Ъ - а > п. Докажите,
что Зх е (a; b): f'{x) < 1 + f2(x).
IX.188**. функция / имеет вторую производную на отрезке [0; а],
причём Ух е (0; а) f(x) + f"(x) > 0. Кроме того, /(0) = f(a) = 0 и
Ух е (0; а) f(x) > 0. Докажите, что а > п.
Доказательство тождеств с помощью производной
Группа А
IX. 189. Докажите тождество:
a) arcsin;*; + arccosjc = —; б) arctga; + arcctga; = —.
2 2
159[ Задачи и упражнения
IX.190. Докажите справедливость тождества:
а) 2arcsimc = arccos(l — 2л:2) при 0 ^ х ^ 1;
б) 2arccosx = arccos(2;c2 - 1) при 0 < х < 1.
1-х2
IX.191. Докажите, что arccos = 2arctg;c при х ^ 0.
л. i X
IX.192. Докажите, что функция
fix) = cos2* + cos2 — + х - cos л: • cos — + x\
принимает одно и то же значение при любом вещественном х.
Найдите это значение.
IX.193. Докажите тождество arctga; + arctg = при х < — 1.
J. 1 X 4
Группа В
IX.194. Придумайте функцию, отличную от константы на отрезке
[0; 1], производная которой равна нулю во всех точках
интервала (0; 1), кроме точек вида хп = —, п е N.
Возрастание и убывание функции
Группа А
Найдите промежутки монотонности функции (IX. 195, IX. 196).
IX.195. а) у = Xs - х2 + х; б) у = хь - Ъх2 + 2;
v -. ч 3 + х2 ч *й ч 1 + х2
в) /(*)= х ; г) fix)= x .
i— 1 х2
IX.196. а) у = yjx + -=; б) у = е~х • х2; в) у = \пх; г) у = Xs - х2 + х.
IX.197. Решите уравнение 5л:5 + 3 • ^]3х + 11 + arcsin(l + х) = 1.
IX.198. Исследуйте на возрастание и убывание функцию
у = х2 - 6х + 8у[х.
Найдите промежутки монотонности (IX.199, IX.200).
IX.199. а) у = sinjc- л/Зсовл:- х; б) у = cosa; ; в) у = tga; - 2х;
v 2 . (к ) 2V3 (п \
r)y=nSin{2X)-—COS{2X)-X-
IX.200. a) y = ix- I)3 • (2jc + З)2; б) у = х2 • в"*2; в) у = —;
х2 — Зх + 2
г) у = ха • ег*9 х > 0, а > 0; д) у = епх - cosrar; е) у = —— -;
X "г ОХ "г ^
1 2х (3 х)3 /
ж) у = - + ——-; з) у = J -(т-; и) у = д/вл:2 - л:4;
X X — 1 IX — ZI
к) у = J2jc3 + 9jc2 ; л) у = . ; м) у =
дМХ "Г L)
160[ Глава IX. Производная и её применения
Группа В
IX.201. При каких значениях параметра а функция возрастает на jR:
a) f(x) = ats + at; б) f(x) = atb + at?
IX.202. При каких значениях параметра а функция f(x) = -Xs + 4х2 -
- ах - 8 возрастает на интервале (1; 2)?
IX.203. При каких значениях параметра а функция
у = (х - а)2 • (х - 2а + 4)2
возрастает на отрезке [0; 1]?
IX.204. Найдите, при каких значениях параметра а функция у = f(x)
строго убывает на (1; +оо): a) f(x) = axs + х; б) f(x) = -xs + ах.
Точки экстремума. Критические точки
Группа А
IX.205. Найдите критические точки и точки экстремума функции:
aj / \Х) - 4 3 х , ) т к ) - 3 2 >
i = е2х — х.
в) f{x) = (х- 2)2 • (х + I)3;
г)
IX.206. Укажите точки экстремума и экстремальные значения функции:
/ / V / — о ■* ' / / V / — о ■* ' / ' V / — о *
Исследуйте функцию на экстремумы (IX.207, IX.208).
IX.207. а) у = х2 • е*; б) г/ = (2л: + 1) • 3/(л;-2)2;
в) у =
IX.208. а) у =
г) У =
х3 - 2х2 - х + 2'
в) у = х - 2 sin2 л:;
д) 1/ = (х - 2) • cos пх sin nx;
я
х2 +1 при л: * О,
2 при х = 0.
(3 - х)2
ж) г/ = In (cos x) — cos x;
и) г/ = л:• Ух- 1;
л) г/ = max{7x - 6л:2; | л:3|};
н) г/ = sin(;c+ l)-|cosx|, л:е (0; п);
о) i/ = sin|;c-3| + cos;x;, jcg(O; я); п) у =
г) г/ = х - 2arctg;c;
е) у = (3 - *2) • е*;
з) у = 1п(лс2 + 1) - 2arctgjc;
к) г/ =
м) у = \х-1\- л/л: + 2;
1 + | cos л: |
2 + cos x + V3 sin
Группа В
IX.209. Найдите, при каких значениях параметра а функция
у = a sin 4х - Юл; + sin 7x + 4ах
убывает на R и не имеет критических точек.
Задачи и упражнения
IX.210. Найдите, при каких значениях параметра а функция
у - - е2х + (1 - а) ех - ах + sin 2
имеет критические точки.
Наибольшее и наименьшее значения функции на промежутке
Группа А
IX.211. Найдите наибольшее и наименьшее значения функции на
промежутке:
a) /(*) = *5 - х - 1, [1; 4]; б) /(*) = ^±j, [0; 2];
в) /(x)=!*.lnx-x.ln2, [|;|]; г) /(*) = tgx-8x, Г-|;|);
д) /(х) = х*, (0; 1]; е) /(*) = ^2- cos*2, x e R.
IX.212. Найдите наибольпгее и наименьшее значения функции
f(x) = cos3* - 2 cos л:
на промежутке
L 2; 4J"
IX.213. Найдите наибольпгее и наименьпгее значения функции
/(*) = 2sin3* + 16 sin2*.
IX.214. Найдите множество значений функции /(*) = cos3* - cos*.
IX.215. Найдите множество значений функции:
а) у = 2* + 3 • V*2" при * g [-2; 2];
б) /(*) = cos8* + sin8* при х е R;
х + 2
в) /(*) = —= при * е (-1; +оо).
у/Х + 1
IX.216. Для любого a е (-оо; 5) найдите наибольшее и наименьшее
значения функции у = Xs - 12* на промежутке [а; 5] как
функции от а.
Группа В
IX.217. Существует ли значение параметра а, при котором наибольшее
и наименьпгее значения функции /(*) = 2*3 — За*2 на отрезке
[-1; 1] достигаются внутри него?
IX.218. При каких значениях а наименьшее значение функции /(*) = *2 + —
на промежутке [1; 2] больше 6? х
IX.219. Найдите множество значений функции /(*) = V4- * + V* + 2.
162; Глава IX. Производная и её применения
IX.220. Для каждого а > -1 найдите наибольшее значение функции
fix) = Xs - \2х на отрезке [-1; а] как функцию от а.
IX.221. Для каждого а > —2 найдите наименьшее значение функции
f(x) = 21 х — х3 на отрезке [-2; а].
max (xs - Зх) при а < О,
IX.222. Постройте график функции f(a) =
х е [а; 0]
0 при а = 0,
max (х3 - Зх) при а > 0.
* е [0; а]
IX.223. Постройте график функции f(a) = min (x3 - х).
х е [а; а + 1]
IX.224. Найдите, при каком а е R наименьшее значение функции
fix) = х3 - 2ах2 +1 на отрезке [0; 1] достигается на его правом
конце.
Группа С
IX.225. Функция / имеет производную на (0; +оо) и непрерывна на
[0; +оо). Пусть /(0) = 0 и /' является возрастающей функцией
fix)
на (0; +оо). Докажите, что gix)= является возрастающей
функцией на (0; +оо).
IX.226. Пусть Р — многочлен степени п, принимающий только
положительные значения на R. Докажите, что многочлен Q(x) =
= Pix) + P'ix) + ... + P^n)ix) также принимает лишь
положительные значения на R.
Текстовые задачи на применение производной
Группа А
IX.227. В данный треугольник впишите прямоугольник наибольшей
площади так, чтобы одна из его сторон лежала на основании, а
противолежащие вершины — на боковых сторонах треугольника.
IX.228. Найдите наибольшую площадь равнобедренного треугольника,
вписанного в круг радиуса г.
IX.229. Число 12 разложите на два слагаемых так, чтобы сумма их
квадратов была наименьшей.
Группа В
IX.230. Из всех трапеций, вписанных в окружность радиуса г так, что
одно из оснований — диаметр, найдите имеющую наибольшую
площадь.
IX.231. Какие размеры имеет прямоугольный параллелепипед
наибольшего объёма, вписанный в шар радиуса г?
IX.232. Через точку А (2; 0,25) проводятся прямые, пересекающие
положительные полуоси в точках В и С. Найдите уравнение
прямой, для которой отрезок ВС наименьший.
Задачи и упражнения
Вторая производная. Производные высших порядков
Группа А
Вычислите вторую производную функции (IX.233, IX.234).
IX.233. a) /(*) = *3 + Зх2 - 7х + 5; б) f(x) = *4 - Зх2 + 2;
в) f(x) = х10 - 9х7 + Xs - х - 1; г) f(x) = (х - I)3.
IX.234. a) f(x) = sin* + cos л:; б) f(x) = 2 sin* + х11 - log2*;
в) f(x) = cos* - x4 + 2* + 2V*; г) /(*) = 2х + log2*;
д) /(л:) = 5л:4 - In* + 4sinx - (0,5)*;
е) f(x) = ех - х + /
Группа В
IX.235. Вычислите /<10°), если:
а) /(*) = *93 + 5*43; б) /(*) = *100 - 2*23;
в) /(*) = *101; г) /(*) = (*2 + * - I)44 • (2*2 - * + I)6;
д) /(*) = sin*; e) /(*) = cos*.
IX.236. Вычислите /(5), если:
а)/М=-Лт; б) /(*)= __0 )_ : в) /(х)= arctgх.
х2- 4л:+ 3'
Выпуклые функции
Группа А
IX.237. Исследуйте на выпуклость функции: а) у = 0,5*; б) i/ = log5*;
в) y = cosx; г) у = Xs.
IX.238. Найдите промежутки выпуклости функции:
*3 _ч *3
a) z/ = arctg*; б) у =
-; в) у =
;; т) у =
- 12*.
() *2+12!
IX.239. Докажите, используя вогнутость функции /(*) = V*,
неравенство V1005 + V1007 ^ 2V1006.
IX.240. Докажите, что каждый многочлен с положительными
коэффициентами, не содержащий нечётных степеней, является чётной
выпуклой функцией.
IX.241. Найдите точки перегиба функции:
а) у = *4 - б*2 + 4; б) у =
в) у = 2*2-*-—;
З-*2'
г) у = х2-Зх-\.
IX.242. Найдите интервалы выпуклости и точки перегиба функции:
ху/х
1641 Глава IX. Производная и её применения
Группа В
IX.243. Докажите, что если дважды дифференцируемая выпуклая на
промежутке функция имеет более одного экстремума на этом
промежутке, то существует интервал, на котором функция
постоянна.
._ . х + Зу . sinx + 3sin# ГЛ ,
ix.244. Докажите, что sin > -, где х, у е [0; п].
4 4
IX.245. При каких значениях а е R функция f(x) = ех + ах3 имеет
точки перегиба?
х + 1
IX.246. Докажите, что график функции у = — имеет три точки пере-
хг + 1
гиба, лежащие на одной прямой.
IX.247. Докажите, что для любых а и 6, таких, что а, Ъ е [0; 1],
а + Ъ = 1, и любых положительных чисел х и у выполняется не-
равенство In (ax + £ш) ^ ——.
IX.248. Докажите, что любой многочлен нечётной степени больше 1
имеет хотя бы одну точку перегиба.
IX.249. При каких значениях параметров а и Ъ точка с координатами
(1; 3) является точкой перегиба функции f(x) = ах3 + Ъх21
Группа С
IX.250. а) Докажите, что если функция / выпукла на [а; 6], то
\/х1э х9 х2 £ [а; Ь], таких, что хг < х < х2У выполняется неравенство
f(x)-f(Xl) f(x2)-f(x)
^ .
X Х-^ Х2 X
Поясните геометрический смысл этого неравенства,
б) Устремляя в неравенстве пункта а) х к хг и к х2, докажите,
что если функция / выпукла и дважды дифференцируема на
[а; Ь], то \/х е [a; b] f"{x) > 0.
IX.251. а) Докажите, что для выпуклой вверх на промежутке функции /,
любых чисел х19 х2, ..., хп из этого промежутка и любых
неотрицательных чисел al9 a2, ..., ал, таких, что аг + а2 + ... + ап = 1,
выполняется неравенство (обобщение неравенства Йенсена)
f(a1x1 + а2х2 + ... + апхп) ^ ajixj + a2f(x2) + ... + anf(xn).
б) Пусть х19 х29 ..., хп е R и al9 a2, ..., ос„ — произвольные
неотрицательные числа, такие, что аг + ос2 4- ... + ап = 1. Докажите,
что справедливо неравенство (агхг + а2х2 + ... + адл:п)2 ^ ахХ1 +
+ ос2*| + ... + ал^.
в) Докажите неравенство (alb1 + a2b2 + ... + anbn)2 ^ (af + ... + а\) х
х (bj2 + ... + b2), верное для любых al9 a2, ..., ал, Ь19 Ь2, ..., 6Л е R.
165| Задачи и упражнения
Построение эскизов графиков функции
Группа А
х^
IX.252. Исследуйте функцию у = —. Постройте её график.
3 1
IX.253. Постройте график функции: a) f(x)= х + ; б) f(x)= * +
IX.254. Исследуйте функцию Ъх + V3- х. Для каждого d укажите
количество корней уравнения Ъх + V3- х = d.
IX.255. Исследуйте функцию f(x)= . Постройте её график.
X X ~~ тс
IX.256. Исследуйте функции из задач vin.74—VIII.79 и постройте их
графики.
IX.257. Постройте график функции:
a) f(x)= х-е~х; б) f(x) = xs - е~х; в) f(x)=e8inx;
г) f(x) = ^arcsin^. д) f(x) = arctgln^; e) f(x) =
I
ж) /(*)=(* + 1).1п2(;с + 1); з) f(x)=xx; и) f(x)=x*.
Доказательство неравенств с помощью производной
Группа А
IX.258. Докажите справедливость неравенства: а) 2у[х> 3 при х>1;
X
б) ех > 1 + х + — при х > 0; в) 1п(1 + х) < х - — + — при х > 0.
2 2 3
О у—
IX.259. Докажите неравенство 2х + -- > Мх при л: ^ 0.
их2
IX.260. Докажите, что: a) sin* < х < tga; при 0 < л: < —; б) cosjc > 1
при х > 0; в) > cos л: при 0 < х < —.
х 2
Группа В
Докажите неравенство (IX. 261, IX. 262).
IX.261. a) tga; > х + — при х > 0; б) sin* < х - ^— + -^- при х > 0.
3 3! 5!
IX.262. а) #- ^— < arctg* < лгпри х>0; б) sinx<^(n - л:)при 0<х<^-;
3 2 2
в) 2аЫп-<Ь2 - а2 при 0<а<Ь.
IX.263. Докажите, что для всех отрицательных х выполняется неравен-
л 2х - 3 х . Л
ство In + — < 0.
х - 7 11
166 Глава IX. Производная и её применения
IX.264. Докажите, что при 0 < хг < х2 < — выполняется неравенство
ix 2
х2
IX.265. Докажите, что при а, Ъ > О неравенство —+ —> ab, если р nq —
положительные числа, такие, что —I— = 1 (неравенство Юнга).
Касательная к графику многочлена. Кратные корни многочленов
Группа С 2
IX.266. Дан многочлен рп (х) = 1 + х + — + ... + —.
а) Докажите, что многочлен рп ни при каком п не имеет
кратных корней.
б) Докажите, что при чётном п многочлен рп не имеет корней.
в) Докажите, что при нечётном п многочлен рп имеет ровно
один корень.
IX.267. Пусть Р — многочлен степени п от одной переменной.
Докажите, что если все корни этого многочлена вещественны, то и все
корни его производной тоже вещественны.
IX.268. Докажите, что каноническая форма многочлена (х - 1)п • Q(x)
имеет хотя бы п + 1 ненулевой коэффициент при Q(x) Ф Э.
IX.269**. Докажите, что если многочлен с рациональными
коэффициентами имеет кратный корень, то он раскладывается в
произведение многочленов с рациональными коэффициентами,
каждый из которых имеет ненулевую степень.
Решение задач с помощью производной
Группа А
IX.270. Найдите множество значений функции у = xlnx — х.
IX.271. Сколько корней имеет уравнение 4е~х • (х2 + х - 5) = 1?
IX.272. Докажите, что х = —1 является единственным корнем
уравнения Xs + Зх2 + 6х + 5 + arctg* + — = 1.
4
IX.273. Сколько корней имеет уравнение х4 — 4х + 2 = О?
IX.274. а) Найдите расстояние от точки М(2; 0) до графика функции
f(X)~ 427(х-2)
б) Найдите расстояние от точки М(0; —2) до графика функции
f(x) = -^ 2, где х > 0.
л/3*3
167 Задачи и упражнения
IX.275. Решите уравнение 2х + - = ifx.
о
IX.276. Найдите все значения параметра а, для каждого из которых
существует только одно Ь, такое, что Ъ2{Ъ + а) = 1, где а, Ъ е R.
Группа В
IX.277. При каких неотрицательных значениях параметра а
наибольшее значение функции f(x)= ах Л— на промежутке [-2; —1] бу-
х
дет наименьшим по модулю (среди всех наибольших значений)?
IX.278. На линии, заданной уравнением logs(y+ l) + log3(3-;c) = 1,
найдите точку, расстояние от которой до прямой Зх - 4г/ - 12 = О
будет наименьшим.
IX.279. При каких значениях параметра а наибольшее значение
функции f(x) = Xs + Ъах2 + 2а на отрезке [-2д/3; 2] достигается в двух
различных точках?
IX.280. Найдите наименьшее значение длины отрезка прямой у = Ь, кон-
цы которого принадлежат графикам функций у = 2х — yjl + x2
и у = 2х.
IX.281. Найдите геометрическое место вершин всех парабол вида
у = х2 + ах + Ь, касающихся прямой у = 4х — 1.
IX.282. Найдите расстояние между графиками функций у = -х2 и у = х+ 1.
IX.283. Сравните (sinl)cosl и (cosl)sinl.
IX.284. Найдите множество значений функции g(x)= fix)- f\ ,
где f(x)= x + ——.
X i X
IX.285. При каких значениях х наибольшее значение функции
f(t) = t3 — 3t2 на отрезке [х — 1; х] будет больше чем —4?
IX.286. При каких значениях параметра а уравнение Xs - ах - а = О
имеет три корня на отрезке [-2; 4]?
IX.287. При каких значениях параметра а уравнение х4 — ах3 + 27 = О
имеет хотя бы один корень, больший 4?
IX.288. При каких значениях параметра а существуют ровно две точки
1 3
на графике функции у = -х4 - -х2 + 2х - 3, касательные в ко-
торых к этому графику параллельны прямой у — ах.
IX.289. При каких значениях параметра а уравнение Xs - ах + 2 = О
имеет хотя бы одно положительное решение?
IX.290. Сколько корней в зависимости от а имеет уравнение
х3 + ах + 1 = О?
1681 Глава IX. Производная и её применения
IX.291. Сколько корней в зависимости от а имеет уравнение: а) ех = ах;
б) е* = ах2?
IX.292. Сколько корней в зависимости от а (а > 0) имеет уравнение
ах = х?
IX.293. Даны два семейства функций, зависящих от параметра U
ft(x) = х • (х - t)2 и gt(x) = х • (х2 - t2), где t > 0.
а) Найдите экстремумы и точки перегиба графиков функций
ft(x) и gt(x), точки пересечения графиков с осями координат
и углы, под которыми графики пересекают оси координат
(в общем виде). Изобразите эскизы графиков обеих функций
в одной системе координат при t = 2.
б) Докажите, что во всех точках между корнями функции ft(x)
выполняется неравенство ft(x) >gt(x).
в) Прямая х = и (0 ^ и ^ t) пересекает графики функций ft(x)
и gt(x) в точках Р и Q соответственно. Для каких значений и
длина отрезка | PQ | будет наибольшей? Докажите, что
касательные к графикам в таких точках (с наибольшей длиной | PQ |)
параллельны друг другу.
г) Найдите ГМТ всех максимумов и минимумов кривых gt(x)
в зависимости от параметра t. Изобразите эти множества на
эскизе графиков из пункта а).
д) Для каждой кривой gt (x) существует прямая, проходящая
через начало координат и пересекающая эту кривую ещё в двух
других точках М и N. При каких значениях t существует ровно
одна прямая указанного вида (т. е. проходящая через точки О(0; 0),
М и N)9 которая пересекает график gt(x) под прямым углом?
IX.294. Дана функция, зависящая от параметра a: fa(x) = 0,25л;4 - а2*2,
а> 0.
а) Найдите корни функции, экстремумы и точки перегиба
в общем виде. Постройте эскиз графика функции при а = 1.
б) Найдите ГМТ всех минимумов графиков функций у = fa(x)
в зависимости от а. Изобразите полученную кривую у = g(x)
в той же системе координат (вместе с эскизом графика из
пункта а)). Объясните, почему ни одна кривая семейства у = fa(x)ne
пересекает график у = g(x) под прямым углом.
в) При а = 1 отрезок, соединяющий точки минимума кривой
У = А(х)> пересекает ось OY в точке А. На кривой у = ft(x) между
её минимумами взяты ещё две точки Б и С так, что ось OY является
осью симметрии треугольника ABC. При каких значениях
абсциссы точки В площадь треугольника ABC будет наибольшей?
Группа С
IX.295. Сравните tg5°3tg9° и tg6°4tgl0°.
IX.296. Уравнение х4 + ах3 + Ъх2 + с = 0 имеет четыре различных
действительных корня. Докажите, что be < 0.
Ц[_3адачи и упражнения
IX.297. Докажите, что если функция / выпукла и f(x) -* с при х —> +оо,
то /'(*) —* 0 при л: —► +оо.
IX.298. Найдите все положительные значения параметра а, при
которых для любого натурального п уравнение f(x) = n имеет
решение, если f(x) = loga + 2x(x2 - 1).
IX.299. Докажите, что если уравнение log^ + 1ах = п + 1 имеет решение,
то а > пе.
IX.300. При каких значениях параметра а уравнение
х4 - ах3 + (3 - 2а)*2 + ах + 1 = О
имеет как положительные, так и отрицательные решения?
IX.301**. Сколько корней в зависимости от а (а > 0) имеет уравнение
IX.302. Дана функция f(x)
j
= /
х — 3
а) Исследуйте функцию и постройте её график.
б) Выясните в зависимости от а, сколько решений имеет
уравнение f(x) = а.
в) Решите уравнение arccos f(x)= —.
4
г) Найдите наибольший положительный угловой коэффициент
касательной к графику у = f(x) на отрезке [0; 2].
д) Сколько корней имеет уравнение
2
= fix)?
Определённый
интеграл
О64. Площадь криволинейной трапеции
1. Проблема определения площади криволинейной трапеций
Пусть дан график функции, принимающей неотрицательные
значения и заданной на отрезке [а; 6]. Рассмотрим фигуру, ограниченную
графиком этой функции, прямыми х = а, х = Ъ и отрезком [а; Ъ\ оси
абсцисс. Такую фигуру называют криволинейной трапецией.
Криволинейную трапецию можно задать аналитически как множество точек
плоскости, координаты которых удовлетворяют системе неравенств
\а ^ х < Ь,
<у< f{x).
Дать строгое определение площади криволинейной трапеции
весьма непросто. Вспомните из курса геометрии, сколь непростым было
определение площади круга. Здесь же криволинейная трапеция может
быть ограничена куда более сложной кривой, нежели окружность.
Пусть на отрезке [а; Ь] дана непрерывная функция у = f(x),
принимающая неотрицательные значения.
Для определения понятия площадь криволинейной трапеции,
ограниченной графиком функции /, прямыми х = а, х = Ъ и осью
абсцисс, поступим следующим образом. Вычислим приближения
площади криволинейной трапеции по недостатку и по избытку с помощью
тех фигур, площади которых мы умеем вычислять.
Для этого разобьём отрезок [а; &], на котором определена функция
y = f(x), точками х19 х2, ..., хп_г на п отрезков (не обязательно
равных). Для удобства записи будем считать а = х0 и Ъ = хп.
Для приближения площади по недостатку построим на каждом из
полученных отрезков как на основании прямоугольник, целиком
лежащий под графиком функции /. Конечно, таких прямоугольников
может быть много, но самый «высокий» из них будет «упираться
в график функции /». Для этого нужно, чтобы высота прямоугольника
была равна наименьшему значению функции / на рассматриваемом
отрезке разбиения (рис. 10.1). Площадь такого прямоугольника
равна произведению длины отрезка разбиения на наименьшее значение
функции на этом отрезке. Символически St = (xi + 1 - xt) • min f(x).
xe [xt; xi+i]
§64. Площадь криволинейной трапеции
У
Рис. 10.1
В результате получится ступенчатая фигура, лежащая в
криволинейной трапеции, площадь которой равна
п-1
п-1
j0 i0 xe[Xi;xi+1]
Таким же образом для приближения площади по избытку построим
на каждом отрезке разбиения как на основании прямоугольник, в
котором лежит часть графика функции, соответствующая данному отрезку
разбиения. Таких прямоугольников можно построить много, но самый
«низкий» из них будет «упираться в график функции /», т. е. иметь
высоту, равную наибольшему значению функции на данном отрезке
разбиения (см. рис. 10.1). В результате получится ступенчатая фигура,
содержащая криволинейную трапецию, площадь которой равна
п-1
/Го
xe[xt;xi+1]
Интуитивно ясно (мы не будем приводить доказательства), что
любое приближение по недостатку не превосходит любого приближения
по избытку (причём не обязательно для одного и того же разбиения
отрезка).
Отметим, что наибольшее и наименьшее значения функции на
отрезках разбиения существуют в силу теоремы Вейерштрасса.
Разобьём отрезок [а; Ь] на большее число частей, делая при этом
все части более и более мелкими.
Очевидно, что множество приближений площади по недостатку
ограничено сверху1, например, числом ф — а) • max f(x). Тогда сущест-
х е [а; Ь]
вует точная верхняя граница таких приближений, которую мы обозна-
1 Велик соблазн сказать, что верхней границей множества таких
приближений является площадь криволинейной трапеции. Однако мы ещё не
доказали, что площадь криволинейной трапеции вообще существует!
1721 Глава X. Определённый интеграл
чим S*. Аналогично можно показать, что существует точная нижняя
граница множества приближений площади по избытку, которую мы
обозначим S*.
Следует отметить, что S* и S* существуют для всех ограниченных
функций (не обязательно непрерывных), заданных на отрезке [а; Ь],
если в определениях этих приближений заменить max на sup, a min на
inf. Значения S* и S* могут быть не равны (см. пример 1), но всегда
S* ^ S*.
Если S* = S*, то это их общее значение и называется площадью
криволинейной трапеции.
Ещё раз отметим, что выше мы определили, что такое площадь
криволинейной трапеции. А именно, это точная верхняя граница
площадей ступенчатых фигур, содержащихся в данной криволинейной
трапеции, равная точной нижней границе площадей ступенчатых
фигур, содержащих данную криволинейную трапецию. Если эти
точные границы не равны, то соответствующая фигура площади не имеет.
Пример 1. Докажем, что криволинейная трапеция, ограниченная
графиком функции Дирихле D, прямыми х = О, х = 1 и отрезком
[0; 1] оси абсцисс, не имеет площади в определённом выше смысле.
тт тл/ ч IX если х gQ9
П Напомним, что D(x) = < _ _ч _
[0, если # е /J\Q.
Пусть отрезок [0; 1] произвольным образом разбит на отрезки.
В каждом из отрезков разбиения есть иррациональное число, а потому
наименьшее значение функции D на любом отрезке разбиения равно 0.
Таким образом, любое приближение по недостатку будет равно 0.
Значит, и точная верхняя граница множества приближений по недостатку
равна 0, т. е. S* = 0.
В то же самое время на любом отрезке разбиения есть
рациональное число. Поэтому наибольшее значение функции D на любом
отрезке разбиения равно 1. Тогда площадь соответствующего
прямоугольника численно равна длине отрезка разбиения, а значит,
приближение по избытку, равное сумме площадей прямоугольников,
численно равно сумме длин отрезков разбиения, т. е. длине отрезка
[0; 1]. Тем самым любое приближение по избытку равно 1. Поэтому
и точная нижняя граница приближений по избытку S* = 1. Таким
образом, S* Ф S*. Полученное неравенство доказывает, что рассмот
ренная криволинейная трапеция не имеет площади. IS
О Мы не приводим доказательства того, что криволинейная
трапеция, ограниченная графиком непрерывной функции, имеет
площадь, но в дальнейшем будем часто пользоваться этим фактом.
Далее вместо слов «площадь криволинейной трапеции,
ограниченной графиком функции /, прямыми х = а, х = Ъ и отрезком [а; Ь]
оси абсцисс» будем писать «площадь под графиком функции / на
отрезке [а; Ь]».
1731 §64. Площадь криволинейной трапеции
2. О вычислении площади
Рассмотрим непрерывную на отрезке [а; Ь] функцию,
принимающую неотрицательные значения, и попытаемся упростить процедуру
нахождения площади криволинейной трапеции по определению.
Для этого будем рассматривать не все приближения по недостатку
и по избытку, как требует определение, а лишь те, которые
соответствуют разбиениям отрезка [а; Ь] на равные части.
Сформулируем без доказательства следующее утверждение.
Утверждение
Пусть криволинейная трапеция ограничена графиком непрерывной
неотрицательной функции. Тогда точная верхняя граница
множества приближений по недостатку, отвечающих разбиениям
отрезка [а; Ь] на равные части, равна точной нижней границе
множества приближений по избытку, отвечающих разбиениям отрезка
[а; Ь] на равные части, и равна площади криволинейной трапеции.
Достаточно вычислять не точные границы указанных множеств,
а пределы соответствующих последовательностей. А именно: если Sn —
это приближение по избытку, отвечающее разбиению отрезка [а; Ь] на
п равных частей, то S* = lim Sn. Аналогично если sn — приближение
П -+оо
по недостатку, то S* = lim sn. Рассмотрим соответствующие примеры.
П -+оо
Пример 2. Вычислим площадь криволинейной трапеции,
ограниченной графиком функции у = х2, прямыми х = О, х = 1 (рис. 10.2).
□ Разобьём отрезок [0; 1] на п равных частей и найдём Sn. Абсциссы
точек деления отрезка имеют вид хь = —. Наибольшее значение у на
отрезке
ГА. £±11
U' п J
длины — достигается в его правом конце. Поэтому
_1
п
П
1
п
или получим Sn =
I2 + 22 + ... + п2
. Для
всех п е N имеет место равенство
I? п9 9 п(п + 1)(2п+1) ,
I2 + 22 + ... + п2 = — (это
равенство можно доказать методом
математической индукции). Поэтому Sn =
22 З1 то 1 ^
, откуда lim Sn = -. Ответ:
n -► оо 3
площадь равна —. й
3
1
п
Рис. 10.2
2_
п
X
174! Глава X. Определённый интеграл
Пример 3. Выясним, на сколько равных частей нужно разбить отрезок
[0; 2], чтобы приближения площади под графиком f(x) = Xs по
недостатку и по избытку отличались меньше чем на 0,1.
о
П Рассмотрим разбиение отрезка [0; 2] на п равных частей длины -
каждая. Так как f(x) = Xs возрастает, то наибольшее её значение на
промежутке достигается в его правом конце, а наименьшее — в левом,
и мы можем составить выражения для Sn и sn:
\з
1 Л
Составим разность: Sn — sn = — (здесь мы использовали то, что все
слагаемые в формулах для Sn и sn9 кроме двух крайних, одинаковы).
Осталось выяснить, при каких п выполнено — < 0,1. Решив это
неравенство, получаем п > 160. Ответ: отрезок следует разбить не
менее чем на 161 часть. Щ
Поскольку площадь под графиком находится между sn и Sn, то
при п^ 161 значения sn и Sn будут отличаться от площади под
графиком менее, чем на ОД.
Приведённым в примере способом можно приближенно вычислять
площадь под графиком, заранее задавая точность приближения.
Пусть отрезок [а; Ь] разбит на п равных частей. Пронумеруем их
от 0 до п - 1. На каждой из частей выберем точку L, где i — номер
h п~г
части, содержащей ^. Составим теперь сумму Rn = ^ /Ч^)- За-
метим, что sn ^ Rn ^ Sn (поскольку формулы для sn и Sn отличаются
от формулы для Rn тем, что вместо произвольного значения функции
на отрезке разбиения в них стоят наименьшее и наибольшее
значения функции на этом отрезке). Так как последовательности sn и Sn
имеют один и тот же предел1 S, то по теореме о сжатой
последовательности последовательность Rn также имеет предел S.
1 Обратите внимание, что последовательность Rn строится так: для
каждого п выбирается набор значений £,., а затем вычисляется значение Rn. Поэтому
одному и тому же значению п может соответствовать бесконечно много
значений Rn. Однако можно показать (например, для непрерывных функций), что,
какими бы ни выбирались наборы значений ^ при различных п, полученные
последовательности Rn имеют предел S.
1751
§64. Площадь криволинейной трапеции
Суммы Rn носят название римановых сумм в честь выдающегося
немецкого математика Б. Римана (с функцией Римана вы могли
встретиться в главе VIII, изучая пределы и непрерывность функций).
Предел последовательности Rn называется интегралом Римана.
орический комментарий
Георг Фридрих Бернхард Риман (1826—1866) — выдающийся немецкий
математик, ученик Гаусса и Дирихле, один из основателей теории функций
комплексной переменной, дифференциальной геометрии и аналитической
теории чисел. Известны дзета-функция Г. Римана, с которой связана одна из
великих нерешённых задач математики, римановы поверхности, риманова
геометрия.
Интересно, что Риман поступил в Геттингенский университет на
богословский факультет, однако страсть к математике оказалась сильнее.
<ий
Пример 4. Вычислим площадь под графиком функции i/ = sin;c на
отрезке [0; я].
0
Рис. 10.3
2л
Зя
5
Л X
П Разобьём отрезок [0; к] на п равных частей и рассмотрим римано-
ву сумму, соответствующую этому разбиению, где в качестве точек ^
1
взяты правые концы отрезков разбиения. Получим Rn = — ^ sin
(на рис. 10.3 изображена фигура, площадь которой численно равна R5).
Для нахождения предела Rn преобразуем выражение
. я 2тг . пп
sin — + sin — + ... + sin —
п п п
п
Умножим и разделим это выражение на sin— и представим каждое
2п
слагаемое вида since «ship числителя дроби как разность косинусов:
176j Глава X. Определённый интеграл
. к . 2л . пп
sin — + sin — + ... + sin — =
п п п
( к Зк Зк 5л (2п - 1
cos cos 1- cos cos 1- ... + cos :
, 2n 2n 2n 2n 2n
cos
(2n
2n
2n
Все слагаемые числителя, кроме первого и последнего, взаимно
уничтожаются. Таким образом, искомая сумма синусов будет равна
л
cos cos
2п
2п
-2 sin • sin-
2
2п
sin-
2п
2 sin —
2n
Теперь найдём
2п
sin-
2п
lim Rn = lim
n —*■ oo n —*■ со
П
sin
sin-
2n
2n
= 2
(так как lim
2vi
.л 1ЧП1
= sin— = 1). Ш
2
Обратим внимание, что в этом примере сумма Римана Rn не
является ни приближением по недостатку sn9 ни приближением по избытку
Sn искомой площади, поскольку в части слагаемых, составляющих i?n,
в качестве значений функции берутся наибольшие значения на
промежутке, а в оставшихся слагаемых — наименьшие (рис. 10.3).
3. Свойство аддитивности площади
криволинейной трапеции
Интуитивно очевидным является следующее свойство:
Свойство (аддитивность площади) ----«----------«----------«—------
1
Пусть функция f непрерывна на отрезке [а; Ь] и принимает на
нём неотрицательные значения. Пусть а^с^Ь, тогда площадь
под графиком функции f на отрезке [а; Ь] равна сумме площадей
под графиком f на отрезках [а; с] и [с; to].
Свойство аддитивности наглядно очевидно и соответствует нашим
представлениям о площади: если фигура составлена из
неперекрывающихся частей, то площадь фигуры равна сумме площадей частей
(рис. 10.4). Однако вспомним, как определялась площадь
криволинейной трапеции. Все свойства площади криволинейной трапеции следует
|77j §64. Площадь криволинейной трапеции
1Л
S=S1+S1
Рис. 10.4
доказывать, исходя из определения, а не наших представлений о том,
что скрывается за словом «площадь». Доказательство
сформулированного свойства не такое простое, и здесь приведено не будет.
4. Площадь криволинейной трапеции
с переменной границей как первообразная
Рассмотрим график функции у = f(x), заданной на отрезке [а; Ь] и
принимающей неотрицательные значения (рис. 10.5). Свяжем с
функцией f(x) функцию S(t), ставящую в соответствие числу t e [a; b]
площадь криволинейной трапеции, ограниченной графиком функции,
прямыми х = а, х = t и отрезком [а; t] оси абсцисс.
178; Глава X. Определённый интеграл
Выясним связь между функциями S(t) и fix) в предположении,
что функция / непрерывна. Для этого придадим переменной t
приращение At и рассмотрим вызванное им приращение AS (см. рис. 10.5),
Пусть At > 0. Тогда AS есть площадь криволинейной трапеции,
ограниченной графиком функции /, прямыми x = tnx = t + At, а также
отрезком [t; t + At] оси абсцисс (обратим внимание, что здесь
использовано свойство площади, сформулированное в предыдущем пункте).
Пусть Мит соответственно наибольшее и наименьшее значения
функции / на отрезке [t; t + At] (эти значения существуют в силу
непрерывности функции / согласно теореме Вейерштрасса). Заметим, что при
фиксированном значении t значения Мит являются функциями
аргумента At, т. е. могут изменяться с изменением At. Однако мы не пишем
аргумент At возле знаков Мит, чтобы не загромождать запись.
Из рисунка 10.5 видно, что
т • At ^ AS ^ М • At, (*)
поскольку криволинейная трапеция, площадью которой является AS,
содержит прямоугольник со сторонами длины т и At и, в свою
очередь, содержится в прямоугольнике со сторонами длины М и At.
Разделим обе части неравенства (*) на At. Получим следующее
неравенство:
т ^ — ^ М. (**)
Пусть теперь At < 0. Аналогично предыдущему (теперь площади
соответствующих прямоугольников будут равны —М • At и —т • At
соответственно, а площадь криволинейной трапеции, взятой на отрезке
[t + At; t], будет равна -AS), получаем неравенство —т • At ^ -AS ^
^ —М • Atj откуда, поделив все части неравенства на —At > 0, вновь
получаем неравенство (**).
Теперь устремим А* к нулю и посмотрим, куда будет стремиться
отношение —. Докажем, что при этом М будет стремиться к fit).
At
D Действительно, М есть значение функции / в некоторой точке tM,
т. е. M = f(tM), где tM e [t; t + At], если Д£>0, и tM e [t + At; t], если
At < 0 (ещё раз обратим внимание на то, что при изменении At может
меняться и tM). Если А* -> 0, то tM —► t (поскольку t ^ tM ^ t + At или
t + At ^ tM ^ t и обе крайние части неравенства стремятся к t при
At -> 0). А тогда в силу непрерывности функции / получим f(tM) -> f(t)
при At —► 0.
Итак, limM= fit). Аналогично можно показать, что и limm= fit),
At-*O At-*O
Тогда из неравенства (**) в силу теоремы о пределе сжатой функции
получим lim — = fit). Заметим, что по определению производной
At^O At
lim — = S'it). Итак, S'it) = fit). Ш
At-*O At
Л^ Площадь криволинейной трапеции
Таким образом, получено следующее удивительное утверждение.
Утверждение "
Площадь криволинейной трапеции, ограниченной графиком
неотрицательной непрерывной функции f, с переменной правой
границей, рассмотренная как функция этой границы, есть
первообразная функции f.
Ясно, что в граничных точках отрезка [а; Ь] имеет смысл говорить
лишь об односторонних производных функции S.
5. Существование первообразной произвольной функции,
непрерывной на отрезке
На основании принятых без доказательства утверждений о
существовании площади криволинейной трапеции, ограниченной графиком
непрерывной функции, и об аддитивности площади криволинейной
трапеции мы доказали, что непрерывная на отрезке [а; Ь] функция,
принимающая неотрицательные значения, имеет первообразную. В
качестве этой первообразной может быть взята функция S(x), ставящая
в соответствие числу х е [а; Ь] площадь под графиком функции / на
отрезке [а; х].
Докажем теперь, что от требования неотрицательности значений
функции / можно освободиться.
ТЕОРЕМА ——————————•-—————^^
Если функция f непрерывна на отрезке [a; to], то она имеет
первообразную на этом отрезке.
П доказательство. По теореме Вейерштрасса функция,
непрерывная на отрезке [а; 6], достигает своего наименьшего значения на этом
отрезке. Пусть т = min f(x). Рассмотрим функцию g(x) = f(x)- т.
х е [а; Ь]
Эта функция на отрезке [а; 6] принимает неотрицательные значения. По
доказанному выше утверждению функция g имеет первообразную,
которую мы обозначим G. Тогда функция F (х) = G (х) + тх будет
первообразной для /. В самом деле, F (х) = G'(x) + т = f(x) - т + т = f(x). Ш
Из доказанной теоремы и теоремы о строении класса первообразных
следует, что любая непрерывная на отрезке функция имеет бесконечно
много первообразных, каждые две из которых отличаются на константу.
6. Выражение площади под графиком
о помощью произвольной первообразной
В пункте 4 было доказано, что для непрерывной функции /,
принимающей неотрицательные значения на отрезке [а; &], площадь S(x)
криволинейной трапеции с переменной правой границей,
рассматриваемая как функция этой границы, есть первообразная функции /.
180| Глава X. Определённый интеграл
П Пусть F — произвольная первообразная функции /. Поскольку S
также является первообразной функции /, она отличается от F на
некоторую константу С, т. е. F(x) + С = S(x). Подставив в это равенство
х-а и учитывая, что S(a) = 0, получим F(a) + C = 0, откуда C = -F(a). Щ
Итак, мы доказали утверждение.
Пусть функция f непрерывна на отрезке [а; Ь] и принимает на нём
неотрицательные значения. Пусть S (х) — площадь под графиком
функции f на отрезке [а; х], тогда для любой первообразной F
функции f верно равенство S (х) = F(x) - F(a).
Из этого равенства, в частности, следует, что площадь под
графиком функции f на отрезке [а; Ь] равна F(b) - F(a).
О65- Определённый интеграл
1. Определённый интеграл непрерывной функции на отрезке
ОПРЕДЕЛЕНИЕ -—--—-————"—^
Пусть на отрезке [а; Ь] задана непрерывная функция f.
Определённым интегралом функции f на отрезке [а; Ь]
называется число F(b) - F(a), где F— некоторая
первообразная функции f на отрезке [а; Ь].
и
Обозначение: J f(x)dx (читается как «интеграл от а до 6 эф от
икс
дэ икс»). °
Замечания. 1) Числа а и Ъ называются пределами
интегрирования^ а функция / — подынтегральной функцией.
2) Обратите внимание на то, что в отличие от неопределённого
интеграла, являющегося классом функций, определённый интеграл —число!
3) На первый взгляд введённое определение зависит от того,
какую именно из многочисленных первообразных взять в качестве F.
Докажем, что это не так.
П Пусть F и Fx — первообразные функции / на отрезке [a; b].
Тогда существует число С, такое, что Fi(x) = F(x) + С. Следовательно,
Fi(b) - Л(а) = (F(b) + С) - (F(a) + С) = F(b) - F(a). Ш
Таким образом, выражение для определённого интеграла не
зависит от того, какую именно первообразную взять, т. е. определённый
интеграл является характеристикой только функции / и отрезка [a; b].
ь
Формула \ f(x)dx = F(b)— -F(a), взятая нами в качестве
определения интеграла непрерывной функции на отрезке, называется
формулой Ньютона — Лейбница.
181, §65. Определённый интеграл
J f(x)dx=S1-S2+S3-S4
Рис. 10.6
b
Мы не будем далее предполагать, что в записи \ f(x)dx обязатель-
а
но а ^ Ъ. Формула Ньютона — Лейбница определяет интеграл и в
случае а> Ъ.
Из предыдущих рассуждений ясно, что для непрерывной неотри-
ь
цательной на отрезке [а; Ь] функции / число \ f(x)dx равно площади
под графиком функции /.
Для произвольной непрерывной на отрезке функции / также мож-
b
но считать, что \f(x)dx равен «площади под графиком» функции /,
а
если принять площади частей, лежащих под осью, отрицательными
(рис. 10.6). 2к
Пример 5. Вычислим \sinxdx.
-п 2п
Г
П По определению получим I sinxdx = -cos(27i)-(—cos(—n)) = -2. IS
-л
Для записи выражения F(b)-F(a) бывает удобно использовать
обозначение F(jc)|^. Такая запись позволяет явно выписать
первообразную, прежде чем подставлять в неё значения пределов интегрирования.
Например, решение предыдущего примера можно записать так:
2л
\ sinxdx = (-cos;c)|^ = -cos(2л)- (-cos(-л)) = -2.
-71 0
Пример 6. Вычислим \ x2dx.
п \x2dx= —
1821 Глава X. Определённый интеграл
о
Пример 7. Найдём J | х - 11 dx.
-1
П способ 1. Найдём первообразную функции \х— 1|. Первообразной
при х > 1 будет — - х + С, а первообразной при л: < 1 будет ——- 4- х + Сх.
Чтобы найти первообразную на всей оси, нужно «склеить» две
найденные ветви, подобрав соотношение между константами. Воспользуемся
непрерывностью искомой первообразной в точке х = 1. Тогда
левосторонний и правосторонний пределы при стремлении к 1 должны быть равны.
lim х
cl = i-
С,
lim I -—
x-*l-
Cv
и, значит, — + С = - + С19 откуда 0 =
1. Возьмём Сг = 0, тогда С = 1.
Итак, на роль первообразной может претендовать функция
1,
хс
х + 1, если х
—— + ху если х ^ 1.
Можно убедиться (см. пример 39 главы IX), что эта функция
действительно является первообразной для функции \х — 1|.
Теперь по формуле Ньютона — Лейбница получим
з
-1 О
Рис. 10.7
способ 2. Мы знаем, что
интеграл от неотрицательной
непрерывной функции — это площадь под
её графиком. Обратившись к
рисунку 10.7, мы видим, что
искомый интеграл равен сумме
площадей равнобедренных
прямоугольных треугольников ABC и CDE,
катет каждого из которых равен 2.
Сумма площадей равна 4. 91
1
Пример 8. Найдём ГVl — x2dx.
□ Для этого воспользуемся первообразной подынтегрального
выражения, найденной в примере 49 главы IX.
1
m Г Гл <Гл
Тогда J VI - x2dx =
Г arcsin х sin (2 arcsin x)
= -. а
183| §65. Определённый интеграл
Конечно, ответ в этом примере ясен сразу. Ведь график у = Vl - х2
на отрезке [0; 1] — это четверть окружности радиуса 1 с центром в
начале координат. Тем самым искомый интеграл — четверть площади
круга радиуса 1.
2. Расширение понятия определённого интеграла
Пример 9. Вычислим [ . Х
D Велик соблазн записать такую цепочку
равенств:
п
dx
j
= arcsin x | _г =
= arcsin 0 - arcsin (-1) = —.
Однако такая запись будет неверна! Ведь
понятие интеграла пока определено лишь для
функций, непрерывных на отрезке между
пределами интегрирования, а в этом примере
подынтегральная функция f(x) = —==== определе-
-1
Рис. 10.8
0
х
на на полуинтервале (-1; 0]. Тем не менее
полученный ответ разумен. Соображения (не
заменяющие определения интеграла в этом случае) могут быть такими:
о
Рассмотрим [ при малых 8 > 0. Здесь подынтегральная
J /i 2
функция определена на отрезке [-1 + е; 0], поэтому
о
dx
j -p^== = arcsin х | ^ + p = arcsin (1-е).
-l+e
Иначе говоря, площадь под графиком подынтегральной функции
на отрезке [-1 + 8; 0] равна arcsin (1-8). Но разумно полагать, что
площадь фигуры, «ограниченной» графиком подынтегральной
функции, прямыми х = -1ил: = 0и отрезком [—1; 0] оси абсцисс, равна
lim arcsin (1 - е) (рис. 10.8). В силу непрерывности функции арксинус
е -»0+
этот предел равен arcsin 1, т. е. —. IS
Рассмотренный пример показывает целесообразность такого
определения.
Глава X. Определённый интеграл
ОПРЕДЕЛЕНИЕ
Пусть функция f непрерывна на интервале (а; Ь) и
существуют пределы Mm F(x) и lim F(x), где F—первообразная
х-*а x-*b
функции f. Тогда определённым интегралом функции f
от а до b называется число lim F(x)- lim F(x).
x-*b x-*a
и
Обозначение: \f(x)dx.
Замечания. 1) Введённое определение не противоречит
предыдущему. Если функция непрерывна на отрезке, то разность пределов
равна разности значений первообразной в граничных точках отрезка
(в силу непрерывности первообразной), т. е. определённому интегралу,
заданному в п. 1.
2) В данном определении можно считать одну или обе границы
интервала символами -оо и +оо.
+ОО -
г ctx
Пример 10. Найдём —-.
1 х i
П Первообразная подынтегральной функции есть функция F(x)=—.
Поэтому [ —- = lim lim = 1. Здесь также удобно приме-
\ X2 *-*+оо^ X) х-+\\ X)
нять обозначение подстановки первообразной, т. е. записать
вычисление так
. Т dx= _1_
' \ х2 ' х
= 0 - (-1) = 1 (под значением функции в точке
+оо подразумевается соответствующий предел). \9\
Пример 11. Рассмотрим функцию f(x) = signx. Согласно ранее
введённому определению эта функция не имеет определённого интеграла
на любом промежутке, содержа-
щем 0, поскольку у неё нет
первообразной на этом промежутке (так
как она не обладает свойством
промежуточного значения, которым,
по теореме Дарбу, должна обладать
-1 производная функции на отрезке).
х Однако эта функция имеет
«площадь под графиком», например,
на отрезке [-1; 2] (рис. 10.9), рав-
ную 1. Поэтому хотелось бы,
чтобы для такой функции было
введено и понятие определённого инте-
Рис. 10.9 грала. Ш
1851 §65. Определённый интеграл
ОПРЕДЕЛЕНИЕ
Пусть функция f имеет на промежутке (а; Ь) конечное
число точек разрыва. Тогда определённым интегралом функ-
(ь \
unnf от а до b jf (x)dx называется сумма интегралов дан-
\а )
ной функции, взятых на промежутках, где она непрерывна.
Напомним, что обозначение (а; Ъ) означает, что рассматриваются
промежутки всех типов с концами в точках а и Ъ независимо от того,
принадлежат ли эти концы промежутку или нет.
Итак, если х19 х2, ..., хп точки разрыва функции f, перечисленные
в порядке возрастания, то по определению
ь *i *2 ь
jf{x)dx= \f(x)dx+\f(x)dx +...+ jf(x)dx.
a a xx xn
Таким образом, возвратившись к примеру 11, получим
2 0 2 0 2
) signxdx = j sign x dx + J sign x dx = j(-l)dx + jldx =
-1 -10 -10
= -*|°1+*lo = -1 + 2=1.
О Итак, мы определили, что такое определённый интеграл для
функций, имеющих на промежутке между пределами
интегрирования конечное число точек разрыва. Именно такие функции мы и
будем интегрировать в дальнейшем. При этом, говоря в условиях теорем
и задач об интеграле таких функций, мы будем предполагать, что он
существует, не упоминая об этом в условии.
3. Общий подход к определению интеграла
Определённый интеграл можно определять в более общем случае
так же, как ранее определялась площадь под графиком. А именно.
Пусть задана функция /, ограниченная на отрезке [а; Ь].
Рассмотрим конечное множество точек этого отрезка т = {х0; х19 х2; ...; хп}, где
точки пронумерованы в порядке возрастания, и а = х0, Ъ = хп. Этими
точками отрезок разбивается на п частей, поэтому множество т часто
называют разбиением отрезка. Составим для данного разбиения две сум-
п-1 п-1
мы: Sx = Y,(xi + i-xi)m sup/(x) и sx = ^(xi + 1- xt)- inff(x), которые
i=0 XE[xi;xi + i] ,= o xe[xitxi + l]
называются соответственно верхней и нижней суммами Дарбу данного
разбиения (отметим, что в § 64 эти суммы фигурировали как
приближения площади под графиком функции по избытку и по недостатку).
186[ Глава X. Определённый интеграл
Можно показать, что любая верхняя сумма Дарбу больше
любой нижней суммы Дарбу (необязательно для одного и того же
разбиения).
Тем самым множество верхних сумм Дарбу, отвечающих
всевозможным разбиениям, ограничено снизу (например, любой нижней
суммой Дарбу) и имеет точную нижнюю границу S*.
Аналогично множество нижних сумм Дарбу ограничено сверху
(например, любой верхней суммой Дарбу) и имеет точную верхнюю
границу S*. Следовательно (по утверждению п. 3 § 6 главы I,
рассмотренному в 10 классе), имеем S* > S*. Если при этом S* = S*, то это
число и называется интегралом функции f на отрезке [а; Ь].
Отметим, что после такого определения интеграла нужно будет
вывести формулу Ньютона — Лейбница, с помощью которой мы ввели
понятие определённого интеграла функций, непрерывных на отрезке.
Это можно сделать так же, как в § 64, заменяя слова «площадь под
графиком» словами «интеграл на отрезке».
Функция, имеющая определённый интеграл на отрезке [а; 6],
называется интегрируемой на этом отрезке.
В примере 1 этой главы показано, что функция Дирихле не
интегрируема на отрезке [0; 1]. В § 64 без доказательства принято
утверждение о том, что непрерывная функция интегрируема (это
утверждение скрыто под словами о том, что существует площадь под графиком
непрерывной функции).
Согласно определению точных верхней и нижней границ из
определения интеграла можно получить такой критерий
интегрируемости функции.
ТЕОРЕМА
Для того чтобы функция была интегрируемой на отрезке [а; Ь]
необходимо и достаточно, чтобы для любого е > 0 существовали
такие разбиения т1 и т2, что SXi - sXg < e.
Приведём здесь следующий любопытный пример.
Пример 12. Докажем, что функция Римана интегрируема на отрезке
[0; 1], и вычислим её интеграл.
□ Напомним, что функция Римана R задана так: она равна 0 во
1 Р
всех иррациональных точках и равна — во всех точках вида —, где
(р; q) = 1, р е Z, q e N.
Выберем произвольное число £ > 0 и рассмотрим все несократимые
дроби —, для которых ->—, т. е. q < —. Таких дробей будет конечное
количество (поскольку возможных значений q будет конечное
количество и для каждого значения q на отрезке [0; 1] имеются не более
1871 §65. Определённый интеграл
q несократимых дробей со знаменателем q). Окружим все эти дроби
непересекающимися окрестностями суммарной длиной, меньшей —. Гра-
ницы этих окрестностей примем за точки разбиения т.
Подсчитаем верхнюю сумму Дарбу для этого разбиения. Она равна
сумме произведений длины отрезка разбиения на максимальное
значение функции в данном отрезке. Имеются несколько отрезков разбие-
ния суммарной длиной, меньшей —, в которых максимальное значение
функции Римана будет большим —, но уж во всяком случае в каждом
из этих отрезков maxR(x) ^ 1. Поэтому вклад всех этих отрезков
в верхнюю сумму Дарбу не превосходит —.
На оставшихся отрезках все значения функции R будут меньше —,
А
а суммарная длина этих отрезков меньше 1. Поэтому вклад этих
отрезков в верхнюю сумму Дарбу также меньше —.
Таким образом, для построенного разбиения т имеем Sx < е.
В то же время нижняя сумма Дарбу для этого разбиения, как
и для любого другого, равна 0, поскольку на любом отрезке есть
иррациональное число, значение функции Римана в котором равно 0.
Таким образом, для построенного разбиения т имеем Sx — sx < 8,
т. е. согласно критерию интегрируемости функция Римана
интегрируема на отрезке [0; 1].
Поскольку нижние суммы Дарбу для любого разбиения равны 0,
то и точная верхняя граница множества нижних сумм Дарбу равна 0.
Поскольку интегрируемость функции Римана уже доказана, то эта
точная верхняя граница и есть значение интеграла функции Римана.
1
Ответ: $R(x)dx= 0. Ш
о
Отметим, что функция Римана не является функцией с конечным
числом точек разрыва на промежутке, поэтому её интеграл не может
быть определён с помощью определения со страницы 185. Более того,
так как функция Римана ни на каком промежутке не обладает
свойством промежуточного значения, то ни на каком промежутке у неё нет
первообразной.
Этот пример показывает, что определение интеграла с помощью
сумм Дарбу является более общим, нежели данное в тексте главы.
Однако, как правило, функции, фигурирующие в задачах школьного
курса, непрерывны на данном промежутке всюду, кроме конечного
числа точек, поэтому для них можно пользоваться определением
(см. с. 185).
188J Глава X. Определённый интеграл
4. Интеграл с переменным верхним пределом
Пусть f — функция, непрерывная на отрезке [а; Ь]. Для данного
X
числа а е [а; Ь] рассмотрим функцию Ф (х) = j f(t)dt, где х е [а; б]1. По
а
формуле Ньютона — Лейбница Ф(х) = F(x) - F(a), где F —
произвольная первообразная функции /. Тогда сама Ф тоже является
первообразной функции /, так как отличается от F на константу. Итак, мы получили
следующую теорему.
ТЕОРЕМА БАРРОУ
Интеграл непрерывной на отрезке функции с переменным верх
ним пределом, рассматриваемый как функция верхнего предела,
есть первообразная подынтегральной функции.
рический комментарий
Исаак Барроу (1630—1677) — английский математик, философ и
богослов. Был учителем И. Ньютона в Кембриджском университете и специально
ушёл с кафедры, которой руководил, чтобы И. Ньютон мог её возглавить.
Один из предшественников И. Ньютона и Г. В. Лейбница в разработке основ
анализа. Нашёл связь между дифференцированием и интегрированием, но
рассматривал её чисто геометрически, так что фактически теоремой Барроу
следует называть утверждение п. 4 § 64.
Известно, что И. Барроу отличался личной храбростью. Путешествуя
в юности, участвовал в схватках с пиратами. Однако по возвращении в Англию
принял сан священника и стал работать в Кембриджском университете.
Пример 13. Найдём наименьшее значение функции F(х) = \ (У1 + tjdt.
□ Для нахождения наименьшего значения возьмём производную
данной функции: по теореме Барроу F'(x) = Ух + х. Видно, что
производная отрицательна при х < 0 и положительна при х > 0. Поэтому
в точке х = 0 функция F имеет минимум. Так как х = 0 — это
единственная критическая точка на области определения функции, то в ней
достигается наименьшее значение функции. Итак, наименьшее
значение функции — это -F(O).
-l
5
4
(мы воспользовались свойствами неопределённого интеграла). Ш
1 Обратите внимание, что это действительно функция переменной х. При
подстановке вместо х конкретного числового значения получается число.
189; §66. Свойства определённого интеграла
- Свойства определённого интеграла
1. Свойства, связанные с арифметическими действиями
Рассмотрим свойства определённого интеграла для функций,
непрерывных на отрезке.
ТЕОРЕМА
Пусть функции f и д непрерывны на отрезке [a; to], к —
произвольная постоянная. Тогда:
b b b
1. J(f(x)+ g(x))dx = jf(x)dx + jg(x)dx.
a a a
b b
2. J(/cf(x))dx = kjf(x)dx.
a a
ebb
3. jf(x)dx + jf(x)dx = \f(x)dx.
4.
ас
b a
D доказательство. 1. Пусть F — одна из первообразных
функции /, G — одна из первообразных функции g9 тогда F + G — одна из
первообразных функции f + g. По формуле Ньютона — Лейбница
получим
J (/ (х) + g (х)) dx = (F (x) + G(x))\ba =
= F(b) + Gib)"- (F(a) + G(a)) = (F(b) - F(a)) + (G(b) - G(a)) =
ь ь
= jf(x)dx + jg(x)dx.
a a
2. Пусть F — одна из первообразных функции /, тогда kF — одна из
первообразных функции kf. По формуле Ньютона — Лейбница получаем
ъ ъ
j(kf(x))dx= (kF(x))\ba = kF(b) - kF(a) = k(F(b) - F(a)) = k\ f(x)dx.
a a c
3. Пусть F — одна из первообразных функции /, тогда Г f(x)dx =
Ь a
= F(c) - F(a), \ f(x)dx = F(b) - F(c). Сложив эти два равенства, полу-
с
с Ь Ь
чим J f(x)dx + j f(x)dx = F(b)- F(a)= jf(x)dx.
a c a
4. Следует непосредственно из определения. W
1901 Глава X. Определённый интег рал
Замечание. В свойстве 3 точка с не обязана лежать между а и Ъ.
Важно лишь, чтобы существовали все интегралы из формулы.
Теорема остаётся верной и для функций, непрерывных на интер-
ъ
вале или полуинтервале, для которых существует j f(x)dx (в этом слу-
а
чае под F(a) нужно понимать \imF(x)), а также и для функций с ко-
х-*а
нечным числом точек разрыва на промежутке.
D Докажем, например, свойство 1 для функций, имеющих
конечное число точек разрыва. Пусть х19 х2, ..., хп — точки разрыва
функций f и g, перечисленные в порядке возрастания (т. е. в каждой из
этих точек либо /, либо g, либо сразу обе эти функции имеют
разрыв). Тогда согласно определению (с. 185) и свойству 3 теоремы для
функций, непрерывных на промежутке, получаем
Ь Х1 Х2 Ь
jf(x)dx = jf(x)dx+jf(x)dx + ...+ jf(x)dx. (*)
a a Xl xn
Здесь определение применяется в том случае, когда в
соответствующей точке терпит разрыв функция /, а свойство 3 теоремы —
когда в соответствующей точке терпит разрыв только функция g.
Ь Х1 Х2 Ь
Аналогично J g (x) dx = j g (x) dx + J g (x) dx + ... + J g (x) dx. (**)
a a Xl xn
Сложив равенства (*) и (**), получим
Ь b (xl xl Л (Х2 *2 >
]f(x)dx + ]g(x)dx= jf(x)dx+jg{x)dx\ + \ jf{x)dx+ Jg{x)dx
a a U a J [Xl *\ )
...+ jf(x)dx+ jg(x)dx\.
\xn xn J
Каждую из сумм в скобках можно заменить на интеграл суммы
функций, а затем воспользоваться определением (с. 185) или
свойством 3 теоремы для непрерывной на промежутке функции (если в
каких-либо из точек х19 х2у ..., хп функция / + g не имеет разрыва). 1
Аналогично доказываются и остальные свойства. j|
„ тт « .. f dx с dx
Пример 14. Найдем + .
JQl + ex JQl+e-x
П Воспользуемся свойством 1 определённого интеграла:
dx A dx
}_dx_ A
i1+eX i
о1+е
dx
-и
1 + ех ех+1
и '
ех )
191) §66. Свойства
определенного интеграла
Отметим, что нахождение первообразных функций из примера 14
гораздо более утомительно, поэтому использование свойств
определённого интеграла здесь оправданно.
2. Свойства, связанные с неравенствами
ТЕОРЕМА ——■—-—■————-^^
1
Пусть f — неотрицательная непрерывная на интервале (а; Ь) (где
Ь>а) функция, не равная тождественно нулю на интерва
ь
(а; Ь). Тогда если существует \f(x)dx, то он положителен.
D доказательство. 1) Пусть F — первообразная функции f.
Поскольку F'(x) = f(x) ^ 0 на интервале (а; Ь), функция F является
неубывающей на интервале (а; Ь) (под F(a) и F(b) следует понимать
соответствующие пределы). Тогда F(b) > F(a), sl потому
ъ
= F(b)-F(a)>0.
2) Если во всех точках интервала (а; Ъ) функция / положительна,
то функция F будет строго возрастать на (a; ft), a тогда разность
ь
F(b) — F(a) будет положительной, т. е. \ f(x)dx > 0.
a
3) Однако в формулировке теоремы стоит строгое неравенство,
даже если функция положительна хотя бы в одной точке. Для
доказательства рассмотрим точку х0 е (а; 6), такую, что f(x0) > 0.
Согласно свойству непрерывной функции существует окрестность точки х0
(окрестность можно выбрать так, чтобы она целиком содержалась
в интервале (а; Ь)), в каждой точке которой значение функции /
положительно. Обозначим границы этой окрестности с и d (с < d).
Ь с d Ь
Тогда J f(x)dx = \ f(x)dx + \ f(x)dx + J f(x)dx. Два крайних слагае-
a a с d
d
мых неотрицательны, а \ f(x)dx > 0, поскольку на промежутке (с; d)
* ь
с г
функция строго положительна (см. 2)). Поэтому I f(x)dx > 0 как сум-
a
ма двух неотрицательных и одного положительного слагаемых. Ш
Утверждение теоремы можно доказать, пользуясь определением
за языке сумм Дарбу. Непрерывная неотрицательная функция имеет
неотрицательную нижнюю сумму Дарбу. Тогда точная верхняя
граница нижних сумм также неотрицательна, а она и есть значение
интеграла. Если же непрерывная неотрицательная функция
положительна хотя бы в одной точке, то она положительна и в некоторой
192J Глава X. Определённый интеграл
окрестности этой точки. Рассмотрев разбиение, в котором одна из |
частей полностью содержится в этой окрестности, получим для этого
разбиения строго положительную нижнюю сумму Дарбу, а тогда и |
точная верхняя граница нижних сумм будет строго положительной 3
да и |
ной. 3
Для функций, имеющих на промежутке конечное число разрывов,
теорему можно сформулировать таким образом:
ТЕОРЕМА
I CUr t IVI А ^ятттштвтштттттттттштвятттттвштттттттттттвятттттттятттвтташшштвшттштттт^тттттттт^ттшштш^шяштттттттштят
ПЕсли функция f неотрицательна на промежутке (а; Ь) и имеет на
нём конечное число разрывов, то jf(x)dx > 0.
Как показывает пример функции, равной 0 всюду, кроме целых
чисел, и равной 1 в целых точках (интеграл такой функции по любому
промежутку равен 0), для разрывных функций нельзя сделать вывод
о строгой положительности интеграла, если функция хотя бы в одной
точке отлична от 0. Однако если точка, в которой функция
положительна, попадает на промежуток, где функция непрерывна, то
интеграл будет положительным. Из этой теоремы следует утверждение.
ТЕОРЕМА (об интегрировании неравенств) ----------—------—————--—
Пусть функции f и д непрерывны на промежутке (а; Ь), причём
b b
Vx e (a; b) f(x) > д(х), тогда \f(x)dx > \g(x)dx. Если же хотя бы
а а
в одной точке х0 выполняется f(x0) > д (х0), то и неравенство
между интегралами будет строгим.
П доказательство. Рассмотрим разность:
b Ь Ь
jf(x)dx- jg(x)dx = j(f(x)-g(x))dx.
a a a
Функция f - g непрерывна и неотрицательна на (a; 6), значит, и её
интеграл неотрицателен. Если же функции fug различаются в
точке х09 то функция f — g будет положительна хотя бы в одной точке, а
тогда и разность интегралов будет положительной, й
я я
Пример 15. Сравним значения интегралов j sin2xdx и jsinsxdx.
о о
П Заметим, что на отрезке [0; л] функции sin2 л: и sin3 л:
непре2л: ^ sin3
рывны, причём sin2л: ^ sin3л:, и имеется точка например, х = — I,
в которой неравенство строгое. По теореме об интегрировании нера-
п п
п п
венств получим J sin2 xdx > J sin3 xdx. Hi
193 §66- Свойства определённого интеграла
Пример 16. Известно неравенство sint < t при t > 0. Проинтегрируем
его на промежутке от 0 до произвольного числа х > 0. Получим
XX п
f Г X
\ sintdt < \tdtj откуда 1 - cosх <—.
0 0
Это неравенство верно при всех положительных х. Можно
интегрировать его дальше и получать новые неравенства, й
Пример 17. Докажем неравенство 1 - cosl < J -dx < —.
iJl-x2 2
□ Для этого запишем неравенство, верное на полуинтервале [0; 1):
и проинтегрируем его. Получим требуемое неравенство. Учитывая, что
каждый знак неравенства становится строгим при некоторых
значениях х, неравенство между интегралами будет строгим. Ш
Замечание. В этом примере есть три особенности.
1. Первообразная функции —== не выражается в явном виде
/1 — эс
через элементарные функции.
2. Не так легко догадаться, какое неравенство нужно
проинтегрировать.
3. Подынтегральная функция не определена в точке х = 1.
Самостоятельно докажите по определению, что J ?ШХп dx существует.
о
3. Применение подстановки при интегрировании
Имеет место следующая теорема:
ТЕОРЕМА (о подстановке в определённом интеграле) ————
Пусть функция ф дифференцируема и её производная
непрерывна на отрезке [а; Р] и ф ([а; Р]) = [a; to], причём ф (а) = а, ф (Р) = to.
Пусть функция f определена и непрерывна на отрезке [a; to],
Р ь
тогда имеет место равенство: Jf((p(f))-cp'(f)cff = jf(x)dx.
□ доказательство. Пусть F — первообразная функции /. Тогда по
теореме о производной композиции функций
1941 Глава X. Определённый интеграл
Тогда
Р в '
Г/(Ф(*))ф'(*)Л = ^(Ф(0)1 = *ЧФ(Р)) - *Чф(ос)) = F(b)-F(a) = jf(x)dx.
Подумайте, зачем в условии теоремы нужна непрерывность q>'(f)7
О Важное преимущество доказанной теоремы состоит в
следующем. Если ранее, основываясь только на формуле Ньютона —
Лейбница, нужно было, вычислив первообразную, вернуться к исходной
переменной и затем подставлять пределы интегрирования, то теперь можно
переходить к интегралу от новой переменной и уже не возвращаться
к старой.
Пример 18. Выясним, при каких значениях а выполнено равенство
5 а
Sdx =
О 3
П Можно, разумеется, просто вычислить соответствующие
интегралы и решить уравнение.
Мы же сделаем замену в первом интеграле: х = t - 3. Тогда исход-
8 а
ное равенство примет вид: j4tdt = j4xdx.
з з
Видно, что а = 8 удовлетворяет этому равенству. Поскольку
фукнем
ция F(a) = jyfxdx возрастает (так как её производная F'(a) = 4а > 0),
з
то каждое своё значение она принимает только один раз, в том числе
8
и значение -F(8) = \4tdt. Ответ: а = 8. Ш
3 1
Пример 19. Найдём [Vl - х2 dx.
О г- -.
П Подставим х = sin t при t e 0; — . Тогда по доказанной теореме
о 4
2 4
Если в примере 19 первообразную можно было найти
непосредственно, то вот пример, где этого сделать нельзя, а метод подстановки
приводит к результату.
dx
Пример 20. Вычислим |
(arcsin x
dx f dx , f dx
f UX = f dX Г
№5j §66. Свойства определённого интеграла
f dx
Рассмотрим I Положим х = —t. Согласно теореме о
подстановке в определённом интеграле получим1
dx f -dt f e*arcsintdt
f dx = f -
:11 + />/агс81пдс {i + e-3
Разумеется, неважно, как обозначена переменная в определённом
интеграле. Поэтому можно записать полученное равенство так:
о
[ *Е = \1
J 1 _L лл/arcsin х • 1
Таким образом,
} ^rcsin =} —
_11 + еа о-*- +
лл/arcsin дс х/у
f /Varcsin дс dx f
=
з
= i. a
Рассмотрим несколько полезных следствий из теоремы о
подстановке.
Следствия из теоремы о подстановке. 1. Пусть/—нечёт-
а
ная непрерывная функция на отрезке [—а; а], тогда \ f(x)dx = 0, т. е.
-а
интеграл нечётной непрерывной функции по промежутку,
симметричному относительно 0, равен 0.
2. Пусть / — чётная непрерывная функция на промежутке [-а; а],
а а
тогда J / (x) dx = 2J / (#) cte.
-а 0
3. Пусть / — непрерывная периодическая функция с главным пе-
Т а + Т
риодом Ту тогда J f(x)dx = J f(x)dx.
0 а
а 0 а
п доказательство. 1. jf(x)dx= j f (x)dx + J /(x)dx.
1 Обратите внимание на то, что во втором интеграле пределы
интегрирования стоят «от большего к меньшему». Это соответствует теореме о
подстановке, поскольку в данном случае ф(£) = -t9 и при этом -1 =ф(1). Затем пределы
интегрирования поменялись местами за счёт знака «-» в числителе второго
интеграла.
196: Глава X. Определённый интеграл
В первом слагаемом осуществим подстановку х = —t:
0 0 0 а
jf(x)dx = jf(-t).(-dt)= j-f(t)(-dt)=-jf(t)dt.
-а а а О
Дальнейшее очевидно.
2. Доказательство аналогично предыдущему.
3. Пусть на промежутке [а; а + Т) находится число kT (k e Z),
тогда:
а + Т kT а+Т
jf(x)dx= jf(x)dx+ jf(x)dx.
a a kT
Рассмотрим каждое слагаемое по отдельности.
Первый интеграл найдём, используя подстановку х = t + (к - 1)Т:
kT Т Т
jf(x)dx= jf(t + (k-l)T)dt= jf(t)dt.
a a-{k-l)T a-{k-l)T
(в последнем равенстве использована периодичность функции /).
Второй интеграл найдём, используя подстановку х = t + kT:
а + Т a + T-kT a-(k-l)T
jf(x)dx= \f(t + kT)dt= jf(t)dt.
kT 0 0
Сложив полученные выражения, получим:
а+Т Т a-(k-l)T т
jf(x)dx= jf(t)dt+ \f(t)dt= \f(t)dt.
a a- (k-l)T 0 0
Геометрический смысл доказательства ясен из рисунка 10.10. Щ
Рис. 10.10
Замечание. Из следствия 3 следует более общее свойство.
СВОЙСТВО ш^тттттттшшттттттштттттшшшштттштттттшттшшштшшшттш^ш^ттттшттттшшш^ттттшштттшттттшшттш^
Интеграл периодической функции одинаков при интегрировании на
любом промежутке длины, равной периоду.
197 §66. Свойства определённого интеграла
2л
Пример 21. Вычислим ) sin3 xdx.
о
□ Период подынтегральной функции равен 2я, и интеграл берётся
по промежутку длины, равной периоду. Тогда по следствию 3 из теоре-
2л л
мы о подстановке (с. 195) J sin3 xdx = \ sin3 xdx.
О -л
Последний интеграл равен 0 как интеграл нечётной функции по
промежутку, симметричному относительно 0 (следствие 1, с. 195).
Решение этого примера с нахождением первообразной и
использованием формулы Ньютона — Лейбница будет существенно сложнее, й
Следующий пример показывает, сколь осторожно нужно
пользоваться теоремой о подстановке и формулой Ньютона — Лейбница.
2л
f dx
Пример 22. Вычислим .
J 2 + cos 2x
П Используем универсальную тригонометрическую подстановку.
2 dx J\
I
\dx
I 2 + cos 2x I 3 + tg2 x
о о о
Применим замену t = tgx. Исходный интеграл равен J = 0.
Однако ответ 0, очевидно, неверен, так как интегрируется
положительная функция, а значит, и значение интеграла должно быть
положительным!
Ошибок здесь допущено несколько.
1. Замена — это функция х = (р(0- В данном случае одному
значению t соответствуют несколько значений х9 отличающихся на п.
2. Даже если бы замена была однозначной (например, если бы
интегрирование велось на промежутке [0; я] и х можно было бы
выразить как функцию от £), функция tga; терпит разрыв в точке х = —.
Функция, выражающая х через t, также будет разрывной, не говоря
уже о её производной!
Поэтому искать этот интеграл нужно по определению. Для этого
найдём первообразную подынтегральной функции.
Используя интегрирование с помощью подстановки в
неопределённом интеграле, получаем, что исходный интеграл равен J -—-9 где t = tgx.
Преобразуем этот интеграл:
dt If dt
J
198' Глава X. Определённый интеграл
Итак, первообразная функции
равна -= arctg Ц^
2 + cos2x V3 V л/3
+С.
Эта формула верна на каждом из промежутков, где непрерывна функция
тангенс, но на каждом из этих промежутков константа своя! Для
нахождения первообразной нужно подобрать константы так, чтобы в точках
х = —их = — части графика «склеились», для чего необходимо равен-
ство односторонних пределов в этих точках.
Пусть первообразная равна F(x) = — arctg
ле
и-
на полуинтерва-
Тогда lim ±= arctg
2V3
Значит, положим F — = —^=, чтобы функция F была непре-
\2) 2V3
рывной. Тогда выполнится равенство lim — arctg -^=- + С = —=,
откуда С - —=. Таким образом, на интервале ^-; -£- | выполнено
V3 ^2 2
- —arctff l&t- I + —
Сравнивая аналогичным образом односторонние пределы при jc->—,
получаем, что на полуинтервале —;
выполнено
Итак, F(x) =
-pr arctg I -4^ при л: g
V3 v /з ;
я
2 '
!)•
Я
Зя
Зя
1 . tgx 2я
-= arctg ~т^- + -;= при
л/3 л/3 л/3
я Зя
Зя о 1
2 J
199, § 67. Применения определённого интеграла
271
Поэтому
dx
2 + cos 2x
2п
о =-7-arctg
1 2£_ JL
arctg
2л
067. Применения определённого интеграла
1. Вычисление площадей
Мы уже знаем, что геометрический смысл определённого
интеграла — площадь под графиком функции. В соответствии с этим верно
следующее утверждение:
Утверждение '
Если на отрезке [а; Ь] даны две непрерывные функции f и д,
графики которых не имеют общих точек на интервале (а; Ь), то площадь
фигуры, ограниченной графиками функций f и д, а также прямыми
ь
х-а и х = Ь, равна f|f(x)- g(x)\dx (рис. 10.11).
Чтобы найти этот интеграл,
нужно выяснить, как
раскрывается модуль, т. е. график какой из
функций находится выше.
Пример 23. Найдём площадь
фигуры, ограниченной графиком
функции у — х2 — 2х и прямой
□ Построим эскизы графиков
этих функций (рис. 10.12). На
участке между точками
пересечения прямой и параболы прямая Рис. 10.11
находится выше параболы.
Найдём пределы интегрирования, решив уравнение х2 — 2х = Зх — 4. Корни
этого уравнения — числа 1 и 4. Искомая площадь равна
y=g(x)
S= j(3x-4-x2 + 2x)dx =
3
= 4,5. Ш
Немного более сложной является задача нахождения площади
фигуры, граница которой состоит из более чем двух графиков.
Пример 24. Найдём площадь фигуры, ограниченной графиком у = х2 — Зх
и касательными к нему, проходящими через точку А (2; -3).
D Заметим, что точка А не лежит на графике функции, поскольку
её координаты не удовлетворяют уравнению этого графика.
200| Глава X. Определённый интеграл
у{ к
х
Рис. 10.12
-3
Рис. 10.13
Прежде всего найдём уравнения касательных и координаты
точки касания. Общее уравнение касательной к графику функции / в
точке графика с абсциссой t имеет вид у = f'(t)(x — t) + f(t), где t —
корень уравнения -3 = f'(t)(2 - t) + f(t) (см. пример 19 гл. IX). Здесь
f(t)=t2 - 3t9 f'(t)= 2t- 3. Решая получившееся уравнение (2t- 3)(2-£)+
+ t2 - 3t = -3, находим '
Для первой точки уравнение касательной у = -х - 1, для второй
у = Зх — 9. Касательные пересекаются в точке с абсциссой х = 2.
Изобразим на чертеже фигуру, площадь которой надо найти (рис. 10.13).
Прямой х = 2 разобьём фигуру на две части и найдём искомую
площадь как сумму площадей этих частей:
2 3
S = \(х2 - Зх - (-х - l))dx + \(х2 - Зх - (Зх - 9))dx =
1 2
г с
= \(х - I)2 dx + [ (х - З)2 dx =
(у -
(ж - З)3
-Ы-1--
1 2
Обратите внимание, что перед тем как интегрировать,
подынтегральные выражения были представлены в виде квадратов1. Это
позволяет более компактно записать первообразную и существенно снижает
риск арифметических ошибок.
ХВ главе IX подробно описано, почему разность правых частей уравнений
квадратичной функции и касательной к ней с точностью до знака является
точным квадратом линейного двучлена.
201 § 67. Применения определённого интеграла
2. Вычисление длин кривых
Пусть на отрезке [а; Ь] дана дифференцируемая функция /,
производная которой непрерывна. Вычислим длину кривой у = f(x) на
отрезке [а; &]. Для этого возьмём достаточно много точек на кривой,
обозначив их Ао, Alf ..., Ап, и соединим их ломаной. Чем «гуще» будут точки,
тем точнее периметр этой ломаной приблизит длину кривой (рис. 10.14).
Ап-г
Ь=хп
Рис. 10.14
Вычислим длину этой ломаной. Длина одного звена
X
По теореме Лагранжа f(xt + г) - f(xt) = f'fa) -(xi + 1- xt), где ^ e (xt; x% + x).
Поэтому AtAi + l = (xi + l - xt)i]l + (Г(^))2 • л-1
Тогда периметр ломаной будет равен ^ (xt + х - х£) • д/l + (Г(^))2 •
i=0
Если теперь разбить отрезок [а; Ь] точками xt на п равных частей, то
длина ломаной будет не что иное, как риманова сумма для функции
Jl + (f'(х))2 . Перейдя к пределу при п —► +оо, получим длину кривой
ъ
графика функции, равной J д/l + (f'(x))2dx.
а
2 -
Пример 25. Найдём длину кривой f(x)- -х2 на отрезке [1; 3].
I 3
□ Найдём производную f'(x)=x2. По формуле длины кривой
получим
2
3
з
х)2
16-
2021 Главах. Определённый интеграл
3. Вычисление пределов последовательностей
Если формула общего члена последовательности представляется
в виде суммы п слагаемых (т. е. число слагаемых растёт с ростом
номера члена), то иногда возможно «увидеть» в этой формуле риманову
сумму для какой-либо функции. В этом случае предел
последовательности есть интеграл данной функции.
(I3 23 п3 ^
Пример 26. Найдём lim —- Н—- + ...Н—- I.
л-оо^П4 П4 П4 )
□ Преобразуем формулу общего члена:
1- (l 2 п?Л г iff*
lim — + — + ...+— = hm - -
4 4 4 ) \
Можно заметить, что последнее выражение есть не что иное, как
риманова сумма для функции f(x) = х3 на отрезке [0; 1]. Поэтому
^r + ^- + ...+^-]= \x3dx= -. Ш
п4 п4 п ) о 4
Вот пример, где соответствующее преобразование «увидеть» труднее.
Пример 27. Найдём lim 1 Ь ... Н
л-оо^п + 1 п + 2 2п
П Вынесем за скобки — и получим
п
—)= lim -
2 I
+... +
п + 1 п + 2 2ny п-^ооп
Теперь видно, что выражение под знаком предела есть риманова
сумма для функции f(x)= — на отрезке [1; 2] (или же для функции
X
g(x) = на отрезке [0; 1]). Таким образом,
X "г J.
2
...+_L|= f^ = ln2. В
Шп [ + + ... + ) f
-юоуп+1 п + 2 2п) J х
4. Физические задачи
Приведём несколько примеров задач с физическим содержанием,
решаемых с применением определённого интеграла.
Пример 28. Материальная точка движется по прямой со скоростью,
зависящей от времени по формуле v(t) = 2t - t2 (отрицательное
значение скорости означает, что тело движется в направлении,
противоположном направлению оси). Какова координата материальной точки
2031 § 67. Применения определённого интеграла
через 10 с после начала движения, если в начале движения
координата точки была равна 0?
Пусть x(t) — координата материальной точки в момент времени t.
Рассмотрим произвольный момент времени t0 и малый промежуток
времени At. Можно считать, что за этот промежуток времени скорость
изменилась пренебрежимо мало по сравнению со значением в точке t0,
а потому координата изменилась на v(to)At (т. е. в течение
промежутка времени At мы считаем движение равномерным со скоростью v(t)).
Тогда общее изменение координаты можно приближённо
вычислить так. Разобьём промежуток времени [0; 10] на п равных малых
участков точками t0 = 0, tl9 ..., tn = 10 и найдём изменение
координаты на каждом участке, а затем эти изменения сложим. Получим фор-
10 п~г
мулу Ах ~ — Х1^*)* т^ем больше будет л, тем точнее будет получать-
/= о
ся значение Ах. Значит, точное значение будет выражено формулой
Г 1
ю
""1
Длг=Ит —У y(t) L Однако эта формула есть не что иное, как
предел римановых сумм, т. е. интеграл функции v(t) на отрезке
[0; 10]. Поэтому
10 10
Ах = \v(t)dt = \(2t - t2)dt = t2 Г - —
J J U -с
о о
10
0
С учётом того что начальная координата была равна 0, получаем
ответ: через 10 с материальная точка окажется в точке оси с
координатой х- -233-. Ш
Пример 29. Полукольцо радиуса R имеет массу т. В центр полукольца
помещена материальная точка массы М. С какой силой полукольцо
притягивает точку?
□ Напомним, что для двух материальных точек, т. е. тел,
размерами и формой которых можно пренебречь, массы которых равны т1
и /п2, а расстояние между ними равно г, сила притяжения направлена
- п т\т2 ,^
от одной точки к другой и ее модуль равен G —-— (G —
гравитационная постоянная).
Однако полукольцо нельзя считать материальной точкой. Поэтому
разобьём полукольцо на п малых участков равной длины, каждый из
которых уже можно считать материальной точкой, найдём векторы
сил притяжения, а затем сложим эти векторы. При этом ясно, что из
соображений симметрии искомая сила будет направлена вдоль
радиуса О А, идущего в середину полукольца, поэтому можно считать лишь
проекции векторов сил притяжения на это направление (рис. 10.15).
2041 Глава X. Определённый интеграл
т
Будем определять положение
точки на окружности углом (р,
который может изменяться от 0 до я.
Для i-ro участка сила
притяжения, с которой он действует на
материальную точку, имеет
модуль G
R2
а проекция этой си-
Рис. 10.15
О
1у
nR2
cos
лы на ось у равна произведению
модуля силы на косинус угла
между вектором силы и осью. В
нашем случае
Mm
л т} ~ Mm (тЛ
— = G - • sin — .
2 п ) nR2 \ п )
Суммируя эти проекции, получим
Но выражение в последних скобках — это риманова сумма для
функции f(x) = sinx, взятой на отрезке [0; л]. Поэтому точное значение мо-
GMm f . ,
дуля силы притяжения равно —— J sin х ах -
2 GMm
R2 '
Ш
Рассмотренные примеры дают представление о том, как в
физических задачах применяется интеграл. Там, где нужно просуммировать
значения, изменяющиеся с течением времени (как в примере 28) или
с изменением положения (как в примере 29), применяется разбиение
на малые промежутки, нахождение «частички» искомой величины,
затем суммирование и подбор подходящей функции, чьей римановой
суммой является данное выражение.
К числу таких задач относятся, например: работа переменной
силы, давление столба жидкости переменной плотности и т. д.
В Задачи и упражнения
Определение площади криволинейной трапеции
Группа А
Х.1. Найдите приближения площади криволинейной трапеции по
недостатку и по избытку для функции f(x) = х2 на отрезке [0; 1],
соответствующие разбиению отрезка на: а) две; б) три; в) четыре
равные части.
Х.2. Найдите по определению площади криволинейной трапеции
площадь под графиком функции h(x) = 2х + 3 на отрезке [1; 3].
205 Задачи и упражнения
Группа В
х.з. На какое наименьшее количество равных частей нужно разбить
отрезок [0; 1], чтобы приближения по недостатку и по избытку
функции g(x) = х4 отличались менее чем на 0,1? Та же задача
для отрезка [-1; 1].
Х.4. Найдите по определению площадь под графиком у = cos 2x на
отрезке 0; — .
L 2 J
Х.5. Существуют ли две неотрицательных функции, заданные на
отрезке [0; 1], под графиком каждой из которых площади нет,
а под графиком их произведения площадь есть?
Х.6. Существуют ли две неотрицательных функции, заданные на
отрезке [0; 1], под графиком каждой из которых площади нет,
а под графиком их суммы площадь есть?
Определение интеграла
Группа А
Вычислите интеграл (х.7—х.ю).
2 1-1
Х.7. a) J(jc3 - 2х2 + х - l)dx; б) J (Jx + Vx1) dx; в) J^/x + ldx;
-1 0 7
л/2 5
2 1 3
Г /7v Г ^ Y* — 9
)l U/A- \ I «->•*• «j
■7f=f; д) J"i~T
_ IV1 ~ Х -1Х Z 2
2 3
Зтс 2тс _7t_
4 3 2
Х.8. a) Jcos2fd^; б) J dx; в) J sin2x • sin3xdx.
n 0 COS— -n
2 2
x.9. a) [(1- 2x)dx; 6)
x.io.
l+ cos л:
x.ll. При каком значении а выполнено равенство:
а За
a) jy/x + ldx = 2; б) j(2x + l)dx = j(3x2 -
-1 a 1
JC+1 2 jc4
X.12. Решите уравнение: a) J sin tdt = 2J cos2^d^; 6) J — = 2.
x-l 0 *2
206, Глава X. Определённый интеграл
2
Х.13. Постройте график функции f(x) = J (2t — x)2dt.
0
jxsdx
x.14. Найдите предел: a)lim^-r——; б) lim —
&-►! О6 — 1 a-*2 >
J V*
J V +
2
X.15. а) Найдите квадратичную функцию /, если известно, что
12 Ч
2
= - J, J f(x)dx = -1 и
6 J 6
6 J 6 J 6
0 1 2
12 3
б) Пусть $ f(x)dx= A, J f(x)dx= В и J f(x)dx = С. Какое равенст-
0 12
во связывает А, Б и С, если известно, что / — линейная функция.
Группа В
Вычислите интеграл (х.16—х.20).
2 1
х.16. а) Jjc|x- l|d:c; б) Jjt(x- |jc|)djc; в) J(2x|x| - x)dx;
0 -з -l
2 3
г) j yj2x-x2dx\ д) j yj6x-x2dx.
1 2
2
4 4
x.17. a) Jmin{x; 4- x}dx; 6) Jmin{jc2 - 2x; 3x- 4}dx;
0 о
4
в) J max{jc2 - 2x; 3x- 4}dx.
о
3 4
X.18. a) J3l*-2ldx; 6) Jmax{4- 2X; 2x}dx.
1 0
2 7C
X.19. a) j| sinx| cos2xdx; 6) J (2sinx + |cosjc|) • |siruc|djc;
_n_ _n_
6 2
20я 10л
в) J д/l + cos2xdx; г) J д/l + sin2xdx.
о о
Tt
n 2
x.20. a) J max {cos x; sinx}dx; 6) J min{V3sinx; cosx}dx.
2071 Задачи и упражнения
Х.21*. Решите уравнение:
T
дс
Х.22. Постройте график функции y = j
1
Х.23. Постройте график функции:
1 1
а) F(t)= Jx- \x- 2t\dx; б) F(x) = j x-\x - 2t\dt.
о
Общий подход к определению интеграла
Группа С х
х.24. а) Найдите J x2 R(x)dx.
-1 1
б) Существует ли Jmin{l — R(x); D(x)}dx (здесь R — функция
о
Римана, D — функция Дирихле)?
Расширение понятия определённого интеграла
Группа В г г
Х.25. Существует ли интеграл: а) | , ; б) | —; в) |-=?
J /1 у2 J X J Jy
о V1"х о о ^х
1
Х.26. При каких значениях а существует J xa dxl
о
Найдите интеграл (Х.27, Х.28).
5 3
Х.27. a) J х2 • sign (х- l)dx; б) J cosjc • signxdx.
-3 -1
з
x.28. a) J (x2 • sign(x - 1) + x • sign(x - 2))dx;
-l
2 Зя
6) J (vW ' sign (x - 1) + sign xjdx; в) J x • sign (cos x) dx.
-2 0
з f x при x ^ 1,
Х.29. Вычислите J f(x)dx, если /(x) = < x2 +1 при 1 < x < 2,
о [2-х при x ^ 2.
3 2
X.30. Вычислите: a) j[2x]dx; 6) J{x2}dx.
0 1
208 Глава X. Определённый интеграл
х+1
0
x3
Интеграл с переменным верхним пределом
Группа А
х.31. Найдите производную функции F, если:
X 1
a) F(x)= jjl + t2dt; б) F(x)= jy/l + t2dt; в) F(x) =
-3 х
X+l X2
г) F(x)= jyll + t2dt; д) F(x)= \yjl + t2dt\ e) F(x) =
x 0 x2
X
x.32. Дана функция g(x)= jt-e~t2dt.
а) Найдите g(2).
б) Найдите множество значений функции g.
в) Составьте уравнение касательной к графику функции g(x)
в точке этого графика с абсциссой х0 = 2.
х
Х.ЗЗ. Дана функция f(x) = J (2 sin2 £ - 3sint)cfr. Составьте уравнение ка-
о
сательной к графику функции, параллельной прямой у = -х + 5.
Группа В ^
х.34. Найдите наибольшее значение функции F(x) = J (3^2 - 4х^ + Зле)Л
при положительных х.
Свойства определённого интеграла,
связанные с арифметическими действиями и неравенствами
Группа А к 2
х.35. Найдите: a) J ех • sin2 xdx + J ex • cos2 xdx; 6) J
0 0 0
Сравните по величине (х.36, х.37).
2 п 2
х.36. a) I sin dx и
2х2 + х + 1
dx; б) J2^2 -cosxdjc и J2*2 -cosxdx.
iL
2
х.37. а) IV2- cosxdx и [2*. cos xdx; б) f . dx и [
•» * J i i --2 ^
0 0 lV1+* 1
х.38. Докажите неравенство:
1
Зтс
4
1 ? :r9 I f Qin r
а) —^< I . dx< —; б) 0< f~ii£
Юл/2 J0A/l^ 10' ' [ х
Задачи и упражнения
Группа В г
С хп
Х.39. Покажите, что lim dx = 0.
Х.40*. Найдите предел lim — | In 1 + -= dx.
х.41. Пусть / — дифференцируемая выпуклая функция, заданная на
отрезке [а; Ь] и принимающая неотрицательные значения.
Докажите неравенство
Х.42. Функция / непрерывна на [а; &] и при всех а и (3, таких,
что а < а < Р < &, выполнено неравенство j f(x)dx > 0. Докажи-
а
те, что f(x) > 0 при всех х е [а; Ь].
Группа С
Х.43. а) Пусть / — непрерывная функция, положительная при х > 0.
X X
Докажите неравенство х\ f(t)dt > \tf(t)dt при х > 0.
о о
х
\tf{t)dt
б) Пусть ф(х)=^ , где /—непрерывная положительная
jf(t)dt
о
функция. Докажите, что функция ф возрастает на (0; -foo).
Х.44. Докажите, что если непрерывная функция / монотонно возраста-
х
ет на [0;+оо), то функция G(x) = — \ f(x)dx монотонно возрас-
0
тает на (0; -foo).
Х.45. Пусть / — функция, непрерывная на отрезке [0; 2], причём
2
J f(x)dx > 0. Докажите, что существует отрезок [а; Ь] с [0; 2], та-
0 г 11
кой, что J f(x)dx > 0, причём —- <Ъ - а < —.
2101 Глава X. Определённый интеграл
Теорема о подстановке в определённом интеграле и следствия из неё
Группа А
х.46. Вычислите интеграл: п
о 7з 7F
х х ; в) f sin3*: • cos2xdx.
7
a) I x-Jl- х2 dx; б) | ,х х ; в) f si
x.47. Найдите наименьшее значение функции F(x)= \\ arctgx \dx.
х.48. Найдите уравнение касательной к графику функции
-1
в точке с абсциссой х0 = 1.
2 Т
Х.49. Докажите равенство Jesin*d:x:= jecosxdx.
Зя
х.50. Вычислите J arctg(sinx)dx.
к
Группа В х
х.51. Решите уравнение \cosn tdt= О при: а) чётном натуральном п;
о
б) нечётном натуральном п.
х.52. Найдите все натуральные значения л, при каждом из которых
х
функция F(x) = J sin" £d£ периодическая.
о
х.53. Пусть / — непрерывная функция, периодическая с главным пе-
х
риодом Т и F(x) = J f(t)dt.
о
а) Приведите пример, показывающий, что функция F может не
быть периодической.
б) Найдите условие в виде равенства, необходимое и достаточное
для того, чтобы функция F была периодической с периодом Т.
в*) Является ли периодической функция
х
F(x) = Jcos* • cos3£ • cos(32*) • ... • cos(32007t)dt?
0
x.54. Вычислите интеграл: a) J n x2 dx; 6) J x dx (обратите
внимание на то, что пределы интегрирования взаимно обратны!).
2111 Задачи и упражнения
~ f sin x , с sin x ,
Х.55. Сравните по величине dx и dx.
* j х j х
О 2л
х
Х.56. Докажите, что J sin dt > О при х > 0.
к . Зя
Вычисление площадей фигур
Группа А
Найдите площадь фигуры, ограниченной линиями (Х.57—Х.61).
Х.57. а) I/ = 7 - х, у = х2 + Зх - 4; б) i/ = х2 - Зх + 5, у = 2х - 1.
Х.58. а) у = л/х, у = х2; б) z/ = x3, z/ = л/х при х ^ 0.
Х.59. a) j/ = 2*-1,j/ = 7- 2W; б) у = 3 - ех, у = 2е~х.
Х.60. а) у = sinx, i/ = cosx при х е [-л; я];
б) z/ = 2 sin х, i/ = tg х при х е 0; — .
Х.61. I/ = arcsinx, у = arcsin2x, у = —-
Х.62. Найдите площадь фигуры, ограниченной графиком функции
у = 2л/х + 1, касательной к нему в точке с абсциссой х0 = 3 и осью:
а) ординат; б) абсцисс.
Х.63. Найдите площадь фигуры, ограниченной графиком функции
у = х2 - Зх + 2 и графиком одной из её первообразных,
проходящим через точку (-1; 6).
Х.64. Найдите площадь фигуры, ограниченной графиком у — х2 + 2х — 4
и касательными к нему, проведёнными в точках с абсциссами
хг = 1 и х2 = 3.
х.65. Найдите площадь фигуры, ограниченной графиком i/ = x2 + 4x + 3
и касательными к нему, проведёнными через точку М (—1; —4).
Группа В
2
х.66. При каком значении а площадь, ограниченная линиями у = -=,
х = 1, х = а, # = 0, в два раза меньше, чем площадь, ограничен-
2
ная линиями у = -=, х = 1, х = 4, у = 0?
Х.67. При каком значении а прямая: а)х = а; б) у = a — делит
пополам площадь фигуры, ограниченной линиями у = -х2 + 4х + 1
и прямой у — 4?
Х.68. Найдите площадь фигуры, ограниченной графиком квадратного
трёхчлена со старшим коэффициентом 1 и двумя касательными
к этому графику, имеющими уравнения у — 4х — 13hi/ = —4х + 3.
212j Глава X. Определённый интеграл
х.69. Запишите в виде кусочно заданной функцию S(a), ставящую
в соответствие числу а площадь фигуры, ограниченной линиями
у = -х2 + ах и у -\х - а\.
х.70. а) Задайте формулой функцию S(a), ставящую в соответствие
числу а площадь фигуры, ограниченной линиями у = х2 + 2х - 3
и у = ах + 1.
б) Найдите наименьшее значение функции S(a).
в) Найдите наименьшее значение площади фигуры,
ограниченной линиями у = х2 + ах + b п у = рх + q, если a, ft, g —
константы (q > &), & р принимает все вещественные значения.
х.71. Найдите квадратичную функцию со старшим коэффициентом 1,
если её график касается прямой у = —2х - 4 и площадь фигуры,
ограниченной этим графиком и прямой у = х, равна 20-.
6
х.72. На графике функции f(x)=Jl296\x\ + 396x найдите все точки
с положительными абсциссами, для которых площадь фигуры,
ограниченной касательной к графику, проведённой через
каждую из таких точек, и самим графиком, равнялась бы 4-.
6
Группа С
х.73. Прямая касается параболы в произвольной точке А.
Параллельно этой прямой проведена хорда параболы ВС. Докажите, что
площадь фигуры, ограниченной параболой и хордой ВС, равна -
3
площади треугольника ABC1.
Х.74. Докажите, что фигура, ограниченная параболой и двумя
касательными к ней, делится на равновеликие части прямой,
параллельной оси параболы, проведённой через общую точку двух
касательных.
х.75. Найдите при произвольном а > 0 такое значение х0, что фигура,
ограниченная прямой, касающейся графика у — ах— 2\1х + 1
в точке с абсциссой х0, самим этим графиком и прямыми х = -1
и х = 2, имеет наименьшую площадь.
Х.76. Пусть числа а, & и с образуют возрастающую арифметическую
прогрессию, причём а > 1. Докажите, что
гг с
—— J
хЭтот результат принадлежит Архимеду, который за 2000 лет до
появления интеграла уже умел считать площади достаточно сложных фигур.
Фактически Архимед разработал методы подсчёта площадей последовательными
приближениями.
Задачи и упражнения
Вычисление длин кривых
Группа В
0; — .
X.78. Найдите длину дуги кривой f(x) = на отрезке [1; V2].
Х.79. Найдите длину дуги кривой у = 1п(х2 - 1) на отрезке [2; 5].
Вычисление пределов последовательностей
Группа В
Х.80. Найдите предел последовательности {хп}, если:
в*) хп = п
Физические задачи
Группа А
Х.81. Тело движется вдоль прямой из состояния покоя в момент
времени t = 0 до момента времени t = -, причём ускорение тела меня-
6
ется по закону a if) = . Какой путь пройдёт тело к тому мо-
л. Т
менту, как скорость станет равна 8 In 2?
Х.82. Точка движется по прямой из состояния покоя в момент времени
t = 0 с начальной скоростью 1 м/с. При этом её ускорение
зависит от времени по закону a(t) = sin* м/с2. Найдите расстояние
между точкой, в которой тело оказалось через 2п с.
Группа В
Х.83. Найдите работу, совершаемую при сжатии идеального газа,
находящегося в цилиндре радиуса i?, если начальная высота поршня
над дном цилиндра равна h, а конечная —, причём сжатие проис-
3
ходит изотермически.
Х.84. Найдите энергию, необходимую для поднятия тела массы m
на высоту Н над поверхностью Земли, если Земля — шар
радиуса R1.
1 Полезно учитывать, что притяжение шара вне его границ такое же, как
материальной точки с массой, равной массе шара, находящейся в его центре.
Это впервые выяснил И. Ньютон.
2141 Глава X. Определённый интеграл
х.85. Найдите энергию, необходимую для того, чтобы выкачать воду
из цилиндрической бочки, радиус основания которой равен Д
а высота равна Н.
Группа С
Х.86. Однородный бесконечный стержень линейной плотности р согнут
в виде угла величины а. На биссектрисе угла поставлена
материальная точка массы т. С какой силой стержень притягивает точку?
Х.87. Найдите массу атмосферы Земли, считая, что Земля — шар
радиуса R и что плотность атмосферы зависит от высоты h над
уровнем Земли по формуле p(h) = р0 • e~h.
Разные задачи
Группа В
х.88. а) Докажите, что для всех натуральных чисел п выполнено
неравенство
б) Докажите, что для всех а > Ь > О выполнено неравенство
, Ъ Ь2-а2
In- < .
а 2аЬ
Х.89. Пусть дано число Т > 0. Докажите, что если для непрерывной
на R функции / при всех вещественных х имеет место равенство
х+Т
\ f(x)dx = 0, то функция / периодична с периодом Т (однако пе-
х
риод Т может быть и не главным).
Группа С \ г Ш24 2
х.90. Вычислите сумму: a) J sinxdx+ \ arcsinxdx; б) \1y[xdx+ \ xlodx.
оо оо
Что объединяет эти два примера?
Х.91. Пользуясь ответом предыдущего номера, вычислите
2L
2 1
J sin7 xdx + J arcsin ifxdx.
о о
x.92. а) Пусть fug — взаимно обратные возрастающие функции,
определённые на [0; +оо). Пусть также /(0) = g(0) = 0. Для
произвольных положительных чисел а и Ь докажите неравенство
a b
J / (х) dx + J g (x) dx^ ab. При каком соотношении между а и Ъ
о о
достигается равенство?
2151 Задачи и упражнения
б) Пусть а > О, Ъ > О и положительные числа р и g связаны ра-
венством — + - = 1. Докажите неравенство — + — > аЪ и выясни-
Р Q Р Q
те, при каком соотношении между а и Ь достигается равенство.
3 3
х.93. Докажите, что 9 < j^Jx4 + ldx + J^/x4 - \dx < 9,0001.
0 (ь х у ь ь
X.94. Докажите неравенство \ f(x)g (x) dx ^ J f2 (x) dx • j g2 (x) dx для
\o J a a
функций fng, непрерывных на [а; Ь]1.
X.95. Дана функция / (х) = д/х2 + х + 7 - д/х2 - х + 1. Докажите неравен-
f 2 f
ство dx + \ f(x)dx ^ 3.
o'w о
x.96. Пусть функция / дифференцируема на отрезке [0; 1] и её
производная непрерывна на [0; 1]. Пусть также /(1)-/(0)=1.
Докажите, что ](f'(x))2dx> 1.
о
х.97. Пусть f(x) = Iog2(2* + а), где а > 0. Докажите неравенство
< 4а для £ > 0.
о
х.98*. Для возрастающей на отрезке [0; 1] непрерывной функции /
докажите неравенство J f(x)dx ^ 2J xf(x)dx.
о о
Х.99**. Пусть р — многочлен степени п. Пусть при всех целых
k е [0; п - 1] выполнено равенство J xkp(x)dx = 0. Докажите, что:
о
а) все корни многочлена р лежат на отрезке [0; 1]; б) среди
корней многочлена нет кратных.
хЭто неравенство называют интегральным неравенством Коши — Буня-
ковского (см. задачу IX.251 в).
В. Я. Буняковский (1804—1889) — знаменитый российский математик,
основные труды которого относятся к теории вероятностей и теории чисел.
Прославился своим капитальным трудом «Основания математической теории
вероятностей», принесшим ему всемирную славу. При этом книга была
написана таким понятным языком, что именно по ней К. Гаусс выучил русский
язык. В. Я. Буняковский также много занимался приложениями математики
к страховому делу, уточнив законы функционирования пенсионных фондов
и страховых компаний. Неравенство было опубликовано В. Я. Буняковским
в 1859 г. Коши доказал дискретный аналог этого неравенства в 1821 г.
Комплексные
числа
Определение комплексных чисел.
Алгебраическая форма записи и арифметические
действия над комплексными числами
1. История открытия комплексных чисел
В 1545 г. в книге итальянского ученого Дж. Кардано1 «Великое
искусство, или Об алгебраических правилах» впервые были
упомянуты числа, которые сам Дж. Кардано называл мнимыми. Они возникли
в процессе решения кубического уравнения в так называемом
«неприводимом» случае (т. е. в случае, когда кубическое уравнение имеет три
вещественных корня).
Не воспроизводя дословно рассуждений Дж. Кардано, рассмотрим
решение уравнения Xs - 13л: -12 = 0. Нетрудно видеть, что его корнями
являются числа -1; -3 и 4. Попробуем решить это уравнение методом,
схожим с методом Кардано. Для этого рассмотрим подстановку х = z + -:
Выберем параметр а так, чтобы взаимно уничтожились слагае-
мые, содержащие множитель z + -. Для этого положим а = —.
z 3
хДжироламо Кардано (1501—1576) — один из выдающихся учёных
своего времени, математик, медик, механик, астролог. Его жизнь напоминает
приключенческий роман: богатство и нищета, европейская известность и
трагическая судьба сыновей (один был казнён за убийство, другой погиб), нищее
детство и забвение в старости, тюрьма инквизиции и азартные игры. Легенда
гласит, что Дж. Кардано покончил жизнь самоубийством, чтобы оправдать
собственный гороскоп. Дж. Кардано предложил для кареты императора
Карла V подвеску, которая используется и теперь под названием карданный
подвес. В математике он может считаться отцом современной алгебры. В своей
«Книге об игре в кости» (1526) он вычислил основные комбинаторные
величины, а также вплотную подошёл к определению вероятности события.
217- §68. Определение комплексных чисел. Алгебраическая форма записи
и арифметические действия над комплексными числами
Умножив на 23 обе части уравнения, получим уравнение
Щ = о,
квадратное относительно новой переменной z3. Казалось бы, мы
решили исходное уравнение (мы можем найти г3, затем 2, а потом
и х). Однако дискриминант этого уравнения будет отрицательным
(d c? (isY 12251 ^ _
— = oz — — = I. Тем не менее хотелось бы получить резуль-
^ 4 V 3 У 27 J
тат. Самое простое — обозначить корень из -1 некоторой буквой, на-
35
пример Z, тогда г3 = 6± —j=i и дальше придётся извлекать корень ку-
3V3
бический из этого числа, находя г.
Можно доказать, что если кубическое уравнение имеет три
различных вещественных корня, то полученное описанным выше методом
квадратное уравнение обязательно будет иметь отрицательный
дискриминант. Так появились квадратные корни из отрицательных чисел, а
затем и комплексные числа.
2. Определение множества комплексных чисел.
Сложение и вычитание, равенство комплексных чисел
ОПРЕДЕЛЕНИЕ
Множеством комплексных чисел называется множество
упорядоченных пар вещественных чисел (а; Ь) с
введёнными на нём двумя операциями сложения (знак операции
обозначается +) и умножения (знак операции обозначается •
или х), определёнными следующим образом:
1) (а; Ь) + (с; of) = (а + с; b + of);
2) (a; b) - (с; of) = (ас - bof; aof + be).
Число a называется вещественной частью комплексного числа
и обозначается Re 2, число Ь называется мнимой частью комплексного
числа и обозначается Im 2.
Обозначение: С — множество комплексных чисел1.
Пример 1. Найдём сумму и произведение чисел гх — (а; 0) и z2 = (b; 0).
П zx + г2 = (а + Ь; 0) и гх • z2 = (а • Ь - 0 • 0; а • 0 + 0 • Ъ) = (ab; 0). Ш
Таким образом, если не записывать нули как второе число в
парах, получаем привычные сумму и произведение вещественных чисел.
1 Кстати, слово «комплексные» применительно к числам зачастую
произносится с ударением на букву «е». Некоторые мотивируют это тем, что числа
комплексные, а комплексными бывают обеды. Другие остряки возражают,
что обеды тоже бывают комплексными: цена вещественная, а еда мнимая.
218| Глава XI. Комплексные числа
Это позволяет считать множество вещественных чисел подмножеством
множества комплексных.
Точнее, существует взаимно однозначное соответствие / между
множеством вещественных чисел R и множеством пар вида (а; 0),
причём f(a + Ь) = f(a) + f(b) и f(ab) = f(a) • f(b), что позволяет не
различать вещественные числа и пары вида (а; 0).
В дальнейшем вместо пары вида (а; 0) мы будем записывать
просто а. Например, вместо (—1; 0) будем писать -1.
Пример 2. Умножим комплексное число (0; 1) само на себя. Получим
□ (0; 1) • (0; 1) = (0 • 0 - 1 • 1; 0 • 1 + 1 • 0) = (-1; 0). Ш
Комплексное число (0; 1) имеет специальное обозначение Z.
Таким образом, результат примера 2 с учётом наших соглашений
о записи вещественных чисел можно записать в виде i2 = -1.
Пример 3. Умножим вещественное число Ь на Z.
□ Запишем эти числа в виде пар и произведём умножение:
(Ь; 0) • (0; 1) = (Ь • 0 - 0 • 1; Ь • 1 + 0 • 0) = (0; Ъ). Ш
Итак, с учётом соглашений о записи вещественных чисел мы
можем записать, что (0; Ь) = Ы.
Наконец, заметим, что (а; Ъ) = (а; 0) + (0; &). Следовательно,
можно записать, что (а; Ь) — а + Ы.
ОПРЕДЕЛЕНИЕ --________-■■——___—_^
Запись комплексного числа (а; Ь) в виде а + Ы, где a, b e Я,
называется алгебраической формой записи комплексного
числа.
В дальнейшем мы часто будем использовать запись z — a + Ы,
подразумевая, что а и & вещественные числа.
Комплексные числа (а; &) и (с; d) равны тогда и только тогда,
когда а — с и Ъ — d, т. е. когда одновременно равны их вещественные
и мнимые части.
Для алгебраической формы записи это же утверждение можно
записать так: числа а + Ы и с + di равны тогда и только тогда, когда
а = с и Ъ - d. Отметим также, что если z - а + fei, то Re z = a, Imz = Ь.
Например, если 2 = 5 — 7/, то Re г = 5 и Im z = -7; если z = 7£, то
Re г = 0 и 1тг = 7; если г = 2, то Re г = 2 и 1тг = 0.
Ненулевые комплексные числа, для которых Re z = 0, т. е. числа
вида Ы (b e R, Ъ Ф 0), будем называть чисто мнимыми числами.
Пример 4. Найдём все вещественные х и у, для которых числа
и = х + i(x + у) и i> = x2 + i(2x — г/) равны.
□ Числа г/ и у равны тогда и только тогда, когда равны их
вещественные и мнимые части, т. е. числа х и у должны быть решением системы
2191 §68. Определение комплексных чисел. Алгебраическая форма записи
и арифметические действия над комплексными числами
f
1
Reu, Г х = х2, f \* = ?'
Imi; [х + у = 2х-у L
12у = х.
Решением системы являются пары (0; 0) и 1; — . В
Пример 5. Найдём все вещественные хиу, при которых вещественная
и мнимая части числа z равны, если z = у2 + ixy + ху — ix2.
□ Rez = у2 + ху, lm z = ху - х2.
Re z = Im 2 <=> i/2 + xi/ = xz/ — x2 <=> x2 + z/2 = 0 <=> x = z/ = 0.
Ответ: x = у = 0. В
Естественной становится операция сложения комплексных чисел,
записанных в алгебраической форме: отдельно складываем
вещественные части и отдельно — мнимые.
Пример 6. Вычислим 5 + 2/4-3 + 7/. □ 5 + 2/ + 3 + 7/ = 8 + 9/. В
Определим вычитание комплексных чисел.
ОПРЕДЕЛЕНИЕ ———■"——-—-—-—-"■——"-—--—---——^^
Разностью комплексных чисел z1 и z2 называется
комплексное число z, в сумме с z2 дающее zv т. е.
Z) - Z2 = Z <^> Z + Z2 = Zv
Выясним, как вычитать комплексные числа.
Пусть zx = a + &/, 22 = с + d/. Будем искать число 2 = zx — z2 в виде
z = х + yi. Тогда по определению разности имеем х + yi + с + di = a + Ы,
откуда х + с + (у + d) i = a + Ы.
Равенство двух комплексных чисел означает равенство их
вещественных частей и равенство их мнимых частей, поэтому
{х + с = а, (х = а — с,
y + d=b 4 [y = b-d.
Таким образом, (а + Ы) — (с + d/) = а - с + (Ь - d)i.
Итак, чтобы найти разность двух комплексных чисел, достаточно
найти разность их вещественных частей и разность их мнимых частей.
Пример 7. Вычислим 3 — 2/ — (3 — 5/).
П 3 - 2/ - (3 - 5/) = 3 - 3 + (-2 + 5)/ = 3/. Ш
3. Умножение комплексных чисел
Попробуем перемножить два комплексных числа в
алгебраической форме не по определению, а как многочлены первой степени с
переменной /:
(а + Ы)(с + di) = ас + bci + adi + bdi2 = ас + (be + ad)i + bdi2.
2201 Глава XI. Комплексные числа
В полученном выражении заменим I2 на —1, получим
(а + Ы)(с + di) = ас - bd + (be + ad)i.
К такому же результату мы придём, если умножим комплексные
числа по определению!
Итак, чтобы перемножить два комплексных числа, записанных
в алгебраической форме, можно перемножить их как многочлены от
переменной Z, а затем заменить i2 на -1.
Пример 8. Вычислим: a) i • (i + 1); б) (2 + i) • (i - 3); в) (5 + 0 • (5 - *)•
П а) £ • (i + 1) = i • i + i = -1 + i;
б) (2 + 0 • (i - 3) = 2/ - 6 - 1 - 3i = -7 - i;
в) (5 + 0 • (5 - 0 = 5 • 5 - Ы + 5/ - i • * = 25 - 5/ + 5/ + 1 = 26. S
Заметим, что операции сложения и умножения комплексных
чисел удовлетворяют всем «естественным свойствам», которым
удовлетворяют вещественные числа.
Свойства сложения и умножения комплексных чисел ——
Пусть и, v \л z — комплексные числа, тогда:
1. и + v = v + и (коммутативность сложения).
2. и - v= v - и (коммутативность умножения)
3. (и + v) +z= и + (v + z) (ассоциативность сложения).
4. (z • и) - v = z • (и • v) (ассоциативность умножения)
5. (z + v) - и = zu + vu (дистрибутивность сложения относительно
умножения).
D доказательство. Докажем, например, свойство 2. Пусть
и = щ + iu2; v = t>! + ш2.
Тогда
U - V = UlVl - U2V2 + (Wit>2 + и2иг)1, 8i V • U = VlUl - V2U2 + (L^l/2 + y2wl)
т. е. (исходя из соответствующих свойств для вещественных
чисел, например, игиг = t^Wx) и - v = v - и, что и требовалось доказать.
Остальные свойства доказываются аналогично. 19 J
Отметим, что естественно ожидать выполнения таких привычных
свойств арифметических действий, поскольку сложение и умножение
комплексных чисел фактически свелись к сложению и умножению
многочленов, а соответствующие свойства арифметических операций
над многочленами верны.
Из этого, в частности, следует, что тождества, верные для
вещественных чисел (например, формулы сокращённого умножения,
формулы для степеней, формула бинома Ньютона и т. д.), справедливы и для
комплексных чисел.
Пример 9. Докажем, что для любых комплексных чисел и и v верно
тождество (и + и)2 = и2 + 2uv + v2.
П (и + и)2 = (и + и) (и + и) = (и + и) и + (и + v)v = и2 + vu + uv + v2 =
= и2 + 2uv + у2.
221; §68. Определение комплексных чисел. Алгебраическая форма записи
и арифметические действия над комплексными числами
При этом мы воспользовались различными свойствами сложения
и умножения комплексных чисел. Например, во втором равенстве мы
применили свойство 5, а в последнем равенстве — свойство 2. В
Поэтому, в частности, в примере 8, в мы могли воспользоваться
формулой (и + v)(u - v) = и2 - v2 и сразу же получили бы
(5 + /) - (5 - /) = 52 - i2 = 26.
Отметим также, что если аей, z = х + yi, то az - ах + ш//, т. е.
умножение комплексного числа на вещественное сводится к
умножению на это вещественное число вещественной и мнимой частей
данного комплексного числа.
Пример 10. Приведём к алгебраической форме записи число: а) £2008;
б) /4/г + К keN; в) (/ + I)802; г) / + 2i2 + З/3 + 4/4 + ... + 2009/2009.
□ a) j2008 = (/2)1004 = (_l)1004 = 1;
б) i4k+ l = i4k • i = (i*)k • i = 1* • i = i;
в) (i -f I)802 = ((i + I)2)401 = (2i)401 = 2401 • i401 = 2401i (в последнем
равенстве мы воспользовались результатом пункта б);
г) нетрудно доказать (аналогично пункту б), что i4k = 1, i4k + 2 = —1,
t4fe + 3 = -i. Таким образом,
* + 2/2 + З*3 + 4/4 + ... + 200Ш2009 = i - 2 - 3/ + 4 + 5/ - 6 + ... + 200Ш =
= /(1 - 3 + 5 -7 + ... + 2009) -f(-2-f4-6 + ...-f 2008) =
= /(502 . (-2) + 2009) + 502 - 2 = 1004 + 1005/. Ш
Пример 11. Найдём все комплексные числа, удовлетворяющие
одновременно условиям z2 = 5 + 12/ и Re z < 0.
D Пусть z = а + Ы и z2 = 5 + 12/. Тогда (а + Ы)2 = а2 - Ъ2 + 2а&/ =
= 5 + 12i, т. е.
2а& = 12.
Из второго уравнения получим а = - (заметим, что 6 = 0 не даёт
с?
решения системы). Подставляя полученное а в первое уравнение, по-
лучим — - &2 = 5, откуда &4 + 5&2 - 36 = 0, тогда Ь2 = -9 или &2 = 4,
первое уравнение вещественных корней не имеет, а второе имеет
корни Ь = ±2.
^»
Из формулы а-- находим соответствующие а - ±3. Таким обра-
Ъ
зом, 2г = 3 4- 2/, г2 = -3 — 2/. Поскольку нужно найти те 2, для которых
Re г < 0, то получим ответ: z = -3 - 2/. В
Пример 12. Может ли произведение двух комплексных чисел, не
являющихся вещественными, быть вещественным числом?
D Да, например чисел 5 + /и5 — /.В
2221 Глава XI. Комплексные числа
К сожалению, оказывается невозможным говорить о том, что одно
из комплексных чисел больше другого. Точнее, невозможно так
сравнивать комплексные числа, чтобы сохранились привычные
свойства арифметических операций с неравенствами и неравенства
между вещественными числами были бы частным случаем неравенств
между комплексными числами. А именно:
ТЕОРЕМА
Невозможно ввести такое определение отношения «)», чтобы
выполнялись следующие свойства.
1. Для любых двух различных комплексных чисел z1 и z2 было бы
выполнено ровно одно из двух отношений z1 )z2 или z2)zv
2. Для двух вещественных чисел а и Ь отношение a) b
выполнено тогда и только тогда, когда а> Ь.
3. Если zy ) 0 и z2 ) 0, то z1 • z2 > 0;
4. Если 0 ) Zi и 0 ) z2> то z1 • z2 > 0.
Q доказательство. Пусть, вопреки утверждению теоремы, ввести
соотношение «)» с указанными свойствами возможно. Сравним тогда
числа i и 0.
Если i ) 0, то по третьему свойству i • i ) 0, т. е. -1 > 0, что
противоречит свойству 2.
Если же 0 ) /, то по четвёртому свойству i • i ) 0, что также
приводит к неравенству -1 > 0, противоречащему свойству 2. Ш
Если же не требовать какой-либо связи между знаком неравенства
и арифметическими действиями, то упорядочить комплексные числа
возможно. Например, a + Ы ) с + di, если a > с. В случае а- с
положим а + Ы) с + di, если b > d. Таким способом можно поставить знак )
между любыми двумя комплексными числами.
Такой способ упорядочивания напоминает упорядочивание слов
по алфавиту, поэтому называется лексикографическим.
4. Сопряжённые комплексные числа
ОПРЕДЕЛЕНИЕ
Сопряжённым числу z = a + bi называется число z-a- bi.
Таким образом, чтобы найти число, сопряжённое данному,
достаточно сменить знак мнимой части данного числа.
Отображение, ставящее в соответствие данному комплексному
числу его сопряжённое, называется сопряжением.
Пример 13. Запишем число, сопряжённое данному: а) -3 - 2Z; б) 2Z; в) 3.
□ Ответ: а) -3 + 2Z; б) -2i; в) 3. Ш
§68. Определение комплексных чисел. Алгебраическая форма записи
и арифметические действия над комплексными числами
Пример 14. Докажем: а) zx + z2 = гг + z2; б) zx •
D б) Пусть zx = аг + bxi и г2 = а2 + b2i. Тогда
=
С другой стороны,
2^- г^" = (ах - bxi)(a2 - b2i) =
т. е. 2j -22 = г^ • 5J, что и требовалось доказать. Равенство из пункта а)
доказывается аналогично. В
Объединим в теорему доказанные в примере 14 свойства
сопряжения и ещё несколько простых свойств.
ТЕОРЕМА (свойства сопряжённых чисел)
Для любых комплексных чисел z, z1 и z2 выполнены следующие
утверждения.
1. Z} + Z2=Ti+Z^ И Zj - Z2 = ZJ - Z^.
3. z = z.
4. ze R <^> z = z.
5. При л eN (z)n = zn.
Пример 15. Найдём пару комплексных чисел^г и w, для которых
одновременно выполняются соотношения 3z - 2w = 1 и "z — iw = -6i.
D Пусть 2 = a + &i, w = с + di. Тогда Зг - 2w = 3(a + bi) - 2(c - di) =
= 3a - 2c + (3& + 2d)i = 1, откуда За - 2c = 1 и 3& + 2d = 0.
Аналогично z - iw = a - bi - i(c + di) = a + d - (b + c)i = -6i, откуда a + d = 0
и b + с = 6. Из полученных четырёх равенств находим a = 3, & = 2,
с = 4, d = -3. Ответ: 2 = 3 + 2/, м; = 4 - 3/. В
5. Деление комплексных чисел
Попробуем определить деление комплексных чисел. Пусть мы
хотим поделить число и на число и. Что это означает? Как обычно
(например, для целых чисел), разделить число и на число v означает
найти такое число w, что w • v = и. Всегда ли это возможно для
комплексных чисел (для целых чисел, очевидно, не всегда), и если возможно, то
как на практике произвести деление комплексных чисел?
Рассмотрим сначала деление произвольного комплексного числа
на вещественное.
Утверждение —"••-■■"••■"••"•■-"■■■•-•--•-■"■"•■-■•■•^^
Пусть z = a + Ы — произвольное комплексное число, х —
вещественное ненулевое число. Тогда существует (и притом
единственное) комплексное число w, такое, что w • x = z.
224| Глава XI. Комплексные числа
П доказательство. Будем искать w в виде w = c + di. Тогда
wx — cx + dxi.
Приравняв число w • х к числу 2, получим
Г о_
°ТКуда
Итак, найдено (и притом единственное) требуемое число w = — + — £. S
Таким образом, получена естественная формула: при х е JfJ, лс ^ О
а+Ы а Ъ. -
выполнено = —I— I, т. е. чтобы разделить комплексное число на
X X X
вещественное, достаточно разделить на это вещественное число
вещественную и мнимую части данного комплексного числа.
Следующий пример показывает, как на практике удобно делить
комплексные числа, сводя деление комплексного числа на
комплексное к делению комплексного числа на вещественное, и демонстрирует
основную идею доказательства теоремы о делении комплексных чисел.
Пример 16. Вычислим: а) -—:; б) \ (напоминаем, что знак дроби
можно рассматривать как запись знака деления).
П а) Умножим числитель и знаменатель на число, сопряжённое
тт 1 1- i
знаменателю. Получим : = :
б) Аналогично пункту а) получим
5-3/ = (5 - 3Q(3 - 2Q _ 9- 1
3 + 21 (3 + 20(3- 20 13
1- i
2
9
" 13
1
2
19
13
i
2
i. Ш
Обоснование правомерности подобного способа действий даёт
следующая теорема:
ТЕОРЕМА |
1} Любое комплексное число и можно разделить на комплексное
I число уф 0, т. е. для любых комплексных чисел ии1/^0 сущест-
\ вует число w, такое, что w • v= и.
Сначала докажем лемму.
ЛЕММА —--———-—■■—-——-___-—-_■—-«--—--—
Для любого комплексного числа уф 0 существует обратное к
нему число w (напомним, что обратным к данному числу
называется число, в произведении с данным дающее 1, т. е. w = -
225 §68 Определение комплексных чисел. Алгебраическая форма записи
и арифметические действия над комплексными числами
□ доказательство леммы. Пусть v = а + Ы. Тогда w = а~ \ явля-
аг + Ъг
ется обратным к числу и. В самом деле,
/ . L-ч а — Ы (a + bi)(a-bi) л _.
ум; = (а + 6i) • д2 + &2 = -—аъ1ьг— = 1. Ш
П доказательство теоремы. Число w—u* — является искомым.
1 Iй
Действительно, w-v - и- -- v - и (число обратное к числу v —
существует по лемме). Ш
Итак, чтобы поделить одно комплексное число на другое,
достаточно записать деление в виде дроби, а затем умножить числитель и
знаменатель дроби на число, сопряжённое знаменателю.
Пример 17. Рассмотрим другой способ решения примера 15.
П Возьмём выражения, сопряжённые обеим частям второго
равенства. Получим г - iw = -6/, что даёт z - i • w = 6/, откуда z + / • w = 6/.
Запишем систему линейных уравнений с неизвестными z и То:
[z + /• w = 6/.
Эту систему можно решить теми же способами, что и систему с
вещественными коэффициентами и вещественными переменными.
Например, методом алгебраического сложения уравнений. Для этого
умножим второе уравнение на 3 и вычтем из полученного уравнения
первое. Получаем в качестве уравнения-следствия (3/ + 2)w = -1 + 18/,
_ -1+18/
откуда w =
2 + 3/
Вычислим То:
-1+18/ (-1+18/)(2-3/) 52 + 39/ 13(4+3/)
= 4 + 3/.
2 + 3/ (2 + 3/)(2-3/) 13 13
Итак, w = 4 + 3/, откуда w = 4 - 3/.
Подставляя найденное значение w во второе уравнение системы,
получаем z + / • (4 + 3/) = 6/, откуда z = 6/ - 4/ + 3, т. е. z - 3 + 2/.
Ответ: 2 = 3 + 2/, w = 4 - 3/. 11
6. Решение квадратных уравнений
Рассмотрим пример.
Пример 18. Докажем, что существует ровно два комплексных числа,
квадрат которых равен -1: / и -/.
D Пусть z = а + Ы и z2 = -1. Тогда (а + &/)2 = а2 - Ь2 + 2а&/ = -1, т. е.
[а2 -Ь2= -1,
[2ab = 0.
22б| Глава XI. Комплексные числа
Из второго уравнения получаем, что а = О, тогда из первого
уравнения Ъ - ±1, или Ъ = О, тогда из первого уравнения а2 = -1 и
решений нет, так как квадрат вещественного числа всегда
неотрицателен. Таким образом, 2 = 0+l-i = i или г = 0 — 1 • i = -t, что и
требовалось доказать. Ш
Пример 19. Решим квадратное уравнение (в комплексных числах)
г2 + 2г + 2 = 0.
□ 22 + 22 + 2 = 0 » (2 + I)2 + 1 = 0 » (г + I)2 = -1, т. е. (см.
пример 18) 2+l = i или 2 + 1 = —i, откуда получаем ответ: zx = -1 + i,
22 = -1 - i. Ш
ТЕОРЕМА ———————--—-——^^
Для любого вещественного числа и ф 0 существует ровно два
комплексных числа, квадрат каждого из которых равен и. При
этом если и > 0, то эти числа вещественные и равны ±Vu, если
же и < 0, то эти числа чисто мнимые и равны ±/'л/-п (символ л/~
обозначает арифметический корень из положительного
вещественного числа).
Q доказательство. Будем искать комплексные числа z = х + г/£,
квадрат которых равен г/, т. е. должно выполняться (х + i/i)2 = i/,
откуда х2 - у2 + 2xi/i = и. С учётом того что и — вещественное число,
получаем систему
[2ху = 0.
Решим систему (1):
Гх2 -I/
1*=0,
- ii2 = w,
х2 - у2 - и,
х= 0,
х2 - у2 = и
f*=0,
Система имеет репгения тогда и только тогда, когда имеет
решения второе уравнение. В свою очередь, второе уравнение имеет
вещественное решение тогда и только тогда, когда и < 0 (по условию и Ф 0).
В этом случае решениями системы будут пары К); yl—uj и уО; —4-и).
Решим систему (2):
х2 - у2 - и \х2 = и.
Система имеет решения тогда и только тогда, когда имеет
решения второе уравнение. В свою очередь, второе уравнение имеет
вещественное решение тогда и только тогда, когда и > 0 (по условию и Ф 0).
В этом случае решениями системы будут пары Ыи; 0J и у-л/и; О).
. Определение комплексных чисел. Алгебраическая форма записи
и арифметические действия над комплексными числами
Таким образом, в случае и < О решениями уравнения z2 — и будут
числа ±iV-w, а при и > О решениями уравнения z2 = и будут
вещественные числа ±у[п. Ш
ТЕОРЕМА (о решении квадратных уравнений)
Квадратное уравнение az2 + bz + с = 0 с вещественными
коэффициентами а^О, Ь и с и отрицательным дискриминантом
(D = b2-4ac<0) имеет два комплексных корня, задаваемых
фОрмуЛОИ Z} р =
2а
П доказательство. Вспомним вывод формулы корней квадратного
уравнения:
az2
= 0
a\z + —
2а
с
h2
4а
z +
2а
Ь2 - 4ас
4а2 '
Согласно предыдущей теореме, применённой для случая
извлечения квадратного корня из отрицательного числа, получим
b i^-(b2- 4ac)
2a ~ 2\a\ '
b i ij- (b2 - 4ac)
2a ~ 2|a] '
Отметим теперь, что как при положительных, так и при
отрицательных значениях а после раскрытия модуля совокупность будет
иметь вид
b iij-(b2 - 4ас)
+ 2^ ~ 2а
Ь_ iyl-(b2- 4ac)
+ ~2а" 2а
откуда и следует искомая формула корней. Ш
Обратим внимание, что можно решать квадратное уравнение
az2 + bz + с = О
- ^ -Ь±л[г> с.
по одной формуле z12 = > не обращая внимания на знак
дискриминанта (правда, при этом нужно понимать, что для
отрицательного дискриминанта под выражением л/D понимается одно из двух
выражений: iyl-D или -iV^J
228* Глава XI. Комплексные числа
Таким образом, квадратное уравнение с вещественными
коэффициентами всегда имеет два корня в С: при D > 0 — два различных
вещественных корня, при D = 0 — два совпадающих вещественных
корня, и при D < 0 — два различных комплексных корня (которые
оказываются комплексно сопряжёнными числами).
Пример 20. Решим квадратное уравнение z2 + Зг + 6 = 0.
□ Согласно выведенной формуле
-3 ± д/9 - 24 -3±V-15 -S
2l'2~ 2 " 2 "~
Ответ запишем в алгебраической форме.
Ответ: ■-- + _;;---__;
О69- Комплексные числа и многочлены.
Основная теорема алгебры
1. Комплексные корни многочлена
с вещественными коэффициентами
Прежде всего, отметим, что рассмотренная нами в 10 классе (см.
главу III) теория, посвященная изучению многочленов с одной
переменной, остаётся верной, если допустить, что переменная и коэффициенты
могут принимать комплексные значения. В частности, сохраняют свою
силу определения и свойства суммы, произведения, композиции и
деления многочленов с остатком, теорема Везу, наличие у многочлена не
большего количества корней, чем его степень, определение многочлена
степени п по его значениям в п + 1 точке, теорема Виета и т. п.
□ Пусть 2 — корень многочлена Р(х) = апхп + ап _ ххп "г + ... + агх + а0
с вещественными коэффициентами. Это значит, что Р(г) = 0, т.е.
ап2п + ап _ г2п " 1 + ... + ах2 + а0 = 0. Рассмотрим равенство выражений,
сопряжённых левой и правой частям этого уравнения. По теоремам о
сопряжённых суммы и произведения с учётом того, что сопряжённое
вещественного числа есть само это вещественное число, в левой части
равенства получим
ауП i п <?П-\ I Л. п У А- П — П 7п
п_ nr_ г о
= ап-(2)п +ап_1-(2)п-1 + ... + а1-2 + а0.
Итак, Р(г)= an-(2)n + an_1-(z)n~1+ ... + аг-2 + а0.Но, с другой
стороны, Р(г)= 0 = 0. Итак, имеемап>(2)п + ап_х-(2)п~г+ ... + аг-2 +
ао=О.Полученное равенство означает, что г является корнем многочлена Р. Ш
ffigj §69. Комплексные числа и многочлены. Основная теорема алгебры
Мы доказали следующую теорему:
ТЕОРЕМА
Если z — корень многочлена Р с вещественными
коэффициентами, то и z — корень многочлена Р.
Если г — вещественное число, то эта теорема ничего не
прибавляет к нашим знаниям о корнях многочлена, поскольку в этом случае
z - г. Если же г — комплексное число, не являющееся вещественным,
то г — ещё один корень многочлена Р.
О Отметим, что попутно доказано равенство P{z)- Р(г), где
Р — многочлен с вещественными коэффициентами.
Пример 21. Известно, что одним из корней уравнения гъ + z + а — О
(a е R) является zx - -1 - 2/. Найдём значение а и остальные корни.
D По доказанной теореме данное уравнение имеет ещё и корень
г2 = -1 + 2£. По теореме Виета сумма трёх корней уравнения равна О,
поэтому
-1 - 21 + (-1 + 20 + 23 = 0,
откуда z3 = 2. По теореме Виета 21г2гг = —а, откуда
(
т. е. а — -10.
Ответ: а = -10, оставшиеся корни равны -1 + 2£ и 2. 11
Замечания. 1) В решении примера существенно использован тот
факт, что уравнение третьей степени обязательно имеет три
комплексных корня (см. далее в п. 2).
2) Конечно, можно было просто подставить в уравнение х = -1 - 2/
и найти из полученного равенства а. Однако вычислений при таком
способе решения требуется больше.
2. Основная теорема алгебры
В 1799 году К. Гаусс1 дал доказательство теоремы, носящей
название основной теоремы алгебры. Эта теорема приводится в двух
равносильных формулировках для многочленов от одной переменной,
коэффициенты и значения переменной в которых могут быть
комплексными числами.
хДо Карла Фридриха Гаусса (который дал 4 доказательства) эту теорему
формулировали А. Жирар (в 1629 г. в форме «Все уравнения алгебры имеют
столько решений, сколько их даёт наименование высшей величины»), Р.
Декарт (1637 г.). Эту теорему доказывали Ж. Даламбер и Л. Эйлер, но в их
доказательствах были некоторые пробелы. В настоящее время известно более
20 доказательств основной теоремы алгебры. Существует даже шутка о том,
что каждый раздел математики имеет своё доказательство основной теоремы
алгебры.
2301 Глава XI. Комплексные числа
ТЕОРЕМА (основная теорема алгебры) ' ———ним|
I 1. Любой многочлен степени п > 0 имеет ровно п корней, если |
каждый корень считается столько раз, какова его кратность.
2. Любой многочлен степени п > 1 имеет хотя бы один корень.
Доказательства основной теоремы алгебры мы приводить не
будем, поскольку оно существенным образом опирается на понятия
и утверждения, выходящие за рамки нашего курса.
□ Покажем, что утверждения 1 и 2 равносильны.
Ясно, что из утверждения 1 следует утверждение 2.
Пусть теперь истинно утверждение 2. Методом математической
индукции докажем истинность утверждения 1 для п ^ 1.
база индукции. При п-\ утверждения 1 и 2 совпадают.
индукционный переход. Пусть произвольный многочлен
степени п имеет ровно п корней с учётом кратности. Докажем, что тогда
произвольный многочлен степени п + 1 имеет п + 1 корень с учётом
кратности.
Рассмотрим произвольный многочлен Р степени п + 1. Согласно
утверждению 2 он имеет комплексный корень х0, а тогда согласно
теореме Безу имеет место равенство Р(х) = (х - xo)Q(x), где Q—
многочлен степени п. Но для Q выполнено индукционное предположение,
т. е. Q имеет ровно п корней с учётом их кратности, а тогда Р имеет
п + 1 корень: п корней многочлена Q и еще корень х0.
Итак, утверждения 1 и 2 равносильны. Ш
В множестве вещественных чисел уравнение х2 = -1 не имело
решений. Введя новое число i, являющееся корнем этого уравнения,
мы выяснили, что теперь любое квадратное уравнение имеет
решение в множестве «новых чисел», получаемых из вещественных чисел
и i с помощью операций сложения и умножения.
Однако вдруг найдётся уравнение четвёртой степени, которое не
имеет решения в множестве этих «новых чисел»? Тогда пришлось бы
заводить новое число у, являющееся корнем этого уравнения, получать
«ещё новые числа» из предыдущих и у и исследовать полученное
множество и уравнения в нём. Основная теорема алгебры избавляет нас от
этого! В множестве комплексных чисел любой многочлен имеет корни.
Этот факт формулируют так: множество комплексных чисел
алгебраически замкнуто.
Можно сказать, что при изучении школьного курса математики мы
«стремились» к алгебраической замкнутости числовых множеств.
Сначала вместо натуральных чисел мы рассматривали целые, что
позволило осуществлять вычитание, т. е. решать линейные уравнения со
старшим коэффициентом 1. Затем рассматривались рациональные числа,
что позволило решать линейные уравнения с произвольными целыми
(и рациональными) коэффициентами. Появление вещественных чисел
ещё больше расширило возможность решения алгебраических уравне-
■■§70. Геометрическое представление и тригонометрическая форма записи
комплексных чисел
ний. И наконец, рассмотрение комплексных чисел полностью закрыло
вопрос о возможности нахождения корней произвольного многочлена.
Отметим, что основная теорема алгебры гарантирует
существование корня любого многочлена степени больше 0, но не говорит о том,
как выразить этот корень через коэффициенты данного многочлена.
Более того, в 1799 г. П. Руффини, а в 1824 г. Н. Абель различными
способами доказали, что не существует формул, выражающих корни
произвольных многочленов степени выше 4 через их коэффициенты
с помощью знаков радикала и арифметических действий.
3. Теорема о разложении многочлена
с вещественными коэффициентами
На основании предыдущих теорем можно доказать теорему:
ТЕОРЕМА ——----—-—-----------——————
Любой многочлен с вещественными коэффициентами, отличный
от константы, раскладывается в произведение линейных
множителей с вещественными коэффициентами и квадратных
трёхчленов с вещественными коэффициентами и отрицательным
дискриминантом.
D доказательство. Доказательство проведём методом
математической индукции по степени многочлена п. Итак, пусть многочлен Р
с вещественными коэффициентами имеет степень п.
база индукции. При п = 1 линейный многочлен Р с
вещественными коэффициентами является произведением одного линейного
множителя.
При п = 2 если квадратный трёхчлен Р имеет корни, то он
раскладывается в произведение линейных сомножителей (может быть,
одинаковых). В противном случае он имеет отрицательный дискриминант.
индукционный переход. Пусть утверждение верно для всех
многочленов с вещественными коэффициентами степени, меньшей
либо равной п. Докажем его для многочленов с вещественными
коэффициентами степени п + 1.
Пусть Р — многочлен степени п + 1. Возможны два случая.
1) Р имеет вещественный корень х0. Тогда Р(х) = (х - х0) Q(x),
где Q — многочлен с вещественными коэффициентами степени я, для
которого выполнено предположение индукции, т. е. многочлен Q
раскладывается в произведение линейных множителей с вещественными
коэффициентами и квадратных трёхчленов с вещественными
коэффициентами и отрицательным дискриминантом. Но тогда и многочлен Р
раскладывается в произведение тех же множителей и множителя (х — х0),
т. е. Р раскладывается в произведение множителей нужного вида.
2) Р не имеет вещественных корней. Тогда по основной теореме
алгебры Р имеет комплексный корень 2, не являющийся
вещественным, а значит, имеет и корень г. Тогда Р(х) = (х - z)(x — ~z)Q(x).
Заметим, что (х — z)(x — г) = х2 - (z + ~z)x + z • г — квадратный трёхчлен
2321 Глава XI. Комплексные числа
с вещественными коэффициентами и отрицательным дискриминантом
(поскольку корни этого трёхчлена не являются вещественными).
Многочлен Q имеет вещественные коэффициенты и степень п— 1, а
значит, для этого многочлена выполнено предположение индукции, т. е.
он раскладывается в произведение множителей нужного вида. Но тогда
и многочлен Р раскладывается в произведение тех же множителей
и множителя х2 — (z + z) х + z • ~z, т. е. Р раскладывается в
произведение линейных множителей с вещественными коэффициентами и
квадратных трёхчленов с вещественными коэффициентами и
отрицательным дискриминантом. Ш
Геометрическое представление
и тригонометрическая форма записи комплексных чисел
1. Изображение комплексных чисел
на координатной плоскости. Модуль комплексного числа
Любое комплексное число z = х + yi можно изобразить точкой А
с координатами (х; у) на координатной плоскости. При этом по оси
абсцисс откладывается вещественная часть комплексного числа, а по
оси ординат — мнимая часть.
Такая координатная плоскость называется комплексной
плоскостью. Ось абсцисс называется вещественной осью, ось ординат —
мнимой осью. Фактически мы получили взаимно однозначное соответствие
между точками комплексной плоскости и комплексными числами.
На рисунке 11.1 отмечены точки А, Б и С, которые соответствуют
числам 0, 2/, 3 - 2/.
Пример 22. Изобразим на комплексной плоскости множество точек,
соответствующих числам, таким, что: a) Imz = 2; б) Rez + Imz = 2;
\ т> г» \ Re z 1
в) Re 12 = 2; г) —- = -.
z- z 2
□ а) Ответ изображён на рисунке 11.2.
б) Пусть z = х + yi. Изобразим все числа 2, для которых х + у = 2,
т. е. у = 2 — х. Ответ изображён на рисунке 11.3.
Imzt
2<
0
2-
В
а ;
Re z
г~ с
Im Zi
2
0
Re z
Рис. 11.1
Рис. 11.2
Рис. 11.3
ИИ §70. Геометрическое представление и тригонометрическая форма записи
комплексных чисел
Im Zi
0
_2
Re г
lm Zi
Re z
Рис. 11.4
Рис. 11.5
Рис. 11.6
в) Пусть z — х + yi. Тогда iz — xi — y и Reiz = -y. Таким образом,
Re 12 = 2 <^> -у = 2 <=$ у = -2. Ответ изображён на рисунке 11.4.
Re 2 х х
г) Пусть 2 = х + #£. Тогда —- = — — = — -. Таким
- Re 2 1
образом, —— = -
z- z 2
\
х2+у2 = 2х,
Далее, х2 + i/2 = 2x
<=> х2 - 2х + i/2 = 0 <=> х2 - 2л: + 1 + у2 = 1 <=> (х - I)2 + у2 = 1, а это
уравнение окружности с центром в точке (1; 0) и радиусом 1. Ответ
изображён на рисунке 11.5 (обратите внимание на выколотую точку (0; 0)). В
В дальнейшем мы часто будем отождествлять комплексные числа
и соответствующие им точки на комплексной плоскости (между ними
существует взаимно однозначное соответствие) и формулировать
задания в виде «изобразите на комплексной плоскости множество точек,
удовлетворяющих данным условиям».
Теперь обратим внимание на ещё одно важное взаимно
однозначное соответствие: каждому комплексному числу z = х + yi можно
поставить в соответствие вектор ОА, где О — начало координат, а точка
А — точка на комплексной плоскости, соответствующая числу z.
Тогда сложение комплексных чисел приобретает
геометрический смысл: комплексные числа складываются так же, как и
векторы, которые им соответствуют, — покоординатно. То есть если числу
2Х = хх + iyx соответствует вектор ОА19 а числу z2 = х2 + iy2
соответствует вектор ОА2, то их сумме zx + z2 = xx + х2 + i(yt + y2) соответствует
вектор ОАХ + ОА2 (рис. 11.6). Более того, при умножении
комплексного числа на вещественное число соответствующий этому комплексному
числу вектор также умножается на это вещественное число.
Отметим также, что сопряжённые комплексные числа
изображаются точками, симметричными относительно вещественной оси.
Пример 23. Концы отрезка заданы точками, соответствующими
комплексным числам и и v. Найдём комплексное число, соответствующее
точке отрезка, делящей его в отношении 1:3, считая от и.
234 Глава XI. Комплексные числа
П Пусть числу и соответствует вектор О А, числу v — вектор ОВ,
а точка С — это точка отрезка АВ, делящая его в отношении
1 : 3, считая от точки А. Тогда, как известно из геометрии,
—*" 1 —*■ 3 —*■
ОС = —ОВ + —ОА. Отсюда получаем, что число, соответствующее точ-
4 4
1 3
ке С, равно w — — у + — и. Ш
4 4
ОПРЕДЕЛЕНИЕ ——————————-^
Модулем комплексного числа z = a + bi называется число
Обозначение: \z\.
Нетрудно заметить, что модуль комплексного числа — это
расстояние от точки, изображающей это число на комплексной
плоскости, до начала координат.
Пример 24. Вычислим модуль числа: а) 3 + 4Z; б) 5i; в) -4; г) 0.
□ а) [3 + 4/1 = д/32+42 = 5.
б) |5*| = |0+5i| = V02 + 55"= 5.
в) |-4| = |-4 + 0/| = д/02+(-4)2 = 4.
г) |0| = |0 + 0/|= V02 + О2 = 0. 11
Заметим, что модуль вещественного числа а + 0/, вычисленный
как модуль комплексного, равен д/а2 +02 = \а\9 т. е. совпадает с
привычным модулем вещественного числа.
Утверждение (свойства модуля) '
Пусть и \л v — произвольные комплексные числа. Тогда верны
следующие равенства:
2. |u + v|<|u| + |v| (неравенство треугольника).
3. и - и=\ и |2.
4. | и | ^ 0 (причём | и | = 0 <=> и = 0).
□ доказательство. Пусть и = а + Ы, v = с + di.
1. | uv | = (а + Ы) (с + di) | = | ас - bd + {ad + be) i \ -
- bd)2 + (ad + be)2 = yj(ac)2 + (bd)2 + (ad)2 + (be)2;
V + (ad)2 + (&c)2,
т. e. \u • у| = 11/1 • |у|, что и требовалось доказать.
§70. Геометрическое представление и тригонометрическая форма записи
комплексных чисел
» (а + с)2 + (Ъ + d)2 ^ а2 + Ъ2 + с2 + d2 + 2д/а2 +
<=> ас + bd ^ д/а2 + Ъ2 • д/с2 + d2.
Последнее неравенство заведомо выполнено, если ас + bd < 0.
Если же ас + bd ^ 0, то после возведения в квадрат получим
неравенство а2с2 + &2d2 + 2abcd ^ а2с2 + a2d2 + &2c2 + b2d29 равносильное заведомо
верному неравенству (be - ad)2 ^ 0.
Кроме того, неравенство ас + bd ^ у/а2 + Ъ2 у/с2 + d2 выражает тот
факт, что скалярное произведение векторов с координатами (a; b)
и (с; d) меньше произведения модулей этих векторов1.
Доказательство свойства 4 очевидно. 51
Заметим, что неравенство 2 мож- im z 11
но было легко обосновать из
геометрических соображений. В самом деле,
пусть числу и соответствует вектор ОА9
числу v — вектор ОВ9 а числу и + v —
вектор ОС = ОВ + ОА (рис. 11.7).
Тогда неравенство |u + i>|^|i/| + |i>|
можно записать в следующем виде:
А(и)
v)
B(v)
Re z
Рис. 11.7
Последнее неравенство является неравенством треугольника.
Кроме того, отметим, что свойство 1 является следствием
свойства 3. Действительно, записав равносильное свойству 1 равенство
\uv\2 = (\u\ \v\)2 и подставив выражение квадрата модуля из свойства 3,
получаем цепочку преобразований:
\uv\2 = (uv) - пи = и • v • п • v = (и • п) • (и • v) = |и|2 • |v|2.
Интересно, что мы получили доказательство тождества
(а2 + &2)(с2 + d2) = (ас - bd)2 + (ad + &с)2,
не прибегая к прямым вычислениям2.
хЭто неравенство является частным случаем неравенства Коши — Буня-
ковского — Шварца, одна из формулировок которого выглядит так: если
(av ..., ап) и (Ь19 ..., bn) — два набора вещественных чисел, то имеет место
неравенство (a1b1 + a2b2 + ... + anbn)2 ^ д/af + а\ Л- ... + а2 • ^jb\ + b\ + ... + b2 ,
причём равенство достигается тогда и только тогда, когда наборы (а19 ..., ап)
и (bl9 ..., 6П) пропорциональны.
2Доказанное тождество иногда называют тождеством Эйлера. Из него,
в частности, следует тот факт, что произведение натуральных чисел, предста-
вимых в виде суммы двух точных квадратов, также представимо в виде
суммы двух точных квадратов. Этот факт был основой для весьма глубоких
результатов теории чисел, полученных П. Ферма и Л. Эйлером.
236 Глава XI. Комплексные числа
Im
А(и)
Пример 25. Найдём расстояние между
точками А и Б на комплексной
плоскости, соответствующими комплексным
числам u = 2 + 3inv = 5 + L
D Числу u - v соответствует вектор
О А - ОВ, а его длина — это расстояние
между точками А и В (рис. 11.8). Таким
образом, расстояние между точками А
и В равно
B(v)
Re z
О Геометрический смысл
выражения | и — v | — это расстояние между
Рис. 11.8 точками, изображающими комплексные
числа и и v.
Воспользуемся этим соображением для решения следующих задач.
Пример 26. Изобразим множество точек на комплексной плоскости,
соответствующих комплексным числам 2, таким, что: а) |г| = 1;
\J) | £ | ^ ± у Л) | 2 — 1\ — .L, с), I ) \£ — I | — \ 2 — х|.
П а) Требуется изобразить множество точек, расстояние от
которых до начала координат равно 1. Это окружность с центром в начале
координат и радиусом 1 (рис. 11.9).
б) Искомое множество — это множество точек, удалённых от
начала координат на расстояние, большее 1, т. е. внешняя часть
плоскости по отношению к окружности пункта а) (рис. 11.10).
в) Расстояние от числа z до числа i равно 1,5. Это окружность
с центром в точке (0; 1) комплексной плоскости и радиусом 1,5
(напомним ещё раз, что, когда речь идёт про расстояние между
комплексными числами, подразумевается расстояние между точками,
изображающими данные числа на комплексной плоскости) (рис. 11.11).
Im Zi
Рис. 11.9
Рис. 11.10
Рис. 11.11
§70. Геометрическое представление и тригонометрическая форма записи
комплексных чисел
г) Расстояния от числа z до чисел * и 1 Im z
равны. Все такие числа находятся на прямой,
являющейся серединным перпендикуляром
к отрезку с концами в точках,
изображающих * и 1. Её уравнение у - х (рис. 11.12).
Заметим, что данный пример можно
было бы решить, не прибегая к
геометрической интерпретации: пусть z — х + yi, тогда
\z-i\ = \z-l\<^>\x + (y-l)i\ = \x-l+yi\<=*
» х2 + (у - I)2 = (х - I)2 + у2 *=> х = у. Ш
Пример 27. Изобразим множество чисел
на комплексной плоскости, таких, что Рис. 11.12
г2 • z2 - 5г- z > -4.
D Можно поступить стандартным способом: обозначить число z = х + yi
и записать данное условие, но мы сначала преобразуем выражение,
данное в условии, пользуясь свойством 3 модуля комплексного числа. В са-
~- |г|2, то данное условие равносильно условию
, откуда |г|2 ^ 1 или \z\2 ^ 4, т. е. (учитывая то, что
0) \z\ ^ 1 или \z\ ^ 2. Ответ показан на рисунке 11.13. Ш
Пример 28. Изобразим на комплексной плоскости множество точек,
удовлетворяющих неравенствам 2<|2*2+1-*|<6.
D Преобразуем выражение, данное в условии:
мом деле, так как z
z
г
2*2 + 1-* =
= 2*
z +
(1-0(-20
= 2
z -
l+i
больше 1, но меньше 3. Ответ
Таким образом, данное условие равносильно условию 1<
1 + i
т. е. расстояние от числа z до числа -
изображён на рисунке 11.14. Ш
Im z
z —
Im Zi
*
- /
1 1 /
: 2\-
0'
V
\
ч
ч
s
ч
ч
ч
ч
' ч
ч
\
1 .'■
2
\
V
\
1
1
/ Re z
Рис. 11.13
Рис. 11.14
238 Глава XI. Комплексные числа
Im2i
-3
\ в
0
0
■ 4
Re z
Рис. 11.15
Пример 29. Выясним, какое наименьшее
значение принимает \г\, если \г + 3/ + 4| = 2.
П Множество точек на комплексной
плоскости, для которых |г + 3£ + 4| = 2 — это
окружность с центром в точке В (-3; -4) и радиусом 2
(рис. 11.15).
Наименьшее значение | z | (равное
расстоянию от z до начала координат О)
достигается в точке А, и равно | О А | = | ОВ \ - | АВ | = = 5 - 2
= 3. В самом деле, для любой другой точки С,
принадлежащей окружности, по неравенству
треугольника \ОС\ + \СВ\ > \ВО\ = | АВ| + |ОА|,
откуда (с учётом того, что | АВ | = | ВС |) следует,
что|ОС|>|ОА|. й
2. Модуль и аргумент комплексного числа.
Тригонометрическая форма записи комплексных чисел
Каждой точке декартовой плоскости (за исключением начала
координат) можно поставить в соответствие пару чисел, первое из
которых положительно и равно расстоянию от начала координат до этой
точки, а второе равно обобщённому углу между радиус-вектором этой
точки и положительным направлением оси абсцисс (рис. 11.16).
Упорядоченная пара чисел, первое из которых
положительно, однозначно определяет
указанным образом положение точки.
Однако каждой точке плоскости
соответствуют бесконечно много пар чисел. В то время
как первое число для данной точки
определяется однозначно, второе число определено
неоднозначно, а именно с точностью до
прибавления 2л/е, k e Z. Эти два числа называются
полярными координатами данной точки1.
Ясно также, почему точка О не имеет
полярных координат: радиус-вектор этой точки
нулевой, а угол между нулевым вектором и
каким-либо другим вектором не определён.
С(23)
Рис. 11.16
1 Таким образом, для задания точки с помощью полярных координат
необходимо задать точку О (называемую полюсом системы полярных
координат), расстояние до которой будет первой координатой (называемой полярным
радиусом), и луч с началом в точке О (называемый полярным лучом), угол
с которым радиус-вектора данной точки будет второй координатой
(называемой полярным углом). Всюду в дальнейшем мы будем считать, что полюс
совпадает с началом координат обычной декартовой системы, а полярный луч
совпадает с положительной полуосью абсцисс.
239: §70. Геометрическое представление и тригонометрическая форма записи
*" комплексных чисел
Полярные координаты данной точки традиционно обозначают
(р; ф), где на первом месте стоит полярный радиус, а на втором —
полярный угол.
Рассмотрим связь между декартовыми и полярными
координатами точки.
Итак, пусть точка плоскости, отличная от начала координат,
имеет декартовы координаты (х; у). Тогда расстояние от неё до начала
координат равно р = ^х2 + у2. При этом в соответствии с определением
тригонометрических функций обобщённых углов имеем
Обобщённый угол ф определяется этой системой однозначно с
точностью до прибавления 2nk, k e Z.
Если же даны полярные координаты (р; ф) точки А, то её декарто-
{х = р cos ф,
у = psinq>.
Пусть ненулевому комплексному числу г - а + Ы соответствует
точка А на комплексной плоскости. Если полярные координаты этой
[а^рсовф,
равны (р; ф), то <
vr Y/ [b = р sinq>.
точки
Итак, z = рсовф + рвтф • i = р(созф + isin(p). При этом, как
отмечалось ранее, р = у/а2 + Ъ2 = \г\.
ОПРЕДЕЛЕНИЕ
Запись ненулевого комплексного числа z в виде
z = p (cosф + /sinф) (где р > 0) называется
тригонометрической формой комплексного числа z.
С учётом того что р = | z |, записать число в тригонометрической
форме можно так: z = | z |(созф + isincp)1.
Число ф называется аргументом комплексного числа z и
обозначается Arg z (впрочем, часто Arg z обозначает множество всех чисел,
которые могут служить аргументами числа z).
1 Тригонометрическую форму записи комплексных чисел можно
воспринимать как произведение вещественного положительного числа р и
комплексного числа, вещественная и мнимая части которого могут быть записаны
соответственно как косинус и синус одного и того же аргумента.
240 Глава XI. Комплексные числа
О 1. Число 0 не имеет тригонометрической формы.
2. Модуль и аргумент комплексного числа являются полярными
координатами точки, изображающей это число.
3. Все числа, являющиеся аргументами данного комплексного
числа, отличаются друг от друга на число вида 2nk, k e Z.
Таким образом, два комплексных числа, записанных в
тригонометрической форме, равны тогда и только тогда, когда равны их
модули, а аргументы отличаются на число вида 2nk, k e Z.
Чтобы избежать неоднозначности, связанной с наличием разных
аргументов, выделяют полуинтервал длины 2л, аргумент из этого
промежутка называют главным аргументом данного комплексного числа
и обозначают arg z.
В качестве такого полуинтервала выбирают либо [0; 2я), либо
[-я; п). Главный аргумент данного ненулевого комплексного числа при
этом определяется однозначно.
Пример 30. Найдём модуль и главный аргумент комплексного числа:
a) 1 + i; б) -2 + 3/; в) -5/.
Im2N,
-3
Рис. 11.17
Re 2
n
2
-51
Рис. 11.19
П а) Отметим число 1 + i на комплексной плоскости (рис. 11.17).
Его модуль равен л/2, его главный аргумент ф равен ^.
б) Отметим число -2 + 3/ на комплексной плоскости. Его модуль
равен д/(-2)2 + З2 = Vl3, его аргумент ф = п - arctg- (рис. 11.18).
в) Модуль числа -Ы равен 5, а вот главный аргумент зависит от
того, каким выбран промежуток главных аргументов. Если главные
аргументы берутся из интервала [0; 2л), то arg (-5/)= —, а если главные
аргументы берутся из интервала [—п; п), Toarg(-5£) = —(рис. 11.19). II
Пример 31. Изобразим множество точек на комплексной плоскости,
таких, что: a) argz = —; б) — ^ argz ^ п; в) argz = —, \z - 1 - i\ = 1.
4 2 4
Re 2
24Ti §70. Геометрическое представление и тригонометрическая форма записи
комплексных чисел
□ а) Ответ на рисунке 11.20. Im.
б) Ответ на рисунке 11.21.
Обратим внимание, что на обоих
рисунках точка (0; 0) выколота — аргумент
числа 0 не определён! ;
в) Изобразим отдельно множество
комплексных чисел 2, таких, что avgz = — (от-
4
крытый луч, часть прямой z/ = x), и таких,
что 12 - 1 - i | = 1 (окружность с центром в точ- Рис. 11.20
ке (1; 1) и радиусом 1) (рис. 11.22). Искомое
множество точек — точки А и В. Ш Im
Пример 32. Запишем в
тригонометрической форме число: а) 1 + Z; б) 3 - VlO;
в) sin 35°-f /cos 145°; г) -5| sin hi cos— ;
(т))-
Im.2i
ч 4л Л-
д) sin Ь i 1 - cos
5 V
□ а) Модуль числа 1 + i равен V2,
аргумент — (см. пример 30), таким образом
4
1 + i = л/2 cos — + i sin — .
v 4 4;
б) Модуль числа 3 - VlO равен VlO - 3,
аргумент п (рис. 11.23). Следовательно,
3 - VlO = (VlO - з) (cos л + i sin n).
в) Преобразуем число sin 35° + i cos 145°
(модуль данного числа равен 1):
sin 35° + i cos 145° =
= cos (35° - 90°) + i sin (90° - 145°) =
= cos (-55°) + /sin (-55°) =
0\
Re г
0\
Рис. 11.22
Re 2
= 1 • cos -
Re 2
Обратим внимание на использование в этом Рис. 11.23
примере формул приведения «наоборот»: мы
знаем, что на первом месте должен стоять косинус числа, а на
втором — синус, и подбираем такие формулы приведения, чтобы синус
и косинус поменялись местами.
242 ГлаваХ!. Комплексные числа
г) Очевидно,
17
17
—5 sin ь /cos— = 5, а для определения
аргумента получим систему
coscp = —sin—,
sincp = —cos—.
17
Подбираем такое преобразование аргумента, чтобы косинус и синус
/ " с- я (2п+ 1) _ч
поменялись местами (т. е. нужно прибавлять — -, п е Z) и каждый
сменил знак. Это замена аргумента: а = -£- - х (т. е. cos — - х = -si
2 V 2 У
и sin -^- - jc = -cos x). В
V 2 )
Зя я 49л
нашем случае получаем ср = —— — = ——.
Следовательно, —5 sin ь i cos — = 5 cos
д) Вычислим модуль данного числа:
Ь i sin
.
sin
4я
Ал 4я ^ . 2 4я (л 4я Y /I I 4я"
1 1-cos-—- = л sin2 — + 1 - cos-— =J2-2cos — =
^ 5 ) у ^v Ъ ) \ 5
OABC — ромб
Тогда для аргумента ср выполнены равен-
. 4я 4я
sin— 1-cos —
5
ства coscp =
о • 2я
2 sin —
о
и
о • 2я '
2 sin—
о
откуда
после тригонометрических преобразований
= cos
получаем
О
Рис. 11-24
Rez
= sin
2JL
5 '
2я_
5 '
т. е. ср можно при-
2я
нять равным —
5
Зя л я
Итак,
Геометрически этот результат виден на рисунке 11.24. В
. 4я -
sin — -fill- cos
5
4я ^ о . 2я ( 2я . , 2я ^
— = 2 sin — cos — + i sin — .
о J 5^5 Ъ )
243, §70. Геометрическое представление и тригонометрическая форма записи
комплексных чисел
3. Умножение и деление комплексных чисел,
представленных в тригонометрической форме
D Перемножим два ненулевых числа, записанных в
тригонометрической форме: гг = 12г | • (cos срх + i sin cpx) и z2 = | z2 | • (cos cp2 + i sin сро).
Алгебраическими формами записи этих чисел являются: zx - \zx\* coscp! +
+ \гг\ sinфх • i и 22 = |z2| • cosф2 + 1221 sinф2 • i. Умножая эти числа, как
записанные в алгебраической форме, получим
2\ ' 22 = 12г I # 1221 cos Ф1 # cos Ф2 ~ 12г I * 1221 sin Ф1 # sin Ф2 +
+ i (| zx I • 1221 cos фх • sin ф2 + I zx I • I z21 sin ф2 • cos ф2) =
= I 211 * I 22 I COS (Ф1 + Ф2) + ^ I 211 * I 22 I sin (Ф1 + Ф2) =
= \2i\ ' |22|(соз(ф1 + ф2) + /8т(ф! + ф2)).
Последняя запись является тригонометрической формой
комплексного числа. Ш
Таким образом, доказана теорема.
ТЕОРЕМА (о произведении комплексных чисел в тригонометрической форме)
1 Модуль произведения двух ненулевых комплексных чисел равен
I произведению их модулей, а одним из аргументов произведения
является сумма аргументов множителей.
Обратим внимание, что мы можем складывать любые аргументы
комплексных чисел, а не только главные аргументы.
Производя действия с числами, записанными в
тригонометрической форме, нужно тщательно следить за тем, чтобы запись
действительно была тригонометрической формой.
Пример 33. Пусть zx - sin— + /cos—, z2 = sinn + icos7T (т.е. zx - 1,
z2 = -/). Найдём zx • z2.
D Если не обратить внимание на то, что запись этих чисел не
является тригонометрической формой, и сложить «аргументы» этих чисел,
Зя . Зя л
то получим число sin— + tcos— = -1, в то время как произведение
этих чисел равно -i. Ш
Из теоремы об умножении комплексных чисел легко вывести
теорему о делении комплексных чисел.
D Действительно, пусть
2i ^ l2il ' (cosa + /sinа) и z2 = \z2\ • (cosP + isinP) —
два числа, записанные в тригонометрической форме, z = \z\ • (coscp +
+ isincp) — искомое частное чисел 2j и г2, т. е.г = —. Тогда по опреде-
22
лению частного комплексных чисел имеем равенство z2 • z = zx, откуда
|г2 • з| = I^J и р + ф = а + 2nk, где k — некоторое целое число (поду-
244 Глава XI. Комплексные числа
майте, откуда появилось слагаемое 2л&), а тогда | z \ - т-^— и ср = а -
\г2\
— Р + 2nk. Как было отмечено ранее, добавление к аргументу 2nk не
изменяет комплексного числа, поэтому в качестве аргумента числа z
можно взять а — р. й
Итак, доказана теорема.
ТЕОРЕМА (о частном комплексных чисел в тригонометрической форме)\
П Модуль частного двух ненулевых комплексных чисел равен
частному их модулей, а одним из аргументов частного является
разность аргументов делимого и делителя.
Если zx = \zx\
• (cosa + /sinа), z2 = \z2\ • (cosP + /sinP), то
p4(cos(ap) + isin(a- p)).
Пример 34. Представим в тригонометрической форме число:
ч ( 2л 2л V 5л . 5л ^ -ч
а) cos— + isin— cos— + *sin— ; 6)
sin24° + /cos 156°
+ isincos+ *sin; 6)
{ 3 3 ){ 6 6) ' cos35°-/sin35°
□ а) По теореме о произведении комплексных чисел, записанных
в тригонометрической форме, их модули перемножаются, а аргументы
складываются. Модуль каждого из сомножителей равен 1, а аргументы
2л 5л о л 2л 5л Зя
— и —-. Значит, модуль произведения равен 1, а аргумент — + — = —
3 6 3 6 2
и
2л ... 2л
cos ь i sin —
3 3
5л . , 5л
cos 1-1 sin —
6 6
Зл , . . Зл
= cos ь i sin —
2 2
б)
sin 24°+ /cos 156°
cos 66°-/sin 66°
= -I.
cos (-66°) + /sin (-66°)
cos35°- /sin35° cos(-35°) +/sin(-35°) cos (-35°) + /sin (-35°)
= cos(-31°) +/sin(-31°). Ш
Пример 35. Изобразим множество точек на комплексной плоскости,
таких, что avgiz = —.
4
П Модуль числа / равен 1, а аргумент —, следовательно, при умноже-
а
нии произвольного комплексного числа на /
его модуль не меняется, а аргумент
увеличивается на —. Таким образом, для того чтобы
Re z
Рис. 11.25
arg/2 = —, необходимо и достаточно, чтобы
4
аргумент числа z равнялся . Ответ изобра-
4
жён на рисунке 11.25. 11
Геометрическое представление и тригонометрическая форма записи
комплексных чисел
Отметим также, что модули ненулевых сопряжённых чисел
равны, а аргументы противоположны1.
Действительно, cos(-cp) + isin(-cp) = coscp - isincp, т. е. смена знака
аргумента меняет знак мнимой части.
4. Формула Муавра2
Из теоремы об умножении комплексных чисел в
тригонометрической форме следует, что при возведении ненулевого комплексного
числа в натуральную степень п (т. е. при умножении комплексного числа
самого на себя п раз) для получения модуля искомого числа достаточно
возвести модуль исходного числа в степень л, а для получения аргумента
искомого числа достаточно умножить аргумент исходного числа на п.
Таким образом, верна формула (р (cos ср + i sin ср))" = рп (cos щ + i sin жр),
где р > 0, п е iV, которую и называют формулой Муавра.
Рассмотрим записанное в тригонометрической форме число
z - р (cos ф + I sin ф)
и запишем в тригонометрической форме обратное число, т. е. число —.
Поскольку 1 = cosO + г sin О, по правилу деления чисел, записанных
в тригонометрической форме, получим — = -(соз(-ф) + i зт(-ф)). Если
теперь обе части этого равенства возвести в натуральную степень п и
применить формулу Муавра, то получим — = — (cos(-mp) + isin(-mp)).
Полученное равенство можно переписать в виде z~n — р~п (cos (-шр) + / sin (-шр).
Это означает, что для возведения комплексного числа, записанного
в тригонометрической форме, в отрицательную целую степень
достаточно возвести в эту степень модуль и умножить на эту степень аргумент,
чтобы получить соответственно модуль и аргумент искомого числа.
Приведённые вычисления показывают, что формула Муавра верна
не только для натуральных, но и для целых показателей степени (для
нулевого показателя формула очевидна, если по определению считать,
что 2° = 1).
Таким образом, выполняется равенство
(р (cos9 + /sin9))n = рл (cosmp + /sinmp), где р > 0, п е Z.
1Мы подразумеваем, что если ф — один из аргументов числа 2, то —ф —
один из аргументов числа i.
2Абрахам де Муавр (1667—1754) — французский математик и механик,
один из создателей теории вероятностей. Поскольку Муавр был гугенотом, то
с 1688 г. жил в Англии, где сблизился с И. Ньютоном. В теории вероятностей
известны предельные теоремы Муавра — Лапласа.
246 Глава XI. Комплексные числа
Пример 36. Вычислим (1 4- V3/J
П Запишем число 1 + v3i в тригонометрической форме.
откуда можно принять ф = —.
о
coscp = -,
sincp = 1"'
Теперь по формуле Муавра получаем
/- /^Л20Ю (п( л . я^2010 О9П1П (
(1 + V3i) =2 cos — + i sin — = 22010 cos
I V 3 SJJ V
2010л . , 2010л
+ i sin
3
3 )
= 22010(cos6707T + isin6707T) = 22010. Ш
Пример 37. Выразим cos 10a через cos a и sin a.
О Воспользуемся равенством
cos 10a = Re (cos 10a + i sin 10a) = Re (cos a + i sin a)10.
По формуле бинома Ньютона
(cos a + /sin a)10 = cos10 a + Cj0cos9a • sin a • i +
+ Cf0cos8a • sin2 a •/+...+ C?0cosa • sin9 a • i9 + i10 • sin10 a.
Заметим, что слагаемые, где i возводится в нечётную степень, будут
чисто мнимыми, а слагаемые, где i возводится в чётную степень, —
вещественными. Так как для решения задачи нужно вычислить вещественную
часть данного выражения, получаем (учитывая, что i2 = — 1, а Z4 = 1 и т. д.)
cos 10a = cos10 a - Cf0cos8a • sin2 a + C140cos6a • sin4 a - Cf0cos4a • sin6 a +
+ Cf0cos2 a • sin8 a - sin10 a. IS
Используя основное тригонометрическое тождество, в правой
части последнего равенства можно получить многочлен относительно
cos a, причём его старший коэффициент будет равен
^10 ~^~ ^10 ~^~ ^10 ~^~ ^10 ~^~ ^10 ~^~ ^10 "" ^ *
Аналогичный результат верен для произвольной степени п:
cos па = Рп (cos a),
где Pn(t) — многочлен степени я, старший коэффициент которого
равен 2п~1. Эти многочлены носят название многочленов Чебышёва
и обладают многими уникальными свойствами.
Таким же образом можно получить аналогичное утверждение для
синусов кратных углов. Сформулируйте и докажите его самостоятельно.
Пример 38. Найдём все комплексные числа 2, пятая степень которых
является вещественным числом.
П 1. Очевидно, число 2 = 0 удовлетворяет условию.
2. Запишем z Ф 0 в тригонометрической форме: z — р(coscp + Zsincp).
Тогда г5 = p5(cos5cp + £sin5cp).
§70. Геометрическое представление и тригонометрическая форма записи
комплексных чисел
Ненулевые вещественные числа (и только
они) имеют аргумент 0 (если они
положительны) или п (если они отрицательны). Поэтому,
чтобы ненулевое комплексное число было
вещественным, необходимо и достаточно, чтобы
его аргумент с точностью до 2nk, k e Z был
равен 0 или п. Итак, получим условие:
2л/е
5ф = 2nk, k e Z,
5ф = п + 2nl, I e Z
Im 2
Ф =
Ф =
5
к + 2nl
, ke Z,
,leZ.
Рис. 11.26
пт
Обе полученные серии можно объединить в одну: ср = —, т е Z.
о
Поскольку значения аргумента, отличающиеся на целое кратное 2я,
соответствуют (при заданном значении модуля) одному и тому же
комплексному числу, достаточно взять лишь произвольные 10 подряд
идущих значений т, поскольку при всех остальных целых т полученные
значения будут отличаться от одного из взятых на целое кратное 2п.
Таким образом, получаем ответ: 0 и все числа вида р (coscp + isincp),
гдер > 0,ф = —, т е {-5; -4; ...; -1; 0; 1; ...; 4}. Множество соответст-
о
вующих точек плоскости изображено на рисунке 11.26. Н
Пример 39. При каких значенияхр среди комплексных чисел 2, таких,
что \г - 1 + £л/з | ^ р, найдётся ровно одно такое, что 24 е R1
D Аналогично предыдущему примеру получаем, что множество
чисел 2, таких, что z4 е Д, состоит из 0 и всех чисел вида р(coscp + isincp),
где р > 0, ср = -—, т е {-4; -3; -2; -1; 0; 1; 2; 3}. На плоскости
соответствующее множество точек является объединением четырёх прямых
(рис. 11.27).
Множество чисел 2, таких, что | z - 1 + /л/31 ^ р, является непустым
лишь при р > 0. При р = 0 оно состоит из одной точки 1 - iV3, не
лежащей ни на одной из изображённых прямых,
а при р > 0 это множество представляет собой
круг радиуса р с центром в точке 1 - ZV3.
Таким образом, нам нужно найти, при каком
радиусе соответствующий круг коснётся одной
из прямых.
На рисунке 11.27 изображён случай
касания (касание будет с прямой О А, поскольку
ZAOK < ^КОВ (ZAOK = 15°, ZKOB = 30°)).
Осталось найти радиус окружности,
касающейся прямой О А.
248i Глава XI. Комплексные числа
Из прямоугольного треугольника OLK получаем LK - OK sin ZLOK.
= 2, ZLOK=15°, sin 15°= sin(45° - 30°) = ^^Д, откуда
ттг л/б- л/2 ^ л/б- л/2 ш
LK = . Ответ: р= - . Ш
2 ^2
{?)71, Корень п-й степени из комплексного числа
1. Корень л-й степени из комплексного числа
Как и в случае с вещественными числами, корнем п-й степени при
натуральном п > 1 из комплексного числа z будем называть такое
комплексное число w, которое при возведении в степень п даёт г, т. е.
wn = 2.
Выясним, из любого ли числа можно извлечь корень п-й степени
и сколько существует корней степени п из данного комплексного числа.
□ Если 2 = 0, то уравнение гип-0 имеет единственный корень w = 0.
Если z Ф 0, запишем его в тригонометрической форме:
2 - 121 (cos a + i sin а).
Поскольку число 0 при возведении в степень п не будет равно
ненулевому числу, 0 не является корнем степени п из ненулевого числа г.
Поэтому корни степени п из числа г можно искать, записав их в
тригонометрической форме: w = p(coscp + isincp). Тогда wn = p"(cosmp + jsinmp),
откуда с учётом равенства wn = 2 и условия равенства двух
комплексных чисел, записанных в тригонометрической форме, получаем
|шр = а + 2nk, +
I— I n n
(где щ\г\ — арифметический корень п-й степени из вещественного
числа 121). Придавая k различные целые значения, мы будем получать
значения w. Ясно, что если два различных значения k отличаются на п, то
соответствующие им значения ср отличаются на 2я, т. е. соответствуют
одному и тому же значению w. Поэтому для получения всех возможных
различных значений w достаточно взять все k е {0; 1; ...; п — 1}. Ш
Итак, доказано следующее утверждение:
Утверждение ----------------
Существуют ровно п корней степени п (п е N, п ^ 2) из ненулевого
числа z = |z|(cos a + /sin а). Все эти корни могут быть заданы форму-
лой w =
При этом символ у/г при ненулевом 2 служит обозначением не
числа, а множества из п чисел. В отличие от случая вещественного
§71. Корень л-й степени из комплексного числа
подкоренного выражения не существует разумного способа
предпочесть один из корней п-й степени оставшимся.
Пример 40. Найдём все корни четвёртой степени из —1.
D Запишем -1 в тригонометрической форме: -1 = cos тс + г sin я.
Тогда корнями четвёртой степени из -1 будут числа
я . , я Зя . . Зя
w0 = cos — + i sin —, w, = cos — + i sm —,
4 4 4 4
5я , . . 5я
Wo = COS h I Sin
4 4
7ях. . 7я
W3 = COS h I Sin
4 4
(нижний индекс корня соответствует тому значению k, при
подстановке которого в формулу корней получается данный корень).
Полученные корни можно записать в алгебраической форме:
J4
Поскольку все корни степени л из данного числа имеют один и тот
же модуль, они располагаются на окружности с центром в начале коор-
гг. - 2я
динат. Так как аргументы корней различаются на —, то корни
располагаются в вершинах правильного гс-угольника (рис. 11.28). Из этого
следует, например, что сумма всех
корней степени п из данного комплексного
числа равна 0, так как сумма векторов,
идущих в вершины правильного
многоугольника из его центра, равна 0.
С другой стороны, корни степени п
из комплексного числа w являются
корнями уравнения zn — w = 0, а тогда по
теореме Виета сумма корней этого
уравнения равна 0. Следовательно, сумма
векторов, идущих в вершины
правильного многоугольника из его центра,
равна 0 (обратите внимание, из
рассмотрений комплексных чисел получен
геометрический факт).
Рассмотрим корни степени п из 1. Одним из этих корней является
само число 1. Остальные корни являются корнями уравнения zn — 1 = 0,
не равными 1, т. е. корнями уравнения zn~x + zn~2 + ... + z + 1 = 0.
Например, корни из 1 третьей степени, отличные от 1, являются корнями
1 л/3
уравнения 22 + 2 + 1 = 0и равны — ± —Z.
В соответствии с общей формулой корней степени п корни из 1 за-
Рис. 11.28
2я& . . 2я& I гл 1 л\
даются формулой ek = cos + ism , где k e {0; 1; ...; п - 1}.
250, Глава XI. Комплексные числа
Отметим следующие свойства корней степени п из 1.
1. ео=1.
2. £к'г1 = гк + 1- Здесь при k + l>n за гк + 1 принимается ег, где
г — остаток от деления k + I на п.
3. г~к = гп_к.
Геометрически свойство 3 означает, что вещественная ось
является осью симметрии многоугольника, вершинами которого являются
корни степени п из 1.
2. Арифметические действия с корнями степени л
Пусть и — один из корней степени п из zX9 w — один из корней
степени п из z2.
Равенство (uw)n = unwn = zxz2 показывает, что uw является одним
из корней степени п из zxz2.
Пусть теперь числа zx и z2 отличны от нуля. Если зафиксировать и
и заставить w пробежать все п различных значений корня степени п
из 22, то произведение uw пробежит все п различных значений корня
степени п из zxz2.
Действительно, если uw1 = uw2, то u(w1 - w2) = 0, откуда wx - w2 = О
(так как и Ф 0), а тогда wx = w2.
Таким образом, различным значениям w соответствуют различные
значения uw. Поскольку мы брали п различных значений w, то мы
получили п различных значений uw, каждое из которых является корнем
степени п из zxz2. Поскольку корней степени п из zxz2 ровно л, то мы
получили все корни степени п из zxz2.
Равенство фг[ • tfz^ = yl^1z2 следует понимать как равенство двух
множеств. В правой части равенства стоит множество корней степени
п из zxz2, а в левой — \ uw: и е фг[\ w e "fz^ }.
Аналогично следует понимать равенство
Рассмотрим квадратное уравнение az2 + bz + с = 0 (а Ф 0) с
комплексными коэффициентами. Так же как в случае уравнения с
вещественными коэффициентами, можно выделить полный квадрат,
г
4az
получив равносильное уравнение \ z + — = г^. Число 2а явля-
^ 2а) 4az
ется корнем второй степени из числа 4а2 (одним из двух). Поэтому
все корни второй степени из числа — получаются, если каждый
4аг
корень второй степени из Ъ2 - 4ас разделить на 2а. Тогда можно за-
Ъ № - 4ас t Ь
писать z Л = (эта запись означает, что число z л может
2а 2а У 2а
251 §71. Корень л-й степени из комплексного числа
Jb2 - 4ас ) -Ь + Jb2 - 4ас
быть равно любому из двух чисел -— , откуда z —
Ad J Ad
(обратите внимание, что перед корнем нет привычного знака ±,
поскольку символ д/&2 — 4ас уже означает множество из двух
комплексных чисел). Итак, с точностью до знака формула корней квадратного
уравнения с комплексными коэффициентами будет такой же, как
и для уравнения с вещественными коэффициентами.
Остановимся подробнее на равенстве ЩЧг = пЦг. При г Ф 0 в
правой части равенства стоит множество из nk корней степени nk из г.
Для каждого из k значений корня степени k из г (обозначим его а)
существует ровно п значений корня степени п из а. Таким образом,
получились nk чисел, составляющих множество, записанное в левой
части равенства. Поэтому равенство Щ^[г = ntfz следует понимать как
равенство двух указанных множеств.
Q72. Применения комплексных чисел
1. Доказательство равенств
л т> 2л 4л 6л
Пример 41. Вычислим значение выражения cos \- cos \- cos —.
□ Заметим, что искомая сумма является вещественной частью
суммы трёх корней седьмой степени из 1. Добавим недостающие
слагаемые так, чтобы получилась вещественная часть суммы всех корней
седьмой степени из 1, равная:
i 2л 4л 6л 8л Юл , 12л
1 + cos — + cos — + cos — + cos — + cos —— + cos ——.
ы 2л 12л 4л Юл 6л 8л
Но cos— = cos , cos— = cos , cos— = cos—, поэтому
7 7 7 7 7 7
л 2л 4л 6л 8л Юл 12л
1 + cos ь cos ь cos ь cos ь cos ь cos =
л п( 2л 4л 6л
= 1 + 2 cos — + cos — + cos —
Поскольку сумма всех корней седьмой степени из 1 равна 0, то и
1 , 2л , 4л , 6л , 8л , Юл , 12л Л
1 + COS Ь COS — 4- COS h COS h COS h COS —— = 0.
А тогда искомая сумма равна —.В
А
Пример 42. Найдём формулу суммы синусов аргументов, образующих
арифметическую прогрессию, т. е.
sin a 4- sin (а + d) + sin (а 4- 2d) + ... 4- sin (а + (n - l)d), где d e JR.
2521 Глава XI. Комплексные числа
□ Заметим, что
since + sin(a + d) + sin(a + 2d) + ... + sin(a + (n - l)d) =
= Im((cosa + /sin a) + (cos (a + d) + *sin(a + d)) + ... +
+ (cos (a + (n - l)d) + isin(a + (n - l)d))).
Рассмотрим число
cos (a + kd) + /sin (a + fed) - (cos a + /sin a) (cos kd + /sin fed),
fe e {0; 1; ...; n - 1}.
Обозначим z0 = cos a + i sin a, q = cos d + i sin d. Тогда cos fed +
+ i sin fed = g*, откуда cos (a + fed) + isin(a + fed) = zoqk.
По формуле суммы геометрической прогрессии для q Ф 1 (если
q — 1, то можно считать d = 27ife, fe eZ, а тогда суммируются я
одинаковых слагаемых, равных sin a) искомая сумма равна
Im(20 + zoq + zoq2 + ... + zoqn ~ г) = Im I z0 _ 1 1-
Рассмотрим множитель:
qn - 1 _ cos nd - 1 + i sin nd _
o . 9nd .o . nd nd
-2 siir2 — + i2 sin cos —
222
а — 1 cosd — 1 + isind o . 9 d .o , d d
4 -2 sin2 — + i2 sin— • cos —
2 2 2
. nd( . nd . nd}
sin— sin icos—
2^2 2 )
. df . d . d
sin— sin г cos —
2 ^ 2 2
Запишем число втф - £созф в тригонометрической форме:
sin ф - i cos ф = cos -^ - ф I - i sin — - ф =
I 2 ] 12 ]
= cos I ф - —
Имеем
sin
nd f nd . nd Л . nd (nd пЛ . . (nd n}
in_.^sin_-_ICOS_j sin_ C08^_.__j + tnn^_.__j
. d ( . d . d\ слгл— (d n\ . . (d n\
in — sin i cos — sm о cos + i sin
2^2 2) 2 U 2j ^2 2)
. nd
. d
sin-
2 f (n - l)d . . (n - l)d
1 cos — + i sin ^—
253] §72. Применения комплексных чисел
Таким образом, получим
sin-
nd
а -
= (cos а + £ since)'
nd
. d
sin —
2
cos
+ i sm
sinT ( ( (n-i)«n . . (
= —— cosr+—^—)+lsm[
sin— v v / v
+ i sin a +
(n -
sin
2
откуда искомая сумма равна
nd
Im
sin
. d
sin—
2
( (п
)s a + —
nd (
sin sin а
-l)d) . . ( (n-
1 + i sin а + ■
(n -
. m
sin-
Конечно, вычисления, которые пришлось произвести, несколько
громоздки, но основная идея — увидеть в записи мнимую часть
суммы комплексных чисел — весьма естественна. В 10 классе мы
находили похожую сумму с помощью искусственного приёма (глава VI,
пример 30), а в данном решении все вычисления естественны.
Вот более сложный пример доказательства тождества.
Л тт я 2я . пп J2n+ 1
Пример 43. Докажем, что sin sin ... • sin = .
2/i + 1 2п + 1 2/i + 1 2п
D Рассмотрим уравнение г2п + 22п~ 1 + ... + г+1 = 0. Его корнями
являются отличные от 1 корни степени 2п + 1 из 1, поэтому
г2л _|_ "у2п — 1 jl. _i_ "у jl. "1 — t *у __ с \ ("У — с \ • » ("У с ^
i<c i...r<Cix — ^<с *^\) v^ ^-'2/ ••• v 2/1/*
Эти корни разбиваются на пары сопряжённых: корню
h -, k е {1; 2; ...; 2п}
Ей = COS h I Sin
* 2/г + 1 2/г
соответствует корень £2^ + 1-/г ~ cos
2я (2n
2n+ 1
Перемножив (г — ел) • (г — г2п +1 _ /г), получаем
(г - ел) - (z - г2п + х
- k) . 2я (2/г
+ i sin —1—
2 О 2Я& , 1
- 22 -22 COS + 1.
Таким образом,
У2п- 1
- 2г cos
2п+1
+ 1\\ 22 -2г cos
2/г+1
+1
22 - 2г cos
2п+1
+1 .
)
254 Глава XI. Комплексные числа
Подставим в полученное равенство 2=1:
2п
= 2- 2cos
2я
2- 2cos
4я
Го о
•... . 2- 2cos
2ЯП
-
2n+
l)
а
Преобразуем правую часть по формуле 2 - 2 cos а = 4 sin2 —:
Л ^ . о я л . о 2я , . о /1Я
2гс + 1 = 4 sin2 г • 4 sin2 •... • 4 sin2
а тогда
2n+ 1
2n+ 1
2n+ Г
2я
nn
откуда следует требуемое тождество. SI
2. Комплексные числа и геометрические преобразования
Рассмотрим умножение произвольного комплексного числа на
вещественное положительное. При этом модуль комплексного числа
умножается на данное вещественное, а аргумент не изменяется.
Таким образом, умножение комплексного числа z на вещественное
положительное число k соответствует применению гомотетии с
центром в О и коэффициентом k к точке, изображающей z (рис. 11.29).
Рассмотрим умножение произвольного комплексного числа z на
комплексное число с модулем 1, т. е. умножение на число вида
cos a + i sin а. При таком умножении | z | не
изменяется, а к аргументу z прибавляется а
(рис. 11.30).
Таким образом, умножение
комплексного числа z на число cos a + i sin а
соответствует повороту изображающей число z точки
на угол а вокруг начала координат.
Итак, умножение на любое ненулевое
комплексное число р (cos a + i sin а) (р > 0)
сводится к умножению на р, т. е. к
гомотетии с коэффициентом р, а затем к
умножению на cos a + /sin а, т. е. к повороту на
угол а.
Прибавление комплексного числа
соответствует параллельному переносу на
вектор, изображающий это число.
Приведём примеры использования этих
соображений.
Пример 44. Дано множество М = {z e С:
\z - 1| ^ 1}, построим множество: а) М;
б) К = {iz + I: z eM}.
П а) Множество М представляет собой
множество точек, удалённых от 1 на рас-
Imzj
0
z/
kz
/
k>0
Rez
Рис. 11.29
z(cosoc + isinoc)
0
Rez
255 §72. Применения комплексных чисел
а) 1т 2
Re z
Re 2
Рис. 11.31
стояние, не превосходящее 1, т. е. круг с центром в точке (1; 0) и
радиусом 1 (рис. 11.31, а).
б) Элементы множества К получаются из элементов М сначала
умножением на £, что соответствует повороту на —, а затем прибавле-
нием 1, что соответствует переносу на горизонтальный вектор
единичной длины. Результат изображён на рисунке 11.31, б. Ш
Вот пример более сложной задачи.
Пример 45. Докажем, что центры квадратов, построенных на
сторонах параллелограмма во внешнюю сторону, являются вершинами
квадрата (рис. 11.32).
D Поместим параллелограмм ABCD на комплексную плоскость
так, чтобы его центр совпал с началом координат.
Рассмотрим векторы ООг и ОО2. Докажем, что ООг X ОО2
и |ООХ| = |ОО2|. Для этого достаточно показать, что эти векторы
получаются один из другого поворотом на —. Повороту вектора на — соот-
ветствует умножение соответствующего комплексного числа на L
Итак, докажем, что 22 = iZ\ (число z2 соответствует вектору ОО2,
а число 2г — вектору ООг).
Выразим число zx через числа а и &, соответствующие вершинам
А и В параллелограмма. Для этого запишем векторное равенство
ООг = OD + DOX. Вектор DOX составляет с вектором DA угол — и имеет
длину, в V2 раз меньшую, нежели длина вектора DA. Поэтому
комплексное число, соответствующее вектору DOX, получается из
комплексного числа, соответствующего вектору DA, умножением на
число с модулем — и аргументом , т. е. на число i.
V2 4 2 2
256| Глава XI. Комплексные числа
Число, соответствующее вектору DA = О А - OD, есть разность
чисел, соответствующих векторам О А и OD, т. е. чисел а и -&. Итак, число,
соответствующее вектору DA, есть а + &, а тогда число, соответствующее
вектору DO!, есть (а + &) i . Таким образом, число гх, соответст-
V2 2 У
вующее вектору ООХ = OD + D01?
равно сумме чисел,
соответствующих векторам-слагаемым, т. е.
Х = -Ь + (а
откуда
а +
2 2
Аналогично получаем
выражение для z2 (можно в уже
полученном выражении заменить -Ъ
на а, а а заменить на &):
Ь + а а - Ь .
+
Рис. ГУ.32
* 2 2
Теперь видно, что действительно
z2 = iZi.
Итак, мы доказали, что ООХ ± ОО2 и |ООХ| = |ОО2|. Аналогично
доказываем, что ОО2 -L ОО3 и |ОО2| = |ОО3|. Это значит, что точки Ol9
О и О3 лежат на одной прямой, причём О — середина отрезка ОгО3.
Аналогично О — середина отрезка О2О4, поэтому четырёхугольник
OiO3O2O4 — параллелограмм. При этом ОХО3 1 О2О4 и ОгО3 = О2О4,
поэтому 0x020304 является ромбом и прямоугольником, т. е.
квадратом. Н &
Геометрические приложения комплексных чисел многообразны.
Многие задачи планиметрии, в том числе и весьма трудные, можно
решить с помощью комплексных чисел.
Комплексные числа и функции комплексных переменных широко
используются в технике. Например, расчёт крыла самолёта
осуществляется с помощью функции
называемой функцией Жуковского. Поэтому тем, кто хочет в
дальнейшем специализироваться в естественно-технических областях, важно
заранее познакомиться с комплексными числами.
§72. Применения комплексных чисел
зторическии комментарии
Ещё до Д. Кардано (1501—1576) метод решения кубических уравнений
был известен итальянскому математику Сципиону дель Ферро, а также был
вновь открыт в 1535 г. талантливым самоучкой Н. Фонтане по прозвищу Тар-
талья (заика), которому на математическом турнире ученик дель Ферро бо-
лонец Марио Фиоре дал тридцать задач, сводящихся к кубическим
уравнениям. Тарталья сумел придумать метод решения кубического уравнения
и победил на турнире.
Упоминавшийся выше Д. Кардано, готовя к изданию книгу «Великое
искусство», выведал этот метод у Тартальи под обещание не печатать его
в книге. Однако через некоторое время он познакомился с бумагами дель
Ферро, где этот метод был опубликован, после чего счёл себя свободным от
обещаний, данных Тарталье, и опубликовал этот метод, обогатив его
решением «неприводимого» случая. Так правило решения кубических уравнений,
а вместе с ним и комплексные числа стали известны.
В книге Р. Бомбелли «Алгебра» (1572 г.) были даны основные правила
действий с числами вида а 4- bv-1, которые достаточно долго называли
мнимыми числами. В течение двух веков мнимые числа числами не считались
(например, И. Ньютоном). Однако с этими числами работали, поскольку их
применение приносило хорошие результаты. И если в конце XVII в. Г.
Лейбниц писал: «Мнимые числа — прекрасное и чудесное убежище
божественного духа, практически амфибия бытия с небытием», то в конце XVIII в. Ж. Ла-
гранж написал: «Одним из важнейших результатов, полученных анализом за
последнее время, я считаю то, что его более не затрудняют мнимые
величины, вычисления с которыми производятся так же, как с вещественными».
Символ / предложил Л. Эйлер в работе, написанной в 1777 г. и
опубликованной в 1794 г. Термин «комплексное число» ввёл в 1803 г. французский
учёный Л. Карно. Геометрическая интерпретация комплексного числа
появилась в работе датского землемера К. Весселя в 1799 г. Однако работа на
датском языке не была замечена, поэтому открытие было повторено в 1806
и 1814 гг. швейцарским учёным Ж. Арганом. Поэтому изображение
комплексного числа называют иногда «диаграмма Аргана».
Изложенная в данной главе теория комплексных чисел как пар
вещественных была построена знаменитым английским (точнее, ирландским)
учёным У. Гамильтоном в 1837 г. Кстати, Гамильтон разработал также правила
действий с векторами, а также продвинул далеко вперёд линейную алгебру,
теорию векторных полей и многие другие разделы математики. В частности,
он открыл пространственное обобщение комплексных чисел — кватернионы,
т. е. упорядоченные четвёрки вещественных чисел. Можно показать, что
построение множества с действиями сложения и умножения, содержащего С
в качестве подмножества, возможно лишь в случае отказа от какого-либо из
свойств действий (например, умножение кватернионов некоммутативно).
258< Глава XI. Комплексные числа
И Задачи и упражнения
Определение комплексных чисел.
Сложение и вычитание, равенство комплексных чисел
Группа А
XI.1. Чему равны мнимая и вещественная части комплексного числа:
a) z = 5 + 2Z; б) z = -3 + i; в) z - -i;
г) z = -2 - 3i; д) 2 = 0; e) 2 = я - i?
XI.2. Вычислите сумму и разность чисел zx и 22, если:
а) гг = 3 + 5i, z2 = 7 - 2i; б) zx = 7 - 2i, 22 = 4 - 2i;
в) 2X = 11 + 7i, 22 = 11 - 3i; r) 2X = 2 - i, 22 = -4i;
д) 2l = 0, z2 = -8 - 9i; e) 2X = -4i, 22 = -5 + 4i.
Какие из полученных чисел являются чисто мнимыми?
комплексными? вещественными?
XI.3. Приведите к алгебраической форме число z = zx- z2 + z3, если:
а) 2X = 2 + i, 22 = 3 - 2i, 23 = 4 + 3i;
б) zx = 3 - i, z2 = -3 + 5i, 23 = 5 - 3i;
в) 2X = i, 22 = 5, z3 = 5 - 4i;
r) 2X = -4 + 6i, 22 = -5 - i, 23 = 7 - 7i.
В каждом случае укажите Imz.
XI.4. При каких значениях вещественного параметра а мнимая и
вещественная части числа z равны:
а) z = -5 + (а2 -7а- 5)/; " б) z = а3 - За + (а2 - 3)/;
в) 2 = а2 - 6а + 7 + (-2а2 - 8а) i?
XI.5. При каких вещественных значениях параметров хну
числа гг и z2 равны, если: а) гг = х2 + jo/£ — 5 + t, 22 = да - у2 + j/i;
б) 2Х = х2 — 3 — i — 5xi, 22 = у - yii
XI.6. Найдите все вещественные значения х, при каждом из которых
верно равенство sinx + icosx = cosx + isin2x.
Умножение и деление комплексных чисел.
Сопряжённые комплексные числа
Группа А
XI.7. Запишите в алгебраической форме число:
a) i(i + 3); б) i(5 - 3i); в) (i - 2)(4i + 3);
г) (5i - l)(2i + 1); д) (1 -f 3i)2(i - 1); e) (1 + O3 (1 - 3i
Xl.8. Напишите число, сопряжённое данному: а) -5 - 3Z; б) л/3 -
в) -0,5 + *; г) 10 + 0,3£; д) 5; е) -4; ж) 3Z; з) -i; и) 0.
XI.9. Приведите к алгебраической форме записи число:
a) (i + l)(i-l); б) (2i + 3)(2i-3);
в) (-2 - 7/)(2 - 70; г) И - 5) (-5 + i).
259 Задачи и упражнения
Х1.Ю. Вычислите: а) /3; б) /6; в) /9; г) /37; д) /95; е) /1006; ж) /2008;
з) /203 + /307 + /16; и) /208 + /207 + /206 + /205; к) /239 + /566; л) /1564 + /1566.
та ч 1 ^ 1 v 5 + 2* ч 2i-l ч 1+* ч 2i-l
Xl.ll. Вычислите: а) -; б) -—:; в) -z—r:; г) ——; д) -—:; е) —-—;
г l + i Ъ-2г 2i+\ l-i 3i+l
. 3-4/
3)
7-2i; 3) 24+Г
xi.12. Вычислите: a) j^ + i^; б) i^ + (l + 2i)3; в) ^".f/ +/10;
;1001 /2008
г^ f ZLi + /347
Г^ ! + j2009 + l *
XI.13. Найдите z из условия (г + i)(l + 2Z) + (1 + г/)(3- 4Z) = 1 + 7/.
XI.14. При каких вещественных значениях х и у равны числа zx и г2,
если 2?! = х2 • (1 + 0 - Зх, z2 = i/2 • (/ - 1) - i?
Х1.15. При каких вещественных значениях хну числа гх и г2 являются
сопряжёнными, если: а) гг = 2х2 — 3/ - 1 + yi; z2 = у + x2i — 3 — 2i;
б) 2Х = (х - if + i/2, z2 = 12 + yi + i?
Xl.16. При каких вещественных значениях jc и i/ числа zx и г2
противоположны (т. е. zx = -г2), если:
а) zt = х + уЧ - 4i + 4; z2 = у + хЧ - 8 - 4i;
xyi + у2- 9х2 __ 29 о
б) 2l" i >22"2T57?
XI.17. При каких значениях параметра а е R число (1 - ai)3 - (2 + ai)2
является: а) вещественным; б) чисто мнимым?
Х1.18. Найдите все 2, такие, что: a) i + Лег = iz; б) i(z + 1) + г Лег = z2.
XI. 19. Найдите все комплексные числа 2, удовлетворяющие условию
2
XI.20. Решите систему уравнений:
x + (3 + i)y = 20 + 5/,
-11 + 16/,
_i _ • х, у е С.
XI.21. Найдите пару комплексных чисел z и w, для которых выполнено
\3z- 2w = 4 + 18/,
|2г" + Зы;= 7 + i.
XL22. Докажите, что z — z тогда и только тогда, когда z —
вещественное число. j—г
XI.23. Докажите, что: a) (zn) = (z)n; б) - = —.
2 2
XI.24. Найдите все комплексные числа, сопряжённые: а) своему
квадрату; б) своему кубу.
260J Глава XI. Комплексные числа
XI.25. Найдите все комплексные числа, квадрат которых равен:
a) Z; б) -i.
XI.26. Для каких чисел z e С выполняется равенство:
а) z2 = ^—-; б) z2 = 3 + 4i; в) 22 = -8 - 6Z?
V3+ i
xi.27. Найдите все комплексные числа, удовлетворяющие условиям:
а) г2 = -7 + 24/ и Re2 < 0; б) г2 = 8 - 6* и Im2 > 0.
XI.28. Решите уравнение: а) г2 + 2г + 1 = 0; б) 22 - 4 Re 2 + 4 = 0.
Группа В
XI.29. Запишите в алгебраической форме число:
a) (i + I)16; б) (i - I)20; в) (/ + I)2008; г) (* - I)2009.
XI.30. Запишите в алгебраической форме число:
/ / \ 239 / , \ 239
а) (1 + 3*)10(1 - Si)10; б) (-3 - iyflO) (3 - iVIo)
(3 + 4Q70(3- 4Q50, (2- 5Q566 (-2- 5Q566
В) " 598 ' Г) (2i- 5)566(5 + 20566
XI.31. Вычислите:
. (3 + 4Q(-l+3Q.
5£^ ^3
3i+ 1 2- i
)U( ° +l^T + 'j(Tn?;
XI.32. Найдите вещественную часть числа 2, если:
XI.33. Вычислите: а) (2 + /)7 + (2 - *)7; б) (1 + 2if + (1 - 2i)5.
xi.34. Вычислите при п е N: а) (1 ^^ .п ; б) ^^.У"
XI.35. Найдите все комплексные числа, для которых выполняется
z 2tZ
условие = г(1 + 2i).
Re z Im 2
Xl.36. Пусть 2Х и г2 — комплексные числа, причём zx • z2 = 0.
Докажите, что 2Х = 0 или 22 = 0.
XI.37. Докажите, что если комплексные числа zx и z2 не являются ве-
Д,
щественными, то < п
14 \Zl-22eR
z9 =
2
2611 Задачи и упражнения
Группа С
XI.38. Вычислите: a) i + i2 + i3 + i4 + ... + i2008; 6) * - i2 + i3 - i4 + ... - i2008;
в) i - 2i2 + 3i3 - 4i4 + ... + 200Ш2009; r) i + 2i2 + 3i3 + 4i4 + ... + 200Ш2009;
д) i + 4i4 + 7i7 + ... + 2008i2008; e) i - 4i4 + If - ... - 2008/2008.
Решение квадратных уравнений
Группа А
XI.39. Найдите все комплексные числа, квадрат которых равен числу:
а) 4; б) -4; в) 0; г) 1; д) -1; е) 11; ж) -33.
XI.40. Решите квадратное уравнение в комплексных числах:
а) х2 + 36 = 0; б) х2+7 = 0; в) х2 + 6х + 34 = 0;
г) х2 + 4х + 29 = 0; д) х2- 10х + 26 = 0; е) х2-6х+ 13 = 0;
ж) х2-4х + 7 = 0;
з) х2 +
+ 9 = 0.
XI.41. Составьте квадратное уравнение с вещественными
коэффициентами, если один из его корней равен:
a) i; б) i + 3; в) 5-i; г) 3 - 21.
Группа В
XI.42. Разложите на множители:
а) х2+ 1; б) х2 + 101;
г) х2 - 6х + 25;
д) и2 + и
2;
в) х2 - 2х + 2;
ч И2 V2
е) +
Комплексные числа и многочлены.
Решение уравнений в комплексных числах
Группа А
XI.43. Вычислите f(u) + f(u), если:
а) f(z) = -223 - 2г2 + Зг - 4 и и = 1 + 2i;
б) f(z) = z4-2z3 + 2z2 -4z + 4nu=2-i.
XI.44. Делится ли многочлен х4 + 2х2 + 4(1 + i) на. х — i + 1?
XI.45. Приведите пример многочлена третьей степени с вещественными
коэффициентами, у которого есть корни: а) 1 и 4 - 7i; б) 2 и 2 - £;
в) докажите, что в пунктах а и б многочлена второй степени с
вещественными коэффициентами и указанными корнями не
существует.
XI.46. Решите уравнение: а) х4 + 4х2 -5 = 0; б) х4 - 5л:2 - 36 = 0;
в) х3 + х2 + х - 3 = 0; г) х3 - 5х2 + 7х + 13 = 0.
XL47. а) При каких значениях параметра a e R число
корнем уравнения 2z3 - a2z2 + 2a2z - a - 2 = 0?
б) При каких значениях параметра a e R число
1+ i
1- i
является
является
корнем уравнения 12z3 + 2a2z2 + 3a2z - 4a + 16 = 0?
Найдите остальные корни данных уравнений при найденных а.
262; Глава XI. Комплексные числа
XI.48. Найдите остаток от деления многочлена f(z) - -5г3 - 2z2 + z - 1
на: a) z - i; б) z + i.
XI.49. Пусть Р — многочлен с вещественными коэффициентами,
причём P(i - 5) = 7 + U P(2i + 7) = 3 + 4i. Найдите Р}~5~"*).
Р(7 — 2/)
Группа В
XI.50. Решите уравнение:
а) г3 + 0,5г2 + 0,5г - 0,5г = 0; б) 4г4 - 17г3 + 12г2 - 17z + 4 = 0;
в) г3 - 4г2 - 4г - 5 = 0; r) z4 - 4zs + 6z2 - 4z - 15 = 0;
д) 23 + 8z2 -f 152 + 18 = 0.
XI.51. Упростите выражение (х - 1 - i)(x - 1 + i){x + 1 + i)(x + 1 - i).
Xl.52. При каких значениях параметров аи b многочлен z3 + 2az2 + bz + l
делится на zs + 1?
xi.53. Остаток от деления многочлена Р наг - i равен £, а от деления на
z + i равен 2. Найдите остаток от деления многочлена Р на z2 +1.
XI.54. Известно, что число 1 + i является корнем уравнения Xs - ах2 +
4- (2а — 2)х — 4 = 0, где а — вещественное число. Найдите а и
остальные корни уравнения.
XI.55. Известно, что уравнение х3 - х2 4- (а 4- 3)х - 4а = 0, где а —
вещественное число, имеет чисто мнимый корень. Найдите а и
корни уравнения.
XI.56. Известно, что уравнение х2 4- 4х + а = 0 (где аей) имеет одним
из своих корней такое число и, что Леи = 2Imi/. Найдите
возможные значения а и при каждом из найденных значений
решите уравнение.
XI.57. При каких вещественных значениях параметра а уравнение
(а - 1)х4 - 4х2 + а + 2 = 0 имеет только чисто мнимые корни?
XI.58. Докажите, что (1 - zx) • (1 - z2) •... • (1 - zn) = п 4-1, если 2Х, г2, ...,
2„ — корни уравнения гЛ + 1 — 1=0, не равные 1.
Группа С
XI.59. Докажите, что если многочлен с вещественными коэффициентами
не имеет вещественных корней, то он представим в виде суммы
квадратов двух многочленов с вещественными коэффициентами.
Изображение комплексных чисел на координатной плоскости.
Модуль комплексного числа
Группа А
XI.60. Отметьте на комплексной плоскости число, укажите его модуль:
a) u-i\ б) и ^ + ^> в) u = -i-5; г) и = 3; д) и = 3 - 4i.
Задачи и упражнения
XI.61. Изобразите множество чисел на комплексной плоскости, таких,
что:
a) Re2 = -1; б) Imz + Rez = 0; в) Im(2 + 0 = 3;
г) Re2z + Imz = 2; д) Reiz = 1; е) Im(2 + 2 + i)> 1;
ж) Im(2(2 + *))>0; з) z • z < 1; и) (г - г)2 ^ г • г.
XI.62. Изобразите множество чисел на комплексной плоскости, таких,
что:
a) Rez2 = 1; б) Im^ = 1; в) г - г + 2г + 2г = 0;
г) 22=ф1±; д) Ьп 2 >1.
V3 + i * ~ 1
XI.63. Пусть множество А задаётся уравнением Re 2 = -Imz.
Изобразите множество чисел и, таких, что:
a) u-z-i; б) и = -z; в) и = z - 1 - i; г) u-~z, где z e A.
XI.64. Пусть множество А задаётся неравенством z • ~z < 4. Изобразите
множество чисел и, таких, что:
а) и = 2 + 2; б) г/ = 2 - 2 + 2£; в) и = г; г) и = 2г, где 2 е А.
XI.65. Найдите расстояние между точками А (и) и Б (у) на комплексной
плоскости, соответствующими комплексным числам:
з) и= 7 - 2i и v = 6 + i; 6)u = 3-4iuv = -4;
в) и = I и v = —i; г) i/ = 0 и у = -3 + 2/.
XI.66. Является ли треугольник А (и), Б (у), C(w) равнобедренным, если:
а) и = 3 + 2/, у = 5 + 2/, ы; = 4 + 6Z;
б) I/ = 2 - Z, у = -2 + 2Z; ы; = -1 - 3Z?
XI.67. Лежат ли на одной прямой точки, соответствующие числам:
а) 0,2 + U 6 + 3Z; б) -4 - 3t, -1 + 3/, 2 + Ш?
XI.68. Три последовательных вершины параллелограмма суть числа:
а) 0; 1 + Z; 1 + 2Z; б) -i; 2 + i; -I + 2i; в) гх; z2; z3.
Какому комплексному числу может соответствовать четвёртая
вершина?
XI.69. Треугольник ABC равносторонний. Точке А соответствует
число и, точке В соответствует число у. Какое число может
соответствовать точке С, если: а) и = -i; v = i; б) и = 0; у = i + 1;
в) м = 2 - 3£; у = 3 - 2Z; г) и = 0; у = 3 + 4Z?
XI.70. Концы отрезка заданы точками, соответствующими
комплексным числам и и у. Найдите комплексное число,
соответствующее: а) середине отрезка; б) точке отрезка, делящей его в
отношении 2:3, считая от и.
XL71. Даны комплексные числа и и у. Найдите комплексное число z,
такое, что и есть середина отрезка с концами в z и у.
XI.72. Изобразите на комплексной плоскости множество точек,
удовлетворяющих условию: а) |г| = 2; б) \z\^l; в) |г + 2/| = 1;
г) |m + 2i+1| = V6; д) |г|=ф-1|; е) |г-1| = |г + 1|.
264J Глава XI. Комплексные числа
XI.73. Из всех чисел 2, удовлетворяющих условию \г - i - 1| = 1,
найдите такие, что: a) \z\ принимает минимальное значение; б)
число с наибольшим модулем; в) число с вещественной частью,
равной 2; г) число с вещественной частью, равной V2.
XI.74. Найдите все комплексные числа 2, для которых выполняется
равенство \z\ = 4/(г - 3).
XI.75. Множество К комплексных чисел задано условием 2 \z + 3i| = \z\.
Найдите все комплексные числа а, такие, что V2X, z2 e К
Группа В Г 1 1
XI.76. Изобразите множества А и Б, если А - \z е С: z - z + —т = 0\,
{ a4 J
В = {z e С: az + az = 2v2}, a = —(1 - i). Найдите комплексные
числа, изображаемые общими точками множеств А и В.
XI.77. Изобразите множество точек комплексной плоскости, удовлетво-
Jz+2*k т (1 П |г-2| 1
ряющих условию: a) L1 ~ ^2; б) Im — \> 1; в) f < -;
\Z ~ /| I 2 2 J |2 + 1| 2
xi.78. Изобразите на комплексной плоскости множество точек,
удовлетворяющих данному неравенству:
а) 3<|3*2 + 1 -i|<9; б) V2 < |(1 - i)z - i\ < 2д/2; в) \zi + 2| ^ |г|.
XI.79. Пересекаются ли множества, заданные условиями:
а) \г-21\ = 1л\г-2\ = 2; б) |г - 21 - 3| = 3 и |г + 2- 3/| = 2;
в) | аг — £ — 11 = 4 и |2-2| = 2; г)|з-1-1|<1и|г-2|<1?
XI.80. Среди всех чисел, удовлетворяющих данному соотношению,
найдите число с наименьп1им и наибольшим модулем: а) \г — 2i\ = 1;
б) \г- 3-4/| = 2; в) |г - 1 - i| = |z - 1 + *|; г) \г - 2| = \г + 4i|.
XI.81. Найдите наименьший модуль комплексного числа 2,
удовлетворяющего условию: а) |z — i\ = \z + V31; б) |z — i\ = |z + v31.
XI.82. Найдите число с наибольшим модулем среди чисел 2, таких, что
\zi- 3i + 4| = |l-iV3|.
XI.83. Даны два комплексных числа zx — 4 + 3/, 22 = 3 + 4£. Изобразите
множество точек 2 на комплексной плоскости, таких, что:
а) |2Х2 - 2Х22| = |222 - 2Х22|; б) \iz - izx\ = \2z - 2z2\-
Xl.84. а) Из всех чисел 2, удовлетворяющих условию z2 - (z)2 = 16i,
найдите такие, что 12 — 51 + | z — Ъц принимает минимальное значение.
б) Из всех чисел 2, удовлетворяющих условию 2*2 = 25,
найдите такие, что | z — 7 \ + | z — li \ принимает минимальное значение.
Задачи и упражнения
XI.85. Известно, что комплексные числа z и 2г — 1 + i имеют
одинаковый модуль. В каких границах может изменяться величина
этого модуля?
XI.86. Известно, что для комплексного числа z выполняются равенства
\г + 101 = л/65 и \г — 2i\ = V13. Найдите все значения, которые
может принимать 1тг.
XI.87. Комплексное число z удовлетворяет условиям |з-13| = 13,
\z + 3i| = 9V2. Найдите возможные значения:
a) Rez; б) \г - 13 + 3/|.
XI.88. Какую фигуру задаёт уравнение az + ~az = 6, если а е С, b e R?
XI.89. Найдите все значения вещественного параметра а, при каждом из
которых векторы, изображающие корни уравнения z2 - 2z + a = 0,
были перпендикулярны.
XI.90. При каких значениях z треугольник с вершинами в точках
0, 2, z2 является равносторонним?
XI.91. Изобразите множество чисел 2, таких, что треугольник с
вершинами в точках i, z - i, z + i является равнобедренным.
XI.92. Докажите, что для любых комплексных чисел или
выполняется неравенство |м-и|>|м|-|и|. Какой геометрический смысл
данного неравенства? Когда данное неравенство обращается в
равенство?
XI.93. Пусть или — различные комплексные числа и|и — u| = |a + i;|.
Докажите, что четырёхугольник, вершины которого находятся
в точках плоскости, соответствующих числам 0, и, и, и + и,
является прямоугольником.
XI.94. Докажите, что для любых комплексных чисел или выполняется
равенство 2(|i/|2 + |и|2) = \и + v\2 + \и - v\2. Данное равенство
называется тождеством параллелограмма. Как вы думаете почему?
Группа С
XI.95. При каких значениях параметра aeR существует единственное
число 2, такое, что |г-/[^0и|г-За|^ 2а?
XI.96. Найдите все действительные числа &, такие, что система нера-
j\z-i\<2,
венств у. ' имеет ровно одно решение на множестве
[\z — 4&I ^ —3&
комплексных чисел.
XI.97. При каких значениях параметрааейне имеет решений система:
'--а\ = 1,
266 Глава XI. Комплексные числа
XI.98. При каких значениях параметра а е R существует хотя бы одно
комплексное число 2, такое, что \г - ai\- a + 4 и 12 - 2|<2?
XI.99. Изобразите на комплексной плоскости множество всех таких
точек 20, что для каждой из них для любого решения z
уравнения: a) \z — 3i| = \z - zo\ выполняется условие z2 Ф ti для
любого положительного t e R; б) |г + 4| = |г — zo| выполняется
условие z2 Ф ti для любого отрицательного t e R.
Модуль и аргумент комплексного числа.
Тригонометрическая форма записи комплексных чисел
Группа А
XI.100. Отметьте на комплексной плоскости число, укажите его
модуль и аргумент: а) и = -i; б) и = —i ——; в) и = --i + —;
£t A £i La
г) и = -i — 1; д) и = 3/ + 4; е) и = — 2 + £.
xi.ioi. Изобразите множество точек 2 на плоскости, для которых:
a) arg2 = ~; б) arg z = 0; в) arg2 = ^-;
о 4
г) arg (г + 0 = ^-; д) arg zi = ^-; е) arg^ = ^-;
4 4 i 4
ж) 0<arg2 ^ -; з) -— <arg2 ^ -; и) arg—— = -я.
Представьте число в тригонометрической форме (XI. 102, XI. 103).
XI.102. а) 1 + i; б)-1 + /л/3; в)16-16л/з/; г)-6л/3-6/; д) — + |i; e) 0.
-
Х1.ЮЗ. а) -/; б) -7; в) i; г) (V3-4)t.
Х1.Ю4. Вычислите: a) cos —^- + i sin —— cos — + i sin -^-
,-vol Я . . Я | ( Я ..Я
б) 3 cos — + i sin — cos — + i sin —
6 6 J у 3 3
ч 2я . . 2я i f 5я . . uu i,. ^ч
в) I cos —- + i sin — 11 cos — + i sin — I (H-1);
о
г) I cos ——
xi.105. Из всех чисел г, удовлетворяющих условию \г - i — l| = 1,
найдите: а) число с наименьшим аргументом; б) число с
наибольшим аргументом; в) число с аргументом —.
3
Задачи и упражнения
XL106. Пусть \z\ = —, arg2 = —. Найдите модуль и один из аргументов
числа 32г4 + 2л/з/.
XI.107. Пусть \z\ = 2, arg2 = —. Найдите модуль и один из аргументов
3
числа 2s - 8i.
Группа В
Х1.Ю8. Изобразите множество точек z на плоскости, для которого:
ч i + 1 ^ч z я
a) arg = -п; б) arg-
i +
л/3
Х1.Ю9. Приведите к тригонометрической форме число:
а) 3 + ц б) -1 + 21; в) -2 - 3Z; г) 3 - 4/.
Xl.no. Приведите к тригонометрической форме число:
a) sin52° + /cos52°; б) -(sin52° + /cos52°);
в) (cos48° - isin48°); г) -cos48° + /sin48°.
XLlll. Приведите к тригонометрической форме число:
a) sin 42° + i cos 148°; б) - (sin 148° + i cos 42°);
в) sin 20° + i cos 70°; r) — —.
cos— + /sin—
XI.112. Приведите к тригонометрической форме число
(sin 26° + /cos 154°) (sin 27° + /cos 153°)
sin 17° + cos 17°
XI
.113. Среди таких комплексных чисел 2, что (г + z)(z - z) = 4/V3,
найдите числа, аргумент которых равен —.
3
XI.114. При каких значениях параметра р среди 2, таких, что
\г - 1 + /л/з| ^ р, найдётся число с аргументом — ?
4
XI.115. Множество точек комплексной плоскости определяется
условием |з + 4 - 3i| < 1. В каких пределах изменяется Re z : Imz?
XI.116. Известно, что \z — 3 —4i|<l. Какие значения может
принимать Imz : Rez?
Х1.И7. Пусть K={z g С: |1 -(/+ 1)г| = |(г+ l)i-f 3|}.
а) Найти все х е К, расстояние от которых до вещественной
оси равно 3.
б) Какие значения принимает модуль чисел из К?
в) Найти множество аргументов чисел из К, принадлежащих
промежутку [0; 2л].
2681 Глава XI. Комплексные числа
Группа С
XI.118. Запишите в тригонометрической форме число:
ч 2я Ал 2п\ ^ 2я .(л 2пЛ
a) sin — + i 1 - cos — ; б) sin — + i\ 1 + cos — ;
5 V 5 У 5 V 5 У
я .(л п\
sin-+ til-cosy I
XI. 119. Запип1ите в тригонометрической форме в зависимости от
параметра Р е [-п; п) число: а) 1 + cos Р - / sin Р; б) (1 + sin Р + i cos p)10;
в) l-itgp;r)2ctgp-2i.
xi.120. Изобразите на комплексной плоскости все такие числа с, что
для каждого из них среди решений уравнения z2 — сг = 0 най-
Зя
дется решение г19 аргумент которого равен —.
Формула Муавра
Группа А
XI.121. Вычислите:
/г— \ 2008 / /— \ 2008 / /— \ 2008
а) (л/3-i) ; б) (l + V3i) ; в) (-1 + Щ ; г) (1 - О2008.
xi.122. Выразите через cos а и sin а: a) sin 10а; б) cos 12а.
Группа В
XI.123. Известно, что г + - = 2cos0. Докажите, что zn + — = 2cosai6.
XI.124. Докажите, что справедлива формула
1 + itgoc
1 + itgna
1 - itga ) 1 - itgna
xi.125. Найдите все вещественные значения параметра а, при каждом
из которых данное число и является корнем данного
уравнения, и решите данное уравнение при найденном значении а.
а)
( "\6
и = sin— - /cos— ; z4 - z3 + (a2 - 3)z2 + az - 3 = 0;
б) и -\ sin — - i cos —I : cos — - i sin —I ; z2 + (a2 - 8) z + 2a +1 = 0;
в) и —
г) и =
8
Зя . Зя
sin 1- icos—
20 20
32
-; zs-(a + 3)z2 + 6a2z + a2 = 5;
-; zs-(a + 6)z2 + 8a2z + a2 = 7.
Задачи и упражнения
XI.126. а) Пусть z — корень уравнения z + - = 1. Найдите z239.
б) Пусть z — корень уравнения z = 1. Найдите 2566.
Группа С
XI.127. Докажите, что cos 1° — иррациональное число.
XI.128. При каких значениях натурального параметра п многочлен
(cos a + xsina)" - cos па - х sin па делится на х2 + 1?
XI.129. Докажите, что хп • sin a - sinna • х + sin (л - l)a делится на
х2 - 2 cos a + 1 при п ^ 2, п е N.
xi.130. Докажите, что хп - sin a — Хп~г sinmx • х + Хп sin (п — 1)а
делится на х2 — 2?uccosa + X2, п е N.
XI.131. При каких значениях натурального параметра п многочлен
Х2п _|_ хп _|_ i делится на многочлен х2 + х + 1?
f cos х + cos у + cos 2 = 0,
XI.132. Известно, что { . . .
[ sin jc + sin г/ + sin 2 = 0.
Докажите, что sin3x = sin3i/ = sin32.
Корень л-й степени из комплексного числа
Группа А
XI.133. Найдите: а) все корни третьей степени из числа -27/; б) все
корни третьей степени из 1; в) все корни третьей степени из (—1);
г) все корни четвёртой степени из числа -8 — 8v3i.
XI.134. Решите уравнение: а) zb = 32; б) 26 = -1.
XI.135. Найдите сумму всех таких чисел 2, что z4 = 1 - iv3. Укажите
одно из этих чисел.
XI.136. Найдите все комплексные числа 2, удовлетворяющие
равенству:
а) (г)4 = (3 - i7з)4; б) (г)3 = (л/3 + iл/3)3.
Группа В
XI.137. Пусть и — корень п-й степени из 1. Вычислите: а) 1 + и +
+ и2 + ... + ип~1; б*) 1 + 2и + Зи2 + ... + пип-1.
Группа С
XI. 138. Вычислите произведение всех корней степени п из 1.
XI. 139. Вычислите cos —^— + cos —^— + ... + cos —.
2fc+l 2fc+l 2fc+l
Xl.140. Докажите, что: а) при п ^ 4 все корни уравнения (z - 1)п = (z + 1)"
располагаются на одной прямой; б) при п> 5 все корни
уравнения (2z - 2)п = (z + 1)" располагаются на одной окружности.
270 Глава XI. Комплексные числа
Комплексные числа и геометрические преобразования
группа а
Х1.141. В какое множество переходит множество, задаваемое
уравнением | z -J | = 1 при отображении ср комплексной плоскости:
а) ф(г) = z; б) ф(г) = z + i + 1;
в) cp(2) = -*z; г) y(z) = (l + i)z.
Группа В
XI.142. Даны два множества Мг = < z: \iz + V2| = ->; М2 = {/г: 2 е М^.
Найдите расстояние между множествами Мх и М2.
XI.143. Пусть множество М точек комплексной плоскости,
соответствующих числам 2, представляет собой окружность с центром
в точке (0; 1) и радиусом 1. Изобразите на комплексной
плоскости множество Mi, состоящее из всех точек, соответствующих
2
числам zX9 таким, что zx — :.
XI.144. Множество М содержит все числа вида z = совф + isincp,
0 ^ ф ^ п. Изобразите множество М19 содержащее все числа
1 — Si
вида со = г • , z e M.
1 + 2/
XI.145. Множество К содержит все комплексные числа z вида z = coscp +
+ isin(p, где — ^ ф ^ п. Изобразите множество Кг комплексных
1 4+2/ - v
чисел у, таких, что v = — • г> гД^ z пробегает множество К.
z 3 — i
Применения комплексных чисел
Группа А
XI.146. Пусть множество А задаётся уравнением \г - 1 - i\ = 1.
Изобразите множество чисел:
a) z; б) -z; в) iz; г) 22, где z e А.
Группа В
XI. 147. Найдите все вещественные значения а, такие, что всякое
комплексное число, удовлетворяющее неравенству \z — l\^\z-a-(a-\-l)i\,
удовлетворяет и неравенству | z — 1 | ^ 1.
\z-4\
\г- 2|
Х1.148. Решите систему уравнений
= 1,
г-2\ _ J_
z-i\ " л/2*
271! Задачи и упражнения
XI.149. Даны точки A (i — 1), B(2i — 1), С (2 — 3i) и множества
S = {г 11 z | = 1} и D = {г 112г - 11 ^ l}.
а) Докажите, что VP e S, АР2 + ВР2 + СР2 = const.
б) Изобразите {г (2/ - 1) + (1 - г) (г - 1), г е £>}.
XI.150. Точки Ао, Ах, А2, А3, А4 — вершины правильного
пятиугольника, О — его центр.
а) Докажите: ОА0 + ОАг + ОА2 + ОА3 + ОА4 = 0.
б) Найдите: 1 + 2 cos ь 2 cos —.
о о
в) Докажите: х16 + х12 + х8 + х4 + 1 ! х4 + х3 + х2 + х + 1.
XI.151. ПуСТЬ 2Х Ф -22 И 23 = .
^1 + Z2 111
а) Докажите, что если г19 22 Ф 0, то точки —, —, — лежат на
одной прямой. * 2 3
б) Докажите, что если z2 — 2^ и 2г Ф 22, то треугольник О2г22
прямоугольный (О — начало координат).
в) Пусть 22 = z^ и |21~2|^1. Найдите наибольпгее значение
отношения площадей треугольников О2г23 и Ozx22.
г) Докажите, что точки О, zlf 22, 23 лежат на одной прямой или
на одной окружности.
XI.152. Пусть Р„(х) = 1 + х + ... + хп.
а) Докажите, что Рп имеет вещественные корни, если и только
если п — нечётно.
б) Пусть zX9 22, ..., 2п — комплексные корни Рп. Докажите, что
(1 - Zl) • (1 - г2) ■ ... • (1 - га) = 1 + п.
XI.153. Докажите, что числа zl9 22, 23 и 24 лежат на одной
окружности именно в таком порядке тогда и только тогда, когда
J? 2 . _J 1 — вещественное положительное число.
Группа С
XI.154. При каких значениях параметров а и Ъ корни многочлена
р (х) = 23 + аг + Ь лежат в вершинах равнобедренного
треугольника?
XI.155. Докажите тождество cos cos •... • cos = —.
м 2n + 1 2n + 1 2n + 1 2n
XI.156. На сторонах треугольника вне его построены равносторонние
треугольники. Докажите, что центры этих треугольников
образуют равносторонний треугольник (треугольник Наполеона).
XI.157. Докажите, что все корни уравнения 1 1 = 0
Z ~ ZX 2- 22 2- 2Ъ
лежат внутри треугольника с вершинами zl9 z2, 23.
272 Глава XI. Комплексные числа
Сюжетные задачи с комплексными числами
Группа А
XI.158. Множество К точек комплексной плоскости задано уравнением
|fe + 2 + 2i| = l.
а) Нарисуйте множество К.
б) Найдите такие точки z e К, расстояние от которых до мни-
13
мои оси равно —.
5
в) Найдите множество значений | z | при z e К.
г) Найдите множество значений argz в [0; 2п) при z e К.
тт л/3 + 3* -л/3 + * yfS-i
xi.159. Даны три комплексных числа: zx — , z2 = , zs = .
Ci £k L*
а) Найдите расстояние от точки zx до фигуры, задаваемой
уравнением | z - zs | = 1.
б) Изобразите множество точек z комплексной плоскости,
таких, что \z2z - zxz2\ = \zsz - z2zs\.
в) Пусть z пробегает все точки отрезка с концами г2, г3,
a U и V — множества, пробегаемые при этом, и = z2z, v = z3z.
Изобразите множество U П V.
г) Пусть z пробегает все точки отрезка с концами г19 zs.
Изобразите множество, пробегаемое z2.
XL160. Пусть А (2г + 1), B(z + 2), C(z2 + 2z) — точки плоскости,
соответствующие указанным комплексным числам.
а) Докажите, что если | z \ = 1, то О А = ОВ (О — начало координат).
б) Докажите, что треугольник ABC подобен треугольнику
с вершинами в точках Ux = 0, U2 = 1, U3 = -(z + 1).
в) Пусть | z | = 1. Найдите множество значений радиусов
окружностей, описанных вокруг треугольника ABC.
г) Пусть | z | = 1. При каком значении z площадь треугольника
принимает наибольшее значение?
XI.161. Пусть A(i — 1), В (2/ — 1), С (2 - 3Z) — точки комплексной
плоскости, S — окружность \z\ = 1, a D — множество комплексных
чисел, заданное неравенством \2z — 1| ^ 1.
а) Докажите, что сумма квадратов расстояний от точки Р е S
до точек А, ВиС постоянна.
б) Изобразите на плоскости точки А и Б и множество чисел
вида 2(2/ - 1) + (1 - z) (i - 1), где z e D.
в) Найдите такую точку Е е D и все такие равносторонние
треугольники с вершинами на S, для которых сумма квадратов
расстояний от их вершин до Е наибольшая.
г) Верно ли, что для всякой точки w из треугольника ABC
найдётся такое число z e D, что w = z • zh - (1 — z) • zj9 (zk, z1 e
e {i - 1, 2i - 1, 2 - 3*})?
и упражнения
XI.162. Пусть А, В, С — точки плоскости, изображающие
комплексные числа и, v, w.
а) При и — 0, v = 1 + i найдите все такие ьиу что треугольник
ABC равносторонний.
б) Пусть и = О, v = 1 + 2/, а число и; является корнем
уравнения 22 = (1 + 2i)z + 3 — 4i. Докажите, что треугольник ABC
равносторонний.
в) Известно, что треугольник ABC равносторонний. Могут ли
действительные и мнимые части чисел и, v, w быть
рациональными?
г) Докажите, что если и2 + v2 + w2 = uv + vw + wu, то
треугольник ABC равносторонний.
Xl.163. Дано число г Ф 1, такое, что е3 = 1. Для данной тройки
комплексных чисел а, &, с рассмотрим числа и = а + Ьг + се2
и v = а 4- бе2 4- се.
а) При а = 0, с = -2ии = 0 определите вид треугольника abc.
б) Докажите, что числа и и у не изменятся, если треугольник
abc подвергнуть параллельному переносу.
в) Докажите, что треугольник abc является равносторонним
тогда и только тогда, когда uv = 0.
г) Изобразите множество значений и для всех треугольников
abc, которые можно накрыть кругом радиуса 1.
XI.164. Дан многочлен p(z) = z3 + az 4- b (a, b, z e C).
а) При a = —i, & = 1 — i найдите корни многочлена р, записав их
в алгебраической форме.
б) Найдите все пары комплексных чисел (а; &), для каждой из
которых один из корней многочлена является серединой
отрезка между двумя другими.
в) Найдите все пары комплексных чисел (а; &), для каждой из
которых корни многочлена р лежат в вершинах
равностороннего треугольника.
г) Докажите, что если \p(z)\ ^ 1 при всех значениях 2,
таких, что \z\ = 1, то а = Ъ = 0.
XI.165. Пусть p(z) = z2 + az + &, где z e С.
а) Пусть Ъ — 1. Верно ли, что при а е R, \а\ ^ 2 корни
многочлена р лежат на окружности с центром в О радиуса 1?
б) Пусть Ь = 1, а е С, |а| < 1. Найдите наименьшее значение
модуля разности корней многочлена р.
в) Пусть 2Х, 22, 23, г4 — вершины квадрата с центром и.
Докажите, что р (zx) + р (z2) + р (zs) + р (24) = Ар (и).
г) Пусть т = тах|р(2)|. Докажите, что |р(г)| ^ яг при всех зна-
|г|=1
чениях г, таких, что |з| < 1.
XI.166. Дан многочлен p(z) = zs + z2, z — комплексное число.
а) Решите уравнение p(z) = 2.
б) Найдите сумму квадратов всех корней уравнения р (z) = 2008.
10—Пратусевич, 11 кл.
2741 Глава XI. Комплексные числа
в) Найдите все действительные значения с, при которых
модули всех корней уравнения p(z) = с не превосходят 1.
г) Существуют ли такие комплексные значения с, при которых
модули всех корней уравнения p{z)- с равны 1?
XI.167. Пусть М = {z е С: \г - 2| = 1} и f(z) = = при а > 0.
а) При а = 1 найдите все корни уравнения f(z) = f(z) = v2,
принадлежащие M.
б) Пусть 21? 22 е М и 2j e й. При каких значениях а
выполняется равенство {zx; z2} = {/Ч^); ?(22)}?
в) При а = 1 нарисуйте множество всевозможных чисел вида
f(z), где z e M.
г) Какие значения может принимать arg f(z) при
всевозможных а и 2 е М?
XI.168. Рассмотрим два комплексных числа zx = 7/ - 1, г2 = 5 + 2,5£.
Пусть if и А соответственно точки, изображающие эти числа на
комплексной плоскости.
а) Найдите все числа 2, такие, что изображающая их точка М
лежит на прямой АК, причём 2 \АМ\ = |J5TM|.
б) Рассмотрим множество Т комплексных чисел 2, таких, что
> 2. Найдите наименьшее значение \г\ для z e Т.
z - z2
в) Пусть f(x) = i/2, и е С. Изобразите на комплексной
плоскости множество чисел и, для которых З2 e T: Ref(z) < 0.
г) При каких положительных значениях а е R для того, чтобы
\г - За - i\ < а, необходимо, чтобы z e T?
XI. 169. Отображение / ставит в соответствие комплексному числу z
число f(z) = uz + (1 - ы)а, где и^Оиа — некоторые
фиксированные комплексные числа.
а) Известно, что arg и = —. Изобразите на плоскости множество
всех значений а, при которых /(l - *л/з) = 1 + /л/3.
б) Изобразите на плоскости множество всех значений а, для
которых найдётся такое значение и, что соответствующее
отображение / переводит точки полуплоскости Im z > 0 в точки
полуплоскости Re 2 > 0.
xi.170. Комплексное число z = а + Ы называют гауссовым, если а и Ъ —
целые числа. Говорят, что гауссово число 2 кратно числу w, если
2 = wu, где w и и — гауссовы числа. Пусть К — множество всех
гауссовых чисел, кратных 1 + 21.
а) Докажите, что если z е К и arg 2 = —, то z кратно 3 - i.
б) Существуют ли числа и, v е К, такие, что arg— = —?
V о
в) Докажите, что для всякого гауссова числа z найдётся число
w е К, такое, что \г - w\ < 1.
i
I
Элементы теории
вероятностей
Случайные события.
Классическое определение вероятности
1. Виды событий
Вокруг нас (а также внутри нас) происходит огромное число
всевозможных событий1. О большинстве этих событий мы и не знаем
(например, вряд ли вы часто задумываетесь о том, что в данный момент
времени многие тысячи клеток вашего организма делятся, а другие
тысячи умирают), другие события нам не интересны, однако есть те,
которые нас живо интересуют, а главное — интересует то, чем эти
события закончатся, каков будет их итог.
Например, мы можем интересоваться итогом футбольного матча,
а также результатом химического опыта, вам наверняка
небезразличен итог выпускного экзамена и т. п.
Итак, событие — это исход некоторого «опыта» в широком
смысле слова (футбольного матча, выпускного экзамена, химического
эксперимента и т. д.). События бывают достоверными, невозможными
и случайными.
Достоверное событие — это событие, всегда наступающее в
результате данного опыта при выполнении одного и того же комплекса
условий.
Например, подброшенный нами на поверхности Земли камень
всегда упадёт вниз (если, конечно, вверху его кто-то или что-то не
задержит). Положенное на поверхность воды бревно будет некоторое время
плавать. В результате реакции щёлочи с кислотой получится соль
и вода. Примеры таких событий можно неограниченно множить.
Наличие таких событий очень важно, поскольку позволяет
предсказывать последствия тех или иных опытов.
Вся наша повседневная жизнь построена на использовании того,
что результаты тех или иных опытов достоверны! Люди строят огром-
1 Здесь мы не будем давать строгого определения события. Для наших
целей вполне достаточно обыденного понимания.
10*
276 Глава XII. Элементы теории вероятностей
ную фабрику или электростанцию, заранее и точно зная, что будет
происходить после её постройки. Большая часть происходящих при этом
событий достоверны в силу законов физики, химии и других наук.
Невозможные события — это фактически отрицания
достоверных. Если подброшенный камень падает вниз на поверхность Земли,
то не упасть он не может. Значит, событие «при подбрасывании вверх
камень не упал» является невозможным (разумеется, при разумных
естественных предположениях).
Нас же будут интересовать случайные события, т. е. такие,
которые в результате одного и того же опыта при одних и тех же условиях
могут как произойти, так и не произойти. Например, если вы будете
бросать монетку, то событие «выпал герб» может как произойти, так
и не произойти. При встрече на футбольном поле двух равных по силе
команд результат встречи непредсказуем (наверное, именно за это
люди так любят футбол).
На первый взгляд об исходе случайного события ничего сказать
нельзя: монетка может упасть любой стороной, футбольные команды
могут сыграть как угодно и т. п.
Однако вряд ли кто-либо станет слишком надеяться на то, что при
бросании монетки 1000 раз монета все 1000 раз упадёт гербом вверх!
Мы разумно полагаем, что выпавших гербов будет около 500 —
возможно, чуть больше, возможно, чуть меньше... Если гербов выпадет
«слишком много», можно заподозрить, что «монетка неправильная»
или «игрок жульничает».
Таким образом, про результат одного бросания монетки мы не
можем сказать ничего определённого, зато про результат 1000 бросаний
уже можно кое-что сказать. Выяснением такого рода
закономерностей, в частности, и занимается теория вероятностей.
2. Пространство элементарных событий
Рассмотрим некоторый опыт (например, результат сдачи ЕГЭ по
математике или измерение длины ползущей гусеницы) и различные
исходы этого опыта. События, наступившие в результате эксперимента,
могут быть разными и включать в себя другие события. Например,
событие «При сдаче ЕГЭ по математике ученик набрал больше 50 баллов»
включает в себя событие «При сдаче ЕГЭ по математике ученик набрал
67 баллов», а также событие «При сдаче ЕГЭ по математике ученик
набрал от 60 до 70 баллов». Событие «При измерении длины гусеницы её
длина больше 5 см» включает в себя событие «При измерении длины
гусеницы её длина составляет от 6 до 8 см», но не включает событие
«При измерении длины гусеницы её длина равна 4,7 см».
Рассмотренные примеры показывают, что некоторые события
«составлены» из более «простых» событий, а «простые» события не
включают в себя других событий (кроме невозможного). Например, событие
«При сдаче ЕГЭ по математике ученик набрал 67 баллов» не включает
в себя никаких других событий. Таким же образом событие «При изме-
277; §73. Случайные события. Классическое определение вероятности
рении длины гусеницы её длина составила ровно 4 см» не включает
в себя других событий (здесь мы пренебрегаем тем, что абсолютно точного
измерения длины добиться невозможно, хотя именно размышления
о погрешностях измерений привели к важным открытиям в теории
вероятностей).
Здесь мы наблюдаем аналогию между понятиями «множество»
«событие». А именно: есть множество некоторых «элементарных
событий», из которых составляются другие события так же, как
множество составляется из своих элементов. При этом разумно
потребовать, чтобы при объединении, пересечении или вычитании
нескольких событий снова получалось событие. Например,
объединение событий описывается фразой «Произошло хотя бы одно из
событий», о пересечении событий можно сказать «Одновременно
произошли оба события», а о разности событий А и В —
«Событие А произошло, а событие В не произошло».
Пока мы ограничимся рассмотрением опыта с конечным числом
исходов, как, например, бросание кубика или сдача ЕГЭ по
математике.
ОПРЕДЕЛЕНИЕ
Множество, состоящее из конечного числа исходов данного
опыта, называется пространством элементарных событий,
если выполняются два условия:
1) опыт может закончиться лишь одним из перечисленных
исходов;
2) опыт не может закончиться никаким другим исходом,
кроме перечисленных.
Событием будем называть некоторое подмножество пространства
элементарных событий. Элемент пространства элементарных событий
(т. е. один из возможных исходов) будем называть элементарным
событием, хотя в отличие от события он не является подмножеством
пространства элементарных событий, а является его элементом.
Элементарные события, составляющие данное событие, называют
также благоприятствующими данному событию.
Достоверным событием называется событие, совпадающее с
пространством элементарных событий. Иначе говоря, достоверному
событию благоприятствует любое элементарное событие.
Невозможным событием называется пустое подмножество
пространства элементарных событий. Иначе говоря, невозможному
событию не благоприятствует ни одно элементарное событие.
Поскольку события — это подмножества пространства
элементарных событий, то с ними можно производить те же операции, что и
с множествами: объединять, пересекать, брать разности и дополнения.
В теории вероятностей имеется своя традиционная терминология.
Например, непересекающиеся события называются несовместными.
278| Глава XII. Элементы теории вероятностей
В более общем случае мы можем дать несколько другое определение:
ОПРЕДЕЛЕНИЕ ——————————————————————
Пусть п — некоторое множество, называемое
пространством элементарных событий. Некоторое множество Z,
состоящее из подмножеств Q, называется множеством событий
(а его элементы — событиями), если выполнены условия:
1) если А е L, В е X, то А П В е I, A U В е Z, А\Б е Z;
2) ft e Z, 0 е Z.
В случае конечного множества Q чаще всего в качестве
множества событий Z мы будем рассматривать множество всех подмножеств
Q, не оговаривая это отдельно.
Пример 1. Опыт состоит в бросании кубика. Тогда пространством
элементарных событий можно считать множество {1;2;3;4;5;6}.
Событие «На верхней грани выпало чётное число» — это множество
А = {2; 4; 6}, событие «На верхней грани выпало число, большее 3» —
это множество В = {4; 5; 6}, событие «На верхней грани выпало чётное
число, большее трёх» — это АПВ = {4; 6}, а событие «На верхней
грани выпало нечётное число, меньшее 4» — это {1; 3}.
С другой стороны, если в условиях решаемой нами задачи нас
интересует не само число, выпавшее на верхней грани кубика, а только
его чётность, то можно считать пространством элементарных событий
множество из двух элементов {ч; н}, соответствующих выпадению
чётного или нечётного числа на верхней грани. Н
Таким образом, одному и тому же опыту можно ставить в
соответствие разные пространства элементарных событий.
Пример 2. Опыт состоит в измерении длины ползущей гусеницы.
Будем считать, что длина гусеницы заведомо лежит в границах от
3 до 6 см. Тогда Q, = [3; 6], элементами Q являются числа, а
элементами множества событий Z могут служить всевозможные числовые
отрезки и интервалы, лежащие в [3; 6], а также всевозможные
множества, получаемые объединениями и пересечениями отрезков
и интервалов, а также дополнениями этих множеств до [3; 6]. В!
3. Определение вероятности
ОПРЕДЕЛЕНИЕ ————————————————
Конечным вероятностным пространством называется
пространство элементарных событий, состоящее из конечного
числа элементов, вместе с заданной на нём функцией р
(называемой вероятностью), ставящей в соответствие каждому
элементу пространства элементарных событий
неотрицательное число так, что сумма значений этой функции по
всем элементам равна 1.
2791 §73. Случайные события. Классическое определение вероятности
Символически: если Q. = {Хг; Х2; ...; Хп}— пространство
элементарных событий и р: Q. —► [0; 1] — данная функция, то
Пример 3. Пусть опыт состоит в бросании кубика, а пространство
элементарных событий есть множество Q = {1;2;3;4;5;6}. Можно
поставить в соответствие каждому элементу множества Q число —. Полу-
6
ченная вероятность соответствует опыту, в котором бросают идеально
симметричный кубик.
Можно поставить в соответствие всем элементам, кроме 5 и 6,
число -> Р(5) = 0, р(6) = —. Полученная вероятность соответствует, напри-
6 3
мер, опыту, в котором бросают кубик, где грани с 5 очками нет, а
вместо неё есть две грани с 6 очками. Щ
ОПРЕДЕЛЕНИЕ —————---———^.__-_______■_■-_.
Пусть задано конечное вероятностное пространство.
Вероятностью события называется сумма вероятностей
составляющих это событие элементов пространства элементарных
событий. Вероятность события, не содержащего
элементарных исходов (невозможного события), по определению
равна 0.
Обозначение: р(А) — вероятность1 события А.
Пример 4. В цехе работает 3 станка, причём в течение часа первый
отказывает с вероятностью 0,1, второй — с вероятностью 0,2, а
третий — с вероятностью 0,3. Никакие два станка не могут отказать
вместе в течение часа. Найдём вероятность того, что в течение часа все
станки будут работать.
D В данном случае пространство элементарных событий состоит из
четырёх элементов: аг соответствует отказу первого станка, р(аг) = 0,1,
аналогично определяются события а2 и а3, причём р(а2) = 0,2 и
р(а3) = 0,3. Оставшийся элемент а4 соответствует случаю, когда ни один
станок не отказал. Посколькур(аг) + р(а2) +р(а3) + р(а4) = 1, получаем
() 04Ш
1 Отметим, что это обозначение вступает в противоречие с тем, что А —
множество элементов, значит, р (А) должно быть образом множества, т. е.
множеством, а в нашем случае р (А) — число, равное сумме значений функции р на
элементах множества А. Тем не менее такое обозначение общепринято и
мотивировано тем, что в случае абстрактных вероятностных пространств
(необязательно состоящих из конечного числа элементов) аргументами функции
вероятности являются не элементарные события, а все возможные события, т. е.
вероятность есть функция, заданная на множестве всевозможных событий.
280i Глава XII. Элементы теории вероятностей
Значения вероятностей берутся из соображений, возникающих
при постановке задачи, т. е. до того, как в дело вступает теория
вероятностей. Например, считая, что монетка симметричная, мы говорим,
что вероятность каждого исхода (герба или решки) равна —. Считая,
что колода состоит из 36 игральных карт, мы полагаем вероятность
вытащить каждую карту равной —. А вероятность того, что вытащен-
36
ная карта окажется тузом, равна сумме 4 слагаемых по — каждое,
36
т. е. — (поскольку событие «вытащен туз» состоит из 4 элементарных
9
событий «вытащен туз пик», «вытащен туз бубен», «вытащен туз
червей», «вытащен туз треф»).
Значения вероятностей событий могут возникнуть из опыта,
обработки долгосрочных наблюдений и множества других соображений.
Например, получение с той или иной степенью точности вероятностей
событий из результатов наблюдений входит в круг вопросов,
которыми занимается математическая статистика.
Подчеркнём: то, откуда берутся значения вероятностей
элементарных событий, не забота теории вероятностей.
4. Свойства вероятности
Непосредственно из определения следуют свойства вероятности,
которые мы объединим в теорему.
ТЕОРЕМА (свойства вероятности) .............
Пусть задано вероятностное пространство Q с функцией
вероятности р, тогда:
1. p(Q)=1,p(0) = O.
2. Если события А и Б не пересекаются, то р (A U Б) = р (Л) + р (Б).
3. Для любого события /\ и его дополнения А выполнено
равенство р(А) = 1 -р(/\).
4. Для любых событий А и Б выполнено равенство р (Л U Б) =
= рИ)+р(Б)-рИПБ).
5. Если АаВ, то р(А)^р (Б).
6. Вероятность любого события не превосходит 1.
□ доказательство. Свойство 1 следует из определения вероятности
и определения события.
Докажем свойство 2. Пусть А = {аг, а2, ..., ak}, В = {bl9 ..., bt}9 где
а19 а2, ..., ak, bl9 ..., bL — элементы пространства элементарных
событий. Тогда, поскольку события А и Б не пересекаются, никакой
элемент множества А не совпадает ни с каким элементом множества В.
281, §73. Случайные события. Классическое определение вероятности
Поэтому A U Б = {а19 ..., ak, bl9 ..., bt}, а тогда по определению
вероятности события
р(А U Б) = p(al) + ... + p(ak) + p(bl) + ... + p{bt) =
р(В)
Свойство 3 следует из свойства 2, применённого к событиям
А и А. Действительно, так как события А и А не пересекаются, то
р(А1) А) = р(А) + р(А). Осталось заметить, что AU4 = Q, а потому
р(А U А) = 1. Итак, 1 = р(А) + р(А), откуда и получается требуемое
равенство.
Свойство 4 получается из формулы AUB = AU (Б\А), верной для
произвольных множеств А и Б. Поскольку множества А и В\А не
пересекаются, имеем
р (A U Б) = р (A) U р (В\А) = р (А) + р (В\А). (*)
В свою очередь, поскольку Б = (В\А) U (Б П А), причём множества
(Б\А) и (Б П А) не пересекаются, по свойству 2 имеем р (Б) = р(В\А) +
+ р(В П А), откуда р(Б\А) =р(В) - р(В П А). Подставив полученное
выражение в равенство (*), получаем требуемое равенство.
Свойство 5 следует из того, что В = A U (В\А), а тогда по
свойству 2 (поскольку А П (Б\А) = 0) получим р(В) =р(А) + р(В\А) >р(А),
так как Р(В\А) > 0.
Свойство 6 следует из свойств 1 и 5, поскольку любое событие
содержится bQ. 1
В случае произвольного пространства событий каждому
событию ставится в соответствие некоторое значение вероятности. Таким
образом, вероятность — это функция р, заданная на множестве I
и принимающая значения в отрезке [0; 1]. Эта функция должна
удовлетворять двум условиям:
2) если А П Б = 0, то р(А U Б) =р(А)
Часть свойств вероятности, сформулированных в теореме для
конечного вероятностного пространства, здесь уже дана в определении.
Свойства 3, 4 и 5 могут быть доказаны так же, как это сделано в
доказательстве теоремы. g|
Каков же практический смысл понятия вероятности?
Предположим, мы производим один и тот же опыт очень много раз
и смотрим, сколько раз произошло интересующее нас событие.
Естественно рассмотреть долю (частоту наступления события), которую
составляют исходы, благоприятствующие событию, среди всех исходов.
Например, если при 1000 бросаний монетки герб выпал 587 раз,
587
то частота выпадения герба равна = 0,587. Если же мы 1000 раз
1000
бросаем игральный кубик и из них 186 раз выпала шестёрка и 124 раза
2821 Глава XII. Элементы теории вероятностей
выпала пятёрка, то доля исходов, благоприятствующих событию «чис-
* л 186+124 п О1
ло выпавших очков больше 4», равна = 0,31.
Если всё увеличивать и увеличивать число опытов, то частота
может стремиться к некоторому предельному значению. Это значение
равно вероятности данного события (так называемый «закон больших
чисел»).
Однако не всегда можно произвести достаточно много опытов,
чтобы с нужной точностью выяснить частоту наступления интересующего
нас события (например, не играть же 1000 матчей между двумя
командами, чтобы выяснить частоту наступления победы одной из
них). Поэтому важно уметь предсказать теоретически эту частоту.
В частности, это один из вопросов теории вероятностей.
Если мы хотим применять результаты теории вероятностей на
практике, значения вероятностей элементарных событий должны быть
не просто «взяты с потолка», но соответствовать потребностям практики.
5. Классическое определение вероятности
Наиболее распространённым является определение вероятности,
называемое классическим. При этом пространство элементарных
событий состоит из конечного числа исходов, каждому из которых
приписывается одна и та же вероятность.
Пусть пространство элементарных событий состоит из п элементов.
Тогда вероятность наступления каждого из этих событий равна —. Если
данному событию удовлетворяют т исходов, то вероятность события
равна —.
Итак, сформулируем классическое определение вероятности.
ОПРЕДЕЛЕНИЕ ————————-——————-—
Вероятность события равна отношению числа исходов,
благоприятствующих данному событию, к общему числу
возможных исходов.
Вероятностное пространство с классическим определением
вероятности является частным случаем конечного вероятностного пространства.
Если вспомнить, что количество элементов множества А
обозначается |А|, то формула классического определения вероятности
выглядит так:
Ещё раз подчеркнём, что эта формула верна лишь в случае
классического определения вероятности, когда возможные исходы равнове-
§ 74. Условная вероятность. Независимые события
роятны. Обычно о том, какие исходы равновероятны, в задаче
говорится прямо или подразумевается интуитивно ясным. Полезно перед
решением задачи выяснить вопрос о том, применимо ли в данной
задаче классическое определение вероятности и если применимо, то какие
именно исходы считаются равновероятными.
Пример 5. Найдём вероятность того, что при случайном выборе двух
различных чисел от 1 до 50 их сумма будет равна 40.
D Интуитивно ясно, что равновероятными будут такие исходы,
как всевозможные пары выбранных чисел. Таким образом,
пространство элементарных событий составится из пар различных чисел.
Таких пар (без учёта порядка чисел в паре) будет С%0 = 25 • 49. Пар,
благоприятствующих исследуемому событию, без учёта порядка чисел
в паре, будет 19. Это пары {1; 39}; {2; 38}; {3; 37}; {4; 36}; ...; {19; 21}.
19
Таким образом, искомая вероятность будет равна .
^о • 4У
Если же считать исходами пары чисел с учётом порядка, то и
числитель, и знаменатель дроби увеличатся в два раза, отчего сама дробь
не изменится. 51
Пример 6. В кармане лежат одинаковые на ощупь монеты двух видов.
Монет I вида 16, а монет II вида 20. Из кармана вытаскивают две
монеты. Оказалось, что монета, вытащенная второй, II вида. Найдём
вероятность того, что монета, вытащенная первой, была I вида.
D Пространство элементарных событий состоит из всевозможных
упорядоченных пар монет, где вторая монета — монета II вида. Нет
оснований полагать, что вероятность вытащить какую-либо пару
отличается от вероятности вытащить другую пару. Таким образом, можно
считать, что все исходы равновероятны.
Всего исходов 35 • 20 (вторую монету можно выбрать 20 способами,
а для каждого выбора второй монеты существуют 35 способов выбрать
первую монету). Исходы, благоприятствующие нашему событию, — это
пары, где первая монета — монета I вида. Таких пар 16 • 20. Таким об-
разом, искомая вероятность равна —. 61
35
(^74. Условная вероятность. Независимые события
1. Условная вероятность
Пусть имеются события А л В — подмножества конечного
пространства элементарных событий Q. Пусть имеет место классическое
определение вероятности, т. е. вероятность каждого элементарного
события равна —, где п — количество элементарных событий.
284, Глава XII. Элементы теории вероятностей
Пусть известно, что произошло
событие В. Какова вероятность того, что
произошло событие А?
Итак, событие Б произошло, а это
значит, что рассматриваются лишь исходы,
благоприятствующие событию В. Таким
образом, произошло сужение
пространства элементарных событий до события В.
Если событие В произошло, то
событие А может произойти, когда исходы, ему
благоприятствующие, будут также
благоприятствовать событию В. Таким образом, если произошло событие В,
то событие А происходит тогда и только тогда, когда происходит
событие А П В.
Тогда вероятность события А, если событие В произошло, равна
отношению количества исходов, благоприятствующих событию А О В,
к количеству исходов, благоприятствующих событию Б, т. е. -—:—j—-.
Разделив числитель и знаменатель на | Q |, получаем искомую вероят-
р(А П В) , ЛП _
ность как — (рис. 12.1).
Р(Б)
ОПРЕДЕЛЕНИЕ
Условной вероятностью события А при условии, что
произошло событие 6, называется число
Обозначение: р(А\В) (читается: вероятность А при условии Б).
Замечания. 1) Формула (1) не определяет условную вероятность
события А при условии, что произошло событие Б, имеющее нулевую
вероятность. С житейской точки зрения это естественно: что можно
предсказывать, если брать во внимание события, имеющие
вероятность, равную нулю!
Таким образом, если вероятность события В равна 0, то
условная вероятность события А при условии, что В произошло, не
определена.
2) Формулу (1) полезно также записать в виде
р(АПВ)=р(А\В).р(В). (2)
Пример 7. Нерадивый ученик выучил один из семи экзаменационных
билетов. Сравним вероятности того, что он сдаст экзамен, если он идёт
сдавать первым или вторым.
П Пусть событие А — ученик сдал экзамен. Оно эквивалентно
тому, что ученик вытащил тот билет, который он знает. Если он идёт
285 § 74. Условная вероятность. Независимые события
первым, то возможных билетов для вытаскивания всего 7, поэтому
вероятность сдать экзамен равна —.
Если же нерадивый ученик идёт вторым, то он может сдать
экзамен лишь в случае, когда выученный им билет не вынут учеником,
шедшим первым. Если событие В — «выученный билет не вытащен
первым учеником», то нас интересует р(А П Б) =р(А\В) • р(В)
(поскольку в этом случае АсВ, то А = А Г) В).
Вероятность того, что «счастливый» билет не вытащен первым
учеником, равна —, т. е. р(В) = —. Перед нерадивым учеником лежит
только 6 билетов. Вероятность вытащить «счастливый» билет теперь
равна —, т. е. р(А\В)= -. Таким образом, интересующая нас вероят-
6 о 6 11
ность по формуле (2) равна р (А Г) В) =—•- = —. Значит, вероятность
7 6 7 -^
сдать экзамен, идя первым и идя вторым, одинакова и равна —. В
Пример 8. В ящике лежат 8 белых и 12 чёрных шаров. Подряд
вытаскивают 2 шара. Найдём вероятность того, что оба извлечённых из
ящика шара будут белыми.
D способ 1. Пусть событие А — «первый извлечённый шар
белый», событие В— «второй извлечённый шар белый». Мы должны
найти р(А П В). Воспользуемся формулой (2). Для этого найдём
способ 2. Рассмотрим в качестве пространства элементарных
событий все возможные пары шаров (с учётом порядка). Этих пар будет
20 • 19. Пар белых шаров, благоприятствующих нашему событию,
будет 8 • 7. Тогда искомая вероятность равна = —. Ш
20 • 19 "о
2. Независимые события
ОПРЕДЕЛЕНИЕ
Событие А называется независимым от события 6, если
р(А\В) = Р(А).
Это определение согласуется с житейским представлением: всё
равно, произошло событие В или нет, вероятность события А от этого
не зависит.
Докажем следующее утверждение.
Утверждение ■■
Если событие А независимо от события В, то событие В
независимо от события А.
2861 Глава XII. Элементы теории вероятностей
П доказательство. По определению независимости события А от
события Б: р(А)= р(А\В)= Р(Апв\ Тогдар (А П Б) =р(А)р(В). От-
Р\В)
сюда р(В)= — = р(В\ А). Полученное равенство р(В) = р(В\ А)
Р(А)
и означает по определению, что событие Б независимо от события А. Ш
Доказанное утверждение позволяет говорить о двух независимых
событиях А и Б, не выделяя, какое именно из них не зависит от другого.
в Не путайте несовместные события с независимыми! Если одно
из несовместных событий произошло, то другое заведомо не
произойдёт, т. е. наступление одного из несовместных событий существенно
зависит от наступления другого. Можно пояснить это и по
определению независимости. Естественно, что условная вероятность одного из
несовместных событий при условии, что произошло другое, равна 0.
Поэтому если вероятность одного из несовместных событий не равна 0,
то оно не будет независимым от другого.
При доказательстве утверждения была получена формула1, для
независимых событий А и В: р(АГ\В) = р(А) - р(В).
Эта формула является основой для практического использования
знаний о независимости событий. Часто при решении задач
информация о независимости событий берётся из практических соображений,
а не из анализа формул.
Например, если двое стрелков, не знающие о существовании друг
друга, стреляют по одной мишени, то события «попадание первого
стрелка в мишень» и «попадание второго стрелка в мишень» будут
независимыми.
Другим примером, где важна независимость событий, может
служить розыгрыш футбольного первенства. Чтобы команды не знали
о результатах друг друга и не «расхолаживались», если от их игры
уже ничего не зависит, матчи проводят в одно и то же время. А если
возникают подозрения, что команда играла не в полную силу, так как
знала результат интересующих её матчей, назначают специальное
расследование.
Пример 9. Найдём вероятность того, что при бросании двух
игральных костей произведение выпавших на них чисел будет нечётным.
П Произведение целых чисел нечётно тогда и только тогда, когда
каждый сомножитель — нечётное число. Поэтому событие
«произведение чисел на двух кубиках нечётно» можно представить в виде А 0 В,
ХВ некоторых учебниках эта формула принимается за определение
независимости событий. Достоинство этого подхода в том, что он позволяет
определить понятие независимости в том числе и для тех событий, вероятность
которых равна 0. В то же время выбранное нами определение ближе к
интуитивному представлению о независимости событий.
2871 § 74. Условная вероятность. Независимые события
где А — «на первом кубике выпало нечётное число», Б — «на втором
кубике выпало нечётное число». Эти два события, очевидно,
независимы (вот использование интуитивного представления о независимости),
поэтому р(А Г) В) = р(А) • р(В). Поскольку р(А) = р(В) = 0,5, то
искомая вероятность равна 0,25. HI
Пример 10. В приборе имеются ровно две ненадёжные детали.
Вероятность выхода из строя первой детали равна 0,8, вероятность выхода
из строя второй детали равна 0,7. Прибор портится, если выходит
из строя хотя бы одна деталь. Найдём вероятность того, что прибор
испортится, если детали выходят из строя независимо друг от друга.
D способ 1. Пусть событие А — «вышла из строя первая деталь»,
событие В — «вышла из строя вторая деталь». Тогда событие «прибор
вышел из строя» — это событие A U Б. По свойству 4 вероятности
p(A\J В) = р(А) + р(В) - р(А Г) В). Поскольку события А и В
независимы, то р(А П Б) = р(А) • р(В). Осталось подставить заданные
числовые значения: p(AUB) = 0,8 + 0,7 - 0,7 • 0,8 = 0,94.
способ 2. Вычислим вероятность противоположного события, т. е.
того, что прибор не выйдет из строя. В обозначениях первого способа это
событие А Г) В. Поскольку события А и Б независимы (объясните
почему), то р(АПВ) =р(А).р(В) = (1-р(А)).(1-р(В)) = 0,2- 0,3 = 0,06.
Тогда искомая вероятность равна 1 - 0,06 = 0,94. Ш
Пример 11. Три охотника стреляют в кабана. Первый попадёт в
кабана с вероятностью 0,4, второй — с вероятностью 0,5, третий — с
вероятностью 0,6. Попадание хотя бы одной пули убивает кабана. Кабан
оказался убит одной пулей. Найдём вероятность того, что он был убит
первым охотником.
D Пусть событие А — «кабан убит одной пулей». Событие Вг —
«попал первый охотник», событие Б2 — «попал второй охотник»,
событие Б3 — «попал третий охотник». Нам нужно найти р(Вг\А).
По определению р(Вг \ А) = —. Событие А П Вг — это собы-
Р(А)
тие «первый охотник попал, а остальные двое не попали». Поскольку
попадание каждого охотника не зависит от результата выстрела
других охотников, вероятность этого события равна произведению
вероятности попадания первого охотника на вероятность того, что второй
и третий не попали:
р(А Г) Вг) = р(Вг) - р(В2). р(В3) =
= р(Вг) • (1 -р(В2)) • (1 -р(В8)) = 0,4 - 0,5 • 0,4 = 0,08.
Теперь вычислим вероятность события А:
р(А) = р(Вг) • р(В^) -р(Щ) + р(В~г) • р(В2) • р(В^) +
+ р(Вг) • р(В2) -р(В3)=р(Вг) . (1 -р(В2)) . (1 -р(В3)) +
+ (1 -р(Вг)) -р(В2) . (1 -р(В3)) + (1 -р(Вг)) . (1 -р(В2)) . р(В3).
288. Глава XII. Элементы теории вероятностей
Подставив числовые значения, получим р(А) = 0,38.
m 0,08 4 А
Тогда искомая вероятность равна = —. Аналогично можно
0,38 19
с * * 0,12 6
найти вероятность того, что кабан был убит вторым охотником: = —.
0,38 19
Наконец, вероятность того, что кабан был убит третьим охотником, рав-
Замечание. Найденные значения вероятностей могут иметь
следующее практическое применение. Если охотники стреляли
одинаковыми пулями и попала только одна из пуль, то нелегко выяснить,
кому должен достаться кабан. В этом случае разумно поделить кабана
пропорционально вероятностям попадания. То есть можно разделить
кабана на 19 одинаковых частей, 4 из которых отдать первому
охотнику, 6 — второму и 9 — третьему.
3. Последовательность независимых испытаний.
Схема Бернулли
Пусть в результате некоторого опыта событие А происходит с
вероятностью р и не происходит с вероятностью q = 1 - р. Пусть, далее,
наступление события А в одном из таких опытов не зависит от
наступления или ненаступления события А в другом таком же опыте.
Примером такого опыта является подбрасывание монетки.
Выпадение герба или решки при одном подбрасывании никак не связано
с выпадением герба или решки в другом подбрасывании.
Произведём п одинаковых опытов подряд и выясним, какова
вероятность того, что событие А в этих опытах произойдёт ровно k раз.
Получившееся в таких предположениях вероятностное пространство
называют схемой Бернулли.
Каким образом событие А может произойти k раз? Например,
событие А происходит в первых k опытах и не происходит в оставшихся
п — k опытах. Вероятность этого равна pkqn~k (поскольку все события
независимы и требуется найти вероятность совместного наступления
п событий). Также событие А может произойти в последних k
опытах и не произойти в первых п — k опытах. Вероятность этого также
равна pkqn~k. При этом два описанных события (наступление
события А в первых k опытах и наступление события А в последних k
опытах) несовместны. Поэтому вероятность наступления хотя бы одного
из этих двух событий равна сумме их вероятностей, т. е. 2pkqn~k. Но
есть и ещё возможности событию А произойти k раз. Всего таких
возможностей С* (количество способов выбрать k номеров опытов,
заканчивающихся наступлением события А), и вероятность реализации
каждой из таких возможностей равна pkqn ~ k. Таким образом,
вероятность наступления события А ровно в каких-то k испытаниях равна
Cknpkqn~k.
2891 § 74. Условная вероятность. Независимые события
Другой способ вычисления этой вероятности состоит в
рассмотрении пространства элементарных событий в виде
последовательностей 0 и 1, где 0 соответствует ненаступлению события А, а 1 —
наступлению события А. Вероятность каждой последовательности из k
единиц и п - k нулей равна pkqn ~ к. Событие А состоит из всех таких
последовательностей, число которых равно Скп. Отсюда также
получаем, что вероятность наступления события А ровно в k опытах из п
равна Cknpkqn~k.
Полученная формула вероятности наступления события А ровно
k раз в п независимых одинаковых опытах называется формулой
Берну лли.
Пример 12. Стрелок попадает в мишень с вероятностью 0,9. Найдём:
а) вероятность того, что стрелок попадёт в мишень ровно 2 раза из
10 выстрелов; б) наиболее вероятное число попаданий в мишень из
10 выстрелов.
D а) По формуле Бернулли указанная вероятность равна
Cf0 • (0,9)2 - (0,1)8 = 0,0000003645.
б) Нужно выяснить, при каком k выражение pk = Cf0 • (0,9)* х
х (0,1)10 " k будет наибольшим. Для этого выясним характер
монотонности последовательности£>£. Проще всего поделить j^ нарк + 1. Если
полученное частное будет больше 1, то pk> pk + l, а иначе pk^Pk + i- Итак,
Pk Cio (0,9)*-(ОД)10-* k+1 ОД _ k+1
Pk+i dV1 (0,9)* + 1-(0Д)9-* 10- k 0,9 90- 9k'
k + 1
Сравним выражение — с 1. Перенесём 1 в левую часть и приведём
90 — 9k
* тх * №k - 89 л о
к общему знаменателю. Итак, необходимо сравнить с 0. С уче-
90 - 9k
том того что k < 10, получим, что данное выражение меньше 0 при
k < 9 и больше 0 при k = 9. Значит, р0 < р19 рг < р2> Р2 < Рз> •••» Ps < Ря
и при этом р9 > р10. Таким образом, наибольшим pk будет при k - 9.
Итак, наиболее вероятно попасть в мишень 9 раз.
Вероятность попасть 9 раз составляет
Cf0 • (0,9)9 - (ОД)1 = 0,387420489!. В
1 Конечно, такой точности в расчётах вероятности на практике не
требуется. Ведь знание вероятности попадания стрелка в мишень, по-видимому,
возникло из практики, а значит, подсчитано с некоторой точностью. Чтобы
получить эту вероятность из опыта с точностью до девятого знака, нужно
произвести порядка 1018 опытов, т. е. выстрелов, что наверняка не было
проделано. Точность вычисления найденной вероятности не может быть выше,
чем точность определения вероятности попадания стрелка в мишень.
290! Глава ХМ. Элементы теории вероятностей
Формула полной вероятности
1. Вывод формулы полной вероятности
Пусть имеются п попарно несовместных событий В19 Б2, ..., Вп,
дающих в объединении всё пространство элементарных событий
(иначе говоря, эти события сами могут считаться элементарными). Такая
система событий иногда называется полной системой событий.
Поскольку для любого события А имеют место равенства
А = А П П = А П (Вг U Б2 U ... U Вп) = (А П Бх) U (А П Б2) U ... U (А П Б„),
причём объединяются попарно несовместные события, то
р(А)=р(А ПВг)+р(А ПБ2) + ... + р(А ПВП).
Применив к каждому слагаемому формулу (2), получаем
р(А)=р(А\В1) • p(Bt) + р(А\В2) ■ р(В2) + ... +р(А\Вп) .р(Вп) (3)
Полученная формула называется формулой полной вероятности.1
2. Примеры применения формулы полной вероятности
Пример 13. В одной из двух одинаковых коробок лежат 8 белых
и 12 чёрных шаров, а в другой коробке — 11 белых и 13 чёрных
шаров. Найдём вероятность того, что, при выборе коробки наугад и
случайном извлечении из выбранной коробки шара, извлечённый шар
окажется белым.
П Пусть событие Вг — «выбрана первая коробка», событие Б2 —
«выбрана вторая коробка». Пусть событие А — «извлечён белый шар».
Тогда р(В1)=р(В2) = 0,5, р(А\В1) = -^, р(А\В2) = ^. Отсюда
о 11109
р(А) = piAlBJ ■ р(Бх) + р(А\В2) ■ р(В2) = 0,5 • ^ + 0,5- ±± = |g. В
Пример 14. В телеграфной линии передают сигналы «точка» и «тире».
Из-за помех на линии четверть всех сигналов «точка» доходит как
сигнал «тире», а треть всех сигналов «тире» доходит как сигнал «точка».
При этом количество посылаемых точек в 6 раз больше количества
посылаемых тире. Найдём вероятность принять сигнал «точка».
О Пусть событие Аг — «послан сигнал „точка"», событие А2 —
«послан сигнал „тире"». Событие Б — «принят сигнал „точка"».
Поскольку система событий Аг и А2 полная, по формуле полной вероятности
имеем:
р(В)=р(В\А1)-р(А1)+р(В\А2)-р(А2). (*)
впервые в явном виде формулу полной вероятности записал П. С.
Лаплас.
2911 §75. Формула полной вероятности
Так как по условию количество посылаемых точек в 6 раз больше
количества передаваемых тире, получаем р(Аг)=—; р(А2)=—. Теперь
О
по условию р(В\Аг)= - (четверть сигналов искажается, а три четверти
доходят нормально), р(В\А2)= — (треть всех сигналов «тире» доходят
3
как сигнал «точка»). Подставим найденное значение в формулу (*)
29
и получим р(В) = —. Условие задачи предполагает, что сигналы не
пропадают по пути, поэтому если не пришёл сигнал «точка», то
пришёл сигнал «тире». Итак, вероятность принятия сигнала «тире»
равна1-р(В)=±|. И
Рассмотрим более сложный пример на применение формулы
полюй вероятности.
Пример 15. Двое игроков играют в игру без ничьих. Изначально
у одного из них а рублей, у другого в наличии Ь рублей. В каждой
партии проигравший игрок отдаёт выигравшему 1 рубль. Игра
заканчивается, когда у одного из игроков заканчиваются деньги.
Какова вероятность выигрыша каждого игрока, если в каждой партии
первый игрок выигрывает с вероятностью р, а проигрывает с
вероятностью 1 - р — ср.
П Обозначим рп вероятность выиграть первому игроку, если у него
имеется п рублей. Очевидно, что р0 = 0, ра + b = 1. Пусть у первого
игрока перед очередной партией п рублей. Вероятность выиграть первому
игроку с этой суммой равна рп. Рассмотрим результат очередной
партии. По формуле полной вероятности рп = рп _ xq + рп + ^р (ведь
вероятность выигрыша всей игры после проигрыша партии равна рп_х, а
вероятность проигрыша партии равна q, вероятность выигрыша всей
игры после выигрыша партии равна р„ + 1, а вероятность выигрыша
партии равна р).
Осталось вывести формулу рп на основании полученной формулы и
условий р0 = 0, ра + ь = 1. Рассмотрим формулу рп - рп _ xq + рп + &.
Запишем её в виде: qpn - qpn_г= ррп + 1 — ррп (здесь мы используем то, что
р + д= 1). Итак, q(pn-pn. i) = р(рп + г - рп). Обозначим sn=pn-pn_l.
Тогда формула приобретёт вид qsn = psn + 1# Иначе говоря, sn + 1= — sn.
Таким образом, последовательность {sn} является геометрической прогрес-
Q
сиеи со знаменателем —.
Р
Имеет место формула
Pn=Po + sx + ... + sn. (**)
292; Глава XII. Элементы теории вероятностей
Осталось применить формулу суммы геометрической прогрессии,
не забыв рассмотреть отдельно случай знаменателя прогрессии,
равного 1, для которого эта формула неприменима (напомним, что р0 = 0).
1) Итак, если р = q, то все члены последовательности {sn} равны s.
Члены последовательности {sn} можно найти, исходя из формулы (**)
и условий р0 = 0, ра + ь=1. Из формулы (**) pn = ns, откуда ра + ь =
= (а + &)s, и значит, s = . Нас интересует ра — вероятность победы
а + b
первого игрока, имеющего а рублей: ра = . Аналогично можно по-
а + b
Ъ
казать, что вероятность выигрыша второго игрока равна .
а + b
Из полученных результатов можно сделать два вывода.
а) Сумма вероятностей выигрыша первого и второго игроков равна 1.
Это означает, что игра закончится с вероятностью 1, несмотря на
то что можно легко представить себе бесконечную игру, например,
если каждую партию выигрывает не тот, кто выиграл предыдущую.
Тем не менее вероятность такой бесконечной игры равна 0.
б) При одинаковом мастерстве игроков вероятность выигрыша
пропорциональна их начальному капиталу.
- -1
р I
2) Пусть теперь р Ф q. Тогда st + ... + sn = sx ^—^ . Подставив
- -1
Р)
вместо п число а + Ь, получим sx -—^ = 1, откуда sx =
Таким образом, рп = —————. Подставив п = а, получим ра = ——'—
Аналогично можно найти вероятность выигрыша второго игрока
(сделайте это самостоятельно). В
3. Формула Байеса
Пусть имеется полная система событий В19 В2, ..., Вп и
вероятности этих событий известны. Событие А таково, что известны условные
вероятности р(А\Вг), р(А\В2), ..., р(А\Вп). Согласно формуле полной
вероятности вероятность события А равна
р(А)=р(А\В1) ■ piBJ + р(А\В2) • р(В2) + ... +р(А\Вп) • р(Вп).
293; §75. Формула полной вероятности
Часто представляет интерес нахождение вероятностей событий В19
В2, ..., Вп, если известно, что событие А произошло. Например, если
орудие стреляет по противнику и вдруг на стороне противника
произошёл сильный взрыв, то весьма велика вероятность того, что взрыв
произошёл, например, из-за попадания в склад боеприпасов. Здесь
событие А — «произошёл сильный взрыв», событие В1 — «произошло
попадание», событие В2 — «не произошло попадание». Сами по себе
вероятности событий Вл и В2 могут быть, например, равны по 0,5 (если
стрельба ведётся наугад), однако знание того, что произошло
событие А, резко повышает уверенность в том, что произошло именно
событие Вг.
Таким образом, речь идёт о необходимости вычисления условных
вероятностей р (Вг | А), р (В21 А), ..., р (Вп | А).
Поскольку р(Ви\ А) = = , то, подставив вы-
р(А) р(А)
ражение р(А) (по формуле полной вероятности), приходим к
следующей формуле:
(В |А) = p(A\Bk).p(Bk)
...+ р(Л|В„).
Эта формула носит название формула Байеса.
дорический комментарий
Томас Байес (1702—1761) родился в Лондоне. Обучался дома, затем по-*
ступил в Эдинбургский университет. Байес помогал отцу-священнику
проводить службу, а вскоре, в 30-х гг. XVIII в., сам стал священником в
пресвитерианской церкви. В 1752 г. он вышел в отставку.
Т. Байес много занимался наукой и в 1742 г. стал членом Лондонского
Королевского общества. Работа, содержавшая рассуждения, которые можно
интерпретировать как формулу Байеса, была напечатана уже после его
смерти. Именно Т. Байес ввёл термин «несовместные события».
Пример 16. Имеются две коробки с шариками. В одной из них 20
белых и 3 чёрных шарика, а в другой — 7 белых и 16 чёрных шариков.
Наугад выбирается коробка, а из нее наугад выбран шарик, который
оказался белым. Найдём вероятность того, что шарик был выбран из
первой коробки.
D Пусть событие А — «выбран белый шарик».
Событие Вх — «шарик выбран из первой коробки».
Событие В2 — «шарик выбран из второй коробки».
Тогда р(А\Вг) = Ц, р(А\В2)= ^, р(Вг) = р(В2) = \.
294! Глава XII. Элементы теории вероятностей
По формуле Байеса р(Вг\А) = -
20 1
23 2 20
1 + _7_.1 27
23 " 2 23 " 2
Ответ: вероятность того, что белый шарик был выбран из первой
коробки, равна —. Ш
л (
Полученный ответ вполне согласуется со здравым смыслом. Если
большая часть белых шариков находится в первой коробке, то
появление белого шарика с большой долей уверенности означает, что шарик
был взят именно из первой коробки.
О 76- Геометрическая вероятность
1. Определение геометрической вероятности
Зачастую многие задачи практики приводят к необходимости
рассмотрения событий, множество исходов которых может
интерпретироваться как некоторое множество точек прямой, плоскости или
пространства.
Пример 17. а) Упоминавшееся в § 73 измерение длины гусеницы
является событием, множеством исходов которого служит отрезок [3; 6].
б) Стрелок стреляет в мишень. Множеством исходов служит
множество точек мишени (если считать, что стрелок наверняка попадает
в мишень, и пренебречь размерами пули).
в) Опытом является определение местоположения отмеченной
молекулы в сосуде. Множеством исходов является множество точек
сосуда, если размерами молекулы можно пренебречь. Ш
ОПРЕДЕЛЕНИЕ ———-———————————————
Пусть множество Q точек на прямой, плоскости или в
пространстве, имеющее меру (т. е. соответственно длину,
площадь или объём), может быть интерпретировано как
множество всех исходов некоторого опыта. Рассматриваются
события, являющиеся подмножествами Q, имеющими меру.
Если вероятность наступления события пропорциональна
его мере (т. е. длине, площади или объёму), то говорят, что
на Q задана геометрическая вероятность.
Например, если наугад бросать точку на отрезок АВ длины 2, то
геометрическая вероятность попадания точки на отрезок CD длины 1
не зависит от того, где именно на отрезке АВ находится отрезок CD.
Более того, эта вероятность равна вероятности попадания точки в про-
Ид § 76. Геометрическая вероятность
извольное множество, состоящее из непересекающихся отрезков
суммарной длины I1, лежащих на отрезке АВ.
Чтобы каждый раз не писать «длина, площадь или объём»
применительно к мере множества (т. е. не рассматривать три формулы
геометрической вероятности для различных размерностей множества Q),
условимся обозначать mes А соответствующую меру множества А (от
французского «mesure» — мера). Если А — подмножество прямой
(или какой-либо кривой), имеющее длину, то mes A — это длина
линии А. Если А — плоская фигура, имеющая площадь, то mes A — это
площадь фигуры А. Если же А — множество точек пространства,
имеющее объём, то mes A — это объём фигуры А.
По определению геометрической вероятности р(А) = kmesA, где
k — коэффициент пропорциональности, не зависящий от события А.
Чтобы найти k, используем естественное соображение о том, что
р(п) = 1. Имеем 1 = femesQ, откуда k = —.
mes £2
Таким образом, имеет место формула геометрической вероятности:
mes A
р(А) =
mes Q
Пример 18. В круг радиуса 1 вписан квадрат. Наудачу в круг кидают
точку. Найдём вероятность того, что она попала в квадрат.
D В данном случае множеством Q является круг и mes fl = п.
Множеством А является квадрат и mes A = 2. Тогда искомая вероятность
- mes A 2 ,-,
будет равна = —. ш
mesQ я
Пример 19. Палку длины 1 наугад распиливают на три части. Найдём
вероятность того, что из этих частей можно составить треугольник.
□ Пусть событие А — «из полученных частей можно сложить
треугольник».
хКак и в случае определения вероятности событий с конечным числом
исходов, далеко не всегда вероятность события, интерпретируемого как
множество точек, пропорциональна мере этого события. Например, вероятность
нахождения какого-либо полезного ископаемого в почве вовсе не
пропорциональна объёму переработанной почвы. На величину этой вероятности влияет
множество факторов, в том числе наличие тех или иных сопутствующих
пород. Фактически некоторые геологические заключения можно
интерпретировать так: «Если в породе встретился минерал А, то вероятность в этой же
породе найти минерал В существенно выше, нежели в противном случае».
Точно так же найти монетку гораздо вероятнее на тех частях суши, где
обитают люди, т. е. вероятность найти монетку на данном участке земной
поверхности существенно зависит не только от его размеров, но и от его
местонахождения. Однако изучение таких вероятностей выходит далеко за рамки
нашего учебника.
296! Глава XII. Элементы теории вероятностей
х 1-х-у у способ 1. Пусть две части (например,
! ' содержащие края отрезка) имеют длины х
Рис. 12.2 л у (рис. 12.2). Тогда третья часть имеет
длину 1 - х — у. Тем самым указание длин
первых двух частей однозначно задаёт длину третьей части, полностью
задавая исход опыта. Таким образом, исход опыта можно
интерпретировать как точку на координатной плоскости с координатами (х; у).
Нарисуем множество всех возможных исходов. Ясно, что обе
величины х и у неотрицательны и их сумма должна не превосходить
длины отрезка. С другой стороны, любые два неотрицательных числа,
сумма которых не превосходит 1, могут служить длинами двух
данных частей исходного отрезка, разбитого на три части.
Поэтому каждой точке множества Q, заданного на координатной
плоскости системой неравенств
I у > 0,
[
соответствует способ разломать
х
единичный отрезок на три части. В то же время каждому способу
разломать единичный отрезок на три части
соответствует точка множества £2. Поэтому можно
говорить о том, что результаты нашего опыта
изображаются (интерпретируются)
множеством ft (рис. 12.3).
Теперь рассмотрим, каким множеством
изображается событие А. Как известно из
курса планиметрии, из трёх отрезков
можно сложить треугольник тогда и только тогда,
когда любой из отрезков меньше суммы двух
оставшихся. Запишем эти условия в виде сис-
1х< у Л-1- х- у,
у < х + 1- х- у, Эта сис-
1-х- у < х + у.
[х<0,5,
тема равносильна следующей < у < 0,5,
[х + у >0,5.
Множество точек, координаты которых
удовлетворяют данной системе, показано на
рисунке 12.4.
Искомая вероятность будет равна
отношению площади треугольника,
изображающего А у к площади треугольника,
изображающего Q, т. е. 0,25. Ответ: вероятность
получения треугольника равна 0,25.
Рис. 12.3
1 х
§ 76. Геометрическая вероятность
способ 2. Пусть хну — расстояния от
точек распила до левого края отрезка '< ' >'
(рис. 12.5). Тогда пара чисел 0 ^ х ^ 1 и У
0 ^ у ^ 1 однозначно задаёт исход опыта, Рис. 12.5
и, наоборот, каждому исходу опыта можно
поставить в соответствие единственную пару чисел, каждое из
которых лежит в отрезке [0; 1].
Интерпретируя пару чисел как координаты точки на плоскости,
можно изобразить множество возможных исходов Q в виде единичного
квадрата.
Длины полученных частей отрезка будут равны min(jc; у), \х — у\,
1 -тах(х; у).
Чтобы из отрезков с такими длинами можно было сложить
треугольник, необходимо и достаточно, чтобы любой из отрезков был
меньше суммы двух других.
Пусть х ^ у. Тогда отрезки, на которые разбит исходный отрезок,
будут равны х, у - хн1 - у. Чтобы из этих отрезков можно было
составить треугольник, необходимо и достаточно выполнения системы не-
1х <1— у + у — х,
у — х < х + 1 — у, т. е. системы
1-у<х + у-х,
\х<0Л
\у < х + 0,5,
Аналогично в случае у ^ х для
возможности построения треугольника
необходимо и достаточно выполнения
системы неравенств
\у > х- 0,5,
[*/<0,5.
Таким образом, множество точек, изображающих событие А, —
это объединение двух прямоугольных равнобедренных треугольников,
взятых без границы (рис. 12.6). Суммарная площадь таких
треугольников равна 0,25, а площадь квадрата, изображающего Q, равна 1.
Поэтому искомая вероятность равна 0,25. Ш
Отметим, что в обоих решениях мы считали интуитивно ясным,
что вероятность можно вычислять как геометрическую, т. е. что
вероятность события пропорциональна мере изображающего его
множества. Никаких доказательных соображений на эту тему приведено
не было!
У i
1-
0,5-
0
/
л
0
/
,5
/
S
s
1 х
Рис, 12.6
298 Глава XII. Элементы теории вероятностей
2. Парадокс Бертрана
«Интуитивный» подход к геометрической вероятности может
привести к парадоксальным следствиям.
Пример 20 (парадокс Бертрана). Наугад берётся хорда окружности.
Найдём вероятность того, что длина этой хорды больше длины
стороны правильного треугольника, вписанного в данную окружность.
П Обозначим за А событие, состоящее в том, что хорда оказалась
длиннее стороны правильного треугольника, вписанного в данную
окружность.
способ 1. Длина хорды окружности данного радиуса зависит от
расстояния от центра окружности до данной хорды. Расстояние от
центра окружности радиуса R до хорды может быть равным любому
числу от 0 до /?.
Очевидно, что расстояние от центра окружности до стороны равно-
R
стороннего треугольника, вписанного в данную окружность, равно —.
R
Если расстояние от центра до хорды больше —, то хорда будет короче
стороны вписанного правильного треугольника, а если меньше, то
хорда будет длиннее. Таким образом исходом опыта является число, равное
расстоянию от центра окружности до хорды, мно-
q жество возможных исходов изображается
отрезком длины Д, а событие А — отрезком длины —,
а потому искомая вероятность равна — : R = -.
способ 2. Можно заранее закрепить один из
концов хорды на окружности. Тогда хорда CD
будет длиннее стороны вписанного правильного
треугольника, если другой её конец попадает на
дугу АВ, отмеченную на рисунке 12.7. Положение
хорды полностью определяется положением
точки D, поэтому множество всех возможных исходов
изображается данной окружностью, а событие А —
дугой АВ. Искомая вероятность равна отношению
длины дуги АВ к длине окружности, т. е. —.
3
способ з. Длина хорды определяется
положением её середины. Чтобы хорда была длиннее
стороны вписанного правильного треугольника,
необходимо и достаточно, чтобы середина хорды
R
находилась в круге радиуса —, концентрическом
с данной окружностью (рис. 12.8). Таким образом,
множество возможных исходов изображается кру-
Рис. 12.7
299[ § 76. Геометрическая вероятность
гом, ограниченным исходной окружностью, а событие А — кругом
вдвое меньшего радиуса. Тогда искомая вероятность равна отношению
1
площадей этих кругов, т. е. —.
4
В чём же причина таких результатов? Причина в
неопределённости понятия «наугад» в формулировке задачи.
В самом деле, в первом решении под словом «наугад»
подразумевается «наугад может быть выбрано любое расстояние до центра
окружности, причём вероятность выбора расстояния из данного отрезка
пропорциональна длине отрезка». Во втором решении под словом
«наугад» подразумевалось «наугад может быть выбрана любая точка
на окружности, причём вероятность выбора точки на дуге
пропорциональна длине дуги». А в третьем решении «наугад» означает «наугад
может быть выбрана любая точка внутри круга, причём вероятность
выбора точки в данной фигуре пропорциональна площади фигуры».
Ясно, что на самом деле в каждом из решений речь шла о своей
задаче. Щ
торический комментарий
Жозеф Луи Франсуа Бертран (1822—1900) — известный французский
математик, экономист и историк науки. Ж. Бертран прослушал курс
Политехнической школы в качестве вольнослушателя, затем стал победителем
конкурса по математике, проводимого в Политехнической школе. Его основные
работы относятся к математической теории электричества, теории
вероятностей и теории чисел. В частности, Ж. Бертран в 1845 г. впервые высказал
гипотезу о том, что между числами п и 2л - 2 (при п > 3) лежит хотя бы одно
простое число. Это утверждение получило название постулата Бертрана, но
в 1850 г. было доказано великим русским математиком П. Л. Чебышёвым.
Однако название «постулат Бертрана» в литературе сохраняется до сих пор.
Рассмотренный выше парадокс Ж. Бертран приводил как обоснование
того, что в событиях с бесконечным множеством исходов нельзя дать
объективного определения вероятности.
Об истории развития теории вероятностей
В течение достаточно долгого времени изучение случайных
явлений сводилось к рассмотрению азартных игр, особенно игры в кости.
В X—XI вв. было определено количество исходов при бросании трёх
кубиков.
В знаменитой книге Л. Пачоли (1445—1514) «Сумма знаний по
арифметике, геометрии, отношениям и пропорциональности» приведено
несколько задач о разделе ставки при прекращении игры до её окончания.
К этим же задачам обращается и Н. Тарталья в книге «Трактат
о мере и числе».
300 Глава XII. Элементы теории вероятностей
Следующим этапом была «Книга об игре в кости» знаменитого
итальянского учёного Д. Кардано (1501—1575). В этой книге в
некоторых частных случаях Д. Кардано ввёл то, что мы назвали
классическим определением вероятности.
Интересными являются также результаты, сформулированные
в книге «О выпадении очков при игре в кости» Г. Галилея (1564—1642),
вышедшей почти через 100 лет после его смерти. Существует легенда,
что Г. Галилей решил так называемую «задачу ландскнехта» (хп.12).
В другой своей книге «Диалог о двух главнейших системах мира»
Галилей также впервые исследовал вопрос об обработке результатов
наблюдений, чем заложил основы современной статистики.
Основы теории вероятностей в современном виде заложили
великие французские учёные Б. Паскаль (1623—1662) и П. Ферма (1601—
1665). В их переписке впервые верно решена задача о разделе ставки.
Следующий толчок развитию теории вероятностей дал великий
голландский учёный X. Гюйгенс (1629—1695). В своей работе «О
расчётах в азартных играх» и других статьях X. Гюйгенс ввёл важные
понятия, относящиеся к теории случайных величин.
Само классическое определение вероятности дано в знаменитой
книге Я. Бернулли (1654—1705) «Искусство предположений». Там же
предложены и подходы к статистическому определению вероятности
как предельной частоте исходов, благоприятствующих данному
событию, а также дана формулировка закона больших чисел.
Дальнейшее развитие теории вероятностей связано с именем
английского математика А. деМуавра (1667—1754), известного нам своей
формулой возведения в степень и извлечения корня из комплексных чисел.
Муавр впервые сформулировал классическое определение вероятности
в современном виде, а также доказал предельную теорему Муавра —
Лапласа, призванную давать приближённое значение вероятностей,
вычисленных по формуле Я. Бернулли при большом числе независимых
испытаний.
Классической книгой, не утратившей своего значения и сегодня,
является «Аналитическая теория вероятностей» П. Лапласа (1749—1827),
с именем которого мы уже встречались ранее. По иронии судьбы сам
П. Лаплас считал, что если известны скорости всех тел и силы, на них
действующие в данный момент времени, то принципиально возможно
полностью рассчитать состояние Вселенной в любой другой момент
времени. Таким образом, теория вероятностей нужна, по мнению П.
Лапласа, лишь постольку, поскольку в распоряжении исследователя нет
достаточных вычислительных мощностей, чтобы, к примеру,
определить средствами механики, какой гранью упадёт подброшенный кубик.
Большую роль в развитии теории вероятностей сыграл
выдающийся русский учёный П. Л. Чебышёв (1821—1894), в 1867 г.
сформулировавший закон больших чисел в формулировке, существенно
уточнённой по сравнению с формулировкой Я. Бернулли.
Понятие случайной величины стало формироваться в связи с
анализом ошибок при измерениях величин. С теми или иными разновидно-
301 Задачи и упражнения
стями случайных величин, не выделяя этого понятия отдельно,
оперировали Я. Вернул ли, П. Лаплас, К. Гаусс и многие другие математики.
По-видимому, первым выделил случайную величину как отдельное
понятие французский физик и математик С. Пуассон (1781—1840). Сами
слова «случайная величина» впервые встречаются в работах ученика
П. Л. Чебышёва, российского математика А. М. Ляпунова (1857—1918).
Основополагающая роль в развитии теории вероятностей, сравнимая
с ролью Евклида в развитии геометрии, принадлежит нашему
соотечественнику, великому математику А. Н. Колмогорову (1903—1987),
который в своей знаменитой работе «Основные понятия теории
вероятностей», опубликованной в 1933 г., сформулировал аксиомы теории
вероятностей, которые поставили её в один ряд с остальными разделами
математики. Тем самым А. Н. Колмогоров избавил теорию
вероятностей от некоторого налета «сомнительности», сопровождавшего её до
появления указанной работы.
Исследования в области квантовой механики показали, что
понятие вероятности лежит в основе строения мира, а все существующие
закономерности являются, по большому счету, вероятностными. Эти
исследования радикально изменили взгляд на теорию вероятностей,
и сегодня никому не придёт в голову заявлять о какой-либо «второ-
сортности» теории вероятностей.
В развитии теории вероятностей сыграли свою роль многие
российские учёные, в том числе А. Я. Хинчин (1894—1959), Ю. В. Линник
(1915—1972), Б. В. Гнеденко (1912—1995), Ю. В. Прохоров (род. 1929)
и многие другие.
И Задачи и упражнения
Виды событий
Группа А
ХП.1. Приведите по три примера: а) достоверных событий; б)
невозможных событий; в) случайных событий.
ХП.2. Будет ли достоверным событием: а) выпадение на двух
игральных кубиках в сумме 6 очков; б) выпадение на двух игральных
кубиках в сумме от 2 до 12 очков?
ХП.З. Является ли невозможным событием: а) выпадение на трёх
игральных кубиках в сумме 18 очков; б) выпадение на трёх игральных
кубиках в сумме 2 очков?
Пространство элементарных событий
Группа А
XII.4. Опишите пространство элементарных событий для следующих
опытов: а) бросание двух игральных кубиков; б) вытаскивание
двух игральных карт подряд из колоды в 36 карт; в) извлечение
одной кости домино; г) 4 раза подбрасывают монетку.
302 Глава XII. Элементы теории вероятностей
XII.5. Укажите все возможные исходы следующего опыта: а)
шахматная партия; б) волейбольный матч.
XII.6. Образуют ли пространство элементарных событий совокупность
следующих исходов при двух выстрелах в мишень: а) «два
раза 10», «один раз 10», «ни одного раза 10»; б) «два раза 10»,
«один раз 10», «один раз 9»; в) «два раза 10», «один раз 10», «два
раза 9»; в) «два раза 10», «один раз 9», «один раз 8», «два раза
меньше 8»?
XII.7. Рассматриваются 4 станка, каждый из которых может либо
работать, либо не работать.
а) Перечислите все элементы какого-либо пространства
элементарных событий Q.
б) Приведите пример двух событий А и В, объединение
которых даёт Q, а пересечение содержит только один элемент Q.
в) Пусть событие А — «работают ровно три станка»,
событие В — «работает хотя бы один станок». Сформулируйте
словесно события A U В, В\А.
XII.8. Двое шахматистов играют партию. Событие А — «выиграл
первый шахматист», событие В — «выиграл второй шахматист».
Какие события нужно добавить к событиям А и В, чтобы
получилось пространство элементарных событий?
Определение и свойства вероятности
Группа А
XII.9. Жулик испортил игральный кубик так, что вероятность
выпадения шести очков втрое меньше, чем вероятности выпадения
любой из остальных граней. Найдите вероятность выпадения:
а) каждой грани; б) чётного числа очков; в) больше трёх очков.
XII. 10. Жулик испортил кубик так, что вероятность выпадения числа
обратно пропорциональна этому числу. Найдите вероятность
выпадения: а) каждой грани; б) чётного числа очков; в) больше
трёх очков.
Классическое определение вероятности
Груп па А
xil.ll. 18 команд разбились на две группы по 9 команд в каждой.
Найдите вероятность события: а) «две заданные команды попали
в одну группу»; б) «три заданные команды не попали в одну
группу».
хп.12. (Задача ландскнехта.) Бросаются три игральные кости. Что
вероятнее: получить в сумме выпавших очков 11 или 12?
ХИ.13. (Задача кавалера де Мере.) Что вероятнее: при бросании 4 кубиков
хотя бы на одном получить шесть очков или при 24 бросаниях
двух костей хотя бы один раз получить два раза по шесть очков?
Задачи и упражнения
ХИ.14. Собрание сочинений в 6 томах стоит на полке в произвольном
порядке. Какова вероятность того, что оно стоит в правильном
порядке слева направо?
ХН.15. Из колоды в 36 карт вынуты наудачу три карты. Какова
вероятность того, что среди вынутых карт: а) будет ровно один туз;
б) будет ровно два туза; в) будет три туза; г) ответьте на те же
вопросы, если три карты вынимаются одна за другой и каждый
раз возвращаются в колоду.
ХИ.16. Деревянный куб, все грани которого окрашены, распилили на
1000 одинаковых кубиков, которые сложили в мешок. Какова
вероятность наугад вытащить из мешка: а) кубик ровно с одной
окрашенной гранью; б) кубик ровно с двумя окрашенными
гранями; в) кубик ровно с тремя окрашенными гранями?
ХП.17. Из колоды подряд извлекаются две карты. Какова вероятность
того, что обе карты будут одной масти?
ХИ.18. Какова вероятность при последовательном извлечении трёх
карт из колоды вытащить: а) тройку, семерку, туза в любом
порядке; б) именно в таком порядке?
ХП.19. Колоду в 36 карт делят на две части по 18 карт. Какова
вероятность того, что в обеих частях окажется поровну карт с
красными и чёрными мастями?
ХИ.20. Из полного набора костей домино извлекают случайным
образом пять костей. Какова вероятность того, что среди этих костей
будет хотя бы одна с шестью очками, если: а) кости
извлекаются и не возвращаются; б) кости извлекаются с возвращениями?
ХИ.21. Имеются пять отрезков, длины которых равны 1, 2, 3, 4, 5.
Какова вероятность того, что: а) из трёх наугад выбранных
отрезков можно составить треугольник; б) из четырёх наугад
выбранных отрезков найдутся три, из которых можно составить
треугольник?
ХП.22. Наугад последовательно выбираются четыре карточки, которые
выкладываются слева направо. Какова вероятность, что
получится чётное число, если карточки выбираются из: а) девяти
карточек, ровно на одной из которых написана каждая из цифр
1, 2, 3, ..., 9; б) неограниченного количества карточек с каждой
цифрой от 1 до 9; в) набора из 18 карточек, содержащего по
2 карточки с каждой из цифр от 1 до 9?
ХИ.23. В наборе содержатся по одной карточке с цифрами от 1 до 8
и некоторое количество карточек с цифрой 9. Наугад
последовательно вытаскиваются три карточки, которые выкладываются
слева направо, образуя запись трёхзначного числа.
а) Сколько в наборе карточек с цифрой 9, если вероятность
получить чётное число равна 0,25?
б) Может ли вероятность получить нечётное число быть
равной 0,4?
3041 Глава XII. Элементы теории вероятностей
ХИ.24. В ящике лежат 100 одинаковых деталей, 10 из которых
бракованные. Какова вероятность того, что среди вынутых наугад
10 деталей не будет ни одной бракованной? Сравните
полученную вероятность с числом 0,5.
ХП.25. Некто забыл номер телефона, состоящий из 7 цифр.
1) Какова вероятность того, что он вспомнит номер с первой
попытки, если:
а) помнит все цифры (и все цифры в номере телефона разные),
но не помнит их порядок;
б) помнит все цифры, кроме одной, и знает, что все они
различны, но не помнит порядка цифр;
в) помнит, что в номер не входили никакие цифры, большие 6,
но не помнит, повторялись ли цифры или нет?
2*) Ответьте на те же вопросы, если на вспоминание номера
даётся 10 попыток.
Группа В
ХП.26. Двое игроков А и В играют в игру «камень-ножницы-бумага».
Каждый показывает одну из этих фигур, причём фигуры
показываются одновременно. Показавший «ножницы» выигрывает
у показавшего «бумага», показавший «камень» выигрывает
у показавшего «ножницы», показавший «бумага» выигрывает
у показавшего «камень». Все остальные результаты считаются
ничейными.
а) Постройте пространство элементарных событий для
описанной игры, к которому было бы разумно применить
классическое определение вероятности.
б) Какова вероятность того, что игра закончится не с ничейным
результатом?
в) Какова вероятность того, что игру выиграет игрок А?
ХП.27. В классе 5 девочек и 16 мальчиков. Случайным образом
выбирают трёх учеников этого класса. Найдите вероятность того, что
среди выбранных учеников будут: а) одни мальчики; б) одна
девочка и два мальчика; в) один мальчик и две девочки;
г) одни девочки; д) дети обоих полов; е) дети одного пола;
ж) хотя бы одна девочка; з) хотя бы два мальчика.
Группа С
XII.28. Ученик знает ответы не на все из 16 вопросов зачёта.
а) Сколько вопросов он выучил, если вероятность того, что он
сможет ответить на оба из случайно выбранных им вопросов, не
меньше — ?
о
б) Сколько вопросов он выучил, если вероятность того, что он
сможет ответить только на один из случайно выбранных им
сразу двух вопросов, равна 0,5?
3051 Задачи и упражнения
в) В каком случае вероятность того, что он сможет ответить на
один случайно выбранный им вопрос, больше, чем вероятность
того, что ему удастся ответить на два (по его выбору) из
случайно выбранных им трёх вопросов?
г) Учитель распределил вопросы случайным образом по восьми
билетам (по два вопроса в каждом). Какова вероятность того,
что ученик в состоянии ответить хотя бы на один вопрос
каждого из билетов, если известно, что он подготовил ответы на
десять вопросов?
ХИ.29. Двое по очереди выбирают числа, по два натуральных числа
от 1 до п (уже выбранное число выбирать нельзя).
а) Какова вероятность того, что среди чисел, выбранных
первым, будет 1, а среди чисел, выбранных вторым, будет 2?
б) С какой вероятностью оба числа первого будут меньше обоих
чисел второго?
в) При п = 8 найдите вероятность того, что сумма чисел,
выбранных первым, будет меньше суммы чисел, выбранных вторым.
г) Пусть рп — вероятность того, что сумма квадратов чисел,
выбранных первым, меньше п2. Найдите limpn.
Условная вероятность
Группа А
ХП.ЗО. Чему равна р(А\А)? Чему равна р(А\А)? При каком условии
невозможно вычислить эти вероятности?
ХН.31. В ящике 10 белых и 12 чёрных шариков. Наугад: а)
одновременно; б) последовательно вынимают два шарика. Какова
вероятность, что эти шарики будут разных цветов?
ХИ.32. В ящике 10 белых и 12 чёрных шариков. Наугад вынимают
шарик и кладут обратно в ящик. После этого снова вынимают
шарик. Какова вероятность, что оба вынутых шарика будут
чёрными?
ХП.ЗЗ. Вероятность попадания стрелка в первую мишень равна 0,6.
Если он попал в первую мишень, то получает право стрелять во
вторую мишень, в которую попадает с вероятностью 0,5.
Какова вероятность попасть во вторую мишень (до того, как стрелок
стреляет в первую мишень)?
ХП.34. Пусть А и В два события с ненулевыми вероятностями. Пусть
р(А\В) >р(А). Докажите, что р(В\А) >р(В).
ХИ.35. Пусть р(А) = а, р(В) = Ъ. Докажите, что р(А \ В) > .
о
XII.36. Некто забыл последнюю цифру номера телефона и набирает её
наугад. Какова вероятность того, что ему понадобится сделать
не более двух звонков?
11—Пратусевич, 11 кл.
3061 Глава XII. Элементы теории вероятностей
XII.37. В ящике имеются белый и чёрный шары. Наугад извлекается
шар. Если извлечённый шар белый, его возвращают в ящик
и добавляют туда ещё два белых шара. Какова вероятность
извлечь чёрный шар: а) во второй раз; б) в четвёртый раз?
Груп па В
XII.38. Два стрелка стреляют по мишени до тех пор, пока один из них
не попадёт. Первый стрелок попадает в мишень с вероятностью
0,3, а второй — с вероятностью 0,4. Какова вероятность того,
что первый стрелок сделает больше выстрелов, чем второй?
XII.39. Двое игроков играют в игру «камень-ножницы-бумага» (см. хи.26)
две партии подряд.
а) Найдите вероятность выигрыша игрока А в обеих партиях,
если он выиграл первую партию.
б) Найдите вероятность выигрыша одной партии каждым
игроком, если первую партию выиграл игрок Б.
в) Найдите вероятность того, что игроки выиграют одинаковое
число партий.
Независимые события
Группа А
XII.40. Пусть А и В — независимые_события. Докажите независимость
событий: а) А и В; б) А и В.
XII.41. В ящике лежат один белый, один чёрный, один красный шары,
а также один шар, в окраске которого присутствуют полоски
всех трёх цветов. Наугад вытаскивают один шар. Событие А —
«вытащен шар, на котором есть белый цвет». Событие В —
«вытащен шар, на котором есть чёрный цвет», событие С —
«вытащен шар, на котором есть красный цвет».
а) Найдите вероятности событий А, Б, С.
б) Независимы ли события А и Б, Б и С, А и С?
в) Независимы ли события А и В Г) С?
г) Независимы ли события Б и A U С?
д) Независимы ли события С к А Г) В Г) С?
XII.42. Автомобильный номер состоит из трёх цифр и может
повторяться сколько угодно раз. Какова вероятность того, что из
номеров трёх подряд встреченных автомобилей:
а) все три номера будут кратны трём;
б) хотя бы два номера будут кратны трём;
в) два номера будут состоять из одних и тех же цифр?
XII.43. При прохождении рентгеновского контроля вероятность
обнаружения брака в детали равна 0,8. Какое наименьшее число раз
деталь должна пройти контроль, чтобы обнаруживать брак с
вероятностью, не меньшей 0,99?
ХИ.44. Детали изготавливают на двух станках. Вероятность того, что
деталь, изготовленная на первом станке, будет первосортной,
Щ_3адачи и упражнения
равна 0,7, а на втором — 0,9. На первом станке изготовили три
детали, а на втором — две детали. Какова вероятность того:
а) что все пять деталей первосортные;
б) четыре детали первосортные, а одна — второсортная;
в) ровно две детали второсортные;
г) не более трёх деталей первосортные?
ХИ.45. Двое по очереди бросают монету. Выигрывает тот, у кого
раньше появился герб.
а) Найдите вероятности выигрыша для каждого из игроков.
б) Решите ту же задачу, если игроков трое.
ХИ.46. Среди выпускников российских школ 24% не сдали ЕГЭ по
математике, 12% не сдали ЕГЭ по русскому языку, а а% не сдали
оба этих экзамена.
а) При а = 3 являются ли независимыми события «случайно
взятый ученик не сдал ЕГЭ по математике» и «случайно взятый
ученик не сдал ЕГЭ по русскому языку»?
б) Существует ли значение а, при котором события пункта а)
являются независимыми? При утвердительном ответе найдите
все такие значения а.
Последовательность независимых испытаний. Схема Бернулли
Группа А
ХИ.47. Двое играют в игру, вероятность выигрыша в каждой партии
которой для каждого из них равна 0,5. Что вероятнее: а) выиграть
три партии из четырёх или пять партий из восьми; б) не менее
трёх партий из четырёх или не менее пяти партий из восьми?
ХН.48. Определите наиболее вероятное число появлений события А
в десяти независимых испытаниях, если в каждом из них
событие А происходит с вероятностью —.
о
ХП.49. Два баскетболиста делают по три броска в корзину. Вероятность
попадания первого при каждом броске равна 0,7, а
второго — 0,8. Найдите вероятность того, что: а) у них будет поровну
попаданий; б) первый попадёт больше раз, чем второй.
ХП.50. Вероятность попадания стрелком в десятку равна 0,8, а в
девятку — 0,2.
а) Найдите вероятность того, что при трёх выстрелах стрелок
наберет не менее 28 очков.
б) Какое наименьшее число раз нужно выстрелить, чтобы хотя
бы один раз попасть в девятку с вероятностью, не меньшей 0,9?
Формула полной вероятности
Группа А
ХП.51. (Задача о разделе ставки.) Вероятность выигрыша партии в
запрещённой игре двух игроков равна 0,5 для каждого из них.
Игра состоит из определённого числа партий, но была прервана
и*
308 Глава XII. Элементы теории вероятностей
до окончания. При этом первому для выигрыша игры осталось
выиграть три партии, а второму — две партии. Как разделить
ставку в игре?
ХИ.52. Из полного набора костей домино извлекаются две кости.
Какова вероятность того, что их можно приставить одну к другой?
XIL53. В одном ящике лежат 6 белых и 13 чёрных шаров, а в другом
ящике — 8 белых и 11 чёрных шаров. Наугад берётся шар из
первого ящика и перекладывается во второй, а затем наугад из
второго ящика вытаскивается шар. Какова вероятность
вытащить белый шар?
ХП.54. В тире имеются три ружья, вероятности попадания из
которых равны 0,4; 0,5; 0,6. Найдите вероятность попадания, если
ружьё берётся наугад.
XII.55. В правом кармане находятся 3 монеты первого вида и 4 монеты
второго вида, а в левом — 6 монет первого вида и 5 монет
второго вида. Наугад переложили 5 монет из левого кармана в
правый, а затем из правого кармана извлекли монету. Какова
вероятность того, что извлечённая монета будет первого вида, если
монеты обоих видов одинаковы на ощупь?
Группа В
ХП.56. В вершине А куба ABCDA1B1C1D1 сидит муха, а в вершине Сг
находится капля клея. Если муха попала в клей, она остаётся там
навсегда. Муха ползёт по ребрам куба, поворачивая в вершине на
каждое из выходящих из вершины рёбер с вероятностью —.
3
а) Какова вероятность того, что муха побывает в вершине С за
первые четыре хода?
б) Какова вероятность того, что за первые десять ходов муха не
прилипнет?
в*) Пусть р(Х) — вероятность, выйдя из вершины X, когда-
нибудь попасть в вершину Сх. Докажите, что если X —
произвольная вершина куба, то р (X) = 1.
ХП.57. Некоторое устройство может находиться в одном из трёх
состояний а, &, с. Из каждого состояния устройство через секунду
переходит в одно из оставшихся состояний с вероятностью 0,5.
Пусть рп(х) (где х е {а, Ь, с}) — вероятность того, что через
п секунд устройство находится в состоянии х, если в начальный
момент оно находится в состоянии а.
а) Вычислите р3(а)> РзФ) и Рз(с)»
б) Может ли при некотором натуральном п вероятность рп(х)
(где х е {a, fe, с}) быть равной -?
3
в) Докажите, что limpn(^)= —.
П-+ОО 3
г*) Докажите, что lim — ]^С* = —.
п-+оо 2nAsi(mod3) 3
Задачи и упражнения
ХП.58. Найдите вероятность того, что при п бросаниях монеты герб
появится нечётное число раз, если: а) монета правильная; б)
монета искривлённая и герб выпадает в два раза чаще, чем решка.
Формула Байеса
Группа А
ХИ.59. В группе экзаменуемых 10 человек. Список экзаменационных
вопросов состоит из 20 вопросов, каждому экзаменуемому
предлагается ответить на 2 случайно выбранных вопроса. Известно,
что 5 учеников знают ответы на все вопросы (отличники), 3
ученика знают ответы на 10 вопросов (троечники), а остальные
двое знают ответы на 5 вопросов (двоечники).
а) Ученик, вошедший первым, ответил на оба вопроса. К какой
из трёх групп он принадлежит с наибольшей вероятностью?
б) Ученик, вошедший первым, ответил только на один вопрос.
Какова вероятность того, что он двоечник?
в) Первый вошедший ученик ответил на 2 вопроса, а второй —
на один вопрос. Какова вероятность того, что они оба
хорошисты? Какова вероятность того, что эти ученики были отличник
и двоечник?
ХИ.60. Три охотника стреляют по кабану. Вероятности попадания
охотников равны 0,5; 0,4; 0,6.
а) Кабан убит двумя пулями. Какова вероятность, что это были
пули первого и второго охотников?
б) В каких долях нужно разделить кабана, убитого двумя
пулями, если не удаётся определить, чьи это пули?
XII.61. На станке изготовлены 5 изделий. При проверке одного
изделия, взятого наугад, оно оказалось бракованным. Какое число
бракованных изделий среди изготовленных наиболее вероятно?
ХИ.62. В ящике имеются 10 шаров, причём каждый из них может
быть белым или чёрным с вероятностью 0,5 независимо от
другого. Наугад извлекли 5 шаров, причём каждый извлечённый
шар возвращался в ящик. Какова вероятность того, что в
ящике нет белых шаров, если все извлечённые шары — чёрные?
Геометрическая вероятность
Группа А
хн.63. В круг вписан равносторонний треугольник. Какова
вероятность того, что наугад брошенная в круг точка попадёт в
треугольник?
ХИ.64. В шар вписана правильная пирамида с прямыми плоскими
углами при вершине. Какова вероятность того, что наугад
брошенная в шар точка попадёт в пирамиду?
310 Глава XII. Элементы теории вероятностей
XII.65. Найдите вероятность того, что квадратное уравнение х2 + рх +
+ q = 0 имеет два различных вещественных корня, если
коэффициенты р и q наугад берутся из отрезка [-1; 1].
XII.66. Какова вероятность, взяв наугад три точки на окружности,
получить: а) тупоугольный треугольник; б) равнобедренный
треугольник?
хи.67. Наугад берутся два числа из отрезка [0; 1]. Какова вероятность
того, что их сумма будет больше 1, а произведение — мень-
ше|?
XII.68. В квадрате ABCD с единичной стороной закрашен треугольник
ABC. Закрасьте какую-либо фигуру так, чтобы события
«попадание в треугольник ABC» и «попадание в закрашенную
фигуру» были: а) независимы; б) равновероятны; в) равновероятны
и независимы.
ХИ.69. Наудачу выбирается число х из отрезка [0; 2] и число у из
отрезка [0; 1]. Найдите вероятность того, что их произведение ху > — ?
хп.70. Наудачу берут числа х е [0; 1]; у е [2; 3].
а) Какова вероятность того, что у - х < 1,5?
б) Найдите число с, если известно, что вероятность того, что
у < х2 + с, равна —.
6
в) Найдите вероятность того, что ху < 0,5.
Груп па В
XII.71. Двое условились встретиться в одном и том же месте
следующим образом. Они независимо друг от друга приходят на
место встречи в промежутке от полудня до часу дня и ожидают
в течение 20 минут, после чего уходят. Какова вероятность
встречи?
ХП.72. Постройте график у=р(а), где р(а) — вероятность того, что:
а) квадратное уравнение х2 + рх + q = 0 имеет два различных
вещественных корня, если коэффициенты р и q наугад берутся
из отрезка [-а; а];
б) квадратное уравнение х2 + рх + q = 0 имеет два различных
положительных корня, если коэффициенты р и q наугад
берутся из отрезка [-а; а];
в) квадратное уравнение х2 + рх + q = 0 имеет два
вещественных корня разных знаков, если коэффициенты р и q наугад
берутся из отрезка [-а; а].
ХП.73*. На плоскости проведено семейство параллельных прямых,
расстояние между любыми двумя соседними равно /. На
плоскость наугад бросают иглу длины а < I. Какова вероятность
того, что игла пересечёт одну из прямых?
равнения
и неравенства
Q77, Некоторые способы решения уравнений
1. Разложение на множители
Один из наиболее эффективных и часто используемых подходов —
приведение уравнения к виду fx(x) • f2(x) • ... • fn(x) = 0. При этом
действует основное правило:
Произведение равно нулю тогда и только тогда, когда хотя бы один
из множителей равен нулю, а остальные имеют при этом смысл.
Пример 1. Решим уравнение (х2 — 4) jx + 1 = 0.
D «Кандидатами в корни» будут числа -2, 2 и -1. Но х = —2 корнем
не является, поскольку при этом значении не имеет смысла второй
множитель л/х + 1. Ответ: {2; -1}. Ж
Правило для произведения применимо и в случае приведения
fix)
уравнения к виду
дя)
дение выражений f(x) и
= 0. В левой части этого уравнения — произве-
1
g(x)
. Возникает дополнительное ограничение:
второй множитель не имеет смысла при g(x) = 0. Можно
сформулировать основное правило так:
Дробь равна нулю тогда и только тогда, когда числитель равен
нулю, а знаменатель имеет смысл и не равен нулю.
Пример 2. Решим уравнение
(х2+ Зх - 4)(х2+ 2х- 3)
= 0.
V9 - х2 (х2 - х - 2)
D Корни числителя — числа -4, -3 и 1. Но при х = -3 знаменатель
обращается в нуль, а при х = — 4 выражение д/9- х2 теряет смысл.
Таким образом, остаётся единственный корень х = 1. Ответ: {1}. IS
I
312 Глава XIII. Уравнения и неравенства
2. Замена переменной
Если в задаче несколько раз встречается какое-то фиксированное
выражение с переменной х, то имеет смысл обозначить его какой-либо
новой буквой1. Вот некоторые примеры уравнений, которые с
помощью замены сводятся к квадратным. Самое известное из них — это
биквадратное уравнение из курса основной школы.
Пример 3. Решим уравнение х4 - х2 - 12 = 0.
□ Введём замену х2 = t. Уравнение сводится к квадратному
уравнению t2 — t — 12 = 0. Его корни t = 4 или t = -3. Поскольку t = х2 ^ О,
то нас устраивает только корень t = 4. Возвращаясь к старой
переменной, получаем уравнение х2 = 4, корнями которого будут числа -2 и 2.
Ответ: {-2; 2}. Ш
Пример 4. Решим уравнение (х - I)4 - х2 + 2х - 73 = 0.
□ Воспользовавшись тем, что (х - I)2 = х2 - 2х + 1, перепишем
уравнение в виде (х2 - 2х + I)2 - (х2 - 2х) - 73 = 0. Дальше у нас есть две
возможности. Если мы введём замену t = х2 - 2х9 уравнение приобретёт
вид (t + I)2 - t — 73 = 0. Решить его не составит труда. А можно
использовать замену t = х2 - 2х + 1. Тогда уравнение примет вид t2 - (t - 1) -
- 73 = 0, откуда t2 - t - 72 = 0. Значит t = 9 или t = -8. Возвращаясь
к переменной х, получим (х — I)2 = 9, откуда х = 4 или х = -2.
Уравнение (х - I)2 = -8 вещественных корней не имеет. Ответ: {-2; 4}. 11
Рекомендации по введению новых обозначений:
1) после введённого обозначения старая переменная должна
исчезнуть;
2) вместе с обозначением полезно описывать его свойства.
Например, если х2 = t, то можно заранее учесть, что t ^ 0. Это позволит
упростить отбор корней (а иногда даже подсказать единственное решение).
Пример 5. Решим уравнение 2х - 1 = 3^J2x — 1.
□ Замена очевидна: t = y/2x- 1, причём полезно учесть, что t > 0.
Уравнение приобретёт вид t2 = 3t> откуда t(t - 3) = 0. Получим
корни уравнения t = 0 или t = 3. Возвращаясь к переменной х, имеем
2х - 1 = 0 или 2х - 1 = 9, откуда х = - или х = 5. Ответ: < -; б}. И
2 [2 J
Пример 6. Решим уравнение х - 14 = Зл/х- 4.
П Здесь замена не бросается в глаза, как в предыдущем примере,
но можно попробовать похожий вариант: пусть t = у/х — 4, тогда
t ^ 0. Выразим х через t:
2
1В замечательной книге В. А. Уфнаровского «Математический аквариум»
этот подход сформулирован в виде «принципа бяки»: «Увидел бяку —
обозначь».
§78. Целые рациональные и дробно-рациональные уравнения
Теперь уравнение примет вид: t2 + 4 - 14 = 3£, откуда t2 — 3t — 10 = 0.
Это уравнение имеет только один неотрицательный корень t = 5.
Возвращаясь к старой переменной: д/х- 4 = 5, откуда х = 29. Ответ: {29}. Ш
3. Подбор корней
Не стоит отказываться и от метода подбора, особенно когда не
получается решение другим методом. Заметим, что в решении не нужно
объяснять, как мы угадали этот корень: достаточно просто показать, что он
удовлетворяет уравнению. Но при этом будет необходимо доказать, что
других корней, кроме предъявленных, уравнение не имеет. Обычно для
доказательства используются соображения монотонности и
ограниченности функций. Для ряда задач это оказывается единственным путём
решения.
Пример 7. Решим уравнение хь = 4 - Зх.
П В левой части уравнения — возрастающая на всей вещественной
оси функция, а в правой части — убывающая на всей вещественной
оси функция. Значит, уравнение имеет не более одного корня.
Подбором находим корень х = 1. Ответ: {1}. Н
Пример 8. Решим уравнение 7 - х2 — х = Jx — 1.
D 00У задаётся неравенством х ^ 1. На ООУ левая часть убывает,
а правая возрастает. Таким образом, уравнение имеет не более одного
корня. Подбором находим х = 2. Ответ: {2}. Ш
(так как
Пример 9. Решим уравнение 1 - х2 = 3
D Очевидно, левая часть уравнения не превосходит
1 - х2 ^ 1), а правая не меньше 1 поскольку х2 + — ^ — и
у 9 9
причём обе части равны 1 лишь при х = 0. Ответ: х = 0. IS
078- Целые рациональные
и дробно-рациональные уравнения
1. Целые рациональные уравнения высших степеней
ОПРЕДЕЛЕНИЕ ———-—-—-—---———•-—--^^
Уравнение вида Р(х) = О(х), где Р и О — некоторые
многочлены от х с вещественными коэффициентами, называется
целым рациональным.
Можно также считать стандартным видом такого уравнения запись
вида Р(х) = 0, где Р — некоторый многочлен от х. Очевидно, любое
уравнение вида Р(х) = Q(x) может быть представлено в виде R(x) = 0.
314' Глава XIII. Уравнения и неравенства
Тогда вопрос о корнях такого уравнения сводится к вопросу о корнях
многочлена. Для многочленов с целыми коэффициентами вопрос о
наличии рациональных корней рассматривался в курсе 10 класса (глава III).
Формула корней квадратного уравнения известна вам с 8 класса,
а формул для корней уравнений высших степеней мы не знаем1. При
решении конкретных практических задач вычислительная техника
и методы вычислительной математики позволяют находить корни
любых уравнений с любой наперёд заданной точностью.
Для нас основным способом решения уравнений степени выше
двух будет угадывание (подбор) некоторых корней и последующее
разложение многочлена на множители.
Этот способ основан на следствии из теоремы Безу: если число а
есть корень многочлена Р, имеющего степень п> то многочлен Р
делится на двучлен (х — а) без остатка, т. е. многочлен можно представить
в виде Р(х) = (х - ос) • Q(x), где Q — некоторый многочлен степени
п - 1. Таким образом, если угадать хотя бы один корень а уравнения
Р(х) = 0 (где degP = n), то можно свести задачу к решению уравнения
степени на единицу меньше: Q(x) = 0, где degQ = п - 1.
Понятно, что начинать приходится с угадывания корня, и встаёт
вопрос: из каких соображений его искать? В § 17 главы III
(«Многочлены») был разобран вопрос о рациональных и целых корнях многочлена
с целыми коэффициентами. Напомним результаты, полученные в этом
параграфе.
Утверждения
1. Если многочлен с целыми коэффициентами и старшим
коэффициентом, равным единице Р(х) =хп + ал_-,хл"1 + ... + а0
имеет целый корень а, то этот корень является делителем
свободного члена, т. е. а0 ; а.
2. Если многочлен с целыми коэффициентами Р(х) = апхп +
+ ап_ -,хл "1 + ... + а0, ап ф 0 имеет рациональный корень - (где
— — несократимая дробь), то р является делителем
свободного члена, a q — делителем старшего коэффициента, т. е.
а0 ; р и ап \ q.
хДля нахождения корней кубического уравнения тоже существует
формула (формула Кардано), а для уравнения четвёртой степени — способ, при
помощи которого его решение сводится к решению некоторого кубического
уравнения (метод Феррари). Но они в нагие время не представляют
практической ценности и их сфера применения ограничена (для знатоков и тех, кто
решил найти формулу Кардано в энциклопедии: попробуйте решить уравнение
Xs — Зх + 1 = 0). А вот для уравнения пятой степени, как доказал
выдающийся норвежский математик Н. X. Абель (1802—1829), вообще не существует
формулы, выражающей его корни через коэффициенты уравнения с помощью
знаков радикала и арифметических действий.
Щ|_§78. Целые рациональные и дробно-рациональные уравнения
Естественно начать поиск корней многочлена с целыми
коэффициентами с проверки наличия у него целых корней, которые следует
искать среди делителей свободного члена.
Если старший коэффициент равен 1, то, как следует из
утверждения, все рациональные корни должны оказаться целыми числами, так
как рациональные корни такого многочлена должны иметь
знаменатель, равный 1. Таким образом, все вещественные корни этого
многочлена либо целые, либо иррациональные числа. Если ни один из
делителей свободного члена такого многочлена корнем не является, то
целых корней (а стало быть, и рациональных) у него нет.
Если старший коэффициент — целое число, не равное ±1, то,
начав с поиска целых корней, мы переходим к перебору всех
несократимых дробей вида —, где р является делителем свободного члена,
ад — делителем старшего коэффициента.
Если в конце концов выяснится, что рациональных корней
многочлен не имеет, то придётся искать какие-то другие подходы к задаче.
Пример 10. Решим уравнение х4 - х3 + 2х2 — 5х + 3 = 0.
□ Поскольку коэффициенты уравнения — целые числа, попробуем
найти какой-нибудь целый корень. (Все прочие вещественные корни,
если они есть, заведомо будут иррациональными, так как старший
коэффициент равен 1.)
Ищем целый корень среди делителей 3: это 1, -1, 3 и -3.
Подстановка показывает, что корень среди этих чисел только один: х = 1. Делим
многочлен Р(х) = х* - х3 + 2х2 - Ъх + 3 на двучлен (х - 1) (например,
уголком или по схеме Горнера). По следствию из теоремы Безу он
разделится нацело. Уравнение приобретёт вид (х - 1)(х3 + 2х - 3) = 0.
Теперь найдём корни многочлена Р\(х) = х3 + 2х - 3. Их мы ищем
среди делителей числа -3, т. е. того же набора чисел: 1, -1, 3 и -3.
Вычислять значения Рг (х) в точках -1, 3 и -3 не нужно, поскольку они не
являются корнями исходного уравнения, а значит, и корнями Рг(х).
А вот Рг(1) = 0, т. е. число 1 является корнем Рх(х).
Повторяя операцию деления, получим Рх (х) = (х - 1) (х2 + х + 3).
Тогда исходное уравнение можно переписать в виде (х - I)2 (х2 + х + 3) = 0.
Поскольку множитель х2 + х + 3 не имеет вещественных корней,
единственным корнем уравнения будет х = 1. Ответ: {1}. Ш
Пример 11. Решим уравнение 8х3 — 16х2 + 8х - 1 = 0.
□ Уравнение не имеет целых корней (кандидаты на эту роль —
делители свободного члена 1 и -1 — корнями не являются). Остаётся
надежда на поиск рациональных корней среди чисел ±—, ±—, ±—.
-* ci 4 о
Подстановкой убеждаемся, что х = — является корнем. Таким об-
разом, после деления (делить удобнее не на х , а на 2х — 1) получим
316 Глава XIII. Уравнения и неравенства
(2х - 1)(4х2 — 6х + 1) = 0. Решив квадратное уравнение 4х2 - 6х + 1 = О,
/l 3 + л/б 3- л/б] ,-.
получаем ответ: 1 -; ; f. IS
[2 4 4 J
Замечание. В примере 11 можно упростить решение, обозначив
t = 2х. Получим уравнение ts — 4t2 + 4t — 1 = 0. Для этого уравнения
нужно подбирать только целые корни, а возможных «кандидатов»
в целые корни только два: числа 1 или -1.
2. Замены в целых рациональных уравнениях
Уравнения, сводящиеся к квадратным
Пример 12. Решим уравнение (х + 1)(х + 2)(х + 3)(х + 4) = 24.
П Группируя в левой части первый множитель с последним, а
второй с третьим, получим (х2 + Ъх + 4)(х2 + 5х + 6) = 24. Теперь замена
становится очевидной. Можно, например, положить t = х2 + Ъх + 4.
Тогда уравнение примет вид £(£ + 2) = 24. Корни этого уравнения t = 4
или £ = -6. Возвращаясь к старой переменной, получим:
1) х2 + Ъх + 4 = 4; х2 + 5х = 0; х = 0 или х = -5;
2) х2 + Ъх + 4 = -6; х2 + 5х + 10 = 0; уравнение не имеет
вещественных корней (D < 0).
Ответ: {-5; 0}. Ш
Замечание. Продемонстрированный приём применим к
уравнениям вида (х + а)(х + Ь)(х + с)(х + d) = А, если а + d = Ъ + с.
Например, совершенно аналогично решается уравнение (х - 1)(х - 2)(х - 3) х
х (х - 4) = 24.
Следующее уравнение весьма напоминает уравнение из
примера 12, но решается с помощью другого приёма.
Пример 13. Решим уравнение (х2 - 7х + 6)(х2 - Ъх + 6) = 1Ъх2.
П Поскольку х = 0 не является корнем уравнения, разделим обе
части уравнения на х2 (каждую из скобок делим на х):
Теперь очевидна замена t = х + —. Уравнение примет вид
(t -7)(t -5) = 15.
Находим корни t = 2 или t = 10.
Возвращаемся к старой переменной, для чего решаем уравнения
х + — = 2 и х + — = 10. Первое из этих уравнений вещественных корней
не имеет, а второе имеет два корня х = 5 ± V19.
Ответ: {5 - Vl9; 5 + Vl9}. H
317 §78. Целые рациональные и дробно-рациональные уравнения
Возвратные уравнения
Уравнение вида апхп + ап_ 1хп~1 + ... + а0 = О, ап Ф О с
вещественными коэффициентами называется возвратным, если ak = an_ k, при
k = О, 1, ..., п (т. е. коэффициенты, «одинаково удалённые от начала
и от конца», равны между собой). Например, 2х3 + 7х2 + 7х + 2 = О
(а3 = а0 = 2, а3 = а2 = 7) или х4 - 7х3 + 14х2 - 7х + 1 = О (а4 = а0 = 1,
Чаще всего мы будем встречаться с возвратными уравнениями
третьей и четвёртой степеней. Их общий вид соответственно будет
ах3 + Ьх2 + Ьх + а = 0, а * О и ах4 + Ьх3 + сх2 + Ьх + а = 0 (а Ф 0).
Рассмотрим подробнее способы решения таких уравнений.
Уравнение ах3 + Ьх2 + Ьх + а = 0 (ап Ф 0) всегда имеет корень х = -1
(как и любое возвратное уравнение нечётной степени!). Осталось
разделить обе части уравнения на х + 1 и решить полученное квадратное
уравнение.
Возвратное уравнение 4-й степени имеет вид ах4 + Ьх3 + сх2 +
+ Ьх + а = 0, а Ф 0. Поскольку а Ф 0, то х = 0 не является корнем
уравнения, а тогда можно обе части уравнения поделить на х2 и получить
уравнение вида
х
Введём замену t = х + —. Если обе части этого равенства возвести
в квадрат, то получится t2 = х2 н—- + 2, откуда х2 н—- = £2 — 2. Таким
образом, исходное уравнение оказывается квадратным относительно
новой переменной t. Дальше, как обычно, находим его корни и,
возвращаясь к старой переменной, решаем уравнения вида х + — = t.
Пример 14. Решим уравнение х4 — 7х3 + 14х2 - 7х + 1 = 0.
D Поделив обе части уравнения на х2 и перегруппировав слагаемые
в левой части, получим х2 н—- — 7\ х-\— +14=0. Положим t = хН—,
{ х2) У х) х
тогда t2 = х2 + -^- + 2 и х2 + -i- = *2 - 2. Получим *2 - 2 - 7t + 14 = 0;
х2
t2 - 7t + 12 = 0, откуда t = 3 или £ = 4.
Возвращаемся к переменной х:
1) х + I = з; х2 - Зх + 1 = 0; х =
х
з; х Зх + 1 0; х ;
х 2
2) х + - = 4; x2-4jc+ 1 = 0; *= 2±л/§.
Ответ: |i±^; ^^; 2 + л/З; 2-7з}. Н
3181 Глава XIII. Уравнения и неравенства
Однородные уравнения
Напомним, что многочлен от двух переменных Р(х, у) называется
однородным порядка k, если все слагаемые многочлена Р(х, у)
являются одночленами одной и той же степени к.
Например, многочлен Р(х, у) = Зх3 - 2ху2 является однородным,
а многочлен Рг(х> у) = Зх3 - 2ху2 + 1, уже нет.
ОПРЕДЕЛЕНИЕ --_«-___—____-___-__-_-_-^^
Уравнение вида Р(х, у) = 0, где Р(х, у) — однородный
многочлен, называется однородным.
Основной способ решения однородных уравнений — деление
обеих частей уравнения на старшую степень одной из переменных (при
этом нужно отдельно оговорить, что будет в случае, когда эта
переменная равна нулю).
Решая однородное уравнение от двух переменных, мы выражаем
одну переменную через другую. Второе уравнение, связывающее
переменные, либо задаётся непосредственно (в этом случае мы говорим об
однородной системе уравнений), либо задано по умолчанию самим
выбором переменных.
Пример 15. Рассмотрим уравнение 2х2 + ху — у2 = 0.
П Если у = 0, то х = 0. Пусть теперь у Ф 0. Разделим обе части урав-
( Л2
I X I X
нения на у2. Получим 2— + 1 = 0. Это квадратное уравнение от-
х 1
носительно t = —. Решив уравнение 2t2 + £—1 = 0, найдём, что t = -
У " 2
или t = -1. Возвращаясь к старым переменным, получим совокупность
~У " 2' „ .. [у = 2х,
Перепишем ее в виде
* = _1. 1у = ~х-
У
Заметим, что последней совокупности удовлетворяет и пара (0; 0).
Объединяя эти два случая, можно переписать уравнение в вице
(2х — у)(х + у) = 0 (этот же результат можно было получить, решив
исходное уравнение как квадратное относительно переменной у с
параметром х).
Добавим к этому уравнению ещё одно условие, связывающее эти
неизвестные. Например, это может быть второе уравнение. Получим
систему
{2х2 + ху - у2 = 0,
х2 + у2 = 5.
§78. Целые рациональные и дробно-рациональные уравнения
Эту систему мы можем решить, выражая из однородного
уравнения одну переменную через другую и подставляя результат во второе
\ у = 2х, \у = -х,
уравнение. Получим < или <
[х2 + у2 = 5 [х2 + у2 = 5.
Свет, [Oi 2), (-1; -2), (|; -||, (-|; |]j. В
Систему, в которой одно из уравнений является однородным,
часто называют однородной системой.
Связь между неизвестными может быть задана и иначе.
Пример 16. Рассмотрим несколько уравнений, сводимых к
однородному уравнению 2и2 + uv - v2 = 0.
D а) Положим и = х2, v = Зх + 4. Получится уравнение
2х4 + х2(3х + 4) - (Зх + 4)2 = 0.
Здесь и и v уже не будут независимыми переменными!
Ранее (при рассмотрении уравнения 2х2 + ху — у2 = 0 в приме-
ре 15) мы уже получили результат в виде совокупности
Возвращаясь к переменной х, получим Зх + 4 = 2х2 или Зх + 4 = -х2.
з
и х =
3-V41
;
„ з-Vii з+ViT
Первое уравнение имеет корни х = или х = , а второе ве-
4 4
щественных корней не имеет (D < 0). Ответ: ,
Если раскрыть скобки, то полученное уравнение 4-й степени не
решается подбором корней, так как все его корни иррациональные.
б) Если взять и = 2х и v = 3х, то получится уравнение 2 • 4х +
+ 2х • 3* - 9* = 0. Мы уже знаем, что — = - или - = -1. Переменные и
v 2 v
и v не будут независимыми, они связаны между собой, например,
и 2* (2Y „ (2Y 1
равенством — = —= — . Тогда, решая уравнение — = —, мы полу-
v 3х \3) уЗ] 2
1 (2\*
чим корень х = log2 — = - log2 2. Уравнение — = —1 решений не име-
з2 з \3)
ет. Ответ: \ -
в) Теперь положим и = \og2x, v = Iog2(2x - 1). У нас получится
уравнение 2 log! х + ^°ё2х ' Iog2(2x - 1) - log2 (2x - 1) = 0.
3201 Глава XIII. Уравнения и неравенства
Из уравнения 2и2 + uv — v2 = 0 мы уже получили совокупность
[v = 2i/, T.
Как и в предыдущем случае, переменные и и v не являются
| у — I/»
независимыми (хотя мы и не будем искать связь между ними в явном
виде). Подставим выражения для и и v в совокупность, и получим
riog2(2x-l)=21og2x,
|_log2 (2х - 1) = -log2x.
Единственный корень первого уравнения системы х = 1, он же
будет единственным корнем второго уравнения. Ответ: {1}.
г) Положим и = sinx, v = cosx. Получится так называемое
однородное тригонометрическое уравнение 2sin2x + sinx • cosx - cos2x = 0.
~ и sin x т» и 1 и л m
Очевидно, — = = tgx. Ранее мы получили — = — или — = -1. Таким
v cosjc v 2 v
образом, tgx = - или tgx = -1. Ответ: < -— + 7m, arctg- + пп: пе zL H
Так же рассматривается однородное уравнение большей степени.
3. Дробно-рациональные уравнения
Р(х)
Уравнение вида —— = 0, где Р и Q — многочлены с вещественны-
Q(x)
ми коэффициентами, называется дробно-рациональным.
Любое дробно-рациональное уравнение сводится к решению
целого рационального уравнения Р(х) = 0, которое является его следстви-
тт - PW л \Р(*)= 0,
ем. Действительно, уравнение = 0 равносильно системе л*,^ п
Первое уравнение системы решается, а нижнее неравенство
проверяется (решать его обычно не нужно, достаточно просто проверить, что
корни верхнего уравнения удовлетворяют условию Q(x) ^ 0). Однако
такой прямолинейный подход не всегда приводит непосредственно
к ответу.
12jc 12jc
Пример 17. Решим уравнение = — + 5.
х2 х + 2
□ Убедившись, что х = 0 не является корнем, и считая в
дальнейшем лс^О, разделим числитель и знаменатель каждой из дробей на х.
Получим
12 _ 12 5
х + х + — + 1
х 2 х
321 §79. Системы алгебраических уравнений и неравенств
2 12 12
Введя замену t = х + —, переходим к уравнению = + 5,
X о t + 1
~ 2
24 12 к . о 5 Л7 2 о
откуда = + 5, а тогда t = 3 или £ = --. Уравнение х + — = 3
2£ — 3 £ ■+■ 1 2 •£
имеет корни х=1их = 2,а уравнение х + — = — не имеет веществен-
х 2
ных корней. Ответ: {1; 2}. Ш
Ещё один специальный приём, который пригоден только для
уравнений особого вида, — это выделение полного квадрата.
х2
Пример 18. Решим уравнение х2 Н = 3.
\Х ~г л.)
П В левой части уравнения находится сумма квадратов. Попробуем
превратить её в квадрат суммы или квадрат разности (смотря, что
окажется удобнее). Для этого прибавим и вычтем в левой части удвоенное
произведение слагаемых х и , получим
| |
X + 1 (X + I)2 * + 1
( у Л2 9 у2 ( у2 V 9 у2
откуда х + 3=0, т. е. + 3=0. Теперь
^ х+1) х+1 \х+1) х+1
х2
очевидна замена t = . Получим квадратное уравнение: £2 + 2£-3 = 0,
х2 х2
1 и
откуда t = 1 или t = -3.
х х
Осталось решить уравнения = 1 и = -3. В первом урав-
1±л/б
нении х = , а второе уравнение не имеет вещественных корней.
Ответ:
- Системы алгебраических уравнений и неравенств
Система — это предикат, записанный в виде конъюнкции
предикатов. Решить систему — значит найти множество истинности этого
предиката.
Таким образом, решениями системы могут быть только такие
значения переменной (пары, тройки, наборы значений переменных),
которые удовлетворяют сразу всем условиям системы.
Решить систему — означает найти все её решения или доказать,
что их нет.
322j Глава XIII. Уравнения и неравенства
Если система не имеет решений, она называется несовместной
(поскольку её условия не могут быть выполнены одновременно ни для
какого набора переменных).
Пример 19. Рассмотрим две системы 1 2 и 1 _
П Графически первая система задаёт всю плоскость, а вот вторая —
прямую у = х. Ясно, что и ответы, записанные в аналитической форме,
будут различны. Для первой системы ответом будет множество всех пар
вида {(х; у): х е R> у е R}> а ответ во второй системе может быть
записан в виде {(х; х): х е R}. ВН
1. Понятия равносильности и следования систем
Определения равносильности и следования для систем даются
в точности так же, как для уравнений или неравенств. Это
естественно, поскольку определения равносильности и следования
формулируются в терминах соотношений между множествами истинности
предикатов.
Итак, пусть даны две системы уравнений или неравенств (1) и (2)
с одинаковым набором неизвестных и с множествами решений Мг и М2
соответственно.
ОПРЕДЕЛЕНИЕ
Системы называются равносильными, если множества их
решений совпадают, т. е. М1 = М2.
Заметим, что, как и в случае уравнений, любые две несовместные
системы с одинаковым набором неизвестных будут равносильны.
ОПРЕДЕЛЕНИЕ —-——-—--———--—"—•-——■—^^
Система (2) называется следствием системы (1), если
М1 с М2, т. е. каждое решение системы (1) является также
решением системы (2).
Следствием системы может быть также уравнение или
неравенство с теми же переменными, если каждое решение системы является
решением этого уравнения (неравенства).
Г х2 + у2 = 1
Пример 20. Следствием системы s _ ' является уравнение
х2 + у2 = ху. Отметим, что это уравнение имеет своим решением лишь
пару чисел (0; 0), которая не является решением исходной системы. Ш
Равносильными преобразованиями систем мы будем называть
такие преобразования, которые приводят к получению равносильной
системы (т. е. не изменяют множества решений).
§79. Системы алгебраических уравнений и неравенств
В дальнейшем в этом разделе мы будем рассматривать системы
с двумя неизвестными.
Если в системе одно уравнение или неравенство заменить
равносильным ему набором условий, а все остальные условия
системы оставить без изменения, то получится система, равносильная
исходной.
Отсюда следует, в частности, что система уравнений \ } f ' л _ Х
[ А (*> У) ~ Si (х, У)=09
равносильна системе \ „ , ч , Л и общим
[ h (х> У) ~ §2 (х> У) = О,
двух уравнений с двумя неизвестными мы можем считать систему
iFl(x,y)=O,
[F2(x,y)=0.
видом системы
Если из одного уравнения системы можно выразить одну
переменную через остальные и подставить это выражение в любые
другие уравнения (неравенства) системы, то получится система,
равносильная исходной.
В этом заключается суть метода подстановки, одного из
наиболее распространённых методов решения систем.
_, [ х + 4 = у3,
Пример 21. Решим систему 1 о
[х2 - у6 = 8.
D Выразим из первого уравнения системы х через у и подставим во
второе уравнение. При этом получится система, равносильная исходной:
fх = у3 - 4, \х = у3 - 4, (х = -3,
\(У* -4)2-у* = 8<=*\у3 = 1 ~ [у = 1.
Ответ: {(-3; 1)}. 11
Важность условия подстановки именно в другие уравнения
системы иллюстрирует следующий пример.
\х3+у3=2,
Пример 22. Рассмотрим систему . 1
[х + у — 1.
D Исходная система равносильна системе
Ux + y)3=-l,
\х3+у3 = 2.
324| Глава XIII. Уравнения и неравенства
_ Гх3 + г/3 + 3ху(х + у) = -1,
Раскроем скобки в первом уравнении:
I:{^+J» = 2?l'(
Подставив вместо х + у и вместо Xs + г/3 их значения, взятые из
исходной системы, придём к системе
[ху = 1,
* +у*= 2.
Решением этой системы является пара (1; 1), которая не является
решением исходной системы! Причина этого парадокса в том, что мы
подставили первое уравнение системы «само в себя» (сравните с
исходной системой). Ш
Если к уравнению системы прибавить другое уравнение этой
системы, предварительно умноженное на произвольное число, а все
остальные условия оставить без изменений, то получится
система, равносильная исходной.
Такой способ действий принято называть методом
алгебраического сложения уравнений в системе. Заметим, что, конечно же, сюда
входит и вычитание одного уравнения из другого, а также переход
одновременно к сумме и разности двух уравнений: системы \ } v
1/2 =#2
f/1 + /2 = £i + £2>
и Г , равносильны.
[А' /2= 8l"82
__ \х + у = а,
Например, система < , равносильна системе i Л
[x-y = b [2y = a-b9
Замечание. Сложение неравенств в системе может не привести
к равносильной системе! Таким образом мы можем получить только
следствие исходной системы, в чём легко убедиться на следующем
\х > 0, .
примере: система \ задает на плоскости первую четверть (первый
[у ^ О
квадрант), неравенство х + у > 0 задаёт часть плоскости выше прямой
jx + y>0,
у = —ху а система \ — часть верхней полуплоскости выше
[у ^ О
§79. Системы алгебраических уравнений и неравенств
а) УЦ_ б)
Рис. 13.1
прямой у = —х (рис. 13.1). Видно, что в множестве, задаваемом
последней системой, содержатся точки, координаты которых не
удовлетворяют исходной системе.
Если к утверждениям системы добавить утверждения её
следствий (в том числе следствие одного из её условий), то получится
система, равносильная исходной.
Это утверждение используется, как правило, при решении
сложных систем уравнений, где оно позволяет упростить отбор решений,
а иногда подсказывает единственно возможное решение.
{ху + yz = 8,
ух + zx = 9,
zx + ху = 5.
Обозначим ху = a, yz = b, zx = с, тогда <j b + с = 9,
[с + а = 5.
Сложив все три уравнения, получим 2а + 2& + 2с = 22. Если
добавить это уравнение к предыдущей системе, получится равносильная
а + b = 8,
Ъ + с = 9,
с + а = 5,
а + & + с = 11,
= 2,
ния к старым переменным, \ yz = 6,
= 3.
система
[а =2,
из которой получим I Ъ — 6, и, после возвраще-
с=3
326, Глава XIII. Уравнения и неравенства
Перемножив три уравнения, получим следствие: x2y2z2 = 36,
откуда xyz = 6 или xyz = -6. Таким образом, исходная система
равносильна системе <
или совокупности систем«
ху = 2,
= 6,
xz = 3,
x2y2z2 = 36
\x-l, fx--l,
Из первой системы: s у = 2, а из второй: i У = -2,
[г = 3, [г = -3.
Ответ: {(1; 2; 3); (-1; -2; -3)}. В
xi/г = 6,
хг/ = 2,
1/2 = 6,
xz = 3
и i
= -6,
ху = 2,
= 3.
Пример 24. Решим систему
х2+у =
= 20.
П Вычитая из первого уравнения системы второе, получим равно-
х2-у2-(х-у)=0, _ j(x-y)(x + y-l)=O,
сильную систему , , 9 = 2Q ^ [х + у2= 20.
Эта система равносильна совокупности систем
и
Решим первую из систем. Подставим х = у во второе уравнение:
гг. a jx= 49 \x= -5,
Таким образом, < . или <
[У = 4 U = -5.
Реп1ая вторую систему, получим
ix=l-y,
x + i/2 = 20
- у -19= 0
х= 1- г/,
г/ =
2
1-V77
2 '
1-V77"
2 '
1-V77
2 '
1 + V77
Ответ: |(4; 4); (-5; -5);
777"
;
\-4тт
JJ"
327| §79. Системы алгебраических уравнений и неравенств
2. Однородные и приводящиеся к однородным системы
Напомним, что если хотя бы одно из уравнений системы является
однородным, то эта система уравнений называется однородной. В
такой системе сначала решается однородное уравнение, в результате
чего одна переменная выражается через другую в явном виде, после
чего для завершения решения используется метод подстановки.
Чаще мы имеем дело с системами, которые тем или иным способом
могут быть сведены к однородным. В частности, если система уравнений
имеет вид \ ' где f(x, у) и g(x, у) — однородные многочлены
одного порядка (т. е. все их слагаемые являются одночленами одной
степени), а а и & — числа, то система приводится к однородной.
Достаточно из второго уравнения, умноженного на а, вычесть первое
уравнение, умноженное на число &. Тот же подход применим, если в правой
части вместо чисел а и Ь стоят подобные одночлены а(х, у) и Ь(х, у).
^ Г х2 — ху + у2 = 3,
Пример 25. Решим систему 1 9 9
[2х2 - ху - у2 = 5.
D Вычтем из второго уравнения системы, умноженного на 3, первое
уравнение, умноженное на 5 (чтобы уничтожить свободные слагаемые
I у2 XU Н~ U —- 3
в правой части). Получится однородная система { о Л Л о ' Л
[х2 + 2ху - 8у2 = 0.
Решая однородное уравнение х2 + 2ху - 8у2 = 0, найдём, что х = 2у
или х = —4у. Исходная система равносильна совокупности систем
\х2 -ху + у2=3,^ \х2 -ху+у2=3,
\х = 2у \х= -4у.
Из первой системы подстановкой получаем < _ что даёт решения
[х= Zy,
\ 2=-
(2; 1) и (-2; -1). Из второй системы получаем у 7' что даёт решения
[х=-4у,
Пример 26. Решим систему i 9 о 9 ч о
[х2у + 2ху2 + у3 = 2.
D Вычитая из второго уравнения удвоенное первое, получим
однородное уравнение -2х3 + х2у + 2ху2 — у3 = 0. Таким образом, исходная
(х3 +у3 = 1,
система равносильна системе ло32
\£х — х у —
2ху2
328; Глава XIII. Уравнения и неравенства
Поскольку у = О не доставляет решения системы, делим обе части
второго уравнения на у3 и приходим к уравнению
21-T-f-T-2-+ 1=0.
У) \У) У
Полагая — = t, решаем уравнение 2t3 - t2 - 2t + 1 = 0, откуда:
t=~l,
t= 1.
Возвращаясь к старым переменным, получаем, что исходная
система равносильна совокупности трёх систем:
1х = -у, \х = -у, \х = у,
2 13+3-1и|3+3-1
Решая эти системы методом подстановки (вторая система
решений, очевидно, не имеет), получаем ответ: \ —; — ; -=; — \\. Ш
3. Симметрические системы. Замена переменных
О симметрических многочленах мы уже говорили ранее, в
главе III учебника 10 класса. Если все уравнения системы имеют вид
Р(х>у> ...) = 0, где левая часть есть симметрический многочлен, то
система называется симметрической.
Общий вид симметрической системы с двумя переменными:
< ч _ п' где f(x, у) и g(x, у) — симметрические многочлены от
двух переменных. Простейшая из таких систем имеет вид
\х + у = а,
[ху = Ъ
[
и сводится по теореме Виета к решению уравнения t2 - at + Ъ = 0. Если
уравнение не имеет корней, то система не имеет решений; если же
уравнение имеет корни tx и t2, то решениями системы являются пары
{X — t^y I X — £2>
У = Ч \у = tx.
Ранее было отмечено, что все симметрические многочлены
выражаются через элементарные симметрические многочлены. В случае
двух переменных это как раз сг = х + у и о2 = ху. Как правило, при
такой замене мы получаем более простую систему уравнений, решая
которую находим значения ах и о2, в результате чего для нахождения х
и у получаем всё те же системы вида
[х + у = а,
[ху = Ъ.
. Системы алгебраических уравнений и неравенств
По той же схеме можно решать симметрические системы от трёх
(и более) переменных. Для трёх переменных элементарными
симметрическими многочленами (через которые выражаются все остальные)
будут ох = х + у + 2, о2 = ху + yz + zxy о3 = xyz. Решая новую систему,
получившуюся в результате такой замены, мы находим olf o2, о3
(х + у +z = а,
ху + yz + zx = b, решения которой по теореме
xyz = с,
Виета получаем как корни кубического уравнения ts - at2 + bt - с = 0.
Для удобства применения этого подхода полезно заранее
научиться выражать через элементарные симметрические многочлены так
называемые степенные суммы — выражения вида Sn = хп + уп для двух
переменных и Sn = хп + уп + zn для трёх переменных. Результат для
наиболее употребительных случаев представлен в таблице.
Симметрические многочлены
от двух переменных х, у
сл=х + у, <з2-ху
S1 =Х + у=<5л
S2 = х2 + у2 = о2 - 2о2
S3 = х3 + у3 = о3 - Зо^з
5А = хл + ул = с* - 4о2о2 + 2о2
Симметрические многочлены
от трёх переменных х, у, z
с1 = х + у + z, о2 = ху + yz + zx,
о3 = xyz
S1=x + y + z = a1
S2 = x2 + y2 + z2 = o2-2o2
S3 = x3 + у3 + z3 = о3 - Зс^с2 + 3o3
Формулы других степеней выводятся по мере надобности.
Например, для двух переменных нетрудно получить формулу S5 = хь + уь =
= cl — 5ofo2 + бс^о^, умножая S4 на Sx и пользуясь результатами, уже
представленными в таблице. Аналогично получаются формулы
степенных сумм для трёх переменных.
\х2 +у2 = 17,
Пример 27. Решим систему \ Л
D Система симметрическая, поэтому выражаем все
симметрические многочлены через элементарные (сг = х + у, С2 = ху):
Решая эту
М = 5*
s й или
f - 2о2 = 17,
! + а2 = 9.
систему стандартным методом
\о2 =
подстановки, получим
16.
3301 Глава XIII. Уравнения и неравенства
Возвращаемся к старым переменным:
{ху = 4 [ху = 16.
Решения первой системы находятся как решения квадратного
уравнения t2 - 5t + 4 = 0. Таким образом,
[х=1,
Л А ИЛИ
[у = 4
Вторая система решений не имеет, поскольку уравнение t2 + It +
+ 16 = 0 не имеет вещественных корней. Ответ: {(1; 4); (4; 1)}. Ш
Замечание. Симметрические системы оказываются полезными
при решении некоторых уравнений высших степеней и
иррациональных уравнений.
Например, решая уравнение (х — 2)6 + (4 - х)6 = 64, удобно ввести
о л „ /ив + vG =64,
замену х - 2 = i/, 4 - х = и и перейти к системе s которую
можно решить стандартным способом.
Другой пример: иррациональное уравнение Цх + 8 + л/8 - х = 2
имеет смысл решать с использованием замены Ух
и>=2,
Тогда ,..А . „.д = 1б
Для уравнения вида tfa- f (x) + tfb + /(jc) = с удобно использовать
замену i/ = ^а - /(х), у = ^Ь + /(л:). Тогда м и у находятся из симметри-
ческой системы
ju + v=c,
[ип +vn = a + b.
Заметим, что уравнения в системе можно также почленно
умножать или делить, но делать это следует с осторожностью, поскольку
такая операция может изменить множество решений: есть опасность
как потери решений, так и приобретения посторонних решений.
\хъу7 = 32,
Пример 28. Решим систему s _
ух у — 128.
□ Если уравнения в системе умножить и разделить одно на другое,
(ху)12 = 212,
2
У -I
получится система
Но эта система не равносильна исходной! Легко видеть, что в
последней системе могут быть всевозможные сочетания знаков х и у,
3311 §79. Системы алгебраических уравнений и неравенств
а в исходной системе хну должны быть одного знака! Поэтому ху > О,
— > 0, и тогда можно перейти к системе \ _ ' из которой х = 2,
х [х — £у*
у=1 или х = -2, у = -1. Ответ: {(2; 1); (-2; -1)}. Ш
4. Метод «оценки»
Иногда удобно сначала показать, что решения системы, если они
есть, должны удовлетворять каким-то жёстким ограничениям, а затем
проверить, какие из наборов неизвестных, удовлетворяющих этим
ограничениям, действительно являются решениями системы. Чаще
всего следствия из исходной системы представляются в виде
неравенств. Для получения этих неравенств используются, как правило,
выделение полного квадрата или классические неравенства (например,
неравенство Коши).
Г х2у2 — 2х + у2 = О,
Пример 29. Решим систему { Л п Л о ' Л
У [2х2 -4x + 3 + ys= 0.
D Заметим, что у Ф 0, и представим систему в виде
2(jc-1)2 = -1-y3 [2(x - I)2 =-1 - ys
Получили единственно возможное значение у = —1. Отсюда х=1
и остаётся проверить, что пара (1; —1) является решением исходной
системы. Ответ: {(1; -1)}. В
Обратите внимание, что в данном решении следствием системы
уравнений от двух переменных выступает система неравенств от одной
переменной.
J J(xy)2(2-(xy)2) = y*+x2(l- х),
Пример 30. Решим систему \ .
[VI + (х + У)2 + (2у3 + х2)х ^ 0.
п _ \у* + х2 - х* = J(xy)2 (2- (ху)2),
D Перепишем систему в виде < ;
[2ysx + xs^ -Jl + (x + y)2.
Если сложить уравнение и неравенство, то в левой части
неравенства будет полный квадрат:
(у3 + х)2 < yl(xy)2(2-(xy)2) - Jl + ix + y)2.
3321 Глава XIII. Уравнения и неравенства
Оценим слагаемые в правой части. Заметим, что (ху)2 (2 - (ху)2) ^ 1
(в этом легко убедиться, обозначив (xy)2 = t), и, значит,
В то же время <Jl + (х + у)2 ^ 1. Таким образом,
j(xy)2(2-(xy)2) - д/1 + (х + у)2 ^ О,
а тогда и (у3 + х)2 ^ 0, откуда у3 + х = 0, и оба радикала в правой части
неравенства равны 1.
Итак, система может иметь решение только в том случае, когда
(ys+x = O, fx + */3 = 0,
выполнены три условия: < 1 + (х + у)2 = 1, Отсюда < х + у — О,
[ (
Первым двум уравнениям удовлетворяют только три пары чисел:
(0; 0), (1; -1) и (-1; 1). Пара (0; 0) отбрасывается, поскольку не
удовлетворяет последнему равенству. Осталось проверить (это
обязательно!), являются ли решениями исходной системы оставшиеся две пары.
Подходит только пара (1; -1). Ответ: {(1; -1)}. И
О80. Уравнения и неравенства с параметром.
Аналитическое исследование
Пусть дан предикат с двумя переменными А(х; а) (например,
уравнение f(x; а) = 0), из которых х считается переменной, а а —
параметром. Если выбрать и зафиксировать какое-то конкретное
значение а и подставить его в предикат, то получится просто предикат с
одной переменной х, причём вид этого предиката и его множество
истинности существенно зависят от выбора конкретного значения
параметра а. Таким образом, например, уравнение с параметром — это
целое семейство уравнений, получаемых при подстановке конкретных
значений а.
При решении задач с параметром мы считаем переменную а
постоянным (но неизвестным) числом, через которое должно быть
найдено значение переменной в уравнении. Параметров может быть и
несколько!
1. Уравнения с параметром
Решить уравнение с параметром означает выяснить, при
каких значениях параметра решения вообще существуют, сколько их,
и в случае их существования дать формулы решения, т. е. выразить
х через параметры.
. Уравнения и неравенства с параметром Аналитическое исследование
Это напоминает составление некоторой программы (алгоритма)
для вычислительной машины (или неопытного пользователя, не
желающего вникать в смысл задачи): если мы берём какое-то конкретное
значение параметра, то для получения решения уравнения пользуемся
такой-то формулой, а если взять другое значение параметра, то
решение получится уже по другим формулам, а вот при таком значении
параметра решений нет вовсе и т. д. Пользователь, «вводя» любое
значение параметра, должен получить полную информацию о решении
уравнения в этих условиях. Отсюда особая форма записи ответа, по
которой можно было бы сразу прочитать, какое будет решение для
каждого значения параметра.
Рассмотрим несколько примеров, где продемонстрируем
некоторые простейшие приёмы работы с параметром.
Пример 31. Решим уравнение ах = 3.
о
О На первый взгляд всё очевидно: х = -. Но на самом деле это
верно, только если а Ф 0, и вовсе не потому, что «на нуль делить нельзя».
Если а — 0, то получается уравнение 0 = 3, не имеющее корней.
о
Ответ: если а Ф 0, то х — —;
а
если а = 0, то х е 0. Ш
О В ответе должны быть перечислены все (!) вещественные
значения параметра а (иначе задача не будет считаться решенной
полностью) и соответствующие этим значениям параметра решения
уравнения.
Пример 32. Решим уравнение ах = За.
О При а Ф 0 сразу получаем х = 3, а вот при а = 0 обе части
уравнения обращаются в нуль, т. е. решением будет любое вещественное число.
Ответ: если а Ф 0, то х = 3;
если а = 0, то х е R. Ш
Пример 33. Решим уравнение (а2 — а)х = За.
D Ясно, что в случае линейного уравнения нужно обратить
внимание на коэффициент при переменной х. Если он отличен от нуля,
можно делить обе части уравнения на этот коэффициент. Но вот если он
равен нулю, то это вовсе не означает, что уравнение не имеет решения.
Нужно подставить соответствующие значения а в исходное уравнение
и решить получившиеся уравнения.
Коэффициент равен нулю при а = 0 или а = 1. Подставляя в
уравнение а = 1, мы получим уравнение 0 = 3, не имеющее решений;
а если подставим а = 0, то получим уравнение 0 = 0, корнем которого
является любое число.
о
Ответ: если а <£ {0; 1}, то х = ;
Q — 1
если а = 0, то х е R;
если а = 1, то решений нет. Ш
334| Глава XIII. Уравнения и неравенства
Пример 34. Решим уравнение = 0.
с\дС — А
□ Сформулированное в § 77 правило «дробь равна нулю, если её
числитель равен нулю, а знаменатель при этом отличен от нуля», приобре-
1х = а,
1 Тогда
ХФ-.
запишем ответ: если а Ф —, то х = а;
Ci
если а = -, то решений нет. Щ
Ci
Пример 35. Решим уравнение ——- = 0.
Х
[xz — 4
П Заменим уравнение равносильной системой \
[xz 4Ф 0.
Разобьём решение на два этапа. На первом этапе (его можно
назвать «грубым решением») решим уравнение ах + 1 = 0. Если а Ф 0, то
х- —; если а = 0, то решений нет.
На втором этапе (произведём «чистку решения»); по
«запрещённым» значениям переменной х найдём значения параметра а, при
которых найденное значение х будет обращать знаменатель в нуль. Для
этого значения х = 2 и х = -2, при которых знаменатель дроби
обращается в нуль, подставим в уравнение ах +1 = 0. Получим а = — на = -
соответственно. , >,
Ответ: если а £ \ —; 0; -L то х = —;
[ 2 2J а
если a g \ —; 0; -к то решений нет. Щ
{ 2 2J
Пример 36. Решим уравнение ах2 = х + а.
□ Начнём с определения вида уравнения (с этого всегда нужно
начинать!). Это уравнение вовсе не при всех значениях а будет
квадратным! При а = 0 наше уравнение превращается в линейное, имеющее
корень х = 0. А вот если а Ф 0, уравнение действительно будет
квадратным. Тогда количество его корней зависит от знака
дискриминанта. Перепишем уравнение в стандартном виде ах2 - х — а = 0.
Дискриминант D = 1 + 4а2 всегда положителен, т. е. уравнение имеет два
различных корня хх = и х2 =
2а * 2а
Ответ: если а = 0, то х = 0;
'l- л/1 + 4а2
если а Ф 09 то х е
§80. Уравнения и неравенства с параметром. Аналитическое исследование
2. Неравенства с параметром
Решение неравенств с параметром обычно существенно сложнее
решения уравнений.
Пример 37. Сравним числа —а и За.
D Если а < О, то -а > За; если а = О, то -а- За; если а > 0, то
-а < За. Ш
Чтобы подчеркнуть сходство и различие в подходах к решению
уравнений и неравенств с параметром, мы будем частично
использовать уже рассмотренные уравнения с параметром, поменяв знак
равенства на какой-либо из знаков неравенства.
Пример 38. Решим неравенство ах > 3.
D Решение зависит от знака коэффициента при х (а не только от
равенства или неравенства этого коэффициента нулю). Действительно,
если мы разделим (умножим) обе части неравенства на отрицательное
число, знак неравенства меняется на противоположный.
о
Ответ: если а > О, то х > -;
а
если а = О, то х е 0;
если а < О, то х < —. Ш
а
Пример 39. Решим неравенство ах ^ За.
D Здесь в ответе тоже будут три случая:
если а > 0, то х ^ 3;
если а = 0, то х е R;
если а < 0, то х > 3. В
Пример 40. Решим неравенство (а2 — а)х > За.
D Для решения этого неравенства, как и в предыдущих примерах,
рассмотрим знаки коэффициента а2 - а. В каждом из пяти случаев:
а < 0, а = 0, 0 < а < 1, а = 1, а > 1, выражение а2 - а либо обращается
в нуль, либо имеет постоянный знак.
о
Ответ: если а < 0 или а > 1, то х > ;
а - 1
если а = 0, то х е 0;
если а = 1, то х е 0;
если 0 < а < 1, то х < . И
а - 1
Пример 41. Решим неравенство ^ 0.
2х - 1
D Это уже не линейное неравенство. Воспользуемся методом
интервалов. Единственный корень числителя — это х = а, корень
знаменателя х = —. Чтобы расположить эти корни на числовой прямой
3361 Глава XIII. Уравнения и неравенства
(рис. 13.2), выясним, как они
расположены относительно друг друга, т. е.
рассмотрим по отдельности случаи 1
111 * 2
а>-,а<-ка=-.
Ответ: если а > -, то х е
2
-; а ;
V2 J
если а = -, то х е 0; рИСш 13.2
если а < -, то х е а; - . Ш
Пример 42. Решим неравенство — > 0.
jc2- 4
П Решим неравенство методом интервалов. Корень числителя х— —
(рассматриваем случай а Ф 0; при а = 0 этого корня нет). Корни
знаменателя х = —2 и х = 2. Нужно расставить эти корни на числовой
прямой. Две точки х = -2 и х = 2 жёстко закреплены, а точка х = —
«бегает» по прямой. Три основных случая взаимного расположения этих
точек изображены на рисунке 13.3: в первом случае точка х = —
находится слева от точки х = — 2, во втором случае она между корнями
знаменателя, в третьем — справа от точки х = 2.
1 о
Итак, первый случаи: — < -2, что равносильно неравенству
< 0, из которого a i
а у & j
В случае — > 2 мы аналогично получим — < 0 и а е I --; 0 I.
а а у 2
В третьем случае -2 < — < 2, откуда а е -оо; -- U -; +оо .
а
-2
-2
1
а
to<
2
X
X
—►
-2
Рис. 13.3
1
а
~~~а
<
<-
>
-2
1
а
2
337! §80. Уравнения и неравенства с параметром. Аналитическое исследование
+
ае(-оо;-|)
X
Расставляем знаки дроби
мого числа а (рис. 13.4).
•Н)
х2- 4
> 0, не забывая учесть знак са-
Теперь необходимо отдельно рассмотреть ещё неучтённые случаи
1
Л 1 1
а = 0, а = -- и а = -.
Пусть а = 0. Исходное неравенство приобретает вид
х2-4
> 0, откуда
отсюда х g (-оо; -2) U (2; +оо).
1 Л(х ~2)
Пусть а — —. Получим
2 х2 - 4
(-оо; -2).
1 ^
Пусть а = -. Аналогично получаем —^
с^ X 4
х + 2
< 0, что даёт
> 0 и х е (2; +оо).
Теперь «собираем» все эти случаи для получения ответа:
если а>-, то хе\ -2; — U (2; +оо);
если а- -, то х е (2; +оо);
если 0<а<|, то х е f ~; -2 J U (2; +оо);
если а = 0, то х е (-оо; -2) U (2; +оо);
если -^ < а < 0, то х е (-оо; -2) U | 2; ^ |;
12—Пратусевич, 11 кл.
3381 Глава XIII. Уравнения и неравенства
если а = --, то х е (-оо; -2);
1
если а < —, то х е
(_oo;-2)ufi;2J. В
Такое реп1ение и правильность полученного ответа трудно
проверить.
- Множества на плоскости,
задаваемые уравнениями и неравенствами
Уравнение с двумя переменными f(x, у) = О (или неравенство
f(x, у) > 0) задаёт на координатной плоскости множество, состоящее
из всех точек, координаты которых удовлетворяют этому уравнению
(или неравенству).
ОПРЕДЕЛЕНИЕ -———————-——^^
Множество всех точек плоскости, координаты которых
удовлетворяют данному уравнению (неравенству), называется
графиком этого уравнения (неравенства).
В частности, график уравнения у = f(x) — это график функции /.
Заметим, что понятие «график уравнения» шире, чем «график
функции»: график функции / является графиком уравнения у = f(x), но
график уравнения вовсе не обязан быть графиком функции.
Пример 43. Построим график уравнения (2х + у)(у — х) = 0.
П Произведение двух множителей равно нулю, если хотя бы один из
них равен нулю (а второй при этом имеет смысл). Поэтому график
уравнения будут составлять те и только те точки, координаты которых
удовлетворяют совокупности _
[_у — х= U.
Значит, искомое множество есть объединение двух прямых у = х и
у = -2х (рис. 13.5). Ш
Пример 44. Построим график уравнения ^^ = 0.
X с*
П Уравнение У±М. 1 = о равносильно системе, в которой к сово-
\\У = -2х,
купности предыдущего примера добавлено условие х - 2 Ф 0: \\у = х,
[хф2.
В результате получаем (рис. 13.6) две прямые с двумя выколотыми
точками (которые высекает на них вертикальная прямая х = 2). В
3391 § 81 Множества на плоскости, задаваемые уравнениями и неравенствами
0/
/■
\ ■
Рис. 13.5
Рис. 13.6
Рис. 13.7
Пример 45. Построим множество, заданное неравенством
(2х + у)(у- х)>0.
Q Понятно, что знак левой части зависит от знаков множителей 2х + у
и у - х. Выше прямой у = —2х множитель 2х + у положителен, ниже —
отрицателен. Аналогично выше прямой у = х множитель у — х
положителен, ниже этой прямой множитель у - х отрицателен. Такой
подход фактически оперирует системами неравенств вида
[2х + у> О,
\у-х>0
(всего четыре системы с разными комбинациями знаков множителей)
(рис. 13.7). В
Более удобным представляется следующий подход: прямые
2х + у = 0 и у — х = О разбивают координатную плоскость на четыре
области, в каждой из которых оба множителя имеют постоянные
знаки. Действительно, знак множителя может измениться лишь при
переходе из области в область через граничную прямую (на которой этот
множитель обращается в нуль). Проверить знаки множителей в
каждой области можно, взяв там контрольную точку (только не на
границе области). А можно просто следить за изменением знаков
множителей при переходе из области в смежную область.
Приведённое рассуждение практически является аналогом метода
интервалов. Назовём этот вариант «методом областей»: здесь вместо
координатной прямой мы используем координатную плоскость, а
вместо точек, разбивающих прямую на интервалы, — линии,
разбивающие плоскость на области.
Отметим, что мы приняли без доказательства то, что знак
функции двух переменных изменяется лишь при переходе через границу
области. Более того, мы не даём описание тех функций, при
определении знака которых применим «метод областей». Это связано с тем,
12*
340 Глава XIII. Уравнения и неравенства
что понятие непрерывности функции двух переменных выходит за
рамки нашего курса. Однако метод областей настолько интуитивно
ясен, а преимущества его применения столь широки, что мы можем
смириться с этой нестрогостью.
Итак, для использования «метода областей» сначала строим
область определения левой части неравенства (включая «вырезанные»
прямые и кривые, ограничивающие эту область) и все прямые и
кривые, на которых какой-либо из множителей обращается в нуль. Эти
линии разбивают координатную плоскость на области, в каждой из
которых выражение в левой части неравенства имеет постоянный знак,
который можно определить, например, при помощи контрольной
точки, взятой из внутренней части области.
Пример 46. Построим множество, заданное неравенством
(2х + у)(у - х) Q
х- 2
□ Запишем уравнения граничных прямых, разбивающие плоскость
на области: у = -2х, у = х, х = 2. Важно не забыть, что штриховую
прямую х = 2 мы, с одной стороны, вырезаем из области определения,
поскольку во всех её точках знаменатель дроби обращается в ноль, а с
другой — знаменатель х - 2 имеет разные знаки
по разные стороны от этой прямой, так что
выражение в левой части меняет свой знак
при переходе через неё.
1\ ^ и ' Далее выбираем контрольные точки в
\У ** I /'/* каждой из семи областей, на которые разбили
У* yf<b плоскость указанные три прямые (рис. 13.8)
\ /\ (или выясняем знак в одной области и
затем отслеживаем изменения знака дроби
при переходе из данной области в смежную
с ней). Ш
Такими методами удобно пользоваться
и при задании множеств уравнениями и
неравенствами с модулем. В качестве граничных
линий, разбивающих плоскость на области,
добавляются линии, на которых выражения
под знаком модуля обращаются в нуль.
Рис. 13.8
Пример 47. Построим график уравнения \х-у+1\ + \х - 2у\ = х.
О Прямые y = x + liiy = — разбивают плоскость на четыре обл
Выясним знаки выражений х - у + 1 и х - 2у. Выбрав контрольную
А ,Л Л^ (
точку (например, А(1; 1)), получим
у
(Х ~ У +1^ 0>
ух — Zy ^ и.
341 §81. Множества на плоскости, задаваемые уравнениями и неравенствами
X
Заметим, что эти неравенства задают область Dx как пересечение
полуплоскостей. Будем это кратко записывать так: Dxx \ о < о '
Тогда уравнение в этой области приобретает вид х - у + 1 +
+ 2у — х = х, а после упрощения у = х — 1.
Аналогично область D2 задаётся системой D2: I ^
[х — 2у ^ О.
Здесь, раскрыв модули, получим у = х + -. Эта прямая не имеет
3
общих точек с областью, поэтому в области D2 не будет точек графика
исходного уравнения.
Область Do задаётся системой Ds: \ _ ^ ^ ' В этой области
[х- 2у > 0.
исходное уравнение превращается в у = -х - 1, которое задаёт
прямую, не имеющую общих точек с рассматриваемой областью.
Наконец, в области 2)4:
х+ 1
х - у + 1 > 0,
х - 2у > 0
рассматриваемое уравнение
примет вид у =
о
Таким образом, графиком исходного уравнения является
объединение двух лучей с общим началом (рис. 13.9). В
Пример 48. Построим множество, задаваемое неравенством
\х - у + 1\ + \х - 2у\ **: х.
□ Возьмём уже построенный график уравнения \х — у+1\ + \х — 2у\ = х.
Он разбивает плоскость на два множества Мх и М2 (внутренняя и внеш-
342 Глава XIII. Уравнения и неравенства
О
Рис. 13.10
X
няя области угла) (рис. 13.10). В
соответствии с «методом областей»
проверяем выполнение неравенства в этих
областях при помощи контрольных
точек (т. е. выясняем знак выражения
| х - у + 11 + | х - 2у | - х). Для ответа нам
подходит множество Мг вместе с
границей, поскольку неравенство было
нестрогим. Ш
Замечание. При работе с
неравенством, когда график уравнения уже
построен, нам вовсе не нужны области
Dl9 D2, Ds, D4, которые мы использовали при построении графика
уравнения! При выборе ответа в неравенстве речь идёт уже о совсем других
областях Мг и М2, на которые разбил плоскость график уравнения.
Таким образом, речь идёт о двукратном применении «метода областей» —
сначала для построения графика уравнения (границы неравенства),
а потом для выбора ответа в неравенстве.
С?)82- Графический метод решения уравнений
и неравенств с параметрами в плоскости (х; а)
Расширим арсенал приёмов решения задач с параметрами. Этому
послужат графические методы.
Можно выделить два основных графических приёма: первый —
интерпретация задачи в плоскости (х; у)> второй — в плоскости (х; а).
Начнем с координатной плоскости (х; а), которая определяет один
из наиболее наглядных и эффективных методов решения задач с
параметрами.
В § 80 мы рассматривали параметр как постоянное (но
неизвестное) число. Между тем формально параметр — это тоже переменная,
причём равноправная с другими переменными, о которых идёт речь
в задаче. При таком взгляде, например, f(x; a) — это функция двух
переменных, a f(x; а) = 0 — уравнение с двумя переменными. Кроме
того, поскольку параметр «уравнивается в правах» с переменной,
имеет смысл завести для него отдельную координатную ось. Так
естественным образом появляется координатная плоскость (х; а). А графики
уравнений с двумя переменными и множества, задаваемые
неравенствами, мы как раз и учились строить в § 81!
Дадим более подробную схему разбора такой задачи.
1. В плоскости (х; а) строим график уравнения f(x; a) = 0.
Заметим, что всегда решение начинается именно с построения
графика уравнения, даже если в задаче речь идёт о неравенстве!
Рекомендация: можно попробовать выразить из уравнения f(x; a) = 0
параметр а как функцию от х, т. е. а = g(x).
343; §82. Графический метод решения уравнений и неравенств с параметрами
в плоскости(х; а)
2. Мысленно проводим всевозможные прямые вида а = const.
Количество точек пересечения такой прямой с графиком
уравнения даёт количество корней при данном значении а.
3. Если нужно решить уравнение (выписать решения, зависящие
от а), то на каждой ветке графика уравнения по отдельности выражаем
х через а («переименовываем ветви»): х = ср(а). Иногда для этой
операции приходится дополнительно разбивать ось Ох на промежутки.
Эти действия обусловлены тем, что решениями уравнения
f(x; a) = О при данном а являются абсциссы точек пересечения прямой
а = const с графиком уравнения. Мы как раз и получаем эти корни
в виде х = ф(а). Теперь можно выписать ответ в уравнении.
4. Если в задаче идёт речь о решении неравенства, то выбираем
и заштриховываем части плоскости, где неравенство выполняется
(«метод областей»).
Решениями неравенства при данном значении а являются
абсциссы тех участков прямой а = const, которые попали в заштрихованные
области. Границами соответствующих промежутков будут корни
уравнения, найденные на третьем этапе.
Продемонстрируем применение описанного метода на примерах.
Пример 49. Найдём в зависимости от а количество решений уравнения
(а + 1 -\х- 1|)(а- 2х2 + 4х) = 0.
«хх Га + 1- \х- 1| = О,
U Исходное уравнение равносильно совокупности Л '
[а - 2х2 + 4х = 0.
В первом уравнении а = |х-1|-1,аво втором а = 2х2 - 4х. График
уравнения представляет собой объединение «уголка» и параболы
(рис. 13.11). Проводим всевозможные прямые а = const. Прямая а = —2
имеет с графиком одну общую точку. При -2 < а < — 1 и при а = 0
прямые пересекают график в двух точках; при -1 < а < 0 и при а > 0 —
в четырёх различных точках. Прямая а = -1 имеет с графиком три
общие точки. Таким образом, ответ читается по рисунку 13.11:
если а < -2, то решений нет;
если а = -2, то решение одно;
если -2 < а < -1, то решений два;
если а = — 1, то решений три;
если — 1 < а < 0, то решений четыре;
если а = 0, то решений два;
если а > 0, то решений четыре. Ш
Пример 50. Решим уравнение
\х + 1| = ах.
D Выразим из уравнения а как
1* + 1|
функцию от х, получим а = -.
Деление обеих частей уравнения
на х не изменит множества его корней
3441 Глава XIII. Уравнения и неравенства
-1
в—1-4-
0
a=const
-1
Рис. /3.72
вид а = 1 + —,
Х=7Г=1
откуда х =
а- 1
ни при каких значениях а,
поскольку при любом значении а
значение х = О не является
корнем уравнения (это можно
увидеть, подставив х = О в исходное
уравнение). Построим график
этой функции на плоскости
(х; а). На рисунке 13.12 видно,
что при а < -1 уравнение имеет
один корень; при -1 < а < О —
два корня; при а = О — один
корень; при 0 < а ^ 1 корней
нет; при а > 1 снова один
корень. На каждой ветке графика
выражаем х через а. Справа от
прямой х = —1 уравнение имеет
Слева от прямой х = -1 график
представлен частью гиперболы а = — 1 , откуда х = —
,
а+1
Ответ: если а ^ — 1, tojc =
а-19
если -1 < а < 0, то хх = -
если а = 0, то х = -1;
если 0 < а < 1, то корней нет;
1
а+1'
а-11
если а > 1, то х =
а- 1
-1
Мо
a=const х
Рис. 13.13
Пример 51. Решим
неравенство \х + 1| ^ ах.
П В предыдущем примере был
построен график уравнения
\х + 1\ = ах. Он разбивает
плоскость на три области М19 М2
и М3. Проверяем выполнение
неравенства в этих областях с
помощью контрольных точек.
Неравенству удовлетворяют
координаты точек из областей Мг
и М3 (рис. 13.13). Напомним, что
решением неравенства при
данном значении а будут абсциссы
тех участков прямой а = const,
которые попали в эти области.
345, §82. Графический метод решения уравнений и неравенств с параметрами
в плоскости (х; а)
Ответ: если а ^ -1, то х е -оо;
если
-1 < a < О, то х е Ц-; —Ц- ;
a + 1 а - 1J
если а = О, то х = —1;
если 0 < а ^ 1, то решений нет;
если а > 1, то х е
г;+оо .
Попробуйте для сравнения решить эту задачу аналитически.
Будет поучительно сравнить результат и затраченные усилия.
Обратимся теперь к примеру 42 из § 80, в котором мы
столкнулись с определёнными сложностями.
Пример 52. Решим неравенство
—
х2- 4
> 0.
D Построим график уравнения
ах + 1
х2- 4
= 0, которое равносильно сис-
теме
a = —,
х
хф -2,
хф2.
А?
•
-2
1
/
#
0
1
2
1
■] 4 :
-—^—
a=constl
i i
Обратите внимание, что мы
изображаем здесь не только
выколотые точки на гиперболе, но
целые «вырезанные» из
плоскости прямые х = -2 и х = 2. Это
принципиально: знак
знаменателя зависит от того, по какую
сторону от каждой из этих
прямых находится точка;
поэтому сами эти прямые участвуют
в разбиении плоскости на
области — подобно тому, как
границами интервалов на прямой
были корни знаменателя дроби
при решении рациональных
неравенств методом интервалов.
Не забудем, что график функции a = тоже должен быть выполнен
х
штриховой линией, поскольку мы решаем строгое неравенство. Всего
на рисунке 13.14 у нас получилось семь областей, из которых нам
подходят Dl9 Ds, D5 и D7. Записываем ответ:
Рис. 13.14
346| Глава XIII. Уравнения и неравенства
если а < --, то х е (-оо; -2) U -; 2 |;
если а = --, то х е (-оо; -2);
-| < а < О, то х е (-оо; -2) U [2; Л;
а = 0, то х е (-со; -2) U (2; +оо);
0< а < |, то х е |-i; -2J U (2; +оо);
если а = -, то х g (2; +оо);
если а > -, то х g -2; — U (2; +оо).
2 у а)
Упомянутая в § 80 симметрия ответа объясняется тем, что
график неравенства центрально-симметричен относительно начала
координат. Ш
А теперь воспользуемся некоторыми примерами § 81. В примере 47
§ 81 мы строили график уравнения \х - у + 1\ + \х - 2у\ = х9 ав
примере 48 — множество, задаваемое неравенством \х — у + 1\ + \х — 2у\^х.
Пример 53. Решим уравнение \х - а + 1\ + \х - 2а\ = х.
□ Воспользуемся уже построенным графиком уравнения (рис. 13.15),
поменяв лишь название вертикальной оси. На каждом из лучей
выразим х через а, у нас получится х = а + 1 для одного луча и х = За - 1 для
другого.
Ответ: если а < 1, то нет решений;
если а = 1, то х = 2;
если а>1, тох1 = а+1, х2 = За — 1. Ш
1
0
/а=
/х-а+
a=const у ^^^
-а+1 х
2= За
х-1
х=
<<-
-1
За-1
:~з~
X
Рис. 13.15
347, §83. Графический метод решения уравнений и неравенств с параметрами
в плоскости (х; у)
ui\
Рис. 13.16
Пример 54. Решим неравенство \х — а + 1\ + \х - 2а\^ х.
П Графический образ неравенства построен в примере 48 § 81
(рис. 13.16). Осталось «прочитать» ответ: если а < 1, то нет решений;
если а = 1, то х = 2; если а > 1, то х е [а + 1; За - 1]. И
Пример 55. Выясним, при каких значениях параметра а имеет
решение система неравенств
(ах + 1 <0,
\х + а > 0.
a)
a =
ax
-i'
J
0
fl<0
a
X
s
1
6N)
ч
ч
ч
i
ч
ч
ч
ч
0
а>0
т
X
s
ч
ч
ч
\
а=-х ns
Ч
-1
-1
' Ч
/ ч
Рис. 13.17
Ответ читается по рисунку 13.17, в.
Ответ: а е (-оо; -1) U (1; +оо). Щ
- Графический метод решения уравнений
и неравенств с параметрами в плоскости (х; у)
Пример 56. Найдём наибольшее и наименьшее значения функции
у = (х - а)2 на отрезке [0; 1] в зависимости от параметра а.
D Графическая интерпретация здесь очевидна. Всё зависит от того,
принадлежит ли абсцисса хо = а вершины параболы у = (х — а)2 отрез-
348 Глава XIII. Уравнения и неравенства
ку [0; 1], и если принадлежит, то к какому из концов отрезка она
ближе (рис. 13.18).
Ответ: если а ^ 0, то min f(x) = /(0) = a2, max fix) = f(l) = (l- a)2;
[0; 1] [0; 1]
если 0<а<-, то min/(x)= f(a)= 0, max/(x)=/(1)=(1-а)2;
2 [0; 1] [0; 1]
если а = -, то min f(x) = f(a) = 0, max f(x) = f(0)= /(1) = -;
если - < a < 1, то min fix) = f(a) = 0, max f(x) = /(0) = a2;
2 [0; 1] [0; 1]
если a > 1, то min f(x) = f(l) = (1 - a)2, max f(x)= f(0) = a2. Ш
[0; 1] [0; 1]
X
Рис. 13.18
Рис. 13.19
Пример 57. Выясним, при каких значениях параметра а уравнение
х - а = |4|х| - 2а21 имеет три различных корня.
□ В данном случае применение графического метода в плоскости
(х; а) связано с определёнными неудобствами: весьма трудно
построить график уравнения. Поступим иначе.
Построим в плоскости (х; у) график функции у = |4|х| - 2а21
элементарными преобразованиями (на рис. 13.19 изображен случай
а Ф 0; случай а = 0 очевиден). Кроме того, имеется семейство
параллельных прямых вида у = х — а. Нас интересуют те прямые этого
семейства, которые пересекают построенный график ровно в трёх точках.
Очевидно, для прямой 1г должно выполняться условие а = , а для
прямой 12 — условие —а = 2а2. Поскольку а Ф 0, получаем а = -2 или
а = --. Ответ: а = -2 или а = --. Щ
349 §83. Графический метод решения уравнений и неравенств с параметрами
в плоскости (х; у)
Чаще всего приходится применять рассуждения в плоскости (х; у)
при работе с определёнными типами иррациональных уравнений с
параметрами.
Пример 58. При каких значениях параметра а уравнение
ах - 1 = д/8х- х2-15
имеет единственное решение?
D Рассмотрим функции у = ах — 1 и у = ^8х - х2 - 15.
График функции у = ^8х — х2 - 15 представляет собой
полуокружность с центром в точке (4; 0) и радиусом 1, расположенную в верхней
полуплоскости, задаваемую сие-
(х- 4)2 + у2 = 1, *У
у> о.
Графики семейства у = ах - 1 —
это прямые, проходящие через
точку А(0; -1) с угловым
коэффициентом а. Такая прямая имеет с
полуокружностью ровно одну общую
точку, либо если она касается её
(в точке М на рисунке 13.20), либо
если она проходит во внутренней
области угла ZBAC, либо если это
сама прямая АС. Легко найти, что Рис. 13.20
угловые коэффициенты прямых
АВ и АС соответственно равны — и —. Угловой коэффициент касательной
5 3
AM определим из условия, что уравнение (ах - I)2 = 8х - х2 - 15
должно иметь совпадающие корни при условии ах > 1 (т. е. дискриминант
о
этого квадратного уравнения должен быть равен нулю!). Отсюда а— —.
15
1
Ответ: —
Пример
система
1 8
а < — или а = —. Ш
59.
\х\
Сколько
*- \у\ = а>
решении имеет
х2 +у2 =
в зависимости от
параметра а?
П Сразу заметим, что при а ^ 0
решений нет. Уравнение х2 + у2 = 1
задаёт окружность с центром в начале
координат и радиусом 1, а вот уравнение
Iх I + IУI = а — множество
«раздувающихся» квадратов (рис. 13.21).
3501 Глава XIII. Уравнения и неравенства
Если квадрат находится внутри окружности, решений нет. С
ростом а квадрат «раздувается» (его вершины имеют координаты (а; 0),
(0; а), (-а; 0), (0; -а)). Решения в системе появятся при а = 1, когда
квадрат окажется вписанным в окружность, причём их будет четыре.
Дальше с ростом а решений станет восемь (окружность пересекает
каждую сторону квадрата в двух точках). При а = V2 стороны
квадрата будут касаться окружности, и решений снова будет четыре. При
а > л/2 система решений не имеет.
Ответ: если а < 1 или а > V2, то решений нет;
если а = 1 или а = V2, то решений четыре;
если 1 < а < л/2, то решений восемь. В
О84. Иррациональные уравнения и системы
Напомним, что иррациональным уравнением мы условно называем
уравнение, содержащее радикалы, под которыми находятся выражения
от переменной х (чаще всего многочлены или алгебраические дроби).
1. Избавление от иррациональности
Утверждение -----------------------------——
Уравнение (f(x))n = (д (х))п при п е N является следствием
уравнения f(x) = g(x).
Символически: f(x) = g(x) => (f(x))n = (g(x))n.
П доказательство. Действительно, если число а есть корень
первого уравнения, то f(a) = g(a), но тогда (f(a))n = (g(a))n> т. е. а является
одновременно корнем второго уравнения. Ш
Легко заметить, что для чётной степени п обратного следствия
нет: например, из уравнения х2 = 4 не следует х = 2.
Замечания. 1) Для чётной степени п = 2k (f(x))2k = (g(x))2k =>
=> |/(х)| = |#(х)|. Таким образом, имеет место следующая
равносильность уравнений: (f(x))2k = (g(x))2k <=> \f(x)\ = \g(x)\.
2) Операция возведения уравнения в нечётную степень п = 2k + 1
есть равносильное преобразование: f(x) = g(x) <=t> (f(x))2k + 1 = (g(x))2k + 1.
Для нас главное то, что операция возведения обеих частей
уравнения в натуральную степень заведомо не приводит к потере корней, но
в случае возведения в чётную степень может привести к появлению
посторонних корней.
В примерах при рассмотрении различных методов и подходов
(включая отбор корней и стандартные виды замен) мы будем, как
правило, ограничиваться уравнениями с квадратными радикалами
(поскольку при работе с радикалами других чётных степеней никаких
3511 §84. Иррациональные уравнения и системы
принципиальных отличий нет) и кубическими радикалами (как
типичным случаем уравнения с радикалами нечётной степени).
Итак, начинаем с уравнений, содержащих квадратные радикалы.
Выясним вопросы, связанные с ООУ: насколько это понятие здесь
полезно и нужно ли начинать решение такого уравнения с поиска ООУ.
Поскольку при возведении в квадрат корни заведомо не теряются,
можно возводить уравнение в квадрат столько раз, сколько
понадобится, чтобы полностью избавиться от иррациональности (это будет
цепочка следствий), а потом полученные корни проверить прямой
подстановкой (если такая подстановка не представляет значительных
вычислительных трудностей). Напомним, что в таком решении
проверка является обязательной частью решения.
Пример 60. Решим уравнение yjx2 + Зх — 3 = 2х — 3.
□ Возведём обе части уравнения в квадрат:
yjx2 + Зх - 3 = 2х - 3 =» х2 + Зх - 3 = 4х2 - \2х + 9;
после упрощения получим х2 — 5х + 4 = 0, откуда _ '
\_х = 4.
Проверка: х = 1 — посторонний корень (при подстановке правая
часть уравнения отрицательна!), корень х = 4 подходит. Ответ: {4}. В
Заметим, что х = 1 будет корнем уравнения д/х2 + Зх - 3 = 3 - 2х,
а х = 4 оказывается в этом случае посторонним корнем.
Кстати, на примере решённого уравнения хорошо видно, что
в данном случае при возведении в квадрат корни уравнения-следствия
попадают в ООУ: область определения исходного уравнения
определялась неравенством х2 + Зх - 3 > 0, но поскольку при возведении
в квадрат мы получаем х2 + Зх - 3 = (2х - З)2, то требуемое
неравенство заведомо выполнено для решений полученного уравнения. Наличие
постороннего корня здесь связано вовсе не с ООУ, а со знаками правой
и левой частей уравнения: необходимо, чтобы эти знаки совпадали!
Более подробно мы обсудим это позже.
Если в уравнении присутствует несколько радикалов, уравнение
приходится возводить в квадрат неоднократно. Для удобства обычно
один из радикалов оставляют в одной из частей уравнения, а все
остальные выражения переносятся в другую часть уравнения (таким образом,
уравнение приводится к виду <yjf(x) = g (x)). Такой приём называется
уединением радикала.
Пример 61. Решим уравнение ^х + 2 - Л/2лГ^~3 = 1.
D Перепишем уравнение в виде ^2х- 3 = д/х + 2 - 1 (т. е. уединим
радикал д/2х - 3); теперь обе части возведём в квадрат:
352 Глава XIII. Уравнения и неравенства
Уединим радикал и возведём обе части в квадрат: 2у/х + 2 = 6 - х;
2 2 8 4
+ 2) = 36 -
+ х
2;
х2 -
р
+ 28 = 0, откуда х = 2 или х = 14.
{}
) у
Проверка: х = 2 подходит, х=Ы — посторонний корень. Ответ: {2}. И
Однако проверку не всегда легко осуществить прямой
подстановкой, например, если корни получившегося уравнения-следствия будут
содержать выражения с радикалами. В этом случае можно
воспользоваться следующими очевидными утверждениями:
Утверждения
= д(х) равносильно системе
1. Уравнение вида yj
f() (e(
\д(х)>о.
2. Уравнение вида yjf(x) = Л/д(х) равносильно любой из систем
lff(x)>0
Пример 62. Запишем решение уравнения из примера 60, используя
переход к равносильным системам:
D д/^+Зх-З = 2x-3<=>
jc2 + 3jc-3=(2x-3)2,
2x - 3 > 0
Iх''
[2х-
- 5х + 4 = 0,
0
<=>
<=> х = 4.11
Отметим, что никаких преимуществ по сравнению с цепочкой
следствий и проверкой не появилось. Однако следующий пример
показывает, что переход к равносильной системе бывает оправдан.
Пример 63. Решим уравнение ^2х + 5 = 4- х.
П При решении уравнения появятся два корня х = 5 - Vl4 и х = 5 + <Jli.
Проверять, получилось ли верное числовое равенство, прямой
подстановкой таких корней затруднительно.
Поступим иначе:
+ 5= (4-х)2,
x2 - Юх н
4-x> О
= 0,
<=>
0
Если в квадрат придётся возводить не один раз, то при каждом
возведении в квадрат добавляются новые ограничения.
353, §84. Иррациональные уравнения и системы
Пример 64. Запишем решение уравнения примера 61, используя
переход к равносильным системам:
4(х + 2) = (6 - х)2, (х2 - 16* + 28 = О,
<=>
1,
Неравенства в системе в данном случае решать необязательно
(равно как и выяснять, какое из них сильнее); достаточно решить
уравнение и проверить, удовлетворяют ли его корни всем этим
неравенствам. Получим
<=> х= 2. 11
Замечания. 1) Обычно выписывать на каждом шаге в
процессе решения всё увеличивающиеся системы не слишком удобно.
Для облегчения процесса решения примера и записи этого
решения полезно понимать, что, во-первых, зачастую неравенства в этих
системах решать не нужно! Уравнения решаются, а неравенства
только проверяются (туда подставляются корни уравнения). Во-вторых,
чаще всего этот подход используется либо в совсем незамысловатых
уравнениях (там это легко сделать), либо в задачах с параметрами
(особенно при использовании графических методов, при построении
множеств на плоскости), либо в случае получения «плохих» корней,
с которыми сложно проводить арифметические операции.
2) Встречаются уравнения, где ответом является целый
промежуток, а не конечное множество чисел (т. е. уравнение на самом деле
представляет собой тождество на некотором множестве). В этом случае
проверка, конечно же, невозможна, а значит, здесь как раз
необходимо накладывать дополнительные условия на корни в виде неравенств;
тогда в ответе появляются множества, задаваемые этими
неравенствами. Соответствующие примеры мы рассмотрим позже.
О Предостережём от стандартной ошибки, которая часто
встречается при решении уравнений: умножение радикалов, т. е. переход от
(fix)
выражения jf{x) • Jg(x) к корню из произведения yjf(x)- g(x), не есть
равносильное преобразование! Область определения второго
выражения шире (f(x) и g(x) должны быть одного знака, но необязательно не-
354J Глава XIII. Уравнения и неравенства
отрицательными), поэтому при таком преобразовании могут появиться
посторонние корни.
Обратный же переход может выглядеть следующим образом:
JV7 •
при / > О, g > О,
Эти соображения могут понадобиться при вынесении множителя
из-под знака радикала или внесении множителя под знак радикала.
Пример 65. Решим уравнение (х — 2) (х + 1) - (х — 2)
= 2.
□ Обозначим (х - 2)
= t. Тогда t2 = (х - 2)(х + 1) и исходное
уравнение приобретёт вид t2 — t — 2 = 0, откуда
=2,
(х-2)
(х-2)
х+1
х-2
= 2,
х-2
= -1.
(1)
(2)
Решим (1):
(х-2)
х- 2>0
= 4, \х2 - х
\х>2
- х - 2 = 4,
= 3.
Неравенство х > 2 в системе возникло как необходимое и
достаточное условие того, что обе части возводимого в квадрат уравнения
имеют одинаковый знак.
Решим (2):
'2=1 \х2-х-2=1у _ „ 1-V13
Ответ:
-Vl3
При распространённом неверном реп1ении этого уравнения
множитель (х — 2) вносится под корень без рассмотрения его знака, в
результате чего второй корень данного уравнения будет потерян. Ж
Вернёмся ещё раз к вопросам, связанным с ООУ. Как видно из всех
разобранных примеров, как правило, можно обойтись вообще без
нахождения ООУ. Уравнение может быть правильно решено даже при отсут-
355j § 84. Иррациональные уравнения и системы
ствии упоминания об ООУ. Более того, верно найденная ООУ и отбор
корней по ней не гарантируют появления посторонних корней, и сама
задача нахождения ООУ оказывается сложной, ненужной, а в некоторых
случаях даже неразрешимой, как показано в следующих примерах.
Пример 66. Решим уравнение ^х3 - х +1 = ^1 - х.
(хз - х + 1 ^ О,
□ ООУ задаётся системой s 'в которой первое неравен-
[1 — х ^ и,
ство мы решать не умеем. В то же время исходное уравнение равносиль-
(хз — х + \= 1 — х9
но системе s ' которая решается устно. Ответ: {0}. IS
[1 — х ^ 0,
Пример 67. Рассмотрим уравнение
П Нахождение ООУ весьма затруднительно. Замена уравнения
равносильной системой тоже не привлекает. А цепочкой следствий получим:
х3 + 4х- 1 - 8^х4 - х = Xs - 1 + 4д/х3 - 1 • у[х + 4х => yjx3 -1 • 4х = 0,
откуда х = 0 или х = 1. Проверкой убеждаемся, что х = 0 —
посторонний корень. Ответ: {1}. Ш
Впрочем, иногда нахождение ООУ даёт единственный ключ к
задаче или существенно облегчает решение.
Пример 68. Рассмотрим уравнение <yjx2 — х + л/2 — х — х2 = у[х - 1.
D ООУ состоит из двух чисел: {0; 1}. Проверкой убеждаемся, что
корнем уравнения является только значение х = 1. Ответ: {1}. В
Вывод: универсальных рекомендаций и рецептов, вообще говоря,
нет. Например, нахождение ООУ, как правило, не нужно, но может
оказаться полезным. Иногда удобнее пользоваться равносильными
системами, иногда удобнее использовать следствия и проверку.
2. Возведение уравнения в нечётную степень
Возведение уравнения в нечётную степень есть равносильное
преобразование:
fix) = g(x) <=> (f(xfk + * = (g(x))2k + K
Однако есть свои особенности, позволяющие упростить
техническую сторону задачи. Имеет смысл обратить на них внимание.
Пример 69. Решим уравнение л/5 + х + л/4-х = 3.
D Возведём обе части уравнения в куб, воспользовавшись
формулой (а + Ь)3 = а3 + Ъ3 + ЗаЬ(а + Ь). Получим равносильное уравнение
356: Глава XIII. Уравнения и неравенства
9 + 3 ^/(5 + х)(4 — х)(л/5 + х + л/4- xj = 27. Мы воспользовались
несколько непривычной формой записи куба суммы, чтобы стало заметным
существенное упрощение: если х является корнем уравнения, то
л/5 + х + у/4-х = 3 по условию задачи. Однако при этом становится
необходимой проверка! Такая подстановка приводит к
уравнению-следствию, причём обратного следствия нет!
Итак,
-х) = 27 => 3^20-х-х2 = 2 =>
=>20-х-х2 = 8=>х2 + х-12 = 0=>х=3 или х = -4.
Проверка показывает, что оба корня подходят. Ответ: {-4; 3}. II
Пример 70. Решим уравнение л/х + 3 + л/5- х = -yfi.
□ Возведя обе части уравнения в куб, получим
8 + 3 syl(x + 3)(5- х) - (Vx + З + Уб- х) = -4.
Если х — корень уравнения, то л/х + 3 + у/5- х = -л/i. Тогда
= -12 <=> ^/4(х + 3)(х- 5) = -4 =>
- 5) = -64 =>х2-2х+1 = 0^>х=1.
Но проверка показывает, что х = 1 не является корнем уравнения!
Ответ: 0. Н
Однако проверку не всегда легко осуществить (например, если
полученные корни содержат громоздкие выражения с радикалами). Тогда
можно воспользоваться следующим соображением: при способе решения,
продемонстрированном в предыдущих примерах, происходит замена
уравнения вида А + В = С на уравнение вида А3 + В3 + ЗАВС = С3.
Поскольку А3 + Б3 - С3 + ЗАВС = ±(А + В-С)((А- В)2 + (В + С)2 + (А + С)2)
(проверьте это самостоятельно), то
А3 + В3 + ЗАВС = С3 <=> ,
х\. — .О — \
Таким образом, если при выполнении равенства А3 + В3 + ЗАВС = С3
не выполняется равенство А = В = -С, то выполняется равенство А + В = С.
Тем самым проверку полученного корня можно осуществлять не
подстановкой в исходное уравнение, а проверкой невыполнения
равенства А — В — —С.
Пример 71. Решим уравнение у/х + 1 + у/х — 1 =
□ Возведя обе части уравнения в куб, получим
2х
357 §84. Иррациональные уравнения и системы
Если х — корень уравнения, то Ух +1 + Ух - 1 = %[Ьх. Тогда
х = з/х2-1. з/5^ => х3 = 5х(х2 - 1) => 4х3 - 5х = 0 => х(4х2 - 5) = 0.
Из последнего уравнения х = О или х = ± —. Первый корень х = О
проверяется легко, а вот с подстановкой двух других возникают
проблемы. Тогда просто убедимся, что эти числа не являются корнями
уравнений Ух + 1 = Ух— 1 = —Убх или х + 1 = х — 1 = —5х, что
очевидно. Ответ: \0; ; —\. В
3. Замена переменной
Введение новой переменной встречается постоянно среди методов
решения задач любого типа. Рассмотрим лишь некоторые
характерные для иррациональных уравнений случаи замен. Воспринимайте все
разобранные варианты замен не как рецепты для заучивания, а как
намёки, которыми можно воспользоваться в сходных ситуациях1.
Пример 72. Решим уравнение Хл/З — х — 5х = 1 + л/3 — х.
□ Введём замену t = л/3— х; тогда t ^ 0 (вместе с введением новой
переменной полезно описывать некоторые её очевидные свойства) и х = 3 -12
(старая переменная должна оказаться выраженной через t). Получим
(3 - t2)t - 5(3 - t2) = 1 + t, откуда ts - Ы2 - 2t + 16 = 0. Среди
делителей числа 16 находим корень уравнения t = 2 и раскладываем левую
часть на множители: (t - 2)(t2 - 3t - 8) = 0. Таким образом, все корни
З-Vil
о 3 + Vil З-Vil п
этого уравнения tx = 2, t2 = , ts = . С учетом ограничения
t>0 остаются только tx = 2 и t2 = . Отсюда находим хг = -1
19 + Зл/il __
их2= .Ш
Пример 73. Решим уравнение 6х2 + 7xVl + х = 24(1 + х).
□ Если, как в предыдущем примере, ввести новую переменную
t = л/l + ху где t ^ 0, то окажется, что через неё неудобно выразить х.
Тем не менее посмотрим, что получилось: 6х2 + Itx - 24t2 = 0 —
уравнение, однородное относительно х и t. Решаем его стандартным
образом (делим на t2, предварительно убедившись, что t = 0 не доставля-
1 Здесь уместно напомнить высказывание замечательного математика
и автора прекрасной трилогии по математике для школьников Д. Пойа:
«Метод — это приём, которым вы воспользовались дважды».
358! Глава XIII. Уравнения и неравенства
о о о I
ет решения) и получаем х = — t или х = —t. Теперь х— —\1 + х или
о 2 3 2
х = —Vl + х. Возводя в квадрат обе части первого уравнения, получим
3 3
хг = 3, х2 = --. Проверка показывает, что х2 = -- — посторонний ко-
8
рень. Аналогично поступаем со вторым уравнением: х3 = --, х4 = 8, но
Г 8] 9
х4 = 8 — посторонний корень. Ответ: < 3; —f. Ш
Пример 74. Решим уравнение л/8 + х + л/8 - х = 2.
. , (и _|_ у = 2
□ Обозначим л/8 + х = i/, v8 - х = v. Тогда s 4 4 _'
при условии
К = 2,
[о2 - 8о2 = 0.
которая не имеет решений.
i/^0, v > 0. Получилась симметрическая система. Используя
симметрические многочлены ог = и + v, O2 = uvy получим
\сх = 29 «1°1 = 2'
[о} - 4а2о2 + 2а| = 16 [16 - 16а2 + 2а2 = 16
Отсюда а2 = 8 или о2 = 0.
тт о JU + V=2,
Для а2 = 8 имеем систему <
[uv = о,
Случай с2 = 0 доставляет пару решений i/ = 2, v = 0 или i/ = 0,
v = 2. Соответственно х = 8 или х = -8. Ответ: {-8; 8}. Ш
Пример 75. Решим уравнение 4х + 24 х- 1 + \х - 2у/х- 1 = 2.
D Введём замену £ = 4х—19 где £ ^ 0, тогда х = ^2 + 1. Получим
д/*2 + 1 + 2f + Jt2 +1- 2t = 2, откуда <yj(t + l)2 + yj(t - I)2 = 2, а значит,
|t+ 1| + U- 1| = 2.
Учитывая, что ^ ^ 0, можно записать: t + 1 + \t — l| = 2. Решением
этого уравнения является отрезок [0; 1]. Таким образом, 4х - 1 ^ 1,
откуда 0 ^ х - 1 ^ 1. Ответ: х е [1; 2]. И
Пример 76. Решим уравнение 4х-1 + 4х + 3 + 2^(х- 1)(х + 3) = 4 - 2х.
П Приведём различные способы решения.
способ 1. Введём замену 4х — 1 = i/, vjc + 3 = у. Отсюда (обратите
внимание, не из уравнения!) и2 + v2 = 2х + 2 и правая часть уравнения
записывается в виде 4 - 2х = 6 - и2 - v2. Уравнение приобретёт вид
и + v + 2i/y = 6 - i/2 - v29 тогда (и + v)2 + (и + v) - 6 = 0.
Обозначим u + v = z, получим уравнение 22 + 2-6 = 0с корнями гг = -3,
22 = 2. Корень 2Х = -3 является посторонним, поскольку z = и + v ^ 0.
Значит, 4х — 1 + 4х + 3 = 2. Решаем последнее уравнение стандартным
способом (уединение радикала и возведение в квадрат). После проверки
остаётся единственный корень х = 1. Ответ: {1}.
3591 § 84. Иррациональные уравнения и системы
способ 2. В процессе решения первым способом было получено
соотношение z = и + v = 2. Далее, для явного нахождения и или v
„ iu + v = 2, ,
можно воспользоваться системой s о о . (второе уравнение следу-
[ir2 - i/z = 4
ет из определения w и v). Разделив второе уравнение на первое, полу-
(u + v = 2, \и = О,
чаем систему-следствие s _ откуда s
^ v — и = ^, [^ у = ^.
Дальнейп1ее решение очевидно.
способ з. При анализе первого решения можно было заметить
более содержательную замену г = у/х — 1 + yjx + 3 (фактически мы к ней
и так пришли, но в два этапа). Значит, этот путь естественно
сократить. Действительно, в этом случае
z2 = 2х + 2
и уравнение сразу приводится к виду z2 + z - 6 = 0. Дальше всё, как
в решении первым способом.
Это весьма распространённый ход в уравнениях, содержащих
конструкцию вида и + v + <Juv.
способ 4. Наиболее рациональным в данном случае будет
решение, связанное со свойствами выражений, составляющих это уравнение.
Областью определения уравнения служит отрезок [1; 2]. На этом
отрезке подкоренное выражение (х — 1)(х + 3) является возрастающей
функцией, а значит, и всё слагаемое J(x - 1) (х + 3) тоже. Таким
образом, левая часть уравнения возрастает на ООУ как сумма трёх
возрастающих функций yjx — 1, у!х + 3 и д/(х — 1)(х + 3), а правая часть
уравнения 4 - 2х строго убывает. Значит, уравнение заведомо имеет не
более одного корня. Таковым оказывается х = 1. Ш
Заметим, что последнее решение выглядит очень компактно и
привлекательно, но нам помогает то, что корень «хороший». В противном
случае, даже зная, что корень только один, мы не смогли бы его
угадать. Хотя такой предварительный анализ уравнения полезен в
принципе, а некоторые уравнения решаются исключительно этим способом.
Об этом следующий пункт.
4. Оценка количества корней. Применение свойств функций
Применение соображений монотонности
Пример 77. Решим уравнение у/7х- 6 + >/5x + 17 = 5.
□ Возведение в куб в данном случае — громоздкая
вычислительная процедура, в то время как сразу видно, что левая часть уравнения
360 Глава XIII. Уравнения и неравенства
есть строго возрастающая функция (как сумма двух возрастающих
функций), а правая — константа. Таким образом, уравнение имеет не
более одного корня, который можно угадать: х = 2. И
Пример 78. Решим уравнение(х - 4)(х - 6)[л/х- 2 + л/3- х) = 3(2х - 5).
□ Избавиться от радикалов в данном случае затруднительно.
Найдём ООУ: х е [2; 3]. Умножим обе части на выражение
у/х— 2 — д/3- х (предварительно убедившись, что корень этого
выражения х=— не является корнем исходного уравнения). Получим
х2 - 10х + 24 = 3\yjx- 2 - л/3- х). На отрезке [2; 3] правая часть
уравнения является возрастающей, а левая — убывающей функцией.
Значит, уравнение имеет не более одного корня. Им оказывается х = 3. Ш
Применение ограниченности функций
Пример 79. Решим уравнение д/х2 - Ах + 5 + д/2х2 - 8х + 17 = 4.
□ Применим соображения ограниченности. Действительно, первое
подкоренное выражение х2 - 4х + 5 = (х - 2)2 + 1 > 1, стало быть, и
д/х2 - 4х + 5 > 1. Аналогично со вторым слагаемым: 2х2 - 8х + 17 ^ 9
и д/2х2 - 8х + 17^3. Таким образом, правая часть уравнения не
меньше 4, а знак равенства возможен только в случае одновременного вы-
\х2 — 4х + 5 = 1,
пол нения условий s 2 Получаем ответ: х = 2. В
Заметим, что этот подход здесь не единственный, и вполне можно
было сделать замену t = х2 — 4х.
Полезными могут оказаться и такие приёмы, как умножение на
сопряжённое выражение, и другие приёмы, подсказанные самой
структурой уравнения.
Пример 80. Решим уравнение ^х2 + 5х + 3 - ^х2 + Зх + 2 = 2х + 1.
□ Умножив на выражение, сопряжённое левой части (не
обращающееся в нуль на ООУ), получим уравнение
2х + 1 = (2х + 1) (V*2 + 5х + 3 + V*2 + Зх + 2) =»
=» (2х + 1) (V*2 + 5х + 3 + V*2 + Зх + 2 - l) = 0.
Один корень очевиден: х =—, второй найдём из уравнения
^х2 + 5х + 3 + д/х2 + Зх + 2 = 1. Это уравнение можно решить
стандартно, а можно сложить с исходным уравнением ^х2 + 5х + 3 - л[х2
361 §84. Иррациональные уравнения и системы
= 2х + 1, что даст нам как следствие у]х2 + 5х + 3 = х + 1. Решив
последнее уравн
{-Н-н
нее уравнение и не забыв про проверку, мы получим х = —. Ответ:
о
5. Системы иррациональных уравнений
Поскольку среди преобразований систем иррациональных
уравнений чаще всего встречается операция возведения в квадрат обеих
частей уравнения, мы не останавливаемся подробно на этом вопросе,
ограничившись напоминанием.
«. т» - 1л/*2 + 4хы - Зу2 = х + 1,
Пример 81. Решим систему уравнении < v v v
[х- у = 1.
□ Возведя первое уравнение системы в квадрат, получим следствие
из исходной системы:
[ д/х2 + 4x1/ - Зу2 = х + 1, _ jx2 + Аху - Зу2 = х2 + 2х + 1, _
\х-у = 1 >\х = у + 1
Uxy - Зу2 - 2х - 1 = 0, _^ Uy2 + 4у - Зу2 - 2у - 2- 1 = О, _
\х = у 4-1 =^[х=1/ + 1
f i/2 + 2у - 3 = О,
[х = у + 1.
Отсюда \ ' или \ ' Проверка (она обязательна) показывает,
[х = Z [х = —Z.
что пара (-2; -3) не является решением. Ответ: {(2; 1)]. Ш
При решении последнего примера можно было воспользоваться
равносильными преобразованиями, если при возведении первого
уравнения в квадрат добавить условие х + 1 > 0 (тогда проверка, конечно,
не нужна!), т. е.
f х2 + Аху - Зу2 = х2 + 2х + 1,
\х=у + 1,
* 0.
А можно было не переписывать систему, а сразу,
воспользовавшись подстановкой х = у + 1, получить вместо первого уравнения
иррациональное уравнение с одной переменной, решить его, а потом
вернуться к системе.
362| Глава XIII. Уравнения и неравенства
\yfx+Jy =
Пример 82. Решим систему
[ /х + 5 + у/у + 3 = 5.
П Подстановка громоздка, поэтому сразу уединим радикалы в урав-
f Jy
нениях и перепишем систему в виде s , . и возведем
[л1х + 5 = 5- у]у + 3
оба уравнения системы в квадрат:
\х = у- бд/у +9, \х=У- 6у[у + 9,
[х + 5 = 25 - lOyjy + 3 + г/ + 3 [x=i/- lO^/j/ + 3 + 23.
Отсюда получаем i/ - 6д/# + 9 = у - 10^1/ +3 + 23 => 5^/j/ + 3 = Зд/z/ + 7.
После возведения в квадрат это уравнение приобретает вид
25у + 75 = 9у + 42^ + 49 =» 8j/ - 21^ + 13 = 0.
Реп1ая это уравнение относительно Jy9 находим Jy = 1 или у[у = —.
8
Таким образом, у = 1 или у = . Возвращаясь к системе (точнее, под-
64
становке х = у - 6<Jy + 9), находим соответствующие значения х. У нас
получилось две пары чисел, которые теперь необходимо проверить
подстановкой в исходную систему, так как решение представляет
собой цепочку следствий. Проверкой убеждаемся, что обе пары являют-
д,
Г121 16911 га
; г. И
\ 64 64 ))
гл La 1ч Г121
ся решениями системы. Ответ: < (4; 1); ;
[ \ 64
Среди систем иррациональных уравнений также встречаются
сводящиеся (обычно посредством удачной замены) к однородным и
симметрическим системам.
. f V5- х = 2у - 6,
Пример 83. Решим систему уравнении <
[2х= 4-
О Введём замену: л/5 - х = и> ^у = v (заметим сразу, что таким
образом и ^ 0 и v ^ 0). Тогда х = 5 - i/2, у = и2. Система приобретает вид
u=2v2-6, iu=2v2-6,
lO-2u2 = 4-v=* \v= 2u2-6.
Теперь симметрия налицо, и можно воспользоваться
стандартными приёмами. Вычитая из первого уравнения второе, получим
и - v = 2v2 - 2и2 =» (и - v)(2u + 2v + 1) = 0. Учитывая, что в силу
условия i/^0, v > 0 второй множитель в нуль не обращается, получаем
(
и = v и соответственно систему
у
(и = v9
[v = 2и2 - 6.
363 §85. Иррациональные неравенства
Тогда 2и2 - и - 6 = 0, отсюда (с учётом того, что и > 0) и = 2.
{и = 2,
' Возвращаясь к старым переменным, имеем
v - I.
Id; 4)}. а
/5-л- = 2, /д:=1,
= 2 ~ Ь - 4.
Q85. Иррациональные неравенства
В большинстве случаев решение неравенств может быть сведено
к решению уравнений, поскольку в нашем распоряжении имеется
метод интервалов. С помощью метода интервалов решение любого
неравенства сводится к нахождению области определения неравенства
(которая ничем не отличается от области определения уравнения!), корней
уравнения, расстановке их на области определения неравенства (далее
ООН) и выборе соответствующих промежутков.
Тем не менее рассмотрим некоторые очевидные утверждения,
помогающие избавиться от иррациональности. Как и в случае
уравнений, их применение оправдано при работе с несложными
неравенствами и в задачах с параметрами.
\f(x)>(g(x))2,
{*(*)< 0,
!/(*) >0;
\f(x)>0,
[g(x)>0;
Замечания. 1) Понятно, что в первом случае при g(x) < 0
неравенство выполнено везде на ООН, которая задаётся условием f(x) > 0.
Если же g(x) ^ 0, то можно смело возводить в квадрат.
Первое условие равносильности может быть записано в более про-
[lg(x)<0,
стом виде: yjf(x) > g(x) <=> \f(x)> 0, (в самом деле, среди решений
_f(x)>(g(x))z
неравенства f(x) > (g(x))2 могут содержаться те х9 при которых g(x) < 0,
но эти значения х> очевидно, являются решениями первой системы, так
что удаление условия g(x) > 0 не может породить «лишних» решений).
364 Глава XIII. Уравнения и неравенства
2) Понятно, что при g(x) ^ 0 второе неравенство не имеет
решений, а условие f(x) ^ 0 нужно потому, что два других неравенства не
обеспечивают автоматического попадания их решений в ООН.
Пример 84. Решим неравенство Зл/б + х - х2 > 4х- 2.
П Неравенство равносильно совокупности двух систем:
\4х — 2 < 0, (если правая часть отрицательна, то
I б + х - х2 > О, неравенство верно для всех х из ООН)
\4х-2> О,
[9(6 +х- х2)>(4х- 2)2.
Решим первую систему:
4х - 2 < О,
6 + х - х2 *>
О
\х<\,
(3-
0
Решим вторую систему:
J4x-2> О,
■х- х2)>(4х-2)2
Объединяем полученные результаты в ответ: х е [-2; 2). IS
Пример 85. Решим неравенство 3V6 + х — х2 < 4х - 2.
D Исходное неравенство равносильно системе
[(6 + jc-jc2)<(4:ic-2)2,
6 + х - х2 > О,
[4л;-2>0.
Преобразовав неравенства системы, получим
х2 - х - 2 > О,
(3-х)(х + 2)>
хе (-оо; -1
-2 ^ х ^ 3,
; +oo),
(2; 3].
Ответ: (2; 3]. 11
Пример 86. Решим неравенство
>л/Т^~
□ VI + х -
Ответ: (0; 1]. 11
1 + х - х3 > VI - х3.
- Xs > 1 - х3, Jх > 0,
о ~ U3 ^ 1
х g (0; 1].
3651 §85. Иррациональные неравенства
Если бы мы стали искать ООН в последнем примере и начали с
решения неравенства 1 + х - Xs > О, решение бы вызвало затруднения.
Другое дело, что можно было решить систему s з о ' которая,
[1-Х ^ U,
собственно, и задаёт ООН. Но приведённое решение явно самое
короткое и очевидное. Такое решение явно выигрывает в сравнении с
применением метода интервалов.
Опять возникает вопрос, что лучше: равносильные системы или
метод интервалов? Метод интервалов — это главный подход. Иногда его
использование осложняется техническими (вычислительными)
сложностями. Поэтому в простейших неравенствах или в неравенствах, где
нахождение области определения затруднено (и порой в неравенствах
с параметрами), имеет смысл не забывать о равносильных системах.
Всё же, как правило, даже в несложных задачах стремление
непременно использовать равносильные системы ведёт к ненужным
техническим усложнениям, в которых легко запутаться. Сравним два способа
решения на следующем примере.
Пример 87. Решим неравенство у/х + 3 < у/х- 1 + у/х - 2.
\х + 3 < 2 х - 3 + 2^1 х - 1 • у/х - 2,
1*+з>о.
Уже здесь нужна внимательность и осторожность: формально
нужно было бы условие у/х — 1 + у/х — 2 ^ 0, но оно выполняется
автоматически, если это выражение определено, а это обеспечивается наличием
множителей у/х — 1 и v^-2 в первом неравенстве. Зато если мы захотим
их перемножить, нам придётся накладывать дополнительное условие,
чтобы сохранить ООН:
-2),
СПОСОБ 1.
| 2у]х2 - Зх + 2 > 6 - х.
х + 3 > О,
х- 1 > 0, [х- 2> 0.
х- 2> 0
Первое неравенство равносильно совокупности двух систем.
Решим его отдельно.
Г6- х< 0,
(х-1)(х- 2)> 0,
- Зх + 2 > 6 - х
|б- х> 0.
ьоо). Во второй -
промежутков -оо; -2 - U 2J-; 6 (рис. 13.22).
V V3J V V3 J
В первой системе ответ х е (6; +оо). Во второй — объединение двух
3661 Глава XIII. Уравнения и неравенства
а)
б)
Я неравенство
выполняется
Рис. 13.23
6 х
Рис. 13.22 Рис. 13.24
Таким образом, вся совокупность равносильна следующей:
х>6
Возвращаясь к исходной системе и учитывая условие х - 2 ^ О,
получаем ответ: 2J—; +оо .
способ 2. ООН исходного неравенства [2; +оо). Решим
соответствующее уравнение Jx + З = у/х-1 + ylx- 2. Его единственный корень
(не забудьте про проверку!) х = 2 J—. Таким образом, вся область
определения оказывается разбита на два промежутка (рис. 13.23).
Выбираем контрольные точки в каждом из них и проверяем
выполнение неравенства. При этом в левом промежутке можно в
качестве контрольной точки взять х — 2 (легче подставлять). Ответ:
№
+ОО
Последнее решение можно было оформить ещё и следующим
образом. Рассмотрим функцию f(x) = -Jx + 3 - у/х — 1 — у/х - 2. Её область
определения D(f) = [2; +оо).
Найдём корни функции f(x), решив уравнение
Единственный корень х
-4-
Теперь на D (/) расставим знаки
функции и выберем множество точек, где значения функции отрицательны
(рис. 13.24). Ш
367 § 86. Иррациональные уравнения и неравенства с параметрами
{^86- Иррациональные уравнения и неравенства
с параметрами
Пример 88. Найдём, при каких значениях параметра а уравнение
у1х + а = х имеет два корня. (В задачах, связанных с определением
количества корней, равные корни считаем, как правило, за один.)
(х + а = х2
П способ 1 (аналитический). Перейдём к системе s ' рав-
[х ^ U,
носильной исходному уравнению. Квадратное уравнение х2 — х — а = О
имеет два различных корня при 2)=1 + 4а>0, т. е. а > —. Система
4
будет иметь два решения, если при этом меньший корень (а значит,
оба) неотрицателен:
2
Из второго неравенства Jl + 4а ^ 1, откуда — ^ а ^ 0. С учётом
4
первого неравенства ответ: — < а
4
способ 2 (графический, в плоскости (х; у)). Построим в
плоскости (х; у) прямую у = х и семейство кривых у = <Jx + а (рис. 13.25). Все
кривые получаются из графика функции у = <s[x сдвигом на -а единиц
вдоль оси Ох. Нам нужно определить те значения параметра, при
которых прямая пересекает кривую ровно в двух точках. При а = 0
решений два. Очевидно, если мы будем сдвигать кривую влево (т. е. при
а > 0), решение будет только одно. Теперь двигаем кривую вправо.
Найдём, при каком а прямая у = х касается кривой g(x) = yjx + a.
Это будет при
Отсюда
Из рисунка 13.25 видно, что при дальнейшем движении вправо
\ а < — корней не будет вовсе. В итоге уравнение имеет ровно два
1 4) 1 ^
корня при — < а ^ 0.
4
368; Глава XIII. Уравнения и неравенства
Ук
- л
Рис. 13.25
О
a=const
Рис. 13.26
Заметим, что точку касания можно найти немного иначе
(например, найти, при каких значениях а прямая х — у является
касательной к графику функции х=у2 — а при у ^ 0; можно сделать, используя
условие равенства нулю дискриминанта уравнения у2 - а = у).
способ з (графический, в плоскости (х; а)). Снова запишем систе-
\х
му, равносильную исходному уравнению:
в виде
[х
а = х2,
но перепишем ее
= х2-
> 0.
х,
В таком виде ясно, что система задаёт просто часть параболы.
Проводим горизонтальные прямые вида а = const. Количество точек
пересечения такой прямой с кривой (рис. 13.26) равно количеству корней
уравнения при данном значении параметра а. Ответ: —<а^ 0. IS
4
Последнее решение, наверное, оставляет самое приятное
впечатление. Жаль только, что не ко всем задачам такие методы удобно
применять. Иногда строить график уравнения — слишком сложная и не
оправдывающая затраченных усилий задача. Тогда нужно искать
другие методы. Но начинать всегда стоит именно с графических методов;
это позволяет увидеть задачу «в целом».
Пример 89. Решим уравнение *Jx + а = х.
П Воспользуемся уже построенным в примере 88 графиком
уравнения. Выразим х через а на ветках параболы стандартным образом. На
левой ветви (слева от оси симметрии параболы, задаваемой уравнением
, а на правой х =
. Ответ можно «прочи-
тать» по рисунку 13.27.
§ 86. Иррациональные уравнения и неравенства с параметрами
Ответ: если а < —, то решений нет;
4
1 1
то х ;
если а = —, то х = -;
если — < а ^ 0, то х =
Пример 90. Решим неравенство yjx + a > х.
П Построим область определения неравенства. Она задаётся
условием х + а ^ 0 или а ^ —х. Теперь решим уравнение у!х + а = х и построим
его график.
I (х + а = х2, \а = х2 - х,
л/х + а = х <=> 1 <=> <
[х > 0 [х > 0.
Часть параболы, задаваемая последней системой, разбивает ООН на
две области, в одной из которых неравенство выполняется (на
рис. 13.28 закрашена), а в другой нет. (Выбор областей был проведён
с помощью контрольных точек.) Осталось записать ответ. Для этого
выражаем на каждой ветке параболы х через а, решив для этого уравнение
х2 - х - а = 0 относительно х. Теперь ответ читается по рисунку 13.28.
Ответ: если а < —, то решений нет;
4
1 1
если а = —, то х = —;
если — < а ^ 0, то х
4
если а > О, то х е -
х=
Рис. 13.27
13—Пратусевич, 11 кл.
Рис. 13.28
3701 Глава XIII. Уравнения и неравенства
Сг)87- Показательные уравнения и неравенства
1. Показательные уравнения
Простейшим из показательных уравнений является уравнение
ах = &, где а > 0, а ф 1. Если Ь ^ 0, то это уравнение не имеет решений.
При Ъ > 0 уравнение имеет единственное решение, которое мы назвали
логарифмом Ъ по основанию а и обозначили х = logafe.
Далее мы будем рассматривать уравнения вида af(x) = ag(x). В
основе решения таких уравнений лежит утверждение.
Если а > О, аФ 1, то уравнение af{x) = ag{x) равносильно
уравнению f(x) = g(x).
Это утверждение, очевидно, следует из свойств показательной
функции (а именно из её строгой монотонности на R). Назовём это
утверждение основной теоремой о показательных уравнениях.
Пример 91. Решим уравнение 5х +х= 51"*2.
П По основной теореме о показательных уравнениях это
уравнение равносильно уравнению х2 + х = 1 - х2, откуда х = -1 или х = —.
-1; —\. Ш
Уравнения вида f(ax) = 0 или f(ag(x^) = 0 решаются с помощью
замены t = ах (или соответственно t = ag(x)). Полезно сразу заметить, что
t > 0 (это сокращает запись решения). Решая уравнение fit) = 0, мы
находим его положительные корни tl9 ..., tk и приходим к совокуп-
ности уравнений
ах= tv
ах = tk,
откуда
х=
х= logatk.
Пример 92. Решим уравнение 22х + 2 + 3 • 2х - 1 = 0.
□ Введём замену t = 2х, где t > 0, тогда 22х + 2 = 4 • (2х)2 = At2.
Получим квадратное уравнение 4£2 + 3£-1 = 0, откуда t = — 1 или t = —. По-
4
скольку t > 0, нам подходит £ = -. Вернёмся к исходной переменной:
4
2х = - <=> 2х = 2~2 <=> х = -2. Ответ: {-2}. В
4
Рассмотрим примеры более сложных показательных уравнений,
решаемых с помощью замены.
371| § 87. Показательные уравнения и неравенства
Пример 93. Решим уравнение 2sin2* + 2cos2* = 3.
D Показатели степени в этом уравнении связаны основным
тригонометрическим тождеством: sin2jc + cos2x = 1. Если положить cos2x = у>
то sin2 х = 1 — у. Мы получим уравнение 2у + 21 ~у = 3, где — 1 ^ у ^ 1.
о
Переписав уравнение в виде 2у + — = 3, заметим, что теперь имеет
2
смысл использовать замену t = 2у. Уравнение приобретёт вид t + — = 3.
Откуда найдём t = 1 или t = 2. Перейдём к уравнениям 2у = 1 и 2у = 2,
откуда г/ = 0 или у = 1. Возвращаясь к переменной х, получим два
уравнения: cos2x = 0 и cos2x = 1, решая которые приходим к ответу:
T>neZ\
Пример 94. Решим уравнение (д/9 - 4л/б j + (д/9 + 4л/б J = 18.
D Заметим, что (9 - 4л/б) (9 + 4л/б) = 1. Тогда
Введём замену t = \л]9 + 4V5 j . Получим уравнение - + t = 18, решая
которое мы найдём t = 9 + 4v5 или £ = 9 - 4V5. В первом случае,
возвращаясь к старой переменной, получим (J9 + 4v5 j = 9 + 4V5, откуда
х = 2. Во втором случае (л/9 + 4v5 ) = 9 — 4V5, или (J9 + 4v5 ) = =,
v ' \v / 9 + 4V5
откуда х = -2. Ответ: {-2; 2}. IS
С заменами специального вида мы встречаемся также в случае
однородного показательного уравнения.
Пример 95. Решим уравнение 4х — 2 • 6* = 3 • 9*.
□ Перепишем уравнение в виде (2*)2 - 2 • 2х • 3х - 3 • (З*)2 = 0. Мы
получили уравнение, однородное относительно переменных и = 2х и
v = 3х. Как и обычно, основной приём — деление на старшую степень
одной из переменных. Получим квадратное уравнение t2 - 2t - 3 = 0
относительно переменной t
= — = — .
Отсюда t = -1 или t = 3, но поскольку t > О, то t = 3. Возвращаясь
(2у Г ]
к старой переменной, получим — = 3 <=> х= log2 3. Ответ: s log2 3f. Щ
\S) 3 I 3 J
13*
3721 Глава XIII. Уравнения и неравенства
Конечно, не всегда такой вид замены сразу бросается в глаза!
Например, в уравнении 32*2 + 6*~9 + 4-15*2 + 3*~5 = 3- 52*2 + 6*~9 это заметно
не сразу, тем не менее это уравнение является однородным
относительно и = 3x2 + Sx~5 и v = 5*2 + 3*"5. Проверьте это и доведите решение
до конца самостоятельно.
О Уделим особое внимание уравнениям вида af(x) = bg(x).
Поскольку два положительных числа равны тогда и только тогда, когда равны
их логарифмы (по произвольному основанию), мы можем
прологарифмировать обе части и получить равносильное уравнение, например,
вида f(x) • lna = g(x) • lnfe, откуда f(x) = g(x) • loga&.
К этому же результату приводит такое рассуждение: общее
решение уравнения af(x) = В имеет вид f(x) = logaB. В данном случае в
качестве В фигурирует В = bg(x).
Пример 96. Решим уравнение 3х -Т2'^ = 21.
□ Уравнение приводится к виду 7х2~1= 3х'1. Это уравнение
равносильно следующему: х2 - 1 = (х - 1) • log7 3 <=> (х - 1) (х + 1 - log7 3) = 0 <=»
х = log7 3-1.
з1
Ответ: \1; log7 — >. Ш
Встречаются показательные уравнения, решение которых связано
с использованием свойств функций (чаще всего монотонности и
ограниченности).
Пример 97. Решим уравнение 3х + 4х = 5х.
□ Поделив обе части уравнения на 4*, получим уравнение
3-\+1
■(5)"
в левой части которого стоит убывающая функция, а в правой —
возрастающая. Значит, уравнение имеет не более одного корня. Проверка
показывает, что х = 2 корень этого уравнения. Ответ: {2}. Ж
Пример 98. Решим уравнение Ы9 - 4л/б V + U/9 + 4л/б j = (yfl8j.
□ Заметим, что это уравнение очень напоминает уравнение из
примера 94, но это сходство кажущееся, и методы решения различны.
Поделив обе части уравнения на (д/9 + 4V5 j , получим уравнение
18
„ 9-4л/б 1 ,
Число рг меньше 1, а это означает, что функция
9 + 4V5
убывает, и вместе с ней вся левая часть уравнения является убываю-
373J §87. Показательные уравнения и неравенства
щей функцией. В правой части уравнения стоит возрастающая функ-
V л:
I 18 I I 18 I
ция — поскольку ■== > 1 . Значит, уравнение имеет не
U + 4V5J V 9+4>/5 )
более одного корня. Этот единственный корень легко угадывается:
х = 2. Ответ: {2}. Ш
Пример 99. Решим уравнение 2х2 + 2~*2 = 1 + cosx.
Q Выражение в левой части уравнения 2х2 н можно представить
в виде t + -, где £ ^ 1, a t + - ^ 2 для t > 0. Таким образом, левая часть
не меньше 2. В то же время правая часть не больше 2 (поскольку
cosx < 1, то 1 + cosx ^ 2). Равенство возможно только в том случае,
когда обе части уравнения равны 2. В левой части это значение
достигается только при х = 0. Проверкой убеждаемся в том, что правая
часть тоже равна 2 при х = 0. Ответ: {0}. Ш
2. Показательные неравенства
При решении показательных неравенств используется
утверждение.
Утверждение
1
Если а> 1, то неравенство af{x)>a9{x) равносильно неравенству
f(x)>g(x);
если 0 < а < 1, то неравенство af{x) > ag{x) равносильно
неравенству f(x)<g(x).
Это утверждение мы назовём основной теоремой о
показательных неравенствах. Оно (как было показано в главе V учебника
10 класса) следует из того, что при а > 1 показательная функция у - а
строго возрастает на R (а вместе с ней и обратная к ней функция),
а при 0 < а < 1 показательная функция у — ах строго убывает на R.
Оговорим отдельно вопрос о том, как записывать обоснование
перехода от неравенства для показательных функций к неравенству для
показателей в случае решения неравенств вида af(x) > ag(x). (Это
обоснование есть необходимая часть в решении показательного
неравенства!) Например, что нужно писать при решении неравенства 52*2 + х > 5?
Нужно понимать, что в основной теореме речь идёт о монотонности
внешней функции а1, которая зависит только от того, что а > 1 или
0 < а < 1 (в данном случае это функция у = 5*). Поэтому краткая
запись выглядит следующим образом:
52х
> 5 <Д 2х2 + х> 1 » (2х - 1)(х + 1) > 0 <=> х е (-оо; -1) U f-; +oo J.
374! Глава XIII. Уравнения и неравенства
Пример 100. Решим неравенство 22х + 2 + 3 • 2х - 1 > 0.
□ Введём замену t = 2х, где t > 0, тогда 22х + 2 = 4 ■ (2х)2 = At2.
Получим квадратичное неравенство 4t2 + 3t — 1 > 0, откуда
*€=(-oo;-l)U \±;
С учётом того что t > О, получаем t > -.
4
Возвращаясь к старой переменной, получим 2х > 2~2, в силу
возрастания функции у = 2х получаем х > —2 (что можно записать так:
2х > 2~2 2й х> -2). Ответ: (-2; +оо). 11
Пример 101. Решим неравенство х • 2х > 8.
П При х ^ 0 неравенство не выполняется. Пусть х > 0. Перепишем
о
неравенство в виде 2х > —. На луче (0; +оо) функция у = 2х строго воз-
X
8 8
растает, а функция у = — строго убывает. Значит, уравнение 2х = —
имеет единственный корень, который легко угадывается: х = 2. А при
о
х > 2 выполняется неравенство 2х > 4 > —. Ответ: (2; +оо). Щ
Рассмотрим примеры показательных уравнений и неравенств с
параметром.
Пример 102. Решим неравенство а2 - 9х + г - 8а • 3х > 0.
П Введём замену t = 3х, t > 0, тогда неравенство можно переписать
в виде (а + t)(a — 9t) > 0. Построим график уравнения (а + t)(a — 9t) = 0
ак i и образ неравенства (а + t)(a - 9t) > 0
' в плоскости (х; а) (рис. 13.29). Получим,
/ _ что если а > 0, то t е 0; - ; если а = 0, то
/ a=9t I 9)
i'
у )
i
' решений нет; если а < 0, то t e (0; -а).
Вернёмся к переменной х: при а > 0
► имеем 3* < - <=> х < log3 -. Аналогично
0 | ^, t 9 9
ч 3*?
чч при а < 0 имеем 3х < -а <=> х < Iog3(-a).
Ответ: если а > 0, то х е
[-oo;log3f);
если a = 0, то решений нет;
Рис- 73-29 если а<0, то х g (-оо; Iog3(-a)). И
375J §88. Логарифмические уравнения и неравенства
Пример 103. Выясним, при каких значениях параметра а уравнение
5 • 25* - (5а + 2) • 10* + 2а • 4х = 0 имеет единственное решение.
П Введём замену t = - , t > 0, получим Ы1 - (5а + 2)t + 2а = 0.
Таким образом, достаточно выяснить, при каких значениях
параметра а уравнение Ы2 - (5а + 2) t + 2а = 0 имеет ровно один
положительный корень. Это происходит, если произведение корней уравнения
tx • t2 < 0 или один корень равен нулю, а второй положителен (tt = 0,
t2 > 0) или, наконец, оба корня совпадают и положительны. В первом
случае согласно теореме Виета имеем — < 0 <=> а < 0. Во втором слу-
о
а = 0 при этом один корень tx = 0, а второй t2 = -
чае а = 0 при этом один корень tx = 0, а второй t2 = - . Наконец, корни
совпадают при условии D = 0. В этом уравнении D = (5a + 2)2 - 40а =
2
= (5а - 2)2, значит, D = 0 при а = —. Проверкой убеждаемся, что при
этом t = -. Ответ: а е (-оо; 0] U ^ -\. Ш
5 [5J
(^88. Логарифмические уравнения и неравенства
1. Логарифмические уравнения
Логарифмическим уравнением мы называем уравнение, содержащее
неизвестное (переменную) под знаком логарифма. Простейшее из таких
уравнений — это logax = b, где a > 0, а Ф 1. Его решением является х — аъ.
В 10 классе была сформулирована теорема: если логарифмы по
одному и тому же основанию от двух чисел равны, то сами числа
равны. Изменив формулировку, мы получим утверждение, которое
назовём основной теоремой о логарифмических уравнениях.
гржден иt
[ Если а >
системе
0, а 9
\f(x)
lff(x)
>
>
, то
0,
0.
уравнение
loga
Цх)
= 1ода
9
(х)
равносильно
Понятно, что на самом деле в системе одно из неравенств является
лишним (оно следует из второго неравенства и уравнения), и можно
использовать любую из систем:
f(x)=g(x), \f(x)=g(x),
f(x)>0 ИЛИЫ
376! Глава XIII. Уравнения и неравенства
Пример 104. Решим уравнение
Iog3(2x + 1) + Iog3(3 - х) = 1 + Iog3(2x - 1).
!2х + 1 > 0,
3 - х> О,
2х - 1 > 0.
Эту систему несложно решить, но мы этого не делаем
принципиально (поскольку иногда решение системы неравенств может
оказаться сложной задачей, а проверить для любого конкретного числа
выполнение этих неравенств обычно несложно). Пользуясь тем, что
1 = Iog33, и складывая логарифмы в обеих частях уравнения,
получаем Iog3((2x + 1)(3 - х)) = Iog3(6x - 3). Отсюда
(2х + 1)(3 -х) = 6х-3=>2х2 + х-6 = 0=*х=- или х = -2.
о
Проверка: х = - является решением уравнения (входит в ООУ),
-Ш-
а х = -2 не является решением (не входит в ООУ). Ответ:
Заметим, что с использованием цепочки равносильных
преобразований решение этой задачи могло быть записано следующим образом:
П Iog3(2x + 1) + Iog3(3 - х) = 1 + Iog3(2x - 1) <=>
1б*-8>0
\2х2 +х-6= 0,
2 2
Такая запись ничем не лучше приведённого выше решения, а при
решении более сложных уравнений может оказаться просто неудобной.
При решении последнего примера мы воспользовались тем, что
1 = 1°ёзЗ. Обратим внимание на то, что любое число можно
представить в виде логарифма с произвольным основанием. Действительно,
для любого числа Ь и положительного числа а Ф 1 имеют место
равенства 1 = logaa и Ъ = \ogaab.
Например: как записать число 3 в виде логарифма по основанию 2?
Ответ: 3 = Iog223 = Iog28.
В частности, нуль можно записать как логарифм единицы по
любому основанию: 0 = logal, где a > 0, а Ф 1.
х + 3
Пример 105. Решим уравнение lg((х - 1)(х + 3)) + lg = 0.
X X
П Здесь нерационально «разбирать уравнение на слагаемые»,
пользуясь формулами логарифма произведения и частного. Воспользуемся
формулой суммы логарифмов.
3771 §88- Логарифмические уравнения и неравенства
Получим lg(x + З)2 = 0, откуда (х + З)2 = 1 =» х = -2 или х = -4.
Учитывая ООУ: (х — 1)(х + 3) > 0, получим, что только х = -4 будет
корнем исходного уравнения. Ответ: {-4}. Ш
Рассмотрим важный приём, который также имеет «подводные
камни»: переход к новому основанию логарифма.
Пример 106. Решим уравнение log2jc+1x = log 2 xx»
□ На первый взгляд естественным представляется поменять
местами основание и аргумент логарифма в данном уравнении (т. е. перейти
к логарифмам по основанию х). Получим = . Ре-
logx(2x+l) log^x2* 1)
шая это уравнение, найдём его единственный корень х = 2. Но
исходное уравнение, очевидно, имеет ещё корень х = 1. При переходе к
новому основанию мы потеряли этот корень за счёт сужения области
определения: во втором уравнении х Ф 1.
Применение формулы \о&0{хЛ f(x) = -—— «слева направо» мо-
жет привести к потере корней, при которых ф(х) ^ 0 или ср(х) = 1 за
счёт того, что правая и левая части в формуле определены на разных
множествах. Использование формулы «справа налево» может
привести к появлению посторонних корней по этой же причине.
В этой ситуации есть выход: переход к логарифму по любому
фиксированному основанию есть равносильное преобразование! Если в
нашей задаче перейти, например, к логарифмам по основанию 2 или
к натуральным логарифмам, то корень не потеряется. Действительно,
\og2x+1x= log <>
Отсюда получится, что х = 1 или х = 2. Ответ: {1; 2}. Ш
О Лучше всегда работать с логарифмами по фиксированному
основанию.
Пример 107. Решим уравнение log2 х = 41og9^ x.
□ Перейдём в правой части уравнения к логарифмам по основанию 3.
! - = 41og x « log! x = ^-^ « log! - = ГП^
log! - = 41og9^ x « log! x = ^-^ « log! - =
2t
Теперь очевидной становится замена t = log3x. Получим t2 = .
Отсюда t = 0, или t = 1, или t = -2. Возвращаясь к старой переменной
378! Глава XIII. Уравнения и неравенства
и решая совокупность уравнений
log3 х = О,
log3 х = 1, получим ответ (провер-
log3 х = -2,
ка здесь не требуется): si; 3; —k IS
Однако встречаются ситуации, где переход к фиксированному
основанию создаёт технические сложности и не позволяет увидеть
подходящую замену. В этом случае преобразования следует производить,
тщательно отслеживая изменение области определения на каждом
шаге, чтобы не потерять и не приобрести корни.
Пример 108. Решим уравнение
logx _ 2*(6х2 - 5х + 1) - log! _ з*(4*2 - 4х + 1) = 2.
П Раскладывая выражения под знаком логарифма на множители,
получаем logi_2jc((2x - 1)(3х - 1)) - log!_3jc(2x - I)2 = 2. А теперь за-
1- 2х> 0,
1 - 2х ф 1,
1 - Зх> 0,
1- Зх* 1.
метим, что ООУ задаётся условиями:
Нам это важно по двум причинам: зная знаки этих выражений,
мы сможем аккуратно применить формулы логарифмирования; кроме
того, мы сразу же получаем ООУ: s 3'
[хфО.
Следствием исходного уравнения является уравнение
log!_2j2x-l| + Iog1_2j3x-l| -21og!_3j2x-l| =2.
Снимая модули и учитывая ООУ, получим 12х — 11 = 1 - 2х, | Зх — 1\ =
= 1 - Зх, и соответственно 1 + log! _ 2лг(1 - Зх) - 2 logi _ Sx(l - 2х) = 2.
2
Введём замену t = logi _ 2лг(1 - Зх). Получим уравнение 1 + t = 2,
х
корни которого t = — 1 или £ = 2.
Возвращаемся к старой переменной:
logi_2jc(l - Зх) = -1 или logi_2jc(l - Зх) = 2.
Решим первое уравнение
logl_2jc(l - Зх) = -1 =* 1 - Зх = т~,
откуда х = 0 или х = -, но оба этих значения не принадлежат ООУ,
6
т. е. корнями уравнения не являются.
379[ §88. Логарифмические уравнения и неравенства
Решим второе уравнение logj _2л:(1 ~ 3jc) = 2 =» 1 - Зх = (1 - 2х)2,
откуда х = 0 или х= —. Первое число не входит в ООУ, поэтому корнем
4
не является. Ответ
■Ш-
Обратимся к уравнениям вида ф(х)/(л:) = ф(х)^(л:). Основной метод
работы с таким уравнением уже был рассмотрен: это логарифмирование
обеих частей уравнения по любому фиксированному основанию,
которое покажется нам удобным в данной задаче. Будем считать, что
область определения такого уравнения задаётся неравенством ф(х) > О,
поскольку речь идёт о возведении в степень с вещественным
показателем. В некоторых учебных пособиях можно встретить отдельный
перебор случаев, когда ф(х) = 0 (в этом случае равенство будет выполнено,
если только f(x) > 0 и g(x) > 0) или когда функция ф принимает целые
отрицательные значения, а функции / и g — целые значения
(подробнее по этому поводу см. с. 247, 248 учебника 10 класса). Мы не
рассматриваем эти случаи и всегда считаем, что ф(х) > 0.
Пример 109. Решим уравнение xlog2X = 4х.
□ ООУ задаётся условием х > 0. Обе части уравнения
положительны, поэтому мы можем рассмотреть равенство логарифмов обеих
частей, например, по основанию 2, т. е. Iog2(xlog2*) = (Iog24x).
Преобразовав обе части этого уравнения, получим log2 х = 2 + log2 x.
Введём замену t = log2x. Корнями уравнения t2 = 2 + t являются числа
2и-1. Решив уравнения log2 х = 2nlog2x = -1, получим ответ: < -; 4^. И
Замечание. Выбор основания, по которому производилось
логарифмирование, был продиктован наличием в показателе степени
выражения log2x. Можно логарифмировать по любому основанию, но
неудачный выбор основания может привести к ненужным техническим
сложностям, связанным с преобразованиями.
Заметим, что приём логарифмирования имеет более широкую
сферу применения. Весьма часто им приходится пользоваться для
сравнения двух чисел или двух выражений, представленных в виде сложных
степеней: вместо самих чисел сравнивают их логарифмы. Например,
в уравнении 10lg2* + xlgx = 20 нет никакого смысла логарифмировать
обе части уравнения. Но идея здесь состоит в том, что слагаемые в левой
части оказываются равны; чтобы доказать это, достаточно
прологарифмировать их по основанию 10. После этого мы сможем переписать
уравнение в виде 10lg2* = 10, которое решается без труда.
Напомним об использовании свойств функций (как всегда при
решении любых типов уравнений). Если решение сразу не «видно», имеет смысл
воспользоваться свойствами функций, входящих в уравнение; может
быть, даже попробовать изобразить их графики. Чаще всего в таких
задачах используются соображения монотонности и ограниченности функций.
380! Глава XII! Уравнения и неравенства
Пример 110. Решим уравнение log2(3 + х) + у/х-1 = 2.
□ ООУ задаётся условием х ^ 1. При этом левая часть уравнения
строго возрастает на [1; +оо) и, стало быть, принимает значение 2 не
более чем в одной точке. Значение х = 1 удовлетворяет уравнению.
Ответ: {1}. Ш
Пример 111. Решим уравнение log|(3 + х) + \х—1 = 2.
О Левая часть уравнения строго возрастает на [1; +оо), и уравнение
имеет не более одного корня. А вот как его подобрать, если это вообще
возможно? Оценим наименьшее значение функции в левой части
уравнения. Оно достигается при х = 1 и равно 4. Тогда для всех х е [1; +оо)
левая часть уравнения не меньше 4, и уравнение корней не имеет.
Ответ: 0. В
2. Логарифмические неравенства
При решении логарифмических неравенств используется
следующее основное утверждение.
Утверждение --■--■—■■■■-■■—--■---■■-----■------■--
Если а > 1, то неравенство logaf(x) > \одад(х) равносильно сис-
ff(х) > д(х),
теме < \ \ „ '
lflf(x)>0;
если 0<а<1, то неравенство \OQaf(x)>\oQag(x) равносильно
системе <! ~v ''
[f(x >0.
Это утверждение мы назовём основной теоремой о
логарифмических неравенствах. Оно следует из того, что при а > 1
логарифмическая функция у = logax строго возрастает на открытом луче (0; +оо)
(а вместе с ней и обратная к ней функция), а при 0 < а < 1 функция
у = logax строго убывает на (0; +оо).
Договоримся о формальной записи обоснования перехода от
логарифмического неравенства к неравенству для функций, стоящих под
знаком логарифма. Напомним, что мы используем при этом
утверждение о монотонности композиции и ссылаемся на характер монотонности
внешней функции. Ещё раз подчеркнём, что если функция ф строго
возрастает, то из неравенства ср(а) > ср(&) следует, что а > Ъ (в частности,
из ср (/(#)) > (p(g(x)) следует f(x) > g(x)). Если же функция ф строго
убывает, то из неравенства ф (а) > ф(&) следует, что а < fe, т. е. знак
неравенства меняется на противоположный (в частности, из ф(/(х)) > y(g(x))
следует f(x) < g(x)). Например, краткая запись части решения
неравенства Iog2(x2 - 2х) > Iog23 может выглядеть так:
log2 t\
log2 (х2 - 2х) > log2 3 =» х2 - 2х > 3.
381[ §88- Логарифмические уравнения и неравенства
А краткая запись части решения неравенства log х (х2 — 2х) > log х 3
может выглядеть так: 2 2
i t\
Ji (x2 - 2x) > logi 3 => x2 - 2x < 3.
2 2
Также можно просто перейти заранее к логарифмам по основанию
больше 1, если позволяет задача, тогда не придётся задумываться об
изменении знака неравенства.
Пример 112. Решим неравенство log3(х2 - 1) + log^(х + 7) ^ -1.
[ х2 - 1 > 0 3
□ ООН задаётся системой s ' решая которую мы получим
х е (-7; -1) U (1; +оо). Далее запишем неравенство в виде
Iog3(x2 - 1) + 1 ^ Iog3(x + 7) <=>
lOgo t\
<=> Iog33(x2 - 1) ^ Iog3(x + 7) => 3(x2 - 1) < x + 7.
Решая последнее неравенство, получим, что х g —; 2 .
Теперь пересечём это
множество с ООН (рис. 13.30). По-
[ч О # О—
--; -1 U (1; 2]. -7 А -1
3 ) 3
Ответ: --; -lj U (1; 2]. 11
- '3.30
Пример 113. Решим неравенство | - | > 1.
. 3 л
Особое место занимают неравенства, содержащие
логарифмические функции с переменным основанием.
Рассмотрим неравенство logax > 0 в общем виде. Если а > 1, то
функция logax строго возрастает, и отсюда х > 1. Если а < 1, то
функция logax строго убывает, и тогда х < 1 (на самом деле 0 < х < 1).
Можно сказать это иначе: выражения (а— 1)и(х-1) имеют
одинаковые знаки, что, в свою очередь, можно записать в виде неравенства
382 Глава XIII. Уравнения и неравенства
(а - 1)(х - 1) > 0. Та же ситуация возникает при рассмотрении
неравенства logax < 0, но там выражения (а — 1) и (х — 1) имеют разные
знаки, что можно записать в виде неравенства (а - 1)(х — 1) < 0.
О logax и выражение (а - 1)(х - 1) имеют одинаковые знаки!
Теперь, вспомнив про ООН, получим равносильную систему:
f(a-l)(x-l)>0,
loga x > 0 <=> 1 х > 0,
[а>0.
Для нестрогого неравенства нужно будет ещё не забыть условие а Ф 1:
0
а > 0,
а Ф 1,
> 0.
Мы будем пользоваться этой записью в следующей форме:
а > 0,
f(x)>0.
Аналогично для неравенства вида loga/(x) > logag(x) получим
равносильную систему:
logaf(x)> logag(x)<=>
Заметим, что все условия кроме первого неравенства задают
область определения неравенства.
Эти системы удобно использовать, если в неравенстве фигурируют
логарифмы с переменным основанием а = ф (х) и при решении
логарифмических неравенств с параметрами.
Пример 114. Решим неравенство logx + 2(x2 — 2) ^ 2.
□ Перепишем неравенство в виде log^. + 2 (х2 — 2) > logx + 2 (х + 2)2 и
перейдём к равносильной системе
+ 1)(х2-2-(х + 2)2)> 0,
х + 2 > 0,
+ 2*1,
2 - 2 > 0,
+ 2)2 > 0.
а > О,
а Ф 1,
/(*)>0,
§88. Логарифмические уравнения и неравенства
Преобразуем первое
неравенство к виду (х+ 1)(-4х - 6) > О
и, решив его методом интервалов,
а)
/
ПОЛУЧИМ X G
Н- -]•
Пересече-
-2 -V2" -1
-2 -f -
Рис. 13.31
-1
V2"
X
ние множеств решений оставшихся
неравенств, образующих систему
х2 - 2 > О,
х + 2 > О,
изображенное на ри-
х + Z Ф 1,
(х + 2)2>0,
сунке 13.31, а, есть область определения исходного неравенства.
Пересекая множество решений первого неравенства с ООН (рис. 13.31, б),
.[-М-
получаем ответ:
Пример 115. Решим неравенство logJC + 2(2x + а) < 1.
□ Неравенство можно переписать в виде
(2x + a)<logx
Оно равносильно системе \ х + 2 > О,
х + а>0.
Условие х + 2 ^ 1 можно не включать в систему, так как первое
неравенство строгое. Обратите внимание: на первом же шаге мы
избавились от логарифмов и получили обычную алгебраическую систему
с параметром. Далее строим график неравенства (х + 1)(х + а - 2) < О
(график уравнения (х + 1)(х + а - 2) = 0 с последующим выбором
областей, рис. 13.32, а). С учётом неравенств х + 2>0п2х + а>0 получаем
графический образ системы (рис. 13.32, б) и на каждой ветви
выражаем х через а. Ответ читается по рисунку 13.32, б.
а) ч-
4 ч а=2-х
Рис. 13.32
384 Глава XIII. Уравнения и неравенства
Ответ: если а < 2, толге
(-§»->
если 2 ^ а < 3, то х е (-1; 2 - а);
если а = 3, то решений нет;
если 3 < а < 4, то х е (2 - а; -1);
если а ^ 4, то х е (-2; -1). В
В заключение ещё несколько слов о неравенствах вида (p(x)fix)>
> ф(х)^(л:). Напомним, что мы считаем здесь ф(х) > 0. Как и в случае
соответствующих уравнений, основным методом является
логарифмирование обеих частей неравенства по любому фиксированному основанию
(рекомендуем сразу брать основание больше 1, чтобы не менялся знак
неравенства).
Иногда из тех же соображений, что и для логарифмических
неравенств с переменным основанием, выводят следующие соотношения:
{ °' <и похожие системы для
других знаков неравенства). Мы считаем излишним отдельное
запоминание этих формул.
Обсудим ситуацию, возникающую с неравенствами вида ф (x)fix) >g(x)
и q>(*)'<*><£(*).
При решении неравенства (p(x)fix) > g(x) имеет смысл рассмотреть
два случая:
1) если g(x) > 0, то логарифмируем обе части неравенства по
фиксированному основанию а > 1;
2) если g(x) ^ 0, то неравенство выполнено везде на области
определения (поскольку левая часть положительна).
Рассмотрим неравенство (p(x)f№ < g(x):
1) если g(x) > 0, то логарифмируем обе части неравенства по
фиксированному основанию а (удобно взять а > 1);
2) если g(x) ^ 0, то решений нет, поскольку в левой части
неравенства стоит заведомо положительное выражение.
Пример 116. Решим неравенство (x2)logzx2 > х.
П ООН: х ^ 0. Рассмотрим два случая:
1) х < 0. В этом случае левая часть неравенства положительна,
а правая отрицательна, т. е. неравенство выполнено.
2) х > 0. Поскольку обе части неравенства положительны, можно
его прологарифмировать по основанию 2, получим log2 (x2)log^x2 > log2 x.
После преобразования получим log2 х2 • log2 х2 > log2 х => 41og2 х > log2 x.
Введём замену t = log2x. Получим 4t2 — t > 0 => t(4t — 1) > 0,
откуда t > - или t < 0.
Если t > -, то возвращаясь к переменной х, имеем
4
log2x > - *=> log2x > Iog224 <=> x > 24.
385! §88. Логарифмические уравнения и неравенства
L-
log2 х\
Если t < О, то log2x < 0 <=> log2x < log2 I <=> 0 < х < 1.
Объединяя все случаи, получаем ответ: (-оо; 0) U (0; 1) U (V2; +оо). В
3. Системы логарифмических и показательных уравнений
и неравенств
При решении систем логарифмических и показательных
уравнений и неравенств также следует постоянно помнить о том, что в
процессе преобразований и применения формул может меняться множество
решений.
Пример 117. Решим систему уравнений
(*2 + i/2)=2-lg5,
\g(x-y)=\g\2.
Область определения системы задается системой двух неравенств:
\х + у > 0,
[х-у >0.
Преобразовав уравнения исходной системы, получим:
\lg(x2+y2)= lg20, _ Jx2 + i/2 = 20, _ fx2 = 16,
- у2) = Igl2 ^ \x2 -y2 = 12 ^ [y2 = 4.
Четыре получившиеся пары чисел (4; 2), (-4; 2), (4; -2), (-4; —2)
нужно проверить на принадлежность области определения системы.
{х + и > 0
' ' а две другие нет.
X I/ > U,
Ответ: {(4; 2); (4; -2)}. Ш
Пример 118. Решим систему
D Из условия очевидно, что х > 0 и х Ф 1. Логарифмируем оба
уравнения по основанию 5, получим
(2i/2-l)log5x = l,
Поскольку х Ф 1, делим первое уравнение системы на второе и по-
2i/2 — 1 1
лучаем -^—— = — =» 6i/2 — 3 = i/2 н- 2 => i/2 = 1. Отсюда сразу находим
у + 2 3
log5 х = 1; х = 5. Дальнейшее очевидно. Ответ: {(5; 1); (5; -1)}. Ш
386 Глава XIII. Уравнения и неравенства
О89- Тригонометрические уравнения и неравенства
В курсе 10 класса уже были рассмотрены элементарные
тригонометрические уравнения (cosx = a, sinx = а, tgx = а, ctgx = а).
Фактически решение тригонометрического уравнения в общем случае состоит
в том, что оно приводится к совокупности элементарных
тригонометрических уравнений. Для этого у нас имеются два основных метода —
разложение на множители и замена переменной.
Иногда оказывается полезным и другой взгляд на
тригонометрические уравнения — как на специальный случай систем
алгебраических уравнений. Действительно, если принять во внимание
основное тригонометрическое тождество, то уравнение /(sinx, cosx) = 0
можно заменить равносильной системой
f{u9v)= 0,
где и = cosx, v = sinx. Но чаще для решения уравнений и систем
применяют тригонометрические подстановки. Поэтому в этом
параграфе мы будем рассматривать «чисто тригонометрические» решения.
Проведём краткий обзор основных видов тригонометрических
уравнений, рассмотренных ранее.
1. Замена переменной. Разложение на множители
Рассмотрим уравнения вида f(t) = 0, где t представляет собой
какую-либо тригонометрическую функцию.
Пример 119. Решим уравнение cos2x + cosx = 0.
□ По формуле cos2x = 2cos2x - 1 сводим уравнение к такому:
2cos2x + cosx -1 = 0.
Получилось уравнение, квадратное относительно t = cosx. Отсюда
cosx = —1 или cos х = —.
я+2яп/
\ °
1
2
|-+2яп
j
n
Ответ:
b— + 2nn; n + 2nn:
Рис. 13.33
Заметим, что при решении
элементарных тригонометрических уравнений
полезно использовать тригонометрическую
окружность. Часто это позволяет
упростить отбор корней или подсказывает, как
записать ответ в более компактной форме.
Так, изобразив обе серии
решений на тригонометрической окружности
(рис. 13.33), мы видим, что они объеди-
§ 89. Тригонометрические уравнения и неравенства
няются в одну: х- — + , fe e Z, или, что то
3 3
же самое, х =
, k e Z.
Пример 120. Решим уравнение
sin2 х + sin2 2x = sin2 Зх.
П Перепишем уравнение в виде
1 - cos 2х + 2 sin2 2х = 1 - cos 6x.
Далее,
2 sin2 2x = cos 2x - cos 6x «
<=> 2 sin2 2x = 2 sin 4x • sin 2х <=>
<=> sin 2x (sin 4x - sin 2x) = 0 <=>
<=> 2sin2x ■ sinx • cos3x = 0. Рис- 13-34
Последнее уравнение равносильно совокупности
X = ПП,
х = "тр где n, k, I e Z.
71 . П1
sin 2x = 0, откуда
cos Зх = 0,
Если расставить эти точки на тригонометрической окружности
(рис. 13.34), станет видно, что окончательный ответ можно записать
в виде двух серий: х = — + — или х = nn, n e Z.
6 3
i
.ш
Ответ: \ — + —; nn: ne Z
о 3
Рассмотрим уравнения вида cosf(x) = cosg(x) (или sin/(x) = sing'(x),
/ = tgg(x)). Чтобы упростить запись, будем говорить об
уравнении cos A = cosB. Конечно, можно решить его с использованием
формулы разности косинусов:
cos А - cosB = 0 <=> 2 sin
А + В
sin
В-А
А + В= 2пп,
В- А = 2nk,
2 2
где n, k e Z.
Но к результату можно прийти иным путем. Напомним, что общее
решение уравнения cos х- а выглядело так: х = ±ф + 2яп, n e Z, где ф —
это какое-то частное решение данного уравнения. В частности, решение
уравнения cosx = cos а можно записать в виде х = ±а + 2nn, n e Z
(поскольку х = а, очевидно, есть одно из решений этого уравнения). Тогда
условие cos A = cos В можно переписать в виде А = ±В + 2nn, n e Z,
а решение уравнения cos/(x) = cosg(x) соответственно получается как
~ [f(x)=g(x) + 2nny , ^
ответ следующей совокупности уравнении: где я, fee Z.
388! Глава XIII. Уравнения и неравенства
Аналогично общее решение уравнения sin х- а представляет собой
^ „ \х = ф + 2пп9 . .
объединение двух серии /г, ft e Z; условие sin A = sin Б
[_Х = 7С — ф + 27Ш
равносильно тому, что
— ТС х5 j
= sing(jc) получается из совокупности
л, ft e Z, а решение уравнения
= 71 -
где п9 k e Z.
Казалось бы, аналогично можно записать, что уравнение tgf(x) =
= tgg(x) равносильно уравнению f(x) = g(x) + пп, п е Z, но это не так,
поскольку область определения второго уравнения может оказаться
шире: например, в первом уравнении должно
быть выполнено условие f(x)* — + пп, п е Z,
а во втором это условие отсутствует.
Уравнение tg/(x) = tg£(x) равносильно системе
У1
5л /
в/
\ s
\/
х—■
я
2
2
\ к
Ve
\°>
1 X
у я
/ 6
7i
-
где
Z.
Пример 121. PeniHM уравнение tgЗх = tg5x.
□ Уравнение равносильно системе
\3х= Ьх + пп,
п где п, k e Z.
Рис. 13.35
лп
Из первого уравнения получаем х = —. Далее расставляем эти точки
на тригонометрической окружности (рис. 13.35), на ней же
выкалываем точки серии х— —I , ft e Z, и получаем ответ: х — пп, п е Z. В
6 3
2. Некоторые тригонометрические замены
Первая из стандартных замен — «универсальная
тригонометрическая подстановка» — уже обсуждалась в 10 классе (VI глава).
Соответствующие формулы используются обычно в двух вариантах:
1. Если f = tgx, то sin2x = -^Ц-, cos2x = —-^-, tg2x = -^
2. Если f = tg-, то sin x = -^-
2 1 + f2
, cos х =
_f tg х =
1-f2
389 § 89. Тригонометрические уравнения и неравенства
Это весьма опасная, хотя порой и удобная подстановка. Дело в том,
что, во-первых, во всех этих формулах левая и правая части определены
на разных множествах (например, sin 2х определён при всех
значениях х, a tgx только при х Ф — + nk, k e Z), и при их применении может
произойти потеря корней (вида х- — +nk, k e Z, если t= tgx). Во-вто-
рых, достаточно часто применение универсальной подстановки
приводит к появлению сложных алгебраических уравнений высоких
степеней. По этим причинам такой подстановки лучше избегать, но если
использовать, то с максимальной осторожностью.
о
Пример 122. Решим уравнение tg2х + sin2х = — ctgx.
3
П Введём подстановку t = tgx и рассмотрим два случая:
1) х = ^- + nk, k g Z. В этом случае tgx не существует, но уравне-
ние превращается в верное равенство! Таким образом, эта серия
входит в множество решений уравнения.
2) Пусть теперь х Ф —ь nk, k e Z. С помощью подстановки урав-
нение преобразуется в равенство н = —, которое сводится
х. Т л. "г Т ОГ
к биквадратному уравнению 2£4 + 3t2 -2 = 0 или (2t2 - l)(t2 + 2) = 0.
Отсюда t = ±-рг.
V2
Возвращаясь к переменной х9 получим: х = ±arctg-pr + nk, k e Z.
f 71 1
Объединяя результаты 1) и 2), получим ответ: I—h nk, ±arctg -=■ + nk:
k G Z}. Ш
Заметим, что, если бы мы выразили все функции в этом
уравнении через sinx и cosx, решение оказалось бы не более громоздким, но
более безопасным.
Сходная ситуация возникает и при применении некоторых
формул тригонометрических преобразований (а именно тех, где в правой
части стоят не всюду определённые функции тангенс или котангенс).
Приведём соответствующий пример.
Пример 123. Решим уравнение tg\х + — = ctgx- 1.
□ Если в левой части уравнения воспользоваться формулой танген-
1+tgJC л 1+tgJC 1 л
са суммы, то мы получим = ctgx— 1, т. е. = 1.
1- tgx 1- tgx tgx
Отсюда находим, что tgx = — => х = arctg— + пп, п е Z.
3 о
390! Глава XIII. Уравнения и неравенства
При этом решении мы потеряли очевидный корень х = — (и, следо-
2
вательно, всю серию х = —h пп). На каком этапе? Очевидно, при при-
, ( Tl} 1+ tgX К гж
менении формулы tghcH— = : в точках —н пп, п е Z, левая
^ 4) 1- tgx 2
часть существует и равна -1, а правая не существует. Таким образом,
применив эту формулу, мы изменили область определения уравнения,
что привело к потере корней. Значит, нужно было разбирать отдельно
два случая: 1) х= — + пп, п е Z (проверка подстановкой); 2) хФ — л-пп,
п е Z, когда мы действительно имеем право использовать формулу
тангенса суммы. Ответ: \ arctg- + пп, — + пп: пе Z>. И
[32 J
Часто оказывается весьма удобной замена t = sinx + cosx.
Пример 124. Решим уравнение sin2x = cosx + sinx.
□ Пусть t = sinx + cosx. Тогда t2 = 1 + 2sinx • cosx = 1 + sin2x,
откуда sin 2x = t2 - 1.
Исходное уравнение преобразуется к виду t2 - t - 1 = 0, откуда
. 1 + S 1-V5 „ „
t = или t = . Возвращаясь к старой переменной, решаем
два уравнения:
1) sin х + cos jc = —-—. С помощью вспомогательного аргумента пре-
г- /7Т ( 71 ^ 1+V5 ( л | 1+V5
образуем уравнение к виду >М cos х = или cos х = —=-,
\ 4) 2 у 4) 2V2
которое решений не имеет, так как ■=- > 1 (проверка обязательна).
2V2
2) sinx + cos x = . Отсюда получаем cos \ х = =-;
г 2 V 4У 2V2
х - — = larccos =- + 2пп, neZ.
4 2>/2
Ответ: \ — ± arccos =- + 2пп: п е Z L S
3. Применение свойств функций
при решении тригонометрических уравнений
Начнём с соображений ограниченности функций, наиболее часто
используемых при решении тригонометрических уравнений. Первое,
что следует принять во внимание, — это оценки множеств значений
функций синус и косинус: \/х ей -И sinx ^ 1 и -И cosx ^ 1.
391, § 89. Тригонометрические уравнения и неравенства
Пример 125. Решим уравнение 2cos4x - sin3jc = 3.
□ Можно, конечно, пробовать преобразовать уравнение. Но
заведомо проще оценить выражение в левой части уравнения: 2cos4x^2
и -sin3x^ 1. Тогда левая часть уравнения не превосходит 3, т. е.
2cos4x - sin3x ^ 3, причём равенство возможно только в том случае,
когда одновременно cos4x=l и sin3x = -l. Уравнение равносильно
/cos4x =1, „ п о _ _
системе < . решением которой является серия — + 2пп> п е Z
(peniaeM уравнение по отдельности и производим отбор общих корней
на тригонометрической окружности). Ответ: \ —v 2пп: п е Z\. Ш
Заметим, что если в предыдущем примере вместо 4х взять,
например, 6х, а вместо Зх взять 5х, то получится уравнение 2 cos 6x -
- sin 5x = 3, которое затруднительно преобразовать традиционными
способами! Однако приведённые соображения остаются в силе.
Соображения ограниченности используются и при решении
следующей задачи:
Пример 126. Решим уравнение cos7x - sin7x = 1.
□ Поскольку |cosx|^l и |sinx|^l, получаем cos7x ^ cos2x и
-sin7x ^ sin2x. Таким образом cos7x - sin7x ^ cos2x + sin2x = 1, причём
равенство возможно только в случае, когда одновременно cos7 х = cos2x
и -sin7x = sin2x.
_ ^ [cos7x=cos2x,
Таким образом, уравнение равносильно системе < . „ . о ре-
[sin7x= sin2x,
шением которой являются две серии: х = 2пп и х— h2nk, n,keZ
(систему peniaeM, нанося точки, изображающие корни каждого из
уравнений, на тригонометрическую окружность).
Ответ: <2пп9 -— + 2пп: neZ>. Ш
I 2 J
Пример 127. Решим уравнение cos3x • cos5x = 1.
□ Уравнение равносильно совокупности двух систем:
[cos3x = 1, fcos3x = -1,
с л или л
cos эх = 1 cos эх = -1.
_ [cos3x=l,
Рассмотрим первую из них: < „ <=>
[cos5x = l
X —
X —
2nk
3 '
2пп
где k, neZ. Отби-
5 7
рая решения на тригонометрической окружности, получим х- 2nk, keZ.
3921 Глава XIII. Уравнения и неравенства
Л „ /cos3x= -1,
Аналогично реп1ение второй системы < „ доставляется
[cos5x = -1
серией х = п + 2nk, k e Z. Две полученные серии корней можно
записать в виде одной.
Ответ: {л/г: k e Z). Ш
В следующих примерах также используется идея ограниченности,
но нелегко догадаться о её использовании.
Пример 128. Решим уравнение 3sinx + 4sin5x • cosx - 5sin3x = 10.
□ Заметим, что сумму 3sinx + 4sin5x • cosx можно рассматривать
как выражение вида asinx + fecosx, где а = 3 и Ь = 4sin5x. Но в
соответствии с методом вспомогательного аргумента
a sin х + Ъ cos х = у/а2 + Ъ2 • sin (х + ф) ^ ^а2 + Ъ2 .
В нашем случае
3 sin х + 4 sin Ъх • cos х ^ д/9 + 16 sin2 Ъх ^ V9 + 16 = 5.
Слагаемое -5sin3x ^ 5. Таким образом, левая часть не
превосходит 10, и равенство возможно, только если рассмотренные выражения
одновременно равны 5. Для этого необходимо, чтобы одновременно
J|sin5x| = 1, Q 7i о
выполнялись равенства у . ft ' н Это происходит при х = — + 2пп,
[sin3x = -1. 2
п е Z. Кажется, мы уже получили ответ. Но это не так! В данном
случае система не равносильна исходному уравнению: для того чтобы
выполнялось равенство 3sinx + 4sin5x • cosx = 5, условие |sin5x| = 1
необходимо, но не является достаточным. При х = — + 2пп это равенство
не выполняется (таким образом, на самом деле при всех х выполнено
неравенство 3sinx + 4sin5x • cosx < 5), а стало быть, уравнение не
имеет корней. Ответ: 0. Ш
Пример 129. Решим уравнение 4cos2x - 4cos23x • cosx + cos23x = 0.
П Сначала попробуем определить вид уравнения. Для этого введём
обозначения u = cosx, u = cos3x. Получим 4и2 - 4uv2 + v2 = 0. Сразу
видно, что однородным уравнение не является. Зато можно попробовать
рассмотреть это уравнение как квадратное относительно переменной
и = cosx. Это уравнение имеет корни, если — > 0, где — = 4cos43x -
4 4
- 4cos23x = 4 cos2 Зх (cos2 3х - 1). Но 4 cos2 Зх (cos2 3х - 1) ^ 0, поэтому
уравнение имеет корни только при — = 0, т. е. cos Зх = 0 или cos2 Зх = 1.
4
Рассмотрим два случая.
3931 § 89. Тригонометрические уравнения и неравенства
1) Если cos3x = 0, то уравнение приобретёт вид 4cos2x = 0, т. е.
fcos3x =0,
мы получим систему < Л решением которой является серия
[cosx = 0,
х = — + 7Ш, п е Z.
2) Если cos23x=l, то уравнение приобретёт вид 4cos2x-4cosx +
' fcos23x=l,
\
+ 1 = 0, откуда cosx = —. Нам осталось решить систему < i
2 cosx = -.
Её реп1ения записываются серией х— ±—н2яп, п е Z.
о
Ответ: \ — 4-пп; ±— + 2пп: пе Z>.
[2 3 J
Ш
Основные приёмы работы с тригонометрическими уравнениями
очень хорошо видны в сюжетах выпускных экзаменов
Санкт-Петербургского математического общества. Приведём здесь один из таких
сюжетов (экзаменационная работа 1991 г.) в несколько изменённом виде.
Пример 130, Дана функция f(x) = cos2x + cosx — 4cos2 —.
а) Найдём множество значений функции /.
б) Найдём количество корней уравнения /(х) = а на отрезке [0; я].
в) Найдём количество корней уравнения f(x) = a на отрезке 0; — .
L 2 J
■_■ \ т-т OO91 9 X 1 + COS X
П а) Поскольку cos2x = 2cos2x - 1 и cos2 — = , можно при-
Ci Ci
вести функцию к виду /(х) = 2cos2x — cosx - 3. Введём замену t = cosx
и рассмотрим функцию g, заданную на
отрезке [—1; 1]: g(t) = 2t2 — t-3. Множества
значений функций / и g совпадают. Гра- -1
фик функции g показан на рисунке 13.36.
Из рассмотрения графика очевидно, что
Искомое множество значений совпадает
с множеством значений E(g) = -3—; 0 .
Ответ: E(f)= Г-3-; ol.
б) Если х е [0; я], то t e [-1; 1] (t
пробегает все значения от -1 до 1). Разобьём
решение на два этапа: сначала выясним,
Рис. 13.36
394 Глава XIII. Уравнения и неравенства
а) */| я сколько корней имеет уравнение cos x = t (в
зависимости от t), а затем — сколько корней имеет
уравнение g(t) = а (в зависимости от а). В нашем
случае уравнение cos x = t имеет единственное
решение при любом te[-l; 1] (на рис. 13.37, а
любая вертикальная прямая пересекает
выделенную дугу ровно в одной точке). Поэтому
количество корней уравнения f(x) = a на отрезке
[0; п] совпадает с количеством корней уравнения
g(t) = а, которое находится по рисунку 13.37, а
стандартным образом (количество точек
пересечения прямой у = а с графиком функции g).
Ответ: если а < -3-, то корней нет;
8
если а = -3-, то корень один;
8
если -3— < а ^ -2, то корней два;
8
если -2 < а ^ 0, то корень один;
если а > 0, то корней нет.
в) По сравнению с пунктом б)
существенно изменилось только одно: количество
решений уравнения cosx = t. На рисунке 13.37,6
видно, что при 0 < t ^ 1 это уравнение имеет
0; — , при -1 < t ^ 0 — два корня, при t = —1 — снова
один корень.
Значит, при рассмотрении графика функции g(t) придётся найти
не только количество корней уравнения g(t) = а, но и определить,
какие это корни (нас интересует расположение этих корней
относительно 0 и -1, поскольку в зависимости от этого каждому t соответствует
разное количество значений х).
Видно, что при а = -3- уравнение g(t) = а имеет один положитель-
8
ный корень, а вместе с ним и уравнение f(x) = a имеет один корень.
При -3— < а <—3 уравнение g(t) = a имеет два положительных
8
корня; тогда уравнение f(x) = a имеет тоже два корня. Но при а = -3
один из корней уравнения g(t) = а равен 0 (ему соответствуют два кор-
71 371 лЧ ,
ня — и — уравнения cosx = £), а второй корень положителен (ему со-
ответствует один корень уравнения cosx = £). Таким образом, при
а = —3 уравнение f(x) = а имеет три корня на отрезке 0; — .
Рис. 13.37
один корень на
3951 § 89. Тригонометрические уравнения и неравенства
Далее, при -3 < а ^ -2 уравнение g(t) = а имеет два корня tx и t2,
причём -1 < tx < О (ему соответствуют два значения х), а 0 < t2 ^ 1
(одно значение х).
При -2 < а < 0 уравнение g(t) = а имеет один корень, причём
-1 < t < О (два значения х).
А вот при а = О единственным корнем уравнения g(t) = а
оказывается t = — 1, которому соответствует единственное значение х, а именно
х = п.
Ответ: если а < -3-, то корней нет;
8
если а = -3 — , то уравнение имеет один корень;
8
если -3- < а < -3, то уравнение имеет два корня;
8
если -3 ^ а ^ -2, то уравнение имеет три корня;
если -2 < а < О, то уравнение имеет два корня;
если а = О, то уравнение имеет один корень;
если а > 0, то корней нет. ®
4. Системы тригонометрических уравнений
Решение систем тригонометрических уравнений, по сути, ничем
не отличается от решения любых других систем. Обычно решение
системы сводится к решению набора тригонометрических уравнений.
И здесь важно понимать, что целочисленные параметры в записи
каждого из решений этих уравнений должны быть разными!
Это связано с тем, что решение уравнения — множество чисел,
обозначенных с помощью целочисленного параметра. Ясно, что это
множество не зависит от того, какой буквой назван этот параметр. Решение
системы заключается в нахождении пересечения множеств чисел.
Пример 131. Решим систему уравнений
- y)= 1,
[cos(x + у) = 0.
D Из первого уравнения системы получаем х- у — —V 2nk, k e Z,
а из второго х + у = — + пп, п е Z. Таким образом, исходная система
равносильна
х - у = - + 2nk,
где k> n e Z
х + у = - + кп,
пп
где ky n е Z.
Последняя система может быть приведена и в качестве ответа.
396j Глава XIII. Уравнения и неравенства
Обратим внимание, что, если бы целочисленные параметры были
71
обозначены одинаковыми буквами, итоговая система
пп
да-
вала бы неверный ответ (например, пара чисел
Н}
является
решением исходной системы, но не является решением последней системы).
5. Тригонометрические неравенства.
Метод интервалов на тригонометрической окружности
Напомним некоторые основные принципы решения элементарных
тригонометрических неравенств. Прежде всего, все элементарные
неравенства вида sinx > a, sinx < а, cosx > а, cosx < а (и соответствующие
нестрогие неравенства) мы будем решать только на тригонометрической
окружности.
Ранее в 10 классе (VI глава, пример 8) было рассмотрено
неравенство cos х > -. В ответе мы получали объединение интервалов вида
Ci
-— + 2nk; -5- + 2nk , ke Z. He имея тригонометрической окружности пе-
3 3 у
ред глазами и не задумываясь над смыслом решения, можно решить,
что, как и для уравнения cosx = а (с решением в виде larccosa + 2nk9
k g Z), мы получили универсальную формулу, но это не так. Поменяем
знак неравенства на противоположный и решим неравенство cos х < —.
Ci
На тригонометрической окружности (рис. 13.38) видно, что нас
интересуют точки, абсциссы которых меньше —. На окружности имеются ров-
Ci
но две точки, абсциссы которых равны —,
Ci
причём одной соответствует серия
аргументов вида — + 2nk, а другой -— + 2nk, однако
3 3
было бы грубой ошибкой записать в ответе
-■5" + 2nk; — + 2nk , k g Z (как мы уже виде-
3 о J
ли, это решение неравенства cosx > —
Ci
Дело в том, что речь идёт о двух разных
дугах, на которые окружность разбивается
этими точками. Чтобы получить верный ре-
Рис. 13.38 зультат, нужно сначала взять решение не-
3971 § 89. Тригонометрические уравнения и неравенства
равенства в пределах одного периода (см. рис. 13.38), а это будет дуга
я 5я1 „ -
—; — . Выбирая дугу, полезно отметить ее стрелкой в положитель-
3 3 у
ном направлении обхода окружности: тогда станет ясно, что в качестве
правой границы интервала нужно взять из серии корней -— + 2nk не
3
71 571 . „ -
—, а — (т. е. корень, соответствующий этой же точке, но больший на
3 3
2я, который будет следующим непосредственно за — решением уравне-
3
ния). Тогда ответ записывается в виде объединения всех таких
интервалов: ^ + 2nk; — + 2nk , где k e Z. Заметим, что с равным успе-
13 3 )
хом мы можем записать его и в виде
Ответ: [ - + 2nk; — + 2nk j, keZ.
( 5л;
I 3
+ 2nk; - — + 2nk |, где k e Z.
3
Обратите ещё внимание на то, что целый параметр п в записи
ответа обязан быть одним и тем же (разными буквами пользоваться
нельзя), поскольку речь идёт об интервалах фиксированной длины,
повторяющихся через 2л.
Пример 132, Решим неравенство sinx ^ —.
3
□ Двум точкам на тригонометрической окружности, имеющим
ординату -, соответствуют серии х = arcsin— + 2пп и х = п — arcsin— + 2пп,
3 3 3
п е Z, причём точке в первой четверти — первая серия, а точке во
второй четверти — вторая серия.
Отмечаем нужную дугу стрелкой в положительном направлении
(рис. 13.39). Если в качестве левого конца отрезка взять число п - arcsin -,
3
то на правом конце должно стоять
число 2л + arcsin-. Если же в ка-
3
честве правого конца отрезка я-arcsin—
взять число arcsin-, то левым
3
концом отрезка должно служить
число -л — arcsin — . В ответ
записываем объединение всех таких
отрезков.
arcsin-g-+27t
Рис. 13.39
398 Глава XIII. Уравнения и неравенства
Ответ: п - arcsin - + 2пп; 2л + arcsin - + 2пп , пе Z.
Ш
Пример 133. PeniHM неравенство tgx > 2.
□ Неравенство можно решить на тригонометрической окружности
(рис. 13.40), если кроме корней уравнения учитывать область
определения тангенса, но проще воспользоваться графиком функции у = tgx
(рис. 13.41).
Рис. 13.40 Рис. 13.41
В пределах одного интервала -—; — решением является интер-
( \
вал arctg 2; — , а на всей оси в силу периодичности тангенса с
периодом л — объединение интервалов arctg 2 + пп; —h пп , п е Z. Ответ:
arctg 2+пп; — + пп , пе Z.M
2 )
Теперь разберём более общий подход, который можно назвать
«метод интервалов на тригонометрическом круге».
Пример 134. Решим неравенство cosx • cos2x > 0.
□ Найдём корни левой части. Они являются решениями совокупно-
„ fcos х = 0,
сти уравнении
[cos2x = 0.
Решением первого из этих уравнений является серия х— —v nk,
k g Z; решением второго уравнения — серия х— —I , п е Z.
Расставим точки, соответствующие этим числам, на
тригонометрической окружности. Для этого в первой серии достаточно рассмотреть
399, § 89. Тригонометрические уравнения и неравенства
fe = O и ft=l (мы попадаем в одну из
71 371
уже отмеченных точек — или — при
всех прочих целых k). Вторая серия
окажется представленной точками,
соответствующими числам —, —,—,
4 4 4
—. Эти точки разбивают тригономет-
4
рическую окружность на интервалы,
в каждом из которых произведение
cosx • cos2x имеет постоянный знак;
его можно определить так же, как
и в обычном методе интервалов, при
помощи контрольной точки, взятой
внутри интервала. Осталось выбрать Рис. 13.42
интервалы положительного знака и
выписать ответ (рис. 13.42).
Но можно и упростить процесс определения знаков выражения на
интервале. Заметим, что при переходе через каждую точку (если
двигаться по окружности в положительном направлении) меняется знак
ровно одного из двух множителей, а значит, и знак произведения. Тогда
достаточно определить знак в каком-либо интервале, а дальше знаки
будут чередоваться (там, где знак произведения положителен, кривая
рисуется вне круга, а там, где произведение отрицательно, — внутри
круга). После этого выберем те участки, которые соответствуют нашему
неравенству (в данном случае интервалы положительного знака, где
кривая находится вне круга), и отметим их стрелками в
положительном направлении (это позволит нам не забыть, что мы двигаемся от
меньшего числа к большему, и не включить случайно в ответ
несуществующий интервал I —; —
4 4
71 Я
вместо ; —
4 4
Запишем ответ в пределах одного круга. С учётом замечания о рас-
( п tcVYtc 37i V. f 57i ЗтО
положении точек он может выглядеть так: —-; — U —; — U —; — .
У 4 4J ^2 4 J у 4 2 )
В силу периодичности вместе с каждым интервалом (а; Ъ) мы включаем
в ответ все интервалы вида (а + 2nk; Ъ + 2nk). Тогда запишем ответ:
(-^ + 2nk; ^ + 2nk) U (|+ 2nk; Ц-+ 2nk) U (Ц- + 2nk; ^+ 2nk\ keZ.m
О Во всех скобках стоит один и тот же параметр k (используется
обязательно одна и та же буква, а не разные!).
Теперь покажем, что следует делать в случае, если главный период
функции оказывается равным не 2я, а, например, произвольному числу
4001 Глава XIII. Уравнения и неравенства
Т > 0. Во-первых, можно просто взять отрезок длиной Т (например,
отрезок [0; Г]) на числовой прямой, решить неравенство на этом отрезке,
а затем прибавить ко всем числам в полученных интервалах Тп, п е Z.
А во-вторых, можно использовать удобную замену, как в следующем
примере.
х
Пример 135. Решим неравенство cos —
П Функция в левой части
cosf >
0.
периодична
с периодом
неравенства
X
Т=12п. Используем замену t = —, тогда неравенство приобретёт вид
6
cos3£ ■ cos 2t > 0, и мы можем решить
его стандартным способом. Из
совокупности уравнении
| = 0,
[cos 2t = 0
получаем
пп
2 '
nk
з'
n,keZ.
Рис. 13.43
Расставляем соответствующие
точки на тригонометрической окружности
в пределах одного круга (рис. 13.43).
При t = 0 левая часть положительна,
и далее, при обходе окружности в
положительном направлении, знак
меняется в каждой из отмеченных
точек. Тогда
t е
-- + 2nk; - + 2nk\ U Г- + 2nk; - + 2nk) U Г— + 2nk; — + 2nk) U
u'ir
U|f.
—— + 2nk , ft e Z.
Умножением на 6 получаем интервалы для значений х. Ответ:
(-n+12nk; n+12nk)[J\ — + 12nk; Зя +12яй ] U (— + 12nk; 5n+12nk)\J
U |77с+12яЛ;^^ + 127сл|и[9я;+127сЛ;—+ 127сЛ|, fceZ.i
В приведённых примерах решения уравнений давали на окружности
несовпадающие точки, и знак левой части менялся в каждой из таких
точек. В общем случае это не так. Можно, конечно, как мы уже
говорили, выяснять знак левой части в каждом из получившихся интервалов,
вычисляя значения в контрольных точках на каждом интервале, но это
достаточно трудно, особенно при большом количестве интервалов.
4011 § 89. Тригонометрические уравнения и неравенства
Поэтому лучше всего смотреть, корнем какого именно множителя
является соответствующее данной точке число и меняет ли этот
множитель знак при переходе через эту точку (например, 2тг является
корнем функции cos х- 1, однако при переходе через соответствующую
точку знак этой функции не меняется). В соответствии с числом
перемен знака множителей в данной точке можно сделать вывод об
изменении или сохранении знака всего произведения.
Всё сказанное выше в равной степени относится и к точкам
разрыва функции, стоящей в левой части неравенства. Очень важно
выявить все точки разрыва функции /. Некоторые из них могут
оказаться «спрятанными»: например, если в неравенстве присутствует
как часть какого-то выражения, то серия х = — + тт, п е Z, участвует
в определении знака функции / наравне со всеми прочими.
Пример 136. Решим неравенство
sin3x-(tgx- л/з) > 0.
D Определим точки, в которых
левая часть неравенства равна 0 или
sin Зх = 0,
не существует:
(послед.
х = - + nl,
няя серия в совокупности —
значения, при которых tg х не определён).
пп
Получим
X =
х = — + nk, n, k, I e Z.
3
2тг/Т^>
n
*! -
Зя З
2
Рис. 13.44
При расстановке точек, соответствующих этим значениям, на
тригонометрической окружности оказывается, что точки — и — встреча-
3 3
ются в двух сериях, каждый множитель меняет в этих точках знак,
таким образом, знак выражения sin Зх • (tg x — V3J в этих точках
меняться не будет. Остальное видно на рисунке 13.44.
Ответ: || + 2пп\ U (| + 2тт; — + 2пп\ U Гп + 2пп; Щ- + 2пп\ U
U Г— + 2пп; 2тг + 2пп\, neZ.i
14—Пратусевич, 11 кл.
402J Глава XIII. Уравнения и неравенства
Вот более сложный пример решения тригонометрического
неравенства.
cos 2* + 3cos x + 2
Пример 137. Решим неравенство
0.
(sin x - 1) sin (x + 3)
Преобразовав числитель и разложив его на множители, перепи-
(2cosjc + 1)(cosjc +
шем неравенство в виде
У1
^ 0.
(sin x - 1) sin(jc + 3)
Заметим, что в числителе есть
множитель, который обращается в нуль, но не
меняет своего знака: cosx+ 1^0 для всех х.
В знаменателе схожая картина, только здесь
множитель неположителен: sinx - 1^0 для
всех х. В связи с этим неравенство удобнее
(2 cos х + l)(cos x + 1)
переписать в виде
(1 - sin x) sin (х + 3)
Найдём корни числителя:
0.
2л-
Рис. 73.45
cos л: = —,
COS X - -1
х = ±
х =
2тт,
п
2тт,
(при переходе через точку х = п + 2тт,
п е Z, знак дроби не меняется!).
fsinx = 1,
с + 3) = О
х = ± + 2пп,
2 п е Z.
Найдём корни знаменателя:
-3 + тт,
Расставляя соответствующие точки в пределах одного круга
(поскольку период дроби равен 2тг) и применяя метод интервалов (рис. 13.45),
|;^ U {л} U 12я-3;^|.(3аме-
получаем результат: х е | п - '6; ^- I U
тим, что здесь появилась одна выколотая точка и одна изолированная.)
Ответ: | п - 3 + 2кп; ^ + 2кп \ , ■£■ + 2кп; - - + 2пп \ U {п + 2кп} U
U (2л -
2пп;1
U ■£ + 2пщ — + 2тт U {тг
у V2 3 J
4тг
2пщ — + 2тг/г
3
Как известно, ответ в тригонометрическом уравнении может быть
записан по-разному, в зависимости от способа решения. Это может
создать определённые сложности при решении неравенств на
тригонометрической окружности: иногда практически невозможно
догадаться, что два разных числовых выражения являются разными формами
записи одного и того же числа (являющегося, например,
одновременно корнем числителя и знаменателя, как в примере ниже).
§ 89. Тригонометрические уравнения и неравенства
<■«« ™ 3 sin 2л: + 4cos2x + 3 . л
Пример 138. Решим неравенство = ^ 0.
ginx+ л/2
D Найдём корни числителя. Если воспользоваться методом
вспомогательного аргумента (что кажется наиболее естественным в данном
случае), мы получим 3 sin 2х + 4 cos 2х =-3 => 5 - sin 2х + - cos 2х = -3=»
V /
=> зт(2л:н-ф) = —, где ф = arctg- или, например, arcsin- . Далее,
5 3 I Ъ)
2х
2х
+
+
ф =
Ф =
-arcsin— + 2тт,
5
з
тс + arcsin —ь 2тсй
5
где
>
k
G
Z
1 . 3 1 , 4
х = — arcsin arctg — + пп9
я 1 3 1 4 v*en,keZ.
х = - + - arcsin - - - arctg - + тг/г,
„ « .. л/2
Найдем корни знаменателя: sinx=
х = ~ + 2тт,
4
4
где
п, k e Z. Выясним, где именно по отношению к корням знаменателя
располагаются корни числителя. Оказывается, число —- является
4
корнем и числителя, и знаменателя! Но увидеть непосредственно, что
одна из серий корней числителя как раз и содержит все числа вида
— + тт, п е Z, трудно. Для этого представим корни числителя в более
4
простом виде.
„ я 1 . 3 1 4
Например, число — + - arcsin arctg - лежит в интервале
А А О А о
(0; тс). В этом интервале число однозначно определяется, например,
своим тангенсом. Поэтому рассмотрим тангенс этого числа:
3 1 4^1 (\ . 3 1
- - — arctg - - -ctg — arcsin — - -
1 + tg -arcsin- • tg -
14*
(l 4"l (l 3
tg -arctg- - tg-arcsm-
404| Глава XIII. Уравнения и неравенства
т-т j_ , ос 1 - cos ос
По формуле tg — = получим
2 sin a
( 3^1 4
, ч 1 - cos arcsin— I
(l • 3^ I 5j 5 1
tg -arcsin- =
2 5J ( 3^
sin | arcsin - i K
о
3
sin arctg—
(как вычислять выражения вида cos arctg - , подробно разбиралось
в § 37 учебника 10 класса).
Таким образом, получаем
1 4- — • —
л 1 31 4^ 32-
- +-arcsin-- -arctg5J = -j-j- = 7.
2 3
Итак, одна из серий корней числителя имеет вид х = arctg 7 и- пп9
п е Z. Аналогичные вычисления для первой серии корней числителя
дают тангенс, равный —1, откуда уже легко догадаться, что сам корень
равен —- + пп, п е Z.
4
Кстати, нахождение именно тангенса выражения, а не его
косинуса мотивировано тем, что применение формул суммы приведёт к
необходимости нахождения функций половинного аргумента, а формулы
для тангенса половинного аргумента наиболее просты.
Кроме того, если при решении соответствующего уравнения запи-
4 3
сать ф не как arctg-, а как arccos-, то один из полученных корней
3 5
числителя окажется равным
1 .31 3 If .3. 3) п
1 .31 3 if .3^ 3) п
--arcsin — - - arccos - = -- arcsin - + arccos - = -—,
2 52 52y о 5у4
поскольку сумма арксинуса и арккосинуса одного аргумента равна —
(см. пример 44 § 37 учебника 10 класса).
Попробуем другой подход к нахождению корней числителя,
а именно сведём соответствующее уравнение к однородному:
3 sin 2х + 4 cos 2х = -3 =>
=> 6 sin х • cos x + 4 cos2 x - 4 sin2 x + 3 (sin2 x + cos2 x) = 0 =>
=Ф sin2 л: - 6 sin л: • cosx - 7cos2x = 0;
очевидно, cos x = 0 решения не доставляет; переходим к уравнению
t2 - 6t- 7 = 0, где t = tgx.
405 § 89. Тригонометрические уравнения и неравенства
Отсюда
x= -1,
X = h ПП,
4
где п, k e Z.
х = arctg 7 + nk,
Вот теперь действительно легко
расставить точки на тригонометрическом
круге и воспользоваться методом интервалов
(рис. 13.46).
Ответ: [ — + 2пп; arctg 7 + 2пп U
Зл_
4
;^ + 2тт
4
Пit
Пit
к + arctg 7 + 27т; — + 2тт |, п е Z.M
Рис. 13.46
6. Отбор решений в тригонометрических уравнениях
и неравенствах
Как и в других уравнениях, при решении тригонометрических
уравнений возникает проблема отбора корней (например, в уравнениях,
содержащих дроби с переменной в знаменателе, или в смешанных
уравнениях, содержащих тригонометрические функции под знаком
радикала или логарифма).
Пример 139. Решим уравнение
= 0.
cos
(Н
Уравнение равносильно системе
fcos3x = 0,
Решая первое уравнение системы, на-
Из
ходим Зх= — + тг/г<=>х=—I , neZ.
2 о 3
Рис. 13.47
второго уравнения хф ьттй,
6
Г. Поскольку левая часть исходного
уравнения имеет период 2тг, можно провести отбор решений в пределах
одного обхода тригонометрической окружности.
406 Глава XIII. Уравнения и неравенства
Расставляя точки первой серии на окружности и исключая из них
точки второй серии (рис. 13.47), получаем ответ в виде объединения
двух серий х=— + ппих=— + nk, п, k g Z.
,[l + nn,l + nk:n,kez\.
твет можно запис
Ответ: \ — + тт, — + nk: n,keZ\.M
[26 J
Замечание. Ответ можно записать также в виде
Порой отбор на окружности (вообще говоря, наиболее надёжный
и предпочтительный способ) оказывается громоздким, и тогда легче
свести его к решению линейных уравнений в целых числах, как это
будет показано в следующем примере.
Зх
Пример 140. Решим уравнение cos2x + cos— = 2.
4
Зх
П Поскольку cos 2х ^ 1 и cos — ^ 1, равенство возможно, только если
4
{cos 2x = 1,
Зх
cos— = 1.
4
Теперь достаточно взять те решения первого уравнения системы,
которые одновременно являются корнями второго.
Проблема состоит в том, что период функции cos — (а вместе с ней
4
и всей левой части исходного уравнения) равен 4тг, а значит, отобрать
корни в пределах одного круга не получится. Эту ситуацию можно
х
обойти, введя замену t — — (тогда мы будем иметь дело с системой
4
l,
\ в которой период левой части равен 2тг; мы уже пользова-
[cos ot = 1,
лись этим приёмом при решении неравенств, см. пример 135). Но
гораздо проще в данном случае выглядит алгебраическое решение.
{х = nk,
Snn где k, n g Z. Найдём общие
х- 3 ,
Q_
элементы двух серий: nk = => 3k = 8п. Поскольку числа 3 и 8 вза-
3
имно просты, k должно быть кратно 8, т. е. k = 8Z, где I e Z. При
таких k корни верхней серии удовлетворяют второму уравнению.
Окончательно имеем х = 8тг/, I e Z. Заметим, что тот же результат мы
получим, если, учитывая, что п \ 3, подставим в нижнюю строку
п = 3/тг, т е Z. Ш
407, § 89. Тригонометрические уравнения и неравенства
Рассмотрим несколько более сложный пример того же типа,
обращая особое внимание именно на алгебраическое решение уравнений
в целых числах в процессе отбора корней.
Пример 141. Решим уравнение = —.
sin х sin 2x sin 4х
П Приведя обе части уравнения к общему знаменателю, переходим
sin 2х • sin 4х - sin х • sin 4х = sin х • sin 2х,
sin х Ф 0,
к равносильной системе \ . Л
sin 2х Ф 0,
L sin 4х Ф 0.
Понятно, что из трёх неравенств достаточно оставить sin4x^0,
поскольку все корни уравнений sin л: = 0и sin 2x = 0 содержатся среди
корней уравнения sin4x = 0. Таким образом, достаточно решить
первое уравнение системы и выкинуть из множества его решений корни,
удовлетворяющие условию sin4x = 0. Решим уравнение:
sin 2x • sin 4х - sin x • sin 4х = sin x • sin 2x »
<=> sin 2x • sin 4х = sin x (sin 2x + sin 4x) <=>
<=> sin 2х • sin 4x = sin л: • 2 sin Зх • cos x » sin 2x • sin 4x = sin 2x - sin Зх <=>
» sin 2x (sin 4х - sin3x) = 0.
Поскольку одно из условий системы sin2x Ф 0, достаточно решить
уравнение sin4x = sin3x.
х = 2пп,
[4х = Зх + 2тт,
Л.у — тг Ят-1-5
sm4x = sin3x » ai, k e Z
1 2тгй
л(2/г + 1) n, /г e Z.
x = —
Очевидно, первая серия не является решением системы. Сложнее
разобраться со второй. Можно расставить все точки этой серии на
окружности, вычеркнуть из них все точки вида — и записать ответ:
4
±— + 2пп; ±— + 2тт; ±— + 2пп: п е
7 7 7
А можно поступить иначе. Решим в целых числах уравнение
к (2п 4- 1) nk и г, тт
= —, где k, n e Z. Получаем целочисленное уравнение
— = —. Отсюда 7k = 8п + 4. Поскольку правая часть уравнения
кратна 4, то и левая должна делиться на 4, а поскольку числа 7 и 4
взаимно просты, то k должно быть кратно 4, т. е. k = 4Z, I e Z.
Подставив это значение в уравнение и разделив обе части на 4, получим
71 = 2п + 1. В правой части этого уравнения стоит нечётное число,
а значит, I тоже должно быть нечётно: I = 2т +1, т е Z. Отсюда
14/тг + 7 = 2п + 1»2я = 14/тг + 6 » п = 7т + 3, т е Z.
408 Глава XIII. Уравнения и неравенства
m n (2n + 1) „
Тогда ответ записывается в виде х = — -, где п е Z,
п Ф Чт + 3, т е Z. (Заметим также, что последнее условие можно
записать в виде п ^ 3 (mod 7).) IS
Перейдём к смешанным уравнениям, в которых возникают
ограничения в виде неравенств.
сильной системе
Пример 142. Решим уравнение д/2sin2х + 2sinx = 0.
□ Уединим радикал: ^J2^xi2x = -2 sin я, а затем перейдём к равно-
J 2 sin 2x = 4 sin2 x,
\ sin л: < 0.
Решая первое уравнение системы,
получим
4 sin х • cos x = 4 sin2 л: »
/ • ч л fsinx = 0,
» sin л: (sin х - cos x) = 0 <=>
Рис. 13.48
< пп; -j- + 2пп: пе z\.
Пример 143. Решим уравнение
( х\ (
log2 cos 2x + — + log^ si
D Перепишем уравнение в виде
Отбирая корни на окружности (рис. 13.48)
(корни первого уравнения заведомо
удовлетворяют условию sinx^O), получим ответ:
5л
Ш
хЛ
sin л: + cos — = 0.
2
log2 | cos 2x + cos— = log2 sin л: + cos — |,
2 / I 2
что, в свою очередь, равносильно системе
cos 2x + cos ~ = sin х -h cos ^,
I 2 2
х
sin x + cos — > 0.
Решая первое уравнение системы, получим cos 2x = sin x
1 - 2 sin2 х = sin x
sinx = -1,
1 Откуда
einx=-.
х = -— + 2пп,
х = — +
6
п, k, I e Z.
409. § 89. Тригонометрические уравнения и неравенства
У и
х
Рис. 13.49
х
Теперь решим неравенство sinх + cos— > 0. Чтобы воспользовать-
ся методом интервалов на окружности, введём замену — = t и
рассмотрим неравенство sin 2t + cos t > 0 (теперь левая часть имеет период 2тг).
Решим неравенство cos t (2 sin t + 1) > 0 стандартным образом на
окружности (рис. 13.49).
Получим t е [-- + 2тт; - + 2пп j U | — + 2тт; Щ- + 2тт), neZ.
Чтобы произвести отбор корней в пределах одного периода,
разумно переписать множество решений первого уравнения в виде
t = —- + пп,
4
t = — + nk, n, k, I e Z.
Отбор корней на тригонометрической окружности показан на
рисунке 13.50.
п
Таким образом, после отбора остаются серии
n,keZ.
Возвращаясь к переменной х, получаем ответ: \ — +4тт; — + 2пп: neZ\.\*
6 6
'}•
410! Глава XIII. Уравнения и неравенства
Отметим, что, поскольку отбираемые корни имеют достаточно
простой вид, можно было производить отбор, непосредственно
подставляя их в условие sinx + cos— > 0.
Вот ещё один пример, связанный с отбором корней. В этом
примере условие, накладываемое на область определения, не является
«чисто тригонометрическим».
Пример 144. Решите неравенство Iog2^_^2 (cos2x- sinx)^ 0.
sinx- 1)> 0,
_ TT cos 2x + sin x > 0
□ Неравенство равносильно системе
2
X ^ U,
2х-х2ф\.
!cos 2x + sin x > 0,
2x - x2 > 0,
2x - x2 ф 1.
Решив неравенство 2х - x2 > 0,
получим x g (0; 2). Из последней строки х Ф 1.
Решим неравенство cos 2x + sin * > 0.
Получим
1-2 sin2 x + sin x > 0 »
» (2 sin л: + 1)(1 - sin я) > 0.
Учитывая, что второй множитель
неотрицателен, т. е. 1 - sin л: > 0 для всех х,
заменяем неравенство системой
I sinх > --,
[sinx Ф 1.
Решение системы изображено на
рисунке 13.51.
Но с учётом того что х е (0; 2), вполне
можно было ограничиться и решением на
числовой прямой. Окончательно ООН
задаётся условием
~0< х < 1,
!<*<§,
Теперь рассмотрим неравенство
Рис. 73.52
0,
411 § 89. Тригонометрические уравнения и неравенства
которое перепишем в виде
(2х - х2 - l)(-2sin2x + sinx) > О <=>
» (х2 -2х+ l)(2sin2x - sinx) > О «
» (х - I)2 • sin х (2 sin * - 1) ^ 0.
Последнее неравенство можно решать
как на тригонометрическом круге (рис. 13.52), так и на числовой
прямой (рис. 13.53). (С учётом ООН достаточно рассмотреть круг в
границах х g [0; 2тг).) г- х
Пересекая полученное множество с ООН, получаем ответ: —; 1 U
( \ ( \ L6 у
U l;f Uf;2.«
7. Уравнения и неравенства,
содержащие обратные тригонометрические функции
Этот тип задач также может быть условно отнесён к нестандартным.
Некоторые примеры уравнений и неравенств, содержащих обратные
тригонометрические функции, были рассмотрены в 10 классе (VI
глава). Здесь мы напомним основные приёмы работы с подобными
уравнениями.
Во-первых, это применение определения в уравнениях, которые
могут быть приведены к виду arcsin/(x) = g(x) (в левой части может
стоять любая из аркфункций), причём особое внимание следует
уделять областям определения и множествам значений аркфункций.
Во-вторых, поскольку такое уравнение, как правило, говорит о
равенстве некоторых аргументов («углов»), то имеет смысл рассмотреть
тригонометрические функции этих аргументов. Напомним, что если
аргументы равны, то равны и тригонометрические функции от них.
Обратное неверно, поэтому, взяв, например, синус обеих частей
уравнения, мы получим только следствие исходного уравнения (скорее
всего, приобретя при этом посторонние корни). Далее посторонние корни
отсеиваются непосредственной проверкой (подстановкой в исходное
уравнение); при этом начинать проверку разумно с принадлежности
корней областям определения входящих в уравнение функций и
сравнения знаков обеих частей уравнения.
ос
Пример 145. Решим уравнение arccos— = 2arctg(x- 1).
А
П способ 1. Возьмём косинус от обеих частей уравнения:
( х\
cos arccos — = cos (2 arctg (x - 1)). (1)
V 2 /
Полученное уравнение является следствием исходного, но не
равносильно ему!
412; Глава XIII. Уравнения и неравенства
Займёмся преобразованием правой части уравнения. Введём заме-
itgy = х-1,
ну у = arctg(x - 1). По определению это означает, что s к к
12 <У <~2'
После замены переменных в правой части уравнения (1) имеем
cos2i/, а по формуле («универсальная тригонометрическая
подстановка») cos2i/ = \~lgg2yy получим cos2j/ = *~ |* ~ g2.
Таким образом, исходное уравнение преобразуется к виду
2 ^
2 jc
г~~
, откуда х = О или х = +V2. Теперь необходимо провести
2 jc2 - 2# + 2
проверку.
Подставим х — 0 в исходное уравнение: arccosO = 2arctg(-l). Это
равенство неверно, поскольку arctg(-l) Ф —.
Подставим х — -V2 в исходное уравнение:
arccos I -— = 2arctg (-V2 - l).
V 2 )
Это равенство неверно, поскольку его левая часть, будучи арккосину-
(п Л г
сом отрицательного числа, лежит в интервале —; тг , а правая, будучи
\2 )
удвоенным арктангенсом отрицательного числа, лежит в интервале (-тг; 0).
Наконец, подставим х = V2 в исходное уравнение. Получим
arccos |^Ч = 2arctg (V2 - l).
Это равенство является верным, поскольку косинусы обеих частей
этого равенства равны (оно было получено из решения соответствующего
уравнения!) и оба числа лежат в промежутке (0; тг), а из равенства
косинусов двух чисел на этом промежутке следует равенство самих
чисел. Ответ: {л/2}.
способ 2. Можно было воспользоваться другой
тригонометрической функцией, в данном случае взять тангенс обеих частей уравнения
(выбор функции, естественно, зависит от самого уравнения). Однако
при таком подходе мы можем потерять решения, при которых обе части
уравнения равны —. Таким образом, кроме получившегося уравне-
{X К
arccos -=-,
которая ре-
2arctg(x-l)=|,
шения не имеет. Но без этого исследования решение будет неполным!
Как видно, способ 1 оказался удобнее.
4131 Задачи и упражнения
способ з. Заметим, что функция /(х)= arccos — является убываю-
щей, в то время как функция g(x) = 2arctg(x - 1) является
возрастающей. Поэтому уравнение f(x) = g(x) не может иметь более одного
решения. Если угадать корень этого уравнения, задача будет решена. II
Одним из наиболее часто встречающихся подходов при решении
неравенств, содержащих обратные тригонометрические функции,
является применение соображений монотонности обратных
тригонометрических функций на их области определения. Но в более сложных
неравенствах этими соображениями пользоваться затруднительно,
поэтому, как и обычно, рекомендация заключается в решении
соответствующего уравнения и использования метода интервалов на области
определения неравенства.
Пример 146. Решим неравенство arccos— > 2arctg(x- 1).
□ Областью определения неравенства
служит отрезок [-2; 2] (поскольку есть
единственное ограничение: -1^ — ^ 1).
Единственным корнем соответствующего уравнения является, как
мы выяснили выше, х = V2. Эта точка разбивает отрезок [-2; 2] на два
множества, в которых мы проверяем выполнение неравенства,
воспользовавшись контрольными точками (рис. 13.54) (в качестве таковых мы
можем для удобства взять х = -2 и х = 2). Ответ: Г-2; V2). 11
В Задачи и упражнения
Уравнения высших степеней
Группа А
Х1П.1. Найдите целые корни уравнения:
а) х3 - 5х + 4 = 0; б) 2х3 + х2 - 13х + 6 = 0;
в) х4 + 2х3 - 4х2 - 8х = 0; г) 4х4 - Их2 + 9х - 2 = 0;
д) х5 + 4х4 - 10х3 - 65х2 - 86х - 24 = 0;
е) хъ + Зх4 - 9х3 - 2\х2 - 10* - 24 = 0.
хш.2. Найдите рациональные корни уравнения:
а) х3 - Зх2 + 2 = 0; б) 2х3 - Зх2 - Зх + 2 = 0;
в) 6х4-7х3-6х2 + 2х+1 = 0; г) Зх4 - 8х3 - 2х2 + 7х - 2 = 0.
хш.З. Решите уравнение:
а) х3 - 7х - 6 = 0; б) х3 + 9х2 + Их - 21 = 0;
в) х3 - 5х2 + Зх + 1 = 0; г) х3 + 7х2 + 4х - 2 = 0;
д) 4х3 + Зх - 2 = 0; е) 6х4 - Их3 + 9х2 - Их + 3 = 0;
ж) 6х5 + 7х4 - 18х3 - 16х2 + х + 2 = 0.
414; Глава XIII. Уравнения и неравенства
хш.4. Решите неравенство:
а) х3 - 7х - 6 > 0;
в) 4л:3 + 3* - 2 > 0;
д) л3 - 4л2 + 5л - 2 ^
0;
б) х3 + 9х2 + Их - 21 < 0;
г) 6л4 - Их3 + 9х2 - Их +
е) х3 - Ъх2 + 8* - 4 < 0.
3 ^ 0;
Замены в целых рациональных уравнениях
Группа А
ХШ.5. Решите уравнение с использованием подходящей замены:
а) Зл4 - л2 - 2 = 0; б) 2л6 - 11л3 - 40 = 0;
в) л2 + 2л + 2|л+ 1| = 7; г) 4л2-12л-5|2л-3|+15 = 0;
д) (л - I)4 - л2 + 2л - 73 = 0; е) (л + 2)4 + 2л2 + 8л - 16 = 0;
ж) (л2 - 2л)2 - Зл2 + 6л - 4 = 0;
з) (л2 - 5л + 7)2 - (л - 3)(л - 2) - 1 = 0;
и) (2л2 + Зл - I)2 - Юл2 - 15л + 9 = 0;
к) 4л2-2|2л-1| = 34 + 4л;
л) л4 + л2 + 4|л2 - *| = 2л3 + 12;
м) л4 + 4л3 = 30 - 7|л2 + 2*| - 4л2;
н) (*+ 1)2(л2 + 2л) = 12;
о) (л - 2)(л - 3)2(л - 4) = 20;
п) л(л + 4)(л + 5)(* + 9) + 96 = 0;
р) (л - 3)(л - 4)(л - 5)(л - 6) = 1680;
с) (2л - 1)(2л + 3)(3л - 2)(3л - 8) + 25 = 0.
Решите уравнение (хш.б, хш.7).
ХШ.6. а) 7 [ л + - ] - 2 [ л2 + - | = 9; б) 4 л2 + 12л + — + -i- = 47;
V х) \ х) хх
в) 2л4 + л3- 11л2 + л + 2 = 0;
д) 2л4 + л3-9л2-2л + 8 = 0;
ж) л4 + 2л3-9л2-6л + 9 = 0;
хш.7. а) (л2 + 2л)2 - (л + 2) (2л - л2) = 6 - (2л - I)2;
б) 2(л2 + л + I)2 - 7(л - I)2 = 13(л3 - 1);
в) 2л4 + л2(л + 2) - 3(л + 2)2 = 0;
г) 4л4 + Зл3 - 14л:2 + Зл + 4 = 0;
е) х4 - 4х3 + 7х2 - 8л + 4 = 0;
з) 9л4 - 6л3 - 18л2 - 2х + 1 = 0;
Д) 20
е) 5
х-2
х+ 1
х-2
х + 1
- 5
+ 12
х + 2
х-1
хг- 4
х2- 1
+ 48
х2- 4
х2- 1
= 0;
= 44
х + 2
*- 1
2х2 + 2х
х2 + 4х - 5 '
415; Задачи и упражнения
Дробно-рациональные уравнения
Группа А
ХШ.8. Решите уравнение:
ч х + 2 л* + 6 л* + 10 а ЛЧ х х + 1 л* + 2 26
а) + + = 6; б) + + = —;
х + 1 л* + 3 х + 5 * + 1 * + 2 * 6
Д)2^ + 2^ = 2; е)
Решите уравнение, используя подходящую замену (хш.9—хш.13).
XIIL9. a)^lp5+ 3|_^ + 4=0; 6)x_±i+ * =_|.
в, ^_ + _Ё_=о. г> _J ^=J_.
х2 + 4 х2 + 5 ' ' х3 + 2 х3 + 3 12'
„ х2 - х х2 - х + 2 л ч 24 15
1
л:2-л: + 1 х2-х-2 '
х2+ 2х + 1 ^ л:2+ 2л: 4-2 7
О1 ^
2* + 3 б' ' х(х + 2) (л: + I)2 " 12'
и) х^-х2- —^—j = 2.
о
ХП1.10. а) — х2 = 3 -
jc2- 4jc + 1
б) 2 2
в)
В)
л:2 -2л: + 2 х2 - 2х + 3 *2 - 2л: +4'
6 | 8 1т
(х + 1)(* + 2) (х- 1)(х + 4)
, 165
1
Xs + Зл*2 - х + 5 л*3 + Зл:2 - х + 2
ч л:2- 2* к 16л:-12 ч ("4л: - 5V f3x + 2V .1
ж)
л:2-10х+15 _ Зл: . л:2 + 5л:+4 л:2-л:+4 13
.11. а) ^26:с+15 - „28:с+15; °' ^27^+4+^2 + ^+4+ 3
в) 2*2+8 + ^ + 11=0; г) (х2 - 6х - 9)2 = х(х2 -Ах- 9);
х л:2+Зл:+4
ч 8л*2 + 8 Юл* _ л ч л*2+Зл* + 6
Д) -^—7^ 7"~i—7 + 7 = 0; е)
л*2 Юл: + 1 л*2 + 1
^7^7i7 + 7 0; е) х + 5х + 615
л*2 - Юл: + 1 л*2 + 1 л*2 + х
416, Глава XIII. Уравнения и неравенства
хш.12. а) х2 + -^—=7; б) x2+*u*=11; в) (-^)\(^У= 90;
(х-3)2 (х + 5)2 x+1) *1^
ч 2 ^ 81*2 АП \ 1 1 10
Группа В , v
хш.13. а) (х2 - 5х + 1)(х2 - 4) = 6(х - I)2; б) х • ^^ • х + ^^ = 6;
х + 1 ^ х + lj
в) х3 + 4 + *2 + 4 + * + - = 6' г) (х + 3)4+(х + 5)4 = 16.
X3 X2 X
Уравнения и неравенства с параметрами
Группа А
Решите уравнение с параметром а е R (хш.14, хш.15).
хш.14. а) (а2 - а)х = 3; б) (а2 - 9)х = а - 3;
в) (За2 + 2а - 1)х = 1 - а2; г) х2 = а;
д) 4х2 + а = 0; е) ах2 = 1.
хш.15. а) а = 1 + -^-; б) ^±^ = 8(х + 1) + 7-
а а(х - 1) а а
. х 2а + х _ 16а2 jc-За 2а + 3_а-5
В^ 2а + л: х - 2а " 4а2 - х2 ' Т) х2 - 9 "" л: + 3 " х-3'
хш. 16. Решите неравенство с параметром а е R:
(^ 2 21
. 2* - 1 х+1 2х-гл .ах х - 1 2* + 3,
В а + 1 " 2(а - 1) " а - 1 ' Г а - 2 3 4
. 2х + 1 а 4- 5 3 ч ах + 1 4а - х а2
Д) J^V^c ^Т > х; е) "^~ ~2~" < У"
хш.17. При каких значениях а неравенство (а2 + 2а - 3)х + За2 - а -
- 14 < 0 выполнено для всех х < 0?
хш.18. При каких значениях а неравенство (а - 2) л: + 2а - 16 < 0
выполнено для всех х, таких, что \х\ ^ 5?
хш.19. Решите неравенство с параметром а е R:
а) х2 - 2(а + 1)х + 4а < 0; б) (а2 - 1)х2 - 2ах + 1 < 0;
в) ах2 + (2а + 1) + а 4- 2 > 0; г) (а + 1)х2 4- ах 4- а < 0.
Множества на плоскости, задаваемые уравнениями и неравенствами
Группа А
ХШ.20. Постройте график уравнения:
б) ^ Zx)f \\2х Ц = 0;
417! Задачи и упражнения
в) 4у2 = х2; г) х2 + у2 = О;
Д) (х2+у2)(у-х-1)= 0; е) (у- х)2 + (у- х2)2 = 0;
(2у + л: - 1)(* - у - 2) = Q (2у + х - 1)(х - у - 2) = Q
2х + у - 1 ' у2 - х2
ХШ.21. Постройте множество, задаваемое неравенством:
а) у > -; б)ху>1; в) х > -; г) —< 1; д) ху(х + у - 1) ^ 0;
>0; з)
+ у - 1 jci/ - 1
и) х > у2; к) 2у + х ^ у2 + 2у ^ 2х + у; л) у[у ^ ^2х - х2 .
Группа В
ХШ.22. Постройте график уравнения:
а) |х + у| = |х| + у; б) |х + у| = х + Ы;
в) |х + у| = |х| + |у|; г) |х + у| = |у| + у;
д) |х| + |у| = 1; е) |х+1| + |х-1| = |у + 1| + |у-1|;
ж) 2|х + у|-|х-2у| = 3у; з) |х - у| - \2х + у| = \х - 11;
и) \у - х\ + х2 = 1; к) у = \у + х2 - Зх|;
л) \у-х\ + \у-х2\ = 2.
ХШ.23. Постройте множество, задаваемое неравенством:
а) \х-2у\-\х + у\^2у; б) \х- Зу\ < \х - у\ - 2у;
о
в) \2х-у\>-у + \х-у\; г) |х2 + у|^у+1;
д) |х + у + 1| + |х-2у|>4.
Группа С
хш.24. Постройте график уравнения:
a) max(x; у) = min(|x|; |у|); б) шах(х; у) = min(x2; у2);
в) max (я; у2) = min(y; х2); г) max(|x|; y + 1) = min(x2; 2x-\-y).
Графические методы решения уравнений и неравенств с параметрами
Группа А
хш.25. При каких значениях а уравнение | х2 - 11 = 2х - х2 + а имеет
единственный корень?
хш.26. При каких значениях а уравнение
(а + 4х- х2- 1)(а+ 1 - \х - 21) = 0
имеет ровно три корня?
Х1П.27. При каких значениях а уравнение (х2 - а)2 - 6х2 + Ах + 2а = 0
имеет ровно три корня?
ХШ.28. При каких значениях а уравнение х2 + 4х — 2\х — а\ + 2 - а = 0
имеет ровно два различных корня?
418 Глава XIII. Уравнения и неравенства
Группа В г
ХШ.29. При каких значениях а система неравенств < не име-
^ [х > 4а
ет решений?
„ fax + 1 < О,
ХШ.ЗО. При каких значениях а система неравенств < _ имеет
[х + а > О
решение?
„ \х2 - (За + 1)х + 2а2 + 2а < О,
ХШ.31. При каких значениях а система s
\х + а2 = О
имеет хотя бы одно решение?
„ f х2 + (5a + 2) jr + 4a2 + 2a < О,
хш.32. При каких значениях а система < о о
[х2 +а2 = 4
имеет хотя бы одно решение?
ХШ.ЗЗ. Найдите все значения параметра а, при которых система
неравенств
[х2 +а + 4х + 3^ О,
< on удовлетворяется лишь при одном х.
У 2ci — х + 2 ^ О
те все значения параметра а, при которых система не!
\х2 - 4х + а ^ О,
< о _ _ удовлетворяется лишь при одном х.
[х* + 2х — За ^ О
ХШ.35. Найдите все значения а, при которых неравенство (х - За) х
х (х - а - 3) < 0 выполняется для всех х из отрезка [1; 3].
хш.36. При каких значениях а множество решений неравенства
(х - а2)(х - а - 4) ^ 0 содержит не более четырёх целых
значений х?
ХШ.37. Найдите все значения параметра а, при каждом из которых
множество решений неравенства (х2 — а) (а — 2х — 8) > 0 не
содержит ни одного решения неравенства х2 ^ 4.
ХШ.38. Найдите все значения параметра а, при которых отрезок [3; 4]
не имеет общих точек с множеством решений неравенства
х + а-
Группа С
ХШ.39. При каких значениях а все решения неравенствах2 + 2\х — а\^5
положительны ?
ХШ.40. Найдите все значения параметра а, при каждом из которых ре-
\х2 +&х- 7-ha ^ 0, ^
шения системы неравенств < о _ образуют на чи-
[х2 +4х+ 7 ^ 4а
еловой оси отрезок длиной 1.
419[ Задачи и упражнения
xni.41. Найдите все значения параметра а, при которых наименьшее
значение функции у = х2 + 2х—1 + \х — а\ больше 2.
ХШ.42. Решите уравнение |х + 3|-а|дг-1| = 4.
ХШ.43. Решите неравенство 2х2 + х - а - 8 ^ \х2 + 2х - 2а - 4\.
хш.44. Решите систему неравенств:
\х2 + Ах + 3 + а < О, (х2 - х-2 + а<0,
а) \2х + а + 6 > 0; ' \х2 - 2х - 3 + 2а > 0.
„ П2;с — а| + |л; + а|^6,
хш.45. При каких значениях а система неравенств <'
[Зх2+2х-4а ^ 0:
а) имеет решение;
б) имеет единственное реп1ение;
в) имеет только отрицательные решения;
г) имеет только положительные решения;
д) имеет только решения, удовлетворяющие условию \х\ ^ 1;
е) имеет хотя бы одно решение, удовлетворяющее условию | х \ < —;
ж) имеет решения, содержащие отрезок -1; — ;
L 4J
з) имеет решения, содержащие не более трёх целых чисел?
и) Решите эту систему для всех значений параметра а.
Системы уравнений и неравенств
Группа А
ХШ.46. Решите систему уравнений:
\х-
б)
ХШ.47. Следует ли из системы < х _ v соотношение:
а) А + h - ё\ + ^2» б) f\- f2 = ё\- e£
д) h ' ё2 = h ' eJ
хш.48. Следует ли из системы { } " 19 соотношение:
I #2 ^ ^2
а) Л + /2 ^ g"l + ^2» б) fi~ f2^ ё\~ §2у В) /l "
г) Л * /2 ^ g"i * #2» Д) т" ^ ~?
/2 &2
420; Глава XIII. Уравнения и неравенства
хш.49. Верен ли переход:
хш.50. Решите систему неравенств, опираясь на графическую
интерпретацию:
у - 2 > х2 + 4х, {у - 10 > х2 - 6х,
\6x-y-l\^2; ' \|2* + у-5|<1.
Сложение и вычитание уравнений. Метод подстановки
Группа А
Решите систему уравнений (хш.51—хш.53).
ч Ux2 + 7у2 = 148, ^ [—Ц- - —Ц- = -,
ХШ.51. а)^о9 , ^ б) < у - 1 у + 1 л:
Зх2 - у2 = 11; 9 к Л
1 * [у2-х-5=0;
у2-ху = -12, Гуз - х3 = 9,
х2-ху = 28; Г) |x2i/ - ху2 = 6;
x2z/ + ху2 = -2.
хш.52. a) V~l "^ ' о б)
[2х + 2\у-1\ = 3; \х + у = х2-у2;
В) [х2 = 4у - 3; Г) \х = у2 - 2у + 2.
хш.53. a) i б) \ '
[х + у = о; [х2 + Зод + 2у2 + 2х + 4у = 0.
Однородные и приводящиеся к однородным системы уравнений
Группа А
ХП1.54. Реп1ите систему уравнений:
ч (Зх2 - 4ху + у2 = 0, ^ч ГЗх3 - 4х2у + ху2 = 0,
a) "s о) \
I Л Т Ul^ — It7) l^'i/ — ^5
4211 Задачи и упражнения
х2 + у2 _ 5
в) \ ху = 2'
х2-у2 = 3;
f х2 + Ay2 = 8,
Ю \х2- Зху = -2;
(*>+„« =28*.
' [2х2-ху + у2 = 8.
Симметрические системы уравнений
Группа А
xiii.55. Решите систему уравнений:
е)
\ х2 + 3 = 2л;у,
I 6л;2 - Иг/2 = 10;
б)
х + у + ху = 7,
ж2 + г/2 + ху = 13;
\х2 -ху + у2 = 7,
а) \х + у=5;
(Г2 . „2 _ 1 7 f г2 — гн + и2 — 1Q
[X +у -к, 1л: ху+у - iy,
[х + лгу+ i/= 9; [л:-л:г/+ у = 7;
|л:2 + г/2+2л: + 2у = 30, Гх-у = 2,
\л:2 + г/2 + л:г/ = 27; ' \х3 - у3 = 8;
Д)
У) =30,
. (х3+х3У3+у3 = 12,
\х + ху+у = 0;
Замена переменных в системах
Группа А
Решите систему уравнений (ХШ.56—хш.60).
[1-1 = -L
ХШ.56. а) \ х у 36' б)
[л:г/2 - х2у = 324;
Группа В
[л:3 +х3у3 +у3 = 17,
1
ХШ.57. а)
в)
2ху
о 21
2ху = —,
5
о 21
+у2 = —;
4
ху(х-у)= 210.
б)
г)
= 136,
ху +
= 30;
2)= 300,
У2 = 37;
422 Глава XIII. Уравнения и неравенства
д)
ж)
ху + — + — + — = 13,
ху у х
ху + У- = 12;
ху у х
2х2 - ху - у2 = 5,
2(у-х)=(2х + у)2+:
у3
в)
XIII.59. а)
в)
Д)
Группа С
ХШ.60.
[х3 = 5х + у,
[у3 = х + Ьу;
У
х
2
^l =12,
Ы
у)
(ху)2 + ху = 6;
х
ху + - = 2(х2 + у2),
X
ху = х2 +у2;
UX2+ 1)(г/2+1)= 10,
е) 1(х + у)(ж|/-1)=3;
ж2 + 2*i/ + 4 = О,
з)
б)
г)
б)
\-(х2+у2)=6,
\У-(х2-у2)=1.
у)(х + 2у)(х + Зг/) = 60,
jc)(i/ + 2л:)(г/ + Зх) = 105;
л; х2 х3
г) 1у У2 У3
[х + у = 3;
(x + y + z = 4,
' \2ху-г2 = Ы.
4-У2 = (2*-3У)2, Г4-г/2 = (^_3г/)2, fx3+!/3 = l,
х2 - ху2 = -9 + 2х; ; \х2 - 4ху2 = -2х - 9; ' [х* + у* = 1.
Иррациональные уравнения
Группа А
Решите уравнение (хш.61, хш.69).
J = х + 3;
ХШ.61. a) -J(x
в) jc + д/Зд: + 7 = 7;
д) V*2 - 36 = ^2* - 1;
б) л/х + 1- 42х + 3 = х + 3;
г) д/(Зл;-1)(4л; + 3) +1 = 3jc;
е)
- 5 =
-2
4231 Задачи и упражнения
ж)
х + 6
==== = V"T». з) *=5-J2*2-14* + 13;
:- х х+ 4 ^
4
и) J2* + 3 + J2* + 5 =
72х + 5
; к) (2* - 1)д/^2 - * - 20 = 12* -
л)
н) 4х
;-18; м)
о)
Р)
- 1 = V* - V* + 8; о) V* - 3 + х = 3 + ^6 - 2х;
п) л/* + х = 3- J5x- 16;
с) V д/
ХШ.62. а) %8 + х + %8-х = 1; б)
в) ^/лг + 34 - Vx-З = 1; г)
д) ЩЪ + х - 2%1Ъ-х = ^/25 - х2.
ХШ.63. а) 9-Д/81-7Л:3 =—; б)
ЛГ+1
= 3.
2' ;
г) фс2 - 4* + 5 + -yjx2 - 4* +13 = -*2 + 4х;
+ 2* +1 + Д~
д)
+ 8* +13 =
е) Jbx2 - 20* + 21 + д/3*2 - 12* +~28 = 8* - 2*2 - 3;
ж) (х - З)2 + 3* - 22 = у/х2 -3* + 7;
- 4V*- 1 + ^ + 8 - 6л/*-Т = 1;
+12;
хш.64. а) х3 +х + ду*3 + * - 2 = 12;
б)
-з/(3-*)(6 + *) = 3;
Группа В
ХШ.66. а)
/2х + 8 = 7; б) Jx + ^f^j
^)Ч(л/^ТТ + ^)2 = 2;
- yjX- у/Х - - / ,
| л т- "V л
= 2;
б) х 4- д/л:2 + 16 =
424 Задачи и упражнения
в) х + ^2х2 + 6х +12 - д/4*2 - 20ж + 25 = 2;
г)
+ 1 - 2х = 1 - х; д) V^x + V~* - л/х +1 = 1.
xiii.67. а) 4х2 + 12xVl-x = 27 (1 + х); б) - - 2 = —
2 2(1+
Jx + 4 + Jx - 4 /—; —
в) = х + ух2 - 16 - 6;
г)
д)
3 - 16;
= 35 -
е) Зж + 2-yJ2x2 - Зл: + 1 = 4 - Vjc — 1 -
ж)
15
XIII.68. а) л/1 + л/л: = 2 - л/1 -
в) %1-х - 1 = 1 - Vx + 2;
п! 5/ и у -U 5/
Ж) '
б) <Jx-2 =
г) V^ + ^^
е) ^97 - х + Vx = 5;
-8 = 2.
ХШ.69. а) V2*2 + 8* + 6 + д/л:2 - 1 = 2х + 2;
б)
в)
б) (лг - 2)^х2 + 2х = (х + 1
2л: - 10
- 2
д) ^2
ж)
з)
ч (39 -
и)
- 2 =
г)
е)
]х + 2
- 1
]х + 2 - Jx - 1
= -1;
- 6 - (х - 6)3/39 - х
5/39 - * - 5/л: - 6
Иррациональные неравенства
Группа А
Решите неравенство (хш.70—хш.76).
хш.70. а) л/х + 3 > х + 1; б) д/(х + 2)(х- 5) < 8 - х;
в) д/Зх2+13х + 4 ^ х - 2; г) 3^-л:2+л: + 6 > -2(2х - 1);
д) J2x + 3 < 1 - Vx + 2.
425 Задачи и упражнения
Jx + 2
хш.71. а) ^ < 1;
б)
Зх- 1
2-х
в) (л/3 + х + х - з) (д/5 + 4х + х - 4) ^ 0;
г) Ух+ 2 + УЗ- х < 3;
д) л/l + х + л/l-x > 1; е) V* + 3 - л/7 - х > д/2х - 8;
J- х + 4х - 3
ч
ж)
2; з) д/2х +1 <
2 —
ч JS-2x- х2
и) ■*—
- х2
ч
к)
х + 10
— X — X2
+ 9
ill2 - х - х2
хш.72. а) д7-9х2 + 6х < Зх;
в) з/х2-х > -х^2;
ХШ.73. а)
в) х- 4 <
х
X2
б) (-9х2 + 6х)з < Зх;
г) (х2 - х)з > -х-2з.
3; б) л/х + 1 + Vx + 13 ^ 6;
(i+ у/тт^у
Группа В
ХШ.74. а
б) J2x-1 н- J3x- 2 < J4x- 3 + J5x - 4;
в) V*2"8x + 15 + V^2 +2x-15
хш.75. а) | 2 - Vx + 2 > х - 2;
б) л/х + л/л: + 7 + 2д/х2 + 7х < 35 - 2х;
(8 - х)д/8 - х 4- (5 4- х
(8 - яОд/б + х + (5 + х)д/8 - х 6
+ х 7#
6'
д) (35 - х)л/35 - л: + (л: -
- 9 > ^
-л; + Vx-9)3;
4
/1-х
2л:+ 9.
ХШ.76. а) х -—- > -1; б*) д/4л:2 + 6х + 2 - ^4x2 + 4х > 2х + 2.
426 Задачи и упражнения
Иррациональные уравнения и неравенства с параметрами
Группа А
Аналитический способ
хш.77. а) При каких значениях а и & множество решений неравенства
Jx- a > J2x- Ь есть полуинтервал [1; 5)?
б) Решите неравенство
х-2
а-1
> а.
в) Решите неравенство ^5х2 + а2 > -Зх.
Графический способ (плоскость (х; у))
хш.78. а) При каких значениях а уравнение у/х — 3 = а — \ х \ имеет
решение?
б) При каких значениях а уравнение л/б- х + у/х + 3 = ах
имеет решение?
в) При каких значениях а уравнение ах + VlO - 6х = 0 имеет
решение на отрезке [-1; 1]?
хш.79. а) При каких значениях а неравенство
4
у/х2 + 4ах + 4а2 + л/х - а
не имеет решений?
б) При каких значениях а неравенство
решения?
в) Для каждого значения а < 0 решите неравенство
2х + у/а2 - х2 > 0.
Графический способ (плоскость (х; а))
ХШ.80. а) Решите уравнение л/х — а = а.
б) Решите уравнение ^J2x- a = х.
- х2 > а — х имеет
J
в) Найдите число решений уравнения ^21 х | - х2 = а в
зависимости от параметра а.
г) При каких значениях а уравнение у]х и- 2а2 (х2 - (а - 1)х - а) = 0
имеет два различных корня?
ХП1.81. а) Решите неравенство д/4:х; + а > х.
б) Решите неравенство
- х2 > -(х- а)при а = 0 и убедитесь,
3
что множество его решений есть отрезок. При каких значени-
ях а множество решении неравенства есть отрезок длиной -?
5
427J Задачи и упражнения
в) При каких значениях а множество решений неравенства
Ху[х - ayfx ^ ах- х2 есть отрезок длиной меньше 1?
г) При каких значениях а множество решений неравенства
х + <у]х2 - 2ах > 1 содержит отрезок -; 1 ?
Применение свойств функции
хш.82. а) Решите уравнение у/а- х - у/а + х = х.
б) Решите уравнение Щх + 4х—а = у/а.
в) Найдите количество корней уравнения
в зависимости от параметра а.
г) Найдите количество корней уравнения ^2х + 8 - а = у/2х + 3
в зависимости от параметра а.
д) При а > 3 решите уравнение у\2а - Зу[х = yjx- 2.
е) Решите уравнение у/а-\-х - у/а- х = ^/2а^.
ж) Ре1ыите уравнение у[х — у/а — х = Va.
Разные методы
2 - 4* + 3 =
Х1П.83. а) При каких значениях а уравнение д/
имеет единственное решение?
б) Решите неравенство (л/х - a) (V#- 1 - 2а) > 0.
в) Регаите неравенство у[х—а ^ 2л: + 1.
г) Решите неравенство у/х + а < а - у[х.
д) При каких значениях а множество решений неравенства
^2ах — х2 ^ а — х содержит отрезок длиной 2 + V2?
е) При каких значениях а множество решений неравенства
д/а2 - л:2 > 2х есть отрезок длиной 4?
Системы иррациональных уравнений
Группа А
Решите систему (хш.84—хш.86)
с - 5 • yJ4- у = О,
-У2 = 9;
= х- 2,
= х + 1,
428, Глава XIII. Уравнения и неравенства
= 3;
jx2+ у2 -
[x3 + 2y3 = 118;
з)
Группа В
I х2 + 2х - у2 + 4у = 7.
ху + у2 = 2у - х;
г)
Системы иррациональных уравнений с параметрами
Группа В
хш.87. При каких значениях параметра а е R система уравнений
\у = у/х- а,
\x= jy-a
имеет единственное решение?
хш.88. При каких значениях параметра а е R система неравенств
\у «S у/х- а,
\x< yjy- a
имеет единственное решение?
хш.89. При каких значениях параметра а е R система уравнений
* имеет ровно два решения?
[а(х-1)= у + 1
429 Задачи и упражнения
Показательные уравнения
Группа А
Решите уравнение (хш.90, хш.95).
О
ХШ.90. а) л/2*~ = 8~з; б) -
в) 16-1 • л/б4*~ = 2*; г) 2^* = 16л/[ ±'
д) 4* • 5*-1 = 0,2 • 203~2*; е) 2*-3* + 1 = 81;
ж) 3*-52*-3 = 45; з) 2* • 3*~х • 52*+ 1 = 250;
и) 41*-Ч = 8; к) 4 • 2C0S* = л/8;
л) 3*-2-3*"2=7; м) 4 • 3*-х + 3* + 1 = 117.
хш.91. а) 9* - 4 • 3* = 45; б) 2* - 8 • 2г* = 7;
в) 4*-i-17 • 2*-3+1 = 0; г) 2 • 4* + 1 - 17 • 2* = 2г* - 10;
Д)
Х1П.92. а) дг • З*"1 + 3 • З^3"* = 3* + х •
б) jc2 • 4^~* + 42+* = 16 • 22^~~х + л:2 • 22*;
в) х2 ■ 6~* + 6^+2 = х2 • 6^* + б2-*;
г) 4*-2-6*= 9*+2;
д) 3 • 4* + 2 • 25* = 5 • 10*;
ж) 4~* - З"*"^ = 32 х - 2"2*-1;
з) 3-4 * + i-92-*= 6-41'*---91"*;
3 2
т_\ Qjc _|_ qjc + 1 _i_ Ojc + 2 _i_ Ojc + 3 Qjc _i_ Qjc + 1 j^
И1 ^j ~г ^ i ^ i ^j — о i о ~г
к) 9-4*+5-6* = 4-9*.
Группа В
ХШ.93. a) 2cos2*= 3-2cos2*-4;
в) (3- 2л/2)* + (3 + 2л/2)х = 34;
ХШ.94. а) 5*2-*+1-2-3*= 3*+1; б) 7*2 + *+1 - 4- 3*+1 = 3*+2;
в) 5* • 8 * = 500; г) 2* • 5 * = 8.
430; Задачи и упражнения
х_
хш.95. а) 2х - З2 = 1; б) 2 • 3* = 7 - х;
в) 12* + (Тб)2* = 13*; г) 2х + 3* + 4х = 9*;
д)
f-T= -
е) f-T= -2л;2+ 6*-9;
ж) 4*-2* + 1 + 5=4cos2-; з) 2* + 22~* = 4sin—;
2t 2
и)
-cosx= 1; к) 4~*2 • sinf -- 2х| = 1;
sin2 2? . „cos2^
л) 2х2 = V2-3*-32*; м) 4sin Т + 4COS Т = ^13 + 6х - Зх2 .
Показательные неравенства
Группа А
Решите неравенство (хш.96—хш.юо).
хш.96. а) \-\ >--; б) \-
в) л/32-2-4*2>83*; г) 125- \-
д) 25 • 0,042* > 0,2* О - *>; е) 3*~ 2 > -^
3
ж) 0,91^+11^ 0,92;
tf
х+5
и) 6^2"9 > 1; к) (lO*2-3*+2)5"* < 1;
Зд:2+2
л) 3-9 * -272*>0; м) -4 ^ З^2-2^"1 - 5 ^ 4;
<0; о) *-£
Х1П.97. a) 4* + 2JC+3> 20; б) —
5ж + 32*2-5ж+1-4>0; г) 9^ГГз+3<28-3^Гз
д) 52*~Т< (3/5)*2.52-2jc + 24; е) 9^ + 32~* < 2- 271"*;
ж) 0,4* - 2,5«i > 1>б. з) 491J;3;i"13^3115 ^ 5-
431| Глава XIII. Уравнения и неравенства
хш.98. а) 5х - Зх +! > 2 • (5*-1 - Зх~2);
б) Зх2 + 2 -5х2~1> 5х2 + 1 + Зх2~Н
в) 2х + 3-х3- 2х <: 16-2*3;
д) 10 • 5х + 2Ж^2 + 5 • 10*;
Группа В
ХШ.99. а)
г) х4 + Зх + 4 > х4 ■ 3х + 81;
е) 24 • 3х + 2Х + 1 > 8 + 6* + 1.
+ 24 - 2 > 3*+ *;
б)
в)
г)
д)
е) 4(2-
6*-6
хш.ЮО. а)
+ 1; б)
Показательные уравнения и неравенства с параметрами
Группа А
хш.101. При каких значениях параметра а е R уравнение 2 • 4х+ 1 +
+ а2 = 2 - 5 • 2х имеет решение?
ХШ. 102. При каких значениях параметра а е R уравнение
32х
— — = а имеет ровно одно решение?
ХШ.103. Решите неравенство а2 - 16* + 1 - 15а • 4х < 0.
ХШ. 104. При каких значениях параметра а е R неравенство 16 • 9* +
+ 91 ~ х - 2 • (4 • 3* + З1" *) ^ а выполнено для всех х ^ 0?
Логарифмические уравнения
Группа А
Решите уравнение (хш.105—Х1И.Ю8).
хш.105. a) V
б)
в) Iog4(x + 2) - Iog4(x - 2) = 2 - Iog48;
г) 2 log2 x + log^ x + log i x = 9;
д) lg(x2 - 1) = lg(x - 1)2 + lg|2 - x|.
ХШ.Ю6. a) Iog2(26 - 2*) = x; 6) 2x(l - Ig5) = lg(4* + 2x - 6);
в) Ig2 + lg(4-JC~1 + 9)= 1 + lg^-*"1 + 1);
r)
432] Задачи и упражнения
хш.107. а) 2 log2 (sin х) = 1°&4 (4 sin2 *);
б) logcos^(2cosx + sin я) = 1;
в) 1 + log/^ cos x = log2 (3—3 sin x);
г) 1°§5 (V2 sin xj = log25 (2 + cos x).
ХШ.108. a) log3log8log2(x + 9) = Iog32 - 1;
б) Iog8(21og3(l + Iog2(l + 31og2x))) = |;
в) log2 (log3 x) + log2 (log9 x) = 1;
r) log5 x2 (2x2 - 8x - 2) = 1 + Iog5_ 2 2;
д) log^ + 2log2logJC + 3(llx2 + 46x + 48) = 0.
ХШ.Ю9. Решите уравнение, используя замену:
a) log2 x + log2 x2 = -1; б) log4 (9x2) + log2 (Зх) = 2;
2
в) log4 x2 - 21og2 (-*) = -1; г) log2 (4x) + log2 (^-] = 8;
2 2 V " У
i ^ ' 1Л
е)
ж) 3 • Jlog^x - log2 (8x) + 1 = 0;
= -т=; и) 21og9x2- 2^^3 = 3;
к) 3 + log^+19 = log /д (х + 1); л)
м) log^2 (я2 + 4х + 4) = log_x (x + 2).
хш.но. Решите уравнение, используя переход к новому основанию
и подходящие замены:
a) Iog3^x3 = log9jcx5; б)
лЛ fi 1псг^ v • 1псг^ v — 1по*Л v р^ 1псг TQv^^ • 1по*2 у— 4*
ж) log4jc 2 • log£ 2 = log^ 2;
4 16
з) 1 + log,, ^- = (lg 4 - 1) • log,, 10.
Решите уравнение (xill.lll, xiii.112).
Xill.lll. a) xloe^3x) = 9; 6) xl^x = 100x;
в) x3+lg^ = 400; r) x^3^-51^^= 0,0001;
31ел:_^_
д) х 1е* = VlO; e)
433. Задачи и упражнения
хш.112. а) (2х- 1)*2 + ** = (2х- 1)*+5; б) х1^3 + З1^ = 54;
в) 4*^* = (х2 + З)1^2; г) 9*Я* = (х2 -
д) (sin х + cos х)~4х = (sin х + cos я)* + 10;
е) (sin x)shl х ~ г = (sin x)cos x.
ХШЛ13. Решите уравнение, используя свойства функций:
а) х = 6 + logj^x; б)
в) ^х2 - х - 2 = log2 (1 - х4); г) xlog2 (х + 1) = logi x + 7;
д) log2 (4х - х2 - 2) = 2l*-2l.
Группа В
Решите уравнение (хш.114, хш.115).
хш.114. a) logx + х(2х3 + 2л:2 - Зх + 1) = 3;
б) log2 ^^ = 3 + log16 х4 - log4 (x - З)2.
хш.115. a) Vlog2(2х2) ■ log4(16х) = log4(х3);
б) log2х• A/logJC8.1ogJC(2x)-2 + 1 = 0;
в) ^^ + 1(х3-9х + 8)- ^^_!(х+ 1) = 3;
г) log^tx + 12)2 + log^ 12x4 = 6;
д) Iog3jc + 7(4x2 + 12х + 9) + log2jc + 3(6*2 + 23х + 21) = 4;
е)
ж)
ХШ.116. Решите уравнение, используя свойства функций:
а) (л/х) х + хlog2 х = 24; б) х2 + (х - 3)log2л: = 4х - 3;
в) log| х+(х- 1) log2 л: = 6 - 2х.
хш. 117. Решите уравнение:
б) 3* 4 = 2^ 2 ;
г)
e) lg3
15—Пратусевич, 11 кл.
434 Глава XIII. Уравнения и неравенства
Логарифмические неравенства
Группа А
Решите неравенство (хш.118—ХШ.130).
хш.118. a) Iog3(4jc - л:2) > 1; б) Iog7(;c2 + 6jc) ^ 1;
в) logj^ (х2 - Зх) > 0; г) logi^ (4л: + х2) > -1;
3 5
е) lg(* - З)2 > \g{Ax - х2 - 3).
хш. 119. a) log2^ + Iog2(^ + 2)> 2;
б) log3 (л:2 - 1) + logi (х + 3) ^ -1;
в) Iog2(* + 1) ^ Iog43(2jc2 + Зх);
ч , х2 - 2х . о
г> bg2 .. о ^ 3.
хш.120. a) logglogi х > -1;
в) logj log
х -
д) lg(^-l)2<
ХШ.121. a) Iog;c2>-1;
в) log,3 < logi fij;
д) log1_JC5>logJC+1f|J;
ж) log2l-l<61og8jc2;
и) log.,.3 • Iog3;(r9> 1;
б)
- I)2; e) lg(l -
б)
г)
е)
з)
-2;
- xf
xf.
<-Iog2_
к) bg3_2^3>log2_;c3.
2-х
ХШ.122. a) log^ 5 + log25 л: ^ -;
б) log,9-log2(3;c)^-2;
в) A/log3^-21og9j|>|; г) log2f|j>31ogiee4;
д) log^x + log^l^-l >0;
хш.123. а)
в)
>2;
е) Iog4;c(2x).log24^1og,
l-log3(2.3*+3)
1-х
^ 2;
6)
r)
X
x-1
log3(9-3-)-3
1.
435 Задачи и упражнения
хш.124. a) log6jcx • log3jcx < 0;
б) log^x • log5jcx > 0;
в) log^lOx + 3) • Iog10jc(3x + 10) > 0;
г) log2jc (6* + 7) • log5jc f 3x + |] < 0.
ХШ.125. а) Iog2_x(3 + x) ^ 1;
в) log^ + 2(x2- 5)>0;
+ х)> 1;
б)
д) log,, (x +1) < logxZ (x2 + 5); e) log*(x + 2) + 2 log* + 2 * > 3;
ж)
>0;
з) log,
- 5
ХШ.126. а) х*1*х > 10х; б) л1х
-r} л/г1о£2>^ > p. r\ rlg;
д) х~3х ~ 8 > х7; е) (4л
ХШ.127. a) logg* + * > 4; б) л: •
Группа В , .
ХШ.128. a) loglog я logi л: > 0;
2 V 7 У
в) Iog|^ + 6|2-log2(x2-x-2)^l; г) |log2(x + 3)-2|^log4x;
д) 2 log 2 л: ^ log2 _ х (2 + х).
1ое1(16л:4-л:2 + 1) ч
хш.129. а) (3* + s-xy*]gx-\g(2x* + 3x) < i; б) х- 3 9 > -;
в) (logjpS)10^»^"^ > 1;
18; в) Iog7(3* + 4*) < х.
6) log, * I logi x I ^ 0;
J
XIII. 130. а) -;
4
24
6) fi
r)(logx+12)log2(f)<l.
^ X* 2*\
Логарифмические уравнения и неравенства с параметрами
Группа А
хш.131. При каких а е R уравнение log 2 Ах + а) = 1 не имеет ренгений?
хш. 132. При каких а е R уравнение
log^^g (2х2 - Зх + 2) = 2logajc_ 6 (х2 + 2* - 4)
имеет единственное решение?
15*
436, Глава XIII. Уравнения и неравенства
хш.133. При каких а е R неравенство Iog2*(3# + а) < 1 не имеет
решений?
хш.134. При каких а е R неравенство log2-*(3* + а) < 1 не имеет
решений?
хш. 135. При каких а е R для всех х е 2; - выполняется неравенство
х е 2; -
fa2- 4 ^
ХШ.136. Решите уравнение log^a • logfl2 = 1.
хш.137. Решите неравенство:
а) log,, (2Va + х) ^ |; б) log2jc + а(х + 2) > 1;
в) Iogx + 2(x2-2x + a)>2; г) loga_x + 1(a2 - 2ах) ^ 2;
д) log^^x^ 1.
Системы логарифмических и показательных уравнений и неравенств
Группа А
Решите систему уравнений (хш.138—хш.142).
хш.138. а) \у ' б) \ .
[х + у = 6; [б^-^512 = 200;
Ixy =
""' {ху = 256,
1024*= {%,
t2x + 2» = -l,
[7-2у-20х= 146;
= 28,
fjc + y = 6, ^ч \х2 +у2 = 68,
хш.139. а) ^. * . _ б) 1, 1 о
[logA: + logi/= 3; [Iog2^-log2i/= 2;
Г4^-у2 = 2>
[log2 (2x + y)- log (2л у) 1; '
log2 (2л - у) = 1; |ху = 27;
15, |^
c=3i' + 1;
[y-3lgx2 = l.
Группа В
XIII. 140. a]
437] Задачи и упражнения
ХП1.141. a) f
б) 11/ * - X ,
[log4y\ogy(y-3x)
в)
[2log5\xy\-loglxyi(x
[x-y =
(log,,,2 (xy - x - 2y + 2) + | log,,_ а(*2 - 4x + 4) = 3,
Группа С
{;°f|lOffl = 'Og|loe-!'1- в)
Тригонометрические уравнения и неравенства
Группа А
Решите уравнение (хш.143—хш.150).
ХШ.143. a) cos 2х + cos л: = 0; б) tgx + 3ctgx = 4;
в) sin — - cos — = sin х; г) 1 - cos (тг - х) + sin —-— = 0;
д) sin3* • cos3x + sin3x • cos3л: = -;
о
е) 2 sin2 2x - 11 sin2 x + 3 cos2 x = 1.
хш.144. a) cos 4х + 2 cos2 х = 0; б) sinx + cosx = 1 + sin2x;
в) cos x - cos 2x = sin Зх; г) cos 2x - cos 8x + cos 6x = 1;
д) sin2 x + sin2 2x = sin2 3x;
е) sinx + sin2x + sin3x + sin4x = 0;
ж) sin 5x + sin x + 2 sin2 л: = 1.
xin.145. a) sin x= sin —; 6) cos3x=cos—;
У 1U
в) cos 5x - sin — = 0; r) tg x = tg 2x;
438J Глава XIII. Уравнения и неравенства
. 1- tgx , о ч cos х + sin x
Д) -—f— = ctg2x; e) : = ctgx;
1 + tgx cos jc — sin x
ж) 2 sin2 ян- л/3 sin2x- 1 = 2cosx.
ХШ.146. a) sin6* + sin4 * • cos2* = sin3 * • cos3* + sinx • cos5*;
б) sin x - cos x - 4 cos2 x • sin x = 4 sin3 x;
в) sin4x - cos4x = sin2x; r)
cos x
Х1П.147. a) 2sinx • sin2x + cos3x = 0;
б) cos 7x • cos 3x = cos 4x;
в) cos x • cos 3x = cos 5x • cos 7x;
ч cos2 jc - sin2 2jc f , л "\ f л
r) = sin \ x + — • sin \x - —
4cos2jc ( 6) у б
sin \ x + sin \x
4cos2jc (^ 6) у б
ХШ.148. a) sin x + sin 2x + sin 3x = cos x + cos 2x + cos 3x;
б) sin2x • sinx + cos2x = sin5x • sin4x + cos24x.
ХШ.149. a) sinx - V3cosx = л/3; б) л/3 sin л: - cos л: = 2cos2x;
в) 3 sinx + 4cosjc = 5; r) 3 sinx + 4 cos x = 5 sin 5x.
ХШ.150. a) |sinx + cosjc| = 1 + sin2x;
б) Icosx - sinx| = 1 + 2sin2x;
в) sin 2x + л/3 (sin x - cos x) = 0.
Решите неравенства (хш.151, ХШ.152).
л/3 1
xni.151. a) sin(37rx) < ^—; 6) costtx < -.
ХШ.152. a) tgx^ 1; 6) ctgx^ -=;
V3
в) tgf|-xl<-V3; r)
д) 2tgx - ctgx < 1; e) tg2x + tgx ^ 0.
Xiii. 153. Постройте график неравенства:
a) sin(x - у) > 0; 6) cos л: • cosy > 0;
ч sin x л ч cos jc л
в) < 0; г) > 0;
sin у cos у
д) arcsin(x + у) < 0; e) arcsin (од) > 0.
Решите неравенство (хш.154—хш.156).
sin jc cos jc p cos 2x sin jc + —
xiii.154. a) \ ^i ^ 0; 6) A- LZ ^ 0;
sin jc (v2 - 2cos jc )
439 Задачи и упражнения
у 2 у у
в) sin — sin2x<0; г) cos — sin— > 0;
2 3 2
v 2 sin x - cos x . ~ ч cos x - sin x . ~
д) ^ 0; e) ^ 0
cos x + sin x 2cos x + sin x
v sin x • cos Зх ~ v cosx-sin 3x
2cos2 x - cosx - 1 1 - sinx - 2sin2 x
cos x (ctg л; + 1)
(sin x + 1) cos x (cos x - 1) sin x
\ 2) ^2
ХШ.155. a) 2sin2x + sinx > 0; 6) 2cos2x + cosx < 0;
в) cos4x + 2cos2x ^ 0; r) sinx + cosx ^ 1 + sin2x;
д) cos x - cos 2x > sin 3x; e) cos 2x - cos 8x + cos 6x ^ 1.
мши. a) 2cosx0- > 0; 6)
cos 2x sin x
os|^s
2 sin x — cos x
в) cos— > sinx; r) cos— ^ sin — ;
2 2 3
д) sin5x > sinx; e)
sin x - cos x - 1
ж) 2 cos 2x + sin 2x >
Решите уравнение (ХШ.157—ХШ.159).
ч cosx л -v 14- sin2x л ч ^wo^n, л
ХШ.157. a) —- = 0; 6) : = 0; в) = 0;
1 4- cos 2x cos x 4- sin x 1 4- tg x
r) = 0; д) tg3x = tgx; e)
cos x — sm x
sin I x —— | 4- cos
ж) — cos x - sin x • tg — =
cos2 x 2 cos x
2 - sin x - cos x
jc
13 J.
cos2 x 1 - sin x
3)
а) ^iz± = q. 6^ ^«^ = o; B) °"x ^ = 0; r) wo" = 0.
cos3x cos3x sin3x sin4x
Группа В
хш.159. а) —— + = — ;
cos x cos x • cos 2x sin x cos 2x • cos 3x
б) cosx(tgx 4- tg3x) = 4sin3x • sin4x;
в) cos Зх • tg 5x = sin 7x; r) tgx - ctg3x + ctg4x = 0;
tg 5x - tg 3x = tg 2x; e^) tg 5x + tg 3x = tg 8x.
Глава XIII. Уравнения и неравенства
Решите уравнение, используя свойства тригонометрических функций
(ХШ.160, ХШ.161).
ХШ. 160. a) cos х + cos 5x = 2; б) sin 7x + cos 2x = -2;
в) sinx • sin5x = 1; г) cos2x • sin5x = 1.
ХШ.161. a) sin (cos x) = cos (sinx); 6) tg (4 sin x) = л/3;
в) ctg(3cosx) = 1.
Решите уравнение (хш.162, хш.163).
хш. 162. a) sinx + cos4x • cosx = -л/2;
б) cos x - л/з cos 3x • sin x = 2;
в) sin2x - sinx • sin3x = —;
4
r) cos2x + 2cosx • cos4x = -1.
xin.163. a) | sin3x| = sin x - — на отрезке 0; — ;
V 4У L 2J
б) cos x - 2 sin 2x - cos 3x = 11 - 2 sin x - cos 2x |;
в) | sin x 4- 2 sin 2x + sin 3x | = 1 + 2 cos x + cos 2x.
xin.164. Решите неравенство:
a) (tg22x + 4)|cos2x|^4; 6) (ctg22x + 4)|sin2x| ^ 4.
Решите уравнение (хш.165, хш.166).
ХШ.165. a) (1 + 2 sin x) cos x + — | = 0;
в) Vsinx H-cosx = 0;
д) Vcosx = л/2 sin—;
2cosx).sin x + — =
6)
r) Vcosx + sinx = 0;
e) ^-cosx = л/2 cos—;
ж) J— + sinx = J sin Зх; з) J- - cos x = J- + cos 3x;
и) yj-cosx = ^J2sin2 x - 1; к) д/l - cos 2x = sin2x;
л) Vsinx H-cosx = cos2x;
m) Vsinx + cos x = sinx - cos x.
хш.166. a) Vl + sinx - Vl + cosx = 1;
6)
sin2x = л/2со8 3х;
в) д/х cos 2x 4- sin x =
4- xsinx;
г) д/х2 sinx + cosx = A/x2cosx+ sinx.
ХШ.167. Решите неравенство:
a)
sinx ^ Vl -hcosx; 6) Vl - sinx > Vcosx;
в) cos x > д/5соз2х- 1; г) sin x ^ д/4со82х- 1;
д) sinx < V2cosx-hl; e) cos x ^ V2sinx + 1.
441, Задачи и упражнения
Решите уравнение (хш.168, хш.169).
ХШ.168. a) log6jc х2 (- cos х - cos Зх) = log6jc x2 (- cos 2x);
Ti П
б) log2^ ^2 (sin x + cos x) = log2x x2 (1 + sin 2x);
в) Iog2(3sinx - cosx) + log2cosx = 0;
r) 31og|(sinx) + Iog2(l - cos2x) = 2;
д)
хш.169. a) cos3x = 1 - tgx • tg2x;
б) sin3x = 1 - tgx • ctg4x;
в) cos x 4- sin \2x - — \ = 3 - л/з sinx;
v 6;
r) cos x - sin \2x + — = 3 + л/3 sin x;
д) -= sin2 x + ^- I + sin 3jc = cos 3x - V2;
е) - 1 - cos2 2x + — + -= sin6x = — cos6x- 1.
Уравнения и неравенства с обратными тригонометрическими функциями
Группа А
Решите уравнение (хш.170, хш.171).
хш.170. а) 2 arccos х + arcsin х = ——; б) arctg4x - arcctg4x = —;
6 3
в) arcsin2 л: + arccos2 л: =
;
г) arccos2 * + 2 arcsin л: • arccos jc = ;
36
д) arcsin 6x + arcsin бл/Зх = -—;
е) arcsin (Зх - 1) + 2arctg4x = arccos (1 - Зх);
ж) arcsin л: + arccos (x - 1) = тг; з) arcsin л: = 2arctgx;
и) arcsinx = arcctgx;
к) arctg(x + 1) - arctg(x - 1) = arctg2;
л) arcsin x + arcsin Гхл/з) = —;
v X Xy[3
м) arcsin— + arcsin—— = arcsinx;
h) 2arccos -■^ I = arccos (x + 3); o) 2arcsinx = arcsin yxy[2j;
442| Глава XIII. Уравнения и неравенства
п) 2 arccos х = arcsin (2л: Vl - x2j;
р) 2 arccos л: = arccos (2л:2 - 1);
2 3 х
с) arccosx = —arcsin2х; т) arccosx— —arccos—;
3 2 2
у) cos (4 arccos x) = —; ф) sin (3 arccos x) = -;
х*) cos (2 arccos x) = arcsin (cos x);
(2 Л . (2 . Л
arccos — arccos x = arcsin — arcsin x .
[n ) [n )
ХШ.171. a) 2 arcsin x • arccos x = 3 arcsin —j= • arccos -7=;
б) arcsin § = ^
. 1 ( хЛ
в) arcsin (1 + I sin x \) = arccos 1 + cos — .
ХШ.172. Решите неравенство:
a) arcsin л: < —; 6) arccos x < —;
3 4
в) arctgx>-—; r) arcctgx>-—;
6 6
ч 2 . n ч 2x ^ n
д) arccos ^ —; e) arccos— ^ —;
1-jc2 jc2+12
ж) arcsin x < arcsin (1 - x); 3) arccos x > arccos (x2);
и) arcsin x > arccos x; к) arctgx > arcctgx;
л) 2 arcsin x > arctg x; м) 2 arcsin x > arccos 3x.
Тригонометрические уравнения и неравенства с параметрами
Группа А
хш.173. При каких значениях параметра а уравнения sin 2x (sin 2х - 1) = О
и (а + 3) sin2 2# - sin 2х • cos 4х - (а + 4) sin 2x = 0 равносильны?
ХШ.174. При каких значениях параметра а уравнения sin x = 2 sin2 x
и sin3x = (a+ l)sinx - 2 (а - l)sin2x равносильны?
хш.175. При каких значениях параметра а уравнения 4 cos2 x ~ cos Зх =
= a cos х - (а - 4) (1 + cos 2х) и 2 cos jc • cos 2x = 1 + cos 2x + cos Зх
равносильны?
хш. 176. При каких значениях параметра а множества решений
уравнений 4 cos2 х = а2 - 6 и 1- cos 2x = - совпадают?
6
ХШ. 177. При каких значениях параметра а число п является периодом
функции f(x) = ?
а - cos х
443j Задачи и упражнения
ХШ. 178. При каких значениях параметра а число — является периодом
функции f(x) = ™s2x ?
За 4- sin 2х
ХШ. 179. Найдите все пары чисел (а, &), при которых равенство
sin (ах + Ъ) = а sin л: + Ь выполнено при всех вещественных х.
ХШ. 180. Найдите все пары чисел (а, &), при которых равенство
a (cos л: - 1) + Ь2 = cos (ах + Ь2) - 1 выполнено при всех
вещественных х.
ХШ.181. Для всех значений параметра а решите уравнение
a (sin2 х - 5 cos2 x) = cos х д/За2 + 5a2tg2x.
ХШ.182. Найдите количество корней уравнения cos x • ctg x - sin x =
= acos2x на отрезке [0; тс].
_ \(tgx-<j3)(x-a)=0,
ХШ. 183. При каких значениях параметра а система < v y
[К х<2
имеет единственное решение?
ХШ.184. При каких значениях параметра а уравнение sin(2-a)x +
+ sin (2 + а)х = 2 имеет решение на отрезке [0; тс]?
ХШ. 185. Решите уравнение
x + a = 2acosf--x| • sinf т
V4 ) V4
ХШ.186. Решите уравнение sin2x(sinx + cos я) = a(sin3x + cos3x).
ХШ.187. Решите уравнение tg2x + 2atgx • cos4x + a2 = 0.
XT „ „ 3cos x + 1
ХШ.188. Найдите количество корней уравнения — = а на отрез-
cos х — 1
ХШ.189. Найдите количество корней уравнения 2cos2jc — cosx — а = О
на отрезке -—; — .
хш.190. Найдите количество решений уравнения 2sin2x - sinx + а = О
Гл 5тс1
на отрезке О; —
ХШ.191. Найдите количество решений уравнения tgx- l = a(sinx — cosx)
в зависимости от положительного параметра а > 0 на отрезке
[0; 2тс].
ХШ. 192. При каких значениях параметра а уравнение cos (д/a2 - х2 j = 1
имеет ровно восемь решений?
444 Глава XIII. Уравнения и неравенства
хш.193. При каких значениях параметра а уравнение ^а + уа + sin x =
= sin л: имеет решение?
хш. 194. При каких значениях параметра а > О неравенство
1
J а выполняется для всех х е \ -—; — |?
хш. 195. При каких значениях параметра а неравенство II sin х- -
ГЛ 2я]о
выполняется для всех х е О; — /
ХШ.196. Для всех значений параметра а решите уравнение sinx +
+ 2 cos ах = 3.
ХШ.197. При каких значениях параметра а неравенство 5а- 5 + sin2x +
+ а(3 — cosx)3 > 0 выполняется для всех х е R?
хш. 198. а) Решите уравнение cosx = д/со8 4л:- cosxh- 1.
б) Выясните, при каких значениях параметра а уравнение
cosx = д/cos 4х - cos x + а имеет решение.
хш.199. а) Решите уравнение Vsinх + cos х - 1 = Jsin2x- -.
б) Выясните, при каких значениях параметра а уравнение
Vsin х + cos х- а - Jsin2x имеет решение.
ХШ.200. При каких значениях параметра а уравнение
у/2 (а - sin х) (а - cos х) = - sin х - cos х + 1
имеет решение?
хш.201. Решите уравнение Va sin x + cos x = Va cos x + sin x для всех
значений параметра a e JR.
Системы тригонометрических уравнений и неравенств
Группа А
Решите систему уравнений (хш.202—хш.205).
{sinx н- sin у = 1,
sin* _ б)
|sin3x- siny + 2sinx = О,
- бху + 5х2 = 0;
f 7sinjc + 5cos(4i/- 2) = 6,
B) \2y = x +1: Г)
445] Задачи и упражнения
д)
ж)
и)
к)
е)
5л
Q
sin2 x + sin2 у = -;
[ д/cos 2л: • cos у = О,
sin2 ян- sin2 i/ = -;
2
JVsinx-cosy = 0,
з)
[2sin2:x;-cos2y-2= 0; | 2 sin2 x - cos 2y-- U 0;
f sin 2x + sin 2y = 0,
[cos (2x + y) + cos i/ = 0;
Г tg 7ГХ + tg ny = 1 - tg nx • tg ny,
[sin л: • cosy = sin у • cosx.
sin л: • siny = —,
XIIL203. а) < 4 б)
[cosx • cosy = —;
J sinx- siny = --,
= -tgy;
1
ХШ.204. a)
sinx-
cosy
1
cosz/
= 2,
= 2;
л/3
sin л: • cosy = —,
л/3
cosx • siny = —;
[cos(x + y) = 2cos(x - y),
Icosjc • cosy = -.
J
tgy = 0,
sin2x+tg2i/ = 1;
в)
= 3 + 12 sin2*,
= 7;
[ sin2 (x + y) + sin (я + y) = 2, [cos x + cos у = 1,
г) j 2cos(x-y)- 1 _ 1 д)
Группа В
XIII.205. a)
в)
. o л/3
sin х- sin2y = —-,
I cos x + cos 2y = —;
I ^
[2 sin л: = -sin у,
= V3cosy;
r)
= smy,
[cosx = sin2y;
fV2 sinx = siny,
л/2 cosx = л/б cosy;
446 Глава XIII. Уравнения и неравенства
Jtg*+sin2y=sin2*, J
Д [2 sin у -cos (х- у) = sinx; e ] cos x • cosy = ^;
f4tg3y = 3tg2x, fctgx+ sin2y = sin2x,
[2 sin x • cos(x — y) = sin у; [2 sin у • sin(x + y) = cosx;
f sin x • cos (x + y) + sin (x + y) = 3 cos (x + y),
ч f sin2 (x + y)+ sin (x + y)= cos2 (x +
[l + cos (я - y) = 2 sin2 (2x + y);
+ cos (x +
JcosxH- 3sinx = 2cosi/, J2cos(2x + y) = cosy,
[cosy 4- 3siny = 2cosx; [2cos(x + 2y) = cosx;
н)
sin л: = sin2z/,
= sin y,
о)
. sin(x + y) = 0,
Х1П.206. При каких значениях параметра а е R система ■
имеет не меньше десяти решений?
{и
ИЛА
I
Повторение
Материал этой главы состоит из задач, решение которых призвано
напомнить, систематизировать и обобщить знания, приобретённые
в ходе изучения курса.
Сюжетные задания взяты из экзаменов Санкт-Петербургского
математического общества (позднее — профильно-элитарный экзамен
в Санкт-Петербурге), составлявшихся под руководством
профессора СПбГУ О. А. Иванова.
Задачи и упражнения
Сюжетные задачи
XIV.1. Дана функция у = 8х - 3 • 2х.
а) Решите уравнение у = -2.
б) Найдите наименьшее значение функции у.
в) Решите неравенство у ^ 4X+*.
г) Сколько на графике функции у пар точек, симметричных
друг другу относительно начала координат?
XIV.2. Дана функция у = 27х - 4 - 3х+1.
а) Решите уравнение у = -9.
б) Найдите наименьшее значение функции у.
в) Решите неравенство у ^ 0.
г) Сколько на графике функции у пар точек, симметричных
друг другу относительно начала координат?
XIV.3. Дана функция у = cos2x + cosx - 4 cos2 —.
а) Выразите у как функцию от cos я.
б) Решите уравнение у = -3.
в) Докажите, что при всех х е R выполнено неравенство у ^ 0.
г) Сколько корней в зависимости от а имеет уравнение у = а на
отрезке [0; тг]?
xiv.4. Дана функция у = 4sin2x + cos4x.
а) Выразите у как функцию от cos2x.
б) Решите уравнение у = 1.
в) Найдите область значений функции у.
448! Глава XIV. Повторение
г) Сколько корней в зависимости от а имеет уравнение г/ = ана
отрезке 0; — ?
xiv.5. Дана функция у = х2 и точка Б(3; 5).
а) Найдите координаты точек касания с графиком данной
функции касательных, проходящих через точку В.
б) Пусть А — точка касания с меньшей абсциссой, а С — точка
касания с абсциссой х = 3. Найти площадь S треугольника ABC.
в) Обозначим через s площадь криволинейного треугольника,
ограниченного отрезками ВС, АВ и дугой АС графика данной
ос
функции. Покажите, что s = —-.
о
г) Сформулируйте и докажите аналогичное утверждение для
произвольной точки В под графика данной функции.
xiv.6. Дана функция f(x) = log| x - 31og| x.
а) Решите неравенство f(x) ^ 0.
б) Решите уравнение f(x) = -4.
в) Выясните, при каких а неравенство f(x) < alog2x
выполняется при х е [2; 4д/2].
г) Выясните, сколько корней в зависимости от а имеет
уравнение f(x) = a.
xiv.7. Дана функция f(x) = log| x - 5 log| x + 8 log3 x.
а) Решите неравенство f(x) < 0.
б) Решите уравнение f(x) = 4.
в) Выясните, при каких а неравенство f(x) > alog3x
выполняется при х g [27; +оо).
г) Выясните, сколько корней в зависимости от а имеет
уравнение f(x) = a.
xiv.8. Дана функция f(x) = sinx • sin3x.
а) Решите уравнение f(x) = 0,5.
б) Найдите наименьшее положительное решение системы
Г/(*)=о,
\cos5x = 1.
в) Найдите область значений функции /.
г) Пусть g(t) — наименьшее значение функции / на отрезке
t; t + — . Найдите наибольшее значение функции g на JR.
xiv.9. Дана функция f(x) = cosx • cos3x.
а) Решите уравнение f(x) = -0,5.
б) Найдите наименьшее положительное решение системы
[/<*)= 0,
I sin 5x = 1.
449 Задачи и упражнения
в) Найдите область значений функции /.
г) Пусть g(t) - наибольшее значение функции / на отрезке
t + — . Найдите наименьшее значение функции g на R.
XIV.10. Дана функция f(x)=-Jx. Точки пересечения прямой х = т
с графиком функции / и осью абсцисс обозначим
соответственно через А(т) и В(т), касательную к графику / в точке А(т)
обозначим 1(т).
а) Докажите, что площадь фигуры, ограниченной графиком /,
* - 2mf(m)
осью абсцисс и прямой х = т, равна -^-^-.
3
б) Пусть С — точка пересечения прямой 1(т) с осью абсцисс.
Найдите отношение площадей криволинейного треугольника
АОС и прямолинейного ABC (О — точка (0; 0)).
в) Пусть М и N — точки графика функции /, такие, что
MN || 1(т). Докажите, что площадь фигуры, ограниченной
прямой MN, осью абсцисс и перпендикулярами к ней из точек М
и N, не превосходит 32.
г) Пусть g — непрерывная неотрицательная функция,
определённая на [0; +оо), такая, что g(4) = 2, и при любом т> 0
площадь фигуры, ограниченной графиком /, осями координат
2mg(m) — , ч г-
и прямой х = т, равна 1-z. Докажите, что g(x) = yjx.
3
xiv.ll. Последовательность {хп} задана рекуррентно:
хг = а, хп + 1=х2п -хп-3.
а) Докажите, что при целых а хп — нечётное число при п ^ 2.
б) Выясните, при каких а последовательность {хп} неограни-
чена.
в) Выясните, при каких а последовательность {хп} есть
геометрическая прогрессия.
г) Пусть а = 4. Докажите, что последовательность {хп} не имеет
предела.
XIV.12. Дана функция f(x) = log2 х • log0>5 I -±- j • log4 f ^ 1.
а) Решите неравенство f(x) ^ 0.
б) PeniHTe уравнение f(x)= f — .
\x J
в) При каких а уравнение f(x) = а имеет ровно два различных
вещественных корня?
г) Пусть Ъ Ф 1, Ь > 0, п(Ь) — число различных корней
уравнения f(x) = f{bx). Постройте график функции п(Ь).
450| Глава XIV. Повторение
xiv.13. Дана функция f(x) = lg I — • lg (l05x) • lg -^— .
\x) V10 7
а) Решите неравенство f(x) ^ 0.
б) Решите уравнение f(x)= f\ — .
в) При каких значениях параметра а уравнение f(x) = а имеет
ровно два различных корня?
г) Пусть Ь Ф 1, Ь > 0, п{Ь) — число различных корней
уравнения f(x) = f(bx). Постройте график функции п.
XIV.14. Даны функции f(x) = sinx, g(x) = cos2x.
а) Вычислите площадь фигуры, ограниченной графиками дан-
7к
ных функции и прямыми х = тг, х = —.
6
б) Пусть А (/тг), В (т) — точки пересечения прямой х = т с
графиками fug. При каких значениях т длина отрезка с
концами в этих точках равна 1?
в) Существует ли отрезок, концы которого лежат на графике
функции /, а середина совпадает с точкой М
г) Изобразите на координатной плоскости множество точек,
являющихся серединами отрезков, концы которых лежат на
графике функции /.
XIV.15. Даны функции f(x) = cosx, g(x) = cos2x.
а) Вычислите площадь фигуры, ограниченной графиками
данных функций и прямыми х = —, х = —.
3 2
б) Пусть А(т), В(т) — точки пересечения прямой х = т с
графиками fug. При каких значениях т длина отрезка с
концами в этих точках равна 1?
в) Существует ли отрезок, концы которого лежат на графике
функции /, а середина совпадает с точкой М\ —; - ?
V 6 4)
г) Изобразите на координатной плоскости множество точек,
являющихся серединами отрезков, концы которых лежат на
графике функции /\
xiv.16. Дана функция loga + 2x(x2 - 1).
а) При а = 0 решите уравнение f(x) = 1.
б) При а = -1 решите неравенство f(x) ^ -1.
в) Изобразите на плоскости множество таких пар (х; а), что
f(x) = 1. При каких а это уравнение имеет решения?
г) Найдите все такие положительные а, при которых
уравнение f(x) = п имеет решение для всех натуральных п.
4511 Задачи и упражнения
XIV.17. Дана функция a + 2^ )
а) При а = -2 решите уравнение f(x) = 1.
б) При а = -3 решите неравенство /(я) ^ -1.
в) Изобразите на плоскости множество таких пар (х; а), что
f(x) = 1. При каких а это уравнение имеет решения?
г) Найдите все такие а > -2, при которых уравнение f(x) = п
имеет решение для всех натуральных п.
XIV. 18. Дана функция f(x) = sin* + cos2x, х е 0; — .
а) Решите уравнение f(x) = 0,5.
б) Найдите длину наибольп1его промежутка монотонности
функции /.
в) Сколько решений в зависимости от а имеет уравнение
f(x) = a?
г) Рассмотрите тело, ограниченное поверхностью, полученной
при вращении графика данной функции относительно
лежащей в плоскости Оху прямой у = т, и плоскостями х = 0,
* = 1,5тг. При каком /тг объём этого тела является наибольшим?
xiv.19. Дана функция f(x) = cosx- х, jcg -тг; — .
а) Решите уравнение f(x) = -1.
б) Найдите длину наибольп1его промежутка монотонности
функции /.
в) Сколько решений в зависимости от а имеет уравнение
f(x) = a?
г) Рассмотрите тело, ограниченное поверхностью, полученной
при вращении графика данной функции относительно лежащей
в плоскости Оху прямой у = т, и плоскостями х = -тг, х = 0,5тг.
При каком m объём этого тела является наименьшим?
XIV.20. Дана функция f(x) = х3 + Зх2.
а) Докажите, что фигуры, ограниченные отрезками
горизонтальных касательных графика этой функции и дугами этого
графика между точками пересечения касательных с графиком,
имеют равные площади.
б) Докажите, что график функции / симметричен
относительно точки А(-1; 2).
в) Докажите, что если некоторая прямая касается графика
функции / в точке с абсциссой х0 (х0 Ф -1), то она
пересекает график в точке с абсциссой -3 - 2х0.
г) Докажите, что всякая прямая, пересекающая график
функции / в трёх точках, одна из которых является серединой
отрезка между двумя другими, проходит через точку А.
XIV.21. Пусть а, Ь, с — длины некоторых отрезков.
а) Докажите, что если а = л/2, Ь - л/з, с = л/7, то из этих
отрезков можно составить остроугольный треугольник.
452j Глава XIV. Повторение
б) Выясните, существует ли треугольник со сторонами а — 1921,
Ь = 2021, с = 2121?
в) Докажите, что если для любого натурального п существует
треугольник со сторонами ап, Ьп, сп, то все эти
треугольники — равнобедренные.
г) Пусть фл — угол треугольника со сторонами 1, v2, v4,
лежащий против средней из них. Докажите, что последовательность
фп монотонна и имеет предел.
xiv.22. Дана функция /(х) = ^Jlog2x.
а) Решите уравнение f(2x2 + 0,5) + Л — ] = /1 4х + — I.
I 4 - х2 \
б) Решите неравенство f\ ^ /(3,5- х).
у 1 4- X2 )
в) Решите для всех а е R уравнение f(2xa) = f(4x).
г) Числа а, &, с образуют возрастающую геометрическую про-
V2 Г
грессию (а ^ 1). Докажите, что f(x)dx ^ /(&).
с —a J
I а
XIV.23. Дана функция f(x) = ylogg^-
а) Решите уравнение /|2x-—] + /[ — ]= /(х2 - 0,5).
V х) \%)
б) Решите неравенство
^ ) У )
в) Решите для всех а е R уравнение f(y[3xaj = f — .
г) Числа а, Ь, с образуют возрастающую геометрическую
прогрессию (а > 1). Докажите, что [ f(x)dx ^ f(b).
с —a J
а
xiv.24. Дана функция / (х) = + .
cosx sinjc
а) При а = 1, Ь = V3 решите уравнение f(x) = 4.
б) При тех же а и & решите неравенство /(х) ^ 0.
в) При а = 1 найти все &, при которых функция убывает на
интервал 0; —
V 3
г) Пусть а > 0, & > 0. Докажите, что уравнение f(x) = 1 имеет
ровно три решения на отрезке [0; 2л] тогда и только тогда,
2 2
когда a3 -h &3 = 1.
XIV.25. Дана функция f(x) =
cos х sin х
а) При & = 1, а = л/3 решите уравнение /(я) = 4.
б) При тех же а и & решите неравенство f(x) ^ 0.
453! Задачи и упражнения
в) При а = 3 найдите все Ь, при которых функция убывает на
'5я
интервал —; тс
6
г) Пусть а > О, Ъ > 0. Докажите, что уравнение /(я) = 8 имеет
ровно три решения на отрезке [0; 2тг] тогда и только тогда,
2 2
когда а3 +&3 = 4.
XIV.26. Дана последовательность {ап}9 где ап+1 = у2 - д/4 - а^ , ах = с > 0.
а) Докажите, что при всех натуральных я выполнено л/2 ^ —— ^ 2.
«п + 1
б) Докажите, что последовательность убывает, и вычислите её
предел.
в) Пусть с- 1. Докажите, что все числа an, ai ^ 2,
иррациональны.
г) Пусть с = 2. Докажите, что lim 2nan = 2тг.
—> оо
xiv.27. Дана функция f(x) = 4 + ax-x2, прямая Z, заданная
уравнением у = 2х + 8, и точка А(0; 4).
а) Найдите все а, при которых прямая I касается графика /.
б) Пусть Р и Q — точки касания прямой I с графиками / (при
найденных выше). Вычислите площадь криволинейного
треугольника, ограниченного отрезком PQ и дугами АР и AQ этих
графиков.
в) Пусть а = 2. Найдите точку графика /, ближайшую к точке
М(-3; 1,5).
г) Найдите наименьшее значение площадей сегментов,
ограниченных графиком функции / и осью абсцисс.
xiv.28. Дана функция f(x) = ———-—.
А — X
а) Пусть а = -2. Решите уравнение f(x + 1) = f(x).
б) Пусть а = 3,5. Решите неравенство f(x) + f(-x) ^ 0.
в) Найдите все значения а, при каждом из которых функция /
монотонна на луче (-оо; 0).
г) Найдите все значения а, при каждом из которых
существует &, такое, что уравнение f(x) = b не имеет решений.
xiv.29. Дана функция f(x) = — —.
4х - 2х
а) Пусть а = --. Решите уравнение f(x - 1) = f(x).
о
21
б) Пусть а = . Решите неравенство f(x) + f(-x) > 0.
4
в) Найдите все значения а, при каждом из которых функция /
монотонна на луче (0; +оо).
г) Найдите все значения а, при каждом из которых
существует Ьу такое, что уравнение f(x) = Ь не имеет решений.
4541 Глава XIV. Повторение
Xiv.30. Пусть fn(x) = cosnx, где п е N.
а) Найдите все * е [1; 2], для которых fb(x) ^ /зС*)-
б) Решите уравнение f5(x) + 2/3(#) = 0.
в) Найдите все значения а, для каждого из которых уравнение
fs(x) = fs(a) имеет ровно два решения на отрезке —; — .
г) Существует ли многочлен q такой, что \fxeR g(sinx)= f2oo9(x)?
xiv.31. Пусть fn(x) = sinnx, где п е N.
а) Найдите все х е [1; 2], для которых fb(x) ^ fs(x)-
б) Решите уравнение f5(x) = 2/з(#)-
в) Найдите все значения а, для каждого из которых уравнение
fAx) - fs(a) имеет ровно два решения на отрезке [0; тг].
г) Существует ли многочлен q такой, что \/xeR q(sinx)= /
xiv.32. Дана функция f(x) = yjx2 + х + 7 - ^х2 - х + 1.
а) Решите неравенство f(x) ^ 1.
б) Найдите множество значений функции /.
в) Докажите неравенство J -—dx + J f(x)dx < 3.
о fM о
г) Найдите все такие k e Z, что f(k) e Q.
XIV.33. Пусть рп(х) = 1 + х + х2 + ... + хп, где п е N.
а) Докажите, что уравнение рп (х) = 0 имеет вещественные
корни тогда и только тогда, когда число п нечётно.
б) Пусть zl9 z2, ..., zn — все корни (в том числе и комплексные)
уравнения рп(х) = 0. Докажите, что
в) Найдите все значения п, при каждом из которых рп (х) • х3+ 1.
г) Докажите, что Хс*;! А(х)= 2ярГ1
XIV.34. Дана функция f(x) = log|x + '.
а) Решите уравнение f(x) = 3.
б) Решите неравенство /(х) ^ -1.
в) Найдите все значения а, при каждом из которых уравнение
f(x) = f(a) имеет единственное решение.
г) Определите число корней уравнения f(x) = f(2x).
Xiv.35. Дана функция f(x) = log| 3 + logi (Зх2).
о
а) Решите уравнение f(x) = 2.
б) Решите неравенство f(x) ^ -2.
в) Найдите все значения а, при каждом из которых уравнение
f(x) = f(a) имеет три решения.
г) Определите число корней уравнения / (х) =
455 Задачи и упражнения
XIV.36. Дана функция f(x) = cos6 л: + sin6 л: + 2а cos2 x.
7
а) Пусть а = —. Найдите корни функции /.
8 Т
б) Найдите все значения а, при каждом из которых J f(x)dx= 0.
в) Найдите все значения а, при каждом из которых функция /
монотонна на отрезке —; — .
г) Вычислите предел lim — Y /1 — - х .
xiv.37. Дана функция f(x) = cos6* + sin6* + 2а sinx • cos я.
13
а) Пусть а = ——. Найдите корни функции /.
8 Т
б) Найдите все значения а, при каждом из которых J f(x)dx— 0.
о
в) Найдите все значения а, при каждом из которых функция /
Г п я!
монотонна на отрезке —; — .
г) Вычислите предел lim — Y /1 — + х .
»-°°nk=i V п )
xiv.38. Последовательность {хп} задана соотношениями хп + 1 = 2х2п - 1,
х0 = -с.
а) Найдите все значения с, при каждом из которых х2 > 0.
б) Докажите, что если с > 1, то эта последовательность
монотонна.
в) Найдите все непостоянные конечные арифметические
прогрессии, образованные последовательными членами
последовательности {хп}.
г) Докажите, что существуют последовательности данного
вида, имеющие сколь угодно большой период.
xiv.39. Дана функция f(x) = logx+1(ax).
а) Известно, что х = 1 - корень уравнения f(x) = 3. Найдите а
и остальные корни этого уравнения.
б) Пусть а = 4,5. Решите неравенство f(x) > f\ — .
\х )
в) Найдите все значения а, при каждом из которых уравнение
f(x) = 3 имеет единственное решение.
г) Докажите, что если уравнение f(x) = n + l(neN) имеет
положительный корень, то а > пе.
456 Глава XIV. Повторение
XIV.40. Дана функция f(x)=\og1_x — .
1 х
а) Известно, что х = корень уравнения f(x) = 2. Найдите а
и остальные корни этого уравнения.
3 ( \\
б) Пусть а — . Решите неравенство f(x) ^ Л — .
16 ух J
в) Найдите все значения а, при каждом из которых уравнение
f(x) = 2 имеет единственное решение.
г) Докажите, что если уравнение f(x) = n, где п е N, имеет
положительный корень, то па < е~г.
xiv.41. Дана функция f(x) = cos ax • cos я.
а) При а = 2 решите уравнение — = 1.
б) Найдите все значения а, при каждом из которых J f(x)dx^O.
о
в) Пусть ха — ближайший к — корень уравнения f(x) = sin*.
Найдите наименьшее значение ха
г) Найдите все значения а, при каждом из которых
ха
xiv.42. Дана функция f(x) = sin ax • sinx.
f(2x)
а) При а = 3 решите уравнение -^—- = -2.
б) Найдите все значения а, при каждом из которых J f(x)dx>0.
о
в) Пусть ха — наименьший положительный корень уравнения
f(x) = cosx. Найдите наименьшее значение ха.
г) Найдите все значения а, при каждом из которых
xiv.43. Даны многочлены /? (х) = ах1998 + Ъ и д(х) = сх1917 + d (а * 0).
а) Найдите наибольп1ее возможное число вещественных
корней уравнения р(х) = д(х).
б) Решите уравнение/?(х) = q(x) при а= 71, & = 3, с = 74, d = 0.
в) Пусть & = 0, с = 1. Найдите все целые значения а и d, при
которых число /?(ai) делится на число q(n) при всех
натуральных значениях п.
г) Пусть d = 0. Найдите все целые значения а, &, с, при
которых число р(п) — q(n) делится на (п - I)2 при всех натуральных
значениях п9 больших 1.
457; Задачи и упражнения
XIV.44. Каждая из граней куба закрашивается целиком белым или
чёрным цветом. Раскраски двух кубов называются
одинаковыми, если эти кубы невозможно различить (при этом их можно
перемещать и вращать в пространстве).
а) Найдите вероятность того, что при случайном
раскрашивании куба все его противоположные грани имеют различные
цвета.
б) Сколько существует различных раскрасок куба?
в) Двое по очереди раскрашивают по одной грани куба.
Раскрасив один куб, они принимаются за следующий. Докажите,
что, независимо от количества имеющихся кубов, второй из
них сможет добиться, чтобы все кубы оказались одинаково
раскрашенными .
г*) Найдите вероятность того, что при случайном
раскрашивании двух кубов их раскраски оказались одинаковыми.
XIV.45. Дана функция f(x) = 2х - ах.
а) Решите неравенство f(3x) > f(2x) + f(x).
б) Найдите все значения а, при каждом из которых уравнение
f(2x) = f(x) + f(x + 1) имеет единственное решение.
в) Пусть а = 0,5. Решите уравнение yjf(x) + х = 0.
г) При а = 1 найдите с точностью до 0,03 положительный
корень уравнения f(x) = 1024.
xiv.46. Дана функция f(x) = ах - 3х.
а) Решите неравенство f(3x) > f(2x) + f(x).
б) Найдите все значения а, при каждом из которых уравнение
f(2x) = f(x) + f(x + 1) имеет единственное решение.
2 I
в) Пусть а = -. Решите уравнение ^J-f(x) = -х.
3
г) При а = 1 найдите с точностью до 0,01 положительный
корень уравнения f(x) = -729.
XIV.47. Дана функция f(x) = cos3 х-a cos2 х • sin х + Ъ cos х • sin2 х - sin3 x.
ч тт « 1 71 ЗЯ
а) Найдите а и Ь, если известно, что числа — и — являются
4 4
корнями функции /.
б) Пусть а = Ъ - -1. Решите неравенство f(x) > 0.
в) При а = —3 решите уравнение f(x) = sin3x.
г) Найдите все пары чисел (а; &), для каждой из которых пери-
од функции / равен —.
3
XIV.48. Дана функция f(x) = cos3 * + a cos2 jc • sin x + b cos x • sin2 x + sin3 x.
а) Найдите а и &, если известно, что числа — и —- являются
4 4
корнями функции /.
б) Пусть а = Ь = -1. Решите неравенство f(x) ^ 0.
458; Глава XIV. Повторение
в) При Ъ = -3 решите уравнение f(x) = cos3x.
г) Найдите все пары чисел (а; &), для каждой из которых пе-
, , ' 2л
риод функции / равен —,
3
xiv.49. Пусть рп — многочлен степени п.
а) Известно, что числа 3 и 7 являются корнями многочлена р2
и р'(3) = 11. Найдите р'(7).
б) Известно, что числа 1 и 2 являются корнями многочлена ps.
Пусть Рд(1) = ^» Рз(2) = 1> пРичём kl > 0. Докажите, что число,
делящее отрезок [1; 2] в отношении k : Z, является третьим
корнем этого многочлена.
в) Пусть Рз(х) = Xs - Зх2 - 1. Найдите все значения а, при
каждом из которых уравнение р3 (х) + ах = 0 имеет ровно два
вещественных корня.
г) Пустьр1000(х) = х(х - 2)(х - 4) • ... • (х - 1998). Найдите все
а ^ 0, при каждом из которых уравнение Рюоо(х) = а имеет
1000 различных вещественных корней.
XIV.50. Дана функция f(x) = Iog2(2* + a).
а) При каком значении а прямая у = касается графика
функции /?
б) Докажите, что /(0) ^ -—.
In 2
в) Пусть а = 0,5. Сколько решений в зависимости от Ъ имеет
уравнение f(x) = — + Ы
г) Пусть а > 0 и t > 0. Докажите, что
2
о
XIV.51. Дана функция f(x) = Iog3(3* + a).
t2
\f(x)dx-f-
< 4а.
а) При каком значении а прямая у = касается графика
функции fl
б) Докажите, что /(0) ^ -—.
2
в) Пусть а = -. Сколько решений в зависимости от Ъ имеет
3
уравнение f(x) = — + &?
3
г) Пусть а > 0 и £ > 0. Докажите, что
jf{x)dx-*l
< а.
_ „ (4cosx- cosy = а,
Xiv.52. Дана система уравнении < . . . ,
[4sin:x;+ sin г/ = &.
а) Решите систему при а = Ъ - 0.
б) Решите систему при а = 4, 6 = -1.
459, Задачи и упражнения
в) Найдите наибольшее значение площади четырёхугольника,
длины последовательных сторон которого равны 3, 1, 3 и 4.
г) Изобразите на плоскости множество всех точек М(а; &), для
каждой из которых система имеет решение.
w „ f4cosx — 3cosz/ = а,
xiv.53. Дана система уравнении < л . Л .
[4Sinx + 3siny = Ь.
а) Решите систему при а = Ъ = 0.
б) Решите систему при а = 3, & = 4.
в) Найдите наибольшее значение площади четырёхугольника,
длины последовательных сторон которого равны 1, 3, 1 и 4.
г) Изобразите на плоскости множество всех точек М(а; &), для
каждой из которых система имеет решение.
XIV.54. Рассмотрим всевозможные последовательности {хп}9 для кото-
Рых хп = ^— •
Z ~ Хп - 1
а) Пусть *о = £' Найдите х2009-
б) Докажите, что если х0 < 1, то последовательность {хп}
монотонна.
в) Найдите множество Со всех чисел, которые не могут являться
начальными членами бесконечных последовательностей {хп}.
г) Найдите множество начальных членов монотонных
бесконечных последовательностей {хп}.
XIV.55. Даны функции f(x) = log^^x и g(x) - f — .
а) Решите неравенство f(x) < g(x). ^ ^
б) Найдите все значения х, такие, что f(x) и g(x) одновременно
являются целыми числами.
в) Найдите все числа с, такие, что уравнение f(x) + g(x) = с
имеет решения.
г) Пусть хп — такое число, что f(xn) = —п, где п —
натуральное число, п ^ 2. Докажите, что хп < .
XIV.56. Даны функции f(x) = log^(x +1)и^(л;)= ——- - 1.
f[x)
а) Решите неравенство f(x) + g(x) > 0. v J
б) Найдите все значения х, такие, что f(x) и g(x) одновременно
являются целыми числами.
в) Найдите все положительные числа d, такие, что уравнение
f(x) — §(х) = d не имеет решения.
г) Пусть хп — такое число, что f(xn) = —, где п — натураль-
^ г» тг 2 In Л
ное число, п ^ 2. Докажите, что хп < .
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Асимптота вертикальная 37
— горизонтальная 38
— наклонная 38
Вероятность 278, 279
— геометрическая 294
— классическое определение 282
— условная 284
Дифференциал 83
Длина кривой 201
Интеграл неопределённый 97
— определённый 180, 184, 185
— с переменным верхним
пределом 188
Интегрирование подстановкой 193
— по частям 105
Касательная 74
Комплексная плоскость 232
Комплексное число 217
— — алгебраическая форма 218
— — аргумент 239
— — вещественная часть 217
— — мнимая часть 217
— — модуль 234
— — тригонометрическая форма 239
Комплексные числа
— — деление 223, 243
— — разность 219
— — умножение 219, 243
— — сопряжённые 222
Конечное вероятностное
пространство 278
Корень п-й степени из комплексного
числа 248
Критерий нестрогой монотонности
функции 112
Неравенство иррациональное 363
— Йенсена 131
— Коши 132
— логарифмическое 380
— показательное 373
— с параметром 385
— тригонометрическое 396
Парадокс Бертрана 298
Первообразная 93
Площадь криволинейной
трапеции 170, 172
Порядок малости 22
Предел «замечательный»
,. sin х ле,
lim ——- 15
*—о х
(1+х)
18
х->0
lim
*— о
18
* —о х
Предел функции 3
— — бесконечный 8
— — левосторонний 8
— — по Гейне 5
— — по Коши 3
— — правосторонний 8
Производная 57
— вторая 123
— композиции 87
— односторонняя 60, 66
— произведения 84
— частного 86
Символ o(f) 22
Система однородная 327
— равносильная 322
— симметрическая 328
Событие 275
— достоверное 275, 277
— невозможное 276, 277
— независимое 285
— случайное 276
Сумма Дарбу 185
— Римана 175
Схема Бернулли 288
Теорема Барроу 188
— Больцано — Коши (первая) 32
— Больцано — Коши (вторая) 33
— Вейерштрасса (первая) 35
— Вейерштрасса (вторая) 35
— Дарбу 111
I
461[ Предметный указатель
— Лагранжа 108
— основная алгебры 229
— Ролля 107
— Ферма 106
Точка критическая 117
— перегиба 130
Угол между графиками функций 78
Уравнение возвратное 317
— дробно-рациональное 320
— иррациональное 350
— логарифмическое 375
— однородное 318
— показательное 370
— с параметром 332
— тригонометрическое 386
— целое рациональное 313
Формула Байеса 293
— Муавра 245
— Ньютона — Лейбница 180
— полной вероятности 290
Функции эквивалентные 21
Функция бесконечно большая 20
— — малая 20
— вогнутая 124
— выпуклая 124, 126
— гладкая 63
— дифференцируемая 82
— интегрируемая 186
— локально ограниченная 11
— непрерывная 24, 25
— Римана 28
Частота наступления события 281
ОГЛАВЛЕНИЕ
Глава VIII. Предел и непрерывность функции 3
§ 44. Понятие предела функции —
§ 45. Некоторые свойства пределов функции 10
§ 46. Вычисление предела функции в точке 13
§ 47. Классификация бесконечно малых функций 20
§ 48. Непрерывность функций 24
§ 49. Непрерывность функций на промежутке 30
§ 50. Свойства функций, непрерывных на отрезке 32
§ 51. Существование и непрерывность обратной функции 37
§ 52. Асимптоты графика функции —
Задачи и упражнения 41
Глава IX. Производная и её применения 56
§ 53. Определение производной —
§ 54. Производные некоторых элементарных функций 69
§ 55. Задача о касательной. Уравнение касательной 73
§ 56. Приближение функции линейной функцией. Дифференциал 80
§ 57. Производная произведения, частного, композиции функций 84
§ 58. Таблица производных. Первообразная 91
§ 59. Неопределённый интеграл 97
§ 60. «Французские» теоремы 106
§ 61. Исследование функции с помощью производной 112
§62. Вторая производная. Выпуклые функции 123
§ 63. Построение эскизов графиков с помощью производной.
Решение задач с помощью производной 133
Задачи и упражнения 142
Глава X. Определённый интеграл 170
§ 64. Площадь криволинейной трапеции —
§ 65. Определённый интеграл 180
§ 66. Свойства определённого интеграла 189
§ 67. Применения определённого интеграла 199
Задачи и упражнения 204
Глава XI. Комплексные числа 216
§ 68. Определение комплексных чисел.
Алгебраическая форма записи и арифметические действия
над комплексными числами —
§ 69. Комплексные числа и многочлены. Основная теорема алгебры 228
§ 70. Геометрическое представление и тригонометрическая форма
записи комплексных чисел 232
463 Оглавление
§ 71. Корень п-й степени из комплексного числа 248
§ 72. Применения комплексных чисел 251
Задачи и упражнения 258
Глава XII. Элементы теории вероятностей 275
§ 73. Случайные события. Классическое определение вероятности —
§ 74. Условная вероятность. Независимые события 283
§ 75. Формула полной вероятности 290
§ 76. Геометрическая вероятность 294
Задачи и упражнения 301
Глава XIII. Уравнения и неравенства 311
§ 77. Некоторые способы решения уравнений —
§ 78. Целые рациональные и дробно-рациональные уравнения .... 313
§ 79. Системы алгебраических уравнений и неравенств 321
§ 80. Уравнения и неравенства с параметром.
Аналитическое исследование 332
§ 81. Множества на плоскости, задаваемые уравнениями
и неравенствами 338
§ 82. Графический метод решения уравнений и неравенств
с параметрами в плоскости (х; а) 342
§ 83. Графический метод решения уравнений и неравенств
с параметрами в плоскости (х; у) 347
§ 84. Иррациональные уравнения и системы 350
§ 85. Иррациональные неравенства 363
§ 86. Иррациональные уравнения и неравенства с параметрами .... 367
§ 87. Показательные уравнения и неравенства 370
§ 88. Логарифмические уравнения и неравенства 375
§ 89. Тригонометрические уравнения и неравенства 386
Задачи и упражнения 413
Глава XIV. Повторение 447
Задачи и упражнения —
Предметный указатель 460
Учебное издание
Пратусевич Максим Яковлевич
Столбов Константин Михайлович
Головин Алексей Николаевич
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
11 класс
Учебник для общеобразовательных учреждений
Профильный уровень
Зав. редакцией Т. А. Бурмистрова
Редактор П. А. Бессарабова
Младший редактор Е. А. Андреенкова
Художник О. П. Богомолова
Художественный редактор О. П. Богомолова
Компьютерная графика А. Г. Въюниковской, О. Ю. Тупикиной
Технический редактор и верстальщик А. Г. Хуторовская
Корректоры И. П. Ткаченко, А. К. Райхчин
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93 — 953000. Изд. лиц.
Серия ИД № 05824 от 12.09.01. Подписано в печать 15.12.09. Формат 70x907i6- Бумага
офсетная. Гарнитура Школьная. Печать офсетная. Уч.-изд. л. 27,9 + форз. 0,5. Тираж 5000 экз.
Заказ № 24159 щ-гз).
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
Открытое акционерное общество «Смоленский полиграфический комбинат».
214020, г. Смоленск, ул. Смольянинова, 1.
К. ГАУСС
(1777- 1855)
Б. РИМАН
(1826-1866)
П. Л. ЧЕБЫШЕВ
(1821 - 1894)
Ж. ДАРБУ
(1842-1917)
А. М. ЛЯПУНОВ
(1857- 1918)
СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ъ ъ
g(x))dx =
а
Ь
\{kf{x))dx =
а
с
а
\f(x)dx = -\f(x)dx
а
А. Н. КОЛМОГОРОВ
(1903 - 1987)
И. М. ВИНОГРАДОВ
(1891 -1983)
ПРОФИЛЬНЫЙ
УРОВЕНЬ
ISBN 978-5-09-017190-8
Учебно-методический комплект
по алгебре и началам математического
анализа для 10-11 классов содержит:
УЧЕБНИКИ для 10 и 11 классов
(авторы М. Я. Пратусевич, К. М. Столбов,
А. Н. Головин)
ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ
для 10 и 11 классов (авторы В. Н. Соломин,
К. М. Столбов, М. Я. Пратусевич)
КНИГИ ДЛЯ УЧИТЕЛЯ
для 10 и 11 классов (авторы М. Я. Пратусевич,
К. М. Столбов, А. И. Головин)
ПРОСВЕЩЕНИЕ
ИЗДАТЕЛЬСТВО