Текст
ПЕРЕВ0ДНАЯ НАУЧНО'ПОПУЛЯРНАЯ ЛИТЕРАТУРА
Йоханнес Леман
УВЛЕКА ТЕЛЬНАЯ
DURCHMATHE
ББК 22.1 Л 44
Научный редактор и автор предисловия — А. П. Савин.
Перевод с немецкого 10. А. Данилова.
Леман И.
Л 44 Увлекательная математика. Пер. с нем.— М.: Знание, 1985.— 272 с., ил.
50 к. 100 000 экэ.
Автор книги Йоханнес Леман, главный редактор научно-популярного математического журнала ГДР «Альфа», собрал в ней несколько сотен задач, среди которых и совсем свежие, и такие, возраст которых исчисляется тысячелетиями. Большое количество иллюстраций делает книгу особенно привлекательной для школьников, которым в первую очередь ока и адресована.
1702010000—037 л ББК 22.1
Л 073(02)—85 28—84 51
© Urania-Verlag Leipzig, Jena, Berlin. Verlag fur popularwissenschaftliche Literatur, Leipzig, 1980.
© Издательство «Знание», 1985 г.
Перевод на русский язык, комментарии, предисловие
УВЛЕКАТЕЛЬНАЯ МАТЕМАТИКА
Johannes Lehmann
KURZWEIL BURCH MATHE
Johannes Lehmann
KURZWEIL
DURCH MATHE
URANIA-VERLAG
LEIPZIG • JENA BERLIN
УВЛЕКАТЕЛЬНАЯ МАТЕМАТИКА
Перевод с немецкого Ю.А. Данилова
Издательство „Знание"
Москва 1985
ПРЕДИСЛОВИЕ
Когда мы перелистываем страницы научно-популярного журнала, то вольно или невольно взгляд, скользнув по иллюстрациям, останавливается на занимательных задачах. Необычность ситуации, неочевидность ответа па поставленный вопрос заинтриговывает нас, и мы начинаем нелегкий поиск пути, ведущего к решению задачи.
Многие считают занимательные задачи средством для приятного времяпрепровождения, отдыха, но если вдуматься, то становится ясной их гораздо более важная роль. Несомненно, что именно занимательные задачи являются одним из самых мощных инструментов развития человеческого интеллекта. Если человеку в течение жизни приходится, скажем, десяток раз оказаться в затруднительном положении, выход из которого можно найти с помощью логических рассуждений, то задачи предоставляют ему такую возможность сотни раз уже в детстве и юности, именно тогда, когда формируется его интеллект. Не зря люди передавали эти задачи устно и письменно из поколения в поколение.
Одной из таких эстафетных палочек является и книга, которую вы держите в руках. Автор собрал в ней несколько сотен задач, среди которых и совсем свежие, и такие, возраст которых исчисляется тысячелетиями. Множество иллюстраций делает книгу особенно привлекательной для школьников, которым она в первую очередь и адресована.
Автор книги Йоханнес Леман, главный редактор научно-популярного математического журнала ГДР «Альфа», считает, что наибольшую пользу занимательные задачи приносят детям 12—13 лет, поскольку до этого у них еще нет достаточного жизненного опыта и запаса знаний.
Представляя книгу И. Лемаиа, хочется отметить чрезвычайно широкую палитру задач, включенных в сборник: от «чисто математических» до таких, которые, казалось бы, к математике не имеют прямого отношения, например: «Как выглядит с изнанки шнуровка тапочек, изображенных на рисунке?» Не менее широк и спектр трудности задач: от совсем легких, решаемых «в уме» первоклассниками, до таких, которые могут заставить надолго задуматься и специалиста с высшим образованием. Правда, нужно отметить, что для решения задач, как правило, достаточно знаний школьников 5—6-х классов. Задачи проверяют не знания, а умение логически рассуждать, они учат этому умению.
В заключение хочется отметить большое количество коротких занимательных историй на математические темы, умело вкрапленных автором в текст книги.
Желаю читателям получить максимум удовольствия в занятиях «интеллектуальной гимнастикой», возможность для которой предоставляет читателю эта книга.
А. 77. Савин
Часть 1
ЗАДАЧИ
Голубыми цифрами набраны номера страниц, на которых начинаются главы с условия* ми задач в первой части книги, черными — номера страниц с решениями в конце книги.
9 17 25 32 39 Пестрые картинки нз разных стран 148 Античные этюды 153 Школьные истории 160 Старое и новое из практики 166 Минуту на размышление 173
47 55 63 Арифметика с птичьего полета 180 Занимательная геометрия 189 Тренировка по современной математике 195
7! 79 86 94 I01 108 116 Математика на каждом шагу 204 Слово знаменитым математикам 213 Наша секция игр 220 Путь, время, скорость 222 Беседы на естественнонаучные темы 230 Напряженное расписание 236 Вокруг циркуля и линейки 245
124 132 139 Игра с числами 253 Огонь математических олимпиад 256 По разным странам 263
Не знание, а изучение, не обладание, а приобретение, не существующее, а грядущее доставляет величайшее наслаждение.
Из письма К. Ф. Гаусса Яиошу Бойяи.
ПЕСТРЫЕ КАРТИНКИ из
Математика не принадлежит какому-нибудь одному народу, она поистине интернациональна. Нет ни одной страны, которая не поддерживала бы с математикой дружеских отношений, не приумножала ее сокровищ и славы.
А. И. Маркушевич
1. Франция. Во время летнего пикника четыре супружеские пары выпили 32 бутылки лимонада. Жены выпили: Жанна—1 бутылку, Жаклнн — 2 бутылки, Колетта — 3 бутылки и Анетта — 4 бутылки. Мужья не уступили женам: месье Пон выпил столько же, сколько его жена, месье Дюбуа — вдвое больше своей жены, месье Пейзан — втрое и месье Фонтен — вчетверо больше своих жен.
Как зовут мадам Пон, Дюбуа, Пейзан и Фонтен?
2. Вьетнам. Эта задача известна с давних времен. Во вьетнамских деревнях старики-рисоводы любят задавать ее молодежи. Так задача переходит от поколения к поколению.
Для кормления 100 буйволов заготовили 100 охапок сена.
Стоящий молодой буйвол съедает 5 охапок сена.
Лежащий молодой буйвол съедает 3 охапки сена.
Старые буйволы втроем съедают 1 охапку сена.
Сколько молодых буйволов стоят, сколько лежат и сколько буйволов старых?
3. Югославия. Расставьте числа (в рамке слева) и знаки арифметических действий ю
4. СССР. На обочине шоссе стоят километровые столбы. Шоссе ведет из пункта А в пункт В. На каждом столбе указано расстояние в километрах как от пункта А, так и от пункта В. Расстояние от Л до В составляет 999 км.
На скольких километровых столбах обе надписи используют только 2 различные цифры?
5. Австрия. «Подальше положишь — поближе возьмешь». Перед нами хитрый крот. Между своей спальней А и выходом Е он проложил хитроумную систему ходов и камер. Каждое утро крот следует из Е в А и по дороге проходит через свою запасную кладовую. Интересно, что отыскивает он ее по определенному правилу. Если крот достигает выхода Е, миновав 3, 5, 7, 9 или 11 промежуточных остановок (обозначенных на плане кружками), то кладовая остается в стороне. Если же крот добирается до выхода Е после четного числа промежуточных остановок, то по до-
роге он непременно наталкивается на запасную кладовую.
Между какими двумя камерами расположена запасная кладовая хитрого крота?
6. Болгария. Отец по имени Николай с сыном и отец по имени Петр с сыном отправились удить рыбу. Число рыб, пойманных Николаем, оканчивается на 2, а число рыб, пойманных его сыном, — на 3, число рыб, пойманных Петром, также оканчивается на 3, а число рыб, пойманных его сыном,— на 4. Число рыб, пойманных нашими рыболовами вместе, совпадает с квадратом некоторого натурального числа.
Как зовут сына Николая?
7. Дания. Рыбаки Адам, Бауэр, Кристиансен и Дазе (сокращенно А, В, С и D — по первым латинским буквам их имен), взвесив свой улов, установили следующее:
(1) D поймал больше, чем С.
(2) А и В вместе поймали столько же, сколько С и D (вместе).
(3) А и D вместе поймали меньше, чем В н С (вместе).
Расположите результаты взвешиваний уловов а, Ь, с и d рыбаков А, В, С и D по величине.
Математик или футболист?
Однажды братья — физик Нильс Бор и математик Гаральд Бор — вместе с приятелем отправились на прогулку по улицам Копенгагена. К удивлению приятеля, прохожие довольно часто здоровались с Гаральдом, Нильса же никто не приветствовал. «По-видимому, математики в Копенгагене котируются высоко»,— заметил приятель. Нильс Бор возразил ему: «Не математики, а Гаральд. Ведь он любимый футболист нашего города!»
8. Венгрия. Учитель начертил на классной доске четырехугольник. Янош утверждал, что это квадрат. Имре считал, что четырехугольник — трапеция. Мария думала, что на доске изображен ромб. Эва назвала четырехугольник параллелограммом. Выслушав каждого и обстоятельно изучив свойства четырехугольника, учитель установил, что ровно 3 из 4 утверждений истинны и ровно 1 утверждение ложно.
Какой четырехугольник начертил учитель на классной доске?
9. Греция. Четырежды пять — двадцать: составьте из любых четырех фигур пентамино прямоугольник со сторонами 4><5.
ABCDEF G Н I J К L
Сколько решений допускает эта задача? (Сторона клетки считается равной единице. Каждая фигура пентамино состоит из 5 квадратов.)
10. США. Джон Гаррис из г. Санта-Барбара изобрел новую игру. «Путешествие перекатывающейся игральной кости». Для того чтобы нам легче было следить за маршрутом игральной кости, выкрасим одну
из ее граней в какой-нибудь цвет. С одного поля шахматной доски на соседнее игральная кость «путешествует», перекатываясь через ребро, совмещенное с общей стороной этих двух полей.
А теперь решим задачу.
Поставьте игральную кость на левое верхнее поле шахматной доски цветной гранью вверх. Можете ли вы указать маршрут, «путешествуя» по которому, игральная кость побывает по одному разу на всех полях шахматной доски и окажется в правом верхнем углу цветной гранью вверх? Во время путешествия из угла в угол цветная грань игральной кости (так гласят правила игры) нигде, кроме начального и конечного поля, не должна быть обращена вверх.
11. ФРГ. На рисунке вы видите различные предметы (бокалы, чашки, бутылки и кувшины), уравновешенные на чашах настольных равноплечих весов.
Сколько бокалов, чашек и бутылок понадобится, чтобы уравновесить 3 кувшина?
12. Бельгия. Найти трехзначные числа вида abc, цифры которых удовлетворяют уравнению
а2 — f,2 — с2—а — b — с
(все 3 цифры числа должны быть различны).
13. Италия. Разделить заданный треугольник с помощью зигзагообразной ломаной на 5 равновеликих частей.
14. ГДР. Во время перемены в классе оставались Ангелика, Бернд, Вольфганг и Мануэла. Кто-то из них разбил стекло. Учитель опросил ребят и получил от каждого по три ответа.
Ангелика: 1. Окно разбила не я.
2. Я сидела в классе и читала.
3. Мануэла знает, кто разбил окно.
Бернд: 1. Это сделал не я.
2. С Мануэлой я уже давно не разговариваю.
3. Окно разбил Вольфганг.
Вольфганг: 1. Я не виноват.
2. Окно разбила Мануэла.
3. Бернд лжет, когда утверждает, будто окно разбил я.
Мануэла: 1. Окно разбила не я.
2. Ангелика разбила окно.
3. Бернд знает, что я не виновата, ведь на перемене мы с ним играли вместе.
Кроме того, каждый из них признался, что из трех ответов два истинных и один ложный.
Кто разбил окно?
АНТИЧНЫЕ этюды
Когда радость особенно велика? Когда удается достичь желаемого.
Фалес Милетский
1. Фу Ши (около 3000 г. до и. э.). В обозначениях Фу Ши
знак ~ означал 6,
знак — — означал 1
и знак ЕЕт-ЕЕЕ означал 3.
а) Что означал знак —?
б) Сколько и каких знаков можно составить из трех сплошных или состоящих из двух разделенных промежутком отрезков линий?
2. Из Древнего Вавилона (около 2000 г. до н. э.). Длина и ’Д ширины вместе составляют 7 ладоней, а длина и ширина вместе — 10 ладоней.
Сколько ладоней составляют длина и ширина в отдельности?
3. Из древнеиндийской математики (около 2000 г. до н. э.). В Древней Индии математика распространялась как своего рода спорт. Для решения сложных задач устраивались состязания в присутствии многочисленных зрителей. Некоторые индийские руководства математики были написаны как учебные пособия по проведению подобных состязаний —
для повышения мастерства любителей умственного спорта. Автор одного из таких учебников писал: «Следуя приведенным здесь правилам, можно придумать тысячи других задач. Подобно тому, как солнце затмевает своим сиянием звезды, слава ученого человека, поставившего и решившего алгебраическую задачу, затмевает славу других ученых в многолюдном собрании». Весь учебник этого автора написан в стихах. Приведем лишь одну из задач, но не в стихотворном, а в прозаическом варианте.
«Пчелы числом, равным квадратному корню из полного числа их во всем рое, сели на куст жасмина, 5 * * 8/» пчел полетели назад к рою. И только одна пчела из того же роя кружилась над цветком лотоса, привлеченная жужжанием подруги, неосторожно угодившей в ловушку сладко благоухающего цветка.
Сколько всего пчел было в рое?»
4. Арифметика древних китайцев (2000 г. до н. э.). В центре квадратного пруда шириной 10 шагов растет камыш, возвышающийся на 1 шаг над поверхностью воды. Если, стоя на берегу водоема, притянуть камыш к середине любой из сторон, то он как раз касается края пруда.
Какова глубина пруда?
5. Пифагор Самосский (около 580—501 гг.
до н. э.). Поликрат (известный из баллады Шиллера тиран с острова Самос) однажды спросил на пиру у Пифагора, сколько у того учеников. «Охотно скажу тебе, о Поликрат»,— отвечал Пифагор.— «Половина моих учеников
изучает прекрасную математику, четверть ис-
следует тайны вечной природы, седьмая часть
молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины».
Сколько учеников было у Пифагора?
6. Греческий крест (около 500 г. до н. э.). Название этой фигуры связано с тем, что древние греки чертили такой крест на хлебах, считая его символом жизни.
Вырежьте из картона (или фанеры) греческий крест, разрежь-
те его, как показано на рисунке, и сложите из получившихся частей квадрат.
7. Евклид (около 300 г. до н. э.). Однажды мула и осла нагрузили зерном. По дороге мул сказал ослу: «Если бы ты уступил мне одну меру своего груза, то я нес бы вдвое больше зерна, чем ты. А если бы я уступил тебе одну меру своего груза, то мы оба несли бы зерна поровну».
Сколько мер зерна нес мул и сколько осел?
8. Из папируса Ринда (около 1700 г. до н. э.). Этот папирус, найденный в конце прошлого века англичанином Риндом, представляет собой фрагмент другого более древнего египетского труда по математике, относящегося, по-видимому, к Ш тыс. до н. э. Приведем две задачи из папируса Ринда.
а) Некий математик насчитал на выгоне
70 коров. «Какую долю от всего стада составляют эти коровы?» — спросил математик у пастуха. «Я выгнал пастись две трети от трети всего стада»,— отвечал пастух.
Сколько голов скота насчитывается во всем стаде?
Встречаются в древнем папирусе и чисто формальные задачи, например следующая:
б) Найдите х из уравнения [7 , 2 \ , 1 ( 2 \1 1
л+——х +—-х + —-х 1|.___=10 [ \ О / □ \ о □
9. Гиппократ Хиосский (около 440 г. до --
н. э.). Гиппократ на- ----\
чертил квадрированные //s\ \
им лунки и установил: I- у / х’ \ I
сумма площадей двух \1/ Мз луночек Mi и М2 (за- а ----------------^в
полнены точками) равна площади треугольника АВС.
Докажите это утверждение.
10. Шен Кан (ум. в 152 г. до н. э.). Три снопа хорошего урожая, 2 снопа среднего урожая и 1 сноп плохого дают 39 доу (старинная китайская мера) зерна. Два снопа хорошего урожая, 3 снопа среднего и 1 сноп плохого дают 34 доу зерна. Один сноп хорошего, 2 снопа среднего и 3 снопа плохого урожая дают 36 доу зерна.
Спрашивается: сколько доу зерна дает 1 сноп хорошего, 1 сноп среднего и 1 сноп плохого урожая?
11. Архимед (287—212 гг. до н. э.). Существует общая формула для вычисления площади двух «арбелосов», или «сапожных ножей»,
покрытых на рисунке точками. Эту формулу вывел Архимед. Вот она:
s=^_.
8
где t — длина отрезка АВ.
Выведите формулу Архимеда.
12. Герои Александрийский (I в. до н. э.). Из-под земли бьют четыре источника. Первый заполняет бассейн за 1 день, второй — за 2 дня, третий — за 3 дня и четвертый — за 4 дня.
За сколько времени наполнят бассейн все 4 источника вместе?
13. Римский математик (около I в. до н. э.). Адвокаты в Древнем Риме имели обыкновение задавать друг другу задачи. Одна из таких задач гласит:
«Некая вдова должна разделить оставшееся после смерти мужа наследство в размере 3500 динариев с еще не родившимся ребенком. По римским законам, если родится сын, то мать получает половину причитающейся ему доли, а в случае рождения дочери мать
получает вдвое больше нее. У вдовы родились близнецы — сын и дочь.
Как разделить наследство, чтобы все требования закона были соблюдены?»
14. Диофант Александрийский (III в. н. э.). По двум данным числам 200 и 5 найти третье число, которое, если его умножить на одно из них, дает полный квадрат, а если его умножить иа другое число, дает квадратный корень из этого квадрата.
15. Великолепную задачку мы находим в собранных много веков назад арабских сказках «1001 ночь» (ночь 458-я):
«Стая голубей подлетела к высокому дереву. Часть голубей села на ветвях, а другая расположилась под деревом. Сидевшие на ветвях голуби говорят расположившимся внизу: «Если бы один из вас взлетел к нам, то вас стало бы втрое меньше, чем нас всех вместе, а если бы один из нас слетел к вам, то нас с вами стало бы поровну».
Сколько голубей сидело на ветвях и сколько под деревом?
16. В старинной персидской легенде «История Морадбальса», также вошедшей в сборник «1001 ночь», мудрец задает юной деве следующую задачу.
«Одна женщина отправилась в сад собрать яблоки. Чтобы выйти из сада, ей нужно было пройти через 4 двери, у каждой из которой стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала ему половину оставшихся яблок. Так же она поступила и с третьим стражником; а
когда она поделилась яблоками со стражником у четвертых дверей, то у нее осталось лишь 10 яблок.
Сколько яблок она собрала в саду?»
Ученик спросил у Евклида: «Какая выгода от того, что изучу все это?» Евклид позвал своего раба и приказал, указывая на юношу: «Дай ему 3 обола! Несчастный должен непременно получать выгоду от того, что он изучает!»
школьные
ИСТОРИИ
Умение решать задачи — такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путем подражания или упражнения.
Дьердь Пойа
1. Учащиеся одного класса написали контрольную по математике. Треть из них неверно решила по 1 задаче, четвертая часть класса неверно решила по 2 задачи, */б — по 3 задачи и */s— неверно решила все 4 задачи.
Сколько учеников правильно решили все задачи, если в классе не более 30 человек?
2. Лучшего математика из 5 «А» класса попросили отгадать натуральное число, о котором его друзья высказали следующие утверждения.
Вольфганг: Это, число простое.
Карин: Это число 9.
Петер: Это число четное.
Росвита: Это число 15.
Известно, что Вольфганг и Карин вместе высказали ровно одно истинное утверждение (так же, как Петер и Росвита).
Что это за число?
3. Для школьной мастерской купили 29 деталей на 29 марок. Детали были трех сортов: по 10 марок, по 3 марки и по 50 пфеннигов за штуку. Каждого сорта куплено не менее 1 детали. Деталей других сортов среди купленных не было.
Сколько деталей каждого из трех сортов куплено?
4. Для нумерации страниц учебника, по словам учителя, потребовалось 6869 цифр. Его хитроумные ученики тотчас же сообразили, сколько страниц в книге.
Как они подсчитали, сколько страниц в учебнике?
5. Двоим друзьям потребовалось вычислить 42—З2. Они заметили, что результат — число 7 — равен сумме оснований квадратов — чисел 4 и 3. Проверив свое открытие на числах 10 и 11, друзья установили, что оно подтверждается и в этом случае: II2—102=21 = 11 + 10. После этого друзья нашли все пары (а, Ь) натуральных чисел а>Ь, для которых разность а2—Ь2 равна сумме а-^-Ь.
Как друзьям удалось найти все такие числа (а, Ь)?
6. Рози тренируется в школьном спортивном кружке. Одно из упражнений — ритмичная ходьба с пружинящими наклонами. Упражнение выполняется на дорожке длиной 30 м, в начале и в конце которой стоят флагштоки. Рози выполняет упражнение так: два шага вперед, наклон, шаг назад, два шага вперед, наклон, шаг назад и т. д.
Сколько шагов она успевает сделать от флагштока до флагштока, если каждый шаг ее равен 50 см?
7. Войдя в класс после перемены, ребята увидели на доске арифметические примеры с пропущенными кое-где числами и знаками действий (недостающие числа и знаки заменены звездочками). Эти примеры придумал учитель математики, большой любитель задач на смекалку.
Восстановите недостающие числа и арифметические действия.
8. Отец обещал сыну за каждую правильно решенную задачу опускать в копилку по 10 пфеннигов. За каждую неправильно решенную задачу сын должен возвращать отцу по 5 пфеннигов. После того как было решено 20 задач, у сына в копилке оказалось 80 пфеннигов.
Сколько задач сын решил неправильно и сколько без единой ошибки?
9. Учитель математики предложил ученикам обойти ходом коня клетки с вписанными частями слов и вспомнить определение, встре-
цщц ецией вы о X
лук против аллель трал ко поло
ны ается ны четыре лар уголь
ро лый две ыв жные тор
наз сто ого ник
чавшееся на одном из уроков. Поразмыслив, ученики справились с задачей.
Что за определение скрыто в клетках таблицы?
10. Перелистывая страницы старинного учебника арифметики «цифирных дел мастера» Йоханнеса Альберта «Пером по линейкам» (около 1750 г.), библиотекарь нашел следующую интересную задачу (по замыслу автора учебника она предназначалась для «людей низкого и подлого сословий и любителям арифметики»).
Два подмастерья одновременно отправились пешком из Виттенберга в Испанию. Первый подмастерье ежедневно проходил по 7 миль. Второй в первый день прошел 1 милю, во второй — 2 мили, в третий — 3 мили и т. д.— в каждый следующий день на 1 милю больше, чем накануне.
Через сколько дней подмастерья встретились?
11. Три девочки задали на перемене своей подруге задачку на сообразительность. Вот что они ей сообщили.
У Уты вдвое больше цветных карандашей, чем у Регины, а у Сабины на 13 карандашей меньше, чем у Регины.
Сколько цветных карандашей у каждой из нас, если, пересчитав все карандаши, мы получили простое число? Оно меньше 50, а сумма его цифр равна 11.
Итак, сколько цветных карандашей у Уты, Регины и Сабины в отдельности ii у всех вместе?
Ум и остроумие
Еще в школьные годы К- Ф. Гаусс неоднократно поражал учителя своим умом и остроумием. Однажды учитель спросил его: «Гаусс, я сейчас задам тебе два вопроса. Если на первый ты ответишь правильно, то на второй можешь не отвечать. Итак, скажи мне, сколько иголок на рождественской елке?» Гаусс без промедления ответил: «67534». «Как ты так быстро сосчитал иголки?»— изумился учитель. «А это уже второй вопрос, господин учитель»,— улыбнулся Гаусс.
12. От числа одну восьмую
Взяв, прибавь ты к ней любую Половину от трехсот,
И восьмушка превзойдет
Не чуть-чуть — на пятьдесят
Три четвертых. Буду рад,
Если тот, кто знает счет, Мне число то назовет.
Эту задачу более 200 лет назад задавал своим ученикам учитель арифметики Иоганн Хемелинг.
13. Учителя Альтман (А), Брендель (В) и Клаузнер (С) преподают в одном классе математику (М), физику (Ф), химию (X), биологию (Б), немецкий язык (Н) и историю (И). Каждый учитель ведет по 2 предмета. Учитель химии живет в одном доме с учителем математики. Альтман — самый молодой из трех преподавателей. Учитель математики часто играет в шахматы с Клаузнером. Учитель физики старше учителя биологии, но младше
Бренделя. Тот из трех учителей, кто старше двух других, живет дальше всех от школы.
Какие предметы преподает каждый из трех учителей?
14. В гимнастическом зале стоит несколько одинаковых по длине скамей. Если спортсмены попытаются сесть по 6 человек на скамью, то одна скамья окажется незаполненной: на ней сядут лишь 3 спортсмена. Если же спортсмены попытаются сесть по 5 человек на скамью, то 4 спортсменам места не хватит.
Сколько спортсменов и сколько скамей в гимнастическом зале?
15. Для вручения наград всех победителей математической олимпиады выстроили в ряд на сцене. «Шестой слева,— заметил Карл,— единственный среди участников олимпиады, набравший полное число баллов». «Совершенно верно,— согласилась Аннерозе,— он стоит десятым справа».
Сколько было победителей олимпиады? Можете ли.вы обобщить задачу?
16. После экскурсии на завод учитель предложил ребятам следующую задачу. Современная техника позволяет изготовлять из металла проволоку толщиной всего 0,002 мм.
Какой длины получится проволока круглого сечения диаметром 0,002 мм из 2 г серебра?
Идщ
новое
ПРАКТИКИ
Много знать еще не означает многое понимать.
Гераклит
1. Греческий математик Митродор (III в. до н. э.) поставил следующую задачу: «Царская корона имеет массу 60 мин (I мина-100 драхм=='/бо таланта) и отлита из сплава золота, меди, свинца и железа. На золото и медь приходится %, на золото и свинец —2/з, на золото и железо —3/з массы короны.
Сколько мин золота, меди, свинца и железа в царской короне?
2. Эратосфен (умер около 195 г. до и. э. в Александрии) с поразительной точностью измерил окружность Земли. Эратосфен знал, что в Сиенне (нынешнем Ассуане), расположенном в Верхнем Египте, Солнце в полдень самого продолжительного дня в году стоит в зените. Измерив в этот день точно в полдень угол, под которым Солнце видно в Александрии, Эратосфен обнаружил, что направление на Солнце отклоняется от отвесной линии на 7,5°. Из собственных измерений Эратосфену было известно, что Александрия расположена в 5000 египетских стадиях к северу от Сиенны. Пользуясь этими данными, Эратосфен вычислил окружность Земли.
а) Чему равна окружность Земли в египетских стадиях?
б) Перевести полученную величину в километры, считая, что 1 египетская стадия равна 184,72 м.
в) Сравнить полученное Эратосфеном значение с современным (около 40 000 км).
3. Задача Этьенна Безу (1730—1783). По контракту работникам причитается по 48 франков за каждый отработанный день, а за каждый неотработанный день с них взыскивается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается.
Сколько дней они отработали в течение этих 30 дней?
4. Мебельная фабрика каждый месяц выпускает на 10 столов больше, чем в предыдущий. За год фабрика выпустила 1920 столов.
Сколько столов было выпущено в июне и в декабре?
5. Шнур для электрической проводки электрик скручивает из двух медных проводов («жил#). Провода могут иметь изоляцию 8 различных цветов: зеленого (3), голубого (Г), белого (Б), красного (К), черного (Ч), желтого (Ж), серого (С) и фиолетового (Ф). Каждый шнур можно маркировать двумя буквами — по цвету изоляции жил, из которых он скручен. Цвета изоляции должны быть непременно различные: если одна жила имеет зеленую изоляцию, то изоляция другой может быть любого цвета, кроме зеленого.
Сколько шнуров различных маркировок может скрутить электрик из жил с изоляцией 8 цветов?
6. Помещение освещается 32 лампами накаливания общей мощностью 1800 Вт. На складе имеется достаточно большой запас ламп по 40, 60 и 75 Вт. Никаких других ламп на складе нет.
Сколькими различными способами можно удовлетворить заявк№,на комплекты ламп для освещения этого помещения?
7. Детали 1—7 вдвинуты в футляр сверху (каждая деталь двигалась строго по вертикали).
В какой последовательности производилась укладка?
8. Деревянная балка круглого сечения весит 300 Н.
Сколько бы весила такая балка, если бы она была вдвое толще н вдвое короче?
9. Томас Алва Эдисон (1847—1931) обладал тонким чувством юмора. Его многочисленные посетители часто удивлялись, почему калитка в саду перед домом великого изобретателя открывается с трудом. Наконец, один из друзей спросил у Эдисона: «Неужели такой технический гений, как ты, не может отрегулировать какую-то калитку?» «Калитка отрегулирована именно так, как надо,— смеясь возразил Эдисон.— Я сделал от нее привод к цистерне, и каждый, кто приходит ко мне, накачивает в цистерну 20 л воды».
Если бы каждый посетитель вместо 20 л накачивал в цистерну 25 л воды, то для заполнения цистерны понадобилось бы на 12 человек меньше.
Сколько воды вмещает цистерна?
10. Какой из этих 8 рисунков маляр нанес на стену изображенным здесь валиком?
И. Двумя грузовыми машинами требуется перевезти 143 т сыра. Грузоподъемность одной машины в 1,5 раза больше, чем другой. Для перевозки всего груза полностью груженной машине меньшей грузоподъемности понадобится совершить 31 рейс и 27 рейсов машине большей грузоподъемности.
Сколько тонн сыра перевозит за 1 рейс каждая машина?
12. Даны проекции тела на две взаимно перпендикулярные плоскости — вид спереди и вид сверху.
Можно ли по этим двум проекциям однозначно восстановить тело или существуют несколько тел, имеющих одинаковый вид спереди и сверху?
13. Сколько носильщиков необходимо нанять путешественнику, намеревающемуся совершить шестидневный переход по пустыне по замкнутому маршруту, если н он сам, и каждый из носильщиков могут нести четырехдневный запас пищи и воды для 1 человека?
14. В одном из залов «Дома занимательной науки» в Ленинграде* посетителям показывали карту. Требовалось обойти все 17 мостов, соединяющих острова н берега Невы, на которых стоит Ленинград, так, чтобы каждый мост оказался пройденным не более 1 раза.
Возможно ли это?
* Подробнее о замечательной деятельности этого уникального научно-просветительиого учреждения, организованного сотрудником комбината наглядной агитации Ленсовета В. А. Камским, известным популяризатором науки Я. И. Перельманом, страстным пропагандистом астрономии В. И. Прянишниковым, писателем Л. В. Успенским и художником А. Я. Малковым, можно прочесть в статье Г. И. Мишкевича «Дом занимательной науки» (Наука и жизнь, 1968, № 3, с. 71— 77).— Примеч. пер.
15. Объем древесины некоторого участка леса увеличивается за год в среднем на 4%. Предположим, что при благоприятных условиях годовой прирост древесины составляет 5%, а при неблагоприятных условиях—всего лишь 3%.
На сколько процентов увеличится объем древесины за 2 года, если вслед за годом с благоприятными условиями выдастся год с неблагоприятными условиями?
16. Бюро услуг принимает заказы на изготовление копий с архивных документов. Изготовить 3 копии стоит 6 марок, 5 копий — 9 марок и 9 копий — 15 марок.
Во сколько марок обойдется заказчику изготовление п копий? (Цена складывается из платы, взимаемой за пользование архивным документом, и стоимости изготовления копий.)
17. В книге 152 страницы, на каждой странице в среднем по 45 строк, в каждой строке (также в среднем)— по 68 знаков.
Сколько страниц понадобится при наборе того же текста более крупным кеглем, если на странице в среднем умещается по 32 строки, а в каждой строке в среднем — по 51 знаку?
18. Собираемый пчелами нектар примерно на 70% состоит из воды. Производимый пчелами мед содержит около 17% воды.
Сколько нектара необходимо для того, чтобы получить 1 кг меда?
19. Имеется 1 000 000 стальных шариков диаметром 1 мм.
Сможет ли один человек поднять их, если все шарики упаковать в ящик?
МИНУТУ нз РАЗМЫШЛЕНИЕ
Искра знания возгорается в том, кто достигает понимания собственными силами.
Из трактата «Лилавати» [ индийского математика Бхаскары (XII в.) |
1. В одном старинном задачнике суд Па-)нса описан следующим образом. Богини Ге->а, Афродита и Афина пришли к юному Па->ису, чтобы тот решил, кто из них прекраснее. 1редстав перед Парисом, богини высказали следующие утверждения.
Афродита: Я самая прекрасная. (1)
Афина: Афродита не самая прекрасная. (2)
Гера: Я самая прекрасная. (3)
Афродита: Гера не самая прекрасная. (4)
Афина: Я самая прекрасная. (5)
Парис, прилегший отдохнуть на обочине дороги, не счел нужным даже снять платок, которым прикрыл глаза от яркого солнца. Но богини были настойчивы, и ему во что бы то ни стало нужно было решить, кто из них самая прекрасная, Парис предположил, что все утверждения прекраснейшей из богинь истинны, а все утверждения двух остальных богинь ложны.
Мог ли Парис, исходя из такого предположения, вынести то решение, которого ожидали от него богини, и если мог, то кто прекраснейшая из богинь?
2. «Абракадабра»— волшебное слово. В прошлом его нередко можно было встретить выгравированным на амулетах: по существовавшему некогда поверью, оно ограждало владельца амулета от болезней и прочих несчастий.
Перед вами 2 конфигурации. Сколькими способами можно прочитать в них слова «абракадабра» и «математика», спускаясь от каждой буквы на одну строку вниз или на одно место правее или левее?
А Б Б Б р р р р р А А А А А А А ккккккккк ААААААААААА ддддддддд А А А А А А А Б Б Б Б Б
Р Р Р К
М М М М М
А А А А А А
Т Т Т Т Т Т Т
ИИИИИИИИ
КККККККК
А
АААААААААА
3. — Куда ты так спешишь?
— На шестичасовой поезд. Сколько еще минут осталось до отправления?
— 50 минут назад с 3 часов прошло вчетверо больше минут, чем сейчас осталось до отправления шестичасового поезда.
Во сколько часов и минут происходил этот диалог?
4. За обеденным столом собрались одни дедушка, одна бабушка, два отца, две матери, четверо детей, три внука, один брат, две сестры, два сына, один свекр, одна свекровь и одна невестка.
На сколько персон минимально должен быть накрыт стол?
5. Маневровая задача. Локомотив должен прибыть на станцию в правом верхнем углу рисунка. Для этого ему необходимо пройти пронумерованные стрелки — одни в прямом направлении, другие в обратном. Железнодорожный путь в некоторых местах преграждают препятствия.
Как должен маневрировать локомотив, чтобы прибыть на станцию?
6. В вагоне метро рядом сидят 5 девушек. Анетта сидит через столько же человек от Бабетты, как Колетта. Доретта сидит через столько же человек от Анетты, как Колетта. Прекрасная Жаиетта сидит между двумя своими лучшими подругами.
Как их зовут?
7. Для того чтобы отгадать задуманное целое число, его необходимо умножить на следующее за ним число и из произведения вычесть задуманное.
Как по полученному результату найти задуманное число?
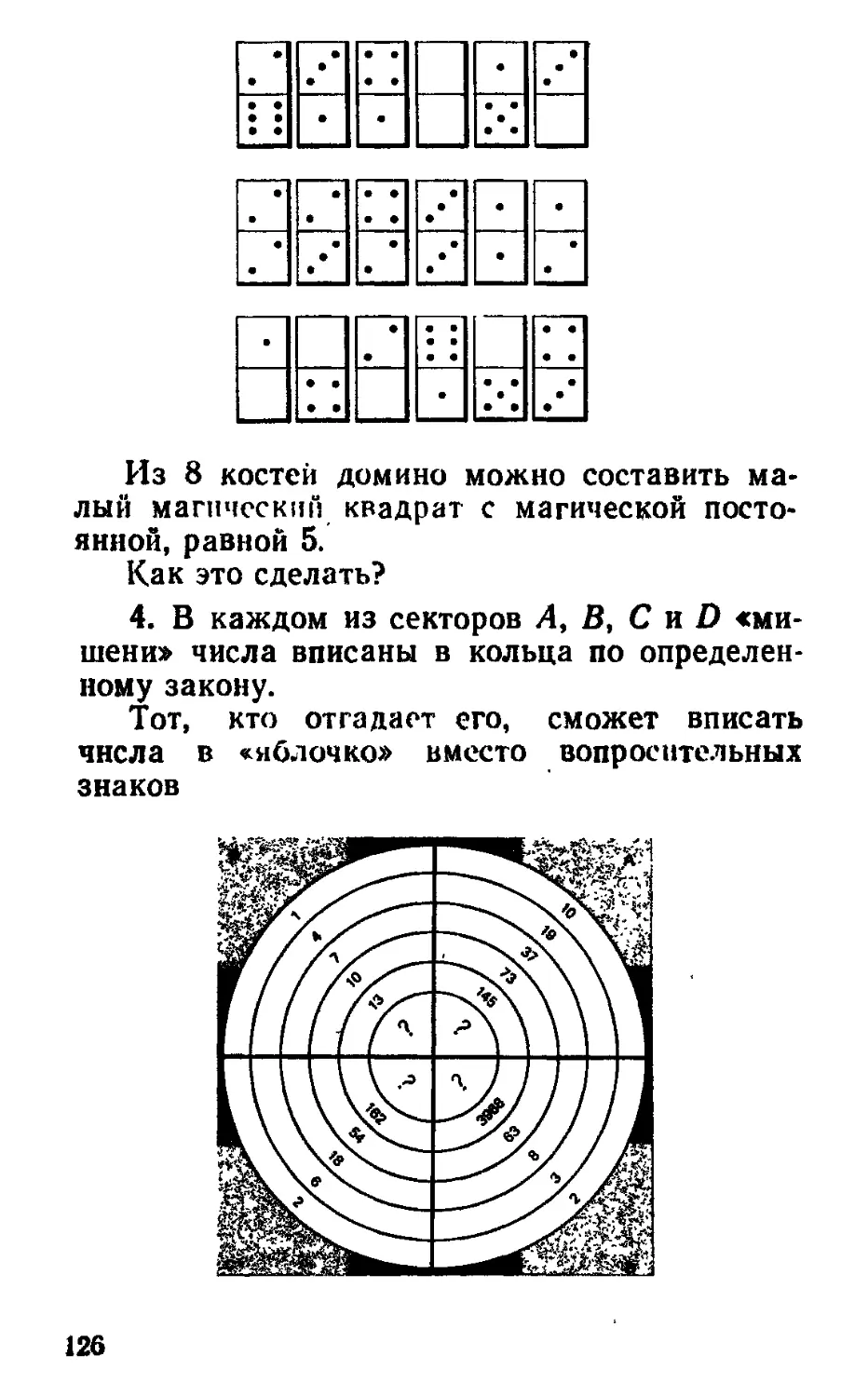
8. а) В верхнем магическом квадрате требуется расставить 9 степеней двойки так, чтобы произведение чисел, стоящих в каждой строке, в каждом столбце и на каждой диагонали, были равны. 21 22 2з
24 2s 26
27 28 2®
б) В нижнем магическом квадрате 9 чисел, вписанных в клетки, требуется расположить так, чтобы произведения чисел, стоящих в каждой стро-ке, в каждом столбце и на 1 а а2
ь ab а2Ь
ь2 аЬ^ А2
каждой диагонали, были рав-
ны а3Ь3, после чего положить а=2, Ь = 3.
9. В каждой из четырех серий фигур верхнего ряда требуется иайти в нижнем ряду ту из четырех фигур, обозначенных буквами А, В, С, D, которой можно, не нарушая логической последовательности, заполнить правый пустой квадрат в верхнем ряду.
D А В С D
D А В С D
- 10. «Четырехзначный номер автомашины моего учителя математики очень легко запомнить,— сообщил Ганс своему приятелю.— Номер симметричен, а сумма его цифр совпадает с числом, образуемым первыми двумя цифрами».
Какой номер у автомашины учителя математики?
11. Моника попросила Марию-Луизу: «Назови мне любое трехзначное число, все цифры которого отличны от нуля и попарно различны. Запиши его на листке бумаги и прибавь к нему все трехзначные числа, которые получаются из него при перестановке цифр»;
И не успела Мария-Луиза вычислить сумму, как Моника назвала ответ.
Как ей удалось так быстро получить результат?
12. Задача из английской газеты «Обс^р-вер». Все звери в зоопарке находятся ие в своих клетках. Служителю необходимо как можно быстрее разместить животных по их клеткам. Поскольку все звери, кроме осла,— хищники, их нельзя помещать вдвоем в одну клетку или выпускать вдвоем в общий вольер, в который открываются клетки.
Какое наименьшее число «переселений» должен произвести служитель зоопарка, что-
бы ге звери оказались в своих клетках? (Предполагается, что в присутствии служителя звери друг иа друга ие нападают.)
13. Известный английский составитель задач по занимательной математике Барнард назвал эту игрушку, известную у нас под названием «мобиль», эквнлябром (производное из «эквилибристики» и «канделябра»).
Какие 2 предмета (2 рыбки, 2 шарика, 2 колокольчика, 2 коромысла или какая-то комбинация
из 2 различных предме-
тов) могут удержать систему в равновесии вместо вопросительного знака? (Вес нитей в отличие от веса коромысла пренебрежимо мал.)
14. В одну из разновидностей игры с игральными костями играют по следующим правилам. Если при бросании кости выпадает четное число, то игрок получает столько «плюс очков», сколько выпало. Если при очередном бросании кости выпадает нечетное число очков, то игрок получает столько «минус очков», сколько выпало.
Игрок бросил кость 5 раз подряд. Два раза выпало одно и то же число очков, а в трех остальных случаях число очков было различным. При подсчете число «плюс очков» совпало с числом «минус очков».
По скольку очков выпадало в отдельных бросаниях?
15. Слова, приводимые ниже под номерами (1) — (4), составлены из тех же букв, что и названия профессий, требующих основательной математической подготовки. Что это за профессии?
(1) ДОЕНИЕ, РАНЖИР
(2) ТРОТИЛ, СМЕСЬ, ОТО*
(3) ВАЛ, МЕТЕЛЬ, ПОРА
(4) РОСТ, ПИ, ГРАММ
16. Задача Л. Эйлера. Некий чиновник купил лошадей и быков за 1770 талеров. За каждую лошадь он уплатил по 31 талеру, а за каждого быка — по 21 талеру.
Сколько лошадей и сколько быков купил чиновник? Сколько решений — одно или несколько — допускает задача?
Общая теория относительности.
арисрметика С
ПТИЧЬЕГО
ПОЛЕТА
Человек, смолоду приученный к догматическому мышлению, к чрезмерному почтению к абстрактным формулам, обречен на постоянные и не очень приятные для него столкновения с жизнью.
Э. Ильенков*
В эпоху Возрождения в XVI в. математика достигала своего расцвета. Введя буквенные обозначения неизвестных величин, Франсуа Виет (1540—1603) формализовал алгебраические преобразования и тем самым сделал решающий шаг. Работы Виета позволили применить алгебраические методы к задачам, в которых величины принимают числовые значения, что намного упростило вычисления.
Большие заслуги в развитии арифметики принадлежат Михаэлю Штифелю (1487— 1567). В 1544 г. вышло из печати его трехтомное сочинение <Arithmetica Integra» (Полная арифметика). В ием автор систематически изложил весь свод математических знаний своего времени.
Эту главу мы начинаем с одной из задач Штифеля.
1. Сумма двух чисел равна 19, а сумма их квадратов равна 205.
Что это за числа?
1. Пусть х н у — натуральные числа.
В следующих примерах требуется заменить звездочки знаками >, < или = так, чтобы получились истинные высказывания.
* Ильенков Э. В. Учитесь мыслить смолоду. М.. Знание, 1977, с. 59.
а) Если *>8, то *4-3 *10.
б) Если 60*=50«/, то * <• у.
в) Если 5*>10 и у>х, то у * 3.
г) Если *>«/, то t/4-2 **4-5-
д) Если х>у, то 60 — х «75 — у.
е) Если у<5, то Зу *17.
3. Найдите 2 различных натуральных числа, удовлетворяющих следующим условиям:
а) их среднее геометрическое на 4 больше меньшего из чисел;
б) их среднее арифметическое на 6 меньше большего из чисел.
4. Выясните, существуют ли натуральные числа, обладающие следующими свойствами.
Остаток от деления такого числа на 3 равен 1, на 4 равен 2, на 5 равен 3, на 6 равен 4.
Если такие числа существуют, укажите наименьшее из них, обладающее всеми нужными свойствами.
5. Сумма двух натуральных чисел равна 90. Сумма 25% первого и 75% второго числа равна 30.
Требуется найти оба числа.
6..В ыберите значения переменных а, b и с из чисел 13, 15 и 20 так, чтобы значение выражения
а(с—Ь) Ь—а
было целым положительным числом.
7. Какое значение принимает выражение а (а-|-2) 4-е (с — 2) — 2ас
при а — с=7?
8. Дано множество
17= {3, 4, 5, 6, 7, 8, 9} и два его подмножества
Л={4, 6, 7} и В={4, 5, 6, 8}.
Из каких элементов состоят следующие множества *?
а) ЛОВ, в) B=U ^В, > д) Л^В б) Л Л В, г) и=и^и,
Математические головоломки
Магический квадрат. Какие целые поло* жительные значения следует придать переменным х, у и z, чтобы суммы трех чисел, стоящих в каждой строке, в каждом столбце и на каждой диагонали, были равны? Найденное решение нетрудно проверить: числа, стоящие в четырех угловых клетках, четны и
* Для тех, кто не знаком с обозначениями операций, принятыми в теории множеств, поясним, что Х()У — множество (называемое объединением множеств X и У), состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств X и У, Х()У — множество (называемое пересечением множеств X и У), состоящее из элементов, принадлежащих как множеству X, так и множеству У; Х^У—множество (разность множества X и множества У, порядок множеств существен!), состоящее из тех элементов множества X, которые не принадлежат множеству У.— Примеч. пер.
образуют арифметическую прогрессию, сумма которой в 4 раза больше числа, стоящего в центральной клетке.
X х + у -10 4z — х
X + Z ' У Z
Z + у - X 2z + у - х 2z
Кросснамбер. Дрезденский математик К. Хайнрих предложил следующий «числовой кроссворд» (кросснамбер). В каждую из 36 клеток следует вписать по одной из цифр О, 1, 2, 9. Возникающие при этом двух-,
трех- и четырехзначные числа «простираются» по горизонтали или по вертикали от клетки с номером до ближайшей ограничительной черты или края большого квадрата. Все эти числа должны удовлетворять следующим условиям.
1 2 3 4 5
6 7 8
9 тА* 10
12 13
15 ‘fS
19 20
По горизонтали. 1. Кратное числа, стоящего под номером 3 по горизонтали. 3. Квадрат числа, стоящего под номером 3 по вертикали. 6. Кратное суммы цифр числа, стояще
го под номером 7 по вертикали. 8. Число с такой же суммой цифр, как у числа, стоящего под номером 16 по вертикали. 9. Кратное квадратному корню из числа, стоящего под номером 14 по вертикали. 10. Кратное числа, стоящего под номером 14 по горизонтали. 12. Число, стоящее под номером 9 по горизонтали. 14. Простое число. 15. Квадрат, являющийся одновременно кубом., 17. Число, стоящее под номером 14 по вертикали. 19. Простое число. 20. Число с суммой цифр, как у числа под номером 3 по вертикали.
По вертикали. 1. Произведение чисел, стоящих под номером 14 по горизонтали, и под номером 18 по вертикали. 2. Кратное числа, стоящего под номером 16 по вертикали. 3. Кубический корень из числа, стоящего под номером 5 по вертикали. 4. Кратное числа, стоящего под номером 3 по горизонтали. 5. Число, одинаково читаемое слева направо в справа налево. 7. Простое число. 10. Кратное числа, стоящего под номером 14 по горизонтали. 11. Кратное числа, стоящего под номером 19 по горизонтали. 13. Простое число. 14. Число, стоящее под номером 17 по горизонтали. 16. Квадратный корень из числа, стоящего под номером 15 по горизонтали. 18. Простое число.
9. При каких целых неотрицательных значениях а, Ь, х, у и z истинны следующие высказывания? (В каждом случае укажите все множество допустимых значений.)
а) 5<а<60, г) 30—(z-z)=z,
б) (х+3)4=4х+12, д) 3(6+1)<10.
в) (5у)+у-4=9у,
Есть ли еще вопросы?
Английский физик П. А. М. Дирак привык выражаться ясно и четко. В конце одного из своих докладов он спросил, обращаясь к аудитории: — Есть ли еще вопросы?
— Я не понял, откуда следует вон та формула,— отозвался один из слушателей.
— Это не вопрос, а утверждение,— возразил Дирак и, обращаясь к аудитории, повторил:
— Есть ли еще вопросы?
10. Найдите все двузначные натуральные (исла, которые равны утроенной сумме своих цифр.
11. Какими цифрами следует заменить а и b (одинаковым переменным соответствуют одинаковые цифры), чтобы выполнялось равенство
(а-+-а)+3(&-|-Ь) =аа+&а?
12. При каком натуральном числе п произведение предшествующего числа и числа, следующего за п, равно 2208?
13. Какие натуральные числа х и у удовлетворяют уравнению
— + _2_ + J_==1? х у ху
14. Можно ли заменить девять неизвестных а, Ь, с, ..., h, i в системе уравнений
девятью цифрами 1, 2, 3, .... 8, 9 так, чтобы равенства не нарушались?
15. Сколькими способами можно заменить переменные а и b числами от 0 до 20, не нарушив неравенства a<Zb?
16. При каких натуральных числах а>Ь>0 выполняется неравенство
_2±*>а.Ь?
а—Ь
17. Укажите любые 2 значения переменных х, t и z, при которых выполняются следующие соотношения:
а) — ; х> —, б) 7 : t<7, в) Л; z«= Л. 2 2 7 2 2
18. Найдите множество решений неравенства
х2+ (х-Ь1)2+ (х+2)2> (х+3)»+ + (х+4)2+(х+5)2.
19. Найдите множество решений уравнения (х2-|-х+1) (2х2-|-2х — 3) = — 3 (1 — х — х2).
20. Найдите все упорядоченные пары (х, у) неотрицательных целых чисел хну, удовлетворяющих системе неравенств
x+f/<4, (1)
2х4-5у>10. (2)
21. Найдите вЬе упорядоченные тройки (х, у, г) неотрицательных целых чисел х, у и z, удовлетворяющие системе уравнений
7хЧ-5и — 2=8, f/+z=ll.
ЗАНИМАТЕЛЬНАЯ
О «сеансах», или беседах, проводимых известным польским математиком Стефаном Банахом (1892—1945), ныне ходят легенды. Банах приглашал своих единомышленников— профессиональных математиков и студентов Львовского университета — в «Шотландское кафе», где обсуждал с ними различные интересные и нередко весьма необычные математические идеи и проблемы. Банах считал, что в непринужденной атмосфере среди отдыхающей публики под звуки музыки и уличного шума, доносящегося из-за зеркальных витрин заведения, его коллегам — юным и зрелого возраста — легче отрешиться от скованности. Накал страстей во время научных споров нередко бывал весьма высоким. К великому неудовольствию официантов необходимые выкладки производились спорящими сторонами тут же на столиках белого мрамора. Во избежание скандала Банах завел толстую книгу. В нее стали записывать наброски решений, которые затем постепенно дополнялись и усовершенствовались. За особо изящные и оригинальные решения участники круглого стола устанавливали специальные призы — от чашки кофе «мокко» до живого гуся. Частым гостем этих бесед был близкий друг Банаха замечательный польский математик Гуго Штейнгауз, известный не только своими научными достижениями, но и как автор многочисленных задач по занимательной математике.
Эту главу мы хотим начать с одной из задач, поставленных Гуго Штейнгаузом.
1. Измерить с помощью линейки длину пространственной диагонали кирпича, имеющего форму прямоугольного параллелепипе-56
да, т. е. расстояние между двумя его наибо* лее удаленными вершинами.
Предлагаемый способ измерения диагонали должен быть применимым на практике, т. е. таким, чтобы его можно было внедрить на производстве. Пользоваться теоремой Пифагора не разрешается.
2. Даны 2 развертки куба: (1) и (2).
Какие из изображенных здесь кубов можно сложить из этих разверток?
3. Каждую из изображенных здесь разверток сложите в куб. (Куб должен быть «замкнут со всех сторон».)
4. а) Трапеция, которую вы видите на ри-сунке, составляет часть равиостороинего треугольника?
Разделите эту трапецию на 4 равновеликие части.
б) Разделите этот невыпуклый шестиугольник на 4 равновеликие части.
5. Кому из девушек адресовано письмо, конверт которого в развернутом виде изображен слева?
6. От одного кубика, помеченного кружком на верхней грани, требуется пройти к другому, т. е. проложить путь либо слева направо, либо справа налево. Ходить можно только по горизонтали и вертикали на столько шагов, сколько очков «выпало» на исходном кубике, т. е. стоит на его верхней грани. (Например, если на верхней грани стоит 5 очков, то при очередном ходе следует сделать 5 шагов, а если на верхней грани стоит 2 очка, то 2 шага.) С каждым ходом направление продвижения меняется. Если при очередном ходе оказывается невозможным сделать нужное число ходов в выбранном направлении, то направление выбрано неверно. В подобных случаях следует попытаться продвинуться в другом направлении.
Вая&)»)Н)В)вЖ
Требуется найти
be de
** MM
9 10 r ~
В каждом случае элементы фигуры, кото-рые требуется найти, изображены голубым Я цветом.
▼
7. Фигуры а, Ь, с, d и е разрезаны на части 1—12, изображенные на рисунке. Части какой фигуры вы видите на каж« дом из этих рисунков?
8. Как сложить из квадрата правильный шестиугольник? (Квадрат разрешается как угодно перегибать и складывать. Размеры шестиугольника несущественны.)
9. Четыре стержня А, В, С и D имеют соответственно длину а, Ь, с и d. Если к стержню А приставить стержень В, то получится стержень такой же длины, как и стержень С, а стержень В имеет такую же длину, какую имеет стержень, составленный из стержней А и D Наконец, длина стержня D — лишь 2/з длины стержня С.
Определить длины Ь, с н d, выбрав за единицу длины а.
10. Из одного листа бумаги требуется сделать заготовку для 16-страннчной тетрадки и, не разрезая, заранее пронумеровать страницы. Левая половина каждого разворота должна иметь четный номер, а правая — нечетный.
Как сложить лист и пронумеровать страницы будущей тетради?
11. Два соседних угла А и В шахматной доски ABCD соединены отрезками прямых с серединой М противоположной стороны. Образовался треугольник AMD.
Сколько полей шахматной доски не имеют с треугольником AMD общих внутренних точек?
ТРЕНИРОВКА
ПО СОВРЕМЕННОЙ
математике
Не клянись именем своего учителя, а приведи доказательство.
Древняя поговорка
1. При повторении темы «Рациональные и иррациональные числа» ученики среди прочих высказали следующие утверждения:
а) Произведение двух различных иррациональных чисел есть всегда иррациональное число.
б) Сумма двух различных иррациональных чисел есть всегда иррациональное число.
в) Сумма рационального и иррационального чисел есть всегда иррациональное число.
Какие из этих утверждений истинны и какие ложны?
2. Доказать, что удвоенное произведение произвольного натурального числа и числа, следующего за ним, на 1 меньше суммы квадратов этого числа и числа, следующего за ним.
3. Прямоугольник составлен из 7 конгруэнтных квадратов.
Доказать, что углы аир удовлетворяют неравенству
26,5°<а+Р<26.6°
4. Знания учащихся в ГДР оцениваются по 5-балльной системе: высшей считается
оценка 1, затем в порядке убывания идут оценки 2, 3 и т. д.
В конце учебного года ученик решил подсчитать свой средний балл. Он знал, что по 6 предметам ему поставили единицу, а по 3 другим предметам — тройку. Оценки по 3 остальным предметам еще не были известны, но ои твердо рассчитывал получить по ним либо 2, либо 3.
Какие оценки ему следовало бы получить, чтобы средний балл был лучше, чем 2?
5. Две задачи Исаака Ньютона.
а) Даны 3 члена геометрической прогрессии. Их сумма равна 19, а сумма их квадратов— 133. Определить эти члены.
б) Даны 4 члена геометрической прогрессии. Сумма двух крайних членов равна 13, двух средних 4. Определить эти члены.
6. Дано линейное неравенство
<3x4-2
5
а) Решить это неравенство в области действительных чисел.
б) Найти следующие множества, перечислив их элементы:
1) множество решений. Pi неравенства в области натуральных чисел;
2) множество решений Ра неравенства в целых числах, удовлетворяющих условию —4<х<1;
3) множество М всех элементов, входящих как в Pj, так и в Ра.
7. На автобусной остановке можно сесть на автобусы, движущиеся по различным маршрутам с интервалами движения 5, 2, 10 и 15 мин.
Какова вероятность того, что первым подойдет автобус, следующий по маршруту с интервалом движения 2 мин?
Как кошка с собакой
а) Построив графики следующих функций в прямоугольной системе координат, вы получите некое «произведение искусства».
Функция Область Авали iji4<xk<h
определения выражение
ь /3 h h ft
h h
I® ho
hi hj IIS fu
4<x<8
8<xs£9
9s£xs£ 10
lOsgxsg 16 16<xsg 18
5sgxsg8
8<x< 10
11 <x< 15
16<x< 18
-—s£x<7
2
.11 <x< 12
14 ^x 15
x = 8
0 = -|-+11 y=2x— 1 v=-7x4-80 0=10 y=x—6 (/=-2x4-21
x 28
3 + 3 0=—6x4-60 0=6 j/=6x—96
2 51
0= -7- x4- -5-0=-6x4-72 z/=6x—84 0=14
б) Перед вами «портрет» кошки. Найдите 14 линейных функций, описывающих отрезки, из которых составлена картинка.
Для тех, кто готовится стать математиком
Юный студент-математик обратился к известному специалисту по теории чисел Э. Ландау, заявляя, будто ему удалось иайти доказательство великой теоремы Ферма, утверждающей, что ни при каком целом п>2 нельзя найти 3 целых числа, х, у и z, которые бы удовлетворяли уравнению Xn-\-y'n=Zn.
Хотя математики всего мира на протяжении вот уже 300 лет пытаются доказать эту теорему, их усилия пока не увенчались успехом. Ландау терпеливо выслушал студента, затем усмехнулся и попросил его решить совсем простенькую математическую задачу, которую тут же продиктовал. Как ни старался студент, решить задачу Ландау ему так и не удалось. И тогда известный профессор дал ему ценный совет: «Прежде чем пытаться потрясти основы науки, необходимо их изучить!»
8. Известная теорема гласит: если плос-кость е пересекает две параллельные плос-кости а и р, то линии пересечения параллель-ны. S
Кто сумеет доказать эту теорему на языке теории множеств?
9. Куб рассечен плоскостью так, что сечение имеет форму равностороннего треугольника, образованного диагоналями некоторых граней куба.
а) Начертить куб с проведенным сечением в косой проекции.
б) Построить развертки обоих тел, на которые распадается куб.
в) Как называется меньшее из этих тел?
10. Перед нами коробка, вмещающая 160 круглых карандашей, если их укладывать в 8 рядов по 20 штук в каждом.
Можно ли и как именно уложить карандаши по-другому, чтобы их вошло в коробку больше 160?
11. В одном проектном институте имеется 3 отдела: А, В и С. При обсуждении одного проекта руководство института условилось придерживаться следующего порядка.
а) Если в обсуждении не принимает участия отдел В, то отдел А также не участвует в обсуждении.
б) Если в обсуждении проекта принимает участие отдел В, то отделы Л и С также участвуют в обсуждении.
Должен ли при этих условиях отдел С принимать участие в обсуждении проекта, если в обсуждении участвует отдел Л?
12. Пусть А, В и С — множества натуральных чисел, относительно которых известно следующее:
(1) Л1|В={2, 3, 4, 5, 6, 7, 8);
(2) B|JC={1,2, 4, 6,8};
(3) CU^={1, 2, 3, 4, 5, 7, 8};
(4) ЛЛВ={2};
(5) ВПС={2, 4, 8} ;
(6) СЛЛ={2};
Какие числа принадлежат каждому из множеств Л, В и С?
Примечание. Под A(JB принято понимать объединение множеств А и В, т. е. множество, содержащее те и только те элементы, которые принадлежат по крайней мере одному из множеств Л и В. Под Л("|В принято понимать пересечение множеств Л и В, т. е. множество, содержащее те и только те элементы, которые принадлежат как множеству А, так и множеству В. (И в объединении, и в пересечении каждый элемент включается только один раз.)*
13. Спичечный коробок имеет длины ребер а=17 мм, 6=37 мм и с=52 мм.
Какой должна быть развертка упаковки для 10 коробков, чтобы расход оберточной бумаги был минимальным?
14. В некоторой местности требуется проложить дороги между четырьмя населенными пунктами А, В, С и D. При обсуждении воз
* Смысл обозначений теоретико-множественных операций пояснен в примечании иа с. 50.— Примеч. пер.
можных вариантов были высказаны следующие пожелания.
а) Одним хотелось бы, чтобы из населенных пунктов Л и 5 выходило по 3 дороги, из населенного пункта С — 2 дороги и из населенного пункта D — 4 дороги.
б) Другие отдавали предпочтение варианту, в котором из каждого населенного пункта выходило бы по 3 дороги.
в) Третьи считали более удобным, чтобы из населенного пункта А выходила одна дорога, а из каждого из остальных населенных пунктов — по 2 дороги.
Каждое ли пожелание могут учесть проектировщики? Должны ли дороги пересекаться?
иии на КАЖДОМ ШАГУ
Ни один человек еще не научился думать, читая в готовом виде записанные мысли другого человека. Научиться думать можно, лишь размышляя самостоятельно. Михай Эмииеску*
1. Однажды мы невольно стали свидетелями следующего разговора.
— Правильно ли я тебя понял? Ты утверждаешь, что состоишь членом шахматного клуба вдвое дольше, чем я.
— Совершенно верно.
— Но насколько мне помнится, ранее ты говорил, что состоишь членом шахматного клуба втрое дольше, чем я?
— Два года назад? Но тогда мой стаж как члена клуба действительно был в 3 раза больше твоего, а сейчас лишь в 2 раза.
Сколько лет каждый из двух собеседников состоит членом шахматного клуба?
2. По обычаю одной восточной страны жене запрещается оставаться без мужа в обществе мужчин. Однажды трем супружеским парам понадобилось переправиться с северного берега реки иа южный. Единственное подручное средство — лодка, вмещающая Двух человек.
В какой последовательности они должны были переправляться, чтобы соблюсти строгий обычай?
3. При распродаже коврижек по 12 и по 17 марок за штуку в кассу за короткое время
* Михай Эмииеску (1850—1889) —румынский и молдавский поэт.— Примеч. пер.
поступило 478 марок. Коврижек каждого сорта было распродано более 10 штук.
Сколько коврижек каждого сорта было распродано?
4. Из 100 коллекционеров 70 собирают старинные монеты, 75 — значки, 80 — этикетки со спичечных коробков и 85 — марки.
Сколько из них увлекаются всеми четырьмя видами коллекционирования сразу?
5. Одна швейцарская община насчитывает 50 членов. Родной язык всех 50 членов общины — немецкий, но
20 из них говорят еще и по-итальянски,
35 из них владеют французским и
10 не знают ни итальянского, ни французского.
Сколько членов общины говорят и по-французски, и по-итальянски?
6. Замечательный венгерский эстрадный вычислитель Ференц Патаки, способный за считанные секунды Неремножить в уме 2 трехзначных числа, выступая в 1979 г. по телевидению, продемонстрировал следующий фокус.
«Умножьте свой размер обуви на 2, прибавьте к произведению 39, умножьте полученную сумму на 50, прибавьте к произведению 29, вычтите из суммы год своего рождения»,— попросил Патаки. К удивлению зрителей каждый из них получил четырехзначное число, две первые цифры которого задавали номер обуви, а две последние — возраст зрителя в конце календарного года.
Объясните, на чем основан фокус Ференца Патаки.
7. Ящик можно обвязать веревкой тремя различными способами.
В каком из трех случаев потребуется самая короткая и в каком самая длинная веревка? (Размеры ящика удовлетворяют неравенству а-}-&> 2с.)
8. Гастрономическая задача.
Рыбу прекрасно готовят тут, Форель отварная — король всех блюд. Вот принят заказ. Все готово. Несут! По порции рыбы на стол подают.
Но что там за шум? То кричат повара, <Для порции нам не хватает стола, И по две на стол мы подать не смогли бы, Остался бы стол чей-то вовсе без рыбы». Вы назвать бы не сумели Нам число порций форели И количество столов Там, где хвалят поваров?
9. Хотя стоимость входного билета в цирке была снижена на 30%, выручка оказалась прежней.
На сколько- процентов возросло число зрителей?
10. Дерево отбрасывает тень длиной 10 м. Столб длиной 3 м отбрасывает тень длиной 2 м.
Чему равна высота дерева?
11. Как выглядит шнуровка левой и правой туфли изнутри?
12. Проехав треть Пути, пассажир скорого поезда' наконец заснул. Когда он проснулся, до станции назначения оставалось проехать половину того расстояния,, которое отделяло его от станции назначения, когда он заснул.
Какую часть пути проехал поезд, пока пассажир спал?
13. Группе туристов ревни А в деревню В.
нужно попасть из де-
Какой путь им выбрать, чтобы добраться побыстрее? (Числа на плане показывают, сколько минут необходимо затратить на прохождение соответствующего участка пути.)
14. Какие из изображенных на рисунке деталей выпилены любителем головоломок и какие добавлены художником?
Шедевр
Математик и поэт, сочинитель эпиграмм Абрахам Готхельф Кестнер (1719—1800) в бытность свою студентом учился необычайно легко, словно играючи, и даже накануне выпускных экзаменов мог позволить себе вместо того, чтобы Сидеть дома, уткнувшись носом в книги, отправиться на прогулку с дочкой своего профессора. Когда же профессор упрекнул его в легкомыслии, Кестнер тотчас же возразил: «Господин профессор, вы же сами рекомендовали своим студентам неукоснительно следовать лучшим образцам. Вашу дочь я считаю совершенством».
15. Предлагаем вниманию читателя четыре примера на сложение, в которых цифры заменены буквами (одинаковые буквы соответствуют одинаковым цифрам, различные — различным). Требуется восстановить цифровую запись всех 4 примеров (знать немецкий язык для этого не обязательно).
а) , EBER, б) , SCHI, в) , AAL г) , ICH
Т ENTE, + LIFT, + AAL + BIN
+ dJue’ SCHON. FANG LIEB
RABb.
TI ERE,
16. 45% поступлений лотереи расходуется на выплату выигрышей.
Сколько билетов стоимостью по 5 франков должны распространить организаторы лотереи, если на выплату выигрыша предполагается израсходовать 87300 франков?
17. На заседании правления садового кооператива обсуждается вопрос о стоимости пригласительного билета на праздник урожая. Расходы на проведение праздника, по мнению членов правления, должны составить не менее 420 марок. Ожидается, что в празднике примут участие 150 членов кооператива и 100 гостей. Расходы решено покрыть за счет продажи пригласительных билетов. Сборы должны составить сумму, несколько превышающую 420 марок. Члены правления считают, что стоимость пригласительного билета для гостей должна превышать стоимость пригласительного билета для членов кооператива, но не более чем в 2 раза.
Сколькими способами можно назначить цены на пригласительные билеты?
18. Сколькими способами можно разменять 1 марку, имея достаточный запас монет достоинством в 1 пфенниг, 5 пфеннигов, 10 пфеннигов, 20 пфеннигов и 50 пфеннигов?
19. Старинная задача на бытовые темы. Ее задавал своим ученикам учитель арифметики Якоб из Кобурга, чей учебник был напечатан в 1599 г. во Франкфурте.
Расстояние между 2 городами составляет 260 миль. Из обоих городов навстречу друг другу выходят 2 гонца. Один из них ежедневно проходит на 2 мили больше, чем другой. Через 12 дней гонцы встречаются.
Сколько миль проходит ежедневно каждый гонец?
слово ЗНАМЕНИТЫМ МАТЕМАТИКАМ
Ничего не сделано, если хоть что-то осталось недоделанным.
Карл Фридрих Гаусс
1. Бхаскара I (VI в.). Найти натуральные числа, дающие при делении на 2, 3, 4, 5 и 6 остаток 1 и, кроме того, делящиеся на 7.
2. Брахмагупта (около 600 г.). Следующая задача заимствована из трактата этого индийского математика. «Если число дней уменьшить на I, затем разделить на 6 и прибавить 3, то получится 7s первоначального числа дней».
Сколь велико число дней?
3. Ал-Хорезми (около 780 г.—850 г.). Разложить число 10 на 2 слагаемых, сумма квадратов которых равна 58.
4. Алкуин (около 800 г.). Король Карл был большим любителем наук и всячески поощрял их развитие. Беседы за его круглым столом нередко переходили в состязания на лучшее решение хитроумных головоломок. Самым известным из. участников этих собраний был математик Алкуин, ученый монах из Ирландии. Он написал несколько элементарных учебников по математике.
Однажды король и Алкуин отдыхали вместе после охоты, и Алкуин в шутку предложил королю прикинуть, за сколько прыжков его гончая настигнет зайца, если первоначально их разделяет расстояние 150 футов, заяц с каждым прыжком удаляется от собаки на 7 футов, а собака бежит быстрее зайца и с
каждым прыжком приближается к нему на 9 футов. Карл был не только искусным охотником, но и знал толк в арифметике.
Что ответил король Алкуину?
5. Леонардо Пизанский (XIII в.). . Этот итальянский математик, известный под именем Фибоначчи, т. е. сына Боначчи, поставил в своей «Книге абака» следующую задачу. Имеется 5 гирь, позволяющих взвесить любой предмет с массой от 1 до 30 кг, если она выражается целым числом килограммов. Все гири при взвешивании разрешается ставить только на одну и ту же чашу весов.
Какие гири понадобятся для, взвешивания 1 кг, 2 кг, .... 30 кг?
6. Абу-ль-Вафа (X в.). Два из трех равновеликих квадратов разрезать на 8 частей так, чтобы из них и из третьего равновеликого квадрата можно было составить квадрат большего размера.
7. Бхаскара II (1114—1185). Одна треть, одна пятая и одна шестая цветов лотоса в венке посвящена богам Шиве, Вишну и Сурье, одна четвертая — Бхавани. Остальные 6 цветов предназначаются почитаемому праведнику.
Сколько цветов лотоса сплетено в венок?
8. Адам Рис (1492—1559). Трое подмастерьев хотели купить дом за 204 гульдена. На покупку первый дал втрое больше денег, чем второй, а второй дал вчетверо больше, чем третий.
Сколько гульденов внес на покупку дома каждый из трех подмастерьев?
9. Мануэль Мосхопулос (около 1453 г.). Этот ученый из Константинополя придумал следующую задачу: расположить числа 0, 1, 2, 14, 15 в вершинах внутреннего и внеш-
него кубов так, чтобы сумма чисел, стоящих у вершин любой замкнутой четырехзвенной ломаной, была равна 30.
10. Иоганн Бутев (1549 г.). В его книге по математике под названием «Логистика» есть такая задача: «Если стоимость 9 яблок, уменьшенная на стоимость 1 груши, составляет 13 динаров, а стоимость 15 груш, уменьшенная на стоимость 1 яблока, составляет 6 динаров, то сколько, спрашиваю я, стоит 1 груша и 1 яблоко?»
11. Георг Мор (1640—1697). Этот датский математик показал, как с помощью циркуля и линейки разделить данную окружность на 4 равные дуги.
12. Исаак Ньютон (1642—1727). В своей «Универсальной арифметике» Ньютон высказал убеждение, что «при изучении наук при
меры полезнее, нежели правила». В «Арифметике» Ньютона среди прочих есть и такая задача.
На трех лугах площадью 3‘/з, 10 и 24 га трава растет одинаково, т. е. с одинаковой густотой и с одним и тем же приростом. После того как на первом лугу 12 коров паслись 4 недели, а на втором лугу 21 корова паслась 9 недель, трава оказалась съеденной настолько, что оба пастбища на время пришлось забросить.
Сколько коров можно пасти на третьем лугу в течение 18 недель?
13. Альберт Эйнштейн (1879—1955). Даже став всемирно известным ученым, Эйнштейн продолжал предлагать вниманию читателей газеты «Франкфуртер цайтунг» различные задачи на сообразительность. Вот одна из них.
Девять кружков образуют вершины 4 малых и 3 больших равнобедренных треугольников. Требуется вписать в эти кружки числа от 1 до 9 так, чтобы суммы чисел, стоящих в вершинах каждого из 7 равнобедренных треугольников, были равны.
14. Христиан Гольдбах (1690—1764) высказал гипотезу о том, что любое четное число, большее 2, представимо в виде суммы 2 простых чисел.
Проверьте гипотезу Гольдбаха для всех четных чисел, меньших 50. (Христиан Гольдбах высказал свою гипотезу в письме Леонарду Эйлеру. Доказательство ее до сих пор неизвестно.)
15. Сриниваса Рамануджан (1887—1920). Английский математик Г. Г. Харди однажды отправился навестить своего друга и сотрудника индийского математика С. Рамануджана в кебе с номером 1729.
— Весьма скучное число,— заметил в разговоре Харди.
— Напротив!—живо возразил Рамануджан.— Это очень интересное число: 1729— наименьшее из чисел, представимых в виде двух кубов двумя различными способами.
Найдите оба разложения числа 1729 в сумму двух кубов.
16. К. Ф. Гаусс (1777—1855) имел обыкновение кодировать свои записи. Знаменательные события своей жизни он кодировал номерами дней, отсчитываемых с рождения до соответствующей даты. * Защитив 16 июля 1799 г. ученую степень доктора, Гаусс закодировал эту дату числом 8113. Самым ранним знаменательным событием, отмеченным в личных записках Гаусса, был день, когда 15-летннй Гаусс занялся проблемой распределения простых чисел. Это произошло на 5343-й день после его рождения, и дата вошла в записи под кодом 5343.
На какой год, месяц и день приходится эта дата?
Пальто Эйнштейна
Эйнштейн встретил как-то раз знакомого. — Господин Эйнштейн, вам непременно следует купить себе новое пальто!— посоветовал тот.
— Зачем?— удивился Эйнштейн.— Ведь в этом городе меня никто не знает.
Через несколько лет они снова встретились в том же городе. Эйнштейн был в том же пальто, давно отслужившем свой век. Знакомый снова посоветовал Эйнштейну купить новое пальто.
— Зачем?— возразил Эйнштейн,— теперь меня здесь знает каждый.
НАША
СЕКЦИЯ
ИГР
sjek *як
Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. Блез Паскаль
1. Построй мостик. Американский матема-
тик Дэвид Гейл изобрел следующую игру. Игровое поле («до-
ска») состоит из черных точек, расставленных в вершинах квадратов, которыми «выложена* часть плоскости. Между рядами черных точек расположены такие же ряды голубых точек. Играют вдвоем: игрок А прово-
• • • • •
•: я г
дит линии черным каран-
дашом, игрок В — голубым Делая очередной ход, каждый игрок соединяет горизонтальным
или вертикальным отрезком две соседние точки своего цвета в одном ряду. Игрок В
стремится провести сплошную черную линию, соединяющую левый край игрового поля с правым. Игрок А стремится соединить сплошной голубой линией верхний край игрового поля с нижним. Игроки совершают ходы по очереди. Выигрывает тот, кому удастся провести сплошную ломаную от одного своего края до другого — построить «мостик».
На этом рисунке вы видите партию в игре Гейла, в которой победителем оказался игрок, делавший ходы голубым карандашом. Играть можно на «досках» любых размеров.
2. Тетракубы. Из обычных детских кубиков, склеивая их гранями по 4, можно изготовить набор так называемых тетракубов (некоторые из них изображены на рисунке).
Предположим, что все тетракубы склеены из игральных костей. Для каких тетракубов сумма очков на видимых гранях наибольшая и для каких наименьшая?
3. Крестики-нолики. . В эту игру играют вдвоем. Каждый из игроков стремится выстроить (по горизонтали, по вертикали, или по диагонали) цепочку из 4 идущих подряд клеток. Ходы делают по очереди. За каждый ход
игрок помечает 1 клетку. Чтобы клетки можно было отличать «по принадлежности», один игрок помечает клетки крестиком, другой — ноликом.
Выигрывает тот, кто первым построит связную цепочку из 4 клеток. На рисунке пока-
зана партия в крестики-нолики, которую выиграл тот, кто ставил крестики.
4. Хальма-соло. Цель игры —перевести 13 фишек, стоящих на серых полях, за возможно меньшее число ходов на голубые поля. Тот, кому удастся осуществить перестроение менее
чем за 20 ходов, может поздравить себя с успешным началом. Немного ф потренировавшись, попытайтесь осуществить перестроение всего за 13 ходов.
Через фишку, стоящую на пути, разрешается перепрыгивать.
5. Лиса и гуси. Четырех «гусей» расставляют у верхнего края шахматной доски (доска может быть ориентирована любым образом — соблюдение шахматных правил не обязательно). Ходят гуси, как обычные шашки,— по диагонали на одно поле от своего края доски. На одном из полей у противоположного края доски гусей поджидает «лиса». Она ходит, как пешка, прошедшая в дамки,— по диагонали на
любое число полей как Брать гусей запрещается. Лиса делает первый ход и стремится достичь противоположного края доски. Ее противник (гусиное стадо) выигрывает в том случае, если гуси смогут поймать лису прежде, чем она достигнет противоположного края
доски.
6. Французская головоломка. Необходимые детали вырезают из дерева или картона (размеры каждый выбирает по своему усмотрению) и укладывают в коробку, днище которой имеет форму прямоугольника, стороны а и b которого относятся, как 4:5. Вырезать необ-
ходимо следующие детали: 4 квадрата со стороной а/4, 6 прямоугольников со сторонами а/4Х°/2 и 1 квадрат со стороной а12. Извлекая из полного набора то одни, то другие детали, можно создавать различные головоломки на перестроение фигур. Приведем лишь 2 из них.
а) Передвигая детали, но не вынимая их из коробки, перевести большой квадрат из угла А в угол В.
б) Передвигая детали, но не вынимая их из коробки, перевести большой квадрат А на место, занимаемое прямоугольником К и дву-мя малыми квадратами G и Н.
7. Пентамино. Каждая фигура пентамино состоит из 5 квадратов, склеенных сторонами.
8. Неусыпное наблюдение. На дорожках городского парка инспектор Леклерк расставил 6 полицейских так. чтобы те могли держать под наблюдением все дорожки парка. Один из полицейских стоит иа перекрестке 34.
Где должны стоять остальные полицейские?
9. Магический квадрат. В китайском варианте игры в домино на клетках 3 костей встречается любое число очков от I до 9. .
Составьте из этих костей магический квадрат.
10. Как угадать исходы бросаний игральных костей. Иоганн Хемелинг, признанный придворный поэт и учитель арифметики и письма города Ганновера, в своей книге «Начала арифметики» (1729 г.) предложил любителям такую задачу.
Некто бросает 3 игральные кости. Ежели ты пожелаешь угадать, сколько очков выпало на каждой кости, то попроси его проделать следующее. Удвоить число очков, выпавших
на первой кости, а затем прибавить 5. Сумму умножить на 5, после чего прибавить к произведению 10. К этому результату пусть он при* бавит число очков, выпавших на второй кос* ти, а сумму умножит иа 10. Наконец, пусть к полученному результату прибавит число очков, выпавших на третьей игральной кости.
Попроси его назвать окончательный результат, вычти в уме 350, и по результату (трехзначному числу) ты сможешь сказать, сколько очков выпало на каждой кости (первая цифра трехзначного числа совпадает с исходом бросания первой кости, вторая — второй и третья — третьей).
(Примеры см. в решении.)
11. Лабиринт. Требуется пройти из А в В так, чтобы символы вдоль маршрута встречались в той же последовательности, в какой они изображены слева от плана лабиринта (считая сверху вниз).
IEEEEEEEB EEQQEBEQ □ЕВВЕЕЕЕ □ЕВИЕЕЕИ ЕЕЕЕЕЕЗВ
EEEEEEEQ EEL3EEEEE ЕЕЕЕЕОЕЕ ЕДЕЕЕШИ ЕЕШЕШИ_____
дЕЕЕЕЕЕЫШИ
1ЕЕИ IGEQ IEEE
ВЕИ еее
12. Играем в кости. Предположим, что мы бросаем 2 игральные кости: красную и белую.
Сколько различных исходов бросаний мы можем получить? (Исход бросания, при котором на красной кости выпадает 1 очко, а на белой 4 очка, легко отличить от исхода бросания, при котором на красной кости выпадает 4 очка, а иа белой 1 очко: исходы этих бросаний различны.)
Сколько различных исходов бросаний возникает в том случае, когда кости не отличаются по цвету?
sm, ВРЕМЯ, СКОРОСТЬ
Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива.
Роже Петер
1. Кто не слышал об одном из самых быстрых поездов мира? Называется он «Хикари» (звук) и курсирует на участке железной дороги Токио—Явата протяженностью 1176,5 км. «Хикари» развивает наивысшую скорость около 210 км/ч. Интервалы между поездами на магистрали составляют 12 мин.
Вычислить среднюю скорость, развиваемую экспрессом «Хикари» на участке Токио— Нагоя (отправление fe 6.00, прибытие в 8.03). Расстояние между этими двумя городами равно 366 км.
Какую среднюю скорость развивает «Хикари» на всем участке от Токио до Яваты (отправление в 6.00, прибытие в 13.01)?
2. Телевидение транслирует оперный спектакль из миланского театра «Да Скала» в Норвегию.
Кто первый услышит начало увертюры к опере: зритель, сидящий в зале театра на расстоянии 25 м от сцены, или телезритель в норвежском городе Хаммерфесте? (Расстояние Милан — Хаммерфест — около 2900 км, скорость звука 340 м/с, скорость распространения электромагнитных волн 300 000 км/с.)
3. а) Парашютист пролетает в свободном падении, не раскрывая парашюта, 80 м.
С какой скоростью он падает в момент раскрытия парашюта (сопротивлением воздуха пренебречь)?
б) С какой скоростью входит в воду спортсмен, прыгающий с 5-метрового трамплина?
4. Легкомысленный мотоциклист несется по улице большого города со скоростью 50 км/ч и прежде, чем успевает затормозить, врезается в «мертвое» препятствие.
С какой высоты он должен был бы лететь в свободном падении, чтобы удар о землю оказался таким же, как при наезде на препятствие?
5. Камертон совершает гармонические колебания. Их можно наблюдать и записать на фотопленке, если к ножке камертона прикрепить зеркальце. При проведении такого эксперимента с камертоном, совершающим ко^ лебания с частотой 440 Гц, было записано 50 колебаний.
Сколько времени длилась запись?
6. Во время летних Олимпийских игр 1976 г. в Монреале бегунья Иоганна Шаллер из ГДР пробежала 100 м с барьерами за 12,77 с. Ее результат был всего лишь на 0,01 с лучше, чем результат советской бегуньи Татьяны Анисимовой.
На сколько Иоганна Шаллер опередила Татьяну Анисимову на финише, если считать, что обе спортсменки бежали дистанцию с постоянной скоростью?
7. Две яхты принимают участие в гонке. Требуется пройти туда и обратно дистанцию 24 км. Одна яхта проходит всю дистанцию с постоянной скоростью 20 км/ч, другая проходит первую половину дистанции со скоростью 16 км/ч, а вторую — со скоростью 24 км/ч.
Почему гонку выиграла первая яхта?
Вопросы на экзамене
В бытность студентом Гёттингенского I университета будущий лауреат Нобелевской премии по физике Макс Борн как-то раз сдавал экзамен астроному Карлу Шварцшильду. Между экзаменатором и экзаменующимся произошел следующий диалог.
Шварцшильд: Что бы вы стали делать, если бы увидели падающую звезду?
Борн: Загадал бы желание.
Шварцшильд: Прекрасно! А потом?
Борн: Потом я взглянул бы на часы, заметил время, определил, из какого созвездия летит падающая звезда, направление ее движения, длину оставляемого ею светящегося следа и т. д., а вернувшись домой, вычислил бы в соответствующем приближении ее орбиту.
Профессор не задал более ни единого вопроса: ответы экзаменующегося его вполне удовлетворили.
Вокруг часов
8. На часах ровно 9.
Через сколько минут стрелки часов (минутная и часовая) совпадут?
9. Минутная стрелка часов имеет длину 2 см, а часовая — 1,5 см.
Найти отношение скоростей, с которыми движутся концы стрелок.
10. Сколько раз в течение суток минутная и часовая стрелки часов образуют прямой угол?
11. Стрелки часов только что совпали.
Через сколько минут они будут «смотреть» в противоположные стороны?
12. На часах Клауса минутные деления нанесены небольшими штрихами. Взглянув на часы в шестом часу пополудни, Клаус обнаружил, что большая стрелка отстает от малой на 3 деления.
Сколько было на часах?
13. Какова минимальная скорость движения, при которой искусственные спутники не падают на Землю?
Эту скорость, называемую первой космической скоростью для Земли, можно найти, предположив, что спутник обращается вокруг Земли непосредственно по ее поверхности (без учета трения). В этом случае радиус орбиты был бы равен 6378 км. Ускорение свободного падения можно принять равным 9,81 м/с2.
14. Плутон — самая дальняя планета нашей Солнечной системы. Она находится на расстоянии около 5 910 000 000 км = 5,91 млрд, км от Солнца.
Сколько времени требуется свету, чтобы преодолеть это расстояние? (Скорость света в вакууме равна 300 000 км/с.)
Выразить полученный результат в минутах и секундах.
15. Криптарифмы. Заменив буквы цифрами от 0 до 9, расшифруйте следующие примеры на сложение (одинаковым буквам соответствуют одинаковые цифры, различным буквам
соответствуют различные цифры) :
, TEMPO , WEG
+ TEMPO f ZE IT
+ TEMPO ---------EILE "
HEKTIК
(Обе надписи — значащие. Первый пример утверждает: «Темп-(-темп+темп=суета», второй — «Путь-(-время=спешка».)
16. Хутора А и В и городок С лежат на одной проселочной дороге (в той последовательности, в которой они перечислены). Из В в С ровно в 6 утра отправляется возница на телеге. Лошади идут со средней скоростью 10 км/ч. ZB тот же день в 7 ч утра из А в С выезжает велосипедист, движущийся со средней скоростью 15 км/ч.
Сколько километров отделяет хутор В от городка С, если расстояние между хуторами А и В равно 5 км и велосипедист прибывает в С на 20 мин раньше возницы?
Когда и на каком расстоянии от С велосипедист догоняет возницу?
17. Спортсмен-саночник уходит со старта с начальной скоростью 18 км/ч и движется с постоянным ускорением 0,8 м/с2.
Через сколько секунд и на каком расстоянии от старта он разовьет скорость 90 км/ч?
18. При постоянном режиме работы машины теплоход проходит некоторое расстояние вверх по течению реки за 41/2 ч, а вниз по течению такое же расстояние за 3 ч.
За какое время преодолеет то же расстояние пустая бутылка, плывущая по течению реки?
19. Машинист пассажирского поезда проехал туннель за 7 мин 30 с, а его коллега, водивший товарные поезда, проехал тот же туннель за 9 мин 30 с. Скорость пассажирского поезда на 4 м/с больше, чем товарного.
Какой длины туннель?
20. Два пассажирских поезда, следующих в противоположных направлениях, встречаются в пути. Скорость первого поезда составляет 45 км/ч, скорость второго — 36 км/ч. Пассажир второго поезда засек по часам, что встречный поезд промелькнул за окном всего за 6 с.
Какой длины был первый поезд?
БЕСЕДЫ
НА
ЕСТЕСТВЕННОНАУЧНЫЕ
Существует еще одна причина, по которой математику надлежит ценить высоко: именно математика придает естественным наукам степень достоверности, недостижимую без нее.
Альберт Эйнштейн
1. Французскими специалистами (в сотрудничестве с их коллегами из СССР) разработан проект шара-зонда для исследования атмосферы Венеры. Требованиям, предъявляемым к оболочке шара, лучше всего отвечает трехслойный материал. Он состоит из алюминиевой фольги на фторуглеродной основе, полиэфирной пленки и ткани из волокон арамида. Один квадратный метр этой легкой оболочки имеет массу 240 г. Для транспортировки полезного груза диаметр шара должен составлять 8 м.
Велика ли масса оболочки. шара-зонда?
2. Пакет из 7 труб наружного диаметра 10 см необходимо связать как можно более короткой лентой.
Чему равна минимальная длина ленты, идущей на обвязку пакета? (Припуск на соединение концов ленты в расчет не принимается.)
3. К клеммам полностью заряженной аккумуляторной батареи мопеда (6В; 4,5А-ч) присоединена лампа (6В; 0,6 Вт).
Сколько времени будет гореть эта лампа, если к батарее не присоединены никакие другие нагрузки?
4. Какие силы действуют на верхний и нижний стержни и нити системы в точках А, В L, М?
5. Футбольный мяч массой 700 г от удара приобретает скорость 18 м/с.
С какой силой бьет по мячу футболист, если продолжительность удара считать равной 0,02 с?
6. Время цикла ЭВМ составляет 1,3 мкс, т. е. для выполнения одной операции ЭВМ требуется 1,3 мкс.
Какой частоте соответствует такое быстродействие? Сколько операций в среднем может выполнить ЭВМ за 1 мин?
7. Микрокалькулятор — вещь необычайно полезная. За считанные доли секунды он выполняет разнообразнейшие математические операции. Но микрокалькулятор — прибор универсальный и может служить не только для серьезных дел, но и для забав. Вот, например, как можно с помощью микрокалькулятора проверить, знаете ли вы немецкий язык. Попытайтесь самостоятельно ответить на каждый из вопросов, а затем, нажав клавиши микрокалькулятора в указанной последовательности и повернув микрокалькулятор на 180°
(«вверх тормашками»), прочтите правильный ответ на индикаторе.
Копытное животное, широко распространенное в южных странах (7; 3; 5; 3).
Приправа (3; 0; 0; 0; 0; +; 5; 5; 0; 5; =).
Слово, противоположное по смыслу слову «темный» (7;-; 1; 0; 0; 0; 7; 3; 4; = ).
8. Двое рабочих переносят груз весом
981 Н (100 кг) на шесте. Расстояние от плеча
одного рабочего до плеча другого -2 м. Груз подвешен на расстоянии 80 см от плеча
рабочего, идущего сзади.
С какой силой давит шест на плечи каждого из рабочих?
9. Какие из грузов /1, В, С и D поднимутся и какие опустятся, если рукоять повернуть в направлении, указанном стрелкой?
10. Пробковый спасательный круг весит 35,ЗН (3,6 кг).
Велика ли его грузоподъемность? (Плотность пробки р=0,2 г/см3.)
11. Петер весит 35 кг (343 Н). При подтягивании на перекладине он поднимает свое тело на 38 см.
а) Какую работу затрачивает Петер на подьем своего тела, подтянувшись 6 раз на перекладине?
б) Какую работу затрачивает Петер, принеся по просьбе матери ведро брикетов весом 10 кг (98,1 Н) из погреба на первый этаж (разность уровней 7,20 м)?
в) В каком случае работа больше?
12. В ледниковый период ледник принес в Центральную Германию множество валунов. В 1903 г. при возведении памятника на месте Битвы народов под Лейпцигом жители окрестных мест принесли 100 валунов почти круглой формы. Из них воздвигли прямую квадратную пирамиду с основанием шириной 5 м и длиной ребра 6,1 м. Промежутки между камнями (составлявшие около 45% объема) для большей прочности заполнили бетоном.
Сколько камня пошло на пирамиду, если его плотность составляет Р=2,6 г/см3?
Метод решения доведен до совершенства, если мы с самого начала в состоянии предвидеть и даже доказать, что он позволяет иам достичь поставленной цели.
Г. В. Лейбниц
13. Криптарифмы. Расшифровать следующие арифметические примеры, заменив буквы цифрами (одинаковым буквам в каждом примере соответствуют одинаковые цифры, различным буквам — различные цифры).
VOLVO х FIAT
MOTOR
. MOON
Т MEN
+ CAN REACH
(1) РАДАР--PPP-PPP.
(2) РАДАР= (PPP)A,
(3) РАДАР
(«ВольвоЧ-Фиат=мотор», «Люди могут достичь Луны».)
14. Театральный бинокль имеет длину 14 см и дает пятикратное увеличение.
Какое фокусное расстояние у его окуляра и объектива?
15. Диаметр заднего колеса велосипеда 70 см. Число зубцов в шестерне, вращаемой педалями, 46, в шестерне на втулке заднего колеса — 16.
Сколько оборотов нужно сделать педалями велосипедисту, чтобы, не используя холостой ход, проехать 120 км?
16. Золото обладает замечательным свойством: его можно раскатать в тончайшие листки толщиной примерно */эооо мм (так называемое сусальное золото).*
Сколько золота пойдет на изготовление 1 м2 сусального золота, если плотность золота р=19,3 г/см3?
17. 105 столбов нужно уложить в штабель 6 рядами так, чтобы в каждом ряду было на 2 столба меньше, чем в предыдущем.
Сколько столбов следует уложить в основание штабеля?
18. Сколько весит чемодан массой 25,00 кг на высоте уровня моря
а) на широте 45е (g=9,81 м/с2);
б) на экваторе (g=9,78 м/с2);
в) на Северном полюсе (g=9,83 м/с2)?
НАПРЯЖЕННОЕ
РАСПИСАНИЕ
Работайте и ищите, не надеясь на молитвы, и вы непременно найдете.
Якоб Штейнер
1. Перед вами выписка из расписания занятий в пятых классах:
Понедельник
5-й класс «А» 5-й класс «Б»
1-й урок Немецкий из. География
2-й урок История Немецкий яз.
3-й урок Физкультура Физика
4-й урок География 'Рисование
5-й урок Физика Математика
6-й урок Рисование Биология
Вторник
5-й класс «А» 5-й класс «Б»
1-й урок Физика Немецкий яз.
2-й ’урок Математика Физика
3-й урок Математика Физкультура
4-й урок Немецкий яз. Математика
5-й урок Биология Немецкий яз.
6-й урок Физкультура —
Определить, какие предметы преподают герр Райхельт, фрау Хельмерт, фрейлен Фишер и герр Вальтер, если известно следующее.
а) Каждый учитель ведет по 2 предмета.
б) Каждый учитель преподает оба своих
предмета и в 5-м классе <А», и в 5-м классе «Б».
в) Фрейлен Фишер занята по вторникам и в 5-м классе «А» и в 5-м классе <Б» только в первые 2 урока.
г) У герра Райхельта по вторникам библиотечный день, так как он учится на заочном отделении аспирантуры.
д) Фрау Хельмерт проводит по понедельникам только 2 урока в 5-м классе «Б», а в остальное время ее можно найти в учительской.
е) У учителя физики рабочий день по понедельникам начинается с третьего урока.
2. Физкультура. На тренировке в школьном спортивном клубе велосипедист получил от тренера задание отработать частоту вращения педалей 120 об/мин при передаче 91,8.
За сколько времени он проезжает отрезок в 200 м и какова его средняя скорость?
(При передаче 91,1 велосипедист за один полный оборот педальной шестерни проезжает 7,26 м.)
3. Русский язык. Составьте из следующих слогов слова, определения которых приведены ниже. Прочитав сверху вниз первые буквы слов, вы узнаете, как называется современная наука, принадлежащая к числу математических и широко применяемая в различных областях науки и техники:
ал — ан — бра — вен — вер — ге — де — ди — е — же — и — ин — ир — ко — коб — куль — ла — ле — ма — мно — му — наль —' не — ни — ность — пе — пре — ра — ре — ромб — са — си — ство — те — фор — ца — ци — цир — эдр — я.
а) Доказываемое утверждение.
б) Наименьшее натуральное число.
в) Задание объекта.
г) Четырехугольник с четырьмя равными попарно параллельными сторонами.
д) Правильный многогранник с 20 граня* ми.
е) Имя одного из членов знаменитого семейства математиков.
ж) Геометрическое преобразование.
з) Отношение между двумя числами.
и) Математическое выражение,
к) Действие.
л) Угловая мера.
м) Совокупность элементов.
н) Раздел математики.
о) Прибор для геометрических построений.
п) Свойство чисел.
р) Повторение одной или нескольких операций.
4. Французский язык.
, ONZE Sachant que:
ONZE est divisible par 11,
VJNGT NEUF est divisible par 3, et V1NGT est divisible par 5.
5. Экономическая география. В одном городе численность пенсионеров составляет 40% численности трудоспособного населения и 25% численности всех жителей.
Какую часть всего населения составляют пенсионеры, Остальные взрослые, а также дети и подростки?
По следам Якоба Штейнера
Песталоцци принял будущего знаменитого геометра, которому тогда едва минуло 18 лет, в свое учебное заведение, не взяв с него никакой платы. Очень скоро преподаватели обратили внимание на необыкновенные способности своего воспитанника.* Так, он мгновенно нашел решение следующей предложенной ему I геометрической задачи на построение.
6. Разделить правильный пятиугольник на 2 равновеликие части прямой, параллельной одной из его сторон.
Эта задача далеко не простая. Проследив шаг за шагом решение Штейнера, читатель сможет в полной мере оценить ясность его мышления. Встречались Штейнеру задачи и потруднее. Если задачу не удавалось решить сразу, воспитанник Штейнер упорно продолжал искать решение до тех пор, пока его усилия не приводили к успеху. Сохрани-! лась приписка Штейнера к решению од-; ной задачи: «Найдено в воскресенье, i 10-го Христова месяца * 1814 г. в час । ночи; решал 34-3+4 часа».
7, Физика, а) Какое давление оказывает стоящий человек весом 588,6 Н (60 кг) на пол, если площадь его подошв составляет 150 см2?
Предположим, что этот человек занимается зимними видами спорта.
б) Какое давление он оказывает при ходь
* Декабря — прим, перев.
бе на лыжах на снежную поверхность, если длина лыж равна 2 м, а средняя ширина составляет 10 см?
в) Округлив, до ближайших целых чисел, найти отношение между давлением, оказываемым стоящим человеком на пол, и давлением, оказываемым Тем же человеком на снежную поверхность при ходьбе на лыжах.
8. Английский язык.
A Dissection Puzzle: A triangle ABC has been dissected into parts X, Y, Z, along lines through M, the mid-point (centre) of AB that are parallel respectively perpendicular to the base BC. Show how the three pieces can be fitted together to make a rectangle, respectively two different parallelograms.
9. Математика. Учитель, решив проверить знания своих учеников, предложил им решить следующую занимательную задачу:
а—b с
d+e--=f g+h=>
О числах а, Ь, .... i известно, что t»
а — сумма всех целых чисел от 2 до 193; &=22-52-72;
с — среднее арифметическое чисел 23 105, 13 830 и 4525;
з,-----
d^V 17 576,
е — 6,25% от 5248;
f — удовлетворяет пропорции;
148 _ 34 112 .
37 f ’
g — число, квадрат которого равен 518 400;
h — число, удовлетворяющее соотношению (Л+4)-13=59 488;
i — наименьшее общее кратное чисел 4, 27 и 49.
В книжном магазине
Луиза: У вас действительно можно купить любую книгу, которая может понадобиться в школе?
Продавщица: Конечно!
Луиза: Тогда дайте мне, пожалуйста, сборник решений всех задач по математике за 7-й класс!
10. Биология. Сердце тренированного спортсмена в течение коротких промежутков времени может развивать огромную мощность. В моменты наивысшего напряжения сердце спортсмена совершает за минуту работу порядка 932 Дж.
Какова мощность, развиваемая сердцем в моменты наивысшего напряжения?
11. Химия. Памятная медаль состоит из сплава меди и серебра. Масса медали равна 20,9 г, а ее объем составляет 2123 мм3.
Из скольких долей серебра и меди (в расчете на 1000) состоит сплав, из которого изготовлена памятная медаль? (Плотность серебра 10,5 г/см3.)
12. Астрономия. На какую высоту над поверхностью Земли следует запустить искусственный спутник, чтобы он мог «висеть» над одной и той же точкой?
(Воспользуйтесь одним из законов Кеплера, а в качестве тела сравнения — Луной. Период обращения Луны вокруг Земли равен примерно 27,33 суток, средний радиус лунной орбиты составляем 384 000 км.)
13. География. Однажды ребята всем классом отправились в поход по горам. Один из школьников начертил профиль рельефа вдоль маршрута, а снизу на узких полосках изобразил возвышенности темными участками, а долины светлыми. Его одноклассники сразу же нашли, какая из полосок /1, В.. G соответ-
ствует изображенному ниже горному массиву. А вы?
вост
ЦИРКУЛЯ линейни
То, чем в прежние эпохи занимались лишь зрелые умы ученых мужей, в более поздние времена стало доступно пониманию мальчишек.
Гегель
1. Астроном Г. К. Шумахер из Альтоны сообщил 22 сентября 1836 г. своему другу К. Ф. Гауссу, что получил от гамбургского астронома К. Л. Румкера следующую задачу вместе с решением.
Дан эллипс и в плоскости эллипса вне его точка Р.
Не пользуясь циркулем, провести из точки Р касательные к эллипсу.
Решение Румкера. Проведем через точку Р любые 4 прямые, пересекающие эллипс.
Пусть А и А', В и В', С их пересечения с эллипсом. Соединим отрезками прямых точки А и В', В и А', С и D', D и С'. Пусть Q — точка пересечения прямых АВ' и А'В, R — точка пересечения прямых CD' и C'D. Прямая, проходящая через точки Q и R, пересекает эллипс в точках Е и F. Точки Е и F принадлежат касательным, проведенным к эллипсу из точки Р.
и С. D и D' — точки
В письме к Гауссу Шумахер добавил, что Румкер провел слишком много прямых и что можно обойтись тремя прямыми, проходящими через точку Р и пересекающими эллипс.
Через несколько дней пришел ответ от Гаусса. По мнению великого математика, Румкер действительно провел слишком много прямых, и можно было бы обойтись тремя прямыми. Но и трех линий слишком много: достаточно двух прямых, проходящих через точку и пересекающих эллипс. '
Располагая этими сведениями, найдите предложенное Гауссом решение. На какой геометрической теореме оно основано?
2. Выдающийся польский физик Леопольд Инфельд в своей книге «Э. Галуа — избранник богов» рассказал об. одном эпизоде, происшедшем с главным героем, когда шестнадцатилетний Галуа учился в Колледже Людовика Великого. Ученики, слушавшие дополнительный курс математики, получили задание на неделю, которое, как это часто бывает, показалось им очень трудным. В первой задаче требовалось по известным сторонам а, Ь, с и d вписанного в окружность четырехугольника найти его диагонали х и у.
В задание входили еще две задачи. К великому удивлению преподавателя математики, полагавшего, что уча- ____
щимся придется затра- с Чс
тить на выполнение за- /Г\ ./у
дания не один час, Галуа Z/ \
решил все три задачи за I/ ь I
15 мин! /
Сможете ли вы ре- у 3"-—/ шить первую задачу? Она \. не так уж проста. ----
3. Среди глав государств своего времени Наполеон Бонапарт (1769—1821) был единственным, кто получил научное образование. Он принимал участие в заседаниях Парижской академии. Во время похода в Египет вместе с наполеоновской армией на берега Нила отправилась научная экспедиция. Наполеон также немного был и математиком. В частности, его интересовала геометрия. По преданию, ему удалось сформулировать и доказать приводимую ниже теорему (хотя ныне авторство Наполеона представляется нам сомнительным). Не вызывает сомнения то, что Наполеон интересовался задачами такого рода и предлагал их математикам. Наполеону посвящен известный английский палиндром (фраза, читаемая одинаково слева направо и справа налево):
ABLE WAS I ERE I SAW ELBA.
(Я многое мог прежде, чем увидел Эльбу).
Теорема Наполеона. Пусть на сторонах произвольного треугольника АВС вне его построены равносторонние треугольники АНВ, ВРС, CQA. Тогда их центры Qt, Qa. и Q3 располагаются в вершинах равностороннего треугольника. Докажите эту теорему.
4. Вычислить площадь каждой фигуры.
С помощью циркуля и чертежного угольника
Невозможные фигуры из голландского математического журнала для школьников «Пифагор»
5. Чему равна (в единицах длины, которые выбраны по осям координат) длина стороны квадрата, равновеликого четырехугольнику с вершинами в точках (1, 0), (17, 0). (13, 12), (0, 7)?
6. От куба отсечены 8 частей, имеющих форму треугольных пирамид (тетраэдров).
Какую долю от объема всего куба составляет объем оставшейся части V-m., ?
7. Периметр прямоугольника равен 40 м. Его длина х и ширина у отличаются не менее чем на 2 м.
Чему могут быть равны наименьшая длина и наибольшая ширина такого прямоугольника?
8. Дан угол 63°. С помощью циркуля и линейки разделить его:
а) на 3 равные части;
б) на 7 равных частей.
9. На каждой стороне квадрата (длиной а) вне его построено по равнобедренному треугольнику, равновеликому квадрату.
Вычислить расстояние между дальними вершинами треугольников, построенных на противоположных сторонах квадрата (вся фигура напоминает 4-конечную звезду).
10. Даны два правильных многоугольника. Число сторон второго многоугольника вдвое больше числа сторон первого. Каждый внутренний угол первого многоугольника на 10° меньше любого внутреннего угла второго.
Найти число сторон каждого из двух многоугольников и их внутренние углы.
11. Задача на сообразительность из передачи венгерского телевидения. Возьмем выпуклый n-угольрик. Предположим, что никакие три из его диагоналей не проходят через одну точку.
В скольких точках пересекаются диагонали нашего «-угольника? (Вершины «-угольника и расположенные вне его точки пересечения прямых, на которых лежат диагонали, в число точек пересечения диагоналей не входят.)
12. Доказать, что вольного треугольника из его сторон.
полупериметр произ-всегда больше любой
13. Одну нз сторон прямоугольника увеличили на 25%.
На сколько процентов следует уменьшить другую сторону, чтобы площадь прямоугольника осталась неизменной?
ИГРА с
числами
Хорошая математическая шутка всегда лучше целой дюжины посредственных математических работ.
Дж. И. Литлвуд
1. От башни нужно пройти в правый нижний угол за 10 шагов, набрав по дороге сумму в 60 очков (суммируются очки, проставленные на тех полях, по которым проходит маршрут).
Кто сумеет быстрее других найти дорогу?
2. Равенство двух дробей, в записи которого использованы все 10 цифр, а сами дроби принимают наименьшие из возможных
значений, имеет вид
1 _ 2
4865 9730
Как выглядит равенство двух дробей, в за-записи которого также использованы все 10 цифр, если дроби принимают наибольшее нз возможных значений?
3. В комплект домино входит 28 костей. Из 18 костей составлен магический квадрат с суммой очков по всем горизонталям, вертикалям и диагоналям (магической постоянной), равной 13.
Из 8 костей домино можно составить малый магический квадрат с магической постоянной, равной 5.
Как это сделать?
4. В каждом из секторов А, В, С и D «мишени» числа вписаны в кольца по определенному закону.
Тот, кто отгадает его, сможет вписать числа в «яблочко» вместо вопросительных знаков
5. Упростите дроби в следующих числовых последовательностях. Если удастся, попытайтесь найти общий член каждой последовательности.
2 . 3 . 4 5
2 ’ 2+4 ’ 2+4+6 ’ 2+4+6+« ’
2 . 2+4 . 2+4+6 . 2+4+6+8 .
3 ’ 3+5 ’ 3+5+7 ’ 3+5+7+9 ’
1 . 1+2 . 1+2+3 . 1+2+3+4 .
1 ’ 1+3 ’ 1+3+5 ’ 1+3+5+7 '
6. Перед вами лабиринт. Темные кольца— стенки, светлые — коридоры между ними. Проходы в стенках проложены только в тех местах, где стоят числа («номера» проходов).
Сумеете ли вы пробраться внутрь лабиринта, набрав по дороге сумму в 500 очков? (Стоя снаружи, вы имеете 0 очков. Минуя очередной проход, вы прибавляете его «номер».)
Числовые узоры
5 5 5 5 5 5 52
2 5 2 5 2 5 2 5 2 5 2 5 25252525 2525252525 252525252525 25252525252525 252525252525 2525252525 25252525 2 5 2 5 2 5
2 5 2 5 2 5
1-1 = 1
11-11= 1 2 1
111-111= 1 2 3 2 1
1111-1111 = 1 2 3 4 3 2 1 '11111-11111 =1 23454321
30864191358025
1 + 3-22
1 + 3 + 5 = 32 1+3+5+7=42 1 +3+5+7+9=52 1 +3 + 5 + 7 + 9 + 11 -62 1+3 + 5 + 7 + 9 + 11 +13 = 72
7 72
4 9
4 9 4 9
4 9
6 6 62
3 6
3 6 3 6
3 6 3 6 3 6
3 6 3 6
3 6
5 5 5 52
2 5 2 5 2 5
2 5 2 5 2 5
25252525 2 5 2 5 2 5
2 5 2 5
2 5
4 4 3 5 5 6
5 9 2 9
30858025
7. Разделить изображенную на рисунке двухрядную полоску на четыре конгруэнтные части так, чтобы сумма чисел в клетках каждой части была равна 34
1 9 16 7 12 5 4 3
8 15 10 2 13 6 11 14
62=36
762=5776
37Q2—141376
(101-65)- 36=1296 (65-36)-101 =2929
(101-36)- 65 = 4225
42 : 3=4-3+2 85 — 63=8+5+6+3 4-23=34 —2
Арифметические курьезы
Заметив закономерность в каждой из по следовательностей чисел, продолжите их.
72=49 672=4 489 6672=444889
1 23456789- 9=111 111 111
12345678 9-18=222 222 222
1 23 4 56 789-27=333 333 333
1-9+2= 11 12-9+3= 111
123-9+4=1111
9-9+7= 88 98-9+6= 888
987-9+5=8888
К121 = 12-1
1331=3+1+3+3+1
(533 — 456=77) (552 — 474 = 78)
151+264= (1«+5»+1») + (23+63+43)
1233=122+332 8833=882+332
8. Вычислите и вы удивитесь!
X] =900 991-863 247 х2=803-202-137 х3=689 976:888 х4= (379+888) —(477+124)
773=456 533
783=474 552
х5= (2997-729) : (81-81)
х6 = 412+ 4324-452
х7= <5-5)4i5-5) + (5:5)
7 ^5 ,.5j + (o-+-5) — (.5 : 5>
9. Венгерский эстрадный вычислитель Патаки поставил трем своим партнерам из зрителей А, В а С следующую задачу.
Партнер. А должен был задумать одно произвольное четное, одно произвольное нечетное число и сообщить одно из них партнеру В, а другое — партнеру С. Партнер В должен был умножить свое число на 2, а партнер С свое число должен был умножить на 3. Полученные произведения партнеры В и С должны были сложить и назвать вслух сумму.
Патаки по сумме сразу же назвал, кому нз двух партнеров В и С партнер А сообщил четное и кому нечетное число.
На чем основан этот фокус?
10. Числа 12 и 60 обладают интересным свойством: их произведение в 10 раз больше их суммы.
12-60=720, 124 60=72.
Существуют ли другие пары натуральных чисел, обладающих тем же свойством?
11. Над двумя различными натуральными числами проделывают четыре операции:
а) находят их сумму;
б) из большего числа вычитают меньшее;
в) находят произведение двух исходных чисел;
г) большее число делят на меньшее.
Сумма результатов всех четырех операций оказывается равной 243.
Что это за числа?
12. С помощью знаков арифметических действий и скобок представить каждое из чисел 1, 2, 10 с помощью четырех семерок,
например (74-7-7) : 7=8.
огонь матемагпичесних олимпиад
С любознательности начинается познание мира. Именно она составляет наиболее характерную и значительную особенность юности, когда формируется личность и знания усваиваются особенно быстро и прочно. Без любознательности, по моему мнению, человек не может развиваться нормально.
Л. Д. Ландау
С 1968 г. проводятся международные математические олимпиады. Ежегодно в этих соревнованиях принимают участие по 8 лучших школьников более чем из 20 стран. Некоторые из приведенных ниже занимательных задач заимствованы из задач, предлагавшихся на олимпиадах.
1. Перед началом бегов на ипподроме четыре знатока из числа зрителей обсуждали шансы фаворитов А, В и С.
(1): «Заезд выиграет А или С».
(2): «Если А будет вторым, то выигрывает В».
(3): «Если А придет третьим, то С не выиграет».
(4): «Вторым придет А или В».
После заезда выяснилось, что три фаворита А, В n С действительно заняли первые три места и что все четыре утверждения знатоков Оказались истинными.
Как фавориты поделили между собой три первых места?
2. Два школьника Эпсилон и Дзета беседуют между собой на досуге.
Эпсилон: Я могу представить число 30 в виде арифметического выражения, содержащего только 3 пятерки и знаки основных действий.
Дзета (после короткого размышления): Ничего удивительного! При любом натуральном //>2 число 30 можно представить в виде арифметического выражения, содержащего ровно п пятерок и знаки основных действий.
Как Дзета может доказать свое утверждение?
3. Из квадратного куска картона со стороной 8 дм нужно вырезать 9 неконгруэнтных разверток куба. Каждая развертка должна складываться в куб с ребром длиной 1 дм.
Доказать, что задача разрешима, й раскроить лист картона, начертив на нем 9 неконгруэнтных разверток куба нужного размера.
4. Фамилия великого математика содержит пять букв. Если буквы алфавита А, Б. В, ..., Ю, Я (без Е) перенумеровать по порядку идущими подряд числами от 1 до 32 и вместо букв, входящих в фамилию математика, подставить их «номера», то окажется, что сумма чисел, соответствующих
(1) первой и второй буквам, равна 40;
(2) первой и третьей буквам, равна 42;
(3) первой и четвертой буквам, равна 36;
(4) первой и пятой буквам, равна 47;
(5) всем пяти буквам, равна 75.
Назовите фамилию великого математика.
5. Обсуждали высказывания, которые начинаются словами: «Если а и b— два отличных от нуля действительных числа, таких, что а^>Ь и |н|< |й1, то...»
А предложил закончить словами «...число а отрицательно».
В предложил закончить словами «...а и b — отрицательные числа».
С предложил закончить словами «...число b отрицательно».
D предложил закончить словами «...ни число а, ни число b не должно быть отрицательным».
Какие из получившихся полных высказываний истинны и какие ложны?
6. На рисунке вы видите четыре концентрических круга. Примем площадь внутрен-.него круга за единицу. Кольцо, заключенное между границами внутреннего и следующего круга, разделено на две конгруэнтные части, помеченные номерами 2 и 3. Следующее кольцо разделено на четыре конгруэнтные части, получившие номера 4, 5, 6 и 7. Наконец, последнее кольцо разделено на 8 конгруэнтных частей с номерами 8, 9, ..., 14, 15.
Как следует выбрать радиусы четырех кругов, чтобы все 15 частей были равновеликими?
7. Вот треугольник не простой, В нем угол АС В — прямой.
А теперь условий узы: с — длина гипотенузы, р — величина не меньшей нужности — Радиус вписанной окружности.
Задача, посильная для школьника: Выразить через них площадь треугольника.
8. Два игрока А и В по очереди берут из большого короба, вмещающего ровно 150 спичек, не менее 1 и не более 10 спичек.
Кто из игроков может обеспечить себе выигрыш? Какая стратегия ведет к выигрышу?
Тот, кто хоть раз пережил радость творческого свершения, не пожалеет никаких усилий, чтобы пережить ее снова. Никакие трудности не остановят его. Его стремление, старание и упорство в преодолении препятствий будут возрастать с каждым новым успехом.
_А. Я. Хннчин
9. Дано конечное множество черных и голубых точек. Некоторые точки соединены отрезками прямых. Точка множества называется «необыкновенной», если более половины исходящих из нее отрезков заканчиваются в точках другого цвета, чем она. Если в данном множестве точек имеются необыкновенные точки, то, выбрав любую из них, перекрасим ее в другой цвет. То же проделаем и 136
с полученным множеством точек, если в нем существуют необыкновенные точки, и т. д.
Доказать, что любое конечное множество черных и голубых точек при любом выборе необыкновенных точек, подлежащий перекрашиванию в другой цвет, после конечного числа перекрашиваний перейдет в множество, не содержащее необыкновенных точек.
10. По преданию, основательница чешского государства принцесса Либуша обещала отдать свою руку тому из трех женихов, кто сумеет решить следующую задачу: «Если бы я дала первому жениху половину слив из этой корзины и еще одну сливу, второму жениху половину оставшихся слив и еще одну сливу, а оставшиеся сливы поделила пополам и. половину их и еще три сливы дала бы третьему жениху, то корзина опустела бы».
Сколько слив в корзине?
11. Гюнтер рассказывает: «Шестизначный номер телефона своей школы я запоминаю следующим образом. Записываю двузначный номер дома, в котором живу, к нему приписываю справа сумму его цифр, а затем приписываю справа сумму двух последних цифр до тех пор, пока не получится шестизначное число. Оно-то и будет номером телефона моей школы.
Должен еще сказать, что в номере,телефона моей школы нег ни одной единицы, а номер дома, где я живу, делится на 3».
Назовите номер дома, в котором живет Гюнтер, и номер телефона его школы.
12. В одном старинном учебнике арифме
тики упоминается о следующей торговой сделке.
Крестьянин хотел купить у торговца несколько голов скота. Торговец запросил за всех одинаковую цену. Крестьянину удалось сбить цену на столько же процентов, сколько грошей он должен был бы уплатить за каждую голову скота первоначально.
Торговцу скотом за каждую голову крестьянин уплатил 21 грош. При первоначальной цене денег хватило бы на покупку трех голов скота. После скидки крестьянин купил больше скота, израсходовав на покупку все свои деньги.
Сколько голов скота купил крестьянин?
Каждая задача, которую я решал, становилась правилом, служившим впоследствии для решения других задач.
Рене Декарт
I. Монголия, В шахматном турнире участвовало 10 шахматистов. Каждый сыграл с каждым по одной партии. Все участники турнира набрали различное число очков. Шахматисты, занявшие первое и второе места, не проиграли ни одной встречи и набрали на 10 очков больше, чем шахматист, занявший третье место. Шахматист, занявший четвертое место, набрал столько же очков, сколько набрали вместе шахматисты, занявшие четыре последних места.
Сколько очков набрали шахматисты, занявшие с первого по шестое места? (За выигранную партию шахматист получает 1 очко, за партию, закончившуюся вничью, оба партнера получают по ’/г очка. Шахматист, проигравший партию, получает 0 очков).
2. Исландия. Неподалеку от деревни расположился летний лагерь спортклуба. В первый день 28 обитателей лагеря приняли участие в соревнованиях по прыжкам в длину, прыжкам в высоту и прыжкам с шестом. Каждый из 28 спортсменов выступил по крайней мере в двух видах программы. 8 спортсменов состязались в прыжках в длину. В прыжках в длину и в прыжках в высоту участников оказалось на 3 больше, чем в прыжках в высоту и в прыжках с шестом. Спортсменов, выступивших в двух номерах программы— и в прыжках в длину, и в прыж
ках в высоту, было столько же, сколько прыгунов с шестом.
Сколько спортсменов выступило во всех трех номерах программы? Попробуйте решить задачу с помощью диаграмм Венна.
3. Польша. Между пятью городами, из которых никакие три не лежат на одной прямой, требуется проложить сеть железных дорог из четырех прямолинейных отрезков. Железнодорожные пути могут пересекаться: в местах пересечений будут построены путепроводы.
Сколько существует вариантов прокладки железнодорожной сети?
4. Англия. Шесть фигурок расположены следующим образом:
Фигурки могут перепрыгивать через одну фигурку, продвигаться вперед, но не могут поворачиваться, ходить назад или отклоняться в сторону.
За какое минимальное число прыжков или шагов фигурки можно перестроить в следующем порядке?
Эти выразительные математические термины построены по образцу и подобию тех, которые предложил своим читателям голландский математический журнал для школьников «Пифагор».
де/ление t'x с Э/иипс па ^Лзбола
отрао+сение трОпеция
1€рёнь пароль бектор гХпербо/id
5. Швейцария. В «Солитер», как говорит само название (от франц, solitaire — одинокий, уединенный, отшельник) играют в одиночку. Доска для этой игры состоит из 37 осо-
бым образом расположенных квадратных полей.
Перед началом игры на всех полях, кроме одного, выбираемого «отшельником», расставляются фишки. Каждый ход состоит в том, что играющий переставляет одну фишку по горизонтали или вертикали через занятое поле на свободное и снимает с доски ту фишку, через которую перепрыгнула фишка, совершившая очередной ход. (Если поля 02 и 03 заняты, а роле 04 свободно, то фишку можно переставить с поля 02 на поле 04, сняв с доски фишку, стоявшую на поле 03.) После каждого хода на доске становится на одну фишку меньше. Цель игры состоит в том, чтобы оставить на доске только одну фишку.
6. Канада. Решите эти два весьма остроумных криптарифма:
, MIX +ALORS
Т FUN TALORS
~г AND + NOUS
MATH + NOUS
L'AVONS
7. Танзания. Каникулы Мбонго продолжались f дней. По его наблюдениям:
(1) дождь шел 7 раз либо с утра, либо к вечеру;
(2) если дождь шел к вечеру, то с утра стояла солнечная погода;
(3) 5 раз к вечеру устанавливалась солнечная погода;
(4) 6 раз с утра стояла солнечная погода.
Сколько дней продолжались каникулы Мбонго?
Сведения не подтвердились
На лекциях по теории групп Феликс Клейн (1849—1925) имел обыкновение рассказывать своим слушателям следующую историю.
На знаменитом Математическом конгрессе, состоявшемся в Париже в 1900 г., во время торжественного заседания были помянуты все выдающиеся математики, скончавшиеся за последние 10 лет, предшествовавших конгрессу. Среди прочих председательствующий назвал специалиста по теории групп профессора Политехнической школы Камилла Жордана, сообщив, что тот родился в 1838 г. и умер 7 ноября 1898 г. Неожиданно в задних рядах поднялась высокая фигура и сообщила ученому собранию, что по крайней мере дата смерти названа явно неверно, поскольку Жордан (а это был он) еще жив. (Камилл Жордан умер 20 января 1922 г. в Милане).
8. Испания. 2=3?
«Доказать» это «равенство» можно следующим образом:
4—10=9—15,
4-10+ 2L=9-154- —, 4 4
2=3.
Где ошибка?
9. Румыния. В одном доме жило несколько супружеских пар с детьми. О них известно, что всех детей было больше, чем взрослых, а взрослых — больше, чем мальчиков. В свою очередь, мальчиков было больше, чем девочек, а девочек — больше, чем семей. В каждой семье был по крайней мере один ребенок, а число детей во всех семьях было различным. У каждой девочки был по крайней мере один брат и не более одной сестры. В одной семье детей было больше, чем во всех остальных семьях вместе.
Сколько семей жило в доме? Сколько девочек было в каждой семье?
Трудная проблема
Во время одной из лекций знаменитому берлинскому математику Ф. Э. Куммеру (1810—1893) понадобилось решить трудную задачу: вычислить 7-9. Он обратился за помощью к слушавшим его лекции студентам. Один назвал число 62, другой — число 65.
— Господа!— возразил профессор Куммер.— Число 7-9 не может быть одновременно равно 62 и 65. Что-нибудь одно!
10. ГДР. Ганс попросил своегб друга Уве: — Задумай какое-нибудь отличное от нуля целое положительное число, умножь его на 5 и прибавь к найденному произведению 2. Затем умножь полученную сумму на 4, прибавь
к новому произведению 3, а сумму умножь на 5. Если ты назовешь мне результат, то я тут же скажу тебе, какое число ты задумал.
Объясните, на чем основан арифметический фокус, показанный Гансом своему приятелю Уве.
Часть 2
РЕШЕНИЯ
148 Пестрые картинки из разных стран 9
153 Античные этюды 17
160 Школьные истории 25
166 Старое и новое из практики 32
173 Минуту на размышление 39
180 Арифметика с птичьего полета 47
189 Занимательная геометрия 55
195 Тренировка по современной матема-
тике 63
204 Математика на каждом шагу 71
213 Слово знаменитым математикам 79
220 Наша секция игр 36
222 Путь, время, скорость 94
230 Беседы на естественнонаучные темы 101
236 Напряженное расписание 108
245 Вокруг циркуля и линейки 116
253 Игра с числами 124
256 Огонь математических олимпиад 132
263 По разным странам 139
ПЕСТРЫЕ КАРТИНКИ ИЗ РАЗНЫХ СТРАН
1. Пусть х, у, z и и — число бутылок лимонада, которое выпили соответственно жены месье Пона, Дюбуа, Пейзана н Фонтена. Всего жены выпили
*+'/+*+«= Ю
бутылок лимонада. Их мужья выпили *+2i/4-3z4-4m
бутылок лимонада, а четыре супружеские пары вместе опустошили
2х-j-3y+4z+5u—32 бутылки лимонада. Подставляя и— 10—х—у—z, получаем 18=3x-j-2y4-z.
Числа х и z должны быть либо оба четными, либо оба нечетными. Значения х=1 и х=2 отпадают, так как каждое из чисел у и z не превосходит 4. При х—4 мы получили бы г—2 и у—2, что невозможно, так как х, у, г и и — различные числа. Следовательно, задача допускает единственное решение: х=3, z=l, у—4, и—2\
х=3 (Колетта Пон), у—4 (Анетта Дюбуа), z—1 (Жанна Пейзан), и—2 (Жаклин Фонтен).
2. Пусть х—-число стоящих, у —число лежащих молодых буйволов иг — число старых буйволов. Тогда
х+Н-г==Ю0, (1)
5х+3^-|- — = 100, О
(2>
</=25-
Так как х и у — натуральные числа, последнее равенство выполняется только при х=0, 4, 8, 12. Задача допускает поэтому следующие четыре решения:
г
х у
О 25
4 18
8 11
12 4
75
78
81
84
3.
4. Пусть а и b - различные цифры. Тогда из них можно составить следующие надписи па километровых столбах:
(aab) или (9 — а, 9—,а, 9 — ft); (aba) или (9 — а, 9 — ft, 9 — а); (baa) или (9 —ft, 9— а, 9 — а)\ (ааа) или (9т-й, 9 — а, 9—а); (ftftft) или (9 — ft, 9 - ft, 9 — ft).
Так как по условию задачи различными должны быть только 2 цифры, то всюду должно выполняться равенство ft=9 — а. Перечислить все 40 возможных случаев после того, как установлено это соотношение, не представляет труда.
5. Хитрый крот устроил запасную кладовую между камерами 10 и II.
6. Так как сумма последних цифр 24-34-4-34-4=12 оканчивается на 2 и не существует квадрата натурального числа, который бы оканчивался на 2, речь идет не о четырех, а лишь о трех рыболовах, т. е. сын одного из любителей рыбной ловли одновременно является отцом другого^ (24-3-|-4=9). Николай не может быть сыном'Петра, так как улов Николая оканчивается на 2, а не на 4, как того требуют условия задачи. Следовательно, Петр сын Николая.
7. Результаты взвешивания уловов а, Ь, с и d удовлетворяют соотношениям
c<d (1), a+b^c-j-d (2), a-hd<&4-c- (3)
Из (2) и (3) при сложении получаем неравенство 2а4-&4-^<6-|-2с-НА откуда 2а<2с и, следовательно, а<_с.
Из (1) и неравенства а<,с заключаем, что
Наконец, из (2) и неравенства полу
чаем d<b. Таким образом, выполняется це-почка неравенства a<zc<zd<b.
Следовательно, самый большой (по весу) улов у рыбака В; за ним следуют D, С и А.
8. Ромб является трапецией и параллелограммом, но не является квадратом. Следовательно, четырехугольник, начерченный учителем на доске, имеет форму ромба.
9. Задача допускает 13 решений, например:
10.
11. Пусть а — число бокалов, b — чашек, с — кувшинов nd — бутылок. Тогда предметы, находящиеся в равновесии на чашах весов на рисунке, позволяют записать следующие уравнения:
. 2а+Ь=2с, 5b—c^-2d, 5a—3c+2d,
из которых следует, что 3c=6d, 3c=5ft+2d, 3c=2a+b+2d, Зс s== л -|- 3b -j- 2d.
Итак, 3 кувшина можно уравновесить либо 6 бутылками, либо 5 чашками и 2 бутылками, либо 2 бокалами, 1 чашкой и 2 бутылками, либо 1 бокалом, 3 чашками и 2 бутылками.
12.
Т2—42—62 = 7—4—6, 92—62—72 = 9—6—7.
Существует ровно 4 таких трехзначных числа: 976, 967, 764, 746.
13. Задача легко решается, если сначала построить треугольник ACD (I), площадь которого составляет» '/s от площади треугольника АВС: для этого достаточно выбрать точку D так, чтобы CD= (’А) СВ.
Продолжая . действовать в том же ду- с
хе, построим треуголь-ник ЛОЕ (II), площадь /// 1 которого составляет ‘А //к vX.
оставшейся части ис- А*“—---------о----~^в
ходного треугольника — треугольника A.BD-. для этого достаточно выбрать точку Е так, чтобы ЛЕ=(*/4) АВ. Затем достаточно выбрать точку F так, чтобы DF—(lfs)DB и, наконец, точку G так, чтобы EG=(42)EB.
14. Обозначим три высказывания первыми буквами имен их авторов и индексами 1, 2, 3, соответствующими номерам, под которыми
высказывания приведены в задаче: Аь А2, А3, Б.ь Б2, Бз, Вь В2, Вз, Mi, М2, М3. Начнем с анализа высказываний Вольфганга. Высказывания Bi и В3 утверждают одно и то же, поэтому они либо оба истинны, либо оба ложны. Но по условию задачи они не могут быть оба ложными. Следовательно, они оба истинны и ложно высказывание В2. Так как В3 истинно, высказывание Б3 ложно, а это означает, что Б1 и Б2 истинны. Так как Б2 истинно, высказывание М3 ложно. Следовательно, высказывания Mi и М2 истинны. Но если М2 истинно, то Ai ложно, А2 и Аз истинны. Итак, окно разбила Ангелика.
АНТИЧНЫЕ ЭТЮДЫ
1. а) Так как— —означает 1, можно предположить, что сплошная верхняя линия соответствует 1, а линии, состоящие из двух разделенных промежутком отрезков, всегда соответствуют 0. Поскольку знаком .......
Фу Ши обозначил число 3, средняя сплошная линия должна соответствовать числу 2 (1+2+ +0=3). Знаком — Фу Ши обозначил число 6, поэтому нижняя сплошная черта должна соответствовать числу 4 (0+2+4=6). Таким образом, знак —— может означать
только число 4 (0+0+4=4).
б) С помощью трех линий, сплошных или состоящих из двух отрезков, разделенных промежутком, можно составить знаки, соответствующие в системе обозначений Фу Ши числам 0, 1, 2, 3, 4, 5, 6, 7.
2. Пусть ширина составляет х ладоней, длина — у ладоней. Тогда
7+У=7, (1)
х+у= 10, (2)
х=10— у. (2')
Подставляя (2') в (1), получаем
+</=7.
у=6.
Затем из (1) находим
—у— +6=7, х=4.
3. Пусть х— число пчел в рое. Тогда
*= / ^~ + j~x+z
(П
Обозначив У 2 через у, преобразуем уравнение (1) (так как у2—х/2, или х=2у2) к виду
4Н- y-«/2+2=2j/’, (2)
2у2 — 9у— 18=0,
откуда
„ 3
«1 = 6, (/2=-
Этим значениям у соответствуют следующие значения х: Х\ = 12, х2=4,5. Так как число пчел в рое может быть только натуральным числом, то _______
|/ ZL + JL -72+2=72.
Итак, в рое было 72 пчелы.
4. По теореме Пифагора *24-52= (Х-Ь1 )2, х24-25=х24-2x4-1, х=12.
Глубина пруда—12 шагов.
10 шагов
5. Пусть х — число учеников Пифагора. Тогда
“Г*+ у-х+3=х>
откуда х=28.
Итак, у Пифагора было 28 учеников.
6.
7. Пусть мул нес х, а осел у мер зерна. Тогда
х-Ь1=2 (у-1), (1)
х-l=i/4-l. (2)
Подставляя x=0-j-2 в (1), получаем
i/+2+l = 2 (у-1), 0=5, Следовательно, x=7, т. e. мул нес 7 мер зерна, а осел 5 мер.
8. а) Пусть х — число голов скота во всем стаде. Тогда
— • — х=70, 3 з
откуда после эквивалентных преобразований 2
— х=70, 2х=-630
находим: х=315.
Итак, во всем стаде было 315 голов скота. /2 1 2 \ 1
б) * + х ' Т =10’
\ о - О У / О
/9 6 3 2 \ 1
4 т -|0-
1121 _ид 20
9. Площадь луночек нетрудно вычислить следующим образом:
Af,+Af2= _2а2+— Ьг+^- - — с2= 8 8 2 8
= ~ (а’+62-с2)+ -у--О
Но так как а2+&2=с2, ai(+ai2= -|L -Л1з, что и требовалось доказать.
10. Пусть 1 сноп хорошего урожая дает х доу зерна, среднего — у доу и плохого — z доу .зерна. Тогда
Зх-|- 2у+ 2==36,
2x-j-3f/“|~ z==:34,
x-j-2y+3z=26,
откуда х=9‘/4, У—4'к, z=23!t.
Итак, 1 сноп хорошего урожая дает Э'Д доу зерна, 1 сноп среднего урожая — 41/* доу и 1 сноп, плохого урожая — 23/4 доу.
11. Пусть S — площадь двух «сапожных ножей», Г| и Г2— радиусы двух внутренних окружностей. Тогда
S=яг2—яг21—ЯГ22, (1)
2г=2г(4-2г2. (2)
К этим двум соотношениям добавим третье
(3)
(высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное отрезков, на которые ее основание делит гипотенузу). Соотношения (2) и (3) преобразуем к виду
(/•1+г2)2=г2, (2')
2гхгг= . (3')
О
Вычитая, получаем /2 n24-r22=r2-----------------—
О
и, подставляя в (1), находим
12. Если все 4 источника заполняют бас сейн за х дней, то
!2х 6х , 4х । Зх __ 12
12 12 12 12 12 ’
12х4-6х+4х4-3х= 12,
25х=12,
Следовательно, чтобы заполнить бассейны из четырех источников, требуется 12/25, т. е. чуть меньше половины дня. 13
13. Пусть доля сына составляет х, дочери у, доля матери z динариев. Тогда
х-Н/4-г=3500, х=2г, у= —• .
следовательно, х—2000, у=500, z=1000.
Таким образом, вдова должна получить 1000 динариев, сын — 2000 динариев и дочь— 500 динариев.
14. Пусть х—число, которое требуется найти. Тогда 200х=у2, (1)
5х=у. (2)
Подставляя (2) в (1), получаем 200х=25х2, 200 = 25х, х =8.
Итак, третье число равно 8. Проверка: 5-8=
—40; 200-8=1600 и У 1600 =40.
15. Пусть х — число голубей, севших на дерево, а у — число голубей, расположившихся под деревом. Тогда
и, кроме того, х—1=04-1. т. е. х=04-2.
Подставляя х=у4-2 в первое уравнение, получаем
(у— 1)-3=Н-2+!/, Зу-3=2у+2, i/=5.
Следовательно, х=у+2=7.
Итак, 7 голубей сели на дерево, а 5 голубей расположились под деревом.
16. Если х — число яблок, собранных женщиной в саду, то первому стражнику досталось х/2 яблок, второй получил х/4 яблок, третий — х/8 яблок и четвертый — х/16 яблок. Так как х/16=10, то х= 160. Следовательно, женщина собрала в саду 160 яблок.
ШКОЛЬНЫЕ ИСТОРИИ
1. Наименьшее отличное от нуля натуральное число, делящееся на 3, 4, 6 и 8, равно 24. Следующее такое число (равное 48) больше 30. Таким образом, в классе всего 24 ученика. Они-то и писали контрольную по математике.
Так как (*/3) -24=8, (»/4) -24=6, ('/б) -24= —4, (’/в)-24=3 и 84-6+4+3=21, контрольную написали с ошибками 21 человек. Следовательно, 3 человека решили все задачи правильно.
2. Если утверждение Вольфганга истинно, то утверждение Карин ложно. Следовательно, число отлично от 9. Это означает, что если утверждение Петера истинно, то простое число должно быть двойкой, и утверждение Рос-виты ложно. Все другие варианты приводят к противоречию. Итак, лучший математик из 5-го «А» должен был назвать число 2.
3. Пусть х — число деталей по 10 марок за штуку, у — число деталей по 3 марки за штуку и г — число деталей по 50 пфеннигов за штуку. Тогда
10х+Зу+0,5г=29, (1)
х+у+г=29, (2)
1«=х<29, (3)
1<у<29, (4)
l«Sz<29 (5)
и, следовательно,
10х+Зу+0,5г=х+у+г, 9х+2у=0,5г,
или, чт,о то же,
18х+4у=г.
Из (1) следует, что х=1. Но тогда 18х4-4у= —г, откуда у=1, при этом z=22 или у—2 (z=26). Условию (2) удовлетворяет только набор значений х—1, у— 2, z—26.
Для школьной мастерской купили 1 деталь по 10 марок за штуку, 2 детали по 3 марки за штуку и 26 деталей по 50 пфеннигов за штуку.
4. Кроме нуля, существует 9 однозначных чисел. Следовательно, число цифр, необходимых для нумерации страниц однозначными номерами, равно 9. Двузначных чисел всего 90. Следовательно, число цифр, необходимых для нумерации страниц с двузначными номерами, равно 90-2=180. Трехзначных чисел 900. Чтобы записать их, потребуется 900-3 цифр. Четырехзначных чисел всего 9000. Для их записи потребуется 9000-4 цифр. Пусть х— число страниц учебника с четырехзначными номерами. Тогда
94-90 -24-900 • 34-х • 4= 6869, х=995.
Число страниц равно числу всех страниц с одно-, двух-, трех- и четырехзначными номерами, т. е.
94-904-9004-995=1994.
Итак, в учебнике 1994 страницы.
5. Требуется найти все пары натуральных чисел (а, Ь) с а>Ь, для которых а2—Ь2=а-^Ь.
По формуле разложения разности квадратов a2—b2— (a-j-b) («—Ь), поэтому требуемое равенство эквивалентно равенству («4-6) X X(а—Ь} — («4-6)- Так как «и b — натуральные числа и а>Ь, то «4-6=/=0. Разделив на «4-6. обе части последнего равенства, получим,
что требуемое свойство чисел а и b эквивалентно равенству а—5=1, или а—1 = Ь. Итак, требуемым свойством обладают все пары (д, Ь) натуральных чисел, в которых а на единицу больше b (Ь и а — последовательные натуральные числа).
6. За 3 шага Рози продвигается вперед на 50 см. Следовательно, сделав 2-3-29=174 шага, она окажется на расстоянии 29 м от старта. Сделав еще 2 шага, Рози достигнет второго флагштока и закончит упражнение.
Итак, двигаясь от одного флагштока до другого, Рози успевает сделать 176 шагов.
7- а) А - -2-= JL а) Деление ООО
Ь) — — — = — Ь) Умножение ' 14 21 42
113
с) — + — = — с) Вычитание
d) ------~ d) Сложение
8 4 8
8. Пусть х — число задач, решенных сыном правильно (за них сын получил от отца 10х пфеннигов), а у — число неправильно решенных задач (за них сыну пришлось вернуть отцу 5у пфеннигов). Тогда
10х—5у=80, х+ у =20, и х=12, «/=8.
Сын правильно решил 12 задач и допустил ошибки при решении 8 задач.
9. Определение, .скрытое в клетках таблицы, гласит: выпуклый четырехугольник, две противоположные стороны которого параллельны, называется трапецией.
10. На седьмой день пути оба подмастерья проходят одинаковое расстояние — по 7 миль каждый. В последующие дни второй подмастерье должен наверстать то расстояние, на которое он отстал от первого подмастерья за первые 6 дней пути. Возникает уравнение:
(7-6) + (7-5) + (7-4) + (7-3) + (7—2) + + (7-1) + (7+1) + (7+2) + (7+3) (7+4) +
(7+5) + (7+6)=7х,
91 = 7х, х=13.
Итак, подмастерья встретятся к исходу 13-го дня.
11. Обозначим число цветных карандашей у каждой из девочек начальной буквой ее имени. Из условий задачи следует, что У=2Р, С=Р—13, У+Р+С<50 и У+Р+С —простое число. Так как
11 = 2+9=3+8=4+7=5+6, простыми числами, меньшими 50, с суммой цифр, равной 11, могут быть только 29 и 47. Подставляя каждое из этих чисел, получаем: 2Р+Р+Р—13=29,
4Р=42, и
2Р+Р+Р—13=47, 4Р=60.
У тре£ девочек всего было 47 цветных карандашей, причем Р=15, У=30, С=2, т. е. у Уты было 30 карандашей, у Регины 15 и у Сабины 2 карандаша.
12. «Тот, кто знает счет», без труда составит уравнение
-£-+150= JLx-f-50, х= 160.
Число, которое требуется найти, равно 160.
13.
1. Учитель химии живет в одном доме с учителем математики =**Х#=М.
2. А младше В и С А<.В, С.
3. Учитель математики играет в шахматы с С=^М#=С.
4. В старше учителя физики, который, в свою очередь, старше учителя биологии =*В>Ф>Б.
5. Старший из учителей живет дальше всех от школы ^старший =/=Х.
Из 3: учитель математики не С.
Из 2 и 4: учитель физики не А.
Из 4 и 5: В не преподает химию и математику, так как он старше двух других учителей по возрасту =^А преподает математику =>/1 не учитель химии.
Из 2 и 4: .4 младше своих коллег =>А преподает биологию.
Из 2 и 4: Л<С<В=>С преподает физику.
Так как В старше своих коллег и не преподает. химию и математику, В учитель немецкого языка и истории =*С учитель химии.
М Ф X Б Н И
ДХ--Х--
В ------ х X
С - X X - - -
14. Пусть х — число скамей и у — число спортсменов в гимнастическом зале. Тогда 6(x-l)4-3=y, (I)
5х+4=0, (2)
* => означает «следовательно».
откуда
6х—6+3=5x4-4
и, следовательно, х=7. Подставляя в (2), находим </=39.
Итак, в гимнастическом зале занимаются 39 спортсменов и расставлено 7 скамей.
15^ Условия задачи позволяют составить уравнение (х — число победителей олимпиады):
х=6+10—1 = 15.
Призовые места в математической олимпиаде заняли 15 человек.
Задача допускает обобщение: если бы школьник, набравший полное число очков, стоял на m-м месте слева и на и-м месте справа, то число победителей олимпиады было бы равно m+n--l.
16. Пусть V—объем 2 г серебра. Тогда
V= —--------——0,1905 см3.
10,5 гсм~3
Пусть х — длина изготовленной из 2 г серебра проволоки (в см). Диаметр проволоки составляет 0,002 мм, ее радиус — вдвое меньше, т. е. равен 0,001 мм = 0,0001 см, и 0,00012лх=0,1905, откуда
х= «0,0606 108 =^6 060 000
3,14
Итак, из 2 г серебра получается около 6 060 000 см = 60 600 м=60,6 км круглой проволоки диаметром 0,002 мм.
СТАРОЕ И НОВОЕ ИЗ ПРАКТИКИ
1. Предположим, что на отливку царской короны пошло х мин золота, у мин меди, г мин
свинца и f мин железа. Тогда *+«/+24-7=60, (1)
•«+//= -60=40, (2)
и
x-hz= — -60=45, (3)
4
x+f= -1-60 = 36. (4)
5
Складывая (2), (3) и (4), получаем 3x+iz+2+f=121, (5)
а вычитая из (5) уравнение (1), находим, что 2х=61, т. е. х=30,5. Подставляя найденное значение х в (2), (3) и (4), вычисляем значения у, г и f:
у=40—30,5=9,5, 2=45—30,5=14,5, f=36—30,5= 5,5.
Итак, на отливку царской короны израсходовано 30,5 мин золота, 9,5 мин меди, 14,5 мин свинца и 5,5 мин железа.
2. Воспользуемся для вычислений горизонтальной системой координат. Радиус Земли пренебрежимо мал по сравнению с расстоянием от Земли до Солнца, и солнечные лучи вполне допустимо считать параллельными. Итак, наблюдатель находится в центре Земли М и видит, что отклонение а=7,5° направления на Солнце от отвесной линии в Александрии равно центральному углу р между
Александрией и Сиенной (как соответственные углы).
а) Окружность Земли и вычислим из пропорции р : 360=5000 : и,
360 • 5000 _ 360 • 5000 ~ 24() 00() Р 7.5 ~
Солнечные лучи
М — Центр Земли А — Александрия В-Сменке a-fi Дуге АВ «8000 егил-стадий
Итак, окружность Земли составляет 240 000 египетских стадий.
б) 240 000-0,18472» «44 333.
Окружность Земли составляет 44 333 км.
в) Полученная Эратосфеном величина отличается от принятого ныне значения на 4333 км.
3. Пусть х — число дней, отработанных работником. Тогда
48х—12(30—х) =0,
откуда х=6.
Итак, из 30 дней отработанными оказались лишь 6.
4. Фабрика выпустила: за январь х=х-(-0-10, за февраль х+10=х+1 • 10, за март х-(-20=х4-2-10,
за декабрь х+110=х-}-11 • 10.
Итого за год 1920= 12х-Ь 10-f-20-f-—-F1Ю. х=105, за июнь х-|-5-10= 155, за декабрь х-|-11 • 10=215.
В июне фабрика выпустила 155, а в декабре 215 столов.
5. ЗГ, ЗБ. ЗК, 34, ЗЖ, ЗС, ЗФ, ГБ, ГК, гч, ГЖ, ГС, ГФ, БК, БЧ, БЖ, БС, БФ, КЧ, КЖ, КС, КФ, ЧЖ, ЧС, ЧФ, же, ЖФ, СФ.
Число различных маркировок двухжильных шнуров с жилами в изоляции различного цвета равно
7+64-5+44-3+24-1 = 28.
Электрик может скрутить шнуры 28 различных маркировок.
6. Пусть х — число ламп мощностью 40 Вт, у— число ламп мощностью 60 Вт и z— число ламп мощностью 75 Вт в комплекте. Тогда 40x+60i/+75z= 1800, (1)
х+у+г=32. (2)
Умножая второе уравнение на 40 и вычитая из (1), получаем
20//+35г=520, откуда
</==26- £.
Это уравнение допускает целые положительные решения у только при z=0, 4, 8, 12.
Следовательно, заявки на комплекты ламп можно удовлетворить следующими тремя способами:
(75 Вт) г 0 4 8 12
(60 Вт) у 26 19 12 5
(40 Вт) х 6 9 12 15
7. Укладка деталей в футляр производилась в следующей последовательности: 2—7— —5— 6—1—3-4.
8. Удвоение диаметра (при неизменной длине) приводит к учетверению веса: после удвоения диаметра балка весила бы 1200 Н. При уменьшении длины балки вдвое вес ее уменьшился бы вдвое, т. е., став вдвое толще и вдвое короче, балка весила бы 600 Н, Итак, толстая короткая балка круглого сечения весит вдвое больше более длинной и тонкой.
9. Пусть х — число посетителей, которое необходимо для заполнения цистерны при условии, что каждый, кто открывает калитку в сад перед домом Эдисона, накачивает в цистерну 20 л воды. Тогда 20х=25 (х—12) и х—60.
Итак, при «норме» 20 л цистерну заполняют 60 посетителей. Следовательно, цистерна вмещает 1200 л.
10. Изображенным на рисунке валиком маляр «накатал» 6 рисунок.
11. Пусть х — грузоподъемность (в т) меньшей машины, у — грузоподъемность большей машины. Тогда
31х+27</= 143, (1)
1,5х=у, (2)
откуда х=2, у=3.
Итак, машина с меньшей грузоподъемностью перевозит за 1 рейс 2 т сыра, а машина с большей грузоподъемностью — 3 т сыра.
12. По проекции на две взаимно перпендикулярные плоскости (вид спереди и вид сзади) тело, вообще говоря, можно восстановить неоднозначно, т. е. весьма многими способами. В частности, это относится к на
шей задаче. Приведем лишь три тела, имеющие те виды спереди и сверху, которые приведены в условиях задачи.
Прямоугольный пармтлапипвд
13. Как видно из схемы, путешественнику достаточно нанять 2 носильщиков (П — путешественник, Н| — первый носильщик, Н2 — второй носильщик, V* — запас пищи и воды на k дней для 1 человека. fe=0, 1, 2, 3, 4).
14. Где бы ни начинался маршрут, обойти все 17 мостов, побывав на каждом из них не более 1 раза, невозможно. На приводимом ниже маршруте по крайней мере 2 моста придется пройти дважды.
15. Пусть и первоначальный объем древесины. По истечении года с благоприятными условиями объем древесины составит
„ , 5-е 105а _ 21а 100 100 20 ‘
По истечении следующего года с неблагоприятными условиями объем древесины составив
21а , 3
20 100
1,0815а.
20 2000
Итак, за 2 года объем древесины возрастет на 8,15%.
16. Цена Р складывается из платы, взимаемой за пользование архивным документом в размере х марок, и стоимости изготовления копий в размере s марок за штуку. Если заказчику требуется п копий, то их изготовление обойдется ему в P=x-f-ns марок.
По условиям задачи при п—3 заказчик
уплачивает P—6—x-}-3s марок, при n=b стоимость заказа составляет P,=9=x4-5s марок. Следовательно,
6—3s=9—5s, откуда 2s=3, или s—1,5. Но тогда х=6— —3-1,5= 1,5.
Цена изготовления 9 копий, приведенная в условиях задачи, служит для проверки и подтверждает правильность полученного решения. Итак, изготовление п копий одного архивного документа обойдется заказчику в Р— 1,5-f-n-1,5 марок.
17. Пусть х — число страниц в книге, набранной более крупным кеглем. Тогда х-32-51 = 152-45-68,
Таким образом, при наборе более крупным кеглем объем книги составит 285 страниц.
18. 1 кг нектара содержит 700 г воды и 300 г твердого вещества, 1 кг меда содержит 170 г воды и 830* г твердого вещества. Составляем пропорцию:
300 : 830= 1 : х, откуда х « 2,77.
Итак, для получения 1 кг меда пчелам необходимо собрать 2,77 кг нектара.
19. Докажем, что все шарики умещаются в кубе с длиной ребра 10 см. Действительно, один слой содержит 100X100=10 000 шариков. Так как размеры куба позволяют поместить в нем 100 слоев, куб с длиной ребра 10 см действительно вмещает 10 000X100=
== 1 000 000 шариков. Масса шариков меньше массы куба, изготовленного из того же материала, так как шарики не заполняют пространство куба целиком. Масса стального куба с длиной ребра 10 см составляет около 7,8 кг, масса шариков меньше и составляет около 4 кг. Такую массу без труда может поднять один человек.
МИНУТУ НА РАЗМЫШЛЕНИЕ
1. Парис мог рассуждать следующим образом.
а) Предположим, что Афина изрекла истину. Тогда Афина — прекраснейшая из богинь, и, по предположению, утверждение (4) ложно. Мы приходим к противоречию, так как Гера не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Афина. Итак, исходное • предположение ложно.
б) Предположим, что истину изрекла Гера. Тогда Гера — прекраснейшая из богинь и, по предположению, утверждение (2) ложно. Мы снова приходим к противоречию, так как Афродита не может быть прекраснейшей из богинь, кодь скоро прекраснейшая из бсгинь Гера. Следовательно, и зто исходное предположение ложно.
в) Предположим, что Афродита изрекла истину. Тогда Афродита — прекраснейшая из богинь. Отрицания утверждений (2), (3) и (5) истинны и подтверждают, что Афродита прекраснейшая из богинь.
Итак, по решению, вынесенному «судом Париса», прекраснейшая из богинь Афродита.
2. Число, стоящее на месте каждой буквы, показывает, сколькими способами можно добраться до нес. спускаясь с вершины конфигурации
1 2 3 2 1 1
1 3 6 7 6 3 1 1 1
2907 3139 2907 1 2 1
8967 1 3 3 1
14 6 4 1
1 5 10 10 5 1
1 6 16 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
29-512
Итак, слово «абракадабра» можно прочитать 8957, а слово «математика» 512 способами.
3. 180 мин отделяют отправление поезда (6 ч) от 3 ч. Число минут, оставшихся до отправления поезда, мы найдем, разложив разность 180—50=130 в сумму двух чисел, одно из которых в 4 раза больше другого, т. е., взяв '/5 от 130. Следовательно, до отправления поезда оставалось 26 мин. Действительно, за 50 мин перед разговором до 6 ч оставалось 504-26=76 мин, т. е. с 3 ч прошло 180—76=104 мин, что вчетверо больше 26 мин, остававшихся в момент диалога до отправления поезда.
Следовательно, диалог происходил в 5 ч 34 мин.
4. Стол должен быть накрыт по крайней мере на 7 персон: для одного дедушки и одной бабушки, образующих супружескую чету, их сына, его жены и их троих детей (внуков родителей сына): одного сына и двух дочерей.
5. Локомотив должен маневрировать следующим образом: двигаясь вперед, миновать стрелку 6, после чего, двигаясь назад, проехать стрелки 6, 8, 5, 3, 4 и 7, а затем, двигаясь снова вперед, миновать стрелки 7 и 1.
6. Девушки сидят в следующем порядке: К—Д—А—Ж—-Б.
Следовательно, лучших подруг Жанетты зовут Анеттой и Бабеттой.
7. х(х-Н)— x-х-.
Чтобы найти задуманное число, достаточно
1в 612 4
8 32 126
266 2 64
3 36 2
4 в 9
18 1 12
9. а) Крест из 4 черточек от картинки к картинке в верхнем ряду (слева направо) поворачивается по часовой стрелке на 45°. Левая точка (на первой картинке) остается при этом на своем месте, а правая при каж-
дом повороте перемещается на одну черточку по часовой стрелке и на четвертой картинке совпадает с другой точкой. Итак, пустой квадрат следует заполнить картинкой А из нижнего ряда.
б) Пустой квадрат следует заполнить картинкой А, так как при движении слева направо малый круг остается на месте, а средний каждый раз поворачивается на 90° по часовой стрелке.
в) Темные треугольники в правом верхнем и в левом нижнем' углах остаются неподвижными. Треугольник в левом верхнем углу при движении слева направо поворачивается каждый раз на 90°, а треугольник в правом нижнем углу поворачивается каждый'раз на 180°. Следовательно, в пустой квадрат следует поместить картинку В.
> г) Переход от картинки к картинке в верхнем ряду можно осуществить, поворачивая куб каждый раз на 90° вокруг оси, проходящей через центры его правой и леврй граней. Следовательно, пустое место на правом конце верхнего ряда следует заполнить картинкой В.
10. Номер автомашины учителя математики выражается четырехзначным числом вида abba, причем
2(ц-|-&)== lOo-f-ft, &=8а.
Следовательно, а может быть только цифрой 1, а b — только цифрой 8.
Итак, автомашина учителя математики имеет номер 1881.
И. Пусть а, Ь, с — 3 различные цифры, каждая из которых больше нуля. Перестав-
ив
ляя их всеми возможными способами, мы получим следующие трехзначные числа: 100а+Ю&+с, 100с4-10а+&, 100Ь4-10с4-а,
100b+10a-t-c. IOOa-HOc-f-Ь, I00c+106+a.
Сумма всех 6 чисел представима в виде: 100(2a+2Z>4-2c)-J-10(2a+2Z>+2c) 4-
4- (2а+2Ь+2с) = 111 (2а+2Ь+2с) = = 222(a4-&4-c)=222Q, -
где Q — сумма цифр любого из 6 трехзпач-ных чисел.
Моника умножила сумму цифр названного Марией-Луизой трехзначного числа на 222.
12. Разместить зверей по их клеткам служитель зоопарка может за 14 переселений, производимых по следующей схеме (см. с. 178, номера клеток идут слева направо).
13. Пусть Р —рыбка, Ш — шарик, К — колокольчик, Кр — коромысло. Тогда
Ш=2Кр, (1)
Р4-Ш=К, (2)
2Р4-К=Р4-Ш4-К4-Кр, (3)
или
Р=Ш4-Кр. (4)
Из (1) и (4) следует, что
Р=3 Кр, (5)
а из (1), (2) и (5) — что
К=5 Кр. (6)
Если х — груз, удерживающий систему в равновесии вместо вопросительного знака, то х=3 Кр+Ш —5 Кр.
Как видно из (6) н (2), равновесие системы не нарушится, если вопросительный знак заменить двумя предметами: одним шариком и одной рыбкой.
14. В отдельных бросаниях выпало 2, 2, 3, 4 и 5 очков (24-24-4=8, 8—5—3=0).
№ п/п 1-я клетка 2-я клетка 3-я клетка
1 Пантера Крокодил Осел
2 Пантера Крокодил *—•
3 Пантера Крокодил Лев
4 — Крокодил Лев
5 Крокодил Лев
6 Крокодил Лев ——
7 Крокодил Лев Осел
8 Крокодил Лев Осел
9 Крокодил Лев Осел
10 ——. Лев Осел
11 Лев — Осел
12 Лев Осел
13 Лев Осел Волк
14 Лев Осел Волк
4-я клетка 5-я клетка Общий вольер
Волк Лев
Осел Волк Лев
Осел Волк —-
Осел Волк Пантера
Осел Волк Пантера
Осел Волк Пантера
__ Волк Пантера
Волк Пантера Пантера
Волк ——
Волк Пантера Крокодил
Волк Пантера Крокодил
Волк Пантера Крокодил
— Пантера Крокодил
Крокодил Пантера —
15. Названия профессий, требующих основательной математической подготовки: (1) радиоинженер: (2) мостостроитель; (3) мореплаватель; (4) программист.
16. Пусть х — число купленных лошадей, у — число купленных быков. Тогда 31x4-210=1770, откуда
210= 1770—31х= 17644-6—21х-10х
0=84—х— .
и 21
Из последнего равенства следует, что число 10х—6, а следсвательно, и 5х—3 должно делиться на 21. Полагая 5х—3=21z, получаем 0=84—х—2z, х=21*+3=42-|- -£±1 . о 5
Так как х — целое число, числитель z-f-З должен делиться на 5, т. е. z=5«—3 и
х=4(5«—3)4-«=21«—12, 0=84—21И4-12—Ю«4-6= 102—31«.
Но 0—положительное число, а поскольку z=5«—3 не может быть равно нулю, то возможны только 3 случая:
«=1, и—2 и «=3.
Итак, задача Эйлера допускает следующие 3 решения:
1) «=1; х=9, 0=71;
2) «=2; х=30, 0=40;
3) «=3; Л=51, 0=9.
Нетрудно проверить, что во всех трех случаях
31x4-210=1770.
АРИФМЕТИКА С ПТИЧЬЕГО ПОЛЕТА
1. Пусть х—первое число. Тогда второе число равно 19—х. По условиям задачи х24-(1Э—х)2==205, т. е. х2— 19x4-78=0. Это квадратное уравнение имеет корни Xi=13 и х2=6.
Итак, в задаче Штифеля речь идет о числах 13 и 6.
2. а) Если х>8, то х4-3>11, и поэтому заведомо выполняется неравенство х4-3>10.
б) Если 60х=50//, то х=5& и y=Gk, где k—натуральное число. Следовательно, х<.у.
в) Если 5х>10, то х>2, а поскольку У>х, то у>3.
г) Так как х>у, должно выполняться равенство x—y+k, где k — некоторое отличное от нуля целое положительное число. Но y~r2<y+k+5, поэтому «/4-2<х4-5.
д) Так как х>у, то х=^4-й, где k — некоторое отличное от нуля целое положительное число. Поскольку 60<75 и y<.y-\-k, справедливо неравенство
60— (#4-fe)<75—у или
60—х<75—у.
е) Если у<5, то 3t/<15 и тем более 3«/< 17.
3. Пусть а и Ь — два числа, удовлетворяющих условиям задачи. Не ограничивая общности, будем считать, что а>Ь. Тогда
|аЬ = Ь-Н. <1)
=а—6. (2)
Из (2) следует, что а-^-Ь=2а—12, пли Ь=а—12. Подставляя это соотношение в (1), получаем
У а (а—12) =а—124-4, а2— 12а—(а-—8)2, а2— 12а=а2— 16а 4*64, а—16, откуда 6=4. Как показывает проверка, числа 16 и 4 действительно удовлетворяют условиям задачи.
4. Выпишем 10 наименьших натуральных чисел, дающих при делении на 6 остаток 4:
4, 10, 16, 22, 28, 34, 40, 46, 51, 58.
Лишь 2 из них, а именно числа 28 и 58 при делении на 5 дают остаток 3.
Из 2 чисел 28 и 58 только число 58 при делении на 4 дает остаток 2. Это же число при делении на 3 дает остаток 1.
Итак, число 58 обладает всеми требуемыми свойствами. Одновременно доказано, что 58 — наименьшее из чисел, удовлетворяющих условиям задачи. Все остальные числа, обладающие требуемыми свойствами, представимы в виде 584*60fe, где k — произвольное натуральное чисдо.
5. Пусть п — первое из двух чисел. Тогда второе число равно 90—п и
25п . 75(90—п) _чп
100 "Г 100
откуда
п__3(90—л) _go
4 4
«4-3(90—«) = 120, «4-270—3«= 120, 2«=150, n—75.
Итак, условиям задачи удовлетворяют числа 75 и 15.
6. Неравенство а(с—b)/(b—а)>0 выполняется в том и только том случае, если либо О-b и Ь>а, либо с<6 и Ь<а, т. е. если либо а<Ь<с, либо а'>Ь>с.
При а<6<с, т. е. при а=13, 6=15, с—20 выражение а (с—b)/(b—а) принимает нецелое значение:
13-(20—15) _ 13-5
15-3 2
При а>Ь>с, т. е. прн а=20, 6 = 15, с=13, получаем
20(13—5) _ 201—2) _8 15—20 —5 " ‘
Итак, приведенное в условиях задачи выражение принимает целое положительное значение при а=20, 6=15, с=13.
7. Подставляя а=с4-7, получаем
(с4-7) (с4-9)4-<*(с—2)—(2с4-14)с= =с24- 16С4-634-С2—2с—2с2— 14с=63.
8. а) ЛиЯ={4, 5, 6, 7, 8},
б) 4f|B={4, 6},
в) В={3, 7, 9},
г) (7=0,
д) Д\В={7}.
Магический квадрат
Пусть Т — сумма чисел, стоящих в каждой строке, в каждом столбце и на каждой диагонали. Тогда
T=x+y+2z—— 2x+2y+5z= =x-l-y+4z—10=2z-f-3y—10= 7z—x.
Мы получаем только 5 из 8 возможных уравнений и 3 тождества. Из четырех первых уравнений находим х=8, r/=9, z=5, Т—27. Полученные значения удовлетворяют пятому уравнению. Следовательно, в клетках магического квадрата стоят числа
в 7 12
13 9 6
в 11 10
Сумма четных чисел в 4 угловых клетках 84-6+12+10=36=4-9 в 4 раза больше числа, стоящего в центральной клетке.
Кросснамбер
9. а) а с (6, 7, 8, .... 58, 59},
б) х = {0, 1, 2, ..., п, п+1, ...},
в) 06{0, 1, 2, .... п, п+1, ...},
10. 10а-|-6=3(а4-Ь), где 1^а^9, 0^6<;9, откуда
~а—2Ь, а — — .
7
Итак, а принимает целое значение лишь при Ь=7 (а=2).
Условиям задачи удовлетворяет единственное двузначное число: 27.
11. а) Пусть о=1. Тогда равенство 2а+6Ь—аа+Ьа
переходит в равенство 24-66=14-6,
1 откуда ь=— .
5
Поскольку b не является ни одним из чисел
О, 1, 2.. 9, то случай а—1 необходимо
исключить.
б) Пусть а=2. Тогда приведенное в условиях задачи равенство переходит в такое: 4+6&=4+&2
или
b(b—6)=0.
Так как б'>0, то из этого квадратного уравнения следует, что 6=6. Итак, одно решение задачи найдено: о=2, 6=6.
в) Пусть а>3. Преобразуем исходное равенство
2а 4-66=аа 4-6“
к виду а(а0~'—2) = 6(6—Ьа~'). Так как о^З, выполняется неравенство
2)>3(32—2) = 21.
С другой стороны,
6(6—Ь°-') = 5<21 при Ь=1,
6(6—6“-*)=4<21 при 6=2,
6(6—6а~')=0<21 при 6=3.
Следовательно, при а^З и 6=1, 2, 3, ... равенство
2а+66=а°+6а не выполняется.
Итак, задача допускает единственное решение, которое дано в случае <б».
12. Число, предшествующее натуральному числу п, равно п—1. Число, следующее за п, равно п+1. По условиям задачи (п—1)Х X(п+1) =2208, или п2=2209.
Следовательно, задача допускает единственное решение в натуральных числах: п=47. Проверка: 46-48=2208.
13. Умножив ибе части уравнения на ху, получим после несложных преобразований: у+х+\=ху, ху—х—у+1, х(у—1)=у+1,
,= У+1
у— 1
Итак, пары натуральных чисел (х, у), удовлетворяющие уравнению, получаются только при yi—2 и #2—3, что соответствует Xj=3 и Х-2—2.
14. Сумма чисел от 1 до 9 равна 45. Она разделена на 3 равные части. Следовательно, каждая из 3 сумм, приведенных в условиях задачи, равна 15.
Итак, задача допускает следующие решения:
1+54-9=2+6+7=34-4+8, 1+6+8=2+4+9=3+5+7.
15. Число 0 меньше каждого из 20 остальных допустимых значений 1, 2, 20 пере-
менных а и Ь. Следовательно, полагая а=0 и придавая b любое из 20 остальных значений, можно составить 20 неравенств а<Ь. При а=1 переменная Ь может принимать только значения 2, 3, 20, т. е. всего 19 раз-
личных значений. Те же рассуждения применимы и при значениях а, равных 2, 3 и т. д. Наконец, при а=19 переменная b может принимать только одно значение: & = 20. Так как 20+19+...+3+24-1 = 210, неравенство а<Ь можно составить 210 способами.
16. Предположим, что неравенству ~^->аЬ удовлетворяет какая-то пара чисел (а, Ь). Так как а и b — натуральные числа и а>Ь, справедливо неравенство а—&^1. Умножая обе части исходного неравенства на а—Ь, получаем
а+Ь>а& (а—b) ^ab, поскольку а—&^1.
Из неравенств а+&>а& и а>& следует, что 2а>аЬ, откуда 2>Ь, т. е. 6=1. При 6= 1 исходное неравенство преобразуется к виду (а+1)/(а—1)>а, откуда а+1>Д2—°> или а2—2а—1<0. Прибавляя к обеим частям последнего неравенства по 2, получаем а2—2а+1<2, т. е. (а—1)2<2.
Последнему неравенству удовлетворяет только одно натуральное число: а=2. Как показывает проверка, пара чисел а=2, Ь—1 действительно удовлетворяет исходному неравенству.
Другой вариант решения задачи.
Преобразуем исходное неравенство:
ab< а+Ь — a~b+2b —и- 26 а-Ь а-b а-Ь
Так как а>Ь, выполняется неравенство
или
а6<2&+1. (1)
Если существует какая-то пара чисел, удовлетворяющих исходному неравенству, то эти же числа должны удовлетворять неравенству (1), которое можно представить в виде Ь(а—2) 1.
По предположению, Ь<а, поэтому натуральное число b может быть равно только 1. Число а может принимать значения 1, 2 и 3. Как показывает проверка, исходному неравенству удовлетворяет единственная пара чисел: а=2, b—i. 17 18 *
17.
а). —> — ; 2х 2
х<1, например, х=0,5; х=0,25.
б) -1<7;
/>1, папример, 1=1,5; t—2.
в) 4=—; 1 2г* 2
z4=l, например, z=l, z——1.
18. х2+х2-|-2х+1+х2+4х+4>
>х2+6х4-9-Н24-8х+ 16-f-x24-10x4-25,
откуда
19. Раскроем гкобки и, перенеся все члены в левую часть уравнения, приведем подобные члены. После этого разложим получившееся выражение на линейные множители:
(x2+*+l) (2х24-2х—3) =—3(1— х—х2);
2x4-j-2x3—3x2+2x3-f-2x2- -Зх+2х2+2х—3= s= —-3 -f- Зх-f- Зх2, 2х4+4х3—2х2—4х=О, х4+2х3—х2—2х=О, х3(х+2)— x(x-f-2) =0, (х+2) (х3-х)=0, (х-l)x(x-f-l) (х+2) =0, х, = 1, х2=0, х3——1, Хц~—2.
20. Если у—0, то х<4, (1)
2х> 10, (2)
т. е. система неравенств не имеет решений.
Если у= 1, то
х<3, (1)
2х>5, и система неравенств также не имеет решений.
Если у—2, то х<2 2х>0, и система неравенств допускает единственное решение: х—1. Если же у=3, то х<1, т. е. система допускает единственное решение: х—0.
При у^4 в силу неравенства (1) х+#<4: система неравенств не имеет решений.
Итак, задача может иметь не более 2 решений. Как показывает проверка, пары чисел 188
(1, 2) и (О, 3) удовлетворяют условиям задачи.
21. Разрешим второе уравнение t/4-z=ll относительно г и подставим z—11—у в первое уравнение:
7x4-5t/—(11—у) = 8, или
7*4-6«/= 19.
Так как х и у — целые неотрицательные числа, должно выполняться неравенство 0^х^2 (в противном случае 7-3=21 >19). Если х=0, то мы получаем уравнение Ъу—19, не имеющее решений в целых числах. Следовательно, х=0 отпадает. При х= 1 мы получаем у—2 и z—9. При х—2 уравнение также не имеет решений в целых числах.
Итак, нсходйая система уравнений может иметь единственное решение: (1, 2, 9). Как показывает проверка, эта тройка чисел действительно удовлетворяет обоим уравнениям.
ЗАНИМАТЕЛЬНАЯ ГЕОМЕТРИЯ
1. Положим кирпич на угол стола так, чтобы 2 его грани совместились с боковыми гранями столешницы. Отметив карандашом на поверхности стола, где проходит грань, перпендикулярная краю стола в точке М, сдвинем кирпич на его длину вдоль края стола так, чтобы грань, располагавшаяся у края стола, совместилась с отметкой 'М. Затем линейкой измерим по воздуху длину отрезка от угла стола до наиболее далекой вершины («угла») кирпича, лежащей в грани,
которая проходит через отметку М перпендикулярно поверхности стола.
Другое решение: уложить линейку так, чтобы ее обрез совпадал с диагональю верхней грани кирпича, и, сдвинув вдоль диагонали на длину диагонали, измерить требуемое расстояние.
2. (1) а, с, d, f. (2) b, с, f.
3.
4.
5. Письмо адресовано Доретте.
6.
7.
Номера рисунков 1 2 3 4 5 6
Фигуры ' а d b d c a
Номера рисунков 7 8 9 10 11 12
Фигуры d b С d e c
1ргбуе1СЯ найти '
= 7273<О8я, S*96,4
W!
2 2
<VSK.' S«e‘‘-откуда (х + 8) х»2, х>8,
SABC * SADB ° .«JImbo,
h (15-h) =20 10, h- 10, s-Sabm"’00
8. Сложим квадрат пополам, отметим линию сгиба Л В, после чего развернем н, сложив пополам в другом направлении, отметим линию сгиба CD. Пересечение линий сгиба
АВ и CD даст нам точку О. Сложив и отметив линии сгиба, разогнем каждую из половин, на которые делит квадрат отрезок CD. Вершину Е правильного шестиугольника мы найдем, наложив угол с вершиной К на остальную часть квадрата так, чтобы точка А осталась на месте, а вершина К легла на сгиб, делящий пополам отрезок АО. Найдя вершину Е, проведем сгиб АЕ, после чего найти вершины /•', G и Н уже не составляет труда.
9. />=5а; с=6о; d=4a
тав, сколько полей шахматной доски целиком попадает в прямоугольные треугольники АВМ и DCM, возникающие при построении па доске треугольника AMD. Так жак треуголь-
ники АВМ и DCM конгруэнтны, достаточно подсчитать, сколько полай целиком помещается в одном из них.
Введем на шахматной доске прямоугольную систему координат, положительные полуоси которой х и у совпадают с лучами АВ и AD. За единицу длины по обеим осям выберем длину стороны поля. Так как и квадрат, и треугольник принадлежат к числу выпуклых многоугольников, любое поле шахматной доски целиком лежит внутри треугольника АВМ, если в этом треугольнике лежат вершины поля. Пусть [х, у] — координаты левой нижней вершины поля. Тогда 3 остальные вершины поля имеют координаты [х-f-l, У1, [х, t/4-l], [х-j-l, t/4-l]- Прямой, проходящей через точки А и ЛТ, соответствует уравнение у=(1/2)х. Поле шахматной доски попадет внутрь треугольника АВМ, если координаты вершин поля удовлетворяют неравенствам
0=ОС7, «/< -L-x, jz+lsS-Lx. (1)
Таким образом, задача будет решена, если мы найдем все упорядоченные пары [х, у] целых чисел, удовлетворяющих неравенствам (1). Придавая х целые значения от О до 7 и находя из неравенств (1) допустимые значения у, получаем:
X 0 1 2 3
У X 4 5 0 6 0 7
У 0; 1 0; 1 0; 1; 2 0; 1; 2
При составлении таблицы третье неравенство, следующее из четвертого, можно отбросить. С полным основанием мы можем отбросить также второе неравенство, так как оно следует из первого и третьего неравенств. Итак, при составлении таблицы достаточно воспользоваться неравенством у^О и первым и четвертым неравенствами (последнее удобнее записать в виде у=~х—I). Мы пслучаем 12 полей, левые нижние вершины которых лежат в точках с координатами
12, 01, [3, 01, [4, 0], [4, I], Г5, 01, [5, 11, |0, 0], [6, 1], [6, 2J, [7, 0], [7, 1], [7, 2].
Столько же полей целиком умещается в треугольнике DCM.
Итак, с треугольником AMD не имеют общих внутренних точек 24 поля шахматной доски.
ТРЕНИРОВКА ПО СОВРЕМЕННОЙ МАТЕМАТИКЕ
1. а) Число У2 п отличное от пего У 8 иррациональны, произведение же этих чисел У2-У8=4 рационально. Следовательно, утверждение <а» ложно.
б) |/2 и —Y2 — два различных иррациональных числа. Их сумма У2-(-(—у2)=0— рациональное число. Следовательно, утверждение «б» ложно.
в) Предположим, что существует рациональное число г и иррациональное число х, сумма которых r-f-x рациональна. Тогда существуют такие целые числа а, Ь=#0, с и d^O,
что г=а/Ь и r-\-x=dd. Следовательно, x=dd—a/b=(bc—ad)/bd, что противоречит предположению об иррациональности числа х. Итак, мы доказали, что утверждение «в» истинно. (То же самое можно доказать иначе, а именно, сославшись на теоремы о том. что разность двух рациональных чисел рациональна.)
2. Пусть п— произвольное натуральное число. Тогда ra-f-l — число, следующее за ним. и удвоенное произведение числа п и следующего за ним числа равно 2п(п-(-1). Сумма квадратов числа п и следующего за ним числа равна /12+(м-|-1)2, а так как по условию задачи удвоенное произведение чисел на 1 меньше суммы их квадратов, должно выполняться равенство
2n(n-(-l)-]-l =/i2-f-(n-f-I)2.
Раскрывая скобки, получаем тождество 2n24-2n+1 — n2-f-n24-2n-(-1, которое выполняется при любом натуральном п, что и требовалось доказать.
3. Нетрудно видеть, что tga=V3. tgp= Ут-По формуле тангенса суммы углов, применимой к данному случаю, получаем:
tg(a+P) =
tga+tgfi
1—tga-tgfl
7
10
21=22.1L=_L
20 21 ’ 20 2
21
т. e. tg (a+p) = ’/2.
Из таблиц тригонометрических функций
находим значения tg 26,5°, tg 26,6Э и убеждаемся, что tg 26,5°<’/2<tg 26,6°. А так как 0°<а<45° и 0°<₽<45°, неравенство тангенсов соответствует неравенству углов 26,5°<а-Ьр<26,6э, что и требовалось доказать.
4. Поскольку l-6-f-3-3=15 и 24—15=9, то для того чтобы средняя оценка по трем остальным предметам была выше 2, сумма оценок по этим предметам должна быть меньше 9. Действительно, 24 : 12=2, но 23 : 12<2. Итак, по остальным трем предметам студенту необходимо получить по крайней мере одну двойку (напоминаем еще раз, что в ГДР принята пятибалльная система, в которой высшей оценкой считается единица).
5. а) В геометрической прогрессии отношение последующего члена к предыдущему постоянно (и называется знаменателем прогрессии). Обозначим знаменатель прогрессии через q. Тогда 3 соседних члена прогрессии можно записать, например, в виде
— , т, mq Ч
(такая запись членов геометрической прогрессии для нас удобнее более привычной записи a, aq, aq2\ разумеется, обе записи эквивалентны: в этом нетрудно убедиться, положив в традиционной записи a—m/q).
По условиям задачи
-!2- +m-}-m<7= 19, (1)
Ч
+m2-HnV=133. (2)
Подставляя x—q-^-i/q, получаем
m(x-|-l) = 19, (Г)
m2(x-f-l) (х—1) = 133, (2')
откуда
19 133
х=——1 п соответственно *2= —г+1-
, т т2
Приравнивая оба выражения для х2, находим:
т=6их= —, а также о= —п а— —. 6 3 2
Итак, условиям задачи удовлетворяют 2 геометрические прогрессии: 4, 6, 9 и 9, 6, 4.
б) Запишем условия задачи в виде двух уравнений:
а-|-а^3=13, (1)
aq-j-aq2=4. (2)
Решив их, мы получим две геометрические прогрессии: Vs. 4/s, l6/s. 64/s и 64/s, I6/s, 4/s, Vs.
6. а) Исходное неравенство 8(2x-f-l)/5< <3x+2 с помощью эквивалентного преобразования приводится к виду 16x4-8<15x4-10, или х<2. Следовательно, ему удовлетворяют все действительные числа, которые меньше 2.
б) 1. Р.-Ц0.1}
2. Р2={—3; —2; —1; 0}
3. Л4= {0}
7. Вероятность, с которой автобусы, следующие по тому или иному маршруту, прибывают на остановку, зависит от относительной частоты, с которой они курсируют на линии. Например, в течение 30 мин на остановку успевают прибыть 6 автобусов, следующих по маршруту с интервалом 5 мин, 15 автобусов, следующих с интервалом 2 мин, 3 ав
тобуса, следующих с интервалом 10 мин, и 2 автобуса, следующих с интервалом 15 мин, т. е. всего 26 автобусов, из которых 15 приходится на долю следующих с интервалом 2 мин. Значит, относительная частота автобусов, следующих по маршруту с интервалом 2 мин, составляет
р2= 11 ж 0,577,
26
т. е. примерно каждый второй автобус следует по маршруту с интервалом движения 2 мин.
Как кошка с собакой
а)
Так как все функции линейны, их графики имеют вид отрезков прямых и, следовательно, однозначно определяются концевыми точками. Например, для функции fa с областью определения 4<:х<^8 и аналитическим выражением #=x/2-f-H началом отрезка служит точка с координатами' х=4; #=24-11 = 13, а концом — точка с координатами х=8;
у=44-11 = 15. Графики всех 14 функций образуют «портрет» собаки, который вы видите на рисунке.
б)
Функ- Область ция определения Аналитическое выражение
h 4<j/sS6 х=1
h 4<0<6 x=-l
/з — 1sSx<1 y=\x / —x-f-5 при — IsgxsgO, 1+0 ’ t x-f-5 при OsS.tsCl.
h 4,5гС</С5 x==0,5
Is 4,5^0^5 x=—0,5 —x-f-4,5
Is —0,5<x^0,5 0=[x|4-4,5= при—О.б^х^О, «4-4,5 'при 0c«C0,5
h —0,25 sg x sg 0,25 у=4
Is -igxgo y=— 3x-bl
Is —O.Ss^xsgO 0=2x4-1
f 10 —0,5gxg7 0=0
hi 0=-x4-7
112 3C*<6 0~2L_j
(l3 Osg0s£2 'X=3
h* l.-£x^3 0=—x-l-5
8. Плоскость а параллельна плоскости р(а||р) в том и только в том случае, если а=р или af|p=0.
Прямая g параллельна прямой h (g||ft) в том и только в том случае, если g—h или £Г1Й=0.
Переходим к доказательству теоремы.
По предположению, аПе#=0. Следовательно, существует прямая g=aQe. Кроме того, РР,е^=0. Следовательно, существует прямая /1=рПе. Так как gee, и fteze, эти прямые лежат в одной общей плоскости, .а именно, в плоскости е. Так как а||р, необходимо различать следующие случаи.
1) а=р=*Я=аПе=рПе—ft, т. е. g\\h.
2) иПр=0=>£ПЛ= (аПе)П (РПе)= afW Пе= (аПР) Л (еПе) = 0Ле= 0-
Следовательно, и в этом случае £||л.
в) Тетраэдр (прямой, неправильный).
10. Можно. Для этого карандаши следует уложить в коробку слоями, содержащими попеременно то 20, то 19 штук. Карандаши верхнего слоя должны располагаться в промежутках между карандашами нижнего слоя. При таком способе упаковки в коробку войдет 5-20+4-19= 100+76= 176 карандашей.
При рекомендуемом нами способе упаковки в коробку войдет более 160, а именно 176 карандашей.
11. Из условия «а» следует, чта если отдел В не принимает участия в обсуждении проекта, то отдел А также не участвует в обсуждении проекта. Иначе говоря, если отдел А принимает участие, то В также участвует в обсуждении проекта (обратное* утверждение). Из условия «б» мы заключаем, что если отдел А принимает участие в обсуждении проекта, то отдел С непременно участвует в обсуждении.
12. Из (4) следует, что число 2 принадлежит как множеству А, так и множеству В. Из (5) мы заключаем, что числа 2, 4 и 8 принадлежат как множеству В, так и множеству С. Таким образом, число 2 принадлежит всем 3 множествам, в то время как числа 4 и 8 не принадлежат множеству А, ибо в противном случае мы пришли бы к противоречию с условием (4).
Из (1). следует, что число 1 не принадлежит ни множеству А, ни множеству В, а из (2) и (3) — что число 1 принадлежит множеству С.
С помощью аналогичных рассуждений мы заключаем из (I), (2) и (3), что
число 3 принадлежит только множеству А, число 5 принадлежит только множеству А, число 6 принадлежит только множеству В, число 7 принадлежит только множеству А.
Итак, множества А, В и С содержат следующие элементы: А={2, 3, 5, 7), В={2; 4, 6, 8}, С={1, 2, 4, 8}.
13. Обозначим длины ребер упаковки 10 спичечных коробков через А, В и С. Предположим, что вдоль ребра А упаковки ребро а спичечного коробка укладывается х раз (Л = ах), вдоль ребра В упаковки ребро b 'спичечного коробка укладывается у раз (В—by) и вдоль ребра С упаковки ребро с спичечного коробка укладывается z раз (C=cz). Собьем упаковки равен АВС=аЬс xyz. Так как abc — объем одного спичечного коробка, то произведение xyz задает число спичечных коробков в упаковке. Следовательно, ху?=10. Так как х, у, z—могут быть только положительными целыми числами, то 202
существует всего 9 возможных вариантов, представленных в следующей таблице:
площади поверхности прямоугольного параллелепипеда, составленного из 10 спичечных коробков (припуски на клапаны, необходимые для склеивания обертки, не учитываются), т. е.
2AB-\-2AC-i-2BC=2(abxy+acxz-i-bcyz).
Поскольку расход бумаги требуется свести до минимума, величина
W =. abxy-4-acxz-A-bcyz
также должна быть минимальной.
В 9 перечисленных выше возможных вариантах величина W принимает значения 28 709, 26 414, 17 054, 24 918, 24 153, 19 718, 17 678, 15 833 и, наконец, 14 558 (при х=5. у—2, 2=1).
Итак, наиболее экономичной по расходу оберточной бумаги оказывается упаковка с х=5, у=5, z=l. Именно ее и используют в торговой сети.
14.
в) Пожелание невыполнимо. Действительно, если бы проектировщики могли учесть все пожелания, то число дорог было бы равно 7, тогда как оно должно быть четным (каждая дорога считается дважды, так как соединяет
б) Первый вариант
два населенных пункта, а подсчет производится по числу дорог, выходящих из каждого пункта).
МАТЕМАТИКА НА КАЖДОМ ШАГУ
1. Условия задачи позволяют записать уравнения (х — стаж одного собеседника, У — другого):
у=2х, (1)
у—2x3 (х—2), (2)
откуда х=4, у=8. Итак, один собеседник состоит в шахматном клубе 8 лет, другой — 4 года.
2. Схема переправы приведена в следую-
Южный берег Северный берег
1 т a, b ХА, а) 1 о а 2 т а, Ь, с 2 о а, b 3 т а, А, Ь, В 3 о а, А 4 т а. А, В, С 4 о А, В, С 5 т А, В, С, а, Ь 5 о А, В, С, а (А, В, а, 6) 6 г А, В, С, а, Ь, с А, а, В, b. С, с А, В, С, с (В, b. С, с) А, В, b. С, с, А, В, С А, В, С, с С, с В, b. С, с &, С а, Ь, с Ь, с (С, с)
щей таблице. Буквы Л, В и С означают мужей, а, b и с — их жен (так что А, а; В, b и С, с — супружеские пары). Число рейсов указано вместе с направлением, в котором лодка пересекает реку: т — туда, о—обратно. В случае, когда имеются 2 варианта, второй вариант указан в круглых скобках.
3. Пусть х — число распроданных коврижек по 17 марок за штуку, у — число распроданных коврижек по 12 марок за штуку. Тогда
17х+120=478, (1)
где х и у — целые положительные числа. Разрешив уравнение (1) относительно у, получаем:
jz=39-x+ 5(2~х).
Так как у — целое число, а 5 и 12 — взаимно простые числа, (2—х) должно делиться на 12, т. е. 2—х=12/, где t—целое число, или х=2—12/. Подставляя х в (2), получаем 0=37+17/.
По условиям задачи х>10 и 0>О, поэтому /=—1 и, следовательно, х=14, 0=20.
Итак, было распродано 14 коврижек по 17 марок за штуку и 20 коврижек по 12 марок за штуку.
4. Из 100 коллекционеров 30 не собирают старинные монеты, 25 не интересуются значками, 20 равнодушны к этикеткам от спичечных коробков и 15 без энтузиазма относятся к филателии, т. е. (30+25+20+15) =90 любителей не занимаются по крайней мере одним из четырех видов коллекционирования.
Следовательно, 10 коллекционеров собирают и монеты, и значки, и этикетки, и мар-
ки. (На рисунке СМ монеты,- Зн — значки, марки.)
5. Из 50 членов общины 10 говорят только на родном (немецком) языке. Остальные 40 членов общины, кроме родного языка, владеют также французским или итальянским языком. Так как
означает старинные
Э — этикетки и М —
20+35=55, а 55—40=
= 15, мы заключаем, что 15 членов общины говорят н по-французски, п по-итальянски.
6. Для любых натуральных чисел а и b из допустимых множеств (размер ботинок и возраст) выполняется тождество
[ (2«+39) • 50+29]— (1979—6) = 100а+&.
7. В первом случае потребуется веревка длиной 4a-j-8c+46, во втором — веревка длиной 4а+4&+4с и в третьем — веревка длиной 6a+4c+6ft.
Самая короткая веревка потребуется во втором случае, так как
4a-f-8c-j-4b >4a-f-4&+4c и 6a-|-4c+6&>4a+46+4c.
Самая длинная веревка потребуется в третьем случае, так как
(4а-+-8с~|-4&)—(4а+46+4с) =4с, (6а+4с+6&)—(4а+4&+4с) = 2а-(-2Ь, а по условиям задачи a-j-b>2c, вследствие чего 2а+2&>4с.
Итак, длины веревок удовлетворяют неравенствам (2)< (1) < (3).
8. Пусть х — число порций рыбы, приготовленных искусными поварами, у — число столов. Тогда
. «/+!=*. (О
2(у-1)=х, (2)
откуда «Н-1=2(у—1) и у=3, х=4.
Итак, повара приготовили 4 порции рыбы, а для гостей была 3 стола.
9. Предположим, что до снижения цен входной билет в цирк стоил х марок (рублей или других денежных единиц), а на представлении побывало п зрителей. Выручка от продажи билетов составила пх марок. После снижения стоимости входной билет стал стоить 0,7х марок, число посетителей возросло на у человек, а выручка осталась прежней, т. е.
nx=(n+tf) jy X, или
пх=
7 7
тГ’+к4'-
3 7
Зп=7у,
«/=—n«0,43n
Итак, число зрителей возросло примерно на 43%.
10. Высота дерева относится к длине отбрасываемой им тени так же, как высота столба к длине своей тени, т. е.
х: 10=3:2 х=15.
Итак. Высота дерева равна 15 м.
12. Так как (*/2) • (2/з) — ‘/з. пассажир проспал ’/з пути. '
13. Цифры у каждой деревни указывают продолжительность в мин самого короткого маршрута, ведущего к ней из пункта А. Кратчайшие маршруты показаны на плане более жирными линиями. Следуя кратчайшим маршрутом, из Л в В можно добраться за 60 мин.
14.
15.
. . 4 846 б) ,1 054 , I 054 , I 065 , 1076
а) + 4 124 + 9 478 + 9 482 + 9 578 + 9 658
+ 9 710 10 532 10 536 10 643 10 734
4- 6 784
25 464
в) Приведем одно из решений:
, 992
+ 992
1 984
г) Приведем два решения:
, 286 , 467
+ 923 "Г 942
1 209 1 409
(Остальные 30 решений этого криптарифма предлагаем желающим найти самостоятельно.)
16. Пусть х — число подлежащих распространению билетов лотереи. Тогда
5-х= 87300-100 = (94(Ю0 .х = 38800
45
Итак, чтобы израсходовать намеченную сумму в 87 300 франков на выплату выигрышей, организаторам лотереи необходимо распространить 38 800 билетов стоимостью по "> франков.
17. Пусть х — стоимость пригласительного билета для члена садового кооператива, а у— для гостя. Если бы сборы от продажи пригласительных билетов должны были составить ровно 420 марок, а стоимость пригласительного билета для члена кооператива была вдвое меньше стоимости пригласительного билета для гостя, то мы получили бы систему уравнений
150х+100у=420, у=2х
п, решив ее, нашли бы, что х=1,20 и у=2,40.
Поскольку задача сформулирована не столь четко («расходы, по мнению членов правления, должны составить не менее 420 марок», «стоимость пригласительного билета для гостей должна превышать стоимость при-210
гласительного билета для членов кооператива, но не более чем в 2 раза»), ее условия можно записать в виде системы двух неравенств:
150х+100// >420, 2х>//.
Существует бесконечно много вариантов цен на пригласительные билеты, удовлетворяющих этим неравенствам. Например, если бы расходы должны были составить не более 500 марок, то 250 участников праздника долж-нй были бы в среднем заплатить по 250 марок. Из множества возможных решений правление могло бы отдать предпочтение варианту, при котором входной билет для члена кооператива стоил бы 1,50 марки, а входной билет для гостя — 2 марки. Выручка от продажи пригласительных билетов составила бы в этом случае 425 марок.
18. Пусть х, у, г, и, v - число монет достоинством 50, 20, 10, 5 пфеннигов и 1 пфенниг соответственно. Задача сводится к решению в целых неотрицательных числах уравнения
50x4-20//4-10г4-5«4-У= ЮО (1) при условии, что х^2, г/^5, zs^lO, u^20 и ц^ЮО.
Все решения уравнения (1) можно было бы найти, прямым перебором, составив таблицу, но такой подход слишком громоздок, так как число решений очень велико.
Мы будем исходить из другого. Прежде всего обратим внимание на то, что суммы 5«4~у и 20//-)-Юг делятся на 10 и поэтому могут принимать только значения 0, 10, 20,
100. Кроме того, х может принимать только значения 0, 1 или 2.
Уравнение 5«+i>=0 допускает единственное решение, удовлетворяющее этим условиям («=и=0), а уравнение 5«+и=10— ровно 3 решения (и=0, о=10; и=1, и=5; и=2, и=0).
В следующей таблице показано, сколько решений, удовлетворяющих всем условиям, допускает уравнение 5«+и=Л при Л=0, 10, 20, ..., 100- и уравнение 20i/+10z=B при В= 100, 90, 80, ..., 10, 0.
А Число решений В Число решений
0 1 100 6
10 3 90 5
20 5 80 5
30 7 70 4
40 9 60 4
50 11 50 3
60 13 40 3
70 15 30 2
80 17 20 2
90 19 10 1
100 21 0 1
При х=0 число решений уравнения (1) равно сумме произведений чисел, стоящих в одной строке во втором и четвертом столбцах (так как Л+В= 100, и любое решение уравнения 5u-]-v=A может сочетаться с любым решением уравнения 20z/+10z=B): 1-6-ЬЗ-5-!-5-5+7.4-|-9-4+11*3+13.3+15-2+ 4-17.2+19-1+21-1 = 1 • (21 + 19)+2-(17+ + 15)+3- (13+11)+4- (9+7)+5- (5+3) + 4-6-1 = 40+64+72+74+40+6=286.
При х--1 число решений уравнения (I)
равно сумме произведений чисел, стоящих во втором столбце в первых шести строках, а в четвертом столбце — в шести последних строках (что соответствует Д+В=50): 1.3+3-34-5-2H-7-2-I-9-1 + 11-1=3- (1+3) + +2- (5+7)+ 1-(9+11) = 12+24+20=56.
Наконец, при х=2 число решений уравнения (1) равно 1 (так как х=2 соответствует Д+В=0).
Итак, уравнение (1) допускает всего 286+56-t-l = 343 решения: 1 марку монетами достоинством в 50, 20, 10, 5 пфеннигов и в 1 пфенниг можно разменять 343 способами.
19. Пусть у — число миль, проходимых за день одним, ах — другим гонцом. Тогда
У=х+2, (1)
12х+12^=260. (2)
Подставляя (1) в (2), получаем 12х+12(х+2) =260, откуда
Таким образом, один гонец проходил за 5 5
день 9 — миль, а другой — 1 11 g- миль.
СЛОВО ЗНАМЕНИТЫМ МАТЕМАТИКАМ
1. Такие числа х должны удовлетворять соотношениям
х=60п+1, х=7а,
где п и a — некоторые целые числа.
Итак, 60«+1 = 7а, откуда
60rt-j-l
7 *
a=8«+ 1"±1.
7
Целым положительным значениям а соответствует n=5, 12, 19, ...
При n=5 x=301,
при л= 12 x=721,
при n=19 x— 1141 и т. д.
Эта задача допускает простое решение, если следовать Бхаскаре. В прошлом веке одному математику для «доказательства» правильности результата, полученного Бхаскарой, понадобилось несколько страниц.
2. Пусть х — число дней. Тогда
Х—1 1 х
6 + 5 '
Число дней равно 85.
3. Пусть х — одно из слагаемых числа 10. Тогда
х2+(Ю—х)2=58,
*1=7, «2 = 3.
Итак, слагаемые, о которых идет речь в задаче Аль-Хорезми, равны 7 и 3.
4. С каждым прыжком гончая уменьшает расстояние, отделяющее ее от зайца и первоначально составляющее 150 футов, на 2 фута: 9—7= 2, 150 : 2= 75.
Гончая догонит зайца за 75 прыжков.
5. Если гири при взвешивании разрешается ставить только на одну чашу весов, то
для взвешивания любой массы ее необходимо представить в виде суммы масс имеющихся гирь. (Разумеется, при взвешивании одной массы любая гиря может быть использована только 1 раз.) Следовательно, если рь р2» Рз» Pi и р5 — массы гирь, то массу Q^30 кг любого тела необходимо представить в виде
Q=ai Pi +а2Р2+язРз+в4Р4+язР5>
где коэффициенты at, а2, аз, at и аз равны либо единице (если соответствующая гиря поставлена на чашу весов), либо нулю (если гиря не поставлена на чашу весов). В такой постановке задачи нетрудно усмотреть аналогию с представлением числа Q в двоичной системе счисления. Массы гирь pi, р2, Рз, р* и рз достаточно выбрать равными 1, 2, 4, 8 и 16 кг.
Сумма масс равна 14-2+4+8+16=31, т. е. больше 30. Кроме того, любое число Q, не • превышающее 30, можно представить в виде
Q=b424+&323+&222+6i2I+&o20,
где коэффициенты &4, b3, b2, и Ьо, как и требуется, равны либо нулю, либо единице.
6.
7. Пусть х — число цветов лотоса в венке. По условиям задачи
fx44x+4-x+-rx+6==x’
откуда х—120.
Итак, венок сплетен из 120 цветов лотоса.
8. Пусть х — сумма денег, внесенная на покупку дома третьим подмастерьем. По условиям задачи
12x-|-4x-f-x=204,
Откуда х=12.
Итак, на покупку дома первый подмастерье дал 144 гульдена, второй внес 48 гульденов, а третий— 12 гульденов.
10. Пусть х — стоимость 1 яблока, а у — стоимость 1 груши в динарах. Тогда
9х—1/=13, (1)
15(/—х=6. (2)
Разрешив (2) относительно х, подставим полученное выражение х=15г/—6 в (1):
134 г/=67,
откуда i/=0,5. Следовательно, х=1,5.
Итак, 1 яблоко стоит 1,5 динара, 1 груша — 0,5 динара.
11. Из' произвольной точки А заданной окружности радиусом АО сделаем подряд 3 засечки так, что АВ — ВС=СО — АО. Вокруг точек А и D как вокруг центров опишем 2 окружности радиусом AC—BD. Пусть Е и Е' — точки пересечения этих окружностей, а F и F' — точки пересечения заданной окружности с окружностью радиуса ОЕ, проведенного из точки А как из центра. Тогда AF — сторона квадрата, вписанного в данную окружность.
Доказательство. В прямоугольном треугольнике ADC по построению AD=2CD и, следовательно, AC2=3CD2. Отсюда мы заключаем, что в прямоугольном треугольнике АЕО
ОЕ2==2АО2,
т. е. OE=AF=AO]/2— сторона квадрата, вписанного в данную окружность.
12. Пусть у — доля, которую составляет прирост травы за 1 неделю от первоначального ее количества на лугу площадью в 1 га. Тогда прирост травы на первом лугу за 1 неделю составит 311зУ долей, а за 4 недели —
з з
Аналогичным образом травы съела за 1 неделю
3’/з«/-4 долей от того количества травы, которое первоначально было на лугу площадью в I га, что эквивалентно увеличению первоначальной площади первого луга до (3*/з+ +40/зУ) га. Коровы съели столько травы, сколько ее было бы в первый день на лугу площадью (31/з+40/зу) га. За 1 неделю 12 коров съели 'А травы, а 1 корова за 1 неделю съела ’/<& всей травы, т. е. столько травы, сколько было первоначально на лугу площадью
1 1 . 40 \ 104-404,
~13 — + — УI = —тп га.
144
ВЫЧИСЛИМ, СКОЛЬКО 1 корова на втором лугу:
прирост травы на 1 га луга за 1 неделю: у, прирост травы на 1 га луга за 9 недель: 9 у, * '
прирост травы на 10 га луга за 9 недель: 90 у.
Итак, для того чтобы прокормить 21 корову в течение 9 недель, хватило бы травы, которая первоначально была на лугу площадью (10+90i/) га, а для того чтобы прокормить 1 корову в течение I недели, хватило бы травы, которая была на лугу площадью
Ю+90у _ 10+90у 9-21 189
Так как, по предположению, все коровы в день съедают одно и то же количество-травы, мы получаем уравнение
10+40у 10+90^'
144 189
и, решая его, находим у—1/2-
Зная недельный прирост травы на 1 га луга, определим площадь пастбища, способного прокормить 1 корову в течение 1 недели:
10+401/ _ 5 144 54 ,а‘
Теперь у нас уже все готово, чтобы ответить на вопрос задачи.
Пусть х — число коров, которых можно пасти на третьем лугу в течение 18 недель. Тогда
И+2«.18.Д- 5 18ж 54
откуда х=36.
Итак, на третьем лугу в течение-18 недель можно пасти 36 коров.
14. 4=2+2 10=5+5
6=3+3 ........
8=5+3 46=41+5
48=43+5
15. 13+123= 1 + 1728= 1729, 93+103 = 729+1000= 1729.
16. От 16 июля 1799 г. интересующую нас дату отделяют 2770 дней, так как 8113— —5343=2700 дней. Из них на 1799 г. прихо
дится 197 дней (а именно: 16 дней в июле, 3-31 дней в январе, марте и мае, 2-30 дней в апреле и июне, 28 дней в феврале). На промежуток времени с 1792 по 1798 г. приходится 2557 дней (5 лет продолжительностью по 365 дней и 2 високосных года по 366 дней). Остается 16 дней (2770—197—2557=16). Отсчитав их назад от 31 декабря 1791 г., мы узнаем, что интересующая нас дата приходится на 15 декабря 1791 г.
НАША СЕКЦИЯ ИГР
2. Наибольшая сумма очков достигается на видимых гранях тетракуба слева (она равна 67 очкам), наименьшая — на видимых гранях «линейного» тетракуба справа (она равна 36 очкам).
7.
8. Полицейским нужно стоять на перекрестках 3, 12, 14, 23, 25 и 34. Действительно, полицейские должны держать под наблюде-
нием все дорожки городского парка: 6 по горизонтали (г), 6 по вертикали (д), 6 по диагонали в одном (д) и 6 по диагонали в другом направлении (е). По условиям задачи один полицейский стоит на перекрестке 34, что приводит к единственному варианту расстановки 5 остальных полицейских:
3 : вз, dj, 65; 14 : вг» гз, ^2» ез‘г 25: дь г5, д3, е>;
12 : вв, д4,
23 : в$, д$, е4",
34 : в4, гв, а6, е2.
9.
10. Пусть х — число очков, выпавших на первой игральной кости, у — число очков, выпавших на второй кости, и z — число очков, выпавших на третьей кости. Тогда
[(2х-|-5) • 5+10+1/] 10+z=s, или
100x+10y+z=s—350.
Пример. Предположим, что на костях выпало 2, 3 и 6 очков. Проделываем вычисления:
2-2=4; 4+5=9; 9-5=45; 45+10=55;
55+3=58; 58-10=580; 580+6=586; 586—350=236.
Итак, на первой кости выпало 2 очка, на второй — 3 и на третьей — 6 очков.
11.
э © я с_и~е-ээ э яиэ я иэ-я и ©-м и й © © © <И Э Я ЛЭ Э ЭИ И © э ив и ©Xte э э © И Я± И И ф и и й© © © ©ф©©ИЯХ>Э©фИИ э ©эя© э яэ и е-я © И ЭН ©Л© и© и э я я э © э ©,я© и Ф © © В (9&3 ©И В В.©Х я л сдо © в э я © и э я © в©эв©©лэяя©э
12. При бросании 1 красной и 1 белой игральной кости общее число исходов равно 6-6=36. Рассмотрим теперь бросание двух неотличимых костей. Если на костях выпадает по одинаковому числу очков, то безразлично, отличимы ли кости или не отличимы. По одинаковому числу очков на каждой из двух костей выпадает в 6 случаях. В остальных 30 случаях из-за неотличимости костей мы отождествляем исходы бросаний попарно, так как не можем сказать, на какой именно кости выпало одно из двух неравных чисел и на какой другое. Следовательно, вместо 30 в случае одинаковых костей мы насчитываем лишь 15 различных исходов.
Итак, при двух, одинаковых костях общее число исходов бросаний равно 21.
ПУТЬ, ВРЕМЯ, СКОРОСТЬ
1. Воспользуемся для вычислений формулой v=s/t
u, = 366 км/мин, v2 = 1176,5 км/мин> 123 421
Vi« 2,976 км/мин, t>i« 178,5 км/ч.
u2« 2,795 км/мин, t>2« 167,7 км/ч.
Итак, на участке Токио — Нагоя «Хикари» развивает среднюю скорость 178,5 км/ч, а на участке от Токио до Яваты — 167,7 км/ч.
2. В обоих случаях вычисления будем производить по формуле s—vt, разрешив ее относительно t.
Милан: «1 = О1Л. Хаммерфест: s2=V2h,
Л = ±_, t2= 21-,
V1 иг
t == 2900
2 300 000
6 «0,0735 с,
t2 «0,0097 с.
Итак, звук долетает до зрителя, сидящего в зале театра, примерно через 0,07 с, а электромагнитные волны доходят до зрителя, сидящего у экрана телевизора в далекой Норвегии, примерно через 0,01 с.
Следовательно, зритель в Хаммерфесте услышит музыку раньше, чем зритель в зале театра.
3. В обеих задачах нам понадобятся формулы для равноускоренного движения: v=gt и s=gt2/2. Исключив /, запишем s как функцию от V.
s=^r> v=gt,
Р*= -51 s= g 11= g2 ’ 2 g2 2g
и2-—2gs,
v=V2gs.
a)
t'i=y2gsi,
i4 = }2-9,81 -80 м/с, th «39,6 м/с «143 км/ч.
6)
t>2=f2gsa, »2=}2-9,8l -5 м/с,
U2~9,9 м/с «35,7 км/ч.
Итак, парашютист к моменту раскрытия парашюта успевает в свободном падении развить скорость примерно 143 км/ч, а прыгун с трамплина входит в воду со скоростью около 35,7 км/ч.
4. Высоту свободного падения s вычислим по формуле v2=2gs:
Так как 50 км/ч=125/э м/с, получаем s=1252/92«9,8 м.
Итак, при свободном падении с высоты 9,8 м удар о землю будет таким же, как при наезде на препятствие со скоростью 50 км/ч.
5, Из соотношений f— ~-и Т= 1—получаем
t=Tn, t—n .
t=50- — «0,114с.
440
Таким образом, запись длилась около 0,114 с. За это время камертон совершил 50 колебаний.
6. Анисимова пробежала дистанцию 100 м за 12,77-4-0,001 = 12,78 с, развив среднюю скорость о=100/12,78 м/с.
Шаллер обогнала Анисимову на расстояние, которое та пробежала за 0,01 с, т. е. на 1,00/12,78-0,01 «7,82 см. Итак, Шаллер на финише была впереди Анисимовой с едва различимым преимуществом около 8 см.
7. Вторая яхта пришла второй потому, что со скоростью 24 км/ч она шла не так долго, как со скоростью 16 км/ч. (Например, если бы дистанция гонки была равна 48 км, то со скоростью 24 км/ч вторая яхта шла бы 24/24=1 ч, а со скоростью 16 км/ч—24/16=*= = 1*/2 ч.) Именно поэтому на прохождение дистанции «туда» она израсходовала больше времени, чем ей удалось выиграть на обратном пути.
Вокруг часов
8. Если часовая стрелка до того, как обе стрелки совпадут, успеет пройти х минутных делений, то минутная стрелка за то же время пройдет (454-х) минутных делений. Так как за одно и то же время часовая стрелка проходит */12 того, что проходит минутная, мы можем составить уравнение х= (454-х)/12, откуда х=47и-
Минутная стрелка совпадает с часовой через 497п мин.
15 « га ,9=
9. Пусть t>t — линейная скорость конца минутной стрелки, а и2 — часовой. Тогда
v,= *_=*£ = см/ч.
6 Ч 1
с2= J1. = = 2=vL5 = _л_ см/
it tt 12 4
ui:t>2=4n: -£L =16:1.
Итак, конец минутной стрелки движется в 16 раз быстрее, чем конец часовой стрелки.
10. За 1 ч часовая^ стрелка описывает угол 30°, а за 1 мин — угол 0,5°. Минутная стрелка за 1 мин описывает угол 6°. Так как 90: (6— —0,5) = 164/ц, минутная и часовая стрелки образуют прямой угол в первый раз через 164/ц мин после того, как обе будут стоять на 12. Поскольку п-164/11 = 24-60, мы получаем п=88 (в это число входят углы в 0, 90°, 180° и 270°, образуемые минутной и часовой стрелками).
В течение суток минутная и часовая стрелки образуют прямой угол 44 раза.
11. Пусть х—промежуток времени (в мин), который должен пройти прежде, чем стрелки расположатся на одной прямой и будут направлены в противоположные стороны. Минусная стрелка успеет пройти за это время х минутных делений циферблата, а часовая— х/12 минутных делений. Когда стрелки расположатся на одной прямой и будут направлены ,в противоположные стороны, их будут разделять 30 минутных делений циферблата. Следовательно, в это время
х—- 12 — 3°»
откуда x==328/ti.
Через 328/ц мин после того, как минутная и часовая стрелки совпадут, они будут «смотреть» в противоположные стороны.
12. В 5°° минутную стрелку отделяют от часовой 25 минутных делений. В тот момент, когда Клаус взглянул на часы, большая стрелка отставала от малой лишь на 3 деления и, следовательно, успела пройти 22 деления. За 1 мин большая стрелка проходит 1 деление, а малая */i2 деления. Следовательно, за 1 мин минутная стрелка догоняет часовую на 1—,/i2=,,/i2 деления, а для того чтобы пройти 22 деления, минутной стрелке понадобится 22 : u/i2=24 мин.
Итак, Клаус взглянул на часы в 524.
13. Для того чтобы тело могло двигаться по круговой орбите вокруг Земли, центростремительная сила Fu должна быть равна силе тяготения Гт. Это равенство достигается только при определенной скорости, так как Р\=ти2/г, FT—mg.
ttlVs ------ =mg,
г
0== i/ 6378 9'81
V iuoo
«7,91 км/с.
Итак, первая космическая скорость составляет 7,91 км/с. 14 *
14. Разрешив уравнение равномерного дви-
жения s=vt относительно /, получим:
<= ^9]0 000000 =(9700с==3281/ мин=5ч 287, мин. 300 000
Чтобы преодолеть расстояние от Солнца до Плутона, свету потребуется 5 ч 28*/з мин.
15.
, 71 568
+ 71568
+ 71568
214 704
Приведем лишь некоторые из 28 решений второго криптарифма:
, 825 , 745 , 472 , 382
1207 ~г~ 3419 Г 6715 7816
2032 4164 7187 8198
16. До места встречи велосипедист успевает проехать на 5 км больше, чем возница, поэтому «вел.—5=«воз. . ПОДСТЭВЛЯЯ «вел. = = 151вел.. «воз. = 10(1вел. +1). ПОЛучаеМ 15/всл.—5=10(/ вел. +1).
откуда /вел. = 3, «вел. = 45, «воз. = 40,’/воз. =4.
Пусть АС—х км и ВС—х—5 км. Тогда
/ t — х~~5
Г вел. — tz" и * век». =* 1
10 10
Кроме того, по условиям задачи
/воз. = (вел. I—.
поэтому
/воз. =
х , _4____х+20
15 1 3 — 15 ’
228
и, следовательно:
х—5 х+20
10 15 '
откуда х—55.
Итак, расстояние между хутором В и то-родком С равно 55 км. Велосипедист догоняет возницу в 10 ч утра, не доезжая 10 км до городка С.
17. Предположим, что спортсмен достигает скорости 90 км/ч за время t на расстоянии з от старта. Если Оо — начальная скорость, а — ускорение, то
о==о0-|-а/,
а
72000 с 3600-0,8
Определим теперь расстояние s:
s=u0^+ —L at2,
s= 18000.254- _JL -0,8-252=375 м.
3600 2
Спортсмен-саночник разовьет скорость 90 км/ч через 25 с после старта, пройдя 375 м пути.
18. За 1 ч теплоход проходит против течения 2/9 расстояния, а по течению — */з расстояния. Разность (равная */9) соответствует удвоенной скорости течения. Следовательно, за 1 ч плывущая по реке пустая бутылка проходит ‘/is расстояния.
Итак, то же расстояние пустая бутылка проплывает за 18 ч.
19. Пусть оп — скорость пассажирского, v т— скорость товарного поезда, а До — разность скоростей. Тогда
«п=«т +Ао.
—= — +Д», <П tT
stf=st п -j-Aof п t т ,
s = ...Wr д ^ОД^Д =8550 м tj — 2
(мы воспользовались здесь тем, что 4 м/с= = 240 м/мип).
Таким образом, длина туннеля равна 8550 м.
20. Скорости встречных поездов складываются:
o=oi+o2=45+36=81 км/ч, и
«И 9РР в = 135 и.
8600
Итак, 135 м.
длина первого поезда составляла
БЕСЕДЫ НА ЕСТЕСТВЕННОНАУЧНЫЕ ТЕМЫ
1. Массу оболочки вычислим по формуле m=Sx, где S — площадь поверхности оболочки, а х—масса ее квадратного метра:
5=4лг2, щ=4лг2-х=4-3,14-42-240«48 200 г.
Масса оболочки шара-зонда равна примерно 48,2 кг.
2. На рисунке показано, как следует расположить 7 труб в пакете (1 труба в центре и 6 соприкасающихся труб вокруг нее), для того чтобы их можно было обвязать самой короткой лентой. Обозначим длину ленты I. Тогда
/==6-10-Ьл-10=10(6-Н0«91,4 см,
т. е. минимальная длина ленты равна 91,4 см.
3. Батарея мопеда обладает зарядом Q=4,5 А-ч. Мощностью электрической лампы называется величина Р=Ш, где U—напряжение, / — сила тока, откуда 1=Р/и= =0,6/6=0,1 А.
Поскольку заряд батареи равен заряду, который пройдет через лампу за время t, Q=it,
t Q 4,5 t= —X = ’ =45 ч.
I 0,1
Итак, лампа будет гореть в течение 45 ч.
4. Л=20 кГ, В= 5 кГ, С=10 кГ, 0=20. кГ,
Е= 5 кГ, F— 5 кГ, G=10 кГ, Я= 5 кГ,
/=10 кГ, А=20 кГ, £=40 кГ, М=40 кГ.
5. По второму закону Ньютона сила, действующая на мяч, равна F=ma, где a—v/t, т. е.
F=m —=0,7- _21_ = 630Н. t 0,02
Итак, футболист бьет по мячу с силой 630 Н.
6. Частота f — это число операций га, выполняемых ЭВМ в единицу времени (за 1 с): f=nlt. При п=1 мы получаем соотношение f=zi/T, где Т — период, т. е. время, необходимое для выполнения одной операции. Отсюда
Если на выполнение одной операции требуется 1,3 мкс, то это соответствует частоте около 770 кГц. За 1 мин такая ЭВМ может выполнить
Г 3"Тб~* 46,2-10е операций.
7. ESEL (осел), SOSSE (соус), hELL (светлый).
Другие задачи такого рода мы предоставляем читателю придумать самостоятельно. Следует иметь в виду, что цифры 0, 1, 3, 4, 5, 7 и 9 на индикаторе перевернутого микрокалькулятора соответствуют латинским буквам О, I, Е, h, S, L, G.
8. Пусть F — сила, с которой шест давит на плечо рабочего, идущего впереди. Тогда по правилу рычага должно выполняться соотношение
F-2=9810,8 (Нм), откуда
F= ЭЗЬОЛ" _ 392 4 Н = 40 кГ. 2
Итак, на плечо рабочего, идущего сзади, шест давит с силой 588,6 Н, а на плечо рабочего, идущего впереди,— с силой 392,4 Н.
9. Грузы А и D поднимутся, грузы В и С опустятся.
10. По закону Архимеда выталкивающая сила Гвыт равна весу вытесненной телом жидкости:
^ВЫТ. = Vpgt
где р=1 г/см3, §’=9,81 м/с2, V—mlp„, m—GIg, рп=0,2 г/см3. Итак,
Гвыт == = Gp = 3W да176Н
£рп Рп 0,2
Подъемная сила и вес спасательного круга направлены в противоположные стороны, поэтому подъемная сила F равна их разности, т. е.
/7=ГВЫТ-С= 176-35,3» 141 Н.
Итак, подъемная сила спасательного круга равна 141 Н (или 14,4 кГ).
11. Работа W по подъему груза G на высоту h равна произведению веса груза на высоту: W—Gh.
а) = GA=35 • 0,38 » 13,3 кГм » 130 Дж;
13,3 кГм-6=79,8»783 Дж;
б) U72=G2ft2=10-7,2=72 кГм»706 Дж;
в)
12. Объем пирамиды связан с длиной стороны а лежащего в основании квадрата н высотой h соотношением V=a'2hl3. По теореме Пифагора Л==У«2—(d/2)2, где s — длина ребра пирамиды, a d— длина диагонали основания. Подставляя численные значения, получаем
V= -~4'9Z =41,42 м3. 3
Из полученного нами полного объема пирамиды следует изъять объем бетона. Разность даст нам объем камней, уложенных в пирамиду.
По условиям задачи 45% объема пирамиды приходится на промежутки между камнями, поэтому общий обьем камней составляет 41,42-0,55 «22,78 м3.
Пусть т — общая масса, V — общий объем и р — плотность камней, уложенных в пирамиду. Тогда m = Vp, откуда т=22,78-2,6«59,2 т.
Итак, в пирамиду уложено около 59,2 т камней.
13.
, MOON. , 9552
.VOLVO, .71671 + MEN. Т 902
+ FIAT, 9 542 + CAN. 382
MOTOR. 81213 REACH. 10836
Может быть, вам удастся найти другие решения?
Три криптарпфма со словом РЛДАР. Из (1) и (2) следует, что А=2. Из (3) и А—2 мы заключаем, что Р2Д2Р=1112, а поскольку 1112= 12321, то Р=1 и Д=3..
14. Пусть fi — фокусное расстояние объектива, /2—фокусное расстояние окуляра.
Т1о условиям задачи
1-/2= 14, Л = 5/2,
откуда ft — 17,5 и /2=3,5.
Фокусное расстояние объектива равно 17,5 см, а фокусное расстояние окуляра — 3,5 см.
15. При одном обороте шестерни, вращаемой педалями, велосипедист проезжает расстояние 5=(46/и)л 0,7«6,32 м (4в/|б~ передаточное отношение от шестерни, вращаемой педалями, к шестерне на втулке заднего колеса). Для того чтобы проехать расстояние 120 км, велосипедисту придется совершить педалями около 19 000 оборотов.
16. Объем 1 м2 сусального золота равен У==100Х100><(79о<юо) = 79 см3, а его масса ш=(79)19,3«2,!4 г.
Итак, на изготовление 1 м2 сусального золота необходимо израсходовать около 2,14 г золота.
17. Пусть х—число столбов, уложенных в основание штабеля. По условиям задачи в 6 рядах должно быть уложено всего 105 столбов, причем в каждом ряду на один столб меньше, чем в предыдущем: .
х+ (х—1) + (х—2) + (х—3) + (х—4 j + + (х—5) = 105,
откуда х=20.
Итак, в основание штабеля следует уложить 20 столбов.
18. Во всех трех случаях вес чемодана равен произведению его массы на ускорение свободного падения: G=tng.
а) 0 = 25-9,81 «245 И;
б) 0 = 25-9,78 «244 Н;
в) 0 = 25-9,83«246 И.
Итак, на широте 45° чемодан весит около 245 Н, на экваторе — около 244 И и на Северном полюсе — около 246 Н.
НАПРЯЖЕННОЕ РАСПИСАНИЕ
1. В двух 5-х классах («А» и «Б») 4 учителя за 2 дня проводят уроки по 8 различным предметам. Условия «а» и <б» и приведенная в условиях задачи выписка из расписания позволяют утверждать, что ни один из четырех учителей не может вести следующие пары предметов: физика — физкультура, физика — математика, физика — немецкий язык. Условие «е» позволяет также исключить комбинации физика - география и физика — история.
Остаются комбинации физика — биология и физика — рисование. Так как по условию «а» комбинация немецкий язык — математика невозможна, по условию «в» фрейлейн Фишер должна преподавать физику. По условию «в» комбинация физика — биология также отпадает. Следовательно, фрейлейн Фишер преподает физику и рисование.
Из условия «г» мы заключаем, что герр Райхельт не может преподавать следующие предметы: физику, немецкий язык, математику, физкультуру и биологию. Так как рисование преподает фрейлейн Фишер, этот предмет также отпадает для герра Райхельта. Следо-236
вательно, герр Райхельт преподает географию и историю.
Выписка из расписания показывает, что комбинации немецкий язык — рисование и немецкий язык - биология подлежат исключению.
Из условия «д» и предыдущих рассуждении следует, что фрау Хельмерт преподает математику и биологий. Остальные два предмета— немецкий язык и физкультуру — преподает герр Вальтер.
2. При передаче 91,8 спортсмен за один оборот педалей проезжает х м, где
„ 7.26-91.8 ,
х— --------«7,32 м/об.
91,1
При заданной частоте вращения педалей (120 об/м) спортсмен проезжает 120-7,32=878,40 м/мин.
Пусть расстояйие 200 м он проезжает за у мин, тогда
«= -J22—мин «13,7 с.
” 878,4
Вычислим скорость:
= 2°0 = 0.2J600 ^ 52 6 км/ч
t 13,7 13,7
Итак, велосипедист проезжает 200 м примерно за 13,7 с, его средняя скорость при этом равна 52,6 км/ч.
3, а) Теорема, б) Единица, в) Определение. г) Ромб, д) Икосаэдр, е) Якоб (Бернулли). ж) Инверсия, з) Неравенство, и) Формула. к) Операция, л) Радиан, м) Множе
ство. в) Алгебра, о) Циркуль, п) Иррациональность. р) Итерация.
4. Перевод с французского: одиннадцать-)--{-девять=двадцать. Учтите, что одиннадцать делится на II, девять—на 3 и двадцать — на 5.
Решение криптарифма:
4- 4829 8 976 'Т.З 805
5. Пусть г% всего населения города составляют пенсионеры, е% — остальные взрослые и k%— дети и подростки. По условиям задачи
г=0,4(г+е), r=0,25(r+e+fe), r-j-e-|-fe= 100,
откуда г=25%; е = 37,5%; 6=37,5%.
Итак, 25% населения города составляют пенсионеры, 37,5% — дети и подростки.
6. Пусть ABCDE — правильный пятиугольник. Разделим его на 2 равновеликие части прямой, параллельной одной из сторон.
Первый шаг к решению состоит в том, чтобы из вершины С опустить на сторону АЕ перпендикуляр CF, служащий осью симметрии пятиугольника. Перпендикуляр CF заведомо делит площадь пятиугольника ABCDE на 2 равновеликие части, но не удовлетворяет условиям задачи, так как не параллелен ни одной из сторон. Пусть G — точка пересечения прямой, проходящей через точку F параллельно стороне АВ, со стороной ВС. Рассмотрим лежащую внутри пятиугольника тра-
пению CEFG (FG\\CE) < и пусть FG—a и CE—b. Диагональ CF трапеции разбивает ее на треугольник CFG площадью /( и треугольник CEF площадью /2, которые, очевидно, относятся между собой, как а : Ь, т. е.
/| : 1?—а : b. (1)
Итак, первоначальная задача сводится теперь к следующей: разделить трапецию CEFG прямой, параллельной основаниям, на 2 части, площади которых относятся между собой как а :Ь.
Пусть Н и К — концы такой прямой и пусть НК=с. Обозначим неизвестное пока расстояние от НК до FG через х, а расстояние от НК до СЕ — через у. Попытаемся найти положение прямой НК аналитически— с помощью введенных нами величин х п у. Площади /| и /2 частей трапеции HFGK и ЕНКС вычислим по формуле площади трапеции:
2Л=(а+<.)х. 212—(Ь-^с)у. (2)
Из соотношений (1) и (2) следует, что а : Ь— (a-f-c)x : {b-\-c)y.
Эту пропорцию нетрудно преобразовать в уравнение 'Следующего вида:
(a+c)ftx— (&+с)ш/=О. (3>
Уравнение (3) линейно относительно неизвестных х и у. Еще одно линейное уравнение мы получим, если применим к трапеции теорему о пучке прямых, пересекающих параллельные прямые. Непосредственно из теоремы следует пропорция
х : у— (с—а) : (&—с), которую нетрудно преобразовать в уравнение (&—с)х-[-(а—с)у~0. (4)
Это уравнение также линейно относительно х и у. Уравнения (3) п (4) должны помочь нам найти длину с отрезка НК. Запишем их в виде системы:
(а4-с)6х—(&4-с)аУ=0, (5)
(Ь—c)x-f-(a—с)у=0.
В систему (5), состоящую из 2 уравнений, входят 5 неизвестных величин. Однако это еще не означает, что мы должны отказаться от ее решения и отложить карандаш в сторону. Приглядевшись к системе уравнений внимательнее, мы обнаружим, что входящие в нее уравнения содержат только члены, линейные по х и у и не содержат свободных членов, т. е. уравнения системы (5) линейны (относительно х и у) и однородны. Мы вправе ожидать, что система уравнений (5) допускает ненулевые решения для х и у, так как расстояния между сторонами FG и СЕ трапеции и отрезком НК заведомо отличны от нуля.
Для того чтобы лучше понять, как обстоит дело с общим решением системы (5), рассмотрим сначала 2 численных примера. Система линейных однородных уравнений
Зх-Ну=0, (6)
6x-(-7i/=0
допускает только решение х=0, у—0. Изменим один из коэффициентов системы (6) и рассмотрим систему линейных однородных уравнений
3x4-4//=О, (7)
6x-j-8y=0.
Значения х=0, у=0 также удовлетворяют уравнениям (7), но это решение уже не единственное — существуют и другие пары чисел, например х=4, //=—3, удовлетворяющие уравнениям (7). Система линейных однородных уравнений (5) принадлежит к числу систем того же типа, что и уравнения (7). Система уравнений (7) обладает важным свойством: если в какой-то линейной комбинации входящих в нее уравнений коэффициент при х обращается в нуль, то коэффициент при у также обращается в нуль, и наоборот. Математики говорят в таких случаях, что уравнения линейно зависимы. В общем случае система двух линейных однородных уравнений имеет вид
aix4-&!//=0, а2х4-&2у=0. Для того чтобы 'такая система допускала отличные от нуля решения (х, у), должна выполняться пропорция
Ц| : /z2= б 1 : &2.
Применим теперь наши познания к системе линейных однородных уравнений (5). Как следует из условия (8), система уравнений (5) допускает отличные от нуля решения х и у в том и только в том случае, если
(а+с)Ь : (Ь—с) = (Ь-{-с)а :(с—а). (9)
Эта пропорция содержит только одну неизвестную величину с. Выразив из соотношения (9) с через а и Ь, мы получим выражение, которое послужит ключом к построению от
резка НК. Умножая обе части равенства (9) на (&—с) (а—с) и перенося все члены в левую часть, преобразуем его к виду
(62—с2)а-Ь(а2—с2) 6=0, откуда
c—^ab.
Итак, длина с отрезка НК, делящего площадь трапеции CEFG в отношении а : Ь, есть среднее геометрическое длин an b оснований трапеции. Для его построения нужно на отрезке длиной как на диаметре полуокружности из общего конца двух отрезков восставить перпендикуляр до пересечения с полуокружностью. Длина этого перпендикуляра как раз и будет равна с.
?. а) 150 см2 ==0,0150 м2;
р=- — =5886 «39,24 кПа.
м S 0,0150
Стоя на полу, человек массой 60 кг создает давление около 39,24 кПа (0,4 атм),
б) 200-10=2000 см2=0,2 м2;
р= ^Ь1«2,943 кПа- (0,03 атм).
Итак, давление, оказываемое лыжниками на снежиую поверхность, составляет 2,943 кПа (0,03 атм).
в) Давления относятся между собой, как 40: 3. '
8. Перевод с английского. Задача на разрезание. Треугольник АВС разрезан иа 3 части X, У и Z двумя прямыми, проходящими через середину М стороны АВ параллельно и перпендикулярно основанию ВС.
Показать, как из этих трех частей можно составить прямоугольник и два различных параллелограмма. Решение показано на рисунке.
9.
18 720--4900= 13 820
26 ’ X 328= 8528
720 +4572= 5292
10. Мощность сердца мы найдем, вычислив работу, производимую им за 1 с:
Р= А = -2И ~ 15,53 Вт (1,6 кГм/с).
t 60
11. Пусть сплав состоит из х долей серебра и у долей меди (если весь сплав принять за 1000 долей).
х 4-г/=1000. (1)
Масса серебра (в г), израсходованного на изготовление медали, составляет 20,9 х/1000, а масса меди — 20,9 у/1000, поэтому серебро занимает объем (в см3) 20,9 х/( 1000-10,5),
а медь — 20,9 yl(1000-8,92), Так как объем медали равен 2,123 см3,
20,9х ।___20,9у __g 123
1000 10,5 "Г 1000-8,92
Подставляя у=1000—х из (1) в (2), получаем
ТЯГ х+ Гй! (Ю00-х) = 2123, (3)
откуда
х ж 624,1
и, следовательно, у=1000—624,1=375,9.
После округления получаем х«625, У «375.
Итак, сплав, из которого изготовлена памятная медаль, состоит примерно из 625 долей серебра и 375 долей меди.
12. Радиус орбиты Луны 6=384 000 км;
радиус орбиты искусственного спутника Земли
период обращения Луны вокруг Земли 6=27,33 суток;
период обращения спутника t\ = 1 сутки.
По третьему закону Кеплера квадраты периодов обращения двух спутников относятся как кубы радиусов их орбит (больших полуосей эллиптических орбит):
: Z22=Z31 : Р2, откуда
,3 _ I2-384 0003
1 27,ЗЗ2
Ц «42 320 км.
Высота над поверхностью Земли составляет 42 320—6370=35 950 км.
Итак, искусственный спутник должен обра
щаться вокруг Земли на высоте около 35 950 км.
13. Горному массиву соответствует полоса D.
ВОКРУГ ЦИРКУЛЯ И ЛИНЕЙКИ
1. Предложенное Гауссом решение использует следующую теорему: точки пересечения поляры р точки Р относительно эллипса совпадают с точками, в которых касательные, проведенные из точки Р к эллипсу, касаются эллипса ♦.
* Гаусс воспользовался теоремой проективной геометрии, которая изучает свойства фигур, не изменяющиеся при так называемых проективных преобразованиях — взаимно-однозначных отображениях, сохраняющих прямые (точки, расположенные до такого преобразования на одной прямой, после преобразования лежат на одной прямой, возможно, отличной от исходной).
Рассматривая окружность, начерченную на листе бумаги, под углом, отличным от прямого, вы увидите эллипс. При этом все прямые, начерченные на том же листе бумаги, останутся прямыми. Следовательно, раз-
2. Ограниченный объем книги вынуждает нас отказаться от чисто геометрического решения задачи, предложенного Галуа.
Приведем более простое решение, использующее теорему косинусов. Так как Z_CDA = = 180°—р и cos(180°—Р)=—cos р, приравнивая правые части равенств
х2==а2+&2—2ab cos р
и
x2=c2+d2—2cd cos(180°—р) = = c24-d24-2cd cos р, получаем
а2+&2—2ab cos p=c2-f-d24-2cd cos р, откуда
2 cos р(a&-f-cd) =a2-f-62—с2—d2,
2e»,S-
ab+cd
Следовательно,
cb-^-cd
Аналогично
,,2 Мвг+<И+«‘.'(Ь2+сг)
Галуа не мог воспользоваться этим решением,
глядывая окружность под любым углом, вы совершаете проективное преобразование (называемое центральным проектированием), и с точки зрения проективной геометрии эллипс не отличается от окружности. Воспользуемся последним обстоятельством и определим поляру относительно окружности: полярой точки Р относительно окружности радиуса R с центром в точке О называется прямая, перпендикулярная лучу ОР и проходящая на расстоянии R?IOP от центра О. (Примеч. лер.)
так как в его время предложенную задачу требовалось решить чисто геометрически.
3. Доказательство теоремы Наполеона. Прежде всего напомним следующую теорему: четырехугольник можно вписать в окружность в том и только в том случае, если сумма двух противолежащих углов его равна 180°. Докажем, что окружности, описанные вокруг трех построенных на сторонах треугольника АВС вне его равносторонних треугольников, пересекаются в одной точке. Действительно, окружности, описанные вокруг треугольников ARB и ACQ, помимо вершины А, пересекаются еще в некоторой точке D, лежащей внутри треугольника ЛВС. Из тео-
ремы об описанном четырехугольнике (примененной к четырехугольникам ARBD и ADCQ) следует, что Z_R-\-2LADB = 180°, Z.Q+Z-ADC= 180°. Кроме того, Z_ADB = =Z_ADC—120° (так как, по предположению,
Z_R = Z_Q=60°). Таким образом, Z_BDC= = 360°—(Z-ADB4-DC) = 120°, а поскольку Z_P=60°, мы получаем Z-P-[-Z_BDC= 180°. Используя еще раз теорему о вписанном четырехугольнике (в «обратном» направлении), мы заключаем, что вершина D четырехугольника BPCD должна лежать на окружности, описанной вокруг треугольника ВРС. Отрезки прямых, соединяющих центры трех равносторонних треугольников (т. е. отрезки OiO2, ОХО3 и О2О3), перпендикулярны общим хордам попарно пересекающихся окружностей, т. е. хордам CD, BD и AD. Следовательно, стороны углов О3О|О2 и BDC взаимно перпендикулярны, а сами углы либо равны, либо в сумме составляют 180°. Аналогичное утверждение справедливо относительно углов OiO2O3 и ADC, О2О3О{ и ADB. Но поскольку сумма внутренних углов треугольника О1О2О3 может быть равна только 180°, каждый из перечисленных нами углов равен не 120°, а 60°, что и требовалось доказать.
4. S=3a&; 5=3а2; S=4a2.
5. Площадь четырехугольника удобнее всего вычислять «по частям», вычитая из площади S„ прямоугольника со сторонами 17X12
площади St, S2 и S3 прямоугольных треугольников:
Sn = 17-12=204,
s _513_ 65 ' 2 2 ’
S2=_L.S3=24.
Итак, площадь четырехугольника равна 144 квадратным единицам, т. е. четырехугольник с вершинами в указанных точках равновелик квадрату со стороной 12.
6. Пусть а — длина ребра куба, Кк — объем . куба. Каждая из 8 отсеченных от куба частей имеет форму пирамиды ABCD, в основании которой лежит равнобедренный прямоугольный треугольник АВС с катетами длиной а/3. Высота пирамиды также равна, а/3, поэтому ее объем составляет
У 1 _L а . а а д3
”3’2’3'33 162 '
Объем оставшейся части куба равен
Итак, объем оставшейся части относится к объему куба, как 77 : 81.
7. Так как х — длина прямоугольника, то его ширина у равна 20—х. По условиям задачи х—(20—х)^г2, откуда х^П.
Итак, длина прямоугольника должна быть не меньше 11 м, а его ширина — не больше 9 м.
8. Пусть P/4Q — угол 63° с вершиной в точке А. Построим равносторонний треугольник произвольных размеров так, чтобы одна из его вершин совпала с точкой А, а одна из
сторон совпала со сто-
роной угла AQ. В результате мы получим угол 3°. Удвоив его и сложив углы 6° и 3°, мы получим угол 9°. Построив угсл 9° на стороне
равностороннего треугольника по ту же сторону, по которую лежит сторона АР исходного угла, мы получим угол 21°, заключенный между вертикалью и другой стороной построенного нами угла. Он составляет треть данного угла. Тем самым мы решили задачу «а». Полученный в процессе построения угол 9° составляет */т данного угла. Тем самым задача <б» также решена. (Откладывая каждый из этих углов от стороны данного угла внутрь, мы получим разбиение угла на соответствующее число равных частей.)
9. Так как каждый из равнобедренных треугольников равновелик квадрату, (l/2)ha=a2, откуда h—2а. Следовательно, расстояние между дальними вершинами равнобедренных треугольников, построенных на противо-
положных сторонах квадрата вне его, равно
2а+а4-2а=5а, т. е. в 5 раз больше длины стороны квадрата.
10. Внутренний угол правильного «-угольника равен
а = — 180°. п
По условиям задачи
?”~2 180°—10°=- ±JL180°. 2п п
откуда п— 18.
Итак, у первого многоугольника 18, а у второго 36 сторон. Внутренний угол правильного 18-уголышка равен 160°, внутренний угол правильного 36-угольнпка равен 170°.
11. Условимся обозначать каждую точку пересечения двух диагоналей четырьмя буквами, стоящими у вершин, которые соединяют эти диагонали. Например, точку пересечения диагоналей АС и BD обозначим ACBD.
Корректна ли предложенная нами система обозначений, т. е. не может ли случиться так, что различные точки получат одинаковые обозначения? Нет, подобное совпадение исключено. Действительно, буквы А, В, С и D могут встретиться нам только в обозначении точки пересечения диагоналей выпуклого четырехугольника ABCD, т. е. диагоналей АС и BD. Кроме тОго, для обозначения точек пересечения диагоналей нам понадобятся все возможные четверки вершин нашего многоугольника. Например, четверка ACEF соответствует точке пересечения диагоналей $Е и CF. Если мы хотим пересчитать все точки пересечения диагоналей, то для этого доста
точно пересчитать все возможные четверки вершин. Итак, число точек пересечения диагоналей совпадает с числом элементов множества всех возможных подмножеств вершин, содержащих по 4 элемента. При п=6 мы найдем число та-
/ ( ких четверок, равное
, чуть быстрее, если
воспользуемся тем, что
В общем случае число точек пересечения диагоналей выпуклого n-угольника, удовлетворяющего условиям задачи, равно
/ п \ / п \
\ 4 ) = U-4'
12. Стороны любого невырожденного треугольника удовлетворяют неравенству треугольника а<6+с. Следовательно,
й—£1-|-2а<а4-6+с> а< -1 (a+b+c) = -Lp,
что и требовалось доказать.
13. Пусть а и Ь — длины сторон прямоугольника, х — отрезок, на который нужно уменьшить одну из сторон. По условиям задачи
(a - x) (b+~-b )=a&,
\ 4 /
5
(a—x)—b—ab, 4
4 a~x= ~a,
5
Итак, для того чтобы площадь прямоугольника не изменилась, другую сторону необходимо уменьшить на 20%.
ИГРА С ЧИСЛАМИ
1. 4+10+5+9+8+64-7+2+1+8=60.
2.
4 __ 1896
5 2370
3. Магический квадрат из 8 костей домино составлен из 4-4 квадратов — половинок костей, т. е. из 16 клеток. Для того чтобы сумма очков была наименьшей, необходимо взять следующие 8 костей: 00, 01, 02, 11,
очков равна 19. Заменив кость 13 на 23, мы увеличим сумму очков до 20 и сможем соста
вить магический квадрат с постоянной, равной 5.
4. Сектор А. Каждое число (кроме первого) равно удвоенному предыдущему числу минус единица. Вместо вопросительного знака нужно вписать число 145-2—1=289.
Сектор В. Каждое число (кроме первого) равно квадрату предыдущего числа минус единица. Вместо вопросительного знака следует вписать число 3968-3968—1 = 15 745 023.
Сектор С. Каждое следующее число втрое больше предыдущего. Вместо вопросительного знака следует вписать число 162-3=486.
Сектор D. Каждое следующее число на 3 больше предыдущего. Вместо вопросительного знака следует вписать число 13-f-3=16.
5.
__n-i-1 _ 1 . n(n-|-l) _ «4-1 . n(«4-l) n ’ (n-f-1)2— 1 «4-2 ’
n(«4~l) _ «4-1
2n2 2n
6. Пробраться внутрь лабиринта, набрав по дороге 500 очков, можно, например, по маршруту 24, 312, 45, 47, 15, 17, 40 или 60, 21, 38, 47, 15. 17 302.
7.
1 - . 9 ’«1 7 ‘ 12 5 4 3
8 , 15 то' 2 ; ,131 6 Н ,14
8. Xt — 777 777 777 777, х2=22 222 222, х3= = 777, х4=666, х5=333, х6=5555, х?=3.
9. Так как партнер В должен умножить свое число на 2, его слагаемое всегда четно. Каким будет второе слагаемое — четным или нечетным, зависит от числа, которое А сообщает партнеру С: если сумма четна, то А сообщил С четное число, а В — нечетное. Если же сумма- нечетна, то А сообщил С нечетное число, а В — четное.
10. Пусть а и ft — два натуральных числа, обладающие требуемым свойством. Тогда
ab= 10(а-)-6), ab — 10a+10ft, ab—10а= 10ft, a(b—10) = 10ft,
106 106—1004-100
6—10 6—10
_ 10(6—10)4-100 _in , 100 6—10 +6—10 ’
Величина a принимает натуральные значения лишь при ft=ll, 12, 14, 15, 20, 30, 35, 60, НО.
Итак, требуемым свойством обладают только пары чисел (11, НО), (12, 60), (14, 35), (15, 30), (20, 20), (30, 15), (35, 14), (60, 12), (НО, Н).
11. Пусть х и у — неизвестные числа, причем х<у. Тогда (х+у) + (х—у)+ху+ — =
2х+ху+ — =243,
2ху+ху2+х=243у, х(2у+у2+1)=243у, х(у+1)2=243у,
243y _ 35t/
(y+D2 («Ж)2 ‘
Поскольку x—натуральное число, знаменатель (iH-1)2 должен быть делителем числа 243, а так как 243=35, (t/4-l)2 может быть только степенью тройки, совпадающей с квадратом некоторого натурального числа. Следовательно, знаменатель (t/4-О2 может быть равен либо З2, либо 34=92, т. е. либо у=2, либо У=8.
При у=2 получаем
х.= 2f|±=54,
при у =8
Итак, числами, над которыми производились операции, были либо 2 и 54, либо 8 и 24.
12.
77:77=1, 7—(74-7): 7=5
7:74-7:7=2, (7-7—7): 7=6,
(74-74-7) : 7=3, (7—7) : 74-7=7,
77: 7—7=4, 7+ (74-7) : 7=9,
(77—7) :7=10.
ОГОНЬ МАТЕМАТИЧЕСКИХ ОЛИМПИАД
1. Так как фавориты А, В и С заняли первые 3 места, возможны только следующие 6 исходов заездов (в колонке справа указаны утверждения, которым противоречат эти исходы) :
a) ABC —
б) ACB (4)
в) ВАС (1)
г) ВСА (1), (4)
Д) CAB (2)
е) СВА (3)
В 5 случаях предполагаемая очередность прихода фаворитов к финишу противоречит по крайней мере одному утверждению. Всем условиям задачи удовлетворяет распределение мест, при котором фаворит А пришел первым, В вторым и С третьим.
2. Дзета может воспользоваться, например, тем, что
5-5+5=30, (1)
5-(5+5: 5) =30 (2)
Так как в левую часть равенства (1) цифра 5 входит 3 раза, утверждение Дзета верно при любом нечетном п, поскольку в левую часть равенства (1) можно при любом п>3 включить (п—3)/2 слагаемых (5—5).
Утверждение Дзета верно н при любом четном п, так как в левую часть равенства (2), которая содержит 4 пятерки, при любом п>4 можно включить (п—4)/2 слагаемых (5—5).
4. Пусть х,, Хо, х3, х4, х5— номера букв, входящих в фамилию великого математика. По условиям задачи
х,-)-х2=40, х,4“Х3=42, откуда х2=40—х,, откуда х3=42—X,,
х,-|-х4= 36, откуда х4=36—х,,
*1+л:5=47, откуда х5=47—х,,
JC,-|-X2-|-X34--)c4"f-JC5— 75. (2)
Подставляя (1) в (2), получаем х1-|-'(40-х1) J- (42-х,) + (36—х,) 4- (47-х,) = = 75, 3X1=90,
откуда х,=30. Следовательно, х2=10, х3=12, х4=6, х3=17.
Номер 30 имеет буква Э,
номер 10 — буква И,
номер 12 — буква Л,
номер 6 — буква Е, номер 17 — буква Р.
Фамилия великого математика Эйлер.
5. Числа а=1 и Ь=—2 отличны от 0. Они удовлетворяют неравенству а>Ь и (поскольку |lj = l, |—2|=2) неравенству |а|<|&|.
Так как число а неотрицательно, то утверждения, высказанные А и В, ложны.
Если а и b — два отличных от нуля действительных числа, таких, что а>b и |а|<|&|, то число b отрицательно. Действительно, если бы число b было неотрицательным, то выполнялось бы неравенство а>Ь>0 и, следовательно, |а|=а>Ь=|&|, что противоречит условию I а] < | b |.
Тем самым доказано, что утверждение С верно, а утверждение D ложно.
6. Пусть гь г2, г3 и г4— радиусы концентрических кругов от центрального до самого большого. Круги .содержат соответственно 1, 3, 7 и 15 равновеликих частей.
Так как площадь каждого круга равна пп (i=l, 2, 3, 4), из условий задачи следует, что площади кругов относятся между собой, как яг 1 :лг2 8лгз : лг4= 1 : 3 : 7^ 15,_откуда (так как г<>0) и: г2 :г3: г4=1 : /3 :/7 :/15.
7. Пусть D, Е nF — основания перпендикуляров, опущенных из центра О на стороны АВ, ВС и СА прямоугольного треугольника АВС, Л.АСВ=90°, АВ—с, OD=OE=OF=p. Поскольку прямоугольные треугольники ODB и ОЕВ, ODA и OFA попарно конгруэнтны,
суммарная площадь всех четырех треугольников равна удвоенной площади треугольника АОВ, т. е. равна ср. Четырехугольник OECF— квадрат со стороной р, поэтому площадь его равна р2.
Следовательно, площадь треугольника АВС равна ср+р2.
8. Заведомо обеспечить себе выигрыш игрок может только в том случае, если существует стратегия, которая гарантирует выигрыш при любых обстоятельствах. Именно такая стратегия существует и в игре со спичками. Предположим, что после очередного хода одного из игроков, например игрока А, число
спичек, оставшихся в коробке, будет делиться иа 11. Сколько бы спичек ни взял, делая следующий ход, его противник — игрок В (йо правилам игры игрок может взять от 1 до 10 спичек), игрок А всегда может дополнить это число до 11. Следовательно, перед любым ходом игрока В число спичек в коробке будет делиться на 11. После конечного числа ходов наступит момент, когда перед очередным ходом игрока В в коробке останется ровно 11 спичек, из которых он может взять не менее 1 и не более 10. Следовательно, после хода игрока В в спичечном коробке непременно останется не менее 1 и не более 10 спичек, и игрок А сможет забрать их, делая свой последний ход.
В рассматриваемом нами случае (коробок перед началом игры вмещает 150 спичек) ситуация складывается следующим образом: игрок Д всегда может обеспечить себе выигрыш, взяв первым ходом 7 спичек (в коробке останется 143 спички, а число 143 делится на 11).
Игрок В не может гарантировать себе выигрыш. Он может выиграть только в том случае, если игрок А нарушит стратегию.
9. Назовем отрезок, соединяющий две точки, «двуцветным», если он соединяет голубую точку с черной или черную точку с голубой, и «одноцветным», если он соединяет 2 голубые или 2 черные точки. Точка является необыкновенной в том и только в том случае, если из нее двуцветных отрезков выходит больше. Если необыкновенную точку перекрасить, то из нее будет выходить больше одноцветных отрезков, чем двуцветных, а все остальные отрезки, не выходящие из перекрашенной точки, останутся такими, какими были. Следова-260
тельно, какую бы точку не выбрать, перекрасив ее, мы уменьшим число двуцветных отрезков. Если бы после конечного числа шагов исходное множество точек не перестало содержать необыкновенные точки, то это означало бы, что существует множество точек, в котором возможно бесконечное число перекрашиваний. Но тогда должна была бы существовать бесконечная строго убывающая последовательность натуральных чисел (каждое из которых соответствовало бы числу двуцветных отрезков), что невозможно. Полученное противоречие доказывает утверждение задачи.
10. Если бы первоначально в корзине было х слив, то первый жених получил бы (х/2-f-l) слив, и в корзине осталось бы х—(х/2-|-1) = =х/2—1 слив. Следовательно, второй жених получил бы (х/2—1 )/2+1 =х/4+1/2 слив и в корзине осталось бы (х/2—1)—(х/4-|-1/2)== =х/4—3/2 слив. Но тогда третий жених получил бы (х/4—3/2)/2-|-3=х/8-4-9/4 слив. Поскольку после этого в корзине не осталось бы ни одной сливы, мы получаем уравнение (х/4—3/2)—(х/8+9/4)=0, откуда х/8=15/4, х=30.
Итак, в корзине было 30 слив. 11
11. Шестизначный телефонный номер в десятичной системе счисления соответствует числу
z=al05+ftl04+cl03+t/102-|-el0+f, где а, Ь, с, d, е, f — натуральные числа. По условию задачи с, а, е, /«С9, цифры Ь, с, d, е, f отличны от 1 и 2^а^9. Если бы а-ЬЬ>10, то сумма двух первых цифр номера телефона школы начиналась бы с 1. Следовательно, a-|-ft=c^9.
Аналогичным образом можно доказать, что 6+c=dC9, c-f-d=eC9, d-f-e=fC9. Предположим, что а^4. Тогда с=4, d=4, мы пришли бы к е=8 и неравенству d-f-e=f^!2, противоречащему условию f<9. Следовательно, а^З, т. е. либо а=1, либо а=3. Предположим, что &>0. Тогда должно было бы выполняться неравенство Ь^2, откуда с^4, и c-f-d=e^lO, что невозможно. Следовательно, b=Q. Так как номер дома, где живет Гюнтер, делится на 3, а=3.
Значит, Гюнтер живет в доме номер 30. Телефон его школы 30-33-69.
12. Предположим, что торговец первоначально запросил за голову скота а грошей. Поторговавшись, крестьянин сбил цену иа а(а/100) грошей и уплатил торговцу
а2 а——=21 грош.
100
Следовательно,
100а—а2=2100, а2—100а 4-2100=0.
Итак, либо а=70, либо а=30.
Если а=30, то у крестьянина было бы 90 грошей, но 90 не делится на 21, поэтому а=30 отпадает. Итак, условиям задачи может соответствовать только а=70.
Поторговавшись, крестьянин сбил первоначальную цену (70 грошей за голову скота) на 70%, т. е. на 49 грошей. Новая цена составила 21 грош за голову скота. Стоимость всей покупки составила 210 грошей. На эти деньги по старой цене можно было бы купить 3 головы. Так как по условиям задачи крестьянин израсходовал на покупку все деньги (210 делится на 21), то он купил 10 голов скота.
ПО РАЗНЫМ СТРАНАМ
1. Встреча между шахматистами, занявшими первое и второе место, закончилась вничью, так как ни один из них не проиграл ни одной партии. Следовательно, шахматист, занявший первое место, набрал не более 8V2> а обладатель второго места набрал не более 8 очков. Шахматисты, занявшие 4 последних места, сыграли между собой ровно 6 партий, поэтому набрали не менее 6 очков. Следовательно, шахматист, занявший четвертое место, набрал не менее 6 очков, а шахматист, занявший третье место,— не менее 6*/2 очка. Но шахматист, занявший третье место, не мог набрать 7 или более очков, так как в противном случае шахматисты, занявшие первое и второе место, набрали бы вместе не менее 17 очков, что невозможно. Следовательно, шахматист, занявший третье место, набрал 6’/2 очка, а шахматист, занявший четвертое место,— ровно 6 очков. Шахматисты, занявшие первое и второе место, набрали в сумме 16’/2 очка. Это возможно только в том случае, если занявший первое место набрал 8‘/г очка, а занявший второе набрал 8 очков. Итак, все 10 участников шахматного турнира набрали в сумме 45 очков (так как всего было сыграно 45 партий), из которых шахматисты, занявшие 6 последних мест, получили 45—(в’/гЧ-вЧ-б’/гЧ-4-6) = 16 очков, а шахматисты, занявшие 4 последних места,— 6 очков. Следовательно, шахматисты, занявшие пятое и шестое места, набрали в сумме 10 очков, что возможно только в том случае, если они получили соответственно 5*/г и 4*/2 очка.
Итак, шахматисты, занявшие первые 6 мест, набрали по 8’/2. 8. 6V2. б’/г и 4*/2 очка.
Примечание. Все условия задачи были бы выполнены и в том случае, если бы партии между шахматистами, занявшими первое и второе, третье и пятое, второе и шестое места, закончились вничью, а во всех остальных партиях победу одержали шахматисты, занявшие более высокое место, чем их партнеры.
2. Во всех 3 номерах программы—в прыжках в длину (Д), в высоту (В) и с шестом (Ш)—приняли участие 6 спортсменов.
3. Как видно из схем, существуют 3 типа вариантов прокладки железной дороги.
1) В первом варианте одному из городов отводится роль железнодорожного узла, в котором сходятся 4 линии. В зависимости от того, какой из городов выбран, проектировщики могут предложить 5 проектов такого типа.
2) Во втором случае одному из городов отводится роль железнодорожного узла, в котором сходятся 3 линии. С тремя остальными городами узел можно связать железнодорожными линиями 4 различными способами (число сочетаний из 4 предметов по три). В каждом варианте пятый город можно связать с одним из трех городов, который соединен ли-
нией с первым городом, поэтому в рассматриваемом случае существует 4-3=12 вариантов прокладки железных дорог. Поскольку в качестве железнодорожного узла можно выбрать любой из 5 городов, то всего существует 5-12=60 вариантов железнодорожных сетей второго типа.
3) В третьем случае никакие 3 железнодорожные линии не сходятся ни в одном из городов. Любой перестановке из 5 городов соответствует железнодорожная сеть, т. е. вариантов прокладки сети существует столько же, сколько перестановок из 5, а именно: 51 = 120. При этом одной и той же последовательности городов соответствуют 2 перестановки (одна перестановка перечисляет города «от начала», другая—«от конца»), поэтому различных железнодорожных сетей вдвое меньше, чем перестановок, т. е. всего их 120: 2=60.
Итак, общее число вариантов прокладки железнодорожной сети достигает 54-604-60= = 125.
4. Обозначим фигурки латинскими буквами а, Ь, с, d, е, f. Для того чтобы перестроить фигурки, достаточно совершить 15 шагов и прыжков:, с—d е—с f—е
d—f f—h b—d
d—f a—b b—d
c—b e—c g—e
f—g d—f e—d
5. Приводимая ниже стратегия принадлежит швейцарцу Г.—К. Ленхарду.
Он показал, что игра доводится до успешного завершения, если ни сумма, ни разность цифр, образующих номер начального поля, не делится на 3. Этому условию удовлетворяют поля с номерами 02, 04, 13, 20, 23, 26, 31, 32, 34, 35, 40, 43, 46, 53, 62 и 64.
В нашем примере (свободно от фишки поле 43) игра проводится следующим образом.
Фишка 45 переставляется с поля 45 на поле 43 (фишка 44 снимается). Фишка 24 переставляется с поля 24 на поле 44 (фишка 34 снимается). Фишка 43 переставляется с поля 43 на поле 45 (фишка 44 снимается). Затем следуют ходы:
46—44, 43—63, 32—52, 03—23, 32—12,
36—34, 51—53, 62—42, 12—32, 02—22,
26—24, 63—43, 23—25, 42—22, 11—31,
63—43, 34—54, 15—35, 40—42, 23—21,
55—53, 64—44, 04—24, 30—32, 20—22,...
6. Первый криптарифм в переводе с английского означает «Мешай забаву с математикой», второй в переводе с французского гласит «Вперед и вперед мы идем».
Криптарифмы допускают, например, следующие решения:
, 138 ,91650 , 91670
+ 920 + 91 650 Т 91670
+ 407 J 4 670 Т 4 650
146S 4 670 "** 4 650
192 640 192 640
7.
День 1-й 2-й 3-й 4-й
С утра К вечеру Солнце Дождь Солнце Дождь Солнце Дождь Солнце Дождь
День 5-й 6-й 7-й 8-й 9-й
С утра К вечеру Солнце Солнце Солнце Солнце Дождь Солнце Дождь Солнце Дождь Солнце
f 6+5+7 =9
Каникулы Мбонго продолжались 9 дней.
8. Ошибка заключается в неэквивалентном преобразовании при извлечении квадратного корня:
9. Предположим, что в доме живут х семей, имеющих У1<у2<Уз<.. <Ух-1 <УхД^~ тей. По условиям задачи
У1+Уа+Уз4-~+Уж-1 <Ух.
Следовательно,
ух>1+2+3+...+ (х-1)= *(У} .
и общее число детей удовлетворяет неравенству
у>2 I.) =х(х—1).
Если во всех семьях вместе имеется и мальчиков и и девочек, то по условиям задачи y>2x>u>v>x,
откуда
4х > и 4- о=у > 2х.
Кроме того, u^2x—1
и, следовательно,
о<2х—2, y=u-l-v^4x—3,
поэтому х{х— 1) <#< (4х—3),
откуда х(х—1)—(4х—3)<0.
Преобразуя последнее неравенство, получаем х2—5х-|-3<0, (2х—5)2<13<16, —4<2х—5<-|-4, 1<2х<9, 1<х<4.
I) При х—2 мы получили бы 2х—4> >«>х=2 и 2х=4>о>х=2, откуда вопреки условиям задачи следовало бы, что и==о=3.
2) При х=3 мы получили бы 2х=6>и> >х=3 и 2х=6>о>х=3. Так как u>v, то и=5, о=4. Следовательно, у=«+и=9= = 1+24-6=1+3+5.
Условиям задачи, согласно которым каждая девочка имеет по крайней мере одного брата и не более одной сестры, удается удовлетворить только в том случае, если в доме живут три семьи, причем в первой семье один ребенок, во второй семье трое детей, в третьей семье пятеро детей, при этом в первой и во второй семье по одному сыну, а в третьей — три сына,
в первой семье 0 дочерей, а во второй и в третьей семье — по две дочери.
Это единственное решение задачи, так как при х=4 мы получили бы
х(х— 1) = 12<1/<4х— 3=13, откуда следовало бы, что
у= 13=1+2+3+7.
В первой семье не может быть дочерей, во второй семье может быть не более одной дочери и в третьей семье — не более двух дочерей. Следовательно,
о<0+1+2+2=5,
а так как
о>х=4,
мы получаем
о=5, и—у—о=13—5=8=2х, что противоречит условию 2х>и.
10. Пусть х — число, задуманное Уве, а п — результат вычислений. Тогда
[(х- 5+2) -4+3] -5=п, 100х+55=п.
Следовательно, задуманное число мы получили, отбросив две последние цифры (55) полученного результата. Пример: если в результате вычислений получилось число 1755, то было задумано число 17 (т. е. х=17).
Йоханнес Леман
УВЛЕКАТЕЛЬНАЯ МАТЕМАТИКА
Главный отраслевой редактор Л. А. Ерлыкин
Редактор Г. Г. Карвовский
Мл. редактор Н. А. Сергеева
Худож. редактор М. А. Бабичева
Художник В. А. Провалов
Техн, редактор С. А. Птицына
Корректор Н. 'Д. Мелешкина
ИБ 6425
Сдано в набор 06.02.8S. Подписано к печати 18.07.85. Формат бумаги 75Х90'/зг. Бумага офсетная № 1. Гарнитура литературная. Печать офсет. Усл. печ. л. 10,62. Усл. кр.-отт. 21.SS. Уч.-нзд. л. 8,82. Тираж 100000 экз.
Заказ Ф-73. Цена 50 коп. Издательство «Знание».
101835, ГСП, Москва, Центр, проезд Серова, д. 4. Индекс заказа 857716.
Издательство Тат. ОК КПСС, г. Казань, ул. Декабристов, 2.