УДК 531
ББК 22.21
В31
Веретенников В. Г., Синиц ын В. А. Метод переменного дей-
действия. - 2-е изд., исправ. и доп. - М.: ФИЗМАТЛИТ, 2005. - 272 с. -
ISBN 5-9221-0569-8.
В книге рассматриваются метод виртуального варьирования и метод пе-
переменного действия как дополняющие друг друга и составляющие общий
аналитический подход, который является концептуальным для естествознания.
На примере механических систем изучается изменение действия в резуль-
результате применения виртуального варьирования, при котором из рассмотрения
исключаются реакции идеальных связей. Таким образом, создаётся своего
рода «инструмент», освоение которого необходимо для учёта ограничений при
исследовании несвободных динамических систем.
Обосновываются и практически применяются новые и более общие фор-
формы принципов. В их числе: принцип освобождаемости и общее уравнение
для несвободных динамических систем; принцип наименьшего отклонения,
принцип изменяемого действия, включающий интегральный принцип равенства
действия и противодействия, вириальный интегральный принцип, интеграль-
интегральный принцип для систем Четаева-Румянцева; принцип изменения нарушения
симметрии, используемый при решении проблем инерционности движения и
гравитации; принцип предикативности (логической и математической строго-
строгости) в механике.
Для студентов, аспирантов, научных сотрудников и преподавателей соот-
соответствующих специальностей.
© ФИЗМАТЛИТ, 2005
ISBN 5-9221-0569-8	© В. Г. Веретенников, В. А. Синицын, 2005

ОГЛАВЛЕНИЕ
Предисловие	 8
Предисловие к первому изданию	 9
Введение	 10
Глава I. Заметки о некоторых основных понятиях	 17
1.	Развитие понятия материальной точки в моделях механики	 17
1.1. Классическое понятие материальной точки A7). 1.2. Модели
точки комплексной массы и точки переменной массы A8). 1.3. Мо-
Модель термодинамической точки A9).
2.	О понятиях скорости и ускорения материальной точки	 21
2.1. Скорость материальной точки и производная по времени её ра-
радиуса-вектора B1). 2.2. Об ускорении материальной точки B2).
3.	К обоснованию принципа Гамильтона	 25
3.1. Из истории «силы» и «действия» B5). 3.2. О выводе принципа
Гамильтона из общего уравнения динамики B8).
4.	О действии и противодействии	 33
4.1.	Основные задачи механики и третий закон Ньютона C3).
4.2.	Принцип равновесия Даламбера и «даламберово равно-
равновесие» C5). 4.3. О силах инерции C7). 4.4. Интегральное
равенство действия и противодействия D1). 4.5. О лоренцовой
«силе торможения» D5).
5.	Об энергии и действии	 47
5.1. Склерономные и реономные системы D7). 5.2. Аналоги тео-
теоремы об изменении кинетической энергии реономных систем D8).
5.3.	Теорема об изменении полной механической энергии E0).
5.4.	Функция Гамильтона и уравнение энергии E1). 5.5. Теоре-
Теорема об изменении кинетического потенциала. Динамический смысл
обобщённой силы для времени E5).
6.	Примеры величин, называемых «действие»	 57
6.1. Функционалы «действие» E7).	6.2. Функции «дей-
«действие» F0).
Глава П. Заметки о способах виртуального варьирования	 62
7.	О дифференцировании	 62
7.1. Дифференцирование функции при неявной зависимости от па-
параметров F2). 7.2. Вариационная производная F5).
8.	Некоторые приёмы и способы варьирования	 66

Оглавление
8.1. Синхронные вариации F6). 8.2. Асинхронное варьирова-
варьирование F6). 8.3. Варьирование по Гельмгольцу F8). 8.4. Расширен-
Расширенное варьирование по Гельмгольцу F9). 8.5. Вариации в скользя-
скользящих режимах реализации связей F9).
9. Уравнения для виртуальных вариаций	 70
9.1. Уравнения для виртуальных вариаций при неголономных
связях G1). 9.2. Виртуальное варьирование связи, представля-
представляющей огибающую G3). 9.3. О варьировании уравнения связи
при двух независимых переменных G4). 9.4. О неравенствах для
виртуальных перемещений при неудерживающих связях G4).
10. О применении неопределённых множителей	 75
10.1. «Заметка о равновесии упругой нити» (М. В. Остроград-
Остроградский) G5). 10.2. Неопределённые множители в задачах на экс-
экстремум функции G7). 10.3. О представлении реакций идеальных
связей G9). 10.4. Неопределённые множители при скользящем ре-
режиме (80). 10.5. О неопределённых множителях при варьировании
функционалов (82). 10.6. О неопределённых множителях в других
задачах (83).
11.0 принципе Герца. Принцип наименьшей кривизны	 84
11.1. Принцип прямейшего пути Герца (85). 11.2. Некоторые на-
направления развития принципа прямейшего пути (90). 11.3. Прин-
Принцип наименьшей кривизны (91).
12.	О принципах несвободных динамических систем	 94
12.1. Принцип освобождаемости по Четаеву (94). 12.2. Свойство
идеальности. Общее уравнение несвободных динамических си-
систем (95). 12.3. Принцип наименьшего отклонения (97). 12.4. Об-
Общее уравнение динамики систем с вероятностными связями (98).
12.5. Принцип освобождаемости для динамических систем (99).
13.	О применении вириалов. Центральное вириальное равенство	 102
13.1.	О вириале количеств движения и вириале системы сил A02).
13.2.	Центральное вириальное равенство A03).
Глава III. Об интегральных принципах	 106
14.	Центральное интегральное равенство	 106
14.1. Центральное уравнение Лагранжа при асинхронном варьи-
варьировании A06). 14.2. Центральное интегральное равенство A07).
14.3. Об изменении действия по Гамильтону и действия по Лагран-
жу при синхронном и асинхронном варьировании A08).
15.	О принципе Гамильтона-Остроградского в теории реономных си-
систем 	 111
15.1. Принцип Гамильтона-Остроградского A11). 15.2. Асинхрон-
Асинхронное варьирование действия вспомогательной склерономной систе-
системы A11). 15.3. Расширенный принцип Гамильтона-Остроградско-
Гамильтона-Остроградского A13).
16.	Обобщение интегрального принципа Гёльдера	 118
16.1. Применение варьирования по Гельмгольцу при выводе прин-
принципа Гёльдера A18). 16.2. Частные формы принципа A19).
16.3. Новое обобщение принципа Гёльдера A20).

Оглавление
17.	Вириальный интегральный принцип. Интегральный принцип
для систем Четаева-Румянцева	 121
17.1. Вириальный интегральный принцип A21). 17.2. Ин-
Интегральный принцип для систем Четаева-Румянцева A22).
17.3. Интегральный принцип изменяемого действия для систем
Четаева A25).
18.	Заметка об евклидовом действии (Э. и Ф. Коссера)	 127
18.1. Аксиомы об однородности и изотропности простран-
пространства A27). 18.2. «Евклидовское действие деформации» A28).
18.3. Евклидовское действие и натуральные системы A29).
19.	О принципе Гамильтона-Остроградского при импульсивных движе-
движениях динамических систем	 132
19.1.	Постановка задачи. Потенциал ударных импульсов A32).
19.2.	Функционал «действие» и условия его стационарности A34).
19.3.	Интегральный инвариант Пуанкаре-Картана A36). 19.4. Об
оптико-механической аналогии для движений с ударами A38).
20.	Об интегральных равенствах для неголономных систем	 142
20.1.	Интегральные равенства Гёльдера, Воронца и Суслова A42).
20.2.	О вариационной форме интегрального принципа для неголо-
неголономных систем A44).
Глава IV. Решение прикладных задач	 146
21.	Модель динамики системы «жёсткое колесо — деформируемый
рельс»	 146
21.1. Механическая схема A46). 21.2. Действие A47). 21.3. Ана-
Анализ связей A49). 21.4. Интегральный принцип. Уравнения движе-
движения системы A50). 21.5. Стационарный режим движения систе-
системы A52).
22.	О качении деформируемого колеса	 156
22.1. Механическая схема A56). 22.2. Вариация функционала
«действие» A58). 22.3. Уравнения для определения формы
кольца A59). 22.4. Условия на границе зоны контакта A60).
22.5. О сопротивлении качению A61).
23.0 квазистатическом скольжении нагрузки на деформируемом
стержне	 162
23.1. «Энергетический парадокс» A62). 23.2. Схема взаимодей-
взаимодействия. Выражение действия деформации A63). 23.3. Энергетиче-
Энергетические соотношения A65).
24.	К оценке частот поперечных колебаний стержня	 165
24.1.	Формула и теорема Релея. Формула Граммеля A65).
24.2.	Оценка точности определения частоты колебаний по форме
изгиба A68). 24.3. Учёт продольных сил инерции A69).
25.	Об устойчивости равновесной формы стержня при изгибе	 170
25.1. Задача Эйлера A70). 25.2. Функционалы потенциальной
энергии A71). 25.3. Уравнения равновесных форм оси стой-
стойки A72). 25.4. Уравнения смежных форм равновесия. Условие
устойчивости прямолинейной формы A73). 25.5. О применении

Оглавление
энергетического метода в задаче об устойчивости формы изгиба
стержня A74).
26.	Уравнения движения систем с линейным деформируемым элемен-
элементом 	 177
26.1. Уравнения движения однородной цепи A77). 26.2. Модель
движения гибкого элемента волнового редуктора A80).
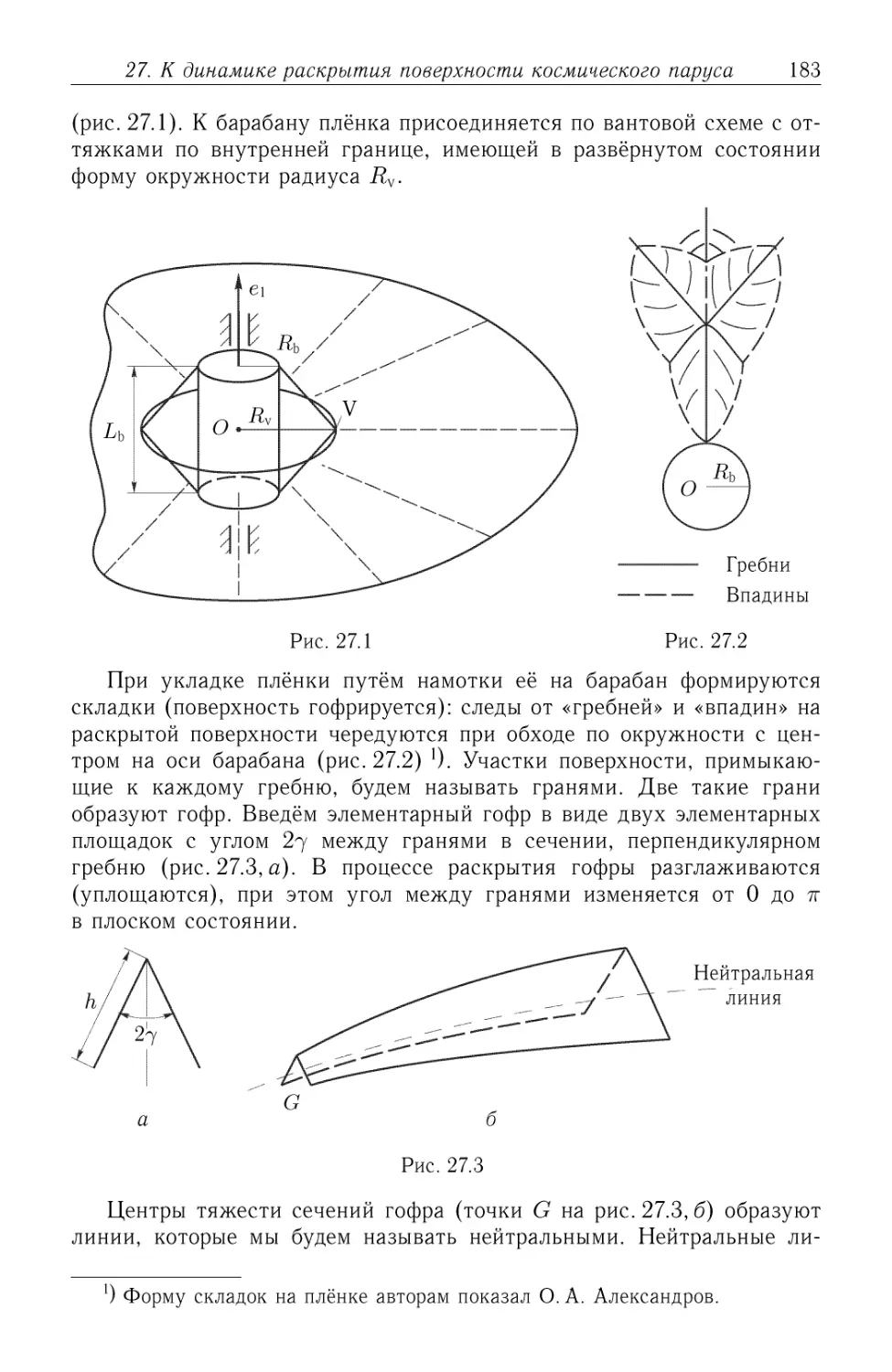
27.	К динамике раскрытия поверхности космического паруса	 182
27.1. Описание процесса раскрытия поверхности паруса. До-
Допущения и приближённые соотношения A82). 27.2. Вывод
уравнений движения оболочки в процессе её развёртывания A85).
27.3. О форме равновесия вращающейся отражающей поверх-
поверхности A90).
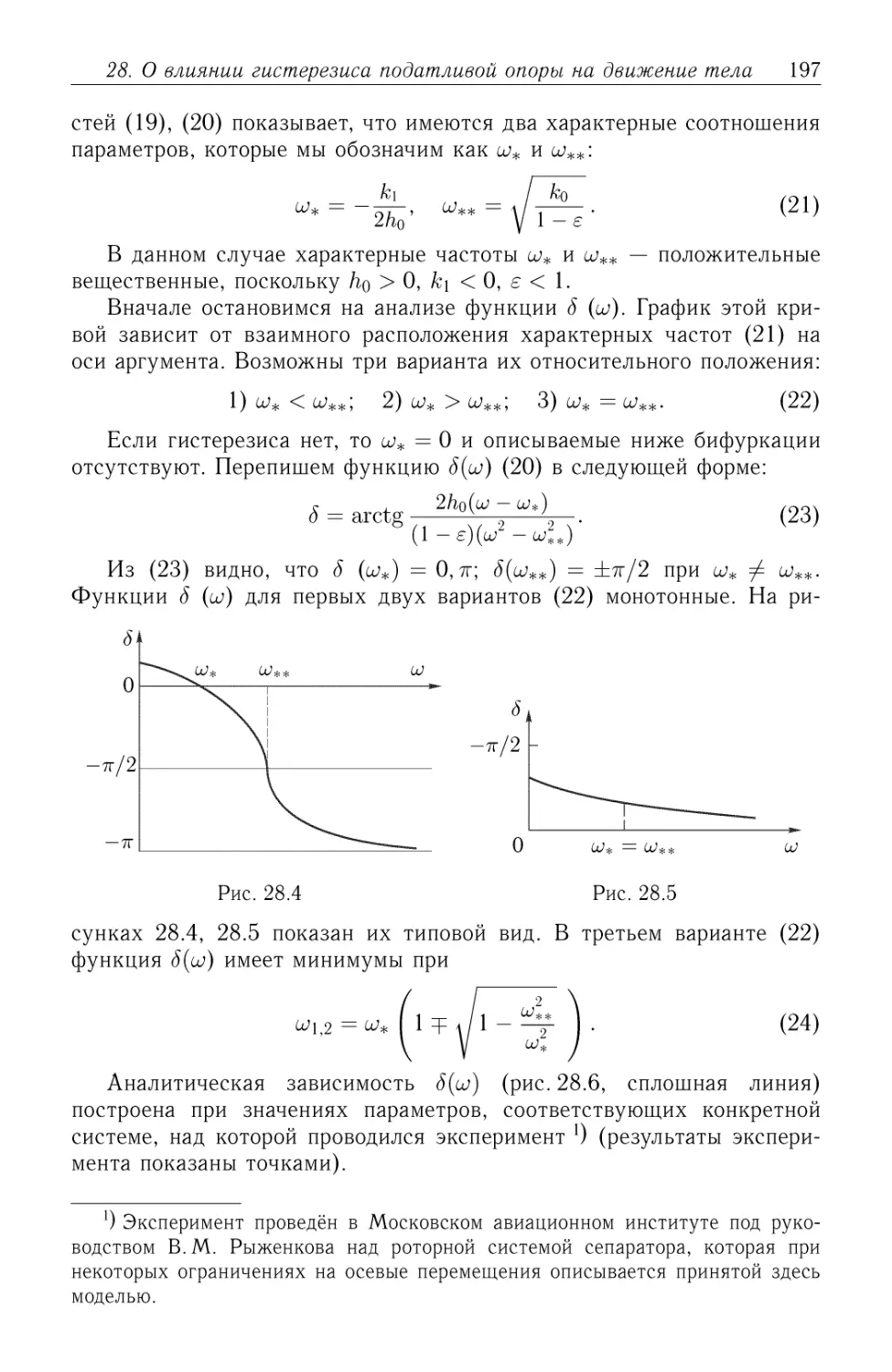
28.	О влиянии гистерезиса податливой опоры на сферическое движение
тела, несущего маховик	 192
28.1. Механическая схема. Общее уравнение динамики си-
системы A92). 28.2. Уравнения движения оси маховика (линейная
модель) A95). 28.3. О влиянии гистерезиса на устойчивость
движения оси маховика A95). 28.4. Влияние гистерезиса на
вынужденные периодические колебания A96).
29.	Построение периодического решения системы с малым параметром 199
29.1. Приведение динамической системы Е. Лоренца к форме си-
систем Н. Четаева A99). 29.2. Несвободная система Четаева B00).
29.3. Условия периодичности движения B00).
30.	Об энергии в динамике точки переменной массы (в первой задаче
Циолковского)	 202
30.1. О моделях точки переменной массы B02). 30.2. Кинетиче-
Кинетическая энергия и работа реактивных сил в системе «ТПМ — изменя-
изменяющая масса» B03). 30.3. О внутренней энергии ракеты B06).
Глава V. Принцип предикативности. Некоторые свойства гамиль-
тоновых систем	 208
31.0 понятии «предикативность» в математике и механике	 208
31.1.	Краткая характеристика понятия «непредикативность» B08).
31.2.	«Определимость» и «предикативность» понятий и правил со-
соответствия по А. Пуанкаре B10). 31.3. Аксиома сводимости Рас-
Рассела. Примеры B16).
32.	О преобразовании времени и функции Гамильтона в склерономных
системах	 221
32.1.	Лемма Уинтнера для гамильтоновых систем B21).
32.2.	Применение леммы Уинтнера и «обращение» времени B23).
32.3.	Свойство взаимности гамильтонианов B24).
33.	Интегральные инварианты и гамильтонова форма уравнений дви-
движения 	 225
33.1. Основной и универсальный классические интегральные инва-
инварианты гамильтоновых систем B25). 33.2. Задача о гамильтоновой
форме уравнений, имеющих инвариант B26). 33.3. О приведе-
приведении уравнений движения динамической системы к гамильтоновой
форме B27).

Оглавление
34.	Об однородных свойствах гамильтонова действия	 232
34.1. Определение квазиоднородной функции B32). 34.2. Об одно-
однородности гамильтонова действия B33).
35.	О реализации реакций и реализации связей	 234
35.1. Идеальные связи и идеальные реакции B34). 35.2. Опреде-
Определение реакций как решение задачи особого оптимального управ-
управления B35).
Глава VI. Принцип инерционности	 238
36.	Масса и принцип инерционности	 239
37.	К задаче о собственном энергоресурсе гравитирующей массы .... 248
37.1. Две схемы формирования гравитирующего тела из бесконечно
удалённой массы B49). 37.2. Эффективный собственный энерго-
энергоресурс массы, из которой формируется шар B52).
38.06 инерционности при релятивистском ограничении скорости. . . . 255
38.1. О наблюдении инерционных свойств B55). 38.2. О массе
и энергии в системе из двух тел B56). 38.3. Кинетический потен-
потенциал частицы и её собственного поля B59). 38.4. Предваритель-
Предварительные заключения B62).
Заключение	 264
Список литературы	 265

Предисловие
По предложению редакции весь прежний материал оставлен без
изменений, но в некоторые заметки первого издания включены до-
дополнительные пункты. Новые заметки вошли в главу IV «Решение
прикладных задач», составили главу V «Принцип предикативности.
Некоторые свойства гамильтоновых систем» и главу VI «Принцип инер-
инерционности».
На характере изложения и тематике заметок отразились новые
впечатления от работ А. Пуанкаре, 150-лет со дня рождения которого
отмечалось в 2004 году. А. Пуанкаре считал, что при кризисе всех
основных принципов физики в начале XX века «пока остаётся вне
сомнений принцип наименьшего действия... он является более общим
и неопределённым» (курсив наш). С этими качествами связана преди-
предикативность понятий (правил, отношений, доказательств), что является
существенным не только в логике, но, по-нашему мнению, и в теории
механики. По-видимому, в математике первым рассматривал опреде-
определимость и предикативность именно А. Пуанкаре. Одной из ключевых
в механике и физике по-прежнему остаётся проблема инерционности
и гравитации, но теперь принцип инерционности приобретает новую,
более общую форму.
При работе над вторым изданием книги авторы имели финан-
финансовую поддержку в рамках научных программ ФЦП «Интеграция»
и НП «Университеты России».

Посвящается памяти наших родителей
Предисловие к первому изданию
Книга написана в форме собрания заметок. В их число входят
некоторые классические результаты с нашими комментариями, содер-
содержание ряда докладов, с которыми авторы выступали на конференциях
и семинарах, а также статей в части, относящейся к рассматриваемым
методам. Заметки логически связывает между собой близость тема-
тематики обсуждаемых вопросов, они сгруппированы по принадлежности
к двум методам: виртуального варьирования и переменного действия.
Эти методы образуют основу аппарата аналитической механики и ис-
используются также в небесной механике, механике сплошных сред,
некоторых разделах теоретической физики, математической физики,
ряда направлений математики и т. д.
В теоретической механике содержание работы было бы отнесено
к разделам «Дифференциальные принципы механики» и «Интеграль-
«Интегральные принципы механики». Здесь мы рассматриваем метод виртуального
варьирования и метод переменного действия как дополняющие друг
друга и составляющие общий аналитический подход, который является
концептуальным для естествознания. На примере механических систем
изучается изменение действия в результате применения виртуального
варьирования, при котором из рассмотрения исключаются реакции
идеальных связей. Таким образом, создаётся своего рода «инструмент»,
освоение которого необходимо для учёта ограничений при исследова-
исследовании несвободных динамических систем.
Надеемся, что наши «Заметки» будут полезны при изучении меха-
механики.
Работа выполнена при финансовой поддержке ФЦП «Интеграция»
и Конкурса грантов по фундаментальным исследованиям в области
технических наук.

Введение
Заметки объединяет аналитический подход, основанный на приме-
применении двух взаимосвязанных методов: метода виртуального варьиро-
варьирования и метода переменного действия. Основы этих методов являются
составной частью содержания современных курсов теоретической ме-
механики [30, 39, 62].
Метод виртуального варьирования возник вместе с принципом «воз-
«возможных» перемещений (принципом виртуальных скоростей Лагранжа
(J.L. Lagrang)) и принципом Даламбера (J. d'Alembert) при объеди-
объединении их в единый принцип Даламбера-Лагранжа, дающий общее
уравнение аналитической механики. С использованием понятия «воз-
«возможных перемещений» задаются реакции связей, в частности с помо-
помощью известного критерия идеальности связей. Принцип «возможных»
перемещений вначале применялся при решении задач статики как
необходимое условие равновесия. Достаточность принципа виртуаль-
виртуальных скоростей для равновесия могла быть доказана только в теории,
описывающей движение, так как «под виртуальной скоростью следует
понимать скорость, которую тело, находящееся в равновесии, готово
принять в тот момент, когда равновесие нарушено, т. е. ту скорость,
какую тело фактически получило бы в первое мгновение своего движе-
движения...» [51]. Здесь мы вместо термина «возможное перемещение» пред-
предпочитаем пользоваться термином «виртуальное перемещение», чтобы
избежать терминологического противоречия, указанного М. В. Остро-
Остроградским [79]: при нестационарных связях виртуальные перемещения
в общем случае не являются возможными в смысле физической ре-
реализации (иначе получилось бы, что «возможные перемещения» не
являются возможными). Термин «виртуальные вариации» применяем,
следуя авторам работ [74, 101], чтобы подчеркнуть, что варьирование
производится в соответствии с требованиями, налагаемыми на вирту-
виртуальные перемещения. Совокупность способов получения виртуальных
вариаций, правила выбора множества последних и условия их приме-
применения составляют метод виртуального варьирования.
Метод виртуального варьирования является непременной составной
частью дифференциальных и интегральных принципов механики на
основе интегралов, называемых «действие».
Исследование роли интегрального принципа стационарного
действия в развитии физики имеется в работе [87]. Гамильтон
(W. R. Hamilton), занимаясь задачей объединения оптики и механики
в единой математической схеме, задачу динамики свёл к задаче отыс-

Введение	11
кания и дифференцирования характеристической функции V движения
системы (действия). «Уравнение, выражающее фундаментальный закон
вариации V, мы назовём уравнением характеристической функции или
законом переменного действия» (цитата по кн. [87]) (курсив наш).
Приёмы и способы изменения действия с целью выявления свойств
движения составляют метод переменного (варьируемого) действия.
В частных случаях движения систем обнаруживается, что действие
имеет стационарное значение и может иметь максимум или минимум.
Тогда говорят о принципе стационарного действия или о принципе
наименьшего действия.
В общем случае метод позволяет вскрыть важные свойства дви-
движений путём сравнения их не только с возможными, но и с невоз-
невозможными (перефразированное высказывание Эддингтона в отношении
принципа Гамильтона [87]). Такая широкая свобода сравнений откры-
открывает целый спектр направлений исследования интегральных свойств
движения на базе современных методов неголономной механики [101],
обратных методов аналитической динамики, движения систем Гельм-
гольца, Биркгофа, Намбу [24], конструктивного подхода к реализации
связей [44] и других приложений математической теории в современ-
современном естествознании. Постоянно происходит расширение области при-
применения метода. Он применяется для описания систем с распределён-
распределёнными параметрами, используется в динамике систем с деформируемы-
деформируемыми элементами, систем, обладающих термодинамическими свойствами,
систем со случайными связями и т.д.
Процесс развития и применения рассматриваемых методов со вре-
времён Мопертюи и до наших дней сопровождается критическими вы-
высказываниями в их адрес. По поводу принципа наименьшего действия
Пуассон (S.D. Poisson, 1838) писал: «Если сравнить принцип наимень-
наименьшего действия с законом живых сил, с законом сохранения центра
тяжести и законом площадей, то мы увидим, что принцип наименьшего
действия является лишь правилом для составления дифференциаль-
дифференциальных уравнений, являющимся ныне бесполезным...» [87] (курсив наш).
Ответ на критику Пуассона дала история, показав, что метод перемен-
переменного действия даёт правило составления уравнений процессов и вне
классической механики. Известны критические высказывания Герца,
ошибка Линделёфа в составлении с помощью принципа Гамильтона
модели движения системы при наличии дифференциальных связей.
В последнее время критике подверглись некоторые математические
модели механических систем с дифференциальными связями (модели,
получаемые с помощью принципа Гамильтона) [126]. В частности,
«неприемлемость» некоторых новых моделей механики в некоторой
мере обусловлена неприятием представлений о «реализации связи».
Здесь мы также изучим модели с различными способами «реализации
связи» и заметим, что этот термин входит в состав «гипотезы о реа-
реализации допустимых связей» в формулировке достаточности принципа

12	Введение
Даламбера-Лагранжа [25]. Термин, оставляя возможность отвлечься
от способа реализации в случае идеальных связей, наполняется новым
содержанием при появлении новых моделей. В частности, модель систе-
системы с идеальными связями может быть получена как предел различных
последовательностей моделей, в которых рассматриваются конкретные
силовые поля, участвующие в создании сил, являющихся реакциями.
Для «конструктивных» способов реализации связей [44] требуется
обобщение представления о виртуальных перемещениях и расширение
сферы применения изучаемых методов. Заметим, что известная [119]
«некорректность Пуанкаре в постановке задачи о теории возмущений»
также может быть устранена с помощью конструктивного построения
физических моделей.
Отрицание новых результатов или неправильное понимание как
старых, так и новых результатов, а также неоправданное ограничение
развития понятий и т.д. часто имеют объяснение в сфере методологии.
Возникает подобная критика из-за неприятия её авторами одной про-
простой, но важной, по нашему мнению, методологической схемы развития
естественнонаучного знания. По этой схеме некая первичная модель
используется при обосновании более общей модели, в которой первич-
первичная является частным случаем (получаемым при некоторых условиях
согласно принципу соответствия). Указанная схема может характери-
характеризовать взаимоотношение теорий (например, квантовой и классической
механики). «Квантовая механика занимает очень своеобразное положе-
положение в ряду физических теорий: она содержит классическую механику
как свой предельный случай и в то же время нуждается в этом
предельном случае для самого своего обоснования» [54]. Связующим
элементом этих механических теорий является «действие». Добавим
также, что описанная ситуация является типичной.
В приведённую выше схему (в несколько более сложном варианте
для физико-математических моделей, когда речь идёт как о физических
свойствах, так и об их математическом описании) укладывается и раз-
развитие отдельных понятий. Уточнение смысла основных применяемых
понятий дано в заметках первой главы работы. Дано обобщение по-
понятия материальной точки (заметка 1), рассмотрены понятия скорости
и ускорения (заметка 2), обсуждается соотношение виртуальных пере-
перемещений и вариаций, используемых в дифференциальных и интеграль-
интегральных принципах (заметка 3). Закон Ньютона о действии и противодей-
противодействии получен как следствие принципа равновесия Даламбера и вто-
второго закона Ньютона. Прослеживается логическая цепь, соединяющая
принцип равновесия Даламбера с уравнениями «даламберова равнове-
равновесия», использующими понятие о силе инерции. Предложено описание
взаимодействия в форме интегрального равенства (заметка 4). Об-
Обсуждаются аналоги теоремы об изменении кинетической энергии для
реономных систем и место функции Гамильтона в уравнении энергии

Введение	13
(заметка 5). Приводятся примеры функционалов и функций «действие»
различного физического смысла (заметка 6).
Содержание второй и третьей глав составляет разработка двух
взаимосвязанных методов: метода виртуального варьирования и метода
переменного действия.
Виртуальное варьирование предполагает использование виртуаль-
виртуальных перемещений, определяющих свойства реакций связей. Таким
путём применение операций вариационного исчисления при варьиро-
варьировании функционала «действие» увязывается с физическим смыслом
учитываемых ограничений. Вспомогательный характер имеет заметка 7
о дифференцировании функции при неявной зависимости от пере-
переменных и о вариационной производной. Способы синхронного, асин-
асинхронного варьирования и способ, применённый Гельмгольцем (и его
расширение), а также варьирование в скользящих режимах реализа-
реализации связей рассматриваются в заметке 8. В заметке 9 обсуждается
составление уравнений для виртуальных вариаций неголономной связи;
связи, представляющей огибающую; связи, зависящей от двух неза-
независимых параметров; неравенства для виртуальных перемещений при
неудерживающих связях. В одном из пунктов заметки 10 полностью со-
содержится (с нашим примечанием) двухстраничная работа М. В. Остро-
Остроградского «Заметка о равновесии упругой нити», написанная им по
поводу одной известной классической ошибки Лагранжа; в других
пунктах рассматривается использование неопределённых множителей
при представлении реакций связей. Некоторое ограничение множе-
множества виртуальных перемещений позволило сформулировать обобщение
принципа наименьшей кривизны Герца для систем с нестационарными
связями (заметка 11). Несвободное движение систем с параметриче-
параметрическими связями (заметка 12) изучается на основе принципа освобож-
освобождаемое™ по Четаеву, сформулированному им в задаче о вынужденных
движениях; составлено общее уравнение несвободных динамических
систем, основные уравнения «немеханической» части которых имеют
первый порядок (в отличие от механической части, основные уравнения
которой второго порядка), предложено общее уравнение динамики си-
систем со случайными параметрами. Центральное вириальное равенство
(заметка 13) выводится с помощью центрального уравнения Лагранжа.
Практическое применение интегральных принципов происходит че-
через составление интегральных равенств, получаемых методом перемен-
переменного действия. Классические примеры таких равенств дают интеграль-
интегральный принцип Гамильтона-Остроградского и интегральные принципы
для неголономных систем.
В методе переменного действия развивается подход, состоящий
в использовании способов синхронного, асинхронного варьирования
и варьирования по Гельмгольцу. Среди полученных интегральных ра-
равенств (заметки 14-17): центральное интегральное равенство, состав-
составленное на основе центрального уравнения Лагранжа при асинхронном

14	Введение
варьировании; обоснование аналога принципа Гамильтона-Остроград-
ского в теории реономных систем; новое обобщение принципа Гёль-
дера, интегральный вириальный принцип и принцип систем Четаева-
Румянцева, содержащих так называемые термодинамические точки,
и т. д. В заметке 18 приведены требования, полученные Э. и Ф. Кос-
сера к форме евклидового действия деформации на изменяемую ли-
линию. Применению интегральных принципов при движениях с ударами
и в неголономных системах посвящены заметки 19, 20.
В качестве примеров приложения разрабатываемой теории анализи-
анализируются (гл. IV) модели механических систем, содержащих абсолютно
твёрдое тело и одномерный деформируемый элемент (стержень, нить).
Модели динамики конкретных механических систем составлены с учё-
учётом замечаний Э. и Ф. Коссера в отношении формы евклидового дей-
действия, замечаний М. В. Остроградского о применении неопределённых
множителей при наличии условных уравнений и т. д.
Полученные результаты исследования динамики конкретных меха-
механических систем имеют, на наш взгляд, самостоятельный прикладной
интерес. В задаче о движении системы «жёсткое колесо — деформируе-
деформируемый рельс» (заметка 21) обнаружено некое псевдоскольжение (на прой-
пройденном пути действительное число оборотов колеса меньше, чем гео-
геометрическое число оборотов). В отличие от известного классического
крипа {creep) [136], обусловленного продольными деформациями осно-
основания и (или) периферии колеса, причиной псевдоскольжения является
поперечная деформация изгиба. В динамике колеса с деформируемым
ободом (заметка 22) наблюдается эффект диссипации, являющийся
причиной сопротивления качению. Свойства деформируемого стержня
изучаются в заметках 23-25. Рассматривается схема перспективного
волнового редуктора.
Основные связующие темы сохранились и для дополнительного
материала, включённого во второе издание. Кинетическая энергия,
кинетический потенциал и действие применяются при исследовании
динамики общих и специальных систем. В их числе: реономные си-
системы (п. 5.5); динамические системы (п. 12.5) и системы Четаева
(п. 17.3), (заметка 29); системы с неевклидовым действием (п. 18.3);
системы с распределёнными параметрами — стержень в задаче об
устойчивости его формы (п. 25.5) и развёртываемая центробежными
силами в космосе поверхность (заметка 27); система с диссипацией
энергии за счёт гистерезиса в опоре (заметка 28); система перемен-
переменного состава (заметка 30); гамильтоновы системы (заметки 32-35);
системы, включающие бесконечно удалённые гравитирующие массы со
сферической симметрией и инерционные объекты, нарушающие общую
симметрию (заметки 36, 37); система, состоящая из релятивистской
частицы и её собственного поля (заметка 38).
Общими являются вопросы учёта ограничений и взаимодействий.
Предложен принцип освобождаемости от связей для динамических

Введение	15
систем (п. 12.5), включающих в себя как частный случай системы
Четаева. Распространение классического принципа освобождаемости
соответствует последовательному включению: классические механиче-
механические системы — системы Четаева (механическая часть и «немеханиче-
«немеханическая» часть) — динамические системы, описываемые обыкновенными
дифференциальными уравнениями. Свойство идеальности связей фор-
формулируется как результат расширенного применения гипотезы Гаусса
о мыслимых движениях механической системы (и виртуального варьи-
варьирования по Лагранжу-Остроградскому). Применение принципа и свой-
свойство идеальности продемонстрированы на примере построения периоди-
периодического решения системы с малым параметром (динамическая система
Лоренца, преобразованная к форме системы Четаева, при наложении
связей) (заметка 29). Неголономной связью является релятивистское
ограничение скорости (сочетание свойств «свободная релятивистская»
частица противоречиво).
Тесно связаны проблема инерционности и проблема гравитации,
становящаяся всё более злободневной по мере её осознания. Предло-
Предложение Э. Маха [64] по расширению аксиоматики Ньютона за счёт
бесконечно удалённых масс учитывается при исследовании инерцион-
инерционности механического движения в форме принципа, названного принци-
принципом изменения нарушения симметрии (заметка 36) (аналог известного
«спонтанного нарушения симметрии» при наблюдениях массы элемен-
элементарных частиц). Нарушение симметрии — исходная посылка появления
так называемого гравитационного парадокса [75]. Обсуждается задача
вычисления энергоресурса бесконечно удалённых масс, из которых
при наличии закона тяготения Ньютона в мысленных экспериментах
формируется тело конечных размеров (шар) (заметка 37). Составлен
кинетический потенциал системы: релятивистская частица — собствен-
собственное поле, обладающее инерционными свойствами (заметка 38).
Может показаться, что заметка 31 не относится к рассматривае-
рассматриваемому методу. Однако это только на первый взгляд. Более того, реко-
рекомендуем ознакомиться с заметкой 31 прежде, чем с остальными, так
как в ней обсуждается предикативность понятий (правил, отношений,
доказательств) — свойств, универсальных для логики, математики
и естествознания. В заметке содержатся практически весь доклад
А. Пуанкаре [91], наши комментарии и примечания, представляющие
собой размышления и попытку лучше понять требования научной
строгости на примерах. Механика весьма подходящий предмет для вы-
выработки отношение к научным результатам, получаемым в мысленных
экспериментах с бесконечно удалёнными массами, с применением вир-
виртуального варьирования, интегральных принципов и интегральных ин-
инвариантов. Первооткрыватель интегральных инвариантов — А. Пуан-
Пуанкаре — широко пользовался принципом наименьшего действия и внёс
свой вклад в его развитие. В то же время он высказывал и свою
неудовлетворённость формой принципа: «Самая формулировка принци-

16	Введение
па наименьшего действия имеет в себе нечто, неприятно поражающее
наш ум. При переходе от одной точки к другой материальная частица,
не подверженная действию какой-либо силы, но подчинённая условию
не сходить с некоторой поверхности, движется по геодезической линии,
т.е. по кратчайшему пути. Эта частица как будто бы знает ту точку,
куда её желают привести, предвидит время, которое она затратит,
следуя по тому или иному пути, и наконец, выбирает путь, наиболее
подходящий. В такой формулировке принципа частица представлена
нам как бы одушевлённым существом, обладающим свободой воли.
Ясно, что следовало бы заменить эту формулировку другой, более под-
подходящей, в которой, выражаясь языком философа, конечные причины
не становились бы явным образом на место причин действующих» [94].
Очевидно, что это не критика принципа изменяемого действия,
а скорее, желание его усовершенствовать.
Заметки могут читаться независимо друг от друга, имеющиеся
ссылки на формулы из других заметок снабжены двойной нумерацией.
Заметки дополняют тематику учебных пособий, написанных с уча-
участием авторов [13, 108, 114].

Глава I
ЗАМЕТКИ О НЕКОТОРЫХ ОСНОВНЫХ
ПОНЯТИЯХ
1. Развитие понятия материальной точки
в моделях механики
В истории механики можно выделить исследования, в которых
вводятся расширения классического понятия материальной точки: точ-
точка комплексной массы, точка переменной массы, термодинамическая
точка. Для объяснения свойств последней здесь предлагается исполь-
использовать гипердействительные числа.
Известно, что объекты (в том числе идеальные, являющиеся мате-
математическими моделями) проявляются только через отношения (в ви-
виде физических взаимодействий, установленных качественно и количе-
количественно с помощью математики). Отношения же и свойства зависят
от системы, в которую объект входит как элемент [50]. Реальные
физические системы и отношения изучает физика, а идеальные свой-
свойства описываются на языке математики (аналогичная ситуация имеет
место и в других естественных науках). Поэтому возникновение (и раз-
развитие) научного понятия сопровождается, условно говоря, созданием
(и обновлением) «словарей» (терминологических и толковых), которые
позволяют осуществлять «переводы» результатов физических экспе-
экспериментов и наблюдений на язык математики и обратно. В качестве
примера обсудим развитие понятия материальной точки в дискретных
механических системах (неквантовых, нерелятивистских).
1.1. Классическое понятие материальной точки. Понятие ма-
материальной точки в классической механике сохранилось со времён
Галилея и Ньютона до наших дней практически в неизменном виде:
положение определяется геометрической точкой в трёхмерном евклидо-
евклидовом пространстве (пространстве R3), а масса описывается с помощью
трёхстолбцового словаря (см. табл.) [137].
В процессе развития понятия записи в «словаре» могут уточняться,
таблица может расширяться за счёт столбцов, где указывалась бы
система, в которой используется модель материальной точки, а также
решаемая задача (проводимое исследование). Даже условие «изоли-
«изолированности» материальной точки в законе инерции Галилея (первый
закон Ньютона) предполагает упоминание об инерциальной системе
отсчёта, что указывает на возможность пополнения словаря инфор-
информацией о новых физических явлениях, соответствующих математиче-

18
Гл. I. Заметки о некоторых основных понятиях
ским моделям пространства и времени (в последнее время открыты
реликтовое излучение, являющееся наилучшим из известных ныне
приближений к инерциальной системе координат, и атомные эталоны
Таблица
Наименование
понятия
1
Масса
Математические
понятия
2
Положительное
число (ш)
Физические понятия
3
Количество вещества в теле. Мера со-
сопротивления тела изменению скорости.
Мера способности тела гравитационно
притягивать другое тело.
времени). В первом столбце таблицы также неявно фигурирует гипо-
гипотеза о тождестве инерционной и тяготеющей масс. Схему словаря для
классического понятия материальной точки примем за основу, отмечая
новые свойства более общих терминов.
1.2. Модели точки комплексной массы и точки переменной
массы. Потребность в понятиях точка комплексной массы и точка
переменной массы возникла при решении конкретных задач динамики
некоторых механических систем.
Примером применения комплексных чисел для описания массы яв-
является представление нецентрального гравитационного поля в задаче
о движении искусственного спутника [33]. Классическая задача двух
центров в небесной механике (Эйлер, Н.Е. Жуковский [38]) в случае
комплексных масс двух притягивающих центров принимает обобщён-
обобщённую трактовку. Отметим, что комплексные массы вводятся одновре-
одновременно для двух точек и используется комплексное пространство С3,
в котором для вычисления «расстояния» принято эрмитово скалярное
произведение. Ограничения на комплексные числа выводятся из требо-
требования, чтобы силовая функция
j-j _ [МП\	[М712
Г\	Г2
где /i — гравитационная постоянная Гаусса (/i = /га, / — универ-
универсальная гравитационная постоянная), т\ и тп^ — массы неподвижных
притягивающих центров М\ и М^, а г\ и г 2 — расстояния от них до
пассивно гравитирующей массы га, имела действительные значения.
Для этого массы притягивающих центров представляются комплексны-
комплексными сопряжёнными числами, а «расстояния» от них до точки с массой га
имеют вид
^	+ (z - Cif , г =1,2.
Здесь с\ и С2 — комплексные сопряжённые числа.

/. Развитие понятия материальной точки в моделях механики 19
Точка переменной массы (A. Cayley, И. В. Мещерский) — термин,
используемый для определения некоторых моделей систем переменного
состава. История развития этого направления динамики рассмотрена
в работах Г. К. Михайлова (см., например, [69]). Заметим, что даже
при малых размерах системы, когда её положение может быть задано
одной геометрической точкой, определение «материальная точка пере-
переменной массы» может служить источником ошибочного учёта внешних
сил. Если силы приложены к материальной точке, то они аксиома-
аксиоматически эквивалентны одной равнодействующей. Однако для точки
переменной массы такой вывод в общем случае сделать нельзя, так
как внешние силы могут быть приложены к разным материальным точ-
точкам, составляющим точку переменной массы (например, «уходящей»
и «остающейся»), даже если эти материальные точки представлять на-
находящимися в одном и том же геометрическом месте. Анализ подобных
моделей имеется в работе [13].
Для описания массы материальной точки в рассматриваемых си-
системах служат математические понятия: комплексное число и функция
времени.
1.3. Модель термодинамической точки. Сразу же отметим, что
при формировании понятия термодинамической точки отношение ме-
механики и термодинамики принимается в некотором смысле противопо-
противоположным традиционному. Обычно термодинамические системы рассмат-
рассматриваются состоящими из материальных точек. «Точки», о которых идёт
речь, ввёл Н.Г. Четаев при формулировке своего принципа [128], наде-
наделив их термодинамическими свойствами. Затем В. В. Румянцев, обос-
обосновывая принцип Четаева, отметил, что изучается физическая система,
которая «состоит из совокупности физически малых материальных
частиц («точек»), рассматриваемых как термодинамические системы,
для каждой из которых определены механические понятия о поло-
положении и движении и физические понятия о внутреннем состоянии,
характеризуемые конечным числом величин, задаваемых числами —
определяющими параметрами» [103]. Для краткости каждую такую
«физически малую материальную частицу» будем называть термодина-
термодинамической точкой.
Полагается, что каждая термодинамическая точка обладает свой-
свойствами материальной точки, и кроме того, характеризуется внутрен-
внутренней энергией, способностью к теплообмену (абсолютной температурой,
энтропией). Системы из термодинамических точек (названные в ра-
работе [14] системами Четаева-Румянцева) удобны для аналитического
исследования и являются обобщением чисто механических систем,
в которых тепловые процессы несущественны. Несмотря на имеющееся
внешнее оправдание существования таких объектов, нельзя считать
удовлетворительной суть данного понятия. Дело в том, что в нём при-
присутствуют противоречивые свойства: детерминированное однозначное

20	Гл. I. Заметки о некоторых основных понятиях
определение положения точки и её вероятностные термодинамические
свойства (описываемые энтропией). Последние невозможно матема-
математически описать без раскрытия внутренней структуры термодинами-
термодинамической точки. Разъяснение возникшего противоречия даёт, на наш
взгляд, представление положения точки в пространстве, координатами
которого являются гипердействительные числа.
Основа противоречия состоит в том, что положение точки детерми-
нированно и однозначно определено в том случае, если используется
пространство, координаты которого — действительные числа. В на-
настоящее время в математике интенсивно развивается так называемый
нестандартный анализ (см., например, [119]). Один из его вариантов
основывается на рассмотрении поля гипердействительных чисел R*,
представляющего собой неархимедово расширение поля действитель-
действительных чисел R. (Напомним аксиому Архимеда: если \х\ < 1/п, для
любого натурального п, то х = 0.) Поле R этой аксиоме удовлетворяет,
а поле R* — нет. Разница состоит в том, что, например, отрезки
[0, 1/п], п = 1,2,..., имеющие лишь единственное общее действитель-
действительное число 0, содержат бесконечно много общих гипердействительных
чисел (которые все называются бесконечно малыми: 0 < Л < 1/п для
любого натурального п). «Числами» являются формальные ряды вида
где а\, р\, а2, /02,... — действительные числа; последовательность
р\,Р2,--- — неограниченно возрастающая. К каждому действительному
числу поле гипердействительных чисел добавляет, как образно говорят,
«ореол» из бесконечно малых чисел. Отмеченные выше противоре-
противоречия снимаются, поскольку появляются новые математические объекты
для описания внутренней структуры и дополнительных физических
свойств «точки».
В число определяющих параметров термодинамической точки, кро-
кроме массы, координат радиуса-вектора г и вектора скорости v, могут
входить переменные параметры /^ и физические постоянные [103].
Изменение определяющих параметров в функции времени представля-
представляет собой некоторый процесс, включающий и механическое движение.
В определение термодинамической точки входит также описание воз-
возможных состояний и процессов, обусловленное её взаимодействиями
с другими телами.
Представление о массе, находящейся не только в точке, задан-
заданной действительным числом, но и «размазанной» по бесконечно ма-
малой окрестности (по её «ореолу»), расширяет понятие классической
материальной точки. Геометрическое пространство R*3 для задания
положений массы позволяет более полно представить пространствен-
пространственные свойства понятий точки переменой массы и термодинамической
точки и даёт возможность применения их в математических моделях
механики (и других физических систем).

2. О понятиях скорости и ускорения материальной точки	21
2. О понятиях скорости и ускорения
материальной точки
Для формирования понятий скорости и ускорения был необходим
метод исчисления бесконечно малых, связанный с именами Ньютона
и Лейбница. Ньютон применяет его в важнейшем из своих произведе-
произведений — «Principia» — только в неявной форме, и лишь спустя полвека
анализ позволил Л. Эйлеру систематически изложить механику в ра-
работе «Механика, т. е. наука о движении, изложенная аналитическим
методом», Петербург, 1736 г. (см. [132]). Современные представления
требуют для этих понятий ещё более сложного математического опи-
описания.
2.1. Скорость материальной точки и производная по времени
её радиуса-вектора. С помощью производной переменного радиуса-
вектора г точки в современных учебниках по теоретической механике
вводится вектор скорости точки:
Сравним производную A) с определением скорости, которое дал
Эйлер: «О всяком теле, которое движется, говорят, что оно имеет
быстроту или скорость, и эта скорость измеряется тем расстоянием,
которое тело, двигаясь равномерно, проходит в данное время» (опреде-
(определение 5, [132]). Далее Эйлер описывает условия мысленного экспери-
эксперимента для измерения скорости: «Скорость, которую имеет движущееся
неравномерно тело в какой-либо точке проходимого пути, должна изме-
измеряться тем расстоянием, которое могло бы пройти в данное время тело,
движущееся равномерно с этой же скоростью» (следствие 2, [132];
курсив наш). Курсивом выделено указание Эйлера на виртуальность
событий 0, происходящих в последующие моменты времени.
Физический смысл, содержащийся в определении Эйлера, в фор-
формуле A) отсутствует. Эта формула может быть использована толь-
только для движений, траектории которых являются кривыми класса С1
(г — непрерывные дифференцируемые функции времени). Для нахож-
нахождения скорости в данный момент времени требуется информация об
однозначном положении точки в момент времени t + dt, т. е. фак-
фактически в «будущем». Задача прогнозирования будущего положения
точки полагается фактически решённой в линейном приближении на
элементарном промежутке времени.
*) Событие в классической механике характеризуется совокупностью опре-
определяющих координат и временем [137].

22	Гл. I. Заметки о некоторых основных понятиях
Отмеченные недостатки лишают скорость A) статуса самостоя-
самостоятельной характеристики (независимой от действительного изменения
положения и изменения времени) 0.
Модификация определения A) с помощью понятия об односто-
односторонних производных пригодна для некоторых движений, траектории
которых содержат угловые точки. Односторонние производные поз-
позволяют описывать движение, при котором в изолированных точках
траектории происходят удары (в числе основных аксиом теории сте-
реомеханического удара — аксиома о конечном изменении скорости
при ударе). Однако уже в задаче о соударении двух тел при наличии
сухого трения в месте контакта для описания изменения скорости (при
фиксированном времени) составляются дифференциальные уравнения
относительно скорости v(iV) как функции монотонно возрастающего
импульса нормальной составляющей реакции в месте контакта (N)
(см., например, [113]).
В моделях точки переменной массы (системы переменного состава)
рассматриваются «непрерывные удары». При этом вектор относитель-
относительной скорости «присоединяющейся» и (или) «отделяющейся частицы»
представляет собой усреднение по некоторому промежутку времени.
Точнее говоря, усредняется импульс, а это значит, что усреднение
происходит не только по времени, но и по пространственному распре-
распределению массы этих «частиц».
Современные представления о физическом смысле скорости матери-
материальной точки, используемые в понятиях кинетической и потенциальной
энергии, действия и других, требуют сопоставления им математических
объектов, называемых обобщёнными функциями (распределениями)
[99, 135]. Так, например, в интегральных принципах, использующих
выражение кинетической энергии, скорости v(?) — функции, интегри-
интегрируемые не менее чем с квадратом, т. е. принадлежащие пространству
распределений L2 2). Если кинетическая энергия является локально
интегрируемой функцией, то ей однозначно сопоставляется (в случае
её существования) обобщённая функция.
2.2. Об ускорении материальной точки. После замечаний в от-
отношении скорости становятся понятными трудности поиска [85] «уско-
«ускорения — физической величины, характеризующей изменение скорости»
х) Этот вопрос, по-видимому, относится к проблеме неопределённости
в классической механике [124] (подобной принципу неопределённости Гейзен-
берга в квантовой механике).
2) Пространство L2 можно рассматривать как наименьшее полное про-
пространство (пополнение относительно Ь2-нормы), содержащее пространство С^
(С^ — пространство непрерывных квадратично интегрируемых функций) [99].

2. О понятиях скорости и ускорения материальной точки	23
в виде производной по времени от A):
dv d y	/оч
w = ^ = ^-	B)
Историку не удалось найти ни у Галилея, ни у А. М. Ампера, ни
у Лагранжа ускорение в форме B). В своём исследовании формиро-
формирования понятия ускорения И. Б. Погребысский отмечает: «Что касает-
касается картезианской механики, то она вообще обошлась без ускорения,
оперируя возрастанием импульса или скорости», а «введение понятия
ускорения как понятия «sui generis», подготовленное Галилеем, каково
бы оно ни было, осуществилось только после Лагранжа. И так как
было уже привычно понятие ускоряющей силы, то это прошло почти
незамечено, в процессе исследований, можно сказать само собой» (кур-
(курсив наш).
Этот результат, по нашему мнению, не случаен, так как без уско-
ускоряющих сил в динамике физический смысл ускорения неясен. Форму-
Формула B) даёт чисто кинематическое представление об изменении «скоро-
«скорости» A) в случае траекторий, принадлежащих кривым класса С2.
Модели механического движения, в которых траектория не явля-
является кривой класса С2, не единичны. Так, в динамике несвободных
систем рассматриваются последовательности моделей, в которых связь
реализуется бесконечно возрастающими силами (движение в «сколь-
«скользящем режиме»). Приведём примеры моделей, в которых возникают
такие режимы.
При бесконечном возрастании коэффициента жёсткости потенци-
потенциальные упругие силы могут обеспечить условие голономной связи.
Движение с ограничением в виде уравнения, линейного относи-
относительно скорости, может рассматриваться как движение относительно
некоторой гипотетической проницаемой сплошной среды [67].
Как известно, в моделях гидромеханики [49] к воздействиям среды
на тело относят вязкие силы сопротивления движению и сопротивле-
сопротивление изменению ускорения путём учёта инерционных свойств идеальной
жидкости с помощью присоединённых масс. Поэтому в качестве сил,
обеспечивающих условие связи, могут использоваться диссипативные
силы вязкого трения при бесконечно возрастающем коэффициенте вяз-
вязкого трения, а также присоединённые массы, возрастающие до беско-
бесконечности [44].
В первом способе реализации связи при отклонении положения
точки от поверхности, заданной уравнением связи, создаются упругие
силы; во втором способе силы вязкого трения противодействуют «ско-
«скорости деформации связи»; наличие присоединённых масс эквивалентно
действию сил, линейно зависящих от ускорения, поэтому третьим спо-
способом реализации связи обеспечивается противодействие «ускорению
деформации связи». Эти способы можно использовать в некоторых
сочетаниях. В результате движения принимают вид соответствующих

24	Гл. I. Заметки о некоторых основных понятиях
скользящих режимов [121], обеспечивающих заданную точность вы-
выполнения условий связи лишь на конечном интервале времени.
Вместо уравнения движения материальной точки в скользящем
режиме имеем дифференциальное включение [13]
raw е Ф,	C)
где га — масса материальной точки; Ф — множество допустимых
векторов (F + R), F — равнодействующая активных сил, a R —
равнодействующая сил реакции, приложенных к материальной точке.
Например, пусть в течение бесконечно малых промежутков вре-
времени At\ и At2 попеременно создаются ускорения wi и W2. Тогда
одним из способов выбора w является доопределение следующего вида
(рис. 2.1):
w = 7W1 + A — 7) W2>
0<7<1> 7 = lim^-, At = Ati+At2, At -> О,
где коэффициент 7 находится из условия выполнения уравнения связи.
0
7711
Х\
Рис. 2.
2
Х2 X
Рис. 2.1
Пример. Одномерная консервативная система двух материальных
точек (рис. 2.2) движется в потенциальном силовом поле с энергией
П = - с{х\ -х2- if,
где с и I — константы.
Изменение разности координат точек происходит по закону
х\ — Х2 = I + J— sin J- (t — to),
п ф , п	,	TTli 7712
Е = Т + П = const, а =	.
ТП\ + 7712
Из D) следует, что при с —> оо потенциальные силы «реализуют»
связь \х\ — Х2\ = /, а относительная скорость точек и относительное
ускорение равны нулю в среднем на периоде.

3. К обоснованию принципа Гамильтона	25
3. К обоснованию принципа Гамильтона
3.1. Из истории «силы» и «действия». В 1744 году Мопер-
тюи для объяснения некоторых оптических и механических явлений
сформулировал «принцип наименьшего действия», в котором термин
«действие» используется в смысле «деятельности», и измеряется это
действие произведением mvs, где т — масса, v — скорость, s — путь,
пройденный телом. Суждение, расширяющее представление о дей-
действии, было высказано Даламбером в связи с происходившим в то
время спором о том, что считать «силой» (производящей «действие»)
при движении тела: импульс mv или живую силу Лейбница mv2?
«Вся трудность... сводится к тому, чтобы определить, следует ли
измерять силу числом препятствий или суммой сопротивлений этих
препятствий. Может показаться более естественным измерять силу
именно последним способом... И тем не менее, поскольку в слове
сила не содержится никакого ясного и точного смысла, помимо со-
соответствующего ей действия, я полагаю, что нужно каждому предо-
предоставить свободу решать данный вопрос по его усмотрению» [32] (кур-
(курсив наш).
Эйлер, пользуясь равенством
mv ds = mv2 dt,	A)
т.е. при ds = vdt, показал, «что для кривой, описываемой брошенным
телом, сумма всех живых сил, находящихся в теле в отдельные мо-
моменты времени, будет наименьшей» [133]. И как отклик на тогдашние
споры, Эйлер в этой же работе отметил: «...таким образом ни те,
кто полагает, что силы следует оценивать по самим скоростям, ни те,
кто — по квадратам скоростей, не найдут здесь ничего неприемле-
неприемлемого».
Примечание. Термин «сила» в контексте приведённых цитат
классиков по своему смыслу отличается от современного примене-
применения этого термина. Однако можно отметить уместность его в данном
тексте и, что немаловажно, согласованность с понятием о действии.
Данную ситуацию можно сравнить (по этому поводу см. замечания
Бертрана [51]) с применением термина «сила» Лагранжем для обо-
обозначения ставших общепринятыми понятий обобщённых сил (набор
которых составляет ковектор для выбранного вектора обобщённых
координат).
Пусть движение материальной точки происходит в потенциальном
силовом поле. Обозначим
Я = Т + П,	B)
где Т = mv2/2 — кинетическая энергия; П — потенциальная энергия.

26	Гл. I. Заметки о некоторых основных понятиях
Перенесём слагаемое из правой части A) в левую часть и восполь-
воспользуемся равенством B):
mvds- (T -U)dt = Hdt.
Обозначив через L функцию Лагранжа:
L = Т - П,	C)
имеем
mv ds — Ldt = Н dt,	D)
или
mvds-Hdt = Ldt.	E)
После интегрирования равенства E) на фиксированном промежутке
времени [to, t\] имеем
и
Umvds-Hdt) = Ibdt.	F)
to
Интеграл в левой части F) является криволинейным по траектории
(в пространстве координат-времени) из начального положения в ко-
конечное. Интегралы в равенстве F) называют действием по Гамиль-
Гамильтону:
a) S=J Ldt, б) S=\j(mvds-Hdt).	G)
to
Если при движении сохраняется полная механическая энергия, т. е.
Я = Т + П = /1 = const,	(8)
то из G) с учётом (8) имеем также
и	si
5 = -h(t\ - t0) + [ 2Т dt, S = -h(t\ -to)+ [ mv ds. (9)
to	s0
Интегралы
tx	sx
W = \2Tdt= I mvds	A0)
to	s0
называются действием по Лагранжу. Исторически они использовались
раньше, чем было обосновано применение действия по Гамильтону G)
в неконсервативном случае. Однако здесь нами принята иная после-
последовательность с целью показать соотношения между действием по
Лагранжу и действием по Гамильтону в виде равенств (9). Заметим,
что при выводе первого из этих равенств с помощью интеграла энер-
энергии (8) в выражении функции Лагранжа произведена замена потенци-

3. К обоснованию принципа Гамильтона	27
альной энергии П. Выражая кинетическую энергию, получим
и
S = -h(U -t0)- \2Udt	A1)
to
Последнее равенство показывает, почему Лагранж не называл свой
принцип принципом наименьшего действия: «рассматриваемый прин-
принцип сводится собственно к тому, что сумма живых сил всех тел от
момента, когда они выходят из заданных точек, до того момента, когда
они приходят в другие заданные точки, является максимумом или
минимумом. Следовательно, его с большим основанием можно было
бы назвать принципом наибольшей или наименьшей живой силы; эта
формулировка имела бы то преимущество, что она была бы общей как
для движения, так и для равновесия; ... мы видели, что при прохожде-
прохождении положения равновесия живая сила всегда бывает наибольшей или
наименьшей» [51].
Принцип, будучи пригодным к задаче о равновесии, полезен, оче-
очевидно, и в случае квазистатических процессов, настолько медленных,
что можно пренебречь кинетической энергией, как, например, в за-
задаче о квазистатическом нагружении стержня скользящей нагрузкой
(см. заметку 23).
Для системы материальных точек, положение которой задаётся
обобщёнными координатами qi (пространство конфигураций), в пере-
переменных Лагранжа q^ t, qi (qi — обобщённые скорости) действие по
Гамильтону имеет вид
и
\L(qitt,qi)dt, q = (qi,...,qn).	A2)
to
При использовании переменных Гамильтона qi, t, pi (pi — обобщён-
обобщённые импульсы):
ft = §,	A3)
интеграл G б) примет следующую форму:
\	A4)
Интегралы, называемые «действие», используются в двух направ-
направлениях: для описания свойств движения и при составлении уравне-
уравнений движения [51]. Интересна роль действия в теориях, граничащих
с классической механикой. Например, в обосновании взаимоотношения
классической и квантовой физики [54] действие используется как мате-
математический объект, позволяющий проводить квантование, а в перспек-
перспективе — и вторичное квантование [106]. Понятие о действии является
основой утверждений в форме принципов.

28	Гл. I. Заметки о некоторых основных понятиях
3.2. О выводе принципа Гамильтона из общего уравнения ди-
динамики. Рассмотрим вывод [25] принципа Гамильтона-Остроградско-
го для голономных систем с помощью общего уравнения динамики:
J2(?k-mkhMrk=O,	A5)
k=\
где Fk — векторы активных сил, приложенных к материальным точкам
с массами га&; г& и г& — радиусы-векторы и ускорения материальных
точек с номерами к; 5г^ — виртуальные перемещения материальных
точек.
Как известно, общее уравнение динамики выражает необходимое
и достаточное условие для того, чтобы движение, совместимое с иде-
идеальными связями, соответствовало заданной системе активных сил.
Общее уравнение A5) справедливо в любой момент времени t и при
любых виртуальных перемещениях; рассматривается общее уравне-
уравнение динамики вместе с уравнениями для виртуальных перемещений.
Из общего уравнения динамики следует столько уравнений движения,
сколько имеется независимых виртуальных перемещений (число по-
последних называется числом степеней свободы системы). Совокупность
уравнений движения включает, кроме уравнений, получаемых путём
приравнивания нулю коэффициентов при независимых виртуальных
перемещениях в A5), также и уравнения связей.
В переменных Лагранжа qi, t, qi (i = 1,...,п) общее уравнение
динамики A5) принимает вид
где Qi — обобщённые силы, qi — обобщённые скорости, T(q,t,q) —
кинетическая энергия, выраженная через переменные Лагранжа.
Напомним, что виртуальные перемещения согласованы со связями
в том смысле, что являются «мысленными перемещениями» материаль-
материальных точек из заданного при фиксированном времени действительного
положения при неизменных действительных скоростях. Следовательно,
при операциях, указанных в общем уравнении динамики, значения
кинетической и потенциальной энергии системы, а также силы (по-
(полагаемые зависящими только от состояния) остаются неизменными.
Пусть траектория действительного движения системы г&(?), к =
= l,...,N (и qi(t), i= 1,...,п), включена в однопараметрическое се-
семейство кривых rk(t,a) (аналогично qi(t,a)) и содержится в нём при
а = 0 [25]. Тогда для вариаций 5г^ и 5qi, равных разностям
5rk = rk(t,a)-rk(t), k=l,...,N,

3. К обоснованию принципа Гамильтона	29
имеют место такие же, как и для виртуальных перемещений 5vk и 5qi,
соотношения:	п
5rk = У^ -^5qj, k=l,...,N.
Поэтому вариации радиусов-векторов 5rk при любом t можно под-
подставить в A5) вместо виртуальных перемещений ^г^. Учитывая имею-
имеющуюся в рассматриваемом случае перестановочность операций d/dt
и д/да (производная по параметру а используется при получении
вариации 5 [25]), т.е.
имеем преобразование
J2 mkrkSrk = — J2 mkrkSrk - 6Т,	A9)
k=\	аг k=\
ГД6	n	, N
5T=J2mkrk5rk и Г=±?т*г|.	B0)
k=\	k=\
При замене виртуальных перемещений вариациями радиусов-векто-
радиусов-векторов виртуальная работа сил потенциального силового поля заменяется
вариацией функции П со знаком минус, т. е. — Ш. Таким образом,
вместо A5) получаем уравнение
5Т-Ш+^2 Fk^k - 4 ? mkrkSrk = 0,	B1)
k=\	dt k=\
где Fk — активные непотенциальные силы. _ _
Применение обозначений Т и П вместо Т и П не вносит какой-
либо путаницы в выражения для действий, поэтому подынтегральные
выражения в действии обычно обозначают так же, как кинетическую
и потенциальную энергию соответственно. Значок «тильда» над ва-
вариацией, отличающий её от виртуального перемещения, также можно
опустить, но при этом вариации, удовлетворяющие тем же уравнениям,
что и виртуальные перемещения, называются виртуальными вари-
вариациями (см. введение). Результат преобразования B1) записывается
в следующем виде:
6T-6n + 6'A-±jr mkrk5rk = 0.	B2)
k=\
N
Здесь 5'А = ? Yk5vk — виртуальная работа активных непотенциаль-
к=\
ных сил (на перемещениях, равных виртуальным вариациям). Штрих
у символа 5 указывает, что результат математической операции не

30	Гл. I. Заметки о некоторых основных понятиях
всегда является результатом варьирования некоторой функции (но,
в частности, 5fU = 5U).
Если перестановочное соотношение A8) не выполняется, то вме-
вместо B2) получаем [58] центральное уравнение Лагранжа:
5Т-5П + 5'А + Y, m^k \Fтку - 5гк] - 4 ? тктк5тк = 0. B3)
к=\	L	1 аг к=\
После интегрирования обеих частей уравнения B2) по времени на
фиксированном промежутке [to, t\] имеем
tl	U	/ дг
5\bdt = - \5'Adt +
to	t0
к=\
B4)
Здесь
означает разность значений при to и t\.
to
Если радиус-вектор при to и t\ не варьировать, т. е. начальное
и конечное положение считать фиксированными, то второй член
в правой части уравнения B4) равен нулю. При этом в отсутствие
непотенциальных активных сил из B4) следует условие стационарно-
стационарности действия по Гамильтону:
и
5 [ L dt = 0	B5)
to
при
Л*(*о) = Л*(*1) = О,	B6)
или интегральный вариационный принцип Гамильтона.
С другой стороны, первое необходимое условие экстремума функ-
функционала B5) в переменных Лагранжа составляют уравнения Эйлера-
Лагранжа [58]:
d dL дЬ А . 1	/о„ч
-тг^-^-= 0, г=1,...,п.	B7)
dt aqi aqi
В случае, когда имеются непотенциальные силы, из B4) (при усло-
условии B6)) следует интегральный принцип Гамильтона:
и	и
s\Ldt = - U'Adt.	B8)
to	t0
Применение принципа Гамильтона для систем с нестационарными
связями обосновано М. В. Остроградским, поэтому свойство B8) при
условии B6) называют также принципом Гамильтона-Остр о град-
градского.

3. К обоснованию принципа Гамильтона	31
Из B8) следуют уравнения Лагранжа второго рода для голономных
систем с непотенциальными обобщёнными силами Qi\
-Л -WT- - ~— = Qi, г=1,...,п.	B9)
dt dqi dqi
Если составить функцию Гамильтона
Я = ^Pi4i -L, H = H(q,t,p)	C0)
г
(значок в виде дуги означает, что обобщённые скорости должны быть
выражены через переменные Гамильтона из равенств A3)), то из
условия стационарности действия B5) следуют уравнения в форме
Гамильтона:	. дН .	дН
qt = W*' Рг = "%' г=1-•••'"•	C1)
В приведённом рассуждении немало недосказанного, вызывающего
вопросы, и различного рода ограничительных предположений.
1.	Сразу же заметим, что это не «вывод», поскольку в условиях
принципа Даламбера-Лагранжа виртуальные перемещения рассматри-
рассматриваются при фиксированном состоянии и времени и никаких изменений
скоростей не допускается, так что кинетическая и потенциальная энер-
энергии при виртуальных перемещениях должны оставаться неизменными.
А что же тогда варьируется? Согласно Э. и Ф. Коссера [48], ^варьи^
руется действие, в котором плотностями являются функции Т и П
(см. уравнение B1)) — действие движения и действие деформации
соответственно. Это не единственный случай, когда одна и та же
функция играет различные смысловые роли (см. ниже о двух ролях
функции Гамильтона).
2.	Используется предположение о наличии свойства перестано-
перестановочности A8) операций варьирования и дифференцирования по вре-
времени, т. е. виртуальные вариации считаются дифференцируемыми
функциями времени, и вариации скоростей равны этим производным.
В общем уравнении динамики в каждый момент времени виртуаль-
виртуальные перемещения могут быть любыми из множества, определяемого
ограничениями, а в общем случае коммутатор d5 — 5d двух дифферен-
дифференциальных операторов d и 5 требует доопределения [74].
В отличие от операции d, операция варьирования 5 выполняется
при фиксированном времени (изохронное варьирование).
3.	Применение в принципе Гамильтона малых вариаций для коор-
координат и скоростей соответствует предположению, что варьированные
траектории находятся в окрестности первого порядка или, ина-
иначе, слабой окрестности траектории действительного движения [127].
Действительное и варьированное состояния сравниваются в одни и те
же моменты времени, т. е. изохронно.

32	Гл. I. Заметки о некоторых основных понятиях
4.	Траектории действительного движения и варьированные траекто-
траектории («окольные пути») сравниваются при одинаковых начальных и оди-
одинаковых конечных положениях (см. B6)) на фиксированном промежут-
промежутке времени, что не позволяет считать обоснованным применение
уравнений движения B7) (а также B9) и C1)), полученных с помо-
помощью интегрального принципа, для определения ускорений в моменты
времени to и t\. В противном случае возникает вопрос: являются ли
условия фиксированности начального и конечного положений связями,
из которых следуют уравнения B6) для виртуальных перемещений,
и не требуется ли рассматривать их «реализацию» с помощью реакций?
Иначе говоря, является ли область интегрирования, в которой вычисля-
вычисляется действие, замкнутой или открытой? При применении общего урав-
уравнения динамики A5) этот вопрос не возникает, так как виртуальные
перемещения на концах временного промежутка могут быть любыми из
множества, определяемого ограничениями, в том числе и не равными
нулю. Однако в отличие от «силовой механики», действие применяется
и при решении проблем квантования, связанных с проблемой краевых
условий. Эти проблемы существуют в механике, математике и физике
(вообще в естествознании).
Математики, например, полагают, что для их целей точное указа-
указание области интегрирования О в выражении «действия» Ldx\ ... dxn
п
является «лишней деталью», и предлагают математический «смысл
иероглифов типа Ldx\ ... dxn (без О!)» [106].
5.	В приведённом обосновании интегрального принципа на основе
общего уравнения динамики A5) остались не затронутыми вопросы
применения их совместно с принципом освобождаемости.
Мысленное освобождение системы от связей на основе принципа
освобождаемости расширяет множество независимых виртуальных пе-
перемещений. Возможно также мысленное наложение новых связей для
реализации «окольных путей».
Принцип освобождаемости предполагает включение в число ак-
активных сил в общем уравнении динамики A5) реакций тех связей,
от которых система освобождена. При этом механические свойства
системы могут составлять только часть свойств более общей системы,
и уравнения связей могут содержать также какие-либо «немеханиче-
«немеханические» параметры, «вынужденно изменяющиеся согласно дифференци-
дифференциальным уравнениям» [129]. Тогда влияние связи на изменение пара-
параметра также может описываться путём включения в уравнение (опи-
(описывающее изменение этого параметра) дополнительного слагаемого,
названного Н. Г. Четаевым «принуждение реакции» (см. также [13]).
Приём введения «принуждений реакции» аналогичен представлению
реакций с помощью неопределённых множителей Лагранжа. Остаются
не рассмотренными только следующие вопросы. Когда можно учиты-

4. О действии и противодействии	33
вать уравнения связей с неопределёнными множителями, а когда —
уравнения для виртуальных вариаций, и как составлять уравнения для
виртуальных вариаций по уравнениям связей? Какие условия требуют
физической реализации с помощью реакций, а какие — нет?
Состав ограничений при применении интегральных принципов ока-
оказывается по сравнению с дифференциальными принципами разнообраз-
разнообразнее: связи могут иметь вид интегральных, интегро-дифференциальных,
интегро-разностных и других соотношений с участием интегрирования.
Обсуждение физического смысла способов реализации связей имеется
в [13, 43, 44] и в гл. II настоящей работы.
6. Функция Я, согласно выражению (8), является энергетической
характеристикой, представляющей полную механическую энергию кон-
консервативной системы, а в действии A4) функция —Н и время t могут
рассматриваться как сопряжённые переменные, где —Н имеет смысл
обобщённого импульса (рп+\ = —Щ, а время t — обобщённой коор-
координаты (qn+\ = t). Тогда для того, чтобы время было равноправной
обобщённой координатой при сравнении с окольными путями, оно
также должно быть варьируемым. Для обобщённого импульса pn+i по
аналогии с C1) можно написать равенство
— = — (' i = -—)	C2)
Равенство C2) является верным и следует также из уравнений C1).
Однако время t в C2) не стало равноправной с другими обобщённой
координатой, поскольку за ней сохранена роль независимой перемен-
переменной. Очевидно, что теперь требуются новый независимый параметр
и новая энергетическая характеристика. Отметим, что в физике при по-
построении квантовой механики небезразлично, представляет некоторая
величина импульс или энергию, так как при этом принимаются разные
аксиомы о квантовании действия, зависящего от данных величин [40].
Подробнее об энергии и о функции Гамильтона см. в заметке 5.
4. О действии и противодействии
Третий закон Ньютона анализируется с помощью принципа равно-
равновесия Даламбера. Приводятся три трактовки понятия «сила инерции»
в уравнении «даламберова равновесия». На основе принципа Гамиль-
тона-Остроградского дано обоснование интегрального равенства дей-
действия и противодействия.
4.1. Основные задачи механики и третий закон Ньютона.
По Ньютону механика «есть учение о движениях, производимых ка-
какими бы то ни было силами, и о силах, требуемых для производства
каких бы то ни было движений, точно изложенное и доказанное».
А «приложенная сила есть действие, производимое над телом, чтобы
изменить его состояние покоя или равномерного прямолинейного дви-
2 В. Г. Веретенников, В. А. Синицын

34	Гл. I. Заметки о некоторых основных понятиях
жения» (И. Ньютон «Математические начала натуральной философии»,
перевод А.Н. Крылова).
В современном понимании механика — это наука о механическом
движении и взаимодействии материальных тел (см., например, [62]).
Из всех взаимодействий в механике, основанной на аксиоматике Нью-
Ньютона, выделено механическое взаимодействие посредством только сил,
подчинённых третьему закону Ньютона (равенства действия и проти-
противодействия). Более того, дополнительно полагается, что силы действия
и противодействия «всегда возникают одновременно и представляют
собой силы совершенно одинаковой природы» [125]. Такие ограничения
на способы «передачи движения» не позволяют с достаточной ясностью
и общностью изучать механическое движение, если для взаимодей-
взаимодействия не представлен (или вообще отсутствует) «перевод» на язык
силовой механики. Этот «перевод» требует, чтобы в описании взаимо-
взаимодействия всегда имелись две силы с указанием реальных материальных
источников силового действия и противодействия (обычно это тела,
обладающие конечной, бесконечно большой или пренебрежимо малой
массой).
Примечание. В учебной литературе иногда объясняют первую
основную задачу следующим образом: «Задача отыскания равнодей-
равнодействующей силы, действующей на материальную точку, по заданным
уравнениям движения решается дифференцированием уравнений дви-
движения. В силу этого решение первой основной задачи динамики всегда
возможно и не представляет затруднений» (цитата из учебника). Ре-
Решение задачи демонстрируется следующим примером. Пусть уравнения
движения точки М (точка движется по эллипсу) имеют вид
х2 у2
x = acoscut, y = bsmcut, —~ + ^ = 1.	(П.1)
а Ь
Определить действующую силу.
Решение. Проводится дифференцирование закона движе-
движения (П. 1) и составляются выражения
Fx = —таи;2 cos cut, Fy = —mbuo2 sinujt.	(П.2)
Исключением времени в (П.2) с помощью (П.1) находится F =
= —muj2r, и задача считается решённой. Однако следуя той же логике,
можно написать
г-,	таи . ,-,	тЪио .
F' = -—v> py = -—x'
и считать, что сила зависит от скорости F(v). Ущербность такой
интерпретации первой основной задачи механики очевидна.
Спектр задач об изменении механического движения оказывается
гораздо шире, чем можно описать с помощью силового воздействия,
и поэтому имеется почва для возникновения парадоксов и спорных

4. О действии и противодействии	35
суждений. Например, гравитационный парадокс, парадокс Даламбера
о сопротивлении движению тела в идеальной жидкости, споры о «ре-
«реальности» даламберовых и эйлеровых сил инерции, разногласия по
поводу существования «источника» противодействия для сил инерции,
а также для силы электромагнитного поля (силы Лоренца), дискуссия
о конструктивных способах реализации связей и т. д.
Поиск выхода из парадоксальной ситуации приводит к более ясному
пониманию изучаемых процессов: обнаруживаются несовершенство мо-
модели, неоднозначная роль перехода к бесконечности, нарушение логи-
логических требований при образовании понятий и прочие несоответствия.
Чаще всего объяснение находится вне теории ньютоновой механики:
в релятивистской динамике, в ньютоновой квантовой динамике, в об-
общей теории относительности и т. д. Здесь мы ограничимся динамикой
Даламбера и аналитической механикой, использующей метод перемен-
переменного действия.
Внесём изменение в редакцию основных задач механики. Откажем-
Откажемся от требования, чтобы в способах передачи движения взаимодействие
тел было сведено непременно к силовому, и первой основной задачей
механики будем считать задачу изучения способов передачи механи-
механического движения, а второй — задачу определения состояния системы
в любой (последующий) момент времени, если её состояние задано
в данный (начальный) момент времени. Задачи решаются в своём
единстве, что и отражено в принципах Даламбера [32], где в качестве
первого и главного предмета механики принимается движение и его
общие свойства.
4.2. Принцип равновесия Даламбера и «даламберово равно-
равновесие». В динамике Даламбера исходным является представление
о том, что взаимодействие тел между собой (или тела и поля) вме-
вместе с его следствием и есть способ передачи движения. В определе-
определении способа передачи движения можно выделить три элемента: два
внутренних, образующих систему, и один внешний. Внешний элемент
необходим для описания изменения движения первых двух, которые
взаимодействуют между собой. В механике Ньютона внешним объек-
объектом для любой механической системы является инерциальная система
отсчёта, включающая евклидово пространство и абсолютное время.
Роль внешнего элемента в задаче о взаимодействии не всегда требуется
специально отмечать, но именно в данном обсуждении она важна
и даёт, на наш взгляд, основные признаки, разделяющие различные
точки зрения на силы инерции и трактовку уравнения «даламберова
равновесия». Путь к этому уравнению попытаемся пройти от принципа
равновесия Даламбера, учитывая, что автор принципа считал термин
«сила» неясным и не связывал с ним «никаких представлений, отлич-
отличных от тех, которые вытекают из принципов...» (динамики Даламбе-
Даламбера) [32].

36	Гл. I. Заметки о некоторых основных понятиях
Принцип равновесия Даламбер включил в число трёх основных
принципов динамики вместе с принципами силы инерции и сложения
движений. Эти три основные принципа позволяют «расширить рамки
механики и сделать подход к этой науке гладким и ровным» [32].
Принцип равновесия предложен Даламбером для описания равнове-
равновесия и свойств передачи движения. «Законы передачи движения сводят-
сводятся к законам равновесия, а законы равновесия... сводятся к законам
равновесия двух равных тел, обладающих двумя равными и противо-
противоположно направленными виртуальными скоростями. В этом последнем
случае движения обоих тел, очевидно, уничтожат друг друга. Отсю-
Отсюда... будет вытекать, что равновесие будет иметь место и в том случае,
когда массы обратно пропорциональны скоростям {виртуальным, наше
примечание)» (см. [32], с. 30). Цитированное условие равновесия при
взаимодействии двух тел (при поступательном движении) или двух
материальных точек Даламбер считает уже всеми признанным. Обозна-
Обозначим виртуальные скорости по Даламберу, т. е. «скорости, с которыми
тела стремятся двигаться», как 5v\, Sw^. Тогда принцип равновесия
Даламбера имеет вид равенства
A)
где т\, ni2 — массы тел (материальных точек).
Виртуальные скорости в данном контексте представляют собой при-
приращения скоростей, пропорциональные ускорениям w&, которые тела
могли бы получить (виртуально) на бесконечно малом промежутке
времени 5t, следующим за рассматриваемым моментом времени, т. е.
k = 1,2.
Поэтому равенство A) можно записать в виде,
miWi+m2W2=0,	B)
или
—miWi — 7T12W2 = 0.	C)
Подставив в равенство B) уравнения второго закона Ньютона:
= F12, m2W2 = F2i,	D)
получаем для силы действия и силы противодействия (третий закон
Ньютона) равенство
Fi2 = -F2i,	E)
где Fi2 — сила, действующая на первое тело со стороны второго,
a F21 — сила, действующая на второе тело со стороны первого.
Таким образом, закон Ньютона о равенстве сил действия и противо-
противодействия получен здесь как следствие принципа равновесия Даламбера
и второго закона Ньютона. При этом использовалась «смесь» двух
разных систем аксиом: из динамики Даламбера и силовой механики

4. О действии и противодействии	37
Ньютона. Третий закон Ньютона, как известно, совместим с аксиомой
об однородности и изотропности пространства, но он более ограничи-
ограничителен, поскольку не позволяет охватить никакие электродинамические
взаимодействия, кроме простого притяжения и отталкивания Куло-
Кулона [137].
Уравнения движения D) (уравнения второго закона Ньютона), за-
записанные в виде
—miWi+Fi2=0, — m2W2 + F2i=0,	F)
в настоящее время называют уравнениями даламберова равновесия
(для каждой материальной точки). Можно заметить, что после сумми-
суммирования равенств F) в предположении E) приходим к равенству C),
т. е. к принципу равновесия Даламбера.
В формулировке даламберова равновесия равенства вида F) рас-
рассматриваются как уравнения равновесия сил с использованием термина
«сила инерции». Однако единой трактовки сил инерции (физической
природы, места приложения и наличия для них сил противодействия)
до настоящего времени нет [26, 41, 83, 105].
4.3. О силах инерции. Обсудим вопросы применения понятия
о силах инерции в равенствах, имеющих смысл равновесия систе-
системы сил.
В ньютоновой механике сила является промежуточной физической
характеристикой, введение которой разделило основную задачу меха-
механики на две части и тем самым позволило существенно продвинуться
вперёд в решении основной задачи механики. Сила в механике Ньюто-
Ньютона является и «причиной» изменения движения и средством «передачи»
движения (см. п. 4.1). Силой инерции называют вектор — raw (далее
этот термин будет уточнён). Поэтому равенство C) может рассмат-
рассматриваться как сумма двух сил инерции. Две силы могут находиться
в равновесии при условии, что они приложены к одной материальной
точке (имеющей массу или являющейся материальным элементом си-
системы, масса которого в пределе принимается равной нулю). Приведём
некоторые суждения о силах инерции.
1. Термин сила инерции введён Кеплером (см. [26]) для вектора,
характеризующего инерционное сопротивление тела при воздействии
на него других тел. Эта сила считается противодействующей и прило-
приложенной к ускоряющему телу (связи). В таком же смысле писал о «силе
инерции» и сам Ньютон. Для этой силы предлагается [41] ввести тер-
термин «ньютонова сила инерции» или «кеплерова сила» и рекомендуется
в изложении основ механики для устранения разночтений различать
ещё одну силу инерции: даламберову. Ньютонова сила инерции —
абсолютная сила. Она является «мерой обратного суммарного воздей-
воздействия рассматриваемого точечного тела на другие тела, вызывающие
ускорение данного. К самому телу она, конечно, не приложена.

38	Гл. I. Заметки о некоторых основных понятиях
«Даламберовы силы инерции — искусственно вводимые векторные
величины... Даламберова сила инерции... — вектор, который условно
считается приложенным к данной материальной точке» [41]. Пола-
Полагается, что в отличие от даламберовых, ньютоновы силы инерции
сопровождаются «противодействиями», и следовательно, удовлетворя-
удовлетворяют третьему закону Ньютона о взаимодействии в виде двух равных
и противоположных сил.
Далее мы также будем пользоваться двумя терминами: сила инер-
инерции Даламбера и сила инерции Ньютона [26, 41]. Соответственно,
введём два обозначения: — raw — сила инерции Даламбера, —raw* —
сила инерции Ньютона. Поскольку силы инерции Ньютона считаются
приложенными к тем же телам, к которым приложены равные им силы
взаимодействия, мы имеем эквивалентность сил (знак «~» является
знаком эквивалентности):
—miw*~F2i, w*=wi,
—ra^wjj ~ F12, w^ = W2.
Наименование векторов —raiw*, — ra^w^ силами инерции Ньютон
считал как нельзя более «вразумительным».
Условия эквивалентности G) дают повод говорить об одновремен-
одновременности появления сил инерции Ньютона (при предположении мгновен-
мгновенности их передачи на расстояние) и тождествественности их природы.
Относительно реальности даламберовых сил инерции имеется
и другое мнение.
2. В работе [105] рассматривается уравнение движения материаль-
материальной точки, записанное (с точностью до обозначений) в виде
-raw + Fi +F2 + ... + Fn =0.	(8)
Здесь
-raw = -raw0T - rawnep - rawA°6,	(9)
где w0T — относительное ускорение; wnep — переносное ускорение;
wao6 _ обобщённое ускорение Кориолиса, которое возникает, когда
переносная система координат вращается или вращается и деформиру-
деформируется.
Слагаемые в правой части равенства (9) называются силами инер-
инерции: относительной, переносной и добавочной соответственно. «В ло-
локальных эффектах проявление действия распределённых по объёму
тела внешних сил инерции согласно законам физики аналогично дей-
действию также распределённых по объёму внешних сил тяжести... С со-
содержательной точки зрения не возникает сомнений в реальности или
фиктивности каких-либо векторных членов в уравнении (см. (8)) и,
в частности, в реальности члена —raw. В ньютоновой механике физи-
физическое пространство евклидово и время абсолютно. Это постулат типа
наложенной связи» (курсив наш) [105].

4. О действии и противодействии	39
Возможность (хотя бы и локально) моделировать силы инерции
силами гравитационного поля (и построение теорий на основе гипотезы
об их эквивалентности) указывает на конструктивный характер данной
точки зрения. Приведём ещё одно наблюдение, состоящее в том, что
переносная сила инерции и сила инерции Кориолиса (эйлеровы силы
инерции) могут моделироваться силой инерции Лоренца. На точечный
электрический заряд в электромагнитном поле действует сила Лорен-
ца[53]
^^ xHj,	A0)
где е — заряд; v — скорость точки; Е и Н — напряжённости элек-
электрического и магнитного полей. Векторы Е и Н выражаются через
скалярный потенциал (р и векторный потенциал А с помощью формул
1 яд
E = -grad(^-^^, H = rotA.	A1)
Сравнив силу Лоренца A0), A1) с выражением эйлеровых сил инерции
в уравнении относительного движения материальной точки массы т
по отношению к жёсткой системе, замечаем их совпадение при
ти2о2 А тс /Лг ,	ч	/1ОЧ
?>=—^Г"> А = —(Vo + юхр),	A2)
где Vo(t) — скорость центра подвижных осей, ю(?) — угловая скорость
подвижных осей; р = (х, у, z) — радиус-вектор положения материаль-
материальной точки относительно центра подвижных осей.
Следовательно, эйлеровы силы инерции в движении по отношению
к подвижным жёстким осям действуют аналогично силе электромаг-
электромагнитного поля со скалярным и векторным потенциалами A2) в абсолют-
абсолютном движении. Сила Лоренца относится к реальным силам, поэтому
ответ на вопрос о природе силы инерции в (8) неоднозначен. Например,
в (9) составляющей силы инерции (вектор —mw0T) может быть придан
смысл гравитационной силы, а другим слагаемым — смысл силы Ло-
Лоренца.
При сравнении точек зрения 1 и 2 существенно то, что одна из
них относится к взаимодействию между телами, а в другой речь
идёт о взаимодействии тела и поля. Различие трудно было усмотреть
на примере представления силы инерции только с помощью грави-
гравитационного поля, так как в классической механике гравитационные
поля создаются гравитирующими телами, что соответствует и первой
точке зрения. Вторая точка зрения в своих доводах выходит за рамки
механики Ньютона и опирается на более «физичные» представления
о пространстве (и времени). Здесь уместно напомнить о современных
теориях, в которых пространство имеет вид гравитирующего вакуума,
и о недавнем A965 г.) открытии так называемого реликтового излуче-
излучения (электромагнитного происхождения). Последнее, благодаря своим
свойствам однородности и изотропности, в настоящее время претен-

40	Гл. I. Заметки о некоторых основных понятиях
дует на роль наиболее точной физической реализации инерциальной
системы (наличие которой составляет содержание закона инерции Га-
Галилея — первой аксиомы Ньютона).
Таким образом, вторая точка зрения допускает для сил инерции Да-
ламбера физическую природу различного происхождения в виде полей
(гравитационного, электромагнитного). Признав реальность даламбе-
ровых сил инерции, для каждого тела получим равновесие двух сил:
—miwi — 7T12W2 = 0, — m2W2 — raiw* = 0.	A3)
Однако и после признания реальности даламберовой силы инерции,
приложенной к телу, для неё не найдена противодействующая. Допол-
Дополнительные возможности поиска ответа этот вопрос даёт ещё одна точка
зрения, в которой в рассмотрение вводится пространство как объект,
участвующий во взаимодействии.
3. При выводе прямой и обратной форм дифференциальных уравне-
уравнений колебаний упругих систем используются две различные отправные
позиции. «В обоих случаях предполагается мысленное расчленение си-
системы путём отделения обладающих массой грузов от упругого скелета
системы. В первом случае записываются законы движения грузов, а во
втором случае — зависимости, определяющие движение безмассово-
безмассового упругого скелета; соответственно первый путь приводит к прямой
форме уравнений движения, а второй путь — к обратной форме этих
уравнений» [83]. Прямая форма уравнений получается, если кинетиче-
кинетическая энергия имеет вид суммы квадратов, а обратная — если суммой
квадратов является потенциальная энергия. Эти два случая иллюстри-
иллюстрируют схемы упругой балки с грузами в виде точечных масс, к которым
приложены заданные силы (рисунки 4.1, 4.2). На рис. 4.2 к упругому
Рис. 4.1
скелету приложены заданные силы и силы инерции (грузы от балки
отделены). Авторы работы [83] отмечают, что понятие об упругом
безмассовом скелете «условно и, в сущности, речь идёт о системе
внутренних связей» (курсив наш). Полагается, что на освобождённую
от массы т связь действует реальная сила. Далее указывается, что
«понятия механической системы и её безмассового каркаса требуется
различать».
Примечание. Пространству можно приписать не только упругие
свойства. Пусть, например, линейная система задана тремя квадратич-
квадратичными формами с постоянными коэффициентами: кинетической энерги-
энергией, потенциальной энергией и диссипативной функцией Релея. Выбо-

4. О действии и противодействии	41
Р2-ГП2У2
Рис. 4.2
ром обобщённых координат одна или одновременно две из этих форм
(знакоопределённые) могут быть представлены в виде суммы квад-
квадратов. Тогда каждому представлению, определяющему форму уравне-
уравнений движения, сопоставляются и соответствующие свойства простран-
пространственного скелета (упругие и (или) диссипативные).
В качестве внутренних безмассовых связей, способных противо-
противодействовать силам любой природы, примем элементы пространства
(в обобщённых координатах — конфигурационного пространства). Об-
Образуем систему, являющуюся наложением двух взаимодействующих
систем [117]. В аксиоматике К. Трусделла наложение имеется для
любых двух, в том числе отделённых, тел и содержит нулевое тело —
пространственный элемент. Пространственному элементу, полученному
в результате наложения, отведём роль промежуточного звена между
взаимодействующими системами. Безмассовые элементы нередко ис-
используются в моделях механических систем (например, пружина, нить,
стержень и т.д.). В данном случае речь идёт об условной внутренней
связи.
Для двух отделённых тел (материальных точек) равновесие сил на
нулевом теле имеет вид равенства C). В полный набор вариантов урав-
уравнений равновесия с применением сил инерции входит также равенство
-m\w* - m2w2 = 0.	A4)
В A4) для ньютоновых сил инерции приняты те же обозначения,
что и ранее в G) и A3), хотя теперь они имеют иное место приложения.
Заметим, что взаимодействия тел в схеме с безмассовыми про-
пространственными элементами снимают все вопросы о дальнодействии
по причине его отсутствия.
Итак, все варианты равенств с участием векторов даламберовых
и ньютоновых сил инерции исчерпаны (из принципа равновесия Далам-
бера C) получены уравнения равновесия A3), A4) для сил на телах:
первом, втором и нулевом). Включение пространственного элемента
в число рассматриваемых тел позволило примирить кажущиеся проти-
противоречивыми точки зрения на силы инерции.
4.4. Интегральное равенство действия и противодействия. По-
Получим закон о действии и противодействии в форме интегрального
равенства для действия.

42	Гл. I. Заметки о некоторых основных понятиях
Напомним, что эквивалентность нулю системы сил записывается
в виде общего уравнения (принцип виртуальных скоростей):
?Ffe<Jvfe=0, или ^Fk5rk = 0.	A5)
k=\	k=\
В уравнении A5) F& — силы известной природы (точнее — из-
известного происхождения: активные и реакции неидеальных связей),
приложенные к материальным точкам (точкам, обладающим инерци-
инерционной массой); 5vk и 5rk — совместимые с идеальными связями вир-
виртуальные скорости и виртуальные перемещения материальных точек
(связи предполагаются стационарными удерживающими). Возможны
некоторые равновесные положения и в системах с нестационарными
связями, но мы ограничимся более простой ситуацией. Равенство A5)
даёт условие эквивалентности нулю сил известного происхождения.
Виртуальная работа даламберовой силы инерции материальной точ-
точки представляется (при условии перестановочности операций d и 5)
в следующей форме:
-mw5r = ~ (mv5r) + 5Т, Т= ^-.	A6)
Пусть имеются не содержащие общих материальных точек две вза-
взаимодействующие механические системы. Обозначим их кинетические
энергии через Т^ (г = 1,2), виртуальные работы сил, не являющих-
являющихся силами взаимодействия, — через 5'А^ (г = 1,2), а виртуальные
работы сил взаимодействия первой и второй систем — через 51 А^
и 5'АB1) соответственно. Применение принципа Гамильтона-Остро-
градского для каждой системы на фиксированном промежутке времени
[t\, ?2] даёт интегральные равенства
dt = O при 5r^ e Dlt A7)
= O при 5т® е D2,	A8)
где D\ и D2 — множества виртуальных перемещений соответствующих
систем. Множество виртуальных перемещений Dq системы, являющей-
являющейся наложением рассматриваемых систем, получаем как пересечение
множеств D\ и D^. Do = D\ П D2.
Для системы, полученной наложением взаимодействующих систем,
имеем интегральное равенство Eг^ — виртуальное перемещение на-

4. О действии и противодействии	43
ложения):
dt = 0 при 5г(о)еД)^0.	A9)
При вычислении виртуальной работы в подынтегральное выражение
в A9) может включаться и виртуальная работа сил инерции.
Равенство A9) имеет следующие частные случаи.
1. В условиях принципа равновесия Даламбера (см. п. 4.2) подста-
подставим в A9) виртуальную работу сил инерции A6). Получаем равенство
dt = O при Sri = 5r2,
B0)
Сомнения в реальности величин в B0) не возникают. Однако из
него непосредственно следует равенство C), которое в «силовой» ак-
аксиоматике создаёт трудности с ответами на подобные вопросы. От-
Отсутствие явной зависимости выражения B0) от сил взаимодействия
позволяет сделать вывод о том, что силы инерции Даламбера могут
иметь любую физическую природу (в том числе разную для взаимодей-
взаимодействующих тел). Тем самым ещё раз подтверждается вспомогательная
роль сил в описании физических процессов.
2.	Форма интегрального равенства A9) содержит как частный слу-
случай третий закон Ньютона E), для которого
Fi2<fri +F2i<fr2)<ft = 0 при 5r{=5r2.	B1)
Из равенства B1) следует равенство E), но только для класса сил,
зависящих от состояния (и времени). При этом исключается, например,
широко применяемая модель взаимодействия с использованием поня-
понятия о присоединённых массах.
3.	Пусть ограничение движениям сплошной однородной идеальной
жидкости доставляет только замкнутая достаточно гладкая (в матема-
математическом смысле — поверхность Ляпунова и без трения) поверхность
недеформируемого тела. Взаимодействие при потенциальном обтекании
свободного абсолютно твёрдого тела (поверхности) при установившем-
установившемся движении может описываться с помощью виртуальных работ
_ F5ro _ Mofy, 5'A^ = -ST&\ B2)
где F, Mo — главный вектор и главный момент внешних сил (за
исключением сил взаимодействия с жидкостью), приложенных к телу
и приведённых к центру О; 5ro, 5q> — виртуальное перемещение

44	Гл. I. Заметки о некоторых основных понятиях
центра и вектор виртуального угла поворота тела; Т^ и Т^ — ки-
кинетическая энергия тела и жидкости соответственно (Т^ выражается
через кинематические параметры движения тела); в частности, при
поступательном движении тела Т^ = m\v2/2, Т^ = ni2V2/2 (ni2 —
присоединённая масса). В общем случае движения тела кинетическая
энергия жидкости при потенциальном обтекании вычисляется по фор-
формуле [49]
тB) _ 1 VA-T/T7-
где Xij (i,j= 1, 2,..., 6) — присоединённые массы тела (коэффициенты,
зависящие от формы тела и массовой плотности среды); Щ (г = 1,2,3)
и Щ (г = 4, 5,6) — координаты вектора скорости полюса и угловой
скорости тела по осям, связанным с телом.
Пример. В работе [18] в модели динамики большого испаряюще-
испаряющегося тела при высокоскоростном входе в атмосферу планеты учитыва-
учитывается присоединённая масса. На больших высотах плотность среды мала
по сравнению с плотностью тела, аналогично соотносятся присоеди-
присоединённая масса и масса тела. Однако малость величины присоединённой
массы по сравнению с массой тела не означает a priori, что ей можно
пренебречь при расчёте силового влияния на тело. Присоединённая
масса при изменении плотности является переменной, и процесс её
изменения вызывает появление реактивной силы, зависящей от быст-
быстроты изменения массы и относительной скорости частиц, изменяющих
состав системы. Относительная скорость частиц, изменяющих присо-
присоединённую массу в покоящейся атмосфере, по величине равна скорости
тела и противоположна ей по направлению. При таком рассмотрении
на этапе возрастания скорости тела (см. «парадокс спутника» [26])
удаётся избежать ошибки в оценке уноса массы тела и получить за-
зависимости относительного уноса массы от условий входа в атмосферу,
от величины пути, пройденного телом, силы притяжения и других
параметров для двух моделей уноса массы.
Если наложение систем содержит материальные точки, то обозна-
обозначив через Т(°) кинетическую энергию наложения, а через 5'А^ —
виртуальную работу внешних сил, приложенных к этим материальным
точкам, имеем интегральное равенство
t = O при Sr^eD0, B3)
где 5fA@l\ 5''А^ — виртуальная работа сил со стороны частей систем,
не вошедших в наложение; Dq — множество виртуальных перемещений
системы, полученной наложением.
Если наложение не содержит объектов, имеющих массу, то из
интегрального равенства B3) следует интегральное равенство A9).

4. О действии и противодействии	45
Очевидно, что эти интегральные равенства представляют собой не
что иное, как интегральный принцип Гамильтона-Остроградского для
специально сформированной системы. Интегральные равенства спра-
справедливы при интегрировании на фиксированном промежутке времени,
на концах которого виртуальные перемещения принимаются равными
нулю.
Интегральная форма позволяет использовать в законе о действии
и противодействии не только силы, зависящие от состояния, но и непо-
непосредственно силы инерции, виртуальная работа которых, в соответ-
соответствии с равенством A6), выражается с помощью вариации выражения
кинетической энергии. Кроме того, интегральные равенства обладают
большими эвристическими возможностями, например, подобным обра-
образом можно формировать интегральные равенства действия и противо-
противодействия для систем, не являющихся натуральными системами, систем
с термодинамическими точками [14] и т.д.
4.5. О лоренцовой «силе торможения». К рассматриваемой про-
проблеме относится также вопрос о «самодействии». Это понятие вводится
в аксиоматике работы [117]. Известен и важный пример из физи-
физики [53] (см. также [98], задача 5.20): при движении материальной
точки с электрическим зарядом в электромагнитном поле происходит
потеря энергии. Эту потерю энергии описывают с помощью лоренцовой
силы торможения, пропорциональной ускорению второго порядка (про-
(производной по времени от ускорения точки), с учётом которой уравнение
движения имеет вид
fflw = е (Е + - х hW ^w.	B4)
V с ) Зс3
Физики отмечают [53] ограниченность этого уравнения, так как
«при отсутствии внешнего поля (Е = 0, Н = 0) оно имеет решение
/Зтс3 г
v = exp —r t
\ 2е
приводящее к абсурдному выводу о неограниченном «самоускорении»
заряда при выходе из поля. Поэтому выражение для лоренцовой силы
применимо лишь в том случае, когда она оказывается малой по срав-
сравнению с силами внешнего поля» [98]. Предлагается искать решение
в два этапа: сначала решить уравнение
raw = е (Е + - х н),	B5)
а затем результат использовать при решении уравнения B4). Иначе
говоря, наличие лоренцовой силы торможения в уравнении B4), не от-
отвечающей требованиям ньютоновой механики, приводит к двум меха-
механическим системам. Первая задана уравнением B5), а вторая не имеет,

46	Гл. I. Заметки о некоторых основных понятиях
к сожалению, единственного описания. В B4) w можно подставлять
в виде функции состояния и ускорения:
f - х HV	B6)
771 V	С	С	J	V '
или в виде функции состояния (выразив в B6) ускорение с помо-
помощью B5)), или, может быть, в виде функции только времени w(?)
(и констант интегрирования) и т. д.
Для того чтобы подставляемую в B4) функцию отличать от уско-
ускорения второго порядка, обозначим её w* (пока не уточняя её вида)
и будем рассматривать уравнение
raw = е (Е + - х HW %w*.	B7)
V с ) Зс3
Убедимся, что при некоторых условиях последнее слагаемое в пра-
правой части уравнения B7) является тормозящей силой. Для этого
умножим обе части равенства B7) скалярно на скорость v. При поло-
положительном знаке произведения w • v движение является ускоренным,
а при отрицательном — замедленным, что является признаком тор-
тормозящего эффекта слагаемых правой части. В полученном равенстве
последнее слагаемое представляем в форме
w*v = A (w*v) - w*w.	B8)
Вид правой части B8) показывает, что после усреднения на доста-
достаточно большом промежутке времени (движение предполагается финит-
финитным) слагаемое, представляющее среднюю мощность силы торможе-
торможения в B7), имеет знак, совпадающий со знаком —(w*w). Этот знак
отрицательный, если ускорение w отлично от нуля и ускорение w*
достаточно мало отличается от w. Заметим, что при w* = 0, согласно
уравнению B7), никакого неограниченного «самоускорения» при выхо-
выходе из поля не происходит. Интересно, что тормозящий эффект имеет
место независимо от структуры «обычных сил» и получен при усло-
условиях финитности (по состоянию и ускорению) и достаточной близости
ускорений: в порождающем и действительном движениях.
Учитывая, что рассматривается нерелятивистский случай {v/c <C
< 1), для оценки малости членов уравнений введём малый параметр
s = г>тах/с, где г>тах — некоторая характерная скорость (например,
максимальная в финитном движении), и представим уравнение B4)
в следующем виде:
ее	2е
olq = —, а\ =
771

?°:
е1:
е2:
е3:
w
W
W
W
@)
A)
B)
C)
= а\
= а\
= ах
(v
(v
(v
@)
A)
B)
X
X
X
н)
н)
н)
+
+
a2w('),
5. Об энергии и действии	47
Пусть векторы Е(?), Н(?) являются функциями времени и решение
представляется в виде ряда по степеням малого параметра [9]:
r = r@)+?r(l)+?2rB) + _	C0)
Припишем верхние индексы и всем кинематическим характеристикам,
имеющим множителем малый параметр в соответствующей степени.
Тогда для нахождения членов ряда C0) можно составить бесконечный
набор уравнений:
C1)
Каждое из уравнений C1) (и далее) имеет структуру второго закона
Ньютона с силами, зависящими только от времени. Таким образом,
метод малого параметра даёт иное доопределение динамической систе-
системы B9) в виде последовательности моделей ньютоновой механики.
5. Об энергии и действии
5.1. Склерономные и реономные системы. В зависимости от
того, являются голономные связи, наложенные на систему, стацио-
стационарными или нестационарными, голономные системы разделяют на
склерономные («твёрдые») и реономные («текущие»). Однако свойство
системы быть реономной или склерономной проявляется только после
того, как выбраны обобщённые координаты q^, г = 1,..., п, и через них
выражены радиусы-векторы материальных точек г& (#,?), k= l,...,N.
Если все радиусы-векторы не зависят явно от времени, т. е. dr^/dt = 0,
то будем называть такую систему склерономной, а в противном слу-
случае — реономной.
Выражения скоростей материальных точек реономной системы по-
после введения обобщённых координат, в отличие от скоростей точек
склерономной системы, в общем случае не являются однородными
относительно обобщённых скоростей:
* = ±& + w- ' = '	»•	«)
где Vk — скорости материальных точек.
Свойство системы быть «реономной» отражает следующая кине-
кинематическая трактовка равенства A). Если в правой части A) векто-
векторы drk/dt рассматривать как переносные скорости точек, то суммы

48	Гл. I. Заметки о некоторых основных понятиях
qi будут соответствующими относительными скоростями
г
точек. Переносные скорости точек склерономной системы равны нулю.
Представление абсолютных скоростей точек в виде суммы относи-
относительной и переносной позволяет также установить смысл «мощности
обобщённых сил» У2 QiQ_i-
г
Мощность системы сил F& в абсолютном движении и мощность
соответствующей системы обобщённых сил связаны соотношением
?*Vvfc = E^ + E*v^-	B)
к	г	к
Из равенства B) следует, что мощность сил F& в абсолютном дви-
движении равна сумме мощности обобщённых сил (мощности сил F& в от-
относительном движении) и мощности сил F& в переносном движении.
Поэтому, например, понятие о гироскопических свойствах сил (сил,
мощность которых тождественно равна нулю) для сил F& и соответ-
соответствующих им обобщённых сил Qi совпадают только в относительном
движении. В склерономной системе мощность сил F& в абсолютном
движении равна мощности обобщённых сил Qi.
Неоднородная зависимость абсолютных скоростей от обобщённых
скоростей в A) приводит к тому, что кинетическая энергия T(q,t,q),
выраженная через обобщённые координаты, обобщённые скорости
и время, является суммой трёх однородных форм относительно обоб-
обобщённых скоростей:
T = T2+Ti+T0,	C)
где Т2, Т\, То — формы второй, первой и нулевой степени соответ-
соответственно.
Кинетическая энергия склерономной системы является только квад-
квадратичной формой с коэффициентами, не зависящими явно от времени,
т. е.	г,гр
Т = Т2, ^=0.	D)
Мощность реакций идеальных нестационарных связей согласно B)
не равна нулю. Тем не менее для реономных систем имеются аналоги
теорем об изменении кинетической энергии и полной механической
энергии в форме, не содержащей реакций идеальных связей. Приведём
вывод этих теорем с помощью уравнений Лагранжа второго рода.
5.2. Аналоги теоремы об изменении кинетической энергии ре-
реономных систем. Умножим каждое из уравнений Лагранжа второго
рода на соответствующую ему обобщённую скорость и просуммируем
полученные равенства:

5. Об энергии и действии	49
Преобразовав слагаемые первой группы в E) по формуле
d (дТ\ . d (дТ . \ дТ..	,а.
*\mqi = *\Mqi)-dqi>	F)
получим возможность использовать однородные относительно обоб-
обобщённых скоростей составляющие кинетической энергии:
г
Учтём выражение производной от кинетической энергии по вре-
времени:	dT дт	дт ^
Подставив F)-(8) в E), получаем известное утверждение теоремы
об изменении кинетической энергии голономной системы в обобщён-
обобщённых координатах, называемое аналогом теоремы об изменении кинети-
кинетической энергии для реономных систем [46]:
При частных предположениях из (9) следуют
—	теорема об изменении кинетической энергии склерономной си-
системы в обобщённых координатах (см. свойства D)):
t = 4?Qiqi;	A0)
г
—	обобщённый интеграл энергии при движении реономной системы
в стационарном силовом поле с потенциальной энергией П(#) при
dT/dt = O (Qi = -дП/dqi):
Т2 - То + П = h = const;	A1)
—	если Т и П не зависят явно от времени, но имеются непотенци-
непотенциальные активные силы, то
г
где Qi — непотенциальные обобщённые силы.
Для склерономной системы из A0) получаем
—	в нестационарном силовом поле
Т=^-П;	A3)
—	в стационарном потенциальном силовом поле
Т + П = const,
т. е. система является консервативной.

50	Гл. I. Заметки о некоторых основных понятиях
Предложим аналог теоремы об изменении кинетической энергии
реономной системы в новой форме. Силы в системе представим в ви-
виде потенциальной и непотенциальной составляющих (если таковые
имеются). Перепишем равенство (9), оставив в левой части только
полную производную по времени от квадратичной формы кинетической
энергии:
dt -±^ЧгЧг	т	dt	+	^ ,
г
где U(q,t) — потенциальная энергия, Qi — непотенциальные обобщён-
обобщённые силы.
Слагаемые в правой части полученного равенства также имеют
смысл мощностей обобщённых потенциальных сил и обобщённых
непотенциальных сил. Последние два слагаемые представляют мощ-
мощность обобщённых потенциальных сил с новой потенциальной энерги-
энергией, равной П — То, а оставшиеся слагаемые — мощность обобщённых
непотенциальных сил, полученных сложением обобщённых сил Qi
исходной системы с «обобщёнными силами» Q* (кавычки поставлены
для того, чтобы подчеркнуть отличие происхождения этих слагаемых):
"*' " 2 ^ at Чз dt'
где ciij(q,t), bi(q,t) — коэффициенты в выражениях Т^ и Т\:
Т = -Та-'-'- Т =ТЬ'-
г,3	г
Таким образом, для реономных систем доказана следующая тео-
теорема: полная производная по времени от квадратичной формы в вы-
выражении кинетической энергии равна сумме мощностей обобщённых
потенциальных сил с потенциальной энергией П — То и обобщённых
непотенциальных сил Qi + Q*.
Приём выделения квадратичной формы в выражении кинетической
энергии удобен при формулировке теорем об энергии при импульсив-
импульсивных движениях [13].
5.3. Теорема об изменении полной механической энергии.
Полная механическая энергия системы Е равна сумме кинетиче-
кинетической C) и потенциальной П энергии:
Е=Т + П.	A4)
Пусть кроме потенциальных сил на материальные точки системы
действуют непотенциальные силы, которым соответствуют непотенци-

5. Об энергии и действии	51
альные обобщённые силы Qi. Мощность потенциальных обобщённых
сил равна разности
f-n.	ов)
Заменив в правой части (9) мощность потенциальных обобщённых
сил выражением A5), имеем
дТ d(T2-T0) _ я й дП
dt+ dt " ^ЯгЪ + dt'
г
откуда следует теорема об изменении полной механической энер-
энергии [25]:
^Д(Г2Г)Ж> L = T-IL.	A6)
Поскольку группа слагаемых в правой части A6) связана с мощно-
мощностью N непотенциальных сил F& равенством вида B):
к	г
теорема A6) принимает следующую форму:
к
Для склерономной системы из A7) получаем
При движении склерономной системы в стационарном потенциаль-
потенциальном силовом поле при непотенциальных силах, являющихся гироско-
гироскопическими, полная механическая энергия сохраняется:
Е = const.
Если dL/dt = 0 и непотенциальные обобщённые силы — гироско-
гироскопические, т.е. Y^ QiQi = 0' то из A6) следует обобщённый интеграл
г
энергии A1).
5.4. Функция Гамильтона и уравнение энергии. Функция Га-
Гамильтона Н связана с функцией Лагранжа L (в условиях преобра-
преобразования Лежандра при переходе от переменных щ к переменным р^)
равенством
h,4)-	A9)

52	Гл. I. Заметки о некоторых основных понятиях
Получим из равенства A9) некоторые энергетические свойства
функции Гамильтона. Подставив в него выражения обобщённых им-
импульсов C.13), находим
Я = V |^& -Ь = 2Т2+Т{- (Г2 + Тх + То - П),	B0)
г
т. е. Я = Т2 - То + П.
Отсюда следует, что в фазовом пространстве (пространство обоб-
обобщённых координат, обобщённых импульсов — пространство QP) обоб-
обобщённо-консервативные системы имеют интеграл энергии (см. A1))
в форме
H(q,p) = const.	B1)
Дифференцируя равенство A9) частным образом по t (при фикси-
фиксированных q и р с учётом разрешимости линейных уравнений C.13)
относительно qi), для частных производных по времени от функции
Гамильтона и функции Лагранжа имеем равенство
dt	dt	K }
(дифференцирование в правой части при фиксированных q и q).
Из аналога теоремы об изменении кинетической энергии (9), под-
подставляя выражение мощности потенциальных сил A5), получаем ра-
равенство
d{T2 - Тр + П) _ „ jx	dL
С учётом B1), B2) из B3) получаем выражение, связывающее
изменение функции Гамильтона во времени в зависимости от мощности
непотенциальных обобщённых сил:
При составлении уравнений движения в переменных Гамильтона
в случае непотенциальных сил можно заметить следующее. Первая
группа уравнений (см. C.31)) не изменится, так как они представляют
собой соотношения в преобразовании Лежандра A9) (при обратном
переходе от переменных pi к переменным qi). Изменение правых частей
второй группы уравнений (см. C.31)) состоит в появлении допол-
дополнительных слагаемых Р^. Таким образом, уравнения движения при
наличии непотенциальных сил имеют следующую форму:
дН .	дН , „	,0-.
®=flfc' ft = -%+P<-	B5)

5. Об энергии и действии	53
Выясним механический смысл слагаемых Р^. Вычисляя производ-
производную Н в B4), с учётом уравнений B5) находим, что дополнительные
слагаемые Pi в B5) обладают свойством
? P%q% = ? Q4i-
г	г
Далее, в преобразовании от qi к pi обобщённые координаты qi и вре-
время t, i= 1,...,п, фигурируют как параметры, для которых, согласно
теореме Донкина [25], справедливы равенства
дВ_ _ _dL_	дВ_ _ _dL
~dq~i ~ % И ~Ж ~ ~dt'
Поэтому, сравнивая уравнения Лагранжа второго рода:
dt\dqj " дЧ
dq
со второй группой уравнений B5), можно увидеть^ что слагаемые Pi
имеют смысл непотенциальных обобщённых сил Qi. Таким образом,
уравнения движения в переменных Гамильтона имеют вид
дН .	дН pr	1	/rtr\
qi = W Pi = ~Wi+Qi' г = 1'-'п'	B6)
где Qi получены из Qi путём выражения обобщённых скоростей через
переменные qi, t, pi.
Вернёмся к вопросу об использовании времени в качестве дополни-
дополнительной обобщённой координаты gn+i и введении сопряжённого с ней
обобщённого импульса рп+\. Набор получаемых переменных состав-
составляет пространство состояний и энергии (пространство QTPH [137]).
Чтобы избежать путаницы, вызванной двумя ролями, которые играет
функция Гамильтона в этом пространстве, кроме рп+\ = —Н использу-
используем также обозначение [137]
Н = u(qi,...,qn+i,pi,...,pn) = -Pn+i
или	B7)
^=Pn+i +u;(<2i,...,gn+i,pi,...,pn) =0.
В симметричной записи это равенство можно представить в виде
уравнения
П (qu ..., qn+\,p\,... ,Рп+\) = 0.	B8)
Уравнение B8) (его называют уравнением энергии [137], а также
вспомогательным условием) налагает на координаты изображающей
точки в пространстве QTPH ограничение в виде Bп + 1)-мерной по-
поверхности энергии. Использование термина «энергия» оправдывается
тем, что применение функции fl(q,p) может быть аналогично примене-
применению функции Гамильтона склерономной системы, имеющей интеграл

54	Гл. I. Заметки о некоторых основных понятиях
энергии B1). Динамическая система определена, если задана поверх-
поверхность энергии и находящаяся на этой поверхности изображающая
точка. Введение функции энергии fl(q,p) вместо поверхности энергии
позволяет расширить рамки динамики в QTPH, рассматривая действие
S= [l>*%	B9)
вместе с дополнительным условием [137]
Q(qi,...,qn+i,pi,...,pn+i) = const.	C0)
Требование, чтобы на сравниваемых траекториях функция энергии
имела одно и тоже значение (изоэнергетическое варьирование), даёт
уравнение для вариаций:
Варьирование функционала B9) (при фиксированных концевых зна-
значениях обобщённых координат q\,...,qn+\) с учётом дополнительного
условия C0) и его вариации C1) приводит к уравнениям, имеющим
гамильтонову форму:
Qi = ^9 Pi = -Qj:> i=l,...,n+l>	C2)
где штрихом обозначено дифференцирование по параметру w, элемен-
элементарное приращение которого определяется равенством
п+1	п+1 д^
Л Pi d(ii = Z^TT" dw'
г=1	г=1 °Vi
По своему смыслу dw — бесконечно малый неопределённый множи-
множитель Лагранжа. Физический смысл независимого параметра w может
быть различен и определяется функцией О. При этом произведение ?lw
имеет размерность действия. Сильные и слабые стороны представления
уравнения энергии в формах B7) или B8) объясняются аналогией
с сильными и слабыми сторонами представления поверхности в трёх-
трёхмерном пространстве с помощью уравнения z = f(x, у) или уравнения
F(x, у, z) =0 соответственно. Для энергии в форме B7) из C2) сразу
следует, что число независимых уравнений — 2п (уменьшить число
уравнений до 2п можно и при использовании энергии в форме B8)).
При этом
tr = 1 и t = w + const,	C4)
и следовательно, в качестве независимого параметра может быть при-
принято время t.

5. Об энергии и действии	55
Совершив такой «круг» в рассуждениях (вначале обобщение от
Я-гамильтоновых систем к О-гамильтоновым системам [137], а затем
обратно — от вторых к первым как частному случаю) можно сделать
следующие наблюдения:
—	в рассматриваемых системах математическое время как частный
случай параметра является однородным и обратимым (см. C4));
—	функция энергии для реономных механических систем, находя-
находящихся в потенциальном силовом поле, имеет вид (см. B0))
— динамическая гамильтонова система может быть задана функ-
функцией энергии (и уравнением энергии О = 0) вместе с элементарным
действием dS и параметром w, для которых имеется дифференциаль-
дифференциальное соотношение (см. C3)):
JC	П+\	rsQ	П+1	лг*
S=^ = X>flk' или 5=Е9^. ? = ?m - SX C5)
Подчеркнём ещё раз, что уравнение энергии даёт ограничение
в дифференциальной форме C1) и приводит к дифференциальному
равенству C5), в котором фигурирует элементарное действие. Для дей-
действия как функционала вариационной задачи функцию энергии можно
использовать также в изопараметрическом ограничении вида
?ldw = const,	C6)
Wo
что даёт ещё один способ задания динамических систем.
5.5. Теорема об изменении кинетического потенциала. Ди-
Динамический смысл обобщённой силы для времени. Пусть голо-
номная реономная система имеет функцию Лагранжа (кинетический
потенциал) в виде полинома второй степени относительно обобщённых
скоростей:
L(q,t,q) = L2 + L{ + Lo,	C7)
где функции 1/2, I/i, I/o являются однородными соответствующих сте-
степеней относительно обобщённых скоростей (индекс указывает степень
однородности). Уравнения движения системы имеют вид
I F "Г = ^' г=1,...,п,	C8)
dt \oqiJ oqi
где qi — обобщённые координаты, q^ — обобщённые скорости, Qi —
непотенциальные обобщённые силы.
Теорему об изменении кинетического потенциала докажем так же,
как и аналог теоремы об изменении кинетической энергии (см. п. 5.2.).

56	Гл. I. Заметки о некоторых основных понятиях
Выполнив над C8) с учётом C7) те же операции, что и в формулах
E)-(8), получаем аналогичное (9) равенство:
aL ^L)_ = E^	C9)
г
Равенство C9) выражает теорему об изменении кинетического потен-
потенциала реономной голономной системы.
Применим теорему C9) при установлении динамического смысла
обобщённой силы для времени, если его рассматривать в качестве
дополнительной обобщённой координаты.
Дополнительная обобщённая координата в аналитической механике
может вводиться для унификации формул реономных и склерономных
систем. Введём дополнительную обобщённую координату gn+i и на
основе функции Лагранжа C7) образуем функцию [22]
V = L2 + Lign+i + Lo^+i,	D0)
однородную относительно обобщённых скоростей с учётом дополни-
дополнительной обобщённой скорости. Для дополнительной обобщённой коор-
координаты имеем уравнение
d ( dL* \ dL* ~
)	Q
где Qn+i — непотенциальная обобщённая сила, соответствующая qn+\.
При заданном законе изменения дополнительной координаты
(qn+\ = qn+\(t)) из уравнения D1) можно найти обобщённую
силу Qn+\. Пусть дополнительная обобщённая координата имеет
также смысл независимой переменной (qn+\ = t). Тогда структуру
обобщённой силы с учётом свойств однородных функций можно
получить по виду функции Лагранжа исходной системы, так как
из D1) имеем равенства
Qn+l = (Li+2Lo)-- ^ = L-(L2- ЬоУ- ^.	D2)
Подставляя C9) в D2), находим
г=\
т. е. обобщённая сила, соответствующая времени в роли дополнитель-
дополнительной обобщённой координаты, равна скорости изменения кинетического
потенциала, уменьшенной на величину «мощности» непотенциальных
обобщённых сил, соответствующих первым п обобщённым коорди-
координатам.

6. Примеры величин, называемых «действие»	57
6. Примеры величин, называемых «действие»
Приведём некоторые примеры, показывающие разнообразие смысла,
вкладываемого в понятие «действие». Обсуждение применения этих
понятий при формировании принципов и получении моделей движения
составляет содержание последующих заметок.
6.1. Функционалы «действие». 1. Действие в форме Якоби.
Действием в форме Якоби называют функционалы, составленные на
основе действия по Лагранжу C.10) при необходимости увеличить или
желании уменьшить число обобщённых координат.
Первая ситуация возникает при стремлении унифицировать форму-
формулы аналитической механики за счёт включения времени (или какой-
либо функции от t) в число обобщённых координат.
Пусть в качестве независимого аргумента вместо времени t исполь-
используется новый независимый параметр т:
* = /(т),	A)
и вводится новая «кинетическая энергия» Т*:
B)
где штрих обозначает дифференцирование по параметру т. Для дей-
действия движения с кинетической энергией B) составляется функционал
C)
Действие (З) содержит время наравне с обобщёнными координата-
координатами, также как и их производные по т. Однако можно заметить, что
зависимость функции Т* в C) от t' не совпадает по форме с зависи-
зависимостью её от обобщённых скоростей. Функция Т* содержит слагаемые
первой, нулевой и минус первой степени относительно tr, тогда как
относительно производных от обобщённых координат q[ (г = 1,...,п)
функция Т* состоит из однородных форм второй, первой и нулевой
степени. Поэтому полной идентичности между tr и обобщёнными ско-
скоростями в выражении Т* нет. Это несоответствие устраняет подход, ко-
который предложил В. А. Вуйичич (см., например, [22]): дополнительная
координата до, совпадающая со временем, включается в кинетическую
энергию по соглашению
T = T2 + Tlq0 + T0ql	D)
Выражение D) является квадратичной формой относительно скоро-
скоростей q0, q\, ..., qn.

58	Гл. I. Заметки о некоторых основных понятиях
Якобиева форма действия живой силы для консервативной системы
может содержать меньшее число обобщённых координат, чем лагран-
жева форма действия. Достигается это тем, что одна из обобщённых
координат принимается в качестве независимой переменной вместо
времени. Функционал «действие» получается следующим путём.
Для консервативных систем, в которых Т + П = h = const, в ка-
качестве независимой переменной Якоби предложил выбирать одну из
обобщённых координат. Интеграл энергии в консервативной системе
можно использовать для исключения дифференциала времени с помо-
помощью равенства
2T(dtf = ]Г aij dqi dqj = 2(h - IL)(dtf.	E)
Величина dt выражается из E) через дифференциалы обобщённых
координат:
м (l l г и и Х'/2
at = I - -тт——г 2_^ а^ dqi d
V	i,j
Подставляя это значение dt в выражение действия живой силы
в форме Лагранжа, получаем якобиеву форму действия живой силы:
2Tdt= \ y/Rdqu	G)
i
i,j=2	m
В случае обобщённо-консервативных систем можно также принять
в качестве независимой переменной одну из обобщённых коорди-
координат [25].
2.	Функционалы «действие» в механике сплошной среды описыва-
описываются в работе [4].
3.	Элемент действия в релятивистской динамике. Вопрос о физиче-
физическом смысле функции Лагранжа в виде разности кинетической и потен-
потенциальной энергий получил разъяснение после создания специальной
теории относительности.
Пусть полная энергия частицы с массой покоя то в поле сил
с потенциальной энергией П(#) есть Е = rriQC2 + П(д) (где с — скорость
света). Время наблюдателя t и собственное время t* частицы связаны
соотношением
dt* =
где v — 3-скорость частицы (в пространстве).

6. Примеры величин, называемых «действие»	59
Преобразуем элемент действия Edt* [4] (в ньютоновском прибли-
приближении v/c <С 1, П/тос2 <С 1):
Edt* = eJi -^ dt= (т0с2 + U(q) - ^ + .Л dt. (8)
После отбрасывания постоянного слагаемого т^с2 в круглых скоб-
скобках в (8) остаётся выражение функции Лагранжа со знаком минус.
К подобному же объяснению приводит преобразование элемента
действия [137] свободной частицы:
rriQcda = rrtocr \ 1 — -у dt,	(9)
с2
где da — элементарная длина дуги траектории в 4-мерном простран-
пространстве-времени (в координатах Минковского):
а г берётся равным +1 или —1 так, чтобы сделать da действительным.
Физический смысл различия между плотностью действия в ис-
исходных выражениях (8), (9) и функцией Лагранжа как плотностью
действия по Гамильтону состоит в следующем: разные знаки соответ-
соответствуют противоположным тенденциям влияния движения на изменение
действия; отброшенные слагаемые, степень малости которых выше,
чем v2/c2, отражают эффекты, игнорируемые в классической механи-
механике; наличие постоянного слагаемого представляет интерес в проблеме
квантования и применения принципов в задачах на равновесие.
4. Функционал «действие» для волновой функции. Математический
аппарат квантовой (нерелятивистской) механики основан на описа-
описании состояния системы частиц с помощью волновой функции Ф(д,?)
(Э. Шрёдингер). Квадрат модуля этой функции задаёт распределение
вероятностей значений координат: |Ф| dV есть вероятность того, что
произведённое над системой измерение обнаружит значения коорди-
координат в элементарном объёме dV конфигурационного пространства [54].
Волновая функция позволяет вычислить вероятности различных ре-
результатов произведённых измерений (под «произведённым измерением»
понимается взаимодействие частиц с «классическим» прибором без
предположения о наличии постороннего наблюдателя).
Систему уравнений для параметров, определяющих волновую функ-
функцию (в форме уравнений Эйлера-Лагранжа), можно получить из усло-
условия стационарности функционала [81]:
, Ф*, ^, ^, УФ, УФ*) dVdt,	A0)

60	Гл. I. Заметки о некоторых основных понятиях
где плотность действия
* = У {Ж * " **Ш + i Н^ф)* (~^V*) + П (q) Ф*Ф. A1)
Звёздочкой отмечены сопряжённые величины; г2 = — 1; ft = /г/Bтг),
/г — постоянная Планка; m — масса; V — оператор Гамильтона. После
подстановки в A1) волновой функции специальной структуры:
Ф = Л/р exp(iS/%),	A2)
лагранжиан A1) принимает вид
Условие стационарности функционала A0) с лагранжианом A3)
приводит в квазиклассическом приближении к уравнению Гамильтона-
Якоби относительно функции S и уравнению неразрывности относи-
относительно плотности вероятности р.
Таким образом, имеем двухуровневую иерархию применения поня-
понятия «действие», соответствующую применениям механики в областях
явлений (микро- и макро-): действие как функционал A0) для волно-
волновой функции и действие S как функция в классической механике.
Соответственно для двух названных областей описания явлений
проблема квантования является двухуровневой, а в общем случае —
многоуровневой [124].
При построении квантовой механики к классическим принципам
добавляются две квантовые аксиомы в виде двух уравнений [40]:
\pdq = nh (квантовое условие),
J	(И)
hv = E\ — Е% (условие частот).
Здесь h — постоянная Планка; v — частота излучения (она может не
быть целым числом); энергия Е нормирована, исходя из некоторого
рационально выбранного нулевого уровня. «Первое уравнение опреде-
определяет избранные или стационарные состояния атома и характеризует
их целым числом п («квантовое число»); второе определяет излучение,
испускаемое при переходе из некоторого начального в некоторое конеч-
конечное состояние, посредством соответствующих энергий Е\ и i?2» [40].
6.2. Функции «действие».
1. Действие в роли одноточечной и двухточечной характеристиче-
характеристических функций, главной функции Гамильтона, производящей функции
для канонических преобразований, описано в работах [25, 137]. На-
Например: «Определим двухточечную характеристическую, или главную,
функцию как лагранжево или гамильтоново действие (они равны) от
точки Б* до точки В вдоль луча...» (см. [137], с. 235). Эта функция
двух точек расширенного координатного пространства (пространства

6. Примеры величин, называемых «действие»	61
событий) может существовать или не существовать, может быть мно-
многозначной и т. д.
2.	Изменение действия при ударе. При импульсивном движении
в случае обобщённых ударных импульсов, имеющих потенциал, дей-
действие по Гамильтону составляется как функционал разрывной вариа-
вариационной задачи (кроме интегралов имеется слагаемое в виде функции,
определяющей изменение обобщённых импульсов при ударе) [107].
3.	Действие как фаза волны вероятности. Действие S в A2) может
рассматриваться как фаза плоской волны вероятности [54].
4.	В диссипативных системах Гамильтона-Якоби [63] функция S
комплексная:
S = Si+iS2, i2 = -l	A5)
где Si =ReS, S2 =
Функции S\ и $2, рассматриваемые как производящие функции,
каждой обобщённой координате ставят в соответствие два обобщённых
импульса:
W M Л) ^
У	dq ' У	dq'
Диссипативная система Гамильтона-Якоби задаётся двумя веществен-
вещественными функциями /i, /2 переменных q, t, p^\ p^ и сводится к уравне-
уравнению Гамильтона-Якоби с комплекснозначной функцией Гамильтона.
Перечень примеров действия может пополняться путём конструиро-
конструирования плотности действия для конкретных задач, в частности за счёт
более общих математических объектов, обладающих определёнными
инвариантными свойствами.

Глава II
ЗАМЕТКИ О СПОСОБАХ ВИРТУАЛЬНОГО
ВАРЬИРОВАНИЯ
7. О дифференцировании
7.1. Дифференцирование функции при неявной зависимости
от параметров. Приведём правила частного дифференцирования при
определении условий стационарности функции (градиента функции)
при наличии ограничений. Будем пользоваться матричными обозначе-
обозначениями.
Скалярная функция
L(x,u), x= [xi,...,xn]T; и = [щ,...,иг]т,	A)
зависит от п параметров состояния х\,... ,хп и г параметров щ,... ,иг,
которые связаны соотношениями (f = [/ь ..., /П]Т)
f(x,u)=0.	B)
Стационарной точкой функции A) в задаче оптимизации векто-
вектора и с ограничениями в виде равенств B) называется такая точка,
для которой dL = О при произвольном значении du, удовлетворяющем
равенству di = О (при этом dx изменяется в зависимости от du так,
чтобы не нарушалось условие df (х, и) = 0) [8].
Дифференциалы функций L и f имеют вид
dL = Lxdx + Lu du,	C)
df = fxdx + fudu,	D)
где
dfn
'' дхп
dfn
\дх\ ''" ' дхп
(аналогично для Lu и ?и).
В стационарной точке должно выполняться равенство df = 0. По-
Поэтому, если матрица fx невырождена, то уравнения D) можно разре-
разрешить относительно dx:
dx = -f-lfudu.	E)
С учётом E) выражение C) представляется в виде
dL=(Lu-Lxf-[fu)du.	F)

7. О дифференцировании
63
Так как в стационарной точке dL должно быть равно нулю для
любого значения du, необходимо, чтобы выполнялись уравнения (их
число — г)
Lu-Lxf~lfu = O.	G)
Левая часть уравнения G) представляет собой частную производ-
производную функции L по и при фиксированном значении f, тогда как Lu —
частная производная функции L по и при фиксированном значении
вектора х. Для того чтобы различать эти частные производные, при-
применяются [131] два термина: «частная производная» и «полная частная
производная», с разными обозначениями:
dL
= Lu и
д
(8)
соответственно.
Очевидно, что прежде чем возникнет задача частного дифферен-
дифференцирования функции, необходимо составить эту функцию и определить
те постоянные условия, при которых находится полная частная произ-
производная.
Пример. Механическая система представляет собой «связку» аб-
абсолютно твёрдого тела и материальной точки. Требуется составить
уравнение связи и найти градиент функции связи. Направление гра-
градиента функции связи должно определять направление натяжения
нити: связка состоит из абсолютно твёрдого тела и материальной точ-
точки, соединённых абсолютно гибкой нерастяжимой безмассовой нитью.
Изучается плоское движение: ма-
материальная точка, нить и сечение,
проходящее через центр масс О
тела, всё время находятся в од-
одной плоскости. На рис. 7.1 показа-
показаны оси О^ и От], связанные с телом
(ось ОС, перпендикулярна плоско-
плоскости движения). Материальная точ-
точка соединена с телом нитью, второй
конец которой прикреплён в точ-
точке К с координатами (/о,0,0), дли-
длина нити — /; сечение поверхности
тела плоскостью имеет вид окруж-
окружности радиуса Iq. Нить натянута
и имеет участок на поверхности те-
тела. Обозначим через N реакцию
связи на материальную точку (сила натяжения нити), а через риг —
радиусы-векторы положения материальной точки относительно цен-
центров G и О (G — центр масс системы, О — центр масс тела) соот-
соотРис. 7.1
ветственно. Введём безразмерный вектор р* = р
р
Ml
(М — масса

64	Гл. И. Заметки о способах виртуального варьирования
тела) с координатами х, у в системе координат Gxy (ось О^ состав-
составляет с осью Gx угол в, который является обобщённой координатой,
определяющей поворот тела относительно осей Gxy). Для описания
движения с наматыванием нити примем, что точка К крепления нити
находится на оси О^ и обозначим через а угол между направлением на
точку касания в месте схода нити с поверхности тела (точка Р) и осью
О?. Ограничимся случаями, когда нить натянута и угол а > 0 (нить
имеет участок, намотанный в положительном направлении отсчёта
угла а).
Возможны разные формы записи условия постоянства длины нити.
Например, в виде уравнения
(р\ (х, у, а) = па + \Jx2 + у2 — п2 —1=0,	(9)
или уравнения [15]
(f2(x, у, а) = —х sin (в + а) + у cos (в + а) + па —1=0.	A0)
В уравнениях (9), A0) угол в = const и п — тоже постоянная
величина. Кроме того, имеет место равенство
n-xcos(S + a) - у sin (в + а) =0.	A1)
Выполнив частное дифференцирование функций ср\ и ср2 по х и у
(при а = const), получаем
Л
-
Jx2 + y2 -n2' Jx2 + y2 -n2 J \l-na' l-naj '
i12)
((P2x,(P2y) = (— sin F + a), cos F + a)).	A3)
Нетрудно проверить, что векторы A2) и A3) имеют разное направ-
направление, причём вектору N коллинеарен только вектор A3) (см. рис. 7.1).
При вычислении полных частных производных функций (9), A0)
учтём соотношения между углом а и координатами х, у:
х = ncosF + а) — A — na) sin (в + а),
у = п sin (в + а) + A — па) cos (в + а).
Для дифференциалов dx, dy, da из A4) имеем равенства
dx = — A — па) cos (в + a) da, dy = — A — па) sin (в + a) da,
,	cos (В + a) , sin (В + a) ,
da = -—-^	'- dx - —-^	'- dy,
1 — na	1 — na
A5)
из которых получаем частные производные
_ cos (В + а)	_ sin (В + а)
х	1 — па	у	1 — па

7. О дифференцировании	65
С учётом A6) находим полные частные производные функции ф\\
o-{^i} = 4>\х +пах = -sin(e + a),
д	A7)
щ Ы = 4>\у + пау = cos (e + «)>
которые совпадают с A3). Градиент функции ср2 при вычислении
полных частных производных при переменном а остаётся тем же
(см. A3)), поскольку при A1) d(f2/da = 0 и
Таким образом, оба уравнения связи, (9) и A0), позволяют найти
направление реакции нити и могут применяться как уравнения связи
при составлении уравнения для виртуальных вариаций.
7.2. Вариационная производная. Операции, выполняемые при
составлении уравнений движения в форме уравнений Лагранжа второ-
второго рода (см. C.29)), представляют собой действие оператора Эйлера-
Лагранжа на функцию Лагранжа L(q,t,q):
/гЧ d dL дЬ . 1	/1ОЧ
ei(L) = — т^-тл-, г=1,...,п.	A8)
4 ' dt aqi aqi
Оператор с противоположным знаком называют также вариацион-
вариационной производной [29]:
— -- — = —.	A9)
dqi dt dqi 5qi'
Пока независимая переменная — одна (например, t), никаких
неудобств с обозначениями производных не возникает: d/dt — полная
производная по времени, д/dqi, d/dqi — частные производные по
обобщённым координатам и по обобщённым скоростям. Однако уже
здесь, рассматривая совокупность переменных Лагранжа (дь t, qi,
i= l,...,n) с учётом зависимости обобщённых координат и обобщён-
обобщённых скоростей от времени (qi(t), qi(t)), можно записать вариационную
производную A9) с помощью понятия полной частной производной:
% dtldqiJ'	K }
Если же независимых переменных несколько, например в случае
непрерывных систем (систем с распределёнными параметрами), то по-
понятие полной частной производной позволяет более чётко записать
вариационную производную. Так, если независимых переменных две: s
и t, а варьируемый функционал для определения функции rj(s, t) имеет
плотность действия (удельный лагранжиан):
3 В. Г. Веретенников, В. А. Синицын

66	Гл. И. Заметки о способах виртуального варьирования
то вариационная производная вычисляется по формуле
д f dJ^\ д
)
dr\ ds I drl
Вариационная производная B1) представляет собой оператор Остро-
Остроградского (точнее Эйлера-Остроградского) и позволяет составлять
уравнения для определения функции r](s, t) из условия стационарности
действия.
8. Некоторые приёмы и способы варьирования
8.1.	Синхронные вариации. Синхронные вариации обобщённых
координат и обобщённых скоростей, применённые в п. 3.2 при обосно-
обосновании принципа Гамильтона с помощью общего уравнения динамики,
были связаны соотношением (перестановочность операций d и 5)
** = dJ?-	<¦>
Более общим является приём вариационного исчисления [131], при
котором изохронно в момент времени t действительному состоянию
Qi(t)> Qi(t) ставится в соответствие варьированное состояние, получае-
получаемое следующим образом. Действительное состояние включается в за-
зависящее от некоторого параметра а семейство функций qi(t,a), qi(t,a)
и полагается содержащимся в нём при а = 0. Вариации получаются
вычислением производной по а при а = 0. При линейной зависимости
от а имеем
(I'll с\ ) — а' \ i \ I с\( ' [ т ) а' [ т с\ ) — а * \ i \ I ^vt7 * (/ ) 1 — I rfi ( / \
Тогда
UQi(t) = °^?,i{t), Sqi(t) = arji(t).
В общем случае возможны неравенства гц ф &. Время t не варьиру-
варьируется, поэтому вариации называются изохронными (их также называют
синхронными). Аналогичные действия производятся при варьировании
функций и функционалов. Например, синхронными являются вирту-
виртуальные вариации, обладающие свойствами виртуальных перемещений
при фиксированном состоянии и времени.
8.2.	Асинхронное варьирование. Варьируемыми можно считать
не только обобщённые координаты и обобщённые скорости, но и время.
Варьирование с изменением времени называется асинхронным [58].
В способе асинхронного варьирования, применявшемся ещё Лагран-
жем, обозначим операцию классического асинхронного варьирования
обобщённых координат и обобщённых скоростей через А:
C)
D)

8. Некоторые приёмы и способы варьирования
67
где At(t) — произвольная бесконечно малая функция времени [58].
Операции варьирования 5 в C), D) являются изохронными и переста-
переставимы с операцией дифференцирования по времени (см. A)) (предпола-
(предполагается, что функции 5qi(t), At(t) принадлежат классу функций С2).
Геометрическая интерпретация асинхронного варьирования опре-
определяется равенствами C), D): пусть q^ = qi(t) — некоторая траек-
траектория системы в действительном движении под действием активных
сил и реакций связей, согласующих движение с наложенными свя-
связями; наряду с траекторией действительного движения рассматрива-
рассматриваются варьированные кривые такие, что точке q^ в момент времени t
на действительной траектории соответствуют точки qi + Aqi в мо-
момент времени t -\- At на варьированной кривой. Точке М траектории
действительного движения ставятся в со-
соответствие точка М\, полученная син-
синхронным варьированием, и точка М^, по-
полученная классическим асинхронным ва-
варьированием (рис. 8.1).
Из C), D) для операций А и d/dt
следуют соотношения [58]
d(AQl) _ д
ML
Sq
¦Qi
E)
Mi
м
Aq
t
At
Рис. 8.1
dt	чг ' *" dt
Далее соотношения вида E) между
производной от вариации и вариацией
производной будем называть перестановочными соотношениями. Эти
соотношения в подынтегральных выражениях удобны при интегриро-
интегрировании по частям.
Операции асинхронного варьирования функции и функционала обо-
обозначим так же, как и вариации варьирования обобщённых координат,
через А. Напомним, что операция 5 выполняется изохронно. При-
Применительно к функции Лагранжа L и функционалу S (действие по
Гамильтону) имеем следующие выражения вариаций:
Ь л , dL А . \ , dL А ,
AL =
SL =
9L
dL ,.
S1
F)
AS = Aj Ldt =
G)
Здесь t\ и t2 —
^2	Ь2
SS = s\bdt= \SLdt
и	и
начальный и конечный моменты времени.

68	Гл. И. Заметки о способах виртуального варьирования
Асинхронное варьирование позволяет в варьированном движении
обобщённо-консервативных систем сохранить одинаковыми значения
интеграла энергии (изоэнергетическое варьирование). Изоэнергетиче-
ское варьирование движения можно считать следствием влияния до-
дополнительно наложенных идеальных стационарных связей (см. [51],
Примечание Бертрана). Однако сам интеграл энергии как связь, тре-
требующую физической реализации с помощью реакций, Бертран не рас-
рассматривает. Выполнение условия изоэнергетичности достигается соот-
соотнесением действительного и варьированного состояний в разные мо-
моменты времени, в частности при прохождении начального и конечного
положений.
8.3. Варьирование по Гельмгольцу. Иной способ варьирования
применил Гельмгольц при выводе своего принципа (см. [113]). Далее
способ, применённый Гельмгольцем, будем называть варьированием
по Гельмгольцу. В отличие от асинхронного варьирования, в этом
способе время как переменная, не варьируется, но варьируется диф-
дифференциал времени dt. (Например, при введении новой независимой
переменной г? вместо t, когда принимается t = ?($), t1 = dt/d'd ^ 0.)
Обозначим через А вариации по Гельмгольцу и покажем, что это
варьирование перестановочно с операцией d/dfi. Способ Гельмгольца
приведём в сравнении со способом асинхронного варьирования.
В качестве вариаций обобщённых координат в способе Гельмгольца
принимаются изохронные вариации
Aft = 5q%.	(8)
Производные от обобщённых координат по новой переменной
(о.[ — dqi/dd) примем со свойством перестановочности: Д<^ = (Д^У-
Преобразуем это равенство с учётом варьирования дифференциа-
дифференциала dt:		 ,
()	' '	'
то есть	,-г-
^t' = t'Aqt+qtAt'.	(9)
Из (9) следуют перестановочные соотношения в способе Гельмгольца:
<&>=** + **<*>.	A0)
Из сравнения A0) и E) следует, что перестановочные соотношения
в способе Гельмгольца и способе асинхронного варьирования совпа-
совпадают с точностью до обозначения (используем его и далее в способе
Гельмгольца):	_
d(At) = A(dt)	МП
dt	dt '	У '
Равенство A1) показывает, что относительное изменение дифферен-
дифференциала времени (отношение вариации A(dt) к дифференциалу dt) в спо-

8. Некоторые приёмы и способы варьирования	69
собе Гельмгольца равно производной от бесконечно малой функции
At в асинхронном варьировании. Однако варьирование обобщённых
координат в способе Гельмгольца производится изохронно (см. (8)),
и это должно учитываться при варьировании функций и функционалов:
dt \
A3)
Варьирование по Гельмгольцу ставит в соответствие точкам q^
действительного движения точки q^ + 5qi в тот же момент времени
(точки М и М\ на рис. 8.1), а скорости в варьированном состоянии
qi + Aqi получаются с учётом соотношения E) (операции А и диффе-
дифференцирование d/dt не переставимы). Интегрированием равенства A1)
каждой кривой, полученной варьированием по Гельмгольцу, сопостав-
сопоставляется функция At в способе асинхронного варьирования.
Примечание. В работе [22] операция асинхронного варьирова-
варьирования C) в реономной голономной системе рассматривается как расши-
расширенное варьирование вспомогательной склерономной системы с п+1
степенями свободы. Заметим, что для дополнительной обобщённой
координаты, которой считается время, в равенстве вида C),
At = iAt + 6t,	A4)
виртуальная вариация 5t должна быть равна нулю, так как вирту-
виртуальные перемещения являются изохронными, т.е. A4) соответствует
тождеству At = At. Последнее, само по себе очевидное обстоятель-
обстоятельство меняет смысл величины At в равенствах C): для склерономной
системы это вариация дополнительной обобщённой координаты. Сле-
Следовательно, теперь равенства C) могут рассматриваться как уравнения
для вариаций Ag^, At. Об условиях, которые налагают на вариации
связи, рассказывается в заметке 9.
8.4. Расширенное варьирование по Гельмгольцу. Положим, что
изменение дифференциала времени производится различно для каж-
каждой обобщённой скорости, т.е. вводятся несколько функций Ar^(t)
со свойствами функции At. Тогда перестановочные соотношения при-
примут вид
Вместе с (8) равенства A5) составляют расширение способа Гельм-
Гельмгольца.
8.5. Вариации в скользящих режимах реализации связей. Вы-
Выше рассматривалось варьирование непосредственно кинематических

70	Гл. И. Заметки о способах виртуального варьирования
параметров состояния (обобщённых координат, обобщённых скоростей
и времени). Влияние на вариации состояния может быть и опосре-
опосредованным через некоторые параметры. Выбор закона изменения этих
параметров, при котором процесс был бы оптимальным, составляет
основную задачу теории управления (а сами эти параметры и называ-
называют управлениями). В несвободном движении роль управлений могут
играть неопределённые множители Лагранжа, с помощью которых
вводятся реакции идеальных связей.
Неопределённые множители входят в уравнения движения линейно
(первая форма уравнений Лагранжа). В уравнениях движения в форме
E.26) реакции связей с неопределёнными множителями включаются
в правые части в число обобщённых непотенциальных сил.
Обозначим для краткости вектор фазовых координат через х и
положим, что в скользящем режиме реализуется одна связь. Тогда
уравнения движения автономной
системы запишутся в виде
Т~!	x = fo(x) + Afi(x), A6)
I 1
I I	где А — скалярный неопределённый
] ] , 2?	множитель; fo(x), f\(x) — вектор-
—v
I
функции фазовых координат.
to	т + е\	U t
!	Нахождение реакции связи из
1 |	условия минимума действия приво-
| !	дит к задаче поиска неопределённо-
	i ¦	го множителя А. В скользящем ре-
режиме (см. заметку 2) для А возмож-
рис g 2	ны «игольчатые» вариации, «дву-
«двусторонние» вариации и более общие
«пакетные» вариации [23]. Двусторонняя вариация — вариация Келли
(Н.Т. Kelley) — показана на рис. 8.2 и описывается соотношениями
{v, te[T,T + e],
-v, te[r + e,T + 2e],	A7)
0, t<? [т,т + 2е].
Варьирование множителя А соответствует изменениям ускорений.
9. Уравнения для виртуальных вариаций
Совокупность уравнений для виртуальных вариаций составляют
уравнения для виртуальных перемещений (задающие направления ре-
реакций связей) или уравнения для вариаций обобщённых скоростей и,
вообще говоря, времени. Уравнения для вариаций обобщённых скоро-
скоростей необходимо рассматривать вместе с перестановочными соотноше-
соотношениями для операций d5 и 5d, так как в числе стандартных операций

9. Уравнения для виртуальных вариаций	71
вариационного исчисления применяется приём «интегрирования по ча-
частям».
Составление уравнений для виртуальных вариаций демонстрирует-
демонстрируется на примере учёта неголономных связей. Показано, что уравнение
голономной связи с параметром является идеальной связью, когда оно
описывает огибающую. Обсуждаются правила виртуального варьиро-
варьирования связей при двух независимых переменных.
9.1. Уравнения для виртуальных вариаций при неголономных
связях. Пусть уравнения идеальных неинтегрируемых связей пред-
представлены уравнениями
fl(q,t,q)=O, /=l,...,r,	A)
разрешимыми относительно обобщённых скоростей. Полагая, что
(?ь ••• ,4k — независимые обобщённые скорости, к = п — г, имеем
4k+i = 4>i(qi,---,qn,t,qi, •••>&), / = 1,... ,r,	B)
где q\,... ,qn, t, 4\, ••• ,4k — переменные Лагранжа. Виртуальные пере-
перемещения 5qi, г = 1,...,п, идеальных связей A), согласно Остроград-
Остроградскому [79] и Четаеву [130], удовлетворяют условиям
i=l
принимающим для связей B) вид
к
Наиболее простым и удобным является предположение о переставимо-
сти операций дифференцирования и варьирования:
54г — -г 5qi, i=l,...,iy.	E)
Свойство E) принималось для вариаций всех обобщённых скоростей
(у = п) при «выводе» принципа Гамильтона для голономных систем
(см. заметку 3) и в подходе Гёльдера при обосновании интегрального
принципа неголономных систем [101]:
и
\5Ldt = 0, 5qi(to)=5qi(ti)=O.	F)
to
В отличие от принципа Гамильтона, интегральный принцип Гёльде-
Гёльдера F) не является вариационным. Кроме того, в случае неголономных
связей кривые сравнения не удовлетворяют уравнениям неголономных
связей.
Сторонники другой точки зрения (П. В. Воронец, Г. К. Суслов) при-
признавали переставимость операций дифференцирования и варьирования

72	Гл. И. Заметки о способах виртуального варьирования
для независимых обобщённых скоростей, число которых в E) v = к.
Для остальных обобщённых скоростей перестановочные соотношения
устанавливались с учётом связей.
Промежуточный между этими двумя точками зрения вариант
(к ^ v ^ п) для связей, линейных относительно обобщённых скоростей,
предложен Ю. И. Неймарком и Н.А. Фуфаевым [74]. Очевидно, что
возможен также вариант выбора соотношений в E) при 1 < v < к.
В последнем случае в выборе вариаций обобщённых скоростей остаётся
произвол, который может быть устранён путём введения дополнитель-
дополнительных (произвольных) соотношений: в виде либо условных уравнений,
либо уравнений для вариаций (число их равно n — r — v).
При v > к после выбора виртуальных перемещений число условий,
которым должны удовлетворять вариации обобщённых скоростей, из-
избыточно (и-\-г > п). Этим объясняется невозможность в общем случае
удовлетворить уравнениям связей A) (или B)) на варьированных кри-
кривых, т. е. 5fi т^ 0.
Варьирование функций связи A) после подстановки E) с учётом
уравнений C) даёт выражение
?§?)•-??«•¦	G)
где использовано обозначение вариационных производных (см. G.19)).
Для функций //, полученных из уравнений B), выражения G)
принимают вид
s=\ dQs	m=\
Если связь с номером / интегрируема, т. е. // = dQ/dt, где Ф(д, t), то
соответствующее выражение G) тождественно равно нулю Efi = 0).
Выражения G) (или (8)) для неинтегрируемых связей могут также
обращаться в нуль в силу уравнений движения при нелинейной зависи-
зависимости от обобщённых скоростей или при специальном выборе вариаций
5qi (см., например, [101]). В этих случаях варьированные состояния
удовлетворяют уравнениям связей.
При v = к также можно обеспечить уравнения связей в варьиро-
варьированных состояниях. Приняв
5qs = jt5qs, s=l,...,k, 8ft = 0, l=\,...,r,	(9)
получим для зависимых вариаций обобщённых скоростей условия
d	k
s=1

9. Уравнения для виртуальных вариаций	73
Связь, заданная уравнением вида G), является голономной, если
существует некоторая функция 4f(q,t) такая, что в каждый момент
времени выполняется равенство 5fi = 5Ф. Иначе говоря, для голоном-
голономной связи имеем (см. G)) общее уравнение
d dfl_dfl дЪ\ _
diW д^ W)qt~ '	( '
которое при учёте уравнений для виртуальных перемещений C) соот-
соответствует системе п — r уравнений. Голономная связь позволяет умень-
уменьшить число обобщённых координат на единицу с помощью уравнения
4f(q, i) = 0, и тогда в варьированном состоянии выполняется уравнение
связи Sfi = 5Ф = 0.
9.2. Виртуальное варьирование связи, представляющей огиба-
огибающую. Рассмотрим уравнения G.9), G.10), имеющие вид голономных
связей. Оба уравнения описывают одно и то же условие: постоянную
длину нерастяжимой нити, но форма их записи различна и кроме
координат имеется зависимость от угла а. Зависимость от угла пред-
представляет собой частный случай параметра (обозначим его тоже а)
в уравнении следующего вида:
F(x,y,a)=0.	A2)
Из теории огибающей семейства кривых с параметром а известно,
что иногда существует кривая, которая касается каждой кривой семей-
семейства в одной или нескольких точках и состоит из этих точек касания.
Координаты точки касания определяются значением параметра а. При
предположении существования и непрерывности частных производных
по х, у и а от функции F(x, у, а) параметрические уравнения огибаю-
огибающей получаются как решения относительно х и у системы уравнений:
F(x,y,a)=0, |^=0.	A3)
Из уравнений G.9) и G.10), описывающих одно и то же условие
связи, только второе удовлетворяет условиям A3). И именно из него
следует уравнение для виртуальных перемещений материальной точки
с координатами х, у:
О Г с-	О Г с-	г\	/ 1 л \
— 5х+—5у = О.	A4)
дх	ду
Таким образом, имеем уравнение для вариаций в форме A4), если
голономная связь с параметром A2) описывает огибающую.
Заметим, что уравнение для виртуальных перемещений можно по-
получить и с помощью уравнения G.9), для которого второе равенство
в A3) не выполнено, однако при этом нужно операцию частного
дифференцирования в A4) заменить операцией полного частного диф-
дифференцирования, предварительно вычислив частные производные от а
по х и у (см. пример в заметке 7).

74	Гл. И. Заметки о способах виртуального варьирования
9.3.	О варьировании уравнения связи при двух независимых
переменных. Связи в системе с двумя независимыми параметрами
(время t и пространственный линейный параметр s) можно разделить
на три категории: условия, налагаемые при всех значениях параметра
(во всём диапазоне их изменения); условия, которые должны выпол-
выполняться при фиксированных значениях одного параметра; и наконец,
условия, которые должны удовлетворяться интегрально для заданного
диапазона изменения параметров. Примеры связей первых двух кате-
категорий применяются в модели качения жёсткого колеса по деформируе-
деформируемому рельсу (см. заметку 21).
При вычислении вариации функционала переменные t и s высту-
выступают как равноправные аргументы. В составлении же уравнений для
виртуальных вариаций роль t и s, вообще говоря, различна. Чтобы
продемонстрировать это различие, возьмём связь, зависящую от двух
определяющих параметров u\(s,t) и U2(s,t) и их производных по t и s
(обозначим производные точкой и штрихом соответственно):
/(?, S, Щ, Щ, U\, Щ, и'\, U2) = 0.	A5)
Реакцию идеальной связи A5), как и в дискретных механических
системах, будем задавать с помощью уравнения для виртуальных ва-
вариаций, получаемого из уравнения связи. В зависимости от наличия
в A5) производных по времени имеем два случая:
1) J^O, i e 1,2;
В случае 1 имеем уравнение для виртуальных перемещений (мат-
(матричная форма записи с обозначением и = (щ,и2)Т):
^г5и = 0, если ^ф 0, jGl,2.	A6)
ди	duj
В случае 2 уравнение для виртуальных вариаций имеет вид
^-5и+%5иг = 0, если %L = 0, j = 1,2.	A7)
ди	ди	duj
Уравнения A7) для связей применяются в прикладных задачах
(см. гл. IV).
9.4.	О неравенствах для виртуальных перемещений при
неудержи вающих связях. Неудерживающие связи, создающие
реакции, математически представляются в виде нестрогих неравенств.
Это связи, которые не могут быть нарушены (в отличие от связей,
которые не должны быть нарушены [12]). Если состояние системы
таково, что в условии связи выполняется строгое неравенство, то

10. О применении неопределённых множителей	75
в данном состоянии система свободна и никаких ограничений на
виртуальные перемещения такая связь не налагает.
Если же состояние системы согласовано с условием связи в виде
равенства (система находится «на связи»), то задачей несвободного
движения является определение влияния связи на движение системы,
а именно: «напряжена» связь (создаёт реакцию) или «ослаблена» (для
действительных ускорений точек выполняется строгое неравенство,
и реакция её равна нулю). Реакции идеальных неудерживающих связей
удовлетворяют неравенству ^ Щ^ ^ 0, из которого следует нера-
к
венство	п
J2(Fk-mkwkMrk^O.	A8)
к=\
Отметим два важные положения, отличающие формирование мно-
множества виртуальных перемещений неудерживающих связей (см., на-
например, [13]).
1.	В множество включаются виртуальные перемещения, которые
оставляют систему «на связи», и те, при которых происходит её
мысленное «ослабление» (виртуальные перемещения пропорциональны
разностям соответствующих мысленных ускорений).
2.	В общее неравенство A8), не опасаясь его нарушить, можно
подставить любые виртуальные перемещения, удовлетворяющие только
тем неравенствам, которые соответствуют связям, не ослабевающим
при действительном движении [7].
10. О применении неопределённых множителей
Учёту варьированного уравнения одной связи в варьированном урав-
уравнении другой связи с применением неопределённых множителей по-
посвящена заметка М. В. Остроградского [80]. Эта заметка приведена
полностью с нашими примечаниями. В ней обсуждается применение
неопределённых множителей на разных этапах дифференцирования
функции, исследуемой на экстремум, а также представление реакций
идеальных удерживающих и неудерживающих связей. Сформулирована
задача оптимального особого управления с использованием в качестве
управлений неопределённых множителей.
10.1. «Заметка о равновесии упругой нити» (М. В. Остроград-
Остроградский). «Профессор Шультен первый указал в печати, что у Лагранжа
вкралась неточность при применении его метода вариаций к равнове-
равновесию упругой нити ([51]); но Шультен не объясняет происхождение этой
неточности, ибо не говорит, по какой причине нельзя принять, как это
сделал Лагранж, что 5ds = 0.
Заметим, что дифференциалы, относящиеся к виртуальным переме-
перемещениям системы и обозначенные в «Аналитической механике» через

76	Гл. И. Заметки о способах виртуального варьирования
5 О, изменяют свои свойства при применении множителей и не соот-
соответствуют тогда виртуальным движениям; так, условному уравнению,
например, L = 0, в уравнении равновесия системы, к которой относится
L = О, соответствует член X5L, где 5L не равно нулю; ибо 5L равно
нулю только тогда, когда 5 соответствует виртуальному перемещению,
между тем 5 в X5L означает произвольное дифференцирование. Вслед-
Вследствие этого в аналитической механике нельзя положить ни 5 ds = 0, ни
5d2s = 0 в дифференциале 5 величины
_ v d2x2 + d2y2 + d2z2 — d2s2 2)
ds
ВмеСТО	2 2	2 2	2 2
с _ d xSd x + d ySd у + d zed z
dsy/d2x2 + d2y2 + d2z2 - d2s2
надо писать
с. _ d2x5d2x + d2y5d2y + d2z5d2z — d2s5d2s e5 ds
' 2 1 Л27/2 i Л2-2 _ ^/2q2	(is
Это последнее выражение для 5е даст верные уравнения равновесия
упругой нити или, лучше сказать, верное выражение натяжения Л,
ибо легко видеть, что варьируемость ds ничуть не меняет уравнений,
относящихся ко всем точкам кривой, и влияет только на выражение Л.
Это замечание имеет общее значение, и его легко пояснить. В самом
деле, если есть некоторое условное уравнение L = 0, обусловленное
свойствами системы, и требуется прибавить к виртуальным момен-
моментам 3) сил, приложенных к системе, такую величину, как [i5M, где
М — функция L, dL, d2L..., то в общее уравнение равновесия системы
будет входить величина 4)
Если положим 5М = 5Р + Q5L + R5dL + S5d2L + ... и примем во
внимание только величины под знаком S 5), то получим выражение
5 [ц5Р + (Л + /zQ - d (fiR) + d2 (fiS) -...ML].
Эта же величина, в предположении, что 5М = 5Р, т. е. когда 5L = О,
будет
1)	Под операцией S понимается варьирование.
2)	Здесь е — угол смежности.
3)	«Момент» здесь означает виртуальную работу.
4)	Здесь S — знак интегрирования, когда оно возникает как предел сумми-
суммирования по всем материальным точкам.
5)	После интегрирования по частям.

10. О применении неопределённых множителей	11
Таким образом, варьируемость L, dL, d2L,... только заменяет Л
на Л + fiQ — d(fiR) + d2(fiS) — ... Следовательно, пишем ли Л или
Л + /iQ — d(/iR) + d2(/iS) — ..., исключение даст всегда один и тот же
результат» [80].
Примечания.
1.	Учёт варьированного уравнения связи с неопределённым множи-
множителем позволяет считать множество виртуальных вариаций свободным
от условия, налагаемого на них этим уравнением, что вполне соответ-
соответствует принципу освобождаемости от связи.
2.	Утверждение 1 распространяется М. В. Остроградским и на свя-
связи, образованные «сложным» образом, когда функция связи М зависит
от функции L и её дифференциалов dL, d2L... связи L = 0, и показы-
показывает, как изменяется множитель при 5L.
3.	Исключение множителя при 5L приводит к одним и тем же урав-
уравнениям равновесия, пишем ли мы Л или Л + /iQ — d(/j,R) + d2(fiS) — ...,
однако разные множители определяют разные реакции при реализации
связей.
4.	Принцип Даламбера позволяет распространить утверждения 1-3
на динамику, что и подтверждается при решении прикладных задач.
Однако остаётся сомнение в возможности безусловной зависимости
связей от функции и её последовательных дифференциалов второго
порядка и выше, которую допускает М. В. Остроградский. Ситуация
здесь, на наш взгляд, аналогична той, которая возникает, когда в чис-
число определяющих параметров системы, кроме параметра, входят его
первая и вторая производные по времени. Параметры, находящиеся
в таком отношении, связаны неголономным соотношением и тоже могут
учитываться с помощью неопределённых множителей.
Пример зависимого уравнения в вариациях даёт уравнение 5е = 0,
т. е. варьирование, при котором сохраняется угол смежности (так на-
называемое изоповоротное варьирование) при условии нерастяжимости
нити 5 ds = 0.
10.2. Неопределённые множители в задачах на экстремум
функции. Необходимое условие стационарности (и выражение гради-
градиента) функции G.1) при наличии ограничений в виде равенств G.2)
можно получить и с помощью неопределённых множителей. Приведём
два подхода.
В первом подходе в стационарной точке равенства dL = 0 и df = 0
(см. G.3), G.4)) рассматриваются как система линейных алгебраиче-
алгебраических уравнений относительно векторов-столбцов dx и du. Из условия
совместности этих уравнений следует, что можно выбрать [8] п посто-
постоянных множителей Ai,...,An так, что
^ + Z>§f = o,	A)

78	Гл. И. Заметки о способах виртуального варьирования
где
у = (х\,...,хп,щ,...,иг).	B)
Уравнение A) показывает, что линейная комбинация строк матрицы
fy = df/dy должна быть равна вектору Ly. В скалярной форме система
уравнений A):
i=\ dxi
/=1 диз
рассматриваемая вместе с уравнениями G.2), позволяет найти и, х и Л.
Уравнение C) можно разрешить относительно Л:
Л- (Г (f)-lf- (dLf	(Ъ
Л — — [bx{Jx) ) — — \~q7J •	\°)
Последнее равенство в E) означает, что величины Л/ являются
частными производными от L по / при постоянном значении и и допу-
допустимом изменении х.
Во втором подходе неопределённые множители Л/ используются при
образовании вспомогательной функции Н:
Н (ж, и, Л) = L О, и) + J2 Xifi (ж'и)-	F)
1=1
Полагается, что для некоторого номинального значения и из ра-
равенств G.2) найдено соответствующее ему значение х, так что Н = L.
Поскольку представляет интерес изменение Н (и L) при изменении
вектора и, то Л выбирается так, чтобы дН/дх = 0, откуда для Л следует
выражение E).
Учитывая, что х определяется из соотношения f(x, и) = 0, получаем
dL = dH=^- du.	G)
ди
Таким образом, дН /ди есть градиент L по и при выполнении усло-
условия f(x, и) = 0. Следовательно, необходимые условия стационарности
функции L (при f(x, и) = 0) представляются с помощью функции Н F)
ввиде	ш=0 ш=0
дх	ди
Перечисленные условия позволяют найти и,х и Л.
Обратим внимание на то, что в этих двух подходах к учёту огра-
ограничений с применением неопределённых множителей последние вво-
вводятся на разных этапах дифференцирования функции, исследуемой на
экстремум. В первом подходе с неопределёнными множителями урав-
уравнения для дифференциалов учитываются, когда функция уже продиф-
продифференцирована, а во втором формируется новая функция, в которую

10. О применении неопределённых множителей	79
включаются с неопределёнными множителями уравнения ограничений,
и затем уже дифференцируется эта новая функция. Результат одинаков
по той причине, что в обоих подходах выполнялись одинаковые диф-
дифференциальные операции.
Заметим, что варьирование также является дифференциальной опе-
операцией. Однако варьирование функции и составление уравнений для
виртуальных вариаций, вообще говоря, проводятся по разным правилам
(см. заметки 8, 9). Исключение составляют системы с идеальными
голономными связями при применении классического изохронного ва-
варьирования (см. п. 8.1). Во всех остальных случаях условия стационар-
стационарности дадут разные уравнения в зависимости от того, на каком этапе
применяются неопределённые множители.
10.3. О представлении реакций идеальных связей. Пусть мате-
материальная точка движется по регулярной гладкой (без трения) поверх-
поверхности (голономная связь):
f(x,y,z,t) = O.	(8)
Функция поверхности непрерывна вместе с производными до второго
порядка включительно по своим аргументам. Связь может создавать
реакцию в направлении градиента функции и с помощью неопреде-
неопределённого множителя Л представляется произведением AV/ (V/ ^ 0).
Уравнения движения материальной точки в декартовых координатах
принимают вид
mx = Fx+X^, my = Fv + \fy, mz = Fz+X^,	(9)
где F — равнодействующая активных сил, приложенных к материаль-
материальной точке; т — масса материальной точки; х, у, z — координаты точки
в декартовой системе.
Число уравнений (8), (9) совпадает с числом неизвестных х, у,
z, А. Выражение множителя Л находится следующим образом. Дважды
дифференцируем по времени уравнение связи (8):
wV/ + d(r,v,?) =0.	A0)
Здесь w и v — ускорение и скорость точки; d(r,v,t) — слагаемые
в продифференцированном уравнении связи, не содержащие ускорения.
Из (9), A0) находится выражение неопределённого множителя:
Из A1) следует, что множитель Лагранжа А, и следовательно,
реакция связи находятся по известной активной силе, массе точки и её
состоянию в данный момент времени (без каких-либо предположений
о способе реализации). Такие реакции называются идеальными.

80
Гл. И. Заметки о способах виртуального варьирования
f(x,y,z,t) =
Рис. 10.1
В отсутствие трения направление реакции по нормали к поверх-
поверхности ещё не обеспечивает свойство идеальности связи. На рис. 10.1
показано разложение реакции неидеальной связи на составляющие.
Направленная по нормали составляющая равна реакции идеальной
связи только для множителя Л, найденного по формуле A1). Малые
неидеальности, вызванные деформируемостью связи, могут означать
наличие неидеальной составляющей, обусловленной упругими силами,
возможно, в сочетании с сила-
силами вязкого трения, пропорцио-
пропорциональными относительной состав-
составляющей скорости точки по отно-
отношению к поверхности [13].
Идеальные реакции не явля-
являются силами естественного вза-
взаимодействия материальных точек
системы с ограничениями, а пред-
представляют собой мысленный об-
образ, искусственно реализуемый
по описанной выше схеме (что
и оправдывает предложенный для
них термин — идеальные реакции). Можно отметить, что идеальные
связи, реализуемые идеальными реакциями, являются частным случа-
случаем сервосвязей (Бёген А.), и способ представления реакций идеальных
связей и сервосвязей един [13].
Способ реализации связи с помощью идеальных реакций освобож-
освобождает нас от анализа физических свойств ограничений. При этом сужа-
сужается класс рассматриваемых траекторий, так как идеальные реакции
находятся совместно с траекториями, являющимися дважды дифферен-
дифференцируемыми функциями времени.
10.4. Неопределённые множители при скользящем режиме.
Идеальные реакции и соответствующие траектории, как уже упоми-
упоминалось, не отражают «физических» свойств, которые уже рассматри-
рассматривались на примере реализации голономной связи упругими потенци-
потенциальными силами с бесконечно большим коэффициентом жёсткости
(см. заметку 2). Действительно, увеличение коэффициента жёсткости
упругой силы в пределе приводит ко всё более частому изменению
направления ускорения, т. е. к движению, называемому идеальным
скользящим режимом. В скользящем режиме траектория не имеет
того порядка гладкости, который соответствует идеальным реакциям.
В нём условия связи могут быть выполнены с заданной точностью
лишь на ограниченном отрезке времени. Найдём механический смысл
неопределённых множителей в реакции связи, полагая что реализация
голономной связи осуществляется потенциальными силами, а неголо-
номной связи — диссипативными силами. Пусть система задана функ-

10. О применении неопределённых множителей	81
цией Лагранжа L в переменных Лагранжа и имеются две идеальные
связи — голономная и неголономная:
f(q,t)=O, <p(q,t,q)=O.	A2)
Уравнения движения системы с неопределёнными множителями,
представляющими реакции идеальных связей, имеют вид
El(L) = X^ + A Et = -f.	A3)
dqi dqi	%
В скользящем режиме условия связей A2) могут нарушаться, по-
поэтому принимаем
f(q,t)=a, tp(q,t,q)=p.	A4)
Введём потенциальную энергию и диссипативную функцию Релея:
П = Щ-, R=4-> c = c0N, k = k0N, со,ко>О, N -> оо.
A5)
Если неголономная связь является линейной относительно обобщён-
обобщённых скоростей, то удвоенная функция R задаёт мощность сил линейно-
линейного вязкого трения в относительном движении [13]. Множество моделей
(с той же функцией Лагранжа, но при разных значениях N в A5))
описывается уравнениями
г-, / гЧ <9П dR	1
Сравнение A3) и A6) с учётом A4) показывает, что
Л = -са, II = -кC, (с = c0N, к = k0N).	A7)
Равенства A7) определяют механический смысл множителей Аи//.
При N ^оо значения а и /3 стремятся к нулю, а их произведе-
произведения A7) — к значениям неопределённых множителей реакций идеаль-
идеальных связей. Однако в отличие от траектории с идеальными связями,
траектории в полученном таким путём скользящем режиме имеют
другой порядок гладкости.
В частности, второе уравнение в A2) может быть следствием пер-
первого, т.е.
/(<?,*)= О, ^	g
Тогда и потенциальные, и диссипативные силы, заданные с помощью
функций A5), будут обеспечивать реализацию одной голономной свя-
связи и
/с
А = — са — ка = —Nkn (а + -^- а
\ ко
При достаточно больших N отношение коэффициентов со/ко будет ха-
характеризовать быстроту затухания величины «деформации» связи (а).

82	Гл. И. Заметки о способах виртуального варьирования
Ещё более общий способ реализации связи можно обеспечить, учиты-
учитывая присоединённые массы [43, 67].
10.5. О неопределённых множителях при варьировании функ-
функционалов. Пусть связь в системе с двумя независимыми аргументами
(например, временем t и линейной координатой одномерного деформи-
деформируемого элемента s) и двумя функциями, зависящими от этих аргумен-
аргументов, имеет вид
/ (?, 5, щ, щ, щ, щ, и\, uf2) = 0.	A8)
Составление уравнений для виртуальных вариаций связи A8) обсуж-
обсуждалось в заметке 9. Если реакция идеальной связи задаётся с помощью
неопределённого множителя Л (s, t), то вариация действия реакции,
в зависимости от того, является связь A8) неголономной или голоном-
ной, содержит слагаемое (и =(u\,U2)):
to So
X^Sudsdt	A9)
ой
U si
ИЛИ
h S2
-рг~ 5и -\—-г 5u I ds dt.	B0)
ou	du )
Сравним применение неопределённого множителя в задаче о несво-
несвободной механической системе с голономной связью с задачей вариаци-
вариационного исчисления. Выражение B0) после интегрирования по частям
преобразуется к виду
J V ди'{
В B1) введено обозначение
Для сравнения приведём результат варьирования при решении ва-
вариационной задачи на экстремум функционала при условии A8). Функ-
Функционал безусловной вариационной задачи содержит слагаемое
^2 S2
\\xfdsdt,	B2)
t\ S\
где хE'0 ~~ неопределённый множитель.

10. О применении неопределённых множителей	83
Составляем вариацию B2):
to So
ds+ | \x^fSudsdt-
ou
si	tx s
t. B3)
U si
Вид вариации B3) показывает, что условие стационарности функ-
функционала безусловной вариационной задачи содержит производную по
времени от неопределённого множителя (х), и следовательно, для
определения \ требуются начальные условия, которые в механиче-
механической постановке задачи отсутствуют (согласно принципу причинности
Ньютона движение должно определяться только состоянием систе-
системы в начальный момент времени). Поэтому траектории неголономной
системы будут принадлежать к решениям вариационной задачи при
дополнительных условиях. Можно показать, что в число этих условий
входят равенства
*2
B4)
df d(df\ d(df\\ ,df]s n
10.6. О неопределённых множителях в других задачах.
1.	О реакциях неудерживающих связей. Для неудерживающей иде-
идеальной связи неопределённый множитель может принимать значения
только одного знака. Если связь не напряжена, то множитель Л равен
нулю. В случае одной неудерживающей связи условие «ухода со связи»
математически соответствует моменту изменения знака неопределён-
неопределённого множителя. Однако если неудерживающих связей несколько, то
изменение знака неопределённого множителя одной (или нескольких)
связей ещё не означает, что именно данная связь (связи) ослабляется.
Это сигнал о том, что модель движения с одним составом напряжённых
связей (рассматриваемых как удерживающие) должна быть заменена
моделью движения с другим составом напряжённых связей. Задача
определения связей, ослабевающих или остающихся напряжёнными
в любой момент времени, решается с помощью принципа наименьшего
отклонения Больцмана-Болотова [7] и его обобщений [13, 109].
2.	Бесконечно малый неопределённый множитель используется при
варьировании расширенного функционала «действие» E.29) при посто-

84	Гл. И. Заметки о способах виртуального варьирования
янной функции энергии О = const E.30) (см. заметку 5). Уравнение
для изоэнергетических вариаций E.31) учитывается с помощью бес-
бесконечно малого множителя dw, определяющего параметр w. По па-
параметру w ведётся дифференцирование при составлении уравнений
движения в гамильтоновой форме E.32).
3.	Неопределённые множители в изопериметрических задачах. Ва-
Вариационные задачи со связями в виде постоянных значений функцио-
функционалов называются изопериметрическими. Правило множителей в этих
задачах состоит в том, что для исследования на безусловный экстре-
экстремум составляется функционал, в подынтегральное выражение которого
включаются подынтегральные выражения функционалов связей с по-
постоянными множителями. Неопределённые множители в изоперимет-
изопериметрических задачах являются константами [127].
4.	В задаче оптимального управления движением неопределён-
неопределённые множители, представляющие реакции, можно рассматривать как
управления, обеспечивающие минимум функционала «действие». При
этом вместо условий на ускорения, которые позволяют находить иде-
идеальные реакции, для устранения неопределённости реакции можно ис-
использовать условия оптимальности управлений. Неопределённые мно-
множители входят в уравнения движения линейно, поэтому возможны
скользящие режимы и особые экстремали [23].
11. О принципе Герца.
Принцип наименьшей кривизны
Тенденции развития механики находят своё концентрированное от-
отражение в принципах, которые, согласно Герцу, представляют основные
образы трёх «картин» механики. В современных курсах теоретической
механики технических университетов менее полно, чем «силовая» ме-
механика Ньютона, представлены «энергетическая» механика Лагранжа,
Гамильтона, Остроградского и «геометрическая» механика Гамильтона,
Герца, Каратеодори. В то же время именно последние две картины
находят широкое применение в современных естественно-научных фи-
физических и общединамических теориях.
Наиболее перспективна, по-видимому, тенденция рационального ис-
использования образов всех трёх картин [16]. К этому наименее подго-
подготовлен подход Герца. Классический принцип прямейшего пути сформу-
сформулирован как «эмпирический основной закон», объединяющий «обычный
закон энергии и принцип наименьшего принуждения Гаусса в одно
утверждение» [27]. Позже Дж.Л. Синг с помощью введённого им
понятия относительной кривизны обосновал более общее утверждение
принципа, допускающее наличие силового поля [137].
На основе принципа наименьшего отклонения одного движения
от другого [13] здесь приводится дальнейшее обобщение принципа

11.0 принципе Герца. Принцип наименьшей кривизны	85
наименьшей кривизны в координатном пространстве Герца. Оно при-
применимо к системам с нестационарными и неудерживающими связями
на множестве траекторий мыслимых движений, в которых касательные
ускорения материальных точек равны касательным ускорениям в их
действительном движении. Из полученного принципа как частный
случай следуют обобщение принципа, данное Сингом, и принцип пря-
прямейшего пути Герца.
11.1. Принцип прямейшего пути Герца. Основные подходы
к изучению механического движения Герц описал в виде трёх «картин»
образов механики, приняв для анализа каждой теории критерии её
допустимости, правильности, целесообразности и простоты [27].
Первая картина даётся «силовой» механикой Ньютона, основанной
на представлениях о пространстве (евклидовом), времени (математи-
(математическом, непрерывном, однородном), массе (одновременно инерционной
и тяжёлой) и силе как мере взаимодействия материальных тел. Вторую
картину составляет «энергетический» подход, использующий понятия
пространства (риманова), времени, массы и энергии и опирающийся на
интегральные принципы.
В основу третьей своей картины Герц положил категории простран-
пространства, времени и массы с широким использованием геометрии систем
материальных точек. При построении третьей картины движения Герц
дополнительно в качестве гипотезы полагает, что «одновременно дей-
действует нечто скрытое (не имеющее особой категории), являющееся
опять-таки движением и массой..., отличающееся от видимого не по
существу, а в отношении наших средств восприятия. Отношения, име-
имеющиеся между пространством и временем, составляют кинематику,
а между массой и временем не существует никакой связи. Между
массой и пространством имеются важные эмпирические соотношения
(пространственные связи, касающиеся только относительного положе-
положения масс между собой в виде однородных линейных уравнений между
первыми дифференциалами положений)» [27].
Новый основной принцип прямейшего пути Герц сформулировал
как эмпирический «основной закон: каждое естественное движение
самостоятельной материальной системы состоит в том, что система
движется с постоянной скоростью по одному из своих прямейших
путей. Это положение объединяет обычный закон энергии и принцип
наименьшего принуждения Гаусса в одно утверждение... Если бы связи
были разрушены (на один момент), то массы рассеялись бы в прямоли-
прямолинейном и равномерном движении... Это первый и последний основной
принцип механики. Из него и допущенной гипотезы скрытых масс
дедуктивно выводится содержание механики» [27]. В предложенном
законе Герц усматривает также объединение первого закона Ньютона
и принципа наименьшего принуждения Гаусса, а в числе преимуществ
отмечает, что «метод бросает яркий свет на разработанный Гамильто-

86
Гл. И. Заметки о способах виртуального варьирования
ном способ рассмотрения проблем механики при помощи характери-
характеристических функций».
Проиллюстрируем применение перечисленных трёх подходов на
простом примере.
Пример. Пусть наблюдается движение материальной точки, на-
находящейся на идеальной сфере постоянного радиуса в отсутствие ак-
активных сил.
В «силовой» механике применяется принцип «освобождаемости от
связей», согласно которому в уравнения движения включаются реак-
реакции связей. В случае идеальных связей для представления реакций
используются неопределённые множители Лагранжа (первая форма
уравнений Лагранжа или, иначе, уравнения Лагранжа первого рода).
Для несвободного движения материальной точки на сфере имеем урав-
уравнения
mxi = A-^-, f = ^ х2 — R = 0,	A)
где т — масса материальной точки, Х{ — декартовы координаты точки,
R — радиус сферы.
При «энергетическом» подходе для описания движения состав-
составляется функционал, например действие по Гамильтону с функцией
Лагранжа L = Т — П, где кинетическая и потенциальная энергия име-
имеют вид
Т =
mRz
(ф2 + ф2 cos2 if),
П = 0.
Здесь R, (р, ф — сферические координаты точки (рис. 11.1).
Из условий стационарности действия по Гамильтону следует, что
движение описывается уравнениями Лагранжа второго рода, с помо-
помощью которых получаем уравнения
движения материальной точки:
ф — ф2 sin ip cos ip = О,
d_
dty
— гр cos
=0.
т-г	dL A dL A
Поскольку — = 0 и — = 0, урав-
уравнения имеют два первых интеграла
(интеграл энергии и циклический
интеграл для циклической коорди-
координаты ф):
ф2 + ф2 cos2 i
= h = const,
Рис. 11.1
ф COS2 (f = фо COS2 (

11.0 принципе Герца. Принцип наименьшей кривизны	87
Следовательно, без ограничения общности отсчёт обобщённых ко-
координат можно выбрать с учётом начальных условий так, что движе-
движение будет происходить по дуге окружности большого радиуса R (при
^0=0 точка движется по меридиану). Условие стационарности функ-
функционала выделяет из всех «окольных путей» действительное движение
(«прямой путь»).
Геометрическая картина движения по Герцу достаточно ясна: пря-
прямейшими на сфере являются дуги окружностей больших радиусов.
Центр сферы и направление скорости точки в каждый момент времени
определяют соприкасающуюся плоскость.
Приведём аналитическое обоснование того, что траектория действи-
действительного движения имеет наименьшую кривизну. Вектор кривизны к
кривой в трёхмерном пространстве определяется как производная еди-
единичного вектора касательной т по длине дуги ds:
dx л ,	dr	, d г	/оч
— =k = kn, %=—, т.е. k=^.	C)
ds	ds	ds2
Выражения элементарной длины дуги траектории в декартовых
координатах и обобщённых координатах (риф имеют вид
3
ds2 = J2dxl ds2 = г2 (d(P2 + cos2 #2) •	D)
i=\
Классический принцип прямейшего пути (при условии движения по
инерции, т. е. с постоянной кинетической энергией) выводится непо-
непосредственно из принципа наименьшего принуждения Гаусса. В каче-
качестве меры принуждения принимается отклонение сравниваемых мысли-
мыслимых движений, среди которых находится и действительное движение,
от действительного же движения системы, полученной из данной осво-
освобождением от всех связей [7]. Поскольку активные силы отсутствуют,
свободная материальная точка имеет ускорение, равное нулю (равно-
(равномерное прямолинейное движение), поэтому принуждение имеет вид
Z	2	E)
Здесь через w обозначено любое мыслимое ускорение, которое при
фиксированном времени и заданном состоянии удовлетворяет условию
связи
u2=0.	F)
Задача выбора действительного движения в множестве мыслимых
с помощью принципа Гаусса сводится к решению задачи на минимум
функции E) при условии F), т.е. для исследования на безусловный
экстремум по ускорению имеем функцию
Z = - mw2 + /i(r w + v2),	G)
где \i — неопределённый множитель.

88	Гл. И. Заметки о способах виртуального варьирования
Примечание 1. Термин «мыслимые движения» мы используем
как синоним для обозначения кинематически возможных движений
(в данном состоянии, в данный момент времени с мыслимыми по Чета-
еву ускорениями) (см. заметку 9). Для мыслимых ускорений специаль-
специального обозначения не вводим (далее такое же обозначение используем
для ускорения в действительном движении), то же самое относится
и к кривизне.
Разложим ускорение точки на касательное и нормальное:
wr = si, wn = kv2n,
и учтём ортогональность векторов г и wr. После этого функция Z G)
и уравнение связи F) принимают вид
Z = Jm(^+^)+/i(rwn+ v2) ,	(8)
v2 - Rkv2 cos a = 0,	(9)
где а — угол между вектором п и радиусом сферы; —тг/2 < а < тг/2.
Можно заметить (см. (9)), что кривизна траекторий кинематически
возможных движений не превосходит величины, обратной радиусу
сферы.
Функция (8) минимизируется по параметрам, характеризующим
мыслимое ускорение. Мыслимое касательное ускорение определяется
одним параметром (ё), а нормальное — двумя параметрами: кривиз-
кривизной к и углом а, который равен двугранному углу между соприкасаю-
соприкасающимися плоскостями мыслимого и действительного движений. Условия
стационарности функции (8) по перечисленным параметрам имеют вид
^г = тё = 0,	A0)
оs
— = mkvA — /iRv2 cos a = 0,	A1)
UK
^ = fikv28ma = 0.	A2)
да
Равенство A0) показывает, что в действительном движении величина
скорости точки постоянна. Поскольку при v ^ 0 реакция связи не равна
нулю (/i ф 0), из A2) следует, что sin a = 0; как следствие (9) находим
кривизну траектории действительного движения:
к = ±.	A3)
С учётом сделанного выше замечания о кривизне мыслимых траекто-
траекторий найденная кривизна A3) является наименьшей из них, а траекто-
траектория, соответственно, прямейшей.
Неопределённый множитель \± определяет реакцию сферы на мате-
материальную точку и находится из уравнения A1). Отметим, что вывод
о равномерности движения (постоянстве кинетической энергии) явился

11.0 принципе Герца. Принцип наименьшей кривизны	89
не следствием принципа наименьшей кривизны, а условием применения
этого принципа в его классической формулировке.
Примечание 2. Пример показывает также необходимость уточ-
уточнения области применения термина «прямой путь» для траектории
в действительном движении. Пусть движение материальной точки про-
происходит в течение достаточно большого промежутка времени, так что
пройденный точкой путь будет иметь длину более половины длины
окружности радиуса R. Тогда, несмотря на то, что действительный
путь является в каждой точке «прямейшим» по Герцу и «прямым»
в интегральном смысле, он не будет кратчайшим, так как расстояние
между начальным и конечным положениями точки короче не по дуге
траектории, а по дуге, дополняющей её до полной окружности. Кро-
Кроме того, для начального и конечного положений точки, являющихся
концами большого диаметра сферы, «прямых» путей бесконечно много.
Точки, через которые могут проходить два или целый пучок прямых
путей, называются сопряжёнными кинетическими фокусами. Известно,
что при достаточной близости начального и конечного положений (ко-
(когда между ними нет фокуса, сопряжённого с начальным положением)
и в общем случае на действительной траектории достигается минимум
действия. Тогда прямой путь является кратчайшим в смысле функцио-
функционала, определяющего «расстояние» между точками.
Геометрическая картина, рассмотренная в примере для одной мате-
материальной точки, естественным образом обобщается на систему матери-
материальных точек. Системе N материальных точек ставится в соответствие
геометрическая точка (изображающая точка) в евклидовом простран-
пространстве 37V измерений с координатами
I ЗЛГ	N
з
№-2 = /x3fc—I =/x3fc = mk, k= l,...,iV,
где rrik — массы материальных точек с номерами k; M — масса
системы; ^ (г = l,...,3iV) — декартовы координаты материальных
точек. Координаты A4) далее будем называть координатами Герца.
Элемент дуги траектории, изображающей точки, имеет вид
I N	| ЗЛГ	ЗЛГ
d(j2 = jfYl тк dsl = jjY, Vi d^i = E dxl	A5)
Аналогично векторам (З), но только размерности 3N, вводятся
радиус-вектор г(х\,... ,жздг), единичные векторы т, п, векторы ско-
скорости v и ускорения w изображающей точки и вектор кривизны её
траектории К:
к = ^4.
da

90	Гл. И. Заметки о способах виртуального варьирования
Дальнейший ход рассуждений проводится по той же схеме, что
и в приведённом выше примере.
Учитывая, что связи — только однородные относительно скоро-
скоростей (катастатические [84]), имеем интеграл энергии (напомним, что
в классической формулировке обобщённые силы отсутствуют), поэтому
касательное ускорение равно нулю и принуждение как отклонение
движения системы от движения тех же, но свободных материальных
точек определяется только нормальными ускорениями. Минимум при-
принуждения
Zw=l-Mw2=l-Mw2n=l-Mv2K2
находится при условии, что выполняются ограничения на ускорение,
следующие из уравнений связей (в данном случае в этих уравнениях
остаются только нормальные ускорения). При нахождении минимума
принуждения по ускорениям, кроме уравнения вида A0), подтвер-
подтверждающего, что движение изображающей точки будет равномерным,
и уравнений связей, получаем систему линейных алгебраических урав-
уравнений относительно компонент вектора кривизны и неопределённых
множителей. Найденный из этих уравнений вектор кривизны имеет
наименьший модуль, что соответствует действительному движению.
11.2. Некоторые направления развития принципа прямейше-
прямейшего пути. Отмечая незавершённость своей работы, Герц пишет:
«...честнее будет признать, что наше понятие допустимых связей носит
характер гипотезы, принятой в виде пробы». «Оказывается также, что
формы силовых функций могут иметь весьма общий характер, и мы
не устанавливаем для них никаких ограничений. Но с другой стороны,
остаётся ещё открытым вопрос, не существует ли среди форм, встре-
встречающихся в природе, хотя бы одна, которая не поддаётся такому объ-
объяснению» ([27], с. 55). Иначе говоря, Герц усматривал необходимость
продолжения исследований принципа как в направлении расширения
гипотезы о допустимых связях, так и в ответе на вопрос о существо-
существовании силовых полей, которые невозможно представить связями.
Напомним, что Герц рассматривал только связи, однородные отно-
относительно скоростей. Более общим является известный класс нестаци-
нестационарных связей, а ещё более общим — класс сервосвязей Бёгена [3].
Кроме того, не ожидая кардинального решения проблемы представле-
представления силовых полей с помощью реакций связей, можно одновременно
изучать принцип Герца для несвободных систем с учётом действую-
действующих сил. Конечно, «чистота» геометрической картины будет нарушена,
так как будут присутствовать образы первой картины, однако более
перспективно, по-видимому, использование образов всех трёх картин.
К обобщениям принципа относится также применение принципа для
систем с неудерживающими связями.
Приложение принципа к консервативным системам становится воз-
возможным на основе концепции Герца о кинетическом происхождении

11.0 принципе Герца. Принцип наименьшей кривизны	91
потенциальной энергии. Согласно этой концепции потенциальная энер-
энергия консервативной системы всегда может быть рассматриваема как
кинетическая энергия так называемых «скрытых» движений. Скрыты-
Скрытыми движениями называют такие движения, при которых изменяются
только циклические (скрытые) координаты. Циклические координаты
в данном случае вводятся искусственно, что приводит к изучению
«расширенной» системы.
Для учёта заданных (активных) сил, не являющихся, вообще го-
говоря, потенциальными, и связей, допускающих применение принципа
наименьшего принуждения, в работе [137] вводится так называемая
динамическая кривизна К&, равная положительному квадратному кор-
корню из выражения
(|)	A7)
Поскольку A7) совпадает с принуждением по Гауссу, принцип
наименьшей (динамической) кривизны К& A7), сформулированный
Сингом, тождествен принципу наименьшего принуждения. Далее бу-
будем изучать свойства траектории, изображающей точки с помощью
понятия кривизны по Герцу A6) {геометрической кривизны [27]),
а также понятия относительной геометрической кривизны двух тра-
траекторий [137], определяемой как модуль разности векторов кривизны
этих траекторий. Например, если траектории 1 и 2 имеют векторы
кривизны Ki и К2, то в равенстве
(K{-K2f = K2l2	A8)
величина К\2 есть относительная кривизна траектории 1 по отношению
к траектории 2.
Понятие относительной кривизны позволяет использовать различ-
различные формы принципа наименьшего принуждения [13], полученные
сравнением отклонений движений друг от друга по мере принужде-
принуждения Гаусса. Обоснование новых формулировок принципа наименьшей
кривизны для систем, в которых имеются и силовые поля, и связи, не
только однородные относительно скоростей (и не только удерживаю-
удерживающие), даётся в п. 11.3.
11.3. Принцип наименьшей кривизны. Получим формулировку
принципа наименьшей кривизны для систем с идеальными удержива-
удерживающими нестационарными связями с помощью принципа наименьшего
отклонения [7]. В этом принципе наряду с данной (несвободной) си-
системой рассматривается так называемая освобождённая система: си-
система, состоящая из тех же материальных точек, движение которых
ограничено лишь частью связей. Материальные точки освобождённой
системы находятся под действием тех же активных сил и имеют то же
состояние. В пространстве координат Герца A4) с евклидовой метрикой

92	Гл. И. Заметки о способах виртуального варьирования
имеем отклонение действительного движения от действительного же
движения освобождённой системы, равное
Z=^M(w-w0J,	A9)
где w, w° — действительное ускорение системы и действительное
ускорение освобождённой системы соответственно.
Составляем условие стационарности функции A9) в множестве
мыслимых движений с мыслимыми ускорениями w*:
5Z = M(w - w°)(w* - w) = 0.	B0)
Каждое из ускорений в B0) представляется в виде суммы касательного
и нормального:
w = wr + v2K, w° = w°T + v2K°, w* = vr* + v2K\ B1)
Для сравнения используем мыслимые движения, в которых мыс-
мыслимые касательные ускорения равны касательному ускорению в дей-
действительном движении, т.е. w* = wr. Тогда уравнение B0) после
подстановки B1) принимает вид
(wr - w°T + v2K - v2K°) (v2K* - v2K) = 0.	B2)
С учётом того, что векторы wT, w^ ортогональны векторам К, К*, при
условии v2 ф 0 из B2) получаем
(К - К0) (К* - К) = 0.	B3)
Произведение в левой части B3) представляется в следующем виде:
(К - К0) (К* - К) = 1- (К - К0J + i (К* - КJ - 1- (К* - К0J.
B4)
Согласно B3) правая часть B4) равна нулю, откуда имеем равенство
(К - К0J + (К* - КJ = (К* - К0J.	B5)
Каждой величине относительной кривизны в равенстве B5) мож-
можно поставить в соответствие стороны прямоугольного треугольника,
каждая из вершин которого условно обозначает тра-
траекторию одного из трёх движений: d — траектория
действительного движения, 5 — траектория мыслимо-
мыслимого движения, д — траектория действительного дви-
движения освобождённой системы (рис. 11.2).
Катеты в этом треугольнике изображают относи-
Рис 11 2	тельную кривизну траектории действительного дви-
движения относительно траектории освобождённой си-
системы и относительную кривизну траектории любого мыслимого дви-
движения (имеющего касательное ускорение, равное касательному уско-

11.0 принципе Герца. Принцип наименьшей кривизны	93
рению системы в действительном движении) относительно траектории
действительного движения, а гипотенуза — относительную кривизну
траектории мыслимого движения относительно траектории освобож-
освобождённой системы.
Из B5) следуют неравенства
(К* - К0J > (К - К0J, (К* - К0J > (К* - КJ. B6)
Неравенства B6) в координатном пространстве Герца выражают
принцип наименьшей кривизны систем с нестационарными удержива-
удерживающими связями: на множестве траекторий мыслимых движений, в ко-
которых касательные ускорения материальных точек равны касательным
ускорениям в их действительном движении, траектория действи-
действительного движения системы со связями имеет наименьшую от-
относительную кривизну по отношению к траектории действительного
же движения системы, полученной освобождением от любой части
удерживающих связей.
Приведём некоторые частные случаи применения полученного
принципа.
1.	Пусть силовое поле активных (заданных) сил отсутствует, в ка-
качестве освобождённой системы принята система свободных материаль-
материальных точек (освобождение от всех связей); соответственно, кривизна
траектории освобождённой системы равна нулю (К0 = 0). Тогда нера-
неравенство B6) принимает вид
(K*f > (КJ,
т. е. кривизна действительной траектории системы является наимень-
наименьшей по сравнению с кривизной траекторий мыслимых движений, в ко-
которых касательные ускорения равны касательному ускорению системы
в действительном движении.
2.	Пусть кроме условий, принятых в 1, дополнительно имеется
предположение, что все связи являются катастатическими. Тогда каса-
касательные ускорения в действительном движении (и мыслимых движе-
движениях, принятых к сравнению) равны нулю и из B5) следует принцип
прямейшего пути Герца, который можно рассматривать как обобщение
закона инерции Галилея: система движется по прямейшему пути (т.е.
по пути наименьшей кривизны) с постоянной по величине скоростью.
Равенство B5) получено как следствие принципа наименьшего от-
отклонения при отыскании действительного ускорения в множестве срав-
сравниваемых мыслимых ускорений, различающихся только нормальными
составляющими (и следовательно, кривизной траекторий).
Аналогичный приём ограничения на принимаемые к сравнению
мыслимые ускорения позволяет получить из других форм принципа
наименьшего отклонения [13] соответствующие утверждения принципа
наименьшей кривизны. Например, из принципа наименьшего отклоне-

94	Гл. И. Заметки о способах виртуального варьирования
ния для систем с неудерживающими связями в форме Больцмана-Бо-
лотова [7, 13] получаем следующую форму принципа наименьшей кри-
кривизны: в координатном пространстве Герца на множестве траекторий
мыслимых движений, в которых касательные ускорения материальных
точек равны касательным ускорениям в их действительном движении,
траектория действительного движения системы со связями имеет
наименьшую относительную кривизну по отношению к траектории
действительного же движения системы, полученной освобождением
от всех неудерживающих и от любой части удерживающих связей.
Обобщение принципа, данное Сингом, и принцип прямейшего пути
Герца являются частными случаями полученных утверждений.
12. О принципах несвободных
динамических систем
Принцип освобождаемости от связей Н.Г. Четаев обобщил на си-
системы, в которых кроме чисто механической части содержатся пере-
переменные параметры, описываемые обыкновенными дифференциальными
уравнениями первого порядка [129]. По современной терминологии та-
такие системы называют динамическими. Если существуют ограничения
на движение, то мы имеем несвободную динамическую систему. В от-
отличие от связей, создающих реакции только на материальные точки
механической системы, в уравнения для параметров несвободной дина-
динамической системы также включаются слагаемые, названные Четаевым
принуждениями реакций. Связи являются условиями, налагаемыми
на состояние материальных точек системы и на значения параметров
в каждый момент времени.
В заметке приведены свойство идеальности, принцип наименьшего
принуждения и принцип виртуальных скоростей для несвободных ди-
динамических систем.
12.1. Принцип освобождаемости по Четаеву. В задаче Четаева
о вынужденных движениях [129] предполагается, что силы, приложен-
приложенные к материальным точкам, могут определяться не только состоянием
и временем, но и некоторыми параметрами. Изменение параметров
описывается обыкновенными дифференциальными уравнениями перво-
первого порядка. Динамика свободной системы задана системой уравнений
второго порядка относительно координат точек и уравнений первого
порядка для параметров:
Wfc = Ffc, k=l,...,n,
fiupu = Фи,..., v = 1,... , га,
где nik — массы материальных точек; w& — ускорения; F& — силы,
зависящие от состояния материальных точек, времени и значений пара-
параметров (rjfe, Vfc, t, pu); \iv — положительные функции координат точек,

12. О принципах несвободных динамических систем	95
времени и параметров; Фи — принуждения, являющиеся функциями
тех же аргументов, что и силы F&.
Пусть состояние материальных точек и значения параметров в каж-
каждый момент времени удовлетворяют уравнениям связей (вообще говоря,
нелинейным относительно скоростей):
V^(ri,vi,...,rn,vn,pi,...,pm,?) =0,
I = 1,...,г < Зп + т.
Обобщение принципа освобождаемости, данное Четаевым, состоит
в том, что наложение связей вида B) влияет и на процесс изменения
параметров через так называемые «принуждения реакций», которые
добавляются в виде слагаемых в уравнения для параметров. Уравнения
несвободной системы по Четаеву принимаются в виде [129]
Fk+~Rk, k=l,...,n,
(о)
[iy'Py = Ф„ + Р„,..., v = 1,... , га,
где Hk — реакции связей, Ру — принуждения реакций.
Уравнения C) рассматриваются вместе с уравнениями B).
12.2. Свойство идеальности. Общее уравнение несвободных
динамических систем. Для задания реакций и принуждений реакций
система B), C) должна быть доопределена. В этих целях использу-
используем аналог свойства идеальности связей. Свойство идеальности связей
в аналитической механике вводится с помощью приёма сравнения
мыслимых движений из одного и того же состояния и может быть
записано в трёх эквивалентных формах:
? (Rfe • Srk) = 0, J2 (Rk • Svk) = 0, J2 (Rk ' Swk) = 0, D)
k=\	k=\	k=\
где 5rk — векторы виртуальных перемещений, 5vk — векторы вирту-
виртуальных скоростей, 5wk — векторы варьированных ускорений. Первая
и вторая совокупности векторов образуются из третьей умножением на
коэффициенты пропорциональности с размерностями [с2] и [с] [13].
Состояние системы с параметрическими связями задаётся в каж-
каждый момент времени t значениями радиусов-векторов rk, скоростей
точек vk и параметров р„. Дифференцированием по времени уравнений
связей B) получаем уравнения, которым удовлетворяют мыслимые
ускорения точек и мыслимые скорости изменения параметров:
По/	т о /
7^~Wk + E i&Pi> + di(ri,vi,...,rn,vn,pu...,pm,t) =0,
k=i °Vk	v=\ °Pv	E)
1 = l,...,r,
где di — слагаемые, не содержащие w^ и ри.

96	Гл. И. Заметки о способах виртуального варьирования
Соответственно для вариаций ускорений ^w^ и вариаций скоростей
изменения параметров 5р„ (при фиксированном состоянии и фиксиро-
фиксированном времени) из E) имеем уравнения
В уравнениях F) величины 5wk и 5ри не обязательно являются
малыми. Приняв пропорциональные векторам Sw^ и 5pv бесконечно
малые виртуальные скорости (по Лагранжу) 5vk и виртуальные изме-
изменения параметров 5ри, имеем также
Очевидно, что критерий идеальности параметрических связей в от-
отсутствие параметров не должен противоречить равенствам D). Поэто-
Поэтому естественно с помощью приёма сравнения мыслимых движений для
реакций и принуждений реакций параметрических связей B) составить
равенство
^2 (R/c^waO + ^ Py^Vv = 0>	(8)
k=\	v=\
или
J2 (Rfc^vfc) + Yl p"sPv = °-	(9)
к=\	v=\
Таким образом, в качестве критерия идеальности параметрических
связей B) принимается равенство (8) или эквивалентное ему равен-
равенство (9).
Умножим каждую группу уравнений C) на ^w^ и 5pv соответствен-
соответственно и просуммируем по индексам к = l,...,n; v= l,...,m. Из полу-
полученных сумм с учётом свойства идеальности (8) (или (9)) составляем
общее уравнение
п	т
У (mkwk - Ffe) 5wk + у {nvpv - PvMpv = 0,	A0)
Е
к=\	v=\
или эквивалентное общее уравнение
п	т
vk + 5Z (№v ~ PvNpv = 0.	A1)
k=\	v=\
Общее уравнение A0) (и A1)) несвободных динамических си-
систем C) с идеальными связями B) является необходимым и доста-
достаточным (при предположении реализуемости реакций и принуждений
реакций) условием того, что действительное движение системы для
заданных сил F& и принуждений Ру согласовано с уравнениями свя-
связей [13].

12. О принципах несвободных динамических систем	97
Доказательство утверждения почти дословно повторяет доказа-
доказательство классического принципа Даламбера-Лагранжа (см., напри-
например, [25]).
В отсутствие параметров р„ уравнение A1) имеет вид общего урав-
уравнения, называемого принципом Журдена:
JT(mkwk-FkMvk = 0.	A2)
k=\
В общем уравнении A2) применяются виртуальные скорости
в смысле Лагранжа и М. В. Остроградского [79], поэтому оно
является следствием любой из двух других эквивалентных форм D)
свойства идеальности связей. Для систем с параметрическими связями
вариантов общего уравнения осталось только два: A0) и A1).
Свойство идеальности в третьей записи в D) приводит, как извест-
известно, к общему уравнению аналитической механики:
f^(mkwk-FkMwk=0,	A3)
k=\
которое является условием стационарности функции принуждения по
Гауссу.
12.3. Принцип наименьшего отклонения. Уравнение с вариаци-
вариациями ускорений A0) также будем рассматривать как условие стационар-
стационарности функции отклонения несвободного движения C) со связями B)
от свободного движения, описываемого уравнениями A).
В качестве меры отклонения движения 1 от движения 2 в момент
времени t примем величину
Z = \t т*К> - wfJ+ f „„(pO) - #f,	A4)
k=\	v=\
A) B)	.A) .B)
где w^y, wykJ и pvJ, pvJ — ускорения точек и скорости изменения
параметров в первом и во втором движении соответственно. Состояния
материальных точек и значения параметров в обоих движениях одина-
одинаковы. Приняв в A4) за первое мыслимое несвободное движение, а за
второе — движение системы, освобождённой от всех связей, получаем
функцию
i(^)
В A5) звёздочкой отмечены мыслимые ускорения точек и мыслимые
скорости изменения параметров, которые удовлетворяют уравнению E)
независимо от действующих сил и принуждений. Действительные
ускорения wk и скорости изменения параметров ри принадлежат мно-
4 В. Г. Веретенников, В. А. Синицын

98	Гл. И. Заметки о способах виртуального варьирования
жеству мыслимых. В качестве вариаций ускорений и скоростей изме-
изменения параметров принимаются разности
5wk = w^ — Wfc, к = 1,... ,n,
<%, = P$-Pv, v = l,...,m.
Функция A5) положительно определена, и условие её стационарно-
стационарности по Wk и pv даёт общее уравнение A0).
Полагая, что общее уравнение A0) при условиях E) и F) имеет
единственное решение, сформулируем результат как принцип наимень-
наименьшего отклонения: в любой момент времени из всех мыслимых дви-
движений истинное движение несвободной динамической системы с иде-
идеальными удерживающими связями имеет наименьшее отклонение от
движения системы, полученной освобождением от всех связей.
Обобщение принципа наименьшего отклонения для несвободных
динамических систем с идеальными связями можно получить в тех же
направлениях, что для принципа Гаусса [13]: при сравнения истинного
движения с движениями системы, полученной освобождением от части
связей, при наличии неудерживающих связей и т. д.
12.4. Общее уравнение динамики систем с вероятностными
связями. Пусть в каждый момент времени положение системы описы-
описывается набором обобщённых координат q\,...,qn механической части
и случайными параметрами рь ... ,рт. Система задана функциями
T = T(q,q,p,t), n = Il(q,q,p,t), R = R(q,q,p,t),	A6)
где Т, П, R — кинетическая, потенциальная энергия и диссипативная
функция Релея соответственно.
Вектор случайных параметров р удовлетворяет стохастическому
дифференциальному уравнению Ито вида [71]
p = <p(q,p,?)+?(q,p,?)V, р(?0) = р0,	A7)
где cp(q, p, t) и \|/(q, p, t) — вектор-столбец и матрица размерности т х /
детерминированных функций, V = [V\(t),... ,Vi(t)]T — вектор-столбец
белых шумов (равный производной по времени от произвольного слу-
случайного процесса с независимыми приращениями).
Во всякий момент времени t на движение системы наложены иде-
идеальные линейные относительно обобщённых скоростей и параметров
связи в виде уравнений
п-\-т
Y^ aij^j + ai = 0, i=l,...,l<m,	A8)
i=i
где тс — вектор с координатами q\,...,qn, P\,---,Pm'> aij> ai ~ диффе-
дифференцируемые функции обобщённых координат и времени. Уравнения
для виртуальных скоростей 5q\,... ,5qn и виртуальных изменений па-

12. О принципах несвободных динамических систем	99
раметров 5р\,... ,5рт (вектор виртуальных вариаций 5п) связей A8)
имеют вид
п-\-т
]Г (HjSttj = 0, i= I,...,/.	A9)
i=i
Ковектор обобщённых сил, соответствующих обобщённым координа-
координатам, считаем допускающим представление
где Q^ и Q^ — вектор-столбец и матрица размерности п х I.
Условие идеальности связей A8) позволяет исключить обобщённые
реакции и принуждения реакций при составлении общего уравнения:
+ д#+(р^Нр=0-B0)
В уравнении B0) может быть проведена подстановка зависимых
виртуальных вариаций вектора <5тс через независимые с помощью урав-
уравнений A9). После этого из общего уравнения B0), приравнивая нулю
коэффициенты при независимых виртуальных вариациях вектора 5п,
получаем п-\-т — I уравнений в стохастических дифференциалах Ито,
по которым с применением обобщённой формулы Ито можно составить
уравнения для распределений вектора состояния системы [71]. Полу-
Полученные уравнения рассматриваются вместе с уравнениями связей A8).
Здесь система отличается тем, что учитывается влияние связи на изме-
изменение параметров через идеальные принуждения реакций по Четаеву.
12.5. Принцип освобождаемости для динамических систем.
Принцип освобождаемости от связей в механике (заключающийся во
введении в уравнения дополнительных слагаемых, называемых реак-
реакциями связей) распространяется на динамические системы, описыва-
описываемые обыкновенными дифференциальными уравнениями при наличии
ограничений на фазовые координаты. Составлено общее уравнение
движения динамических систем с идеальными связями, частными слу-
случаями которых являются системы Н. Г. Четаева (см. п. 12.1) и системы
с производными высших порядков [88]. Теория применяется при по-
построении уравнений для медленных переменных в системах с малым
параметром (не равным нулю). В качестве примера рассматривается
автоколебательная система с инерционным возбуждением, к которой
приводится динамическая система Лоренца (E.N. Lorenz) [73].
1. Принцип освобождаемости от связей. Реакции идеальных связей.
Принцип освобождаемости от связей для несвободных динамиче-
динамических систем получается как естественное обобщение приёма, приме-
применённого Н. Г. Четаевым в работе [129], а свойство идеальности связей
формулируется как результат расширенного применения гипотезы Гаус-
Гаусса о мыслимых движениях механической системы (см. [88]).

100	Гл. И. Заметки о способах виртуального варьирования
Моделью физического процесса (или процесса другой природы)
является динамическая система, которая, будучи свободной (без огра-
ограничений), описывается обыкновенными дифференциальными уравне-
уравнениями:
x = f(x,?), хеГ,	B1)
где х — вектор фазовых координат размерности п (фазовое простран-
пространство с евклидовой метрикой); координаты вектора f — дифференци-
дифференцируемые функции своих аргументов; t — время; точкой обозначена
производная по времени.
Пусть движение системы B1) вынужденно изменяется удерживаю-
удерживающей связью, уравнение которой имеет вид
р(х,*)=0,	B2)
где (р — непрерывная дифференцируемая регулярная функция (для
простоты считаем, что она одна).
Известно, что связь B2) реализуется с помощью реакций — воздей-
воздействий того же физического содержания, что и описываемые функциями
в правых частях соответствующих уравнений системы B1).
Принцип освобождаемости состоит в том, что несвободная система
рассматривается как свободная, которая описывается уравнениями
x = f(x,?)+r*	B3)
совместно с уравнением связи B2). В правых частях уравнений B3)
реакциями г* являются объективные воздействия, изменяющие со-
составляющие фазовой скорости некоторых отмеченных (согласно свой-
свойствам системы) фазовых координат (обозначим этот вектор через х* =
= (х\,..., х\, 0,..., 0), I ^ п; координаты вектора г* с номерами от Z + 1
до п принимаются равными нулю).
Например, в механических системах такие «отмеченные» фазо-
фазовые координаты определяются аксиомами Ньютона (это обобщённые
скорости в механике Лагранжа и обобщённые импульсы в динами-
динамике Гамильтона). Если в системе B1) некоторые фазовые координаты
являются производными по времени от других фазовых координат,
то реакция вводится только в уравнение с производной наиболее
высокого порядка. В случае, когда динамическая система содержит
подсистему, являющуюся чисто механической, реакциями в этой под-
подсистеме являются обобщённые силы, которые соответствуют силам
реакции.
Модель B2), B3) требуется доопределить: нужна информация,
относящаяся к проблеме реализации связей. Вопрос о способах реали-
реализации связей является одним из основных в динамике несвободных си-
систем. Отвлечься от способа реализации связей, как и в аналитической
механике, позволяет представление о свойстве идеальности связей,
которое формулируется с помощью понятия о виртуальных вариациях

12. О принципах несвободных динамических систем	101
(в механике им соответствуют виртуальные перемещения, виртуальные
скорости, вариации ускорений по Гауссу).
Расширим область применения гипотезы Гаусса о виртуальном ва-
варьировании в механике следующим образом: при составлении урав-
уравнений для виртуальных вариаций неизменными принимаются время
и те фазовые координаты, в уравнения которых реакции не входят.
Соответственно получаем варьированное уравнение связи:
V?x*.(bc*=O, V?x* = |^,	B4)
где 5х* — вектор виртуальных вариаций (бесконечно малых вирту-
виртуальных изменений координат вектора х* не нарушающих условие свя-
связи B2)).
Для множества виртуальных вариаций, удовлетворяющих уравне-
уравнению B4), аксиоматически вводим критерий (необходимое и достаточ-
достаточное условие) идеальности связи:
г* • 5х* = 0.	B5)
При предположении, что связь B2) является идеальной, реакция
представляется с помощью неопределённого множителя Л в виде г* =
= А(?>х*. Множитель Л находится из уравнения, получаемого путём
дифференцирования уравнения связи с последующей подстановкой в
него уравнений несвободного движения.
2. Общее уравнение динамических систем.
С учётом свойства идеальности B5) и уравнений B3) получаем
общее уравнение динамических систем вида B1):
[x-f(x,?)]-(bc*=0.	B6)
Общее уравнение B6) рассматривается вместе с уравнениями свя-
связей вида B2) и уравнениями для виртуальных вариаций вида B5). Для
динамических систем B3) общее уравнение B6) не содержит реак-
реакций идеальных связей, из него следует столько уравнений движения,
сколько имеется независимых виртуальных вариаций. Таким путём
из уравнений несвободной системы исключаются реакции идеальных
связей.
Частным случаем рассматриваемых динамических систем являются
системы с производными высших порядков [88] и системы, включаю-
включающие механическую часть, описываемую дифференциальными уравне-
уравнениями второго порядка (системы Четаева; см. п. 12.1).
Приложение принципа демонстрируется на примере автоколебатель-
автоколебательной системы с инерционным возбуждением [73] (в форме системы
Четаева) (см. заметку 29).

102	Гл. И. Заметки о способах виртуального варьирования
13. О применении вириалов.
Центральное вириальное равенство
Рассматривается применение вириала [13, 55] системы векторов,
являющихся динамическими величинами. Составлен вириальный диф-
дифференциальный принцип динамики физической системы, модель кото-
которой предложена В. В. Румянцевым [103] при обосновании принципа
Н.Г. Четаева. Обсуждаемый подход может быть использован при ре-
решении задач термомеханики.
13.1. О вириале количеств движения и вириале системы сил.
Вириалом системы векторов а& относительно некоторого центра назы-
называется скалярная величина ^а^г^, где г& — радиусы-векторы точек
к
приложения векторов относительно центра [55]. Исторически понятие
о вириале введено Р. Клаузиусом в его теореме о вириале (см., напри-
например, [29]), в которой вириалом была названа величина — ^ ( У
Х к
(F& — векторы сил, ( ) — знак усреднения по времени). Мы будем
пользоваться приведённым выше определением для физических вели-
величин, представляемых векторами.
Обозначим через Vo вириал количества движения системы матери-
материальных точек относительно центра О:
У0 = ^2тк^кГк,	A)
к
где гпь и Vfc — массы и скорости материальных точек, к = 1,... ,7V.
Пример 1. Целесообразность использования понятия о вириале
количества движения показывает задача о соударении двух одинаковых
однородных шаров. Пусть движение шаров является поступательным
с одинаковыми по величине скоростями по прямой, соединяющей цен-
центры шаров, удар абсолютно упругий в предположениях стереомеха-
нической теории, ударные активные силы отсутствуют. Как известно,
в доударном и послеударном состояниях системы одинаковы её ос-
основные динамические величины (количество движения, кинетический
момент и кинетическая энергия). Однако между шарами происходит
«обмен движениями», который перечисленные динамические величины
не отражают. В тех же условиях за время движения вириал количества
движения изменяется, и это изменение нетрудно найти с помощью
теоремы об изменении вириала количества движения.
Теорема об изменении вириала количества движения: производ-
производная по времени вириала количества движения системы, вычисленного
относительно некоторого центра, равна сумме удвоенной кинетической
энергии системы и вириала системы сил относительно того же центра.
Доказательство состоит в непосредственном дифференцировании
по времени обеих частей равенства A). Дифференцируя выражение A)

13. О применении вириалов. Центральное вириальное равенство 103
по времени и используя второй закон Ньютона, получаем равенство
(центр неподвижный)
?	B)
к
где Т — кинетическая энергия системы. Что и требовалось доказать.
Для движения в осях Кёнига получаем равенство, аналогичное
равенству B) и выражающее теорему об изменении вириала количества
относительного движения:
= rfc-rc,	C)
где VI — вириал количества относительного движения в осях Кёнига,
вычисленный относительно центра масс С; 7J — кинетическая энергия
относительного движения в осях Кёнига; гс — радиус-вектор положе-
положения точки С в инерциальных осях.
Теорема об изменении вириала количества движения в инте-
интегральной форме. Интегрируя равенство B) на фиксированном проме-
промежутке времени [ti,^], получаем равенство
*2	h
V0{t2) - V0(ti) = J 2Tdt + J ? Fk*k dt.	D)
Пример 2. Приращение вириала количества движения системы,
описанной в примере 1, получаем по формуле D). При вычислении
интегралов в правой части D) с учётом исчезающе малой продолжи-
продолжительности удара первое слагаемое равно нулю, а второе равно вириалу
импульсов сил, создающих поле ускорений (однородное).
Пример 3. Пусть система представляет собой абсолютно твёрдое
тело. Тогда из C) следует равенство
= -2I?.	E)
Пример 4. Если движение системы материальных точек является
финитным, то усредняя по времени (на периоде или бесконечно боль-
большом промежутке времени) равенства B), C), в пределе имеем
.	F)
к	к
Первое равенство в F) (теорема Р. Клаузиуса о вириале) является
одним из основных законов в кинетической теории газов.
13.2. Центральное вириальное равенство. Рассмотрим меха-
механическую систему с идеальными удерживающими связями, возмож-
возможно, неголономными, зависящими от скоростей. Согласно принци-

104	Гл. И. Заметки о способах виртуального варьирования
пу освобождаемости уравнения движения материальных точек име-
имеют вид
mkwk=Fk+Rk, k = I	iV,	G)
где mk и wk — массы и ускорения точек; Fk и Rk — равнодействующие
активных сил и сил реакций, приложенные к точке с номером к
(обозначение Fk, в отличие от п. 13.1, сохранено только для активных
сил); N — число материальных точек.
Теорема об изменении вириала количества движения B) для дви-
движений, описываемых уравнениями G), имеет форму
T>0 = 2T + EF^ + ER^V	(8)
к	к
Применим к равенству (8) операцию изохронного варьирования (см. за-
заметку 8). Переход в варьированное состояние осуществляется следу-
следующим способом: действительное состояние включается в зависящее
от параметра а семейство функций rk(t,a), vk(t,a) и полагается, что
оно содержится в этом семействе при а = 0. Операция варьирования
состояния заключается в вычислении производной по а (а = 0).
Обсуждение варьирования ускорений приведём ниже, а пока из
равенства (8) формально имеем
5V0 = 25T + Y. Yk5vk + Е 5F^k + E R^ + E 5Rkrk. (9)
к	к	к	к
Положим, что вариации 5гк являются виртуальными. Тогда
O,	A0)
к	к
где 5'А — виртуальная работа активных сил. Второе равенство выра-
выражает свойство идеальности связей.
Подставляем A0) в равенство (9):
5V0 = 25T + 5'А + Е № + SRk) rk.	A1)
к
Обсудим варьирование в последней группе слагаемых в правой ча-
части A1) вместе с варьированием ускорений. Напомним, что виртуаль-
виртуальные вариации 5гк должны удовлетворять уравнениям для виртуальных
перемещений, число которых равно числу независимых удерживающих
связей (обозначим это число через /). Кроме того, виртуальным вари-
вариациям 5гк могут быть поставлены в соответствие разности ускорений
wfc — wb гДе wfc — мыслимые ускорения по Четаеву, удовлетворяющие
условиям связей в фиксированный момент времени в действительном
состоянии. Будем использовать только мыслимые ускорения, близкие
действительным, т. е.
5rk=r5wk, 5wk =wfk -wk, к = I,... ,N,	A2)

13. О применении вириалов. Центральное вириальное равенство 105
где r — не равный нулю скалярный множитель, имеющий размерность
квадрата времени.
Рассмотрим два варианта дальнейших преобразований равен-
равенства A1). Оба они связаны с имеющейся свободой выбора 5гк,
5vk, k= 1,...,7V.
1.	Мыслимые ускорения w^ будем рассматривать как имеющие
место в некотором движении в результате действия активных сил Ffk
и соответствующих реакций R'k тех же связей, что и в исходной
системе. Тогда имеются уравнения, аналогичные G):
mkvr'k = F'k + B!k, k=l,...,N.	A3)
Обозначив через 5Fk = F'k - Fk и 5Rk = R'k - Rk, к = 1,... ,7V, из G)
и A3) для вариаций ^w^ A2) находим равенства
mk5v/k = 5Fk + 5Rk, k= 1,...,ЛГ.	A4)
Последнюю сумму в A1) заменяем суммой из равенства A4). Получаем
равенство
SV0 = 25Т + 6'А + J2 mk5wkrk.	A5)
к
2.	Приведём другой вариант вывода равенства A5). Наложим на
вариации 5vk условия в виде перестановочных соотношений: 5vk =
=	, к = 1,...,7V. Тогда, как известно [58], имеем центральное
уравнение Лагранжа:
-J ? mkvk6rk = 5Т + 5'А,	A6)
аг к
вычитание которого из A1) даёт равенство
? mk5wkrk = J2 EFk + 5Rk) rk.	A7)
к	к
С учётом A7) равенство A1) также принимает вид A5).
Таким образом, оба варианта преобразований A1) привели к равен-
равенству A5), которое, как и A6), можно назвать центральным. Однако
поскольку оно содержит вириалы вариаций ускорений по Гауссу, мы
назовём его более полно: центральное вириальное равенство.
Центральное вириальное равенство A5) может рассматриваться как
общее уравнение. Далее оно используется при выводе интегральных
принципов в вириальной форме (см. заметку 17).

Глава III
ОБ ИНТЕГРАЛЬНЫХ ПРИНЦИПАХ
Составляются интегральные равенства, представляющие собой вы-
выражения изменения действия при варьировании. В качестве действия
рассматриваются классические действия по Гамильтону, по Лагранжу
и вириальная форма действия для систем Четаева-Румянцева. Обоб-
Обобщения интегральных равенств получены при рассмотрении истинной
траектории и варьированных кривых при совместном применении син-
синхронного и асинхронного варьирования. Даётся обоснование расши-
расширенного принципа Гамильтона-Остроградского в теории реономных
систем. На основе способа варьирования по Гельмгольцу сформулиро-
сформулированы новые обобщения принципа Гёльдера.
14. Центральное интегральное равенство
При совместном использовании синхронных и асинхронных вари-
вариаций получен расширенный аналог (обобщение) центрального урав-
уравнения Лагранжа. На основе этого уравнения составлено интеграль-
интегральное равенство (называемое здесь центральным интегральным равен-
равенством), связывающее действие по Лагранжу и действие по Гамильтону.
Полученное интегральное равенство позволяет находить синхронные
и асинхронные вариации действия при различных вариантах задания
условий варьирования концевых точек траектории. Из центрального
интегрального равенства как частные случаи следуют классические
принципы стационарного действия и другие интегральные выражения
изменения действия при варьировании.
14.1. Центральное уравнение Лагранжа при асинхронном ва-
варьировании. Центральным уравнением Лагранжа по предложению
Гамеля называют равенство [58]
J	6T + 6'A,	A)
аг к=\
где rrtk^k — количества движения, 5г^ — виртуальные перемещения
материальных точек; Т — кинетическая энергия системы; 51А — вир-
виртуальная работа всех активных сил.

14. Центральное интегральное равенство	107
Уравнение A) получается непосредственным дифференцированием
с последующим учётом общего уравнения динамики при предположе-
предположении свойства переставимости
^ 5vk, k=\,...,N.	B)
В отсутствие свойства B) имеем общее центральное уравнение Лагран-
жа [58]:
N	N
d
dErk)
dt
-6vk\. C)
k=\	k=\
Предполагая использовать далее асинхронные вариации:
Arfc = 5rk + vfc At, fc=l,...,JV,	D)
составим также «элементарную работу количеств движения» на пере-
перемещениях Дг&:
J2 mkvkArk.	E)
к=\
Вычислим производную по времени от выражения E), предвари-
предварительно сделав подстановку B) и учитывая A):
-^ J2 mkVkAvk = 5fA + 5T+^- BTAt).	F)
at k=l	at
Равенство F) является обобщением центрального уравнения Лагран-
Лагранжа. В частном случае, при At = 0, из F) следует центральное урав-
уравнение Лагранжа A). В отсутствие свойства B) с учётом общего цен-
центрального уравнения Лагранжа C) получаем равенство
у N	,	N	I
-| Yl ™kVkArk = 5fA + 5T+^- BTAt) + ]Г mkvk
at f—\	at	f—\	lll	i
G)
Равенство G) является расширенным аналогом общего центрального
уравнения. Из G), в частности, следуют уравнения F), C), A).
14.2. Центральное интегральное равенство. Будем называть
интегралы по времени на промежутке [to,ti] от центральных равенств
центральными интегральными равенствами. Интегрируя по времени
равенство F), получаем
- BTAt)
и
(8)
Заметим, что произведение 2TAt имеет смысл элементарного дей-
действия по Лагранжу на промежутке времени At (At(t) — бесконечно
малая функция времени). При использовании обобщённых координат

108	Гл. III. Об интегральных принципах
в равенстве (8) следует учитывать условия, налагаемые на виртуальные
перемещения неголономными связями (и условия голономных связей,
не учтённых выбором обобщённых координат).
14.3. Об изменении действия по Гамильтону и действия по
Лагранжу при синхронном и асинхронном варьировании. Ле-
Левая часть интегрального равенства (8) представляет собой выраже-
выражение, которое равно нулю при предположениях принципа Гамильтона-
Остроградского. Действительно, если кривые сравнения получаются
изохронным виртуальным варьированием (At = 0) и при условиях на
концах
=O,	(9)
то при этом также и Ar/C(to) = Avk(t\) = 0 (см. D)), т.е. правая
часть (8) будет равна нулю, и тогда приходим к принципу Гамильтона-
Остроградского:
и
^	5'А) dt = O.	A0)
Представим центральное интегральное равенство (8) в виде фор-
формулы для изохронной вариации действия по Гамильтону. Для этого
в составе активных сил выделим потенциальные силы, виртуальная
работа которых равна — 5U, и введём функцию Лагранжа L = Т -^И.
После этого равенство (8) можно записать в следующей форме E'А —
виртуальная работа активных непотенциальных сил):
5 \Ldt = - 5fAdt+ I ]Г mkvkArk - 2TAt 1
to	t0	^ k	'
A1)
В частности, если кривые, полученные асинхронным варьировани-
варьированием, проходят через концы истинной траектории в моменты времени
k=l,...,N,	A2)
то для изохронной вариации действия по Гамильтону получим формулу
ti
A3)
to
• [Ldt = - U'A<ft-BTA?)
to	t0
Таким образом, равенство нулю изохронной вариации действия по
Гамильтону:

14. Центральное интегральное равенство	109
выполняется при условии A2) и равенстве
= 0,	A4)
*\	и
5fAdt + BTAt)
to
т. е. если сумма интеграла от виртуальной работы непотенциальных
сил и приращения виртуального действия по Лагранжу BTAt) на
промежутке времени [to,ti] равна нулю.
Принцип стационарного действия Лагранжа для голономных кон-
консервативных систем:
= 0,	A5)
to
выведем также из центрального интегрального равенства (8).
С учётом условий, при которых получено равенство A5), централь-
центральное интегральное равенство (8) можно переписать в виде
и
2-| (TAt)\ dt = 0.	A6)
to
Преобразуем подынтегральное выражение A6) к виду
25Т + 2TAt + 2Tj (At) = 2AT + 2Tj (At)	A7)
и используем асинхронную вариацию интеграла [58]:
A\Fdt= (AF + F^(Atj) dt.	A8)
to	t0
Поэтому из A6) окончательно получаем принцип стационарного
действия Лагранжа A5).
Для вывода формулы асинхронной вариации действия по Гамиль-
Гамильтону обратимся к интегральному равенству A1). При условиях на
концах A2) перепишем A1) в следующей форме:
а	и
f- BTAt)) dt = -\ 5rAdt.	A9)
Для подынтегрального выражения A9) составим цепочку равенств:
5L + 2TAt + 2T-f (At) = AL + EAt + 2T^- (At) =
(ЛЬ	(ЛЬ
(At) + (EAt), B0)
где Е = T + П — полная механическая энергия.

B1)
to
ПО	Гл. III. Об интегральных принципах
Подставляя результат преобразования B0) в A9), находим инте-
интегральное равенство
и	и
A\Ldt = - \5'Adt-(EAt)
to	t0
При асинхронном варьировании из B1) следует условие стационарно-
стационарности действия по Гамильтону:
и
A^Ldt = 0,	B2)
to
если приняты предположения A2) и выполнено равенство
и
И = 0.	B3)
B4)
to
t0
to
Из B1) нетрудно получить также выражение асинхронной вариации
действия по Лагранжу для неконсервативных систем:
и	и
А [ 2Tdt = -2 [ 5fAdt - BTAt)
to	t0
Изохронная вариация действия по Лагранжу непосредственно сле-
следует из центрального интегрального равенства (8) (или из B4)): при
условиях на концах A2) получаем
и	и
s\2Tdt = -2\ 5rAdt - (ATAt)
to	t0
Для полноты выпишем ещё одно несколько более общее, чем принцип
Гамильтона-Остроградского A0), интегральное равенство:
и
[ (ST + 5'A) dt = - BTAt)
to
Полученные интегральные равенства A3), B1), B4)-B6) пред-
представляют собой различные частные формы записи центрального инте-
интегрального равенства (8). Однако, как известно, полезность формулы
определяется не только содержанием, но и формой её представления
и, добавим ещё, способом, которым она получена. Поэтому сделаем
следующие примечания.
1.	Действие здесь рассматривалось как характеристика, не завися-
зависящая от способа варьирования.
2.	Интегральные равенства, в которых фигурируют только изо-
изохронные вариации и функция At(t), можно получить также приме-
B5)
to
B6)
to

15. О принципе Гамильтона-Остр о градского	111
нением способа варьирования по Гельмгольцу (см. заметку 8). При-
Примечательно, что в формулах фигурируют только значения вариаций
времени на концах промежутка [to, ^i]- Поэтому для того, чтобы, на-
например, равенство B6) приняло вид принципа Гамильтона-Остроград-
ского A0), достаточно положить At (to) = At(t\) = 0 (не требуется
условия At(t) = 0).
3. Условия вида A4), B3) полезны тем, что выделяют множе-
множество сравниваемых варьированных кривых, в котором действие имеет
стационарное значение. Ситуация противоположна той, когда ищется
условие стационарности при ограничениях; здесь, напротив, получены
условия (ограничения на варьирование), при которых истинное движе-
движение доставляет функционалу «действие» стационарное значение.
15. О принципе Гамильтона-Остроградского в теории
реономных систем
Стремление к унификации формул аналитической механики при-
приводит к идее рассматривать реономные системы как склерономные
с п+1 обобщённой координатой, включив в это число время. Здесь
изучается вспомогательная склерономная система, построенная на ос-
основе функционала «действие» по Якоби. Обсуждается обоснование
расширенного принципа Гамильтона-Остроградского вспомогательной
системы с применением асинхронного варьирования. Получены урав-
уравнения движения и условия трансверсальности.
15.1.	Принцип Гамильтона-Остроградского. Согласно этому
принципу движение реономной системы с п степенями свободы удо-
удовлетворяет интегральному равенству
*2	h	п
5 J Ldt + J 5'Adt = 0, 5'А = ]Г Q^,	A)
где L — функция Лагранжа, 5qi — виртуальные перемещения, Qi —
непотенциальные обобщённые силы. Промежуток времени и концы
траектории фиксированы, варьирование функционала «действие» по
Гамильтону в A) — изохронное.
15.2.	Асинхронное варьирование действия вспомогательной
склерономной системы. Исходной реономной системе A) сопо-
сопоставляется вспомогательная склерономная система по способу Якоби
(см. п. 6.1). В этой системе время t рассматривается как дополни-
дополнительная обобщённая координата и вводится независимый аргумент г

112	Гл. III. Об интегральных принципах
(t = /(т), df/dr > 0). Вспомогательная система задаётся функцией L*
Лагранжа:
L*=T*-n*, T* =t'T (q,tX\ П.* =t'Il(q,t),	B)
где Т* — новая кинетическая энергия F.2), П* — новая потенциальная
энергия, штрихом обозначены производные по т.
Действие по Гамильтону вспомогательной системы представляет
функционал
\L*dr, tj = f(Tj), j = 1,2.	C)
Начальное и конечное значения аргумента (г\ и т^) фиксированы.
Воспользуемся асинхронными вариациями обобщённых коорди-
координат (8.3), для которых после перехода к новому аргументу г имеем
равенства
t'Aqi-q'iAt = t/5qi, i=l,...,n.	D)
Операции А и d/dr переставимы, т. е.
, At' = (Atj.	E)
Будем в дальнейшем равенства D) рассматривать как связи, а ра-
равенства E) использовать при интегрировании по частям.
Вначале проделаем обычные операции вариационного исчисления
при варьировании А на примере функционалов, составляющих дей-
действие C). Варьируем интеграл функции Т*:
Т2	Т2
A J T* dr = J AT* dr.	F)
n	n
Раскроем в F) подынтегральное выражение:
Слагаемые в правой части G), содержащие А<^ и At', с учётом пере-
перестановочных соотношений E) интегрируются по частям. В результате
выражение F) преобразуется следующим образом:
' I
Г2
At dr. (8)

15. О принципе Гамильтона-Остр о градского	113
Найдём вариацию А интеграла от функции П*:
А [ П* dr = [ АП* dr,	(9)
где П* = tfU(q,t), U(q,t) — потенциальная энергия исходной системы.
Во вспомогательной системе функция П* линейно зависит от t',
что придаёт ей форму обобщённого потенциала. Если же обобщённый
потенциал V (линейно зависящий от обобщённых скоростей [25]) име-
имеется в исходной системе:
V = '?Ui(q,t)qi + Ik(q,t),	A0)
г
то во вспомогательной системе ему соответствует функция V*, также
имеющая форму обобщённого потенциала:
v* = ^ЫъЫ + г'ЫчЛ), * = /(т).	(и)
г
Различие состоит в том, что в исходной системе обобщённый потенци-
потенциал A0) является в общем случае неоднородной функцией обобщённых
скоростей, а во вспомогательной системе относительно производных q[,
t' функция V* становится однородной функцией первой степени.
С учётом перестановочных соотношений E) получаем преобразова-
преобразование вариации (9):
А
[ П* dr = UAt Т2 + \^2 |5 (txA^ - ^At) dr.	A2)
Аналогичными действиями находим вариацию интеграла от функ-
функции V* A1):
т2
r2
-J:
dt
q'At dr + f V Я± (t'Aq, - q'At) dr. A3)
15.3. Расширенный принцип Гамильтона-Остроградского.
Получим аналог принципа Гамильтона-Остроградского для вспомо-
вспомогательной системы на основе функции Лагранжа L* B). С учётом

114
Гл. III. Об интегральных принципах
равенств D) для вариаций обобщённых координат и времени состав-
составляем интегральное равенство
AL* + t'5'A
- q'{At - ?
dr = 0,
A4)
где Xi(r) — неопределённые множители Лагранжа.
Первое слагаемое в A4) варьируется так же, как и (8) (достаточно
заменить Т* на L*, а затем учесть B) и (9)). Перегруппировав слагае-
слагаемые, преобразуем равенство A4) к виду
от ,
d (дт*
= 0. A5)
В силу независимости вариаций А^ (г = l,...,n), At и 5qi
(г = 1,...,п) к равенству A5) может быть применена основная лем-
лемма вариационного исчисления [131]. Приравняв нулю коэффициенты
при независимых вариациях в подынтегральном выражении и внеин-
тегральную часть равенства A5), получаем дифференциальные урав-
уравнения
d_( дТ*\ дТ* , дП
dr
t — Xit =0, г = I,..., n,
A7)
значения неопределённых множителей
Xi = Qi i = 1,... ,n,
и равенство
= 0.
A8)
A9)

15. О принципе Гамильтона-Остр о градского	115
Равенства A6)—A9) являются следствием интегрального равен-
равенства A4). Из A9) на концах траектории вспомогательной системы
имеем условия трансверсальности:
= 0, j = 1,2. B0)
Уравнения A6), A7) с учётом равенств A8) представляют собой
уравнения движения вспомогательной системы. Действительно, под-
подстановка в A6) и A7) неопределённых множителей, равных, соглас-
согласно A8), соответствующим непотенциальным обобщённым силам, при-
приводит к уравнениям [22]
-?-г) --*— = -*-*-+tQi> г=1,...,п,	B1)
dql ) dqi	dqi
dr \dt' ) dt ~ 2_. ^ * 2^ V»*'
Так как
^С = ?^, г=1,...,п, (•)/ = 4(')^^	B3)
уравнения B1) совпадают с классическими уравнениями Лагранжа
второго рода C.29) исходной реономной системы. Равенство B2) с учё-
учётом выражений B3) и равенств
(9Г* _,,дТ_
dt ~ dt'
где Тъ и То — квадратичная форма и форма нулевой степени отно-
относительно обобщённых скоростей в выражении кинетической энергии,
принимает вид аналога теоремы об изменении кинетической энергии
реономных систем E.9). В частности, в случае потенциального поля
получаем
дТ , d (гп m\	дП
Согласно равенству A9) для исходной реономной системы требуется
выполнение условия
2 = 0. B4)

116	Гл. III. Об интегральных принципах
Равенство B4) выполняется, если на концах промежутка времени
движения исходной реономной системы выполняются условия транс-
трансверсальности:
/	\ \
= 0, j=l,2.	B5)
Очевидно, что равенства B5) выполняются, если равны нулю
виртуальные вариации на концах траектории: 5qi(t\) = fo/ife) = 0,
г = 1,... ,п, и кроме того, At\ = АЬъ = 0, так как приняты равенства
Aqi = qiAt + 5qi, г=1,...,п	B6)
(сравните с равенствами D)).
Полученный результат позволяет сделать вывод о том, что инте-
интегральное равенство A4) на фиксированном промежутке [тьтг] явля-
является некоторым расширением принципа Гамильтона-Остроградского.
Расширение обеспечивается за счёт введения неопределённых множи-
множителей, которые позволяют рассматривать как независимые обе группы
вариаций: асинхронные (и At) и изохронные. Если на какие-либо из
них наложены ограничения в виде уравнений, то они также могут быть
учтены с неопределёнными множителями.
Пример 1. Пусть виртуальные перемещения связаны уравнением
Y^ a>i(q, tMqi = 0.	B7)
г
Соответственно, для системы с функцией L* B), с учётом уравне-
уравнений D) и B7), для вариаций переменных имеем интегральное равен-
равенство
"г	i
AL* + vt1 ]Г diSqi + ]Г Х{ (t'Aqi - q[At - t'Sqi) \ dr = 0, B8)
где v(t), Xi(r) — неопределённые множители Лагранжа.
При произвольных вариациях 5qi, i= 1,...,п, из B8) по основной
лемме вариационного исчисления, как и следовало ожидать, имеем
равенства вида A8):
Xi = vdi г = 1,..., п,
подстановка которых в A6), A7) даёт соответственно равенства
d (дТ*\ дТ* , дП ,, ,, п • 1	/опч
— —- - ^— + jr-t -vtdi =0, г=1,...,п,	B9)
dr \ d J dq dq
d

15. О принципе Гамильтона-Остр о градского	117
Используя для производных функции Т* равенства B3), в переменных
исходной системы имеем уравнения движения
d (дТ\ _ дТ _ _дП	. _	.« v
Из C0) (а также из уравнений движения C1)) следует утверждение
теоремы об изменении кинетической энергии реономной системы:
У**-L .^ UJ / ГТ~\	ГТ~\ \ 		X	/ ^-^-LJ-	\ •	/QO\
г
Для нахождения неопределённого множителя v в равенствах C1),
C2) требуется также уравнение связи, которому соответствуют уравне-
уравнения для виртуальных перемещений B7). Связь может быть голономной
или неголономной линейной относительно обобщённых скоростей с ко-
коэффициентами Оь{.
Рассмотрим пример, в котором условия наложены на асинхронные
вариации.
Пример 2. Пусть асинхронные вариации удовлетворяют урав-
уравнению
]Г a,i(q, t)Aq{ + ao(q, t) At = 0.	C3)
При составлении интегрального равенства вида A4) требуется допол-
дополнительно учесть условие C3). Это можно сделать, включив в подын-
подынтегральное выражение левую часть равенства C3) с неопределённым
множителем. Предварительно для удобства сравнения с примером 1
в C3) сделаем подстановку B6). Кроме того, включим в подынтеграль-
подынтегральное выражение с неопределённым множителем v выражение
C4)
Коэффициент при v в C4) соответствует идеальной связи только в слу-
случаях, когда
At = 0 или J2 aiQi + «o = O.	C5)
i
Первое равенство в C5) определяет условие изохронного получения
виртуальных перемещений, а второе задаёт определённый вид уравне-
уравнения связи. В этих случаях получаем уравнения B9) и равенство
0,	C6)
из которого с учётом уравнения связи C5) также следует аналог
теоремы об изменении кинетической энергии для исходной системы.
Другой путь, не предполагающий использования неопределённых
множителей, состоит в том, чтобы выразить зависимые вариации через

118	Гл. III. Об интегральных принципах
независимые. В работе [22] это делается следующим образом. В каче-
качестве принципа принимается интегральное равенство
7*2	То
A J T* dr + J (j2 QMi) tf dr = 0,	C7)
где Qi — обобщённые силы.
Функции 5qi в C7) выражаются с помощью B6). Выкладки про-
проводятся с заменой функции L* на функцию Т* при предположении
независимости вариаций Aqi (i = l,...,n) и At. Результат отличается
тем, что слагаемое с потенциальной энергией не входит в условия на
концах:
|
(-Т2 + Го)Д*^ | = 0.
Из интегрального равенства C7) находим, что движение описывает-
описывается уравнениями Лагранжа второго рода и имеет место аналог теоремы
об изменении кинетической энергии.
16. Обобщение интегрального принципа Гёльдера
Показано, что интегральное равенство обобщённого принципа Гёль-
Гёльдера справедливо также для кривых сравнения, полученных варьиро-
варьированием по Гельмгольцу. Принцип Гамильтона-Остроградского и прин-
принцип стационарного действия Лагранжа выводятся как частные случаи.
Предложено новое обобщение принципа Гёльдера [17].
16.1. Применение варьирования по Гельмгольцу при выводе
принципа Гёльдера. Применим варьирование по Гельмгольцу при
выводе интегрального равенства в обобщённом принципе Гёльдера.
Проинтегрируем вариацию (8.12) по времени на фиксированном вре-
временном промежутке:
С учётом перестановочных соотношений (8.10) и равенства (8.11)
после интегрирования по частям равенство A) преобразуется к ви-
виду (At = At)
+. ^i _ ,	.
dL d dL \ -г- ,, . dL d f к ^
	— I Aqi dt — qi —:	\Ат/
to у i L \	/
to
B)

16. Обобщение интегрального принципа Гёльдера	119
При условиях на концах
Aft(*o)=Aft(*i)=O, i= l,...,n,	C)
перепишем равенство B) в следующей форме:
to г
В качестве вариаций обобщённых координат в D) возьмём вир-
виртуальные вариации (Aqi = 5qi). Тогда, принимая во внимание общее
уравнение аналитической динамики и условия на концах C), из равен-
равенства D) получаем интегральное равенство
л т , V^ . dL d , к ч , г/
AL+y п.—- — (Ат)+ 6'
Интегральное равенство E) по виду совпадает (с точностью до обо-
обозначений) с обобщённым принципом Гёльдера, полученным [102] при
интегрировании асинхронной вариации функции AL (первое выраже-
выражение в (8.6)). Однако здесь функция L варьируется по Гельмгольцу,
и поэтому имеется различие кинематического смысла условий на кон-
концах: кривые, варьированные по Гельмгольцу, проходят через начальное
и конечное положения системы в моменты времени to и t\, а кри-
кривые, полученные асинхронным варьированием — в моменты времени
16.2. Частные формы принципа. Приведём некоторые частные
специализации варьирования в E).
1. Пусть d(Ar)/dt = 0. Тогда равенство E) принимает вид принципа
Гамильтона-Остроградского:
и
[ EL + 5'A) dt = 0.	F)
to
Кроме классического принципа Гамильтона-Остроградского, по-
получаемого изохронным варьированием (Дт = 0), принятому условию
можно сопоставить расширенный вариант принципа, получаемого асин-
асинхронным варьированием. Например, условию d(Ar)/dt = 0 удовлетво-
удовлетворяет также функция At = cdt, где с = const, т. е. могут рассматривать-
рассматриваться асинхронно варьированные кривые, получаемые путём бесконечно

120	Гл. III. Об интегральных принципах
малого сдвига вдоль оси времени на величину, пропорциональную
элементарному промежутку времени dt.
2. Изоэнергетическое варьирование в обобщённо-консервативных
системах. При Qi = 0, dL/dt = 0 и связях, однородных первой сте-
степени относительно обобщённых скоростей, имеет место обобщённый
интеграл энергии Якоби: Т% — То + П = h = const (T2, Т\, То — формы
второй, первой и нулевой степени относительно обобщённых скоро-
скоростей в выражении кинетической энергии системы; П — потенциальная
энергия). Для вариаций, сохраняющих интеграл энергии, равенство E)
преобразуется к следующему виду:
и
Д [^&!^<й = 0.	G)
I г
Действительно (ср. (8.13)),
и
Qi^^dt =
?
а(Е*|П+^*?^1Л- (8)
Поскольку в данном случае ^ Чг^~ = 2Т2 + Т\ = L + h, правая часть
i	^
равенства (8), согласно интегральному равенству E) (с учётом обо-
обозначения (8.11)), равна нулю. Таким образом, при «изоэнергетиче-
ском» варьировании (способом Гельмгольца) функционала «действие»
по Лагранжу имеем принцип стационарного действия для обобщённо-
консервативных систем:
(9)
to
Действие по Гамильтону в данном случае не является стационарным:
и	и
А [ (L + К) dt = 0, т. е. ~K\Ldt = h [Ar (t0) - Ar (tx)].
to	t0
16.3. Новое обобщение принципа Гёльдера. Получим на основе
расширения способа варьирования по Гельмгольцу (см. (8.8), (8.15))
соответствующее ему новое обобщение принципа Гёльдера.
Повторив те же, что и при выводе E), выкладки при интегри-
интегрировании AL, получаем интегральное равенство, выражающее новое
обобщение принципа Гёльдера:
и
|^ ^Ц|	]	A0)

17. Вириальный интегральный принцип	121
Из A0) при Ari(t) = Ar(t), i = 1,...,п, следует равенство E)
(обобщённый принцип Гёльдера).
В заключение отметим, что принцип, предложенный Гёльдером
в форме интегрального равенства
и
\6Ldt = 0,
to
где 5 — символ изохронного варьирования, применяется как для го-
лономных, так и для неголономных систем (подробнее см. в замет-
заметке 20).
17. Вириальный интегральный принцип.
Интегральный принцип для систем
Четаева-Румянцева
Получена вириальная форма интегрального принципа механики.
Составлен [14] интегральный принцип динамики физической системы,
модель которой предложена В. В. Румянцевым [103] при обосновании
принципа Н. Г. Четаева [128]. Обсуждаемый подход может быть ис-
использован при решении задач термомеханики.
17.1. Вириальный интегральный принцип. Используем цен-
центральное вириальное равенство A3.15) при выводе интегрального прин-
принципа в вириальной форме. Интегрируем равенство A3.15) по времени
на фиксированном временном промежутке:
J 5V0 dt = JB5T + 5f A) dt + J ]T mk6vrkrk dt.	A)
и	и	и k
Допуская перестановочные соотношения, на том же промежутке вре-
времени интегрируем центральное уравнение Лагранжа A3.16):
tl I
\(ST + 5'A)dt.	B)
I
С учётом равенств A3.12) имеем перестановочность операции 5 и ин-
интегрирования по времени в левой части A). Поэтому, приняв во вни-
внимание B), из A) получаем
mk5vkrk
7
к
= EТ + J2 mk5wkrk) dt.	C)
к
k)
Пусть наряду с траекторией действительного движения между на-
начальным и конечным состояниями рассматривается кривая, которая

122	Гл. III. Об интегральных принципах
получена изохронным варьированием по правилам, описанным в за-
заметке 13. При этом считаем фиксированными начальный и конечный
моменты времени, а также начальные и конечные скорости точек, т. е.
5vk = 0, h=\,...,N, при t = t\ и t = t2-	D)
Тогда равенство C) примет вид
Ч ,
к
Интегральное равенство E) и условия на концах D) составляют вири-
альный интегральный принцип. Формулировка его очевидна и выража-
выражает свойство действительного движения.
17.2. Интегральный принцип для систем Четаева-Румянце-
ва. Рассмотрим физическую систему, состоящую из «совокупности
физически малых материальных частиц («точек»), рассматриваемых
как термодинамические системы, для каждой из которых определе-
определены механические понятия о внутреннем состоянии, характеризуемые
конечным числом величин, задаваемых числами — определяющими
параметрами» [103]. Понятие термодинамической точки обсуждалось
в заметке 1. Силы, действующие на частицы, делятся на три группы:
Fk — силы, зависящие от состояния, времени и физических констант;
Фк — внутренние силы взаимодействия, которые зависят, кроме того,
от переменных физических параметров; Ик — силы реакции идеальных
связей, зависящие от переменных физических параметров. Для данной
модели физической системы путём рассуждений, аналогичных приве-
приведённым при выводе A3.15), получаем
5V0 = 25Т + 6'A(F) + 6'А(Ф) + ? rnk5wkvk,
к	SR\
5fA(F) = ]Г Fk5rk, 5'А(Ф) = ]Г Ф^г*.	[ }
к	к
Взаимосвязь механического движения и термодинамических процессов
проявляется через переменные физические параметры. Обозначим их
через fiki (индекс указывает номер частицы к и номер параметра г, со-
соответствующего этой частице). Пусть в уравнениях внутренних связей,
зависящих от переменных параметров, не содержится скоростей точек,
т. е. они имеют вид
f(rk,tJLki,i) = 0	G)
и в отсутствие варьирования переменных параметров являются идеаль-
идеальными. При этом виртуальные вариации 5гк и вариации параметров 5fiki
для связи вида G) удовлетворяют уравнению
кг

17. Вириальный интегральный принцип	123
Коэффициенты aki в (8) являются некоторыми функциями от гк, №*, t.
Вид этих функций определяется конкретной физической системой.
Если включить физические параметры в параметрическое семейство
/iki(<%?)' содержащее действительные значения /^(?) ПРИ а = 0, то
В действительном процессе и любых возможных процессах [103]
имеем уравнение притока тепла, равносильное закону сохранения
энергии:
AQ = AU + АА(Ф), A*Q = A*U + А*А(Ф),	(9)
где AQ, A*Q — приток тепла к телу извне, равный сумме притоков
тепла к частицам в действительном и возможном движениях соответ-
соответственно; AU, A*U — приращения внутренней энергии U (внутренняя
энергия системы принимается равной сумме внутренних энергий ча-
частиц); АА(Ф), А*А(Ф) — работа сил Фк на действительном и возмож-
возможном перемещениях [103] из положения rk, fiki (в момент времени t).
Вычитая в (9) из второго уравнения первое, получаем для виртуальных
изменений соответствующих величин
5'Q = 5U + 5'А (Ф),	A0)
где 5'Q — виртуальный приток тепла к системе извне; 5U — вирту-
виртуальное изменение внутренней энергии; 5'А(Ф) — виртуальная работа
сил Фк. Подставляя 5'А(Ф) из A0) в F), находим
5V0 = 2ST + 5'A(F) + 5fQ-5U + J2 mk5wkrk.	A1)
к
Интегрированием по времени с учётом переставимости операции 5
и интегрирования из A1) получаем равенство
l\ (	\
= 25Т + 5fA(F) + 5'Q-5U + J2 ™кЫкгк dt. A2)
' *Л	к	)
Пусть фиксированы начальный t\ и конечный t^ моменты времени,
а также вириалы количеств движения в эти моменты времени, т. е.
5Vq = 0 при t = t\ и t = ?2-	A3)
Тогда равенство A2) принимает вид
[ B5Т + 5'A(F) +5'Q-5U + Y1 ^ik5wkrk) dt = 0.	A4)
и	k
Интегральное равенство A4) и условия на концах A3) составляют
вириальный интегральный принцип для физической системы [14].

124	Гл. III. Об интегральных принципах
Пример. Прямолинейный однородный стержень массы т враща-
вращается вокруг неподвижной оси, перпендикулярной стержню и проходя-
проходящей через его торец. Ось вращения установлена в идеальных опорах,
внешние активные силы отсутствуют. При равномерном нагреве (по
длине) длина стержня / связана с температурой # линейным законом
расширения:
l k(ti) a(ti) = 1+х(#-#0),	A5)
где /о — длина стержня при температуре #о> >с — постоянный коэффи-
коэффициент теплового расширения.
Переменным физическим параметром в данной системе является
температура #, а частицами — элементарные массы dm, по условию
расположенные на прямой. Направим ось Ох вдоль стержня (центр О
поместим в точке пересечения оси вращения и стержня). Координаты х
элементарных масс и параметр # связаны уравнением
х = хоа($),	A6)
где xq — координата элемента dm при # = #о-
Составим равенство A4). При варьировании кинетической энергии
стержня Т = Ju2/2, где J = ml2/3 — момент инерции стержня отно-
относительно оси вращения, и — величина угловой скорости, имеем
5T=^-5J + Ju5u.	A7)
Вариации 51 и 5х связаны с вариацией 5д соотношениями
(см. A5), A6))
51 15$ 5	5$	A8)
Через вариацию 5д выражается и вариация внутренней энергии:
A9)
где с/(#) — коэффициент теплоёмкости стержня при постоянной длине.
Последняя группа слагаемых в равенстве A4) в данной задаче сво-
сводится к интегралу по длине недеформированного стержня (при # = #0)-
- [ 5(со2х)х dm = -2Jco5u; - cu2KaJ05$, J = J0a2.	B0)
После подстановки A7), A9), B0) с учётом A8) интегральное
равенство A4) принимает вид
[ [S'
[	] dt = 0.	B1)
to
Равенство B1) выполняется на произвольном заданном промежутке
времени, если
8^1	B2)

17. Вириальный интегральный принцип	125
Из B2) следует, что «виртуальная теплоёмкость» (при к > 0) для
вращающегося стержня меньше, чем теплоёмкость при постоянной
длине с/. В отсутствие некомпенсированного тепла 5'Q = fidS, где S —
энтропия стержня [103]. Пусть при этом к{$ — #о) <С 1 и с/ = const.
Тогда из B2) находим выражение для приращения энтропии:
S = (q-xJ0u;02)ln|-.	B3)
Пример показывает, что предложенный принцип позволяет связать
термодинамические величины с механическими. В частности, подтвер-
подтвердилось, что энтропия не выражает чисто тепловые свойства, а связана
также с локальными перемещениями масс. В данной задаче деформи-
деформирование не является термоупругим; в отсутствие же деформирования
(при к = 0) из B3) следует выражение, совпадающее с энтропией
в теории термоупругости для недеформированной среды [86].
17.3. Интегральный принцип изменяемого действия для си-
систем Четаева. Составим принцип изменяемого действия для дина-
динамических систем, имеющих в своём составе кроме «механической»
также «немеханическую» часть, описываемую обыкновенными диф-
дифференциальными уравнениями первого порядка, которые называются
системами Четаева (см. п.п. 12.1, 12.2):
mkwk = Fk, k= l,...,n,
B4)
[iy'Py = Ф1/, у = 1,... ,m,
где тк — массы материальных точек; w& — ускорения; F& — силы,
зависящие от состояния материальных точек, времени и значений пара-
параметров гk, Vfc, t и ри; [iv — положительные функции координат точек,
времени и параметров; Ф^ — принуждения, являющиеся функциями
тех же аргументов, что и силы F&.
Пример. Форму систем Четаева имеют автоколебательные систе-
системы с инерционным самовозбуждением [73]. В таких системах генера-
генерация колебаний происходит за счёт инерционности цепи обратной связи,
приводящей к так называемому инерционному взаимодействию между
динамическими переменными. В простейшем случае соответствующие
уравнения колебаний имеют вид
х + 25х + ljqX = —ку + / (х, х, у),
у + jy = ах + (р(х, х, у),
где 5 — коэффициент трения, 7 — параметр инерционности, к и а —
коэффициенты линейной связи между переменными, / и (р — нелиней-
нелинейные функции.

126	Гл. III. Об интегральных принципах
Пусть состояние материальных точек и значения параметров систе-
системы B4) в каждый момент времени удовлетворяют уравнениям связей
(вообще говоря, нелинейным относительно скоростей):
гр1 (n, vi,... ,rn, vn,pi,... ,pm,t) =0, I = 1,... , г < 3n + m. B5)
Наложенные связи вида B5) влияют на процесс изменения параметров
через так называемые принуждения реакций; тогда уравнения несво-
несвободной системы по Четаеву принимаются в виде [129]
mkwk=Fk+Rk, k=l,...,n,
Hvftv = Ф„ + Р„, v = 1,... , га,
где Ик — реакции связей, Ри — принуждения реакций.
Уравнения B6) рассматриваются вместе с уравнениями B5).
Если связи вида B5) являются идеальными, то общее уравнение
динамики несвободной системы имеет вид (см. A2.11))
? (mkwk - FkMvk + f) (№„ - Ф„) 5Vu = 0,	B7)
к=\	v=\
где 5vk — виртуальные скорости (по Лагранжу), 5ри — виртуальные
изменения параметров.
Общее уравнение динамики несвободной системы, получаемой из
свободной системы B4) путём включения в правые части уравнений
реакций и принуждений реакций идеальных связей B5), является
необходимым и достаточным (при предположении реализуемости) усло-
условием того, что действительное движение системы для заданных сил F&
и принуждений Ф^ согласовано с уравнениями связей [13].
Из общего уравнения динамической системы с идеальными связями
B7) при условии перестановочности операций d5 и 5d следует равен-
равенство	,
5Т + 5'А = Т Y, Рг5рг + |1] ГПкТкбТк,	B8)
где 5Т — вариация кинетической энергии механической части системы;
5'А — виртуальная работа сил механической части системы; 5pi — вир-
виртуальные вариации определяющих параметров немеханической части
системы; г — множитель, имеющий размерность времени Erk = r5vk).
Для определения коэффициента г имеем равенство
TJ2Pi5pi = j:PiSpi.	B9)
Если принимается постоянное значение коэффициента г, то при
фиксировании значений параметров на концах траектории и условии
перестановочности операций d и 5 имеем также

18. Заметка об евклидовом действии	127
Интегрирование равенства B8) на фиксированном замкнутом интерва-
интервале времени [to,ti] при фиксированных положениях материальных точек
системы и фиксированных значениях параметров на концах траекто-
траектории даёт для рассматриваемых динамических систем интегральный
принцип:
^	и	и
J ET + 5'A) dt = J г ]Г Р{5р{ dt.	C0)
to	t0
Таким образом, изменение действия механической части системы Чета-
ева отличается от изменения действия по Гамильтону-Остроградскому
на интеграл по времени от величины, пропорциональной «виртуальной
работе принуждений реакций». Коэффициент пропорциональности удо-
удовлетворяет равенству B9).
18. Заметка об евклидовом действии
(Э. и Ф. Коссера)
«Заметка о теории Евклидовского действия» представляет «главный
интерес этого нового тома», как отмечено в предисловии книги [48],
в которой помещена заметка Э. и Ф. Коссера. Далее П. Аппелль
пишет: «Известно, что в современной механике господствуют две ве-
величины: энергия, зависящая от разности Т — U, и действие, выра-
выражаемое посредством суммы Т + U» (смысл обозначений здесь очеви-
очевиден). Э. и Ф. Коссера удалось «извлечь всё наиболее существенное
(из теорий Гамильтона и Гельмгольца — ред.) и установить прямое
определение действия, форма которого может быть перенесена во все
области Естественной философии. Отправная их точка заключается
в том соображении, что действие, в том виде, как его ввёл Мопертюи,
является инвариантом в группе евклидовых перемещений...» Из ре-
результатов, полученных Э. и Ф. Коссера, приведём только рекомендации
относительно формы «действия деформации на изменяемую линию»
(плотности действия), которым мы следуем при решении прикладных
задач, и формулы внешней силы и внешнего момента в точке, учитывая
их важность для понимания аксиом механики.
18.1. Аксиомы об однородности и изотропности пространства.
Евклидовская группа перемещений включает поступательные переме-
перемещения и повороты, что соответствует аксиоме об однородности и изо-
изотропности пространства соответственно. Совокупность уравнений дви-
движения имеет одну и ту же форму для всех координатных систем,
полученных одна из другой переносом начала координат и поворотом
вокруг оси (при равномерном прямолинейном движении центра имеем
галилееву группу преобразований [30]). Принимаются собственные
ортогональные преобразования, т. е. не включаются отражения (инва-
(инвариантность по отношению к отражениям от плоскости означала бы

128	Гл. III. Об интегральных принципах
эквивалентность правых и левых винтов: кинематических и силовых).
Рассматриваемое преобразование точно соответствует перемещению
абсолютно твёрдого тела. С аксиомой об однородности и изотропности
связан вопрос об условиях, которым должна удовлетворять система
сил, действующих на материальные точки системы. Очевидно, что
аксиома выполняется, если все внешние силы рассматривать прило-
приложенными к жёсткой конфигурации, совпадающей с конфигурацией
материальных точек, составляющих систему, а внутренние силы под-
подчиняются третьему закону Ньютона. Аксиома «о равенстве действия
и противодействия» в виде третьего закона Ньютона (см. заметку
4) совместима с аксиомой об однородности и изотропности, но сужает
класс сил, не позволяя охватить электродинамические взаимодействия.
Электродинамические взаимодействия имеют релятивистское истолко-
истолкование (вводится аксиома однородности и изотропности пространства-
времени, согласно которой уравнения, определяющие движение систе-
системы, должны быть инвариантны относительно собственного преобразо-
преобразования Лоренца [137]).
18.2. «Евклидовское действие деформации». Рассмотрим кри-
кривую, описываемую точкой Мо, координаты которой относительно трёх
неподвижных прямоугольных осей Ox, Оу, Oz представляют функции
одного и того же параметра, например дуги so, отсчитываемой от
определённого начала в определённую сторону. С точкой Мо по кривой
перемещается трёхгранник, направляющие косинусы которого являют-
являются функциями того же параметра. Сплошная совокупность (одного из-
измерения) таких трёхгранников называется изменяемой линией [48]. Со-
Сообщим трёхграннику бесконечно малое перемещение (поступательное
и поворот) и обозначим через М начало координат в новом положении.
Сплошная совокупность одного измерения трёхгранников с началом
в точке М называется деформированным состоянием рассматриваемой
изменяемой линии [48].
Возьмём функцию W от двух бесконечно близких положений трёх-
трёхгранника с началом в М, т.е. от so, координат х, у, z точки М,
направляющих косинусов трёхгранника и от их первых производных
по so.
Требуется ответить на вопрос: какова должна быть форма функ-
функции W для того, чтобы изменение интеграла W dso, распростра-
распространённого на какой-нибудь участок траектории точки Мо, равнялось
нулю, когда совокупность всех трёхгранников свободной изменяемой
линии, взятой в своём деформированном состоянии, подвергается од-
одному и тому же произвольному дифференциальному преобразованию
группы евклидовых перемещений.
Интеграл Wdso, взятый между точками Aq и Bq линии (Мо),
представляет действие деформации на деформированную линию между
соответствующими точками А и В кривой (М). На поставленный

18. Заметка об евклидовом действии	129
вопрос авторы работы [48] дали следующий ответ: искомая функция W
имеет замечательную форму:
w(So,tvX,p,q,r).	A)
Здесь W — плотность действия деформации в точке деформированной
линии. Смысл обозначений в A) следующий. Предположим, что so
меняется и играет роль времени; обозначим при этом через ^о, щ, (о
проекции скорости Mq на оси связанного с ней трёхгранника, а через
Ро> Уо, го — проекции на те же оси мгновенной угловой скорости этого
трёхгранника. Аналогичные количества для трёхгранника, связанного
с М, обозначены через ?, rj, ?, р, q, r. Линейный элемент кривой,
описываемой точкой М, определяется формулой
ds2 = (?2 + rf + С2) ds20.	B)
Рассматривая изменение действия деформации на деформирован-
деформированную линию между точками Aw В линии (М), имеем
\ W
J
A
dso =
Ao
M5X) ds0,	C)
где 5y — виртуальное перемещение точки М; 5% — виртуальный пово-
поворот трёхгранника Мх'у1 z1, связанного с М, в соответствующих точках
траектории;
р _ (dW_ dW_ dW^\ L _ (dW_ dW_ dW_
V <9? ' dr] ' д( J '	\ dp ' dq ' dr
_ d dW dW dW
x' " ds0 д? + q д( Г dr] '
d dW , aV^ dW ,
{x'yfz'\ ?,ri
Циклическая перестановка индексов, указанных в фигурных скобках
(по три), позволяет записать два другие, не выписанные в D) выра-
выражения проекций силы и момента; F и М — внешняя сила и внешний
момент в точке М, отнесённые к единице длины недеформированной
линии; Р Л и L л — внешнее усилие и внешний момент деформации
в точке А, аР п hL L —в точке В.
18.3. Евклидовское действие и натуральные системы. «Клас-
«Классические системы, в которых силы имеют обычный потенциал П(<^,?)
или обобщённый потенциал V(qi,t,qi), мы будем называть натураль-
натуральными. Для таких систем функция Лагранжа L является функцией
второй степени от обобщённых скоростей, т. е. представляется выраже-
выражением L = 1/2 + L\ + I/o, где 1/2 — положительно определённая квадра-
5 В. Г. Веретенников, В. А. Синицын

130	Гл. III. Об интегральных принципах
тичная форма относительно обобщённых скоростей» [25]. Функции L^,
Li, I/O являются однородными соответствующих степеней относительно
обобщённых скоростей (индекс указывает степень однородности):
L = 1/2 + 1/1 +1/0-	E)
Функциями Лагранжа второй степени относительно обобщённых
скоростей описываются ньютоновские механические системы, если для
них принято декартово описание, поскольку тогда действие является
«евклидовым» (см. п. 18.2). Если функция Лагранжа в виде многочлена
второй степени относительно обобщённых скоростей E) имеет гессиан
по обобщённым скоростям, отличный от нуля, то уравнения Лагранжа
второго рода разрешимы относительно обобщённых ускорений.
Понятие «натуральная система» по своему смысловому содержанию
является более широким, чем приведённое выше. К «натуральным» си-
системам естественно относить любые динамические системы, аксиома-
аксиоматика которых имеет научные физические основания. Тогда, например,
релятивистская частица, описываемая функцией Лагранжа (коэффи-
(коэффициент при dt в формуле C8.15)), не будет считаться «ненатуральной»
на том лишь основании, что выражение функции L не является по-
полиномом второй степени относительно скорости. Системы с функцией
Лагранжа вида E) далее будем называть системами с евклидовым
действием.
Обобщённый потенциал в определении натуральной системы пред-
представляет собой линейную функцию от обобщённых скоростей:
V(q,q,t) = 1?Vi(q,t)qi + Vo.	F)
г=1
Покажем, что системы с обобщённым потенциалом F) являются
частным случаем систем с интегральным ограничением
и
[ V (q, t, q) dt = const	G)
to
(интегральное изопериметрическое условие).
и
Отыскание экстремума действия L (q, t, q) dt при условии G) пред-
*о
ставляет собой изопериметрическую задачу на безусловный экстремум
функционала (см., например, [127])
и
J F (q, t, q) dt, F (q, t,q)=L (q, t, q) + XV (q, t, q),	(8)
to
где A — множитель Лагранжа.

18. Заметка об евклидовом действии	131
Уравнения прямого изопериметрического пути, получаемые приме-
применением оператора Эйлера-Лагранжа к функции F(q,t,q) (8), имеют
множитель Л у группы слагаемых, определяемых функцией V (q, t, q).
Поэтому получаемые уравнения можно рассматривать как некоторое
обобщение уравнений движения системы с функцией Лагранжа E)
и обобщённым потенциалом F) (последние получаются при Л = 1).
В частности, если функция Лагранжа и обобщённый потенциал не
зависят явно от времени (dF /dt = 0), то в системе G), (8) имеется
первый интеграл:
1/2 — I/O ~ ^^о — const,
аналогичный обобщённому интегралу энергии Якоби. Постоянный
множитель Лагранжа (Л = const) находится из условия G). Обыч-
Обычные обобщённо-консервативные системы являются частным случаем
(Л = 1) рассмотренной системы.
Примером систем с неевклидовым действием являются динамиче-
динамические системы Биркгофа (см., например, [24]), элементарное действие
которых имеет вид
Г п
^2 Ri(q,t)qi — B(q,t) dt,	(9)
г=1
где функция В называется биркгофианом; Ri(q,t) — дифференцируе-
дифференцируемые функции своих аргументов.
Сравним обобщённый потенциал F) с выражением в квадратных
скобках в (9): они совпадают с точностью до обозначений, поэтому
результаты применения к ним оператора Эйлера-Лагранжа (см. фор-
формулу C.27)) также будут иметь одинаковую форму.
Пусть динамическая система имеет действие по Пфаффу [24] в виде
интеграла
и
\A(q,t,q)dt,	A0)
to
где роль функции Лагранжа играет выражение
?).	(И)
г=1
Вторая форма уравнений Лагранжа с функцией A1) (применение
оператора Эйлера-Лагранжа) приводит к дифференциальным уравне-
уравнениям движения системы Биркгофа [24]:
dq%	dt
lj(q,t) dRi(q,t)

132	Гл. III. Об интегральных принципах
Матрица коэффициентов при обобщённых скоростях в уравнениях A2)
кососимметричная. Прослеживается аналогия с известным свойством
обобщённого потенциала F) создавать (в числе прочих) также обоб-
обобщённые гироскопические силы.
19. О принципе Гамильтона-Остроградского
при импульсивных движениях динамических систем
Рассматривается движение динамических систем, описываемых
уравнениями Гамильтона, при действии обобщённых ударных сил,
мгновенные ударные импульсы которых имеют потенциал. В этом
случае уравнения движения определяются из условия стационарности
функционала вариационной задачи Больца [127], где интегральная
часть является действием по Гамильтону. Показано, что при потен-
потенциальности ударных импульсов имеет место интегральный инвариант
Пуанкаре-Картана. Обсуждается применение полученных результатов
к исследованию натуральных систем с разрывами обобщённых импуль-
импульсов, происходящими в результате мгновенного изменения обобщённого
потенциала.
19.1. Постановка задачи. Потенциал ударных импульсов.
Пусть движение динамической системы описывается уравнениями
Гамильтона:
dQi_dH dPi__dH
Ж~^? ~dt~ %+Уг' г-1'""п'	W
где Н — функция Гамильтона динамической системы; qi, pi (i =
= l,...,n) — канонические переменные; Qi — обобщённые ударные
силы.
Обозначим через Si импульсы ударных обобщённых сил за время
удара г (обобщённые ударные импульсы):
г
Si = lim \Qidt, i = l,...,n.	B)
Qi-ooJn
При действии мгновенных ударных импульсов уравнения импуль-
импульсивного движения в соответствии с A) и B) получаем в виде
(it - ЯГ = °> Pt-Pr = si' i=h-,n.	C)
Индексы «плюс» и «минус» указывают на принадлежность значений
переменных моментам времени до и после удара.
Известно, что движение системы A) на интервалах времени, на
которых отсутствуют ударные силы Qi, может рассматриваться как
непрерывная последовательность канонических преобразований, по-
порождённая функцией Н. Подобно этому, наложим на обобщённые

19. Импульсивные движения динамических систем	133
ударные импульсы ограничения, при выполнении которых уравнения
импульсивного движения C):
qt=Q7> Pt=V7+Si, i=l,...,n,	D)
являются каноническими преобразованиями переменных #г-, рг-.
Необходимые и достаточные условия каноничности преобразования
состоят в том, чтобы скобки Лагранжа удовлетворяли следующим
равенствам [25]:
fc~ %} = 0, [p~Pk] = 0> [Ofc ] = c5ik-	E)
Здесь с — валентность канонического преобразования; 5ik — символ
Кронекера.
Составляем скобки Лагранжа для преобразования D):
Из условия E) для равенств F) следует, что преобразование D)
будет каноническим, если ударные импульсы обобщённых сил удовле-
удовлетворяют равенствам
—- =0, г ф к, 1 + —- = с, г = к.
дРк	дРк
Условия G), налагаемые на ударные импульсы Si, будут, очевидно,
выполнены, если принять их в виде
Si = (c- \)р~ + Ft(q-,..., q~,t)+ сг	(8)
при dFi/dq^ = dFk/dq~, г, к = 1,..., п.
Здесь ^ — некоторые постоянные, определяемые условиями, с по-
помощью которых задаётся момент удара (см. ниже).
Ударные импульсы (8) при с = 1 (далее речь будет идти только об
импульсивных движениях, соответствующих унивалентным канониче-
каноническим преобразованиям) определяются некоторой функцией П, которую
мы назовём потенциалом ударных импульсов. Поскольку поле удар-
ударных импульсов (8) образуется как результат наложения двух полей,
в функции П также выделим слагаемые, линейно зависящие от ^
(г = 1,... ,п) и t:
П = -По - J2 ад - cot.	(9)
г=1
С помощью потенциала П ударные импульсы определяются аналогично
силам потенциального силового поля:
Si = -^, i=l,...,n.	A0)

134	Гл. III. Об интегральных принципах
Однако поле ударных импульсов отличает то, что его действие лока-
локализовано во времени, т. е. происходит мгновенное наложение и снятие
поля.
С учётом (9) запишем производящую функцию К канонического
преобразования D) в виде
_	....,q~,t).	(И)
i=\
Действительно, производящая функция A1) приводит к канони-
каноническому преобразованию, соответствующему импульсивному движе-
движению D):
дК _ + сШ_ _ _ дК_ _ _ _ + . _
A2)
Здесь q~, pf (i = 1,..., n) — независимые переменные.
Заметим, что некоторая характеристика X(q,t,p) динамического
процесса при изучаемом импульсивном движении изменяется так, что
для скобок Пуассона справедливо равенство (ХН)~ = (ХН)+ [25].
В частности, интеграл, не зависящий от времени, сохраняет своё зна-
значение.
19.2. Функционал «действие» и условия его стационарности.
Покажем, что в случае потенциального поля ударных импульсов на
действительном движении динамической системы имеет место усло-
условие стационарности функционала, составленного в виде суммы функ-
функции —П и действия по Гамильтону. При этом фиксируются начальный
и конечный моменты времени (to и t\), начальное и конечное поло-
положение системы, а также обобщённые координаты (не обязательно все)
и (или) момент времени приложения ударных импульсов.
В момент времени t~ начинается импульсивное движение, которое
описывается производящей функцией A1). Обозначим через L функ-
функцию Лагранжа и введём в рассмотрение функционал
J = -II0(q-,...,q-,t)+ [ Ldt+ [ Ldt.	A3)
to	t+
Мгновенное приложение ударных импульсов, при котором обоб-
обобщённые координаты не изменяются, а также фиксирование некоторых
обобщённых координат и, возможно, времени приложения удара при-

19. Импульсивные движения динамических систем	135
водят к равенствам
Ф/ = qf -qf = 0, / = 1,...,п, Фп+1 = ?+ -?" =0,
ф/ =<h-n-\ ~ai-n-\ =0, / = n + 2,...,r <2n+ 1,	A4)
Фо = t~ - a0 = 0,
где as (s = 0, 1,...,r — n — 1) — фиксированные постоянные.
Отыскание условий минимума J A3) при ограничениях A4) явля-
является разрывной вариационной задачей [12]. Необходимое условие ста-
стационарности функционала с последующим переходом к каноническим
переменным (pi = dL/dqi) приводит к уравнениям A) на интервалах,
на которых отсутствуют ударные импульсы (Qi = 0), и равенствам
Pi =-^=> Р\t = ^T> г=1,...,п,
дФ и+ дФ Л гт , ^
Я- = --, Я+ = ---, Ф = -По + Y.
ох	ох	/=0
Здесь pi (I = 0, 1,...,г) — неопределённые постоянные множители.
Исключая из уравнений A5) неопределённые множители pi (I =
= 1,..., п + 1), получаем
+	0
Pi=Pi -^-^+
<*Ь	A6)
Из сравнения A6) и A2) видно, что постоянные q (г = 0, 1,..., п)
в (9) должны быть выбраны равными соответствующим неопределён-
неопределённым множителям, т. е.
При г= 1,...,Г-П- 1,
q = 0 при г > г — п — 1.
Если момент времени t~ не фиксирован, то следует также при-
принять со = 0.
Таким образом, на действительном движении динамической систе-
системы в условиях принципа Гамильтона-Остроградского при приложе-
приложении потенциальных ударных импульсов A0) выполняется необходимое
условие стационарности функционала J:
SJ = О, J = -П + 5, S= \ Ldt+ \ Ldt,
to	t+
где S — действие по Гамильтону.

136
Гл. III. Об интегральных принципах
Для определения постоянных q (г = 0, 1,..., п), входящих в функ-
функцию П, привлекается вторая группа уравнений A4) в соответствии
с условиями A7).
Полученное утверждение принципа Гамильтона-Остроградского
естественным образом распространяется на случай конечного
(фиксированного) числа моментов приложения мгновенных ударных
импульсов с потенциалами вида (9).
19.3. Интегральный инвариант Пуанкаре-Картана. Покажем,
что в случае потенциальных ударных импульсов в системе A) име-
имеет место интегральный инвариант Пуанкаре-Картана. С этой целью
рассмотрим расширенное фазовое Bп + 1)-мерное пространство пере-
переменных qi, t, pi (рис. 19.1). В этом пространстве выберем замкнутую
трубку прямых путей с контуром С0, определяющим начальное состо-
состояние системы в момент времени ?0- На трубке выделим замкнутую
кривую С~ охватывающую её и имеющую с каждой образующей лишь
одну общую точку. Контур С~ характеризует состояние системы перед
Рис. 19.1
ударом и, вообще говоря, является произвольным, так как условия,
определяющие момент приложения ударных импульсов, могут быть
заданы различным образом. Полагая, что преобразование D) — вза-
взаимно однозначное, дополним его равенством ?+ = t~ (мгновенность
удара) и построим контур С+. При последующем движении системы он
задаёт новую трубку прямых путей, на которой выделим произвольный
замкнутый контур С\ охватывающий эту трубку.

19. Импульсивные движения динамических систем	137
Две полученные трубки пересекаются в подпространстве qi, г =
= l,...,n, t. Для каждой из них имеем интегральные инварианты
Пуанкаре-Картана [25].
Обозначим через S^ и S^ действие по Гамильтону вдоль образу-
образующих трубок от кривой С0 до кривой С~ и от С+ до С1:
to(a)	t+(a)	г~[
Здесь L — функция Лагранжа, выраженная через канонические пе-
переменные; а — параметр, с помощью которого уравнения кривых
представляются в виде qi = qi(a), p% = Pi{pt), i = 1,..., n, t = t(a).
При любом а имеем [25]
l
^_ ^-HSt
jo	L V
Найдём сумму SS^ и SS^ с учётом A4):
6S = SSW + 6S& =
[	]l	l-Pi)K + (H+ - H~)St- A8)
(Sq~ =6q+, 6t-=6t+).
После подстановки в A8) равенств A2) и интегрирования по а для
замкнутых контуров С0 и С1 получаем
Е Pi6* ~ H5t
Таким образом, значение интегрального инварианта Пуанкаре-Кар-
Пуанкаре-Картана при разрывах фазовых координат данного вида сохраняется.
Пример. В качестве примера системы с разрывами фазовых ко-
координат рассмотрим момент перехода натуральной системы из одной
области пространства состояний в другую с различными обобщёнными
потенциалами. Обобщённый потенциал описывается выражением вида
г=\
где Ai (i = 0, 1,..., п) — функции обобщённых координат и времени t.
Обобщённые импульсы определяются равенствами
дЬ дТ , . 1
Pi = wt- = -7ГТ- - А{, г = 1,...,п
dq dq

138	Гл. III. Об интегральных принципах
(где Т — кинетическая энергия), из которых следует, что разрывы пер-
первого рода функций Ai приводят к разрывности обобщённых импульсов.
Момент мгновенного изменения обобщённого потенциала характеризу-
характеризуется условиями
vt-VT = -Af + Ar, i= l,...,n.
Если для разностей в правых частях этих равенств существует
функция П((/1,... ,qn,t) такая, что
л- л+ дП	л
Ai -At = —, г = 1,...,п,
1	г dqi
то все предыдущие рассуждения и выводы справедливы.
Не только интегральный инвариант, но и скобки Пуассона других
механических величин инвариантны по отношению к такому преоб-
преобразованию обобщённого потенциала. Используя терминологию, при-
принятую в теории поля, назовём функцию Aq скалярным потенциалом,
а (А\,... ,Ап)т — векторным потенциалом. Тогда имеющаяся неодно-
неоднозначность потенциалов позволяет выбрать их так, чтобы скалярный
потенциал был равен нулю. Для этого достаточно выполнения условия
(при импульсивном движении оно может быть выполнено только непо-
непосредственно после окончания приложения ударной силы)
Отмеченное свойство известно в теории поля [53] как калибро-
калибровочная (или градиентная) инвариантность физических величин по от-
отношению к такому же преобразованию потенциала поля лоренцовой
силы [25].
Отметим, что в выражении функции Лагранжа реономных систем
роль скалярного и векторного потенциалов могут играть члены нулевой
формы и набор коэффициентов линейной формы относительно обоб-
обобщённых скоростей соответственно.
19.4. Об опти ко-механической аналогии для движений с уда-
ударами. Известна аналогия оптических явлений и непрерывных (без
ударов) механических явлений (см., например, [1, 4]).
В данном пункте показано, что аналогию с волновой теорией света
Гюйгенса имеет динамика расширенной системы (расширение системы
производится на основе метода Лиувилля за счёт введения допол-
дополнительных переменных, сопряжённых с обобщёнными координатами
и обобщёнными импульсами [1]). Аналогия механики с корпускуляр-
корпускулярной теорией света Ферма распространяется на движения с ударами,
имеющими потенциал ударных импульсов и не меняющими значения
обобщённого интеграла энергии.
Рассмотрим систему, движение которой на интервалах времени
между ударами (непрерывное движение) описывается каноническими

19. Импульсивные движения динамических систем	139
переменными q^ pi, i= l,...,n (обобщёнными координатами и обоб-
обобщёнными импульсами), и функцией Гамильтона Я:
дН	дН . 1	/от
*=flfc' Л = "%' *=1—^	B0)
В некоторые дискретные моменты времени происходит ударное вза-
взаимодействие материальных точек системы с неудерживающей связью:
п-\
<in=Y^asQs> as = as(qi,'~,qn,t)-	B1)
s=\
Ограничимся изучением движения с одним ударом, момент которого
определяется условием вида
Vo(qi,...,qn,t)=O-	B2)
Получим замкнутую систему уравнений импульсивного движения
(позволяющую находить обобщённые скорости после удара) с помощью
понятия о коэффициенте восстановления (х) [113]:
p+ + asp+ =p~ +asp-, s = l,...,n- 1,
_ n-i _	/	n-\ _ \	B3)
s=\	V	s=l
где индексами «минус» и «плюс» отмечены доударные и послеудар-
послеударные значения переменных соответственно, а символ «~» указывает,
что обобщённые скорости заменяются союзными выражениями (через
обобщённые импульсы).
Аналогия между механикой и волновой теорией света Гюйгенса
основана на представлении процесса движения с помощью канониче-
канонических уравнений Гамильтона. В общем случае при ударе преобразование
переменных состояния не является каноническим. При этом и разрыв-
разрывное движение (включающее, кроме участков непрерывного движения,
также импульсивное движение) исходной системы не имеет указанной
аналогии.
Покажем, что оптико-механическая аналогия распространяется на
системы, в которых кроме переменных (qit pit i= l,...,n), удовле-
удовлетворяющих уравнениям B0), B3), введены дополнительно две группы
переменных — ^ и щ, г= 1,...,п, сопряжённые соответственно с qi
и pi. Систему, движение которой описывается An переменными — qi,
Pi, ?ь Ци далее будем называть расширенной. Для того чтобы имела
место аналогия с волновой теорией света Гюйгенса, импульсивное дви-
движение расширенной системы должно быть каноническим преобразо-
преобразованием. Построение расширенной системы проведём на основе метода
Лиувилля приведения уравнений к канонической форме [1]. Кроме
уравнений B0), B3), которым должны удовлетворять переменные %

140	Гл. III. Об интегральных принципах
Pi, потребуем также, чтобы на участках непрерывного движения рас-
расширенной системы выполнялось условие стационарности действия по
Гамильтону исходной системы с функцией Лагранжа L:
г=\
Тогда функция Гамильтона Н* расширенной системы имеет вид
i	^ +т— .	B4)
i={ x -^t l dpi %dqi)'
Функция Н* определяет уравнения для сопряжённых перемен-
переменных ?i, rji на участках непрерывного движения:
1	дШ дН , А д2Н , , ч , А <92Я
дН ™ д2Н ( с. , ™ д2Н	,ОЛЧ
4i = "^=g^^(pi"^)+g^^4i- B6)
Если ввести обозначения Q = ^ - pit то уравнения B5), B6) при-
примут вид уравнений в вариациях Пуанкаре:
¦ " д2н , " д2н
д2н
Функционал в вариационном принципе Гамильтона-Остроградско-
го в случае разрывных движений имеет вид
/ = П + 5.	B7)
Необходимые условия стационарности функционала B7) включают
следующие выражения для доударных и послеударных значений пере-
переменных <^, гц\
с- _ _ дП .+ _ дП - _ _ дП + _ дП .
2n	l	B8)
/=0
где Ф/ = 0 (/ = 1,..., п) — символическая запись равенств, полученных
из B3); Ф/ = q~l_n — Ч[-п = ® (I = п-\- \,..., 2п) — условия непрерывно-
непрерывности обобщённых координат (непрерывность времени в B3) уже учте-
учтена); pi (I = 0, 1,..., 2п) — неопределённые множители (постоянные),

19. Импульсивные движения динамических систем	141
для определения которых привлекаются уравнения B2), B3) и условия
непрерывности обобщённых координат.
Равенства B8) имеют вид свободных унивалентных канонических
преобразований с производящей функцией П и независимыми пере-
переменными q~, р~, qf, pf, г = 1,...,п [25]. Эти переменные могут
рассматриваться как независимые за счёт учёта в функции П условных
уравнений, выражающих зависимости между переменными, с неопре-
неопределёнными множителями р\.
Заметим, что каноническое преобразование переменных состояния
расширенной системы можно получить и в более общем случае, когда
замкнутая система уравнений импульсивного движения составлена при
других ограничениях и функции Ф/ принадлежат классу С1.
Таким образом, канонический формализм Гамильтона распростра-
распространяется на разрывное движение расширенной системы. Отсюда следует
вывод об оптико-механической аналогии динамики расширенной систе-
системы и волновой теории света Гюйгенса (оптико-механическая аналогия
Гамильтона, основанная на представлении движения с помощью груп-
группы канонических преобразований).
Примечание. Известно, что в случае системы со стационарны-
стационарными связями при одной неудерживающей абсолютно упругой {к = 1)
мгновенной связи уравнения движения могут быть приведены к кано-
канонической форме (без расширения системы) путём замены переменных.
Аналогию с оптическим принципом Ферма, известную для непре-
непрерывного движения [25], обнаруживаем, используя соотношение между
действием B7) и действием по Лагранжу для обобщённо-консерватив-
обобщённо-консервативных систем:
W = Tl + S + h(tx -t0),	B9)
в случае, когда значение обобщённого интеграла энергии Н = h при
ударе не меняется.
Действительно, из принципа взаимности вариационных задач на
условный экстремум следует, что экстремали в задаче на минимум
функционала B7) при фиксированном времени движения совпадают
с экстремалями задачи на минимальное время движения при фик-
фиксированном (или стационарном) действии / B7). Поэтому из B9)
непосредственно получаем, что стационарному значению действия /
соответствует стационарное значение функционала быстродействия.
Таким образом, движение с ударами, имеющими потенциал ударных
импульсов, в случае обобщённо-консервативных систем имеет анало-
аналогию с оптическим принципом Ферма.
Полагаем, что аналогию с колебательными процессами световых
явлений (оптико-механическую аналогию Н. Г. Четаева) для механи-
механических движений с ударами также следует искать в классе движений
с потенциалом ударных импульсов, к которому при определённых тре-
требованиях относится движение расширенной системы.

142	Гл. III. Об интегральных принципах
20. Об интегральных равенствах
для неголономных систем
Принцип Гамильтона, рассматриваемый как вариационный прин-
принцип стационарного действия, справедлив только для голономных си-
систем. Невозможность непосредственного распространения интеграль-
интегральных принципов, установленных для голономных систем, на неголоном-
ные системы была отмечена ещё Герцем [27]. Он обратил внимание
на то, что не всякие две точки конфигурационного пространства мо-
могут быть соединены траекторией системы с неинтегрируемой диффе-
дифференциальной связью. Первым, кто предложил интегральный принцип,
пригодный для неголономных систем, по-видимому, был Гёльдер: его
принцип имеет форму интегрального равенства, не являющегося усло-
условием стационарности функционала; он был получен при предположе-
предположении перестановочности операций d и 5 (см. заметку 16). При этом,
во-первых, варьированные траектории не удовлетворяют уравнениям
неголономных связей, и во-вторых, уравнения движения неголономной
системы не совпадают с уравнениями Эйлера вариационной задачи
Лагранжа. Обсуждению этих двух вопросов посвящена обширная ли-
литература с начала двадцатого века и до настоящего времени. Приведём
некоторые результаты [101].
20.1. Интегральные равенства Гёльдера, Воронца и Суслова.
Рассматривается неголономная система, заданная функцией Лагранжа
L(q,t,q) = Т — П, с идеальными независимыми неголономными свя-
связями:	п
fl = 'JTauqi + ao = 0, /=1,...,г.	A)
г=1
Здесь qi и qi — обобщённые лагранжевы координаты и обобщённые
скорости; t — время; T(q,t,q) = Т2 + Т\ + То — кинетическая энергия
системы; Та — однородные относительно обобщённых скоростей qi
степени а функции (а = 0, 1,2); П — потенциальная энергия; au(q,t),
ao(q,t). В силу независимости связей A) их можно представить в раз-
разрешённом виде:
Qk+i = Vi(q\,'-,qn,q\,'-,qk,t), / = l,...,r,	B)
приняв qs (s = 1,..., к = n — г) за независимые обобщённые скорости.
Виртуальные перемещения 5qi удовлетворяют уравнениям
= 0, 1= l,...,r,	C)
г=1
принимающим для связей B) вид
-?bls6qs, 1=1,...,г.	D)
s=l

20. Об интегральных равенствах для неголономных систем	143
Интегральное равенство Гёльдера
и
\5Ldt = O	E)
to
при
5qi(to) = 5qi(tl)=O, i=l,...,n,	F)
справедливо как для голономных, так и для неголономных систем при
допущении перестановочности операций d и 5:
% = |(%),	G)
для всех переменных (г = 1,...,п). После изохронного варьирования
в подынтегральном выражении E) получаем
Исключив с помощью B) из выражения кинетической энергии
зависимые обобщённые скорости, получаем функцию
$(<?!,...,gn,gb...,gb?),	(9)
вариация которой связана с вариацией кинетической энергии равен-
равенством	г
1=\
Подстановка A0) в E) приводит к интегральному равенству Ворон-
Воронца (форма Воронца принципа Гамильтона) (при условии F)):
дТ	1
——Eqk+i — S<Pi) dt = O.	A1)
I	1—f uqk+i
to'
Свойство G) можно оставить только для независимых обобщённых
скоростей, т. е.
а для зависимых с учётом B) принять выражения
Sqk+l = jt Fqk+i) - J2 Aks+lS(ls,
s=rl	A3)
~ dt dqs dqs ^ dqk+v dqs '
Символ 5 означает вариацию функции, содержащей зависимые скоро-
скорости, в смысле A2), A3).

144	Гл. III. Об интегральных принципах
При таком способе варьирования кривые сравнения в первом при-
приближении удовлетворяют уравнениям связей.
Используя соотношения A2), A3) в интегральном равенстве (8),
получаем интегральное равенство Суслова (форма Суслова принципа
Гамильтона):
A4)
при условиях F).
Все три приведённые интегральные равенства в общем случае не
представляют собой вариационного принципа стационарного действия
для неголономных систем. Принцип стационарного действия для него-
лономных систем при некоторых условиях имеет вариационную фор-
форму [101].
20.2. О вариационной форме интегрального принципа для
неголономных систем. Вариационной задаче на условный экстремум
функционала (действие по Гамильтону) с условиями A) сопоставляется
задача на безусловный экстремум функционала
L*dt,	A5)
to
A6)
где Х\ — множители Лагранжа.
Необходимое условие стационарности функционала A6):
L*dt = O,	A7)
to
состоит в выполнении уравнения
y^W=0.	A8)
Сравним уравнение A8) с общим уравнением динамики. Общее
уравнение динамики голономной системы с функцией Лагранжа L
и идеальными связями A) имеет вид
dL_8L_y^ 8^\
dqi dqi *f dqi J
где Л/ — множители связей.

20. Об интегральных равенствах для неголономных систем	145
Уравнения A8) и A9) совпадают, если имеет место равенство
2>(|-Ш%=°-	B0)
1,1
При этом
Xi = -Xv 1=1,..., г.	B1)
Условие B0) необходимо и достаточно (А. С. Сумбатов, см. [101]) для
того, чтобы некоторое решение qi(t) уравнений несвободой системы
с множителями связей (при связях A)) находилось среди решений
уравнений, полученных из A8), A). Соответственно интегральный
принцип Гамильтона для неголономной системы имеет характер вариа-
вариационного принципа стационарного действия A7) только для движений,
удовлетворяющих равенству B0).
Покажем, что при указанных условиях можно получить канониче-
каноническое представление уравнений движения в новых переменных qi, t, тг^:
тг< = ^,	B2)
dq
с помощью функции Гамильтона Н\, получаемой в результате преоб-
преобразования [98]
Нх (q, тг, t) = maxf ? тг*& - L \ ft = о).	B3)
В переменных Гамильтона qi, t, щ для функции Н\ уравнения движе-
движения имеют вид	о„	о„
*=a5i7' " = -%•	B4)
Уравнения B4) при условии B0) (и B1)) равносильны уравнениям
с множителями связей:
dpi r	dqi ^ dqi
Таким образом, при выполнении условия B0) движения неголоном-
неголономной системы описываются каноническими уравнениями B4), которые
могут быть положены в основу описания с помощью принципа стацио-
стационарного действия в вариационной форме [101]:
to *
равносильного (при условиях на концах F)) принципу Гёльдера E).

Глава IV
РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ
21. Модель динамики системы
«жёсткое колесо — деформируемый рельс»
Изучается качение жёсткого колеса по деформируемому упругому
рельсу, лежащему на вязкоупругом основании. Ранее [20, 115] при со-
составлении модели системы использовалась приближённая теория Бер-
нулли-Эйлера. Здесь применяется уточнённая теория изгиба стержней
(СП. Тимошенко). С помощью принципа Гамильтона-Остроградского
составлены уравнения движения. Показано, что связи, описывающие
условия контакта, создают реакции в виде силы и пары. Дана оценка
величины псевдоскольжения, обусловленного поперечными (в отличие
от классического крипа) деформациями. Найдены две характерные
скорости стационарного качения колеса, разделяющие области каче-
качественно различного движения рельса.
21.1. Механическая схема. Рассматривается плоское движение
системы «жёсткое колесо — деформируемый рельс». Ось колеса яв-
является осью динамической симметрии, рельс моделируется однород-
однородной балкой, испытывающей поперечный изгиб в условиях гипотезы
плоских сечений. В недеформированном состоянии рельс расположен
Ун
	———
Ox
у\
(
{
У\
О
\)
к
-Ре,
хх
XI
S9
Рис. 21.1
горизонтально на вязкоупругом основании. Внешние по отношению
к системе активные силы, приложенные к колесу, приведены к его
центру и включают силу (представленную в виде двух составляющих
Fe\ и —Рв2) и пару с моментом М (рис. 21.1). Примем следующие
обозначения: w(s,t) — поперечное перемещение точки нейтральной
линии рельса с горизонтальной координатой s (s e [51,52]), параллель-
параллельное оси O\Y\ инерциальной системы координат в момент времени ?;

21. Динамика системы «жёсткое колесо — деформируемый рельс» 147
so G [51,52] — координата той точки нейтральной линии рельса 1о,
которой соответствует точка К на линии контакта l\\ ijj(s,t) — угол
поворота плоского сечения балки; х\, у\, # — координаты центра
масс О колеса и угол его поворота (Oxyz — оси координат, связанные
с колесом).
Составим модель динамики системы с помощью метода переменного
действия, состоящего в распространении принципа Гамильтона-Остро-
градского на системы с распределёнными параметрами. Для примене-
применения этого принципа требуются функционал действия по Гамильтону
и изменение действия за счёт активных непотенциальных сил и сил
реакций связей, не учтённых выбором определяющих параметров.
21.2. Действие. Действие по Гамильтону S строится на основе
функции Лагранжа L = Т — П (где Т — кинетическая энергия системы,
П — её потенциальная энергия):
5= Ibdt,	A)
и
где [t 1, ^2] — фиксированный отрезок времени. Кинетическая энергия
системы складывается из кинетической энергии круглого колеса при
плоском качении и кинетической энергии рельса:
_ ю	. S2
(pw + Jip ) ds,	B)
Si
где пг и Jq — масса и момент инерции колеса относительно оси
симметрии соответственно; р и J ds — линейная массовая плотность
и момент инерции элементарной массы рельса относительно оси, пер-
перпендикулярной плоскости движения и проходящей через соответству-
соответствующую точку нейтральной линии; точка означает дифференцирование
по времени t.
Примечание 1. С помощью параметра J характеризуются про-
продольные силы инерции. Иногда эта величина трактуется как «момент
инерции единицы длины стержня относительно центральной оси», но
это не так. Малость отношения высоты сечения к длине балки не явля-
является, вообще говоря, достаточным основанием возможности пренебречь
членами с коэффициентом J в B) (и соответственно в уравнениях
движения).
Составим функционал потенциальной энергии. Потенциальными
считаем внутренние упругие силы изгиба балки и линейные упругие
силы основания.
Используем уточнённую теорию С. П. Тимошенко, в которой функ-
функционал потенциальной энергии имеет вид [4]
s2
j [^ + hty-w'^ds,	C)

148	Гл. IV. Решение прикладных задач
где к\ — коэффициент, зависящий от модуля упругости и геометрии
поперечного сечения рельса (пропорциональный h4; h — характерный
размер поперечного сечения); кз — коэффициент, определяемый по мо-
модулю сдвига и геометрии поперечного сечения (пропорциональный h2)
и учитывающий также неравномерность касательных напряжений по
сечению; штрихом обозначено дифференцирование по s.
Слагаемые в C) имеют следующий механический смысл: первое
слагаемое — потенциальная энергия упругих изгибающих моментов
и зависящих от них перерезывающих сил, а второе — потенциальная
энергия дополнительных упругих перерезывающих сил.
Примечание 2. В теории Бернулли-Эйлера потенциальная
энергия имеет вид интеграла
где к — изгибная жёсткость рельса. Этот функционал можно по-
получить из C) подстановкой равенства ф = w' (далее это условие
будет рассматриваться как связь) и равенства, получаемого из него
дифференцированием по s. Однако, в отличие от C), функционал
потенциальной энергии в теории Бернулли-Эйлера не удовлетворяет
требованиям, предъявляемым к функционалам, представляющим дей-
действие деформации [48], в части порядка производной от функции w
по аргументу s (плотность евклидового действия деформации, как
показали Э. и Ф. Коссера, не должна зависеть от производных второго
порядка; см. также заметку 18). Кроме того, этот функционал не
является голономным в смысле работы [4] (в голономном функционале
подынтегральное выражение может зависеть от вторых производных
только линейно).
С учётом линейных упругих сил деформации основания, на котором
лежит рельс, потенциальная энергия системы представляется функци-
функционалом	S2
И = - \ [к\ф; + k2w + к$(ф — wf) ] ds,	D)
где &2 ~~ жёсткость основания.
При кинетической энергии B) и потенциальной энергии D) функ-
функция Лагранжа представляется в виде двух слагаемых:
L = L0+\Ads, LQ = ^{x\+y\)+J-^-,
А	2	2	E)
Л = i \pw2 + JiJ - кхф'2 - k2w2 -к3(ф- w'f].
Изменение действия по Гамильтону A) при варьировании опре-
определяющих координат и их производных (с учётом перестановочных

21. Динамика системы «жёсткое колесо — деформируемый рельс» 149
соотношений) находим по правилам вариационного исчисления [131]:
и	и г~-
q\ =x\(t),
^"AdsdtJ1-^^ д1дА] д1дА
J J	J J ^ Vj [
t\ S\	t\ S\ J
G)
Ul(s,t) = w(s,t), U2(s, t) = 1p(s, t),
где
duj dt [ duj J ds [ дщ J	j
представляет собой оператор Эйлера-Остроградского (операция над
выражением в фигурных скобках является полной частной производ-
производной [131]). В выражения F), G) не включены слагаемые, относящиеся
к моментам времени t\, t2 и точкам с координатами s = s\, s = s2.
Структура функционала диссипативных сил вязкого трения часто
принимается [20] аналогичной структуре функционала потенциальной
энергии. Однако вопрос об экспериментальном подтверждении суще-
существования материалов, в которых внутренняя диссипация энергии про-
пропорциональна скорости деформирования (материал Кельвина-Фойхта),
остаётся открытым [112]. Учтём только малые силы внешнего вязкого
трения, действующие на рельс, с диссипативным функционалом следу-
следующего вида:	S2
D = - e(d\ip2 + d2w2) ds,	(8)
2 J
где d\, d2 — коэффициенты вязкого трения; г — малый параметр.
Изменение действия за счёт виртуальной работы сил вязкого тре-
трения, заданных функционалом (8), имеет вид
- d2w5w^j ds dt.	(9)
U si
Изменение действия за счёт виртуальной работы внешних активных
(заданных) сил, приложенных к жёсткому колесу, находится так же,
как обычно в аналитической механике.
21.3. Анализ связей. Общие свойства связей в системе с не-
несколькими независимыми параметрами (в данной задаче это t и s)
рассмотрены в п. 9.3.
Упоминавшееся в примечании 2 условие
f = ^-w' = 0	A0)

150
Гл. IV. Решение прикладных задач
будем рассматривать как идеальную связь. Реакция идеальной связи
задаётся с помощью уравнения для виртуальных вариаций, получаемо-
получаемого из уравнения связи A0):
5f = 5i/;-5w' = O.	A1)
Условия в месте контакта колеса и рельса также являются связями.
Положим, что при качении колеса в месте контакта отсутствует про-
проскальзывание. Тогда имеем равенство скоростей материальных точек
колеса и рельса, находящихся
в точке К (рис. 21.2):
х\ + rb cos a = —hwfQ cos a,
у\ + гё sin a = —hw'o sin a + wq.
A2)
В A2) и на рис. 21.2 нижний
индекс 0 указывает на то, что па-
параметр принимается при s = so,
где so — координата точки ней-
нейтральной линии 1о, которой соот-
соответствует точка К на линии каса-
касания 1\ (в недеформированном со-
состоянии нейтральная линия совпа-
совпадает с осью О\Х\, а линия каса-
касания 1\ задаётся уравнением Y\ = h\
2h — высота рельса); г^о = w(so,t);
фо = ip(so, t); а — угол между вертикалью и радиусом ОК; ср — угловая
координата точек обода колеса (^о соответствует точке К в месте
контакта). Соответственно имеется равенство [20]
2/1
О
Рис. 21.2
а =
A3)
Отдельно взятое равенство A3) представляет собой чисто кинематиче-
кинематическое соотношение. Однако учитывая в точке контакта равенство
tga = wf0,	A4)
после исключения а из A3) и A4) получаем связь между физическими
параметрами. Ограничив область исследования неравенствами \а\ <С 1,
\w'0\ <C 1, из A2) и A3), A4) получаем уравнения для виртуальных
вариаций:
5х\ + rStf = —h5w'o, 5y\
= —hw'o5w'o
= 5w'o, A5)
где г — радиус колеса.
Уравнения связей и уравнения для виртуальных вариаций вместе
с функционалами (см. п. 21.2) определяют модель движения системы.
21.4. Интегральный принцип. Уравнения движения системы.
Получим уравнения движения системы с помощью интегрального

21. Динамика системы «жёсткое колесо — деформируемый рельс» 151
принципа для интервала изменения s, состоящего из двух равных
частей — [si,so) и Eо>52]> ПРИ s\ = —b, s2 = b и достаточно большом
значении b [20].
Составляем интегральное равенство принципа Гамильтона-Остро-
градского:
^2	^2 ^2
t\ S\
l \[-e(diip5il;+ d2w5w) + \Eф - 5w')]dsdt +
t\ S\
f (FSxi - PSy{ + МЩ dt + f /ii (Sxi + r<W + h6w'o) dt +
ra^i? + hw'o5w'o - 5w0) + i/(*i? - 6w'o)] dt = 0, A6)
5uj(s,t\) = 5uj(s,t2) =0, j = 1,2,
где A(s,?), /Jii(t), fi2{t), v(t) — неопределённые множители Лагранжа,
задающие реакции связей. В подынтегральном выражении A6) вариа-
вариации произвольны.
Раскрываем первое слагаемое в A6) по формулам F), G) с учётом
перестановочных соотношений 5ф' = Eф)', 5w' = Ew)f. После интегри-
интегрирования по частям, приравнивая нулю коэффициенты при вариациях
5х\, 5у\, Si!), 5w, 5ф, получаем дифференциальные уравнения
тх\ -
тух =
Jo^ = М + /
кхф" + к3(ф
k2w + /сз^^7 -
-Р + /Х2
Х1Г + /Х2П
di^- A = 0,
d2^ - Ах = 0
A7)
A8)
A9)
B0)
B1)
и условия сопряжения в точке s = sq
-v + /xift + МЧ =0'	B2)
-A(s0 - 0, t) + AE0 + 0, t) - fi2(t) = 0.	B3)
Полученные уравнения дополняются условиями непрерывности опре-
определяющих координат и их производных по s (до второго порядка)
в месте контакта, граничными условиями (uj(s\,t) = Uj(s2,t) — 0)»
уравнениями связей и начальными условиями.
Вид правых частей уравнений A7)—A9) показывает, что реакция
рельса на колесо состоит из силы, приложенной в точке К, и пары,
момент которой направлен по оси колеса. Момент реакции v можно
трактовать как момент трения качения. Равенство B2) означает, что
главный момент этой реакции относительно центра, лежащего на ней-
нейтральной оси, равен нулю, т. е. реакция рельса на колесо имеет рав-
равнодействующую, проходящую через этот центр. Таким образом, имеем

152	Гл. IV. Решение прикладных задач
обоснование предложения, сделанного в [20]: «считать, что реакция,
возникающая в точке К, переносится в соответствующую точку ней-
нейтральной линии с координатой sq...». Неравенство нулю момента ре-
реакции относительно точки контакта отражает тот факт, что физически
контакт колеса и рельса не является точечным. Аналогичную ситуацию
имеем при учёте момента трения качения с помощью коэффициента
трения качения (получаемого на основе моделей с деформируемыми
телами или экспериментально).
Неопределённый множитель A(s, t) имеет смысл перерезывающей
силы (см. B0)) в сечениях рельса. Перерезывающая сила в сечении
рельса с координатой s = so (см. B3)) претерпевает разрыв, равный по
величине вертикальной составляющей реакции колеса на рельс.
Уравнения B0), B1) в отсутствие связи A0) и диссипации совпа-
совпадают с уравнениями, полученными в работе [122].
Примечание 3. В работе [122, с. 115] дан вывод дифференци-
дифференциального уравнения собственных поперечных колебаний балки (урав-
(уравнение С. П. Тимошенко) из чисто физических соображений (потенци-
(потенциальная энергия при этом не использовалась) и показан его волновой
характер.
Подставив уравнение связи A0) в уравнения B0), B1), имеем
Зф - кхф" + edxi) - Л = 0,	B4)
pw + k2w + ed2w - А' = 0.	B5)
Сопоставление B4), B5) с уравнениями, полученными в отсутствие
связи A0), приводит к выводу о том, что идеальная связь A0) мо-
может быть реализована бесконечным увеличением жёсткости балки при
сдвиге (&з —> оо) (переход от теории Тимошенко к теории Бернулли-
Эйлера).
Исключив множитель А и координату ф (с учётом уравнения свя-
связи A0)), из уравнений B4), B5) находим уравнение для определения
прогиба рельса:
k\ww — Jw" + pw — ed\w" + sd2w + k2w = 0, s ф s§. B6)
Если закон изменения прогиба w(s,t) получен, то из B4), B5)
(с учётом уравнения связи A0)) находится дополнительная перерезы-
перерезывающая сила, обусловленная реакцией. В частности, это может быть
сделано в стационарном режиме движения.
21.5. Стационарный режим движения системы. Стационарный
режим движения системы характеризуется постоянной скоростью оси
колеса, постоянной угловой скоростью и неизменным положением точ-
точки контакта в системе координат, поступательно перемещающейся
с осью, а также постоянным значением мощности диссипативных сил,
т. е. когда
х\ = с, у\ = const, ё = const, a = const, D = const, B7)

21. Динамика системы «жёсткое колесо — деформируемый рельс» 153
где с — скорость оси колеса, D — значение функционала (8).
Подстановка B7) в уравнения связей и в уравнения движения
A8)—B0) приводит к равенствам
с + rficosa = — Jiw'q cos a, rfisina = — hw^sina + wq, B8)
^ = O.	B9)
Из B7) и B8) с учётом сделанных выше предположений о малых
величинах имеем
щ = const = —cw'q, c-\-r\$ = 0 (wq = $, r\=r-\-h). C0)
Мгновенный центр вращения колеса в общем случае смещён на
величину г\а по горизонтали относительно точки нейтральной линии
рельса, имеющей координату so- Поэтому, согласно C0), на пройденном
пути действительное число оборотов колеса x\/Bnr\ cos а) в общем
случае отличается от геометрического числа оборотов х\/Bтгг), т.е.
проявляется своего рода псевдоскольжение. Известное [136] явле-
явление крипа (creep) обусловлено продольными деформациями основания
и (или) периферии колеса, здесь же причиной псевдоскольжения явля-
является поперечная деформация.
При стационарном движении выполняется равенство (см. A9), B9))
M-nF + Pna = 0.	C1)
Из C0), C1) получаем кинематическое и динамическое выражения
для угла а (при с > 0):
С	Г\Р
которым соответствуют три варианта относительного расположения
колеса и рельса (рис. 21.3):
а)	а > 0, щ < 0 при r\F - М > 0;
б)	а<0, w0>0 при nF-M<0;	C3)
в)	а = 0, wo = 0 при r\F = M.
Сравнение мощности активных сил GV(a) = Мё + Fc) и мощности
всех внешних сил (N = Мд + Fc + Pwo = 0), приложенных к колесу,
приводит к равенству — 2D = Рщ, где D — значение функционала (8)
диссипативных сил. Из последнего равенства следуют два вывода:
1) сила Р в стационарном движении постоянна; 2) из трёх вариан-
вариантов C3) возможны лишь варианты а и в, причём варианту в соответ-
соответствует модель без диссипации энергии (г = 0 в (8)). Для консерва-
консервативной системы при с ф 0 имеем: а = 0, касательная к нейтральной
линии — горизонтальна (wf0 = 0), г^о = 0. В этом случае пригодна
кинематическая интерпретация [20] движения оси колеса: гипотетиче-
гипотетическое колесо радиуса г\ с центром в точке О катится без скольжения

154
Гл. IV. Решение прикладных задач
по горизонтальной направляющей, совпадающей с недеформированной
нейтральной линией.
Система координат, связанная с осью колеса, в стационарном режи-
режиме является инерциальной. В таких осях удобно использовать коорди-
координату ? = s — ct для точек рельса перед колесом (s > sq) и координату
С = ct — s для точек рельса позади колеса (s < so). Функции W(?)
и w(s,t) (W(?) = u;(s,t)) имеют производные, связанные равенствами
вида
w = — с
dW
W
, dW
W = -jr-,
w = с
2d2W
. „	d3W
w = -c
¦3 '
w =
C4)
(аналогично для функций Ф(?) = ifj(s,t)). Производные от функции
W(Q = w(s,t) (они отличаются знаком в нечётном порядке) имеют вид
dW
—,
/ dW .. 2
w = — ^r—, w = с
w" = c
d3W
w" =
d2W
C5)
(аналогично для функций Ф(?) = ip(s,t)).
Подставив C4), C5) в B6), получаем соответственно уравнения
(оставляем одинаковое обозначение производных по переменным (и ()
(fci - Jc2)Ww + edxcWf" + pc2W/x - d2c^' + /c2W = 0, ? > 0, C6)
(fei - Jc2)WIV - edicW7" + pc2W/x + d2c^' + /c2W = 0, С > 0. C7)
В консервативном случае уравнения C6) и C7) совпадают:
(fci - Jc2)Ww + pc2W" + /c2W = 0,	C8)
что соответствует симметрии решений относительно оси Оу\. Можно
заметить, что порядок уравнения для консервативной системы тот же,
что и уравнения, полученного с учётом внешнего вязкого трения.

21. Динамика системы «жёсткое колесо — деформируемый рельс» 155
Корни характеристического уравнения, соответствующего уравне-
уравнению C8), вычисляются по формулам
n ±J	2 , A ^pc
у 2{k\ — Jc )
C9)
Величина Д в C9) представляется в виде произведения (А =
D0)
Характерные скорости с\ (см. D0)) и с2 (с\ = к\/J = \/к\к2 /(цр)),
причём с2 > с\, разделяют весь диапазон скоростей на области, в ко-
которых форма рельса качественно различна. Скорость с\ является кри-
критической скоростью в том смысле, что в области с < с\ существуют
нетривиальные решения уравнения C8), удовлетворяющие граничным
условиям (значение критической скорости, найденное в [20], получает-
получается при /i = 0).
Учёт параметра J, как показывает выражение D0), снижает значе-
значение критической скорости с\ и приводит к появлению второй характер-
характерной скорости с2.
В области скоростей 0 < с < с\ корни характеристического уравне-
уравнения, соответствующего уравнению C8), имеют вид ±a±iC. Поэтому
форма нейтральной оси рельса описывается уравнением
W(?) = Сх ехр [(-а + г/?)?] + Сх ехр [(-а - г/?)?], ? > 0, D1)
где С\ и С\ — комплексные постоянные интегрирования (С\ — ком-
комплексное число, сопряжённое с числом С\)\ другие постоянные инте-
интегрирования равны нулю согласно условиям на бесконечности. Заме-
Заменой ? на С получаем уравнение, аналогичное D1):
W(C) = С2 ехр [(-а + г/3)С] + С2 ехр [(-а - г/3)(], С > 0.
При скоростях с > с2 корни характеристического уравнения — веще-
вещественные (dzcji, ±^2), а условия на бесконечности можно удовлетво-
удовлетворить при специальном выборе постоянных интегрирования.
В области скоростей с2 > с > с\ корни характеристического уравне-
уравнения — чисто мнимые: dzicji, ±ioo2 (oo\ < ио2). В этой области параметров
условия на бесконечности нетривиально не удовлетворяются, но можно
ожидать, что учёт малого вязкого сопротивления изменит ситуацию.
Найдём малые поправки к корням характеристического уравнения
консервативной системы в области скоростей с2 > с> с\.

156	Гл. IV. Решение прикладных задач
Составляем характеристическое уравнение, соответствующее урав-
уравнению C6), в форме
(fci - Jc2)(Dn + г5L + edic(Dn + е5K + pc2(Dn + e5J -
- sd2c(Dn + eS) + k2 = 0 (n= 1,...,4), D2)
где величины Dn C9) удовлетворяют уравнению C8), а г5 — малые
приращения. С учётом малых первого порядка относительно е из D2)
находим, что корни ±icj\, ±icj2 получают поправки e5j (j = 1, 2), где
6j = -(-\y^2+^jl (j=l,2;51>0;S2<0).	D3)
Следовательно, форма нейтральной оси рельса перед колесом опи-
описывается уравнением:
W(O = С, ехр [(е62 + iw2)i] + С, ехр [(е62 - ico2)$ , ? > 0. D4)
Характеристическое уравнение для C7) имеет вид
(fci - Jc2)(Dn + e5)A - sdxc(Dn + s5f + pc2(Dn + ?<5J +
+ ed2c(Dn + eS) + k2 = 0 (n=l,...,4). D5)
Далее имеем
6j {iy	Ul>2Sl<0t62>0)>
и поправка е5\ к корням dzicji является отрицательной. Соответственно
получаем решение уравнения C7):
Ж,(С) = С2 ехр [(^! + io;i)C] + С2 ехр [(^! - гол )С], С > 0, D6)
описывающее форму нейтральной оси рельса позади колеса. Для опре-
определения постоянных интегрирования в функциях D4) и D6) имеем ра-
равенство этих функций и равенство их производных (с учётом различия
знаков в нечётных производных) до третьего порядка включительно
в точке ? = С = 0. Форма нейтральной оси рельса имеет вид двух зату-
затухающих гармоник: гармоника перед колесом имеет больший декремент
и меньший период по сравнению с гармоникой позади колеса.
22. О качении деформируемого колеса
Рассматривается плоское стационарное качение колеса по прямоли-
прямолинейной направляющей (модель В. Г. Вильке). Колесо состоит из жёст-
жёсткого диска и деформируемой периферии [21], инерционные свойства
которой представляет абсолютно гибкое нерастяжимое кольцо.
22.1. Механическая схема. В качестве модели колеса возьмём
жёсткий динамически-симметричный круглый диск и тонкое однород-
однородное кольцо, которое в недеформированном состоянии образует окруж-

22. О качении деформируемого колеса
157
ность радиуса г, концентричную диску. К периферии относится кольцо
и безынерционные соединения, создающие упругие силы при смещении
точек кольца от их положений относительно диска в недеформиро-
ванном состоянии системы. Положим, что качение колеса является
плоским стационарным движением по недеформируемой прямолиней-
прямолинейной направляющей.
Колесо совершает движение в однородном поле силы тяжести,
контактируя без проскальзывания с прямолинейной горизонтальной
направляющей. В стационарном движении центр масс колеса движется
равномерно и прямолинейно.
Известно, что перемещение элементов деформируемой системы
можно представить в виде перемещения её как целого (поступательное
перемещение и поворот недеформированной конфигурации) и дефор-
деформационных перемещений относительно жёсткой системы, связанной
с недеформированной конфигурацией. Недеформированная конфигура-
конфигурация кольца определяет положение его как целого (окружность ра-
радиуса г).
Положение материальных точек кольца зададим [21] в средних осях
кольца (далее просто средние оси) вектором R с помощью переменных
Эйлера в полярных координатах (С — центр масс кольца, рис. 22.1):
= [г + и(ф)]ег
A)
где (р — полярный угол (отсчитываемый от вертикали); и и v —
радиальное и поперечное деформационные перемещения; ег и е^ —
орты полярной системы координат. На рис. 22.1 введены следующие
обозначения: d — вектор посту-
поступательного перемещения средних
осей относительно центра О дис-
диска; г* — радиусы-векторы материаль-
материальных точек недеформированного коль-
кольца в осях, связанных с диском;
w* — перемещения материальных то-
точек кольца относительно диска.
Условие нерастяжимости кольца
имеет вид (см. A))
(ЖJ = [(и' - vf +
+ (г + и + v'J]d(p2 = r2d(p2,
\
\
\
B)
Рис. 22.1
где штрих означает дифференцирова-
дифференцирование по (р.
Из равенства B) следует нелинейное уравнение связи:
(и1 - vJ + 2r(u + v1) + (и + v1J = О,
C)

158	Гл. IV. Решение прикладных задач
из которого в линейном приближении по и, v, uf, v' имеем условие
и + v1 = О,	D)
являющееся уравнением связи.
22.2. Вариация функционала «действие». Будем считать коль-
кольцо состоящим из двух участков, составленных из материальных точек,
находящихся вне зоны контакта и в зоне контакта соответственно.
Участок в зоне контакта принимаем прямолинейным (хорда с централь-
центральным углом 27), абсолютные скорости точек этого участка равны нулю.
Получим выражение кинетической энергии участка, находящегося вне
зоны контакта. При стационарном качении колеса (см. рис. 22.1) отно-
относительно осей, движущихся поступательно вместе с центром масс С,
деформированная конфигурация является неизменной, поэтому вме-
вместо двух независимых переменных можно рассматривать одну. Неза-
Независимое изменение координаты ср при переходе от одного элемента
кольца к другому в фиксированный момент будем рассматривать как
перемещение, происходящее за элементарный промежуток времени dt.
Обозначив dip = uidt, где uj — постоянная угловая скорость, находим
(см. A)) выражение скорости элементарной массы кольца относительно
осей Кёнига с центром в точке С:
— = и {и' - v)er + и {г + и + г/)е«р.	E)
Поскольку указанные оси являются инерциальными, примем их за
основную систему координат. В отсутствие внешних горизонтальных
сил и внешнего момента относительно оси колеса форма кольца при
стационарном движении симметрична относительно вертикали; при
этом поворот средних осей относительно диска равен нулю; точка С
лежит на оси Оу (d = dey); центральный угол 7 (т = ^ ~~ ^i)> опираю-
опирающийся на зону контакта, делится осью пополам. Кинетическая энергия
кольца представляется выражением
J [(и1 -vf + (r + u + v'J] d<p + ...,	F)
где р — масса единицы длины кольца. В формуле F) не выписано
постоянное слагаемое.
Кольцо находится в поле постоянных радиальных сил, в поле ли-
линейных упругих сил взаимодействия с диском и в однородном поле сил
тяжести, так что сила F, отнесённая к единице длины кольца, имеет
вид [21]
F = (с0 - cxu)er - c2ve(f + pg,	G)
где со — константа (радиальное усилие соег обеспечивает круговую
форму кольца в свободном состоянии; в пневматике, например, оно
создаётся давлением); с\, с2 — постоянные коэффициенты жёсткости

22. О качении деформируемого колеса	159
(с2 ^> с\); g — ускорение свободного падения в однородном поле си-
силы тяжести. Виртуальная работа этих сил, действующих на участок
вне зоны контакта, является полной вариацией функции А = —П
(П — потенциальная энергия):
5А= [ (FrSu + F^Svydcp,
—ч>\
Fr = с\(а — и — Ь\ cos(p), Fp = — с^{у — Ь^ sincp),
где а = со/сь bi = d-\- pg/c\\ Ь^ = d-\- pg/c2. Вариация действия по
Гамильтону для участка кольца вне зоны контакта имеет вид
t,	(9)
и
где 5Т и 5А берутся из выражений F) и (8).
22.3. Уравнения для определения формы кольца. Рассмотрим
условие нерастяжимости кольца как идеальную связь C), виртуальные
вариации которой удовлетворяют уравнению
(V - v)Euf - 5v) + (r + и + vf)Eu + 5vf) =0	A0)
и перестановочным соотношениям 5?/ = (Su)f, 5v' = (feO. Воспользо-
Воспользовавшись принципом освобождаемости, составляем виртуальную работу
реакции связи, действующую на элемент кольца, в виде произведения
неопределённого множителя X(s,t) и выражения, стоящего в левой
части уравнения A0). Теперь не требуется выполнения уравнения A0)
(и равенства 5и + 5v' = 0). Физический смысл множителя связи Л
установим, сопоставив виртуальную работу реакции связи и вирту-
виртуальную работу силы натяжения N нити, моделирующей кольцо, на
виртуальном перемещении 5и (при прочих вариациях, равных нулю).
Виртуальная работа силы натяжения N в линейном приближении
равна работе реакции на перемещении недеформированного элемен-
элемента, т. е.
Xr5u = -Ndip5u.	A1)
Из A1) следует, что	ЛТ
Л = -^.	A2)
В результате виртуальная работа сил натяжения вне зоны контакта 5 А
представляется интегралом
J N[(uf-v)Euf-5v) + (r + u + v/)Eu + 5v/)] dip. A3)
Прибавляя к интегралу (9) изменение действия за счёт реакции связи,
получаем интегральное равенство принципа Гамильтона-Остроград-

160	Гл. IV. Решение прикладных задач
ского:	,
L2
¦5A + 5fA)dt = O.	A4)
После интегрирования по частям, приравняв нулю коэффициенты при
5и и 5v, из A4) получаем равенства
„ _v,_r)=Fr + "'	^
С помощью представления силы натяжения в виде двух слагаемых
(см. [21]): N = No + rq((p), где q вместе со своей производной по ср
является малой величиной, из уравнений A5) выделяем слагаемые
нулевого порядка малости, которые позволяют найти постоянную со-
составляющую: No = cor + рси2г2. После этого в линейном приближении
относительно и, v, q и их производных имеем
ри2 (и" - v1 - т) = Fr + Щг~2 (и" - v1 - т) - q,
A6)
poo2 (uf — v) = F^ + Щг 2 (uf — v) + q''.
Для исключения переменной составляющей реакции дифференцируем
первое уравнение в A6) по (р, складываем результат со вторым урав-
уравнением и получаем
cor -1 (и'" - v" + u'-v) = -F'r - Fy.	A7)
Уравнение A7) и уравнение связи D) составляют систему, описы-
описывающую деформационные перемещения точек кольца. Краевые условия
определяются условиями на границе зоны контакта.
22.4. Условия на границе зоны контакта. Пусть при вертикаль-
вертикальной нагрузке Р (учитывающей вес кольца) параметры колеса обеспе-
обеспечивают малость угла 7 G ^ 1> %1 ~ центральный угол, опирающийся
на зону контакта). Тогда внутри зоны контакта выполняются равенства
та	dR
\хех = rj, т = —— = ех,
ds
из которых следует, что
v(vi) = v(ip2) = 0, и\ч>х + 0) = -и\ч>2 - 0) = -п. A8)
Конфигурация кольца (и зоны контакта) симметрична относительно
вертикали, и величина угла 7 определяется выражением (с точностью
до обозначений [21])
27 = -г-^-
где d = (Р — 2тггр)[тгг(с1 + С2)}~\ и'_ = и'((р\ — 0).

22. О качении деформируемого колеса	161
Значение и'_ находим из условия трансверсальности на свободном
конце[127]:	/мх
где Л — подынтегральное выражение функционала «действие» (и' вхо-
входит только в выражение кинетической энергии F)). Отсюда с учётом
равенства A8) следует, что и'_ = 0.
Примечание. Сделанный вывод имеет ясное физическое со-
содержание [21]. Сначала находится постоянная составляющая силы
натяжения Щ = c\ar + pV2 (V = иг). Затем к объяснению привле-
привлекается известный физический эффект, состоящий в том, что с уве-
увеличением угловой скорости вращения гибкое кольцо под действием
центробежных сил в пределе приобретает свойства абсолютно твёрдого
тела, и тогда зона контакта должна стягиваться в точку G = 0).
Последнее возможно (при найденном выражении 7V0), только если
в A9) и'_ =и'(ух -0) =0.
Поэтому в число граничных условий включаем равенства
u'(<pi - 0) = и'(ч>2 + 0) = 0.	B0)
Полученные уравнения и условия в угловых точках позволяют най-
найти форму деформированного кольца (см. [21]).
22.5. О сопротивлении качению. Переход частицы кольца в зо-
зону контакта сопровождается ударным изменением скорости от некото-
некоторого значения до нуля при абсолютно неупругом ударе (или квазипла-
квазипластическом процессе). Покидают зону контакта частицы кольца также
импульсивно, приобретая вертикальную конечную скорость в резуль-
результате импульса силы натяжения. Эти два процесса приводят к сопро-
сопротивлению качению. В отличие от работы [21], в которой в качестве
причины диссипации принимались силы линейного вязкого трения со-
соединений кольца и диска, здесь мы замечаем, что система не является
консервативной и в отсутствие вязкого трения.
Непосредственно перед приходом частиц кольца в контакт с осно-
основанием они имеют вертикальную скорость у_:
У- = —ио [г/cos 7 + (г + vf) sin 7] ~ — Vj.	B1)
Подставляя в B1) выражение для 7> получаем зависимость у- от
скорости колеса:
*- = -»tw	B2)
где Ь = rBac\ + c\d + pg).
Можно заметить, что «потерянная» скорость (и скорость, приобре-
приобретаемая в другой угловой точке) согласно зависимости B2) от скорости
колеса имеет максимум, который достигается при V* = ^/Ь/2р.
Переменность состава частиц кольца в зоне контакта при ударном
характере выхода из этой зоны означает наличие в «задней» угловой
б В. Г. Веретенников, В. А. Синицын

162	Гл. IV. Решение прикладных задач
точке вертикальной реактивной силы, создающей момент сопротивле-
сопротивления rp^2V2 относительно центра кольца. Абсолютно неупругие удары
в «передней» угловой точке приводят к потере энергии, которая может
быть компенсирована приложением в центре колеса силы p/y2V2/2.
Отметим, что найденные величины момента и силы сопротивления
пропорциональны квадрату малого угла (в работе [21] задача решалась
с точностью до первой степени 7)-
Таким образом, постоянная скорость колеса невозможна без допол-
дополнительных активных сил.
23. О квазистатическом скольжении нагрузки
на деформируемом стержне
Рассматривается деформирование защемлённого упругого стержня
при квазистатическом скольжении по нему сосредоточенной нагрузки.
Эта задача неоднократно обсуждалась в связи с кажущимся «исчез-
«исчезновением» части работы силы, известным в литературе под названием
«энергетический парадокс» [82]. Обсуждается способ реализации на-
нагрузки, уточняющий постановку задачи и позволяющий дать ещё одно
разъяснение парадокса.
23.1. «Энергетический парадокс». На упругую нерастяжимую
консольную балку действует сосредоточенная сила Р (рис. 23.1). Точка
её приложения к балке определяется координатой ?. В положении
равновесия малый поперечный про-
прогиб балки описывается функци-
функцией w(x,?). Происходит медленное
перемещение нагрузки от места за-
защемления к концу балки (величи-
(величина ? меняется от нуля до I). Стати-
Статический прогиб в месте приложения
нагрузки равен w(?,?). Нагрузка на
Рис. 23.1	правом конце балки при х = ? = I
даёт прогиб /, т. е. w(l, I) = /. В этом
положении, как сказано в [82], «потенциальная энергия деформации
балки равна Pf/2. Разумеется, она накоплена в результате работы,
которую совершает сила Р при постепенном опускании точки её при-
приложения на величину /. Однако если вычислять работу силы Р как
произведение Pf, то получается результат, вдвое больший потенци-
потенциальной энергии деформации. Возникает вопрос: куда израсходована
вторая половина этой работы?». Разъяснение парадокса, приведённое
в цитированной книге, основано на введении скорости скольжения
и переходе к распределённой нагрузке (и обратно). Сделан вывод о том,
что результат вычисления работы силы, прилагаемой к материальным
точкам балки, не зависит от скорости движения и в любом положении

23. О квазистатическом скольжении нагрузки	163
составляет ровно половину потенциальной энергии упругих сил балки.
Источник парадоксальности состоит в несоблюдении известного прави-
правила вычисления работы силы [1]: при вычислении элементарной работы
силы, как действительной, так и виртуальной, вектор силы скалярно
умножается на элементарное (соответственно виртуальное) перемеще-
перемещение материальной точки. Потенциальная энергия деформации балки
вычислена правильно, работа силы Р, прилагаемой к материальным
точкам балки, также равна Pf /2, а работы, равной Pf, просто нет, так
как / — перемещение геометрической точки.
Дополним схему элементами, реализующими нагрузку. Допустим,
что нагрузка обеспечивается взаимодействием стержня и весомой ма-
материальной точки. Работа силы Р, приложенной к материальной точке,
при вертикальном перемещении на величину / равна Pf. Парадоксаль-
Парадоксальный вопрос остался, только теперь он относится к системе «стержень —
материальная точка». Для ответа на него необходимо уточнить способ
реализации взаимодействия материальной точки и стержня.
23.2. Схема взаимодействия. Выражение действия дефор-
деформации. Пусть объектом, создающим перемещающуюся нагрузку,
является материальная точка М, скользящая по балке (например,
Р — сила тяжести в однородном потенциальном поле). Тогда Pf —
работа силы этого поля, приложенной к материальной точке М.
Квазистатическая постановка задачи предполагает равновесие М
в каждом положении.
Пусть стержень идеально гладкий. Тогда для равновесия матери-
материальной точки на стержне потребуется приложить к ней некоторую го-
горизонтальную силу F. На рис. 23.2 показаны реакция N, направленная
по нормали к кривой, описывающей
прогиб стержня, и дополнительная
горизонтальная сила F. В равновес-
равновесном положении материальной точки
имеем уравнение
P + F + N = 0.	(I)
При малости угла между каса-
тельной к кривой, описывающей про-
прогиб стержня, и осью Ох справедливо следующее соотношение между
величинами сил Р и F:
F = Pwf „ w' = ^-, \wf\ «1.	B)
х=?	ox
Можно заметить, что теперь стержень нагружается силой давления
в направлении нормали, а не силой постоянного направления.
Составим действие деформации (термин Э. и Ф. Коссера, см. за-
заметку 18) потенциальных полей сил F, Р и поля внутренних упругих
сил стержня. Нулевой уровень потенциальных силовых полей при-

164	Гл. IV. Решение прикладных задач
мем в недеформированном горизонтальном положении стержня при
расположении сосредоточенной нагрузки в месте защемления (? = 0).
Переменной ? отведём такую же роль, какую играет время t в принципе
Гамильтона. Различие физических размерностей аргументов несуще-
несущественно, поскольку применение теории размерностей позволяет пере-
переходить к безразмерным параметрам, поэтому подобную замену пере-
переменных делать не будем, а аналогичную величину назовём действием
деформации.
Действие деформации потенциального поля силы F на стержень
равно нулю, а действие деформации потенциального поля силы Р на
стержень определяется выражением
оо **e
Потенциальная энергия внутренних сил балки по теории изгиба
стержней Бернулли-Эйлера имеет вид следующего функционала:
?	1	2
U=l- \k(w"fdx+Uk(w"fdx, w" = ^,	D)
0	?
где к = EJ — жёсткость балки на изгиб (постоянная).
Соответственно действие деформации внутренних упругих сил
стержня равно
-\lldC	E)
о
Суммируя C) и D), имеем действие деформации потенциальных полей
сил F, Р и потенциального поля внутренних упругих сил балки:
о о
где П имеет вид D).
Функционал F) в рассматриваемом приближении совпадает с дей-
действием при нагружении стержня только силой Р. По правилам вир-
виртуального варьирования и вариационного исчисления из F) следу-
следует дифференциальное уравнение, решение которого с учётом усло-
условий в месте защемления даёт известное уравнение упругой ли-
линии [82]:
—— C? — х) при U ^ х ^ 4,
G)
—у- (Зх - ?) при х > ?.
о/с
Используем уравнения G) для проверки энергетических соотношений.

24. К оценке частот поперечных колебаний стержня	165
23.3. Энергетические соотношения. В данной схеме к балке
прикладывается сила —N, имеющая составляющие, равные силам Р
и F. При этом составляющая Р совершает работу, которая, как по-
показано в [82], равна потенциальной энергии внутренних упругих сил
балки. Сила F, приложенная к балке, работу не производит, так как
она в любом положении перпендикулярна перемещению материальной
точки.
С другой стороны, сила F, приложенная к материальной точке М,
совершает работу. Выражение для элементарной работы этой силы при
перемещении точки М имеет вид
\=idi.	(8)
Для сравнения на рис. 23.3 показаны перемещение материальной точки
М в положение М\ и перемещение М —> М' точки стержня. Находим
полную работу силы F при перемещении точки М к концу балки:
Р?2	Р213
О
Подставляя в (9) значение /, равное Р/3/C&) согласно уравнениям G),
получаем для силы F работу —Р//2,
т. е. в точности равную «потерянной»
работе.
Таким образом, при выбранной схе-
схеме реализации имеется баланс энер-
энергии: работа, совершённая силами Р
и F при перемещении материальной
точки, равна энергии внутренних упру-	OQ Q
г^	г^ИС. Zo.o
гих сил стержня. Заметим, что в рас-
рассмотренной постановке нельзя сделать вывод о независимости решения
от скорости скольжения, так как в равенстве A) для материальной
точки должна быть учтена сила инерции.
24. К оценке частот поперечных колебаний стержня
Рассматриваются способы определения частот изгибных колебаний
однородного прямолинейного стержня, основанные на формулах Ре-
лея и Граммеля (см. [83]). С помощью принципа Гамильтона-Остро-
градского проведён анализ точности вычисления частот колебаний по
принятой форме изгиба стержня. Получены аналоги формул Релея
и Граммеля, учитывающие влияние продольных сил инерции.
24.1. Формула и теорема Релея. Формула Граммеля. Идея ме-
метода Релея в применении к колебаниям стержня при предположениях
технической теории изгиба состоит в следующем. Форма колебаний

166	Гл. IV. Решение прикладных задач
является функцией одной пространственной координаты z\
/ = /(*).	A)
где z — координата текущего сечения стержня; / — прогиб оси в том
же сечении. Свободные малые линейные колебания описываются зави-
зависимостью
w(z,t) = f(z)sinu)t,	B)
где uj — постоянная циклическая частота колебаний.
Выражения кинетической и потенциальной энергии стержня при
изгибе соответственно имеют вид
I
Т* 2 j	/о\
= — mw az,	(о)
о
I
11 — — гьЦу (Х/6,	Цу — Ш ,	\^/
О
где / — длина стержня; к — жёсткость на изгиб (к = El); ip(z) —
угол поворота сечения; m(z) — линейная массовая плотность стержня;
штрихом обозначена производная по z, а точкой — производная по
времени t.
Подставив B) в выражения C) и D), получаем
1 = - uj cos [ujt) га/ az,	E)
/<fe.	F)
Равенство ф = w' будем рассматривать как идеальную связь, реализу-
реализуемую потенциальными перерезывающими силами с бесконечно боль-
большим коэффициентом жёсткости. Поскольку система — консервативная
и Т + П = const, отсюда следует формула Релея:
UJ
2
= k(ffdz
О
\mfdz\ .	G)
- о	J
Формула Релея G) даёт точное значение собственной частоты коле-
колебаний uj в том случае, когда f(z) является собственной формой. Если
же вместо собственной формы подставляется некоторое приближение
(обозначим эту функцию f*(z) и будем называть её «форма изгиба»
стержня), то аналогичная формула для приближённых вычислений
имеет вид
p2=\k(f:fdz\\mf!dz] .	(8)

24. К оценке частот поперечных колебаний стержня
167
«Релею принадлежит не только вывод формулы, но и доказатель-
доказательство очень важной теоремы: при любом выборе формы колебаний f(z),
удовлетворяющей кинематическим условиям задачи, формула даёт зна-
значение основной частоты р, всегда более высокое, чем истинное значе-
значение основной частоты» [83].
Приведённая редакция теоремы кажется небезупречной. Вначале
о терминах. Собственная форма колебаний не выбирается, а опре-
определяется при решении задачи вместе с частотой собственных коле-
колебаний. Допущение о том, что в формуле (8) функция f(z), удовле-
удовлетворяющая кинематическим условиям задачи, может быть «любой»,
становится источником недоразумений. Примерами являются формы
изгиба, представленные на рис. 24.1. Приняв форму изгиба рис. 24.1, а,
автор примера (см. [83] со ссылкой на С. А. Бернштейна) полагал, что
О
Рис. 24.1
нашёл приближённую собственную частоту р = 0 (см. (8) при f" = 0),
и привёл форму изгиба (рис. 24.1, б), якобы исправляющую «порок»,
заключающийся в нарушении плавности упругой линии. Однако зна-
значение частоты р = 0 противоречит теореме Релея, а форма изгиба
рис. 24.1,6 по той же формуле даёт в пределе бесконечно большое
значение частоты.
Заметим, что обе формы изгиба, изображённые на рис. 24.1, не
могут рассматриваться как приближённые собственные формы стерж-
стержня: они противоречат предположению о близости деформированной
и истинной линий, поскольку не выполнено исходное условие линейной
теории о малости производной угла ф' (см. в п. 24.3 более полную
модель). Анализу форм изгиба
рис. 24.1, приведённому в [83],
фактически соответствует двух-
стержневая система, схема ко-
которой представлена на рис. 24.2.
Сопротивление изгибу в узле
шарнирного соединения стержней
изображено в виде спиральной
пружины с жёсткостью с. Оче-
Очевидно, что при с = 0 получим равную нулю собственную частоту, а при
с —> оо частота стремится к бесконечности.
В
Рис. 24.2

168	Гл. IV. Решение прикладных задач
Из равенства
получается известная
ттах = итах
формула Граммеля:
1 г 1 "^2
р2 = га/| dz
0
/с
- о
-dz
-1
(Ю)
где Миз = р2МИЗ;^МИЗ(г) — изгибающие моменты, вызываемые на-
нагрузкой mf*p2 (Миз — изгибающий момент, вызываемый условной
нагрузкой га/*, т.е. в р2 раз меньшей, чем силы инерции).
Считается, что формула Граммеля A0) всегда позволяет (при од-
одних и тех же аппроксимационных формулах) находить более близкие
к точным собственные частоты, чем формула Релея. Одной из причин
этого является отсутствие в формуле Граммеля операции дифферен-
дифференцирования приближённой функции, что, как известно, всегда ведёт
к возрастанию ошибок.
Получим оценку ошибок частот колебаний на основе анализа дей-
действия по Гамильтону.
24.2. Оценка точности определения частоты колебаний по
форме изгиба. Составим для рассматриваемой системы с функцией
Лагранжа L = Т — П действие по Гамильтону
г
S=\Ldt,	A1)
о
где [0, г] — фиксированный промежуток времени.
Состоянию, приближённо заданному функцией /* и частотой р*,
соответствует действие
г
#*=|(Т*-П*)^,	A2)
о
где	г
ll2\f!dz,	A3)
kf':2dz.	A4)
о
Полагая, что действие на истинном движении имеет минимум, для
близких движений, к которым отнесём приближённое, получаем
5*-5^0.	A5)
Из условия A5) следует неравенство для средних значений функций
Лагранжа:
(Г*-П*)-(Г-П)^0.	A6)

24. К оценке частот поперечных колебаний стержня	169
Подставляем в A6) средние значения интегралов
г	г
- sin2 atdt = - — -— sin 2ат, - cos2 atdt = - + -— sin 2ат.
r J	2 4ат	т J	2 4ат
О
Получаем
pi
2 Л + 1 8'т2и;т)А- (\ - -^—8'т2и;г)в, A7)
где	I	I
A= Imfdz, В = \kff2dz
о	о
(для А*, В* имеют место аналогичные выражения, если вместо f(z)
использовать f*(z)). Поскольку uj2 = В/А (см. G)), неравенство A7)
принимает вид
л 2 А*р* . ~	В*р* . о	D sin2a;r / л 2 тэ\ /iq\
Учитывая, что на промежутках времени, больших, чем период соб-
собственных колебаний, приближённое решение всё менее удовлетворяет
требованиям, предъявляемым к варьированным движениям в принципе
Гамильтона-Остроградского, примем г = 2тг/и;. Тогда для приближён-
приближённых значений р = р* = ^/В*/А* неравенство A8) выполняется, если
г^Ъо.	A9)
UJ J
Из A9) следует, что приближённое значение частоты, вычисленное
по формуле Релея в принятых предположениях, находится в диапазоне
1,25а; >р> ио.	B0)
Напомним, что дополнительно было принято условие близости при-
приближённого действия к минимальному значению действия, достигае-
достигаемому на истинном движении.
24.3. Учёт продольных сил инерции. Для учёта инерции пово-
поворота поперечных сечений введём в рассмотрение угол поворота сече-
сечений ф. Тогда кинетическая и потенциальная энергии стержня имеют
вид функционалов:
T=^Umw2 + Jip2)dz, n = ^lki/;'2dz,	B1)
о	о
где Jdz — момент инерции элементарной массы стержня относительно
оси, перпендикулярной плоскости колебаний и проходящей через соот-
соответствующую точку нейтральной линии.

170
Гл. IV. Решение прикладных задач
Система является консервативной, поэтому, следуя идее метода
Релея, получаем обобщение формулы (8):
1	\l	1
Р2 = \ KfJf dz \{mfl + J/:2) dz .	B2)
о	L о
Если /*(z) является собственной формой f(z), то формула B2) даёт
точное значение квадрата собственной частоты: р2 = со2. Обобщение
формулы^Граммеля получается, если в A0) подставлять изгибающий
момент Миз, вызываемый условной нагрузкой (га/* + J/*).
Сравнение формулы Релея (8) и её обобщения B2) показывает, что
учёт продольной силы инерции стержня при поворотах приводит, как
и следовало ожидать, к уменьшению частоты поперечных колебаний.
25. Об устойчивости равновесной формы стержня
при изгибе
Решаемая задача относится к проблеме потери устойчивости при
появлении смежных форм равновесия стержня. Дифференциальные
уравнения, описывающие равновесную форму стержня, составляются
с использованием уточнённой
теории С. П. Тимошенко. Пре-
Предельный переход к прибли-
приближённой теории осуществля-
осуществляется путём введения некото-
некоторой идеальной связи, реак-
реакция которой представляет со-
собой момент распределённой
пары, реализуемой перерезы-
перерезывающими силами. Получено
условие устойчивости прямо-
прямолинейной формы шарнирно
опёртой стойки при действии
продольной силы.
25.1. Задача Эйлера.
История одного из направ-
направлений решения проблемы
устойчивости форм равнове-
равновесия упругих систем восходит
N
I
-N
Рис. 25.1
Рис. 25.2
к задаче, поставленной Эй-
Эйлером. Им было составлено уравнение формы оси шарнирно опёртой
стойки, сжимаемой продольной силой (рисунки 25.1, 25.2). Первона-
Первоначально принятая Эйлером схема сил привела к уравнению, на основа-
основании которого автор заключил, что стойка вообще не может потерять
устойчивость, однако при повторном рассмотрении это показалось ему

25. Об устойчивости равновесной формы стержня при изгибе 171
«не только парадоксальным, но и весьма подозрительным» [83]. Разъ-
Разъяснение ошибки состояло в необходимости учёта при составлении
уравнения для моментов горизонтальных реакций (реакций, перпенди-
перпендикулярных оси стойки в недеформированном состоянии).
Дифференциальное уравнение, получаемое после дифференцирова-
дифференцирования интегродифференциального уравнения моментов в состоянии рав-
равновесия, имеет вид [83]
EJ^ + (qz + P)%L = N,	A)
dz	dz
где q — постоянная интенсивность распределённой нагрузки; Р —
постоянная сжимающая сила на верхнем конце стойки; z — абсцисса
произвольного сечения стойки, изменяющаяся от нуля до / (/ — длина
стержня); w(z) — прогиб оси; EJ — постоянная по длине стержня
изгибная жёсткость; N — горизонтальная составляющая реакции.
Решение уравнения A) должно удовлетворять следующим усло-
условиям:	2
w = О, ^=0 при z = 0 и z = L	B)
dz
Число граничных условий B) превышает число постоянных интегри-
интегрирования в общем решении уравнения A), что в отсутствие N в A)
и привело Эйлера к ошибке (в следующей публикации уравнение A)
решалось им при Р = 0, и прежний вывод о неограниченной устойчи-
устойчивости стойки был отвергнут) [83].
Будем считать, что в схеме сил (см. рисунки 25.1, 25.2) распреде-
распределённая нагрузка равна нулю (q = 0), но учтём влияние жёсткости на
сдвиг. Уравнения равновесных форм получим из условия стационарно-
стационарности потенциальной энергии.
25.2. Функционалы потенциальной энергии. Составной частью
действия по Гамильтону является функционал потенциальной энергии.
В уточнённой теории С. П. Тимошенко для описания положения
стержня используются два определяющих параметра: w(z) и ip(z) (ф —
угол поворота поперечного сечения). Функционал потенциальной энер-
энергии имеет вид [4]
/
^2 + k2(il>-w'J] dz,	C)
где fci — коэффициент, зависящий от модуля упругости и геометрии
поперечного сечения рельса (пропорциональный /i4; h — характерный
размер поперечного сечения); к% — коэффициент, определяемый по мо-
модулю сдвига и геометрии поперечного сечения (пропорциональный h2)
и учитывающий также неравномерность касательных напряжений по
сечению. Слагаемые в C) имеют следующий механический смысл:
первое слагаемое — потенциальная энергия упругих изгибающих мо-

172	Гл. IV. Решение прикладных задач
ментов и зависящих от них перерезывающих сил, а второе — потенци-
потенциальная энергия дополнительных упругих перерезывающих сил.
С учётом продольных перемещений точки приложения силы Р
потенциальная энергия системы имеет вид функционала:
П = \\ [kl^2 + k2 № ~ W^ ~ Puj/2} ds'	D)
si
Равенство
ф = w1	E)
будем рассматривать как идеальную связь.
Примечание. Если мы подставим равенство E) и результат его
дифференцирования по z в C), то согласно теории Бернулли-Эйлера
получим функционал потенциальной энергии внутренних упругих сил
при изгибе стержня:
\\{kw)dz,	F)
о
где к — изгибная жёсткость (EJ); штрихом обозначено дифферен-
дифференцирование по z. В заметке 21 показано, что связь E) может быть
реализована упругими потенциальными силами (см. второе слагаемое
в подынтегральном выражении D)). Здесь эту связь учтём в вариа-
вариационной задаче с множителем Лагранжа, который в данном случае
(см. условия в п. 9.3) совпадает с множителем связи.
В задаче на безусловный экстремум требуется варьировать функци-
функционал П, составленный с учётом выражения D) и связи E):
П =
S2
I f \кхф'2 + к2(ф- w'f - Pw'2 + 2А (<ф - w')] dz, G)
где X(z) — неопределённый множитель.
При составлении уравнений формы оси стойки будем использовать
потенциальную энергию G).
25.3. Уравнения равновесных форм оси стойки. Равновесные
формы должны удовлетворять условиям стационарности функциона-
функционала G), т.е. <Ш = 0.
Варьирование выражения G) согласно правилам вариационного ис-
исчисления [131] приводит к необходимости выполнения внутри интер-
интервала интегрирования уравнений Эйлера-Лагранжа:
dz du'i dm	w

25. Об устойчивости равновесной формы стержня при изгибе 173
где А(щ,и^) — подынтегральное выражение в G), щ = ф, и2 = w;
а также к условию на концах интервала интегрирования:
2	z=l
]Г (и[5щ) = 0.	(9)
Применение оператора (8) к подынтегральному выражению в G)
даёт следующие уравнения:
к\ф" - к2(ф - w') - Л = 0,	A0)
(к2 - P)w" - к2ф' - X1 = 0.	A1)
Из возможных вариантов граничных условий, удовлетворяющих (9),
примем условия, аналогичные B):
w = 0, ф1 = 0 при z = 0 и z = l.	A2)
В отсутствие связи E) уравнения формы оси при равновесии име-
имеют вид
к\ф" - к2(ф - wf) =0,	A3)
(к2 - P)w" - к2ф' = 0.	A4)
При наличии связи E) (и уравнения, полученного дифференциро-
дифференцированием E)) из A0), A1) получаем уравнения
к\ф" — X = 0, Pw" + X! = 0.	A5)
Как и следовало ожидать, реакция связи E), представленная в A5)
неопределённым множителем Л и его производной Лх, имеет смысл
момента и перерезывающей силы соответственно. Сравнение A5) с A3)
и A4) показывает, что реализация связи E) может осуществляться
внутренними упругими силами при к2 —> оо (при этом достигается
предельный переход (ф — w') —> 0).
25.4. Уравнения смежных форм равновесия. Условие устой-
устойчивости прямолинейной формы. Проведём анализ уравнений A3),
A4). При к2 ^ Р форм равновесия, кроме прямолинейной, нет.
Пусть к2 > Р. Из A4) следует первый интеграл (с\ — постоянная
интегрирования):
/	7 /	7	1^2	^ 1	/ 1 Г- \
W — ЬЦ) = С\, 0 = 	 > 1.	\1в)
Используя A6), находим общее решение A3), A4) (А, а, с2 — посто-
постоянные интегрирования):
/ а • ( i \ i ci 2 к^Оэ — 1)
ф = Asmiuz + а) +	-, ujz = —^	-,
С1	A7)
w =	cos (ujz -\- а) — -—— z + С9,
и	6—1
о;= y(±s±r), s,r = 0,1,2,3,...	A8)

174
Гл. IV. Решение прикладных задач
С учётом граничных условий A2) имеем уравнения формы изгиба
стержня:
, АЫ . GГП \	а 1 о	/1Л\
w = ±—sin l-rz , n = 0,l,2 .,	A9)
которые возможны (см. A6)—A8)) при следующих значениях продоль-
продольного сжимающего усилия:
р* _
где
I2
п = 1,2,...
B0)
Для оценки устойчивости прямолинейной формы стержня восполь-
воспользуемся теоремой Лагранжа-Дирихле. Достаточно, как известно, чтобы
потенциальная энергия F) в равновесном состоянии имела строгий
минимум. В окрестности устойчивого положения (в котором потенци-
потенциальная энергия равна нулю) должно выполняться неравенство П > 0.
Это неравенство выполняется на кривых A9), рассматриваемых как
уравнения формы стержня в варьированном состоянии, при условии
Р < Poi (Pq\ = 7v2k\/l2). Таким образом, при п = 1 появление смежной
формы равновесия происходит при меньшей сжимающей силе, чем
потеря устойчивости (в отличие от предельного случая бесконечно
большой сдвиговой жёсткости: к% —> оо (см. B0)).
25.5. О применении энергетического метода в задаче об устой-
устойчивости формы изгиба стержня. Обсуждается применение энерге-
энергетического метода при определении критической силы и оценке устойчи-
устойчивости прямолинейной формы в классической задаче Эйлера об изгибе
стержня. Получена формула расчё-
расчёта критической силы при дополни-
дополнительном учёте свойства сжимаемо-
сжимаемости стержня.
1. Идея применения метода в тео-
теории устойчивости упругих систем.
Энергетический метод введён в
теорию упругости Кирхгофом A850)
и применялся СП. Тимошенко [116]
и другими авторами. Применительно
к задаче о форме консольной бал-
балки, нагруженной продольной силой
постоянного направления вдоль оси
балки в недеформированном состо-
состоянии (рис. 25.3), идея этого метода
излагается так [116]: «Допустим, что
произошло боковое смещение, пока-
показанное на рис. 25.4; тогда энергия де-
деформации увеличивается вследствие
того, что к энергии сжатия прибавляется энергия изгиба стержня.
В то же время потенциальная энергия нагрузки уменьшается сообраз-
I
Рис. 25.3
Рис. 25.4

25. Об устойчивости равновесной формы стержня при изгибе 175
но с понижением точки приложения. Это уменьшение потенциальной
энергии является просто работой, произведённой нагрузкой в результа-
результате понижения верха стержня. Если AV означает энергию деформации
стержня, а АА — работу, произведённую нагрузкой вследствие изгиба,
то можно сделать заключение, что прямая форма сжатого стержня
будет устойчивой, если
AV - АА > 0;
она будет неустойчивой, если
AV - АА < 0.
Критическое значение нагрузки, при котором прямолинейная форма
равновесия переходит из устойчивого состояния в неустойчивое, опре-
определяется из уравнения AV = АА» (здесь мы для удобства используем
букву А вместо обозначения, принятого в оригинале).
Левые части приведённых выше неравенств равны потенциальной
энергии упругих сил изгиба и внешней силы Р (см. рис. 25.4). По-
Полагается, что изогнутая ось описывается уравнением (/ — боковое
смещение точки приложения сил)
а потенциальная энергия вычисляется по формуле (EJ — жёсткость при
изгибе)
j
где М — изгибающий момент:
v)=Pfcos^.	B3)
Энергетический метод используется для определения критической
силы, которая согласно Эйлеру определяется как «сила, требующая-
требующаяся для самого малого наклонения колонны». В концепции «упругой
устойчивости» полагается, что критическая сила обнаруживается при
появлении новых форм равновесия. «Предполагается, что при достаточ-
достаточно малых нагрузках равновесие упругой системы устойчиво и что оно
остаётся таковым вплоть до первой точки разветвления форм равнове-
равновесия, за которой исходная форма равновесия становится неустойчивой»
[6]. В литературе отмечается [83] парадокс в оценке устойчивости,
который, однако, не возникнет, если при вычислении потенциальной
энергии изгиба подставить момент не по формуле B3), а считать
(см. [83]), что «изгибающий момент, определяемый деформациями оси
(её кривизной) в смежных, вообще говоря, неравновесных состояниях:
М = EJ^».	B4)
dz

176	Гл. IV. Решение прикладных задач
В постановке задачи упоминается энергия сжатия, которая в ана-
анализе [83, 116] не фигурирует, как если бы она не зависела от изгиба
(в данном случае — малого линейного приближения). Поэтому най-
найденное энергетическим методом в работах [83, 116] эйлерово значение
критической силы
р	- ^EJ	/ОС\
-* Крит —	2	\АО)
следует относить только к несжимаемым стержням.
2. Расчёт критической силы при учёте сжимаемости стержня.
Стержень однородный, испытывает плоский изгиб. Потенциальная
энергия деформации стержня при изгибе в плоскости уог и сжатии
выражается формулой
где N — упругая сила, перпендикулярная плоскости сечения; EF —
жёсткость на сжатие;
Mx = -EJv", N = -p(l-^Y	B7)
штрихом обозначены частные производные по z. Приняв за нуле-
нулевой уровень потенциальной энергии прямолинейную форму (сжатого)
стержня, имеем
При изгибе стержня его конец,	к которому приложена сила Р,
сместится на величину
1	I
РA-г/2) , PI	P Г /2 ,
dz-	= -]V dZ
о	о
т. е. в сторону защемлённого конца, и величина работы этой силы будет
соответственно равна
v'2dz'	B9)
о
Из равенства AV = АА величин B8), B9) с учётом B7) для кривых
B1) после дифференцирования и интегрирования имеем (при / ^ 0)
равенство

26. Системы с линейным деформируемым элементом	177
Учитывая выражение эйлеровой критической силы B5), из C0) по-
получаем
^^f	C1)
Смысл полученного выражения следующий: при значениях силы Р,
вычисленных по формуле C1), стержень имеет, кроме прямолиней-
прямолинейной формы, также другие равновесные состояния вида B1). Из C1),
в частности, при соотношении параметров A12F = 3tt2J следует, что
сила Р равна критической силе Эйлера (т. е. как и для несжимаемого
стержня). К тому же результату приводит и вычисление потенциальной
энергии изгиба по схеме СП. Тимошенко [116].
3. Замечание об оценке устойчивости.
Авторы цитированных выше работ в оценке устойчивости применя-
применяют формулировку, аналогичную теореме Лагранжа-Дирихле. Однако
напомним, что теорема Лагранжа-Дирихле доказана для дискретных
консервативных систем с конечным числом степеней свободы и даёт
достаточное условие устойчивости по Ляпунову для изолирован-
изолированного положения равновесия. Выделенные курсивом условия теоремы
Лагранжа-Дирихле в приведённом выше суждении об устойчивости
прямолинейной формы стержня не выполняются. Это замечание от-
относительно применения теоремы Лагранжа-Дирихле в данной задаче
показывает целесообразность проведения дальнейших исследований на
основе более строгой математической теории устойчивости для систем
с распределёнными параметрами (см., например, [111]). Энергетиче-
Энергетический метод при этом может быть использован при формировании мер
отклонения от равновесного состояния, которые при вычислении по-
потенциальной энергии по формулам B2) и B6) являются разными.
В полном объёме задача об устойчивости может решаться только
в динамике.
26. Уравнения движения систем с линейным
деформируемым элементом
Приводятся уравнения плоского движения цепи, подвешенной за
один конец в однородном поле силы тяжести. Рассматривается одна из
схем применения поперечной бегущей волны, являющейся движителем
в волновом редукторе непрерывного вращения. Составлены уравнения
для определения формы гибкого элемента волнового редуктора.
26.1. Уравнения движения однородной цепи. Конфигурация
цепи при плоском движении определяется двумя координатами, явля-
являющимися функциями двух аргументов [19]:
x(s,t), y(s,t), 0<s<l, ti<t<t2,	A)

178	Гл. IV. Решение прикладных задач
где х и у — декартовы координаты элемента цепи, координата s в есте-
естественном способе задания движения отсчитывается от точки подвеса
цепи, / — длина цепи, t — время.
Связи, наложенные на перемещения, имеют вид
x@,t)=0, 2/@,*)= 0, х'2 + у'2- 1 =0.	B)
Последнее равенство в B) имеет смысл условия нерастяжимости,
а штрихом в нём обозначены частные производные по s. Из B) следуют
условия для вариаций:
5х = 5у = 0 при s = 0, х'5х' + у'5у' = 0.	C)
Составляем функцию Лагранжа:
D)
где g — ускорение свободного падения в однородном поле силы тя-
тяжести, р — массовая линейная плотность (далее примем её равной
единице).
Умножаем последнее уравнение в C) на неопределённый множи-
множитель Л, складываем с вариацией подынтегрального выражения в функ-
функционале D), составляем интегральное равенство принципа, интегриру-
интегрируем последнее по частям и приравниваем нулю коэффициенты при 5х
и 5у. В результате получаем уравнения
х + \х" + AV -9 = 0, у + \у" + АУ = 0.	E)
Уравнения E) вместе с уравнением связи B) образуют систему для
определения х, у и Л. Неопределённый множитель Л в E) представляет
реакцию связи и равен (со знаком минус) силе натяжения цепи, отне-
отнесённой к плотности р. Физическая адекватность уравнений E) очевид-
очевидна, так как они являются проекциями основного уравнения динамики
нити на неподвижные декартовы оси. Таким образом, вариации в C)
являются виртуальными.
Далее будем использовать обобщённую координату (p(s,t) — угол
между касательной к цепи и вертикалью. Координаты элемента цепи
выражаются через угол (р следующим образом:
x(s, t) = J cos <p(?, t) d?, у(s, t) = J sin <p(?, t) d?,	F)
о	о
где ? @ < ? < /) — текущая координата элементов цепи. Интегральные
выражения F) приводят к тому, что уравнения движения относитель-
относительно (р становятся интегродифференциальными, но при этом условие

26. Системы с линейным деформируемым элементом	179
нерастяжимости B) и уравнение для вариаций C) выполняются тож-
тождественно и имеет место свойство перестановочности, поскольку
x'(s, t) = cos (p(s, t), y'(s, t) = sin (p(s, t),
s	s
Г	Г
x = — sin </?(?, t)(p d?, у = cos </?(?, t)(p d?,
о	о
s	s
Sx = ~\sin4>(€> t)fy(€>l) С Sy = Jcos<p(f, tNip(?, t) d^ G)
о	о
5x'(s, t) = — sin (p(s, tM(p(s, t), 5y'(s, t) = cos (p(s, tM(p(s, t),
s	s
Sx = -\ sin <p(?, t)^(^, t) d?, Sy = [ cos <p(?, t)^(^, t) d^.
о	о
Из уравнений E), исключая Л, а затем — Лх, получаем
У = (g-x)cos(p-ysm(p,
уо)
(х — g) sin ip — \ipf — у cos cp = О,
где	s
Я = - J [Ф (?, 0 sin (^ (^, t) + ф2 (е t) cos <p Й, t)] dg,
о
s
У = \[Ф (С t) cos р (С, t) - ^ (?, t) sin ^ (^, t)] dC
0
Учитывая механический смысл множителя Л, применим принцип
Даламбера к участку цепи s < ? < I. Равенство нулю суммы главных
векторов (активных сил, сил инерции и реакций) в проекциях на
касательную и нормаль к кривой даёт уравнения для определения Л
и (р:
i	i
Л = - cos <p(s, t)Ug- x(?, t))d? + sin <p(s, t) \ y(?, t) dg,
i	i
sin (p(s, t)j(g- x(?, t))<% + cos ф, t) J y(?, t) di = 0,
s	s
где	^
(C t) \[Ф (v> t) sin ^ (Vi t) + ^2 (??> 0 cos ^ I7?'
о
s
У(€> t) = \ [Ф (?7> t) cos (p (rj, t) — ф2 (rj, t) sin cp (rj, t)] drj.
о
Уравнения движения в формах (8) и (9) являются интегродиффе-
ренциальными, только в первых уравнениях выполняется однократное

180
Гл. IV. Решение прикладных задач
интегрирование, а во вторых — двукратное. Выражение \' в (8) можно
получить из (9).
26.2. Модель движения гибкого элемента волнового редук-
редуктора. Свойства бегущих волн на протяжённых деформируемых эле-
элементах используются в различных инженерных устройствах. В частно-
частности, редуцирующее свойство (волна движется по телу гораздо быстрее,
чем само тело) составляет основу принципа действия волновых меха-
механизмов — редукторов.
1.	Принцип работы волнового редуктора. Схема волнового меха-
механизма непрерывного вращения показана на рис. 26.1. Принцип работы
редуктора состоит в следую-
следующем 0: идеальная гибкая нерас-
нерастяжимая нить / охватывает сво-
своей внутренней стороной жёсткие
круговые цилиндры 3 и 4; ци-
цилиндр 4 (обкатной ролик) свобод-
свободно вращается на оси О\ ведущего
звена (водила) 5, вращающегося
вокруг оси О. Внешняя сторо-
сторона нити / катится по внутренней
поверхности цилиндра 2, концен-
концентричного цилиндру 3.
Если цилиндр 3 неподвижен
(жёстко закреплён), а цилиндр 2
подвижен, то вращение водила
вызывает качение нити по по-
поверхности цилиндра 3. Скорость
вершины А гребня волны передаётся подвижному цилиндру 2, который
получает медленное вращение в сторону вращения водила. Соответ-
Соответственно имеем волновой редуктор попутного вращения.
Если неподвижен цилиндр 2, а цилиндр 3 — подвижный, то являясь
ведомым звеном, он получит медленное вращение в сторону, проти-
противоположную вращению водила 5. Это волновой редуктор встречного
вращения.
На примере волнового редуктора попутного вращения поставим
задачу определения формы гибкого элемента /.
2.	Уравнения для определения формы гибкого элемента волнового
редуктора. Пусть происходит стационарное движение, при котором во-
водило вращается с постоянной угловой скоростью и. В схеме попутного
вращения происходит редукция, и цилиндр 2 вращается с угловой
скоростью U02 = va/R2, где i?2 — радиус цилиндра 2, скорость точки А
va = сс;(|От4| — R), R — радиус цилиндра 3.
X
Рис. 26.1
1) Добролюбов А. И. Скольжение, качение, волна. — М: Наука, 1991.

26. Системы с линейным деформируемым элементом	181
Для нахождения формы нити составим уравнения для определения
малых отклонений от линейной формы в недеформированном состоя-
состоянии (рис. 26.1): w = (v,u) (где v — перемещение вдоль оси ОХ, па-
параллельной недеформированному прямолинейному участку нити между
цилиндрами, и — вдоль оси OY), так что координаты точки имеют
значения
? = x + v(x,t), rj = R + u(x,t)-	(Ю)
Из условия нерастяжимости гибкого элемента ds = dx (ds — диффе-
дифференциал дуги) имеем
%2 №2
,dxj ' \дх) '
или, пользуясь A0),
v' = -±(u'2+v'2),	A1)
где штрихом обозначены частные производные по координате s = х.
Считая перемещения и и их производные и' малыми, из последнего
равенства находим, что производные v1 и перемещения v будут вели-
величинами второго порядка малости.
В стационарном движении в осях, вращающихся вместе с води-
лом, нить совершает равноскоростное движение со скоростью ujR.
Связь A1) налагает на виртуальные вариации условие
5v' + u'5u' + v'5v' = 0.	A2)
Учитывая, что система координат OXY вращается вокруг оси OZ,
получаем выражение квадрата скорости элемента нити с координата-
координатами A0):
V2 = [х + v - (R + и)ио}2 + [и + (х + г;) uj}2 , x = uoR, A3)
где точкой обозначены частные производные по времени.
Варьируем действие, состоящее в данном случае только из действия
движения, определяемого кинетической энергией частиц со скоростя-
скоростями A3), и интегрируем «по частям» с учётом изменения действия за
счёт виртуальной работы связи A2) с неопределённым множителем А.
Приравняв нулю коэффициенты при независимых виртуальных вариа-
вариациях, получаем уравнения
и + 2uov - ио2и + AV - Ruo2 = 0,
A4)
v - 2пио - vuo + \v" + X' A + vr) - Ruo2 = 0.
В стационарном режиме будем вместо двух аргументов использо-
использовать один: С = х + uoRt, и введём преобразование u(x,t) = U(Q,
v(x,t) = W(C), \(x,t) = Л(С). Тогда и' = dU/дС и = uoRdU/d( (ана-
(аналогично для функций v(x,t) и W, а также X(x,t) и Л(()). Приняв во
внимание замечание о том, что продольные деформационные переме-

182	Гл. IV. Решение прикладных задач
щения v и их производные имеют второй порядок малости, из второго
уравнения в A4) имеем приближённое уравнение:
Л' - 2ou2RU' - uu2R = О,
имеющее первый интеграл
Л = 2uj2RU + ou2R( + const.
Первое уравнение в A4) в новых переменных с учётом полученного
интеграла приводится к обыкновенному дифференциальному уравне-
уравнению, позволяющему определить форму гибкого элемента на свободном
участке.
27. К динамике раскрытия поверхности
космического паруса
Искусственная поверхность, полученная в космосе развёртыванием
мягкой оболочки, может применяться для отражения и (или) погло-
поглощения солнечного света (с целью создания аккумуляторов солнечной
энергии) и мобильной направленной транспортировки энергии в задан-
заданные районы Земли или для энергообеспечения космических объектов.
Поверхность может применяться и в дальнем космосе вблизи границ
областей притяжения планет как космический парус, использующий
давление солнечной радиации.
Традиционно полагается, что поверхность получается в результате
сборки большой космической конструкции из элементов, имеющих
некоторую жёсткость. Последнее обстоятельство отодвигает решение
многих неотложных космических задач в отдалённую перспективу.
В некоторых ситуациях выход состоит в том, чтобы в качестве ос-
основного элемента поверхности использовать тонкую мягкую оболочку.
Тонкая мягкая оболочка с малой массовой плотностью удобна для
вывода её на орбиту, так как её компактная упаковка возможна и про-
проста для развёртывания (при специальной схеме укладки). Форма её
в развёрнутом состоянии может поддерживаться за счёт центробежных
сил инерции во вращательном движении [89]. Развёрнутая поверх-
поверхность представляет собой основу для сборки конструкции заданного
назначения. В простейших задачах (маховик, зонт, отражатель, парус)
достаточно развернуть поверхность, и она может выполнять своё назна-
назначение, если имеется управление ориентацией и стабилизация заданного
направления оси вращения.
27.1. Описание процесса раскрытия поверхности паруса. До-
Допущения и приближённые соотношения. Отражающая поверхность
паруса представляет собой тонкую однородную плёнку, которая в свёр-
свёрнутом виде имеет форму гофрированной поверхности, уплощающейся
при раскрытии. Перед началом раскрытия она специальным образом
уложена на барабане цилиндрической формы радиуса R\> и длиной Ь\>

27. К динамике раскрытия поверхности космического паруса
183
(рис. 27.1). К барабану плёнка присоединяется по вантовой схеме с от-
оттяжками по внутренней границе, имеющей в развёрнутом состоянии
форму окружности радиуса RY.
Рис. 27.1
^—^— Гребни
— — — Впадины
Рис. 27.2
При укладке плёнки путём намотки её на барабан формируются
складки (поверхность гофрируется): следы от «гребней» и «впадин» на
раскрытой поверхности чередуются при обходе по окружности с цен-
центром на оси барабана (рис. 27.2) 0. Участки поверхности, примыкаю-
примыкающие к каждому гребню, будем называть гранями. Две такие грани
образуют гофр. Введём элементарный гофр в виде двух элементарных
площадок с углом 2^ между гранями в сечении, перпендикулярном
гребню (рис. 27.3, а). В процессе раскрытия гофры разглаживаются
(уплощаются), при этом угол между гранями изменяется от 0 до тг
в плоском состоянии.
Нейтральная
"~~ линия
Рис. 27.3
Центры тяжести сечений гофра (точки G на рис. 27.3, б) образуют
линии, которые мы будем называть нейтральными. Нейтральные ли-
х) Форму складок на плёнке авторам показал О. А. Александров.

184
Гл. IV. Решение прикладных задач
нии, как показывает форма складок на рис. 27.2, разветвляются. Появ-
Появление новых ветвей нейтральной линии вызвано тем, что с увеличением
расстояния от оси барабана (вдоль нейтральной линии) при заданной
длине образующей барабана на его поверхности укладывается большая
площадь отражающей поверхности паруса.
Условимся считать, что нейтральные линии расположены в одной
плоскости, перпендикулярной оси, и описываются параметрически с по-
помощью полярных координат. В качестве параметра принимаем коорди-
координату s — длину дуги нейтральной линии от точки крепления к бара-
барабану (К) до центра G рассматриваемого элемента гофра. Изменение
формы нейтральной линии во времени означает, что полярные коор-
координаты (р, ср) текущей точки являются функциями двух независимых
аргументов (s, t).
Грань элементарного гофра имеет форму прямоугольника со сто-
сторонами ds и h (рис. 27.4). Элементарный гофр расположен вдоль
касательной к нейтральной линии с единичным вектором т, который
Рис. 27.4
Рис. 27.5
составляет угол v с радиальным направлением полярных координат ер
(рис. 27.5). Таким образом, для определения положения элементарного
гофра и его конфигурации вводятся четыре определяющих параметра:
p(s,t), <p(s,t), l(s,t), v{s,t).
Для этих параметров приближённо выполняются равенства
s).
N
2тгр = 2Nh sin 7 cos v при h
(i)
B)
где N — число гофров на окружности радиуса р.
Из выражений B) следует не зависящее от числа N соотношение:
р = (i?b + s) sin 7 cos z/	C)
Очевидно, что при 5 = 0 должно выполняться равенство р = R^.
Однако равенство C) показывает, что для этого угол 7 не должен быть
равен 0. Действительно, крепление плёнки к барабану по окружности

27. К динамике раскрытия поверхности космического паруса 185
требует, чтобы гофр, примыкающий непосредственно к барабану, также
«уплощался», и тогда угол 7 = тг/2. Подобные переходные участки име-
имеют малую протяжённость и ими можно пренебречь. То же самое можно
сказать об участках, где происходит переход от гребня к впадине
(гофр «выворачивается», образуя своего рода «карманы», в которых при
укладке может «упаковаться» воздух).
Грани, примыкающие к одному гребню, в уложенном состоянии
касаются друг друга и на каждом обороте вокруг барабана равномерно
удаляются от оси на одинаковое расстояние. Подобным свойством
обладает архимедова спираль:
р = Rb + aip.	D)
Примем уравнение D) в качестве начального условия при t = 0.
Будем считать, что р,(р — полярные координаты точки на нейтральной
линии; а — не зависящий от s параметр.
Полагаем также, что влияние внешних сил и внутренних дисси-
пативных сил на промежутке времени раскрытия поверхности паруса
пренебрежимо мало.
27.2. Вывод уравнений движения оболочки в процессе её
развёртывания.
1. Применение принципа Гамильтона-Остроградского. Принятое
описание простейших элементов (их однотипно изменяемая конфигу-
конфигурация и расположение) задаёт структуру раскрываемой поверхности
и позволяет использовать интегральные принципы изменяемого дей-
действия для составления уравнений её движения. Для относительного
движения в осях, жёстко связанных с барабаном, согласно принципу
Гамильтона-Остроградского имеем интегральное равенство следующе-
следующего вида:
и	и
5 J L^ dt + J [5rA (F) + 5rA (Ф) + 5rA (R)] dt = 0.	E)
о	о
Здесь 5 — знак изохронной вариации; l/r) — функция Лагранжа
раскрываемой поверхности паруса:
L(r) = Т(г) _ Uf	F)
где Т(г) — кинетическая энергия раскрываемой поверхности паруса
в относительном движении, П — суммарная потенциальная энергия сил
инерции поступательного переносного движения и центробежных сил
инерции; 5' A (F) — виртуальная работа активных непотенциальных
сил; 5' А (Ф) — виртуальная работа непотенциальных сил инерции;
5'A (R) — виртуальная работа реакций неидеальных связей и идеаль-
идеальных связей, не учтённых выбором определяющих параметров; [0, t\] —
фиксированный отрезок времени течения рассматриваемого процесса

186	Гл. IV. Решение прикладных задач
раскрытия; на концах промежутка состояние системы при варьирова-
варьировании также фиксировано.
Рассматриваемая система является распределённой (с одномерным
распределением), поэтому
.dm, dm = 2fihds,	G)
где Л — удельный лагранжиан элементарного гофра массой dm; \i —
масса единицы поверхности паруса.
Элементарный гофр соединён с другими гофрами как в продольном
(т), так и в поперечном (п) направлениях. Уравнения, описывающие
эти условия, рассматриваем как связи.
2. Уравнения связей. Определяющие параметры A) не являются
независимыми. Условие B) и учитываемые далее (в плоском случае)
кинематические соотношения выражают наложенные связи, уравнения
которых запишем в следующем виде:
р — ho(s) sin 7 cos z/ = 0, ho = — h(s);
7Г
p'2 + pV2 -1=0, piff - sin v = 0.	(8)
Штрихом в (8) и далее обозначены частные производные по s, т. е.
d/ds. Связи, описанные уравнениями (8), имеют следующий меха-
механический смысл. Первое уравнение в системе (8) (условие B)) уже
обсуждалось выше. Здесь оно представлено в более общем виде, так
как возможно уточнение вида зависимости ho(s). Второе уравнение —
геометрическое выражение квадрата длины элемента нейтральной ли-
линии (dsJ; третье — условие ориентации элементарного гофра вдоль
нейтральной линии.
Будем рассматривать уравнения (8) как уравнения идеальных свя-
связей. Для левых частей этих уравнений, а также для определяющих
параметров введём единообразные обозначения:
fj(u,u')=0, j = 1,2,3, и = (щ,и2,щ,щ),	(9)
где щ = р, щ = (р, щ = 7, Щ = v.
По правилам виртуального варьирования, используя векторно-мат-
ричную запись, имеем
-J^-ЬиЛ—Ц- 5иг = 0, 7 = 1,2,3,	A0)
ди	ди	J	v ;
где 5и, 5и' — виртуальные вариации параметров и, и'. Применяя равен-
равенство A0) к уравнениям системы (8), получаем уравнения для вирту-
виртуальных вариаций:
5р — ho(s) cos7cos uSj + ho(s) sin7 sin v5v = 0,
pr 5pr + ptpr25p + p2(pf5(pf = 0,
cpf5p + p5cpf — cos vbv = 0.	A1)

27. К динамике раскрытия поверхности космического паруса
187
Учёт уравнений для виртуальных перемещений с множителями свя-
связей Xj(s,t) (неопределёнными множителями Лагранжа) означает осво-
освобождение системы от этих связей и даёт в интегральном равенстве E)
слагаемые вида
5'A
(R)=
о i=1
ди1
ds.
A2)
Силовые характеристики определяются множителями Лагранжа,
которые и являются коэффициентами пропорциональности при вычис-
вычислении реакций связей.
3. Вычисление лагранжиана и виртуальной работы сил инерции.
Для получения функции Лагранжа вычислим удельные величины,
отнесённые к массе dm элементарного гофра с учётом переменности
его конфигурации, положения и ориентации. Ограничимся плоским
случаем, когда корпус КА имеет угловую скорость и угловое ускорение,
направленные по оси паруса (еь см. рис. 27.1).
Составим выражение кинетической энергии одного гофра плёнки
в относительном движении в осях, жёстко связанных с барабаном:
Т{г) = I
2
— A + 6cos27O2
ту (Ф + ^) sin2 7
dm.
A3)
В A3) и далее точкой обозначены частные производные по t, т.е. d/dt,
и производные по t от функций, зависящих только от t.
Принимая центр масс паруса за начало отсчёта инерциальной систе-
системы и полагая, что плёнка нерастяжимая, а соединение гофров идеально
гибкое, находим выражение потенциальной энергии центробежных сил
инерции:
П = —-
I + Е (р2 + - /i2sin27) — рр — - /i2sin27nn dm,
1 О
О cos2 7
О 0 sin2 7
О
О
A4)
где ft — переносная угловая скорость, состоящая из угловой скорости
корпуса космического аппарата (ю) и угловой скорости вращения бара-
барабана относительно корпуса (<^iei); Е — единичный тензор; рр, пп —
тензоры, записанные в форме диадных произведений векторов.
Тензор I составлен в проекциях на естественные оси нейтральной
линии; по своему смыслу это сумма тензоров инерции граней элемен-
элементарного гофра относительно их собственных центров масс.

188
Гл. IV. Решение прикладных задач
Диадные произведения и вектор переносной угловой скорости пред-
представляем в тех же осях:
рр =
cos2 v
nn =
0 0 0
0 1 0
0 0 0
— sin v cos v 0
— sin v cos v sin v 0
0	0	0
П = @, 0, г + vp
где г — проекция угловой скорости корпуса КА на ось паруса.
После подстановки выражений A5) в A4) потенциальная энергия
центробежных сил принимает вид
A5)
кг
(г + ф\) dm.
A6)
Для вычисления виртуальной работы вращательных и кориолисо-
вых сил инерции имеем [58]
-овращ
Qi =-
дщ
(или i = p,(p,j,
?*(ко )'	A7)
где K.Q — главный момент количества относительного движения
элементарного гофра относительно центра О (точки пересечения оси
паруса и оси динамической симметрии корпуса; см. рис.27.1):
e\dm.
A8)
Для обобщённых сил инерции, отнесённых к единице длины ds,
оставим те же обозначения, что и в A7), и используем нижние индек-
индексы, соответствующие обозначениям определяющих параметров. Выпол-
Выполним операции, указанные в A7). С учётом A8) находим обобщённые
вращательные силы инерции, отнесённые к единице длины:
двращ = ^ двращ = 2^ (р2 + & gin Л (^ + ^) ?
2/х/г3
sin7 (г + ф\),
A9)
и обобщённые кориолисовы силы инерции, отнесённые к единице дли-
длины (h = 0):
= (г
фх)
)кор _ _fA
(г-
B0)

27. К динамике раскрытия поверхности космического паруса 189
Выражения A9), B0) позволяют получить выражение виртуальной
работы сил инерции:
5'А(Ф) = \J2 {Q?*m + Q7PMUlds.	B1)
Таким образом, найдены все слагаемые в интегральном равен-
равенстве F) принципа изменяемого действия. Равенство F) выполняется,
если коэффициенты при независимых виртуальных вариациях опреде-
определяющих параметров равны нулю. Остаётся найти эти коэффициенты
и получить уравнения движения.
4. Уравнения относительного движения паруса при плоском развёр-
развёртывании. Выполним преобразования равенства E), обычные при при-
применении интегральных принципов.
После варьирования первого слагаемого в E) по определяющим
параметрам и их производным (по обоим аргументам) и применения
операции интегрирования «по частям» с учётом перестановочных со-
соотношений находим, что коэффициенты при независимых виртуальных
вариациях равны вариационным производным от плотности лагранжи-
лагранжиана (L = Л2/хЛ; см. G)):
— = -( — ) + -{ —1-—, г= 1	4,	B2)
6щ dt I дщ J ds у дщ J дщ '
где — {•} и — {•} — полные частные производные.
Вычисляем вариационные производные B2) от плотности лагран-
лагранжиана (L), составленной из разности подынтегральных выражений A3)
и A6):	6L
— = \р - рф2 - р (г + фх) J 2/ih,
о , д Г 2 ¦ , 7/г2
2М^|^+ —
12 /v
+ -^— 672 - 7 (9? + i>f + 3 (r + <?i J sin 27,
B3)
5L rt , a f 7h2
Слагаемые, получаемые при преобразовании виртуальной работы
реакций A2) с учётом уравнений для виртуальных вариаций A1),
сразу включим в уравнения. Тогда
?Ь _ Окор , д , 2Л /2 - У ' - Л " + А х - О
?р р	2

190	Гл. IV. Решение прикладных задач
^ - QI7 - А,/i0cos 7 cos i; = 0,
g	_ дкор + Ai h() gin 7 gin y _ дз cos y = q
В B4) используются выражения, приведённые выше (см. B0) и B3)).
Уравнения B4) вместе с уравнениями связей (8) составляют за-
замкнутую систему относительно семи неизвестных функций (четырёх
определяющих параметров и трёх множителей связи). Это уравнения
в частных производных второго порядка относительно двух аргумен-
аргументов. Начальные условия предоставляет уравнение D), а также значения
7E,0) = 0, v(s,0) = тг/2 и уравнения связей (8). Процесс развёртыва-
развёртывания характеризуется неравенствами v(s,t) < 0, p'(s,t) > 0, (p(s,t) < 0.
Можно заметить, что последние два уравнения в B4) позволяют
выразить неопределённые множители Ль Аз через остальные перемен-
переменные (и их производные). После этого из первых двух уравнений на-
находятся Л2 и \'2. Остаётся одно уравнение для четырёх определяющих
параметров, которые связаны тремя уравнениями связей (8) (с помо-
помощью этих уравнений тригонометрические функции от v выражаются
через другие переменные). Следовательно, система сводится к одному
уравнению в частных производных для одной неизвестной функции от
двух аргументов. Указанные выкладки громоздки для «ручной» работы,
но алгоритм их проведения достаточно прозрачен и может быть реали-
реализован в процессе разработки программного обеспечения вычислений.
Составленные уравнения описывают развёртывание, которое назва-
названо плоским, так как нейтральная линия в процессе движения предпо-
предполагается плоской, лежащей в плоскости, перпендикулярной оси паруса.
В этой плоскости гофр является абсолютно гибким, но рассматривается
как жёсткий в плоскости второй кривизны нейтральной линии.
Представленная модель, с одной стороны, является частным случа-
случаем более детальных моделей, а с другой — сама может использоваться
для составления упрощённых расчётных моделей.
27.3. О форме равновесия вращающейся отражающей поверх-
поверхности. При действии только центробежных сил инерции нейтральные
линии гофров развёрнутой поверхности являются прямыми, располо-
расположенными в одной плоскости (невозмущённой плоскости). Последняя
перпендикулярна оси паруса.
Пусть в направлении, перпендикулярном к невозмущённой плоско-
плоскости, падает световой поток. Тогда в стационарном движении элементар-
элементарный гофр будет находиться в относительном равновесии под действием
трёх сил: N — растягивающего усилия в направлении касательной;
D — силы, обусловленной давлением и действующей в направлении
нормали; Фцен — центробежной силы инерции (рис. 27.6).
Обозначим отклонения точек нейтральной линии гофра от невоз-
невозмущённой плоскости через u(s). В условиях равномерного вращения
отражающей поверхности с абсолютной угловой скоростью О в линей-

27. К динамике раскрытия поверхности космического паруса
191
След невозмущенной
плоскости
Нейтральная
линия гофра
Рис. 27.6
ном приближении, \и'\ « 1 (а = г/, sin а = г/, cos а = 1), составляем
уравнение относительного равновесия элементарного гофра (проекции
сил на нормаль к нейтральной линии):
Dda = (u2pdm)v!.	B5)
В B5) приняты те же обозначения, что и в п. 2:
da = 2hsin/yds, dm = 2hfids, p = R\> + s.	B6)
Из B5) с учётом B6) получаем дифференциальное уравнение с
разделяющимися переменными:
, D sin 7
du =	тг1-
(Дь + s)'
B7)
Принимая в B7) sin 7 = const (в развёрнутом состоянии sin 7 ~ 1)
и интегрируя уравнение B7) при граничном условии
u(sY) = щ,
находим
D
Rb + s
B8)
Выбором конструктивных параметров можно обеспечить значе-
значение щ, равное нулю.
Уравнение B8) отклонения нейтральной линии от невозмущённой
плоскости показывает, что в стационарном режиме равновесная форма
отражающей поверхности является вогнутой (к направлению внешнего
потока, перпендикулярному невозмущённой плоскости). Величина от-
отклонения нейтральной линии гофра изменяется по логарифмическому
закону B8).

192
Гл. IV. Решение прикладных задач
28. О влиянии гистерезиса податливой опоры
на сферическое движение тела, несущего маховик
Исследуется движение оси динамической симметрии абсолютно
твёрдого тела, несущего маховик, ось которого совпадает с осью сим-
симметрии тела. Система находится в однородном поле силы тяжести.
Центр тяжести системы расположен выше непо-
неподвижной точки (рис. 28.1). Учитывается внеш-
внешнее вязкое трение. Сопротивление отклонению
оси тела от вертикали оказывает радиальная
податливая опора, обладающая упругими свой-
свойствами и гистерезисом. Показано, что реакция
этой опоры представляется силовым полем, по-
получаемым в результате применения компози-
композиции оператора Гамильтона и оператора поворота
к силовой функции (после линеаризации это
поле позиционной неконсервативной силы).
Получены условия устойчивости по Ляпу-
Ляпунову вертикальной ориентации оси тела. При
изучении линейных периодических вынужден-
вынужденных колебаний найдены три типа зависимо-
зависимостей сдвига фазы колебаний от частоты. Од-
Одна из этих зависимостей имеет точку миниму-
минимума и точку максимума. Теоретические выводы
подтверждены результатами физического экспе-
эксперимента, проведённого над роторной системой
сепаратора, имеющего подобную механическую
схему.
Рис. 28.1
28.1. Механическая схема. Общее уравнение динамики си-
системы. Система (несущее тело-маховик) состоит из двух динами-
динамически-симметричных абсолютно твёрдых тел с общей осью симмет-
симметрии и неподвижным центром в точке О (рис. 28.1). В инерциаль-
ных осях 0{;Г]( (орты i,j,k) положение оси симметрии Oz задаёт-
задаётся углами а,/3 (а,C,ф — корабельные углы), определяющими также
связанные с несущим телом оси Oxyz с ортами Ii, i2, 1з (рис. 28.2).
Положение системы задаётся обобщёнными координатами а, /3, ф, ср.
Маховик вращается равномерно относительно собственной оси Oz:
fj(r) = (p\3i ф = const = и.
Составляем выражение для кинетической энергии системы:
т = in •
п •
A)
где 0(°) — тензор инерции системы для точки О; П — угловая

28. О влиянии гистерезиса податливой опоры на движение тела 193
скорость несущего тела (в осях
Oxyz):
, B)
@("г) _ тензор инерции маховика
для точки О (J — момент инерции
относительно оси Ог).
Потенциальная энергия одно-
однородного поля силы тяжести с уско-
ускорением свободного падения g, па-
параллельным оси О( (при нулевом
уровне в вертикальном положении
оси ротора):
Ug=MgL(i3k-\), C)
где М — масса системы; L — расстояние от точки О до центра тяжести
системы.
Составляем функцию Лагранжа:
Рис. 28.2
L = Т - Пп
D)
из которой, с учётом выражений A) и C), следует, что обобщённые
координаты ф, ср являются циклическими.
Условие постоянства угловой скорости собственного вращения ма-
маховика рассматриваем как идеальную связь с уравнением для вирту-
виртуальной вариации
ф — const = 0, 5(р = 0.	E)
Принцип Гамильтона-Остроградского для рассматриваемой систе-
системы записывается как
(SL +
5'A) dt = 0,
F)
где Л — неопределённый множитель идеальной связи E); 5rA — вир-
виртуальная работа непотенциальных сил.
Непотенциальные силы представлены моментом внешних сил вяз-
вязкого трения относительно центра О (—z/fi; v — неотрицательная
константа) и силами со стороны радиальной опоры, контактирующей
с валом несущего тела в точке Р, находящейся достаточно близко к оси
симметрии (см. рис. 28.1).
Отклонению оси тела от вертикали оказывает сопротивление ради-
радиальная опора со свойствами упругости и гистерезиса. Упругие свойства
считаем заданными с помощью силовой функции U.
7 В. Г. Веретенников, В. А. Синицын

194
Гл. IV. Решение прикладных задач
R
Учёт влияния гистерезиса материала при разработке математиче-
математических моделей динамики и рекомендаций по их практическому приме-
применению относится к первой основной задаче механики и представляет
самостоятельный интерес. Для учёта гистерезиса воспользуемся при-
приёмом, применяемым при составлении модели внутреннего неупруго-
неупругого сопротивления [112]: вектор силы сопротивления деформированию
считаем отклонённым на некоторый угол 7 от вектора реакции, полу-
полученного в предположении, что сопротивление является чисто упругим
(рис. 28.3). Угол 7 — /VBtt), где /i — коэффициент поглощения, ха-
характеризующий гистерезисные потери на цикле «нагрузка-разгрузка».
В общем случае полной ясности построения этой модели сопротив-
сопротивления нет [112], однако в рассматриваемой системе указанный при-
приём имеет прозрачный физический смысл, который поясняет рис. 28.3.
На рисунке показан контакт вала и по-
податливой опоры как малая конечная об-
область (в окрестности точки Р) в виде двух
зон: «нагружаемой» и «разгружаемой». Ка-
Качественно гистерезис проявляется в том,
что в нагружаемой зоне создаётся реак-
реакция Ri большей величины по сравнению
с величиной реакции R2 в разгружаемой
зоне. Результат такого учёта гистерезиса
приводит в рассматриваемой модели к по-
появлению сил, называемых собственно кон-
консервативными [66] или неконсервативными
позиционными силами (силы, линейно за-
зависящие от обобщённых координат с ко-
сосимметрической матрицей коэффициен-
коэффициентов). Все аналитические выкладки сохра-
Рис. 28.3
няются как при положительном, так и при отрицательном значении
угла 7- Для численных расчётов, сравниваемых далее с эксперимен-
экспериментальными данными, принят угол, при котором реакция оказывает «со-
«сопротивление» движению, имеющему место в отсутствие гистерезиса.
В этом случае полученные частотные характеристики качественно
и количественно близки результатам физического эксперимента.
В приведённом объяснении закономерности, моделирующей гисте-
гистерезис, нетрудно усмотреть некую аналогию с законом сухого трения
и законом трения качения. Возможно, что закономерность для учёта
гистерезиса также должна иметь разрывный характер (с изменением
знака угла 7)- Более полное исследование требует проведения допол-
дополнительных экспериментов.
Силовое поле, получаемое поворотом оси потенциального поля,
математически можно записать с помощью оператора (°V) (см. [13]),
представляющего собой композицию оператора Гамильтона и оператора
поворота, последовательно действующих на силовую функцию.

28. О влиянии гистерезиса податливой опоры на движение тела 195
Соответственно виртуальная работа непотенциальных сил опреде-
определяется выражением Eгр — виртуальное перемещение точки Р)
5'А = (°VU)Srp - и ft • (iiSa + ]5C + \36ф).	G)
Теперь мы имеем все слагаемые для вывода уравнений динамики
на основе равенства F). Приравнивая коэффициенты при независимых
виртуальных перемещениях по обобщённым координатам нулю, полу-
получаем четыре уравнения движения и уравнение связи для определения
обобщённых координат и неопределённого множителя.
Для циклических обобщённых координат с учётом уравнения связи
находим первые интегралы уравнений движения:
дТ
ф = const при Л + Qy = 0, —г + уф = const.	(8)
Второе равенство в (8) означает, что реакция связи E) уравнове-
уравновешивает обобщённую силу Qp, соответствующую обобщённой коорди-
координате (р.
28.2. Уравнения движения оси маховика (линейная модель).
В линейном приближении по а, C и а, C уравнения для соответствую-
соответствующих обобщённых координат отделяются:
Аа + JuoC — MgLa = — cl2a cos 7 — cl2 C sin 7 — ua,
A/3 — Juoa — MgL/3 = — cl2f3 cos 7 + cl2a sin 7 — z//3,
где с — коэффициент жёсткости податливой опоры; / — расстояние от
точки О до места установки податливой опоры (точка Р), I > г.
Запишем оба уравнения (9) в виде одного для комплексной пере-
переменной и = а + г/3, г2 = — 1:
и + 2 (/го + h\i)u + (fco + k\i)u = О,
9ь v 9h	Juj h clcos^-MgL ,
= A'	= ~^4~'	= 	A	'	=A
Заметим, что учёт гистерезиса в данной системе соответствует появле-
появлению в уравнениях движения обобщённых сил, называемых «собственно
неконсервативными» [66].
28.3. О влиянии гистерезиса на устойчивость движения оси
маховика. Рассмотрим влияние гистерезиса (sin 7 7^ 0) на устойчи-
устойчивость тривиального решения и = 0 уравнения A0) по отношению к ма-
малым возмущениям начальных условий. В данном случае уравнение A0)
является уравнением возмущённого движения. Поиск решения в форме
и = Hexp(i\t) приводит к общему решению
и = Hiex.p(i\it) +Я2ехр(гА2?),	A1)
где Н\, В.2 — комплекснозначные постоянные интегрирования; Ль Л2 —
корни характеристического уравнения
Л2 + 2(/ц - hoi)X - (к0 + кхг) = 0.	A2)

196	Гл. IV. Решение прикладных задач
Решая уравнение A2) относительно Л, имеем
Ai>2 = -Ы + hoi ± у (hi - h0iJ + k0 + M .	A3)
Подкоренное выражение A3) является комплексным числом m-\-in,
и корень из него равен (а, Ъ — действительные числа)
Для устойчивости решения и = 0 необходимо, чтобы мнимые части
корней т -\- in A3) были неотрицательны (ho ± Ь ^ 0), т. е.
ш + л/m2 + п2 ± л/2 An > 0.	A5)
Из A5) следует, что в отсутствие внешнего вязкого трения (у = 0)
при наличии гистерезиса G ^ 0) «спящая» вертикальная ориентация
оси неустойчива. При знаке строгого неравенства имеет место асимп-
асимптотическая устойчивость.
28.4. Влияние гистерезиса на вынужденные периодические
колебания. Введём периодическое силовое возмущение в правую
часть уравнения A0):
и + 2(ft0 + hii)u + (k0 + kxi)u = Qeiujt.	A6)
Частное решение A6) (где Go, G\ — вещественные величины)
u* = Geiujt, G = Go + Gxi,	A7)
соответствует вынужденным колебаниям с частотой возмущения.
Подставив A7) в A6) и приравняв коэффициенты при веществен-
вещественной, а также при мнимой частях в обеих частях равенства, получаем
уравнения для определения Go и G\, из которых находим
Go = Щ, Gx = -Щ, р=-и;2- 2hxuj + fc0,
В	В
q = 2h0u + ki, В = ^p2 + q2.	A8)
Соответственно частное решение A7) имеет вид
Выраженные через параметры системы A0) амплитуда Q/B и сдвиг
фазы 5 вынужденных колебаний имеют вид
|= .	<*">	A9)
^[A-е)ш2-к0]2 + Bк0со + к[J
2hoou + к\	J
1-е)ш -ко	Л
Коэффициент г характеризует вытянутость эллипсоида инерции
системы для точки О. Рассмотрим случай, когда г < 1. Вид зависимо-

28. О влиянии гистерезиса податливой опоры на движение тела 197
стей A9), B0) показывает, что имеются два характерные соотношения
параметров, которые мы обозначим как и* и и**\
о;* =-
м
/о 1 \
B1)
В данном случае характерные частоты оо* и оо** — положительные
вещественные, поскольку ho > 0, к\ < 0, г < 1.
Вначале остановимся на анализе функции 5 (и;). График этой кри-
кривой зависит от взаимного расположения характерных частот B1) на
оси аргумента. Возможны три варианта их относительного положения:
1) uj* < а;**; 2) а;* > а;**; 3) а;* = и;**.	B2)
Если гистерезиса нет, то оо* = 0 и описываемые ниже бифуркации
отсутствуют. Перепишем функцию 5(и) B0) в следующей форме:
= arctg -
B3)
Из B3) видно, что S (о;*) = 0,тг; 5(и;**) = ±тг/2 при uj* ^ uj**.
Функции 5 (и) для первых двух вариантов B2) монотонные. На ри-
Рис. 28.4
Рис. 28.5
сунках 28.4, 28.5 показан их типовой вид. В третьем варианте B2)
функция 5(uj) имеет минимумы при
B4)
Аналитическая зависимость 5(и) (рис. 28.6, сплошная линия)
построена при значениях параметров, соответствующих конкретной
системе, над которой проводился эксперимент 0 (результаты экспери-
эксперимента показаны точками).
1) Эксперимент проведён в Московском авиационном институте под руко-
руководством В. М. Рыженкова над роторной системой сепаратора, которая при
некоторых ограничениях на осевые перемещения описывается принятой здесь
моделью.

198
Гл. IV. Решение прикладных задач
ил	uj^ 200 а;* 400
Рис. 28.6
UJ2 600 LJ, С
Для изучения амплитуды вынужденных колебаний A9) функция
Q(uo) принята в виде (d, uom = const)
Q(u) =d(cu2 +cu2m).	B5)
Зависимость B5) моделирует (хотя и не всегда [83]) влияние экс-
эксцентриситета е центра масс маховика; d = moloe/A; uom = л/g/lo ; mo,
/о — масса ротора (маховика) и расстояние от точки О до центра масс
маховика. Обозначим амплитуду вынужденных колебаний через U(u).
Тогда из A9) с учётом B5) имеем
U(lo) =
B6)
р= A -
-ui2
q =
График функции U(u) B6), построенный расчётным путём для
параметров конечной системы, показан на рис. 28.7 сплошной линией,
а результаты экспериментальных
измерений отмечены точками.
В области, близкой к резонансной
частоте сл**, в эксперименте на-
наблюдалось нарушение устойчивого
режима работы роторной системы.
Отличие теории и эксперимента
объясняется, в частности, тем,
что теоретически рассматривались
только вынужденные колебания
U, мкм
40
20
0 ои** 200 400
Рис. 28.7
600 ои, с"
с частотой, равной частоте пери-
периодического возмущения, которая
для удобства сравнения с измерениями принята равной «роторной»
частоте (угловой скорости маховика). Очевидно, что реально имеются
также вынужденные колебания с собственной частотой и частотами
других источников возмущений. Процедура анализа этих колебаний
в линейной теории известна.

29. Построение периодического решения системы с малым параметром 199
29. Построение периодического решения системы
с малым параметром
Применим уравнение несвободного движения (см. п. 12.5) при по-
построении периодического решения для системы с малым параметром,
к которой приводится динамическая система Е. Лоренца (Е. N. Lorenz)
[59, 73]. Методы и схемы построения решений систем с малым пара-
параметром обычно [70] относятся к системам, в которых порождающее ре-
решение получено при равенстве нулю малого параметра (/i = 0). Из си-
системы Лоренца система с малым параметром получается при условии
0 < /i <С 1; по смыслу это автоколебательная система с инерционным
возбуждением, на которую налагаются идеальные связи, обеспечиваю-
обеспечивающие заданное решение, а по форме — система Четаева (см. п. 12.1).
Условия для реакций дают дополнительные уравнения для началь-
начальных условий при нахождении периодического решения.
29.1. Приведение динамической системы Е. Лоренца к форме
систем Н. Четаева. Системой Лоренца называют систему обыкновен-
обыкновенных дифференциальных уравнений третьего порядка [59, 73]:
х\ = — а(х\ — Х2), х'2 = ах\ — х% — х\х%, х'% = — Ъх% + х\Х2, A)
где а, а и Ъ — постоянные положительные коэффициенты; штрих
означает производную по независимой переменной т.
Примечание. Система Лоренца была получена при составлении
математической модели конвективного движения в подогреваемом слое
жидкости. Вопрос адекватности такой модели конвективного движения
не является предметом нашего обсуждения, но также может быть
рассмотрен с позиций предлагаемого подхода. Большой объём исследо-
исследований, посвященных системе A), сделал её по сути классическим ма-
математическим объектом (см., например, [59, 73]); среди решений этой
системы есть отвечающие устойчивым и неустойчивым положениям
равновесия, регулярные колебания и хаотические движения с широким
сплошным спектром, стохастические колебания. К уравнениям Лорен-
Лоренца при некоторых предположениях исследователи сводят (см., напри-
например, [73]) уравнения для медленных амплитуд напряжённости поля,
поляризации и разности населённостей в лазерах и мазерах, уравнения
генераторов с нелинейностью. Исследуются различные комплексные
формы уравнений Лоренца и т. д.
Продемонстрируем изложенную в п. 12.5 методику построения
несвободной порождающей системы при решении задачи отыскания
периодических движений системы A).
Переход в A) к новым переменным
fe"' 7? = МЛЖз" 2а Ч' М*=(<г+1)т. »= , , ,f B)

200	Гл. IV. Решение прикладных задач
приводит к уравнениям (см., например, [73])
|	8	).	C)
В уравнениях C) при больших значениях а коэффициент fi может
рассматриваться как малый параметр.
Система C) получена преобразованием переменных при условии,
что /i т^ 0 [73]. Модель порождающей системы, получаемой при /i = 0,
выпадает из класса моделей, описываемых уравнениями C).
29.2.	Несвободная система Четаева. Поступим иначе: вместо
«волевого» выбора консервативного нелинейного осциллятора в каче-
качестве порождающей системы, получаемой при /i = 0, построим несво-
несвободную систему при 0 < /i <C 1, имеющую решение, совпадающее
с «порождающим решением». Этим путём мы также изменяем класс
рассматриваемых моделей, но введение реакций — это более конструк-
конструктивный способ обеспечить движение системы с заданными свойствами.
Несвободную систему получим путём введения идеальных связей,
при наличии которых постоянными являются полная механическая
энергия «механической части» (первое уравнение в системе C)) и пе-
переменная Г].
Указанные связи представляются уравнениями
?2 + G7 - 1)^2 + ^ = 2Е = const, г] = const.	D)
Выражение Е по форме совпадает с полной механической энергией.
Из уравнений связей D) по правилам, описанным в п. 12.5, для
виртуальных вариаций 5?, 5rj получаем уравнения
2?<*? + ?2<fy = 0, 5г] = 0.
Учитывая реакции идеальных связей с помощью неопределённых мно-
множителей Ai и А2, имеем уравнения несвободного движения:
ё+(»?-1)е + е3 = ё(-д + 2А,)> т? =-м/(е??) + Ai?2 + а2. E)
Вместе с уравнениями E) для определения множителей Ai и А2
рассматриваются уравнения связей D), дифференцируя которые по t,
с учётом уравнений движения E) находим
fl	F)
29.3.	Условия периодичности движения. Будем рассматривать
переменные Е и т\ как «медленные» переменные исходной системы,
а в выражениях Е и rj, получаемых с учётом уравнений E), выделим

29. Построение периодического решения системы с малым параметром20\
слагаемые, являющиеся реакциями (обозначим их ге и rv соответ-
соответственно):
^2 ^(Л^ + Ч	A,?2 + A2,	G)
где Ai и А 2 имеют вид F).
Реакции обеспечивают свойства D), при которых изменение «быст-
«быстрой» переменной (?) является периодическим при любых начальных
условиях (удовлетворяющих этим уравнениям). Выберем из всех дви-
движений то, на котором реакции G) в среднем по времени на периоде Т
равны нулю:
]п(№>?(*)) dt = O, i = E,ri.	(8)
о
Примечание. В системах с малым параметром равенство нулю
средних значений всех реакций на конечном периоде Т решений урав-
уравнений означает, что уравнения, получаемые усреднением на периоде
несвободной системы, совпадают с укороченными уравнениями свобод-
свободной системы.
Прежде чем воспользоваться уравнениями (8), найдём закон изме-
изменения «быстрой» переменной (?(?)). Из уравнений D) непосредственно
следует интеграл (при начальных значениях to = 0, ?о — О, Со > 0)
±	2E-(V-l)e-^-	(9)
о /т
В периодическом движении при некотором значении t координата ?
достигает своего наибольшего значения (d); при этом
2Е = (г]- I)d2 + y.	A0)
Интеграл в (9) с учётом выражения A0) после замены переменной с
помощью равенства ?2 = d2(l — B) преобразуется к нормальной форме
Лежандра:
cot =
l -C2)(l -/СЧ2
и = л/г] - 1 + d2 , k2 = ^, 7] + d2>\.	A1)
2(JL>
Обращение интеграла A1) является эллиптическим синусом Якоби
с модулем к, т.е. ( = sn(ujt;h). Возвращаясь к исходной переменной ?
(с учётом тождества для функций Якоби: sn2 (и; к) + сп(и; к) = 1),
имеем
).	A2)

202	Гл. IV. Решение прикладных задач
Соответственно период колебаний (действительный) Т = 4K(k)/u),
где К (к) — полный эллиптический интеграл Якоби первого рода в
нормальной форме с модулем к.
Равенства (8) с учётом реакций G) и выражения /G7, ?) (см. C))
имеют вид
A3)
0	0	0
Уравнения A3) совпадают с уравнениями, полученными в рабо-
работе [73]. Однако имеется принципиальное отличие их приложения, со-
состоящее в том, что здесь это уравнения для несвободной системы, они
позволяют найти начальные условия, при которых движение является
периодическим, а реакции в среднем на периоде равны нулю (см. (8)).
30. Об энергии в динамике точки переменной массы
(в первой задаче Циолковского)
Модели точки переменной массы используются при изучении ре-
реактивного движения, в том числе в теории полёта ракет. Из решения
первой задачи К. Э. Циолковского следует возможность сообщения
ракете в свободном пространстве неограниченно большой скорости
за конечное время; естественно возникает вопрос: может ли ракета
достичь скорости света? В научной литературе обсуждаются вопросы
создания с помощью реактивного принципа объектов, обладающих
большой энергией при полном расходе массы (ситуация, для класси-
классической механики парадоксальная). Актуальными становятся проблемы
полётов со скоростями, при которых нельзя пренебречь релятивистски-
релятивистскими эффектами (см. [104]).
В данной заметке приведён анализ энергетических соотношений
в условиях классической задачи Циолковского в системе «точка пере-
переменной массы (ТПМ) — изменяющая масса (уходящие частицы непо-
непосредственно перед их отделением и отделившаяся масса)». В конечной
форме получено выражение работы реактивной силы, приложенной
к ТПМ и создающей кинетическую энергию ТПМ и кинетическую
энергию изменяющей массы непосредственно перед отделением частиц.
Получено выражение внутренней энергии, необходимой для реализа-
реализации реактивного принципа (с учётом работы реактивной силы, прило-
приложенной к отделяющимся частицам). Показано, что в случае полного
расхода массы (га —> 0) полная работа реактивных сил в системе
целиком идёт на создание кинетической энергии изменяющей массы
и ожидать появления нового безмассового объекта, обладающего энер-
энергией, не приходится.

30. Об энергии в динамике точки переменной массы	203
30.1.	О моделях точки переменной массы. Переменность мас-
массы в классической динамике является следствием изменения соста-
состава [68] и (или) внутренних движений в системах, представляемых для
описания кинематики геометрической точкой, но имеющих протяжён-
протяжённость [76].
Основная задача механики о силах сохраняет своё значение и в ди-
динамике систем точек переменной массы и становится ещё более слож-
сложной: в уравнения движения включаются реактивные силы. Уравнение
движения точки переменной массы при отсутствии внутренних движе-
движений и присоединяющихся масс имеет вид
m^=F + P, P = mvr,	A)
cue
где т — масса частиц, составляющих ТПМ; v — абсолютная скорость
точки в инерциальной системе; F — равнодействующая внешних сил
(за исключением взаимодействия с изменяющими массами), приложен-
приложенных к точке; Р — импульсная (ударная) реактивная сила (И. В. Ме-
Мещерский, A. Cayley); vr — относительная скорость элементарной массы
\dm\ относительно точки переменной массы; точкой обозначена произ-
производная по времени (d/dt).
Известно, что второму закону Ньютона ((mv)" = F) также мож-
можно придать форму уравнения движения точки переменной массы
(при vr = — v).
Полагаем, что отделяющаяся частица представляется точечной мас-
массой (в более общем случае вводится понятие эффективной скорости
истечения). Различные варианты описания модели с учётом приложе-
приложения внешних сил к разным частям ТПМ как системы переменного
состава «ТПМ — отделяющаяся частица» имеются в работе [13], в том
числе с учётом переменного состава связей.
Классической задачей, решаемой с помощью модели ТПМ, является
первая задача К. Э. Циолковского. Из её решения следует возможность
сообщения ракете неограниченно большой скорости за конечное время.
В процессе движения ракеты работа реактивной силы, приложенной
к ней, увеличивается. Должна ли при этом увеличиваться полная
энергия ракеты? В результате полного расхода массы ракета как объект
прекращает своё существование. Каков тогда материальный носитель
энергии, равной работе реактивной силы, приложенной к ракете? Воз-
Возникает своего рода энергетический парадокс, удовлетворительное разъ-
разъяснение которого можно получить только на основе анализа системы,
включающей как ТПМ, так и изменяющую массу.
30.2.	Кинетическая энергия и работа реактивных сил в си-
системе «ТПМ — изменяющая масса». Рассмотрим решение зада-
задачи Циолковского о поступательном прямолинейном движении раке-
ракеты в свободном пространстве при действии только реактивной силы

204	Гл. IV. Решение прикладных задач
(в уравнении A) F = 0):
-г» dm	.	/гьЧ
Р = -^-vr, vr = const.	B)
При расходовании массы до величины т ракета приобретает ско-
скорость (начальную скорость ракеты без ограничения общности прини-
принимаем равной нулю), величина v которой связана с массой ракеты т
формулой Циолковского:
v = — vv In —,	C)
m0
где то — масса ракеты в начальный момент времени.
Из формулы C) следует, что в результате расходования всей массы
ракете сообщается неограниченная по величине скорость.
Вычислим работу реактивной силы и кинетическую энергию ра-
ракеты.
Работа приложенной к ракете реактивной силы на промежутке вре-
времени [0, t] вычисляется как интеграл от мощности силы B) (используем
одинаковые обозначения для граничных значений массы и скорости
и их текущих значений в качестве переменных под знаком интеграла):
m
v
0	то
В правой части равенства D) первое слагаемое — кинетическая
энергия ракеты. Учитывая соотношение C), имеем кинетическую энер-
энергию ракеты Т как функцию начального и конечного значений массы
ракеты:
()
га0/
Рассмотрим механический смысл последнего члена в выражении D).
Примечание 1. В научной литературе последнее слагаемое
в D) не всегда имеет удовлетворительную трактовку. В работе [104]
полагается, что формулой D) можно пользоваться для вычисления
«полной переменной энергии Е, равной работе реактивной силы тяги на
перемещениях ракеты». В результате следует парадоксальное суждение
о возможности в пределе при т —> 0 получить безмассовый объект,
обладающий энергией. Интеграл противоположного знака фигурирует
в теоремах об изменении кинетической энергии точки переменной мас-
массы. Для получения этого слагаемого к реактивной силе в [76] делается
«добавка» — вектор mv/2. Затем «добавка» и реактивная сила объеди-
объединяются в «добавочную силу». Смысловое назначение этой добавки —
диссипация энергии, равной кинетической энергии изменяющей массы
перед отделением составляющих её частиц. Однако реальной силы, со-
соответствующей этому вектору, нет («добавка» не является ни внешней,
ни внутренней силой, не имеет противодействующей силы); он фор-

30. Об энергии в динамике точки переменной массы	205
мально добавляется для придания теореме об изменении кинетической
энергии точки переменной массы того же вида, что и вид теоремы об
изменении кинетической энергии точки постоянной массы.
Нетрудно убедиться в том, что последнее слагаемое в D) имеет
смысл кинетической энергии частиц, изменяющих массу, непосред-
непосредственно перед их отделением, т. е. когда они ещё находятся в соста-
составе ракеты. Суммативная величина кинетической энергии изменяющей
массы до сообщения частицам относительной скорости (обозначим её
через Т~) равна
mo — m
Т~ =	—У-1- d/ji, /1 = то — m (d/i = —dm = \dm\), F)
о
где /i — величина отделившейся массы.
При возвращении к исходной переменной m интеграл F) принимает
форму последнего интеграла в D), т.е.
—-—- dm.	G)
2	v ;
ra0
Таким образом, имеем
A = T + T~.	(8)
С учётом зависимости скорости ракеты от массы C) интеграл в G)
вычисляется в конечной форме:
Ts-=mo,r2-^[(ln^2-21n^ + 2l.	(9)
(Ю)
m0/	m0
Соответственно
2	2 Г	9
mv .	2 mvr Л my ол m . о
=	1- mn??z	—l In — — 2 In	h 2
2 \\ moj	m0
Подстановкой E) в A0) находим выражение полной работы реактивной
силы, приложенной к ракете:
A = mov, ( I	1	In— .	(II)
V mo mo mo/
Составляем выражение кинетической энергии отделившихся ча-
частиц (Т+):
m	m	m	m
Т+ = - f (v + Vr) dm = - f v- dm - f vvr dm - [ у dm. A2)
m0	m0	m0	m0
Смысл первого слагаемого в A2) рассмотрен выше (см. F) и G)).
Второе слагаемое равно взятой со знаком минус работе А реактивной

206	Гл. IV. Решение прикладных задач
силы, приложенной к ракете (см. D)). Третье слагаемое — кинетиче-
кинетическая энергия относительного движения отделившихся частиц (Тг):
т
Tr = - J |dm = (mo-m)|	A3)
Получим выражение работы внутренних сил взаимодействия в си-
системе «ракета — отделяющиеся частицы». Внутренними силами явля-
являются реактивная сила Р, приложенная к ракете, и противодействующая
ей сила —Р, приложенная к отделяющейся частице. Элементарные им-
импульсы реактивной (Pdt) и противодействующей (—Р di) сил сообщают
материальным точкам с массами т и \dm\ приращения скоростей dv
и vr соответственно. Для вычисления работы воспользуемся теоремой
Томсона и Тета в теории импульсивных движений (см., например,
[13]): работа ударной силы при ударе равна произведению импульса
этой силы на вектор средней скорости (для доударного и послеударного
значений скорости) материальной точки, к которой приложена ударная
сила:	t	t
®	v+(v+dv)	v + (^ + Vr)dt,	A4)
о	о
где А^ — работа внутренних ударных сил в системе. Опуская малые
второго порядка и переходя к другой независимой переменной (массе),
с учётом равенства C) выражение A4) преобразуем к виду
т
m)^=Tr.	A5)
\?L
га0
Приращение кинетической энергии системы происходит вследствие
совершения работы реактивными силами (теорема об изменении кине-
кинетической энергии системы постоянного состава):
Т+ + Т = А^.	A6)
Имеем также равенство (где As — работа реактивной силы, дей-
действующей на отделяющиеся частицы)
выражающее теорему об изменении кинетической энергии отделивших-
отделившихся частиц.
30.3. О внутренней энергии ракеты. Кинетическая энергия си-
системы (левая часть равенства A6)) представляет собой приращение
внешней энергии, а правая часть — расход внутренней энергии, т. е.
W	m)^-.	A7)

30. Об энергии в динамике точки переменной массы	207
Начальное значение приращения внутренней энергии A7), очевид-
очевидно, равно нулю (АЕ(г\то,то) = 0). Полёт ракеты до полного расхо-
расходования массы (при т —> 0) в правой части A7) требует приращения
внутренней энергии A^W(mo,O) = —movf/2 (знак минус показывает,
что внутренняя энергия убывает).
Составляем выражение полной переменной энергии ракеты Е в виде
суммы внутренней и внешней энергии:
Е = Е® + АЕ^г\т0, т) + ^,	A8)
где щ ' — начальный запас внутренней энергии.
Из A8) следует, что для обеспечения полного расхода изменяющей
массы начальный запас внутренней энергии должен удовлетворять
неравенству
Я<° > ?f-.	A9)
Примечание 2. Понятие внутренней энергии в классической
механике неявно фигурирует в стереомеханической теории удара,
в частности в теоремах об энергии Карно-Остроградского. В неупругой
фазе удара часть кинетической энергии трансформируется во внут-
внутреннюю энергию, а фаза восстановления представляет в некотором
смысле обратный процесс. Пример с трансформацией внешней энергии
во внутреннюю и обратно (но уже с другой целью) в задаче о движении
летательного аппарата с прямоточным воздушно-реактивным двигате-
двигателем имеется в работе [13], где показано, что энергия, выделяющаяся
при внешнем трении и используемая как внутренняя энергия для
создания реактивных сил, может обеспечить при некоторых условиях
ускоренное движение ракеты, несмотря на наличие сил сопротивления
и отсутствие других ускоряющих сил, кроме реактивной.
Предельный переход при т^Ов формулах (9) и A0) даёт сов-
совпадение значений работы реактивной силы А, приложенной к ракете,
и кинетической энергии Т~ частиц перед их отделением:
A = f~= mov^.	B0)
Иначе говоря, работа реактивной силы, приложенной к ракете,
идёт на создание кинетической энергии, уносимой изменяющей массой
после отделения. Никакого энергетического парадокса нет.
Отметим любопытное совпадение: при относительной скорости, рав-
равной скорости света (vT = с), из B0) следует
А = Т-= гщс2 = Ео.	B1)
Согласно формуле для энергии в специальной теории относительности
величина Ео в релятивистской динамике равна «собственной энергии»
частицы с «массой покоя», равной то-

Глава V
ПРИНЦИП ПРЕДИКАТИВНОСТИ.
НЕКОТОРЫЕ СВОЙСТВА
ГАМИЛЬТОНОВЫХ СИСТЕМ
В философии, логике, математике, физике и в любой другой сфере
деятельности с применением научного знания требуются анализ отно-
отношений между понятиями, проверка логической чистоты и математиче-
математической строгости. Одно из свойств применяемых математических поня-
понятий, названное в работе А. Пуанкаре [91] предикативностью (и непре-
непредикативностью), необходимо учитывать и в механике. Это относится
и к методам принципа изменяемого действия, которые, как отметил
А. Пуанкаре, несут в себе «неопределённость».
О непредикативности понятий известно из логики; непредикатив-
непредикативные понятия и доказательства в математике также обсуждались ра-
ранее [91], [5], [93]. В философии неоднозначные категории и противоре-
противоречивые понятия используются в диалектическом методе (демонстрацию
приложений этого метода в физике дал Аристотель [2]). Дискуссия
в конце XIX — начале XX века, в которой участвовали Больцман,
Пуанкаре, Цермело и другие великие учёные, показала, что матема-
математическая физика не может обходиться без противоречивого понятия
«бесконечного».
Непредикативные доказательства отличаются тем, что в них ис-
используются доказываемые положения или их следствия. Решение задач
с помощью предположений, принимаемых уже в процессе решения,
использование «нестрогих» или «некорректных» суждений — всё это
может служить причиной парадоксальных выводов и «неправильных»
умозаключений. Высказывания типа: «если не грешить против логики,
то нельзя получить никаких научных результатов», не могут убедить
нас не замечать «курьёзные доказательства» или «бег по кругу» и не
искать выхода из подобных ситуаций.
31. О понятии «предикативность»
в математике и механике
31.1. Краткая характеристика понятия «непредикативность».
Предикат — языковое выражение, обозначающее некоторое свойство
или отношение [31]. Слово «предикативный» (definit) означает «опре-
«определимый», поэтому уже само по себе сочетание слов «непредикативное
определение» содержит в себе противоречие. Возможность сформу-
сформулировать определение имеется не всегда. Например, свойства, полу-

31. О понятии «предикативность» в математике и механике 209
чаемые через постулат [93] (или через абстракцию (см. [31]) по
некоторым правилам, обнаруживаются в самих изучаемых предметах.
Определение двух понятий А и А' непредикативно (по Расселу),
если А упоминается в определении понятия А', и обратно. Определение
называется непредикативным, если с его помощью некоторый объект
вводится через множество, включающее этот объект в качестве своего
элемента (определяемое уже включено в определяющее). Например,
«Верхней границей множества действительных чисел называется самое
большое число этого множества, т. е. число, которое больше любого
числа этого множества». Здесь определяемое включено в множество
действительных чисел и тем самым участвует в его формировании.
Подобные определения рассматриваются как определения с «порочным
логическим кругом».
Непредикативность часто является следствием стремления иссле-
исследователя понять причины физических явлений, в результате которого
из четырёх основных причин нередко «три... сводятся в одну, ибо
«что именно есть» и «ради чего» — одно и то же, а «откуда первое
движение» — по виду одинаково с ними...» [2]. «Ради чего» — это
некоторым образом цель, которая вольно или невольно присутствует
в результатах, поэтому естественно её рассматривать ещё и как причи-
причину, влияющую на весь процесс (без процесса оказывается, как сказал
поэт: «...Нашёл кончину, ради которой родился» (Эврипид)). В ин-
интегральных принципах шире, по сравнению с дифференциальными,
выражается участие «цели» и «стремление» к некоторой оптимальности
при нахождении закона движения.
Одним из источников непредикативности является понятие бес-
бесконечного. За пояснением смысла бесконечного обратимся к физике
Аристотеля [2]. «... теоретическое рассмотрение бесконечного является
вполне подходящим для физика» (а не только для философа или
математика). Рассмотрение бесконечного имеет свои трудности, так
как много невозможного следует и за отрицанием его существования,
и за признанием. ... бесконечное существует таким образом, что всегда
берётся иное и иное и взятое всегда бывает конечным, но всегда
разным и разным (курсив наш). ... бесконечное имеется там, где беря
известное количество, всегда можно взять что-нибудь за ним... Так
что бесконечное не следует брать как определённый предмет, например
как человека или дом, а в том смысле, как говорится о дне или
о состязании, бытие которых не является определённой сущностью,
а всегда находится в возникновении и уничтожении, и хотя является
конечным, но всегда иным и иным. ... бесконечное скорее подходит под
определение части, чем целого, так как материя есть часть целого...
и в мире мысли «большое» и «малое» должны охватывать мыслимые
предметы».
Из сказанного о бесконечном следует непредикативность правила
его формирования.

210	Гл. V. Принцип предикативности
Непредикативность не должна восприниматься a priori как отрица-
отрицательная оценка, а скорее, лишь как важная характеристика применяе-
применяемых понятий, отношений, выводов, причём с обязательным выявлением
по возможности всех обстоятельств, приводящих к противоречиям. Эта
дополнительная характеристика позволяет многие, на первый взгляд,
бесполезные результаты воспринимать как естественный промежуточ-
промежуточный этап и искать возможность разорвать «порочный круг», перевести
«непримиримую» борьбу в сферу противоречий, кажущихся противо-
противоречий, а может быть и дополнений.
Если непредикативность не замечена, то полученный «логический
круг» может продлить жизнь некоторым научным «парадигмам». И на-
наоборот, замеченный парадокс, возникший по причине непредикативно-
непредикативности, нередко принимается в качестве предлога для полного «ниспро-
«ниспровержения» теории, тогда как более ценным является поиск иных суще-
существующих (согласно аксиоме о сводимости Рассела) способов задания
множеств, в которые включается определяемый объект, независимо от
имеющегося непредикативного определения. Выявление непредикатив-
непредикативности позволяет установить наличие «нестрогости» в математических
доказательствах, причины возникновения «парадоксов», «порочных ло-
логических кругов» в рассуждениях и т. д.
Смысл слов «предикативное отношение» мы даём не в виде опреде-
определения, а пытаемся раскрыть его, опираясь на работы А. Пуанкаре [91],
[93] и анализируя примеры «непредикативных» понятий, правил, соот-
соответствий.
31.2. «Определимость» и «предикативность» понятий и правил
соответствия по А. Пуанкаре. Анализу на предикативность подле-
подлежат «отношения», устанавливаемые «правилами соответствия». Пра-
Правило соответствия предполагает «классификацию», которая меняется
(или не меняется) в зависимости от введения новых элементов. Каж-
Каждый новый элемент имеет своё «определение». Поэтому первичными
являются «определимость» понятия, а также его атрибут быть «преди-
«предикативным» или «непредикативным». Эта цепочка, ведущая к смыслу
«предикативности отношений», выстраивается, следуя работе А. Пу-
Пуанкаре [91] (только последними звеньями этой цепочки с атрибутом
непредикативности являются «правила соответствия» и «отношение»,
устанавливаемое «правилами соответствия»). Поскольку считается, что
«разъяснение значения слова „предикативный", данное в лекции, не
совсем ясно» [5], приведём с нашими комментариями (и примерами)
значительную часть (в противном случае потребовалось бы неоднократ-
неоднократное цитирование с перекрывающимися контекстами) доклада А. Пуан-
Пуанкаре в Гёттингене на тему: «О трансфинитных числах» (доклад пятый,
1909) [91].
«Господа! Сегодня мой доклад посвящен понятию трансфинитного
кардинального числа Ч и прежде всего я хочу поговорить об од-

31. О понятии «предикативность» в математике и механике 211
ном кажущемся противоречии, которое якобы содержит это понятие.
Но прежде чем начать, я хотел бы сделать следующее предварительное
замечание: по моему мнению, предмет мыслим только тогда, когда
его можно определить конечным числом слов. Предмет, определимый
конечным числом слов, я буду для краткости называть просто опреде-
определимым. С этой точки зрения неопределимый предмет просто немыслим.
Аналогично я буду называть закономерность высказываемой, если её
можно высказать за конечное число слов.
Г-н Ришар доказал, что множество определимых предметов счётно,
т.е. кардинальное число этого множества есть Щ. Доказательство
совсем просто: пусть а — число слов в словаре, тогда п словами можно
определить самое большее ап предметов 2\ Если теперь разрешить п
неограниченно возрастать, то, как нетрудно видеть, даже в этом случае
невозможно выйти за пределы счётного множества. Следовательно,
мощность множества мыслимых предметов была бы равна Щ. Г-н Шен-
флис возразил против этого доказательства, заметив, что с помощью
одного-единственного определения можно задать несколько, даже бес-
бесконечно много предметов. В качестве примера он приводит определение
функций-констант. Такое возражение неприемлемо потому, что опреде-
определения этого типа задают не отдельные предметы, а их совокупность,
в нашем примере — множество функций-констант, и это множество
представляет собой один-единственный предмет. Итак, выдвинутое
г-ном Шёнфлисом возражение необоснованно.
Как известно, Кантор доказал, что континуум не счётно-бесконе-
счётно-бесконечен 3); это противоречит доказательству Ришара. Возникает вопрос:
какое из двух доказательств верно. Я утверждаю, что оба доказатель-
доказательства верны и что противоречие, о котором идёт речь, лишь кажущееся.
Для обоснования этого утверждения я приведу новое доказательство
теоремы Кантора. Предположим, что задан отрезок АВ и правило,
по которому каждой точке этого отрезка4) поставлено в соответствие
целое число. Для простоты условимся обозначать точки соответствую-
соответствующими им целыми числами. Разделим наш отрезок двумя произвольно
выбранными точками А\ и А% на три части, которые назовём подо-
трезками первой ступени; каждую из этих частей, в свою очередь,
разделим на три части и получим подотрезки второй ступени; мысленно
представим себе этот процесс продолженным до бесконечности, причём
длины подотрезков у каждой границы должны уменьшаться. Точка
1 принадлежит одной или, самое большее (когда точка 1 совпадает
с точкой А\ или точкой А2), двум подотрезкам первой ступени, и
следовательно, заведомо существует один подотрезок первой ступени,
которому точка 1 не принадлежит... Продолжив наш метод..., мы
получим в итоге последовательность отрезков, обладающих следую-
следующими свойствами: каждый из них содержится во всех предыдущих
отрезках и один из отрезков n-й ступени не содержит ни одну из точек
с номерами от 1 до п— 1. Из первого свойства следует, что должна

212	Гл. V. Принцип предикативности
существовать по крайней мере одна точка, общая для всех отрезков;
тогда как из второго свойства следует, что номер этой точки должен
быть больше любого конечного числа, т. е. этой точке невозможно
поставить в соответствие ни одно из чисел Ч
Из какого предположения мы исходили в этом примере? Мы при-
приняли предположение о правиле, по которому каждой точке отрезка
поставлено в соответствие некоторое целое число. Затем нам удалось
определить точку, которой не соответствует никакое число. В этом
отношении приведённые выше различные доказательства теоремы не
отличаются. Но прежде всего необходимо установить правило. По Ри-
Ришару, такое правило, по-видимому, существует, но Кантор доказал
противоположное. Можно ли найти выход из создавшейся дилем-
дилеммы? Проанализируем, как надлежит понимать слово «определимый».
Мы берём перечень всех конечных утверждений и вычёркиваем из
него все утверждения, которые не определяют никакой точки. Остав-
Оставшиеся утверждения мы поставим в соответствие целым числам. Ес-
Если теперь мы снова просмотрим наш перечень, то в общем случае
можно показать, что некоторые из ранее вычеркнутых утверждений
придётся оставить. Действительно, утверждения, в которых шла речь
о правиле соответствия, ранее не имели значения, так как точки
не были поставлены в соответствие целым числам. Теперь же эти
утверждения обрели значение и поэтому должны оставаться в нашем
списке. Если бы мы изменили правило, по которому устанавливает-
устанавливается соответствие между точками и целыми числами, то та же самая
трудность повторилась бы, и так до бесконечности. Но именно в этом
и заключается разрешение кажущегося противоречия между Ришаром
и Кантором. Пусть Mq — множество целых чисел, М\ — множество
точек нашего отрезка, определяемых всеми конечными утверждениями,
сохранившимися в нашем перечне после первого вычёркивания, G\ —
правило, устанавливающее соответствие между Мо и М\. Правило G\
порождает новое множество определимых точек М^. Но множеству
М\ + М2 соответствует новое правило G<i, которое, в свою очередь,
порождает новое множество Мз и т. д. Доказательство Ришара учит
нас, что там, где я оборву применение нашего построения, всегда
существует некоторое правило соответствия, тогда как Кантор дока-
доказывает, что наше построение можно продолжать сколь угодно долго.
Таким образом, между доказательствами Ришара и Кантора никакого
противоречия не возникает.
Видимость противоречия связана с тем, что правилу соответствия
по Ришару недостаёт одного свойства, которое я назову «предикатив-
«предикативностью», заимствуя это выражение у одного английского философа.
(По Расселу, у которого я заимствую этот термин, определение двух
понятий А и А' не предикативно, если А упоминается в определении
понятия А!, и наоборот.) Под предикативностью я понимаю следующее.
Каждое правило соответствия предполагает определённую классифи-

31. О понятии «предикативность» в математике и механике 213
кацию. Я называю соответствие предикативным, если лежащая в его
основе классификация предикативна. Что же касается классификации,
то я называю её предикативной, если она не изменяется от введения
новых элементов. В этом смысле правило соответствия Ришара не
предикативно; более того, введение предложенного им правила соот-
соответствия изменяет классификацию утверждений на имеющие значение
и на не имеющие значения. То, что в этом случае имеется в виду
под атрибутом «предикативный», лучше всего пояснить на примере.
Если мне требуется упорядочить множество, распределив образующие
его предметы по некоторому числу коробок, то могут представиться
два случая: либо упорядоченные предметы в конце концов окажутся
на своих местах, либо мне придётся всякий раз, когда я буду класси-
классифицировать новый предмет, извлекать какой-то другой предмет (или
другие предметы) из той коробки (или тех коробок), в которой он
(или они) находились. В первом случае я называю классификацию
предикативной, во втором — непредикативной. Хороший пример непре-
непредикативного определения привёл Рассел: пусть А — наименьшее число,
для определения которого требуется более ста немецких слов. Число А
должно существовать, так как с помощью ста слов можно определить
лишь конечное количество чисел. Но определение, которое мы выше
дали числу А, содержит меньше ста слов; таким образом, число А и
определимо, и неопределимо.
Цермело высказал возражение против отказа от непредикативных
определений, ссылаясь на то, что в таком случае пришлось бы от-
отказаться от большей части математики, например от доказательства
существования корня алгебраического уравнения.
Как известно, это доказательство состоит в следующем.
Дано алгебраическое уравнение F(x) = 0. Доказывают, что у \F(x)\
должен быть минимум. Пусть xq — то значение аргумента, при котором
достигается минимум, следовательно,
\F(x)\>\F(xo)\.
Отсюда далее следует, что |.F(#o)| — 0. Такое определение F(xq) не
предикативно, так как значение F(xq) зависит от множества значений
F(x), к которому оно принадлежит.
Я не могу останавливаться на обосновании этого возражения. Дока-
Доказательство можно преобразовать так, чтобы непредикативные опреде-
определения из него исчезли. Для этого я рассмотрю совокупность значений
аргумента вида (га + in)/p, г = л/—Т, где га, п и р — целые числа.
Я могу воспользоваться теми же рассуждениями, что и прежде, но
значение аргумента, при котором достигается минимум \F\, вообще
говоря, не принадлежит к рассматриваемым значениям аргумента. Тем
самым мы избегаем круга в доказательстве5). От каждого матема-
математического доказательства можно потребовать, чтобы оно содержало

214	Гл. V. Принцип предикативности
только предикативные определения и т.д., так как в противном случае
доказательство нестрого...
Что же касается второго трансфинитного кардинального числа Hi 6),
то я не совсем убеждён в том, что оно существует. Мы приходим
к нему через рассмотрение множества ординальных чисел мощности
Но; ясно, что это множество должно иметь более высокую мощность.
Спрашивается, однако, замкнуто ли оно, чтобы мы могли говорить
о его мощности, не впадая при этом в противоречие. Актуальной
бесконечности здесь во всяком случае не существует.
А как обстоит дело со знаменитой проблемой континуума? Можно
ли вполне упорядочить точки пространства? Что мы под этим по-
понимаем? Возможны два случая. Во-первых, мы можем утверждать,
что правило вполне упорядочения высказываемо за конечное число
слов; тогда это утверждение не доказуемо, и даже г-н Цермело не
претендует на то, чтобы представить такое доказательство. Но мы
допускаем и такую возможность, что правило невыразимо с помощью
конечного числа слов. В этом случае я не могу придать утверждению
никакого смысла, оно для меня — «пустой звук». В этом и заключается
трудность. И в этом же причина споров по поводу почти гениальной
теоремы Цермело. Эти споры весьма примечательны: одни отвергают
постулат выбора, но тем не менее считают доказательство правильным,
другие считают постулат выбора приемлемым, но не признают доказа-
доказательство 7\
Я могу говорить на эту тему ещё несколько часов, но не в силах
решить проблему».
Комментарии.
^ Трансфинитные числа — обобщение понятия порядковых чисел
для бесконечных множеств. Если множество может быть сделано
вполне упорядоченным различными способами, то одинаковые карди-
кардинальные числа (обобщение количественных чисел) могут быть заданы
различными трансфинитными числами (в случае конечных множеств
эти понятия совпадают) [60].
2) В этом месте А. Пуанкаре, как и Ришар, признаёт только объек-
объекты, а не классы, и потому не принимает возражение Шёнфлиса. Од-
Однако далее А. Пуанкаре сам отступает от данного ограничения, когда
использует понятие отрезка и понятие точки (см. комментарии 3, 4).
Можно согласиться с Дж. Д. Биркгофом [93] в том, что понятие класса
ограничивает обсуждение проблемы, однако мы не согласны с тем, что
понятие класса ограничивает взгляды А. Пуанкаре на проблему. На-
Напротив, А. Пуанкаре не отрицает полезность непредикативных понятий
и правил соответствия и демонстрирует применение «аксиомы своди-
сводимости» Рассела, допускающей существование иного способа задания
элементов множества не через это множество.

31. О понятии «предикативность» в математике и механике 215
3)	Континуум (непрерывное), конечно, не сводится к дискретному
и просто не сопоставим с числами. Представление о «непрерывном» от-
отрезке и «дискретных» точках делает противоречивым суждение о том,
что «отрезок состоит из точек». Например, если точки представлять
как единые неделимые элементы, а отрезок считать сплошным непре-
непрерывным, то возникающее противоречие приводит к выводу [2], что
прямая (и любой её отрезок) не составляется из точек. Принимая
в качестве «слов» слова «отрезок» и «подотрезки», состоящие из точек,
А. Пуанкаре вслед за Кантором поступает, как и Шёнфлис, вводя
«слова», означающие целый класс. Это тоже делает несравнимыми
доказательство Ришара и доказательство Кантора (см. также коммен-
комментарий 4).
4)	Представление об отрезке как множестве, состоящем из «то-
«точек», приводит к непредикативности, так как «точки», в свою оче-
очередь, определяются через множество (с помощью правила образования
«точек» путём вложения «подотрезков»). «Подотрезки» представляют
собой подмножества, эквивалентные отрезку. При отказе от аксиомы
Архимеда (см. заметку 1) в результате вложения отрезков мы не будем
иметь того, что называется точкой. Таким образом, множество (отре-
(отрезок) составляется из элементов (точек), которые сами определяются
через свойства этого множества. Следовательно, и в доказательстве
Кантора используются непредикативные понятия и правила.
Приведём пример образования элементов множества с помощью
непредикативного приёма (только в обратном порядке: от точки к от-
отрезку). Составляем счётно-бесконечный ряд:
Сумма любого конечного числа членов этого ряда даёт одну из двух
чередующихся «точек», которые можно принять за «концы непрерыв-
непрерывного отрезка». Ничто не мешает принять в качестве суммы ряда также
любые другие числа для точек, расположенных внутри этого отрезка
(например, иррациональные). Иррациональные числа — это символы
нового (по сравнению с рациональными числами) правила «вставле-
«вставления» новых «точек» на отрезке. Получается, что счётная бесконечность
и непредикативное правило образования элементов множества с помо-
помощью натуральных чисел позволили построить «континуум»? (Сравните
с результатом в комментарии 6.)
5)	Вводя более широкое числовое множество (множество комплекс-
комплексных чисел вместо множества действительных), А. Пуанкаре на этом
примере демонстрирует применение аксиомы сводимости Рассела.
6)	«Долгое время оставался открытым вопрос: существует ли такое
кардинальное число с, что Щ < с < Hi? Оказалось, однако, что как
утверждение о существовании такого с, так и отрицание этого утвер-
утверждения совместимы с общепринятой аксиоматикой теории множеств»
(см. [65]). (Сравните с комментарием 4.)

216	Гл. V. Принцип предикативности
В современной алгебре трансфинитными числами (трансфинитами,
порядковыми числами, ординальными числами и ординалами) называ-
называют элементы вполне упорядоченного множества. Например, множество
целых чисел становится вполне упорядоченным, если его элементы
расположить в следующем порядке (здесь «<» — знак упорядочения,
а не сравнения величин):
7) Аксиому Цермело A904 г.) называют также принципом произ-
произвольного выбора, согласно которому для любой системы непустых
непересекающихся множеств существует функция, сопоставляющая
каждому множеству один его элемент [60]. Иначе говоря, предполага-
предполагается, что из каждого множества произвольной системы непустых и не
имеющих общих элементов множеств можно сразу выбрать по одному
элементу. На эту аксиому опирался Цермело в доказательстве теоремы
о возможности всякое множество сделать вполне упорядоченным (пол-
(полное упорядочение состоит в установлении отношения порядка следова-
следования и требовании, чтобы в каждом подмножестве существовал первый
элемент). Аксиома Цермело вызвала много споров, ряд математиков
не признал её, а следовательно, не считает установленной и теорему
о возможности вполне упорядочить произвольные множества.
Противоречие опять возникает вследствие непредикативности.
В теореме Цермело понятие выбора и понятие вполне упорядоченного
множества связаны и используется непредикативное правило. Выбрать
можно актуально или виртуально, т. е. «по природе» или «для нас»
(Аристотель). Актуальный выбор требует существования также
множеств, «лишённых» выбранных элементов (множеств, получаемых
после удаления выбранных элементов). Выбранный актуально элемент
и лишённое этого элемента множество являются непредикативными
понятиями. Виртуальный выбор (без удаления) элементов состоит
в том, что делается «указание» на выбираемый элемент, который тем
самым приобретает ещё один признак; следовательно, меняется набор
признаков, по которому составлено множество. Последнее означает
непредикативность отношения правила выбора элемента и правила
формирования множеств, в которых делается выбор элементов, так как
при каждом выборе даётся новое определение множества, в котором
ведётся упорядочение.
31.3. Аксиома сводимости Рассела. Примеры. «Я предоставляю
слово автору (Расселу, наше примечание), так как не уверен в том, что
правильно понял его мысль: „Мы предполагаем, что всякая функция
эквивалентна для всех её значений некоторой предикативной функции
того же самого аргумента"» [93].

31. О понятии «предикативность» в математике и механике 217
В современной логике предикация рассматривается как частный
случай функциональной зависимости. Предикатами называются функ-
функции, значениями которых служат высказывания [31].
На основе иерархии типов Рассела А. Пуанкаре применил аксиому
сводимости при построении предикативной функции. «Предложение
(предикат, наше примечание) будет определённого порядка в иерархии
типов, и этот порядок не будет одним и тем же, каково бы ни было х
(неопределённый предмет, наше примечание), так как он будет зави-
зависеть от порядка х. Функция будет называться предикативной порядка
fc+ 1, когда х порядка к. После этих определений смысл аксиомы всё
ещё не очень ясен, и несколько примеров не помешают» [93]. Приведём
примеры, демонстрирующие использование аксиомы.
Пример 1. Покажем, что в доказательстве существования корня
алгебраического уравнения (см. п. 31.2) Пуанкаре практически исполь-
использует аксиому сводимости. Обсудим этот пример несколько подробнее,
воспользовавшись приведёнными определениями и расширив иерархию
типов аргумента.
Итак: «Дано алгебраическое уравнение F(x) = 0. Доказывают, что
у \F(x)\ должен быть минимум. Пусть хо — то значение аргумента,
при котором достигается минимум, следовательно
\F(x)\>\F(xo)\.
Отсюда далее следует, что |.F(#o)| — 0. Такое определение F(xq) не
предикативно, так как значение F(xq) зависит от множества значений
F(x), к которому оно принадлежит».
Для переменной х устанавливаем иерархию типов, присваивая им,
например, следующий порядок:
—	нулевой, если х G Z (Z — множество целых чисел);
—	первый, если х G R (R — множество действительных чисел);
—	второй, если х G С (С — множество комплексных (плоских)
чисел);
—	третий, если х G Р (Р — множество пространственных комплекс-
комплексных чисел) 0.
1) Пространственным комплексным числом называют [37] выражение
z + о j , где z и а — комплексные числа вида и-\- v i , ? + rj i , а символы г ,
j — мнимые единицы, таблица умножения которых задаётся в следующем
виде:
i i — j j — — 1 у г j = j i = к, (ijJ = (jiJ=k2=l.
Тогда, например, в множествах Z, IR, С уравнение х2 — 1 = 0 имеет корни
xi;2 = =Ы, а в множестве пространственных комплексных чисел Р, кроме того,
имеет «пространственные корни»: хз,4 = ±к = ±i j = ±j i , где г = л/^Т,
j = \/~Г- Действительно, х\л =k2 = (ijJ = l, и следовательно, это

218	Гл. V. Принцип предикативности
Для этих множеств имеем включение: Ъ С R С С С Р, т. е. каж-
каждое из них включает в себя предыдущее. Поэтому высказываниям
относительно значений F(xo) можно присвоить порядок, на единицу
больший, чем порядок её аргумента. В доказательстве существования
корня алгебраического уравнения А. Пуанкаре вместо непредикативно-
непредикативного определения значения F(xq) (xq G R) использовал принадлежащий
более широкому множеству аргумент второго порядка, для которого
определение (дефиниция) значения F(xq) предикативно.
В связи с примером в сноске на с. 217 поставим вопрос: сколько
решений имеет квадратное уравнение х2 — 1 = 0? Ответ не единствен-
единственный: одно (в области натуральных чисел); два (в множествах Z, R, С);
четыре (в множестве Р) и т. д.
Пример 2. Непредикативны такие дополнительные понятия, как
случайное и детерминированное (в смысле не вероятностное), абсолют-
абсолютное и относительное, непрерывное и дискретное и т. д.
В работе [94] А. Пуанкаре отмечает неполноту (непредикативность)
классического определения вероятности: «Определение, скажут, —
очень просто: вероятность какого-нибудь события есть отношение чис-
числа случаев, благоприятствующих этому событию, к полному числу
возможных случаев... приходится дополнить (это определение, наше
примечание), говоря: «...при условии, чтобы эти случаи были равно-
равновероятны». Замена термина «равновероятны» словами «несовместимы
и равновозможны» не отменяет непредикативность классического опре-
определения.
Иной подход (аксиоматический) к построению теории вероятно-
вероятностей предложен А. Н. Колмогоровым. Здесь также рассматривается
множество О элементарных событий, но, кроме того, вводится мно-
множество ^5 подмножеств элементарных событий (алгебра множеств),
удовлетворяющее ряду требований. Первое из этих требований (см.,
например, [28]), имеющее вид
О G 9, 0GS @ — пустое множество),
как нетрудно заметить, представляет собой применение аксиомы сво-
сводимости Рассела (вводится расширение множества элементарных со-
событий).
Примечание. «Проблема детерминизма и тесно связанная с ней
проблема корректного определения случайного, вводящего в детер-
детерминизм вероятность» видится Луи де Бройлю [57] следующим обра-
образом: «Согласно современным представлениям явления на этом уровне
(атомном, наше примечание) происходят чисто случайно, и если на
макроскопическом уровне нам кажется, будто мы располагаем неким
точным законом, то это происходит лишь потому, что макроскопиче-
тоже корни многочлена. Отметим, что в множестве Р имеются делители ну-
нуля: о = (?+ J)(?- J).

31. О понятии «предикативность» в математике и механике 219
ские явления представляют собой статистическое среднее огромного
числа элементарных явлений. Эта точка зрения прямо противоположна
классической точке зрения на природу случайности, которую разде-
разделял ещё Пуанкаре. Согласно классической точке зрения лишь строго
детерминированный закон соответствовал глубокому слою физической
реальности, а статистический закон был лишь его макроскопическим
проявлением. Согласно современной точке зрения, наоборот, статисти-
статистический закон играет основную роль, а детерминированный служит
лишь его макроскопическим проявлением». В этих высказываниях Луи
де Бройля отражаются его собственные переходы от одной крайней
точки зрения к другой, имеющей в науке название «господствующая
парадигма». Возможно, поэтому ему не удалось заметить многосторон-
многосторонность взглядов А. Пуанкаре при решении вероятностных проблем ([94],
глава XI «Исчисление вероятностей»; [95] («Замечания о кинетической
теории газов»)). «Знание», «незнание» и его различные степени в кон-
контексте работы [94] также относятся к вероятностному подходу.
Непредикативность возникает при попытке ввести время («абсолют-
(«абсолютное», объективное) путём наблюдения (всегда относительного, субъ-
субъективного) явлений, на которые влияет суточное вращение Земли.
К недостаткам способов измерения времени с использованием явле-
явлений, на которые влияет суточное вращение Земли, А. Пуанкаре отнёс
следующий. «Один из факторов какого-либо явления есть скорость
вращения Земли; если эта скорость меняется, она представляет собой
фактор, который не остаётся больше идентичным при повторении этого
явления. Но принять эту скорость постоянной значит предположить,
что мы умеем измерять время. (Цитируется Калинон (A. Calinon) —
наше примечание). Измерение времени с использованием причин не
позволяет нам полностью выйти из порочного круга». Пуанкаре при-
приходит к выводу: «Одновременность двух событий или порядок их сле-
следования, равенство двух длительностей должны определяться таким
образом, чтобы формулировка законов природы была настолько про-
простой, насколько это возможно. ... все эти правила, все эти определения
являются лишь плодом... соглашения» [96], которое стало основой
принципа относительности.
Пример 3. Развитие теории через непредикативные отношения
даёт история обоснования уравнений Гамильтона-Якоби. Первоначаль-
Первоначально было показано, что уравнению Гамильтона-Якоби удовлетворяет
главная функция Гамильтона (W), которая позволяет получить конеч-
конечные уравнения движения.
Примечание. Главная функция Гамильтона представляет собой
действие по Гамильтону, вычисленное при переменном верхнем пределе
и выраженное через начальные и текущие значения обобщённых коор-
координат. Будучи производящей функцией канонического преобразования
начальных значений обобщённых координат и импульсов в их теку-
текущие значения, главная функция позволяет ответить на вопрос: какие

220	Гл. V. Принцип предикативности
начальные импульсы надо сообщить системе в начальном положении,
чтобы она в назначенный момент времени пришла в заданное конечное
положение (см., например, [58]).
Главная функция удовлетворяет уравнению Якоби и является его
полным интегралом вида W = W(q\,... ,qS:a\,... ,as,t), в котором по-
постоянные равны начальным значениям обобщённых координат.
Если известно решение задачи Коши (закон изменения обобщённых
координат и импульсов как функция времени и начального состоя-
состояния), то действие вычисляется через начальные значения обобщённых
координат, импульсов и время. Последующее исключение начальных
обобщённых импульсов даёт выражение главной функции.
Однако в результате возникает порочный круг: для написания ко-
конечных уравнений движения (закона движения) нужна функция W,
а для составления этой функции нужно знать конечные уравнения
движения. Определение полного интеграла в виде главной функции
Гамильтона для нахождения закона движения непредикативно по от-
отношению к решению с заданными начальными условиями, которое
находится с помощью полного интеграла в виде главной функции
Гамильтона. Этот порочный круг разорвал Якоби, показавший, что
конечные уравнения могут быть написаны при помощи произвольного
полного интеграла S уравнения Гамильтона-Якоби (приём расшире-
расширения множества, в которое включено одно из понятий, участвовавших
в непредикативном определении).
Дальнейшее обобщение метода Якоби дал А. Пуанкаре. В задаче
возмущённого движения он предложил [92] увеличить число степеней
свободы голономной системы так, чтобы стало возможно применять
метод вариации постоянных и каноническую форму уравнений возму-
возмущённой системы.
Пример 4. Преобразование одной конкретной гамильтоновой си-
системы к другой её гамильтоновой форме представляет собой пример
непредикативного правила. Непредикативность отсутствует при ка-
канонических преобразованиях сопряжённых переменных (за счёт рас-
расширения множества преобразуемых систем), так как каноническое
преобразование не связано с конкретной функцией Гамильтона: оно
преобразует любую гамильтонову систему снова к гамильтоновой фор-
форме. Сопряжённые величины (переменные, числа, функции, уравнения
и т.д.) всегда непредикативны.
В заключение отметим, что при сопоставлении аксиомы сводимо-
сводимости и принципа индукции А. Пуанкаре не пришёл к выводу об их
сравнительной общности. Если иметь в виду только математическую
индукцию и пропозициональные функции, то можно заметить, что при-
применение аксиомы сводимости возможно и для аргументов предметного
содержания.
Приведённые примеры показывают, что следовать принципу преди-
предикативности удаётся, переходя от пропозициональных функций непре-

32. О преобразовании времени и функции Гамильтона	221
дикативных аргументов к пропозициональным функциям от предика-
предикативных аргументов (область значений этих функций составляют вы-
высказывания).
Принцип предикативности, как и другие принципы, имеет высокую
степень неопределённости и не даёт конкретных рекомендаций, а от-
относится скорее к аналитической работе ума. Интуитивно он широко
используется в логике и математике, но ещё не вполне оформился
в статусе общего научного принципа естествознания.
При изучении свойств гамильтоновых систем попутно обращается
внимание на ситуации, в которых используются непредикативно опре-
определённые понятия, непредикативные правила и доказательства.
32. О преобразовании времени и функции Гамильтона
в склерономных системах
При «изоэнергетической» редукции гамильтоновых систем [118]
и регуляризации уравнений [34] применяется преобразование незави-
независимой переменной в гамильтоновых системах. Следуя [34], мы называ-
называем правило преобразования леммой Уинтнера 0.
32.1. Лемма Уинтнера для гамильтоновых систем. Соглас-
Согласно лемме Уинтнера [118] решение автономной гамильтоновой си-
системы (q(t),p(t)) e М2п с функцией if(q, р), принадлежащее уров-
уровню H(q, p) = h, эквивалентно решению гамильтоновой системы с га-
гамильтонианом
Я(Ч,р,Л) = (Я(Ч,р)-/1)О(Ч,р)	A)
при новой независимой переменной т, полученной с помощью замены
t —> г вдоль траектории (q(t), p(t)):
— = '	B)
dt G(q(i),p(i))'	*• '
где G(q, p) — гладкая, не обращающаяся в нуль скалярная функция.
При этом решение (q(r), р(т)) G М2п принадлежит уровню Н = 0.
Доказательство леммы состоит в непосредственном подсчёте про-
производной:
dp dp dt „, ,,Л ,.ЛЛдН dG(H-h) ,и u,dG
dr dt dr	v v J v n <9q	<9q	v	J <9q
x) Применение леммы позволяет получить новую картину движения с за-
замедлением времени вблизи нерегулярной точки в уравнениях плоской задачи
трёх тел (в нерегулярной точке лемма и производящая функция канонического
преобразования не применимы).

222	Гл. V. Принцип предикативности
(аналогично для производной dq/dr). На энергетическом уровне
H(q, p) = h эти равенства являются уравнениями Гамильтона (штри-
(штрихом далее мы будем обозначать производные по переменной г):
C)
что и доказывает лемму.
Покажем, что элементарные действия по Гамильтону сопоставля-
сопоставляемых гамильтоновых систем равны и не зависят от вида гамиль-
гамильтонианов (они зависят только от величины энергетических уровней).
Действительно, с учётом B) для элементарных действий «новой» и ис-
исходной систем имеем равенство
^2 Pidqi — Hdr = ^2 Pi^Qi ~ Hdt + hdt.	D)
Из D) следует, что при Я = 0 и Я = /i на любых конечных
интервалах времени с учётом его преобразования или обращения,
J
о	о
величины действия одинаковы.
Согласно лемме при преобразовании времени с применением функ-
функции G = if (q, р) — а (где а — константа; а ф К) структуру A) имеет
гамильтониан
, р, h) = (Я(Ч, р) - h) (H(q, p)-a).	E)
Рассматриваемое преобразование независимой переменной в данном
случае сводится к умножению времени на постоянный множитель.
Примечание. Аналогичные уравнения получаются, если принять
функцию Гамильтона в виде
„* (Я - аJ
2
Здесь также можно усмотреть преобразование независимой переменной
с функцией G = Н — а (а ф К). Однако в отличие от леммы Уинтне-
ра, мы имеем непредикативное преобразование, так как при каждом
преобразовании система переходит на разные энергетические уровни.
Кроме того, элементарное действие системы с гамильтонианом Я* как
показывает равенство
^2 Pidqi - H*dr = ^^pidqi - — dt + ^ dt,
г	i
отличается от элементарного действия по Гамильтону исходной си-
системы. Однако отличие представляет собой полный дифференциал,

32. О преобразовании времени и функции Гамильтона	223
и поэтому происходит известное «преобразование симметрии» (см.,
например, [36]), позволяющее получить те же уравнения движения, но
изменяющее величину действия на фиксированном интервале времени.
32.2. Применение леммы Уинтнера и «обращение» времени.
Применим лемму Уинтнера при сопоставлении решений системы, име-
имеющей гамильтониан Я, с решениями системы, имеющей гамильтони-
гамильтониан A) (в форме, позволяющей различать значения энергетического
уровня исходной системы):
а)	Я(q, р, а) = (Я(Ч> р) - а) (Я(Ч> р) - /3) при а ф /3;
F)
б)	H(q,p,C) = (H(q,p)-C)(H(q,p)-a) при /3 ф а.
Лемма Уинтнера позволяет в случаях Fа) и F6) получить следую-
следующие сопоставления:
а)	решению системы с гамильтонианом Я на энергетическом уровне
hj= а ставится в соответствие решение системы с гамильтонианом F)
H(q, р, а) = const = х на уровне х — 0;
б)	решению системы с гамильтонианом Я на энергетическом уровне
hj= /3 ставится в соответствие решение системы с гамильтонианом F)
H(q, р, /3) = const = х на уровне \ = 0.
Оба проведённые сопоставления определяются преобразованием
независимой переменной t —> т, которое состоит (см. B)) в умножении
независимой переменной на постоянный множитель (размерность мно-
множителя сохраняет размерность «действия»):
а)	г = -№, tf = (/3-a)-\
G)
б)	т = Ш, tf = (C-а)-{.
Заметим, что при преобразовании t —> г множители в случаях Gа)
и G6) отличаются лишь знаком. Иначе говоря, сопоставление траек-
траекторий сопровождается так называемым обращением нового времени
(г —> — г). Для определённости положим /3 > а, т. е. # > 0 и для со-
сокращения записи примем следующие обозначения: Га для траектории
q(r), р(т) при г > 0 гамильтоновой системы if(q, р, а) = х на уровне
^ = 0; Га для траектории гамильтоновой системы H(q, р,а) = х на
уровне х = 0 с обращенным «новым» временем, т.е. q(—r), р(—т);
аналогично (с заменой а на /3) обозначаются траектории Г^ и Г^.
Тогда наблюдаемое свойство для траекторий Г^ и Г^" (траектории q(?),
р(?) при ? ^ 0 системы с гамильтонианом Я = /г на уровнях h = a
и /г = /3 соответственно) можно сформулировать следующим образом:
траекториям Г^ и Г^" ставятся в соответствие траектории Та
и Г^ соответственно.

224	Гл. V. Принцип предикативности
Введём в рассмотрение также «обращенное» «старое» время, ко-
которому соответствуют траектории q(—?), р(—?), обозначаемые далее
через Г~ и Г^" для гамильтоновой системы Н = ft на уровнях h = a
и ft = C соответственно. Варианты сопоставления траекторий очевидны
и даются условиями F) и G):
—	траектории Т~ ставится в соответствие траектория Та;
—	траектории Т^ ставится в соответствие траектория Г^.
32.3. Свойство взаимности гамильтонианов. Обобщим задачу
преобразования независимой переменной, допустив, что в гамильтони-
гамильтониане A) значение Н = ft может быть не равным значению а (а ф ft).
Такое допущение принималось и в гамильтониане F6), но взамен
аналогичную роль начинал играть второй сомножитель. Составим га-
гамильтониан:
H(q, p) = (H(q, p) - a) G(q, p), a = const.	(8)
Из (8) при а = ft, в частности, получается гамильтониан A), для
которого применима лемма Уинтнера. В отличие от A) и F), при а ф h
требуется найти условия, при которых решение гамильтоновых уравне-
уравнений системы с гамильтонианом (8) имеет первый интеграл:
H(q, p) = const.	(9)
Необходимое и достаточное условие состоит в тождественном ра-
равенстве нулю скобки Пуассона: {Н, Н} = 0. Раскрывая выражение
в левой части этого равенства, с учётом (8) и (9) находим, что тожде-
тождество имеет место
при h = а либо при h Ф а и {G, Н} = 0,
т.е. когда функции G и Н находятся в инволюции. Иначе говоря,
если рассматривать систему с гамильтонианом G(q, p), то в этой си-
системе (как и в системе с гамильтонианом Н) имеется первый инте-
интеграл #(q, p) = const = h.
Используем ещё один имеющийся первый интеграл, G = const =
= g, при составлении симметричных функций Гамильтона (аналогич-
(аналогично F)):
а)	H(q,p,a) = (#(q, р) - a) (G(q, р) -/3) при ft = а, g ф /3;
б)	G(q,p,/3) = (G(q,p)-/3)(tf(q,p)-a) при h ф a, g = C.
Лемма Уинтнера позволяет в случаях A0а) и A06) получить сле-
следующие сопоставления:
а) решению системы с гамильтонианом Н на энергетическом уровне
ft = а ставится в соответствие решение системы с гамильтониа-
гамильтонианом A0): H(q, р, а) = const = \ на уровне \ — 0;

33. Интегральные инварианты и гамильтонова форма уравнений 225
б) решению системы с гамильтонианом G на энергетическом уровне
gj= C ставится в соответствие решение системы с гамильтонианом A0):
G(q, р, /3) = const = х на уровне \ — 0-
Оба сопоставления сделаны при преобразовании независимой пе-
переменной t —> г, которое состоит (см. B)) в умножении независимой
переменной на постоянный множитель (размерность множителя сохра-
сохраняет размерность «действия»):
а)	т = М, $ = {д-13)-\
б)	т = Ш, •d = {h-a)-\
Согласно A1) обращение времени при сопоставлении траекторий
происходит при C > д и при а > h соответственно.
33. Интегральные инварианты и гамильтонова форма
уравнений движения
33.1. Основной и универсальный классические интегральные
инварианты гамильтоновых систем. Пусть при движении гамильто-
новой системы сохраняется интеграл (интегральный инвариант, откры-
открытый Пуанкаре)
г=\
с
где С — замкнутый односвязный контур на одной и той же трубке
прямых путей для одновременных состояний (в момент времени ?);
интегрирование ведётся по параметру а @ < а < /);
Pi=Pi(t,a), 5qi = 5qi(t,a) (г = 1,... ,n).	B)
При а = 0 и а = / на контуре, охватывающем трубку, имеем одну
и ту же точку в фазовом пространстве обобщённых координат — обоб-
обобщённых импульсов (пространство (Q,P): обозначение работы [137]);
5qi — изохронные виртуальные вариации (см. заметку 8).
Интеграл 1\ сохраняет своё значение для всех моментов времени
(инвариант) и называется универсальным интегральным инвариан-
инвариантом Пуанкаре.
Обычно (см., например, [25]) доказательство инвариантности ин-
интеграла 1\ получают с помощью основного интегрального инварианта,
установленного Картаном позже. Основной интегральный инвариант
(интегральный инвариант Пуанкаре-Картана) также представляет со-
собой криволинейный интеграл:
C)
=i	I
8 В. Г. Веретенников, В. А. Синицын

226	Гл. V. Принцип предикативности
Синхронные вариации в выражении A) и асинхронные в выражении
C) связаны равенствами
поэтому из C) при At = 0 следует A).
В фазовом пространстве (QTPH), полученном расширением за счёт
добавления сопряжённых переменных t и —Н, интеграл C) является
интегральным инвариантом, и варьирование, не являясь изохронным,
может рассматриваться как синхронное по отношению к новому неза-
независимому параметру г (см. ниже). Поэтому вместо C) будем писать
J^PMi-HStl =inv.	D)
Криволинейный интеграл D), взятый вдоль произвольного одно-
связного замкнутого контура, не меняет своего значения при произ-
произвольном смещении (с деформацией) этого контура вдоль трубки пря-
прямых путей. Замкнутая трубка прямых путей описывается уравнениями
qi = qi(t,a), Pi=Pi(t,a), t = t(a) (г=1,...,п)	E)
при условиях
qi(t,O)=qi(t,l), Pi(t,O)=Pi(t,l), t(O)=t(l) (i=l,...,n).
Варьированию 5 в D) соответствует операция дифференцирования по
параметру а.
33.2. Задача о гамильтоновой форме уравнений, имеющих ин-
инвариант. Пусть движение системы описывается дифференциальными
уравнениями первого порядка для сопряжённых фазовых переменных:
%	f	,р)	F)
(г= 1,...,п),
и имеется интегральный инвариант. Требуется установить условия, при
которых система F) имеет гамильтонову форму.
Достаточно просто доказывается [25], что система F) имеет инте-
интегральный инвариант A), если она является гамильтоновой:
* = ^? Р* = -% (* =!.-.«)•	G)
Предпосылки простоты вывода в том, что имеются две группы
сопряжённых переменных, qi (i = 1,..., п) и pi (г = 1,..., п), и контур
в криволинейном интеграле располагается на трубке прямых путей,
т. е. траекторий, доставляющих стационарное значение функционалу
«действие».

33. Интегральные инварианты и гамильтонова форма уравнений 227
Для системы F), имеющей интегральный инвариант вида C), также
известно обратное утверждение: «инвариантность интеграла Пуан-
каре-Картана может быть положена в основу механики, так как
из этой инвариантности вытекает, что движение системы подчиняется
каноническим уравнениям Гамильтона» [25]. Однако теперь ситуация
является более сложной, поскольку в интегральном инварианте исполь-
используется ещё одна пара сопряжённых переменных. Наличие в интеграль-
интегральном инварианте C) функции Н и условие, что система имеет вид G)
с гамильтонианом Я, дают лишь тривиальный случай по совпадению.
Причины, по которым доказательство обратного утверждения для ин-
интегрального инварианта Пуанкаре-Картана, приведённое в [25], мы не
считаем убедительным, будут отмечены ниже.
Поэтому продолжим поиск условий, при которых система F) имеет
интегральный инвариант вида D).
33.3. О приведении уравнений движения динамической си-
системы к гамильтоновой форме. Пусть система дифференциальных
уравнений первого порядка F) имеет единственное решение, непре-
непрерывно зависящее от начальных условий так, что для любой трубки
траекторий системы инвариантен интеграл (относительный интеграль-
интегральный инвариант первого порядка)
= inv,	(8)
¦ г=1	-I
где G = G(q,t,p) — непрерывная дважды дифференцируемая функция;
интеграл (8) (вычисленный вдоль охватывающего трубку замкнутого
контура) не изменяет своей величины при произвольном смещении
точек контура вдоль образующих трубки.
Требуется найти соотношение между функцией G и функция-
функциями Qi, Pi, при котором уравнениям F) можно придать гамильтонову
форму.
Вначале будем следовать доказательству, приведённому в рабо-
работе [25]. Изменим только некоторые обозначения: новую независимую
переменную обозначим г (вместо /i); произвольную положительную
функцию обозначим ф^,г,р) (вместо iv(q,t,p)) и G (вместо Н). Вве-
Введение тиф дополняет систему F) ещё одним уравнением:
dq\	dqn dpi	dpn dt	,	/Оч
Q\ '" Qn P\ '" Pn 1
Примечание 1. Ранее в теории реономных систем (см. замет-
заметку 15) принималась явная (недифференциальная) зависимость новой
независимой переменной от времени, т. е. такая, как если бы функ-
функция ф зависела только от t. Здесь же функция ф зависит также и от
фазовых координат. Для новой независимой переменной г должно быть
принято некоторое начальное значение.

228
Гл. V. Принцип предикативности
Для прямых путей, образующих данную трубку, при новой незави-
независимой переменной имеем параметрические уравнения:
qi = qi(r,a), Pi=Pi{r,a), t = t(r,a)
(i= l,...,n; O^a^l).
Обход замкнутого контура при изменении параметра а от а = 0 до
а = I даёт одну и ту же точку.
Поскольку интеграл (8) инвариантен, имеем
где буква d означает дифференциал по параметру т. Выполняем диф-
дифференцирование под знаком интеграла (8):
Г Г п	1
О = ck ^{dpiSqi + PidSqi) - dG5t - Gd5t .	A0)
Написав 5dqi и 5d? на месте dSqi и d5t (условие перестановочности
операций: 5d = d5) и проинтегрировав по частям вдоль замкнутого
контура, получаем
0 =
- dG5t + 5Gdt I =
i=\
*
^d*Jft|. A1)
Примечание 2. Далее в работе [25] выполняется деление
последнего равенства на d[i = dt/тг (в обозначениях [25]), в результате
которого в подынтегральное выражение вводится множитель iv(q,t,p).
Затем делается вывод о том, что «выражение, стоящее под знаком ин-
интеграла, должно быть полным дифференциалом при произвольном мно-
множителе тг». Однако функция, которую мы ввели и обозначили через ф
(вместо тг), в каждом определённом преобразовании не может быть
произвольной (в первую очередь знакопеременной), как этого требует
основная лемма вариационного исчисления (в частности, ф должна
обеспечивать монотонное изменение независимой переменной). Далее
в работе [25] вариации 5qi,5pi,5t рассматриваются как независимые,
т. е. игнорируется существование условного уравнения dt — irdfi = 0,
налагающего ограничение на вариации переменных. Доказательство
заканчивается утверждением о том, что функции Qi, Pi выражаются
через функцию Н в интегральном инварианте D) согласно равенствам
Q	P	A)

33. Интегральные инварианты и гамильтонова форма уравнений 229
т. е. в тривиальном случае. Применение одинакового обозначения (Н)
для функции в интегральном инварианте и искомого гамильтониана
системы не позволяет различить в доказательстве свойство единствен-
единственности и тривиальности. Для общности естественно не считать эти
функции одинаковыми (что и сделано нами выше).
Продолжим решение поставленной задачи. Получим уравнения, для
которых имеет место инвариант (8) и выполняется последнее уравнение
в (9). Для этого уравнения имеем следующую зависимость между ва-
вариациями:
(|^	^Ц^	A2)
При составлении A2) выполнено синхронное варьирование относи-
относительно новой независимой переменой E т = 0). Уравнение для вариа-
вариаций A2) учтём с неопределённым множителем Л (г):
Щ(И-5фAт),	A3)
включив его как слагаемое в подынтегральное выражение A1). Выпол-
Выполнив интегрирование по частям с учётом того, что 5Х = 0, имеем
+ ( -dG + —dt- X-^- dT]5ty
, . dG ,, л дф , \ х
—dqiJr^—dt — X^-dT)opi , . ^ , _
Фг	Фг / J	V	<^t
A4)
Вариации переменных в A4) могут рассматриваться как незави-
независимые.
Разделим равенство A4) на йт и приравняем нулю коэффициенты
при независимых вариациях 5qi,5pi,5t. Получаем уравнения
, _ I dG ,дф , _ .dG .dij)
dG _ ,dG _ ^ф
где штрихом обозначены производные по г и подставлено уравне-
уравнение t' = ф.
Вернёмся в уравнениях A5) к исходной независимой переменной t:
. _ dG X dф . _ dG X dф
dG _ dG X dф

230	Гл. V. Принцип предикативности
Видно, что правые части уравнений A6) для сопряжённых перемен-
переменных qi,Pi имеют гамильтонову форму:
дН .	дН / • 1	\
с функцией Гамильтона
A9)
В общем случае функцию ip(q,t,p), а также множитель Л требуется
найти. Получим соответствующие уравнения.
Приравниваем правые части уравнений A6) и правые части уравне-
нии F):	п -dG А ^ р _ до х дф
dpi ф dpi	oqi гр oqi
Умножая равенства первой группы B0) на дф/dqi, а равенства
второй группы — на дф/dpi и затем суммируя по индексу, получаем
уравнение, которому должна удовлетворять функция ф:
где {ф, G} — скобка Пуассона функций ф и G.
Аналогично, умножая равенства первой группы B0) на dG/dqi, a
равенства второй группы — на dG/dpi и затем суммируя по индексу,
получаем уравнение, которому удовлетворяет множитель Л:
B2)
где {In^,6/} — скобка Пуассона функций Ыф и G.
Из B1) и B2) следует равенство
дф D\	(dG ~ , dG D\	/OQ4
^Pi)=^?feQi + Pi) B3)
которое, как нетрудно проверить, представляет собой необходимое^
достаточное условие того, что сопряжёнными являются также t и —Н:
'=¦¦ f=#
Таким образом, система F), имеющая интегральный инвариант (8),
приведена к гамильтоновой форме с гамильтонианом A9).
Рассмотрим некоторые частные случаи.
1. Тривиальный случай: рассматриваемая система уже имеет га-
гамильтонову форму, и интегральный инвариант (8) является интеграль-
интегральным инвариантом Пуанкаре-Картана, т. е.
п dG . и 8G
Q	P

33. Интегральные инварианты и гамильтонова форма уравнений 231
Тогда из A8), A9) следует, что функция ф = 1. Иначе говоря, пре-
преобразованием независимой переменной является либо тождество, либо
постоянный сдвиг.
2. Случай, когда система F) уже имеет гамильтонову форму ви-
вида G) с не зависящим от времени гамильтонианом (Н) и инвариант (8)
с функцией G. Тогда для выполнения равенств B1) и B2) достаточ-
достаточно, чтобы функции G и ф были первыми интегралами в инволюции
({ip,G} = 0) обобщённо-консервативной системы.
Проведённые выкладки позволяют сделать следующее утвержде-
утверждение. Если для траекторий системы F) имеются фазовые трубки прямых
путей и интегральный инвариант вида (8), то система имеет гамильто-
гамильтонову форму с гамильтонианом A9).
Вместо тривиального случая 1, в котором то, что требуется дока-
доказать, предполагается имеющим место по совпадению, здесь получены
уравнения B1) и B2) для определения функции ip(q,t,p) и множите-
множителя Л и формула гамильтониана A9).
В заключение заметим, что дополнительное уравнение для вспомо-
вспомогательной переменной г можно принять в другом (неголономном) виде:
N{r,qXp)dt-M{r,qXp)dr = Q, М > 0, N > 0. B5)
Можно также использовать голономное (в явной или неявной форме)
уравнение
Т — f(q>t,p), или (p(r,q,t,p) = 0,
или полуголономное уравнение (представляющее собой полный диффе-
дифференциал)
N(t, q, t, p)dt - М(т, q, t, p)dr = dU(r, q, t, p) = 0.
В отличие от (9), преобразование B5) зависит также и от новой
независимой переменной г. Варьирование равенства B5) (синхронное
относительно новой переменной) для вариаций 5qi,5t,5pi даёт урав-
уравнение
5Ndt + N5dt - 5Mdr = 0,	B6)
где для 5М (и аналогично для 5N) справедливо выражение
дм я+
St
)	qi + > 1— 5pi + ?
^-^ dqi	^-^ dpi	dt
i	i
Учёт уравнения B6) с неопределённым множителем в подынтегральном
выражении вариации инварианта позволит рассматривать вариации
5qi,5t,5pi как независимые. Дальнейшие выкладки по составлению
условий «гамильтоновости» формы уравнений F), имеющих интеграль-
интегральный инвариант (8), могут быть проведены по той же схеме, что и для
уравнения (9).

232	Гл. V. Принцип предикативности
34. Об однородных свойствах гамильтонова действия
На основе метода размерностей даётся расширенное определение
квазиоднородной функции фазовых координат, частным случаем ко-
которой являются автономные квазиоднородные функции и функции,
однородные по Эйлеру.
Показано, что элементарное действие и уравнения Гамильтона бу-
будут инвариантными по отношению к преобразованию подобия, если
суммы показателей квазиоднородности сопряжённых величин равны
между собой. При этом преобразование Лежандра даёт функцию
Лагранжа, которая является квазиоднородной той же степени, что
и функция Гамильтона.
34.1. Определение квазиоднородной функции. Дадим опреде-
определение квазиоднородной функции, используя изменение масштабов фа-
фазовых координат z\,...,zn и времени t (преобразование подобия):
zx -> a9lzu...,zn -^a9nzn, t -> a9n+1t,	A)
где а ф 0; t > 0; g\,... ,gn,gn+\ — вещественные числа.
Пусть время t и фазовые координаты z\,...,zn являются аргу-
аргументами дифференцируемой функции f(z\,..., zn,t). Будем называть
f(z\,..., zn,t) квазиоднородной функцией степени до с показателями
квазиоднородности д\,...,gn,gn+i, если в области определения функ-
функции при а ф 0 выполняется равенство
f(a*zi,...,tfnzn,tfn+4,)=tf<>f(zi,...,zn,t)-	B)
Приведём некоторые свойства квазиоднородных функций, кото-
которые могут быть использованы при интегрировании дифференциальных
уравнений и в других математических преобразованиях.
1.	Тождественному преобразованию переменной соответствует по-
показатель квазиоднородности, равный нулю.
2.	Если все показатели квазиоднородности равны единице (д\ = ...
. . . = дп = 1), ТО фуНКЦИЯ v(z\, ... , Zn) CO СВОЙСТВОМ
v(az\,..., azn) = a9ov(z{ ,...,zn)	C)
является однородной степени до (а ф 0). Для однородных функций
вида C) известна формула Эйлера:
Y,z^=9ov.	D)
г=\	г
Формулу Эйлера D) можно получить из равенства C), если его
продифференцировать по а и принять а = 1.
3.	Функция v(z\,..., zn) (не зависящая от времени):
v(a9lzx,...,a9nzn)=a9»v(zx,...,zn),	E)

34. Об однородных свойствах гамилыпонова действия	233
является квазиоднородной степени до с показателями квазиоднородно-
квазиоднородности д\,...,дп (см., например, [45]). После дифференцирования квази-
квазиоднородной функции E) по а при значении а = 1 имеем равенство
t9iZi^r(z)=gov(z).	F)
Из F) следует, что квазиоднородная функция степени до в случае
одинаковых показателей квазиоднородности (д\ = ... = дп = д) являет-
является однородной степени до/д.
Если для некоторых переменных показатели квазиоднородности
равны нулю, а для других — одинаковы, то функция со свойством F)
является однородной по соответствующей части переменных.
34.2. Об однородности гамильтонова действия. Гамильтоново
действие вдоль кривой в расширенном конфигурационном простран-
пространстве определяется интегралом, в котором подынтегральное выражение
имеет вид
J^PidQi-Hdt,	G)
г
где qi,pi — обобщённые координаты и обобщённые импульсы; Н, t —
функция Гамильтона и время.
Функция Гамильтона в G) определяет уравнения
дН .	дН	,оч
q> = w>' ft = "%-	(8)
Пусть функция Гамильтона является квазиоднородной функцией
вида
H(agiquah^pu...,ag"qn,ah"pn,agt) = ahH(qupu...,qn,pn,t) (9)
степени h с показателями квазиоднородности g\,h\,... ,gn,hn,g. Тогда
элементарное действие G) и уравнения (8) будут инвариантными по
отношению к преобразованию подобия A), если показатели квазиод-
квазиоднородности и степень квазиоднородности функции Н удовлетворяют
равенствам
giJrfii=gJrfi^ г=1,...,п.	A0)
Равенства A0) означают, что при данном преобразовании суммы
показателей квазиоднородности сопряжённых величин равны.
Заметим, что степень квазиоднородности функции Н в равен-
равенствах A0) играет также роль показателя квазиоднородности величины,
сопряжённой с независимой переменной (временем), а суммы пока-
показателей (включая и правую часть равенства) дают значение степени
действия. При условиях A0) преобразование Лежандра даёт функцию
Лагранжа, которая является квазиоднородной той же степени, что
и функция Гамильтона.

234	Гл. V. Принцип предикативности
35. О реализации реакций и реализации связей
35.1. Идеальные связи и идеальные реакции. Восходящий
к Лагранжу классический способ составления уравнений несвободного
движения состоит в том, что реакции представляются в виде произ-
произведений неопределённых множителей и коэффициентов в уравнени-
уравнениях для виртуальных вариаций (уравнения Лагранжа первого рода).
Неопределённые множители (соответственно и реакции), найденные
с помощью уравнений связей, в каждый момент времени зависят от
положений, скоростей и масс материальных точек. Полученные таким
путём реакции идеальных связей для сокращения записей будем на-
называть идеальными реакциями (идеальных связей). В невырожденных
случаях идеальные реакции обеспечивают траектории, не нарушающие
условия идеальных связей.
Оснований считать, что свойства идеальных связей указывают на
какое-либо природное происхождение идеальных реакций, нет. Тем не
менее идеальные реакции интересны уже тем, что, например, в случае
стационарных связей они не совершают механическую работу и об-
обладают известным дифференциальным свойством минимальности [61];
поэтому они могут рассматриваться как управляющие воздействия
с очевидными критериями оптимальности. Идеальные реакции, не яв-
являясь силами естественного взаимодействия материальных точек си-
системы с ограничениями, представляют собой математический объект,
получаемый по описанной выше схеме (что и оправдывает предложен-
предложенный для них термин — идеальные реакции). В этом, на наш взгляд,
и заключается смысл известного утверждения о том, что «реакции
идеальных связей не зависят от способа реализации связи» [3].
Способ реализации связи с помощью идеальных реакций освобож-
освобождает от анализа физических свойств ограничений математика, но не
физика. В физике к понятию «идеальная связь» приходят в предельном
случае потенциального поля (при бесконечном возрастании коэффици-
коэффициента жёсткости), когда происходит «вымораживание» степени свободы
и возникает кинематическое условие в виде голономной связи [29],
[123]. Таким образом, в задачу реализуемости связи включается так-
также задача реализации реакций. Если идеальная реакция голономной
связи реализуется упругими силами с бесконечно большим коэффици-
коэффициентом жёсткости, то идеальные реакции линейной неголономной связи
можно реализовать линейными вязкими силами (при бесконечном уве-
увеличении коэффициента вязкого трения), введением «присоединённых
масс» (стремящихся к бесконечности) и т.д. (см. [42], [13]). Упомяну-
Упомянутый «физический» подход называется также конструктивным [44].
Реализация связи с помощью идеальных реакций является одним
из способов реализации реакций сервосвязей: в отличие от идеальной,
реакция сервосвязи может содержать касательную составляющую, но

35. О реализации реакций и реализации связей	235
направление её также задаётся уравнениями для виртуальных переме-
перемещений.
Идеальные реакции и соответствующие траектории, как уже упо-
упоминалось, не отражают «физических» свойств, которые иллюстриро-
иллюстрировались на примере реализации голономной связи упругими потенци-
потенциальными силами с бесконечно большим коэффициентом жёсткости.
Действительно, увеличение коэффициента жёсткости упругой силы
в пределе приводит ко всё более частому изменению направления
ускорения, т.е. к движению, называемому идеальным скользящим
режимом. В этом случае траектория не имеет того порядка гладкости,
который соответствует идеальным реакциям. В скользящем режиме
условия связи могут быть выполнены с заданной точностью лишь
на ограниченном отрезке времени, тогда как уравнения, полученные
с учётом идеальных реакций, можно использовать для анализа и на
бесконечном интервале времени.
Единственность движений со связями, реализуемыми идеальными
реакциями, зачастую позволяет при исследовании ограничиться ис-
использованием условий, получаемых на основе анализа первой вариации
функционала. Из условий второго порядка в задачах минимизации дей-
действия обычно упоминаются только сопряжённые кинетические фокусы,
причём в виде оговорки, что их не должно быть между начальной
и конечной точками траектории.
35.2. Определение реакций как решение задачи особого оп-
оптимального управления. Рассмотрим метод определения реакций,
основанный на использовании условий оптимальности в особых случа-
случаях [23], когда нет единственного решения при определении идеальных
реакций идеальных связей.
Вместо условий на ускорения, которые можно получить из урав-
уравнений связей, для устранения неопределённости реакции обратимся
к принципу наименьшего действия. Иначе говоря, будем решать задачу
определения реакций как задачу оптимального управления движени-
движением. В качестве критерия оптимальности примем действие, а в роли
управлений будем рассматривать неопределённые множители. Неопре-
Неопределённые множители входят в уравнения движения линейно, поэтому
здесь применимы методы теории особых оптимальных управлений [23].
Постановку задачи рассмотрим на примере автономной механи-
механической системы с одной идеальной (вообще говоря, неголономной)
связью. Уравнения движения с неопределённым множителем в канони-
канонических переменных qi, Pi (i = 1,... ,п) имеют вид
<2г = -о-, Рг = —rr-+Qi + Abi(q,p),	A)
и Pi	uqi
где H(q, p) — функция Гамильтона; Qi — обобщённые непотенци-
непотенциальные активные силы; A^(q, р) — обобщённые силы реакции связи,
А(?) — скалярный неопределённый множитель (кусочно-непрерывная

236	Гл. V. Принцип предикативности
функция), коэффициенты Ь{ находятся из уравнения, полученного вир-
виртуальным варьированием уравнения связи
a(q,p)=0.	B)
Коэффициенты Ь{ могут быть выбраны и из других соображений,
например, если уравнение B) представляет сервосвязь.
Минимизируемое действие является функционалом на фиксирован-
фиксированном промежутке времени \ЦЛ\\-
и
)	C)
Примем для фазовых координат единое обозначение: х\,...,Х2П>
и введём ещё одну координату, #2п+ь Для перехода от задачи Лагран-
жа с функционалом C) к задаче Майера-Больца. В пространстве
с координатами х\,... ,#2n+i с учётом уравнений A) и функционала C)
имеем в векторной форме уравнения
, te [to,t\],	D)
дН с Л	\ АО) дН
Значения координат в начальный и конечный моменты времени должны
удовлетворять условию связи B). Поэтому критерий оптимальности
задачи терминального управления со скалярным управлением А име-
имеет вид
«/(A) =X2n+\(ti) +va(xl(ti),...,x2n(ti)) ^min,	E)
А
где /i — постоянный неопределённый множитель, который находится
с учётом уравнения связи в момент времени t\\
)=0.	F)
Относительно функций f(°) и f^1) полагаем, что они дифферен-
дифференцируемы достаточное число раз. Введём дифференцируемую вектор-
функцию \|/(?), сопряжённую с вектором х, и составим гамильтониан Н
задачи оптимального управления D)-F):
Н = VTf@) + A?TfA) = Я0(х,?) + АЯ!(х,?),	G)

35. О реализации реакций и реализации связей 237
..,X2n).	(9)
Реакцию связи будем называть особой, если коэффициент при мно-
множителе Л в гамильтониане G) тождественно равен нулю:
Я,(х,?) = 0.	(Ю)
При этом на отрезке [to.ii] выполняется и тождество
|я,(х>?)=0.	A1)
Полная производная по времени в A1) вычисляется вдоль траекто-
траекторий канонически сопряжённых переменных х(?), \|/(?), поэтому с помо-
помощью скобок Пуассона {...,...} для двух функций она представляется
в виде	,
±	A2)
Hl(x,v) = {H0,Hl}
Поскольку в A2) скобка Пуассона при Л тождественно равна нулю
(в силу свойства скобок Пуассона), равенство A1) не содержит мно-
множителя Л. Вычисляем вторую производную по времени:
Последнее равенство принимает вид уравнения
из которого находится множитель Л, а также особая реакция (если
коэффициент при Л не равен нулю).
Неопределённые множители могут быть представлены в роли управ-
управлений и в процедуре формирования пакетных вариаций ускорений. При
этом появляется возможность использовать условия оптимальности,
называемые условиями второго порядка. Действие в исходной системе
доставляет минимизируемый функционал; исходная система уравнений
дополняется системой уравнений для сопряжённых переменных. Про-
Производится «игольчатое» варьирование множителя для использования
условия оптимальности первого порядка, а также двусторонние и па-
пакетные вариации для определения оптимальных реакций с помощью
условий второго порядка.

Глава VI
ПРИНЦИП ИНЕРЦИОННОСТИ
Продолжим изучение инерционных свойств материи, начатое в мо-
моделях материального объекта, положение которого определяется од-
одной точкой (см. заметку 1). Термин «инерционность» кажется нам
более подходящим для обозначения исследуемого физического явле-
явления (оставим термин «инертность» для характеристики химических
превращений); кроме того, более созвучны исторически принятые со-
сочетания «закон инерции» и «центр инерции», которые наполняются
новым содержанием с тех пор, как обнаружены инерционные свойства
энергетических полей. Всплеск интереса к закону инерции наблюдался
в конце XIX в. и в начале XX в. [64], в период зарождения принципа
относительности в физике [90]. Проблема до сих пор не потеряла своей
актуальности и требует повышенного внимания в настоящее время
и в ближайшем будущем.
Физические поля и различные виды энергии проявляют свойства,
подобные свойствам, которые характеризует масса. Потребовалась де-
детализация определения массы: «масса покоя» («собственная масса»),
«релятивистская», «продольная», «поперечная», «электромагнитная»,
«топологическая», «нулевая», «отрицательная», «масса античастиц»,
«масса, эквивалентная энергии», «масса полевая», «активная грави-
гравитационная», «пассивная гравитационная», «универсальная элементар-
элементарная», «масса динамической системы», «масса, невыделимая из полной
массы...», «массэргия» и т.д. (см. [134], [78], [100]). Приведённый
«спектр» применения понятия массы (или непризнания какого-либо
из перечисленных понятий) показывает, что принцип инерции или,
в более общем виде, «концепция инерционности» ещё не сформирова-
сформировались. Детализация в определениях потребовалась в связи с изучением
взаимодействий тел, полей и ограничения в виде выделенной в природе
скорости движения, равной скорости света в вакууме и играющей
особую роль в электромагнитных и других явлениях.
Понятие «масса» естественно рассматривать в совокупности с по-
понятиями энергия, импульс (количество движения), момент импульса
и действие, которые связаны с пространством, временем и движением.
Поэтому определение массы должно быть включено в систему основ-
основных понятий механики.

36. Масса и принцип инерционности	239
36. Масса и принцип инерционности
Исследование природы движения, состоящего в перемене места
с течением времени, без понятия массы невозможно («Природа мас-
массы — вопрос № 1 современной физики» [78]). Проблемы с применением
термина «масса» требуют как анализа возникновения релятивистских
понятий, так и нового отношения к основам классической механи-
механики. Сравнение показывает, что инерционная и гравитационная массы
проявляются в ситуациях, сопровождаемых явлением, которое можно
характеризовать как «изменение нарушения симметрии». Этому прин-
принципиальному положению требуется конкретизация, содержащая указа-
указания о том, о какой симметрии идёт речь, в чём состоит её нарушение
и как происходит изменение этого нарушения. Например, в физике
элементарных частиц наблюдается появление массы при «спонтанном
нарушении калибровочной симметрии». Естественно провести анализ
подобных ситуаций в классической механике.
Обсудим свойства массы в аксиоматических соотношениях меха-
механики с учётом концепции Маха [64] о бесконечно удалённой массе,
которую мы используем для представления о сферической симметрии,
нарушениях этой симметрии и изменениях этих нарушений.
Перечислим свойства массы в классической механике.
1.	Масса является мерой количества вещества, количества материи.
2.	Масса замкнутой системы равна сумме масс составляющих её
тел (независимо от их движений и взаимодействий).
3.	Масса изолированной системы тел сохраняется (не меняется со
временем).
4.	Масса тела не меняется при переходе от одной системы отсчёта
к другой; в частности, она одинакова во всех инерциальных системах
отсчёта.
5.	Масса тела является мерой его инерционности (инерционная
масса равна гравитационной массе; см. п. 6).
6.	Массы тел являются источником их гравитационного притяже-
притяжения друг к другу (гравитационная масса равна инерционной массе;
см. п. 5).
7.	Тела, имеющие массу, характеризуются кинетической энергией,
импульсом, моментом импульса и действием.
8.	Масса бесконечно удалённой (от наблюдателя) Вселенной рас-
распределена относительно него однородно и сферически-симметрично.
9.	Масса тела как инерционная характеристика проявляется в моде-
моделях с изменением нарушения симметрии Вселенной, введённой в п. 8.
В принципе инерции Галилея масса не упоминается, а в принципе
инерции А. Пуанкаре ей отводится роль коэффициента, который удобно
ввести в вычисления [94].

240	Гл. VI. Принцип инерционности
Предмет обсуждения фигурирует в пп. 1-9 то как свойство, то как
количество, то как вещество, то как тело (то как существующее, то
как возникающее), т.е. в тех многочисленных «обличьях», в которых
представляется нам и масса.
Формулировки первых шести перечисленных свойств близки по
содержанию свойствам, приведённым в статье [78], где проведено их
сравнение со свойствами массы в теории относительности. Понятие
массы как меры (см. свойство 1) по сути «доклассическое» (связанное
с философскими категориями), но возврат к этой стороне понятия
оказался неизбежным и в «постньютоновской» механике. Далее мы не
будем разграничивать указанные периоды.
Среди равноправных инерциальных систем (свойство 4) выделим
как логически «первичную» ту инерциальную систему координат, в
которой изолированная материальная точка покоится.
Об эквивалентности инерционной (свойство 5) и гравитационной
(свойство 6) масс будет говориться ниже в задаче двух тел (см. при-
пример 2).
К свойству 7 добавим, что понятия работы силы и импульса силы
имеют смысл, если сила приложена к материальной точке (в том числе
и в тех моделях, где массой этой материальной точки пренебрегается).
В перечень динамических величин включаем также действие, которое,
в отличие от других динамических величин, является интегральной
характеристикой.
Пункт 8 выражает необходимость учёта бесконечно удалённых
масс: «...даже в простейшем случае, в котором мы как будто занимаем-
занимаемся взаимодействием только двух масс, отвлечься от остального мира
невозможно (курсив наш). Дело именно в том, что природа не начи-
начинает с элементов, как мы вынуждены начинать» [64]. Распределение
массы должно быть таковым, чтобы пространство было однородным
и изотропным (и тогда оно описывается геометрией Евклида). Без
обращения к бесконечно удалённым массам не удастся рассматривать
задачи об энергоресурсе тела (см. заметку 37) и скрытых движениях.
Пункт 9 выражает новое для классической механики наблюдение за
проявлением свойства тела «иметь инерционную массу» и «изменением
нарушения симметрии» бесконечной Вселенной.
Остановимся на данном вопросе несколько подробнее. Удалённые
массы мы примем во внимание (в рассуждениях, а не во взаимодей-
взаимодействиях), начиная с аксиом о движении одного тела.
Пусть наблюдатель (и с ним система отсчёта) движется вме-
вместе с изолированной материальной точкой поступательно, равномерно
и прямолинейно («первичная» инерциальная система). Тогда матери-
материальная точка постоянно находится в начале координат и Вселенная
остаётся сферически-симметричной: нарушения симметрии нет (и из-
изменения тоже). Однако и масса никак не проявляется: скорость тела
равна нулю (все динамические величины равны нулю, и действие в том

36. Масса и принцип инерционности	241
числе, причём на любом интервале времени) независимо от величины
массы тела. Поэтому непосредственно «масса покоя» как свойство
тела в «первичной» инерциальной системе в классической механике
не проявляется. Масса наблюдается в опытах, а наличие последних
автоматически означает нарушение симметрии. Выход из этого логи-
логически порочного круга состоит в том, что покоящемуся телу масса
просто приписывается после принятия постулата о её эквивалентности
массам в других («не первичных») инерциальных системах, в которых
тело не покоится, динамические величины не равны нулю, а действие
изменяется равномерно с течением времени. Отсюда и эквивалентность
массы во всех инерциальных системах. Полагается, что свойство иметь
массу и притом такой же величины, сохраняется независимо от того,
рассматривается тело в движении или в покое.
В чём усматривается нарушение симметрии, если для описания
движения изолированной материальной точки используется «не пер-
первичная» инерциальная система?
Пусть инерциальное движение (материальной точки) наблюдается
теперь из другой инерциальной системы отсчёта, в которой изоли-
изолированная материальная точка движется равномерно и прямолинейно.
Тогда и появляется масса как характеристика, участвующая в фор-
формировании всех названных динамических величин. Заметим, однако,
что этому сопутствует изменение нарушения сферичекой симметрии
Вселенной (далее просто «изменение нарушения симметрии»). Дей-
Действительно, центр однородно распределённых удалённых масс теперь
находится (вместе с наблюдателем) в начале координат, а материальная
точка — уже не в её центре и (или) с течением времени смещается
относительно этого центра. Вселенная, включающая, кроме удалён-
удалённых масс, также и рассматриваемую материальную точку, перестала
быть симметричной для наблюдателя: имеется нарушение симметрии,
которое изменяется вместе с перемещением материальной точки. По-
Получается, что Вселенная (её модель) зависит от тех правил, по ко-
которым наблюдатель формирует её в бесконечности? Действительно,
таково непредикативное понятие бесконечного (подробнее см. замет-
заметку 31): модель бесконечной Вселенной включает мысленный процесс
достраивания «видимой Вселенной» (область её расширяется вместе
с нашими знаниями: извне, изнутри, на границе и т.д.) к некоему
образу бесконечной Вселенной (отсюда, в частности, и так называемый
гравитационный парадокс [75]).
Во втором законе Ньютона фигурирует сила, приложенная к ма-
материальной точке и сообщающая ей ускорение, что также позволяет
выявить её массу. Этому опять сопутствует изменение нарушения
симметрии, поскольку для силы неявно предполагается наличие её
материального носителя («источника») — силового поля.
Таким образом, масса изолированного находящегося в покое (в
«первичной» инерциальной системе) тела не является «первичным»

242	Гл. VI. Принцип инерционности
понятием (не наблюдаема по определению). Это относится и к массе
как характеристике «количества вещества». Информация о массе тела,
находящегося в покое, вносится из других («не первичных») инер-
циальных систем, в которых кинетическая энергия, импульс, момент
импульса и действие содержат коэффициент, называемый массой.
Если полагать, что инерционность — «врождённое» свойство тел,
то нет оснований сомневаться в наличии свойства тела иметь массу
и в покое. Однако это означает принятие доклассического понимания
массы, что не входит в нашу задачу. Таким образом, нужно признать,
что релятивистские теории имеют логически небезупречный классиче-
классический ориентир — «массу тела в состоянии покоя». Последнее относится
к термину «масса» («масса покоя», «собственная масса»), принимае-
принимаемому в теории относительности и совпадающему с классической, как
выяснилось, «не первичной» массой. Поскольку все массы в клас-
классической механике эквивалентны, в релятивистских теориях вопрос
о пересмотре соответствия пока не ставится.
Напротив, в классической механике для соответствия её реляти-
релятивистской теории требуется ответить на вопрос: можно ли приписать
энергию (Eq) телу с массой (то), находящемуся в покое? Притом так,
чтобы энергия Eq = moc2 (где с — некоторая скорость) имела меха-
механический смысл. Для ответа на поставленный вопрос воспользуемся
классической моделью точки переменной массы (см. пример 1).
Примечание. Соответствие между наблюдением массы и «из-
«изменением нарушения симметрии» давно известно в физике элементар-
элементарных частиц: «...оказывается, принципы симметрии, справедливые на
изначальном уровне, не проявляются на уровне наблюдаемых непо-
непосредственно на опыте величин, например масс частиц. ...механизм
спонтанного (т. е. самопроизвольного, наше примечание) нарушения
калибровочной симметрии приводит к появлению масс у промежуточ-
промежуточных бозонов и тем самым к различиям во внешних проявлениях сла-
слабых и электромагнитных взаимодействий» [72]. С экспериментальным
подтверждением существования бозонов есть много неясного, но для
фотонов наблюдение их массы и «изменение нарушения симметрии»
происходят при образовании и аннигиляции пар электронов и пози-
позитронов. Спонтанные нарушения симметрии как закономерность ис-
используются в доказательстве существования античастиц [120]. Термин
«изменение нарушения симметрии» можно детализировать, отметив,
в частности, возможную «регулярность» изменения. В термодинами-
термодинамических процессах имеются изменения нарушения симметрии, которые
описываются как «стохастические». «Регулярные», «стохастические»
и «спонтанные» изменения нарушения симметрии наблюдаются как
закономерности в микро-, макро- и мегамире. Соотнесение характера
изменения с определённой масштабной областью не является, вооб-
вообще говоря, однозначным, поскольку наблюдение изменения нарушения

36. Масса и принцип инерционности	243
симметрии происходит при участии наблюдателя (факте его присут-
присутствия и его представления о симметрии).
Таким образом, свойства 8, 9 выражают некоторый принцип, рас-
распространяемый нами на классическую механику и названный измене-
изменением нарушения симметрии.
Предлагаемое название принципа является достаточно общим
(и неопределённым) и включает в себя как обсуждаемый принцип
инерционности для сферически-симметричной Вселенной, так
и принцип спонтанного нарушения калибровочной симметрии при
взаимодействии элементарных частиц.
Приведём примеры «изменения нарушения симметрии».
Пример 1. Рассмотрим точку переменной массы в задаче о пря-
прямолинейном движении ракеты в свободном пространстве при посто-
постоянной относительной скорости с отделяющихся частиц (первой задаче
К.Э. Циолковского; см. заметку 30). Пусть начальная скорость ракеты
равна нулю, начальная масса — гао, текущая масса ракеты — га. Для
удобства возьмём предельный случай полного расхода массы (га —> 0);
тогда имеем следующие соотношения (см. формулы C0.19), C0.20),
C0.16)):
^ б)Т-=ш0с2, в)Т+ = ^,	A)
где Eq — начальный запас внутренней энергии, необходимой для
реализации реактивного принципа; Т~ — суммативная кинетическая
энергия частиц непосредственно перед их отделением (при скорости
равной текущей скорости ракеты); Т+ — суммативная кинетическая
энергия частиц непосредственно после их отделения (с последующим
свободным движением).
«Масса» гао в выражении Aа) участвует в оценке внутренней энер-
энергии, за счёт которой реализуется реактивный принцип (информация
о ракете в её начальном состоянии). Ракета как носитель своей внут-
внутренней энергии находится в определённом месте в определённое время.
Нарушения симметрии нет, но и параметр гао не описывает внешние
инерционные свойства, а скорее является параметром во внутренней
энергетической информационной характеристике.
Какой смысл имеет коэффициент гао в выражении A6)? Выражение
для Т~ является результатом суммирования кинетических энергий
изменяющих масс в их состояниях непосредственно перед отделением.
Частицы находятся в разных местах (пространственно) и скорости
их вычисляются в разные моменты времени (термин «суммативность»
подчёркивает, что величина не относится к системе, существующей
единовременно). Величина Т~ не является кинетической энергией си-
системы в обычном понимании этого слова. Она равна работе реактивной
силы, приложенной к ракете, но работа эта идёт также и на создание

244	Гл. VI. Принцип инерционности
кинетической энергии, уносимой изменяющей массой после её отде-
отделения (поэтому возможно заблуждение, что ракета может дать нам
объект, имеющий большую энергию, но не имеющий массы). Таким
образом, можно говорить о массе то в выражении A6) как о коли-
количестве вещества, не составляющего никакой системы, имеющей инер-
инерционную характеристику то- Иначе говоря, масса есть, а системы нет
(специальная теории относительности даёт противоположный пример:
система есть, а «массы нет»; см. заметку 38). Замечание это не новое,
например, «Г. Герц определяет массу как „число одинаковых частиц,
сравниваемое с числом материальных частиц, находящихся в некото-
некоторой выбранной части пространства в определённое время. Понятие
материальной частицы — понятие внутренней интуиции, с помощью
которого мы соотносим определённую точку пространства в данный
момент времени с определённой точкой пространства в другой мо-
момент времени"» (цитата из [134]). Определение системы материальных
частиц требует введения единой для всех частиц системы отсчёта
(системы координат и математического времени).
Энергия частиц непосредственно после отделения (формула Aв))
сохраняется и в дальнейшем свободном их движении. Вместе с отде-
отделившимися частицами должна также уноситься та часть внутренней
энергии, которая имеется сверх значения в правой части формулы Aа).
Пример показателен тем, что во всех соотношениях A) фигурирует
одна и та же величина массы, однако в выражениях энергии она
играет совершенно разные роли: в формулах Aа) и A6) это количество
вещества, не представляющее инерционные свойства. Закон сохране-
сохранения энергии (как суммы внутренней и кинетической энергии) для
начального и конечного состояний системы (см. 1(а) и Aв)) выполня-
выполняется (с учётом последнего замечания о возможности уноса внутренней
энергии). Появился термин «изменяющая» масса (И. В. Мещерский),
т. е. масса, не составляющая единой механической системы при вы-
вычислении кинетической энергии частиц перед их отделением. Отделив-
Отделившиеся частицы распределяются по линии, что нарушает сферическую
симметрию распределения массы вокруг ракеты; происходит изменение
этого нарушения.
Пример 2. Закон гравитационного притяжения Ньютона сформу-
сформулирован для двух тел (малого размера по сравнению с расстоянием
между ними). В этом случае из любой (инерциальной) системы на-
наблюдается нарушение сферической симметрии, и следовательно, про-
проявляются массы обоих тел (mi и т^). Свяжем инерциальную систему
с общим центром масс двух тел и обозначим радиусы-векторы тел
через ri и г2:
= 0.	B)

36. Масса и принцип инерционности	245
Если ввести вектор относительного положения тел: г = ri — г2, то
7712	7711	/оч
r	г, г2 =	¦	г.	C)
ГГЦ + ТП
ri	г, г2
7711 + ТП2	ГГЦ + ТП2
Тогда кинетическая энергия системы выражается через относитель-
относительную скорость тел и приведённую массу /i [52]:
т = Еф ^ш^	D)
2	^ 7711 + 7712
(положение первого тела задаётся относительно второго).
Потенциальная энергия, зависящая только от расстояния между те-
телами, сохраняет свой вид: П(г). Пусть П(г) — потенциальная энергия
притяжения по закону Ньютона (G — гравитационная постоянная), т. е.
П(г) = Gmirm2 .	E)
При разных коэффициентах пропорциональности гравитационных
масс т^рав, Ш2рав инерционным массам тп\, m2 для обоих тел возник-
возникла бы неоднозначность соответствия инерционной и гравитационной
массы при стремлении инерционных масс к одной величине (был бы
нарушен принцип детерминированности Ньютона). Для центра грави-
гравитации имеем
m;paBr1+m^paBr2 = 0.	F)
т~»	грав	грав
В случае пропорциональности гравитационных масс тп{ , ш2
инерционным массам тп\, тп^ с одинаковым коэффициентом пропорци-
пропорциональности центр тяжести с весами, пропорциональными гравитацион-
гравитационным массам, согласно F) совпадает с центром инерции B). Квадрат
коэффициента пропорциональности между инерционной и гравитаци-
гравитационной массами в E) может быть без ограничения общности включён
в гравитационную постоянную G.
Задача двух тел свелась к задаче о движении одной материальной
точки относительно осей, связанных с материальной точкой массы тп^
(неинерциальные оси), с функцией Лагранжа
т _ fir2 Gm\m2	/7ч
L~~2	—'	G)
Модель динамики в задаче двух тел привела к понятию «приведённая
масса» и понятию «центр масс», который для изолированной механи-
механической системы предоставляет инерциальную систему отсчёта, а также
к выводу о пропорциональности «инерционной» и «гравитационной»
масс для согласования с аксиомами и принципами механики.
Гравитационное притяжение двух тел, как мы видим, также сопро-
сопровождается нарушением симметрии и его изменением при движении тел.
Пример 3 (опыт Ньютона). Два тела на разных концах связы-
связывающей их и вращающейся в плоскости верёвки создают натяжение.
Нарушение симметрии, создаваемое инерционными массами, в данном

246	Гл. VI. Принцип инерционности
случае не является «статичным», а изменяется, поскольку изменяется
расположение этих масс.
Пример 4. Регулярная прецессия по инерции динамически-сим-
динамически-симметричного тела демонстрирует регулярное «изменение нарушения сим-
симметрии». Инерционные свойства тела характеризуются тензором инер-
инерции. Гироскопический момент при вынужденной регулярной прецессии
направлен так, чтобы «стремились» совместиться две оси: ось быстрого
собственного вращения и ось прецессионного вращения (правило Жу-
Жуковского). При совпадении этих осей имеем «спящий» волчок, который
удивляет свойством сохранять направления своей оси в пространстве.
Вращающийся по инерции однородный шар даёт пример циклического
движения, в котором сохранение симметрии лишь кажущееся, посколь-
поскольку в каждый момент времени на место одних масс приходят другие
равные им массы с такими же скоростями.
Пример 5. Гравитационный парадокс. Считается, что «... приме-
применение закона Ньютона для вычисления гравитационного поля, создава-
создаваемого всем веществом в бесконечной Вселенной, ведёт к противоречию,
названному гравитационным парадоксом» [75]. Непредикативность по-
понятия о бесконечном (см. заметку 31) и обсуждаемый принцип позво-
позволяют найти другое объяснение этого парадокса.
Парадокс состоит в следующем. Полагается, что «Вселенная в сред-
среднем равномерно заполнена небесными телами так, что средняя плот-
плотность вещества в очень больших объёмах пространства одинакова».
В предположении, что вначале Вселенная «пуста», проводятся два
мысленных эксперимента по её построению. В первом эксперименте
сферически-симметричная однородная Вселенная строится добавлени-
добавлением сферических слоев вокруг точечного пробного тела. Гравитационные
силы, действующие на тело, в этом случае уравновешены. Во втором
эксперименте сначала выделяется однородный шар и пробное тело
помещается на его поверхность. На пробное тело должна действовать
отличная от нуля сила притяжения. Затем бесконечная Вселенная
строится последовательным добавлением сферических слоев той же
плотности с центром в центре шара. Эти слои не изменяют силу
гравитационного взаимодействия пробного тела и шара. В первом
эксперименте сила гравитационного взаимодействия равна нулю, а во
втором отлична от нуля.
В первом эксперименте нет противоречия принципу инерционности
(не проявляются ни инерционная, ни гравитационная массы). Во вто-
втором эксперименте имеется нарушение симметрии (но нет изменений
этого нарушения): пробное тело неподвижно относительно центра и не
может проявить своих инерционных свойств, но ему приписывается
гравитационная масса (пассивная). Казалось бы, мы имеем ситуацию,
в которой различаются гравитационная и инерционная массы. Однако
возникший парадокс лишает нас такой возможности: отсутствует про-
проявление инерционной массы (согласно принципу инерционности) и мы

36. Масса и принцип инерционности	247
имеем неопределённость гравитационного взаимодействия, а соответ-
соответственно, и гравитационных масс.
Возможны два выхода из сложившейся ситуации: либо не вво-
вводить гравитационные массы при отсутствии изменения нарушения
симметрии (так же, как и инерционные); либо так изменить условия
эксперимента, чтобы происходило изменение нарушения симметрии.
По сути оба выхода предполагают одно: соблюдение принципа изме-
изменения нарушения симметрии не только для инерционной, но и для
гравитационной массы. В свою очередь, это означает, что требуется
отказаться от модели покоящихся инерционных и гравитационных масс
во Вселенной. Ещё один недостаток модели, принятой в «эксперимен-
«экспериментах», приведших к гравитационному парадоксу, состоит в том, что
пробное тело характеризуется лишь пассивной гравитационной массой
(притягивается, но не притягивает), что нарушает закон равенства
действия и противодействия, «позволяя» первоначально выделенному
шару находиться «в покое». Таким образом, рассматриваемый принцип
в классической теории позволил прийти к известному выводу о «неста-
«нестационарности» Вселенной. Изменение нарушения симметрии происходит
также и в циклических системах (см. пример 4). Поэтому уже из
классической теории следует, что материальная точка, обладающая
массой, является моделью со скрытыми движениями и внутренней
энергией.
Таким образом, гравитационный парадокс демонстрирует не условия
ограничения закона Ньютона (которые имеются объективно), а разные
правила построения моделей, имеющих различные свойства и, как
следствие, неодинаковость гравитационной силы. С равным успехом
можно считать парадоксальными неодинаковые значения кинетической
энергии, импульса, кинетического момента, действия при наблюдении
тела в разных инерциальных системах координат, имеющих разные
скорости, а затем делать выводы о непригодности принципа инерции
Галилея. Конечно, аналогия не полная. Вместо принципа Галилея более
подходящими для сравнения являются условия гидродинамического
принципа Даламбера движения относительно идеальной среды (с инер-
инерционной массой).
Условия гравитационного парадокса позволили с помощью принци-
принципа изменения нарушения симметрии выявить свойство пробного тела
иметь гравитационную (пассивную) массу, если тело и наблюдатель
находятся в разных местах.
Гравитационная сила должна быть тем больше, чем дальше тело
от наблюдателя (в качестве инструмента наблюдатель использует шар,
в центре которого он находится, с радиусом, равным расстоянию до
пробного тела). Чтобы тело находилось в покое, нужна ещё одна сила,
тоже пропорциональная расстоянию, но не притягивающая, а отталки-
отталкивающая. Этим свойством обладает центробежная сила инерции, однако
для её появления придётся отказаться от возможности наблюдать поко-

248	Гл. VI. Принцип инерционности
ящееся тело в инерциальной системе из другого места. Движение тела
не может быть и прямолинейным (для выбора направления движения
в условиях гравитационного парадокса нет достаточного основания).
Наблюдения за циклическими движениями приводят к открытию зако-
закона площадей.
Упоминание сил инерции означает, что опять придётся использовать
понятие инерционной массы, т. е. логический круг зависимости между
наблюдениями гравитационной и инерционной массы замкнулся. Прин-
Принципиальный вывод не сделан, однако можно извлечь некоторую пользу
и из самого процесса рассуждений.
Попутно мы ещё раз убедились, что однородная бесконечная Все-
Вселенная, гравитирующая по закону Ньютона, при нарушении сфериче-
сферической симметрии не может быть стационарной (точнее, нет возможности
наблюдать покоящееся тело в инерциальной системе на расстоянии).
На примере пробного тела явной стала роль понятия пассивной гра-
гравитационной массы, с помощью которого можно более точно очертить
условия задачи о гравитационном парадоксе: Вселенная имеет актив-
активную гравитационную массу («вырезанный» в ней шар используется как
инструмент наблюдателя) по отношению к пробному телу, которому
приписывается только пассивная гравитационная масса. Модели пас-
пассивной гравитационной массы широко применяются и в других зада-
задачах, где только одно тело (с массой, большей по сравнению с массами
других тел системы) полагается активно гравитирующим; наоборот,
в ограниченной задаче трёх тел (см., например, [62]) одно из них
(сравнительно малой массы) принимается пассивно гравитирующим.
Нарушения симметрии вследствие присутствия активных и пассив-
пассивных гравитационных масс различны, соответственно получаем разные
модели силовых и инерционных свойств. Заметим также, что примене-
применение моделей тел с пассивной гравитационной массой нарушает принцип
равенства действия и противодействия гравитационных сил.
Самый общий вывод из сказанного состоит в том, что, с одной
стороны, масса является мерой инерционных свойств, препятствующих
изменению движения, а с другой — первопричиной движения.
37. К задаче о собственном энергоресурсе
гравитирующей массы
Под ресурсом мы понимаем, как и обычно, запас энергии, которую
можно трансформировать в какие-либо другие виды энергии. Полага-
Полагается, что имеется начальная потенциальная энергия, и если она пре-
превышает минимальное значение потенциальной энергии, то возможно
использование ресурса в целях создания кинетической энергии или
получения других видов энергии. «В этом смысле указанная разность
характеризует собственный энергетический ресурс системы» [30], ко-

37. К задаче о собственном энергоресурсе гравитирующей массы 249
торый вычисляется как работа, совершаемая потенциальными силами
при формировании тела из элементарных масс, изначально находя-
находящихся в бесконечном удалении, где они не взаимодействуют между
собой. Формирование тела представляет собой образование неоднород-
неоднородности в каком-либо месте Вселенной и, по предположению, не сопро-
сопровождается появлением неоднородности в другой её части. Если тело
представляет собой однородный шар, то происходит переход от одной
сферической симметрии к другой сферической симметрии: в первой
из них гравитационные взаимодействия скомпенсированы, а во второй
появляется тело, создающее потенциальное гравитационное поле.
37.1. Две схемы формирования гравитирующего тела из беско-
бесконечно удалённой массы. На бесконечности гравитационный потен-
потенциал принимается равным нулю. Формируемое тело создаёт поле гра-
гравитационных сил всемирного тяготения по закону Ньютона. Скорости
материальных точек в начале и в конце мысленного эксперимента рав-
равны нулю. Очевидно, что гравитационные силы притяжения совершат
положительную работу. Энергоресурсом (согласно приведённому выше
определению) обладает масса, из которой «создаётся» тело, и в этом
смысле будем называть его собственным гравитационным энергоре-
энергоресурсом. Вопрос о механизме «возмещения» энергии, затраченной на
формирование тела так, чтобы сохранялся общий баланс энергии в си-
системе, включающей сформированное тело и бесконечно удалённую её
часть, оставим открытым.
Проведём подсчёт энергетического гравитационного ресурса массы
М при формировании из неё однородного шара радиуса R. Плотность
шара равна р = 3M/DirR3). Гравитационный потенциал шара V(r) на
расстоянии г от центра шара (см., например, [30])
{GM	. п
	,	если г ^ R,
СМ	A)
^-(ЗЯ2-г2),	если r<R
(где G — универсальная гравитационная постоянная).
Найдём энергетические затраты на формирование шара по двум
схемам мысленных экспериментов, приводящим к одному и тому же
известному результату.
А. Рассмотрим схему «создания» шара путём его последовательного
«наращивания» до тех пор, пока шар не примет нужные размер и мас-
массу. В результате будет получен потенциал A). Материальные точки
«мысленно» перемещаем из бесконечности, где достигается максимум
потенциальной энергии, и присоединяем к «промежуточному» шару
массы т и радиуса а. В качестве материальной точки принимается
элементарная масса dm, которая после присоединения распределяется
по сферическому слою радиуса а и толщины da (по эквипотенциальной
поверхности).

250	Гл. VI. Принцип инерционности
Согласно A) работа гравитационных сил, действующих на массу
dm, при перемещении её из бесконечности на поверхность шара массы
т и радиуса а равна
dA= — dm.	B)
Выражение зависимости массы т от радиуса шара а: т = 4тга3р/3,
подставляем в B) и вычисляем полную работу гравитационных сил по
формированию шара:
п
где О — объём, занимаемый телом.
Интеграл в правой части последнего равенства имеет смысл мо-
момента инерции шара относительно своего центра CMR2/5). Таким
образом, в результате сформирован шар и гравитационными силами
выполнена работа
„=»§?.	C,
Б. Вывод формулы энергетического гравитационного ресурса из
теории потенциала.
При формировании системы заданной конфигурации работа сил
потенциального поля (см. [30])
А = 1 ? т№,	D)
г=1
где Vi — потенциал, созданный всеми остальными материальными точ-
точками (кроме неё самой), в точке пространства, где должна находиться
масса mf.
Vl = G (
Гравитационный потенциал внутри однородного шара вычисляется по
формуле A):
У(г) = |^(ЗЯ2-г2).	E)
Умножая E) на dm и составляя для вычисления работы по формуле
D) выражение
, 1 f3GM2 GM
снова имеем значение работы C).
Примечание. Двумя способами получена работа, противополож-
противоположная той, «которую необходимо затратить, чтобы всю массу данного
тела удалить в бесконечность» [35] (в цитированном источнике форму-
формула работы по непонятной причине имеет коэффициент 5/6 вместо 3/5).

37. К задаче о собственном энергоресурсе гравитирующей массы 251
Убедимся в том, что поле A) обладает ресурсом (Э), равным рабо-
работе C):	о^л.2
Переход к интегрированию вместо суммы D) даёт формулу
А = i J VpdU,	(8)
п
где V — потенциал точки в объёме, занимаемом телом, которую мы
используем во второй схеме формирования шара.
Перемещаем элементарные массы из бесконечности на своё место
в области будущего шара в неизменном гравитационном поле, экви-
эквивалентном гравитационному полю шара массы М и радиуса R. Пере-
Перемещение элемента dm из бесконечности составляется из двух этапов:
перемещения на поверхность шара радиуса R, а затем с поверхности
внутрь этого шара с образованием сферического слоя. При этом работа
будет равна 2А. Действительно, при перемещении элемента dm на
обратном ходе цикла суммарная работа сил тяготения
А , л 3GM2 GM г 2 ло	/п\
А\ + А2 =	^- - —Т rzpdU.	(9)
2R3 2R3 J^
Интеграл в правой части последнего равенства есть момент инерции
шара относительно центра, поэтому
Ц? = 2А.	A0)
Во второй схеме считается, что поле уже имеется, а массу ещё
только предстоит доставить на своё место. Последнее возможно, когда
поле отделено от массы и существует само по себе, т. е. оно должно
быть физическим. Поэтому и работа получилась по величине вдвое
большая, чем энергоресурс. В результате, кроме введённого по предпо-
предположению физического поля, появляется гравитирующее тело, имеющее
такое же потенциальное поле (математическое).
Применение формул (9), A0) неявно предполагает эквивалентность
физического поля (без предположения о наличии масс, его создающих)
и массивного тела с потенциальным математическим гравитационным
полем. Вторая схема строилась в условиях, когда физическое поле
было «отделено» от массы. В мысленных экспериментах с «пробными»
телами, наоборот, их масса рассматривается отдельно от собственного
поля.
Теперь становятся очевидными условия применения определений
«пассивная» и «активная» гравитационная масса. Пассивную гравита-
гравитационную массу определяют как объект гравитационного притяжения
или как массу, склонную к восприятию гравитации. Активная гравита-
гравитационная масса характеризует материальный источник гравитационного
поля.

252	Гл. VI. Принцип инерционности
Приведённое рассуждение о «формировании» шара, конечно же,
не может претендовать на статус способа создания шара в смысле
возникновения неоднородности в однородной Вселенной. В принятой
постановке очень многое чрезмерно схематично, в том числе статич-
статичность масс и их перемещение на бесконечно большое расстояние без
ограничения скорости. В рассмотренных схемах формирования тел
можно проследить роль принципа изменения нарушения симметрии
(см. заметку 36). Изменение нарушения симметрии происходит при
«переносе» выделенного элемента на своё место.
37.2. Эффективный собственный энергоресурс массы, из ко-
которой формируется шар. Из того, что свободные гравитационно
взаимодействующие тела не могут находиться в покое, следует неста-
нестационарность всей Вселенной [75]. Поэтому при оценке собственно-
собственного энергоресурса в мысленном эксперименте по формированию шара
(из бесконечно удалённых материальных частиц) будем принимать во
внимание их движение. В формуле C) собственного гравитационного
ресурса это свойство не использовалось.
Вначале напомним, что «эффективный» потенциал учитывает грави-
гравитацию и центробежные силы инерции (являющиеся потенциальными).
Рассмотрим систему, включающую абсолютно твёрдый однородный
шар радиуса а, имеющий массу га, и материальную точку, масса
которой равна т\. Гравитационное взаимодействие однородного шара
и материальной точки по закону Ньютона позволяет изучать движение
центра шара и материальной точки в условиях задачи двух тел.
Сведение к задаче двух тел происходит следующим образом. На-
Начало координат помещается в инерциально движущемся центре масс
системы. После введения вектора относительного положения матери-
материальной точки относительно центра шара (г) кинетический потенциал
системы преобразуется к виду
^+Тс-П(г), [I = ттх ,	A1)
2	т -\- т\
где \i — приведённая масса; Тс — кинетическая энергия массы шара
относительно собственных осей Кёнига; П(г) — потенциальная энергия
взаимодействия шара и точки.
Кинетическая энергия Тс в процессе движения до контакта с эле-
элементарной массой остаётся постоянной. После введения обобщённых
координат г, (р и соответствующих обобщённых скоростей
• 2 -2 , 2-2
rz = г -\- гАфА
и система описывается функцией Лагранжа
отличающейся от функции A1) на аддитивную константу.

37. К задаче о собственном энергоресурсе гравитирующей массы 253
Функция Лагранжа A2) формально представляет некоторую гипо-
гипотетическую материальную точку с массой, равной приведённой массе,
движущуюся в поле неподвижного центра с полярными координатами г
и ср.
В системе, представленной лагранжианом A2), имеется цикличе-
циклический интеграл (постоянный обобщённый импульс, сопряжённый с цик-
циклической обобщённой координатой ф)
Ру = цг2ф = к = const,	A3)
имеющий смысл момента импульса гипотетической материальной точ-
точки относительно оси, проходящей через центр шара перпендикулярно
плоскости.
Составив сумму кинетической и потенциальной энергий, с учётом
интеграла A3) получаем функцию Рауса:
вид которой показывает, что после игнорирования циклической коор-
координаты в преобразованной системе роль потенциальной энергии играет
функция, называемая «эффективной» потенциальной энергией:
эф ^ + ()
2/лг
Слагаемое &2/B/хг2) называют центробежной энергией [52].
Далее вместо постоянного момента импульса удобнее будет исполь-
использовать постоянную а, равную удвоенной секториальной скорости:
а = г2ф = -,	A4)
т. е. закон площадей. Тогда
Пэф = П(г) + ^.	A5)
Получим формулу, оценивающую энергетический ресурс массы,
формирующей однородный шар массы М и радиуса R путём переме-
перемещения элементарных масс dm из бесконечности в поле эффективного
потенциала по схеме А (см. п. 37.1). Кинетическую энергию Тс в энер-
энергоресурс массы, образующей шар, не включаем.
Элементарная масса dm как точка мысленно перемещается на по-
поверхность шара массы т (и радиуса а) в силовом поле потенциальной
энергии A5), а затем распределяется в виде сферического слоя с тол-
толщиной da и плотностью, равной плотности шара. Из гравитационного
потенциала по закону Ньютона и центробежного потенциала с учё-
учётом полученного выражения эффективной потенциальной энергии A5)

254	Гл. VI. Принцип инерционности
составляем эффективный потенциал УЭф, действующий на единичную
пробную массу:
ЛТ / ч Gm(a) а (а)
а	2а
т(а) = -тгра , Р
где G — универсальная гравитационная постоянная.
По формуле (8), учитывая, что /i = dm = pdfl, составляем выраже-
выражение работы в поле с эффективным потенциалом A6):
Подставляем в A7) значение
dQ = An a2 da
и интегрируем по а. Интеграл от первого слагаемого вычислен ранее
(см. C)). Поэтому A7) принимает следующий вид:
А=*^-*МШ-, 5(R)=Ja2(a)da.	A8)
о
Из A8) следует, что при одинаковой секториальной скорости для
всех перемещаемых элементарных масс эффективный энергоресурс
определяется выражением
а 3GM2 ЗМа2
В отличие от гравитационного энергоресурса G) эффективный
энергоресурс A9) может иметь отрицательный знак и быть равным
нулю.
Отсюда уже можно делать заключения, выходящие за пределы
модели. Например, положительный энергоресурс массы наводит на
мысль о возможности его естественного расходования при «конденса-
«конденсации» масс, а отрицательный способствует тенденции их «разбегания».
Нулевому ресурсу соответствует «компенсация» взаимного влияния
двух учтённых факторов (возможно, основных). Условия, при которых
массы будут «разбегаться», полезно знать при прогнозе изменений,
ожидаемых для уже имеющихся скоплений масс. При положительном
знаке ресурса возникает вопрос: как массы «узнают», в какой шар (по
размерам и массе) им объединяться? Например, чисто гравитационный
энергоресурс масс G) может оцениваться от нуля (на бесконечности)
и до бесконечности, если мысленно попытаться собрать конечную мас-
массу в «материальную точку». Для одной и той же массы эффективный

38. Об инерционности при релятивистском ограничении скорости 255
энергоресурс A9) как функция радиуса шара имеет значения от нуля
(на бесконечности) до некоторого максимума, затем уменьшается до
нуля и становится отрицательным неограниченной величины.
Примечание. В 1900 г. А. Пуанкаре показал, что фотон с энер-
энергией Е должен обладать инерционной массой т = Е/с2 (где с — ско-
скорость света в вакууме). Соответственно, рассматривая ресурс энергии
при трансформации массы в световую (электромагнитную) энергию как
предельный для массы М, составим равенство
Е = Мс2 = Э + X,	B0)
где X — другие виды энергоресурсов. Полагая их неотрицательными
(X ^ 0), получаем ограничение на эффективный энергоресурс A9)
(Э < Мс2) и соотношение
~	„	М . 5с2
Ьсли константа площадей равна нулю, то имеем неравенство —- ^ ^—^,
К oGr
ограничивающее отношение массы к радиусу для шаров, образуемых
из бесконечно удалённых масс.
38. Об инерционности при релятивистском
ограничении скорости
К самым релятивистским объектам относится фотон, для которого
А. Пуанкаре установил меру инерции: т = Е/с2 (где Е — энергия
фотона, с — скорость света в вакууме). Фотон движется со скоростью
света, в теории относительности это безмассовая частица, а т —
мера присущей телу (электромагнитной) энергии. «В 1905 г. Эйнштейн
выступил в печати с утверждением, что если тело теряет энергию
путём излучения (электромагнитного, наше примечание), то масса
тела уменьшается приблизительно на величину потерянной энергии,
умноженной на 1/с2» [138]. Более общим, чем равенство Е = тс2,
выражением соотношения массы и энергии считается единое опреде-
определение импульса в виде универсального утверждения (Планк, 1908 г.),
а не только утверждения для случая электромагнитного излучения.
«В 1911 г. Лоренц показал, что необходимо включать в рассмотрение
любые виды энергии» [138]. Означает ли это, что в общую сумму энер-
энергий надо включать и потенциальную энергию сил инерции? Например,
силы инерции поступательного движения имеют потенциал, зависящий
от ускорения. Тогда и масса должна зависеть от переносного ускоре-
ускорения. Ответ на поставленный вопрос могут дать только эксперименты.
38.1. О наблюдении инерционных свойств. Начнём с вопроса:
почему фотон не имеет массы покоя? Типичными являются следующие
ответы: потому что в специальной теории относительности нет системы

256	Гл. VI. Принцип инерционности
отсчёта, в которой фотон покоится, или «у безмассовой частицы нет си-
системы координат, в которой она покоится». Есть и более убедительный
ответ. «Оказывается, что фотоны, которые движутся со скоростями с
относительно любой системы отсчёта, состоящей из материальных ча-
частиц с нулевыми массами (по-видимому, имеются в виду массы покоя,
наше примечание), отличными от нуля, относительно друг друга могут
двигаться с любыми скоростями*» [100].
Таким образом, если наблюдатель — реальный (его система от-
отсчёта движется со скоростью меньшей, чем скорость света, и связана
с телами, имеющими массу покоя), то у него просто нет возможности
приписать фотону массу покоя, поскольку он не может обеспечить
своим движением (по определению) относительную скорость фотона,
равную нулю. Вообразим себе наблюдателя, движущегося как другой
фотон. Оказывается, что тогда наблюдаемому фотону можно приписать
любую относительную скорость, в том числе и равную нулю (но си-
система отсчёта такого наблюдателя не может состоять из тел, имеющих
массу покоя). Можно представить себе и третьего, виртуального,
наблюдателя с системой отсчёта, движущейся с бесконечной скоростью
по отношению к реальному наблюдателю. Тогда каждый из двух на-
наблюдателей (реальный и виртуальный) для одного тела (не обязательно
фотона) находит свою относительную скорость (и и v, причём одна
из них больше скорости света), эти две скорости направлены в одну
сторону и связаны соотношением uv = с2, одна из них удовлетворяет
прямому преобразованию Лоренца, а другая — обратному (см. [100]).
Относительно реального и виртуального наблюдателей скорость фо-
фотона одинакова и равна скорости света. Введению трёх таких систем
отсчёта соответствует положительная, равная нулю и отрицательная
масса наблюдаемого объекта, но и системы отсчёта должны строиться
из объектов, имеющих положительную, равную нулю и отрицатель-
отрицательную массу соответственно. Поскольку фотон не может иметь строго
постоянной скорости, число наблюдателей не может быть меньше трёх
(один из них — реальный, и он может пользоваться информацией,
теоретически получаемой с позиций двух других наблюдателей).
38.2. О массе и энергии в системе из двух тел. Приведём
известную [78] оценку массы покоя атома водорода.
Атом водорода, состоящий из протона и электрона, имеет энергию
покоя Eq, представляемую «с хорошей степенью точности... суммой
четырёх слагаемых»:
Ео = гпрс2 + гаес2 + Т + П,	A)
где тр — масса протона; ше — масса электрона; Т и П — кинети-
кинетическая и потенциальная энергия электрона (обозначения кинетической
и потенциальной энергии заменены на традиционные для классической
механики). «Потенциальная энергия П обусловлена взаимным притя-

38. Об инерционности при релятивистском ограничении скорости 257
жением электрических зарядов протона и электрона, которое не даёт
электрону улететь от протона. Из теории, исчерпывающе проверенной
опытом, следует, что
где ve — скорость электрона в атоме водорода. Отсюда масса атома
водорода
Ео	meve	/Оч
ГПц = ~y = ГПр + Ше — 	2~.	(о)
с	2с
Таким образом, масса атома водорода на несколько стотысячных
доли массы электрона меньше, чем шр + ше» [78].
Очевидно, что при выводе формулы C) использован некий «гибрид»
классических и релятивистских понятий. Тем не менее процедура вы-
вычисления массы атома позволяет обнаружить так называемый дефект
массы: масса частицы, состоящей из двух частиц, меньше суммы их
масс. Поэтому продолжим обсуждение на том же уровне строгости,
условно называя тела «протон» и «электрон», а систему — «атом».
Отметим, что потенциальная энергия в формуле A) является только
электростатической, а формула B) напоминает не вполне строго запи-
записанную теорему о вириале.
На первый взгляд, внутренняя энергия атома должна кроме энергии
масс содержать ещё и кинетическую энергию электрона, и тогда вместо
«дефекта» получился бы «избыток» массы. Но так было бы, если бы
в правую часть выражения C) не была включена потенциальная энер-
энергия. Следовательно, за «дефект массы» (отрицательный вклад в вы-
выражение массы) ответственна отрицательная потенциальная энергия
(отрицательный энергоресурс). Этот ресурс проявится, в частности,
в том, что при разрушении атома водорода потребуется энергия, не
меньшая по величине, чем энергоресурс («энергия связи»). Попыта-
Попытаемся объяснить «дефект массы» и роль других видов потенциальной
энергии, не учтённых в C). Предположение о возможности пренебречь
гравитационным ресурсом протона и электрона преждевременно, так
как в модели шара малых размеров этот собственный гравитационный
ресурс велик (см. заметку 37).
Примечание 1. Конечно, можно было бы сослаться на приве-
приведённое выше в категоричной форме правило: при оценке массы нужно
учитывать все виды энергии и во всём пространстве. Но именно это
«правило» и требует более убедительного логического обоснования,
чем те, которые нам известны из работ начала XX века. Остаётся
вопрос: почему же всё-таки энергия, существующая, судя по назва-
названию, в потенции, представляется как уменьшение реальной массы?
Или иначе, в духе физики Аристотеля [2]: как здесь преодолевается
«противопоставление бытия в возможности или в потенции бытию
актуальному, находящемуся в состоянии реализации, завершения или
9 В. Г. Веретенников, В. А. Синицын

258	Гл. VI. Принцип инерционности
энтелехии ...»? «Наряду с термином „энтелехия", и даже чаще, Ари-
Аристотель пользуется термином энергия, но с несколько иным оттенком.
Энергия обозначает переход потенции в её реализацию, деятельность,
акт; энтелехия — завершение этой деятельности» (примечание к [2]).
Пример потенции дают бесконечно удалённые массы (и их энергоре-
энергоресурс), из которых формируется тело с относящимися к нему энерге-
энергетическими свойствами. Поэтому потенциальная энергия как энергия
положения, зависящая исключительно от расположения тел, представ-
представляет бытие актуальное (она потенциальна только в смысле возможной
трансформации в другие виды энергии) и в потенции по Аристотелю
не находится.
Соотношение между средними значениями кинетической и потен-
потенциальной энергии даёт теорема о вириале в следующей форме:
2(Г> = -(virF).	D)
Треугольные скобки означают, что берётся усреднённое по времени
значение заключённой в них величины. Вириалом силы (vir(F)) мы
называем скалярное произведение Fr силы на радиус-вектор точки её
приложения (по сравнению с вириалом Клаузиуса знак изменён на
противоположный и отсутствует усреднение по времени).
Если потенциальная энергия является однородной функцией сте-
степени s относительно расстояния от электрона до центра, практически
совпадающего с центром протона, то
virF = Fr = -^r = -sU.	E)
or
Поэтому теорема о вириале D) для однородных функций принима-
принимает вид
2(Т)=5(П).	F)
Потенциальная энергия сил притяжения зарядов имеет степень
однородности s = — 1. Поэтому соотношение F) показывает, что вме-
вместо C) мы имеем равенство
тн = шр + ше	2 (Т) -	G)
с
Или иначе, выразив среднее значение кинетической энергии через
среднее значение потенциальной энергии и снабдив её нижним индек-
индексом, указывающим принадлежность к полю притяжения электрических
зарядов, получаем
тн = шр + гае + —2 (Пэл) •	(8)
2с
Пусть теперь внутреннее движение в атоме водорода представля-
представляется моделью электрона и протона в задаче двух тел (см. заметку

38. Об инерционности при релятивистском ограничении скорости 259
37). Применим теорему о вириале D) в условиях движения электрона
относительно протона. Тогда
Т = ШрШе Г2 ^	,дч
Шр + тпе 2
Взаимодействие зарядов учтём в прежней форме и добавим эффек-
эффективную потенциальную энергию, состоящую из потенциальной грави-
гравитационной энергии (Пграв) и потенциальной энергии центробежных сил
(Пцен). Для этой модели теорема вириала F) даёт равенство
2(Г) = 51 ((Пэл) + (Пграв)) + 52(Пцен),
51 =-1, 52 = -2.	A0)
Соответственно вместо правой части (8) получаем выражение
Шр + Ше Н	2 ((Пэл) + (Пграв)) ,
2с
/П \ —
\А1Грав/ — —
где г — средний радиус орбиты электрона в движении около протона.
Формула A1) показывает, что
—	дефект массы атома не зависит от потенциальной энергии цен-
центробежных сил;
—	гравитационное поле притяжения увеличивает дефект массы
атома.
Если атом движется с постоянным ускорением, то нетрудно убе-
убедиться, что при периодическом круговом движении электрона среднее
значение вириала переносной силы инерции стремится к нулю (с уве-
увеличением времени усреднения).
Можем ли мы выражение A1) считать значением массы рассматри-
рассматриваемой системы? Утвердительное суждение преждевременно, так как
неясно, где находится отрицательная масса, называемая «дефектом
массы».
Отметим также, что теорема о вириале D) получена при условии
финитного движения. Финитность движения позволяет ввести для
системы с внутренними движениями «массу покоя», которая характе-
характеризует среднюю по времени энергию.
38.3. Кинетический потенциал частицы и её собственного
поля. На основе аналога действия по Мопертюи и аналога действия
по Гамильтону получено элементарное действие для релятивистской
частицы. Построено элементарное действие системы «частица — соб-
собственное поле» («внешняя субстанция», «эфир», «физический вакуум»).
А. Аналог действия по Мопертюи для частицы.
В ньютоновской динамике элементарное действие по Мопертюи
представляет собой произведение импульса материальной точки на
элементарное перемещение (см. C.1)).

260	Гл. VI. Принцип инерционности
В релятивистской динамике используется четырёхмерное простран-
пространство с интервалом между событиями
ds2 = e(dx2 + dy2 + dz2 - c2dt2),	A2)
где с — фундаментальная постоянная (скорость света); г = ±1.
Будем рассматривать временно-подобные события (г = — 1), в кото-
которых смещение происходит из прошедшего в будущее:
ds = ida, da = cdt*, г2 = -1.	A3)
Здесь dt* — элементарный промежуток времени в собственной системе
частицы:	^
,, * at	1	о v	/1 л \
dt = —,	7 = ^^^,	Р = -,	A4)
7	\/^^	с'
где v — 3-скорость частицы (координатами её являются производные
от пространственных координат по времени).
С учётом A2), A3) составляем аналог действия по Мопертюи для
релятивистской частицы:
moVds = —mocda = —moc2/y~ldt,	A5)
где то — масса покоя частицы; V = гс — модуль 4-скорости в специ-
специальной теории относительности (чисто мнимое число).
Коэффициент при dt в A5) (обозначим его Lm)
Lm = -moc27	A6)
имеет смысл кинетического потенциала частицы в системе наблюда-
наблюдателя.
Б. Аналог действия по Гамильтону для частицы.
В собственной системе скорость частицы равна нулю, поэтому ин-
инвариантность элементарного действия по Гамильтону при переходе от
находящегося в этой системе наблюдателя к другому, для которого
скорость частицы отлична от нуля, имеет вид равенства
-H*dt* =Lmdt.	A7)
Поскольку здесь Н* = тос2, с учётом A4) из A7) снова получаем
кинетический потенциал частицы A6). Знак кинетического потенциала
частицы получен однозначно, и поэтому не требуется искусственного
сравнения с функцией противоположного знака (сравните с [137]).
В. Аналог действия по Гамильтону для системы «частица — соб-
собственное поле».
Кинетическая энергия Т релятивистской частицы определяется вы-
выражением
Т = ш0с2G-1),	A8)
где то — масса покоя; 7 ~~ вещественное число, поскольку мы рас-
рассматриваем временно-подобные движения.

38. Об инерционности при релятивистском ограничении скорости 261
Разложение выражения A8) по степеням отношения v/c:
A9)
показывает, что его первый член совпадает с кинетической энергией
в классической механике.
В A8) имеется слагаемое
ш0с27,	B0)
неограниченно возрастающее с увеличением скорости, что приводит
к трудностям в его использовании.
Примечание 2. Описанная ситуация нередко встречается в фи-
физике. «Можно подсчитать энергию взаимодействия частицы самой с со-
собой через виртуальные кванты. Однако такой подсчёт привёл к удруча-
удручающе нелепому результату. Эта энергия, а значит, и собственная масса
заряженной частицы получилась бесконечно большой. Фотонная «шу-
«шуба» электрона, а значит, и он сам весят бесконечно много! Несомненно,
взаимодействие с собственным полем должно вносить какой-то вклад
в массу частицы. Но не бесконечный же! Выход из трудностей до сих
пор не найден» [72].
Ситуация сравнима с парадоксом Даламбера в гидродинамике [49],
когда получается бесконечная кинетическая энергия системы «тело —
сплошная среда», если в бесконечности скорость среды не равна нулю.
Только в случае с частицей уже нет «массовой» среды, поэтому, как
и для электрона, можно ввести «собственное поле» частицы, имеющее
инерционные свойства.
Будем рассматривать энергию B0) как полную энергию системы,
включающей частицу и внешнее по отношению к ней «собственное
поле». Эта энергия наблюдается в системе реального наблюдателя. Бу-
Будем называть его первым. Первому наблюдателю не удаётся различать
энергии частицы и её собственного поля.
Вторым назовём наблюдателя, покоящегося в собственной системе
частицы. Для него не наблюдаема та часть энергии, которой обладает
собственное поле. Вообще говоря, и энергия частицы (шос2) является
лишь информацией о собственной энергии. О ненаблюдаемой энергии
второй наблюдатель узнаёт от первого (также информация). Она вы-
вычисляется как разность
Е-т0с2=Т*,	B1)
где Е = шос27-
Недоступная наблюдению для второго наблюдателя величина Т*
равна (см. A8)) кинетической энергии, известной первому наблюдате-
наблюдателю. Только эта кинетическая энергия отнесена к собственной системе
частицы.

262
Гл. VI. Принцип инерционности
Одинаковое элементарное действие для собственного поля в систе-
системах обоих наблюдателей соответствует равенству
T*d?* = L^dt,
B2)
где Ьц — кинетический потенциал собственного поля («присоединён-
(«присоединённый кинетический потенциал»):
= тос A-7 )•
B3)
Примечание 3. В классической теории с абсолютным време-
временем (dt* = dt) ненаблюдаемая для второго наблюдателя кинетическая
энергия Т* равна кинетической энергии Т в осях первого наблюдате-
наблюдателя; в этом случае нет потребности в энергии покоя массового тела.
К понятию «собственной» энергии тела ttiqc2 привело релятивистское
ограничение скорости.
При /3 = 0 имеем L^ = 0 (при традиционном представлении о кине-
кинетическом потенциале имело бы место равенство нулю разности кине-
кинетической и потенциальной энергий). В предельном случае /3=1, когда
нет массы покоя (и самой весомой частицы), кинетический потенциал
собственного поля B3) имеет значение, равное собственной энергии
тела (тос2).
Из A6) и B3), предполагая аддитивность этих кинетических по-
потенциалов, составляем суммарный кинетический потенциал системы
«частица — собственное поле»:
2
0
тос2
^^
0
^^
,25
0
У
,5
/
У
/0,75
j
J\ 01
L = L
= m0c2(l -
)
B4)
В классическом приближении
из B4) следует выражение, отли-
отличающееся на аддитивную констан-
константу от «живой силы» BТ), фигури-
фигурирующей в действии по Лагранжу
(см. формулу C.10)).
На рис. 38.1 показано из-
изменение кинетических потенциа-
потенциалов A6), B3) и B4) в зависимо-
сти от аргумента /З2 в пределах
0 ^ /З2 ^ 1, т.е. в диапазоне ско-
скоростей от нуля до скорости света A ^ 7 < °°)- Для наблюдателя,
покоящегося в собственной системе частицы, кинетические потенци-
потенциалы 1/@) = Lm@) = —тос2, что соответствует значению потенциаль-
потенциальной энергии тос2 (информация о внутренней энергии частицы). При
скорости, равной скорости света (/3 = 1), значения кинетических по-
потенциалов составляют 1/A) = ^A) = тос2, т.е. остаётся только поле,
энергия которого равна собственной энергии покоившегося тела.
рис 38 1

38. Об инерционности при релятивистском ограничении скорости 263
38.4. Предварительные заключения. В предварительных заклю-
заключениях (п. 11 статьи [97] A895) «К теории Лармора» А. Пуанкаре)
читаем: «Опыт дал множество фактов, которые допускают следующее
обобщение: невозможно обнаружить абсолютное движение материи,
или, точнее, относительное движение весомой материи и эфира. Всё,
что можно сделать, — это выявить движение весомой материи относи-
относительно весомой материи. ...невозможность выявить движение материи
относительно эфира, а также равенство, которое, несомненно, имеет
место между действием и противодействием без учёта действия мате-
материи на эфир, представляют собой два факта, связь которых кажется
очевидной. Может быть, оба пробела будут заполнены одновременно».
В модели системы, описанной в п. 38.3, энергии частицы и соб-
собственного поля с точки зрения двух наблюдателей также не разделены
и никакого относительного движения частицы и её собственного поля
не наблюдается. Однако мы надеемся, что предложенная схема с двумя
кинетическими потенциалами составных частей системы «частица —
собственное поле» будет полезна, и не только в случае электромагнит-
электромагнитных полей.
Если успех действительно достигнут, то в этом заслуга тех двух на-
наблюдателей, которые не соперничают, доказывая каждый свою право-
правоту, а сотрудничают, понимая, что дополняют друг друга. Даже один
«универсальный» наблюдатель (принимающий позицию то первого, то
второго наблюдателя) не может заменить двух, так как лишён наблю-
наблюдения с той позиции, где его нет. Напомним, что есть ещё и третий —
виртуальный — наблюдатель (см. п. 38.1): его возможности полностью
ещё не раскрыты, но когда вместо частицы образуется объект, не
имеющий массы покоя, виртуальный наблюдатель заменяет второго
и вместе с первым констатирует это событие, наблюдая только поле.
Наличие в B4) присоединённого кинетического потенциала означа-
означает, что релятивистская частица не является полностью изолирован-
изолированной, поскольку имеется её собственное поле.
Отметим также некоторые другие обстоятельства изучения движе-
движения релятивистских частиц методами теоретической механики. Огра-
Ограничение скорости релятивистской частицы не позволяет считать её
свободной по определению: ограничение величины скорости представ-
представляет собой неголономную связь в пространстве-времени (другое дело,
что пока не вполне ясно, как она реализуется). Известно, что при
выводе уравнений движения условие неголономной связи не должно
быть использовано в функции Лагранжа, как это было сделано в A5).
Эта связь неидеальная: в уравнении движения релятивистской части-
частицы [78] в составе сил имеется слагаемое, противоположное скорости.

Заключение
В настоящей работе мы сосредоточили внимание на применении
метода виртуального варьирования и метода переменного действия
в области механики в связи с изучением классических дифферен-
дифференциальных и интегральных принципов. Метод переменного действия
позволяет изучать основные образы всех трёх «картин» механики:
силовой, энергетической и геометрической. Без понятия о действии не
обходятся и в других областях естествознания. Вспомним, например,
принцип неопределённости в квантовой механике; законы сохранения
и симметрии уравнений движения в математической физике; теорию
интегральных инвариантов; построение аналитической динамики си-
систем Гельмгольца, Биркгофа и Намбу и т. д. Эти и многие другие
направления исследования остались вне рамок книги. Обобщая сказан-
сказанное, можно заметить важнейшую роль понятия о действии в развитии
теории несвободных динамических систем и в становлении новой па-
парадигмы науки в целом. Достаточно отметить, что понятие о действии
стоит в одном ряду с понятиями энтропии и информации, которые
являются концептуальными для естествознания.
Полагаем, что изучение метода переменного действия и его при-
применений станет одной из фундаментальных составляющих не только
естественнонаучного, но и технического, и гуманитарного образования.

Список литературы
1.	Лппель П. Теоретическая механика. Т. 1. 2. — М.: Физматгиз, I960.
2.	Аристотель. Физика. — М.: Гос. социально-экономическое изд-во,
1936. - 190 с.
3.	Беген А. Теория гироскопических компасов Аншютца и Сперри и общая
теория систем с сервосвязями. — М.: Наука, 1967. — 171 с.
4.	Бердичевский В. Л. Вариационные принципы механики сплошной сре-
среды. - М.: Наука, 1983.
5.	Биркгоф Дж.Д. Гёттингенские лекции Пуанкаре // Последние работы
А. Пуанкаре. — Москва-Ижевск: НИЦ «Регулярная и хаотическая дина-
динамика», 2001.
6.	Болотин В. В. Неконсервативные задачи упругой устойчивости. — М.:
Гостиздат, 1961.
7.	Болотов Е.А. О принципе Гаусса // Известия физико-математического
об-ва при Казанском ун-те. — Казань, 1916.
8.	Брайсон А., Хо Ю-Ши. Прикладная теория оптимального управления /
Пер. с англ. — М.: Мир, 1972.
9.	Веретенников В. Г. Устойчивость и колебания нелинейных систем. — М.:
Наука, 1984.
10.	Веретенников В.Г., Синицын В.А. Интегральный принцип равенства
действия и противодействия // Сб. Научно-методических статей Теорети-
Теоретическая механика. Вып. 24. — М.: Изд. Московского университета, 2003.
С. 15-22.
11.	Веретенников В.Г., Синицын В.А. К динамике точки переменной мас-
массы // Российско-американский журнал: Актуальные проблемы авиацион-
авиационных и аэрокосмических систем: процессы, модели, эксперимент. №2A6).
Т. 8. 2003. С. 90-102.: Казанский гос. Тех университет — Embry-Riddle
Aeronautical Univercity, Казань — Daytona Beach.
12.	Веретенников В.Г., Синицын В.А. Разрывная вариационная задача опти-
оптимизации процессов управления // ПММ. 1972. Т. 36. Вып. 2. С. 357-360.
13.	Веретенников В.Г., Синицын В. А. Теоретическая механика. Дополнения
к общим разделам. — М.: Изд. МАИ, 1996.
14.	Веретенников В.Г., Синицын В. А. Интегральный принцип динамики си-
систем Четаева-Румянцева // VII-я Четаевская конференция «Аналитич.
мех., устойчивость и управление движением». Тезисы докл. — Казань,
1997. Сб.
15.	Веретенников В.Г., Синицын В.А. К динамике связки: абсолютно твёр-
твёрдое тело — материальная точка // Межведомственный сборник «Актуаль-
«Актуальные проблемы классической и небесной механики» / Под ред. С. Д. Фур-
ты. - М.: ТОО «Эльф», 1998. С. 33-39.
16.	Веретенников В.Г., Синицын В.А. Принцип наименьшей кривизны //
Второе Всероссийское совещание-семинар заведующих кафедрами теоре-

266	Список литературы
тической механики. Тезисы докл. Москва, 11-16 октября 1999 г. — М.:
Христианское изд-во, 1999. С. 11-12.
17.	Веретенников В.Г., Синицын В.Л. К изучению интегральных принципов
механики // Сб. Научно-методических статей «Теоретическая механи-
механика». - М.: Изд. МГУ, 2000. Вып. 23. С. 21-29.
18.	Веретенников В.Г., Синицын В.Л. К динамике большого тела в атмосфе-
атмосфере планеты // Вестник МАИ. Т. 6, № 1. — М.: Изд. МАИ, 1999. С. 50-53.
19.	Вилъке В. Г. Аналитические и качественные методы в динамике систем
с бесконечным числом степеней свободы. — М: Изд. МГУ, 1982.
20.	Вилъке В. Г. О качении жёсткого колеса по деформируемому рельсу //
ПММ. 1995. Т. 59. Вып. 3. С. 512-517.
21.	Вилъке В.Г., Синицын В.А. Стационарный режим качения колеса с вяз-
коупругой периферией // Изв. АН МТТ. 1997. № 3. С. 39-46.
22.	Вуйичич В.А., Козлов В.В. К теории реономных систем // Вестн. МГУ.
Сер. 1, Математика, механика. 1995. №5. С. 79-85.
23.	Габасов Р., Кириллова Ф.М. Особые оптимальные управления. — М.:
Наука, 1973. - 256 с.
24.	Галиуллин А. С, Гафаров Г.Г., Малайшка Р.П., Хван A.M. Аналити-
Аналитическая динамика систем Гельмгольца, Биркгофа, Намбу. — М.: Ред.
журнала «Успехи физических наук», 1997.
25.	Гантмахер Ф.Р. Лекции по аналитической механике. Изд. 2-е. — М.:
Наука, 1966.
26.	Геронимус Я. Л. Теоретическая механика. Очерки об основных положени-
положениях. — М.: Наука, 1973.
27.	Герц Г. Принципы механики, изложенные в новой связи. — М.: Изд. АН
СССР, 1959.
28.	Гнеденко Б. В. Курс теории вероятностей. Изд. б-е. — М.: Наука, Физ-
матлит, 1988. — 448 с.
29.	Голдстейн Г. Классическая механика / Пер. с англ. — М.: Наука, 1975.
30.	Голубев Ю.Ф. Основы теоретической механики. Изд. 2-е. — М.: Изд.
МГУ, 2000.
31.	Горский Д.П., ИвинА.А., Никифоров А. Л. Краткий словарь по логике. —
М.: Просвещение, 1991. — 208 с.
32.	Даламбер Ж. Динамика. — М.-Л.: Госиздат, 1950.
33.	Демин В. Г. Движение искусственного спутника в нецентральном поле
тяготения. — М.: Наука, 1968.
ЗА. Демин В.Г., Косенко И.И., Красилъников П. С, Фурта С.Д. Избранные
задачи небесной механики. Уч. пособие / Под ред. П. С. Красильникова. —
Ижевск: Ред. журнала «Регулярная и хаотическая динамика». — Изд. дом
«Удмуртский ун-т», 1999 г. — 211 с.
35.	Дибай Э.А., Каплан С. А. Размерности и подобие астрофизических вели-
величин. — М.: Наука, 1976. — 400 с.
36.	Добронравов В. В. Основы аналитической механики. — М.: Высшая шко-
школа, 1976. - 263 с.
37.	Елисеев В. И. Введение в методы теории функций пространственного
комплексного переменного // Сб. статей. — М.: Тип. НИАТ, 1990. —
190 с.

Список литературы	267
38.	Жуковский Н.Е. К вопросу о движении материальной точки под при-
притяжением одного и двух центров / Соч. Н. Е. Жуковского. Юбилейное
издание A870-1910 гг.). Т. 1. — М: Тип. Императорского Московского
Ун-та, 1912. С. 185-189.
39.	Журавлев В. Ф. Основы теоретической механики. — М.: Наука, 1997.
40.	Зоммерфельд А. Волновая механика / Пер. С. 1-го нем. — М.-Л.: Госте-
хиздат, 1933.
41.	Ишлинский А.Ю. К вопросу об абсолютных силах и силах инерции
в классической механике // Сб. научно-методических статей «Теоретиче-
«Теоретическая механика». Вып. 23. — М.: Изд. МГУ, 2000. С. 3-9.
42.	Козлов В. В. К вопросу о реализации связей // ПММ. 1991. Т. 56. Вып. 4.
С.692-698.
43.	Козлов В. В. Конструктивный метод обоснования теории систем с неудер-
живающими связями // ПММ. 1988. Т. 52. Вып. 6. С. 883-894.
44.	Козлов В. В. Конструктивный подход к обоснованию динамики систем
со связями (к 200-летию «Аналитической механики» Лагранжа) // Сб.
Научно-методических статей. Теоретическая механика. — М.: Изд. МПИ,
1990. Вып. 20. С. 8-15.
45.	Козлов В. В. Симметрии, топология и резонансы в гамильтоновой меха-
механике. — Ижевск: Изд. Удмуртского гос. Ун-та, 1995. — 429 с.
46.	Козлов В.В., Колесников Н.Н. О теоремах динамики // ПММ. 1978.
Т. 42. Вып. 1. С. 28-33.
47.	Космодемьянский В. А. Об определении реакций при вращательном дви-
движении твёрдого тела относительно неподвижной оси // Сб. научно-ме-
научно-методических статей «Теоретическая механика». — М.: Изд. МГУ, 2000.
Вып. 23. С. 58-70
48.	Коссера Э. Ф. Заметка о теории евклидовского действия // В кн. П. Ап-
пелль. Руководство теоретической (рациональной) механики. — М.: Типо-
литогр. Т-ва И.Н. Кушнерев и К°. 1911. Т. 3. С. 612-682.
49.	Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. —
М.-Л.: Госиздат, 1948. Т. 1.
50.	Кузнецов И.И., Идлис Г.М., Гутина В.Н. Естествознание. — М.: Изд.
фирма «Агар», 1996.
51.	Лагранж Ж. Аналитическая механика. Изд. 2-е. — М.-Л., 1950. Т. 1.
52.	Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. I. Механика. Изд.
4-е. - М.: Наука, 1988. - 216 с.
53.	Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. П. Теория поля.
Изд. 6-е. - М.: Наука, 1973. - 504 с.
54.	Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. III. Квантовая
механика. Изд 3-е. — М.: Наука, 1974. — 752 с.
55.	Леви-Чивита Г., Амалъди У. Курс теоретической механики / Пер.
с итал. - М.: Ин.-лит. 1952. Т. 1. Ч. 1.
56.	Лоренц Э. Детерминированное непериодическое течение // Странные
аттракторы. — М.: Мир, 1981. — С. 88-116. Lorenz E.N. Deterministic
Nonperiode Flow // J. Atmos. Sci. 1963. V. 20, № 2. P. 130-141.
57.	Луи де Бройль. Анри Пуанкаре и физические теории // А. Пуанкаре.
Избранные труды. Т. III. - М.: Наука, 1974. С. 703-711.
58.	Лурье А. И. Аналитическая механика — М: Физматгиз, 1961.

268	Список литературы
59.	Малинецкий Г.Г., Потапов А. Б. Современные проблемы нелинейной ди-
динамики. — М.: Эдиториал УРСС, 2000. — 335 с.
60.	Мантуров О.В., Солнцев Ю.К., Соркин Ю.И., Федин Н.Г. Толковый
словарь математических терминов / Под ред. В. А. Диткина. — М.: Про-
Просвещение, 1965. — 539 с.
61.	Маркеев А. П. О принципе Гаусса // Сб. научно-методических статей
«Теоретическая механика». - М.: Изд. МГУ, 2000. Вып. 23. С. 29-44.
62.	Маркеев А. П. Теоретическая механика. — М.: Наука, 1990.
63.	Маслов В. П. Асимптотические методы решения псевдодифференциаль-
псевдодифференциальных уравнений. — М.: Наука, 1987.
64.	Мах Э. Механика. Историко-критический опыт её развития / Пер. С. б-го
нем. изд. — Ижевск: Ред. журнала «Регулярная и хаотическая механика»,
2000. - 455 с.
65.	Мельников О.В., Ремесленников В.И., Романьков В.А. и др. Общая ал-
алгебра. Т. 1. Серия СМБ / Под общей ред. Л. А. Скорнякова. — М.: Наука,
Физматлит, 1990. — 591 с.
66.	Метелицын И. И. Некоторые теоремы об устойчивости движения некон-
неконсервативных систем // Избр. тр. — М.: Наука, 1977. С. 38-45.
67.	Мещерский И. В. Дифференциальные связи в случае одной материальной
точки // Сообщения и протоколы заседаний Математического об-ва при
Харьковском ун-те. 1887. Ч. П.
68.	Мещерский И. В. Уравнения движения точки переменной массы в общем
случае // В кн. И. В. Мещерский. Работы по механике тел переменной
массы. Изд. 2-е. — М.: Госиздат, 1952. — 280 с.
69.	Михайлов Г. К. К истории систем переменного состава // Изв. АН СССР.
МТТ. №5. С. 11-51.
70.	Моисеев Н.Н. Асимптотические методы нелинейной механики. Изд.
2-е. - М.: Наука, 1981. - 400 с.
71.	Мощук И.К., Синицын И.Н. О стохастических неголономных системах //
ПММ. 1990. Т. 54. Вып. 2. С. 213-223.
72.	Мякишев Г.Я. Элементарные частицы. Изд. 3-е, перераб. — М.: Наука,
Гл. редакция физ.-мат. литературы, 1979. — 179 с.
73.	Неймарк Ю.И., Ланда П. С. Стохастические и хаотические колебания. —
М.: Наука, 1987. - 424 с.
74.	Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. — М.:
Наука, 1967.
75.	Новиков И.Д. Эволюция вселенной. Изд. 3-е, ПНТП. — М.: Наука,
1990. - 189 с.
76.	Новоселов В. С. Аналитическая механика систем с переменными масса-
массами. — Л.: Изд-во Ленинградского ун-та, 1969. — 240 с.
77.	Общая алгебра. Т. 1. Серия СМБ / О. В. Мельников, В.Н. Ремесленни-
Ремесленников, В. А. Романьков, Л. А. Скорняков, И. П. Шестаков. Под общей ред.
Л. А. Скорнякова. — М.: Наука, Физматлит, 1990. — 591 с.
78.	Окунь Л. Б. Понятие массы (масса, энергия, относительность) // УФН.
1989. Т. 158. Вып.З. С. 511-530.
79.	Остроградский М.В. О принципе виртуальных скоростей и о силе инер-
инерции / Избр. тр.: Изд. АН СССР, 1958. С. 270-279.

Список литературы	269
80.	Остроградский М.В. Заметка о равновесии упругой нити / Поли. собр.
трудов в трёх томах. — Киев: Изд. АН Укр.ССР. 1959. Т. 1. С. 116-117.
81.	Павленко Ю.Г. Гамильтоновы методы в электродинамике и в квантовой
механике. — М.: Изд. МГУ, 1985.
82.	Пановко Я. Г. Механика деформируемого твёрдого тела. — М.: Наука,
1985.
83.	Пановко Я.Г., Губанова И.И. Устойчивость и колебания упругих систем.
Современные концепции, парадоксы и ошибки. Изд. 4-е. — М.: Наука,
1987.
84.	Парс Л. А. Аналитическая динамика / Пер. с англ. — М., 1971.
85.	Погребысский И. Б. Формирование понятия ускорения / В кн. Исследо-
Исследования по истории физики и механики 1993-1994. — М.: Наука, 1997.
С.218-222.
86.	Подстригая Я. С, Ломакин В. А., Коляно Ю.М. Термоупругость тел неод-
неоднородной структуры. — М.: Наука, 1984.
87.	Полак Л. С. В. Р. Гамильтон и принцип стационарного действия. — М.-Л.:
Изд. АН СССР, 1936.
88.	Поляхов П.П., Зегжда С.А., Юшков М.П. Теоретическая механика. —
Л.: Изд-во Ленингр. ун-та, 1985. — 536 с.
89.	Поляхова Е.Н. Космический полёт с солнечным парусом. — М.: Наука,
1986.
90.	Принцип относительности. Сборник работ по СТО. — М.: Атомиздат,
1972.
91.	Пуанкаре А. О трансфинитных числах // Последние работы А. Пуанка-
Пуанкаре. — Москва-Ижевск: Ижевск НИЦ «Регулярная и хаотическая динами-
динамика», 2001.
92.	Пуанкаре А. Об обобщении метода Якоби / Последние работы А. Пу-
Пуанкаре. — Москва-Ижевск: Ижевск НИЦ «Регулярная и хаотическая
динамика», 2001. С. 25-28.
93.	Пуанкаре А. Последние мысли // Анри Пуанкаре о науке. — М.: Наука,
Физматлит, 1983. С. 405-520.
94.	Пуанкаре А. Наука и гипотеза // Анри Пуанкаре о науке. — М.: Наука,
Физматлит, 1983. С. 5-152.
95.	Пуанкаре А. Замечания о кинетической теории газов // А. Пуанкаре.
Избранные труды. Т. III. — М.: Наука, 1974.
96.	Пуанкаре А. Измерение времени // А. Пуанкаре. Избранные труды.
Т. III. - М.: Наука, 1974. С. 419-428.
97.	Пуанкаре А. К теории Лармора // Принцип относительности. — М.:
Атомиздат, 1973. С. 8-9.
98.	Пятницкий Е. С. Динамика неголономных систем // Сб. Научно-методи-
Научно-методических статей «Теоретическая механика». — М.: Изд. МГУ, 2000. Вып. 23.
С. 72-86.
99.	Рихтмайер Р. Принципы современной математической физики / Пер.
с англ. — М.: Изд. «Мир», 1982.
100.	Родимое Б. П. Автоколебательная квантовая механика. Изд. 2-е. — Томск:
Изд. Томского ун-та, 1976. — 408 с.
101.	Румянцев В. В. Об интегральных принципах для неголономных систем //
ПММ. 1982. Т. 46. Вып. 1. С. 3-12.

270	Список литературы
102.	Румянцев В. В. О некоторых вопросах аналитической механики // Про-
Проблемы аналитической механики и управления движением. — М.: ВЦ АН
СССР, 1985. С. 20-35.
103.	Румянцев В. В. О совместимости двух основных принципов динамики
и о принципе Четаева // Проблемы аналитической механики, теории
устойчивости и управления. — М.: Наука, 1975. С. 258-267.
104.	Седов Л. И. К релятивистской теории полёта ракеты // Об основных
моделях в механике. — М.: Изд. МГУ, 1992.
105.	Седов Л. И. Очерки, связанные с основами механики // Сб. научных
трудов, посвященных памяти акад. М. А. Лаврентьева. — Новосибирск:
Наука, 1983. С. 224-243.
106.	Симметрии и законы сохранения уравнений математической физики / Под
ред. A.M. Виноградова, И.С. Красильщика. РАЕН Ин-т Диффеотопии. —
М.: Факториал, 1997.
107.	Синицын В. А. О принципе Гамильтона-Остроградского при импульсив-
импульсивных движениях динамических систем // ПММ. 1981. Т. 45. Вып. 3.
С. 488-493.
108.	Синицын В. А. Связи в механике / Уч. пособие. — М.: МАИ, 1983.
109.	Синицын В.А. О принципе наименьшего принуждения для систем
с неудерживающими связями // ПММ. 1990. Т. 54. Вып. 6.
ПО. Синицын В. А. Развитие понятия материальной точки в моделях механи-
механики // Научные чтения по авиации, посвященные творческому наследию
Н.Е.Жуковского. Программа и тезисы докладов. — М.: ИИЕТ РАН,
2000. С. 9.
111.	Сиразетдинов Т.К. Устойчивость систем с распределёнными параметра-
параметрами. — Новосибирск: Наука, 1987.
112.	Сорокин Е. С. К теории внутреннего трения при колебаниях упругих
систем. — М.: Госиздат по строит., архитектуре и строит, материалам,
I960.
113.	Суслов Г.К. Теоретическая механика. — М.-Л.: Госиздат, 1944.
114.	Теоретическая механика. Вывод и анализ уравнений движения на ЭВМ /
Под ред. В. Г. Веретенникова. — М.: Высшая школа, 1990.
115.	Тимошенко СП. Прочность и колебания элементов конструкций // Избр.
работы. — М.: Наука, 1975.
116.	Тимошенко СП. Устойчивость упругих систем. — М.: Гостехиздат, 1955.
117.	Трусделл К. Первоначальный курс рациональной механики сплошных
сред. — М.: Мир, 1975.
118.	Уинтнер А. Аналитические основы небесной механики / Пер. с англ. —
М.: Наука, 1967. - 523 с.
119.	Успенский В. А. Что такое нестандартный анализ? — М.: Наука, 1987.
120.	Фейнман Р.Ф. Почему существуют античастицы / УФН. 1989. Т. 157.
Вып. 1. С. 163-183.
121.	Филиппов А. Ф. Дифференциальные уравнения с разрывной правой ча-
частью. - М., 1985.
122.	Филиппов А. П. Колебания деформируемых систем. — М.: Машиностро-
Машиностроение, 1970.
123.	тер Хаар Д. Основы гамильтоновой механики / Пер. с англ. — М.: Наука,
1974.

Список литературы	271
124.	Хазен A.M. Введение меры информации в аксиоматическую базу механи-
механики. 2-е дополненное издание. — М.: Рауб, 1998.
125.	Хайкин С.Э. Силы инерции и невесомость. — М.: Наука, 1967.
126.	Харламов П. В. Неприемлемость некоторых математических моделей ме-
механических систем с дифференциальными связями // ПММ. 1991. Т. 56.
Вып. 4. С. 683-692.
127.	Цлаф Л.Я. Вариационное исчисление и интегральные уравнения. — М.:
Наука, 1966.
128.	Четаев Н.Г. Из записной книжки. A939, 23.10) / В кн. Устойчивость
движения. Работы по аналитической механике. — М.: Изд. АН СССР,
1962. С. 490-499.
129.	Четаев Н.Г. О вынужденных движениях / В кн. Устойчивость движе-
движения. Работы по аналитической механике. — М.: Изд. АН СССР, 1962.
С. 329-334.
130.	Четаев Н.Г. О принципе Гаусса / В кн. Устойчивость движения. Работы
по аналитической механике. — М.: Изд. АН СССР, 1962. С. 323-326.
131.	Элъсголъц Л.Э. Дифференциальные уравнения и вариационное исчисле-
исчисление. — М.: Наука, 1969.
132.	Эйлер Л. Основы динамики точки. «Классики естествознания». — М.-Л.:
ОНТИ-НКТП СССР, 1938.
133.	Эйлер Л. Метод нахождения кривых линий, обладающих свойствами
максимума либо минимума, или решение изопериметрической задачи. —
М.: Гостехиздат, 1934.
134.	Jammer M. Concepts of Mass in Classical and Modern Physics. — Cam-
Cambridge: Harvard Univ. Press, 1961. (Джеммер М. Понятие массы в клас-
классической и современной физике / Пер. с англ. и комментарии Н.Ф. Ов-
Овчинникова. — М.: Прогресс, 1967. — 254 с.)
135.	Mikusinsi /., Sikorski R. The elementare theory of distributions (II).
Warszawa, 1961. (Рус. пер. Микусинский Я., Сикорский Р. Элементарная
теория обобщённых функций. — М.: ИЛ., 1963).
136.	Rocard Y. LTnstabilite en Mecanique. Automobiles. Avions. Ponts sus-
pendus. Masson ET Cie, Editeurs — Paris, 1954. (Рокар И. Неустойчивость
в механике / Пер. с фр. — М.: Ин. лит., 1959.)
137.	Synge J.L. Classikal dinamics. — Springer-Verlag / Berlin-Gottingen-Hei-
delberg, 1960. (Синг Дж.Л. Классическая динамика. — М.: Физматгиз,
1963).
138.	Whittaker E.A. History of the Theories of Aether and Electrisity. V. 2 -
London: Nelson, 1953. (Уиттекер Э. Теория относительности Пуанка-
Пуанкаре и Лоренца // Принцип относительности: Сб. работ по специальной
теории относительности / Сост. А. А. Тяпкин. — М.: Атомиздат, 1973.)
С. 205-231.

Научное издание
ВЕРЕТЕННИКОВ Виктор Григорьевич
СИНИЦЫН Валерий Александрович
МЕТОД ПЕРЕМЕННОГО ДЕЙСТВИЯ
Редактор О. А. Пекина
Оригинал-макет: В.В. Худяков
ЛР №071930 от 06.07.99. Подписано в печать 26.01.05.
Формат 60x90/16. Бумага офсетная. Печать офсетная. Усл. печ. л. 17.
Уч.-изд. л. 18,7. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ОАО «Ивановская областная типография»
153008, г. Иваново, ул. Типографская, 6.
E-mail: 091-018@adminet.ivanovo.ru
ISBN 5-9221-0569-8
985922 105699