Автор: Кечиев Л.Н.
Теги: аппаратные средства техническое обеспечение компьютерные технологии цифровая электроника
ISBN: 978-5-94833-024-2
Год: 2007
Текст
ПРОЕКТИРОВАНИЕ
ПЕЧАТНЫХ ПЛАТ
ЦИФРОВОЙ
БЫСТРОДЕЙСТВУЮЩЕЙ
АППАРАТУРЫ
Серия «Библиотека ЭМС»
Л.Н. Кечиев
Проектирование печатных плат
для цифровой быстродействующей
аппаратуры
ООО «Группа ИДТ»
Москва
2007
УДК 004.3
ББК 32.973.26-02
КЗЗ
Серия основана в 2003 году
Серия издается под редакцией журнала «Технологии ЭМС»
Главный редактор серии — Кечиев Л.Н.,
д. т. н., профессор
Кечиев Л.Н.
КЗЗ Проектирование печатных плат для цифровой быстродействую-
щей аппаратуры / Л.Н. Кечиев — М.: ООО «Группа ИДТ», 2007. -
616 с.: ил. — (Библиотека ЭМС).
ISBN 978-5-94833-024-2
Впервые в отечественной литературе рассматривается полный комплекс воп-
росов проектирования печатных плат для быстродействующей цифровой аппара-
туры. Дается характеристика современной и перспективной элементной базы,
рассматриваются электрофизические параметры печатных плат и линий передач
в их составе. Большое внимание уделено методам анализа помех в цифровых уз-
лах. Отдельно рассмотрен один из важнейших вопросов — проектирование шин
питания и заземления в составе плат. Детально представлен материал по проек-
тированию дифференциальных пар, которые все шире применяются в печатных
платах. Излучения от печатных плат и их восприимчивость к электромагнитным
помехам рассмотрены в контексте электромагнитной совместимости, базовые
сведения о которой необходимы каждому разработчику. В завершение рассматри-
ваются некоторые аспекты САПР печатных плат, применение которых важно для
создания быстродействующих печатных узлов, а также влияние технологии на
конечные показатели плат.
Изложение материала ориентировано на инженерную аудиторию, иллюстри-
руется многочисленными практическими примерами и сопровождается конкрет-
ными рекомендациями и правилами проектирования.
Книгу можно рассматривать как развернутый справочник. Она может быть по-
лезна разработчикам печатных плат, студентам и аспирантам соответствующих спе-
циальностей, а также её можно рекомендовать в качестве учебного пособия в си-
стеме повышения квалификации и профессионального мастерства.
Издание книги одобрено Гильдией профессиональных технологов приборо-
строения.
УДК 004.3
ББК 32.973.26-02
Все права защищены. Никакая часть настоящей книги не может быть воспроизве-
дена или передана в какой бы то ни было форме и какими бы то ни было средствами,
будь то электронные или механические, включая фотокопирование и запись на маг-
нитный носитель. При нарушении авторских прав применяются меры в соответствии
с нормами Российского законодательства в области авторских прав.
ISBN 978-5-94833-024-2
© Кечиев Л.Н., 2007
© ООО «Группа ИДТ», 2007
Перепечатка запрещена
Памяти друга
профессора Петрова Бориса Викторовича
и учителей
профессора Князева Алексея Дмитриевича
и
профессора Литвака Игоря Иосифовича
посвящаю
Оглавление
Содержание............................................................4
Предисловие...........................................................9
Глава 1. Печатные платы в цифровых системах............................ 13
1.1. Тенденции развития электронных средств и проблемы проектирования
печатных плат....................................................... 13
1.1.1. Развитие методов проектирования и конструкций печатных плат.. 13
1.1.2. Стратегия разработки и верификации плат....................21
1.2. Элементы цифровой обработки информации..........................33
1.2.1. Цифровые системы и передача сигналов.......................34
1.2.2. Стандарты передачи сигналов и семейства логических микросхем.37
1.2.3. Помехи в системе при работе микросхем .....................48
1.2.4. Вольтамперные характеристики цифровых схем.................52
1.2.5. Электрические соединения на плате..........................56
1.2.6. Цифровой сигнал в электрических соединениях................57
1.2.7. Контрольная диаграмма, джиттер и расфазировка..............64
1.3. Номенклатура и параметры корпусов микросхемы....................67
1.3.1. Микросхемотехника и печатные платы ........................67
1.3.2. Корпуса микросхем для монтажа в отверстия..................68
1.3.3. Корпуса для поверхностного монтажа.........................76
1.3.4. Корпуса с матрицей шариковых выводов BGA...................79
1.3.5. Корпуса с размерами кристалла..............................90
1.3.6. Электрические параметры корпусов ИС........................92
1.3.7. Методология моделирования корпусов микросхем............. 105
1.4. Материалы для печатных узлов.................................. 109
1.4.1. Материалы для корпусирования кристаллов.................. 109
1.4.2. Материалы для печатных плат............................... ПО
1.4.3. Материалы с высокой магнитной проницаемостью............. 121
Глава 2. Электрофизические параметры печатного монтажа.................123
2.1. Полное сопротивление и электрические модели печатного монтажа..... 123
2.1.1. Описание целостности сигнала в решениях и терминах полного
сопротивления.................................................. 124
2.1.2. Полные сопротивления реальных и идеальных элементов цепей.... 125
2.1.3. Полные сопротивления во временной области
2.1.4. Полные сопротивления в частотной области................. 129
2.1.5. Эквивалентные схемы компонентов.......................... 132
2.1.6. Выбор моделей............................................ 134
2.2. Сопротивление и его модели.................................... 137
2.2.1. Физические основы сопротивления.......................... 137
2.2.2. Объемное удельное сопротивление материала................ 141
2.2.3. Сопротивление на единицу длины проводника................ 142
2.2.4. Поверхностное сопротивление.............................. 142
2.2.5. Скин-эффект и распределение тока по сечению проводника....... 144
Содержание
5
2.3. Электрическая емкость в печатном монтаже...................... 150
2.3.1. Основные определения..................................... 150
2.3.2. Классификация электростатических систем.................. 153
2.3.3. Общие свойства электрической емкости..................... 154
2.3.4. Электрический ток в конденсаторах........................ 156
2.3.5. Емкость и конфигурация проводников....................... 157
2.3.6. Плоскопараллельный конденсатор........................... 158
2.3.7. Диэлектрическая проницаемость............................ 159
2.3.8. Эффективная диэлектрическая проницаемость................ 160
2.3.9. Емкость между слоями платы............................... 162
2.3.10. Погонная емкость........................................ 165
2.4. Методы расчета электрической емкости в печатном монтаже....... 167
2.4.1. Классификация методов расчета емкости.................... 167
2.4.2. Инженерные методы оценки емкости......................... 168
2.4.3. Емкость металлизированных отверстий...................... 175
2.5. Физические основы индуктивности............................... 179
2.5.1. Понятие индуктивности.................................... 180
2.5.2. Парциальная индуктивность................................ 184
2.5.3. Эффективная индуктивность проводников.................... 187
2.5.4. Собственная и взаимная индуктивность контура............. 192
2.5.5. Система электропитания и индуктивность контура питания... 193
2.5.6. Индуктивность контура с прямоугольными пластинами........ 194
2.5.7. Индуктивность контура и переходные отверстия............. 195
2.5.8. Индуктивность контура с плоскостями, содержащими матрицу
отверстий с гарантированным шагом............................... 197
2.5.9. Взаимная индуктивность контуров.......................... 198
2.5.10. Индуктивность нескольких элементов...................... 198
2.5.11. Вихревые токи и индуктивность........................... 199
Глава 3. Линии передачи в печатном монтаже.............................202
3.1. Линии передачи и их модели.....................................202
3.1.1. Модели линии передачи.....................................202
3.1.2. Однородные линии передачи.................................205
3.1.3. Скорость распространения сигнала в линии..................207
3.1.4. Пространственное разрешение при распространении сигнала....210
3.1.5. Понятие электрически длинной и короткой линии передачи.....211
3.1.6. Мгновенное полное сопротивление линии передачи............216
3.1.7. Волновое сопротивление....................................216
3.1.8. Путь возвратного тока в линии передачи....................218
3.1.9. Возвратный путь в смежных слоях МПП.......................220
3.1.10. Модель линии на основе £С-звеньев........................227
3.1.11. Расчет волнового сопротивления с помощью приближенных
соотношений......................................................228
3.1.12. Частотная зависимость волнового сопротивления............234
3.2. Линии передачи с потерями......................................234
3.2.1. Влияние потерь в линиях передачи на качество функционирования
цифрового узла...................................................235
3.2.2. Контрольная диаграмма.....................................237
3.2.3. Механизмы потерь в линии передачи.........................239
3.2.4. Коэффициент рассеяния.....................................240
3.2.5. Модель линии передач с потерями...........................243
6
Содержание
3.2.6. Волновое сопротивление линии передачи с потерями..........247
3.2.7. Скорость распространения сигнала в линии с потерями.......247
3.2.8. Ослабление в линии с потерями.............................248
3.2.9. Полоса пропускания линии передачи.........................255
3.2.10. Поведение линии с потерями во временной области..........258
Глава 4. Обеспечение целостности сигнала в печатном монтаже............260
4.1. Целостность сигнала в электронных модулях......................260
4.1.1. Целостность сигнала и проектирование печатных плат........260
4.1.2. Однородность линий передачи и помехи отражения............263
4.1.3. Перекрестная помеха в межсоединениях......................264
4.1.4. Помехи в шинах питания....................................265
4.1.5. Джиттер цифрового сигнала.................................267
4.1.6. Нарушение целостности сигнала за счет скин-эффекта........271
4.1.7. Режим общего вида.........................................274
4.1.8. Электромагнитные помехи...................................276
4.1.9. Методология проектирования печатных плат и печатных узлов..278
4.2. Целостность сигнала в коротких и длинных одиночных линиях
передачи............................................................279
4.2.1. Короткие линии передачи...................................279
4.2.2. Длинные линии передачи....................................280
4.2.3. Отражения в линиях передачи...............................286
4.2.4. Помехи отражения в длинных линиях передачи................290
4.2.5. Определение формы сигнала в однородной линии с линейными
нагрузками ......................................................292
4.2.6. Определение формы сигнала в однородной линии
с нелинейными нагрузками.........................................296
4.2.7. Согласование линии передачи...............................305
4.2.8. Особенности согласования ЭСЛ-схем.........................313
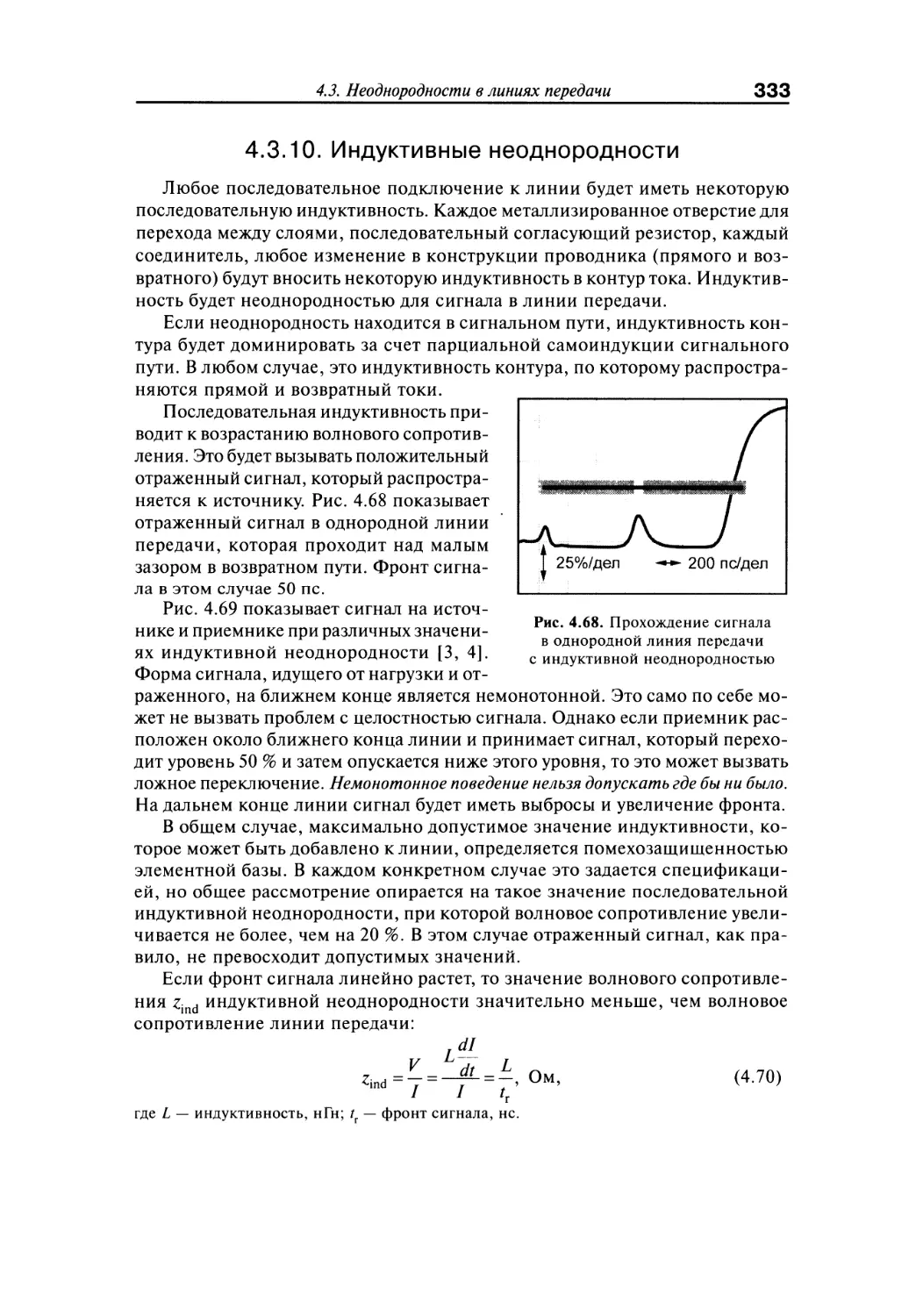
4.3. Неоднородности в линиях передачи...............................316
4.3.1. Плоскость как возвратный проводник линии передачи.........316
4.3.2. Возвратный путь в аналого-цифровых платах.................318
4.3.3. Разветвления..............................................320
4.3.4. Шлейфы....................................................321
4.3.5. Емкостная нагрузка в конце линии..........................322
4.3.6. Емкостная нагрузка в середине линии.......................325
4.3.7. Повороты сигнальных проводников...........................328
4.3.8. Металлизированные отверстия...............................329
4.3.9. Нагрузки, распределенные по длине линии...................331
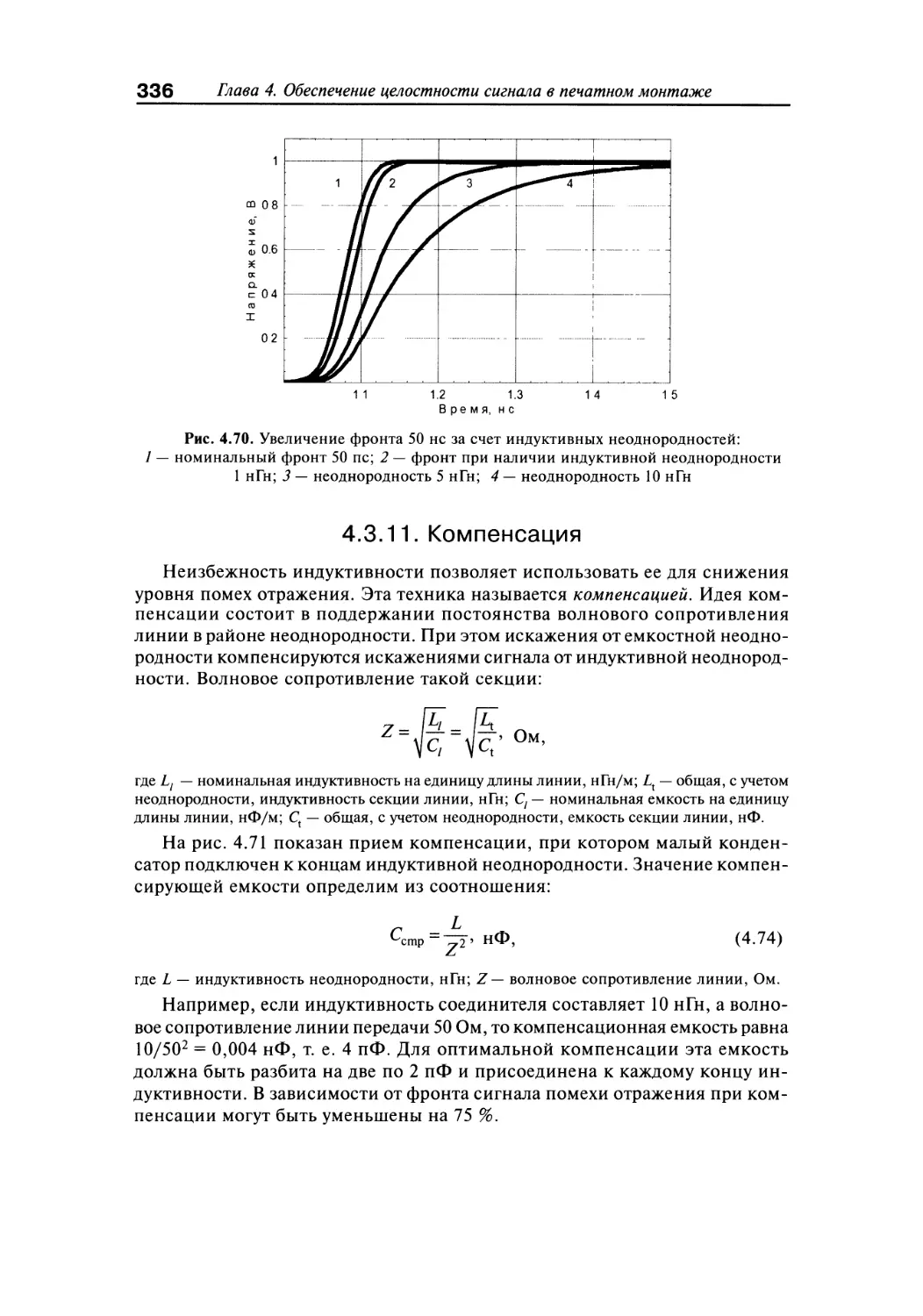
4.3.10. Индуктивные неоднородности...............................333
4.3.11. Компенсация..............................................336
4.3.12. Последовательно соединенные короткие отрезки линии.......337
4.3.13. Соединители как неоднородность линий передачи..........338
4.4. Перекрестные помехи в связанных линиях передачи................341
4.4.1. Перекрестные помехи и суперпозиция........................341
4.4.2. Механизм связи активной и пассивной линий.................342
4.4.3. Модели описания перекрестных помех........................343
4.4.4. Перекрестные помехи в коротких линиях.....................344
4.4.5. Перекрестные помехи в длинных линиях передачи.............346
4.4.6. Коэффициенты перекрестной помехи в длинной линии..........350
4.4.7. Емкостные параметры связанных линий.......................359
Содержание
7
4.4.8. Матрица емкостей и расчет................................360
4.4.9. Индуктивная матрица......................................363
4.4.10. Способы снижения уровня перекрестных помех..............364
4.4.11. Защитные трассы.........................................365
4.4.12. Перекрестная помеха и диэлектрическая проницаемость.....368
4.4.13. Перекрестные помехи и джиттер...........................368
4.4.14. Коммутационные помехи...................................370
4.4.15. Методы снижения перекрестных помех......................372
Глава 5. Проектирование шин питания и заземления......................373
5.1. Система питания и заземления..................................373
5.1.1. Полное сопротивление системы питания.....................373
5.1.2. Стратегия и правила проектирования слоев питания.........376
5.1.3. Потенциальный слой с сетчатым рисунком...................379
5.1.4. Топология сплошных слоев питания и опорного напряжения...384
5.1.5. Структура набора слоев МПП...............................389
5.2. Помехи в шине питания и их устранение.........................398
5.2.1. Особенности систем питания цифровых микросхем............398
5.2.2. Развязывающие конденсаторы в электронных модулях.........406
5.2.3. Минимизация полного сопротивления системы питания........422
5.3. Рекомендации по проектированию шин питания и заземления.......426
Глава 6. Дифференциальная пара в печатном монтаже.....................429
6.1. Передача дифференциальных сигналов............................429
6.1.1. Основы дифференциальной передачи сигналов................429
6.1.2. Конструкция дифференциальной пары........................432
6.1.3. Дифференциальное полное сопротивление несвязанных линий..434
6.1.4. Влияние связи между линиями..............................436
6.2. Полное сопротивление дифференциальной пары....................440
6.2.1. Дифференциальное полное сопротивление....................440
6.2.2. Распределение возвратного тока в дифференциальной паре...441
6.2.3. Нечетная и четная моды...................................443
6.2.4. Дифференциальное полное сопротивление и полное
сопротивлениенечетной моды......................................446
6.2.5. Полное сопротивление режима общего вида и четной моды....447
6.3. Сигналы дифференциального и общего вида и компоненты
напряжения нечетной и четной мод...................................448
6.3.1. Скорости мод и перекрестная помеха на дальнем конце
дифференциальной пары......................................450
6.3.2. Модель идеальной связанной линии или идеальная
дифференциальная пара...........................................453
6.3.3. Согласование дифференциального и общего сигналов.........454
6.3.4. Согласование низковольтных ЭСЛ схем......................458
6.4. Преобразование дифференциального сигнала в сигнал общего вида.460
6.4.1. Расфазировка.............................................460
6.4.2. Асимметрия...............................................463
6.4.3. Сигналы общего вида и электромагнитные помехи............464
6.5. Помехи в дифференциальной паре................................468
6.5.1. Перекрестная помеха между одиночной линией
и дифференциальной парой.......................................468
6.5.2. Неоднородности в возвратном пути.........................471
8
Содержание
6.6. Расчет параметров дифференциальной пары.........................473
6.6.1. Расчет параметров нечетной и четной мод...................473
6.6.2. Матрица волновых сопротивлений............................475
6.7. Рекомендации по проектированию дифференциальной пары...........477
Глава 7. Печатные платы и элементы ЭМС.................................484
7.1. ЭМС как показатель качества электронной аппаратуры ............484
7.1.1. ЭМС и качество изделия ...................................484
7.1.2. Система технического регулирования в области ЭМС..........488
7.1.3. Понятие «электрического размера»..........................491
7.1.4. Общие единицы измерения ЭМС...............................493
7.2. Помехоэмиссия от печатных узлов................................500
7.2.1. Ближняя и дальняя зоны излучаемого поля...................500
7.2.2. Токи в дифференциальном и общем режиме....................501
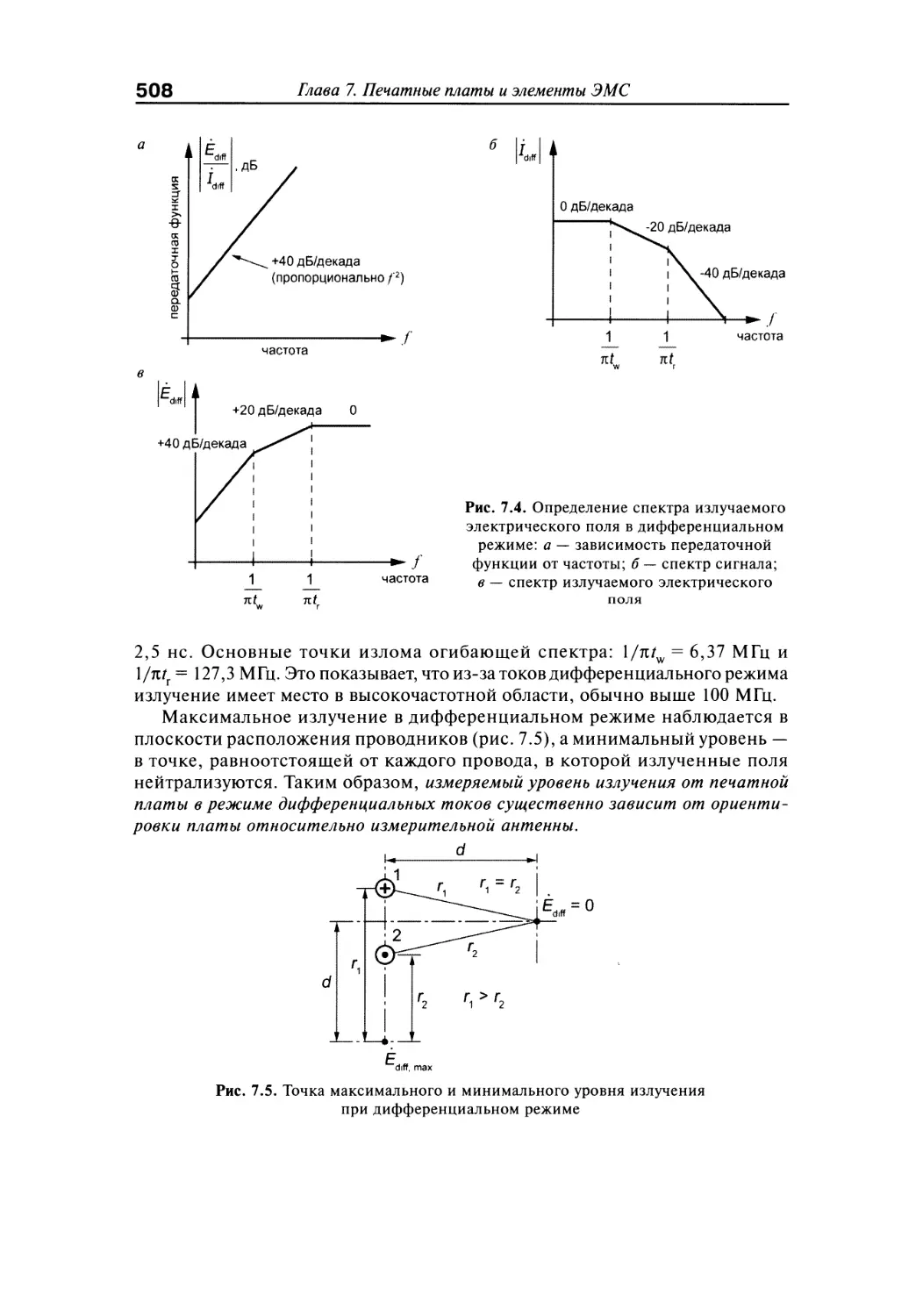
7.2.3. Модель излучения тока дифференциального режима............505
7.2.4. Модель излучения тока синфазного режима...................509
7.3. Восприимчивость печатных плат..................................512
7.4. Экранирование печатных узлов...................................518
7.4.1. Принцип действия электромагнитного экрана.................518
7.4.2. Механизмы работы экрана при различных видах излучения.....520
7.4.3. Электро- и магнитостатическое экранирование...............522
7.4.4. Практика экранирования....................................524
7.5. Соединение печатного узла с шасси..............................526
Глава 8. Конструкторско-технологическое проектирование: модели и системы
автоматизации проектирования...........................................531
8.1. Тенденции в развитии САПР......................................531
8.1.1. Целостность сигнала и САПР................................531
8.1.2. Использование специализированного программного обеспечения
в области целостности сигнала и ЭМС...............................533
8.1.3. Программы предтопологического и посттопологического
анализа...........................................................536
8.2. Решение задач целостности сигналов в САПР......................544
8.2.1. Перекрестные помехи и их моделирование....................544
8.2.2. Сопротивление шин питания и заземления....................546
8.2.3. Учет индуктивностей.......................................548
8.3. Структура и задачи САПР печатных плат..........................549
8.3.1. Структура перспективных САПР..............................549
8.3.2. Комплексность решений при проектировании плат в САПР......563
8.3.3. Моделирование и симуляция в проектировании печатных плат...566
8.3.4. Методы моделирования цифровых узлов электронных приборов... 571
8.4. Технологические факторы и целостность сигнала..................579
8.4.1. Модели и инструметарий....................................579
8.4.2. Оценка влияния технологических факторов...................581
8.5. Сводка САПР печатных плат с учетом ЭМС и целостности сигнала....596
Условные буквенные обозначения......................................601
Латинские .......................................................601
Греческий........................................................607
Литература..........................................................609
Предисловие
Впервые печатные платы появились в составе радиоэлектронной аппарату-
ры более полувека назад. С тех пор, несмотря на многочисленные попытки при-
менить альтернативные решения, они остаются на лидирующих позициях, а в
последние годы благодаря успехам технологов печатные платы остались прак-
тически без конкуренции, являясь основной сборочной единицей современной
аппаратуры любого назначения от сотового телефона до крупного радиолока-
ционного комплекса. С повышением быстродействия цифровых систем, при про-
ектировании печатных плат на первое место выступили вопросы электродина-
мического анализа, помехозащищенности, обеспечения требований электромаг-
нитной совместимости (ЭМС) и ряд других, с которыми разработчики плат ранее
не встречались. Успешно проектируя многие годы платы для систем умеренно-
го быстродействия, конструктор не всегда может почувствовать ту грань, после
которой его прошлый опыт и интуиция, основанная на нем, перестают работать.
Традиционные решения не приносят успеха, а новых знаний зачастую не хвата-
ет. К сожалению, информация о новых подходах к проектированию печатных плат
в отечественной литературе практически отсутствует, а зарубежные источники
труднодоступны и разрозненны. В настоящей книге сделана попытка на основе
собственного многолетнего опыта проектирования плат, чтения лекций в вузе
и в системе повышения квалификации, а также на основе обобщения передо-
вого отечественного и зарубежного опыта проектирования высокоскоростных
цифровых систем впервые в отечественной литературе осветить новые подходы
к проектированию печатных плат и печатных узлов для цифровых систем высо-
кого и сверхвысокого быстродействия.
Развитие цифровых систем идет под знаком повышения быстродействия. На
это направлены усилия разработчиков и изготовителей интегральных микросхем,
системотехников и схемотехников, конструкторов и технологов радиоэлектрон-
ных и электронных устройств и систем. В условиях конкурентной борьбы на со-
временном рынке электронных средств только совместные усилия всех групп раз-
работчиков могут привести к успеху. Технические решения должны быть выве-
рены и обоснованы, что сократит время доводки и отладки аппаратуры, в том
числе и на уровне печатных узлов. Это особенно важно в части параметров по-
мехозащищенности и ЭМС, по которым изделия подлежат обязательной серти-
фикации перед появлением на рынке.
В этих условиях меняется содержание задач, которые приходится ре-
шать конструктору, разрабатывающему печатные платы. Традиционно для
относительно низкочастотной аппаратуры требовалось решить в основном
топологические задачи по безошибочной трассировке печатного монтажа, а
некоторые особенности функционирования платы подсказывал разработчик
принципиальной схемы. При проектировании плат для быстродействующих
10
Предисловие
систем таких «подсказок» накапливается слишком много, что исключает эффек-
тивную работу конструктора. Он должен быть сам достаточно квалифицирован
для принятия технических решений в новой изменившейся ситуации, для веде-
ния конструктивного диалога со схемотехником, а также для анализа результа-
тов испытаний и измерений. Если настоящая книга поможет в этом, автор бу-
дет считать свою задачу выполненной. При ее написании основной акцент сде-
лан на физический уровень строгости изложения, а доступный инженеру матема-
тический аппарат применялся для более глубокого понимания сути рассматри-
ваемых явлений и процессов.
Первая глава показывает комплексность задачи проектирования печатных
плат, которую необходимо рассматривать как органическую часть проектирования
цифровой системы. Электрические параметры сигнала, конструкторские пара-
метры корпусов микросхем, характеристики применяемых материалов оказы-
вают непосредственное воздействие на конечный продукт, на те или иные ре-
шения. Прогнозирование конечного результата возможно на адекватной моде-
ли печатного узла в виде виртуального прототипа, на примере которого показано
взаимодействие различных групп разработчиков.
Во второй главе рассматриваются электрофизические параметры печатного
монтажа. Разработчик платы должен понимать, что в быстродействующих уст-
ройствах любое изменение рисунка монтажа, ширины и длины проводников,
диаметров металлизированных отверстий и других факторов приведет к изме-
нению электрических и физических параметров монтажа (емкость, индуктив-
ность, волновое сопротивление и др.), что скажется на качестве обработки сиг-
нала. Иногда эти изменения мало заметны, но чем выше быстродействие, тем
сильнее зависимость электрофизических параметров межсоединений от конст-
рукции платы, и тем более обоснованы и продуманы должны быть решения. Для
инженерной оценки наиболее важных параметров приведены справочные фор-
мулы, графики и примеры.
Третья глава посвящена одному из центральных вопросов проектирования
печатаных плат — формированию линий передачи цифрового сигнала. Непре-
менное условие качественной обработки сигнала заключается в создании печатных
плат с контролируемым волновым сопротивлением. В главе детально рассмот-
рены вопросы формирования и расчета линий передач без потерь и линий с по-
терями, которые начинают сказываться на высоких скоростях передачи инфор-
мации.
В четвертой главе рассматривается совокупность вопросов, которые объеди-
няются термином «целостность сигнала». Это понятие относится ко всем при-
чинам, которые вызывают отклонение формы цифрового сигнала от идеальной.
В начале главы дается общая характеристика этих причин, которые детально
разбираются в последующих разделах главы. К ним, прежде всего, относятся пе-
рекрестные помехи и помехи, связанные с рассогласованием длинных линий
передачи. Показано, как конструкторские решения при проектировании платы
влияют на данные помехи, и даны рекомендации и практические способы по
обеспечению целостности сигнала в межсоединениях печатных плат.
Помехи в шинах питания и заземления типичны для цифровых устройств.
Снижение уровня этих помех во многом достигается конструкторскими мето-
дами и установкой развязывающих конденсаторов. Здесь с особой остротой стоит
вопрос о взаимопонимании разработчика схемы, в прерогативу которого входит
Предисловие
11
назначение типов и номиналов этих конденсаторов, и конструктора, который
управлением соответствующими параметрами рисунка печатного монтажа и
расположением потенциальных слоев может существенно улучшить ситуацию
или свести на нет усилия схемотехника. В пятой главе детально анализируются
вопросы проектирования шин питания и заземления, а также даются соответ-
ствующие методики расчета и практические рекомендации.
Перспективному направлению в проектировании печатных плат — диффе-
ренциальной передаче сигнала с помощью дифференциальных пар — посвяще-
на шестая глава. Следует отметить, что применение дифференциальных пар в ряде
случаев является единственным решением для создания цифровых узлов с пре-
дельно высоким быстродействием и одновременно с наилучшими характерис-
тиками ЭМС. Устройства с гигабитной скоростью обработки информации пре-
имущественно строятся на дифференциальных парах. Несмотря на уже имею-
щийся опыт их применения, в отечественной литературе практически отсутствуют
сведения о теории и практике построения дифференциальных пар на печатных
платах. Материалы главы в определенной мере восполняют этот пробел. Здесь
же дается описание работы дифференциальной пары, методов снижения уров-
ня помех в них и способов реализации на печатных платах.
В седьмой главе показан механизм генерирования электромагнитных помех
от проводников печатного монтажа и индуцирования помех в межсоединениях
платы при воздействии на нее электромагнитного поля. Приведенные простые
модели и методы расчета помех позволяют выполнять необходимые оценки на
этапе проектирования платы и принимать решения по снижению уровня излу-
чаемых помех и повышению стойкости цифрового узла к воздействующим по-
мехам. Достаточно жесткие требования, которые выдвигаются к современной
электронной аппаратуре с позиций электромагнитной совместимости, требуют
принятия ряда дополнительных мер по ее обеспечению, в том числе экраниро-
вания. Хотя это очень важное направление выходит за рамки книги, в главе при-
ведены некоторые наиболее общие сведения, а также примеры выполнения эк-
ранов в печатных узлах.
Говоря о печатных платах, нельзя не затронуть системы автоматизации про-
ектирования плат. Это отдельное направление, широко освещенное в технической
литературе. Наиболее продвинутые САПР содержат в своем составе подсисте-
мы оценки целостности сигнала, но максимальный эффект от их применения
возможен только тогда, когда пользователь сможет квалифицированно задать
исходные параметры и оценить полученный результат, т. е. будет достаточно
подготовлен с позиций целостности сигнала и смежных вопросов, относящих-
ся к этой проблеме. В восьмой главе приводятся сведения о решении основных
задач целостности сигнала в наиболее мощных САПР, кратко описываются под-
системы и прикладные программы обеспечения целостности сигнала.
Перспективные направления в сфере автоматизации проектирования осно-
ваны на применении моделей высокого уровня. В главе приводится краткий обзор
существующих подходов к моделированию цифровых узлов, среди которых можно
выделить IBIS-описания. Это относительно новое направление в моделирова-
нии цифровых систем, наиболее пригодное для проектирования цифровых уз-
лов на печатных платах.
В завершении восьмой главы освещаются вопросы влияния технологических
факторов на качество проектируемого печатного узла. Приведенные материалы
12
Предисловие
позволяют говорить о том, что для быстродействующих узлов технологический
процесс должен контролироваться более жестко, в том числе и по ряду параметров,
которые до настоящего времени не принимались во внимание.
При изложении материала автор постарался придать ему инженерную направ-
ленность, приводя многочисленные практические примеры и подчеркивая пра-
вила и рекомендации проектирования. В определённой мере книга может слу-
жить справочником по разработке печатных плат для высокочастотных прило-
жений. Кроме этого, монография может быть полезна студентам и аспирантам
соответствующих специальностей, а для систем повышения квалификации и
профессионального мастерства специалистов ее можно рассматривать в качестве
учебного пособия.
Автор выражает признательность своим коллегам за помощь в подготовке
материалов для книги. Это, прежде всего, к.т.н. А. В. Алешину за выполнение всех
аналитических расчетов, выполненных с применением пакета Mathematica, и
проверку корректности формул, А. В. Соловьеву и Нисану А. В. за проведение рас-
четов с применением пакета ELCUT, Н. В Лемешко, выполнившему исследова-
ния цифровых узлов на основе IBIS-описания, К. А. Марченкову, который, бу-
дучи одновременно прекрасным художником и специалистом в области проекти-
рования электронных средств, взял на себя труд по иллюстрированию книги, а также
О. С. Гердлер, проделавшей большую работу по подготовке материалов к главе 8.
Все пожелания и замечания, направленные в адрес редакции,
будут с благодарностью приняты.
Глава 1
Печатные платы в цифровых
системах
1.1. Тенденции развития электронных
средств и проблемы проектирования
печатных плат
1.1.1. Развитие методов проектирования
и конструкций печатных плат
Общая характеристика
Основной чертой развития цифровой техники в последние годы является по-
вышение быстродействия. Это ставит перед разработчиками электронных средств
и, в том числе, печатных плат ряд новых задач. Понятие «высокое быстродей-
ствие» весьма расплывчато и зависит от конкретного проекта. Как будет пока-
зано в последующих главах, относительная граница высокого быстродействия
при рассмотрении печатных плат может начинаться с частот 50 МГц. В настоя-
щее время от 50 до 60 % печатных плат работают именно в этом частотном ди-
апазоне. Для систем телекоммуникаций, где требования к быстродействию
особенно высоки, цифровые системы должны работать с сигналами, фронты
которых составляют доли наносекунд, что соответствует частотам в сотни и ты-
сячи мегагерц [1—4]. Однако большинство проектировщиков слабо информи-
рованы о тех новых задачах, которые возникают при конструировании быстро-
действующих электронных модулей и печатных плат для них. Это во многом
объясняется рядом причин: отсутствием опыта проектирования быстродейству-
ющих устройств; отсутствием должных знаний в области физических явлений
и процессов, которые необходимо учитывать при проектировании плат; разроз-
ненностью этапов проектирования (схемотехнических, электрофизических, то-
пологических, технологических); относительно слабой поддержкой САПР та-
ких задач проектирования, как целостность сигнала, обеспечение электромаг-
нитной совместимости и т. п.
14
Глава 1. Печатные платы в цифровых системах
Не определено Нет данных
Более 200 МГц
8%
9%
41%
25°/о
Менее 50 МГц
Рис. 1.1. Распределение
проектируемых печатных плат
по частотному диапазону
на начало 2000 г.
151-200 МГц
101-150 МГц<Й'%,1
Повышение частот приводит к проявлению «паразитных» параметров в то-
пологических элементах печатных плат (проводниках, экранах, шинах питания),
а также в компонентах (индуктивность выводов и т. п.), устанавливаемых
на платы. Кроме этого, работа цифровых микросхем на повышенных частотах
имеет определенные особенности, которые сказываются на конструкции
печатной платы. На системном уровне повышенное быстродействие требу-
ет учета влияния конструкции платы и особенностей передачи сигнала в ней
на общие показатели системы.
Важным фактором, подтверждающим необходимость освоения методов
проектирования печатных плат повышенного быстродействия, является не-
прерывное увеличение доли цифровой техники и увеличение ее быстродей-
ствия в суммарном объеме продукции.
По оценкам специалистов [5—7] в бли-
жайшие годы до 90 % печатных плат бу-
дут создаваться для цифровых систем по-
вышенного быстродействия. Причем но-
менклатура продукции занимает огром-
ный спектр — от мобильных телефонов
до уникальных изделий специального
назначения. Распределение проектиру-
емых плат по частотному диапазону на
начало 2000 года представлено на
рис. 1.1, из которого видно, что доля вы-
сокочастотных плат к этому времени уже
составляла примерно 50 %, и она непре-
рывно растет.
Повышению быстродействия способствует применение новых конструк-
торско-технологических направлений, а именно — новых конструкций кор-
пусов интегральных микросхем, увеличение числа выводов на один корпус,
применение технологии монтажа на поверхность и миниатюризации ком-
понентов [8—12, 46]. Согласно прогнозу [13], к 2006 году число выводов ком-
понентов должно возрасти до 1200, а шаг выводов должен стать 0,5—0,1 мм.
При этом увеличивается плотность монтажа на плате, что, кроме техноло-
гических трудностей, определяет усложнение задач, связанных с проблемой
целостности сигнала и электромагнитной совместимости (ЭМС).
Перечислим некоторые основные задачи, которые возникают при проек-
тировании печатных плат для быстродействующей цифровой аппаратуры:
• минимизация перекрестных помех;
• минимизация помех отражения;
• устранение помех по шинам питания;
• устранение «отрыва» заземления цифровых микросхем;
• обеспечение минимальной системной задержки;
• обеспечение требований ЭМС и другие.
Эти задачи требуют рассмотрения процессов и явлений, существенным
образом влияющих на деградацию цифрового сигнала. При длительности
51-100 МГц
1.1. Тенденция развития электронных средств...
15
фронта цифрового сигнала 1 нс и менее необходимо комплексное решение
этих и ряда других задач. В противном случае у разработчика печатных плат
практически нет никаких шансов на успех. Конечным результатом решения
этих задач является рациональная топология и конструкция печатной пла-
ты, а также компоновка печатного узла (электронного модуля).
Следует отметить еще два важных момента. Во-первых, проектирование
высокоскоростных печатных плат следует рассматривать как часть комплек-
сного этапа проектирования печатного узла, при котором только совмест-
ное рассмотрение схемотехнических, конструкторских и технологических
аспектов создания печатного узла позволит достичь успеха.
В-вторых, необходимо иметь в виду, что печатный узел является важнейшей
сборочной единицей электронной аппаратуры, от которой зависит качество
функционирования конечного продукта. Чем более выверены и обоснова-
ны будут решения на стадии проектирования, тем короче и дешевле будет этап
экспериментальной отработки, и тем быстрее изделие появится на рынке.
В условиях жесткой конкурентной борьбы этот фактор имеет очень большое
значение.
Разработка топологии печатных плат ведется с помощью тех или иных
систем автоматизации проектирования (САПР). Алгоритмы трассировки не-
прерывно совершенствуются, но для многих САПР топологические задачи
оторваны от задач анализа прохождения сигнала по линиям передачи в со-
ставе платы и оценки качества функционирования печатного узла. Даже если
подобные процедуры включены в состав наиболее продвинутых САПР, ал-
горитмы и суть выполняемых задач, как правило, скрыты от пользователя,
что не позволяет судить о качестве решаемых задач, развивать их и творчес-
ки применять для новых изделий с более высокими параметрами быстродей-
ствия. Пользователь САПР должен понимать, как взаимоувязаны задачи то-
пологического проектирования и другие задачи, основанные на электрофи-
зическом анализе, без решения которых даже идеально разведенная плата
может оказаться неработоспособной.
Место и стратегия проектных решений
Потребность в создании плат высокого быстродействия изменила фило-
софию проектирования. Историческое развитие подходов к принятию про-
ектных решений и состава САПР печатных плат прошло несколько этапов,
которые отражали потребности промышленности и уровень техники на со-
ответствующий период.
Первый этап может характеризоваться состоянием дел до 1980 года, когда
еще проблема создания быстродействующих систем практически не ставилась,
ограничиваясь только отдельными проектами. В этот период трассировка пе-
чатных плат проводилась при достаточно большом шаге координатной сет-
ки, число выводов микросхем было относительно невелико. При разработке
плат основным считалось удовлетворение критериев решения топологичес-
ких задач [14]. Именно на это были ориентированы соответствующие алгоритмы
и программы. Практика создания относительно низко скоростных плат в этот
16
Глава 1. Печатные платы в цифровых системах
период не требовала серьезных доработок и учета электрических и электро-
динамических процессов, происходящих в печатной плате при работе уст-
ройства.
Последующие два десятилетия отмечались бурным развитием цифровой
техники и микроэлектроники во всех приложениях, включая бытовую тех-
нику. Резко возросли скорости обработки информации, совершенствовалась
конструкция корпусов микросхем, многократно увеличилось число их вы-
водов, повысились требования к срокам и стоимости разработки. Конкурен-
ция на рынке достигла такого уровня, что промедление в 6 месяцев может
привести к тому, что продукт окажется неконкурентоспособным. Сложность
проектирования печатных плат возросла настолько, что специалист уже не
мог опираться на интуитивные решения, основанные на прежнем опыте раз-
работки.
Повышение быстродействия требовало представлять плату как некото-
рый распределенный элемент электрической схемы, который во многом опре-
деляет ее функционирование. На основе рассмотрения отдельных процессов
и явлений были разработаны проектные нормы и решения, которые служи-
ли рекомендациями при создании плат. Эти правила формулировались в кон-
структорско-технологических понятиях (например, «длина проводника не
более ...»), что определяло разрыв между функциональными требованиями
и качеством конечного продукта.
Совершенствование САПР, требования к сокращению сроков проекти-
рования заставили развивать подходы, основанные на анализе виртуально-
го прототипа и верификации проектных решений [7, 15—17]. Тем не менее,
в большинстве подходов топологическое проектирование было отделено от
электрического моделирования, что требовало взаимодействия специалис-
тов различного профиля, передачи данных из одного программного продукта
в другой. В конечном итоге это усложняло процесс проектирования.
В настоящее время при создании быстродействующих плат на первое место
выходят требования к помехозащищенности платы и ее электрическим па-
раметрам. Именно электрические параметры и характеристики подлежат ве-
рификации, что проявляется в новых глобальных оценках конструкции пла-
ты, а именно:
• задержка в трассе предпочтительней ее длины;
• уровень перекрестных помех предпочтительней расстояния между про-
водниками;
• применение дифференциальных пар предпочтительней, чем одиноч-
ных линий;
• минимизация индуктивностей цепей питания, возвратных токов и за-
земления предпочтительней топологических рекомендаций по их про-
ектированию.
Историческое развитие подходов к проектированию печатных плат на-
глядно представлено на рис. 1.2.
Процесс моделирования интерактивный и охватывает все стадии созда-
ния печатного узла: схемотехническое проектирование, конструирование
1.1. Тенденция развития электронных средств...
17
Физические
параметры
Временные
параметры
Электрические
параметры
Топологические
нормы и —
правила
Электроди-
намические
параметры
Печатная
плата
Технологические
нормы и правила
Рис. 1.2. Развитие норм и правил
проектирования быстродействующих
печатных плат
и технология. Чем на более
ранних стадиях будет приня-
то решение по удовлетворе-
нию тех или иных требова-
ний целостности сигнала и
электромагнитной совмести-
мости, тем меньше будут ито-
говые затраты и сроки созда-
ния аппаратуры. Эта концеп-
ция носит название «сдвиг
влево». Для реализации этой
концепции разработчик пе-
чатных плат должен обла-
дать знаниями о процессах и
явлениях, относящихся к более
ранним стадиям создания ап-
паратуры, например, к кон-
цептуальным и схемотехни-
ческим аспектам цифровой обработки информации, механизмах работы циф-
ровых интегральных микросхем и т. п. Конечно, конструктор не должен
заменять соответствующих специалистов, но он обязан квалифицированно
взаимодействовать с ними.
Тенденции в конструкциях плат
Конец XX и начало XXI века ознаменовались значительными достижени-
ями в области информационных технологий. Персональные компьютеры,
мобильные телефоны, автомобильная электроника и многие другие изделия
массового спроса придали ускорение новым методам создания печатных плат
и печатных узлов. Здесь, прежде всего, следует отметить монтаж на поверх-
ность, создание новых видов корпусов для интегральных схем, а также но-
вых технологических приемов изготовления печатных плат: создание мик-
ропереходов, сверхплотный монтаж, применение встроенных пассивных
элементов и др. Зарождаясь как уникальные технологии, они со временем
стали доступны для массового производства. Производители технологичес-
кого оборудования обеспечили поддержку этим процессам, и в настоящее
время проектировщик плат должен опираться на новые технологические
нормы [8, 10]. Наглядно прогресс в области создания печатных плат пред-
ставлен на рис. 1.3.
Соответствующие изменения происходят в развитии интегральных мик-
росхем. Уменьшение размеров элементов полупроводниковых структур при-
вело к повышению быстродействия микросхем, увеличению их степени ин-
теграции и повышению функциональной сложности. При этом резко воз-
росло число выводов у корпусов, и видоизменилась их конструкция. Все это
сказывается как на топологических аспектах проектирования плат, так и на
их электрических характеристиках.
18
Глава 1. Печатные платы в цифровых системах
Рис. 1.3. Конструкции печатных плат:
а — начало 70-х годов прошлого века;
б — современные решения
Наглядное представление о направлениях развития технологии печатных
плат дает рис. 1.4.
Одним из важных направлений в создании плат для цифровых электронных
средств является реализация протоколов для высокоскоростной передачи дан-
ных: 3 Гбит/с с увеличением до 10 Гбит/с [11, 18, 19]. При таких скоростях
передачи информации добавляются новые задачи: учет дрожания фронтов
сигнала (джиттер), разности появления выходных сигналов на выводах мик-
росхемы (расфазировка), учет потерь в проводниках и диэлектрике платы,
применение дифференциальной передачи сигналов.
Повышение быстродействия диктуется также и развитием архитектуры
асинхронной обработки информации. Такова новая технология третьего по-
коления (3GIO) фирмы Intel, которая предполагается как стандартная для
PCI Express™. В ней применена последовательная асинхронная обработка как
1990
2000
2010
Рис. 1.4. Ускорение развития технологий печатных плат
1.1. Тенденция развития электронных средств...
19
альтернатива классической параллельной синхронной. Она требует работы
на частотах более 500 МГц. На рис. 1.5 представлены данные для ведущих
мировых производителей, показывающие распределение печатных плат по
быстродействию.
Такие частоты требуют более тонких подходов к созданию моделей и их
верификации, а основным типом линии передачи сигналов на плате в этом
случае становится дифференциальная пара.
Технология создания печатных плат опирается на использование слоис-
тых структур и металлизированных сквозных, слепых и глухих отверстий [8,
20]. Современные достижения в области корпусирования интегральных мик-
росхем, а именно, создание корпусов с большим числом выводов — с мат-
рицей шариковых выводов (BGA) [12], многовыводных микросхем с разме-
рами не более 125 % от размеров кристалла (CSP) — стимулировали разви-
тие встроенных слоистых структур и микропереходов (рис. 1.6) [8, 21, 22].
Рис. 1.5. Процентное распределение высокоскоростных плат для цифровых
систем по классической (синхронная параллельная) технологии
и технологии 3GIO
Матрица шариковых выводов
с большим числом выводов
Рис. 1.6. Обеспечение межсоединений с высокой плотностью за счет
применения дополнительных многослойных структур и микропереходов
20
Глава 1. Печатные платы в цифровых системах
Микропереходы позволили увеличить плотность печатного монтажа.
Особенно важно то, что уменьшение диаметра отверстия позволило сместить
его на контактную площадку. Это устранило проводники между контактной
площадкой для установки микросхем и контактной площадкой металлизи-
рованного отверстия (рис. 1.7) [11], как это выполнялось по традиционной
технологии. Устранение проводников не только увеличивает плотность мон-
тажа, но и уменьшает индуктивность соединения, что положительно сказы-
вается на целостности сигнала.
Стремление обеспечить целостность сигнала в гигагерцовом час-
тотном диапазоне приводит конструкторов и технологов к принципиально
новым решениям. Примером является печатная плата с экранированными
линиями передачи [26]. Для создания линии передачи используются три слоя
(рис. 1.8), на которых формируются верхняя часть экрана, сигнальные про-
водники и нижняя часть экрана. Лазерной технологией формируются канавки,
разделяющие сигнальные проводники, которые далее заполняются медью.
Это обеспечивает полностью экранированную линию передачи в составе
платы. Для обеспечения типового волнового сопротивления глубина канавки
должна быть 300...500 мкм, а минимальная ширина линии 0,7 мм. Для срав-
нения укажем, что типовая глубина микроперехода составляет 50... 100 мкм.
Не обсуждая технологические особенности получения подобных экраниро-
ванных линий, можно отметить ее очень высокие показатели в части поме-
хозащищенности.
При выборе материала следует учитывать, что при скорости передачи ин-
формации 1 Гбит/с и более тангенс угла диэлектрических потерь материала
основания платы должен быть минимальным (желательно не более 0,001).
Для этих целей применяют новые материалы, например, Rogers.
Еще одним перспективным направлением в проектировании печатных
плат является применение встроенных в толщу платы пассивных компонентов
(резисторов, конденсаторов, индуктивностей), которые используются, на-
пример, для согласования линий (резисторы) или развязки (конденсаторы).
Рис. 1.7. Переходные отверстия
вне контактных площадок (слева),
выполненные по традиционной
технологии, микропереходы,
встроенные в контактные
площадки (справа)
Экран
Рис. 1.8. Экранированная линия пе-
редачи в составе печатной
платы
1.1. Тенденция развития электронных средств...
21
Обобщая, можно отметить следующие основные моменты.
❖ Цифровая техника развивается в сторону повышения скорости пере-
дачи и обработки информации как за счет увеличения быстродействия
элементной базы, так и за счет совершенствования архитектуры вы-
числительных комплексов.
♦ ♦♦ Успехи в развитии микроэлектроники и корпусировании кристаллов
микросхем привели к созданию компонентов с большим числом вы-
водов, высокой степени интеграции и высоким быстродействием, что
непосредственно влияет на топологию и электрические параметры пе-
чатных плат и печатных узлов.
❖ Высокое быстродействие печатных узлов требует решения новых за-
дач по его обеспечению, препятствием для которого являются элект-
рические параметры платы и корпусов микросхем.
❖ Повышению конкурентоспособности продукции и снижению стоимо-
сти разработки способствует внедрение концепции «сдвига влево» работ
по комплексному обеспечению быстродействия печатных плат.
❖ Проектирование печатных плат для цифровых систем высокого быс-
тродействия должно базироваться на адекватных моделях, учитываю-
щих электрофизические процессы в плате, влияющие на качество про-
хождения сигнала.
❖ Разработчик печатных плат должен обладать расширенными знания-
ми об этапах проектирования аппаратуры, предшествующих разработке
платы и следующих за ней, для возможно более полного учета элект-
рофизических параметров и характеристик компонентов и материа-
лов, формирующих среду передачи сигналов.
1.1.2. Стратегия разработки и верификации плат
Традиционные подходы к созданию электронных средств предполагали
получение на заключительных этапах создания аппаратуры опытного образца
и его отладку. В современных условиях такой подход не может быть принят,
поскольку он слишком дорог и требует значительного времени, из-за чего
продукция на рынок будет попадать с большим опозданием. Выходом из этой
ситуации является применение верификации проекта с использованием
виртуального прототипа. Под верификацией понимают установление рабо-
тоспособности технического средства на его возможно полной модели (вир-
туальном прототипе) с использованием программных средств. Успешное
выполнение этой стадии возможно только при тесном взаимодействии в
едином цикле разработки специалистов, отвечающих за системо- и схемо-
техническую часть проекта, и специалистов, разрабатывающих топологию
печатной платы и конструкцию печатного узла [23-25].
Верификация проектных решений имеет существенное значение по сле-
дующим основным причинам:
• многие решения по конструкции быстродействующих плат не могут
быть приняты на основе интуиции и прошлого опыта;
22
Глава 1. Печатные платы в цифровых системах
• для обоснования проекта платы требуются определенные знания в об-
ласти схемотехники, теоретических основ электротехники и электро-
динамики, которыми не всегда владеют разработчики плат;
• для быстродействующих плат это, практически, единственный способ
проверить качество работы проектируемого узла до выполнения фи-
зической модели и внести соответствующие коррективы, если они
необходимы.
Процедура верификации становится не только инженерной проблемой,
но и проблемой бизнеса. Нельзя быть на рынке в числе первых, но с нера-
ботающей и не сертифицированной аппаратурой. Совершенство моделей, за-
ложенных в виртуальный прототип, и программно-инструментальных средств
позволяет получить в процессе верификации результаты, которые максималь-
но приближены к реальным. Ясно, что в данном случае процесс создания
аппаратуры идет с максимальной скоростью и с минимальной стоимостью.
Но при этом встает ряд важнейших вопросов: какие модели использовать?
насколько они обоснованы? какова область их применения? Ниже на эти воп-
росы будут даны ответы, которые соответствуют современному уровню по-
нимания электродинамических процессов, происходящих в быстродейству-
ющих печатных платах.
Уровни верификации могут быть различны: на уровне интегральной мик-
росхемы, на уровне печатной платы и печатного узла, на уровне блоков, си-
стемы и т. д. Естественно сложность моделей при возрастании иерархичес-
кого уровня увеличивается, так же как и необходимые вычислительные ре-
сурсы. В контексте книги речь идет только о моделях на уровне печатной платы
и печатного узла.
Физический прототип
Основными этапами создания печатного узла являются концептуальное
схемотехническое проектирование, конструкторско-топологическое и тех-
нологическое проектирование, а также его производство. На этапе концеп-
туальной проработки формулируются требования к основным параметрам
изделия, его архитектуре и конструкции. На этапе схемотехнического про-
ектирования разрабатывается принципиальная электрическая схема узла,
проводятся необходимые расчеты электрических и тепловых режимов, оп-
ределяются временные параметры работы цифрового узла. На этапе конст-
рукторско-топологического проектирования решаются задачи размещения
компонентов и трассировки печатных проводников, расположения шин
питания и заземления. Как отмечалось выше, для быстродействующих плат
критерием качества выполнения топологических задач является удовлетво-
рение электрическим требованиям к топологии. В свою очередь, эти требо-
вания формируются исходя из особенностей функционирования узла. Да-
лее изделие запускается в производство. После прохождения сертификаци-
онных испытаний оно поступает на рынок.
При «ручном» методе проектирования размещение и трассировка выпол-
нялись без участия САПР, опираясь только на опыт и знания разработчика.
1.1. Тенденция развития электронных средств...
23
Рис. 1.9. Исторически ранняя верификация базировалась на физическом
прототипе
При этом обязательно требовалось создавать физическую модель (опытный
образец), на которой отлаживались схемные решения и конструкция платы.
Опытный образец продукции служил фактически физическим прототипом,
на котором проводилась верификация (рис. 1.9).
Выявленные в процессе такой верификации ошибки подлежали исправ-
лению либо простыми приемами (например, установкой перемычек), либо из-
менениями в принципиальной схеме. В худшем случае требовались существен-
ные изменения, приводящие к полному пересмотру проекта. Как правило,
требовалось многократное тестирование прототипа для выявления всех недо-
статков. В ряде случаев время на отладку узла было соизмеримо со временем
разработки его первоначального варианта. Многократное повторение цикла
«изготовление прототипа — обнаружение проблемы — решение проблемы —
изготовление нового прототипа» затягивало разработку, а для быстродейству-
ющих плат такой подход вообще оказался непригодным. Это объясняется тем,
что исправления, внесенные в прототип, по своим электрофизическим пара-
метрам не будут соответствовать конечному продукту. Например, навесная про-
волочная перемычка в многослойной печатной плате, при помощи которой
удалось устранить некоторый дефект, имеет электрофизические параметры,
совершенно отличные от печатного проводника, внесенного в документацию
вместо этой перемычки.
В отмеченные выше исторические периоды произошло поэтапное внедрение
САПР. Эти системы охватывают в настоящее время стадии схемотехнического
и топологического проектирования, технологической подготовки производ-
ства и изготовления, а также инженерных расчетов (в англоязычной лите-
ратуре: Computer-Aided Design — CAD/Computer-Aided Manufacturinge — САМ/
Computer-Aided Engineering — CAE), что позволило объединить все этапы в
единое направление автоматизации проектирования электронной аппара-
туры (Electronic Design Automation — EDA).
Достижения в области микроминиатюризации, повышение тактовых
частот и сокращение фронтов сигналов привело к вычленению из общих задач
верификации проектных решений таких направлений, как целостность сиг-
нала, тайминг, электромагнитная совместимость. Это разделение вызвано,
с одной стороны, возросшей сложностью получения комплексной всеобъ-
емлющей модели, а с другой — тем, что при решении отдельных задач уда-
ется обеспечить желаемое качество изделия более экономными средствами.
Рассмотрим возможные ситуации, связанные с влиянием времени, необхо-
димого для отладки прототипа на время появления продукта на рынке (рис. 1.10).
24
Глава 1. Печатные платы в цифровых системах
Рис. 1.10. Взаимосвязь времени выхода на рынок и отладки физического
прототипа:
7 — время выхода новой продукции на рынок; 2 — время, необходимое для
отладки прототипа; 3 — время, отводимое для других стадий создания изделия;
4 — ситуация, при которой время отладки прототипа диктует сроки появления
продукции на рынке; 5 — ситуация, при которой прототип не может быть
отлажен, что препятствует выходу продукции на рынок
С одной стороны, усложнение печатных плат, повышение частот, приме-
нение больших интегральных схем привело к увеличению сроков создания фи-
зических прототипов и их отладки, что характеризуется прямой 2. С другой
стороны, конкурентная борьба на мировом рынке требует постоянного сокра-
щения сроков появления на нем новой продукции (прямая /). В настоящее
время этот срок для большинства изделий широкого применения составляет
5...6 месяцев. Поэтому время, которое отводится на другие этапы создания
печатных узлов, непрерывно сокращается (зона 5). Уже в настоящее время на-
ступает ситуация, когда создание физического прототипа будет стратегичес-
ки невыгодным, поскольку либо сроки его отладки будут сдерживать появле-
ние продукции на рынке (ситуация 4), либо прототип вообще не может быть
отлажен, и продукция не поступит на рынок (ситуация 5).
Почему может сложиться ситуация, при которой физический прототип вы-
сокочастотного печатного узла не может быть отлажен? Современная микро-
электронная аппаратура реализуется на БИС, которые выполнены в корпусах
с большим (иногда до 1000 и более) числом выводов на многослойных печат-
ных платах. Учитывая широкий диапазон частот, который типичен для таких
узлов, любой контрольный вывод служит антенной и вносит искажения в по-
1.1. Тенденция развития электронных средств...
25
казания тестирующей аппаратуры. Высокочастотный сигнал, проходящий по
проводникам во внутренних слоях многослойной печатной платы, вообще не
доступен для контроля. Кроме этого, даже если удастся провести измерения и
по их результатам потребуется внести изменения в физический прототип, то в
большинстве случаев эта процедура не даст должного результата. Это объясня-
ется тем, что после отладки прототипа соответствующие изменения будут вне-
сены в конструкторскую документацию и реализованы в том виде и в той тех-
нологии, которая принята для конечного продукта. Поэтому нет никакой га-
рантии, что после изготовления нового дорогостоящего физического прототипа
МПП не придется вносить новых изменений. Чем выше быстродействие узла,
тем безнадежней может оказаться ситуация бесконечного хождения по кругу
«прототип — отладка — новый прототип — отладка — новый прототип — ...».
Таким образом, для высокоскоростных печатных узлов применение вир-
туального прототипа позволяет устранить противоречие между желаемой ско-
ростью поступления изделия на рынок и длительностью отладки прототи-
па. Кроме этого, именно виртуальный прототип позволяет реализовать упо-
мянутую выше концепцию «сдвига влево».
Верификация в проектировании плат
Процесс верификации позволяет выбрать рациональное техническое
решение. Если для верификации используется максимально полная модель
объекта, то говорят о параметрической верификации. Для сложных объектов, к
которым относятся печатная плата или печатный узел, модель, лежащая в
основе параметрической верификации, может иметь чрезвычайную слож-
ность, а во многих случаях она не может быть получена. Кроме этого, ком-
плексная модель требует для анализа весьма больших вычислительных ре-
сурсов. Поэтому рационально упростить модель объекта, например, рассмот-
рев раздельно тепловые и электродинамические процессы в печатном узле
и печатной плате (при этом следует быть уверенным в слабом взаимодействии
или полной независимости этих процессов). Для быстродействующих циф-
ровых узлов, реализованных на печатных платах, целесообразно использо-
вать следующие типы верификации:
• параметрическая;
• временная;
• целостности сигнала,
• электромагнитной совместимости.
Рассмотрим их более детально.
Параметрическая верификация
Параметрическая верификация предполагает установление рабо-
тоспособности устройства с учетом всех его схемотехнических и кон-
структорских параметров. Особенность процедуры верификации в данном
случае заключается в комплексной модели, которая включает в себя:
• модель электрической схемы,
• модель конструкции изделия.
26
Глава 1. Печатные платы в цифровых системах
Построение полной электродинамической модели конструкции изделия
представляет весьма сложную задачу. Поэтому в ряде случаев ограничива-
ются только моделью электрической схемы, которая используется на этапе
автоматизированного схемотехнического проектирования. При этом абст-
рагируются от физической конструкторской реализации этой схемы, что
вносит существенные погрешности в результаты выполнения этапа парамет-
рической верификации для быстродействующих печатных узлов.
Следует иметь в виду, что чем выше частотный диапазон сигналов, обра-
батываемых проектируемым устройством, тем важней иметь его адекватную
модель конструкции.
Пример. При моделировании электрической схемы сложно учесть емкости электри-
ческих соединений между ее компонентами. Типичный пример: невозможно учесть ем-
кость линии передачи, не зная ее реальной длины, которая выявляется только после эта-
па топологического проектирования. Индуктивность шины питания невозможно учесть
на этапе моделирования схемы, поскольку, как и в первом случае, неизвестны конфигу-
рация шины, ее длина, ширина и другие параметры, от которых зависит индуктивность.
Поэтому комплексная модель не может быть получена на этапе схемотехнического про-
ектирования. Кроме этого, еще ряд параметров конструкции принципиально невозмож-
но учесть на этапе моделирования схемы.
Полная модель конструкции платы может быть
получена только после завершения всех конструктор-
ских работ при создании аппаратуры.
Рассмотрим фрагмент цифрового узла (рис. 1.11),
конструкция которого показана на рис. 1.12. В дан-
ном случае печатная плата расположена в непосред-
ственной близости от металлического корпуса.
Попытаемся составить модель данного фрагмен-
та конструкции для выполнения этапа параметри-
ческой верификации.
проводник
Рис. 1.11. Фрагмент
принципиальной схемы
цифрового узла
Рис. 1.12. Фрагмент конструкции цифрового устройства
1.1. Тенденция развития электронных средств...
27
Модель фрагмента принципиальной схемы включает в себя на данном эта-
пе только модели элементов интегральных схем. Полнота модели сейчас не
обсуждается.
Эта модель дополняется идеальными моделями элементов, которые фор-
мируются в реальной конструкции. В данном случае такими параметрами яв-
ляются:
1. Электрическая суммарная емкость линии CTL = Сп + С12.
2. Емкость Cmnt монтажа, емкость Ц входа и Со выхода микросхемы. Ти-
повое значение емкости монтажа составляет 3...5 пФ на одну пайку при
качественном монтаже, а входные и выходные емкости приводятся в
технических условиях на микросхемы.
3. Индуктивность шины питания LSB может быть определена после раз-
работки конструкции платы и всего устройства.
4. Индуктивность возвратного пути для тока и шины заземления £GND,
определяющая полное сопротивление шины заземления. Для радио-
электронной аппаратуры предъявляются очень жесткие требования по
значению этого сопротивления, оно должно составлять не более, чем
несколько десятков мОм. Увеличение сопротивления заземления может
быть вызвано коррозией, ослаблением винтового соединения, исполь-
зованием тонкого провода и т. д.
В том случае, если корпус изделия выполнен из стали, то его магнитные
свойства изменят показатели среды распространения сигнала, и линии пере-
дачи, расположенные рядом со стенкой корпуса, будут иметь параметры, от-
личающиеся от параметров линий, расположенных в центре платы.
С учетом отмеченных факторов, полная модель будет выглядеть, как по-
казано на рис. 1.13.
Даже при значительных упрощениях, принятых в примере, видно разли-
чие между полной моделью и моделью электрической схемы. Комплексная мо-
дель значительно превосходит по сложности модель принципиальной схемы,
но ряд ее параметров может быть получен только после разработки конструкции.
Во многих случаях точный учет
Рис. 1.13. Полная модель фрагмента
цифрового узла
всех электрических параметров кон-
струкции невозможен, поэтому ог-
раничиваются приближенными мо-
делями, экспериментальными дан-
ными, эвристическими решениями
и пр. Практически во всех случаях
приходится использовать другие ти-
пы верификации.
Временная верификация
Временная верификация явля-
ется частным случаем параметри-
ческой верификации. Она приме-
нима к цифровым узлам.
28
Глава 1. Печатные платы в цифровых системах
Целью временной верификации является установление временных соот-
ношений между событиями срабатывания микросхем в системе. При про-
ектировании цифровых систем составляются временные диаграммы, кото-
рые жестко связаны с осью времени. На этой оси фиксируются «события сра-
батывания» логических элементов. Вся логика работы любого цифрового
устройства жестко и однозначно увязана с временными диаграммами. При
этом все интервалы времени также очень точно определены. Совокупность
задач при проектировании платы, решение которых направлено на поддер-
жание заданных временных соотношений в цифровых схемах, называется тай-
минг. Таким образом, основная цель временной верификации заключается
в решении задач тайминга [27—29].
Тайминг отражает цифровую суть информационного сигнала, в отличие
от проблемы целостности сигнала, при которой к цифровому сигналу при-
меняется аналоговое рассмотрение. Типичное рассмотрение задач таймин-
га ассоциируется с выбором элементной базы, логическим проектировани-
ем и задержкой сигнала в межсоединениях, в частности, выполненных на пе-
чатных платах. К сожалению, проектировщик электронных средств часто
может видеть только малую часть всех факторов, которые нарушают времен-
ные соотношения в системе (рис. 1.14).
Если временные параметры элементной базы известны на концептуаль-
ном и схемотехническом уровне, а логическое проектирование оперирует аб-
страктными моделями, то задержки в межсоединениях становятся известными
на постопологическом этапе. Поэтому виртуальный прототип является наи-
лучшим вариантом для определения проблем тайминга и поиска путей уст-
ранения возникших нарушений временных соотношений в системе.
Для решения задач тайминга могут быть использованы различные инст-
рументальные средства, но разработчик должен понимать суть проблемы и
видеть многообразие взаимоувязанных факторов, влияющих на тайминг.
В качестве примера рассмотрим фрагмент цифрового устройства (рис. 1.15),
содержащий схему совпадения — базовый вентиль 2И-НЕ.
При работе фрагмента схемы логический «О» на выходе Y микросхемы-
нагрузки появляется, когда на оба входа XI и XI поданы логические «1». Важно,
Рис. 1.14. Распределение времен задержек распространения сигнала по различным эта-
пам создания аппаратуры
1.1. Тенденция развития электронных средств...
29
Рис. 1.15. Фрагмент схемы цифрового
устройства, содержащей схему Рис. 1.16. Временная диаграмма
совпадения работы схемы совпадения
чтобы приход этих сигналов был в один и тот же момент времени. В против-
ном случае на выходе микросхемы-нагрузки появится логическая «1». Это,
конечно, будет ошибкой, в результате которой работа цифровой системы будет
нарушена.
Проведем анализ работы схемы. Для этого рассмотрим временную диаг-
рамму (рис. 1.16) работы схемы совпадения.
Предположим, при выполнении топологии мы получили /2 > 1{. Примем,
что скорость распространения сигнала в линиях передачи на печатной пла-
те одинакова. Тогда понятно, что при синхронном выходе сигналов с выхо-
дов драйверов получим /2 > ина вход нагрузки сигналы приходят не од-
новременно, т. е. имеет место расфазировка. Таким образом, только в момент
t2 (рис. 1.16) на выходе возникает логический «О», а в интервал времени от tx
до /2 на входе XI присутствует логическая «1», на входе XI присутствует ло-
гический «О» и на выходе — логический «О». Следовательно, во временном
интервале (/2 — /}) на выходе микросхемы-нагрузки присутствует логический
сигнал, который может рассматриваться как помеха (на рисунке отмечена
серым цветом) длительностью А/ = /2 — tv
Таким образом, топологические особенности конструкции платы обус-
ловили более позднее срабатывание микросхемы-нагрузки, чем предпола-
галось на этапе логического проектирования. Результатом может быть сбой
в работе аппаратуры.
Аналогичный результат может быть получен при одинаковой длине про-
водников, но при различной скорости распространения сигнала в них, ко-
торая определяется наличием диэлектрических и магнитных материалов в кон-
струкции линий передачи. Эта ситуация типична для случая, когда одна линия
расположена в наружном слое, а другая — во внутреннем слое многослой-
ной печатной платы.
Рассмотренный пример условный. В реальной ситуации необходимо до-
полнительно учитывать более тонкие механизмы нарушения временных со-
отношений. Временная верификация, которая оперирует точными моделями
30
Глава 1. Печатные платы в цифровых системах
линий и микросхем, позволяет оценить с повышенной точностью все пара-
метры тайминга в системе. Следует обратить внимание, что этот пример ил-
люстрирует отмеченную выше новую парадигму проектирования: «задание
задержек предпочтительней заданию длин проводников».
В результате выполнения этапа временной верификации устанавливает-
ся работоспособность изделия, и при необходимости вносятся коррективы
в предыдущие этапы проектирования. Наиболее дешевый способ изменения
конструкции - корректировка топологии, дороже — смена проектных норм,
и наименее предпочтительный путь — это замена элементной базы.
Верификация целостности сигнала и ЭМС
Разработчики цифровых систем оперируют идеализированным представле-
нием цифрового сигнала: либо прямоугольной, либо трапецеидальной формы.
В реальном мире нет идеальных сигналов, а из-за ряда причин цифровой сиг-
нал искажается по форме и становится ближе к аналоговому сигналу (рис. 1.17).
Обеспечение целостности сигнала сводится к мерам, которые приближают по
форме реальный сигнал к идеальному.
Причины, вызывающие искажения сигнала, многочисленны и могут быть
вызваны перекрестными помехами, отражениями от несогласованных нагру-
зок и т. п. В последующих главах вопросы целостности сигнала будут рассмот-
рены более детально. Верификация целостности сигнала позволяет интег-
рировано проанализировать влияние всех значимых причин на форму сиг-
нала, выявить факторы недопустимых искажений и реализовать меры по их
устранению. При анализе целостности сигнала могут быть одновременно ре-
шены задачи тайминга.
Устаревшая стратегия проектирования, использующая физический
прототип, была основана на экспериментальном определении иска-
жений цифрового сигнала и поиске путей их устранения. Как отме-
чалось ранее, это приводило к длительным циклам создания прото-
типов, его исследования и переделок.
По мере развития методов анализа и средств автоматизации проектирова-
ния, удалось часть задач верификации вычленить в тайминг и целостность
сигнала на уровне печатного узла и печатной платы, создавая для этих целей
виртуальный прототип печатного узла (рис. 1.18) [30]. Очевидно, что это су-
Рис. 1.17. Реальный сигнал в цифровой системе имеет аналоговый вид
1. 1. Тенденция развития электронных средств...
31
Корректировка схемы
Рис. 1.18. Виртуальный прототип печатного узла и печатной платы
в цикле создания изделия
ся важной при отладке устройств в целом. Эта ситуация типична для настоя-
щего времени.
В будущем по мере развития знаний в сфере описания электродинами-
ческих процессов в сложных печатных платах, увеличения мощности вычис-
лительных средств удастся решить задачи параметрической верификации и
заменить физический прототип виртуальным (рис. 1.19).
Согласно концепции «сдвига влево», т. е. переноса тяжести разработок
на более ранние стадии проектирования, верификация целостности сигна-
ла может не выделяться в отдельный этап, а может интегрироваться в про-
цесс проектирования. Первым шагом в этом направлении является встраи-
вание методов анализа целостности сигнала в процесс топологического про-
ектирования (рис. 1.20). Это позволит вносить коррективы в размещение
компонентов и трассировку непосредственно в ходе проектирования платы.
Дальнейшее развитие состоит в охвате верификацией (задачами целост-
ности сигнала, тайминга и ЭМС) этапов схемотехнического и концептуаль-
ного проектирования (рис. 1.21).
Подобный интегрированный процесс создания электронного оборудова-
ния и печатных узлов, в частности, сокращает обратные связи между стадиями
От этапа
концептуального
проектирования
Корректировка схемы
Рис. 1.19. Виртуальный прототип в цикле создания изделия
Верификация
(виртуальный
прототип)
Разработка
схемы
Топология
Производство
Рис. 1.20. Верификация целостности сигнала интегрированная
в стадию топологического проектирования
32
Глава 1. Печатные платы в цифровых системах
Верификация
Концепция L Р“;Р”?га L Топология L
схемы
Производство
Рис. 1.21. «Сдвиг влево» верификации целостности сигнала
проектирования, что сокращает сроки проектирования и повышает качество
проектных решений.
Обобщая подходы к проектированию печатных плат и печатных узлов, пе-
речислим основные задачи верификации проектных решений, которые да-
лее будут рассмотрены детально. Кроме временной верификации (тайминг)
и верификации целостности сигнала, необходим анализ электромагнитной
совместимости узла, а также симуляция цифровых и аналоговых сигналов.
Вопросы ЭМС должны быть рассмотрены при анализе любой электрон-
ной аппаратуры, поскольку готовое изделие обязательно сертифицируется
на соответствие требованиям ЭМС [31]. Таким образом, верификация про-
ектных решений при создании печатных плат и печатных узлов может быть
представлена в виде, показанном на рис. 1.22.
Раскроем содержание задач анализа и верификации.
Тайминг:
• задержка распространения сигнала в линиях передачи;
• системная задержка из-за влияния емкости и индуктивности печатных
проводников;
• системная задержка, вызванная помехами отражения в линиях передач;
• расфазировка сигналов и джиттер их фронтов.
Целостность сигнала:
• управление волновым сопротивлением линий передач;
• анализ перекрестных помех;
• анализ влияния нагрузки линии передачи;
• влияние «отрыва» заземления при работе цифровых микросхем;
• определение рациональной структуры многослойных печатных плат;
• анализ линий передач в виде дифференциальных пар.
Электромагнитная совместимость:
• уровень помехоэмиссии от печатного узла;
• кондуктивные помехи по шинам питания;
• восприимчивость к излучаемым помехам от внешних источников.
Основными результатами решения этих задач являются:
для концептуальной стадии:
• рекомендации о реализуемости требований технического задания по
быстродействию;
• рекомендации по выбору материалов и технологии изготовления плат
и сборки печатных узлов;
1.2. Элементы цифровой обработки информации
33
Топология
Поведенческое
моделирование
Симулирование аналоговых
и цифровых сигналов
Производство
Рис. 1.22. Задачи верификации при проектировании печатных плат
и печатных узлов
• типы корпусов микросхем;
для стадии схемотехнического проектирования:
• уточнение требований к электрическим параметрам микросхем;
• получение рекомендаций по установке помехоподавляющих и согла-
сующих компонентов;
• получение рекомендаций по выбору корпусов микросхем;
для стадии топологического проектирования:
• выработка топологических норм и рекомендаций для трассировки
платы;
• получение данных для расположения компонентов на плате;
• определение требований к шинам питания и заземления и рекомен-
дации по их расположению;
• определение структуры МПП;
• определение требованиям к экранам и их расположению.
1.2. Элементы цифровой обработки
информации
Для более глубокого понимания влияния электрических параметров пе-
чатных плат на процессы, происходящие в электронных модулях при циф-
ровой обработке информации, проектировщик должен ориентироваться в ба-
зовых понятиях, которые относятся к этой проблеме. Тенденции в этой об-
ласти непосредственно влияют на основные показатели печатных плат.
2 1527
34
Глава 1. Печатные платы в цифровых системах
1.2.1. Цифровые системы и передача сигналов
Одно из стратегических направлений в развитии цифровых систем обра-
ботки информации состоит в увеличении их производительности. Она может
быть увеличена следующими основными методами: за счет повышения сте-
пени интеграции элементной базы; применением быстродействующих интег-
ральных схем, улучшением компиляторов; применением высокопроизводи-
тельной архитектуры; увеличением разрядности шин команд и данных; при-
менением параллельной обработки; увеличением тактовой частоты и другими
методами, которые относятся как к концептуальному и схемотехническому
уровню создания электронных средств, так и к этапам конструкторско-тех-
нологической реализации. Для достижения максимальной производительности
все быстродействующие компоненты системы в идеале должны быть объеди-
нены на одном кристалле. Однако технологические трудности позволяют ис-
пользовать данный подход лишь в достаточно простых случаях. Практически
все электронные средства имеют в своем составе отдельные узлы, и основной
проблемой становится обеспечение связи быстродействующих частей систе-
мы. Поскольку непрерывно повышается быстродействие систем и их частей,
то должна увеличиваться и пропускная способность этих связей. На печатных
платах реализуется большая часть подобных межсоединений, поэтому мето-
ды их проектирования должны учитывать глобальную тенденцию повышения
быстродействия.
Существуют три основных способа повышения пропускной способности со-
единения — увеличение тактовой частоты, увеличение разрядности шин при
параллельной обработке информации и увеличение скорости распространения
сигнала в межсоединениях. На уровне печатной платы увеличение разряднос-
ти усложняет конструкцию платы. Увеличение скорости распространения сигнала
ограничено параметрами применяемых диэлектрических материалов. Повыше-
ние тактовых частот связано с применением быстродействующих микросхем,
которые генерируют сигналы с короткими фронтами. Это существенно расши-
ряет частотный диапазон информационных сигналов, что требует особого вни-
мания крещению задач целостности сигнала и электромагнитной совместимости.
Таким образом, повышение быстродействия приводит к усложнению архитек-
туры и конструкции системы и увеличению затрат на ее реализацию. Для оп-
тимизации конструкции платы необходимо применение верификации работы
системы с целью оценки ее производительности. Параметрами, влияющими на
точность оценки, являются: адекватность модели, точность модели и соответ-
ствие модели области ее использования.
Рассмотрим некоторые показатели цифровых систем более подробно.
Повышение производительности
Для увеличения производительности цифровой системы необходимо про-
извести такие изменения, которые позволяют достичь более высоких частот
синхронизации и/или передачи большего количества данных за один такт.
Основными факторами, которые доступны системному проектировщику на
1.2. Элементы цифровой обработки информации
35
концептуальном уровне для повышения производительности, являются выбор
архитектуры, разрядность шин, скорость передачи данных, стандарт пере-
дачи данных, элементная база, компоновка и топология системы. Эти фак-
торы должны быть сбалансированы для достижения требуемой производи-
тельности в рамках подходящей стоимости, заданного времени разработки
и при допустимом уровне искажений сигнала, восприимчивости к электро-
магнитным возмущениям и помехоэмиссии.
При выборе архитектуры для достижения высокой эффективности необ-
ходимо разбивать системы таким образом, чтобы быстродействующие соеди-
нения применялись только там, где необходимо. Но не следует забывать, что
добавочная производительность имеет цену: большее число контактов, бо-
лее сложная маршрутизация на системной плате и большее количество по-
мех от дополнительного переключения дополнительными драйверами.
Другой способ увеличения пропускной способности соединения состоит
в простом увеличении разрядности и скорости канала связи. Так удвоение раз-
рядности шины дает непосредственное удвоение ее пропускной способнос-
ти, однако при этом требуется большее число контактов на корпусах микро-
схем, большая площадь для их размещения на печатной плате и увеличение
числа линий передач. Дополнительные драйверы занимают дополнительную
площадь на кристаллах, что приводит к рассеиванию большей мощности и
создает больший уровень помех.
Увеличение скорости шины также увеличивает ее пропускную способность,
причем без использования дополнительных физических ресурсов, но дан-
ный подход приводит к значительному усложнению конструкции печатной
платы и ухудшению помеховых характеристик межсоединений, а также к уве-
личению потребляемой мощности.
Развитие шин расширения персонального компьютера иллюстрирует исполь-
зование этих методов для увеличения пропускной способности шины. Перво-
начально шина ISA была 16-разрядной и тактировалась на частоте 8,3 МГц, что
позволяло получить пиковую пропускную способность шины 16,6 Мбит/с. Для
увеличения производительности была разработана 32-разрядная шина PCI с
частотой 33,3 МГц, что позволило получить пиковую пропускную способность
133 Мбит/с. Дальнейшее повышение производительности включало увеличение
разрядности шины до 64 и скорости до 66,6 МГц, таким образом, была дос-
тигнута пиковая производительность в 533 Мбит/с. Но каждое приращение
разрядности и тактовой частоты шины потребовало усложнения топологии меж-
соединений, увеличения площади печатной платы и кристаллов, а также ус-
ложнения системы синхронизации и применения новых типов корпусов. Все
эти недостатки препятствуют повышению производительности при параллель-
ной передаче информации.
Одно из перспективных направлений в архитектуре систем, как отмеча-
лось выше, состоит в переходе на последовательную асинхронную передачу
информации. При этом, естественно, отсутствуют отмеченные выше недо-
статки параллельной передачи, но многократно возрастают частоты. При-
мером может служить протокол последовательной передачи данных USB
э *
36
Глава 1. Печатные платы в цифровых системах
(Universal Serial Bus), который применяется для построения компьютерных
сетей и подключения периферийного оборудования. Конструктивно соеди-
нители USB выполнены одинаково для всех устройств, что облегчает их ком-
мутацию в единую систему. Сокращение номенклатуры кабелей и соедини-
телей для компьютерных приложений является одной из целей внедрения
данного протокола. Через один USB порт может быть запитано до 127 пери-
ферийных устройств, имеющих USB-порты.
Первая версия протокола USB 1.1 предназначается для передачи инфор-
мации со скоростью 12 Мбит/с. Вторая версия USB 2.0 обладает существен-
но большим быстродействием 480 Мбит/с. Повышение быстродействия при-
водит к повышению восприимчивости оборудования и шин передачи данных
к возмущающим электромагнитным воздействиям. Кроме этого, при высоком
быстродействии линии передачи сигналов становятся весьма критичными к
любым неоднородностям в линии. Например, установка ограничителя пере-
напряжения для защиты микросхемы от импульсов тока электростатическо-
го разряда приведет к увеличению емкостной нагрузки и, как следствие, к сни-
жению быстродействия [32].
Распределение мощности
Более высокие уровни интеграции микросхем дают возможность обрабо-
тать большее количество данных за один такт, но это означает, что микро-
схему необходимо обеспечить большей мощностью. Паразитные параметры
корпусов микросхем хотя и очень малы, но, учитывая высокие скорости из-
менения токов и напряжений при переключении, могут вызвать значитель-
ные колебание напряжения относительно номинального напряжения источ-
ника питания или заземления. Кроме этого, из-за специфики работы выход-
ных каскадов цифровых микросхем (особенно серий ТТЛ) в шине питания
возникают кратковременные импульсы тока потребления очень высокой ин-
тенсивности. Высокая скорость изменения тока потребления приводит к па-
дению напряжения на шине питания и снижению напряжения питания во
время переключения микросхемы. При неудачной топологии шины питания
напряжение на выводе питания микросхемы может выйти за минимально до-
пустимые пределы. Устраняют помехи этого вида установкой развязываю-
щих конденсаторов, что влияет на топологию платы. К этим конденсаторам
предъявляются особые требования, которые будут рассмотрены в последу-
ющих разделах.
Топология и нагрузка
Топология проводников на печатной плате играет критическую роль
в определении максимальной частоты сигнала, которая может быть достигну-
та на плате. Самое быстрое соединение — непосредственная кратчайшая связь
двух устройств по линии передачи с контролируемым волновым сопротивлением
и соответствующими схемами согласования для поглощения любых отражений
от нагрузки или источника сигнала. Любое отклонение от этой схемы понизит
максимально достижимую частоту. В частности, когда необходимо связать три
1.2. Элементы цифровой обработки информации
37
или более устройства, невозможно достижение полного согласования, и возни-
кающие отраженные сигналы приведут к снижению быстродействия.
Для создания разветвленных соединений используются два основных при-
ема, которые заключаются в использовании подключения шлейфом или звез-
дой. При подключении шлейфом компоненты располагаются вдоль одной про-
тяженной шины и связываются с ней короткими отводами. Основная задача при
этом состоит в том, чтобы шина и отводы имели минимальную длину. При под-
ключении звездой каждое устройство связано с центральным компонентом
линиями передачи, и ключевой задачей топологии является обеспечение их рав-
ной длины.
После топологии емкостная нагрузка — следующий наиболее критичес-
кий аспект, определяющий скорость соединения. Суммарная емкость линии
передачи, включая емкости металлизированных отверстий и поворотов сиг-
нальных проводников, является главной составляющей емкости нагрузки
драйвера, питающего линию передачи. Кроме этого, каждый вывод компо-
нента увеличивает емкостную нагрузку за счет входной или выходной емкости
кристалла и емкости вывода корпуса микросхемы. Так большое число уст-
ройств (как в подсистемах памяти) приводит к медленному нарастанию фрон-
та сигнала из-за большого времени заряда этих емкостей. Дополнительная
емкостная нагрузка появляется, главным образом, из-за особенностей кон-
струкции корпусов компонентов, качества пайки, наличия устройств элек-
тростатической защиты и состояния высокого входного сопротивления в ряде
серий микросхем.
Для повышения качества сигнала в электрически длинных линиях пере-
дачи и достижения более высоких скоростей должны использоваться согла-
сующие резисторы, предотвращающие нежелательные отражения. Эти ре-
зисторы также могут замедлить передачу сигналов, увеличивая время заря-
да паразитных емкостей, а параллельное согласование на выходе линии
передачи дополнительно увеличивает потребляемую мощность. Любое со-
гласование увеличивает число деталей, стоимость и сложность платы и пе-
чатного узла. Проблема отражений сигнала в длинных линиях передачи и их
согласования будет детально рассмотрена в последующих разделах.
1.2.2. Стандарты передачи сигналов
и семейства логических микросхем
Номенклатура семейств логических микросхем
Цифровая система может успешно работать только в том случае,
если выход драйвера и вход приемника работают на согласованном
нижнем и высоком уровне. В цифровой технике применяются микро-
схемы, в которых логические операции выполняются набором базо-
вых вентилей [33]. Каждый из этих вентилей выполняет вполне опре-
деленную элементарную логическую функцию («И», «НЕ», «ИЛИ» и
т. п.), но схемотехнические решения создания вентилей различны. Они
38
Глава 1. Печатные платы в цифровых системах
определяются технологическими достижениями микроэлектроники, про-
стотой построения схемы и другими причинами. В настоящее время все циф-
ровые логические микросхемы делятся на логические семейства, для кото-
рых характерно общее схемное решение, единая технология и определенные
параметры входных и выходных сигналов. В технической документации ого-
вариваются стандартные параметры сигнала, статическая и динамическая по-
мехоустойчивость и ряд других требований. Каждое семейство микросхем име-
ет большое число разновидностей как по функциональной сложности, так
и по степени интеграции, но в любом случае параметры входа/выхода у все-
го логического семейства одинаковы и совпадают с параметрами элементар-
ного вентиля (за который часто принимают вентиль «2И-НЕ»). Это свойство
удобно использовать для верификации частных решений, оперируя только
простейшим вентилем, что существенно упрощает анализ, делает его более
прозрачным.
В табл. 1.1 представлены основные параметры драйверов, а в табл. 1.2 —
базовых семейств логических интегральных схем [4, 33]. Все микросхемы
можно разделить на два основных класса в зависимости от принятой техно-
логии и схемотехнического решения: биполярные и полевые. Среди бипо-
лярных наибольшее распространение получили схемы на основе транзистор-
Таблица 1.1
Параметры драйверов основных семейств логических интегральных схем
Серия Напряжение питания, Ks, В Выходное напряжение низкого уровня, KOL, В Выходное напряжение высокого уровня, У()И, В Требование к нагрузке
min max min max
ТТЛ 5± 10% 0,4 2,4 Не оговорены
НВТТЛ 3,3 ±10 % 0,4 2,4
GTL 1,2 ± 5 % 0,4 К,-0,4 Ks
HSTL 1,5 ±0,1 0,4 Ks-0,4
ЭСЛ -5,2 ± 5 % -1,810 -1,620 -1,025 -0,880 50 Ом со сме- щением -2 В
ПЭСЛ 5,0 ± 5 % 3,190 3,380 3,975 4,120 50 Ом
НВПЭСЛ 3,3 ± 5 % 1,490 1,680 2,420 50 Ом
LVDS 1,474 50 Ом
Примечание.
ТТЛ — транзисторно-транзисторная логика; НВТТЛ — низковольтная транзис-
торно-транзисторная логика (с пониженным напряжением питания); GTL —
(Gunning transceiver logic) — низковольтная высокоскоростная логика; HSTL —
(High-speed transceiver logic) — высокоскоростная логика; ЭСЛ — эмиттерно-свя-
занная логика на переключателях тока; ПЭСЛ — позитивная эмиттерно-связан-
ная логика; НВПЭСЛ — низковольтная позитивная эмиттерно-связанная логи-
ка; LVDS — низковольтная передача дифференциальных сигналов.
1.2. Элементы цифровой обработки информации
39
Таблица 1.2
Параметры приемников основных семейств логических интегральных микросхем
Серия Напряже- ние пита- ния, в Выходное напряжение низкого уровня, ^оиВ Выходное напряжение высокого уровня, ^он> В Тип линии
min max min max
ТТЛ 5±10 % 0,8 2,0 Одиночная
НВТТЛ 3,3±10 % -о,з 0,8 2,0 rss-o,3 То же
GTL 1,2±5 % Kref-0,05 r„f-0,05 Псевдодиффе- ренциальная
HSTL 1,5±0,1 -о,з 0,05 Kss - 0,3 То же
ЭСЛ -5,2±5 % -1,810 -1,620 -1,025 -0,880 Дифферен- циальная
ПЭСЛ 5,0±5 % 3,190 3,380 3,975 4,120 То же
НВПЭСЛ 3,3±5 % 1,490 1,825 2,235 2,420
LVDS 0,9 1,5 1,1 1,7
Примечание.
Опорное напряжение Kref = 2 Kss/3 для максимального значения входного напряжения
низкого уровня KILmax для микросхем GTL, HSTL и Kref = Kss/2 для минимального значе-
ния входного напряжения высокого уровня К1Нтш.
но-транзисторной логики (ТТЛ-схемы) и микросхемы на переключателях
тока — эмиттерно-связанная логика (ЭСЛ-схемы). Среди микросхем на по-
левых транзисторах базовыми можно считать микросхемы на комплементар-
ной МОП-структуре (КМОП-схемы). В каждом из этих направлений суще-
ствует много разновидностей, которые отличаются быстродействием, уровнем
питающих напряжений, конструкций корпуса и другими параметрами. У про-
ектировщика есть широкий выбор микросхем для реализации концептуальных
идей, но этот выбор должен быть обоснован, в том числе и с позиций про-
ектирования печатной платы и печатного узла. Например, стандартная ТТЛ-
серия была модернизирована путем добавления диодов Шоттки в базовую
схему. Новая разновидность ТТЛШ-схемы отличается более высоким быст-
родействием, но и меньшей помехоустойчивостью. В свою очередь, схемы
ТТЛШ также имеют разновидности, которые отличаются потребляемой мощ-
ностью и быстродействием.
Две цепи, имеющие различные стандарты обработки информации, не могут
работать совместно и требуют устройств по преобразованию стандартов, но
две цепи, использующие один стандарт и построенные на разных семействах
микросхем, могут работать совместно, однако скорость работы будет опре-
деляться самым медленным семейством.
Одним из основных показателей быстродействия микросхемы яв-
ляется длительность фронта /г импульса, типичные значения которо-
го для основных логических семейств составляют: ЭСЛ — 0,7... 1 нс; ТТЛ —
около 10...20 нс; ТТЛШ — 3...5 нс; КМОП — 3...50 нс.
40
Глава 1. Печатные платы в цифровых, системах
Повышение быстродействия микросхем реализуется за счет:
• совершенствования схемного решения вентиля (уменьшения числа
компонентов в вентиле, изменения режимов его работы);
• совершенствования технологии (снижение проектных норм, переход
на технологии менее 0,2—0,3 мкм; снижение геометрических размеров
элементов “автоматически” приводит к повышению быстродействия,
это объясняется снижением паразитных емкостей в полупроводниковой
структуре);
• применения новых материалов для подложек ИМС, например арсе-
нида галлия.
Временные параметры цифровых интегральных схем
Временные параметры характеризуют быстродействие микросхем, которое,
в свою очередь, будет определять и потенциальную производительность системы.
В предыдущих разделах, давая характеристику микросхемам, мы оперировали
термином «быстродействие». Этот показатель определяется временными соот-
ношениями при переключении микросхемы, и, хотя он интуитивно понятен,
необходимо этот параметр определить более четко для получения количественных
оценок для анализа.
Процесс переключения логического
элемента определяется временными па-
раметрами цифрового сигнала, который
представлен на рис. 1.23. Задача разработ-
чика печатных плат состоит в поддержа-
нии целостности (неизменности по фор-
ме) этого сигнала при его распростране-
нии в межсоединениях плат.
Для проектирования печатных плат
интерес представляют следующие пара-
метры сигнала:
• /г — время перехода микросхемы из со-
стояния логического нуля в состояние
логической единицы (длительность
фронта импульса), которое определяется интервалом времени между
моментами достижения уровня 10 и 90 % установившейся амплитуды
импульса;
• — время перехода микросхемы из состояния логической единицы в
состояние логического нуля (длительность спада импульса), которое
определяется интервалом времени между моментами достижения уров-
ня 90 и 10 % установившейся амплитуды импульса;
• td — время задержки распространения сигнала (в общем виде) опреде-
ляется как интервал времени между соответствующими точками формы
сигнала при его распространении в определенной среде, например, в
микросхеме или в линии передачи;
• г — длительность импульса на уровне 0,9;
Рис. 1.23. Временные параметры
элементарного вентиля,
определяющие
быстродействие
1.2. Элементы цифровой обработки информации
41
• — длительность импульса, измеряемая на уровне 0,5 его амплиту-
ды; при работе системы она может быть произвольна; наибольший
интерес представляет минимальная длительность импульса, при ко-
торой сохраняется требуемая работоспособность системы.
Минимально возможная длительность импульса при цифровой обработке
сигнала зависит от многих параметров — применяемых микросхем, потерь
в линиях передачи, помех в линиях передачи. Важно, чтобы при максимальной
тактовой частоте приемник смог различить отдельный импульс и четко от-
личить его от соседнего. В этом случае каждый бит информации будет чет-
ко воспринят. Чем выше частота следования битовых импульсов, тем слож-
нее распознавать их в потоке. Далее эти вопросы будут рассмотрены более
подробно, и на примере контрольной диаграммы будут проиллюстрирова-
ны возможные погрешности в передаче информации при высокой частоте
следования импульсов.
Опираясь на рассмотрен-
ные временные параметры,
можно оценить потенциаль-
ную высшую тактовую часто-
ту, при которой может функ-
ционировать микросхема.
Типовой тактовый цикл tc
представлен на рис. 1.24. При
минимальной длительности
цикла /c(min) определяется
максимальная тактовая час-
тота /тах работы вентиля:
1
^c(min)
max
(1.1)
Минимальная длительность цикла будет при равной минимальной дли-
тельности fw(min) импульсов и интервала между ними (цикл обозначается как
50/50). В свою очередь, принято, что минимальная длительность /w(min) тра-
пецеидального импульса примерно в 5 раз должна превосходить длительность
фронта, т. е. 7w(min) = 5/r. С учетом этого Zc(min) = Ю/г, и максимальная частота
определится по формуле
А»—- (1-2)
Приведем пример. Определим максимальную тактовую частоту для мик-
росхемы с длительностью фронта tx = 1 нс. Согласно формуле (1.2) опреде-
лим максимальную тактовую частоту для нашего идеализированного случая:
4ах= 1/1Ч= 1/(10 110-9) = юо1о6Гц.
Таким образом, максимальная тактовая частота для данной микросхемы
составляет 100 МГц. В реальной ситуации, при реализации устройства на
42
Глава 1. Печатные платы в цифровых, системах
печатной плате быстродействие, которое можно назвать системным, будет
ниже из-за влияния параметров конструкции платы и корпусов микросхем.
При совместном рассмотрении сигнала на входе и выходе вентиля мож-
но получить дополнительные временные параметры, связанные с распрос-
транением сигнала внутри микросхемы. На рис. 1.25 показаны основные вре-
менные соотношения для сигналов цифровых схем:
• rd— время задержки распространения сигнала внутри микросхемы;
• /оп — время включения микросхемы;
• ts — время установления сигнала;
* zoff— время выключения микросхемы;
* Zd(on) — вРемя задержки распространения сигнала внутри микросхемы
при ее переключении из состояния логического нуля в состояние ло-
гической единицы;
* Zd(ofT) — время задержки распространения сигнала внутри микросхемы
при ее переключении из состояния логической единицы в состояние
логического нуля.
Рис. 1.25. К определению временных соотношений в цифровых схемах
при работе на резистивную нагрузку
1.2. Элементы цифровой обработки информации
43
Основной оценкой быстродействия можно считать время задержки рас-
пространения сигнала Zd, а для анализа частотных свойств сигнала и пара-
метров печатного монтажа наиболее часто используется значение фронта
сигнала Гг. В общем случае эти параметры не равны между собой, но в инже-
нерной практике используют приближенное соотношение: Zd ~ tT.
Помехоустойчивость цифровых микросхем
Помехоустойчивость определяет стойкость системы к воздействию помех
за счет применения алгоритмов обработки сигналов и специальных схемо-
технических приемов, то есть помехоустойчивость закладывается на этапе
функционального и схемотехнического проектирования. В большинстве слу-
чаев помехоустойчивости недостаточно для качественной работы аппаратуры.
Повышению стойкости электронных средств к внешним электромагнитным
воздействиям способствуют специальные меры, которые закладываются на
этапе проектирования и конструирования (экранирование, заземление, ра-
циональный монтаж ит. п.).
Совокупность всех предпринятых мер обеспечивает помехозащищенность
всей аппаратуры. Таким образом, термин «помехоустойчивость» применим
в большей степени к схемотехническим аспектам проектирования, а термин
«помехозащищенность» — к конструкции в целом. Применительно к циф-
ровым микросхемам, которые являются основным компонентом электрон-
ных модулей на печатных платах, их помехоустойчивость определяется осо-
бенностями построения базового вентиля определенной серии микросхем.
В процессе работы интегральные микросхемы испытывают воздействия
поступающих на вход помех, источниками которых могут быть:
• проводники печатных плат, в которых происходят динамические про-
цессы переключения;
• токи и напряжения, наведенные от сторонних источников электромаг-
нитных помех;
• токи и напряжения, вызванные электростатическими разрядами (ЭСР).
В определенной мере печатный узел защищен от внешних электромагнитных
воздействий экранированием и другими средствами на уровне аппаратуры.
Большую опасность представляют помехи от соседних элементов платы и от
ЭСР. При работе в условиях помех микросхемы должны обладать определен-
ной помехоустойчивостью. Она определяется как способность микросхемы со-
хранять заданное качество функционирования при воздействии на нее вне-
шних помех с регламентируемыми параметрами в отсутствие дополнительных
средств защиты от помех, не относящихся к принципу действия или постро-
ения микросхемы. Параметры помехоустойчивости оговариваются в норма-
тивной документации. Здесь важно обратить внимание на два момента.
Во-первых, помехоустойчивость обусловлена конкретными схемными и
конструкторскими решениями, принятыми при создании микросхем. Посколь-
ку входные каскады и конструкции корпусов в пределах логического семей-
ства однотипны, то и параметры помехоустойчивости в пределах семейства оди-
наковы, хотя они различны для различных семейств.
44
Глава 1. Печатные платы в цифровых системах
Во-вторых, помехоустойчивость оговаривается только по отношению к по-
мехам с определенными параметрами — форма, амплитуда и т. п. Если поме-
ха отличается от регламентируемой, то опираться на приведенные в докумен-
тации значения помехоустойчивости нельзя.
Если уровень помехоустойчивости недостаточен, то применяются допол-
нительные средства защиты от помех, например, ограничители помех, раз-
вязывающие конденсаторы или экранирование. В этом случае говорят о по-
мехозащищенности узла, аппаратуры или системы.
Для цифровых микросхем задают статическую и динамическую помехо-
устойчивость [33, 34].
Статическая помехоустойчивость
Рассмотрим (рис. 1.26) временную диаграмму переключения микросхемы,
на которой представлены возможные искажения сигнала. Хорошо видно, что
по своей сути цифровой сигнал в реальной ситуации представляет собой ана-
логовый сигнал. Стандартами заданы определенные уровни напряжений:
Ин — номинальный уровень высокого напряжения, соответствующий ло-
гической 1;
VL — номинальный уровень низкого напряжения, соответствующий ло-
гическому 0;
Ион — минимальное напряжение логической «1» на выходе микросхемы,
которое воспринимается еще как логическая 1; другими словами, это мини-
мально допустимый уровень логической 1;
HOL — максимальное напряжение на выходе микросхемы, которое воспри-
нимается еще как логический 0; это максимально допустимый уровень ло-
гического 0;
И^тах — максимальный уровень низкого напряжения на входе микросхе-
мы, при котором сохраняется оговоренная работоспособность микросхемы;
Время
Рис. 1.26. Уровни сигналов и допустимые уровни статической
помехоустойчивости
1.2. Элементы цифровой обработки информации
45
^iHmin — минимальный уровень высокого напряжения на входе микросхе-
мы, при котором сохраняется оговоренная работоспособность микросхемы;
Кгг_ — пороговое напряжение на входе микросхемы при изменении вход-
ного напряжения от высокого уровня к низкому;
Кгг+ — пороговое напряжение на входе микросхемы при изменении вход-
ного напряжения от низкого уровня к высокому.
Переключение микросхемы происходит в том случае, если напряжение
на ее входе перейдет определенный пороговый уровень. Если на вход мик-
росхемы поступает от драйвера низкий уровень (KOL), то при возрастании
входного напряжения и достижении им уровня KIL на выходе микросхемы
происходит изменение логического состояния. Аналогично, если на входе
микросхемы имеется высокий уровень напряжения (Кон), то при его снижении
до уровня И1Н произойдет изменение логического состояния на выходе мик-
росхемы. Таким образом, уровни И1Н и KIL являются порогами срабатывания
микросхемы. Уровни статической помехоустойчивости определяются следу-
ющим образом:
относительно высокого напряжения:
^н=’/он-Инт!п;
относительно низкого уровня:
Ж = •
L ILmax OL
Пример. Для ТТЛ-схемы определены следующие уровни: KIL < 0,8 В, И1Н > 2 В, KOL < 0,4 В,
Ион > 2,4 В. Тогда уровни статической помехоустойчивости равны NMH = = =
В целом, чем выше быстродействие микросхемы, тем ниже ее помехоус-
тойчивость, особенно динамическая. Следует отметить, что помехи относи-
тельно нижнего уровня более опасны, чем относительно высокого уровня.
Параметры сигналов и показатели статической помехоустойчивости цифро-
вых микросхем приведены в технических условиях на них.
Дифференциальная технология передачи сигналов не имеет уровней по-
мехозащищенности, которые соотносятся с уровнями стандартных схем. Это
происходит потому, что при дифференциальной передаче происходит подав-
ление помех общего вида, попадающих на оба входа приемника. Хотя диф-
ференциальная передача сигналов обладает повышенной помехозащищен-
ностью, помехи значительного уровня все равно могут привести к сбоям. Более
детально дифференциальная передача сигналов рассмотрена в главе 6.
Динамическая помехоустойчивость
В печатном монтаже в основном преобладают динамические процессы, свя-
занные с изменением во времени токов и напряжений в межсоединениях. Эти
изменения индуцируют токи и напряжения, воспринимаемые в виде помех в
проводниках на платах. Поэтому импульсные помехи более типичны для элек-
тронного модуля и должны быть проанализированы в первую очередь.
Способность интегральных схем противостоять импульсным помехам, ко-
торые поступают на вход микросхем, определяется характеристикой дина-
мической помехоустойчивости. В реальной ситуации импульсные помехи могут
46
Глава 1. Печатные платы в цифровых системах
иметь достаточно сложную форму, но характеристика динамической помехоу-
стойчивости определяется по отношению к прямоугольному импульсу Для луч-
шего понимания этой характеристики рассмотрим эксперимент по ее получе-
нию (рис. 1.27). В ее состав входят: генератор испытательных сигналов, мик-
Рис. 1.27. Схема экспериментального
получения характеристики
динамической помехоустойчивости
росхема, для которой определяется по-
мехоустойчивость, индикатор срабаты-
вания микросхемы.
Генератор сигналов — это имитатор
импульсных помех, который позволяет
1 2
3
Рис. 1.28. Представление импульсных
помех: 1 — прямоугольной формы; 2 —
трапециидальной формы; 3 — треу-
гольной формы;
4 — экспоненциальной формы
управлять параметрами импульсов.
Форма импульсов должна быть макси-
мально приближена к форме реальных
помех, но технически наиболее просто
генерировать прямоугольный импульс
(рис. 1.28). Кроме этого, он наиболее
богат спектральными составляющими,
что соответствует худшему случаю.
Генерирование импульсов с управ-
ляемыми параметрами является весь-
ма сложной задачей. При использова-
нии прямоугольного импульса в каче-
стве тестирующего возникает проблема
исследования микросхем предельного
быстродействия. При этом генератор
сигналов должен быть построен на эле-
ментах, быстродействие которых на по-
рядок выше быстродействия тестиру-
емой микросхемы.
Переменными величинами здесь
являются амплитуда напряжения Ип
импульса помехи и длительность (п
импульса помехи. Для получения характеристики возможно проведение вы-
числительных экспериментов, что снижает ограничение на форму и пара-
метры импульсов, но требует адекватной модели испытуемой микросхемы,
что не всегда просто осуществить.
Индикатор — простейшее безынерционное устройство, например, свето-
диод, фиксирующее события переключения ИМС.
Для получения характеристики динамической помехоустойчивости про-
водят ряд измерений, фиксируя состояние индикатора, приписывая, напри-
мер, знак «+» событию срабатывания микросхемы, а знак «-» — отсутствию
срабатывания. Результаты эксперимента отражаются на графике в коорди-
натах (tn, Ип).
После проведения серии экспериментов и получения совокупности то-
чек «+» и «—», между точками можно провести границу в виде гиперболи-
ческой кривой. Зона выше кривой называется зоной неустойчивой работы,
1.2. Элементы цифровой обработки информации
47
зона под кривой — зоной устойчивой работы микросхемы. Граница между
этими зонами и есть характеристика динамической устойчивости (рис. 1.29).
При длительности помехи меньше Zn min микросхема работает устойчиво
при очень высокой амплитуде помехи, но эта длительность настолько мала,
что практически исключает наличие таких помех. При поступлении на вход
микросхемы весьма коротких импульсов помех значительной амплитуды их
заряд мал, входные емкости не успевают перезарядиться за время, соответ-
ствующее длительности помехи, и напряжение на входе микросхемы не пре-
восходит допустимое.
При увеличении длительности помехи характеристика динамической по-
мехоустойчивости стремится к уровню статической помехи.
При повышении быстродействия площадь зоны устойчивой работы умень-
шается. Например, это можно проследить при переходе от ТТЛ к ТТЛШ. На
рис. 1.30 показаны условные характеристики динамической помехоустойчи-
вости ТТЛ-схем и ТТЛШ-схем. Последние, являясь более быстродействую-
щими, имеют меньшую площадь зоны устойчивой работы. Поэтому поме-
ха, не опасная для ТТЛ, может оказаться недопустимой для ТТЛШ.
Характеристика динамической помехоустойчивости используется при про-
ектировании печатных плат для оценки возможного нарушения работоспособ-
ности цифровых узлов при наличии индуцированных помех, например пере-
крестных. Зная амплитуду и длительность помехи, нанеся эти параметры в ка-
честве координат на характеристику динамической помехоустойчивости, по
расположению соответствующей точки можно судить о потенциальной опас-
ности помехи. При расположении точки в зоне неустойчивой работы помеху сле-
дует считать недопустимой.
При подобном анализе следует учитывать, что характеристика динами-
ческой помехоустойчивости получена для прямоугольных импульсов, а формы
реальных импульсов или их приближенные описания могут отличаться от пря-
моугольной (см. рис. 1.28).
Если ведется разработка аппаратуры на определенной серии микросхем, то
один раз полученная усредненная характеристика для типового вентиля может
Рис. 1.29. Характеристика
динамической помехоустойчивости
V
п
^пТТЛ Тп
Рис. 1.30. Сравнительные
характеристики динамической
помехоустойчивости
ТТЛ-схем и ТТЛШ-схем
48
Глава 1. Печатные платы в цифровых, системах
быть применима для всей серии. При смене элементной базы характеристика
должна быть получена заново. В нормативно-технической документации в обя-
зательном порядке приводится статическая помехоустойчивость, и в ряде слу-
чаев — характеристика динамической помехоустойчивости.
1.2.3. Помехи в системе при работе микросхем
Существует множество факторов при работе цифровых узлов, приводящих
к возникновению помех, обусловленных особенностями работы микросхем. Наи-
более существенные из них: «звон», перекрестные помехи и электромагнитное
излучение от печатного узла. Под общим термином «звон» обычно понимают
затухающие колебания, которые вызываются рядом причин, важнейшими из
которых являются коммутационные помехи при переключении цифровой мик-
росхемы, помехи, связанные с импульсным потреблением тока в динамичес-
ком режиме, а также помехи, определяемые степенью рассогласования линии
передачи и нагрузки. Каждый из этого вида помех требует более детального рас-
смотрения, что будет сделано в последующих разделах.
Помехи значительного уровня могут сказаться на надежности системы
и качестве выполнения ею своих функций. В конечном итоге способность
противостоять помехам и уровни помех, которые генерируются в системе,
зависят от элементной базы.
Коммутационные помехи
Коммутационные помехи возникают в системе при переключении мик-
росхемы. Они возникают из-за наличия индуктивности в системе питания
и заземления и проявляются в виде подскока опорного напряжения (земли) и
сдвига динамического порога.
Подскок опорного напряжения
Подскок опорного напряжения для цифровых микросхем представляет собой
кратковременное возрастание напряжения заземления во время динамических про-
цессов переключения. Основную роль в этом
процессе играет индуктивность выводов
корпуса микросхемы, на которой во время
изменения тока, протекающего по ней,
возникает некоторое падение напряжение.
На рис. 1.31 показана модель КМОП-схе-
мы в корпусе. Здесь Lx представляет индук-
тивность вывода заземления, Л2 — вывод
питания Ксс, и £3 — вывод выхода. Сопро-
тивление полупроводниковой структуры
токам разряда нагрузки представлено как
Rx, а нагрузка представлена емкостной С,
и резистивной Rx составляющими.
При переключении микросхемы из вы-
сокого напряжения в низкое (рис. 1.310
Рис. 1.31. Модель корпуса
в режиме: а — логической
единицы; б — логического нуля
1.2. Элементы цифровой обработки информации
49
ток протекает от нагрузки через вывод заземления микросхемы. Фактически это
ток разряда емкости нагрузки, который протекает через индуктивность выво-
да и сопротивление полупроводниковой структуры выходного каскада микро-
схемы. Изменение тока разряда за время коммутации вызывает падение напря-
жения VL на индуктивностях выводов:
где L — суммарная индуктивность выводов корпуса микросхемы, по которым протекает
выходной ток; А/ — изменение тока; А/ — интервал времени изменения тока.
Таким образом, индуктивность Z, между точками функционального зазем-
ления и внутренней опорной точкой микросхемы вызывает падение напря-
жения, которое и характеризует «подскок» опорного напряжения. В этом случае
напряжение опорной точки внутри микросхемы имеет напряжение, отличное
от нулевого уровня функционального заземления. Подскок напряжения су-
щественно снижает уровень помехозащищенности микросхемы за счет сме-
щения опорного напряжения. В отдельных случаях это явление может вызвать
триггерный эффект приемника за счет помех на выходе драйвера, что приве-
дет к появлению нежелательного бита на выходе приемника.
Следует отметить, что «нулевой уровень» функционального заземления —
также определенная условность, поскольку при некорректном проектирова-
нии системы заземления она обладает повышенным полным сопротивлени-
ем, которое на высоких частотах вызывает аналогичный эффект «подскока»
напряжения заземления относительно Земли. Исходя из этого формулируются
требования к шинам и системе заземления, которые обеспечивают минималь-
ное полное сопротивление [35].
Уровень напряжения подскока обычно вызывается несколькими важней-
шими факторами:
• числом одновременно переключаемых выходов;
• расположением выводов и их конструкцией;
• скоростью переключения (крутизной фронта);
• уровнем питающего напряжения;
• типом нагрузки и ее расположением;
• технологией, которая используется для изготовления микросхемы и
при ее корпусировании.
Число одновременно переключаемых микросхем определяет амплитуду
суммарного тока, протекающего в системе заземления. Поскольку каждый
вывод может быть представлен в виде последовательной индуктивности и со-
противления, то их параллельное включение приведет к снижению этих сум-
марных параметров, что, в свою очередь, вызовет увеличения коммутацион-
ных токов. Чем больше одновременно переключаемых выводов, тем боль-
ше будет ток в системе заземления и подскок напряжения. Однако, если цепь
заземления подключить к микросхеме через ряд параллельных выводов, то
их суммарная индуктивность снизится, что приведет к уменьшению напря-
жения подскока.
50
Глава 1. Печатные платы в цифровых системах
Крутизна фронта непосредственно определяет скорость изменения тока
A//At, а следовательно, падение напряжения на индуктивности выводов и
шины питания. Чем выше быстродействие микросхемы, тем больше скорость
изменения тока и больше уровень подскока напряжения.
Расположение и форма выводов непосредственно влияют на их индуктив-
ность. Чем длиннее вывод заземления внутри корпуса и чем ближе к круго-
вой форме поперечное сечение вывода, тем больше его индуктивность и
больше подскок напряжения.
Уровень питающего напряжения определяет диапазон изменения напря-
жения на выходе микросхемы, а следовательно, входных и выходных токов.
Чем выше напряжение питания, тем, в конечном счете, будет больше под-
скок напряжения.
Тип нагрузки имеет существенное значение. Худший случай — сосредо-
точенная емкостная нагрузка. В этом случае подскок будет максимальный,
поскольку при этом ток разряда/заряда будет максимальный. Значительно
меньший уровень подскока и падения напряжения на шине питания будет
при распределенной емкостной нагрузке.
Принятая технология исполнения микросхем определяет параметры бы-
стродействия, и чем они выше, тем больше подскок напряжения. Кроме этого,
технология определяет режимы работы полупроводниковых элементов. Так
КМОП-схемы обладают более резким изменением тока при переключении,
чем биполярные схемы. Это вызывает более резкий подскок напряжения, что
следует учитывать при конструировании плат. БиКМОП-схемы сочетают по-
ложительные факторы КМОП и биполярных схем, включая меньший под-
скок, чем для большинства КМОП-схем.
Как отмечалось выше, использование в одном корпусе некоторого числа па-
раллельных выводов питания и заземления позволяет снизить влияние эффекта
подскока напряжения за счет уменьшения суммарной индуктивности выводов.
Динамический порог
Динамическое изменение порога срабатывания микросхемы является ре-
зультатом подскока напряжения. Это явление называется: «динамический порог
напряжения при низком входном напряжении» (Voltage Input Low Threshold
Dynamic — VILD) и «динамический порог напряжения при высоком входном
напряжении» (Voltage Input High Threshold Dynamic — VIHD).
Этот эффект вызывается сдвигом напряжений при подскоке напряжения
заземления и провале напряжения питания. Особенно опасен динамический
сдвиг порогового напряжения, когда он соизмерим с допустимым уровнем
статической помехоустойчивости. В этом случае схема может находиться в
некотором непредсказуемом состоянии. Отмеченное явление может прояв-
ляться только в особых случаях, например, при одновременном переключении
в одном направлении нескольких микросхем, работающих на сосредоточен-
ную нагрузку.
Наиболее эффективное средство устранения подскока напряжения и ди-
намического сдвига порога достигается корректным проектированием сис-
1.2. Элементы цифровой обработки информации
51
темы заземления и развязкой, что будет детально рассмотрено в последую-
щих разделах.
Коммутационные помехи в системе питания
Аналогично рассмотренному явлению подскока напряжения заземления
подобный эффект возникает при переключении микросхемы из низкого уров-
ня в высокий (рис. 1.31 а), но при этом индуктивность £2 вывода питания кор-
пуса микросхемы будет вызывать снижение напряжения питания, которое
поступает на кристалл микросхемы. Снижение напряжения питания проис-
ходит на значение KSB:
(1.3)
где A/s — изменение тока потребления при переключении микросхемы; А/ — интервал вре-
мени изменения тока (как правило, А/ = /г).
В этом случае, если напряжение Исс, поступающее на кристалл, будет мень-
ше допустимого, то работоспособность микросхемы не будет гарантирова-
на. Это напряжение равно
^СС = Н>8 - ^SB, (1-4)
где Kss — напряжение источника питания, подведенное к выводу микросхемы, KSB — па-
дение напряжения на выводе питания микросхемы.
При последующем рассмотрении системы питания на печатной плате будет
показано, что к индуктивности вывода микросхемы следует прибавить ин-
дуктивность шины питания, соединяющей микросхему с фильтром питания.
Система питания является причиной возникновения коммутационных по-
мех, которые генерируются изменяемыми токами в шинах и слоях питания
и заземления в составе плат. Эти изменения определяются различием потреб-
ляемой мощности при изменении состояния микросхем. Высокоскоростные
и мощные микросхемы требуют для переключения значительных мощнос-
тей, поскольку они работают на линии передачи, нагруженные на согласу-
ющие резисторы относительно малых номиналов. Если система питания спро-
ектирована не корректно, то изменение мощности потребления при пере-
ключении микросхемы приведет к резкому изменению токов в шинах питания.
При этом индуктивность шины питания вызовет изменение напряжения на
ней и приведет к сдвигу напряжения питания.
Временное снижение напряжения питания на выводах микросхемы при-
водит к сокращению времени задержки распространения сигнала в ней во
время переключения, которое принимает прежнее значение после переклю-
чения микросхемы. Эти вариации времени задержки являются одной из со-
ставляющих дрожания фронта сигнала по времени — джиттера.
При проектировании плат управление коммутационными помехами в сис-
теме питания осуществляется минимизацией индуктивности шины питания
при трассировке путем уменьшения ее длины и увеличения ее ширины. Для
52
Глава 1. Печатные платы в цифровых системах
МПП для шины питания отводится отдельный слой или слои. Положительно
сказывается разнесение слоев питания и заземления для высокоскоростных
и низкоскоростных зон платы.
Развязка
Локальная развязка является эффективным средством снижения провалов
напряжения питания при переключении микросхем. Развязка выполняется
конденсаторами, которые подключаются к шине питания и выводу питания
микросхем. Значение емкостей конденсаторов изменяется в зависимости от
частоты переключения и параметров конструкции платы. Число конденсато-
ров определяется желаемой развязкой.
Конденсаторы должны устанавливаться на минимальном расстоянии от
микросхемы, должны обладать минимальной собственной индуктивностью и
индуктивностью выводов. Правильный выбор конденсаторов и вариантов их
установки на плате — очень серьезная задача в обеспечении целостности сиг-
нала. Она детально рассматривается в пятой главе.
1.2.4. Вольтамперные характеристики цифровых схем
Вольтамперные характеристики (ВАХ) цифровых микросхем определя-
ют зависимость напряжений от токов на входах и выходах микросхем.
Эти характеристики снимаются при медленных изменениях параметров («по
точкам»), что определяет их статический характер. Для каждой из вышеопи-
санных серий микросхем вольтамперные характеристики имеют вполне оп-
ределенные конфигурации.
Для элементарного вентиля различают:
• входную ВАХ;
• две выходных ВАХ (одна для состояния логической 1 на выходе мик-
росхемы, другая — для состояния логического 0).
Выбор системы координат для ВАХ
Для описания ВАХ микросхем примем следующую систему координат: по
оси х будем откладывать значение входного или выходного тока /, а по оси у зна-
чение соответствующего напряжения И В выбранной системе координат угол
наклона некоторой прямой пропорционален, с учетом масштаба, сопротивле-
нию, либо статическому, либо динамическому. При линейной ВАХ (рис. 1.32<?)
Рис. 1.32. Вольтамперные характеристики: а — линейная; б — нелинейная
1.2. Элементы цифровой обработки информации
53
этот угол определяется самой характеристикой. При нелинейной ВАХ (рис. 1.325)
касательная в какой-либо ее точке будет определять динамическое сопротив-
ление для малого сигнала в этой точке.
Значение угла в градусах зависит от выбранного масштаба по оси тока и
напряжения и определяется по выражению
0 = arctg Rt— , град.,
I mi)
где R, — сопротивление (входное, выходное), описываемое ВАХ, Ом; mv — масштабный
коэффициент по оси И, мм/В; mt — масштабный коэффициент по оси /, мм/А.
Таким образом, выбранная система координат позволяет наглядно соот-
нести возрастание сопротивления и увеличение угла наклона соответствую-
щей прямой. Знание ВАХ микросхем, которые используются для построения
цифровых схем электронного модуля, необходимо для анализа помех отражения
и рационального выбора способа согласования линий передач на плате.
Отметим, что в справочной литературе часто встречается иное располо-
жение координатных осей. При этом угол наклона прямой будет пропорци-
онален проводимости.
ВАХ ТТЛ-схем
ВАХ реальных микросхем сугубо нелинейные [33]. Они представляются
в выбранной системе координат некоторыми характерными кривыми, вид
которых типичен для определенных серий микросхем (ЭСЛ, ТТЛ, КМОП)1.
Для каждой серии существует семейство из трех ВАХ. Например, для ТТЛ-
схем семейство содержит:
• входную ВАХ (рис. 1.33);
• выходную ВАХ (рис. 1.34) для состояния логической 1 на выходе мик-
росхемы — выходная ВАХ(1);
• выходную ВАХ для состояния логического 0 на выходе микросхемы —
выходная ВАХ(О).
При нанесении всех ВАХ на один график (рис. 1.35) получается весьма
информативная картина, по которой можно судить о работоспособности си-
стемы, построенной на данной серии микросхем.
Для двух последовательно включенных вентилей точка «Л» пересечения
входной ВАХ и выходной ВАХ(1) характеризует схему в статическом состо-
янии логической единицы. Точка «В» пересечения входной ВАХ и выходной
ВАХ(О) характеризует схему в статическом состоянии логического нуля. Уро-
вень нуля для ТТЛ-схем может составлять приблизительно 0,5 В, уровень еди-
ницы — около 3,5 В. Каждая кривая имеет границы рабочей области. При
Здесь и далее вид ВАХ дается приближенно для качественной оценки параметров и
физических процессов. Конкретный вид ВАХ можно найти в соответствующей справоч-
ной и нормативной документации.
54
Глава 1. Печатные платы в цифровых системах
Рис. 1.33. Входная
ВАХ ТТЛ
Рис. 1.34. Выходные ВАХ ТТЛ: а — для
состояния логической 1 на выходе; б — для
состояния логического 0 на выходе
Рис. 1.35. Семейство
ВАХ ТТЛ
Рис. 1.36. Входные и выходные ВАХ ЭСЛ:
7 — входная ВАХ; 2 — выходная ВАХ для
состояния логической 1; 3 — выходная
ВАХ для состояния логического 0; 4 —
входная ВАХ согласованной нагрузки
выходе параметров за пределы этой области работоспособность микросхе-
мы не гарантируется. Поэтому при использовании семейства ВАХ для про-
ведения расчетов или анализа работоспособности экстраполяция характе-
ристик недопустима.
ВАХ ЭСЛ
ЭСЛ-схемы имеют отрицательное напряжение питания (—5,2 В). Они при-
меняются только с согласованными линиями передачи, и при их работе ис-
пользуют дополнительные источники питания (—2 В) для улучшения режима
согласования.
На рис. 1.36 показаны: входная ВАХ (^Ц)), выходная ВАХ для состоя-
ния логической единицы (1) и выходная ВАХ для состояния логического нуля
(0). Пунктирная прямая соответствует линейной входной (реальной) харак-
теристике, которая имеет место после согласования линий передачи.
Обозначение выходных характеристик «0» или «1» — условно, посколь-
ку ЭСЛ-схемы имеют инвертирующий выход. Поэтому уровни логической
единицы и нуля могут быть взяты произвольно. В реальной ситуации линейная
входная характеристика смещается вправо, обеспечивая статический уровень
«1», равный минус 0,7 В, и уровень «0» — минус 1,7 В.
1.2. Элементы цифровой обработки информации
55
ВАХ КМОП-схем
Вольтамперные характеристики КМОП-
схем (рис. 1.37) не имеют принципиальных
отличий от ВАХ ТТЛ-схем, хотя форма ха-
рактеристик несколько отличается. Преж-
де всего, входная ВАХ имеет вертикальный
участок, практически совпадающий с осью
напряжения. Это говорит о чрезвычайно
высоком входном сопротивлении КМОП-
схем. Во-вторых, напряжение логическо-
го нуля равно нулевому напряжению, а на-
пряжение логической единицы равно на-
пряжению питания при предельно низких
токах потребления в этих режимах [36]. Это
определяет повышенный уровень помехо-
защищенности схем. Приведенные харак-
теристики учитывают наличие во входных
каскадах схем защиты от перенапряжений.
Входные и выходные сопротивления
Рис. 1.37. ВАХ КМОП-схем: 1 -
входная характеристика; 2 — выход-
ная характеристика для низкого со-
стояния на выходе; 3 — выходная ха-
рактеристика для высокого состоя-
ния на выходе (ВАХ даны для
напряжения питания +5 В)
микросхем
Входные и выходные сопротивления микросхем при нелинейных ВАХ
пропорциональны углу наклона касательных в некоторых точках (/, И, опре-
деляющих режим работы микросхемы. Это динамическое сопротивление
при малых уровнях сигналов в окрестностях рабочей точки. Нелинейный
характер ВАХ показывает, что входные и выходные сопротивления микро-
схем также нелинейные. Имеются только отдельные участки относитель-
но линейного сопротивления, которые в малой степени влияют на работу
микросхемы.
Следует учитывать некоторые особенности приемников цифровых сиг-
налов. Входы быстродействующих микросхем, как правило, имеют встро-
енные схемы защиты от перенапряжений, в том числе и от электростати-
ческого разряда (ЭСР), выполненные на полупроводниковых элементах [32].
Эти элементы защиты вносят дополнительные емкости, которые влияют на
форму фронта сигнала и вносят дополнительную задержку его распростра-
нения. Выбор схемы защиты — задача комплексная. Поскольку встроен-
ная защита позволяет поглотить разряд относительно малой энергии, при-
меняются дополнительные навесные защитные устройства. Эти устройства
подключаются между сигнальными проводниками и шинами питания и за-
земления. Емкость защитных устройств добавляется к емкости нагрузки —
и если она относительно велика, то это приведет к дополнительным сис-
темным задержкам распространения сигнала. Поэтому одно из основных
требований при выборе устройств защиты от перенапряжений состоит в
минимизации их емкости. Современные варисторы и перспективные ус-
тройства защиты от перенапряжений обладают емкостью в единицы и доли
56
Глава 1. Печатные платы в цифровых системах
пикофарад. Поэтому соответствующая модель приемника при верификации
состоит из схем защиты от ЭСР, емкости и входного сопротивления.
1.2.5. Электрические соединения на плате
Цифровые системы используют передачу немодулированного сигнала, и
поэтому электрические соединения должны проводить постоянный ток. Поэтому
для соединения компонентов требуется два проводника — по одному провод-
нику (сигнальному) ток протекает от драйвера к нагрузке, по другому (возврат-
ному) ток возвращается от нагрузки к драйверу. Таким образом, путь тока все-
гда замкнут в виде некоторого контура, а система сигнального и возвратного про-
водника образует линию передачи.
В печатных платах для быстродействующей аппаратуры конфигурация этих
проводников становится очень важной, и возвратный проводник должен быть
спроектирован так же тщательно, как и сигнальный. Межсоединения обычно
характеризуются выполняемой функцией, типом корпусов микросхем, под-
ключаемых к ним, видом переходных и монтажных отверстий, расположенных
вдоль соединения, конструкций проводника и т. д. Если совокупность пря-
мого и возвратного проводника не изменяется по сечению на протяжении
длины соединения, то такое соединение формирует однородную линию пе-
редачи, которая имеет специальные свойства, позволяющие проводить бо-
лее детальное моделирование с меньшими временными затратами. Если со-
единение по длине имеет изменения по ширине, применяемым материалам,
включению межслойных переходов и других конструктивных параметров, то
соединение становится неоднородной линией передачи, а элементы, наруша-
ющие однородность линии, являются в общем случае неоднородностями.
Наличие неоднородностей усложняет анализ линий передачи и процесса
прохождения по ней электрических сигналов. Понятие линии передачи по-
зволяет построить теоретический базис для анализа целостности сигналов,
тайминга и электромагнитной совместимости.
Основные типы одиночных линий передач представлены на рис. 1.38. На
печатных платах электрические соединения могут быть выполнены в виде коп-
ланарных, микрополосковых, полосковых и заглубленных линий передач. В коп-
ланарной линии сигнальный и возвратный проводники расположены в одной
плоскости, что удобно при односторонних печатных платах. В микрополоско-
вой линии проводник располагается над слоем возвратных токов, а в полоско-
вой линии проводники располагаются между слоями возвратных токов. Заглуб-
ленная линия формируется из микрополосковой путем нанесения поверх сиг-
нального проводника относительно толстого слоя диэлектрика. В двойной
полосковой линии проводники, расположенные во внутренних слоях, ориен-
тируются ортогонально, что минимизирует емкость между ними. Проводящие
плоскости, по которым протекают возвратные токи, могут подключаться к по-
тенциалу питания или заземления. Далее эти проводящие плоскости будем на-
зывать потенциальными слоями.
В конструкции печатных плат применяют все разновидности полосковых
и микрополосковых линий передач, а для выполнения межблочных и межпри-
1.2. Элементы цифровой обработки информации
57
Рис. 1.38. Типы линий передачи: 1 — копланарная; 2 — полосковая; 3 — заглубленная;
4 — микрополосковая; 5 — двойная полосковая; 6 — коаксиальная; 7 — витая пара
борных соединений применяют коаксиальные кабели и витые пары. Следует
отметить, что витая пара является одним из самых перспективных типов ка-
бельного соединения, которое обеспечивает весьма высокие скорости пере-
дачи информации. Она особенно эффективна при балансном включении. В ряде
случаев базовые особенности витой пары используются для выполнения со-
единений на печатной плате, которые обладают малой помехоэмиссией и малой
восприимчивостью к внешним электромагнитным помеховым полям.
В составе печатных плат лучшими электрофизическими параметрами об-
ладают полосковые линии, но они требуют не менее трех слоев для реализа-
ции. Это означает, что они могут быть использованы только в составе мно-
гослойных печатных плат (МПП). Как будет показано дальше, полосковая
и двойная полосковая линия являются базовыми звеньями при структурном
проектировании МПП.
При создании МПП требуется использовать несколько полосковых или мик-
рополосковых линий, надстраиваемых друг над другом в определенной после-
довательности (стек). Рациональный выбор этой последовательности позволяет
добиться положительных дополнительных эффектов в целостности сигнала и
показателях ЭМС. Детально метод проектирования МПП будет рассмотрен ниже.
Для обоснованного конструирования соединений необходимо четко пред-
ставлять физические процессы, происходящие в них при передаче цифро-
вого сигнала, возможные модели их описания и область их применения, что
будет предметом детального рассмотрения в последующих разделах.
1.2.6. Цифровой сигнал в электрических соединениях
Цифровой сигнал представляет собой последовательность импульсов, не-
сущих биты информации. Последовательность битов и их функциональное
назначение в потоке битов определяется протоколами передачи данных. Су-
ществует достаточно много протоколов различного назначения и различной
сложности, но основные усилия разработчиков направлены на повышение
достоверности передаваемой информации при повышении быстродействия.
58
Глава 1. Печатные платы в цифровых системах
Это следует рассматривать как глобальную тенденцию. В любом случае при
произвольных протоколах сигнальный уровень, определяющий скорость и
качество передачи одного бита информации, во многом будет определять ка-
чество функционирования цифровой системы. Выше рассмотрены времен-
ные параметры цифрового сигнала. Для проведения более детального ана-
лиза прохождения сигнала по линии передачи удобно представить его в ча-
стотной области [37].
Трапецеидальный импульс
Наилучшим приближением к реальному импульсу цифрового сигнала мо-
жет считаться сигнал с огибающей трапецеидальный формы. Рассмотрим пос-
Рис. 1.39. Последовательность импульсов
трапецеидальной формы,
расположенных симметрично оси t = О
ледовательность импульсов, пока-
занную на рис. 1.39, где сигнал за-
дается соотношением:
7
где rw — ширина импульса на уровне 0,5; —
длительность перехода из одного устойчи-
вого состояния в другое; принимая равен-
ство фронта и спада импульса, имеем /г =
= tf = /t; Ин — высокий уровень сигнала.
Поскольку последовательность импульсов периодическая, она может быть
представлена в виде ряда Фурье:
/ \ v-' I 2тсл ।
V(r) = aQ +2^и cos ----------1 >
И = 1 I Г /
где коэффициенты ряда определяются по формулам:
2'c/f2 , 4'c/f2 , . f 2;
ao=- J v(f)dt и an=- J -
lc 0 0 \
Рассчитав интегралы, можем записать:
V(/) = KH^
. I mitw ] . mtt
sin —- sin —1 z
, I tc J Uc ) ( 2лп
1+2E / \ \ •cos —z
। nnt^ । । nnt{ । v
4
(1.6)
(1.7)
Поскольку амплитуда каждой частотной составляющей описывается как
Г 2тш
cos с частотой сол = 2ял//с, то ее можно представить функцией sin(x)/x.
к *с )
1.2. Элементы цифровой обработки информации
59
а
б
Рис. 1.40. Функция sin(x)/x: а — график; б — энергетический спектр
Функция sin(x)/x и ее спектр представлены на рис. 1.40. Огибающая спектра
вначале снижается пропорционально 3 дБ/декаду, когда х = 0,4425л, огиба-
ющая начинает снижаться пропорционально 20 дБ/декаду (6 дБ/октаву). Пер-
вый множитель sin(x)/x в (1.7) дает точку излом 2,78//w, после которой оги-
бающая имеет наклон 20 дБ/декаду. Вторая точка излома 2,78/rt обусловле-
на вторым множителем sin(x)/x в (1.7).
После нее огибающая имеет наклон 40 дБ/
декаду. Результат приведен на рис. 1.41.
Поэтому рассмотрение такого параметра,
как ширина полосы пропускания BW, дол-
жно быть в большей мере основано на ана-
лизе фронта/спада импульсов, чем на их
ширине. Чтобы точно моделировать фронт
трапецеидального импульса, требуется
Рис. 1.41. Огибающая спектра для
трапецеидального импульса,
показанного на рис. 1.39
рассматривать спектральные составляю-
щие, попадающие в полосу частот:
со = 5,56//. (1.8)
min ’ ' г v '
60
Глава 1. Печатные платы в цифровых системах
При этом для воспроизведения фронта сигнала необходимо передать набор
гармоник с частотами не менее
/п,т1п = “т.п/2я, (1.9)
т. е.
/п min = 0,085//.
•'ll, min ’ ' г
Учитывая приближенный характер определения полосы пропускания, ее
значение можно записать как
/n.min“ BW= ГЦ, (МО)
где /г — длительность фронта сигнала, с.
Эта оценка используется для определения необходимого числа гармоник,
которые следует пропустить без искажений по линиям передачи для обеспе-
чения неискаженной формы информационного сигнала.
Другой подход основан на определении необходимого для качественно-
го воспроизведения сигнала гармоник, считая за фундаментальную частоту
частоту следования импульсов. Принимается, что для четкого распознава-
ния импульса требуется приблизительно десять гармоник, как это видно из
рис. 1.42. При меньшем числе гармоник наблюдаются существенные иска-
жения формы сигнала. Если фундаментальная частота равна
f= 1 /
то спектр сигнала определяется частотой
BW . = 10 / t.
min ' с
Учитывая, что минимальная длительность импульса приближенно равна
5/г, получаем tc = 10/г. Окончательно BW =1//г, т. е. данная оценка совпадает с
ранее полученной оценкой (1.10).
Рис. 1.42. Последовательность импульсов трапециидального вида
с = 0,5/с и от Гс/ tr =10, построенных с помощью ряда Фурье,
с числом п гармоник, изменяющимся от 3 до 20
1.2. Элементы цифровой обработки информации
61
В качестве примера рассмотрим систему, работающую с тактовой частотой
100 МГц и с переключениями по фронту Период цикла /с = 10 нс. Если время
фронта/спада импульса составляет 20 % периода, то /г= 2 нс. Таким образом,
требуемая полоса пропускания для соединения составляет 1/(2-10~9 с) = 500 МГц.
Экспоненциальный фронт и спад
Трапецеидальный импульс, рассмотренный выше, в реальной ситуации имеет
экспоненциальный фронт и спад из-за влияния постоянной времени заряда ем-
костных нагрузок. Описание импульса для этого случая дается выражением [4]
1-^“' А^
1-е“а'с/2
(1.П)
1-
где параметр а — коэффициент крутизны фронта и спада, tc — время цикла (ширина им-
пульса равна 0,5/с).
Время фронта/спада импульса непосредственно связано с а. На рис. 1.43 по-
казано несколько импульсов с различным значением коэффициента крутизны
фронта а. Напомним, что длительность фронта определяется между уровнями
10 % и 90 % установившегося напряжения.
Используя преобразование Фурье, можно получить спектры сигналов с
различными фронтами. Анализ показывает, что высокочастотные компоненты
определяют малую длительность фронта.
Время
Рис. 1.43. Экспоненциальный импульс с различным фронтом и спадом: 1 — длитель-
ность фронта 0,35/с; 2 — 0,26/с; 3 — 0,14Гс; 4— 0,069/с; 5— 0,034/с; 6 — 0,017/с; 7 —
0,0086/с; 8 — 0,0043/с (время дано в относительных единицах /с = 1)
62
Глава 1. Печатные платы в цифровых системах
Рис. 1.44. Восстановление импульса с экспоненциальным фронтом и спадом по его
спектральным составляющим; tr = 0,14Zc; полоса пропускания: 1 — 0,25/г; 2 — 0,5/г;
3 - 1//г; 4 - 2//г; 5 - 4/Гг
Чтобы оценивать ширину полосы пропускания BW, требуемую для точного
представления экспоненциальных импульсов, следует рассмотреть влияние ог-
раничения спектра на форму импульса. При длительности фронта 0,14/с фор-
мы импульсов при различной ширине полосы пропускания соединения пред-
ставлены на рис. 1.44. Графики показывают, что форма импульса заметно не улуч-
шается после достижения ширины полосы пропускания, равной 4//г, где tr —
длительность фронта. Вполне приемлемая форма импульса получена для ши-
рины полосы пропускания, равной 1//г. Таким образом, и в этом случае получе-
на оценка полосы пропускания как BW = 1//г. В том случае, если длительности
фронта и спада не равны, следует учитывать параметр, имеющий меньшее зна-
чение. Чаще всего именно фронт имеет минимальное значение.
Простейшая модель электрического соединения
Наиболее простой вариант передачи сигналов по линии передачи соот-
ветствует электрически короткой линии, которая может быть смоделирова-
на простейшей АС-схемой (рис. 1.45). Драйвер представлен как линейная
схема с выходным сопротивлением г0, а емкостная нагрузка моделируется ем-
костью С. Напряжение на конденсаторе равно:
Рис. 1.45. Простейшая
АС-цепь, применяемая
для оценки полосы
пропускания соединения
v0(r) = v(/)(l-e-'/'bc).
При t > 0 время достижения заданного напря-
жения определяется как
r(v0) = -r0Cln( 1 - v0).
Длительность фронта, т. е. интервал време-
ни между уровнями 10 % и 90 % установившегося
значения, равна
1.2. Элементы цифровой обработки информации
63
/r=r(O,9)-/(O,l) = -roCln^l-^j = 2,197roC. (1.12)
Если принять уровень порога срабатывания на уровне 50 % установивше-
гося значения, то время его достижения будет
/0 5 = /(0,5) = г0С1п(1 - 0,5) = О,69гоС.
Если г0С представляет собой постоянную времени ZTL соединения:
Ttl — г0С, (1.13)
то задержка в срабатывании микросхемы из-за влияния соединения будет со-
ставлять примерно 0,7ttl. Это дополнительная системная задержка, опре-
деляемая конструкцией линий передачи и емкостными нагрузками.
При произвольном входном сигнале напряжение на входе линии будет оп-
ределяться выражением
(') = *TL -+ vo-
Передаточная функция этой цепи
Я(со) =---!---.
1 + JCOTL
Энергетический спектр будет равен
I"W|°, .г
1 + ((OTTL)
На низких частотах, когда 1 << (cottl)2, частотная характеристика прак-
тически равномерна и с повышением частоты начинает спадать. Полоса про-
пускания определяется по частоте среза сосо, на которой спад достигает 50 %,
т. е. 3 дБ. Тогда из условия
1 _ 1
2 I + ^cc/Ctl)2
учитывая (1.12), получаем сосо = 2,197//г, или^0 = 0,35//г. Следует отметить, что
полученный результат соответствует простейшей модели соединения в виде
фильтра нижних частот. При более точном моделировании мы приходим к ранее
полученной приближенной оценке полосы пропускания BW = 1 / /г.
Таким образом, в зависимости от желаемой точности полоса пропуска-
ния межсоединения, необходимая для качественной передачи цифрового
сигнала, может быть оценена из соотношения BW ~ (0,35... 1.0) / /г.
64
Глава 1. Печатные платы в цифровых системах
1.2.7. Контрольная диаграмма, джиттер
и расфазировка
С повышением быстродействия проблема целостности в электронных мо-
дулях на печатных платах сигнала усугубляется. Помехи различного вида и ис-
кажения формы цифрового сигнала могут достичь такого уровня, что работа
модуля станет невозможной. Для верификации проекта печатной платы в этом
случае требуется учет таких факторов конструкции платы, которые при низ-
кочастотных приложениях не учитывались. Например, необходимо модели-
ровать переходные металлизированные отверстия в МПП и потери в лини-
ях передачи.
В низкочастотных приложениях линии передачи на печатных плат как бы
«прозрачны» для информационных сигналов. По мере повышения быстро-
действия электрофизические параметры начинают сказываться в большей
мере. В устройствах, работающих на тактовых частотах в сотни и тысячи
мегагерц (единицы гигагерц), амплитуда сигнала, при его прохождении от
драйвера до приемника, снижается в среднем на 50% из-за потерь в линиях
передачи. Приближенная оценка дает следующую рекомендацию: пробле-
ма целостности сигнала становится существенной, если выдерживается сле-
дующее численное неравенство:
/>25ГГ, (1.14)
в котором / — длина линии передачи, мм, а /г — длительность фронта цифрового сигнала, нс.
Это означает, что при фронте сигнала в 1 нс, проблема целостности сиг-
нала возникает при длине линии передачи, превышающей 25 мм. Большинство
линий передач на печатных платах превышает это значение. В последующих
разделах эта оценка будет уточнена, но ее порядок остается неизменным.
При синхронной параллельной передаче информационного сигнала ис-
пользуются многоразрядные шины, которые соединяют драйверы с соответ-
ствующими приемниками.
По мере повышения разрядности для увеличения мощности вычислений
требуется значительное число линий в составе шины, что приводит к услож-
нению топологии платы и конструкции печатного узла. Поэтому на смену
параллельной синхронной организации передачи данных приходит после-
довательная асинхронная передача данных, при которой существенно упро-
щается конструкция шины передачи данных, не требуется разводка цепей син-
хронизации, уменьшается число контактов соединителей, но для сохране-
ния высокой производительности необходимо повышать частоту инфор-
мационного сигнала. Она может достигать 10 ГГц. В настоящее время мож-
но говорить о гигагерцовом диапазоне частот, и эти подходы становятся все
более распространенными.
Значительный эффект дает комплексное применение параллельной и пос-
ледовательной передачи. В этом случае параллельная обработка ведется в уст-
ройствах нижнего уровня (например, на уровне микросхемы), а последова-
1.2. Элементы цифровой обработки информации
65
тельная передача осуществляется между устройствами более высокого уровня
(например, на уровне печатного узла).
На гигагерцовых частотах передачи сигналов проявляются такие особен-
ности линий передач, как потери и электрические характеристики металли-
зированных отверстий. Потери определяются резистивными свойствами
печатных проводников и нагревом основания печатной платы. Они приво-
дят к уменьшению амплитуды сигнала (ослаблению) и размыву фронта сиг-
нала при его прохождении по трассе. Эти явления особенно сильно прояв-
ляются для высоких частот и более детально рассмотрены далее.
Другим значимым фактором, который может существенным образом вли-
ять на целостность сигнала, являются металлизированные отверстия, рас-
положенные вдоль трасс печатной платы. Их расположение зависит от ре-
зультатов этапа топологического проектирования, а электрические парамет-
ры — от размеров и толщины металлизированного покрытия. Искажения
сигнала определяются емкостью и индуктивностью отверстия. Моделирование
[4] показывает, что шесть металлизированных отверстий вдоль трассы, по ко-
торой распространяется сигнал с фронтом 0,5 нс, вносит дополнительную
задержку в 100 пс.
Особое внимание следует уделять конструированию путей протекания воз-
вратных токов, не допуская появления неоднородностей в нем в виде щелей,
отверстий и т. п.
Для контроля целостности сигнала в гигабитных приложениях исполь-
зуются контрольные диаграммы.
Многие явления, которые происходят при распространении информаци-
онного сигнала в линях передачи, изучаются на примере одиночного пере-
пада напряжения или одиночного импульса. Этот подход традиционен и
удобен для анализа синхронных систем.
При анализе асинхронных систем и систем, в которых используется пре-
образование «параллельное—последовательное—параллельное» (SERDES),
применяется контрольная диаграмма (в англоязычной литературе она носит
название «eye diagram», поскольку ее вид на экране осциллографа напоми-
нает очертания глаза; иногда можно встретить название «глазковая диаграм-
ма»). Она является результатом отражения на экране осциллографа протя-
женной случайной последовательности битов, когда их изображения накла-
дываются друг на друга (рис. 1.46). В результате полученная фигура напо-
минает очертание глаза человека. Когда «глаз открыт», вероятность распо-
знавания битов на приемной конце линии передачи высокая. По мере «за-
крытия глаза» (рис. 1.47) вероятность распознавания снижается. Размытость
фронта сигнала известна как «джиттер» [100]. Канал передачи данных с боль-
шим джиттером имеет большую вероятность битовых ошибок (BER) и яв-
ляется неработоспособным.
В реальной ситуации драйвер, генерирующий сигнал, за счет различных
эффектов создает некоторую случайную временную флуктуацию временных
параметров информационных сигналов. Дополнительно увеличивают джит-
тер особенности прохождения сигнала по линиям передачи, особенно при
3 1527
66
Глава 1. Печатные платы в цифровых системах
Рис. 1.46. Контрольная диаграмма — «глаз открыт»
Рис. 1.47. Контрольная диаграмма — «глаз закрыт»
дифференциальной передаче сигнала. Принято считать, что джиттер не дол-
жен занимать более 1 % битового интервала, в котором он распределен по нор-
мальному закону. Более детально явление джиттера рассмотрено в главе 3.
При высокоскоростной передаче данных, кроме отмеченных выше фак-
торов, на качество передачи информации влияет расфазировка rsk (в англо-
язычной литературе — параметр skew), которая определяется как разность
времен распространения сигналов между отдельными линиями передачи в
составе многоразрядной шины.
Основной вклад в расфазировку и джиттер вносят линии переда-
чи. При проектировании печатных плат необходимо принимать меры для ми-
нимизации этих параметров.
Для организации параллельных межсоединений применяются линии пе-
редачи на плате различных конструкций. Основными факторами, которые
влияют на расфазировку, являются длина, тип линии и качество ее изготов-
ления, а также параметры применяемых материалов. Для покупных много-
проводных кабельных изделий параметр расфазировки определяется произ-
водителем и задается в пикосекундах на единицу длины. Чем длиннее линия
передачи, тем больше суммарная расфазировка.
Высококачественные кабели обеспечивают минимальное значение рас-
фазировки на единицу длины, которое составляет от 30 пс/м до 120 пс/м в
1.3. Номенклатура и параметры корпусов микросхемы
67
зависимости от качества кабеля. Общее значение расфазировки складыва-
ется с учетом значения этого параметра для трасс на печатных платах, соеди-
нителей и кабельных межплатных и межблочных соединений. В типичной
ситуации соединители мало влияют на суммарную расфазировку. В настоя-
щее время на рынке доступны соединители с «нулевой расфазировкой».
Требование минимальной расфазировки для трасс в составе шин передачи
данных накладывает определенные ограничения на их топологию и конст-
рукцию, что должно обеспечивать одинаковое время задержки распростра-
нения сигнала в каждой трассе шины.
1.3. Номенклатура и параметры корпусов
микросхемы
1.3.1. Микросхемотехника и печатные платы
Элементная база современной электронной аппаратуры становится все
более сложной как по выполняемым функциям, так и по технологическим
и конструкторским решениям. Среди основных тенденций развития микро-
схемотехники можно отметить увеличение быстродействия и степени интег-
рации, что влечет за собой увеличение числа выводов компонентов и сни-
жение размеров шага их размещения. Эти направления взаимосвязаны: по-
вышение степени интеграции, как следствие уменьшения проектных норм
создания микросхем, приводит к повышению быстродействия за счет умень-
шения емкостных паразитных параметров вентилей на кристалле. Это создает
новые дополнительные проблемы для проектировщиков печатных плат. Для
того, чтобы глубже понять их, необходимо рассмотреть конструкции корпусов
микросхем, устанавливаемых на печатные платы, и их электрофизические
параметры, которые вносят вклад в нарушение целостности сигнала, и уро-
вень помех по шинам питания и заземления.
Число компонентов на кристалле непрерывно возрастает и отвечает за-
кону Мура, который был сформулирован в начале 60-х годов XX века на заре
развития микроэлектроники. Он гласит, что ежегодно число транзисторов
в кристалле микросхемы удваивается. Со временем этот показатель геомет-
рической прогрессии был скорректирован на коэффициент 1,5. В настоящее
время практически каждые два года происходит удвоение числа транзисто-
ров в кристалле. Современные большие интегральные схемы (БИС) содер-
жат более 100 миллионов транзисторов. С увеличением числа транзисторов
растет и набор функций, которые могут быть выполнены на одном кристалле,
и резко растет число выводов корпусов микросхем, которое может достигать
нескольких сотен, и для коммутации они требуют достаточного много мес-
та на печатной плате. При этом очевидно желание снизить размеры корпу-
сов и выводов, а также уменьшить топологические нормы (шаг расположе-
ния выводов) при проектировании печатных плат. Кроме этого, возраста-
ет стоимость физического прототипа, для создания которого требуются
3*
68
Глава 1. Печатные платы в цифровых системах
дорогостоящие БИС и печатные платы, выполненные по предельным топо-
логическим и технологическим нормам.
Современные подходы к проектированию быстродействующих систем тре-
буют учета всех факторов, которые в конечном итоге влияют на быстродей-
ствие. Моделирование схемы не даст приемлемого результата, если не будут
учтены параметры корпусов и выводов микросхем. В свою очередь, корпус
микросхемы проектируется с учетом электрических, механических, терми-
ческих процессов, которые в совокупности определяют функциональную при-
годность микросхемы, ее надежность и экономические показатели.
В настоящее время производители микросхем используют большое число
различных типов корпусов, которые отличаются расположением кристалла,
размерами, конструкцией и числом выводов, применяемыми материалами и
другими показателями. Каждая конструкция обладает определенными элек-
трическими характеристиками, которые в той или иной мере влияют на фун-
кциональные параметры электронных модулей. Бурно развивается направле-
ние, связанное с дальнейшей микроминиатюризацией, при котором размеры
корпуса не превосходят 1,25 размера кристалла. Оно получило название «кор-
пусирование в масштабе кристалла» (Chip scale packaging— CSP). Следует учесть,
что требования рынка накладывают свой отпечаток на конструкции корпусов:
минимизация стоимости, технологичность, развитая номенклатура.
Ниже рассмотрены основные конструкции корпусов и их параметры, ко-
торые должны быть учтены при создании виртуального прототипа и при
анализе функционирования электронных модулей на печатных платах. Сле-
дует отметить, что детальное рассмотрение конструкций корпусов интеграль-
ных микросхем требует изучения не только электрических, но и тепловых и
механических характеристик, которые из-за направленности книги выходят
за ее рамки. Кроме этого, номенклатура корпусов настолько велика и попол-
няется настолько динамично, что ее полное рассмотрение не представляет-
ся возможным. Однако те общие вопросы, которые рассмотрены ниже, дают
некоторую методическую основу для анализа в конкретной ситуации.
1.3.2. Корпуса микросхем для монтажа в отверстия
Номенклатура корпусов для монтажа в отверстия
Несмотря на бурное развитие технологии монтажа на поверхность для со-
здания электронных модулей, все еще значительную долю рынка занимают
микросхемы в корпусах, предназначенных для монтажа в отверстия печатных
плат. Пластмассовые корпуса для монтажа в отверстия выпускаются в различ-
ных вариантах, но наибольшее распространение имеют пластмассовые корпу-
са для установки в металлизированные отверстия печатных плат (рис. 1.48я) или
в специальные колодки (рис. 1.486), которые установлены на плату. В последнем
случае облегчается ремонт изделия и замена компонента, но наличие дополни-
тельного коммутирующего узла может негативно отразиться на электрических
параметрах корпуса. На рис. 1.49 представлена классификация основных типов
1.3. Номенклатура и параметры корпусов микросхемы
69
Рис. 1.48. Установка выводов корпусов в сквозные металлизированные отверстия (а)
и в специальные монтажные колодки (б)
Пластмассовые корпуса
С рядным
расположением
выводов
С двухрядным расположением
выводов
P-DIP
SHRINK DIP
Компактный с двухрядным
расположением выводов
Пластмассовый корпус
Монтаж
в панель
--- PPGA
С матрицей штыревых
выводов
(вид снизу)
Рис. 1.49. Классификация основных типов корпусов для монтажа в отверстия
корпусов, предназначенных для установки в отверстия печатных плат. Подоб-
ные корпуса содержат штыревые выводы, за счет которых выполняется меха-
ническое крепление корпуса и электрическое соединение при помощи пайки.
Рассмотрим эти типы корпусов более подробно1 [6, 33, 38, 39].
1 Здесь и далее использованы обозначения корпусов, принятые производителями; для
перевода в отечественные аналоги следует использовать соответствующие справочники.
70
Глава 1. Печатные платы в цифровых системах
Пластмассовый корпус с двухрядным расположением выводов PDIP
Корпуса с двухрядным расположением выводов, предназначенные для мон-
тажа в металлизированные отверстия, имеют 24, 28, 32, 40, 64 вывода, распо-
ложенные с шагом 2,54 мм. Компактный корпус имеет шаг между выводами
1,60... 1,96 мм. При использовании коммутационных колодок они могут быть
использованы для монтажа на поверхность. Первый вывод отмечен ключом.
Внешний вид корпуса представлен на рис. 1.50.
Рис. 1.50. Внешний вид пластмассового корпуса с двухрядным расположением выводов
Керамические корпуса
Номенклатура керамических корпусов представлена на рис. 1.51.
Керамические корпуса с двухрядным расположением выводов CD1P пред-
ставляют собой корпус прямоугольной формы с шагом установки выводов
Керамические корпуса
Монтаж в колодки
CPGA - Ceramic Pin Grid Array
Керамический корпусе матрицей выводов
Монтаж в отверстия
или в колодки
C-DIP - Ceramic Dual in-Line Package
Керамический корпус с двухрядным расположением
выводов
Корпус с прозрачным окном
2,54 мм. Выводы покрыты ли-
бо золотом, либо припоем.
Материал выводов — медный
сплав или ковар. Длина выво-
да, пригодная для монтажа, —
3,18...4,06 мм.
Керамический корпус
CERDIP (см. рис. 1.48, б) с
двухрядным расположением
выводов с впаянным прозрач-
ным окном отличается от кор-
пуса CDIP наличием в центре
корпуса на его верхней сторо-
не прозрачного для ультрафи-
Стеклокерамический корпус
с двухрядным расположением выводов
Монтаж в отверстиях, наличие прозрачного окна
CERDIP - Ceramic Dual in-Line Package
Рис. 1.51. Номенклатура керамических корпусов
олетового света окна, за счет
которого возможно перепрог-
раммирование электрически
изменяемых постоянных запо-
минающих устройств, которые
монтируются в корпусе.
1.3. Номенклатура и параметры корпусов микросхемы
71
Корпуса со штырьковыми выводами (Pinned Packaging)
Корпуса с двухрядным расположением выводов (DIP) можно отнести к
одним из ранних. Они широко используются и до настоящего времени для
интегральных микросхем, которые устанавливаются на печатные платы с ме-
таллизированными отверстиями. По мере по-
вышения требований к электрическим харак-
теристикам корпусов появились пластмассовые
корпуса с матрицей штыревых выводов {plastic
pin grid array — PPGA) (рис. 1.52) и корпуса с пе-
ревернутым кристаллом и матрицей штыревых
выводов (Flip Chip Pin Grid Array — FC—PGA), ко-
торые имеют улучшенные электрические и тер-
мические характеристики. Корпуса этих разно-
видностей содержат органический материал, и
основное различие заключается в организации
электрического соединения внутренних про-
водников. Для пластмассовых корпусов боль- Рис’ 1,52‘ МатРица штырьковых
выводов
шое внимание уделяется организации отвода
теплоты от кристалла. Установка корпусов PPGA и FC-PGA предусматри-
вается в контактные панели. Внутренние проводники вне кристалла выпол-
нены из меди, что обеспечивает минимальное их сопротивление и задержку
распространения сигнала.
Развитием конструкций корпусов с матрицей штыревых выводов явля-
ются микро-корпуса (Micro Pin Grid Array — \iPGA), число выводов которых
достигает 615 с шагом 1,27 мм, а также новые корпуса, выполненные по тех-
нологии матрицы органических контактных площадок (Organic Land Grid
Array — OLGA) для мобильных персональных компьютеров. Эти корпуса от-
личаются меньшей толщиной и малой массой. Для установки этих корпусов
применяются стеклотекстолитовые промежуточные контактные узлы, снаб-
женные штырями, для установки корпусов на плату. Конструкция этих кон-
тактных узлов может предусматривать установку корпусов OLGA по техно-
логии поверхностного монтажа.
Геометрия и материалы корпусов
Пластмассовый корпус PPGA
Корпус содержит печатные платы на тонких основаниях, через которые про-
ходит штыревой вывод (рис. 1.53). Диэлектрический материал плат выбира-
ется из соображений высокой температурной стабильности и представляет со-
бой стеклотекстолит на основе связующего на основе композиции эпоксид-
ной смолы и бисмалеимида триазина (Bismaleimide Triazine — ВТ) с рабочей
температурой от 170 °C до 190 °C. Проводники выполнены из меди, и для луч-
шего качества соединения их окончания покрыты золотом поверх никеля. Теп-
лосток выполнен из меди, покрытой никелем. Штыревые выводы выполне-
ны из ковара и покрыты золотом поверх никеля и должны быть полностью ок-
ружены припоем после установки в отверстие печатной платы и пайки.
72
Глава Г Печатные платы в цифровых системах
Рис. 1.53. Фрагмент сечения корпуса PPGA
Рис. 1.54. Корпус PPGA — вид
сверху
Корпус PPGA (рис. 1.54) включает
медный теплосток, покрытый никелем, и
восемь дискретных конденсаторов. Кон-
денсаторы используются для развязки по
шине питания и заземления с целью улуч-
шения электрических характеристик ком-
понента.
Приведем (табл. 1.3) некоторые основ-
ные параметры корпуса PPGA на приме-
ре корпуса с 296 выводами, которые мо-
гут влиять на электрические характерис-
тики межсоединений.
Основные конструкторские параметры корпуса PPGA
Таблица 1.3
Параметр Значение, мм
минимальное максимальное
Размер стороны корпуса 49,43 49,63
Диаметр вывода 0,40 0,51
Длина вывода 3.05 3,30
Шаг установки выводов 2,29 2,79
Корпус FC-PGA
В основе конструкции корпуса лежит структура тонкой печатной платы
(рис. 1.55). Печатная плата из стеклотекстолита с эпоксидным связующим
покрыта не армированной смолой. Проводники выполнены из меди, а вы-
воды — из ковара, покрытого золотом поверх никеля. Они присоединяются
за счет высокотемпературной пайки.
1.3. Номенклатура и параметры корпусов микросхемы
73
Рис. 1.55. Сечение корпуса FC-PGA
Корпус FC-PGA может включать комбинацию дискретных конденсато-
ров и резисторов. Назначение конденсаторов такое же, как у корпуса PPGA, —
улучшение показателей функционирования за счет устранения или миними-
зации помех по шинам питания и земли. Резисторы имеют различное назна-
чение. Все дискретные компоненты расположены в специально отведенной
зоне в центре корпуса на стороне выводов.
Основные конструкторские параметры корпусов FC-PGA приведены в
табл. 1.4.
Таблица 1.4
Основные конструкторские параметры корпуса FC-PGA (количество выводов 370)
Параметр Значение, мм
минимальное максимальное
Размер стороны корпуса 49,428 49,632
Диаметр вывода 0,431 0,483
Длина вывода 3.048 3,302
Шаг установки выводов 2,54 - номинальный
Корпус J1PGA
Промежуточный элемент коммутации для кристаллодержателей типа
OLGA содержит медное покрытие (примерно 25 мкм) на стеклянной осно-
ве, слой стеклотекстолита на основе эпоксидной смолы. Это основание ис-
пользуется для установки штырей из медного сплава или ковара, припаян-
ных в виде матрицы через отверстия внутри подложки.
В этом случае материал корпуса OLGA и элемента коммутации одинаков,
что обеспечивает одинаковые значения температурного коэффициента рас-
ширения и наилучшие условия эксплуатации в собранном состоянии.
Элемент коммутации требует контактные площадки диаметром 0,609 мм,
расположенные с шагом 1,27 мм, что соответствует шагу установки выводов.
74
Глава 1. Печатные платы в цифровых системах
Для электрической коммутации с монтажом платы выполняются контакт-
ные площадки диаметром 0,78 мм с шагом 0,635 мм по направлению X и Y
по отношению к площадкам корпуса. Контактные площадки штырей и ша-
риковых выводов соединяются проводниками шириной 0,254 мм. На рис. 1.56
иллюстрируется эта топология.
Материал штырей — медный сплав или ковар — выбран из-за высоких элек-
трических характеристик при соединении. Допуск на форму штыревого вы-
вода составляет примерно 0,050 мм. Он покрывается слоем никеля 0,002 мм
и затем слоем золота 200 мкм для обеспечения надежного контакта гнездом
устройства коммутации с малым переходным сопротивлением.
Конструкция узла установки штыря показана на рис. 1.57. Номинальный
диаметр штыря составляет 0,304 мм. Размер буртика составляет по толщине
максимум 0,254 мм и номинальный диаметр 0,609 мм. Область штыря, кото-
рая пригодна для контактирования, определяется при вдавленном состоянии
от нижней стороны коммутационного устройства до основания штыря и рав-
на номинально 1,25 мм. Она включает зону диаметром 0,965 мм и высотой 0,254
мм, в которой расположен буртик и зона плавного перехода к пайке.
После фиксации штыревого вывода в коммутационном устройстве пайкой
используется припой 95 % Sn, 5 % Sb. Высота выступающей части припоя не
должна превышать 0,050 мм над плоскостью расположения контактных пло-
щадок для того, чтобы гарантировать отсутствие взаимодействия с трафаре-
том для нанесения паяльной пасты в процессе пайки при сборке OLGA.
Штыревые выводы расположены в виде матрицы по всей поверхности кор-
пуса. Отдельные параметры корпусов pPGA представлены в табл. 1.5.
Рис. 1.56. Топология контактных площадок под шариковые выводы и штыри при шаге
координатной сетки 1,27 мм (все размеры в мм)
1.3. Номенклатура и параметры корпусов микросхемы
75
Открытая область
паяльной маски,
диаметр 0,61 мм
Диаметр
контактной
площадки
1,04 мм
Высота пайки
0,051 мм
Окончательный
диаметр отверстия
0,35 мм
Зазор
0,25 мм
Диаметр зоны
0,76 мм
Длина вывода
1,25 мм
Диаметр контактной
площадки 0,787 мм
Открытая область
паяльной маски,
диаметр 0,76 мм
Рис. 1.57. Узел установки штыревого вывода корпуса pPGA
Таблица 1.5
Основные конструкторские параметры корпусов pPGA (количество выводов 615)
Параметр Значение, мм
минимальное номинальное максимальное
Ширина корпуса 32,41 32,56 32,71
Длина корпуса 36,60 36,75 36,90
Диаметр вывода - 0,30 0,36
Длина контактной части вывода 1,19 1,25 1,31
Шаг установки выводов - 1,27 -
Керамический корпус с матрицей штырьковых выводов (CPGA)
Керамический корпус с матрицей штыревых выводов (Ceramic Pin Grid Array
CPGA) имеет число выводов от 68 до 387, шаг установки выводов 2,54 мм и с
возможным уменьшением до 1,275 мм при числе выводов более 240.
Кристаллодержатели
Безвыводные кристаллодержатели (рис. 1.58) имеют шаг расположения
выводов 1,27 мм, число выводов 68.
76
Глава 1. Печатные платы в цифровых системах
Безвыводной кристаллодержатель
LCC - Leadless Chip Carrier
Безвыводной кристаллодержатель
Монтируется в контактную панель
Рис. 1.58. Керамический безвыводной кристаллодержатель
1.3.3. Корпуса для поверхностного монтажа
Номенклатура корпусов для поверхностного монтажа
Технология поверхностного монтажа является наиболее перспективной для
создания разнообразных электронных устройств — от изделий специального
назначения до продукции массового спроса. Эта технология незаменима при
крупносерийном и массовом производстве, например, мобильных телефонов.
Уменьшение габаритов компонентов приводит к сокращению индуктивное-
Пластмассовые корпуса для
монтажа на поверхность
SSOP - Shrink Small
Outline Package
SOJ - Small
Outline Package
TSOP - Thin Small
Outline Package
PSOP - Plastic Small
Outline Package
Малый пластмассовый корпус
с двухрядным расположением
выводов.
Форма выводов - “крыло чайки”
Узкий малый корпус с двухрядным
расположением выводов
Форма вывода - “крыло чайки"
Малый корпус с двухрядным
расположением выводов.
Форма вывода - J-образная
Тонкий малый корпус с
двухрядным расположением
выводов.
Форма вывода - ‘крыло чайки"
PLCC - Plastic Leader
Chip Carrier
Пластмассовый выводной
кристаллодержатель.
PQFP - Plastic
Quad Flatpack
Пластмассовый плоский корпус
с четырехсторонним
расположением выводов
QFP - Quad
Flatpack
Плоский корпус
с четырехсторонним
расположением выводов
FLATPACK
Плоский корпус
с планарными выводами
PBGA/H-PBGA/HL-PBGA
Plasitic Ball Grid Array
MICRO BGA
Пластмассовые корпуса
с матрицей шариковых
выводов
Рис. 1.59. Классификация корпусов микросхем для монтажа на поверхность
1.3. Номенклатура и параметры корпусов микросхемы
77
тей их выводов и сокращению длин проводников, что является весьма поло-
жительным фактором. Но особенности этой технологии требуют применения
микросхем в корпусах, которые отвечают требованиям технологического про-
цесса и применяемого оборудования. Классификация корпусов микросхем для
монтажа на поверхность приведена на рис. 1.59.
Практически все компоненты для монтажа на поверхность поставляются
в носителях (например, на лентах-носителях), предназначенных для заправ-
ки автоматизированных или автоматических станков установки компонентов.
Рассмотрим некоторые корпуса более подробно.
Пластмассовый малый корпус с плоскими
боковыми выводами PSOP/SSOP
Корпус PSOP имеет 44 (корпус SSOP — 48 или 56) вывода в виде «крыла
чайки» (рис. 1.60). Конфигурация корпуса — прямоугольная, выводы рас-
положены с шагом 1,27 мм (SSOP — 0,8 мм). Толщина корпусов примерно
2,95 мм. Финишная обработка выводов припоем.
Уменьшенный малый корпус с боковыми выводами SSOP
Корпус SSOP имеет 56 выводов в виде «крыла чайки» (рис. 1.60). Конфи-
гурация корпуса — прямоугольная, выводы расположены с шагом 0,8 мм. Тол-
щина корпусов примерно 1,27 мм. Финишная обработка выводов припоем.
Малый корпус с J-образными боковыми выводами SOJ
Корпус SOJ имеет 20 или 24 вывода J-образной формы (рис. 1.61). Кон-
фигурация корпуса — прямоугольная, выводы расположены с шагом 1,27 мм.
Толщина корпуса примерно 2,6 мм.
Рис. 1.60. Вывод в виде «крыла чайки»
А 0,13 Мах
0,76
Рис. 1.61. Вывод J-образной формы корпусов для монтажа на поверхность
(все размеры в мм)
78
Глава 1. Печатные платы в цифровых системах
Тонкий малый пластмассовый корпус с боковыми выводами TSOP
Корпус TSOP имеет от 32 до 56 выводов в виде «крыла чайки» (рис. 1.60). Кон-
фигурация корпуса — прямоугольная, выводы расположены с шагом 0,5 мм. Тол-
щина корпусов примерно 2,95 мм. Финишная обработка выводов припоем.
Пластмассовый выводной кристаллодержатель PLCC
Кристаллодержатель имеет число выводов от 28 до 84, расположенных с
шагом 1,27 мм по его периметру. Форма кристаллодержателя квадратная (толь-
ко при числе выводов 28 и 32 — прямоугольная). Его толщина лежит в диа-
пазоне от 2,5 до 3,9 мм. Форма вывода — J-образная (рис. 1.61); выводы по-
крыты припоем.
Пластмассовый плоский корпус PQFP
Корпус квадратной формы PQFP имеет от 84 до 196 выводов, располо-
женных с шагом 0,625 мм по его периферии. Поставляется в носителях, ко-
торые предназначены для применения в автоматах установки компонентов
на поверхность. Форма выводов — «крыло чайки», финишное покрытие —
припой.
Внешний вид корпуса PQFP представлен на рис. 1.62.
Плоский корпус с выводами на четырех сторонах QFP
Корпус (рис. 1.63) имеет от 44 до 208 выводов, расположенных с шагом
0,8 мм (44, 48, 80, 100, 128 выводов), 0,65 мм (64, 160 выводов), 0,50 мм (80,
144, 176, 208 выводов). Форма корпуса либо квадратная, либо прямоуголь-
ная (80, 100 выводов). Форма выводов — «крыло чайки». Корпус имеет раз-
новидности SQFP Shrink QFP — уплотненный QFP (80,100, 128, 208 выво-
дов) и TQFP — Thin QFP — тонкий QFP (100, 144, 176 выводов).
Рис. 1.62. Внешний вид корпуса PQFP
1.3. Номенклатура и параметры корпусов микросхемы
79
Lt.jp О |А|В1С|
Е1 Е
D2*
[с]
Рис. 1.63. Внешний вид корпуса QFP/TQFP/SQFP
Рис. 1.64. Пластмассовый корпус с планарными выводами
Пластмассовый плоский корпус с планарными выводами Flatpack
Плоский пластмассовый корпус для поверхностного монтажа (рис. 1.64)
имеет прямоугольную форму и 68 выводов, расположенных с шагом 1,275 мм.
1.3.4. Корпуса с матрицей шариковых выводов BGA
Пластмассовые корпуса с матрицей шариковых выводов (Plastic Ball Grid
Array — PBGA) становятся наиболее распространенными при создании элект-
ронной аппаратуры. Одним из главных преимуществ этих корпусов является воз-
можность создания большого числа (до нескольких сотен) выводов. Они созда-
ются в виде полусфер припоя под основанием корпуса, которые при установке
80
Глава Г Печатные платы в цифровых системах
на контактные площадки подвергаются расплавлению и обеспечивают механи-
ческое и электрическое соединение корпуса с монтажом платы. Невозможность
упругой деформации шариковых выводов предъявляет высокие требования к
плоскостности основания платы. В процессе пайки шариковые выводы само-
центрируются, что позволяет несколько снизить требования к точности уста-
новки компонентов и расположению контактных площадок. Обычно шаг ус-
тановки выводов BGА составляет 1,27 мм, что больше, чем для QFP и PQFP. Это
несколько упрощает сборку и монтаж электронных модулей.
Электрические и тепловые характеристики корпусов BGA могут быть луч-
ше, чем у QFP и PQFP. Корпуса BGA имеют сокращенный цикл «проекти-
рование — производство» и могут быть применены для построения много-
кристальных корпусов (few-chip-package — FCP) и многокристальных моду-
лей (multi-chip modules — MCM).
Корпуса BGA имеют несколько разновидностей:
• корпуса, спресованные сверху пластиком (PBGA)\
• корпуса на ленточном носителе (tape BGA—TBGAy,
• корпуса, покрытые сверху высокотемпературным металлом (HLPBGA)\
• теплостойкие корпуса (high thermal BGA — H-PBGAs),
• низко-профильные корпуса (low-profile BGA — LBGA),
• корпуса с малым шагом установки выводов (fine-pitch BGA — FBGA).
На базе H-PBGA фирма Intel разработала одну из последних версий кор-
пусов (OLGA) по технологии перевернутого кристалла (Flip Chip — FC), при
которой кристалл устанавливается на матрицу контактных площадок, выпол-
ненную на органической подложке.
Из-за малых размеров корпусов BGA по технологии FC обеспечивается
малая индуктивность проводников, которые соединяют кристалл с выводами.
Параметры корпусов BGA
Расположение выводов
Типичная матрица шариковых выводов представлена на рис. 1.65. Шариковые
выводы из припоя расположены в четыре ряда вдоль каждой стороны корпуса.
При расположении кристалла в центре, трассы, которые идут от кристалла к
угловым выводам, значительно длиннее, чем трассы, идущие к выводам, рас-
положенным в центре рядов. Длина выводов имеет большое значение при оп-
--- Угловые выводы
Центральные выводы
а
Наружный ряд выводов
Внутренний ряд выводов
Тепловые контакты (опция)
Рис. 1.65. Компоновка матрицы шариковых выводов:
а — вид на шариковые выводы, б — распределение выводов
1.3. Номенклатура и параметры корпусов микросхемы
81
ределении их индуктивности. В табл. 1.6 приведены примерные параметры со-
противления (7?), индуктивности (Z) и емкости (Q для проводников максималь-
ной длины для внешних (колонки «О») и внутренних (колонки «/») рядов вы-
водов (см. рис. 1.65) для низко-профильных корпусов BGA и корпусов с малым
шагом установки выводов. Кроме этого, в таблице приведены значения взаим-
ной индуктивности (М) и взаимной емкости (Ст) между угловыми и централь-
ными проводниками. В реальной ситуации топология соединительных провод-
ников определяется конкретной конструкцией, и заранее определить ее, а сле-
довательно, и электрические параметры проводников, достаточно трудно.
Моделирование корпусов, которые имеют плоскости для расположения
шин питания и заземления, должно проводиться комплексно с учетом кон-
фигурации путей возвратных токов. Сигнал распространяется по сигналь-
ным проводникам в нагрузку и возвращается к источнику по шинам пита-
ния и заземления. Высокочастотные компоненты возвратного тока имеют
тенденцию располагаться рядом с путем прямого тока. Это означает, что плот-
ность тока в плоскости не является однородной и постоянной. Поэтому не-
возможно дать значение индуктивности только для одного сигнального про-
водника, а необходимо учитывать и конфигурацию пути возвратного тока,
т. е. рассматривать совокупность пути прямого и возвратного тока как линию
Таблица 1.6
Параметры RLC для некоторых типов корпусов BGA
Тип Размер корпуса, мм R, Ом £, нГн Л/, нГн
угол центр угол центр угол центр
О / О / О / О / О 1 О I
PBGA-208 23x23 1,2 0,8 0,9 0,6 9,0 6,0 5,5 2,5 6,0 4,5 3,5 1,5
PBGA-388 35x35 1,8 1,2 1,35 1,о 14,0 10,0 8,0 4,5 9,0 6,5 5,0 3,0
LBGA-196 15x15 1,4 0,2 0,3 1,7 0,9 1,2 0,6 о,з 0,45
FBGA-81 9x9 0,025-0,075 0,4-1,5 0,03-0,1
Тип Размер корпуса, мм С, пФ Q, пФ
угол центр угол центр
О I О I О I О I
PBGA-208 23x23 0,2 о,1 0,15 0,1 0,35 0,15 0,15 0,1
PBGA-388 35x35 0,3 0,1 5 0,25 0,18 0,5 0,25 0,25 0,15
LBGA-196 15x15 0,08 0,04 0,04 0,1 0,10 0,10
FBGA-81 9x9 0,04- 0,06 0,03-0,075
82
Глава 1. Печатные платы в цифровых системах
передачи. Если пути сигнального (прямого) тока и возвратного расположе-
ны в непосредственной близости друг от друга (что справедливо на высоких
частотах), то может быть рассчитана индуктивность на единицу длины этой
совокупности проводников. В табл. 1.7 и табл. 1.8 приведены параметры ин-
дуктивности, емкости и сопротивления для корпусов EBGA. Значение ин-
дуктивности в колонке £tl (табл. 1.7) дано для линии передачи, образован-
ной сигнальным проводником и возвратной плоскостью. Аналогично зна-
чение емкости относится к этой части плоскости.
Таблица 1. 7
Индуктивность проводников в корпусах EBGA
Тип корпуса Число выводов £, нГн Л/, нГн Л/, нГн L,,. нГн
угол центр угол центр угол* центр*
1 2 3 1 2 3
EBGA 215 5,0- 7,8 2,5- 4,0 2,9- 3,8 1,4- 2,0 2,8- 4,0 2,2- 3,2 2,0- 2,8 2,0- 2,5 1,4- 2,2 1,2- 1,5 4,0
368 7,5 - 10,5 6,5- 8,0 2,5- 4,0 2,5- 3,5 3,1 - 4,0 2,5- 3,0 2,5- 2,8 1,8- 3,0 1,5- 2,0 1,1 - 1,5 4,0
Примечание. * Значение взаимной индуктивности дано для трех слоев; слой 1 — ближай-
ший к плоскости питания (заземления); слой 3 — наиболее удаленный.
Таблица 1.8
Сопротивление (Ом) и емкость (пФ) проводников в корпусах EBGA
Тип корпуса Размер корпуса, мм Число выводов R С с: с; Сп1 (для плоскостей)
угол центр собствен- ная’ взаимная4
EBGA 27x27 215 0,75- 0,90 0,60- 0,80 0,08- 0,12 0,10- 0,14 1,10 - 1,50 0,6- 1,2 5,0-8,0
40x40 368 1,00 - 1,30 0,7- 1,0 0,30- 0,50 0,10 - 0,20 1,20 - 1,80 1,5-2,0 14,5-50
Примечания.
1. Частичная емкость между проводниками.
2. Частичная емкость между проводником и плоскостью.
3. Собственная емкость дана для плоскости, ближайшей к плоскости заземления
платы. Собственная емкость относительно других слоев заземления платы принята
равной 0.
4. Взаимная емкость дана между ближайшими соседними плоскостями. Эта емкость,
если она возникает относительно шины питания, будет способствовать развязке.
1.3. Номенклатура и параметры корпусов микросхемы
83
Проводные соединения внутри корпуса
Для получения индуктивности и сопротивления электрических соединений
внутри корпуса, необходимо учесть длину проводников. Для одиночного про-
водника индуктивность может быть рассчитана только для всей длины. Если
рядом расположен возвратный провод (как отмечалось выше), то индуктивность
может быть рассчитана на единицу длины. В табл. 1.9 приведены значения ин-
дуктивности для соединительных проводников внутри корпусов различных ти-
пов. Емкость проводников пренебрежимо мала и опущена в таблице. Взаимная
индуктивность характеризует связь между соседними проводниками в корпу-
се. Видно, что из-за малой длины проводниковых соединений эти значения ми-
нимальны для корпусов CSP и LLP. Значение «эффективная индуктивность» дает
значения L и Мпри взаимном влиянии ближайших соседних проводников друг
на друга. Для других случаев следует приводить более тонкий анализ.
Таблица 1.9
Индуктивность одиночных проводников в корпусах различного типа
Длина, мм Индуктивность провода (для CSP и LLP), нГн Эффективная индуктивность (для всех проводников), нГн
L М12 М13 L М12 М13
0,50 0,32 0,14 0,09 0,45 0,19 0,12
1,00 0,78 0,39 0,28 1,09 0,55 0,39
2,00 1,83 1,04 0,78 2,57 1,46 1,12
3,00 2,99 1,80 1,40 4,19 2,52 1,96
4,00 4,22 2,62 2,09 5,91 3,67 2,93
5,00 5,50 3,48 2,82 7,70 4,87 3,95
Материалы для корпусов
Корпус BGA содержит кристалл, установленный на плате на основе ВТ с
двусторонней металлизацией медью. Кристалл присоединен проволочными
проводниками к выводам.
Плата имеет четыре слоя, что позволяет отвести два слоя под питание и
землю. Это улучшает электрические и термические характеристики микро-
схем. Кристалл и соединительные проводники герметизированы заливкой
в компаунд. Переходные отверстия в плате обеспечивают трассировку от вы-
водных штырей к шариковым выводам (эвтектический припой 63/37 Sn/Pb)
на обратной стороне. Термические характеристики могут быть улучшены при-
менением теплостока, который устанавливается, например, при помощи про-
водящей эпоксидной смолы. В некоторых типах корпусов (например, H-BGA),
которые отличаются повышенной мощностью рассеяния, кристалл обрат-
ной стороной ставится непосредственно на теплосток, контактирующий с
системой охлаждения модуля.
Корпуса H-BGA по технологии перевернутого кристалла содержат кристалл,
припаянный на органическую подложку, которая содержит от 4 до 10 медных
84
Глава 1. Печатные платы в цифровых системах
слоев и соответствующего числа изоляционных слоев между ними. Медные слои
соединяются металлизированными отверстиями. Смола ВТ усиливается стек-
лотканью, формируя органическую подложку. Шариковые выводы из припоя
(3 % Sn, 97 % Pb) на поверхности кристалла соединяются с контактными пло-
щадками для пайки (60% Sn, 40% Pb) на органической подложке в установке для
пайки. Это соединение формирует механическое и электрическое соединение
между перевернутым кристаллом и корпусом OLGA. Зазор между подложкой
и кристаллом заполняется эпоксидной смолой. Эта заливка обеспечивает до-
полнительную механическую прочность конструкции, защищает соединение
между кристаллом и подложкой, а также минимизирует термические напряжения
в кристалле, которые возникают из-за рассогласования термических коэффи-
циентов расширения материалов кристалла и подложки.
На рис. 1.66, 1.67, 1.68 показаны упрощенные сечения некоторых разно-
видностей корпусов BGA.
Кристалл над платой
Компаунд-|
Печатная плата
на основе ВТ
1OX5UO
____I I ________\_____
------О’ООО------------оооон
Шариковые выводы из припоя
Рис. 1.66. Сечение корпуса PBGA
Медный теплосток
UUUU
Печатная плата-
на основе ВТ
Кристалл
OUUU
Герметизация -
Шариковые выводы
L под теплостоком L из припоя
Рис. 1.67. Сечение корпуса HL-PBGA
Шариковые Кристалл
Слоистый
пластик ВТ
выводы
кристалла
поверх
основания
Шариковые выводы из припоя
OOUOOOOOOOUUOUOU
Рис. 1.68. Сечение корпуса H-PBGA по технологии перевернутого кристалла
1.3. Номенклатура и параметры корпусов микросхемы
85
Применение корпусов BGA
Корпуса BGA используются для создания электронных модулей с высо-
кими термическими и электрическими характеристиками. Они требуют умень-
шенного шага расстановки шариковых выводов, что обеспечивает более
высокую плотность размещения контактов входа/выхода, чем QFP и PGA.
В итоге обеспечиваются меньшие размеры электронного модуля.
Корпуса с матрицей шариковых выводов обеспечивают меньшую длину
электрических соединений, что приводит к снижению их индуктивности. До-
статочно большое расстояние между контактными площадками обеспечи-
вает более свободные допуски при монтаже и установке компонентов. Экс-
плуатационные свойства корпуса выше корпусов с выводами, поскольку от-
сутствуют проблемы, связанные с механическим повреждением выводов при
формовке. Эти характеристики определили широкое применение корпусов
BGA для создания микропроцессоров, микроконтроллеров, заказных мик-
росхем, систем памяти, компонентов персональных компьютеров и другой
продукции микроэлектроники. Малая толщина и уменьшенная площадь ос-
нования особенно полезны, когда требуются малые габариты электронного
модуля, например, в космических приложениях.
Контактные площадки под корпуса BGA
Большинство корпусов BGA имеет контактные площадки, сформирован-
ные паяльной маской для прикрепления шариковых выводов. Контактные пло-
щадки под шариковые выводы, выполненные на печатной плате, должны быть
близки или идентичны по размерам контактным площадкам на корпусе мик-
росхемы. Это способствует выравниванию термических напряжений, что спо-
собствует продлению срока службы компонента.
Контактные площадки, определяемые паяльной маской
(Solder Mask Defined (SMD) Pad)
Уточним понятие контактной площадки, определяемой паяльной маской
(solder mask defined — SMD). Эскиз SMD-площадки показан на рис. 1.69. Мед-
ная площадка должна иметь диаметр больше, чем необходимо. После покры-
тия площадки паяльной маской открытая (рабочая) часть контактной пло-
щадки будет меньше. Для этого типа маски можно отметить следующие осо-
бенности:
• преимущество SMD-площадок
заключается в увеличении адге-
зии меди к поверхности за счет
перекрытия контактной площад-
ки паяльной маской. В том слу-
чае, когда применяются эпоксид-
ные системы, у которых низкая
адгезия, это важнейшее условие;
• одним из недостатков SMD-пло-
щадок является то, что усталост-
Паяльная
маска
Рис. 1.69. К определению понятия
контактной площадки SMD
86
Глава 1. Печатные платы в цифровых системах
ная долговечность, определяемая длительными циклами испытаний на
надежность, меньше, чем для площадок, сформированных без маски.
Контактные площадки без маски
Контактные площадки без маски (Non-Solder Mask Defined Pad — NSMD),
иногда называемые металлическими или медными, показаны на рис. 1.70. Они
имеют паяльную маску, открывающую большую часть, чем медная область.
Рис. 1.70. Контактные площадки
без паяльной маски (Non-SMD)
Размер площадки контролируется при
травлении меди. Это основной фактор,
снижающий точность по сравнению с
паяльной маской, которая контролиру-
ется при фотопроцессе. Размеры
NSMD-площадки изменяются больше
по сравнению с SMD-площадками.
Однако, поскольку нет необходимости
делать край меди выступающим за па-
яльную маску, площадка может быть
сделана меньше, что обеспечит больше
места для размещения трасс между площадками. Совмещение рисунков со-
ответствует точности формирования медных элементов рисунка, которая зна-
чительно больше, чем точность нанесения рисунка паяльной маски.
Топологические расчеты по определению влияния форм контактных пло-
щадок на плотность трассировки можно найти в [8, 21].
Топологические элементы плат под корпуса BGA
Ниже приведены основные требования трассировки под корпуса BGA,
включая размеры контактной площадки, переходные отверстия и трассировку.
Важно обеспечить определенную внешнюю зону вокруг корпуса BGA для ре-
монтных работ. Размеры этой зоны определяются типом применяемого ре-
монтного оборудования.
Маршрутизация и размер контактной площадки
Большинство типов корпусов BGA имеет четыре или пять рядов шари-
ков припоя, расположенных так, что между соответствующими контактны-
ми площадками можно проложить одну или две трассы в четырехслойной
плате. Для этого должны выполняться следующие условия.
• Когда прокладывается одна трасса между площадками, производствен-
ные ограничения на ширину проводников и зазоров становятся пре-
валирующим фактором.
• Когда прокладываются две трассы между площадками, то для диаметра
площадки 0,6 мм требуется ширина проводника и зазор между ними
в 0,125 мм; при диаметре площадки 0,5 мм ширина проводников и за-
зоров должна составлять 0,15 мм. На рис. 1.71 ирис. 1.72 показаны при-
меры трассировки при диаметре контактной площадки 0,5 мм. Если
эти размеры площадок приемлемы, то решение, в первую очередь, оп-
1.3. Номенклатура и параметры корпусов микросхемы
87
Рис. 1.71. Пример № 1 трассировки при установке корпусов ВСА(верхний сигнальный
слой): 1 — диаметр контактной площадки 0,6 мм; 2 — диаметр металлизированного
отверстия 0,3 мм; 3 — диаметр круговой зоны в маске 0,6 мм; 4 — диаметр контактной
площадки 0,5 мм; 5 — зазор 0,15 мм; 6 — ширина проводников 0,15 мм
Рис. 1.72. Пример № 2 трассировки при установке корпусов BGA (верхний сигнальный
слой): 1 — диаметр контактной площадки 0,6 мм; 2 — диаметр металлизированного
отверстия 0,3 мм; 3 — диаметр круговой зоны в маске 0,6 мм; 4 — диаметр контактной
площадки 0,5 мм; 5 — зазор 0,125 мм; 6 — ширина проводников 0,125 мм
ределяется превалирующими производственными технологическими
факторами в отношении ширины проводников и зазоров.
• Когда требуется большая ширина трассы, проложенной между площад-
ками, альтернативным решением является прокладка трасс/зазоров ши-
риной 0,125/0,125 мм или 0,15/0,15 мм внутри места расположения BGA
площадок с последующим расширением до максимальной ширины
трассы; при этом следует иметь в виду, что изменение ширины про-
водника приведет к появлению неоднородности в линии передачи, что
в ряде случаев может оказаться недопустимым.
88
Глава 1. Печатные платы в цифровых системах
Один из вариантов схем трассировки показан на рис. 1.71. Трассы от двух
первых рядов шариковых выводов располагаются на верхнем сигнальном слое,
а трассы от двух внутренних рядов - на нижнем слое платы. В этом случае
требуются переходные металлизированные отверстия между контактными
площадками. При использовании топологии, показанной на рис. 1.72, пер-
вые три ряда выводов трассируются на верхнем сигнальном слое, а внутренние
слои выводов трассируются на нижнем слое платы. В этом случае уменьша-
ется число металлизированных переходных отверстий.
Топологические ограничения на ширину печатных проводников и другие то-
пологические элементы непосредственно влияют на возможность создания на
печатной плате линий передач с требуемыми электрическими параметрами.
Разнесение контактных площадок с помощью переходных отверстий
(Plated Through Hole (РТН) Isolation)
Тщательное проектирование топологии требует точного определения фор-
мы контактной площадки при ее разнесении относительно металлизирован-
ного отверстия. Если металлизированное переходное отверстие расположено
внутри контактной площадки (традиционное решение), то будет наблюдаться
нежелательное проникновение припоя в полость отверстия. Количество этого
затекшего припоя будет зависеть от многих факторов, включая качество ко-
нечной обработки отверстия и вариации толщины его покрытия. Поэтому
результаты в этом случае непредсказуемы и качество паяного соединения
может быть очень низким, что приведет к уменьшению площади сечения пе-
рехода. Из-за этого соединение может иметь пониженный срок службы, и,
как следствие, может быть снижен срок службы аппаратуры. Поэтому более
предпочтительно контролировать качество конечной пайки, чем случайные
параметры процесса пайки. Все переходные металлизированные отверстия,
0,6 или 0,7
диаметр отверстия
паяльной маски
0,5 или 0,6
диаметр контактной
площадки
0,25
ширина трассы
0,75
диаметр шарика
припоя
0,4 или 0,35
0,675 или 0,6 диаметр
диаметр контактной металлизированного
площадки отверстия
Рис. 1.73. Взаимное расположение металлизированного отверстия и контактной
площадки; паяльная маска должна закрывать металлизированное отверстие
(размеры в мм)
1.3. Номенклатура и параметры корпусов микросхемы
89
расположенные между шариковыми выводами корпуса BGA, должны быть
закрыты паяльной маской. Это предполагает, как минимум, что отверстие
будет закрыто паяльной маской в верхней части. Нижняя сторона также может
быть закрыта. На рис. 1.73 показано взаимное расположение металлизиро-
ванного отверстия и контактной площадки под шариковый вывод.
Качество основания платы
Качество монтажа компонентов BGA зависит от параметров основания пе-
чатной платы и процедуры контроля процесса пайки. Одним из требований яв-
ляется требование к плоскостности основания, которое непосредственно зависит
от размеров платы. Типовые спецификации производителей позволяют иметь
изгиб до 0,01 мм (1 %). Для компонентов с размерами корпуса 35 мм это экви-
валентно изгибу 0,35 мм в области основания корпуса. Очевидно, что для больших
корпусов (более 20 мм) компонентов периферийные выводы корпусов или BGA
могут припаиваться к основанию с этим значением изгиба. В наиболее качествен-
ных изделиях предпринимаются меры для обеспечения изгиба меньше значе-
ния 0,010 мм, рекомендованного индустриальными стандартами.
Точность позиционирования
Расположение
Корпуса BGA обладают исключительно высокой способностью к самоцен-
трированию, т. е. способностью шариковых выводов устанавливаться при пайке
по центру контактной площадки за счет сил поверхностного натяжения при-
поя при максимальной температуре пайки. По-
этому возможны достаточно широкие изменения
в координатах контактных площадок. Основное
правило для корпусов BGA заключается в том,
что допустимое смещение долж- но быть не бо-
лее 50 % от размеров контактной площадки. Это
иллюстрируется на рис. 1.74.
При смещениях выводов на расстояния более
50% от размеров контактной площадки увеличи-
вается вероятность короткого замыкания элемен-
тов монтажа мостиками припоя при пайке.
Требуемые параметры установки корпусов
BGA должны быть обеспечены технологическим
оборудованием, применяемым при сборке и мон-
таже, и они должны контролироваться операци-
Контактная площадка
Рис. 1.74. Смещение шарико-
вого вывода относительно
расположения контактной
площадки
ями оптического или рентгеновского контроля.
Электрические характеристики корпусов BGA
Электрические характеристики корпусов BGA значительно лучше, чем
корпусов со штырьковыми выводами. Это объясняется более качественным
выполнением печатного монтажа основания корпуса и отсутствием длинных
90
Глава 1. Печатные платы в цифровых системах
штыревых элементов. Сокращение длины трасс между шариковыми выво-
дами, проходящими через металлизированные переходные отверстия к про-
водящим и заземляющим слоям платы в корпусе микросхемы, снижают па-
разитные электрические параметры.
1.3.5. Корпуса с размерами кристалла
Технология, конструкция и применение корпусов, размеры которых не пре-
вышают 1,2...1,25 размера кристалла (Chip Scale Package — CSP), является от-
носительно новым направлением в корпусировании микросхем, зарождение
которого может быть отнесено к началу XXI века. Варианты конструкций кор-
пусов насчитывают более 50 типов, одним из которых является корпус pBGA
(Intel®) [38], отличающийся широкими возможностями и удобством приме-
нения в различных приложениях. В наибольшей степени CSP-корпуса исполь-
зуются для создания элементов перепрограммируемой памяти. Развитие под-
ходов на основе CSP идет настолько бурно, что приходится рассматривать не-
которые усредненные показатели, типичные на момент написания книги.
Для применения CSP имеется целый ряд причин. Одно из главных преиму-
ществ CSP — снижение размеров корпусов относительно традиционных кор-
пусов с периферийным или матричным расположением выводов. В основном
это объясняется применением техники BGA. За счет расположения межсоеди-
нений под корпусом BGA удается снизить число межсоединений на печатной
плате. Требования к точности расположения корпусов BGA рассмотрены выше.
Размеры корпусов и их параметры
Корпус p,BGA
Корпус pBGA является наиболее типичным представителем направления
CSP. Размеры корпуса определяются в основном размерами кремниевого кри-
Рис. 1.75. Корпус pBGA
сталла. Корпус (рис. 1.75)
имеет матрицу шариковых
выводов, установленных с
шагом 0,75, и сохраняет все
преимущества, связанные с
уменьшением размеров кри-
сталла. Конструкция корпу-
са содержит слои эластомера,
которые развязывают усилия,
определяемые коэффициен-
тами температурного расширения кристалла и материала печатной платы при
изменениях температуры.
По мере снижения размеров кристалла в этом типе корпуса должен сни-
жаться и шаг размещения выводов для того, чтобы размеры корпуса соответ-
ствовали размеру кристалла. При типовом шаге 0,75 мм уменьшенный шаг
может достигать 0,5 мм.
1.3. Номенклатура и параметры корпусов микросхемы
91
Наборные конструкции CSP Intel®
Другой разновидностью технологии CSP является конструкция корпуса и
микросхемы, которая формируется путем набора кремниевых кристаллов в виде
многоуровневой структуры — «наборные CSP» (Intel®). Они также применя-
ются для создания элементов памяти, например SRAM и Flash, путем их объе-
динения в единую конструкцию (рис. 1.76). Расположение кристаллов один
над другим существенно сокращает площадь микросхемы по отношению, на-
пример, к многокристалльным модулям. Хотя данная конструкция может
иметь больший шаг (0,8 мм) расположения шариковых выводов, чем pBGA
(0,75 мм), общая площадь, занимаемая наборными CSP, меньше, чем для двух
отдельных компонентов.
0,8 мм
Рис. 1.76. Конструкция микросхем «наборный CSP»
Упрощенный BGA
Упрощенный корпус BGA (рис. 1.77) спроектирован для флэш-памяти.
Для него применяется больший шаг (1,0 мм) расположения шариковых вы-
водов, что упрощает монтаж. Другим преимуществом этого типа корпуса яв-
ляется его постоянный размер при различной емкости памяти. Это обеспе-
чивает длительный жизненный цикл систем памяти (5...7 лет) путем заме-
ны одной микросхемы другой, более совершенной.
Отличительной чертой корпуса, кроме увеличенного шага выводов, яв-
ляется применение увеличенного диаметра шарикового вывода из эвтекти-
ческого припоя и тонкого ВТ-слоя жесткого основания. Эта комбинация
обеспечивает высокую надежность компонента за счет заливки и максималь-
ного разнесения кристалла и основания печатной платы, что снижает нагрузки
из-за их различных ТКР.
Золотые Герметизирующая
увеличения 1 мм Жесткая
надежности (увеличенный шаг) подложка
Рис. 1.77. Упрощенный корпус BGA
92
Глава 1. Печатные платы в цифровых системах
Требования к конструкции платы для CSP
В большинстве случаев для корпусов CSP используются такие же платы,
как и для корпусов BGA. Приведем сравнительные требования для тополо-
гических элементов печатных плат под корпуса pBGA, упрощенные BGA и
наборные CSP (табл. 1.10).
Таблица /. 10
Сравнительные требования для печатных плат под корпуса pBGA, упрощенные BGA
и наборные CSP (размеры в мм)
Элемент pBGA, CSP pBGA, CSP Наборный CSP Упрощенный BGA
Шаг выводов 0,5 0,75 0,8 1,0
Диаметр контактной пло- щадки по шариковый вывод 0,28 0,30 0,30 0,30
Диаметр открытой зоны в паяльной маске 0,35 0,43 0,43 0,43
Минимальный зазор между маской и металлом 0,050 0,050 0,05
Максимальная ширина трассы 0,10* 0,07** 0,127 0,127 0,23
Типовой зазор 0,16 0,187 0,23
Максимальный диаметр контактной площадке около металлизированного отверстия 0,51 0,51 0,71
Максимальный диаметр металлизированного отверстия при сверлении 0,25 0,25 0,46
Диаметр металлизирован- ного отверстия, окруженного контактной площадкой 0,10
* Номинальная ширина проводников.
* * Ширина проводников между контактными площадками.
1.3.6. Электрические параметры корпусов ИС
Применение корпусов
Наличие интегральных микросхем в различных корпусах определяет воз-
можность их выбора для конкретных условий эксплуатации и приложений.
Во внимание должны приниматься назначение устройства, его массогаба-
ритные показатели, возможность автоматизации процесса производства,
сборки, монтажа и контроля, экономические факторы. Если компоновка ус-
1.3. Номенклатура и параметры корпусов микросхемы
93
тройства требует минимальных габаритов, то наиболее пригоден корпус с на-
бором кристаллов — наборный CSP. При создании систем памяти с исполь-
зованием флэш и SRAM предпочтение следует отдавать корпусам «наборный
CSP». Корпуса этого типа обеспечивают уникальные требования по мини-
мизации размеров изделия. Это особенно необходимо для таких устройств,
как сотовые телефоны, карманные компьютеры, системы глобального по-
зиционирования (GPS) и т. п. При малых габаритах и повышенной надеж-
ности при применении однокристальных компонентов наиболее пригоден
корпус pBGA.
Для ряда изделий основным показателем является не минимальный га-
барит, а минимальная стоимость, например, при производстве печатных плат.
В этом случае предпочтение следует отдавать упрощенным корпусам BGA,
которые имеют шаг установки шариковых выводов 1 мм. Это облегчает трас-
сировку платы и ее сборку и монтаж. Кроме этого, увеличенный диаметр ша-
риковых выводов (0,45 мм) и применение в корпусе микросхемы жесткого
основания из ВТ позволяют повысить качество паяного соединения в ши-
роком температурном диапазоне.
Роль электрических параметров корпусов
Для цифровых устройств наблюдается постоянное повышение скорости
обработки информации при одновременном снижении уровней питающих на-
пряжений. Постоянно возрастает функциональная сложность БИС, которые ре-
ализованы в корпусах той или иной конструкции. Роль корпуса заключается в
механической защите кристалла микросхемы и обеспечении возможности ме-
ханической и электрической коммутации с внешней схемой. Поэтому важно по-
нимание того, как конструкция корпуса влияет на электрические параметры и
характеристики микросхемы. При существенном влиянии ожидаемые от кри-
сталла показатели производительности и качества сигнала могут быть не дос-
тигнуты из-за влияния на них конструкции корпуса и применяемых в нем ма-
териалов. Таким образом, корпус микросхемы формирует ту первичную элект-
ромагнитную обстановку, которая окружает кристалл и влияет на целостность
сигнала. При установке корпуса на плату эта обстановка испытывает влияние
конструкции и материалов платы, что вызывает дополнительные искажения сиг-
нала. Эти факторы должны быть учтены, как отмечалось выше, на возможно более
ранних этапах проектирования путем создания виртуальных прототипов и ин-
тегрирования анализа целостности сигнала в процесс проектирования.
Ввиду сложности строгого теоретического описания всех параметров кор-
пуса и определения их значений на данном этапе следует использовать как
теоретические, так и экспериментальные методы.
Суть заключается в переводе физических свойств корпуса в определен-
ные электрические характеристики, которые должны быть скомбинирова-
ны с электрическими параметрами исходной принципиальной схемы. Типич-
ными характеристиками являются сопротивление на постоянном токе — R,
индуктивность — £, емкость — С и волновое сопротивление — Z, определен-
ные для различных структур в корпусе.
94
Глава 1. Печатные платы в цифровых системах
Модель корпуса должна содержать две части, которые необходимы для пол-
ного понимания тех электрофизических процессов, которые происходят при
работе кристалла. Первая описывает модель выводов вход/выход, которые
определяют путь прохождения сигнала от кристалла к печатной плате. В за-
висимости от желаемой точности рассмотрения, размеров выводов, парамет-
ров сигнала модель может быть представлена в виде:
• сосредоточенных идеальных элементов или в виде распределенных па-
раметров;
• одиночного проводника, однопроводной или многопроводной линии
передачи.
Модели на сосредоточенных элементах адекватно отражают процессы на
постоянном токе или относительно низких частотах. При высоких частотах
модели в виде распределенных параметров более полно отражают такие эф-
фекты, как задержка, отражения сигнала от неоднородностей и перекрест-
ные помехи.
Вторая компонента комплексной модели корпуса относится к системе рас-
пределения питания. Подобно модели выводов, система распределения пи-
тания в корпусе может моделироваться в виде набора сосредоточенных эле-
ментов или в виде распределенных. Совместное использование сосредото-
ченных и распределенных элементов приводит к эквивалентной цепи на
парциальных элементах. Модель на сосредоточенных элементах может опи-
сать характеристики на постоянном токе, например, падение напряжения на
шине питания при постоянном токе, однако для комплексного анализа бо-
лее тонких процессов, которые проявляются при динамических режимах пе-
реключения, необходимы представления шин питания и заземления в виде
распределенных элементов.
Экспериментальное определение электрофизических параметров и харак-
теристик корпуса обычно завершает разработку корпуса микросхемы. Эта про-
цедура требует очень тщательной проработки, но, если она выполнена кор-
ректно, экспериментальные данные служат для проверки адекватности те-
оретической модели.
Ниже представлены следующие основные электрические параметры кор-
пусов, конструкция и особенности применения которых были рассмотрены
ранее:
• CPGA (ceramic pin-grid array),
• PPGA (plastic pin-grid array),
• H-PBGA (high thermal plastic ball grid array),
• TCP (tape carrier package),
• OLGA (organic land-grid array),
• FC-PGA (flip-chip pin-grid array).
• ММ-PQFP (multilayer molded),
• CQFP (ceramic quad flatpack),
• PLCC (plastic leaded chip carrier),
• QFP, SQFP, TQFP (quad flatpack),
• TSOP, PSOP (small outline packages).
1.3. Номенклатура и параметры корпусов микросхемы
95
Основные электрические параметры корпусов микросхем
Сопротивление постоянному току (J?dc)
Сопротивление постоянному току (7?dc) в обычном случае проявляется в
виде падения напряжения V= IRdc на соответствующем элементе корпуса,
по которому протекает ток. Особенно важен этот параметр для путей про-
текания токов питания и заземления. Сопротивление постоянному току для
вывода корпуса определяется через площадь S его сечения и длину /, а так-
же через удельное сопротивление р материала вывода:
Ade —
Керамические корпуса имеют относительно высокое сопротивление выво-
дов, поскольку металлизация вольфрамовым сплавом, который применяется
в этой технологии, имеет высокое удельное сопротивление. Пластмассовые и
органические корпуса имеют значительно меньшее сопротивление выводов, по-
скольку в них применяется металлизация медью и медными сплавами, удель-
ное сопротивление которых в 6... 12 раз меньше вольфрамовых сплавов.
Сопротивление вызывает потерю напряжения в проводниках и выводах
корпуса. Постоянный ток равномерно распределен по сечению проводни-
ка, но на высоких частотах ток начинает оттесняться к поверхности провод-
ника (скин-эффект), и его сопротивление увеличивается при возрастании
частоты, т. е. эффективное сечение вывода уменьшается. На переменном токе
сопротивление проводника линейно зависит от длины, но нелинейно — от
площади сечения и частоты.
Электрическая емкость (Q
Электрическая емкость С определяется длиной и размерами сечения вы-
вода, расстоянием между выводом и шиной заземления или питания, диэлек-
трической проницаемостью окружающих материалов, числом выводов, обра-
зующих емкость. Чем выше быстродействие, тем меньше допустимая емкость.
Относительная диэлектрическая проницаемость ег изоляционных матери-
алов, которые используются при изготовлении керамических корпусов, лежит
в диапазоне 8... 10, а материалов, применяемых при изготовлении пластмас-
совых корпусов, — в диапазоне 4...6. Классические формулы для расчета ем-
кости пригодны только для простых конфигураций электродов, и они мало при-
годны для точной оценки емкости выводов корпусов. Для этих целей приме-
няются численные методы расчета и специальное программное обеспечение.
Простейшая формула для определения емкости плоского конденсатора,
состоящего из двух электродов, без учета краевых эффектов имеет вид:
где S — площадь плоского электрода; е — абсолютная диэлектрическая проницаемость
материала, разделяющего пластины; t — расстояние между пластинами.
96
Глава 1. Печатные платы в цифровых системах
Из формулы видно, что при повышении диэлектрической проницаемо-
сти емкость возрастает. Для снижения емкости предпочтительней применять
материалы с малым значением диэлектрической проницаемости.
Емкость, которая существенно влияет на работоспособность микросхе-
мы, можно разделить на емкость нагрузки, емкость между выводами, развя-
зывающую емкость.
Емкость нагрузки есть общая емкость вывода относительно всех окружа-
ющих проводников. Емкость между выводами определяется как взаимная ем-
кость между ними. Емкость нагрузки соответствует диагональным элемен-
там емкостной матрицы, полученной для короткозамкнутых цепей, а емкость
между выводами — внедиагональным элементам этой матрицы. Взаимная ем-
кость между выводами и взаимная индуктивность между ними определяет
электромагнитное взаимодействие между двумя выводами.
Развязывающая емкость является емкостью между выводами питания и
выводами заземления. В керамических корпусах PGA, в которых применя-
ются плоскости питания и заземления, развязывающая емкость формиру-
ется между этими плоскостями и дополняется дискретным развязывающим
конденсатором. В пластмассовых корпусах PGA развязывающая емкость
обычно выполняется в виде дополнительного дискретного конденсатора.
Развязывающая емкость служит как «резервуар» энергии, часть которой воз-
вращается в буфер в процессе переключения. Это снижает провал напряже-
ния питания и отрыв потенциала земли на пути протекания тока от пита-
ния к земле, рассмотренные ранее.
Большое значение имеет частичная емкость проводника относительно
плоскости заземления. Расчет емкости можно провести по справочным фор-
мулам, приведенным в [40].
Индуктивность (£)
Индуктивность L— коэффициент пропорциональности между магнитным
потоком, пронизывающим некоторый контур, сцепленный с ним, и током,
протекающим в этом контуре. Индуктивность зависит от размеров и формы
контура, а также от магнитной проницаемости окружающей среды. Этот ас-
пект весьма важен для определения перекрестных помех и синхронных по-
мех коммутации. Приведенное классическое определение индуктивности
предполагает, что индуктивность относится к некоторому контуру. Однако
контур может быть сегментирован, и для каждого сегмента может быть оп-
ределена собственная парциальная индуктивность и взаимная парциальная
индуктивность. Этот подход наиболее широко используется для анализа ин-
дуктивных явлений в межсоединениях, в том числе и в составе корпусов мик-
росхем. Например, индуктивность штырькового вывода есть его собствен-
ная парциальная индуктивность.
Другой используемый термин — индуктивность «открытого контура», ко-
торый относится к контуру, который не замкнут с двух сторон. Мы можем рас-
сматривать отрезок линии передачи как открытый контур, а общую индуктив-
ность его — как индуктивность открытого контура. Индуктивности, которые
1.3. Номенклатура и параметры корпусов микросхемы
97
используются для анализа таких явлений, как задержка сигнала или перекрест-
ные помехи, являются в основном индуктивностями открытого контура.
Когда для анализа электрических характеристик используются парциаль-
ные индуктивности, следует четко понимать направление токов в каждом сег-
менте. Неправильное предположение относительно направления тока мо-
жет привести к ошибочному результату. Термин «путь возвратного тока»
следует использовать для усиления важности понимания направления тока
в каждом рассматриваемом сегменте.
Значение индуктивности определяется длиной вывода, размером его сече-
ния, расстоянием между выводами, расстоянием между плоскостью питания
и заземления, магнитной проницаемостью материалов проводников и числом
задействованных выводов. Эмпирическое правило гласит, что меньший по пло-
щади контур обладает меньшей индуктивностью. Эта базовая концепция будет
полезна при рассмотрении корпусирования и проектирования систем в целом.
Каждый сигнальный путь должен иметь близко расположенный и подобный
по конфигурации возвратный путь. Имеются расчетные формулы для опре-
деления индуктивности, которая зависит от физической геометрии структу-
ры и пути возвратного тока [41]. Некоторые классические проблемы могут быть
решены в закрытой форме, но для реальных сложных задач необходимо при-
менение специальных программных средств на основе численных методов.
Рассмотрим определение индуктивностей сегмента более подробно.
Для замкнутого контура индуктивность L связывает магнитный поток Ф
и ток /, наведенный в этом контуре
Ф = £/.
ЭДС е самоиндукции в контуре, при изменении тока / в нем, определя-
ется выражением
В корпусах микросхем сигнал распространяется через сигнальные выво-
ды (на вход или на выход) и возвращается через выводы питания. Замкну-
тый контур формируется посредством сигнальных выводов и выводов питания
и заземления.
Возможно определение парциальной ин-
дуктивности для сегмента (открытого кон-
тура) и раздельное определение парциаль-
ной индуктивности для каждого сегмента.
Это позволяет проектировщику определить
путь возврата сигнального тока и помехи по-
средством симуляции. Далее это позволяет
определить общую индуктивность контура
«сигнальный вывод—вывод питания (или за-
земления)» или дифференциальную пару, ис-
пользуя парциальные собственные и взаим-
ные индуктивности (рис. 1.78).
Рис. 1.78. Индуктивность
сигнального (открытого) контура
98
Глава 1. Печатные платы в цифровых системах
Следует различать индуктивность на постоянном и переменном токе. Ин-
дуктивность на постоянном токе определяется в предположении, что ток про-
текает равномерно по всему сечению проводника. На переменном токе про-
является скин-эффект и эффект близости, за счет которых ток оттесняется
к периферии проводника и сосредотачивается на стороне, ближайшей к со-
седнему проводнику. Это сказывается на значении индуктивности.
Волновое сопротивление (Z)
Волновое сопротивление — один из важнейших параметров, который ха-
рактеризует линию передачи, которая в любом случае содержит два провод-
ника — сигнальный (вывод) и возвратный, как правило, вывод питания или
заземления. При моделировании трасс в корпусах обычно используются мо-
дели линий передач на распределенных элементах, поскольку именно такое
описание позволяет проанализировать времена задержки распространения
сигнала. Модели на сосредоточенных элементах не могут быть применены
для анализа задержек сигнала в корпусе.
Волновое сопротивление линии передачи в общем виде определяется через
емкостные и индуктивные параметры линии по формуле
z=# °и'
где и С1 — удельные (на единицу длины) индуктивность и емкость линии.
Волновое сопротивление не зависит от длины линии. Это важный пара-
метр, определяющий уровень отраженного сигнала от любой неоднородно-
сти. В корпусе микросхемы такими неоднородностями являются точки со-
пряжения между кристаллом и проводником, соединяющим его с платой внут-
ри корпуса, и между платой и выводом. Значение уровня помех, вызванных
отражениями, зависит от рассогласования между волновым сопротивлени-
ем и сопротивлением нагрузки. Например, при типичном волновом сопро-
тивлении трассы на печатной плате 50 Ом необходимо выполнить волновое
сопротивление выводов корпуса, также близким к 50 Ом. Типичное значе-
ние волнового сопротивления трасс в керамическом корпусе CPGA состав-
ляет 42 Ом, а для трасс в пластмассовом корпусе — 47 Ом.
Частотные ограничения параметров R-L-C
Цифровой сигнал содержит широкий спектр синусоидальных составля-
ющих. До тех пор, пока минимальная длина волны для составляющей с мак-
симальной частотой превышает погонную длину проводника, применима
модель на сосредоточенных R-L- С элементах. Для цифровых микросхем мо-
дель на сосредоточенных элементах применима при максимальной длине (мм)
вывода 60/г, где tT — длительность фронта, нс. Когда применяются модели на
сосредоточенных элементах, важно знать, какой параметр (по постоянному
или переменному току) должен быть использован. В табл. 1.11 приведены ча-
стотные ограничения на параметры корпусов [6]. Модель на основе линии
1.3. Номенклатура и параметры корпусов микросхемы
99
Таблица 1.11
Частотные ограничения R-L-C параметров
Параметр Применимость частотного диапазона для корпусов
с выводными рамками с печатными платами
Сопротивление (постоянный ток) От постоянного тока до 500 кГц От постоянного тока до 5 МГц
Сопротивление (переменный ток) От 500 кГц и выше От 5 МГц и выше
Индуктивность (постоянный ток) От постоянного тока до 10 МГц От постоянного тока до 100 МГц
Индуктивность (переменный ток) От 10 МГц до частоты, для которой применима модель на сосредоточенных параметрах От 100 М Гц до частоты, для которой применима модель на сосредоточенных параметрах
Емкость От постоянного тока до частот, для которых можно пренебречь диэлектрическими потерями
передачи или распределенных параметров должна быть использована на вы-
соких частотах.
Перекрестные помехи
Перекрестные помехи относятся к нежелательным сигналам, которые пе-
редаются за счет переноса электромагнитной энергии от одной линии пере-
дачи к другой. Уровень помех определяется характеристиками драйвера и при-
емника сигналов, характеристик трасс, параметрами переключения. Одним
из важных факторов, определяющих уровень перекрестных помех, являет-
ся близость трасс и протяженность параллельного участка линий. Чем длинней
параллельный участок между двумя и более линиями и чем они ближе, тем
выше уровень перекрестных помех между ними. Приближение линий к плос-
костям питания или заземления снижает уровень перекрестных помех.
Модель перекрестных помех в межсоединениях корпусов
По мере уменьшения размеров компонентов и снижения напряжения пи-
тания эффект перекрестных помех становится более выраженным. Усилия
разработчиков должны быть направлены на снижение уровня перекрестных
помех, и необходим их предварительный анализ на виртуальном прототипе.
Простейшая модель включает три параллельных сигнальных проводника, рас-
положенных на минимальном для принятой технологии расстоянии друг от
друга (рис. 1.79). В табл. 1.12 представлены усредненные индуктивные, а в
табл. 1.13 — усредненные емкостные парамет-
ры для рассматриваемой системы проводни-
ков в корпусах CPGA, PPGA,TCP, H-BGA,
OLGA и FC-PGA. Эти параметры определя-
ют взаимную связь между проводниками и
уровень перекрестных помех в них. Отметим,
ZODJ СО
Рис. 1.79. Модель проводников
для определения перекрестных
помех в корпусе микросхемы
100
Глава 1. Печатные платы в цифровых системах
Таблица 1.12
Индуктивные параметры, определяющие взаимную связь проводников
Индуктивный параметр, нГн/см Тип корпуса
GPGA PPGA TCP H-PBGA OLGA FC-PGA
ЛИ 4,26 3,39 5,71 3,39 3,20 2,329
£22 4,30 3,42 4,94 3,42 3,15 2,329
£33 4,30 3,42 4,94 3,42 3,15 2,329
£12 0,79 0,46 2,43 0,46 0,85 0,214
£13 0,79 0,46 2,43 0,46 0,85 0,214
£23 0,18 0,082 1,33 0,082 0,31 0,055
£31 0,79 0,46 2,43 0,46 0,85 0,214
£21 0,79 0,46 2,43 0,46 0,85 0,214
£32 0,18 0,082 1,33 0,082 о,31 0,055
Таблица 1.13
Взаимные емкостные параметры
Емкостный параметр, пФ/см Тип корпуса
GPGA PPGA TCP H-PBGA OLGA FC-PGA
СИ 2,80 1,60 1,25 1,60 1,65 1,707
С22 2,68 1,56 1,23 1,56 1,75 1,707
СЗЗ 2,68 1,56 1,23 1,56 1,75 1,707
Cl 2 -0,49 -0,21 -0,48 -0,21 -0,33 -0,126
С13 -0,49 -0,21 -0,48 -0,21 -0,33 -0,126
С23 -0,022 -0,0092 -0,094 -0,0092 -0,001 -0,008
С31 -0,49 -0,21 -0,48 -0,21 -0,33 -0,126
С21 -0,49 -0,21 -0,48 -0,21 -0,33 -0,126
С32 -0,022 -0,0092 -0,094 -0,0092 -0,001 -0,008
что взаимные емкостные параметры, приведенные в табл. 1.13, имеют отри-
цательные знаки, которые соответствуют определению матрицы взаимных
параметров. Эти данные следует рассматривать как ориентировочные, а для
более точного их определения необходимы экспериментальные исследова-
ния или применение численных методов расчета.
1.3. Номенклатура и параметры корпусов микросхемы
101
Помехи синхронной коммутации
Конечной стадией проектирования корпуса является анализ помех син-
хронной коммутации (ПСК). Имеются два проявления этих помех в момент
одновременного переключения вентилей из одного состояния в другое:
• помехи, которые возникают на шинах питания и заземления при ком-
мутации,
• нарушение временных соотношений.
Первый тип помех — помехи синхронной коммутации — возникает в ши-
нах питания и заземления при реакции их индуктивностей на изменение тока
потребления в системе. Второй тип помех определяется как разность времен
переключения одиночного бита и последовательности битов. Проектиров-
щик должен ориентироваться на худший случай переключения для того, чтобы
быть уверенным в работоспособности в любой ситуации.
Основным правилом, следуя которому можно минимизировать помехи
синхронной коммутации, является четкое определение возвратного пути и
минимизации индуктивности в нем.
Модели корпусов для устоявшихся технологий
В табл. 1.14 и 1.15 представлены основные электрические параметры раз-
личных распространенных корпусов микросхем [6, 38]. Это типовые значе-
ния; уточненные параметры должен предоставлять производитель. При уве-
личении числа выводов значение параметров возрастает.
Параметры корпусов микропроцессоров (Intel)
Ниже приведены параметры перспективных корпусов микропроцессоров
фирмы Intel [38]. Модель контура питания дана для типичной для микропро-
цессоров конфигурации. Все параметры для модели линии передачи и зна-
чения индуктивности рассчитаны для высоких частот. Сопротивления рас-
считаны для постоянного тока. Индуктивности рассчитаны с учетом влия-
ния плоскости заземления.
Модели выводов входа/выхода
Проволочные соединения, штырь и контактная площадка моделируют-
ся последовательными резисторами и индуктивностями. Сигнальные трас-
сы представляются линиями передачи с удельными параметрами R-L-C и
волновым сопротивлением Z. На рис. 1.80 представлена типовая модель
сигнального вывода, а в табл. 1.16 даны типичные значения паразитных
параметров для корпусов CPGA, PPGA, H-PBGA, OLGA и FC-PGA. Пред-
полагается, что корпуса установлены в контактные гнезда, поэтому приве-
денные параметры включают параметры гнезда в виде элементов, подклю-
ченных к корпусу.
Для корпусов с перевернутым кристаллом (OLGA и FC-PGA) проволоч-
ные выводы заменяются шариковыми выводами кристалла и соединение через
них происходят без применения трасс на плате корпуса.
102
Глава 1. Печатные платы в цифровых системах
Таблица 1.14
Параметры корпусов CQFP и МКМ
Электрический параметр Обозначение CQFP МКМ
типовое значение типовое значение
Суммарная индуктивность вывода и сигнальных проводников, нГн А + £w 6,6...10,2
Суммарное сопротивление вывода и сигнального проводника, мОм к+к 81...115
Индуктивность вывода, нГн г 3,3
Сопротивление вывода, Ом rl 0,004
Индуктивность проводников, нГн К 5,0...6,0
Сопротивление проводников (вход/выход), Ом ^W.o 0,8...0,9
Емкость вывода, пФ С, 4,0...5,0 0,5...2,2
Индуктивность шины питания, нГн 1,5...2,5 0,2...0,3
Сопротивление шины питания, Ом 0,2...0,4 0,034
Индуктивность проводников, соединяяющих кристалл с выводами, нГн к 3,0 3,8...5,3
Сопротивление проводников, соединяя- ющих кристалл с выводами, Ом К 0,08 9...12
Емкость слоя питания относительно слоя земли, пФ Cs„ 170,0...240,0 0,090...0,210
Таблица 1.15
Параметры корпусов PQFP, PLCC, QFP, SQFP/TQFP
Электрический параметр Тип корпуса
PQFP PLCC QFP SQFP/TQFP
Сопротивление соединитель- ного провода и вывода RL, (Д + RJ, мОм 62,9-116,9 56,7 - 78,4 60,9- 108,6 61,5-122,6
Индуктивность соединитель- ного провода Г и вывода /,, (/» + /,), нГн 5,3-13,2 4,1-10,3 4,8-10,8 4,0-12,6
Емкость вывода, С{, пФ 0,2- 1,0 0,2- 1,3 0,1 -0,6 0,2- 1,0
Поскольку геометрия корпусов TCP сильно отличается от многослойных
корпусов, для них пригодна другая эквивалентная схема (рис. 1.81). Модель
содержит три сегмента линии передачи с различными параметрами, которые
представляют различные части сигнального пути внутри корпуса. Типичные
значения параметров даны в табл. 1.17
1.3. Номенклатура и параметры корпусов микросхемы
103
Рис. 1.80. Модель сигнальных выводов в корпусе с многослойной подложкой
Таблица 1.16
Параметры сигнальных выводов для корпусов с многослойной подложкой
Электрический параметр Обозна- чение Корпус с проволочным соединением Корпус с перевернутым кристаллом
CPGA PPGA H-PBGA OLGA FC-PGA
Сопротивление проволоки/шарикового вывода кристалла, мОм *и/*вмр 126...165 136...188 114...158 2 0,06
Индуктивность проволоки/шарикового вывода кристалла, нГн As/^bmp 2,3...4,1 2,5...4,6 2,1...4,1 0,02 0,013
Сопротивление трассы, мОм/см R 1200 66 66 590 120
Индуктивность трассы, нГн/см L 4,32 3,42 3,42 3,07 2,33
Емкость трассы, пФ/см С 2,47 1,53 1,53 1,66 1,707
Волновое сопротивление трассы, Ом Z 42 47 47 43 38,5
Сопротивление вывода/шарикового вывода корпуса, мОм ^ВМР 20 20 0 8 20
Индуктивность вывода/ шарикового вывода корпуса, нГн к 4,5 4,5 4,0 0,75 2,9
Диапазон длин трасс, мм 1 8,83...26,25 6,60...42,64 4,41...22,24 3,0...18,0 10,0...42,6
104
Глава 1. Печатные платы в цифровых системах
Внутренняя Внешний
трасса Разветвление вывод
Сегмент 1 Сегмент 2 Сегмент 3
L, R, С, Z L, R, С, Z L, R, С, Z
Рис. 1.81. Модель сигнального вывода для корпуса TCP
СК
CU
X
си
т
ф
С
си
си
с;
с
Таблица 1.17
Электрические параметры сигнальных выводов корпусов TCP
Электрический параметр Сегмент трассы
Вывод (сегмент 1) разветвление (сегмент 2) вывод микросхемы (сегмент 3)
Сопротивление сегмента, мОм/см 352 290 144
Индуктивность сегмента, нГн/см 6,48...8,84 6,43...8,81 7,56...9,77
Емкость сегмента, пФ/см 0,58...0,83 0,13...0,19 0,12...0,16
Волновое сопротивление сегмента, Ом 89...124 183...256 220...288
Длина сегмента, мм 0,90...4,0 0,05...11,8 0,91...3,25
Модель контура питания
Существует несколько различных методов моделирования контура пита-
ния. Основное правило гласит: более распределенная модель — более точ-
ная модель. Но из-за ряда трудностей эта модель используется редко. Впол-
не приемлема более простая модель на сосредоточенных элементах, как по-
казано на рис. 1.82, параметры которой приведены в табл. 1.18. Здесь также
учтены параметры гнезда.
Рис. 1.82. Модель на сосредоточенных элементах контура питания
1.3. Номенклатура и параметры корпусов микросхемы
105
Таблица 1.18
Параметры модели контура питания
Электрический параметр Обозна- чение Тип корпуса
CPGA PPGA TCP H-PBGA OLGA FC-PGA
Сопротивление провод- ника с напряжением питания Fss, мОм Л» 5,5 2,0 6,0 4,1 0,5 1,2
Индуктивность провод- ника с напряжением питания Kss, нГн ^sw 150 150 150 198 15 64,4
Сопротивление провод- ника с опорным напря- жением, мОм Ло 5,5 2,0 6,0 4,1 0,5 1,2
Индуктивность провод- ника с опорным напряжением, нГн 4 150 150 150 217 15 64,4
1.3.7. Методология моделирования корпусов
микросхем
Точное моделирование поведения корпусов и их влияния на целостность
сигнала и тайминг — сложная задача. Во многих случаях для определения кри-
тического поведения достаточно промоделировать только некоторые выводы
входа/выхода. Для моделирования системы питания необходимо промодели-
ровать контур, по которому протекает ток питания: источник питания — шина
питания — микросхема — заземление. Параметры, которые должны учитываться
при моделировании, зависят от желаемой точности моделирования, наличия
инструментария и вычислительных возможностей.
Модель выводов вход/выход
Модель сигнальных выводов содержит набор электрических параметров,
которые влияют на целостность сигнала. Для корпусов микросхем (PGA), в
которых используются проволочные соединения кристалла с выводом, мат-
рица штырьковых выводов, путь прохождения сигнала включает проволоч-
ное соединение, трассу, металлизированное отверстие, штырь и металлизи-
рованный стержень.
Для высококачественной продукции разработаны корпуса OLGA и FC-
PGA. Для этих корпусов путь сигнала включает выводы в виде шариков при-
поя, соединяющих кристалл и корпус, трассу, металлизированное отверстие,
штырь или контактную площадку. Если необходимо проанализировать пе-
рекрестные помехи, то для этого необходимо учесть паразитные параметры
соседних выводов. В простейшем случае предполагается, что пара выводов
работает независимо от других.
Ключевым фактором для адекватности модели является определение пути
возвратного тока. Для примера, при анализе индуктивности проволочных
106
Глава 1. Печатные платы в цифровых системах
соединений к сигнальным выводам сближение токов возвратного пути со-
ответствует приближению проволочных соединений питания или заземле-
ния. Если этот эффект не включать в анализ, тогда расчетное значение ин-
дуктивности соединения выводов будет больше действительного, посколь-
ку не будет учтен эффект взаимной индуктивности близко расположенных
проводников. При анализе сигнальных трасс необходимо идентифицировать
близко расположенные токонесущие плоскости, которые обеспечивают путь
возвратного тока. Наиболее часто применяются модели полосковых или мик-
рополосковых линий, в которых путь обратного тока располагается в плос-
костях, окружающих сигнальный проводник.
Адекватная модель базируется на применении типичной геометрии вы-
водов. Перекрестные помехи определяются для худшего сценария, при ко-
тором расстояние между трассами минимально. Для индивидуального ком-
понента применяются программные средства для решения электродинами-
ческой задачи для двумерной или трехмерной области. В первую очередь,
интерес представляют электрические параметры R, £, С, Z, а также матри-
цы взаимных емкостей и индуктивностей для анализа перекрестных помех.
Модели помех синхронной коммутации обычно включают взаимные эф-
фекты между сигнальными линиями и систему распределения питания. Для
адекватного моделирования необходима комплексная модель, основанная
на 3D расчетах, но при некоторых допущениях пригодна более простая мо-
дель на сосредоточенных элементах.
Простейшая конфигурация модели сиг-
нального вывода для корпуса PPGA пока-
зана на рис. 1.83. Значения параметров R^
и Со не зависят от конструкции корпуса.
Индуктивность корпуса £р = + Ll вклю-
чает индуктивность проволочных соеди-
нений, индуктивность Ll штырьков и гнез-
да. Емкость корпуса Ср содержит емкости
трасс, штырьковых выводов и гнезда. Ин-
дуктивность штыря и гнезда определяется
как для одиночного элемента, и типичное значение составляет 4,5 нГн. Типич-
ная емкость гнезда составляет 1,0 пФ.
Компромисс между точностью и комплексностью
Моделирование корпуса представляет, с одной стороны, точные знания,
а с другой — искусство. В идеальном случае хотелось бы иметь абсолютно точ-
ную модель для последующего анализа, но это представляет огромные труд-
ности, а в ряде случаев ее получить невозможно. При этом следует учиты-
вать, с одной стороны, имеющиеся вычислительные ресурсы, а с другой - не-
обходимость получения комплексной модели.
Разумным подходом является построение модели на базе RLC-параметров,
которые могут быть рассчитаны на основе инженерных формул в закрытом виде.
Однако при этом требуется понимать, насколько адекватна полученная модель.
«о LP
Рис. 1.83. Структура модели
сигнального вывода буфера корпуса
с штырьковыми выводами
1.3. Номенклатура и параметры корпусов микросхемы
107
Это может быть определено после проведения экспериментальных исследова-
ний и сравнения расхождений между теоретическими и экспериментальными
результатами. В общем случае для моделирования одиночного вывода с успе-
хом может быть использована двумерная аппроксимация для печатных трасс и
проводников. Трехмерное моделирование обычно требуется для описания шты-
ревых выводов и металлизированных отверстий. Это может быть точно выпол-
нено с помощью программ анализа электромагнитных полей.
Достаточно большой объем моделирования может потребоваться для мо-
делирования контуров питания. Например, плоскость питания может иметь
тысячи металлизированных переходных отверстий, что значительно увели-
чит объем вычислений, если параметры этих отверстий ввести в программы
расчета. Выявление возможных путей упрощения задачи моделирования мо-
жет быть проведено только после изучения практических и эксперименталь-
ных данных.
Сопоставление моделей
Ключевым вопросом при разработке модели является вопрос о типе моде-
ли, которую можно построить на сосредоточенных элементах или на основе
линии передачи. Модели на основе линий передачи должны быть исполь-
зованы, если
'г < 2/pd/.
где tx — фронт импульса; Zpd — время задержки распространения электромагнитной вол-
ны в линии передачи; / — длина линии передачи.
Значение Zpd определяется свойствами среды. При отсутствии магнитных
материалов, что соответствует реальной ситуации, время задержки распро-
странения в линии передачи определяется по формуле
^pd =3’3\/ЁГХ/’ НС>
где 3,3 — время задержки распространения электромагнитной волны на единицу длины
в свободном пространстве, нс/м; ег — относительная диэлектрическая проницаемость изо-
ляционных материалов линии передачи.
Например, типовое значение длины трассы в керамическом корпусе со-
ставляет приблизительно 25 мм. При относительной диэлектрической про-
ницаемости керамики 10 получаем
2^ х / = 2 х 3,3 Ло х 0,025 = 0,52 нс.
Это значение одного порядка для фронта tr цифрового сигнала в совре-
менных системах. Поэтому для моделирования трасс в корпусах следует при-
менять модель линии передачи. В тех случаях, когда требуется моделировать
время задержки в трассах в корпусах, следует применять модель на основе
линии передачи. Более простая модель на сосредоточенных элементах не
может промоделировать задержки сигнала. Ее следует применять тогда, когда
108
Глава 1. Печатные платы в цифровых системах
задержка в корпусе не является определяющей в общей системной задерж-
ке сигнала. Существующая тенденция уменьшения фронта информацион-
ного сигнала приводит к тому, что задержка сигнала в корпусах становится
более критичной, и необходима модель на основе линии передачи
Частотно-зависимые эффекты
Другой фактор, который должен быть учтен при моделировании корпу-
сов и их выводов, заключается в учете частотной зависимости параметров мо-
дели. Напомним, что при постоянном токе ток протекает равномерно по всему
сечению проводника или вывода. На высоких частотах проявляется скин-
эффект, за счет которого ток оттесняется к периферии проводника. Чем выше
частота, тем ближе к поверхности проводника протекает основная часть тока.
Эта область называется скин-слоем. Толщина этого слоя зависит от материала,
геометрии сечения и частоты. Поскольку толщина скин-слоя уменьшается
с частотой, то с частотой изменяются такие параметры, как сопротивление
проводника и его индуктивность.
Распределение тока в сечении также зависит от близости к другим про-
водникам, этот эффект называется эффектом близости.
Простейшая модель трасс в корпусе определяется на постоянном токе и
используется для оценки параметров на высокой частоте и расчета квазиста-
тической индуктивности. Поскольку длительность фронта цифровых сигналов
уменьшается, спектр расширяется, что требует учета частотно-зависимых эф-
фектов. Поэтому модели должны быть дополнены частотно зависимыми ре-
зисторами и индуктивностями. Параметры таких моделей должны быть рас-
считаны с помощью программных средств путем решения уравнений Макс-
велла.
Концепция распределенного питания
Другая область моделирования, которая необходима, но не так очевидна,
как ранее рассмотренная, — распределенная система питания и ее развязка.
При ее проектировании следует учитывать несколько основных правил.
Существуют два типа развязки — по высокой и низкой частоте. Низко-
частотная развязка используется преимущественно в фильтрах источников
питания для управления помехами от источника питания. Высокочастотная
развязка используется на печатных платах, в корпусах и кристаллах для ус-
транения помех синхронной коммутации. Когда развязывающий конденсатор
расположен в корпусе, он должен быть размещен по возможности ближе к
кристаллу для минимизации паразитной индуктивности, которая присуща
элементам электрического соединения конденсатора и кристалла. Важно, что-
бы используемый для развязки конденсатор обладал минимальной паразитной
индуктивностью и сопротивлением выводов. Это особенно важно для раз-
вязки на высокой частоте. В общем случае, низкочастотная развязка требу-
ет конденсаторов большой емкости, которым присущи значительные индук-
тивности. Высокочастотные конденсаторы должны быть минимального раз-
мера для уменьшения паразитной индуктивности.
1.4. Материалы для печатных узлов
109
Для моделирования системы питания необходимо применять по возмож-
ности адекватную модель развязывающего конденсатора, отражающую осо-
бенности его работы на высоких частотах, а также элементов его соедине-
ния с кристаллом.
Рассмотренные выше эффекты, явления и параметры, относящиеся к кор-
пусам микросхем, необходимы для комплексного решения задач обеспече-
ния целостности сигнала, а также для более точной оценки вклада, который
вносят параметры корпусов в искажение сигнала, по сравнению с парамет-
рами печатных плат.
Все рассмотренные подходы к построению моделей межсоединений в кор-
пусе микросхемы полностью масштабируются на задачи обеспечения цело-
стности сигнала при проектировании печатных плат, которые рассмотрены
в последующих главах книги.
1.4. Материалы для печатных узлов
Свойства материалов, которые применяются для создания печатных уз-
лов, во многом определяют электрические и физические параметры, а так-
же характеристики готового изделия.
1.4.1. Материалы для корпусирования кристаллов
Материалы для корпусирования характеризуются большим перечнем па-
раметров и характеристик. В контексте книги остановимся только на элек-
трических параметрах, которые необходимы для составления модели корпуса
и понимания физических процессов, происходящих при распространении
сигнала в линиях передачи печатных узлов. В качестве примера приведем фи-
зические параметры материалов для корпусов микросхем (табл. 1.19 и 1.20),
а для выводов и выводных рамок микросхем — в табл. 1.21.
Таблица 1.19
Электрофизические параметры материалов для корпусов ИМС
Параметр Материал
оксид алюминий ковар компаунд стекло сплав Си(90 %) - W медь
Удельное электрическое сопротивление, Ом см 104 49 х 106 5х 106 > 10" <6х10‘ < 2 хЮ 6
Относительная диэлектрическая проницаемость на частоте 1 МГц 7,9...10,0 - <5,0 11,5 - -
110
Глава 1. Печатные платы в цифровых системах
Таблица 1.20
Параметры материалов для корпусов TCP
Параметр Материал
полиимид адгезив катаная медная фольга электролити- ческая медная фольга герметик
Удельное электрическое сопротивление, Омсм > 1 х 10 s > 10'5 1,7 х 106 1,7х 106
Относительная диэлектрическая проницаемость 3,5(1 кГц) 3,0 (1 кГц) - - 3,8 (1 кГц)
Таблица 1.21
Сопротивление материалов для выводов и выводных рамок ИМС
Параметр Материал
медный сплав MF202 сплав "Alloy 42" ковар ТАМАС5 CDA 194 OLIN 7025 EFTEC 64Т
Удельное электри- ческое сопротив- ление, Омсм 5,7 х 106 57 х 106 49 х 106 4,9 х 106 2,6х 106 4,3 х 106 2,3 х 106
1.4.2. Материалы для печатных плат
Материалы для печатных плат имеют весьма существенное влияние на ка-
чество функционирования электронного модуля. Это определяется тем значе-
нием, которое оказывают параметры материалов на электрические характери-
стики линий передач на печатных платах. Особенно важен выбор материалов
для электронных модулей, работающих на частоте более 1 ГГц. Рассмотрим ос-
новные параметры наиболее распространенных материалов [80, 42—45].
Диэлектрическая проницаемость
Диэлектрическая проницаемость е является, пожалуй, наиболее важной
характеристикой диэлектрических материалов, которые применяются при
изготовлении печатных плат и корпусов микросхем. Она характеризует по-
ляризацию диэлектриков под действием электрического поля. Согласно
закону Кулона диэлектрическая проницаемость является величиной, пока-
зывающей, во сколько раз сила взаимодействия двух свободных зарядов в
диэлектрике меньше, чем в вакууме. Диэлектрическая проницаемость мате-
риала зависит от его структуры и химического состава, давления, темпера-
туры и других внешних факторов. В общем случае диэлектрическую прони-
цаемость представляют комплексной величиной
e = e'-ze*
(1.18)
1.4. Материалы для печатных узлов
111
Параметры е' и е" зависят от частоты со и времени т релаксации, которое
определяет время поляризации диэлектрика при наложении электрическо-
го поля. Отношение (тангенс угла диэлектрических потерь)
— = tg5 (1.19)
£
определяет диэлектрические потери в среде.
Сдвиг фаз 8 зависит от соотношения времен т и периода колебания
/с = 2л/со. При т << Гс (со << 1/т) говорят о низкой частоте, а при т >> t — о
высоких частотах. На низких частотах диэлектрическая проницаемость прак-
тически не зависит от частоты и будет равна £, а на высоких такая зависи-
мость наблюдается. Это будет определять потери в линиях передачи, рабо-
тающих на высоких частотах.
В общем случае скорость vc распространения электромагнитной волны в
вакууме (скорость света) определяется диэлектрическими и магнитными свой-
ствами среды:
где ц0 — магнитная постоянная, равная 1,256 мкГн/м; е0 — диэлектрическая постоянная,
равная 8,86 пФ/м.
Фазовая скорость распространения электромагнитных волн в произволь-
ной среде определяется по формуле:
’ (L2I)
где ц = |тор,.и е = еоег — абсолютная магнитная и диэлектрическая проницаемость, соот-
ветственно; цги ег — соответственно относительная магнитная и диэлектрическая про-
ницаемость материала; ц0 и е() — соответственно магнитная и диэлектрическая посто-
янная.
Применительно к электрической емкости относительная диэлектричес-
кая проницаемость материала показывает, во сколько раз увеличится емкость
конденсатора Со, если заменить воздух между его обкладками на некоторый
диэлектрик
Се = £ГСО, (1.22)
где С£ — емкость конденсатора, заполненного диэлектрическим материалом.
Относительные проницаемости (магнитная и диэлектрическая) опреде-
ляются свойствами применяемых материалов. Например, для немагнитных
материалов = 1, для стали = 100...800. Для диэлектриков £г равна: для
воздуха 1, для полихлорвинила и т. п. диэлектриков — 2,8...3,2, для влагоза-
щитных лаков — примерно 4, для оснований печатных плат (гетинакс, стек-
лотекстолит различных марок и т. п.) — 4...6.
112
Глава 1. Печатные платы в цифровых системах
Анализ формулы (1.21) позволяет сделать ряд полезных для практики про-
ектирования выводов. Для линий передачи необходимо применять только
немагнитные материалы. При этом цг= 1 и скорость распространения элек-
тромагнитной волны будет максимальной для данного случая. При введении
магнитного материала в конструкцию линии скорость падает, поскольку при
этом значение станет больше единицы. Расположенные рядом с линией
передачи магнитные материалы (например, корпус электронного средства)
снижают фазовую скорость.
При отсутствии магнитных материалов в конструкции линии передачи
принимаем = 1, тогда скорость распространения электромагнитной вол-
ны будет
1 _ 1
v=7^=v^’ о-**)
где = £ — коэффициент укорочения длины волны, который показывает, во сколько
раз уменьшается скорость распространения синусоидальной электромагнитной волны в
линии передачи; для коаксиальных кабелей этот коэффициент приводится в справочных
данных; vc — скорость распространения электромагнитной волны в свободном пространстве
(скорость света).
Окончательно получаем
V = / ^.
Таким образом, в линиях передачи скорость электромагнитной волны сни-
жается пропорционально корню квадратному из относительной диэлектрической
проницаемости изоляционного материала в составе линии. Поэтому в быстро-
действующих печатных платах предпочтение следует отдавать материалам с
малой диэлектрической проницаемостью.
Эффективная диэлектрическая проницаемость
При разработке быстродействующих систем стремятся применять мате-
риалы с минимальной диэлектрической проницаемостью. Достигается это
следующими основными путями:
• разработкой и применением новых материалов, для которых мини-
мизируется ег для сплошного материала. По современным данным,
для материалов, используемых для печатных плат, достигнуто значе-
ние гг > 1,8. Получить меньшее значение в настоящее время не уда-
ется из-за существования определенных физических и химических ог-
раничений;
• применением комбинированных материалов и специальных техничес-
ких решений, направленных на увеличение доли воздуха в готовом ма-
териале (например, вспениванием исходного диэлектрического мате-
риала); чем больше будет объемная доля воздуха в материале, тем ближе
к единице будет значение его относительной диэлектрической прони-
цаемости. В этом варианте формируется кусочно-однородная диэлек-
трическая среда.
1,4. Материалы для печатных узлов
113
На рис. 1.84 приведен пример кусочно-одно-
родной среды в микрополосковой линии, выпол-
ненной на двухсторонней печатной плате. Элек-
трическая емкость между сигнальным провод-
ником и слоем возвратных токов определяется
интегрированным действием трех диэлектричес-
ких сред: воздуха, паяльной маски и диэлектри-
ческого основания платы. Через каждую из этих
сред проходят силовые линии электрического
поля, и оценить усредненное значение диэлек-
трической проницаемости можно, введя поня-
тие эффективной диэлектрической проницаемо-
Паяльная Сигнальный
маска проводник
Основание
Слой
возвратных
токов
Рис. 1.84. Пример форми-
рования кусочно-однород-
ной среды в печатной плате
сти кусочно-однородной среды.
Расчет эффективной проницаемости в общем случае может быть выпол-
нен только с применением численных методов расчета. Подобный пример
можно найти в главе 8.
Для определения эффективной диэлектрической проницаемости экспе-
риментальным методом можно воспользоваться выражением
С0
(1.24)
где Се — реальная емкость некоторого конденсатора при наличии кусочно-однородной
среды; Со — емкость того же конденсатора при удалении диэлектрика и замене его воз-
духом.
Для эффективной проницаемости может быть получено малое значение,
определяемое объемной долей воздуха в составе диэлектрика: ге#> (1,1 ... 1,7).
Используя значение zeffi можно определить удельное время задержки рас-
пространения сигнала в линии передачи:
pd~v_v /ГТ” ’ ^eff' нс/м>
с У eff
(1.25)
где 3,3 нс/м — удельная задержка электромагнитной волны в свободном пространстве
(величина, обратная скорости света).
Эта простая формула очень полезна для инженерной оценки временных
соотношений в системе. При анализе дифференциальной пары (глава 6) не-
обходимо определить скорости распространения различных мод сигнала —
дифференциальной и общего вида. Для дифференциальной пары, располо-
женной на наружном слое печатной платы, каждому режиму будет соответ-
ствовать свое значение эффективной проницаемости, а следовательно, и ско-
рости распространения соответствующей моды. Как будет показано, это при-
водит к дрожанию фронта сигнала (джиттеру).
Очевидно, что выражение (1.25) может быть использовано при однород-
ном диэлектрике, когда Ее^- =
114
Глава 1. Печатные платы в цифровых системах
Диэлектрические потери
При распространении сигнала по линии передачи происходит поглоще-
ние энергии в материале основания платы, вызывая ее нагрев. Рассеяние энер-
гии приводит к снижению амплитуды сигнала и увеличению фронта сигна-
ла на выходе линии передачи. Чем больше потери энергии в материале, тем
больше деградация фронта сигнала и больше вероятность возникновения меж-
символьных помех при передаче данных. Свойство материала по рассеянию
энергии характеризуется коэффициентом рассеяния, или тангенсом угла ди-
электрических потерь (1.19):
t g Рассеянная энергия _ Резистивные потери
Полная энергия Проводимость
Чем меньше значение этого коэффициента, тем предпочтительней при-
менение материала для создания быстродействующих плат. Коэффициент рас-
сеяния зависит от частоты нелинейно, поэтому значение этого коэффици-
ента должно указываться для определенной частоты. Существенное прояв-
ление потерь наблюдается с частоты 1 ГГц.
Значение ослабления может быть оценено по формуле [45]
5 = 90/tg5^e^, дБ/м. (1.26)
Приведем в качестве примера параметры некоторых диэлектрических ма-
териалов, применяемых для изготовления печатных плат [44]. В табл. 1.22
даны параметры материалов для цифровых приложений. Они пригодны для
применения в МПП, и ряд из них выпускается в виде фольгированных. Для
этих материалов используется электролитическая фольга, что обеспечивает
ровную блестящую поверхность, которая способствует хорошему воспроиз-
ведению тонкого рисунка топологических элементов.
Материалы ВТ Epoxy, Cyanate Ester, Polyimide разработаны для замены FR4
в приложениях, которые требуют экстремальной механической стабильности.
Очень высокими электрическими параметрами отличается материал Rogers 4003.
Материалы, рекомендованные для аналоговых приложений (на примере
материалов корпорации Rogers Corp.), приведены в табл. 1.23 [44]. Все ма-
териалы фольгированные и имеют как электролитическую фольгу, так и ка-
таную фольгу.
Различие между материалами для аналоговых и цифровых приложений
заключается в следующем:
• материалы для аналоговых приложений обычно имеют меньшее зна-
чение относительной диэлектрической проницаемости, что обеспечи-
вает большую стабильность на высоких частотах и при изменении тем-
пературы;
• материалы для аналоговых приложений имеют меньший допуск на тол-
щину диэлектрического основания;
• фольга материалов для аналоговых приложений может быть как элек-
тролитической, так и катанной; для цифровых приложений фольга при-
меняется только электролитической;
1.4. Материалы для печатных узлов
115
Таблица 1.22
Диэлектрические материалы для цифровых приложений
Материал (на 1 МГц) Допуск на толщину, мкм tg <5
FR4 (стеклотекстолит) 3,9-4,6 ±(25-50) 0,02-0,03
FR408 3,4-4,1 ±(25-50) 0,01-0,015
ВТ Epoxy 3,9-4,6 ±(25 -50) 0,015-0,02
Cyanate Ester 3,5-3,9 ±(25 -50) 0,009
Polyimide 4,0-4,5 ±(25 -50) 0,01
GETEK 3,5-4,2 ±(25 -50) 0,012
Nelco 4000-13 3,7 (на 1 ГГц) ±25 0,01
Nelco 4000-13SI 3,5 (на 1 ГГц) ±25 0,009
Nelco 6000 3,5 (на 1 ГГц) ±25 0,008
Nelco 6000SI 3,2 (на 1 ГГц) ±25 0,003 - 0,005
Speedboard N (препрег) 3,0 ±25 0,02
Speedboard С(препрег) 2,6-2,7 ±25 0,004
Arion 25/Rogers 4003 3,4 (на 10 ГГц) ±25 0,0027
DriClad(IBM) 4,1 0,011
RogersRF35 3,5 0,0018
Таблица 1.23
Диэлектрические материалы для аналоговых приложений
Материал Ег(на 10 МГц) Допуск на толщину, мкм tg 8 Возможность применения в МПП
Rogers Ultralam 2000 2,4-2,6 ±12,5 0,0019 нет
Rogers 5870 2,3 ±12,5 0,0012 нет
Rogers 5880 2,2 ±12,5 0,0009 нет
Rogers 6002 2,94 ±12,5 0,0012 да
Rogers 3003 3,0 ±25 0,0013 да
Rogers 6006 6,15 ±12,5 0,0019 нет
Rogers 6010 10,2 ±12,5 0,0023 нет
Rogers 3006 6,15 ±25 0,0025 да
Rogers 3010 10,2 ±25 0,0035 да
• только отдельные материалы для аналоговых приложений могут при-
меняться в МПП, а материалы для цифровых приложений все пригодны
для таких применений;
116
Глава 1. Печатные платы в цифровых системах
• обычно коэффициент потерь материалов для аналоговых приложений
на порядок лучше, чем у материалов для цифровых приложений.
Следует отметить, что стоимость материалов с низкими показателями мо-
жет отличаться на два порядка от стоимости высококачественных материа-
лов. Так материал RogersRF35 в 5 раз дороже FR4.
Рассмотрим более детально механизм потерь в диэлектрике.
Ток через конденсатор задается уравнением:
dV
I = С0 —= C0cocos(coz),
где / — ток, текущий через конденсатор; Со — емкость конденсатора; (о — угловая часто-
та, в рад/с; V — амплитуда синусоидального напряжения, приложенного к конденсатору.
В идеальном конденсаторе потерь нет. В нем ток отстает от напряжения
на л/2. Если идеальный конденсатор заполнить диэлектриком с относитель-
ной проницаемостью ег, то емкость пропорционально возрастет.
Ток через идеальный конденсатор, заполненный идеальным, свободным
от потерь диэлектриком, будет расти пропорционально диэлектрической
проницаемости и будет отставать от напряжения на 90°, а следовательно, ни-
какая мощность рассеиваться не будет, т. е. в идеальном конденсаторе нет
диэлектрических потерь.
Тем не менее реальные диэлектрики имеют некоторое сопротивление. Когда
реальные материалы устанавливают между металлическими пластинами кон-
денсатора с напряжением постоянного тока, то будет существовать некоторый
ток, который течет через конденсатор. Обычно его называют током утечки. Этот
эффект может быть смоделирован идеальным резистором. Сопротивление
утечки является следствием нахождения материала между пластинами конден-
сатора. Для микрополосковой линии передачи, которую можно представить
в виде плоского конденсатора, ток утечки можно определить по формуле:
D /и> 1 /
^рт=;т (,27>
Ток утечки, который течет через это сопротивление, определяется по фор-
муле
, _ V _r/ h
1к8’Г Г? (Г28)
1kg • ГУ
где Akg — ток Утечки через диэлектрик; V— напряжение; Alkg — сопротивление утечки, свя-
занное с диэлектриком; р — объемное сопротивление для тока утечки диэлектрика; о —
объемная электропроводность для тока утечки диэлектрика (р = 1/о); / — длина участка,
по которому протекает ток утечки; и> — ширина участка; h — толщина диэлектрика между
обкладками конденсатора (сигнальным и возвратным путем).
Ток утечки, проходящий через резистор, совпадает по фазе с напряжением.
Этот ток определяет мощность рассеяния в материале и, соответственно, по-
тери. Мощность, рассеянная на резисторе, с приложенным к нему постоян-
ным напряжением, будет определяться по формуле:
1.4. Материалы для печатных узлов
117
где: V — напряжение на резисторе, В; R — сопротивление резистора, Ом.
Поскольку для большинства диэлектриков объемное сопротивление очень
большое (около 1012 Омсм), то для линии передачи длиной 250 мм с волно-
вым сопротивлением 50 Ом, шириной w = 2h, сопротивление утечки состав-
ляет около 1011 Ом. Результирующая потеря мощности через это сопротив-
ление будет незначительной, менее, чем 1 нВт.
Тем не менее для большинства материалов удельное сопротивление ма-
териала зависит от частоты и уменьшается по мере ее возрастания. Это яв-
ляется следствием появления тока утечки. Есть два механизма утечки через
диэлектрик. Первым является движение ионов. Это основной механизм для
постоянных токов, но его вклад в общую проводимость мал.
Второй механизм связан с переориентацией постоянных электрических
диполей в материале. Чем больше частота синусоидального напряжения, тем
больше ток и меньше объемное удельное сопротивление на этой частоте.
Поэтому сопротивление материала уменьшается с увеличением частоты.
Удельная электропроводность материала обратно пропорциональна удель-
ному сопротивлению, а = 1/р. Объемное удельное сопротивление материа-
ла уменьшается с частотой, в то время как объемная удельная электропро-
водность с частотой растет. Большинство диэлектриков ведет таким образом:
их удельная электропроводность является константой на постоянном токе,
пока не будет достигнута определенная частота, а затем начнет увеличивать-
ся пропорционально частоте. Рис. 1.85 показывает изменение объемной про-
водимости материала FR4 с частотой. Рост начинается с частоты около 10 Гц.
На более высоких частотах движение диполей играет большую роль, и утеч-
ка тока через реальный конденсатор растет при повышении частоты. Этот
ток будет синфазным с напряжением и будет похож на резистивный. На еще
Рис. 1.85. Зависимость объемной проводимости диэлектрика при изменении частоты
118
Глава 1. Печатные платы в цифровых системах
более высоких частотах сопротивление утечки будет уменьшаться, и мощ-
ность рассеивания увеличится из-за нагрева диэлектрика. Эффективное
вращение диполей переводит электрическую энергию в механическую энер-
гию. Взаимодействие диполей с соседями и остальной частью основы поли-
мера заставляет материал нагреваться.
Фактическая поглощенная энергия слишком мала, чтобы вызывать значи-
тельное повышение температуры. Для предыдущего примера линия переда-
чи с волновым сопротивлением 50 Ом даже при частоте 1 ГГц имеет сопротив-
ление утечки диэлектрика менее 1 кОм и мощность рассеяния менее 10 мВт.
В линиях передачи диэлектрические диполи забирают энергию из энер-
гии сигнала и вызывают уменьшение уровня сигнала в конце линии. Чем
больше частота, тем больше утечка переменного тока — удельная электро-
проводность, и тем больше потеря мощности в диэлектрике.
Коэффициент рассеяния
Описать рассмотренное свойство материала можно коэффициентом рас-
сеяния. Тогда объемная удельная электропроводность диэлектрика будет оп-
ределяться формулой
о = 27r/E0£rtg 8, (1.29)
где f — частота синусоидального колебания, Гц; е0 — диэлектрическая постоянная, е0 =
= 8,89-10-14 Ф/см; ег— относительная диэлектрическая проницаемость; tg 5 — тангенс угла
диэлектрических потерь (коэффициент рассеяния), безразмерная величина:
tg 8 ~ ирОтах,
где п — плотность числа диполей в диэлектрике; р — дипольный момент, значение заряда
на разнос зарядов в диполе; (?тах — сдвиг диполя в приложенном поле.
С ростом частоты диполи колеблются быстрее, что приводит к росту тока
и увеличению удельной электропроводности. Важно иметь в виду, что в оп-
ределении коэффициента рассеяния, как тангенса угла 8, символ 8 не имеет
отношения к толщине скин-слоя, который также обозначается греческой
буквой 8. Не следует путать два этих обозначения.
В реальных материалах движение Qmax диполей замедлено, и эта способ-
ность зависит от структуры материала. Более плотное расположение дипо-
лей, которое удерживается полимерами, имеет малую диэлектрическую про-
ницаемость и низкий коэффициент рассеяния.
Диэлектрики с низкой диэлектрической проницаемостью (например, теф-
лон, кремниевая резина, полиэтилен) обладают очень низким коэффициентом
рассеяния.
Для большинства диэлектриков, применяемых для печатных плат, можно
принять коэффициент рассеяния постоянным и слабо зависящим от часто-
ты. Однако могут быть определенные изменения коэффициента рассеяния от
партии к партии, а также этот коэффициент может изменяться в зависимос-
ти от технологических процессов обработки диэлектрика. Повышенное вла-
гопоглощение приводит к увеличению числа молекул воды, что приведет к
увеличению коэффициента рассеяния. В гибких пленках из полиимида или
каптона влажность может удвоить коэффициент рассеяния.
1.4. Материалы для печатных узлов
119
Для комплексного описания электрических свойств диэлектрических мате-
риалов требуются два показателя. Диэлектрическая проницаемость показы-
вает, как материал увеличивает емкость и снижает скорость распростране-
ния сигнала в линии. Коэффициент рассеяния характеризует число диполей и
их подвижность и показывает, как увеличивается проводимость при увеличе-
нии частоты. Оба показателя слабо зависят от частоты и будут изменяться
от партии к партии материала.
Более детально с характеристиками материалов, которые применяются
при изготовлении печатных плат, можно познакомиться в [8, 20].
Потери в проводниках
Последовательное сопротивление току проявляется во время его распро-
странения к нагрузке и возврата к источнику. Оно определяется удельным
сопротивлением проводника и его сечением, через которое протекает ток.
Постоянный ток распределен по сечению проводника равномерно, и сопро-
тивление печатного проводника равно:
Я = р—, Ом, (1.30)
где р — удельное объемное сопротивление материала проводника, Ом см; / — длина про-
водника, см; W— ширина проводника, см; t — толщина проводника, см.
Возвратный ток в полосковых и микрополосковых линиях передачи про-
текает по широким проводящим слоям. Сопротивление этих слоев очень мало
и поэтому может не учитываться. Для медного проводника шириной 0,125 мм,
толщиной 35 мкм и длиной 250 мм сопротивление постоянному току соста-
вит 0,1 Ом.
Объемное удельное сопротивление меди, как и всех других металлов, по-
стоянно до частот 100 ГГц. На первый взгляд, и сопротивление проводника
может приниматься постоянным. На самом деле при повышении частоты со-
противление проводника увеличивается из-за влияния скин-эффекта. Суть
этого эффекта заключается в оттеснении тока к периферии проводника, что
приводит к уменьшению эффективного сечения проводника.
Толщина 6 скин-слоя определяется соотношением:
8=77’мм- <L3"
где f — частота синусоидального колебания, МГц; ц — абсолютная магнитная проницае-
мость материала проводника, о — проводимость материала проводника.
Для медного проводника ц = ц0 = 1,256 мкГн/м, о =5,8-107 См/м, что по-
зволяет рассчитать толщину скин-слоя по формуле
5=667177,мкм- (| 32)
Если сигнал частотой в 1 ГГц проходит по медному проводнику, то ток
концентрируется на поверхности проводника в слое толщиной 2,1 мкм. Это
120
Глава 1. Печатные платы в цифровых системах
Микрополосковая г------Сигнал
линия ш
приближенное значение. На са-
мом же деле расположение рядом
с сигнальным проводником воз-
Путь возвратного
тока
Полосковая
линия
Путь возвратного
тока
Рис. 1.86. Распределение тока в проводни-
ках толщиной 0,035 мм в составе линий
передачи с волновым сопротивлением
50 Ом, с частотой сигнала в 10 МГц.
Более темный тон показывает
большую плотность
вратного проводника приводит к
перераспределению тока по сече-
нию проводников из-за эффекта
близости. Плотность тока увели-
чивается на сторонах проводника,
обращенных друг к другу. Пример
распределения тока по сечению
проводников в микрополосковой
линии на частоте 10 МГц показан
на рис. 1.86 [4]. Точный расчет рас-
пределения тока по сечению про-
водников для этого случая возмо-
жен только с применением чис-
ленных методов.
Для частот выше 3,6 МГц толщина скин-слоя будет меньше толщины про-
водника, типичное значение которой составляет 35 мкм.
Распределение тока по сечению проводника происходит под воздействием
следующего эффекта: ток стремится распространяться по пути с наимень-
шим полным сопротивлением, что на высоких частотах соответствует пути
с наименьшей индуктивностью контура. Поэтому условные нити тока в каж-
дом проводнике стремятся распространяться как можно разрозненнее, чтобы
уменьшить парциальную самоиндукцию каждого проводника, и одновремен-
но ток в обратном направлении в возвратном проводнике будет распрост-
раняться по возможности ближе к сигнальному току, чтобы увеличить пар-
циальную взаимную индуктивность между двумя потоками.
Это означает, что для всех важных частотных компонентов сигнала распре-
деление тока в проводниках печатных плат ограничено толщиной скин-слоя,
и сопротивление всегда будет зависеть от частоты, если она больше 3,6 МГц.
В таком режиме скин-слой ограничивает рабочую толщину проводника, по ко-
торой протекает ток. В этом случае сопротивление R проводника должно быть
описано уравнением:
Я = р—, Ом,
wo
(1.33)
где р — удельное сопротивление материала, Ом см; / — длина проводника, см; w — шири-
на проводника, см; 5 —толщина скин-слоя, см.
Таким образом, последовательное сопротивление проводника в линии пе-
редачи будет увеличиваться с увеличением частоты. Вопрос о том, как эта за-
висимость сопротивления от частоты влияет на потери, будет поднят далее.
1.4. Материалы для печатных узлов
121
1.4.3. Материалы с высокой магнитной
проницаемостью
Если относительная магнитная проницаемость материала больше 1, то маг-
нитное поле внутри материала усиливается относительно немагнитного ма-
териала. Только три металла, образующих группу ферромагнетиков, имеют
проницаемость более 1: железо, никель и кобальт. Большинство сплавов, в
состав которых входят эти металлы, имеют относительную проницаемость
более 1. Примером может служить феррит, широко используемый в радио-
электронике, содержащий железо и кобальт, проницаемость которого око-
ло 1 000. В межсоединениях используются два распространенных сплава: Alloy
42 и ковар (Kovar). Проницаемость этих материалов может достигать 100...500.
Это достаточно высокая проницаемость для того, чтобы повлиять на частот-
ные свойства межсоединений (сопротивление, индуктивность), выполнен-
ных из этих материалов.
Для проводников из ферромагнетиков собственная индуктивность провод-
ника будет определяться внутренней и внешней самоиндукцией. Все линии
магнитного поля, соответствующие внешней самоиндукции, расположены толь-
ко в воздухе, который имеет относительную проницаемость 1. Поэтому внешняя
самоиндукция проводника из ферромагнетика точно такая же, как и у немаг-
нитного материала, например, меди. Одинаковый ток в магнитном и немагнит-
ном проводнике вызывает одинаковое магнитное поле на 1 Атока в них.
Внутреннее магнитное поле в ферромагнитном проводнике из-за действия
магнитной проницаемости будет усилено. На низких частотах индуктивность
этого проводника очень высокая, но на частотах более I МГц, из-за скин-эф-
фекта собственная индуктивность становится сравнимой с индуктивностью
медного провода такого же размера.
Толщина скин-слоя, в котором протекает ток на высоких частотах, для
ферромагнитных проводников значительно меньше, чем у медного провод-
ника из-за высокой магнитной проницаемости. Например, никель с объемной
проводимостью 1,4-107 См/м и проницаемостью около 100, имеет глубину
скин-слоя:
мкм>
где f — частота синусоидального сигнала, МГц.
Это в 5 раз меньше, чем для меди.
На определенной частоте сечение, по которому протекает ток в никеле-
вом проводнике, будет значительно тоньше, чем в медном проводнике. Кроме
этого, объемное удельное сопротивление никелевого проводника выше.
Поэтому значение последовательного сопротивления никелевого проводника
будет больше медного примерно в 10 раз, а следовательно, сопротивление
выводов из ковара или Alloy 42 на высоких частотах может быть очень вы-
соким по сравнению с немагнитными выводами.
122
Глава 1. Печатные платы в цифровых системах
Рис. 1.87. Распределение тока
в микрополосковой линии,
покрытой никелем (темные
участки соответствуют боль-
шей плотности тока): 1 — ни-
келевое покрытие; 2 — сиг-
нальный проводник из меди;
3 — диэлектрическое основа-
ние платы; 4 — слой протека-
ния возвратных токов
Поверхность микрополосковой линии на пе-
чатной плате часто покрывается слоем никель/зо-
лото для улучшения процесса присоединения
компонентов к печатному монтажу Слой нике-
ля фактически не действует на электрические
свойства трассы, поскольку он расположен на
стороне проводника, противоположной относи-
тельно возвратного пути. Токи протекают по пути
с наименьшим полным сопротивлением, поэто-
му прямой и возвратный токи текут на поверхно-
стях проводников, расположенных ближе друг к
другу (эффект близости). При покрытии медно-
го проводника никелем, ток течет по меди, по-
скольку покрытие нанесено на стороне с мини-
мальной плотностью тока (рис. 1.87).
Это одна из причин, по которой покрытие се-
ребром выводов из Alloy 42 или ковара обеспе-
чивает немагнитный путь по внешней поверхности проводника из магнитного
материала на высоких частотах.
Для сечения произвольной формы точное определение конфигурации
скин-слоя — достаточно трудная задача и может быть решена с помощью чис-
ленных методов и специальных программных средств.
_____________Глава 2_____________
Электрофизические параметры
печатного монтажа
2.1. Полное сопротивление и электрические
модели печатного монтажа
2.1.1. Описание целостности сигнала в решениях
и терминах полного сопротивления
В высокоскоростных цифровых системах сигнал представляется в виде
переменных токов или переменных напряжений. Эти переменные сигналь-
ные параметры взаимодействуют с электрическими параметрами межсоеди-
нений, что приводит к искажениям сигнала. На высоких частотах искаже-
ния сигнала настолько значительны, что его нельзя рассматривать как циф-
ровой с четко выраженными статическими состояниями и некоторым мо-
нотонным переходом из одного состояния в другой. Сигнал приобретает не-
которую произвольную форму, напоминая аналоговый. Для оценки воздей-
ствия электрических параметров печатных проводников и других топологи-
ческих элементов на искажения сигнала необходимо детальное рассмотре-
ние этих параметров и, в первую очередь, полного сопротивления меж-
соединения. Полное сопротивление — ключевой электрический параметр пе-
чатного монтажа.
Полное сопротивление £ определяется отношением напряжения к току [37]:
V Id2 ( т И
г = 7 = ? + “ |2|>
где И— действующее значение напряжения в цепи; /—действующее значение тока в цепи;
R, L, С — последовательно соединенные активное сопротивление, индуктивность и ем-
кость некоторой цепи; со — круговая частота, на которой определяется полное сопротив-
ление цепи.
Величина в круглых скобках в выражении (2.1) называется реактивным
сопротивлением х. Она имеет размерность сопротивления. Член со£, учитыва-
ющий реакцию самоиндукции, называется индуктивным сопротивлением х£,
124
Глава 2. Электрофизические параметры печатного монтажа
а член l/(coQ, учитывающий реакцию емкости, называется емкостным со-
противлением хс:
7 I 7 I
Х = СО£-------, Xi = COL, Хг =------
соС L с соС
(2.2)
Зная полные сопротивления межсоединений, можно точно рассчитать ис-
кажения сигнала и внести соответствующие коррективы в конструкцию пе-
чатной платы в процессе проектирования. Если известно, как геометрия цепи
и свойства материалов влияют на ее полное сопротивление, тогда можно дол-
жным образом спроектировать поперечное сечение линии передачи, топо-
логию сигнальных проводников, шин питания и заземления, выбрать мате-
риалы и другие элементы конструкции платы так, чтобы достичь желаемого
полного сопротивления.
Полное сопротивление описывает очень важные электрические свойства
межсоединений. Знать полное сопротивление межсоединений и задержку рас-
пространения сигнала в них — значит иметь почти исчерпывающую инфор-
мацию об электрических свойствах межсоединений, а следовательно, и об
искажении сигнала в них.
Существуют четыре основные задачи обеспечения целостности сигналов,
каждую из которых можно описать, используя понятие полного сопротив-
ления [4, 24, 25, 47].
I. Искажения сигнала, возникающие при отражении от мест изменения
полного сопротивления в межсоединениях. Это — помехи отражения.
Если полное сопротивление постоянно на пути распространения сиг-
нала, то не будет отражений и искажений сигнала. Эффекты затуха-
ния сигнала при его распространении вызваны шунтирующим воздей-
ствием сопротивления.
2. Перекрестные помехи возникают из-за переноса энергии электрическими
и магнитными полями, которые образуются при взаимодействии линий
передач. Взаимная емкость и взаимная индуктивность между элемента-
ми межсоединений участвуют в образовании полного сопротивления.
3. Помехи в шинах питания и заземления при коммутации цифровых мик-
росхем определяются значениями полных сопротивлений шин. При
снижении их полных сопротивлений условия работы цифровой сис-
темы улучшаются.
4. При наличии в линиях передачи помех дифференциального и общего
вида следует уметь управлять значением полного сопротивления для этих
составляющих с целью избирательного подавления соответствующих
помех. Необходимо увеличивать полное сопротивление для синфазного
тока, что приводит к уменьшению уровня синфазных помех.
Не только проблемы, связанные с целостностью сигнала, лучше описыва-
ются с помощью понятия полного сопротивления, но и методы проектирова-
ния для обеспечения целостности сигнала также основаны на этом понятии.
Существуют модели, по которым определяются полные сопротивления
для реальных межсоединений. Полное сопротивление характеризует среду
2.1. Полное сопротивление и электрические модели печатного монтажа 125
распространения сигнала, обеспечивающую желаемый режим работы устрой-
ства. Например, сближение слоев питания и заземления в МПП приводит к
увеличению емкости шины питания относительно земли и, соответственно,
к уменьшению полного сопротивления шины питания и улучшения ее ре-
жима работы.
Если будет определено, как физическое расположение межсоединений
влияет на их полное сопротивление, то можно описать процесс прохожде-
ния сигналов в них и принять наиболее рациональное решение по конструк-
ции платы и топологии сигнальных проводников.
Полное сопротивление — это тот фактор, который помогает объединить
физические и электрические параметры при проектировании печатных плат.
Стратегия проектирования заключается в необходимости обеспечить выпол-
нение требований к значению полного сопротивления и осуществления его реа-
лизации в конструкции платы.
В процедуре верификации, стараясь обеспечить оптимальные характерис-
тики физической системы, переходят от физической структуры к эквивалент-
ной электрической модели. Полное сопротивление результирующей электри-
ческой модели определяет, как параметры межсоединения влияют на напряжение
и ток сигнала. Используя какую-либо программу для моделирования электри-
ческих схем, можно предсказать, каковы будут формы напряжения источника
в результате воздействия на них полного сопротивления межсоединения.
Наконец, важно предсказать форму анализируемого сигнала, определить,
происходит ли искажение его формы или прочие отклонения от технических
требований, а затем сделать вывод, насколько приемлем разрабатываемый
вариант конструкции платы, или же он должен быть видоизменен. В целом,
процесс создания элементов электронного устройства, места и роли физичес-
кого и виртуального прототипа детально рассмотрен ранее в главе 1.
Одна из важных задач проектирования плат состоит в нахождении пол-
ного сопротивления каждого из элементов цепей, влияющих на целостность
сигнала и ЭМС, используя эквивалентную электрическую схему, и в вычис-
лении полного сопротивления для комбинации элементов цепи, что позво-
лит описать поведение любой модели.
2.1.2. Полные сопротивления реальных
и идеальных элементов цепей
Электрический термин «полное сопротивление» имеет точное определение
на базе соотношения между током, протекающим через компонент, и напря-
жением на нем. Это базовое соотношение применяется к любому двухполюс-
ному прибору, такому, как резистор, развязывающий конденсатор, вывод
корпуса микросхемы или соединения в печатных платах. Когда есть больше,
чем два вывода, определение полного сопротивления более сложное, так как
следует принимать во внимание дополнительные клеммы.
Для двухполюсных приборов определение полного сопротивления дано
выражением (2.1). Например, если напряжение на резисторе 5 В и через него
126
Глава 2. Электрофизические параметры печатного монтажа
протекает ток в 0,1 А, то сопротивление должно быть 5В / 0,1А = 50 Ом. Это
определение полного сопротивления применимо абсолютно во всех ситуа-
циях, в частотной и временной области, для любого реального прибора. Видно,
что полное сопротивление цепи идеального резистора с сопротивлением R
равно его активному сопротивлению z = R.
Существует два крайних случая:
1) Открытый контур, в котором ток не течет. Если ток через прибор для
любого напряжения обращается в нуль, то полное сопротивление будет равно
бесконечности. Полное сопротивление открытого контура (режим холостого
хода) очень велико.
2) В режиме короткого замыкания, при котором напряжение равно нулю,
полное сопротивление всегда будет равно 0 Ом.
При анализе конструкций элементов и узлов электронных средств раз-
деляют два типа компонентов — идеальные и реальные. Параметры реаль-
ных приборов поддаются измерению. Это приборы, которые физически су-
ществуют, и чьи электрофизические параметры реально влияют на функци-
онирование изделия.
Идеальные устройства — это математическое описание (математические
модели) элементов цепи, которые имеют точные конкретные значения. Ма-
тематические модели могут воспроизводить работу реальных приборов с той
или иной степенью приближения, которая зависит от точности математичес-
кого описания реальных процессов и адекватности трактовок физических
явлений. Математическая формулировка теории электрических цепей при-
менима только для идеальных приборов. Модели реальных приборов состав-
ляются из комбинации идеальных приборов.
Очень важно различать реальные и идеальные элементы цепи [4, 49].
Полное сопротивление любого реального физического электрического со-
единения или пассивного компонента может быть измерено. Измерить па-
раметры идеальных элементов цепи невозможно, также как невозможно рас-
считать полное сопротивление любого реального элемента цепи. Другими сло-
вами: рассчитать можно только идеальные компоненты, а экспериментально
исследовать можно только реальный компонент. Поэтому важно четко пред-
ставлять различие между реальными компонентами и идеальными элемен-
тами цепи (рис. 2.1).
Одна из основных задач при создании виртуального прототипа разраба-
тываемой платы состоит в определении эквивалентной схемы проектируе-
мой цепи, состоящей из идеальных элементов, полное сопротивление которых
приближается к реальному значению. Если подобный переход будет выпол-
нен, то у разработчика появляется инструмент анализа, при помощи кото-
рого он может отлаживать виртуальный прототип изделия. Модель цепи
должна быть приближена к реальной конструкции, и всегда важно оценить
степень приближения.
При создании моделей используются четыре идеальных двухполюсных эле-
мента цепи, комбинация которых описывает реальный объект: резистор (про-
водимость), конденсатор, индуктивность и линия передачи.
2.1. Полное сопротивление и электрические модели печатного монтажа 127
Обычно первые три элемента называ-
ют сосредоточенными элементами цепи,
в том смысле, что их свойства могут быть
«сосредоточены» в одной точке. Элемент
«линия передачи» — это модель с распре-
деленными параметрами, которая наилуч-
шим образом моделирует электрические
соединения. При определенных условиях
модель с распределенными параметрами
может быть замещена моделью на сосре-
доточенных элементах [48]. Идеальные
элементы цепи имеют точное значение,
которое описывает их взаимодействие с то-
ками и напряжениями.
Эквивалентная электрическая модель
цепи представляет собой идеализирован-
Рис. 2.1. Развязывающий конденсатор
в корпусе 1206 (о), смонтированный
на плате, и его эквивалентная модель
(б), составляющая комбинацию иде-
альных элементов цепи: R - 0,5 Ом,
L = 1.78 нГн, С =0,67 нФ.
ное электрическое описание реальной структуры. Это приближение основа-
но на использовании идеальных элементов цепи. Адекватная модель обеспе-
чивает полное сопротивление, которое соответствует полному сопротивлению
реального прибора. На этой модели разрабатываемой конструкции можно про-
гнозировать, каковы будут искажения сигнала, и какой будет взаимодействовать
с другими сигналами. Для оценки адекватности модели необходимо знать по-
ведение идеальных элементов.
2.1.3. Полные сопротивления во временной области
Полное сопротивление идеального резистора
во временной области
Для каждого из четырех базовых элементов цепи можно записать зави-
симость, которая показывает, как напряжение и ток связаны между собой.
Соотношение между напряжением и током для идеального резистора зада-
ется известным соотношением:
V= IR,
(2.3)
где V — напряжение на резисторе, В; I — ток через резистор, A; R — сопротивление рези-
стора, Ом.
Во временной области полное сопротивление идеального резистора со-
гласно определению будет
z = V/I=(IR)/I = R.
(2.4)
Это говорит о том, что полное сопротивление резистора постоянно и не
зависит от тока через резистор или напряжения на нем.
128
Глава 2. Электрофизические параметры печатного монтажа
Полное сопротивление идеального конденсатора
В идеальном конденсаторе рассматривается соотношение между зарядом,
запасенным между двумя пластинами, и напряжением на них. Емкость иде-
ального конденсатора определяется соотношением:
C = Q/U, (2.5)
где С — емкость, Ф; V— напряжение между пластинами, В; Q— заряд, запасенный меж-
ду пластинами, К.
Значение емкости конденсатора описывает эту емкость как отношение
запасенного заряда к разности напряжений на обкладках. Большая емкость
означает возможность накопить большой заряд при малом напряжении.
Полное сопротивление конденсатора может быть вычислено при условии,
что известен ток через конденсатор и напряжение на нем. Если напряжение на
конденсаторе меняется, то считается, что через конденсатор течет ток. В дей-
ствительности при изменении потенциала на одной обкладке конденсатора на
другой обкладке индуцируется заряд противоположного знака. При этом кон-
денсатор при изменении напряжения ведет себя так, как будто через него про-
текает ток.
Выразив в (2.5) заряд через емкость и напряжение и взяв производную от
обеих частей полученного выражения, можно записать новое соотношение
тока и напряжения:
I=dQ/dt = C-dV/dt,
где / — ток через конденсатор; Q — заряд пластин конденсатора; С — емкость конденса-
тора; V — напряжение на конденсаторе.
Если напряжение близко к постоянному, то ток через конденсатор прак-
тически равен нулю. Используя это соотношение, можно рассчитать полное
сопротивление идеального конденсатора:
_ И _ V
Zc~f~cd--' (2.6)
Э/
Это выражение говорит о том, что полное сопротивление конденсатора за-
висит от формы напряжения на нем. Если крутизна изменения напряжения
велика (т. е. напряжение меняется очень быстро), то ток через конденсатор
велик, а полное сопротивление мало. Конденсаторы большой емкости име-
ют малое полное сопротивление.
Полное сопротивление идеальной катушки индуктивности
Напряжение на идеальной катушке индуктивности определяется выражением:
Э/
Г = , (2.7)
dt
где L — индуктивность катушки; / — ток через катушку.
2.1. Полное сопротивление и электрические модели печатного монтажа 129
Из формулы следует, что напряжение на катушке индуктивности зависит от
того, как быстро меняется ток через нее. Если ток постоянен, то напряжение
на катушке равно нулю. Если ток через катушку быстро меняет свое значение,
это вызовет большое падение напряжения на индуктивности. В данном случае
индуктивность есть коэффициент пропорциональности между напряжением и
скоростью изменения тока. Большое значение индуктивности означает, что малое
изменение тока генерирует большое напряжение на индуктивности.
Часто возникают вопросы о направлении, в котором происходит перепад
напряжения. Если изменить направление протекания тока на противополож-
ное, то полярность наведенного (индуцированно-
го) напряжения поменяется. Легче всего запомнить
полярность напряжения, посмотрев перепад на-
пряжения на резисторе.
При протекании постоянного тока через рези-
стор, ток течет от положительного контакта к от-
рицательному. Так же происходит в индуктивно-
сти: ток протекает в направлении от плюса к ми-
нусу. Это показано на рис. 2.2.
Используя это базовое определение индуктив-
ности, можно вычислить полное сопротивление
катушки индуктивности как отношение напряже-
ния на зажимах катушки к току через катушку
индуктивности:
I г
+ —I I---
dl/dt
Рис. 2.2. Напряжение на
катушке индуктивности
для изменяющегося тока
по направлению такое же,
как на резисторе при
протекании через него
постоянного тока
_У _ dl/dt
4-i-L—r
(2.8)
Хотя полное сопротивление катушки индуктивности хорошо определе-
но, его неудобно использовать во временной области. Если ток через катушку
быстро изменяется, то ее полное сопротивление большое; если скорость
изменения тока через катушку индуктивности незначительна, то полное
сопротивление очень мало. Для постоянного тока полное сопротивление
катушки индуктивности близко к нулю. Полное сопротивление катушки
индуктивности очень сильно зависит от формы тока через нее.
В частотной области полные сопротивления определяются несколько
проще.
2.1.4. Полные сопротивления в частотной области
Описание поведения идеального компонента в частотной области рассмат-
ривается при синусоидальных сигналах: синусоидального тока и напряже-
ния. Синусоиды имеют три параметра: частоту, амплитуду и фазу. Общепри-
нято описывать фазу в радианах. Угловая частота со связана с частотой/си-
нусоидального сигнала соотношением со= 2л/ где угловая частота измеряется
в рад/с, а частота синусоидального сигнала в Гц (1/с).
5
130
Глава 2. Электрофизические параметры печатного монтажа
Время
Рис. 2.3. Синусоиды тока через идеальный
элемент и напряжения на нем
Важно иметь в виду, что все
основные элементы цепи и меж-
соединения — это линейные уст-
ройства, т. е. при прохождении
через них синусоидального сиг-
нала определенной частоты не
возникает новых частотных со-
ставляющих. Амплитуда тока си-
нусоидальной волны может иметь
смещенную фазу по отношению
к напряжению, но их частоты бу-
дут одинаковы (рис. 2.3). Когда
берется отношение двух синусоид, нужно учитывать их амплитуды и разность
фаз между ними.
Отношение двух синусоидальных волн — это пара значений, содержащих
информацию об их амплитудах и фазах при определенном значении часто-
ты. Абсолютная величина отношения амплитуд двух синусоидальных волн
дает значение полного сопротивления:
I*l=l7|- Ом.
Полное сопротивление любого элемента цепи — это два числа, модуль и фаза
для каждого значения частоты. Значения полного сопротивления и фаза пол-
ного сопротивления могут быть зависимы. Отношение амплитуд или фаза мо-
жет изменяться с частотой. При описании полного сопротивления в частотной об-
ласти необходимо точно знать, для какой частоты производится это описание.
В частотной области полное сопротивление может быть описано комп-
лексными числами, то есть, используя действительную и мнимую часть. Это
позволяет формализовать решение с использованием комплексных чисел,
что упрощает вычисления полного сопротивления в сложных цепях. В ком-
плексном числе заложена необходимая информация — модуль и фаза.
Рассмотрим протекание синусоидального тока через резистор и синусо-
идальное напряжение, которые связаны через сопротивление R резистора:
V = /Osin(co/)J?.
Если взять отношение напряжения к току через резистор, можно убедиться,
что это в точности будет значение сопротивления:
V _ /0 sin(cor) • 7?
I /0 sin(coz)
(2.9)
Для резистора полное сопротивление не зависит от частоты, и сдвиг фаз
равен нулю. Полное сопротивление идеального резистора не меняется в ши-
роких диапазонах частот.
2.1. Полное сопротивление и электрические модели печатного монтажа 131
Ток через конденсатор — это производная от напряжения, то есть уже ко-
синусоидальная волна:
, J(K0sin(co/)) _ IZ z ч
1 =С-------------= CcoK0cos(co/). (2.10)
Из этого выражения видно, что амплитуда тока будет увеличиваться с ча-
стотой, даже если амплитуда напряжения постоянна. Чем больше частота, тем
больше амплитуда тока через конденсатор. Следовательно, полное сопротив-
ление конденсатора будет уменьшаться с ростом частоты согласно формуле:
_У _ Уоsin(coz) _ 1 sin(coz)
Zc I CcoH0cos(co/) соС cos(coz) (2.11)
Очевидно, модуль полного сопротивления конденсатора равен 1 /соС. Так,
если угловая частота увеличивается, полное сопротивление уменьшается. Даже
если значение емкости постоянно при изменении частоты, полное сопротив-
ление все равно будет уменьшаться с частотой.
Сдвиг фаз между волнами синуса и косинуса в данном случае равен —90°.
Когда запись ведется в комплексном виде, то —90° в комплексном виде — это
—У, и полное сопротивление конденсатора равно —j/оэС.
Определим в качестве примера полное сопротивление развязывающего
конденсатора, установленного в цепи питания, на частоте 1 ГГц, который
имеет емкость 10 нФ. Принимаем конденсатор за идеальный. Такой идеальный
конденсатор будет иметь полное сопротивление:
Zc = 1 / (2тс х 1 ГГцх 10 нФ) ~ 1/(6 х 109 х 10 х 10"9) = 1/60 ~ 0,016 Ом.
Это весьма малое полное сопротивление. Если реальный развязывающий кон-
денсатор работает как идеальный, полное сопротивление будет около 16 мОм
на частоте 1 ГГц. Конечно, на низкой частоте полное сопротивление будет больше.
При 1 Гц полное сопротивление этого конденсатора будет около 16 МОм.
Используем частотную область для анализа индуктивности. При прохождении
синусоидальной волны через индуктивность падение напряжения на ней будет:
>z , J(/nsin(co/)) , z ч
V = L dt—- = £w /0 cos(co/).
Видно, что при постоянной амплитуде тока напряжение на индуктивно-
сти будет расти с увеличением частоты. Это означает, что полное сопротив-
ление индуктивности растет с частотой.
Используя базовое определение полного сопротивления, выражение для
его определения может быть преобразовано следующим образом:
_ V _ со£ • /0 cos(co/) _ cos(cor)
Zl I /Osin(cor) sin(co/) (2.12)
132
Глава 2. Электрофизические параметры печатного монтажа
Модуль полного сопротивления растет с частотой, даже если значение ин-
дуктивности постоянно.
Разность фаз в случае индуктивности между волнами напряжения и тока
составляет +90°, что в комплексной форме соответствует у, и полное сопро-
тивление индуктивности записывается в виде:
zL =j(dL.
В реальном развязывающем конденсаторе индуктивность зависит от фор-
мы тела конденсатора и его выводов. Пусть грубая оценка истинной индук-
тивности конденсатора будет 2 нГн. Тогда полное сопротивление последо-
вательной индуктивности реального конденсатора на частоте 1 ГГц прибли-
женно будет:
ZL = 2л: х 1 ГГц х 2 нГн х 6 х 1х109 х 2х10-9 = 12 Ом.
Для развязывающего конденсатора это слишком большое значение. Же-
лательно иметь его не более 0,1 Ом. Из приведенных примеров видно, что
полное сопротивление реального конденсатора с учетом его суммарной ин-
дуктивности почти на два порядка выше, чем идеального.
Значения сопротивления, емкости, индуктивности идеальных резисторов,
конденсаторов, индуктивностей постоянны при изменении частоты. В случае
идеального резистора его полное сопротивление постоянно при изменении
частоты. При увеличении частоты полное сопротивление конденсатора будет
уменьшаться, а для индуктивности полное сопротивление будет увеличиваться.
Важно понимать, что для идеального конденсатора или индуктивности, даже
если значение емкости и индуктивности абсолютно постоянно с частотой,
полное сопротивление меняется при изменении частоты.
2.1.5. Эквивалентные схемы компонентов
Поведение полного сопротивления реальных межсоединений на печат-
ной плате может быть приближенно промоделировано комбинацией идеаль-
ных элементов в виде эквивалентной схемы, или модели.
Эквивалентная схема фактически представляет собой виртуальный про-
тотип. Для ее построения необходимо знать топологию электрической цепи,
реализованной на плате, значения параметров всех компонентов и всех элек-
трофизических параметров топологических элементов. Однако значения этих
параметров не всегда удается определить на этапе проектирования, и часто
эквивалентная схема ограничена только базовыми элементами модели. Ис-
следование этой схемы проводится на этапе параметрической верификации
виртуального прототипа.
Важно иметь в виду, что эквивалентная схема есть не что иное, как набор
идеальных элементов, которые используются для моделирования поведения ре-
альных межсоединений.
Это всегда ограничивает возможности по описанию реальных процессов
в межсоединениях за счет эквивалентных схем. Степень приближения мо-
2.1. Полное сопротивление и электрические модели печатного монтажа 133
жет быть оценена путем экспериментальных исследований. Для каждой
модели необходимо определить два важных момента: насколько адекватна
структура модели, и какова область ее применения, например, по частотно-
му диапазону. Чем выше частотный диапазон работы реального устройства,
тем больше ожидаемые расхождения между результатами анализа эквивален-
тной схемы и экспериментом.
Опыт говорит, что всегда следует начинать рассмотрение с простейшей
модели с последующим ее усложнением до получения приемлемого результата.
Рассмотрим пример. Определим полное сопротивление развязывающего кон-
денсатора, который подключен к выводу питания интегральной микросхемы.
Можно ожидать, что этот реальный компонент может быть промоделирован в
виде простого конденсатора. Но насколько адекватна эта простейшая модель
на высоких частотах? Для приближения к реальной ситуации на высоких час-
тотах следует учитывать активное сопротивление и индуктивность элементов
подключения конденсатора (выводов конденсатора, соответствующих отрезков
печатных проводников). Это означает, что к модели первого порядка в виде
одиночной емкости С следует добавить элементы 7? и L для получения модели
второго порядка. Реальный развязывающий конденсатор описывается его пол-
ным сопротивлением, которое должно учитывать параметры самого конденсатора
и элементов его подключения. На рис. 2.4 представлены результаты измерений
[4], выполненных на частотах от 10 МГц до 5 ГГц, и анализа модели первого и
второго порядка для конденсатора 0,67 нФ.
Видно, что простейшая модель удовлетворительно работает на низких ча-
стотах. Поэтому простейшая модель в виде идеального конденсатора емко-
стью 0,67 нФ является приемлемой моделью, но только до частот 70 МГц.
Для высоких частот следует применять более точную модель, представляю-
щую последовательное соединение идеального конденсатора, сопротивления
Рис. 2.4. Сравнение результатов моделирования
конденсатора с экспериментальными данными:
1 — модель первого порядка; 2 — модель второго порядка;
3 — экспериментальные результаты
134
Глава 2. Электрофизические параметры печатного монтажа
и индуктивности. При правильном выборе этих параметров поведение мо-
дели будет хорошо отражать реальность (рис. 2.4) до высоких частот (5 ГГц).
Полное сопротивление модели второго порядка определяется по формуле
^(со) = Я + j\ со£——
V соС
Это показывает, что при точном выборе параметров модели из идеальных эле-
ментов можно достаточно точно моделировать поведение реальных объектов.
2.1.6. Выбор моделей
Затраты время,усилия,
стоимость
Рис. 2.5. Зависимость между
адекватностью модели
и затратами для достижения
результата
Модели для электрических соединений и пассивных устройств могут быть
созданы исходя из экспериментов или расчетов. В любом случае, сначала
нужно определить топологическую модель печатной платы. Синтезируемая
модель постоянно балансирует между адекватностью и простотой, а так же
между временем и усилиями, необходимыми для
достижения результата. В общем случае, высо-
кая адекватность требует больших материальных
и временных затрат (рис. 2.5). Наиболее раци-
онально начать с простейшей модели, усложняя
ее до получения желаемой адекватности.
Когда межсоединение представлено в виде
электрически короткой линии, то простейшая
модель, с которой можно начать анализ, содержит
набор сосредоточенных электрических элементов.
Когда межсоединение однородное и электрически
длинное, то лучшей моделью замещения будет
идеальная модель линии передачи.
Как отмечалось выше, простейшей моделью
сосредоточенных элементов является обособ-
ленное сопротивление, индуктивность, или ем-
кость. Далее простейшим вариантом будет набор двух из них, затем трех и
так далее. Ключевым фактором, с помощью которого можно определить не-
обходимость усложнения исходной модели, является полоса пропускания,
которой должна соответствовать модель. Однако каждая широкополосная
модель должна также обеспечивать хорошее соответствие на низких часто-
тах, иначе моделирование переходных процессов, которые могут иметь низ-
кочастотные составляющие внутри сигналов, будет неточным.
Для пассивных одиночных элементов, таких, как резисторы, предназна-
ченные для монтажа на поверхность, развязывающие конденсаторы и филь-
тры, могут быть использованы различные модели. На рис. 2.6 иллюстрируются
идеальные схемы замещения перечисленных выше элементов на разных час-
тотах (в низкочастотных и высокочастотных областях). Как показано выше для
случая с развязывающим конденсатором, однокомпонентная модель хорошо
2.1. Полное сопротивление и электрические модели печатного монтажа 135
работает на низких частотах, а широкополосная
модель работает до частот 5 ГГц. Полосу пропус-
кания модели не так легко оценить.
Многие межсоединения могут быть представ-
лены в виде электрически коротких (это поня-
тие раскрывается в главе 3) линий, и к ним мо-
гут применяться простейшие электрические мо-
дели замещения. Такой моделью для печатных
проводников является простой конденсатор. На
рис. 2.7 показаны графики полного сопротивле-
ния микрополосковой линии длиной 25 мм, по-
лученные экспериментально и теоретически для
модели первого и второго порядков. Моделью
первого порядка выступает простейший конден-
сатор с полосой пропускания около I ГГц. Мо-
делью второго порядка является последователь-
ная индуктивность L и параллельная емкость С
с полосой пропускания около 2 ГГц. Таким образом, если заявленная поло-
са пропускания будет меньше, чем 1 ГГц, то простой идеальный конденса-
тор может быть использован как точная модель этого межсоединения, а при
полосе около 2 ГГц следует применить АС-модель.
Лучшая модель электрически длинной линии передачи — это идеальная
модель линии передачи в виде распределенной линии. Этот элемент рабо-
тает как на низких, так и на высоких частотах. На рис. 2.8 показаны изме-
ренное сопротивление микрополосковой линии передачи длиной 25 мм и
теоретически рассчитанная характеристика модели идеального элемента. Рас-
хождения минимальны на всей полосе пропускания.
На низкой
частоте
На высоких
частотах
Реальные элементы
R С
Простейшие на-
чальные модели компонен-
тов или электрических со-
единений на низких
и высоких частотах
Рис. 2.6.
Рис. 2.7. Измеренное полное сопротивление печатного проводника длиной 25 мм
и теоретически рассчитанное сопротивление модели первого и второго порядков:
7 — емкостная модель первого порядка; 2 — АС-модель второго порядка;
3 — экспериментальные данные
136
Глава 2. Электрофизические параметры печатного монтажа
Рис. 2.8. Замеренное сопротивление микрополосковой линии связи и теоретически
рассчитанная модель идеального элемента распределенной линии:
7 — идеальная модель; 2 — экспериментальные данные
Идеализированная схема резистора может моделировать действительное
поведение реального резистора вплоть до необычайно высокой частоты. Су-
ществуют три общепринятые технологии производства резистивных компо-
нентов: выводной, для монтажа на поверхность (SMD-резистор) и интегри-
рованные пассивные устройства (IPD-резистор). На рис. 2.9 показаны экс-
периментальные зависимости полного сопротивления от частоты этих резис-
тивных компонентов. Идеальный резистор имеет постоянное сопротивле-
ние на всех частотах. Эта простая модель совпадает с реальным резистором
на низких частотах, но имеет ограниченную полосу пропускания, зависящую
от технологии изготовления резисторов.
Идеализированный резистор будет иметь постоянное сопротивление на
всей частотной области. Как можно видеть, поведение IPD-резистора совпа-
дает с идеальным резистивным элементом по всей измеряемой частотной
полосе (5 ГГц). SMD-резисторы являются хорошей аппроксимацией идеа-
Рис. 2.9. Измеренное полное сопротивление трех различных резистивных компонен-
тов: 1 — выводное сопротивление; 2— SMD-резистор; 3 — IPD-резистор
2.2. Сопротивление и его модели
137
лизированных резисторов вплоть до 2 ГГц. Точность моделирования зависит
от геометрии монтажа и расположения на плате. Выводные резисторы при-
ближаются к идеальному резистору на частотах до 500 МГц. Далее наблюда-
ется возрастающее расхождение между реальным компонентом и идеальной
моделью. Главный эффект, появляющийся на высоких частотах и вызываю-
щий отмеченное расхождение, — это влияние индуктивных свойств реально-
го резистора. Модель с широкой полосой пропускания обязательно будет со-
держать индуктивные элементы и, вполне вероятно, — емкостные элементы.
Наличие топологической модели печатной платы — это только часть ре-
шения задачи. Другая часть заключается в определении значений электрофи-
зических параметров из результатов измерений, с помощью эмпирических пра-
вил, аналитических аппроксимаций и численных методов расчетов исходя из
геометрических свойств и свойств материала для каждого топологического эле-
мента. Точность модели будет зависеть от того, насколько хорошо можно за-
менить реальную геометрию стандартными шаблонами, для которых имеет-
ся хорошая аппроксимация, или от того, насколько хорошо мы сможем при-
менить численные методы анализа. В том случае, когда нужны грубые, при-
ближенные результаты, можно использовать эвристические правила.
2.2. Сопротивление и его модели
2.2.1. Физические основы сопротивления
Электрические свойства межсоединений связаны с определенным распо-
ложением проводников и диэлектриков и их взаимодействием с электричес-
кими и магнитными полями сигнальных токов и напряжений. Понимание
связи между геометрическими размерами и электрическими свойствами дает
объяснения того, как сигнал взаимодействует с физической моделью соеди-
нительного проводника и как она влияет на целостность сигнала и другие
виды помех в печатном узле.
Ключ к улучшению электрофизических параметров проектируемой платы,
отвечающей требованиям целостности сигнала, заключается в возможности
точного прогнозирования электрических характеристик устройства на уров-
не виртуального прототипа и эффективной оптимизации этих параметров для
получения заданных электрических характеристик.
Все электрические свойства некоторого объекта могут быть полностью
описаны уравнениями Максвелла [48, 50]. Эти четыре уравнения описыва-
ют электрические и магнитные поля, а также граничные условия в зависи-
мости от структуры проводника или диэлектрика. В принципе, имея достаточно
мощный компьютер с соответствующим программным обеспечением, мож-
но, введя схему расположения всех элементов печатной платы и исходные на-
пряжения, рассчитать желаемые электрические и магнитные поля. Эти урав-
нения дают наиболее полный и общий конечный результат, показывающий,
соответствует ли данная плата техническим требованиям. Важно отметить,
что возможность определения всех изменяющихся во времени электрических
138
Глава 2. Электрофизические параметры печатного монтажа
и магнитных полей не дает понимания того, что следует изменить или доба-
вить для получения нужных результатов. Из-за сложности описания печат-
ной платы пока не существует способа ее точного и полного моделирования
с помощью уравнений Максвелла.
Процесс проектирования — интуитивный процесс. Новые идеи — продукт
фантазии и творчества. Электродинамическое рассмотрение нужно не для чис-
ленного решения уравнений Максвелла, а для понимания сути происходящих яв-
лений и процессов.
Каждая модель состоит из двух основных частей: топологии схемы и зна-
чений параметров каждого элемента схемы. Отправной точкой при модели-
ровании межсоединений является использование различных комбинаций трех
идеальных сосредоточенных элементов схемы (резисторов, емкостей, индук-
тивностей) или идеальной модели линии передачи (распределенного элемен-
та — Г-элемента). В следующей главе будет подробно рассмотрено понятие
линии передачи и определены ее параметры.
Физический вид Электрический вид
Рис. 2.10. Физическое и электрическое
представление микрополосковой линии
передачи
Моделирование линии передачи —
это переход от физического объекта,
описываемого такими геометрическими
параметрами, как длина, ширина и тол-
щина проводников, входящих в ее со-
став, к его эквивалентной схеме, описы-
ваемой с помощью R-, L-, С-элементов,
например, как показано на рис. 2.10.
Следующим шагом после разработ-
ки топологии схемы межсоединения яв-
ляется нахождение значения параметров. Задача состоит в переводе геометри-
ческих параметров и свойств материала в эквивалентные параметры идеальных
R-, С-, L-, или Г-элементов. В данном разделе рассматривается, как сопротив-
ление определяется геометрическими параметрами и свойствами материала.
В первом приближении сопротивление электрического соединения рассмат-
ривается как идеальный резистор.
Выбрав фрагмент топологии печатного проводника таким образом, что-
бы он соответствовал элементу идеального резистора, можно использовать
один из трех аналитических методов нахождения значений параметров, ос-
новываясь на специфике геометрии соединения.
Модель проводника в виде идеального
Рис. 2.11. Описание геометрических
параметров проводника
резистора — всего лишь одно из хороших
приближений для анализа межсоединения.
Такая аппроксимация приемлема для про-
водника, у которого поперечное сечение
меньше его длины, что вполне подходит
для анализа печатных проводников. На
рис. 2.11 показаны фрагмент проводника
и его геометрические параметры, необхо-
димые для определения сопротивления.
2.2. Сопротивление и его модели
139
В случае, когда проводник имеет размеры поперечного сечения меньше
его длины, сопротивление может быть рассчитано следующим образом:
Л = р4 (2.13)
Л
где R — сопротивление, Ом; р — удельное сопротивление, Омсм; / — расстояние между
концами соединения, см; S = wt — площадь поперечного сечения, см2; w — ширина про-
водника, см; t — толщина фольги, см.
Удельное сопротивление меди равно 1,68 мкОмхсм. Тогда при длине пе-
чатного проводника 10 см, ширине 0,1 см и толщине фольги 35 мкм полу-
чим значение его сопротивления 48 мОм. Это позволяет иметь приближен-
ную оценку сопротивления печатного проводника на постоянном токе как
0,5 Ом на длине 1 м при ширине проводника 1 мм.
Для оценки сопротивления печатных проводников с определенной тол-
щиной фольги удобно воспользоваться формулами
R = 0,48—, Ом, при толщине фольги 35 мкм, (2.14)
w
Я = 0,96—, Ом, при толщине фольги 17 мкм, (2.15)
w
где / — длина проводника, м; w — ширина проводника, мм.
Для удобства определения сопротивления на рис. 2.12 приведены соот-
ветствующие графики, дающие значение сопротивление на 1 м длины.
Удельное сопротивление медной фольги и металлизированных покрытий
отличается от удельного сопротивления натуральной металлической меди [8].
Они имеют следующие усредненные значения:
чистая отожженная медь — 1,72 мкОмсм,
медная фольга — 1,75 мкОмсм,
Рис. 2.12. Зависимости удельного (на 1 м) сопротивления печатных проводников от их
ширины и толщины: 1 — толщина фольги 17 мкм; 2—35 мкм
140
Глава 2. Электрофизические параметры печатного монтажа
медное гальванопокрытие — (1,8—2,5) мкОмсм,
химически осажденная медь — (2—100) мкОмсм.
Реальная толщина проводников на печатных платах отличается от номи-
нальной толщины фольги. В табл. 2.1 [8] приведены реальные значения ме-
таллической толщины проводников в печатных платах.
Таблица 2.1
Реальные значения металлической толщины проводников
Масса единицы площади Толщина, мкм
унция/кв. фут г/кв.м номинальная внутренние слои (без металлизации) внешние слои после металлизации
0,5 152,5 17.2 12 45
1 305 34,3 28 60
2 610 68,6 64 100
3 915 103,0 98 130
4 1220 137,0 130 170
Учитывая возможный разброс удельных сопротивлений материалов, уча-
ствующих в формировании сопротивления проводника, а также в плохо про-
гнозируемых погрешностях геометрических параметров печатных проводников,
оценка активного сопротивления проводников печатного монтажа на посто-
янном токе и низких частотах проводится приближенно. Как будет показано
ниже, это сопротивление имеет значительно меньший эффект, чем сопротив-
ление проводника, вызванное скин-эффектом на высоких частотах.
Для проводников, которые используются для соединения кристаллов с вы-
водами внутри корпусов микросхем, из-за малости сечения проводника его со-
противление может быть относительно высоким. Например, сопротивление
золотого провода диаметром 25 мкм и длиной 2 мм составляет около 0,1 Ом.
Если ширина проводника изменяется ступенчато, то, очевидно, его сум-
марное сопротивление будет определяться суммой сопротивлений отрезков
проводника, имеющих постоянную ширину. При плавном изменении ши-
рины ее следует усреднить по длине проводника.
В сигнальных проводниках протекают относительно малые токи, но при
контроле печатных плат в тестовых режимах токи в проводниках могут дос-
тигать больших амплитуд. При протекании тока по проводнику из-за активных
потерь происходит его разогрев. Температура проводника повышается, что
вызывает дополнительное сопротивление пропорционально температурному
коэффициенту сопротивления. Связь между током, параметрами проводника
и его температурой задается эмпирическим уравнением [51, 52]
/= 22,6Д7Ю’445()’68, А,
где ДТ — приращение температуры, °C; S — площадь сечения проводника, мм2.
Формула получена аппроксимацией экспериментальных данных, поэтому
точность расчетов для конкретных данных не будет высокой.
2.2. Сопротивление и его модели
141
Для более четкого понимания свойств сопротивления рассмотрим более
детально такие понятия, как объемное удельное сопротивление материала,
сопротивление на единицу длины и поверхностное сопротивление.
2.2.2. Объемное удельное сопротивление материала
Объемное удельное сопротивление р — это основное свойство материала,
присущее всем проводникам. Объемное удельное сопротивление измеряется
в Ом-длина, например Ом м или Ом см. Оно должно иметь такую размерность,
чтобы связанное с ним сопротивление измерялось в омах. Из формулы «удель-
ное сопротивлениедлина/(длина-длина) = сопротивление» видно, что удельное
сопротивление должно измеряться в единицах «Ом-длина».
Объемное удельное сопротивление — это свойство, не связанное с формой или
с объектом, это свойство самого материала.
Удельное сопротивление р обратно пропорционально удельной проводи-
мости о:
р = I/O. (2.17)
Единица измерения проводимости, 1/Ом, — сименс (См). Таким образом,
удельная проводимость измеряется в См/м.
В табл. 2.2 даны значения удельного сопротивления основных проводя-
щих материалов, применяемых при создании электронной аппаратуры.
Необходимо отметить, что значения удельного сопротивления одного и того
же материала в разных условиях могут различаться на 10 %. Например, зна-
чение объемного удельного сопротивления медной фольги колеблется между
1,5-1,8 мкОм см, в зависимости от способа ее получения. Чем более пористый
Таблица 2.2
Значения удельного сопротивления проводниковых материалов
Материал Удельное сопротивление, мкОмсм Материал Удельное сопротивление, мкОм см
Серебро 1,47 Стеклоткань с серебряным наполнителем ~10
Медь 1,68 Олово 10,1
Золото 2,01 Эвтектический сплав олова/свинец 15
Алюминий 2,61 Вывод корпуса 19,3
Молибден 5,3 Ковар 49
Вольфрам 5,3 А11оу42 57
Никель 6,2 Эпоксидная смола с серебряным наполнителем ~300
142
Глава 2. Электрофизические параметры печатного монтажа
материал, тем выше его удельное сопротивление. Если нужно знать удель-
ное сопротивление с меньшей погрешностью, чем 10 %, нужно измерить его
для конкретного образца.
Термин «объемное удельное сопротивление» используется по отношению
к внутренним свойствам материала. Это отличает его от «сопротивления на
единицу длины» и от «поверхностного сопротивления».
2.2.3. Сопротивление на единицу длины проводника
Когда сечение проводника однородно подлине, например в проводе или
в печатном проводнике, сопротивление межсоединения будет пропорцио-
нально его длине. При однородном сечении сопротивление на единицу длины
будет постоянным и вычисляется в общем случае по формуле (2.13).
Несмотря на то, что сопротивление на единицу длины зависит от параметров
сечения проводника, некоторая усредненная оценка для типичных значений
размеров сечения должна быть известна проектировщику. Это помогает опе-
ративно оценить ожидаемый результат при разработке проекта. Так сопротив-
ление золотого проволочного соединения составляет 0,04 Ом/мм, а печатно-
го проводника при толщине фольги 35 мкм — 0,5 Ом/м. Зная длину трассы,
легко сделать приближенную оценку ее сопротивления.
В технической литературе зарубежных авторов часто применяют обозна-
чение проводов согласно коду AWG (American Wire Gauge). Перевод этих обо-
значений в эквивалентный диаметр дан в табл. 2.3. Например, провод 22AWG,
который часто используется в компьютерных системах, имеет диаметр 0,025".
Его сопротивление на единицу длины составляет R{ = 0,5 мОм/см.
Таблица 2.3
Соответствие диаметров провода и его кода AWG
КодАУ/С Диаметр, дюйм (мм) Сопротивление, Ом, надлине 100 м (при р = 1,74 мкОм см)
24 0,0201 (0,510) 8,55
22 0,0254 (0,645) 5,38
20 0,0320 (0,813) 3,38
18 0,0403 (1,024) 2,13
16 0,0508 (1,290) 1,34
14 0,0640(1,626) 0,84
12 0,0808 (2,052) 0,53
10 0,1019 (2,588) 0,33
2.2.4. Поверхностное сопротивление
Для электрических соединений, выполняемых на керамических, стекло-
текстолитовых и т. п. основаниях, таких, как печатные платы, токопроводя-
щие трассы выполняются из однородных слоев проводящего материала. Все
проводники на каждом слое имеют практически одинаковую толщину. В том
2.2. Сопротивление и его модели
143
случае, если ширина трассы одина-
кова по всей длине (рис. 2.13), она
может быть разделена на п квадратов,
п = l/w, где /—длина трассы, w— ши-
рина трассы.
Сопротивление трассы можно
посчитать по формуле:
Толщина
Ширина, \\
Длина, I
Рис. 2.13. Деление однородной по ширине
трассы на квадраты
£ Я
tW \tj\w
(2.18)
Первый множитель, (р//), постоянен для каждой трассы, выполненной
на слое, толщиной t. Таким образом, одинаковые проводящие слои будут иметь
одинаковые объемные сопротивления и толщину. Этому выражению дано спе-
циальное название — поверхностное сопротивление, которое равно
^sq = p/r. (2.19)
Второй множитель, (//w) в выражении (2.18), определяет наименьшее число
квадратов, на которое может быть разделена поверхность трассы. Теперь фор-
мулу для расчета сопротивления трассы можно переписать в следующем виде:
R = (2.20)
Единицей измерения поверхностного сопротивления также является ом.
В случае п = 1 сопротивление между концами квадратной трассы будет так-
же и сопротивлением слоя. Таким образом, поверхностное сопротивление
относится к единичной площади проводника. Это означает, что сопротив-
ление квадратного слоя не зависит от значения стороны квадрата. Этот факт
получил отражение в наименовании величины поверхностного сопротивле-
ния — «Ом на квадрат» (Ом/квадрат).
Поверхностное сопротивление зависит от объемного сопротивления и
толщины слоя. Для западных производителей в типичных печатных платах,
изготовленных из слоев медного проводника, толщина меди описывается как
вес меди на квадратный фут (Табл. 2.2). Такое описание появилось с того дня,
когда толщина медного покрытия стала измеряться с помощью панели в один
квадратный фут и взвешиваться. Медное покрытие, площадью в 1 квадратный
фут и толщиной в 35 мкм, весит 1 унцию (около 28 г). Медное покрытие тол-
щиной 17,5 мкм весит 14 г (0,5 унции). Основываясь на толщине и объемном
сопротивлении меди, делаем вывод: поверхностное сопротивление медного
покрытия толщиной 35 мкм составляет примерно 0,5 мОм/квадрат.
В отечественной промышленности толщина фольги для печатных плат
задается непосредственно в микрометрах, и ее типовое значение составляет
35 и 17,5 мкм.
Полезно запомнить, что поверхностное сопротивление медного покрытия
толщиной 35мкм составляет 0,5мОм на квадрат. Трасса шириной в 0,125мм
и длиной 125мм имеет 1000 квадратов, соединенных последовательно, и ее со-
противление будет 0,5 Ом.
144
Глава 2. Электрофизические параметры печатного монтажа
Рис. 2.14. Сопротивление на единицу длины
для трасс различной ширины с толщиной
медного покрытия в 35 мкм и 17,5 мкм
Поверхностное сопротив-
ление — это важная характе-
ристика проводящего слоя.
Если известно поверхност-
ное сопротивление слоя, то
можно рассчитать сопротив-
ление проводника на едини-
цу длины и общее сопротив-
ление проводника, выпол-
ненного в металлизирован-
ном слое. Зная ширину трас-
сы w и ее длину /, сопротив-
ление на единицу длины рас-
считывается по формуле:
(2.21)
Рис. 2.14 иллюстрирует изменение сопротивления на единицу длины для
трасс различной ширины с толщиной медного покрытия 35 мкм и 17,5 мкм.
Меньшее сопротивление имеет наиболее широкая трасса, как и ожидалось.
Для трассы в 0,125 мм шириной, часто использующейся во многих печатных
платах, типичным является медное покрытие в 35 мкм, которое имеет удельное
сопротивление 0,008 Ом/мм. Тогда трасса длиной 125 мм имеет сопротив-
ление 0,008 Ом/мм х 250 мм = 2 Ом.
Важно не забывать, что эти сопротивления рассчитываются, как и все ос-
тальные сопротивления, на постоянном токе или, по крайней мере, на низ-
ких частотах. Далее будет показано, что сопротивление трассы будет увели-
чиваться с частотой вследствие скин-эффекта. Объемное сопротивление про-
водника не изменится, но изменится распределение тока по сечению про-
водника. Высокочастотные составляющие сигнала будут распространяться
в тонком слое около поверхности проводника. Их интенсивность сильно
уменьшается при углублении в толщу проводника. У трасс с толщиной мед-
ного покрытия 35 мкм сопротивление начинает увеличиваться примерно с
3 МГц пропорционально квадратному корню из частоты. Скин-эффект ока-
зывает влияние и на индуктивность проводника.
2.2.5. Скин-эффект и распределение тока
по сечению проводника
Изменение сопротивления и индуктивности проводников связано с рас-
пределением тока по сечению проводника. Следует разделять режимы работы
по постоянному току и по переменному току. При постоянном токе или при
относительно низких частотах распределение тока по сечению будет равно-
мерным. При высоких частотах это распределение будет резко неравномер-
2.2. Сопротивление и его модели
145
Сплошной
медный
проводник
Силовые линии
внутренней
индуктивности
Силовые линии
внешней индуктивности
Рис. 2.15. Линии магнитного потока при постоянном токе сплошного медного провода
ным, что приводит к существенным изменениям сопротивления и индуктив-
ности проводника. Методически удобно рассмотреть скин-эффект на при-
мере проводника круглого сечения.
При анализе индуктивности следует рассматривать линии магнитного
поля, окружающие проводник. Эти линии частично расположены и внутри
проводника и определяют собственную индуктивность проводника. Это ил-
люстрируется на рис. 2.15.
Можно разделить собственную индуктивность на внутреннюю £int и вне-
шнюю Zext. Линии внутреннего магнитного поля расположены в толще ме-
талла, по которому протекает ток. Если распределение тока в сечении изме-
нится, то изменится и расположение линий внутреннего магнитного поля
и внутренняя самоиндукция.
Линии внешнего магнитного поля расположены вне пределов проводника,
и они не будут изменяться с частотой.
Рассмотрим два цилиндра распределения тока
в сечении сплошного проводника, которые имеют
одинаковую площадь (рис. 2.16). Поскольку пло-
щадь сечения цилиндров одинакова, то в них про-
текает одинаковый постоянный ток. Каждый из то-
ковых цилиндров имеет одинаковое число линий
магнитного поля во внешней области относительно
внешнего цилиндра. Число линий магнитного поля
определяется только суммарным током, который
охватывается этими линиями. Во внутренней об-
ласти внешнего цилиндра нет линий магнитного
поля, поскольку там нет токов этого цилиндра.
Ток внутреннего цилиндра имеет больше линий
внутренней самоиндукции, поскольку он имеет
Рис. 2.16. Два цилиндра
распределения тока в оди-
ночном сплошном медном
проводнике, имеющие оди-
наковую площадь сечения
большее расстояние от линий тока до внутренней стенки проводника. При
приближении линии тока к центру проводника увеличивается общее число
линий магнитного поля вокруг этого тока.
Токи, расположенные ближе к центру проводника, будут иметь большее число
линий магнитного поля на один ампер тока и более высокую самоиндукцию, чем
токи, расположенные ближе к поверхности проводника.
146
Глава 2. Электрофизические параметры печатного монтажа
При переменном токе каждая спектральная компонента тока будет про-
текать по пути с минимальным полным сопротивлением. Путь тока с боль-
шой индуктивностью будет обладать и большим полным сопротивлением.
Чем выше частота, тем выше будет полное сопротивление индуктивности,
и тем больше будет тенденция в поиске для тока пути с минимальной индук-
тивностью. Это приводит к распределению тока около внешней поверхнос-
ти проводника.
На высоких частотах токи в проводниках стремятся расположиться в тон-
кой области (скин-слое) около поверхности проводника.
К сожалению, имеется только несколько геометрических форм сечения
проводников, при которых геометрия распределения высокочастотного тока
по сечению может быть определена с достаточной точностью. Это, прежде
всего, провод круглого сечения. Для каждой частоты распределение тока
подчиняется экспоненциальному закону, согласно которому плотность тока
уменьшается к центру проводника (рис. 2.17).
Для скин-слоя принято равномерное распределение тока по его толщи-
не 5. Толщина скин-слоя зависит от частоты, проводимости металла, его маг-
нитной проницаемости и определяется формулой:
(2.22)
где 6 — глубина скин-слоя, м; о — проводимость материала, См/м; ц() — магнитная по-
стоянная, 4л • 10 7 Гн/м; — относительная магнитная проницаемость; f — частота, Гц.
Для меди с проводимостью 5,6х107 См/м и относительной магнитной про-
ницаемостью, равной 1, глубина скин-слоя составляет
5 = 66
’ мкм,
(2.23)
где f — частота, МГц.
Рис. 2.17. Распределение тока по сечению сплошного проводника (темная область —
большая плотность тока): слева — аппроксимация реального распределения; справа —
аппроксимация при допущении равномерного распределения тока в скин-слое
2.2, Сопротивление и его модели
147
Рис. 2.18. Толщина скин-слоя для меди в зависимости от частоты
На частоте 1 МГц глубина скин-слоя для меди составляет 66 мкм. На рис. 2.18
показано изменение толщины скин-слоя для меди в зависимости от частоты в
сравнении с толщинами проводников на печатных платах (35 мкм и 17,5 мкм).
Из графика видно, что скин-слой имеет толщину 35 мкм на частоте около 3,5 МГц
и толщину 17,5 мкм — на частоте приблизительно 10 МГц. Ниже этих частот
можно принять для соответствующих толщин проводников распределение тока
по сечению равномерным и не зависящим от частоты. В том случае, когда тол-
щина скин-слоя меньше толщины проводника, распределение тока, сопротив-
ление и индуктивность будут зависеть от частоты.
В реальных условиях всегда имеется как прямой путь тока в нагрузку, так
и путь возвратного тока от нагрузки к генератору. Это образует контур тока,
который обладает определенной самоиндукцией. При увеличении частоты
полное сопротивление контура тока из-за самоиндукции будет увеличиваться,
и ток в обоих проводниках будет перераспределяться таким образом, чтобы
уменьшить полное сопротивление или уменьшить самоиндукцию. Это пе-
рераспределение называется эффектом близости. Для печатного проводни-
ка в присутствии плоскости заземления условные нити тока будут стремиться
расположиться на ближайших друг к другу сторонах проводящих слоев.
Для определения этого перераспределения рассмотрим эффект уменьше-
ния самоиндукции контура при сближении прямого и обратного токов. В любом
случае токи в проводниках будут перераспределяться, поскольку токи проти-
воположного направления всегда стремятся быть ближе друг к другу, а токи
одного направления стремятся отдалиться друг от друга.
Точное распределение токов в каждом проводнике определяется на ос-
нове баланса двух явлений. Внутри каждого проводника нити тока одного
направления стремятся отдалиться друг от друга для уменьшения их парци-
альной самоиндукции. В то же время нити токов, текущих в противополож-
ных направлениях в прямом и обратном проводнике, стремятся сблизиться
для уменьшения их парциальной взаимной индуктивности. В результате нити
148
Глава 2. Электрофизические параметры печатного монтажа
Рис. 2.19. Распределение тока в проводнике круглого сечения диаметром 0,5 мм
и в сигнальном проводнике микрополосковой линии передачи, толщиной 35 мкм.
Более темные участки соответствуют более высокой плотности тока
тока распределяются по сечению проводников некоторым образом. Точное
значение этого распределения может быть определено только с применением
специальных программных средств.
На рис. 2.19 [3] показаны результаты моделирования распределения тока
в проводниках плоского кабеля диаметром 0,5 мм. На низких частотах толщина
скин-слоя соизмерима с толщиной проводника, и видно, что распределение
тока по сечению достаточно равномерно. На частоте 100 кГц толщина скин-
слоя в меди составляет 0,2 мм, что соизмеримо с диаметром провода, и скин-
эффект проявляется в незначительной степени. На частоте 1 МГц толщина скин-
слоя составляет 66 мкм, и скин-эффект ярко выражен. При увеличении час-
тоты этот эффект становится еще более выражен. Распределение тока всегда
будет таким, что полное сопротивление контура будет минимальным.
На этом же рисунке (рис. 2.19) показано распределение тока в микропо-
лосковой линии с толщиной меди 35 мкм. Видно, что на частоте 1 МГц рас-
пределение тока практически равномерно, но по мере роста частоты нерав-
номерность усиливается. Ток стремится к поверхности сигнального провод-
ника, расположенной ближе к плоскости возвратных токов, что обеспечивает
уменьшение полного сопротивление контура прямого и обратного тока.
По мере увеличения частоты из-за скин-эффекта уменьшается эффектив-
ное сечение протекания тока и увеличивается сопротивление проводника.
Когда глубина скин-слоя меньше геометрических размеров сечения провод-
ника, то при увеличении частоты площадь сечения, через которое протекает
ток, уменьшается пропорционально корню квадратному из частоты. При этом
сопротивление на единицу длины линии увеличивается также пропорциональ-
но квадратному корню из частоты.
2.2. Сопротивление и его модели
149
Рассмотрим микрополосковую линию передачи с медным покрытием
толщиной 35 мкм, шириной 0,125 мм. Сопротивление 7?dc единицы длины
проводника на постоянном токе равно
^dc = р / Wt,
где р — объемное удельное сопротивление; w — ширина сигнального проводника; t — гео-
метрическая толщина сигнального проводника.
На частотах более 10 МГц существенно проявляется скин-эффект, и со-
противление проводника будет зависеть от частоты. Сопротивление /?ас пе-
ременному току единицы длины проводника на высокой частоте в этом случае
определяется по формуле
^c=P-U (2.24)
wo
где 8 — толщина скин-слоя.
Из формул видно, что отношение сопротивлений 7?ac/7?dc = //5. На час-
тоте 1 ГГц глубина скин-слоя для меди составляет 2 мкм, и сопротивление
на высоких частотах для рассматриваемого проводника будет в 17,5 раз больше
(35/2 = 17,5), чем на постоянном токе. С повышением частоты сопротивле-
ние будет расти.
Рассмотрим зависимость индуктивности от частоты. На низких частотах
индуктивность определяется суммой £int + Zext. На высоких частотах суммар-
ная индуктивность будет определяться только внешней индуктивностью £ext,
и переход к этому значению будет на той частоте, при которой глубина скин-
слоя будет соизмерима с геометрической толщиной проводника. Индуктив-
ность выше этой частоты будет постоянна.
Расчеты внутренней и внешней индуктивности для проводников прямо-
угольного сечения являются трудной задачей: она может быть решена толь-
ко с применением специальных программных средств.
На рис. 2.20 показан результат расчета самоиндукции на единицу длины
контура микрополосковой линии. Видно, что из-за влияния скин-эффекта ин-
дуктивность на низких частотах больше, чем на высоких на соответствующее
0 100 200 300 400 500 600 700 800 900 1000
Частота. МГц
Рис. 2.20. Значение самоиндукции микрополосковой линии
150
Глава 2. Электрофизические параметры печатного монтажа
значение внутренней самоиндукции. Снижение индуктивности системы пря-
мого и возвратного проводника может быть объяснено тем, что сближение
высокочастотных токов противоположного направления в проводниках из-
за эффекта близости приводит к увеличению компенсации магнитных полей
от этих токов. При этом суммарная индуктивность снижается. На частотах более
100 МГц ток распределен в тонком слое около поверхности проводника, и
индуктивность далее при увеличении частоты не изменяется.
Когда говорится о самоиндукции контура тока, наиболее часто имеется
в виду высокочастотное ограничение, связанное с распределением тока около
поверхности проводника. Понятие «высокая частота» относится к такой ча-
стоте, при которой токи протекают около поверхности проводника, и их
плотность не зависит от геометрической толщины проводника. Как было
показано выше, для печатных проводников с толщиной фольги 35 мкм «вы-
сокая частота» начинается приблизительно с 3,5 МГц.
2.3. Электрическая емкость в печатном
монтаже
2.3.1. Основные определения
Комплексное рассмотрение модели печатной платы требует учета магнитных
и электрических полей. Индуктивность соотносится с магнитным полем для
заданной геометрии проводников с током. Аналогично электрическая емкость
соотносится с электрическим полем электрических зарядов, которые распо-
ложены на проводниках платы. В простейшем случае объектом анализа является
электрическая емкость между двумя проводниками. Но печатная плата содер-
жит значительное число проводников, поэтому в данном случае рассмотре-
ние сводится к рассмотрению многопроводных линий, и задача требует более
сложных решений, основанных на матричном представлении результатов [3,
4, 48, 50, 53, 54]. Ввиду важности понятия электрической емкости для проек-
тирования печатных плат, рассмотрим его детально.
Между зарядами и потенциалами любых проводников существует одно-
значная линейная связь, для выражения которой вводится понятие элект-
рической емкости. В зависимости от вида рассматриваемой электростати-
ческой системы различают емкость уединенного проводника, емкость меж-
ду двумя проводниками и емкости в системе многих проводников.
Емкостью уединенного проводника называют скалярную величину, харак-
теризующую способность проводника накапливать электрический заряд и
равную отношению заряда проводника к его потенциалу при условии, что
все другие заряженные проводники бесконечно удалены.
Если обозначить заряд уединенного проводника через 0, а его потенци-
ал через U, то в соответствии с приведенным определением емкость этого
проводника в воздушной среде выразится формулой:
Cq=Q/U. (2.25)
2.3. Электрическая емкость в печатном монтаже
151
Емкостью между двумя проводниками называют скалярную величину,
равную абсолютному значению отношения электрического заряда одного из
проводников к разности их потенциалов при условии, что эти проводники
имеют одинаковые по значению, но противоположные по знаку заряды и что
все другие заряженные проводники бесконечно удалены. Подобная систе-
ма называется электро нейтральной.
Если заряды проводников равны ±0, а их потенциалы имеют значения
и U2, то в соответствии с приведенным определением емкость между этими
проводниками в воздушной среде выражается формулой:
(2.26)
Устройство из двух разделенных диэлектриком проводников (обкладок),
предназначенное для использования емкости между ними, называют кон-
денсатором, поэтому емкость между двумя проводниками иногда называют
также конденсаторной емкостью.
Обобщением введенных понятий на случай системы с произвольным ко-
нечным числом проводников является понятие собственных и взаимных
частичных емкостей. Разделение понятий собственной и взаимной частич-
ной емкости носит в значительной степени условный характер. Действитель-
но, любую систему из п проводников, занимающую конечный объем, мож-
но условно рассматривать как систему из п + 1 проводника, где проводни-
ком (п + 1) является сфера бесконечно большого радиуса, имеющая нулевой
потенциал. В новой системе собственную частичную емкость любого про-
водника, кроме (п + 1), можно интерпретировать как взаимную частичную
емкость между этим проводником и указанной сферой.
Собственной частичной емкостью проводника, входящего в систему
многих тел, называют скалярную величину, равную отношению заряда это-
го проводника к его потенциалу при условии, что все проводники системы
(включая и рассматриваемый) имеют одинаковый потенциал.
Взаимной частичной емкостью между двумя проводниками, входящими в
систему многих тел, называют скалярную величину, равную отношению за-
ряда одного из рассматриваемых проводников к потенциалу другого, при ус-
ловии, что все проводники, кроме последнего, имеют потенциал, равный нулю.
В соответствии с введенными определениями связь между зарядами и по-
тенциалами в системе п проводников выражается следующими уравнениями:
е, =С„1/, +C12(t/,-U2) + ... + C]n(U}-Un),
Q2=c2i(u2-ul)+c22u2+...+c2„(U2-u„),
(2.27)
Q„ = сп1(ип - и,)+сп2(ип - и2)+...+сти,
где Ct и Ц — заряд и потенциал проводника i (i = 1, 2, ..., п); Сц — диагональный эле-
мент матрицы есть собственная частичная емкость проводника i (i = 1, 2, ..., л); Clk —
152
Глава 2. Электрофизические параметры печатного монтажа
внедиагональный элемент матрицы есть взаимная частичная емкость между проводниками
/ и k (i, к = 1, 2, п\ i * к), при этом Clk = Cki, Qt — заряд проводника /.
Свойства емкостной матрицы (2.27) хорошо известны [50, 58], и они за-
ключаются в следующем:
Су=Сл, i,J = 1,2,...,п,
Сп >0, / = 1,2,...,п,
Сд<0, I* j = \,2,...,n,
7=1
(2.28)
Для одиночной линии (п = 1) из емкостной матрицы может быть полу-
чен важнейший параметр линии передачи — волновое сопротивление:
vC
(2.29)
где у — скорость распространения электромагнитной волны в диэлектрической среде линии;
С — емкость линии на единицу длины, что соответствует элементу Су, который характе-
ризует емкость между сигнальным и возвратным проводником в линии передачи.
01- Ц Ц,
Рис. 2.21. Система двух
проводников в присут-
ствии третьей плоскости
возвратных токов с по-
тенциалом, равным 0
Если рассматриваются два проводника, напри-
мер, как показано на рис. 2.21, то этот случай бу-
дет соответствовать дифференциальной паре, ко-
торая детально рассмотрена в главе 6.
Для нее возможны два режима работы [59], ко-
торые соответствуют четной и нечетной моде рас-
пространения сигналов в линиях. При четной моде
потенциалы линий одинаковы, и их можно принять
Ц = U2 = 1. Тогда из (2.27) получаем
G,even = (C,.l + C,.2),/=l,2 (2.30)
со значением волнового сопротивления для каждой линии
Z,even v(Czl+C,2)’ ' 1,1 (2'31)
Для режима нечетной моды потенциалы проводников противоположны,
т. е. = +1, U2 = -1. Тогда получаем
0,odd = (Czl - С,2), /= 1, 2 (2.32)
и волновое сопротивление
^/odd i/->4’ L 2.
v(C,.1-Cz2)
(2.33)
2.3. Электрическая емкость в печатном монтаже
153
Из этого выражения можно сделать важный вывод о том, что режимы ра-
боты дифференциальной пары создают различные условия распространения
сигнала в ней в зависимости от характера сигнала. Для полосковой линии, рас-
смотренной в качестве примера, диэлектрическая среда распространения элек-
тромагнитной волны однородна, и, следовательно, скорость v ее распростра-
нения, которая используется в выражениях (2.31) и (2.33), постоянна. Для мик-
рополосковых линий передачи, у которых сигнальные проводники лежат на
границе раздела двух диэлектрических сред, для различных режимов скорос-
ти распространения сигнала будут различны. Это привнесет еще большее раз-
личие между четным и нечетным режимами работы дифференциальной пары.
Данное явление детально рассматривается в главе 6.
2.3.2. Классификация электростатических систем
Применительно к печатному монтажу под электростатической системой
понимается любая совокупность заряженных проводников и окружающих их
диэлектрических сред. Электростатические системы могут быть классифици-
рованы по числу и форме проводников и структуре диэлектрических сред.
Число п проводников, образующих электростатическую систему, опреде-
ляется с учетом их возможных соединений. При этом система, образован-
ная соединением нескольких проводников, рассматривается как один про-
водник, а влияние соединительных проводников на значение емкости во всех
случаях считается пренебрежимо малым. В зависимости от значения п раз-
личают уединенные проводники, системы из двух проводников (в том чис-
ле конденсаторы) и системы многих заряженных тел (п > 3).
Типизация геометрических форм проводников приводит к их делению на
провода, плоские пластины, а также незамкнутые и замкнутые оболочки.
Последние эквивалентны в электростатических системах сплошным провод-
никам той же формы (за исключением тех случаев, когда внутри оболочек
расположены другие заряженные проводники).
При рассмотрении проводов принимается, что их сечения неизменны по
всей длине, причем линейные размеры сечения значительно меньше длины
провода и расстояний до других проводников. Кроме того, во всех случаях,
когда не оговорено противное, принимается, что сечение провода является
круглым. Этот случай не подходит для анализа печатных плат, но полезен для
рассмотрения физических эффектов, как, например, это сделано при изу-
чении эффекта близости.
При рассмотрении пластин и оболочек предполагается, что их толщина
постоянна по поверхности и во всех случаях, когда не оговорено противное,
пренебрежимо мала.
Одним из распространенных типов электростатических систем являют-
ся так называемые плоскопараллельные системы. Они могут быть применены
при расчете емкости в тех случаях, когда форма проводников и структура окру-
жающих их диэлектрических сред таковы, что электростатические поля в этих
средах можно считать неизменными подлине проводников и лежащими строго
154
Глава 2. Электрофизические параметры печатного монтажа
в плоскости, перпендикулярной проводнику, а алгебраическая сумма заря-
дов всех проводников равна нулю. Поэтому в дальнейшем принято, что число
проводников, образующих любую плоскопараллельную систему, п > 2 (для
уединенных проводников суммарный заряд всегда отличен от нуля, и пото-
му задача расчета их емкости с помощью плоскопараллельных систем лишена
физического смысла), а все величины, характеризующие емкость в таких си-
стемах, отнесены к единице длины проводников.
Структура рассматриваемых диэлектрических сред определяется простран-
ственным распределением диэлектрической проницаемости. С этой точки
зрения все рассматриваемые диэлектрические среды разделяются на одно-
родные (е = const) и неоднородные. Последние могут быть, в свою очередь,
разделены на неоднородные среды с непрерывно изменяющейся диэлектри-
ческой проницаемостью и кусочно-однородные среды, состоящие из одно-
родных подобластей. Кусочно-однородные среды классифицируются по типу
границ, разделяющих однородные подобласти; простейшими из них явля-
ются слоистые среды, в которых границами однородных подобластей явля-
ются параллельные плоскости (помимо этого, могут быть выделены кусоч-
но-однородные среды с секториальным разделением однородных подобла-
стей, а также с цилиндрической, с сферической и другой, более сложной,
формой границ). Слоистые среды наилучшим образом описывают печатные
платы, в том числе многослойные.
При рассмотрении электростатических систем, содержащих кусочно-од-
нородные среды, обычно выделяют такие системы, в которых все проводни-
ки целиком расположены в одной из однородных подобластей. Пусть диэлек-
трическая проницаемость среды в этой подобласти равна £р а в какой-либо
граничащей с ней подобласти — еп. Тогда в зависимости от отношения £|/£ц
могут быть выделены следующие характерные случаи.
Если Ej/Eu >> 1, то границу упомянутых подобластей можно приближенно
считать непроницаемой для силовых линий электростатического поля и
потому рассматривать ее как поверхность некоторой условной среды с ну-
левой диэлектрической проницаемостью. Такая граница называется непро-
ницаемой.
Если Е^Ец « 1, то границу указанных подобластей можно приближен-
но считать эквипотенциальной, т. е. рассматривать ее как поверхность не-
которой условной среды с бесконечно большой диэлектрической проница-
емостью. Такая граница называется проводящей.
Замена реальных границ однородных подобластей проводящими или не-
проницаемыми позволяет в ряде случаев получить двусторонние оценки
значения емкости и установить некоторые общие ее свойства [40, 55—57].
2.3.3. Общие свойства электрической емкости
Основное свойство электрической емкости заключается в том, что она
зависит только от геометрических параметров проводников и диэлектричес-
кой проницаемости окружающей среды. В связи с этим ниже сформулирова-
2.3. Электрическая емкость в печатном монтаже
155
ны некоторые общие положения, выражающие зависимость емкости от ка-
ких-либо из этих параметров при фиксированных значениях других. Эти по-
ложения могут быть полезны для предварительных инженерных оценок ем-
кости в конструкции плат, которые потом могут быть уточнены тем или иным
методом расчета. Они могут быть сгруппированы следующим образом:
• варианты конструкций, при которых значение диэлектрической про-
ницаемости однородной среды имеет определенное фиксированное
значение;
• геометрические параметры проводников неизменны, но возможно из-
менение диэлектрических свойств среды;
• электростатическая система неизменна, но имеются плоские грани-
цы раздела диэлектрических сред.
Рассмотрим эти варианты более детально.
1. Фиксированное значение диэлектрической проницаемости однородной среды
и переменные параметры геометрии проводников.
1.1. Отношения емкостей в двух геометрически подобных системах про-
водников равны отношению сходственных размеров этих систем. Другими
словами, чем больше размер объекта, тем больше емкость системы. Это,
например, означает, что емкость более широкого проводника будет больше
емкости узкого.
1.2. Емкости (на единицу длины) в геометрически подобных плоскопа-
раллельных системах двух или более проводников равны между собой. Это
означает, что при пропорциональном изменении ширины проводников и за-
зоров между ними в плоскопараллельной системе проводников (например,
шина передачи данных) емкостные параметры не изменятся.
1.3. Емкость любого уединенного проводника больше емкости любой его ча-
сти, рассматриваемой как другой уединенный проводник. Это означает, что, если
возможно рассчитать емкость какого-либо топологического элемента, то ем-
кость этого элемента всегда будет больше, чем емкость отдельного его фрагмента.
1.4. Емкость любого уединенного проводника меньше суммы емкостей всех
его частей, рассматриваемых как отдельные уединенные проводники. Если
возможно рассчитать емкости всех фрагментов топологического элемента
платы, то сумма этих фрагментарных емкостей будет больше, чем емкость
этого уединенного топологического элемента.
2. Фиксированные геометрические параметры проводников и изменяющая-
ся диэлектрическая проницаемость среды.
2.1. Отношение емкостей двух систем проводников равно отношению ди-
электрических проницаемостей окружающих их однородных сред, т. е. при
изменении значения диэлектрической проницаемости емкость системы
проводников пропорционально изменяется.
2.2. Увеличение диэлектрической проницаемости в любой части рассмат-
риваемой среды приводит к увеличению емкости (такое увеличение происходит,
в частности, при нанесении лакового покрытия на поверхность платы).
3. Заданы параметры электростатических систем, содержащие плоские
границы раздела сред.
156
Глава 2. Электрофизические параметры печатного монтажа
3.1. Емкость между любым проводником и проводящей плоскостью рав-
на удвоенному значению емкости между этим проводником и его зеркальным
отражением относительно этой плоскости. Это означает, что внесение в кон-
струкцию платы слоев питания и заземления приведет к увеличению емкос-
ти проводников. Несмотря на это, введение таких плоскостей является одним
из действенных приемов организации линий передач (полосковых, микропо-
лосковых и др.) с заданными электрофизическими параметрами линий.
3.2. Емкость между двумя проводниками, которые расположены симмет-
рично плоской границе раздела двух сред с различными диэлектрическими
проницаемостями, равна полусумме значений емкости между теми же про-
водниками в однородных средах с этими диэлектрическими проницаемос-
тями. Фактически речь идет об эффективной диэлектрической проницаемо-
сти, которая в случае симметричного расположения проводников относи-
тельно границы раздела сред равна полусумме диэлектрических проница-
емостей этих сред. Примером подобного расположения проводников явля-
ются проводники в односторонних печатных платах, расположенные на гра-
нице раздела между основанием платы и воздухом. В этом случае эффективная
проницаемость приблизительно равна полусумме относительной проница-
емости основания (например, для FR4 £ = 4) и проницаемости воздуха, равной
1:ес#=2,5.
В ряде случаев перечисленные свойства электрической емкости позволяют
получить инженерные оценки емкостных параметров без сложных вычислений.
2.3.4. Электрический ток в конденсаторах
В идеальном конденсаторе нет протекания постоянного тока между двумя
электродами, которые разделены диэлектриком, но переменный ток через кон-
денсатор протекает, и его значение определяется из следующего уравнения:
/ = де=сж
Д/ dt ’
(2.34)
где / — ток, проходящий через конденсатор; & Q — изменение заряда на конденсаторе; А/ —
время, за которое изменяется заряд; С — электрическая емкость; dV — изменение напря-
жения между электродами; dt — временной период изменения напряжения.
Электрическая емкость является мерой тока, протекающего через пару
электродов, когда напряжение между ними меняется. Если емкость большая,
то имеет место большой ток для постоянной скорости dV/dt изменения на-
пряжения по времени. Полное сопротивление большой емкости низкое.
В реальной ситуации в пространстве между электродами конденсатора ток
не течет, а происходит перезаряд электродов. Внешнее проявление этого
эффекта будет напоминать процесс протекания тока через конденсатор при
изменении напряжения на его электродах. Этот «фиктивный» ток называ-
ется током смещения.
При разработке конструкции печатной платы электродами некоторого кон-
денсатора являются печатные проводники, которые могут быть расположены
2.3. Электрическая емкость в печатном монтаже
157
в одной плоскости или в различных плоскостях в МПП. В линиях передачи
электродами конденсатора являются сигнальный проводник и слой возврат-
ного тока в микрополосковой линии или два слоя возвратных токов в полос-
ковой линии. При распространении электромагнитной волны вдоль линии в
области фронта сигнала передачи происходит заряд элементарных емкостей
линии, вызывая токи смещения. При рассмотрении моделей линий передачи
в следующей главе этот процесс будет рассмотрен более детально.
2.3.5. Емкость и конфигурация проводников
Фактическое значение емкости между двумя проводниками зависит от
числа силовых линий электрического поля, соединяющих эти проводники.
Чем больше силовых линий, соединяющих проводники, тем большая спо-
собность накопления заряда этими проводниками.
Емкость зависит от размеров и геометрической формы проводников. С не-
многими исключениями, большинство формул, которые связывают геомет-
рическую форму с емкостью, являются приближенными. Всегда можно исполь-
зовать некоторую коммерческую программу для расчета электрического поля,
чтобы точно вычислить емкость между каждой парой проводников. Однако
есть несколько конфигураций электродов, где существуют хорошие прибли-
жения между расчетными и экспериментальными значениями емкости. Если
эти варианты не всегда имеют практическое значение, они полезны для по-
лучения более глубокого представления о взаимосвязи между параметрами
объекта и его емкостными характеристиками. Один из таких вариантов — это
емкость между двумя концентрическими сферами, расположенными одна внут-
ри другой. Емкость С между этими двумя сферами:
С = 4ле0 , пф
где е0 — диэлектрическая постоянная, 0,0885 пФ/см; г — радиус внутренней сферы, см;
гь — радиус внешней сферы, см.
Когда радиус внешней сферы в 10 раз больше внутренней, то емкость сферы
считается по следующей приближенной формуле:
С= 4л£0г, пФ.
Например, сфера, радиусом 1 см или диаметром 2 см, имеет емкость С =
= 4л х 0,0885 пФ/см х 1 см = 1,1 пФ. Таким образом, емкость шара с радиу-
сом 1 см примерно равна 1 пФ.
Эта важная зависимость говорит о том, что любой проводник, изолиро-
ванный в пространстве, имеет небольшую емкость относительно Земли. Она
не становится предельно малой, а имеет определенное минимальное значе-
ние, которое определяется размерами проводника. Чем ближе проводник к
поверхности Земли, тем больше значение емкости.
Роль Земли в реальных условиях выполняет система заземления, при
помощи которой на металлические элементы конструкции (потенциальный
158
Глава 2. Электрофизические параметры печатного монтажа
слой в печатной плате, корпус, шасси, рамы и т. п.) подается нулевой потен-
циал. От того, насколько действительно этот потенциал равен нулю, зави-
сит качество функционирования аппаратуры. Одна из причин неравенства
нулю потенциала на элементах заземления заключается в «подскоке» напря-
жения заземления за счет падения напряжения на индуктивности выводов
микросхем при их переключении. Это падение напряжения может достигать
долей вольт, что приводит к отсутствию нулевого потенциала на соответству-
ющем выводе кристалла микросхемы.
Приведенные оценки показывают, что даже относительно малые по длине
электрические соединения, имеющие емкость около 2 пФ, на частоте I ГГц
обладают полным сопротивлением около 100 Ом.
2.3.6. Плоскопараллельный конденсатор
Наиболее распространенное приближение для проводников печатного
монтажа — плоскопараллельный конденсатор. Для случая двух плоских пла-
стин, как показано на рис. 2.22, находящихся на расстоянии h друг от друга,
с площадью пластин Уис наличием воздуха между ними, емкость С опре-
деляется по формуле:
С = е0—, пФ, (2.35)
п
где линейные размеры Л и h задаются в единой размерности, е0 — диэлектрическая посто-
янная Х,85 пФ/м.
Рис. 2.22. Плоскопараллель-
ный конденсатор как модель
емкости в двухслойной плате
Например, два проводника площадью около
1 см2, разделенные воздухом, расположенные на
расстоянии 1 мм друг от друга, имеют емкость
С= 0,0885 пФ/см х 1 см2/0,1 см ~ 0,9 пФ. Для
инженерных оценок можно принять эту емкость
равной 1 пФ.
Зависимость (2.35) указывает важную харак-
теристику всех конденсаторов. Чем больше рас-
стояние h между проводниками, тем меньше ем-
кость и наоборот. Эта зависимость использует-
ся при проектировании шин питания и заземления в составе МПП. Сбли-
жение до минимальных расстояний слоев питания и заземления приведет к
возрастанию емкости между ними, что положительно скажется на работос-
пособности системы. Минимальное расстояние определяется, с одной сто-
роны, пробивной прочностью применяемых диэлектрических материалов,
а с другой стороны — технологическими ограничениями. В настоящее вре-
мя на рынке можно найти предельно тонкие материалы (толщина единицы
микрометров) для этих целей, что обеспечивает значительные емкости между
слоями в платах. Подробнее проектирование системы питания на плате и роль
упомянутой емкости будут рассмотрены в главе 5.
Формула (2.35) для определения емкости плоскопараллельного конден-
сатора является приближенной, поскольку она не учитывает краевой эффект
2.3. Электрическая емкость в печатном монтаже
159
по периметру пластин. Чем меньше зазор между пластинами или шире пла-
стины, тем лучше это приближение. В общем случае реальная емкость больше
определенной по приближенной формуле из-за вклада краевых эффектов,
учет которых представляет определенные трудности. Существует грубое эм-
пирическое правило: если расстояние между пластинами равно боковому
размеру пластины, то есть конденсатор представляет собой куб, то реальное
значение емкости отличается от приближенной в большую сторону в два раза
за счет вклада краевых эффектов.
Применение более точных методов расчета (см. главу 8) позволяет учесть
влияние краевых эффектов.
2.3.7. Диэлектрическая проницаемость
Диэлектрическая проницаемость характеризует внутренние свойства по
всему объему диэлектрика. Метод измерения относительной диэлектрической
проницаемости диэлектрика состоит в сравнении емкостей двух проводни-
ков, когда они окружены воздухом, Со, и когда они полностью находятся в
диэлектрическом материале — С£. Относительную диэлектрическую прони-
цаемость определяют как:
ег=С£/С0. (2.36)
Далее для сокращения записи, если это не будет вызывать неоднознач-
ности, емкость в диэлектрической среде будем записывать как С.
Чем выше диэлектрическая проницаемость, тем больше емкость. Диэлек-
трическая проницаемость будет увеличивать емкость между двумя провод-
никами независимо от их формы, если только все пространство около про-
водников заполнено однородным материалом. Конкретные значения про-
ницаемости для различных материалов приведены в главе 1.
Для большинства материалов, применяемых при создании печатных плат,
относительная диэлектрическая проницаемость составляет 3,5...5,6. Это го-
ворит о том, что емкость между двумя проводниками увеличится примерно
в 4 раза по сравнению с воздушной средой при их расположении в толще
МПП. Важно помнить, что диэлектрическая проницаемость большинства по-
лимеров будет меняться в результате условий обработки, степени отвержде-
ния и использования добавочных материалов. Так же может существовать не-
которая зависимость проницаемости от частоты. Поэтому следует принимать
относительную проницаемость на 10 % больше, чем у измеряемого образца,
что соответствует худшему случаю.
Диэлектрическая проницаемость материала прямо связана с числом ди-
полей и их размерами. Материал, состоящий из молекул с множеством ди-
полей, например, вода, будет иметь высокую относительную диэлектричес-
кую проницаемость (около 80). А материал с малым количеством диполей,
такой, как воздух, будет иметь низкую диэлектрическую проницаемость,
равную 1. Наиболее низкая диэлектрическая проницаемость у некоторых
твердых, гомогенных (как, например, тефлон) материалов — около 2.
160
Глава 2. Электрофизические параметры печатного монтажа
У некоторых керамических материалов, например, титанат бария, ди-
электрическая проницаемость будет более 5000, что позволяет использовать
этот материал для создания конденсаторов высокой удельной емкости. Ди-
электрическая проницаемость может уменьшаться из-за присутствия в ма-
териале воздуха. Вспененные материалы, к примеру, имеют диэлектричес-
кую проницаемость, близкую к 1. В том случае, если диэлектрическая среда
состоит из ряда материалов, то ее диэлектрические свойства характеризуются
эффективной диэлектрической проницаемостью. Ее значение можно опре-
делить экспериментально, как показано выше.
Для повышения системного быстродействия диэлектрическая проница-
емость основания печатной платы должна быть минимальной, поскольку
скорость распространения сигнала в линиях передачи определяется парамет-
рами среды. Для однородной диэлектрической среды:
1
V = Vc—7=,
X
(2.37)
где vt. — скорость электромагнитной волны в свободном пространстве (скорость света
ЗхЮ8 м/с); ег — относительная диэлектрическая проницаемость.
Физико-химические ограничения в настоящее время не позволяют по-
лучить гомогенный материал с относительной диэлектрической проницае-
мостью менее 2, однако, добавляя воздух в диэлектрик (вспенивая его), можно
приблизить значение относительной диэлектрической проницаемости к 1.
Подобный прием используется для создания изоляции в коаксиальных ка-
белях, но для оснований печатных плат он не пригоден.
Диэлектрическая проницаемость будет изменяться с изменением часто-
ты. Этот эффект проявляется на относительно высоких частотах. Например,
для частот от 1 МГц до 10 МГц, диэлектрическая проницаемость стеклотек-
столита меняется от 4,8 до 4,4. Однако в диапазоне от 1 ГГц до 10 ГГц диэ-
лектрическая проницаемость стеклотекстолита может быть постоянной.
Точное же значение диэлектрической проницаемости для стеклотекстолита
зависит от относительного количества эпоксидной смолы и стеклоткани. Для
определенности необходимо точно оговаривать частоту, при которой изме-
ряется диэлектрическая проницаемость материала.
2.3.8. Эффективная диэлектрическая проницаемость
В любом поперечном сечении, где диэлектрик полностью окружает про-
водники, все силовые линии электрического поля будут проходить через
пространство с одной и той же диэлектрической проницаемостью, как, на-
пример, в полосковой линии передачи. Однако, если диэлектрик не рас-
пределен равномерно вокруг проводников, то некоторые силовые линии
будут проходить через воздух, а другие — через диэлектрик. Пример рас-
пределения силовых линий в микрополосковой линии передачи показан на
рис. 2.23.
2.3. Электрическая емкость в печатном монтаже
161
Рис. 2.23. Силовые линии электрического
поля в микрополосковой линии
В том случае, когда диэлектри-
ческая среда состоит из совокупно-
сти отдельных фрагментов различ-
ных диэлектриков, внутри которых
диэлектрические свойства остаются
неизменными, говорят о кусочно-
однородной диэлектрической сре-
де. Наличие кусочно-однородного
диэлектрика увеличивает емкость
между сигнальным проводником и
землей, но насколько? Ответ на этот
вопрос можно дать, используя ин-
тегральную оценку относительной
диэлектрической проницаемости
сложных кусочно-однородных сред через понятие эффективной диэлектри-
ческой проницаемости — ге&
Если диэлектрическая проницаемость — это отношение емкости запол-
ненного диэлектриком конденсатора к емкости конденсатора в воздухе (ва-
кууме), то эффективная диэлектрическая проницаемость — это отношение
емкости конденсатора, заполненного кусочно-однородной диэлектрической
средой, к емкости того же конденсатора, заполненного воздухом.
Первым шагом при подсчете эффективной диэлектрической проницае-
мости, является вычисление погонной емкости Со между двумя провод-
никами в воздушной однородной среде. Далее проводники помещают в ис-
следуемый кусочно-однородный материал и снова вычисляют погонную ем-
кость С. Эффективная диэлектрическая проницаемость вычисляется как
Е< = ПО-
ТОЧНО провести вычисления эффективной диэлектрической проницаемо-
сти линии связи можно только с использованием программ расчета полей.
Эффективная диэлектрическая проницаемость — очень важная характери-
стика, так как от нее напрямую зависит скорость распространения сигнала
в линии передачи. Ее знание необходимо для наружных слоев платы, в ко-
торых проводники лежат в кусочно-однородных средах, содержащих осно-
вание платы, воздух, лаковое покрытие, паяльную маску. Анализ таких сред
выполнен в главе 8.
На рис. 2.24 показано, как зависит эффективная диэлектрическая про-
ницаемость микрополосковой линии (см. рис. 2.23) от ее ширины. Сигналь-
ный проводник в данном случае лежит на границе раздела стеклотекстоли-
та и воздуха. Диэлектрическая проницаемость стеклотекстолита равна 4. Если
проводник очень широкий, то большинство силовых линий проходит через
материал основания, и значение эффективной диэлектрической проницае-
мости приближается к 4. Когда же проводник узкий, большинство силовых
линий проходит через воздух, и эффективная диэлектрическая проницаемость
оказывается меньше 3 из-за вклада низкой диэлектрической проницаемости
162
Глава 2. Электрофизические параметры печатного монтажа
о 0 0 25 0 5 0 75
Ширина проводника мм
Рис. 2.24. Эффективная диэлектрическая проницаемость микрополосковой линии
с толщиной диэлектрика 0,127 мм в зависимости от ширины проводника
воздуха. Подобное изменение эффективной проницаемости приведет к из-
менению скорости распространения сигнала в линии передачи, которая в
данном случае становится зависимой от ширины проводника.
Если добавить достаточно толстый слой диэлектрика в верхней части мик-
рополосковой линии, то силовые линии, проходившие через воздух, будут
проходить через материал с более высокой диэлектрической проницаемос-
тью, и емкость линии увеличится. Когда линия закрыта диэлектриком, она
называется заглубленной микрополосковой линией. Если толщина покры-
тия такова, что определенная часть силовых линий проходит через воздуш-
ную среду, то такая линия называется частично заглубленной микрополос-
ковой линией. Например, такая линия формируется при нанесении паяль-
ной маски или слоя лака.
Линия, у которой все силовые линии охвачены диэлектриком, называется пол-
ностью заглубленной микрополосковой линией. На рис. 2.25 изображена карти-
на электрического поля для трех различных вариантов микрополосковых линий.
Какова толщина слоя диэлектрика поверх микрополосковой линии, чтобы
покрыть все силовые линии и получить диэлектрическую проницаемость, рав-
ную диэлектрической проницаемости базового материала? Эта задача решает-
ся при использовании программы расчета полей. На рис. 2.26 показана вычис-
ленная погонная емкость микрополосковой линии с толщиной диэлектрика
0,127 мм и шириной проводника 0,25 мм в зависимости от толщины добавлен-
ного верхнего слоя диэлектрика с диэлектрической проницаемостью 4.
Видно, что толщина верхнего слоя диэлектрика должна быть равна ши-
рине проводника, чтобы полностью покрыть все силовые линии.
2.3.9. Емкость между слоями платы
Анализ емкости между сигнальным и потенциальным слоями в интеграль-
ных микросхемах или в МПП проводится при условии полного заполнения
слоя медной фольгой. Это позволяет рассматривать емкость между слоями
2.3. Электрическая емкость в печатном монтаже
163
Рис. 2.25. Электрическое поле микрополосковых линий с различной толщиной
диэлектрического покрытия:
а — микрополосковая линия без покрытия; б — частично заглубленная линия;
в — полностью заглубленная линия
Рис. 2.26. Погонная емкость микрополосковой линии в зависимости от толщины
верхнего слоя диэлектрика
как емкость между двумя параллельными пластинами. В главе 5 показано,
что для того, чтобы уменьшить просадку напряжения системы питания, важно
иметь определенное число развязывающих конденсаторов, установленных
между шиной питания и заземления. Их емкость С будет предотвращать
падение напряжения питания в интервале времени переключения микросхе-
мы. Если в кристалле рассеивается мощность Р, Вт, а допустимая просадка
напряжения составляет 5 % от номинального напряжения питания Исс, В,
то интервал времени, при котором просадка не превысит допустимого зна-
чения при емкости С развязывающего конденсатора, определяется как
И2
Д? = СхО,О5-^, с, (2.38)
где С— емкость конденсаторов; Ф; Исс — напряжение питания, В; Р— потребляемая мощ-
ность, Вт.
К примеру, время, за которое емкость 1 нФ будет обеспечивать допусти-
мое напряжение питания при мощности рассеяния 1 Вт и номинальном на-
пряжении 3,3 В, составляет: Д/= 1-10-9х0,05 х 3,32/ 1 = 0,5-10-9 с. Если учесть,
что просадка напряжения по длительности приближенно равна длительности
164
Глава 2. Электрофизические параметры печатного монтажа
фронта сигнала, то полученное значение 0,5 нс в большинстве случаев недо-
статочно. Для уверенной развязки более типично значение 5 мкс. В этом слу-
чае необходимая емкость будет 10 мкФ, что обеспечит достаточную развязку.
При конструировании МПП в качестве одного из развязывающих кон-
денсаторов используется конденсатор, образованный слоями питания и за-
земления. Используя аппроксимацию этой емкости в виде конденсатора из
параллельных пластин, можно установить эффективность развязки. В МПП
со смежными сигнальным и потенциальным слоями мы можем оценить ем-
кость между ними:
С = еоег—, ПФ, (2.39)
п
где е() — диэлектрическая постоянная 8,85 пФ/м; ег— относительная диэлектрическая про-
ницаемость материала, установленного между слоями; S — площадь поверхности слоев,
образующих емкость, м2; h — расстояние между слоями, м.
Пусть площадь конденсатора составляет 10 см2, диэлектрическая прони-
цаемость стеклотекстолита 4, расстояние между слоями 0,025 см, тогда ем-
кость, образованная пластинами, будет
С= 0,0885 пФ/см х 4 х (10 см2/ 0,025 см) - 142 пФ.
Если микросхемы размещены на плате площадью 250 см2, тогда общая раз-
вязывающая емкость между сигнально-потенциальными слоями составит
всего 3,5 нФ. Это почти на три порядка меньше требуемой емкости в 10 мкФ.
Какой интервал времени эта емкость сможет поддержать необходимое на-
пряжение? Используя соотношение (2.38), получим, что время, за которое
емкость 3,5 нФ будет обеспечивать развязку, составит 1,9 нс. Это достаточ-
но малый интервал времени, учитывая, что эта емкость проявляется через
выводы микросхемы, и ее действие частично компенсируется полным сопро-
тивлением выводов. Кроме того, емкость, уже встроенная в корпус некото-
рых типов микросхем, обычно в сотни раз больше емкости между слоями.
Основным достоинством конденсатора, образованного металлизированными
слоями печатной платы, является малая постоянная времени из-за его пре-
дельно низкой индуктивности и сопротивления.
В общем случае емкость между слоями в многослойной печатной плате иг-
рает роль конденсатора с малой постоянной времени. Такой конденсатор обес-
печивает развязку в первоначальный момент времени коммутации до подклю-
чения конденсаторов большей емкости, но меньшего быстродействия, которые
установлены на плате.
В том случае, если толщина диэлектрика может быть сделана малой, его
диэлектрическая проницаемость высокой, то емкость между слоями может
быть относительно высокой, что повысит эффективность этого плоского
конденсатора. На рис. 2.27 показано изменение емкости на единицу площади,
для четырех различных диэлектрических постоянных 1,4, 10 и 20. Очевид-
но, если задачей является увеличение емкости на единицу площади, то путь
к ее решению состоит в использовании тонких диэлектрических слоев и
высоких диэлектрических проницаемостей.
2.3. Электрическая емкость в печатном монтаже
165
Рис. 2.27. Емкость между слоями на единицу площади при различных диэлектрических
проницаемостях и при различной толщине диэлектрика между слоями
К примеру, новый усовершенствованный материал фирмы ЗМ (США) под
торговой маркой С-Ply состоит из титаната бария в полимерной матрице. Его
относительная диэлектрическая проницаемость — 20, а толщина слоев 8 мкм.
Если установить его между слоев, ламинированных с каждой стороны слоем
меди толщиной 17 мкм, емкость на единицу площади составит 2,14 нФ/см2.
Для площади 250 см2 развязывающая емкость составляет 535 нФ, что примерно
в 150 раз больше, чем при традиционных решениях. При этом интервал удер-
жания напряжения составляет 289 нс, что вполне достаточно для удовлетво-
рительной развязки.
2.3.10. Погонная емкость
Путь сигнального и обратного тока многих межсоединений рассматри-
вается при условии постоянства площади поперечного сечения линии пере-
дачи. Исходя из этого, емкость между прямым и обратным проводником
определяется длиной межсоединения, и ее удобно выразить через погонную
емкость, т. е. емкостью на единицу длины линии. Погонная емкость Cf ос-
тается постоянной, пока линия передачи однородна, т. е. имеет постоянное
по длине сечение.
В частном случае общая емкость С между путями сигнального и обрат-
ного тока будет определяться как
С = С{1, пФ, (2.40)
где С7 — погонная емкость линии передачи, пФ/м; / — длина линии передачи, м.
Существуют три вида сечений проводников, для которых имеются тео-
ретически точные расчетные соотношения для определения погонной емко-
сти: коаксиальный кабель, двухпроводная линия (два параллельных провод-
ника круглого сечения) и провод круглого сечения над плоскостью. Эти
166
Глава 2. Электрофизические параметры печатного монтажа
\\
микрополосковая линия
полосковая линия
Рис. 2.28. Поперечное сечение микрополосковой и полосковой линии передачи
системы проводников хорошо изучены, и в литературе имеются формулы для
расчета их погонной емкости.
В печатном монтаже наиболее часто используется микрополосковая и по-
лосковая линия передачи (рис. 2.28). В микрополосковой линии сигнал рас-
пространяется по проводнику, расположенному выше диэлектрического слоя,
а возвратный ток протекает по плоскости, расположенной под проводником.
В полосковой линии путь обратного тока протегает по двум плоскостям, а
сигнальный проводник расположен между ними. Вне зависимости от того,
протекает или нет постоянный ток в двух плоскостях, для высокочастотных
сигналов они рассматриваются как короткозамкнутые, и возвратный ток сим-
метрично распределяется между ними. Диэлектрик в полосковой линии пол-
ностью окружает сигнальный проводник.
В обоих случаях погонная емкость линии передачи может быть рассчитана.
Для этого можно воспользоваться формулами, рекомендованными стан-
дартом IPC. Погонная емкость микрополосковой линии дается как
0,26(1,41 + £_) 0,26(1,41 + е )
) -----^2, пФ/см
5,98/z^ । in Г 7 5 ^ms |
0,8w + Z J I ’ w J
(2.41)
где гг — относительная диэлектрическая проницаемость основания платы; hms — толщи-
на диэлектрика, см; w — ширина проводника, см; t — толщина проводника, см.
Для инженерной оценки полезно помнить, что для микрополосковой линии
при ширине w проводника в два раза больше, чем толщина hms диэлектрика, и
при диэлектрической проницаемости, равной 4, погонная емкость составляет
около 1 пФ/см.
Погонная емкость полосковой линии передачи приблизительно равна
с = 0,558,
In
1,9Л5
0,8w +1
0,55ег
1п| 2,4^
I W
пФ/см,
(2.42)
где hs — толщина диэлектрика, см; w — ширина линии, см; t — толщина проводника, см.
Например, если толщина диэлектрика hs в 2 раза больше ширины и> про-
водника, погонная емкость будет примерно 1,4 пФ/см при ег = 4.
Важно отметить что, хотя толщина проводника присутствует в парамет-
рах, при требованиях высокой точности к результатам расчетов эти форму-
лы использовать нельзя.
2.4. Методы расчета электрической емкости в печатном монтаже
167
Обычно значение погонной емкости линии передачи с волновым сопро-
тивлением 50 Ом составляет около 1,4 пФ/см.
2.4. Методы расчета электрической
емкости в печатном монтаже
2.4.1. Классификация методов расчета емкости
Методы расчета электрической емкости можно разделить на аналитические
и численные. Аналитические методы, в свою очередь, делятся на строгие те-
оретические и основанные на методе конформных преобразований [40, 60,
61]. Численные методы реализуются с применением программных средств,
в основе которых лежат два базовых метода: метод граничных элементов и
метод конечных элементов. Для практики представляют интерес методы, по-
зволяющие применительно к конфигурации сечения линий передач прово-
дить расчеты для кусочно-однородных сред. Этому условию отвечают мето-
ды на основе конформных преобразований [24, 40, 55] и численного метода
граничных элементов [62].
При расчете емкости в общем случае обычно известны лишь геометричес-
кие параметры системы проводников и диэлектрическая проницаемость ок-
ружающей среды. Поэтому, исходя из определения емкости (2.26), необходи-
мо либо рассчитать заряды проводников, задавшись их потенциалами, либо,
наоборот, найти потенциалы проводников, задавшись значением зарядов.
Обе эти задачи могут быть строго решены на основе расчета электроста-
тического поля рассматриваемой системы проводников. Действительно, зная
распределение потенциала электростатического поля Uв пространстве, ок-
ружающем проводники, можно найти заряды каждого из них с помощью
соотношения
где Qt — заряд проводника /; St — поверхность проводника /; N — внешняя нормаль к по-
верхности проводника, е — диэлектрическая проницаемость среды.
Заряд уединенного проводника может быть определен также по формуле
/ 2) TJ \
О = 4л£ , (2.44)
v Л->о
где 5 = 1/R; R — расстояние от поверхности проводника.
Эта формула более удобна для расчетов, чем (2.43), так как позволяет исклю-
чить интегрирование по поверхности и ограничиться исходными данными о за-
висимости потенциала лишь от одной координаты, тогда как при использова-
нии (2.43) необходимо знать пространственное распределение потенциала.
168
Глава 2. Электрофизические параметры печатного монтажа
В тех случаях, когда строгий теоретический расчет электростатического
поля не может быть выполнен, используются специальные методы расчета
емкости, основанные либо на установлении точной или приближенной связи
заряда проводника непосредственно с потенциалом его поверхности (мето-
ды непосредственного определения емкости), либо на преобразовании элек-
тростатических систем и приближенной оценке истинных значений емкос-
ти (вспомогательные методы).
Постановка задач по расчету емкости зависит от выбора исходных вели-
чин (зарядов или потенциалов), которые, в свою очередь, определяются видом
рассматриваемой системы проводников.
При расчете емкости уединенного проводника можно задать произволь-
но его потенциал или заряд. Если положить, в частности, потенциал равным
единице, то заряд уединенного проводника будет численно равен его емко-
сти. При расчете емкости между двумя проводниками, что имеет место при
анализе линий передач, как правило, можно задаваться лишь их зарядами,
причем должно соблюдаться условие электронейтральности Q2 = — Qx.
Потенциалы обоих проводников в общем случае не могут быть выбраны
произвольно, так как они связаны соотношением Ux / U2 = — (С22 / Си), сле-
дующим из выражения (2.27) при п = 2, Qx = -Qr
Задание потенциалов в качестве исходных величин возможно лишь в не-
которых частных случаях, например, следующих.
1. Система двух проводников симметрична относительно некоторой плос-
кости. В этом случае Сп = С22 и при Qx = —Q2, Ux = - U2 = А, где A — произ-
вольное значение.
2. Размеры одного из проводников велики по сравнению с размерами
другого. При этом Сп >> С22, Схх/ С22 ~ 0, т. е. Ux = О, U2 = А, где А — произ-
вольное значение.
При расчете частичных емкостей и коэффициентов электростатической
индукции в системе многих проводников исходными величинами могут яв-
ляться в общем случае лишь их потенциалы.
Так, при расчете собственной частичной емкости потенциалы всех про-
водников системы должны быть приняты равными одному и тому же про-
извольному постоянному значению, а при расчете взаимной частичной ем-
кости между проводниками /и к потенциал одного из них может быть выб-
ран произвольно, а потенциалы всех остальных проводников должны быть
приняты равными нулю.
На этих подходах основаны все методы расчета емкости, которые можно
разделить на две основные группы — методы непосредственного определе-
ния емкости и вспомогательные методы определения емкости.
2.4.2. Инженерные методы оценки емкости
Для инженерной оценки электрической емкости, которая дает в ряде
случаев точный результат и может быть выполнена по аналитическим выра-
жениям, наиболее пригоден метод на основе конформных преобразований
2.4. Методы расчета электрической емкости в печатном монтаже
169
[40] . Эти преобразования позволяют электрическое поле, описанное в од-
ной систем координат XY, привести при помощи функции преобразования
к другой системе координат т|£ (рис. 2.29). В электрическом поле силовые
линии и линии равного потенциала (эквипотенциали) ортогональны. При
конформных преобразованиях это принципиально важное свойство элект-
рического поля сохраняется, что позволяет получить две абсолютно иден-
тичные с позиций электростатики системы, но с различными конфигурациями
электродов. Емкости между электродами в этих системах одинаковы. Если
одна из систем рассчитывается тривиально (например, по формуле для плос-
кого или цилиндрического конденсатора), то, получив после преобразова-
ния новые координаты тривиальных электродов, легко рассчитывается ис-
комая емкость.
В качестве иллюстрации приведем пример. Рассмотрим некоторую сис-
тему криволинейных электродов, образующих конденсатор (рис. 2.29). Пре-
образуем исходную систему электродов к базовой, которая имеет расчетные
формулы. В данном случае это плоский конденсатор, формула для расчета
емкости которого хорошо известна.
Каждая точка в исходной системе задается своими координатами:
а[С¥а|, ral); rAI); a2(Xa2, Ya2); b2(Xb2, Yb2).
После преобразований получаем точки базовой системы в новой систе-
ме координат:
а2^а2^а2^^ ^2^
Координаты базовой системы зависят от координат точек исходной сис-
темы и функции преобразования: т|,£ =f(X, Y, F). Параметры электрическо-
го поля при конформных преобразованиях не изменяются; изменяется только
его внешний вид. Поэтому электрическое поле некоторой системы электродов
полностью сохраняет свои интегральные показатели после конформных пре-
образований, но конфигурации электродов и, соответственно, поля видоиз-
меняются. Таким образом, становятся известными параметры сечения, что
позволяет по известной формуле рассчитать искомую емкость.
Ключевым моментом в процедуре преобразования является поиск функ-
ции преобразования F. Если такая функция найдена, то задача будет решена.
Рис. 2.29. Иллюстрация конформного преобразования электростатической задачи:
слева — исходная система, справа — базовая, имеющая расчетные формулы
170
Глава 2. Электрофизические параметры печатного монтажа
Поиск функции преобразования выделяется в отдельную математичес-
кую проблему. Поэтому в инженерной практике используются уже готовые,
ранее найденные функции преобразования. Они сведены в справочники,
которыми инженеры пользуются в своей практической деятельности [40].
Формулы для расчета, как для проводного, так и для печатного монтажа,
приведены в [57].
Для обоснованного применения рассматриваемого метода расчета емкости
в инженерной практике следует учитывать его принципиальные особенно-
сти. Они заключаются в следующем.
1. Задача может быть решена в случае, если известна функция преобра-
зования (например, из литературы).
2. Метод применим только для решения квазистатических задач, при
которых максимальный размер сечения электростатической системы
существенно меньше длины волны синусоидального сигнала перемен-
ного тока. Это условие соблюдается для всех проводников печатных
плат.
3. Метод применим только для однородных диэлектрических сред. Ку-
сочно-однородные среды могут быть рассчитаны только в отдельных
частных случаях.
4. Метод конформных преобразований, как правило, оперирует с беско-
нечно тонкими элементами, поэтому исходная система электродов дол-
жна быть представлена в виде некоторой модели, содержащей такие
элементы.
5. Расчетная система должна иметь, как минимум, одну плоскость сим-
метрии.
Рис. 2.30. Расчетная модель
фрагмента печатной платы: а —
система проводников; б — при-
ведение к однородному диэлект-
рику; в — расчетная модель
Рассмотрим иллюстративный пример по
расчету электрической емкости копланарной
системы проводников (рис. 2.30). Решим
данную задачу методом конформных преоб-
разований.
Наличие кусочно-однородной среды (ди-
электрика и воздуха) — это дополнительная
трудность для расчета, ибо нарушаются ус-
ловия однородности среды. Поэтому необ-
ходимо привести диэлектрическую среду к
однородной. Помещаем пластины в одно-
родную среду и при этом оговариваем пара-
метры среды путем задания ее эффективной
диэлектрической проницаемости:ге^=/(ег1 ,
ег2). Поскольку метод оперирует бесконеч-
но тонкими пластинами, приводим систему
к виду, где толщина пластин равна нулю. Так
как система имеет ось симметрии, возможен
расчет ее емкости методом конформных пре-
образований.
2.4. Методы расчета электрической емкости в печатном монтаже
171
Формулы для расчета приведены ниже (табл. 2.4) [40, 57]. Емкость опре-
деляется по формуле
С = 8,85Ee/7cz/, пФ, (2.45)
где 8,85 — диэлектрическая постоянная, пФ/м; е^ — эффективная диэлектрическая про-
ницаемость диэлектрической среды; — нормированная емкость на единицу длины, без-
размерная величина; / — длина системы проводников, м.
В МПП проводники расположены в однородной среде, т. е. Е^ОСНОвание)-
Из (2.45) видно, что расчету подлежит только нормированная емкость сг
Методика расчета электрической емкости в печатном монтаже с помощью
справочных формул, полученных методом конформных преобразований,
сводится к следующим шагам.
1. Вычисление модулей к и дополнительных модулей к' полных эллип-
тических интегралов первого рода К, К . Модуль к определяется гео-
метрическими размерами расчетного сечения, и выражения для опре-
деления к, К, К приводятся в справочных таблицах (табл. 2.4), а до-
полнительный модуль А7 определяется из соотношения k' = \]l-k2.
2. Определение модулярного угла а = arcsin к и дополнительного моду-
лярного угла а' = arcsin А7.
3. Определение эллиптических интегралов £и Г как функции соответ-
ственно модулярного и дополнительного модулярного углов по таб-
лицам полных эллиптических интегралов первого рода, приведенных,
например, в [63].
4. Вычисление нормированной емкости с{ = f{K, К ) по соотношениям,
приведенным в справочных таблицах и связывающим геометрические
параметры сечения линии и значение ct.
При расчетах удобно использовать аппроксимацию К и К многочлена-
ми [63], в которых используется параметр т и дополнительный параметр т',
причем т + т' =1. Параметры могут быть определены через модули эллип-
тических интегралов: т = к2\ т' ={к/ )2.
Рис. 2.31. Относительный объем воздушной среды в двусторонних платах
и микрополосковой линии
Формулы для расчета емкости в печатном монтаже [40, 57]
Таблица 2.4
№ Сечение С, т = А2, тх — А^ 8e#
1 е1 a d b 2* К' т - т = аЬ/[(а + d)(b + </)] = (/i - /2)(^з ~ z?) ’ <'|+'2)('з+'2» tt см. (5.5) . (£Г2 ~ £Г1) r! £rl 2 К
h 62
2 Е1 a d I 2А К' т = а/(а 4- d) т _(1-г2)(г3-г2> 1 (1 + Г2)(Г3+/2) ( см. (5.5) c , (Sr2-£,1) £ £'> 2 К
h E2
3 Е1 a d a К' к "Ii = m = [d/ '(d + 2a)]2 / 7i(d+2a)] I/Sh 4Й ] (£Г2 ~ £ri) К 2 Kx
h £2 н па 4h]
4 , a d b d i 3 I । 2a/J 2 +b/d Го \ +b/d + a/d)( 1 + а/d + b/d) H ^)( 1 4- q2)] :м. (5.5) (£r2 ~ £rl) ^1 К Л 2 Kt
1 — к в
h «2 тх + <72)/l(l Н <7р?2 <
Глава 2. Электрофизические параметры печатного монтажа
2.4. Методы расчета электрической емкости в печатном монтаже
173
Окончание табл. 2.4
3 Л 'у г , и, N (р3-г73) [ил/Ё^ + О -п)7Ё^] Значения п см. на рис. 2.31
т = Zf, тх — m=\[/(\ + 2d/b}]2 тх = 1/(1 + q2) q2 см. (5.5) —_— , при b / h« 1 '"(4) —, при b / 2h< 1 |п(81)
О'
Сечение е, ~Н"ГГ г—J к» ь-—1 Ь|| I е2 ь Г чГ .! 3 Q ч[ | ij3 3 я
40 оо
174
Глава 2. Электрофизические параметры печатного монтажа
Для 0 < т < 1 аппроксимирующие многочлены имеют следующий вид:
К= К(т) = [я0 + а{т' + а2(т')2] + [Z>0 + b{m' + b2(m')2] + ln( 1/m') + е(т);
/С = К(т') = [я0 + а}т + а2т2] + [£0 + Ьхт + Ь2т2] + 1п(\/т) + е(ш); (2.46)
| е(лп)| < 3-Ю’5; aQ = 1,3862944; = 0,1119723; а2 = 0,0725296; bQ = 0,5;
= 0,1213478; b2 = 0,0288729.
В большинстве случаев при вычислении с( приходится вычислять отно-
шения К/1С или К /К. Для ускорения расчетов их можно определить по гра-
фику (рис. 2.32) как функцию параметра т.
При вычислении параметра т по выражениям, приведенным в табл. 2.4,
необходимо вычислить ряд вспомогательных коэффициентов Г,, Г2, /3, q2
по следующим выражениям [40]:
ti = (exp - 1) / (exp Xz- + 1), i = 1, 2, 3;
X, = n(2b + d) / 2Л;
X2 = nd / 2h\
X3 = n(2a + J) / 2A; <2-47)
_ sh(7ta / 2Zi)sh[tt(a + b + 2d)/2h]
q'~ sh(nrf/2A)sh[n(Z> + </)/2A] ’
_ sh2(7t/>/4/0
41 - sh(ju//2A)sh[n(/»+(/)/2A)]'
Значения rz- по вычисленным \ — можно определить из графика, приве-
денного на рис. 2.33.
Пример расчета.
В качестве примера рассмотрим одностороннюю печатную плату с проводниками разной
ширины (рис. 2.34). Рассчитаем емкость между проводниками (табл. 2.4, п. 1).
Рис. 2.32. Отношение К (К как функция параметра
т (0,00129 < т < 0,99954)
2.4. Методы расчета электрической емкости в печатном монтаже
175
л,
Рис. 2.33. Зависимость r;.(Xz)
Рис. 2.34. Односторонняя печатная
плата с проводниками разной
ширины
Зададим геометрические параметры проводников и значения относительных диэлек-
трических проницаемостей основания и окружающей среды: а = 1 мм; d= 1 мм; Ь = 3 мм;
h = 2 мм; ег1 = 1; ег2 = 6; I = 1 м.
Методика расчета электрической емкости линии связи в печатном монтаже при по-
мощи справочных формул, полученных методом конформных преобразований, сводит-
ся к следующим операциям.
1. Определяем параметр т:
т = ab / [(а + d)(b + d)] = 1 • 3 / [(1 + 1)(1 + 3)] = 0,375.
2. По графику К / К{т) (рис. 2.32) получаем К / К= 1,5 для т = 0,375 (более точные
значения получены после расчета всех вспомогательных коэффициентов) и рассчитыва-
ем cz=2^/K'= 1,33.
3. Рассчитываем вспомогательные коэффициенты:
= 5,49779; Х2 = 0,785398; Х3 = 2,35619.
По графику rz(Xz) (рис. 2.33) определяем = 0,991842; t2 = 0,373685; t3 = 0,826851 (более
точные значения могут быть получены после расчета всех вспомогательных коэффициентов).
4. Находим параметр т{ = 0,170876.
5. По графику К / К(т) (рис. 2.32) получаем К{ = 1,41563 для = 0,9 (более точ-
ные значения могут быть получены после расчета всех вспомогательных коэффициентов).
6. Эффективная диэлектрическая проницаемость
р - ₽ + ~8/4 ) - 2 97
7. Погонную емкость для заданной системы проводников рассчитываем по формуле (2.45):
С = 8,85ее#- с{- /= 8,85 • 2,98362 • 1,78058 • 1= 34,9 пФ/м.
Значение погонной емкости для линий передачи позволяет определить индуктивность,
волновое сопротивление, удельное время задержки распространения сигнала и другие па-
раметры линии, необходимые для проектирования платы. Эти вопросы рассмотрены в сле-
дующей главе.
2.4.3. Емкость металлизированных отверстий
В печатных платах выполняются металлизированные отверстия для меж-
слойных переходов или для монтажа компонентов. Различают следующие раз-
новидности металлизированных отверстий (рис. 2.35) [8]:
176
Глава 2. Электрофизические параметры печатного монтажа
Рис. 2.35. Металлизированные отверстия в МПП: 1 — глухие отверстия; 2 — слепое
отверстие (межслойный переход); 3 — сквозное отверстие
• сквозные отверстия, предназначенные для монтажа компонентов и для
межслойных переходов;
• глухие отверстия, предназначенные для соединения наружных и внут-
ренних слоев платы; глубина этих отверстий определяется расстоянием
между верхним слоем платы и нижним соединяемым слоем;
• слепые отверстия (внутренние межслойные переходы), предназначен-
ные для соединений внутренних слоев платы; их глубина определяется
расстоянием между соединяемыми слоями.
Емкость металлизированного отверстия создает неоднородность в линии
передачи и дополнительную распределенную емкостную нагрузку. В общем
случае, чем больше диаметр и длина отверстия, тем больше его емкость. По-
этому при наличии сквозных отверстий суммарная толщина МПП должна быть
минимальной. Поверхностный монтаж не требует применения металлизиро-
ванных отверстий для установки компонентов и по этой причине является более
предпочтительным. На значение емкости сквозного металлизированного от-
верстия влияет зазор между стенкой отверстия и металлизацией внутренних
слоев МПП. Для снижения емкости отверстия следует увеличить этот зазор.
Емкость металлизированного отверстия суммируется с емкостью линии
передачи, и общая емкость нагрузки, подключенная к выходу драйвера, ста-
новится ограничивающим фактором при передаче высокочастотных сигна-
лов. На рис. 2.36 наглядно представлены результаты моделирования прохож-
дения синусоидального сигнала по линии передачи, содержащей металли-
зированное отверстие [64, 65]. При частоте сигнала 2 ГГц (рис. 2.36я) он
проходит по линии практически без потерь. При частоте 4,6 ГГц (рис. 2.360
сигнал претерпевает существенные ослабления после прохождения отверстия.
Рассмотрим обобщенную конструкцию металлизированного отверстия
(рис. 2.37). Его емкость зависит от диаметра и глубины отверстия, диэлект-
рической проницаемости материала основания платы, диаметра зазора между
проводящими внутренними слоями платы, через которые проходит отвер-
стие. Если отверстие сквозное, то его глубина равна толщине платы.
На рис. 2.38 показаны конфигурации сечения отверстия диаметром 0,6 мм
и зазора в слое МПП при различных вариантах зазора между отверстием и
плоскостью металлизации. В табл. 2.5 и табл. 2.6 представлены значения ем-
2.4. Методы расчета электрической емкости в печатном монтаже
177
Рис. 2.36. Емкость металлизированного отверстия в линии передачи как фильтр
высокочастотных составляющих сигналов: а — частота 2 ГГц проходит по линии
передачи; б — частота 4,6 ГГц существенно ослабляется
Возвратный ток
Сигнальный ток
отверстие
проводящего слоя
Рис. 2.37. Металлизированное отверстие в МПП
а
кости сквозных металлизированных отверстий при различных параметрах от-
верстия и зазора [64, 65].
Значения емкости металлизированных
отверстий при их различных параметрах
представлены на рис. 2.39 и 2.40 [64,65].
Согласно ранее рассмотренным свой-
ствам электрической емкости при необхо-
димости оценить емкость отверстия с дру-
гими геометрическими параметрами следует
использовать соответствующий коэффици-
ент пропорциональности. Например, при
сокращении длины отверстия в два раза, его
емкость уменьшится также в два раза. Если
все размеры рассматриваемого сечения пла-
ты изменятся в п раз, то емкость отверстия
не изменится.
Отмеченное выше отрицательное дей-
ствие емкости отверстия, приводящее к
Рис. 2.38. Конфигурация сечения
отверстия диаметром 0,6 мм и зазо-
ра в слое МПП: слева — диаметр
кругового зазора 1,32 мм, справа —
размер малой оси эллиптического
зазора 1,32 мм
178
Глава 2. Электрофизические параметры печатного монтажа
Зависимость электрической емкости от значения зазора
Таблица 2.5
Толщина платы, мм Диаметр отверстия, мм Диаметр кругового зазора, мм Емкость, пФ
2,5 0,6 1,06 0,952
2,5 0,6 1,32 0,722
2,5 0,6 1,57 0,812
Таблица 2.6
Зависимость электрической емкости от толщины платы
Толщина платы, мм Диаметр отверстия, мм Диаметр кругового зазора, мм Емкость, пФ
3,8 0,6 1,32 1,060
2,5 0,6 1,32 0,722
1,25 0,6 1,32 0,374
Рис. 2.39. Зависимость емкости и индуктивности слепого металлизированного
отверстия от его геометрических параметров (относительная проницаемость
основания платы 4, 3)
уменьшению полосы пропускания линии передачи, может быть частично ус-
транено сокращением длины отверстия следующими тремя способами:
• применением слепых переходных отверстий минимально необходи-
мой длины вместо сквозных переходных отверстий;
• применением микропереходов между первым и вторым слоем [8];
• применением технологии обратного высверливания (рис. 2.41) [64, 65].
При технологии обратного высверливания сквозное металлизированное
отверстие высверливается с обратной стороны платы на той части, где нет
соединения поверхности отверстия с контактными площадками внутренних
слоев платы.
2.5. Физические основы индуктивности
179
Рис. 2.40. Зависимость емкости сквозного металлизированного отверстия от
его параметров (относительная проницаемость основания платы 4)
Металлизированное
отверстие
Сигнальный
слой
Сверло
Рис. 2.41. При технологии обратного высверливания сокращается неиспользованная
часть металлизированного отверстия
2.5. Физические основы индуктивности
2.5.1. Понятие индуктивности
Индуктивность является одним из основных электрических параметров,
которые в полной мере определяют целостность сигнала и уровень электро-
магнитных помех в электронных модулях на печатных платах. Индуктивность
играет важную роль в распространении сигнала в линиях передачи, в уров-
не связи между сигнальными линиями, в работе системы питания и зазем-
ления, а также в обеспечении ЭМС.
В большинстве случаев задачей проектировщика является уменьшение
индуктивности проводников, шин питания и заземления. Это может быть
180
Глава 2. Электрофизические параметры печатного монтажа
достигнуто конструкторскими методами при разработке топологии печатной
платы и выбором материалов. В отдельных случаях целью разработки яв-
ляется обеспечение необходимого значения индуктивности для достиже-
ния заданного волнового сопротивления.
Для понимания и конструкторских способов управления значением ин-
дуктивности необходимо четко представлять физическую суть индуктивно-
сти и способов управления ее параметрами.
Классическое рассмотрение индуктивности связано с рассмотрением
катушки индуктивности и линий магнитного потока от нее [37, 41]. Ток /,
текущий в проводящем контуре, создает в окружающем пространстве маг-
нитное поле, причем магнитный поток Ф = LI. Коэффициент пропорцио-
нальности L называется индуктивностью, или коэффициентом самоиндук-
ции контура. С математической точки зрения, индуктивность определяется
как интеграл плотности магнитного потока через поверхность. Эти опреде-
ления правильны, но не очень полезны в практической деятельности. Как
обнаружить «катушку индуктивности» в конструкции платы? Как вычислить
интеграл в реальной ситуации? Следует так трактовать индуктивность, что-
бы ее определение и управление ею было доступно инженеру в практичес-
кой деятельности. Это базируется на трех фундаментальных принципах:
1) вокруг любой нити тока существует замкнутый контур силовых линий
магнитного поля;
2) индуктивность есть число линий магнитного потока при токе в про-
воднике, выраженном в амперах (Вб/А);
3) когда число силовых линий магнитного поля вокруг проводника из-
Рис. 2.42. Линии магнит-
ной индукции вокруг
нити тока
меняется, появится напряжение между концами проводника.
Рассмотрим эти положения более подробно.
Положение 1. Вокруг любой нити тока существует замкнутый контур си-
ловых линий магнитного поля (рис. 2.42).
При рассмотрении проводников протекающие
в них токи удобно представлять в виде бесконечно
тонких элементарных нитей тока. При постоянном
токе или при относительно низких частотах распре-
деление этих нитей тока по сечению проводника
будет равномерным. По мере возрастания частоты
происходит перераспределение расположения ни-
тей тока по сечению за счет скин-эффекта и эффекта
близости.
Вокруг каждой нити тока существуют линии
магнитной индукции, плотность которых в про-
странстве по мере удаления от линии поля падает (рис. 2.42). Направление
линий связано с направлением тока правилом правого винта.
Силовые линии магнитного поля всегда замкнуты, круговые и всегда охва-
тывают некоторый ток.
Интенсивность линий магнитного потока вокруг нити тока определяет-
ся в веберах. На значение этой величины, в первую очередь, влияет значе-
2.5. Физические основы индуктивности
181
ние тока в проводнике. При удвоении тока удваивается и число линий маг-
нитного потока. Во-вторых, на число линий магнитного потока влияет длина
проводника: более длинный провод имеет большее число линий. В-третьих,
на число линий влияет форма сечения провода. Это эффект второго поряд-
ка, и влияние его более тонко. Как будет показано ниже, если площадь се-
чения увеличивается, число линий магнитного потока будет меньше. В-чет-
вертых, наличие вблизи проводника с нитями тока других нитей тока изме-
няет суммарный магнитный поток. Это важный фактор при рассмотрении
влияния возвратных токов в линиях передачи. Если прямые и возвратные токи
расположены рядом, то общее число линий магнитной индукции должно быть
просуммировано с учетом их направлений. Наличие диэлектрических мате-
риалов не влияет на магнитные свойства.
На магнитное поле не действует присутствие диэлектрических материа-
лов. Они не изменяют число линий магнитной индукции вокруг нитей тока.
Металлические проводники из нескольких магнитных материалов (фер-
ромагнетики), например, железо, никель или кобальт, будут обладать сум-
марными магнитными свойствами этих материалов. Эти материалы имеют
относительную магнитную проницаемость цг больше 1. Если линии магнитной
индукции находятся внутри этих материалов, то индуктивность увеличит-
ся. Однако это относится только к линиям напряженности магнитного поля
внутри проводника. Выводы микросхем выполняются из двух основных
материалов: сплава Alloy 42 и ковара (Kovar), которые являются ферромаг-
нетиками. Немагнитные материалы проводников, например, медь, серебро,
олово, алюминий, свинец, золото не влияют на индуктивность.
Положение 2. Индуктивность определяется как отношение числа линий маг-
нитного потока на один ампер тока, протекающего в проводнике.
Индуктивность есть число линий магнитного потока (вебер), которые ок-
ружают нить тока со значением один ампер. Следует принимать во внимание
только общее число линий магнитного потока, а не их концентрацию.
Единица измерения индуктивности — генри, равная отношению вебер/
ампер. Для большинства проводников индуктивность будет составлять весьма
малую часть генри — миллигенри (10-6 Гн) и наногенри (10-9 Гн). Индуктив-
ность можно определить как
L=N/I, (2.48)
где L — индуктивность, Гн; N — число линий магнитного потока вокруг проводника, Вб;
I — ток через проводник, А.
Это отношение для рассматриваемого проводника постоянно. Если ток уве-
личится в два раза, то число линий магнитного потока также увеличится в два
раза. Индуктивность проводника не зависит от тока, который протекает по
нему. Значение индуктивности определяется в основном геометрией проводника
и его магнитными свойствами.
Для проводника — источника магнитного поля — следует рассматривать са-
моиндукцию и взаимную индуктивность. Если ток образует контур, вокруг кото-
рого подсчитываются линии магнитного потока, то для него рассматривается
182
Глава 2. Электрофизические параметры печатного монтажа
Рис. 2.43. Линии маг-
нитного потока вокруг
одного проводника яв-
ляются результатом
собственного тока и
тока в другом провод-
нике
индуктивность контура и парциальная индуктивность. Наконец, если рассмат-
ривается магнитное поле около определенного отрезка межсоединений, по
которому протекает весь ток, используются термины: полная индуктивность,
индуктивность цепи или эффективная индуктивность.
Наличие нескольких физических явлений и соответствующих терминов
вносит определенные трудности в анализ индуктивности межсоединений на
плате, что требует корректного применения этих терминов.
Самоиндукция и взаимная индуктивность
Отдельный проводник с током представляет собой идеализированную
картину. В этом случае число линий магнитного потока вокруг него было бы
легко рассчитать. Однако, когда есть токи в других близко расположенных
проводах, их линии магнитного потока могут окружать много других про-
водников с током. Рассмотрим два расположенных
рядом проводника, обозначенные а и Ь, как пока-
зано на рис. 2.43. Если бы ток был только в одном
проводе а, то имелось бы некоторое число силовых
линий вокруг него, что определяло бы его индук-
тивность.
Предположим, что некоторый ток протекает во
втором проводнике Ь. Тогда некоторые линии маг-
нитного потока от провода b охватывают первый про-
вод а. Поэтому вокруг провода а существуют линии
магнитного поля от его собственного тока и от тока
соседнего проводника Ь. В этом случае линии маг-
нитного потока от собственного тока проводника
определяют самоиндукцию, а от тока расположен-
ного рядом проводника — взаимоиндукцию.
Линии самоиндукции — это линии магнитного по-
тока вокруг проводника, которые возникают в резуль-
тате только его собственных токов. Линии взаимоиндукции — это линии маг-
нитного потока, полностью окружающие провод, которые являются результа-
том тока в другом проводнике.
Каждая линия магнитного потока, которая образуется проводником b и
идет вокруг провода а, должна охватывать оба проводника. Таким образом,
линии взаимной индукции «связывают» два проводника. Если мы удаляем
второй проводник от первого, то число линий взаимной индукции вокруг
обоих проводников уменьшится. При сближении число линий взаимной ин-
дукции увеличится.
Но что происходит с общим числом линий магнитной индукции вокруг
первого проводника? Если токи в проводниках имеют одинаковое направ-
лении, то направление линий магнитной индукции вокруг них будет одина-
ковое. Поэтому общее количество линий магнитной индукции вокруг пер-
вого проводника будет суммой собственных линий (самоиндукции) и линий
от второго проводника.
2.5. Физические основы индуктивности
183
Однако, если направление токов в проводниках противоположное, направ-
ления линий самоиндукции и взаимоиндукции вокруг первого провода бу-
дут противоположные. При этом количество линий взаимоиндукции вычи-
тается из линий самоиндукции, и общее число линий магнитной индукции
вокруг первого провода будет уменьшено в результате присутствия располо-
женного рядом провода с противоположным направлением тока.
Важно отметить, что индуктивность проводника есть в действительно-
сти его самоиндукция. Самоиндукция провода не зависит от наличия тока в
другом проводнике.
Взаимная индуктивность определяется как отношение числа линий маг-
нитного потока вокруг провода к току в один ампер в другом проводе. Еди-
ницы измерения взаимной индуктивности — генри.
Взаимная индуктивность имеет два очень необычных свойства. Первое
заключается в том, что взаимная индуктивность симметрична, т. е. для двух
проводников она не зависит от того, в каком проводнике течет ток, а также
от того, каковы размер или форма каждого провода.
Вторая особенность состоит в том, что взаимная индуктивность между лю-
быми двумя проводниками никогда не может быть больше, чем самоиндукция
любого из них. Каждая линия взаимной магнитной индукции от стороннего
проводника должна также быть линией самоиндукции того же проводника.
Так как взаимная индуктивность между двумя проводниками не зависит, от
какого проводника возбуждается поле, то она должна всегда быть меньше,
чем наименьшая самоиндукция из этих двух проводников.
Положение 3. Напряжение в проводнике индуцируется при изменении маг-
нитного потока, охватывающего проводник.
Особое свойство магнитного потока состоит в том, что, когда общее число
линий магнитного потока вокруг участка провода изменяется по любой при-
чине, возникает напряжение по всей длине проводника. Созданное напря-
жение непосредственно связано с тем, как быстро изменяется общее число
линий магнитного потока:
V=NL
At ’
где V— напряжение, индуцированное вдоль проводника; AN— число меняющихся линий
магнитного потока; At — время, за которое они изменяются.
Число линий магнитного потока вокруг провода определяется через его ин-
дуктивность и протекающий по нему ток: N = L х /, где L — самоиндукция
участка провода. Созданное (индуцированное) напряжение связано с индук-
тивностью провода и скоростью изменения тока в нем следующим образом:
AN _L Al _LdI
At At dt '
(2.49)
Индуцированное напряжение иллюстрирует важную роль индуктивности в
проблеме целостности сигнала.
184
Глава 2. Электрофизические параметры печатного монтажа
Рис. 2.44. Напряжение,
вызванное на одном про-
воднике (а) из-за изме-
няющегося тока в дру-
гом (Ь) проводнике
Индуцированное напряжение приводит к нежела-
тельным эффектам в линиях передачи, перекрестным
помехам, коммутационным помехам в шинах пита-
ния и заземления и другим электромагнитным явле-
ниям, нарушающим целостность сигнала.
В печатных платах ток, протекающий в одном
проводнике, наводит эдс индукции в другом про-
воднике (рис. 2.44). При этом обычно использует-
ся термин «наводка», описывающий помеху в смеж-
ном проводнике. В этом случае напряжение помех
Ип можно определить по формуле:
где М — взаимная индуктивность между двумя проводами; I — ток во втором проводе, из-
меняющийся за время t.
В реальной конструкции, когда существует значительное число провод-
ников разнообразной топологии, необходимо четко определять направления
всех токов, которые являются источниками магнитного потока.
2.5.2. Парциальная индуктивность
Ток всегда протекает по замкнутому контуру, хотя в предыдущем приме-
ре рассматривалась только часть проводника, по которому протекает ток.
Когда говорят о парциальной индуктивности, предполагается, что остальной
части контура не существует. Данное предположение не значит, что эта часть
контура игнорируется, но в понимании парциальной индуктивности прини-
мается, что не существует других токов, кроме рассматриваемой секции про-
водников. Концепция парциальной индуктивности есть сугубо математичес-
кая конструкция. Эта индуктивность не может быть измерена, поскольку
отсутствует возможность изолировать фрагмент проводника.
В реальной ситуации невозможно получить парциальный ток; всегда полу-
чают только полный ток контура. Однако концепция парциальной индуктив-
ности является эффективным инструментом для понимания и расчета других
свойств индуктивности, особенно, если неизвестно, какова оставшаяся часть
контура.
Парциальная индуктивность имеет две разновидности: парциальная са-
моиндукция и парциальная взаимная индуктивность. То, что рассматрива-
лось выше, составляет парциальную индуктивность секции двух проводни-
ков. Когда анализируют индуктивность вывода корпуса микросхемы, индук-
тивность соединительного штыря или печатного проводника, всегда имеют
дело с парциальной самоиндукцией соответствующего элемента межсоеди-
нений.
2.5. Физические основы индуктивности
185
Точное определение парциальной самоиндукции и взаимной индукции
базируется на математических расчетах числа линий магнитного потока,
сопряженных с определенной секцией проводника. Число линий магнитного
потока на I А тока в секции есть парциальная самоиндукция этой секции
проводника. Очевидно, если секцию сделать длиннее, парциальная индук-
тивность возрастет.
Если рядом с первой секцией расположить вторую секцию проводника,
то число линий магнитного потока на 1 А тока во втором сегменте, сопря-
женное с первым сегментом, и есть парциальная взаимная индуктивность
между двумя секциями.
Очевидно, что в реальной ситуации нет возможности создать обособлен-
ные секции проводников. Всегда приходится иметь дело с контуром тока, со-
держащем сигнальные проводники, по которым ток течет от драйвера к на-
грузке, и возвратные проводники, по которым ток течет от нагрузки к драй-
веру. Однако подобную абстракцию можно выполнить математически, но
нельзя проверить экспериментально. Тем не менее, парциальные индуктив-
ные параметры являются мощным инструментом для улучшения конструкции
платы и управления ее индуктивными параметрами, которые могут быть из-
мерены.
Существует только несколько геометрий проводников с корректной ап-
проксимацией для расчета парциальной самоиндукции [37, 41]. Парциаль-
ная самоиндукция L прямолинейного круглого проводника в воздушной среде
может быть рассчитана с точностью до нескольких процентов, используя про-
стую формулу:
£ = 0,2/
3
4
нГн,
(2.50)
где г — радиус провода, мм; / — длина провода, мм.
Например, для провода диаметром 0,2 мм и длиной 25 мм парциальная
самоиндукция равна:
£ = 0,2-25
2 • 25 Л 3
0,1 ) 4
= 27,5, нГн.
Полученный результат определяет полезное правило: парциальная самоин-
дукция провода составляет примерно 1 нГн/mm. Иногда полезно пожертвовать
точностью для получения оперативного решения.
Выше отмечалось, что парциальная самоиндукция возрастает при увели-
чении длины провода. Но из формулы (2.50) видно, что это увеличение идет
быстрее линейного, поскольку множитель в квадратных скобках содержит
параметр длины. Физически это объясняется взаимодействием магнитных
потоков секций при увеличении их числа.
Парциальная самоиндукция уменьшается при увеличении площади сечения про-
водника. Если радиус провода увеличить, нити тока раздвинутся, и парциальная
186
Глава 2. Электрофизические параметры печатного монтажа
самоиндукция уменьшится. При уменьшении плотности тока число линий
магнитного потока будет уменьшаться.
Важное свойство', приуменьшении плотности тока уменьшается парциальная
самоиндукция.
Для круглого провода парциальная самоиндукция изменяется обратно про-
порционально натуральному логарифму радиуса, что говорит о слабой зави-
симости от площади сечения. Для плоских проводников, например, для ши-
рокого ленточного проводника, парциальная самоиндукция более чувстви-
тельна к плотности тока. Это очень важное положение, которое говорит о
том, что минимальной индуктивностью будет обладать печатный проводник
максимальной ширины.
Оценим парциальную самоиндукцию некоторых элементов межсоединений.
Печатный проводник от конденсатора к металлизированному отверстию дли-
ной 1,25 мм имеет парциальную самоиндукцию 1 нГн/ммх1,25 мм = 1,25 нГн.
Металлизированное отверстие в плате толщиной 1,6 мм имеет парциальную са-
моиндукцию 1 нГн/ммх1,6 мм = 1,6 нГн. Эти значения приближенные, но дают
хорошую инженерную оценку на первых шагах проработки конструкции. В даль-
нейшем они могут быть уточнены аналитическими или численными методами.
Как уточненные расчеты, так и инженерные оценки парциальной самоиндук-
ции тонких проводов практически совпадают [4].
Парциальная взаимная индуктивность между двумя сегментами провод-
ников определяется числом линий магнитного потока от проводника одного
сегмента, которые сопрягаются с проводником другого сегмента. В общем случае,
парциальная индуктивность между двумя проводниками есть малая часть их пар-
циальной самоиндукции и резко уменьшается при разнесении проводников. Пар-
циальная взаимная индуктивность Ммежду двумя прямолинейными круглыми
проводниками приблизительно может быть рассчитана по формуле:
,, Л , (2М , d (d
М = 0,21 In — -1+-- —
UJ / <2/
, нГн,
(2.51)
где / — длина проводников, мм; d — расстояние между осями проводников, мм.
Эта формула учитывает эффекты второго порядка. Она может быть уп-
рощена при расстоянии между проводниками значительно меньшем, чем
длина проводников (J << /):
М = 0,21 In — -1 . нГн.
I d J
(2.52)
Это модель первого порядка, при которой игнорируются некоторые эф-
фекты взаимодействия проводников. На рис. 2.45 показаны сравнительные
расчеты взаимной индуктивности между двумя круглыми проводниками при
изменении межосевых расстояний. Видно, что при увеличении парциальной
взаимной индуктивности более чем на 20 % парциальной самоиндукции (т. е.,
когда взаимная индуктивность значительна), аппроксимация первого порядка
довольна хорошая.
2.5. Физические основы индуктивности
187
Рис. 2.45. Парциальная взаимная индуктивность между двумя круглыми проводниками
длиной Ю мм: / — модель первого порядка; 2 — модель второго порядка
Например, пусть каждое из двух проводных соединений длиной 10 мм име-
ет парциальную самоиндукцию 9 нГн. Если они расположены на расстоянии
1 мм друг от друга, то их взаимная парциальная индуктивность составит 4 нГн.
В этом случае при протекании тока в 1 ампер в одном проводе будет генери-
роваться 4 нГн х 1 А = 4 нВб линий магнитного потока, сцепленных с вто-
рым проводом. Отношение парциальной взаимной индуктивности двух про-
водов к их парциальной самоиндукции составляет примерно 50 % при ука-
занном выше разнесении.
Полезное правило (см. рис. 2.45)\ если расстояние между двумя проводнико-
выми сегментами больше их длины, их взаимная индуктивность составляет мень-
ше 10 % парциальной самоиндукции любого проводника и часто может быть иг-
норирована.
Концепция парциальной индуктивности является базовой для всех аспек-
тов оценки индуктивных параметров. Все другие формы индуктивности могут
быть описаны в терминах парциальной индуктивности. Модели корпусов и
соединительных элементов базируются на парциальной индуктивности. Мо-
делирование и расчет 3D и SPICE на самом деле оперируют парциальной ин-
дуктивностью.
При оптимизации конструкции и ее индуктивных параметров использует-
ся представление о парциальной индуктивности.
2.5.3. Эффективная индуктивность проводников
Рассмотрим контур, образованный проводниками, как показано на рис.
2.46. Эта конфигурация обычна для всех линий передач, шин питания и за-
земления. Пара проводников может быть рядом расположенными сигналь-
ным и возвратным выводами в корпусе интегральной схемы, или они могут
быть сигнальным проводником и плоскостью заземления, которая служит
возвратным проводником в печатной плате.
188
Глава 2. Электрофизические параметры печатного монтажа
Проводник b
Рис. 2.46. Контур, содержа-
щий прямой и обратный
проводники
Проводник а Если по контуру протекает ток, то линии маг-
нитного потока замыкаются вокруг каждого из
этих двух проводников. Если поменять направ-
ление тока в контуре, то направление линий маг-
нитного потока вокруг каждого проводника из-
менится. Напряжение, индуцированное в каж-
дом проводнике, зависит от того, как быстро
изменяется общее количество линий магнитного
потока, сопряженных с этими проводниками.
Поскольку токи в проводнике а и b протекают в противоположных направ-
лениях, общее число линий магнитного потока, замыкающихся вокруг этой
части контура, есть разность между магнитными потоками двух проводни-
ков. Это при токе в контуре 1 ампер определяет эффективность индуктив-
ность части контура.
Эффективная индуктивность части контура — это общее количество ли-
ний магнитного потока, замыкающихся вокруг только этой части, при токе в
контуре один ампер.
Можно определить эффективную индуктивность одного проводника в при-
сутствии второго проводника, основываясь на понятии парциальной индук-
тивности одиночного проводника. Обозначим парциальную собственную ин-
дуктивность проводников La и Lb. Взаимную парциальную индуктивность
обозначим Lab. Ток в каждом проводнике, одинаковый по значению, но про-
тивоположный по направлению, обозначим I.
Вокруг проводника b существует Nb = ILb линий магнитного потока от его
собственного тока. В то же время некоторые из линий магнитного потока,
замыкающиеся вокруг проводника Ь,— это линии магнитного потока от тока
в проводнике а. Число линий, приходящих от проводника а и замыкающихся
вокруг проводника Ь, равно:
N,=L,-I. (2.53)
ab ab у 7
Так как ток в проводнике а движется в направлении, противоположном
направлению тока в проводнике Ь, линии потока от тока в проводе а, замы-
кающиеся в проводнике Ь, будут направлены противоположно линиям по-
тока, возникающим от тока в этом проводнике. Поэтому общее число линий
магнитного потока, замыкающихся вокруг проводника Ь, равно:
^=Nb-Nab=(Lb-Lab)-I. (2.54)
Это полное число линий магнитного потока вокруг проводника Ь, образу-
ющихся из-за тока в контуре, на которое оказывают влияние токи всех сег-
ментов контура. Разность (Lb — Lab) назовем эффективной индуктивностью
проводника Ь. Она определит напряжение, которое будет создано в одном про-
воднике контура при изменении тока в нем. Когда один из проводников — про-
водник возвратного тока, тогда напряжение, созданное на нем, называется на-
пряжением «подскока» напряжения заземления.
2.5. Физические основы индуктивности
189
Напряжение «подскока» заземления, возникающее в возвратном провод-
нике, равно:
TZ Г di /г г \dl
V^ = ^ = (Lb~Lab^ (2.55)
где Hgb — напряжение подскока напряжения заземления; — эффективная индуктивность
только возвратного проводника; 1 — ток в контуре; Lb — парциальная собственная индук-
тивность возвратного проводника; Lab — парциальная взаимная индуктивность между воз-
вратным проводником и прямым проводником.
Если цель состоит в том, чтобы минимизировать падение напряжения на
возвратном проводнике, то есть только два подхода. Первый заключается в
уменьшении скорости изменения тока в контуре. Это достигается снижением
граничной частоты спектра сигнала за счет увеличения его фронта.
Второй подход состоит в том, что следует найти все возможные способы
для уменьшения эффективной индуктивности Для этого существует только
два варианта: уменьшить парциальную собственную индуктивность провод-
ника и увеличить парциальную взаимную индуктивность между двумя про-
водниками. Уменьшение собственной индуктивности достигается за счет уко-
рочения и увеличения ширины проводника, насколько это возможно (в МПП
используется вся плоскость слоя платы для возвратного проводника). Уве-
личение взаимной индуктивности между прямым и возвратным проводни-
ком достигается их возможным сближением.
Подскок напряжения заземления — это напряжение между двумя точками
в контуре заземления, между которыми меняется ток. Подскок напряжения
заземления является основной причиной коммутационных помех и радиопомех.
Он, прежде всего, связан с эффективной индуктивностью возвратного провод-
ника. Для уменьшения уровня подскока напряжения заземления есть два основ-
ных пути: уменьшить парциальную собственную индуктивность возвратного
проводника, используя короткие и широкие соединительные проводники, или уве-
личить частичную взаимную индуктивность между двумя проводниками.
При сближении проводников эффективная индуктивность составляет:
L^ = Lb — Lab, и при увеличении взаимной парциальной индуктивности она
уменьшается.
Рассмотрим пример. Если используется провод диаметром 0,025 мм, то
парциальная самоиндукция при длине провода 2,5 мм составляет 2,5 нГн.
Когда расстояние между центрами проводников составляет более 2,5 мм, то
парциальная взаимная индуктивность будет меньше 10 % от парциальной са-
моиндукции, и индуктивность одного провода примерно равна его парци-
альной самоиндукции (в случае его автономного рассмотрения). Когда про-
водники сближаются на расстояние 0,125 мм между центрами, взаимная
индуктивность увеличивается, что приводит к снижению эффективной ин-
дуктивности одного провода до 1,3 нГн, т. е. она снижается примерно на 50 %.
Меньшая индуктивность вызывает меньшее падение напряжения на ней и
уменьшает помехи, связанные с подскоком напряжения.
190
Глава 2. Электрофизические параметры печатного монтажа
При эффективной индуктивности 2,5 нГн и приращении тока в этом про-
воднике 100 мА за 1 нс (достаточно типичное значение для линий передач),
уровень подскока напряжения заземления составляет
Kgb = 2,5 нГн х 0,1 А/1 нс = 250 мВ.
Это уровень помехи. При индуктивности 1,3 нГн напряжение помех ста-
новится равным
Kgb= 1,ЗнГнх0,1 А/1 нс = 130 мВ,
т. е. значительно меньше.
Важное правило', сближение прямого и обратного провода приводит к сни-
жению эффективной индуктивности провода.
Рассмотрим другой случай. Предположим, что оба провода несут ток в
одном направлении. Отметим, что при этом токи по проводникам протека-
ют от независимых источников. Что произойдет, если в этом случае сближать
провода (выводы)?
В этом случае токи в проводах текут в одинаковых направлениях, их маг-
нитные поля ориентированы одинаково, и поток от второго провода добав-
ляется к потоку первого провода. Эффективная индуктивность одного про-
вода будет равна
(2.56)
Если целью является снижение эффективной индуктивности выводов
питания, то при конструировании следует уменьшать насколько возможно
парциальную самоиндукцию провода и парциальную взаимную индуктив-
ность проводов. Это достигается увеличением сечения провода и максималь-
ным разнесением проводов друг от друга.
На рис. 2.47 показаны зависимости индуктивных параметров одного из пары
проводов длиной 2,5 мм, которые несут одинаковые и противоположные токи.
Рис. 2.47. Индуктивные параметры одного провода длиной 2,5 мм в присутствии
второго провода при различных направлениях токов в них: 1 — парциальная
самоиндукция; 2 — парциальная взаимная индукция; 3 — общая индуктивность (токи
одного направления); 4 — общая индуктивность (токи противоположного направления)
2.5. Физические основы индуктивности
191
VL, У=0
Рис. 2.48. Расположе-
ние металлизирован-
ных отверстий на кон-
тактных площадках
развязывающего кон-
денсатора: вверху —
традиционное реше-
ние; внизу — оптими-
зированное для сниже-
ния индуктивности и
уровня помех по пита-
нию и заземлению
Чем больше разнесены провода и чем больше их длина, тем меньше их эф-
фективная индуктивность отличается от парциальной собственной индук-
тивности. При сближении проводов эффективная индуктивность снижает-
ся при протекании токов в противоположных направлениях и увеличивает-
ся при протекании токов в одном направлении.
Полезное правило: для минимизации общей индуктивности каждого провод-
ника в системе питания следует по возможности разносить параллельные токи
одного направления на максимальное расстояние, а параллельные токи различ-
ного направления следует сближать на минимальное расстояние.
В качестве примера рассмотрим металлизирован-
ное отверстие, которое соединяет контактную пло-
щадку для установки развязывающего конденсатора
с плоскостью питания Исс и плоскостью возвратных
токов У = 0, как показано на рис. 2.48. Расстояние
между слоями составляет 0,5 мм, а диаметр металли-
зированных отверстий — 0,25 мм, расстояние s2 боль-
ше длины отверстия, а расстояние 5! меньше длины
отверстия. Использование параллельных металлизи-
рованных отверстий имеет ряд преимуществ.
Если расстояние s между центрами отверстий
больше длины отверстия (0,5 мм), их парциальная
взаимная индуктивность будет очень мала, и они не
будут взаимодействовать. Общая индуктивность каж-
дого отверстия будет фактически равна собственной
парциальной индуктивности. При наличии ряда па-
раллельных отверстий, которые соединяют контак-
тную площадку с плоскостями питания и заземления,
будет снижена общая индуктивность соединения про-
порционально числу отверстий. Чем большее число
параллельных отверстий будет в соединении, тем
меньше будет эквивалентная индуктивность. Парци-
альная индуктивность металлизированного отверстия
приведена на рис. 2.39.
На рис. 2.48 значение s2 должно быть, по край-
ней мере, более 0,5 мм. Аналогично, если это возможно, отверстия с проти-
воположными токами должны быть расположены на минимальном рассто-
янии друг от друга. При расстоянии между отверстиями меньше длины этих
отверстий эффективная индуктивность уменьшится. По возможности раз-
мер должен быть меньше 0,5 мм.
Полезное правило', для минимизации общей индуктивности пути протека-
ния тока расстояние между центрами металлизированных отверстий, по ко-
торым протекает ток одного направления, должно быть, по крайней мере, больше
длины отверстия; при протекании в отверстиях токов противоположных на-
правлений расстояние между центрами отверстий должно быть меньше дли-
ны отверстия и чем меньше, тем лучше.
192
Глава 2. Электрофизические параметры печатного монтажа
2.5.4. Собственная и взаимная индуктивность контура
Собственная индуктивность замкнутого контура с током, или самоиндук-
ция контура, определяется как общее число линий магнитного потока, по-
рожденных в замкнутом контуре с током в 1А, которые распределены по всем
участкам контура.
Для замкнутого контура с двумя проводниками а и b (токи текут в них в
противоположных направлениях (см. рис. 2.46) его собственная индуктив-
ность определяется по формуле
L = L - L. + Lh - L. = L+ Lh- 2Lh, (2.57)
a ab b ab a b ao> v 7
где La — частичная самоиндуктивность проводника a; Lb — частичная самоиндуктивность
проводника b\ Lah — частичная взаимная индуктивность между проводниками а и Ь.
Эти отношения показывают, что при сближении проводников индуктив-
ность контура уменьшается, поскольку взаимная частичная индуктивность
возрастает, а частичная самоиндукция остается неизменной.
Часто для снижения индуктивности контура требуют уменьшать его пло-
щадь. Это в общем случае верно, но только частично. Площадь действительно
определяет общее число линий магнитного потока контура, окружающих
каждый проводник. Но, кроме площади, большое значение имеет форма
контура и взаимное расположение проводников, которые образуют его.
Для примера на рис. 2.49 показаны два различ-
(j ных контура, площади которых одинаковы. Они
--------► будут иметь различную индуктивность, так как ча-
Г стичная взаимная индуктивность между провод-
никами различна. Чем ближе располагаются про-
А А водники с противоположным направлением тока,
тем больше их частичная взаимная индуктивность
и меньше результирующая индуктивность контура.
Как видно, основной механизм уменьшения самоин-
В s дукции контура заключается в увеличении частич-
ной взаимной индуктивности между прямым и об-
1 ратным проводом за счет их сближения. Конечно,
Рис 2 49 Два конт а п?и этом следует уменьшать и площадь контура.
одинаковой площади, Есть Две важных геометрии контуров, которые
но с различной имеют хорошие аналитические приближения для
индуктивностью расчета индуктивности контура: круглый и прямо-
угольный.
Для круглого контура индуктивность определяется по формуле:
Г
Z = l,26r lnl — I, нГн, (2.58)
где г — радиус контура, мм; d — диаметр провода, из которого сформирован контур, мм.
Например, провод диаметром 0,2 мм, который образует круговой контур
с радиусом 20 мм, имеет индуктивность 151,2 нГн.
2.5. Физические основы индуктивности
193
Как видно из формулы, индуктивность контура имеет нелинейную зави-
симость от его площади или периметра. Она пропорциональна натурально-
му логарифму от радиуса контура. Чем больше периметр, тем больше частич-
ная самоиндукция каждой секции, на которые можно разбить периметр кон-
тура, но при этом отдаляются токи противоположного направления в контуре,
а следовательно, снижается их взаимная индуктивность.
Однако индуктивность контура приблизительно пропорциональна радиусу
контура. Если периметр контура увеличить, то его индуктивность увеличится.
Для рассмотренного примера длина окружности при радиусе контура 2 см
составляет 12,56 см. При этом удельная индуктивность кругового контура бу-
дет 151,2/12,56 =12,0 нГн/cm. Это значение можно принять как инженерную
оценку удельной индуктивности кругового контура.
Прямоугольный контур (рис. 2.49В), имеющий два протяженных сбли-
женных проводника круглого сечения, обладает индуктивностью
/25^
Л = 0,4/-1п1 — I, нГн, (2.59)
где / — длина проводников, мм; 5 — расстояние между осями проводников, мм; d — диа-
метр провода, мм.
Например, индуктивность контура из провода диаметром 0,2 мм, длиной
20 мм и шириной 0,25 мм, составляет 7,3 нГн, т. е. 3,65 нГн/см.
Это соотношение показывает: индуктивность контура, содержащего два
параллельных провода, прямо пропорциональна длине проводников. Она уве-
личивается пропорционально натуральному логарифму расстояния между
проводниками.
В случае, когда сечение сигнального и возвратного проводов постоянно
по длине, индуктивность может быть рассчитана на единицу длины, как
показано выше.
Для контуров произвольного сечения индуктивность можно рассчитать
по методикам, изложенным в [41].
2.5.5. Система электропитания и индуктивность
контура питания
Ряд важных задач обеспечения качества функционирования цифровых
узлов на печатных платах связан с контуром системы электропитания и за-
земления. При конструировании платы должна быть обеспечена предельно
низкая индуктивность этого контура.
Система электропитания должна вырабатывать постоянное напряжение
для питания микросхем, а шины питания и заземления должны обеспечи-
вать подачу этого напряжения на соответствующие выводы микросхем. В за-
висимости от серии микросхем номинальное напряжение питания может
составлять от 5 до 3,3 В или 2,4 В. Микросхемы серии ЭСЛ требуют отрица-
тельного напряжения питания.
7 1527
194
Глава 2. Электрофизические параметры печатного монтажа
Особое внимание следует уделять уровню помех в системе питания, ко-
торые в большинстве случаев проявляются в виде пульсаций. Как правило,
уровень помех должен быть не более 5% от номинального значения напря-
жения питания. К сожалению, стабилизатор источника питания не в состо-
янии устранить изменения напряжения питания, вызванные влиянием ин-
дуктивности выводов питания и заземления микросхем, шин питания и за-
земления, металлизированных отверстий и других топологических элементов
платы на пути тока от стабилизатора до кристалла микросхемы и обратно.
При изменении тока в шине питания на ее индуктивности возникает па-
дение напряжения, вызывающее провал питающего напряжения на соответ-
ствующих выводах микросхем. Чтобы привести к минимуму этот провал, не-
обходимо поддерживать полное сопротивление системы электропитания ниже
определенного значения. Если полное сопротивление будет достаточно низ-
ким, то снижение падения напряжения может быть поддержано ниже 5% раз-
решенной пульсации.
Малое полное сопротивление шины питания обеспечивается двумя приема-
ми: добавлением развязывающих конденсаторов для удержания низкого полно-
го сопротивления на низких частотах и уменьшением индуктивности контура
между развязывающими конденсаторами и контактными площадками микро-
схем для удержания низкого полного сопротивление на высоких частотах.
Более детально проектирование шин питания и заземления, а также тре-
бования к развязывающим конденсаторам, их выбору и установке рассмот-
рены в главе 5.
2.5.6. Индуктивность контура с прямоугольными
пластинами
Индуктивность контура, в котором путь тока проходит по плоскостям сло-
ев печатной платы (рис. 2.50), зависит от парциальной самоиндукции каждой
плоскости и взаимной парциальной индуктивности между этими плоскостями.
Расширение плоскости, что способствует более свободному распределению нитей
тока в ней, снижает ее парциальную самоиндукцию и снижает индуктивность
контура. Удлинение плоскости увеличивает ее парциальную самоиндукцию и
увеличивает индуктивность контура. Сближение плоскостей увеличивает пар-
циальную взаимную индуктивность и
снижает индуктивность контура. Кон-
тур, содержащий пластины, — хорошая
модель контура питания в МПП, когда
слой питания и слой возвратных токов
расположены рядом.
Индуктивность контура, содержа-
щего два проводника (пластины), у ко-
торых ширина w существенно больше
расстояния h между ними, определя-
ется приближенной формулой:
/
h
Рис. 2.50. Геометрия пути тока, проте-
кающего по слоям платы; направление
прямого тока противоположно направ-
лению обратного тока
2.5. Физические основы индуктивности
195
г , /
L = [ioh-, нГн, (2.60)
W
где ц() — магнитная постоянная 1,256 мкГн/м; h — расстояние между плоскостями, м; / —
длина плоскостей, м; w — ширина плоскостей, м.
Если рассматривается квадратная пластина, т. е. w = /, то отношение этих
параметров равно 1, и поэтому индуктивность в этом случае не зависит от
ширины и длины. Поэтому часто удобно использовать определение индук-
тивности на единицу площади.
При установке тонкой диэлектрической прокладки между квадратными
проводящими пластинами толщиной, например 0,05 мм, приближенная
оценка индуктивности контура, содержащего квадратные пластины, дает
следующее значение:
L =1,256 мкГн/м х 5-Ю"5 м = 6,2864-10-5 мкГн = 63 пГн.
При увеличении толщины диэлектрической прокладки индуктивность
контура увеличивается и уровень помех увеличивается.
Полезное правило', расстояние между сигнальной плоскостью и плоскостью
заземления или питания должно быть по возможности меньше для снижения
индуктивности контура и уменьшения уровня помех.
2.5.7. Индуктивность контура и переходные отверстия
Выше рассматривалось равномерное распределение тока по ширине плос-
кости. Однако ток в плоскостях не течет строго от одного конца плоскости
к другому. На плоскости имеются много точек контакта, в которых проис-
ходит концентрация тока: контакты выводов микросхем и конденсаторов,
переходные отверстия. Если ток концентрируется в точке контакта (рис. 2.51),
то индуктивность контура увеличивается.
Рис. 2.51. Концентрация тока около переходных отверстий
7
196
Глава 2. Электрофизические параметры печатного монтажа
Точный расчет индуктивности в этом случае может быть выполнен толь-
ко с применением специальных программных средств. Поэтому часто исполь-
зуют некоторые приближения, которые приемлемы в инженерной практи-
ке. Рассмотрим пример, когда исходный вариант усложняется включением
двух переходных отверстий на концах квадратных плоскостей, через кото-
рые протекает ток контура [4]. Отверстия имеют диаметр 0,25 мм, и рассто-
яние между их центрами составляет 0,625 мм, подобно тому, как выполне-
ны отверстия в печатной плате.
На рис. 2.52 показано распределение тока в сплошной пластине и в пла-
стинах с переходными отверстиями (более темные участки соответствуют
большей плоскости тока) [4]. Видно, что при наличии переходных отверстий
ток концентрируется около них, что способствует увеличению индуктивно-
сти. Приближенное решение для пластин без отверстий (рис. 2.52а), полу-
ченное по (2.60), дает значение индуктивности 63 пГн, а экспериментальное
значение составляет 62 пГн. Видно, что рассмотренная для этого варианта
аппроксимация вполне приемлема.
Во втором случае при протекании тока по пластинам и переходным от-
верстиям (рис. 2.520 индуктивность контура составляет 252 пГн, что в 4 раза
выше, чем для однородной плоскости. При меньшей области концентрации
тока индуктивность увеличивается в меньшей степени.
Полезное правило: индуктивность контура, содержащего пластины с метал-
лизированными переходными отверстиями диаметром 0,25мм, примерно в 4раза
больше индуктивности аналогичного контура с однородными пластинами.
Индуктивность контура, ассоциируемого с развязывающим конденсато-
ром, будет в основном определяться индуктивностью, вызванной концент-
рацией тока, а не расстоянием между кристаллом и конденсатором. В пер-
вом приближении, общая индуктивность контура конденсатора слабо зависит
от степени приближения к кристаллу. Устанавливая развязывающий конден-
сатор близко к мощному кристаллу, высокочастотные токи в возвратной
плоскости могут быть локализованы около кристалла. Это будет минимизи-
ровать напряжение подскока заземления, которое может привести к поме-
хам общего вида на внешних кабелях и нарушить ЭМС.
а б
Рис. 2.52. Распределение тока в сплошной пластине (а) и при наличии в ней
переходных отверстий (б)
2.5. Физические основы индуктивности
197
2.5.8. Индуктивность контура с плоскостями,
содержащими матрицу отверстий
с гарантированным шагом
Во многих конструкциях печатных плат на проводящих слоях использу-
ется матрица отверстий, расположенных с определенным шагом. Примером
может служить компоновка корпусов BGA, набор контактов соединителя и
др. Эти отверстия в медном слое покрывают плоскости питания и заземле-
ния и необходимы для того, чтобы избежать контакта с металлизированны-
ми отверстиями. Необходимо знать, как они влияют на индуктивные пара-
метры контура, включающего плоскости.
В первом приближении следует ожидать, что индуктивность увеличится.
Но насколько? Ответить на этот вопрос можно, только проведя точные вы-
числения с помощью специальных программных средств.
Рассмотрим вначале две одинаковые плоскости, каждая со стороной 6,25 мм,
разделенные расстоянием 0,05 мм, которые содержат два отверстия (рис. 2.53я).
С одной стороны отверстия закорочены плоскостью. Ток в контур поступает через
левое отверстие, протекает по нижней плоскости, выходит через правое отвер-
стие. Верхняя плоскость, которая видна на рисунке, является плоскостью воз-
вратных токов.
В другой паре плоскостей матрица отверстий создана в каждой плоско-
сти. Каждое отверстие имеет диаметр 0,5 мм и расстояние между центрами
0,625 мм (рис. 2.53d). Поэтому открытая область составляет примерно 50 %
от общей плоскости пластин. Для каждого из двух случаев распределение тока
было рассчитано при помощи ЗБ-программ [4] и показано на рис. 2.53. Видно,
что при наличии матрицы отверстий ток стягивается в узкие каналы между
отверстиями, что приводит к увеличению индуктивности.
Расчеты дают значения индуктивности 192 пГн с двумя отверстиями и
243 пГн при матрице отверстий, т. е. индуктивность увеличивается примерно
а б
Рис. 2.53. Распределение тока в плоскостях при наличии (а) и при отсутствии (6) отвер-
стий (светлые области соответствуют более высокой плотности тока)
198
Глава 2. Электрофизические параметры печатного монтажа
на 25 % и на 50 % относительно однородной области. Для снижения индук-
тивности диаметр отверстий должен быть по возможности меньше, и, конеч-
но, плоскости должны быть как можно ближе.
Важно отметить, что любые отверстия и щели в плоскостях, нарушающие
равномерность распределения тока, приводят к увеличению индуктивности.
Оптимальными соединениями питания и заземления для снижения индуктив-
ности являются плоскости максимально возможной ширины, расположенные
на минимальном расстоянии друг от друга. Когда используется очень тонкий
диэлектрик между плоскостями, то индуктивность контура между корпусом
развязывающего конденсатора и контактной площадкой кристалла уменьша-
ется. Это снижает уровень помехи по шинам питания и способствует ЭМС.
При повышении быстродействия требования к необходимости примене-
ния диэлектриков с минимальной толщиной повышаются.
2.5.9. Взаимная индуктивность контуров
Если имеется два независимых контура тока, то между ними существует
взаимная индуктивность. Взаимная индуктивность есть число линий магнит-
ного потока, вызванных током в один ампер в одном контуре, которые ох-
ватывают провод с током второго контура.
При изменении тока в одном контуре создаваемое напряжение в другом
контуре составляет
Vn=M^’ (2-61)
где Vn — индуцированное напряжение в одном контуре; М— взаимная индуктивность между
двумя контурами; di/ dt — скорость изменения тока в другом контуре.
Напряжение помех возникает только в том случае, когда происходит из-
менение тока. Помехи этого типа называются помехами переключения, или
синхронными коммутационными помехами. В ряде источников встречает-
ся термин «помехи типа дельта /».
Наиболее важно для снижения уровня коммутационных помех уменьшать вза-
имную индуктивность между контурами. Это может быть достигнуто раз-
несением контуров. Взаимная индуктивность между контурами не может быть
больше, чем собственная индуктивность меньшего контура. Поэтому для сни-
жения взаимной индуктивности необходимо снижать собственную индуктив-
ность контуров.
Взаимная индуктивность определяет уровень перекрестных помех меж-
ду сигнальными проводниками. Эта проблема обсуждается в главе 4.
2.5.10. Индуктивность нескольких элементов
Парциальная индуктивность ассоциируется с одиночным элементом меж-
соединения, который имеет два контакта. Результирующий контур содержит
последовательно соединенные эти элементы. Для двух отдельных индуктив-
2.5. Физические основы индуктивности
199
ц
Рис. 2.54. Топология
формирования пар-
циальной индуктив-
ности: последова-
тельная (наверху) и
параллельная (внизу)
ных элементов межсоединений возможны два спосо-
ба соединения: «конец с началом» (последовательно),
«начало с началом и конец с концом» (параллельно).
Эти две конфигурации показаны на рис. 2.54.
После соединения новый элемент имеет два выво-
да и некоторую эквивалентную индуктивность. При
последовательном соединении для начала примем за эк-
вивалентную индуктивность сумму двух парциальных
собственных индуктивностей. Но каково проявление
взаимной индуктивности? Учет взаимной индуктивно-
сти делает определение эквивалентной индуктивности
более сложным. Для последовательной комбинации двух
парциальных индуктивностей результирующая индук-
тивность L^. определяется по формуле:
4enes=^ + ^ + 2£l2- (2.62)
Эквивалентная индуктивность £parallel при параллельном включении пар-
циальных индуктивностей:
т _ ^1^2 —
parallel“£1+Z2-2£l2’ (2’62)
где £, — парциальная самоиндукция одного элемента; £2 — парциальная самоиндукция
другого элемента; Ln — парциальная взаимная индуктивность между элементами.
Когда парциальная взаимная индуктивность равна 0, а парциальная са-
моиндукция одинакова, то это приводит к хорошо известным выражениям
для включения двухполюсников: при последовательном включении суммар-
ная индуктивность равна удвоенному значению самоиндукции элемента, а
при параллельном включении — половине самоиндукции элемента.
При одинаковой самоиндукции двух элементов и при наличии взаимной
индуктивности £12 = Л/получаем для последовательного включения
Series = 2(£ + М),
а при параллельном включении:
^parallel — ’
где L — парциальная самоиндукция каждого элемента; М— взаимная индуктивность элементов.
Если целью является снижение эквивалентной индуктивности двух па-
раллельных путей тока, необходимо снизить до возможного уровня взаим-
ную индуктивность между ними путем разнесения.
2.5.11. Вихревые токи и индуктивность
При высокочастотном изменении тока в одном проводнике во втором
проводнике за счет взаимной индукции возникает некоторое напряжение.
Это напряжение вызывает ток в проводнике, т. е. изменение тока в одном
200
Глава 2. Электрофизические параметры печатного монтажа
проводнике вызывает изменение тока в другом. Будем называть токи во втором
проводнике вихревыми.
Геометрия контура влияет на вихревые токи, которые, в свою очередь, вли-
яют на самоиндукцию проводника и самоиндукцию контура тока. Геометрия про-
является, когда контур является достаточно большой проводящей поверхнос-
тью, например, слоем фольги платы или стороной металлического корпуса.
Простейший пример проявления вихревых токов можно рассмотреть при
расположении круглого проводника над металлической поверхностью. Важ-
но иметь в виду, что металлическая поверхность может быть некоторым про-
извольным проводником, в котором может развиваться напряжение. Потен-
циал проводящей плоскости не имеет значения. Когда ток протекает в про-
воде, некоторое число линий магнитного потока от этого тока пересекает
проводящую плоскость. Это определяется взаимной индуктивностью между
проводом и плоскостью. При изменении тока в проводе в плоскости наводятся
вихревые токи, которые, в свою очередь, создают свои магнитные поля.
Наведенные токи располагаются в плоскости точно под проводом, как бы
представляя обратный проводник (рис. 2.55). Это «зеркальное изображение»
тока, которое принимается во внимание при расчете электрических и маг-
нитных полей [37]. Суммарное магнитное поле от реального провода и его
изображения будет сформировано так, как будто отсутствует проводящая
плоскость, и только прямой и обратный проводники создают магнитные поля
различного направления.
Поскольку направление токов и векторов магнитных полей противополож-
но, суммарное поле есть разность полей прямого и обратного провода. Это
приводит к неожиданному эффекту уменьшения парциальной самоиндукции
провода. Если ток распределен вблизи поверхности плоскости, которая не имеет
электрического контакта с контуром, то это будет уменьшать индуктивность
контура. Чем ближе провод к плоскости, тем больше эффект от вихревых то-
ков и ниже парциальная самоиндукция провода. На рис. 2.56 показано распре-
деление тока в проводе и вихревых токов в плоскости на частоте 1 МГц.
В печатном проводнике два про-
водника прямоугольного сечения
представляют собой сигнальный и
возвратный проводники линии пе-
редачи, которая имеет некоторую
удельную (на единицу длины) само-
индукцию. Если однородная прово-
Реальный
ток
__Проводящая
плоскость
Изображение
тока
Рис. 2.55. Зеркальное изображение
провода относительно реального
Рис. 2.56. Распределение тока на частоте
1 МГц в круглом проводнике над металли-
ческой поверхностью и вихревых токов в
ней (темные участки соответствуют боль-
шей плотности тока)
2.5. Физические основы индуктивности
201
Рис. 2.57. Распределение токов в печатном монтаже и зависимость самоиндукции
контура проводников в зависимости от расстояния до плоскости
дящая плавающая (с произвольным потенциалом) плоскость расположена
рядом с проводниками, самоиндукция контура будет уменьшена за счет вих-
ревых токов в плоскости. На рис. 2.57 показано распределение токов в пе-
чатном монтаже и зависимость самоиндукции контура проводников в зави-
симости от расстояния до плоскости.
В этом примере ширина проводников 0,125 мм и расстояние до плоско-
сти 0,250 мм. Интервал между внутренними краями проводников 0,5 мм.
Как видно, вихревые токи играют заметную роль, если расстояние до пла-
вающей плоскости меньше, чем зазор между проводниками. Присутствие близко
расположенной проводящей плоскости всегда уменьшает самоиндукцию контура.
Завершая рассмотрение индуктивности в печатном монтаже, следует сде-
лать одно важное замечание. В большинстве случаев при корректном про-
ектировании печатных плат формируется система близко расположенных
прямых (сигнальных) и возвратных проводников, образующих линию пере-
дачи. Для нее справедливо соотношение:
(2.64)
где Lt — индуктивность линии на единицу длины; С; — емкость линии на единицу длины;
ц, е — соответственно абсолютная магнитная и диэлектрическая проницаемость среды, в
которой расположены прямой и возвратный проводники.
При неизменных параметрах среды произведение (2.64) постоянно, что по-
зволяет определить значение удельной индуктивности следующим образом:
Ll=\iz/ СГ (2.65)
Это позволяет во многих случаях, представляющих практический инте-
рес, определять индуктивность, опираясь только на знание методов расчета
электрической емкости. Детально параметры линий передачи рассматрива-
ются в следующей главе.
Глава 3
Линии передачи в печатном
монтаже
3.1. Линии передачи и их модели
3.1.1. Модели линии передачи
Подлинней передачи понимается система прямых и обратных проводников
достаточной протяженности, расположенных в непосредственной близости друг
от друга, формирующих единое электромагнитное поле, которое распростра-
няется в этой системе преимущественно от источника к приемнику. Сумма то-
ков прямых проводников равна сумме токов обратных проводников (рис. 3.1).
Модель элементарного отрезка линии передачи на сосредоточенных иде-
альных элементах показана на рис. 3.2.
В линиях передачи, которые формируются на печатных платах, распро-
страняются плоские электромагнитные волны — Т-волны, поскольку раз-
меры поперечного сечения линий различных конструкций, которые могут
быть реализованы на платах, значительно меньше минимальных длин волн
Источник
Ток прямой
Ток возвратный
Сигнальный провод
Приемник
Возвратный провод
Длина
Рис. 3.1. Линия передачи из двух любых протяженных проводников
Рис. 3.2. Обобщенная модель элементарного отрезка линии передачи
3.1. Линии передачи и их модели
203
даже на частотах в единицы гигагерц. «Прямой» ток или проводник означа-
ет направление от источника к приемнику, а «обратный» — от приемника к
источнику. Аналогично падающая электромагнитная волна распространя-
ется от источника к приемнику, а отраженная волна — от приемника к ис-
точнику. В общем случае линия передачи может быть с произвольным чис-
лом прямых и обратных проводников. В составе печатных плат в качестве
обратного проводника может выступать слой питания или заземления. По-
этому линии можно классифицировать на двух-, трех- и многопроводные.
Рассмотрим более детально модель элементарного отрезка линии передачи,
которая представлена на рис. 3.2. Как видно, она состоит из последовательно-
го соединения сопротивления R и индуктивности L и параллельного соедине-
ния проводимости Gm емкости С. Совокупность этих идеальных параметров на-
зывается первичными электрическими параметрами линии, они детально рассмот-
рены в главе 2. Здесь же подчеркнем наиболее важные моменты.
Сопротивление Охарактеризует активные потери в линии. Оно содержит
две составляющие. Первая представляет собой сопротивление постоянно-
му току или токам низкой частоты. Вторая составляющая определяется со-
противлением на высоких частотах, при которых начинает проявляться скин-
эффект. В этом случае ток протекает по скин-слою, и понятие «высокая ча-
стота» относится к частотам, при которых толщина скин-слоя будет меньше
толщины проводника, которая для печатного монтажа определяется толщиной
фольги 35 мкм или 17,5 мкм.
Индуктивность L определяется конструкцией линии и применяемыми ма-
териалами. Для снижения индуктивности линии в ней не должно применяться
магнитных материалов. Кроме этого, наличие магнитных материалов при-
водит к нежелательному снижению скорости распространения электромаг-
нитной волны в линии.
Электрическая емкость Сопределяется также конструкцией линии и при-
меняемыми материалами. Для шин питания эта емкость должна быть по
возможности больше, а для сигнальных линий — по возможности меньше
или определяемой из заданного волнового сопротивления.
Проводимость Gопределяется утечками в изоляционном материале линии.
Для современных изоляционных материалов, которые применяются при со-
здании печатных плат, токи утечки весьма малы, что позволяет пренебречь этим
параметром. Однако на высоких частотах (сотни мегагерц) потери в диэлект-
рике становятся заметными и начинают влиять на целостность сигнала.
До частот примерно 1 ГГц линию передачи рассматривают как линию без
потерь, т.е. принимают R = 0; G= 0. Погонная емкость С, и погонная индук-
тивность Zz образуют волновое сопротивление — вторичный электрический
параметр'.
Значение волнового сопротивления для линий передачи на печатных платах
может быть реализовано в диапазоне 40... 120 Ом, но общепринято выполнять
204
Глава 3. Линии передачи в печатном монтаже
линии передачи с волновым сопротивлением 50 Ом. Такие платы называют-
ся платами с управляемым (контролируемым) волновым сопротивлением.
Для линий передачи, в которых существует Т-волна, действует фундамен-
тальное соотношение LtCt = const для данной конструкции линии. Эта по-
стоянная зависит от диэлектрических и магнитных свойств материалов,
которые применяются при изготовлении линии (цис — абсолютная магнитная
и диэлектрическая проницаемости среды, соответственно). В общем случае
£ZCZ = це. Это выражение играет важную роль при проектировании линий
передачи, поскольку позволяет ограничиться знанием только методов рас-
чета электрической емкости для определения всех важнейших параметров
линии. Таким образом, зная погонную емкость линии передачи определен-
ной конструкции, можно найти значение ее индуктивности:
' С,
(3.2)
Тогда волновое сопротивление будет определяться выражением
(3.3)
Модели для линий передач могут быть различны в зависимости от желае-
мого приближения
к
L
=.С
Рис. 3.3. Модель
линии без потерь
с±: g
Рис. 3.4. Модель
линии с потерями
R L
реальной ситуации. Для относительно низкочастотных
приложений модель линии без потерь (рис. 3.3) обла-
дает приемлемой адекватностью. На высоких частотах,
что характерно для быстродействующих систем, следует
дополнительно учитывать последовательное активное
сопротивление и потери в диэлектрике. В этом случае
модель (рис. 3.4) будет описывать линию с потерями.
Очень часто в линии передачи одну из линий, по
которой протекает возвратный ток, называют землей.
Более корректно использовать термин «возвратный
проводник», поскольку его основная роль заключает-
ся не в заземлении, а в организации пути с малым пол-
ным сопротивлением для возвратных токов.
Многие проблемы в печатных платах, касающиеся
целостности сигнала, появляются благодаря плохо
спроектированным возвратным проводникам. При
разработке линий передач следует акцентировать вни-
мание на роли возвратного проводника в обеспечении качества функциони-
рования цифрового узла.
Когда второй провод обозначается землей, подразумевается, что его фун-
кция заключается в организации стока токов в систему заземления в произ-
вольном месте. Это абсолютно неверно'. Путь высокочастотного возвратно-
го тока будет «зеркально отражать» трассу сигнального тока. Как показано
в предыдущей главе, на высоких частотах индуктивность замкнутого контура
3.1. Линии передачи и их модели
205
из сигнального и возвратного проводника минимизируется, когда возврат-
ный провод будет расположен настолько близко к сигнальному, насколько
позволит конструкция линии передачи.
Когда сигнал распространяется вдоль линии передачи, электромагнит-
ное поле формируется между сигнальным и возвратным проводниками.
Поэтому в линии передачи важную роль играют оба проводника. Когда они
выполнены одинаково, как, например, в витой паре, безразлично, какой
проводник будет назван сигнальным, а какой — возвратным. Когда же один
проводник отличается от другого, как в микрополосковой или полосковой
линии передачи, необходимо оговорить назначение каждого проводника; в
данном случае принимается в качестве сигнального проводника узкий про-
водник, а в качестве возвратного — плоскость.
Когда сигнал попадает в линию передачи, он распространяется вдоль ли-
нии со скоростью распространения электромагнитной волны, которая опре-
деляется свойствами материалов,
используемых в конструкции ли-
нии. При отсутствии магнитных ма-
териалов, что имеет место в печат-
ном монтаже, скорость распростра-
нения сигнала в линии будет опре-
деляться диэлектрической прони-
цаемостью диэлектриков, входящих
в состав линии. Сигнал — это все-
гда разность потенциалов между
двумя соседними точками на сиг-
нальном и возвратном проводниках
(рис. 3.5).
Если известно волновое сопротивление, которое встречает сигнал на своем
пути, всегда можно рассчитать ток, связанный с сигналом. Связь межу напря-
жением падающей волны и током падающей волны задается формулой
Рис. 3.5. Отображение сигнала,
зафиксированного во времени,
в произвольной точке линии
где — соответственно напряжение и ток падающей волны
Эти общие принципы применяются ко всем типам линий передачи, как
к одиночным, так и к дифференциальным.
3.1.2. Однородные линии передачи
В основе классификации линий передачи лежит форма их сечения. Дву-
мя общими особенностями сечений, которые существенно определяют элек-
трические свойства линий передачи, являются: однородность поперечного
сечения вдоль всей длины и идентичность сигнального и возвратного про-
водников в линии.
206
Глава 3. Линии передачи в печатном монтаже
Витая пара
Копланарная
линия
Коаксиальный кабель
Микрополосковая Заглубленная
линия
линия
Рис. 3.6. Примеры поперечных сечений однородных линий передачи, наиболее часто
используемых в электрических соединениях
Полосковая Полосковая
симметричная несимметричная
линия
линия
Когда поперечное сечение линии неизменно вдоль всей ее длины, как,
например, в коаксиальном кабеле, линия передачи называется однородной.
Примеры различных однородных линий передачи представлены на рис. 3.6.
Витая пара и коаксиальный кабель приведены для общности рассмотрения
конструкций межсоединений, а остальные типы линий используются в пе-
чатном монтаже.
Однородные линии передачи входят в состав печатных плат с управляе-
мым волновым сопротивлением.
Все высокоскоростные соединения должны быть спроектированы как одно-
родные линии передачи.
К неоднородным линиям передачи относятся линии, у которых размеры
сечения и/или свойства материалов меняются вдоль линии. Например, если
расстояние между двумя проводниками или их ширина не постоянны, а из-
меняются, то это неоднородная линия. Пара выводов в двухрядном корпусе
(типа DIP) или плоском корпусе (типа QFP) является неоднородными ли-
ниями. Соседние линии в соединителях, как правило, являются неоднород-
ными линиями передачи. Печатные платы, которые не имеют четко выра-
женного возвратного проводника (например, односторонние), в большин-
стве случаев содержат неоднородные линии передачи. Неоднородные линии
передачи приведут к проблемам целостности сигнала. Подобные линии сле-
дует избегать, исключая случаи, когда они электрически короткие.
Одной из задач обеспечения целостности сигнала при проектировании пла-
ты является выполнение всех соединений в виде однородных линий передачи и
минимизация длины всех неоднородных линий передачи.
Другой особенностью, оказывающей влияние на проектирование печатных
плат, является то, насколько идентичны прямой и возвратный проводники в
составе линии передачи. Когда они при одинаковой длине имеют одинаковую
форму и размеры сечения, то появляется симметрия в конструкции линии, и
3.1. Линии передачи и их модели
207
такая линия называется сбалансированной или симметричной. Например, витая
пара симметрична, если в ней применены одинаковые проводники. Это позволяет
использовать витую пару в балансном включении. В копланарной линии (рис.
3.6), если два узких проводника одинакового сечения расположены рядом друг
с другом в одной плоскости, то она является сбалансированной.
Примером несбалансированной линии является коаксиальный кабель, т. к.
центральный проводник в нем существенно отличается по форме сечения от
внешнего проводника. Полосковые, микрополосковые, заглубленные линии
также являются несбалансированными.
В общем случае, для большинства линий передачи качество сигнала и пере-
крестная помеха не будут зависеть от того, сбалансирована линия или не сба-
лансирована. Однако на помехи по шинам заземления и помехоэмиссию будут
оказывать сильное влияние особенности формы возвратного проводника.
Особое внимание к симметричности линий передач следует уделять при про-
ектировании дифференциальных пар (это детально рассмотрено в главе 6). Яв-
ляется ли линия передач однородной или неоднородной, сбалансированной
или несбалансированной, у нее есть только одно назначение: переносить сигнал
от одного конца к другому с приемлемым уровнем искажения.
3.1.3. Скорость распространения сигнала в линии
Скорость распространения сигнала в линии передачи зависит от материа-
лов, которые окружают проводники, и от того, насколько быстро изменяющиеся
магнитные и электрические поля взаимодействуют с сигналом, который мо-
жет их создавать и распространяться в пространстве вокруг проводников линии
передачи.
Рассмотрим эффекты, возникающие при
распространении сигнала в линии передачи
(рис. 3.7). Сигнал представляет собой разность
потенциалов между сигнальным и возвратным
проводниками, что определяет наличие между
проводниками электрического поля.
Скорость распространения сигнала зави-
сит от того, насколько быстро могут форми-
Рис. 3.7. Электрическое поле,
создаваемое в линии передачи,
при распространении сигнала
в линии
роваться изменяющиеся электрические и маг-
нитные поля между проводниками и затем
распространяться в материалах, окружающих
сигнальный и возвратный проводники.
Очевидно, что в сигнальном и возвратном
проводнике должен протекать ток, чтобы доставить заряды, формирующие
электрическое поле. Этот ток, протекающий вдоль проводника, будет созда-
вать магнитное поле.
Скорость распространения электромагнитной волны в материале опре-
деляется свойствами материалов, окружающих проводники, которые про-
низаны электрическими и магнитными полями.
208
Глава 3. Линии передачи в печатном монтаже
Скорость v распространения фронта сигнала в произвольной среде оп-
ределяется как:
1
/еецц ’ (3.5)
где е0 — диэлектрическая постоянная 8,85х10-12 Ф/м; ег — относительная диэлектричес-
кая проницаемость материала; р0 — магнитная постоянная 4лх10-7 Гн/м; цг— относительная
магнитная проницаемость материала.
Подставив значения диэлектрической и магнитной постоянной, получаем:
2,99х108 /
У =--.--- , м/с. (3.6)
В воздухе, где относительная диэлектрическая проницаемость и относи-
тельная магнитная проницаемость равны 1, скорость распространения элек-
тромагнитной волны есть скорость света vc, равная 2,99x108 м/с.
Практически все материалы, из которых выполняют линии передачи в пе-
чатной плате, включая металлы и все диэлектрики, не содержащие ферро-
магнитные материалы, имеют относительную магнитную проницаемость рг,
равную 1.
Относительная диэлектрическая проницаемость ег диэлектриков, входя-
щих в конструкцию линии, больше 1 (для воздуха er = 1). Для большинства
материалов, которые используются для изготовления оснований печатных
плат, она равна приблизительно 4...5,6 (см. главу 1). Это означает, что ско-
рость электромагнитной волны в линиях передачи всегда будет меньше ско-
рости света, а именно:
м/с’ (3-7)
где vc — скорость света в свободном пространстве м/с.
Кусочно-однородные диэлектрические среды характеризуются эффектив-
ной диэлектрической проницаемостью, значение которой используется вме-
сто относительной проницаемости. Во второй главе при рассмотрении ем-
костных параметров печатного монтажа рассматриваются ее способы опре-
деления. Для микрополосковой линии эффективную проницаемость можно
определить по приближенной формуле [67]
£e#= 0’475£r+0’67- (3.8)
Для удобства расчетов можно воспользоваться графиком, представлен-
ным на рис. 3.8
Формула (3.8) не учитывает краевые эффекты, которые при изменении
ширины сигнального проводника вносят различный вклад в значение эф-
фективной проницаемости. Более точное значение эффективной проница-
емости может быть получено за счет поправочного коэффициента кг, значение
которого можно рассчитать по формуле [67]
кг = 0,9646 + 0,02941n w - 0,0941 Ams - 0,0101 er, (3.9)
3.1. Линии передачи и их модели
209
Рис. 3.8. Зависимость эффективной диэлектрической проницаемости от относительной
проницаемости для микрополосковой линии
где w — ширина проводника, мм; hms — толщина диэлектрика в микрополосковой линии,
мм; ег — относительная диэлектрическая проницаемость материала платы.
На рис. 3.9 приведены графики зависимости поправочного коэффици-
ента от ширины проводника и толщины диэлектрика для материала осно-
вания платы FR4 сег=4.
При известном значении поправочного коэффициента скорость (3.7)
распространения электромагнитной волны в микрополосковой линии можно
уточнить по формуле
у
v=kz—^=, м/с.
Х
(3.10)
В некоторых материалах диэлектрическая проницаемость может меняться
с частотой. Другими словами, скорость электромагнитной волны в материале
Рис. 3.9. Зависимость коэффициента кг от параметров микрополосковой линии
для толщин диэлектрика от 1 до 5 мм
210
Глава 3. Линии передачи в печатном монтаже
может зависеть от частоты. В общем случае, диэлектрическая проницаемость
уменьшается с увеличением частоты. Это приводит к увеличению скорости
распространения электромагнитной волны в материале с увеличением час-
тоты. Отмеченный эффект проявляется на очень высоких частотах (тысячи
мегагерц). В большинстве наиболее часто используемых в печатных платах
материалов, таких как стеклотекстолит, диэлектрическая проницаемость ме-
няется очень слабо в интервале частот от 500 МГц до 10 ГГц.
В зависимости от содержания эпоксидной смолы в стеклоткани, ди-
электрическая проницаемость стеклотекстолита меняется от 4,0 до 5,6. Это
приводит к простому, легко запоминающемуся обобщению: скорость элек-
тромагнитной волны в большинстве проводников на печатной плате примерно
в два раза меньше скорости света в вакууме.
Время задержки распространения сигнала Zdl в зависимости от длины /
линии передачи вычисляется как:
/
'di="> с, (3.11)
где / — длина линии передачи, м; v — скорость распространения сигнала в линии, м/с.
Это означает, что, распространяясь вдоль линии передачи длиной 150 мм,
выполненной на стеклотекстолите, задержка распространения сигнала со-
ставляет примерно 1 нс, что соизмеримо с фронтом сигнала.
Во многих случаях более удобно использовать удельное время Zd задерж-
ки распространения сигнала (на единицу длины), которое является величиной
обратной скорости:
1
(3.12)
Учитывая (3.7), получаем удобную для инженерных расчетов формулу:
Zd =3,3Л/ё7, нс/м, (3.13)
где 3,3 — величина, обратная скорости света в вакууме, нс/м; ег — относительная (эффек-
тивная) диэлектрическая проницаемость материала основания платы.
Для стеклотекстолита (относительная проницаемость 4) удельная задер-
жка равна 6,6 нс/м.
3.1.4. Пространственное разрешение
при распространении сигнала
Любой цифровой сигнал имеет определенное время нарастания (фронт),
которое измеряется от уровня 0,1 до уровня 0,9 относительно установивше-
гося значения. При распространении сигнала вдоль линии, его фронт занимает
на линии передачи определенный отрезок d, который зависит от длительности
фронта и скорости распространения сигнала в линии (рис. 3.10). Этот отре-
зок назовем пространственным разрешением.
3.1. Линии передачи и их модели
211
Пространственное разрешение dопределяет-
ся по формуле:
d = /r-v, м, (3.14)
где Гг — длительность фронта, с; v — скорость распрост-
ранения сигнала в линии, м/с.
Например, если скорость распространения
сигнала составляет 1,5-108 м/с, а фронт — 1 нс,
то за интервал времени, равный длительности
фронта, сигнал проходит 0,15 м, что определя-
ет его пространственное разрешение. Именно в
этой области, которая перемещается вдоль ли-
Рис. 3.10. Пространственное
разрешение, соответствующее
фронту сигнала
нии со скоростью распространения сигнала, происходит динамическое вза-
имодействие линий передачи.
Пространственное разрешение играет большую роль при анализе согла-
сования линий передач и определении размеров неоднородностей вдоль линии
передачи, которые могут оказать воздействие на целостность сигнала.
3.1.5. Понятие электрически длинной и короткой линии
передачи
Предполагается, что поперечный размер линии передачи много меньше
ее длины, поэтому в данном рассмотрении линии представляются в виде нитей
тока бесконечно малого сечения. Отметим, что следует различать погонную
длину / линий, которую можно измерить инструментом, и электрическую
длину линии. Это понятие характеризует модели и режимы работы линии.
Различают электрически короткие и электрически длинные линии передачи.
Далее для краткости определение «электрически» будем опускать в тех слу-
чаях, когда это не приведет к разночтениям.
Режимы работы коротких и длинных линий имеют принципиальные раз-
личия, и для их анализа применяются различные модели. Поэтому важно четко
проводить классификацию линий передач, которая может быть выполнена
как в частотной, так и во временной области. Рассмотрим эти подходы.
Анализ линии в частотной области
Максимальная частотная компонента /тах в спектре сигнала определяет
минимальную длину Xmin электромагнитной волны в диэлектрической сре-
де линии передачи:
X . = v /fm„, м, (3/15)
min ' •'max’ ’ \ / /
где v — скорость распространения электромагнитной волны в линии передачи, м/с; /тах —
максимальная частота в спектре сигнала, 1/с.
Так, для сигнала с шириной спектра 300 МГц, который распространяет-
ся в полосковой линии в составе МПП со скоростью 1,5* 10-8 м/с, минимальная
длина волны составляет 0,5 м.
212
Глава 3. Линии передачи в печатном монтаже
Электрически короткой называется линия, у которой погонная длина /sl
будет существенно меньше минимальной длины волны /sl << Xmin. Электри-
чески длинной называется линия, у которой погонная длина /и не меньше
минимальной длины волны /п > Xmin. Для надежной оценки вводят коэффи-
циент запаса 0,1...0,2, что позволяет более строго определять электрически
короткую линию как:
Zsl = (0,1...0,2)Xmin.
(3.16)
Рис. 3.11. Электрически короткая линия
и ее типовые модели
В ответственных приложениях все остальные линии следует считать элек-
трически длинными.
Для короткой линии напряжения токи во всех точках по длине линии в оп-
ределенный момент времени имеют соответствующие одинаковые значения.
Короткие линии моделируются сосре-
доточенными идеальными элемента-
ми, и их типовые модели представля-
ют собой электрическую емкость или
индуктивность (рис. 3.11). Когда и ка-
кую модель использовать? Модель в
виде емкости рекомендуется приме-
нять при анализе схем, в которых уп-
равление ведется напряжением и отно-
сительно малы токи в цепях. Примером
могут служить КМОП-схемы в виду
малых токов, протекающих в них. Мо-
дель в виде индуктивности использу-
ется в цепях с достаточно большими то-
ками. В общем случае наиболее широ-
ко применяется емкостная модель.
Можно дать следующую общую реко-
мендацию по моделям электрически ко-
ротких линий'. в случае анализа быстро-
действующих систем (в основном цифровых) предпочтительной моделью явля-
ется емкостная модель. Индуктивная модель предпочтительна для шины питания.
Для длинной линии характерно непостоянство напряжений и токов вдоль
линии в определенный момент времени. Длинная линия может быть пред-
ставлена в виде линии с распределенными параметрами или в виде набора
из п элементарных звеньев. В простейшем случае такими элементарными
звеньями являются £С-звенья, набор которых моделирует линии с распре-
деленными параметрами без потерь (рис. 3.12). При необходимости учета по-
терь модель усложняется. Этот случай детально будет рассмотрен в следую-
щих разделах.
Каково же должно быть число звеньев и? С увеличением числа звеньев по-
вышается точность моделирования и соответственно результатов расчета.
Однако при этом возрастает потребность в вычислительных ресурсах. Таким
образом, важно снижать и, не теряя точности расчетов. При п = 1 фактически
3.1. Линии передачи и их модели
213
получается модель короткой линии, ко-
торая совершенно не отражает процес-
сы, происходящие в длинной линии.
При этом возможны очень грубые ошиб-
ки в оценках целостности сигнала. По-
этому существует некоторый минималь-
ный предел числа звеньев для модели
электрически длинной линии.
Для определения минимально необ-
ходимого числа звеньев для моделирова-
ния длинной линии передачи, по кото-
рой распространяется сигнал с опреде-
ленным спектром, представим отдельное
£С-звено (рис. 3.12) в виде фильтра ниж-
них частот (ФНЧ). Частота среза^0 это-
го фильтра должна быть не ниже макси-
мальной частоты /тах в спектре сигнала,
распространяющегося по линии:
Рис. 3.12. Электрически длинная
линия и ее типовая модель
J со •'max*
Частота среза для ФНЧ рассматриваемой структуры определяется по фор-
муле
J_ I 1
п N LnCn
/со
(3.17)
где £л, Сп — соответственно индуктивность и емкость одного звена.
Одновременно должно удовлетворяться требование к значению волнового
сопротивления, которое должно быть известно:
Совместное решение этих уравнений дает значение параметров элемен-
тарных моделирующих звеньев:
£ - с =___!__
п л/со’ п
(3.18)
Конкретное число п звеньев определяется следующим образом:
С/
(3.19)
где Cj — полная емкость линии передачи; Сп — емкость элементарного звена, рассчитан-
ная как элемент ФНЧ из условия (3.18).
214
Глава 3. Линии передачи в печатном монтаже
Пример, Рассмотрим длинную линию передачи на печатной плате, по которой распро-
страняется сигнал с фронтом 1 нс. Ранее было показано, что для качественной передачи
фронта этого сигнала необходимо по линии передать как минимум 300 МГц. Примем по-
гонную длину линии 1 м, диэлектрическая проницаемость платы 4, волновое сопротив-
ление 50 Ом при общей емкости линии 130 пФ.
Скорость электромагнитной волны в линии для этого случая, как было определено
выше, составляет 1,5108 м/с, а минимальная длина волны в спектре сигнала - 0,5 м, что в
два раза меньше длины линии.
Вычисляем по (3.18) индуктивность и емкость одного звена:
L 50
" ~ 3,14-300-1 0
= 53-10-’, Гн, С„ =
1
3,14-300-1041-50
= 21,2-10~12,Ф.
Таким образом, индуктивность звена равна 53 нГн, а его емкость 21,2 пФ, что позволя-
ет определить число звеньев, при котором моделирование линии передачи даст приемле-
мый результат: п > 130 / 21,2. Очевидно, что следует принять, по крайней мере, 7 звеньев.
Отсюда следует полезная рекомендация.
При моделировании длинной линии передачи с волновым сопротивлением 50 Ом
в печатной плате при фронте сигнала 1 нс следует принимать не менее семи LC-
звенъев на один метр линии. Число звеньев растет обратно пропорционально дли-
тельности фронта сигнала, который распространяется в линии.
В любом случае для моделирования длинной линии число звеньев на еди-
ницу длины (1 м) должно быть не менее 3.
Анализ линии во временной области
Рассмотрим распространение информационного сигнала по линии пере-
дачи. Время распространения сигнала от начала до конца линии составляет:
rdl= /7d>нс’ (3.20)
где /d — удельная задержка распространения сигнала в линии, нс/м; / — длина линии, м.
Через интервал времени zdl электромагнитная волна достигнет конца
линии, где ее энергия частично поглощается нагрузкой и частично отража-
ется (в общем случае). К драйверу через интервал времени 2/dl придет отра-
женный импульс.
Совместив перепад напряжения на выходе драйвера с отраженным сиг-
налом, можно получить три варианта суммарного сигнала.
Первый вариант: приход отраженного сигнала совпал с окончанием фронта
информационного импульса, т. е. выдерживается соотношение:
Zr = 2/dl = 2Z-rd, (3.21)
где /d — удельная задержка распространения сигнала, определяемая параметрами диэлек-
трической среды линии передачи, нс/м; / — погонная длина линии, м.
Длину линии, определенную из приведенного равенства, назовем крити-
ческой и обозначим /С1. Ее длина равна:
А.
2'd’
(3.22)
3.1. Линии передачи и их модели
215
Как видно, протяженность линии критической длины зависит от пара-
метров сигнала, который распространяется в ней. При повышении быстро-
действия погонная длина этой линии уменьшается. Этот параметр является
своеобразным шаблоном, при помощи которого можно «рассортировать»
линии на электрически длинные и короткие.
Пример. Определим критическую длину линии для полосковой линии в составе МПП
(ег = 4) для сигнала с фронтом 1 нс.
Удельное время распространения сигнала определяется соотношением:
/d = 3,3^/^, нс/м, т. е. rd = 6,6 нс/м.
Откуда получаем критическую длину линии:
V
t. I t
Рис. 3.13. Примеры искаже-
ний сигнала: а — короткая
линия; б — длинная линия
Классификация линий передачи на плате проводится путем сравнения с
полученной критической длиной следующим образом: при меньшей длине
линия относится к электрически короткой, при большей длине - к электри-
чески длинной.
Второй вариант: отраженный сигнал пришел до окончания фронта сигна-
ла. Этот случай соответствует электрически коротким линиям, длина которых
меньше критической. Для короткой линии спра-
ведливо неравенство: /sl < /с1, т. е. 2/dl < tr. Приход
отраженного сигнала во время нарастания фронта
информационного сигнала приводит к монотон-
ному искажению фронта, что является типичным
для короткой линии (рис. 3.13а). Также, как и при
частотном подходе, для уверенной оценки вво-
дят некоторый коэффициент запаса, и длина ко-
роткой линии в ответственных приложениях оп-
ределяется из неравенства /sl < (0,1 ...0,2)/с1.
Третий вариант: отраженный сигнал пришелся
на плоскую часть импульса, что соответствует ре-
жиму электрически длинной линии, для которой
справедливо следующее неравенство: /п > /с1, т. е.
2/di > tr (рис. 3.13d). Этот режим является наибо-
лее опасным и может привести к серьезным на-
рушениям целостности сигнала и тайминга.
Отметим, что в случае неопределенности,
когда длина / произвольной линии лежит в диа-
пазоне (0,1...0,2)/с1 < / < /с1, ищутся компромиссные решения. Для ответствен-
ных систем и узлов эту линию принимают в виде электрически длинной, для
менее ответственных — в виде электрически короткой. В первом случае ус-
ложняется анализ, но повышается точность решения; во втором случае анализ
упрощается, но возможны существенные погрешности в определении цело-
стности сигнала, что скажется на этапе отладки физического прототипа.
216
Глава 3. Линии передачи в печатном монтаже
3.1.6. Мгновенное полное сопротивление линии
передачи
Мгновенный ток в линии всегда пропорционален напряжению, т. е. ли-
ния ведет себя как линейный резистор. При продвижении электромагнит-
ной волны вдоль линии ее полное сопротивление подобно резистивной на-
грузке. Единица измерения полного сопротивления — омы.
Мгновенное полное сопротивление плинии передачи, которое сигнал
встречает при своем распространении, можно определить по формуле:
VI 1 г- 3300 г- „
Z= — = ~— = —--xfcr Ом,
I Сру Ст/ С, v
(3.23)
где С1 — емкость линии на единицу длины, пФ/м; v — скорость распространения элект-
ромагнитной волны в диэлектрике линии, м/с; vc — скорость света в свободном простран-
стве, м/с; ег — относительная диэлектрическая проницаемость материала линии.
Мгновенное полное сопротивление зависит от двух параметров, каждый
из которых полностью определяется конструкцией линии, а именно, сече-
нием линии, определяющим ее емкость, и диэлектрическими свойствами
материала. Пока эти параметры постоянны, сигнал при распространении
вдоль линии будет «видеть» постоянное полное сопротивление.
Например, если относительная диэлектрическая проницаемость состав-
ляет 4 и емкость на единицу длины 120 пФ/м, мгновенное полное сопротив-
ление будет
3300
120
3.1.7. Волновое сопротивление
Если полное сопротивление не изменяется по длине линии, то такая ли-
ния называется однородной линией передачи. Для нее мгновенное полное со-
противление является волновым сопротивлением линии Z, которое задается в
омах. Это один из самых важных электрических параметров линий переда-
чи, который должен выдерживаться с достаточной точностью при проекти-
ровании печатной платы. Волновое сопротивление не зависит от длины линии
и определяется аналогично (3.23) по формуле:
(3.24)
В большинстве случаев линии передачи в печатные платы выполняются
с волновым сопротивлением 50 Ом. Как правило, при выборе материалов для
основания плат возможности ограничены, а управление сопротивлением ве-
дется за счет вариации удельной емкости:
' z v
где Z — требуемое волновое сопротивление, Ом.
(3.25)
3.1. Линии передачи и их модели
217
Например, если Z= 50 Ом, то при конструировании платы на материале FR4
(ег = 4) должны быть выбраны такие геометрические параметры полосковой
линии передачи, чтобы обеспечивалась удельная емкость Cz= 132 пФ/м.
Если линия неоднородна, т.е. ее параметры изменяются по длине, то для
всей линии нет единого значения волнового сопротивления. Оно может быть
определено только для отдельных однородных участков линии передачи.
Однородные линии передачи, для которых волновое сопротивление посто-
янно по длине и заранее предопределено, называются линиями с контроли-
руемым волновым сопротивлением.
Все высокоскоростные цифровые узлы, выполненные на платах с размерами больше
пространственного разрешения и работающие на частотах более 100 МГц, дол-
жны быть выполнены на платах с контролируемым волновым сопротивлением.
Рассмотренные ранее (см. рис. 3.6) типы сечений линий передачи при
постоянстве сечения по их длине будут линиями передачи с контролируемым
волновым сопротивлением. Изменяя размеры элементов сечения, можно из-
менить емкость и индуктивность линии и тем самым изменить ее волновое
сопротивление. Волновое сопротивление шины питания, которая формиру-
ется из близко расположенных слоев питания и заземления, должно быть
минимальным, в общем случае менее 1 Ом. Это достигается значительным
увеличением емкости шины как конструкторскими способами, так и установкой
дополнительных фильтрующих и развязывающих конденсаторов. Сигнальные
трассы с узкими проводниками будут иметь повышенное волновое сопротив-
ление, типичное значение которого лежит в диапазоне от 60 до 90 Ом.
Линия передачи представляет собой направляющую систему, определя-
ющую траекторию распространения электромагнитной волны в печатной
плате вдоль сигнального и возвратного проводников. При этом, как отме-
чалось выше, скорость распространения будет определяться сложной диэ-
лектрической средой, входящей в состав конструкции линии.
В свободном пространстве электромагнитные волны распространяются
без направляющих систем, и волновое сопротивление этого пространства оп-
ределяется двумя фундаментальными величинами: диэлектрической и маг-
нитной постоянной:
Z= I—= 120л-377, ом.
(3.26)
Это фундаментальная константа. Интенсивность излучения антенной мак-
симально, когда ее волновое сопротивление равно 377 Ом.
Существует только одно фундаментальное значение волнового сопротив-
ления — 311 Ом. Значение волнового сопротивления линий передачи может быть
практически любым и ограничивается только технологическими условиями.
Если возможно реализовать линии передачи на плате в широком диапазоне
значений волновых сопротивлений, почему именно 50 Ом задается в большин-
стве случаев? Важно понимать, что в этом значении нет ничего фундаменталь-
ного или магического. Исторически это значение было принято как стандарт
218
Глава 3. Линии передачи в печатном монтаже
для кабелей связи, предназначенных для передачи сообщений на большие
расстояния [68]. Оказалось, что при волновом сопротивлении 50 Ом и ряде
других значений минимизируются потери при передаче сигналов на боль-
шие расстояния. Преемственность технических решений определила один
из факторов в пользу этого значения волнового сопротивления. Вторым фак-
тором является то, что при значении волнового сопротивления 50 Ом удов-
летворяется определенный компромисс между быстродействием и помехо-
защищенностью узла. В высокочастотных печатных платах есть большое число
параметров, определяющих выбор значения волнового сопротивления. Не-
которые из них показаны в табл. 3.1. Использование высокого волнового со-
противления приведет к большему уровню наводок. Малое волновое сопро-
тивление приводит к снижению уровня наводок и меньшим вносимым за-
держкам, но при этом возрастают потери мощности. Это следует учитывать
в высокочастотных системах.
Таблица 3.1
Выбор значения волнового сопротивления
Свойство Малое Z Большое Z
Цена платы лучше хуже
Вносимая задержка лучше хуже
Перекрестные наводки лучше хуже
Цена разъема хуже лучше
Технологичность хуже лучше
Потери энергии хуже лучше
Ослабление сигнала хуже лучше
Каждая система имеет свой оптимум значения волнового сопротивления.
В общем случае, это очень размытый оптимум, и конкретное значение выбранного
волнового сопротивления не столь критично, как его постоянство по всей сис-
теме.
Волновое сопротивление линии передачи - это тот параметр, который
требует совместного обсуждения разработчика принципиальной схемы и кон-
структора печатной платы. Длинные линии передачи должны быть согласо-
ваны, для чего в схему вводятся согласующие резисторы. Если при конст-
руировании печатной платы линия передачи не будет иметь требуемого вол-
нового сопротивления, то установка согласующих резисторов окажется
бесполезной. Важно и допустимое отклонение волнового сопротивления от
номинального значения. Далее при рассмотрении помех отражения мы воз-
вратимся к проблеме согласования линий передач.
3.1.8. Путь возвратного тока в линии передачи
Следует всегда помнить, что ток протекает по замкнутому контуру. Он
начинается в источнике и возвращается к нему. В линиях передачи принима-
ем, что сигнальный (прямой) проводник служит для подвода тока от источ-
3.1. Линии передачи и их модели
219
ника к нагрузке, а обратный путь тока расположен в проводящей среде, ко-
торая находится рядом с прямым проводником. При постоянном токе возврат-
ный ток всегда протекает по пути с наименьшим активным сопротивлением,
но для переменного тока обратный ток будет стремиться располагаться рядом
с прямым путем. Чем выше частота, тем ближе конфигурация пути обратного
тока и прямого. При этом уменьшается полное сопротивление возвратного пути.
Для полосковых и микрополосковых линий обратный путь протекает по ме-
таллизированным слоям, расположенным рядом с сигнальным проводником.
Любые возмущения, которые имеют место в возвратном токе на пути его
распространения, будут приводить к возмущениям в сигнальном токе и нару-
шат целостность сигнала. Поэтому для быстродействующих систем важно
уделять внимание не только сигнальному проводнику, но и проводнику, несуще-
му возвратный ток. Однородность сигнального и возвратного проводника обес-
печивает однородность волнового сопротивления.
В том случае, если в качестве возвратного проводника используется плос-
кость, то обратный ток распределяется в ней определенным образом. Точ-
ное описание этого распределения зависит от частоты и может быть полу-
чено только с помощью специальных программных средств. Однако для
инженерной практики можно дать некоторую приближенную оценку.
В качестве примера на рис. 3.14 показано расчетное распределение тока в
сигнальном и возвратном проводнике в полосковой и микрополосковой ли-
нии передачи на частотах 10 и 100 МГц [4]. Ширина сигнального проводника
в обоих случаях равна 0,125 мм и толщина 17,5 мкм. Из рассмотрения можно
сделать два важных вывода. Во-первых, сигнальные токи из-за скин-эффек-
та протекают только по внешней стороне проводника. Во-вторых, возвратные
токи в проводящем слое концентрируются вблизи сигнального проводника.
Сигнальный проводник может иметь любую топологию, и возвратный ток на
плоскости будет следовать ей. Чем выше частота, тем ближе к сигнальному
____ 10 МГц
KZZ1
I — ..—I I —111 .1
100 МГц <=>
Рис. 3.14. Распределение тока в сигнальном и возвратном проводниках
в микрополосковой (слева) и полосковой (справа) линии передачи на частотах
10 и 100 МГц (темные места соответствуют большей плотности тока)
220
Глава 3. Линии передачи в печатном монтаже
проводнику расположен возвратный ток. Это эффект близости, который про-
является достаточно заметно уже на частотах около 10 МГц. Анализ результа-
тов вычислений показывает, что ширина зоны, в которой протекает возврат-
ный ток, примерно в три раза больше ширины сигнального проводника.
При сближении прямого и обратного токов происходит снижение индук-
тивности линии передачи и уменьшение ее волнового сопротивления.
В любом случае, путь обратного тока будет формироваться таким образом,
что индуктивность контура тока будет минимальна. Любая неоднородность на
пути возвратного тока будет приводить к увеличению индуктивности, а следо-
вательно, волнового сопротивления, увеличивая искажения сигнала.
3.1.9. Возвратный путь в смежных слоях МПП
В составе МПП используется несколько потенциальных слоев, которые
могут рассматриваться как плоскости расположения путей возвратных то-
ков. Особый интерес представляет расположение возвратного тока в слое,
рядом с которым расположен другой потенциальный слой.
Рассмотрим фрагмент конструкции МПП (рис. 3.15). Видно, что возврат-
ный ток преимущественно протекает по поверхности среднего слоя 2, которая
ближе к сигнальному проводнику. Согласно законам индукции на другой
поверхности этого слоя наводятся токи противоположного направления,
которые, в свою очередь, наводят токи в слое 3. Средний слой 2 — плаваю-
щий, а слой 3 подключен к общей шине.
Точное распределение тока в слоях с учетом скин-эффекта будет зависеть
от частоты. В общем, распределение тока в каждом слое будет таким, чтобы
минимизировать общую индуктивность в сигнальном контуре. Результаты
моделирования распределения токов в слоях МПП при толщине проводни-
ков 0,05 мм на частоте 20 МГц показаны на рис. 3.16.
Драйвер линии в этом случае нагружен на две последовательно соединен-
ные линии передачи, а именно: линию, сформированную сигнальным про-
водником и слоем 2, и линию, сформированную двумя слоями 2 и 3, как по-
казано на рис. 3.17. Полное сопротивление последовательно соединенных
линий равно:
Z= + ^2-3*
Рис. 3.16. Распределение тока в системе
проводников: верхний проводник —
сигнальный; нижний слой — возвратный;
средний слой — плавающий
Рис. 3.15. Фрагмент конструкции
МПП: 1 — сигнальный проводник;
2 — слой с возвратным током;
3 — соседний проводящий слой
3.1. Линии передачи и их модели
221
Рис. 3.17. Физическая конфигурация подключения линий передач
и ее эквивалентная схема
При малом сопротивлении Z2_3, суммарное сопротивление будет близко к Zx_r
Таким образом, драйвер фактически нагружается линией передачи, которая сфор-
мирована сигнальным проводником и ближайшей плоскостью, независимо от того,
какая плоскость является в действительности возвратной и подключена к драй-
веру. Причем на этой плоскости не должно быть стороннего напряжения (ни пи-
тания, ни земли).
Волновое сопротивление Z2 3 линии между двумя плоскостями должно
быть сравнительно меньше, чем линии, состоящей из сигнального провод-
ника и плавающей плоскости. Волновое сопротивление Z линии из двух
широких (h « w) пластин протяженностью 1 м может быть приближенно оп-
ределено по формуле [3]:
Z = 377- ’ Ом (3.27)
W Ver
где h — толщина диэлектрической прокладки между пластинами; w — ширина пластин;
ег — относительная проницаемость диэлектрика, разделяющего пластины.
Например, для стеклотекстолита с ег= 4, при ширине плоскости 50 мм и
зазором между ними 0,25 мм, волновое сопротивление будет
Z = 377^1 = 0,94 Ом.
Это значительно меньше типового сопротивления линии передачи 50 Ом.
Малое волновое сопротивление желательно для шин питания.
Для минимизации волнового сопротивления между смежными проводящими
плоскостями следует использовать по возможности более тонкий диэлектрик.
Это увеличит связь между слоями и будет обеспечивать путь с низким полным
сопротивлением для возвратного тока, расположенного вблизи сигнального тока.
На рис. 3.18 показано сечение четырехслойной МПП с переходом сигналь-
ного тока с первого на четвертый слой через металлизированное отверстие.
222
Глава 3. Линии передачи в печатном монтаже
Рис. 3.18. Сечение четырехслойной
МПП с переходом сигнального тока
с первого на четвертый слой через
металлизированное отверстие
Для горизонтальной однородной линии
передачи путь возвратного тока легко
определить. В первой половине пути
высокочастотный (более 10 МГц) воз-
вратный ток протекает в поверхностном
слое 2. В правой части возвратный ток
протекает на поверхности слоя 3.
Несколько сложней определить,
как будет протекать возвратный ток
при протекании сигнального тока по
металлизированному отверстию, ко-
торое соединяет слои МПП. Здесь так-
же соблюдается общий принцип ми-
нимизации общей индуктивности пути тока. Металлизированное отверстие
в МПП обеспечивает резкое изменение направления тока, но оно достаточ-
но короткое (определяется толщиной платы), а плоскости имеют низкое
полное сопротивление. Поэтому вносимая неоднородность будет достаточ-
но мала. Это типично для многослойных конструкций печатных плат. Если
нет ограничений по стоимости, то расположение проводящих плоскостей на
минимальном расстоянии друг от друга и с минимальным зазором от метал-
лизированного отверстия — оптимальное правило проектирования.
Для минимизации общего числа слоев необходимо использовать соседние
потенциальные слои с различными напряжениями. Если слой 2 несет 5 В, а
слой 3 — 0 В, то между ними нет соединения по постоянному току. Как же
протекает возвратный ток из плоскости 3 к плоскости 2?
Между этими плоскостями имеется электрическая емкость. Отверстие имеет
гарантированный зазор, отделяющий металлизацию отверстия от потенци-
альных плоскостей. Возвратный ток будет распределен по внутренней по-
верхности плоскости и связан через емкость «плоскость-плоскость». Наве-
денный ток в проводящих плоскостях будет растекаться от зоны отверстия
со скоростью распространения электромагнитной волны в диэлектрике.
Возвратные токи показаны на рис. 3.19. Два слоя (2 и 3), в которых проте-
кает возвратный ток, формируют линию передачи, и возвратный ток будет
Сигнал
Сигнал
Рис. 3.19. Путь возвратного тока при переходе
от слоя 2 к слою 4 при емкостной связи между
слоями
«видеть» полное сопротивле-
ние, которое является мгно-
венным полным сопротивле-
нием системы двух плоско-
стей.
Когда возвратный ток пе-
реходит с плоскости на плос-
кость (плоскости изолирова-
ны по постоянному току), воз-
вратный ток будет связан че-
рез емкости между этими
плоскостями и будет ветре-
3.1. Линии передачи и их модели
223
чать на своем пути сопротивление, равное мгновенному полному сопротивле-
нию линии передачи, созданной этими плоскостями.
За счет этого сопротивления возвратный ток будет создавать некоторое
падение напряжения на своем пути, которое называется «подскок напряжения».
При большом полном сопротивлении возвратного пути увеличивается напря-
жение подскока и в системе заземления увеличивается уровень помех.
Одной из главных задач проектирования возвратного пути является мини-
мизация его индуктивности для минимизации подскока напряжения. Главным
приемом минимизации волнового сопротивления является расположение потен-
циальных слоев питания и опорного напряжения на минимальном расстоянии друг
от друга.
Емкость и индуктивность переходного отверстия зависят от его раз-
меров. Чем больше радиус, тем больше его емкость и меньше индук-
тивность. Точное значение емкости между отверстием и плоскостью
можно получить с применением специальных программных средств.
Однако можно построить простейшую модель для оценки полного со-
противления и оптимизации наборных конструкций и минимизации
подскока напряжения заземления.
Для расчета сопротивления растекания между двумя слоями необходи-
мо рассчитать емкость на единицу длины радиальной линии передачи и ско-
рость сигнала. Емкость на единицу длины есть изменение емкости. Общая
емкость возвратного пути (емкость между пластинами):
$
С = гогг- (3.28)
и область растекания тока между слоями:
S=nP. (3.29)
Объединяя (3.28) и (3.29), получим емкость между слоями, которая уве-
личивается с расстоянием как:
С = £0£г—, (3.30)
где е0 — диэлектрическая постоянная, 8,85 пФ/м; ег — относительная диэлектрическая про-
ницаемость изоляционного материала между слоями; S — область перекрытия плоскостей
протекания возвратного и сигнального тока; h — расстояние между слоями; г - увеличи-
вающийся радиус связанного круга, который расширяется со скоростью распространения
электромагнитной волны.
Увеличения емкости на единицу приращения радиуса (dC/drY
С,=2леое—. (3.31)
' 0 h
При растекании возвратного тока по плоскости от отверстия емкость
увеличивается. Мгновенное полное сопротивление для возвратного тока
между слоями при этом будет
224
Глава 3. Линии передачи в печатном монтаже
, I Л * 3” * „ *
7=;ГТ^'мГ |З ЗД
где Cz — емкость связи на единицу длины между слоями; v — скорость распространения
электромагнитной волны в диэлектрике; h — расстояние между слоями, мм; г — радиус,
мм, зоны растекания возвратного тока, увеличивающийся со скоростью v; vc — скорость
света в вакууме.
Например, если толщина диэлектрика (ег = 4) между слоями 0,25 мм, то
полное сопротивление для возвратного тока на расстоянии 25 мм от отвер-
стия составляет
0 25
Z = 60—^ = 0,3 Ом.
25^4
Это сопротивление достаточно мало. Видно, что чем больше расстояние
от отверстия, тем меньшее сопротивление будет испытывать ток возврата,
и тем меньше будет подскок напряжения в системе заземления.
Можно оценить изменение сопротивления рассматриваемого возвратного
тока (сопротивление которого включено последовательно с сигнальным
током) по времени. Поскольку возвратный ток растекается со скоростью элек-
тромагнитной волны в материале и г = vt, тогда
z = 60-4= = 60—4= = 60- = 200-, Ом, (3.33)
Гу/Е,. Vly/E, 1
где h — расстояние между слоями, м; v - скорость распространения электромагнитной волны
в диэлектрике, м/с; г — радиус зоны растекания, м, возвратного тока, увеличивающийся
со скоростью v; vc — скорость света в вакууме, м/с; t — время распространения возврат-
ного тока, нс.
Например, для расстояния между слоями 0,25 мм (25-10-5 м) полное сопро-
тивление для возвратного тока после первых 0,1 нс будет Z= 200x25-10-5 /
/ 0,1 = 0,5 Ом. В первоначальный момент времени фронт сигнала встреча-
ет на своем пути сопротивление 0,5 Ом. Если амплитуда сигнала будет 1 В в
линии с волновым сопротивлением 50 Ом, то первые 0,1 нс, за которые, напри-
мер, сигнал достигнет отверстия, его амплитуда составит 1 В / 50 Ом = 20 мА.
Тогда подскок напряжения за счет перехода со слоя на слой за первые 0,1 нс
будет 20 мА х 0,5 Ом = 10 мВ.
Если переключается одновременно 10 сигналов, переходя со слоя на слой
с волновым сопротивлением 0,5 Ом, то суммарный ток будет 200 мВ на пол-
ном сопротивлении возвратного пути. Теперь подскок напряжения достиг-
нет 200 мА х 0,5 Ом = 100 мВ, а полученные 100 мВ составят 10 % от ампли-
туды сигнала. Фактически это напряжение помех, которое прикладывается
к возвратному пути и «отрывает» вывод заземления микросхемы от системы
заземления цифрового узла.
Наибольшее сопротивление будет в первоначальный момент процесса пе-
реключения. Именно в этот момент и будет максимальный подскок напря-
жения заземления. На рис. 3.20 показано изменение во времени полного со-
3.1. Линии передачи и их модели
225
Рис. 3.20. Сопротивление возвратному току между слоями при распространении
сигнала по металлизированному отверстию
противления возвратному току между слоями при распространении сигна-
ла по металлизированному отверстию для расстояния между слоями 0,05 и
0,25 мм. Из графика видно, что это сопротивление имеет существенное зна-
чение только в начальный интервал времени, меньший 0,5 нс.
Анализ показывает, что при коротком фронте и одновременной коммута-
ции нескольких линий, проходящих через металлизированные отверстия, может
возникать значительное напряжение подскока в возвратном пути. Единственный
путь устранения этого явления состоит в снижении полного сопротивления воз-
вратного пути.
При проектировании плат необходимо учитывать следующие рекомендации.
1. Сигнальный путь, проходящий через слои платы посредством метал-
лизированного отверстия, должен всегда пересекать проводящие слои
для организации возвратного пути с некоторым полным сопротивле-
нием. Слои должны быть закорочены металлизированными переход-
ными отверстиями в непосредственной близости к сигнальным метал-
лизированными отверстиям.
2. Расстояние между потенциальными слоями с различными постоянны-
ми напряжениями должно быть по возможности минимальным.
3. Поверхность слоя, по которому протекает возвратный ток, не должна
иметь препятствий для его движения на расстоянии, которое преодо-
левает электромагнитная волна за время фронта сигнала. В противном
случае полное сопротивление возвратного пути может быть высоким.
Добавление развязывающего конденсатора между слоями питания и за-
земления снизит полное сопротивление возвратного пути. Дискретный кон-
денсатор будет обеспечивать низкое полное сопротивление возвратного пути
для тока, протекающего от одной плоскости к другой.
Для обеспечения эффективности реальный конденсатор должен удерживать
полное сопротивление между слоями для высокочастотных составляющих спек-
тра сигнала на уровне, меньшем, чем 5 % от 50 Ом, или менее 2,5 Ом.
8 1527
226
Глава 3. Линии передачи в печатном монтаже
Частота Гц
Рис. 3.21. Полное сопротивление конденсатора емкостью 1 нФ и индуктивностью
контура 0,5 нГн
В высокочастотных приложениях следует использовать компоненты с ми-
нимальным полным сопротивлением, т. е. с минимальной последовательной
индуктивностью. На рис. 3.21 показано изменение полного сопротивления
реального конденсатора емкостью 1 нФ с индуктивностью контура 0,5 нГн.
Реальный конденсатор будет обеспечивать малое полное сопротивление
для возвратного пути для частот до 1 ГГц. Конденсатор емкостью более 1 нФ
не даст ощутимого эффекта, поскольку низкочастотные компоненты будут
испытывать низкое полное сопротивление между слоями в любом случае.
Для конденсаторов, которые используются для снижения полного сопротив-
ления возвратного пути, более важно иметь малую последовательную индук-
тивность, чем большую емкость, например, более 1 нФ.
При индуктивности конденсатора более 0,5 нГн могут быть проблемы с
повышенным сопротивлением на частотах выше 1 ГГц.
Конденсатор между слоями с различными постоянными напряжениями не
будет эффективным средством для снижения подскока напряжения заземле-
ния. Это может внести улучшение в низкочастотном диапазоне, но не реша-
ет проблем на высоких частотах. В МПП основной путь снижения помех со-
стоит в применении предельно тонких диэлектриков.
Токи, наведенные в слоях платы, распространяются к краям слоев и от-
ражаются от них, вызывая напряжения между двумя слоями. Поскольку
полное сопротивление между слоями мало, меньше 1 Ом, созданное напря-
жение так же мало. Для минимизации помех слои платы должны быть на
минимальном расстоянии друг от друга. Падающие и отраженные волны
наведенных токов между слоями определяют резонансные явления. Затуха-
ния при этом определяются потерями в проводниковых и диэлектрических
материалах. Период колебаний определяется временем пробега электромаг-
нитной волны до края платы. Для плат с размерами стороны 250...500 мм ре-
зонансные частоты лежат в диапазоне от 150 до 300 МГц. Это определяет ча-
стотный диапазон работы развязывающих конденсаторов между слоями с раз-
3.1. Линии передачи и их модели
227
личными постоянными напряжениями. Однако для частот, которые опреде-
ляются фронтом сигнала, требуются, как показано выше, более высокочас-
тотные конденсаторы.
Отмеченные проблемы становятся все более актуальными, особенно при
длительности фронта менее 100 пс. Детально проблемы проектирования шин
питания и заземления рассмотрены в главе 5.
3.1.10. Модель линии на основе LC-звеньев
Для моделирования задержки распространения сигнала и волнового сопро-
тивления должна применяться более сложная модель в виде распределенных
параметров. Эта модель, как было
показано ранее, может быть замеще- Сигнал
на моделью на сосредоточенных эле-
ментах, содержащих емкости и ин-
дуктивности (рис. 3.22).
Каждый сегмент моделируется
парциальной самоиндукцией и пар-
циальной взаимной индуктивностью
с возвратным путем. Для несбалан-
сированной линии передачи, кото-
рой, например, является микро по-
Возвратный ток
-------------Длина--------------►
Рис. 3.22. Модель на основе £С-звеньсв
лосковая линия, парциальная само-
индукция сигнального и возвратного проводника различны. В практических
случаях парциальная самоиндукция сигнального проводника может быть в де-
сятки раз больше парциальной самоиндукции возвратного проводника, посколь-
ку сигнальный проводник во много раз уже возвратного.
В линиях передачи сигнальный и возвратный проводники расположены рядом
и образуют токовый контур. Поэтому парциальные самоиндукции не играют
особенной роли, а основную роль играет индуктивность контура. В данной мо-
дели индуктивность линии передачи моделирует индуктивность контура тока.
При увеличении числа сегментов (компонентов L и С) точность моделиро-
вания увеличивается. В предельном случае, при бесконечном увеличении числа
звеньев, мы приходим к модели удельного конденсатора Cz и удельной ин-
дуктивности контура Az. Это — первичные электрические параметры линии
передачи.
При малых элементарных отрезках с параметрами LCрежимы в линии опи-
сываются телеграфными уравнениями, которые позволяют определить по-
стоянное мгновенное полное сопротивление в каждом узле модели, которое
численно равно волновому сопротивлению линии Z. Кроме этого, можно
определить удельную задержку Zd распространения сигнала в линии от ее на-
чала до конца. Эти параметры определяются формулами:
2=Д '..=ж
(3.34)
228
Глава 3. Линии передачи в печатном монтаже
где Z— волновое сопротивление, Ом; — индуктивность контура на единицу длины ли-
нии передачи, Гн; С1 — емкость на единицу длины линии передачи, Ф; /d — удельное вре-
мя задержки распространения электромагнитной волны, с; v — скорость распростране-
ния электромагнитной волны в линии передачи, нс/м.
Из этих соотношений можно получить важные зависимости, которые могут
оказаться полезными при конструировании печатных плат:
1) соотношение между индуктивными и емкостными параметрами линии:
из выражения
получаем
, мкГн, (3.35)
где £г — относительная диэлектрическая проницаемость основания платы для полоско-
вой линии (эффективная проницаемость для микрополосковой линии); Cz — емкость ли-
нии на единицу длины, пФ.
2) соотношения между волновым сопротивлением и скоростью распро-
странения электромагнитной волны
С1=-Г = -Г^г, L,=- = -^, С,=^,нф, £ = ?dZ,Hru,
vZ vcZ v vc Z
где Z — волновое сопротивление, Ом; /d — удельная задержка сигнала в линии, нс/м.
Например, линия с волновым сопротивлением 50 Ом и с диэлектричес-
кой проницаемостью изоляционного материала 4 имеет удельную емкость
С{ = 2/(3-108х50) = 130-10~12 Ф/м, т. е. 130 пФ/м.
Индуктивность на единицу длины этой линии составляет
£/= (2x50)/ ЗЮ8 = 0,333-Ю-6, Гн/м, т. е. 333 нГн/м.
Если задержка в линии составляет 1 нс на длине 1 м, а ее волновое сопро-
тивление 50 Ом, то общая емкость линии должна быть С= 1/50 = 0,020 нФ,
а индуктивность L = 1x50 = 50 нГн.
Отмеченные соотношения относятся к любой однородной линии пере-
дачи. Они так же могут быть получены из рассмотрения сечения линии либо
с помощью приближенных аналитических соотношений, либо с примене-
нием специальных программ расчета, которые будут рассмотрены ниже.
3.1.11. Расчет волнового сопротивления с помощью
приближенных соотношений
При конструировании печатных плат всегда имеется информация о параметрах
сечения сигнальных проводников, толщинах и параметрах изоляционных ма-
териалов и в целом о геометрии печатного монтажа и конструкции платы.
3.1. Линии передачи и их модели
229
В зависимости от сложности сечения линии передачи можно воспользо-
ваться тремя подходами:
• эвристическими правилами,
• аппроксимацией результатов экспериментальных исследований при
помощи аналитических выражений,
• численными методами анализа полей.
Эвристические правила применимы при расчете простейших сечений, на-
пример, полосковых и микрополосковых линий передач. Они сформулиро-
ваны на основе ранее прове-
денных расчетов или экспе-
риментальных оценках и
полезны для предваритель-
ной проработки конструк-
ций. По мере накопления
опыта проектирования и
выполнения соответствую-
щих расчетов конструктор
пополняет собственную ба-
зу правил проектирования.
микрополосковая линия полосковая линия
Рис. 3.23. Масштабное представление сечений
микрополосковой и полосковой линий передачи
с волновым сопротивлением 50 Ом;
для микрополосковой линии w = 2hms,
для полосковой линии hs = 2и’
На рис. 3.23 показано масштабное представление микрополосковой и полос-
ковой линий передач с волновым сопротивлением 50 Ом, которые выпол-
нены на стеклотекстолите.
Например, полезное правило: для линии передачи с волновым сопротивлени-
ем 50 Ом необходимо выдержать для микрополосковой линии ширину проводника
в два раза больше толщины диэлектрика, а для полосковой линии — в два раза
меньше толщины диэлектрика.
Для строгого аналитического расчета пригодны только три геометрии се-
чения проводников: коаксиальная структура, двухпроводная линия и сис-
тема «провод над плоскостью» с проводниками круглого сечения. Печатный
монтаж ввиду специфики сечения проводников может быть рассчитан только
с помощью методов конформных преобразований или численными методами.
Эти подходы рассмотрены во второй главе при анализе методов расчета элек-
трической емкости.
Аппроксимация в виде приближенных аналитических соотношений мо-
жет заменить в некоторых случаях применение программных средств. Рас-
чет волнового сопротивления для линии без потерь может быть выполнен
через емкостные и индуктивные параметры линии передачи. Методы расчета
этих параметров обсуждались во второй главе. При необходимости непос-
редственного вычисления волнового сопротивления можно воспользоваться
сводкой расчетных формул для линий передач в печатных платах, которая
представлена в табл. 3.2 [69—72]. Для упрощения расчетов по этим форму-
лам построены графики для определения зависимости волнового сопротив-
ления от параметров линий, а также для определения ширины проводника
при различных конструкциях линии передачи для получения волнового со-
противления 50 Ом (ег = 4, t = 0,035 мм) (рис. 3.24-3.27).
Таблица 3.2
Сечение линии
Формулы для расчета волнового сопротивления линий передач на печатных платах
Волновое сопротивление, Ом
Ширина проводника для получения
заданного волнового сопротивления, см
Микрополосковая линия
w
Z = . 60 In -----------------
70,47г, +0,67 0,67(0,8»+/)
при w < 2h ошибка не превышает 3 %
8eff= 0,475£г+ 0,67
w =
_______7>46Ч™ . 1 25/
/ Z JO, 4755г.+0,67 \
ехр 60--------------
Полосковая линия
ч
0,67tt(0,8w+Z)
при h3-t> 2w, hs > 4t
Заглубленная линия
где = £г
Двойная полосковая линия
l,9(2Zzs +г)
0,8и> + /
230 Глава 3. Линии передачи в печатном монтаже
Примечание, t — толщина печатного проводника, остальные обозначения геометрических параметров ясны из приведенных рисун-
ков. Размерность всех геометрических параметров, входящих в формулы, должна быть одинаковой.
j о Q
232
Глава 3. Линии передачи в печатном монтаже
0 4 0 6 0.8 1 1 2 1 4
Толщина, мм
Рис. 3.25. Графики для проектирования полосковой линии (окончание):
1 — hs = 1,5 мм; 2 — hs = 1,0 мм; 3 — hs = 0,3 мм
Рис. 3.26. Графики для проектирования заглубленной линии (/zms = 0,5 мм):
7 — А = 0,9 мм; 2 — h = 0,7 мм; 3 — h = 0,5 мм
vlllo villa villa
3.2. Линии передачи с потерями
233
Рис. 3.27. Графики для проектирования двойной полосковой линии (hs = 1 мм):
1 — h\ = 0,8 мм; 2 — h\ = 0,7 мм; 3 — h\ = 0,6 мм
Если пренебречь толщиной трассы то волновое сопротивление будет
зависеть только от соотношения толщины диэлектрика и ширины сигналь-
ного проводника.
В первом приближении волновое сопротивление полосковой и микрополосковой
линий передачи зависит от соотношения толщины диэлектрика и ширины сиг-
нального проводника. До тех пор, пока это соотношение будет постоянным,
будет постоянным и волновое сопротивление. При пропорциональном измене-
нии этих параметров волновое сопротивление не изменится.
Указанные приближенные соотношения позволяют рассчитать значения
волнового сопротивления с точностью до 10 %. Для получения более точных
результатов необходимо воспользоваться численными методами расчета, ко-
торые рассмотрены в главе 8.
234
Глава 3. Линии передачи в печатном монтаже
3.1.12. Частотная зависимость волнового
сопротивления
Для модели линии без потерь, которая часто используется для анализа
целостности сигнала, волновое сопротивление определяется по формуле:
z=>
В том случае, если диэлектрические свойства изоляционных материалов
не изменяются с частотой, не будет изменяться и емкость линии передачи.
Современные материалы имеют достаточно стабильные параметры, которые
практически не изменяются с частотой. При очень высоких частотах начи-
нают проявляться потери в линиях передачи. Этот случай детально будет рас-
смотрен ниже.
Индуктивность, как показано в предыдущих разделах, будет изменяться
с частотой из-за скин-эффекта и эффекта близости. Индуктивность конту-
ра будет максимальна на низких частотах и снижается по мере повышения
частоты из-за оттеснения тока к поверхности проводников и сближения токов
противоположного направления. Поэтому можно ожидать, что волновое со-
противление будет с частотой уменьшаться, достигнет некоторого постоян-
ного значения на высокой частоте и далее будет практически постоянным.
При этом все токи будут протекать в тонком скин-слое около поверхности
проводников. Анализ показывает, что при увеличении частоты спад сопро-
тивления начинается на частоте примерно 1 МГц и практически заканчива-
ется на частоте 50 МГц. Общий спад значения волнового сопротивления со-
ставляет примерно 7 Ом, или меньше 15 %.
На частотах более 50 МГц волновое сопротивление линии передачи посто-
янно и не изменяется с частотой. Это «высокочастотное» волновое сопротив-
ление и является тем значением, которое используется в проектных решениях.
3.2. Линии передачи с потерями
3.2.1. Влияние потерь в линиях передачи
на качество функционирования цифрового узла
Если сигнал с крутым фронтом распространяется по линии передачи, то
он на ее выходе будет иметь фронт более пологий, т. е. длительность фронта
увеличится (рис. 3.28). Это увеличение происходит из-за потерь в линии пе-
редачи, что влияет на межсимвольные помехи и форму контрольной диаграммы.
Потери в проводниках — это принципиальная проблема целостности сиг-
нала для любых сигналов с частотой более одного 1 ГГц, проходящих через
линию передачи длиннее 250 мм, что типично для высокоскоростных при-
ложений.
3.2. Линии передачи с потерями
235
н с
Рис. 3.28. Измеренные сигналы на входе и выходе линии передачи с волновым
сопротивлением в 50 Ом и длиной 900 мм: 1 — сигнал на входе; 2 — сигнал на выходе
Основная причина увеличения фронта сигнала при его распространении
в реальных линиях передачи заключается в том, что высокочастотные ком-
поненты этого сигнала быстрее ослабляются, чем низкочастотные.
Наиболее простой способ проанализировать потери, зависящие от час-
тоты, — это рассмотреть проблему в частотной области. С другой стороны,
эта проблема зависит от времени, для чего следует рассмотреть прохожде-
ние сигнала в линии передачи во временной области.
Если бы потери не зависели от частоты, и низкочастотные компоненты
сигнала ослабевали бы так же, как высокочастотные, то сигнал уменьшался
бы по амплитуде по мере прохождения по линии, но время прохождения всех
частотных составляющих сигнала было бы одинаковым. Эффект ослабления
мог бы быть скомпенсирован усилением на конце линии. Фронт, время рас-
пространения сигнала, а также дрожание (джиттер) фронта сигнала не из-
менялись бы из-за постоянного по частоте ослабления.
При распространении сигнала в реальных линиях с потерями амплиту-
ды высокочастотных компонентов сигнала уменьшаются, в то время как низ-
кочастотных — остаются практически неизменными. Полоса частот сигна-
ла уменьшается из-за этого избирательного ослабления частотных состав-
ляющих, что приводит к увеличению длительности фронта. Эти изменения
в форме сигнала приводят к деградации качества функционирования циф-
рового узла.
Если искажения фронта сигнала увеличиваются, то уровень битового
сигнала будет зависеть от того, насколько долго предыдущий сигнал нахо-
дится в высоком или низком состоянии. При быстрой последовательности
импульсных сигналов с малым интервалом между ними, короткий импульс
не успеет достичь при длительном фронте установившегося состояния, что
приведет к нарушению битовой последовательности. Это определяет меж-
символьные помехи, что иллюстрируется на рис. 3.29.
236
Глава 3. Линии передачи в печатном монтаже
Рис. 3.29. Псевдослучайная последовательность битов с частотой 5 ГГц: слева — фронт
значительно короче интервала между битами, справа — фронт соизмерим с периодом
следования битов; при этом возникают межсимвольные помехи
Межсимвольные помехи — одно из важнейших проявлений частотно за-
висимых потерь и деградации фронта импульса. Это приводит к снижению
разницы между высоким и низким уровнем сигнала на приемнике, что уве-
личивает битовые ошибки.
Одним из распространенных и наглядных способов описания качества
сигнала на приемнике после прохождения линии с потерями является кон-
трольная диаграмма. При этом симулируется и измеряется псевдослучайная
последовательность битов, которая служит образцом всех возможных бито-
вых потоков. Каждый принятый цикл выбирается из цифрового потока и на-
кладывается на предыдущий цикл. Так сотни циклов накладываются друг на
друга. Этот набор наложенных импульсов называется «контрольной диаграм-
мой». Условно ее можно представить как открытые глаза (рис. 3.30). На ри-
сунке показана контрольная диаграмма сигнала частотой в 5 ГГц в случай-
ном битовом потоке с малыми и большими потерями [4]. Большие потери
выражаются в «закрытии глаза» и увеличении джиттера, что проявляется в
расширении перекрывающихся областей. Сокращение свободной области
диаграммы есть показатель количества битовых ошибок: чем больше «глаз»
закрыт, тем больше этих ошибок. В то же время широкое раскрытие этой
диаграммы говорит о возможности малого количества битовых ошибок и хо-
рошем качестве сигнала. Ширина в горизонтальном направлении в месте пе-
рекрещивания линий диаграммы есть мера джиттера. Прямое следствие ча-
Рис. 3.30. Контрольная диаграмма сигнала частотой в 5 ГГц в случайном битном
потоке. Слева — малые потери. Справа — сигнал той же структуры, но с большими
потерями, которые выражаются в «закрытии глаза» и увеличении джиттера,
что проявляется в расширении перекрывающихся областей
3.2. Линии передачи с потерями
237
стотно зависимых потерь в линии и непрямое измерение межсимвольных
помех проявляется в «закрытии глаза» (см. рис. 3.30).
3.2.2. Контрольная диаграмма
Контрольная диаграмма — эффективный инструмент визуализации прояв-
ления потерь в линии передачи. Рассмотрим поток битовых данных (рис. 3.31)
с логической единицей в виде высокого уровня и логическим нулем в виде низкого
уровня. Если эту последовательность наблюдать на экране осциллографа, то
первым будет бит, расположенный справа. Далее при сдвиге по времени мы уви-
дим следующий бит. Так со временем можно наблюдать всю последовательность
(справа налево): 0—1 — 1—0—1—0—0— ... и т. д.
Если в какой-либо точке цепи наблюдать большое число битов в потоке
данных и фиксировать только три последних бита, то возможны только во-
семь вариантов комбинаций битов. Эти комбинации показаны на рис. 3.32
(направление потока показано стрелкой).
Если одновременно наблюдать большое число битов, проходящих точку на-
блюдения, и наложить их друг на друга в одном изображении, то мы увидим
фигуру, представленную на рис. 3.33. Это идеальная контрольная диаграмма.
На данной контрольной диаграмме видно, что переход между логическими
уровнями четкий и предсказуемый. Верхний и нижний допустимый уровень
показан на рисунке. Вертикальные линии ограничивают временной интервал,
Рис. 3.31. Битовый
поток данных
Рис. 3.32. Восемь возможных комбинаций из трех битов
в потоке данных (чтение данных должно проводиться
справа налево)
низкого уровня
высокого уровня
Рис. 3.33. Возможные комбинации, наложенные друг на друга, из трех битов,
проходящих через точку наблюдения
238
Глава 3. Линии передачи в печатном монтаже
на котором не будет логических ошибок. Если поток данных дискретный меж-
ду этими моментами, данные будут всегда корректные.
Когда в линии имеются потери, это приводит к ослаблению высокочас-
тотных составляющих спектра сигнала, что вызывает искажение формы сиг-
нала. Контрольные диаграммы для различных условий приведены на рис. 3.44.
Эти диаграммы показывают только результат, но не говорят о том, что не-
обходимо делать.
Одним из приемов схемотехнического улучшения качества сигнала явля-
ется применение активной и пассивной коррекции. Активная коррекция
заключается в применении усилителей с предыскажениями, а пассивная
коррекция — в установке пассивных параллельных АС-фильтров со специ-
альными характеристиками. Рассмотрение этих приемов выходит за рамки
настоящей книги.
Как было показано, при проектировании печатных плат существуют три
основных фактора, которые влияют на качество контрольной диаграммы.
1. Емкостная неоднородность, связанная с металлизированными отвер-
стиями.
2. Потери в проводниках.
3. Потери в диэлектрике.
Первое решение по устранению деградации фронта сигнала и улучшению
контрольной диаграммы заключается в минимизации числа переходных
отверстий. Затем оптимизация размеров отверстий, применение круговых
зазоров для отверстий в слоях, согласование емкости переходного отверстия
с индуктивностью контура сигнального и возвратного пути таким образом,
чтобы отверстие аппроксимировалось отрезком линии передачи с волновым
сопротивлением, равным волновому сопротивлению линии передачи на плате.
Данный прием напоминает технику компенсации для соединителей.
Общая емкость Cvia отверстия между сигнальным и возвратным путем
должна быть:
г' _ ^via
via Z2 ’
где £via — индуктивность металлизированного отверстия; Z— волновое сопротивление ли-
ний передачи на плате.
Например, если индуктивность контура, к которому подключено метал-
лизированное отверстие, составляет 0,3 нГн, типичное для 6-ти слойной МПП,
а волновое сопротивление линии, к которому подключено отверстие, состав-
ляет 50 Ом, то общая емкость отверстия должна быть Cvia = 0,3-10~9/2500 =
= 0,12-10-12 Ф, т. е. 0,12 пФ. Она должна быть распределена между верхним
и нижним слоями равномерно по длине отверстия. Это значение меньше, чем
можно выполнить при изготовлении платы.
Известно, что индуктивность контура сигнального отверстия и его воз-
вратного пути составляет примерно 0,5 нГн/мм.
Чем меньше площадь контактной площадки и больше гарантированный за-
зор между отверстием и плоскостями внутренних слоев МПП, к которым не
подключается отверстие, тем меньше деградация фронта сигнала.
3.2. Линии передачи с потерями
239
Ширина проводника определяет потери в нем и толщину диэлектрика при
определенном волновом сопротивлении линии передачи. Чем шире провод-
ник и тоньше диэлектрик, разделяющий сигнальный и возвратный провод-
ники, тем меньше потери в линии передачи. Но во многих случаях ширина
проводника не может быть слишком большой, и это является ограничива-
ющим фактором.
Если необходимо снизить ослабление, то, в первую очередь, следует увели-
чить ширину проводников, избегая, если возможно, проводников, ширина которых
меньше 0,125мм. С другой стороны, выполнять проводники шире 0,25мм не сле-
дует, поскольку в этом случае будут существенные потери в диэлектрике FR4.
Если первые два шага выполнены, то деградацию фронта можно умень-
шить выбором диэлектрического материала с минимальным коэффициен-
том рассеяния. Это подчеркивает важность выбора диэлектрических мате-
риалов с определенными свойствами.
3.2.3. Механизмы потерь в линии передачи
Как было показано выше, первая приближенная модель линии переда-
чи — это набор £С-звеньев. Эта модель часто принимается в качестве моде-
ли линии без потерь. Она позволяет определить два главных свойства линии:
волновое сопротивление и время задержки распространения сигнала в ней.
Но данная модель не позволяет определить потери в линии, и для учета этих
потерь она должна быть дополнена.
В процессе распространения сигнала в линии передачи могут возникать
потери энергии в пяти следующих проявлениях.
1. Потери на излучение.
2. Связь с соседними трассами.
3. Потери от рассогласования волновых сопротивлений.
4. Потери в материале проводников.
5. Потери в диэлектрических материалах.
Потери на излучение влияют на параметры ЭМС, и обычно энергия,
потерянная вследствие излучения, очень мала по сравнению с другими по-
терями, и эти потери не имеют особого влияния на общие потери в линии
передачи на печатных платах.
Связь с соседними проводниками очень важна, поскольку может влиять
на ухудшение фронта сигнала. Этот эффект можно детально смоделировать
и прогнозировать сигналы в обоих проводниках — активном и пассивном.
Этот вопрос относится к анализу перекрестных помех и будет рассмотрен
ниже.
Неоднородность волнового сопротивления может очень сильно влиять на
искажение передаваемого сигнала. Это будет оказывать прямое влияние на
ухудшение фронта сигнала на входе приемника. Даже проводник абсолют-
но без потерь будет иметь существенное ухудшение фронта сигнала на вы-
ходе линии из-за неоднородности волнового сопротивления. Это требует тща-
тельного анализа помех отражения, что рассмотрено в следующей главе.
240
Глава 3. Линии передачи в печатном монтаже
Время, пс
Время, пс
Рис. 3.34. Контрольные диаграммы для 5 ГГц псевдослучайного битного потока.
Слева— малые потери. Справа — та же битная структура, также без потерь,
но с неоднородностью в виде четырех последовательных металлизированных
отверстий, каждое из которых имеет емкость 1 пФ
Если фронт ухудшается из-за отсутствия высокочастотных компонентов
сигнала, то следует понять, где происходят потери. Емкостная или индук-
тивная неоднородность не будет сама по себе способствовать поглощению
энергии. Высокочастотные компоненты сигнала отразятся и вернутся к своему
источнику, после чего, в конце концов, они будут поглощены и рассеяны либо
в согласующих резисторах, либо в полном сопротивлении источника.
На рис. 3.34 дан пример для псевдослучайного битового потока с частотой
5 ГГц и более, проходящего через короткий идеальный проводник без потерь с
четырьмя последовательными металлизированными отверстиями, каждое из
которых представляет нагрузку в 1 пФ, т.е. с общей емкостной нагрузкой в 4 пФ
[4]. В результате наблюдается заметное ухудшение фронта сигнала.
Последние два механизма возникновения потерь показывают основные
причины потерь в линиях передачи, не учтенные в других моделях. Потери
в проводниках относятся к потере энергии в прямом и возвратном провод-
никах линии передачи и вызваны их активным последовательным сопротив-
лением. Потери в диэлектрике определяются свойствами материала и харак-
теризуются тангенсом угла диэлектрических потерь tan(5) материала.
В общем случае, для типичного проводника шириной 0,2 мм с волновым со-
противлением 50 Ом потери в диэлектрике (стеклотекстолите) гораздо больше,
чем потери в проводнике, при частоте сигнала более 1 ГГц.
3.2.4. Коэффициент рассеяния
Использование параметра tan(5) при оценке потерь в линии не отвечает тре-
бованиям их точного описания. Это не более, как параметр свойства материа-
ла, который характеризует число свободно двигающихся диполей в материале
и является показателем увеличения подвижности с увеличением частоты.
Ток, протекающий через реальный конденсатор, имеет две компоненты.
Одна компонента относится к току, который имеет точный сдвиг по фазе
относительно изменения напряжения на обкладках конденсатора. Он соот-
ветствует току идеального конденсатора без потерь. Другая компонента тока
точно совпадает по фазе с приложенным напряжением. Это напоминает ток
через идеальный резистор и моделирует потери. Эти две компоненты фор-
3.2. Линии передачи с потерями
241
мально основывают комплексное число. Напряжение в комплексной фор-
ме записывается в виде:
v =Voe’“'.
Ток через конденсатор определяется формулой
(3.36)
(3.37)
(3.38)
а в комплексной форме
I = j(j)CV0.
Ток / через идеальный конденсатор без потерь сдвинут по фазе на 90° от-
носительно приложенного напряжения. Если конденсатор в вакууме имеет
емкость Со, то после заполнения его диэлектриком с относительной диэлек-
трической проницаемостью £г, ток через идеальный конденсатор:
I = ушегС0И0. (3.39)
Из этого выражения видно, что если диэлектрическая проницаемость ха-
рактеризуется вещественным числом, то ток через конденсатор увеличива-
ется только по амплитуде без изменения сдвига фазы. Если проницаемость
комплексная, то ее вещественная часть увеличивает ток без изменения фазы,
а мнимая часть будет переводить напряжение в ток в фазе с приложенным
напряжением, и это будет увеличивать потери.
Для того, чтобы привести вещественную часть тока в точное фазовое со-
ответствие с напряжением, определим комплексную диэлектрическую про-
ницаемость с отрицательным мнимым членом в форме:
£Г=£'Г-Х? (3.40)
где ег — комплексная относительная диэлектрическая проницаемость; Ег — веществен-
ная часть комплексной диэлектрической проницаемости; £г — мнимая часть комплекс-
ной диэлектрической проницаемости.
Знак минус введен в это выражение формально. При этом вещественная
часть тока сдвигается в положительном направлении и становится точно в
фазе с напряжением. Вещественная часть новой комплексной диэлектричес-
кой проницаемости в действительности есть то, что обычно называется ди-
электрической проницаемостью.
То, что традиционно называется диэлектрической проницаемостью, на самом
деле есть вещественная часть комплексной диэлектрической проницаемости.
Ее мнимая часть описывает компоненту, которая создает ток в фазе с прило-
женным напряжением и определяет потери.
Определим ток через идеальный конденсатор с потерями следующим об-
разом:
/ = усоегС0К0 = уоХе'г - X )С0И0 = ;сое'гСоИо + о)е'С0И0, (3.41)
где Со — емкость конденсатора в свободном пространстве; Ио — амплитуда прикладывае-
мого синусоидального напряжения.
242
Глава 3. Линии передачи в печатном монтаже
Рис. 3.35. Представление
комплексной диэлектрической
проницаемости на комплексной
плоскости
Комплексное число можно представить в
виде вектора на комплексной плоскости
(рис. 3.35). Угол, который составляет вектор с
вещественной осью, называется углом диэлек-
трических потерь 8.
Тангенс угла диэлектрических потерь есть
отношение мнимой части к вещественной и
называется коэффициентом рассеяния:
tan 8 = —
£.
откуда
(3.42)
е* = е' tan 8.
(3.43)
Имеется договоренность, что удобней использовать tan 8, чем мнимую
часть комплексной диэлектрической проницаемости. Поэтому веществен-
ная часть и tan 8 комплексно описывают свойства диэлектрического мате-
риала. Из выше приведенных выражений можно соотнести сопротивление
утечки для линии передачи с мнимой частью диэлектрической проницаемости
и коэффициентом рассеяния:
R -
lkg Re(/) со£*С0И0 co£/tan8C0 со-tan 8С
(3.44)
При любой конфигурации проводников геометрические параметры, вли-
яющие на емкость между проводниками, будут также влиять на сопротив-
ление утечки между ними. Это легко видеть на примере конденсатора с па-
раллельными пластинами. Для плоскопараллельного конденсатора емкость
равна
с = е<)е',р
откуда
5_ С
Л £0£'г *
Сопротивление между двумя пластинами определяется по формуле
_ I.EqE;
о 5 о С
Комбинация этой формулы с выражением (3.44) для сопротивления между
проводниками приводит к взаимосвязи между объемной проводимостью ма-
териала на постоянном токе и коэффициентом рассеяния:
д __ 1 ере' _ 1
о С co-tan 8С’
3.2. Линии передачи с потерями
243
что позволяет записать выражение для проводимости диэлектрического
материала
о = еое' со tan 8. (3.45)
В этих формулах: о — объемная проводимость диэлектрического материала
на постоянном токе; £0 — диэлектрическая постоянная; е' — вещественная
часть комплексной диэлектрической проницаемости; £* — мнимая часть ком-
плексной диэлектрической проницаемости; tan 8 — коэффициент рассеяния;
8 — угол диэлектрических потерь; R — сопротивление утечки между провод-
никами; С — емкость между проводниками; h — толщина диэлектрика меж-
ду проводниками; S — площадь проводников; со — угловая частота, равная
2л/ где / — частота синусоидального сигнала.
Даже если коэффициент рассеяния слабо зависит от частоты, видно, что про-
водимость диэлектрика на переменном токе будет линейно увеличиваться с час-
тотой из-за наличия члена со. Рассеяние мощности пропорционально проводимос-
ти и также будет линейно увеличиваться с частотой. Это фундаментальная основа
проблемы потерь в линии передачи при рассмотрении целостности сигнала.
3.2.5. Модель линии передач с потерями
Два основных фактора влияют на ослабление сигнала в линии передачи:
последовательное сопротивление проводников прямого и возвратного пути
и параллельное сопротивление, определяемое через потери в диэлектрическом
материале. Оба этих сопротивления зависят от частоты: последовательное со-
противление увеличивается из-за скин-эффекта, а параллельное сопротив-
ление уменьшается из-за коэффициента рассеяния диэлектрического мате-
риала и вращения диполей его молекул.
Эти элементы, которые ранее были опущены при упрощенном рассмот-
рении модели линии передачи, следует восстановить при анализе линий
передачи с потерями. Линия передачи с потерями будет характеризоваться
дополнительно к волновому сопротивлению и времени задержки распрост-
ранения сигнала, коэффициентом рассеяния диэлектрического материала и
сопротивлением Rt на единицу длины. Это сопротивление является суммой
двух составляющих: сопротивления Adc проводников на постоянном токе и
сопротивления Яас скин-слоя на высокой частоте:
= Л1с + ^ас-
К каждому звену модели линии без потерь добавляется последовательное
сопротивление и параллельная проводимость (рис. 3.36). Таким образом, звено
линии с потерями будет содержать: С — емкость линии, L — собственная ин-
дуктивность контура, R — последовательное сопротивление проводников,
G — параллельная проводимость, характеризующая потери в диэлектрике,
которая равна:
r=_L=_1
co-tanSC (3.46)
244
Глава 3. Линии передачи в печатном монтаже
Рис. 3.36. Модель линии с потерями
Эта модель может быть описана дифференциальными уравнениями — так
называемыми «телеграфными уравнениями». Добавление частотно зависи-
мых параметров усложняет анализ, поскольку в частотной области его надо
будет проводить для каждой отдельной частоты с последующей сверткой ре-
зультатов. Уравнения показывают, что волновое сопротивление линии переда-
чи, скорость распространения синусоидального сигнала в ней, а также ослаб-
ление сигнала зависят от частоты. Это важное отличие линии с потерями от
линии без потерь.
После преобразования точные значения волнового сопротивления, ско-
рости распространения электромагнитной волны и ослабления на единицу
длины определяются формулами [53]:
+ co£z
Z ^б’1+соС,°м’
(3.47)
^(я2 + со2/.2)(G/2 + со2С2) + or Z.zCz - RtGt м/с,
| )(G'2 + "^L‘C< + RiGl ’ Hn/M-
(3.48)
(3.49)
Эти громоздкие выражения сложно применить в инженерной практике.
Поэтому часто используют некоторую промежуточную модель - линию с ма-
лыми потерями. При этом должны соблюдаться условия: R{ <<c^Ll и Gt <<coCz.
Для проводника толщиной 35 мкм последовательное сопротивление на
частотах выше 10 МГц будет увеличиваться пропорционально корню квад-
ратному из частоты, а значение co£z будет увеличиваться линейно. На этой
частоте отмеченные неравенства уже будет выполняться, но на более высо-
ких частотах они будут выдерживаться более строго.
Определим сопротивление на постоянном токе для линии передачи длиной
/ = 1 м с шириной проводника w, м, толщиной t = 35 мкм, учитывая, что удель-
ное сопротивление меди р = 1,8-10“8 Ом м:
Я/=рА 7? = 1,810~8 ' ^(Лом/м.
wt w-35-10 w
(3.50)
3.2. Линии передачи с потерями
245
Начиная с некоторых частот, ток в проводнике протекает в скин-слое,
имеющим толщину менее 35 мкм. Толщину проводника при этом следует
заменить на толщину 5 скин-слоя, которая для меди равна
5 = 66-10‘3^, м (3.51)
где f — частота синусоидального сигнала, Гц.
Тогда сопротивление проводника на частотах, на которых проявляется
скин-слой, увеличится по сравнению с (3.50) в Z/8 раз:
n 1 л-4 г\ / г» 5x35*10 1Л-4 г~, 2,5 у гт
Я/=—Ю4Ом/м; Rt =--------—----з-Ю^*7/=—Ю 77/, Ом/м. (3.52)
w8 wx66*10-3 w ’
Если при некоторой частоте толщина скин-слоя будет больше толщины
проводника, то сопротивление не будет зависеть от частоты, и его можно
определить по формуле (3.50).
Для оценки примем, что индуктивность на единицу длины линии пере-
дачи составляет приблизительно 250 нГн/м для линии с волновым сопротив-
лением 50 Ом.
Определим параметры, при которых будут выполняться условия малых
потерь со£/>> Rr Для этого построим график изменения сопротивления по
частоте (рис. 3.37). Из него видно, что после некоторой частоты fb сопротив-
ление проводника увеличивается. Эта частота соответствует равенству тол-
щины скин-слоя и толщины проводника t= 8. Из формулы (3.52) получаем
, 6621П_6 4356 6
4 =—Ю =——Ю 6, Гц, (3.53)
W W
где w — ширина проводника, м.
Рис. 3.37. Изменение сопротивления печатного проводника по частоте:
1 — индуктивное сопротивление при большом волновом сопротивлении;
2 — индуктивное сопротивление при малом волновом сопротивлении
246
Глава 3. Линии передачи в печатном монтаже
Например, при ширине проводника 0,1 мм (1 • 10~4 м) частота fb, начиная
с которой индуктивное сопротивление будет больше активного сопротивле-
ния, равна примерно 435 кГц.
Определим частоту, начиная с которой выполняется неравенство оо£/ >> 7?z
для линии с малыми потерями при различных волновых сопротивлениях. При
относительно большом волновом сопротивлении и, следовательно, большой
индуктивности, индуктивное сопротивление изменится по прямой 1 (рис. 3.37),
а при малом волновом сопротивлении — по прямой 2 (рис. 3.37). Граничной
частотой, выше которой соблюдается неравенство od£z > R{, в первом случае
будет/[, аво втором — /2. Для принятого выше значения индуктивности
250 нГн/м на частоте fb = 435 кГц индуктивное сопротивление равно od£z =
= 435-103-250-10_9 = 0,1 Ом. Сопротивление при номинальной толщине про-
водника 35 мкм и ширине 0,1 мм, вычисленное по формуле (3.50), равно 5 Ом.
Это позволяет говорить, что изменение индуктивного сопротивления соответ-
ствует прямой 2 (рис. 3.37). Для определения частоты/2 составим неравенство,
учитывая выражение (3.52). На единицу длины линии получаем
2тг/х250-Ю’9»—10’7Т7- (3.54)
W
Откуда частота синусоидального сигнала
где w — ширина проводника, м.
При задании в формуле значения w в миллиметрах, значение частоты будет
получено в мегагерцах. При ширине проводника 0,1 мм частота, выше ко-
торой справедлива модель линии с малыми потерями, равна
f 0,025 _ .
f = ——т = 2,5 МГц.
(0,1)2
Можно заключить, что для линии передачи с шириной проводника шире 0,1 мм
режим с малыми потерями для синусоидальной частоты будет выше 2,5 МГц. Чем
выше частота, тем ближе модель линии к модели линии без потерь.
Следует учитывать, что полученная оценка приближенная, поскольку здесь
не учитывалось возможное технологическое изменение толщины и ширины
проводника, а также то, что значение погонной индуктивности может отли-
чаться от конкретного случая. Тем не менее, она хорошо отражает физичес-
кие эффекты в проводнике и характер основных зависимостей.
Проводимость диэлектрика будет уменьшаться с частотой, а емкость прак-
тически будет неизменна. Режим с малыми потерями будет иметь место, когда
Gz << coCz. Это произойдет, когда tan(6) << 1. В настоящее время все изоля-
ционные материалы имеют коэффициент рассеяния менее 0,02 (см. главу 1),
и межсоединения всегда могут быть рассмотрены в режиме с малыми ди-
электрическими потерями.
3.2. Линии передачи с потерями
247
Таким образом, для печатных плат режим с малыми потерями для провод-
ников с шириной 100 мкм и шире начинается с частоты 2,5 МГц, ниже которой
должны располагаться основные частотные компоненты сигнала. Это наибо-
лее распространенная модель для анализа высокоскоростных линий передач.
3.2.6. Волновое сопротивление линии передачи
с потерями
В идеальной линии передачи с потерями ее волновое сопротивление ста-
новится комплексным и зависимым от частоты (см. (3.47)). После преобра-
зований вещественная и мнимая части волнового сопротивления для линии
с малыми потерями будут:
действительная часть Re(^) - , мнимая часть Im(Z) = 0.
Эти приближенные выражения для линии с малыми потерями становят-
ся точными для линии без потерь. Ошибка приближения для линии с малы-
ми потерями меньше 1 % на частотах, более 10 раз превышающих гранич-
ную частоту, которая, как определено выше, составляет примерно 2,5 МГц
для линии передачи с шириной сигнального проводника 100 мкм.
Абсолютное значение волнового сопротивления, которое приближается
к экспериментально полученному, составляет:
Mag(Z) = 7Re(Z)2 + Im(Z)2.
На относительно низких частотах из-за емкостного характера линии ее
полное сопротивление достаточно высокое. По мере повышения частоты
полное сопротивление линии уменьшается и на частоте примерно 10 МГц ста-
билизируется на определенном уровне, которое соответствует значению
волнового сопротивления. Это соответствует режиму электрически длинной
линии с малыми потерями.
Таким образом, при режиме с малыми потерями потери в линии переда-
чи могут не учитываться.
3.2.7. Скорость распространения сигнала в линии
с потерями
Решение телеграфных уравнений для линии с потерями дает значение ско-
рости распространения синусоидального сигнала в линии (см. (3.48)). В ре-
жиме с малыми потерями (индуктивное сопротивление и коэффициент по-
терь значительно меньше 0,1) скорость электромагнитной волны в линии ап-
проксимируется выражением:
1
-’Ж' (з-56)
248
Глава 3. Линии передачи в печатном монтаже
Рис. 3.38. Отношение скорости распространения сигнала в линии передачи с
потерями и в линии без потерь
Это точно соответствует скорости сигнала в линии без потерь, т. е. в режи-
ме с малыми потерями скорость распространения сигнала не зависит от потерь.
Из точного выражения (3.48) скорости видно, что для определенной ча-
стоты она постоянна и будет изменяться с частотой. Этот эффект называет-
ся дисперсией, и в данном случае она вызвана наличием потерь в линии. На
рис. 3.38 показано отношение скорости распространения сигнала в микро-
полосковой линии передачи с потерями и в линии без потерь с проводни-
ком шириной 75 мкм на стеклотекстолите [4]. Волновое сопротивление ли-
нии 50 Ом. Дисперсия вызвана потерями в проводнике и диэлектрике.
Действие потерь заключается в большем снижении скорости на низких
частотах, чем на высоких. На низких частотах доминирует последовательное
резистивное полное сопротивление над индуктивным сопротивлением. Это
определяет большие потери и большее снижение скорости. Из-за дисперсии
высокочастотные составляющие распространяются быстрее, чем низкочастот-
ные. Во временной области высокочастотные составляющие будут достигать
конца линии первыми, приводя к увеличению длительности фронта. Однако,
если потери будут достаточны для заметного влияния на деградацию фронта,
то воздействие от ослабления будет более значительным, чем от дисперсии.
Для худшего случая конструкции линии с проводником шириной 75 мкм в
стеклотекстолите режим с малыми потерями начинается с 10 МГц. В этом ре-
жиме скорость не зависит от частоты и дисперсия от потерь пренебрежимо мала.
3.2.8. Ослабление в линии с потерями
Для оценки интенсивности ослабления используются децибелы (дБ) или
неперы (Нп). Амплитуда синусоидального сигнала на входе линии, обозна-
ченная Vin, проходя по линии, уменьшается в зависимости от потерь в линии.
На рис. 3.39 показана амплитуда синусоидального сигнала = 1 В частотой
1 ГГц, проходящего вдоль линии с шириной проводника 0,25 мм и волновым
3.2. Линии передачи с потерями
249
Рис. 3.39. Амплитуда синусоидального сигнала 1 ГГц, проходящего вдоль линии
с шириной проводника 0,25 мм и волновым сопротивлением 50 Ом в стеклотекстолите
сопротивлением 50 Ом в стеклотекстолите (диэлектрическая проницаемость 4).
Ослабление сигнала составляет 5 дБ на 250 мм длины линии передачи.
Видно, что уменьшение амплитуды вдоль линии идет по экспоненте.
Напряжение в любой точке d линии может быть записано (по основанию е)
в виде:
V(d)=Vine-A=Vine-da, (3.57)
где d — расстояние точки рассмотрения от начала линии; Vin — амплитуда входного сиг-
нала; А — общее ослабление, Нп; а — ослабление на единицу длины, Нп/м.
Разность уровней сигнала в 1 Нп соответствует их отношению, равному
основанию натуральных логарифмов е= 2,7. В этом случае отношение стано-
вится безразмерной величиной, но обозначаемой как непер. Например, если
ослабление составляет 1 непер, то амплитуда сигнала на выходе линии будет
\/е = 0,37, т. е. 37 % от амплитуды на входе линии. Если ослабление 2 непера,
то ослабление составит 1/е2 = 13 % от входного напряжения. Таким образом,
в общем случае ослабление в некоторой точке d определяется через отноше-
ние выходной и входной амплитуд напряжения:
А=~ hr- ’ Нп- (3-58)
\ "in )
Если потерь в линии нет, то отношение амплитуд будет равно 1 и значе-
ние потерь равно 0. Если в линии присутствует ослабление, отношение ам-
плитуд будет меньше единицы, и по правилам логарифмирования итоговый
результат будет положительным.
250
Глава 3. Линии передачи в печатном монтаже
Чаще ослабление оценивается в децибелах:
A = -201/^1 дБ.
\ "in J
(3.59)
Тогда напряжение V(d) в некоторой точке d можно определить по формуле:
r(rf) = /,J0^/20 = J<„-10 *20-, <3-60>
где А — общее ослабление, дБ; а — ослабление на единицу длины, дБ/м; d — дистанция, м.
Исторически логарифмическая шкала бел (Б) была предложена для оценки
восприятия звука. Она оказалась удобной для взятия отношений в большом
динамическом диапазоне. Чаще используется одна десятая часть бела — де-
цибел (дБ).
При определении отношения мощностей используют формулу:
Л = 101ё[т4 дБ. (3.61)
V0 )
Например, если мощность увеличивается в 1000 раз, то значение Ар со-
ставляет 30 дБ. Уменьшение мощности до уровня 1 % (т.е. снижение в 100 раз)
соответствует ослаблению 101g(10~2) = -20 дБ.
Весьма часто используется значение 3 дБ для описания, например, избира-
тельных свойств фильтров и других устройств. Это значение ослабления мощ-
ности соответствует ее 50 % изменению. Действительно, при усилении 10 lg(2) =
= 10 0,3 = 3, т. е. Ар = 3 дБ, а при ослаблении 10 lg(0,5) = 10-(—0,3) = -3, т. е.
Ар = 3 дБ.
Для двух напряжений, например, Ио и Vv их логарифм отношения г =
= lg(И//^о> является безразмерной величиной, и, строго говоря, для ее опи-
сания нельзя использовать децибелы, поскольку они применяются при отно-
шении двух мощностей или энергий. Для измерения отношений амплитуд на-
пряжений или токов необходимо выполнить дополнительные преобразования.
Учитывая, что мощность P^V^/R и измерения отношений всех физических
величин должны вестись на одном и том же сопротивлении А, то
( р\ ( У2} ( V \
lOlgU =101g V =201gV , дБ.
V ro J v о J v о 7
Например, изменение напряжения в 10 раз составляет 20 дБ. Заметим, что
при этом мощность изменится в 100 раз, что даст также 20 дБ при отноше-
ниях мощностей. Изменение напряжения на 50 % соответствует 6 дБ, а 3 дБ
соответствует изменению напряжения на 30 %. При определении в децибе-
лах суммарного ослабления набора отрезков линии необходимо сложить
значения ослаблений каждого отрезка.
3.2. Линии передачи с потерями
251
Пересчет неперов в децибелы ведется по соотношению 1 дБ = 0,1151 Нп,
т. е. при известном значении ослабления в неперах значение в децибелах по-
лучается следующим образом: А (дБ) = 8,86-Л (Нп).
При распространении синусоидального сигнала вдоль линии его ампли-
туда уменьшается по экспоненте. Общее ослабление, измеренное в децибел-
лах, увеличивается с увеличением длины линии. Для стеклотекстолита типо-
вое значение ослабления составляет 1 дБ/250 мм на частоте 1 ГГц. Это озна-
чает, что при прохождении каждых 250 мм сигнал ослабляется на 1 дБ, и его
амплитуда на выходе отрезка линии становится равной Vout/Vin = 10“1/20 = 0,89
от входного сигнала, т. е. 89 %.
Ослабление на единицу длины обычно задается в единицах «непер/ед.
длины» и обозначают ап (3.49). В режиме с малыми потерями:
ап ~ 2+ Нп/ед. длины. (3.62)
При задании ослабления на единицу длины в децибелах, дБ/длина, по-
лучаем:
adb = 4,34^-^-+ G)Z^, дБ/ед. длины. (3.63)
В этих формулах: 7?z — последовательное сопротивление на единицу длины;
G{ — параллельная проводимость на единицу длины; Z — волновое сопро-
тивление линии, Ом.
Видно, что ослабление не зависит от частоты, если последовательное со-
противление и параллельная проводимость не зависят от частоты. В этом
случае фронт сигнала при прохождении по линии уменьшается по ампли-
туде, но не изменяется по форме, поскольку все частотные компоненты ос-
лабляются одинаково.
В реальной ситуации, как было показано выше, потери в проводнике и
диэлектрике зависят от частоты, и ослабление будет увеличиваться с ростом
частоты. Высокочастотные составляющие будут ослабляться больше, чем низ-
кочастотные. Это приводит к уменьшению полосы пропускания линии и рас-
ширению фронта сигнала. Общее ослабление adb сигнала при этом будет
adb adb,R + adb,D>
(3.64)
где adb R — ослабление в проводнике:
Л п \
adb,R
дБ/ед. длины,
(3.65)
adb D ~ ослабление в диэлектрике:
ам d = 4,34-G/Z, дБ/ед. длины.
(3.66)
252
Глава 3. Линии передачи в печатном монтаже
В режиме, когда ограничивающим фактором является скин-эффект, как
было показано выше, сопротивление полосковой линии на единицу длины
приблизительно составляет:
2 5 7 г-
y[f, Ом/м,
w
где w — ширина проводника, м; f - частота, Гц.
Тогда ослабление в проводнике будет
(2 S _____A Ff
Ч/b.R =4,34 -^Ю-7V7 =1Н0-7^, дБ/м,
wZ ) wZ '
где w — ширина проводника, м; f — частота, Гц; Z — волновое сопротивление, Ом.
Для приближенных оценок можно воспользоваться формулой
а</*,к=ЗО—, дБ/м,
wZ
(3.67)
где f — частота, ГГц; w — ширина проводника, мм; Z — волновое сопротивление, Ом.
Для линии передачи с Z= 50 Ом получаем
ал,я=°,6—, дБ/м.
W
(3.68)
График для определения удельного ослабления линии передачи с волно-
вым сопротивлением 50 Ом представлен на рис. 3.40.
Например, на частоте 1 ГГц, линия с волновым сопротивлением 50 Ом и
шириной проводника 0,25 мм будет иметь ослабление на единицу длины
Рис. 3.40. Зависимость удельного ослабления в проводниках от частоты;
ширина проводника: 7 — 0,1 мм; 2 — 0,2 мм; 3 — 0,5 мм; 4 — 1,0 мм
3.2. Линии передачи с потерями
253
Отношение выходного напряжения к входному при этом будет Vout/ Vin =
= 10-2’75/2°, что примерно составляет 75%. Снижение амплитуды сигнала про-
исходит из-за потерь в линии передачи. Оценка потерь выполнена прибли-
женно, но она пригодна для использования в инженерной практике. Точные
решения могут быть получены на основе численных методов.
Общее ослабление проводника некоторой длины составляет
A(ib,R = l'adb,R> ДБ- (3.69)
Эксперименты [4] подтверждают, что, начиная с частоты примерно 10 МГц,
значения ослабления за счет потерь только в проводниках, полученные с
помощью численных методов, практически совпадают с полученными выше.
Для диэлектриков проводимость для любого сечения линии определяет-
ся по формуле:
Gj= wtan 8-Cz, (3.70)
а волновое сопротивление — по формуле:
(3.71)
Из этих двух соотношений ослабление на единицу длины можно опреде-
лить следующим образом:
л/£ л/£
adb,D =4,34G/Z = 4,34artan8-C/-^—!:- = 4,34(O'tan8—дБ/м,
(3.72)
где со — круговая частота, рад/с; Cz — емкость линии на единицу длины, Ф; ег — эффек-
тивная диэлектрическая проницаемость материала основания платы; vc — скорость света
в вакууме, м/с.
Если учесть, что со = 2л/ тогда:
o.dbD =90f tan8yl^, дБ/м, (3.73)
где f — частота, ГГц.
Интересно, что удельное ослабление не зависит от геометрии проводни-
ка. Например, при увеличении ширины проводника увеличиваются емкость
и проводимость, но волновое сопротивление будет уменьшаться. Поэтому
результат останется неизменным.
Ослабление из-за диэлектрических потерь определяется только свойства-
ми диэлектрических материалов и не может быть изменено за счет геомет-
рии сечения линии.
Для стеклотекстолита с проницаемостью 4 коэффициент рассеяния tan8
составляет 0,02. На частоте 1 ГГц ослабление линии на единицу длины на
данном материале будет 90 х 1 х 0,02 х 2 = 3,6 дБ/м. Это значение несколь-
ко выше, чем ослабление для проводников, равное 2,75 дБ/м, для линии пе-
редачи с волновым сопротивлением 50 Ом, шириной проводника 0,25 мм на
254
Глава 3. Линии передачи в печатном монтаже
частоте 1 ГГц. Это говорит о том, что на частоте 1 ГГц на данном материале
ослабление из-за потерь в диэлектрике несколько больше, чем ослабление
из-за потерь в проводнике. На высоких частотах ослабление из-за диэлект-
рика будет расти быстрее, чем ослабление от проводника, которое становится
менее важным на высоких частотах. Для частот более 1 ГГц диэлектричес-
кие потери доминируют. Поэтому выбору диэлектрического материала для
основания высокоскоростных печатных плат следует уделять особое внима-
ние. Перспективные материалы (см. главу 1) имеют коэффициент рассеяния
на порядок меньше, чем стеклотекстолит.
Учитывая разнообразие эффектов, рассмотренных выше, поясним неко-
торые базовые термины для однозначного их понимания:
• потери — основной термин, относящийся ко всем видам потерь в ли-
ниях передачи;
• ослабление — уменьшение мощности при передаче сигнала или умень-
шение амплитуды. При измерениях в децибеллах ослабление будет
увеличиваться линейно при увеличении длины линии. Когда изме-
рения выходного напряжения даются в процентах напряжения от
входного напряжения, то ослабление будет увеличиваться экспонен-
циально по длине линии;
• ослабление на единицу длины — уменьшение мощности в децибелах, от-
несенное на единицу длины, как параметр линии передачи является
константой. Удельное ослабление есть внутренний параметр линии и
не зависит от ее длины;
• коэффициент рассеяния — специфическое внутреннее материальное свой-
ство всех диэлектриков, которое измеряется числом диполей и скоро-
стью их перемещения в переменном поле. Это свойство определяет ди-
электрические потери и может незначительно зависеть от частоты;
• угол диэлектрических потерь — угол на комплексной плоскости меж-
ду вектором комплексной диэлектрической проницаемости и веще-
ственной осью;
• tan 6 — тангенс угла диэлектрических потерь на комплексной плоско-
сти, который есть отношение мнимой части комплексной диэлектри-
ческой проницаемости к вещественной части комплексной диэлектри-
ческой проницаемости; известен также как коэффициент рассеяния;
• вещественная часть диэлектрической проницаемости — вещественная часть
комплексной диэлектрической проницаемости есть термин, который ас-
социируется с тем, как диэлектрик будет увеличивать емкость между двумя
проводниками, а также как будет снижаться скорость распространения
сигнала в линии передачи; это внутреннее свойство материала;
• мнимая часть диэлектрической проницаемости — термин, который ас-
социируется с поглощением энергии электрического поля из-за дви-
жения диполей. Это внутреннее свойство материала, определяемое чис-
лом диполей и скоростью их перемещения;
• комплексная диэлектрическая проницаемость — фундаментальное внут-
реннее свойство материала, которое показывает, как электрическое поле
3.2. Линии передачи с потерями
255
будет взаимодействовать с материалом. Его вещественная часть пока-
зывает, как материал будет влиять на емкость, а мнимая часть пока-
зывает, как материал будет воздействовать на проводимость утечки.
Когда рассматриваются линии передачи с потерями, важно точно опре-
делиться с упоминаемыми терминами. Ослабление зависит от частоты. Од-
нако коэффициент рассеяния материала или другие свойства материала, как
правило, слабо зависят от частоты. Единственный способ точно определить
свойства материала и степень их влияния на характеристики линии переда-
чи — экспериментальные исследования реальных материалов. Как правило,
относительная стабильность по частоте диэлектрической проницаемости и
коэффициента рассеяния сохраняется по частоте вплоть до 10 ГГц. Дальней-
шие измерения показывают, что частотная зависимость этих параметров на-
чинает проявляться на частотах более 14 ГГц.
3.2.9. Полоса пропускания линии передачи
Если импульс, который распространяется по линии передачи, обладает
широким спектром, то при наличии потерь высокочастотные составляющие
ослабляются более интенсивно, чем низкочастотные. Это явление эквива-
лентно уменьшению полосы пропускания межсоединения. Рассмотрение
такого параметра, как полоса пропускания межсоединения, полезно для ана-
лиза поведения линии при передаче высокочастотных сигналов. В первой
главе уже определялась граничная частота, которую необходимо передать для
заданного фронта сигнала.
Существует фундаментальная связь между полосой пропускания межсо-
единения и потерями в линии передачи. Чем длинней линия, тем больше вы-
сокочастотные потери и уже ее полоса пропускания. Если имеется возмож-
ность определить полосу пропускания, ограниченную потерями, то можно
прогнозировать влияние ослабления на параметры сигнала.
Полоса пропускания определяется по уровню -3 дБ. Для каждой точки
d вдоль линии передачи необходимо рассчитать частоту, которая соответствует
уровню ослабления 3 дБ, что и определит полосу пропускания BWTL линии
в этой точке.
Рассматривая режим, в котором доминируют диэлектрические потери, мы
можем игнорировать резистивные потери. Тогда общее ослабление на час-
тоте f при расстоянии d дается:
AD =uD-d = 9t}f tanSy&d, дБ, (3.74)
где aD — ослабление на единицу длины в диэлектрике, дБ/м; ег — вещественная часть ком-
плексной диэлектрической проницаемости; d - длина линии передачи, м;/— частота си-
нусоидальной волны, ГГц; tan 5 — коэффициент рассеяния материала.
Полоса пропускания BWTL линии для отрезка d равна частоте, при кото-
рой амплитуда сигнала падает на 3 дБ, т. е. AD = 3. Делая соответствующие
подстановки, получаем:
256
Глава 3. Линии передачи в печатном монтаже
TL 9ОЧапб7Ё7 d ЗОЧапб^/ё^ d' ГГц, (3.75)
где d — длина отрезка линии передачи, м.
Из этого выражения видно, что чем больше длина, тем уже полоса про-
пускания и ниже частота, на которой ослабление увеличивается на 3 дБ. Кроме
этого, чем больше коэффициент рассеяния, тем уже полоса.
Длительность фронта идеального импульса равна 0, а его спектр бесконе-
чен. Если спектр сигнала будет ограничен, то его фронт составит как минимум:
0,35
/r-BWTL’HC’ <3-76>
где BWT[ — полоса пропускания линии передачи, ГГц.
Для линии передачи с потерями длительность фронта ZrTL импульса, ко-
торая ограничена полосой пропускания линии передачи, определяется сле-
дующим образом:
zrTL =0,35><30Чап6Л/Ё7х^ = 1О,5Чап6Л/Ё7xJ, нс, (3.77)
где tan 5 — коэффициент рассеяния материала; ег— вещественная часть комплексной ди-
электрической проницаемости; d - длина отрезка линии, м.
Например, для линии передачи с потерями, на основе стеклотекстолита FR4
(ег = 4) с коэффициентом рассеяния 0,02, на отрезке 25 мм фронт сигнала, ог-
раниченный параметрами линии, будет составлять 10,5 х 0,02 х 2 х 0,025 « 10 пс.
При длине линии 250 мм минимальный фронт, ограниченный полосой про-
пускания, будет 100 пс. Это означает, что любой импульс с фронтом существенно
меньше 100пс, поступивший на вход такой линии, на выходе будет иметь фронт
100 пс. Все высокочастотные компоненты спектра импульса будут абсорби-
рованы в материале диэлектрика и переведены в теплоту.
Полезное правило: фронт сигнала при распространении по линии передачи
на основе стеклотекстолита будет увеличиваться примерно на 10 пс на каж-
дые 25 мм дистанции.
В табл. 3.3 приведены значения удельного расширения фронта сигнала
(пс/м) за счет потерь в диэлектрике. Отметим, что для материала RogersRF35
на основе Teflon этот параметр меньше 40 пс/м. В том случае, если сигналь-
ный проводник очень узкий, то значение этого параметра будет больше из-
за потерь в проводнике.
При аппроксимации фронта trjn импульса, поступающего на вход линии,
функцией Гаусса и при произвольной его длительности, после прохождения
импульса по линии с потерями, его фронт определяется как
!гои,=^г,„+ГП1- <3-78)
где /гТ1 — собственный фронт сигнала, определяемый параметрами линии.
В этой формуле все временные параметры задаются в единой размерности.
3.2. Линии передачи с потерями
257
Таблица 3.3
Фронт сигнала, свойственный различным материалам, при учете только диэлектрических
потерь в линии передачи
Материал Ег tan5 Собственный фронт, ZrTL, пс/м
Стеклотекстолит FR4 4,0...4,7 0,02 400
DriClad (IBM) 4,1 0,011 216
GETek 3,6...4,2 0,013 280
Бисмалеимид Триазин (ВТ) 4,1 0,013 280
Полиимид/стеклоткань 4,3 0,014 320
Cyanate Ester 3,8 0,009 188
NelcoN6000SI 3,36 0,003 60
RogersRF35 3,5 0,0018 36
Например, пусть импульс с фронтом 50 пс поступает на линию с собствен-
ным фронтом 400 пс/м, длина которой 0,2 м. Длительность фронта, опреде-
ляемая потерями, на выходе линии составляет 400 пс/м х 0,2 м = 80 пс. Ито-
говое значение фронта на выходе линии составляет
tI0UI = >/502+802 = 94 пс.
Фронт Гг TL, определяемый параметрами линии, должен быть не более 50 %
от фронта Гг сигнала, поступающего на линию. В противном случае искаже-
ния фронта выходного сигнала будут весьма значительны. Это позволяет
сформулировать требование к допустимой длине линии передачи:
rrTL d< 0,5/r. (3.79)
Для линии передачи на стеклотекстолите получаем:
400 d< 0,5/г.
Тогда длина линии должна удовлетворять следующему требованию:
d< 1,25-10-3Гг, м,
где tr — фронта сигнала, пс.
Если фронт сигнала задается в наносекундах, то ограничения на длину
проводников задаются соотношением
d < 1,25rr, м.
Таким образом, при выполнении линии передачи на стеклотекстолите ее длина
должна быть не более 1,25 м при фронте сигнала 1 нс. Если фронт сигнала со-
ставляет 0,1 нс, то допустимая длина линии будет 125мм. В этом случае можно
не учитывать потери в диэлектрике линии. Как будет показано ниже, это ог-
раничение менее жесткое по сравнению с ограничением, связанным с помехами
отражения из-за рассогласования линий.
9 1527
258
Глава 3. Линии передачи в печатном монтаже
3.2.10. Поведение линии с потерями
во временной области
Фронт сигнала определяется между уровнями 10% и 90 % от установив-
шегося значения. Он хорошо аппроксимируется функцией Гаусса, но при
наличии потерь форма сигнала изменяется, и данная аппросимация не мо-
жет применяться.
На рис. 3.41 представлены фронты импульсов при прохождении по ли-
нии с волновым сопротивлением 50 Ом длиной 400 мм на FR4 с коэффици-
ентом рассеяния 0,01 [4].
При корректном моделировании линии с потерями частотно зависимыми
элементами удается достаточно точно определить параметры сигнала в ней. На
рис. 3.42 показаны результаты моделирования с различной степенью учета по-
терь. Здесь моделируется прохождение сигнала по линии с потерями длиной 750
Рис. 3.41. Экспериментальное определение фронтов импульсов при прохождении
по линии длиной 400 мм: 1 — сигнал на входе; 2 — сигнал на выходе
Рис. 3.42. Моделирование с различной степенью учета потерь: 1 — без потерь;
2 — потери только в проводнике, 3 — потери в проводнике и диэлектрике
3.2. Линии передачи с потерями
259
Рис. 3.43. Моделирование прохождения сигнала с тактовой частотой 1 ГГц по линиям
с потерями различной длины: 1 — входной сигнал; 2 — на выходе линии длиной 0,5 м;
3 — на выходе линии длиной 1 м
мм с фронтом примерно 50 пс и с
шириной трассы 0,2 мм, обобщен-
ный коэффициент рассеяния про-
водника и диэлектрика принят 0,02.
Если для анализа использовать
генератор с тактовой частотой 1 ГГц,
то сигналы на входе и выходе линий
длиной 0,5 м и 1 м будут выглядеть,
как показано на рис. 3.43. Линии
выполнены на FR4, ширина трассы
0,2 мм.
Влияние потерь удобно отра-
жать на контрольной диаграмме.
На ней виден один цикл сигнала,
и диэлектриках 2-х металлизированных
отверстий
Рис. 3.44. Контрольные диаграммы для раз-
личных вариантов учета потерь
в линии передачи
и по ее открытости можно судить
о наличии межсимвольных помех.
На рис. 3.44 показана симулиро-
ванная контрольная диаграмма для
50-омной линии, длиной 0,9 м на FR4 без потерь и с различными потерями:
только в проводниках, в проводнике и в диэлектрике, в проводнике, диэлек-
трике и при наличии металлизированных отверстий с емкостью 0,5 пФ на каж-
дом конце линии. Ширина линии 0,2 мм. Источник имел период следования
битов 200 пс, что соответствует частоте 5 Гбит/с.
Видно, что при значительных потерях контрольная диаграмма почти не
имеет открытых областей, что не позволяет использовать данную линию для
передачи импульсов с такой частотой. Необходимо предпринять меры по кор-
ректировке конструкции линии, чтобы диаграмма «раскрылась».
Глава 4
Обеспечение целостности сигнала
в печатном монтаже
4.1. Целостность сигнала в электронных
модулях
4.1.1. Целостность сигнала и проектирование
печатных плат
На одной из конференций прозвучало справедливое выражение: «Всех
проектировщиков можно разделить на две категории: одни уже встретились
с проблемой целостности сигнала, другие обязательно встретятся с ней». Дей-
ствительно, проблема обеспечения целостности сигнала выходит на ведущие
позиции при проектировании цифровых систем в связи с увеличением их бы-
стродействия. Решение этой проблемы возможно только на основе анализа
электромагнитных процессов, которые происходят в печатной плате при рас-
пространении сигнала по линиям передачи, с учетом реальных нагрузок [25,
30, 47]. Ряд задач решается на основе приближений или численных методов
расчета и рассмотрены в предыдущих разделах книги. В общем случае, про-
блема целостности сигнала непосредственно связана с проблемой таймин-
га. Любое искажение формы информационного сигнала относительно иде-
альной приводит к нарушению временных соотношений в системе обработки
информации. Ранее уже рассматривались возможные последствия подобного
явления — возникновение межсимвольных помех. Поэтому одной из важ-
нейших целей обеспечения целостности сигнала является корректная работа
цифровых систем при высоких скоростях обработки информации.
В цифровых системах сигнал в виде логических нулей и единиц распро-
страняется между компонентами схемы. Уровню логической единицы, как
правило, соответствует высокий уровень напряжения, а уровню логическо-
го нуля — низкий. Конкретные значения этих напряжений зависят от серии
микросхем. В реальных компонентах эти уровни задаются с некоторым до-
пуском. Для приемного устройства логической единице соответствует напря-
4.1. Обеспечение целостности сигнала в печатном монтаже
261
Рис. 4.1. Идеальная форма
входного цифрового сигнала
Рис. 4.2. Реальная форма цифрового
сигнала на входе приемника
жение более некоторого порогового уровня KIHmin входного напряжения, а
логический ноль будет восприниматься, если напряжение будет ниже ниж-
него порогового уровня KILmax (рис. 4.1).
Если форма сигнала на входе приемника приближается к идеальной, то
будут четко определены уровни логического 0 и 1, что обеспечит коррект-
ную работу системы. В реальной ситуации фронт сигнала претерпевает из-
менения по ряду причин: наличие потерь в линии передачи, отражения от
несогласованных нагрузок, возникновение перекрестных помех, резонанс-
ные явления. Это приводит к искажениям формы сигнала (рис. 4.2), кото-
рый становится по сути аналоговым, со всеми присущими ему атрибутами:
выбросы, провалы, «звон» и т. п.
Процесс работы цифрового устройства основан на событиях переключения
микросхем, которые объединены определенной логикой работы при помо-
щи временных диаграмм, и процесс обработки данных привязан к синхро-
низирующим импульсам, а моменты переключения драйвера и приемника
задаются с некоторым допуском. Если в зоне между И1Н и KIL (рис. 4.1) про-
исходит искажение фронта сигнала, то приемник не может четко определить
логический уровень, и его состояние может оказаться не определенным, что
приведет к нарушению функционирования системы.
Как было показано в первой главе, у команды разработчиков продукта есть
только один шанс продвинуть свой продукт на рынок: изделие должно пре-
восходно работать с первой попытки. Чем раньше в цикле проектирования
будут устранены и опознаны проблемы целостности сигнала и ЭМС, тем
больше шансов, что продукт будет конкурентоспособен.
При увеличении тактовой частоты, опознание и решение проблемы цело-
стности сигнала становятся более трудными. Успеха добьется тот, у кого про-
блемы с целостностью сигнала и с осуществлением эффективности процесса
проектирования устранены. Именно включение новых правил проектирова-
ния, новых технологий и новых методов анализа позволяет добиться высокого
качества продукции и выполнить работу в более короткие сроки.
Процесс проектирования очень часто интуитивный и творческий. Техни-
ческое понимание проблемы целостности сигнала очень важно для дости-
жения приемлемого результата настолько быстро, насколько это возможно.
262 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Все специалисты, которые занимаются разработкой цифровых систем, долж-
ны представлять, как их технические решения влияют на конечный продукт.
При тактовой частоте до 10 МГц основные требования при проектирова-
нии печатных плат или узлов сводились к трассировке проводников в двух-
слойных платах и повышению надежности изделия. Электрические свойства
межсоединений не были важны, потому что не затрагивали работу системы.
В этом случае говорят, что межсоединения были «прозрачны к сигналам».
Например, устройство, генерирующее импульс с фронтом 10 нс и тактовой
частотой 10 МГц, могло удовлетворительно работать даже в том случае, если
трассировка платы была выполнена без учета электрофизических парамет-
ров печатного монтажа.
Современные изделия работают на значительно более высоких частотах
с очень короткими фронтами. Для большинства плат эффект целостности
сигнала следует принимать во внимание с тактовых частот более, чем 100 МГц,
или для фронта сигнала короче, чем 1 нс. Этот режим называют высокочас-
тотным или быстродействующим режимом. В этом режиме межсоединения
больше «не прозрачны» к сигналам, и, если не учесть этого фактора, то воз-
никнут одна или несколько проблем целостности сигнала.
Целостность сигнала относится, в ее самом широком смысле, ко всем
проблемам, которые возникают в быстродействующих узлах и устройствах.
Все эти проблемы попадают в одну из следующих категорий:
1. Тайминг.
2. Внутриаппаратурные помехи.
3. Межсистемные электромагнитные помехи.
Тайминг — это сложная область, связанная с временными соотношени-
ями в системе. В определенный промежуток времени должен произойти ряд
событий, связанных с обработкой дискретной информации, которая физи-
чески представляется в виде сигналов. Нарушение последовательности этих
событий во времени приведет к нарушению работоспособности изделия.
Некорректная конструкция платы, отсутствие должного временного анализа
прохождения сигналов по линиям передачи в плате приведет к упомянутым
нарушениям.
Внутриаппаратурные помехи проявляются в виде «звона», помех отраже-
ния, перекрестных помех, помех переключения, немонотонности фронтов
сигнала, скачков напряжения в шине питания и заземления, затухания, дис-
персии и т. п. Все они относятся к свойствам межсоединений и воздейству-
ют на форму цифрового сигнала, приводя к его искажению. Вышеупомяну-
тые эффекты связаны с проблемами целостности сигнала и с одним из сле-
дующих источников внутриаппаратурных помех:
1. Электрофизические параметры и режим одиночной линии передачи.
2. Электромагнитное взаимодействие между двумя и более линиями.
3. Нарушения в системе распределения энергии и заземления.
4. Излучение от печатных узлов.
Эти проблемы играют важную роль во всех межсоединениях — от внут-
реннего межсоединения в кристалле и корпусе микросхемы до шкафа и
4.1. Обеспечение целостности сигнала в печатном монтаже
263
стойки цифровой системы. На всех иерархических уровнях принципы и
эффекты остаются неизменными, а отличия заключаются в физической
структуре объекта — определенных геометрических размерах и матери-
альных свойствах.
4.1.2. Однородность линий передачи и помехи
отражения
Линия передачи сигналов определяется качеством выполнения сигналь-
ного и возвратного путей. Любые изменения поперечного сечения или гео-
метрической формы проводников на пути прохождения токов изменяют
волновое сопротивление линии и соответственно влияют на форму сигна-
ла. Эти изменения волнового сопротивления называются неоднородностями.
Каждая неоднородность вызывает определенные искажения сигнала от его
первоначальной формы. Примером неоднородностей геометрического ха-
рактера может служить изменение ширины сигнального проводника, нали-
чие ответвления от проводника; неоднородностей топологического харак-
тера — переход со слоя на слой, разрыв в плоскости заземления; неоднород-
ностей схемно-конструктивного характера — наличие соединителя на конце
линии передачи, несогласованная нагрузка на конце линии. Наиболее рас-
пространенная неоднородность имеет место на конце линии передачи, где
имеет место высокое или низкое сопротивление.
Даже с идеальными согласованными нагрузками, топология платы может
радикально затронуть качество сигнала. Когда трасса делится на 2 отрезка с
различным волновым сопротивлением, то в месте разделения произойдет
изменение сопротивления, и часть сигнала отразится от места стыка обрат-
но к источнику, пока остальная часть сигнала будет продолжать распрост-
раняться к нагрузке в искаженной форме.
Воздействие любой неоднородности на сигнал зависит от длительности
фронта сигнала. Поскольку фронт становится короче, то искажения увеличатся.
Это означает, что неоднородность, которая не была проблемой в плате, рабо-
тающей, например, на частоте 33 МГц, может стать проблемой при 100 МГц.
На рис. 4.3 показано искажение сигнала с различными фронтами при его рас-
пространении по печатному проводнику длиной 150 мм. Нагрузка не подклю-
чена к линии передачи, а фронт сигнала на ее входе составляет в одном слу-
чае 3 нс, в другом — 1 нс. Видно, что при фронте 3 нс никаких существенных
проблем не возникает, а при фронте 1 нс появляется «звон».
Чем выше тактовая частота и меньше длительность фронта импульса, тем
более важно сохранять волновое сопротивление линии передачи постоян-
ным при прохождении сигнала вдоль нее. Одно из решений состоит в реа-
лизации печатного монтажа с контролируемым волновым сопротивлением
даже внутри корпуса микросхемы, например, как это необходимо в случае
применения корпусов BGA. Когда в корпусах не используется контролиру-
емое волновое сопротивление, например, рамка с внешними выводами, важно
сделать эти выводы коротким, как в корпусах CSP.
264 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Время
Рис. 4.3. Искажение сигнала с различными фронтами при его распространении
по линии передачи: 1 — фронт сигнала 3 нс; 2 — фронт сигнала 1 нс
4.1.3. Перекрестная помеха в межсоединениях
Когда один проводник несет сигнал, то на нем развивается некоторое
напряжение, и в нем протекает определенный ток. Электрические и магнит-
ные поля от токов и напряжений в активной линии взаимодействуют с рас-
положенными рядом проводниками (пассивные линии) и, согласно законам
индукции, наводят в них токи и электрические заряды. Эти наведенные токи
и заряды за счет входных и выходных сопротивлений компонентов, подклю-
ченных к пассивной линии, создают на концах линии наведенные напряжения
помех, которые называются перекрестными помехами. Помеховые напряжения
могут быть достаточно высокими. Согласно принципу суперпозиции, они
могут складываться с полезными сигналами и, в конечном счете, помеховые
напряжения сами по себе или совместно с полезным сигналом могут повлиять
на работоспособность системы.
Если между цепями существует индуктивная и емкостная связь, то это обес-
печивает путь для попадания нежелательных сигналов (помех) из одной цепи в
другую.
Детально механизм возникновения перекрестных помех и их расчет рас-
смотрен ниже. В качестве примера на рис. 4.4 показана перекрестная поме-
ха в начале и в конце пассивной линии передачи. В активной линии сигнал
имеет амплитуду 200 мВ. Видно, что на ближнем конце амплитуда помехи
составляет 13 %, а на дальнем конце — 60 % от уровня сигнала.
При проектировании линий передач в печатных платах, особенно мно-
гослойных, в качестве возвратного пути используются слои металлизации.
Наличие таких слоев снижает магнитную и электрическую компоненту связи
между отдельными линиями, причем уровень этих компонент примерно
одинаков. Любое нарушение однородности возвратного пути в слое метал-
лизации будет приводить к увеличению связи между линиями. Так, в случае
сужения возвратного проводника увеличивается индуктивная связь между
4.1. Обеспечение целостности сигнала в печатном монтаже
265
Рис. 4.4. Перекрестная помеха на ближнем и дальнем концах пассивной линии:
1 — помеха на ближнем конце; 2 — помеха на дальнем конце
двумя линиями, которая становится более интенсивной, чем емкостная. В
этом случае индуктивная составляющая помехи превосходит емкостную
составляющую.
Режимы, при которых превалирует индуктивная составляющая в индуци-
рованной помехе, характеризуются различными терминами, а именно: «ком-
мутационные помехи», «помехи типа дельта-Z», «подскок напряжения», «син-
хронные помехи коммутации» (SSN) или «синхронные коммутационные
выходные (SSO) помехи». Все эти типы помех определяются собственными
и взаимными индуктивностями прямых и возвратных проводников.
Минимизация выходных коммутационных помех достигается тщатель-
ным проектированием выводов корпусов микросхем и печатного монтажа,
при котором минимизируется взаимная индуктивность между прямым и
возвратным проводниками.
Приемы, при которых минимизируется индуктивная и емкостная связь
между линиями передачи, сводятся к увеличению расстояния между ними
(разнос), уменьшению длины взаимодействующих участков линий, приме-
нению материалов с низкой диэлектрической проницаемостью, снижению
длительности фронта сигнала.
4.1.4. Помехи в шинах питания
Помехи в печатных платах возникают не только в сигнальных проводни-
ках, но и в шинах питания и заземления, подходящих к каждому корпусу мик-
росхем. При изменении тока потребления во время работы микросхемы про-
исходит уменьшение напряжения питания и увеличение напряжения на шине
заземления. Это происходит из-за влияния индуктивности шин питания, за-
земления и выводов корпусов микросхем. При номинальном напряжении
питания 2,5 В возможно изменение этого напряжения на 125 мВ и более.
266 Глава 4. Обеспечение целостности сигнала в печатном монтаже
В высокопроизводительных микропроцессорах и микросхемах специаль-
ного назначения наблюдается тенденция уменьшения напряжения питания,
но увеличение потребляемой мощности. Это, в первую очередь, вызвано
стремлением повысить быстродействие микросхем. В каждом цикле потреб-
ляется определенная энергия. При повышении частоты переключения энергия
цикла остается неизменной, но за единицу времени ее поглощается больше,
что приводит к большей поглощаемой мощности для всего устройства, вслед-
ствие чего увеличивается перепад тока потребления за один цикл и снижа-
ется допустимый уровень помех. Поскольку напряжение питания микросхем
уменьшается, а уровень тока растет, любая просадка напряжения в шине
питания становится все более серьезной проблемой.
Целью проектирования распределенных систем питания и заземления явля-
ется минимизация их полного сопротивления.
На рис. 4.5 показан тренд максимально допустимого полного сопротив-
ления распределенной системы питания для высокопроизводительного мик-
ропроцессора Sun Microsystems, из которого видно жесткое выполнение
указанного выше требования [70].
Понимая физическую суть полного сопротивления, которая рассмотре-
на во второй главе, можно дать общие рекомендации по снижению полного
сопротивления системы питания. Эти рекомендации получат свое обосно-
вание далее, но в общем они сводятся к следующему [73]:
• следует располагать шины питания и заземления (возвратные провод-
ники) на минимальном расстоянии друг от друга; это расстояние оп-
ределяется в МПП минимально возможной толщиной диэлектричес-
кой прокладки между проводящими слоями;
• необходимо применять развязывающие конденсаторы с низкой индук-
тивностью (собственной и выводов);
• целесообразно распределять подачу напряжения питания между не-
сколькими параллельными выводами микросхемы;
• следует отдавать предпочтение применению развязывающих конден-
саторов, встроенных в корпуса микросхемы.
Год
Рис. 4.5. Тренд максимально допустимого полного сопротивления распределенной
системы питания для высокопроизводительных микропроцессоров Sun Microsystems
4.1. Обеспечение целостности сигнала в печатном монтаже
267
Современные подходы к конструированию печатных плат и новые мате-
риалы способствуют применению ультратонких диэлектрических материа-
лов, устанавливаемых между слоями питания и заземления в составе МПП.
Одним из таких материалов является диэлектрик С-Ply корпорации ЗМ
(США), толщина которого может быть 8 мкм, а относительная диэлектри-
ческая проницаемость 20. Применение этого материала позволяет сблизить
слои питания и заземления до минимальных расстояний, что приводит к
существенному возрастанию емкости между слоями питания и заземления
и снижению индуктивности контура «питание — заземление» в составе МПП.
Худший случай соответствует применению стеклотекстолита FR4, при ко-
тором уровень помех может достигать 0,75 В. Лучший случай — применение
материала С-Ply, при котором практически отсутствуют помехи.
4.1.5. Джиттер цифрового сигнала
В синхронных цифровых системах при выполнении каждого цикла выд-
вигаются жесткие временные требования к ряду параметров. Они включают
время задержки распространения сигнала внутри микросхемы, все задержки
переключения вентиля, фронт и спад сигнала, время установки и удержания,
а также расфазировку — разность между моментом прихода синхроимпульса
и появлением сигналов данных на каждом выходе микросхемы. После про-
хождения сигнала по линии передачи при определенных условиях происхо-
дит временной сдвиг фронтов сигналов относительно идеального положения,
причем для одной последовательности битов сдвиг фронтов различных битовых
импульсов может быть различным. Тайминг предполагает знание всех состав-
ляющих временных затрат на один цикл.
Важным параметром, описывающим вариации временных параметров
цикла, которые могут изменяться от цикла к циклу, является джиттер.
Джиттер определяется как кратковременная вариация расположения циф-
рового сигнала относительно его идеального положения на оси времени [4,
74, 75]. Источники джиттера можно разделить на две категории: случайные
и детерминированные. Случайные источники описываются нормальным
законом распределения с некоторым стандартным отклонением. Их прогно-
зировать невозможно. Детерминированные источники определяются несо-
вершенством среды распространения сигнала, и они могут прогнозироваться.
При решении задач тайминга можно задать допуск, который охватывает все
временные параметры. Широкий допуск необходим для обеспечения коррек-
тной работы системы.
Чем короче цикл, тем более точно должны быть определены все состав-
ляющие тайминга. Ниже показана природа детерминированного джиттера,
средства уменьшения его значения, а также приемы устранения искажений,
связанных с ним.
При наличии адекватной модели можно определить значение джиттера
для каждой ситуации и его влияние на работоспособность системы. В ре-
жиме малых потерь один из типов детерминированного джиттера возникает
268 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Сечение линий
Рис. 4.6. Три связанные
линии передачи: пассивная
линия (в центре) находится
под воздействием активных
линий; внизу — сечение
фрагмента многопроводной
линии передачи
из перекрестных помех между соседними линиями в шинах передачи дан-
ных. Для понимания источника перекрестных помех, которые индуцируют
джиттер, можно рассмотреть механизм его образования путем точного мо-
делирования и оптимизировать показатели конечного продукта.
Перекрестная помеха, которая индуцирует
джиттер, появляется тогда, когда битовый сигнал
в активной линии воздействует на синхронный
сигнал в соседней линии передачи битовой ин-
формации. Для примера на рис. 4.6 показано рас-
положение трех линий передач в шине данных и
их сечение. Шина выполнена в виде набора па-
раллельных микрополосковых линий с шириной
проводников и зазорами, равными 0,125 мм. Каж-
дая линия имеет длину 225 мм и волновое сопро-
тивление 50 Ом. Между линиями существует до-
статочно сильная электромагнитная связь. Связь
центрального проводника с линиями за предела-
ми, указанными на рисунке, весьма слабая, и ее
можно не учитывать.
Центральная линия — это пассивная линия,
и интерес представляет момент времени, когда
сигнал в ней достигнет дальнего конца, на кото-
ром имеется приемник. Две соседние линии с каждой стороны пассивной ли-
нии находятся в активном режиме. Они могут быть как в статическом состо-
янии, так и в динамическом режиме с дополнением битовой последователь-
ности к пассивной линии. По шине данных передается параллельный код,
и на вход каждой линии синхронно могут подаваться различные логические
уровни: либо одинаковые (на всех линиях присутствуют логические едини-
цы), либо дополняющие (на линиях присутствуют как логические нули, так
и логические единицы).
Симуляция времени пробега в пассивной линии показана на рис. 4.7 [4].
На нем показан сигнал на входе приемника, подключенного к выходу пас-
сивной линии, для трех состояний активных линий: линии в статическом со-
стоянии, обе линии переключаются с одинаковой битовой последователь-
ностью, и линии переключаются с дополняющей к пассивной линии бито-
вой последовательностью. Общее время задержки распространения сигнала
в пассивной линии составляет примерно 1,5 нс при отключенных активных
линиях. Видно, что это время изменяется в пределах ±0,1 нс, или около 7 %
общего времени задержки распространения, и зависит от битовой последо-
вательности в активных линиях.
Когда активная линия передает такую же последовательность, как и пас-
сивная линия, задержка пассивной линии увеличивается, а когда активные
линии передают дополняющую последовательность, время уменьшается. Это
одна из составляющих детерминированного джиттера. Если его вариации не
лежат в допустимых пределах, система может давать сбои.
4.1. Обеспечение целостности сигнала в печатном монтаже
269
Рис. 4.7. Сигнал на входе приемника, подключенного к выходу пассивной линии, для
трех состояний активных линий: 7 — линии в статическом состоянии; 2 — активные
линии переключаются с одинаковой битовой последовательностью; 3 — линии
переключаются с дополняющей к пассивной линии битовой последовательностью;
4 — выход драйвера
Часто перекрестные помехи рассматриваются через емкостную и индук-
тивную связь. Перекрестные помехи, которые детально рассмотрены в пос-
ледующих разделах главы, на дальнем конце линии и джиттер, вызванный
перекрестными помехами, имеют общую природу. Значение джиттера не
зависит от общей перекрестной помехи и от фронта сигнала. Детерминиро-
ванный джиттер, вызванный взаимодействием линий, зависит от вариаций
скорости электромагнитной волны в этих линиях. Он может быть исключен
тщательным проектированием шин передачи данных. Можно иметь систему
с высоким уровнем перекрестных помех, но с малым джиттером.
Удельное время задержки распространения сигнала по однородной ли-
нии передачи зависит от относительной диэлектрической проницаемости гг
диэлектрика в конструкции линии:
/d=3,3^, нс/м. (4.1)
При диэлектрической проницаемости материала основания платы, рав-
ной 4, задержка в линии длиной 225 мм составляет 3,3x2x0,225 = 1,48 нс. Если
учесть дополнительную задержку (приблизительно 0,1 нс), вызванную дег-
радацией фронта из-за входной емкости 2 пФ для вентиля, приближенно
получим итоговое время задержки 1,6 нс. При передаче по соседним лини-
ям одинаковых битовых сигналов эффективная проницаемость диэлектри-
ческой среды будет отличаться от эффективной проницаемости при допол-
няющих сигналах на соседних линиях. Любое изменение диэлектрической
проницаемости из-за того или иного сочетания битовых сигналов в сосед-
них линиях приведет к изменению времени задержки распространения. Это,
в свою очередь, приведет к джиттеру.
270 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.8. Электрическое поле одиночной
микрополосковой линии передачи
Ответ на вопрос, как битовая пос-
ледовательность воздействует на диэ-
лектрическую проницаемость, лежит в
рассмотрении краевых эффектов в ли-
нии. На рис. 4.8 показано электричес-
кое поле одиночной микрополосковой
линии передачи. Видно, что силовые линии проходят по воздуху и диэлект-
рику, их конфигурация говорит о большом краевом эффекте. В данном слу-
чае на краевой эффект приходится до 50 % силовых линий, определяющих
емкость. Это случай кусочно-однородной среды, рассмотренной в предыду-
щих разделах книги, и он характеризуется эффективной диэлектрической про-
ницаемостью
При близком расположении соседних линий передачи они попадают в
электрическое поле данной линии, что определяет перекрестные помехи из
одной линии в другую. Наличие активных соседних линий изменяет крае-
вой эффект пассивной линии, который зависит от битовой последователь-
ности в активных линиях. Когда активные линии несут одинаковый с пас-
сивной линией сигнал, то их заряды одинаковы, и между ними нет силовых
линий. Поэтому практически все силовые линии пассивной линии переда-
чи будут замыкаться через диэлектрический материал на слой заземления.
Для этого случая следует принять эффективную диэлектрическую проница-
емость линии, равную проницаемости диэлектрика, и задержка сигнала бу-
дет максимальна.
Когда активные линии имеют противоположные битовые сигналы, то си-
ловые линии частично пройдут по воздуху и будут замыкаться на соседних
проводниках. В этом случае эффективная диэлектрическая проницаемость
будет меньше, чем в первом случае, и задержка сигнала будет минимальна.
Рассмотренные случаи иллюстрируются на рис. 4.9.
Таким образом, эффективная диэлектрическая проницаемость зависит от
битовой последовательности в активных линиях. Различные проницаемос-
Рис. 4.9. Электрическое поле
для трех линий передач: 1 —
заряды линий при передаче
одинаковых битов в актив-
ных и пассивных линиях;
2 — заряды линий при переда-
че дополняющих битов в ак-
тивных и пассивных линиях
ти при различных режимах в линиях вызывают
различные задержки распространения сигнала.
В данном примере при сильной связи между
тремя линиями передачи детерминированный
джиттер из-за изменения краевых эффектов и
эффективной диэлектрической проницаемости
составляет ±0,1 нс при номинале 1,6 нс.
Один из путей снижения детерминированно-
го джиттера заключается в уменьшении перекры-
тия краевым полем соседних трасс за счет их раз-
несения. Например, разнесение проводников на
расстояние, равное удвоенной ширине провод-
ника (общее правило для снижения перекрест-
ных помех на ближнем конце линии), приводит
к уменьшению джиттера на 40 %. Однако разне-
4.1. Обеспечение целостности сигнала в печатном монтаже
271
Рис. 4.10. Распределение поля в полосковой линии передачи
сение проводников не пригодно для плат с высокой плотностью печатного
монтажа.
Для увеличения доли силовых линий электрического поля, которые про-
ходят через диэлектрик при любом варианте передачи битовых последователь-
ностей в активных линиях, следует использовать заглубленные и полосковые
линии передачи, типичные для внутренних слоев МПП. В них детерминиро-
ванный джиттер практически отсутствует даже при достаточно близком рас-
положении проводников. Пример картины электрического поля в полоско-
вой линии дан на рис. 4.10, из которого видно, что силовые линии в любом
случае проходят только через диэлектрическое основание платы. Это означает,
что диэлектрическая проницаемость всегда неизменна, и задержка сигнала в
любом случае не изменяется. Для измерения межсимвольных помех при слу-
чайной последовательности битов используется контрольная диаграмма.
4.1.6. Нарушение целостности сигнала
за счет скин-эффекта
При распространении вдоль линии передачи импульсного сигнала его
форма претерпевает изменение в результате действия двух основных факторов:
ослабления и дисперсии. Важнейшим источником ослабления и дисперсии
является скин-эффект, который проявляется в большей мере для тех линий,
у которых размеры поперечного сечения соизмеримы с толщиной скин-слоя,
т. е. для линий передачи в прецизионных печатных платах, на подложках гиб-
ридных интегральных микросхем, в кристаллах интегральных микросхем и
т. п., а также для линий передачи значительной протяженности. В 3 главе де-
тально рассмотрен процесс распространения сигнала в линии с потерями,
поэтому здесь остановимся только на основных моментах, дополняющих воп-
росы целостности сигнала.
При наличии дисперсии скорость распространения различна для различ-
ных частотных составляющих спектра импульсов. Если ослабление и скорость
одинакова для всех частот, то форма сигнала не изменяется, но его ампли-
туда уменьшается с увеличением расстояния от начала линии.
272 Глава 4. Обеспечение целостности сигнала в печатном монтаже
В линии передачи последовательные потери R определяются конечной
проводимостью проводника, а параллельные потери G— утечками изоляци-
онного материала. В идеализированном случае они не зависят от частоты, и
ослабление определяется по формуле
(4.2)
Фазовая постоянная
R,G,
4®2Z/C/
g/2 , Ri
8cd2C,2 8co2Z?
(4.3)
является функцией частоты, что вызывает искажения формы импульса. На
практике для линии с малыми потерями сопротивление ^определяется скин-
эффектом, a (7Z= О для применяемых диэлектрических материалов.
В случае согласованной линии передачи помехи за счет скин-эффекта,
которые приводят для импульсных сигналов к увеличению длительности
переходных процессов, могут быть определены по графикам, представлен-
ным на рис. 4.11 [53, 57]. На них приведены нормализованные отклики линии
передачи на воздействие напряжения с линейно нарастающим фронтом дли-
тельностью Гг, не зависящие от физических параметров линии и являющие-
ся функцией нормированного времени
f = (t-T)/B, (4.4)
где В — коэффициент, зависящий только от физических параметров линии:
16L,
Для плоских проводников шириной W!
(4.5)
(4.6)
для проводников круглого сечения радиуса г.
(4.7)
Графики на рис. 4.11 даны для нормированных длительностей фронта
(4.8)
Для линий передачи, у которых известен коэффициент затухания, напри-
мер коаксиальные кабели, коэффициент В удобно определить по формуле
4.1. Обеспечение целостности сигнала в печатном монтаже
273
2
5 = (4.9)
где f— частота, на которой измеряется затухание; ГГц; а — затухание на частоте, дБ/м;
I — длина линии, м.
Коэффициент затухания может быть вычислен по формуле
TkJco/2
«= S;7Z (4.Ю)
Если он задан в Нп/м, то пересчет его значения проводится по соотно-
шению
а [Нп/м] = 0,115а [дБ/м].
Для определения длительности фронта сигнала на выходе линии с поте-
рями при помощи графиков (рис. 4.11) вычисляют коэффициент В по (4.5),
Рис. 4.11 (начало). Нормированные отклики линии на воздействие ступенчатой
функции для различных нормированных длительностей фронтов: а — для /гп = 0...20;
б - /гп = 0...200; в - /гп = 0...2000
274 Глава 4. Обеспечение целостности сигнала в печатном монтаже
500 750 1000 1250 1500
f
Рис. 4.11 (окончание)
Рис. 4.12. Задержка распространения сигнала,
вызванная влиянием скин-эффекта: 1 — фронта
сигнала без учета скин-эффекта; 2 — фронт сигнала
с учетом скин-эффекта
нормированную длительность фронта по (4.8), и ось времени на графиках
приводят к значениям t= ВГ + Г, где Т — время пробега электромагнитной
волны от начала до конца линии. Настоящий расчет действителен только для
согласованных линий.
Результаты расчетов позволяют определить дополнительную задержку Аг
сигнала в линии, вызванную искажениями фронта или спада импульса из-
за влияния скин-эффекта:
— *0,5о ~ *0,5/’ (4.И)
где /0 5; — время достижения порогового уровня 0,5 на входе линии; /0 5о — время дости-
жения нормированного порогового уровня 0,5 на выходе линии.
Рис. 4.12 иллюстрирует соотношение (4.11).
Для уменьшения А/, как следует из (4.10), следует увеличивать волновое
сопротивление линии.
4.1.7. Режим общего вида
Площадь контура тока — только одна из проблем ЭМС, которая должна
быть учтена при проектировании печатаных плат. Другой, не менее важной
проблемой является проблема режима общего вида.
4.1. Обеспечение целостности сигнала в печатном монтаже
275
Режим общего вида рассматривается как противоположность режима диф-
ференциального вида. Эти режимы связаны с направлением сигнальных и
помеховых токов, протекающих в системе сигнальных и возвратных провод-
ников. Дифференциальный режим — это обычный режим передачи полез-
ных сигналов по двум проводникам, организованным в виде линии переда-
чи. По сигнальному проводнику ток течет в нагрузку, а по возвратному — от
нагрузки к источнику, т. е. токи имеют противоположное (дифференциаль-
ное) направление. Следуя этой логике, режим общего вида должен отличаться
одинаковым направлением токов в сигнальном и возвратном проводниках.
Согласно закону Кирхгоффа, все токи текут по замкнутому контуру. Но если
в режиме общего вида они текут в одинаковом направлении, то как они воз-
вращаются в источник? Некорректный ответ на этот вопрос приведет к неточ-
ностям в определении дифференциального режима, а также внесет неясность
в методы передачи дифференциального сигнала и построения дифференци-
альных трасс. Эти понятия будут уточнены позже.
Рассмотрим одиночную трассу, например полосковую линию передачи. Оп-
ределим дифференциальный режим применительно к этой трассе. Для устра-
нения проблем ЭМС возвратный путь должен располагаться близко к сигналь-
ному пути. Часть тока zd сигнала в диффе-
ренциальном режиме распространяется в
нагрузку по сигнальному проводнику и
возвращается к источнику по возвратному
пути, который расположен точно под сиг-
нальным проводником (рис. 4.13) в потен-
циальном слое платы. Другая часть сиг-
Рис. 4.13. Токи дифференциального
/d и общего / режима
нального тока распространяется от источ-
ника к нагрузке и возвращается к источ-
нику другим, непредусмотренным путем.
Это — ток / режима общего вида.
Возникновение токов общего вида происходит в следующих случаях. Во-
первых, если слой протекания возвратных токов не является идеальным про-
водником. Поэтому этот проводник обладает некоторой индуктивностью
(предполагается — малой). Во-вторых, это может быть ток за счет деления
возвратного тока на составляющую /d, протекающую по предусмотренному
пути (по слою заземления), и составляющую zc, протекающую по непредус-
мотренному пути. Большая вероятность возникновения непреднамеренно-
го пути имеется при использовании экранированного кабеля или шлейфа,
подключенного к трассе. При широком спектре сигнала высокочастотные
составляющие через паразитные емкости находят сторонние проводящие эле-
менты, которые формируют непреднамеренный возвратный путь.
Основная сложность заключается в том, что установить путь возвратного
тока общего режима достаточно трудно, а во многих случаях невозможно. Они
могут формировать с сигнальным током контур значительной площади, что про-
тиворечит базовому требованию по обеспечению ЭМС: контур тока должен быть
минимальной площади при максимальном сближении прямых и возвратных
276 Глава 4. Обеспечение целостности сигнала в печатном монтаже
путей. Поэтому излучение от платы может быть достаточно интенсивным.
Сигнал в режиме общего вида при относительно малой амплитуде может
вызвать большие проблемы ЭМС, чем сигнал дифференциального вида зна-
чительной амплитуды, что будет показано в главе 7.
Учитывая выше сказанное, режим общего вида определим как ток / ко-
торый протекает как по сигнальному, так и по возвратному проводнику в
одном направлении и возвращается по непреднамеренному пути к источнику
(рис. 4.14).
Рис. 4.14. Составляющие тока
общего вида
Предполагается, что токи общего вида
протекают по пути, которые не предусмот-
рены проектом. Любая комбинация сиг-
нального и возвратного токов может быть
представлена в виде компонентов диффе-
ренциального и общего видов (рис. 4.14).
Предположим, что сигнальный ток состав-
ляет 10000 мкА (10 мА), а возвратный ток
на слое заземления под сигнальным про-
водником несколько меньше — 9950 мкА.
Это означает, что 50 мкА протекают по ка-
кому-то другому пути. Тогда дифференциальная и общая компонента (рис. 4.14)
будут: /d = 9975 мкА и ic = 25 мкА.
Поскольку токи в режиме общего вида непредсказуемы, они трудно под-
даются управлению. Но применение нескольких правил проектирования
может существенно улучшить ситуацию, а именно:
• по возможности для всех трасс следует использовать возвратный про-
водник в виде металлических слоев;
• проблема режима общего вида несущественна для полосковых линий
передач, у которых сигнальный проводник расположен между двумя
потенциальными слоями; по возможности все критические трассы
следует выполнять в виде полосковых линий передач;
• следует минимизировать наличие шлейфов и подобных ответвлений
от скоростных линий передачи, а также устранять возможность про-
текания токов по непредусмотренным путям;
• поскольку все сигнальные токи, в конечном счете, протекают от слоя
питания через драйвер к приемнику и от него через слой заземления воз-
вращаются к слою питания, то следует минимизировать длину этого пути.
Это требует применения в МПП попарного расположения слоев пита-
ния и заземления при минимальном расстоянии между слоями.
4.1.8. Электромагнитные помехи
Тактовая частота работы перспективных печатных узлов превышает 100 МГц
и может достигать нескольких гигагерц. Несколько первых гармоник цифро-
вого сигнала располагается в пределах полосы частот общественной связи: те-
левидения, УКВ и FM радио, сотовые телефоны и средства индивидуальной связи
4.1. Обеспечение целостности сигнала в печатном монтаже
277
(PCS). Это означает: существует возможность того, что электронные узлы со-
здадут электромагнитные помехи (ЭМП), если их помехоэмиссия не останет-
ся ниже приемлемого уровня [31, 57]. К сожалению, если не предпринять спе-
циальных мер, помехоэмиссия усилится на высоких частотах. Интенсивность
излучаемых возмущений в дальней зоне от токов общего вида (протекающих в
проводниках платы в одном направлении) будет расти линейно с частотой, а от
токов дифференциального типа (протекающих в противоположных направле-
ниях) будет расти пропорционально корню квадратному от частоты. С ростом
тактовой частоты уровень помехоэмиссии неизбежно растет.
Проблема возникновения ЭМП и их воздействия на аппаратуру относится
к сфере электромагнитной совместимости (ЭМС) [31, 57, 73], для существо-
вания которой требуются три компоненты: источник помех, среда распрос-
транения помех и рецептор помех. Каждый источник, вызывающий проблемы
целостности сигнала и рассмотренный выше, будет источником ЭМП.
Следует выделить два наиболее общих источника ЭМП'. 1) преобразование
некоторого дифференциального сигнала в сигнал общего вида; 2) подскок зазем-
ления на печатной плате, генерирующей токи общего вида на внешних экрани-
рованных кабелях, у которых экран заземлен с одного конца. Дополнительные
помехи могут исходить от внутренних источников помехоэмиссии при слабой
эффективности экранирования корпуса печатного узла.
Основные источники помехоэмиссии — цепи заземления и питания. Часто
те же самые технические решения, которые способствуют низкому уровню
помех в шине питания, оказываются также полезными для снижения поме-
хоэмиссии.
Источник помехоэмиссии можно изолировать, группируя высокоскоро-
стные элементы платы далеко от того места, где они могли бы излучать.
Экранирующий корпус минимизирует помехоэмиссию, и многие проблемы
неудачной конструкции платы могут быть устранены с помощью эффектив-
ного экрана.
Изделие с эффективным экраном все равно должно иметь кабели, под-
ключающие его к внешнему миру. Как правило, кабели, простирающееся вне
экранированного корпуса, действуют как излучающие антенны. Правильное
применение ферритов на всех кабелях, особенно для витой пары, сильно
уменьшит действие кабелей как антенн.
Полное сопротивление соединителей ввода-вывода, особенно полное со-
противление соединителей на пути возвратного тока, драматично затронет
шумовые напряжения, которые могут возникать от излучающих токов. При-
менение экранированных кабелей с соединителями с согласованным полным
сопротивлением способствует минимизации уровня помехоэмиссии.
К сожалению, для некоторой физической системы повышение тактовой
частоты будет также увеличивать уровень помехоэмиссии и приведет к ус-
ложнению решения проблемы ЭМС. В седьмой главе детально будет рассмот-
рен механизм излучения от печатных плат, способы снижения уровня поме-
хоэмиссии, а также снижение восприимчивости платы к внешним электро-
магнитным возмущениям.
278 Глава 4. Обеспечение целостности сигнала в печатном монтаже
4.1.9. Методология проектирования печатных плат
и печатных узлов
Два важных вывода, которые можно положить в основу методологии про-
ектирования печатных плат для быстродействующих цифровых систем, вы-
текают из рассмотрения проблем целостности сигнала, рассмотренных выше.
Во-первых, каждая проблема усугубляется вследствие повышения частоты
обработки информации в связи со скоростью изменения тока или напряже-
ния. Обычно эти изменения представляют в виде дифференцирования dl/dt
или dV/dt. При повышении частоты скорости изменения токов и напряже-
ний увеличиваются. Неизбежно, что с ростом частоты все более серьезны-
ми будут проблемы, связанные с помехами, а сложность решения этих за-
дач будет возрастать. Как отмечалось в первой главе, при глобальной тен-
денции увеличения быстродействия электронной аппаратуры проблемы, не
оказывающие влияния на одни проекты, могут быть фатальными в других
проектах при создании систем следующего поколения.
Во-вторых, эффективное решение проблем целостности сигнала базиру-
ется на понятиях полных сопротивлений межсоединений. Если мы имеем
четкое представление о полном сопротивлении и сможем при конструиро-
вании платы установить соответствие параметров конструкций линий передач
и их полного сопротивления, то можно успешно решить проблемы целост-
ности сигнала на этапе проектирования.
Наиболее рационально построить методологию проектирования печатной
платы и печатного узла на основе подходов, изложенных в первой главе и ба-
зирующихся на понятии виртуального прототипа. В ряде случаев достаточно
физического уровня строгости для построения виртуального прототипа, с
последующим более строгим математическим расчетом его необходимых па-
раметров.
Можно выделить пять ключевых аспектов методологии, следуя которой
можно добиться максимального сближения параметров виртуального и фи-
зического прототипа.
1. Понять происхождение проблем целостности сигнала и ЭМС и общего
направления их решения.
2. Конкретизировать общие направления в виде определенных правил
проектирования для каждого конкретного изделия.
3. Провести декомпозицию задач, выделяя критические направления, со-
здавая модели для каждого компонента, критической цепи и системы в
целом и выполняя моделирование на локальном и системном уровнях.
4. Рационально построить процесс проектирования с учетом стоимос-
ти, времени выполнения и риска, с учетом концепции «сдвига влево».
5. Провести экспериментальные исследования в течение всего цикла про-
ектирования, чтобы уменьшить риск и повысить уверенность в каче-
стве проектных решений. Разработчики печатных плат должны уча-
ствовать в экспериментальной отработке проектируемых плат совмест-
но со схемотехниками.
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 279
Методология базируется на понимании физических процессов и явлений,
происходящих в печатной плате при функционировании изделия, а также на
моделировании и экспериментальных исследованиях.
Моделирование (создание виртуального прототипа) — это прогнозиро-
вание функционирования системы перед созданием физического прототи-
па аппаратуры. Для низкочастотной аппаратуры требовалось моделировать
отдельные критические цепи, которые были чувствительны к эффектам це-
лостности сигнала. Это были, как правило, шины синхронизирующих им-
пульсов, а также некоторые высокоскоростные шины. В изделиях с такто-
вой частотой до 100 МГц около 5—10 % цепей являются критическими. В из-
делиях с тактовыми частотами 200 МГц и выше более 50 % цепей критические,
что требует моделирования практически всей системы.
Во всех быстродействующих изделиях должно быть выполнено моделирование
на системном уровне, чтобы точно предсказать эффекты целостности сигнала.
Чтобы прогнозировать электрические параметры изделия, которые явля-
ются, как правило, действующими значениями напряжения и тока в различ-
ных узлах, необходимо перевести физический проект в электрическое описание.
Это может быть достигнуто одним из двух способов. На уровне цепей физи-
ческий проект может быть преобразован в эквивалентную схему, которая ис-
пользуется для прогноза напряжений и токов в любом узле. Электродинами-
ческая модель позволяет провести анализ во всей полноте. Она позволяет мо-
делировать электрические и магнитные поля в любой области пространства,
основываясь на физическом проекте. Зная электрические и магнитные поля,
можно создать модель функционирования межсоединений, которая затем
может быть использована при анализе эквивалентных схем, или электричес-
кие и магнитные поля могут быть преобразованы в напряжение и токи, что-
бы показать функционирование цепи.
Электродинамический подход является наиболее полным, но математи-
ческие трудности решения задач в этом случае могут быть непреодолимы-
ми. Поэтому необходимо разумно сочетать менее строгие методы анализа,
базирующиеся на цепевых подходах, с электродинамическим решением от-
дельных задач при обоснованных ограничениях и упрощениях. Именно та-
кой подход принят в данной книге.
4.2. Целостность сигнала в коротких
и длинных одиночных линиях передачи
4.2.1. Короткие линии передачи
Емкостной или индуктивный характер линии передачи проявляется в элек-
трически коротких линиях. В этом случае линия может быть замещена сосре-
доточенными реактивными элементами, и рассмотрение работы двух венти-
лей (рис. 4.15), соединенных этой линией, дает следующие результаты.
280 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.15. Короткая линия передачи при
емкостном характере линии
и индуктивном характере линии (внизу)
Если схема D1 с выходным сопро-
тивлением г0 вырабатывает ступенча-
тое напряжение Ион, то на входе эле-
мента D1 с входным сопротивлени-
ем г{ при г0 << г{ напряжение из-за
реактивного характера линии изме-
няется по закону
^2= W1 -exp(-r/TTL)], (4.12)
где ttl — постоянная времени линии.
При емкостном характере линии
TTL
(4.13)
при индуктивном —
TTL = £/ri- (4.14)
Интерес представляет время задержки распространения сигнала в цепочке
каскадно соединенных цифровых вентилей. Если принять порог Vrr сраба-
тывания вентиля D2 на уровне 0,5 высокого логического уровня Ин, т. е.
Игг = 0,5Ин, (4.15)
то время достижения этого порога (системная задержка) составит
A/=0,7ttl. (4.16)
Таким образом, видно, что для уменьшения системной задержки распрост-
ранения сигнала необходимо снижать постоянную времени линии за счет умень-
шения емкостных или индуктивных параметров линии.
Поскольку для линий передачи произведение постоянно при неизмен-
ных параметрах среды, уменьшение емкости линии приводит к увеличению
ее индуктивности. Поэтому при выборе конструкторского приема снижения
постоянной времени необходимо учитывать особенности применяемых мик-
росхем. Например, для микросхем на МОП-структурах при малых управля-
ющих токах и достаточно высоких напряжениях следует стремиться уменьшать
емкость линии, а для микросхем на биполярных транзисторах — выбирать
некоторые компромиссные параметры линии, обеспечивающие задержку, вно-
симую линией, не превышающую время переключения интегральной микро-
схемы. Учитывая, что для большинства серий микросхем ограничивающим фак-
тором по быстродействию является допустимая емкость нагрузки, то емкост-
ная модель короткой линии передачи более предпочтительна.
4.2.2. Длинные линии передачи
Для электрически длинных линий ситуация значительно сложней. В за-
висимости от фазы и амплитуды отраженного сигнала, погонной длины
линии, удельной задержки распространения сигнала возможны различные
варианты типовых искажений сигнала.
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 281
Процесс распространения сигнала в длинной линии в общем виде пред-
ставляется как последовательность падающих и отраженных электромагнит-
ных волн, распространяющихся соответственно от драйвера линии к нагрузке
и от нагрузки к драйверу. Отраженные волны возникают при неполном по-
глощении энергии сигнала нагрузкой. Если отраженный сигнал не поглотится
в драйвере, то возникает повторная падающая волна, и процесс переотра-
жений будет продолжаться до тех пор, пока не будет достигнуто некоторое
устойчивое состояние — логический 0 или 1. Время пробега электромагнитной
волны до конца линии определяется погонной задержкой распространения
сигнала в линии td и погонной длиной линии /
T=tdxl, нс, (4.17)
где td — удельная задержка распространения сигнала в линии, нс;
td=3,3^, нс/м, (4.18)
I — длина линии, м; гг — относительная диэлектрическая проницаемость материала ос-
нования платы (для полосковой линии); для других конструкций заменяется на эффек-
тивную проницаемость (см. главу 3).
Сигнал в любой точке линии есть сумма всех падающих и отраженных волн
(принцип суперпозиции), которые существуют к данному моменту време-
ни в линии. Если рассмотреть,конец линии, то видно, что уровень сигнала
меняется с дискретностью 2 Т. При осциллографическом наблюдении подоб-
ного сигнала четко видно ступенчатое изменение напряжения (рис. 4.16).
Для качественного анализа типовых искажений сигнала рассмотрим процесс
переключения в конце линии из 0 в 1 (рис. 4.176). Отметим на осциллограмме
пороговый уровень Как видно, время достижения порога, при котором про-
исходит переключение микросхемы нагрузки, составляет 3 Г. В более неблаго-
приятной ситуации возможно достижение порога в моменты 5 Тп даже 7 Г. В этих
случаях снижение системного быстродействия А/ определяется разностью
между моментом достижения порога и физической задержкой (например,
At" = ЗТ- Т=2Т). Таким образом, может быть внесена существенная погреш-
ность во временные диаграммы, рассчитанные для идеализированных условий.
Рис. 4.16. Осциллограммы фронта (а) и спада (б) импульса при наличии отражений
от нагрузки и драйвера
282 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Другой возможный случай заключается в наличии существенного провала
напряжения, который может перейти порог срабатывания и будет воспри-
ниматься как логический ноль (рис. 4.17<?). Такие ошибки чреваты тем, что
микросхема воспринимает два импульса вместо одного. В этом случае необ-
ходимо принять меры, чтобы минимизировать провал и обеспечить целост-
ность сигнала.
Еще один возможный вариант искажений сигналов в длинной линии
(рис. 4.17г) при переключении из «О» в «1» приводит к наличию значитель-
ных отрицательных выбросов на входе линии. Это чрезвычайно опасно, осо-
бенно для входных каскадов микросхем, которые подключены к входу ли-
нии, поскольку отрицательные напряжения могут вывести их из строя при
отсутствии соответствующей защиты.
При некоторых условиях (например, уменьшение погонной длины ли-
нии) искажение сигнала (рис. 4.17<?) за счет отражений напоминает «звон»
(рис. 4.18).
Таким образом, качественный анализ возможных искажений в длинных
линиях связи показывает, что они разнообразны по форме, представляют
существенную потенциальную угрозу целостности сигнала и качеству функ-
ционирования аппаратуры. Проектирование длинных линий в печатном
монтаже требует повышенного внимания. Эта задача становится все более
актуальной, поскольку при повышении быстродействия все больше линий передач
на печатных платах переходят в разряд электрически длинных, опыта проек-
тирования которых у разработчика плат, как правило, нет.
Рис. 4.17. Сигналы в длинной линии при переключении сигнала из 0 в 1: а — длинная
линия и диаграмма координата — время; б — дополнительная системная задержка
равна 2 Г; в — провал в уровне сигнала; г — наличие отрицательных по амплитуде
импульсов в начале линии
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 283
Время, нс
возникающие
Рис. 4.18. Искажения,
из-за многократных отражений сигнала
Например, при замене ТТЛ-схем
на ТТЛШ-схемы допустимая длина
короткой линии сократится пример-
но в три раза, и часть электрически
коротких линий станет электричес-
ки длинными линиями. Отмеченное
обстоятельство необходимо учиты-
вать при модернизации электрон-
ных средств.
Какое волновое сопротивление
должен иметь источник, подклю-
ченный к началу линии передачи?
Если сигнал распространяется вдоль линии, ток, текущий от источника в
линию, равен току фронта сигнала. Полное сопротивление источника дол-
жно быть равно мгновенному сопротивлению линии, пока сигнал распрос-
траняется вдоль линии. Ток в линии прямо пропорционален приложенно-
му напряжению.
Элемент цепи, в котором протекает определенный ток при определенном
приложенном напряжении, — идеальный резистор. Когда сигнал начинает
распространяться вдоль линии, в линии протекает неизменный ток, и линию
можно представить как сопротивление, подключенное к источнику. Не су-
ществует параметра, по которому источник сможет отличить линию от ре-
зистора, пока сигнал распространяется вдоль линии.
Когда говорят, что волновое сопротивление кабеля или линии составля-
ет 50 Ом, имеется в виду, что мгновенное отношение тока к напряжению для
сигнала, распространяющегося в этой линии, будет равно 50 Ом. В началь-
ной стадии, когда время сопоставимо со временем распространения сигна-
ла до конца линии, входное сопротивление линии равно 50 Ом.
В любом случае очень важна разница между полным сопротивлением,
мгновенным сопротивлением и волновым сопротивлением. Говоря «сопротив-
ление», сложно понять, о каком конкретно сопротивлении идет речь, что
приводит к двусмысленности.
Значение сопротивления, измеряемого на входе линии после подачи сигнала
в линию, изменяется со временем от нуля до бесконечности в зависимости от
конструкции линии, от того, что подключено к ее выходу, от длины линии и
способа измерения сопротивления.
Мгновенное полное сопротивление линии передачи — отношение напряжения
к току сигнала, распространяющемуся вдоль линии. Если линия однородна
по всей длине, мгновенное сопротивление будет одинаковым на всей длине
линии передачи. Однако оно может меняться в неоднородностях, например,
в конце линии. Если конец линии разомкнут (холостой ход), сигнал встре-
тит бесконечное сопротивление на конце линии. Если линия разветвляет-
ся, мгновенное сопротивление скачкообразно изменится в этой точке.
Волновое сопротивление линии — физическая характеристика линии, оп-
ределяемая геометрией и свойствами материалов. Оно равно мгновенному
284 Глава 4. Обеспечение целостности сигнала в печатном монтаже
сопротивлению, которое встречает сигнал, распространяющийся в этой
линии.
Всегда следует уточнять, о каком сопротивлении идет речь, или опреде-
лять это по контексту. Зная различие, можно избежать неясностей.
Когда время нарастания меньше времени распространения сигнала до
конца линии и его прихода к источнику, выходной каскад «видит» линию
передачи как омическое сопротивление, равное волновому сопротивлению.
Несмотря на то, что на конце длинной линии может быть разрыв, начало
линии выглядит как резистор.
Время распространения сигнала связано с диэлектрической проницаемо-
стью материала и длиной линии. Время нарастания для выходных каскадов
логических схем часто меньше наносекунды, и межсоединение длиннее не-
скольких сантиметров выглядит как длинная линия, которая ведет себя как
резистивная нагрузка на выходной каскад в течение перепада напряжения.
Это одна из важнейших причин, почему длина линий передачи должна учи-
тываться.
В высокоскоростных системах соединение длиной больше нескольких санти-
метров не ведет себя как разрыв для выходного каскада. Когда линия достаточно
длинная, ее сопротивление может изменяться во времени. Это свойство силь-
но зависит от сигнала, распространяющегося в линии.
По данному критерию практически все соединения в высокоскоростных
цифровых системах должны рассматриваться как длинные линии, и в них
должны учитываться эффекты, влияющие на целостность сигнала. Для ли-
нии передачи на плате длиной 8 см время распространения сигнала до на-
грузки и обратно составляет около 1 нс. Если интегральная схема, управля-
ющая линией, имеет время нарастания сигнала меньше 1 нс, сопротивление
в начале линии будет равно волновому сопротивлению линии. Для выход-
ного каскада микросхемы это будет аналогично омическому сопротивлению.
Если время нарастания много больше 1 нс, линия будет выглядеть как кон-
денсатор, т. е. разрыв.
Время Траспространения сигнала до конца линии — очень важный пара-
метр линии. Для выходного каскада микросхемы в интервал времени 2 Глиния
может быть замещена резистором. На рис. 4.19 показан график зависимос-
ти времени Тот длины линий с диэлектриками из воздуха (er = 1), стекло-
текстолита FR4 (ег = 4), и керамики (ег = 10). В большинстве систем такто-
вая частота больше 200 МГц, и время нарастания сигнала меньше 0,5 нс. Для
этих систем все проводники, длиннее 4 см, выглядят как резистор на про-
тяжении времени нарастания сигнала.
Рассмотрим режим возбуждения длинной линии. Высокоскоростной
драйвер, возбуждающий линию передачи, в первоначальный момент времени
t< /"воспринимает линию как линейное сопротивление, равное волновому.
Эквивалентная схема для этого случая показана на рис. 4.20.
Драйвер может быть смоделирован источником напряжения и его выход-
ным сопротивлением. Источник напряжения вырабатывает напряжение вы-
сокого уровня, которое зависит от серии микросхем: ТТЛ — примерно 3,5 В,
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 285
Рис. 4.19. Зависимость удвоенного времени распространения сигнала в линиях
из различных диэлектрических материалов
Рис. 4.20. Возбужде-
ние линии передачи
и эквивалентная схе-
ма в первоначальный
момент времени
КМОП — от 1,5 до 5 В и более, некоторые системы
памяти — 3,3 В, скоростные процессоры — 2,4 В.
Значение выходного сопротивления также зависит
от серии микросхем. В большинстве случаев это сопро-
тивление нелинейно и определяется выходными вольт-
амперными характеристиками вентиля в состоянии ло-
гического 0 и логической 1 (см. 1 главу). Для предва-
рительных оценок можно ориентироваться на типич-
ное значение, которое составляет от 5 до 60 Ом. При
переключении микросхемы из-за действия этого со-
противления только часть напряжения, которое выра-
батывает источник напряжения, поступает на выход-
ные выводы микросхемы.
Напряжение F<TL, поступающее на вход линии при переключении мик-
росхемы из состояния логического 0 в состояние логической 1, может быть
рассчитано из эквивалентной схемы (рис. 4.20) по следующему выражению:
^1TL -^ОН| Г
(4.19)
где Ион — выходное напряжение высокого уровня; Z — волновое сопротивление линии;
г0 — выходное сопротивление.
Видно, что, когда выходное сопротивление высокое, напряжение, посту-
пающее на линию, будет мало. Это нежелательная ситуация. На рис. 4.21
показана зависимость относительного значения поступающего на линию с
волновым сопротивлением 50 Ом напряжения от выходного сопротивления
драйвера. При выходном сопротивлении 50 Ом только 50 % напряжения
поступает на вход линии, т. е. при напряжении источника напряжения 3,3 В
на линию поступит только 1,65 В. Этого может не хватить для нормальной
286 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.21. Зависимость относительного значения напряжения, поступающего на линию
с волновым сопротивлением 50 Ом, от значения выходного сопротивления драйвера
работы микросхемы-нагрузки. При уменьшении выходного сопротивления
драйвера напряжение на входе линии возрастает.
Для максимального сближения значений напряжения, поступающего на
линию, и источника напряжения необходимо выходное сопротивление ис-
точника делать значительно меньше волнового сопротивления.
Устройства с малым выходным сопротивлением (10 Ом и меньше) часто
называются драйверами линии. КМОП схемы устаревшей технологии не по-
зволяли строить драйверы линии, поскольку их выходное сопротивление было
от 90 до 130 Ом. Для быстродействующих цифровых систем печатный мон-
таж выполняется в виде линий передач с волновым сопротивлением 50 Ом,
поэтому КМОП-схемы драйверов линии должны выполняться с возможно
малым выходным сопротивлением.
4.2.3. Отражения в линиях передачи
Если сигнал, распространяющийся по линии передачи, встретит изменение
волнового сопротивления, то часть энергии сигнала отразится, а форма про-
шедшей части сигнала будет искажена. Сигнал будет претерпевать измене-
ния в каждой точке, в которой происходит изменение волнового сопротивле-
ния. Воздействие на сигнал изменений волнового сопротивления вызывает наи-
большие нарушения целостности сигнала.
Отражения сигнала происходят всякий раз, когда изменяется значение
волнового сопротивления. Они могут происходить в любом месте топологии
линии передачи, например, на углах при повороте трассы, при наличии пе-
реходных отверстий, ответвлений и разветвлений проводника. Поняв меха-
низм образования помех, вызванных отражениями (помех отражения) в каж-
дом случае, можно спроектировать наиболее рациональную топологию печат-
ного монтажа и предпринять обоснованные меры по устранению негативного
влияния помех отражения.
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 2&7
Задача проектирования состоит в том, чтобы создать такую линию пере-
дачи на плате, в которой мгновенное значение волнового сопротивления оста-
ется неизменным по ее длине.
В первую очередь, это означает, что волновое сопротивление линии дол-
жно оставаться неизменным, т. е. линия должна быть однородной. Отсюда и
все возрастающее значение имеют методы и приемы управления волновым
сопротивлением. Например, такие, как уменьшение длины шлейфов, исполь-
зование хабов вместо разветвления трасс, применение топологии «от точки
к точке» и ряд других приемов, призваны стабилизировать значение волно-
вого сопротивления.
Во-вторых, это управление конструкторскими параметрами линий пере-
дачи с целью выполнения их с определенным волновым сопротивлением, а
также применение специальных схем согласования, которые обеспечивают
равенство волнового сопротивления линии и сопротивления нагрузок. Это
обеспечивает отсутствие отражений на концах линий передачи. В данном слу-
чае требуются согласованные усилия схемотехников, которые выбирают схему
согласования и значения ее параметров, и конструкторов печатных плат.
Те места линий передачи, в кото-
рых произошло изменение волново-
го сопротивления, называются нео-
днородностью волнового сопротив-
ления или просто неоднородностью.
Например, место стыка двух участ-
ков линии передачи (рис. 4.22) с раз-
личными волновыми сопротивлени-
ями является неоднородностью.
Уровень отраженного от неоднородности сигнала зависит от степени
изменения волнового сопротивления. Степень изменения волнового сопро-
тивления характеризуется коэффициентом отражения. Часть энергии сигнала,
которая прошла неоднородность, характеризуется коэффициентом прелом-
ления. Свойство электромагнитной волны отражаться от границ раздела двух
участков с различными значениями волнового сопротивления является ос-
новным источником проблем с качеством передаваемого сигнала в пределах
локальной линии.
Чтобы минимизировать нарушения целостности сигнала, возникающие
из-за отражений, нужно выполнять следующие четыре основных правила
проектирования высокоскоростных плат.
1. Применять управляемое волновое сопротивление для линий передач
на плате.
2. Обеспечить согласование линий.
3. Использовать такую топологию, чтобы минимизировать воздействия
от разветвлений линии.
4. Минимизировать любые геометрические неоднородности.
Возвратимся к примеру с двумя состыкованными участками (рис. 4.22) с
различными значениями волнового сопротивления. В момент достижения
ц Ч Ч
Рис. 4.22. Изменение сигнала при измене-
нии волнового сопротивления: часть энер-
гии сигнала отразится, а оставшаяся часть
продолжит движение, но будет изменена
288 Глава 4. Обеспечение целостности сигнала в печатном монтаже
падающей волной точки сопряжения двух участков, в каждом из них суще-
ствует одинаковое напряжение падающей волны и отраженной ее части, а
также одинаковый ток, протекающий через проводник. Другими словами,
на границе раздела сред напряжение и ток не могут измениться. Можно за-
писать два соотношения = И2 и Ц = /2, но = Vx/Zv а /2 = K2/Z2. И если
значения волновых сопротивлений двух участков различны, все эти соотно-
шения теряют свою справедливость, так как тогда Ф /2, Ф И2, следователь-
но, Vx/Zx Ф V2/Z2 и /2Z2 Ф I{ZV
По принципу сохранения энергии, если созданный сигнал отразится от
границы раздела участков, то он должен вернуться в источник. Падающая
электромагнитная волна Kf движется по направлению к границе раздела уча-
стков, в то время как отраженная волна Vr движется от границы раздела к
источнику. Преломленная волна Vv прошедшая границу, продолжает движе-
ние к нагрузке.
Для того, чтобы в обоих участках были одинаковые значения амплитуд
напряжений, необходимо выполнить следующее условие:
rf- Кг = иг (4.20)
Аналогичное условие для токов выглядит несколько иначе. С учетом на-
правлений токов можно записать:
= Ц (4.21)
Окончательное уравнение для нахождения значений волновых сопротив-
лений участков выглядит так:
^f_Z. ^r_Z. K_Z
T'2' (4.22)
Используя выражение (4.21) для токов и уравнения (4.22) для значений
волновых сопротивлений областей, получаем:
Z, z2
Учитывая соотношения между напряжениями (4.20), получаем:
У{
Zl Z, z2 ’
откуда после преобразований значение амплитуды отраженного
можно определить через амплитуду сигнала, подошедшего к месту
v{ z2 + z, r’
где И - амплитуда отраженной электромагнитной волны; Kf- амплитуда падающей элек-
тромагнитной волны; кт — коэффициент отражения по напряжению.
сигнала
стыка:
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 289
Амплитуда отраженной волны может быть рассчитана через коэффици-
ент отражения:
Kr=Jtr-Kf. (4.24)
Чем больше будет разница значений волновых сопротивлений двух участ-
ков, тем большая часть энергии сигнала отразится от границы раздела этих уча-
стков. Так, например, если сигнал с амплитудой 1 В распространяется по ли-
нии с волновым сопротивлением 50 Ом и переходит в смежную область с вол-
новым сопротивлением также 50 Ом, то он не претерпевает никаких изменений.
В этом случае коэффициент отражения равен 0 и отражение отсутствует. Если
изменить значение волнового сопротивления второго участка до 75 Ом (на-
пример, переход от печатной платы на коаксиальный кабель), тогда коэффи-
циент отражения будет равен (75 - 50)(50 + 75) = 0,2, и значение амплитуды
отраженного сигнала будет 0,2 В. Коэффициент отражения не зависит от ам-
плитуды входного сигнала. Он показывает, во сколько раз амплитуда отражен-
ного сигнала будет меньше амплитуды входного сигнала.
Важно отметить, что коэффициент отражения рассчитывается как от-
ношение разности значений волновых сопротивлений двух областей к сумме этих
значений. Это соотношение играет важную роль в анализе длинных линий.
На рис. 4.23 наглядно показано изменение амплитуд падающих, отражен-
ных и преломленных волн в месте сопряжения двух участков с различными
волновыми сопротивлениями. В этом случае падающая волна Vf в первом
участке, достигая места сопряжения, вызывает преломленную волну во
втором участке. Амплитуда преломленной волны связана с амплитудой па-
дающей волны коэффициентом преломления kt\
Vx=kx - Kf, (4.25)
kt = lZ2/(Z2 + Zx). (4.26)
Как видно, при Z2 > Zx амплитуда преломленной волны больше ампли-
туды падающей волны, а при Z2 < Zx — меньше. Для рассмотренного выше
примера амплитуда преломленной волны будет
Kt= [2 • 75 /(50 + 75)] Vf = 1,2 Vf.
X
Рис. 4.23. Отражения от места стыка двух участков: а — соединение двух участков
с различными волновыми сопротивлениями; б — временные диаграммы
10 1527
290 Глава 4. Обеспечение целостности сигнала в печатном монтаже
При переходе от витой пары с Zj = 110 Ом на печатный монтаж с Z2 = 50 Ом
возможно снижение амплитуды сигнала:
Kt= [2 • 50 /(50 + 110)] Kf= 0,625
Это приведет к снижению логического уровня, например, стандартной
ТТЛ-схемы до 2,2 В для логической 1, что резко ухудшит помехозащищен-
ность системы, а это в большинстве случаев недопустимо.
Важно отметить, что отмеченные изменения в амплитуде падающих, от-
раженных и преломленных волн характерны только для момента, когда па-
дающая волна достигла точки стыка двух участков. Если длительность им-
пульса велика, то со временем в неоднородной линии установится опреде-
ленный режим, который будет соответствовать конечному логическому
состоянию. Дальнейшие расчеты позволят определить конкретные искаже-
ния сигнала и временные соотношения.
К наиболее существенным типам неоднородностей в печатном монтаже,
которые влияют на качество сигнала, следует отнести:
• изменения геометрических размеров проводников и их конфигурации;
• изменения волнового сопротивления линий (например, за счет изме-
нения расстояния между сигнальным проводником и экраном) или па-
раметров среды;
• включения по длине линии конструктивных элементов, представляющих
собой дискретные неоднородности, таких, как отверстия, шлейфы и т. п.
Исследование влияния неоднородностей на качество сигнала в общем
случае весьма затруднено, и анализ целесообразно проводить на ЭВМ по
следующей схеме:
• аналитическое или экспериментально-теоретическое построение мо-
дели неоднородности;
• построение модели линии передачи совместно с моделями неоднород-
ностей;
• анализ на ЭВМ прохождения сигнала через линию связи с неоднород-
ностями с помощью полученной модели.
Наиболее трудоемкий — первый этап, и от его выполнения во многом
зависит успешное решение задачи.
В зависимости от характера неоднородности происходит искажение формы
информационного сигнала, причем отраженный от неоднородности сигнал,
попадая на вход микросхемы, может нарушить работоспособность устрой-
ства. Для простейших моделей неоднородностей в [57] приведены парамет-
ры отраженных сигналов при воздействии идеального ступенчатого напря-
жения и сигналов с реальным временем нарастания фронта.
4.2.4. Помехи отражения в длинных линиях передачи
Повышение быстродействия элементов приводит к увеличению относи-
тельного числа длинных линий передачи в печатных платах. Искажения
сигнала в этих линиях (помехи отражения) вызваны отражением сигналов
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 291
от несогласованных нагрузок и неоднородностей, распределенных по дли-
не линии. Эти помехи могут приводить к снижению быстродействия систе-
мы и нарушению ее функционирования. При согласовании линий уровень
помех отражения сводится к минимуму, но при этом резко ухудшаются энер-
гетические показатели системы, снижаются уровни информационных сиг-
налов, что требует в ряде случаев установки специальных передающих и
приемных устройств. Поэтому при конструировании аппаратуры необходимо
уметь оценивать помехи отражения в длинных линиях и обоснованно выби-
рать методы их снижения [76—78].
Далее рассмотрены два основных случая работы длинной линии переда-
чи: с линейными и нелинейными нагрузками. Первый случай интересен более
простым описанием и физическим представлением происходящих процес-
сов. Это позволяет более детально разобраться в механизме образования помех
отражения при работе линии передачи. Второй случай более близок к реальной
ситуации, поскольку входные и выходные сопротивления микросхем нели-
нейные. Однако нелинейные нагрузки требуют более сложных методов расчета
и моделирования, которые могут быть выполнены в большинстве случаев
только с применением ЭВМ [79, 80].
Для инженерных оценок можно выделить два основных метода опреде-
ления формы сигнала при наличии помех отражения.
1. Аналитический метод, основанный на вычислении коэффициентов
отражения.
2. Графический метод расчета, основанный на применении метода харак-
теристик.
Каждый из методов имеет свои особенности и области применения. Ана-
литический метод основан на расчете коэффициентов отражения и итера-
ционном определении амплитуд падающих и отраженных волн с последую-
щим их суммированием. Метод применим только для линейных нагрузок,
что существенно ограничивает его использование при анализе реальных
систем, построенных на микросхемах.
Графический метод [34, 76—80], реализующий метод характеристик реше-
ния дифференциальных уравнений, отличается высокой точностью, доступ-
ностью применения, возможностью оперативного анализа и наглядностью.
Последнее качество особенно важно для проведения экспресс-анализа вли-
яния волнового сопротивления линий передачи на целостность сигнала. Уни-
версальность метода позволяет использовать его и в случае линейных нагрузок,
а учитывая простоту реализации, им можно пользоваться как основным ин-
струментом.
В обоих методах погрешность решения будет определяться достоверно-
стью задания исходных данных, а именно уровнями напряжений, формой
вольт-амперных характеристик и т. п. Далее более подробно будут рассмот-
рены оба метода определения формы сигнала в начале и в конце однород-
ной линии передачи.
10
292 Глава 4. Обеспечение целостности сигнала в печатном монтаже
4.2.5. Определение формы сигнала
в однородной линии с линейными нагрузками
Обобщенное представление длинной линии дано на рис. 4.24. На вход
линии подключен драйвер в виде генератора напряжения Kd (/) с выходным
линейным сопротивлением го, а на
выходе линии подключена линей-
ная нагрузка Rv Напряжение на на-
грузке J^(t). Напряжение в начале
линии в точке s обозначим ^TL(0,
а в конце линии в точке г соответ-
ственно HoTL(z).
В общем случае электрические
процессы в длинной линии описы-
ваются дифференциальными урав-
нениями в частных производных
гиперболического типа — телеграфными уравнениями, которые для одиноч-
ной линии без потерь имеют вид (х — координата вдоль линии)
г 4(0
О—г—►
* Z
о
S
M(t)
Рис. 4.24. Обобщенное представление
длинной линии с линейными нагрузками
дх dt’
- = -С—
дх dt
(4.27)
Как отмечалось, процесс распространения электромагнитной волны в
длинной линии при наличии отражений связан с формированием падающих
и отраженных Кг электромагнитных волн. В любой точке линии напряже-
ние в любой момент / является суммой всех падающих и отраженных волн,
существующих в данный момент в линии.
Коэффициент отражения кГ в конце линии определяется по соотношению
r rf R{+Z’
(4.28)
В зависимости от значения кг различают режим согласованного при R{ = Z
и кг = 0 и несогласованного включений линии для всех остальных случаев.
При этом коэффициент отражения изменяется в пределах -1 < кг < +1. Знак
«—» означает, что отраженная волна имеет противоположную фазу относи-
тельно падающей волны, а знак «+» говорит, что фазы падающей и отраженной
волны совпадают.
В режиме согласованного включения падающая волна полностью погло-
щается в нагрузке и отраженная волна отсутствует. При этом форма сигнала
на входе и выходе линий не искажается. Более детально различные приемы
согласования линий передач и соответствующие рекомендации будут рассмот-
рены ниже.
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 293
В режиме несогласованного включения падающая волна, достигнув на-
Рис. 4.25. Линия передачи в режиме
холостого хода; коэффициент отражения
равен 1
грузки, отражается от нее полностью или частично, и амплитуда отражен-
ной волны определяется выражением (4.24).
Рассмотрим подробнее три особых случая нагрузки. В каждом случае вол-
новое сопротивление линии будет 50 Ом.
Первый случай соответствует режиму холостого хода = °°Дг = +1),т.е.
на выходе линии нагрузка отсутствует. В нем отраженная волна имеет ту же
фазу и амплитуду, что и падающая, т. е. Vr = Kf. Если рассмотреть напряжение,
возникающее на конце разомкнутой
линии, можно наблюдать две волны.
Одна из них является падающей вол-
ной, например, с амплитудой 1 В.
Другая, отраженная волна, которая
также имеет амплитуду 1 В, будет рас-
пространяться в обратном направле-
нии. Общий размах напряжения на
конце линии будет равен сумме этих
двух напряжений, т. е. 2 В (рис. 4.25).
Напряжение на конце разомкнутой
линии передачи есть сумма напряже-
ния падающей и отраженной волны.
Второй особый случай соответствует короткому замыканию между сиг-
нальным и возвратным проводником на конце линии передачи. В данном
случае отраженная волна имеет по отношению к падающей волне противо-
положную фазу, но одинаковую с ней амплитуду: И = -Kf. Когда сигнал с
амплитудой 1 В распространяется по проводнику, то отраженный сигнал будет
иметь амплитуду -1 В. Напряжение на нагрузке при этом будет суммой на-
пряжений падающей и отраженной волны, или 0 В.
Третий важный момент относительно сопротивления на конце линии — ког-
да сопротивление соответствует по значению волновому сопротивлению ли-
нии. Это достигается, например, установкой параллельного резистора 50 Ом
на конце линии передачи с волновым сопротивлением 50 Ом. Коэффициент
отражения в этом случае будет равен 0, т. е. отражение отсутствует. Это наи-
более важный режим — режим согласования.
Для произвольной нагрузки линии сопротивление на ее конце может
лежать между нулем и бесконечностью, а коэффициент отражения будет иметь
значение в пределах от —1 до +1. На рис. 4.26 показана зависимость между
сопротивлением нагрузки и коэффициентом отражения для линии переда-
чи сопротивлением 50 Ом.
Если волновое сопротивление нагрузки меньше волнового сопротивле-
ния, то коэффициент отражения будет отрицательным. Например, если вол-
новое сопротивление линии равно 50 Ом, а на ее конце установлено сопротив-
ление 25 Ом, то коэффициент отражения будет равен (25 - 50)/(25 + 50) =
= — 1/3. Если падающая волна амплитудой 1 В достигнет конца линии, то
отраженная волна будет иметь амплитуду —0,33 В. В этом случае суммарное
294 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.26. Коэффициент отражения для линии передачи с волновым сопротивлением
50 Ом при изменении сопротивления нагрузки
напряжение на конце линии будет суммой падающей и отраженной волн, т. е.
(1 + (-0,33)) В = 0,67 В.
Рассмотренный механизм отражения характерен только для первой фазы
процесса. Последующие фазы связаны с возникновением повторных пада-
ющих и отраженных волн.
В общем случае, отраженная от нагрузки волна распространяется в ли-
нии по направлению к драйверу. Если выходное сопротивление драйвера не
равно волновому сопротивлению линии, то возникает вторая падающая волна
с амплитудой
= (4-29)
где ks - коэффициент отражения в начале линии (со стороны драйвера):
ks — (ro — Z)/(ro+Z). (4.30)
Аналогичные рассуждения позволяют для линии с линейными нагрузками,
несогласованной как со стороны нагрузки, так и со стороны генератора, за-
писать амплитуды всех падающих и отраженных волн и далее вычислить ам-
плитуду сигнала в любой момент времени в начале или конце линии. Посколь-
ку коэффициенты отражения в общем случае меньше единицы, то, как пра-
вило, достаточно нескольких слагаемых для определения формы сигнала в
начале и в конце линии.
Напряжение в линии в установившемся (статическом) режиме определя-
ется выражением
D
KiTL=KoTL = Kdrv—1—. (431)
Vo + Л1)
Наглядное представление о параметрах сигнала в длинной линии дает диа-
грамма координата-время (рис. 4.27). На ней область, ограниченная осями
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 295
координат, разделена на треуголь-
ные зоны, для которых параметры
сигнала постоянны и определяются
как суммы падающих и отраженных
волн, условно изображенных выше
этой зоны. Моменты Т, 2 Г, 3 Т,... со-
ответствуют временам пробега элек-
тромагнитной волны от начала до
конца линии.
С помощью диаграммы можно
получить параметры сигнала в линии
с линейными нагрузками в любой мо-
мент t времени в произвольной точ-
ке хлинии. Например, для t= ЗГ, х =
= 0,8/, из диаграммы получаем
Рис. 4.27. Диаграмма координата-время
И(х,Г) = KiTL(0)[l + *r(l + ks)].
Для построения диаграммы необходимо знать начальное условие, т. е. ам-
плитуду напряжения падающей волны при t = 0,
х = 0. Это напряжение поступает от генератора на
вход линии в первоначальный момент времени.
Схема замещения драйвера, нагруженного на ли-
нию передачи, для этого момента времени пред-
ставлена на рис. 4.28. Из нее видно, что напряже-
(4.32)
Рис. 4.28. Схема замещения
драйвера и длинной линии
при t = 0
ние на входе линии определяется выражением
Помехи отражения зависят от знаков коэффициентов отражения ks и kr,
и характер помех может быть ступенчато возрастающим или затухающим при
одинаковых знаках, или осциллирующим при различных знаках (табл.4.1).
Характер переходного процесса в длинной линии
Таблица 4.1
Сопротивление Коэффициент отражения Характер процесса
со стороны драйвера co стороны нагрузки k k
<Z <Z <0 <0 Осциллирующий
<z >Z <0 >0 Осциллирующий
>z >Z >0 >0 Ступенчатый
>z <z >0 <0 Осциллирующий
296 Глава 4. Обеспечение целостности сигнала в печатном монтаже
4.2.6. Определение формы сигнала в однородной линии
с нелинейными нагрузками
Рассмотренные выше методы анализа переходных процессов в длинных
линиях могут быть применены только в некоторых частных случаях, когда
выходное сопротивление драйвера и сопротивление нагрузки замещаются
активными линейными сопротивлениями. При проектировании линий пе-
редачи для быстродействующих и сверхбыстродействующих цифровых си-
стем в качестве драйвера и нагрузок используются цифровые микросхемы,
входные и выходные сопротивления которых нелинейные. В этом случае
наиболее эффективным для оценки искажений сигнала является примене-
ние метода характеристик, существенное достоинство которого — возмож-
ность графической интерпретации. При графическом задании вольт-ампер-
ных характеристик в качестве нелинейных граничных условий можно избе-
жать ряд серьезных трудностей, возникающих при оперативных расчетах
помех отражений.
Суть метода характеристик сводится к следующему [57, 77]. Телеграфные
уравнения, описывающие распространения сигнала в длинной линии, яв-
ляются уравнениями гиперболического типа. Для гиперболической систе-
мы с постоянными коэффициентами и операторами
Л|[И,/] = Л1^ + Д^,
dx dt
dt dx
(4.34)
Существуют два семейства характеристик, дифференциальные уравнения
которых имеют вид:
dx/A^dt/k^, (4 35)
dx/Ах = dt/*к2В2.
Для каждой характеристики первого семейства х — at = dx — характерис-
тики падающей волны (ХПВ) — выполняется условие
V + kxI= const. (4.36)
Вдоль характеристики второго семейства х + at= d2 — характеристики от-
раженной волны (ХОВ) — выполняется условие
V- k2I = const. (4.37)
В (4.36) и (4.37) коэффициенты кх и к2 определяются из выражений
кх = \ХС2/ Ах; к2 = Х2С2 / Ах,
где
Х12=±л/Д; Д =
Ах кВ2
ХС2 Dx
(4.38)
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 297
Для рассматриваемых телеграфных уравнений
= 1; = Ц В2 = С; С2 = 1.
Характеристические значения операторов системы Xj 2 находятся из урав-
нения
X12=±VZ/C=±Z; fc1=+Z; k2 = -Z.
Таким образом, вдоль ХПВ получаем
Kf + ZIf= dv (4.39)
а вдоль ХОВ
Kr-z/r = d2. (4.40)
Уравнения (4.39), (4.40) в координатной плоскости И, / представляются
в виде прямых с углами наклона соответственно
-0z= arctg (ZmJ (4.41)
0Г = +0Z = arctg {Zmv/ mJ, (4.42)
где mv, mt — масштабные коэффициенты по осям И, мм/В, и /, мм/А.
Постоянные d} и d2 определяются граничными условиями задачи, а именно
входной и выходными вольтамперными характеристиками (ВАХ) интеграль-
ных микросхем, подключенных к линии передачи.
При определении искажений сигнала микросхемы генератора и нагруз-
ки замещаются нелинейными двухполюсниками, характеризующимися сво-
ими ВАХ. Для генератора используются выходные ВАХ для состояний ло-
гического 0 и 1, а для нагрузки — входная ВАХ.
Вид ВАХ определяется схемотехническими особенностями построения
входных и выходных каскадов микросхем, и они могут быть получены либо
теоретически, либо экспериментально (см. главу 1). На рис. 4.29 приведены
ВАХ для различных драйверов и нагрузок. Для них приняты следующие обо-
значения:
И01 (/)— выходная ВАХ генератора для состояния лог. 1;
ИО0(/) — выходная ВАХ генератора для состояния лог. 0;
Kf(/) — входная ВАХ нагрузки.
Для линейных нагрузок (рис. 4.29л) наклон прямой входной ВАХ VJI) оп-
ределяется углом (рис. 4.296)
0/ = arctg (Rxmv / wz), (4.43)
а наклон прямых выходных ВАХ ИО0(/) и И01(/) — углом
0drv = arCtg (rQmv I (4-44)
298 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.29. Включение различных нагрузок и их ВАХ: а — схема включения линейных
генератора и нагрузки; б — ВАХ линейных генератора и нагрузки; в — схема включения
активных нелинейных генератора и нагрузки (НД — нелинейный двухполюсник);
г — типовые ВАХ ТТЛ-схем; д — типовые ВАХ ЭСЛ-схем
Для определения помех отражения методом характеристик, кроме гра-
ничных условий, необходимо знать начальные, т. е. состояния анализируе-
мой системы при t — 0. Если генератор в начальный момент вырабатывает
ступенчатое напряжение с амплитудой Kdrv, то начальное условие определя-
ется напряжением l<TL(0), поступающим на вход линии. Схема замещения
генератора, нагруженного на линию, при t = 0 представлена на рис. 4.28, и
l<TL(0) определяется соотношением
KiTL(0) = iZ. (4.45)
Графически эта зависимость представляется в координатах (И, Г) в виде
прямой, построенной под углом
0Z = arctg (Zmv / /и,.) (4.46)
к оси абсцисс из точки с координатами /(—0); К(—0), соответствующей ре-
жиму работы в начале линии до момента переключения. При анализе рабо-
ты цифровых микросхем этими точками являются точки статического со-
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 299
Рис. 4.30. Определение начальных условий (для ТТЛ-схем): а — при переключении
из 0 в 1; б — при переключении из 1 в 0
стояния логического 0 при переключении из «0» в «1» или состояния логи-
ческой 1 при переключении из «1» в «0». Значение HiTL(0) определяется гра-
фически как точка пересечения прямой (4.45) и выходной ВАХ И01 (/) при пе-
реключении драйвера из «0» в «1» или выходной ВАХ ИО0(/) при переключе-
нии драйвера из «1» в «0».
На рис. 4.30 показан графический расчет ^TL(0) (равному выходному на-
пряжению И0(г) генератора) для ТТЛ-схем при переключении драйвера из 0
в 1 и из 1 в 0. Нагрузочную прямую (4.45) не следует путать с ХПВ и ХОВ.
Если необходимо, можно определить выходной ток /о(0) в момент t = 0.
Найденное значение HiTL(0) является амплитудой падающей волны, ко-
торая начинает распространяться вдоль линии от драйвера к нагрузке. Связь
между током и напряжением в падающей волне определяется ХПВ, из ко-
торой следует
Ef=(-Z)/f + Jr (4.47)
Это уравнение прямой с угловым коэффициентом —Z, проходящей через
точку dx на оси ординат. Для построения этой прямой нет необходимости
искать jj , поскольку известна другая точка, принадлежащая этой прямой,
а именно точка Л[/о(0); Ио(0)] (рис. 4.30), определяющая начальные условия.
Поэтому ХПВ проводят под углом —9Zчерез точку A &Q пересечения с ВАХ,
определяющей граничные условия на нагрузке V\(J) (рис. 4.31).
Падающая волна, достигнув несогласованной нагрузки, отражается от нее.
В момент Т прихода падающей волны к нагрузке параметры сигнала долж-
ны совместно удовлетворять двум уравнениям, описывающим ХПВ и ВАХ
нагрузки. Графическим решением этой системы уравнений является точка
пересечения ХПВ и — точка В (рис. 4.31).
После отражения от нагрузки по направлению к драйверу начинает рас-
пространяться отраженная волна, характеристика которой представляет
прямую, которая описывается выражением
Kr=Z/r+J2, (4.48)
с угловым коэффициентом Z. Здесь постоянную J2, как ранее и dv определять
нет необходимости, поскольку известна точка В, принадлежащая этой прямой.
300 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.31. Графическая интерпретация метода характеристик при расчете линий,
связывающих ТТЛ-схемы: а — метод характеристик; б — осциллограммы сигналов
в начале и в конце ГоТЕ(/) линии
Поэтому ХОВ строится из точки В под углом 07и проводят ее до пересече-
ния с ВАХ генератора.
Отраженная волна достигает драйвера в момент 2 Т, и режим в линии, со-
ответствующий точке Сна рис. 4.31, определяется совместным учетом ХОВ
и ВАХ ИО0(/) или И01(7) в зависимости от состояния генератора после пере-
ключения. Далее путем последовательных построений ХПВ и ХОВ получа-
ют значения токов и напряжений в линии, соответствующих точкам D, Е, ...
для моментов ЗТ, 4Т,.... Построения завершаются по достижении окрестно-
сти точки, соответствующей устойчивому состоянию микросхемы при / —>
т. е. уровню логического 0 или 1. Для получения зависимостей от времени
входного 1<TL(O) и выходного KoTL(r) напряжения в линии (рис. 4.31) удобно
воспользоваться табл. 4.2.
Конечным шагом определения формы сигнала является построение ос-
циллограмм сигналов в начале и в конце линии (рис. 4.310. Режим в начале
линии описывают точки А, С, Е, ... и т. д., лежащие на ВАХ, принадлежащей
началу линии, а режим на конце линии определяют точки В, D, Е, ..., лежа-
щие на входной ВАХ микросхемы нагрузки. Перенеся эти точки на график
зависимости напряжения от времени и учитывая, что изменение состояния
на концах линии происходит в дискретные моменты времени, а именно, в
Таблица 4.2
Характерные точки осциллограммы сигнала
Место наблюдения осциллограммы Время Примечание
0 т 2Т ЗТ 4Г 5Т
Начало линии А А С С Е Е Точки расположены на выходной ВАХ
Конец линии К(-0) В В D D F Точки расположены на входной ВАХ
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 301
начале линии в моменты 0, 2 Г, 4 Г,а в конце линии в моменты Г, ЗГ, 5 Г,...,
получаем описание фронта сигнала в начале и в конце линии (рис. 4.316).
Ниже приведены в качестве примера несколько расчетов, выполненных
для линий, соединяющих ТТЛ-схемы. Во всех случаях размерности по оси
тока — амперы, а по оси напряжения — вольты.
Переключение драйвера из 0 в 1
Исходные ВАХ определены по паспортным данным микросхем и описа-
ны в виде массива точек с последующей кусочно-линейной аппроксимаци-
ей. На рис. 4.32 представлены построенные ВАХ и характеристики падаю-
щих и отраженных волн. Для примера взято малое волновое сопротивление,
поэтому угол построения нагрузочной прямой и характеристик падающих
и отраженных волн также относительно мал. Полученные осциллограммы
представлены на рис. 4.33. Предположим, что пороговое напряжение для
микросхем равно 2,5 В. Из осциллограммы для конца линии (рис. 4.336) видно,
что момент достижения порога срабатывания составляет 3 Т. Это время на 2 Т
превосходит ожидаемое, определяемое только скоростью распространения
сигнала в линии. Очевидно, что подобная ситуация недопустима. Ее можно
исправить двумя путями. Во-первых, можно увеличить значение волнового
сопротивления, что приведет к росту амплитуды первой ступеньки напря-
жения на выходе линии. Во-вторых, устранение искажений формы сигнала
можно добиться корректным согласованием линии.
Переключение драйвера из 1 в О
Методика определения формы сигнала остается неизменной, но на пер-
вом шаге строится нагрузочная прямая под углом 9Z из точки начального
статического состояния — логической «1» (рис. 4.34). Графики осциллограмм
для начала линии и для конца линии представлены на рис. 4.35. На этом примере
можно отметить появление значительного (—0,8 В) отрицательного выброса на
Рис. 4.32. Вольтамперные характеристики /О0(/), И01(7), ^(7) и характеристики
падающих и отраженных волн при переключении драйвера из 0 в 1
302 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Т, относительные единицы
3
25
2
со
> 1.5
1
05
0
Рис. 4.33. Осциллограммы при переключении драйвера из 0 в 1: а — начало линии;
б — конец линии
Г, относительные единицы
Рис. 4.34. Вольтамперные характеристики и характеристики падающих и отраженных
волн при переключении драйвера из 1 в О
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 303
Рис. 4.35. Осциллограммы при переключении драйвера из 1 в 0: а — начало линии;
б — конец линии
конце линии передачи. В том случае, если микросхема-приемник не имеет встро-
енной защиты, это может привести к непредсказуемым последствиям.
Здесь уместно сделать следующее замечание. При использовании ВАХ
микросхем не допускается их экстраполяция за пределами рабочей области
графиков, полученных либо экспериментально, либо взятых из технической
документации. Если при построении характеристик падающих и отраженных
волн не будет найдена хотя бы одна точка их пересечения с рабочим участком
ВАХ, это означает, что микросхема работает вне допустимого режима.
Переключение драйвера из 0 в 1 при коротком замыкании
на конце линии
Короткое замыкание соответствует сопротивлению нагрузки, равному
нулю. Поэтому ВАХ нагрузки будет представлять прямую с нулевым углом
наклона, т. е. совпадающую с осью тока (рис. 4.36). Очевидно, что при этом
изменятся статические режимы логического 0 и 1, что видно на графиках.
304 Глава 4. Обеспечение целостности сигнала в печатном монтаже
I, А
Рис. 4.36. Вольтамперные характеристики и характеристики падающих и отраженных
волн при коротком замыкании на конце линии
Рис. 4.37. Осциллограммы сигналов при коротком замыкании на выходе линии:
а — начало линии; б — конец линии
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 305
Построение нагрузочной прямой ведется из логического 0 с последую-
щим построением характеристик падающих и отраженных волн, имеющих
вид спирали. Из полученных осциллограмм (рис. 4.37) видно, что отрица-
тельный выброс имеет место в начале линии и может быть приложен к вхо-
ду микросхемы, которая присоединена к началу линии короткой линией. Это
может иметь отрицательные последствия.
Приведенные примеры показывают, что если характеристики падающих
и отраженных волн образуют зигзагообразную траекторию, то осциллограмма
будет иметь ступенчатый вид, а если траектория характеристик спиралевидная,
то осциллограммы будут иметь осциллирующий характер.
4.2.7. Согласование линии передачи
Способы согласования для одиночной линии
Эффективным средством устранения помех отражения в линиях переда-
чи является согласование, при котором путем установки согласующих рези-
сторов добиваются равенства сопротивления нагрузки и (или) выходно-
го сопротивления драйвера волновому сопротивлению линии. При этом для
линейных нагрузок коэффициенты отражения на входе или выходе линии
будут равны нулю, и отсутствуют отраженные волны, искажающие форму сиг-
нала. Для нелинейных нагрузок коэффициенты отражения в зависимости от
характера нелинейности будут равны нулю только в отдельных точках диа-
пазона изменений токов и напряжений. В практических случаях подобный
аспект не сможет существенно повлиять на качество согласования.
В зависимости от способа согласования различают согласование по входу
и по выходу линии. Следует отметить, если устраняется отражение сигнала хотя
бы на одном конце линии, то помехи отражения сводятся к минимуму.
В качестве основного объекта согласования выберем двухточечную топо-
логию, при которой одному драйверу соответствует одно приемное устрой-
ство. Существуют следующие способы согласования двухточечной тополо-
гии (рис. 4.38) [4, 77, 80]:
• последовательное согласование одиночным резистором на входе линии;
• параллельное согласование одиночным резистором на выходе линии;
• согласование на выходе линии при помощи делителя напряжения;
• согласование на выходе линии по активной схеме;
• согласование на выходе линии при помощи 7?С-цепи.
Понимание причин возникновения отражения позволит предотвратить их,
выбрав наиболее приемлемую схему согласования, и, следовательно, добиться
неискаженной формы сигнала.
Согласование по входу линии
При таком согласовании последовательно с драйвером, у которого, как
правило, выходное сопротивление г0 меньше волнового сопротивления Z
линии, устанавливается согласующий резистор 7^ (рис. 4.39а), сопротивление
которого определяется из соотношения:
^ti=Z-r0. (4.49)
306 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.38. Способы согласования одиночной линии передачи: а — последовательное
в начале линии; б — параллельное в конце линии; в — с помощью делителя
напряжения; г — активная схема согласования; д — с помощью 7?С-схемы
(S — источник сигнала; L — приемник сигнала)
При согласовании микросхем по входу линии сопротивление нагрузки со
стороны драйвера равно Zh является суммой нелинейного выходного сопро-
тивления драйвера и линейного сопротивления последовательного согласу-
ющего резистора.
Граничные условия на выходе линии для этого случая задаются входной ВАХ
микросхемы, являющейся нагрузкой линии, а на входе линии — двумя выход-
ными ВАХ генератора (для состояния логического 0 и 1), которые представля-
ют собой сумму ВАХ микросхемы и линейного согласующего резистора. Прак-
тически это прямые под углом, пропорциональным —Z. Далее, согласно мето-
ду характеристик, строим (в примере принимаем переключение из 0 в 1):
• нагрузочную прямую, которая проходит под углом, пропорциональ-
ным +Z;
• характеристику падающей волны под углом пропорциональным —Z;
• осциллограммы сигналов на концах линии (рис. 4.39<?).
После выполнения первого этапа, как видно из графика, получена точка
пересечения нагрузочной прямой с суммарной ВАХ Ко1(/) микросхемы и со-
гласующего резистора, которая определяет начальные условия задачи (ре-
жим в начале линии). На рис. 4.39d показано графическое определение ме-
тодом характеристик формы сигнала для входа и выхода линии, а на рис. 4.39<?
приведены соответствующие осциллограммы. Поскольку угол наклона
0 - arctg
/ „ \ I ^тЛ,
(ro + Ati)-^ = arctg Z-t
т, т.
(4.50)
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 307
Рис. 4.39. Согласование по входу линии: а — схема замещения; б — графическая
интерпретация метода характеристик; в — временные диаграммы (7 — уровень
логической 1 до согласования)
ВАХ генератора с учетом установленного согласующего резистора равен углу
наклона характеристики падающей волны, то при ее построении она совпадает
с ВАХ генератора и непосредственно попадает в точку установившегося ре-
жима, что говорит об отсутствии искажений формы сигнала.
На этом процесс распространения электромагнитной волны в линии
передачи заканчивается.
Анализ осциллограмм показывает, что на выходе линии сигнал представлен
без искажений, а на входе сигнал имеет характерное искажение в виде од-
ной ступеньки. Длительность этой ступеньки равна времени пробега элект-
ромагнитной волны от начала до конца линии и обратно к началу. Если к входу
линии подключен ряд микросхем короткими шлейфами, то ступенчатое
напряжение в отмеченный интервал времени попадает на вход этих микро-
схем и может вызвать сбои в работе системы.
На рис. 4.40 представлены построения при расчете помех отражения ме-
тодом характеристик при согласовании на входе линии. Итоговые осциллог-
раммы в начале и в конце линии представлены на рис. 4.41. Отчетливо вид-
на ступенька, искажающая фронт сигнала на входе линии.
Данная схема согласования отличается пониженной мощностью потреб-
ления и простотой реализации, но ее недостатком является наличие иска-
жений сигнала на входе линии и увеличенной постоянной времени линии.
Целесообразно на этапе предтопологического моделирования оценить по-
следствия согласования по входу линии.
При последовательном согласовании на входе линии форма сигнала на выхо-
де линии не искажается, а на входе линии искажения сигнала вызваны прихо-
дом волны, отраженной от несогласованной нагрузки. При этом для микросхем,
подключенных короткими отрезками к входу длинной линии, искаженный сиг-
нал может рассматриваться как помеха.
308 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.40. Графическое определение формы сигнала при согласовании в начале линии
Т относительные единицы
Т. относительные единицы
Рис. 4.41. Осциллограмма напряжения при согласовании в начале линии:
а — начало линии; б — конец линии
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 309
Согласование на выходе линии передачи
Простейший способ согласования на выходе линии заключается в уста-
новке согласующего резистора 7^0 параллельно нагрузке (рис. 4.42), поскольку
входное сопротивление нагрузки всегда значительно больше волнового со-
противления линии. Сопротивление согласующего резистора определяется
при этом из условия
^to + ^l
откуда
ZRX
Rx-Z
(4.51)
При Rx »/получаем сопротивление согласующего резистора, равное вол-
новому сопротивлению линии передачи: Яго = Z. На рис. 4.42 показаны по-
строения по определению формы сигнала методом характеристик. До согла-
сования ВАХ нагрузки строилась под углом
0! = arctg 7^— .
т.
После установки согласующего резистора ВАХ нагрузки должна быть по-
строена под углом 0t = 0Z. Поэтому в начальный момент напряжение на входе
линии (амплитуда падающей волны) равно установившемуся значению. Из
рис. 4.42<? видно, что форма сигнала как в начале, так и в конце линии не ис-
кажается.
Рис. 4.42. Согласование на выходе линии: а —схема замещения; б —графическая
интерпретация метода характеристик; в — временные диаграммы (1 — уровень
логической 1 до согласования)
310 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Расчетные характеристики и осциллограммы сигналов при согласовании
в конце линии представлены на рис. 4.43 и 4.44. Согласно методике, необ-
ходимо построить (переключение из 0 в 1):
• нагрузочную прямую из точки статического режима до момента пере-
ключения, которая в случае согласованной линии проходит под углом
0Z из начала координат,
• осциллограммы в начале и в конце линии (рис. 4.44).
В этом случае характеристики падающих и отраженных волн отсутствуют.
При согласовании по выходу линии нагрузочная прямая, которая стро-
ится под углом 0Z, совпадает с ВАХ согласующего резистора. Поэтому на
первом же шаге построений мы попадаем в конечную точку, определяющую
статический режим. Построенные осциллограммы сигналов для начала и
конца линии показывают, что информационный сигнал не искажается по
форме.
Можно сделать вывод: при согласовании на выходе линии обеспечивается не-
искаженная форма сигнала как на входе, так и на выходе линии.
Согласование на выходе линии приводит к значительному снижению
уровней установившихся напряжений в ней, что обусловливает дополнитель-
ные энергетические затраты. Очевидно, что пониженный уровень напряжения
должен превышать порог срабатывания микросхемы нагрузки и обеспечи-
вать нормальный входной ток. Применение параллельного согласования на
выходе линии, например, для стандартных ТТЛ-схем, может не обеспечить
на выходе линии уровень логической 1. Поэтому в ряде случаев применяют
более сложные согласующие схемы, обеспечивающие нормальные уровни ло-
гического 0 и 1, необходимые втекающие и вытекающие токи микросхем драй-
вера и нагрузки в состояниях логического 0 и 1. Такими согласующими схе-
мами являются делители напряжения и применение 7?С-цепи.
Рис. 4.43. Графическое определение формы сигнала при согласовании в конце линии
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 311
Т, относительные единицы
Т, относительные единицы
Рис. 4.44. Осциллограммы напряжения при согласовании в конце линии: а — в начале
линии; б — в конце линии
Согласование на выходе линии с использованием делителя напряжения
и RC-цепочки
Перечисленным выше требованиям повышения экономичности согласу-
ющей схемы удовлетворяет схема, содержащая резистивную цепочку (делитель
напряжения) (рис. 4.45), один из резисторов 7^о1 которой включен между
шиной питания (Kss) и сигнальным проводником, а другой R^q1 — между сиг-
нальным проводником и шиной заземления. Входное сопротивление нагрузки
при подобном согласовании, если входное сопротивление микросхемы вы-
сокое, определяется как параллельное включение этих резисторов:
Ло=^=^оЛо2/(^о1 + ^о2)- (4-52)
Выбор 7?t01 и Ato2 может быть проведен на основании рассмотрения ВАХ
драйвера и нагрузки линии (рис. 4.456). Для резистивной цепочки ВАХ пред-
ставляется в виде прямой V = Е + RXQI с угловым коэффициентом At0, т. е.
312 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.45. Согласование на выходе линии с помощью делителя напряжения: а — схема
включения; б — графическая интерпретация метода характеристик
построенной под углом 0Z и отсекающей на оси Котрезок Е. Напряжение сме-
щения Е вычисляется по формуле:
^SsAo2
*tol + ^to2
(4.53)
Сопротивления /^о1 и /^о2 должны обеспечивать соответствующие токи
/j и /0 в состояниях логического 0 и 1 при непременном удовлетворении ус-
ловия (4.52). Как видно из графика (рис. 4.45), при наличии смещения не-
сколько увеличивается уровень напряжения логической 1, что способству-
ет более экономичным режимам работы цифровой системы. По сравнению
с одиночным резистором эта схема уменьшает ток от драйвера, но несколь-
ко увеличивает ток потребления от источника питания.
Разновидностью согласования по выходу линии является применение
активной схемы (рис. 4.38г), когда смещение на входе приемника создается
при помощи дополнительного источника питания. Недостатком такой схе-
мы является наличие дополнительного источника питания и применение
резисторов.
При согласовании на выходе линии при помощи 7?С-схемы (рис. 4.38д)
нагрузкой линии является полное сопротивление цепочки RC. В ней значе-
ние сопротивления R должно быть равно волновому сопротивлению линии.
При очень большой емкости увеличивается время достижения порога сра-
батывания микросхемы нагрузки. Емкость меньше 100 пФ ослабляет эффек-
тивность согласования. При такой схеме отсутствует путь постоянного тока
через согласующую цепочку к возвратному проводнику, поэтому постоян-
ный ток не влияет на режим согласования. Эта схема согласования требует
баланса по постоянному току при формировании сигнала: сигнал половину
периода находится в высоком состоянии и половину периода — в низком.
Согласование по переменному току используется наиболее часто, если ис-
пользуется более чем одна нагрузка.
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 313
4.2.8. Особенности согласования ЭСЛ-схем
ЭСЛ-схемы являются наиболее быстродействующими, и поэтому вопросам
согласования линий передачи для них необходимо уделять особое внимание.
Согласно техническим условиям ЭСЛ-схемы применяются только с согла-
сованием.
Семейство ВАХ ЭСЛ-схем имеет характерную форму (рис. 4.46), поскольку
напряжение питания этих микросхем отрицательное. При этом входная ха-
рактеристика почти сливается с вертикальной осью напряжения, и без со-
ответствующих корректив работоспособ-
ность микросхем при работе друг на друга
не обеспечивается. Установка согласую-
щих резисторов со смещением на выхо-
де линий обеспечивает необходимые ус-
ловия работы ЭСЛ-схем.
Наличие в ЭСЛ-схемах выходных кас-
кадов с разомкнутыми эмиттерами требует
для минимизации задержки точного под-
бора постоянной времени, определяемой
Рис. 4.46. Типовые ВАХ ЭСЛ схем
емкостью нагрузки и сопротивлением со-
гласующего резистора.
Согласование линий связи ЭСЛ-схем наиболее эффективно и экономично
при параллельном включении на выходе линии резистора с сопротивлением
Ato = Z, подключенного к дополнительному источнику питания £ss = —2 В, т. е.
согласование ведется по активной схеме (табл. 4.3, п. 1). При этом ВАХ нагруз-
ки описывается уравнением
K = £ss+V
(4.54)
и представляет собой прямую с угловым коэффициентом 7^, отсекающую на оси
напряжения отрезок —2 В (рис. 4.47). Потребность в дополнительном источнике
питания является определенным недостатком рассматриваемой схемы согла-
сования. При использовании только одного
основного источника питания согласова-
ние на выходе линии можно выполнить с
помощью резистивной цепочки, как рас-
сматривалось выше (табл. 4.3, п. 2), назна-
чение которой аналогично назначению со-
гласующего резистора со смещением.
При установке ЭСЛ-схем вдоль длин-
ной линии (табл. 4.3, п. 4) последняя со-
гласуется на конце с помощью резисто-
ра с сопротивлением при подаче на него
смещения —2В. Для уменьшения искаже-
ний сигнала в линии отводы от нее долж-
Рис. 4.47. ВАХ при согласованной
по выходу линии
ны быть минимальной длины.
314 Глава 4. Обеспечение целостности сигнала в печатном монтаже
При последовательном согласовании на входе линии (табл. 4.3, п. 3) со-
противление согласующего резистора Rx выбирается из условия
^=Z-ro, (4.55)
где г0 — выходное сопротивление ЭСЛ-схемы, равное приблизительно 7 Ом.
Расчет формы сигналов для согласованной линии передачи, соединяю-
щей ЭСЛ-схемы, представлен на рис. 4.49, а осциллограммы сигнала для входа
и выхода линии показаны на рис. 4.48.
Сопротивление RE выбирается из условия надежной работы выходного
каскада ЭСЛ-схемы и определяется из соотношения
Re= 10Z-Ati. (4.56)
Рис. 4.48. Вольт-амперные характеристики ЭСЛ-драйвера и несогласованной нагрузки
и характеристики падающих и отраженных волн
Т. относительные единицы
Рис. 4.49 (начало). Осциллограммы сигнала в несогласованной линии передачи
для ЭСЛ-схем: а — начало линии, б — конец линии
4.2. Целостность сигнала в коротких и длинных одиночных линиях передачи 315
Т, относительные единицы
Рис. 4.49 (окончание)
Коэффициент разветвления на конце последовательно согласованной линии
(табл. 4.3, п. 5) ограничивается сопротивлением согласующего резистора. При
увеличении сопротивления или коэффициента разветвления увеличивается
Способы согласования ЭСЛ-схем
Таблица 4.3
№п /п Схема включения согласующих резисторов Номинальное сопротивление резисторов, Ом Примечание
1 2 3 4
1 K = z Необходим дополнитель- ный источник питания
2 -5,2 В ? iH г~1 z Ur-1 jjK Z 50 75 100 150 К. 130 195 260 390 Кг 81 121 162 243 Используется основной источник питания Приведенные значения сопротивлений даны в омах
3 А -5,2 В Д, = 7-7 ЯЕ = 10Z- R,, Используется основной источник питания; выходное сопротивление ЭСЛ-схемы принято 7 Ом
316 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Окончание табл. 4.3
2
3
4
Ш’-
-2 В
R» = z
-5,2 В
/<i>0,4Z
Используется основной источник
питания;
п- число линий;
— демпфирующий резистор
Необходим
дополнитель-
ный источник
питания
П
падение напряжения на согласующем резисторе и снижается помехозащищен-
ность схемы. Поэтому для рассматриваемого случая последовательный резис-
тор R^ в начале линии используется скорее для демпфирования линии с целью
уменьшения амплитуды выбросов или провалов, и его сопротивление меньше
волнового сопротивления линии и в худшем случае равно нулю. Минимальное
сопротивление демпфирующего резистора выбирается из условия
^>0,47.
При этом сопротивление резистора RE определяется по формуле
Дь_107-^
4.3. Неоднородности в линиях передачи
4.3.1. Плоскость как возвратный проводник линии передачи
Если для однородной линии основные проблемы связаны с отражениями
от нагрузки в конце и начале линии, то для неоднородной линии наличие любой
неоднородности приводит к отражению энергии сигнала и нарушению его це-
4.3. Неоднородности в линиях передачи
317
лостности. Именно неоднородная линия в большинстве случаев реализуется
на плате, поэтому знание механизма воздействия неоднородностей на цело-
стность сигнала позволит принять адекватные конструкторско-технологические
меры по сохранению целостности сигнала и устранению проблем тайминга.
Даже если печатная плата разработана с управляемым волновым сопротивле-
нием, практически всегда на пути распространения сигнала имеются неодно-
родности. Наиболее типичные из них:
• щель в возвратном проводнике (плоскости);
• разветвление сигнального проводника;
• шлейфовое ответвление от сигнального проводника;
• нагрузка в конце линии передачи;
• емкостная нагрузка в середине линии;
• входная емкость вентиля;
• поворот сигнального проводника;
• металлизированные переходные или сквозные отверстия;
• индуктивные неоднородности;
• соединители.
Главное воздействие, которое оказывает неоднородность, — это внесение
искажений в форму сигнала и локальное изменение полного сопротивления
линии передачи. Один из основных вопросов, возникающих при проекти-
ровании печатных плат, состоит в допустимом уровне искажений сигнала из-
за отражений от неоднородностей.
Опыт проектирования говорит, что уровень отраженного сигнала не должен
превышать от 5 до 10% номинальной амплитуды сигнала. Так, для перепада 3,3
В уровень отраженного сигнала не должен превышать, в худшем случае, 330 мВ,
а в особо ответственных цепях эти помехи не должны превышать 165 мВ. Сле-
дует отметить, что меньший уровень помех обходится дороже, поскольку тре-
бует более деликатных конструкторских и технологических решений. Кроме
этого, чем точнее локализована причина отражений, тем эффективней будут
средства устранения этих помех. В ряде случаев для этого пригодны инженер-
ные оценки и апробированные рекомендации, но в особо сложных случаях не-
обходимо применение соответствующих программных средств. Ниже более де-
тально рассмотрены основные неоднородности в линиях передачи.
Рассмотрим сигнальный проводник над непрерывной плоскостью. Ток
сигнала распространяется по проводнику и возвращается по плоскости.
Согласно законам индукции, распределение тока по плоскости будет таким,
при котором полное сопротивление контура будет минимальным. Поэтому
возвратный ток будет концентрироваться в плоскости непосредственно под
сигнальным проводником. Площадь контура тока будет определяться дли-
ной трассы и расстоянием между прямым и возвратным проводниками. Всегда
следует стремиться к минимизации площади контура при одновременном
сближении прямого и возвратного проводников. Это снижает полное сопро-
тивление линии передачи и уменьшает излучение от платы.
На рис. 4.50 показана типовая конструкция линия передачи: в одном слое
расположен сигнальный проводник, а во втором — проводящий слой, служащий
318 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.50. Щель в возвратном
проводнике, выполненном в виде
плоскости
возвратным проводником. В этом слое
выполнена щель, которая нарушает од-
нородность возвратного проводника.
Видно, что щель препятствует про-
теканию возвратного тока вдоль пря-
мого проводника. Возвратный ток вы-
нужден огибать щель, что приводит к
увеличению индуктивности контура в
месте расположения щели. Следова-
тельно, на этом участке волновое со-
противление линии увеличивается, а от
места стыка участков линии передачи
с различными волновыми сопротивлениями возникают помехи отражения.
С позиций ЭМС петля возвратного тока вокруг щели может служить излу-
чателем и способствовать помехоэмиссии.
Постоянный ток питания микросхем не имеет высокочастотных состав-
ляющих, и его возвратный путь может располагаться на произвольном по-
тенциальном слое. Но при работе микросхем возникают высокочастотные
помехи в шине питания, и, если не предпринять соответствующих мер, уро-
вень этих помех будет весьма высок, что повлияет на целостность сигнала и
параметры ЭМС. Для снижения уровня помех следует уменьшить площадь
контура, образованного током, поступающим в нагрузку, и током, который
возвращается от нагрузки к источнику. Это достигается сближением слоев
питания и заземления. Строго говоря, слой заземления следует рассматривать
именно как слой возвратного тока. Для еще большего уменьшения площа-
ди контура используют развязывающие конденсаторы, при помощи которых
слои питания и заземления по высокой частоте закорочены.
4.3.2. Возвратный путь в аналого-цифровых платах
Применение принципа зонирования приводит к разнесению высокочас-
тотных и низкочастотных узлов на плате, мощных и восприимчивых, ана-
логовых и цифровых. Кроме этого, на плате могут применяться компонен-
ты, имеющие различные номинальные напряжения питания, например 3 и
5 В. В этом случае слой заземления, который расположен на обратной сто-
роне двусторонней печатной платы и служит для протекания возвратных
токов, должен быть разделен на соответствующие зоны.
Рассмотрим различные варианты зонирования для аналого-цифровых
узлов [81, 82]. В простейшем случае потенциальную плоскость разделяют на
две зоны (рис. 4.51). При таком разделении одного потенциального слоя щель
в нем полностью прервет возвратные токи, которые должны повторять кон-
фигурацию сигнальных проводников. Единственный путь, по которому может
протекать возвратный ток, в данном случае должен быть организован толь-
ко посредством внешних проводников, соединяющих потенциальные уча-
стки с источником питания и точкой заземления, как показано на рис. 4.52.
4.3. Неоднородности в линиях передачи
319
Аналоговая земля
Проводники
Цифровая земля
Рис. 4.51. Строгое разделение
плоскостей возвратных токов
на две зоны: аналоговую
и цифровую
Аналоговая земля
о
о Проводник
Цифровая земля ,
Внешнее соединение
-------- Источник
питания и
точка
заземления
Рис. 4.52. Контур возвратных токов при
строгом разделении на аналоговую
и цифровую зону
В этом случае образуются токовые контуры значительной площади из-за
разнесения прямых и возвратных токов. Это приведет к значительному воз-
растанию уровня перекрестных помех и помехоэмиссии.
Для сокращения площади контуров необходимо соединить зоны заземле-
ния, но при этом остается вопрос: как рационально выполнить соединение зон?
На рис. 4.53 показан вариант конфигурации слоя заземления платы и не-
приемлемый вариант расположения сигнального проводника. В этом случае
проводник, несущий цифровой сигнал, располагается над слоем заземления,
который «обслуживает» аналоговый узел. Поэтому в этом слое будут инду-
цироваться возвратные токи, вызывающие помеховые напряжения в анало-
говом узле. Если возвратные токи протекают, как показано на рисунке, в обход
щели, то увеличивается площадь контура, что ухудшает показатели ЭМС. Оба
варианта плохи. В идеале этот проводник должен располагаться строго над
участком слоя заземления, отведенным для цифрового узла. При этом надо
помнить, что зона, занимаемая возвратным током, примерно в 3 раза боль-
ше ширины сигнального проводника. Сигнальный проводник следует распо-
лагать только над слоем заземления, который соответствует зоне расположения
соединяемых компонентов.
В данном случае зоны аналоговой и цифровой земли соединены в одной
точке, но в стороне от прокладки сигнальных трасс.
Индуцированные помехи
в аналоговой зоне
Цифровая зона
Рис. 4.53. Неприемлемый вариант располо-
жения сигнального проводника
аналого-цифрового узла
Рис. 4.54. Одноточечное соединение
зон в потенциальном слое
320 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Аналоговая зона
АЦП/ЦАП
Ситуация улучшится, если отдельные зоны потенциального слоя соединить
в узкой области, поверх которой будут располагаться проводники (рис. 4.54).
В этом варианте возвратные токи будут протекать под сигнальными провод-
никами, и площади токовых контуров будут минимизированы. Недостатком
подобного соединения участков заземления является усложнение трассировки.
Можно ли обойтись без щели в потенци-
альной плоскости? Если учесть, что высоко-
частотные токи протекают строго под сиг-
нальными проводниками, являясь как бы их
зеркальными отражениями на потенциаль-
ной плоскости, то при строгом расположе-
нии сигнальных проводников в соответству-
ющих зонах, обеспечивается разделение и
возвратных токов. Тогда зоны будут разделе-
ны некоторой условной границей, и щель в
потенциальном слое можно не выполнять.
Для корректного перехода между зонами на
этой границе следует расположить аналого-
цифровые (цифро-аналоговые) преобразователи (рис. 4.55). Этот вариант наи-
более предпочтительный.
Возвратный ток Сигнальный
ток
Цифровая зона
Рис. 4.55. Условное разделение
потенциального слоя на анало-
говую и цифровую зону
4.3.3. Разветвления
Достаточно часто приходится выполнять разветвления трасс в виде знака
Y (Y-разветвление). Разновидности подобных разветвлений показаны на
рис. 4.56. Вариант «а» соответствует разветвлению длинной линии на две длин-
ных линии без изменения волнового сопротивления. Очевидно, что нагруз-
кой первого отрезка электрически длинной линии с волновым сопротивлением
50 Ом будет являться параллельное включение двух полных сопротивлений по
50 Ом, т. е. 25 Ом. При этом коэффициент отражения от точки разветвления
будет равен (25 — 50)/(25 + 50) = 1/3, что вызовет существенные помехи отра-
жения. Уровень отраженного сигнала будет составлять примерно 33 % от уровня
падающей волны, что существенно больше допустимых 5... 10 %.
Имеются два возможных варианта корректно выполнить У-разветвления,
каждый из которых обеспечивает отсутствие отражений от подобной неодно-
родности и, следовательно, сохранение целостности сигнала.
50 Ом
50 Ом
< 50 Ом
50 Ом
<100 Ом
50 Ом
50 Ом
Рис. 4.56. Различные варианты У-разветвления
а — некорректное разветвление длинной линии;
б — корректное разветвление длинной линии;
в — разветвление при наличии первоначального
отрезка короткой линии
4.3. Неоднородности в линиях передачи
321
Первый вариант показан на рис. 4.56d, при котором две трассы после точки
разветвления выполняются с волновым сопротивлением 100 Ом каждая. Парал-
лельное соединение двух сопротивлений по 100 Ом обеспечивает нагрузку 50 Ом
для первоначального участка линии передачи. В этом случае, очевидно, линии
с волновым сопротивлением 100 Ом должны быть согласованы на концах.
Второй вариант показан на рис. 4.56в. В данном случае разветвление
выполняется настолько близко к драйверу, что первоначальный отрезок линии
становится электрически короткой линией, и неоднородность не оказыва-
ет существенного влияния на целостность сигнала. Отрезки линий с волно-
вым сопротивлением 50 Ом должны быть согласованы.
Учитывая проблемы, которые вносят разветвления в обеспечение цело-
стности сигнала, от них по возможности следует отказываться, выполняя
соединения «точка — точка» и используя драйверы с несколькими параллель-
ными выходами.
4.3.4. Шлейфы
Шлейфы представляют собой короткий сегмент трассы, который отхо-
дит от основной линии передачи, часто с контролируемым волновым сопро-
тивлением. Они соединяют контактные пло-
щадки и присоединенные к ним компоненты к
основной трассе. На рис. 4.57 показаны 4 вари-
анта выполнения шлейфов. Варианты 51 и S3
распространены наиболее широко. Вариант S2
приводит к достаточно длинным шлейфам и
должен быть исключен из применения в высо-
коскоростных платах. В противном случае оди-
ночный проводник служит аналогом штыревой
антенны.
Рис. 4.57. Варианты
выполнения шлейфов
Вариант шлейфа 54 неприемлем, поскольку в этом случае шлейф высту-
пает в качестве антенны. Он может образоваться в процессе перетрассиров-
ки по недосмотру. Никогда не следует допускать выступающие ненагружен-
ные шлейфы подобного рода.
В любом случае следует минимизировать длину шлейфов или исключать их.
При проектировании шлейфов действует такое же правило, как и при
других неоднородностях: если время распространения сигнала в шлейфе
меньше 20 % длительности фронта сигнала, то помехами отражения можно
пренебречь. Например, при скорости распространения сигнала в стеклотек-
столите примерно 0,15 м/нс и при фронте сигнала 1 нс, допустимая длина
шлейфа составляет 0,15 х (0,2 х 1) = 0,03 м, т. е. 30 мм.
Практическая рекомендация: длина шлейфов в печатном монтаже при фрон-
те сигнала 1 нс не должна превышать 30 мм. Длина шлейфа уменьшается об-
ратно пропорционально длительности фронта.
11 1527
322 Глава 4. Обеспечение целостности сигнала в печатном монтаже
4.3.5. Емкостная нагрузка в конце линии
Все реальные вентили имеют некоторую входную емкость, типичное зна-
чение которой составляет 2 пФ. Дополнительно сигнальный вывод микро-
схемы может иметь емкость относительно вывода возвратного пути около 1
пФ. Если на конце линии подключена, например, группа из трех элементов
памяти, то общая емкость может достигать 10 пФ. Кроме этого, следует учи-
тывать емкость монтажа, которая имеет значения 3...5 пФ. Таким образом,
суммарная емкость нагрузки на выходе линии передачи может достигать 15
пФ и более.
Падающая электромагнитная волна, достигая конца линии, встречает
полное сопротивление емкостной нагрузки, отличное от ее волнового сопро-
тивления. Полное сопротивление гс емкости во временной области опреде-
ляется как:
V _ V
Zc~
dt
(4.57)
где С — емкость конденсатора; V — мгновенное напряжение сигнала на конденсаторе.
Если фронт сигнала короче, чем изменение напряжения на конденсаторе,
тогда в начальной стадии напряжение будет расти значительно быстрее и полное
сопротивление будет низким. Но по мере заряда конденсатора, скорость за-
ряда JE/J/уменьшается. Когда конденсатор зарядится, напряжение на нем будет
меняться медленно. Это будет вызывать повышение полного сопротивление
конденсатора. Со временем конденсатор полностью зарядится, и будет соот-
ветствовать полностью разомкнутой линии (режиму холостого хода).
Коэффициент отражения будет также изменяться со временем. Отражен-
ный сигнал вначале предельно мал, а затем начинает расти и достигает уровня,
который соответствует разомкнутой линии. Точное значение параметров
сигнала зависит от волнового сопротивления линии (Z), емкости конденса-
тора и фронта сигнала. Моделирование работы линии [4] при емкостной
нагрузке в 2, 5 и 10 пФ показано на рис. 4.58. Фронт сигнала равен 0,5 нс.
Линия согласована в начале.
Наличие емкости приводит к затягиванию фронта сигнала. Увеличение
постоянной времени заряда объясняется зарядом емкости через согласую-
щий резистор на входе линии. Можно оценить новое значение фронта на
выходе линии и увеличение системной задержки, т. е. времени перехода че-
рез пороговый (средний) уровень. Предположим, что фронт сигнала соот-
ветствует изменению напряжения при заряде АС-цепи, которое возрастает
по экспоненциальному закону. Постоянная времени заряда будет
тс = RC. (4.58)
По определению, постоянная времени показывает, что напряжение воз-
растает на 1/е, т. е. на 37 % от конечного значения напряжения. При изме-
рении фронта от 10 % до 90 % установившегося значения перепад уровней
4.3. Неоднородности в линиях передачи
323
Время, нс
Рис. 4.58. Работа длинной линии передачи на емкостную нагрузку 2 (кривая 2), 5 (3)
и 10 пФ (4); для сравнения даны результаты при работе линии в режиме холостого хода
(кривая 1)
напряжения составляет 80 %. Это в 2,2 раза превышает значение 1/е. Новая
постоянная времени равна
т10/90 = 2,2тс = 2,2-А-С. (4.59)
Для конца линии передачи с емкостной нагрузкой в качестве резистора
выступает волновое сопротивление линии передачи, а в качестве емкости —
емкость нагрузки. В этом случае постоянная времени для описания фронта
будет приближенно определяться как
т10/90 = 2,2-ZC. (4.60)
324 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Например, если линия передачи имеет волновое сопротивление 50 Ом и
емкостную нагрузку 15 пФ, тогда постоянная времени т10/90 будет
2,2 х 50 х 15-10“12 = 1,65-10“9 с, т. е. 1,65 нс. Если фронт сигнала драйвера мень-
ше, чем это значение, наличие емкостной нагрузки на конце линии будет доми-
нировать и будет определять длительность фронта на входе приемника. Если
фронт сигнала драйвера больше, чем т10/90, то емкость на конце линии уве-
личит длительность фронта приблизительно на это значение.
Всегда следует оценивать постоянную времени т10/90, которая зависит от
волнового сопротивления линии и емкостной нагрузки на входе приемника. Когда
она соизмерима с фронтом сигнала на входе линии, емкостная нагрузка на дальнем
конце линии будет влиять на тайминг.
Конденсатор действует совместно с линией передачи как ЛС-фильтр,
приводя к увеличению системной задержки. Фронт 10/90 преломленного
сигнала будет увеличиваться, также как и время достижения порога на уровне
0,5. Время т10/50 достижения этого значения приближенно будет равно
тю/50 = 0,5(2,2-Z-C) == Z-С, нс, (4.61)
где Z — волновое сопротивление, Ом; С — емкость нагрузки, нФ.
Увеличение задержки до достижения уровня 0,5 будет определяться как
Д/= 7?C=0,5ZC, пс, (4.62)
где: Д? — увеличение времени задержки до достижения уровня 0,5, нс; Z— волновое со-
противление линии, Ом; С — емкостная неоднородность, пФ.
Коэффициент 0,5 вводится потому, что линия перед конденсатором за-
ряжает его, а линия за конденсатором — разряжает. Поэтому эффективное
полное сопротивление заряжающегося конденсатора составляет половину
волнового сопротивления линии.
Например, для линии с волновым сопротивлением 50 Ом и с неоднород-
ностью в 2 пФ постоянная времени т10/90 согласно (4.59) будет равна 2,2 х 50 х
х 2 = 220 пс. Время достижения порога на уровне 0,5 составит по (4.61) 100 пс,
а дополнительная задержка Д/будет = 50 пс. На рис. 4.59 представлены резуль-
таты моделирования прохождения сигнала с фронтом 100 пс при трех емкос-
тных неоднородностях 2 пФ, 5 пФ, 10 пФ. Видно, что они вносят дополни-
тельную задержку в 50, 125 и 250 пс. Это очень близко к реальной ситуации.
Трудно выполнить неоднородности менее 1 пФ (контактные площадки,
металлизированные отверстия, тестовые контакты и т. п.). Каждая емкост-
ная неоднородность в 1 пФ создает дополнительное увеличение длительно-
сти фронта на значение, равное 0,5 х 50 х 1 = 25 пс. В высокочастотных при-
ложениях, в которых фронт может быть 50 пс, каждое металлизированное
отверстие (типовая емкость 2 пФ) будет увеличивать его длительность на 50 пс.
Таким образом, одно металлизированное отверстие удваивает длительность
фронта.
Единственный путь снизить влияние емкостных неоднородностей —уменьшение
волнового сопротивления. Чем меньше волновое сопротивление, тем меньше добав-
ленная длительность фронта для одной и той же емкостной неоднородности.
4.3. Неоднородности в линиях передачи
325
Время, нс
Рис. 4.59. Увеличение фронта из-за емкостных неоднородностей 2 пФ (кривая 2); 5 пФ
(кривая 3); 10 пФ (кривая 4); линия с волновым сопротивлением 50 Ом; исходный
фронт — 50 пс (кривая 1)
4.3.6. Емкостная нагрузка в середине линии
Контрольные контактные площадки, выводы микросхем или малые шлей-
фы в середине линии будут действовать подобно сосредоточенному конден-
сатору. На рис. 4.60 показан отраженный и преломленный сигнал в линии
передачи с малой емкостью в середине трассы. Линия согласована в начале.
Фронт сигнала составляет 0,5 нс. Графики даны для случая, когда емкость
отсутствует, а также когда емкость конденсатора составляет 2, 5 и 10 пФ [3].
Поскольку в начальной стадии конденсатор имеет низкое полное сопротив-
ление, отраженный к источнику сигнал будет иметь небольшой отрицатель-
ный провал. Если приемник будет присоединен недалеко от переднего кон-
ца трассы, этот провал может вызвать проблемы, поскольку вносит немоно-
тонность в форму фронта.
Прошедший сигнал в первоначальный момент времени может не созда-
вать большого воздействия на первый проходящий сигнал, но после отра-
жения от конца линии он возвратится к источнику. Затем сигнал снова до-
стигнет конденсатора, и такой же сигнал, но с отрицательным знаком, бу-
дет отражен к дальнему концу. Это отражение к приемнику будет в виде
отрицательного напряжения и уменьшит сигнал на входе приемника, вызывая
отрицательный выброс перед фронтом импульса. Если некоторая емкость Стах
приемлема для некоторого фронта /г, то при уменьшении фронта максимально
допустимая емкость будет также уменьшаться. Отношение Zr/Cmax должно быть
больше, чем некоторое допустимое значение. Это отношение измеряется в омах.
Но для какого элемента определено это полное сопротивление? Полное со-
противление конденсатора дается выражением (4.57). Если напряжение V
326 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Время, нс
Рис. 4.60. Отраженный и преломленный сигнал в линии передачи с малой емкостью
в середине трассы: 1 — без емкости; 2 — емкость 2 пФ; 3 — емкость 5 пФ;
4 — емкость 10 пФ
фронта растет линейно со временем, тогда dV/dt равно V/tv и полное сопро-
тивление будет
V
Ом, (4.63)
где С — емкость неоднородности, нФ; tr — фронт сигнала, нс.
Полное сопротивление zc шунтирует волновое сопротивление линии в
течение длительности фронта и вызывает отражения. Это иллюстрируется
4.3. Неоднородности в линиях передачи
327
Рис. 4.61. Емкостная неоднородность как шунтирующее сопротивление между
сигнальной и возвратной линией
на рис. 4.61. Для того, чтобы это сопротивление не оказывало существенного
воздействия на целостность сигнала, полное сопротивление конденсатора
должно быть больше, чем волновое сопротивление линии передачи, т. е.
Zc>> Z. Предположим zc > 10Z. Тогда с учетом (4.63) ограничения на емкость
и длительность фронта будут определяться выражением:
tA->10Z- (4.64)
^max
Отсюда максимально приемлемая емкость, еще не вызывающая проблем
с помехами отражения, определяется из неравенства:
^тах < । > нФ, (4.65)
где Z — волновое сопротивление линии передачи, Ом; tr — фронт сигнала, нс.
Например, если волновое сопротивление равно 50 Ом, максимально до-
пустимая емкость будет равна:
Стах< —— = 0,002 Гг, нФ,
тах 10 50 г ’
или Стах = 2/г, пФ, если фронт задается в наносекундах.
Практическое правило: для того, чтобы емкостная неоднородность в сере-
дине линии не создавала проблем с помехами отражения, численно значение ем-
кости в пФ не должно быть больше двукратной длительности фронта в нс.
Если фронт 1 нс, то емкость не должна быть более 2 пФ. Если емкост-
ная неоднородность составляет 4 пФ, то фронт сигнала должен быть более
2 нс. При фронте 0,2 нс емкостная неоднородность не должна превышать
0,1 пФ, что предъявляет очень высокие требования к однородности линии.
При несоблюдении этого условия проблемы с обеспечением целостности
сигнала присутствуют.
328 Глава 4. Обеспечение целостности сигнала в печатном монтаже
4.3.7. Повороты сигнальных проводников
Если сигнальный проводник линии передачи имеет поворот на 90°, то это
будет являтся неоднородностью, которая вызывает отражения сигнала и его
искажения. На рис. 4.62 показано влияние неоднородности в виде двух по-
воротов сигнального проводника при фронте сигнала 50 пс; ширина про-
водника 1,625 мм, угол каждого поворота 90°; возвратный проводник выпол-
нен в виде металлизированного слоя платы.
Поворот на 90° эквивалентен увеличению ширины проводника для сиг-
нала, который распространяется по линии. Это увеличивает емкость на этом
участке, что является неоднородностью. Изменение угла до 45° и округле-
ние углов поворота сводит влияние неоднородности на нет.
Можно приблизительно оценить значение неоднородности при поворо-
те на 90°. На рис. 4.63 показана модель для оценки неоднородности. Доба-
вочная (к повороту на 45°) область металла определяется меньше, чем одним
квадратом, и, при весьма приблизительной аппроксимации, может быть
представлена половиной площади квадрата.
Емкость Ссгп поворота может быть вычислена через емкость Csq квадрата:
С = 0,5С .
cm ' sq
Емкость на единицу длины для заданного волнового сопротивления равна:
С, = 3,3^.
' Z
Если длина отрезка проводника равна его ширине, емкость поворота будет
равна
w./p WAZE
С._=0,5С/м’ = 0,5-3,3—^ = 1,65—пФ,
сгп 1 Z Z
(4.66)
где С1 — емкость на единицу длины, пФ/м; w — ширина сигнального проводника, мм; Z —
волновое сопротивление, Ом; ег — относительная диэлектрическая проницаемость осно-
вания платы. Если сигнальный проводник расположен в первом или в последнем слое МПП,
Рис. 4.62. Неоднородность в виде
двойного поворота линии передачи
Рис. 4.63. К оценке неоднородности при
повороте трассы: 7 — излишек фольги,
равный по площади 0,5 квадрата
4.3. Неоднородности в линиях передачи
329
то вместо относительной проницаемости следует использовать значение эффективной про-
ницаемости.
Например, для сигнального проводника шириной 1,65 мм, расположен-
ного в толще МПП (ег = 4), оценка емкости при повороте трассы на 90° со-
ставляет 1,65/50 х 1,65 х 2 = 0,1 пФ. Для приближенного рассмотрения об-
щей емкости неоднородности в виде двойного поворота этот результат сле-
дует умножить на 2, т. е. емкостная неоднородность составит 0,2 пФ.
Полезное правило', емкостная неоднородность (в пикофарадах) двойного
поворота на 9(/ линии с волновым сопротивлением 50 Ом приближенно равна
1/10 ширине проводника в миллиметрах.
Дополнительная задержка для данной неоднородности будет составлять,
согласно (4.62), 0,5 х 50 х 0,2 = 5 пс.
4.3.8. Металлизированные отверстия
Металлизированные отверстия следует рассматривать как неоднородности
в линии передачи. В низкочастотных приложениях их влияние на целостность
сигнала было незначительное, однако при длительности фронтов цифрового
сигнала менее 1 нс их влияние следует учитывать.
На рис. 4.64 представлены результаты [3] экспериментальной проверки
однородной линии передачи при наличии и отсутствии металлизированно-
го отверстия в центре линии. Длина линии 375 мм, число слоев МПП 10, фронт
сигнала 50 пс, емкость отверстия 0,4 пФ.
Рассмотрим прохождение сигнального тока по проводникам сигнальных
слоев и металлизированному отверстию между ними (рис. 4.65) [83—85].
Из рис. 4.65 видно: в области металлизированного отверстия путь возврат-
ного тока не следует за сигнальным током, что определяет появления нео-
днородности. Параметры этой неоднородности зависят от размеров метал-
лизированного отверстия. Простейший случай соответствует расположению
Рис. 4.64. Передача сигнала по
линии передачи: 1 — металлизи-
рованное отверстие под соеди-
нитель; 2 — без отверстия; 3 —
одиночное отверстие для уста-
новки вывода компонента
Рис. 4.65. Протекание токов в МПП
через металлизированное отверстие: 7,
4 — сигнальные слои; 2 — слой зазем-
ления; 3 — слой питания
330 Глава 4. Обеспечение целостности сигнала в печатном монтаже
сигнального и возвратного путей в соседних слоях (микрополосковая линия)
без переходного отверстия. При малом заглублении небольшая неоднородность
в возвратном пути не скажется на качестве функционирования. При большом
Рис. 4.66. Эквивалентная схема
металлизированного отверстия
заглублении ответ на вопрос о топологии воз-
вратного пути не очевиден.
Эквивалентную схему металлизированно-
го отверстия можно представить в виде П-об-
разной схемы (рис. 4.66).
Емкость сквозного металлизированного
отверстия определяется по формуле [84]:
Cvla=0,055£r/?- пФ
(4.67)
где ег — относительная диэлектрическая проницаемость материала основания платы; h —
толщина платы (длина отверстия), мм; D\ — диаметр контактной площадки, мм; D2 — ди-
аметр кругового зазора между металлизацией внутренних слоев и металлизированным от-
верстием, мм (см. рис. 4.65).
Из формулы видно, что при уменьшении диаметра DI сверления емкость
отверстия будет уменьшаться.
Приведем пример. Примем следующие параметры металлизированного отверстия, вы-
полненного в МПП на материале FR4 (ег = 4): h = 2 мм, ZH = 0,55 мм, D2 = 0,8 мм. Подста-
вив эти значения в формулу (4.67), получаем значение емкости металлизированного отверстия
0,968 пФ. Каждая емкость в модели отверстия будет иметь значение 0,484 пФ.
Дополнительная задержка от одиночного отверстия в линии с волновым
сопротивлением 50 Ом составляет 0,5 х 50 х 0,968 « 24 пс. Это позволяет сфор-
мулировать практическое правило: каждое металлизированное отверстие
вносит увеличение в системную задержку примерно на 25 пс.
Последовательная индуктивность в модели отверстия вычисляется по
формуле [9, 84]
(4.68)
где h — толщина платы (длина отверстия), мм; d — диаметр сверления, мм.
Пример. Рассчитаем индуктивность металлизированного отверстия, если диаметр свер-
ления d= 0,3 мм. Тогда Lvia =1,71 нГн.
Индуктивность и емкость металлизированного отверстия приводят к рас-
ширению фронта сигнала.
Для сохранения целостности сигнала возможны различные варианты.
Один заключается в установке развязывающих конденсаторов между слоем
питания и слоем заземления у каждого переходного отверстия. Другой ва-
риант вообще запрещает переход трассы со слоя на слой, что, очевидно,
неприемлемо. Эффективно сокращение длины отверстий за счет примене-
ния слепых и глухих отверстий.
4.3. Неоднородности в линиях передачи
331
4.3.9. Нагрузки, распределенные по длине линии
Емкостная нагрузка может быть распределена по длине линии. Напри-
мер, шлейфы с контактами соединителей емкостью 2 пФ каждый, располо-
женные через каждые 50 мм по длине шины, или вентили с входной емкос-
тью 3 пФ, распределенные через каждые 20 мм по шине памяти. Линия пе-
редачи с распределенной однородной емкостной нагрузкой называется нагру-
женной линией.
Каждая неоднородность представляется областью с малым волновым со-
противлением. Когда длительность фронта мала по сравнению со временем
прохождения сигнала между неоднородностями, каждая из них представляется
дискретной неоднородностью. Когда фронт больше времени пробега меж-
ду неоднородностями, области с малым волновым сопротивлением перекры-
ваются, и усредненное значение волнового сопротивления снижается.
На рис. 4.67 показан пример отраженных сигналов с тремя различными
фронтами в нагруженной линии [3, 4]. Пять емкостных неоднородностей по
3 пФ распределены через каждые 25 мм в линии передачи с волновым сопро-
тивлением 50 Ом. Последние 250 мм не имеют распределенной нагрузки. Каж-
дый конденсатор имеет собственный фронт 10/90, определяемый по (4.60)
как 2,2 х 0,5 х 50 х 3 = 150 пс. Даже если фронт сигнала на входе линии ра-
вен 50 пс, то после прохождения первой неоднородности он увеличится до
150 пс и будет увеличиваться при прохождении каждой неоднородности на
это значение.
Первые пять конденсаторов еще воспринимаются как дискретные нео-
днородности, но далее фронт сигнала будет настолько размыт, что неодно-
родности становятся неразличимыми. В том случае, если фронт больше вре-
мени прохождения расстояния между неоднородностями, линия передачи
с распределенной емкостной неоднородностью представляется в виде линии
Время, нс
Рис. 4.67. Отраженный сигнал в нагруженной линии с временем распространения
0,15 нс между емкостными неоднородностями 3 пФ при длительностях фронта 0,05 нс
(кривая 1); 0,15 нс (кривая 2); 0,5 нс (кривая 3); 1 нс (кривая 4)
332 Глава 4. Обеспечение целостности сигнала в печатном монтаже
с волновым сопротивлением уменьшенного значения. Такая нагруженная
линия образуется при увеличении емкости за счет распределенных тополо-
гических элементов печатного монтажа. Высокий уровень распределенной
емкости в линии определяет ее низкое волновое сопротивление и значитель-
ное время задержки распространения сигнала.
В однородной ненагруженной линии передачи длиной / волновое сопро-
тивление и время задержки распространения сигнала определяются по фор-
мулам:
z=Jf’'Л=1^'
где Z— волновое сопротивление ненагруженной линии, Ом; Lt — индуктивность на еди-
ницу длины линии; Cz — емкость на единицу длины ненагруженной линии; / — длина ли-
нии; rdl — время задержки распространения сигнала в ненагруженной линии.
При наличии однородной распределенной нагрузки в виде одинаковых
емкостей Ср расположенных на расстоянии друг от друга, распределенная
емкость на единицу длины увеличивается от Cz до (Cz + C/Jj). Это изменяет
волновое сопротивление и время задержки распространения линии до сле-
дующих значений:
(4.69)
где Zt — волновое сопротивление нагруженной линии, Ом; Zz — индуктивность на еди-
ницу длины линии, Гн/м; Q — индуктивность отдельной дискретной емкости, Ф; — рас-
стояние между дискретными емкостями, м; rdl/ — время задержки распространения нагру-
женной линии, с.
В линии передачи с волновым сопротивлением 50 Ом емкость на единицу
длины составляет приблизительно 130 пФ/м. Когда емкостная неоднородность
соизмерима с этим значением, волновое сопротивление и время задержки рас-
пространения будут заметно изменяться. Например, нагрузки в 3 пФ от входной
емкости вентиля микросхемы памяти, которые расположены через 25 мм по
шине памяти, добавят емкость нагрузки 120 пФ/м. Волновое сопротивление
нагруженной линии в этом случае уменьшится до значения Zz =0,7Z, а время
задержки распространения сигнала увеличится до l,4/dl.
Поскольку волновое сопротивление линии уменьшилось, значение согла-
сующего резистора должно быть также уменьшено. Этот факт часто остает-
ся за пределами внимания разработчиков, которые ориентируются только
на номинальное значение волнового сопротивления. Возможным решени-
ем является компенсация емкостной неоднородности изменением ширины
проводника таким образом, чтобы повысить волновое сопротивление. Это
можно, например, выполнить сужением проводника между емкостными нео-
днородностями, что приведет к возникновению распределенной индуктив-
ной неоднородности, которая может компенсировать емкостную.
4.3. Неоднородности в линиях передачи
333
Рис. 4.68. Прохождение сигнала
в однородной линия передачи
с индуктивной неоднородностью
4.3.10. Индуктивные неоднородности
Любое последовательное подключение к линии будет иметь некоторую
последовательную индуктивность. Каждое металлизированное отверстие для
перехода между слоями, последовательный согласующий резистор, каждый
соединитель, любое изменение в конструкции проводника (прямого и воз-
вратного) будут вносить некоторую индуктивность в контур тока. Индуктив-
ность будет неоднородностью для сигнала в линии передачи.
Если неоднородность находится в сигнальном пути, индуктивность кон-
тура будет доминировать за счет парциальной самоиндукции сигнального
пути. В любом случае, это индуктивность контура, по которому распростра-
няются прямой и возвратный токи.
Последовательная индуктивность при-
водит к возрастанию волнового сопротив-
ления. Это будет вызывать положительный
отраженный сигнал, который распростра-
няется к источнику. Рис. 4.68 показывает
отраженный сигнал в однородной линии
передачи, которая проходит над малым
зазором в возвратном пути. Фронт сигна-
ла в этом случае 50 пс.
Рис. 4.69 показывает сигнал на источ-
нике и приемнике при различных значени-
ях индуктивной неоднородности [3, 4].
Форма сигнала, идущего от нагрузки и от-
раженного, на ближнем конце является немонотонной. Это само по себе мо-
жет не вызвать проблем с целостностью сигнала. Однако если приемник рас-
положен около ближнего конца линии и принимает сигнал, который перехо-
дит уровень 50 % и затем опускается ниже этого уровня, то это может вызвать
ложное переключение. Немонотонное поведение нельзя допускать где бы ни было.
На дальнем конце линии сигнал будет иметь выбросы и увеличение фронта.
В общем случае, максимально допустимое значение индуктивности, ко-
торое может быть добавлено к линии, определяется помехозащищенностью
элементной базы. В каждом конкретном случае это задается спецификаци-
ей, но общее рассмотрение опирается на такое значение последовательной
индуктивной неоднородности, при которой волновое сопротивление увели-
чивается не более, чем на 20 %. В этом случае отраженный сигнал, как пра-
вило, не превосходит допустимых значений.
Если фронт сигнала линейно растет, то значение волнового сопротивле-
ния £ind индуктивной неоднородности значительно меньше, чем волновое
сопротивление линии передачи:
L-~
^=j = ~f-=L, Ом, (4.70)
где L — индуктивность, нГн; /г — фронт сигнала, нс.
334 Глава 4. Обеспечение целостности сигнала в печатном монтаже
05 1 15 2 25 3 35 4
Рис. 4.69. Сигнал с фронтом 50 пс на источнике и приемнике при наличии
индуктивной неоднородности 0, 1, 5 и 10 нГн (соответственно кривые 1, 2, 3, 4)
Оценка максимально допустимой индуктивной неоднородности, при которой
волновое сопротивление индуктивного участка будет меньше 20 % номиналь-
ного волнового сопротивления линии передачи, определяется из неравенства:
^nd<0.2Z,
откуда с учетом (4.70) получаем значение максимальной допустимой по-
следовательной индуктивности:
Апах<0’27Ч’нГн’ (4.71)
где Z — волновое сопротивление линия передачи, Ом; tx — фронт сигнала, нс.
4.3. Неоднородности в линиях передачи
335
Например, если номинальное волновое сопротивление линии передачи
50 Ом и фронт сигнала 1 нс, то максимально допустимая последовательная
индуктивность составит около 0,2 х 50 х 1 = 10 нГн.
Практическое правило: для линии передачи с волновым сопротивлением 50 Ом
максимально допустимое значение индуктивности (в наногенри) в 10раз чис-
ленно превосходит длительность фронта сигнала (в наносекундах). И обрат-
но, если известна индуктивность L (в наногенри) неоднородности, то длитель-
ность фронта сигнала, при котором отраженный сигнал не превосходит допу-
стимого уровня, составляет (в наносекундах) L/10.
Базируясь на этой оценке, можно получить фронт сигнала для согласу-
ющих резисторов с аксиальными выводами и поверхностно монтируемого
(ПМ). Последовательная индуктивность при аксиальных выводах составляет
10 нГн, а для ПМ-резистора — 2 нГн.
Наименьшая длительность фронта для компонента с аксиальными выводами,
при которой отражения не вызывают проблем, составляет примерно 10нГн/10~
- 1 нс, а для ПМ-резистора — 2 нГн/IO ~ 0,2 нс.
Когда фронт сигнала переходит в субнаносекундный диапазон, компо-
ненты с аксиальными выводами не должны применяться из-за высокой ин-
дуктивности выводов. При фронте 0,1 нс необходимо применять только ПМ-
компоненты. Наиболее важная особенность ПМ-резистора заключается в от-
сутствии выводов и наличии близко расположенного возвратного пути.
Индуктивная неоднородность, отвечающая требованиям отражения, также
увеличивает системную задержку. Длительность фронта 10/90 преломленного
сигнала определяется значением последовательной индуктивности:
, , L L
'г=2,2—= нс, (4.72)
а увеличение системной задержки
Д/ = 0,5-|, нс, (4.73)
где L — последовательная индуктивность контура для неоднородности, нГн; Z — волно-
вое сопротивление линии передачи, Ом; А/ — дополнительная системная задержка, оп-
ределяемая как дополнительное расширение фронта на уровне 0,5, нс.
Например, для неоднородности 10 нГн в линии передачи с волновым со-
противлением 50 Ом фронт составит по (4.72) 10/50 = 0,2 нс. На уровне 0,5
дополнительное расширение фронта будет 0,1 нс, что определит дополни-
тельную системную задержку момента переключения микросхемы нагрузки.
На рис. 4.70 [4] показан номинальный фронт 50 нс, а также фронты сигна-
лов при наличии индуктивной неоднородности 1, 5 и 10 нГн. Видно, что про-
исходит соответствующее увеличение системной задержки относительно но-
минального значения на 10, 50 и 100 пс.
336 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.70. Увеличение фронта 50 нс за счет индуктивных неоднородностей:
1 — номинальный фронт 50 пс; 2 — фронт при наличии индуктивной неоднородности
1 нГн; 3 — неоднородность 5 нГн; 4 — неоднородность 10 нГн
4.3.11. Компенсация
Неизбежность индуктивности позволяет использовать ее для снижения
уровня помех отражения. Эта техника называется компенсацией. Идея ком-
пенсации состоит в поддержании постоянства волнового сопротивления
линии в районе неоднородности. При этом искажения от емкостной неодно-
родности компенсируются искажениями сигнала от индуктивной неоднород-
ности. Волновое сопротивление такой секции:
°".
где L{ — номинальная индуктивность на единицу длины линии, нГн/м; Lt — общая, с учетом
неоднородности, индуктивность секции линии, нГн; С, — номинальная емкость на единицу
длины линии, нФ/м; Ct — общая, с учетом неоднородности, емкость секции линии, нФ.
На рис. 4.71 показан прием компенсации, при котором малый конден-
сатор подключен к концам индуктивной неоднородности. Значение компен-
сирующей емкости определим из соотношения:
г _ L
^cmp ^2 ’ нФ, (4.74)
где L — индуктивность неоднородности, нГн; Z — волновое сопротивление линии, Ом.
Например, если индуктивность соединителя составляет 10 нГн, а волно-
вое сопротивление линии передачи 50 Ом, то компенсационная емкость равна
10/502 = 0,004 нФ, т. е. 4 пФ. Для оптимальной компенсации эта емкость
должна быть разбита на две по 2 пФ и присоединена к каждому концу ин-
дуктивности. В зависимости от фронта сигнала помехи отражения при ком-
пенсации могут быть уменьшены на 75 %.
4.3. Неоднородности в линиях передачи
337
Рис. 4.71. Компенсация индуктивной неоднородности
Компенсация может быть применена ко всем индуктивным и емкостным
неоднородностям: металлизированным отверстиям, резисторам и т. п. Реали-
зовать компенсационный элемент в отдельных случаях можно путем коррек-
тировки топологического рисунка. Например, емкостный элемент можно по-
лучить соответствующим увеличением ширины сигнального проводника.
Основной целью разработки конструкции платы и топологии является со-
здание однородной линии передачи на всех ее топологических участках.
4.3.12. Последовательно соединенные
короткие отрезки линии
Зачастую приходится изменять ширину сигнального проводника, напри-
мер, при прокладке трассы между близко расположенными контактными пло-
щадками. При этом изменяются электрофизические параметры линии пе-
редачи, что приводит к изменению волнового сопротивления на отрезках
линии с различными значениями ширины сигнальных проводников. При
уменьшении ширины проводника возрастает волновое сопротивление ли-
нии из-за увеличения индуктивности и снижения емкости на данном топо-
логическом фрагменте. Возникает вопрос: насколько меняется волновое со-
противление, и, начиная с какой длины топологического фрагмента линии,
могут возникнуть проблемы целостности сигнала?
Если рассмотреть два последовательных участка линии передачи, имею-
щие соответственно волновые сопротивления и Z2, то значение коэффи-
циента отражения в точке их соединения определяется следующим образом:
Например, если волновое сопротивление первого участка 50 Ом, а вто-
рого — 75 Ом, то коэффициент отражения будет равен 0,2.
Эти изменения волнового сопротивления вызывают помехи отражения.
Чтобы помехи отражения, а следовательно, коэффициент отражения были
менее 5 %, следует поддерживать изменения волнового сопротивления в
пределах 10 %.
Максимальная длина Jdsc участка с измененным волновым сопротивле-
нием должна быть такой, чтобы время задержки распространения сигнала в
нем не превосходило 20 % длительности фронта сигнала:
(4.76)
338 Глава 4. Обеспечение целостности сигнала в печатном монтаже
или
л 0,2/г _ 0,2/г
Jdsc<V=U7^’M’ (4-77)
где ^dsc — приемлемая максимальная длина неоднородности линий, м; td — удельная за-
держка распространения сигнала в линии передачи, нс/м; tT — длительность фронта сиг-
нала, нс.
Максимально допустимая длина отрезка неоднородности для линии пе-
редачи на стеклотекстолите (ег = 4) составляет
О It
Jdsc = ’ r = Q,Q3O-/г, м, или dd = 30 •/, мм,
use 3 3 2 r use r
где tr — длительность фронта сигнала, нс.
Например, при длительности фронта 1 нс максимально приемлемая длина
неоднородного отрезка линии составляет 30 х 1 = 30 мм. Из формулы (4.77)
видно, что чем больше будет диэлектрическая проницаемость материала ос-
нования платы, тем меньше будет максимально допустимая длина неодно-
родного участка линии. При фронте 0,5 нс отрезок неоднородной линии
длиной меньше 15 мм не будет вызывать проблем целостности сигнала для
материала FR4 (ег = 4), а для стеклотекстолита марки СФ с ег = 5,6 макси-
мально допустимый отрезок неоднородности будет составлять 13 мм.
4.3.13. Соединители как неоднородность
линий передачи
В печатных платах повышенного быстродействия из-за массогабаритных
ограничений для коммутаций линий передачи в ряде случаев приходится ис-
пользовать низкочастотные соединители. Они не должны заметно изменять
волновые сопротивления коммутируемых линий. Если это требование дос-
таточно хорошо удовлетворяется для специальных высокочастотных соеди-
нителей, то при использовании более дешевых низкочастотных соедините-
лей в высокочастотных цепях в линии передачи вносятся существенные нео-
днородности и происходит нарушение целостности сигнала.
Выбор и оценку соединителей с позиций целостности сигнала и ЭМС
необходимо проводить с учетом следующих основных факторов: волнового
сопротивления, экранирующих свойств, материала контактов, электричес-
ких параметров, в том числе характеризующих фильтрующие свойства, ме-
ханических характеристик, экономических особенностей применения.
На топологию возвратного пути следует обращать пристальное внимание
при выполнении соединения между отдельными платами. Рис. 4.72 показывает
формирование контура большой площади при невозможности разместить
прямой и возвратный проводники рядом при назначении контактов соеди-
нителя.
4.3. Неоднородности в линиях передачи
339
Рис. 4.72. Формирование контура большой площади при невозможности разместить
в соединителе прямой и обратный проводники рядом
Если при трассировке платы будет использован контакт ^соединителя,
то площадь контура будет минимальна, что будет способствовать более вы-
сокому качеству передачи сигнала. Этот пример подчеркивает важность трас-
сировки платы с учетом применяемых соединителей, а также показывает, что
конструкция соединителя должна обеспечивать близость расположения
прямого и возвратного проводников.
Другой пример топологии показан на рис. 4.73. Сигнальный проводник
присоединен к металлизированному отверстию из группы отверстий для
установки компонента или соединителя. Возвратный проводник присоеди-
нен к другому отверстию на обратной стороне платы. Для варианта 1 кон-
тур, образуемый сигнальным и возвратным проводниками, имеет максималь-
ную площадь. Вариант 2 лучше, поскольку для него площадь контура мень-
ше. Наиболее удачным является вариант 3, при котором площадь контура,
ограниченная прямым и сигнальным проводниками, будет минимальна.
Вариант 2 показывает, почему необходимо иметь минимальный диаметр
контактных площадок и возможность заужения проводников. Это необхо-
димо для возможности прокладки проводников между контактными площад-
ками, но при этом следует оценить возможное изменение волнового сопро-
тивления, как рассмотрено выше.
Для варианта 3 необходимо комплексно решать задачу цоколевки ком-
понента и трассировки платы.
Одним из главных источников излучения от электронной аппаратуры яв-
ляются соединительные кабели. Для снижения уровня излучаемых непредна-
меренных электромагнитных помех они экранируются, что требует применения
OfOOO ооооо Сигнальный ток
ooootoo ооодоо D
। Возвратный ток
I I I ---------
I I I
I I I
I I I
1 2 3
Рис. 4.73. Практика трассировки проводников в группе металлизированных отверстий
1 — неудачное решение, приводящее к контуру большой площади; 2 — улучшенный
вариант, 3 — лучший вариант с минимальной площадью контура
340 Глава 4. Обеспечение целостности сигнала в печатном монтаже
совместимых экранированных соединителей. Ряд фирм выпускает полнос-
тью экранированные соединители, корпус которых либо металлический, либо
выполнен из термопласта с металлизацией. Для обеспечения контакта между
корпусами соединителя и аппаратуры устанавливается упругая прокладка,
выполненная из бронзы толщиной 0,15 мм, покрытая слоем блестящего олова.
Наилучшим материалом для контактов соединителя является золото.
Серебро и палладий по рабочим характеристикам уступают ему. Серебро не
поддается окислению, но на нем формируется пленка сульфида, а медь,
никель, вольфрам, молибден и латунь подвержены окислению и другим воз-
действиям окружающей среды. На покрытии из чистого олова могут вырас-
тать дендриты — кристаллические отростки, длина которых достаточна для
замыкания с соседними цепями. Предотвратить рост дендритов может на-
несение покрытий из сплавов на основе олова. Отличными параметрами ха-
рактеризуется сложное многослойное покрытие (слой золота нанесен на спе-
циальный слой палладия, который, в свою очередь, осажден на подслой из
никеля). При этом драгоценные металлы используются весьма экономично.
Электрические параметры соединителей во многом определяются его кон-
струкцией, способом подсоединения проводов к соединителю, применяемыми
материалами. При анализе работы линий передачи, содержащих соедини-
тели, недостаточно учитывать только переходное сопротивление контакта.
Необходимо принимать во внимание емкостные и индуктивные параметры его
конструкции и места присоединения провода или кабеля к соединителю.
Основными способами присоединения провода или кабеля к соединителю
являются: пайка, накрутка, обжатие, контакт металл — металл (за счет сме-
щения изоляции провода), сварка. Каждый способ обладает определенны-
ми преимуществами и имеет недостатки как в отношении электрических и
эксплуатационных, так и технологических характеристик.
Для постоянных соединений наиболее часто используется пайка, и каче-
ство соединения определяется материалами соединяемых элементов, составом
припоя и режимом пайки. При соединении накруткой провод плотно нави-
вается на твердый стержень призматической формы, процесс хорошо авто-
матизируется и обеспечивает достаточно приемлемое качество соединений
на низких частотах и не применим для высокочастотных соединений. Об-
жатие выполняется вокруг проводника с помощью металлической втулки.
Оно обычно применяется для сращивания двух проводов, присоединения
металлических наконечников к проводникам и т. п. в низкочастотных цепях.
Накрутка и обжатие не применяются для высокочастотных соединений.
С целью снижения затрат труда и уменьшения стоимости монтажных работ
для плоских кабелей используется присоединение проводов за счет проре-
зания изоляции с последующим зажимом проводников. Можно предполо-
жить, что в данном случае происходит нарушение однородности волнового
сопротивления, но если соединитель согласован по волновому сопротивле-
нию с линией передачи, то малый размер неоднородности не будет существен-
но сказываться на целостности сигнала. Тем не менее при длительностях
фронта сигнала менее 1 нс этот вопрос требует детальной проработки.
4.4. Перекрестные помехи в связанных линиях передачи
341
В перечень основных электрических параметров соединителей входят
следующие:
1) сопротивление или падение напряжения в милливольтах;
2) максимальный рабочий ток через контакт при допустимом перегреве;
3) максимально допустимый кратковременный ток через каждый контакт;
4) максимально допустимое напряжение;
5) испытательное напряжение;
6) сопротивление изоляции;
7) максимальная частота сигнала;
8) волновое сопротивление;
9) вносимые потери;
10) емкость между контактами и т. д.
Параметры 1,7—9 можно отнести к таким, которые непосредственно вли-
яют на качество информационного сигнала в аппаратуре, а емкость между
контактами (п. 10) обусловливает перекрестные помехи в соединителе.
Для оценки влияния электрических параметров соединителя с подсоеди-
ненными к нему тем или иным способом проводниками на качество сигнала
необходимо знать схему замещения узла соединения. Эффективным для по-
лучения этих параметров является метод импульсной рефлектометрии [86-88],
который с успехом может быть применен при анализе неоднородностей в ли-
ниях связи.
4.4. Перекрестные помехи в связанных
линиях передачи
4.4.1. Перекрестные помехи и суперпозиция
Перекрестные помехи — это одна из важнейших проблем обеспечения це-
лостности сигнала и ЭМС [4, 19, 73, 89—91]. Механизм перекрестных помех
заключается в передаче электромагнитной энергии из активной цепи в пас-
сивную соседнюю цепь. На печатной плате перекрестным помехам подвержены
линии передачи, которые расположены в непосредственной близости от ли-
ний передач, в которых происходят динамические процессы переключения из
одного логического состояния в другое. При взаимодействии линий различают
перекрестную помеху на ближнем к драйверу конце пассивной линии и на даль-
нем конце, на нагрузке. Напряжение помех на дальнем конце линии представ-
ляет больший интерес, т. к. от него зависят условия переключения микросхе-
мы нагрузки, а, следовательно, системная задержка.
Запас помехоустойчивости микросхемы нагрузки определяется ее харак-
теристикой динамической помехоустойчивости (см. главу 1). Практика про-
ектирования показывает, что уровень перекрестных помех в 5 % еще приемлем
для надежной работы цифрового устройства. Например, если амплитуда
цифрового сигнала 3,3 В, то максимальная амплитуда перекрестной поме-
хи может быть не более 160 мВ. К сожалению, уровень помех, появляющихся
342 Глава 4. Обеспечение целостности сигнала в печатном монтаже
в линиях передачи на плате, часто бывает больше, чем 5 %. Поэтому важно
уметь определять напряжение помех, распознавать причину возникновения
недопустимых уровней помех и обоснованно применять методы и средства
минимизации помех в печатных узлах. По мере повышения быстродействия
понимание причин возникновения перекрестных помех и умение разрабо-
тать плату с пониженным уровнем помех в печатном монтаже становится все
более актуальным.
При анализе перекрестных помех важную роль играет принцип суперпо-
зиции. Принцип суперпозиции применим для всех пассивных линейных
систем. В общем случае, множество сигналов в цепях не влияет друг на дру-
га и совершенно не зависит друг от друга. Это означает, что значение напря-
жения, которое может быть подано на пассивную линию из активной линии,
совершенно не зависит от напряжения, которое может уже присутствовать
в пассивной линии. Суммарное напряжение в пассивной линии есть сумма
сигналов, которые могут присутствовать в пассивной линии, и помех, ин-
дуцированных из активной линии. Если две или более активных цепи создают
помехи в какой-либо пассивной линии, то уровень помех в ней есть сумма
помех от всех источников. Эти помехи могут иметь разные временные па-
раметры, зависящие от формы напряжения в активных линиях.
4.4.2. Механизм связи активной и пассивной линий
Электрические и магнитные поля линий передачи приблизительно на 50 %
сосредоточены между прямым и возвратным проводником, а 50 % не огра-
ничены каким-либо конкретным пространством между проводниками и рас-
пространяются в окружающей среде. Их можно назвать внешними полями,
определяющими краевые эффекты.
Конечно, интенсивность внешних полей очень
быстро уменьшается по мере удаления от проводника.
На рис. 4.74 показаны внешние поля микрополоско-
вой линии передачи и их взаимодействие со второй
цепью при различных расстояниях до нее. Когда
пассивная линия относительно далеко, то они прак-
тически не взаимодействуют и перекрестная поме-
ха отсутствует. Когда пассивная линия находится в
непосредственной близости от активной линии, то
происходит сильное взаимодействие линий и присут-
ствует перекрестная помеха.
Снизить уровень помех в пассивной линии можно различными путями:
разнесением проводников, сокращением длины взаимодействующих учас-
тков линий, установкой дополнительных экранирующих проводников, из-
менением параметров сигнала в активной линии. Последний способ может
оказаться единственным при повышенной плотности печатного монтажа.
Взаимодействие линий можно описать с помощью модели, используя
понятия взаимной емкости и индуктивности [57, 89].
Рис. 4.74. Внешние
поля вблизи активной
линии: 1 — активная
линия; 2— пассивная
линия
4.4. Перекрестные помехи в связанных линиях передачи
343
Между двумя цепями в системе всегда будут некоторые взаимодействия
емкостного и индуктивного характера, возникающие из-за их внешних по-
лей. Говоря о емкостной и индуктивной связях, всегда нужно иметь в виду
взаимную емкость и взаимную индуктивность.
Умение прогнозировать перекрестную помеху исходя из конфигурации цепи —
важнейший шаг в обеспечении целостности сигнала и качественного проекти-
рования. Прогноз основан на определении взаимной емкости и взаимной ин-
дуктивности на основе геометрии сечения связанных линий.
Как правило, при анализе перекрестных помех механизм емкостной и ин-
дуктивной связи рассматривается раздельно, хотя, естественно, обе состав-
ляющие присутствуют в образовании перекрестных помех. В отдельных слу-
чаях заранее можно сказать о превалирующем влиянии емкостной или ин-
дуктивной составляющей. При наличии единой потенциальной плоскости
для двух сигнальных проводников (наиболее частый случай) основную роль
играет емкостная составляющая. Когда возвратный путь не является плос-
костью, а представляет собой, например, одиночный вывод в корпусе или
одиночный контакт в соединителе, то в этом случае преобладает индуктив-
ная составляющая. Помехи в пассивной цепи в этом случае зависят от ско-
рости изменения тока dl/dt в активной цепи, что имеет место при фронте и
спаде сигнала в активной линии. Принято помехи подобного вида относить
к коммутационным помехам.
4.4.3. Модели описания перекрестных помех
Самый фундаментальный способ описания помех задается в терминах эк-
вивалентной модели связанных линий [89]. Этот способ моделирования
позволяет, учитывая специфику геометрии и согласования, прогнозировать
форму кривой напряжения. Чтобы моделировать связь линий передачи, могут
быть использованы две различные модели.
Первая основана на понятии общей и дифференциальной моды распро-
странения сигнала и применима скорее к дифференциальным парам, кото-
рые будут рассмотрены в шестой главе.
Альтернативная, широко используемая модель
описания связи между линиями использует прибли-
жение П-секционной модели с сосредоточенными
параметрами. В этой модели каждая из двух линий
передачи описана моделью П-секционной схемы с
сосредоточенными параметрами, и связь между ни-
ми описана элементами взаимной индуктивности и
взаимной емкости. Эквивалентная модель цепи
только одной секции показана на рис. 4.75.
Каждая одиночная линия передачи описывается
емкостью на единицу длины (Cz), а контур само-
индукцией на единицу длину (Zz). Связь описыва-
ется взаимной емкостью на единицу длины (Ст1),
Рис. 4.75. Эквивалентная
схема одной секции
П-секционной модели
связанных линий передачи
344 Глава 4. Обеспечение целостности сигнала в печатном монтаже
а петля — взаимоиндукцией на единицу длины (Afz). Для пары однородных
линий передачи взаимная емкость и взаимная индуктивность распределены
равномерно вдоль двух линий. Взаимные емкостные и индуктивные пара-
метры зависят от длины связанных линий. Чтобы описать эти параметры, ис-
пользуется простой формализм, основанный на матрицах.
Полностью две связанные линии передачи можно описать четырьмя линей-
ными параметрами (собственными и взаимными емкостными и индуктивны-
ми параметрами). Если рассматривается связь более чем двух линий передачи,
модель будет иметь более сложный вид. Между каждой парой линий передач
есть взаимные параметры, и размерность задачи резко возрастает.
Конечно, подобное описание — это некоторое приближение. Фактичес-
ки контуры емкостной и индуктивной связи между сигнальной и возврат-
ной линией распределены однородно вдоль всей длины. Эта распределен-
ная связь аппроксимируется дискретными элементами, распределенными рав-
номерно по всей длине. Чем меньше эти дискретные элементы и чем их,
соответственно, больше, тем точнее приближение. Количество необходимых
секций, как показано в предыдущей главе, зависит от требуемой полосы
пропускания и времени задержки распространения сигнала. Их минималь-
ное число для корректного моделирования будет равно:
п > 10 BW /r,
где BW — требуемая полоса пропускания модели; гг — время задержки распространения
сигнала в каждой линии передачи.
В зависимости от электрической длины линий следует рассмотреть две
задачи: перекрестные помехи в коротких линиях и в длинных линиях. В ко-
ротких линиях модель содержит только одно звено емкостных и индуктив-
ных параметров, а в длинной — рассчитанное выше число звеньев. Для длин-
ной линии может быть применен анализ на основе общего описания емко-
стной и индуктивной связи между линиями передачи. Для длинных линий
различают помехи на ближнем и дальнем конце пассивной линии. Очевид-
но, что для коротких линий нет смысла вводить различие между помехами
на ближнем и дальнем концах пассивной линии.
4.4.4. Перекрестные помехи в коротких линиях
Схема замещения для определения перекрестных помех в короткой ли-
нии представлена на рис. 4.76. Следует помнить, что для короткой линии
уровень сигнала по всей длине линии одинаков. Пассивная линия нагруже-
на на выходное сопротивление г0 драйвера и на входное сопротивление г{
микросхемы нагрузки.
Рассмотрим два случая:
• действует только емкостная связь;
• действует только индуктивная связь.
Во всех случаях предполагается, что обратное влияние пассивной линии
на активную отсутствует.
4.4. Перекрестные помехи в связанных линиях передачи 345
Источник |-| Активная линия |-| ПриемниТ]
| ИсточниТН Пассивная линия L-рГриемник |
Рис. 4.76. Модель связанных коротких линий
Емкостная связь
Схема замещения пассивной линии при ем-
костной связи представлена на рис. 4.77.
Определим эквивалентную резистивную на-
грузку:
Рис. 4.77. Схема замещения
пассивной линии
(4.78)
где ro, Tj — соответственно выходное сопротивление драй-
вера и входное сопротивление нагрузки.
Закон изменения фронта сигнала в активной линии соответствует линейно
нарастающему напряжению
К(/) = ^нЛ
(4.79)
где Ион — выходное напряжение высокого уровня; tx — фронт сигнала.
Для определения напряжения помехи на сопротивлении R можно исполь-
зовать операторный метод. Пропуская математические выкладки, получаем
следующий результат. Напряжение перекрестной помехи в произвольный мо-
мент времени будет равно:
у _К)Н 1 .ttl
rct"-----~t--- l~e ’ (4.80)
V 7
где Ион — выходное напряжение высокого уровня; R — эквивалентная резистивная нагрузка;
Ст — взаимная емкость между активной и пассивной линией; tr — фронт сигнала; ttl —
постоянная времени линии, которая определяется выражением
TTL — + Oi)’ (4.81)
где CTL — емкость короткой линии передачи.
346 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.78. Перекрестная помеха
в короткой линии
Графически эта помеха показана на
рис. 4.78. Наибольший интерес пред-
ставляет максимальное значение пере-
крестной помехи Kct max, которое дос-
тигается в момент времени t = /г. Под-
ставляя это значение времени в (4.80),
после упрощений получаем
V - ^он ’
c,max ~ A(CTL+Cm) + /r ’
а при tv « ttl максимальное значение
помехи будет
Л _ ^ОН '
ct max fi fi
CTL +Cm
(4.82)
Индуктивный характер связи
Схема замещения для этого случая представлена на рис. 4.79. Максималь-
ное напряжение помех определяется через ток в активной линии передачи:
= Л/— = м
dt
V
Т ct max
Рис. 4.79. Схема замещения индуктивной
связи коротких линий
М
'г ’
(4.83)
где М— взаимная индуктивность меж-
ду линиями передачи; Д/ — макси-
мальный перепад тока в активной
линии; Гг — фронт сигнала в активной
линии.
Учитывая, что входное сопро-
тивление микросхемы значитель-
но выше выходного сопротивле-
ния драйвера, т. е. г{ » г , на-
пряжение помехи развивается на
входном сопротивлении мик-
росхемы нагрузки.
4.4.5. Перекрестные помехи в длинных линиях передачи
Схема взаимодействия согласованных длинных линий передачи при обра-
зовании перекрестных помех представлена на рис. 4.80. Изменение тока для
взаимодействующих элементов активной (индекс 1) и пассивной (индекс 2)
линий на расстоянии х можно записать в виде системы уравнений [57, 89]:
^х\ _ dQx\ _ ^х2 _ dQxi
dx dt ' dx dt '
(4.84)
4.4. Перекрестные помехи в связанных линиях передачи
347
2
Рис. 4.80. Взаимодействие длинных линий при образовании перекрестных помех
где /х1, 1х2 — токи на расстоянии х для активной и пассивной линий; Qxl, Qx2 — заряды на
единицу длины на расстоянии х для активной и пассивной линии.
При распространении электромагнитной волны приращения магнитно-
го потока на ее фронте вызывает эдс:
dx Jr dx Jr
(4.85)
где Ил1, Vx2 — напряжение на активной и пассивной линии, вызванное изменениями маг-
нитных потоков; Фх1, Фх2 — полный магнитный поток на фронте волны в активной и пас-
сивной линиях на расстоянии х.
Используя третью группу формул Максвелла, связывающих заряд емко-
сти и напряжения на телах, на основании уравнений (4.84) и (4.85) имеем:
2d
2x2
Qi
Qi
(4.86)
q2
С22 Уп
где С, ], С22 — соответственно емкость активной и пассивной линии относительно возврат-
ного проводника на единицу длины (собственная частичная емкость); С21 = С12 = —СП1 —
емкость между линиями на единицу длины (взаимная частичная емкость).
Рис. 4.81. Взаимодействие контуров тока активной и пассивной линий
348 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Активную и пассивную линии передачи можно представить как два кон-
тура, удаленных на некоторое расстояние друг от друга (рис. 4.81). По кон-
туру активной линии течет ток /р а по контуру пассивной линии — ток /2.
Для этого случая можно записать:
Ф1=Фц+Ф12- Ф2 = Ф22 + Ф21 > (4.87)
где Oj — полный магнитный поток контура тока 1; Ф2 — полный магнитный поток кон-
тура 2; Фи — магнитный поток контура 1 от тока в нем; Ф22 — магнитный поток контура
2 от тока в нем; Ф12 — магнитный поток, пронизывающий контур 1, от тока в контуре 2;
Ф21 — магнитный поток, пронизывающий контур 2, от тока в контуре 1.
Потокосцепление \|/ связано с числом витков GJ контура и его магнитным
потоком Ф соотношением:
V = G5 • Ф. (4.88)
Учитывая, что \|/ = £•/, где L — индуктивность контура, и принимая чис-
ло витков равным 1, получаем
Ф = £/. (4.89)
Тогда уравнения для магнитных потоков (4.87) запишем для рассматри-
ваемых линий в следующем виде:
ф*1 _ Ai Д2
®х2 ^22 Лс2
(4.90)
где £н, £22 — индуктивность единицы длины для активной и пассивной линии соответ-
ственно; Z12 = L2l = М — взаимная индуктивность между линиями.
Подставляя (4.90) в (4.85), (4.86) и (4.85) в (4.84), принимая Сн = С22 = С/?
£н = Z22 = £z, получаем систему дифференциальных уравнений, описываю-
щих токи и напряжения во взаимодействующих линиях передачи:
х\ _ ^Ух2
dx 1 dt т dt
х2 _ ^^х2 _
dx 1 dt т dt
dV„1 dl' 1 iz^^x2
----— = £,—— + M—
dx dt dt
^^x2 _ £ x2 1 ^х\
dx 1 dt dt
(4.91)
Решая уравнения, описывающие состояние пассивной и активной линий
передачи, необходимо найти напряжение и ток в пассивной линии 2, инду-
цированные прохождением волны напряжения и тока в активной линии 1.
Решение можно получить операторным методом. Пропуская громоздкие
выкладки, запишем конечные формулы для расчета импульсной помехи на
концах пассивной линии передачи.
4.4. Перекрестные помехи в связанных линиях передачи
349
Напряжение KNEXT перекрестной помехи на ближнем конце пассивной
линии (NEXT) не зависит от длины линии и определяется соотношением:
NEXr’4 С, L, он’
(4.92)
а напряжение KFEXT помехи на дальнем конце пассивной линии (FEXT) оп-
ределяется соотношением
_1(ст АфУон
(4-93)
В этих формулах С/? Z, — собственные частичные емкости и индуктивно-
сти линий передачи на единицу длины; Cm, М — взаимные частичные емкость
и индуктивность между линиями; / — длина связанных линий; у — скорость
распространения электромагнитной волны в линии передачи; Кон — ампли-
туда высокого уровня выходного напряжения драйвера в активной линии;
tr — фронт перепада напряжения в активной линии.
Длительность помехи в пассивной линии на ближнем конце равна 2/d/, а
на дальнем конце — равна длительности фронта tT.
При
С/ А’
(4.94)
на дальнем конце пассивной линии нет напряжения помехи. Это условие со-
блюдается только при расположении линий в однородной диэлектрической
среде, например, выполненных в виде полосковых линий.
Формы перекрестных помех в пассивной длинной линии передачи и их
параметры представлены на рис. 4.82.
Рис. 4.82. Форма перекрестных помех в длинных линиях передачи
350 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Ранее на рис. 4.4 показаны напряжения помехи, измеренные в пассивной
линии, соседствующей с активной линией, управляемой драйвером с быст-
ро нарастающим сигналом с амплитудой перепада 200 мВ [4]. В этом случае
использовались две микрополосковые линии передачи с волновым сопро-
тивлением 50 Ом длиной 10 см. Активная линия и пассивная линия согла-
сованы, поэтому отражения сигнала в них практически отсутствуют. Видно,
что перекрестные помехи на разных концах пассивной линии отличаются друг
от друга. Уровень HNEXT находится приблизительно на отметке 13 мВ. Таким
образом, при сигнале 200 мВ имеем уровень помех на ближнем конце около
6,5 %. Очевидно, что значение этого коэффициента будет зависеть от интен-
сивности связи, например, от расстояния между линиями. Одним из спосо-
бов уменьшения этого коэффициента является увеличение этого расстояния.
Помеха ^FEXT на дальнем конце пассивной линии имеет другую форму.
На дальнем конце помех нет с момента старта сигнала до того момента, когда
он дойдет до этого конца. Поскольку индукционные процессы происходят
при изменении токов или напряжений, т. е. во время фронта или спада, то
ширина импульса помехи будет равна длительности фронта или спада сиг-
нала в активной линии. На примере, рассмотренном выше, это значение
находится на отметке примерно 60 мВ. При сигнале 200 мВ этот уровень
соответствует 30 %. Это очень большое значение.
4.4.6. Коэффициенты перекрестной помехи
в длинной линии
Четыре важных положения определяют уровень перекрестных помех:
• значение мгновенного индуцированного напряжения и тока помехи в
пассивной линии зависит от параметров сигнала в активной линии; чем
больше скорость изменения этих параметров, тем выше уровень помех;
• уровень помех определяется взаимными емкостными и индуктивны-
ми параметрами на единицу длины линии; чем проводники ближе, тем
больше взаимные параметры и выше уровень помех;
• при увеличении скорости распространения сигнала увеличивается
уровень помех в пассивной линии, поскольку расширяется зона вза-
имодействия при постоянной длительности фронта сигнала;
• уровень емкостной и индуктивной составляющей помехи не зависит
от длительности фронта, поскольку при изменении фронта протяжен-
ность области взаимодействия изменяется обратно пропорционально;
очевидно, что для электрически длинной линии область взаимодей-
ствия короче длины линии.
Протяженность Jctk области взаимодействия определяется скоростью
сигнала в линии передачи и длительностью фронта сигнала следующим со-
отношением:
^ctk =tr-v = м, (4.95)
V£r
4.4. Перекрестные помехи в связанных линиях передачи
351
где tr — фронт сигнала, нс; v — скорость электромагнитной волны в активной линии пе-
редачи, м/нс; 0,3 — значение скорости электромагнитной волны в свободном простран-
стве, м/нс; ег — относительная диэлектрическая проницаемость материала основания пе-
чатной платы.
Если фронт сигнала 1 нс, а линия передачи выполнена на стеклотексто-
лите с относительной проницаемостью 4, то длина области взаимодействия
составляет 0,165 м, т. е. 165 мм. Для длинной линии это значение должно быть
меньше погонной длины линии. По мере повышения быстродействия про-
тяженность области взаимодействия становится меньше длины большинства
линий передач на печатной плате. Для этого случая амплитуда помехи HNEXT
на ближнем конце пассивной линии не будет зависеть от протяженности
линий передач. Область взаимодействия, несущая объемный заряд в актив-
ной линии, иллюстрируется на рис. 4.83.
Емкостно-связанные токи, определяющие процесс заряда распределен-
ной емкости линии, втекают в пассивную линию только в зоне взаимодей-
ствия. Встречая на своем пути в пассивной линии одно и то же волновое со-
противление с обеих сторон зоны взаимодействия, этот ток будет равномерно
распределяться в пассивной линии. Половина индуцированного тока будет
протекать по направлению к ближнему концу пассивной линии, а вторая
половина — по направлению к дальнему концу линии.
Эти токи будут создавать на сопротивлениях, подключенных к концам
пассивной линии, емкостную составляющую напряжения помех: ^NEXT(C) —
на ближнем конце, KNEXT(C) — на дальнем конце.
После того, как фронт сигнала прошел в активной линии расстояние, равное
длине зоны взаимодействия, ток на ближнем конце пассивной линии достигнет
постоянного значения. После того как сигнал в активной линии через интер-
вал времени достиг дальнего конца, взаимодействие линий прекратилось,
но наведенный ток от дальнего конца пассивной линии все еще продолжает
протекать к началу этой линии. Он продолжит течь к ближнему концу пассивной
линии в течение времени задержки распространения /pd. Таким образом, про-
должительность протекания емкостной составляющей тока помехи на ближ-
нем конце пассивной линии составляет 2rpd. Форма напряжения помехи на
ближнем конце пассивной линии, вызванной емкостной составляющей свя-
зи между линиями, более детально показана на рис. 4.84.
Рис. 4.83. Область объемного заряда
в зоне фронта сигнала
Рис. 4.84. Типичная характеристика
емкостно-сопряженного напряжения
на ближнем конце пассивной линии
352 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Половина емкостно-сопряженного тока в пассивной линии распростра-
няется в прямом направлении к дальнему концу со скоростью, равной ско-
рости распространения сигнала к дальнему концу активной линии. На каж-
дом шаге вдоль этого пути половина наведенного тока добавляется к уже су-
ществующему току, который распространяется в прямом направлении.
На дальнем конце пассивной линии напряжение помех отсутствует до
момента достижения фронтом сигнала конца активной линии. Совпадающий
с сигналом прямой емкостно-сопряженный ток достигает дальнего конца.
Если фронт сигнала линейный, емкостно-сопряженный ток перекрест-
ной помехи будет представлять собой короткий прямоугольный импульс, дли-
тельностью, равной фронту (/г). Напряжение помехи, развиваемое на сопро-
тивлении нагрузки на дальнем конце пассивной линии, показано на рис. 4.85.
Генерируя положительное напряжение в активной линии, ток помехи в
пассивной линии будет протекать по сопротивлению нагрузки от линии к воз-
вратному проводнику. Это направление принимается за положительное.
Индуктивно-сопряженные токи ведут себя подобно емкостно-сопряжен-
ным. Изменение тока dl/dt в активной линии через взаимную индуктивность
индуцирует напряжение в пассивной линии.
Изменяющийся ток в активной линии распространяется вдоль линии, имея
положительное направление от сигнального проводника к возвратному, об-
разуя контур тока. Согласно законам индукции, направление наведенного
тока в контуре пассивной линии будет противоположно направлению тока,
который вызвал его. Поэтому направление индуктивно-сопряженного тока
в пассивной линии будет противоположно направлению тока в активной
линии, т. е. от конца линии к ее началу (рис. 4.86). Генерироваться ток будет
в зоне взаимодействия, определяемой фронтом сигнала и скоростью распро-
странения сигнала в активной линии.
Учитывая направления емкостно-сопряженных токов и индуктивно-сопря-
женных токов в пассивной линии, видим, что на ближнем конце пассивной
линии эти токи складываются, а на дальнем конце линии — вычитаются, что
отражено в (4.92) и (4.93) знаками алгебраических сумм в круглых скобках.
^FEXT(C)
Рис. 4.85. Типичная характе-
ристика емкостно-сопря-
женного напряжения на
дальнем конце пассивной
линии
Активная линия Пассивная линия
Индуцированный ток
Рис. 4.86. Направление токов при индук-
тивном механизме взаимодействия линий
4.4. Перекрестные помехи в связанных линиях передачи
353
Обратно направленный индуктивно-сопряженный помеховый ток име-
ет такой же вид, как и емкостно-сопряженный ток. Он начинается из 0 и будет
возрастать с ростом сигнала от генератора, достигая некоторого постоянного
значения.
После того, как фронт сигнала достигнет сопротивления нагрузки в даль-
нем конце активной линии, в пассивной линии все еще будет существовать
обратно направленный индуктивно-сопряженный ток помехи. Необходим
интервал времени, равный времени распространения сигнала в линии, для
того, чтобы наведенный ток достиг ближнего конца пассивной линии. Форма
индуктивно-сопряженного тока на дальнем конце пассивной линии будет
производной фронта сигнала по времени в активной линии.
Помеха на ближнем конце пассивной линии определяется токами, про-
текающими через согласующий резистор на ближнем конце линии переда-
чи. Вид этой помехи по форме совпадает с формой помехи, показанной на
рис. 4.84. Можно отметить следующие четыре важных фактора, типичных для
этого вида помех.
1. Если длина участка связанных линий больше, чем участок взаимо-
действия (длинная линия), то помеховое напряжение будет достигать
некоторого постоянного уровня. Амплитуда максимального напря-
жения определяется как перекрестные помехи на ближнем конце ли-
нии (NEXT). Обычно это записывается как отношение напряжения
помехи на ближнем конце пассивной линии к сигналу в активной ли-
нии, и оно определяется коэффициентом перекрестных помех на ближ-
нем конце kn = VJ Va.
2. Если участок связанных линий короче участка взаимодействия (линия
короткая), тогда напряжение помех на ближнем конце будет иметь вид
импульса с максимальной амплитудой, которая меньше уровня посто-
янного напряжения NEXT. Эта амплитуда определяется длиной участ-
ка связи и участка взаимодействия. Например, если длина участка на-
сыщения для фронта 1 нс составляет 125 мм для FR4 и длина участка
связи составляет 100 мм, тогда уровень помех Vb/Va = NEXT х 100/
/ 125 = NEXT х 0,8. На рис. 4.87 показано напряжение перекрестных
помех на ближнем конце пассивной линии, когда длина участка связи
изменяется от 20 % длины зоны взаимодействия до удвоенной длины
этой зоны [4]. Фронт сигнала 0,8 нс, скорость распространения сигна-
ла 0,16 м/с, что определяет длину зоны взаимодействия как: 0,8 нс х
х 0,16 м/с = 0,13 м. Следует помнить, что при длительности фронта мень-
ше удвоенного времени пробега электромагнитной волны до конца ли-
нии, линия считается электрически короткой.
3. Общая длительность помехи на ближнем конце линии не более 2/pd.
Если время задержки распространения сигнала на участке связи со-
ставляет 1 нс, то длительность помехи на ближнем конце линии бу-
дет не менее 2 нс.
4. Фронт импульса помехи равен фронту сигнала.
12 1527
354 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.87. Напряжение перекрестных помех на ближнем конце пассивной линии,
когда длина участка связи изменяется от 20 % зоны взаимодействия до удвоенной
длины этой зоны: 1 — длина 25 мм; 2 — длина 75 мм; 3 — длина 125 мм (длина зоны
взаимодействия); 4 — длина 155 мм; 5 — длина 250 мм
Коэффициент кп перекрестной помехи на ближнем конце пассивной линии
будет зависеть от взаимной индуктивности и взаимной емкости:
к =1 £п/+^
” 4 С, L,
(4.96)
где Ст1 — взаимная емкость на единицу длины между линиями; — емкость сигнально-
го проводника на единицу длины; М{ — взаимная индуктивность на единицу длины; Ll —
индуктивность сигнального проводника на единицу длины.
При сближении двух линий взаимные индуктивные и емкостные парамет-
ры возрастают, и уровень помех увеличивается.
На рис. 4.88 даны расчетные значения коэффициента связи для полоско-
вой и микрополосковой линий передачи при увеличении расстояния между
проводниками. Волновое сопротивление линий 50 Ом, материал FR4, шири-
на проводников 0,125 мм, расстояние увеличивается от 0,1 мм до 1,25 мм. Видно,
что при зазоре более 0,25 мм (удвоенная ширина проводника) для полоско-
вой линии перекрестная помеха на ближнем конце практически равна нулю.
Практическое правило: максимально приемлемое значение перекрестной
помехи на ближнем конце составляет не более 5 % от размаха сигнала.
Если пассивная линия входит в состав шины передачи данных, то это
значение следует снизить до 2 %. Это вызвано тем, что помехи от двух со-
седних линий на каждой стороне суммируются.
Практическое правило: зазор между сигнальными проводниками должен быть,
по крайней мере, больше ширины проводников. При этом уровень NEXT будет
менее 2 %. В худшем случае при нескольких активных линиях, расположен-
ных с двух сторон от пассивной линии, уровень NEXT будет не более 5 %.
Из графиков (рис. 4.88) можно сформулировать два правила, которые
применимы для линий передачи с волновым сопротивлением 50 Ом, выпол-
4.4. Перекрестные помехи в связанных линиях передачи
355
Рис. 4.88. Расчетное значение коэффициента связи для полосковых и микрополоско-
вых линий передачи: 1 — полосковая линия; 2 — микрополосковая линия
ненных на FR4 с проницаемостью 4. Первое правило: перекрестная помеха
на ближнем конце зависит от ширины проводника и зазора между провод-
никами. Определенную роль играет и толщина диэлектрика. В табл. 4.4 по-
казана зависимость коэффициента кп от параметров конструкций линий с
волновым сопротивлением 50 Ом на стеклотекстолите с проницаемостью 4.
Таблица 4.4
Коэффициент NEXT в зависимости от параметров конструкции
Зазор между активной и пассивной линией, s Коэффициент NEXT, кп, %
микрополосковая линия полосковая линия
S = W 4,4 6,5
s =2w 1,9 1,9
s = 3w 1,0 0,57
Второе правило: помеха на дальнем конце линии зависит от тока, кото-
рый протекает через сопротивление нагрузки. Форма сигнала на дальнем
конце линии показана на рис. 4.85. При рассмотрении помех на дальнем конце
линии можно отметить четыре важных аспекта.
1. Помеха не возникнет, пока сигнал не достиг конца линии, т. е. с за-
держкой Помеха распространяется к концу пассивной линии со ско-
ростью распространения сигнала в активной линии.
2. Форма напряжения помехи на дальнем конце пассивной линии есть
производная фронта сигнала. Ширина импульса помех равна длитель-
ности фронта информационного сигнала. На рис. 4.89 показана фор-
ма помехи на дальнем конце пассивной линии при различных длитель-
ностях фронта сигнала. Волновое сопротивление линии передачи со-
ставляет 50 Ом, длина участка связи 250 мм. Видно, что при увеличении
длительности фронта, амплитуда помехи снижается, а ее длительность
увеличивается.
12
356 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Время, пс
Рис. 4.89. Помеха на дальнем конце пассивной линии при различных длительностях
фронта сигнала: 1 — фронт 0,5 нс; 2 — фронт 1 нс; 3 — фронт 2 нс
3. Пиковое значение помехи зависит от длины участка связи. При уве-
личении длины участка пиковое значение увеличивается.
4. Коэффициент FEXT непосредственно показывает пиковое напряжение
помехи на дальнем конце пассивной линии Ffext, обычно по отноше-
нию к напряжению сигнала в активной линии, Va, FEXT = УрЕхт/Кс ^то
напряжение зависит от двух факторов (длины участка связи и фронта
сигнала), дополняющих факторы, которые определяются сечением
линий передачи.
Коэффициент Zy связи на дальнем конце линий (FEXT) определяется
следующим образом:
_ ^FEXT _ ^ctk £ _ ^ctk J_ I Cml _
Va tr f tr 2v [ C, L, ?
k =J_
f 2v ( С/ L, ;
(4.97)
(4.99)
где KFEXT — напряжение на дальнем конце пассивной линии, К — напряжение на сигналь-
ной линии; Jctk — длина области взаимодействия между двумя линиями; v — скорость рас-
пространения сигнала в линии; Ст1 — взаимная емкость на единицу длины; Cz — собствен-
ная частичная емкость на единицу длины; М{ — взаимная емкость на единицу длины.
Как видно из формулы, коэффициент связи Ау.на дальнем конце линии
зависит только от внутренних параметров линии, относительной емкостной
и индуктивной связи и скорости распространения сигнала. Он не зависит от
длины участка связи и от фронта сигнала. Обратная величина этого коэф-
фициента 1/Ау.задается в размерности скорости м/с. Что это за скорость?
В действительности это разность в скоростях распространения четной и
нечетной моды сигнала. Другими словами, рассматривая помехи на дальнем
конце линии, видно, что они в действительности возникают, когда четная
4.4. Перекрестные помехи в связанных линиях передачи
357
мода имеет скорость, отличную от скоро-
сти нечетной моды. Это происходит в
микрополосковой линии, когда сигналь-
ный проводник лежит на границе диэлек-
трических сред. В однородной диэлект-
рической среде, характерной для полос-
ковой линии передачи, диэлектрическая
проницаемость постоянна и не зависит от
формы электрического поля, вызванно-
го приложенным напряжением. В этом
Рис. 4.90. Обобщенное представление
помехи на дальнем конце линии
при линейном фронте сигнала
случае четная и нечетная моды имеют
одинаковую скорость, и помеха на дальнем конце пассивной линии отсут-
ствует. Это явление будет детально рассмотрено в шестой главе при изуче-
нии дифференциальных пар.
Практическое правило: если проводники линии передачи расположены в од-
нородной диэлектрической среде, как, например, в полосковой или заглубленной
линии передачи, то относительные взаимные индуктивные и емкостные пара-
метры будут одинаковы. В этом случае помеха на дальнем конце пассивной линии
отсутствует.
В противном случае при неоднородной диэлектрической среде эффектив-
ная диэлектрическая проницаемость зависит от распределения электричес-
кого поля между прямыми и возвратными проводниками. Это будет опре-
делять различие относительных емкостных и индуктивных взаимных пара-
метров, в результате чего появляется помеха на дальнем конце линии.
Часто используется параметр v х который безразмерен:
Используя понятие FEXT, можно записать:
FEXT = ^E£XL= -к = *&-.у.к
К, tr-V /г
(4.100)
Коэффициент vx ^является внутренним параметром, который зависит
только от сечения связанных линий. Он описывает помеху на дальнем кон-
це линии. Когда время задержки в зоне взаимодействия равно фронту, т. е.
Zpd = /г, и v х kf= 5 %, то помеха на дальнем конце пассивной линии будет со-
ставлять 5 %. Если длина зоны взаимодействия удвоится, то напряжение
помехи вырастет до 10 %.
На рис. 4.91 показано, как изменяется v х Ау для микрополосковой линии
передачи на FR4 с волновым сопротивлением 50 Ом и шириной проводни-
ка 0,125 мм. Из кривой можно сформулировать практическое правило: если
ширина проводника равна зазору, то значение vx к. будет равно 4 %. Напри-
мер, при фронте 1 нс, длине зоны взаимодействия 150мм (скорость 150мм/нс),
358 Глава 4. Обеспечение целостности сигнала в печатном монтаже
S
Зазор, мм
Рис. 4.91. Расчетное значение ух к^ для линии передачи на FR4 с волновым
сопротивлением 50 Ом
помеха на дальнем конце близко расположенных активной и пассивной линии
будет v х kfx tpd/tT = 4 % х 1 = 4 %.
Практическое правило: для линии передачи с волновым сопротивлением 50 Ом
на FR4 при равенстве ширины проводников и зазора между ними, перекрестная
помеха на дальнем конце линии равна — 4 % X Гр(Д.
Если активные линии расположены с обеих сторон пассивной линии на
одинаковом расстоянии, равном ширине проводников, то напряжение по-
мехи будет 8 % при rpd = гг. При уменьшении длительности фронта пробле-
ма перекрестных помех усугубляется.
Одним из приемов снижения перекрестных помех является разнесение
активной и пассивной линий. При ширине w сигнального проводника ко-
эффициент v х kj в зависимости от относительной ширины s зазора изменяется
следующим образом [4].
Табл. 4.5
Значение коэффициента v х к{ в зависимости от зазора
Относительная ширина зазора, 5 Коэффициент ух %
и> 4,0
2и> 2,2
Зи> 1,4
4.4. Перекрестные помехи в связанных линиях передачи
359
4.4.7. Емкостные параметры связанных линий
Определение емкостных параметров в связанных линиях передачи пред-
ставляет собой не тривиальную задачу. Она значительно сложнее, чем опре-
деление емкости в одиночной линии передачи, которое рассматривалось
ранее. Рассмотрим этот вопрос более подробно.
Представим систему активных и пас-
сивных линий передачи в виде набора па-
раллельных проводников над возвратной
плоскостью, на которой задано опорное
напряжение, например, О В [3,4]. Каждой
сигнальной линии может быть присвоен
порядковый номер (рис. 4.92) от 1 до 5.
Возвратный проводник маркируется как
1 2 3 4 5
Возвратный проводник
Рис. 4.92. Пять связанных линий
передач
проводник 0.
Каждая пара проводников в этом наборе имеет взаимную емкость, а каж-
дая сигнальная линия имеет емкость относительно возвратного проводника.
Емкость между первым и вторым проводниками обозначается как С12, между
1 и 3 — как С13 и т. д. Емкость между сигнальным и возвратным проводника-
ми обозначается для удобства последующего матричного представления как
Ci j, С22, С33, Cw С55. Все емкостные параметры в данном случае могут быть пред-
ставлены в виде матрицы размером 5x5. Эквивалентная схема связанных линий
и соответствующая матрица значений параметров приведена на рис. 4.93.
В этой матрице диагональные элементы описывают емкости между сиг-
нальными и возвратными проводниками, а внедиагональные — взаимные
емкости. Для однородных линий передач каждый элемент в матрице — это
емкость на единицу длины, обычно в пФ/мм.
Матрица — это доступный, удобный и простой способ учесть все значения
емкостей. Рассмотренная выше матрица построена на основе схемы замеще-
ния с использованием теории цепей. Реальные значения для каждой емкости
^12 ^1з С14 С15
С22 С23 С24 С25
С32 &зз С34 С35
^42 ^43 ^44 £45
С52 £53 С54 С55
Рис. 4.93. Эквивалентная емкостная модель пяти связанных линий передач
и соответствующая матрица значений параметров
360 Глава 4. Обеспечение целостности сигнала в печатном монтаже
1 2 4 5
110,7 5,94 0,630 0,315 0,197
5,94 105,6 5,866 0,630 0,315
0,630 5,866 105,31 5,866 0,630
0,315 0,630 5,866 105,6 5,94
0,197 0,315 0,630 5,94 110,7
Рис. 4.94. Пять связанных линий передачи
и матрица емкостей, пФ/м
как элемента матрицы могут быть
найдены с помощью вычислений
или измерений. Когда нужны более
точные значения емкостей, необхо-
димо применять анализатор двумер-
ных полей, например, программный
комплекс ELCUT [92 —95]. Пример
рассчитанной емкостной матрицы
для пяти линий передач с шириной
сигнальных проводников 0,125 мм
каждый и находящихся на расстоянии 0,125 мм друг от друга приведен на
рис. 4.94 [4].
В этом конкретном примере все линии имеют волновое сопротивление
50 Ом. Видно, что емкость между проводниками 1 и 3 незначительна по срав-
нению с емкостью между проводниками 1 и 2. Чем дальше расположены
трассы друг от друга, тем быстрее уменьшаются внедиагональные элементы,
и тем меньше емкостная связь между соответствующими проводниками.
Видно, что взаимная емкость между первым и вторым проводниками состав-
ляет примерно 5 % от собственной частичной емкости первого проводника,
а емкость между первым и третьим проводниками только 0,6 %. Очевидно,
если линии будут отдаляться друг от друга, то значения емкостей будут умень-
шаться, но при пропорциональном изменении всех размеров сечения мно-
гопроводной линии результаты останутся неизменными. Если изменить
ширину одной линии, то это, в первую очередь, повлияет на диагональные
элементы этой линии и на ее связь со смежными трассами.
В емкостной матрице на основе теории цепей главное помнить, что каж-
дый ее элемент — это значение параметра элемента цепи, которое появля-
ется в эквивалентной схеме. Значение каждого элемента может быть прове-
рено непосредственным измерением емкости между двумя соответствующими
проводниками. Это, к примеру, определит емкостно-связанный ток, кото-
рый потечет между каждой парой проводников при заданном .
4.4.8. Матрица емкостей и ее расчет
Если матрица получена при помощи уравнений Максвелла, то говорят о
Максвелловской емкостной матрице. Как и ранее рассмотренная матрица,
она является емкостной, но определение ее параметров отличается. Макс-
велловская матрица получается при решении дифференциальных уравнений,
описывающих поле, с учетом граничных условий [48]. Для электростатической
задачи это уравнение Лапласа. Для решения уравнений необходимо задать
граничные условия, которые включают в себя параметры материалов, гео-
метрию границ и потенциалы на проводниках.
Возвратимся к примеру набора из пяти проводников (рис. 4.95). Возврат-
ный проводник обозначен «0», на него подается потенциал 0 В. Расчет ем-
костной матрицы происходит согласно следующему алгоритму.
4.4. Перекрестные помехи в связанных линиях передачи
361
Рис. 4.95. Пять проводников и пример гранич-
ных условия для расчета матрицы емкостей
1. Потенциал 1 В подается поочередно на каждый проводник, подав на
все остальные проводники напряжение О В.
2. При заданных граничных условиях решается уравнение Лапласа для
определения потенциалов в произвольных точках пространства.
3. Когда найден потенциал, электрическое поле рассчитывается по по-
верхности каждого проводника.
4. Общий заряд каждого проводника получается после интегрирования
электрического поля по поверхности проводника.
5. Исходя из зарядов каждого проводника, рассчитывается Максвеллов-
ская емкостная матрица:
9*=тг> (4101>
ик
где Cjk — элемент емкостной матрицы, соответствующей взаимной частичной емкости между
проводниками j и к; — заряд на проводнике J; Uk — потенциал на проводнике к.
Процедура повторяется, перемещая на каждом шаге потенциал 1 В на
другой проводник и подавая потенциал О В на все остальные проводники.
Определение Максвелловской емкостной матрицы отличается от емко-
стной матрицы, полученной на основе теории цепей. Элементы последней
являются значениями параметров соответствующей эквивалентной схемы.
Значение каждого элемента есть непосредственно измеренное значение тока
емкостной связи, который протекает между каждой парой проводников для
данной скорости dV/dt между ними.
Каждый элемент Максвелловской матрицы показывает, какой заряд будет
на одном проводнике, когда на другом будет потенциал 1 В, а все другие про-
водники будут заземлены. Это весьма специфические условия, которые мо-
гут привести к недопониманию.
Расположим потенциал +1 В на проводнике 3 (рис. 4.95), а на все другие
проводники подадим потенциал О В. Этот положительный заряд будет вы-
зывать отрицательные заряды на всех рядом расположенных проводниках.
Отрицательный заряд будет индуцироваться на плоскости заземления и на
каждом из четырех проводников, соединенных с возвратным проводником.
Фактически в этом случае все остальные проводники представляют собой не-
который один обобщенный проводник, распределенный в пространстве,
состоящий из нескольких соединенных фрагментов. Значение заряда, ин-
дуцированного на каждом проводнике, есть показатель емкостной связи с
проводником, имеющим потенциал 1 В. Условное распределение зарядов для
данного примера показано на рис. 4.96.
Из определения Максвелловской матрицы следует, что емкость между
проводником 3 и плоскостью возвратного проводника, которая является
362 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Рис. 4.96. Распределение зарядов
в системе пяти проводников при подаче
на проводник 3 напряжения 1 В
диагональным элементом матрицы, есть отношение заряда Q3 на проводнике
3 к потенциалу U3 на нем:
/^ _ й
(4.102)
Все остальные проводники соединены с возвратным проводником, т. е.
емкость проводника определяется относительно слоя возвратного проводника
и всех других проводников, которые соединены с ним. Эта емкость часто назы-
вается нагрузочной емкостью проводника.
Диагональный элемент Максвелловой матрицы есть емкость проводника,
определяемого относительно слоя возвратного проводника и всех других провод-
ников, которые соединены с ним; диагональный элемент цепевой матрицы есть
емкость проводника относительно только возвратного пути. Элемент мат-
рицы Максвелла — нагрузочная емкость — будет всегда больше диагонального
элемента цепевой матрицы.
Внедиагональный элемент матрицы Максвелла, например, между провод-
никами 3 и 2, определяется по формуле:
(4.103)
где С23 — емкость между проводниками 2 и 3; Q2 — заряд на проводнике 2; U3 — потенциал
на проводнике 3 при условии, что остальные проводники имеют потенциал равный 0 В.
Поскольку индуцированный заряд на проводнике 2 отрицателен и инду-
цированный заряд на любом другом проводнике так же отрицателен, все вне-
117,8 -5,94 -0,630 -0,315 -0,197
-5,94 118,3 -5,816 -0,630 -0,315
-0,630 -5,866 118,34 -5,866 -0,630
-0,315 -0,630 -5,866 118,3 -5,94
-0,197 -0,315 -0,630 -5,94 117,8
Рис. 4.97. Расчетная емкостная матри-
ца Максвелла, пФ/м, для набора мик-
рополосковых линий передач с волно-
вым сопротивлением 50 Ом
диагональные элементы емкостной
матрицы отрицательны. В действи-
тельности отрицательный знак озна-
чает, что заряд на проводнике 2 будет
отрицателен, когда потенциал в 1 В
будет приложен к проводнику 3.
Пример матрицы Максвелла для
рассматриваемой системы 5 микропо-
лосковых линий передачи представлен
на рис. 4.97.
Одна матрица легко конвертирует-
ся в другую. Внедиагональные элемен-
ты матриц одинаковы, но с различны-
4.4. Перекрестные помехи в связанных линиях передачи
363
ми знаками. Однако диагональные элементы отличаются, и они конверти-
руются следующим образом:
ЭД=^(с),
c,(c)=fq.(M), (4-Ю4)
/
где СуЛ/), С^.(С) — диагональные элементы емкостной матрицы Максвелла и целевой, со-
ответственно; С/М), С/С) — внедиагональные элементы матрицы Максвелла и целевой,
соответственно.
Из формулы видно, что для получения диагональных элементов матри-
цы Максвелла необходимо сложить все элементы соответствующей строки
целевой матрицы. Аналогично следует поступить и при определении диаго-
нальных элементов целевой матрицы. Операцию сложения следует прово-
дить с учетом знаков внедиагональных элементов.
Значения элементов матрицы зависят от взаимного положения проводни-
ков, близости возвратного слоя, наличия между проводниками проводников
с потенциалом 0 В. По мере разнесения проводников взаимная емкость умень-
шается. Когда зазор превышает двойную ширину сигнального проводника или
четыре толщины диэлектрика, наличие соседней трассы практически не бу-
дет оказывать влияния на диагональные емкостные коэффициенты матриц.
Внедиагональные элементы также зависят от геометрии и присутствия дру-
гих проводников. Наличие проводника между трассами уменьшает значение
этих элементов матрицы.
Когда расстояние между проводниками равно ширине проводников, емкость
связи между соседними проводниками примерно 6 пФ/м. Это составляет око-
ло 5 % от диагонального элемента (собственной частичной емкости). Когда рас-
стояние между проводниками составляет 3 ширины проводника, емкостная связь
будет примерно 1 пФ/м, или 0,9 % диагонального элемента. Если в это расстояние
установить еще один проводник, емкостная связь снизится до 0,64 пФ/м, или
0,6 % диагонального элемента.
Проводник, установленный между активной и пассивной линиями, на-
зывается защитным проводником.
4.4.9. Индуктивная матрица
Индуктивность всегда соотносится с самоиндукцией контура, которая оп-
ределяется через парциальную самоиндукцию сигнального и возвратного
путей и их взаимной индуктивности:
Ll=Lss+Lsr~2M^ (4.105)
где Ll — индуктивность линии передачи на единицу длины; Lss — парциальная самоин-
дукция сигнального проводника на единицу длины; Lsr — парциальная самоиндукция воз-
вратного проводника; М— парциальная взаимная индуктивность между сигнальным и воз-
вратным проводниками на единицу длины.
364 Глава 4. Обеспечение целостности сигнала в печатном монтаже
1 4 5 В индуктивной матрице диаго- нальные элементы есть самоиндук- ция контура каждого сигнального и
295,95 39,84 11,50 5,39 3,46 возвратного пути. Внедиагональны-
39,84 293,86 39,21 11,30 5,40 ми элементами являются взаимные
11,50 39,21 293,54 39,20 11,65 индуктивности контуров между
5,39 11,30 39,20 293,16 39,68 каждой парой сигнальных и воз-
3,46 5,40 11,65 39,68 295,12 вратных путей. Удельная индуктив-
Рис. 4.98. Индуктивная матрица, ность задается в Гн/м.
нГн/м, системы линий передач На рис. 4.98 представлена ин-
дуктивная матрица для пяти микро-
полосковых линий передач. Ширина проводников и расстояние между ними
0,125 мм.
Комбинация емкостной и индуктивной матриц содержит всю информацию
о связанных линиях передачи. Из этих данных могут быть вычислены все не-
обходимые параметры для определения перекрестных помех.
4.4.10. Способы снижения уровня перекрестных помех
Можно рекомендовать следующие основные способы снижения перекре-
стных помех на дальнем конце линии передачи.
1. Увеличение расстояния между проводниками. При увеличении зазо-
ра с 5 = w до 5 = 3w помеха уменьшается на 65 %. При этом, конечно,
уменьшается плотность расположения проводников на печатной плате.
2. Уменьшение длины зоны взаимодействия. При этом снижается амп-
литуда перекрестных помех. Например, если фронт 0,5 нс, задержка
Zpd в зоне взаимодействия составляет менее 0,1 нс, то напряжение по-
мехи на дальнем конце линии будет 4 % х 0,1/0,5 = 0,8 %. Это примерно
соответствует линиям в BGA корпусе.
3. Покрытие линий диэлектрическим материалом, что делает среду более
однородной. Это может быть, например, толстая паяльная маска. На рис.
4.99 показана зависимость коэффициента vx Zy при различной толщи-
не диэлектрического покрытия с диэлектрической проницаемостью 4,
равной проницаемости FR4, при зазоре, равном ширине проводника.
Добавление диэлектрического покрытия увеличивает помеху на ближнем
конце и уменьшает волновое сопротивление линии. Для заглубленной ли-
нии при толщине покрытия, равной примерно пяти значениям ширины
проводника, можно считать, что линии расположены в однородном ди-
электрике. Это поведение объясняется краевыми эффектами электричес-
кого поля, которые существуют между отдельными проводниками и между
проводниками и возвратным проводником, и пронизывают окружающее
диэлектрическое пространство. В некоторых случаях при толщине покры-
тия, равной толщине основания слоя (примерно 0,075 мм), помеха на
дальнем конце линии равна 0. Оптимальная толщина покрытия зависит
от геометрии топологических рисунков и диэлектрической проницаемо-
4.4. Перекрестные помехи в связанных линиях передачи
365
Толщина покрытия мм
Рис. 4.99. Зависимость коэффициента vx Ay при различной толщине
диэлектрического покрытия
сти. Даже тонкая паяльная маска будет обеспечивать заметное уменьшение
помех на дальнем конце линии.
4. Переход на полосковые линии. В этом случае линии расположены в
однородном диэлектрике и помехи на дальнем конце равны нулю. При
более тонком рассмотрении диэлектрик печатных плат также неодно-
роден. Он состоит из препрега и стеклянных волокон, поэтому диэ-
лектрическая проницаемость материала неоднородна. Это может выз-
вать небольшой уровень перекрестных помех.
5. Применение защитных трасс, расположенных между активной и пас-
сивной линиями передачи.
Разнесение линий передачи позволяет снизить уровень помех до 5 %. При
дальнейшем разнесении площадь платы используется не рационально. В неко-
торых случаях, особенно при смешанном расположении аналоговых и циф-
ровых устройств, требуется очень большое ослабление перекрестных помех.
Например, чувствительный высокочастотный приемник, подключенный к пас-
сивной линии, может потребовать ослабления в 100 дБ цифровых сигналов в
активной линии, что соответствует уровню 0,001 %. Часто в этой ситуации
помогает установка защитной трассы. Но это требует корректного техничес-
кого и топологического решения.
4.4.11. Защитные трассы
Защитная трасса устанавливается между активной и пассивной линия-
ми с целью обеспечения необходимой эффективности экранирования. При-
меры установки защитных трасс показаны на рис. 4.100. Они могут устанав-
ливаться как в полосковых, так и в микрополосковых линиях, хотя в полос-
ковых линиях их установка не так актуальна, поскольку в них трассы более
развязаны из-за действия двух экранов.
366 Глава 4. Обеспечение целостности сигнала в печатном монтаже
1 _ 1
1 1
1 1
Рис. 4.100. Пример
установки защитных
трасс (1)
Рассмотрим три варианта топологии, которые при-
водят к уменьшению перекрестных помех.
1. Исходный вариант: две близко расположенные
линии, шириной 125 мкм с зазором 125 мкм.
2. Увеличение расстояния между проводниками на
максимально возможное (380 мкм).
3. Увеличение расстояния до 380 мкм и установка
защитной трассы в зазоре.
Пиковое значение помехи в пассивной линии, ра-
зомкнутой на конце и расположенной рядом с актив-
ной линией, составляет 130 мВ. Это около 4 %. Разнесение трасс снижает
уровень помех до 39 мВ (около 1,2%). Это примерно в 3,5 раза лучше. Когда
встроена защитная трасса, разомкнутая на левом конце, т. е. плавающая,
помеха в пассивной линии в действительности слабо увеличивается. Одна-
ко, если защитная трасса нагружена на согласующие резисторы с двух кон-
цов, помеха уменьшается до 25 мВ, или составляет 0,75 %. Когда защитная
трасса закорочена на концах, помеха в пассивной линии снижается до 22 мВ,
т. е. составляет 0,66 %.
Практическое правило: при увеличении расстояния между проводниками
помеха уменьшается примерно 3,5раза, а при дополнительной установке защит-
ной трассы, закороченной на обоих концах, помеха уменьшается еще в два раза.
Защитная трасса фактически играет роль экрана, перехватывая силовые
линии электрического поля между сигнальными проводниками. Оно создает
дополнительный возвратный путь для сигнальных токов, что приводит к
снижению индуктивности сигнального контура. Но это происходит только
при закорачивании защитной трассы на обоих концах. В противном случае
она может только ухудшить ситуацию.
Сигнал, распространяющийся по активной линии, будет генерировать на-
пряжение помех на защитной трассе. Возвратный помеховый сигнал защитной
трассы достигнет закороченного ближнего конца защитной трассы и отразит-
ся с коэффициентом отражения —1. Это означает, что увеличенная помеха на
ближнем конце защитной трассы при движении ее в обратном направлении будет
уничтожена совпадающей, отрицательной, отраженной помехой ближнего конца,
распространяющейся в прямом направлении по защитной трассе.
Закорачивание концов защитной трассы будет устранять любую помеху на
ближнем конце, которая приходит по защитной трассе.
В длинных линиях помеха распространяется на дальний конец защитной
трассы и отражается в этой точке с коэффициентом отражения — 1. Таким об-
разом, в защитной трассе будут падающие и отраженные волны, которые, в свою
очередь, будут потенциальными источниками помех. Если потери в защитной
трассе малы, то помехи на дальнем конце линии будут продолжать переотра-
жаться, действуя как низкоуровневый источник помех в пассивной линии.
Если на защитной трассе расположить по длине металлизированные от-
верстия, закорачивающие трассу, то они будут воздействовать на генерацию
помех двумя путями. Помеха дальнего конца защитной трассы будет гене-
4.4. Перекрестные помехи в связанных линиях передачи
367
рироваться только в областях между отверстиями. Уменьшение расстояния
между отверстиями приведет к снижению максимального напряжения по-
мех дальнего конца на защитной трассе. Увеличение числа отверстий также
снижает напряжение помех.
Металлизированные отверстия в защитной трассе непосредственно не вли-
яют на связь между активной и пассивной линией, но способствуют подавле-
нию напряжения помех, которое генерируется в защитной трассе.
На рис. 4.101 показаны помехи в пассивной линии при установке металли-
зированных отверстий в защитной трассе [3, 4]. Длина микрополосковых ли-
ний 250 мм с защитной трассой между ними. Одна из них имеет по одному ме-
таллизированному отверстию на каждом конце, а другая — с 11 металлизиро-
ванными отверстиями, расположенные через каждые 25 мм. Сигнал в активной
линии имеет амплитуду 3,3 В, фронт 0,7 нс и нижнюю частоту 25 МГц. Видно,
что максимальный уровень помех в пассивной линии составляет 35 мВ, или 1 %.
Индуцированная помеха не изменяется, поскольку она не зависит от числа
отверстий, а определяется связью между активной и пассивной линиями при
наличии защитной трассы. Отверстия способствуют снижению уровня помех
от защитной трассы, что устраняет дополнительную составляющую помехи.
Практическое правило: металлизированные отверстия должны распреде-
ляться вдоль защитной трассы так, чтобы на зону взаимодействия приходи-
лось, по крайней мере, 3 отверстия. Это будет гарантией перекрытия помех
дальнего конца с отрицательным отражением, что вызовет устранения напря-
жения помех в защитной трассе.
Например, если фронт 1 нс, а зона взаимодействия составляет 1 нс х
х 0,15м/нс = 0,15 м, то расстояние между отверстиями составит 0,15/3 = 0,05 м.
Если фронт будет 0,7 нс, то расстояние между отверстиями составит 35 мм.
Дальнейшее сближение отверстий не даст дополнительного эффекта, но уве-
личит стоимость платы.
Время, нс
Рис. 4.101. Помехи в пассивной линии при установке металлизированных отверстий
в защитной трассе: 1 — защитная трасса с 11 закороченными отверстиями;
2 — защитная трасса с 2 закороченными отверстиями
368 Глава 4. Обеспечение целостности сигнала в печатном монтаже
В полосковой линии применение защитной трассы не столь обязательно, и
применение металлизированных отверстий вдоль этой трассы не требуется.
Наличие защитной трассы приводит к уменьшению волнового сопротив-
ления пассивной линии на несколько процентов в зависимости от размеров
проводников.
Кроме этого, на высокой частоте следует учитывать скин-эффект и эф-
фект близости. Перераспределение тока требует пересчета емкостных и ин-
дуктивных параметров линии.
4.4.12. Перекрестная помеха и диэлектрическая
проницаемость
Помеха на ближнем конце определяется суммой емкостной и индуктив-
ной составляющих: (Ст/Сп + Л//£и). Очевидно, что индуктивная связь не
зависит от диэлектрических свойств материалов, которые окружают провод-
ники, но при увеличении диэлектрической проницаемости материалов,
окружающих линии передачи, увеличивается емкость Си между прямым и
обратным проводами. Однако взаимная емкость Ст между двумя сигналь-
ными линиями также будет увеличиваться. Поэтому перекрестная помеха в
полосковой линии не возрастет. При уменьшении диэлектрической прони-
цаемости волновое сопротивление будет увеличиваться относительно 50 Ом,
и для ее снижения до 50 Ом необходимо уменьшить толщину диэлектрика,
сблизив прямой и обратный проводники в каждой линии. Именно это при-
ведет к уменьшению перекрестных помех.
Практическое правило: снижение диэлектрической проницаемости приве-
дет к уменьшению перекрестных помех, но только опосредованно. Низкая диэ-
лектрическая проницаемость требует сближения сигнального и обратного про-
водников для обеспечения заданного волнового сопротивления, которое приве-
дет к малому уровню перекрестных помех.
Применение материалов с малой диэлектрической проницаемостью приве-
дет к уменьшению перекрестных помех при одинаковом шаге трассировки или
к снижению шага при одинаковых ограничениях на уровень помех. В конечном
итоге это приведет к уменьшению размеров платы при заданных ограничениях
на уровень перекрестных помех.
4.4.13. Перекрестные помехи и джиттер
В микрополосковой линии имеется скрытая связь между уровнем пере-
крестных помех и таймингом. Это происходит из-за комбинации асиммет-
рии диэлектрических материалов и различия краевых электрических полей
между сигнальными проводниками, зависящими от набора передаваемых
данных [19, 75]. В полосковых линиях эта зависимость практически отсут-
ствует.
Рассмотрим три микрополосковых линии передач длиной 250 мм, шириной
0,125 мм, расположенных с зазором 0,125 мм. Центральная линия пассив-
4.4. Перекрестные помехи в связанных линиях передачи
369
Активная линия
в состоянии,
противоположном
пассивной
пассивная активная пассивная Активная И
в одинаковом
| возвратный проводник | СОСТОЯНИИ
Рис. 4.102. Электрическое поле для активных и пассивной линий при различных
сигналах в них
ная, а внешние линии — активные. Номинальное время rdl задержки распро-
странения сигнала в пассивной линии составляет 1,6 нс.
Время задержки распространения сигнала в пассивной линии будет за-
висеть от вида напряжения в активных линиях. Когда активная линия пере-
ключается в состояние, противоположное пассивной линии, время задерж-
ки распространения сигнала уменьшается. Если активная линия имеет та-
кой же сигнал, как в пассивной линии, то время задержки увеличивается.
Форма поля показана на рис. 4.102, и она определяет различные эффектив-
ные диэлектрические проницаемости и скорости распространения сигнала.
На рис. 4.103 показаны три ситуации для комбинации сигналов в актив-
ных и пассивной линиях, а на рис. 4.104 — форма сигналов на выходе пас-
сивной линии для этих комбинаций.
Когда активная линия отключена, время задержки распространения сиг-
нала в пассивной линии определяется только эффективной диэлектричес-
кой проницаемостью материала диэлектрика и воздуха поверх линии.
Отмеченный эффект, наблюдаемый при передаче случайного потока би-
товых данных, является одной из составляющих джиттера. Он возникает
только при близко расположенных активных и пассивных линиях, когда
сказываются эффекты связи. При значительном разнесении устраняются
перекрестные помехи, и время задержки распро-
странения сигнала в пассивной линии не будет
зависеть от сигналов в активной линии.
Активная линия
>
>
>
Рис. 4.103. Три ситуации для комбинации сигналов
в активных и пассивной линиях: вверху — актив-
ные линии выключены, /dl = 1,6 нс; в середине —
активные и пассивная линия несут одинаковые
сигналы, Zdl = 1,7 нс; внизу — сигналы в активных
линиях противоположны сигналу в пассивной
линии, Zdl = 1,5 нс
Активная линия
VVV VVV VVV
370 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Время, пс
Рис. 4.104. Сигнал на выходе пассивной линии для различных комбинаций сигналов
в активной линии: 1 — активные линии несут сигнал противоположный пассивной
линии; 2 — активные и пассивная линии несут одинаковые сигналы; 3 — одиночная линия
4.4.14. Коммутационные помехи
Когда возвратный путь в линии передачи не является однородной плос-
костью, или диэлектрический материал достаточно асимметричен, тогда
индуктивная связь значительно превосходит емкостную, и помехи будут
определяться взаимной индуктивностью контуров. Это явление обычно
проявляется в малых локальных зонах, таких, как выводы микросхем, соеди-
нители, области печатной платы, в которой возвратный путь прерывается
щелью. В этом случае связь может быть смоделирована сосредоточенной ин-
дуктивностью.
Помехи, которые генерируются в пассивной линии за счет этой индук-
тивности, проявляются только при наличии изменения тока dl/dt в актив-
ной линии за время длительности фронта. Поэтому эти помехи называются
коммутационными помехами, или помехами типа дельта I.
Подскок напряжения заземления — одна из форм проявления коммута-
ционных помех в особых случаях, когда существует некоторый обходной
возвратный путь. Можно указать три способа уменьшения этого эффекта. Для
этого следует:
1. Увеличить число возвратных путей так, чтобы не было возможности
найти еще один неучтенный возвратный путь.
2. Увеличить ширину и уменьшить длину возвратного пути с целью ми-
нимизации его парциальной самоиндукции.
3. Располагать сигнальный путь рядом с возвратным путем для умень-
шения их парциальной взаимной индукции.
Даже в том случае, если нет альтернативного возвратного пути, перекре-
стная помеха между двумя или более линиями передачи будет определяться
взаимной индуктивностью. Взаимная индуктивность контура в корпусах
микросхем и соединителях часто является доминирующим фактором.
4.4. Перекрестные помехи в связанных линиях передачи
371
Оценка взаимной индуктивности двух контуров может быть проведена на
простой модели. Когда сигнал проходит по одной паре штыревых контак-
тов в соединителе (активные выводы), происходит внезапное изменение тока
в контуре при прохождении фронта сигнала. Это вызывает (за счет взаим-
ной индуктивности) появление индуцированного напряжения в соседнем,
пассивном контуре. Это напряжение Vb примерно равно:
vb = Md-^ = M^, В) (4106)
где М — взаимная индуктивность между активным и пассивным контуром, нГн; 1а — из-
меняющийся ток в активной линии, В; Z — типовое значение волнового сопротивления
(около 50 Ом) для рассматриваемого сигнала в активном и пассивном контуре, Ом; Va —
напряжение сигнала в активной линии, В; tr — фронт сигнала, нс.
Приемлемое значение коммутационной помехи зависит от общей помехоу-
стойчивости. Опыт говорит, что это значение должно составлять от 5 до 10 %
от размаха сигнала.
Если приемлемый уровень помех определен, то можно рассчитать мак-
симальнодопустимую индуктивность Ммежду активной и пассивной цепями:
M=^trZ, нГн, (4.107)
* а
где Z— волновое сопротивление, Ом; Va, Vb — соответственно напряжение сигнала в ак-
тивной и пассивной линиях, В; /г — фронт сигнала, нс.
Для примера примем Уь/Уа = 0,05, Z= 50 Ом, /г = 1 нс. Тогда получим
максимально допустимую взаимную индуктивность 2,5 нГн. При уменьше-
нии фронта скорость изменения тока dl/dt увеличивается, и следует умень-
шить взаимную индуктивность для удержания уровня коммутационных по-
мех в заданных пределах.
Практическое правило: для удержания коммутационных помех на приемлемом
уровне между парой сигнальных и возвратных путей, взаимная индуктивность
контуров между ними должна быть менее 2,5 нГн х фронт сигнала (нс).
При фронте 0,5 нс взаимная индуктивность не должна быть более 1,25 нГн,
что представляет значительные трудности при создании корпусов микросхем
и соединителей. Можно назвать три геометрии, которые приводят к сниже-
нию взаимной индуктивности:
• сокращение длины контура, что типично для корпусов CSP;
• разнесение активного и пассивного контуров, что трудно выполнить
в миниатюрной аппаратуре;
• сближение прямого и возвратного путей, что снижает парциальную са-
моиндукцию, а также и волновое сопротивление; это, в свою очередь,
может привести к новым проблемам, связанным с неоднородностью
линии передачи.
Практическое правило: минимальная длительность фронта, нс, ограничен-
ная допустимым уровнем коммутационных помех, составляет tx > М/2,5 нГн.
372 Глава 4. Обеспечение целостности сигнала в печатном монтаже
Это определяет максимальную тактовую частоту на уровне 10 х (l/tr) =
= 250 МГц/М нГн. Период равен 10 х tr.
Например, если взаимная индуктивность между парой сигнальных путей
составляет 1 нГн, максимальная рабочая частота будет 250 МГц. Если будет
пять активных пар, которые индуцируют помехи в пассивную линию, и каждая
из них имеет взаимную индуктивность 1 нГн, то максимальная частота бу-
дет 250 МГц/5 = 50 МГц.
4.4.15. Методы снижения перекрестных помех
Перекрестные помехи никогда не могут быть полностью устранены, но
они могут быть существенно снижены. Это может быть достигнуто следую-
щими приемами, которые рассматривались в этой главе:
• увеличение шага расположения сигнальных трасс;
использование проводящих слоев для возвратного пути;
снижение длины связанных линий;
преимущественное использование полосковых линий передач;
• уменьшение волнового сопротивления линий передачи;
использование материалов с малой диэлектрической проницаемостью;
сближение сигнальных и возвратных трасс в корпусах микросхем и со-
единителях;
использование защитных трасс с закорачивающими металлизирован-
ными отверстиями на концах и по длине.
Важно экономически оценивать применяемые приемы для снижения
конечной стоимости изделия.
Глава 5
Проектирование шин питания
и заземления
5.1. Система питания и заземления
5.1.1. Полное сопротивление системы питания
Система питания на печатной плате должна выполняться в виде потен-
циальных слоев, которые обладают наименьшей индуктивностью. Наиболее
приспособлены для реализации такой системы конструкции МПП, в кото-
рых в виде потенциальных слоев выполняются слои с напряжением питания
и слои опорного напряжения (как правило, с потенциалом О В), в которых
протекают возвратные токи. От корректного проектирования взаимосвязан-
ных систем питания и заземления во многом зависит правильность функци-
онирования электронной системы и уровень помех в ней.
Широкое распространение получили системы распределенного питания,
которые состоят из одного мощного источника напряжения питания и ряда
локальных преобразователей постоянного напряжения, преобразующих на-
пряжение этого источника в требуемые уровни напряжения [108]. Незави-
симо от схемы разводки питания необходимо принимать во внимание про-
блемы подавления помех, которые непрерывно усложняются в связи с по-
вышением быстродействия элементной базы и снижением уровней питающих
напряжений.
По мере повышения быстродействия резко увеличивается мощность по-
требления цифровых систем, что заставляет создавать микросхемы с малым
уровнем питающих напряжений. В настоящее время наиболее распространен-
ными значениями напряжения питания для современных цифровых систем
на печатных платах являются 5; 3,3; 2,5; 1,8 и даже 1,2 В. Наблюдается тен-
денция к снижению напряжения питания, уровень которого к 2009 году до-
стигнет 1 В [98]. Кроме основного напряжения питания, для работы системы
могут потребоваться дополнительные источники питания. Например, для ра-
боты ЭСЛ-схем требуется дополнительный источник питания с напряжени-
ем —2 В для смещения согласующих резисторов.
374
Глава 5. Проектирование шин питания и заземления
Для работы аналоговых и цифровых узлов требуются, как правило, раз-
дельные источники питания. Одна из причин применения раздельных ис-
точников заключается в изоляции помех по шинам питания.
Поскольку все токи протекают в замкнутых контурах, то ток потребления
микросхемы протекает от источника к нагрузке и возвращается по некоторо-
му пути к источнику. Путь протекания тока обладает некоторым полным со-
противлением, от значения которого зависит качество функционирования
цифрового узла. Широкое применение технологии КМОП для построения
микропроцессоров и заказных БИС обуславливает непрерывное увеличение
степени интеграции микросхем, что при повышенной скорости обработки
информации требует все больше мощности. При одновременном снижении
питающих напряжений это приводит к резкому возрастанию токов потребле-
ния, протекающих по проводникам питания и заземления. Все это требует все
меньшего значения полного сопротивления ZpDS систем распределенного
питания. По оценкам специалистов [104], начиная с 1990 года, когда типовое
значение ZpDS составляло 250 мОм, оно уменьшается в пять раз при появле-
нии нового поколения компьютерной техники. В настоящее время типовое
значение полного сопротивления системы питания составляет 0,4 мОм. Это
весьма малое значение должно обеспечиваться комплексом мер, принятых как
на этапе схемотехнического проектирования, так и на этапе конструирования
электронной аппаратуры, в том числе, печатной платы.
В зависимости от типа печатной платы (односторонняя, двусторонняя,
многослойная) у конструктора имеются те или иные возможности управле-
ния полным сопротивлением системы питания и заземления. В любом слу-
чае следует стремиться к минимизации полного сопротивления шин пита-
ния и заземления, что в полной мере может быть реализовано только в мно-
гослойных печатных платах. Общая концепция проектирования шин питания
и заземления остается неизменной: минимизация площадей контуров токов,
сближение прямого и возвратного проводников, управление полным сопротив-
лением, которое, в отличие от линий передач, в данном случае должно быть
минимальным. В контексте рассматриваемой проблемы прямой проводник
является проводником, по которому ток потребления поступает на вывод
питания микросхемы, а возвратным проводником является проводник с
некоторым (чаще всего нулевым) опорным напряжением. Этот возвратный
проводник при организации функционального заземления включается в
систему заземления установки и обычно называется «землей». Более детально
познакомиться с проектированием и организацией систем заземления элек-
тронной аппаратуры в зданиях и помещениях можно в [95, 105].
Быстродействующие цифровые системы, как следует из материалов пре-
дыдущих глав, могут быть созданы только на МПП. В них имеется возмож-
ность не только организовать линии передачи с управляемым волновым
сопротивлением, но и рационально спроектировать шины питания и зазем-
ления. Для этих целей в структуре МПП под напряжение питания и опор-
ное напряжение отводятся отдельные потенциальные слои, не занятые сиг-
нальными проводниками. Но это базовое положение требует уточнения и
5.1. Система питания и заземления
375
детального анализа для обоснованного принятия решения по реализации
выше отмеченной концепции.
Полное сопротивление проводников вызывает градиент напряжения вдоль
них. Он связан с протеканием токов в потенциальном слое, которые необ-
ходимы для заряда/разряда паразитных емкостей и развязывающих конден-
саторов. Изменение напряжения в 250 мВ в потенциальной плоскости не
является исключительным для печатных плат.
Отклонение напряжения по поверхности потенциального слоя от экви-
потенциальности является причиной помех, которые генерируются в самом
устройстве. Для надежного функционирования системы должны быть пред-
приняты меры по устранению этих помех, т. е. обеспечению эквипотенци-
альности потенциальных слоев на высоких частотах.
Слой питания в совокупности со слоем опорного напряжения на высо-
кой частоте может быть представлен в виде линии передачи. Ранее было
показано, что контроль волнового сопротивления облегчается при исполь-
зовании в качестве возвратного проводника проводящего слоя. Далее сово-
купность прямого и возвратного проводника в системе питания будем на-
зывать шиной питания.
Широкий спектр цифрового сигнала при коротких фронтах, а также осо-
бенности работы выходных каскадов цифровых интегральных микросхем
создают условия для возникновения в системе питания импульсных комму-
тационных помех, основным методом борьбы с которыми являются сниже-
ние полного сопротивления шины питания и системы заземления за счет
уменьшения индуктивности шины питания и установка развязывающих
конденсаторов [4, 73, 101].
Пульсации напряжения питания при работе цифровых микросхем вы-
зывают изменения времени задержки распространения сигнала в микро-
схеме, которое зависит от напряжения питания. Например, изменение на-
пряжения питания от 3,6 В до
2,4 В может привести к измене-
нию задержки распростране-
ния сигнала в микросхеме от
I нс до 1,2 нс. Эти изменения
напряжения питания, вызван-
ные кратковременными поме-
хами в системе питания, обус-
лавливают появление эффекта
дрожания фронта импульса и
являются одной из составляю-
щих джиттера. На рис. 5.1 на-
глядно показано возникновение
джиттера как разности времен
задержек распространения сиг-
нала в микросхеме при пульса-
циях напряжения питания [100].
Напряжение, В
Амплитуда выходного
напряжения
Задержка при Усс 2.4
Задержка при Усс 3.6
Джиттер как разность задержек
при Усс 2.4 В и Усс 3.6 В
Рис. 5.1. Образование джиттера как результат
пульсаций напряжения питания
376
Глава 5. Проектирование шин питания и заземления
Типовое значение
1--к—-1----1----1---1---1---1---1---1----
1 Гц 1 кГц 1 МГц 1 ГГц Частота
Рис. 5.2. Обеспечение постоянства полного сопротивления системы питания по частоте
за счет применения фильтров в стабилизаторах напряжения, электролитических
и керамических развязывающих конденсаторов и межслойного конденсатора
в структуре МПП
На рис. 5.2 наглядно иллюстрируются основные компоненты управления
полным сопротивлением системы питания с целью поддержания его посто-
янства по частоте на необходимом уровне за счет применения фильтров в ста-
билизаторах напряжения, электролитических и керамических развязываю-
щих конденсаторов и межслойного планарного конденсатора в структуре
МПП. Видно, что фильтры стабилизатора напряжения обеспечивают низ-
кое полное сопротивление только до частот единицы килогерц, электроли-
тические развязывающие конденсаторы, устанавливаемые на плате эффектив-
ны до 1 МГц, а керамические развязывающие конденсаторы — до частот в не-
сколько сотен мегагерц. Для поддержания низкого полного сопротивления
системы питания в более широком диапазоне необходимо использовать
планарный конденсатор, образованный слоями питания и опорного напря-
жения в составе МПП. При проектировании печатных плат необходимо
обеспечить эффективную работу всех отмеченных средств.
5.1.2. Стратегия и правила проектирования
слоев питания
Напряжения питания в составе МПП распределены по отдельным сло-
ям. Для каждого из значений напряжения отводится отдельный слой или
несколько слоев. Отдельный слой или слои отводятся и для опорного напря-
жения (О В). Для каждого слоя с напряжением питания необходимо отводить
смежный слой с опорным напряжением.
При проектировании слоев питания необходимо определить:
• число слоев,
5.1. Система питания и заземления
377
• их топологический рисунок,
• их местоположения в структуре многослойной платы (стек).
Для высокочастотных приложений необходимо разделять цифровую и ана-
логовую шины питания. Вообще проблема помех должна быть доминирую-
щей при проектировании высокоскоростных печатных плат. Рассмотрим две
линии передачи с общей опорной плоскостью (рис. 5.3). Возвратный высо-
кочастотный ток стремится располагаться под сигнальным проводником и
за счет его распределения занимает некоторую область под проводниками.
За счет перекрытия зон протекания возвратных токов, часть возвратных токов
одного проводника оказывается
под другим сигнальным провод-
ником. Поэтому все помехи из
одной цепи могут за счет этого
индуцироваться в другую цепь.
Для предотвращения этого явле-
ния следует попытаться изоли-
ровать возвратные токи различ-
ных цепей (источников и рецеп-
торов помех), как показано на
рис. 5.3, вариант 2. Для линий
передач это явление детально
рассмотрено при анализе неод-
нородностей в плоскости воз-
вратных токов. Применительно
к шинам питания можно сделать
Слой проводников Распределение
иииии тлид я гпло
Слой возвратных токов
Слой проводников Распределение
Слой возвратных токов
Рис. 5.3. Распределение тока в плоскости для
двух линий: 1 — линии имеют связь за счет вза-
имодействия возвратных токов; 2 — разделение
плоскости заземления предотвращает
взаимодействие возвратных токов
вывод, что максимальное разделение возвратных слоев будет в том случае,
если для каждого источника питания отвести отдельный возвратный слой.
Соединение возвратных слоев с системой заземления
При корректном проектировании все возвратные цепи в плате и в системе
должны иметь один потенциал, равный 0. Обеспечение этого важнейшего
требования эквипотенциальности может быть достигнуто при одноточечном
соединении всех возвратных слоев. Рассмотрим более детально этот момент.
Предположим, что на печатной плате имеется секция аналогового и циф-
рового сигналов, а также возвратные плоскости для этих сигналов в виде двух
фрагментов, соединенных в двух или более точках. При этом из-за неэкви-
потенциальности проводящих слоев создаются условия, при которых возврат-
ный ток может распространяться по обоим фрагментам возвратной плоскости,
и возможно протекание токов по контуру, который включает в себя оба фраг-
мента и две соединительных точки (рис. 5.4). Этот контур называется кон-
туром заземления. Часто этот эффект не очевиден, и его действие часто не
анализируется, хотя оно включает проблемы ЭМС, мощности рассеяния и
температурного режима.
Простейшим способом контроля контура заземления является применение
одноточечного соединения между фрагментами возвратной плоскости. Это
378
Глава 5. Проектирование шин питания и заземления
Рис. 5.4. Образование контура заземления:
1 — раздельные слои питания; 2 — раз-
дельные слои возвратных токов; 3 — две
точки соединения слоев возвратных токов;
4 — контур заземления
исключает возникновение контура.
Но при этом встает вопрос: где рас-
полагать эту точку?
В некоторых системах, особен-
но включающих материнские и до-
черние печатные платы, плоскости
проектируются так, что они образу-
ют подсоединение звездой к единой
точке, обычно на первичном источ-
нике питания. Если используется
распределенная система питания на
плате, слои могут быть соединены
вместе в одной точке резистором с «нулевым» сопротивлением (например,
проволочной перемычкой) или с ферритовой бусинкой. Ферритовая бусин-
ка используется для подавления высокочастотных спектральных компонентов,
обеспечивая соединение между слоями по постоянному току. При высокой
эффективности фильтрации в системе питания применение ферритового
элемента может не потребоваться.
В аналого-цифровых системах необходимо иметь отдельные системы слоев
питания и заземления для цифровых узлов и для аналоговых узлов. Часто
соединение слоев заземления этих частей производится в одной точке не-
посредственно под микросхемами (или в непосредственной близости от них)
с помощью перемычки или ферритовой бусинки.
Перекрытие потенциальных слоев
Для уяснения влияния перекрытия потенциальных слоев рассмотрим
пример. Часть плоскости питания аналоговой цепи перекрывает часть плос-
кости возвратных токов питания цифрового узла (рис. 5.5). Емкость между
слоями будет определяться площадью перекрытия, расстоянием между слоями
и диэлектрической проницаемостью изоляционного материала между метал-
лическими слоями. Это может быть конденсатор достаточно малой емкос-
Рис. 5.5. Перекрытие плоскостей вызывает емкостную связь между отдельными
5.1, Система питания и заземления
379
ти, но, тем не менее, он может обеспечить путь для протекания токов помех
из одной части цепи к другой.
Важной частью решения топологических задач при проектировании плат
является расположение компонентов таким образом, чтобы их отдельные
плоскости питания и заземления были эффективно сгруппированы вместе
и не перекрывались.
5.1.3. Потенциальный слой с сетчатым рисунком
Однородность волнового сопротивления — одно из основных требова-
ний при проектировании линий передачи в высокоскоростных печатных пла-
тах. В том случае, если в конструкции платы применяются сплошные потен-
циальные слои для формирования полосковых и микрополосковых линий
передач, их волновое сопротивление не изменяется при смещении сигналь-
ного проводника параллельно потенциальному слою. По технологическим
соображениям в ряде случаев сплошные металлизированные слои заменя-
ются в МПП сетчатыми. При этом регулярная неоднородность в слое воз-
вратных токов изменяет значение волнового сопротивления линий переда-
чи. Кроме этого, существенно усложняется расчет электрофизических пара-
метров линий передачи, который теперь не может быть выполнен при помощи
имеющихся аналитических приближений, а требует применения численных
методов расчета [106].
Рассмотрим полосковую линию передачи, в которой потенциальные слои
имеют определенный регулярный рисунок, чаще всего выполненный в виде
ортогональной сетки. На рис. 5.6 представлено сечение сдвоенной полосковой
линии передачи в составе МПП с типовыми размерами. Потенциальные слои
в описываемой конструкции выполняются в виде ортогональной сетки. Ти-
повая конфигурация сетки показана на рис. 5.7. Оценим следующие харак-
теристики:
• зависимость волнового сопротивления линии передачи от угла меж-
ду направлением сигнального проводника и линий сетки (рис. 5.8);
Рис. 5.6. Фрагмент сечения МПП: 1 — по-
тенциальный слой; 2 — слой сигнальных
проводников (направление X); 3 — слой
сигнальных проводников (направление У);
4 — потенциальный слой; 5 — диэлектрик
Рис. 5.7. Экранная сетка
(размеры в мм)
380
Глава 5. Проектирование шин питания и заземления
1250 мкм
а б
Рис. 5.8. Варианты взаимного располо-
жения сигнального проводника и сетки
экрана: а — проводник параллелен лини-
ям сетки; б — проводник расположен
под углом 45° относительно линий сетки
• зависимость волнового сопротив-
ления от параллельного смещения
сигнального проводника относи-
тельно экранной сетки.
Проводники и линии сетки экрана
расположены, как показано на рис. 5.8d,
со следующими параметрами конст-
рукции:
• диагональный шаг сетки экрана —
1250 мкм;
• расстояние между плоскостями сиг-
нальных проводников — 250 мкм
(рис. 5.6);
• толщина фольги для всех слоев —
35 мкм;
• диэлектрик изотропный с относительной диэлектрической проница-
емостью 5,8 (стеклотекстолит).
Расстояние h между экраном и ближайшим сигнальным слоем может ва-
рьироваться установкой прокладок для изменения номинального значения
волнового сопротивления линии.
Рассматриваемый фрагмент был рассчитан с использованием численного
метода конечных элементов. Фрагмент был формализован с помощью пря-
моугольных подобластей, что позволило учесть все особенности его конст-
рукции, вплоть до толщины проводников и экранов. Граничные условия
задавались с учетом симметрии конструкции так, чтобы распространить
полученные результаты на протяженные элементы платы.
Для первой оценки сравниваются предельные варианты расположения сет-
чатого экрана относительно проводников (рис. 5.8): а — сигнальный провод-
ник расположен параллельно линиям сетки, и б — сигнальный проводник
расположен по диагонали к линиям сетки. Нормированные значения вол-
нового сопротивления Z/zr при различной ориентировке сигнального про-
водника относительно сетки потенциального слоя приведены на рис. 5.9 при
нулевом смещении (X = 0). Эти данные показывают, что волновое сопротив-
ление линии передачи, у которой сигнальный проводник расположен по ди-
агональному направлению сетки, имеет волновое сопротивление примерно
в два раза больше, чем при расположении проводника над линиями сетки.
Это объясняется значительным уменьшением удельной емкости линии пе-
редачи при расположении проводников по диагональному направлению. Не-
допустимо большое изменение волнового сопротивления в данном случае при-
ведет к существенной неоднородности волновых сопротивлений различных
линий передач в пределах платы. Обратим внимание, что приведенные на рис.
5.9 зависимости соответствуют данным, принятым в примере. Если разме-
ры конструкции платы пропорционально изменятся, то численные резуль-
таты расчетов останутся неизменными.
5.1. Система питания и заземления
381
Рис. 5.9. Зависимость волнового сопротивления от смещения сигнального проводника
относительно сетки экрана: 1 — вариант «а», w = 1 мм; 2 — вариант «а», w = 2 мм;
3 — вариант «б», w = 1 мм; 4 — вариант «б», w = 2 мм
Оценим изменение волнового сопротивления при параллельном смеще-
нии проводников для двух вариантов их расположения (рис. 5.8). Результа-
ты расчета приведены на графике (рис. 5.9). Из этих данных видно, что пре-
дельное смещение проводника для варианта «а» вызывает отклонения зна-
чений волнового сопротивления более, чем на 100 %, а для варианта «б» —
около 80 %. Это позволяет сформулировать рекомендацию: для обеспечения
однородности линий передачи потенциальный слой должен выполняться без
каких-либо рисунков; если по технологическим соображениям требуется
использовать сетчатый рисунок на потенциальных слоях, то сигнальные про-
водники должны быть ориентированы по диагонали сетки этого рисунка.
Для анализа можно воспользоваться расчетами, показывающими изме-
нение параметров линий передач от конструкции потенциальных слоев при
различных значениях ширины w сигнального проводника:
• зависимость изменения волнового сопротивления при ширине линий
экранной сетки 150, 200 и 250 мкм от толщины диэлектрика (рис. 5.10);
• зависимость волнового сопротивления от ширины линий экрана при
различных значениях ширины проводника и толщины диэлектрика
(рис. 5.11);
• зависимость волнового сопротивления от ширины сигнального про-
водника при толщине диэлектрика 197 мкм (рис. 5.12);
• зависимость относительного изменения волнового сопротивления от
смещения проводника для определенных конструкций печатных плат
(рис. 5.13).
Для инженерных расчетов удобно использовать аналитические соотно-
шения, которые получены полиномиальной аппроксимацией зависимостей,
представленных на рис. 5.13. Общий вид выражения при этом имеет вид
dZ = А(Х? + В(Х)2 + CX + D.
(5.1)
382
Глава 5. Проектирование шин питания и заземления
в
Ширина линий сетки экрана, мкм
Рис. 5.10. Зависимость волнового сопротивления от толщины диэлектрика при различ-
ных значениях ширины сигнального проводника и линий сетки экрана: а — ширина ли-
ний сетки экрана 150 мкм, ширина проводников 150 мкм (1), 200 мкм (2), 250 мкм (3);
б — ширина линий сетки экрана 200 мкм, ширина проводников 150 мкм (1), 200 мкм (2),
250 мкм (3); в — ширина линий сетки и толщина диэлектрика изменяется: w = 150 мкм,
h = 197 мкм (1), w = 200 мкм, h = 197 мкм (2), w = 250 мкм, h = 227 мкм (3)
5.1. Система питания и заземления
383
Рис. 5.11. Зависимость
волнового сопротивления от
толщины диэлектрика
и ширины проводников:
1 — w = 150 мкм;
2— w = 200 мкм;
3 — w = 250 мкм
Рис. 5.12. Зависимость
волнового сопротивления
от ширины сигнального
проводника и ширины
линий экранной сетки
при h = 197 мкм:
1 — = 150 мкм;
2 — w3 = 200 мкм;
3 — сплошной экран
Рис. 5.13. Зависимость
относительного изменения
волнового сопротивления
от смещения проводника:
1 — h = 102 мкм, w = 150 мкм,
и>э = 150 мкм;
2— h = 102 мкм,
w = 200 мкм, и>э = 200 мкм;
3 — h = 127 мкм,
w = 150 мкм, и>э = 150 мкм;
4— h = 197 мкм,
w = 150 мкм, и>э = 150 мкм.
384
Глава 5. Проектирование шин питания и заземления
Значения коэффициентов Л, В, Си £>для вариантов 1—4 (рис. 5.13) пред-
ставлены в табл. 5.1.
Таблица 5.1
Коэффициенты полиномиальной аппроксимации
Вариант Значения коэффициентов
А В С D
1 0,1020 - 1,2560 2,6190 - 1,5286
2 0,0639 - 0,9726 2,7992 -2,0571
3 0,0417 - 0,5270 1,0167 -0,5286
4 0,0361 - 0,4774 1,2651 -0,8714
Полученные результаты позволяют сделать следующие выводы:
• волновое сопротивление линий связи в МПП с сетчатыми экранами
определяется не только геометрическими размерами линии, но и вза-
имным расположением и ориентацией экрана и сигнального провод-
ника;
• уменьшение ширины проводника сужает вариацию волновых сопро-
тивлений в зависимости от смещения проводника относительно эк-
рана;
• поворот координатной сетки экрана на угол 45° относительно коор-
динатной сетки проводника позволяет уменьшить влияние смещения
сигнального проводника относительно экрана на электрические па-
раметры образованной ими линии связи.
5.1.4. Топология сплошных слоев питания
и опорного напряжения
Идеальный слой питания и опорного напряжения должен быть сплошным
без каких-либо прорезей и других пробельных элементов. Однако, если даже
отсутствует регулярный сетчатый рисунок потенциальных слоев, на них все
равно имеются определенные топологические элементы, которые нарушают
сплошность фольги слоя. К таким элементам, в первую очередь, относятся кру-
говые зазоры около металлизированных отверстий, которые проходят сквозь
потенциальные слои. С увеличением числа выводов у компонентов таких от-
верстий становится больше, и однородность потенциальных слоев претерпе-
вает существенные нарушения. Напомним, что высокочастотные возвратные
токи, которые протекают по слою с опорным напряжением, располагаются
точно под сигнальным проводником и занимают по ширине полоску примерно
в три раза шире, чем ширина сигнального проводника. Для соблюдения од-
нородности путей возвратных токов на них не должны располагаться проре-
зи, щели, отверстия и т. п. По некоторым источникам [109], для устранения
проблемы ЭМС размер топологической неоднородности на потенциальном
слое не должен превышать 1/100 длины волны для максимальной частоты в
спектре сигнала.
5.1. Система питания и заземления
385
Если избежать неоднородностей нельзя, то необходимо выдерживать оп-
ределенные рекомендации по прокладке сигнальных проводников, которые
позволят свести влияние неоднородностей к минимуму.
Следует иметь в виду, что концентрация зарядов на потенциальном слое про-
исходит около краев слоя меди: по периферии платы и около границ неодно-
родностей. Поэтому сигнальные проводники с высокочастотными сигналами
(с фронтами 2 нс и менее) должны располагаться на расстоянии не менее 10 мм
от края платы или неоднородности. Относительное распределение возвратных
токов в бесконечном потенциальном слое при близко расположенном сигнальном
проводнике (микрополосковая линия) дается соотношением
/(</)=
(5.2)
где hms — толщина диэлектрика (принимается меньше ширины проводника); d— текущая
координата.
При конечных размерах потенциального слоя плотность тока на его гра-
ницах несколько увеличивается. График зависимости (5.2) представлен на
рис. 5.14. Как отмечалось ранее, 95 % возвратного тока протекает в области
утроенной ширины провод-
ника, если она меньше тол-
щины диэлектрика, или ут-
роенной толщины диэлект-
рика в противном случае. В
этой зоне нежелательно рас-
полагать металлизированные
отверстия и другие топологи-
Рис. 5.14. Плотность возвратного тока
в потенциальном слое
ческие элементы, нарушаю-
щие равномерность протека-
ния возвратных токов. Это
относится и к зоне по периметру платы (примерно 10 мм), где наблюдается
повышенная плотность протекания возвратных токов.
Каждый потенциальный слой, обладая определенной распределенной ин-
дуктивностью и емкостью, имеет свои резонансные частоты, которые зави-
сят от размеров слоя, наличия в нем различных неоднородностей, окружа-
ющей среды. Резонансные явления, как правило, ухудшают параметры ЭМС
конструкции, поэтому необходимо выбрать рациональный размер платы, а,
следовательно, и потенциального слоя. Резонансные частоты прямоуголь-
ной проводящей пластины определяются по формуле [109]:
//,\2 \2
f = 150 - J| -1- + —
/res Н 1 J I w J
МГц,
(5.3)
где kt, kw — целые числа 0, 1, 2, 3 и т. д., определяющие моды резонанса; / — длина пласти-
ны, м; w — ширина пластины, м.
13 1527
386
Глава 5. Проектирование шин питания и заземления
Как правило, интерес представляет первая мода резонанса (kt = kw = 1),
тогда из (5.3) следует
/res=-^-’ МГц,
(5.4)
где D — диагональ пластины, м.
При значительном числе металлизированных отверстий, что типично для
печатных плат на современной элементной базе, слои питания и опорного
напряжения становятся перфорированными, поскольку они имеют множе-
ство круговых пробельных мест, обеспечивающих зазор между слоем и про-
ходящими через него металлизированными отверстиями (рис. 5.15). С по-
зиций производителя плат эти круговые пробельные места желательно вы-
полнять максимального диаметра, а с позиций целостности сигнала и ЭМС
их следует выполнять с минимально возможным диаметром. Это противо-
речие разрешается, во-первых, рациональной трассировкой, позволяющей
рассредоточить отверстия таким образом, что они не будут создавать суще-
ственной локальной неоднородности. Во-вторых, переходом на более совер-
шенный технологический процесс с высокоплотным монтажом и микропе-
реходами. В отдельных случаях при использовании САПР топологические
нормы, например, радиусы скругления, заложенные в систему, могут при-
вести к погрешностям рисунка, которые в конечном итоге приведут к суще-
ственным неоднородностям [109]. Это иллюстрируется на рис. 5.16. Во всех
случаях слияние круговых зон увеличивает влияние неоднородности.
Частично эти погрешности могут быть устранены при контроле рисунка
печатного монтажа и при настройке программ прорисовки топологии в САПР.
Однако увеличение диаметра круговых зон может возрасти при длительном
использовании фотошаблона, что требует регулярной проверки качества
рисунка монтажа.
При трассировке многоразрядных шин воз-
никает ситуация, при которой круговые зоны
большого диаметра сливаются, создавая в плос-
кости возвратных токов щель, препятствую-
Рис. 5.15. Круговой зазор в потенциальном
слое вокруг металлизированного отверстия
Рис. 5.16. Погрешности рисун-
ка, приводящие к слиянию то-
пологических элементов: 7 —
круговые зоны слишком близко
расположены друг к другу; 2 —
диаметр зон слишком велик;
3 — задается слишком большой
радиус скругления
5.1. Система питания и заземления
387
щую протеканию этих токов (рис. 5.17). Устранить этот дефект можно умень-
шением диаметров круговых зон (рис. 5.18), но малые зазоры между круговыми
зонами создают для возвратных токов повышенное сопротивление. Таким
образом, в данном случае недостаток полностью не устраняется, а технологи-
ческие трудности изготовления платы возрастают. Наилучшим выходом из
положения является перераспределение проводников в шине и, соответственно,
перестановка круговых зон (рис. 5.19). При этом значительные зазоры между
ними не будут препятствовать протеканию возвратных токов.
Рис. 5.17. Неприемлемая неод-
нородность в потенциальном
слое при слиянии круговых зон
Рис. 5.18. Устранение слияния
круговых зон за счет уменьшения
их диаметра
13*
388
Глава 5. Проектирование шин питания и заземления
На рис. 5.20 показаны некоторые типичные ошибки трассировки, кото-
рые приводят к нарушению однородности путей возвратных токов. Они сво-
дятся к пересечению трассой щелей в потенциальном слое, по которому
протекают возвратные токи, а также к слишком близкому расположению
трассы к щелям и круговым зазорам около металлизированных отверстий.
Рис. 5.19. Минимизация неоднородностей за счет перераспределения круговых зон
Рис. 5.20. Типичные ошибки трассировки
5.1. Система питания и заземления
389
Следует обратить внимание на то, что при изготовлении МПП по техноло-
гии металлизации сквозных отверстий все потенциальные слои платы про-
низаны отверстиями.
5.1.5. Структура набора слоев МПП
Структура набора слоев МПП (стек) имеет решающее значение для обес-
печения целостности сигнала и ЭМС печатного узла. Рациональная струк-
тура должна отвечать двум основным требованиям. Во-первых, все линии
передачи в составе МПП должны иметь одинаковое (как правило, 50 Ом)
волновое сопротивление. Это заставляет выполнять линии передачи в виде
микрополосковых линий в наружных слоях и полосковых линий во внутрен-
них слоях МПП. Во-вторых, расположение потенциальных слоев с напря-
жением питания и с опорным (нулевым) потенциалом должно обеспечивать
минимальное полное сопротивление для шин питания и заземления. Реали-
зовать эти два важнейших требования можно на основе структурного мето-
да проектирования МПП. При этом основной целью является удовлетворе-
ние требуемых электрических параметров линий передач в составе платы и
требований минимизации помех по шинам питания.
Кроме этого, технология автоматизированной пайки и сборки печатно-
го узла, при которой происходит существенный нагрев печатной платы, тре-
бует выдерживать «баланс меди» в МПП. Суть этого требования заключает-
ся в равенстве площадей медной фольги, оставшихся на основаниях слоев
печатной платы, симметричных относительно центральной плоскости МПП:
площадь фольги на первом слое должна быть равна площади фольги на пос-
леднем слое, площадь фольги на втором слое должна быть равна площади
фольги на предпоследнем слое и т. д. Поскольку потенциальные слои (пи-
тания и опорного напряжения) имеют практически 100 % заполнение медью,
то они должны быть симметричны в составе платы. Заполнение сигнальных
слоев зависит от их топологии. Для выравнивания заполнения для различ-
ных сигнальных слоев на них следует оставлять участки нефункциональной
меди, которая должна иметь потенциал 0 В.
Многослойная печатная плата содержит, как правило, четыре типа метал-
лизированных слоев:
• слой контактных площадок, который может содержать некоторое число
сигнальных проводников, особенно при применении корпусов с боль-
шим числом выводов;
• сигнальный слой, в котором расположены только сигнальные провод-
ники преимущественно в одном направлении;
• потенциальный слой, на который подается напряжение питания; если
для работы требуется несколько питающих напряжений, то для каж-
дого отводится отдельный слой;
• потенциальный слой с опорным напряжением, по которому протекают
возвратные токи; как правило, на эти слои подается нулевой потен-
циал, и они соединяются с системой заземления устройства.
390
Глава 5. Проектирование шин питания и заземления
Кроме этого, в конструкции МПП применяются отдельные неметалл и-
зированные диэлектрические слои в виде технологических прокладок.
Число сигнальных слоев определяется топологией платы на этапе топо-
логического проектирования, а минимальное число потенциальных слоев
определяется принципиальной схемой изделия, и оно может существенно
увеличиться из-за электрических требований к плате. Тип корпуса микро-
схемы определяет ограничения на толщину платы, если выводы устанавли-
ваются в отверстия платы. Для поверхностно-монтируемых компонентов
таких ограничений нет, они будут определяться технологией изготовления
платы и, прежде всего, выполнением металлизированных отверстий. Как было
показано ранее, емкость и индуктивность металлизированного отверстия
зависит от его глубины, поэтому толщина быстродействующей платы дол-
жна быть минимальной. При структурном подходе толщина платы строго
обоснована требуемыми электрическими параметрами, которые реализуются
в сигнально-потенциальных звеньях платы.
Сигнально-потенциальные звенья МПП
Сигнально-потенциальным звеном является элементарная составляющая
часть МПП, состоящая из минимально необходимого для выполнения за-
данных электрических параметров набора слоев платы. Число слоев в звене
определяется его конструкцией и требуемыми электрическими параметра-
ми линий передачи. Каждое звено фактически представляет полосковую или
микрополосковую линию передачи или их разновидности. При двухслойном
расположении сигнальных проводников взаимная связь линий, расположен-
ных в различных слоях, должна быть минимальна.
Для создания МПП используются четыре базовых сигнально-потенциаль-
ных звена. Для удобства введем обозначения для различных слоев: С — сиг-
нальный слой, Е — потенциальный слой (питание и земля). Это позволяет
определить сигнально-потенциальные звенья МПП следующим образом:
• звено СЕ с одним сигнальным и одним потенциальным слоем, в ко-
тором реализуются микрополосковые линии передачи;
• звено ССЕ с двумя сигнальными и одним потенциальным слоем, в ко-
тором реализуются сдвоенные микрополосковые линии передачи (про-
водники на сигнальных слоях расположены ортогонально);
• звено ЕСЕ с одним сигнальным и двумя потенциальными слоями для
создания полосковых линий;
• звено ЕССЕ с двумя сигнальными и двумя потенциальными слоями
для создания сдвоенных полосковых линий передачи (проводники на
сигнальных слоях расположены ортогонально).
Дополнительно может применяться технологический (Т) слой, который
устанавливается первым и/или последним и предназначен для размещения
только контактных площадок. Отметим, что термин «слой» относится к слою
медной фольги на диэлектрическом основании.
Рассмотрим методику проектирования сигнально-потенциальных звеньев,
взяв для примера метод металлизации сквозных отверстий, при котором
5.1. Система питания и заземления
391
используются тонкий односторонний фольгированный стеклотекстолит и
тонкие стеклотекстолитовые технологические прокладки.
Звено типа СЕ
Конструкция звена СЕ (рис. 5.21) представляет собой микрополосковую
линию. Диэлектрические прокладки устанавливаются между слоями С и Е,
и их число позволяет изменять расстояние между сигнальным и потенциаль-
ным слоями, тем самым управляя электри-
ческими характеристиками линий передачи.
Введем следующие обозначения: t — тол-
щина фольги, Ad — толщина диэлектрического
основания каждого слоя, Ag — толщина одной
прокладки; к — число прокладок; kh^ — сум-
марная толщина прокладок, которая должна
быть не меньше, чем оговорено технологичес-
кими соображениями. Суммарная толщина
ЛСЕ звена СЕ очевидным образом определяется
из геометрии сечения звена (рис. 5.21):
Сигнальный проводник
Диэлектрические
прокладки
I I \кЛ
Потенциальный слой ±
е h
Рис. 5.21. Конструкция звена СЕ
6CE = 2(r+//d) + ^g. (55)
Различают два варианта компоновки звеньев: однополярный и разнопо-
лярный набор слоев.
При однополярном наборе ориентировка всех слоев в составе платы оди-
накова, например — фольгой вверх, как на рис. 5.21. Достоинство этого ва-
рианта заключается в использовании единой координатной сетки при раз-
работке топологии всех слоев платы.
В разнополярном наборе ориентировка слоев в составе платы различна.
Недостаток этой конструкции заключается в использовании различных по
ориентации координатных сеток при разработке топологии сигнальных слов.
Далее рассматриваем только однополярный набор слоев.
Исходным для расчета звена является заданное значение волнового со-
противления Z, Ом, линий передачи, которое должно быть одинаковым для
всех линий в пределах платы.
Как показано в 3 главе, волновое сопротивление линии передачи есть
функция от диэлектрических параметров среды и линейных размеров сече-
ния линии: толщины t проводников, их ширины w и расстояния Ams между
сигнальным и потенциальным слоями. Расстояние /zms между сигнальным и
потенциальным слоями можно изменять за счет числа прокладок в конст-
рукции звена, и его значение можно рассчитать по формуле:
/ims =0,1675(0,8w + r)exp
(5.6)
где w — ширина проводника, мм; / — толщина слоя фольги, мм; — эффективная ди-
электрическая проницаемость при расположении сигнального проводника на наружных
слоях печатной платы; Z — волновое сопротивление микрополосковой линии, Ом.
392
Глава 5. Проектирование шин питания и заземления
Рис. 5.22. Зависимость толщины Ams для микрополосковой линии при Z = 50
Эффективная проницаемость определяется по формуле
ее#= 0’475ег+0’67’ (5.7)
где ег — относительная диэлектрическая проницаемость основания платы.
Если волновое сопротивление равно 50 Ом, то формула (5.6) упрощается:
Л™ = 0,1675 (0,8w +1) ехр(о,83>/ё^). (5.8)
График зависимости hms (5.5) от ширины проводника при толщине фольги
35 мкм представлен на рис. 5.22.
Зная значение Ams, легко (см. рис. 5.21) определить число прокладок:
Таким образом, если ширина проводников выдержана на минимальных
технологических нормах, то единственным средством управления волновым
сопротивлением в звене СЕ при заданном материале основания является число
прокладок.
Звено типа ССЕ
Конструкция звена типа ССЕ показана на рис. 5.23.
Сигнальные проводники на соответствующих слоях располагаются орто-
гонально, что снижает взаимные электрические параметры между линиями.
При этом взаимная емкость сводится к минимуму, а взаимная индуктивность
практически равна нулю. Малое значение взаимной емкости между линия-
ми в сигнальных слоях позволяет представить исходное звено ССЕ в виде двух
независимых более простых звеньев С(х)Е и C(j)E. Условные обозначения
в скобках показывают ориентировку сигнальных проводников на слое. Расчет
этих звеньев ведется так же, как и ранее рассмотренного звена СЕ, с неко-
торыми особенностями, которые показаны ниже.
5.1. Система питания и заземления
393
Количество прокладок для зоны а
(рис. 5.23) выбирается минимальным
(£min), а для зоны количество прокла-
док зависит от исходных электричес-
ких параметров линии.
Очевидно также, что при равенстве
ширины и wy проводников на сиг-
нальных слоях и неравенстве расстоя-
ний Ams(x) и Ams(j) волновые сопротив-
ления линий передач, которые образо-
ваны сигнальными проводниками на
разных слоях и одной возвратной плос-
костью, будут различны. Как уравнять
волновые сопротивления? Для этого
следует увеличить ширину проводни-
ков на удаленном от потенциального
слоя сигнальном слое. В нашем случае
ширина wx выбирается из условия Zx =
= Zy. Это вносит определенные трудно-
сти в проектирование звена.
Сигнальный проводник
|С(Х)----
'.[ Г" I
Диэлектрические
прокладки
------ К^-пА
Сигнальный проводник
ПУ)-
Диэлектрические
прокладки
6)1 I
^ms(y)
Потенциальный слой
Рис. 5.23. Конструкция звена ССЕ
Звено типа ЕСЕ
Звено ЕСЕ (рис. 5.24) представляет со-
бой полосковую линию передачи со ста-
бильными электрическими параметрами.
Это звено обладает рядом положитель-
ных свойств по сравнению с рассмотренны-
ми ранее звеньями: стабильностью парамет-
ров и возможностью с высокой точностью
прогнозировать значение волнового сопро-
тивления. Следует отметить, что в каждом
зазоре между слоями находится одинаковое
Рис. 5.24. Структура звена
ЕСЕ
число прокладок.
В данном звене определяющим разме-
ром, от которого при заданной ширине
проводника зависит волновое сопротивле-
ние, является расстояние As между экрани-
рующими плоскостями. Относительно небольшая асимметрия централь-
ного проводника практически не влияет на значение волнового сопротив-
ления. Симметричность можно улучшить, перераспределяя прокладки в
зазорах.
Суть проектирования звена остается неизменной: через заданное волновое
сопротивление определяется расстояние между потенциальными слоями, а
затем, зная толщины применяемых слоев диэлектрических и фольгирован-
ных материалов, рассчитывают необходимое число прокладок.
394
Глава 5. Проектирование шин питания и заземления
Рис. 5.25. Зависимость расстояния между потенциальными слоями для полосковой
линии с Z= 50 Ом
Расстояние между потенциальными слоями определяется по формуле
As = 0,526(0,8w + /)exp
60
(5.10)
где w — ширина проводника, мм; t — толщина слоя фольги, мм; ег — относительная диэ-
лектрическая проницаемость материала основания платы; Z — волновое сопротивление
полосковой линии, Ом.
Для волнового сопротивления 50 Ом это расстояние определяется по
формуле
Рис. 5.26. Структура
звена ЕССЕ
hs =0,526(0,8w + /) exp(0,83 ZA/^7j. (5.11)
Графически зависимость (5.11) при разной
ширине проводников представлена на рис. 5.25
Звено типа ЕССЕ
Конструкция звена ЕССЕ показана на
рис. 5.26. Если на сигнальных слоях сигналь-
ные проводники расположены ортогонально,
то исходное звено может быть представлено
в виде двух независимых более простых зве-
ньев ЕС(х)Е и ЕС(у)Е. Эти звенья рассчиты-
ваются аналогично рассмотренному выше
звену ЕСЕ. Размером, определяющим значе-
ние волнового сопротивления, является рас-
стояние между потенциальными слоями.
Звенья ЕСЕ и ЕССЕ позволяют сформи-
ровать достаточно хорошо экранированные
5.1. Система питания и заземления
395
полосковые линии передачи. Электрические параметры в этих конструкциях
наиболее стабильны. Эти два типа звеньев наиболее пригодны для форми-
рования МПП с большим числом слоев.
Формирование структуры МПП
Проектирование отдельных звеньев — только первый шаг в создании МПП.
Следующий шаг состоит в формировании из отдельных звеньев полной струк-
туры МПП. Этому этапу следует уделять должное внимание, поскольку от
его выполнения будет зависеть качество МПП и обеспечение целостности
сигнала в ней. Основное требование на этапе формирования структуры МПП
можно сформулировать следующим образом: при объединении сигнально-
потенциальных звеньев в структуру МПП волновое сопротивление линий
передач в составе звеньев не должно измениться.
Это требование может быть выполнено только в том случае, если после-
довательно набирать звенья, ориентируя их потенциальными слоями друг к
другу. Если это требование не выполнить, то появляются емкости сигнально-
го проводника одного звена относительно потенциального слоя другого зве-
на, что приведет к изменению волнового сопротивления линии передачи.
Наглядно процесс набора структуры МПП с любым числом слоев может
быть представлен с использованием графа набора структуры (рис. 5.27). Граф
набора помогает скомпоновать МПП с задан-
ным волновым сопротивлением линий пере-
дачи. В качестве вершин графа выступают
сигнально-потенциальные звенья (СЕ, ЕСС,
ЕСЕ и ЕССЕ). Для наглядности обозначение
звеньев удобно записывать в той последова-
тельности слоев, в которой они будут установ-
лены в плате. Например, обозначения СЕ-ЕС
и ЕС-СЕ соответствуют четырехслойной пла-
те, состоящей из двух звеньев с различной
последовательностью сигнальных и потенци-
альных слоев. Первая структура (СЕ-ЕС) от-
вечает сформулированному выше требова-
нию, поскольку потенциальные слои высту-
пают в качестве экранов между звеньями,
предотвращая влияние линий передач одного
звена на линии другого. Для второй структуры
МПП (ЕС-СЕ) требование не выполняется
Рис. 5.27. Граф набора
структуры МПП
из-за того, что на электрические параметры сигнального проводника одно-
го звена оказывает влияние потенциальный слой другого звена.
Из приведенного примера ясно, что для устранения влияния одного зве-
на на другое при их объединении в структуру МПП необходимо, чтобы зве-
нья были обращены друг к другу только потенциальными слоями. Для сни-
жения полного сопротивления системы питания и формирования планарного
конденсатора в паре соседних потенциальных слоев один слой должен быть
396
Глава 5. Проектирование шин питания и заземления
отведен под питание, а другой, играющий роль возвратного проводника, дол-
жен быть заземлен.
Порядок составления графа набора структуры МПП следующий: между
вершинами графа, которые соответствуют сигнально потенциальным зве-
ньям, вводятся ориентированные ребра (рис. 5.27), которые показывают воз-
можную последовательность набора структуры платы. Базовые звенья, как
отмечено выше, в составе платы могут объединяться только экранными сло-
ями друг к другу. Таким образом, например, комбинации ЕС-СЕ и ЕС-ЕС
являются запрещенными комбинациями при наборе, а разрешена в этом
случае только комбинация СЕ-ЕС.
Первый и последний слои МПП могут быть технологическими, несущими
только контактные площадки. Влияние такого слоя на параметры звена
определяется после анализа рисунка слоя. Если на этом слое расположены
контактные площадки и проводники (например, как при установке корпу-
сов BGA), то этот слой должен рассматриваться как сигнальный.
Граф носит универсальный характер. С его помощью можно, продвига-
ясь по некоторому пути, получить структуры МПП с любым числом слоев.
Наиболее рационально к технологическому звену присоединить звенья типа
СЕ и ССЕ или использовать наружный сигнальный слой звена СЕ (или ССЕ)
в качестве технологического. Симметричная структура МПП, получаемая при
помощи графа, способствует выдерживанию баланса меди.
Для получения структуры МПП с заданным числом слоев необходимо
найти путь в графе от вершины Т слева до вершины Т справа, проходя по
ребрам графа. Определяющим фактором при построении пути является число
сигнальных слоев.
Очевидно, что поиск желаемой структуры МПП по графу не всегда удо-
бен. Поэтому на основе графа найдены все возможно допустимые структу-
ры МПП, которые сведены в таблицу базовых структур (табл. 5.2). Струк-
туры названы базовыми, поскольку в них применяются только сигнально-
потенциальные звенья. Понятно, что увеличить число потенциальных слоев
можно, разместив их между сигнально-потенциальными звеньями, напри-
мер, следующим образом: СЕ-Е-ЕС. При этом волновые сопротивления
линий передач не изменятся. Установка одного потенциального слоя при-
ведет к перемещению структуры МПП вправо по строке таблицы на один
столбец. Структуры с дополнительными потенциальными слоями назовем,
в отличие от базовых, производными.
Анализ таблицы позволяет сделать несколько важных выводов.
1. При заданном числе сигнальных слоев может быть получено произ-
вольное число структур МПП, отличающихся числом потенциальных
слоев. Их минимальное число определяется принципиальной схемой
проектируемого цифрового узла (число питающих напряжений, об-
щий проводник, дополнительные источники питания).
2. Существует область неприемлемых сочетаний числа сигнальных и по-
тенциальных слоев, при которых невозможно реализовать требование
однородности волнового сопротивления в МПП. При заданном чис-
5.1. Система питания и заземления
397
Базовые структуры МПП
Таблица 5.2
Количество сигнальных слоев Количество потенциальных слоев
1 2 3 4 5 6
1 СЕ ЕСЕ
2 ССЕ ЕССЕ СЕ-ЕС
3 ССЕ-ЕС СЕ-ЕСЕ-ЕС
4 ССЕ-ЕСС СЕ-ЕССЕ-ЕС СЕ-ЕССЕ-ЕС СЕ-ЕСЕ-ЕСЕ-ЕС
5 ОБЛАСТЬ СЕ-ЕССЕ-ЕСС ССЕ-ЕСЕ-ЕСС СЕ-ЕСЕ-ЕСЕ-ЕС СЕ-ЕСЕ-ЕССЕ-ЕС
6 НЕПРИЕМЛЕМЫХ ССЕ-ЕССЕ-ЕСС СЕ-ЕСЕ-ЕССЕ-ЕС СЕ-ЕССЕ-ЕСЕ-ЕСС ССЕ-ЕСЕ-ЕСЕ-ЕСС
7 СОЧЕТАНИЙ КОЛИЧЕСТВА БАЗОВЫХ И ПОТЕНЦИАЛЬНЫХ СЛОЕВ СЕ-ЕССЕ-ЕССЕ- ЕСС ССЕ-ЕСЕ-ЕССЕ- ЕСС
ле сигнальных слоев выход из этой области возможен только за счет
искусственного увеличения потенциальных слоев, что соответствует
сдвигу вправо по строке таблицы. Например, если задано 5 сигналь-
ных слоев, то реализовать требования однородности волнового сопро-
тивления можно только с четырьмя и более потенциальными слоями,
выполняя следующие базовые структуры: СЕ-ЕССЕ-ЕСС или ССЕ-
ЕСЕ-ЕСС.
Окончательный выбор структуры при наличии альтернативных вариан-
тов проводится с учетом принятой технологии изготовления платы, конст-
рукции печатного узла и экономических соображений. Например, если плата
содержит значительное число слоев и предназначена для установки выводов
компонентов в металлизированные отверстия, то следует удостовериться, что
суммарная толщина платы не будет превосходить минимально допустимую
длину выводов компонентов с учетом технологического припуска на пайку
(рис. 5.28). Для данного варианта толщина ЛрсЬ платы ограничена следующим
соотношением:
V^z2- Ьмм, (5.12)
где /2 — длина вывода, пригодная для монтажа, мм; 1 мм — выступающая часть вывода,
определяемая технологией пайки, мм.
398
Глава 5. Система питания и заземления
Рис. 5.28. Монтаж компонента
в металлизированное отверстие
Значение /2 — это минимальная длина
вывода с учетом допуска: /2 = /2ном - 8.
При установке на плату микросхем с пла-
нарными выводами и поверхностно-монти-
руемых компонентов, ограничения на ее тол-
щину, связанные с монтажом микросхем,
отсутствуют. При этом следует помнить, что
платы меньшей толщины имеют металлизированные отверстия меньшей ин-
дуктивности и емкости.
Второе ограничение на толщину платы связано с качеством металлизации
отверстия. Соотношение между диаметром отверстия и толщиной платы оп-
ределяется принятой технологией изготовления платы и может варьировать-
ся в достаточно широких пределах. Увеличение толщины печатной платы сверх
отношения толщины к диаметру отверстия 4:1 приводит к значительным ос-
ложнениям в обеспечении надежности металлизированных отверстий.
Если при проектировании МПП приходится учитывать оба ограничения,
то принимается тот вариант структуры, у которого будет минимальная толщина
ЛрсЬ. При окончательной оценке следует принимать во внимание допустимые
отклонения на толщины отдельных слоев и диэлектрических прокладок. Сум-
марный допуск на толщину 8рсЬ печатной платы есть сумма допусков на тол-
щины отдельных слоев и прокладок. Если, например, число слоев п = 10, а
допуск на толщину одного слоя: б = ±0,03 мм, то брсЬ = 0,03x10 = 0,3 мм. Тол-
щина платы, таким образом, будет: ЛрсЬ = ЛрсЬ nom ± 0,3 мм, где ЛрсЬ nom — но-
минальный размер толщины МПП, который при выборе варианта структуры
вычисляется из соотношения:
^pcb, nom ^pcb ^pcb*
Это гарантирует, что в худшем случае толщина МПП не превысит допус-
тимого значения.
5.2. Помехи в шине питания и их устранение
5.2.1. Особенности систем питания цифровых
микросхем
Подключение вентиля к шине питания
При работе цифрового узла происходит изменение тока потребления за
достаточно короткое время, соизмеримое с длительностью фронта сигнала.
При этом скорость изменения тока в шине питания становится весьма зна-
чительной, что вызывает падение напряжения на индуктивности шины пи-
тания. Это может привести к заметным нарушениям работоспособности
цифровых узлов. Для устранения помех подобного типа применяются раз-
личные методы конструкторского и схемотехнического характера. К конст-
рукторским методам можно отнести приемы снижения индуктивности шины
5.2. Помехи в шине питания и их устранение
399
питания и повышения ее емкости. К схемотехническим методам относится,
в первую очередь, установка развязывающих конденсаторов. Однако эффек-
тивность работы этих конденсаторов во многом определяется способом их
монтажа и размещением на плате.
Существуют две стратегии применения развязывающих конденсаторов,
которые приводят к различным результатам. Первая, традиционная точка
зрения, предполагает, что развязывающий конденсатор есть малая батарея,
а вторая — что конденсатор изменяет полное сопротивление шины питания
для достижения некоторого определенного низкого уровня для распределен-
ной системы питания. Это должно быть справедливо для всех высоких час-
тот, которые присутствуют в спектре сигнала. В общем случае справедливы
оба подхода, хотя между ними имеются определенные различия [103].
Из всех семейств микросхем именно для ТТЛ схем особенности функци-
онирования системы питания проявляются наиболее полно. Поэтому далее
именно эта серия будет взята за основу при рассмотрении наиболее важных
аспектов проектирования шин питания и заземления. Определяющим фак-
тором в генерации помех по шинам питания является работа наиболее мощ-
ного выходного каскада, который для ТТЛ и КМОП серий микросхем пост-
роен по схеме составного инвертора. Она содержит два ключа, которые по-
очередно подключают выход драйвера к шине питания или к шине опорного
напряжения (заземления). В первом случае на выходе микросхемы имеет место
высокий уровень напряжения, а во втором — низкий.
Для более детального уяснения особен-
ностей работы системы питания цифровых
микросхем рассмотрим простейший ТТЛ-
вентиль, выполняющий операцию инвер-
тирования НЕ (рис. 5.29). Если на вход вен-
тиля приходит логический ноль, выходной
транзистор ТЗ включается, и на выходе вен-
тиля формируется логическая единица, т. е.
происходит логическая операция инверти-
рования. При подаче на вход вентиля логи-
ческой единицы ключ ТЗ запирается и от-
крывается ключ Т4. При этом выход мик-
Рис. 5.29. Типичный вентиль ТТЛ
(функция НЕ)
росхемы подключается через сопротивление
р-п перехода транзистора Т4 к шине опорного напряжения. Ток, потребляемый
вентилем, в состоянии логической единицы не равен току, который потребля-
ет вентиль в состоянии логического нуля. Поэтому за время переключения, ко-
торое приближенно равно длительности фронта /г, в шине питания произойдет
изменение тока со скоростью Д/Д. Но, как только ток в проводнике начнет
изменяться, в контуре тока происходит падение напряжения, пропорциональ-
ное самоиндукции контура, в данном случае контура шины питания:
^sb _ Asb“~’
(5.13)
400
Глава 5. Система питания и заземления
где £SB — индуктивность контура протекания токов потребления; А/ — модуль разности
токов потребления в статических состояниях; Гг — фронт сигнала.
В первом приближении разность токов потребления определяется через
данные спецификации на вентиль:
A^-|^sb ^sb|’
(5.14)
где /$в, /gB — соответственно ток потребления в состоянии логического 0 и в состоянии
логической 1 (известны из спецификации).
Упрощенная схема подключения вентиля к шине питания показана на
рис. 5.30.
Рис. 5.30. Эквивалентная упрощенная
схема подключения вентиля с учетом
индуктивности шины питания
Видно, что напряжение на вен-
тиле будет определяться при нали-
чии падения напряжения на индук-
тивности шины питания выраже-
нием:
^CC = KSS-^SB’ (5.15)
где Исс — напряжение питания на соот-
ветствующем выводе корпуса вентиля;
Kss — напряжение питания источника пи-
тания; KSB — падение напряжение на ши-
не питания (5.13).
Падение напряжения на индук-
LSB шины питания про-
тивности
исходит только во время изменения тока потребления в процессе переклю-
чения вентиля, и значение индуктивности будет определяться ее конструк-
торскими параметрами: формой сечения, расстоянием от плоскости опорного
напряжения, материалами.
Оценить индуктивность в односторонних и двухсторонних платах мож-
но будет только после компоновки узла и трассировки, но в любом случае в
этих платах не удается достичь минимального полного сопротивления шины
питания, необходимого для работы быстродействующих систем. Это мож-
но обеспечить только в МПП, когда для слоев питания и возвратных токов
(заземления) отводятся отдельные слои, расположенные на минимальном
расстоянии друг от друга.
Скорость изменения тока в шине питания при переключении вентиля оп-
ределяется перепадом тока и временем переключения. Выше перепад тока
вычислялся как разность тока потребления в состояниях логической 1 и
логического 0. Однако из-за особенностей работы выходных каскадов вен-
тилей это может привести к значительным погрешностям, поскольку реаль-
ный перепад тока будет во много раз больше, и он определяется режимом
сквозных токов. Это явление часто остается скрытым от разработчика, что
приводит к существенным погрешностям при проектировании быстродей-
ствующих цифровых узлов.
5.2. Помехи в шине питания и их устранение
401
Сквозные токи выходных каскадов вентилей
Для уяснения причин образования сквозных токов рассмотрим работу
выходного каскада ТТЛ-вентиля в различных стадиях переключения более
детально (рис. 5.31).
Выходной каскад включает в себя составной инвертор на транзисторных
ключах ТК1 и ТК2. Когда ТК1 находится в проводящем состоянии, а ТК2
заперт, на выходе вентиля имеет место логическая 1 (рис. 5.31 я). Когда ТК2
находится в проводящем состоянии, а ТК1 заперт, на выходе вентиля при-
сутствует логический 0 (рис. 5.310. В статических режимах, как отмечалось,
потребляемый ток соответствует спецификации вентиля. Сложней дело об-
стоит на стадии переключения (рис. 5.310, когда оба ключа в определенный
момент оказываются в проводящем состоянии. Это объясняется невозмож-
ностью быстрого выхода транзисторных ключей из режима насыщения, ко-
торый типичен для ТТЛ-схем. В ЭСЛ-схемах транзисторы работают в линей-
ных режимах, что определяет меньшую инерционность ключевых элементов.
В интервале времени, когда оба ключевых элемента ТК1 и ТК2 находятся
в проводящем состоянии от шины питания к опорной плоскости, протекают
сквозные токи, значение которых могут на порядок и более превосходить токи
потребления в статических режимах. Таким образом, более точное значение
перепада тока А/в выражении (5.13) определяется сквозными токами, типич-
ными для конкретной серии микросхем. К сожалению, этот параметр не все-
гда указан в документации на микросхемы, что требует проведения экспери-
ментальных исследований или тонких моделей выходных каскадов для рас-
чета значений этих токов. Перепад сквозного тока принято обозначать А/, и
помехи, вызванные им, часто определяются как «помехи типа дельта /». Си-
туация усугубляется при одновременном синхронном переключении венти-
лей на плате. При этом суммарный сквозной ток увеличивается пропорцио-
нально числу переключаемых вентилей, что способствует возникновению син-
хронных коммутационных помех в шине питания и заземления.
Значительное падение напряжения на шине питания может привести к
тому, что напряжение на вентиле будет меньше допустимого, а это приведет
к нарушению работы цифрового узла. Рассмотрим изменение токов потреб-
ления /SB и напряжения питания Исс вентиля (рис. 5.32).
Состояние
статической
единицы
Состояние
статического
нуля
Рис. 5.31. Токи выходных каскадов ТТЛ-схем в различные стадии переключения
Стадия
переключения
из “0” в “1” или
из “1”в“О”
402
Глава 5. Система питания и заземления
Рис. 5.32. Диаграмма работы шины питания
Работоспособность микросхемы
гарантируется только в том случае,
когда ее напряжение питания не
выходит за поле допуска (рис. 5.32).
Во время протекания по шине пи-
тания сквозных токов падение на-
пряжения на ее индуктивности оп-
ределяется выражением (5.13), ко-
торое для расчетов имеет вид:
^sb^^sb-^-’ мВ, (5.16)
где £SB — индуктивность шины питания,
нГн; А/— перепад сквозного тока, мА; /г —
фронт сигнала, нс.
Падение напряжения KSB может оказаться столь велико, что напряжение
питания Исс микросхемы выйдет за поле допуска на интервале времени А/
(рис. 5.32), на котором снижается помехозащищенность микросхемы, и ее
работоспособность не гарантируется. В этом случае требуется скорректировать
технические решения при проектировании платы таким образом, чтобы глу-
бина провала напряжения на выводах питания микросхемы не выходила за
пределы допуска.
Подскок напряжения заземления
Возвращаясь к работе выходного каскада ТТЛ-вентиля (рис. 5.316), видим,
что ток протекает по контуру, содержащему распределенные индуктивности
цепи заземления. Аналогично рассмотренному выше, падение напряжения в
цепи заземления при изменении тока в ней определяется соотношением:
J'GND - A^NDy-’ (5.17)
где £gnd — индуктивность контура на участке протекания токов заземления; Д/ — сквоз-
ной ток; /г — фронт сигнала.
Следует отметить, что все положения, относящиеся к понятиям индук-
тивности, которые рассматривались во второй главе, полностью примени-
мы для контуров, в которых протекают токи потребления (от источника в
нагрузку) и токи заземления (от нагрузки к источнику). Поэтому индуктив-
ность контура протекания токов потребления будет зависеть от частичной
собственной индуктивности путей протекания токов потребления, частич-
ной собственной индуктивности путей протекания токов заземления и вза-
имной индуктивности между этими путями. Все эти три параметра шины пи-
тания могут изменяться в зависимости от конструкции платы и выводов
корпусов микросхем. Напомним, что под «шиной питания» понимается со-
вокупность проводников питания и заземления, образующих контур тока.
5.2. Помехи в шине питания и их устранение
403
В рассматриваемом примере выходной сигнал вентиля при переключении
из 1 в 0 теперь есть сумма напряжения логического перепада и напряжения,
которое генерируется на индуктивности, включенной между цепью опорно-
го уровня внутри микросхемы и печатного узла. Если этот суммарный сигнал
достаточно велик, то он может быть воспринят последующим вентилем как
логическая 1, что приведет к сбою в работе узла. Это явление, которое в об-
щем виде рассматривалось ранее, при работе цифровой микросхемы называ-
ется подскоком напряжения заземления. На рис. 5.33 иллюстрируется эффект
подскока напряжения заземления. На выход драйвера поступает сумма напря-
жений с выходного каскада и напряжения, которое развивается на индуктив-
ности системы заземления. Это добавочное напряжение, которое развивает-
ся только во время переключения, есть подскок напряжения заземления. Видно,
что в этом случае результирующий сигнал достигает порога срабатывания с не-
которым запаздыванием относительно неискаженного сигнала, что привно-
сит дополнительную системную задержку в работу цифрового узла.
На графике горизонтальная линия показывает нижний пороговый уро-
вень. Действие подскока напряжения заземления может быть интерпрети-
ровано одним или обоими вариантами.
1 . Для некоторой точки во времени сигнал оказывается большим по ам-
плитуде на уровень подскока напряжения заземления.
2 . Эффективное время распространения сигнала снижается, поскольку
порог достигается позже номинального времени, т. е. увеличивается
системная задержка.
При значительном числе одновременно переключающихся микросхем эф-
фект подскока напряжения заземления усиливается, поскольку растут токи
переключения.
Простая модель для анализа подскока напряжения заземления показана
на рис. 5.34.
Внешние компоненты, нагружающие выходы микросхемы, имеют емко-
стные нагрузки С1— Сп. Емкостная нагрузка определяет ее заряд согласно ра-
венству
Q = v/c.
j t Напряжение
Сигнал
/ Результирующий сигнал
Подскок напряжения заземления
Нижний уровень порога
переключения
Время
Рис. 5.33. Влияние подскока напряжения заземления на функционирование
цифрового узла
404
Глава 5. Система питания и заземления
Переключающиеся
выходы
Статичный выход
Заземление платы
Рис. 5.34. Модель для анализа подскока заземления
Необходимый заряд увеличивается, если увеличивается напряжение или
уменьшается емкость. Окружение микросхемы и путь возвратного тока имеют
некоторую индуктивность (отмеченную на рисунке, как £1, £2 и £3). Индук-
тивность £1 — это индуктивность проводников присоединения кристалла к
выводу микросхемы, £2 — индуктивность вывода и места соединения мик-
росхемы с платой, включая контактную панель, если она установлена, £3 —
индуктивность трассы возвратных токов между выводом микросхемы и точ-
кой, где эта трасса соединяется с шиной заземления устройства или с источ-
ником питания. Увеличенный заряд многих емкостей, подключенных к ли-
нии передачи, вызывает значительный ток разряда при переключении из 1
в 0 и, соответственно, увеличенный уровень подскока напряжения заземления.
Хотя бросок тока весьма короткий по времени, но его амплитуда достаточ-
но велика и может вызвать переключение других микросхем на плате.
Для минимизации индуктивности £2 не следует применять коммутаци-
онные панели для установки микросхем на плату. При установке панели
напряжение подскока может возрасти на 100 % [107]. По сравнению с ин-
дуктивностью панели индуктивность трассы £3 существенно меньше, а при
рациональном конструировании МПП ею можно пренебречь.
Методы предотвращения помех по шине питания и заземления
При проектировании цифровых узлов следует уделять серьезное внимание
методам предотвращения помех в шинах питания и заземления. Существую-
щие методы можно разделить на две основные группы: во-первых, конст-
рукторский метод снижения полного сопротивления шины питания, во-вто-
рых, схемно-конструкторский метод снижения отрицательного действия сквоз-
ных токов, провала напряжения питания и подскока напряжения заземления.
Каждая группа методов реализуется различными способами. Кроме того, нельзя
забывать одно из основных правил проектирования цифровых узлов — быст-
родействие микросхем должно быть минимально необходимым для выполнения
заданных функций. Это приведет к уменьшению крутизны фронта сигнала и,
следовательно, скорости изменения тока в шине питания, что положительно
скажется на работоспособности цифрового узла.
5.2. Помехи в шине питания и их устранение
405
Метод, основанный на уменьшении полного сопротивления шины пи-
тания, реализуется на этапе конструкторского проектирования печатной
платы. Для этого могут быть применены следующие способы:
• уменьшение собственной частичной индуктивности проводников пи-
тания и заземления посредством увеличения площади их сечения;
• изменение формы сечения проводников шины питания на более плос-
кую;
• сокращение длины шины питания;
• увеличение емкости проводников питания относительно плоскости
возвратных токов (заземления) за счет увеличения площади.
Следует помнить, что для однородной линии передачи произведение LC
удельных параметров — величина постоянная. Это справедливо так же для
шины питания, как совокупности проводников питания и опорного напря-
жения. Поэтому увеличение емкости проводников питания относительно про-
водников опорного напряжения соответствует снижению индуктивности
шины питания.
Снижение собственной частичной индуктивности проводников может
быть достигнуто с учетом следующих особенностей [41]. При равных пло-
щадях сечения плоский проводник имеет меньшую индуктивность. Физи-
чески это объясняется более свободным распределением условных нитей тока
по сечению проводника, в итоге снижается взаимная индуктивность между
ними, и в результате уменьшается ин-
дуктивность проводника. Изменение
индуктивности за счет изменения фор-
мы сечения уединенного проводника
показано на рис. 5.35.
Для снижения индуктивности ши-
ны питания в печатных платах и дру-
гих конструкциях должны выполнять-
ся в виде совместного расположения
проводников питания и возвратных то-
ков, разнесенных на минимальное расстояние. Поскольку в этом случае
направление токов в проводниках противоположное, то и электромагнит-
ные поля вокруг них также имеют противоположные направления. Проис-
ходит частичная компенсация этих полей, и чем ближе сигнальная линия к
возвратной, тем полнее компенсация и меньше суммарная индуктивность.
В МПП имеются наиболее широкие возможности по снижению индуктив-
ности шины питания, поскольку, как показано выше при обсуждении струк-
туры МПП, для подвода питания и для возвратных токов отводятся отдель-
ные слои, имеющие максимальные размеры для разрабатываемой платы. При
этом, чем ближе слой питания к слою возвратных токов (заземления), тем
больше емкость образованного планарного конденсатора. Роль этого кон-
денсатора в работе системы питания рассмотрена ниже. Как правило, пла-
нарный конденсатор только частично способен снизить полное сопротивле-
ние шины питания. Для высокоскоростных приложений требуется установка
^1 $2 ^1 < Ц < Ц /^<4
ezzzzzzzzzzj VZZZZZZ2 Хф/
Sv L1 S2, L2 S3, L3
Рис. 5.35. Изменение индуктивности
проводника за счет изменения формы
его сечения (5р S2, S3 — площади
сечения проводников 1, 2, 3)
406
Глава 5. Система питания и заземления
дополнительных развязывающих конденсаторов. По технической реализа-
ции этот способ полностью совпадает с приемами, относящимися ко второму
методу, и детально будет рассмотрен ниже.
Второй метод предотвращения помех реализуется на этапе схемотехни-
ческого проектирования введением дополнительных емкостей в шину пи-
тания путем установки развязывающих конденсаторов, место и способ ус-
тановки которых определяются на этапе конструирования платы. Это весь-
ма действенный метод снижения помех по шинам питания и обеспечения
целостности сигнала и требований ЭМС, но его эффективность в очень боль-
шой мере зависит от топологии печатного монтажа, типа, способа и места
установки конденсатора. Эти вопросы требуют детального рассмотрения.
5.2.2. Развязывающие конденсаторы
в электронных модулях
Контуры токов в цепочке вентилей
В электронных модулях логические вентили соединены каскадно, как по-
казано на рис. 5.36. Уточним понятие контуров тока для группы вентилей.
Рис. 5.36. Два каскадно
соединенных вентиля
Логические цепи проектируются таким
образом, чтобы уровни логических сигна-
лов находились внутри известного и опре-
деленного диапазона. Это позволяет пос-
ледующему вентилю четко определять ло-
гический уровень на выходе предыдущей
схемы. Если помехи будут соизмеримы с
уровнями полезных сигналов, то возмож-
ны ошибки при переключении микросхем
и при работе цифрового устройства.
Возможные причины возникновения
помех на входе вентиля были рассмотре-
ны ранее (например, помехи отражения,
перекрестные помехи), но существуют еще
факторы, которые существенно влияют на
функционирование электронных модулей. Рассмотрим ситуацию, которая
представлена на рис. 5.37. Две логических схемы соединены последовательно
и питаются от одного источника питания Ксс. Как отмечалось, проводники
питания и заземления имеют некоторую индуктивность, которая включена
между источником питания или опорной плоскостью и соответствующими
выводами микросхем. Эти индуктивности определяются конструкцией то-
пологических элементов печатной платы: потенциальными слоями, контак-
тными площадками, металлизированными отверстиями и переходами меж-
ду контактными площадками, конструкцией выводов микросхем и т. п. Сле-
дует помнить, что токи всегда текут в замкнутом контуре, проходя по всем
компонентам, которые встречаются в этом контуре.
5.2. Помехи в шине питания и их устранение
407
Рис. 5.37. Фрагмент пути тока при логическом 0 на выходе первой микросхемы
Рис. 5.38. Развязывающий конденсатор как средство устранения пути тока через
индуктивность
Для устранения отрицательного действия индуктивностей около микро-
схемы устанавливается развязывающий конденсатор (рис. 5.38), соединяя
проводник питания и заземления. В этом случае импульсный ток в процес-
се переключения микросхем преимущественно будет протекает через кон-
денсатор, а не через индуктивности проводников, соединяющих микросхе-
му с источником питания. Кроме этого, существенно сокращается площадь
контура тока и, следовательно, снижается уровень помехоэмиссии.
Выбор типов и количества развязывающих конденсаторов
Несмотря на принципиальную простоту варианта с установкой развязы-
вающих конденсаторов, остаются вопросы, которые необходимо решить при
проектировании печатного узла: какова емкость конденсатора? можно ли
408
Глава 5. Система питания и заземления
использовать более одного конденсатора? где располагать конденсаторы? как
соединять их с платой?
Некоторые ответы на эти вопросы можно найти на рис. 5.39. Из приве-
денных кривых видно, что заряд, поддерживаемый штатным источником
питания микросхем, не может обеспечить необходимую длительность пере-
пада напряжения. Установка развязывающего конденсатора большой емкости
позволяет улучшить ситуацию. Временной отрезок, на котором поддержи-
вается высокий уровень заряда, относительно всех остальных вариантов
развязки максимальный, но за счет своих габаритов и паразитных индуктив-
ных параметров этот конденсатор обладает худшими свойствами по поддер-
жанию крутого фронта сигнала. Конденсатор меньшей емкости обладает
большим быстродействием, но его заряда не хватает на длительное поддер-
жание тока. Планарный конденсатор, образованный плоскостями питания
и заземления в структуре МПП, обладает относительно небольшой емкос-
тью, но минимальными паразитными индуктивными параметрами, что по-
зволяет ему практически отслеживать фронт сигнала, но, к сожалению, весьма
короткий интервал времени. По мере создания новых материалов с высокой
диэлектрической проницаемостью и малой толщиной удается увеличивать
емкость планарного межслойного конденсатора, и его эффективность воз-
растает. Планарные конденсаторы обладают высоким быстродействием и
малой индуктивностью; они имеют ряд особенностей:
• заряд распределен по плоскостям и не локализован;
• при больших габаритах планарного конденсатора, его эффективность
будет определяться только зоной, ограниченной дистанцией, которую
проходит сигнал в диэлектрике конденсатора за время фронта [99];
например, если задержка распространения сигнала в материале FR4
составляет примерно 1 нс на 150 мм, то при фронте 1 нс зона эффек-
тивного заряда будет не более 150 мм.
В общем случае, чем ближе кривая заряда конденсатора к форме переход-
ного процесса, тем предпочтительней этот конденсатор.
Напряжение
Заряд, необходимый для нормальной работы
/ZY / Заряд, поддерживаемый
П \/ Л \ источником питания
п Л 1 X /\ Заряд от блокировочного
' II 1\/ \ / \ конденсатора большой
II / V V \ емкости
11 I Л /\ \ Заряд от конденсатора
Ц / /1 / ----г---меньшей емкости, но
I / / \ / \ \ более быстрого
1/7 / \___\ Заряд от планарного
II/ /у V V конденсатора
и// \\Время
Рис. 5.39. Иллюстрация влияния различных типов развязывающих конденсаторов
при переключении вентиля
5.2. Помехи в шине питания и их устранение
409
На форму кривой заряда основное отрицательное воздействие оказыва-
ют индуктивность корпуса конденсатора и индуктивность его выводов. Чем
меньше суммарная индуктивность конденсатора, тем предпочтительней он
для использования в качестве развязывающего. Кроме этого, при размеще-
нии конденсатора на плате на удалении от микросхемы начинает сказываться
время задержки распространения в соединительных печатных проводниках
и их индуктивность. Более жесткие ограничения вызываются индуктивны-
ми параметрами конденсаторов и соединительных проводников.
Исходя из рассмотренных выше соображений, напрашивается комплек-
сное решение. Например, можно установить конденсатор достаточно боль-
шой емкости (например, 0,1 мкФ) для накопления значительного заряда и
конденсатор малой емкости (например, 0,01 или 0,001 мкФ) для быстрого
заряда и разряда. Одновременно при высоком быстродействии потребуется
использовать планарный конденсатор. Например, для кремниевых кристаллов
требуется применение конденсаторов с малым последовательным сопротив-
лением (ESR-конденсаторов), монтируемых на поверхность платы от 0,01 мкФ
до 0,1 мкФ, устанавливаемых параллельно. Дополнительный конденсатор
0,001 мкФ, параллельный этим конденсаторам, позволяет отфильтровать вы-
сокочастотные помехи (более 100 МГц).
Полное сопротивление развязывающего конденсатора
Полное сопротивление z идеального конденсатора дается выражением:
1 1
гс-(оС-2л/С’ Ом’ (518)
где f — частота, Гц; С — емкость конденсатора, Ф.
Это соотношение представлено на графике в виде зависимости полного со-
противления от частоты (в логарифмическом масштабе), имеющей вид прямой
Рис. 5.40. Частотная характеристика полного сопротивления идеального и реального
развязывающего конденсаторов
410
Глава 5. Система питания и заземления
Рис. 5.41. Эквивалентная
схема реального
развязывающего
конденсатора
на рис. 5.40. Прямая линия показывает, что для
идеального конденсатора обеспечивается очень
большое полное сопротивление на низких час-
тотах и очень малое на высоких частотах.
Однако в реальном конденсаторе присутствует
некоторая индуктивность, которая определяется
конструкцией корпуса и выводов конденсатора,
а также способом его установки на плату. Поверх -
ностно-монтируемые компоненты имеют мини-
мальную индуктивность от 5 до 10 нГн, а осталь-
ные типы навесных конденсаторов имеют большие значения индуктивности.
Поэтому реальный конденсатор может быть замещен схемой, представленной
на рис. 5.41, в виде последовательно соединенных идеальных компонентов —
емкости и индуктивности.
Полное сопротивление реального конденсатора определяется суммой ком-
плексных сопротивлений индуктивности (jwL) и емкости (1//соС= -j/озС). У
индуктивности реактивная составляющая zL = со£, а у емкости zc = -1/соС.
Активные составляющие комплексного сопротивления идеальной емкости и
индуктивности равны нулю. Тогда полное сопротивление последовательно со-
единенной идеальной емкости индуктивности определяется выражением:
Z = |^ + *c| =
2лД----—
2л/С
(2л/)2£С-1
(5.19)
Эта функция представлена кривой на рис. 5.40. Следует отметить, что на
низких частотах она совпадает с характеристикой идеального конденсато-
ра, а после минимума происходит резкий рост полного сопротивления из-
за влияния индуктивности. Минимум достигается на частоте саморезонан-
са, которая определяется из условия равенства нулю числителя формулы, а
именно:
f 1
/=^Ж- г“’ (5 М)
где L — индуктивность конденсатора, Гн; С — емкость конденсатора, Ф.
Это частота собственного резонанса конденсатора. На этой частоте пол-
ное сопротивление конденсатора теоретически равно 0, а при наличии по-
терь оно очень близко к 0.
В качестве примера рассчитаем частоту собственного резонанса для кон-
денсатора с параметрами С= 0,01 мкФ и L = 10 нГн. Подставив эти значе-
ния в формулу (5.20), получаем
/ =---7=----1 =16 10б. п,
глуюю-’хо^гю-6 ц’
5.2. Помехи в шине питания и их устранение
411
Таким образом, частота резонанса выбранного конденсатора составляет 16 МГц.
После резонанса (зарезонансная область) полное сопротивление конден-
сатора растет и имеет индуктивный характер (формально фаза сдвигается по-
ложительно в зарезонансной области). В зарезонансной области конденса-
тор может быть использован, пока его полное сопротивление все еще оста-
ется малым, и индуктивный характер не проявляется в полной мере.
Выбор числа конденсаторов
Сколько развязывающих конденсаторов действительно необходимо?
Можно приблизительно оценить необходимую суммарную емкость конден-
саторов, полагая, что они обеспечивают питание микросхемы зарядом в те-
чение некоторого периода времени Д/. За это время напряжение на конден-
саторе будет понижаться на Д И, т.к. его заряд, протекающий через микросхему,
изменяется на Д£):
ДИ= Д(2/ С, (5.21)
где С — емкость конденсатора.
Каков ток /, проходящий через микросхему? Очевидно, это зависит от спе-
цификации микросхемы и будет меняться в зависимости от сигнала, прохо-
дящего через нее. Можно приблизительно оценить предполагаемую мощность
Употребления микросхемы, которая зависит от напряжения Ии среднего тока,
проходящего через нее. Учитывая среднюю мощность потребления, значе-
ние среднего тока потребления микросхемы будет равно:
I = P/V. (5.22)
Этот ток должен поддерживаться разрядом некоторого конденсатора
емкостью С за время Д/, что определяется уравнением:
Если известен допуск 8 на уровень напряжения питания, например, 5 %
(0,05) от номинального значения, то это уравнение позволяет связать вре-
мя и емкость развязывающего конденсатора, а именно:
И2
Д/ = 8С—. (5.24)
Если известно значение развязывающей емкости, то легко определить
время поддержания напряжения питания в пределах допуска. В том случае,
если задано время провала напряжения питания, то легко определить зна-
чение необходимой емкости развязывающих конденсаторов:
1 РА/
Ф, <5.25>
где А/ — время, за которое происходит разряд конденсатора, с; 8 — допуск на напряжение
питания; С — емкость развязывающего конденсатора, Ф; V— напряжение питания, В; Р —
мощность рассеивания микросхемы, Вт.
412
Глава 5. Система питания и заземления
Например, если для типовой микросхемы памяти мощность потребления
1 Вт, напряжение питания 3,3 Вс 5 % разрешенной пульсацией, то можно
вычислить общее значение развязывающей емкости:
С = —----!^- ДГ = 2 ДГ, ф.
0,05 3,32
Если, например, конденсатор должен среагировать на изменение напря-
жения быстрее, чем за 10 мкс, то емкость конденсаторов должна быть, по
крайней мере, 2x10 мкс = 20 мкФ. В противном случае провал напряжения
питания превысит 5 %.
Почему бы не использовать один конденсатор 20 мкФ для обеспечения
требуемой развязки? В реальных конденсаторах есть контур, сформирован-
ный связью между выводами конденсатора и выводами микросхемы. Эта ин-
дуктивность контура, находящаяся в последовательном соединении с иде-
альной емкостью, заставляет полное сопротивление реального конденсато-
ра увеличиваться с ростом частоты.
На рис. 5.42 показан график замеренного полного сопротивления развя-
зывающего конденсатора 0603. Индуктивность определяется контуром, ко-
торый образован соединениями в плате между выводами конденсатора. При
увеличении частоты достигается точка саморезонанса. Выше этой частоты
полное сопротивление начинает увеличиваться и совершенно не зависит от
его емкости. Оно будет ассоциироваться только с индуктивностью контура.
Если мы хотим уменьшить полное сопротивление развязывающих конден-
саторов в более высоком диапазоне частоты, нам необходимо уменьшить ин-
дуктивность ассоциированных с ними контуров, а не увеличивать емкость.
Измерение d
петли Z
Рис. 5.42. Измеренное полное сопротивление развязывающего конденсатора 0603
емкостью 1 нФ
5.2. Помехи в шине питания и их устранение
413
Ключевой особенностью развязывающих конденсаторов является то, что на
высокой частоте полное сопротивление связано исключительно с индуктивно-
стью контура, которую можно назвать последовательной эквивалентной ин-
дуктивностью. Снижение полного сопротивления развязывающего конденсатора
на высокой частоте означает снижение индукции контура полного пути — от
контактных площадок микросхемы до развязывающего конденсатора.
Измеренная индуктивность контура шести развязывающих конденсато-
ров типа 0603 с различными значениями емкости показана на рис. 5.43. Их
полное сопротивление на низкой частоте радикально отличается, так как они
имеют различный порядок значений емкости. Однако на высокой частоте их
полное сопротивление одинаковое, потому что у них единая топология на
тестируемой плате.
Единственный путь снижения полного сопротивления развязывающего кон-
денсатора на высокой частоте — это снижение самоиндукции его контура.
Наилучшие пути снижения индуктивности контура развязывающего кон-
денсатора следующие:
1) поддерживать короткие межслойные отверстия путем установки шин
питания и заземления близко к поверхности;
2) использовать конденсаторы малых размеров;
3) использовать очень короткие соединения между контактными площад-
ками конденсатора и межслойными отверстиями к ниже находящим-
ся слоям;
4) использовать параллельно несколько конденсаторов.
Если индукция контура взаимодействует с одним развязывающим конден-
сатором и их индуктивность составляет 2 нГн, с максимально разрешенной ин-
дуктивностью 0,1 нГн, тогда требуется как минимум 20 параллельных конден-
саторов для получения эквивалентной требуемой индуктивности контура.
Для снижения индуктивности должна быть разработана топология соеди-
нения развязывающего конденсатора и микросхемы с учетом отмеченных
выше рекомендаций.
Частота, Г ц
Рис. 5.43. Измеренная индукция контура шести различных конденсаторов типа 0603
с емкостью, варьируемой от 10 пФ до 1 мкФ, но с одинаковой топологией
414
Глава 5. Система питания и заземления
Я
L
Рис. 5.44. Эквивалентная
схема конденсатора
с ПЭС
Последовательное эквивалентное сопротивление (ESR)
Для снижения уровня передаточной функции при резонансе применяют
конденсаторы с последовательным сопротивлением R. Эквивалентная схе-
ма подобного конденсатора (рис. 5.44) содержит последовательно включенную
емкость, индуктивность и сопротивление, которое
называется: «последовательное эквивалентное со-
противление» (ПЭС — ESR). Это сопротивление
очень мало и обычно не учитывается в эквивален-
тных схемах, также как и сопротивление параллель-
ное емкости, которое моделирует токи утечки.
ПЭС играет важную роль в применении развя-
зывающих конденсаторов. Пиковое значение пе-
редаточной функции при резонансе обратно про-
порционально значению ПЭС. Отмеченный выше
эффект достаточно очевиден. Менее очевидно вли-
яние ПЭС на поведение общего полного сопротив-
ления распределенной системы питания, когда
значительное число конденсаторов включено параллельно. В этом случае при
анализе следует учитывать следующие моменты:
1) при использовании двух конденсаторов с близкими частотами собствен-
ных последовательных резонансов, собственный резонанс системы из
этих конденсаторов будет лежать между резонансными частотами от-
дельных конденсаторов;
2) минимальное значение функции полного сопротивления меньше, чем
ПЭС, и это значение уменьшается по мере сближения частот саморе-
зонанса конденсаторов;
3) с позиций полного сопротивления системы небольшое значение ПЭС
лучше, чем предельно низкое значение.
Уточним эти положения.
Рассмотрим конденсатор емкостью С, с индуктивностью L и ПЭС, рав-
ном R. Индуктивность должна учитывать собственную индуктивность кон-
денсатора, индуктивность его выводов, а также индуктивность соответству-
ющих топологических элементов установки конденсатора. Полное сопротив-
ление в этом случае определяется по следующей формуле:
z = R + j^L + 1 / jcoC = R +j(co£ - 1 / coQ,
где co — круговая частота, co = 2л/
Резонанс появляется, по определению, когда коэффициент при /равен
0. Тогда резонансная частота будет равна
(5.26)
1
(0=-7=
(5/27)
и полное сопротивление будет равно R, т. е. последовательному эквивален-
тному сопротивлению.
5.2. Помехи в шине питания и их устранение
415
Рассмотрим теперь набор из п идентичных конденсаторов, соединенных
параллельно. При этом параметры каждого конденсатора будут Сп = пС, Ln =
= L/n, Rn = R/n. Полное сопротивление системы теперь определяется как
R .( &L 1
“ + 7---------- •
п у П (ЯПС J
(5.28)
Рис. 5.45. Включение
конденсаторов
параллельно
Резонансные частоты системы определяются, как и ранее, при равенстве
О коэффициента при у, т. е. из условия со£/л =1/соиС. Видно, что значение ре-
зонансной частоты не изменилось, и оно равно резонансной частоте одиноч-
ного конденсатора. Параллельное соединение конденсаторов не изменяет ре-
зонансную частоту, но это увеличивает емкость, снижает индуктивность и
ПЭС по сравнению с одиночным конденсатором. Как видно из (5.28), па-
раллельной установкой определенного числа развязывающих конденсаторов
можно регулировать полное сопротивление системы питания на резонанс-
ных частотах. Результирующая кривая полного сопротивления имеет тенден-
цию к расширению по сравнению с одиночным конденсатором.
На печатной плате, как правило, используется боль-
шое число развязывающих конденсаторов одинакового
значения. Однако в реальной ситуации эти конденса-
торы имеют определенный допуск на значение емкос-
ти, и поэтому их, строго говоря, нельзя считать полно-
стью идентичными. Рассмотрим два конденсатора раз-
личной емкости, включенных параллельно (рис. 5.45).
Примем для простоты Rl = R2 = R, а также Cl > С2 и
£1 > L2. Это означает, что частота резонанса конден-
сатора 1 меньше частоты резонанса конденсатора 2.
Определим полное сопротивление набора конденса-
торов. Реактивная составляющая сопротивления конден-
саторов определяется соотношениями:
ТЛ 1 1
х} - со£1------, хэ = (tiL2-------
1 (ОСГ 1 2 <оС2
(5.29)
Тогда их полные сопротивления определяются по формулам:
= R +jx{, z2 = R+jx2.
При параллельном включении конденсаторов полное сопротивление
набора будет:
1 _(R + jxi)(R + Jxl)
_L + _L 2R+j(xl+x2)
Zi г2
(5.30)
416
Глава 5. Система питания и заземления
Из этого выражения можно определить действительный и мнимый чле-
ны, умножая числитель и знаменатель на (27? — j(xx+ х2)). Тогда действительная
часть будет
7?^2(т?2 -x1x2) + (^i + х2)2
47?2 +(jq + х2)2
(5.31)
а мнимая —
Im(z) =
(xi +*2)(^2 +хл)
47?2 +(xj +х2)2
(5.32)
Определим амплитуду и фазу полного сопротивления. Амплитуда сопро-
тивления:
|г| = ^Re(^)2+ 1т(г)2,
(5.33)
а фаза:
9 = tan 1
lmU) |
ReW ’
(5.34)
Кривая полного сопротивления как функция частоты показана на рис. 5.46.
Резонанс появляется (по определению), когда мнимый член равен нулю.
Это также есть точка, в которой фазовый угол равен 0. Полное сопротивле-
ние в этой точке равно действительному члену в выражении полного сопро-
тивления.
Рис. 5.46. Полное сопротивление двух параллельных конденсаторов различной емкости
5.2. Помехи в шине питания и их устранение
417
Мнимый член равен 0 при двух условиях:
= — х2, А2 = — х}х2. (5.35)
Первое условие представляет полюс между частотами саморезонанса двух
конденсаторов и определяет частоту системного резонанса (антирезонанса)
между частотами резонанса.
Предполагая R малым, второе условие появляется только тогда, когда или
хр или х2 малы, что справедливо для окрестностей соответствующих частот
резонанса. Кроме этого, х} и х2 должны быть противоположных знаков, по-
скольку значение R2 должно быть положительным. Поэтому точка систем-
ного резонанса должна быть между частотами резонанса отдельных конден-
саторов, и она не должна быть равна им (кроме предельного случая R = 0).
Из рассмотренного видно, что частоты системного резонанса различны, кроме
случая, когда ПЭС равно 0. В этих точках полное сопротивление уменьша-
ется до значения R.
На частоте саморезонанса конденсатора С1 х} = 0 и амплитуда полного
сопротивления в точке х{ = 0 равна
|г|=»Ец.
1 1 '|4К1+^
Это меньше А для любого положительного (R > 0) значения R. В пределе
оно равно R для R « х2 и равно R/2 при R » х2. Результат будет аналогичен
для частоты саморезонанса конденсатора 2 при х2 = 0.
Минимальное значение функции полного сопротивления достигается на
частоте, отличной от частоты системного собственного резонанса, а также
отличной от частот саморезонанса конденсаторов. Это значение будет меньше
ПЭС (R) при соединении двух конденсаторов в параллель. Частоты собствен-
ных резонансов сближаются при увеличении числа конденсаторов.
Если Xj = —х2 = х, тогда Im(z) будет равна 0 по определению. Точка анти-
резонанса будет расположена между частотами саморезонанса конденсато-
ров 1 и 2. В этой точке полное сопротивление будет:
R х2
z = — +—•
2 2R
(5.36)
При малых значениях R оно обратно пропорционально R и может иметь
очень большое значение, если R « х. Это дает очень высокое полное сопро-
тивление около анти-резонансной частоты. Если R имеет значение от 1 до 10,
то это значение полного сопротивления может поддаваться управлению. Но
если R » х, тогда полное сопротивление на частоте антирезонанса пример-
но равно R/2. Это меньше, чем полное сопротивление в точке резонанса. Важно,
что пик полного сопротивления в точке антирезонанса может быть меньше, чем
полное сопротивление в точке резонанса.
Как может быть, что z = R в точке минимума резонанса и в точке максимума
при системном антирезонансе? Напомним, что Нравно ПЭС конденсатора.
14 1527
418
Глава 5. Система питания и заземления
Поэтому кривая полного сопротивления (приближенно) будет иметь неко-
торое плато с уровнем z = R на антирезонансной частоте, если:
R=x{ = -x2. (5.37)
Это очень существенный вывод. При малом значении ПЭС для получе-
ния плоской кривой полного сопротивления Xj и х2 должны быть малы на
антирезонансной частоте. Это означает, что частоты резонансов конденса-
торов должны быть расположены близко друг к другу, и, следовательно, при
малом ПСЭ требуется больше конденсаторов для получения относительно
плоской кривой полного сопротивления [110].
Низкое значение ПСЭ требует большего числа конденсаторов для достижения
сглаженного отклика. Небольшое увеличение ПСЭ приводит к сглаживанию
кривой отклика с более управляемым антирезонансным пиком.
Более сложные случаи с несколькими конденсаторами ESR могут быть про-
анализированы только с применением ЭВМ. На рис. 5.47 показана расчетная
кривая зависимости полного сопротивления от частоты для наборов из 100,
150 и 200 конденсаторов с ПЭС 0,01 Ом [4]. Видно, что в этом случае сфор-
мирована относительно плоская часть характеристики в диапазоне частот от
1 до 1000 МГц. При увеличении числа конденсаторов значение полного сопро-
тивления на плато снижается. При одном и том же числе конденсаторов даль-
нейшее снижение значения ПЭС приведет к некоторому снижению значения
полного сопротивления на плато, но при этом появятся небольшие резонан-
сные пики. Поэтому значение ПЭС должно быть обосновано.
Проблема выбора типа и количества конденсаторов в большей мере от-
носится к системо- и схемотехническим этапам проектирования печатных
узлов. Но ее понимание необходимо конструктору для обоснования реше-
ний при трассировке платы.
Можно спроектировать систему питания с заданной формой кривой пол-
ного сопротивления на всех частотах с малым числом конденсаторов. Для
этого необходимо следовать следующим основным рекомендациям:
Рис. 5.47. Расчетная кривая зависимости полного сопротивления набора конденсаторов
от частоты и количества конденсаторов: 7—100 конденсаторов;
2—150 конденсаторов; 3 — 200 конденсаторов
5.2. Помехи в шине питания и их устранение
419
• внимательно выбирать тип конденсаторов, принимая во внимание зна-
чение емкости и частоту саморезонанса;
• применять планарные конденсаторы, образованные потенциальными
слоями МПП;
• предпочтительней применять широкий диапазон значений емкостей
конденсаторов и частот саморезонанса (определенных с учетом индук-
тивности конденсатора и его монтажа), чем применять конденсаторы
с одинаковыми емкостями;
• выбирать конденсатор с некоторым относительно небольшим значе-
нием ПСЭ.
Расположение конденсатора не особенно важно, если выполнены требо-
вания по минимизации индуктивности, за исключением случаев, когда бы-
стродействие требует располагать конденсаторы с учетом скорости распро-
странения сигнала (примерно 150 мм/нс).
Для уменьшения низкочастотных помех (ниже 1 кГц), вызванных системой
питания, на входе печатной платы следует установить помехоподавляющий
фильтр, например, в виде электролитического конденсатора емкостью от 10
до 100 мкФ [107]. Если на плате используется стабилизатор напряжения, то
конденсатор ставится непосредственно около его вывода, с которого снима-
ется напряжение для питания компонентов. Этот конденсатор не только сни-
жает низкочастотные помехи, но и является источником экстра-токов, потреб-
ляемых при коммутационных процессах.
Для повышения эффективности фильт-
рации следует использовать нерезонансные
поверхностно монтируемые ферритовые по-
мехоподавляющие элементы. Они распола-
гаются последовательно с источником пи-
тания между ними и помехоподавляющими
конденсаторами. Ферритовый элемент по-
давляет высокочастотные компоненты по-
мех в цепи питания (рис. 5.48).
10 мкФ
Рис. 5.48. Включение
помехоподавляющих элементов
в цепь питания
Размещение и подключение конденсаторов
Минимизация индуктивности развязывающего конденсатора и его при-
соединительных проводников является одним из важнейших требований.
Исходя из этого, конденсатор должен устанавливаться на минимально воз-
можном расстоянии от вывода питания и заземления микросхемы. Но где
должны быть расположены два конденсатора? Ответ здесь единственный.
Конденсатор малой емкости должен быть расположен на минимальном рас-
стоянии от микросхемы, поскольку он обеспечивает быстрый заряд/разряд.
При этом надо учитывать два основных момента:
• развязывающий конденсатор должен располагаться ближе к плоско-
сти опорного напряжения,
• индуктивность топологических элементов, по которым протекает ток
от конденсатора к выводу микросхемы, должна быть минимальная.
14:
420
Глава 5. Система питания и заземления
Контактные
конденсатор
Широкий и
короткий
проводник
Рис. 5.49. Расположение контактных площадок конденсаторов и металлизированных
отверстий
Рассмотрим некоторые практические варианты установки развязываю-
щих конденсаторов. Например, следует использовать широкие, короткие
проводники между металлизированным отверстием и контактной площад-
кой конденсатора; металлизированное отверстие должно быть рядом с кон-
тактной площадкой (рис. 5.49) [107].
Проводники, проходящие от выводов питания к слою питания (или к раз-
вязывающему конденсатору), должны быть широкими, насколько возмож-
но. Это уменьшает последовательную индуктивность проводников и, следо-
вательно, уменьшает потери напряжения от источника питания до вывода
питания и снижает уровень подскока напряжения заземления.
Способ подключения конденсатора должен обеспечить минимизацию по-
мех, проникающих в плоскость опорного напряжения. Это может быть обес-
печено минимизацией индуктивности пути протекания тока при переклю-
чении микросхемы. Следует учитывать, что металлизированное отверстие име-
ет большую удельную индуктивность, чем линия передачи. Можно реко-
мендовать следующие приемы для минимизации индуктивности при подклю-
чении конденсатора:
• выбирать конденсаторы с низкой собственной индуктивностью и ин-
дуктивностью выводов;
• использовать контактные площадки и металлизированные отверстия
с минимальной индуктивностью;
• рассмотреть возможность применения планарного конденсатора в ка-
честве малого быстрого конденсатора;
• располагать малый конденсатор ближе к плоскости опорного напря-
жения;
• отдавать предпочтение применению компонентам для монтажа на по-
верхность.
На рис. 5.50 показаны примеры установки поверхностно-монтируемых раз-
вязывающих конденсаторов. Индуктивность соединения снижается по мере
сокращения длины присоединительных проводников и увеличения числа па-
раллельных металлизированных переходных отверстий. Максимальный эф-
фект по снижению индуктивности достигается использованием технологии
микропереходов.
Обобщая рекомендации по монтажу развязывающих конденсаторов,
можно сформулировать следующие правила:
5.2. Помехи в шине питания и их устранение
421
Очень
Хорошо Лучше лучше вариант
Пример установки компонентов типа 0508, 0612 и т.п.
Рис. 5.50. Примеры установки поверхностно-монтируемых развязывающих
конденсаторов
• для снижения индуктивности соединений их длина должна быть как
можно меньше, а ширина — больше;
• следует уменьшать расстояние между плоскостью расположения сиг-
нальных проводников и плоскостью опорного напряжения; это при-
водит к сокращению длины металлизированных отверстий и сниже-
нию площади контура протекания токов; напомним, что парциальная
индуктивность металлизированного отверстия составляет приблизи-
тельно 1 нГн на 1 мм длины отверстий;
• если металлизированные отверстия несут противоположные по направ-
лению токи (например, питание и заземление), то эти отверстия сле-
дует располагать на минимально возможном расстоянии друг от друга
(желательно не более 1 мм); например, два металлизированных отвер-
стия диаметром 0,5 мм, по которым протекают токи противоположно-
го направления, имеют суммарную индуктивность 1,2 нГн при рассто-
янии между ними 5 мм, и только 0,53 нГн при расстоянии между ними
1 мм [109];
• по возможности металлизированные отверстия следует располагать па-
раллельно для протекания тока в одном направлении; снижение ин-
дуктивности будет больше, если эти отверстия расположить дальше друг
от друга;
• увеличение диаметра металлизированного отверстия приводит к сни-
жению его парциальной индуктивности; однако отверстия большого ди-
аметра требуют увеличения диаметра кругового зазора в потенциальных
слоях, что, как было показано выше, ухудшает параметры ЭМС и це-
лостности сигнала цифрового узла.
Традиционные требования проектирования печатных плат требуют на-
личия термической защиты контактных площадок за счет наличия узкой
422
Глава 5. Система питания и заземления
перемычки между ними и проводниками. При этом предполагается, что ус-
ловия групповой пайки будут лучше, поскольку перемычка препятствует от-
воду теплоты с контактной площадки. С позиций целостности сигнала по-
добная перемычка обладает повышенной индуктивностью и вносит неодно-
родность в параметры линии. Эта рекомендация может быть применима
только для плат с установкой выводов компонентов в сквозные металлизи-
рованные отверстия, а для плат с микропереходами только при необходимо-
сти. При этом следует искать компромисс между требованиями целостнос-
ти сигнала и ЭМС и технологичностью.
5.2.3. Минимизация полного сопротивления
системы питания
Одно из основных требований при проектировании быстродействующих
цифровых узлов заключается в минимизации полного сопротивления рас-
пределенной системы питания для высоких частот в спектре сигнала.
Идеальный отклик
При размещении развязывающих конденсаторов на плате создается рас-
пределенная система питания с высоким полным сопротивлением на посто-
янном токе, но низким на высоких частотах. Если рассматривать только одну
микросхему, невозможно оптимизировать всю систему питания. Для этого
необходим комплексный подход, учитывающий работу всех микросхем в
составе печатного узла.
Для идеальной системы можно предположить бесконечно большое пол-
ное сопротивление на постоянном токе и предельно низкое полное сопро-
тивление на всех других частотах (рис. 5.51). Кривая показывает приближе-
ние, к которому следует стремиться.
Рис. 5.51. Идеализированная зависимость полного сопротивления системы питания
от частоты
5.2. Помехи в шине питания и их устранение
423
Планарный конденсатор
Существенную роль в снижении полного сопротивления распределенной
системы питания играет планарный конденсатор, который создается в МПП
за счет расположения слоев питания и опорного напряжения на минималь-
ном расстоянии друг от друга. Чем меньше будет расстояние между слоями,
тем больше будет емкость подобного конденсатора. Это расстояние опреде-
ляется минимальной толщиной диэлектрических прокладок, выпускаемых
промышленностью, которые могут быть установлены между потенциальными
слоями в процессе производства МПП. Основным достоинством планарного
конденсатора является его малая индуктивность. Определим емкость, которую
можно реализовать в планарном конденсаторе:
8,85-е,. х5х(и-1)
С =------пФ, (5.38)
а
где £г — относительная диэлектрическая проницаемость диэлектрического материала (ег = 1
для воздуха, гг = 4 для FR4); S — область перекрытия плоскостей, м2; d — расстояние между
слоями, м; п — число слоев.
При расчете следует учитывать уменьшение площади перекрытия за счет
отверстий и других топологических элементов.
Достижимая емкость для типичных значений составляет 1,6...5,3 нФ/дм2.
Учитывая, что у планарного конденсатора практически отсутствует индуктив-
ность, характеристика его полного сопротивления будет приближаться по
форме к характеристике идеального конденсатора (зависимость 1, рис. 5.52/7).
Для примера в табл. 5.3 приведены значения удельной емкости и распределен-
ной индуктивности планарного конденсатора, выполненного в структуре МПП
на стеклотекстолите (FR4, ег~ 4) при различной толщине диэлектрика [9].
Анализируя частотные зависимости полного сопротивления набора кон-
денсаторов (рис. 5.52/7), можно видеть, что применение планарного конден-
сатора еще больше расширяет частотный диапазон малых значений полно-
го сопротивления. На рис. 5.526показана суммарная кривая для набора кон-
денсаторов, из которых видно, что полное сопротивление менее 200 мОм будет
выдерживаться на всем диапазоне частот, начиная с 1 кГц.
Однако данный вариант имеет и определенные недостатки. Все ниспа-
дающие кривые определяют емкостный характер конденсаторов, все вос-
ходящие кривые определяют индуктивный характер конденсатора, а точ-
ки пересечения кривых определяют частоту резонанса последовательного
Таблица 5.3
Удельная индуктивность и емкость плоского конденсатора
Толщина диэлектрика, мкм Индуктивность, пГн/квадрат Удельная емкость, пФ/см2
102 130 35
51 65 70
25 32 140
424
Глава 5. Система питания и заземления
а
б
Рис. 5.52. Полное сопротивление системы питания: а — содержащей (7) планарный
конденсатор 950 пФ, (2) 200 конденсаторов по 0,01 мкФ и (5) 20 конденсаторов
по 50 мкФ; б — суммарная характеристика
ZC-контура. Во всех резонансных точках полное сопротивление бесконеч-
но мало (теоретически), а передаточная функция — максимальна по моду-
лю. На этих частотах помехи будут распространяться по всей системе без со-
кращения длины путей возвратных токов, что приведет к повышенному уров-
ню излучения от платы.
Множество развязывающих конденсаторов
Расширить частотный диапазон малых значений полного сопротивления
системы питания можно за счет установки на плату множества развязываю-
щих конденсаторов. Рассмотрим вариант установки на плату п одинаковых
развязывающих конденсаторов. Пусть п = 200, емкость С каждого конден-
сатора 0,01 мкФ, индуктивность L — 1 нГн. Эти конденсаторы, установлен-
ные около выводов микросхем, можно считать соединенными параллельно.
В этом случае комбинированный эффект набора конденсаторов на систему
питания будет соответствовать применению одного конденсатора суммар-
ной (Сх п) емкости 2,0 мкФ, но при индуктивности только 0,05 нГн (L/ri),
5.2. Помехи в шине питания и их устранение
425
Рис. 5.53. Изменение значений полного сопротивления конденсаторов: 1 — идеальный
одиночный; 2 — реальный одиночный; 3 — множество параллельных конденсаторов
поскольку конденсаторы соединены параллельно. Характеристика этого мно-
жества конденсаторов показана на рис. 5.53 одновременно с характеристи-
кой идеального одиночного конденсатора 0,01 мкФ и реального конденса-
тора 0,01 мкФ с соответствующими индуктивными параметрами. Отметим,
что набор из 200 конденсаторов имеет ту же резонансную частоту, что оди-
ночный конденсатор.
Отметим два момента. Во-первых, полное сопротивление набора конден-
саторов на некоторой частоте значительно ниже, чем одиночного конден-
сатора. Во-вторых, диапазон частот, в котором полное сопротивление ниже
определенного уровня, значительно шире для множества конденсаторов, что
соответствует основной стратегии снижения полного сопротивления. Таким
образом, одно из решений снижения полного сопротивления системы питания
в широком частотном диапазоне заключается в использовании большого числа
параллельных конденсаторов.
Расширение диапазона номиналов конденсаторов
Для снижения полного сопротивления на более низких частотах можно до-
бавлять конденсаторы различных номиналов. Например, добавить 20 конден-
саторов по 50 мкФ. Но большие конденсаторы будут иметь значительную ин-
дуктивность — до 20 нГн на конденсатор. Общий эффект при этом показан на
рис. 5.54 совместно с характеристикой 200 конденсаторов емкостью 0,01 мкФ
каждый. Видно дальнейшее расширение частотного диапазона с малым зна-
чением полного сопротивлением. Если объединить фрагменты двух характе-
ристик для значений полного сопротивления, например, не более 1 Ом, то
частотный диапазон будет простираться от 100 Гц до 3 ГГц. Таким образом,
расширяя номенклатуру конденсаторов, можно получить более широкий диа-
пазон малых полных сопротивлений системы питания.
426
Глава 5. Система питания и заземления
Рис. 5.54. Частотная зависимость полного сопротивления: 1 — 200 параллельных
конденсаторов по 0,01 мкФ, 10 нГн; 2—20 конденсаторов по 50 мкФ, 20 нГн
5.3. Рекомендации по проектированию
шин питания и заземления
Система питания
Приведем сводку основных рекомендаций, детально обоснованных в на-
стоящей главе. Это позволит уменьшить полное сопротивление системы
распределенного питания в широком диапазоне частот, снизит до минималь-
ного уровня помехи по шинам питания и заземления, минимизирует подскок
напряжения заземления.
• Для быстродействующих цифровых систем следует применять МПП,
которые обеспечивают разделение слоев питания и сигнальных слоев.
• Слои питания и слои опорного напряжения должны образовывать пла-
нарный конденсатор; для увеличения его емкости эти слои должны на-
ходиться на минимально возможном расстоянии (желательно, чтобы
толщина диэлектрика между двумя слоями была не более 0,125 мм).
• Между металлизированным отверстием и контактной площадкой кон-
денсатора должны применяться широкие, короткие проводники.
• Металлизированное отверстие должно быть рядом с контактной пло-
щадкой, а еще лучше — непосредственно в контактной площадке (мик-
ропереход).
• Проводники, проходящие от выводов питания к слою питания (или к
развязывающему конденсатору), должны быть широкими, насколько
возможно. Это уменьшает последовательность индуктивности провод-
ников и поэтому уменьшает потери напряжения от источника пита-
ния до вывода питания: аналогичное требование должно выдерживаться
и для системы заземления, что снижает возможность сильного подскока
напряжения заземления.
5.3. Рекомендации по проектированию шин питания и заземления
427
• Для устранения помех в системе питания применяют развязывающие
конденсаторы.
• Размещают развязывающие конденсаторы так близко, насколько воз-
можно к выводам питания и заземления микросхем.
• Для расширения частотного диапазона малых значений полного со-
противления системы питания номенклатура развязывающих конден-
саторов должна быть широкой.
• Следует избегать применения контактных панелей для корпусов мик-
росхем, когда это возможно.
• Необходимо уменьшать число выходов микросхем, которые могут пе-
реключаться одновременно, и/или распределяют эти выходы равно-
мерно по всей плате.
• Если возможно, располагают (или назначают) переключающиеся вы-
воды ближе к выводу заземления.
• Целесообразно в микросхемах и соединителях размещать выводы пи-
тания и заземления рядом друг с другом: при этом полная индуктив-
ность будет уменьшена взаимной индуктивностью, поскольку токи в
этих выводах противоположны по направлению.
• Металлизированные отверстия для соединения контактной площадки
конденсаторов со слоем питания и заземления должны иметь максималь-
ный диаметр для минимизации индуктивности соединения конденса-
тора; этот эффект можно получить при использовании ряда параллель-
ных металлизированных отверстий относительно малого диаметра,
расположенных на максимально большом расстоянии друг от друга.
• Металлизированные отверстия, соединяющие контактные площадки
конденсатора со слоями питания и заземления, по которым протека-
ют токи противоположного направления, должны располагаться на
минимальном расстоянии друг от друга.
• Для минимизации индуктивности развязывающих конденсаторов пред-
почтение следует отдавать поверхностно-монтируемым компонентам.
• Следует использовать ESR-конденсаторы. Значение ПЭС должно быть
менее 400 мОм.
• Каждый вывод заземления корпуса микросхемы должен быть связан
с плоскостью опорного напряжения индивидуально.
Если система питания аналого-цифрового узла имеет одну и ту же плос-
кость заземления для аналоговых и цифровых узлов, то может иметь место
нежелательное взаимодействие между двумя типами цепей. В этом случае
следующие предложения помогут уменьшить уровень помех:
• следует использовать отдельные слои питания для аналогового и циф-
рового фрагмента узла,
• слои возвратных токов (опорного напряжения) должны располагать-
ся рядом со слоями питания,
• размещение аналоговых и цифровых компонентов, а также сигналь-
ных проводников между ними, допускается только поверх соответству-
ющих участков возвратной плоскости,
428
Глава 5. Система питания и заземления
Аналого-
цифровая
микросхема
иа
Зазор между
зонами
Участок
плоскости
возвратных
токов
цифровой
системы
Участок
плоскости
возвратных
токов
аналоговой
системы
Общий
участок
заземления
Рис. 5.55. Пример возможного разделения плоскости возвратных токов на зоны
• развязку между цифровой и аналоговой системой питания можно вы-
полнить за счет ферритовых помехоподавляющих элементов.
Рекомендуется разделять цифровые и аналоговые слои питания, что можно
обеспечить дополнительным введением слоев питания. В отдельных случа-
ях такое разделение можно получить корректным разделением на участки
одной плоскости возвратных токов. Пример такого разделения на локаль-
ные зоны показан на рис. 5.55 [107]. Напомним, что в этом случае сигналь-
ные проводники цифровых сигналов и аналоговых сигналов должны прохо-
дить строго над соответствующими участками плоскости возвратных токов.
Глава 6
Дифференциальная пара
в печатном монтаже
6.1. Передача дифференциальных сигналов
6.1.1. Основы дифференциальной передачи сигналов
Построение систем обработки цифровой информации на основе специально
сформированных дифференциальных сигналов является одним из наиболее
перспективных направлений в развитии цифровой техники [117]. Это отно-
сительно новое направление в создании сверхбыстродействующих систем.
Первый стандарт ANSI/EIA-644-1995, рассматривающий основные вопросы
описания и применения дифференциальной передачи сигналов, появился
только в 1995 году. Дальнейшие разработки показали, что дифференциальная
передача сигналов становится многоцелевым стандартным интерфейсом,
позволяющим передавать информацию со скоростью 100 Мбит/с и выше,
вплоть до гигабитного уровня. Устройства на основе дифференциальной пе-
редачи сигналов отличаются высокими показателями по быстродействию,
параметрам ЭМС и целостности сигнала [3]. Для передачи дифференциаль-
ных сигналов в печатном монтаже используется дифференциальная пара — две
линии передачи с сильной связью между ними. Как будет показано ниже, чем
больше электромагнитная связь между линиями, тем выше качество переда-
чи сигнала.
Для передачи дифференциального сигнала используются два выхода драй-
вера с целью подачи сигналов по двум линиям передачи. Одна линия несет
один бит информации, а другая — его дополнение. Информационный сиг-
нал заключен в разнице между сигналами в этих линиях.
Передача дифференциального сигнала по паре линий имеет следующие
основные преимущества перед передачей сигнала по одиночной линии:
• скорость изменения тока di/dt на выходах драйвера значительно ниже,
чем у драйвера одиночной линии; это определяет меньший уровень из-
лучения от платы и потенциально меньший уровень электромагнит-
ных помех;
• дифференциальный усилитель в приемнике может иметь большее уси-
ление, чем усилитель одиночного сигнала;
430
Глава 6. Дифференциальная пара в печатном монтаже
• распространение дифференциального сигнала по сильно связанной
дифференциальной паре более устойчиво к перекрестным помехам и сосре-
доточенным неоднородностям в возвратном проводнике;
• распространяемый по дифференциальной паре дифференциальный
сигнал будет менее подвержен коммутационным помехам, так как каждый
сигнал имеет свой возвратный путь в окружающей среде; точность выдер-
живания временных соотношений выше, чем в одиночной линии.
Помимо преимуществ использования дифференциального сигнала суще-
ствуют и недостатки. Самый существенный из них заключается в возмож-
ности возникновения электромагнитных помех (ЭМП) (так называемая са-
моэмиссия). В составе дифференциального сигнала присутствуют компонен-
ты дифференциального и общего вида и, если этот сигнал должным образом
не сбалансирован или не отфильтрован, то присутствует сигнал общего вида,
которые в конечном итоге будут служить причиной ЭМП.
Второй недостаток заключается в том, что для передачи дифференциаль-
ного сигнала необходимо вдвое больше сигнальных линий, чем для переда-
чи одиночного сигнала. И, наконец, недостаточно проработанная теория пе-
редачи дифференциального сигнала усложняет практическую реализацию
дифференциальных пар.
Анализ показывает, что в настоящее время более 90 % плат имеют контро-
лируемые волновые сопротивления, а в ближайшие годы ожидается, что более
90% плат будут иметь дифференциальные пары. Одна из самых используемых
сигнальных схем — это схема низковольтных дифференциальных сигналов1.
При передаче сигналов по одиночной линии передачи между сигнальным и
возвратным проводниками существует некоторое напряжение, которое прини-
мают за сигнал в этой линии. При передаче сигнала по дифференциальной паре
вдобавок к двум сигналам в каждой линии появляется еще и напряжение, яв-
ляющееся разностью между потенциалами двух сигнальных проводников. Это
дифференциальное напряжение, или дифференциальный сигнал. На рис. 6.1
показано, как эти напряжения измеряются в дифференциальной паре.
В LVDS два проводника используются для переноса отдельного бита ин-
формации. Каждый сигнал изменяется в пределах от 1,125 В до 1,375 В и
переносится по отдельной линии передачи. Напряжение одиночного сигнала,
Рис. 6.1. Измерение напряжений сигналов в дифференциальной паре
1 В англоязычной литературе —LVDS
6.1. Передача дифференциальных сигналов
431
Рис. 6.2. Напряжения типичного дифференциального сигнала в LVDS: 1 — Кр 2 — И2
измеренное между сигнальным и возвратным проводниками в каждой ли-
нии, показано на рис. 6.2.
На приемном конце присутствует напряжение Vx первой линии и И2 вто-
рой линии. Дифференциальный усилитель измеряет дифференциальное на-
пряжение между этими двумя линиями и выводит дифференциальный сигнал'.
(6.1)
где И, — сигнал первой линии относительно общего возвратного проводника; И2 — сигнал
второй линии относительно общего возвратного проводника.
Помимо специально созданного дифференциального сигнала, который
несет информацию, существует некоторый сигнал общего вида, который оп-
ределяется как среднее напряжение, появляющееся в обеих линиях:
Исотт=|(И+(Л2)- (6.2)
Эти определения дифференциального сигнала и сигнала общего вида приме-
нимы для всех сигналов. Любой произвольный сигнал, генерируемый в паре ли-
ний передач, может быть полностью и единственным образом описан комби-
нацией компонентов общего и дифференциального сигналов.
Одиночный сигнал на каждой линии относительно возвратного провод-
ника может быть восстановлен из дифференциального сигнала и сигнала
общего вида:
— ^comm Kliff ’ ^2 — ^comm — KlifT• (6.3)
432
Глава 6. Дифференциальная пара в печатном монтаже
Время, нс
Рис. 6.3. Компоненты общего и дифференциального сигналов LVDS:
1- ^2-
1’ z’ comm’ din
Из рис. 6.3 видно, что дифференциальный сигнал в каждой линии изме-
няется от — 0,25 В до + 0,25 В, т. е. его суммарное изменение составляет 0,5 В.
Следует обратить внимание на присутствие в каждой линии очень большой
компоненты сигнала общего вида в виде постоянного напряжения с ампли-
тудой 1,25 В. Это в два с половиной раза больше, чем дифференциальный
сигнал.
В идеальных условиях сигнал общего вида в каждой линии строго оди-
наковый и не будет содержать информацию. При этом он не будет влиять на
целостность сигнала или работу системы. К сожалению, как мы увидим ниже,
даже небольшое расхождение в конструкции одной из линий дифференци-
альной пары при практической реализации печатной платы может привес-
ти к появлению переменной составляющей в сигнале общего вида. Это при-
ведет к возникновению двух очень важных проблем:
• если значение сигнала общего вида становится слишком большим,
входной усилитель дифференциального приемника может перенасы-
титься; это приведет к неточному чтению дифференциального сигнала;
• любое изменение сигнала общего вида может послужить причиной
порождения чрезмерных электромагнитных помех.
Термины «дифференциальный» и «общий» всегда относятся к свойствам сиг-
нала и никогда к свойствам дифференциальной пары линий передачи. Кор-
ректность применения этих терминов позволяет более точно понять осно-
вы построения дифференциальной пары и управления её параметрами.
6.1.2. Конструкция дифференциальной пары
Дифференциальная пара состоит из двух линий передачи. Каждая линия
может представляет собой, например, обычную полосковую или микропо-
лосковую линию передачи, рассмотренную в предыдущих главах книги. Рас-
положенные в непосредственной близости друг от друга, две линии образу-
6.1. Передача дифференциальных сигналов
433
1
2
3
4
Рис. 6.4. Наиболее распрост-
раненные виды поперечных
сечений дифференциальных
пар: 1 — компланарная; 2 —
микрополосковая; 3 — по-
лосковая; 4 — развернуто-
связанная полосковая
ют дифференциальную пару. В принципе, из
любых двух линий передачи можно образовать
дифференциальную пару. Подобно тому, как су-
ществует ряд конфигураций поперечных сечений
для одиночных линий передач, так же есть раз-
новидности поперечных сечений и для диффе-
ренциальных пар линий передач. На рис. 6.4
представлены наиболее распространенные виды
поперечных сечений дифференциальных пар,
реализуемых на печатных платах.
Хотя, в общем случае, любые две линии пе-
редачи могут образовать дифференциальную
пару, существует пять особенностей, которые
важны при передаче широкополосных сигналов.
Перечислим их.
1. Наиболее важная особенность дифференциальной пары состоит в том,
что она должна иметь однородное поперечное сечение по всей длине и
обеспечивать постоянное волновое сопротивление для разных сигна-
лов. Это гарантирует минимальные отражения и искажения сигнала.
2. Вторым важным свойством является то, что временная задержка линий
должна быть согласована так, чтобы фронт и спад сигналов в отдель-
ных линиях были точно и четко определены. Любое различие во вре-
менной задержке между двумя линиями или иное рассогласование
между ними приведут к тому, что дифференциальный сигнал будет
преобразован в сигнал общего вида.
3. Обе линии передачи должны быть конструктивно полностью идентич-
ны. Ширина сигнальных проводников и толщина диэлектрического
слоя между двумя линиями должны быть одинаковы. Эта свойство
называется симметрией. Не должно быть никаких асимметрий, вроде
наличия контактной площадки для тестирования или сужений толь-
ко на одной линии и т.п. Любая асимметрия преобразует дифферен-
циальные сигналы в сигнал общего вида.
4. Линии в паре должны иметь одинаковую длину. Это поможет поддер-
живать одинаковую временную задержку и минимизировать расфази-
ровку сигналов.
5. Электромагнитная связь между двумя проводниками не обязательна,
но важное преимущество дифференциальных пар — помехоустойчи-
вость — теряется, если ее нет. Связь между двумя линиями передачи в
составе дифференциальной пары позволит дифференциальным сиг-
налам распространяться с меньшими помехами, возникшими от дру-
гих активных цепей, чем одиночным сигналам. Чем больше связь, тем
более устойчивыми будут дифференциальные сигналы к внешним
возмущениям и несовершенствам конструкции.
Пример дифференциальной пары линий передачи, с распространяющимся
дифференциальным сигналом, показан на рис. 6.5. В этом примере сигнал
434
Глава 6. Дифференциальная пара в печатном монтаже
Положение вдоль линии
1
О
Положение вдоль линии
1
О
diff 1 2 Положение вдоль линии
Рис. 6.5. Дифференциальная пара с сигналом, распространяющимся по каждой линии,
и дифференциальным сигналом между двумя линиями
в одной линии изменяется от 0 до 1 В, а другой — от 1 до О В. Так как сигналы
распространяются вдоль длинных линий передачи, они имеют некоторое рас-
пределение напряжения по длине, как, например, показанное на рисунке.
Дифференциальный сигнал по определению есть разность сигналов в
линии: — И2); он показан на рис. 6.5 в виде перепада в 2 В от —1 до +1 В.
В то же время существует сигнал общего вида, который равен 0,5( Vx + И2).
В нашем примере сигнал общего вида будет равен 0,5(1 + 1) = 0,5 В, и его ам-
плитуда будет постоянна вдоль всей линии.
Наиболее важной особенностью дифференциальной пары является нали-
чие полного сопротивления, которое встречает на своем пути дифференциальный
сигнал. Оно называется дифференциальным полным сопротивлением.
6.1.3. Дифференциальное полное сопротивление
несвязанных линий
Полное сопротивление, согласно определению, — это отношение напря-
жения сигнала к току сигнала. Настоящая формулировка является базисом
для расчёта дифференциального полного сопротивления. Для успешного ре-
зультата очень важно правильно определить напряжение и ток сигнала.
Наиболее простой для анализа является ситуация, когда между двумя
линиями, образующими дифференциальную пару, нет электромагнитной
связи. Целесообразно на первом этапе рассмотреть именно такой случай, а
потом учесть связь между линиями и определить её влияние на значение
дифференциального полного сопротивления.
Слабая связь линий передачи в составе дифференциальной пары обеспе-
чивается их достаточным разносом, например, размещением с зазором, рав-
ным не менее удвоенной ширины сигнальных проводников. В этом случае
6. 1. Передача дифференциальных сигналов
435
каждая линия может рассматриваться как одиночная линия, и она будет
обладать волновым сопротивлением Z, равным, как правило, 50 Ом. Как
рассмотрено в предыдущих главах книги, волновое сопротивление линии
передачи определяется как отношение напряжения ^падающей волны к току
^падающей волны. Следовательно, ток /f, проходящий по сигнальному про-
воднику и по пути возврата, рассчитывается по следующему уравнению:
т Kf
Л=рА, (6.4)
где — амплитуда падающей волны, В; Z — волновое сопротивление одиночной линии
передачи, Ом.
Направление токов в линиях передачи соответствует направлениям вы-
ходных токов драйвера: при передаче логической 1 выходной ток вытекает
из драйвера, а при передаче логического 0 выходной ток втекает в драйвер.
Например, когда сигнал от 0 до 1 В подается на одну линию, и в то же время
сигнал от 1 до 0 В подается на другую линию, то в каждой из линий появля-
ется токовая петля. В первой линии ток будет равен 1= 1/50 = 0,020 А, и он
протекает от начала к концу линии и возвращается по возвратному пути. Во
второй линии ток также будет равен 20 мА, но направление его протекания
будет противоположно. Он будет протекать от возвратного проводника к сиг-
нальному, в котором будет продвигаться от конца к началу линии.
Фронт дифференциального сигнала, распространяющийся по линии, —
это дифференциальный сигнал между двумя проводниками линии. Размах
Kdiff дифференциального сигнала в два раза превышает напряжение на лю-
бой линии: Kdiff = 2 Vv В нашем примере этот размах составляет 2 В, и фронт
дифференциального сигнала распространяется к концу линии. В то же вре-
мя, если наблюдать за сигнальными проводниками линий, то становится ясно,
что ток 20 мА в одной линии течет от драйвера к нагрузке, а в другой — от
нагрузки к драйверу, т. е. образована некоторая горизонтальная токовая петля
из двух сигнальных линий. В действительности в возвратной плоскости су-
ществуют возвратные токи от каждого сигнального проводника, но поскольку
их направление противоположно, они компенсируют друг друга. Поэтому
однородность возвратной плоскости при дифференциальном сигнале не столь
важна, как в одиночной линии. При нарушении равенства амплитуд дифферен-
циальных сигналов в возвратной плоскости возникает нескомпенсированный ток,
амплитуда которого будет равна разности сигнальных токов.
По определению полного сопротивления, оно рассчитывается для диф-
ференциального сигнала по формуле:
Zdiff=^ = ^X = 2Z, (6.5)
7f yf
где Zdiff — дифференциальное полное сопротивление, т. е. сопротивление, которое встре-
чает дифференциальный сигнал при распространении вдоль линии; Kdiff— размах диффе-
ренциального сигнала; 1{ — ток сигнала в одиночной линии передачи; — напряжение
436
Глава 6. Дифференциальная пара в печатном монтаже
между сигнальным проводником и плоскостью возвратных токов одиночной линии; Z —
волновое сопротивление одиночной линии.
Видно, что дифференциальное полное сопротивление при слабой связи линий
передачи в составе дифференциальной пары равно удвоенному волновому сопро-
тивлению одиночной линии. Если сопротивление каждой линии равно 50 Ом,
то дифференциальное полное сопротивление пары будет 100 Ом.
При передаче дифференциального сигнала по дифференциальной паре
в случае рассогласования линий с нагрузкой возникнут помехи отражения,
которые приведут к нарушению целостности сигнала. Как было показано в
главе 4, для устранения помех отражения необходимо согласовывать линии
передачи, приравнивая сопротивление нагрузки к волновому сопротивлению
линии. В случае дифференциальной пары один из способов устранения от-
ражения сигнала заключается в установке согласующего резистора на кон-
цах обеих линий. Значение сопротивления согласующего резистора, при
котором отражения отсутствуют, должно быть равно сопротивлению, кото-
рое встречает дифференциальный сигнал при распространении вдоль линии,
а именно:
Рис. 6.6. Сопротивление
между каждой линией и
путём возврата тока в
дифференциальной паре
и эквивалентное сопро-
тивление между двумя
линиями сигнала
/Jt = Zdiff=2Z. (6.6)
Дифференциальное сопротивление также может
рассматриваться как эквивалентное сопротивление
двух одиночных линий, как показано на рис. 6.6.
Каждый сигнал встречает при распространении по
дифференциальной паре одновременно сопротивле-
ние двух линий. Поэтому эквивалентное сопротив-
ление двух линий, или дифференциальное сопротив-
ление, представляет последовательную комбинацию:
Zdiff = Z + Z=2Z. (6.7)
В реальной ситуации два важных фактора услож-
няют анализ дифференциальной пары в отличие от
рассмотренного выше варианта её построения на
слабо связанных линиях передачи. Во-первых, до-
бавляется эффект от связи двух линий, а во-вторых,
усиливается роль сигнала общего вида, его генера-
ции и способов управления.
6.1.4. Влияние связи между линиями
При наличии связи между линиями появляются взаимные электрические
параметры на единицу длины: CmZ и М{. (по умолчанию эти элементы отве-
чают матрицам параметров SPICE). При этом собственные частичные ем-
костные параметры будут изменены за счет перехвата части силовых линий
соседней трассой, поэтому емкость линии на единицу длины С; будет умень-
шаться, а Ст1 будет увеличиваться. Однако нагрузочная емкость Ц = Cz + Cm/
существенно не изменится. На рис. 6.7 показаны емкостные параметры С7и
6.1. Передача дифференциальных сигналов
437
Сечение линий
Эквивалентная схема
1 - 2
s
Рис. 6.7. К определению емкостных параметров связанных линий
Таблица 6.1
Значение емкостных параметров связанных полосковых линий
Зазор s между проводниками в значениях их ширины w С,, пФ/см Ст„ пФ/см Ср пФ/см
5= w 1,22 0,16 1,38
s= 2w 1,28 0,04 1,32
5= 3w 1,31 0,01 1,32
Примечание. Материал основания FR4, ширина проводников 0,125 мм.
Ст/ связанных линий, а в табл.6.1 приведены численные значения емкост-
ных параметров в зависимости от зазора между проводниками полосковой
линии с волновым сопротивлением 50 Ом [3, 4].
Индуктивные параметры Ln и Мг будут изменяться при сближении трасс
следующим образом: £и останется практически неизменной, a Mt будет уве-
личиваться. При зазоре, равном утроенной ширине проводника, эти значе-
ния составляют до 1%, что пренебрежимо мало. По мере сближения линий
электромагнитная связь между проводниками увеличивается. При зазоре, рав-
ном ширине проводника, она составляет в относительных единицах Cm//Cz
или менее 15%.
Когда линии разнесены, волновое сопротивление одной линии переда-
чи не зависит от волнового сопротивления другой линии и зависит только
от её удельной собственной емкости и диэлектрических свойств материала
основания платы:
(6.8)
где с — скорость света в свободном пространстве; Cz — емкость линии передачи на еди-
ницу длины; ег — относительная диэлектрическая проницаемость материала основания
платы.
Присутствие соседней линии изменяет волновое сопротивление первой
линии за счет эффекта близости и, если на вторую линию подать потенциал
0 В, т. е. возвратный и соседний сигнальный проводники находятся под од-
ним потенциалом, то волновое сопротивление первой линии будет определяться
нагрузочной емкостью, т. е. Cz = Сг Поскольку при сближении трасс нагрузочная
емкость возрастает, волновое сопротивление линии 1 уменьшается.
438
Глава 6. Дифференциальная пара в печатном монтаже
Работа дифференциальной пары должна быть рассмотрена в двух вари-
антах. В первом, по линиям передаются оппозитные сигналы (как показано
на рис. 6.5), во втором случае по линиям передаются одинаковые сигналы.
Рассмотрим их детально.
Передача оппозитных сигналов
При передаче оппозитного сигнала дифференциальная пара передает
сигнал с размахом Kdiff = 2 V\ =2Kf. На фронте Kf падающей волны в первой
линии будет возникать ток через Сн за счет dVJdt между линией 1 и возвратной
плоскостью. Кроме этого, возникает ток из линии 1 к линии 2 за счет изме-
нения напряжения между ними dV^/dt.
Ток в одной сигнальной линии при наличии связи будет определяться
как [3]:
/l=vzr(c/^+cm'^]=vzr'^(с,+2ст/)- (6.9)
Но С, = Ct + Ст/, тогда
Л = v 'r+ст/). (6.Ю)
В этих формулах: v — скорость распространения сигнала в линии; /г —
фронт сигнала; Cz — емкость на единицу длины между прямым и возвратным
проводниками линии передачи; Kf — напряжение падающей волны между сиг-
нальным и возвратным проводниками; CmZ — емкость между сигнальными
проводниками на единицу длины; Kdiff—дифференциальное напряжение меж-
ду сигнальными проводниками; С1 — нагрузочная емкость одной линии.
Из формулы (6.10) видно, что при сближении линий сигнальный и воз-
вратный токи в одной линии будут возрастать из-за увеличения взаимной
емкости Ст/.
Если при неизменном напряжении увеличивается ток, то это вызвано
снижением волнового сопротивления одиночной линии при передаче по
соседней связанной линии оппозитного сигнала.
Передача одинаковых сигналов
Запитаем линию 2 точно таким же сигналом, как и первую линию. В этом
случае при одинаковых потенциалах на линиях взаимная емкость между ними
равна нулю, т. е. Ст1 = 0. Поэтому нагрузочная емкость линии 1 будет равна
только собственной емкости линии (Сх = Cz), т. е. драйвер линии 1 будет «ви-
деть» меньшую емкость для заряда выходным током, чем в первом случае.
В этом случае ток в линии 1 будет:
Ix=vt, (6.11)
dt dt
где v — скорость распространения сигнала в линии; Гг — фронт сигнала; Иг — напряжение
падающей волны между сигнальным и возвратным проводниками; С1 — емкость на еди-
6.1. Передача дифференциальных сигналов
439
ницу длины между прямым и возвратным проводниками линии передачи; Ct — нагрузоч-
ная емкость одной линии; Ст/ — емкость между сигнальными проводниками на единицу
длины.
Из формулы видно, что при подаче на линии дифференциальной пары оди-
наковых сигналов ток одной линии уменьшается, что вызвано увеличением вол-
нового сопротивления линии.
Обобщение режимов работы
Обобщая рассмотрение режимов работы, видим, что волновое сопротив-
ление одной линии вблизи другой изменяется в зависимости от способа запит-
ки второй линии, а именно:
• если вторая линия находится в искусственно низком состоянии и со-
единена с возвратной плоскостью, то волновое сопротивление линии
будет близко к волновому сопротивлению несвязанной линии;
• если вторая линия несет сигнал, оппозитный относительно первой
линии, то волновое сопротивление первой линии будет меньше вол-
нового сопротивления несвязанной линии;
• если вторая линия имеет сигнал, аналогичный сигналу первой линии,
то волновое сопротивление первой линии будет выше волнового со-
противления несвязанной линии.
Изменение волнового сопротивления первой линии при увеличении за-
зора между проводниками дифференциальной пары при различных вариантах
подачи сигнала во вторую линию (ширина проводника 0,125 мм) показано
на рис. 6.8 [3]. Из графика видно, что при зазоре, равном утроенной шири-
не проводника, линии оказываются практически не связанными.
При применении дифференциальной пары по линиям передаются оппо-
зитные сигналы, и поэтому при сближении проводников волновое сопротив-
ление одной линии будет уменьшаться, и максимальное изменение составит,
между проводниками,кратное ширине проводника
Рис. 6.8. Изменение волнового сопротивления одной линии при увеличении зазора
между проводниками: 1 — вторая линия подключена к возвратной плоскости;
2 — на трассах противоположные сигналы; 3 — на трассах одинаковые сигналы
440
Глава 6. Дифференциальная пара в печатном монтаже
как видно из графика, примерно 12 %. Дифференциальное полное сопротив-
ление с учетом связи будет приблизительно в два раза больше волнового со-
противления каждой линии.
Когда трассы сближены на расстояние меньше трех размеров ширины
проводника, присутствие второй линии будет влиять на волновое сопротив-
ление первой линии.
6.2. Полное сопротивление
дифференциальной пары
6.2.1. Дифференциальное полное сопротивление
При рассмотрении дифференциальной пары при максимальной связи
необходимо дополнительно формализовать задачу. Сложность возникает при
определении падения напряжения на дифференциальном полном сопротив-
лении. Решение задачи может быть получено теоретически с применением
достаточно сложных алгоритмов и программных средств. Однако для инже-
нерной практики проще использовать приближенный подход, предложен-
ный в [112].
Для гранично-связанной микрополосковой линии (рис. 6.4) на стекло-
текстолите приближенное значение дифференциального полного сопротив-
ления находится из уравнения:
^diff
= 2Z 1-0,48 expl-0,96-^- ,
I Ans ,
Ом,
(6.12)
где Z— волновое сопротивление несвязанной одиночной линии передачи; s — расстояние
от края до края между трассами, мм; hms — толщина диэлектрика между сигнальной трас-
сой и плоскостью возврата, мм.
Для гранично-связанной полосковой линии (рис. 6.4) передачи из стек-
лотекстолита дифференциальное полное сопротивление рассчитывается из
уравнения:
^diff
1с
-2,9^-
> Ом,
(6.13)
где Z — волновое сопротивление несвязанной одиночной линии передачи; s — расстоя-
ние от края до края между трассами, мм; hs — общая толщина диэлектрика между плос-
костями возвратных токов.
Оценка точности, проведенная путем сравнения с численными метода-
ми расчета [69], говорит, что погрешность расчета не превышает 10 % для
диапазона значений волновых сопротивлений от 20 до 150 Ом. При этом
следует принимать во внимание, что расчет волнового сопротивления оди-
ночной несвязанной линии также ведется с некоторым приближением.
6.2. Полное сопротивление дифференциальной пары
441
Аппроксимации никогда не должны использоваться при завершении проек-
та. На этом этапе следует привлекать апробированные программные средства,
которые позволяют выполнить расчеты поля с высокой точностью.
6.2.2. Распределение возвратного тока
в дифференциальной паре
Когда расстояние между линиями велико и связь между ними мала, то при
дифференциальном сигнале в них существует ток в каждой сигнальной ли-
нии и ток противоположного на-
правления равного значения в воз-
вратном пути. На рис. 6.9 показ*ано
распределение тока в проводниках
дифференциальной пары на частоте
100 МГц, волновое сопротивление —
50 Ом, ширина проводника 0,125 мм,
зазор 0,375 мм, толщина проводни-
ков 35 мкм.
Ток в проводнике 1 направлен от
наблюдателя, а возвратный ток под
Ф ©
1 2
________МН____________МН___________
©_____________________ф
Возвратный проводник
Рис. 6.9. Распределение тока в проводниках
дифференциальной пары на частоте
100 МГц. Более светлые места
соответствуют большей плотности тока
ним течет к наблюдателю. В линии 2 ток в сигнальном проводнике направ-
лен к наблюдателю, а в возвратном проводнике — от наблюдателя. При от-
носительно большом расстоянии между проводниками возвратные токи в иде-
альном случае распределены так, что нет их перекрытия. Но даже при сла-
бой взаимосвязи все равно в возвратной плоскости имеется некоторое пере-
крытие возвратных токов, что вносит помехи в работу дифференциальной
пары. Любое изменение распределения возвратного тока будет изменять диф-
ференциальное полное сопротивление пары трасс.
Кроме этого, волновое сопротивление определяется расстоянием между
сигнальным проводником и возвратной плоскостью. При увеличении это-
го расстояния снижается емкость одиночной линии, что приводит к увели-
чению её волнового сопротивления, а следовательно, и дифференциально-
го полного сопротивления.
Расчет показывает, что при сближении сигнальных проводников до рас-
стояния, равного ширине проводника, перекрытие распределения обратных
токов будет незначительно.
Когда связь между сигнальным и возвратным проводниками значительно
больше, чем связь между соседними сигнальными трассами в дифференциаль-
ной паре, тогда возвратные токи различны, четко определены в плоскости и
слабо перекрываются. Нарушение распределения возвратных токов очень сильно
влияет на дифференциальное полное сопротивление пары.
По мере удаления возвратной плоскости распределение возвратного тока
расширяется и будет полностью перекрываться и компенсировать друг дру-
га. При этом присутствие возвратной плоскости не будет уже играть роли в
формировании дифференциального полного сопротивления.
442
Глава 6. Дифференциальная пара в печатном монтаже
Расчеты, выполненные для связанных микрополосковых линий с шири-
ной проводника и зазором в 0,125 мм, показывают, что волновое сопротив-
ление одиночной линии возрастает при увеличении толщины диэлектрика,
а дифференциальное полное сопротивление достигает значения 140 Ом и далее
практически не изменяется. Это относится к варианту, когда возвратные токи
полностью перекрываются, что соответствует расстоянию до возвратной
плоскости 0,375 мм, или утроенной ширине проводника.
На рис. 6.10 показана зависимость волнового сопротивления одиночной
полосковой линии и дифференциального полного сопротивления двух трасс
от расстояния между плоскостями заземления. Ширина сигнального провод-
ника 0,125 мм, расстояние между сигнальными проводниками 0,250 мм.
Видно, что при расстоянии более 1,25 мм дифференциальное сопротивле-
ние не зависит от расстояния между плоскостями.
Практическое правило: когда расстояние до возвратной плоскости равно или
более, чем расстояние между внешними краями двух сигнальных проводников,
распределение токов в возвратном проводнике перекрывается, и наличие воз-
вратной плоскости не играет роли в формировании дифференциального полно-
го сопротивления пары. В этом случае возвратный ток одной сигнальной линии
полностью соответствует возвратному току другой линии, что справедливо
для дифференциального сигнала.
Приведенные примеры иллюстрируют важное правило работы дифферен-
циальной пары: когда связь между любым сигнальным проводником и воз-
вратной плоскостью велика по сравнению со связью между сигнальными
проводниками, важнейшую роль начинает играть ток в возвратной плоско-
сти; наличие возвратной плоскости — важный фактор определения диффе-
ренциального полного сопротивления пары.
Когда связь между двумя сигнальными проводниками значительно больше,
чем связь между сигнальными проводниками и возвратной плоскостью,
Расстояние hs. мм
Рис. 6.10. Зависимость волнового сопротивления одиночной полосковой линии
и дифференциального полного сопротивления пары от расстояния между плоскостями
возвратных токов: 1 — дифференциальное сопротивление; 2 — волновое сопротивление
одиночной линии
6.2. Полное сопротивление дифференциальной пары
443
имеется участок перекрытия возвратных токов, за счет чего происходит их
компенсация. В этом случае наличие возвратной плоскости не играет роли,
и она не влияет на значение дифференциального сопротивления. В этом случае
возвратная плоскость может быть удалена без влияния на конечный результат,
что в действительности будет означать, что вторая линия несет возвратный
ток первой линии.
Практическое правило: для связи между двумя трассами большей, чем связь
между трассами и возвратным путем, расстояние для ближайшей плоскости
должно быть в два раза больше, чем интервал между сигнальными линиями.
Не является ли теперь дифференциальная пара с удаленной возвратной плос-
костью обычной одиночной копланарной линией передачи? В этом случае сиг-
нал так же формируется между двумя сигнальными проводниками и похож на
дифференциальный сигнал в дифференциальной паре с удаленной возврат-
ной плоскостью. Волновое сопротивление одиночной копланарной линии
передачи, расположенной на тонком диэлектрике, аналогично дифференци-
альному полному сопротивлению связанных микрополосковых линий с воз-
вратной плоскостью, удаленной на большое расстояние.
В большинстве межсоединений на печатных платах связь между сигналь-
ным проводником и возвратной плоскостью значительно больше, чем связь
между двумя сигнальными проводниками, поэтому возвратные токи в плос-
кости играют существенную роль. В этом случае положение о наличии воз-
вратных токов в соседнем сигнальном проводнике будет ошибочным.
Однако, если возвратный путь нарушен (например, участок этого пути
удален), то это приведет к изменению режима связи, что вызовет изменение
сопротивления и неоднородность в линии передачи. В этом случае необхо-
димы специальные меры по усилению связи в области неоднородности.
В соединителях, в которых обычно связь «контакт-контакт» больше, чем
«контакт-возвратный путь», справедливо предполагать, что возвратный ток
в одном контактном выводе вызывается сигнальным током в другом контакт-
ном выводе.
6.2.3. Нечетная и четная моды
Если в одной линии дифференциальной пары на вход подать перепад
напряжения от 0 до 1 В, а вторую линию оставить в положении О В, то мож-
но определить перекрестную помеху на дальнем конце линии 2. При этом
сигнал на линии 1 будет искажаться. На рис. 6.11 представлена форма на-
пряжения на двух связанных микрополосковых линиях; одна линия переклю-
чается из 0 в 1 В, вторая линия находится на уровне О В.
При работе линий возможны два случая.
Первый относится к одинаковым сигналам, приложенным к каждой ли-
нии, например, переход из 0 до 1 В в каждой линии. В этом случае отсутствует
изменение напряжения между сигнальными проводниками, поэтому нет
емкостной связи между ними. Индуцированный ток в одной линии будет
точно таким же, как и во второй, поскольку скорости изменения тока в каждой
444
Глава 6. Дифференциальная пара в печатном монтаже
Позиция вдоль линии
Рис. 6.11. Форма напряжения на двух связанных микрополосковых линиях; одна линия
переключается из 0 в 1 В, вторая линия — О В: 1 — V(, 2 — V2
линии одинаковы. В результате форма напряжения, которая распространя-
ется вдоль линий, будет одинакова в каждой линии (рис. 6.12а).
Во втором случае на линиях присутствуют оппозитные сигналы, например,
перепад напряжения из 0 в 1 В в одной линии и из 0 в -1 В в другой линии.
Сигнал первой линии будет генерировать на конце линии 2 перекрестную
помеху в виде отрицательного импульса (как это показано в главе 4). Это будет
снижать сигнал на линии 1 по мере распространения. Одновременно отри-
цательный импульс в линии 2 будет генерировать положительный импульс
перекрестной помехи на дальнем конце линии 1. Амплитуда этого положи-
тельного импульса помехи в линии 1 будет точна такая же, как и уменьше-
ние амплитуды сигнала в линии 1 из-за потерь, связанных с переносом энергии
помех в линию 2. Поэтому форма напряжения в дифференциальной паре будет
распространяться без искажений (рис. 6.12d) [3].
Эти два характерных режима неискаженной передачи сигнала по диффе-
ренциальной паре соотносятся с двумя специальными состояниями возбуж-
дения дифференциальной пары, которые называются модами дифференци-
альной пары.
Когда напряжение на линиях одинаково — это четная мода, когда напря-
жения на линиях оппозитны — нечетная мода. Для двух линий в дифферен-
циальной паре существуют только две моды. Для набора трех связанных линий
существуют три моды, для четырех линий — четыре моды, при которых сиг-
налы передаются без искажений.
Моды есть внутреннее свойство дифференциальной пары. Конечно, по диф-
ференциальной паре может быть передано напряжение любой формы, но когда
6.2. Полное сопротивление дифференциальной пары
445
Рис. 6.12. Форма напряжения на микрополосковых линиях дифференциальной пары
при запитке четной (а) и нечетной (6) модой: 1 — Ир 2 — И2
эта форма согласована с одним из этих состояний, сигнал, распространяющийся
по линии, будет иметь специальные свойства. Понятие моды используется для
описания этих специальных свойств.
Введение понятий четной и нечетной мод позволяет определить эти спе-
циальные свойства симметричной дифференциальной пары. Например, как
показано выше, полное сопротивление для сигнала в одной линии зависит
от близости другой и формы напряжения в ней. Введенные понятия позво-
ляют сформулировать это явление по-другому. Определим полное сопротив-
ление одной линии, когда пара находится в режиме нечетной моды, как полное
сопротивление нечетной моды линии. Волновое сопротивление в режиме
четной моды определяется как полное сопротивление четной моды линии.
Нечетная мода часто некорректно определяется как дифференциальная
мода. Если нечетная мода приравнивается к дифференциальной моде, то
можно ошибочно назвать полное сопротивление для нечетной моды полным
сопротивлением дифференциальной моды. Подобное утверждение размы-
вает разницу между этими понятиями.
446
Глава 6. Дифференциальная пара в печатном монтаже
Рис. 6.13. Распределение электрического поля в режимах нечетной (слева)
и четной (справа) мод
Если проводники в паре симметричны, т. е. полностью идентичны, то форма
напряжения мод обусловлена только формой приложенного напряжения. Если
проводники не симметричны, то формы напряжения четной и нечетной мод
не одинаковы. Понятие симметричности линий дифференциальной пары очень
важное и требует особого внимания при реализации дифференциальной пары.
Точное описание режимов этих мод можно определить только при исполь-
зовании программ анализа электрических полей. На рис. 6.13 показана кар-
тина электрического поля в дифференциальной паре на основе микрополос-
ковых линий в различных режимах. Здесь очевидна разница в направлении
силовых линий, что определяет различные электрофизические параметры
дифференциальной пары в различных режимах работы.
Дифференциальный сигнал соответствует возбуждению нечетной моды, а
сигнал общего вида создает четную моду для симметричной, связанной микро-
полосоковой дифференциальной пары. Четная и нечетная моды относятся к внут-
реннему состоянию дифференциальной пары. Теперь можно говорить о полном
сопротивлении в режиме нечетной моды и в режиме четной моды.
Не следует путать понятие дифференциального сигнала и режим нечетной
моды. Это различные факторы. Существует дифференциальный сигнал, полное
сопротивление нечетной моды и дифференциальное полное сопротивление.
Полное сопротивление нечетной моды есть полное сопротивление одной
линии, когда пара возбуждается нечетной модой. Дифференциальное пол-
ное сопротивление есть полное сопротивление рассматриваемого дифферен-
циального сигнала, который распространяется по дифференциальной паре.
6.2.4. Дифференциальное полное сопротивление
и полное сопротивление нечетной моды
Как отмечалось выше, дифференциальное полное сопротивление есть пос-
ледовательная комбинация полных сопротивлений каждой линии к обще-
му возвратному пути. Когда связь отсутствует, дифференциальное полное
сопротивление есть двойное значение волнового сопротивления каждой
линии. Когда линии сближены настолько, что их связь имеет определенное
значение, волновое сопротивление изменяется.
Когда пара работает в режиме нечетной моды, говорят о полном сопро-
тивлении нечетной моды. Как показано на рис. 6.14, дифференциальное пол-
ное сопротивление есть удвоенное значение полного сопротивления нечет-
6.2. Полное сопротивление дифференциальной пары
447
ной моды. Дифференциальное полное сопро-
тивление определяется как
^=2 -Zodd, (6.14)
где Zdiff — дифференциальное полное сопротивление;
Zodd — волновое сопротивление одной линии, когда
пара запитана нечетной модой.
Для расчета или измерения дифференциаль-
ного полного сопротивления следует рассчи-
тать или измерить полное сопротивление не-
четной моды линии и умножить его на 2.
Полное сопротивление нечетной моды есть
полное сопротивление одной линии, когда пара
запитывается нечетной модой.
Z = Z' . + Z .. = 2хZ_
din odd odd odd
Рис. 6.14. К определению диф-
ференциального полного сопро-
тивления при возбуждении
нечетной модой
Расчет дифференциального сопротивления для микрополосковых связан-
ных линий дается формулой (6.12), а для полосковых связанных линий — (6.13).
На графике (рис. 6.15) представлено относительное изменение дифферен-
циального сопротивления в зависимости от параметра s/h, где h равно Ams
для микрополосковой линии или для полосковой.
Рис. 6.15. Относительное изменение полного дифференциального сопротивления
6.2.5. Полное сопротивление режима общего вида
и четной моды
Сигнал общего вида приводит к четной моде. При распространении это-
го сигнала вдоль линии сопротивление линии будет определяться как вол-
новое сопротивление четной моды. Сигнал общего вида испытывает сопро-
тивление параллельных линий (рис. 6.16). Тогда
Z Z 1
у _ even even _ _ у
^comm у у -^even’ (6.15)
even even
где ^comm — волновое сопротивление дифференциальной пары в режиме сигнала общего
вида; Zcvcn — волновое сопротивление линии, когда пара запитана четной модой.
448
Глава 6. Дифференциальная пара в печатном монтаже
Рис. 6.16. К определению волно-
вого сопротивления четной
моды при возбуждении линии
сигналом общего вида
Паяльная
маска
Основание
платы
Рис. 6.17. Покрытие трассы
паяльной маской
Для двух несвязанных 50-Омных линий пе-
редачи, составляющих дифференциальную па-
ру, полное сопротивление нечетной и четной
моды одинаково — 50 Ом. Дифференциальное
полное сопротивление будет 2 х 50 Ом =
= 100 Ом, а полное сопротивление для сигна-
1
ла общего вида будет — х 50 Ом = 25 Ом.
Расчеты [3] показывают, что для типовых производственных значений то-
пологических элементов печатного монтажа дифференциальное полное со-
противление и полное сопротивление для сигнала в режиме общего вида слабо
зависят от связи. Увеличение связи уменьшает дифференциальное полное
сопротивление только на 10 %.
При покрытии микрополосковой линии паяльной маской происходит
изменение волновых сопротивлений пары. На рис. 6.17 показан эффект
покрытия трассы паяльной маской. Поскольку силовые линии поля в нечет-
ной моде проходят через маску, то именно в этом режиме влияние маски будет
больше, чем в режиме сигнала общего вида.
Поэтому важно принимать во внимание наличие паяльной маски, что мо-
жет привести к изменению дифференциального полного сопротивления бо-
лее, чем на 10 %.
6.3. Сигналы дифференциального и общего
вида и компоненты напряжения нечетной
и четной мод
Сигнал произвольного вида можно представить в виде набора двух ком-
понент:
• дифференциальная компонента — разность между двумя напряжени-
ями на каждой линии;
• компонента общего вида — среднее значение двух напряжений на линиях.
Для симметричной дифференциальной пары дифференциальный сигнал
распространяется в нечетной моде, а сигнал общего вида распространяется
в четной моде. Понятия четной и нечетной моды могут быть использованы
для описания произвольного сигнала. Компоненты четной моды, Keven, и не-
четной моды, Kodd, задаются через напряжения на линиях пары следующи-
ми соотношениями:
6.3. Сигналы дифференциального и общего вида и компоненты напряжения... 449
Kxid -*diff “И ^even “ ^comm ~ 2^ (6.16)
Компонента нечетной моды распределяется в равных по модулю, но с про-
тивоположными знаками, по линиям передачи, а именно
V =V =V -V
v odd v diff v 2-
Сигналы в линиях можно теперь представить состоящими из компонент
четной и нечетной мод следующим образом:
И “ ^even + 2 K)dd’ ^2 — ^even “ Kxid • (6.17)
В этих формулах: Keven — компонента напряжения, распространяющаяся
в четной моде; Kodd — компонента напряжения, распространяющаяся в не-
четной моде; Kj — напряжение сигнала в линии 1 по отношению к общему
возвратному проводнику; И2 — напряжение сигнала в линии 2 по отноше-
нию к общему возвратному проводнику.
Например, если в одной линии дифференциальной пары сигнал изменя-
ется от 0 до 1 В, а в другой линии неизменное напряжение О В, тогда распро-
страняющееся вдоль линии напряжение имеет компоненту четной моды
Keverl = 0,5 х (1 + 0) = 0,5 В и компоненту нечетной моды Kodd = 1 — 0 = 1 В.
Таким образом, в дифференциальной паре одновременно распространяет-
ся компонента 0,5 В четной моды, которая встречает волновое сопротивле-
ние четной моды каждой линии, и компонента 1 В нечетной моды, которая
встречает волновое сопротивление нечетной моды каждой линии. Описание
сигнала в терминах нечетной и четной моды иллюстрируется на рис. 6.18.
Дифференциальный Сигнал общего
сигнал вида
Нечетная мода Четная мода
+
Рис. 6.18. Три эквивалентных описания сигнала в дифференциальной паре:
напряжения в каждой линии (слева); дифференциальный сигнал и нечетная мода
(в центре); сигнал общего вида и четная мода (справа)
450
Глава 6. Дифференциальная пара в печатном монтаже
Компоненты четной и нечетной моды независимы. Они распространя-
ются независимо друг от друга и не взаимодействуют друг с другом. Каждая
компонента будет испытывать различные волновые сопротивления для каж-
дой сигнальной линии и может распространяться с различной скоростью.
Когда диэлектрический материал полностью окружает проводники, ди-
электрическая среда становится однородной и гомогенной. В этом случае
напряжение любой формы будет распространяться по дифференциальной
паре без искажений. Для полосковых линий дифференциальных пар в тол-
ще МПП нет перекрестных помех на дальнем конце линии, и сигнал в ней
распространяется без искажений.
6.3.1. Скорости мод и перекрестная помеха
на дальнем конце дифференциальной пары
Каждая модовая компонента распространяется в линии передачи со своей
скоростью. Напомним, что скорость распространения электромагнитной
волны в направляющей системе зависит от диэлектрической проницаемос-
ти материалов, окружающих сигнальный и возвратный проводники. Если
линии передачи выполнены в виде полосковых линий, то диэлектрик одно-
роден, и скорость распространения электромагнитной волны не зависит от
формы напряжения и картины электрического поля, которое формируется
в линии передачи. Электрическое поле в дифференциальной паре на полос-
ковых линиях полностью расположено в диэлектрике между сигнальными
проводниками и возвратными плоскостями. Четная и нечетная моды в та-
кой линии распространяются с одинаковой скоростью.
Если дифференциальная пара построена на микрополосковых линиях пе-
редачи, то её диэлектрическая среда будет кусочно-однородной, поскольку
между сигнальными проводниками и возвратным слоем расположен диэлек-
трический слой, например, стеклотекстолит, а сверху проводников — воз-
душное пространство или некоторая слоистая композиция из паяльной маски,
влагозащитного лака, воздуха. Поэтому в этом случае эффективная диэлек-
Рис. 6.19. Электрическое поле в дифферен-
циальной паре для нечетной (слева) и чет-
ной (справа) мод
трическая проницаемость, а следо-
вательно, и скорость распростране-
ния электромагнитной волны зави-
сит от режима работы лини. Судить
о значении эффективной диэлект-
рической проницаемости при раз-
личных режимах работы дифферен-
циальной пары можно по картине
электрического поля (рис. 6.19). При
нечетной моде определенная часть
силовых линий электрического по-
ля проходит через воздух (считаем,
что покрытие отсутствует), а при
четной моде — в основном через
6.3. Сигналы дифференциального и общего вида и компоненты напряжения... 451
толщу диэлектрика. Эффективная диэлектрическая проницаемость в первом
случае становится меньше, чем во втором, поэтому нечетная мода имеет боль-
шую скорость распространения, чем четная мода. Разность скоростей может
достигать 10 %. Для точного определения скоростей распространения мод
необходимо знать значение эффективной диэлектрической проницаемости
кусочно-однородных сред, окружающих проводники. Это достаточно сложная
задача, и для её решения необходимо применять численные методы анали-
за поля. Она рассмотрена ранее в главе 2.
По мере разнесения проводников значения скоростей четной и нечетной
мод сближаются и становятся одинаковыми, поскольку распределение поля
в каждой линии при их слабом взаимодействии становится одинаковым. При-
ближенно можно считать, что при зазоре между микрополосковыми лини-
ями передачи в дифференциальной паре, равном учетверенной ширине про-
водника, скорости четной и нечетной моды одинаковы.
Например, при близко расположенных линиях скорость нечетной моды
составляет приближенно 0,20 м/нс, а четной моды — 0,17 м/нс. Если сигнал
на линии будет иметь только дифференциальную компоненту, то она будет
распространяться со скоростью 0,20 м/нс. Если на линию подается сигнал
общего вида, то он будет распространяться со скоростью 0,17 м/нс.
Для дифференциальной пары длиной 250 мм время задержки td odd рас-
пространения нечетной моды составит 250 мм/200 мм/нс = 1,25 нс, а время
zd even Распространения четной моды составит 250 мм/170 мм/нс = 1,47 нс. При
этом разность этих времен (расфазировка) составит:
/d_even-'d_odd= 137 - 1,25 = 0,22 нс.
Разница времён задержки распространения четной и нечетной мод в 220 пс
в ряде случаев может оказаться несущественной, но она приводит к возрастанию
помех на дальнем конце линий.
Поскольку компоненты распространяются с разной скоростью, то фор-
ма фронта сигнала, который является суммой напряжений этих компонент,
будет изменяться.
Если на линии 1 распространяется перепад от 0 до 1 В, а линия 2 нахо-
дится под напряжением 0 В, то линия 1 становится активной, а линия 2 пас-
сивной в понятии перекрестных помех. Мы можем описать сигнал на двух
линиях как дифференциальный сигнал, представленный в нечетной моде,
и в виде сигнала общего вида, представленного в виде четной моды. Сигнал
общего вида равен 0,5 В на линии 1 и 0,5 В на линии 2. Дифференциальный
сигнал равен 0,5 В на линии 1 и -0,5 В на линии 2. Это показано на рис. 6.20.
В микрополосковой линии нечетная компонента (дифференциальный сигнал)
достигнет конца линии быстрее четной (сигнал общего вида). Сигнал на даль-
нем конце линии 2 будет получен объединением сдвинутых по фазе друг отно-
сительно друга дифференциальной компоненты —0,5 В и компоненты общего
вида +0,5 В. Это создает напряжение помех на дальнем конце линии 2.
Помехи на дальнем конце связанных линий передач определяются токами ем-
костной связи за вычетом токов индуктивной связи (как было рассмотрено ранее)
452
Глава 6. Дифференциальная пара в печатном монтаже
Рис. 6.20. Описание сигнала на активной и пассивной линии в виде дифференциальной
и общей компоненты дифференциальной пары: 1 — сигнал в одиночной линии;
2 — компонента четной моды; 3 — компоненты нечетной моды
или как сумма сдвинутой по времени дифференциальной компоненты и компо-
ненты общего вида. Эти два подхода совершенно эквивалентны.
Оценим помеху на дальнем конце при линейном фронте сигнала [3]. На
рис. 6.21 представлен сигнал на линии 2 как сумма дифференциальной ком-
поненты и компоненты общего вида. Помеха на дальнем конце есть сумма
этих компонент в конце линии с учетом их взаимного временного сдвига. Ам-
плитуда дифференциальной компоненты равна 1/2 напряжения на линии 1,
т. е. 0,5 V{. Время задержки между приходом дифференциальной компонен-
ты (скорость моды vodd) и компоненты общего вида (скорость моды veven) будет
составлять
ЛТ = —--------—
^even ^odd
(6.18)
Начальная часть сигнала определяется линейным фронтом, и максималь-
ное напряжение помех в конце линии 2 определяется следующим образом:
1
1
1
у =-У . —= J-K
FbXT 2И 2И
V
Keven
1
^odd
= -иг-
2 tr
^odd
v
’even у
(6.19)
где HFEXT — пиковое напряжение помехи на дальнем конце пассивной линии 2; V\ - напря-
жение на активной линии 1; / — длина участка связанных линий; А Г— разница времен рас-
пространения дифференциальной и общей компоненты; /г — фронт сигнала; veven — скорость
распространения сигнала в четной моде; — скорость распространения сигнала в нечетной
моде.
Из рассмотренного выше можно сделать следующие выводы:
• чем больше разность скоростей мод, тем больше уровень помех;
• в полосковой линии скорости мод одинаковы и помехи на дальнем
конце пассивной линии отсутствуют;
• если дифференциальная компонента на линии 2 имеет отрицательную
полярность, то и помеха имеет такую же полярность;
• если разница времен прихода мод к концу линии меньше длительно-
сти фронта, то помеха будет возрастать при увеличении длины линии;
если эта разница будет больше длительности фронта, то максималь-
ный уровень помехи в линии 2 будет составлять 0,5 V\.
6.3. Сигналы дифференциального и общего вида и компоненты напряжения... 453
Критическая длина /sat связанных линий, при которой достигается зна-
чение KFEXT = 0,5 рассчитывается следующим образом:
Lt =...J tx——> м, (6.20)
V V
*even Kodd
где tr — длительность фронта сигнала, нс; vodd — скорость распространения сигнала в ре-
жиме нечетной моды, м/нс; veven — скорость распространения сигнала в режиме четной
моды, м/нс.
Например, при сильно связанных микрополосковых линиях и при фронте
сигнала 1 нс критическая длина составляет
Lt ~ | I — 1Д4, м.
0Д7~0^
Очевидно, что в любом случае уровень помех на дальнем конце пассив-
ной линии не должен превышать допустимого значения.
6.3.2. Модель идеальной связанной линии
или идеальная дифференциальная пара
Помехи на ближнем конце, KNEXT, и на дальнем конце, KFEXT, в паре свя-
занных линий передачи будут определяться соответствующими коэффици-
ентами связи следующим образом:
ИчЕХТ - LL> J'FEXT - >
(6.21)
454
Глава 6. Дифференциальная пара в печатном монтаже
где И — напряжение в активной линии; кп — коэффициент связи перекрестных помех для
начала пассивной линии; к,— коэффициент связи перекрестных помех для конца пассивной
линии; /с(к — длина области связи; Гг — длительность фронта сигнала в активной линии.
Коэффициенты перекрестных помех можно вычислить через значения
полных сопротивлений четной и нечетной мод в следующем виде:
17-7 1 (
fa _ _ ^even ^odd fa _ _ _
2 Zeven +Zodd’ f 2( V<
(6.22)
> АА V
odd even у
Помехи на ближнем конце линии непосредственно зависят от разности
волновых (полных) сопротивлений нечетной и четной мод. Разнесение трасс
уменьшает разницу между волновыми сопротивлениями нечетной и четной
мод и снижает уровень связи. При разнесении трасс их взаимное влияние
мало, и волновое сопротивление линии не зависит от сигнала в другой ли-
нии. В этом случае волновые сопротивления для четной и нечетной мод
одинаковы, и помеха на ближнем конце будет равна 0.
Подобный подход позволяет моделировать пару связанных линий как диффе-
ренциальную пару. Модель идеальной дифференциальной пары может моделиро-
вать работу дифференциальной пары или пары независимых связанных линий.
Идеальная дифференциальная пара определяется четырьмя параметрами:
• волновое сопротивление для нечетной моды,
• волновое сопротивление для четной моды,
• время задержки распространения нечетной моды,
• время задержки распространения четной моды.
Если линия передачи выполнена в виде полосковой линии, то скорости
четной и нечетной мод одинаковы, и для ее описания необходимо только три
параметра. Точное значение параметров может быть получено только с при-
менением программ расчета электрических полей.
6.3.3. Согласование дифференциального
и общего сигналов
Для согласования дифференциального сигнала устанавливается согласу-
ющий резистор между сигнальными проводниками (рис. 6.22). Сопротивление
этого резистора должно быть равно дифференциальному полному (волно-
Рис. 6.22. Согласование дифференциаль-
ного сигнала в дифференциальной паре
вому) сопротивлению.
Сигнал общего вида на обеих ли-
ниях имеет достаточно высокий
уровень постоянного напряжения.
Для него наличие этого резистора
не имеет значения, и линия в этом
режиме является не согласованной.
Если нарушена симметрия диффе-
ренциальной пары, то нарушается
баланс сигналов общего вида, в ли-
6.3. Сигналы дифференциального и общего вида и компоненты напряжения... 455
Рис. 6.23. Согласование сигнала общего вида
нии возникают отраженные сигналы, которые приходят к началу линии и вы-
зывают искажения информационного сигнала.
Согласование не устраняет сигнал общего вида, но предотвращает искажение
информационного сигнала от него. Согласование помогает снизить электромаг-
нитные помехи от сигнала общего вида. Более важная задача — устранить
источник дисбаланса сигнала общего вида.
Один из способов согласования сигналов общего вида заключается в ус-
тановке согласующих резисторов между линией и возвратной плоскостью
(рис. 6.23). Параллельное соединение согласующих резисторов должно быть
равно волновому сопротивлению для сигнала общего вида. Если волновое
сопротивление для сигнала общего вида равно 25 Ом, то каждый резистор
должен быть по 50 Ом.
Плохо, когда используется эта схема для согласования сигналов общего
вида, поскольку при этом дифференциальные сигналы не будут согласова-
ны, за исключением специальных случаев отсутствия связи между линями.
Эквивалентное сопротивление, которое будет видеть дифференциальный
сигнал в этой схеме согласования, — последовательное соединение двух со-
гласующих резисторов, 4 х Zcomm. Только в случае Zeven = Zodd эти резисторы
равны дифференциальному волновому сопротивлению. По мере увеличения
связи волновое сопротивление общего вида будет увеличиваться, а диффе-
ренциальное волновое сопротивление будет уменьшаться.
Если необходимо, следует применять метод согласования, который од-
новременно будет согласовывать сигналы обоих типов [ИЗ]. Это может быть
выполнено двумя топологиями, каждая из которых содержит три резисто-
ра. Это П- и Т-образные схемы включения (табл. 6.2).
В П-образном включении значения резисторов могут быть рассчитаны на
основе следующих соображений. Эквивалентное сопротивление для сигнала
общего вида должно быть равно волновому сопротивлению сигнала общего
вида, а для дифференциального сигнала — дифференциальному волновому со-
противлению. Для сигнала общего вида параллельная комбинация двух рези-
сторов /?2 должна быть равна волновому сопротивлению в режиме общего вида:
^eq — ^2 — ^comm — ^even ’
где 7?cq — эквивалентное сопротивление, которое «видит» сигнал общего вида; Я2 — зна-
чение сопротивления резистора R2; Zcomm — полное сопротивление для сигнала общего вида
456
Глава 6. Дифференциальная пара в печатном монтаже
Таблица 6.2
Схемы согласования дифференциальных пар
Топология Эквивалентная схема Значение параметров
*1 *2
П-образная П-образная & п топология 1U —н=Н 17 7 р _ ^"^even ^odd 1 7 —7 ^even odd ^2 = ^even
Т-образная Т-образная ¥ топология MJ A, == Z . □ 1 odd II n 3 1
в дифференциальной паре; Zeven — волновое сопротивление для четной моды в дифферен-
циальной паре.
Из этого выражения следует, что
*2 = Zeven- (6.23)
Эквивалентное сопротивление 7?eq, которое «видит» дифференциальный
сигнал, есть параллельная комбинация резистора R{ с последовательной ком-
бинацией двух резисторов R2:
р — 17
Aeq ” d . d - zz>odd >
I Jv2
где R} — значение сопротивления резистора 7^; R2 — значение сопротивления резистора
Л2; ZdifT — волновое сопротивление дифференциального сигнала в дифференциальной паре;
Zodd — волновое сопротивление сигнала общего вида в дифференциальной паре.
Поскольку R2 = Zeven, мы можем рассчитать значение R} как
17 7
п _ ^^even ^odd
1 Z — 7 (6.24)
^even "^odd
При слабой связи Zeven « Zodd « Z, тогда R2 = Zm R{ = и П-образная то-
пология преобразуется в обычную схему согласования для одиночной линии.
Для типичной связанной дифференциальной пары волновое сопротив-
ление нечетной моды может быть 50 Ом и четной моды — 55 Ом. В этом случае
в П-топологии резисторы R{ = 1 кОм, а резистор R2 = 55 Ом. Эта комбина-
ция обеспечивает 100 Ом для дифференциального волнового сопротивления
и 27,5 Ом для волнового сопротивления общего вида.
Для Т-образной топологии дифференциальный сигнал будет «видеть» эк-
вивалентное сопротивление R^n в виде последовательной комбинации рези-
eq
сторов R{:
A?q = ^diff = 27?! = 2ZQdd,
6.3. Сигналы дифференциального и общего вида и компоненты напряжения... 457
где Rx — сопротивление каждого из резисторов R{ \ Zdiff — полное сопротивление для диф-
ференциального сигнала в дифференциальной паре; Zodd — полное сопротивление для
сигнала общего вида в дифференциальной паре.
Из этого выражения следует, что
= 2odd- (6.25)
Эквивалентное сопротивление l?eq, которое видит сигнал общего вида, оп-
ределяется последовательным соединением двух параллельных резисторов
Rx и резистора Т?2:
^eq — ^comm — + ^2 — ^even •
Учитывая, что R{ = Zodd, определим значение R2:
^2 — (^even — ^odd )• (6.26)
При Т-топологии при слабой связи Zeven « Zodd « Z, схема согласования
переходит к двум резисторам R{, которые включены по традиционной схе-
ме для одиночной линии, каждый из которых равен волновому сопротивле-
нию для нечетной моды. Центральное ответвление накоротко подключает-
ся к возвратному пути.
Если волновое сопротивление нечетной моды 50 Ом и волновое сопро-
тивление четной моды 55 Ом, то Т-образная схема включает два последова-
тельных резистора между сигнальными линями по 50 Ом каждый и резис-
тор 2,5 Ом между центральной точкой и возвратным путем.
Важным обстоятельством выбора стратегии согласования является воз-
можное увеличение нагрузки драйвера по постоянному току. В обоих случаях
имеется некоторое сопротивление между каждым сигнальным проводником
и возвратной плоскостью для полного сопротивления четной моды. При
снижении волнового сопротивления четной моды увеличивается ток, выте-
кающий из драйвера. Типичный дифференциальный драйвер не может обес-
печить работу на низкоомный резистор по постоянному току, подключен-
ный к низковольтному выходу так, что практически невозможно согласовать
сигнал общего вида. Поэтому, как отмечалось выше, предпочтительней уст-
ранить причины возникновения дисбаланса сигнала общего вида и согла-
совывать дифференциальный сигнал.
Развитие Т-схемы согласования связано с применением развязывающего кон-
денсатора (рис. 6.24). В этой топологии резисторы выбираются из ранее рассмот-
ренных условий, а конденсатор — исходя из постоянной времени сигнала об-
щего вида, которая должна быть больше длительности фронта сигнала. Это
Рис. 6.24. Т-образная схема согласования с конденсатором
для минимизации постоянного тока
458
Глава 6. Дифференциальная пара в печатном монтаже
обеспечит малое полное сопротивление конденсатора по сравнению с пол-
ным сопротивлением резисторов в полосе частот сигнала. В первом прибли-
жении емкость конденсатора выбирают из соотношения:
RC=5tr.
Приняв R = Zcomm, получаем
(7 -
с ” у ’ нФ,
^comm
где R — эквивалентное сопротивление для сигнала общего вида, Ом; С — емкость конден-
сатора, нФ; tr — длительность фронта сигнала, нс; Zcomm — полное сопротивление для
сигнала общего вида в дифференциальной паре, Ом.
Например, если волновое сопротивление общего вида составляет 25 Ом,
фронт 1 нс, емкость конденсатора должна быть около 5 нс/25 Ом = 0,2 нФ
или 200 пФ.
6.3.4. Согласование низковольтных ЭСЛ схем
Низковольтные ЭСЛ-драйверы дифференциальных сигналов имеют на-
пряжение питания 3,3 В. Стандартные схемы согласования требуют приме-
нения источника дополнительного питания напряжением Vcc — 2 В = 1,3 В,
что может усложнить цифровой узел и систему [102, 114]. На рис. 6.25 пока-
зана стандартная схема согласования дифференциальной пары с низковольт-
ными ЭСЛ-схемами.
Схема может быть упрощена, если дополнительного источника питания
не требуется, как показано на рис. 6.26. Это наиболее распространенная схема
согласования. Разновидностью её может служить схема согласования, пред-
ставленная на рис. 6.27. В ней используются три резистора, что несколько
экономичней с позиций потребляемой мощности, чем схема с четырьмя
резисторами (рис. 6.26). Во всех случаях согласующие резисторы должны быть
расположены на минимально возможном расстоянии от приемника сигналов.
В особых случаях для снижения уровня сигнала в режиме общего вида ис-
пользуются последовательные конденсаторы, установленные в сигнальные
Рис. 6.25. Стандартная схема согласования дифференциальной пары на низковольтных
ЭСЛ-схемах
6.3. Сигналы дифференциального и общего вида и компоненты напряжения... 459
Рис. 6.26. Согласование дифференциальной пары на низковольтных ЭСЛ-схемах
с дополнительным источником питания
Рис. 6.27. Вариант согласования дифференциальной пары на низковольтных
ЭСЛ-схемах без дополнительного источника питания
проводники. Подобная схема рекомендуется только для высокоскоростных
приложений при балансе сигнала по постоянному току, например, при цикле
50/50, Манчестерском коде и некоторых других. На рис. 6.28 и рис. 6.29 по-
казаны схемы согласования с уровнями смещения 1,3 В и 2 В соответствен-
но со стороны приемника. Это смещение играет роль сигнала общего вида.
Резисторы RI, установленные в начале линии, должны быть размещены как
можно ближе к драйверу, а резисторы R2 и R3 должны размещаться ближе к
приемнику.
Рис. 6.28. Согласование дифференциальной пары при связи только по переменному
току со смещением Исс = 1,3 В
460
Глава 6. Дифференциальная пара в печатном монтаже
Рис. 6.29. Согласование дифференциальной пары при связи только по переменному
току со смещением Ксс = 2 В
6.4. Преобразование дифференциального
сигнала в сигнал общего вида
Вся информация при использовании дифференциальной пары содержится
только в дифференциальном сигнале. Поэтому при проектировании диффе-
ренциальной пары в составе печатной платы для обеспечения целостности
сигнала следует:
• применять линии с контролируемым дифференциальным волновым
сопротивлением;
• минимизировать любые неоднородности в дифференциальной паре;
• согласовывать дифференциальные сигналы на дальнем конце.
Дополнительные источники искажений дифференциального сигнала —
это расфазировка и асимметрия линий.
Искажения из-за расфазировки и асимметрии зависят от степени связи
между линиями, они могут появляться в любой дифференциальной паре, как в
микрополосковой, так и в полосковой линии.
6.4.1. Расфазировка
Одна из составляющих расфазировки заключается в разности моментов
переключения двух выходов дифференциального драйвера. Она будет иска-
жать дифференциальный сигнал. На рис. 6.30 показан сигнал на входе при-
емника с расфазировкой драйвера, которая изменяется от 20 % до 200 % от
длительности фронта. Общее правило гласит, что расфазировка не должна
превышать 20 % от длительности фронта для избежания добавок во время
задержки распространения сигнала и искажений фронта дифференциального
сигнала. Любая расфазировка будет непосредственно влиять на проблему
тайминга и допустимые временные искажения.
Другая компонента расфазировки может создаваться различием времен
задержки распространения между двумя линиями в паре. Для удержания рас-
фазировки меньше 20 % от фронта сигнала разность длин сигнальных про-
6.4. Преобразование дифференциального сигнала в сигнал общего вида 461
Время, нс
Рис. 6.30. Сигнал на входе приемника с расфазировкой драйвера, которая изменяется
от 20 до 200 % от длительности фронта: 1 — 20 %; 2 — 50 %; 3 — 100 %; 4 — 200 %.
водников (при равной скорости распространения дифференциального сиг-
нала) должна быть не более 20 % области связи. Это условие требует выдер-
живать разность А/ между длинами сигнальных проводников не более сле-
дующего значения:
AZ=0,2/rv, (6.27)
где Гг — длительность фронта сигнала, с; v — скорость дифференциального сигнала, м/с.
Если скорость сигнала принять приблизительно 0,15 м/нс и фронт 1 нс,
тогда область связи, соответствующая фронту, составит 0,15 м. Длины сиг-
нальных проводников в дифференциальной паре не должны различаться
более, чем на 0,2 х 0,15 м/нс х 1 нс =0,03 м. Это условие выполнить не трудно,
но при меньшей длительности фронта эта разность будет пропорционально
меньше. Так, при фронте 0,1 нс различие в длинах сигнальных проводников
дифференциальной пары не должно превышать 3 мм, что может существенно
усложнить трассировку.
Другое ограничение на разность длин сигнальных проводников в диффе-
ренциальной паре может быть получено исходя из требований ЭМС. При
наличии расфазировки для дифференциальной компоненты в возвратной
плоскости потекут токи, определяемые разностью токов в сигнальных ли-
ниях. На рис. 6.31 показана качественная осциллограмма сигнала при отсут-
ствии расфазировки, из которой видно, что в любой момент времени разность
(без учета их направления) токов положительного и отрицательного сигна-
лов будет равна нулю. При наличии расфазировки, например, трасса с сиг-
налом (-) короче, чем трасса с сигналом (+) (рис. 6.32), на некотором вре-
менном интервале / разность токов не будет равна нулю, что вызовет проте-
кание разностного тока в возвратной плоскости. Это, в свою очередь, вызовет
повышенный уровень помех в дифференциальной паре.
Эта проблема может быть рассмотрена с другой стороны. При отсутствии рас-
фазировки разность импульсных дифференциальных сигналов в точности равна
462
Глава 6. Дифференциальная пара в печатном монтаже
Рис. 6.31. Момент переключения приемника в дифференциальной паре при отсутствии
расфазировки
Момент
Рис. 6.32. Осциллограмма токов в сигнальных проводниках дифференциальной пары
при наличии расфазировки
нулю, но при наличии расфазировки в сигнальной линии возникает разно-
стный импульс, длительность которого определяется разностью фаз при при-
ходе импульсов на вход дифференциального приемника [115]. Импульс по-
мехи может выглядеть, как показано на рис. 6.33. Этому импульсу будет со-
ответствовать возвратный ток в возвратной плоскости. Видно, что изменение
тока происходит за короткое время, соизмеримое с длительностью фронта
импульса. Это может создать проблемы в области ЭМС.
Допустимая разность фаз при расфазировке не должна превышать 1...2 гра-
дуса. Например, для импульсов, следующих с частотой 100 МГц, длительность
периода составит 10 нс. Если скорость распространения импульсов 0,15 м/нс в
FR4, то дистанция, пройденная за период, составит 1,5 м, а сдвиг на один гра-
дус составит 1,5/360 = 0,004 м, т. е. 4 мм. Таким образом, разность длин сигнальных
проводников в дифференциальной паре не должна превышать 4 мм. Соответ-
ственно для тактовых частот 500 МГц допустимая разность длин проводников
не должна превышать 0,8 мм! Это весьма жесткое условие, которое трудно реа-
лизовать при трассировке печатной платы.
Следует обратить внимание на следующее обстоятельство. Разность длин
сигнальных проводников в дифференциальной паре не имеет отношения к задерж-
6.4. Преобразование дифференциального сигнала в сигнал общего вида 463
Рис. 6.33. Импульс помехи на входе дифференциального приемника из-за расфазировки
ке сигнала в линии передачи, на которую ориентируются при синтезе времен-
ных диаграмм. Она определяется требованиями целостности сигнала и ЭМС.
6.4.2. Асимметрия
Другой потенциальный источник искажений дифференциального сигнала
- асимметрия, которая заключается в нарушении идентичности конструкций
связанных линий в дифференциальной паре. Искажений сигнала не будет
только при идеальной симметрии двух линий дифференциальной пары, что
практически трудно осуществить. Например, наличие контактной площад-
ки на одной из линий приведет к изменению емкости этой линии, что вне-
сет асимметрию и приведет к искажениям. Наличие металлизированного
отверстия вносит дополнительную задержку примерно 8 пс [116]. Даже раз-
личное расстояние сигнальных проводников одной дифференциальной пары
от стенок корпуса может внести существенную асимметрию, если дифферен-
циальная пара расположена на краю платы.
Любая асимметрия приводит к преобразованию дифференциального сигна-
ла в сигнал общего вида, т. е. вызывает несбалансированный ток в возвратной
плоскости. Если драйвер и приемник не чувствительны к сигналам общего
вида, уровень этого сигнала не имеет существенного значения. Это очень
полезное свойство, позволяющее улучшить показатели электромагнитной со-
вместимости печатного узла, поскольку внешние электромагнитные возму-
щения вызывают именно помехи общего вида. Дифференциальный прием-
ник — типичный пример устройства, которое не реагирует на сигналы об-
щего вида, т. е. имеет высокую степень режекции сигналов общего вида
(common-mode rejection ratio — CMRR), тем не менее необходимо любым спо-
собом минимизировать сигналы общего вида, которые могут появляться
намеренно или непреднамеренно, проникая через экраны, кожухи, аперту-
ры или по кабельным вводам.
Асимметрия преобразует дифференциальный сигнал в сигнал общего вида.
464
Глава 6. Дифференциальная пара в печатном монтаже
Время, нс
Рис. 6.34. Сигнал на входе приемника на дальнем конце с расфазировкой 20 % при
согласовании дифференциальной и общей компоненты: 1 — Kdifr; 2 — Кр 3 — Kcomm; 4 — И2
Даже если общий и дифференциальный сигналы полностью согласова-
ны, все еще есть возможность образования сигнала общего вида из-за асим-
метрии. На рис. 6.34 показан сигнал на входе приемника на дальнем конце
с расфазировкой 20 %, вызванной асимметрией, при согласовании диффе-
ренциальной и общей компонент по Т-образной схеме. Видно, что присут-
ствует небольшой звон, который усиливает проблему ЭМС. При увеличении
расфазировки сигнал общего вида увеличивается даже при полном его со-
гласовании.
Даже очень малая асимметрия приводит к сигналу общего вида значитель-
ной интенсивности. Поэтому необходимо минимизировать все асимметрии.
6.4.3. Сигналы общего вида и электромагнитные
помехи
Наибольший уровень электромагнитных помех (ЭМП) возникает при
наличии сигнала общего вида при соединении печатного узла с межблочным
монтажом [118, 119]. Если, например, неэкранированная витая пара присо-
единяется к дифференциальной паре на печатной плате (рис. 6.35), то на ка-
бель может быть передан дифференциальный и общий сигналы. Дифферен-
циальный сигнал несет полезную информацию. Витая пара очень слабо из-
лучает электромагнитную энергию от дифференциального сигнала. Но сигнал
общего вида, который присутствует на кабеле, будет способствовать излу-
чению энергии.
По какому пути будет возвращаться сигнал общего вида? На печатной плате
сигнал общего вида возвращается через возвратный слой в составе платы. Когда
сигнал переходит с платы на витую пару, её непосредственное присоединение
к возвратному слою печатной платы отсутствует. Это не проблема для диффе-
ренциального сигнала, поскольку возможно спроектировать узел соединения
так, что дифференциальное волновое сопротивление линии на плате будет со-
6.4. Преобразование дифференциального сигнала в сигнал общего вида 465
Рис. 6.35. Схема пути тока общего вида при соединении витой пары к печатной плате
гласовано с дифференциальным волновым сопротивлением витой пары. В этом
случае неоднородность, связанная с переходом от платы к кабелю, для диф-
ференциального сигнала будет практически отсутствовать.
В неэкранированной витой паре возвратный путь для сигнала общего вида
буквально есть Земля или другой соответствующий проводник, если необхо-
димо. Для него практически невозможно выдержать некоторое определенное
волновое сопротивление для качественной передачи возвратных токов сигнала
общего вида. Это может вызвать значительное рассогласование между сигна-
лом общего вида в печатной плате и в витой паре. На высоких частотах воз-
вратный путь обычно определяется доминирующим действием паразитных ем-
костей между землей печатной платы и заземленного шасси корпуса. Емкость
только в 1 пФ имеет полное сопротивление на частоте 1 ГГц около 160 Ом.
По мере распространения сигнала по витой паре, возвратный ток непре-
рывно связывается с ближайшим проводником через паразитную емкость
между витой парой и проводником. Это показано на рис. 6.35.
Значение тока общего вида на витой паре будет зависеть от напряжения
сигнала общего вида, поступающего в кабель, и полного сопротивления,
которое «видит» сигнал общего вида в кабеле:
V
4™=/^ А, (6.28)
^comm
где ^comm ““ сигнал общего видя, поступяющий ня витую пяру, В; Zcomm — полное сопро-
тивление витой пяры для сигняля общего видя, Ом.
Этот ток будет излучать электромагнитные помехи, уровень которых не
должен превышать установленные нормы.
Напряженность электрического поля, которое генерируется аппаратурой
(помехоэмиссия), измеряется в единицах вольт на метр (В/м). В нормативных
документах уровни помехоэмиссии регламентируются как по значениям, так
и по условиям измерения. Например, ГОСТ Р 51318.22-991 предусматривает
1 ГОСТ Р 51318.22-99 (СИСПР 22-97). Совместимость технических средств электро-
мягнитняя. Рядиопомехи индустрияльные оборудовяния информяционных технологий.
Нормы и методы испытяний.
466
Глава 6. Дифференциальная пара в печатном монтаже
нормы напряженности поля от оборудования информационных технологий
при измерениях на расстоянии 10 м, приведенные в табл.6.3.
Требования Федеральной комиссии связи (США) FCC, р. 15 (1999) для
цифровой техники несколько отличны. Так, для аппаратуры класса А напря-
женность поля внутри определенного частотного интервала измеряется в стан-
дартных условиях на расстоянии 3 м от изделия, а допустимый уровень на-
пряженности соответствует данным, приведенным в табл. 6.4.
Эти нормы можно задать в виде определенных границ на графике зави-
симости напряженности от частоты (рис. 6.36). Из графика видно, напри-
мер, что допустимая напряженность электрического поля на частоте 100 МГц
составляет 150 мкВ/м.
Таблица 6.3
Нормы помехоэмиссии согласно ГОСТ Р 51318.22-99
Полоса частот, МГц Напряженность поля, дБ (мкВ/м)
класс А класс Б
30...230 40 30
230...1000 47 37
Таблица 6.4
Нормы помехоэмиссии согласно требованиям FCC
Полоса частот, МГц Напряженность поля, мкВ/м
30...88 100
88...216 150
216...960 200
выше 960 500
50 100 500 1000 5000 10000
Частота, МГц
Рис. 6.36. Задание допустимой напряженности электрического поля при испытаниях
аппаратуры на соответствие требованиям ЭМС
6.1. Передача дифференциальных сигналов
467
Можно оценить напряженность излучаемого электрического поля от сигнала
общего вида в витой паре, аппроксимируя витую пару как электрическую мо-
нопольную антенну Дальняя зона, в которой действуют электродинамические
процессы распространения электромагнитных волн, начинается примерно с рас-
стояния 1/6 длины волны. Поэтому расстояние 3 м, которое требуется для из-
мерений, соответствует границе дальней зоны для 16 МГц. В дальней зоне на-
пряженность электрического поля для монопольной антенны составляет [3]:
£ = 4лЮ-7//сотт|, (6.29)
К
где 4отт — ТОК сигнала общего вида витой пары, А; Е — напряженность электрического
поля на расстоянии R, В/м; f — частота синусоидальной волны в компоненте тока обще-
го вида, Гц; / — длина излучающего отрезка витой пары, м; R — расстояние от витой пары
до точки, в которой производится измерение, м.
Например, если сигнал общего вида составляет 100 мВ, волновое сопро-
тивление сигнала общего вида в витой паре 200 Ом, то ток общего вида со-
ставляет 0,1 В/200 Ом = 5-10~4 А. Если длина витой пары 1 м, а расстояние,
на котором производится измерение, составляет 3 м, то напряженность из-
лучаемого поля на 100 МГц составит:
Е = 4л10"7 • 108 • 5 • КГ4 • | = 20 • 10’3. В/м.
Видно, что напряженность поля составляет 20000 мкВ/м, что более, чем
в 100 раз превышает нормы. Этот пример позволяет сделать очень важный
вывод: даже малые токи общего вида могут создавать излучения в кабелях,
которые превышают нормы ЭМС.
В главе 7 этот анализ будет проведен более детально.
Для снижения уровня помехоэмиссии от токов общего вида в витых па-
рах можно рекомендовать три следующих основных приема.
1. Следует минимизировать преобразование дифференциального сигна-
ла в сигнал общего вида, устраняя асимметрию линий передач и расфазировку
сигналов.
2. Следует применять экранированную витую пару для организации в ней
пути возвратного тока общего вида. Использование экранированного кабе-
ля может даже увеличить значение тока общего вида, поскольку полное со-
противление может быть ниже из-за близости возвратного проводника к
сигнальному проводнику. Если экран присоединен к шасси, ток в экране будет
иметь противоположное направление на внутренней стороне экрана. Сиг-
нал общего вида тогда должен протекать по коаксиальной геометрии — ухо-
дить по витой паре в качестве жилы кабеля и возвращаться по внутренней
стороне экрана. При такой геометрии внешнее электрическое и магнитное
поле должны отсутствовать, и излучения от тока общего вида не будет. Этот
вариант требует низко индуктивного соединения между экраном и шасси.
3. Увеличить полное сопротивление пути тока общего вида за счет установки
ферритовых помехоподавляющих изделий (ФППИ) в виде втулок, шайб и т. п.
468
Глава 6. Дифференциальная пара в печатном монтаже
Рис. 6.37. Установка ФППИ на витую пару для снижения
токов общего вида
Широко используются ферритовые цилиндрические втулки, через которые про-
пускается кабель (рис. 6.37). Они обладают высокой индуктивностью, что при-
ведет к увеличению волнового сопротивления цепи, проходящей через феррит.
Если дифференциальный сигнал протекает через проводник, находящийся
внутри ФППИ, он не создает магнитного поля в феррите из-за оппозитно-
го направления тока в проводниках. Только сигнал общего вида, протекаю-
щий по проводникам в одном направлении, у которых возвратный провод-
ник расположен вне ФППИ, будет создавать магнитное поле, пронизываю-
щее феррит. Поэтому токи общего вида будут испытывать высокое полное
сопротивление и, следовательно, будут уменьшаться по амплитуде. Это при-
ведет к снижению уровня помехоэмиссии.
Второй вид ФППИ применяется в основном для витых пар. Он представ-
ляет собой ферритовое кольцо, через которое пропускается несколько вит-
ков витой пары. В этом случае сопротивление для токов общего вида резко
возрастает, и помехоэмиссия от них снижается.
Ферритовое кольцо для дифференциальной пары может быть встроено в
соединитель. Например, ряд разновидностей соединителей RJ-45 имеют по-
добные ФППИ. При этом полное сопротивление для сигналов общего вида
может быть увеличено на 99 %, т. е. на 40 дБ, что приводит к устранению по-
мехоэмиссии, вызванной асимметрией и расфазировкой в дифференциаль-
ной паре на печатной плате.
6.5. Помехи в дифференциальной паре
6.5.1. Перекрестная помеха между одиночной линией
и дифференциальной парой
На рис. 6.38 показана схема определения перекрестной помехи от актив-
ной одиночной линии на пассивную дифференциальную пару. Для миними-
зации дифференциальной помехи в дифференциальной паре необходимо,
чтобы связь между линиями дифференциальной пары была бы максимальна,
6.5. Помехи в дифференциальной паре
469
1
сильная связь
1
слабая связь
Время, нс
Рис. 6.38. Дифференциальная помеха в дифференциальной паре от активной
одиночной линии: 1 — слабая связь в паре; 2 — сильная связь в паре
(вверху: 1 — активная линия)
а связь между активной линией и линиями дифференциальной пары была бы
минимальна. Если расположить активную линию передачи близко от диффе-
ренциальной пары, то некоторое напряжение будет индуцироваться в пассивной
дифференциальной паре при переключении активной линии. Наведенное на-
пряжение будет одинаковой полярности в каждой линии дифференциальной
пары. Очевидно, что при близком расположении активной линии и диффе-
ренциальной пары большее напряжение будет индуцироваться в той линии диф-
ференциальной пары, которая ближе к активной линии. Чем сильнее связа-
ны линии в дифференциальной паре, тем ближе по значению будут наведен-
ные напряжения в этих линиях.
В общем случае, помехи, которые индуцируются в каждой линии пары,
имеют одинаковую полярность, и на дифференциальный сигнал будет вли-
ять помеха, амплитуда которой есть разность наведенных в каждом провод-
нике напряжений, т. е. дифференциальная помеха. Это основное свойство
сильно связанных линий дифференциальной пары при относительно боль-
шом расстоянии между парой и активной линией.
На рис. 6.39 показана дифференциальная помеха от одиночной активной
линии в дифференциальной паре, построенной на полосковой линии, диф-
ференциально согласованной на дальнем конце и имеющей на ближнем конце
низкое полное сопротивление, типичное для драйвера [3]. Графики постро-
ены для двух случаев связи линий в составе дифференциальной пары — силь-
ной и слабой.
В этой конфигурации активная линия расположена на расстоянии, равном
ширине сигнального проводника от ближайшего проводника пары. Оценим
470
Глава 6. Дифференциальная пара в печатном монтаже
два различных уровня связи в дифференциальной паре. При сильной связи рас-
стояние между сигнальными проводниками равно ширине проводника, а при
слабой связи — расстояние между проводниками равно удвоенной ширине про-
водника. Для проводников дифференциальной пары проводник, расположен-
ный дальше от активной линии, будет иметь с ней более слабую связь.
Дифференциальная помеха есть разность между уровнями помех на каж-
дой линии. В приведенном примере при слабой связи дифференциальная по-
меха составляет 1,3%, что примерно в два раза меньше, чем при сильной свя-
зи. Так, при уровне сигнала в активной линии 3,3 В дифференциальная по-
меха составит 40 мВ. Если с другой стороны пассивной дифференциальной пары
находится вторая активная линия, переключающаяся в противоположном на-
правлении, то на паре произойдет сложение помех, и суммарный уровень
достигнет значения 80 мВ. Это практически предельное допустимое значение.
Помехи общего вида есть среднее напряжение в каждой линии дифферен-
циальной пары. На рис. 6.39 показаны помехи общего вида для сильной и
слабой связи между линиями в дифференциальной паре. Помехи этого вида
не будут сильно зависеть от связи с дифференциальной парой. При сильной
связи уровень помех составляет 2,1 %, а при слабой — 1,5 %.
Сильная связь линий в дифференциальной паре будет уменьшать диффе-
ренциальную помеху, но увеличивать помеху общего вида. Перекрестная по-
меха — один из типичных путей возникновения токов общего вида в дифферен-
циальной паре. Даже в том случае, если линии в дифференциальной паре спро-
ектированы полностью симметрично, перекрестная помеха будет создавать
напряжение общего вида в дифференциальной паре. Поэтому всегда важно
ослаблять помехи общего вида путем установки ФППИ, в особенности для
присоединенных витых пар.
1
сильная связь
1
слабая связь
Рис. 6.39. Помехи общего вида в дифференциальной паре: 1 — слабая связь в паре;
2 — сильная связь в паре (вверху: 1 — активная линия)
6.5. Помехи в дифференциальной паре
471
Практическое правило. Для минимизации помех дифференциального вида от
активной одиночной линии следует усиливать связь между линиями дифферен-
циальной пары. При этом расстояние между активной линией и дифференци-
альной парой необходимо предельно увеличить.
Дифференциальная помеха между двумя дифференциальными парами
меньше, чем между одиночной линией и дифференциальной парой. Диффе-
ренциальная помеха может быть до 1 %, а помеха общего вида — до 2 %.
6.5.2. Неоднородности в возвратном пути
Неоднородности в возвратном пути токов, как было рассмотрено ранее
для одиночных линий передачи, являются источниками искажений инфор-
мационного сигнала. Для дифференциальной пары также предъявляются
высокие требования к однородности возвратного пути. Одними из самых
распространенных видов неоднородностей в фольгированных слоях платы,
в которых расположены возвратные пути токов, являются зазоры между раз-
личными участками фольги и другие пробельные участки. Зазоры в возвратном
пути часто изолируют одну зону платы от другой. Они также появляются, когда
в двухсторонних платах плоскость питания одновременно используется как
опорный слой или применяется разделение участков питания. В ряде слу-
чаев зазор появляется непреднамеренно, когда зона около отверстия в воз-
вратном слое перетравлена. В этом случае любая сигнальная линия, которая
проходит около отверстия, будет иметь неоднородность в возвратном пути.
При расположении сигнального проводника перпендикулярно зазору, этот
участок линии передачи будет восприниматься как индуктивная неоднород-
ность. На рис. 6.40 показаны отраженный и прошедший сигналы с фронтом
100 пс в 50-омной линии с зазором шириной 25 мм в середине возвратного
пути [3]. Фронт сигнала, прошедшего неоднородность, очень сильно увели-
чивается из-за последовательной индуктивности.
Время, пс
Рис. 6.40. Отраженный и прошедший сигналы с фронтом 100 пс в 50-омной линии
с зазором шириной 25 мм в середине возвратного пути: 7 — отраженный сигнал;
2 — прошедший сигнал
472
Глава 6. Дифференциальная пара в печатном монтаже
Один из путей устранения этого явления — использование конденсато-
ра с низкой индуктивностью для перекрытия зазора в потенциальном слое
и обеспечения низкого полного сопротивления возвратного пути. Но в этом
случае трудно обеспечить широкий частотный диапазон.
Другой путь избавиться от неоднородности, вызванной зазором между
участками фольги, заключается в использовании дифференциальных пар.
На рис. 6.41 показана типичная ситуация. Сигнал стартует в зоне 1 (микро-
полосковая линия), проходит зазор с удаленным возвратным проводником
и проходит зону 3 (микрополосковая линия).
В зонах 1 и 3 дифференциальное волновое сопротивление дифференци-
альной пары составляет 90 Ом. В средней зоне слой возвратного тока уда-
лен. При ширине проводников и зазоре между ними 0,125 мм и при толщи-
не диэлектрика под проводниками 0,0675 мм, дифференциальное волновое
сопротивление становится 160 Ом. Для повышения однородности линии
необходимо в зонах 1 и 3 возвратную плоскость расположить от проводни-
ков на расстоянии, по крайней мере, равном интервалу между сигнальны-
ми проводниками. В этом случае дифференциальное волновое сопротивле-
ние не будет зависеть от расположения возвратной плоскости. Этот техни-
ческий прием позволяет построить модель цепи для изучения влияния этой
неоднородности на качество дифференциального сигнала. На рис. 6.42 по-
врем я, ПС
Рис. 6.42. Дифференциальный сигнал с фронтом 100 пс, прошедший и отраженный
от зазора в возвратной плоскости; ширина зазора 25 мм: 1 — отраженный
дифференциальный сигнал; 2 — прошедший дифференциальный сигнал
6.6. Расчет параметров дифференциальной пары
473
казан дифференциальный сигнал с фронтом 100 пс, прошедший и отраженный
от зазора в возвратной плоскости; ширина зазора 25 мм. Видно, что диффе-
ренциальный сигнал претерпевает минимальные искажения.
Использование дифференциальной пары с сильной связью — один из путей пе-
редачи широкополосного сигнала в районе с плохо определенной возвратной плос-
костью.
Следующие условия говорят о преимуществах в стоимости и технологич-
ности сильной связи между линиями в дифференциальной паре:
• повышается плотность межсоединений, функциональная плотность
платы и конечная стоимость платы снижается;
• снижается уровень дифференциальных помех;
• неоднородность дифференциального волнового сопротивления из-за
несовершенства возвратного пути уменьшается.
6.6. Расчет параметров
дифференциальной пары
6.6.1. Расчет параметров нечетной и четной мод
Напомним, как определяется волновое сопротивление и удельная задержка
распространения сигнала в одиночной линии без потерь:
где Z — волновое сопротивление одиночной линии передачи; Z, — индуктивность линии
на единицу длины; С, — емкость линии на единицу длины; td — удельное время задержки
распространения сигнала.
Для дифференциальной пары можно расширить эту модель, включив связь
между линиями. На рис. 6.43 показана одна секция из «-секционной модели на
сосредоточенных элементах для пары связанных линий с емкостной и индук-
тивной матрицей SPICE. Параметры мат-
рицы получены с помощью программных
средств. Эта модель используется для полу-
чения модели для определения волнового
сопротивления для четных и нечетных мод.
Когда пара запитывается нечетной мо-
дой, то волновое сопротивление одной ли-
нии есть волновое сопротивление нечет-
ной моды. Эквивалентная емкость одной
линии равна:
Codd=C'|| + 2C|2=C1 + C12, (6.30)
где Codd — емкость на единицу длины сигналь-
ного проводника относительно возвратного пути
Рис. 6.43. Одна секция из «-сек-
ционной модели на сосредото-
ченных элементах для пары свя-
занных линий с емкостной и ин-
дуктивной матрицей SPICE
474
Глава 6. Дифференциальная пара в печатном монтаже
одной линии, когда пара запитывается нечетной модой; Си — диагональный элемент ем-
костной матрицы SPICE; С12 — внедиагональный элемент емкостной матрицы SPICE; Сх —
нагрузочная емкость сигнальной линии, равная Сп + С12.
При нечетной моде ток входит в сигнальную линию 1 и возвращается по
возвратному пути. Одновременно ток, выходящий из линии 2, входит в его
возвратный путь. В этом случае вокруг линии передачи 1 будет магнитное поле
взаимной индукции от сигнала линии передачи 2. Это поле будет иметь на-
правление, противоположное самоиндукции линии 1. Эквивалентная индук-
тивность контура линии 1 будет уменьшена за счет тока линии 2. Эта индук-
тивность, когда пара запитывается нечетной модой, определяется как
^odd ~ ^\\~ ^12’ (6.31)
где Aodd — индуктивность на единицу длины контура, включающего сигнальный и возврат-
ный проводник одной линии, когда пара запитывается нечетной модой; Lx j — диагональный
элемент индуктивной матрицы; £12 — внедиагональный элемент индуктивной матрицы.
Из этих двух выражений волновое сопротивление нечетной моды и вре-
мя задержки распространения могут быть рассчитаны по следующим фор-
мулам:
7 = Лхк! = А1 ~^2
odd Vcodd К,+с12’ <632)
rd_odd “ V^oddQdd “ \ (Л 1 (6.33)
Когда пара запитывается четной модой, емкость между сигнальным и
возвратным проводниками уменьшается за счет экранирования соседней трас-
сой, которая имеет тот же потенциал, что и трасса 1. Эквивалентная емкость
линии на единицу длины при четной моде равна
С = см = С, - с1?,
even 11 1 12’
где С] ( — диагональный элемент емкостной матрицы SPICE; С12 — внедиагональный эле-
мент емкостной матрицы SPICE; — нагрузочная емкость сигнальной линии, равная
С, 1 + С12.
При четной моде ток вытекает из сигнальной линии 1 и возвращается по
возвратному пути в потенциальной плоскости. Аналогично ток, вытекающий
из линии 2, возвращается по возвратному пути в потенциальной плоскости.
Таким образом, при четной моде направление контуров тока для проводни-
ка 1 совпадает с направлением контура тока в проводнике 2. Поэтому направ-
ление полей самоиндукции совпадает, и эквивалентная индуктивность £even
контура линии 1 при четной моде будет:
^even — ^11 + ^12’ (6.34)
где £п — диагональный элемент индуктивной матрицы; £12 — внедиагональные элемен-
ты индуктивной матрицы.
Волновое сопротивление и время задержки распространения при четной
моде определяются по формулам:
6.6. Расчет параметров дифференциальной пары
475
7
even
^cven
с
even
1Л1 + ^12
G ~^12
(6.35)
^deven V^even^even \ А2 )(G ^12 )•
(6.36)
Это наиболее фундаментальное описание, которое показывает, как вне-
диагональные элементы, С12 и £12, описывают влияние связи на волновое со-
противление и время задержки распространения для каждой моды. При уси-
лении связи внедиагональные элементы увеличиваются, волновое сопротив-
ление нечетной моды уменьшается, а волновое сопротивление четной моды
увеличивается.
6.6.2. Матрица волновых сопротивлений
Матрица волновых сопротивлений описывает дифференциальную пару
или две связанные линии и может быть развита на п связанных линий. Это
описание такое же фундаментальное, как и описание матрицами емкостных
и индуктивных параметров, однако имеются и определенные различия.
Матрица полных сопротивлений показывает, как соотносятся ток и напря-
жение в каждой линии дифференциальной пары. Следующий анализ иллю-
стрирует построение матрицы полных сопротивлений для двух связанных
линий [3, 4, 53]. Подобный подход может быть развит на п связанных линий.
Применение матрицы не требует знания деталей конструкции линии, сим-
метрии или свойств материалов.
Две линии передачи показаны на рис. 6.44.
Произвольный сигнал в линиях передачи
описывается токами и напряжениями. Если
связи между линиями нет, то напряжение в
каждой линии не зависит от режима в другой
линии. В этом случае напряжение V\ в линии
1 и напряжение И2 в линии 2 определяется
через токи и /2 в каждой линии будет
2
Рис. 6.44. Напряжения и токи
в линиях передачи
^,=7,/,, K2 = Z2/2>
где Zp Z2 — соответственно волновое сопротивление линии 1 и линии 2.
При наличии связи между линиями возникают перекрестные помехи.
Связь можно описать матрицей волновых сопротивлений, каждый элемент
которой определяет ток в одной линии, вызванный напряжением в другой
линии. Через матрицу волновых сопротивлений напряжения на линии 1 и 2
описываются выражениями:
V. = znl{ + Z12/2, r2 = Z21/1 + Z22/2. (6.37)
Диагональные элементы ZH, Z22 матрицы волновых сопротивлений есть
волновое сопротивление каждой линии, когда в другой линии нет тока. Когда
476
Глава 6. Дифференциальная пара в печатном монтаже
связь отсутствует, диагональные элементы преобразуются в то, что ранее было
названо волновым сопротивлением Zлинии передачи.
Внедиагональные элементы матрицы описывают уровень связи, но их роль
недостаточно интуитивно понятна. Рассмотрим матричные внедиагональ-
ные элементы Z12 и Z21. В действительности это не волновые сопротивления
между линией 1 и линией 2. Элемент Z12 определяет значение напряжения,
которое генерируется на линии 1 на один ампер тока в линии 2. Аналогично
элемент Z21 определяет индуцированное напряжение в линии 2 на 1 ампер
тока в линии 1. Учитывая это, можно говорить о взаимном полном сопро-
тивлении:
7 7 -К2
Z21"7^’ (6.38)
При слабой связи внедиагональные элементы малы, и их можно принять
равными нулю.
Из этого описания можно идентифицировать волновые сопротивления
при четной и нечетной модах в терминах матрицы волновых сопротивлений.
Когда дифференциальный сигнал прикладывается к двум линиям, имеет место
нечетная мода. По определению при нечетной моде ток в одной линии ра-
вен и противоположен по направлению току в другой линии, или 1{ = -/2.
Основываясь на этом определении, вычислим напряжение на линии 1:
И = “ Z12^1 = ” Z12^’
Откуда волновое сопротивление нечетной моды линии 1 равно:
у
Zoddl =~j~ = Z\ \ “^12- (6.39)
Аналогично при четной моде токи в линиях одинаковы — /2. Напряжение
на линии 1 для четной моды равно
И = Z11A + Z12^1 “ + Z12^
Волновое сопротивление четной моды линии 1:
^evenl — у — ^11 + ^12- (6.40)
Для линии 2, очевидно, можно получить аналогичные выражения, поскольку
конструкция линий симметрична. Напомним, что выше даны приближенные
выражения (6.12) и (6.13) для расчета этих волновых сопротивлений.
При принятом определении полное сопротивление нечетной моды одной
линии есть разность между диагональным и внедиагональным элементом
матрицы полных сопротивлений. При усилении связи увеличивается значение
внедиагональных элементов и уменьшается дифференциальное полное со-
противление. Полное сопротивление четной моды одной линии есть сумма
диагональных и внедиагональных элементов. При увеличении связи внедиа-
6.7. Рекомендации по проектированию дифференциальной пары
477
тональные элементы увеличиваются, и полное сопротивление для четной
моды увеличивается.
В большинстве случаев при анализе дифференциальных пар для расчета
элементов емкостных и индуктивных матриц, а также матриц полных сопро-
тивлений необходимо применять численные методы расчета и соответству-
ющие программные средства.
6.7. Рекомендации по проектированию
дифференциальной пары
Рассмотренные выше основы работы дифференциальной передачи сиг-
нала позволяют обоснованно подойти к техническим решением по реали-
зации дифференциальной пары на печатных платах. Дифференциальная
передача сигналов имеет ряд преимуществ перед передачей сигнала по оди-
ночной линии передачи: меньший провал напряжения в шине питания,
меньший уровень ЭМП, лучшая помехозащищенность (отношение сигнал/
шум), меньшая чувствительность к потерям. Любой сигнал в дифференци-
альной паре может быть описан дифференциальной компонентой и компо-
нентой общего вида. Каждая компонента будет иметь различное волновое
сопротивление и время задержки распространения. Поскольку дифферен-
циальный сигнал имеет в сигнальных проводниках равные, но противопо-
ложные токи, то отсутствуют возвратные токи в каких-либо других путях. По
этой причине однородность возвратных путей не столь важна. Если диффе-
ренциальная пара пересекает границу между аналоговой и цифровой частью
устройства, то взаимодействие этих частей будет сведено к минимуму. В этом
случае легко разделить системы питания.
Дифференциальная пара может быть полностью описана волновыми со-
противлениями нечетной и четной мод, а также временем задержки распро-
странения для каждой моды. Волновое сопротивление нечетной моды есть
волновое сопротивление на одной линии, когда пара запитывается нечетной
модой. Связь между линиями в паре будет увеличивать дифференциальное
волновое сопротивление.
Параметры дифференциальной пары могут быть рассчитаны точно только
с применением программных средств, но для инженерной практики прием-
лемые результаты могут быть получены с помощью приближенных методов
расчета.
Особое внимание при проектировании дифференциальной пары следу-
ет уделить устранению причин возникновения помех, связанных с сигнала-
ми общего вида. Один из наиболее частых источников ЭМП есть сигнал
общего вида, приходящий от витой пары. Путь снижения ЭМП сводится к
минимизации асимметрии между двумя линиями в дифференциальной паре
и добавлению ферритового помехоподавляющего изделия на внешний ка-
бель для снижения сигнала общего вида. При создании дифференциальной
пары на печатной плате именно симметрии двух связанных линий, входящих
478
Глава 6. Дифференциальная пара в печатном монтаже
в её состав, следует уделить самое пристальное внимание. Суммарная асим-
метрия дифференциальной пары, вызванная погрешностями конструирова-
ния печатной платы, не должна вызывать расфазировку более 150 пс [ 119]. Это
примерно соответствует разности длин проводников линии в 20 мм на FR4.
На высоких частотах (более 500 МГц) на параметрах дифференциальной
пары начинают сказываться свойства материалов основания печатной пла-
ты. Стеклотекстолит из-за своей неоднородной диэлектрической структуры
оказывается непригоден для создания высококачественных дифференциаль-
ных пар. Например, проводники могут быть расположены, как показано на
рис. 6.45. При этом проводник «+» оказывается над стекловолокном, и за счет
более высокой диэлектрической проницаемости стекла скорость распрост-
ранения электромагнитной волны в этой линии передачи оказывается меньше
средней. Проводник «-» расположен над областью, преимущественно запол-
ненной эпоксидной смолой с меньшей, чем у стекла, диэлектрической про-
ницаемостью, и скорость электромагнитной волны в данной линии будет
выше средней. Средняя скорость определяется по формулам, приведенным
в главах 2 и 3, исходя из значения относительной диэлектрической прони-
цаемости, приведенного в спецификации на материал основания. Для стек-
лотекстолита FR4 это значение равно приближенно 4, и оно является, фак-
тически, эффективной диэлектрической проницаемостью кусочно-однород-
ной среды, состоящей из стекла и эпоксидной смолы. Расфазировка для
рассмотренного случая может достигать 5 % от времени распространения
сигнала вдоль линии передачи [119]. Возможным приемом устранения от-
меченного явления является изменение ориентировки линий передачи от-
носительно направления нитей основания платы, например, расположив их
относительно друг друга под углом от 30° до 60°.
В сверхвысоком частотном диапазоне предпочтение следует отдавать
специальным полимерным материалам, однородным по своей структуре,
например, G-TEK. В первой главе приведены основные параметры подоб-
ных материалов, применяемых для создания высокоскоростных печатных
плат. Стоимость подобных материалов и, следовательно, плат будет замет-
но выше, чем плат на стеклотекстолите.
Применение дифференциальных пар повышает требования к технологи-
ческому процессу покрытия печатной платы. Неравномерность диэлектри-
ческого покрытия изменяет параметры диэлектрической среды вокруг про-
водников, влияя на скорость распространения сигнала в них. Толщина по-
Стекловолокно Стекловолокно Эпоксидная
(нити основы)
(нити утка)
смола
Рис. 6.45. Пример асимметрии дифференциальной пары, вызванной применением
6.7. Рекомендации по проектированию дифференциальной пары
479
крытия проводников в дифференциальной паре должна быть одинакова, а
для прогнозирования функциональных параметров дифференциальной пары
желательно знать точное значение диэлектрической проницаемости покры-
тия. К сожалению, этот показатель не всегда известен, и он имеет большой
разброс от партии к партии материалов, применяемых для покрытия плат.
Ниже приведены базовые рекомендации, которые обеспечат высокое
качество дифференциальной пары и, следовательно, будут способствовать
сохранению целостности сигнала на высоких частотах и минимизации по-
мех в цифровом узле.
Сигнальные проводники
1. Сигнальные проводники должны располагаться на минимальном рас-
стоянии друг от друга на всем протяжении, начиная с контактных площа-
док около драйвера и заканчивая контактными площадками около прием-
ника. Это увеличивает связь между линиями в дифференциальной паре, что
всегда положительно сказывается на её параметрах. Для избежания неодно-
родности в дифференциальном волновом сопротивлении это расстояние
должно быть строго постоянным по всей длине трасс.
2. Для минимизации расфазировки длина сигнальных проводников дол-
жна быть одинакова, независимо от наличия поворотов. При различной длине
проводников моменты прихода дифференциальной компоненты на вход
приемника будут различны, что приведет к определенной расфазировке.
Совместно с расфазировкой, вызванной другими причинами, например,
параметрами элементной базы, это может превысить допустимый уровень.
Особую тщательность при трассировке следует соблюдать при создании плат
для микросхем с большим числом выводов, например BGA. На рис. 6.46 пока-
заны примеры трассировки дифференциальных пар, в которых выдержано
Рис. 6.46. Примеры трассировки дифференциальных пар при высокой плотности
металлизированных отверстий
480
Глава 6. Дифференциальная пара в печатном монтаже
равенство длин сигнальных проводников при высокой плотности металли-
зированных отверстий.
3. Число неоднородностей в линиях, включая металлизированные отвер-
стия, должно быть сведено к минимуму. Наилучший вариант соединения -
расположение проводников без перехода со слоя на слой.
4. Любая нежелательная электромагнитная связь дифференциальной пары
со сторонними объектами и/или паразитная нагрузка, например, емкостная,
должны быть устранены или иметь одинаковое значение для каждой линии.
Для анализа электромагнитной связи необходимо рассматривать не только
печатную плату, но и компоновку всего устройства, в который входит печатный
узел, поскольку, например, элементы крепления, стенки и крышки корпуса
могут быть теми объектами, емкость которых не была учтена при проекти-
ровании платы. На рис. 6.47 показаны некоторые примеры «паразитных» свя-
зей, которые нарушают симметрию дифференциальной пары:
• влияние соседней линии передачи;
• наличие отверстия в диэлектрике, что нарушает однородность диэлек-
трической среды для одной из линии;
• расположение дифференциальной пары рядом с краем потенциального
слоя или щели в нем, что изменяет емкостные параметры ближайше-
го к краю или границе щели проводника;
• расположение пары рядом с участком фольги в сигнальном слое, что
также изменяет локальные емкостные параметры соседнего с участ-
ком фольги проводника;
• расположение дифференциальной пары рядом с металлическими эле-
ментами крепления или корпуса; это локально изменяет емкостные па-
раметры проводника, а в том случае, если металл магнитный, то око-
ло металлического элемента увеличится магнитная проницаемость
среды распространения сигнала, что приведет к уменьшению скоро-
сти распространения сигнала на этом участке линии.
Рис. 6.47. Некоторые примеры «паразитных» связей, нарушающих симметрию
дифференциальной пары
6.7. Рекомендации по проектированию дифференциальной пары
481
5. Для избежания возникновения неоднородностей повороты проводни-
ков предпочтительней выполнять под углом 45° или в виде дуги, избегая
выполнения поворотов под углом 90°.
Согласование дифференциальной пары
1. Согласование дифференциальной пары ведется для дифференциаль-
ного сигнала (обязательно) и для сигналов общего вида. Допуск на согласу-
ющие резисторы задается не более ±5 %.
2. Располагать согласующий резистор следует как можно ближе к входу
приемника, не далее 7 мм [118].
3. Желательно использовать поверхностно-монтируемые компоненты,
например чип-резисторы 0603 или 0805.
Минимизация электромагнитных помех
1. При расположении в одном слое для минимизации перекрестных по-
мех одиночные линии передачи должны удаляться на максимально возможное
расстояние (не менее 12 мм [118]) от дифференциальной пары.
2. В составе МПП дифференциальные пары и одиночные линии долж-
ны располагаться в различных слоях, которые разделяются экранами в виде
потенциальных слоев опорного напряжения и питания (рис. 6.48).
3. Применение дифференциальных пар на основе полосковых линий
передач приводит к снижению уровня электромагнитного излучения по срав-
нению с применением микрополосковых линий.
4. Применение полосковых линий в составе МПП имеет следующие
особенности: скорость распространения сигнала в них примерно в 1,5—2 раза
меньше, чем в микрополосковых линиях, необходимы дополнительные пе-
реходные металлизированные отверстия, требуется большее число слоев для
создания дифференциальных пар, из-за увеличенной емкости имеются оп-
ределенные трудности для обеспечения точного значения дифференциаль-
ного волнового сопротивления (около 100 Ом).
5. Для обеспечения максимальной электромагнитной связи между лини-
ями в одной паре и минимальной связи с линиями в другой паре рекомен-
дуется выдерживать следующие топологические размеры:
• расстояние s между проводниками в одной паре должно быть менее
удвоенной ширины w проводника;
• расстояние d между соседними парами должно быть более удвоенно-
го зазора s между проводниками в дифференциальной паре;
Дифференциалиные
парЫ
Слой питания
Слой опорного
напряжения
Одиночные линии
Рис. 6.48. Структура фрагмента МПП с дифференциальными парами
16 1527
482
Глава 6. Дифференциальная пара в печатном монтаже
w s w d
Микрополосковая линия
w s w d
Полосковая линия
Рис. 6.49. Размеры дифференциальных пар на полосковых и микрополосковых линиях
• толщина h платы или слоя МПП должна быть больше зазора 5 между
проводниками в паре.
Указанные соотношения иллюстрируются на рис. 6.49.
6. Установка развязывающих конденсаторов должна проводиться с уче-
том рекомендаций, данных в главе 5.
Установка соединителей
1. Драйверы и приемники дифференциальных пар следует располагать
как можно ближе к соответствующим контактам соединителей. Топология
присоединения трасс дифференциальной пары к соединителю может явиться
существенной неоднородностью. Этот участок не должен превышать 5 мм.
Примеры топологии узла коммутации дифференциальной пары показаны на
рис. 6.50. Для варианта неудачной трассировки, показанного слева, слиш-
ком велика разница длин короткого и длинного проводника каждой пары,
что может вызвать недопустимую расфазировку. Для удачного решения, по-
казанного справа, длины обоих проводников в каждой паре одинаковы.
2. Для снижения уровня помех в зоне соединителя для каждой линии диф-
ференциальной пары устанавливаются последовательные ферритовые поме-
хоподавляющие элементы. Разрабатываются новые помехоподавляющие ком-
поненты, ориентированные на применение в дифференциальных парах. При-
мером может служить комбинированный ££С-фильтр типа X2Y рис. 6.51 [119].
3. Соединитель должен обеспечивать минимальную собственную расфа-
зировку и минимальный уровень перекрестных помех.
4. Длины выводов соединителя, по которым передаются сигналы диффе-
ренциальной пары, должны быть одинаковы для минимизации расфазировки.
(о §)q)q)§i§)q)S
Короткий
проводник
Длинный
Хорошо
проводник
Плохо
Рис. 6.50. Примеры неудачной (слева) и рациональной топологии узла коммутации
дифференциальной пары
6.7. Рекомендации по проектированию дифференциальной пары
483
Рис. 6.51. Установка фильтров в дифференциальной паре
5. Для снижения перекрестных помех вывод заземления соединителя
желательно располагать между выводами дифференциальной пары.
6. Крайние выводы не следует задействовать под дифференциальные
пары; их следует заземлить.
7. Все незадействованные выводы соединителя должны быть надлежа-
щим образом нагружены.
Глава 7
Печатные платы и элементы ЭМС
7.1. ЭМС как показатель качества
электронной аппаратуры
7.1.1. ЭМС и качество изделия
В настоящее время электромагнитная совместимость (ЭМС) является
одним из важнейших качественных показателей электронной аппаратуры,
которые подлежат сертификации. ЭМС характеризуется двумя основными
свойствами: восприимчивостью к внешним электромагнитным возмущениям
и помехоэмиссией — способностью создавать электромагнитные помехи для
других радиоэлектронных средств. Показатели этих параметров нормируются
и подлежат строгому контролю, и, если они не отвечают нормативной до-
кументации, аппаратура не может пройти сертификационные испытания.
В этом случае необходимы доработки, что задерживает появление изделия
на рынке. Эта ситуация детально обсуждается в главе 1.
Повышение восприимчивости электронных изделий к электромагнитным
воздействиям происходит параллельно с увеличением электромагнитного
загрязнения окружающей среды. Повышение восприимчивости обусловле-
но использованием интегральных микросхем для решения новых задач, а
также тех задач, которые ранее выполнялись с использованием электроме-
ханических и аналоговых устройств, что сопровождается уменьшением элек-
тромагнитной энергии, потенциально необходимой для нарушения функци-
онирования электронных систем [31, 96].
Расширение применения средств радиосвязи означает увеличение чис-
ла одновременно работающих радиопередатчиков и возрастание средней
напряженности радиочастотных электромагнитных полей, воздействующих
на электронное оборудование. Кроме того, распространение электронных
цифровых устройств означает возрастание помехоэмиссии низкого уровня,
воздействующей на радиоприем.
Все страны активно проводят техническую политику по регулированию
ЭМС [31, 120]. Облегченный режим обеспечения ЭМС, который ранее почти
7.1. ЭМС как показатель качества электронной аппаратуры
485
повсеместно существовал в Европе, кардинально изменен в результате при-
нятия Европейской комиссией Директивы ЭМС № 89/336/ EEC, введенной
с 1 января 1992 г. Существует общепризнанное мнение, что Директива ЭМС
является наиболее всесторонней, сложной и, возможно, наиболее придир-
чивой Директивой, когда-либо исходившей из Брюсселя.
Обеспечение свободного движения товаров между государствами являет-
ся важнейшей целью развития мировой торговли. Все государства вводят для
изготовителей товаров стандарты и устанавливают ответственность за их на-
рушение для обеспечения качества и безопасности товаров, защиты пользо-
вателей и т.д. Определенные различия в процедурах и требованиях играют роль
технических барьеров в торговле и приводят к раздробленности мирового рынка
и повышению стоимости товаров, так как изготовители должны модифици-
ровать свою продукцию применительно к различным национальным рынкам.
Детальные технические требования на компоненты и аппаратуру устанавли-
ваются в стандартах, разрабатываемых международными (МЭК, МСЭ), реги-
ональными (СЕН, СЕНЕЛЕК и ЕТСИ) и национальными органами по стан-
дартизации. Соответствие требованиям этих стандартов будет доказывать
соответствие существенным требованиям каждой директивы.
В начале 2000 г. Европейской комиссией был опубликован документ, ус-
танавливающий определенные критерии, соблюдение которых может обес-
печить разработку европейских директив «Нового подхода» в относительно
единообразном стиле.
Во время подготовки Директивы ЭМС независимо от нее были приняты
другие директивы «Нового подхода», которые могут оказать влияние на не-
которые отрасли электротехнической и электронной промышленности, а
именно:
• Безопасность игрушек (88/378/ЕЕС);
• Неавтоматические взвешивающие устройства (90/384/ЕЕС);
• Медицинские изделия (93/42/ЕЕС);
• Активные имплантируемые медицинские изделия (90/385/ЕЕС);
• Безопасность машин (89/392/ЕЕС);
• Приборы для сжигания газового топлива (90/396/ЕЕС);
• Лифты (95/16/ЕС);
• Телекоммуникационное оконечное оборудование (98/13/ЕС);
• «Ин-витро» диагностические медицинские устройства (98/79/ЕС);
• Радио- и телекоммуникационное оконечное оборудование (99/5/ЕС).
Дополнительно к указанному перечню имеются две другие директивы,
которые имеют отношение к Директиве ЭМС, хотя и не относятся к дирек-
тивам «Нового подхода». Это так называемые «Низковольтная Директива»
(LVD) (72/23/ЕЕС) и «Автомобильная Директива ЭМС» (95/54/ЕС). Низко-
вольтная Директива имеет отношение к безопасности продукции, а не к
вопросам ЭМС, но, учитывая требования Директивы о маркировании про-
дукции знаком соответствия СЕ, в настоящее время знак соответствия СЕ
удостоверяет соответствие продукции как требованиям Низковольтной Ди-
рективы, так и всем другим применимым директивам «Нового подхода».
486
Глава 7. Печатные платы и элементы ЭМС
Директива о радио- и телекоммуникационном оконечном оборудовании
(99/5/ЕС) вступила в силу 8 апреля 2000 г. с переходным периодом до 7 апреля
2001 г.; после этой даты все оборудование, относящееся к области применения
указанной Директивы, должно соответствовать ее требованиям. Данная Дирек-
тива представляет собой развитие ранее принятой Директивы о телекоммуни-
кационном оконечном оборудовании (89/13/ЕС). Имея область применения,
охватывающую телекоммуникационное оконечное оборудование всех назначе-
ний и радиооборудование всех назначений, эта Директива заменяет Директи-
ву ЭМС применительно к указанному оборудованию. При этом требования ЭМС
сохранены, хотя на этот счет имеются небольшие изменения. Точно определе-
но оборудование, которое исключено из области применения Директивы о ра-
дио- и телекоммуникационном оконечном оборудовании, в том числе:
• аппараты, используемые исключительно для обеспечения обществен-
ной безопасности, обороны, государственной безопасности и государ-
ственной деятельности в области выполнения уголовного законода-
тельства;
• морское оборудование, оборудование гражданской авиации и управ-
ления воздушным движением (для указанного оборудования приме-
няются отдельные предписания);
• оборудование для радиолюбителей, радиовещательные приемники,
кабельные системы и провода связи.
Введение Директивы о радио- и телекоммуникационном оконечном обо-
рудовании фактически привело к фундаментальному изменению способов
регулирования, относящихся к указанному оборудованию, которое ранее на
национальном и общеевропейском уровне было объектом режима утверж-
дения типа. Целью введения указанной Директивы явилось в основном уп-
рощение и облегчение процедур и уменьшение объема существенных требо-
ваний в соответствии с подходами Европейского союза, что можно рассмат-
ривать как быструю реакцию на нужды рынка.
Директива о радио- и телекоммуникационном оконечном оборудовании
вводит требования Низковольтной Директивы и Директивы ЭМС и позво-
ляет в дальнейшем применять для указанного оборудования режимы оцен-
ки соответствия, уже введенные в указанных директивах. Важнейшим отли-
чием является исключение нижнего допустимого предела напряжения для
применения требований Низковольтной Директивы (50 В переменного тока
и 75 В постоянного тока). Это означает, что требования безопасности при-
менимы даже к портативным аппаратам с батарейным питанием, имея, на-
пример, в виду обязательное применение норм излучений, обеспечивающих
безопасность. Поэтому мобильные портативные радиопередатчики должны
быть объектом оценки соответствия этим нормам.
Одобрение типа радиопередатчиков упразднено при одновременном вве-
дении дополнительных требований по эффективному использованию радио-
частотного спектра с тем, чтобы исключить влияние помех. Это не мешает
национальным органам власти применять ограничения, касающиеся управ-
ления спектром с применением процессов лицензирования, но они не должны
7.1. ЭМС как показатель качества электронной аппаратуры
487
навязывать в этой связи режим одобрения типа. Введено требование инфор-
мировать соответствующие национальные органы власти в случае намере-
ния разместить на рынке оборудование, которое использует негармонизи-
рованное распределение спектра. В случае необходимости органы власти
должны выдвинуть возражение в течение четырех недель.
Директива также позволяет Европейской комиссии вводить дополнитель-
ные требования для оборудования определенных классов, но до настояще-
го времени такие требования не вводились.
Особого внимания заслуживают требования к оконечному оборудованию,
направленные на то, чтобы исключить передачу помех в сети или такие ре-
жимы функционирования оборудования, которые вызывают неприемлемое
ухудшение обслуживания других пользователей. Эти аспекты ЭМС тради-
ционно регулировались с использованием процессов одобрения типа, однако
существует опасение, что если оставить процесс регулирования и установ-
ления требований к оборудованию в том же виде, как он существовал ранее,
то это повредит общеевропейской гармонизации применительно к сектору
проводной связи и промышленности средств связи.
Директива ЭМС 89/336/ЕЕС применяется к аппаратам, способным со-
здавать электромагнитные помехи, или к тем, качество функционирования
которых подвержено воздействию таких помех. Под «аппаратом» понима-
ется любой электрический и электронный прибор, оборудование и установка.
Существенно то, что область применения Директивы охватывает все аппа-
раты, питание которых осуществляется от источника электрической энер-
гии, независимо от того, является ли указанным источником общественная
распределительная электрическая сеть, электрическая батарея или специа-
лизированная питающая сеть (источник).
Под электромагнитной помехой понимается любое электромагнитное яв-
ление, которое может ухудшить качество функционирования аппарата безот-
носительно к частоте или механизму связи. Таким образом, эмиссия всех из-
лучаемых электромагнитных помех, а также помех, распространяющихся в
кабелях, а равно и устойчивость к электромагнитным полям, низкочастотным
сетевым помехам, кондуктивным переходным и радиочастотным помехам,
электростатическим разрядам и импульсным помехам, вызванным молниевыми
разрядами, относятся к области применения Директивы ЭМС. Ни одно элек-
тромагнитное явление, касающееся электромагнитной совместимости, не ис-
ключено из области применения Директивы ЭМС.
Существенные требования базовых нормативных документов в области
ЭМС заключаются в том, что аппараты должны быть изготовлены таким об-
разом, чтобы:
• создаваемые ими электромагнитные помехи не превышали уровня,
обеспечивающего функционирование радио- и телекоммуникацион-
ного оборудования и других аппаратов в соответствии с назначением;
• аппараты имели достаточный уровень собственной устойчивости к
электромагнитным помехам, позволяющий им функционировать в со-
ответствии с назначением.
488
Глава 7. Печатные платы и элементы ЭМС
Цель установления существенных требований заключается в том, чтобы
защитить функционирование не только радио- и телекоммуникационного
оборудования, но и любого другого оборудования, которое может быть вос-
приимчивым к электромагнитным помехам, например оборудования инфор-
мационных технологий или управления процессами. В то же время различ-
ное оборудование должно быть в состоянии нормально функционировать в
любой обстановке, в которой было бы разумным ожидать его использования.
Несмотря на установление указанных требований, любое государство име-
ет право принять специальные меры, относящиеся к введению аппарата в эк-
сплуатацию, направленные на преодоление имеющихся или ожидаемых про-
блем в области обеспечения ЭМС, связанных с размещением аппаратов в оп-
ределенных местах, или защитой общественных телекоммуникационных
сетей, или обеспечением работы служб безопасности. Соответствие суще-
ственным требованиям должно быть удостоверено с использованием одно-
го из двух основных способов: способа самосертификации применительно
к требованиям гармонизированных стандартов ЭМС или способа подготовки
технического файла конструкции.
Эти требования применяются для всех аппаратов, которые размещают-
ся на рынке или вводятся в эксплуатацию. Печатные платы и цифровые узлы
на их основе являются основными компонентами практически всех аппаратов,
систем и установок, которые работают во всех сферах деятельности челове-
ка. Поэтому от качества их проектирования во многом зависит, насколько
выполняются требования ЭМС. Конструктор должен осознавать, насколь-
ко важно удовлетворить параметры ЭМС на стадии проектирования изде-
лия, и должен владеть основными методами и средствами обеспечения по-
вышения стойкости электронных узлов к воздействию внешних электромаг-
нитных возмущений, а также приемами снижения помехоэмиссии.
Более подробно о стандартизации в области ЭМС и основных методах
проектирования аппаратуры с учетом ЭМС можно познакомиться в [31].
7.1.2. Система технического регулирования
в области ЭМС
Решение вопросов ЭМС становится в настоящее время неотъемлемым
элементом деятельности предприятий-разработчиков и изготовителей тех-
нических средств (ТС), в том числе печатных узлов; организаций, осуществ-
ляющих проектирование и монтаж установок, состоящих из электротехни-
ческих, электронных и радиоэлектронных аппаратов и систем; предприятий
электроэнергетического комплекса; органов государственного надзора и
контроля; организаций сферы подтверждения соответствия (испытательных
лабораторий ЭМС, органов по сертификации продукции).
Опыт развитых стран показывает, что для эффективного решения проблем
ЭМС необходимо осуществлять техническое регулирование в области элек-
тромагнитной совместимости, включающее установление обязательных тре-
бований к продукции, осуществление субъектами хозяйственной деятельности
7.1. ЭМС как показатель качества электронной аппаратуры
489
обязательного подтверждения соответствия и выполнение государственными
органами надзорных и контрольных функций. Устойчивое развитие стран и
конкурентоспособность изделий их промышленности в современных усло-
виях во многом зависят от эффективности применяемых форм и способов
технического регулирования в области ЭМС.
Европейская система технического регулирования основана на установ-
лении для аппаратов, систем и установок различного назначения жестких тре-
бований ЭМС и на применении относительно мягких способов обязатель-
ного подтверждения соответствия, позволяющих изготовителю, использу-
ющему гармонизированные стандарты ЭМС, декларировать соответствие на
основе собственных доказательств.
В России до настоящего времени отсутствует законодательный акт, ус-
танавливающий единые правовые основы технического регулирования в об-
ласти ЭМС, а обязательные требования, относящиеся к электромагнитной
совместимости, устанавливаются в государственных стандартах Российс-
кой Федерации и межгосударственных стандартах. На основании законов
РФ от 10 июня 1993 г. № 5141-1 «О стандартизации» и от 10 июня 1993 г.
№ 5151-1 «О сертификации продукции и услуг» федеральными органами
исполнительной власти организовано подтверждение соответствия техни-
ческих средств (ТС) требованиям ЭМС в ряде систем обязательной серти-
фикации продукции. Таким образом, главный акцент при осуществлении
в настоящее время технического регулирования в области ЭМС делается
на государственное регулирование, осуществляемое федеральными орга-
нами исполнительной власти в сферах своих полномочий. Развитие рыноч-
ных отношений и интеграция в мировое сообщество требует ускоренного
развития нормативной базы, которая позволит отечественным изделиям со-
ответствовать европейским требованиям ЭМС и устранит ограничения по
доступу российских предпринимателей на рынок ЕС и других стран миро-
вого сообщества.
С 1 июля 2003 г. вступил в силу Федеральный закон «О техническом ре-
гулировании», положения которого отражают условия рыночной экономи-
ки, присоединение России к Всемирной торговой организации, устранение
барьеров в торговле, необходимость обеспечения конкурентоспособности
отечественной продукции.
В соответствии с Федеральным законом «О техническом регулировании»
предусмотрена разработка и принятие общего Технического регламента «Об
электромагнитной совместимости». Таким образом, поставлена задача по со-
зданию в РФ единой системы технического регулирования в области ЭМС,
по существу, аналогичной европейской системе технического регулирования
в этой области.
В соответствии с Федеральным законом «О техническом регулировании»
при обязательной сертификации соответствие продукции требованиям об-
щего Технического регламента «Об электромагнитной совместимости» должно
подтверждаться сертификатом соответствия, выдаваемым заявителю орга-
ном по сертификации.
490
Глава 7. Печатные платы и элементы ЭМС
Проблемы ЭМС не ограничиваются случаями, описанными выше. Все боль-
шее значение приобретают проблемы, связанные с тем, что электронная аппа-
ратура всех видов становится более восприимчивой к внешним электромагнит-
ным помехам. Это явление становится все более заметным по двум причинам:
во-первых, постоянно увеличивается распространение и взаимодействие элек-
тронных изделий во всех сферах повседневной жизни, и, во-вторых, современное
оборудование с микропроцессорами и пластмассовыми корпусами обладает, как
правило, худшей устойчивостью к электромагнитным помехам. Восприимчи-
вость к помехам сегодня является основной проблемой электронных устройств
многих видов, особенно тех, для которых обеспечение нормального функцио-
нирования является жизненно важным по причинам, связанным с безопасно-
стью или экономикой. Системы управления автомобилями или авиацией яв-
ляются примерами, относящимися к первой категории, банковское дело и те-
лекоммуникационные сети — примерами второй категории.
В настоящее время каждая компания, которая изготавливает или импор-
тирует электрические или электронные изделия, должна принять необходи-
мые меры, чтобы указанные изделия соответствовали требованиям ЭМС. Это
означает, что каждая служба предприятия должна быть осведомлена о вопросах
электромагнитной совместимости.
Требования ЭМС, бесспорно, влияют на конструирование изделия. Поэтому,
в первую очередь, группа конструирования и разработки должна быть осве-
домлена о вопросах, относящихся к обеспечению ЭМС. Электромагнитная
совместимость зависит от того, каким образом отдельные изделия соединя-
ются вместе, так что необходима осведомленность по этим вопросам и про-
изводственного отдела. ЭМС зависит также от способов установки изделия на
месте эксплуатации, поэтому вопросы обеспечения ЭМС оказывают влияние
на работу специалистов, осуществляющих установку, техническое обслужи-
вание изделий и разрабатывающих документацию для пользователя.
Поскольку электромагнитная совместимость должна быть обеспечена для
каждого отдельного узла и блока, вопросы ЭМС оказывают влияние на работу
отдела испытаний. От обеспечения ЭМС зависят стратегия маркетинга и цено-
вая политика, таким образом, указанные вопросы оказывают влияние на рабо-
ту отделов ценообразования и маркетинга и, в конечном счете, на жизнеспособ-
ность предприятия и выполнение им своих обязательств. Поэтому старший уп-
равленческий персонал должен хорошо разбираться в вопросах обеспечения ЭМС.
В долгосрочной перспективе выполнение сотрудниками отдела ЭМС пред-
приятия обязанностей, связанных с повышением в каждом действующем под-
разделении уровня знаний, относящихся к электромагнитной совместимости,
может оказаться излишним, учитывая, что решение вопросов обеспечения ЭМС
становится, по мере развития, естественной частью функционирования каждого
подразделения. Тем не менее, необходимо выполнение указанных ниже задач:
• проверка соблюдения принципов ЭМС при создании каждого ново-
го изделия на всех стадиях его разработки и создания прототипа и кон-
сультирование, при необходимости, по вопросам изменения конструк-
ции с целью обеспечения ЭМС;
7.1. ЭМС как показатель качества электронной аппаратуры
491
• составление и контроль выполнения плана обеспечения ЭМС и пла-
на испытаний в области ЭМС для каждого изделия;
• надзор за проведением предварительных испытаний и испытаний на
соответствие как в условиях предприятия, так и при взаимодействии с вне-
шними испытательными лабораториями;
• поддержание высокого уровня знаний стандартов ЭМС и законодатель-
ных актов, применяемых для изделий компании;
• поддержание связи с отделами разработки, производства, испытаний, ус-
тановки и технического обслуживания, продаж и ценовой политики с целью
обеспечения соответствия их стратегии требованиям ЭМС.
Перечень задач, вероятно, может быть более детализирован, но и приве-
денный выше служит подтверждением того, насколько широка область дея-
тельности персонала, отвечающего за обеспечение ЭМС. Не менее важна ква-
лификация в области ЭМС специалистов, участвующих на всех стадиях в со-
здании изделия. В первой главе рассмотрены стадии проектирования и
прототипирования аппаратуры, в том числе печатных плат и печатных узлов.
Из этого рассмотрения видно, что учет требований ЭМС на ранних этапах
проектирования существенно снизит итоговые затраты, поскольку существенно
сократят объем корректив и доработок.
Ниже приведены основные сведения по обеспечению требований ЭМС
при проектировании печатных плат.
7.1.3. Понятие «электрического размера»
Один из важных параметров для понимания сути явлений и процессов, про-
исходящих в печатной плате и в аппаратуре в целом, — «электрический размер»
[121]. Печатную плату в общем виде можно рассматривать как некоторую из-
лучающую электромагнитную структуру. Будем считать, что излучающая элек-
тромагнитная структура — это любая структура, состоящая из проводников,
проводящих ток. «Электрический размер» наиболее важен в определении эф-
фективности электромагнитной связи структуры с другими объектами.
Электрические размеры измеряются в длинах волны. Длина волны пред-
ставляет собой расстояние, которое электромагнитная волна должна прой-
ти, чтобы фаза сдвинулась на 360°. Строго говоря, это имеет отношение к
одному типу волны: однородной плоской волне. Свойство сдвига по фазе
также связано с временем распространения волны между двумя точками.
Достаточно просто определить электрические размеры платы или другой
электромагнитной структуры в терминах длин волн. Длины волн обознача-
ются символом X. Для начала предположим, что электромагнитные волны
распространяются в среде без потерь. В этом случае длина волны может быть
рассчитана по известной формуле:
X=v//, (7.1)
где v — скорость распространения электромагнитной волны в данной среде; f — частота
синусоидального колебания.
492
Глава 7. Печатные платы и элементы ЭМС
При импульсном сигнале частота определяется как максимальная частота
спектра сигнала, что определяет минимальную длину волны.
Электрический размер некоторой структуры в длинах волн можно выра-
зить следующим образом:
ke=ds/X, (7.2)
где ds — максимальный физический размер структуры, м; X — минимальная длина волны
в спектре сигнала, м.
Электрические размеры структуры зависят от физических величин: час-
тоты возбуждения и скорости распространения электромагнитной волны в
среде, в которую структура помещена. Печатная плата является электрически
малой, если ее наибольшее значение ds намного меньше, чем длина волны,
ке « 1 или ds« X. Обычно неравенство задают в следующем виде
JS<O,1X. (7.3)
Скорость распространения электромагнитной волны в свободном про-
странстве обозначается v0 и приблизительно составляет ЗхЮ8 м/с. Для сво-
бодного пространства диэлектрическая и магнитная постоянные обознача-
ются соответственно как р0 и е0 и определяются следующим образом:
£о ‘10 9’ Ф/м, (приближенное значение),
Зол
р0 = 4л-10“7, Гн/м, (точное значение).
Скорость распространения электромагнитной волны определяется соот-
ношением:
1 8
= I—= 310 , м/с(приближенное значение). (7.4)
о
Для непроводящей среды, отличной от свободного пространства, скорость
распространения электромагнитной волны может быть выражена через от-
носительную диэлектрическую и магнитную проницаемость среды следую-
щим образом:
где е — относительная диэлектрическая проницаемость; — относительная магнитная
проницаемость.
Из (7.5) видно, что скорость распространения электромагнитной волны
в линиях передачи на стеклотекстолите FR4 с ег = 4, = 1 будет в два раза
меньше скорости распространения сигнала в свободном пространстве, а
следовательно, и длина волны для какой-либо частоты будет в два раза меньше.
Параметры других материалов приведены в главе 1.
7.1. ЭМС как показатель качества электронной аппаратуры
493
Очень важно правильно вычислить электрические параметры материала на
определенной частоте. Для этого необходимо помнить, что один метр равен
длине волны на частоте 300 МГц в свободном пространстве (воздухе). Длина
волны в свободном пространстве может быть легко рассчитана на другой ча-
стоте, соответственно масштабируя размеры. Для этого необходимо помнить,
что с увеличением частоты длина волны уменьшается и наоборот. Например,
длина волны на частоте 50 МГц равна 1 м х 300 МГц/50 МГц = 6 м. Длина волны
на частоте 2 ГГц (1 ГГц = 1000 МГц) равна 300/2000 = 0,15м, т. е. 15 см. В ди-
электрической среде длина волны должна быть уменьшена пропорциональ-
но корню квадратному из значения относительной диэлектрической прони-
цаемости этой среды.
Электрические размеры печатной платы или другой электромагнитной
структуры должны быть рассчитаны так, чтобы можно было определить,
является ли данный объект электрически малым, т. е выполняется ли усло-
вие ds < 0, IX или нет. Если он является электрически малым, то при анализе
объекта можно применить более простые подходы и вычисления, чем в слу-
чае, если он будет электрически большой. Например, применяются законы
токов и напряжений Кирхгофа наряду с моделированием цепей на сосредо-
точенных элементах, если наибольший размер платы является электричес-
ки малым. Если плата является электрически большой, то мы можем исполь-
зовать только уравнения Максвелла (или упрощенные уравнения Максвел-
ла), чтобы описать задачу. С таким подходом мы встречались, например, при
классификации линий передачи на электрически длинные и короткие.
Один из способов определения электрических показателей платы заклю-
чается в вычислении длины волны на интересующих сверхвысоких частотах
и затем коэффициента kQ по (7.2). Например, рассмотрим плату на FR4 (ег = 4),
которая имеет максимальный размер 300 мм, работающую на частоте 500 МГц
(максимальная частота спектра сигнала). Минимальная длина волны в воздухе
составит 300/500 = 0,6 м, а в диэлектрике 0,6/7? = 0,3 м. Очевидно, что не-
равенство (7.3) в данном случае не выполняется. Это означает, что при про-
ектировании печатной платы происходящие в ней электродинамические
процессы должны быть рассмотрены с позиций электродинамики, а приме-
нение упрощенных моделей требует серьезного обоснования.
7.1.4. Общие единицы измерения ЭМС
Первичные электрофизические параметры, представляющие интерес в
области ЭМС, — это кондуктивная помехоэмиссия (напряжение измеряется
в вольтах, а ток — в амперах) и излучаемая помехоэмиссия (напряженность
электрического поля измеряется в вольтах на метр (В/м), а напряженность
магнитного поля измеряется в амперах на метр (А/м). С этими первичными
величинами связаны величины мощности, измеряемые в ваттах (Вт), или
плотность потока мощности, измеряемая в ваттах на квадратный метр (Вт/м2).
Числовой диапазон этих величин в задачах ЭМС может быть весьма широким.
Например, электрическое поле может иметь значения в диапазоне от 1 мВ/м
494
Глава 7. Печатные платы и элементы ЭМС
до 200 В/м. В этом динамическом диапазоне представлено более восьми
порядков величин (108). Для удобства представления этих широких диапа-
зонов единицы измерений, применяемые в ЭМС, выражаются в децибелах
(дБ). Эта размерность использовалась ранее при рассмотрении линий передач
с потерями.
Числовой диапазон, выраженный в децибелах, намного меньше. Напри-
мер, диапазон напряжений 108 В равен 160 дБ. Как мы увидим далее, суще-
ствуют также и другие причины для выражения этих величин в децибелах.
Для удобства использования следует уметь оперировать величинами, кото-
рые выражены в децибелах. Также необходимо понимать значения величин
ЭМС, когда они выражены в децибелах.
Для пояснения соответствующих преобразований рассмотрим усиление
сигнала в некотором усилителе, который работает на постоянную нагрузку.
Для него можно получить отношения для определения коэффициента уси-
ления в децибелах:
Г /J ]
для мощности — дБ = 101og101 — ,
V2 )
для напряжения — дБ = 20 logj0 —
<V2.
для тока — 4B-201og10 1 .
V2 7
(7.6)
(7.7)
(7.8)
Абсолютные уровни мощности, напряжения или тока, выраженные в
децибелах, дают значения относительно некоторого опорного значения.
Например, значение напряжения обычно выражается относительно 1 мкВ
и обозначается как 1 дБмкВ:
г о пт I Вольт
дБмкВ = 20 log10 --—
I 1 мкВ
Например, значение напряжения 1 В равно 120 дБмкВ, поскольку
1В
20 login I------——-г— I = 20 log10106 = 120 дБмкВ.
101. 1 мкВ = Ю^В J 10
Обычно говорят, что «1 В равен 120 дБ относительно 1 мкВ» или «1 В на
120 дБ выше 1 мкВ».
Аналогично значение 350 мВ равно:
20 log, 0 р5^0----^ = 201og10 (350 • 103) = 110,88 дБмкВ.
7.1. ЭМС как показатель качества электронной аппаратуры
495
Если абсолютное значение менее 1 мкВ, то это дает отрицательное зна-
чение децибел. Например, значение 0,1 мкВ равно — 20 дБмкВ.
Другие величины измеряются в стандартных единицах измерения: дБмВ
(относительно 1 мВ), дБмА (относительно 1мА) и в дБмкА (относительно
1 мкА). Это дается выражениями:
дБмВ = 201og10|
I 1мВ }
( 1А
дБмкА = 20 log10 -- ,
ЦмкА )
Л 1А Л
дБмА = 20^10 .
^1мА )
Мощность выражается по отношению к микроваттам (дБмкВт) или от-
носительно милливатта (дБмВт, или равнозначное обозначение дБм), как,
например:
Г О 1П1 ( 1Вт
дБмкВт = 101og10 ---- ,
ЦмкВт )
Г г о 1Л1 ( 1Вт
дБм = дБмВт = 10 log10 - .
I^ImBt )
Заметим, что при обозначениях относительных величин напряжения и тока
используются обозначения дБмВ, дБмА, за исключением обозначения мощ-
ности, дБм, например:
15 мВ - 15000 мкВ = 83,52 дБмкВ = 23,52 дБмВ,
630 мА = 630000 мкА = 115,99 дБмкА = 55,99,
250 мВт = 250000 мкВт = 53,98 дБмкВт = 23,98 дБм.
Обозначение дБм используется как более простая запись обозначения дБмВт.
Излучающее электромагнитное поле приводится в терминах (значениях)
напряженности электрического поля, которое измеряется в вольтах на метр,
В/м, или в значениях напряженности магнитного поля, имеющую единицы
измерения ампер на метр, А/м. Относительные единицы измерения в зада-
чах ЭМС сводятся к 1 мкВ/м, 1 мВ/м, 1 мкА/м или 1 мА/м, как дБмкВ/м,
дБмВ/м, дБмкА/m и дБмА/m соответственно. Например, один из пределов,
разрешенный нормативными документами напряженности излучаемого
электрического поля, равен 100 мкВ/м. Это значение преобразуется к
40 дБмкВ/m. Соответственно данные единицы измерения преобразуются та-
ким же образом для напряжения и тока:
( 1В/м
дБмкВ/м = 20 log10 ----- ,
Ц мкВ/м )
496
Глава 7. Печатные платы и элементы ЭМС
Г хВ
ио-6 в,
дБмкА/м = 201og10 ------
Ц мкА/м
Не менее важно уметь конвертировать (преобразовать) единицы измере-
ния, приведенные в децибелах, в их абсолютные значения. Для этого исполь-
зуется логарифм числа п с основанием т:
1оМ = п.
Это означает: чтобы получить значение числа Л, необходимо т возвести
в степень п\
тп = А.
Поэтому можно преобразовать число п, приведенное в децибелах, к его
абсолютному значению, выполнив указанные преобразования. Например,
108 дБмкВ равны:
108 дБмкВ = 20 log10
Таким образом, абсолютное значение в вольтах, В, в этом выражении равно:
Х = |01О8 дБмкв/20 х 10-6 = 0,2512 В.
Преобразования для других размерностей задаются выражениями:
Вольт = 10дБмкВ/2Ох10—6^
Вольт = ЮдБмВ/20х 10“3,
Вольт = 10дБмкВ/1Ох 10—6,
Вольт = 10дБмВ/10хЮ-3.
Можно рекомендовать следующую последовательность преобразований:
1. Необходимо поделить величину, подлежащую преобразованию, на 20
(если это напряжение или ток) или на 10 (если это мощность).
2. Затем нужно возвести число 10 в степень, определяемую результата-
ми первого шага.
3. Умножить результат на 10-6 для дБмкВ, дБмкВт и дБмкА или на 10-3
для дБмВ, дБм или дБмА.
Этих правил следует придерживаться также для величин электрического
и магнитного полей в дБмкВ/м, дБмВ/m, дБмкА/m или дБмА/m, где они
преобразуются подобно напряжению и току, то есть, используя выражение
201og10. Например, интенсивность электрического поля, равная 44 дБмкВ/м,
приводится к 158,49 мкВ/м следующим образом:
Вольт = Ю44 дБмкВ/20хЮ—6 = 0,00015849 В/м = 158,49 мкВ/м.
7. 1. ЭМС как показатель качества электронной аппаратуры
497
Точно так же 56 дБм преобразуется в 398 Вт:
Вольт = ю56дБмкВ/10хЮ-3 = 398,107, Вт.
Преимущества представления в задачах ЭМС физических единиц в дБ, а
не в абсолютных значениях заключаются в переводе больших чисел в мень-
шие и упрощении ряда преобразований. При этом используются известные
свойства логарифмов. Напомним основные из них:
logmM х В) = log^ + logm5,
log^* = fclog^,
( д A
10gm -jj = 10gm^-10gmB.
Заметим, что:
10gm(^ + В)* log^ + logm5.
Эти очень важные свойства делают преобразование единиц измерения в
области ЭМС более простыми, если они выражены в дБ. Например, рассмот-
рим преобразование напряжения к дБмкВ:
201og10 = 201og10 (Вольт) - 201og1010"6 = 201oglo (Вольт) + 120.
Здесь преобразовано напряжение к дБВ (дБ относительно 1 В) взятием
201og10 от напряжения, а затем прибавлением числа 120, чтобы получить
значение в дБмкВ. В табл. 7.1 приведен пересчет чисел в значения децибел
при расчете напряжений и токов, а также мощностей.
Эти свойства могут также применяться для получения достоверно точных
оценок величин в децибелах без использования калькулятора. Чтобы убедить-
ся в этом, приведем некоторые простые числа к децибелам, используя дан-
ные табл. 7.1.
Операция приведения 10 к целочисленным множителям (положительным
или отрицательным) весьма проста. Из всех чисел от 1 до 9 двумя наиболее
используемыми числами являются 2 и 3. Заметим, что отношение двух на-
пряжений или токов, значение которого равно 2, приблизительно дает 6 дБ,
а если отношение равно 3-10 дБ. Для мощности отношение 2 дает прибли-
зительно равно 3 дБ, а для отношения 3—5 дБ. Очевидно, что отношение 10
для напряжений даст значение 20 дБ, а для отношения мощностей — 10 дБ.
Эти значения могут использоваться для оценки величин в децибелах, рас-
писав число как результат произведений чисел 10, 2 и 3. Например, если
отношение напряжений равно 25, то это соответствует приближенно 28 дБ.
Приближенная оценка выглядит следующим образом:
25 - 24 = 3 x 2 x 2 x 2.
498
Глава 7. Печатные платы и элементы ЭМС
Таблица 7.1
Приведение чисел к децибелам
Порядок Напряжение или ток, дБ Мощность, дБ
106 120 60
105 100 50
104 80 40
101 60 30
102 40 20
10 20 10
9 19.08 9.54
8 18.06 9.03
7 16.9 8.45
6 15.56 7.78
5 13.98 6.99
4 12.04 6.02
3 9.54 4.77
2 6.02 3.01
1 0 0
10 ' -20 -10
10 2 -40 -20
10 1 -60 -30
Следовательно:
20 log10 25 = 20 log10 24 = 20 log10 (3 х 2 х 2 х 2) =
= 20 log10 3 + 20 log10 2 + 20 log10 2 + 20 log10 2 =
= 10 + 6 + 6 + 6 — 28, дБ,
или, например:
201og10360 = 201og10(3x2x3x2xl0) = 10 + 6 + 10 + 6 + 20 = 52, дБ, (51,126).
101og10 = 10 log101 — 10 l°gi()l 80 = 0 — 10 l°g10 (2 х 3 X 3 х 10) =
= -3-5-5-10 = -23, дБ, (-22,52).
Точное значение приводится в круглых скобках. Приняв во внимание
данные рассуждения, можно оценивать число в децибелах и конвертировать
7.1. ЭМС как показатель качества электронной аппаратуры
499
число, выраженное в децибелах, к его абсолютному значению. Например,
значение напряженности электрического поля, равное 86 дБмкВ/м, может
быть представлено в виде 86=204-204-204-20+6. Таким образом, 86 дБмкВ/м
соответствуют (приблизительно):
86 дБ/мкВ/м = 10 х 10 х 10 х 10 х 2 = 2 х 104 = 20 000 мкВ/м,
или 20 мВ/м. Точное значение равно 19952,62 мкВ/м.
Способность децибел (и логарифмов) преобразовывать большие числа в
меньшие означает, что можно проводить некоторые относительно грубые
приближения и при этом получать реальную (разумную) оценку числа в де-
цибелах. Рассмотрим пример, с которым мы уже встречались при оценке
потерь в линии передачи.
Потери в линии передачи определяются потерями в проводниках и в ок-
ружающем диэлектрике. В нормальном частотном диапазоне использования
первичные потери происходят из-за потерь в проводниках. Сопротивление
проводников возрастает прямо пропорционально jf из-за скин-эффекта.
Однако потери в линии передачи должны быть определены на каждой час-
тоте, которая входит в состав спектра импульсного сигнала.
Потери мощности в линии определяются как разность между входной мощ-
ностью и мощностью, которая имеет место на выходе линии. Вместо этого
удобнее вычислять потери как отношение выходной мощности к входной:
А = -^ = е2а1,
^out
где Pin — входная мощность; Pout — выходная мощность; а — коэффициент затухания; / —
длина отрезка линии передачи.
Удобно для линий передачи приводить потери в размерности дБ/длину.
Этим подразумевается, что
А = 101og10e2a/ = 20a/-log10e = 8,686а/,
где длина / линии принимается некоторой определенной, например, 1 м. Для коаксиаль-
ных кабелей эта длина принимается 100 м.
Измерив входную и выходную мощность при заданной длине линии при
согласованной нагрузке, получаем значение ослабления, выраженное в де-
цибелах:
А = Р — Р
'дБ 2 in дБх 7 out дБх’
где дБх обозначает мощность, приравненную к некоторому уровню х. Как правило, ис-
пользуется уровень одного милливатта (дБм).
Можно получить коэффициент затухания на некоторой частоте как
_А(4 /4; 8=0)
а~ 8,686 / ’
где / — длина, которую используют изготовители для определения потерь.
500
Глава 7. Печатные платы и элементы ЭМС
Например, если для линии передачи 100 МГц получены потери 0,15 дБ на
длине 1 м, то коэффициент затухания будет равен
а=о /or 1 = 1710 3> Нп/м.
О,ОоО1 '
Важно помнить, что определение потерь в линиях передачи предполага-
ет, что линия согласована. В противном случае это определение потерь не
имеет никакого отношения к потерям в линии.
7.2. Помехоэмиссия от печатных узлов
7.2.1. Ближняя и дальняя зоны излучаемого поля
Рассмотрим важные механизмы образования электромагнитных полей в
печатном узле и их распространение по направлению к измерительной ан-
тенне, которая используется для проверки на соответствие требованиям ЭМС.
Нормативными документами предусмотрены требования к диапазону изме-
ряемых частот — от 30 МГц до, возможно, 40 ГГц, если изделие будет прода-
ваться в США (требования FCC) и от 30 МГц до 1 ГГц, если изделие будет
продаваться за пределами США (CISPR1 22). ГОСТ Р 51318.22-992 предус-
матривает нормы напряженности поля от оборудования информационных
технологий при измерениях на расстоянии 10 м. Область распространения
электромагнитного поля может быть разделена на две зоны в зависимости
от относительного расстояния от источника излучения. Ближняя зона огра-
ничена расстоянием, которое равно Х/2тс, где X — длина волны синусоидаль-
ного колебания. Если расстояние от источника больше этого значения, то
говорят о дальней зоне. В ближней зоне превалирует либо емкостная, либо
индуктивная составляющая электромагнитного поля в зависимости от типа
(модели) излучателя, т. е. имеют место индукционные процессы. В дальней
зоне независимо от типа источника излучения распространяется сформиро-
ванная плоская электромагнитная волна, для которой волновое сопротив-
ление равно волновому сопротивлению свободного пространства 377 Ом.
Дистанция, на которой устанавливается измерительная антенна соглас-
но требованиям, например, FCC составляет 3 м для изделия класса В и 10 м
для изделия класса А. При нижней частоте измерений 30 МГц длина волны
синусоидального колебания составляет 10 м и граница ближней зоны рас-
положена от источника излучения (испытуемой аппаратуры) на расстоянии
10/2тс, что приблизительно равно 1,6 м. Для C1SPR 22 соответствующее рас-
1 Специальный комитет по радиопомехам Международной электротехнической комис-
сии (МЭК).
2 ГОСТ Р 51318.22-99 (СИСПР 22-97). Совместимость технических средств электро-
магнитная. Радиопомехи индустриальные оборудования информационных технологий.
Нормы и методы испытаний.
7.2. Помехоэмиссия от печатных узлов
501
стояние составляет 10 м для изделия класса В и 30 м для изделия класса А.
Поэтому при испытаниях изделия, расположенные на расстоянии 3 м и бо-
лее, находятся в зоне дальнего поля для всех видов измерений.
Структура поля излучения в ближнем поле более сложная, чем в дальнем
поле. Некоторые преобразования, допустимые для дальнего поля, неприме-
нимы для ближнего поля, хотя они часто используются. Примером может
служить правило обратного расстояния, которое используется для приведения
излучения, измеренного на одном расстоянии, к другому расстоянию. Это
подразумевает линейную зависимость поля от расстояния измерения, т.е. про-
исходит увеличение (уменьшение) поля с уменьшением (увеличением) рас-
стояния измерения, что справедливо только для дальней зоны. Рассмотренные
ниже простые модели для прогнозирования помехоэмиссии от проводников
и печатных узлов применимы для дальней зоны. Для простоты представле-
ния предполагается, что для данных моделей измерительная антенна находится
в дальней зоне излучения, хотя это не обязательно может соответствовать пол-
ному требуемому диапазону измерений.
На первом этапе необходимо рассмотреть свойства излучения нежелатель-
ных антенн в системе, которыми являются проводники печатных плат и другие
металлические конструкции печатных узлов, например, корпусов. Простые
модели позволяют выявить факторы, вызывающие излучения, интенсивность
которых превышает установленные ограничения. Эти модели получены для
идеальных условий, например, пары изолированных проводников в свобод-
ном пространстве. Основной целью построения этих моделей является по-
нимание механизма возникновения помехоэмиссии и методов управления
ее уровнем на этапе конструирования печатной платы и печатного узла.
7.2.2. Токи в дифференциальном и общем режиме
Дифференциальный режим и режим общих токов были описаны в главе 6
при рассмотрении дифференциальной пары. Рассмотрим линию передачи, со-
стоящую из пары параллельных проводников на печатной плате, длиной / и
разнесенных на расстояние s, как показано на рис. 7.1а [121].
Предположим, что токи в одном и том же поперечном сечении направ-
лены вправо, и обозначим их как Ц и /2. Будем рассматривать излучение в
частотной области, поэтому токи будут комплексными величинами. Они могут
быть разложены на компоненты дифференциального и общего режима сле-
дующим образом:
I\ — /comm + /diff, Il — /comm-'/diff • (7«9)
Токи дифференциального режима Zdiff и /comm токи режима общего вида
могут быть получены из исходных токов, как это было сделано при анализе
дифференциальных пар, в следующем виде:
(7.10)
2 2
502
Глава 7. Печатные платы и элементы ЭМС
Рис. 7.1. Модели линии передачи для дифференциального и общего режима:
1 — сигнальный проводник; 2 — возвратный проводник; а — линия передачи
на печатной плате; б — дифференциальный режим; в — общий режим
В поперечном сечении линии, токи дифференциального режима равны
по значению, но имеют противоположные направления. Они несут инфор-
мацию и являются желательными. Идеальные модели линий передачи в пе-
чатной плате, которые рассматривались ранее, могут быть использованы для
прогнозирования только этих токов.
Токи режима общего вида (синфазного) являются нежелательными токами,
вызывающими повышенный уровень помехоэмиссии от печатного узла и
кабелей, которые подсоединены к нему. Они не являются необходимыми для
обеспечения работы электронных устройств. С помощью идеальных моде-
лей линий передач нельзя спрогнозировать токи синфазного режима. Как
правило, токи синфазного режима существенно меньше токов дифференци-
ального режима. Однако они часто производят большее излучение, чем токи
дифференциального режима.
1.2. Помехоэмиссия от печатных узлов
503
Рассмотрим излученные электрические поля в плоскости проводников и
в точке, лежащей на расстоянии d от средней линии. Конфигурация для то-
ков дифференциального режима изображена на рис. 7. Id. Заметим: из-за того,
что токи дифференциального режима равны, но противоположно направлены,
излучаемые от них электрические поля будут также противоположно направ-
лены и будут частично компенсировать друг друга. Эта компенсация не бу-
дет полной, так как проводники не совпадают. Поэтому суммарная напря-
женность электрического поля £diff будет отлична от нуля и будет опреде-
ляться разностью между различными компонентами излучения, как показано
на рис. 7.Id.
Теперь рассмотрим механизм излучения, вызванного токами синфазного
режима. Поскольку токи синфазного режима имеют одинаковое направление,
то их составляющие излученных электрических полей будут складываться, обра-
зуя суммарное излучаемое электрическое поле £Comm • Напряженность этого
поля может быть во много раз больше, чем поля от токов дифференциально-
го режима. Таким образом, токи режима общего вида способны создать суще-
ственные уровни излучения. Множество факторов, таких, как эффект близос-
ти проводящих плоскостей и других структурных асимметрий, могут создать
токи режима общего вида. Некоторые примеры асимметрий линий передачи,
вызванных конструкцией печатных проводников, рассмотрены в главе 6.
Для приближенного количественного анализа пары параллельных провод-
ников применимы простые модели излучения, вызванного токами, протека-
ющими в этих проводниках. Хотя случай двух параллельных проводников пред-
ставляет собой только малое подмножество возможных вариантов располо-
жения токонесущих проводников, расположенных на плате, он, тем не менее,
представляет собой важную и легко ана-
лизируемую структуру. На этом примере
можно лучше понять механизм излуче-
ния, который может быть применен для
анализа других структур. Основной метод
определения поля излучения пары парал-
лельных проводников базируется на
принципе суперпозиции и состоит в со-
вмещении излученных полей от каждого
проводника.
Рассмотрим два проводника, распо-
ложенных параллельно, как показано на
рис. 7.2.
Два провода расположены на оси у сфе-
рической системы координат и параллель-
ны оси z. Провод 1, по которому течет ток
/1 (г), расположен в точке у = -s/2, а про-
вод 2, ПО которому течет ТОК h(z) , рас- Рис- Модель излучающей системы
w проводников
положен в точке у =s/2. Каждый из этих
504
Глава 7. Печатные платы и элементы ЭМС
токов является функцией расстояния z вдоль провода. Заметим, что эта общая
задача может использоваться для описания случая, показанного на рис. 7.1.
Для случая с токами дифференциального режима приняты условия
11 (z) = /difr (г) и ^2 (г) = (г) ? а для случая с токами общего вида приня-
ты условия /1(г) = /сотт (г) и Л(г) = /сотт (^). Если будет определено значе-
ние поля Ее,ant излучения в дальней зоне каждой антенны, то, предполагая, что
точка измерения находится в дальней зоне, можно определить совокупное излу-
чаемое поле путем суперпозиции полей каждой антенны как:
^E0,ant = ^E0,antl + £e,ant2, (7.11)
где поле в дальней зоне каждой антенны может быть определено по форму-
ле [121]:
. . е-УРо'/
Ее ,antz — М/——F(0), (7.12)
где Ij — ток в центре антенны; ДО) — коэффициент усиления антенны, определяемый ее
диаграммой направленности, зависит от угла 0 и принимается максимальным; М — коэф-
фициент, зависящий от типа антенны; г. — расстояние от проводника до точки наблюдения.
Коэффициенты М и F(0) для диполя Герца равны
л/ = уПоРо/ = у2л.1о-6././)
4л (7.13)
F(0) = sin 0.
Этот результат является верным для отрезков тока, которые являются
электрически очень короткими, что позволяет предположить, что ток в каждой
точке антенны имеет одну и ту же амплитуду и фазу. Для полуволновых ди-
полей (/ = 0,5Х), которые имеют синусоидальное распределение токов, можно
записать:
м=А=/бо,
2л
^(0)=
COS —71 COS 0
[2
sin0
(7.14)
От начала координат можно провести вектор г расстояния до точки из-
мерения и два параллельные вектора rl и г2 из центров проводников, как
показано на рис. 7.2. Можно обозначить эти расстояния в значении рассто-
яния гот середины пары проводников. Расстояние Д, показанное на рис. 7.2,
определяется как
Д = -5sin0sin6.
2
(7.15)
7.2. Помехоэмиссия от печатных узлов
505
Таким образом,
/j=r + A, r2 = r + A. (7.16)
Подставив выражения (7.15) и (7.16) в (7.12) и совместив результаты,
согласно (7.11), получим следующее выражение:
£e,ant =М^^р|^м + /2^7р')Л р(е), (7.17)
полагая, что эти две антенны идентичны (два диполя Герца или два полувол-
новых диполя и т.п.) и приблизительно г~ Гр^в знаменателе. Фазовые зна-
чения зависят от электрического расстояния, £0 ri = 2nri • Хо, поэтому здесь
нельзя сделать подобные приближения и следует подставить выражение (7.16).
Полученный результат будет использоваться для случая токов дифференци-
ального режима и для токов режима общего вида в последующих разделах. На-
помним, что выражение (7.17) получено из предположения, что точка измере-
ния (измерительная антенна) находится в дальней зоне. Если это предположение
будет нарушено, то простые последующие модели будут неадекватны.
7.2.3. Модель излучения тока дифференциального
режима
Чтобы упростить результирующую модель, представим каждый провод как
диполь Герца. Для этой модели характерны два важных предположения:
• длины / проводников достаточно физически малы, и точка измерения
удалена от них на достаточное расстояние, поэтому векторы расстоя-
ния от каждой точки на антенне к точке измерения приблизительно
параллельны;
• распределение токов (по амплитуде и фазе) является постоянным по
длине линии.
Для измеряемого расстояния 3 м в соответствии с первым предположени-
ем необходимо, чтобы максимальная длина проводника была не более метра.
Предположение о постоянном распределении токов в проводниках является
приемлемым приближением при условии, что проводники электрически ко-
роткие на интересующей нас частоте. Это значительно упрощает результаты
и применяется во многих практических задачах. Например, печатный провод-
ник длиной 0,5 м равен длине волны Хо в свободном пространстве на частоте
600 МГц. Этот же проводник на частоте 100 МГц будет в шесть раз короче длины
волны, и распределение токов вдоль него является приблизительно постоян-
ным. Печатный проводник длиной 250 мм составляет 1/12 длины волны на
частоте 100 МГц, и распределение токов в нем будет практически постоянным
на частоте ниже 100 МГц. Для более коротких проводников применимость рас-
смотренной модели будет справедлива на более высоких частотах.
Определим излученные поля в точке, лежащей на перпендикуляре к ли-
нейным проводникам и лежащей в плоскости расположения проводников,
506
Глава 7. Печатные платы и элементы ЭМС
Рис. 7.3. Излучение от токов
дифференциального вида
как показано на рис. 7.3. Для постоянного рас-
пределения тока максимальное значение излу-
ченных полей будет в этой точке, находящейся
на расстоянии dот оси симметрии системы про-
водников. Еще раз важно подчеркнуть, что точка
измерения находится в дальней зоне.
Излученные поля могут быть определены, со-
гласно предположению о постоянном распреде-
лении токов в проводниках, приняв каждый про-
вод за диполь Герца и подставив выражение (7.13)
в (7.17). Дополнительно в выражении (7.15) при-
нимаем 9 = 90° и ф = 90° (чтобы поле было в плос-
кости проводов) так, чтобы А = 5/2. И, наконец,
так как рассматриваются токи дифференциаль-
ного режима, необходимо подставить
11 = /diff, /2 =-/diff
(7.18)
в выражение (7.17). В результате максимальная напряженность поля для диф-
ференциального режима будет определяться выражением
£difr,max =y-2n l0-7^^e-^rf(e-^/2 -е-^/2) =
d v 7
fji (\ \ (7.19)
= -4 л• Ю"7-7 /dlfirsin| Ip s I.
d ^2 ° )
В этом выражении произведена замена е*А — e~jA — 2/ sin А, где А = Рол/2.
Заменив
1П 71 S Tt'S'f , г
= =-----— = 1,05-10 V/
2 X v0
и полагая, что разнесение 5 проводов является электрически малым, можно
принять
sin(Po-s/2)s|V/2,
и выражение для расчета амплитуды напряженности поля (7.19) становится
более компактным:
£diff,max = 1,316 10~14 /diff Z , В/М, (7-2°)
d
где / difi — ток линий передачи в дифференциальном режиме, А; /— частота, которая пред-
ставляет интерес, Гц; / — длина отрезка линий передачи, м; 5 — расстояние между провод-
никами, м; d — расстояние между центром набора проводников и точкой размещения из-
мерительной антенны, м.
7.2. Помехоэмиссия от печатных узлов
507
Направление вектора напряженности электрического поля будет парал-
лельно проводникам.
В качестве примера рассмотрим печатную плату с проводниками длиной
0,5 м, которые разнесены на расстояние 1,25 мм. Предположим, что по ним
течет ток дифференциального режима с частотой 30 МГц. Определим мак-
симальный уровень тока дифференциального режима, который создает по-
мехоэмиссию в плоскости проводов на расстоянии 3 м (d = 3) (в худшем
случае), что соответствует уровню класса A FCC (40 дБмкВ/м или 100 мкВ/м
на частоте 30 МГц). Значение тока рассчитывается из выражения (7.20) по
следующей формуле:
/difF
/^diff, max d
\,3\6f2bs
•IO14. A.
(7.21)
Подставив соответствующие значения, получаем:
/diff
___________100 10~6 3____________
1,31б(30 106)2 0,5-(1,25 10-3)
1014 =4010\
или /diff = 40 мА.
В общем случае, формула для максимального значения излучения, приве-
денная в выражении (7.20), является достаточной для инженерной оценки.
При прохождении импульсного сигнала по линиям передачи ситуация
несколько изменится. Рассмотрим информационный или синхронизирую-
щий сигнал трапециевидной формы с фронтом /г и периодом следования /с.
Заметим из выражения (7.20), что передаточная функция, связывающая мак-
симальное полученное значение электрического поля с током, изменяется
пропорционально площади контура S = /5 и квадрату частоты, и она опреде-
ляется по формуле:
£diff ,max
Aiiff
(7.22)
где константа К равна К= 1,316х 10“ 14/J = 4,39х10-15 для расстояния d= 3 м,
заданного требованиями FCC измерения класса В. Таким образом, ампли-
тудно-частотная характеристика этой передаточной функции увеличивает-
ся пропорционально квадрату частоты, т. е. с интенсивностью +40 дБ/дека-
ду (рис. 7.4я). Перемножение этой передаточной функции и спектра сигна-
ла (рис. 7.46), полученного для трапециевидной формы сигнала в главе 1, дает
результирующий спектр (рис. 7.4в) искомой интенсивности электрическо-
го поля [121]. Заметим, что результирующее значение спектра излучаемого
электрического поля увеличивается от +40 дБ/декаду до частоты l/7t/w, где
Zw — длительность импульса, затем увеличивается как +20 дБ/декаду до ча-
стоты 1/я/г, и является плоским выше этого значения.
Как пример, рассмотрим последовательность импульсов на частоте 10 МГц,
имеющих 50 % коэффициент заполнения (/с = 2zw) и длительность /г фронта
508
Глава 7. Печатные платы и элементы ЭМС
Рис. 7.4. Определение спектра излучаемого
электрического поля в дифференциальном
режиме: а — зависимость передаточной
функции от частоты; б — спектр сигнала;
в — спектр излучаемого электрического
ПОЛЯ
2,5 нс. Основные точки излома огибающей спектра: l/7t/w = 6,37 МГц и
1 /л/г = 127,3 МГц. Это показывает, что из-за токов дифференциального режима
излучение имеет место в высокочастотной области, обычно выше 100 МГц.
Максимальное излучение в дифференциальном режиме наблюдается в
плоскости расположения проводников (рис. 7.5), а минимальный уровень —
в точке, равноотстоящей от каждого провода, в которой излученные поля
нейтрализуются. Таким образом, измеряемый уровень излучения от печатной
платы в режиме дифференциальных токов существенно зависит от ориенти-
ровки платы относительно измерительной антенны.
Рис. 7.5. Точка максимального и минимального уровня излучения
при дифференциальном режиме
1.2. Помехоэмиссия от печатных узлов
509
Максимальное значение излучаемого электрического поля, как видно из
(7.22), зависит от квадрата частоты, площади Is контура, амплитуды тока.
Поэтому, чтобы уменьшить уровень помехоэмиссии на определенной часто-
те из-за токов дифференциального режима, необходимо:
1) уменьшить уровень тока;
2) уменьшить площадь контура при одновременном сближении прямо-
го и возвратного проводников.
Вариант 1 требует решений на концептуальном уровне при определении
применяемой элементной базы, поскольку уровни токов в проводниках оп-
ределяются функциональными причинами. Снижения частотного диапазона
и уменьшения частот точек излома передаточной характеристики можно
добиться уменьшением тактовых частот, что приведет к увеличению /w и дли-
тельности фронта Zr и спада импульса.
Вариант 2, связанный с уменьшением площади контура, необходимо
применять на ранних стадиях проектирования. Эта проблема в разных ас-
пектах обсуждалась в предыдущих разделах.
Правильный выбор функционального назначения соединителей, устанав-
ливаемых на плате, может также снизить помехоэмиссию от токов диффе-
ренциального режима. Если по каким-либо причинам выводы соединителя
задействованы так, что сигнальный и возвратный токи разнесены на отно-
сительно большое расстояние, то образуется контур значительной площа-
ди, приводящий к заметной помехоэмиссии от дифференциальных токов. Сле-
дует изменить расположение выводов соединителя так, чтобы прямой и воз-
вратный проводники были смежными. При этом площадь контура между ними
уменьшится, и уровень помехоэмиссии снизится. Разумные рассмотрения
решения такого типа обеспечивают проектировщику плат уменьшение уровня
помехоэмиссии «бесплатными» методами. Уменьшение площади наиболее эф-
фективно за счет сближения проводников с дифференциальными токами. Именно
сближение проводников приведет к заметному уменьшению помехоэмиссии.
7.2.4. Модель излучения тока синфазного режима
Вышеупомянутые результаты достаточно просто
изменить для того, чтобы рассмотреть случай токов
синфазного режима, показанный на рис. 7.6.
В данном случае предположим, что проводники
могут быть рассмотрены как диполи Герца, и точка
измерения находится (для максимального значения из-
лучения) в плоскости проводников на расстояние d от
центральной оси. Как и в предыдущем случае, прини-
маем, что точка измерения находится в дальней зоне.
Токи режима общего вида равны по амплитуде и име-
ют одинаковое направление:
/1 = II— /comm. (7.23)
Рис. 7.6. Излучение
от токов в режиме
общего вида
510
Глава 7. Печатные платы и элементы ЭМС
Наложение полей двух диполей Герца, как было сделано ранее для токов
дифференциального режима (в выражении (7.19)) следует заменить знак «ми-
нус» на знак «плюс», так как токи режима общего вида направлены в одном
направлении), дает:
Ecomm,max = J2* '1 ~ 1 e~^d (e~^S/2 + ) =
d ' '
fi / (\ A <7-24)
= _4n.lO-72-™E£e-^dcos lp05 .
J 1^2 )
В этом выражении произведена замена е^А + е~'А = 2/ cos/l, где А = P0s/2.
Заменив
и предположив, что расстояние 5 между проводниками электрически малое
настолько, что
cos(P0s/2) = 1,
выражение (7.24) может быть записано в следующей форме:
j 257 1 о । ~^сотт I I
d
Е comm, max
(7.25)
где /comm — ток линий передачи в режиме общего вида, А;/— частота, которая представ-
ляет интерес, Гц; / — длина отрезка линий передачи, м; d — расстояние между центром на-
бора проводников и точкой размещения измерительной антенны, м.
Направление вектора напряженности электрического поля будет парал-
лельно проводникам.
Рассмотрим пример, который был приведен выше для дифференциаль-
ных токов. Примем те же параметры проводников платы: проводники раз-
несены на расстояние 1,25 мм, длина проводников 0,5 м, и по ним течет ток
режима общего вида с частотой 30 МГц. Определим уровень тока, который
будет соответствовать требованиям на помехоэмиссию для аппаратуры класса
В по требованиям FCC (40 дБмкВ/м или 100 мкВ/м на частоте 30 МГц на рас-
стоянии 3 м). Значение тока можно получить, решив уравнение (7.25) отно-
сительно тока общего вида:
/comm —
| -Fcomm,max | d ^5
1,257 //
(7.26)
Подставив в это выражение численные значения параметров, получаем
/comm
10- = 16.10-
1,257-(30 106)0,5
или / = 16 мкА.
comm
7.2. Помехоэмиссия от печатных узлов
511
Следует обратить внимание, что для получения одной и той же напряжен-
ности электрического поля в некоторой точке дальней зоны требуется существен-
но меньшее значение тока общего вида, чем тока дифференциального режима.
В общем случае, формула для максимального излучения, приведенная в
выражении (7.25), является достаточной для оценки уровня помехоэмиссии.
Для сигнала трапециевидной формы предположим, что его форма совпа-
дает с формой тока дифференциального режима. Строго говоря, включение
ферритового помехоподавляющего элемента, который рассматривался в
предыдущей главе, для подавления токов общего вида будет сказываться на
форме сигнала, прошедшего через этот элемент. Но, принимая форму тока
общего вида такой же, как и дифференциальных токов, мы имеем худший
случай. Заметим из выражения (7.25), что передаточная функция, связыва-
ющая максимум полученного электрического поля с током, зависит линей-
но от длины линии / и от частоты /:
7Tcomm,max
I comm
(7.27)
где константа К= 1,257 х 10 6/d = 4,19 х 10х7для расстояния измерения d = 3 м (класса В
требований FCC).
Таким образом, амплитудно-частотная характеристика передаточной
функции увеличивается с интенсивностью +20 дБ/декаду (рис. 7.7 а). Пере-
множение этой передаточной функции и спектра сигнала, показанного на
рис. 7.76, полученного для трапециевидной формы импульса, дает резуль-
тирующий спектр (рис. 7.7в) интенсивности излученного электрического
поля. Заметим, что результирующий спектр электрического поля увеличи-
вается с интенсивностью +20 дБ/декаду до частоты l/7t/w, затем он постоя-
нен до частоты 1 /тс/г и уменьшается с интенсивностью —20 дБ/декаду при ча-
стотах больше этого значения. Продолжим пример, приведенный выше для
последовательности импульсов с частотой 10 МГц, имеющих 50 % коэффи-
циент заполнения и длительность фронта импульса 2,5 нс. Точки излома ха-
рактеристики остаются неизменными — l/nZw = 6,37 МГц и l/7Ur = 127,3 МГц,
но излучение из-за токов синфазного режима располагается в более низком
частотном диапазоне, обычно ниже 200 МГц.
Поскольку токи в режиме общего вида текут в одном направлении, в даль-
ней зоне (на относительно большом расстоянии) пара проводников может
рассматриваться как одиночный провод. Поэтому уровень максимального
излучения от токов общего вида не зависит от положения точки измерения.
Таким образом, излучение тока общего вида пары параллельных проводников не
чувствительно к вращению платы вокруг оси симметрии проводников. Макси-
мальное значение излученного электрического поля изменяется в зависимости
от частоты, длины линии и уровня тока режима общего вида. Поэтому, что-
бы уменьшить излучение на определенной частоте из-за токов режима общего
вида, следует:
512
Глава 7. Печатные платы и элементы ЭМС
Рис. 7.7. Определение спектра излучаемого
электрического поля в режиме общего
вида: а — зависимость передаточной
функции от частоты; б — спектр сигнала;
в — спектр излучаемого электрического
поля
1) уменьшить уровень тока;
2) уменьшить длину линий.
Вариант 1 можно получить, уменьшив пиковые уровни токов и/или уве-
личив длительность фронта импульса и/или уменьшив частоту повторения
импульсов, так как при этом сместятся в область низких частот две точки
излома, l/7r/w и 1/л/г спектра импульса.
Вариантом 2, сокращением длины линий, необходимо воспользоваться
на ранних этапах проектирования электрических соединений. В печатной
плате это может вызвать определенные топологические проблемы. Наибо-
лее эффективным средством подавления помехоэмиссии от токов общего вида
является применение ферритовых помехоподавляющих изделий. В печатных
узлах следует использовать специальные ФППИ, выпускаемые в виде ком-
понентов для печатных плат.
7.3. Восприимчивость печатных плат
Восприимчивость изделия к излучению других электронных устройств рас-
сматривается путем получения упрощенных моделей, которые дают значе-
ния напряжений и токов, наведенных в системе параллельных проводников
падающей плоской электромагнитной волной. Восприимчивость аппаратуры
к внешним электромагнитным возмущениям является важным аспектом ЭМС
изделий высокого качества.
7.3. Восприимчивость печатных плат
513
Соблюдение регулирующих пределов излучения (и кондуктивной эмиссии)
является абсолютно необходимым для того, чтобы представлять на рынке циф-
ровые электронные средства. Однако, как было отмечено ранее, с точки зрения
электромагнитной совместимости, только соблюдение регулирующих пределов не
является достаточным, чтобы считать завершенным проектирование изделия. Если
изделие восприимчиво к внешним помехам, например, излучению от радиопе-
редатчиков и радаров, или восприимчиво к грозовому или электростатическо-
му разряду (ЭСР), то будет нарушено функционирование изделия.
Упрощенная модель [121] будет пригодна для инженерной оценки уров-
ня восприимчивости. Рассмотрим структуру из параллельных проводников
линии передачи длиной /, которая возбуждается плоской электромагнитной
волной, как показано на рис. 7.8я.
Провода разнесены на расстояние 5 и имеют сопротивления нагрузки As
в точке х = 0 (начало линии) и R{ в точке х = I (конец линии). Провода па-
раллельны оси х.
Целью прогнозирования восприимчивости является определение напряже-
ний Ks на входе линии и V\ — на выходе линии, при воздействии синусо-
идального установившегося электрического поля £ в виде плоской волны,
электромагнитной
волны
Рис. 7.8. Модель восприимчивости печатной платы: а — воздействие продольной
электромагнитной волны; б — наведенные токи и напряжения в элементарном отрезке
линии передачи
17 1527
514
Глава 7. Печатные платы и элементы ЭМС
при изменении ее поляризации и направления распространения. Две ком-
поненты возбуждающей электромагнитной волны вызывают индуцирован-
ные напряжения. Это компонента возбуждающего электрического поля, ко-
торая перпендикулярна оси линии передачи, Elt = Еу (в плоскости проводников
и перпендикулярно им), и компонента возбуждающего магнитного поля, ко-
торая является нормалью к плоскости расположения проводников, Н'п = Н[ (пер-
пендикулярно плоскости проводников), как показано на рис. 7.8д. Линия пе-
редачи характеризуется удельными параметрами: индуктивностью Az и ем-
костью Cz, как было рассмотрено в главе 3. Для длинной линии модель линии
формируется набором АС-звеньев.
Определим удельные источники и Д, индуцированные возбуждающей
волной, исходя из следующих соображений. Сначала рассмотрим нормаль-
ную компоненту вектора интенсивности возбуждающего магнитного поля,
//'. Закон Фарадея показывает, что это вызывает эдс е в контуре, ограниченном
проводниками:
е = у(0Ц0|я„</5=уй)И0Дх j Hndy, (7,28)
5 у=0
где S — площадь контура; 5 — размер зазора между проводниками,
Данная индуцированная эдс может рассматриваться как источник напря-
жения, чья полярность, согласно закону Ленца, вызывает ток и соответству-
ющее магнитное поле, которое препятствует любому изменению возбужда-
ющего магнитного поля. Таким образом, для вектора интенсивности возбуж-
дающего магнитного поля отрицательного направления z (в страницу) поло-
жительный конец источника будет слева. Для отрезка Дх удельный источник
напряжения можно получить, поделив результат (7.28) на Дх:
К(х) = Лоц0 J H„dy. (7 29)
^=0
Удельный источник тока / имеет направление +у и определяется векто-
ром возбуждающего электрического поля, который является поперечным к
линии и имеет направление +у. Его значение равно [121 ]:
5 5
4=-ушС/ | E',dy = -jwCl j E‘ydy. (7 30)
_у=0 _у=0
Данный источник является дуальным по отношению к ys. Возбуждающее
электрическое поле вызывает напряжение между двумя проводниками, ко-
торое порождает ток смещения в полном сопротивлении удельной емкости
1/С/соСуДх) между ними.
Модель, изображенная на рис. 7.8, также применима к возбуждающим
полям, в виде неоднородных плоских волн, таких, как магнитные поля от
7.3. Восприимчивость печатных плат
515
близлежащих трансформаторов, но в этом случае возбуждающие поля вы-
числить достаточно трудно.
От удельной модели можно перейти к уравнениям линии передачи (теле-
графным уравнениям), которые связывают напряжение и ток вдоль линии.
Точное решение этих уравнений не является необходимым для инженерной
оценки, и поэтому будет получено приближенное решение.
Упрощенное рассмотрение предполагает, что линия передачи является
электрически короткой на интересующей частоте; то есть I « Хо. Если ли-
ния электрически короткая, то можно сосредоточить распределенные пара-
метры, используя при рассмотрении всей линии только одно звено, изобра-
женное на рис. 7.86.
При этом следует заменить Дх на /, умножив удельные параметры и ис-
точники на полную длину линии /. Хотя наведенные напряжения могут быть
рассчитаны из этой модели для электрически коротких линий, можно сде-
лать окончательное упрощение для получения простейшей модели, которая
применима для различных практических ситуаций.
В простейшей модели нет необходимости рассматривать удельные индук-
тивные и емкостные параметры. Кроме того, если расстояние между провод-
никами намного меньше, чем длина проводника, и поэтому также электри-
чески короткое, то векторы поля существенно не меняются вдоль попереч-
ного сечения провода (по координате у). Поэтому интегралы в источнике
относительно у могут быть заменены значениями расстояния 5 между про-
водниками, что позволяет получить следующие выражения для индуциро-
ванных напряжений и токов для всей линии на длине /:
Ks/ = >gotf'5,
(7.31)
JJ = jwClE‘S,
где 5 — площадь контура
S=sl. (7.32)
Упрощенная модель линии показана на рис. 7.9. Из этой модели, используя
принцип суперпозиции, легко вычислить индуцированные напряжения на
концах линии:
' 5 Е'"
+ К1
R\ . / Ui ^R\ г , ri (7-33)
+ К\ + К\
Это простейшая модель, которая дает полезные оценки эффектов воздей-
ствия внешних полей, как показано в следующих примерах.
Рассмотрим пример в виде условной линии передачи на печатной плате
длиной 1 м, которая включена, как показано на рис. 7.10я. Проводники линии
за счет толщины диэлектрика разнесены на 1,25 мм. Входное и выходное
17*
516
Глава 7. Печатные платы и элементы ЭМС
R
S
-jaC^s-E}
I
17 0R.
Рис. 7.9. Упрощенная модель линии передачи при анализе восприимчивости
50 Ом
7'4,42 мВ )22,1 мВ
Рис. 7.10. Оценка восприимчивости при продольном возбуждающем
электрическом поле
полное сопротивление равно Rs = 10 Ом и R{ = 50 Ом. Волновое сопротивле-
ние линии передачи равно 50 Ом, а электрическая емкость Cz на единицу длины
составляет примерно 130 пФ/м. Таким образом, входное сопротивление меньше
волнового сопротивления линии, а выходное равно волновому, т.е. линия со-
гласована по выходу Воздействующая однородная плоская волна имеет час-
тоту 100 МГц и распространяется в плоскости ху в направлении у, перпенди-
кулярно к линии. Линия имеет длину Хо/3 на частоте 100 МГц. Это является
критическим для линии, которая будет рассматриваться как электрически
короткая, и для ее описания уже желательно использовать распределенную
модель линии передачи. В нашем случае для упрощения предположим, что
линия электрически короткая и используется упрощенная модель, показан-
ная на рис. 7.9.
Вектор напряженности электрического поля имеет амплитуду Ef= 10 В/м
и поляризован в направлении х. Вектор напряженности магнитного поля на-
правлен в отрицательном z (от наблюдателя) направлении согласно свойствам
однородных плоских волн и равен И = 7?/Z0 = 10/120л = 2,65-10’2 А/м. Таким
7.3. Восприимчивость печатных плат
517
образом, поперечная к линии компонента электрического поля является ну-
левой, и помеха будет вызвана только компонентой магнитного поля, кото-
рая является нормальной к плоскости проводников. Поэтому индуцирован-
ные источники, полученые из выражения (7.31), будут представлены как
И5/ = / (о ц0Я' •5 = у-2лх108-4лх10“7—-(1x1,25-10-3) = /26,5, мВ.
^0 v
Поскольку нет никаких составляющих электрического поля, которые
являются поперечными к оси линии, соответствующий источник тока отсут-
ствует. Эквивалентная схема показана на рис. 7.10d, откуда мы вычисляем
напряжение в начале и в конце линии, рассматривая сопротивления в этих
точках как параллельные. Тогда
Й=——/26,5 = у'4,42, мВ,
s 10 + 50
Й =——у 26,5 = /22,1, мВ.
1 10 + 50
Во втором примере рассмотрим ту же линию передачи, как в первом при-
мере, но с другим направлением воздействующей волны (рис. 7.11а).
Волна распространяется вдоль оси линии по направлению х, и вектор ин-
тенсивности электрического поля поляризован в направлении у (перпенди-
кулярно линии). Вектор напряженности магнитного поля направлен по на-
правлению z (к наблюдателю) и нормально к плоскости проводников. Тогда
а
50 Ом
/26,5 мВ
-/13,75 мВ
10 Ом
-/12,75 мВ
50 Ом
Рис. 7.11. Оценка восприимчивости при поперечном возбуждающем
электрическом поле
518
Глава 7. Печатные платы и элементы ЭМС
эквивалентные источники определяются следующим образом, учитывая, что
со = 2л/:
VJ = j 2nf • ц0Я' • 5 = j • 2лх 108 • 4лх 1 О*7/ • (1 х1,25• 10’3) = /26,5, мА,
А)
/s/ = /-2n/ C, £' S = /-2nxl08 130xl0’1210 (lxl,2510’3)« /1,0, мА.
Эквивалентная схема для этого случая показана на рис. 7.116. Следует
обратить внимание на полярность эквивалентного источника напряжения.
Положительный вывод этого источника находится справа, так как воздей-
ствующее магнитное поле направлено к наблюдателю (из страницы). Напря-
жения на выводах рассчитываются согласно (7.33):
К =----— /26,5 • 10-3 — 10 50 /1,0 = -/12,75, м В
s 10 + 50 10 + 50 ’
Й =---—— /26,5 • 10*3 - 10 50 /1,0 = -/13,75, мВ
1 10 + 50 10 + 50
Заметим, что из-за направления воздействующего магнитного поля и ре-
зультирующего эквивалентного источника напряжения, суммарное напря-
жение от двух эквивалентных источников вычитают из Р[, но добавляют к Ks.
7.4. Экранирование печатных узлов
7.4.1. Принцип действия электромагнитного экрана
Обеспечение требований ЭМС на уровне печатного узла — задача комп-
лексная, решаемая на всех этапах проектирования аппаратуры — от выбора
элементной базы до конструирования изделия в целом. К средствам обес-
печения ЭМС, которые стали уже классическими, относятся:
• зонирование, связанное с компоновкой устройства;
• фильтрация;
• экранирование;
• заземление.
Каждый из этих вопросов требует особого детального рассмотрения.
В контексте книги частично были рассмотрены вопросы зонирования, филь-
трации и заземления применительно к проектированию печатных плат. Эк-
ранирование рассматривалось только как составная часть проектирования
линий передач в части требований установки потенциальных слоев. В насто-
ящем разделе будут уточнены основные понятия, связанные с экранирова-
нием, и даны практические рекомендации по выполнению экранов в печатных
узлах. Основной акцент сделан не на математическую точность изложения,
а на физические аспекты проблемы, которые позволят принять правильное
решение. Для более точных количественных оценок следует обратиться к спе-
7.4. Экранирование печатных узлов
519
циальной литературе. Следует обратить внимание, что вопрос об экраниро-
вании на уровне печатного узла должен решаться в комплексе вопросов эк-
ранирования аппаратуры в целом, поскольку нерациональный выбор экра-
нов и их распределение между конструктивными иерархическими уровня-
ми приведет к неоправданному возрастанию материальных затрат, увеличению
габаритов аппаратуры и ее утяжелению. Более подробно с комплексом во-
просов по обеспечению ЭМС для электронных средств можно познакомиться
в [31, 122].
На вопрос о принципе действия электромагнитного экрана можно дать
два ответа, которые внешне отличаются друг от друга, но, в сущности, оди-
наковы.
Первый формулируется следующим образом. Под действием первично-
го поля (поле источника) на поверхности экрана индуцируются заряды, а в
его толще — токи и магнитная поляризация. Эти заряды, токи и поляриза-
ция создают вторичное поле. От сложения вторичного поля с первичным
образуется результирующее поле, которое в защищаемой области пространства
оказывается слабее первичного. Этот ответ позволяет рассматривать работу
экрана на любых частотах, включая частоту, равную нулю.
Второй ответ гласит: принцип действия электромагнитного экрана состоит
в том, что, отражая и направляя поток энергии, создаваемый источниками
поля, экран отводит его от защищаемой области пространства, не допуская
в эту область.
Единая суть обоих ответов ясна из того, что сам механизм отражающего
и направляющего действия экранов на потоки электромагнитной энергии
неразрывно связан с возникновением на его поверхности и в толще материала
экрана зарядов, токов и поляризации.
Количественная оценка эффективности экранирования определяется следу-
ющим образом:
S = 10^[падающая энергия / пропущенная энергия], дБ, (7.34)
где «падающая энергия» — это энергия в точке измерения до установки экрана, а «пропу-
щенная энергия» — энергия в той же точке, но уже после установки экрана. Это выраже-
ние определяется как потеря, и поэтому 5 всегда положительна.
Степень ослабления, обеспечиваемая экраном, зависит от трех механиз-
мов. Первый — это отражение волны от границы «воздух — экран». Второй —
поглощение электромагнитной волны по мере ее прохождения через метал-
лическую стенку экрана. Третий — повторное отражение, которое имеет место
при достижении волной противоположной стороны экрана. Более тонкие
механизмы прохождения электромагнитных волн через экран рассматривают
многократные переотражения волны внутри экрана между его стенками. Для
худшего случая переотражения можно не рассматривать. Количественно
высокая эффективность экранирования достигается при значениях 100—120
дБ, хотя это требует очень тщательного проектирования экрана. Получить
большие значения эффективности весьма сложно из-за наличия различных
неоднородностей в экране (отверстий, щелей и т.п.).
520
Глава 7. Печатные платы и элементы ЭМС
В общем случае, экран не только ослабляет, но и искажает поле источника
в защищаемой области. Поэтому его эффективность экранирования оказыва-
ется различной для электрической и магнитной составляющих поля и от коор-
динат точки измерения. Это обстоятельство существенно затрудняет коли-
чественную оценку эффективности экранирования.
Для напряженности двух полей, измеряемых в одной среде с определен-
ным волновым сопротивлением, выражение (7.34) будет выглядеть для элек-
трического поля
5= 201g(£’/ £j/r), дБ, (7.35)
для магнитного поля
5=20^(Я/Я5А),дБ, (7.36)
где Е — напряженность электрического поля до установки экрана в некоторой точке про-
странства; Esh — напряженность электрического поля в той же точке после установки эк-
рана; Н— напряженность магнитного поля до установки экрана; Hsh — напряженность маг-
нитного поля после установки экрана.
Очевидно, что при создании несущих металлических конструкций элек-
тронных средств можно предусмотреть технические решения, обеспечива-
ющие необходимые экранирующие свойства конструкции. Но без специаль-
ных мер подобные решения не обеспечат необходимой эффективности ос-
лабления электромагнитного поля. Магнитное экранирование на низких
частотах является самой сложной практической задачей. Оно, как правило,
существенно усложняет и утяжеляет конструкцию.
7.4.2. Механизмы работы экрана при различных
видах излучения
При анализе вопросов ЭМС рассматривают рецептор и источник помех.
Рецептор — объект, который находится под воздействием электромагнит-
ных помех. Восприимчивость печатного узла, рассмотренная выше, относится
к плате как к рецептору помех. Чем выше быстродействие микросхемы, тем
чувствительней она как рецептор. Рецептором, в общем случае, может выс-
тупать практически любой элемент конструкции, начиная от корпуса изде-
лия и заканчивая выводами микросхемы, которые обладают хотя бы мини-
мальным антенным эффектом. Рецепторы могут различаться по их чувстви-
тельности к воздействию различных полей.
Источники помех разделяют на источники естественного и искусствен-
ного происхождения. Все многообразие источников может быть сведено к
двум основным типам.
Источники с высоким волновым сопротивлением. Для них эквивалентная схема
или модель может быть представлена в виде штыря (антенна-штырь). В окрес-
тностях этого штыря формируется относительно интенсивное электрическое поле
и слабое магнитное поле. Это определяет весьма высокое (приблизительно
3000 Ом) волновое сопротивление среды в непосредственной близости от штыря.
7.4. Экранирование печатных узлов
521
Источники помех, модель которых может быть представлена в виде то-
ковой петли, формируют интенсивное магнитное поле и слабое электрическое
в непосредственной близости от источника. Это определяет достаточно ма-
лое волновое сопротивление среды в окрестностях источника (приблизитель-
но 30 Ом).
В наиболее общей модели имеет место процесс переноса электромагнитных
волн от источника к рецептору — помехоэмиссия. Экранирование направле-
но на обеспечение электромагнитной совместимости источника и рецепто-
ра помех.
Высокое и низкое волновое сопротивление среды характерно только в не-
посредственной близости от источника помех. По мере удаления от источ-
ника волновое сопротивление Zсреды стремится к волновому сопротивле-
нию свободного пространства 377 Ом. Принято считать, что при расстоянии,
равном Х/2я, плоская электромагнитная волна полностью сформирована, и
волновое сопротивление для нее составляет 377 Ом. Рис. 7.12 иллюстрирует
изменение волновых сопротивлений различных источников при увеличении
расстояния. Из графика видно, что можно выделить три зоны действия ис-
точников: ближняя, дальняя и переходная. Границей ближней и дальней зоны
считается значение Х/2я. Например, для частоты 100 МГц длина волны со-
ставляет 3 м, и граница между ближней и дальней зоной будет расположена
на расстоянии примерно 0,5 м. Чем выше частота, тем ближе к источнику будет
находиться граница между ближней и дальней зоной. На очень высоких ча-
стотах практически все пространство будет соответствовать дальней зоне.
Понятие дальней зоны использовалось выше при оценке помехоэмиссии и
восприимчивости печатного узла.
Для выделенных зон характерны следующие особенности.
1. Ближняя зона (расстояние до источника меньше чем Х/2л). Здесь пре-
имущественно действует механизм индукции с достаточно четким раз-
делением на магнитную и электрическую составляющие, что требует
отдельного рассмотрения электрического и магнитного экранирова-
ния.
2. Переходная зона — зона формирования плоской электромагнитной
Рис. 7.12. Зоны экранирования
522
Глава 7. Печатные платы и элементы ЭМС
3. Дальняя зона (расстояние до источника больше, чем Х/2л) — зона дей-
ствия плоской электромагнитной волны (Т-волны), для которой сле-
дует рассматривать электромагнитное экранирование.
Таким образом, при анализе экранирования необходимо разделять зада-
чи локализации электрического, магнитного и электромагнитного полей.
К сожалению, тип источника известен только в частных случаях, например,
трансформатор как источник магнитного поля. Поэтому экранирование в
ближней зоне требует тщательного анализа типа источника. Очевидно, что
для дальней зоны тип источника не имеет значения - в любом случае будет
сформирована плоская электромагнитная волна.
7.4.3. Электро- и магнитостатическое экранирование
В подавляющем большинстве случаев электромагнитные экраны делаются
из металла: меди, алюминия, стали. Электростатическое и магнитостатическое
поля являются частными видами электромагнитного поля, а электростати-
ческий и магнитостатический экраны являются частными видами электро-
магнитного экрана.
Электростатическое экранирование в ближней зоне
В ближней зоне электрическое и магнитное поля рассматриваются как ква-
зистатические, поэтому картины электрического и магнитного полей при со-
ответствующих частотах и картины статических полей совпадают. Выводы,
полученные для статического случая, пригодны для использования в опреде-
ленном диапазоне частот, пока соблюдается условие ближней зоны. В ней про-
водим, по сути, экранирование статического поля. Роль экрана в этом случае
заключается в перехвате силовых линий электрического поля, связывающих ис-
точник и рецептор помех. Индуцированные заряды на экране следует отвести
на землю, поэтому электростатический экран должен быть надежно заземлен.
Эффективность электростатического экрана практически не зависит от
параметров проводящего материала (проводимости, толщины), а в основном
зависит от конструкции экрана, а именно, наличия щелей, отверстий и других
неоднородностей, их размеров и ориентации. Чем меньше подобных неодно-
родностей, тем выше эффективность экранирования. Потенциальные слои
печатных плат являются вполне эффективными экранами для силовых ли-
ний электрического поля, нормальных к ним.
Экран устанавливается как можно ближе к источнику помех. В конструк-
циях печатного узла эта рекомендация может быть выполнена, когда источник
находится в его пределах. Когда же источник находится вне пределов дося-
гаемости или его невозможно экранировать, экранируют рецептор.
Магнитостатическое экранирование
Механизм работы магнитостатического экрана заключается в шунтиро-
вании силовых линий магнитного поля. Эффективность экранирования прямо
пропорциональна магнитной проницаемости ц и толщине экрана. Поэтому
7.4. Экранирование печатных узлов
523
для магнитного экранирования необходимо применять материалы, которые
имеют максимальную магнитную проницаемость — стали, пермаллои и другие
магнитные сплавы с высоким значением ц. Магнитные экраны, как прави-
ло, отличаются большой массой, сложностью изготовления и высокой сто-
имостью исходных материалов. Неоднородности в виде щелей, отверстий,
плоскостей разъема не должны препятствовать силовым линиям магнитно-
го поля.
Отметим, что медные слои печатной платы «прозрачны» для магнитного
поля и не оказывают на него никакого влияния.
Магнитный экран заземляют только из соображений электробезопасно-
сти, хотя для обеспечения эффективной работы это не требуется.
Электромагнитное экранирование
Механизм электромагнитного экранирования основан на отражении элек-
тромагнитных волн от границ раздела сред «воздух — экран» и поглощении
энергии при прохождении волны в толще стенки экрана. Эффективность
электромагнитного экранирования оценивается по формуле
S = R + А + В, дБ, (7.37)
где R — потери на отражение от границы «воздух — экран»; А — потери на поглощение; В —
потери на многократные переотражения.
Вклад этих компонентов в общую эффективность различен. Потери В на
переотражения составляют 2—3 дБ, что существенно меньше, чем вклад других
слагаемых. Поэтому этот параметр не учитывают. При толщинах материалов
0,3 мм и более основной вклад в общее ослабление вносят потери на погло-
щение, которые составляют около 9 дБ на каждый скин-слой. Если принять
во внимание, что на высоких частотах толщина скин-слоя составляет еди-
ницы микрометров, то для конструкционного материала толщиной примерно
0,5 мм эффективность экранирования будет составлять несколько сот децибел.
Для медной фольги толщиной 35 мкм на частоте 100 МГц толщина скин-слоя
составляет 6,6 мкм. Эффективность экранирования такой фольги только с
учетом потерь на поглощение составит
35
5= Л = —9 = 47,7 дБ,
т. е. ослабление более, чем в 100 раз.
Чем выше частоты, тем эффективнее электромагнитное экранирование.
Однако на практике достичь суммарной эффективности экранирования Sболее
120 дБ весьма сложно из-за наличия неоднородностей в экране. Поэтому
эффективность экрана определяется не столько выбором материалов, а кон-
струкцией экрана: наличием щелей, отверстий и других неоднородностей. По
этой причине теоретические оценки эффективности экранирования носят
весьма условный характер, поскольку теоретические трудности не позволяют
получить адекватные модели экранов с предсказуемыми и непредсказуемыми
неоднородностями, возникающими в реальной ситуации.
524
Глава 7. Печатные платы и элементы ЭМС
7.4.4. Практика экранирования
Выбор материала экрана проводится, исходя из обеспечения заданной эф-
фективности экранирования в рабочем диапазоне частот при соответству-
ющих ограничениях: влияния на экранируемый объект, массо-габаритных
параметров, а так же устойчивости против коррозии, обеспечения механи-
ческой прочности, технологичности конструкции и т.д. При конструирова-
нии печатного узла выбор экранирующих материалов достаточно ограничен.
Медная фольга, применяемая для создания печатных плат, выполненная
в виде потенциальных слоев, играет роль экрана. На высоких частотах по
экрану протекают возвратные токи, и требования, выполнение которых не-
обходимо для эффективной работы экрана в составе линий передач, сфор-
мулированы в предыдущих главах книги.
При повышенных требованиях к экранированию, например, дифференци-
альных пар, применяют специальный конструкторский прием по созданию ка-
нала для полосковой линии, в котором дополнительно к экранным слоям с
двух сторон формируется «стенка» из металлизированных отверстий [119], как
Рис. 7.13. Формирование экраниро-
ванной дифференциальной пары
показано на рис. 7.13. Дифференциальная
пара должна быть расположена симметрич-
но относительно стенки металлизирован-
ных отверстий. Для эффективной работы
системы отверстий в качестве экрана, они
должны быть расположены на расстоянии
не более 1/10 минимальной длины волны,
которая определяется для максимальной
частоты в спектре сигнала. Подобный при-
ем можно использовать для повышения
симметрии дифференциальной пары при
наличии неоднородности (края платы, от-
верстия, щели в возвратном слое и т. п.).
Не следует забывать, что наличие стенки
металлизированных отверстий изменит волновое сопротивление линии пере-
дачи, и для его точного определения потребуется использовать программы рас-
чета трехмерных электрических полей.
Для экранирования отдельных фрагментов печатного узла или узла в целом
на плату могут устанавливаться специальные экраны. Наиболее подходящим
для этих целей материалом являются медь и медные сплавы. Эти материалы
обеспечивает приемлемое значение эффективности экранирования при элек-
тростатических полях и при электродинамическом экранировании. Магнит-
ное экранирование решается на уровне аппаратуры и помещения. При раз-
работке подобных экранов и способов их крепления на печатной плате сле-
дует обеспечивать возможность автоматизированной сборки и монтажа.
Поверхность экрана должна быть эквипотенциальной. При соединении
с шиной заземления потенциал на экране будет 0 В. Следует помнить, что
по экрану протекают возвратные токи высокой частоты, поэтому заземле-
7.4. Экранирование печатных узлов
525
ние экрана должно обладать низким полным сопротивлением на тех макси-
мальных частотах, которые характерны для проектируемого цифрового узла.
Это принципиально отличает систему функционального заземления от за-
земления, выполняемого с целью обеспечения электробезопасности. Поэтому,
проектируя систему экранирования, большое внимание следует уделить обес-
печению низкого полного сопротивления соединения экрана с системой
заземления аппаратуры. Один из важнейших принципов, заложенных в по-
добные проектные решения, состоит в обеспечении непрерывности экрани-
рования. Согласно этому принципу все экраны в аппаратуре, системе, уста-
новке должны представлять собой непрерывную металлическую оболочку с
минимальными нарушениями целостности экрана в местах соединения его
отдельных фрагментов [35]. Поэтому, рассматривая экраны печатного узла,
необходимо одновременно проектировать узлы их соединения с системой за-
земления аппаратуры и экранами присоединяемых кабелей. На рис. 7.14 по-
казан пример полного экранирования печатного узла [119]. Отметим неко-
торые особенности данной конструкции, отвечающие принципу непрерыв-
ности экранирования:
• потенциальные слои (1 и 5) платы служат экранами и должны соеди-
няться металлизированными отверстиями, расположенными друг от
друга на расстоянии не более О, IX, где X — длина волны в материале
основания платы, соответствующая максимальной частоте в спектре
сигнала;
• экраны (3) должны присоединяться к экранирующему слою платы по
всему периметру системой металлизированных отверстий, расположен-
ных на расстоянии не более О, IX;
• соединитель (7) должен быть экранированным и присоединяться к эк-
ранирующим слоям платы по всему периметру;
Рис. 7.14. Пример полностью экранированного печатного узла: 1 — верхний
потенциальный слой с напряжением О В; 2 — сигнальные трассы, защищенные
потенциальными слоями; 3 — экраны отдельных зон узла; 4 — металлизированные
отверстия, соединяющие верхний и нижний экранирующие слои; 5 — нижний
потенциальный слой (экран); 6 — трассы к соединителю внутри платы;
7 — экранированный соединитель; 8 — экран кабеля
526
Глава 7. Печатные платы и элементы ЭМС
Рис. 7.15. Пример частично экранированного печатного узла: 1 — неэкранированный
кабель; 2 — фильтры на каждый неэкранированный ввод; 3 — фильтры на каждый
неэкранированный проводник, который входит или выходит из экранированной зоны;
4 — экран; 5 — верхнее и нижнее экранирующее кольцо, соединенные стенкой метал-
лизированных отверстий по периметру платы; 6 — единый нижний экранирующий
слой под экраном; 7 — локальный экранирующий слой; 8 — экранированные
соединитель и кабель
• кабель должен находиться в экране (8), который соединяется с экра-
ном соединителя по периметру.
В том случае, когда не требуется полного экранирования цифрового узла,
все неэкранированные кабели должны иметь на входах/выходах фильтры. Для
эффективной работы эти фильтры должны соединяться с землей способом,
обеспечивающим низкое полное сопротивление на высоких частотах. При-
мер для этого случая показан на рис. 7.15. Следует обратить внимание на то,
что все неэкранированные вводы/выводы должны иметь фильтры.
7.5. Соединение печатного узла с шасси
Любой печатный узел, в конечном счете, устанавливается на шасси. Под
шасси в контексте ЭМС понимается некоторая металлическая конструктивная
единица, служащая для механического крепления печатных узлов и других
элементов аппаратуры. Конечно, в отдельных случаях шасси может быть из
пластмассы, но при этом она должна обладать определенными проводящи-
ми свойствами, которые обеспечиваются соответствующими добавками. По
своей конфигурации шасси может быть как простой пластиной, на которую
устанавливается печатный узел, так и сложной деталью или сборочной еди-
ницей. Важно, чтобы в любом случае обеспечивалась эквипотенциальность
металлической конструкции. Если она состоит из отдельных деталей, то со-
единение между ними должно иметь предельно низкое полное сопротивле-
ние на высоких частотах. Поэтому шасси можно рассматривать как некото-
рую обобщенную опорную плоскость с заданным потенциалом, как прави-
ло, О В. В этой опорной плоскости будут протекать токи, наведенные близко
7.5. Соединение печатного узла с шасси
527
расположенными кабелями и проводниками печатной платы. Шасси может
играть роль экрана, но не обязательно.
Потенциальные слои платы с опорным потенциалом (как правило, О В)
должны соединяться с шасси соединением с низким полным сопротивлением.
На рис. 7.16 показана типичная установка печатного узла на поверхность
металлического шасси.
Важным фактором обеспечения эквипотенциальности является миними-
зация полного сопротивления электрического соединения печатного узла с
шасси. Одним из таких соединений является узел механического крепления
(рис. 7.17), который выполняется с помощью резьбовых разъемных соеди-
нений и втулок, обеспечивающих необходимый зазор между шасси и печатным
узлом. Контактная площадка (2) под крепеж соединяется со слоем с нуле-
вым потенциалом при помощи набора металлизированных отверстий (7), рас-
положенных по окружности. Это приводит к снижению индуктивности элек-
трического соединения и, следовательно, к снижению его полного сопро-
тивления.
Места контактов металлических деталей не должны коррозировать в те-
чение всего срока эксплуатации, что требует соответствующих гальванических
покрытий. Если используется невыпадающая втулка, то должны быть пред-
приняты конструкторско-технологические меры по устранению коррозии
между шасси и втулкой и такого соединения, которое не приведет к возрас-
танию полного сопротивления в месте стыка втулки и шасси.
Кроме непосредственного соединения, рассмотренного выше, в ряде
случаев для расширения частотного диапазона малых значений полного со-
противления соединения платы с шасси,
а в отдельных случаях для их электричес-
кой изоляции, применяют соединение с
помощью конденсатора. Этот конденса-
тор должен обладать минимальной индук-
тивностью (1-2 нГн), поскольку каждая
дополнительная индуктивность в 1 нГн
добавляет 6,3 Ом в полное сопротивление
между платой и шасси на частоте 1 ГГц.
Рис. 7.17. Механическое крепление
печатного узла: 1 — край печатной
платы; 2 — контактная площадка
крепежного отверстия; 3 — металли-
ческая втулка; 4 — крепежный болт
или винт; 5 — край внутреннего
слоя с потенциалом О В; 6 — отвер-
стие в плате для крепежа; 7— круго-
вое расположение металлизирован-
Механическое
крепление узла
Проводники
располагаются
близко к шасси
Рис. 7.16. Пример установки печатного
528
Глава 7. Печатные платы и элементы ЭМС
3
Рис. 7.18. Пример универсального узла соединения:
1 — контактная площадка для непосредственного
соединения (не соединена с плоскостью О В);
2 — металлизированное отверстие к слою О В;
3 — контактные площадки для установки
конденсатора, резистора или перемычки
Однако при применении дополнительного конденсатора возможны непред-
сказуемые резонансы с паразитными параметрами конструкции.
Для устранения структурных резонансов соединение может осуществляться
с помощью демпфирующего резистора. В [122] рекомендовано при необхо-
димости устанавливать резистор с сопротивлением от 47 до 100 Ом, что сни-
жает добротность системы при резонансах.
Из-за сложности происходящих процессов трудно прогнозировать, ка-
кое именно соединение или их комбинация обеспечивает наилучшие усло-
вия функционирования узла на высоких частотах. Это может быть сделано
при отладке физического прототипа, для чего удобно предусмотреть возмож-
ность установки дополнительно перемычки, конденсатора или резистора в
месте механического крепления платы, как показано на рис. 7.18.
Один из важных вопросов, который следует решить при разработке со-
единения печатного узла с шасси, заключается в выборе числа точек соеди-
нения. Классический подход к проблеме заземления заключается в реали-
зации принципа одноточечного заземления, при котором шины заземления
отдельных устройств соединяются в одной точке. При этом отсутствуют кон-
туры токов в системе заземления, что положительно сказывается на парамет-
рах ЭМС. Для высокочастотных печатных узлов этот принцип требует кор-
ректив. Ранее было показано, что одна из самых серьезных проблем при работе
цифрового узла с позиций ЭМС — это преобразование сигналов дифферен-
циального вида в сигналы общего вида. Именно они являются причиной
наиболее существенных излучений от узлов и аппаратуры в целом. Для сиг-
налов общего вида, протекающих по проводникам печатной платы, возврат-
ным проводником является шасси. Поэтому, чем однородней будет возврат-
ный путь по шасси и чем меньше будет полное сопротивление соединения
между платой и шасси, тем меньше будет уровень токов общего вида, а
следовательно, и меньший уровень излучений. Снижению упомянутого пол-
ного сопротивления способствует увеличение числа точек соединения, ко-
торые рекомендуется выполнять на углах платы, в местах ввода/вывода вы-
сокочастотных сигналов и около высокочастотных и мощных компонентов,
например, тактовых генераторов, мощных микропроцессоров.
Снижению уровня излучений от токов общего вида будет способствовать сбли-
жение печатного узла и шасси. Шасси и плата формируют некоторую линию
передачи, открытую с торцов. Это вызывает значительные краевые эффекты и
7.5. Соединение печатного узла с шасси
529
приводит к высокому уровню излучения. Чем ближе печатный узел будет к шасси,
тем в меньшей степени проявятся краевые эффекты, и уровень излучения бу-
дет снижен. Это наглядно иллюстрируется на рис. 7.19. Рекомендуется рассто-
яние между шасси и печатным узлом выдерживать не более половины длины
волны для максимальной частоты в спектре сигнала. Кроме этого, уменьшение
зазора между платой и шасси повышает частоты структурных резонансов.
Частоты структурных резонансов зависят от размеров и конструкции
шасси. На резонансных частотах увеличивается помехоэмиссия и повыша-
ется восприимчивость технического средства к внешним электромагнитным
воздействиям. Все это ухудшает показатели ЭМС электронных средств.
Для печатной платы, закрепленной по углам, длиной / и шириной w со
сплошными потенциальными слоями, установленной на некотором рассто-
янии от шасси, которое существенно меньше габаритных размеров платы,
частоту первого резонанса можно определить по формуле [119]:
ГГц,
(7.38)
где /, w — соответственно длина и ширина печатной платы, мм.
Например, для платы с размерами 160 х 120 мм, установленной на высо-
те 5 мм от шасси, первая резонансная частота будет 0,75 ГГц.
Если плата закреплена только на двух углах одной стороны, резонансная
частота будет
(7.39)
При проектировании платы точки крепления узла должны выбираться,
исходя не только из прочностных соображений, но и позиций ЭМС. Можно
рекомендовать правило «одной двадцатой длины волны» [119], при котором
Рис. 7.20. Пример расстановки
точек крепления печатного узла
по правилу «одной двадцатой ..г»
Рис. 7.19. Снижения уровня излучения
за счет сближения шасси и печатного узла
530
Глава 7. Печатные платы и элементы ЭМС
расстояние между точками крепления не должно превышать значение Х/20,
где X — длина волны в свободном пространстве при максимальной частоте
в спектре сигнала. Пример расположения точек крепления по правилу «од-
ной двадцатой...» показан на рис. 7.20.
Конечно, в зависимости от конкретной ситуации могут быть предложе-
ны и реализованы другие способы крепления, в том числе и с использова-
нием пружинных контактов для выдвигающихся печатных узлов, но в лю-
бом случае расстояние между точками крепления или пружинными зажимами
не должно превышать значения 1/20.
В заключение отметим, что для этажерочной конструкции, когда одна
плата располагается над другой, все рассмотренные выше рекомендации по
снижению полного сопротивления узлов крепления, устранению резонан-
сов и условий существования токов общего вида остаются в силе.
________________Глава 8__________________
Конструкторско-технологическое
проектирование: модели и системы
автоматизации проектирования
8.1. Тенденции в развитии САПР
8.1.1. Целостность сигнала и САПР
В данной главе рассмотрены вопросы обеспечения целостности сигналов
и ЭМС в современных САПР печатных плат. С наступлением эры субмикрон-
ных и нанометровых технологий (0,18 микрон и ниже) интегральные схемы
стали работать на высоких частотах и потреблять больший ток и мощность при
меньших напряжениях питания. Это привело к более активному проявлению
эффектов индуктивного и емкостного характера как на уровне корпусов мик-
росхем, так и на печатных платах. Предыдущие главы книги показали, что
широкий спектр других эффектов электромагнитной природы в межсоедине-
ниях печатной платы, который можно было не учитывать в проектах элект-
ронных средств предыдущего поколения, стал ключевым фактором для обес-
печения правильного функционирования и высокой производительности
перспективных цифровых систем. В современных условиях проблема взаимо-
связи таких параметров, как быстродействие, потребляемая мощность, цело-
стность сигналов, ЭМС и надежность, стала столь же актуальной, как и про-
блема снижения площади кристалла для устройств предыдущего поколения.
Очевидно, что новые задачи, которые встали перед проектировщиками
печатных плат, не могли не найти отражения и в развитии САПР. Если на первых
этапах применение САПР для проектирования печатных плат ограничивалось
топологическими задачами и технологическим сопровождением, то по мере
того, как проблемы обеспечения целостности сигнала и ЭМС становились более
актуальными, ведущие производители САПР начали включать определенные
процедуры и подсистемы в свою продукцию. Начало 2005 года ознаменова-
лось выходом ряда новых версий популярных систем проектирования печат-
ных плат. Часть из них претерпела незначительные изменения, часть была
532
Глава 8. Конструкторско-технологическое проектирование...
полностью обновлена, но все без исключения расширили свои возможности
в направлении целостности сигнала и ЭМС.
Многие современные электронные приборы, особенно видео- и телеком-
муникационное оборудование, требуют повышения скорости передачи дан-
ных. Новейшие интерфейсные микросхемы позволяют при помощи систем
стабилизации (equalization) и предварительной коррекции (pre-emphasis)
противостоять ограничениям полосы пропускания, неминуемо возникаю-
щим в высокоскоростных соединениях. Применение таких интегральных схем
дает возможность инженеру избежать дорогостоящих доработок объедини-
тельных панелей, таких, как перетрассировка или замена материала платы.
Тем не менее, основная тяжесть в обеспечении целостности сигнала и ЭМС
ложится на плечи разработчика плат.
Обобщая весь предыдущий материал, можно отметить, что распределенная
емкость и индуктивность печатных проводников, взаимная индуктивность
и емкость близлежащих проводников, наличие неоднородностей в сигнальных
и возвратных проводниках, несогласованность длинных линий, высокие
полные сопротивления шин питания и заземления и многие другие эффек-
ты приводят к тому, что процесс проектирования платы и печатного узла
становится итерационным. Даже при применении виртуального прототипа
необходим физический прототип, после испытаний которого в него вносятся
определенные изменения. Наличие виртуального прототипа сокращает срок
и стоимость проектирования, но полностью устранить все недочеты можно
только при тестировании реальной конструкции.
Для моделирования электронной системы на этапе создания виртуального
прототипа в основном используются пакеты прикладных программ. В них
этапы схемотехнического моделирования и разработки топологии печатных
плат или интегральных схем разделены. Сначала проводится моделирование
электронных схем без учета паразитных эффектов, присущих реальным то-
пологиям, а затем после разработки конструкции моделирование повторя-
ется с их учетом. Эта процедура охватывает с той или иной полнотой задачи
обеспечения целостности сигналов и ЭМС. В данной главе содержится крат-
кий обзор наиболее известных программ анализа целостности сигналов с
целью иллюстрации возможностей САПР в этой сфере.
Комплексный подход к проектированию электронных систем показывает,
что в настоящий момент инженер всегда имеет альтернативу, которая зак-
лючается в:
• использовании традиционных методов совершенствования печатных
плат и объединительных панелей (расширение сигнальных дорожек,
замена на другой материал платы и т.п.);
• применении новейших микросхем с алгоритмами стабилизации или
предварительной коррекции сигнала.
Окончательный выбор решения на концептуальном уровне зависит от кон-
кретного применения, экономической целесообразности, доступности материа-
лов и компонентов. Следует отметить еще одно обстоятельство. Проектиро-
вание печатаных плат имеет много общего с разработкой металлизации кри-
8.1. Тенденции в развитии САПР
533
Все
Другие
31%
Zuken
15%
Рис. 8.1. Распределение
мирового рынка САПР
печатных плат (2003 г.)
Cadence
21%
Mentor
Graphics
33%
сталлов и плат для их установки в корпусах микросхем. Эта общность, преж-
де всего, касается вопросов топологии, целостности сигналов и проектиро-
вания шин питания и заземления. Наи-
большие успехи в решении этих задач, как
показывает анализ, достигнуты в САПР
интегральных микросхем. Поэтому в гла-
ве приведены сведения о некоторых про-
цедурах, предназначенных для проектиро-
вания микросхем и имеющих методичес-
кое единство с вопросами проектирования
печатных плат, но не получивших пока в
этой сфере должного развития.
На мировом рынке в настоящее время
выявилось преимущественное положение
трех ведущих производителей САПР пе-
чатных плат: Mentor Graphics, Cadence, Zuken. В совокупности они занимают
(по данным 2003 г.) около 70 % мирового рынка (рис. 8.1). В Европе САПР
Mentor Graphics занимает 54 % рынка. Ниже будут рассмотрены состав и
задачи, решаемые этими системами при проектировании печатных плат.
8.1.2. Специализированное программное
обеспечение в области целостности
сигнала и ЭМС
Уровень развития современных САПР электронных средств открывает
широкие возможности для разработчиков печатных плат. Наряду с комплек-
сными системами проектирования (OrCAD, Protel 99, ACCEL EDA, P-CAD,
Power PCB и др.) на рынке информационных технологий широко представ-
лены специализированные программные пакеты для анализа целостности
сигналов и ЭМС: Signal Integrity, QUIET, Omega Plus, FIDELITY, ANSYS,
ePlanner, EMC-Engineer, FLO/ЕМС и др. Большинство из них являются до-
полнительными модулями к системам проектирования и имеют специаль-
ные интерфейсы для импорта проектов, а также для экспорта изменений,
внесенных в проект, обратно в систему проектирования.
При проведении анализа эффектов на печатных платах разработчики часто
приходят к выводу, что использование инструментов анализа целостности
сигналов — это единственный способ исследования этих эффектов путем мо-
делирования. Тем более, что большинство автоматизированных пакетов
проектирования уже имеют встроенные модули — анализаторы целостнос-
ти сигнала (например, в Power РСВ модуль Signal Integrity). Анализ целост-
ности сигнала основан на составных моделях, которые позволяют оценить
искажения формы сигнала еще на стадии проектирования платы. Но этого
не достаточно для выявления причин возникновения нарушений в работе
печатных узлов.
S
ф
S
1ф I
|§|
151
i$ ।
I х I
I 00 I
Н
S
V
Сбои по питанию
Возмущения между
проводниками
Уменьшение
индуктивности
проводника L
Увеличение
емкости
проводника С
Увеличение
площади
сечения
проводника S
Помехи
отражения
Согласование,
устранение
неоднородностей
Увеличение момента
инерции сечения про-
водника за счет более
плоской его геометрии
Использование
нескольких слоев
(МПП)
Восприимчивость
к внешним ЭМ
возмущениям
Уменьшение площади
петли S, образуемой
проводником,
сближение прямого
и возвратного
проводников
Установка
согласующих
резистров
Изменение
топологии
(МПП)
Сбои из-за
некорректного
заземления
Уменьшение
активного
сопротивления и
индуктивности
заземления
Применение
развязывающего
конденсатора
Рис. 8.2. Основные задачи по обеспечению ЭМС при проектировании печатных плат
/
Л
/ \
f \
1
I'D I
J
ф
X
S
ф
534 Глава 8. Конструкторско-технологическое проектирование...
8.1. Тенденции в развитии САПР
535
Эффективный анализ целостности сигнала и ЭМС предполагает иссле-
дование с использованием различных методов моделирования. В идеале
анализ должен не только указывать на существование проблем, но и помо-
гать обнаруживать их причины: помехи или восприимчивость. Включение
эффективного анализа целостности сигнала и ЭМС в процесс проектирования
печатных плат — это шаг в направлении сокращения затрат. Оценка воспри-
имчивости узла и обнаружение источников нежелательных возмущений
позволит избежать повторного проектирования и обеспечит повышение его
качества в целом.
На начальных стадиях проектирования инструментальные средства ана-
лиза целостности сигнала позволяют быстро определить, будет ли разраба-
тываемая плата удовлетворять всем требованиям специфики поведения сиг-
нала. Но инструменты анализа целостности сигнала не обеспечивают выяв-
ления причин нарушений в работе или возникновения паразитных эффектов
и полезны только для некоторых стандартизированных случаев.
Рассмотрим возможные случаи проявления электромагнитных возмуще-
ний. Плата может являться каналом распространения электромагнитных
возмущений (ЭМВ) (рис. 8.2) [123, 124]. Чем меньше это сказывается на
работоспособности платы и ее окружения, тем более отвечающей требова-
ниям ЭМС она является.
Проектирование быстродействующих устройств требует предварительных
расчетов, позволяющих учесть влияния параметров платы на показатели
обеспечения целостности сигнала и ЭМС на стадии проектирования. Для
проведения расчетов электрических параметров необходимо построение
адекватных моделей составляющих частей печатной платы, некоторые из них
могут быть представлены, например, как линии передачи.
Рис. 8.3. Классификация прикладных программ в области ЭМС
536
Глава 8. Конструкторско-технологическое проектирование...
Исследования в этих направлениях можно проводить с использованием спе-
циализированных инструментальных средств, подразделяющихся по этапам
проектирования (рис. 8.3). Несмотря на удобный интерфейс, программное
обеспечение зарубежных производителей в большинстве своем не имеет под-
робной документации на русском языке, что вызывает определенные трудности
для части пользователей, недостаточно хорошо владеющих английским язы-
ком. Основными производителями данных продуктов являются такие компа-
нии, как Mentor Graphics, Cadence, Zuken, Innoveda, Ansoft, Altium и др.
Для проведения исследований посттопологического проектирования мо-
гут использоваться следующие инструментальные средства анализа ЭМС:
Omega Plus, Signal Integrity Analyzer, BoardSim, XTK и др. Провести более эф-
фективное исследование проблемы электромагнитных помех позволяет исполь-
зование программных средств предтопологического анализа (LineSim, ePlanner,
BLAST, QUIET, QUIET Expert и др.) на ранних стадиях цикла проектирова-
ния изделия, когда составляющие модели недоступны, и анализ ведется по
эквивалентным схемам. Такой подход позволяет снизить временные и финан-
совые затраты в процессе проектирования изделий, отвечающих требовани-
ям целостности сигнала и ЭМС. Для проведения электромагнитного модели-
рования могут использоваться следующие программные продукты: FLO/EMC,
Microwave Office, IE3D, FIDELITY, HFSS, SimLab и др.
8.1.3. Программы предтопологического
и посттопологического анализа
Приведем краткую характеристику программных продуктов предтополо-
гического и посттопологического анализов.
HyperLinx — средство анализа целостности сигналов и ЭМС. В настоя-
щее время включает два продукта: LineSim и BoardSim. Первая программа
предназначена для предварительной оценки проблем ЭМС, а вторая — для
более подробного посттопологического анализа целостности сигналов, пе-
рекрестных помех и параметров ЭМС. Имеются средства моделирования пе-
рекрестных помех и анализа ЭМС, которые позволяют рассчитать наводи-
мые сигналы в цепях, их спектры, а также оценивать электромагнитное из-
лучение вокруг них с учетом режима переключения и сравнивать с разре-
шенными пороговыми значениями.
LineSim позволяет представить печатный узел в виде эквивалентной схемы,
микросхемы и дискретные элементы которой представляются соответствующими
IBIS-моделями (I/O Buffer Information Specification models), а печатные провод-
ники на плате — моделями линий передачи. Библиотеки компонентов содер-
жат около 7000 моделей и легко могут быть пополнены. Пользователь может
получить начальную информацию о работоспособности после задания после-
довательности слоев платы. Результат анализа позволяет конкретизировать
требования к топологии, а модуль — передать их в систему проектирования.
BoardSim работает с реальным чертежом платы. В данный модуль может
быть загружен проект плат, разработанный практически в любом современ-
8.1. Тенденции в развитии САПР
537
ном пакете проектирования. Имеются средства расчета полных сопротивле-
ний проводников с учетом многослойной структуры платы, оценки степе-
ни согласования их с нагрузкой и оптимизации топологии для решения про-
блемы целостности сигналов.
ePlanner — предтопологическое средство анализа. Позволяет провести
оценку проекта на этапе разработки базовой концепции. Например, можно
построить графические модели топологий цепей с помощью разного рода
«мастеров». Это позволяет рассмотреть различные подходы к проектирова-
нию. Модуль предоставляет разработчику оптимальное решение для задания
ограничений в проекте еще до начала разработки платы в САПР. После того,
как по окончательно разработанной принципиальной схеме будет сформи-
рован список соединений, модуль ePlanner может быть использован совме-
стно с системой управления ограничениями для наложения ограничений на
критические параметры сигналов в проекте.
Предложенные топологии, ограничения на сигналы и варианты оконеч-
ных устройств могут моделироваться для оценки их влияния на временные
показатели и качество сигналов. Разработчик имеет возможность изменять
любые физические свойства, которые воздействуют на временные и каче-
ственные параметры сигналов, например, длину проводников, их волновые
сопротивления или скорость распространения сигнала в них. Исследование
перекрестных искажений может производиться с помощью метода подбора,
использующего модели индуктивно связанных линий, в которых можно ва-
рьировать различные параметры, например, зазор между проводниками, длину
связи, расположение слоев платы и свойства материалов. Затем предвари-
тельные оценки параметров уточняются и передаются вместе со списком
соединений в среду проектирования плат.
Blast — модуль, предназначенный для статического анализа временных
характеристик. Тщательно анализирует проводники и определяет задержку
в них, что позволяет на этапе проектирования плат выявить нарушения за-
данных временных параметров сигналов. Предварительная оценка задержек
в проводниках позволяет оптимизировать топологию на этапе трассировки.
Имеется полная интеграция с программой ХТК, благодаря чему можно по-
лучить уточненные данные на посттопологическом этапе.
Традиционные программы моделирования логических схем обеспечивают
функционирование проекта, когда он состоит из компонентов, имеющих средние
или типичные значения временных задержек. Модуль Blast решает задачи по-
строения проектов с использованием элементов, у которых определены мини-
мальные или максимальные временные характеристики. Он моделирует худший
случай с точки зрения временных параметров и позволяет сделать вывод о ра-
ботоспособности проекта. Мощной функциональной возможностью программы
является многообразие методов определения значений задержек межплатных
соединений, что позволяет плавно увеличивать точность вычислений.
ХТК — специализированный инструмент для анализа целостности сиг-
налов и перекрестных искажений в сложных многослойных платах. Это сис-
тема посттопологического анализа. После проведения подробного анализа
538
Глава 8. Конструкторско-технологическое проектирование...
всего проекта, с учетом заранее заданных критериев, генерируется отчет с опи-
санием всех выявленных нарушений. В программе используются собствен-
ные оригинальные алгоритмы, позволяющие повысить скорость анализа. Па-
раметрический и статистический анализ проводится методом Монте-Кар-
ло. Модуль поддерживает широкий набор моделей устройств.
Имеется комплекс трансляторов для загрузки топологий, разработанных
в разнообразных системах проектирования. Встроенная система просмотра
топологии облегчает пользователю поиск в проекте критических мест бла-
годаря средствам визуализации в отчетах. Все найденные нарушения отобра-
жаются на топологии специальными маркерами. После этого производится
интерактивный анализ сигналов в отдельных цепях или классах цепей. За-
тем проводится поиск возможного решения выявленных проблем. Модуль
позволяет получить параметрические данные, например, матрицы «паразит-
ных» емкостей и индуктивностей, используемые для моделирования пере-
крестных эффектов, а также диэлектрических потерь в изолирующих мате-
риалах, потерь за счет скин-эффекта.
QUIET — расширенный модуль ХТК, полезен на всех этапах разработки
проекта. Позволяет проводить анализ электромагнитных помех на систем-
ном уровне, в том числе в цепях питания и заземления; анализ целостности
сигналов и перекрестных искажений на уровне отдельных плат. Также есть
возможность задать стратегию трассировки для наиболее критических цепей,
определить стратегию распределения нагрузки в цепи, разрешить проблемы
межслойных связей в платах, установить наборы правил проектирования для
программ и др. Данная программная среда позволяет решить проблемы ЭМИ
с помощью метода подбора, учитывает дифференциальные и синфазные ис-
точники помех. Поддерживается широкий набор библиотек элементов и со-
вместимость с IBIS и SPICE моделями.
На стадиях предтопологического анализа QUIET позволяет: задать стра-
тегию трассировки для наиболее критических цепей, определить стратегию
распределения нагрузки в цепи, разрешать проблемы межслойных связей в
платах, устанавливать правила проектирования, передаваемые в САПР. При
посттопологическом анализе будет смоделировано поведение всех цепей пла-
ты, и информация о рассчитанных значениях будет занесена в отчет, где будут
выделены критические цепи.
В процессе анализа модуль QUIET учитывает и моделирует множество
самых разнообразных паразитных эффектов, встречающихся в сложных
платах. Например, контуры, образуемые корпусами микросхем, замкнутые
контуры проводников на плате, обрывы заземления, наличие паразитных
связей между близко расположенными проводниками, отвод теплоты, шумы
в цепях заземления. Модуль QUIET позволяет выявить и оценить даже трудно
обнаруживаемые источники помех, которые могут быть легко пропущены при
обычном контроле размещения компонентов на плате. Например, это мо-
гут быть пересечения двух или нескольких проводников на разных слоях с
возникновением слабой связи в точке пересечения или высокочастотное
шунтирование входных или выходных цепей.
8.1. Тенденции в развитии САПР
539
EMC-Engineer — отдельное средство управления моделированием ЭМС,
которое может использоваться как дополнительный компонент к САПР платы
(EDA). Быстрые методы моделирования для анализа целостности сигнала
объединены с физическими критериями проверки, что позволяет миними-
зировать затраты времени на проверку качества платы. Программа имеет
специально разработанный быстрый имитатор целостности сигнала, исполь-
зует метод граничных элементов (МГЭ), внедрены новые алгоритмы луче-
вого анализа, которые эффективны при идентификации источника излуче-
ния. Позволяет проводить расчеты волновых сопротивлений и временных
задержек.
Наряду с быстрыми методами в программе предложена довольно каче-
ственная визуализация результатов. Полученные результаты могут быть сис-
тематизированы и представлены в виде электронной таблицы.
Omega Plus — данный пакет предназначен для высокоскоростного ана-
лиза целостности сигнала и моделирования ЭМС, он также использует МГЭ
и позволяет решать задачи экранирования платы:
• экранирование одной группы микросхем от другой;
• анализ линий связи с учетом перекрестных помех и потребностей в эк-
ранировании.
Также пакет позволяет проводить расчет паразитных эффектов и моде-
лировать электромагнитное излучение на стадии трассировки. Анализ цело-
стности сигналов может быть проведен до и после выполнения трассиров-
ки платы. Имеется средство контроля выполнения технологических ограни-
чений. Отдельные модули предназначены для создания собственных моделей
источников сигналов и нагрузок, проведения более детального анализа в
частотной области. Рассчитываются комплексные амплитуды токов и напря-
жений и напряженности электрического и магнитного полей на заданных ча-
стотах. При превышении допустимого уровня излучения диагностируется цепь
или область платы, вносящая наибольший вклад в уровень излучения, и
производится повторная трассировка, изменяются типы компонентов, вво-
дятся слои металлизации и проводятся другие мероприятия на этапах от
виртуального прототипирования до изготовления реальной конструкции.
Signal Integrity — модуль анализа целостности сигналов, встроенный в си-
стему Protel 99 SE. Все элементы проводников на плате представляются здесь
в виде отрезков линий передачи, после чего проводится расчет переходных
процессов при воздействии на них импульсных сигналов. При этом прохож-
дение сигналов через микросхему не моделируется. Помимо расчета формы
сигнала в каждом узле проводника здесь выполняется анализ перекрестных
искажений. Особенностью данного модуля является то, что здесь не учиты-
ваются физические эффекты, связанные с распределением токов в провод-
никах земли и питания. Эти цепи считаются идеальными.
По итогам моделирования формируются правила проектирования, кото-
рые не контролируются при интерактивной трассировке, а используются только
при проверке правил проектирования (DRC) в пакете. В ходе проверки фор-
мируется отчет с указанием списка нарушений. Затем необходимо провести
540
Глава 8. Конструкторско-технологическое проектирование...
детальное моделирование в модуле Signal Integrity указанных в отчете цепей.
При нарушении допустимых значений полных сопротивлений моделирование
может не потребоваться — достаточно изменения ширины проводников ука-
занных цепей.
StatMod — трехмерная программа электромагнитного моделирования, ба-
зирующаяся на МКЭ, предназначена для предтопологического анализа.
Основными задачами являются: размещение элементов и расположение
проводников. Моделирование проводится в частотной области с высокой
степенью точности. Может использоваться для решения следующих задач:
вычисление текущего распределения в любой трехмерной структуре, моде-
лирование и вычисление магнитных связей линий передачи, трехмерное вы-
числение емкостей в произвольных структурах плат, визуализация тока, на-
пряжение и распределения плотности нагрузки.
FLO/ЕМС может использоваться в разработке и моделировании плат, с
целью определения любых потенциальных проблем ЭМС. Базируется на
методе матриц линии передачи (transmission line matrix — TLM) для моде-
лирования электромагнитного поля в трехмерном пространстве и времени.
TLM-метод подходит для моделирования электромагнитных полей, провод-
ников и схем. Данная программа может использоваться для определения плот-
ности, оптимального размещения и емкости развязывающих конденсаторов,
требуемых для подавления электромагнитных помех в многослойной плате.
Microwave Office — распространенный программный пакет, включающий
в себя два модуля: VoltaireXL (пакет моделирования линейных и нелинейных
схем) и EMSight (система трехмерного электромагнитного моделирования
СВЧ систем). EMSight представляет собой графическую среду для быстрого
анализа электромагнитных явлений, которые часто встречаются в высоко-
частотных интегральных схемах, монолитных микросхемах и высокоскоро-
стных цифровых печатных платах. Модуль при расчетах использует метод
моментов (ММ). Анализ проводится внутри ограниченной многослойной
области прямоугольной формы, причем боковые границы области всегда пред-
ставляются как идеальные проводники, в то время как верхняя и нижняя гра-
ницы области могут иметь потери. Количество анализируемых слоев, меж-
слойных соединений и внешних выводов не ограничено.
Графические возможности системы EMSight позволяют пользователю
исследовать цветное трехмерное, анимационное изображение токов высокой
частоты, на котором отображается не только амплитуда, но и направление
этих токов, что позволяет получить более полное представление о поведе-
нии СВЧ структур.
IE3D позволяет проводить моделирование и расчет конструкций на элек-
тродинамическом уровне — это новая технология для выполнения точного
анализа и проектирования сложных печатных схем в диапазоне СВЧ. Элект-
родинамический расчет предполагает применение электродинамических ме-
тодов расчета, в отличие от методов теории цепей. IE3D — интегральный элек-
тромагнитный имитатор и пакет оптимизации для анализа и проектирования
3-мерных микрополосковых антенн и печатных схем высокой частоты.
8.1. Тенденции в развитии САПР
541
Основная операция IE3D — составление и решение интегрального урав-
нения, полученного с помощью функций Грина. В IE3D можно моделиро-
вать электрический ток на металлической структуре и магнитный ток, пред-
ставляющий распределение напряженности электрического поля на метал-
лической апертуре. Программа использует ММ и имеет много положительных
особенностей для моделирования планарных и объемных схем и антенн в
слоистой диэлектрической среде. Однако ММ имеет некоторый свойствен-
ный ему недостаток в моделировании трехмерных диэлектрических, волно-
водных структур и структур с сильно неравномерным распределением напря-
женности электрического поля. По этой причине компания Zeland предста-
вила электромагнитный имитатор FIDELITY.
FIDELITY использует метод конечных разностей (МКР) для решения
уравнений Максвелла во временной области, применяемый в 3-х мерном элек-
тромагнитном имитаторе. Имитатор позволяет моделировать ЭМС для мик-
роволновых схем, компонентов, антенн и других высокоскоростных и вы-
сокочастотных схем. Использование МКР позволяет учитывать влияние силь-
ных и слабых источников напряжения и тока, получать результат в широкой
полосе частот, обрабатывать сложные диэлектрики, структурируя его про-
ще, чем ММ и МКЭ.
HFSS (High Frequency Structure Simulator) — мощный пакет программ, вы-
числяющий электромагнитные поля для пассивной трехмерной структуры
произвольной формы. Позволяет разработчикам заниматься сложными трех-
мерными, высокочастотными структурами, такими, как микроволновые филь-
тры, соединители, волноводы и антенны. HFSS построен на методе конечных
элементов (МКЭ), используя такие методы, как автоматическое адаптивное
генерирование и деление ячеек, МКЭ для векторов поля и адаптивную раз-
вертку. Программа автоматически вычисляет кратные адаптивные решения до
определяемого пользователем критерия сходимости. Решения для поля, най-
денные из уравнений Максвелла, точно предсказывают все дисперсионные ха-
рактеристики, существующие типы волн, преобразования типов волн, поте-
ри в материалах и на излучения. Анализ антенн, СВЧ линий передачи, пере-
ключающих схем, волноводных элементов, фильтров ВЧ и трехмерных неодно-
родностей сводится к визуализации структуры, точному определению мате-
риала, идентификации выводов и характеристик поверхностей.
ANSYS — многоцелевой программный пакет для проведения анализа в
широком круге инженерных дисциплин (прочность, теплофизика, динамика
жидкостей и газов и электромагнетизм) использует МКЭ. Для решения во-
просов ЭМС предназначен модуль EMAG — электро- и магнитостатика, низ-
ко- и высокочастотный анализ, нестационарные задачи и пр.
Momentum — программа для электромагнитного моделирования планарных
устройств, предназначенная для улучшения точности расчета пассивных ВЧ
и СВЧ цепей и моделей схемы. Momentum учитывает реальные конфигурации
конструкции, моделируя связь и паразитные эффекты, и может анализировать
многослойные произвольные структуры. Преимущество Momentum перед
другими планарными электромагнитными моделирующими устройствами —
542
Глава 8. Конструкторско-технологическое проектирование...
интегрированный интерфейс и взаимодействие с комплексом программ ADS
(Advanced Design System). Это позволяет пользователям выполнить и элек-
тромагнитный, и схемотехнический анализ.
Хотелось бы заметить, что для проведения отдельных исследований в ка-
честве инструмента моделирования может использоваться программный ком-
плекс ПА-9 (программа анализа, разработанная на кафедре САПР МГТУ им.
Баумана, представляет собой открытый комплекс). Специалисты КГТУ им.
А.Н. Туполева, например, применяют данный комплекс для анализа задер-
жек, перекрестных помех, емкостных характеристик, а также в процессе про-
ведения многокритериальной оптимизации ЭМС межсоединений цифровых
плат генетическими алгоритмами [125].
Как видно из приведенного обзора, к сожалению, пока нет универсаль-
ного продукта для анализа целостности сигналов и оценки параметров ЭМС.
Прикладные программные средства, используемые для проведения рас-
четов, можно классифицировать по методологической базе (рис. 8.4). В при-
веденной классификации под оригинальным алгоритмом разработчика по-
нимается использование определенной комбинации методов расчета, подо-
бранной изготовителем программного обеспечения.
Таким образом, разработчик платы должен принять решение о целесооб-
разности использования того или иного математического метода в каждом
конкретном случае и затем сделать выбор рациональной программной сре-
ды, которая позволит провести анализ на основе выбранного метода. Наи-
более оптимальным решением пока остается комбинированный метод ис-
пользования нескольких программных продуктов при проектировании платы.
Некоторая условная обобщенная последовательность применения программ-
Метод граничных
элементов (МГЭ)
EMC-Engineer,
Omega Plus
Метод конечных
элементов (МКЭ)
HFSS, ANSYS,
EMFlex StatMod
Прикладные программы
в области ЭМС
на стадии проектирования
Метод конечных
разностей (МКР)
FDTD, FIDELITY,
Celia, SEMCAD
Метод моментов
(ММ)
EMSight, IE3D,
WIPL-D
Метод матриц
линии передачи
(TLM)
Оригинальный
алгоритм
разработчика
FLO/EMC
XTK, HyperLmx,
Blast, QUIET
Рис. 8.4. Классификация программных продуктов в области ЭМС по методологической
основе
8.1. Тенденции в развитии САПР
543
Проектирование ПП с учетом требований ЭМС
Рис. 8.5. Прикладное программное обеспечение в проектировании печатных плат
ных средств при создании печатных плат и печатных узлов, отвечающих
требованиям целостности сигнала и ЭМС, представлена на рис. 8.5.
Отдельно следует отметить развитие программного обеспечения, ориен-
тированного на проведение испытательных процедур. Такие продукты раз-
рабатываются по принципу интеллектуальных испытательных программных
систем, тесно взаимодействующих с аппаратным обеспечением испытаний.
Примерами таких комплексных систем являются TILE, EMITest. Приведем
их краткую характеристику.
TILE (глобальная объединенная лабораторная среда) — гибкая инструмен-
тальная программная среда для контроля над испытаниями. Она состоит из
системы управления приборами, библиотек методов определенных измерений
и испытаний помехоустойчивости, библиотек инструментальных устройств
544
Глава 8. Конструкторско-технологическое проектирование...
и базы данных. Тестовая задача представляется в виде блок-схемы, каждое дей-
ствие на которой (определение частоты, амплитуды, уровня модуляции, ка-
либровка и т.д.) может быть отредактировано, что позволяет пользователю через
графический интерфейс проводить настройку каждого шага испытаний.
EMITest — программное обеспечение для управления испытаниями в об-
ласти ЭМС. Изначально разрабатывалось для внутреннего использования
фирмой СКС Laboratories, но в процессе развития показало свою конкурен-
тоспособность на мировом уровне и совместимость с разнообразным испы-
тательным оборудованием. Состоит из следующих блоков: 1) анализ на из-
лученную и кондуктивную эмиссию; 2) анализ на помехозащищенность;
3) программы калибровки и спецификации. Все испытательные данные могут
экспортироваться в Excel.
Использование специализированного программного обеспечения позво-
ляет включить в процесс проектирования платы анализ ЭМС на каждом этапе.
Такой подход (рис. 8.5) ведет к сокращению излишних материальных и вре-
менных затрат, позволяет избежать повторного проектирования и повысит
качество проекта.
8.2. Решение задач целостности сигналов
в САПР
8.2.1. Перекрестные помехи и их моделирование
Программы электродинамического анализа в составе САПР печатных плат
требуют согласования с этапом топологического проектирования, что позво-
ляет создать некоторую комплексную среду проектирования платы. Рассмот-
рим взаимодействие процедур электродинамического анализа и топологи-
ческого проектирования на примере минимизации перекрестных помех в
линиях передачи печатного монтажа.
Современные методы анализа перекрестных искажений применяются после
разработки топологии, когда программа моделирования схемотехнического
уровня (например, Spice), использующая специальные модели и векторы,
пытается проанализировать все паразитные эффекты на подложке и иденти-
фицировать проблему. Обнаруженные проблемные фрагменты платы, как
правило, решаются корректировкой топологии. Самые современные систе-
мы используют специальные дополнительные методы моделирования, позво-
ляющие анализировать временные эффекты в статическом режиме на тран-
зисторном и вентильном уровнях, или специальные программы моделирова-
ния, способные решать задачи по расчету и идентификации помех. Однако, в
целом, процедура анализа перекрестных искажений, возникающих из-за па-
разитных емкостных и индуктивных связей, достаточно утомительна, и решение
любой идентифицированной проблемы требует больших усилий. Рекомендации
по ручному исправлению работают лишь для узкого круга практических за-
дач. В общем случае, такой подход требует нескольких последовательных ите-
8.2. Решение задач целостности сигналов в САПР
545
раций постановки задачи и моделирования, что может привести к значитель-
ному увеличению времени проектирования.
Поскольку задачи целостности сигнала и ЭМС желательно идентифици-
ровать до топологического проектирования, существуют другие системы,
производящие анализ перекрестных искажений уже во время размещения и
трассировки схемы. В них используется набор эвристических правил, кото-
рые служат критериями первичной идентификации проблем перекрестных
искажений (например, максимально допустимое значение длины двух парал-
лельных проводников) на этапе трассировки платы, после чего автоматически
запускается программа моделирования, производящая более детальный ана-
лиз данного участка топологии. Как только критическое место будет выяв-
лено, автотрассировщик попробует изменить топологию таким образом, чтобы
увеличить расстояние между данными цепями или разместить их в разных
слоях. Для большинства сложных и высокоскоростных плат это может по-
требовать значительных усилий по разрыву и восстановлению проводников
без гарантии полного решения проблемы в автоматическом режиме.
Улучшенный подход к трассировке заключается в принудительном огра-
ничении на длину любых двух параллельно проложенных проводников.
Однако он базируется на эмпирических данных и не отражает всю физику
эффекта перекрестных помех, где присутствует зависимость от сигналов в
разных цепях. Указанное ограничение может оказаться неоправданно жес-
тким, что приведет к перегрузке программы трассировки. Кроме того, здесь
не может быть определена средняя длина цепей, максимально подвержен-
ная перекрестным искажениям, и проблема сохранится. Ряд компаний уже
сообщили о существовании интеллектуальных систем автотрассировки,
правильно понимающих эффекты перекрестных искажений, но они еще не-
совершенны и могут привести к перегрузке трассировщика из-за чрезмер-
но жестких ограничений. В случае отсутствия точной информации о време-
ни прихода сигналов на приемники, оценка перекрестных искажений может
быть выполнена с большим запасом, что также пагубно отразится на резуль-
татах трассировки.
Идентификация проблем перекрестных искажений на этапах трассировки
или обработки уже готовой топологии является слишком запоздалой, исполь-
зование же системы анализа на посттопологическом этапе и вовсе неприем-
лемо из-за значительного увеличения времени проектирования. Новый подход
ориентируется на раннее выявление перекрестных искажений и их подавление
во время размещения или глобальной трассировки, что достигается непре-
рывной обработкой моделей. Здесь физическое проектирование прогрессивно
разделено на небольшие ячейки с оптимизацией связности, синхронизации,
мощности и перегрузки на всех этапах, включая анализ перекрестных иска-
жений.
Основой для решения проблем перекрестных искажений является интег-
рированный, инкрементный статический анализатор временных характери-
стик, учитывающий паразитные физические процессы и имеющий механизм
экстракции АС-схем замещения связанных цепей. В самых современных
18 |>2
546
Глава 8. Конструкторско-технологическое проектирование...
инструментах такой анализатор временных характеристик позволяет смоде-
лировать перекрытие фронтов сигналов в различных цепях и выявить потен-
циально опасные места схем. Так как на данном этапе в проекте еще не имеется
никакой информации о топологии устройства, для выявления проблемных
мест может быть использован статистический метод.
Сложность моделей связей снижается с понижением ее уровня. Один из
подходов решения задачи заключается в том, что пассивные цепи с сигна-
лами, которые являются потенциальными жертвами перекрестных искаже-
ний, будут иметь дополнительные признаки, предписывающие системе гло-
бальной трассировки выполнить для этих цепей или большие зазоры, или эк-
ранирование, или повторную разводку в системе локальной трассировки.
Локальный трассировщик представляет собой бессеточную (основанную
на точных геометрических формах) систему автоматической трассировки,
позволяющую изменять ширину проводников и зазоры между ними с целью
подавления перекрестных помех. Он включает механизмы, позволяющие
напрямую связать ограничения, направленные на снижение перекрестных
искажений, с весовыми оценками качества трассировки и избежать влияния
искажений на длительность фронтов и задержки в цепях. Аналогичным об-
разом производится анализ помех, возникающих в результате наличия па-
разитных связей. Здесь вместо анализа вклада перекрестных помех в задер-
жку тракта производится моделирование формы наведенного сигнала в цепи-
приемнике. Если наведенный сигнал превышает порог, заранее заданный для
логической схемы, управляемой данной цепью, то нарушение будет выяв-
лено и устранено локальным трассировщиком.
8.2.2. Сопротивление шин питания и заземления
Проблема помех по шинам питания и заземления становится все бо-
лее актуальной. Ранее было показано, что динамические процессы в этих
цепях во время переключения микросхем приводят к коммутационным
помехам различного вида. Однако при протекании большого тока в ре-
зистивных цепях питания или заземления проявляется статическое падение
напряжения. Напомним, что даже если статическое падение напряжения
в шинах питания и заземления незначительно, то динамическое падение
напряжения при переключении микросхем весьма велико, и большая часть
проблем проектирования шин питания и заземления связана именно с этим
явлением. В результате этого нарушается целостность сигнала и снижа-
ется помехозащищенность изделия. По мере перехода к субмикронным
технологиям, проблема коммутационных помех становится еще более
актуальной из-за следующих факторов:
• увеличения токов, связанного с увеличением числа устройств в про-
екте, а также с большим потреблением каждого устройства;
• увеличения сопротивления проводников за счет уменьшения их сечения
и числа межслойных соединений;
• снижения напряжения питания до 1,5 В и ниже.
8.2. Решение задач целостности сигналов в САПР
547
Например, на полном сопротивлении 1 Ом при токе 1 А падение напря-
жения составляет 1 В, что соответствует 2/3 от напряжения питания 1,5 В.
В этом случае в микросхеме может произойти отказ по одной из следующих
причин:
• ухудшение характеристик (снижается быстродействие схемы относи-
тельно теоретически рассчитанной);
• функциональные сбои (изменяется длительность фронтов и уровни сиг-
налов);
• ненадежное функционирование (снижается запас помехоустойчивости).
Из-за снижения напряжения в цепи питания во фронтах импульсов по-
являются дополнительные задержки. В общем случае, эти проблемы долж-
ны быть выявлены на этапе виртуального прототипирования. Если пробле-
му решать на этапе физического прототипирования, то усилия по иденти-
фикации проблемного элемента схемы могут привести к существенному
увеличению длительности цикла производства. В большинстве проектов
двусторонних плат разработчики пытаются избежать возможного проявле-
ния описываемых эффектов путем использования неоправданно широких
шин питания и специальной топологии. Однако соответствующее этому
сокращение доступных для трассировки ресурсов в современных условиях
недопустимо.
В последнее время различные компании-производители систем САПР
предлагают собственные инструменты для динамического анализа паразитных
падений напряжения в цепях питания и заземления в моменты переключе-
ния. Как правило, для точной оценки падения напряжения необходима про-
грамма моделирования на транзисторном уровне. Во время размещения и
трассировки схемы список ее соединений, необходимый для запуска програм-
мы моделирования, как правило, отсутствует, а сам запуск может занять много
времени и привести к неоправданному замедлению процесса проектирова-
ния. Требование значительных вычислительных ресурсов накладывает огра-
ничения на посттопологический анализ устройства и может стать причиной
задержки передачи проекта в производство. Благодаря использованию мо-
делей питания на уровне вентилей, можно будет отказаться от списка соеди-
нений. Однако требуемые в этом случае вычислительные ресурсы еще слиш-
ком велики, чтобы допустить проведение анализа по мере практического
размещения и трассировки схемы. Присутствует также проблема зависимо-
сти результатов, полученных на транзисторном и вентильных уровнях мо-
делирования, а также реальных характеристик кристалла.
Решение задачи устранения паразитного падения напряжения кроется в
раннем их обнаружении: на этапах размещения и глобальной трассировки.
В этом случае нагрузки могут быть получены достаточно точно, и еще оста-
ется определенная свобода для размещения ячеек, благодаря чему устраня-
ются проблемы синхронизации и некоторые другие проблемы субмикрон-
ных технологий.
Структура системы питания должна быть определена на этапе виртуаль-
ного прототипирования, так как она сильно влияет на трассировку сигнальных
18*
548
Глава 8. Конструкторско-технологическое проектирование...
цепей, перегрузку трассировщика и размещение ячеек на последующих этапах.
Для анализа паразитного падения напряжения все токи внутри ячеек сум-
мируются и представляются в виде одного источника тока. Такие источни-
ки располагаются в некоторой сетке питания. Далее по результатам работы
быстрого анализатора падений напряжения строится цветовая карта прогрева
кристалла и производится корректировка сети питания для минимизации
паразитных эффектов. Как правило, сеть питания строится со значительным
запасом. Анализ позволяет получить оптимальные значения ширины про-
водников на различных участках сети питания и выиграть значительное ко-
личество места на кристалле или плате. Если изначальная сеть питания не
удовлетворяет рассчитанным значениям токов в ячейках, то ширина провод-
ников будет увеличена, а возможно, и будут добавлены дополнительные
проводники. Пользователь может провести также анализ «что, если» и выя-
вить дополнительные пути оптимизации проекта.
Радикальным приемом устранения большинства проблем, связанных с
проектированием шин питания и заземления, является применение МПП
и рациональный выбор развязывающих конденсаторов, как это показано в
главе 5.
8.2.3. Учет индуктивностей
По мере того, как частота синхронизации превысила 500 МГц, в кристаллах
микросхем и на печатных платах стали весьма заметны индуктивные эффекты,
способные отрицательно влиять на целостность сигнала и ЭМС печатного
узла. Моделировать абсолютно все индуктивные связи и эффекты самоин-
дукции в устройстве нет никакой необходимости, так как индуктивный эф-
фект является критическим только для цепей с высокочастотными сигналами,
эффект самоиндукции является важным только для относительно длинных
цепей, а эффект взаимоиндукции влияет только на относительно длинные
параллельные участки связанных линий передачи. Чтобы снизить индуктив-
ные эффекты, наиболее важно обеспечить правильный путь возврата высо-
кочастотных токов. Эта задача чрезвычайно затруднена для автоматических
инструментов размещения и трассировки, так как в настоящее время нет до-
статочно точного механизма анализа происходящих индуктивных эффектов.
Для схем, критичных к индуктивным эффектам, существуют специаль-
ные рекомендации по проектированию, которые базируются на выводах и
положениях, детально рассмотренных в предыдущих главах книги. Наибо-
лее общая рекомендация сводится к необходимости расположения рядом
сигнального и возвратного проводников. Чем ближе друг к другу они рас-
положены, тем меньше их суммарная индуктивность. В печатных платах это
требование конкретизируется в МПП при выборе расстояния между сигналь-
ными и потенциальными слоями для линий передач и минимизации рассто-
яния между потенциальными слоями для шин питания и заземления. В ме-
таллизации интегральных микросхем эти технические решения видоизме-
няются, но их физическая суть остается неизменной.
8.3. Структура и задачи САПР печатных плат
549
/Хк о Полярность ЭДС, возникающей
вследствие протекающих токов
Рис. 8.6. Добавление инверторов для подавления индуктивных эффектов
в высокоскоростных цепях
Индуктивные эффекты критичны для цепей с высокочастотными сигна-
лами. Для длинных проводников современные инструменты проектирова-
ния автоматически добавляют инверторы (рис. 8.6), чем достигается подав-
ление ЭТИХ Эффектов. Лучший же способ заключается в том, чтобы осуще-
ствить такую глобальную и локальную стратегию трассировки, которая
устраняет потребность в подробном моделировании и анализе индуктивных
эффектов.
8.3. Структура и задачи САПР печатных плат
8.3.1. Структура перспективных САПР
САПР фирмы MENTOR GRAPHICS
Любая система проектирования печатных плат представляет собой слож-
ный комплекс программ, обеспечивающий сквозной цикл, начиная с про-
рисовки принципиальной схемы и заканчивая генерацией управляющих
файлов для оборудования изготовления фотошаблонов, сверления отверстий,
сборки и электроконтроля. Однако условия современного рынка наклады-
вают дополнительные требования на эти системы.
Как отмечалось выше, ведущие позиции занимает компания Mentor
Graphics. Имея собственную систему проектирования печатных плат Mentor
BoardStation, компания продолжает развивать линии продуктов Expedition
РСВ и PADS PowerPCB. Ключом к успеху компании явилась ориентация на
современные интегрированные среды проектирования для Windows. Маршрут
проектирования PADS включает создание проекта, топологическое проек-
тирование, анализ и верификацию. Его отличают следующие возможности:
550
Глава 8. Конструкторско-технологическое проектирование...
• проектирование высокоскоростных плат (определение правил; трас-
сировка; анализ);
• повторное использование на логическом и физическом уровне;
• корпусирование BGA, CSP; трассировка под любым углом;
• неограниченная сложность проекта;
• трассировка по заданным правилам;
• управление атрибутами, ограничениями и вариантами.
Описание проекта ведется средством DxDesigner, которое включает сле-
дующие процедуры:
• систему навигации проекта, обеспечивающую быстрый просмотр и ана-
лиз иерархии проекта;
• окно схемного редактора, обеспечивающее быстрый поиск, выделе-
ние и редактирование компонентов и цепей;
• редактор ограничений, позволяющий вводить ограничения непосред-
ственно в принципиальную схему;
• редактор атрибутов, обеспечивающий многообъектное редактирова-
ние атрибутов проекта;
• повторное использование отработанных узлов принципиальной схе-
мы с атрибутами.
В создании проекта используется пакет I/O Designer, обеспечивающий
сквозную интеграцию проектов FPGA и печатных плат, оптимизацию задер-
жки распространения сигнала, целостность сигнала и минимизацию помех,
системную оптимизацию распределения выводов FPGA.
Пакет Expedition РСВ представляет сейчас наиболее мощное решение в
области проектирования плат. Пакет обеспечивает современные технологии
трассировки, включая дифференциальные пары, обеспечивая высокую плот-
ность трасс. При этом требования к параметрам печатных плат охватывают
весь диапазон, представляющий практический интерес, а именно:
• размер: меньше 5 кв. см; больше 2600 кв. см;
• число слоев от 1 до 40;
• в среднем 3 и более ПЛИС на плате;
• число компонентов более 9000; число цепей более 12 000; число отрезков
более 90 000;
• число металлизированных отверстий более 37 000, использование мик-
ропереходов;
• возможность размещения более 100 деталей на 10 см2;
• возможность применения корпусов BGA, CSP, СОВ, DCA;
• учет технологии изготовления платы.
Основу системы составляет среда AutoActive, позволяющая реализовать
такие функции, как предтопологический анализ целостности сигналов, ин-
терактивная и автоматическая трассировка с учетом требований высоко-
частотных плат и специальных технологических ограничений, накладыва-
емых использованием современной элементной базы (например, примене-
ние корпусов с шариковыми выводами BGA). Единая среда позволяет с
помощью модуля ICX моделировать наводки в проводниках непосредствен-
8.3. Структура и задачи САПР печатных плат
551
Рис. 8.7. Автоматическое из-
менение формы проводника с
контролируемой длиной при
перемещении конденсатора в
пакете PADS PowerPCB
но при прокладке трассы или шины и контролировать превышение ими
заданного уровня.
В пакет Expedition РСВ входит трассировщик высокочастотных трасс HSR.
Он позволяет:
• учитывать физические ограничения при трассировке: задержку рас-
пространения; параллелизм трасс, ограничения на длину трасс с уче-
том необходимости согласования, дифференциальных пар;
• интегрироваться с редактором ограничений;
• поддерживать различную топологию трасс.
У продукта Expedition РСВ можно отметить
только один недостаток — его высокую сто-
имость, что является существенным препятстви-
ем для проникновения на российский рынок и
его освоения малыми предприятиями.
Другой продукт компании MENTOR — сис-
тема PADS PowerPCB — предлагает более деше-
вое решение. Эта система имеет лучший авто-
трассировщик BlaseRouter, поддерживающий
все необходимые при трассировке высокочас-
тотных плат функции (рис. 8.7).
САПР Mentor Graphics позволяет провести
полный цикл верификации платы. При этом
используются следующие подсистемы:
• HyperLynx, ICX/Tau, Quiet Expert — анализ целостности сигналов и
электромагнитной совместимости;
• BetaSoft Board — анализ теплового режима печатного узла;
• IDF Interface — двунаправленный интерфейс в CAM/CAD (UGS, Pro
Engineer, Solid Works,...);
• Fablink XE/Pro — пост-обработка для повышения технологичности про-
изводства.
Пакет HyperLynx — наиболее мощный в области анализа целостности сиг-
нала. Он имеет модули предтопологичекого (HyperLinks LineSim) и постто-
пологического (HyperLinks BoardSim) анализа, тесно взаимодействующие с
системой контроля ограничений.
• LineSim и LineSim — предварительный анализ целостности сигналов
во временной и частотной областях до разработки печатной платы
(предварительные модели печатных проводников в виде отрезков линий
передачи вставляются в схему вручную на основе предположительных
соображений о топологии печатной платы);
• BoardSim и BoardSim — анализ целостности сигналов во временной и
частотной области после разработки печатной платы (но до изготов-
ления фотошаблонов).
Пакет ICX выполняет верификацию целостности сигнала, обеспечивая
анализ высокой точности, в том числе наихудшего случая. Анализ может про-
водиться для многоплатных систем в интерактивном и пакетном режимах.
552
Глава 8. Конструкторско-технологическое проектирование...
Важной особенностью является возможность анализа размещения компо-
нентов и трассировки по электрическим требованиям.
Пакет Таи выполняет исчерпывающую временную верификацию до и после
трассировки платы.
В Mentor Graphics Design Kits имеются готовые блоки и библиотеки мо-
делей компонентов (SI Design Kits), которые используются для анализа це-
лостности сигнала. Это модели Spice, IBIS, VHDL-AMS и другие, поставля-
емые изготовителями микросхем ИС (Xilinx, Altera, Micron, NVIDIA). В набор
включены также описания и правила проектирования ввода/вывода FPGA,
а именно полное описание выводов семейств FPGA и правил их распреде-
ления (Xilinx, Altera, Lattice, и др.).
САПР фирмы CADENCE
Следующей по мощности предлагаемых решений идет компания CADENCE.
Для верхнего уровня проектирования предлагается пакет РСВ Design Studio.
В качестве редактора печатных плат здесь используется программа Allegro, по-
зволяющая разрабатывать многослойные и высокоскоростные платы с высокой
плотностью размещения компонентов. В качестве штатного модуля авторазме-
щения и автотрассировки здесь используется программа SPECCTRA, управля-
емая обширным набором правил проектирования и технологических ограни-
чений. Анализ целостности сигнала и ЭМС топологии платы выполняется с
помощью специального модуля SPECCTRAQuest SI Expert, а для предваритель-
ного анализа проекта и подготовки наборов правил проектирования используется
модуль SigXplorer.
Другой продукт компании CADENCE, пакет OrCAD рекомендуется как
более легкое и дешевое решение для проектирования печатных плат. В по-
следнее время продукт почти не развивается, о чем косвенно свидетельствуют
номера последних версий (9.1, 9.2, 9.22, 9.23). Данный пакет рассматрива-
ется фирмой CADENCE как приоритетная система ввода проектов и моде-
лирования: модули Capture CIS и PSpice сейчас поставляются в составе па-
кета РСВ Design Studio [126]. В самую последнюю версию системы OrCAD
вошли новые возможности синтеза и моделирования цифровых логических
схем NC Sim. Редактор печатных плат OrCAD Layout имеет три различные
конфигурации с разными функциональными возможностями. В проекте
платы здесь могут присутствовать до 30 слоев, 16 из которых могут быть сиг-
нальными. Имеются встроенные средства авторазмещения и автотрассировки,
а также интерфейс с программой SPECCTRA.
САПР фирмы ZUKEN
Третьим по популярности в мире является достаточно мощный продукт —
Visula компании ZUKEN. Продукты этой компании обеспечивают сквозной
цикл проектирования и предлагают эффективные средства моделирования и
синтеза программируемой логики с последующей разработкой печатной платы.
Здесь имеется стандартный набор инструментария, а также собственные сред-
ства авторазмещения и автотрассировки. Следует отметить, что компания
8.3. Структура и задачи САПР печатных плат
553
Рис. 8.8. Трехмерное моделирование платы и узла средствами компании Zuken
ZU KEN также предлагает пользователям интегрированные средства трехмер-
ного твердотельного моделирования разрабатываемых устройств (рис. 8.8).
В состав системы входит пакет Board Designer — разработка топологии пе-
чатных плат. Эта объектно-ориентированная среда включает следующие под-
системы:
• групповая совместная разработка проектов;
• мощные средства планирования топологии;
• интеллектуальная система выделения компонентов;
• анализ тепловых режимов;
• поддержка встроенных компонентов;
• поддержка шаблонов трассировки компонентов;
• базы данных материалов;
• средства повторного или заимствованного проектирования;
• средства просмотра редактирования ЗЭ-вида платы;
• средства оптимизации набора слоев и плотного монтажа;
• возможность управления вариантами проекта;
• настраиваемый пользовательский интерфейс;
• генератор отчетов.
САПР фирмы ALTIUM
Австралийская компания ALTIUM, благодаря умелой инвестиционной
политике, смогла свести до минимума потери, связанные со спадом рынка
высоких технологий в 2002 году. В августе 2002 года компания выпустила в
свет пакет Protel DXP, представляющий собой продолжение собственной ори-
гинальной линии продуктов Protel. Этот пакет обеспечивает сквозной цикл
554
Глава 8. Конструкторско-технологическое проектирование...
проектирования смешанных аналого-цифровых печатных плат с использо-
ванием программируемой логики фирм XILINX и ALTERA. Весь инструмен-
тарий реализован на базе интегрированной среды проектирования Design
Explorer, работающей под управлением операционной системы Windows ХР.
К имевшимся ранее средствам посттопологического анализа целостности сиг-
налов добавилась возможность выполнять предтопологический анализ. Но
главным новшеством системы Protel DXP должен был стать топологический
автотрассировщик Situs, призванный реализовать новый подход к автома-
тической разводке плат.
На фоне полной мобилизации усилий на разработку пакета Protel DXP
компания ALTIUM продолжает развивать свой второй пакет проектирова-
ния печатных плат P-CAD 2002. Эта система остается достаточно популяр-
ной в России, что скорее определяется привязанностью наших разработчи-
ков к названию Р-CAD (в свое время фирма ALTIUM сделала умелый мар-
кетинговый ход, переименовав пакет ACCEL EDA в P-CAD). В последних
версиях основные изменения затронули в основном пользовательский ин-
терфейс, который стал больше походить на Protel.
Основу системы Protel 2004 составляет программная оболочка Design
Explorer, которая интегрирует в себе различные модули, выполняющие оп-
ределенные функции проектирования, например, редактор принципиальных
схем, редактор печатных плат, автотрассировщик, программу моделирова-
ния, интерфейсы импорта и экспорта, САМ средства. Среда Design Explorer
представляет собой полностью 32-разрядное приложение, предназначенное
для работы под управлением операционных систем Windows 2000/ХР и ис-
пользующее технологию клиент-сервер.
Одной из самых важных частей системы Protel 2004 является программа ввода
проектов nVisage, которую нельзя отождествлять с обычным редактором прин-
ципиальных схем. На самом деле редактор схем является лишь составной этой
программы наряду с редактором библиотек символов, текстовым редактором
списков соединений и описаний на языке VHDL, программой смешанного
аналогово-цифрового моделирования, синтеза логики для ПЛИС и др.
В отличие от системы Р-CAD, ввод проекта в котором ограничивается лишь
вводом схем (пусть даже многолистовых), система Protel 2004 изначально пред-
назначена для построения проекта изделия сверху вниз: аппарат - блок - су-
блок — модуль — ячейка — плата — компонент (ПЛИС). Проект Protel 2004
представляет собой специальный служебный файл, содержащий ссылки на
отдельные документы и обеспечивающий доступ к ним в рамках среды про-
ектирования Design Explorer. Отдельные документы проекта могут храниться
на жестком диске компьютера или на соседних машинах в рамках локаль-
ной вычислительной сети, причем допускаются множественный доступ к од-
ним и тем же файлам и использование одного документа в разных проектах,
что обеспечивает уникальные возможности групповой разработки. Отметим,
что проекты бывают четырех типов: проекты печатных плат (РСВ), програм-
мируемой логики (FPGA), VHDL описания (Embedded) и интегрированные
библиотеки компонентов (Integrated Library).
8.3. Структура и задачи САПР печатных плат
555
В редакторе принципиальных схем применяется несколько видов иерар-
хии, причем один из них ранее применялся только в «тяжелых» САПР для
построения многоканальных проектов. Подобные функции дают возможность
пользователям избавиться от необходимости копировать подчиненные ли-
сты по числу одинаковых каналов. Достаточно нарисовать схему канала один
раз и правильно связать ее с вышестоящим листом. При моделировании или
передаче проекта в редактор печатных плат система автоматически размно-
жит описанные каналы, присвоит компонентам уникальные позиционные
обозначения и добавит необходимые связи. Многоканальная структура про-
екта сохранится и в редакторе печатных плат: все компоненты определен-
ного канала будут автоматически привязаны к так называемой «комнате» раз-
мещения (Room), что облегчит их последующее размещение и трассировку
связей, благодаря уникальной функции Copy Room Format.
Редактор схем Protel 2004 имеет дискретность 0,01 дюйма, что составля-
ет около 0,25 мм. Так как для оформления схем, согласно требованиям ЕСКД,
достаточно дискретности 0,5 мм, то рекомендуется рисовать схемы в умень-
шенном масштабе.
САПР Sigrity
SpeedXP Suite — система анализа электромагнитной совместимости, це-
лостности сигналов и перекрестных искажений на печатных платах и в кор-
пусах интегральных микросхем.
Пакет SpeedXP представляет собой интегрированную среду анализа це-
лостности сигналов и перекрестных искажений на сложных печатных пла-
тах и кристаллах интегральных микросхем. В состав пакета входят два само-
стоятельных приложения, имеющих единый интерфейс и общую базу дан-
ных: Speed2000 и PowerSI. Новый продукт XcitePI, предназначенный для
моделирования проблем электромагнитной совместимости в корпусах и под-
ложках высокоскоростных интегральных схем.
Speed2000
Программа Speed2000 — это пакет анализа проблем электромагнитной со-
вместимости с оригинальным вычислительным ядром, работающий во вре-
менной области. Главным отличием его от аналогичных продуктов других про-
изводителей является то, что шины заземления и цепи питания, в том числе
выполненные в виде внутренних слоев питания и заземления, здесь не счи-
таются идеальными.
Благодаря такому подходу стало возможным резко повысить точность
оценки уровней сигналов, наводимых не только в соседних проводниках, но
и в проводниках, расположенных на разных слоях, разделенных экранами.
Отметим, что подобные возможности недоступны ни в одном другом совре-
менном пакете анализа — компания Sigrity выступает здесь пионером.
Мощные средства трехмерной визуализации позволяют посмотреть рас-
пространение помехи по внутреннему слою заземления к различным ком-
понентам на плате. Наглядность процессов, происходящих в моделируемом
556
Глава 8. Конструкторско-технологическое проектирование...
устройстве, позволяет оптимально подобрать положение развязывающих
конденсаторов и их номиналы.
PowerS I
Программа PowerSI выполняет аналогичные функции, но ее ядро работа-
ет в частотной области. Здесь можно рассчитать спектры сигналов и помех в
различных проводниках печатной платы, оценить частотные характеристики
отдельных узлов микросхемы, оптимизировать размещение экранов.
Программы Speed2000 и PowerSI дополняют друг друга и позволяют в рам-
ках одного продукта полностью перекрыть все возможные вопросы, связанные
с электромагнитной совместимостью. В дополнение к ним в состав пакета
SpeedXP входит программа BroadBand SPICE, предназначенная для экстракции
SPICE схем замещения устройств, описанных матрицами 5-параметров, что дает
возможность учитывать их в пакетах моделирования на основе ядра HSPICE.
XcitePI
Программа предназначена для моделирования проблем электромагнит-
ной совместимости в корпусах и подложках высокоскоростных интеграль-
ных схем. Учитываются эффекты распространения не только в сигнальных
проводниках, но и в цепях питания и земли всего стека слоев.
САПР Quantic ЕМС
Compliance — система посттопологического анализа электромагнитной
совместимости на печатных платах. Пакет Compliance канадской компании
Quantic-ЕМС позволяет оценивать влияние конструктивных особенностей
Рис. 8.9. Интефейс анализа целостности сигнала в системе Compliance
8.3. Структура и задачи САПР печатных плат
557
печатных плат на их электрические характеристики (рис. 8.9), а также мо-
делировать электромагнитную совместимость устройств еще до изготовле-
ния реальных конструкций, тем самым сокращая сроки и стоимость проек-
тирования при значительном повышении качества.
Пакет Compliance представляет собой дальнейшее развитие хорошо за-
рекомендовавшей себя программы Omega PLUS, предназначенной для ра-
боты на персональных компьютерах под управлением ОС Windows. Различ-
ные модули позволяют анализировать целостность сигналов, перекрестные
искажения, временные задержки, время установления сигналов и помехоу-
стойчивость, а также электромагнитное излучение нижней и верхней сторон
печатной платы в широком диапазоне частот.
Большой набор трансляторов позволяет импортировать в систему проекты
печатных плат, разработанных в таких популярных пакетах, как P-CAD (ACCEL
EDA), SPECCTRA, Mentor BoardStation, OrCAD, Protel, PADS PowerPCB и др.
MicroSim Polaris
В состав системы моделирования аналого-цифровых электронных схем Design
Center компании MicroSim (в начале 1998 г. объединилась с фирмой OrCAD)
включены программы Polaris и PCBoards. Первая из них предназначена для
анализа целостности сигналов, вторая представляет собой графический редактор
печатных плат. В результате система Design Center получила новое качество —
возможность сквозного проектирования печатных плат, и популярность ее сразу
же возросла. Однако программы Polaris и PCBoards оказались не полностью
совместимыми, в связи с чем Polaris исключили из состава последней версии
пакета программ DesignLab 8.0, заменившего Design Center. Тем не менее, Polaris
все же можно использовать, принимая во внимание ряд ограничений.
Во-первых, ее можно применять совместно с редакторами печатных плат
других систем: P-CAD, ACCEL EDA (вместе с утилитой DBXSIMU), PADS,
BoardStation фирмы Mentor Graphics и др. Файлы печатных плат, созданные
с помощью MicroSim PCBoards, приходится предварительно преобразовы-
вать в формат Р-CAD с помощью конвертора M2S.
Во-вторых, при создании печатных плат следует использовать английскую
систему единиц (при работе в метрической системе возникают грубые ошибки).
В-третьих, следует иметь в виду, что программа Polaris имеет два режима:
• Native, предусматривающий комплексное создание принципиальных
схем и печатных плат и затем проведение анализа целостности сигналов;
• External, предусматривающий анализ целостности сигналов на осно-
вании информации о топологии печатной платы.
Для проведения моделирования необходимо создать только схемы подклю-
чения генераторов сигналов и нагрузок. При этом в базе данных печатной платы
должны быть указаны параметры пассивных компонентов (сопротивлений
резисторов, емкостей конденсаторов и т. п.), а в библиотеке PSpice — иметь-
ся математические модели остальных компонентов.
Также отметим, что для анализа целостности сигналов не всегда нужно про-
водить трудоемкое моделирование с учетом электрофизических параметров
558
Глава 8. Конструкторско-технологическое проектирование...
печатных плат, большей частью достаточно ограничиться также выполняемыми
программой Polaris расчетами емкостей, индуктивностей и сопротивлений
потерь печатных проводников, волновых сопротивлений и запаздывания
сигналов, коэффициентов связей смежных проводников.
Viewlogic ХТК
Программа ХТК компании Viewlogic Systems (разработка фирмы Quad
Design Technology) предназначена для анализа целостности сигналов в циф-
ровых устройствах, реализуемых на печатных платах и гибридных интеграль-
ных схемах. Результаты анализа ошибок суммируются в отчете, в котором
приводятся данные о перекрестных помехах, задержках и выбросах сигна-
лов, немонотонных фронтах импульсов, распределении потенциалов в це-
пях «земли» и напряжениях логических уровней (рис. 8.10). Программа ХТК
функционирует в среде Windows 95/NT, Sun и др. и поддерживает форматы
следующих пакетов САПР: ACCEL EDA, Cadence Allegro, SPECCTRA, Mentor
Graphics BoardStation, PADS PowerPCB, Xynetix Encore, Zuken-Redac Visul.
Рис. 8.10. Программа ХТК совместно с пакетом Workview Office позволяет провести
тестирование ячейки памяти
AMPredictor
Пакет программ AMPredictor компании АМР предназначен для анализа
влияния неидеальностей соединителей, контактных панелей, цепей комму-
тации и межсоединений на качество обработки цифровых сигналов. Пакет
состоит из следующих модулей:
8.3. Структура и задачи САПР печатных плат
559
Рис. 8.11. Схема устройства дополняется в пакете AMPredictor моделями цепей питания
и разъемов, и после редактирования топологии печатной платы выполняется
моделирование
• AMPSPICE Circuit Simulator — программа моделирования, позволя-
ющая с высокой точностью рассчитывать характеристики линий пе-
редачи и анализировать такие эффекты, как повышение уровня помех,
перекрестные помехи, отражения и задержки распространения сигна-
лов в рассматриваемых устройствах;
• Connector Noise Analyzer — анализ уровня шума, обусловленного на-
личием разъемов;
• Model Library Manager — менеджер библиотек математических моде-
лей компонентов; разъемов, цепей заземления и т. п.;
• РСВ Structure Analyzer — расчет эквивалентных электрических схем
печатных проводников на основе анализа двухмерных электромагнит-
ных полей;
• Net Topology Editor — центральная программа пакета, с помощью ко-
торой составляются списки соединений анализируемого устройства и
подключаются модели генераторов сигналов и измерительных прибо-
ров, необходимые для моделирования;
• Power/Ground Plane Analyzer — расчет распределения потенциалов по
постоянному току на плоскостях металлизации «земли» и питания;
• IBIS-to-AMPSPICE Converter — преобразование IBIS-файлов моделей
интегральных схем в формат программы моделирования AMPS PICE;
• AMPSPICE Interpreter — преобразование моделей МОП-транзисторов
программы HSPICE в формат AMPSPICE;
• On-Line Education and Help — руководство по применению пакета.
560
Глава 8. Конструкторско-технологическое проектирование...
Пакет программ AMPredictor (рис. 8.11) функционирует в среде Windows
95/NT.
Hyper Suite 4.5
Программа Polaris и подобные ей позволяют моделировать прохождение
сигналов в реальных печатных платах, при этом они учитывают подробные
модели всех электронных компонентов (транзисторов, операционных уси-
лителей, цифровых интегральных схем, разъемов и пр.), что требует суще-
ственных затрат времени. Меньшую степень подробности обеспечивает па-
кет программ HyperSuit 4.5. Печатные проводники по-прежнему представ-
ляются в виде отрезков линий передачи, учитывается взаимная индуктивность
близлежащих проводников, однако электронные компоненты имитируют-
ся лишь входными и выходными комплексными сопротивлениями. Это дает
возможность, подключив модели генераторов сигналов, рассчитать частот-
ные характеристики отдельных трасс прохождения сигналов с учетом реальных
нагрузок и интерференционных искажений, что может быть достаточно для
предварительной оценки работоспособности печатных плат. Для моделиро-
вания входных и выходных комплексных сопротивлений интегральных схем
применяется ставший общепризнанным стандарт IBIS. Пакет программ
HyperSuit имеет трансляторы с графическими редакторами печатных плат
ACCEL P-CAD РСВ, Cadence Allegro, Mentor Graphics BoardStation, OrCAD
Layout, PADS, Protel Advanced РСВ и др.
Пример анализа целостности сигнала
Рассмотрим в качестве примера проверку платы мультивибратора с по-
мощью пакетной проверки правил проектирования (DRC) в системе Protel
DXP. Сначала принудительно введем в проект нарушение, которое затем об-
наружим. Сделаем ширину проводника, подходящего к транзистору VT1, 1
мм (рис. 8.12).
Рис. 8.12. Описание проводника в системе Protel DXP
8.3. Структура и задачи САПР печатных плат
561
Ширина проводника изменится, а фун-
кция автоматической проверки правил про-
ектирования сразу выявит связанные с этим
нарушения и подсветит конфликтующие
объекты (рис. 8.13). Следует обратить вни-
мание, что редактирование проводника вы-
полняется как изменение параметров обыч-
ного объекта. Если бы использовалась фун-
кция интерактивной трассировки, то
система отследила бы нарушение и не по-
зволила выполнить некорректную опера-
цию. В данном случае проводник воспри-
нимался как обычная линия, поэтому изме-
нение было выполнено.
Так как редактор печатных плат поддер-
живает очень широкий набор правил про-
ектирования, нарушение некоторых из них не может быть выявлено в ходе
автоматической (on-line) проверки DRC, то по завершении разводки платы
рекомендуется выполнить пакетную (batch) проверку DRC. Выполним эту
проверку.
На экране откроется отчет, содержащий описание выполненных проверок,
в котором будут содержаться два сообщения о выявленных нарушениях:
Рис. 8.13. Отображение нарушений
на чертеже платы
Processing Rule: Width Constraint (Min=0.3048mm)(Max=0.3048mm)
(Preferred=0.3048mm) (All)
Violation Track (18mm,37mm)(19.46mm,28mm)Top Layer Actual
Width =lmm
Rule Violations :1
Processing Rule :Clearance Constraint (Gap=0.2mm)(All), (All)
Violation between Pad VT1-1(19.27mm, 37mm) Multi-Layer and
Track (18mm, 37mm)(19.46mm, 28mm)Top Layer
Rule Violations :1
Первая запись сообщает, что выявлен проводник на верхнем слое, ширина
которого равна 1 мм, в то время, как правило, Width Constraint задает ши-
рину, равную 0.3048 мм. Вторая запись сообщает, что нарушено правило
контроля зазора между проводниками разных цепей Clearance Constraint, и
это очень хорошо видно на рис. 8.13.
Информация о том, что зазор оказался меньшим 0,2 мм, показана на
рис. 8.14.
На экране появится окно Design Explorer Information с сообщением, что рас-
стояние между указанными линией и контактной площадкой равно 0,1735 мм
(рис. 8.15). Далее разработчик должен сам решать, устраивает его такой за-
зор или нет. Если зазор достаточен, то следует изменить имеющееся правило
проектирования или создать новое, относящееся только к данным объектам,
562
Глава 8. Конструкторски-технологическое проектирование...
Рис. 8.14. Просмотр описания нарушения зазора
Design Explorer Information
1 ) Distance between
Track(18mm,37mmXI9.46mm,28mm)Top Layer and
Pad Х/Г1-1 (19.27mm. 37mm) Multi-Layer is
0.1735mm (8.833mil)
L_°±_J
Рис. 8.15. Результат измерения расстояния между двумя объектами
с меньшим значением допустимого расстояния. Если нет, то следует умень-
шить ширину проводника. В нашем случае лучше вернуться к начальному
значению ширины.
Мы рассмотрели одно из простейших нарушений, но этого достаточно,
чтобы понять, как работает система проверки правил проектирования DRC.
В ходе работы над сложными проектами разработчику придется выявлять и
исправлять сотни подобных нарушений, но есть один момент, на который
следует обратить особое внимание.
Система Protel DXP имеет модуль анализа целостности сигналов, позволя-
ющий оценить искажения сигналов, а также взаимные наводки в проводниках
разработанной платы. Аналогичные модули имеются почти во всех системах про-
ектирования печатных плат, но в системе Protel DXP он интегрирован непосред-
ственно в редактор плат и позволяет выполнять первичный анализ на уровне DRC.
Критерии оценки качества сигналов задаются специальными правилами про-
ектирования из категории Signal Integrity. При пакетной проверке запускается
система моделирования сигналов в проводниках платы и, если искажения сиг-
нала превышают определенный уровень, генерируется и заносится в отчет ин-
формация о нарушении. В дальнейшем выявленное нарушение служит подсказкой
при более подробном анализе электромагнитной совместимости [127].
8.3. Структура и задачи САПР печатных плат
563
8.3.2. Комплексность решений при проектировании
плат в САПР
Легко заметить, что мощность всех перечисленных выше программных
комплексов в значительной мере определяется встроенными средствами
анализа целостности сигнала и ЭМС. В этой связи нельзя не отметить не-
которые специализированные программы, направленные на комплексное
решение задач проектирования и изготовления печатных плат. Эти программы
охватывают отдельные вопросы электрофизического анализа, целостности
сигналов, анализа теплового режима, технологической подготовки произ-
водства и ряд других.
Большинство современных программ анализа ЭМС используют модели
микрополосковых линий, рассматривая шины питания и заземления идеаль-
ными, и не учитывают распределение токов в них. Однако наиболее точные
решения могут быть получены при электродинамическом подходе при ана-
лизе электрофизических параметров печатных плат. Пионером в данной
области выступила компания SIGRITY, которая разработала пакет Speed ХР.
Эта программа использует не упрощенные модели, а численные методы ре-
шения электродинамических задач, благодаря чему стало возможным иссле-
дование распространения помех по внутренним слоям питания (рис. 8.16).
Однако наличие столь мощной математики делает программу почти на по-
рядок дороже продуктов ближайших конкурентов, которые предпринимают
Рис. 8.16. Анализ помех в слое заземления в пакете Speed 2000 компании Sigrity
564
Глава 8. Конструкторско-технологическое проектирование...
попытки реализовать аналогичные методы в своих системах, как, например,
компания Mentor Graphics.
Из программ, реализующих классический подход к анализу ЭМС, следует
отметить компанию QUANTIC ЕМС, предлагающую на рынок продукт Omega
PLUS. Помимо обычного анализа целостности сигналов и перекрестных ис-
кажений, здесь могут быть получены спектры излучения платы в заданном
диапазоне частот, уровни токов в проводниках, а также интенсивность элек-
трического и магнитного полей над платой.
Отдельной задачей проектирования печатных плат является тепловой ана-
лиз. Наиболее мощным решением в этой области является программа ВЕТА
Soft-Board компании DYNAMIC SOFT ANALYSIS. Здесь также имеются ин-
терфейсы импорта проектов из всех выше перечисленных продуктов, богатые
библиотеки моделей и материалов. В процессе расчета могут быть получены
температуры отдельных компонентов, карты прогрева плат, градиент темпе-
ратур. Отметим, что программа BETA Soft-Board поставляется как штатное
средство теплового моделирования для продуктов MENTOR GRAPHICS.
Другая программа теплового анализа Sauna компании THERMAL
SOLUTIONS позволяет моделировать поведение не только плат, но и бло-
ков и шкафов. Здесь присутствуют обширные библиотеки компонентов и ма-
териалов. Имеется специальный графический редактор, позволяющий про-
рисовывать конфигурацию оборудования. Система дает возможность назна-
чать специальные рабочие циклы с учетом включения и выключения внешних
источников питания.
Английская фирма FLOMERICS предлагает пользователям свой пакет
Flotherm, главной особенностью которого является интерфейс, построенный
на базе современных интернет-технологий на основе обычного браузера. Про-
грамма позволяет моделировать отвод теплоты от микросхем, упакованных
в современные корпуса PBGA и TBGA, а также позволяет учитывать техно-
логию поверхностного монтажа перевернутых кристаллов. Компания
NATIONAL SEMICONDUCTOR включила в состав своего программного
комплекса Webench специальный модуль Webtherm, позволяющий получать
цветную карту градиента температур для платы, построенный на базе вычис-
лительного ядра Flomerics.
Из российских программ следует отметить коммерческий пакет теплово-
го моделирования ТРИАНА (АСОНИКА-Т), разработанный специалистами
Красноярского государственного технического университета (КГТУ) и Мос-
ковского государственного института электроники и математики (МИЭМ).
В состав пакета входит редактор, позволяющий формировать геометрическую
модель исследуемой печатной платы или гибридной интегральной схемы, а
также специализированный модуль подготовки тепловых моделей. Программа
имеет интерфейс с современными системами проектирования печатных плат
P-CAD 2002, Protel DXP, OrCAD 9.2, Allegro, SPECCTRA, а также co стары-
ми, но все еще распространенными в России, версиями P-CAD 4.5 — 8.7. Кроме
того, пакет может обмениваться данными с тепловизионным диагностичес-
ким комплексом ТЭРМИД РЭС.
8.3. Структура и задачи САПР печатных плат
565
Важным этапом проектирования печатных плат является подготовка уже
разработанного проекта к производству (CAM-системы). Под этим подра-
зумевается генерация управляющих файлов для изготовления фотошабло-
нов, станков для сверления отверстий, оборудования для автоматического
тестирования плат и расстановки компонентов. Как правило, все системы
проектирования печатных плат имеют встроенные средства генерации таких
файлов, тем не менее, имеется ряд задач, которые необходимо выполнять в
специально предназначенных для этого продуктах.
Одним из наиболее мощных CAM-систем является пакет Genesis 2000
компании РСВ Frontline. Эта программа ориентирована на мощные аппа-
ратные платформы, работающие под управлением операционной системы
UNIX, что определяет ее относительно высокую стоимость. Основная осо-
бенность пакета Genesis 2000 — высокий уровень автоматизации обработки
топологий. Здесь имеются специальные средства верификации и корректи-
ровки, которые позволяют увеличить технологичность платы и учесть осо-
бенности производства на данном предприятии. Широкий набор интерфейсов
импорта/экспорта позволяет обмениваться данными с большинством изве-
стных систем проектирования печатных плат.
Более доступные по цене, но достаточно мощные средства САМ предла-
гаются на рынок сразу несколькими производителями. Прежде всего, здесь
следует отметить наиболее популярную в России программу САМ350 компа-
нии DOWNSTREAM TECHNOLOGIES. Ранее облегченная версия этого про-
дукта поставлялась с пакетом ACCEL EDA, поэтому имела схожую с ней иде-
ологию и позволяла загружать проект платы не в виде набора Gerber файлов,
а файл РСВ с сохранением информации об электрических связях. Вышедшая
в марте 2003 новая версия 8.0 получила полностью обновленный пользователь-
ский интерфейс, усовершенствованные средства контроля правил DRC и DFM,
улучшенные средства генерации списков соединений с учетом сквозных, слепых
и глухих переходных отверстий. Отметим, что в качестве основного стандар-
та обмена данными сейчас принят формат ODB++, содержащий полную ин-
формацию о проекте и поддерживаемый большинством систем управления
ресурсами предприятия.
Другая американская компания — PENTALOGIX, ранее известная как
LAVENIR, предлагает пользователям линейку продуктов, самым мощным из
которых является CAM-Master. Ранее эти продукты были ориентированы на
собственные фотоплоттеры серии Pulsar. Но летом 2002 компания отказалась
от выпуска фотоплоттеров и сфокусировалась на разработке исключитель-
но программного обеспечения. Последние версии продуктов PENTALOGIX
предоставляют специалистам все необходимые средства подготовки печат-
ных плат к производству, отличительной особенностью которых является
поддержка языка макроскриптов Visual Basic for Application.
Компания WISE предлагает на рынок программу GerbTool. Эта программа
хорошо известна пользователям системы проектирования OrCAD, так как
долгое'время поставляется в составе этого пакета как штатный САМ-модуль.
Здесь имеется полный набор инструментов первичной подготовки проектов
566
Глава 8. Конструкторско-технологическое проектирование...
плат к производству: обработка топологий, генерация файлов сверления и
фрезерования, средства верификации и улучшения технологичности.
Нельзя не упомянуть программу CAMtastic компании ALTIUM. Эта програм-
ма была изначально разработана фирмой INNOVATIVE CAD Software и сейчас
в разных исполнениях поставляется бесплатно в качестве штатного САМ-средства
совместно с пакетами P-CAD 2002 и Protel DXP. Как автономный продукт сей-
час поставляется только самая последняя версия CAMtastic DXP, построенная
на базе интегрированной среды проектирования Design Explorer. В дополнение
к обработке формата Gerber введена качественная поддержка формата ODB++.
Появился макрорекордер, позволяющий автоматизировать большинство про-
цедур с помощью специального языка Client Basic.
Компания VALOR предлагает собственные решения по автоматизации
процесса производства печатных плат Trilogy 5000 и Enterprise 3000. Эти
системы позволяют моделировать процесс производства, выявлять наибо-
лее критичные его этапы и оптимизировать, поэтому являются не просто
САМ, а скорее ERP-системами. Они тесно взаимодействуют с системами
проектирования печатных плат и позволяют проанализировать качество
размещения компонентов на плате, а также трассировку. Специальные биб-
лиотеки Valor Part Library содержат достоверную информацию о большин-
стве компонентов и позволяют получать реалистичный трехмерный вид платы.
Основным форматом обмена данными между различными частями системы
является ODB++, который компания VALOR разработала и успешно внедряет
через организацию OSA (Open Systems Alliance). В будущем на базе формата
ODB++ будет разработана спецификация IPC-2581 [1].
8.3.3. Моделирование и симуляция в проектировании
печатных плат
Моделирование и описание объекта
Есть три типа средств электрического моделирования, которые описы-
вают схожие явления в межсоединениях при прохождении сигнала.
1. Электромагнитные (ЭМ) модели, которые строятся на основе уравне-
ний Максвелла и моделируют электрические и магнитные поля в раз-
личных местоположениях в частотной или временной области; это наи-
более полное описание.
2. Модели цепи, которые решают дифференциальные уравнения, соот-
ветствующие различным элементам цепи, и включают соотношения
тока и напряжения по Кирхгоффу, чтобы рассчитать напряжения и токи
в различных узлах цепи в частотной или временной области.
3. Программы поведенческого моделирования, которые используют мо-
дели, основанные на таблицах, линиях передачи и других моделях пас-
сивных элементов, основанных на передаточных функциях, которые
быстро рассчитывают напряжения и токи в различных узлах, преиму-
щественно во временной области.
8.3. Структура и задачи САПР печатных плат
567
Рассмотрим целостность сигнала с позиций уравнений Максвелла. Эти
уравнения описывают, как проводники и диэлектрики взаимодействуют с
электрическим и магнитным полями. В конце концов, сигналы - это не что
иное, как распространение электрических и магнитных полей. Когда моде-
лируются электрические и магнитные поля, межсоединения и все пассив-
ные компоненты должны быть представлены в виде проводников и диэлек-
триков со связанной с ними формой и свойствами материала.
Драйверы генерируют падающую электромагнитную волну, и уравнения
Максвелла используются для прогнозирования взаимодействия волны с про-
водниками и диэлектриками. Формы и свойства материалов определяют гра-
ничные условия, при которых уравнения Максвелла имеют решение. В ин-
женерной практике нет необходимости решать их вручную. Падающая элек-
тромагнитная волна взаимодействует со структурой и материалами и может
быть определена в каждой точке пространства. Эти поля могут моделироваться
либо во временной, либо в частотной области.
Некоторые явления могут моделироваться только с помощью электромаг-
нитной модели. Обычно эта модель необходима, когда межсоединения весьма
неоднородны и электрически длинные (подобно щели, пересекающей путь
возвратного тока), когда преобладают эффекты электромагнитного харак-
тера (резонансы внутри корпусов и соединительных проводов) или когда
необходимо моделировать явления электромагнитных помех.
Сложность описания во всей полноте электродинамических процессов в
конструкции печатного узла не позволяет решить уравнения Максвелла для
него с помощью лучших на сегодняшний день аппаратных средств ЭВМ и
средств программного обеспечения, за исключением простейших устройств.
Дополнительным ограничением является то, что большая часть современ-
ного программного обеспечения требует достаточно высокой квалификации
пользователя со знанием основ теории электромагнитного поля.
Значительно проще модели на основе теории цепей. Эти средства моде-
лирования представляют сигналы в виде напряжений и токов, а различные
проводники и диэлектрики преобразуются в идеальные основные элемен-
ты электрической цепи, такие, как резисторы, конденсаторы, индуктивно-
сти и их комбинации.
Теория цепей не менее правильна, чем электромагнитный подход. Неко-
торые проблемы в области целостности сигнала легче понимаются, и их ре-
шения легче определяются при использовании описания на уровни цепей,
нежели при описании электродинамическими моделями. Есть некоторые
ограничения на то, что может моделироваться при помощи цепевых моде-
лей. Электромагнитные явления, связанные с некоторыми видами помех,
резонансов и анализа неоднородностей при распространении электромаг-
нитной волны, не могут быть учтены в расчетах, выполненных при помощи
цепевых моделей.
Самой популярной программой моделирования цепи является SPICE
(программа моделирования с ориентацией на интегральные схемы). Первая
версия была создана в университете Беркли (США) в начале 1970-х годов как
568
Глава 8. Конструкторско-технологическое проектирование...
средство для прогнозирования работы транзисторов на основании их струк-
туры и свойств материалов. Если вводится описание схемы в специальном
формате, то с помощью программных средств решаются дифференциальные
уравнения для каждого элемента цепи, затем вычисляются напряжения и токи
либо во временной области (моделирование переходных процессов), либо в
частотной области (моделирование по переменному току). Существует более
30 коммерчески доступных версий SPICE, включая некоторые бесплатные
студенческие/демонстрационные версии, доступные для загрузки в Интернете.
Программы поведенческого моделирования используют таблицы и спе-
циализированные функции преобразования, чтобы моделировать напряжения
и токи. Их главное преимущество перед программами анализа цепей заклю-
чается в скорости вычисления. Многие программы поведенческого модели-
рования используют запатентованные средства моделирования и оптимизи-
рованы для специфических типов цепей, таких, как цепи линии без потерь,
связанные линии передачи и т. п.
Расчетные модели цепей
Инженерная деятельность — это постоянный акт балансирования меж-
ду полученными результатами и затратами (материальными и временными)
на их получение. Анализ целостности сигнала и ЭМС, как и большинство
других задач, не является исключением. Постоянно приходится балансировать
между качеством полученного решения и его точностью и затратами на по-
лучение результата.
Цель всех программ виртуального прототипирования заключается в ускорении
создания изделия в сегодняшнем рынке глобальной конкуренции, которое от-
вечает должным образом требованиям спецификации проекта, за минимальные
сроки, с минимальной стоимостью в рамках обоснованного риска.
Это достаточно трудная задача. Инженер, занимаясь проектированием
печатных плат, опираясь на свои знания и опыт, приходит к определенному
техническому решению в отборе лучшего технологического варианта и оп-
тимальных правил проектирования на возможно ранних стадиях разработ-
ки проект.
Наиболее важный инструмент в комплекте инструментов любого специ-
алиста — гибкость в принятии решений, которая заключается в способнос-
ти быстро оценивать влияние разносторонних факторов на конечный резуль-
тат, например, как выбор геометрии, материальных свойств и правил про-
ектирования затронет качественные показатели системы. Чем раньше в цикле
проекта будет установлена взаимосвязь параметров изделия и их влияние на
конечный продукт, тем короче цикл создания продукта и ниже его стоимость.
Помочь в решении этой проблемы могут три уровня приближения, на основе
которых можно прогнозировать качество функционирования изделия или его
электрические параметры и характеристики. Эти три подхода включают:
• эвристические правила;
• аналитические приближения;
• численное моделирование.
8.3. Структура и задачи САПР печатных плат
569
Каждый подход представляет различный
баланс близости к реальности (то есть, точно-
сти, времени и усилий, которые требуются для
получения ответа). Это иллюстрируется на
рис. 8.17. Конечно, результаты этих подходов
не могут быть оценены путем измерений. Од-
нако применение корректной техники анали-
за может иногда сокращать цикл проектиро-
вания до 10 % от первоначальной оценки.
Эвристические правила — простые соот-
ношения, сформулированные таким образом,
что они легко запоминаются и помогают ин-
туитивным решениям. Примером такого рода
правил может являться следующая формули-
Рис. 8.17. Баланс между точ-
ностью и требуемыми усилия-
ми для трех уровней анализа
ровка: самоиндукция короткого провода приблизительно равна 1 нГн/мм.
Если проводник имеет длину 10 мм, то, согласно этому правилу, его индук-
тивность составит 10 нГн.
Эвристические правила должны быть первым шагом при любом анали-
зе, если только поставленная задача не настолько проста, что может быть
решена просто здравым смыслом. Когда решаются более серьезные задачи,
эвристические правила могут ускорять поиск решения более, чем в десять
раз. Ближе к началу цикла проектирования изделия, когда задачи решают-
ся укрупненно, выбор направлений проектирования и технологий может
сэкономить средства и время.
Эвристические правила, по определению, не являются точными, но дают
быстрый ответ. Их не следует использовать на заключительной стадии проек-
тирования — они должны использоваться для развития инженерной интуиции
и обеспечения решений, которые послужат основой на последующих стадиях.
В частности, в настоящей книге эвристические правила выделены курсивом.
Аналитические приближения задаются в виде формул, которые имеют
ценность в той области значений параметров, для которой они определены.
При помощи формул можно быстро ответить на вопрос «что, если...». Эти ма-
тематические модели идентифицируют основные параметры первого поряд-
ка и связь между ними. Аналитические соотношения позволяют выявить ко-
эффициенты влияния параметров, входящих в формулу, на выходной параметр.
Формулы могут устанавливать точные отношения между двумя или больше
параметрами. Например, отношение между частотой и периодом F = 1/Т
является точным и может быть сформулировано в виде некоторого опреде-
ления. Очевидно, что погрешность расчета, определяемая средством вычис-
ления, не может считаться в этом случае погрешностью формулы. Другие
аналитические соотношения, заданные в виде формул, могут соответство-
вать реальности только приблизительно. Это связано с теми ограничения-
ми и допущениями, которые приняты при выводе формулы. На базе таких
приближенных соотношений определение сформулировать нельзя, но можно
дать те или иные рекомендации практического характера. В этом случае всегда
570
Глава 8. Конструкторско-технологическое проектирование...
следует волноваться относительно точности приближения, которое может из-
меняться от 1 до 50 % или больше. Для сложных процессов и явлений, опи-
сываемых аналитически, трудно прогнозировать точность приближения.
В инженерной практике во многих случаях приемлемой считается погреш-
ность 10—20 %, а в ряде случаев и более. Конечно, все зависит от степени риска
при принятии конкретного решения.
Важнейший способ подтвердить результаты вычислений — эксперимен-
тальная проверка. В свою очередь, эта процедура может потребовать значи-
тельных усилий и материальных затрат для обеспечения адекватных условий
проведения экспериментов. Кроме этого, для оценки степени расхождения
теоретических и экспериментальных данных должны применяться соответ-
ствующие методы обработки результатов экспериментов.
Никогда не следует полагаться на приближения, погрешность которых не
оценена или сомнительна.
Для расчета электрофизических параметров, которые связывают парамет-
ры материалов и геометрию их границ в конструкции платы, имеются более
точные методы на основе численных методов решения уравнений Максвелла.
Эти методы реализуются при помощи специальных программ — солверов
(solver — решающая программа). Они предназначены для определения па-
раметров электрических, магнитных и электромагнитных полей, используя
определенные граничные условия на проводниках и диэлектриках. Для ре-
шения уравнений в солверах применяются различные методы: метод гранич-
ных элементов (МГЭ), метод конечных элементов (МКЭ), метод моментов
(ММ) и др. Выше при классификации программных средств предтопологи-
ческого и посттопологического проектирования указаны методы, на кото-
рых построены соответствующие продукты.
При однородной геометрии поля вдоль одной из координат задача рас-
чета поля сводится к плоскопараллельной (двумерной), что существенно
упрощает решение задачи. При неоднородном поле требуется трехмерное рас-
смотрение поля, и соответствующий программный продукт становится до-
статочно сложным и дорогим.
Перед использованием солверов всегда важно иметь результаты, проверен-
ные для некоторых тестовых вариантов, близких к тем, которые подвергаются
расчету. Каждый пользователь должен настоять на подобной проверке программ-
ного продукта у разработчика или продавца, чтобы убедиться, что он работает
должным образом. Это дает доверие к качеству полученных результатов.
Обеспечивая высокую точность полученных результатов, применение
солверов требует высокой квалификации, длительного времени и определен-
ных материальных затрат. Но полученные результаты наиболее близки к
реальным значениям. Среди отечественных солверов следует отметить про-
дукт ELCUT [92], построенный на МКЭ, который обладает широкими воз-
можностями при расчете электрических и магнитных полей.
При умелом использовании комбинации из этих трех рассмотренных выше
подходов, удается сбалансировать точность оценок, сроки проектирования
и риск для обеспечения желаемого качества продукта.
8.3. Структура и задачи САПР печатных плат
571
8.3.4. Методы моделирования цифровых узлов
электронных приборов
Цифровые системы и их модели
В настоящее время цифровые устройства применяются практически во
всех областях приложений электронной техники. Достоинствами цифровых
устройств являются высокая точность их функционирования, сложные ал-
горитмы работы, хорошо отлаженная технология производства и т. д.
Цифровые системы и узлы (ЦУ), разрабатываемые сегодня, являются чрез-
вычайно сложными и могут содержать сотни и тысячи цифровых интеграль-
ных схем. В силу этого объем проектных работ становится настолько большим,
что «ручное» ведение работ по созданию проекта нового ЦУ становится не-
целесообразным. Действительно, сроки, отводимые на проектирование нового
цифрового устройства, в настоящее время сократились до 6—12 месяцев. Столь
жесткие временные требования обусловлены конкуренцией фирм-произво-
дителей электронной техники, и задержки с выводом на рынок новой продукции
грозят фирмам крупными финансовыми потерями.
Использование вычислительных систем является необходимой составля-
ющей процесса проектирования подавляющего большинства ЦУ. Особое
значение имеет моделирование. Оно позволяет создать виртуальный прототип
будущего устройства и его частей, что дает возможность избежать необхо-
димости использования макетов. Моделирование дает возможность устано-
вить работоспособность еще не созданного устройства и выявить его элект-
рические и другие характеристики. Оно должно проводиться с использова-
нием адекватных моделей всех элементов системы.
Для возможности проведения моделирования ЦУ, например, выполненного
в виде печатного узла, и получения адекватных результатов модели компонентов
системы должны обладать определенными свойствами. Они должны быть
экономичными, т. е. требовать при выполнении расчетов с использованием
САПР минимального количества машинной памяти, и быть достаточно про-
стыми и точными. Последние два требования трудно сочетаются друг с дру-
гом, так как практика показала, что попытки учесть все характеристики элек-
тронных узлов приводят к столь существенному повышению размерности чис-
ленной задачи, решаемой вычислительной системой или компьютером, что
она не может быть решена даже для печатных узлов средней сложности.
Однако в практике моделирования далеко не всегда требуется получить
предельно точный результат. В общем случае использование той или иной
модели является компромиссом между ее сложностью и точностью отраже-
ния свойств радиоэлемента.
Задача моделирования цифровых узлов и систем может быть решена на ос-
новании моделей интегральных микросхем, составленных разными способами.
В зависимости от подхода и метода составления моделей они имеют разное
назначение, сложность и точность описания электрических свойств и логики
функционирования. В контексте книги будут рассмотрены только основные
572
Глава 8. Конструкторско-технологическое проектирование...
подходы к представлению информации о цифровых узлах и микросхемах, на ос-
новании которой проводят моделирование цифровых узлов, и дана их общая
характеристика [129—135]. Это язык описания электронных схем SPICE, язы-
ки спецификации логических систем VHDL и AHDL и формат IBIS представ-
ления данных об электрических свойствах цифровых интегральных схем (ЦИС).
Классификация моделей микросхем
Цифровые интегральные схемы представляют собой изделия микроэлек-
тронной техники со сложным устройством. Они состоят из множества по-
лупроводниковых ключей, которые при работе микросхемы находятся боль-
шую часть времени в открытом либо закрытом состоянии. Помимо ключей,
которые иногда называют вентилями, схемотехника предусматривает наличие
в микросхеме других пассивных и активных элементов. Схемы сложных
интегральных устройств типа микропроцессоров, запоминающих устройства
и др. состоят из сотен тысяч и миллионов элементов.
Моделирование проводится на основании их математических моделей. Ма-
тематическая модель — это совокупность математических элементов (чисел,
переменных, векторов и т.п.) и соотношений между ними, которые с требу-
емой для проектирования точностью описывают свойства проектируемого
объекта. На каждом этапе проектирования используется свое математичес-
кое описание объекта, причем сложность его должна быть согласована с воз-
можностями анализа с применением вычислительных систем. Это приводит
к необходимости иметь для одного объекта несколько моделей различного
уровня сложности, что и характерно для всех указанных выше языков опи-
сания ЦИС при проектировании ЦУ.
Все математические модели могут быть по уровню сложности подразделены
на полные модели и макромодели. Полные модели объекта проектирования
получают путем непосредственного объединения моделей компонентов с
формированием общей системы уравнений. Макромодели представляют со-
бой упрощенные математические модели, аппроксимирующие полные.
Макромодели делят на две группы: факторные и фазовые модели. Фак-
торные модели предназначены для использования на следующих этапах про-
ектирования в качестве моделей компонентов. Фазовые модели использу-
ются на том же этапе проектирования, на котором их получают, и служат для
сокращения размерности решаемой задачи.
По способу получения математические модели делят на физические и фор-
мальные. Физические модели получают на основе изучения физических за-
кономерностей функционирования объекта, так что структура уравнений и
параметры моделей имеют ясное физическое толкование. Формальные мо-
дели получают на основе измерения и установления связи между основны-
ми параметрами объекта в тех случаях, когда физика работы его известна не
достаточно полно. Как правило, формальные модели требуют большего числа
измерений и по своей природе являются локальными, справедливыми вблизи
тех режимов, в которых производились измерения. Иногда такие модели на-
зывают «черным ящиком».
8.3. Структура и задачи САПР печатных плат
573
Для проведения моделирования печатного узла информация о содержа-
щихся в нем микросхемах должна быть представлена в той или иной форме.
Обычно фирмы-разработчики интегральных компонентов обеспечивают сво-
бодный доступ как к справочной информации (которой, безусловно, мало
для выполнения точного моделирования), так и к моделям микросхем.
В настоящее время справочная информация по интегральным компонен-
там представляется в виде значений их основных их параметров и графиков,
а также предельных эксплуатационных характеристик. Естественно, что с
увеличением сложности внутреннего устройства объем информации, необ-
ходимой для первоначального выбора ЦИС той или иной серии для исполь-
зования в конкретном устройстве, существенно возрастает.
Информация, необходимая для моделирования ЦИС в составе какого-либо
цифрового узла, также увеличивается в объеме с возрастанием сложности фун-
кционирования и внутреннего устройства. Она может быть представлена в
виде таблиц, графиков, а также в текстовом формате.
В случае рассматриваемых основных языков моделирования SPICE, VHDL,
AHDL и IBIS информация о функционировании и свойствах входящих в циф-
ровой узел микросхем представляется в текстовых формах, которые воспри-
нимаются различными средствами автоматизированного проектирования.
Ниже они будут рассмотрены подробнее.
Языки описания логических систем VHDL и AHDL
Язык VHDL (Very high speed integrated circuits Hardware Description Language)
является фактически международным стандартом в области автоматизации про-
ектирования цифровых систем. Это входной язык многих современных САПР
как заказных, так и программируемых логических интегральных схем (ПЛИС)
и программируемых пользователями матриц. VHDL предназначен, в первую
очередь, для спецификации — точного описания проектируемых систем и их
моделирования на начальных этапах проектирования — алгоритмическом и
логическом. С помощью VHDL можно моделировать схемы с учетом реаль-
ных временных задержек.
VHDL — это мощный язык, который позволяет описывать поведение, т. е.
алгоритмы функционирования цифровых узлов и цифровых интегральных схем
при их проектировании, а также проводить иерархическое функционально-
структурное описание систем. Он имеет средство для описания ряда асинх-
ронных процессов, регулярных структур и в то же время имеет все признаки
языка программирования высокого уровня.
Язык VHDL был разработан в США по инициативе министерства обороны.
В1987 г. VHDL был принят в качестве стандарта ANSI/IEEEE Std. 1076-1987
(VHDL'87). В 1999 г. утвержден стандарт ANSI/IEEEE Std. 1076.1-1999 (VHDL-
AMS), который включает расширение, дающее возможность описание мо-
делей аналоговых и смешанных схем.
Логические системы проектируются на базе хорошо формализованного
вполне строгого и сравнительно простого аппарата булевой алгебры. В рамках
этого математического аппарата доказано, что любая логическая система
574
Глава 8. Конструкторско-технологическое проектирование...
может быть скомпонована из ограниченного количества простых объектов,
называемых элементами. Т.к. все элементы булевой алгебры имеют функци-
ональное описание, т.е. каждому элементу может быть поставлена в соответ-
ствие некоторая логическая функция, то найдется такая функция и для ком-
позиции конечного числа таких элементов. Эта функция и является мате-
матической моделью логической системы. Поэтому проблема декомпозиции
сложной системы на простые элементы решается достаточно легко.
Обычно в САПР предусмотрено автоматическое преобразование модели
цифровой системы в виде набора логических функций в структуру элемен-
тов на кристалле. Таким образом, если проектировщик доверяет САПР вы-
полнение этапов компоновки, размещения и трассировки, то ему остается
только создать модель проектируемой системы, понятную для САПР. Если
это сделано для какого-либо цифрового узла, то легко решается и проблема
его моделирования.
Языки VHDL и AHDL очень похожи как по командному базису, так и по
возможностям описания цифровых систем и ПЛИС. Отличие между ними
состоит в том, что VHDL создавался как язык описания цифровых устройств
вообще, a AHDL ориентирован на ПЛИС и другие микросхемы фирмы Altera.
Это значит, что он имеет более узкую «специализацию», но, поскольку был
создан для микросхем с определенной архитектурой, то позволяет наиболее
полно использовать ее особенности.
Крупнейшие фирмы-производители программного обеспечения САПР в
области микроэлектроники используют языки VHDL и AHDL в качестве ис-
ходного описания проекта. Эти языки развиваются, им посвящены междуна-
родные конференции, выходят научные журналы, в которых изучаются про-
блемы использования VHDL и AHDL. VHDL стал языком разработки между-
народных проектов, в том числе осуществляемых с помощью всемирной
компьютерной сети. Знакомство с этим языком способствует эффективной
работе по созданию разнообразной электронной аппаратуры на современной
элементной базе сверхбольших интегральных схем.
Таким образом, с точки зрения задачи моделирования цифровых устройств,
языки VHDL и AHDL и САПР на их основе обеспечивают логический рас-
чет на ранних этапах проектирования. Эти языки пригодны также для мо-
делирования цифровых микросхем. Их достоинствами является наглядность
и сравнительная простота, широкая распространенность и универсальность.
Эти языки не предназначены для расчета электрических схем будущего циф-
рового узла, но без проведения отладки функционирования средствами САПР
с применением VHDL и других подобных языков создание сложных устройств
становится очень затруднительным. Возможность проведения моделирова-
ния цифрового узла на стадии их проектирования — неоспоримая практи-
ческая польза и несомненное достоинство VHDL.
В соответствии с приведенной выше классификацией модели, которые
анализируют САПР на языках VHDL и AHDL, можно отнести к полным
физическим моделям, представленным в виде совокупности элементарных
ячеек. Они могут быть как фазовыми, так и факторными.
8.3. Структура и задачи САПР печатных плат
575
SPICE как метод моделирования цифровых узлов
Язык и система SPICE (Simulation Program with Integrated Circuit Emphasis)
были созданы более двадцати лет назад в Department of Electrical Engineering
and Computer Sciences, University of California, Berkeley. Язык предназначен для
описания электрических цепей разной сложности, и он используется для рас-
чета схем во временной и частотной областях, а также в статическом режиме.
Эти типы расчетов используются в инженерной практике наиболее часто. При
проведении моделирования все элементы схемы заменяются их математичес-
кими моделями. Таким образом, SPICE-модели являются полными.
Язык SPICE и системы на его основе используются во многих САПР;
существуют разные их модификации. Например, в системе OrCAD 9.2 ис-
пользуется программа PSPICE. Заметим, что в системе OrCAD предусмот-
рен расчет логических устройств на основе булевой алгебры. Помимо PSPICE
существуют и другие программы: WinSPICE (некоммерческая программа, рас-
пространяется свободно), HSPICE, XSPICE и др. Языки, используемые во
всех системах, имеют незначительные отличия и дополнения по сравнению
с изначальной версией SPICE.
Язык SPICE может быть использован для моделирования цифровых уз-
лов с использованием только электрических сигналов. Это подразумевает ис-
пользование полных SPICE-моделей микросхем. Основная сложность, воз-
никающая при полном моделировании внутренней электрической схемы
микросхемы при автоматизированном проектировании, связана с размерно-
стью вычислительной задачи и высоким порядком систем уравнений, опи-
сывающих цифровой узел. Уже для микросхем средней степени интеграции
объем вычислений становится неоправданно большим.
Одним из методов, позволяющих существенно сократить размерность за-
дачи, является использование макромоделей. Однако их удается построить
только для очень ограниченного класса цифровых элементов — триггеров и
логических элементов.
Еще одной трудностью, возникающей на пути полного схемотехническо-
го моделирования цифрового узла на основе SPICE-моделей составляющих
его элементов, является отсутствие в свободном доступе принципиальных
электрических схем, тем более с номиналами пассивных и характеристиками
активных элементов. Напротив, большинство крупных фирм старается сохра-
нить эту информацию в тайне (особенно для новых разработок). В техничес-
кой документации на микросхемы они лишь иногда приводят структурную схе-
му, которая не дает практически ничего для составления SPICE-моделей.
Поэтому в настоящее время производители микросхем практически прекра-
тили распространение их SPICE-моделей. Все большее развитие получает но-
вый подход к моделированию микросхемы, основанный на IBIS-описании.
Моделирование цифровых узлов на основе IBIS-спецификации
Моделирование цифровых узлов с позиций целостности сигнала и ЭМС
оказывается весьма непростой задачей. Для ее решения необходимо было
использовать новый подход. Специалисты остановились на формальных
576
Глава 8. Конструкторско-технологическое проектирование...
макромоделях микросхем, и результатом их работы стало появление нового
типа моделей — IBIS (I/O Buffers Information Specification, или информаци-
онная спецификация буферов ввода/вывода) [129].
Потребность в разработке нового формата представления данных возникла
вследствие сочетания ряда обстоятельств. Основными причинами явились
необходимость обмена информации между организациями, которые зани-
маются производством изделий микроэлектронной техники и аппаратуры,
в которой они применяются, и все возрастающая сложность SPICE-моделей
ИС. При формировании общих принципов построения IBIS-спецификации
и выборе параметров моделей входных и выходных буферов была удачно
учтена необходимость возможности работы с этим форматом САПР различ-
ного назначения, введена система приоритета параметров и предусмотрена
различная глубина описания моделей. Все это регламентируется стандартом,
который принимается основными организациями, поддерживающими IBIS.
Один из последних принятых стандартов имеет версию 4.2 [129] (вторая
половина 2004 г.). Практически все документы, связанные с IBIS, находят-
ся в открытом доступе в сети Интернет.
Сущность IBIS заключается в том, что в спецификации приводится описа-
ние свойств только входных и выходных буферов ЦИС, причем под буфером
(термин широко используется в стандарте) понимается часть схемы, непосред-
ственно связанная с тем или иным сигнальным выводом [130—134]. Распрост-
ранение сигналов внутри микросхемы не моделируется. Сами буферы представ-
ляются в виде схем замещения, которые показаны на рис. 8.18 и рис. 8.19.
Сигнал
на
входном
буфере
Рис. 8.18. Стандартная модель входного буфера в IBIS-моделировании
0В
Управляющий
сигнал
специальной
формы г—\
GND_
Clamp
-4+VCC
POWER_
Clamp
R_pkg L_Pk9 Выход
C_pkg
С_сотр
Рис. 8.19. Стандартная модель выходного буфера в IBIS-моделировании
8.3. Структура и задачи САПР печатных плат
577
Рассмотрим рис. 8.18 и рис. 8.19. Здесь C_pkg, L_pkg и R_pkg представ-
ляют собой физические характеристики вывода ИС — емкость «на землю»,
индуктивность и активное сопротивление. По IB IS-стандарту при описании
конкретной микросхемы можно задавать как одинаковые для всех выводов
параметры (при задании характеристик корпуса), так и индивидуально. Как
правило, эти характеристики одинаковы для всех выводов, поскольку с тех-
нологической точки зрения наиболее удобен корпус, в котором все выводы
одинаковы. Но бывают и исключения (это обычно связано с внутренним
устройством микросхемы).
В качестве GNDClamp и POWER_Clamp обозначены ограничивающие
диоды. Пока напряжение питания лежит в интервале от 0 до +Vcc, оба дио-
да заперты, и ток через них практически не течет. Но если напряжение вы-
ходит за этот интервал, то такой режим работы, как правило, аварийный,
вызывает весьма существенный ток через один из диодов. В зависимости от
типа логики, при напряжениях на входе микросхемы вне указанных преде-
лов переходы полевых и биполярных транзисторов могут оказываться в ин-
версном режиме, что приведет к протеканию через переход достаточно боль-
шого тока. Его также необходимо учитывать при моделировании. Но в слу-
чае упрощения, а также при других типах логики они могут быть исключены.
Диоды POWER-Clamp и GND Clamp иногда называют антизвонными, так
как они гасят колебательные процессы, которые возникают при высоких ча-
стотах включения.
Емкость С_сотр отражает наличие инерционных свойств буферов. При
этом емкость, как правило, рассматривается на шину заземления. Однако
такой подход справедлив только в том случае, если индуктивность и сопро-
тивление питающей шины невелики. В противном случае, емкости входа
(выхода) микросхемы не могут быть объединены в одну эквивалентную,
поскольку шины питания и заземления не будут замкнуты накоротко по
переменному току.
В отдельных случаях обнаруживается необходимость включения парал-
лельно емкости нелинейного сопротивления, которое отражает поведение
входного буфера в статическом режиме при различном напряжении на нем.
Это сопротивление не входит в стандартную модель, но может быть описа-
но в рамках IBIS. Однако, согласно IB IS-стандарту, это не делается, чтобы
не усложнять процесс моделирования. Такое упрощение означает, что вход
микросхемы не потребляет тока, что допустимо не для всех типов логики.
Кроме рассмотренных элементов моделей, на рис. 8.19 условно изображе-
ны два источника тока, которые обозначены как Pull down и Pull up. Это ус-
ловные обозначения нелинейных сопротивлений, которые включаются соот-
ветственно к шинам заземления и питания. Их сопротивления меняются при
переключении выходного буфера в противоположное логическое состояние, а
в статическом режиме зависят только от напряжения на них. В режиме логи-
ческой единицы сопротивление Pull_up мало, сопротивление Pull down вели-
ко, в состоянии логического нуля сопротивление Pull up велико, Pull down —
мало. Когда значение сопротивления Pull_up или Pull_down мало, ток через него
19'/, 1527
578
Глава 8. Конструкторско-технологическое проектирование...
зависит от напряжения на нем и моделирует выходную ВАХ соответственно в
режимах логической единицы или логического нуля.
Заметим, что схема на рис. 8.19 достаточна для моделирования переход-
ных процессов в выходном буфере и получения при моделировании графи-
ков сквозных токов. Однако эта схема обладает существенным недостатком.
Дело в том, что для реальной цифровой микросхемы всегда имеется какое-
либо минимальное время переключения, причем, какой бы короткий фронт
не имелся у входного сигнала, переключение всегда займет время, большее,
чем некоторое ненулевое минимальное значение. Оно примерно составля-
ет единицы наносекунд. Устранить эффект такого «феноменального» быст-
родействия, сделав модель более адекватной, можно при помощи специальной
схемы, ограничивающей минимальное время переключения.
Выходной буфер управляется сигналом специальной формы. Это может быть
трапецеидальный сигнал, ограниченный значениями 0 и 1 В. Сигнал такого
вида иногда называют нормированным. Он может быть сформирован на ос-
новании преобразования входного сигнала, поступившего на какой-либо вход-
ной буфер. Переключение осуществляется за счет зависимости сопротивле-
ний Pull_up и Pull_down от уровня нормированного сигнала.
Для того чтобы входные и выходные буферы функционировали взаимо-
связанно, необходимо входные сигналы привести к нормированному виду.
Схема, при помощи которой обрабатывается входной сигнал и формирует-
ся управляющий выходной, называется внутренней логикой, или, согласно
принятой в IBIS терминологии, логикой уровня и активации.
Моделирование с использованием IBIS-моделей проводят на этапе про-
ектирования печатных плат [130]. При его выполнении все микросхемы за-
меняются совокупностью IBIS-моделей их буферов, проводится анализ того,
как распространяется сигнал в печатном узле от микросхемы к микросхеме,
и оцениваются искажения сигналов при распространении в элементах пе-
чатного монтажа. Смена логического состояния выходных буферов обеспе-
чивается непосредственно программой моделирования и не зависит от ло-
гического состояния на входе.
Однако IBIS-модели можно использовать и при моделировании с исполь-
зованием языка SPICE и систем на его основе. В этом случае внутреннюю
часть схемы заменяют такой схемой замещения, чтобы она выполняла ин-
тересующие пользователя логические функции, а входные и выходные бу-
фера — их IBIS-моделями. Это позволяет существенно расширить область
применения IBIS-моделей и получить возможность моделировать те свой-
ства цифрового узла, которые интересуют разработчика. Моделирование
можно провести несколько раз, чтобы оценить, как функционирует тот или
иной цифровой узел.
В настоящее время наблюдаются две важные тенденции в области IBIS.
Первая из них — это массовый переход от SPICE к IBIS-моделям микросхем.
Вторая заключается в том, что IBIS в своем развитии все больше сближает-
ся с VHDL и другими подобными языками. Файлы с IBIS-описанием мик-
росхем могут быть дополнены VHDL-описанием логики ее функциониро-
8.4. Технологические факторы и целостность сигнала
579
вания. Такое сочетание языков разного назначения в стандарте IBIS назы-
вают мультиязычным расширением.
Рассмотрены наиболее распространенные подходы к моделированию
цифровых узлов, каждый из которых применим на определенных стадиях
проектирования и дает точный результат при использовании по назначению.
Все они имеют свои перспективы развития, преимущества и недостатки.
Наиболее перспективным является совместное использование IBIS и VHDL
для описания электрических свойств и логики функционирования микро-
схем, на основе чего можно проводить моделирование цифровых узлов на
печатных платах на разных этапах проектирования.
8.4. Технологические факторы
и целостность сигнала
8.4.1. Модели и инструментарий
Проектирование высокоскоростных плат требует построения адекватных
моделей для анализа целостности сигнала и ЭМС. Уровни достигнутого
быстродействия повышают чувствительность конструкции к различного рода
вариациям параметров материалов, размеров элементов конструкции и ха-
рактеристик компонентов. В предыдущих главах неоднократно подчерки-
валось, что технологические аспекты производства печатных плат оказывают
существенное влияние на ее электрофизические параметры. Появление новых
материалов, развитие технологии микропереходов, увеличение разрешаю-
щей способности и другие технологические факторы способствуют получе-
нию все более совершенных конструкций плат. При этом происходит уточ-
нение моделей, которые подлежат анализу. Так, если для относительно низ-
кочастотных плат расчет емкости между проводниками можно было
проводить по упрощенным выражениям, которые не учитывают толщину про-
водников, то при сближении значений зазоров между проводниками и их
толщины учет последнего параметра становится обязательным. Как отме-
чалось выше, на заключительном этапе проектирования следует применять
как можно более адекватные модели и методы расчета, обеспечивающие мак-
симальную точность. В подавляющем числе случаев таким расчетным ин-
струментом являются солверы электрических и магнитных полей или элек-
тродинамических задач.
В настоящем разделе рассмотрим достаточно актуальную задачу влияния
влагозащитного покрытия на электрические параметры микрополосковой
линии передачи. При нанесении влагозащитного покрытия формируется заг-
лубленная линия передачи, диэлектрическая среда которой становится кусочно-
однородной, состоящей из четырех сред: воздух — паяльная маска — лак —
диэлектрик (рис. 8.20). Точное определение электрических параметров такой
линии передачи возможно только численным методом. Для этих целей исполь-
зуем солвер ELCUT [92].
|9 *
580
Глава 8. Конструкторско-технологическое проектирование...
Рис. 8.20. Модель микрополосковой линии передачи: 1 — диэлектрическое основание;
2 — влагозащитное покрытие; 3 — паяльная маска
ELCUT — программа моделирования двумерных полей методом конеч-
ных элементов — разработанная и представленная на рынке петербургской
компанией ТОР с 1991 г.
Спектр задач, решаемых данной программой, очень широк: электроста-
тика, электрическое поле постоянных или переменных токов, магнитоста-
тика, магнитное поле синусоидальных токов и нестационарное магнитное
поле, стационарное и нестационарное температурное поле, а также упругое
напряженное состояние.
Дружественный пользовательский интерфейс, простота описания даже
самых сложных моделей, широкие аналитические возможности комплекса
и высокая степень автоматизации всех операций позволяют разработчику
полностью сосредоточиться на своей задаче.
ELCUT представляет небольшой, но удобный набор инструментов для
работы с геометрическими объектами, включая перемещение, копирование
и размножение объектов. Геометрические формы создаются в терминах вер-
шин и соединяющих их ребер, прямых и дугообразных. Мощный геометри-
ческий процессор сам отслеживает образование замкнутых подобластей. Он
также разрешает иметь в расчетной области изолированные вершины, ви-
сячие ребра, многосвязные области и прочие геометрические усложнения.
Имеется двухсторонняя связь с системами САПР через файлы DXF и дина-
мический импорт двумерных эскизов из SolidWorks.
Специальная технология, включенная в редактор модели, позволяет ав-
томатически создавать гладкую сетку, подходящую для модели. Источники
и граничные условия полностью независимы от сетки и могут быть измене-
ны в любое время.
Достоинством ELCUT является необычайно быстрое решение задачи. Эф-
фективность решения по ряду оценок не имеет себе аналогов в индустрии.
Более того, время решения задачи увеличивается с ростом размерности по-
чти линейно (в степени 1,1), против стандартного квадратичного роста.
Интерактивный постпроцессор позволяет просмотреть результаты расче-
та в различных формах представления: линии поля, цветные карты, графики
различных величин вдоль произвольных контуров и пр. Можно также вычислять
различные интегральные величины на заданных линиях, поверхностях или
объемах. Постпроцессор обеспечивает вывод таблиц и рисунков в файлы для
дальнейшей обработки или качественной графической печати.
8.4. Технологические факторы и целостность сигнала
581
ELCUT это полноценное Windows приложение, которое было разработано
специально для этой платформы и полностью использует все преимущества
современных компьютеров. Солвер может эффективно применяться для
решения различных инженерных задач. В данном случае он применен для
определения электрофизических параметров линий передач, которые могут
изменяться при изготовлении платы [135]. Задача, по сравнению с ранее рас-
смотренными, усложнена наличием кусочно-однородной среды, состоящей
из диэлектрического основания, паяльной маски, влагозащитного покры-
тия и воздуха.
8.4.2. Оценка влияния технологических факторов
На первом этапе оценим параметры микрополосоковой линии передачи
без покрытия со следующими параметрами: ширина проводника — w; тол-
щина проводника — Zcnd; толщина основания — Ams; относительная диэлек-
трическая проницаемость материала основания платы — ег.
В главе 2 приведены аналитические выражения для расчета волнового со-
противления и электрической емкости подобной линии. Для сформулиро-
ванной в данном разделе задачи аналитические формулы не пригодны, и един-
ственным инструментом решения становится солвер.
Как неоднократно отмечалось, значение волнового сопротивления линии
передачи должно составлять 50 Ом. В реальной ситуации погрешности из-
готовления платы приведут к погрешностям этого значения, которые для бы-
стродействующих систем не должны превышать ±1—2 %. Значение волнового
сопротивления при следующих параметрах микрополосковой линии: ег= 4,5,
w = 0,9 мм, rcnd = 0,035 мм, /?ms = 0,5 мм, будет равно Z = 49,254 Ом.
Полученные параметры были использованы для создания модели линии
связи в программе ELCUT. Для анализа влияния различных параметров ли-
нии передачи на значение времени задержки распространения сигнала и вол-
нового сопротивления на следующем этапе анализа в модель были добавле-
ны слои паяльной маски и влагозащитного покрытия.
Модель линии передачи в солвере ELCUT
Модель линии передачи в солвере ELCUT представляет собой подложку
из диэлектрического материала с металлическим слоем заземления на ниж-
ней стороне, и токоведущей дорожкой — проводником на верхней стороне.
Дополнительно на верхней стороне имеются слои паяльной маски и влаго-
защитного покрытия (рис. 8.21).
Рис. 8.21. Модель линии передачи в солвере ELCUT
582
Глава 8. Конструкторско-технологическое проектирование...
Параметры модели представлены в табл. 8.1.
Таблица 8.1
Параметры модели микрополосковой линии в солвере ELCUT
Параметр Значение
Ширина подложки, мм 10
Толщина подложки, Ams, мм 0,5
Диэлектрическая проницаемость подложки, ег 4,5*
Ширина полигона заземления, мм 10
Толщина полигона заземления, мкм 35
Ширина проводника, w, мм 0,9
Толщина проводника, Zcnd, мкм 35
Ширина слоя паяльной маски, мм 10
Толщина слоя паяльной маски, мкм 30*
Диэлектрическая проницаемость паяльной маски 3,5*
Ширина слоя влагозащитного покрытия, мм 10
Толщина слоя влагозащитного покрытия, мкм 75*
Диэлектрическая проницаемость влагозащитного покрытия 2,5*
Примечание. * Изменяется при анализе влияния этого параметра на время задержки рас-
пространения сигнала и волновое сопротивление линии связи.
Поскольку в ELCUT не может быть открытых областей с заданными свой-
ствами, подложка окружена экраном диаметром 50 мм. Внутри экрана на-
ходится воздух, относительная диэлектрическая проницаемость которого
составляет 1.
Далее для решения задачи необходимо построить сетку конечных элемен-
тов. ELCUT использует единственный тип конечного элемента — треуголь-
ник первого порядка. Генератор сетки может работать полностью автомати-
чески либо учитывать пожелание пользователя по сгущению или разреже-
нию сетки в отдельных участках модели.
В расчетах электрических параметров описываемой модели сетка конечных
элементов генерировалась автоматически (рис. 8.22). Среднее количество
узлов сетки — 50 000.
Для каждой подобласти (в терминологии ELCUT-блока) необходимо за-
дать диэлектрическую проницаемость. Проводники создаются контурами,
для которых задается определенный потенциал. Поскольку электростатичес-
кое поле не проникает внутрь проводящего массива, нет необходимости мо-
делировать внутреннюю структуру проводников, а достаточно задать их гра-
ницы.
В данной модели потенциал проводника составлял 1 В, потенциал по-
лигона заземления и экрана 0 В. Вид сетки вблизи проводника показан на
рис. 8.23.
8.4. Технологические факторы и целостность сигнала
583
Рис. 8.22. Построение сетки конечных элементов
Анализ влияния параметров модели
Для проверки правильности получаемых результатов при каждом изме-
нении геометрической модели проводился следующий расчет.
1. Для всех блоков была задана диэлектрическая проницаемость er = 1.
В результате расчетов были получены энергия поля и погонная
емкость проводника Со.
2. Затем для всех блоков была задана диэлектрическая проницаемость ег =
= 4,5 и также посчитаны энергия поля И^и погонная емкость провод-
ника С£.
3. Далее по формуле С£ / Со рассчитывалась эффективная диэлект-
рическая проницаемость, которая, исходя из задаваемых параметров
модели во втором пункте, должна быть равна 4,5.
584
Глава 8. Конструкторско-технологическое проектирование...
Рис. 8.23. Вид сетки конечных элементов вблизи проводника
Погрешность расчетов во всех случаях не превышала ±0,17%, что являет-
ся показателем точности расчетов, проводимых в данной программе. На по-
следующих шагах проведено исследование влияния конструкторско-техноло-
гических параметров на электрофизические параметры линии передачи.
Влияние паяльной маски
Расчет проводился на модели, которая не включала слой влагозащитно-
го покрытия. Это позволило упростить модель, а также получить данные,
которые потребовались в дальнейшем для анализа влияния влагозащитно-
го покрытия.
Влияние толщины паяльной маски приведено в табл. 8.2.
Поскольку толщина паяльной маски не варьируется в широких пределах
и составляет 30±5 мкм, изменение ее толщины от максимума до минимума
практически не влияет на значение волнового сопротивления. Разброс зна-
чения волнового сопротивления составляет лишь 0,2 Ом, а времени задер-
жки распространения сигнала — 0,024 нс/м.
Влияние значения диэлектрической проницаемости паяльной маски
представлено в табл.8.3.
Диэлектрическая проницаемость паяльной маски для различных матери-
алов лежит в пределах от 3 до 4. Для получения более полной картины, а также
принимая во внимание возможное появление новых технологических мате-
риалов, расчет проводился для значений диэлектрической проницаемости
от 2 до 7.
8.4. Технологические факторы и целостность сигнала
585
Таблица 8.2
Результаты расчета влияния толщины паяльной маски
Толщина паяльной маски, мкм Энергия поля, Дж Погонная емкость, Ф/м Эффективная диэлектрическая проницаемость Время задержки распространения сигнала, нс/м Волновое сопротивле- ние, Ом
25,0 6,255Е-11 1,251Е-10 3,42928 6,11104 49,35264
30,0 6,280Е-11 1,256Е-10 3,44298 6,12324 49,25431
35,0 6,304Е-11 1,261Е-10 3,45669 6,13542 49,15656
Таблица 8.3
Результаты расчета влияния значения диэлектрической проницаемости паяльной маски
Диэлектри- ческая про- ницаемость Энергия поля, Дж Погонная емкость, Ф/м Эффективная диэлектрическая проницаемость Время задержки распростране- ния сигнала, нс/м Волновое сопротивле- ние, Ом
2,0 6Д64Е-11 1,233Е-10 3,37993 6,06692 49,71157
3,0 6,245Е-11 1,249Е-10 3,42379 6,10615 49,39214
3,2 6,259Е-11 1,252Е-10 3,43202 6,11348 49,33293
3,4 6,273Е-11 1,255Е-10 3,44024 6,12080 49,27393
3,6 6,287Е-11 1,257Е-10 3,44572 6,12568 49,23471
3,8 6,301Е-11 1,260Е-10 3,45395 6,13298 49,17606
4,0 6,314Е-11 1,263Е-10 3,46217 6,14028 49,11763
5,0 6,377Е-11 1,275Е-10 3,49507 6,16938 48,88594
6,0 6,435Е-11 1,287Е-10 3,52796 6,19835 48,65750
7,0 6,490Е-11 1,298Е-10 3,55811 6,22478 48,45088
Видно, что изменение времени задержки распространения сигнала в ин-
тервале значений диэлектрической проницаемости от 3 до 4 составило
0,158 нс/м, а разница волновых сопротивлений составила 1,26 Ом.
Влияние диэлектрической проницаемости паяльной маски на волновое
сопротивление линии передачи представлено на рис. 8.24, а влияние диэлек-
трической проницаемости паяльной маски на время задержки распростра-
нения сигнала — на рис. 8.25.
Влияние значения диэлектрической проницаемости подложки
печатной платы
Диэлектрическая проницаемость подложки печатной платы оказывает
наиболее сильное влияние на время распространения сигнала и волновое со-
противление линии передачи. Этого результата следовало ожидать. Поскольку
20 1527
586
Глава 8. Конструкторско-технологическое проектирование...
ЕТ
Рис. 8.24. Влияние диэлектрической проницаемости паяльной маски на волновое
сопротивление
£(
Рис. 8.25. Влияние диэлектрической проницаемости паяльной маски на время
задержки распространения сигнала
подложка, по сути, является диэлектриком, находящимся между двумя об-
кладками конденсатора — полигоном заземления и проводником, то изме-
нение диэлектрической проницаемости материала подложки приводит к наи-
более сильному изменению параметров линии передачи. В табл. 8.4 представ-
лены результаты расчета влияния значения диэлектрической проницаемости
подложки печатной платы на параметры линии передачи.
Разница между максимальным и минимальным временем задержки рас-
пространения сигнала при изменении диэлектрической проницаемости пе-
чатной платы от 4 до 5,5 составила 0,86 нс/м. Разница между крайними зна-
чениями волнового сопротивления составила 6,49 Ом, что составляет почти
13 % от номинального. Это весьма значительное отклонение, что говорит о
необходимости жестко контролировать значение относительной диэлектри-
ческой проницаемости основания печатной платы.
8.4. Технологические факторы и целостность сигнала
587
Таблица 8.4
Результаты расчета влияния значения диэлектрической проницаемости подложки
печатной платы на параметры линии передачи
Диэлектричес- кая проницае- мость Энергия поля, Дж Погонная емкость, Ф/м Эффективная диэлектричес- кая прони- цаемость Время задержки распространения сигнала, нс/м Волновое сопротивление, Ом
4,0 5,836Е-11 1Д67Е-10 3,19901 5,90231 51,09797
4,1 5,957Е-11 1Д91Е-10 3,26480 5,96269 50,58050
4,2 6,079Е-11 1,216Е-10 3,33333 6,02495 50,05786
4,3 6,201Е-11 1,240Е-10 3,39912 6,08411 49,57106
4,4 6,323Е-11 L265E-10 3,46765 6,14514 49,07878
4,5 6.444Е-11 L289E-10 3,53344 6,20316 48,61973
4,6 6,566Е-11 1,313Е-10 3,59923 6,26064 48,17333
4,7 6.687Е-11 1,337Е-10 3,66502 6,31760 47,73900
4,8 6.808Е-11 1,362Е-10 3,73355 6,37639 47,29884
4,9 6,929Е-11 1,386Е-10 3,79934 6,43233 46,88754
5,0 7,051Е-11 1,410Е-10 3,86513 6,48778 46,48678
5,1 7,172Е-11 L434E-10 3,93092 6,54276 46,09613
5,2 7,293Е-11 1,459Е-10 3,99945 6,59955 45,69949
5,3 7,414Е-11 1,483Е-10 4,06524 6,65361 45,32820
5,4 7,534Е-11 1,507Е-10 4,13103 6,70723 44,96581
5,5 7,655Е-11 1,531Е-10 4,19682 6,76043 44,61197
На рис. 8.26 представлен график зависимости волнового сопротивления мик-
рополосковой линии передачи от значения диэлектрической проницаемости
основания печатной платы, а на рис. 8.27 — зависимость времени задержки рас-
пространения сигнала от диэлектрической проницаемости основания платы.
Определенный интерес для анализа представляет картина электрического
поля исследуемой линии передачи. Солвер ELCUT позволяет визуализиро-
вать рассчитанное электрическое поле в виде эквипотенциалей и векторов
напряженностей поля. В качестве примера на рис. 8.28 приведена картина
электрического поля микрополосковой линии.
Влияние влагозащитного покрытия
Относительная диэлектрическая проницаемость влагозащитного покрытия
может меняться от 2,0 в случае акрилового покрытия до 5,2 в случае урета-
нового покрытия. Разница в значениях волнового сопротивления для этих
20*
588
Глава 8. Конструкторско-технологическое проектирование...
Рис. 8.26. Влияние диэлектрической проницаемости подложки печатной платы
на волновое сопротивление
Рис. 8.27. Влияние диэлектрической проницаемости подложки печатной платы
на время задержки распространения сигнала
крайних случаев составляет почти 1 Ом, а время задержки распространения
сигнала при этом увеличивается на 0,13 нс/м. Если обратиться к предыду-
щим главам книги, то это значение, например, для дифференциальных пар,
следует признать недопустимо большим. Поэтому этот технологический
аспект должен быть решен на концептуальном уровне, и замена покрытия
от партии к партии печатных узлов может быть недопустимой. Выборочные
расчетные данные по влиянию значения диэлектрической проницаемости
влагозащитного покрытия на параметры микрополосковой линии переда-
чи приведены в табл. 8.5, а на рис. 8.29 и рис. 8.30 показаны зависимости вол-
нового сопротивления и удельного времени задержки распространения сиг-
нала от относительной диэлектрической проницаемости покрытия платы.
Толщина влагозащитного покрытия в зависимости от способа нанесения
и материала может изменяться в очень широких пределах. Нанесение покры-
тия приводит к увеличению эффективной диэлектрической проницаемое-
8.4. Технологические факторы и целостность сигнала
589
Рис. 8.28. Картина поля при диэлектрической проницаемости подложки печатной
платы ег = 4
ти среды линии передачи и, как следствие, к увеличению погонной емкости
линии и снижению ее волнового сопротивления. Единственная возможность
оценить влияние толщины на изменение параметров линии в данном слу-
чае заключается в применении солвера.
«г
Рис. 8.29. Влияние диэлектрической проницаемости влагозащитного покрытия
на волновое сопротивление
590
Глава 8. Конструкторско-технологическое проектирование...
£г
Рис. 8.30. Влияние диэлектрической проницаемости влагозащитного покрытия
на время задержки распространения сигнала
Таблица 8.5
Результаты расчета влияния диэлектрической проницаемости влагозащитного
покрытия на параметры линии
Диэлектричес- кая прони- цаемость Энергия поля, Дж Погонная емкость, Ф/м Эффективная диэлектричес- кая проницае- мость Время задержки распростране- ния сигнала, нс/м Волновое сопротивле- ние, Ом
2,0 6,396Е-11 1,279Е-10 3,50603 6,17905 48,80943
2,1 6,4О6Е-Н 1,281Е-10 3,51151 6,18388 48,77132
2,5 6,444Е-11 1,289Е-10 3,53344 6,20316 48,61973
3,0 6,489Е-11 1,298Е-10 3,55811 6,22478 48,45088
3,5 6,532Е-11 1,306Е-10 3,58004 6,24393 48,30226
4,0 6,572Е-11 1,314Е-10 3,60197 6,26303 48,15500
4,5 6,611Е-11 1,322Е-10 3,62390 6,28206 48,00907
5,0 6,648Е-11 1,ЗЗОЕ-1О 3,64583 6,30104 47,86447
5,5 6,684Е-11 1,337Е-10 3,66502 6,31760 47,73900
6,0 6,720Е-11 1,344Е-10 3,68421 6,33412 47,61452
6,5 6,754Е-11 1,351Е-10 3,70340 6,35059 47,49101
7,0 6,787Е-11 1,357Е-10 3,71985 6,36468 47,38590
7,5 6,820Е-11 1,364Е-10 3,73904 6,38107 47,26415
8,0 6,852Е-11 1,370Е-10 3,75548 6,39509 47,16054
8.4. Технологические факторы и целостность сигнала
591
В результате проведенного анализа выявилась нелинейная зависимость из-
менения волнового сопротивления от толщины покрытия. В реальных услови-
ях толщина покрытия может варьироваться от 25 мкм (в случае нанесения
париленового покрытия) до 500 мкм в случае нанесения методом погружения
в нижней (по отношению к ванне с материалом) части печатного узла. Случаи
с еще большей толщиной влагозащитного покрытия были рассчитаны, чтобы
понять характер зависимости. При очень больших толщинах покрытия дальней-
шее изменение толщины перестает оказывать сильное влияние на распростра-
нение сигнала. Это объясняется тем, что эффективная диэлектрическая прони-
цаемость среды вблизи проводника практически не меняется, т. е. линия пере-
дачи становится практически заглубленной. Полученный результат может быть
использован для определения максимального поверхностного слоя диэлектри-
ческого покрытия, при котором параметры становятся независимыми от тол-
щины покрытия. В табл. 8.6 приведены результаты расчета влияния толщины
влагозащитного покрытия на параметры линии передачи, на рис. 8.31 — влия-
ние толщины влагозащитного покрытия на волновое сопротивление, а на
рис. 8.32 — на время задержки распространения сигнала.
Неровный характер кривой на графиках объясняется тем, что при моде-
лировании тонких покрытий толщиной 25— 50 мкм нельзя игнорировать тол-
щину металлического проводника (рис. 8.33). Покрытие, образно говоря,
«огибает» проводник, что вносит определенную погрешность в расчеты, так
Таблица 8.6
Результаты расчета влияния толщины влагозащитного покрытия
Толщина влагозащит- ного покры- тия, мкм Энергия поля, Дж Погонная емкость, Ф/м Эффективная диэлектричес- кая проницае- мость Время задержки распространения сигнала, нс/м Волновое сопротивле- ние, Ом
25 6,353Е-11 1,271Е-10 3,48410 6,15970 48,96280
50 6,413Е-11 1,283Е-10 3,51700 6,18871 48,73329
75 6,444Е-11 1,289Е-10 3,53344 6,20316 48,61973
100 6,492Е-11 1,298Е-10 3,55811 6,22478 48,45088
200 6,634Е-11 1,327Е-10 3,63761 6,29393 47,91854
300 6,734Е-11 1,347Е-10 3,69243 6,34118 47,56147
400 6,808Е-11 1,362Е-10 3,73355 6,37639 47,29884
500 6,864Е-П 1,373Е-10 3,76371 6,40209 47,10899
1000 7,008Е-11 1,402Е-10 3,84320 6,46935 46,61922
2000 7,084Е-11 1,417Е-10 3,88432 6,50386 46,37182
4000 7Д08Е-11 1,422Е-10 3,89803 6,51533 46,29022
14000 7Д16Е-11 1.423Е-10 3,90077 6,51762 46,27395
592
Глава 8. Конструкторски-технологическое проектирование...
Рис. 8.31. Влияние толщины влагозащитного покрытия на волновое сопротивление
Рис. 8.32. Влияние толщины влагозащитного покрытия на время задержки
распространения сигнала
как предсказать толщину и контуры на углах проводника довольно сложно,
поскольку это зависит, в том числе, от вязкости материала.
При нанесении покрытий толщиной более 75 мкм толщиной проводни-
ка можно пренебречь (рис. 8.33).
Влияние ширины полигона заземления
Во второй главе было сформулировано правило, согласно которому при
ширине возвратного проводника в микрополосковой линии более утроенной
ширины сигнального проводника, электрические параметры линии переда-
чи не изменяются. Проверка, выполненная точным методом численного ана-
лиза, показывает правильность данного утверждения. В табл. 8.7 приведены
результаты расчета влияния ширины возвратного проводника на парамет-
ры линии передачи, на рис. 8.34 график зависимости ширины возвратного
8.4. Технологические факторы и целостность сигнала
593
Рис. 8.33. Модели с различной толщиной влагозащитного покрытия:
с толщиной 50 мкм (слева) и 75 мкм (справа)
Таблица 8.7
Результаты расчета влияния ширины полигона заземления
Ширина возврат- ного про- водника, ММ Погонная емкость в вакууме, Ф/м Погонная емкость, Ф/м Эффективная диэлектрическая проницаемость Время задержки распространения сигнала, нс/м Волновое сопротивле- ние, Ом
0,20 2,385Е-11 6,551Е-11 2,74675 5,46920 84,34677
0,40 2,655Е-11 7,989Е-11 3,00904 5,72437 72,39157
0,60 2,871Е-11 9Д87Е-11 3,19993 5,90316 64,91768
0,90 ЗД19Е-11 1,061Е-10 3,40173 6,08645 57,95636
1,35 3,352Е-11 1Д90Е-10 3,55012 6,21778 52,78870
1,80 3,476Е-11 1,248Е-10 3,59033 6,25290 50,61967
2,25 3,540Е-11 1,271Е-10 3,59040 6,25295 49,70408
2,70 3,577Е-11 1,280Е-10 3,57842 6,24251 49,27221
3,15 3,600Е-11 1,284Е-10 3,56667 6,23225 49,03799
3,60 3,612Е-11 1,286Е-10 3,56035 6,22674 48,91838
4,50 3,630Е-11 1,288Е-10 3,54821 6,21611 48,75905
5,40 3,636Е-11 1,288Е-10 3,54235 6,21098 48,71880
6,30 3,642Е-11 1,289Е-10 3,53926 6,20827 48,65977
7,20 3,644Е-11 1,289Е-10 3,53732 6,20656 48,64641
8,10 3,647Е-11 1,289Е-10 3,53441 6,20401 48,62640
9,00 3,648Е-11 1,289Е-10 3,53344 6,20316 48,61973
10,00 3,649Е-11 1,289Е-10 3,53247 6,20231 48,61307
594
Глава 8. Конструкторско-технологическое проектирование...
Рис. 8.34. Влияние ширины возвратного проводника на волновое сопротивление
линии передачи
IV, м м
Рис. 8.35. Влияние ширины полигона заземления на время задержки
распространения сигнала
проводника на волновое сопротивление линии, а на рис. 8.35— на удельное
время задержки распространения сигнала. Из приведенных данных видно:
при ширине возвратного проводника больше 2,7 мм (что составляет 3w, при
w = 0,9) параметры линии передачи практически не меняются.
Предельное изменение параметров линии передачи
Для того, чтобы оценить максимально возможную разницу между мини-
мальным и максимальным волновым сопротивлением, а также максималь-
ным и минимальным удельным временем задержки распространения сигнала,
был проведен расчет худших случаев. Максимальная удельная задержка рас-
пространения достигается при минимальном волновом сопротивлении, а ми-
нимальная удельная задержка распространения сигнала — при максималь-
ном волновом сопротивлении.
8.4. Технологические факторы и целостность сигнала
595
Таблица 8.8
Конструкторско-технологические параметры линий передачи при предельных
значениях волнового сопротивления
Конструкторско-технологические параметры линии передачи Значение параметров
при минимальном Z при максимальном Z
Толщина подложки, мм, 0,5 0,5
Относительная диэлектрическая проницаемость подложки 5,5 4,0
Толщина слоя паяльной маски, мкм 35 25
Диэлектрическая проницаемость паяльной маски 4 3
Толщина слоя влагозащитного покрытия, мкм 500 25
Относительная диэлектрическая проницаемость влагозащитного покрытия 5,2 2,0
Минимальное и максимальное значение волнового сопротивления обес-
печивается при параметрах линии передачи, приведенных в табл. 8.8.
Таблица 8.9
Электрофизические параметры линий передачи при предельных значениях волнового
сопротивления
Электрофизические параметры линии передачи Значение параметров
при минимальном Z при максимальном Z
Энергия поля в вакууме, Дж 1,824Е-11 1,823Е-11
Погонная емкость в вакууме, Ф/м 3,648Е-11 3,647Е-11
Энергия поля, Дж 8,963Е-11 5,673Е-11
Погонная емкость, пФ/м 179,4 113,5
Эффективная диэлектрическая проницаемость 4,91776 3,11215
Удельное время задержки распространения сигнала, нс/м 7,31809 5,82162
Волновое сопротивление, Ом 41,21239 51,82039
Результаты расчетов дают следующие параметры линии передачи в пре-
дельных случаях.
Расчеты показывают, что максимальная разница между минимальным и мак-
симальным волновым сопротивлением составляет более 10 Ом (более 20 % от
номинального значения 50 Ом), при этом время задержки распространения
сигнала изменяется на 1,5 нс/м. Это весьма большие изменения, которые могут
иметь очень серьезные последствия. Достаточно напомнить, что допустимое
рассогласование линии передачи не должно превышать 5 %. В данном же случае
при согласовании линии с волновым сопротивлением 50 Ом должен быть ус-
тановлен согласующий резистор также с сопротивлением 7^ = 50 Ом. Но если
596
Глава 8. Конструкторско-технологическое проектирование...
в процессе изготовления платы получено минимальное сопротивление Zmin =
= 40 Ом, то коэффициент отражения будет
к _ ~ ^min _ 50-40 п I I
^+Zmin 50 + 40 ’ ’
т. е. коэффициент отражения равен 11 %, что больше допустимого, исходя
из требований целостности сигнала.
Приведенный анализ позволяет сделать два важных вывода, а именно:
• уточненные модели линий передач и топологических элементов печатных
плат и их параметры на заключительном этапе отработки проекта мо-
гут быть получены только с помощью численных методов анализа элек-
трического и магнитного поля и соответствующих программных средств;
• комплексный подход к созданию печатных плат для быстродействую-
щих цифровых систем требует непременного учета влияния техноло-
гических факторов на конечные показатели целостности сигнала.
8.5. Сводка САПР печатных плат
с учетом ЭМС и целостности сигнала
В данном разделе в виде справочного материала приведена сводка неко-
торых САПР и программных средств, которые ориентированы на решение
задач целостности сигнала и ЭМС при проектировании печатных плат и
цифровых узлов.
Система и программные средства Состав
Applied Wave Research (www.mwoffice.com) • Microwave Office 2004 — система сквозного про- ектирования и моделирования СВЧ устройств. • Visual System Simulator 2004 — пакет моделиро- вания радиотехнических систем на уровне фун- кциональных блоков. • Analog Office 2004 — пакет проектирования вы- сокочастотных интегральных микросхем. • AWR SI 2005 Design Suite — пакет анализа цело- стности сигналов в высокочастотных печатных платах.
Dynamic Soft Analysis (www.betasoft-thermal.com) • BETAsoft-Board — программа моделирования тепловых процессов в печатных платах. • BETAsoft-MCM — программа моделирования теп- ловых процессов в интегральных схемах.
Computer Simulation Technology (www.cst.de) • CST Microwave Studio — система трехмерного мо- делирования СВЧ устройств на платформе PC. • CST Design Studio — система обработки резуль- татов моделирования, полученных с помощью разных программ.
8..5. Сводка САПР печатных плат с учетом ЭМС и целостности сигнала 597
• CST EM Studio — система анализа низкочастот- ных устройств.
Harvard Thermal (www.harvardthermal.com) • TASPCB — система моделирования тепловых процессов в печатных платах. • TAS — система анализа трехмерных конструкций произвольной формы.
Sigrity (www.sigrity.com) SpeedXP Suite — программа анализа целостности сиг- налов, перекрестных искажений и электромагнит- ной совместимости на печатных платах и в корпу- сах интегральных микросхем. Speed2000 • Программа Speed2000 — это пакет анализа про- блем электромагнитной совместимости с ориги- нальным вычислительным ядром, работающий во временной области. PowerS I • Программа PowerSI выполняет аналогичные функ- ции, но ее ядро работает в частотной области. Здесь можно рассчитать спектры сигналов и по- мех в различных проводниках печатной платы, оценить частотные характеристики отдельных узлов микросхемы, оптимизировать размещение экранов. XcitePI • Программа предназначена для моделирования проблем электромагнитной совместимости в кор- пусах и подложках высокоскоростных интеграль- ных схем. Учитываются эффекты распростране- ния не только в сигнальных проводниках, но и в цепях питания и земли всего стека слоев.
Quantic EMC (www.quantic-emc.com) Compliance — система посттопологического анали- за электромагнитной совместимости на печатных платах. • Пакет Compliance канадской компании Quantic- ЕМС позволяет оценивать влияние конструктив- ных особенностей печатных плат на их электри- ческие характеристики, а также моделировать электромагнитную совместимость устройств еще до изготовления реальных конструкций, тем са- мым сокращая сроки и стоимость проектирова- ния при значительном повышении качества.
Downstream Technologies (www.downstreamtech.com) САМ350 — система подготовки печатных плат к про- изводству.
PCB Frontline (www.frontline-pcb.com) Genesis 2000 — система подготовки печатных плат к производству.
598
Глава 8. Конструкторско-технологическое проектирование...
Aldec (www.aldec.com) • Active-HDL — Active-HDL — среда проектирова- ния цифровых устройств. • Riviera — программа верификации сложных ASIC и FPGA проектов.
КГТУ ТРиАНА — отечественная система моделирования тепловых процессов в электронном оборудовании.
Институт машиноведения УРО РАН Aplite — отечественная система визуального конт- роля качества фотошаблонов и печатных плат на лю- бой стадии изготовления.
FreeStyle Team • TopoR — отечественная программа автотрасси- ровки печатных плат. • АиТОР — отечественная программа авторазмеще- ния компонентов на печатных платах.
ConnectEDA ELECTRA — адаптивный бессеточный автотрасси- ровщик.
Pulsonix Pulsonix — сквозная система проектирования печат- ных плат.
Altium Limited (www.altium.com) • Protel 2004 — система сквозного проектирования печатных плат. • Nexar 2004 — система ввода и моделирования проектов. • CAMtastic 2004 — система подготовки печатных плат к производству. • P-CAD 2004 (ACCEL EDA) — система сквозно- го проектирования печатных плат. • Вспомогательные продукты для P-CAD 2004.
CADENCE • РСВ Design Studio — пакет верхнего уровня про- ектирования. • Allegro — редактор печатных плат, позволяющий разрабатывать многослойные и высокоскорос- тные платы с высокой плотностью размещения компонентов. • SPECCTRA — штатный модуль авторазмещения и автотрассировки; управляет обширным набо- ром правил проектирования и технологических ограничений. • SPECCTRAQuest SI Expert — модуль анализа це- лостности сигнала и ЭМС топологии платы. • SigXplorer — модуль предварительного анализа проекта и подготовки наборов правил проекти- рования.
CADSTAR — система проектирования печатных плат среднего уровня сложности • CADSTAR 3D — система трехмерного проекти- рования конструкции печатных плат. • CADSTAR SI-Verify — система анализа электро- магнитной совместимости печатных плат.
8.4. Технологические факторы и целостность сигнала
599
• CADSTAR TopSPICE — модуль смешанного ана- лого-цифрового моделирования. • CADSTAR MRPLINK — интерфейс связи с сис- темами планирования материальных ресурсов (MRP).
CR-5000 - мощная система сквозного проектирования печатных плат, включает • System Designer — система ввода проектов, вклю- чающая редактор принципиальных схем. • Board Designer — мощный редактор печатных плат. • Board Producer — модуль подготовки проектов пе- чатных плат к производству. • Layout Tool — средства подготовки библиотек эле- ментов. • ЕМ Designer — мощная система трехмерного про- ектирования конструкции печатных плат. • Hot-Stage — система анализа целостности сигна- лов и электромагнитной совместимости.
MENTOR GRAPHICS Пакет Expedition РСВ представляет мощное реше- ние в области проектирования плат. Основу систе- мы составляет среда AutoActive, позволяющая реа- лизовать такие функции, как предтопологический анализ целостности сигналов, интерактивная и ав- томатическая трассировка с учетом требований вы- сокочастотных плат и специальных технологических ограничений, накладываемых использованием со- временной элементной базы (например, примене- ние корпусов с шариковыми выводами BGA).
MicroSim • Polaris — программа предназначена для анализа целостности сигналов. • PCBoards представляет собой графический редак- тор печатных плат.
Quad Design Technology ХТК — программа компании Viewlogic Systems пред- назначена для анализа целостности сигналов в циф- ровых устройствах, реализуемых на печатных платах и гибридных интегральных схемах. Результаты ана- лиза ошибок суммируются в отчете, в котором при- водятся данные о перекрестных помехах, задержках и выбросах сигналов, немонотонных фронтах импуль- сов, распределении потенциалов в цепях «земли» и на- пряжениях логических уровней.
AMP AMPredictor — пакет программ предназначен для ана- лиза влияния неидеальностей соединителей, контакт- ных панелей, цепей коммутации и межсоединений на качество обработки цифровых сигналов. Пакет состо- ит из следующих модулей: • AMPSPICE Circuit Simulator — программа моде- лирования, позволяющая с высокой точностью
600
Глава 8. Конструкторско-технологическое проектирование...
рассчитывать характеристики линий передачи и анализировать такие эффекты, как повышение уровня помех, перекрестные помехи, отражения и задержки распространения сигналов в рассмат- риваемых устройствах; • Connector Noise Analyzer — анализ уровня шума, обусловленного наличием разъемов; • Model Library Manager — менеджер библиотек математических моделей компонентов, разъе- мов, цепей заземления и т. п.; • РСВ Structure Analyzer — расчет эквивалентных электрических схем печатных проводников на основе анализа двухмерных электромагнитных полей; • Net Topology Editor — центральная программа пакета, с помощью которой составляются списки соединений анализируемого устройства и под- ключаются модели генераторов сигналов и изме- рительных приборов, необходимые для модели- рования; • Power/Ground Plane Analyzer — расчет распреде- ления потенциалов по постоянному току на плоскостях металлизации «земли» и питания; • IBIS-to-AMPSPICE Converter — преобразование IBIS-файлов моделей интегральных схем в фор- мат программы моделирования AMPSPICE; • AMPSPICE Interpreter — преобразование моде- лей МОП-транзисторов программы HSPICE в формат AMPSPICE.
HyperLinx HyperSuit 4.5 — пакет программ для анализа целост- ности сигнала по упрощенной модели, когда печат- ные проводники представляются в виде отрезков линий передачи, для которых учитывается взаимная индуктивность близлежащих проводников, однако электронные компоненты замещаются лишь входны- ми и выходными комплексными сопротивлениями.
Условные буквенные обозначения
А — амплитуда тока или напряжения
А — ослабление (по умолчанию дБ)
Ап — ослабление, непер
BW — полоса пропускания
С — электрическая емкость
Се — емкость конденсатора при наличии диэлектрика
Со — электрическая емкость в воздушной среде
Свр — емкость развязывающего конденсатора
Сстр — компенсирующая емкость
Ссгл — электрическая емкость поворота сигнального проводника
С — входная емкость микросхемы
С/ — емкость проводника на единицу длины
Cj — емкость на единицу длины нагруженной линии передачи, емкость на-
грузки
ct — нормированная емкость (безразмерная величина)
CL — собственная емкость вывода интегральной микросхемы
Ст — взаимная емкость
m
Cml — частичная взаимная емкость на единицу длины линии
С? t — емкость монтажа
mnt
Сп — электрическая емкость звена в модели линии связи
Со — выходная емкость микросхемы
Ср — собственная емкость корпуса интегральной микросхемы
CSB — емкость слоя питания относительно слоя возвратного тока в печатной
плате
С — электрическая емкость квадрата площади линии передачи
s4
Ct — суммарная емкость единицы длины линии
CTL — общая емкость линии передачи
Cvia — электрическая емкость металлизированного отверстия
d — расстояние, пространственное разрешение, дистанция
Jctk — область взаимодействия связанных линий
Jdsc — длина неоднородности линии передачи
— расстояние между равномерно распределенными емкостными нагруз-
ками
ds — максимальный размер проводящей структуры
Е — напряженность электрического поля
е — эдс самоиндукции
602
Условные обозначения
Е — энергия
Esh — напряженность электрического поля при наличии экрана
Ess — напряжение смещения согласующего резистора, включенного па-
раллельно выходу линии; напряжение дополнительного источника пи-
тания для смещения согласующего резистора
Е— напряженность возбуждающего электрического поля
Е0 ant— напряженность электрического поля, излучаемого антенной в оп-
ределенном направлении q
f — частота
fco — частота среза
/пах — максимальная частота синхронизации, тактовая частота
Xes — частота электрического резонанса проводящей пластины
G — проводимость
Gt — проводимость на единицу длины
Н — напряженность магнитного поля
Н‘ — напряженность возбуждающего магнитного поля
h — толщина диэлектрического слоя, основания, прокладки
Я(со) — передаточная функция
hCE — толщина звена типа СЕ в составе МПП
Ad — толщина диэлектрического слоя
h{ — толщина фольги
Aems — толщина заглубленной линии
hg — толщина диэлектрической прокладки
Ams — толщина диэлектрика в микрополосковой линии
Лрсь — толщина печатной платы
Лрсь nom — номинальная толщина платы
hs — толщина диэлектрика в полосковой линии
Hsh — напряженность магнитного поля при наличии экрана
/ — ток, переменный ток
/ — ток, постоянный ток
/ — амплитуда тока на линии 1 дифференциальной пары
/2 — амплитуда тока на линии 2 дифференциальной пары
/с — ток заряда емкости
Is — индуцированный ток на единицу длины линии передачи
4в — ток потребления микросхемы
4в — ток потребления микросхемы в состоянии логического О
^sb — ток потребления микросхемы в состоянии логической 1
/ — ток режима общего вида
zd — ток дифференциального режима
/f — ток падающей волны
/FExt ~ ток перекрестной помехи в конце пассивной линии
/ — входной ток вентиля
/1к — ток утечки
/NExt ~ ток перекрестной помехи в начале пассивной линии
Условные обозначения
603
/0 — выходной ток вентиля
/г — ток отраженной волны
Is — индуктивный удельный ток
/s — ток источника, постоянный
1{ — ток преломленной волны
К — константа при оценке помехоэмиссии
к — коэффициент отражения
кг — поправочный коэффициент при расчете эффективной диэлектрической
проницаемости
kQ — электрический размер
kt — целое число, определяющее моды резонанса по длине металлической
пластины
kf — коэффициент перекрестных помех на дальнем конце пассивной линии
кп — коэффициент перекрестных помех на ближнем конце пассивной линии
кх — коэффициент отражения в конце линии передачи
к$ — коэффициент отражения в начале линии передачи
kt — коэффициент преломления
к^ — целое число, определяющее моды резонанса по ширине металлической
пластины
/ — длина проводника, вывода микросхемы
L — индуктивность
— эффективная индуктивность
/с1 — длины линии передачи критической электрической длины
£стр — компенсирующая индуктивность
£ext — внешняя индуктивность
ZGND — индуктивность системы заземления
Lint — внутренняя индуктивность
ZL — индуктивность вывода микросхемы
Zj — индуктивность проводника на единицу длины
/п — длина электрически длинной линии
Ln — индуктивность звена в модели линии связи
£р — индуктивность соединительных проводников и выводов внутри кор-
пуса микросхемы
^parallel — индуктивность параллельно соединенных элементов
/ — длина участка связанных линий, при которой достигается максимум
помех на конце пассивной линии
ZSB — индуктивность шины питания
Aeries — индуктивность последовательно соединенных элементов
/sl — длина электрически короткой линии
Zsp — индуктивность слоя питания
Lsr — парциальная самоиндукция возвратного проводника
Lss — парциальная самоиндукция сигнального проводника
Zsw — индуктивность проводника питания в корпусе микросхемы
Zt — суммарная индуктивность единицы длины линии
604
Условные обозначения
£TL — общая индуктивность линии передачи
£via — индуктивность металлизированного отверстия
£w — индуктивность провода круглого сечения
М — взаимная индуктивность
mt — масштаб по оси тока, деление/А
Afz — частичная взаимная индуктивность на единицу длины линии
mv — масштаб по оси напряжения, деление/В
п — число звеньев, уравнений и т. п.
N — число линий магнитного потока
NMn — уровень статической помехоустойчивости цифровой микросхемы от-
носительно высокого логического уровня
NML — уровень статической помехоустойчивости цифровой микросхемы от-
носительно низкого логического уровня
Р — мощность
PD — мощность рассеяния
Pin — мощность на входе линии передачи
Pout — мощность на выходе линии передачи
Q, q — заряд
— сопротивление скин-слоя
R, г — сопротивление
Яас — сопротивление переменному току
Явмр ~ сопротивление шарикового вывода микросхемы
/?с1с — сопротивление постоянному току
ЯЕ — дополнительное сопротивление при согласовании ЭСЛ-схем на вхо-
де линии
Я — эквивалентное сопротивление
— входное сопротивление
Rl — сопротивление вывода микросхемы
Я1 — сопротивление нагрузки
R{ — сопротивление проводника на единицу длины
7?ikg — сопротивление утечки
го — выходное сопротивление
Я8 — сопротивление резистора, подключенного к началу линии
7?SB — сопротивление шины питания
Rvn — поверхностное сопротивление
Asw — сопротивление проводника питания в корпусе микросхемы
Rt — согласующий резистор
Я1 comm — эквивалентное согласующее сопротивление в режиме сигнала об-
щего вида
diff — согласующее сопротивление в дифференциальном режиме
— согласующий резистор на входе линии
7?to — согласующий резистор на выходе линии
Aw — сопротивление проводника круглого сечения
Условные обозначения
605
— демпфирующий резистор, включенный последовательно на вход ли-
нии /, которая параллельно с другими линиями подключена к выходу
ЭСЛ—схемы
s — зазор между проводниками печатного монтажа
S — площадь, эффективность экранирования
Т — время пробега электромагнитной волны от начала до конца линии пе-
редачи
t — время, толщина печатного проводника
/0 5i — время достижения уровня 0,5 на входе линии
/0 5о — время достижения уровня 0,5 на выходе линии
Гс — длительность цикла
rd — удельное время задержки распространения сигнала в линии передачи
zd(ofo ~ время задержки распространения сигнала при переключении мик-
росхемы из 1 в 0
/d(on) — время задержки распространения сигнала при переключении мик-
росхемы из 0 в 1
zd even “ УДельное время задержки распространения четной моды
/d odd — удельное время задержки распространения нечетной моды
Zdl — время задержки распространения сигнала на длине /
/f — длительность спада импульса
/off — время переключения при выключении
/оп — время переключения при включении
Гр — длительность импульса
tpd — время задержки распространения сигнала в линии передачи
/г — длительность фронта импульса
/rin — длительность фронта импульса на входе линии
Ггп — нормированная длительность фронта импульса
/rout ~ длительность фронта импульса на выходе линии
/rTL — длительность фронта импульса, определяемая параметрами линии пе-
редачи
/s — время установления сигнала
/sk — время расфазировки
/t — время перехода из одного устойчивого состояния в другое
/w — длительность импульса
/cnd — толщина печатного проводника
U — потенциал
v — скорость
И, v — напряжение
— амплитуда напряжения на линии 1 дифференциальной пары
И2 — амплитуда напряжения на линии 2 дифференциальной пары
Иа — максимальное напряжение в активной линии
Иь — максимальное напряжение в пассивной линии
vc — скорость света в вакууме
606
Условные обозначения
Исс — напряжение питания коллекторное (постоянный ток), напряжение на
выводе питания микросхемы
^comm — амплитуда напряжения сигнала общего вида
Kct — напряжение перекрестной помехи в короткой линии передачи
^diff— Дифференциальное напряжение
Kdrv — напряжение перепада генератора драйвера
Veven — скорость распространения четной моды
Kf — напряжение падающей волны
Ирехт — напряжение перекрестной помехи на дальнем конце пассивной длин-
ной линии передачи
Иеехт(С) — напряжение на дальнем конце пассивной линии, вызванное ем-
костной связью
ИрЕхт(Г) ~ напряжение на дальнем конце пассивной линии, вызванное ин-
дуктивной связью
Иь — напряжение отскока напряжения
^gnd — падение напряжения в цепи заземления
Ин — высокий логический уровень
И[(/) — входная ВАХ микросхемы
Ин max — максимальный уровень высокого входного напряжения
Ин min “ минимальный уровень высокого входного напряжения
Иьтах ~ максимальный уровень низкого входного напряжения
Htmin — минимальный уровень низкого входного напряжения
Ить — входное напряжение линии передачи
Kj — наведенное напряжение в конце линии передачи
VL — напряжение, вызванное индуктивностью
VL — низкий логический уровень
Ип — напряжение шумов, амплитуда импульса помехи
Ичехт — напряжение перекрестной помехи на ближнем конце пассивной
длинной линии передачи
Ичехт(С) — напряжение на ближнем конце пассивной линии, вызванное ем-
костной связью
Ичехт(Ь) — напряжение на ближнем конце пассивной линии, вызванное ин-
дуктивной связью
ИО0(7) — выходная ВАХ микросхемы в состоянии логической О
ИО1(7) — выходная ВАХ микросхемы в состоянии логической 1
vodd — СК°РОСТЬ распространения нечетной моды
Ион — выходное напряжение высокого уровня
K0L — выходное напряжение низкого уровня
HjTl — выходное напряжение линии передачи
И — напряжение отраженной волны
Kref ~ напряжение опорного уровня
Условные обозначения
607
Игг — пороговое напряжение
И — наведенное напряжения в начале линии передачи
И — индуцированное напряжение на единицу длины линии передачи
И(/) — вольт-амперная характеристика, учитывающая выходное сопротив-
ление драйвера и последовательный согласующий резистор; относится
к входу линии
KSB — падение напряжение на шине питания
Hss — напряжение источника питания, постоянный ток
Kt — напряжение преломленной волны
w — ширина проводника
юэ — ширина линий сетки на потенциальном слое
— энергия электрического поля в свободном пространстве
Wd — энергия электрического поля в диэлектрике
wsh — ширина линий экранной сетки в печатной плате
х — реактивное сопротивление
хс — емкостное сопротивление
xL — индуктивное сопротивление
Z — волновое сопротивление
Z — полное сопротивление
Zo — волновое сопротивление свободного пространства (377 Ом)
Zc — полное сопротивление емкости
Zconim “ волновое сопротивление в режиме сигнала общего вида
Zdiff — дифференциальное волновое (полное) сопротивление
Zeven — волновое (полное) сопротивление в режиме четной моды
zic — входное полное сопротивление в режиме общего вида
£id — дифференциальное входное полное сопротивление
^ind ~ полное сопротивление индуктивности
£is — входное полное сопротивление одиночной линии
Zz — волновое сопротивление нагруженной линии передачи
ZL — полное сопротивление индуктивности
Zo — выходное полное сопротивление
Zodd — волновое сопротивление в режиме нечетной моды
£odd — дифференциальное полное сопротивление
£os — выходное полное сопротивление одиночной линии
ZpDs — полное сопротивление системы распределенного питания
Греческие
а — коэффициент ослабления
aD — коэффициент ослабления за счет потерь в диэлектриках
aR — коэффициент ослабление за счет потерь в проводниках
5 — толщина скин-слоя
5рсЬ — допуск на толщину платы
608
Условные обозначения
Al — разность длин сигнальных проводников дифференциальной пары
Д/ — перепад тока в шине питания при переключении микросхемы
At — системная задержка
£ — абсолютная диэлектрическая проницаемость
£0 — диэлектрическая постоянная
£е^ — эффективная диэлектрическая проницаемость (относительная)
ег — относительная диэлектрическая проницаемость
0j — угол наклона прямой в координатах (/, V), пропорциональный сопро-
тивлению нагрузки
О, — угол наклона прямой в координатах (/, V), пропорциональный сопро-
тивлению согласующего резистора
0Z— угол наклона прямой в координатах (/, У) пропорциональный Z
X — длина волны электромагнитных колебаний
Хо — длина волны электромагнитных колебаний в свободном пространстве
Хе — длина волны электромагнитных колебаний в некотором диэлектрике
ц — абсолютная магнитная проницаемость
ц0 — магнитная постоянная
эффективная магнитная проницаемость (относительная)
цг — относительная магнитная проницаемость
р — удельное объемное сопротивление материала
о — удельная объемная проводимость материала
т1О/5о — постоянная времени, равная интервалу времени между моментами
достижения уровня 0,1 и 0,5
тю/9о — постоянная времени, равная интервалу времени между моментами
достижения уровня 0,1 и 0,9
тс — постоянная времени конденсатора
тп — длительность импульса помехи
ttl— постоянная времени линии передачи
Ф — магнитный поток
сосо — круговая частота среза
G5 — число витков контура тока
Литература
1. Guidelines for Designing High-Speed FPGA PCBs. AN-315, 2004, February,
ver. 1.1. Altera Corporation.
2. Board Systems Design and Verification Mentor Graphics Corporation, 2001, 15 p.
3. Bogatin E. Signal Integrity — Simplified. Prentice — Hall PTR, 2003. — 608 p.
4. Brooks D. Signal Integrity Issues and Printed Circuit Board Design. — Prentice
Hall PTR. 2003. - 432 p.
5. Bowie C. RF Circuit Design, Library of Congress Cataloging — Publication Data,
1982. -p. 174.
6. Electrical Performance of Packages. National Semiconductor. Application Note
1205. August 2001.
7. Holden H. HDIs Beneficial Influence on High-Frequency. Signal Integrity. Mentor
Graphics. Part 1 - 1 - 12 p., Part 2 - 2 - 7 p. Westwood Associates, West Haven, CT,
USA.
8. Медведев A.M. Печатные платы. Конструкции и материалы / А.М. Медве-
дев. — М.: Техносфера, 2005. — 304 с.: ил.
9. Virtex-4 РСВ Designer’s Guide. UG072(l.l)/Xilinx, September 9, 2004.
10. Barbetta M., Dickson J. Registration Techniques for Advanced Technology PCBs.
Printed Circuit Design&Manufacture. 2004, № 12, p. 38-42.
11. Resso M., Gneiting T., Modler R., Roe J. Investigating Microvia Technology for
10 Gbps and Higher Telecommunication Systems. DesignCon 2005, 12 p.
12. Pulliam W. Designing With BGAs. Printed Circuit Design. 2002, № 3,
p. 30-34.
13. VerguldM. Trends in Electronic Packaging and Assembly for Portable Consumer
Products, www.smtinfocus.com.
14. Лунд П. Прецизионные печатные платы. Конструирование и производ-
ство: пер. с англ. / П. Лунд. — М.: Энергоатомиздат, 1983. — 360 с.
15. Isaac J., Wiens D. The Future of PCB Design. Mentor Graphics Corporation.
16. Maxfield C., Wiens D. System Solutions: Redefining Systems Design for the
Electronics. Community Achieving New Levels of Performance, Quality, Scalability, and
Affordability!. Mentor Graphics Corporation. Tech. Publication. September 2000.
17. Wiens D. Printed Circuit Board Routing at the Threshold. Advanced Techno-
logy for the New Millenniumio 2000. Mentor Graphics.
18. Hargin B. 3,125 Gbps with your Hair on Fire Simulation-Based Signal-Integrity
Analysis of Digital Interconnects at Multi-Gigabit Speeds High-Speed Systems Design.
Mentor Graphics Corporation.
19. Noise, Cross-talk, Jitter, Skew, and EMI. Section 6. Backplane Designer’s Guide.
2002. Fairchild Semiconductor Corporation MS500736. 11 p.
610
Литература
20. Пирогова Е.В. Проектирование и технология печатных плат: учебник /
Е.В. Пирогова. - М.: ФОРУМ: ИНФРА-М, 2005. - 560 с.
21. Медведев А.М. Печатные платы. Плотность межсоединений. «Технологии
приборостроения», № 3 (15), 2005. - С. 3-9.
22. Медведев А.М. Печатные платы. Токонесущие способности цепей. «Тех-
нологии приборостроения», № 3 (15), 2005. С. 16-19.
23. Кечиев Л.Н., Смирнов С. Н. Система автоматизированного проектирова-
ния печатных плат с учетом требований внутриаппаратурной ЭМС: труды VIII
Межд. симпозиума по ЭМС. - Вроцлав, 1986, Ч. 2. - С. 676-683.
24. КечиевЛ.Н. Методы анализа печатных плат быстродействующих устройств.
IV Межд. симпозиум по ЭМС и электромагнитной экологии ЭМС-2001. Сбор-
ник научных докладов. - СПб, 2001. - С. 154-163.
25. Кечиев Л.Н., Алешин А.В., Шнейдер В. И. Обеспечение целостности сигнала
при проектировании печатных плат: сборник докладов VIII НТК по ЭМС и элек-
тромагнитной безопасности. ЭМС-2004. - СПб.: ВИТУ, 2004. — С. 331-336.
26. Tourne J. Micro-machining of Trenches to Form Shielded Transmission Lines.
Printed Circuit Design&Manufacture. 2004, № 4, p. 34—37.
27. Hogan M. Circuit Timing Analysis: Mastering A Lost Art Timing and Signal Integrity
Technical Marketing Engineer for High-Speed Design Tools. September 2001.
28. Hogan M. Advanced Routing Techniques: The Importance of Timing. April 2003.
Mentor Graphics Corporation 2003.
29. Hogan M. A Matter of Timing. Printed Circuit Design & Manufacture. 2004,
№ 12, p. 22-27.
30. Кечиев Л.Н., Шнейдер В.И. Современные проблемы обеспечения ЭМС и
целостности сигнала электронных модулей быстродействующих цифровых элек-
тронных средств. «Технология ЭМС», 2004, № 4.— С. 50—59.
31. Уилльямс Т. ЭМС для разработчиков продукции: пер. с англ. / Т. Уильямс. —
М.: Издательский дом «Технологии», 2004. — 540 с.
32. КечиевЛ.Н. Защита электронных средств от воздействия статического элек-
тричества: учебное пособие для вузов. / Л.Н. Кечиев, Е.Д. Пожидаев. — М.:
Издательский Дом «Технологии», 2005. — 352 с.
33. Цифровые интегральные микросхемы: справочник / П.П. Мальцев,
Н.С. Долидзе, М.И. Критенко и др. — М.: Радио и связь, 1994. — 240 с.
34. Скарлетт Д. Транзисторно-транзисторные логические интегральные схемы
и их применение: пер. с англ. / Д. Скарлетт. — М.: Мир, 1974. — 288 с.
35. ЭМС для систем и установок /Т. Уиллямс, К. Армстронг — М.: Издатель-
ский Дом «Технологии», 2004 г. — 508 с.
36. Transmission-Line Effects Influence High Speed CMOS. Fairchild Semicon-
ductor, AN-393, 1998. - 8 p.
37. Нейман Л.Р. Теоретические основы электротехники: учебник для вузов: в
2 т. — 3-е изд., перераб. и доп. — Л.: Энергоиздат. Ленингр. отд-ние, 1981. — Т. 2. —
416с.
38. Intel. Package Databook: 1 — Introduction, 2 — Package/Module/PC Card
Outlines and Dimensions, 4 — Performance Characteristics of 1C Packages.
39. IPC-D-317A, «Design Guidelines for Electronic Packaging Utilizing High-Speed
Techniques,» January 1995, IPC. — 220 p.
Литература
611
40. Иоссель Ю.Я. Расчет электрической емкости / Ю.Я. Иоссель, Э.С. Коча-
нов, М.Г. Струнский. — 2-е изд., перераб. и доп. — Л.: Энергоиздат, Ленинград,
1981. - 288 с.
41. Калантаров П.Л. Расчет индуктивностей: справочная книга / П.Л. Калан-
таров, Л. А. Цейтлин. 3-е изд., перераб. и доп. — Л.: Энергоатомиздат. Ленингр. отд-
ние, 1986. - 488 с.
42. Base Materials for High Speed, High Frequency PC Boards Rick Hartley, March
2002, Published in PCB & A
43. Потапов Ю.В. Решаем проблемы ЭМС. Технологи и материалы: печатные
платы, 2002, №2. — С. 92-95.
44. Hartley R. The Impact of Material Selection. Printed Circuit Design. 2002, № 3,
p. Ю-14, 44, 45.
45. Leys D. Best Materials for 3—6 GHz Design. Printed Circuit Design & Manufac-
ture. 2004, № 11, p. 34-39.
46. I EC 60194:2006. Printed board design, manufacture and assembly — Terms and
definitions. — 120 p.
47. Алешин А.В., Кечиев Л.Н., Шнейдер В.И. Обеспечение целостности сигнала
при проектировании печатных плат: сборник докладов VIII НТК по ЭМС и элект-
ромагнитной безопасности. ЭМС-2004. - СПб, ВИТУ, 2004. - С. 331-336.
48. Кечиев Л.Н. Численные методы определения емкостных параметров мно-
гопроводных линий связи / Л.Н. Кечиев, А.Ю. Воробьев, С.А. Королев, П.В. Сте-
панов. — М.: Изд-во МГИЭМ, 1999. — 77 с.
49. Handbook of Electronic System Design/Ed. by Harper C.A. — N.Y., 1980. —
659 p.
50. Кечиев Л.Н. Численные методы анализа многопроводных линий связи /
Л.Н. Кечиев, А. Ю. Воробьев, С. А. Королев, П. В. Степанов. — М.: Изд-во
МГИЭМ, 2000. - 50 с.
51. Jouppi М. Current and Conductors. Printed Circuit Design & Manufacture. 2003,
№ 5, p. 33-38.
52. Brooks D. Temperature Rise in PCB Traces. www.ultraCAD.com. 1998. — lip.
53. Matick R. Transmission Lines for Digital and Communication Network. — N.Y.,
1969. - 360 p.
54. Кечиев Л.Н. Метод граничных элементов в анализе коммутационных плат /
Л.Н. Кечиев, О.С. Гердлер, И.В. Степанов. — М.: Изд-во МГИЭМ, 2001. — 56 с.
55. КечиевЛ.Н., Тумковский С.Р., Шевцов М.А. Расчет электрофизических па-
раметров линий связи на начальной стадии проектирования с применением ма-
тематического пакета Mathematica: сборник докладов VII Российской НТК по
ЭМС. - Изд. ВИТУ, СПб, 2002. - С. 266-271.
56. Кечиев Л.Н., Цирин И.В. Численный метод расчета паразитных емкостей
элементов РЭА сложной конфигурации: труды VII Межд. симпозиума по ЭМС. —
Вроцлав, 1984, ч. 2. - С. 695-701.
57. Князев А.Д. Конструирование радиоэлектронной и электронно-вычисли-
тельной аппаратуры с учетом электромагнитной совместимости / А.Д. Князев,
Л.Н. Кечиев, Б.В. Петров. — М.: Радио и связь, 1989. — 224 с.
58. Kammler D. Calculation of Characteristics Admittances and Coupling Coefficients
for Strip Transmission Lines. IEEE Trans, on MTT. 1968, v. MTT-16, № 11, p. 925—937.
612
Литература
59. Справочник по расчету и конструированию СВЧ полосковых устройств /
С.И. Бахарев, В.И. Вольман, Ю.Н. Либ и др. - М.: Радио и связь, 1982. — 328 с.
60. Лаврик В.И. Справочник по конформным отображениям / В.И. Лаврик,
В.Н. Савенков. — Киев: Наукова думка, 1970. — 252 с.
61. Лаврентьев М.А. Методы теории функций комплексного переменного /
М.А. Лаврентьев, Б.В. Шабат. — М.: Наука, 1973. - 736 с.
62. Дубицкий С.Д. ELCUT — конечно-элементный анализ низкочастотного элек-
тромагнитного поля. - EDA Express, № 12, октябрь 2005. — С. 24-29.
63. Справочник по специальным функциям с формулами, графиками и ма-
тематическими таблицами / под ред. М. Абрамовица, И. Стигана. — М.: Наука,
1979. - 832 с.
64. Jonson Н. High-Speed Signal Propagation. Н. Jonson and Signal Consulting,
2002, p. 5.1-5.3.
65. Cohen T. Practical Guidelines for the Implementation of Back Drilling Plated
Through Hole Vias in Multi-gigabit Board Application. Web ProForum Tutorials,
p. 1—20. — http://www.iec.org.
66. Jonson H. Via Inductance. High-Speed Digital Design. Online Newsletter, v. 6,
№ 04. www.sigcon.com/Pubs/news/6_04.htm
67. Brooks D. Microstrip Propagation Times. Slower Than We Think. Ultra CAD
Design, Inc., 2002, 10 p.
68. Гроднев И.И. Линии связи: учебник для вузов / И.И. Гроднев, С.М. Вер-
ник. — 5-е изд., пераб. и доп. — М.: Радио и связь, 1988. — 544 с.
69. Patel G., Rothstein К. Signal Integrity Characterization of Printed Circuit Board
Parameters. — TERADYNE, 2002. — 8 p.
70. Brooks D. PCB Impedance Control: Formulas and Resources. Printed Circuit
Design Magazine, 1998, March, p. 4.
71. Burkhardt A. J., Gregg C.S., Staniforth J.A. Calculation of PCB Impedance. —
p. 6.
72. IPC-2141. Controlled Impedance Circuit Board and High-Speed Logic Design.
1996.
73. Кечиев Л.Н., Гердлер О. С, Шевчук А.А. Задачи обеспечения ЭМС при про-
ектировании печатных плат. «Технологии ЭМС», 2002, № 2. — С. 32—40.
74. An Introduction to Jitter in Communication Systems. Maxim, AN 1916, Mar.
06, 2003. - p. 8.
75. Garat G., Bogatin E. Determining Deterministic Jitter. Mentor Graphics. February
2004.
76. Кечиев Л.Н. Алешин А. В. Расчет помех отражения в линиях связи. «Тех-
нологии ЭМС», 2002, № 2. - С. 53-56.
77. Кечиев Л.Н. Расчет помех отражения в линиях связи быстродействующих
цифровых устройств: учеб, пособие / Л.Н. Кечиев, А.В. Алешин, С.Р. Тумковс-
кий, А.А. Шевчук. — М.: Изд-во МИЭМ, 2002. — 86 с.
78. Кечиев Л.Н.. Алешин А.В. Расчет помех отражения в длинных линиях свя-
зи с применением пакета Mathematica. V Международный симпозиум по ЭМС
и электромагнитной экологии: сборник науч, докладов. — СПб, 2003.
79. Кечиев Л.Н., Алешин А. В. Расчет характеристик коротких и длинных линий
с помощью пакета Mathematica. Электромагнитная совместимость и интеллекту-
Литература
613
альные здания: сборник науч, трудов / под ред. Л.Н. Кечиева, П. В Степанова. — М.:
«ФЭД+», 2000.
80. Кечиев Л.Н., Алешин А. В., Тумковский С. Р., Шевчук А. А. Разработка про-
граммы расчета помех отражения в линиях связи печатных плат с применением
пакета Mathematica и возможностью использования через всемирную сеть Ин-
тернет. Электромагнитная совместимость и проектирование электронных средств:
сборник научн. трудов / под ред. Л. Н. Кечиева. — М.: Изд-во МИЭМ, 2002. —
С.46-49.
81. Line Driving and System Design. National Semiconductor, AN-991, 1995. —
46 p.
82. Ott H. Partitioning and Layout of a Mixed-Signal PCB. Printed Circuit Design,
2001, June, p. 8-11.
83. Me Morrow S. Handling Signal Return Current. Printed Circuit Design. 2002,
№ 9. - P. 12-14, 16.
84. Riazi A. Via Modeling for High-Speed Simulation. Part 2. Printed Circuit
Design&Manufacture. 2003, № 10, p. 38-40.
85. Kohlmeier P.Via Modeling. Printed Circuit Design & Manufacture. 2005, № 12,
p. 26-28.
86. Глебович Г. В. Широкополосные линии передачи импульсных сигналов /
Г. В. Глебович, И. П. Ковалев. — М.: Сов. радио, 1973. — 230 с.
87. Кечиев Л. И, Хабарова Л. В. Помехи в соединителях линий передач быс-
тродействующей аппаратуры: труды VII Междунар. симпозиума по ЭМС. Ч. I. —
Вроцлав, 1984.- С. 495-501.
88. Кечиев Л.Н., Хабарова Л. В., Зима М. А. Разработка модели соединителя для
быстродейсвующей аппаратуры. «Радиотехника», 1989, № 3. — С. 29—30.
89. Hill D., Cavcey К., Johnk R. Crosstalk Between Microstrip Transmission Lines.
IEEE Trans, on EMC, 1994, v. 36, № 4, p. 314-321.
91. White, Donald R. A Handbook on Electromagnetic Interference and Compa-
tibility, Volume 3. Gainesville, Va: Don White Consultants, 1987. — 870 p.
92. ELCUT. Руководство пользователя. - Производственный кооператив TOP —
СПб, 2005. - 257 с.
93. Дубицкий С.Д. ELCUT 5.1 — Платформа разработки приложений анализа по-
лей. —Exponenta Pro. «Математика в приложениях», № 1(5), 2004. — С. 20—26.
94. Дубицкий С. Д., Поднос В. Г. ELCUT — Инженерная система моделирова-
ния двумерных физических полей. «CADMaster», 2001. № 1.— С. 17—21.
95. Кечиев Л.Н. Заземление электронного оборудования в системах телеком-
муникаций / Л.Н. Кечиев, П.В. Степанов. — М.: МИЭМ, 2001. — 82 с.
96. Кечиев Л.Н., Степанов П.В. ЭМС: стандартизация и функциональная бе-
зопасность /Л.Н. Кечиев, П.В. Степанов. - М.: МИЭМ, 2001. — 82 с.
97. Harrer И, Pros Н., Winkel, Т.-М., Becker W.D., Stoller H.I., Yamamoto М., Abe
S., Chamberlin D.J., Katopis G.A. First and second-level Packaging for the IBM eServer
z900. IBM, v. 46, № 4/5, 2002, p. 1-16.
98. Chitwood S., Zheng J. IR Drop in High-Speed IC Packages and PCBs. Printed
Circuit Design&Manufacture. 2005, № 4, p. 16—18.
99. Fang J., Zhao J. Low-Impedance Power Delivery over Broad Frequencies. Printed
Circuit Design&Manufacture. 2003, № 9, p. 26—28.
614
Литература
100. Li Р. Designing for Minimal Jitter When Using PI49FCT3805D/32805 Clock
Buffers. Pericom, AN 24, 2000. - 3 p.
lOl. Djordjevic A.R., Sarkar T.K. An Investigation of Delta-I Noise on Integrated
Ciruits. IEEE Trans, on EMC, 1993, v. 35, № 2, p. 134-147.
102. Taking Advantage of ECL Minimum-Skew Clock Drivers. Fairchild Semicon-
ductor Corp. AN 817, 2000. — 10 p.
103. Hubing Т.Н., Drewniak J.L., Van Doren T.P., Hockanson D.M. Power Bus
Decoupling on Multilayer Printed Circuit Boards. IEEE Trans, on EMC, 1995, v. 37,
№ 2, p. 155-166.
104. Smith L., Anderson R., Forehand D., Pelc T., Roy T. Power Distribution System
Design Methodology and Capacitor Selection for Modern CMOS Tehnology. IEEE Trans,
on Advanced Packaging, 1999, v.22, № 3, p. 16—32.
105. Кечиев Л.Н., Степанов П.В. ЭМС и информационная безопасность в
системах телекоммуникаций/Л.Н. Кечиев, П.В. Степанов. - М.: Издательский
Дом «Технологии», 2005. — 320 с.
106. Кечиев Л.Н., Гердлер О. С., Шевчук А. А. Анализ влияния конструкции сет-
чатых экранов на волновое сопротивление линий связи в многослойных печат-
ных платах. «Технологии ЭМС», 2002, № 2. — С. 41—43.
107. Kjar М. High Speed Layout Design Guidelines. - Freescale Semiconductor,
AN2536, 2005. - 26 p.
108. Куэстад Ф. Проектирование систем распределенного питания. «Элект-
роника», 1990, № 7. — С. 39—48.
109. Armstrong К. Advanced РСВ design and Layout for EMC. Part 4 — Reference
Planes for 0 V and power. EMC&Compliance Journal, 2001, p. 13—43.
110. Brooks D. ESR and Bypass Capacitor Self-Resonant Behavior: How to Select
Bypass Caps, www.ultracad.com.
111. Cain D. The Effects of ESR and ESL in Digital Decoupling Applications. - AVX
Corp., 1997. — 5 p.
112. Mears J. Transmission Line RAPIDESIGNER Operation and Applications
Guide/ AN-905, National Semiconductor Corporation, 1996. — 28 p.
113. KauferS., Crisafalu K. Terminating Differential Signals on PCBs. «Printed Circuit
Design magazine», March 1999. p. 25
114. Ma J. Termination Schemes and Design Guidelines for 3.3V LVPECL Driver. —
Pericom Semiconductor Corp./ AN 73, 2004. — 2 p.
115. Poniatowski S. High Speed Transmission with LVDS Link Devices. AN-1059.
National Semiconductor. June 1998. — 6 p.
116. Riazj A. TDR for Differential Pair Characterization. Part 2. Printed Circuit
Design&Manufacture. 2005, № 12, p. 30—31.
117. Low-Voltage Differential Signaling. — Web Pro Forum Tutorials, 15 p. -
www.iec.org
118. Board Design Guidelines for LVDS Systems. Altera. White Paper. 2000, v. 1. -
P. 6.
119. Armstrong K. Advanced PCB design and Layout for EMC. Part 6 — Transmission
Lines - 3rd. EMC&Compliance Journal, 2001, p. 1—30.
120. Кечиев Л.Н., Алешкина H.B., Степанов П.В. Основы сертификации элек-
тронных средств: учеб, пособие /Л.Н. Кечиев, Н.В. Алешкина, П.В. Степанов. —
М.: МИЭМ, 2002. - 94 с.
Литература
615
121. Paul C. Introduction to Electromagnetic Compatibility. — Wiley Inter Science,
1992. - 766 p.
122. Электромагнитная совместимость подвижных объектов: учебное посо-
бие / Балюк Н.В., Болдырев В.Г., Булеков В.П. и др. — М.: Изд-во МАИ, 2004. —
648 с.
123. Кечиев Л.Н., Гердлер О.С., Шевчук А.А. Задачи обеспечения ЭМС при про-
ектировании печатных плат. Электромагнитная совместимость и проектирование
электронных средств: сборник науч, трудов / под ред. Л.Н. Кечиева. — М.: Изд-
во МИЭМ, 2002. - С. 17-32.
124. Юркевич Л.В. Прикладные программы в области ЭМС: сборник докла-
дов VII Российской научно-технической конференции по ЭМС, 2002. — СПб,
2002. - С. 574-578.
125. Чермошенцев С.Ф. Многокритериальная оптимизация электромагнитной со-
вместимости межсоединений цифровых печатных плат генетическими алгоритмами:
сборник научных трудов Всероссийского симпозиума «Проблемы ЭМС технических
средств» / под ред. Л.Н. Кечиева. — М.: МИЭМ, 2002. — С. 72—74.
126. PCB Design Studio: технология от Cadence — прорыв в проектировании
печатных плат. — http://www.cadmaster.ru
127. Пример анализа целостности сигнала в программе Protel DXP — http://
www.eltm.ru
128. Потапов Ю. Обзор САПР печатных плат — EDA Expert, 4/2003.
129. IBIS-standart, ver. 4.2C. — IBIS open forum, 2004. — 117 c.
130. КечиевЛ.Н., Лемешко H.B. Использование IBIS-моделей для создания вир-
туальных прототипов электронных устройств. «Технология приборостроения»,
2005, № 2 (14). - С. 41-52.
131. Кечиев Л.Н. Методы экспериментального определения выходных емко-
стей LVDS-буферов для IBIS-моделей. Электромагнитная совместимость, про-
ектирование и технология электронных средств/Л.Н. Кечиев, Н.В. Лемешко. -
М.: Изд. МИЭМ, 2004. - С. 39-45.
132. Кечиев Л.Н., Лемешко Н.В. Построение модели элементарного цифро-
вого устройства на основании его IBIS-описания. Моделирование нелинейных
сопротивлений, емкостей и индуктивностей. Электромагнитная совместимость,
проектирование и технология электронных средств. — М.: Изд. МИЭМ, 2004. —
С. 29-39.
133. КечиевЛ.Н., Лемешко Н.В. Методы моделирования цифровых узлов элек-
тронных приборов. «Технологии приборостроения», 2006, № 1 (17). — С. 36—43.
134. КечиевЛ.Н., Лемешко Н.В. Моделирование помех в шинах питания циф-
ровых устройств на основе IBIS-описания интегральных схем. «Технологии ЭМС»,
2006, № 1 (16). - С. 9-18.
135. Кечиев Л.Н., Соловьев А.В. Методика анализа влияния технологических
факторов печатных плат на их электрофизические параметры «Технологии при-
боростроения», 2006, № 1 (17). — С. 24—35.
Книги издательской группы компаний ООО «Группа ИДТ» можно
приобрести
> В издательстве
123182, Россия, Москва, пл. Академика Курчатова, д. 1, стр. 3
(ст. м. «Октябрьское поле»)
Контактное лицо: Смолин А.М.,
тел. (495) 609-6897 (доб. 220); e-mail: smolin@techizdat.ru
Интернет-магазин: www.techizdat.ru
> В магазинах
«Библио-Глобус», «Московский Дом Книги», «Дом технической книги»,
«Молодая Гвардия», Торговый Дом книги «Москва»,
«Дом книги» в Братеево, «Новый книжный», «Библиосфера»,
«Республика», Санкт-Петербургский Дом Книги»
Кечиев Леонид Николаевич
ПРОЕКТИРОВАНИЕ ПЕЧАТНЫХ ПЛАТ
ДЛЯ ЦИФРОВОЙ БЫСТРОДЕЙСТВУЮЩЕЙ
АППАРАТУРЫ
Главный редактор К.Н. Стась
Исполнительный директор А.В. Фионичев
Выпускающий редактор Т.А. Рыбакова
Верстка В. В. Семёнов
Художник Е.А. Егорова
Иллюстрации К. В. Марченков
Корректор Э.А. Веденяпина
Подписано в печать 19.06.2007. Формат 70x100/16
Бумага офсетная №1. Печать офсетная. Усл. печ. л. 43,12
Тираж 2000 экз. Заказ № 1527
ООО «Группа ИДТ»
123098, Россия, Москва, ул. Маршала Новикова, д. 5
Тел./факс (495) 609-68-99, www.techizdat.ru
Отпечатано с готового оригинал-макета
на ОГУП «Областная типография «Печатный двор»
432049, г. Ульяновск, ул. Пушкарева, 27.
ПРОЕКТИРОВАНИЕ ПЕЧАТНЫХ ПЛАТ
для
ЦИФРОВОЙ БЫСТРОДЕЙСТВУЮЩЕЙ АППАРАТУРЫ
Кечиев Леонид Николаевич
— доктор
технических наук, профессор, акаде-
мик Международной академии инфор-
матизации, обладатель диплома Про-
фессионального инженера России,
лауреат конкурса инженеров России.
Заведующий кафедрой «Радиоэлек-
тронные и телекоммуникационные
устройства и системы» МИЭМ. Один из
ведущих специалистов России в облас-
ти конструирования радиоэлектронных
средств и электромагнитной совмести-
мости. Член правления Гильдии профессиональных техноло-
гов приборостроения. Возглавляет Комитет по ЭМС Москов-
ского правления Союза научных и общественных объедине-
ний. Главный редактор журнала «Технологии ЭМС».
Область научных интересов — проектирование электронных
средств с учетом ЭМС. Автор более 200 научных работ в этом
направлении, в том числе в составе авторских коллективов
книг «Конструирование радиоэлектронной и электронно-
вычислительной аппаратуры с учетом ЭМС» (1989), «Электро-
магнитная совместимость подвижных объектов» (2004), «Защи-
та электронных средств от воздействия статического электри-
чества» (2005), «ЭМС и информационная безопасность в систе-
мах телекоммуникаций» (2005).