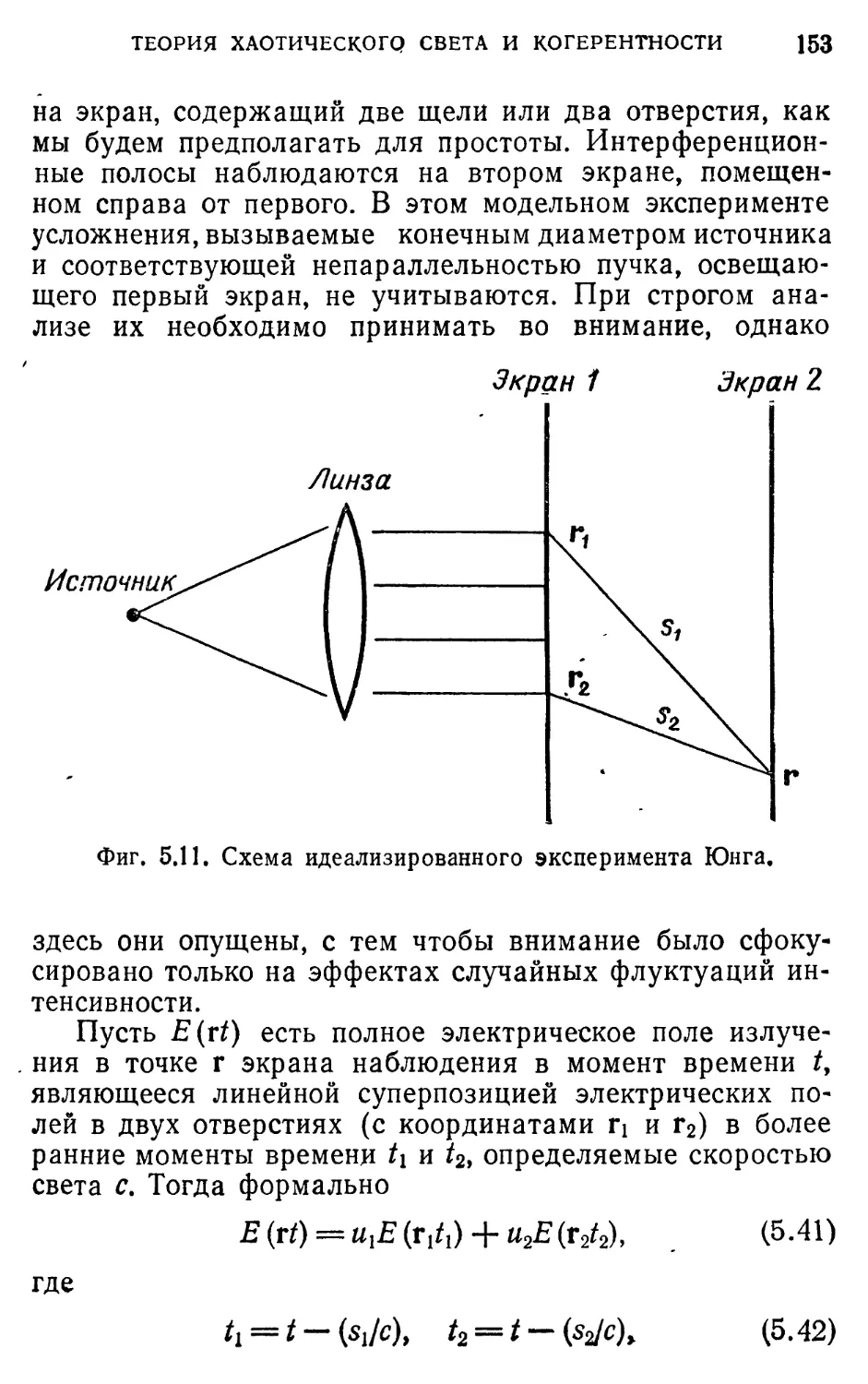
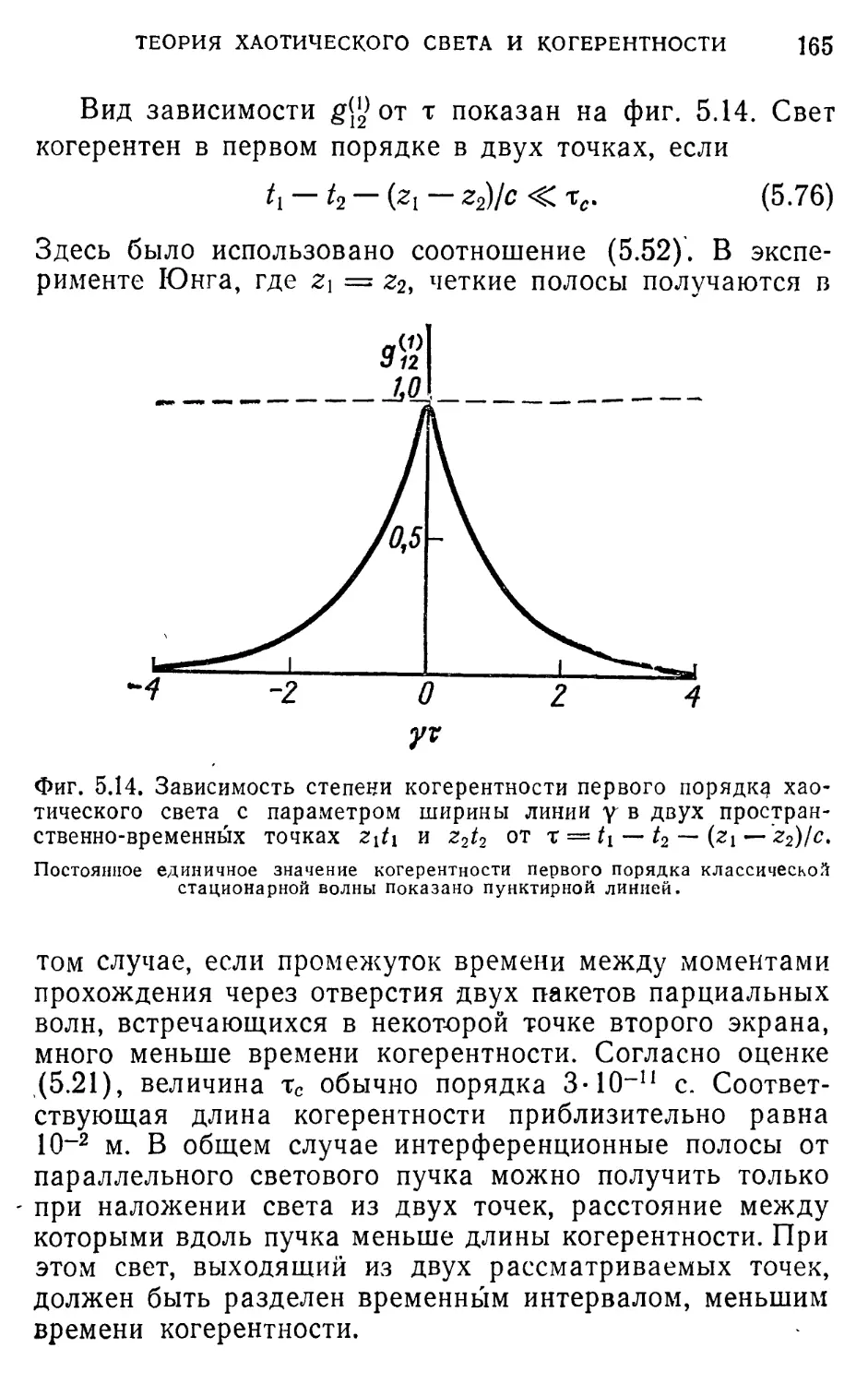
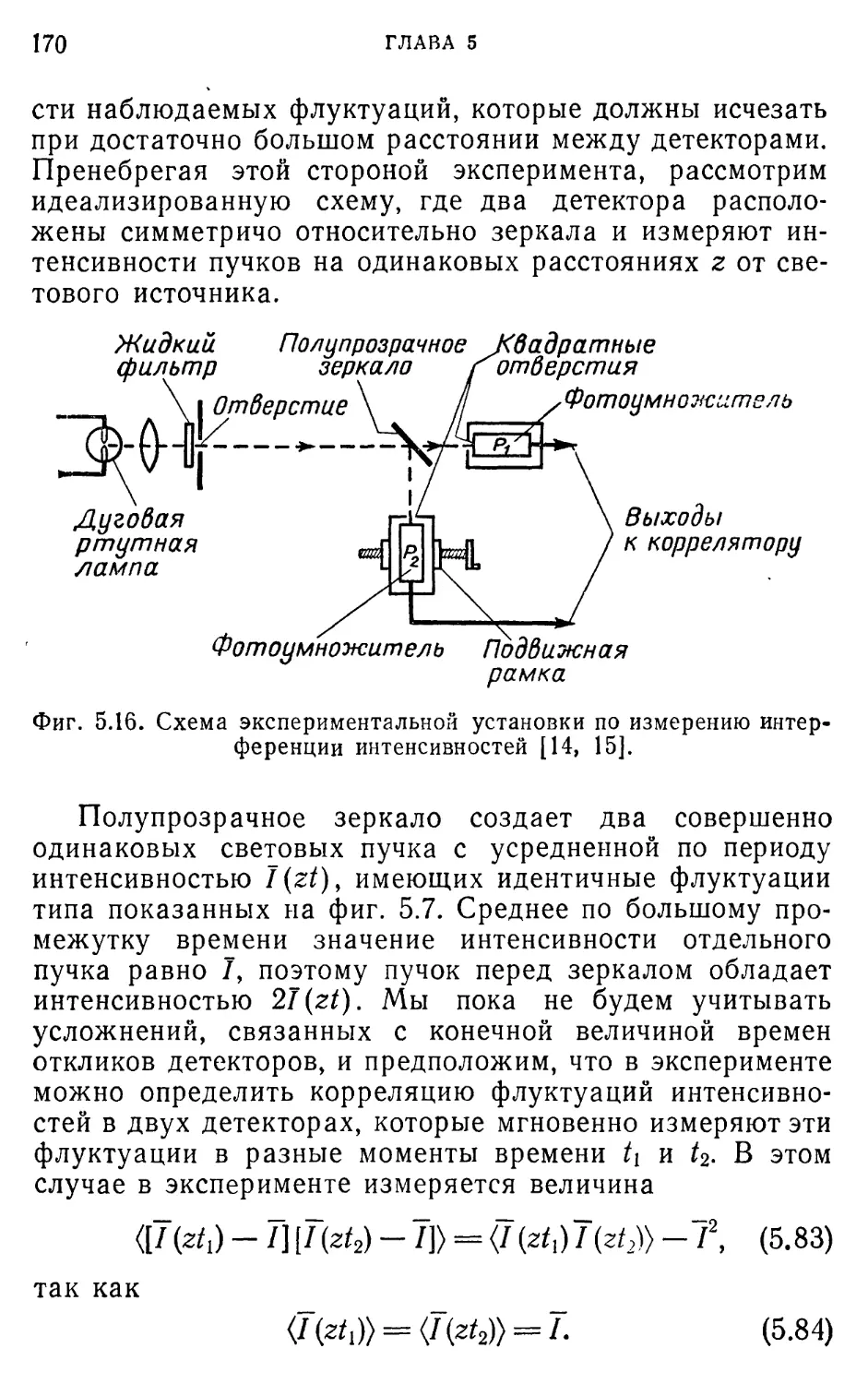
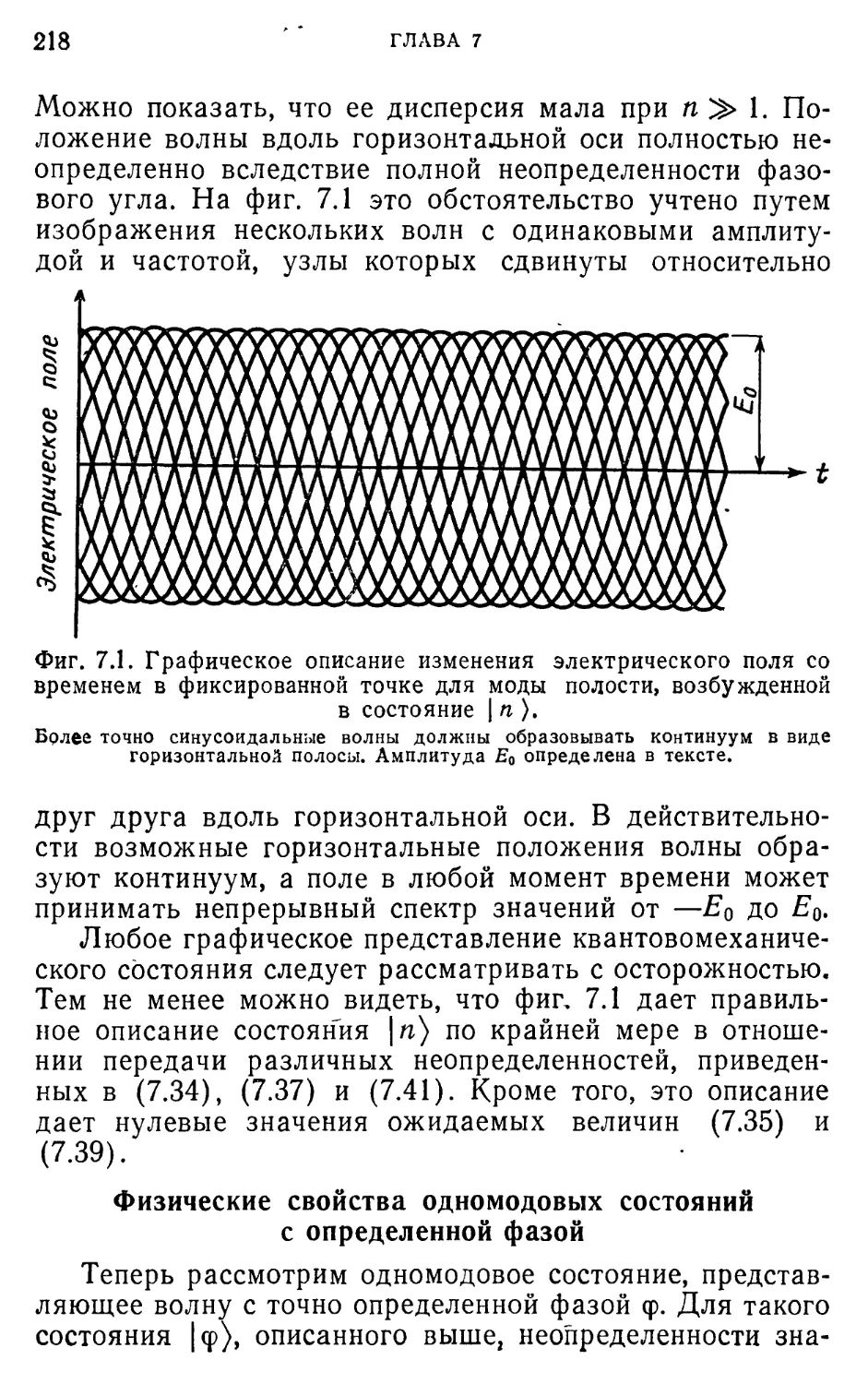
Автор: Лоудон Р.
Теги: теория света физика электромагнетизм спектроскопия переводная литература издательство мир квантовая оптика
Год: 1976
Текст
Rodney Loudon
The Quantum Theory
Of Light-
Clarendon Press. Oxford
1973
Р. Лоудон
Квантовая теория
света
Перевод с английского
А. А. КОЛОКОЛОВА
под редакцией
проф. Г. В. СКРОЦКОГО
Издательство «Мир»
Москва 1976
УДК 535.14
Книга представляет собой учебник, в котором
детально освещены основы квантовой теории
электромагнитного излучения в оптическом диапазоне и его
взаимодействия с веществом. В кнше содержится практически
весь нужный для понимания материал, так что у
читателя не возникнет необходимости обращаться к каким-
либо дополнительным руководствам. В виде задач
рассмотрено около 75 различных важных проблем квантовой
оптики. Представлены и проиллюстрированы все
основные методы описания взаимодействия излучения с
веществом. Даже при изложении традиционных вопросов
автор обычно обращается к работам последних лет,
поэтому все разделы книги отвечают современному уровню
знаний.
Книга предназначена для аспирантов и студентов
старших курсов, специализирующихся в области
квантовой оптики, квантовой электроники, теории
взаимодействия излучения с веществом, физики и техники лазеров,
спектроскопии.
Редакция литературы по физике
This translation of The Quantum Theory
of Light A st edition 1973) is published
by arrangement with The Oxford
University Press
© Oxford University Press 1973
© Перевод на русский язык, «Мир», 1976
Р. Лоудон
КВАНТОВАЯ ТЕОРИЯ СВЕТА
Редактор В. И. Самсонова
Художник А. И. Когановский Художественный редактор В. К. Самойлов
Технический редактор Т. А. Максимова
Сдано в набор 26/IX 1975 г. Подписано к печати 25/11 1976 г.
Бумага тип. № 3 84X108V32=7\63 бум. л. 25,62 усл. печ. л. Уч.-изд. л. 23,79.
Изд. № 2/8456. Цена1р.85 к. Зак. 885
ИЗДАТЕЛЬСТВО «МИР» МосТсва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени Ленинградская типография № 2
имени Евгении Соколовой Союзполиграфпрома при Государственном
комитете Совета Министров СССР по делам издательств, полиграфии
и книжной торговли. 198052, Ленинград, Л-52, Измайловский проспект, 29«
20405-072
Л 041@1)—76 72_7в
Предисловие редактора
Быстрое развитие квантовой электроники и квантовой
оптики привело к появлению на мировом книжном рынке
большого числа книг, предназначенных для читателей
с самым различным уровнем подготовки. Перед их
авторами стояла задача изложить результаты исследований,
опубликованные в специальных научных журналах.
Лучшие из этих книг уже переведены на русский язык.
Среди них учебники Ф. Бертена (изд-во «Мир», 1971) я
Р. Пантела и Г. Путхофа (изд-во «Мир», 1972),
вышедшие под одинаковыми названиями «Основы квантовой
электроники», и монографии У. Люиселла «Излучение и
шумы в квантовой электронике» (изд-во «Наука», 1972)
и А. Ярива «Квантовая электроника и нелинейная
оптика» (изд-во «Сов. радио», 1973). Этот перечень, по
мнению редактора, удачным образом дополняется
настоящей книгой.
Каждая из перечисленных книг по-своему
оригинальна. Их авторам пришлось отобрать из большого и не
всегда согласующегося материала, обладавшего к тому
же различной научной ценностью, то, что прошло
испытание временем и уже более или менее устоялось.
Предлагаемая вниманию читателей книга Р. Лоудона,
никоим образом не перекрываясь по содержанию с
отмеченными выше монографиями, содержит свежее,
добротное и ясное изложение широкого круга вопросов,
причем автор обращает особое внимание на физическую
сторону рассматриваемых явлений. Содержащиеся
6
ПРЕДИСЛОВИЕ РЕДАКТОРА
в книге задачи органически дополняют излагаемый
теоретический материал.
Книга предназначена для читателя, знакомого с
основами теории поля и квантовой механики в размере
программ физических и инженерно-физических факультетов
вузов. Математические выкладки проведены в ней
достаточно подробно, для того чтобы все опущенные
вычисления можно было восстановить, не прибегая к
дополнительной литературе. При изложении традиционных
разделов квантовой оптики, таких, найример, как
излучение абсолютно черного тела или вопрос об импульсе,
переносимом электромагнитным полем и т. п.гавтор
подходит с современной точки зрения и связывает их с
теоретическими и экспериментальными работами,
выполненными в последние годы. Сравнительно скупые ссылки
на оригинальные работы предназначены скорее для
освещения истории вопроса.
Несмотря на широкий охват материала, относящегося
к квантовой оптике, в книгу не вошел ряд важных
вопросов квантовой теории света. В частности, не
рассматриваются когерентные эффекты в двухуровневых
системах: сверхизлучение [1—3], световое, или фотонное, эхо
[4—7], явление самоиндуцироваиной прозрачности [8—12],
оптические нутации и т. п. В настоящее время эти
эффекты, составляющие обширную область квантовой
оптики (и радиофизики), интенсивно изучаются как
теоретически, так и экспериментально. Следует заметить, что
эти вопросы еще не нашли "отражения не только в
учебной, но и в монографической отечественной литературе.
Для более глубокого ознакомления с теорией
основных когерентных эффектов в двухуровневых системах,
кроме упомянутых обзорных работ [5, 10, 12] можно
рекомендовать книги [13, 14]. Новейшие достижения в
области использования лазерного излучения для
спектроскопии сверхвысокого разрешения подробно
рассмотрены в монографии [16].
Автор настоящей книги любезно прислал для ее
русского издания список замеченных в английском издании
опечаток, а также сделал некоторые исправления в
тексте. Все они были учтены при редактировании книги.
ПРЕДИСЛОВИЕ РЕДАКТОРА-
7
Редактор выражает благодарность проф. Р. Лоудону
за предисловие, специально написанное им для русского
издания книги.
Мы надеемся, что учебная монография Р. Лоудона
принесет большую пользу и доставит удовольствие
широкому кругу научных работников, инженеров,
аспирантов и студентов, специализирующихся в области
квантовой электроники и когерентной квантовой оптики.
проф. Г. Скроцкий
Москва
МФТИ
сентябрь 1975 г.
ЛИТЕРАТУРА
1. Dicke R. Я., Phys. Rev., 93, 99 A954).
2. Фаин В. М.у УФН, 64, 274 A958), в кн. Квантовая радиофизика,
т. 1, изд-во .«Сов. радио», 1972.
3. Stenholm S., Phys. Lett., 6c, № 1 A973).
4. Kurnit N. Л., Abella I. £>., Hartman S. A., Phys. Rev. Lett., 13,
567 A964); Phys. Rev., 141, 391 A966).
5. Abella I. D., Echoes at optical frequencies, в кн. Progress in
optics, v. 7, p. 141, North-Holland, Amsterdam — London, 1969.
6. Ораевский А. Я., УФН, 91, 181 A967).
7. Известия АН СССР, сер. физ. 37, № ю A973).
8. McCall S. L., Hahn E. L., Phys. Rev. Lett., 18, 908 A967); Phys.
' Rev., 183, 457 A969).
9. Slusher R. £., Gibbs H. M., Phys. Rev., 5A, 1634 A972); Phys.
Rev., 6A, 1255 A972).
10. Крюков П. Г., Летохов В. С, УФН, 99, 169 A969).
И. Lamb G. L.y jr. Rev. Mod. Phys., 43, 99 A971).
12. Полуэктов И. Л., Попов Ю. М.у Ройтберг В. С, УФН, 114, 97
A974).
13. Nussenzveig H. M.y Introduction to quantum optics, Gordon and
Breach, London — New York —Paris, 1973.
14. Арекки Ф., Скалли М., Хаген Г., Вайдлих В., Квантовые
флуктуации излучения лазера, изд-во «Мир», 1974.
15. Летохов В. С, Чеботаев В. Я., Принципы нелинейной лазерной
спектроскопии, изд-во «Наука», 1975»
Предисловие автора к русскому изданию
Русское издание этой книги стало возможным
благодаря усилиям пррф. Г. В. Скроцкого по осуществлению
перевода, поэтому я считаю своим приятным долгом
поблагодарить его за проделанную работу.
.Содержание книги не отличается от содержания
английского издания 1973 г., за исключением нескольких
улучшений. Некоторые из рассмотренных проблем, в
частности статистика фотонов, неупругое рассеяние света
и нелинейная оптика, продолжают оставаться
развивающимися' областями исследования, в которых имеются
интересные достижения. Однако эта книга была
задумана в качестве вводного курса, поэтому в ней не было
сделано попытки охватить новейшие достижения.- За
последние несколько /лет основы квантовой теории света
не испытали каких-либо существенных изменений,
поэтому можно надеяться, что читатели СССР найдут
представленный здесь материал достаточным для
понимания настоящего и будущего развития квантовой
теории света.
Л Лоудон
Ист Бергхольд, Суффолк, Англия
1975
Предисловие автора
Все сведения по квантовой теории, необходимые для
объяснения экспериментов по изучению света и его
взаимодействия с веществом, до недавнего времени могли
быть изложены в соответствующей главе учебника по
квантовой механике. Знания теории скоростей переходов
для поглощения и излучения света атомом было
достаточно для понимания большинства спектроскопических
экспериментов. В книгах, посвященных теории
электромагнитного излучения и его взаимодействия с веществом,
таких, как «Квантовая теория излучения» Гайтлера, в
основном рассматривались фотоны высоких энергий, а
также обсуждались всевозможные ухищрения,
необходимые для учета релятивистских поправок и
перенормировок, устраняющих расходимость.
Относительно простые теоретические методы,
требуемые для анализа света видимого диапазона, были
пересмотрены в связи с изобретением лазера в 1960 г.
Объяснение экспериментов, в которых использовался лазерный
свет, привело к необходимости расширения ранее
развитой теории в нескольких направлениях. Высокая
интенсивность лазерного света делает возможным
наблюдение процессов, являющихся слишком слабыми для их
обнаружения с помощью света от обычного источника.
Наиболее впечатляющим примером служит совокупность
нелинейных оптических процессов, которые удалось
наблюдать только с изобретением лазера. Лазерный свет
как по своей природе, так и по интенсивности отличается
от света, получаемого от обычных тепловых источников.
10
ПРЕДИСЛОВИЕ АВТОРА
Это вызвало быстрое развитие теоретических методов,
на основе которых можно объяснить когерентные и
статистические свойства световых пучков от источников
разного типа. Для понимания внутренних механизмов
действия самого лазера требуется более тщательный анализ
взаимодействия атомов с электромагнитным излучением,
чем это необходимо при обсуждении других источников
света.
Изобретение лазера не только сделало возможным
проведение экспериментов нового типа, но также привело
к более детальному исследованию процессов,
наблюдавшихся ранее с помощью некогерентного света.
Примерами таких процессов могут служить рассеяние света
атомами и детектирование света с помощью
фотоэффекта. В каждом случае для получения более точных
результатов экспериментального исследования требуется
соответственно более тщательный теоретический анализ,
чем тот, который до этого казался адекватным.
Цель настоящей книги заключается в детальном
изложении основ теории, необходимой для понимания
свойств света и его взаимодействия с атомами. На
протяжении всей книги мы стремились к возможно более
простому изложению теории, лежащей ъ основе
последних достижений в данной области физики.
Следует подчеркнуть, что эта книга является сугубо
теоретической. Хотя необходимость объяснения
экспериментов определяла выбор теоретического материала и
экспериментальные результаты иногда использовались
для иллюстрации расчетов, однако за такими деталями,
как конструкция фотоэлемента или типы оптических
резонаторов, используемых для создания реальных
лазеров, читатель должен обращаться к другим источникам.
Мы предполагаем, что читатель знаком с основами
квантовой механики, электромагнитной теории и
статистической механики на уровне студентов старших
курсов. Действительно, изложение первых глав доступно
для студентов старших курсов, а материал первой
половины книги получен на основе записи курсов лекций,
прочитанных для студентов-выпускников и аспирантов
первого года обучения. Уровень второй половины книги
соответствует более подготовленным аспирантам и на-
ПРЕДИСЛОВИЕ АВТОРА
II
учным работникам, специально интересующимся
рассмотренными вопросами.
Предполагается, что последние главы, посвященные
оптике фотонов, теории лазера, рассеянию света и
нелинейной оптике, должны служить введением во все еще
активно развивающиеся области исследований. В конце
каждой из этих глав имеется список дополнительной
литературы, необходимый для понимания более
современных научных статей. Поскольку по замыслу эта книга
должна служить учебником, автор не стремился
приводить ссылки на оригинальные работы, содержащие
изложение теоретических расчетов, и все вычисления в ней
проведены без указания на источники.
Выбор материала определялся различными
ограничениями, из которых наиболее существенным являлось
ограничение области частот электромагнитного излучения,
в которой справедливы получаемые результаты.
Особенно большое внимание уделено теоретическим
требованиям к экспериментам с использованием видимого
света. Однако приближения, которые необходимо
сделать для описания видимого диапазона, пригодны и в
более обширной области частотного спектра. Нижний
предел этой области определяется из условия, что при
комнатной температуре на соответствующей частоте
должно отсутствовать заметное тепловое возбуждение.
Это определяет нижний предел по частоте порядка
1013 Гц, лежащий э далекой инфракрасной области.
Самые высокие рассматриваемые частоты должны
быть такими, чтобы фотоны еще не могли передать
взаимодействующим с ними электронам энергию,
достаточную для приобретения ими скорости, близкой к скорости
света. Если скорость электрона должна быть меньше
одной десятой скорости света, то частота фотона должна
быть меньше 1018 Гц. Понятия «видимый свет» и
«оптические частоты» будут использоваться для обозначения
частотной области от 1013 до 1018 Гц, хотя, строго говоря,
свет является видимым только в узкой полосе частот
вблизи 5-1014 Гц.
Далее, выбор материала ограничен природой
вещества, с которым рассматривается взаимодействие света,
Всюду предполагается, что атомы или молекулы нахо«
12
ПРЕДИСЛОВИЕ АВТОРА
дятся в газообразном или жидком состоянии и
ориентированы случайным образом. В частности, в книге нет
анализа важных изменений, происходящих с некоторыми
оптическими эффектами в тех случаях, когда атомы
расположены в регулярной кристаллической структуре.
Выбор тематики, особенно для последних глав, также до
некоторой степени произволен. Например, можно было
бы включить анализ эффектов, связанных с
распространением импульса, таких, как фотонное эхо,
самоиндуцированная прозрачность, а также теорию импульсного
лазера. Однако, по мнению автора, рассмотренные в
книге вопросы представляют более общий интерес, чем
те, которые были опущены.
В тексте имеется около 75 задач. Часть из них
предназначена для воспроизведения некоторых этапов
довольно кратких выводов, другие служат интересными ил*
люстрациями более общих результатов. Во всех
вычислениях используется система СИ.
В заключение дается замечание об использовании
классической и квантовой теории. В книге имеются
вычисления, данные на основе классической теории, на
основе так называемой полуклассической теории, в
которой свет описывается классически, а атомы — квантово-
механически, и на основе последовательной квантовой
теории, в которой квантовая механика используется для
описания как,света, так и атомов. В частности,
классическая и полуклассическая теории^применяются в первых
главах книги. Эти вычисления имеют то преимущество,
что они иногда позволяют исследовать излучательные
процессы на основе наглядных классических моделей.
В действительности существует мнение, что почти все
излучательные процессы могут быть описаны с помощью
соответственно расширенных полуклассических теорий
без применения квантовой механики к
электромагнитному полю. Мы не придерживаемся этой точки зрения и
предполагаем, что свойства фотонов можно строго
исследовать только на основе теории квантованного
электромагнитного поля излучения. Поэтому в гл. 6
описывается квантовая теория электромагнитного поля, а в
последующих главах эта теория применяется ко
множеству проблем. Теория квантованного поля сама по себе
ПРЕДИСЛОВИЕ АВТОРА
13
проста, и если понять ее основные положения, то такую
теорию нетрудно использовать даже для описания
простых процессов, когда полуклассическая теория дала бы
правильный ответ.
Автор благодарен д-ру Е. Ф. Пайку из Королевского
научно-исследовательского центра по изучению радаров
за консультации по теориям когерентности и
экспериментов по счету фотонов, д-рам Л. Р. Уолкеру и
Д. П. Гордону из фирмы «Белл Телефон» за помощь
в изложении теории лазера. Миссис Сильвия Сюзман
любезно провела машинные численные расчеты, я
миссис Мэри Лоудон выполнила численное интегрирование.
Автор благодарен миссис Мейри Киммит, миссис
Дорис Лоудон и мисс Джил Сандерсон за их тщательную
подготовку рукописи.
Разрешение на полное или частичное воспроизведение
таблиц и графиков было любезно получено от
следующих авторов и издателей: фиг. 5.5 от проф. Г. А. Хауса
и Американского института физики; фиг. 5.16 от проф.
Р. Хенбери Брауна и Королевского общества; фиг. 9.5,
9.7 и 10.9 от д-ра Е. Р. Пайка и Института физики;
фиг. '9.8 от проф. Ф. Т. Арекки и издательской фирмы
«Норс-Холланд»; фиг. 11.4 и 11.5 от проф. М. Гаврила и
Американского института физики; фиг. 11.7 и 11.8 от
проф. Д. Л. Миллса и Американского института физики;
фиг. 12.3 от д-ра Г. Р. Вебера и Института инженеров
по электронике и радиоэлектронике.
Р. Лоудон
Ист Бергхольд, Суффолк
1972
Глава 1
Формула Планка для излучения
и коэффициенты Эйнштейна
Квантовая теория света возникла в 1900 г., когда
Планк [1] открыл возможность объяснения измерений
спектрального распределения электромагнитной энергии,
излучаемой тепловым источником, на основе постулата
о квантовании энергии гармонического осциллятора.
Иначе говоря, гармонический осциллятор с угловой
частотой со может иметь только такие значения энергии,
которые равны целому числу основных квантов йсо, где
h = h/2n и h — постоянная Планка. В 1905 г. Эйнштейн
[2] показал, что фотоэффект может быть объяснен с
помощью гипотезы о корпускулярности электромагнитного
излучения. Квант излучения был назван фотоном
значительно позже, в 1926 г. [3]. Работы Планка и Эйнштейна
во многом положили начало развитию квантовой
механики.
Другое главное направление в создании квантовой
теории было связано с объяснением атомных спектраль-
• ных линий. Взаимодействие электромагнитного
излучения с атомами рассматривалось Эйнштейном [4] а
1917г.1). Его теория поглощения и испускания света-
атомом, основанная на простых феноменологических
рассуждениях, приводит, однако, к правильным
предсказаниям и до сих пор часто используется. Мы начнем наше
изложение квантовой теории света так же, как эта
теория развилась исторически — с теорий Планка и
Эйнштейна.
1) Работы [1, 2, 4] переведены на английский язык и подробно
обсуждаются в книге Тер Хаара [11],
16
ГЛАВА I
Уравнения Максвелла
Классическая теория электромагнитного излучения
основана на уравнениях Максвелла, переживших
введение квантовой механики. В гл. 6 мы увидим, что в
строгой квантовой механике электрическое и магнитное поля
Е и Н заменяются операторами. Тем не менее квантово-
механическая теория электромагнитного поля основана
на уравнениях Максвелла. Классическое описание
электрического и магнитного полей будет сохранено в первых
пяти главах. Гипотезу квантов можно косвенно ввести
в классическую теорию как дополнительное условие при
вычислении энергии электромагнитного поля.
Электромагнитное поле будет далее рассматриваться
только в немагнитных средах, где уравнения Максвелла
имеют вид
VXE = -[x04?b AЛ)
VXH=e0f+ J, A.2)
ejV.E = cr, y A.3)
VH=0. A.4)
Здесь 8о и |io — электрическая и магнитная
проницаемости свободного пространства, сг и J — плотности
заряда и тока. Использование тождества
V . ?ХН=0 A.5)
позволяет исключить Е и Н из уравнений A.2) и A.3)
и получить уравнение непрерывности
Для среды, содержащей только связанные заряды,
величины а и J можно выразить через поляризацию Р
обычным способом [5]:
a = -rV.P, A.7)
dt
J = 4£. A.8)
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 17
Формулы A.7) и A.8) согласуются с уравнением
непрерывности A.6). С учетом A.7) и A.8) уравнения
Максвелла A.2) и A.3) принимают вид
VXH={(e0E + P), A.9)
V.(e0E + P) = 0. A.10)
Эти уравнения используются в последующих главах;
сейчас рассматривается электромагнитное поле в свободном
пространстве, где уравнения A.2) и A.3) записываются
следующим образом:
?ХН=е0Д|, A.11)
V.E = 0. A.12)
Уравнение для электромагнитных волн в свободном
пространстве получается исключением Н из уравнений
A.1) и A.11):
VXVXE^-^^b A.13)
Здесь скорость света с определяется выражением
с = (в0\1оГУ2. A.14)
Использование тождества
VXVXE = V(V.E)-V\ A.15)
дает уравнение
Магнитное поле Н удовлетворяет точно такому же
уравнению.
Возможными решениями волновых уравнений
являются плоские бегущие волны
Е (г/) = Е0 exp (ik • г — /со/), A.17)
Н (rt) = H0 exp (ik . г — ш/). A.18)
Здесь волновой вектор к может быть ориентирован в
произвольном направлении, а его модуль определяется
формулой
к = со/с. A.19)
18
ГЛАВА 1
При комплексной форме записи поля всегда следует
помнить, что физически измеримыми являются только
его вещественные части. Для решений, данных в A.17) и
Е
\
^^* > *»k
Фиг. 1.1. Относительные направления векторов Е, Н и к для
электромагнитной волны.
A.18), исходные уравнения Максвелла A.1) и A.11)
принимают вид
к X Е = cojioH, к X Н = - со80Е. A.20)
Следовательно, векторы к, Е и Н должны быть
взаимно ортогональными, как показано на фиг. 1.1, а
величины полей связаны соотношением
Я = (e0M>I/2 £. A.21)
Для каждого направления волнового вектора к имеются
два независимых направления поляризации
электрического вектора Е.
В случае электромагнитной волны, занимающей
ограниченную прямоугольную область пространства,
решения уравнения A.16) удобнее взять с вещественными
пространственными частями, которые можно записать
в виде
/sin kxx\ /sin kuy\ /sin kzz\
^^-^U* J U*;J (cos A J «P <-'«<>• C-22>
Такие же решения существуют для магнитного поля
Н(г/). Теперь для каждого значения волнового вектора к
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ, ЭЙНШТЕЙНА 19
имеются семь решений, соответствующих различным'
комбинациям синусов и косинусов; при этом вектор к
находится в положительном октанте (где все его
составляющие kXi ky и kz положительны).
Плотность мод поля в полости
Электромагнитное излучение обычно удобцо
рассматривать как заключенное в полости. Хотя некоторые
эксперименты со светом проводятся в точно определенной
оптической полости, выделение какой-либо реальной
экспериментальной полости часто является невозможным.
Тем не менее полость удобно вводить в теоретическое
рассмотрение для ограничения исследуемого
пространства конечным объемом. Это служит лишь теоретическим
приемом, и конечные результаты обычно не зависят от
размера, формы и природы предполагаемой полости1).
Для максимального упрощения вычислений была
выбрана полость в форме куба со стороной L, направление
осей которого показано на фиг. 1.2. Стенки полости
предполагаются идеально проводящими, поэтому
тангенциальная составляющая поля должна соответственно
равняться нулю на границах полости. .
Формула Планка описывает спектральное
распределение электромагнитного излучения внутри полости в
тепловом равновесии при температуре Т. Это излучение
называется излучением черного тела; оно обладает
таким же частотным распределением, как и излучение
идеального черного тела при температуре Т. Вычисление
частотного распределения состоит из двух частей.
Сначала определяется координатная зависимость поля в
полости и находится выражение для числа различных мод
возбуждений ноля. Во второй части рассматривается
временная зависимость поля и вычисляется энергия
каждой возбужденной моды при температуре Т.
х) Плотность термодинамических функций, описывающих
равновесное тепловое излучение, не зависит от размеров, формы и
природы стенок полости только в том случае, когда линейные размеры
полости много больше средней длины волны равновесного излучения.
Рассмотрение величины поправок, обусловленных конечными
размерами полости, см. в работе [12]. — Прим. ред.
20
ГЛАВА 1
Первая часть вычислений является полностью
классической. Решение уравнений Максвелла, взятое из
A.22) и удовлетворяющее граничным условиям, имеет
следующие составляющие:
Ех (rt) = Ех (t) cos (nvxx/L) sin (nvyyJL) sin (nv2z/L),
Ey (rt) = Ey (t) sin (nvxx/L) cos Gtvyy/L) sin (nv2z/L), A.23)
E2 (rt) = Ez (t) sin (tcvxx/L) sin (nvyy/L) cos (nv2z/L),
где величина E(/) не зависит от координат и
v„ v„, v2 = 0, 1, 2, 3, ... . A.24)
Кроме тогог на целые числа v накладывается
ограничение, состоящее в том, что одновременно равняться нулю
Фиг. 1.2. Геометрия оптической полости.
может только одно из них, так как если два или три
числа v равны нулю, то поле E(rf) также равно нулю
и в полости нет электромагнитного поля.
Легко проверить, что поле Е(г^), определенное в
A.23), удовлетворяет граничным условиям на стенках
полости, например Ех(т1) =0 при у = 0, L и z — 0, L.
Граничным условиям можно было бы полностью
удовлетворить при замене косинусов синусами, однако при
этом было бы невозможно удовлетворить уравнению
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 21
Максвелла A.12) во всей полости. Для решения A.23)
это уравнение ведет к условию
Ех @ (nvJL) + Еу (t) (iiVy/L) + Ег (t) (nvJL) = 0. A.25)
Волновой вектор к определяется своими составляющими
kx = nvx/L, ky = 7ivy/L, kz = nvz/L; A.26)
при этом уравнение A.25) принимает вид
k.E(f)=0. "A.27)
Последнее уравнение выражает просто условие
ортогональности поля Е(/) волновому вектору к, и для
каждого значения к опять имеются два независимых
направления Е(/).
Граничные условия выделяют дискретные значения
компонент волнового вектора, определяемые целыми
числами vx, vy и vz. Каждый набор целых чисел (vx, Vy, vz)
определяет моду поля излучения в полости и с учетом
двух направлений поляризации соответствует двум
степеням свободы поля. Любое возбуждение
электромагнитного поля можно представить в виде суммы таких
мод поля. Разрешенные значения вектора к можно
изобразить в виде трехмерной точечной решетки, причем
постоянная решетки равна n/L. На фиг. 1.3 показана часть
решетки, для которой числа v*, vy и vz не превышают 4.
Теперь следует получить выражение для числа мод
поля с величиной волнового вектора, лежащей между
значениями J и Н dk. Искомое число просто равно
числу точек решетки в октанте сферического слоя,
ограниченного поверхностями с радиусами k и k + dk.
Предполагая объем слоя достаточно большим по сравнению
с объемом свободного пространства (я/LK,
окружающего каждую точку решетки, найдем, что требуемое
число мод поля определяется следующей формулой:
^{4jik2dk){7t/Ly3X2. A.28)
Здесь последний множитель учитывает две возможные
поляризации.
По определению плотность мод поля phdk есть число
мод поля в единице объема полости, волновой вектор
22 ГЛАВА 1
которых лежит в определенной области. Поэтому из
A.28) получим
9kdk = tfdkl7i2. A.29)
Этот результат справедлив в общем случае и не зависит
от природы полости, использованной для его получения.
Фиг. 1.3. Разрешенные волновые векторы к для полости в форме
куба со стороны L.
Отметим, что точки, в которых две или три компоненты kx, k и kz обращались
бы в нуль, отсутствуют..
Соотношение A.19) между k и со позволяет
преобразовать A.29) в выражение для плотности мод р^со с
частотами, лежащими между значениями со и со + do:
Рю da> = со2 d(o/n2c3. A.30)
В следующих главах встретятся выражения, которые
необходимо просуммировать по модам поля. Используя
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 23
плотность мод из A.29) и A.30), такие суммы можно
преобразовать в интегралы по k или со:
Yj -» \ WW*2) dk-> J {V<s>2/n2c3) dffl, A.31)
k
где V — объем полости и при суммировании в левой
части A.31) для каждого волнового вектора к
учитываются две независимые поляризаций.
Квантование энергии поля
О пространственной зависимости электромагнитного
поля уже сказано достаточно. На второй стадии
вычислений определяется величина энергии, запасенной в
каждой моде поля при температуре Т. Уравнение для
временной зависимости электрического поля получается
путем подстановки решений A.23) в волновое уравнение
A.16). Используя A.19), получаем
д2Е (t)/dt2 = — со2Е (*). A.32)
Решение этого уравнения простого гармонического
движения можно выбрать в виде
Е (/) = Е0 ехр (— /со/), A.33)
где Е0 — постоянный вектор, который в классической
электромагнитной теории может иметь произвольную
величину.
Согласно классической теории, энергия
электромагнитного поля определяется интегралом
Y S (*оЕ2 + VoH2) dV, A.34)
по полости
где Е и Я — значения вещественных электрического и
магнитного полей. Для рассматриваемой моды поля
комплексное электрическое поле определяется
формулами A.23) и A.33). Энергию поля удобно усреднить по
периоду колебаний, поскольку изменение энергии за
период обычно недоступно для измерения. Среднее за
период легко находится с помощью теоремы,
сформулированной в виде следующей задачи.
24
ГЛАВА I
Задача 1.1. Теорема для среднего за период. Покажите,
что если зФ и $ являются комплексными
величинами, изменяющимися со временем как
ехр(—Ш), то среднее за период колебаний
значение произведения вещественных частей
зФ и $ дается выражением
(Re а) X (Re Я) = ± Re {азГ), A-35)
где звездочка означает комплексное
сопряжение.
Теорему для среднего за период можно применить
к выражению для энергии A.34), где электрический
вектор для рассматриваемой моды поля находится из A.23)
и A.33). Если использовать соотношение A.21) между
величинами электрического и магнитного полей, то
энергия поля запишется в виде
\ \ s0\E(vt)?dV. A.36)
по полости
Именно в этом месте вводится гипотеза квантования
Планка. В классической теории энергия поля,
определяемая формулой A.32), может принимать любое
положительное значение, поскольку амплитуда Е0 в A.33)
может иметь любую величину. Поле Е(/), однако,
удовлетворяет уравнению гармонического осциллятора A.32).
Если это уравнение рассматривать квантовомеханически
(детали приводятся в гл. 6), а не классически, то
энергия осциллятора может принимать только дискретные
значения:
Еп=(п+~)Л<й9 л = 0, 1,2, 3, ... . A.37)
Мы соответственно припишем эти разрешенные
значения электромагнитной энергии моды, определяемой
формулой A.36):
1 J B0\E(Tt)\2dV = {n + j)h^ A.38)
по полости
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 25
Очевидно, что это условие квантования накладывает
ограничения на возможные значения амплитуды Е0 в
A.33). Однако обсуждать эти следствия сейчас нет
необходимости; мы рассматриваем поля как классические
величины и накладываем условие квантования только на
энергию поля. При более глубоком подходе
электромагнитное поле необходимо рассматривать как квантовоме-
ханическую систему, что сделано в гл. 6, но для многих
задач описанный выше
п
полуклассическии подход
является вполне
адекватным.
Таким образом,
сущность квантовой теории
поля излучения
заключается в том, что с каждой
модой поля связывается
квантовый гармонический
осциллятор. Схема
уровней такого осциллятора
приведена на фиг. 1.4.
Когда энергия моды опреде*
ляется выражением A.38),
соответствующий
осциллятор находится в своем
п-ы возбужденном
состоянии. При п=0 осциллятор
находится в своем
основном состоянии, но в поле
все же имеется конечная
энергия Уг^со. Это энергия
нулевых колебаний, ее
значение обсуждается в
гл. 6. В большинстве экспериментов результаты
наблюдения зависят от того, насколько энергия возбуждения
превышает энергию основного состояния. В состоянии
с энергией £п, кроме энергии нулевых колебаний, имеется
п квантов с энергией fico. Эти кванты называются
фотонами. Поэтому, когда поле имеет энергию Еп, говорят об
п фотонах, возбужденных в моду поля излучения. Если
электромагнитная энергия в моде увеличивается (умеиь^
О
Рождение
фотона
Уничтожение
фотона
*
2 ha)
-yfiOi
2^@
2#fc>
jbui
- о
Фиг. 1.4. Первые шесть
энергетических уровней для квантового
гармонического осциллятора.
26
ГЛАВА 1
шается) на один квант, то говорят, что был рожден (уни-»
чтожен) фотон. На фиг. 1.5 показано несколько нижних
уровней гармонических осцилляторов, связанных с
первыми десятью модами поля и расположенных в порядке
»*Wz 011 101 110 111 210 201 120 021 102 012
х У
coL/лс VI V? V? \tf VF V5 у/5 VF л/5 л/5*
Фиг. 1.5. Схема энергетических уровней гармонического
осциллятора для первых десяти мод поля, расположенных в порядке
увеличения частоты.
Эти моды соответствуют десяти наиболее близким к началу координат точкам
на фиг. 1.3. Строго говоря, для того чтобы учесть для каждого вектора к две
независимые поляризации, каждый уровень должен быть нарисован дважды.
возрастания частоты. Отметим, что для каждого из этих
осцилляторов имеются две моды с независимыми
поляризациями.
Формула Планка
В тепловом равновесии при температуре Т
вероятность теплового возбуждения осциллятора моды на п-й
возбужденный уровень дается обычным множителем
Больцмана
_ ехр(-р£„) _ exp(-frzto) „ щ
п ^ ехр <- р£») Z ехр (~ $пЫ)'
п п
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 27
где
t=l/kBT, A.40)
a kB — постоянная Больцмана. При написании формулы
A.39) было использовано выражение для квантованной
энергии A.37) и опущен член 7г J со, имеющийся во всех
экспонентах числителя и знаменателя выражения A.39).
Формула Планка не зависит от энергии нулевых
колебаний, и к тому же в 1900 г. существование нулевых
колебаний Планку было неизвестно. Отметим, что при
применении теплового распределения Больцмана к
гармоническому осциллятору каждому уровню был приписан
одинаковый вес и не учитывалось различие в числах
фотонов, соответствующих разным уровням. Такой метод
корректен для нахождения свойств фотонов при тепловом
равновесии 1).
Знаменатель выражения A.39) представляет собой
геометрическую прогрессию, которую можно легко
просуммировать:
£ ехр (— рлгйсо) = {1 — ехр (— р/ко)}. A.41)
п
Следовательно,
рп = ехр (— рлАо) {1 — ехр (— р/гсо)}. A.42)
Таким образом, среднее число фотонов Я, возбужденных
.в моду поля при температуре 7", дается выражением
п=£пРп, A.43)
п
поэтому необходимо вычислить сумму
Yj п ехр (— р/гйсо) = — {д/д (р/ш)} ]С ехР (~ Р^Асо) =
п п
= ехр (— р/ко) {1 — ехр (— р/гсо)}; A-44)
при этом была использована формула A.41). Среднее
число фотонов, полученное из A.43), имеет вид
Й = 7аГ~\ Г* A-45)
ехр фйсо) —1 N '
) См. также анализ Д. Тер Хаара в сборнике [6],
28 . глава i
Этот важный результат представляет собой функцию
распределения Планка. Ее зависимость от частоты
осциллятора или фотона со показана на фиг. 1.6.
Результаты A.30) и A.45), определяющие
соответственно число мод поля излучения в единице объема
с частотой в интервале от со до со + dco и среднюю
энергию ййсо каждой такой моды при температуре Г, можно
объединить ^ля нахождения средней плотности энергии
излучения lFr((o)dco в этих модах при температуре Т:
WT (со) dco = Морю dсо = /гйсо3 я?со/я2с3 =
ЙСО3 d(d ,. ддч
~ JtV exp(Pfiffl)-1 * l1#4D'
Последнее выражение есть формула Планка для
плотности энергии излучения Wt((o). Зависимость
величины Wt((o) от рйсо приведена на фиг. 1.7.
В случае высоких и низких температур формула
Планка немного упрощается. При 1гвТ ^> йсо экспоненту
можно разложить в ряд и получить
¥т (со) « со2/я2с3р {kBT > Йсо). A.47)
Эта формула для плотности энергии излучения была
получена Рэлеем [7] в 1900 г. незадолго до того, как
Планк нашел правильное выражение. Формула Рэлея
является классическим пределом, который получается
из формулы Планка при устремлении квантовой
постоянной Планка Ь к нулю.
При низких температурах, когда kBT <С йсо,
экспонента очень велика, и поэтому
¥т (со) « (Йсо3/л2с3) ехр (- р/ш) (kBT < A©). A.48)
Оба приближения формулы Планка непригодны в том
случае, когда величина йсо сравнима с kBTy т. е.
рйсо « 1.
Максимум теплового распределения энергии
излучения приходится на частоту соМакс, которую можно найти,
дифференцируя выражение A.46) по со. В результате по-
лучтш
Aow = 2,W. A.49)
8
n
Фиг. 1.6. Среднее число тепловых фотонов п с частотой со,
возбужденных при температуре Т ф = \/kBT).
t,5r
Фиг. 1.7. Формула Планка для зависимости плотности энергии
электромагнитного излучения от частоты со и температуры
т (р = щвт).
30
ГЛАВА I
Последнее выражение представляет собой один из
способов записи закона смещения Вина [8], открытого
в 1893 г.
Полная плотность энергии фотонов в полости
получается интегрированием выражения A.46):
? — Ь °r x3dx n2k4T4
\^WA^)d^ = 1^^^\^r^^-^Er. A.50)
о о
Здесь для определенного интеграла было подставлено
его значение я4/15. Пропорциональность полной
плотности энергии четвертой степени температуры является
законом Стефана — Больцмана для излучения, который
был сформулирован в 1879 г. Если ET(rt) есть полное
электрическое поле, определяемое всеми модами поля
излучения в полости при температуре Г, то полную
плотность электромагнитной энергии можно записать в
другом виде с помощью формулы A.36):
оо
\ WT @) do> = {ll2V) \ e3\ ET (rt) \2dV. A.51)
0 ПО ПОЛОСТИ
Эквивалентность выражений A.51) и A.50) будет
использована в гл. 3.
Коэффициенты Эйнштейна А и В
Механизмом, с помощью которого можно изменять
число фотонов в полости, является поглощение или
испускание фотонов атомами или молекулами стенок полости.
Рассмотрим основные процессы взаимодействия между
электромагнитным излучением и атомами. Эти процессы
можно исследовать на основе простой
феноменологической теории, развитой Эйнштейном. Теория Эйнштейна
позволяет качественно понять множество излучательных
процессов, например поглощение и рассеяние света
атомами и усиление световых пучков в лазерах.
Теория Эйнштейна основана на некоторых физически
разумных постулатах относительно поглощения и
испускания фотонов атомами. Все эти постулаты можно
строго доказать с помощью квантовомеханического рас-
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ, ЭЙНШТЕЙНА 31
смотрения процессов взаимодействия (см. гл. 8). Однако
в теории Эйнштейна квантовая механика явно не
используется, за исключением того, что атомные
энергетические уровни считаются дискретными, а энергию
электромагнитного поля удобно (хотя это и несущественно)
рассматривать как квантованную.
Проще рассматривать взаимодействие излучения не
с атомами стенок полости, а с некоторыми атомами или
E2iN2,gz
B21W(sa>)
EuNug1
Спонтанное Поглощение Вынужденное
испускание испускание
Фиг. 1.8. Три основных вида излучательных процессов.
молекулами, помещенными внутри полости. Допустим,
что в полости находится газ, состоящий из N
одинаковых атомов, причем каждый атом имеет пару связанных
состояний с энергиями Ех и Е2, и пусть
П(о = Е2 — Е1. A-52)
Для такой системы возможны процессы с сохранением
энергии, в которых фотоны с частотой со испускаются или
поглощаются атомами, совершающими переходы между
двумя состояниями. Допустим, что два атомных уровня
являются мультиплетами с кратностью вырождения g\
и g2; всеми остальными атомными уровнями для
простоты пренебрежем. Числа N\ и N2 атомов в состояниях
с энергиями Е\ и Е2 будем называть населенностями
соответствующих уровней. Схема уровней приведена на
фиг. 1.8.
С точки зрения эксперимента замкнутая полость,
содержащая атомы и тепловое излучение, не представляет
собой особенно интересную систему. Для изучения
взаимодействия между атомами и излучением необходимо
32
ГЛАВА !
проделать более сложный и тщательно продуманный
эксперимент. Например, можно послать пучок излучения
с частотой со через полость и измерить долю
интенсивности пучка, потерянную в полости. В типичном
эксперименте усредненная за период плотность энергии
излучения с частотой со превышает тепловую часть плотности
энергии WT((o) на величину We (со), которая
представляет вклад некоторого внешнего источника
электромагнитного излучения. Следовательно, полная плотность
энергии дается выражением
W {<*) = ¥? (со) + ¥Е (со). A.53)
В общем случае величина ШЕ(ы) является функцией
координат внутри полости, а внешнее излучение не имеет
пространственно-изотропного распределения, но сейчас
эти свойства не учитываются.
Вероятности поглощения и испускания фотона
определяются следующим образом. Если атом находится в
состоянии 2, то имеется конечная вероятность в единицу
времени А2\ спонтанного перехода атома в нижнее
состояние 1 с испусканием фотона, обладающего энергией
ЙСО.
Теперь рассмотрим атом в состоянии 1. В отсутствие
какого-либо излучения с частотой со переход атома в
состояние 2 невозможен, поскольку в таком переходе
энергия не сохраняется. Однако при наличии излучения с
плотностью энергии t^(co) переход вверх 1-^2 может
произойти за счет поглощения фотона. Предположим, что
скорость такого перехода пропорциональна IF (со) с
коэффициентом пропорциональности SJ2.
Эти два процесса интуитивно представляются
разумными, но не столь очевидно, что присутствие излучения
с плотностью энергии IF (со) увеличивает также скорость
перехода из верхнего состояния в нижнее. Однако
позднее будет доказано, что такое увеличение скорости пере-
хода_должно иметь место, поэтому обозначим его через
В2\ Щсо). Этот третий излучательный процесс
называется вынужденным излучением. Скорости переходов
для всех трех процессов показаны на фиг. 1.8.
Необходимо подчеркнуть, что три коэффициента
Эйнштейна А2и В[2 и В2\ определены таким образом, что
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 33
они не зависят от №(о). Коэффициенты Эйнштейна
зависят только от свойств двух рассматриваемых атомных
состояний, причем эта зависимость определяется
методами квантовой механики (см. гл. 3). Пока будем
рассматривать эти коэффициенты как феноменологические
постоянные. Пропорциональность скор_остей поглощения
и вынужденного излучения величине W((o) справедлива
только в том случае, когда плотность энергии медленно
меняется с частотой со вблизи частоты перехода.
Рассмотрим влияние трех скоростей переходов на
населенности уровней N\ и N2. Уравнение для скоростей
изменения N\ и N2- имеет вид
dNJdt = - dN2/dt = N2A2l - NXB[2W (со) +
+ N2B2[W(®). A.54)
Это уравнение будет решено после обсуждения
соотношений, существующих между коэффициентами
Эйнштейна.
Случай теплового равновесия
Кинетическое уравнение A.54) справедливо в общем
случае, однако некоторые полезные результаты можно
получить при рассмотрении специального случая
теплового равновесия. При любом условии равновесия
населенности уровней постоянны, а поэтому из A.54)
получим
N2A2l - N{B[2W{<u) + N2B2lW (g>) = 0. A.55)
Для теплового равновесия,-когда внешнее излучение,
вводимое в полость, отсутствует, плотность энергии в
A.55) представляет собой просто тепловой вклад Wr(co),
а решение уравнения A.55) для этой величины имеет
вид
^^-(WB,-B2l- 0-56)
При тепловом равновесии населенности уровней N\
w*N2 связаны законом Больцмана
NilN2 = {g, exp (- ?£,)}/{& exp (- p£2)} =
= (&/&) exp фАю)- A.57)
2 Зак. 885
34
ГЛАВА 1
Здесь величина E определена в A.40). Тогда из A.56)"
WT (со) = A2l/{(gjg2) exp (РА©) В12 - £21}. A.58)
Последнее выражение для №т(со) следует из
определений коэффициентов Эйнштейна и применения
распределения Больцмана к населенностям атомных уровней.
Однако этот результат должен согласовываться с
формулой Планка A.46) для плотности энергии излучения при
тепловом равновесии. Выражения A.58) и A.46) равны
друг другу при всех температурах Т только тогда, когда
выполняются соотношения
(Bi/g2)Bl2 = B2l, A.59)
(Н®3/л2с3)В2[ = А21. A.60)
Таким образом, три коэффициента Эйнштейна
являются взаимосвязанными, а скорости всех переходов
между данной парой уровней могут быть выражены через
значение одного коэффициента. Из A.58) видно, что без
введения процесса вынужденного излучения
согласованность между теорией Эйнштейна и формулой Планка
не могла быть достигнута. В гл. 8 будет показано, что
этот процесс естественно возникает в строгой теории
излучения фотонов.
Сравнение формулы Планка A.46) с выражением
A.60) показывает, что при тепловом равновесии
B2lWT(<*) = A2ln. A.61)
Иначе говоря, скорость вынужденного теплового
излучения равна скорости спонтанного излучения, умноженной
на среднее число фотонов в каждой моде поля излучения
С частотой перехода со. Сумма двух скоростей излучения
имеет вид
B2lWT (со) + А2{ = А21 (п + 1). A.62)
*
Интересно рассмотреть отношение двух скоростей
излучения как функцию частоты фотона со. Из A.45) и
A.61) получим
A2JB2lWT (со) = 1/й = ехр (ПфвТ) - 1. A.63)
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 35
Для полости, поддерживаемой при комнатной темпера-
гуре (Г = 300 К), показатель экспоненты b(o/kBT равен
единице для излучения с длиной волны
Я « 50 мкм, A.64)
которая соответствует частоте порядка 6-Ю12 Гц в
дальней инфракрасной области спектра. Следовательно, для
излучения с длиной волны 50 мкм и большей,
соответствующей микроволновой4 или радиочастотной области,
выполняются неравенства
ft© < kBT и Л21 < B2{WT (со), A.65)
а для излучения в ближней инфракрасной, видимой,
ультрафиолетовой или рентгеновской областях —
Йсо > kBT и A2l » B2lWT{a>). A.66)
Отсюда видно, что для частот, малых по сравнению
с 6-Ю12 Гц, скорость вынужденного теплового
излучения значительно больше скорости спонтанного
излучения, а для частот, больших по сравнению с 6-Ю12 Гц,
скорость спонтанного излучения превосходит скорость
вынужденного теплового излучения. /
Флуктуации числа фотонов
Процессы поглощения и испускания фотонов
вызывают флуктуации числа фотонов в каждой моде поля
излучения в полости. Флуктуации характеризуются
определенным временным масштабом, который детально об«
суждается в гл. 5. Однако некоторые усредненные
свойства флуктуации можно получить без знания их
временных масштабов. В дальнейшем будет использована
эргодическая теорема статистической механики (см.,
например, [9]) !), согласно которой усредненные по
времени величины эквивалентны величинам, усредненным по
большому числу совершенно одинаковых систем,
каждая из которых поддерживается в фиксированном
состоянии. Воображаемый набор одинаковых систем назы-
!) Эквивалентность средних значений по ансамблю и по
времени рассматривается в книге Киттеля [10],
2*
36
ГЛАВА 1
вается ансамблем, системы в ансамбле распределены по
всем их возможным состояниям в соответствии с
распределением вероятностей для рассматриваемой системы.
В случае фотонов в определенной моде поля полости
следует представить себе ансамбль, состоящий из одной
и той же моды поля, находящейся в большом числе
одинаковых полостей. В ансамбле каждая мода полости
имеет некоторое фиксированное число фотонов. Та часть
мод полости, которые содержат п фотонов, определяется
функцией Рп, приведенной в A.42). Среднее число
фотонов п уже было вычислено с помощью формулы A.43).
Результат этого вычисления [формула A.45)] можно
равным образом рассматривать как среднее по ансамблю
или как среднее по времени числа фотонов в данной
моде одной реальной полости. Согласно эргодической
теореме, которая подробно обсуждается в гл. 5, оба
средних значения равны.
Распределение вероятностей Рп можно также
использовать для определения величины флуктуации числа
фотонов п относительно среднего значения п. Сначала
более подробно исследуем вид распределения Рп.
Подставляя из A.45)
ехр (- р/ш) = й/A + п) A.67)
в A.42), получаем выражение
Ря = {п)п1A +«)'+", A.68)
которое удобно для изображения зависимости Рп от п
для данного значения я. Некоторые примеры такой
зависимости приведены на фиг. 1.9. Вероятность Рп дает
распределение результатов, которые были бы получены
для большого числа последовательных измерений числа
фотонов в выбранной моде полости. Из приведенных
зависимостей видно, что значение п = О всегда имеет
наибольшую вероятность реализации, а величина Рп
монотонно уменьшается с ростом п. Это уменьшение
обусловлено уменьшением больцмановской вероятности
заселения высших уровней гармонического осциллятора моды.
Вероятность Рп не имеет какой-либо особенности при
п = п, среднее значение не соответствует какому-нибудь
пику в распределении Рп. Флуктуацию числа фотонов
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 37
можно характеризовать среднеквадратичным
отклонением распределения An. По определению
(ДлJ= £ (п- пJРп = ~^-(пJ. A.69)
п
Второй момент распределения п2 может быть найден
точно таким же методом, какой был использован в A.44),
0,5
0,4
0,3
0,2
0,1 -
р
" О
г
f'
-
/Г=/
^s
J
П П п « «
0,2-
0,1
О
0,1 ~ „
п = 5
П П П л
П П П n n n
О
п = 10
ИППППППпппп
о
8 10 12 14
Фиг. 1.9. Распределение вероятностей для числа фотонов в одной
моде поля излуч#шя для трех значений среднего числа фотонов п.
для определения первого момента п. Используя A.41) и
A.45), получаем
п
= {I — ехр (— РМ} {д/д (рйсо)}2 Е ехр (— рлйю) =
38
ГЛАВА 1
С учетом этого результата для п2 среднеквадратичное
отклонение принимает вид
hi = {{hJ + n}4\ A.71)
Видно, что величина флуктуации числа фотонов п всегда
больше среднего значения п в соответствии с большой
шириной распределения вероятностей, показанного на
фиг. 19. Для больших п выражение A.71) стремится
к виду
Дя=Д + -^ (п>1). A.72)
Теория экспериментов по счету фотонов детально
описана в гл. 9. Необходимо отметить, что результаты,
полученные выше на основе эргодическои теоремы, строго
справедливы только для идеализированного
эксперимента, в котором число фотонов измеряется ~ мгновенно.
В любом реальном эксперименте имеются ограничения,
определяемые временем разрешения аппаратуры, а
полученные результаты зависят от относительных величин
времени разрешения и временного масштаба,
характеризующего флуктуации числа фотонов.
В заключение укажем другой способ записи
распределения вероятностей Рп для тепловых фотонов.
Исключая экспоненту из A.57) и A.67), получаем
n/(l+n) = glN2/g2Nb A.73)
или
n = g{N,l{g2Nx-g[N2). A.74)
Здесь, как и на фиг. 1.8, g и N обозначают
соответственно кратности вырождения и населенности двух
атомных уровней с -разностью энергий йсо. Тогда
выражение A.68) можно переписать следующим образом:
и распределение фотонов при тепловом равновесии
полностью выражено через величины, связанные с
атомными энергетическими уровнями.
Конечно, населенности уровней N\ и N2 также
испытывают флуктуации, обусловленные испусканием и по-
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 39
глощением фотонов атомами. Величины N\ и N2, которые
появились в приведенных выше уравнениях, строго го*
воря, представляют собой средние населенности
атомных уровней. На протяжении всей книги наибольшее
внимание будет уделено свойствам фотонов, а не атомов,
поэтому флуктуации величин N\ и N2 специально не
исследуются.
Случай высоких частот
В последующих главах основной интерес для нас
будут представлять излучательные процессы, которые
играют важную роль в экспериментах с использованием
электромагнитного излучения в ближней инфракрасной,
видимой и ультрафиолетовой областях спектра. Для
таких экспериментов плотность энергии We(®) светового
пучка от внешнего источника всегда намного больше
плотности энергии Wt(u>) теплового излучения внутри
оптической полости. Далее, эти частоты достаточно
велики для применимости неравенств A.66), а потому
скорость спонтанного излучения намного больше скорости
вынужденного теплового излучения. Согласно A.59),
скорость поглощения теплового излучения также мала.
Эти рассуждения вместе с критерием A.64)
показывают, что для процессов, происходящих на частотах
порядка КЗ^Гц и выше, плотностью энергии теплового
излучения WE(ti>) можно пренебречь. Такие частоты мы
будем называть оптическими, а электромагнитное
излучение— светом, хотя излучение видимо только в узкой
области частот около частоты 1015 Гц. Конечно,
поглощение и вынужденное излучение, вызываемые внешним
излучением с плотностью энергии Й?я(со), по-прежнему
являются важными процессами и должны быть сохранены*
Если пренебречь тепловым вкладом TFr((o), то величину
W(q)) в A.53) можно использовать для описания
плотности энергии излучения от внешних источников
света и опустить индекс Е, поскольку в этом случае
остается только один вид плотности энергии излучения,
который следует рассматривать.
Как видно из A.57), при комнатной температуре
тепловая населенность возбужденных атомных состояний в
40 ГЛАВА 1
области оптических частот пренебрежимо мала. Здесь
будут рассмотрены эксперименты с атомами, имеющими
одно низколежащее состояние, называемое атомным
основным состоянием, и большое число оптических
возбужденных состояний. Если нижний уровень Е\ на
фиг. 1.8 принять в качестве основного состояния, то при
тепловом равновесии все атомы находятся в этом
состоянии и N\ = N. Данный атомный верхний уровень Е2
можно возбудить с помощью внешнего светового пучка,
частота которого со точно подобрана для удовлетворения
условия A.52). В этом случае говорят, что свет
резонансен атомному переходу между состояниями 1 и 2. Таким
образом, для многих исследований можно ограничиться
анализом основного атомного состояния и одного из
возбужденных состояний, пренебрегая при этом всеми
остальными состояниями и рассматривая систему как
двухуровневый атом.
Для последующего удобно получить некоторые
результаты для двухуровневого атома. Населенности
данного атома должны удовлетворять соотношению
Nx + N2=N. A.76)
Предположим далее, что оба уровня невырожденны
(gi == g = 1), поэтому два коэффициента В равны
между собой в соответствии с A.59). Следует подчеркнуть,
что, хотя условия A.59) и A.60) на коэффициенты
Эйнштейна получены при рассмотрении случая теплового
равновесия, в действительности* эти условия справедливы
в общем случае, поскольку коэффициенты не зависят от
величины W((x)) и температуры.
В двухуровневом случае индексы у коэффициентов А
и В можно опустить ввиду равенства величин В\2 и В2\.
Тогда уравнение для скоростей перехода A.54)
упрощается и принимает вид
dNJdt = - dNJdt = N2A + {N2 - N{) BW. A.77)
Здесь молчаливо предполагается, что W есть плотность
энергии на частоте со. В большинстве экспериментов
величина W зависит от координат внутри полости,
поэтому в гл. 2 будет показано, как рассматривать этот
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 41
случай. Если зависимостью от координат пренебречь, то
уравнение A.77) зависит только от времени и может
быть решено стандартными методами.
Задача 1.2. Доказать, что общее решение уравнения
A.77), удовлетворяющее условию A.76),
имеет вид
Ni = {n4 - N[A + *g } е*Р I ~ (Л + 2 В W) t] +
vu + bw) J8)
A+2BW
где N\ — начальное значение N\ при t = 0.
Решение N2 легко находится из условия
A.76).
Некоторые специфические процессы для атома, в
котором эффективны два уровня, исследуются в
следующей главе вместе с процессом, в теории которого
существен учет трех атомных уровней. В принципе методом
кинетического уравнения, в которое входят коэффициенты
Эйнштейна, можно рассматривать любое число
энергетических уровней.
В заключение настоящей главы сделаем несколько
замечаний относительно области применимости свойств
коэффициентов Эйнштейна, полученных на основе
анализа теплового равновесия. Выше было указано, что
условия A.59) и A.60) выполняются независимо от
величины W. Это правильное утверждение, однако следует
также учитывать и пространственное распределение
плотности энергии. При тепловом равновесии плотность
излучательной энергии Шт(ы) распределена в
пространстве изотропно. Используемые в экспериментах
световые пучки таким свойством обычно не обладают;
например, очень часто удобно работать с
плоскопараллельным световым пучком. Поэтому необходимо
рассмотреть возможность применения соотношений,-
полученных для А и Ву в случае анизотропного светового
пучка.
42
ГЛАВА 12
Эти соотношения остаются справедливыми для
систем, в которых излучение взаимодействует с газом или.
жидкостью, состоящими из атомов или молекул. В
дальнейшем будут рассматриваться именно такие системы.
В газе или жидкости атомы и молекулы имеют
случайные ориентации, а потому взаимодействие излучения с
газом является изотропным, даже несмотря на то, что
взаимодействие с отдельным атомом или молекулой
может быть анизотропным. Усредненный по всем
направлениям коэффициент В не зависит от геометрии
светового пучка, используемого в эксперименте.
Большая осторожность необходима при анализе
взаимодействия света с веществом в твердом состоянии,
когда образующие твердое тело атомы или молекулы
могут быть жестко ориентированы в общем для всех
атомов или молекул направлении. В этом случае объемный
материал может иметь сильно анизотропные оптические
свойства, поэтому коэффициенты Эйнштейна должны
использоваться с осторожностью. В дальнейшем будут
рассматриваться атомы или молекулы только а^газе или
жидкости, где преобладает оптическая изотропия.
В последующих вычислениях символ п часто будет
использоваться для обозначения среднего числа фотонов
в световом пучке, а не как среднее число тепловых
фотонов, возбужденных в каждую моду полости {формула
A.45)]. Многие из уравнений настоящей главы,
содержащие Я, несправедливы для нового значения п.
Например, в световом пучке с частотой со и разбросом частот
Асо, имеющим п фотонов в объеме полости У, средняя
плотность энергии W на единичном интервале частот
определяется выражением
W= йА©/7 Асо. A.79)
Этот результат заменяет выражение A.46) для
теплового равновесия, и, конечно, формула A.61)
неприменима в случае нетеплового равновесия.
v
ЛИТЕРАТУРА
1. Plank M, Verh. dt. phys. Ges., 2, 202 A900).
2. Einstein Л., Ann. der Phvs., 17, 132 A905).
3. Lewis G. N.} Nature, US[ 874 A926), •
ФОРМУЛА ПЛАНКА ДЛЯ ИЗЛУЧЕНИЯ И КОЭФФИЦ. ЭЙНШТЕЙНА 43
4. Einstein Л., Phys. Zs., 18, 121 A917).
5. Panofsky W. К. Я., Phillips M.t Classical electricity and
magnetism, Addison-Wesley, Reading, 1955, pp. 20, 118.
6. Quantum Optics, ed. R. Glauber, Academic Press, New York, 1969,
P- I-
7. Rayleigh, Lord, Phil. Mag., 49, 539 A900).
8. Wien W., Ber. Berlin Akad. Wiss. (9 Feb. 1893).
9. Farquhar I. £., Ergodic theory in statistical mechanics, Interscien-
ce, London, 1964.
10: Kittel C, Thermal physics, Wiley, New York, 1969, p. 32.
11, Ter Haar D., The old quantum theory, Pergamon, Oxford, 1967.
12*. Колоколов А. А., Скроцкий Г. В., Оптика и спектроскопия", 36,
217 A974), "
Глава 2
Теория простых оптических процессов
В настоящей главе будут рассмотрены процессы,
происходящие при прохождении светового пучка через
полость, заполненную атомным или молекулярным газом.
Классическая и полуклассическая теории, развитые в
предыдущей главе, дают правильное объяснение
множества различных оптических процессов. Цель настоящей
главы заключается в том, чтобы проиллюстрировать
некоторые наиболее важные применения этих теорий.
Однако приводимые ниже вычисления выявляют
некоторые недостатки теории взаимодействия света с
атомами, созданной Эйнштейном. Сама теория не дает
никакого способа вычисления значения коэффициентов А и
В, соответствующих данному атомному переходу. Для
этого следует обратиться к квантовомеханической теории
вероятностей переходов. Вычисление значений
коэффициентов Эйнштейна описывается в гл. 3. Крохме того, тео-,
рия Эйнштейна не дает удовлетворительного объяснения
ширины линии атомных переходов. Переходы происходят
не на строго определенной частоте, а в интервале частот,
измерение распределения которых может дать полезную
информацию для теоретического анализа. Для
проведения такого анализа необходимо найти выражения для
восприимчивости, зависящей от частоты. Вывод этих
выражений составляет основное содержание гл. 4.
На всем протяжении этих более сложных вычислений
теория Эйнштейна продолжает давать адекватную
теоретическую модель взаимодействия излучения с атомами,
а коэффициенты Эйнштейна — подходящую меру вели-
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ
45
чины взаимодействия. Поэтому пока будет
использоваться феноменологическая теория Эйнштейна,
изложенная в предыдущей главе.
Макроскопическая теория поглощения
Атомный газ в полости можно рассматривать как
диэлектрическую среду, а распространение
электромагнитных волн через полость описывать на основе
классической электромагнитной теории. Прежде чем подробно
исследовать микроскопическую природу процесса
поглощения, удобно суммировать соответствующие
результаты электромагнитной теории поглощения света
диэлектриком.
Поляризация диэлектрика пропорциональна
приложенному электрическому полю
Р = е0хЕ. B.1)
Здесь % — диэлектрическая восприимчивость.
Восприимчивость является функцией частоты со приложенного
поля, а ее вид зависит от энергетических уровней и
волновых функций атомов, образующих диэлектрик.
Свойства электромагнитных волн в изотропном
диэлектрике можно получить с помощью подстановки
поляризации Р из B.1) в уравнения Максвелла A.9) и
A.10). Решения для Е и Н по-прежнему имеют такой
же вид, как в A.17) и A.18), но теперь волновой вектор
к связан с частотой соотношением
(ВД2=1+х, B.2)
которое в предельном случае свободного пространства
Х = 0 переходит в A.19). Величина 1+Х называется
диэлектрической постоянной; конечно, она является
константой только в смысле независимости от Е, поскольку
ее величина зависит от частоты.
В общем случае восприимчивость является
комплексной величиной и записывается в виде
Y=v/ + /v". B.3)
46
ГЛАВА 2
Корень квадратный из выражения B.2) обычно
записывается следующим образом:
he/® = т| + in. B.4)
Определенные здесь величины г\ и к являются
соответственно показателем преломления и коэффициентом
экстинкции. Сравнение вещественных и мнимых частей
выражения B.2) после подстановки в него формулы
B.4) приводит к системе уравнений
Ч2-и2=1+х', B.5)
2цх = %". B.6)
Эти уравнения можно использовать для определения
частотной зависимости ц и х, если известна зависящая
от частоты восприимчивость.
Рассмотрим электромагнитную волну, у которой
волновой вектор к направлен вдоль оси г. Согласно
формулам A.17) и A.18), пространственная и временная
зависимости величин Е и Н даются выражением
ехр / (kz — со/) = ехр | ш (— — А — ^^- \ , B.7)
где было использовано уравнение B.4). Поля Е и Н в
диэлектрике остаются ортогональными как друг к другу,
так и к волновому вектору к, как показано на фиг. 1.1,
однако теперь величины полей связаны следующим
соотношением:
Н = (80/^о),/2 (Ч + йе) Е, B.8)
которое легко получается из B.4) и A.1). В свободном
пространстве соотношение B.8) переходит в A.21).
Интенсивность электромагнитной волны I,
определяемая как энергия, проходящая через единицу площади
в единицу времени, дается обычным вектором Пойнтинга
О]1):
1 = ЕХН. B.9)
1) Интенсивность обычно определяется как скалярная величина,
равная энергии, проходящей в единицу времени через единичную
площадь, нормальную к направлению потока энергии, — Прим. ред.
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 47
Как и при рассмотрении плотности электромагнитной
энергии в гл. 1, из физических соображений правильнее
работать с потоком энергии, усредненным по периоду
колебаний. Согласно A.35), величина усредненного по
периоду вектора Пойнтинга имеет вид
/ = ]-80^|Е(г/)|2. B.10)
Здесь вместе с B.8) была дополнительно использована
ортогональность векторов Е и Н. Поскольку
зависимость Е от координат и времени определяется
выражением B.7), формула B.10) показывает, что величина 7
зависит только от координат. Если /0 есть усредненная
по периоду интенсивность при z = 0, то можно записать
следующее соотношение:
Г(г) = /0ехр(-/С2), B.11)
где
К = 2ш/с. B Л 2)
Определенная таким образом величина К называется
коэффициентом поглощения. На расстоянии, равном 1//С,
интенсивность электромагнитной волны уменьшается в е
раз по сравнению с ее начальным значением.
Свойства микроскопических процессов
Вид комплексной восприимчивости % определяется
свойствами атомов, образующих диэлектрик. Полное
выражение для восприимчивости х выведено в гл. 4 и 8.
В настоящей главе рассматривается связь между
восприимчивостью и теорией поглощения и испускания
Эйнштейна. Сначала необходимо более детально
обсудить свойства трех основных процессов,
рассматриваемых в теории Эйнштейна.
Предположим, что имеется излучение в виде точно
определенной моды полости, причем частота света
резонансна с атомным переходом, описываемым
коэффициентами Эйнштейна Л и В. На фиг. 2.1 показана
направленность трех процессов, которые могут иметь место.
Наиболее важная особенность заключается в том, что свет,
создаваемый вынужденным испусканием возбужденных
48
ГЛАВА 2
атомов, принадлежит той же моде полости, что и
падающий свет, вызывающий испускание, и обладает точно
такими же фазовыми свойствами, что и падающий пучок.
Следовательно, вынужденное испускание стремится
усилить интенсивность падающего пучка при сохранении
неизменными других его свойств. Эти характерные
особенности вынужденного излучения доказываются в гл. 8
и 10.
о
>
Атом
в основном состоянии
^ BW= вероятность поглощения
о
«о
с»
§: Атом
*о в возбужденном состоянии
—ь- 4 »»
g- \ BW - вероятность
5 \ вынужденного испускания
\
А = вероятность
спонтанного испускания
Фиг. 2.1. Направленность процессов поглощения, вынужденного и
спонтанного испускания.
В то же время свойства света, возникающего при
спонтанном излучении* совершенно не зависят от свойств
падающего пучка, и потому излучаемый свет может
принадлежать любой моде полости, удовлетворяющей
закону сохранения энергии. Таким образом, направление
спонтанно излученного света имеет случайную
ориентацию относительно направления распространения
падающего светового пучка, а его фаза произвольна.
После того как свет и атомы достигли стационарного
состояния, средние числа атомов в нижнем и верхнем
состояниях (N\ и N2) остаются постоянными. Благодаря
процессам поглощения число фотонов fico в пучке света,
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 49
проходящем через атомный газ, непрерывно
уменьшается. Возбужденные таким образом атомы со
временем переходят в свои основные состояния и могут
возвращать фотоны в пучок при вынужденном испускании.
Если бы происходили только эти два процесса, то при
достижении стационарного состояния пучок проходил бы
через атомный газ без изменения своей интенсивности.
Однако в силу того, что некоторые атомы возвращаются
в основное состояние путем спонтанного испускания
фотона, доля поглощенной энергии, определяемая
отношением
AJ(A + BW) = 1/{1 + (ttW/ftco3)}, B.13)
переизлучается в произвольных направлениях, причем
только малая часть этой энергии случайно излучается в
направлении падающего пучка.
Следовательно, спонтанное излучение приводит к
рассеянию света и последующему ослаблению падающего
пучка. Такое рассеяние является микроскопическим
источником коэффициента поглощения, определенного в
B.12). Необходимо подчеркнуть, что, хотя мы
употребляем термин «коэффициент поглощения», энергия,
теряемая падающим пучком в стационарных условиях, не
поглощается атомами, а рассеивается1). Одно и то же
основное явление можно экспериментально изучать либо
с помощью измерения коэффициента поглощения, либо
с помощью определения интенсивности рассеянного
света. Теория коэффициента поглощения приводится
ниже в настоящей главе, а рассеяние света подробно
рассматривается в гл. 11.
Как видно из фиг. 2.1, относительная роль
вынужденного и спонтанного излучения определяется
величиной отношения BW/A. Для BW/A = 1 две скорости
излучения равны между собой. Определим некоторые
приближенные численные величины для интенсивности Свето-
1) Это утверждение справедливо только для атомов и простых
молекул. В случае сложных ^молекул заметная часть энергии
возбуждения может преобразовываться в энергию молекулярных
колебаний и тепловую энергию. Более подробное рассмотрение таких
процессов см. в книге [4]. — Прим. ред.
50
ГЛАВА 2
вого пучка. В случае видимого света с частотой в
области 5.10м Гц
со« 3- 1015 Гц B.14)')
и каждый фотон обладает энергией
. Й©« 3- 1(Г19 Дж. B.15)
Определяя плотность мод поля согласно формуле A.30)
pttrf© = (©2/nV)rfco « 3,4- 104dco м-3, BЛ6)
для плотности энергии при BW/A = 1 получаем
следующее выражение:
W rfco = (Л/В) rfco = (/ш3/я2с3) do « 1(Г14 do Дж . м"А BЛ 7)
Здесь бцла использована формула A.60). Интенсивность
светового пучка, требуемая для равенства скоростей
вынужденного и спонтанного излучений, получается точно
так же, как в формуле B.33), умножением выражения
B.17) на скорость света (предполагается, что пучок
распространяется в свободном пространстве, где показатель
преломления равен единице). В результате получим
7rf©«3 • 10~~6dcD Вт . м. B.18)
Типичное значение ширины узкой линии испускания
обычного спектроскопического светового источника
порядка 1010 Гц, что соответствует величине dec, равной
2я-1010 Гц. Интенсивность светового пучка с такой
шириной, требуемая для достижения равенства BW = A,
согласно формуле B.18), приблизительно равна
2«105 Вт'М-2. Это значение можно лучше понять,
обращаясь к табл. 2.1. Из этой таблицы видно, что даже
самая мощная из обычных световых источников ртутная
лампа создает световую интенсивность, недостаточную
для равенства скоростей вынужденного и спонтанного
испускания. Для таких световых пучков почти все
фотоны, поглощенные атомами, переизлучаются в процессе
1) Здесь круговая частота измеряется в герцах. В советской
научной литературе для измерения круговой частоты используется
специальная единица измерений радиан в секунду, — Прим. ред.
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 51
спонтанного испускания и потому их число в падающем
пучке уменьшается. Из табл. 2.1 также видно, что
значения BW, которые сравнимы с А или превышают его,
можно достичь с помощью лазерных световых
источников, в частности импульсных лазеров. В этом случае
вынужденное испускание существенно и характер
распространения света меняется. Условия BW<^A и
BW^A приводят к различным видам поглощения или
усиления, описанным ниже в этой главе.
Таблица 2,1
Приблизительные порядки следующих величин:
усредненной по периоду интенсивности, амплитуды
электрического поля, плотности числа фотонов
и числа фотонов в одной моде полости для основных
видов еветовых источников !)
Ртутлая лампа
Лазер непрерывного
действия
Импульсный лазер
Вт-м~~2
10*
10* '
1012
Е,
В-м"
103
103
107
n/V,
м-3
101*
101*
1Q22
фотоны/мода
ю-2
109
1017
') Данные для ртутной лампы относятся к линии излучения на длине
волны 253,7 нм и являются верхними пределами параметров выходного
излучения обычных спектроскопических источников. Данные для лазеров
являются скорее типичными величинами, а не верхними пределами.
Оптическое возбуждение атомов
В качестве предварительного шага к выводу
микроскопического выражения для коэффициента поглощения
рассмотрим населенности атомных уровней,
получаемые с помощью светового пучка. Предположим, что
N атомов находятся в такой тонкой полости, что при
пррхождении пучка через атомный газ его
интенсивность меняется на незначительную величину. Пусть
пучок с постоянной плотностью энергии W включается в
момент времени ^ —0, когда все атомы находятся в
своих основных состояниях. Тогда, согласно A.76) и
52
ГЛАВА 2
A.78), число атомов в возбужденных состояниях в
более поздний момент времени / определяется выражением
No =
NBW
A+2BW
=- {1 - ехр (- (Л + 2BW) t)}. B.19)
Зависимость величины N2 от времени приведена на
фиг. 2.2.
1,0 г
я;
/
2 _3
(A + 2BW)t
Фиг. 2.2. Число атомов, возбужденных в верхние состояния
в момент времени /.
Для коротких промежутков времени, когда
{A + 2BW)t< 1,
B.20)
число возбужденных атомов возрастает линейно со
временем t:
N2=NBWt. B.21)
В случае больших промежутков времени, когда
(A + 2BW)t> 1, B.22)
число возбужденных атомов приближается к своему
значению в стационарном состоянии:
N2=NBWJ(A + 2BW).
B.23)
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ
53
В самом начале включения светового пучка атомы
переходят в возбужденные состояния и энергия
передается от света к атомам. После достижения
стационарного состояния атомы содержат постоянную величину
запасенной энергии
N2h(a = =■ = z-^rz — B.24)
и передача энергии от излучения уменьшается.
Результат взаимодействия между светом и атомами заклю-
0,5
5?
BW/A
Фиг. 2.3. Зависимость доли атомов, находящихся на верхнем уровне
в стационарном состоянии, от интенсивности пучка, измеряемой
в единицах BWJA.
чается в перераспределении пространственных
направлений распространения фотонов.
На фиг. 2.3 показано значение N2 в стационарном
состоянии. Для обычных световых источников, для которых
BW<^A, величина N2 много меньше N и большинство
атомов остается в основных состояниях. В этом
случае вторым членом в знаменателе выражения B.23)
можно пренебречь, и в результате величина N2
пропорциональна плотности энергии падающего светового пучка.
Для мощных лазерных световых источников, когда
значение BW приближается к А или превосходит его,
зависимость N2 от интенсивности становится нелинейной.
54
ГЛАВА 2
Кривая N2/N приближается к значению 1/2 для Bw > A.
Нелинейное поведение населенности называется
насыщением атомного перехода. В экспериментах с
использованием обычных световых пучков эффектами насыщения
можно, как правило, пренебречь. Однако в теории
экспериментов, использующих лазерные световые источники,
а также в теории действия самого лазера эти эффекты
становятся важными. В эксперименте, описанном выше,
достичь условия N2 > N\ невозможно.
Если теперь падающий пучок снова выключить, то
возбужденные атомы возвращаются в основные
состояния, а запасенная в них энергия, определяемая
формулой B.24), переизлучается в виде фотонов. Пусть N2
есть населенность возбужденного уровня в
стационарном состоянии, найденная по формуле B.23), а момент
времени t = О переопределен и обозначает момент
выключения падающего пучка. Если в A.77) плотность
энергии пучка W положить равной нулю, то кинетическое
уравнение принимает вид
dN2/dt = -N2A, B.25)
а его решение есть
N2 = Nlexv(—At). B.26)
Каждый атом, переходящий из возбужденного состояния
в основное, испускает квант йо, поэтому интенсивность
излучаемого света также уменьшается как ехр(—At).
Наблюдение этого флуоресцентного излучения является
экспериментальным методом измерения коэффициента
Эйнштейна А.
Величина, обратная Л, обозначается тя,
А = 1/тд, B.27)
и называется флуоресцентным или излучательным
временем жизни рассматриваемого перехода.
Результаты B.19), B.21) и B.23) для N2 относятся
к средней населенности атомного возбужденного
состояния. С другой стороны, отношение N2/N можно
рассматривать как вероятность нахождения выбранного атома
в его возбужденном состоянии. Конечно, при поглощении
и переизлучении фотонов отдельный атом совершает не-
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 55
однократные переходы вверх и вниз, причем эти переходы
происходят в случайные интервалы времени в
соответствии с данными вероятностями поглощения и
испускания. Когда система достигает стационарного состояния,
величина N2/N, определяемая формулой B.23), равна
той доли времени, которую отдельный атом проводит в
возбужденном состоянии.
Микроскопическая теория поглощения <-
Рассмотрим теперь прохождение светового пучка
через атомный газ, находящийся в протяженной полости,
где происходит значительное ослабление пучка. Наша
цель заключается в нахождении связи между скоростью
затухания и, следовательно, коэффициентом поглощения,
и коэффициентами теории Эйнштейна.
Допустим, что стационарное состояние уже
достигнуто. Тогда из кинетического уравнения A.77) получим
N2A = (N{ - N2) BW.% B.28)
Скорость рассеяния энергии пучка за счет
спонтанного излучения есть N2Ab^. Чистая скорость потерь
энергии пучка равна скорости N\BWb(of с которой энергия
забирается из пучка в процессе поглощения, минус
скорость возвращения энергии в пучок благодаря
вынужденному испусканию N2B,Wn(i). В стационарном
состоянии два способа вычисления изменения энергии пучка
должны быть идентичными и давать одинаковые
результаты как в формуле B.28).
Для вычисления скорости затухания пучка будем
использовать правую часть формулы B.28), однако
сначала необходимо усовершенствовать описание атомных
переходов. До сих пор предполагалось, что все атомы
имеют одинаковую точно определенную частоту перехода
со. Однако, как описывается в гл. 4 и 5, даже при
рассмотрении для каждого атома одной и той же пары
уровней всегда существует некоторый статистический
разброс частот фотонов, которые могут поглощаться или
испускаться атомами. Пусть F(u)d(u есть та часть
переходов, в которых частота фотонов лежит в малом
интервале Ло около частоты со. На фиг, 2.4 показано типичное
56
ГЛАВА 2
изменение F(co) с частотой, причем площадь под кривой
нормирована к единице.
Рассмотрим пока только те переходы, для которых
частота со лежит в определенном интервале. В
стационарном состоянии, когда число атомов на нижнем уровне
равно Nu а на верхнем N2i скорость изменения энергии
Фиг. 2.4. Доля переходов, в которых частота поглощенного или
испущенного фотона равна со.
пучка в_интервале частот rfco равна —(N\— N2)F((o)'X
XdaBWh®.
Пусть световой пучок распространяется вдоль оси г.
Благодаря затуханию пучка плотность энергии W
является функцией г. Рассмотрим перпендикулярный оси z
тонкий слой полости, имеющий толщину dz и площадь
поперечного сечения а, как показано на фиг. 2.5.
Энергия пучка в этом слое на интервале частот rfco равна
Wdaadz, где величина W предполагается не зависящей
от координат внутри слоя.
Если V есть полный объем полости, то adz/V —
относительное число атомов, находящихся в рассматривав-
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ
57
мом слое. Условие энергетического баланса имеет вид
(d/dt){Wd(*adz) = — {Nl—N2)F{(o)d(x>BWh(i>adz/V; B.29)
преобразуя это выражение, получаем
dW/dt = — {N{ — N2)F((o) BWhnlV. B.30)
Коэффициент поглощения /С, введенный в B,11),
определяет пространственное изменение интенсивности
пучка 7, тогда как теория Эйнштейна дает уравнение для
л
Idio
/
dz
< >
/
Площадь а
/
(I+gdz)du>
Фиг. 2.5. Тонкий слой полости, перпендикулярный направлению
распространения пучка.
временной зависимости плотности энергии пучка W.
Поэтому уравнение B.30) необходимо переписать для
интенсивности.
Левую часть уравнения B.30) можно преобразовать,
приравнивая скорость потерь энергии внутри слоя,
определяемую левой частью уравнения B.29) со знаком
минус, скорости втекания энергии в слой через его
границы. Если Td(x) есть интенсивность пучка в интервале
частот между со и со + dco, то, согласно фиг. 2.2,
- (д/dt) {Wdaa dz) = —a{dT/dz) dz rfco, B.31)
или
dW/dt = dl/дг.
B.32)
Для преобразования правой части уравнения B.30)
заметим, что коэффициент Эйнштейна В обычно
определяется так же, как в гл. 1, где рассматривается
электромагнитная волна,, падающая на один атом в свободном
58
ГЛАВА 2
пространстве, плотность энергии которой связана с элек^
трическим полем уравнением, сходным с A.51).
Интенсивность, используемая в определении коэффициента
поглощения, приведена в B.10), поэтому сравнение
формул A.51) и B.10) дает
W = T/cr\. B.33)
Подставляя B.32) и B.33) в уравнение B.30),,получаем
требуемое уравнение для пространственной
зависимости 7:
dl/dz = - (N{ - N2) P (со) (Bha/Vcr)) 7 B.34)
Для вырожденных энергетических уровней последнее
уравнение обобщается путем введения множителя g2/g\
для члена N\. Однако последующий анализ ограничен
случаем g\ = g2> где дополнительный множитель равен
единице.
Решение уравнения B.34) более сложно, чем это
может показаться на первый_взгляд, так как сами
величины N\ и N2 зависят от W и, следовательно, от 7.
Согласно B.23) и B.33),
Nx- N2= NA/{A + 2BW) = NA/{A + BВ//ст|)}, B.35)
и уравнение B.34) можно переписать в виде
2ВТ \ дТ NBhaF (со)
-(* +—)
/ \ Лсг\ ) dz Vcr\
B.36)
Здесь мы пренебрегли слабой частотной зависимостью
величины А по сравнению с быстрым изменением
функции F((x))i показанной на фиг. 2.4.
Рассмотрим решение уравнения B.36) в двух
предельных случаях. Как было показано выше в этой главе,
для всех обычных световых пучков второй член в
скобках левой части уравнения B.36) (равный 2BW/A)
много меньше единицы.' Если этим членом пренебречь,
что соответствует пренебрежению числом возбужденных
атомов N2, то уравнение B.36) можно проинтегрировать
и получить
l(z)=7Qexp(-Kz), B.37)
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 59
где
K = NBh®F{®)IVc<4. B.38)
Выражение B.37) совпадает с B.11), поэтому
коэффициент поглощения К B.38) совпадает с
коэффициентом поглощения, определенным в B.12).
Измерение затухания пучка позволяет
непосредственно получит.ь коэффициент поглощения. Из B.38) видно,
что величина К изменяется с частотой таким же
образом, как изображенное на фиг. 2.4 распределение частот
атомных переходов, но только умноженное на
дополнительные зависящие от частоты коэффициенты. Для
экспериментального определения зависимости К от частоты
со необходимо использовать световые пучки переменной
частоты, частотный интервал которых узок по
сравнению с распределением частот переходов.
Теория Эйнштейна не дает информации о форме
линии поглощения. Интегрирование по со обеих частей
уравнения B.38) после перенесения множителя Ьы/сц в
левую часть уравнения приводит к равенству
{Ксфсо) d® = NB/V. B.39)
Здесь была использована нормировка функции формы
линии ^(со). Следовательно, измерение значений К и ц
дает возможность экспериментального определения
величины В. Дл~я разреженного атомного газа значение ц
близко к значению показателя преломления для
свободного пространства, равного единице. Ширина
большинства линий поглощения мала по сравнению с теми
частотами со, для которых величина К весьма велика, поэтому
на ширине линии поглощения значение со почти не
меняется. В этом случае величина В прямо
пропорциональна площади под кривой зависимости К от частоты
со. Функциональный вид К обсуждается в гл. 4.
Результат B.39) можно переписать через интеграл
мнимой части восприимчивости %" по частотному
распределению рассматриваемой линии поглощения:
\jX,fd(^ = hNBJV. B.40)
Здесь были использованы формулы B.6). и B.12).
60
ГЛАВА 2
Теперь рассмотрим решение уравнения B.36) в
другом предельном случае светового пучка .очень большой
интенсивности, когда 2BW/A много большее единицы, а
зависимость атомных населенностей от W становится
нелинейной, как описывалось раньше. В этом случае
первым членом в скобках уравнения B.36) можно
пренебречь и получить следующее решение:
Т(г) - /0 = — (NAftoF (cu)/2F) z. B.41)
Следовательно, вместо быстрого экспоненциального
уменьшения интенсивности, определяемого для
небольших интенсивностей коэффициентом В, в B.41) мы имеем
линейное уменьшение I(z) с расстоянием z вдоль
полости со скоростью, определяемой коэффициентом Л.
Уменьшение поглощения по мере приближения
атомного перехода к насыщению обусловлено приближением
скорости рассеяния энергии пучка Л^Лйсо к ее
максимальному значению 1/2^АЬ(а. Любое дальнейшее
увеличение интенсивности пучка 7 не может привести к
пропорциональному увеличению скорости рассеяния, а
поэтому относительное изменение I при прохождении
через газ уменьшается. Макроскопическая теория
поглощения, основанная на уравнениях Максвелла, в
условиях насыщения неприменима. При измерениях
коэффициента поглощения /С, очевидно, следует избегать
насыщения, если результаты будут описываться на основе
теории, приводящей к уравнению B.39).
Инверсия населенностей: лазер
Согласно уравнению B.34), интенсивность пучка при
прохождении через атомный газ растет в том случае,
когда число возбужденных атомов N2 превышает число
атомов в основном состоянии N\. Зависимость роста
интенсивности от z точно такая же, как в B.34), только
теперь коэффициент поглощения отрицателен. Условие
N2 > N\ известно как условие инверсии населенностей
или как условие отрицательной температуры,
поскольку из применения распределения Больцмана A-57)
к случаю N2 > N\ следует, что температура Т
отрицательна. В более общем случае вырожденных энергетиче-
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 61
В
Ъ*Р
121
Чз
V
B21W
1
*23
ских уровней условие роста интенсивности пучка есть
N2> (g2/gl)N\.
Конечно, при тепловом равновесии инверсия населен-
ностей никогда не может быть достигнута, а раньше мы
показали, что этого нельзя достигнуть и с помощью
резонансного поглощения света на частоте перехода двух
состояний. Однако инверсии населенностей для уровней
1 и 2 можно достичь с помощью
экспериментов, использующих
другие энергетические уровни
атома. В самом простейшем
способе используются три
уровня. Чтобы сделать
анализ наиболее простым,
рассмотрим случай, когда все три
уровня являются
невырожденными.
Схема переходов показана
на фиг. 2.6. Теперь основное
состояние атома обозначим как
уровень <?, а его первое и
второе возбужденные состояния —
как уровни 1 я 2. Для
возбуждения перехода 3-+2 используется пучок с плотностью
энергии.Wp, поэтому N2 атомов находятся в
возбужденном состоянии 2. Используемый таким образом световой
пучок называется накачкой, относительное число атомов
NdN, возбужденных накачкой, обычно мало и имеет
величину порядка К)-6. Следовательно, переход 3-+2 далек
от насыщения.
Атом на уровне 2 может излучать свет, совершая
переходы вниз 2->1 или 2-*3, а атом на уровне 1 может
вернуться в основное состояние 3. Ниже будет показано,
что для определенных значений коэффициентов
Эйнштейна можно достичь условия N2 > N\ и, следовательно,
усиливать свет с частотой со = (Е2 — Е\)/Ь.
Уравнения, описывающие скорости переходов в
трехуровневой системе, являются простыми обобщениями
кинетических уравнений для двухуровневой системы. Все
виды переходов показаны на фиг. 2.6. Коэффициенты
Эйнштейна должны иметь индексы, обозначающие те
Фиг. 2.6. Схема атомных
энергетических уровней и
скорости переходов для
трехуровнего усилителя
света.
62
ГЛАВА 2
уровни, к которым они относятся. Предположим также,
что, кроме излучательнои энергии пучка накачки, имеется
свет с частотой со и некоторой плотностью энергии W.
Допустим, что только три рассматриваемых уровня
населены, поэтому
NX + N2 + NZ = N. B.42)
Три кинетические уравнения имеют вид
dN2/dt = — N2A2l — N2A23 +
+ WPB23 (N3 - N2) - WB2{ (N2 - Nx), B.43)
dNxldt = N2A2l - NxAl3 + WB2X {N2 - Nx), B.44)
dN3/dt = N2A23 + NXAX3 - WPB23 (M3 - N2). B.45)
В соответствии с формулой B.42) сумма трех скоростей
равна нулю.
В стационарном состоянии все временные
производные можно положить равными нулю. Получающиеся в
результате уравнения позволяют найти решения для на-
селенностей уровней N\, N2 и N3i выраженные через N,
W и Wp. Эти выражения несколько громоздки, и
основные свойства стационарных решений можно объяснить
более просто следующим образом. Определим скорость
накачки г как
r=~WpB23(N3-N2)/N. B.46)
Отсюда Nr есть скорость, с которой атомы под действием
накачки переводятся в состояние 2. Тогда условия
стационарного состояния из уровней B.44) и B.45),
принимают вид ,
N2 (А2Х + B2lW) = Nx (Л.з + B2[W) B.47)
и
N2A23 + NxAl3 = Nr. B.48)
Из B.47) сразу видно, что для выполнения неравенства
^2 > Ni должно удовлетворяться условие
А21 < Ахз. B.49)
Короче говоря, атомы, возбужденные в состояние 2,
должны относительно медленно переходить в состояние
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ ч 63
/, откуда они быстро переходят в основное состояние.
Решения уравнений B.47) и ^2.48) имеют вид
N = N(A2l+B2lW)r 5Q)
1 Л13(Л23 + A2i) + B21W (Л13 + Л2з)
и
N N(A» + B2lW)r 251)
Ац (Л23 + Ап) + B2lW (Л13 + Л23)
Атомный газ, для которого выполняется условие
B.49), может усиливать излучение с плотностью энергии
W. При некоторых соответствующих изменениях знака
эта теория сходна с вышеизложенной теорией
поглощения света. Структура выражения для N2 — N\,
полученного из B.50) и B.51), сходна со структурой выражения
для N\ — jV2 в случае поглощения, определяемого
формулой B.35). Из B.50) и B.51) следует, что для
небольших интенсивностей усиливаемого пучка величина N2 —
— N1 фактически не зависит от W. В этом случае
интенсивность пучка растет экспоненциально с расстоянием,
проходимым пучком в газе. С другой стороны, для
высоких интенсивностей пучка величина N2 — N\ обратно
пропорциональна интенсивности пучка, а переход между
уровнями 1 и 2 приближается к насыщению. При этом
усиление уменьшается и интенсивность пучка растет с
расстоянием только линейно. Подробные результаты для
двух предельных случаев даны в следующей задаче.
Задача 2.1. Показать, что в случае усиления аналогом
уравнения B.36) является следующее
выражение:
где
; Ы4 + ^)Л B.53)
° А13 + А23 В21 Х '
q _ r(Al3 — A2l) NB2ln<dF(a) /2 54)
Ai3(A23 + A21) Vcx\ V *
Общее решение уравнения B.52)
определяется выражением
In (//То) + {G - 70)//Л = Gz, B.55)
И
ГЛАВА 2
которое в предельных случаях низкой и
высокой интенсивности преобразуется к виду
Т(г) = Т0 exp {Gz) (Г < 1С) B.56)
и
7(z) = 7Q + IcGz (/>/,). B.57)
Общее решение для двух значений /о
представлено на фиг. 2.7,
О 5 Ю 15
Gz
Фиг. 2.7. Кривые, иллюстрирующие рост интенсивности
электромагнитной волны в усиливающей среде для двух значений
отношения 70//с.
Ле1КО видеть область экспоненциального и линейного роста. Пунктирная
кривая построена на основе выражения B.56).
Описанный выше усилитель света называется
трехуровневым лазером. Лазер может так же работать, как
самовозбуждающийся осциллятор, поскольку даже
если плотность энергии W первоначально отсутствует, то
благодаря вероятности спонтанного перехода А2\ может
появиться излучение с частотой со. Такой осциллятор
может создавать световые пучки очень высокой интенсив-
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 65
ности (см. табл. 2.1), поэтому нелинейные эффекты,
связанные с насыщением активного перехода, играют
важную роль в определении характеристик выходного пучка.
Возможны другие типы лазеров, в которых используются
более сложные схемы энергетических атомных уровней.
Теория трехуровневого лазера, кратко описанная выше,
значительно расширена в гл. 10.
Давление излучения
Каждый из фотонов, образующих бегущую
электромагнитную волну с волновым вектором к, обладает
импульсом Ьк. В этом отношении их поведение аналогично
поведению других частиц в квантовой механике и
согласуется с соотношением де Бройля между длиной волны
и импульсом частицы. В любом взаимодействии фотонов
с другими частицами полный импульс должен
сохраняться. Реальность импульса фотона была замечательно
продемонстрирована Комптоном, наблюдавшим в 1922 г.
сохранение импульса при рассеянии фотонов
электронами (комптоновское рассеяние кратко рассматривается
в гл. 11). Комптон использовал взаимодействие
рентгеновских фотонов со свободными электронами, когда
эффекты фотонного импульса особенно важны. Однако
импульс фотонов может привести к интересным следствиям
даже при взаимодействии фотонов видимого диапазона,
обладающих небольшой энергией, с относительно
тяжелыми атомами.
Рассмотрим влияние импульса фотонов на три
основных взаимодействия пучка света с атомным газом,
показанные на фиг. 2.1. В процессе поглощения от светового
пучка к поглощающему атому передается импульс Ьк.
В результате атом приобретает параллельную пучку
скорость Ьк/М, где М — масса атома. Если возбужденный
атом впоследствии переходит в основное состояние за
счет вынужденного испускания, то испущенный фотон
уносит импульс Ьк, параллельный падающему пучку, а
атом теряет приобретенную ранее скорость.
Однако если возбужденный атом впоследствии
переходит в основное состояние за счет спонтанного
испускания, то направление импульса, унесенного испущенным
3 Зак. 885
66
ГЛАВА 2
фотоном, с равной вероятностью лежит в любом участке
полного телесного угла 4я, центр которого находится
в атоме. Таким образом, атом приобретает скорость
отдачи в некотором случайном направлении, поэтому
предварительно приобретенная атомом компонента скорости
в среднем не теряется.
Отсюда следует, что каждое поглощение фотона, за
которым следует спонтанное испускание, в среднем
передает от фотонов к атомам импульс Ьк. Это утверждение
справедливо независимо от того, достигла ли система
«атом + излучение» стационарного состояния или нет.
В этом заключается отличие от передачи атомам энергии
возбуждения йсо, которая, как было подчеркнуто в связи
с формулой B.24), уменьшается при достижении
стационарного состояния. Передача импульса атомам
эквивалентна давлению, производимому на газ излучением^
При наличии плотности излучательной энергии W на
частоте со, резонансной переходу между атомным
основным состоянием и одним из возбужденных состояний,
скорость изменения полного атомного импульса П
пропорциональна разности между скоростями поглощения и
вынужденного излучения
dU/dt = Ьк {Nx - N2) BW. B.58)
В стационарном состоянии, когда выполняется уравнение
B.28), скорость передачи импульса принимает вид
dU/dt = HkN2A, B.59)
откуда явствует прямая пропорциональность между
dU/dt и скоростью спонтанного излучения, ожидаемая
из приведенного выше обсуждения.
Задача 2.2. Оцените скорость передачи импульса в
зависимости от величин W и t для эксперимента,
описываемого уравнением B.19), когда
световой пучок падает на газ из атомов,
находящихся в начале эксперимента в своих
основных состояниях. Рассмотрите результат
в предельных случаях большого и малого
значений W, большого и малого времени t.
ТЕОРИЯ ПРОСТЫХ ОПТИЧЕСКИХ ПРОЦЕССОВ 67
Эшкин [2] наблюдал действие давления излучения при
ускорении частиц, много больших, чем описанные здесь
атомы. Он использовал шарики из латекса диаметром
порядка 1 мм, взвешенные в воде и облучаемые
лазерным световым пучком. По-видимому, аналогичные
эффекты должны наблюдаться при давлении излучения на
атомы газа, откуда можно получить некоторые полезные
следствия. Например, в газе, состоящем из смеси атомов
двух типов, из которых атомы только одного типа имеют
переход на частоте со, падающий световой пучок
оказывает давление только на атомы этого типа.
Следовательно, с помощью подходящего устройства камер можно
было бы осуществлять разделение атомов двух типов [2].
В частности, поскольку электронные энергии
возбуждения разных изотопов одного атома, вообще говоря,
немного различны, то этот метод можно было бы
использовать для разделения изотопов.
Другое применение давления излучения следует из
передачи импульса фотонов лазерного пучка электронам
проводимости полупроводника [3]. Ускоренные таким
образом электроны создают заметный ток, и этот эффект
можно использовать для измерений интенсивности
лазерных световых импульсов. Теория таких экспериментов
должна строиться на основе зонной структуры
полупроводников, однако основной процесс является другим
проявлением импульса фотонов1).
ЛИТЕРАТУРА
1. Panofsky W. К. #., Phillips AL, Classical electricity and
magnetism, Addison-Wesley, Reading, 1955, p. 161.
2. Ashkin A., Phys. Rev. Lett., 24, 156 A970).
3. Gibson A. F., Kimmitt M. F., Walker A. C, Appi. Phys., Lett., 17,
75 A970).
4*. Теренин Л. //., Фотоника молекул красителей, изд-во «Наука»,
1967.
5*. Эшкин Л., УФН, 110, 101 A973).
6*.Аскарьян Г. А., УФН, ПО, 115 A973).
1) Краткое и ясное изложение проблемы давления лазерного
излучения имеется в работах [5, 6]. — Прим. ред.
3*
Глава 3
Квантовая теория коэффициента
Эйнштейна В
Коэффициенты Эйнштейна можно рассматривать как
феноменологические параметры, определяемые
экспериментальным путем для интересующих нас атомных
переходов. В то же время поглощение и испускание света
атомами можно исследовать теоретически, пользуясь
методами квантовой механики. Результаты исследования
удобно представлять в виде теоретических выражений
для коэффициентов Эйнштейна. Хотя эти выражения
часто непригодны для точных оценок, они позволяют
судить о тех факторах, которые влияют на величину
коэффициентов Эйнштейна, а иногда и определять их
относительную величину для соответствующих переходов.
В настоящей главе коэффициент Эйнштейна В
вычисляется на основе квантовой механики. При этом
используется полуклассическая теория, в которой
электромагнитное поле описывается классически, а атомные
состояния—квантовомеханически. Точно такие же
выражения для коэффициентов Эйнштейна получаются и втом
случае, когда как атом, так и свет рассматриваются
квантовомеханически (см. гл. 8). Как и в предыдущей главе,
будем предполагать, что тепловое возбуждение высоко-
лежащих атомных состояний отсутствует и что
единственными атомными уровнями, участвующими во
взаимодействии с излучением, являются основное состояние
атома и одно из его возбужденных состояний, которое
отстоит от основного состояния по энергии на
расстояние, равное энергии светового кванта. Поэтому в
дальнейшем все атомы могут рассматриваться как квантово-
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 69
механические системы, имеющие только два
эффективных уровня, со всеми вытекающими отсюда
упрощениями теории.
Квантовая механика процессов, зависящих
от времени
Коэффициент Эйнштейна В дает скорость, с которой
изменяется во времени состояние системы в процессах
поглощения и вынужденного испускания.
Соответствующее квантовомеханическое рассмотрение должно
начинаться с рассмотрения временного волнового уравнения
(см., например, [1])
3%W = ihdx¥/dt. C.1)
Здесь Ж — квантовомеханический гамильтониан,
зависящий, вообще говоря, от времени, а 4я — зависящая от
времени волновая функция. В этой книге везде знаком
Л в дальнейшем обозначаются величины, являющиеся
квантовомеханическими операторами.
Рассмотрим сначала изолированный атом в
отсутствие поля излучения. В этом случае гамильтониан ато-
ма Же слагается из кинетической и потенциальной
энергий составляющих его частиц и не зависит явным
образом от времени. В учебниках по квантовой механике1)
показано, что при не зависящем от времени гамильто-
ниане, подобном Же> волновое уравнение C.1) имеет
решения вида
Ч'„ (г/) = ехр (- ВДА) фя (г). C.2)
Зависящая от времени волновая функция 4я п
оказывается произведением зависящего от времени фазового
множителя и не зависящей от времени волновой
функции г|)п(г), которая удовлетворяет уравнению на
собственные значения энергии Еп:
%ЕЪп(г) = ЕпЪп(г). C.3)
В этом уравнении индекс п означает решения,
соответствующие различным значениям энергии Е7и а аргумент
-
1) См. работу [1], стр. 38,
70
ГЛАВА 3
т характеризует координаты всех частиц, образующих
атом. Очевидно, что соотношение C.3) является как раз
тем условием, при котором волновая функция вида C.2)
удовлетворяет уравнению CJ) с гамильтонианом Же
вместо гамильтониана Ж.
Состояния, описываемые волновой функцией C.2) и
уравнением C.3), называются стационарными атомными
состояниями. Они обладают тем свойством, что когда
атом находится в одном из этих состояний, то среднее
значение любой наблюдаемой величины не зависит от
времени, если при этом соответствующий ей оператор
также явно не зависит от времени. Система, помещенная
в одно из стационарных состояний ее полного
гамильтониана, остается в нем во все последующие моменты
времени. Во многих случаях зависящим от времени
фазовым множителем в C.2) можно пренебречь, и поэтому
под волновой функцией понимается только ее
пространственная часть г|эп(г). Однако при рассмотрении
зависящих от времени процессов, таких, например, как
поглощение и испускание света атомом, эти фазовые
множители должны учитываться.
При вычислении коэффициента В будут учитываться
только два атомных уровня, имеющие волновые функции
^i(r) и г|J(г) с собственными значениями энергии
соответственно Е\ и Е2, так что
ЖЕ^2(т) = Е2^2(т).
Соответствующие зависящие от времени волновые
функции записываются в виде
Wl(rt) = exp(-iElt/h)*i(r),
W2 (r/) = ехр (- iE2t/h) ф2 (г). F'Ъ}
В дальнейшем мы часто будем говорить о волновых
функциях W и ф, не рассматривая их явного аналитического
вида. При этом всегда будем помнить, что зависящий от
времени фазовый множитель входит в волновую
функцию ? и не входит в волновую функцию \f>. В этом
случае схема энергетических уровней такая же, как на
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 71
фиг. 1.8, но только теперь частота перехода обозначается
через (о0:
Нщ = Е2 — Е{. C.6)
Во всех последующих вычислениях волновые функции
\fi и \Ь2 предполагаются известными.
Рассмотрим теперь случай, когда на атом действует
электромагнитное излучение. С электромагнитной волной
связаны электрическое и магнитное поля, изменяющиеся
в пространстве и во времени. Их взаимодействие с
атомом приводит к тому, что у него появляется
дополнительная электромагнитная энергия, которая может быть
представлена гамильтонианом Ж^ добавляющимся
к гамильтониану свободного атома спое. /1вный вид
гамильтониана 26i будет кратко обсужден в дальнейшем,
в данный момент этот оператор рассматривается как
некий оператор общего вида, зависящий от координаты г
и времени t. Тогда полный гамильтониан принимает вид
об = ав]? ~\- <?#/. C.7)
Поскольку гамильтониан Ж зависит явно от времени, то
волновое уравнение C.1) уже не имеет решений в виде
стационарных состояний типа C.2) и C.3).
Выражение для коэффициента Эйнштейна 5i2,
связанного с поглощением излучения, можно получить
следующим образом. Предположим, что в некоторый
момент времени атом находится в своем состоянии «фь Бла-
годаря наличию в гамильтониане члена Жг состояние
г]?1 не является стационарным и имеется конечная
вероятность того, что в более поздний момент времени
атом будет обнаружен в состоянии г|?2. Эту вероятность
можно выразить через скорость перехода из состояния 1
в состояние 2 и, следовательно, связать с
коэффициентом В. Необходимая информация содержится в
зависящей от времени волновой функции атома W, получаемой
решением уравнения C.1).
Если частота света близка к соо, то лишь два
выделенных атомных состояния принимают участие в излу-
чательных процессах, поэтому в любой момент времени
72
ГЛАВА 3
волновая функция должна быть линейной комбинацией
следующего вида:
Y (rt) = С{ (t) Т, (rt) + С2 (/) ¥2 (rt). C.8)
Смесь состояний меняется со временем, однако
можно потребовать, чтобы волновая функция 4?(rt) была
всегда нормирована
J | ¥ (rt) р dV = | С, (О I2 +1 С2 @ |2 = I. C.9)
Здесь была использована формула C.5) и
предполагалось, что функции \|)i(r) и ty2(r) ортонормированы.
Коэффициенты Ci и С2 не зависят от координат.
Подстановка выражения C.8) в уравнение C.1) дает
уравнение для коэффициентов С\ и С2, которое с
помощью формул C.4), C.5) и C.7) можно упростить и
привести к виду
Ж, (С,¥, + С2Ча) = /А (V, -^- + У2 Щ. C.10)
Умножая это уравнение слева на комплексно
сопряженную функцию W* и интегрируя по всему пространству,
получаем
С] J ^\Ж^Х dV + С2 ехр (— m0t) J ф!ад2 dV = ih dCrfdt.
C.11)
Здесь были использованы формулы C.5) и C.6). Для
матричных элементов гамильтониана Mi удобно ввести
сокращенные обозначения
hfu = $ф13М>,£*У, Й/,2= 5^/*2dy и т. д., C.12)
после чего уравнение C.11) упрощается:
Cxfn + С2 ехр (- ШоО /i2 ='dCJdt. C.13)
Аналогично, умножая уравнение C.10) слева на W2i
получаем
C{exp(i(oQt)f2l+C2f22 = idC,/dt. C.14)
Уравнения C.13) и C.14) не зависят от координат,
а матричные элементы ? являются известными функ-
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 73
циями времени, если функциональный вид гамильтониана
Жг определен. Уравнения C.13) и C.14) можно в
принципе решить и найти значения С\ и С2 как функции
времени, а затем определить волновую функцию ^{vt) по
формуле C.8).
Вид гамильтониана взаимодействия
Полный вид гамильтониана взаимодействия
электромагнитного поля с атомом довольно сложен, поэтому его
подробное обсуждение отложено до гл. 8. Однако для
EQcos(kz-a)t)
к
и H0cos(kz-a)t)
Фиг. 3.1. Система координат, используемая для описания атома &
электромагнитной волны.
вычисления коэффициента В достаточно знания
основных свойств взаимодействия.
Рассмотрим изображенный на фиг. 3.1 атом,
состоящий из ядра с зарядом Zey окруженного Z электронами,
каждый из которых имеет заряд —е. Атом
взаимодействует с поляризованной электромагнитной волной,
имеющей компоненты электрического и магнитного
полей, изображенные на фиг. 3.1, где атомное ядро
выбрано в качестве начала координат. В настоящей главе
для описания временной зависимости полей
используются вещественные функции.
74
ГЛАВА 3
Типичные значения радиусов орбит атомных электронов
определяются величиной боровского радиуса
а0 = 4ле0Н2/те2 « 5 • КГ11 м, C.15)
где т — масса электрона. Боровский радиус намного
меньше длины волны электромагнитного излучения, если
частота излучения не превышает величину порядка
1018 Гц. Для таких частот
ka0<l, C.16)
поэтому пространственное изменение электрического и
магнитного полей на расстоянии порядка размера атома
очень мало. Тогда в хорошем приближении членом kz
в косинусе, описывающем пространственную зависимость
полей, можно пренебречь.
Полный электрический дипольный момент атома
можно записать в виде —eD, где
z
D = Zr/. C.17)
Основной вклад в гамильтониане взаимодействия
обусловлен потенциальной энергией электрического диполя
C.17) в электрическом поле Е0 cos cof, поэтому
гамильтониан 36i можно записать в виде
3@1 = eD- E0cosGtf. C.18)
Другие вклады в гамильтониан взаимодействия Ж\
подробно рассматриваются в гл. 8, где показано, что они
малы по сравнению с гамильтонианом C.18).
Гамильтониан взаимодействия §6i {формула C.18)]
является вещественным и нечетным, иначе говоря
меняет знак при инверсии координат относительно ядра,
когда координаты Tj заменяются на —г,-. Отсюда
следует, что подынтегральные выражения в матричных
элементах tfw и ^22, определенных в C.12), являются
нечетными функциями координат, поэтому
соответствующие интегралы должны обращаться в нуль:
/и = /22 = 0. C.19)
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 75
Если волновые функции атомных состояний i|)i и ip2
имеют противоположную четность, то недиагональные
матричные элементы f\2 и f2\ совсем не обязательно
должны обращаться в нуль, причем, согласно C.12),
эти матричные элементы связаны соотношением
/12=^21. C.20)
Поскольку на фиг. 3.1. поле Е0 направлено вдоль оси х,
явный вид матричного элемента ?\2 дается выражением
/12 = {eE0Xl2/h) cos со/, C.21)
где
#12=^№М1Л C.22)
Здесь X есть ^-компонента вектора D, а интегрирование
производится по координатам всех электронов.
Матричный элемент ?\2 состоит из зависящего от времени
члена cos со/, умноженного на численный коэффициент,
для которого удобно иметь простое обозначение.
По определению
Г12 = еЕ0Х12/Н, C.23)
и выражение C.21) принимает вид t
fl2 = T[2cos(i>t. C.24)
Рассмотрим, напримегр, переход 1S->2P в атоме
водорода. С учетом спинового квантового числа электрона
основное состояние 15 вырождено двукратно, а
состояние 2Р шестикратно. Однако спиновое квантовое число
при атомном переходе не может изменяться, поскольку
гамильтониан взаимодействия C.18) не зависит от спина
электрона. Таким образом, для данного спинового
квантового числа основного состояния имеются три
разрешенных относительно перехода состояния 2Р. Кроме
того, для электромагнитной волны, поляризованной
вдоль оси ху интеграл в выражении для Т\2 равняется
нулю для всех состояний, за исключением состояния
2РХ. Величина Т\2 вычисляется в следующей задаче.
76
ГЛАВА 3
Задача 3.1. Докажите, что для состояний атома водорода
ih = n-V.fl-v, exp (- r/aQ), C.25)
^ = 2/2я-1/2а-5/^ехр(--^) C.26)
выполняется соотношение
У12 = 21'% еЕ0а0/Шп. C.27)
Частота перехода между состояниями C.25)
и C.26) есть
со0= —со^, C.28)
где
Л©я = теА1Ъ2пЧуг\ C.29)
Покажите, что для выполнения равенства
Тп = соо требуется величина поля Е0
порядка 3-Ю11 В-м-1.
Для полей Е0 почти всех световых пучков (см.
табл. 2.1) выполняется неравенство
Г12 < ©о- C.30)
Очень мощные световые пучки требуют специального
анализа и рассматриваются в гл. 12.
Скорость перехода
Используя формулы C.19), C.20) и C.24), основные
уравнения C.13) и C.14) можно упростить:
Tl2 cos со/ ехр (— m0t) С2 = * dCJdt C.31)
и
У и cos Ы ехр (i(u0t) С{ = / dCJdt. C.32)
Для двухуровневой системы последние уравнения
являются точными.
Задача 3.2. Докажите, что величина |Ci|2+ |C2|2 не
меняется со временем, обеспечивая таким
образом выполнение условия нормировки C.9)
на всем протяжении процессов, зависящих от
времени.
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В J7
К сожалению, несмотря на их простоту, уравнения
гC.31) и C.32) решить в общем случае трудно, поэтому
следует искать приближенные решения, основанные на
неравенстве C.30), которое выполняется для двух
данных частот соо и со, входящих в уравнения C.31) и C.32).
Прежде чем искать приближенные решения, полезно
рассмотреть специальный случай, когда эти уравнения легко
решаются.
Задача 3.3. Рассмотрите решение уравнений C.31) и
C.32) для специального случая со = 0, когда
электрическое поле, действующее на атом,
постоянно во времени. Покажите, что в этом
случае величина С2 удовлетворяет уравнению
^-Шо^г + \Г12?С2 = 0. C.33)
Докажите, что если при t = 0 атом
находится в своем нижнем состоянии ifi, то значение
|С2|2 определяется выражением
| с212 = 24|Г12'2 sin2{(со2 + 4Г212I/* //2),
C.34)
а значение |Ci|2 можно найти из условия
нормировки C.9). Обе величины |Ci|2 и
|С2|2 представлены на фиг. 3.2 в виде
функции времени для нереально большого
значения отношения \Ti2\/(Ooy указанного на
графике. Период колебаний этих величин
определяется временем
/o=^frfk?F* C35)
Величины |Cj|2 и |С2|2 есть зависящие от
времени вероятности нахождения атома в его
нижнем и верхнем состояниях. Для более
реальных значений \Т\2\2 вероятность
нахождения атома в его возбужденном
состоянии очень мала и в максимуме достигает
величины порядка 4 \Т12 р/со2).
78
ГЛАВА 3
Вычисление коэффициента Эйнштейна В в принципе
сходно с решением приведенной выше задачи, однако
теперь уравнения C.31) и C.32) необходимо решить для
случая, когда частота со близка к частоте перехода щ.
Вновь примем, что в момент времени t = О атом нахо-
1,0
0,5
\Г12\/ь>о
Фиг. 3.2. Вероятности \С{\2 и \С2 \2 нахождения атома в
нижнем и верхнем состояниях при действии приложенного постоянного
поля.
Предполагается, что при f=0 атом находится в невозмущенном нижнем
состоянии.
дится в своем нижнем состоянии г|)ь поэтому граничные
условия имеют вид ,, & *- •
d @) = 1 и С2@) = 0. C.36)
Величина |С2@|2 опять есть вероятность нахождения
атома в верхнем состоянии \р2 в момент времени t.
Скорость \C2(t)\2/t, с которой возрастает вероятность
нахождения атома в его возбужденном состоянии,
является скоростью квантовомеханического перехода.
Сравнивая эту скорость с определениями В\2 на фиг. 1.8,
получаем
Bl2W(<*)=\C2{t)\% C.37)
где Щсо)—усредненная по периоду плотность энергии
электромагнитной волны, показанной на фиг, 3.1. Следо-
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 79
вательно, вычисление величины C2(t) дает требуемое
квантовомеханическое выражение для В[2.
При отсутствии точного решения1) уравнений C.31)
и C.32) неравенство C.30) наводит на мысль о
возможности получения выражений для С\ и С2 в виде ряда по
степеням Y\2. Если начальные значения С\ и С2 {формула
C.36)] подставить в левые части уравнений C.31) и
C.32) и проинтегрировать по времени, то в первом
приближении получим следующие временные зависимости
величин С\ и С2:
С{ (/) = 1
и
C.38)
Подставляя эти решения в левые части уравнений C.31)
и C.32) и еще раз интегрируя по времени, получаем
второе приближение, в котором величина C2(t) остается без
изменения, а уточненное выражение для Ci(t)
принимает вид
С{ @ = 1 +1 Г12 f X (функция /). C.39)
Теперь можно найти третье приближение и т. д. Для
связанных уравнений таким образом получается
итерационное решение, в котором C\(t) выражается в виде
ряда по четным степеням \У\2\, a C2(t)—в виде ряда
по нечетным степеням Т\2 или Т\2. Предполагается, что
при выполнении условия C.30) оба ряда быстро
сходятся.
Согласно C.23), эти ряды можно также
рассматривать как разложения по степеням электрического поля
Е0. Плотность энергии волны связана с Е0 соотношением
уе^02==5^((о)йсо, C.40)
которое после интегрирования по объему становится
сходным с соотношением A.51). Сравнение членов с оди-
1) Уравнения C.31) и C.32) были численно решены в работе
[2]. В этой работе можно найти кривые временной зависимости
\C2(t) |2 для нескольких значений щ — со.
80
ГЛАВА 3
наковыми степенями Е0 в левой и правой частях
равенства C.37) показывает, что требуемое выражение для
В\2 можно получить, если величину C2(t) вычислить с
точностью до членов первого порядка по Ед или,
эквивалентно, по Т\2- Для этой цели достаточно уже первого
приближения {выражение C.38)].
Члены более высокого порядка по Е0, входящие в
выражение для C2{t)y в соответствии с приведенным выше
анализом дают скорости перехода, пропорциональные
второй и более высоким степеням величины Щсо). Такие
переходы относятся к области нелинейной оптики, где
линейная теория поглощения и излучения Эйнштейна
неприменима. Они не наблюдаются в экспериментах с
обычными световыми пучками, но играют важную роль в
случае интенсивных световых пучков, получаемых в
импульсных лазерах, когда неравенство C.30) может не
выполняться. Рассмотрение процессов нелинейной оптики
мы отложим до гл. 12, а здесь ограничимся линейным
случаем, где адекватным решением является выражение
C.38).
Второй член в линейном решении C.38) для С2@
намного больше первого члена. Рассмотрим случай,
когда частота света со точно равна со0 и выражение C.38)
принимает вид
С2 (t) = — (/Fi2/2coo) [exp (too*) sin ©о* + co0t]. C.41)
В дальнейшем будет получено, что характерный период
времени ty в течение которого происходят атомные
переходы, обычно порядка Ю-7 с или больше, тогда как
типичное значение частоты со о из B.14) порядка 1015 Гц.
Поэтому неравенство
coQt > 1 C.42)
выполняется очень хорошо для интервалов времени /,
интересующих нас при данном расчете. Другими словами,
проходит много периодов колебаний электромагнитного
поля, прежде чем вероятность атомного возбуждения
достигнет значительной величины. Следовательно, второй
член в скобках выражения C.41) намного больше
первого члена, и это утверждение остается справедливым,
когда частота со близка, но не равна точно со0.
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 81
Таким образом, в хорошем приближении первым
членом в основном решении C.38) можно пренебречь и
переписать это решение в виде
|C2(/)P=ir,2Psin2j^;//2}. C.43)
Когда частота со точно равна соо, вероятность атомного
возбуждения возрастает со временем квадратично:
\C2(t)\2 = j\Tl2\2t2 (со = со0), C.44)
но если частота со отличается от частоты соо, то
зависимость |С2@|2 от времени имеет колебательный
характер.
На фиг. 3.3 показана зависимость величины |С2@|2
от частоты со при фиксированном значении времени t.
С возрастанием t величина максимума кривой растет
пропорционально t2, а нули функции смещаются вдоль
горизонтальной оси к началу координат.
Выражение C.43) является требуемым решением для
вероятности перехода атома в его возбужденное
состояние за время t. Однако, прежде чем этот результат
связать с измеряемой скоростью перехода, его необходимо
преобразовать. До сих пор предполагалось, что частота
перехода со0 является строго определенной величиной,
которой можно приписать математически точное значение.
Это предположение не соответствует условиям любого
реального эксперимента, в котором всегда имеется
некоторая неопределенность значения соо- Все
спектроскопические приборы имеют конечное разрешение, поэтому
измеряемые частоты спектральных линий определяются
с точностью до некоторой величины Асо. Даже если
рассмотреть идеальный эксперимент с совершенным
разрешением по частоте, то все равно имеется более
фундаментальное ограничение, обусловленное собственными
ширинами самих спектральных линий. Различные
источники уширения частот атомных переходов описываются
в гл. 4 и 5. Хотя некоторые из этих источников можно,
по крайней мере в принципе, устранить, однако
вследствие процесса спонтанного испускания всегда
существует неустранимая составляющая неопределенности
82
ГЛАВА 3
значения Дсо. Следовательно, величина неопределенности
Дсо для значения соо зависит от множества факторов и
может существенно меняться от эксперимента к экспе-
\СМ)[
-4 л It -2л/1 0 2л/1 4лIt
со-со0
Фиг, 3.3. Зависимость вероятности | С212 нахождения атома на его
верхнем уровне в момент времени t от частоты возбуждающего
света со.
Ордината кривой при g)=uH есть 1/4 | У и I212.
рименту. Приведем типичное значение Дсо, которое
следует иметь в виду;
Дсо~109Гц. C.45)
Неопределенность величины со0 можно учесть путем
интегрирования выражения для |С2@|2 по области Дсо.
Интерпретируя теперь со0 как центр распределения
частот перехода и учитывая формулы C.23) и C.40),
запишем выражение C.43) в виде
О*+ 72 А©
0)о —1/2 Дсо
Будем предполагать, что плотность энергии излучения
имеет постоянное значение Щсоо) на всей области Дсо,
72 АО)
Г ,7^, ч sin2 {(со0 — со) t/2} * /о лс\
\ W (со) г-^ гН-1 асо. C.46)
J v J (со0 —соJ v
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 83
Тогда выражение C.46) можно переписать следующим
образом:
| С2 (t) |2 = {2е21 Xl212 W Ы/е0Й2} Л C.47)
где
©о+'/г А@
sin» f(«o - «)//2L д {гА8)
Зависимость значения интеграла / от До и t приведена
на фиг. 3.4. Два предельных значения этого интеграла
tAco
Фиг. 3.4. Зависимость значения интеграла, определенного в C.48),
от t (сплошная кривая).
Пунктирная кривая построена на основе линейного приближения C.50).
можно записать аналитически. Из фиг. 3.4 видно, что
для малых значений ^Дсо подынтегральное выражение
является почти константой, поэтому
I = \t2 Aco (*Дсо< 1).
C.49)
Для больших значений tAco интегрирование в C.48)
производится почти по всей области под кривой на фиг. 3.3
84
ГЛАВА 3
и предельное значение интеграла имеет вид {3]
I = jnt (/Дсо> 1). C.50)
Линейная по t предельная зависимость C.50)
изображена пунктирной линией на фиг. 3.4. Как видно из
фиг. 3.4, точное значение / описывается кривой с
небольшими модуляциями, обусловленными нулями функции,
показанной на фиг. 3.3. С увеличением значения /Асо
линейная зависимость становится все более и более
хорошим приближением.
Согласно уравнению C.37), коэффициент Эйнштейна
В связан с теорией поглощения, в которой вероятность
возбуждения атома пропорциональна промежутку
времени ty прошедшему после включения поля. Это
соответствует линейной временной зависимости /, описываемой
выражением C.50) квантовой теории поглощения.
Комбинируя формулы C.47) и C.50), получаем
I C2 (t) |2 = ш?21 Xl212 W (co0)//edft2. C.51)
Последний результат будет нами использован для
получения квантовомеханического выражения для
коэффициента В.
Обычно квадратичной временной зависимостью /,
описываемой выражением C.49), можно пренебречь, так
как эта зависимость реализуется для очень коротких
промежутков времени, когда вероятность возбуждения
|С2(/)|2 настолько мала, что является ненаблюдаемой
величиной. В большинстве экспериментов наблюдаемые
переходы соответствуют более значительным
промежуткам времени /, когда сплошная линия на фиг. 3.4 служит
хорошим приближением для точной зависимости /.
Существование начальной квадратичной зависимости / от
/ можно качественно объяснить следующим образом.
Фурье-компоненты электромагнитной волны с
фиксированной частотой, но конечной длительности t
распределены по частотному интервалу порядка 2n/t (см.
вычисление ударного уширения в гл. 5). Следовательно, для
времени t, меньшего 2я/Асо, только доля энергии волны,
равная ?Дсо/2я, приходится на распределение атомных
частот перехода Доо, и вероятность возбуждения за вре-
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 85
мя t пропорциональна /2Дсо. С другой стороны, для
времени t, большего 2я/Дсо, вся падающая на атом
электромагнитная энергия может быть сосредоточена внутри
частотного интервала Дсо; в этом случае нет
дополнительного множителя tA(x)/2n, а вероятность возбуждения
просто пропорциональна t.
Линейное приближение, реализованное в выражении
C.51), должно, очевидно, нарушаться для таких
промежутков времени, когда величина \C2(t) |2, согласно C.51),
больше единицы, что противоречит условию нормировки
C.9). Однако для больших промежутков времени число
возбужденных атомов можно определить с помощью
уравнений B.19) — B.23), если только величина
коэффициента В уже вычислена. При таких больших
промежутках времени нарушение линейного приближения
обусловлено членами более высокого порядка по У°\2 в
разложениях Ci(t) и C2(t).
Выражение для коэффициента В
Теперь вычисление коэффициента Эйнштейна В в
принципе закончено. Однако, прежде чем записать
результат, необходимо рассмотреть переход от расчета,
проведенного для одного атома, к расчету для случая
газа, состоящего из одинаковых атомов.
Допустим, что возмущение Ж\ действует
одновременно на большое число одинаковых атомов N. В момент
времени t каждый атом будет с вероятностью |Ci|2
находиться в своем нижнем состоянии \р\ и с вероятностью
|С2|2 — в своем верхнем состоянии if>2. Поэтому средние
числа атомов в этих двух состояниях определяются
выражениями
Af1 = j/V|C,|2 и N2 = N| С212. C.52)
Тогда из условия нормировки C.9) следует, что
населенности уровней удовлетворяют требованиям сохранения
числа атомов A.76). Формулы C.52) можно
использовать для установления связи между квантовомеханиче-
скими амплитудами вероятности нахождения атома в
определенных состояниях С\ и С2, вычисленных для од-
86
ГЛАВА 3
ного атома, и населенностями уровней большого числа
одинаковых атомов.
Однако даже в случае газа из одинаковых атомов
или молекул пространственные ориентации
соответствующих электронных состояний меняются случайным
образом от атома к атому или от молекулы к молекуле.
Полезно привести выражение для коэффициента В, в
котором случайные пространственные ориентации уже
точно учтены. Пусть е есть единичный вектор в
направлении электрического поля электромагнитной волны,
которое выбрано в качестве оси х на фиг. 3.1. Матричный
элемент Х\2 можно записать в виде
*,2 = e-D12> C.53)
где
а вектор D определен в C.17).
Для данной пары состояний \fi и г|J вектор Di2 имеет
определенную пространственную ориентацию, которая
в газе меняется случайным образом вследствие случай*
ных ориентации атомов и молекул. Чтобы получить
коэффициент В для газа, используя выражение C.51),
величину |^i2|2 необходимо усреднить по всем случайным
ориентациям вектора D12. Требуемая усредненная
величина содержит среднее значение cos2 6, где 6 — угол
между векторами Di2 и е. Поскольку
cos4) = -~, C.55)
то, производя в C.51) замену
\Xl2f^\JTJ==±\Dl2\2 C.56)
и сравнивая выражения C.37) и C.51), получаем
следующий квантовомеханический результат для
коэффициента Эйнштейна:
Bl2 = 7ie2\Dl2\2/3e0h2. C.57)
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 87
В отсутствие падающей электромагнитной волны га-
мильтониан 2&i обращается в нуль, а состояния \|)i и г|>2
вновь становятся стационарными состояниями полного
гамильтониана, который теперь сводится к одному га-
мильтониану Же- Переходы из состояния / в состояние
2 не могут происходить даже тогда, когда энергия
состояния 2 меньше энергии состояния 1.
Полуклассический метод настоящей главы не включает процесса
спонтанного излучения, поэтому для удовлетворительного
анализа необходимо использовать квантованное поле
излучения. Такой анализ проводится в гл. 8. Однако
правильное выражение для коэффициента А можно найти,
комбинируя общие соотношения между
коэффициентами Эйнштейна, приведенные в A.59) и A.60), с кван-
товомеханическим выражением для В\2, В результате
получим
= ficO30gl = gl*4|Pl2l2 C58ч
21 я2с3£2 12 Зле0£2Йс3 *
Величины коэффициентов А можно легко вычислить
для случая атома водорода. Рассмотрим переходы
между состояниями IS и 2Р. Имеются три 2Р-состояния,
обладающие одинаковыми скоростями перехода из
состояния IS, поэтому величина общего для трех 2Р-со-
стояний коэффициента Bi2 в три раза больше величины,
даваемой формулой C.57), в которой Di2 есть
матричный элемент между состоянием 15 и одним из трех 2Р-
состояний. Принимая g\ = 1, g2 =3 и используя C.15),
C.27) и C.28), получаем
вУ0)Р12|2 те{0
421 = ——гт~= я ч 5*6 з =^6' Ю8с. C.59)
Отсюда излучательное время жизни состояния 2Я,
определяемое по формуле B.27), равно 1,6-Ю-9с. Линия
испускания или поглощения на переходе 15 ■«-*■ 2Р лежит
в ультрафиолетовой области. Скорости некоторых
переходов в атоме водорода показаны на фиг. 3.5; отметим
тенденцию к уменьшению скоростей переходов при
уменьшении частоты перехода, что согласуется с зависимостью
коэффициента А от величины со3.
88
ГЛАВА 3
Для сравнения со скоростью спонтанного испускания,
данной в C.59), укажем, что скорость вынужденного
излучения для того же перехода в случае пучка с интен-
/7=4
/7=3
/7=2
В
П = 1
Фиг. 3.5. Скорости спонтанных переходов между некоторыми
нижними уровнями водорода, измеряемые в единицах Ю6 с-1.
Численные значения взяты из работы [4].
сивностью 104 Вт-м-2 и частотной шириной 2я-1010 Гц
(см. табл. 2.1) равна
£21Ц7(со) = 3. Ю7 с
-I
C.60)
Дельта-функция Дирака
Метод, использованный в настоящей главе для
вычисления коэффициента Эйнштейна В, широко
распространен, поэтому полезно привести результат в такой
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 89
форме, которая облегчит его применение к другим
проблемам.
Рассмотрим дельта-функцию Дирака, которую можно
определить следующим образом:
*/ \ 2 1- sin2 {(со0 — со) t/2] /о яп
6((D0-(D) = -hrn (^ _ ю),', • C.61)
Согласно соотношению C.50),
оо
J 6(©о — ©)Ло=1. C.62)
Дельта-функция иллюстрируется пределом кривой,
изображенной на фиг. 3.3, при бесконечном значении t, где
все нули функции собраны в начале координат, а
значение функции при со = соо стремится к бесконечности
таким образом, чтобы площадь под кривой сохранялась
постоянной. В пределе вся площадь под кривой
сконцентрирована при со = о)о, а во всех остальных точках
дельта-функция равна нулю. Следовательно, уравнение
C.62) можно переписать в более общем виде:
0J
Uk-coMco^1' еСЛИ «> < «о < со2, C63)
J @ во всех других случаях.
Определение, приведенное в C.61), можно
использовать для доказательства основного свойства
дельта-функции. Пусть /(со) —любая функция со, несингулярная при
со = со0. Рассмотрим интеграл
@2 С02
W(o)N(co0-co)rfco = -^lim ^ /(со) sin2/(<Po "У* d<o.
J ' Ч ' V U ' Я /->оо J @H — СОJ /
©I 0>1
C.64)
Заменяя переменные интегрирования
х = (со —со0)/, C.65)
90
ГЛАВА 3
получаем
со2
W (о>) 6 @О — со) da> =
0)!
@J-C0n) t
= 4-Hm \ f[(x/t) + <^-2£g2-dx
@>i —СО0) t
оо
2 и ч Г sin2(x/2) - . .
= — /(со0) J ^—^ dx, если щ<щ< со2,
— оо
= /(о>о). C.66)
Следовательно, включение дельта-функции в интеграл
выделяет такое значение подынтегрального выражения,
которое определяется нулевым значением аргумента
дельта-функции.
Кроме частного определения дельта-функции через
предел C.61), существуют другие представления дельта-
функции. Критерий для возможного представления
дельта-функции заключается в том, что должно выполняться
соотношение C.64). Поэтому справедливость каждого
представления необходимо доказывать на основе
рассмотрения интеграла в левой части соотношения C.64).
Некоторые примеры представлений дельта-функции даны
в следующих задачах.
Задача 3.1. Докажите следующие возможные
представления дельта-функции Дирака:
т
б(о0 — со) = — lim \ exp [i (<о0 — со) t] dt>
Zn Г-»оо J
C.67)
6 (со0 — со) = 77— lim -г ггп—г • C.68)
v и ' 2л; g^Q (со0 — (*У + е2 v '
Некоторые полезные свойства дельта-функции,
используемые в ее преобразованиях, можно установить с
помощью анализа основного интеграла в левой части
соотношения C.64). Наиболее широко используемые
свойства дельта-функции приводятся в следующей задаче.
КВАНТОВАЯ ТЕОРИЯ КОЭФФИЦИЕНТА ЭЙНШТЕЙНА В 91
Задача 3.2. Докажите следующие свойства дельта-
функции:
б (со — со0) = б (со0 — со), C.69)
6 (со0 - М = (\/\ Ь\) 6 [(соо/6) - со] C.70)
и
б {@} — СО) (С02 — СО)} =
6 (@! — СО) + 6 @2 — СО)
~"~ I ©1 — Ю2 |
C.71)
Здесь Ь — константа. В каждом случае
равенство означает тот факт, что обе части
уравнения дают один и тот же результат при
умножении их на некоторую функцию и
интегрировании.
При выводе выражения для коэффициента В
использовалось решение, определяемое формулой C.50) для
промежутков времени t, больших по сравнению с
характерными временами 1/со0 и 1/Асо, определяющими
результаты экспериментального наблюдения поглощения света.
В этом пределе больших времен удобно ввести дельта-
функцию в представлении C.61) и переписать
выражение C.43) следующим образом:
I C2 (t) |2 = (я | Г12121/2) 6 @О - со). C.72)
Выражение C.72) более компактно, а интегрирование
по области частот Асо проводится элементарно, если
использовать соотношение C.66).
Результат C.72) можно применить к любому
процессу перехода, где зависящая от времени часть
гамильтониана пропорциональна cos co£; только величина
матричного элемента Ти различна для разных процессов.
Необходимо подчеркнуть, что дельта-функция обладает
высокой сингулярностью и может иметь физический
смысл только в том случае, когда она стоит под знаком
интеграла и интегрирование производится по аргументу
дельта-функции. Тем не менее дельта-функция широко
используется в уравнениях, как, например, в C.72). Во
всех этих случаях необходимо иметь в виду, что
интегрирование будет проведено на более поздней стадии
вычислений и до получения физически измеримых величин.
92 ГЛАВА 3
ЛИТЕРАТУРА
i. Dlcke R. #., Wittke J. P., Introduction to quantum mechanics,
Addison-Wesley, Reading, 1960, p. 102.
2. Salzman W. R., Phys. Rev. Lett., 26, 220 A971).
3. Dwight H. B.t Tables of integrals, Macmillan, New York, 1961,
p. 221 (См. перевод: Г. Б. Двайт, Таблицы интегралов, изд-во
«Наука», 1966.)
4. Bethe H. Л., Salpeter E. £., Quantum mechanics of one- and two-
electron atoms, Springer-Verlag, Berlin, 1957, p. 226 (См. перевод:
Г. Бете, Э. Солпитер, Квантовая механика атомов с одним и двумя
электронами, Физматгиз, 1960.)
Глава 4
Восприимчивость, зависящая от частоты
Прохождение электромагнитной волны через
атомный газ определяется показателем преломления и
коэффициентом экстинкции, введенными в уравнении B.4).
Например, коэффициент поглощения прямо
пропорционален коэффициенту экстинкции в выражении B.12). Эти
величины являются функциями частоты
электромагнитной волны со и очень быстро меняются с со в окрестности
частоты атомного перехода.
Теория Эйнштейна предсказывает скорости
поглощения и испускания для светового пучка, распределение
частот которого занимает область частот, где атомный
переход приводит к значительному поглощению. Эта
теория дает выражение B.39) для интегрального
коэффициента поглощения, однако не позволяет определить
частотную зависимость параметров т|, х или К. Из B.5) и
B.6) видно, что эти частотные зависимости
определяются частотной зависимостью восприимчивости %. Эта
зависимость обеспечивает информацию, необходимую для
полного описания распространения электромагнитной
волны.
В настоящей главе будут описаны общие свойства
функции восприимчивости и рассмотрены два метода ее
вычисления. Сначала обсуждается классическая теория
восприимчивости. Метод рассмотрения очень прост и
дает возможность понять природу взаимодействия
излучения с атомами. Затем будет показано, что квантовая
теория восприимчивости приводит к результату,
сходному с классическим выражением.
94
ГЛАВА 4
Определение восприимчивости
Наше изложение удобно начать с уточнения
определения восприимчивости, приведенного в начале гл. 2.
Рассмотрим эксперимент, в котором на атомный газ
действует электрическое поле, описываемое вещественной
функцией E(t). He уточняя вид функции E(t),
предположим, что ее можно разложить в интеграл Фурье по
частотным составляющим £(со)
оо
£@= \ Е (со) ехр (- Ш) da>. D.1)
— с»
Фурье-коэффициенты £(со) определяются обратным
преобразованием
оо
£•(©) = A/2я) [ E{t)txp(mt)dt. D.2)
— оо
Чтобы поле E(t) было вещественным, коэффициенты
разложения £(со) должны удовлетворять соотношению
£(-©) = £•(©). D.3)
Поле E(t) можно рассматривать как приложенное
к атомам возмущение, под действием которого они
поляризуются. Если функция P(t) есть атомная поляризация
в момент времени t> то ее тоже можно разложить в
интеграл Фурье
оо
P(t)= \ Р (со) ехр (- Ш) dm. D.4)
— оо
Восприимчивость %(со) определяется соотношением
Р(со)==8оХ(со)£(со). D.5)
Необходимо отметить, что, как и в случае вычисления
коэффициента В в предыдущей главе, отклик атомов на
приложенное поле линеен по £(со) только для не
слишком сильных полей. В случае полей мощных лазерных
световых пучков в правой части формулы D.5)
существенны члены, содержащие более высокие степени £(со).
Обусловленные этими членами нелинейные оптические
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ 95
процессы рассматриваются в гл. 12; в настоящей главе
поля предполагаются достаточно слабыми, чтобы
линейная восприимчивость %(со) обеспечивала адекватное
описание атомной поляризации.
Подстановка соотношения D.5) в D.4) дает
оо
P(t) = e0 \ х(а>)Е(а)ехр(—Ш)Aа>. D.6)
— оо
Вещественное поле создает вещественную поляризацию,
поэтому, для того чтобы величина P(t) была
вещественной, восприимчивость должна удовлетворять
соотношению
Х(-а) = Х». D-7)
Разделение восприимчивости %(о)) на вещественную и
мнимую части таким же образом, как в B.3), приводит
к равенствам
х'(-со) = х» D.8)
И
0С"(-со) = -х'». D.9)
Эти равенства называются кросс-соотношениями для
восприимчивости; они показывают, что х(оз) необходимо
вычислить только для полей вида £(о))ехр(—/со/), где со —
положительная частота. Кросс-соотношения
обусловлены лишь условием, что вещественное воздействие
должно вызвать вещественный отклик.
Классическая теория восприимчивости
В классической теории восприимчивости N атомов в
объеме V описываются N гармоническими
осцилляторами с затуханием, обладающими массой т и зарядом
—е. Рассмотрим данную частоту атомного перехода соо.
Допустим, что некоторая часть /0 из N гармонических
осцилляторов имеет естественную частоту я>о. Сначала
определим вклад этих осцилляторов в %(со), а вкладом всех
остальных осцилляторов пренебрежем. Электромагнитная
волна с электрическим полем Е = £0ехр(—/со/),
поляризованная в направлении х} возбуждает вынужденные
96
ГЛАВА 4
колебания. Так же, как на фиг. 3.1, рассмотрим атом,
помещенный в начало координат, и пренебрежем
пространственным изменением электрического поля.
Уравнение движения осциллятора имеет вид
т (X + ТХ + (*1Х) = -еЕ=-еЕ0 ехр (- Ш). D.10)
Здесь точки обозначают производные по времени, J? —
смещение заряда относительно его положения
равновесия. Сила трения пгТХ описывает потерю энергии
колеблющимся зарядом за счет излучения электромагнитных
волн. Излучение ускоренным зарядом является
классическим аналогом квантового процесса спонтанного
излучения. В гл. 11 показывается, что потерю энергии
осциллятором можно описать, как в уравнении D.10), с помощью
силы трения, пропорциональной скорости, если положить
Г = £>2со2/6яе0тс3. D.11)
Решение уравнения D.10) имеет вид
Х= , , ~f . гч . D-12)
а поляризация атомного газа, обусловленная
смещенными зарядами foN осцилляторов, дается выражением
р _ _ toNeX _ tpNe2E0 ехр (— Ш) ,. - дч
V tnV (со2 - со2 - /с&Г) "
Отсюда в соответствии с определением D.5) получим
зосприимчивость
(ю)в 'Mwv DЛ4)
©q — СО — 1@1
В окрестности атомного перехода на частоте со0 это
классическое выражение для зависящей от частоты
восприимчивости можно использовать для нахождения
изменений показателя преломления г] и коэффициента
поглощения К, которые экспериментально более доступны.
Согласно формулам B.5) и B.6),
©«S (со2, — ©2)
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ 97
И
X" = 2т]н =
со^соГ
(ш§ - ш2J + со2Г2 •
D.16)
где 5 — безразмерная величина
S = ?0Ne2/eQmV<i>lt
D.17)
характеризующая силу взаимодействия между
осциллятором и электромагнитной волной. Из формул D.15) и
Фиг. 4.1. Изменение с частотой вещественной и мнимой частей
восприимчивости для значений параметров S = Vo Г = со0/20.
D.16) видно, что величины %' и х" подчиняются кросс-
соотношениям D.8) и D.9).
Зависимость х' и %" от частоты для выбранных
частных значений S и Г/шо показана на фиг. 4.1, а
соответствующее изменение ц и х, полученное из D.15) и
D.16), приведено на фиг. 4.2. При этом предполагалось,
что центральная резонансная частота щ намного больше
параметра затухания Г. В этом случае функция %" имеет
значительную величину только при условии, что частота
со близка к coo- Для таких значений о в выражении
4 Зак. 885
98
ГЛАВА 4
D.16) всюду, кроме члена, содержащего со — со0, можно
в хорошем приближении заменить со на соо и в
результате получить
X
//
2*1* = 7^3
£со0Г/4
(со0 - со)^ + (Г/2)»
Это выражение пропорционально функции
F ( \ — Г/2Я
^L^)— (o0 - ©J + (Г/2)а '
(Г<©0). D.18)
D.19)
которая описывает распределение частот для лоренцевои
формы линии. Функция D.19) изображена на фиг. 4.3.
Фиг. 4.2. Изменение с частотой показателя преломления г\ и
коэффициента экстинкции к для значений параметров S = У4» Г = (о0/20„
Константы в знаменателе выражения D.19) выбираются
из условия обычной нормировки
\ FL (со) rfco = 1.
D.20)
Как показано на фиг. 4.3, полная ширина лоренцевои
линии на половине ее максимальной высоты точно
равна Г.
Для экспериментаторов часто представляет интерес
коэффициент поглощения /С, связанный с коэффициен-
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ 99
том экстинкции к простым соотношением B.12). Как по«
казано на фиг. 4.2, зависимость х от частоты со в общем
случае несимметрична относительно соо- Если исключить
из выражения 2 цк зависящий от частоты показатель
преломления т|, то симметричная лоренцева форма этого
Ширина =Г
-1 0 1
(и>-аH)/Г
Фиг. 4.3. Нормированная функция лоренцевой формы линии.
выражения искажается, причем величина искажения
определяется величиной cdoS/Г. Если последняя мала по
сравнению с единицей, то показатель преломления на
всех частотах мало отличается от единицы, и в
результате из B.12) и D.18) получим
К = (щ -S$+\r/2)> <Г « «о- "oS/Г « О. D.21)
Следовательно, в этом пределе коэффициент поглощения
имеет лоренцеву форму.
Классический результат D.14) относится к одной
частоте атомного перехода, Восприимчивость газа из ато-
4*
100
ГЛАВА 4
мов, имеющих много частот возбуждения со;, вычисляется
путем разделения N гармонических осцилляторов на
отдельные группы fiN, в которых осцилляторы имеют
частоту о)г и параметр затухания Гг\ Тогда восприимчивость
определяется суммой членов, сходных с выражением
D.14), причем каждой группе осцилляторов
соответствует один член суммы:
e0mV t-r1 cof. — от — /соГ^
где
ЕЛ=1. D.23)
i
Когда частота со близка к одной из частот со*, то
соответствующий член в сумме D.22) доминирует и остальными
вкладами часто можно пренебречь.
Квантовомеханическая теория восприимчивости,
описанная ниже, предсказывает частотную зависимость,
очень похожую на зависимость классического результата
D.22). Однако квантовая теория позволяет получить
выражения для величин /и которые не определяются
классической теорией, и показывает, что параметры
затухания Гг в общем случае не описываются классическим
результатом D.11).
Поток энергии
Интересно рассмотреть, каким образом выполняется
закон сохранения энергии в классической теории
взаимодействия электромагнитной волны с атомным или
молекулярным газом. Мы исследуем случай, когда частота
со близка к данной частоте атомного перехода оз0.
Рассматривая уравнения Максвелла A.1) и A.2), где
плотность тока J заменена скоростью изменения
поляризации Р, как и в уравнении A.8), нетрудно получить
следующий результат (см., например, {1, 2]):
\ Е X Н . ds = - J (е0Е . Ё + Ц0Н • Н + Е . Р} d*% D.24)
S If
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ 101
где v — произвольный объем, окруженный поверхностью
5. Используя D.10) и D.13), последний член в
подынтегральном выражении справа можно преобразовать к виду
Е Р = {/QNm/V) (Х + ГХ + со2*) х =
= (f0Nm/2V) (djdt) (X2 + со2*2) + (f0NmT/V) X\ D.25)
Таким образом, подынтегральное выражение
представляет собой сумму полной производной по времени и
члена, содержащего параметр затухания Г,
обусловленный силой трения.
Полную энергию в единице объема газа удобно
обозначить через Wt\ эта величина состоит из вклада поля
излучения Шизл и вклада атомов WaT, описываемых
гармоническими осцилляторами классической модели.
Следовательно,
Wt = WWUi + Wn9 D.26)
где
Гнзл = \ (е0Е2 + \х0Н>) D.27)
и
^ат = (f0Nm/2V) {P + со2*2). D.28)
Здесь величина Wn3Jl аналогична плотности энергии
Щсо), введенной в гл. 1, но только последняя относится
к энергии в единичном частотном интервале, поэтому для
нахождения полной энергии излучения она должна быть
проинтегрирована как по объему, так и по частоте. В
настоящем расчете предполагается, что электромагнитное
поле имеет одну частоту возбуждения.
На основе определения вектора Пойнтинга (формула
B.9)] уравнение D.24) можно переписать в виде
J I • ds + $ (/0NmTX2/V) A> = — J (dWrfdt) d». D.29)
S ir V
Теперь величина /0ЫтТХ2 представляет собой скорость,
с которой f0N гармонических осцилляторов теряют
энергию за счет силы трения. Таким образом, уравнение
D.29) выражает закон сохранения энергии в газе,
причем члены слева являются скоростями потерь энергии
102
ГЛАВА 4
в объеме v за счет переноса энергии через поверхность
объема v и диссипации, а интеграл справа есть полная
скорость потерь энергии, запасенной в объеме v.
Теорию можно более тесно связать с измеряемыми
величинами, если различные выражения для энергии
усреднить по периоду колебания. Применяя теорему о
среднем за период {формула B.35)] к выражениям
D.27) и D.28), получаем
^изл = |е0A+п2 + >с2)|£Р, D.30)
^ат = (f^mjAV) (со2 + со2) | X |2. D.31)
Здесь была использована формула B.8).С помощью
выражения D.12) WaT можно переписать следующим
образом:
- _ /0Ые2 со2 + <4 2
AmV (со2) - со2J + со2Г2 v
Усредненная по периоду полная плотность энергии
в газе, получаемая из выражений D.15), D.16), D.26),
D.30) и D.32), имеет вид
Wt = { 8, {Bштрс/Г) + т]2} | Е |2. D.33)
Этот результат отличается от часто используемого
выражения для плотности энергии, в котором отсутствует
первый член в скобках. Обычное выражение не
содержит энергию, запасенную в атомах, и эквивалентно
результату D.33) только тогда, когда частота
электромагнитной волны достаточно удалена от частоты атомного
перехода соо-
Уравнение для энергии D.29) можно также
переписать в усредненном по периоду виде. Из формул D.27)
и D.48) видно, что в стационарных условиях, когда
колебания имеют временную зависимость вида ехр(—Ш),
усреднение по периоду приводит к следующему
результату;
dWt/dt = 0 (стационарное состояние). D.34)
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ ЮЗ
Поэтому уравнение D.29) принимает вид
J T • ds + J (/оЛГтГсо21 X \2/2V) dv = 0, D.35)
s to
где I—усредненный по периоду вектор Пойнтинга,
определенный в B.10). Диссипация энергии в объеме v за
счет сил трения компенсируется потоком энергии внутрь
объема v через его поверхность.
Если поступление электромагнитной энергии
устранить, то I = 0 и только два интеграла по объему
останутся отличными от нуля в уравнении D.29). После
усреднения по периоду подынтегральные выражения этих
интегралов можно приравнять друг к другу и получить
уравнение
dWt/dt = - /оЛГтГсо21 X \2/2V. D.36)
В противоположность результату D.34) для
стационарного состояния теперь плотность энергии уменьшается со
временем. В отсутствие электромагнитного вклада в
энергию имеем Wt = Wam, и выражение D.31) можно
использовать для записи скорости диссипации при ш = ©о:
dWJdt = — ГГат (со = ©о). D.37)
Следовательно, скорость релаксации энергии, запасенной
в атомах, равна параметру затухания Г в классической
модели.
Задача 4.1. Правильное вычисление скорости потока
энергии vE через газ в стационарных
условиях должно учитывать оба вклада в
плотность энергии Wt в выражении D.26).
Следовательно, если скорость vE определяется
формулой
vB=Wi9 D.38)
докажите, что
I/O* = (Ч/с) + (Я/Г). D.39)
104
ГЛАВА 4
Сравните зависимость от частоты скорости
vE и групповой скорости vg, определяемой
обычным образом:
vG = dco/dk = с {г\ + со (dri/^co)}. D.40)
Докажите, что при нулевом затухании Г = 0
скорость vq — vE.
Соотношения Крамерса — Кронига
Восприимчивость х(со), введенная в D.5),
определяет отклик атомов на воздействие в виде приложенного
электрического поля. Восприимчивость принадлежит
классу функций, называемых функциями отклика. Такие
функции имеют некоторые общие свойства, не зависящие
от какой-либо частной теоретической модели системы,
которую они описывают. Мы проиллюстрируем эти
свойства для случая восприимчивости, определяемой
выражением D.14), а затем укажем, как данные свойства
можно установить в общем случае.
Классический результат для восприимчивости D.14)
можно записать в виде
ЛЧ/ COi — С02 V СО — СОд СО — 0J / Х '
где разделение на отдельные слагаемые осуществлено
при помощи введения двух частот:
со, = - \i (Г - (Г2 - 4®g)'/.} D.42)
и
<о2 = -1 / {Г + (Г2 - 4со2)'/*}. D.43)
Положения частот coi и оJ на комплексной плоскости
частот показаны на фиг. 4.4. Эти положения зависят от
того, больше или меньше величина Г удвоенной частоты
2оо, но в обоих случаях полюса лежат ниже
вещественной оси в нижней полуплоскости.
Некоторые важные свойства, известные как
соотношения Крамерса — Кронига, или дисперсионные соотно-
ВОСПРИИМЧИВОСТЬ", ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ Ю5
шения, можно вывести для восприимчивости в форме
выражения D.41). Рассмотрим интеграл
оо
J @ — @ '
D.44)
— оо
где 9* обозначает главное значение интеграла в смысле
Коши [2], определяемое в виде предела
00 /©—б оо ч
J © ~Й 6-»0\ J © — © J СО —СО /
-оо ч-оо 00 + 6 '
D.45)
Путь интегрирования для / лежит вдоль вещественной
оси комплексной плоскости со7, как показано на схеме
фиг. 4.5, а,
оъ-плоскость
Ч oj,
)<0)t
х
OJ1
х
(лJ
Г>2а><
Г<2оH
Фиг. 4.4. Расположения полюсов восприимчивости в комплексной
плоскости частоты.
Требуемый интеграл может быть вычислен с по-
мощью контурного интегрирования. Пусть Л, В и С--»
интегралы от точно такого же подынтегрального
выражения, что и в D.44), но вычисленные по контурам,
обозначенным этими буквами на фиг. 4.5,6—г. Различ-s
ные интегралы удовлетворяют соотношению
1 = А-В-С. D.46)
Поэтому значение / определяется путем вычисления трех
стоящих справа интегралов.
106
ГЛАВА 4
Подынтегральное выражение имеет три полюса: один,
указанный на фиг. 4.5, а, при а/ = со, и два других
полюса, которые нас не интересуют, лежащие в нижней
а>'-плоскость
-оо
О)
^тт*—
6-
оо
а
6
£2l
Фиг. 4.5. Контуры интегрирования, используемые для получения
соотношений Крамерса — Кронига.
Радиус контура в виде большой полуокружности в действительности бесконечен.
полуплоскости при о7 = coi и о/ = оJ. Интеграл А
берется по замкнутому контуру, не содержащему полюсов,
причем внутри контура подынтегральное выражение
регулярно. По теореме Коши {2]
А = 0. D.47)
Контур для интеграла В содержит лишь очень большие
значения |со'|, для которых подынтегральное выражение
' ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ Ю7
пропорционально (со')~2. Поскольку длина контура равна
rtlo/l, то величина В порядка (со'), и, следовательно,
для контура бесконечного радиуса
5 = 0. D.48)
В результате остается только интеграл С по контуру в
виде полуокружности с центром в полюсе при со' = со.
Согласно теореме вычетов [3],
С = — шх(ю). D.49)
Таким образом, интеграл / из D.44) определяется
следующим выражением:
оо
tax (со) = ^ J -|Д^- *»'. D.50)
— оо
Отметим, что, несмотря на комплексные значения о/,
использованные в выводе, конечный результат D.50)
содержит только вещественные физические частоты.
Соотношения Крамерса — Кронига получаются с
помощью разделения вещественной и мнимой частей
уравнения D.50):
оо
Х"(в) —-L* $-£^Л»' D.51)
— оо
и
оо
*»=Ч^ \ ■£¥***'• <4-52)
—оо
С другой стороны, кросс-соотношения D.8) и D.9)
можно использовать для ограничения областей
интегрирования только положительными частотами со':
оо
Х'>) = --^-Р^' D.53)
" J CD — CD-
CD — CD*
0
И
оо
*Ы = $*\*£Щ<1«. D.54)
л CD — СО
о
108
ГЛАВА 4
Прежде чем обсудить важность и полезность
соотношений Крамерса — Кронига, сделаем замечание об их
общности. Выше они были получены на основе частного
выражения D.41) для восприимчивости, которое в свою
очередь основывается на частной модели атомов. Однако
при выводе уравнения D.50) были использованы только
два свойства выражения для %((х>): 1) положения
полюсов coi и оJ ниже вещественной оси и 2) более быстрое
уменьшение, чем со-1, при больших значениях со.
Сначала рассмотрим положения полюсов функции
Х((о). Из общих рассуждений можно математически
доказать, что полюсы функции отклика должны лежать в
нижней полуплоскости [4, 5]. Детали соответствующих
немного громоздких теорем здесь не приводятся. С
физической точки зрения эти теоремы зависят только от
принципа причинности, согласно которому отклик
системы не может предшествовать вызывающему его
воздействию. В данном случае если электрическое поле E(t)
начинает действовать на атомы после некоторого
времени i0i то поляризация P(t) может быть отличной от
нуля только при t > t0. Принцип причинности вводит
асимметрию между временем t <Z t0 и временем / > t0,
которая, как можно показать математически, ведет к
асимметрии в области частот, определяемой полюсами
функции отклика, которые всегда лежат ниже
вещественной оси.
Для модели атомов в виде классического
осциллятора принцип причинности проявляется в условии
положительности величины Г. Поляризация, вызванная
приложенным полем, должна со временем затухать, а
возможности создания поляризации до приложения поля не
существует. Положительность Г обеспечивает
расположение частот coi и оJ, определяемых формулами D.42)
и D.43), ниже вещественной оси. Следовательно,
соотношения Крамерса — Кронига для восприимчивости и
других видов функции отклика могут быть доказаны в
общем случае, если можно доказать второе необходимое
свойство: более быстрое, чем от-1, уменьшение %(ш) при
больших значениях о).
Соотношения Крамерса — Кронига показывают, что
вещественная и мнимая части восприимчивости очень
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ ]Q9
тесно связаны. Действительно, знания одной части
восприимчивости на всех положительных частотах
достаточно для вычисления интеграла в D.53) или D.54) и,
следовательно, для полного определения другой части
восприимчивости на всех частотах. Это свойство часто
является полезным в таких экспериментах, где легче
измерить одну часть восприимчивости %(со), чем другую.
Соотношения Крамерса — Кронига показывают, что из
существования зависящей от частоты вещественной
части %'((о) следует существование ненулевой мнимой
части %"((о). Поведение величин %'((i)) и %"(а0,
проиллюстрированное на фиг. 4.1, типично для связи между
двумя функциями, определяемой соотношениями
Крамерса — Кронига. В любой теории или экспериментальном
измерении острый максимум функции 5с"((о) должен
сопровождаться резким изменением знака функции х'((о).
Задача 4.2. Докажите, что
оо
J @ — СО2
о
и, следовательно, мнимая часть
восприимчивости равна нулю, если вещественная часть
постоянна.
Задача 4.3. На основе точного вычисления интегралов
докажите, что классическое выражение для
восприимчивости D.14) удовлетворяет
соотношениям Крамерса — Кронига.
Восприимчивость, определяемая выражением D.14),
на котором было основано приведенное выше
рассмотрение, относится к случаю одной атомной частоты
перехода. Однако точно так же можно было бы использовать
выражение D.22) для атомов, имеющих много частот
переходов; поскольку полюсы каждого члена в сумме
D.22) лежат ниже вещественной оси, то точно такие же
соотношения Крамерса — Кронига можно доказать для
восприимчивости более общего вида.
Соотношения Крамерса — Кронига можно также
получить для вещественной и мнимой частей выражения
.AгЬх),/з> т. е. для показателя преломления и коэффи-
по
ГЛАВА 4
циента экстинкции, определенных в B.4). Эти
соотношения имеют вид
х(в)__^Л-Л£1^/ D.56)
71 J CD — CO2
О
И
00
„(„j-l-^CJ^fcldo'. D.57)
31 J со — со2
о
Характерное сочетание острого пика функции и (со) с
изменением знака функции г] (со) — 1 проиллюстрировано
на фиг. 4.2.
Правила сумм
Важным применением соотношений Крамерса — Кро-
нига является вывод правил сумм. Для любого атомного
или молекулярного газа существует такая большая
частота сомакс, что на частотах со, больших соМакс, значения
%" и % пренебрежимо малы и газ является прозрачным.
Чтобы получить правило сумм для восприимчивости,
запишем уравнение D.54) для частоты со, большей соМакс>
в следующем приближенном виде:
оо
%' (со) = - B/жо2) J о/х" ((о') Ло' (со > сомакс). D.58)
О
В этом приближении электроны ведут себя так, как
если бы для очень высоких частот со, рассматриваемых
в D.58),они были свободными,поскольку отсутствие
поглощения на частотах выше соМакс означает, что величина
л со много больше любой энергии связи электрона. В этом
случае частотная зависимость вещественной части
восприимчивости имеет простой вид, который можно
получить из классического выражения D.22). Это
выражение удобно немного обобщить путем рассмотрения
атома, имеющего Z электронов, как это использовалось
в вычислениях гл. 3. Тогда высокочастотный предел
вещественной части выражения D.22) принимает вид
%' (со) = - ZNe?/e0mV<*2 (со > сомакс). D.59)
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ Ш
Здесь каждый из Z электронов дает вклад, равный
вкладу одного свободного электрона. В дальнейшем в
настоящей главе (см. формулу D.114)] будет доказано,
что высокочастотный предел восприимчивости,
вычисленный методом квантовой механики, согласуется с
выражением D.59).
Теперь, комбинируя формулы D.58) и D.59),
получаем
оо
J со%" (со) dco = nZNe2/2eQmV. D.60)
о
Результат такого типа называется лравилом сумм, а
частный пример D.60) называется правилом сумм
Томаса — Рейхе — Куна. Оно выполняется в общем случае
для всех видов атомов и молекул. В правой части
равенства D.60) единственной переменной является
электронная плотность ZN/V. Следует отметить, что правило
сумм D.60) относится к интегралу по полному спектру
поглощения атомов; интеграл, приведенный ранее в
B.40), относится к одному атомному переходу.
Задача 4.4. Предполагая справедливость соотношений
Крамерса — Кронига D.56) и D.57) для
х(со) и rj(co), докажите, что
сох (со) dco = nZNe?IAb0mV. D.61)
о
Отсюда покажите, что коэффициент
поглощения К (со) подчиняется правилу сумм
оо
0
Квантовая теория восприимчивости
Квантовомеханическое выражение для
восприимчивости можно получить с помощью вычислений, подобных
тем, которые использовались в гл. 3 для нахождения
коэффициента В. Мы снова рассмотрим газ Z-электрон-
112
ГЛАВА 4
ных атомов, на которые действует возмущение в виде
электромагнитной волны с частотой со, лежащей вблизи
частоты атомного перехода соо. Как и в гл. 3, мы
исследуем сначала один атом, взаимодействие которого с
электромагнитной волной описывается гамильтонианом 36i
из C.18). Затем результат, найденный для одного атома,
соответственно усредняется для получения аналогичного
результата для газа, состоящего из атомов или молекул,
ориентированных случайным образом.
Гамильтониан §ei описывает атомное возмущение,
созданное приложенным электрическим полем Е0 cos со/,
которое содержит компоненты с положительной (-\-со)
и отрицательной (—а)) частотами. В соответствии с
формулой D.1) приложенное поле запишем в виде
Е @ = 1 Е0 {ехр (- Ш) + ехр (Ш)}. D.63)
Действие электрического поля на атомный газ создает
поляризацию P{t), определяемую уравнениями D.4) и
D.5). В специальном случае, когда поле E(t)
описывается формулой D.63),
Р (t) = y е0£о (Х (о) ехр (— Ш) + х (— ») ехр (/со/)}. D.64)
Метод вычисления заключается в нахождении
поляризации P(t) с помощью квантовой механики и последующем
определении восприимчивости %(со) путем сравнения
полученного выражения с результатом D.64).
Сначала рассмотрим вклад в поляризуемость газа
одного пробного атома. Допустим, что приложенное
электрическое поле направлено вдоль оси х, как на фиг. 3.1.
Параллельный оси х электрический дипольный момент
атома определяется ожидаемым значением следующей
величины;
z
— ]С £*/ = — еХ,
где X есть лг-компонента вектора D, введенного в C.17),
Таким образом, в момент времени t, когда атомная вол-
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ ЦЗ
новая функция есть ^(t), для электрического дипольного
момента имеем
d @ = - J ЧГ (*) еХЧ @ dV. D.65)
Здесь интегрирование производится по координатам всех
Z электронов.
Как и в гл. 3, допустим, что частота со близка к
частоте соо одного атомного перехода между двумя
атомными состояниями \р\ и г|J, обладающими энергиями Е\
и Е2. Оставшиеся атомные уровни энергии пока не
учитываются, и поэтому общий вид волновой функции
определяется выражением
= Сх @ ifo ехр (- 1Ехф) + С2 @ ф2 ехр (- iE2t/ti). D.66)
Здесь были использованы формулы C.5) и C.8), в
которых зависимость функций ty\ и ty2 от координат опущена.
Зависящие от времени коэффициенты должны
находиться путем решения уравнений C.31) и C.32)
ТХ2 cos со/ ехр (— /coqO C2 = iC{ D.67)
и
Г*12 cos со/ ехр (too*) Cx = iC2f D.68)
на которые наложены определенные граничные условия.
Подставляя выражение D.66) в D.65), находим
d{t) = -e {CIC2X12 ехр (- m0t) + C*2CiX2i ехр (м>о*)}, D.69)
где величина Xi2 определена в C.32). Здесь было
использовано свойство
Хп=Х22 = 0, D.70)
аналогичное C.19). Из определения Х\2 следует
*21=*12, D.71)
а потому дипольный момент D.69) является
вещественной величиной, как и ожидалось из физических
соображений.
Используя формулы D.67) и D.68), коэффициенты
С\ и С2 можно исключить из выражения D.69) и полу-
114
ГЛАВА 4
чить уравнение для d(t), записанное через известные
величины. Дифференцируя выражение D.69) по t,
получаем
d(t) = — e {{С\С2 + С\С2 - 1щСгС2) Xi2 exp (- /©<>*) +
+ {C2Ci + С2С1 + /©0С2С1) X2i ехр (/©о/)}. D.72)
Согласно определению C.23),
Tl2 = eE0Xl2/h, D.73)
поэтому из уравнений D.67) и D.68) легко показать, что
члены уравнения D.72), содержащие производные
величин С\ и С2, сокращаются.
Еще одно дифференцирование уравнения D.72)
приводит к следующему результату:
d (t) = ш0е {(CiC2 + С1С2 — /СО0С1С2) Xi2 exp (— ш00 —
- (C2Ci + С2Сх + modCi) X2i exp (ш0/)} =
= Bе2щ \ Xl2 I2 EQ cos ©//ft) {| d |2 - I C212} - ©grf (/). D.74)
Здесь на последнем этапе были использованы формулы
D.67) — D.69) и D.73).
Теперь дипольный момент одного атома необходимо
связать с поляризацией газа. Соответствующие
рассуждения будут точно такими же, какие были использованы
при вычислении коэффициента В. Если в объеме V
имеется N одинаковых атомов, то коэффициенты С\ и С2
связаны с атомными населенностями соотношением
C.52). Мы предполагаем, что приложенное
электрическое поле слабое, так что атомные населенности
испытывают пренебрежимо малое возмущение относительно
своих значений при тепловом равновесии. Поэтому в
уравнении D.74) величиной |С2|2 можно пренебречь, а
|Ci|2 положить равной единице. Случайные ориентации
атомов учитываются пугем замены C.56), и в
результате уравнение D.74) принимает вид
d (t) + ©2d (t) = 2Ao01 D1212 E0 cos ©*/3ft. D.75)
Теперь величина d(t) описывает средний дипольный
момент одного атома в момент времени t, и макроскопиче-
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ Ц5
екая поляризация газа определяется простым
выражением:
Р (t) = Nd (t)/V. D.76)
Дифференциальное уравнение D.75) легко решается.
В результате восприимчивость, получаемая из сравнения
формул D.76) и D.64), имеет вид
Зе0йк ©q — со
Это квантовомеханическое выражение для
восприимчивости очень похоже на классический результат D.14),
если в последнем уравнении пренебречь параметром
затухания Г. Действительно, в пределе нулевого затухания
результаты становятся идентичными, если /0 в
классической теории определяется выражением
/0 = 2mGH|D12|2/3/L D.78)
Удивительное сходство между результатами
классической и квантовой теории обусловлено тем замечательным
обстоятельством, что ожидаемое значение d(t) атомного
дипольного момента, вычисленное в строгом
соответствии с законами квантовой механики, удовлетворяет
уравнению для гармонического осциллятора с внешней
вынуждающей силой D.75). Аналогичное уравнение D.10)
является исходным для классической теории.
Квантовомеханическое выражение для
восприимчивости газа из атомов, имеющих много частот переходов со*,
можно получить на основе обобщения метода,
использованного в случае одной частоты перехода соо. Нетрудно
показать, что различные атомные возбужденные
состояния дают независимые вклады в восприимчивость,
причем каждый вклад описывается выражением, похожим
на выражение D.77). В качестве волновой функции
основного состояния мы по-прежнему используем \ри а
типичную волновую функцию возбужденного состояния
обозначим через i|>t-. Если энергия: возбужденного
состояния «фг есть Асог, то полная восприимчивость имеет вид
116
ГЛАВА 4
где
0и=$1|>;0ф,£*У. D.80)
Квантовый результат опять похож на соответствующий
классический результат D.22) в пределе нулевого
классического затухания.
Задача 4.5. Докажите, что соотношение D.78) между
классической величиной /0 и квантовомеха-
ническими величинами обеспечивает
соответствие между проинтегрированной площадью
под кривой классической восприимчивости
%", описываемой формулой D.18), и кванто-
вомеханическим результатом.
Учет затухания в квантовой теории
Сравнение восприимчивостей D.77) и D.79) с
результатами классической теории, не учитывающей затухание,
было необходимо, так как использованные до сих пор
квантовомеханические уравнения не содержат эффектов
спонтанного испускания. Полная квантовая теория
взаимодействия света с атомами включает три основных
взаимодействия, определенных, например, на фиг. 2.1.
Однако использованная выше полуклассическая теория
учитывает только процессы поглощения и вынужденного
испускания. Вычисление восприимчивости, основанное на
полной квантовомеханической теории, автоматически
включает эффекты спонтанного испускания. Такая
теория описывается в гл. 8. Тем rie менее хорошее
приближение строгого результата можно получить с помощью
феноменологического учета затухания, обусловленного
спонтанным испусканием, в теории, приводящей к
выражению D.77).
Легко видеть, что использованная выше теория не
может учесть спонтанного испускания. В отсутствие
приложенного электромагнитного поля величина Е0 равна
нулю и матричный элемент У°\2 обращается в нуль. Из
уравнений D.67) видно, что в этом случае значения С\
и С2 постоянны независимо от их начальных значений,
что противоречит известной физической ситуации, где
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ Ц7
возбужденный атом должен в конечном счете перейти
в основное состояние путем спонтанного испускания
фотона.
Положение можно исправить, если в левую часть
уравнения D.68) добавить член, описывающий
спонтанное испускание. В качестве обобщенного уравнения
примем
У9*2 cos со/ ехр (/©оО С{ — 1уС2 = iC2. D.81)
В отсутствие внешнего электрического поля уравнение
D.81) можно сразу проинтегрировать и получить
С2 (t) = С2 @) ехр (— yt). D.82)
Если в газе, состоящем из N атомов, при t = 0
возбуждено N2 атомов, то число возбужденных атомов в
момент времени t, определяемое формулами C.52) и
D.82), имеет вид >л
N2=N°2exp{—2yt). D.83)
Сравнение последнего выражения с формулой B.26)
показывает, что введение дополнительного члена в
уравнение D.81) приводит к правильной скорости затухания
флуоресценции, если
2у = Л21. D.84)
В проводимых ниже вычислениях уравнение D.67) не
используется, поэтому нет необходимости рассматривать
его преобразование с целью учета спонтанного
испускания.
Восприимчивость находится путем подстановки в
D.69) выражений для коэффициентов С\ и С2. Этот
метод похож на определение коэффициента Эйнштейна В
в гл. 3 в том смысле, что для С\ и С2 требуются решения
с точностью до первого порядка по Е0 или, эквивалентно,
по Т\2. До приложения поля начальные условия
заключаются в том, что все атомы находятся в основных
состояниях. Осциллирующее электрическое поле
вызывает в каждом атоме переходы между состояниями,
так что имеется некоторая вероятность нахождения
атома в возбужденном состоянии. Однако поле
предполагается настолько малым, что в левой части
уравнения D.81) величину С\ можно положить равной единице.
118
ГЛАВА 4
В этом случае интегрирование дает решение для С2,
справедливое в первом порядке теории возмущений по
Г12.
В отличие от коэффициента Эйнштейна В,
относящегося к неравновесному состоянию, в котором энергия
передается от поля излучения к атому, восприимчивость
относится к стационарному состоянию, где в принципе
атомы должны подвергаться действию электрического
поля бесконечно долго. Поэтому в уравнении D.81)
нужно взять неопределенный интеграл. В результате
получим следующее выражение:
С2 (*) = - 4-rh\ ехр {/ ((°° + о) ° + ехр {/ ((°° ~ m) H D.85)
* v 7 2 L ©о + ю — /у ©0 — © — гу J
Поскольку величина |С2@|2 порядка \Т\2\2> то условие
нормировки
\C{(t)\2 + \C2(t)\2=l D.86)
показывает, что значение С\ (t) отличается от единицы
на величину порядка \Т\2\2. Следовательно, в первом
порядке теории возмущений по Т\2 необходимо положить
С, (/)=1. D.87)
Дипольный момент d(t) одного атома находится с
помощью подстановки формул D.85) и D.87) и D.69):
Л (А — е21 Xl212 ^° | ^р (/сор , ехр (—Ш) ,
ехр (-/©0 ехр (/со/) |
со0 + о) + *Y ©о — © + *Y J
Здесь было использовано выражение D.73). Определяя
теперь поляризацию газа, состоящего из одинаковых
атомов, по формуле D.76), где произведена замена C.56),
учитывающая случайные ориентации атомов, и
сравнивая полученный результат с D.64), получаем следующие
выражения для восприимчивости:
И
Х{-*)="У№( J . + Цг-). D-90)
л v ' 3e0bV \ ©о + © — *Y ©о — со + /y /
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ Ц9
Это квантовомеханическая форма восприимчивости,
найденная для случая одной частоты перехода при учете
затухания на основе приближения D.81). Результаты
данного приближения подтверждаются более строгим
расчетом в гл. 8.
Нетрудно видеть, что восприимчивость, определенная
в D.89), удовлетворяет общему условию вещественности
D.7) и имеет два полюса, лежащие в нижней половине
комплексной плоскости в точках соо — iy и —соо — iy, как
показано на правой части фиг. 4.4. Если скомбинировать
два слагаемых в выражении D.89), то при больших
частотах со восприимчивость уменьшается как о"-2. Поэтому
соотношения Крамерса — Кронига D.51), D.52)
выполняются и их нетрудно доказать точно.
Отметим, что введение затухания, обусловленного
спонтанным испусканием, с помощью уравнения D.81)
приводит к выражению"для восприимчивости %{ы),
похожему на результат D.77) без учета затухания, но
только частота со заменяется на со + iy. Эта замена
пригодна дЛя преобразования квантовомеханических
выражений с целью учета затухания в довольно общем
случае. Она будет использована в гл. 11 и 12 для учета
затухания и эффектов ширины линии в выражениях,
полученных для нулевого затухания.
Задача 4.6. Докажите, что если классическое значение
/о определяется формулой D.78) и скорости
затухания из D.84) связаны с классическим
параметром затухания Г соотношением
Г = 2у = А21, D.91)
то классическое выражение D.14) для
восприимчивости совпадает с квантовомехани-
ческим результатом D.89), но только со2 в
знаменателе классического результата
заменяется в квантовомеханическом выражении
на cOq + Y2-
Эквивалентность классического параметра Г и
коэффициента Эйнштейна А следует с очевидностью из
результатов, полученных ранее. В теории Эйнштейна
показывается, что скорость затухания определенного числа
возбужденных атомов, а следовательно, и энергии, запа-
120
ГЛАВА 4
сенной атомами, равна, как вытекает из B.26),
коэффициенту А. Сравнение с аналогичным классическим
результатом D.37) показывает, что параметр Г играет в
классической теории осциллятора точно такую же роль,
что и коэффициент Эйнштейна А2\ в квантовой теории.
В случае спонтанного перехода атома водорода из
состояния 2Р в состояние 15 параметры Г и А2\, согласно
формуле C.59), имеют величину 6-Ю8 с-1. Таким
образом, благодаря спонтанному испусканию
соответствующая линия поглощения атома водорода обладает
шириной порядка 108 Гц в единицах частоты (но не круговой
частоты). Эта ширина чрезвычайно мала, поэтому в
большинстве экспериментов наблюдаемые ширины
атомных линий поглощения определяются другими
механизмами, например эффектом Доплера или атомными
столкновениями, которые будут рассмотрены в гл. 5.
Однако в принципе эти дополнительные процессы ушире-
ния всегда можно уменьшить каким-либо способом,
например охлаждая газ или уменьшая его давление. С
другой стороны, невозможно уменьшить скорость
спонтанного испускания, поэтому ширина А2\ является
наименьшей шириной, которую можно достичь для данного
перехода1). Эта ширина линии спонтанного испускания
называется естественной шириной спектральной линии.
Сдвиг центральной резонансной частоты к значению
(u>o + Y2)ly4 упомянутый в задаче 4.6, приводит к тому, что
полюсы квантовомеханического выражения для
восприимчивости всегда располагаются так, как показано в
правой части фиг. 4.4, и никогда — как показано в левой
части этой фигуры. Однако для оптических частот перехода
величина у/ы0 обычно мала, поэтому различиями между
классическими и квантовомеханическими результатами
можно пренебречь. Все квантовомеханические
выражения для т|, к и К получаются из D.89) и имеют
частотные зависимости, подобные частотным зависимостям их
классических аналогов и рассмотрение, проведенное для
классического расчета, по-прежнему применимо.
') Это утверждение справедливо, если возбужденный атом
находится в свободном пространстве [10, 11]. — Прим. ред.
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ 121
Чтобы учесть затухание в квантовомеханическом
результате D.79) для восприимчивости атомов,
обладающих многими переходами, необходимо произвести замену
со на со + i\i в 1-м члене суммы. Здесь 2у*— полная
скорость спонтанного испускания i-ro возбужденного
уровня. В действительности выражение для
восприимчивости, учитывающее затухание в случае многих переходов,
содержит некоторые тонкости, поэтому подробное
рассмотрение отложено до гл. 8.
Квантовомеханические вычисления восприимчивости
и коэффициента Эйнштейна В очень похожи, и в общем
случае эти две величины связаны соотношением B.40).
Коэффициент В является довольно грубой
характеристикой. Он определяет скорость поглощения для пучка
электромагнитного излучения, распределение частот которого
перекрывает всю ширину атомной линии поглощения.
Определим более тонкую характеристику перехода, а
именно скорость перехода 1/т, с которой N одинаковых
атомов в объеме V возбуждаются при поглощении
излучения с точно определенной частотой со.
Как показано в гл. 2, для обычных световых пучков
испускание излучения обусловлено в основном
спонтанными переходами, поэтому энергия, поглощаемая
атомами, не возвращается в световой пучок. Скорость
изменения плотности энергии излучения на частоте со равна
величине — йсо/Ут, которая в классической теории
соответствует скорости изменения плотности энергии
излучения за счет силы трения и определяется отрицательным
значением подынтегрального выражения во втором члене
уравнения D.35). Приравнивая эти эквивалентные
выражения, находим соотношение
- Йсо/Ут = - ДМпГсо21 X \2/2V, D.92)
которое с помощью формул D.12) и D.16) можно
переписать в виде
l/t = J/x"80|£|2/2ft. D.93)
Следовательно, введенное выше время перехода
пропорционально мнимой части восприимчивости, и поэтому
подстановка квантовомеханического выражения для %"
определяет квантовомеханический результат для 1/т,
122
ГЛАВА 4
Выражение для коэффициента В было получено в
гл. 3 путем вычисления скорости перехода в пределе
очень узкой линии перехода. В этом случае соотношение
D.93) между скоростью перехода и восприимчивостью
может быть доказано точно.
Задача 4.7. Докажите, что для положительных частот о>
в пределе нулевой ширины линии мнимая
часть выражения D.89) принимает вид
Х"(<в) = ,*8'з1УЯа(ио-Р). D-94)
Путем сравнения с C.72) покажите, что
скорость перехода, определяемая формулой
1/т = АПС2@Р/*, D.95)
точно удовлетворяет общему результату
D.93). В пределе у~^0 связь между
коэффициентом В и скоростью перехода
описывается выражениями C.37) и D.95),
Силы осцилляторов
Величина вклада данного атомного возбужденного
состояния г|^ в восприимчивость обычно измеряется
силой осциллятора /ц для перехода из основного
состояния tyi в возбужденное состояние г|)г-, определяемой
следующим образом:
fu = Bma>i/3h)\Dli\2. D.96)
Эта величина, также называемая /-значением перехода,
безразмерна. Силы осцилляторов можно использовать
для того, чтобы переписать выражение D.79);
Х(ш)в^2__!^. D.97)
В этом виде квантовомеханическая восприимчивость
очень похожа на классическое выражение D.22).
Действительно, формула D.78) для /0 классической теории
точно совпадает с формулой D.96) для /\2. Завершая
перечисление сходств между классической и квантово-
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ 123
механической теориями, укажем, что силы осцилляторов
удовлетворяют правилу сумм, аналогичному
классическому уравнению D.23).
Рассмотрим сначала атом, имеющий только один
электрон. Если х и рх являются х-компонентами
координаты и импульса электрона, то, согласно обычному
коммутационному соотношению,
[х, РЛ = *А. D.98)
Считая атомные волновые функции нормированными,
вычисляем матричные элементы обеих сторон равенства
D.98) для основного состояния
A1 хрх -^11) = $ т|>; (хрх - рхх) ф, dV = ih. D.99)
На всех последующих стадиях для матричных
элементов будет использоваться более компактное обозначение
Дирака, приведенное в левой части уравнения D.99).
Из условия полноты следует [6—8]
£ |/><*1=1- D.100)
i
Здесь суммирование ведется по всем состояниям атома.
Двухкратное использование этого условия в
соотношении D.99) дает следующее равенство:
Z (О \х \i)(i\px 11>- A1 px \i){i\x 11» = Ih. D.101)
i
Силы осцилляторов, определенные в D.96), зависят
только от матричных элементов координат, поэтому
следующий шаг заключается в замене матричных элементов
импульса в равенстве D.101). Гамильтониан для
электронов, использованный в уравнении C.3), должен иметь
вид
ЖЕ = № + Р\ + fil)/2m) + V (г), D.102)
где V(r) — потенциальная энергия атома. Поскольку
координата х коммутирует с импульсами ру и р2, то
[*, #*] = D%т) [х, рх-\ =
= {'km) ([*, рх] рх - рх [рХУ х]) = ihpx/m. D.103)
124
ГЛАВА 4
Возьмем матричный элемент уравнения D.103) между
состояниями xpi и г|)г:
A | хЖЕ - ЖЕх I I) = (/A/m) <1 I p х\ />. D.104)
Поскольку функции opi и г|п являются собственными
функциями гамильтониана Же с собственными
значениями, различающимися на величину энергии
возбуждения йсог, то правую часть уравнения D.104) можно
упростить следующим образом:
(l\px\i) = -im<i>l(l\x\i>. D.105)
Сопряженное соотношение имеет вид
A\рх\1) = 1тщA\х\1). D.106)
Теперь матричные элементы импульса из уравнения
D.101) можно исключить и получить соотношение
Z B/п©,)/А 1A \х |/> |2 = 1. D.107)
i
Очевидно, что точно такое же соотношение можно
доказать при замене х на у или г, поэтому суммирование
всех трех аналогичных соотношений дает
Z Bтю,/ЗЙ) | гн I2 = Е /и = 1, D.108)
где Пг — краткое обозначение матричного элемента
(l|r|i). Полученный результат называется правилом
/-сумм (правилом сумм для сил осциллятора).
Замечательно, что квантовомеханические силы осцилляторов
подчиняются точно такому же правилу сумм, как и доли
//, на которые разделяются N осцилляторов в
классической теории восприимчивости.
Правило /-сумм можно проиллюстрировать на
примере атома водорода. Только Я-состояния имеют
отличные от нуля матричные элементы вектора г для
перехода в основное состояние 15. Соответствующие
величины для перехода в 2Р-состояние, которые следует
подставить в D.96), были вычислены в C.27) и C.28). Пол-
пая сила осциллятора для трех вырожденных
возбужденных состояний имеет вид
/ls> 2Р = 213/39 = 0,416. D.109)
ВОСПРИИМЧИВОСТЬ, ЗАВИСЯЩАЯ ОТ ЧАСТОТЫ 125
Значения сил осциллятора 1) вплоть до перехода в
состояние с п = 5 приведены в табл. 4.1. Отметим, что на
переходы в непрерывный спектр атома водорода
приходится почти половина полной силы осциллятора и почти
три четверти силы осциллятора, соответствующей
переходам в дискретный спектр, приходится на 2Р-состояния.
Таблица 4.1
Значения силы осциллятора для переходов из lS-состояния
атома водорода
п
Л$>/гР
2 3 4 5 ...
0,416 0,079 0,029 0,014 ...
Дискрет-
ные Копти- Резуль-
состояния нуум тат
0,565 + 0,435 = 1,000
Различные другие правила сумм можно доказать
такими же методами, которые использовались для
получения соотношения D.108). Наиболее важным из них
является обобщение на случай атома с Z электронами.
Вывод правил не очень сложен, поэтому некоторые из них
приведены в виде задач.
Задача 4.8. Рассмотрите атом с Z электронами, для
которого матричный элемент Dh в выражении
для силы осциллятора D.96) определен в
соответствии с формулами C.17) и C.54).
Докажите, что обобщение правила /-сумм
имеет вид
Y./u = Z- D.110)
i
Задача 4.9. В более общем случае силу осциллятора /ц
можно определить для перехода между
двумя возбужденными состояниями \J)j и %. По
определению
/И = B/и/ЗЙ) (щ - <о}) | D;, |2, D.111)
где вектор Dj* находится очевидным
образом по аналогии с формулой C.54). Дока-
1) Числа взяты из книги [9J,
126 ГЛАВА 4
жите, что для любого состояния \|)j
Zftl=z. D.П2)
Задача 4.10. Докажите, что
£(о,*иУп=0. D.113)
i
Здесь Хц и Yi\ — различные декартовы
компоненты векторов Dh и D^.
Для частоты со, намного большей всех частот
переходов сог, восприимчивость, определяемая выражением
D.97), принимает вид
X(°>e-WE'" = -I$5r (•>•!)• DЛ14)
i
Здесь было использовано правило /-сумм D.110).
Выражение D.114) является точно таким же
высокочастотным пределом, как и предел, использованный D.59) для
нахождения правила сумм Томаса — Рейхе — Куна
D.60). Эти два правила сумм можно рассматривать как
две формулировки одного физического закона.
ЛИТЕРАТУРА
1. Panofsky К. W. #., Phillips M.y Classical electricity and magnetism,
Addison-Wesley, Reading, 1955, p. 160.
2. Hewson A. C, An introduction to the theory of electromagnetic
waves, Longmans, London, 1970 p. 12.
3. Arfken G.t Mathematical methods for physicists, Academic Press,
New York, 1966.
4. Toll J. 5., Phys. Rev., 104, 1760 A956).
5. Hamilton /., Progress in nuclear physics, ed. O. R. Frisch, vol. 8,
Pergamon, Oxford, 1960, p. 145.
6. Dirac P. A. M.y The principles of quantum mechanics, 4th ed.
Clarendon Press, Oxford, 1958, p. 63.
7. Messiah Л., Quantum mechanics, vol. 1, North-Holand Publ. Co.,
Amsterdam, 1961, p. 270.
8. Anderson E. £., Modern physics and quantum mechanics,
W. B. Saunders Co., Philadelphia, 1971, p. 223.
9. Bethe H. Л., Salpeter E. £., Quantum mechanics of one- and two-
electron atoms, Springer-Verlag, Berlin, 1957, p. 265. (См. перевод:
Г. Бете, Э. Солпитер, Квантовая механика атомов с одним и
двумя электронами, Физматгиз, 1960.)
10*. Drexhage /(. Я. в кн. Progress in optics, North-Holland Publ. Co.,
Amsterdam — London, v. 12, 1974, p. 164.
11*. Быков В. [J,t Квантовая электроника, № 7, 1557 A974),
Глава 5
Теория хаотического света
и когерентности
В трех предыдущих главах были описаны явления,
происходящие при распространении светового пучка
через атомный газ. Для характеристики светового пучка
было достаточно средней плотности энергии W или
интенсивности 7, которые в общем случае являются
функциями координат.
Для понимания многих экспериментов, в которых
используется свет, необходимо более детальное знание
характеристик интенсивности пучка. Как кратко
обсуждалось в гл. 1, число тепловых фотонов в полости
испытывает флуктуации, приводящие к соответствующим
флуктуациям интенсивности светового пучка.
Флуктуации интенсивности имеют характерный временной
масштаб и среднеквадратичное отклонение, величины
которых определяют возможности некоторых экспериментов.
Настоящая глава посвящена в основном изучению
флуктуации интенсивности световых пучков и их роли
в оптических экспериментах. Мы начнем с обсуждения
тех факторов, которые определяют частотное
распределение света, излучаемого обычным источником. Те же
самые факторы вызывают временные флуктуации
интенсивности пучка; мы рассмотрим статистические свойства
флуктуации интенсивности. Теоретический анализ
некоторых интерференционных экспериментов приведет к
рассмотрению когерентности световых пучков.
Когерентность пучка, временные флуктуации и распределение
частот— проявления одних и тех же физических свойств
излучающих атомов, образующих световой источник.
128
ГЛАВА 5
Важно различать два типа световых источников.
Обычным спектроскопическим источником является
газоразрядная лампа, где различные атомы возбуждаются
за счет электрического разряда и испускают фотоны
независимо друг от друга. Форма линии испускания
определяется статистическим распределением скоростей
атомов и случайными столкновениями, как описано ниже.
Обычный световой источник такого типа называется
хаотическим источником. Тепловая полость и лампа
накаливания служат другими примерами хаотических
источников. Световые пучки от хаотического светового
источника любого типа описываются статистически
одинаковым образом, и только параметры статистического
распределения изменяются от одного хаотического
светового пучка к другому.
Иным видом светового источника может служить
лазер, имеющий совершенно другие статистические
свойства. В настоящей главе эти свойства лазерного света
лишь кратко упоминаются, а их подробное рассмотрение
этложено до гл. 10.
Доплеровское уширение
Хаотический свет удобно исследовать на примере
света от газоразрядной лампы. Возбужденные разрядом
атомы испускают свет в процессе своего излучательного
перехода на более низкие энергетические уровни.
Рассмотрим линию испускания, соответствующую переходу
атома с возбужденного энергетического уровня Е2 в
основное энергетическое состояние Е\.
Имеются три механизма, которые в основном
ответственны за частотное распределение излученного света.
Первым из них является сам процесс излучательного
перехода. В предыдущей главе было показано, что
существование процесса спонтанного излучения ведет к уши-
рению линии поглощения, которая приобретает лорен-
цево частотное распределение с шириной Г,
определяемой коэффициентом Эйнштейна А. Это распределение
приведено в D.19). Вычисление линии испускания
показывает, что она имеет точно такую же форму и
естественную ширину, как и соответствующая линия поглоще-
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 129
ния. Естественная ширина является наименьшей
возможной шириной линии испускания. Два других вклада
в ширину линии обусловлены движением атомов,
которое приводит к столкновениям между атомами и
соответствующему ударному уширению, а разброс скоростей
атомов вызывает доплеровский разброс частот
испускаемого света. Сначала рассмотрим доплеровский механизм
уширения; при этом всеми другими вкладами в ширину
линии удобно пренебречь. Сравнение и суммарный учет
различных вкладов оставлены на конец главы.
Допустим, что атом, возбужденный на энергетический
уровень £, имеет скорость v2. Этот атом испускает
фотон с энергией йсо и переходит на более низкий
энергетический уровень Е\. Фотон обладает импульсом fik, где
k = со/г, поэтому его испускание приводит к отдаче
атома, который в результате приобретает новую
скорость Vj. Полные импульсы системы до и после
испускания должны быть равны
Mv2 = Mvl + hk. E.1)
Здесь М — масса атома. Условие сохранения энергии
имеет вид
Е2 + ±Ми1 = Е{+± Mv\ + ft©. E.2)
Пусть 09 есть частота света, излучаемого атомом,
который до и после излучения имеет нулевую скорость
Нщ = Е2 — Е{. E.3)
Исключение величин vf, £1 и Е2 из E.2) и
использование формул E.1) и E.3) приводит к уравнению
йсо0 = й© — Av2k + h2k2l2M. E.4)
Если направление волнового вектора испущенного
фотона к принять за ось г, то уравнение E.4) можно
переписать в виде
©0 = © ~ (®0§/с) + (А©2/2Мс2). E.5)
Величины в правой части уравнения E.5) имеют
следующие типичные порядки:
vlh « 10~5, НфМс2« 1(Г9. E.6)
б Зак. 885
130
ГЛАВА 5
Следовательно, со очень мало отличается от соо и
последним членом в правой части уравнения E.5) можно
пренебречь, поэтому
со = —-^тгт'« «>о f 1 + —) • E.7)
Таким образом, частота излучаемого света испытывает
доплеровский сдвиг, обусловленный составляющей
начальной скорости атома в направлении волнового
вектора испущенного фотона.
Следовательно, частотное распределение света,
излучаемого в направлении оси z всеми атомами в
газоразрядной лампе, отражает распределение компонент
скоростей атомов газа. Согл-асно распределению Максвелла
для скоростей [1], относительная вероятность того, что
атом газа при температуре Т имеет z-компоненту
скорости, заключенную между vz и vz + dvz, есть
ехр[-у рМ (vzJ~\dvz =
^ехрГ-^рМс2^""^2!^-^, E.8)
|_ 2 со0 J ©0
где
$=\jkBT. E.9)
Здесь для перехода от распределения скоростей к
эквивалентному распределению частот было использовано
соотношение E.7). Выражение, стоящее в правой части
равенства E.8), есть частотное распределение
излучаемого света, которое называется гауссовой функцией, а
форма линии — гауссовой.
Максимум гауссовой функции приходится на со = «о,
а половина максимальной интенсивности линии
соответствует частоте, определяемой из уравнения
1 = ехр[- - (Шс2 (со - со0J/(о2]. E.10)
Следовательно, полная ширина линии с доплеровским
уширением на половине ее максимальной высоты равна
.Д = 2оHB1п2/р/Ис2),/2. E.11)
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ
131
С другой стороны, ширину линии можно выразить через
среднеквадратичную ширину б гауссова распределения.
TFLUo) или AFAui)
Гауссова функция
-4-3-2-101254
Ы-ш0)/Г или (<о-ОH)/А
Фиг. 5.1. Сравнение нормированных лоренцевой и гауссовой
функций форм линии.
Обе функции в соответствующих масштабах имеют одинаковую ширину,
равную единице.
Нетрудно показать, что
6 = (©g/pM?2)* = Л/2 B In 2)ч\ E.12)
Функцию, описывающую гауссову форму линии,
удобно определить следующим образом:
FG (со) = Bяб2)",/2 ехр [- (со - со0O262]. E.13)
132
ГЛАВА б
Здесь постоянная перед экспонентой обеспечивает
нормировку
5^@0)^@=1. E.14)
Гауссова функция FG((o) и лоренцева функция Fl(<u)\
определенная в D.19), изображены для сравнения на
фиг. 5.1. Обе линии имеют на полувысоте одинаковую
ширину, т. е. А = Г, причем площади под кривыми
равны единице. Из фиг. 5.1 видно, что гауссова кривая
имеет более острый максимум и спадает быстрее вне
центральной области. Напротив, лоренцева кривая имеет
крылья, простирающиеся на некоторое расстояние вне
области пика.
Ударное уширение
Столкновения между атомами в газовом разряде
могут быть важным источником уширения линии
испускания. Обстоятельный анализ ударного уширения довольно
сложен B, 3]. Здесь мы рассмотрим только те детали
процесса ударного уширения, которые необходимы для
иллюстрации природы этого механизма.
Основное внимание направим на ту же самую пару
атомных состояний, которая использовалась выше.
Однако теперь доплеровский и естественный (излучатель-
ный) вклады в ширину линии не учитываются, поэтому
атомы излучают свет с частотой соо, определенной в E.3).
Пренебрежение излучательной шириной линии
эквивалентно предположению, что излучательное время жизни
тд, определенное в B.27), велико по сравнению с
некоторым другим временным масштабом системы, в данном
случае средним временем между атомными
столкновениями.
Рассмотрим отдельный возбужденный атом,
излучающий свет с частотой соо. Можно представить, что
волновой цуг электромагнитного излучения непрерывно
испускается атомом до тех пор, пока атом не испытывает
столкновения. Во время столкновения энергетические
уровни излучающего атома сдвигаются под действием
сил взаимодействия между двумя сталкивающимися
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 133
атомами. Следовательно, во время столкновения
излучаемый волновой цуг прерывается. Когда волна с
частотой coo восстанавливается после столкновения,* все ее
характеристики совпадают с характеристиками этой волны
до столкновения, за исключением фазы, которая не
связана с фазой волны до столкновения.
E(t) t *+г
Фиг. 5.2. Амплитуда электрического поля волнового цуга,
излучаемого отдельным атомом.
Вертикальные линии обозначают столкновения, разделенные временами
свободного пробега, для которых указано их среднее значение т0. Величина @0То
выбрана нереально малой, чтобы показать случайные изменения фазы, вызванные
столкновениями.
Если длительность столкновения достаточно мала, то
любым излучением, испущенным во время столкновения,
можно пренебречь, тогда как частота света сдвигается
относительно соо- В этом случае эффект ударного ушире-
ния можно адекватно описать на основе модели, в
которой каждый возбужденный атом всегда излучает на ча-*
стоте соо, однако во время каждого столкновения
происходит случайное изменение фазы излучаемой волны.
Наблюдаемый разброс излучаемых частот обусловлен тем,
что волна разбивается на конечные цуги, фурье-компо-
ненты которых содержат частоты, отличные от соо.
Волновой цуг, излучаемый отдельным атомом,
схематично изображен на фиг. 5.2, где показана временная за-
висимость амплитуды электрического поля E(t) в фикси-
134
ГЛАВА 5
рованной точке наблюдения. Момент столкновения
обозначается вертикальной линией, за которой следует
случайное изменение фазы волны. Согласно кинетической
теории газов (см. {1]), вероятность p{%)dx того, что вре-
2л
л
О
2л
;,
f
л
О
Фиг. 5.3. Временная зависимость фазы ф волнового цуга,
изображенного на фиг. 5.2.
мя свободного пробега атома лежит в интервале от т до
т + dx, определяется выражением
р (т) dx = A/т0) ехр (— т/т0) dx, E.15)
где среднее время свободного пробега т0 может быть
записано как
1 _ Ad2N ( n \h
Тп _ V
(w)"- <5Л6>
Здесь 'd — расстояние между центрами атомов во время
столкновения, а остальные обозначения имеют прежние
значения. Времена свободного пробега на фиг. 5.2
выбраны в соответствии с распределением вероятностей,
приведенным в E.15). Временное изменение фазы цуга
волны, изображенного на фиг. 5.2, показано на фиг. 5.3.
Рассмотрим один период свободного пробега атома,
который начинается в момент ^о и имеет продолжитель-
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 135
ность т. Комплексную амплитуду поля можно записать
следующим образом:
Е (t) = Е0 ехр (— i(x>Qt + /ф) (t0 < t < t0 + т), EЛ 7)
где ф — фаза волны для данного свободного пробега, а
Е0 и соо одинаковы для любого свободного пробега. Поле
E(t) в E.17) можно так же, как в D.1), представить
в виде интеграла Фурье, тогда амплитуда на частоте со
определяется согласно D.2):
Е (со) = — \ Е0 ехр (— ш01 + щ + Ш) dt =
и
Е0 ,. , \± \ - \ ехР U (© — ©о) т) ~ 1 /г ю\
= 2^ехр0 (а- ©о)/о + "Р> <(«,-£,) • EЛ8>
Таким образом, усредненная по периоду интенсивность
излучения, испущенного за данный промежуток времени,
имеет частотное распределение
/(co)~|£(o>)P = (-|J ^^rg^ • E-19)
Вид частотного распределения E.19) приведен на
фиг. 5.4.
В любой момент времени полная интенсивность
излучения состоит'из вкладов большого числа возбужденных
атомов. Времена свободного пробега различных атомов
распределены в соответствии с выражением для
вероятности E.15), а поэтому для нахождения полной
интенсивности величину, показанную на фиг. 5.4, следует
умножить на вероятность р(х) и проинтегрировать по т:
оо
т i \ If sin2 {(©о — со) т/2} , \ \ л
/«*,„(©) ~ -^\ (^г^р ехр (- т/то) dx =
о
= ((D0-fflJ + (l/ToJ # E,20)
Следовательно, частотное распределение линии
испускания с ударным уширением имеет лоренцеву форму,
характеризующуюся шириной 2/то, которая в два раза
больше средней скорости соударений.
На фиг. 5.2 величина соото имеет нереальное малое
значение 60. Для плотности газа, соответствующей дав-
136
ГЛАВА 5
лению 105 Па при комнатной температуре, реальное
знамение времени столкновений есть
To«3.10"nc. E.21)
Если для видимого света принять, как и в B.14),
(о0«3.1015Гц, E.22)
то
со0т0« 9 • 104. E.23)
Для этих значений волновой цуг, излучаемый одним
атомом, между двумя последовательными столкновениями
Пи»)
О 1 2
Ы-о>0)г/2я
Фиг. 5.4. Частотное распределение света, излучаемого отдельным
атомом за время свободного пробега т.
совершает в среднем около 15000 колебаний, поэтому
ударная ширина линии примерно в 100 раз больше
естественной ширины линии излучения, полученной для
значения А из C.59). Интересно отметить, что для
использованных выше значений параметров доплеровская
ширина {формула E,11)] примерно равна ударной ширине
линии.
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 137
Составная форма линии испускания
Выражения E.11) и E.16) явно показывают, как
можно с помощью выбора экспериментальных
параметров сделать доплеровскую и ударную ширины сколь
угодно малыми. Обе эти ширины пропорциональны
корню квадратному из температуры, а ударная ширина
пропорциональна также плотности газа, или, эквивалентно,
125 г
100 -
2Г
75
50
25
ч
О
5 10 15
Давление, мм pm. cm.
Фиг. 5.5. Изменение с давлением ширины лазерного перехода в
молекуле С02 (по данным работы [4]).
давлению газа. По этой причине ударное уширение
иногда называют уширением за счет давления.
Используя газовый разряд, поддерживаемый при достаточно
низкой температуре, можно в принципе наблюдать
линию испускания, обладающую только неустранимым из-
лучательным уширением. Кроме того, регулируя
давление газа, можно менять величину ударной ширины
относительно величин доплеровской и излучательной ширин.
На фиг. 5.5 приведена зависимость некоторых
экспериментальных результатов {4] для ширины линии
перехода на длине, волны 10,6 мкм в СОг от давления газа,
138
ГЛАВА 5
На этой зависимости ясно виден ожидаемый линейный
по давлению вклад ударного уширения. Величина
других вкладов в ширину линии определяется по точке
пересечения прямой с осью ординат при нулевом давлении.
В этом случае остаточная ширина в основном
обусловлена доплеровским уширением, а излучательная ширина
мала вследствие малой частоты перехода. Благодаря
использованию низких давлений и соответственно низких
плотностей A5 мм рт. ст. ^2-103 Па) ударная ширина
также намного меньше ширины, приведенной в E.21).
Когда вклады доплеровского, ударного, а также,
возможно, и излучательного уширений сравнимы по
величине, необходимо определить составную форму линии,
обусловленную этими тремя процессами. Рассмотрим
сначала комбинацию механизмов, приводящих к ушире-
нию линии, которые по отдельности определяют форму
линии, описываемую функциями /^(о) и /^(со).
Соответствующая составная форма линии описывается
функцией
оо
F(<o)= $ Fl (w) F2 (со + Щ — w) dm. E.24)
— оо
Здесь ©о — общая центральная частота для двух
распределений. Можно сказать, что интегрирование в E.24)
связывает с каждой частотной компонентой
распределения F\ уширенное распределение, которое соответствует
механизму, приводящему к распределению F2.
Очевидно, что с помощью повторных применений
уравнения E.24) можно объединить любое число
механизмов, приводящих к уширению линии. Отметим также,
что окончательная форма линии не зависит от порядка
объединения вкладов и величина интеграла в E.24)
инвариантна относительно перемены мест функций F\ и F2.
Некоторые применения уравнения E.24), приводящие
к простым результатам, описаны в следующих задачах.
Задача 5.1. Если два источника уширения приводят к
лоренцевым формам линии с ширинами Т\ и
Т2у то докажите, что полная линия также
является лоренцевой и имеет ширину {5]
Г = Г! + Г2. E.25)
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 139
Задача 5.2. Проведите такие же вычисления для случая
двух механизмов, ведущих к гауссовым
формам линии, и покажите, что составная линия
также является гауссовой с шириной Д,
определяемой уравнением
Л2 = А? + Д|, E.26)
где Ai и Аг — ширины линии для отдельных
механизмов.
К сожалению, интегрирование в E.24) нельзя
провести аналитически в том случае, когда форма одной линии
лоренцева, а другой — гауссова. Однако для этого
важного случая, который реализуется, например, когда
одновременно важны доплеровское и ударное уширения,
имеются полезные численные таблицы {6—8].
Соответствующая форма линии называется фогтовской и
является промежуточной между лоренцевой и гауссовой
формами линии.
Процессы, уширяющие линию, можно разбить на две
большие категории, которые характеризуются разными
качественными свойствами и связаны с двумя основными
формами линии. Одна категория содержит такие
источники уширения, в которых благодаря статистическому
распределению некоторых параметров, определяющих
частоту перехода, разные атомы поглощают или
излучают свет, немного различный по частоте. Такие
процессы уширения обычно приводят к гауссовой форме
линии. Доплеровское уширение принадлежит к этой
категории, причем скорость атома является соответствующим
статистическим параметром. Атомы, излучающие на
данной частоте, в принципе отличаются от остальных
атомов своей компонентой скорости, параллельной
излученному световому пучку. Другим примером служит
испускание света атомами, внедренными в кристалл; при
этом флуктуации локального напряжения могут вызвать
сдвиги частоты атомных переходов. Эти эффекты
принадлежат к категории механизмов неоднородного
уширения.
Лоренцева форма линии соответствует механизмам
однородного уширения, когда каждый поглощающий или
140
ГЛАВА 5
излучающий атом идентичен остальным атомам.
Например, для процессов излучательного или ударного ушире-
ния в принципе нет экспериментального способа
определения принадлежности света определенной частоты к
отдельной группе атомов. В этих случаях ширина Лео
обусловлена средним временем Aty в течение которого
атомный переход не возмущается. В соответствии с квантово-
механическим принципом неопределенности или
свойствами преобразования Фурье
ДюД*>1, E.27)
что согласуется с точными результатами для излучатель-
ных и ударных процессов.
Временная зависимость хаотического светового пучка
В случае хаотического источника зависимость
распределения интенсивности светового пучка от частоты
определяется суммарным влиянием излучательного, доп-
леровского и ударного уширений. Частотное
распределение можно измерить, например, с помощью решеточного
спектрометра и отсюда сделать заключение о физических
параметрах атомных переходов, ответственных за
излучение света. Обычная спектроскопия связана с
измерением таких частотных распределений.
Другие виды экспериментов со световыми пучками
требуют, однако, более детального знания зависящих от
времени свойств электрического поля и интенсивности
излучения. Так обстоит дело во многих
интерференционных экспериментах, примеры которых рассматриваются
НиЖе в настоящей главе. В то же время существуют
световые пучки со столь малыми частотными ширинами,
Что методами обычной спектроскопии их нельзя
разрешить. Как следует из E.27), узкая линия испускания
соответствует большой длительности тех процессов в
источнике, которые определяют ширину линии. В таких
случаях может оказаться полезным исследование свойств
светового пучка на основе изучения временной
зависимости. Анализ таких измерений, подробно обсуждаемый
в гл. 9, требует более тщательного исследования того,
какие зависящие от времени свойства источника влияют
на излучаемый свет.
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 141
Из рассмотрений, проведенных выше, следует, что
спектральное распределение излученного света
определяется теми же параметрами, которые определяют
временную зависимость характеристик атомов излучающего
источника. Эта тесная связь особенно отчетливо видна
в теории ударного уширения, поэтому теорию временных
свойств светового пучка удобно развивать для источника,
в котором атомные столкновения вызывают основное
уширение. Пренебрежения доплеровским и излучатель-
ным процессами уширения несколько уменьшает
общность расчета, однако принципы теории одни и те же для
любого хаотического светового источника. В
последующем рассмотрении используется классическая
электромагнитная теория, а квантование света не учитывается.
Существование фотонов приводит к дополнительным
эффектам, зависящим от времени, которые описываются
в гл. 9.
Временные свойства светового' пучка с ударным уши-
рением легко получить, развивая метод вычисления
частотного профиля линии излучения. Вид волнового цуга,
испущенного отдельным атомом, показан на фиг. 5.2.
Для этого частного атома, скажем имеющего номер /,
временную зависимость амплитуды электрического поля
Ei(t) волны в фиксированной точке наблюдения можно
записать следующим образом:
Ех (/) = Е0 ехр [— m0t + /ф! (/)]. E.28)
Это выражение похоже на E.17). Здесь cpi@—фаза,
изображенная на фиг. 5.3; она остается постоянной в
течение времени свободного пробега, а при каждом
столкновении ее значение резко меняется.
Полная испущенная волна описывается суммой
членов, подобных выражению E.28), причем каждому
излучающему атому соответствует один член. Если имеется v
таких атомов, то полная амплитуда электрического поля
дается выражением
E(t) = E{(t) + E2(t)+ ... +Ev(t) =
= Е0 ехр (— ш00 {ехр [/ф! (t)] +
+ ехр [ир2 (*)] + ... + ехр [fq>v (*)]} =
= Е0 ехр (— /g>q0 a (t) ехр [ир (/)]. E.29)
142
ГЛАВА 5
Здесь каждому атому были приписаны одинаковая
амплитуда Е$ и частота соо, однако фазы для различных
атомов совершенно не связаны. Для простоты
предполагается, что наблюдаемый свет имеет фиксированную
поляризацию, поэтому электрические поля можно
складывать алгебраически.
fc(t)'
РСО
Фиг. 5.6. Диаграмма Эргенда, на которой показаны амплитуда a (t)
и фаза ф (t) результирующего вектора, образованного большим
числом единичных векторов, фазовые углы которых выбраны
случайным образом.
Формальное суммирование фазовых коэффициентов
в последней строке выражения E.29)
проиллюстрировано на фиг. 5.6. Поскольку каждый из фазовых
коэффициентов фь ф2, ..., фУ имеет различные случайные
изменения, подобные тем, которые показаны на фиг. 5.3,
амплитуда a(t) и фаза q(t) имеют различные значения
в разные моменты времени. Вещественное электрическое
поле, получаемое из E.29), состоит из несущей волны
с частотой соо, обладающей случайной амплитудной и
фазовой модуляциями. Частота фурье-разложения
модулированной волны распределена около со0 таким же
образом, как в случае линии, имеющей ударное уширение
E.20).
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 143
Разрешить колебания амплитуды £@> происходящие
на частоте несущей волны, практически невозможно.
Хорошее экспериментальное время разрешения имеет
величину порядка 10~9 с, что на шесть порядков больше, чем
требуется для обнаружения колебаний на частоте соо,
данной в E.22). Следовательно, для сравнения с
экспериментом теоретические результаты необходимо
усреднить по периоду колебаний несущей волны. Среднее за
период значение вещественного электрического поля из
E.29) равно нулю. Согласно B.10), усредненная по пе-
риоду^ интенсивность пучка в свободном пространстве
есть
T(t) = {еиС|£@ I2 = 1 г0с'Еу (t). E.3Э)
Интенсивность /(/) все еще содержит временную
зависимость, обусловленную случайной амплитудной
модуляцией a(t).
На фиг. 5.7 и 5.8 показаны виды флуктуации
интенсивности и фазы пучка, полученные на основе численного
моделирования светового источника с ударным ушире-
нием, в котором точное суммирование фазовых
коэффициентов в формуле E.29) проводилось для большого
числа атомов v. Изменение фазы для каждого атома
имеет вид, показанный на фиг. 5.3, где времена
свободного пробега распределены согласно вероятностному
закону E.15). Горизонтальные временные масштабы для
/(/) и (p(t) на фиг. 5.7 и 5.8 определяются только
величиной среднего времени пробега то, указанного на
графиках.. Из графиков видно, что значительные изменения
интенсивности и фазы могут происходить на временном
интервале порядка то, а на временных интервалах At <C
«С то эти величины примерно постоянны.
Кроме флуктуации интенсивности и фазы, свет от
хаотического источника испытывает также флуктуации
плоскости поляризации, меняющейся во времени
случайным образом. Это изменение было исключено из данной
теории с помощью допущения о фиксированной
поляризации.
Учет излучательного и доплеровского уширений
изменил бы детали приведенного выше рассмотрения, однако
lit)
Фиг. 5.7. Временная зависимость усредненной по периоду
интенсивности хаотического светового пучка, полученная при помощи
численного моделирования.
Среднее время между столкновениями to имеет величину, указанную на
графике. Пунктирная линия обозначает среднее значение интенсивности,
усредненной по времени, много большему t0. (Вычисления проводились миссис
С. Сюзман.)
2яг
«М
^ *
О
г\
м
Фиг. 5.8. Временная зависимость фазы волны, испущенной
источником с ударным уширением линии.
График пвлучен на основе вычислений, использованных для фиг. 5.7»
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 145
флуктуации интенсивности и фазы остались бы
сходными с флуктуациями, изображенными на фиг. 5.7 и 5.8.
Для любой комбинации механизмов, уширяющих линию,
существует некоторое характерное время, аналогичное
времени то для ударного уширения, которое определяет
временной масштаб случайных флуктуации. Это
характерное время обычно называется временем
когерентности Тс светового пучка. Его величина имеет порядок
обратной спектральной ширины линии. Связь между
временем когерентности тс и обычным определением
когерентности рассматривается ниже в этой главе.
Во всех последующих теориях основное внимание
будет уделено таким световым пучкам, у которых ширина
частотного распределения мала по сравнению со средней
частотой, иными словами, тем случаям, когда величина
сооТс много больше единицы. Из фиг. 1.7 видно, что свет,
излучаемый нагретой полостью (излучение черного тела),
имеет ширину частотного распределения, приблизительно
равную средней частоте, и потому не попадает в эту
категорию.
Длина пути
К = сг„ E.31)
связанная с временем когерентности, называется длиной
когерентности. График зависимости усредненной по
периоду интенсивности от времени в фиксированной точке
пучка, приведенный на фиг. 5.7, можно было бы также
рассматривать как график зависимости интенсивности
от расстояния z вдоль пучка в фиксированный момент
времени. В этом случае ось абсцисс была бы
переобозначена как ось г, а среднее время to как \с. В данный
момент времени усредненная по периоду интенсивность
изменяется мало на расстояниях, малых по сравнению с Хс,
но на расстояниях порядка Хс или больших происходят
значительные изменения^ интенсивности. Временной и
пространственный масштабы флуктуации пучка связаны
простым размерным множителем с. Для
рассматриваемых пучков длина когерентности всегда много больше
длины волны света.
146
ГЛАВА 5
Флуктуации интенсивности хаотического света
Флуктуации интенсивности, показанные на фиг. 5.7,
можно измерить экспериментально только тогда, когда
имеется детектор со временем отклика, меньшим
времени когерентности тс. В большинстве случаев
флуктуации интенсивности I(t) происходят слишком быстро для
прямого наблюдения, а потому измеряются флуктуации,
усредненные по времени отклика детектора. Пренебрегая
этими экспериментальными трудностями, допустим, что
существует некоторый способ мгновенных измерений
усредненной по периоду интенсивности.
Среднее значение большого числа измерений
интенсивности 7@, проведенных за период времени, большой
по сравнению с тс, легко вычислить. Согласно формуле
E.29),
Щ^
= | ехр[/ф! {t)\ + ехр [/ф2 (*)] + . • • + exp [/<pv (*)] l2=v. E.32)
Здесь черта означает усреднение по большому
промежутку времени. Для времен, больших по сравнению с тс,
средние значения кросс-членов от разных излучающих
атомов равны нулю. То, что остается после усреднения,
представляет единичный вклад каждого атома в
значение a2(t).
Средняя по большому промежутку времени
интенсивность 7 находится с помощью подстановки выражения
E.32) в E.30)
/ —ye0c£ov. E.33)
Это значение 7 равняется просто усредненной по периоду
интенсивности света, излученного отдельным атомом,
умноженной на v. Величина 7 для флуктуирующей
интенсивности, изображенной на фиг. 5.7, указана пунктирной
горизонтальной линией. Здесь везде предполагается, что
световой источник является стационарным, т. е.
усредненная по большому интервалу времени интенсивность 7
фиксирована и не зависит от данного большого
интервала времени, выбранного для измерения интенсивности.
Любое измерение интенсивности пучка независимо от
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 147
времени отклика детектора должно приводить к
одинаковому значению усредненной по большому интервалу
времени интенсивности 7. Эта средняя интенсивность
обычно используется в теориях, описывающих
прохождение света через поглощающие среды, как, например,
в гл. 2 и 4.
Теперь рассмотрим отдельные измерения мгновенной
интенсивности. Из фиг. 5.7 видно, что результат
измерения T(t) нельзя предсказать точно. Можно точно
определить только статистическое распределение результатов
серии экспериментов. Статистические свойства
интенсивности I(t) могут быть определены из E.30), если
известно статистическое распределение значений a(t).
Из E.29) и фиг. 5.6 видно, что в любой момент
времени t значение a(t) равно расстоянию, пройденному из
центра диаграммы Эргенда за v шагов единичной длины
в случайных направлениях, определяемых углами cpi@>
Фг@> .•••> <Pv@- Соответствующее вычисление является
примером задачи о «случайном блуждании», хорошо
известной в теории стохастических процессов {9]. Пусть
p[a(t)] есть вероятность того, что конечная точка
случайного блуждания, состоящего из v шагов, лежит в
единичной площадке около точки с координатами a(t) и ср@
на фиг. 5.6. Результат, определяемый теорией
случайного блуждания, для данной задачи имеет вид [10]
Р [а (<)] = A/nv) exp [- «* (,)/v]f E.34)
причем p[a(t)] не зависит от ср@» как ЭТ0 И ожидалось
из физической природы задачи, и нормирована
следующим образом:
с» 2л
J da (t) J a (t) p [a {t)] dq> @=1. E.35)
0 0
Распределение вероятностей E.34) есть гауссова
функция, вид которой показан на фиг. 5.9. Такое же
распределение имеет место для любого хаотического
светового пучка, поэтому свет от хаотического источника
иногда называется гауссовым светом. Важно не путать
гауссово распределение амплитуды |£(/)| с
распределением частот пучка, которое может быть гауссовым, ло-
148
ГЛАВА 5
ренцевым или описываться промежуточной функцией.
Здесь предполагается механизм ударного уширения,
поэтому в действительности распределение частот лорен-
цево.
«(f) sin<£Ш
: *: • >
л'
i
' • '•"'•■v-." _* • * *
•/•'•л •. . • . •
a(t)COS0(f)
•• • »
\
Фиг. 5.9. Распределение вероятностей для амплитуды и фазы
электрического поля хаотического светового пучка.
Плотность затемнения пропорциональна вероятности того, что й {t) и Ф (t) имеют
значения,, определяемые соответствующей точкой комплексной плоскости.
Отметим, что вероятность имеет наибольшее значение в начале координат и не
зависит от фазы (р@«
С помощью выражения E.30) распределение
вероятностей для a(t) можно преобразовать в распределение
вероятностей для интенсивности 7(t).
Задача 5.3. Докажите, что при мгновенном измерении
усредненной по периоду интенсивности
вероятность получения ее значения в интер*
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 14$
вале от T(t) до 7@ +dl(t) равна p[I(t)]X
Х#@.где
р[Т (*)] = A/7)ехр[—7@/7], E.36)
а 7 определяется из E.33). Отметим, что
наиболее вероятное значение I(t) всегда
равно нулю.
Распределение вероятностей для случайных
блужданий, строго говоря, относится к результатам большого
числа блужданий, которые все начинаются из начала
координат. Для рассматриваемой задачи конечная точка
каждого блуждания определяет амплитуду а и фазу ф
светового пучка. Теория случайного блуждания
приписывает определенную вероятность каждому возможному
значению а и ф. Набор световых пучков со всеми
возможными амплитудами и фазами образует
статистический ансамбль типа упомянутого в гл. 1. Каждый
световой пучок ансамбля имеет фиксированные значения а
и ф, а распределение интенсивности, приведенное в
E.36), строго справедливо для такого ансамбля пучков
с фиксированными значениями амплитуды и фазы.
Эта ситуация, конечно, является результатом
теоретических построений и не соответствует типичному
эксперименту с использованием хаотического света, где,
возможно, имеется только один световой пучок, амплитуда
и фаза которого флуктуируют так, как описано выше.
Мы хотим использовать распределение вероятностей,
приведенное в E.36), для описания результатов серии
измерений мгновенной интенсивности одного и того же
пучка в разные моменты времени t. Связь между двумя
типами распределений находится с помощью эргодиче-
ской теоремы, уже упоминавшейся в гл. 1, согласно
которой средние по ансамблю и по времени могут быть
эквивалентными.
Очевидно, что в случае данного вычисления два
измерения мгновенной интенсивности одного и того же пучка
в одной и той же точке, но в разные моменты времени,
разделенные промежутком, меньшим тс, не могут быть
статистически независимыми. В этом случае в течение
промежутка времени между одним измерением и после-
150
ГЛАВА 5
дующим изменяются только некоторые из фазовых углов
<Pi@> Ф2@> •••» <Pv@» поэтому на диаграмме Эргенда
между двумя соответствующими случайными
траекториями имеется лишь небольшое различие. Однако для
двух разных измерений, разделенных промежутком
времени, много большим времени когерентности, почти все
фазовые углы различны. При этом случайные
траектории определяются статистически независимыми
случайными выборками v фазовых углов, и именно поэтому
можно использовать распределение E.36). Таким
образом, для применения эргодической теоремы в настоящем
вычислении необходимо выполнение следующих условий:
1) каждое измерение усредненной по периоду
интенсивности должно проводиться за время, меньшее тс; 2) вся
совокупность измерений должна занимать время,
большее тс.
Рассмотрим эксперимент, удовлетворяющий этим
условиям. Среднее значение n-й степени мгновенной
интенсивности обозначим через (In(t)). Теоретическое
значение этого среднего может быть вычислено на основе
распределения E.36)
оо
</*(*)) = A/Г) J Г(t) exp [- T{t)lT] dT{t) = п\ Т. E.37)
о
Следовательно, средние значения степеней мгновенной
интенсивности просто связаны с соответствующими
степенями 7.
Среднеквадратичное отклонение усредненной по
периоду интенсивности определяется выражением
((? (t)) - (T(t)Jjh =7. E.38)
Таким образом, величина флуктуации равняется средней
интенсивности, что качественно видно на фиг. 5.7.
Аналогичный результат был получен в A.71) или A.72) для
флуктуации числа тепловых фотонов в одной моде
полости.
Приведенные выше результаты для флуктуации
интенсивности справедливы для любого хаотического
светового пучка, причем единственное изменение при
переходе от одного источника к другому заключается в изме-
ТЕОРИЯ ХАОТИЧЕСКОГО CBFTA И КОГЕРЕНТНОСТИ 151
нении параметра 7 и временного масштаба тс, на
котором происходят флуктуации. Несмотря на большие
флуктуации 7(t), время когерентности тс обычно настолько
мало, что наблюдать эти флуктуации экспериментально
трудно, а их влияние на экспериментальные результаты
часто мало. Обобщение уравнения E.38), учитывающее
конечное время отклика детектора, приводится ниже
в E.94).
При помощи немного искусственного способа можно,
однако, создать световой пучок, флуктуации
интенсивности которого легко наблюдаются. Такой пучок может
быть создан путем рассеивания лазерного света на
маленьких полистироловых шариках, взвешенных в воде
A1]. Небольшие доплеровские сдвиги частоты
рассеянного света обусловлены броуновским движением
шариков. Взвесь представляет замедленную модель
излучающего газа, причем точно определенная лазерная частота
заменяет частоту атомного перехода. В этом случае
время когерентности тс порядка Ю-1 с, поэтому
флуктуации интенсивности видны невооруженным глазом.
Описанный выше хаотический световой пучок можно
сравнить с классической волной (обладающей
стабильной амплитудой и фазой), которая часто
используется в теоретическом анализе оптических
экспериментов. Предполагая, что волна распространяется вдоль оси
г, запишем ее электрическое поле как
Е (zt) = Е0 exp (ikz — i<uQt + /<p), E.39)
где в противоположность хаотическому полю E.29)
значения амплитуды и фазы фиксированы. На фиг. 5.10
показано изменение электрического поля со временем в
фиксированной точке наблюдения. Применять статистику
к классической стационарной волне нет необходимости,
поскольку усредненная по периоду интенсивность
постоянна и не испытывает флуктуации. Результат,
аналогичный соотношению E.37), имеет вид
</"(/)> = Г, E.40)
а среднеквадратичное отклонение равно нулю.
Степень зависимости результата оптического
измерения от статистических свойств используемого светового
152
ГЛАВА б
пучка различна для разных экспериментов. Некоторые
примеры описаны ниже. Результат многих
экспериментов один и тот же независимо от того, применяется ли
хаотический пучок или стабильная волна. В других
случаях результат полностью зависит.от величины
флуктуации или шума в пучке. Как будет показано в гл. 7 и 10,
пучок от лазера аппроксимирует классическую
стационарную волну без шума типа изображенной на фиг. 5.10,
fWV
Фиг. 5.10. Изменение электрического поля классической
стационарной волны со временем в фиксированной точке наблюдения.
Таким образом, определение влияния статистических
свойств света на результаты оптических экспериментов
представляет практический интерес.
Интерференционные полосы в эксперименте Юнга
Интерференционный эксперимент Юнга является
примером измерения, результат которого зависит от
флуктуации интенсивности. Этот эксперимент будет
проанализирован весьма детально, с тем чтобы понять условия,
при которых хаотическая природа светового источника
влияет на видность интерференционных полос.
Эксперимент довольно прост, однако его анализ иллюстрирует
некоторые общие принципы, присущие целому классу
оптических экспериментов.
На фиг. 5.11 показан упрощенный вариант
эксперимента Юнга. Хаотический свет от точечного источника,
сформированный линзой в параллельный пучок, падает
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 153
на экран, содержащий две щели или два отверстия, как
мы будем предполагать для простоты.
Интерференционные полосы наблюдаются на втором экране,
помещенном справа от первого. В этом модельном эксперименте
усложнения, вызываемые конечным диаметром источника
и соответствующей непараллельностью пучка,
освещающего первый экран, не учитываются. При строгом
анализе их необходимо принимать во внимание, однако
Экран 1
Экран 2
Линза
Источник
Фиг. 5.11. Схема идеализированного эксперимента Юнга.
здесь они опущены, с тем чтобы внимание было
сфокусировано только на эффектах случайных флуктуации
интенсивности.
Пусть E(rt) есть полное электрическое поле
излучения в точке г экрана наблюдения в момент времени ty
являющееся линейной суперпозицией электрических
полей в двух отверстиях (с координатами х\ и г2) в более
ранние моменты времени t\ и t2t определяемые скоростью
света с. Тогда формально
Е (rt) = щЕ {г А) + u2E(r2t2), E.41)
где
*i = < — {sjc)9 t2 = t — {s^c),
E.42)
154
ГЛАВА 5
а коэффициенты щ и и2 обратно пропорциональны
расстояниям S\ и s2 соответственно, которые определены на
фиг. 5.11. Коэффициенты щ и и2 зависят от геометрии
эксперимента, например от размера отверстий, однако в
данном вычислении их точный вид неважен; эти
коэффициенты чисто мнимые, поскольку вторичные волны,
излучаемые отверстиями, сдвинуты на фазе на я/2
относительно исходного светового пучка {12, 13].
Дифракционные.эффекты на самих отверстиях не учитываются.
Интенсивность света в точке г, усредненная по
периоду колебаний, имеет вид
T(rt) = ±e0c\E(rt)\2 =
= 1 е0с (| щ I21Е (гА) I2 + | и2121 Е (r2t2) |2 +
+ Ыи2 Re [£• (гЖ) Е (г2Щ. E.43)
Здесь был использован тот факт, что щ и и2 являются
чисто мнимыми величинами. Интенсивность 7 (rt) сходна
с интенсивностью, определенной в E.30).
Полосы в интерференционном эксперименте Юнга
обычно записываются на фотографическую пластинку
или наблюдаются невооруженным глазом. В каждом
случае время записи больше времени когерентности тс
хаотического света, поэтому для сравнения теории с
экспериментом I(rt) необходимо усреднить по временному
промежутку, большему тс. Обозначая по аналогии
с E.33) это среднее значение T(rt) через 7 (г) и
усредняя выражение E.43), получаем
7(г) = <T(rf)> = \ г0с {| щ I2 <| Е (Т&) I2) + | и212 (| Е (v2t2) i2) +
+ 2и\и2 Re (E* (nti) E (r2t2))}. E.44)
Угловые скобки в E.44) обозначают средние
значения по временам, много большим тс. Считая световой
источник стационарным, эти средние значения можно
вычислить на основе эргодической теоремы как средние
по ансамблю для статистического распределения,
описывающего поле, созданное источником. Точное значе-
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 155
ние последнего в выражении E.44) члена, усредненного
по времени, определяется формулой
т
(Е*(г^)Е(т212)) = Нт | y $ £*(гЛ)£(г2| tx+t2l) dt{ \,
E.45)
где
*2i=*2-'i. E.46)
Среднее E.45) называется корреляционной функцией
первого порядка для полей в
пространственно-временных точках (ri^i) и (r2t2). Оно явно зависит только от
комбинации времен t2\y равной разности между
временами измерения полей.
Из E.44) видно, что интенсивность на втором экране
состоит из трех слагаемых. Первые два описывают
интенсивности света, пропускаемые каждым отверстием в
отсутствие другого отверстия. Эти два члена не
приводят к каким-либо интерференционным эффектам.
Интерференционные полосы возникают благодаря члену,
содержащему корреляционную функцию полей от двух
отверстий.
Вычисление корреляционной функции первого порядка
Сущность корреляционной функции можно лучше
всего понять на примере подробного вычисления для
определенного светового источника. Рассмотрим важный
случай стационарного хаотического светового источника,
излучающего свет с лоренцевым частотным
распределением, как в случае линии испускания с ударным уши-
рением.
Предположим, что свет, падающий на первый экран
в эксперименте Юнга, распространяется вдоль оси г, а
его плоский волновой фронт перпендикулярен оси z.
Оптическая полость для данной задачи является
одномерной, и нормальные моды — это плоские волны с
волновым вектором к, параллельным оси z. Интервал Ак
между значениями волновых векторов соседних мод
определяется по аналогии с выражением для трехмерного
случая, рассмотренного в гл. 1:
Ak = n/L, E.47)
156
ГЛАВА 5
где L — длина полости. Такое одномерное описание
эксперимента Юнга является идеализацией практической
ситуации, однако оно достаточно реально, чтобы
показать наиболее существенные свойства корреляционной
функции.
Сначала рассмотрим математическое описание
хаотического светового пучка типа показанного на фиг. 5.7, где
только часть пучка внутри полости длины L
представляет интерес. Предположим, что полость имеет идеально
прозрачные стенки, поэтому пучок проходит сквозь них
без поглощения или отражения. Роль полости
заключается в выделении определенной области пучка; часть
пучка вне полости не учитывается.
Электрическое поле света в полости испытывает
случайные флуктуации, рассмотренные ранее, величину
которых можно описать так же, как в E.29).
Электрическое поле в полости E(zt) в произвольный момент
времени t удобнее выразить в виде фурье-суммы по
нормальным модам
Е (zt) = 2 Ek exp (ikz — ш*0> E.48)
к
где
cok = ck. E.49)
Комплексные коэффициенты Фурье Ей имеют амплитуду
и фазу, которые можно определить только статистически
в соответствии со случайными свойствами хаотического
света. В принципе амплитуды и фазы можно измерить
экспериментально, причем их величины различны в
разные моменты времени, так как свет проходит через
полость, и измеряются характеристики различных частей
распространяющегося пучка.
Число вкладов заметной величины от различных
нормальных мод в разложении E.48) зависит от длины
полости L и длины когерентности света Яс, определенной
в E.31). Допустим сначала, что полость очень коротка:
L < %е. E.50)
В соответствии с проведенным ранее рассмотрением
усредненная по периоду интенсивность пучка в каждый
момент времени почти постоянна на всей длине полости
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 167
Не зависящая от координат интенсивность флуктуирует
во времени так же, как показано на фиг. 5.7.
Интервал Асо между частотами соседних мод полости
определяется из E.47) и E.49)
Дсй = яс/£. E.51)
С другой стороны, за ширину предполагаемой лоренце-
вой линии излучения можно взять 2у, где величина у
связана со временем когерентности тс так же, как в
случае линии с ударным уширением, форма которой описана
в E.20):
Y = 1/V E.52)
С помощью формул E.31), E.51) и E.52) условие
E.50) для короткой полости может быть преобразовано
к виду
у < Дсо/я. E.53)
Следовательно, спектральная ширина светового пучка
много меньше частотного интервала между
нормальными модами очень короткой полости. В этом случае
с помощью пучка можно значительно возбудить только
одну моду полости. Пусть полость имеет такую длину L,
что частота одной из ее мод совпадает с центральной
частотой соо линии испускания. Тогда величина волнового
вектора возбужденной моды определяется выражением
kQ = ©о/с E.54)
Случай короткой полости проиллюстрирован в
верхней части фиг. 5.12. Интенсивность одной возбужденной
моды флуктуирует с временным масштабом порядка тс«
Интенсивность, средняя за период наблюдения, большой
по сравнению с тс, равна среднему значению за большой
промежуток времени интенсивности 7, определенному в
E.33). Отсюда следует, что
(| Еь I2) = 2Т/еос E.55)
Теперь рассмотрим противоположный предельный
случай очень длинной полости:
L » кс. E.56)
158
ГЛАВА 5
Интервал между нормальными модами Асо
удовлетворяет неравенству
у > До/л, E.57)
поэтому внутри ширины линии излучения лежит большое
число мод полости. Случай длинной полости иллюстри-
а
со
о
О}
......Ш1
ml
if
к
1ш
llu
<t)t
О)
Фиг. 5.12. Частотный спектр хаотического светового пучка в
полости, длина которой L много меньше длины когерентности Хс (а)
и много больше Кс (б).
а —частотный интервал между нормальными модами так велик, что только
одна мода падает в частотную область, изображенную на графике; б
—частотный интервал между модами полЪсти показан много большим, чем это
следует из условия L > Я, . На обеих частях фигуры высота спектральной
компоненты указывает ее интенсивность, усредненную по промежутку времени, много
большему времени когерентности.
руется на нижней части фиг. 5.12. Среднее значение по
ансамблю (\Ek\2) является лоренцевой функцией
частоты моды (Oft, поэтому можно положить
<1 Ek i2) = яг т \о. 2.
41 к l ' (ю0 — ©лJ + y2
где ^ — константа пропорциональности.
E.58)
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 159
Эту константу можно выразить через усредненную по
большому промежутку времени интенсивность 7. По
определению
/ = j e0c (| Е (zt) |2> =
fcfe'
Здесь было использовано разложение E.48). При k ф k'
амплитуды нормальных мод Ей и £V являются
случайными независимыми переменными, имеющими нулевые
средние значения. В результате средние значения по
ансамблю в правой части выражения E.59) обращаются
в нуль, если k Ф k'\
(Е\Ек) = О (k ф k'). E.60)
В выражении E.59) остаются только те члены, для
которых k = k\ поэтому
7=~е0с£<|£*|2>. E.61)
к
В случае очень длинной полости, когда выполняется
условие E.57), распределение мод внутри линии можно
приближенно рассматривать как континуум и заменить
сумму по k интегралом. По аналогии с трехмерным
результатом A.31) в одномерном случае имеем
оо оо
]Г -> (L/я) jj dk ~> (Line) \ d<uh. E.62)
k о о
Таким образом, из E.58) и E.61) получим
оо
Т= *ЪГ\ (со0 - JAJ + V2 U?<°fe = Т Б°^; E'63)
постоянную *ё можно исключить из выражения E.58).
В результате _
(|Ек |2) = -2L У ■. E.64)
41 *' ' e0L (со0 — юЛJ + Y v '
160
ГЛАВА 5
Интенсивности спектральных компонент в нижней
части фиг. 5.12 были изображены в соответствии с ло-
ренцевой формой выражения E.64). Интенсивность
каждой нормальной моды флуктуирует около своего
среднего значения по временному закону, определяемому
прохождением светового пучка через полость. Временной
масштаб этих флуктуации т/ определяется скоростью,
с которой изменяется распределение интенсивности при
прохождении пучка. Для времен, меньших L/c,
распределение интенсивности смещается на расстояние,
небольшое по сравнению с размером полости, поэтому фурье-
амплитуды Eh меняются очень мало. Для времен порядка
L/c или больше часть пучка внутри полости полностью
меняется, поэтому фурье-амплитуды соответственно
испытывают большие изменения. В этом случае временной
масштаб флуктуации Ей определяется величиной L/c и
за время флуктуации можно принять
т^ = L/c. E.65)
Эта величина играет роль, аналогичную роли тс в случае
короткой полости. Следовательно, временной масштаб
флуктуации увеличивается с увеличением длины полости.
Частотное уширение, связанное с временем т/, является
величиной такого же порядка, что и межмодовое
расстояние Дсо, определенное в E.51). Дальнейшее
увеличение длины большой полости приводит к еще более
плотно расположенным модам, но не увеличивает общую
ширину 2у распределения возбужденных мод.
Теперь можно приступить к вычислению
корреляционной функции первого порядка. Предположим, что длина
полости велика согласно условию E.56).
Корреляционная функция, определяющая интенсивность полос в
E.44), имеет вид
(Е* (V,) Е (z2t2)) = Z (ЕкЕк,) ехр {/ (- kzx +
+ (Okh + kfz2 — ©Иг)} = Z (I Ek I2) exp (r'Oftt), E.66)
к
где
* = h — к — (zi ~ z2)/c. E.67)
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ
161
Здесь были использованы формулы E.48), E.49) и
E.60). Подставляя выражение E.64) для (\Eh\2) в
E.66) и заменяя сумму интегралом, найдем
— оо
(F (гА) Е (z2t2)) = -^ J "Р!У> d*h. E.68)
-о- - (S
В случае узкой линии излучения нижний предел-
интегрирования можно без существенного изменения значения
-сю
оо
Фиг. 5.13. Контуры интегрирования в комплексной плоскости для
интеграла E.68).
интеграла заменить на — оо, после чего интеграл
вычисляется с помощью контурного интегрирования. Полюсы
подынтегрального выражения и контуры интегрирования,
соответствующие т>0 и т < 0, показаны на фиг. 5.13.
В результате интегрирования получаем
— оо
у ехр (Шкт)
(и - vy + Y2 d®k = л ехр {1щх — Y М). E.69)
6 Зак. 885
162
ГЛАВА 5
Подстановка выражения E.69) в E.68) приводит к
требуемому результату для корреляционной функции
<£* (г,*,) Е (*.&)> = B//е0с) ехр {1щх - y I т I). E.70)
Следует подчеркнуть, что при нахождении
корреляционной функции E.70) были использованы два
различных свойства светового источника: во-первых,
независимость и случайный характер значений коэффициентов
различных нормальных мод, что характерно для любого
хаотического источника и выражено соотношением
E.70), и, во-вторых, распределение частот излучаемого
света по большому числу мод полости, что является
необходимым условием для замены суммы интегралом
в E.62).
Интенсивность полос и когерентность первого порядка
Интенсивность полос в эксперименте Юнга можно
теперь определить, подставляя выражения E.59) и E.70)
в E.44). Два отверстия имеют одинаковую координату
z, поэтому формула для интенсивности приводится к виду
7(г) = Т{ I их I2 + 11/212 + 2«1Ы2ехр(— Y | т |) cos со0т}. E.71)
Здесь т определяется согласно E.42) и E.67):
х — — (s{ — s2)/c. E.72)
Видность полос в точке г на втором экране обычно
определяется выражением
ПОмакс - Шиин = 2Ц1 ехР (- У 1 *1 - *2 l/c) ,д 73ч
+ / (г)мин I «1 I2 + |"г|2
В центре второго экрана на фиг. 5.11, где щ = и2 и S\ =
= 52, видность полос равна единице, а вне оси, где
г г ф и2 и S\ ф 52, — меньше единицы.
Влияние хаотической природы светового источника на
видность полос отражено экспоненциальным членом в
выражении E.73), который в принципе приводит к
полному исчезновению интерференционных полос для
значений 5Ь достаточно сильно отличающихся от значения
52. Однако из E.71) видно, что для узкой линии излуче-
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 163
ния с соо > у член, содержащий косинус, успевает очень
много раз изменить знак, прежде чем величина т станет
достаточно большой и уменьшение экспоненциального
члена приведет к исчезновению интерференционных
полос. Для времени когерентности и частоты,
определенных в E.21) и E.22), на втором экране имеется около
104 четких интерференционных полос, расположенных
симметрично вокруг оси экспериментальной установки.
В реальном интерференционном эксперименте Юнга
хаотическая природа света обычно не является самой
важной причиной исчезновения полос. Конечная
протяженность источника в направлении, перпендикулярном оси,
которая не учитывалась в проведенном выше анализе,
часто бывает наиболее важным ограничивающим
фактором, и в действительности имеются методы определения
угловых диаметров удаленных световых источников,
например звезд, на основе наблюдения исчезновения
интерференционных полос (см. [13]).
Таким образом, хаотические свойства светового
источника, принятые при расчете интерференционных
полос, оказывают очень малое воздействие на результат
эксперимента. Правильное в основном теоретическое
выражение можно было бы получить, полагая источник
идеально стабильным и монохроматическим, с выходным
излучением типа волны, изображенной на фиг. 5.10.
Действительно, именно такой подход к анализу
интерференционных явлений описан в большинстве учебников;
сильные флуктуации интенсивности и фазы излучения от
хаотического источника, изображенные на фиг. 5.7 и 5.8,
оказывают небольшое влияние на типичный
классический интерференционный эксперимент.
Конечно, относительно небольшая роль хаотического
характера источника является результатом допущения
о малой ширине линии испускания источника.
Экспоненциальные множители в E.71) или E.73) имели бы
большое значение в случае хаотического источника, у
которого ширина излучения сравнима со средней частотой,
как, наприхмер, у теплового излучения полости. В другом
предельном случае настолько узкой линии излучения, что
можно было бы прямо наблюдать флуктуации
интенсивности, обычный анализ интерференции был бы недоста-
6*
164
ГЛАВА 5
точным. Самое большое возможное для хаотического
источника время когерентности обычно порядка 10~9с,
поэтому можно, как правило, предполагать, что
экспериментальное время разрешения много больше тс.
Свойства светового пучка, существенные для
интерференционного эксперимента, удобно выразить через
понятие "оптической когерентности. Говорят, что в двух
пространственных или временных точках свет является
когерентным, если при сложении он может в принципе
создать интерференционные эффекты. Примером
является свет из двух, отверстий в интерференционном
эксперименте Юнга. В большинстве классических
интерференционных экспериментов возможная величина
интерференционных эффектов определяется когерентностью
первого порядка используемого светового пучка.
Степень когерентности первого порядка для полей в
пространственно-временных точках (r^i) и (г2^)
описывается функцией g"A)(ri^r> i^), К0Т0Рая Для краткости
обозначается как g\lJ. Эта величина определяется через
корреляционную функцию первого порядка как
g{i)(Tt гП = ^ = i(£*(Mi)£(r2/2))l /5?4ч
В 1гА>гА)-*12. ((|£Wl)|2)(|£(r2,2)|2))v2- №)
Здесь угловые скобки указывают на необходимость
усреднения по ансамблю при статистическом определении
поля E(rt). Говорят, что в точках (v\t\) и (гг^г) свет
когерентен в первом порядке, если gW=l, некогерентен,
если g^ = 0, и частично когерентен при промежуточных
значениях #$.
В качестве первого примера когерентности
рассмотрим хаотический световой источник с лоренцевым частот^
ным распределением, использованный выше для теории
эксперимента Юнга. После подстановки выражений
E.59) и E.70) в E.74) степень когерентности первого
порядка принимает вид
£A) (*А, 22*2) = ехр {— y I *i — *2 — (*i — 22)/с I) =
= ехр(-уМ). E.75)
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 165
Вид зависимости g$ от т показан на фиг. 5.14. Свет
когерентен в первом порядке в двух точках, если
*i - h - (*i — г2)/с < хе. E.76)
Здесь было использовано соотношение E.52). В
эксперименте Юнга, где Z\ = z2, четкие полосы получаются в
В12
Ж
0,5
~4 -2 0 2 4
ух
Фиг. 5.14. Зависимость степени когерентности первого порядка
хаотического света с параметром ширины линии у в двух
пространственно-временных точках Z{ti и z2t2 от т = t\ —• t2 — (z\ — z2)/c.
Постоянное единичное значение когерентности первого порядка классической
стационарной волны показано пунктирной линией.
том случае, если промежуток времени между моментами
прохождения через отверстия двух пакетов парциальных
волн, встречающихся в некоторой точке второго экрана,
много меньше времени когерентности. Согласно оценке
E.21), величина тс обычно порядка 3-Ю-11 с.
Соответствующая длина когерентности приблизительно равна
10~2 м. В общем случае интерференционные полосы от
параллельного светового пучка можно получить только
- при наложении света из двух точек, расстояние между
которыми вдоль пучка меньше длины когерентности. При
этом свет, выходящий из двух рассматриваемых точек,
должен быть разделен временным интервалом, меньшим
времени когерентности.
166
ГЛАВА 5
Задача 5.4. Докажите, что степень когерентности
первого порядка для хаотического света с
гауссовым частотным распределением, средне-
Фиг. 5.15. Зависимость степени когерентности первого порядка
хаотического света с гауссовым частотным распределением,
имеющим среднеквадратичную ширину б, от т.
Сравните с фиг. 5.14 для лоренцева частотного распределения.
квадратичная ширина которого б определена
в E.12), дается выражением
£^=ехр(-4б2т2)' E-77>
В этом случае время когерентности есть
хс « 1/6 E.78)
и имеет точно такое же качественное
значение, что и время когерентности для
лоренцева распределения. Степень когерентности
первого порядка, определяемая выражением
E.77), показана на фиг. 5.15.
Классическая стационарная волна, определенная в
E,39) и изображенная на фиг. 5.10, представляет
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 167
пример излучения с другими когерентными свойствами.
В этом случае корреляционная функция первого
порядка определяется без всякого усреднения по ансамблю,
поскольку поле не обладает статистической
неопределенностью
(Е* (z^,) Е (z2t2)) = El exp (ш0т) = B//е0с) exp (/ю0т). E.79)
Здесь значение т приведено в E.67). Таким образом, по
определению когерентности первого порядка E.74)
£$=1. E.80)
Пучок когерентен в первом порядке во всех
пространственно-временных точках, и можно сказать, что он
полностью когерентен в первом порядке. Результат E.80)
совпадает с результатом, который получается при
устремлении параметра ширины линии у к нулю в выражении
для хаотического пучка E.75) (эквивалентно тс-^ оо).
Между двумя предельными случаями хаотического
пучка и классической стационарной волны имеются
другие световые пучки, для которых когерентность первого
порядка можно легко вычислить. Примеры таких пучков
дают понятие об условиях, необходимых для получения
когерентного света.
Задача 5.5. Рассмотрите одномерную полость,
содержащую хаотический световой пучок с
неопределенным временем когерентности, и
предположите, что вклады в поле от всех
нормальных мод полости, кроме одной, можно
было бы устранить с помощью фильтра.
Оставшийся одномодовый пучок испытывает
случайные флуктуации интенсивности,
характерные для хаотического света.
Докажите, что равенство E.80) тем не менее
выполняется, т. е. пучок в первом порядке ко-
, герентен во всех парах
пространственно-временных точек полости.
Задача 5.6. Рассмотрите стабильный световой пучок,
созданный путем возбуждения двух мод по-
168
ГЛАВА 5
лости, электрическое поле которого имеет
вид
Е (zt) = Ех exp (ikxz — mj) +
+ E2 exp (ik2z — m2t). E.81)
Докажите, что этот световой пучок
когерентен в первом порядке для всех пар точек.
Выше были приведены примеры некоторых общих
условий, при которых свет может иметь полную
когерентность первого порядка. Эти условия выполняются, если
либо возбуждена только одна мода полости, либо поле
можно точно определить без статистического описания.
Если пучок состоит из более чем одной моды и
обнаруживает статистические флуктуации, то выполнение
равенства E.80) для всех пар точек невозможно.
Задача 5.7. Рассмотрите световой пучок, созданный,
как и в E.81), путем возбуждения двух мод
полости, однако теперь обе моды
испытывают независимые случайные гауссовы
флуктуации. Докажите, что если средние за
большой промежуток времени
интенсивности обеих мод одинаковы, то выполняется
соотношение
gg = cos {1 (со! - 02) т }. E.82)
Классическая теория оптики связана с явлениями,
наблюдаемыми при помощи хаотического светового
источника, для которого когерентность первого порядка
определяется выражением E.75). Интерференционные
эксперименты, подобные эксперименту Юнга, построены
таким образом, чтобы использовать когерентность первого
порядка. Такое использование возможно при выполнении
условия E.76).
Новейшее развитие оптики вышло за пределы
классической теории. Лазерное излучение имеет когерентные
свойства, которые можно менять от когерентных свойств
излучения хаотического источнику до когерентных
свойств классической стационарной волны. Кроме того,
были проведены эксперименты, где прямо измерялись
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 169
флуктуации интенсивности излучения от хаотического
источника. Такие эксперименты зависят от когерентных
свойств света более высокого порядка.
Интерференция интенсивностей
и когерентность высших порядков
В противоположность описанным выше классическим
интерференционным экспериментам рассмотрим теперь
интерференционный эксперимент другого типа,
выполненный Хенбери Бряуном и Твиссом [14, 15], в котором
флуктуации интенсивности хаотического света
непосредственно определяют получаемый результат. Этот
эксперимент, детально рассматриваемый в гл. 9, важен не
только вследствие полученных результатов, но также
потому, что он положил начало целой новой области
эксперимента. Эксперимент Хенбери Брауна и Твисса можно
анализировать на разных уровнях сложности. Анализ,
проведенный здесь, аналогичен тому, который
использовался в случае эксперимента Юнга. Он показывает, как
понятия классической интерференционной теории следует
расширить, чтобы они включали эксперимент Хенбери
Брауна и Твисса.
Экспериментальная аппаратура схематически
показана на фиг. 5.16. Чтобы устранить все излучение, кроме
одной линии испускания спектра ртути на длине волны
435,8 нм, свет от ртутной дуговой лампы пропускается
через фильтр. С помощью полупрозрачного зеркала
пучок разделяется на две равные части. Интенсивность
каждой части измеряется фотоумножителем, принципы
работы которого описываются в гл. 9. Затем флуктуации
выходных токов двух детекторов перемножаются в
корреляторе. Проинтегрированное по большому промежутку
времени значение этого произведения дает величину
флуктуации интенсивности.
Один из детекторов установлен на передвижной
рамке таким образом, чтобы его положение можно было
менять относительно неподвижного детектора в
горизонтальном направлении. Это позволяет совмещать или
полностью разделять апертуры детекторов относительно
отверстия, что может служить способом проверки реально-*
170
ГЛАВА 5
сти наблюдаемых флуктуации, которые должны исчезать
при достаточно большом расстоянии между детекторами.
Пренебрегая этой стороной эксперимента, рассмотрим
идеализированную схему, где два детектора
расположены симметричо относительно зеркала и измеряют
интенсивности пучков на одинаковых расстояниях z от
светового источника.
Жидкий Полупрозрачное Квадратные
фильтр зеркало f отверстия
-j^V—V
Дуговая
ртутная
лампа
Фотоумножитель
Выходы
к коррелятору
v
Фотоумножитель Подвижная
рамка
Фиг. 5.16. Схема экспериментальной установки по измерению
интерференции интенсивностей [14, 15].
Полупрозрачное зеркало создает два совершенно
одинаковых световых пучка с усредненной по периоду
интенсивностью T(zt)y имеющих идентичные флуктуации
типа показанных на фиг. 5.7. Среднее по большому
промежутку времени значение интенсивности отдельного
пучка равно 7, поэтому пучок перед зеркалом обладает
интенсивностью 27 (zt). Мы пока не будем учитывать
усложнений, связанных с конечной величиной времен
откликов детекторов, и предположим, что в эксперименте
можно определить корреляцию флуктуации
интенсивностей в двух детекторах, которые мгновенно измеряют эти
флуктуации в разные моменты времени t\ и t2. В этом
случае в эксперименте измеряется величина
<[/ (zt,) - I] [I (zt2) - I)) = (/ (zt,) I (zt2)) - I2, E.83)
так как
</(z/,)) = (/(z/2)) = /.
E.84)
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 171
Здесь угловые скобки обозначают такое же усреднение,
как в E.45).
Корреляционная функция для эксперимента Хен-
бери Брауна и Твисса очень похожа на корреляционную
функцию, которая встречалась в эксперименте Юнга, но
только теперь в корреляционную функцию входит
интенсивность пучка, а не электрическое поле.
Корреляционная функция в E.83) представляет собой частный
случай корреляционной функции более общего вида:
</Wi) ТШ) = (\ е0сJ (| Е (*,*,) р| Е (z2t2) I2) =
= A г0сJ (Е* (zA) E*(z2t2) E (z2t2) E (*,*,)>. E.85)
Расположение членов во второй строке формулы E.85)
подчиняется соглашению о таких выражениях,
называемых корреляционными функциями второго порядка.
Функция корреляции второго порядка для
хаотического света определяется таким же способом, как и
функция корреляции первого порядка. Разлагая
электрическое поле пучка по плоским волнам, как и в E.48), и
подставляя это разложение в E.85), получаем
T{z]tl) I (z2t2) = (j e0c) Y, {ЕкДкДкгЕк) X
К\, Kit &3» &4
X exp {i {— kxz{ + ©!*, — k2z2 + cu2/2 +
+ kzz2 — co3f2 + k±zx — ©4*0}, E.86)
где
щ = ckx и т. д. E.87)
Четыре комплексных коэффициента Фурье в E.86)
являются независимыми случайными переменными с
нулевыми средними значениями, поэтому в сумме E.86)'
существуют только два вида членов, для которых
средние значения по ансамблю в правой части уравнения не
обращаются в нуль. Ненулевые члены получаются при
выполнении условий
( kx = k3 ( kx = k4
X k2 = &4 \k2 = kz. \ * *
172 ГЛАВА 5
Таким образом, выражение E.86) упрощается и
принимает вид
</(гА) 7B^2» =
= (т 8^ьJ Z(| ^|2)(| Ек*12) [ехр W^-0*) т> + ^ <5-89)
Здесь величина т определена в E.67). С помощью E.61)
и E.66) правую часть можно выразить через
корреляционную функцию первого порядка:
<7Wi) /W2)> = (у *осJ1 (Я* (*A) £ Ш) I2 + 7V E.90)
Следовательно, корреляционная функция второго
порядка для любого хаотического светового источника
определяется величиной, соответствующей корреляционной
функции первого порядка.
До сих пор не детализировалось частотное
распределение светового пучка. Если предположить длинную
полость, как в E.56), и многомодовое возбуждение, как на
нижней части фиг. 5.12, то для лоренцевой линии
испускания корреляционная функция первого порядка из
E.70) дает
G(^1)/~(^2)) = /2{exp(-2Y|T|)+ 1}. E.91)
Отметим, что среднее значение квадрата интенсивности
в одной и той же точке пространства удовлетворяет
следующему соотношению:
G2(^)) = 2/2, E.92)
которое было доказано в E.37) для всех хаотических
световых пучков.
Предсказываемый результат эксперимента Хенбери
Брауна и Твисса получается при подстановке выражения
E.91) в E.83):
<[/(**,) - 7] [I(zt2) - /]> = 72ехр(- 2Y| fi - U |). E.93)
В эксперименте непосредственно измеряются флуктуации
интенсивности хаотического светового пучка. В случае
классической волны имеем I(zt) = T для всех
точек zt и предсказываемый результат равен нулю.
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 173
В действительности результат E.93) не может
служить реальным предсказанием для практического
эксперимента, где невозможно провести мгновенное
измерение интенсивности пучка. Всегда существует некоторое
минимальное время отклика детектора тг, такое, что
измеренная интенсивность является средней за время хг.
Рассмотрим эксперимент Хенбери Брауна и Твисса, где
«мгновенные» интенсивности измеряются одновременно
двумя детекторами с одинаковым временем отклика хг
Если дополнительное усреднение по времени отклика
детектора обозначить второй парой угловых скобок, то
предсказываемый экспериментальный результат примет
вид
«(/(г*,) -Т)GШ -/)» =
т т
г г
=-V 5 л, \ (TW - Т, (T(zt2) - 7)> dt2 =
Хг -
г О О
= ~4"т {ехр (- 2Ytr) - 1 + 2утг}. E.94)
Здесь были использованы формулы E.83) и E.91). Этот
результат проиллюстрирован на фиг. 5.17.
Для очень короткого времени отклика детектора,
когда
Ytr< 1, E.95)
или, эквивалентно, из E,52),
тг < т„ E.96)
правая часть уравнения E.94) переходит в 72, что
согласуется с E.38) и E.93) для случая одновременного
измерения мгновенных интенсивностей. В
противоположном случае большого времени отклика, когда
ухг > 1 или хг > хСУ E.97)
выражение E.94) принимает вид
((№,) - 7] (I[zt2) - 7]» = ^-. E.98)
174
ГЛАВА 5
Отсюда следует, что корреляции интенсивностей
уменьшаются с увеличением времени отклика детектора.
Оригинальные измерения корреляции интенсивностей
проводились [14, 15] с использованием световых источников и
детекторов, для которых величины ухг были порядка 105.
Флуктуации, измеряемые для таких больших
относительно тс значений тг, очень малы по сравнению с 72,
Фиг. 5.17. Величина коррелированных флуктуации интенсивности
хаотического света, имеющего лоренцево частотное распределение
с параметром ширины линии у.
Время обоих детекторов равно х .
поэтому успех эксперимента зависит от прямой
регистрации коррелированных флуктуации интенсивностей,
а не много больших коррелированных интенсивностей.
В проведенных выгце вычислениях, как и при анализе
интерференционного эксперимента Юнга, световой пучок
предполагался поляризованным. Существование в непо-
ляризованном световом пучке двух независимых
поляризаций легко учесть. Это приводит к дополнительным
множителям 2 или 4 в некоторых выражениях, и они,
конечно, существенны при сравнении теории и
эксперимента. Однако физические принципы явления
интерференции интенсивностей остаются без изменения.
Из приведенных выше выражений видно, что
эксперименты по интерференции интенсивностей можно ис-
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 175
пользовать для определения параметра ширины линии у.
Эксперимент Хенбери Брауна и Твисса зависит от
временного разрешения флуктуации интенсивности
хаотического света. Напротив, в обычном спектроскопическом
эксперименте свет исследуется на основе частотного
разрешения. Спектроскопия временного разрешения
рассматривается в гл. 9, где учитываются эффекты
квантования поля излучения.
Свойства светового пучка, используемые в
экспериментах по интерференции интенсивностей, можно
выразить с помощью расширения понятия когерентности. По
аналогии с определением когерентности первого порядка
в E.74) определим степень когерентности второго
порядка световых полей в пространственно-временных
точках (r{ti) и (г2*2) следующим образом:
£B)(Г1*1> T2fV Г2^ *Vl) — ё?2 =
__ (E*(r1tl)E*(r2t2)E(T2t2)E(Tltl)) ,-QQv
~ <|E(ri*i)|2><|£(r2^|2> * К '
Здесь угловые скобки снова обозначают средние по
ансамблю. Отметим, что эта функция представляет собой
частный случай более общей 4>УНКВДИ когерентности
второго порядка, в которой четыре поля берутся в
четырех разных пространственно-временных точках, однако
именно функция E.99) адекватна эксперименту
Хенбери Брауна и Твисса, в котором впервые была измерена
когерентность второго порядка. Говорят, что свет в
точках (T\t\) и (г2^) когерентен во втором порядке, если
одновременно выполняются условия
«$=1. £(i22)=1- E-100)
Когерентность второго порядка хаотического света
связана с когерентностью первого порядка простым
общим соотношением, справедливым независимо от
частотного распределения света. Используя E.90) и
определения g\l] и g$ [формулы E.74) и E.99)], получаем
*1? = («йJ+1. E-101)
Как было показано в связи с результатом E.75),
хаотический свет всегда можно рассматривать как когерент*
176
ГЛАВА 5
иый в первом порядке при условии, что точки (r^i) и
(гг^г) достаточно близки друг к другу. Однако в пределе,
определяемом неравенством E.76), которое
обеспечивает степень когерентности первого порядка, равную
единице, когерентность второго порядка равна 2
согласно формуле E.101). Хаотический свет не может быть
когерентным во втором порядке в соответствии с
определением E.100) при любом выборе
пространственно-временных точек. В эксперименте Хенбери Брауна и Твисса
измеряется величина, пропорциональная отклонению от
когерентности второго порядка g$— 1.
В случае одномерного хаотического светового пучка
с лоренцевым частотным распределением когерентность
первого порядка определяется выражением E.75), а
степень когерентности второго порядка, получаемая из
E.101), имеет вид
.£Й = ехр(-27|т|) + 1, E.102)
где т находится из E.67). Для хаотического света с
гауссовым частотным распределением соответствующий
результат получается с помощью E.77):
g<|) = ехр (—б2т2) + 1. E Л 03)
Зависимость когерентности второго порядка от т для
этих двух типов хаотических пучков изображена на
фиг. 5.18. Отметим, что степень когерентности второго
порядка хаотического света приближается к степени
когерентности второго порядка когерентного света при
больших значениях ух или бт в отличие от степени
когерентности первого порядка, изображенной на фиг. 5.14
и 5.15, где хаотический свет приближается к
когерентному при малых значениях ух или бт.
Классическая стационарная волна E.39),
приведенная на фиг. 5.10, имеет следующую корреляционную
функцию второго порядка:
(I (г&) T(z2t2)) = 72, E.104)
так как усредненная по периоду интенсивность равна
постоянной величине 7. Тогда из E.99) следует
соотношение
^=1, E.105)
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 177
которое вместе с формулой E.80) показывает, что
стационарная волна когерентна во втором порядке во всех
пространственно-временных точках. В- этом случае
коррелированные флуктуации в эксперименте Хенбери
Брауна и Твисса обращаются в нуль, как указывалось ранее.
Точно такой же результат E.105) получается для поля,
лB)
J//2
Стационарная волна
Гауссово
распределение
Лоренцево
распределение
-2
-1
0
YT или 6т
Фиг. 5.18. Степени когерентности второго порядка хаотического
света, имеющего гауссово и лоренцево частотные распределения с
параметрами ширин линии 6 и y соответственно.
Постоянная единичная степень когерентности второго порядка классической
стационарной волны показана пунктирной линией.
описываемого выражением E.81) и образованного в
результате сложения двух классических стационарных волн.
Степени когерентности первого и второго порядков,
определенные в E.74) и E.99), являются лишь первыми
двумя членами иерархии функций когерентности. Можно
рассмотреть обобщенный интерференционный
эксперимент, результат которого зависит от корреляций
электрических полей в произвольном числе
пространственно-временных точек. Результат Любого подобного измерения
. зависит некоторым образом от иерархии функций коге-
178
ГЛАВА 3
рентности. Степень когерентности n-го порядка может
быть определена следующим образом [16]:
_ (E* (T\h) ... E* (rntn) E (rn+\tn + \) ♦ • • E (г2п*2п))
((\E{Tltl)\*)...{]E(rntn)\*){\EJL rn+i*/i+1) I2) • • • (I ESSinhn) I2))
E.106)
Очевидно, что формулы E.74) и E.99) представляют
собой частные случаи этого общего определения.
В наши планы не входит сколько-нибудь детальное
исследование общих свойств когерентного света n-го
порядка, поскольку в отношении эксперимента наибольший
интерес обычно представляют когерентности первого и
второго порядков. Однако следует отметить два простых
результата. Когда точки набора (rn+i^n+i), ..., (Sinhn)
совпадают с соответствующими точками набора
(Гп^п), ..., (nfi), корреляционная функция в E.106)
содержит интенсивность в п различных точках. В случае
классической стационарной волны можно точно так же,
как при нахождении gf^, доказать, что
g{n){r{tu ..., rntn\ rntny ..., r^j) = 1 для всех п. E.107)
На основе очевидного обобщения определения
когерентности второго порядка в E.100) можно сделать вывод,
что классическая стационарная волна когерентна во
всех порядках.
Для хаотического светового пучка не имеется столь
же простого результата. Однако можно привести очень
частный случай, когда все точки в выражении E.106)
являются одной и той же пространственно-временной
точкой (rt). Тогда корреляционная функция совпадает с
выражением, вычисленным в E.37), и в результате
g{n)(rt, ..., rt\ г/, ..., vt) = n\. E.108)
Теория, изложенная в настоящей главе, включая
теорию эксперимента Хенбери Брауна и Твисса, анализ
которого в действительности больше соответствует
некоторой области квантовой оптики, была построена на основе
классической физики. Теория когерентности пересматри-
ТЕОРИЯ ХАОТИЧЕСКОГО СВЕТА И КОГЕРЕНТНОСТИ 179
вается в гл. 9 на основе квантования поля излучения.
Понятия, введенные в настоящей главе, остаются в
основном справедливыми, однако методы вычисления функций
когерентности при квантовомеханическом подходе
совершенно иные.
Задача 5.8. Рассмотрите пучок, образованный путем
пропускания классической стационарной волны
постоянной интенсивности I/f через
периодически окрывающийся и закрывающийся
затвор. Здесь / — число, меньшее единицы,
которое обозначает промежуток времени, в
течение которого затвор открыт.
Следовательно, средняя интенсивность прерываемого
пучка равна 7 независимо от /. Докажите,
что когерентность п-го порядка в одной
пространственно-временной точке (rt) есть
&n)(rt, ..., Tt\ rt, ..., г*) = Гя+1- E.109)
Этот результат показывает, что при выборе
достаточно малых значений / величина gln)
может достигать любых, сколь угодно
больших значений, исключая случай п— 1,
когда степень когерентности первого порядка
равна единице независимо от /.
ЛИТЕРАТУРА
1. Jeans /., An introduction to the kinetic theory of gases, Cambridge
University Press, Cambridge, 1940, § 90.
2. Weisskopf V.f Phys. Z., 34, 1 A933).
3. Hindmarsh W. R.y Atomic spectra, Pergamon, Oxford, 1967.
4. Bridges T. /., Haus H. A., Hoff P. W., Appl. Phys. Lett., 13, 316
A968).
5. Park D., Am. Journ. Phys., 39, 682 A971).
6. Davies J. Т., Vaughan J. M., Astrophys. J., 137, 1302 A963).
7. Elste G.t Z. Astrophys., 33, 157 A953).
8. Hummer D. J, Mem. R. Soc, 70, part 1 A965).
9. Wax N. (ed), Selected papers on noise and stochastic processes,
Dover, New York, 1954.
10. Chandrasekhar S., Rev. Mod. Phys., 15, 1 A943).
11. Pike E. R., In Quantum optics (ed. Key S. M., Maitland A.),
Academic Press, New York, 1970, p. 127,
iou
X ЛЛБЛ U
12. Longhurst R. 5., Geometrical and physical optics, Longmans,
London, 1957, p. 188.
13. Born M.y Wolf E.y Principles of optics, Pergamon, Oxford, 1970,
p, 374. (См. перевод: М. Борн, Э. Вольф, Основы оптики, изд-во
«Наука», 1970.)
14. Hanbury Brown /?., Twiss R. Q., Nature, 177, 27 A956).
15. Hanbury Brown R.t Twiss R. Q., Proc. Roy. Soc, A242, 300 A957) j
A243, 291 A958).
16. Glauber R. /., Quantum optics and electronics (ed. DeWitt C.f
A. Blandin, C. Cohen-Tannoudji), Gordon and Breach, New York,
1965, p. 63. (См. перевод в сб, «Квантовая оптика и радиофи«
зика», изд-во «Мир», 1966,)
Глава 6
*• • - -
Квантование поля излучения
Все описанные до сих пор вычисления были
основаны на теории, в которой электрическое Е и магнитное
Н поля излучения считались классическими
переменными, тогда как атомы рассматривались квантовомеха-
нически. Условия квантования были наложены на
энергию поля излучения в гл. 1 при выводе формулы Планка,
но в остальном понятие фотона играло небольшую роль
для последующей теории. Такая полуклассическая
теория излучения приводит к правильным теоретическим
выражениям для широкого класса величин;
действительно, при некоторой модификации и обобщении
полуклассическая теория оказалась способной объяснить
почти все оптические эксперименты, выполненные
приблизительно до 1960 г.
Однако, несмотря на успех полуклассической теории
излучения, принято считать, что квантовая механика дает
лучшее современное описание физических явлений, а
потому наиболее полное описание поля излучения следует
искать в квантовой механике, где наблюдаемые поля Е
и Н описываются квантовомеханическими операторами.
Теория квантованного поля излучения приводит к
строгим выражениям для наблюдаемых величин,
характеризующих поле излучения и его взаимодействие с атомами.
Справедливость любой полуклассической или
феноменологической теории излучения может быть доказана
только ее способностью воспроизводить результаты
квантовой теории поля.
Квантованное поле излучения необходимо
использовать для объяснения многих современных
экспериментов, где измеряются величины, понятие о которых лежит
за пределами представлений любой полуклассической
182
ГЛАВА 6
теории. В классе экспериментов, называемом квантовой
оптикой и описываемом в гл. 9, для получения
информации о свойствах светового поля используются
детектирование и счет отдельных фотонов. Эксперименты по счету
фотонов можно полностью понять только на основе
теории электромагнитного поля, включающей понятие
фотона. Что касается возможных состояний светового поля,
то лишь часть состояний, разрешенных квантовой
теорией поля, может быть описана классически. Например,
состояние электромагнитного поля с определенным
числом возбужденных фотонов, которое нетрудно
рассмотреть в квантовой теории поля, не может быть описано на
основе классической теории поля.
Настоящая глава посвящена применению квантовой
механики к электромагнитному полю. В последующих
главах будет показано, как некоторые результаты
полуклассической теории могут быть доказаны с помощью
последовательной квантовомеханической теории.
Например, снова кратко выводятся скорости переходов для
процессов поглощения и испускания, а хаотический
световой пучок заново пересматривается. В этих примерах
квантовая теория излучения приводит к новой точке
зрения на простые излучательные процессы.
Вся эффективность и простота
квантовомеханической теории станет очевидной позднее в более сложных
вычислениях. Теория лазера, описанная в гл. 10, служит
примером расчета, где полное поведение системы можно
получить, лишь используя квантованное поле излучения.
Теориям восприимчивости, описанным в гл. 8, и теориям
процессов излучения высших порядков, анализируемых
в гл. 11 и 12, можно частично сопоставить расширенную
полуклассическую теорию, однако в математическом и
физическом планах эти теории легче создать на основе
квантованного поли.
Описание классического электромагнитного поля
с помощью потенциалов
Квантовая теория поля излучения имеет некоторое
сходство с классической теорией. В квантовой теории
полевые векторе должны рассматриваться как операторы,
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
183
а не как алгебраические величины классической теории,
тем не менее обе теории базируются на уравнениях
Максвелла. Конечно, вывести квантовую теорию из
классических уравнений невозможно, однако переход к
квантовой механике легче осуществить, если сначала
уравнения классической электромагнитной теории
преобразовать к более подходящему виду. Как указывалось в гл. 1,
квантование осуществляется путем замены уравнения
классического гармонического осциллятора
соответствующим квантовомеханическим уравнением. Первая
задача настоящей главы заключается в том, чтобы
представить классические уравнения в такой форме, в
которой зависимость от переменных поля такая же, как в
уравнении для гармонического осциллятора, что удобно
для перехода к квантовой механике.
Векторный потенциал электромагнитного поля играет
важную роль з процедуре квантования, поэтому мы
начнем с обзора свойств классических скалярного и
векторного потенциалов ф и А соответственно. Потенциалы
можно использовать для записи уравнений Максвелла
A.1) и A.4) в более компактной форме. Четвертое из
этих уравнений удовлетворяется тождественно, если Н
определить через потенциал А согласно уравнению
^0H=VXA, F.1)
где магнитная проницаемость свободного пространства
(Но введена для удобства записи последующих уравнений.
Тогда из тождества
'VXV<p = 0, F.2)
где ф — скалярная функция, следует, что первое
уравнение Максвелла удовлетворяется тождественно, если ф
определяется по формуле
V<p = -E-4f, F.3)
или эквивалентно
dt
^-ж- (е-4)
Если потенциалы известны, то уравнения F.1) и F.4)
позволяют найти поля Н и Е,
184
ГЛАВА б
Потенциалы можно в принципе определить из
уравнений, получаемых в результате подстановки выражений
F.1) и F.4) в оставшиеся уравнения Максвелла A.2)
и A.3):
V(V-A)-V2A+^V9+^-^ = M F.5)
— е0У2ф — e0V • -jf = a. F.6)
Здесь были использованы формула A.14) и тождество
A.15). Это полевые уравнения, которые определят поля,
созданные данным распределением заряда а и тока J.
Поскольку в левых частях уравнений F.5) и F.6)
имеются члены, содержащие как А, так и ф, эта форма
уравнений довольно сложна. Уравнения можно
упростить, накладывая на потенциалы А и ф некоторое
дополнительное условие. Важно понимать, что выражения
F.1) и F.3) для потенциалов А и ф не полностью
определяют вид этих потенциалов. Потенциалы можно в
некоторых пределах менять без изменения наблюдаемых
полей Е и Н. Преобразование потенциалов А и ф,
обладающее таким свойством, называется калцбровочлым
преобразованием.
Допустим, что А0 и ф0 представляют собой решения
уравнений поля для данных о и J. Тогда электрическое
и магнитное поля Е и Н определяются уравнениями
F.4) и F.1).Рассмотрим калибровочное преобразование
к новой паре потенциалов А и ф, определяемых
формулами
А = А0 - V2 F.7)
и
Ф = Фо + -^г> F.8)
где S — произвольная функция координаты г и времени
t. Из уравнения F.4) видно, что при калибровочном
пребразовании поле Е не меняется. Соответствующая
инвариантность поля Н, получаемого из F.1), следует
из тождества F.2), которое также справедливо для
функции S.
1
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ 185
Калибровка для электромагнитного поля
определяется некоторым условием, налагаемым на А и <р,
которое может быть реализовано посредством
калибровочного преобразования произвольной пары решений полевых
уравнений для данных а и J. Необходимо подчеркнуть,
что практически измеряемые поля Е и Н никоим образом
не зависят от выбора калибровки для Аиф, Тем не
менее свободу выбора, обусловленную калибровочной
инвариантностью, часто можно использовать для
значительного упрощения вычислений Е и Н.
Кулоновская калибровка
Говорят, что электромагнитное поле имеет кулонов-
скую калибровку, если векторный потенциал
удовлетворяет условию
V.A = 0. F.9)
Позднее будет видно, что кулоновская калибровка
удобна для квантования электромагнитного поля. В случае
поля, первоначально определяемого некоторой парой
потенциалов А0 и ф, всегда можно С9вершить
преобразование к кулоновской калибровке с помощью
преобразования типа F.7) и F.8), где функция S должна быть
решением уравнения
V23 = V-A0. F.10)
Необходимо отметить, что даже при наложении условия
кулоновской калибровки {уравнение F.9)] потенциалы
все еще не определены полностью. Дальнейшие
преобразования потенциалов, удовлетворяющих кулоновской
калибровке, возможны, если для S выполняется
уравнение
V2E = 0. F.11)
Кулоновская калибровка выбирается отчасти потому,
что в результате уравнения поля F,5) и F.6) упро-
щаются и принимают вид
-V2A + Jt|£- + tt|-V<P = M F.12)
186
ГЛАВА б
И
-У2Ф = -^. F.13)
Теперь скалярный потенциал ф удовлетворяет уравнению
Пуассона из электростатики, формальное решение
которого есть [1]
^-ik\j0Fjd3r'- <6Л4)
Здесь координатная зависимость а и ф явно указана.
В общем случае эти величины зависят также от времени,
однако в уравнение Пуассона / явно не входит.
Плотность зарядов, которую следует использовать в
интеграле F.14), соответствует тому же моменту времени, в
который требуется определить ф. Скалярный потенциал
в кулоновской калибровке ведет себя так, как будто он
мгновенно «узнает» распределение плотности заряда во
всем пространстве.
Уравнение поля F.12), определяющее А, все еще
является сложным благодаря наличию члена, содержащего
Ф, однако этот член можно исключить следующим
образом. Согласно теореме Гельмгольца (см., например, {2]),
любое векторное поле может быть представлено в виде
суммы двух компонент, одна из которых имеет равную
нулю дивергенцию, а другая — равный нулю ротор.
В случае плотности тока J эту сумму можно записать как
J = Jr + JL, F.15)
где
V. Jr = 0, F.16)
VXJL = 0. F.17)
Здесь Jr называется поперечной, или соленоидальной,
компонентой, a Jl — продольной, или безвихревой,
компонентой.
После разделения J на две части уравнение
непрерывности A.6) можно переписать в виде
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
187
Благодаря свойству F.17) векторная полевая
компонента Jl может быть выражена через некоторый
скалярный потенциал, скажем г|э:
J£ = Vi|). - F.19)
Подстановка выражения F.19) в F.18) приводит к
уравнению
сравнение которого с F.13) показывает, что функции \р
и ф должны быть связаны соотношением
Тогда из F.19) получим
Jz. = e0v4j. F.22)
Теперь, используя F.15) и F.22), уравнение поля
F.12) можно упростить и привести к виду
-^А+^г^ = Мг, F.23)
где скалярный потенциал уже исключен. В учебниках
по теории поля [1] показывается, что решение уравнения
F.23) имеет вид
А И)-■£■ J T7=FT ^ -F-24)
где
t' = t- |г~г'1 , F.25)
Таким образом, выражение для векторного потенциала
в точке г в момент времени / явно учитывает влияние
конечной скорости света на запаздывание действия тока
в удаленной точке г', приходящего в точку г.
Наблюдателю в точке г может быть известно только то
распределение тока в точке г', которое существовало в более
раннее время t\ определяемое формулой F.25).
Формальные решения задачи вычисления поля,
созданного плотностями заряда о и тока J, описываются
188
ГЛАВА в
уравнениями F.14) и F.24) для ф и А. Данная форма
этих уравнений является следствием предполагаемого
условия калибровки F.9), однако теория калибровочной
инвариантности, кратко изложенная выше, показывает,
что получаемые поля Е и Н не должны зависеть от
условия калибровки.
Не следует искать большого физического смысла в
самих потенциалах ф и А. Например, из простого анализа
выражения F.14) следует, что изменение знака
плотности заряда в точке г' ведет к немедленному изменению
скалярного потенциала ф в точке г. Это противоречит
требованию теории относительности, заключающемуся
в том, что любая информация, содержащаяся в
электромагнитном поле, может передаваться только с конечной
скоростью с. Тем не менее можно показать (см.,
например, [3]), что измеряемые в точке г поля Е и Н в момент
времени t зависят от плотностей заряда и тока,
существовавших в точке г' вл более раннее время t\ определяемое
формулой F.25), и поэтому релятивистские принципы не
нарушаются. Выражение F.14) для скалярного
потенциала может противоречить постулату о конечной
величине скорости света, поскольку ф не является
наблюдаемой величиной. Непосредственный физический смысл
можно приписать только полям Е и Н.
Электрический вектор Е также можно представить
в виде поперечной и продольной частей:
Е = Ег + EL, F.26)
где
V.Er = VXEL = 0. F.27)
Из F.4) видно, что обе части вектора Е могут быть явно
записаны следующим образом:
Ег = - 4г <6'28)
и
EL = - Уф. F.29)
Тогда из тождества F.2) и условия кулоновской
калибровки F.9) следует, что эти компоненты удовлетворяют
уравнению F.27), Согласно уравнению Максвелла A.4),
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
189
магнитный вектор Н является поперечным и не имеет
продольной компоненты.
Большое преимущество кулоновской калибровки для
проблемы поля излучения и его взаимодействия с
зарядами и токами заключается в разделении уравнений поля
и уравнений Максвелла на две различные части.
Продольная часть связана со скалярным потенциалом <р, как
в уравнении F.29), а соответствующее уравнение поля
есть F.13). Из уравнения Максвелла A.3)
V-EL = -f, F.30)
fc0
и плотность продольного тока, получаемая из F.22) и
,F.29), определяется выражением
дЕ
h=-^-et- F.31)
Последние два * уравнения описывают поля, созданные
зарядами, согласно законам электростатики.
С другой стороны, поперечная часть поля связана
с векторным потенциалом А уравнением F.28).
Соответствующее уравнение поля F.23) имеет форму волнового
уравнения, а уравнения Максвелла A.1) — A.4) для
поперечного поля принимают вид
VXH=e0-/ + Jr, F.33)
V.Er = 0 F.34)
и
V . Н = 0. F.35)
Уравнения F.32) — F.35) описывают электромагнитные
волны. В соответствии с уравнениями F.23) и F.33),
электромагнитные волны определяются только
поперечной частью плотности тока Jr.
Необходимо подчеркнуть, что разделение уравнений
на статическую часть, связанную с плотностью заряда, и
динамическую часть, связанную с ^ электромагнитными
волнами, является формальным следствием условия ку-
190
ГЛАВА б
лоновской калибровки. Это разделение служит примером
тех преимуществ вычислений, которые могут быть
достигнуты при выборе соответствующих условий калибровки.
Свободное классическое поле
В оставшейся части главы мы рассмотрим
электромагнитное поле в области пространства, где
Jr = 0, F.36)
и, следовательно, согласно F.23),
Поле в такой области пространства называется
свободным. В теории взаимодействия излучения с атомами
требуется решение более сложной задачи, в которой Jr
описывает поперечный ток, созданный атомными
электронами. Взаимодействие излучения с атомами
анализируется в гл. 8.
Квантование электромагнитного поля осуществляется
на основе замены классического векторного потенциала
А квантовомеханическим оператором А. Последнее
преобразование, которое будет проделано над классическим
полем, приводит к форме классических уравнений,
позволяющей ^непосредственно перейти к квантовомеханиче-
скому описанию электромагнитного поля.
, Рассмотрим область пространства, имеющую форму
куба со стороной L, аналогичную кубической полости,
изображенной на фиг. 1.2. Однако теперь «полость»
рассматривается просто как область пространства без
каких-либо реальных границ. Вместо решений в виде
стоячих волн, приведенных в A.23) и A.24), выберем
решения для поля в виде бегущих волн, как в A.17) и A.18),
и наложим на них периодические граничные условия.
Кроме того, в отличие от вычисления, проведенного в
гл. 1, мы будем использовать векторный потенциал А, а
не поля Ей Н.
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
191
Учитывая эти предварительные замечания, векторный
потенциал в полости можно разложить в ряд Фурье:
А = £ {Ак @ ехр (/к • г) + А*к (/) ехр (- /к • г)}. F.38)
к
Здесь компоненты волнового вектора к принимают
значения
Vx Vy V2
kx=2n-j-t ky = 2jt-7-, k2 = 2n-jT, F.39)
где
v*, V v2 = 0, ±1, ±2, ±3, .... F.40)
Плотность определенных таким образом мод равна
плотности мод, определяемых формулами A.24) и A.26).
Условие кулоновской калибровки F.9) удовлетворяется,
если
к ■ Ак (*) = к • А! (*) = 0. F.41)
Для каждого волнового вектора к существуют два
независимых направления вектора A^(t).
Различные фурье-компоненты векторного потенциала
А независимы и должны по отдельности удовлетворять
уравнению поля F.37), поэтому
1 д2\к (/)
k*Ak(t) + v-^- = 0 F.42)
и Ak(/) удовлетворяет точно такому же уравнению.
Следовательно, фурье-коэффициенты являются решениями
простого гармонического уравнения
02Ак(О л ■
-J^ + u>lAk(t) = 0, F.43)
где
©k = c&. F.44)
Электромагнитное поле квантуется путем
преобразования уравнения F.43) в квантовомеханическое уравнение
гармонического -осциллятора. Чтобы показать, как можно
осуществить такое преобразование, полезно перейти к
описанию осциллятора с помощью эффективных
координаты и импульса, связанных с модой полости.
192
ГЛАВА б
С этой целью мы вычислим классическую энергию
нормальной моды полости, определяемой волновым
вектором к. В качестве решения уравнения F.42) можно
взять
Ak@ = Akexp(— ШкО, F.45)
тогда полный векторный потенциал F.38) принимает вид
А = Z{Akexp (—td)kt + *k«r) + Akexp(*a>kf—/к • г)}. F.46)
Усредненная по периоду энергия одной моды к равна
«Гк = ^- \ (вД + ^Щ) dV, F.47)
ПО ПОЛОСТИ
где черточки обозначают среднее значение за период, Ек
и_ Нк — электрическое и магнитное поля моды. Из
формулы F.1), F.4) и F.46) получим
Ек = шк {Ак ехр (— i(okt + /к • г) — Ак ехр (шк/ — /к • г)},
F.48)
Нк = -—-к X {Акехр (— mkt + /к • г) —
— А; ехр (шк* - /к . г)}. F.49)
Из F.41) и F.44) следует, что величины Ек и
Нк связаны соотношением A.21), как это и ожидалось
для свободной электромагнитной волны. Подстановка
формул F.48) и F.49) в F.47) и вычисление средних по
времени значений приводит к выражению
ffk = 2е07со2кАк . А*к, F.50)
где
V = L\
Модовые переменные Ак и Ак можно заменить
обобщенной «пространственной» координатой моды Qk и
обобщенным «импульсом» моды Як согласно
преобразованиям
Ак = Dв01Ч)-% О А + iPu) h F-5D
И
А; = Dе/со2)-1/2 (cokQk - iPk) гк. F.52)
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
193и
Координаты Qk и Рк являются скалярными величинами,
поскольку векторные свойства величин Ак и Ак были
выделены путем введения для моды единичных векторов
поляризации е^.
На основе формул F.51) и F.52) энергия одной моды
[выражение F.50)] преобразуется к виду
$b=Y(Pl + <Ql)' F-53)
Последнее выражение точно совпадает с выражением
для энергии классического гармонического осциллятора
с единичной массой, или, что то же самое, это
выражение представляет собой обычный гамильтониан для
классического гармонического осциллятора. Таким образом,
проблема векторного потенциала, связанного с модой
полости, была сделана формально эквивалентной
проблеме классического гармонического осциллятора.
Полный классический гамильтониан для излучения в
полости получается простым суммированием выражения для
одной моды F.53) по всем к и двум независимым
направлениям £к-
Квантовомеханический гармонический осциллятор
Теперь электромагнитное поле квантуется
посредством преобразования Qk и Рк в квантовомеханические
операторы координаты q^ и импульса рк. Прежде чем
перейти к такому преобразоваию, теорию квантовомеха-
нического осциллятора удобно представить в форме,
которая наиболее пригодна для квантования поля.
Квантовомеханический гамильтониан для
одномерного гармонического осциллятора с единичной массой
имеет вид
^==j(P2 + coY). F-54)
где р и $ подчиняются обычному коммутационному со-
- отношению
[<?, р] = iti. F.56)
, Определим пару операторов а и а+ для замены q и р
u = Bh<o)~y2{(oq + ip) F.56)
7 Зак. 885
194
ГЛАВА 6
И
<jf = BА©Г'/г {щ - ifi), F.57)
или, совершая обратный переход,
^=AУ/2(а + й+), F.58)
p=-i (^У (й - ^- F-59)
Операторы с и а" называются соответственно
операторами уничтожения и рождения для гармонического
осциллятора. Как станет ясно в дальнейшем, эти
операторы чрезвычайно полезны благодаря их простым
свойствам. Однако они не описывают наблюдаемые величины
гармонического осциллятора.
Из формул F.56) и F.57) получим
йЧ = BА©) (Р2 + ©2<?2 + mqp - mPq) =
= (ЙсоГ1 [Ж - y А©) • F.60)
Здесь были использованы выражения F.54) и F.55).
Аналогично
й&* = (А©)~! (Ж + у А©). F.61)
Коммутатор для новых операторов легко находится из
этих результатов:
[й, а+] = й&* - а+й = 1. F.62)
Используя F.60), гамильтониан можно переписать
в виде
Ж = Нсо (аЧ +y). F.63)
Часто встречающаяся комбинация операторов acft
называется оператором числа частиц для гармонического
осциллятора. Мы обозначим его как
п = йЧ. F.64)
При выводе формулы Планка в гл. 1 мы уже
использовали известный результат A.37), заключающийся в том,
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
195
что собственными значениями оператора п являются
нуль и положительные целые числа. Теперь этот
результат будет строго получен в процессе исследования
свойств операторов а и а+.
Пусть \п) есть собственное состояние гамильтониана
гармонического осциллятора с собственным значением
Еп. Уравнение для собственных значений имеет вид
Ж\п)=ы(аЧ +1)|м><=£„|л). ^ F.65)
Умножая обе части этого уравнения слева на а+
П®(аЧЧ + ^а^\п)==ЕпаЦп) F.66)
и используя для преобразования первого члена в правой
части уравнения F.66) коммутатор F.62), получаем
уравнение
Йсо (а?й& - й* + ~ d+) | п) = Endf | п), F.67)
которое можно преобразовать к виду
Асо (йЧ + у) а+1 п) = Ш+1 п) = (Еп + Ао) й* \ п). F.68)
Это последнее выражение снова имеет вид
уравнения на собственные значения энергии. Отсюда следует,
что состояние а^\п) есть собственное состояние энергии
гармонического осциллятора с собственным значением
Еп -+- Ъы. Если определить новые собственное состояние
и собственное значение как
\п+1) = й*\п) F.69)
и
Еп+\ =Еп + Н(д, F.70)
то уравнение F.68) можно переписать следующим
образом:
#|/1+1> = £я+1|л + 1>. F.71)
Эти результаты показывают, что если имеется некоторый
энергетический уровень гармонического осциллятора ЕПу
то существует другой уровень, расположенный выше пер-
7*
196
ГЛАВА 6
вого на величину йсо. Таким образом, энергетические
уровни располагаются на одинаковом расстоянии друг
от друга, образуя лестницу.
Как и в классической
механике, здесь не существует
ограничения на максималь*
ную энергию гармонического
осциллятора, а поэтому
лестница из уровней
простирается вверх до бесконечности.
Схема уровней
гармонического осциллятора
приведена на фиг. 6.1.
Для исследования
нижней части лестницы уровней
умножим уравнения на
собственные значения энергии
F.65) слева на а. Тогда пре*
образования, подобные тем,
на основе которых совершен
переход от F.66) к F.68),
приводят к уравнению
>
^
л
а
f
Еп+
En
En-
c2 г
hu>
_ з
f7 = fto
E0--zbco
Фиг. 6.1. Схема энергетических
уровней для квантовомеханиче-
ского гармонического
осциллятора, показывающая роли опе-
раторов рождения а и
уничтожения а в добавлении кванта
энергии Йсо к энергии
возбуждения или его вычитании.
Ш\п) = (Еп — Йо>) d| п).
F.72)
Следовательно, состояние
а\п) есть собственное
энергетическое состояние с
собственным значением Еп—йсо.
Если мы введем определения
|/i—1> = й|л> F.73)
и
Еп-х = Еп-Ы% F.74)
то уравнение F.72) преобразуется к виду
3§|я—1) = £„_!! л—1>. F.75)
Таким образом, лестница энергетических уровней
простирается вниз с равными шагами йсо. Однако эта лестница
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
197
должна быть ограничена снизу, так как кинетическая и
потенциальная энергии осциллятора являются
положительными величинами и собственные значения не могут
быть отрицательными. Пусть |0) есть основное
состояние с энергией £,0. Для основного состояния уравнение
F.72) дает
Жа | 0} = {Е0 - Йсо) а | 0). F.76)
Поскольку, согласно гипотезе, нет собственных
состояний с энергией, меньшей энергии основного состояния, то
единственное решение уравнения F.76), согласующееся
с такой физической интерпретацией, определяется
выражением
й\0) = 0. F.77)
Условие основного состояния F.77) можно использовать
для определения Е0, поскольку уравнение на
собственные значения F.65) для основного состояния принимает
вид
Ж\0) =1й©|0> = £0|0>. F.78)
Поэтому
£0 = 1/jcd, F.79)
и из F.70) следует обычный результат для
гармонического осциллятора
Еп = (п + 4") йсо> л = 0, 1, 2, ... . F.80)
На фиг. 6.1 показана схема энергетических уровней и
указаны роли операторов й и а+ соответственно в
уничтожении или рождении кванта feco в энергии
возбуждения осциллятора и, следовательно, в совершении
перехода на одну ступеньку лестницы вверх или вниз.
Состояния \п) являются собственными состояниями одно-
временно операторов Жий:
А\п) = й*й\п) = п\п). F.81)
Собственное значение оператора h указывает число
квантов йсо, возбужденных выше основного состояния
осциллятора.
198
ГЛАВА 6
В проведенном анализе нормировка собственных
функций \п) не рассматривалась. Если эти функции
нормировать, то в уравнениях, связывающих разные
собственные состояния, появляются дополнительные
множители. Записывая условия нормировки как
<л — 1 |я — 1) = (п\п) = (п+1 \п+1) = 1, F.82)
рассмотрим влияние этих условий на уравнение F.73).
Чтобы функции п) и \п—1) были нормированными,
в уравнение F.73) необходимо ввести численный
множитель Wn'.
фп\п— 1> = й|л>. F.83)
Умножая обе части уравнения F.83) слева на их эрми-
тово-сопряженные выражения
(п - 1 \VnVn \п - 1) = (п \йЧ \п) F.84)
и учитывая формулы F.81) и F.82), получаем
\<Vnf = nm F.85)
Как обычно, примем фазу нормировочной константы
равной нулю, тогда уравнение F.83) принимает вид
а\п) = пЦп- 1). F.86)
Такой же анализ уравнения F.69) приводит к
результату
й*\п) = {п + \)у'\п+ 1). F.87)
В последующем мы будем отдавать предпочтение
уравнениям F.86) и F.87), а не F.69) и F.73), поскольку
желательно работать с нормированными собственными
функциями. Отметим, что условие основного состояния
F.77) входит в общий результат F.86) как частный
случай.
Собственные состояния гармонического осциллятора
с разными энергиями, конечно, ортогональны, поэтому из
F.86) и F.87) следует, что единственные отличные от
нуля матричные элементы операторов а и й+ имеют вид
<я — 1 \й\п) = п\ F.88)
(п+1\й+\п) = (п+1Iк. F.89)
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
199
Матричные элементы каждого эрмитова оператора О
удовлетворяют условию [5]
<П6|/> = </|6|/>*. F.90)
Очевидно, что а и а+ не являются эрмитовыми
операторами, а потому, согласно общим принципам квантовой
механики [4], они не могут описывать наблюдаемые
величины. Однако их свойство уничтожения или рождения
кванта энергии при действии на собственное состояние
энергии осциллятора легко понять с физической точки
зрения. Простые свойства матричных элементов'
(формулы F.88) и F.89)] операторов уничтожения и
рождения делают их более удобными для использования по
сравнению с операторами координаты и импульса, с
которыми они связаны соотношениями F.58) и F.59).
Задача 6.1. Докажите, что п-е возбужденное состояние
осциллятора можно выразить через основное
состояние согласно формуле
\п) = (п\Г h Wn\ 0>. F.91)
Задача 6.2. Выражая q и р через й и а*1*, докажите, что
(п\?\п) = ш(п + т) F-92)
и
(п \р\ п) = ha>m (n +-j). F.93)
Задача 6.3. Докажите, что
(л + 3) (я + 2) (п | (dfK йЧ* | п) =
= {п-1){п-2){п\а3(й+)*й\п). F.94)
Задача 6.4. Проверьте правильность соотношений
[й, (d+J] = 2df, [a2, Uf] = 2й F.95)
и в общем случае, когда п — целое
положительное число,
[й, {й*)п~\ = п (d+)"-1 и [йя, й+] = пйп-К F.96)
Отсюда докажите равенство
[а, ехр Fd+)] = Й ехр (|М+). F.97)
200
ГЛАВА 6
Квантование поля
Электромагнитное поле квантуется путем связывания
квантовомеханического осциллятора с каждой модой к
поля излучения. Мода, к которой относится квантовоме-
ханический оператор, обозначается индексом;
следовательно, d£ и ак — операторы рождения и уничтожения
кванта энергии йоок моды электромагнитного поля
полости с волновым вектором к. Эти кванты представляют
собой фотоны с волновым вектором к; число фотонов к,
возбужденных в полости, определяется собственным
значением мк соответствующего оператора числа частиц
nk = d£dk и может иметь значения 0, 1, 2, ... . Уровень
возбуждения моды к определяется собственным
состоянием |пк) оператора /гк. При действии на состояние
!|/гк) операторы рождения и уничтожения для моды к
подчиняются найденным выше правилам F.86) и F.87):
дк\пк) = п11>\пк-1) F.98)
и
йк|лк> = (лк + 1),/,|лк+1>- F'99)
Состояния полного поля излучения в полости можно
определить, задавая числа фотонов Як,, ^к2, пьА, ...,
возбужденных в полный набор мод полости кь к2, к3, ... •
При подсчете нормальных мод необходимо помнить,
что для каждого волнового вектора к существуют
два независимых направления вектора поляризации
моды ек. Однако удобно не вводить явное обозначение
поляризации моды, поскольку оно значительно
усложнило бы обозначения. Поэтому мы примем, что один
символ к обозначает как волновой вектор, так и
поляризацию моды. В соответствии с этим условием фраза «дай*^
ная нормальная мода к» означает, что волновой вектор
и поляризация этой моды определены.
Состояние полного поля можно записать как | Як,, Як2,
Пк3, ...), тогда при условии определенного
упорядочения мод полости, как, например, на фиг. 1.5, состояние
полного поля определяется набором чисел. Поскольку
различные моды полости независимы, то состояние пол-
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
201
ного поля можно записать в виде произведения
отдельных мод:
V "к2> *к3> • ' ') = | Пь) | "к,) | "к,) ' • • • F« 10°)
Будем всегда предполагать, что состояния отдельных
мод полости нормированы. Отсюда следует, что полное
состояние поля F.100) также будет нормировано.
Оператор, относящийся к данной моде к, действует только
на фотоны данной моды. Например,
V U ' ™U * ^1г ' • • • J *^1г > • • • /
к/ I к1 к2 К3 К/ '
= (пк. + 1У/2\пк^ \> \> •••> \ +]> •••)> F.101)
что является просто результатом применения правила
F.99) к произведению состояний F.100).
Обозначение F.100) имеет довольно сложный вид,
поэтому иногда состояние полного поля будет кратко
обозначаться следующим образом:
1К}> = КЖ>К>- • F-Ю2)
Здесь символ \{пь}) обозначает полный набор чисел,
определяющих уровни возбуждения всех 'гармонических
осцилляторов, связанных с модами полости. Разумеется,
число этих осцилляторов бесконечно. Состояния |{як})
образуют полный набор состояний электромагнитного
поля в полости, ес'ли каждый член п\. из набора {п^}
может принимать как нулевое значение, так и все целые
положительные значения.
О базисных состояниях поля сказано достаточно.
Теперь, используя формулы F.51) и F.52), классические
векторные потенциалы Ак и А£ для моды к,
выраженные через Рк и Qk, можно превратить в квантовомеха-
нические операторы, выраженные через рк и $к> с
помощью непосредственных подстановок:
Ak = De0^->kQk + /Pk)ek-*
-> (ЧМГ'А Ык + >А) \=(lijy * а А. №• юз)
- (\У<УУг (Мк - <А) h - B^к:У й1\- (е- Ю4)
202
ГЛАВА 6
На последних этапах вывода этих выражений были
использованы соотношения F.56) и F.57).
Таким образом, переход от классической к квантовой
механике заключается в замене классических
коэффициентов Фурье Ак и Ак оператором уничтожения dk и
оператором рождения dj, умноженными на численный
коэффициент и единичный вектор. Квантовомеханическое
выражение для полного векторного потенциала
получается путем подстановки выражений F.103) и F.104)
в F.46):
я=Е (i^f г* к ехр н v+* ■г)+
+ а\ ехр (ta)kt — /к • г)}. F.105)
Отметим, что теперь векторный потенциал является
оператором, поэтому обращаться с ним необходимо в
соответствии со свойствами операторов йк и й\.
Соответствующие результаты для операторов элект-
рического и магнитного полей Ек и Нк моды к
получаются с помощью сходных подстановок в формулы
F.48) и F.49):
л ( ^0к \Ч*
Ек =' уШоу) ек idk ехР (- Ч' +/к -г) -
— а\ ехр (шк* - /к ■ г)}, F.106)
йк=' Ы^/2к х 8к {К ехр (- ч<+* ■г) -
— й\ ехр (шк* — ik • г)}. FЛ07)
В результате операторы для полных поперечных
электрических и магнитных полей принимают вид
Ег = ЕЁк, F.108)
к
Н = Енк. F.109)
к
В качестве первого примера вычисления с использова-
нием операторов поля Ек и Нк рассмотрим
электромагнитную энергию моды к, находящейся в состоянии, где
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
203
возбуждено пк фотонов. Классическая формула F?47)
для энергии поля теперь запишется как
#k=4 J <«к|вДк.Ёк + ц0Нк.Нк|пк)^, F.110)
по полости
где черта снова обозначает усреднение по периоду,
которое следует провести после вычисления матричного
элемента.
Задача 6.5. Докажите, что
8оК |Ек * Ек К) = ^("к | Нк • Нк| пк) = Т\Пк + Т J
F.111)
и, следовательно, энергия моды есть
*к = (як+т)И- F-П2>
Отметим, что в действительности усреднение
по периоду не требуется, так как матричный
элемент не зависит от времени.
Результат, полученный для энергии моды, конечно,
является обычным выражением для энергии
гармонического осциллятора, как это предполагалось в выводе
формулы Планка в гл. 1. Однако теперь выражение для
энергии является следствием более последовательной
теории квантования электромагнитного поля,
выполненного на более высоком уровне, соответствующем
выражению F.105) для оператора векторного потенциала
А. Необходимо отметить, что выбранная процедура
квантования должна обеспечивать для энергии выражение
вида F.112). Иными словами, выбор численных
множителей при переходе к квантовомеханическим операторам
определяется условием, что в классической и квантовой
теориях энергия моды должна записываться так же, как
для гармонического осциллятора.
Гамильтониан полного электромагнитного поля в по-
лости Жя, состоящий из суммы членов, подобных
выражению F.63), обозначим как
**=£ к 0*&+-§-)• FЛ13)
к
204
ГЛАВА б
Тогда полная энергия излучения для состояния мод
полости |{^к)) представляет собой сумму вкладов энергии
отдельных мод F.112):
^-Е^-ЕК+т)***- (ели)
к к
Поток энергии классического электромагнитного поля
описывается вектором Пойнтинга, определенным в B.9).
Аналогичный квантовомеханический вектор Пойнтинга I
может быть определен следующим образом:
1 = £ 'к. F.115)
к
Здесь It— вектор Пойнтинга для одной моды:
Ik-EkXHk. F.116)
В случае одномодового состояния, в котором имеется nk
возбужденных фотонов, ожидаемое значение вектора
Пойнтинга легко вычисляется.
Задача 6.6. Докажите, что
(пк IК К) = тг (д + i)hk- F-117>
Поток энергии для моды к пропорционален
импульсу фотона этой моды Ьк.
Задача 6.7. Докажите коммутационное соотношение
[Жя, А] = «АЁГ. F.118)
Задача 6.8. Докажите, что запись гамильтониана поля
излучения в виде
Жн = 1 \ (е0Ё2г + ц0Н2) dV F.119)
эквивалентна выражению F.113),
Энергия нулевых колебаний
Состояние электромагнитного поля, в котором во всех
модах поля нет фотонов, т. е.
/,ь1 = лк, = лк= ••• =0, F.120)
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
20*
называется вакуумным состоянием поля. Это состояние
обладает тем интересным свойством, что, несмотря на
отсутствие фотонов, его полная энергия отлична от нуля.
Согласно формуле F.114), энергия вакуумного
состояния есть
#о = £уК- F.121)
к
Величина <^0 называется энергией нулевых колебаний
поля. Она равна сумме энергий основных состояний
гармонических осцилляторов, связанных со всеми модами
поля.
Результат A.31), полученый в гл. 1 для стоячих волн,
справедлив также для бегущих волн, рассматриваемых
в настоящей главе, поэтому суммирование в F.121)
можно с помощью преобразования A.31) заменить
интегрированием. В результате энергия нулевых колебаний
принимает вид
Jr0=$
VJial
2^da>k. F.122)
Величины разрешенных частот сок не имеют верхней
границы, поэтому интеграл F.122) быстро расходится, а
энергия нулевых колебаний соответственно не
ограничена. Смысл энергии нулевых колебаний трудно
объяснить удовлетворительным образом, а ее бесконечное
значение является слабым местом теории квантованного
электромагнитного поля.
К счастью для теории квантованного поля,
оказывается, что при выборе теоретических результатов для
сравнения с экспериментом никаких трудностей,
связанных с существованием бесконечной энергии нулевых
колебаний, не возникает. Еще не удалось разработать
экспериментов, в которых прибор регистрировал бы отклик,
пропорциональный энергии нулевых колебаний. В
реальных экспериментах отклик всегда пропорционален
некоторому изменению полной энергии
электромагнитного поля. Бесконечная энергия нулевых колебаний
составляет известную трудность квантовой теории
излучения, однако она не приводит к каким-либо
бесконечным результатам в конкретных предсказаниях теории»
206
ГЛАВА б
В подавляющем большинстве экспериментов
измеряемый отклик пропорционален энергии возбуждения поля
относительно энергии нулевых колебаний. Обозначим эту
энергию штрихом:
§' = Ш-Шь = ^£ь F.123)
к
где
#£ = Аок/1к. F.124)
Например, результат эксперимента по измерению
интенсивности светового пучка пропорционален &\ а не &.
Теория экспериментов такого типа подробно обсуждается
в гл. 9.
Существует небольшой класс экспериментов, в
которых измеряется некоторое изменение энергии самих
нулевых колебаний1). Рассмотрим замкнутую полость в
форме куба, в которой находится электромагнитное поле,
описываемое решениями в виде стоячих волн,
приведенными в A.23) и {1.24). Как указано на фиг. 1.5,
наименьшая возможная частота поля в такой полости дается
выражением
cok = _2^1. F125)
Эта частота должна быть нижним пределом в интеграле
F.122), определяющим энергию нулевых колебаний в
замкнутой полости. Таким образом, энергия нулевых
колебаний зависит от длины ребра куба L, поэтому ее
можно уменьшить, изменяя величину L. На стенки
полости действует соответственно сила, обусловленная
энергией нулевых колебаний. Сила такого типа иногда
называется дальнодействующей силой Ван-дер-Ваальса.
Она была измерена [5] для случая незамкнутой полости,
образованной парой параллельных пластинок,
расположенных на небольшом расстоянии друг от друга. Больше
эта тема обсуждаться не будет, так как объяснение
экспериментов, рассматриваемых в последующих главах, не
1) Рассмотрение различных вопросов, связанных с нулевыми
колебаниями поля, имеется в работах [7—9]. — Прим. ред.
КВАНТОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
207
зависит от энергии нулевых колебаний. Более полное
обсуждение эффектов энергии нулевых колебаний можно
найти в работе {6].
ЛИТЕРАТУРА
1. Panofsky W. К. Я., Phillips М.у Classical electricity and
magnetism, Addison-Wesley, Reading, 1955, p. 10.
2. Morse P. M.y Feshbach. Я., Methods of theoretical physics, McGraw-
Hill, New York, 1953, p. 53 (см. перевод: Ф. М. Морс, Г. Феш-
бах, Методы теоретической физики, ИЛ, 1958, т. I).
3. Brill О. L., Goodman В., Am. Journ. Phys., 35, 832 A967).
4. Dicke R. Я., Wittke J. P., Introduction to quantum mechanics, Ad-
dison-Wesley, Reading, I960, p. 92.
5. Kitchener J. A, Prosser A. P., Proc. Roy. Soc, A242, 403 A957).
6. Power E. A.y Introductory quantum electrodynamics, Longmans,
London, 1964, ch. 3.
7*. Левин М. Л.у Рытое С. М, Теория равновесных тепловых
флуктуации в электродинамике, изд-во «Наука», 1967.
S*.Boyer Т. Я., Phys. Rev., 182, 1374 A969); ID 2257 A970).
9*. Колоколов А. Л., Скроцкий Г. В., Оптика и спектроскопия, 35, 393
A973).
Глава 7
Состояния квантованного поля
излучения
Квантование поля излучения производится, как и в
предыдущей главе, путем сопоставления каждой моде
поля квантовомеханического гармонического
осциллятора. При переходе к квантованному полю естественно
работать с состояниями |nk), в которых мода полости к
содержит пк возбужденных фотонов. Состояния полного
поля |{як}), определенные в F.102), образуют удобный
полный набор для описания электромагнитного поля в
полости. Однако нет никаких оснований предполагать,
что электромагнитное поле реальных световых пучков
можно описать на основе предположения о том, что
возбуждено одно из частных состояний |{ftk}). Более общее
состояние системы включает некоторую линейную
суперпозицию базисных состояний |{як}). Было найдено, что
реальные световые пучки соответствуют таким линейным
суперпозициям. Приготовление состояния поля
излучения, в котором число фотонов в моде к равно
определенному собственному значению пк, является на практике
трудной, хотя в принципе и разрешимой
экспериментальной проблемой.
Задача настоящей главы заключается в анализе
различных возможных типов состояний поля. Между видами
световых пучков в классической и квантовомеханической
теориях можно провести некоторые параллели.
Например, в гл. 5 было показано, что имеются два совершенно
различных типа классических световых пучков. В случае
классической стационарной волны, изображенной на
фиг. 5.10, электрическому полю световой волны в каждой
состояния квантованного поля излучения 209
точке и в каждый момент времени можно было
приписать определенную величину, приведенную в E.39).
Напротив, электрическое поле светового пучка от
хаотического источника можно было бы определить, только
применяя понятие вероятности того, что поле в некоторой
точке наблюдения и в некоторый момент времени имеет
данные амплитуду и фазу.
В- квантовой механике можно установить
аналогичное различие между двумя типами световых пучков.
Поле светового пучка, в котором все фотоны
находятся в некотором определенном состоянии,
описывается линейной комбинацией состояний |{ftk}) и
называется чистым состоянием поля излучения. Однако если
можно определить лишь набор вероятностей нахождения
фотонов в нескольких состояниях, соответствующих
линейным комбинациям состояний |{/iij), то состояние
системы называется статистической смесью. Будет
показано, что классическая стационарная волна и
хаотический пучок являются классическими пределами
фотонных состояний, принадлежащих в квантовой механике
соответственно категориям чистых состояний и
статистических смесей.
Мы начинаем главу с анализа чистых состояний; для
большинства выводов достаточно рассмотрения только
одной моды поля излучения. Статистические
распределения вводятся в квантовую механику с помощью
оператора плотности, общие свойства которого кратко
рассматриваются перед его применением к статистическим
смесям поля излучения.
В дальнейшем будет видно, что квантование
обусловливает специфические квантовомеханические свойства
электромагнитного поля. Например, нельзя
рассматривать волну, амплитуда и фаза которой одновременно
точно определены. Как обычно, в квантовой механике
точность измерения ограничена соотношениями
неопределенности.
Операторы фазы фотонов
В начале главы мы ограничимся рассмотрением
отдельной моды электромагнитного поля к, имеющей
определенную поляризацию. Принимая это во внимание, ин-
210
ГЛАВА 7
деке к можно опустить у всех переменных, описывающих
данную моду, а полевые величины А, Е и Н записывать
как скаляры.
В классической теории световых волн комплексную
амплитуду волны удобно записывать в виде
произведения вещественной амплитуды на фазовый множитель,
как в формуле E.17). Если эту процедуру выполнить для
классического векторного потенциала F.46), то можно
положить
Лк = А) ехр (/ф), G.1)
поэтому вклад одной моды равен
А = А0 {ехр (— Ш + /к • г + /<р) +
+ ехр (Ш — /к • г — /ф)}. G.2)
В квантовой механике также удобно провести
разделение на амплитудный и фазовый множители аналогично
выражению G.1). Для этого в квантовомеханическое
описание поля необходимо ввести понятие фазы.
Квантовомеханйческий оператор векторного
потенциала одной моды, получаемый из F.105), имеет вид
+ d+exp(/©/ — /kT)}. G.3)
Таким образом, аналогом выражения G.1) является
разделение оператора а на произведение операторов
амплитуды и фазы. Точного способа, которым должно
производиться такое разделение в квантовой механике, в
действительности нет, и потому в определении квантовоме-
ханического оператора фазы имеется соответствующая
степень произвола. Основные соображения заключаются
в том, что в соответствующем пределе квантовомехани-
ческая фаза должна иметь то же значение, что и
классическая фаза, и должна быть связана с эрмитовыми
операторами, чтобы являться (хотя бы в принципе)
наблюдаемой величиной.
Рассмотрим оператор фазы ф, определяемый
соотношением [1]
Л = (Л+!)'''ехр (/ф), G.4)
состояния квантованного поля излучения 21!
где п — оператор числа частиц, приведенный в F.64).
Эрмитово сопряженное соотношение имеет вид
й+ = ехр(-/ф)(й+1I/2. G.5)
Определенный таким образом оператор ф будет принят
в качестве квантовомеханической фазы
электромагнитного поля, аналогичной классической фазе. Как будет
показано позже, в соответствующем пределе свойства
квантовомеханической фазы приближаются к свойствам
классической фазы.
Основные свойства оператора фазы можно
определить из известных свойств операторов рождения и
уничтожения, а также оператора числа частиц. Согласно
G.4) и G.5),
ехр(/ф) = (Я + 1Г1/2а " G.6)
и
ехр (- щ) = d+ (A + 1Г1/2. G.7)
Поскольку из F.62) и F.64) следует
йа* = п+1, G.8)
то из G.6) и G.7) получим
ехр(/ф)ехр(-/ф)=1. G.9)
Отметим, однако, что произведение с обратным
порядком экспоненциальных операторов не равно единице.
С помощью формул F.81), F.86) и F.87) можно
легко вычислить результаты действия операторов
ехр(/ф) и ехр(—*ф) на состояние \п)
ехр (/ф) | п) = (А + 1)/2 л1/* | п -• 1> =
\п— 1) для пФО,
G.10)
-
0 для п = 0,
ехр(-/ф)|/г) = а+(/г + 1)"",/2|п) = |л+1>. G.11)
Отсюда не равные нулю матричные элементы этих двух
экспоненциальных операторов даются выражениями
<л — 1 | ехр (*ф) | я) = 1 G.12)
и
(п+ 11 ехр (— /ф) J /г> = 1. G.13)
212
ГЛАВА 7
Все остальные матричные элементы обращаются в нуль.
Эти результаты сходны с матричными элементами F.88)
и F.89) операторов уничтожения и рождения, но только
выражения G.12) и G.13) не включают нормировочные
множители матричных элементов F.88) и F.89).
Приведенные выше уравнения описывают
формальные свойства операторов фазы, возникающих при
разложении операторов а и eft на операторы амплитуды
и фазы. Из G.12) и G.13) видно, что операторы exp(/q)
и ехр(—/ф) не удовлетворяют соотношению F.90), а
потому не являются эрмитовыми операторами и не
описывают наблюдаемые свойства электромагнитного поля.
Однако их можно скомбинировать для получения другой
пары операторов:
cos ф = 1 (ехр (/ф) + ехр(— /ф)} G.14)
и
sin ф = j. {ехр (*ф) — ехр(— /ф)}, G.15)
не равные нулю матричные элементы которых имеют ъид
(п — 11 cos ф | п) — (п | cos ф [ п — 1) = y G.16)
и
<я — 11sin ф |«> == — </i | sinф |л — 1> = ^. GЛ7)
Эти матричные элементы удовлетворяют соотношению
F.90), поэтому операторы cos ф и sin ф являются
эрмитовыми и будут приняты в качестве квантовомеханиче-
ских операторов, описывающих наблюдаемые свойства
фазы электромагнитного поля.
Задача 7.1. Докажите коммутационное соотношение
[cos ф, sin ф] = ^г fo* (Л + I) й - 1}. G.18)
Отсюда покажите, что все матричные
элементы этого коммутатора равны нулю, за
исключением диагонального матричного
элемента для основного состояния
<01 [cos ф, sin ф] 10) = - -57. G.19)
состояния квантованного поля излучения 213
Задача 7.2. Докажите коммутационные соотношения
[А, й] = - d G.20)
[Л, df] = d*. G.21)
Отсюда покажите, что
[А, ехр (/ф)] = — ехр (/ф), G.22)
[А, ехр (- /ф)] = ехр (- *ф) G.23)
и
[А, cosq>] = —/sinq>, G.24)
[Я, sinq>] = /cosq>. G.25)
Приведенные выше коммутационные соотношения
показывают, что операторы числа частиц и фазы не
коммутируют. Следовательно, в принципе невозможно найти
состояния поля излучения, являющиеся одновременно
собственными состояниями этих двух операторов, а
поэтому нельзя одновременно точно определить амплитуду
электромагнитной волны, связанную с /г, и фазу,
связанную с соэф или этф. Результаты измерений амплитуды
и фазы подчиняются соотношениям неопределенности,
найденным обычным путем из G.24) и G.26) [2, 3]:
ДяА cos ф ^ — | (sin ф) |, G.26)
ДяД sin ф > у | <cos ф) |. G.27)
Здесь А обозначает среднеквадратичное отклонение
следующей за А величины, полученное в серии измерений
для состояния поля, в котором операторы соэф и этф
имеют соответствующие ожидаемые значения (соэф) и
(sin ф). Некоторые примеры использования этих
соотношений неопределенности для числа фотонов и фазы
описываются ниже в этой главе.
Мы показали, таким образом, что разделение
операторов рождения и уничтожения на операторы амплитуды
и фазы {формулы G.4) и G.5)] по аналогии с
классическим результатом G.1) приводит к фазовым операторам,
не коммутирующим с оператором амплитуды.
Получающиеся в результате соотношения неопределенности
характерны для квантованного поля излучения.
214
ГЛАВА 7
Состояния с точно определенной фазой фотонов
Состояния гармонического осциллятора \п),
являющиеся одновременно собственными состояниями
энергии и оператора числа частиц /г, уже обсуждались.
Теперь мы исследуем природу состояний |ср), которые
являются собственными состояниями операторов фазы.
Для описания фазовых свойств поля излучения мы
ввели два оператора: соэф и sin ф. В обычном
представлении электромагнитной волны фаза является одной
величиной, поэтому ее квантовомеханическое описание с
помощью двух различных операторов не кажется
необходимым. Можно было бы выбрать один из операторов
фазы, а другой оператор исключить из дальнейших
вычислений. С другой стороны, эти два оператора образуют
симметричную пару, и сохранение обоих операторов не
связано с большими дополнительными трудностями.
Удивительное свойство операторов фазы заключается
в том, что они не коммутируют между собой, согласно
соотношению G.18). Отсюда следует невозможность
построения состояний, которые были бы одновременно
собственными состояниями обоих операторов соэф и этф.
Однако благодаря тому, что, как показано в G.19),
только один из бесконечного числа матричных
элементов их коммутатора отличен от нуля, оказывается
возможным построение состояний, являющихся
одновременно-собственными состояниями как соэф, так и эшф
в.некотором предельном смысле.
Рассмотрим состояние |ср), определяемое рядом
| <р) = lim (s + 1)"'/2 £ ехр (ш<р) | п). G.28)
Это состояние представляет собой линейную комбинацию
всех собственных состояний оператора числа частиц |/г),
каждое из которых взято с весом, равным фазовому
множителю ехр(тф). Нормировка и ортогональность
состояний \п) обеспечивают нормировку состояния
<Ф|Ф>=1. G.29)
Отметим, что в сумме G.28) каждое собственное
состояние энергии \п) имеет одну и ту же амплитуду E-f:l),/2t
состояния квантованного по^я излучения 215
монотонно уменьшающуюся до нуля при бесконечном
увеличении s. С помощью формул G.10), G.11) и G.14)
находим
cos<p|(p)=-i lim(s+ 1)",/2( У exp(mqp)|/2- 1)+
+ У ехр(шф)|п+ 1) ) = С08ф|ф) + т lim {s+ 1)~У2 X
Х[ехр(/5ф)|5+1)--ехр{/E+1)ф}|5>-ехр(-/ф)|0)]. G.30)
Следовательно, за счет членов, стоящих в квадратных
скобках выражения G.30), состояние |ф) не является
точным собственным состоянием оператора cos<p.
Однако в пределе s->oo эти члены стремятся к нулю и
G.30) становится уравнением для собственных значений.
Диагональный матричный элемент оператора coscp,
полученный из G.30), имеет вид
(ф | cos ф | ф) = cos ф {l — lim (s + 1)"~ } = cos ф. G.31)
S->oo
Таким же способом можно показать, что
(ф| зтф|ф) = $тф{1 — lim (s + 1)"" } = зщф. G.32)
S-»oo
Матричные элементы квадратов операторов фазы также
можно легко вычислить и получить в пределе s->oo
(ф | cos2 ф | ф) = cos2 ф, (ф | sin2 ф | ф) = sin2 ф. G.33)
Последние результаты показывают, что во многих
вычислениях состояние |ф), определенное в G.28), можно
рассматривать как собственное состояние сразу двух
операторов coscp и sin ф с наблюдаемым фазовым углом ф*
Строго математически правильнее было бы говорить не
о том, что |ф) есть точное собственное состояние
операторов фазы, а о том, что оно является состоянием, в
котором, согласно результатам G.31), G.32) и G.33),
неопределенности измеряемых значений операторов cos<p и
216 ГЛАВА 7
sin ф одновременно обращаются в нуль1). Отсутствие
точных собственных состояний, общих для операторов
cos ф и этф, является следствием того, что коммутатор
G.18) не равен нулю.
Задача 7.3. Рассмотрите интеграл перекрытия F|ф)
двух различных фазовых состояний |6) и
|ф), определенных по формуле G.28).
Докажите, что величина (8|ф) стремится
к нулю при s -> оо, если 6 ф ф.
Физические свойства одномодовых состояний
с определенным числом фотонов
Состояние с определенным числом фотонов \п) и
фазовое состояние |ф) описывают возбуждения
электромагнитного поля в одной моде оптической полости.
Определим физическую природу таких возбуждений и сравним
их с видами возбуждений, рассмотренных в классической
электромагнитной теориу.
Сначала изучим одномодовое состояние, где
возбуждено точно п фотрнов. Для такого состояния \п)
неопределенность числа фотонов равна нулю
Д/г = 0. G.34)
Используя G.14) и G.15), получим для операторов фазы
<^г | cos ф | п> = </г | sin ф | /г> = 0 G.35)
и
{у ДЛЯ П ф 0,
, G.36)
-г ДЛЯ П = 0.
Таким образом, если исключить из рассмотрения
состояние с п = 0, неопределенности фазы принимают вид
Д cos ф = A sin ф = 2~v\ G.37)
*) Строгое рассмотрение свойств различных состояний, которые
могут быть определены в связи с фазовыми операторами, см. в
работе [1],
состояния квантованного поля излучения 217
Отметим, что выражения G.34), G.35) и G.37)
согласуются с соотношениями неопределенности G.26) и
G.27).
Полученные выше результаты показывают, что с
физической точки зрения электромагнитная волна,
соответствующая состоянию \п), имеет определенную
амплитуду, однако ее фазовый угол ф, определяемый
выражениями G.35) и G.36), с равной вероятностью принимает
любое случайное значение, лежащее между 0 и 2я.
Эти свойства можно проиллюстрировать графически,
изображая распределение электрического поля,
связанного с возбужденным состоянием \п). Оператор
электрического поля для одной моды, согласно F.106), дается
выражением
Е = i (jjj?) 2 № ехР (— ш + ik ' г)"""
— af ехр (Ш — /к • г)}. G.38)
Ожидаемые значения ё и Ё2 для состояния \п)
определяются формулами
(п\Ё\п) = 0 G.39)
и
<П|^1л>=4^(п+т)« G-40)
которые согласуются с выражением F.111).
Следовательно, среднеквадратичное отклонение электрического
поля есть
**-E-Г(»+тГ- СМ.)
Графическое представление одномодового
возбуждения для состояния \п) приведено на фиг. 7.1, где
показана зависимость электрического поля в некоторой
фиксированной точке полости от времени. Поле осциллирует
как синусоидальная волна с известной частотой со.
Приведенный выше анализ показывает, что амплитуда
электромагнитной волны может быть описана величиной
218
ГЛАВА 7
Можно показать, что ее дисперсия мала при п 3> 1.
Положение волны вдоль горизонтальной оси полностью
неопределенно вследствие полной неопределенности
фазового угла. На фиг. 7.1 это обстоятельство учтено путем
изображения нескольких волн с одинаковыми
амплитудой и частотой, узлы которых сдвинуты относительно
Фиг. 7.1. Графическое описание изменения электрического поля со
временем в фиксированной точке для моды полости, возбужденной
в состояние | п ).
Более точно синусоидальные волны должны образовывать континуум в виде
горизонтальной полосы. Амплитуда £0 определена в тексте.
друг друга вдоль горизонтальной оси. В
действительности возможные горизонтальные положения волны
образуют континуум, а поле в любой момент времени может
принимать непрерывный спектр значений от —Е0 до Е0.
Любое графическое представление квантовомеханиче-
ского состояния следует рассматривать с осторожностью.
Тем не менее можно видеть, что фиг. 7.1 дает
правильное описание состояния \п) по крайней мере в
отношении передачи различных неопределенностей,
приведенных в G.34), G.37) и G.41). Кроме того, это описание
дает нулевые значения ожидаемых величин G.35) и
G.39).
Физические свойства одномодовых состояний
с определенной фазой
Теперь рассмотрим одномодовое состояние,
представляющее волну с точно определенной фазой ф. Для такого
состояния |ф), описанного выше, неопределенности зна-
состояния квантованного поля излучения 219
чений операторов фазы обращаются в нуль в пределе
5-> оо
д cos ф = Д sin ф = 0. G.43)
Однако число фотонов в моде полости теперь
неопределенно. Согласно выражению G.28), определяющему
состояния |ф) через состояния \п)9 получим
<ФIЛ|ф> = lim (s + l)_iyrt= lim\s G.44)
И
s
(ф|/г2|Ф)== lim (s+ir'Yy= lim ^2s+1> . G.45)
Следовательно, ожидаемые числа фотонов, а также их
неопределенность Дп обращаются в бесконечность. Тем
не менее отношение этой неопределенности к среднему
числу фотонов конечно:
Ап =3~Л G.46)
(ф|д|ф) v
Найдено также, что левые части соотношений
неопределенности G.26) и G.27) для состояния J ф) обращаются
в бесконечность, если предельный переход s->-oo
осуществляется после вычисления произведения
неопределенностей.
Ожидаемое значение электрического поля,
полученное с помощью выражения G.38), равно
<<р|£|ф> =
* S
= -2 (^г)'/2 sin (k-г - «D/ + Ф)Шп (s + I)"' £ (п + 1)V'.
/2=0
G.47)
При больших значениях 5 сумма расходится как s3/2 и
приводит к расходящемуся ожидаемому значению
электрического поля. Неопределенность электрического поля
также оказывается бесконечной. Однако колебания
электрического поля имеют определенную фазу, как это
ожидалось для состояния |ф).
220
ГЛАВА 7
На фиг. 7.2 приведено графическое представление од-
номодового состояния |ф). По оси ординат снова
отложено электрическое поле в некоторой фиксированной
точке внутри полости. Волна представляет собой
суперпозицию бесконечного числа волн с различными
амплитудами, соответствующими различным значениям п.
Фиг. 7.2. Графическое описание изменения электрического поля со
временем в фиксированной точке для моды полости, возбужденной
в состояние | ф >.
В результате сложения всех показанных составляющих получается
электрическое поле, ожидаемое значение которого резко меняется от + оо до — оо за
каждый полупериод.
Каждая вспомогательная волна имеет одну и ту же
частоту со и фазу ф, поэтому узлы суммарной волны
располагаются в строго определенных точках оси абсцисс.
В соответствии с G.44) и G.46) число фотонов в моде
полости полностью не определено, поэтому изображение
волны полностью размазано в вертикальном
направлении.
Фазовое состояние |ср) обладает несколько
странными свойствами. Из выражения G.44) видно, что сред-
состояния квантованного поля излучения 221
няя энергия возбуждения этого состояния должна быть
бесконечной, поэтому в реальном эксперименте
возбуждение моды полости в состояние |<р) было бы
невозможно. Основание для рассмотрения состояния |ср)
заключается в том, что оно реализует один из предельных
случаев для значений связанных неопределенностей
числа фотонов и фазы. Фиг. 7.1 и 7.2 иллюстрируют
противоположные предельные случаи в областях значений An
и Acoscp или эквивалентно A sin ср. Выбор состояния
с точным значением одного из параметров приводит к
полной неопределенности значения другого параметра.
Ситуация аналогична той, которая связана с известным
соотношением неопределенностей для координаты и
импульса в квантовой механике частиц, где собственные
состояния операторов координат и импульсов обладают
соответственно полными неопределенностями импульса
и координат частиц.
Когерентные фотонные состояния
Ни одно из одномодовых состояний \п) или |ф),
показанных на фиг. 7.1 и 7.2, не имеет сходства с
изображенной на фиг. 5.10 временной зависимостью
классической электромагнитной волны со стабильной
амплитудой и фиксированной фазой. Интересно исследовать
такие состояния квантованного поля излучения, свойства
которых в пределе больших амплитуд аналогичны
свойствам классической электромагнитной волны. Эти
состояния, обозначаемые в дальнейшем через |а), по
причинам, которые будут понятными из рассмотрения
квантовой теории когерентности в гл. 9, называются
когерентными состояниями поля излучения {4]. Когерентные
состояния"! а) важны не только потому, что из всех кван-
товомеханических состояний они наиболее близки к
классической электромагнитной волне, но также и потому,
что лазер (описанный в гл. 10), работающий при
значительном превышении порога, генерирует излучение,
находящееся в когерентном возбужденном состоянии.
Когерентное состояние
между состояниями \п) и
а) является промежуточным
ф) в том смысле, что ни
амплитуда, ни фаза этого состояния точно не определены,
222
ГЛАВА 7
однако обе эти величины имеют распределение с
наименьшим среднеквадратичным отклонением. В механике
частиц квантовым состоянием, наиболее
соответствующим классической частице, является волновой пакет,
имеющий аналогичное распределение для своих
координат и импульса.
Рассмотрим свойства состояния |а), определенного
через линейную суперпозицию собственных состояний
оператора числа частиц E]:
оо
|а>=ехр(-1|аР)Х-^|я>. G.48)
В этом выражении а может быть любым комплексным
числом, и в результате определенные таким образом
когерентные состояния образуют двойной континуум,
соответствующий непрерывным областям изменения
вещественной и мнимой частей а. Легко проверить, что
состояние |а) нормировано, т. е.
(а|а>=ехр(~[а|2)^-^===1. G.49)
п
Однако состояния для двух различных комплексных
чисел а и р не ортогональны
<«i0-«p(-1i«p-!ippJ-^-
п
= exp(-i-|a2|--i|p|2 + a*p), G.50)
т. е.
|<a|p>p = exp(-|a-p|2). G.51)
Из определения G.48) следует, что когерентных
состояний |а) намного больше, чем состояний \п). Состояния
|а) образуют переполненный набор состояний для
гармонического осциллятора, а их неортогональность
является следствием этой переполненности. Тем не менее
отметим, что, согласно G.51), состояния |а) и |р)
становятся приблизительно ортогональными, когда величина
| ос — р| много больше единицы.
состояния квантованного поля излучения 223
Когерентные состояния являются собственными
состояниями оператора уничтожения, поскольку
й|а) = ехр(-||ар)£-^«'/2|/г-1> = а|а>. G.52)
П
Следовательно, комплексное число а, обозначающее
когерентное состояние, является собственным значением
оператора уничтожения. Отметим, однако, что состояние
|а) не есть собственное состояние оператора рождения,
поскольку сумму по п, аналогичную сумме в G.52),
нельзя преобразовать таким образом, чтобы снова
получить когерентное состояние в случае а+|сс). Другой
подход к когерентному состоянию заключается в том, чтобы
уравнение для собственных значений G.52) выбрать
в качестве определения когерентного состояния. Тогда
разложение G.48) можно получить как одно из
следствий нового определения [4].
Соотношение F.91) можно использовать, чтобы
переписать определение когерентного состояния G.48)
следующим образом:
,а)=ехр(-1|ар)£-^|0> =
П
= ехр (аЗ* - у I a I2) I 0). G.53)
Задача 7 А. Докажите, что оператор рождения af не
имеет нормируемых собственных состояний.
Задача 7.5. Результат
exp{6)&Lp(d)==exv(e + d+±[69d]) G.54)
можно доказать [5] для любой пары
операторов с иЙ, коммутирующих со своим
коммутатором
1М*. <*]] = tf. [*,<*]] = 0. G.55)
Используя G.54), запишите уравнение G.53)
в более компактной форме:
| а) = ехр (ай* — ай) 10>. G.56)
224 ГЛАВА 7
В G.56) экспоненциальный оператор
эквивалентен оператору рождения когерентного
состояния.
Величину а иногда удобно выразить через амплитуду
и фазу. В качестве обозначения фазового угла (arga)
мы выберем 9 и запишем
a = \a\eiQ. G.57)
Физические свойства
одномодовых когерентных состояний
Свойства моды полости, возбужденной в когерентное
состояние |а), можно определить методами,
применявшимися в этой главе раньше для анализа состояний с
определенным числом фотонов \п) и состояний с
определенной фазой |ф). Ожидаемые значения оператора числа
частиц имеют вид
<a|n|a> = exp(-|a|2)£i^rt = |a|2, G.58)
П
<о| й2 |а> = ехр(-| а |2)£ -^^ =
П
= exp(-|a|2JJ^r-{»(«-l) + "} = !a|4 + [a|2) G.59)
отсюда среднеквадратичное отклонение
Дп = | a [, G.60)
и относительная неопределенность числа фотонов в моде
полости есть
Ап =|аГ!. G.61)
<о|Л|о>
Эти результаты показывают, что |а|2 есть среднее
число фотонов в моде полости, а среднеквадратичное
отклонение от этого среднего значения равно корню
квадратному из среднего числа фотонов. Относительная
неопределенность числа фотонов, приведенная в G.61),
обратно пропорциональна корню квадратному из среднего
состояния квантованного поля излучения 225
числа фотонов и уменьшается с ростом степени
возбуждения моды полости. Последний результат можно
сравнить с нулевой неопределенностью числа фотонов
[формула G.34)] для состояния \п) и постоянной
относительной неопределенностью [формула G.46)] для состояния
|ф>-
Из определения G.48) следует, что вероятность
нахождения п фотонов в моде дается выражением
|(/2|а)|2 = ехр(-|ар)^, G.62)
которое представляет собой пуассоновское
распределение вероятностей (см. [6] и фиг. 9.4) около среднего
значения |а|2; среднеквадратичное отклонение от этого
распределения дается обычной формулой G.60).
В случае когерентных состояний ожидаемые значения
фазовых операторов описываются довольно сложными
выражениями [7]. Мы ограничимся оператором coscp, для
которого, используя формулы G.12), G.13), G.48) и
G.57), получим
<а|С08ф|а> = 4ехр(-|ар)У-^ <*+<*<* д
п
На1созеехр(-|ар)У ,'"f* . G.63)
*—' п\ (п + 1)/2
п
Таким образом, ожидаемое значение оператора cos ф
пропорционально косинусу фазы величины а. Аналогично
<а| соз2ф | а) = у - техр (-1 а |2) +
+ | а |2 (cos2 в - -J") ехр (-1 а |2) У ]-^ т. G.64)
п
К сожалению, аналитическое вычисление сумм в
G.36) и G.64) невозможно. Однако эти суммы немного
упрощаются, когда среднее число фотонов в моде много
больше единицы. Тогда можно использовать следующие
8 Зак. 885
226 ГЛАВА 7
асимптотические разложения [7], приводимые здесь без
доказательства:
у [а]2* _ехрAа[2)/1 1_ , \
Ln\{n + \jl*~ |а| V 8|ap"t"'eV'
|а|2>1,
G.65)
Лп
El а Г ^
пЦ(л + 1)(^ + 2)},/2
=^w!!IA-w----)- ia'2»L <7-66)
Таким образом, для больших чисел фотонов ожидаемые
значения фазы принимают вид
<а | cos ф | а> = cos G A — -gj^p" + •••)' *а|2>1> G'67>
<а| cos2 ф 1 а) = cos2 8 - cos^ в~342 -..., а2>1, G.68)
и, следовательно, неопределенность фазы есть
Асо5ф = -||^_, |аР>1. G.69)
Из G.60) и G.69) следует, что произведение
Неопределенностей описывается выражением
ДМ cos ф = j sin 6, | a |2 > 1. G.70)
Можно получить результат, аналогичный формуле G.67),
который показывает, что ожидаемое значение оператора
sin ф равно sin 9 при большой величине |а|2. Таким
образом, для большого среднего числа фотонов
когерентное состояние |а) имеет минимальное произведение
неопределенностей, допускаемое соотношением G.26). Из
выражений G.61) и G.69) видно, что относительные
неопределенности числа фотонов и фазы изменяются как
|а|-1, а потому с увеличением среднего числа фотонов
соответственно увеличивается точность определения
амплитуды и фазы волны.
состояния квантованного поля излучения 227
Эти свойства можно увидеть более отчетливо,
вычисляя ожидаемое значение электрического поля в
когерентном состоянии. С помощью определения G.38) получаем
<а|£|а> =
~~ ' ( 2 °V ) 2 ^ еХР ^~~" *Ф* ~^~ ^ ' Г) ~ а* ехР У®* "" * # Г)} ==s
= -2 (^г),/2| а | sin (k • г - at + В). G.71)
Здесь мы использовали соотношение
(а | df | а) = а*.
Аналогично
(а | В | а> = (-|^г) {41 а Р sin2 (к . г - ©* + в) + 1}, G.73)
и, следовательно, среднеквадратичное отклонение
электрического поля есть
Отметим, что в отличие от результатов двух предыдущих
разделов, где были использованы приближения,
справедливые для волн с большой амплитудой, результаты
данного параграфа применимы независимо от амплитуды
волны.
Временная зависимость электрического поля в
фиксированной точке полости показана на фиг. 7.3 для трех
когерентных состояний |а), имеющих один и тот же
фазовый угол, но три разных значения среднего числа
фотонов. Поскольку неопределенность Д£, приведенная в
G.74), не зависит от амплитуды волны, то точность
определения волн улучшается с увеличением |а|2. Из фиг. 7.3
видно, что по мере увеличения среднего числа фотонов
в когерентном состоянии изменение электрического поля
становится все более похожим на изменение
классической волны (ср. фиг. 5.10).
Можно показать, что когерентное состояние |а)
является лишь одним из видов квантовомеханического
состояния электромагнитного поля, которое можно
прямо связать с классической электромагнитной
G.72)
8*
228
ГЛАВА 7
волной (подробное обсуждение этого соответствия см. в
работе [8]). Конечно, когерентное состояние проявляет
характернее свойства квантовомеханической
неопределенности, рассмотренные выше. Однако все эти эффекты
Фиг. 7.3. Графическое описание изменения электрического поля со
временем в фиксированной точке для моды полости, возбужденной
в состояние | а ).
Изменения поля приведены для трех различных значений среднего числа
фотонов 1 а |2, причем во всех этих случаях используется различный вертикальный
масштаб. Неопределенности значении поля указаны вертикальными ширинами
2АЕ синусоидальных волн. Эти неопределенности можно также рассматривать
как обусловленные неопределенностью амплитуды, связанной с An, и
неопределенностью фазы, связанной с Д cos Ф.
становятся практически несущественными в
классическом пределе, когда величина |а|2 много больше
единицы. Другие виды возбуждений в полости, например
состояния с определенным числом фотонов \п)% не
стремятся к классическому пределу, когда число фотонов
много больше единицы.
Изменение классического электрического поля,
полученное из выражения для векторного потенциала А
G.2), имеет вид
Е = — 2©А0 sin (k • г — со/ + ф). G.75)
Из сравнения G.75) с G.71) видно, что в классическом
пределе когерентное состояние |а) соответствует клас-
состояния квантованного поля излучения 229
сической волне, фаза которой равна фазе величины a, a
амплитуда электрического поля связана с
^соотношением
-2соЛа = -2A^г)'/2|а|. G.76)
Из квантовомеханического рассмотрения процессов
детектирования световых пучков в гл. 9 будет видно, что,
несмотря на очевидную неопределенность различных
наблюдаемых характеристик когерентного состояния, это
состояние полностью когерентно.
Оператор плотности
До сих пор все вычисления в этой главе были
связаны с чистыми состояниями поля излучения для одной
моды оптической полости, иначе говоря, с состояниями,
которые можно выразить в виде некоторой определенной
линейной комбинации базисных состояний с
определенным числом фотонов \п). Не представляет труда
обобщить чистые состояния на случай полного поля
излучения в полости, когда это состояние полного
электромагнитного поля образуется обычным образом с помощью
произведения состояний отдельных мод. В результате
любое вычисление для многомодового поля сводится к
серии вычислений для отдельных одномодовых полей.
Более радикальное обобщение описанной выше
теории требуется для анализа статистически смешанных
состояний поля излучения, когда нет точного определения
состояния поля, а имеются только вероятности
наблюдения поля в области возможных состояний. Эти
статистически смешанные состояния удобно рассмотреть до
обсуждения многомодовых состояний поля. Чистое
состояние представляет собой частный случай статистической
смеси, поэтому оба состояния можно анализировать в
рамках общей теоретической схемы.
Рассмотрим некоторое электромагнитное поле
полости, для которого известна вероятность PRy того, что поле
находится в состоянии \R). Здесь R— индекс,
пробегающий набор чистых состояний, достаточный для описания
поля. В случае одной моды полости состояния \R) могли
230 ГЛАВА 7
бы быть состояниями с определенным числом фотонов
|п), фазовыми состояниями |ф), когерентными
состояниями |а) или некоторыми другими чистыми
состояниями. В случае полного поля полости состояния \R) были
бы всеми возможными произведениями одномодовых
состояний, причем в каждое базисное состояние \R)
входило бы по одному состоянию для каждой моды полости.
Состояния, приведенные в F.102), образуют возможный
набор состояний \R), построенный на основе
одномодовых состояний с определенным числом фотонов.
Состояние, описываемое вероятностью PRl является
статистической смесью; величины Рп для данного набора чистых
состояний \R) содержат всю имеющуюся информацию
об этом состоянии.
Хаотический световой пучок служит примером поля,
которое в квантовой механике должно рассматриваться
как статистическая смесь. Из классического анализа,
приведенного в гл. 5, ясно, что природа хаотического
светового источника исключает возможность какого-либо
точного предсказания состояния поля излученного света.
Вероятностное описание — единственно возможное как в
классической, так и квантовомеханической теории
хаотического света.
Другим примером статистической смеси служит
тепловое возбуждение фотонов в моде полости, описанное
в процессе вывода формулы Планка в гл. 1. Наиболее
подробным описанием, которое можно дать в этом
случае, является описание на основе вероятности
возбуждения Рп п фотонов при температуре Г, определенное в
A.42). Распределение Рп является примером общего
распределения PR, введенного выше.
В общем случае результат эксперимента, который
можно провести со световым пучком, зависит от среднего
по ансамблю значения некоторой наблюдаемой
величины. Например, для определения флуктуации числа
фотонов, полученного в A.71), требуется знать среднее по
ансамблю значение п2, а для нахождения интенсивности
интерференционных полос, описанной в E.44),требуется
вычисление среднего по ансамблю значения
произведения электрических полей. Рассмотрим некоторую
'наблюдаемую величину О, определяемую квантовомехани-
состояния квантованного поля излучения 231
f
ческим оператором б. Для чистого состояния- \R)
среднее значение наблюдаемой величины равно (/?|E|7?),
поэтому для статистической смеси, описываемой
распределением вероятностей Рд, среднее по ансамблю
значение наблюдаемой величины дается выражением
@) = ZPr(R\0\R). G.77)
R
Будем предполагать, что Pr — нормированное
распределение вероятностей
2>*=1. G.78)
R
Формула G.77) является основным выражением,
позволяющим делать полезные предсказания для известных
статистических смесей поля излучения. Однако
выражение G.77) удобно записать в другой форме, с которой
обычно легче работать и которая приводит к более
изящным выражениям для средних значений по ансамблю.
Пусть \S) описывает полный набор состояний
рассматриваемого поля, a S есть индекс, принимающий ряд
значений. Тогда, согласно условию полноты D.100),
Z|5)<S|=1. G.79)
Подставляя эту единичную величину в выражение G.77)
сразу после оператора E, получим
<o> = Z^Z<fl|6is><sii?> = ZZMs.ltf><*|6|s>.
R S R S
G.80)
Оператор плотности р определяется выражением
(9, 10]
P=ZPr\R)(RI G.81)
Поэтому среднее значение О, приведенное в G.80),
может быть записано в виде
<0> = Z<S|p6|S>. G.82)
Оператор плотности содержит точно такую же
информацию, как и распределение вероятностей Рд, и является
232
ГЛАВА 7
определенным в том случае, если распределение PR
задано для данного набора чистых состояний \R).
Преимущество оператора плотности заключается в простоте
получения с его помощью средних значений различных
наблюдаемых величин.
Общий результат G.82) не зависит от частного
полного набора состояний |5), выбранного для вычисления.
Это очевидно из способа введения состояний ]5), а
также может быть прямо доказано. Пусть | Т) — некоторый
другой полный набор состояний поля излучения. Дважды
применяя условие полноты и подставляя единичную
величину G.79) до и после оператора р<5 в G.82), получим
<0> = Z I £ (SI Т) (Т | рб | Г) <Г | S). G.83)
. S Т Т'
Здесь индексы Г и Г7 пробегают по одному и тому же
полному набору состояний. Если предположить, что
состояния \Т) ортонормированы, то преобразование выра-,
жения G.83) с использованием G.79) дает
(О) = £ £ £ <г \S)(s\t)(t\ 01 Г)='£(п рб |г>.
S Т Т' Т
G.84)
Поскольку (О) не зависит от конкретного полного
набора состояний, используемого для вычисления
среднего значения, то уравнение G.84) можно переписать
следующим образом:
<0>=Sp(p6). G.85)
Здесь след (шпур) оператора представляет собой сумму
диагональных матричных элементов оператора для
любого полного набора состояний. Этот результат
полностью эквивалентен основному выражению G.77).
Распределение вероятностей Pr содержит физическую
информацию о поле излучения, необходимую для
вычисления средних по ансамблю. Важно правильно выбрать
конкретный полный набор чистых состояний \R)y
который будет использоваться в определении распределения
вероятностей. Этот выбор должен быть сделан таким
образом, чтобы сохранить всю имеющуюся информацию о
состоянии системы. Приведенные рассуждения можно
состояния квантованного поля излучения 233
.лучше всего понять на основе конкретных примеров,
приведенных ниже в этой главе.
Необходимо отметить, что сами матричные элементы
оператора р имеют различные свойства для разных
полных наборов состояний. Для набора \R)9 используемого
для построения р, отличны от нуля только диагональные
матричные элементы
(Rf I Р I Я"> = I PR (R' \R)(R\ R") = PvbR'ir. G.86)
R
Однако типичный матричный элемент некоторого
другого полного набора состояний имеет вид
(T\p\r) = ZPR(T\R)(R\T'), G.87)
R
и нет никаких общих условий, накладываемых на
состояния | Г) и | Т'), для которых правая часть выражения
G.87) отлична от нуля. Единственный общий результат
дается выражением
spp = Z<:np|:r> = lP* = i, G.88)
Т R
которое можно рассматривать как частный случай
выражения G.85), где оператор б есть просто число. Для
любого состояния поля излучения всегда существует
некоторый полный набор состояний \R), для которого
оператор плотности имеет только диагональные матричные
элементы, как в G.86).
Операторы плотности для чистых состояний
Чистое состояние можно рассматривать как частный
случай статистической смеси, когда одна из вероятностей
PR равна единице, а все остальные значения PR равны
нулю. В этом случае, согласно G.81), оператор
плотности имеет вид
Р = |Л><Я1 G.89)
и поле излучения с определенностью находится в данном
чистом состоянии \R). Поэтому статистическое описание
становится излишним. Тем не менее понятие оператора
плотности остается справедливым и для чистого состоя-
234
ГЛАВА 7
ния. Некоторые более простые свойства оператора
плотности удобно проиллюстрировать на примере чистого
состояния. Один результат, справедливый только для
оператора плотности чистого состояния,
Р2=Р, G.90)
нетрудно доказать, используя G.89).
Легко построить операторы плотности для различных
видов одномодовых чистых состояний, рассмотренных
раньше в этой главе. Оператор плотности для ноля в
одном из состояний \п)у в котором имеется точно п
фотонов, запишется просто как
0 = \п){п\. G.91)
Единственный отличный от нуля матричный элемент для
состояния с определенным числом фотонов имеет вид
<м|р|п>=1. G.92)
Отсюда среднее значение наблюдаемой, описываемой
оператором E, в соответствии с G.85) дается
выражением
(О) = Sp (| п) (п | б) = (п | О | я), G.93)
где для вычисления следа используется полный набор
состояний с определенным числом фотонов. Выражение
в правой части уравнения G.93) точно такое же, какое
обычно используется для вычисления среднего значения
для состояния \п). В частном случае чистого состояния
формализм оператора плотности приводит ко всем
обычным результатам.
Аналогичным образом можно построить оператор
плотности для одного из состояний с определенной
фазой |ф) или для одного из когерентных состояний |а):
Р = |ф>Ы " G.94)
р = |а)(а|. G.95)
Рассмотрим подробнее оператор плотности для
когерентного состояния, представляющий больший физический
интерес.
состояния квантованного поля излучения 235
Из нормировки когерентных состояний в G.49)
следует, что оператор плотности G.95) удовлетворяет
соотношению
<сг|р|а>=1, G.96)
которое аналогично соответствующему результату G.92)
для случая состояний с определенным числом фотонов.
Однако из неортогональности различных когерентных
состояний, описываемой выражением G.50), следует, что
(а|р|а) не является единственным отличным от нуля
матричным элементом оператора плотности р,
определенного в G.95). Действительно, каждый матричный
элемент оператора р для когерентного состояния отличен от
нуля. Эта особенность обусловлена упомянутой выше
переполненностью состояний |а). Чтобы использовать
некоторые положения обычной теории оператора
плотности в случае когерентных состояний, их необходимо
осторожно и продуманно расширить [И], а некоторые
связанные теоремы — обобщить. Для проводимых ниже
вычислений не потребуется таких обобщений, поскольку в них
используются в основном операторы плотности,
выраженные через состояния с определенным числом фотонов
\п).
Теперь рассмотрим общий матричный элемент
оператора плотности чистого когерентного состояния G.95)
для состояний с определенным числом фотонов.
Используя G.48), получим
(«|р|п') = ехр(-|а|2)-^^. G.97)
(п\п I)'2
Таким образом, оператор плотности чистого когерентного
состояния имеет отличные от нуля недиагональные
матричные элементы для состояний с определенным числом
фотонов. Этот пример показывает важность выбора для
выражения оператора плотности таких соответствующих
состояний \R), чтобы не было потеряно никакой
информации о состоянии системы. Полностью описать чистое
когерентное состояние |а) с помощью диагонального
оператора плотности, построенного на состояниях с
определенным числом фотонов \п), невозможно, так как
такой оператор плотности имел бы нулевые недиагональ-
236
ГЛАВА 7
ные матричные элементы (n|p|/i') и информацию,
содержащуюся в выражении G.97) для п Ф п\ нельзя было
бы получить.
Недиагональные матричные элементы оператора
плотности особенно важны при вычислении средних
значений операторов б, имеющих отличные от нуля
недиагональные матричные элементы (п|0|м'). Рассмотрим,
например, одногуюдовый оператор электрического поля,
приведенный в G.38). Среднее электрическое поле,
найденное с помощью формулы G.85), где след вычисляется
на основе состояний с определенным числом фотонов,
дается выражением
<£> = £<«|р£|гс> =
П
:==i (le^r) 2 Z ^пI Р 'п ~~ ^пУ*ехр(~~ Ш + /к ' г^ ~~
п
- {п | р | п + 1) {п + 1)Уг ехр {Ш - /к • г)}. G.98)
Если в первом члене, стоящем в фигурных скобках,
заменить п на п+ 1, то
<£)=-2A^г)'/22](п + 1),/Чт{<п+1|р|п)Х
П
X ехр (- Ш + & • г)}. G.99)
Очевидно, что состояние поля излучения может иметь
отличный от нуля средний вектор электрического поля
только тогда, когда оператор плотности имеет отличные
от нуля недиагональные матричные элементы вида
(я+1|р|я). Для чистого когерентного состояния |а) из
формул G.57) и G.97) следует, что
(n+llpU) = exp(-|al2 + /9) 'q|2"+1l.l/l - G.100)
п\ (п + 1)/2
Подстановка последнего выражения в G.99) приводит к
точно такому же результату, который был получен
предварительно в G.71).
Диагональный матричный элемент оператора
плотности для состояний с определенным числом фотонов
(п\р\п) дает вероятность того, что в состоянии поля,
состояния квантованного поля излучения 237
описываемом оператором р, находится п фотонов.
Диагональный матричный элемент оператора плотности
чистого когерентного состояния, полученный из G.97),
воспроизводит результат G.62), найденный ранее для
вероятностного распределения по состояниям с
определенным числом фотонов.
Чистые состояния полного полд излучения
рассматриваются таким же образом. Теперь состояние \R) в G.89)
описывает все моды полости. Если, например, каждая
мода полости имеет определенное число возбужденных
фотонов, то \R) является одним из состояний |{nk}),
определенных в F.102), а оператор плотности есть
Р = I К}) (К) I = I "к,) I "*,) | "кз) • • ' К | ("к, | ("к, |-
G.101)
В качестве другого примера можно было бы взять
состояние поля, в котором каждая мода полости находится
в определенном когерентном состоянии, В этом случае
состояние полного поля можно записать в виде
| К}> = I «kl>| «kj> |%>--- G-102)
а соответствующий оператор плотности для многомодо-
вого когерентного состояния — в виде
р = 1Ы)<Ы1- G-юз)
Другие чистые состояния полного поля описываются
аналогично. В любом случае матричный элемент оператора
р записывается как произведение матричных элементов,
каждый из которых относится к отдельной моде полости,
поэтому переход от одномодового случая к многомодово-
му не приводит к появлению новых физических свойств.
Статистически смешанные состояния поля излучения
Важная практическая роль оператора плотности
становится очевидной при его применении к анализу
статистически смешанных состояний. В качестве первого
примера рассмотрим тепловое возбуждение фотонов в одну
моду полости, поддерживаемой при температуре Т, Эта
238
ГЛАВА 7
задача рассматривалась в гл. 1 при выводе формулы
Планка. Вероятность Рп возбуждения п фотонов
приведена в A.42). Тогда, согласно определению G.81),
оператор плотности, построенный на основе состояний с
определенным числом фотонов, дается выражением
Р = 2 Рп \п) (п I = (!— ехР (— Рйс°)} Z ехр (— р/гйсо) | п) (п |,
п п
G.104)
где
P^-tV' GЛ05>
В этом случае состояния \п)- являются правильным
базисом для оператора плотности, поскольку тепловое
распределение дает информацию только о вероятностях
нахождения системы в ее различных собственных
состояниях энергии, а состояния с определенным числом
фотонов являются собственными состояниями энергии
фотонной системы.
Выраженный через состояния с определенным числом
фотонов оператор плотности для теплового
распределения фотонов имеет только диагональные матричные
элементы. Поэтому, согласно выражению G.99), которое
справедливо как для чистых состояний, так и для
статистических смесей, среднее электрическое поле всегда
равно нулю. Если ввести среднее число возбужденных
тепловых фотонов п, то оператор плотности можно
записать в другой форме.
Согласно определению G.85),
n = (n) = Sp(pu+u). G.106)
Задача 7.6. Используя для вычисления среднего числа
фотонов п формулы G.104) и G.106),
покажите, что оператор плотности можно
выразить следующим образом;
p=£A+*wV'|n)<nl- <7Ло7>
п '
Отметим, что алгебра этого вычисления
аналогична преобразованию, проведенному
в A.44),
состояния квантованного поля излучения 239
Задача 7.7. Покажите, что оператор плотности для одно-
модового теплового излучения G.104) может
быть записан в следующей эквивалентной
форме:
р = {1 — ехр(— рй©)}ехр(— $ПъйЧ). G.108)
Здесь экспонента определяется ее
обычным разложением в степенной ряд.
Рассмотрим теперь тепловое возбуждение всех мод
полости. Состояния |{^к}) Для всей совокупности мод
образуются из произведений состояний с определенным
числом фотонов для отдельных мод полости таким же
образом, как в F.102). Поскольку различные моды поля
независимы, полный оператор плотности является
произведением вкладов различных мод. Следовательно,
оператор плотности, общий вид которого дается выражением
Р = 1,}Ры\{пк})({пк}\, G.109)
>
в случае теплового излучения определяется путем пере-
1 1 /- \nk//i i - \^ + пк
множения коэффициентов (Пк) /A+Як) Для всех
мод, с тем чтобы получить полную вероятность
V> = n7rrjW GЛ,0)
к 0 + /2к)
I
В этих выражениях Як есть среднее число фотонов,
возбужденных в моду к, а символы {/гк} обозначают набор
чисел Як,, ftk2, Як3, ... и т. д. фотонов, возбужденных
в каждую моду полости. Суммирование в G.109)
производится по каждому возможному набору чисел {/гк}.
Следовательно, оператор плотности для поля
теплового излучения в полости, полученный из G.109) и
G.110), имеет вид
/- \^к
p = IlKM*Jin-^W GЛП)
{пк} к V + пк)
240
ГЛАВА 7
Задача 7.8. Для' оператора плотности, приведенного в
G.111), непосредственно докажите
выполнение условия нормировки
Spp = l G.112)
и покажите, что среднее число фотонов в
полости есть
п = 2 ^.. G.113)
к
Средние числа фотонов Як в выражении G.111)
связаны с частотой моды сок и температурой Т
соотношением A.45)
йк = {ехр (рЙок) - I}. G.114)
При использовании для пк формулы G.114) оператор
плотности G.111) в основном содержит ту же
информацию, что и результаты расчетов на основе распределения
вероятностей для теплового излучения, использованного
при выводе формулы Планка. Однако выражение G.111)
применимо не только к тепловому распределению
фотонов, но также к широкому классу возбуждений, в
котором статистические свойства излучения света имеют
соответствующий случайный характер. Например, в гл. 10
показывается, что оператор плотности для света,
излучаемого источником, атомы которого поддерживаются на
более высоком уровне возбуждения по сравнению с
уровнем при тепловом равновесии, имеет точно такой же вид,
как в случае теплового излучения. Из этого не следует,
что спектральное распределение излучения такое же, как
в случае теплового равновесия, и средние числа
фотонов Як, конечно, не даются формулой G.114), а
определяются природой возбуждения случайного поля.
В частности, оператор плотности G.111) относится к
световому пучку, излучаемому хаотическим источником,
и определяет способ, при помощи которого классическому
рассмотрению хаотического света, описанному в гл. 5,
можно придать квантовомеханическую форму. Например,
оператор р в G.111) является правильным оператором
плотности для пучка с лоренцевым частотным
распределением, излучаемого хаотическим источником, если пред-
состояния квантованного поля излучения 241
положить, что величина якозк имеет лоренцеву
зависимость ОТ (Ок-
Задача 7.9. Покажите, что выражение E.64) можно
преобразовать таким образом, чтобы оно
определяло среднее число фотонов
nk = мк (со0 - cok)* + y2 ' GЛ15)
возбужденных в моды квантованного поля
излучения пучком с лоренцевым частотным
распределением и площадью поперечного
сечения а. Этот результат используется в гл. 9
для вычисления квантовомеханической
когерентности пучка с лоренцевым частотным
распределением.
Из приведенных выше замечаний следует, что
оператор плотности для полного поля излучения G.111) имеет
широкую применимость в случае хаотического света.
Операторы плотности для полного поля можно, конечно,
построить на базисе других полных наборов состояний
мод полости или на базе переполненного набора
состояний |{ак}), определенных в G.102). Однако физические
проблемы, которые будут обсуждаться в последующих
главах, включают либо многомодовый хаотический свет,
для описания которого подходит выражение G.1 И),
либо одномодовые возбуждения, для которых оператор
плотности упрощается. Поэтому мы не рассматриваем
другие возможные виды операторов плотности для
полного поля.
Для случайного возбуждения фотонов такого же типа,
как хаотический свет, одномодовый^оператор плотности
G.107) не дает никакой информации о временном
масштабе флуктуации числа фотонов. Квантовомеханиче-
ские средние, которые можно найти с помощью
оператора плотности, аналогичны средним по классическому
ансамблю, описанным в гл. 5, причем на тип
эксперимента, который должен быть проведен для сравнения
с теоретическими предсказаниями, накладываются такие
же условия, как и при классическом описании поля. В об-
242
ГЛАВА 7
щем случае экспериментальные средние должны
вычисляться из серии экспериментов, длительность которой
велика по сравнению с временем флуктуации, однако
каждое отдельное измерение должно быть проведено в
течение промежутка времени, короткого по сравнению с
периодом флуктуации.
Классическое описание зависимости частотного
спектра возбуждения нормальных мод от длины полости с
помощью лоренцевой функции, приведенной в связи с
фиг. 5.12, остается справедливым для квантованного
поля, но с некоторыми очевидными изменениями
терминологии. Выводы относительно величины времени
флуктуации в одной моде для полостей, длины которых
больше или меньше длины когерентности, по-прежнему
остаются справедливыми. В частности, для длинной в
смысле определения E.56) полости, где возбуждено
много нормальных мод, скорость флуктуации в каждой
моде определяется разностью частот соседних мод Доз,
введенной в E.51). В этом случае многомодовыи
оператор плотности, определяемый выражением G.111), куда
подставлены значения nk из G.115), зависит от y и,
следовательно, содержит информацию о времени
когерентности Тс(= 1/y) пучка в целом.
Резюмируя, можно сказать, что, хотя оператор
плотности для каждой отдельной моды полости не дает
информации о временной зависимости возбуждения моды,
многомодовыи оператор плотности для пучка, частотные
компоненты которого распределены по многим модам,
все же содержит величину времени когерентности пучка.
Как в классической, так и в квантовой теории световой
пучок можно полностью описать с помощью
распределения интенсивности поля или чисел фотонов только в том
случае, если нормальные моды расположены плотно по
отношению к распределению частотных компонент
светового пучка.
Задача 7.10, Рассмотрите квантовомеханические аналоги
классических возбуждений в виде пары мод
полости, описанных в задачах 5.6 и 5.7.
Пусть индексы 1 и 2 обозначают состояния
двух мод. Покажите, что возбуждение, наи-
СОСТОЯНИЯ КВАНТОВАННОГО ПОЛЯ ИЗЛУЧЕНИЯ 243
более близкое к описываемому
классическим выражением F.81), представляет
собой чистое состояние с оператором
плотности
р = |а1>|а2><а2|<а11. G.116)
Выведите соотношение между ось «2 и
классическими полями Е\ и £2, при котором
квантовое поле имеет своим классическим
пределом выражение E.81).
Покажите, что для случайного возбуждения
мод, описанного в задаче 5.7, квантовоме-
ханический оператор плотности имеет вид
оо с»
Ш=0 п2=0 ,0 \ -Г )
G.117)
Здесь п — среднее число фотонов в каждой
моде и предполагалось, что выражение
G.111) справедливо для любого случайного
возбуждения.
' ЛИТЕРАТУРА
1. Susskind JL, Glogower /., Physics, 1, 49 A964).
2 Ландау Л. Д., Лифшиц Е. М.у Квантовая механика, Физматгиз,
1965.
3. Louisell W. Я„ Phys. Lett., 7, 60 A963).
4. Glauber R. /., Phys. Rev., 131, 2766 A963).
5. Messiah A., Quantum mechanics, vol. 1, North-Holland Pub. Co.,
Amsterdam, 1964, p. 442.
6. Kittel C, Thermal physics, Wiley, New York, 1969, Appendix G,
p. 395.
7. Carruthers P., Nieto M. Af., Phys. Rev. Lett., 14, 387 A965).
8. Vinson J. F., Coherence optique, classique et quantique, Dunod,
Paris, 1969, PL 2, Ch. 1.
9. Ziman J. M.y Elements of advanced quantum theory, University
Press, Cambridge, 1969, p. 94.
10. Louisell W. #., Radiation and noise in quantum electronics,
McGraw-Hill, New York, 1964, Ch. 6. (См. перевод: У. Люиселл,
Излучение и шумы в квантовой электронике, изд-во «Наука»,
1972.)
11, Glauber R, /., Quantum optics (ed. by Kay S. M. and Maitland A.)
Academic Press, London, 1970, p. 53,
Глава 8
Взаимодействие поля излучения
с атомом
В гл. 7 были рассмотрены свойства только свободного
поля излучения, т. е. поля в пространстве, свободном от
частиц, взаимодействующих с излучением. В то же
время все эксперименты по генерации и измерению световых
пучков включают взаимодействие электромагнитных
волн с атомами, и настоящая глава посвящена изучению
теории этих взаимодействий.
Классический гамильтониан
для взаимодействующих полей и зарядов
Как и в случае свободного поля излучения,
рассмотрение удобно начать с классической теории.
Последующий переход к квантовой механике может быть выполнен
обычным образом — путем замены классического
гамильтониана квантовомеханическим гамильтонианом.
Согласно формулам F.13) и F.23), уравнения
электромагнитного поля в кулоновскои калибровке имеют вид
-У2ф = (т/е0 (8.1)
и
-У2А + ^гА = Мг. (8.2)
Здесь точки обозначают дифференцирование по времени.
Электрическое и магнитное поля определяются из
выражений F.28), F.21) и F.1):
Ег = — А, (8.3)
EL = -Vq>, (8.4)
Mf^VXA, (8.5)
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 245
а условие кулоновской калибровки имеет вид
V-A = 0. (8.6)
Теория свободного поля, описанная в гл. 7 и в последнем
разделе гл. 6, основана на решении уравнения (8.2) для
нулевого поперечного тока Jr. Теперь мы должны решить
задачу, определяемую приведенными выше уравнениями
для отличных от нуля плотностей заряда а и тока J.
Мы выполняем обычный переход от классической
механики к квантовой, при котором на промежуточных
этапах классические уравнения движения (8.1) и (8.2)
записываются сначала в лагранжевой форме, а затем в га-
мильтоновой. Подробные вычисления отнимут довольно
много времени, поэтому здесь мы приведем лишь
схематический вывод, достаточный для того, чтобы указать
основные преобразования, выполняемые в классической
механике, однако без некоторых основных доказательств
О, 2].
Будем считать, что плотности зарядов и токов
обусловлены электронами и ядрами некоторого модельного
атома типа показанного на фиг. 3.1. Считается, что масса
ядер достаточно велика, для того чтобы они в основном
покоились в начале координат. Если вектор г,- описывает
положение /-го электрона' и Z есть полное число
электронов, то плотности заряда и тока могут быть записаны
следующим образом:
ст = — Z еб (г - г/) + Zed @), (8.7)
J = - Е ei-,6 (r - rj). (8.8)
i
Неподвижные ядра не создают тока. Модельный атом
точно такой же, как в гл. 3, поэтому позже будет видно,
что приближенный гамильтониан взаимодействия,
полученный в C.18), является лишь соответствующим
пределом более точного результата.
Вид лагранжиана L для системы^ «атом + излучение»
мы сначала постулируем, а затем покажем, что этот
лагранжиан дает правильные классические уравнения дви-
246 " ГЛАВА 8
жения для электронов и полей. Рассмотрим лагранжиан
0,4]
1=S т mf /•+т S (8оЕ2 ~ ^и2) <^ -
— $a<pdy+ Jj-ArfK. (8.9)
Сначала выведем уравнение движения для /-го
электрона. Координаты электрона можно явно ввести в (8.9)
путем подстановки выражений (8.7) и (&.8) для а и J:
+ е J] {ф (гу) - гу • А (г,)} - Z«p @). (8.10)
Здесь аргументами функций ф и А являются координаты
точек, в которых эти функции должны вычисляться.
Импульс, сопряженный vjy равен
Р/ = -тг- = тг/ — еА (г,), (8.11)
dry
а уравнения движения даются обычным выражением
Af4U- = 0. (8.12)
dt V ^Г/ / ^г/
Задача 8.1. Докажите, что уравнение движения
электрона, полученное из (8.12), можно записать
в виде
mr, = ->Е (г/) - W/ X Н (г/). (8.13)
Выражение в правой части уравнения есть
обычная сила Лоренца [5], действующая на
электрон.
Таким образом, лагранжиан (8.9) дает правильное
уравнение движения частицы. Рассмотрим теперь элек-
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 247
тромагнитную часть системы. Заметим, что L можно
записать в виде
L==Eim^/+T^ ${W + A2-c2(VXAJ}rfF~
/
- \oydV + \iT-AdV. (8.14)
Здесь были использованы формулы (8.3) — (8.5), а
также соотношения
J EL • Ег rfK = J Уф . A rfF = — J ф? • A rfK = 0 (8.15)
и
J JL • A dV = 80 \ Vq> . A dV = — е0 \ ф (V . A) dV = О,
(8.16)
вытекающие из кулоновской калибровки и F.22).
Зависящую от переменных поля часть лагранжиана удобно
выразить через плотность лагранжиана J?, поэтому
положим
L = YJ\mv)+\SdV, (8.17)
где
к.
2 = j eo {(V<pJ + А2 - с2 (V X АJ} - стер + Jr . А. (8.18)
Импульсы, сопряженные А и ф, определяются
обычным образом из плотности лагранжиана
гА = -^ = еэА (8.19)
И
г«=щ-=0' (8-20)
Уравнения движения для полей находятся из плотности
лагранжиана 3? путем обобщения1) уравнения (8.12), в
1) Уравнение движения, связанное с плотностью лагранжиана,
выводится в работе [4],
248 ГЛАВА 8
котором учитывается замена L на 2>\
А-(Щ + У -±-(-^-)-^- = о, (8.21)
dt \д%, ) .J-* dxi \д(д%,1дх\) д2> » v '
где Хг — декартовы координаты и 5£ может обозначать
либо ф, либо компоненту вектора А.
Задача 8.2. Докажите, что уравнения движения для ф и
А, полученные из (8.21), совпадают с
уравнениями поля (8.1) и (8.2).
Следовательно, постулированный лагранжиан (8.9)
содержит три правильных классических уравнения
движения для rj, ф и А.
Классический гамильтониан системы Ж теперь легко
получить из классического лагранжиана L и
сопряженных импульсов обычным способом:
& = Z Р'' ■ Г' + \ (ГА • А + V) dV ~ L- (8-22)
Для последующего перехода к квантовой механике в
описании движения частиц необходимо вместо г,
использовать pj. С помощью (8.11) плотность тока (8.8) можно
записать следующим образом:
i = - ir £ (р/ + ек (г,)) 6 (г - Г/), (8.23)
тогда формулы (8.11), (8.14), (8.19) вместе с (8.20)
позволяют записать гамильтониан в виде
м=-к Z р/ (р/ +ек W> + e° S*2 dV -
i
-iZ (P/+eA (r')J - Те° S^V(PJ+ A2-c2(V X AJ} dV+
+ J <r<p dv + -J- £ (p,- + eA (r,)) • A A7) =
=iZ(p/+eAM2+
+ J 60 \ {A2 - (V<pJ + c2 (V X AJ} dV + J oq> rfF. (8.24)
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 249
Гамильтониан связанной системы «атом +
излучение» может быть записан в различных .эквивалентных
формах. Используя формулы (8.3) — (8.5) и (8.7),
перепишем его в следующем виде:
М = Ш £(р/ + еА (Г>)J + Т S (eoEr + ^oH2) dV -
i
-js^EldV-eJ^vM+ZeviO). (8.25)
В этой форме записи гамильтониана первый член
представляет кинетические энергии электронов и энергию их
взаимодействия с полем излучения А, второй член
является энергией поля излучения, а три последних члена
описывают статические потенциальные энергии
электронов и ядер.
Мультипольное разложение гамильтониана
Теперь классический гамильтониан (8.25) можно было
бы преобразовать к квантовомеханическому виду
обычным способом, а члены, описывающие взаимодействие
между полем излучения и атомными электронами,
использовать для определения свойств различных
процессов излучения. Однако, прежде чем перейти к расчетам
процессов излучения, гамильтониан (8.25) удобно
преобразовать к другому эквивалентному виду. Для наших
целей этот гамильтониан можно улучшить двумя
способами. В гамильтониане (8.25) взаимодействие между
полем излучения и электронами полностью описывается
векторным потенциалом А, а не имеющими более
понятный физический смысл электрическими и магнит-ными
полями излучения Ег и Н. Далее, векторный потенциал
в (8.25) должен вычисляться в точках нахождения Tj
всех электронов, тогда как в связи с уравнением C.16)
было указано, что электромагнитные поля на расстоянии
порядка размера атома меняются мало. С помощью
калибровочного преобразования, которое сейчас будет
рассмотрено, часть гамильтониана, описывающую
взаимодействие, можно выразить через величины Ет и Н, а
250
ГЛАВА 8
также через их градиенты в точке нахождения ядер,
выбранной за начало отсчета.
Отвлечемся пока от гамильтониана и рассмотрим
потенциальную энергию V атома, изображенного на
фиг. 3.1 во внешнем поле Ег(г). Согласно законам
электростатики, величину V можно вычислить как работу,
требуемую для перемещения каждого из Z отрицательных
зарядов — е, первоначально расположенных в точке
нахождения заряда ядра Ze, в соответствующее
положение Tj. Кулоновские взаимодействия между зарядами при
вычислении, конечно, не учитываются, поскольку
определяется вклад в потенциальную энергию только внешнего
поля Ег(г). Этот вклад описывается выражением
г/
У = £*$Ег(г).Ж\ (8.26)
/ о'
Согласно C.16), интересующие нас поля Ег(г) слабо
меняются в интервале между 0 и г,-, поэтому поле можно
разложить в быстро сходящийся ряд Тейлора:.
Ег(г) = Ет@) + (r-V) Ег @) + ±{т.У?Ет{0) + ..., (8.27)
где операторы V действуют только на Ег(г), а после
дифференцирования, величина г для поля полагается
равной нулю. Потенциальная энергия, определяемая
формулой (8.26), принимает вид
^ = ^{l + ^-rrV + l(rrVJ+...}rrEr@), (8.28)
или
V = eYjeXP{rri[l)~l ггЕг@). (8.29)
/ у
Здесь для компактной записи ряда (8.28) была
использована функция exp(rj-V), определенная через свой
степенной ряд.
С другой стороны, энергию V можно записать
следующим образом:
V=\ET{r)-P(r)dV9 (8.30)
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 251
где Р(г)—поляризация атома, записанная через муль-
типольное разложение
P(r) = e£{r/--lr/(r/.V) +
+ ^-r/(r/-VJ- ...}б(г). (8.31)
Подставляя Р(г) в интеграл (8.30) и интегрируя по
частям, для того чтобы операторы V действовали на Ег,
легко проверить, что получающееся выражение для
потенциальной энергии V (8.30) совпадает с (8.28).
Первый член мультипольного разложения
поляризации атома пропорционален дипольному моменту атома
eD = Zery, (8.32)
определенному в C.17). Второй член пропорционален
квадрупольному моменту
/
третий член пропорционален октупольному моменту и
т. д.
Возвратимся теперь к гамильтониану взаимодействия.
Приведенное выше отступление наводит на мысль о том,
что часть членов, описывающих взаимодействие в (8.25),
может быть представлена в виде (8.28) или (8.29), а
оставшиеся члены зависят только от магнитного поля.
Это ожидаемое разделение гамильтониана можно
реально осуществить с помощью калибровочного
преобразования F.7) и F.8), где калибровочная функция
2 = ijA(r).P(r)dF. (8.34)
Здесь А (г) —векторный потенциал, входящий в
гамильтониан (8.25), Р(г)—поляризация атома, определенная
в (8.31). Очевидно, что S является функцией координат
всех электронов г,.
252
ГЛАВА 8
Рассмотрим сначала преобразованный скалярный
потенциал, который легче вычислить. Согласно F.8),
новый потенциал в' точке г? дается выражением
<Р (Г/) + 3, = Ф(Г/) - 1 $ Ег (г) • Р/ (г) dV =
exp (rf • V) — 1
= Ф(г7) ^фУ г7.Ег@). (8.35)
Здесь были использованы формулы (8.3) и (8.31);. Sj и
Pj — зависящие от г,- части функций S и Р соответственно.
Видно, что подстановка <р(г;-) из (8.35) в исходный
гамильтониан (8.25) точно приводит к ожидаемой формуле
(8.29) для взаимодействия электрического поля
излучения Ег с атомом.
Преобразованный векторный потенциал в точке г;,
определенный из F.7) и (8.34), имеет вид
А (г,) - VyE = А (Г/) -1V, $ А (г) • Р (г) dV. (8.36)
Интеграл можно прямо вычислить, подставляя
разложение Р(г) из (8.31) и применяя оператор V/, но это
вычисление трудоемко. Если векторный потенциал А (г,-)
также разложен в ряд Тейлора в начале координат, то
члены правой части формулы (8.36) можно
перегруппировать и получить
А(г;) - V,3 = - ц0 {^+ !•(!•/ • V) +
+ |-(r,-VJ+ ...)r,XH@). (8.37)
Здесь были использованы формула (8.5) и тождество
Г/ X (V X А @)) = V (г, • А @)) - (г, • V) А @). (8:38)
В этом выражении оператор V действует только на А (г),
причем после выполнения всех операций величина г
полагается равной нулю. То же самое справедливо для
(8.37), где оператор V действует только на поле Н.
Выражение (8.37) для преобразованного векторного потен-
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 253
диала может быть записано более компактно с помощью
экспоненциального оператора, использованного в (8.29):
ехр(г,- V)(rr V — 1)
А (г,) - VyS = [х0 U(rMVJ " Н @) X г,. (8.39)
Таким образом, преобразованный векторный потенциал
зависит только от магнитного поля излучения в начале
координат.
Гамильтониан в новой калибровке получается путем
подстановки *в (8.25) выражений (8.35) и (8.39) для
<р(П) и А (г,-):
1 v-i ( exp(rr V)(rr V — П + 1 ч 12
-2^L{P/ + ^0 P(/ lr)!Vy } Н@)Хг,} +
i
+ Zecp @) + e £ ехр^\У~1 Г/. Ег @). (8.40)
/ 1
Теперь взаимодействие поперечного поля излучения с
электронами полностью выражено через электрический и
магнитный векторы излучения, определенные в точках
нахождения атомных ядер.
Скалярный потенциал ф(г) по-прежнему описывает
статистические кулоновские взаимодействия между
зарядами, a El — соответствующее электрическое поле.
С учетом (8.1) и (8.4) получаем
le0\EldV=\e3\(V^dV =
= -~e0\^2^dV = ^\a(pdV; (8.41)
кулоновские члены гамильтониана после подстановки
плотности заряда из (8.7) могут быть преобразованы
следующим образом:
1 е0 J El dV = -1 е £ Ф (г,) + 1 Ze<p @). (8.42)
254
ГЛАВА 8
Тогда полный гамильтониан принимает вид
^=^-£{р/+^о (,;.V (н(о)хгу)} +
+ Т J № + Ho**2) dV -1 е J] Ф (гу) +
+1Zecp@) + е£ "Р^/'у-1 Г/. Ег@)в (8 43)
/ j
Здесь члены, соответствующие кулоновской энергии,
содержат множитель 72, поскольку каждая пара
заряженных частиц дважды учтена при вычислении
потенциальной энергии.
Электрическое дипольное приближение
До сих пор все вычисления в этой главе были чисто
классическими. Переход от классического гамильтониана
(8.43) к квантовомеханическому можно осуществить
заменой векторов pj, Ет и Н соответствующими квантозо-
механическими операторами1).
В то же время экспоненты удобно разложить в ряд.
Так как величины Tj порядка боровского радиуса а0 и
оператор градиента при действии на поля Н или Ет
имеет величину порядка волнового числа излучения &,
то из C.16) ясно, что последовательные члены
разложения экспоненты быстро уменьшаются. Мы сохраним в
выражении (8.43) только первый не обращающийся в
нуль член, содержащий Н@), и два первых не
обращающихся в нуль члена, содержащих Ег@).
При переходе к квантовой механике с учетом
сохраненных членов разложения экспонент гамильтониан
можно записать следующим образом:
аё = <5х?£ -р Ztwr "г 5©/i (8.44)
где Же — гамильтониан изолированного атома,
записанный в тех же обозначениях, которые были использованы
1) Полностью квантовомёханическое преобразование выражения
(8.25) в (8t43) имеется в работе [1], см, также [6],
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 255
в гл. 3:
^=Е£-т*1> <г/>+т Z^ @)> (8'45)
/ /
УЧ
и Жя — гамильтониан свободного поля излучения,
имеющий форму F.119):
&к = \\{Ф\ + Ф*)М* (8.46)
Гамильтониан взаимодействия атома с полем излуче-
ния Жт содержит четыре слагаемых:
Ж1 = ЖЕО + ЖЕ§ + Жмо + ^wz.5 (8.47)
соответствующие члены слева направо описывают
электрическое дипольное взаимодействие
ЖЕО = eZrrET{0) = eD- ЁГ @), (8.48)
электрическое квадрупольное взаимодействие
**Q = T*£ (г' • ?)(f/" Ег @)) = - V . Q • Ег О) (8.49)
и магнитное дипольное взаимодействие
&мо = fr Н @). М, (8.50)
где последнее выражение упрощено введением оператора
полного углового момента атома
. М = Ег/ХР/. (8.51)
Последний член в гамильтониане взаимодействия
(8.47) является нелинейным, поскольку он
пропорционален квадрату вектора магйитного поля:
2 2
Этим членом мы пока пренебрежем, так как он
описывает нелинейные процессы, но мы рассмотрим его в гл. 11
и 12, где будет показано, что он имеет пренебрежимо
256
ГЛАВА 8
малую величину даже для тех процессов, где его вклад
отличен от нуля *).
Порядки величин трех линейных гамильтонианов
можно сравнить при помощи грубой оценки входящих в
них членов. Примем, что вектор г, имеет величину
порядка боровского радиуса а0, приведенного в C.15),
угловой момент М — порядка Ъ, VE— порядка kET @) =
= — Ег@) и частота со — порядка частоты атомного
перехода соо, определенной в C.28). Тогда
Ет @) 4яе0Й2
<7W
ED
me
Ет @) 3eh
и
~ Я @) НеЬ Ет @) ей
MD 2m 2mc
Отсюда видно, что электрическое квадрупольное и
магнитное дипольное взаимодействия имеют одинаковую
величину, которая меньше величины электрического ди-
польного взаимодействия на порядок безразмерного
множителя
4й£йГ«Т5Г' <8-54>
называемого постоянной тонкой структуры. Высшие
члены разложения экспонент в (8.43) по степеням iy V,
которыми мы пренебрегли в (8.47), меньше ЖЕэ на
величину порядка постоянной тонкой структуры во второй
или более высокой степени.
Как обсуждалось в гл. 3 и будет позднее показано
в этой главе, скорость поглощения или испускания
излучения при атомном переходе между состояниями i|)i и \р2
пропорциональна квадрату матричного элемента
(tpi|5^i|i|J). Из предыдущего рассмотрения следует, что
если матричный элемент (i|?i |<Жг]г|J) отличен от нуля, то
1) Другой вывод гамильтониана взаимодействия с точностью до
четырех первых членов, имеющихся в (8.47), без использования
потенциалов А и ф см. в работе [7].
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 257
вкладом остальных членов разложения Mi в (8.47)
можно несомненно пренебречь. Пренебрежение всеми
членами, кроме Med, эквивалентно допущению о
равенстве нулю волнового вектора излучения и называется
дипольным приближением. Вычисление в гл. 3
проводилось в этом приближении, поскольку пространственное
изменение электрического поля излучения не
учитывалось.
Большинство интенсивных атомных линий
поглощения и испускания видимого участка спектра относится
к переходам, в которых электрический дипольный
матричный элемент отличен от нуля. Такие переходы
называются разрешенными электрическими дипольнымц пе-
реходами. Взаимодействия Med и Mud могут быть су-
щественны при (\pi \Med\^2) = 0, когда электрический
дипольный переход запрещен. Если матричный элемент
(^i|<3^eq|^2) или (\|5i|«3^md|i|52) отличен от нуля и
наблюдается поглощение или испускание, то переход
называется разрешенным в электрическом квадрупольном или
магнитном дипольном приближении соответственно.
Общие законы, определяющие условия, при которых
разрешены или запрещены различные типы переходов,
детально рассматриваются в книгах, посвященных
атомным спектрам [8—10]. Здесь мы отметим лишь
простейшее правило отбора, которое вытекает из соображений,
четности. Координаты электрона г,- являются нечетными
функциями, поэтому при инверсии Tj величины D и Med
меняют знак. Отсюда следует, что матричный элемент
(^i|<3^ed|^2) может быть отличен от нуля только тогда,
когда функции \|?i и \|J имеют противоположную четность,
как указывалось в гл. 3. В то же время величины Q и
М четны, поэтому матричные элементы операторов Meq
и Mmd могут быть отличны от нуля только для
волновых функций i|)i и г|J одинаковой четности.
Во всех последующих вычислениях мы будем
рассматривать только электрические дипольные переходы,
хотя в большинстве случаев не составило бы труда за-
*>. Х"Ч Х»»
менить Med на Meq или Mmd- Как показывают строгие
вычисления, приведенные в настоящей главе, в диполь-
9 Зак. 885
258
ГЛАВА 8
ном электрическом приближении гамильтониан
взаимодействия поля излучения с атомом имеет такой же вид,
как и гамильтониан, полученный в гл. 3 на основе
простого энергетического рассмотрения.
Вторичное квантование гамильтониана атома
Если для определения полевых операторов Ег@) и
Н @) использовать результаты гл, 6, то члены
гамильтониана (8.44), относящиеся к излучению, можно выразить
через операторы рождения и уничтожения. Операторы
рождения и уничтожения удобно также ввести для
атомных членов гамильтониана. Тогда полный гамильтониан
можно записать в виде произведения алгебраических
величин и операторов рождения и уничтожения. Такая
форма особенно удобна при применении теории к
сложным излучательным процессам, в которых происходят
многократные взаимодействия света с атомами.
Рассмотрим гамильтониан атома Ж (8.46); пусть \х)
есть его стационарное состояние с энергией йшг-,
26E\i) = h<*i\i). (8.55)
Согласно условию полноты D,100),
£|*Ж=1. (8.56)
Здесь суммирование производится по всем собственным
функциям Же как дискретного, так и непрерывного
спектра. Повторное использование условия полноты
приводит к тождеству
#£ = £|0<'1#*Е|/></1. (8.57)
i i
Из (8.55) и условия ортонормированности собственных
функций оператора Же следует, что
(i \§вЕ | /) = tuofii,, (8.58)
поэтому формула (8.57) преобразуется к виду
щ = 2 hu>i | i) (i |. (8.59)
i
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 259
Рассмотрим теперь действие произвольной
комбинации \i){j\ на некоторое состояние атома |/). В силу ор-
тонормированности собственных функций
100'1/> = 10в//. (8.60)
Следовательно, применение оператора \i){j\ к состоянию
атома |/) дает состояние |i), если исходное состояние
атома есть |/), и нуль во всех остальных случаях.
Другими словами, Ю01 есть такой оператор, который,
действуя на атомное состояние |/), преобразует его в
состояние |/). Можно сказать, что оператор \i)(j\ уничтожает
состояние атома |/) и рождает состояние атома |/).
В соответствии с этим языком оператор \i){j\
принято обозначать аналогично с операторами рождения и
уничтожения фотонов. Определим Ь\ и hi как операторы
рождения и уничтожения атомного состояния \i) и
введем новое обозначение
!>Vb,^\i)(i\; (8.61)
при этом уравнение (8.60) запишется в виде
Ь]Ь} | /) = | I) б/Л (8.62)
Отметим, *Гто поскольку при взаимодействии атома с
фотонами видимого диапазона новые электроны не могут
родиться, а старые электроны уничтожиться и возможен
лишь переход электрона из одного состояния в другое,
то атомные операторы должны всегда записываться
в виде пары операторов рождения и уничтожения.
Теперь гамильтониан атома (8.59) можно записать
следующим образом:
&E = Xib<*ib\bi. (8.63)
i
Такое преобразование известно как вторичное
квантование гамильтониана. Согласно этой терминологии,
обычная квантовомеханическая процедура определения
стационарных состояний и их энергии рассматривается как
первое квантование движения электронов атома. Во
вторичном квантовании гамильтониан записывается через
9*
260
ГЛАВА 8
стационарные решения, которые считаются уже
известными. Гамильтониан в форме вторичного квантования
удобен для расчета взаимодействия атома с некоторой
другой физической системой, такой, как, например, поле
излучения. Атомный гамильтониан (8.63), форма записи
которого похожа на форму записи излучательной части
гамильтониана Жя, приведенной в (8.46), принимает
точно такой же вид, как выражение F.113):
^« = I>k («fA + j) • (8-64)
к
Здесь электрическое и магнитное поля выражены через
операторы рождения и уничтожения фотонов.
Остается выразить гамильтониан взаимодействия
Ж-ed через электронные операторы рождения и
уничтожения. Согласно формуле (8.48), электронные коорди-
наты входят в Жев только через вектор D,
определяемый как сумма радиусов-векторов всех электронов
атома. Двукратное использование условия полноты
(8.56) приводит к тождеству
D = ZI i) (i ID £ | /) </ H £ DtJ | i) (j I, (8.65)
i i i> i
где
• D/7 = </|D|j>. (8.66)
Подстановка обозначений, определенных в (8.61),
приводит к записи D в форме вторичного квантования:
D = £ Dijbttj. (8.67)
i, i
Результат (8.63) для гамильтониана, записанного в
форме вторичного квантования, является частным случаем
более общего выражения (8.67), справедливого тогда,
когда оператор недиагонален в представлении
стационарных состояний.
Теперь электрическое дипольное взаимодействие
(8.48) вторично квантуется путем подстановки D из
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 261
(8.67) и Ег@) из F.106) и F.108), где величина г
принимается равной нулю:
к i, f
X [^к ехр (— /©к*) — ^к ехр (ш^)] $?£/• (8.68)
Электрическое квадрупольное и магнитное дипольное
взаимодействия могут быть вторично проквантованы
таким же способом, однако здесь не~ приводится каких-либо
точных формул для этих членов гамильтониана и
рассмотрение ограничено только случаем разрешенных
электрических дипольных переходов.
Теперь полный гамильтониан системы «атом +
излучение» записан в форме вторичного квантования. Все
свойства гамильтониана как оператора содержатся в
операторах рождения и уничтожения фотонов, а остальные
коэффициенты являются обычными числами,
переменными или векторными величинами.
Часто необходимо рассматривать часть
электрического дипольного гамильтониана, относящуюся к паре
выделенных состояний атома, скажем |1) и |2), с
энергиями ficoi и й©2. Поскольку в (8.68) либо iy либо /
может быть равно 1 или 2, то соответствующая часть ЖЕи
имеет вид
i E fyk {К ехр (— mkt) — й\ ехр (i(okt)) (b\b2 + 6*5,), (8.69)
где
( й<°к \к
и вектор D2i был положен равным Di2, что справедливо
для вещественных волновых функций if>i и if>2. Все члены
в (8.68), у которых / =/, обращаются в нуль, поскольку,
как указывалось в связи с обсуждением выражения
C.19), они определяются диагональными матричными
элементами нечетного оператора D.
Преимущество формализма вторичного квантования
заключается в простоте, с которой различные типы
процессов взаимодействия, разрешенные гамильтонианом
262
ГЛАВА 8
SISed, могут быть представлены графически. Если
перемножить члены, находящиеся в скобках в выражении
(8.69), то получим четыре разных члена, каждый из ко-
<«
а к 4У 5kV b.
•£^ а
2
А . А
iA bi
в
^>-г*
Ьо Ъл
Фиг. 8.1. Диаграммы, иллюстрирующие четыре типа электрического
дипольного взаимодействия.
Волнистые линии описывают фотоны, прямые линии — состояния атома. Все
четыре диаграммы рассматриваются в тексте. Линия, стрелка которой направлена
к точке взаимодействия, соответствует фотону или состоянию атома,
уничтоженному в процессе взаимодействия; линия, стрелка которой направлена из
точки взаимодействия, соответствует рожденным фотонам или атомным
состояниям. В каждой диаграмме начальное состояние находится справа, а
конечное состояние — слева от точки взаимодействия.
торых при действии на соответствующее начальное
состояние дает некоторое конечное состояние системы
«атом + излучение». Эти четыре члена могут быть
описаны диаграммами фиг. 8.1. Начальное состояние
соответствует правой части каждой диаграммы, а конечное
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 263
:остояние, в которое система переходит под действием
эператора <Жея, соответствует левой части диаграммы.
Допустим, что состояние |2) имеет большую энергию,
чем состояние 11), т. е. йсо2 > йсоь На фиг. 8.1
поглощение фотона к, сопровождающееся возбуждением атома
из состояния |1) в состояние |2), описывается
диаграммой б, а обратный процесс испускания фотона —
диаграммой в. Процессы, представленные первой и четверо
гой диаграммами, не соответствуют разрешенным
процессам поглощения и испускания, поскольку в этом
случае равенство энергий начального и конечного состояний
невозможно. Однако такие члены, не сохраняющие
энергию, имеются в Жег>, и, как будет видно в* гл. 11 и 12,
они могут давать определенный вклад в излучательные
процессы более высокого порядка, когда энергия сохра-<
няется в конечном состоянии, но не сохраняется в
некоторых промежуточных состояниях.
Вычисление скоростей поглощения
и испускания фотонов
В качестве первого применения вторично прокванто-
ванного гамильтониана взаимодействия вычислим
скорости поглощения и испускания фотонов атомом, который
может совершать переходы между состояниями |1) и
|2). Это точно та же задача, которая была рассмотрена
в гл. 3 на основе полуклассической теории излучения.
Однако полуклассическая теория не может строго учесть
спонтанное излучение, а поэтому в C.58) излучательное
время жизни атома было найдено из соотношений между
коэффициентами Эйнштейна А и В. Прямое вычисление,
проводимое ниже, автоматически учитывает спонтанное
излучение и дает строгое обоснование
феноменологической теории Эйнштейна.
Обозначим через \пъ, 1) состояние объединенной
системы «атом + излучение», где атом находится в
состоянии |1) и в моде к имеется пк фотонов. Такое же
обозначение может быть использовано для других
комбинированных состояний. Весьма просто записать матричные
элементы оператора Жеи для процессов поглощения и
264
ГЛАВА 8
испускания фотонов, описываемых диаграммами бив
на фиг. 8.1. Если учесть формулы F.98), F.99) и (8.62),
то матричный элемент для поглощения фотона дается
выражением
(пк-1, 2\ЖЕ0\пк, l) = %kexp(-/(V)nV% (8.71)
а для испускания — выражением
(пк + 1, 11 ЖЕО | пк, 2) = - %к ехр (/с0кГ) (пк + 1),/2. (8.72)
При работе в представлении вторичного квантования
существенно, чтобы волновая функция начального
состояния системы находилась справа, а волновая функция
конечного состояния — слева от всех матричных элементов.
Пользуясь приведенными выше матричными
элементами, можно методом теории возмущений, зависящих от
времени, вычислить скорости поглощения и испускания*
фотонов. Рассмотрим сначала процесс поглощения. Пусть
в момент / = 0 атом находится в своем нижнем
состоянии 11) и на него падает пучок фотонов с волновым
вектором к. В обозначениях гл. 3 вероятность возбуждения
атома в состояние |2) в более поздний момент времени
Нравна |С2@12- Согласно C.72),
I C2 (t) |2 = (я | Г12121/2) б (со0 - со), (8.73)
где
со0 = со2 — со1# (8.74)
Матричный элемент перехода, приводящий к этому
результату, равен
(НТ12/2)ехр{-Ш)у (8.75)
поскольку в обсуждении, следующем за формулой C.41),
было показано, что член с ехр (Ш) в разложении
временного множителя cos co^ дает пренебрежимо малый
вклад.
Эти результаты из гл. 3 можно использовать для
вычисления скорости поглощения с учетом квантования
поля. Матричный элемент, приведенный в (8.71), имеет
такую же временную зависимость, что и
полуклассический матричный элемент в (8.75), а поэтому выражение
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 265
для скорости перехода (8.73) можно переписать,
заменив 72^12 на ркпЧ2 и со на сок, что дает
| С2 (t) |2 = 2jt/kV6 Oo ~ О- (8-76)
Скорость перехода пропорциональна числу фотонов nk
в пучке, т. е. энергии пучка
#'к = пкЛик, (8.77)
определенной в F.124); выражение (8.76) можно
переписать в виде
С2 (t) |2// = Bя/к1у/шк) б (со0 - ©к). (8.78)
Эти результаты применимы к пучку фотонов, начальное
состояние которых есть \пъ) и число которых,
следовательно, точно определено. В гл. 9 показано, что для
пучка фотонов в некотором более общем состоянии
уравнения для скоростей переходов обобщаются путем замены
ftk средним числом фотонов пк, а в остальном
приведенные выше результаты остаются без изменения.
Формулу для коэффициента Эйнштейна В можно
получить из (8.78) способом, аналогичным
использованному в гл. 3. Для излучения с частотой (Ok плотность
энергии iF(o)k) определяется выражением, аналогичным
C.40):
%'k = V]W(<uk)d(ok. (8.79)
После усреднения по случайным ориентациям вектора
D12 в соответствии с выведенным в полуклассической
теории выражением C.57) получим
В12 = яе2|012р/ЗвоА2. (8.80)
Аналогичным образом можно исследовать процесс
испускания фотона. Допустим, что в момент / = 0 атом
находится в возбужденном состоянии |2), и вычислим
вероятность нахождения атома в состоянии |1) в более
поздний момент времени /. В обозначениях гл. 3 эта
вероятность равна C\(t)\2 и вычисления проводятся так
же, как и для процесса поглощения, только вместо (8.71)
266
ГЛАВА 8
должен быть использован матричный элемент испускания
(8.72). В результате получим
| С, (t) |2 = 2я/к (пк + 1) й (со0 - сок). (8.81)
Эта величина представляет собой вероятность перехода
атома в состояние |1) с испусканием фотона,
обладающего определенным волновым вектором к.
Множитель /гк + 1 в формуле (8.81) дает два
слагаемых в выражении для скорости испускания фотона.
Слагаемое, линейное по як, определяет скорость,
пропорциональную числу уже имевшихся фотонов к, и
соответствует вынужденному излучению. Этот член в формуле
(8.81) идентичен правой части выражения (8.76) и
приводит к скорости излучения, равной скорости
поглощения фотона. Это равенство двух скоростей, доказанное
здесь квантовомеханическим способом, эквивалентно
равенству коэффициентов Эйнштейна В\2 и В2\ для двух
невырожденных состояний, полученному в A.59).
Отметим, что при вторичном квантовании гамильтониана
взаимодействия вынужденное излучение появляется
естественным образом. Далее, из матричного элемента (8.72)
видно, что при вынужденном излучении фотон имеет
такой же волновой вектор к и такое же направление
поляризации (обозначение которой, согласно договоренности,
заключенной в гл. 6, учтено в индексе к), как и у
имевшихся до излучения фотонов /гк. Эти свойства
вынужденного излучения были сформулированы без
доказательства при обсуждении фиг. 2.1.
Слагаемое в выражении (8.81), не зависящее от nk,
соответствует спонтанному излучению, так как здесь
переходы происходят даже при полном отсутствии какого-
либо излучения (пк = 0). Отметим, что множитель
ик+1, который в (8.81) определяет отношение
скоростей вынужденного и спонтанного излучений для
определенного фотона к, похож на множитель Я+ 1, равный
отношению двух скоростей в A.62), когда среднее число
тепловых фотонов в одной моде полости равно п.
Спонтанно излученный фотон может иметь любую
ориентацию волнового вектора, разрешенную геометрией
полости, и в этом отношении он отличается от фотона
вынужденного излучения, который всегда должен иметь такой
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 267
же волновой вектор и такую же поляризацию, как и у
фотонов, вызывающих излучение.
Следовательно, полная скорость спонтанного
излучения получается суммированием выражения (8.81) для
излучения в отдельную моду полости к по всем модам
полости. Тогда излучательное время жизни тя дается
выражением
*/** = | С{ (t) fft = 2я £ /кб (со0 - сок). • (8.82)
к
Эта формула является частным случаем общего
результата, известного под названием золотого правила Ферми,
который дает скорость перехода 1/т из начального
состояния \i) в совокупность конечных состояний \f) под
действием возмущения Жъп.
1/т = Bя/Д2) £ I <fl *ю I г) Р б (со, - cof). (8.83)
f
Здесь ficoi и bat — энергии системы до и после перехода.
Для рассматриваемой задачи в начальном состоянии
фотоны отсутствуют и атом находится в состоянии |2), а
конечные состояния соответствуют различным фотонам
к, которые могут быть испущены при переходе атома в
состояние |1). Для рассматриваемого перехода золотое
правило, которое в общем случае будет доказано в гл. 11,
сводится к формуле (8.82).
Для завершения оценки величины тя необходимо в
выражении (8.82) от суммирования по к перейти к
интегралу по сок и результат усреднить по всем
направлениям вектора к, как это было сделано в A.31) и C.56),
Из (8.70) и (8.82) получаем
\/Xr = Аоз | DJ2 |2/3jte0ftcV (8.84)
Согласно B.27), величина 1/тя равна коэффициенту
Эйнштейна А2и а поэтому выражение (8.84) точно
совпадает с результатом C.58) полуклассической теории
излучения для двух невырожденных уровней атома.
Проведенные выше вычисления показывают, как
различные процессы, рассматриваемые в теории поглощения
и излучения света Эйнштейна, автоматически появляются
в вычислениях с квантованным полем излучения. Все
268
ГЛАВА 8
скорости переходов могут быть непосредственно
вычислены без каких-либо феноменологических рассуждений,
характерных для полуклассического подхода. Хотя в
настоящей главе все полученные до сих пор результаты
просто подтверждают формулы, выведенные менее
сложными методами, в последующих вычислениях будет
видно, что при использовании квантованного поля
излучения анализ сложных процессов можно провести
быстрее, ^ем при любом феноменологическом или
полуклассическом подходе.
Переход к представлению Шредингера
Проведенные выше вычисления вероятностей
переходов основаны на теории возмущений, зависящих от
времени, развитой в гл. 3. Основным уравнением
является зависящее от времени волновое уравнение C.1), где
гамильтониан Ж, как и в C.7), представлен в виде
суммы гамильтониана атома Же и гамильтониана взаи-
модействия Mi. Гамильтониан взаимодействия зависит
от времени и рассматривается как причина переходов
между собственны ми состояниями оператора Же>
В электрическом дипольном приближении можно
записать волновое уравнение
{ЖЕ + ЖЕО @) Т (t) = ih dW (t)/dt. (8.85)
Здесь явно указаны зависящие от времени функции. Точ-
ные выражения для Же и Жев приведены в формулах
(8.63) и (8.68), откуда можно видеть, что временная за-
висимость оператора ЖевA) обусловлена электрическим
вектором поля излучения Ёт. При рассмотрении
взаимодействия между атомом и излучением на основе
уравнения (8.85) используются зависящие от времени
операторы для излучения и не зависящие от времени
операторы для атома.
Как показано в учебниках по квантовой механике
{11], данная задача может быть рассмотрена в
нескольких различных представлениях. Представления
отличаются характером временной зависимости квантовоме-
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 269
ханическнх уравнений. Предельнььми случаями являются
шредингеровское представление, когда операторы не
зависят от времени, а вся временная зависимость
содержится в волновой функции, и гейзенберговское
представление, когда волновые функции не зависят от времени, а
вся временная зависимость заключена в операторах.
Волновое уравнение (8.85) записано в смешанном
представлении, в котором гамильтониан атома определен
в шредингеровском представлении, а полевая часть
гамильтониана— в гейзенберговском* представлении.
Иногда всю систему удобно описывать в шредингеровском
представлении, как это сделано, например, в конце
настоящей главы при вычислении восприимчивости атома.
Временная зависимость исключается из полевой части
гамильтониана простым преобразованием волновой
функции.
Определим новую функцию Ф@> связанную с "*F@
соотношением
ф (t) = ехр (- ткЩ W (/), (8.86)
**, ^_^
где Жв. — гамильтониан поля излучения (8.46).
Подставим функцию (8.86) в волновое уравнение (8.85)
{ЖЕ + ЖЕ0 Щ ехр {^-) Ф (/) =
= ih eXp (i -J-) | i _& ф {t) + -±L j (8.87)
и умножим полученное уравнение (8.87) с обеих сторон
слева на ехр(—хЖцЦЪ)
| ЖЕ + Ж % +
(8.88)
Ич
Здесь была использована коммутация операторов Же и
0VR.
Зависящий от времени член гамильтониана, стоящий
в левой части уравнения, может быть сильно упрощен.
270
ГЛАВА 8
Задача 8.3. Используя коммутационные соотношения
G.20) и G.21), доказать, что
а ехр {i(oafdt) = ехр {ш {а+й + 1) t) й (8.89)
и
df ехр (i(odfdt) = ехр {/© {аЧ - 1) 0 df, (8.90)
где а^ и а — операторы рождения и
уничтожения для произвольного гармонического
осциллятора, и, следовательно, показать, что
ехр (— t3SRt/h) ЖЕ0 @ ехр (№кф) = ЖЕВ @).
(8.91)
Таким образом, волновое уравнение (8.88)
преобразуется к виду
{ЖЕ + ЖЯ + ЖЕО) Ф (t) = ih ^p-. (8.92)
Здесь записанный без временной зависимости оператор
Med будет обозначать электрический дипольный
гамильтониан (8.68), где время t принято равным нулю:
k it I
Гамильтониан в (8.92) совсем це зависит от времени, так
как преобразование (8.86) перенесло временную
зависимость с поля излучения на волновую функцию Ф@-
Такое же преобразование можно провести для полного
гамильтониана взаимодействия §6i (8.47); в результате
получается точно такое же волновое уравнение, как урав-
нение (8.92) при замене Жев на <5^j при t = 0.
Физические выводы, которые можно сделать из
нового волнового уравнения (8.92), идентичны
получающимся из исходного уравнения (8.85). Преобразованное
уравнение симметрично относительно атомных и
полевых членов полного гамильтониана и часто является
более удобным при вычислениях, в которых как атом, так
и излучение рассматриваются квантовомеханически.
В то же время иногда удобнее сохранить
гейзенберговское представление операторов поля излучения с учетом
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 271
их явной временной зависимости. Выбор представления
определяется удобством вычислений. Развитие
основанной на уравнении (8.92) теории возмущений, зависящих
от времени, описано в гл. 11, и в первом приближении
оно приводит к тому же результату, который был
получен в гл. 3 на основе волнового уравнения (8.85).
Теперь рассмотрим часть гамильтониана в шрединге-
ровском представлении, относящуюся к одной паре
энергетических уровней атома. Двухуровневый атом
подробно изучен в предыдущих главах, где подчеркивалось,
что экспериментальные условия часто выделяют
определенную пару атомных состояний; поэтому двухуровневый
атом является очень хорошим теоретическим
приближением. Снова рассмотрим два состояния атома |1) и |2),
разделенные по энергии на йооо. Если энергию нижнего
состояния |1) принять за нуль, то гамильтониан атома
(8.63) преобразуется к виду
ЖЕ = НщЫЬ2. (8.94)
Операторы, входящие в гамильтониан, можно
упростить введением операторов перехода, определяемых
следующим образом:
й+ = 6^1=|2><1| (8.95)
и
ft = 5+52 = |l) B|. (8.96)
Следовательно, оператор я+ переводит атом из его
основного состояния в возбужденное состояние, а оператор я
вызывает обратный переход. Свойства операторов я+ и
я легко получаются из их определения. Например, если
учесть (8.61) и предположить, что состояния
нормированы, то
А*й = |2><1|1><2| = 52$2 (8.97)
и аналогично
Ц^ = Ь\Ь\. (8.98)
Следовательно, гамильтониан атома (8.94) можно
переписать в виде
ЖЕ = Пщк^к. (8.99)
272
ГЛАВА 8
Электрический дипольный гамильтониан можно
преобразовать аналогично. Согласно формуле (8.65), вектор D,
записанный в форме вторичного квантования, имеет вид
D = D12(ftf+ ft). C.100)
Здесь учитываются только состояния |1) и |2). Тогда
соответствующая часть электрического дипольного
гамильтониана из (8.68), где время t положено равным
нулю, равна
$вЕО = i Z ft,k (йк - йП (ft+ + ft); (8.101)
k
величина Ь^к определена в (8.70). Члены, получающиеся
при перемножении выражений в скобках, описываются
четырьмя диаграммами на фиг. 8.1.
Полный гамильтониан для двухуровневого атома,
взаимодействующего с полем излучения, полученный из
(8.64), (8.99) и (8.101), имеет вид
w <Я/> I 'уЬ i <ч2>
<лэ — аЬ£ -j" ato ^ -р &&ED —
= ft©0ft+ft + £ йо)ка+ак + IZ hv К ~ й1) (ftt + ")• (8-102)
к к
Здесь в 36 r была опущена энергия нулевых колебаний
в соответствии с замечанием в конце гл. 6. Этот
гамильтониан простого вида приводит к результатам,
совпадающим с полученными в начале главы для скоростей
поглощения и излучения в случае переходов между
уровнями 11) и |2), он особенно удобен для определения
более сложных свойств взаимодействия излучения с двумя
уровнями.
Диагонализация гамильтониана
системы «атом + излучение»
Одним из проявлений взаимодействия излучения с
парой атомных уровней, которое можно рассчитать при
помощи гамильтониана (8.102), является вклад переходов
между двумя уровнями в зависящую от частоты
восприимчивость газа, состоящего из одинаковых атомов.
Классические и полуклассические выражения для восприим-
* чивости получены в гл. 4, где было подчеркнуто, что
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 273
спонтанное излучение учтено лишь феноменологически.
Теперь мы в состоянии дать более строгий расчет
восприимчивости без какого-либо произвола в учете
затухания, обусловленного спонтанным излучением. Будет
показано, что более точный результат в основном
совпадает с результатами более ранних приближений, хотя и
отличается от них в деталях.
Сначала рассмотрим систему, состоящую из одного
атома в полости, который описывается гамильтонианом
(8.102). Если бы в гамильтониане отсутствовало взаимо-
действие Жев, то наша система (атом в полости) имела
бы энергетический спектр, изображенный в верхней
части фиг. 8.2, где соо — частота возбуждения атома, сок —
частота квазинепрерывного спектра собственных мод
полости. В отсутствие Жев падающий световой пучок не
взаимодействовал бы с атомом и проходил через полость
без рассеяния и соответствующего поглощения.
Если теперь учесть взаимодействие Жев, в котором
оставлены только сохраняющие энергию члены,
соответствующие диаграммам б и в на фиг. 8.1, то
гамильтониан принимает вид
Ж = Йсо0я+л; -(- 2 ^°\^k^k +г' 2 ^я (^f^k ~~ я£я). (8Л03)
к к
Введение взаимодействия ЖЕв приводит к двум
следствиям: во-первых, к установлению связи между
атомным возбуждением и падающим светом, а во-вторых,
к установлению связи между атомным возбуждением и
всеми модами полости. Если мы учтем перво'е
следствие, то получим поглощение светового пучка только
при условии точного равенства его частоты со частоте соо,
как и в случае результата C.72), содержащего б-функ-
цию. Именно второе следствие приводит к затуханию,
которое обусловлено спонтанным излучением и должно
быть включено в вычисления, чтобы получить правильное
квантовомеханическое выражение для восприимчивости.
Метод, используемый ниже, служит прежде всего для
исследования задачи об атоме, помещенном в замкнутую
полость, в отсутствие падающего светового пучка.
Поскольку в выражении (8.103) содержатся члены взаимо-
o>*
Падающий
световой
пучок
а> ———
\
Воз5уж- /////I
денное I////'-
атомное Ш/Л-
состоя* ш*~
' fs~:
ш.
%
0)i
3
с:
U>2
связь &eL
ED
О)
Падающий
световой
пучок
/А-
/#>
"/,:'
W+/
»3
а:
§
*t
Л2
•Ct
+
Фиг. 8.2. В верхней части фигуры по вертикали отложены частоты
трех основных компонент взаимодействия внешнего падающего
светового пучка с атомом, помещенным в полость с квазинепрерывным
спектром электромагнитных мод. Пунктирные линии соединяют
возбужденное состояние атома с состояниями излучения,4с которыми
оно связано электрическим дипольным взаимодействием. В нижней
части фигуры изображена та же система, после того как была
проведена диагонализация взаимодействия возбужденного состояния
атома с модами полости для получения смешанных атомно-полевых
возбуждений | /).
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 275
действия, то собственные состояния \i) связанной
системы «атом + излучение» являются суперпозициями
атомного возбуждения и моды полости. В принципе
каждая мода полости получает некоторую долю атомного
возбуждения, однако в действительности эта доля
существенна только для тех мод, частота которых со^ близка
к соо. Состояния \i) диагонализуют гамильтониан (8.103),
поэтому можно записать
£e\i) = hXi\i\ (8.104)
где bhi — соответствующее собственное значение
энергии.
Теперь внешний световой пучок, падающий на атом
в полости, взаимодействует через Жев не с одним узким
атомным переходом на частоте со0, а с набором
смешанных возбуждений \i), занимающих область частот А,*.
Сила взаимодействия пучка с возбужденным состоянием
\i) пропорциональна величине его атомной
составляющей, и каждое возбуждение дает соответствующий вклад
в поглощение падающего пучка. Поэтому поглощение
распределено по некоторому интервалу частот, а
функциональная зависимость поглощения от частоты по
определению является естественной формой линии
поглощения рассматриваемого атомного перехода.
Взаимодействие падающего света с атомом в полости после диаго-
нализации изображено графически в нижней части
фиг. 8.2. Конечно, мы получим, что только смешанные
состояния \i) с энергией ftku близкой к йсоо, достаточно
сильно взаимодействуют с пучком.
В общем случае восприимчивость атома в полости
можно найти, суммируя вклады переходов между
основным состоянием системы (где атом находится в
состоянии |1) и в поле излучения нет возбужденных фотонов)]
и всеми смешанными возбужденными состояниями |Л.
Эти состояния по определению являются точными
собственными состояниями гамильтониана (8.103), и
поэтому они не обладают каким-либо излучательным
затуханием и взаимодействуют только с падающим
световым пучком. Точное выражение для восприимчивости
такого набора состояний определяется формулой D,79),
276
ГЛАВА 8
которая для данного случая может быть записана в виде
* (с°)=-Щг £ |D"|2*(я< ~ <о)~1+{Xi+фГ'^ (8-105)
где разложение знаменателя на слагаемые удобно для
дальнейшего использования.
В феноменологическом подходе, описанном в гл. 4,
влияние квазиконтинуума мод полости, изображенного
в верхней части фиг. 8.2, было учтено введением
скорости излучательного распада возбужденного состояния
атома, а падающий световой пучок взаимодействовал с
этим единственным затухающим возбужденным
состоянием. В данном методе вычисления падающий световой
пучок взаимодействует с большим числом близко
расположенных незатухающих состояний, каждое из которых
является суперпозицией возбужденного состояния атома
и одной моды полости. Несмотря на большие различия
между двумя методами вычислений, как будет видно из
сходства полученных результатов, феноменологический
подход часто является очень хорошим приближением.
Число мод полости удобно ограничить большим, но
конечным числом N, чтобы можно было использовать
конечные матрицы. Разумеется, в действительности число
N бесконечно, поэтому в конце вычисления должен быть
сделан переход от конечного N к бесконечному.
Волновые векторы мод полости можно записать как кь к2, ...,
..., kNj а соответствующие операторы рождения и
уничтожения— как df, dp d£, d2; ... а\1Угйм. Гамильтониан
(8.13) можно представить в виде матричного
произведения
G0
тг
= [nf
а; а<
*я
©о
©!
C02
l?N
.- ~~ l?N
П
A.
a0
= a++ (© + >) a, (8.106)
где a+ — строка, составленная из операторов рождения,
а — столбец, составленный из операторов уничтожения,
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 277
(о и д.—диагональная и недиагональная квадратные
матрицы.
Квадратная матрица эрмитова, поэтому ее диагона-
лизация в принципе возможна с помощью унитарного
преобразования [12]
U(© + f)lTI = *. (8.107)
Здесь U — унитарная матрица, которую следует
определить, % — диагональная матрица, элементами которой
являются N + 1 собственных значений для смешанных
возбуждений, определяемых уравнением (8.104).
Операторы в однострочной матрице
д^аЧг1 (8.108)
являются операторами рождения для смешанных
состояний; состояние \i) получается из основного состояния,
где атом находится в состоянии |1) и нет возбужденных
фотонов, с помощью оператора рождения \х\:
10 = АЛ О- <8Л09)
Элементами одностолбцовой матрицы
£=Ua (8.110)
являются соответствующие операторы уничтожения Д*.
Формула для восприимчивости (8.105) может быть
выражена через элементы матрицы U. Согласно
формуле (8.100), матричный элемент D, входящий в %((о),
определяется выражением
Dn = D12</|ft+ + ft| 1> = 012(/|я;*| 1). (8.111)
Из формулы (8.108) следует
a+=Vu, (8.112)
и первые элементы однорядовых матриц, стоящих в
правой и левой частях уравнения (8.112), дают
ft+ = EATtf#i. (8.113)
Если это выражение для й+ подставить в формулу
(8.111), то из ортогональности смешанных возбуждений
278
ГЛАВА 8
\i) и формулы (8.109) видно, что в выражении (8.113)
только член с / = 1 дает ненулевой вклад, а потому
Dn = D12C/n.
(8.114)
Тогда зависящая от частоты восприимчивость (8.105)
может быть записана в виде
х(®)=-етг1,)'2|2Е|С/»|г^~<а) + (л'+шГ|Ь
i
(8.115)
Записанное через неизвестные величины 11ц и Я*
выражение для %(со) необходимо преобразовать в эквивалент1-
ное выражение, определяемое через известные
элементы матриц о) и у уравнения (8.106). Формулы для
некоторых комбинаций элементов 0ц и Я*, содержащихся
в (8.115), найти относительно просто. Нет необходимости
определять всю матрицу U, поскольку требуется знание
только некоторых сумм ее матричных элементов.
Умножение уравнения (8.107) справа на U дает новое
уравнение
и((д + ^) = Ш, (8.116)
которое можно тождественно переписать в матричной
формег
U\i Ui2 f/13 • • • "ltf + l
^22 ^23 • • • ^2М+\
Uz\ U$2 ^33 ' • • ^ЗЛГ + 1
X
°°0 1?[ 1?2 • • • l?N
— iyx ©j .
—ly2 ®2
Я1С/Ц Я1С/12 Я1С/13 ... Ait/itf+i
Л2С/21 A2C/22 ^2^23 • • • ^2^2N+l
Я3С/31 Я3С/32 A3f/33 ... h$U3N+1
••••»••••♦•••••
@
Arte. 117)
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ
279
Если стоящие слева матрицы перемножить, то сравнение
соответствующих элементов с обеих сторон матричного
уравнения приводит к следующему уравнению:
N
ип%
'2Ж+,у*=^/
ft=l
Л
для элементов первого столбца и к уравнению
(8.118)
(8.119)
для всех остальных элементов.
Из уравнения (8.119) следует
Я, — со
Ut
i
l¥=U
(8.120)
7-1
и в результате все элементы унитарной матрицы могут
быть выражены через элементы первого столбца;
U =
£/31
iUu?
\\г\
я1-а1
Я2-со1
Я3""®1
^11*2
Я1""®2
'^21*2
Я2-со2
//731^2
Я3-®2
*^п*
\\ГЫ
Я1 — Ш^
^91Я
21^ЛГ
Я2-со^
/С/.
31 ^ЛГ
A3~°V
f/
ЛГ+Il
iUN + \\?N
%
N + \
CO
Л/" —
(8.121)
Оставшиеся матричные элементы Un входят в
выражение для восприимчивости (8.115); согласно формуле
(8.114), сила дипольного электрического взаимодействия
в i-u смешанном состоянии пропорциональна Un.
Столбцы любой унитарной матрицы удовлетворяют
соотношениям нормировки и ортогональности A2]
£ВД*=в/а, (8.122)
i
поэтому нормировка первого столбца приводит к
равенству
Е|С/«Р=1, (8-123)
280
ГЛАВА 8
а из ортогональности первого столбца ко всем остальным
столбцам следует
z
Ut
^-©k
= 0.
(8.124)
Здесь «к — частота произвольной моды из N мод полости.
После умножения уравнения (8.124) на произведение
величин сок — Xj, гДе каждый сомножитель соответствует
одному из N + 1 собственных значений Xj, после
изменения знака получим
Z^trII(*-V)-o.
(8.125)
Это уравнение есть полином порядка N относительно сок-
Его решением^ является каждая из N частот сок
собственных мод полости. Следовательно, частоты сок являются
собственными корнями уравнения (8.125), в котором
частоты сок заменены на со, поэтому левая часть уравнения
(8.125) может быть записана в виде произведения
сомножителей СО — СОк'
Un |2
Е-ЙЕ-Пс-ад-П<—*
(8.126)
Из (8.123) видно, что коэффициенты при со^ в обеих
частях уравнения равны единице, поэтому в правой части
уравнения (8.126) не требуется постоянного множителя.
Из (8.126) следует, что
П К ~@)
(8.127)
i
ипГ _
Xt — со
П>/-«о'
и восприимчивость (8.115) можно записать в виде
хМ-зЗИ0»^
П к - ®) П к+«о
к + к
(8.128)
Д(Я/-со) П(я/ + Ш)
/ i
Неизвестные элементы унитарной матрицы из
восприимчивости исключены, и последний шаг заключается в
исключении неизвестных собственных значений Xj.
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 281
Из (8.118) и (8.120) получим уравнение
Умножим обе стороны этого уравнения на произведение
сомножителей Кг— соь где каждый сомножитель
соответствует одной из N частот сок собственных мод полости.
После перегруппировки получим
Л| — соо — ^ л7^^ } П(А'~ ®к) = °- (8Л30)
к ) к
Этому уравнению порядка N -\- \ по Кг удовлетворяет
каждое из iV-f 1 собственных значений Кг. Используя
метод, подобный примененному для преобразования
формулы (8.125) в (8.126), можно найти
|0_(Оо_^_£1_|д{(О_Шк)=Д((й_Лг). (8.131)
Чтобы получить искомое выражение для
восприимчивости, записанное через известные величины, произведения
сомножителей Kj — со и Кг + со можно исключить из
(8.128) с помощью уравнения (8.131):
xM = Z£i%JL( _!_ .+
e2lDi2l2 ( J
3eQhV J co0 - со - £ *k/(ok ~ со)
+ ^—. тЦпт-Т—rl- (8-132)
/co0+co-2^k/K + co) j
Этот результат для восприимчивости двухуровневого
атома является точным в рамках гамильтониана (8.103),
однако необходимо помнить, что этот гамильтониан сам
является приближением полного гамильтониана (8.102)„
В гл. 11 будет видно, что члены, опущенные в
приближении (8.103), играют важную роль в описании рассеяния
света. Несмотря на это, при вычислении
восприимчивости они дают пренебрежимо малый вклад.
ZO^
1 i/lftDrt О
Излучательная ширина линии и частотный сдвиг
Сравнение выражения (8.132) с полуклассическим
результатом D.89) показывает, что эти два выражения
похожи, но феноменологический параметр у
полуклассической восприимчивости заменен в (8.132) двумя
различными членами, зависящими от частоты со, на которой
измеряется восприимчивость. Два знаменателя в
выражении (8.132) удобно разделить на мнимую и
вещественную части. При проведении суммирования по к
необходимо соблюдать некоторую осторожность. Теперь
ограничение на конечное число N мод полости к будет снято,
а'суммирование по к заменено интегрированием. Из
требований причинности, аналогичных обсуждавшимся в
гл. 4, следует, что полюса функции %(со) должны
лежать в нижней полуплоскости со. Этому условию можно
удовлетворить путем добавления к со бесконечно малой
мнимой части ie, величина которой впоследствии
принимается равной нулю.
Тогда, используя формулы A.131) и (8.70), сумму
в первом знаменателе выражения (8.132) можно
записать в виде
V V Л у Г g2u)klPl2l2 1
lim > т- = ltm \ г о * * г- асок.
e_>0Z^j сок — со — ie е->о J Зп~е0пс3 сок — а> — te
к
(8.133)
Здесь множитель 3 в знаменателе получается в
результате усреднения по углам, как и в формуле C.56).
Интеграл берется по положительной оси cor, и знаменатель
как функция сок имеет полюс в верхней полуплоскости.
Соответствующий контур интегрирования показан на
фиг. 8.3, а результат интегрирования может быть
записан в виде суммы двух слагаемых:
ОО о О О ОО С) О .О
- e^cot 10,о I dat, с еЖ ID, u
о о
(8.134)
Здесь интеграл в смысле главного значения получается
при интегрировании вдоль прямой контура, а интеграл,
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 283
содержащий б-функцию, является вкладом от полуобхода
полюса. Отметим, что последний интеграл согласуется
с б-образным представлением уравнения C.68),
с*)к-плоскость
О)
"СГ
^- оо
Фиг. 8.3. Контур интегрирования для выражения (8.133).
Результат суммирования выражений (8.133) и (8.134)
может быть записан следующим образом:
л
"™Е«,Лк-/6=Аи+'у(«>>>
к
(8.135)
где
Д(ш)=^5
°° e2co^|DI2|2 tfco,
6я2е0£с3 шк — со *
(8.136)
Вычисляя интеграл, входящий в мнимую часть
выражения (8.134), получим
е2сй31 Di212
6яе0Йс3
Y(co)
(8.137)
В тех же обозначениях сумма, входящая во второй
знаменатель выражения (8.132), имеет вид
limY
2
в->0Г «к + <° + i&
к
= А(—со) —/у(—со). (8.138)
Для любой положительной частоты со имеем
Y (— со) = 0, <о>0,
(8.139)
поскольку интегрирование в формуле (8.134)
производится только по положительным частотам сок и
особенность функции 6(о)к+_о)) исключена, Однако восприим-
284
ГЛАВА 8
живость также определена и для отрицательных частот
о, на что было обращено внимание при обсуждении
выражения D.6). Для этих частот функция у((о) равна
чулю, а у(—со) ф 0. Вещественная часть А(со) в общем
случае не равна нулю как для отрицательных, так и для
лоложительных частот.
После подстановки выражений (8.135) и (8.138) в
формулу для восприимчивости (8.132) получим
( \ = Ne21 р'° I2 / ! l
Х ^ Зе0ЙК I со0 - со - А (со) - iy (со) ~*~
Н z w * , ,. , Л. (8.140)
' со0 + © — А (— со) + iy(— со) J ч
Легко проверить, что это выражение удовлетворяет
общему требованию, сформулированному в D.7).
Наиболее интересным экспериментально
наблюдаемым эффектом, связанным с атомным переходом на
частоте сось является поглощение, или, точнее, рассеяние,
имеющее место для света с частотой со, близкой к соо.
Для положительной частоты со только первый член в
скобках формулы (8.140) имеет мнимую часть, поэтому
форма линии поглощения определяется выражением
1т*(@) - 3e0bV K-cd-AHP+yMco) • <8Л41>
Функциональная форма Imx(co) похожа на лоренцеву
форму линии D.19), но является более сложной,
поскольку обладает сдвигом частоты А и параметром
ширины линии у, зависящими от частоты со.
Рассмотрим сначала член А (со) в знаменателе
выражения (8.141). Интегрирование в (8.136) выполнить
нетрудно, однако подынтегральное выражение при больших
частотах cor пропорционально со£, и, следовательно,
интеграл на верхнем пределе расходится, приводя к
бесконечному значению А (со). Бесконечное значение А (со)
делает мнимую часть Imx(co) в (8.141) равной нулю для
всех конечных частот, что не согласуется с наблюдением
атомных линий поглощения на конечных частотах.
В течение многих лет расходимость А (со) была
неразрешимым противоречием между квантовой теорией
излучения и экспериментальной спектроскопией. Это проти-
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 285
воречие преодолел Бете [13]1) в 1947 г. с помощью
метода, известного под названием перенормировки масс.
Бете указал, что расходимость может быть в основном
связана с массой электрона. Обнаружено, что энергия
свободного электрона имеет бесконечное слагаемое,
обусловленное взаимодействием электрона с полем
излучения. Иначе говоря, кажущаяся масса электрона
увеличена на бесконечную величину по сравнению с массой
электрона, не взаимодействующего с полем излучения.
Поскольку электрон невозможно изолировать от поля
излучения, то экспериментально измеряется именно
первая масса. Отождествление измеряемой массы электрона
с теоретической массой после перенормировки,
произведенной для учета энергии взаимодействия с полем
излучения, в основном устраняет расходимость А (со).
Мы не воспроизводим здесь детального вычисления
А (со); найдено, что для устранения остаточной
логарифмической расходимости (после перенормировки масс) в
области релятивистских частот должно быть введено
обрезание интервала интегрирования в (8.136). Эти
рассмотрения лежат за пределами настоящей книги, а
интересующийся читатель сможет найти хорошее изложение
вычисления в других книгах [15]2).
Расчеты для атома водорода показывают, что
величина А (со) равна нулю, если только одно из состояний,
участвующих в переходе, не является 5-состоянием.
Даже при А (со) фО перенормированный сдвиг А (со) всегда
очень мал по сравнению с частотой возбуждения и слабо
зависит от со. Например, сдвиг А (со) для состояния
водорода 22Si/2 приблизительно равен 109Гц, что почти на
шесть порядков меньше частоты возбуждения состояния
с п = 2. Таким образом, влияние величины А (со) состоит
в очень малых кажущихся сдвигах частот атомных
линий поглощения. На частоте соо основного возбужденного
уровня этот сдвиг может быть вычислен с пренебрежимо
малой ошибкой. Существование сдвигов уровней было
') Эта статья перепечатана в [14].
2) В анализах, проводимых в этой и предыдущей работах,
взаимодействие между электроном и полем измерения записывается в
виде А • р, как и в (8.25). Анализ, основанный на записи
взаимодействия в виде Е • г, как и в (8.48), см. в [16],
286
ГЛАВА 8
впервые показано Лэмбом и Резерфордом в
экспериментах по излучаГтельным переходам между состоянием
водорода 225i/2 и несмещенным состоянием 2!Р1/2.
Расщепление А (со) между этими уровнями известно под
названием лэмбовского сдвига.
Благодаря малой величине и слабой зависимости от
со влияние А (со) сводится к небольшому сдвигу
максимума линии поглощения без существенного изменения
формы линии. В последующих формулах Сдвиг Д(со0)
будет включен в величину со0, которую мы
переопределим как частоту возбуждения верхнего атомного
состояния с учетом всех излучательных сдвигов уровней.
Как следует из (8.137), параметр ширины линии у
пропорционален со3 и не является постоянным, как это
предполагалось в феноменологической теории затухания,
изложенной в гл. 4. Частотная зависимость параметра у
приводит к небольшому отклонению зависимости (8.41)
от лоренцевой кривой и вызывает слабый сдвиг
максимума в Imx(co) относительно соо. Однако для узких
линий поглощения, обычно встречающихся в атомной
спектроскопии, эти искажения чрезвычайно малы. Сдвиг пика
поглощения очень мал даже по сравнению с
обсуждавшимся выше малым .сдвигом Д(со).
Для большинства целей параметр у((о) можно
положить постоянным и равным его значению при со = соо-
Сравнение формул (8.84) и (8.137) показывает, что
2у{щ) = -±- = А21. (8.142)
Это равенство согласуется с соотношением D.91) для
феноменологической константы затухания. Таким
образом, в соответствии с выводами, полученными ранее с
использованием менее строгих методов, излучательная
ширина линии Im%(co), определяемая формулой (8.141),
равна коэффициенту Эйнштейна А для перехода между
уровнями.
В результате описанных выше приближений
выражение (8.141) принимает вид
lm%(®) = Nel]*f -. ?(,".) (8.143)
. лч ' Зг0ЬУ (со0 — соJ + у (©о) v
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 287
Это выражение имеет лоренцеву форму и согласуется
с мнимой частью первого члена феноменологической
формулы для восприимчивости D.89). Различие с теорией,
изложенной в гл. 4, обусловлено вкладом в Imx(co)
второго члена выражения D.89). В более точной теории
соответствующий вклад равен нулю, поскольку параметр
у(—со) для положительных частот обращается в нуль,
как и в (8.139). Однако для частот со, близких к соо,
второй член выражения D.89) очень мал по сравнению с
первым членом, поэтому феноменологический результат
близок к выражению (8.143). Основной вывод из более
точного рассмотрения заключается в том, что для узких
линий поглощения (т. е. у <С соо) учет затухания,
обусловленного спонтанным излучением, посредством
добавления мнимой части iy к частоте со в выражение для
восприимчивости без затухания является очень хорошим
приближением-, если величина у определяется
соответствующим коэффициентом Эйнштейна Л, как в формуле
(8.137).
В случае точного резонанса (со = соо) выражение
(8.143) принимает вид
т , v Ate2|Di2|2 2kNc* NX3 fQ 1/|/П
Зе0йКу (со0) Fcdq AtCV
Здесь была использована формула (8.137), а X = 2яс/соо
есть длина волны излучения при резонансе. Этот
замечательный результат показывает, что мнимая часть
восприимчивости в максимуме линии поглощения зависит
только от концентрации атомов и длины волны
излучения и не зависит от всех микроскопических параметров,
связанных с атомным переходом.
Восприимчивость многоуровневых атомов,
зависящая от частоты
Восприимчивость, полученная выше на основе диаго-
нализации матрицы, относится к одному атомному
переходу между основным состоянием |1) и возбужденным
состоянием |2). Рассмотрим теперь более реальный
случай газа, состоящего из атомов, обладающих набором
возбужденных состояний, переход в которые из основ-
288
ГЛАВА 8
ного состояния разрешен в электрическом дипольном
приближении. Восприимчивость без учета затухания,
обусловленного спонтанным излучением, была получена
в D.79).
Электрический дипольный гамильтониан
взаимодействия для многоуровневого атома приводится в (8.93).
Как и в случае гамильтониана (8.103) для
двухуровневого атома, он снова может быть упрощен путем
сохранения только тех членов взаимодействия, для которых
поглощение фотона сопровождается переходом атома на
более высокий уровень, а испускание фотона —
переходом атома на более низкий уровень.
Спектр поглощения атома определяется мнимой
частью восприимчивости, поэтому мы рассмотрим только
эту часть восприимчивости. К сожалению, при расчете
многоуровневой системы довольно трудно учесть
эффекты спонтанного излучения с той же точностью, что и
в двухуровневом случае. Метод диагонализации
матрицы для многоуровневого атома становится очень
громоздким, поэтому предпочтительней использование
других методов, принадлежащих области теории многих
частиц. Однако эта теория выходит за пределы
настоящей книги и необходимые результаты для
многоуровневого атома будут приводиться без доказательства.
Обобщение формулы (8.143) на случай
многоуровневого атома имеет вид
0)£ < О)
ImX((o) = £
где
Ne* (о — OfK
18jte§VfiV
у \Ofl\\Dn\
Zj и, — <о— IV,- (со)
СОу <0)
(.л- V 1
*\Dt ,?(*-<,>,?
(8.145)
бЯБпЙС3
(8.146)
Восприимчивость многоуровневого атома переходит в
выражение (8.143) в случае двухуровневого атома, где
накладываемые на матричные элементы Т>ц и D*i
ограничения по четности приводят к тому, что индекс i может
относиться только к состоянию 2, а индекс / — только к
состоянию 1. Аналогично в (8.146) индекс / может
обозначать только состояние 1, а индекс i — только состояние
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 289
2, и параметр ширины линии Y2(w) идентичен параметру
Y((o), определенному в (8.137).
Вид мнимой части восприимчивости (8.145)
показывает, что максимум поглощения соответствует случаю,
когда со равна одной из частот возбуждения со*. Это,
конечно, является ожидаемым свойством восприимчивости
многоуровневого атома, которое также справедливо и
для классического результата D.22). Однако в отличие
от классического результата восприимчивость (8.145) не
может быть строго записана в виде суммы отдельных
вкладов возбужденных состояний, разрешенных в
электрическом дипольном приближении, поскольку квадрат
модуля содержит смешанные члены, соответствующие
различным возбужденным состояниям атома.
Многоуровневая восприимчивость была записана в
наиболее строгом виде (8.145) для последующего
использования в гл. 11 при рассмотрении рассеяния света
атомами. Эксперименты по рассеянию света обычно
проводятся со светом, частота которого лежит между
частотами атомных резонансов со*, где эффекты
интерференции между различными возбужденными состояниями
дают большой вклад в сечение рассеяния.
С другой стороны, эксперименты по поглощению
обычно связаны с измерением на частотах со, близких к
резонансным частотам (ог-, где существен вклад только
одного данного возбужденного состояния, а вкладом всех
остальных уровней можно пренебречь. Действительно,
сколько-нибудь существенное поглощение на частотах,
лежащих между резонансными частотами, где величина
Im%((o) мала, обычно обнаружить трудно. В этих
условиях эксперимент по поглощению должен зафиксировать
слабое изменение интенсивности проходящего пучка
света, вызываемое атомами, тогда как в эксперименте
по рассеянию наблюдается непосредственно теряемый
пучком свет, который незамаскирован относительно
большой интенсивностью исходного пучка. Следовательно,
эксперимент по рассеянию света принципиально является
более чувствительным методом изучения Imx(co) на
частотах со, лежащих между частотами атомных
резонансов, как это далее обсуждается в гл. 11.
Ю Зак. 885
290
ГЛАВА 8
В случае вычисления спектра поглощения, где частота
со всегда близка к одной из частот сог-,
интерференционен.
со
У*
"'54
чУи
"У52
751
Сл>,
Уб5
-<*5
t Ув4
"У63
"Уб2
0}4
CJ,
Уб1
У5
Ув
ш1
Фиг. 8.4. Отдельные вклады в полные параметры ширин линии уъ (со)
и Ye (о>) Двух энергетических уровней атома, где ю5 < со и соб > со.
Горизонтальные линии изображают уровни атома, вертикальные линии
—возможные переходы, дающие вклад в полные параметры.
ными, или кросс-членами, в выражении (8.145) можно
пренебречь и получить
ЫШ-^Y. |Р"'>A.. (8.147)
Зе0Й7
(со; — со) -t-Yj(co)
Здесь была использована формула (8.146) с учетом
того, что индексы / в (8.145) и / в (8.146) пробегают
один и тот же набор атомных состояний.
ВЗАИМОДЕЙСТВИЕ ПОЛЯ ИЗЛУЧЕНИЯ С АТОМОМ 291
Теперь восприимчивость многоуровневого атома
представлена в виде суммы членов, каждый из которых
аналогичен восприимчивости двухуровневого атома (8.143),
Параметр ширины линии для каждого уровня равен
сумме вкладов от всех состояний с меньшей энергией.
Полный параметр ширины линии yi(<o) полезно
представить в виде суммы отдельных вкладов
Y*(co)= Z Yi/И, (8.148)
где
и полный параметр согласуется с выражением (8.146).
Сравнение с формулой C.58), справедливой в общем
случае для любой пары уровней, дает
2уиЫ = Аи. (8.150)
Таким образом, ширина уровня возбужденного
состояния многоуровневого атома получается обобщением
результата (8.142), в котором суммируются скорости
спонтанного перехода на все уровни, лежащие ниже данного.
На фиг. 8.4 показаны вклады в полные параметры
ширин линий от двух уровней атома, причем частота
одного из них больше со, а частота другого меньше со.
ЛИТЕРАТУРА
1. Power E. Л., Introductory quantum electrodynamics, Longmans,
London, 1964.
2. Atkins P. W., Woolley R. G., Proc. Roy. Soc, A319, 549 A970).
3. Dicke R. H.y Wittke J. P., Introduction to quantum mechanics, Ad-
dison-Wesley, Reading, 1960.
4. Goldstein //., Classical mechanics, Addison-Wesley, Reading, 1950.
(См. перевод: Г. Голдстейн, Классическая механика, Гостехиздат,
1957.)
5. Lorentz H. A.f The theory of electrons, Dover, New York, 1952,
p. 14. (См. первод: Г. А. Лорентц, Теория электронов,
Гостехиздат, 1956.)
6. Fiutak /., Can. Journ. Phys., 41, 12 A963).
7. Hansen Л. £., Amer. Journ. Phys., 39, 653 A971).
8. Bethe H. A., Salpeter E. £., Quantum mechanics of one- and two-
electron atoms, Springer-Verlag, Berlin 1957, section 66. (См, пе-
10*
292
ГЛАВА 8
ревод: Г. А. Бете, Э. Солпитер, Квантовая механика атома с
одним и двумя электронами, Физматгиз, 1960.)
9. Condon Е. U., Shortley G. #., The theory of atomic spectra,
Pergamon, Oxford, 1967, p. 78. (См. перевод: Е. Кондон, Г. Шортли,
Теория атомных спектров, ИЛ, 1949.)
10. Hindmarsh W. R., Atomic spectra, Pergamon, Oxford, 1967, p. 78.
11. Ziman J. M., Electronics of advanced quantum theory, University
Press, Cambridge, 1969, Ch. 3.
12. Margenaw #., Murphy G. M., The mathematics of physics and
chemistry, Van Nostrand, Princeton, 1956, Ch. 10.
13. Bethe H. Л., Phys. Rev., 72, 339 A947).
14. Quantum electrodynamics ed. J. Schwinger, Dover, New York,
1958, p. 139.
15. Sakurai J. /., Advanced quantum mechanics, Addison-Wesley,
Reading, 1967.
16. Power E. Л., Zienau S., Phil. Trans. Roy. Soc, 251, 427 A959).
Глава 9
Оптика фотонов
Цель настоящей главы заключается в рассмотрении
теории различных оптических экспериментов, которые
могут быть проанализированы в рамках квантовой
теории света. Квантование поля излучения требует
пересмотра определения когерентных свойств. Классическая
теория, описанная в гл. 5, основана на предположении о
том, что электрическое поле Е может быть в принципе
измерено в произвольной точке светового пучка.
Изложение квантовой теории когерентности должно
начинаться с исследования вопроса о том, до какой степени
в этой теории можно действительно определить
электрическое поле светового пучка. Для понимания свойств
светового пучка, доступных измерению, необходимо
проанализировать квантовую теорию прибора, используемого
для измерения параметров световых пучков.
Квантовомеханический анализ оптических
экспериментов имеет два основных следствия. Во-первых, он
дает более глубокое понимание классических
интерференционных экспериментов, но при этом показывает, что
в общем случае квантование электромагнитного поля
очень мало влияет на наблюдаемые явления в таких
экспериментах. Во-вторых, квантование ведет к
возможности проведения экспериментов нового типа, где
измеряются распределения фотонов в световых пучках. Эти
эксперименты лежат в основе наблюдений в квантовой
оптике; они включают прямое детектирование фотонов,
а поэтому лежат за переделами классической оптики.
294
ГЛАВА 9
Фотоэффект
Действие почти всех устройств, измеряющих
интенсивность светового пучка, основано на поглощении части
светового пучка, энергия которой преобразуется в другой
вид энергии. К этой категории относятся фотопластинка,
фотоумножитель и болометр. Для определения точного
вида квантовомеханического оператора, описывающего
наблюдаемую интенсивность, полезно детально
рассмотреть процесс измерения интенсивности. В гл. 6 было
показано, что определенная стандартным образом энергия
поля содержит бесконечную энергию нулевых колебаний,
поэтому важно отчетливо показать, что любое
экспериментальное измерение интенсивности не зависит от этой
бесконечной энергии.
Удобно ограничиться подробным анализом одного из
применяемых устройств. В качестве объекта анализа
выберем фотоумножитель, или фотодетектор. Такой же
анализ применим к другим методам измерения
интенсивности. Действие фотодетектора основано на
фотоэффекте, при котором поглощение атомом фотона вызывает
возбуждение электрона из связанного состояния в
свободное состояние, что позволяет ему совсем покинуть
атом. Фотодетектор представляет собой в сущности
такое устройство, при помощи которого освобожденный
электрон посредством лавинного процесса создает
другие свободные электроны, до тех пор пока электронный
ток не достигнет величины, достаточной для измерения.
,С помощью тщательно сконструированных
фотодетекторов возможна регистрация процессов ионизации атомов
отдельными фотонами. Фотодетектор позволяет
определить интенсивность светового пучка, измеряя скорость
ионизации атомов, которая в свою очередь
пропорциональна скорости попадания фотонов на фотодетектор и4
следовательно, интенсивности пучка.
Рассмотрим скорость ионизации отдельного атома в
фотодетекторе пучком фотонов. Теория фотоэффекта
похожа на вычисление скорости поглощения фотонов,
приведенное в гл. 8, но только в данном случае электрон в
конечном атомном состоянии может покинуть атом.
Простейшим возможным примером служит ионизация атома
ОПТИКА ФОТОНОВ
295
водорода в основном состоянии 15 при поглощении
фотона с волновым вектором к, частотой сок и поляризацией
е^. Величина волнового вектора q освобожденного
электрона определяется законом сохранения энергии
Йсок = йю* + (ЛУ/2/я), (9.1)
где Ьсоя — энергия основного состояния водорода,
определенная в C.29)
H(oR = те4/32пЦН2 = Щ2та\. (9.2)
Здесь а0 — боровский радиус, определенный в C.15).
Строго говоря, волновой функцией конечного
состояния электрона должно быть одно из решений,
принадлежащих непрерывному спектру уравнения Шредингера
для атома водорода. Однако эти решения математически
сложны, поэтому мы используем приближенную
волновую функцию, справедливую в том случае, когда энергия
фотона много больше начальной энергии связи
электрона
ЙС0к ^ ЙСОя. (9.3)
В этом случае кинетическая энергия свободного
электрона намного больше кулоновской энергии связи йсод, и
в хорошем приближении можно пренебречь влиянием ку-
лоновского потенциала на волновую функцию свободного
электрона. Тогда в качестве волновой функции конечного
состояния можно взять плоскую волну
^ = J/-,/2exp(/q.r). (9.4)
Отметим, что из неравенства (9.3) и формул (9.1) и
(9.2) следует
q > 1/а0, (9.5)
и длина волны свободного электрона много меньше бо-
ровского радиуса.
Предполагается, однако, что длина волны падающего
фотона намного больше а0. Например, если величина
i«k порядка 100 йсоя, то простая оценка дает, что длина
волны фотона
Л = 2я/6^10~"9 м (9.6)
296
ГЛАВА 9
намного больше боровского радиуса, равного 5-10~п м.
Поэтому взаимодействие между излучением и атомом
можно рассматривать в электрическом дипольном
приближении, в котором координата электрона, входящая
в оператор электрического поля, заменена координатой
атомного ядра. Для последующего обсуждения
когерентности удобно принять, что ядро расположено не в начале
системы координат, как это считалось раньше, а в
некоторой точке, определяемой вектором гь Тогда оператор
электрического дипольного взаимодействия (8.48)
запишется в виде
3%ED = er-ET(rl), (9.7)
где г — вектор, определяющий положение единственного
электрона относительно ядра водорода.
В вычислениях настоящей главы используется
смешанное представление, в котором операторы
электромагнитного поля зависят от времени. Оператор
электрического поля, определенный в F.106) и F.108), удобно
разделить на две части. Для момента времени t\
положим
Ёг {T{t{) = Ё+ (гА) + Ё~ (гА), ' (9.8)
где
Ё+ (г,*!) = / X (fi(Ok/2e0l/)V2ekdk ехр (— шф + & • г,) (9.9)
к
И
^(r^) = -/Z (A©k/2e0^)Vf MkeXP04'l - * * ri)« (9Л°)
Процесс поглощения фотона, сопровождаемый
возбуждением фотоэлектрона в момент tu описывается
диаграммой, сходной с диаграммой фиг. 8.1,6, а
соответствующий матричный элемент похож на матричный
элемент (8.71). Прежде всего мы предположим, что фотоны
первоначально находятся в состоянии | Пк) с точно
определенным числом фотонов. Если \Rf) есть фотонное
состояние после фотоэлектронной эмиссии, то матричный
элемент процесса определяется выражением
(f I #bd 10=<#/> ч k • [Ё+ (v.) + r OvOl In» IS>-
(9.11)
ОПТИКА ФОТОНОВ
297
Очевидно, что конечное электронное состояние
обладает большей энергией, чем начальное, поэтому реальные
переходы возможны только для процессов, в которых
происходит поглощение энергии электромагнитного поля.
Следовательно, только компонента электрического поля,
содержащая операторы уничтожения фотонов, дает
х
Электрон
kbk
Фотон
4(Лр)
Атом
+~z
Фиг. 9.1. Система координат, используемая при вычислении
скорости фотоэлектронной эмиссии.
вклад, отличный от нуля, и матричный элемент после
факторизации принимает вид
(/1 ^ed Ю = в (R, | Е+ (г,/,) | лк> • <q | г | IS). (9.12)
Исследуем сначала атомную часть матричного эле-
' мента, для которой необходимые волновые функции
приведены в (9.4) и C.25). Рассмотрим систему координат,
в которой волновые векторы падающих фотонов
параллельны оси г, а их векторы поляризации параллельны
оси х, как показано на фиг. 9.1. Направление волнового
вектора эмиттированного фотоэлектрона определяется
сферическими полярными углами G и <р, причем направ-
298
ГЛАВА 9
ление оси z выбрано в качестве полярной оси, а
азимутальный угол ф измеряется от оси х.
Задача 9.1. Докажите, что
/ , ИО\ . 32л'2q , sin 9 cos©
<q|ek.r|lS> = — i ~
^4* tf+ajj
/32я '2 sin 8 cos ф
V2„6/2/75
Vl2aj2q
(9.13)
Здесь на последнем этапе было использовано
неравенство (9.5).
Теперь скорость перехода для фотоэффекта можно
получить с помощью золотого правила Ферми (8.83).
Вычислим полную скорость перехода 1/т для всех
процессов, в которых фотоны с частотой сок поглощаются
атомами и вызывают эмиссию электрона. В соответствии
с (8.83) мы должны просуммировать по всем конечным
фотонным состояниям \Rf) и учесть все конечные
волновые векторы электрона q. Тогда из (9.12) и (9.13)
1 2яГ> Г»|/п ,й+/ п, ч 12 210яе2 sin2 0 cos2 ф ч,
v=^L Ll^f|E (ri<i)ink>i —Vay0 x
Rf q
Ь bq-
\ 2ma'd 2m J
(9.14)
Измерение фотонной интенсивности
Рассмотрим зависимость скорости фотоэлектронных
переходов от поля излучения. Согласно (9.14),
электромагнитное поле входит в выражение для скорости
перехода через множитель
Z|(i?f|£+(ri^i)|nk>|2 =
= Е </*k I Ё~ (Т&) I Rf) (Rf IE+ {nti) | nk>. (9.15)
Rf
Суммирование в принципе производится по всем
возможным состояниям поля излучения, причем любые
ограничения на конечное состояние обусловлены свойствами
ОПТИКА ФОТОНОВ
299
матричных элементов Ё+ и £~", а не ограничением на
суммирование по Rf. Следовательно, к состояниям поля
излучения можно применить условие полноты D.100)
£| *,)<*, 1=1- (9.16)
На основе соотношения (9.16) уравнение (9.15)
преобразуется к виду
Z | (Rf | Ё+ (nti) | пк) |2 = | <лк | Ё~ {пи) Ё+ (nti) | пк). (9.17)
Скорость, с которой атом под действием поля
излучения в состоянии |nk) испускает фотоэлектроны,
пропорциональна, таким образом, ожидаемому значению
оператора E-(rit\)E+(riti) в состоянии |як). Если
интенсивность светового пучка определяется по измерению
тока, созданного пучком в фотодетекторе, то оператор,
соответствующий наблюдаемой интенсивности, есть
E-(rit\)E+(r\ti) с некоторым численным коэффициентом.
Для одномодового светового пучка, где все фотоны
имеют одинаковый волновой_вектор к, наблюдаемую
интенсивность светового пучка I можно определить
следующим образом:
I = Bе0Л/сок) (пк | Ё~ (nti) Ё+ (vitx) \ пк). (9.18)
В одномодовом случае из (9.9) и (9.10) следует, что
И' (г,/,) Ё+ (г,/,) = (К/Ч^)Кйк = (Н/2во^) V (9-19>
Здесь пк— оператор числа фотонов. Тогда
(пк | £" (rrfi) Ё+ (nti) | пк) = (Йсок/2еоЮ пк. (9.20)
Отсюда наблюдаемая интенсивность пучка (9.18) дается
выражением
Г= {c2hk/V) nk, (9.21)
которое полностью аналогично F.117), но только вклад
нулевых колебаний исключен.
Отметим, что в одномодовом случае интенсивность I
не зависит от Т\ и t\. Квантовомеханическая
интенсивность пучка, введенная в (9.18), аналогична усредненной
300
ГЛАВА 9
по большому промежутку времени классической
интенсивности I, введенной в гл. 5. Из (9.20) видно, что отклик
фотодетектора пропорционален средней плотности
фотонов в световом пучке.
До сих пор вычисление 1/т относилось к полю
излучения, находящемуся в некотором чистом состоянии \п^)у
однако результаты легко обобщить на случай
статистически смешанного состояния. Пусть вероятность
нахождения пучка в начальном состоянии \п^) определяется
вероятностью PrtJc. Формула (9.14) для скорости
перехода по-прежнему справедлива, но только различные
компоненты \пк) начального состояния должны быть
просуммированы с весом Рпк. Обобщение формулы
(9.17) можно записать следующим образом:
Z Рпк ("к IE' (nti) E+ (nti) | пк) = Sp [p£~ {nti) £+ (ri*i)],
пк
(9.22)
где р — оператор плотности, определенный в G.81). Здесь
было использовано равенство выражений G.81) и G.77).
В случае одномодового пучка обобщение формулы
(9.18) имеет вид
Г= Bе0с2к/сок) Sp [p£- (г,/,) Ё+ (г^,)]. (9.23)
Наблюдаемая интенсивность по-прежнему не зависит от
И и tu поэтому выражения (9.21) и (9.22) также
справедливы, если величину пк заменить средним числом
фотонов п в статистической смеси
п = Z Рпкпк. (9.24)
пк
Если возбуждено больше одной моды, то при
условии параллельности волновых векторов различных
фотонов интенсивность, наблюдаемая с помощью
фотодетектора, дается выражением
ИгА) = 2г0с Sp [р£~ (г^) Ё+ (r{t{)l (9.25)
которое теперь зависит от Т\ и t\. Однако для пучка с
узким частотным распределением произведение операторов
Ё~ё+ не содержит слагаемых, осциллирующих со средней
частотой пучка. Квантовомеханическая интенсивность
ОПТИКА ФОТОНОВ
301
(9.25) аналогична усредненной по периоду классической
интенсивности I(t), определенной в E.30). В этом
случае для получения аналога классической интенсивности
7 необходимо усреднение интенсивности 7(r^i) no
большому промежутку времени.
Интенсивность, измеряемая фотодетектором,
пропорциональна ожидаемому значению произведения
операторов £_£+. Этот отклик не пропорционален ожидаемой
величине оператора ЕЁ, вычисленной в F.111) и
содержащей вклад нулевых колебаний от каждой моды к поля
излучения независимо от того, содержатся в пучке
фотоны данной моды к или нет. Следовательно, можно
утверждать, что энергия нулевых колебаний не дает никакого
вклада в наблюдаемую энергию поля, которая всегда
определяется величиной %' из F.123), а не <% из F.114).
Теперь мы вернемся к вычислению скорости
фотоэлектронного перехода (9.14), которая принимает вид
t=L г^от 4Wk"l^J- (9-26)
г^ЬаУ
Здесь были использованы формулы (9.17) и (9.21), а в
б-функции опущен член h2/2mal в соответствии с
неравенством (9.5).
Суммирование по q можно заменить интегрированием
таким же образом, как в A.31). Пусть dQ— элемент
телесного угла, внутри которого лежит вектор q. Тогда
£ -* is? \ \ ? didQ- (9-27)
q
Здесь множитель 2, введенный в A.31) и учитывающий
две независимые поляризации фотона, должен быть
опущен, поскольку фотоэлектрон не имеет поляризации.
Вычисляя интеграл по q на основе свойства б-функции
C.70), получаем следующее выражение для скорости
перехода (9.26):
1 Г / 2т \11г Ae2hzh sin2 6 cos2 го _,~ /Г1 ЛОЧ
7=\ ("Г") т/ 4 5 */, dQ- (9«28)
Экспериментальные и теоретические результаты по
величине фотоэффекта обычно приводятся в виде попе-
302
ГЛАВА 9
речного сечения а, а не скорости перехода 1/т.
Поперечное сечение имеет размерность площади и определяется
как отношение скорости потерь энергии светового пучка,
обусловленных фотоэффектом, к скорости потока
энергии пучка фотонов через единичную площадь,
перпендикулярную к направлению его распространения. Скорость
потерь энергии равна ficok/т, интенсивность пучка,
согласно (9.21), равна cha^n/V, следовательно,
о = V/xnc (9.29)
и выражение для а легко получить из (9.28).
Дифференциальное поперечное сечение определяется
так же, как и поперечное сечение, только оно относится
к скорости потерь энергии фотонного пучка на
возбуждение фотоэлектронов с волновым вектором q, лежащим
в телесном угле dQ. Дифференциальное поперечное
сечение находится путем дифференцирования о по Q.
В результате из (9.28) и (9.29) получим
da /2m \V* Ае2Ьъ sin2 8 cos2 ф ,Q on\
dil \ Ь ) л;е0ст4а^(о^2
Основными свойствами дифференциального
поперечного сечения являются обратная пропорциональность его
величины частоте фотона в степени 7/г и
предсказываемая угловая зависимость. Наиболее вероятное
направление эмиссии электрона параллельно вектору
поляризации фотона, и дифференциальное поперечное сечение
уменьшается до нуля, когда вектор q перпендикулярен
efc. На высоких частотах, где поперечное сечение
фотоэффекта мало, наиболее вероятно рассеяние фотонов, а
не их поглощение в процессе фотоэффекта. Комптонов-
ское рассеяние фотонов на электронах кратко
обсуждается в гл. 11.
Необходимо подчеркнуть, что теория, приводящая к
формуле (9.30), является приближенной, причем
основное приближение состоит в использовании плоской волны
(9.4) в качестве волновой функции фотоэлектрона.
Точная кулоновская функция дает несколько отличные
результаты [1]. Наиболее сильное отличие проявляется в
том случае, когда энергия /ко^ лишь немного больше
пороговой величины ft(ort и волновые функции свободного
ОПТИКА ФОТОНОВ
303
состояния совсем не похожи на плоские волны.
Отклонение приближения (9.30) от точного результата при
малых значениях fiook показано на фиг. 9.2. Приближенная
теория также непригодна на больших частотах, когда
величина 1/6 становится сравнимой с боровским радиу-
\
\
CJ
5:
<*j
§•
с:
\
Г \
\ \
\ \
\ \
\ \
-\ \
\ N
\ \
\ \
X. ^
\^ ^^
^"Чц^ v*^
^*^^| *^«*.вв
1 1 1 -
1
J
u>K/o)R
Фиг. 9.2. Поперечное сечение фотоэффекта в произвольных
единицах как функция частоты фотона.
На графике показана лишь низкочастотная область, где энергия фотона не
слишком велика по сравнению с энергией связи электрона. Сплошная кривая
соответствует точному результату из [1], пунктирная кривая —приближенному
результату (9.30).
сом и электрическое дипольное приближение
неприменимо или когда энергия ficok становится сравнимой с тс2
и необходимо использовать релятивистские волновые
функции.
Тем не менее приближенная теория достаточно
реалистична для того, чтобы передавать основные свойства
фотоэффекта. Главная цель обсуждения этого эффекта
заключается в определении сущности измерения
световой интенсивности с помощью фотодетектора.
Использование лучшего приближения для волновых функций или
304
ГЛАВА 9
рассмотрение вместо .атома водорода какого-либо
другого атома изменяет лишь атомную часть скорости
перехода, а вывод о том, что состояние поля излучения
входит в скорость перехода через множитель, определенный
в (9.21) или (9.23), остается справедливым. Анализ
других типов устройств для измерения интенсивности
приводит к прежнему выводу о том, что наблюдаемая
интенсивность описывается оператором вида Ё~Ё+ с
некоторым алгебраическим множителем.
Когерентные свойства фотонов
Квантовомеханическое описание измерения
интенсивности светового пучка можно использовать при
получении теоретических выражений для любых
экспериментально измеримых величин, зависящих от интенсивности
световых пучков. Мы рассмотрим переход к квантовоме-
ханической теории интерференционных экспериментов.
Классическое описание этих экспериментов дано в гл. 5,
где показано, что величины, измеряемые в
интерференционных экспериментах, зависят от первой, второй или
более высоких степеней когерентности используемого
светового пучка. Квантовая теория интерференции
соответственно описывается на основе подходящим образом
определенных квантовомеханических степеней
когерентности !).
Рассмотрим сначала интерференционный эксперимент
Юнга, классическое описание которого дано в гл. 5.
Можно провести параллельное квантовомеханическое
описание этого эксперимента, рассматривая на
фотодетекторе или каком-либо другом приемнике света,
расположенном в некоторой точке экрана наблюдения,
суперпозицию полей излучения от двух небольших отверстий.
Теория такой суперпозиции во многом сходна с
классическим анализом, с той лишь разницей, что классичес-
ская интенсивность, пропорциональная среднему по
ансамблю от £*£, должна быть заменена откликом кван-
1) Начало квантовой теории когерентности было в основном
положено Р. Глаубером. Подробности можно найти в его работах,
опубликованных в сборниках [2, 3].
ОПТИКА ФОТОНОВ
305
товомеханического детектора, пропорциональным
среднему значению оператора интенсивности В~Ё+.
Соответствующие вычисления приводят к квантовоме-
ханической степени когерентности первого порядка,
аналогичной классическому выражению E.74) и
определяемой формулой
В № V2j-g12 [(g-(Ml)g+{Ml)>(g-(r2/a)g+(raW>]V,
(9.31)
Здесь мы использовали для степени когерентности
первого порядка точно такое же обозначение, что и в
классическом случае, и эта величина сохраняет свой
физический смысл как мера способности света в
пространственно-временных точках (v\t\) и (г2^) образовывать при
сложении полей интерференционную картину. Угловые
скобки в правой части выражения (9.31), как и в
классическом выражении, обозначают усреднение по
ансамблю, но само усреднение проводится в соответствии с
формулой G.85):
(Ё- (г,*,) Ё+ (r2t2)) = Sp [рЁ~ (гА) £+ (г2/2)]. ■ (9.32)
Аналогично производится усреднение по ансамблю в
знаменателе. В специальном случае, когда фотоны
находятся в чистом состоянии, три средних по ансамблю в
(9.31) сводятся к ожидаемым значениям тех же
комбинаций операторов.
, Общие свойства квантовомеханической когерентности
первого порядка иллюстрируются рассмотрением
некоторых простых специальных случаев.
Задача 9.2. Докажите, что световой пучок, состоящий из
одной моды излучения, возбужденной в
состояние \п) или когерентное состояние |а),
имеет когерентность первого порядка, т. е.
для всех пар пространственно-временных
точек gW = 1.
Покажите, что мода, возбужденная в
произвольное чистое состояние, имеет
когерентность первого порядка. Этот результат можно
получить с помощью разложения чистого со-
306
ГЛАВА 9
стояния по полному набору состояний с
точно определенным числом фотонов \п).
Задача 9.3. Докажите, что мода излучения,
возбужденная в произвольное статистически смешанное
состояние, имеет когерентность первого
порядка. Этот результат можно доказать с
помощью вычисления величины g\1^ для
произвольного одномодового оператора
плотности р с учетом в разложении Ё~ и £+только
членов, относящихся к возбужденной моде.
Полученные результаты показывают, что любое одно-
модовое возбуждение имеет когерентность первого
порядка. Это свойство является общим как для квантово-
механического, так и для классического определения
когерентности первого порядка.
Квантовомеханические когерентные свойства
световых пучков, состоящих из нескольких возбужденных мод,
более разнообразны.
Задача 9.4. Рассмотрите возбуждение полного поля в
состояние |{ак}), определенное в G.102), в
котором каждая мода находится в
когерентном состоянии. Используя основное свойство
когерентных состояний G.52), докажите, что
|{ак}) когерентно в первом порядке.
Хотя чистое состояние |{ctk}) имеет полную
когерентность первого порядка, тем не менее это не является
общим свойством чистых состояний, в которых
возбуждено больше одной моды. Следующая задача
иллюстрирует данное утверждение простым примером.
Задача 9.5. Рассмотрите чистое состояние, в котором
один фотон возбужден в каждую из двух
мод kj и к2, причем соответствующие частоты
равны coi и «2- Докажите, что степень
когерентности первого порядка определяется
выражением
£</2) = [2@^ cos {(k, - к2) . (г, - г2) -
. ~ (<°i — ®2) (?i ~" Я) + ®i + ®i]y,/(®i + ®г)-
(9.33)
ОПТИКА ФОТОНОВ
307
Свет когерентен в первом порядке для
любой пары пространственно-временных точек
только тогда, когда два фотона находятся
в одной моде.
Классический результат, заключающийся в том, что
свет когерентен в первом порядке, если поле может быть
точно определено без использования статистики,
переходит в квантовую механику в виде утверждения о том, что
любое чистое состояние вида |{aij) когерентно в первом
порядке. Квантовомеханическая когерентность первого
порядка не является общим свойством многомодовых
чистых состояний.
Степень когерентности первого порядка многомодовой
статистической смеси можно легко определить из (9.31),
если известен оператор плотности. Особенный интерес
представляет случай хаотического света, для которого
оператор плотности определен в G.111). Степень
классической когерентности первого порядка для хаотического
света была вычислена в E.75).
Задача 9.6. Рассмотрите хаотический световой пучок с
оператором плотности р, определенным в
G.111). Докажите, что степень
когерентности первого порядка определяется
следующей формулой:
«12
Z ак®к ехр очт)
к
к
(9.34)
где
x = U — *2 — A/©к) к-(Г! — Га). (9.35)
Если пучок имеет лоренцево распределени
частот, при котором, как и в G.115),
ttkO>k
/*^/
(°>о - икJ + У'
(9.36)
308
ГЛАВА 9
и все волновые векторы параллельны, то
покажите, что
g$=exp(-YM). (9.37)
Это выражение эквивалентно классическому результату
E.75). Классический и квантовомеханический выводы
степени когерентности первого порядка для хаотического
светового пучка приводят к одинаковым результатам.
Подводя итоги, можно сказать, что в некоторых
случаях, включая хаотический и когерентный свет, причем
последний в квантовой механике описывается
состояниями |{ак}), приведенные выше результаты
подтверждают выводы классической теории для экспериментов,
зависящих от когерентности первого порядка.
Когерентные свойства состояний |{ак}\еще больше увеличивают
их сходство со стационарными волнами классической
теории, на что было указано раньше в гл. 7. Однако
интерференционные свойства других видов чистых
состояний, которые могут встретиться в квантовой механике,
должны определяться, как было показано на примере
задачи 9.5, квантовой когерентностью первого порядка.
Состояния |{ак}) являются специальным классом
состояний; другие виды квантовомеханических состояний не
всегда имеют классический аналог.
Когерентность высших порядков
Степень когерентности второго порядка, классическое
определение которой дано в E.99), определяется кван-
товомеханически таким же образом, как и степень
когерентности первого порядка. Когерентность второго
порядка' можно ввести, как и в гл. 5, на основе анализа
опыта Хенбери Брауна и Твисса. Интенсивности
измеряются фотодетекторами, как показано на фиг. 5.16, и
квантовомеханический анализ эксперимента должен
заключаться в вычислении скорости одновременной
регистрации фотонов двумя фотодетекторами. Вычисление по
схеме, описанной ранее в настоящей главе, снова
приводит к выражениям, сходным с выражениями
классической теории, с той лишь разницей, что произведения
ОПТИКА ФОТОНОВ
309
классических полей вида ЕЕ* заменяются произведением
пары операторов £~Ё+.
Эти вычисления ведут к следующему определению
квантовомеханической степени когерентности второго
порядка:
= (ё~ (Г|/,) Е- (r2t2) Е + (r2t2) Е+ (ntt)) (g 38,
<£-(г,*,J7 + (rltl))(E"(T2t2)E-¥ (га/а)> *
Здесь усреднение по ансамблю членов, стоящих в
угловых скобках, производится при помощи оператора
плотности, как и в (9.32). При новом определении
когерентности второго порядка отклик в эксперименте Хенбери
Брауна и Твисса остается пропорциональным g"^ — 1.
Детальный вывод формулы (9.38) здесь не приводится,
однако читатель может обратиться к теории скорости
одновременного поглощения двух фотонов, изложенной
в гл. 12, где пропорциональность между этой скоростью
и числителем выражения (9.38) получена более строго.
Когерентность второго порядка для различных одно-
модовых чистых состояний, описанных в гл. 7, вычислить
нетрудно. Результаты даны в следующих задачах.
Задача 9.7. Покажите, что состояние с определенным
числом фотонов \п) имеет следующую
степень когерентности второго порядка:
8А2 = "^~ ДЛЯ П>2>
п (9.39)
g$ = 0' для п = 0 или 1.
Эта величина всегда меньше единицы,
поэтому если бы можно было создать световой
пучок с определенным числом фотонов, то
в опыте Хенбери Брауна и Твисса была бы
получена отрицательная корреляция.
Задача 9.8. Покажите, что фазовое состояние |ф),
определенное в G.28), имеет следующую степень
когерентности второго порядка:
g<!>=4. (9.40)
310
ГЛАВА 9
Состояние с точно определенной фазой дает
положительную корреляцию в эксперименте
Хенбери Брауна и Твисса.
Задача 9.9, Докажите, что когерентное состояние |а)
имеет следующую степень когерентности
второго порядка:
£<|> = 1. (9.41)
Таким образом, согласно определению
E.100), состояние |а) когерентно во втором
порядке, а потому световой пучок в этом
состоянии дает в опыте Хенбери Брауна и
Твисса нулевую корреляцию.
Видно, что в отличие от когерентности первого
порядка, которая для одномодовых возбуждений всегда
равна единице, степень когерентности второго порядка
имеет разные значения для разных одномодовых
возбуждений.
Степень когерентности второго порядка для
статистических смесей в некоторых простейших случаях
вычислить нетрудно.
Задача 9.10, Рассмотрите хаотический световой пучок в
оптическом резонаторе, где по условию все
нормальные моды, кроме одной, исключены
с помощью фильтра, как и в задаче 5.5.
Оператор плотности для одной оставшейся
моды определен в G.107). Докажите, что
gf2> = 2. (9.42)
Степень когерентности второго порядка для
нефильтрованного хаотического пучка
исследуется в задаче 9.13.
Задача 9.11. Докажите, что степень когерентности
второго порядка любого одномодового
светового пучка можно выразить через среднее
число фотонов п и средний квадрат числа
фотонов п2 следующим образом;
gft = Eq±. (9.43)
ОПТИКА ФОТОНОВ
311
Вычисление когерентности второго порядка многомо-
довых возбуждений обычно значительно сложнее, и
поэтому мы исследуем только два предельных случая: мно-
гомодовое когерентное состояние и многомодовое
хаотическое состояние.
Задача 9.12. Рассмотрите определенное в G.102)
многомодовое возбуждение |{ак}), где каждая
мода находится в когерентном состоянии.
Используя оператор плотности G.103),
докажите, что
«$=1. (9.44)
Этот результат вместе с результатом
задачи 9.4 прзказывает, что состояние |{ccid)
когерентно во втором порядке.
Задача 9.13. Рассмотрите многомодовый хаотический
пучок, оператор плотности которого
определен в G.111). Докажите, что степень
когерентности второго порядка имеет вид
8\
B) =
Е якюк ехр (/о)кт)
к
(?ЯЛУ
+ l=(g(lI2)J+1-
(9.45)
Здесь была использована формула (9.34),
Квантовомеханическая когерентность
второго порядка хаотического светового пучка
совпадает с классическим выражением
E.101).
Как и в классической теории, степени когерентности
первого и второго порядков являются лишь первыми
членами в иерархии функций когерентности, и можно было
бы поставить обобщенный интерференционный
эксперимент, результат которого определялся бы когерентностью
произвольного порядка. Квантоврмеханическое определе-
312
ГЛАВА 9
ние когерентности n-го порядка, заменяющее
классическое определение E.106), имеет вид
_l(£""(r^i) ... Е" (rntn)E+ {Tn+jtn + i) ... Е+ (r2nt2n))\ .g ,
Степени когерентности первого и второго порядков,
определенные в (9.31) и (9.38), являются частными случаями
этого более общего определения.
Степень когерентности n-го порядка определяет
измеряемый отклик в эксперименте, где каким-либо способом
одновременно регистрируются п фотонов. Пример такого
эксперимента можно найти в гл. 12, где показано, что
скорость одновременного поглощения трех фотонов
светового пучка, сопровождаемого испусканием одного
фотона третьей гармоники, пропорциональна g{3\
Когерентность /г-го порядка имеет два простых
свойства, аналогичных классическим результатам E.107) и
E.108). Рассмотрим сначала многомодовое когерентное
состояние |{ак}). Из определения Ё+ в (9.9) и свойства
когерентных состояний G.52) следует, что |{оск}) —
собственное состояние оператора £+:
£+ (г*) i Ы> =
= i E [(ftcok/280FI/2 ак ехр (- mkt + /к • г)] | {ак}>. (9.47)
к
Следовательно, в случае чистого состояния |{<Хк})
числитель и знаменатель выражения (9.46) для g^
содержат произведения коэффициентов, похожих на члены в
квадратных скобках формулы (9.47) и их комплексное
сопряжение. Более тщательный анализ показывает, что
в действительности числитель и знаменатель идентичны,
и в результате получаем
g{n) (г^ь • •> ГА; гп+1*я+1, • • -I *2nhn) = 1 Для всех п.
(9.48)
Таким образом, квантовомеханическое когерентное
состояние имеет точно такие же когерентные свойства, что
и классическая стационарная волна, и является
когерентным во всех порядках. В любых интерференционных экс*
ОПТИКА ФОТОНОВ
313
периментах, как бы сложны они ни были, квантовомеха-
ническое когерентное состояние создает такие же
интерференционные картины и корреляции полей, какие
получились бы при расчете для классической
стационарной волны. Именно благодаря этому свойству базисные
состояния |а) получили название когерентных
состояний.
В противоположном пределе многомодового
хаотического состояния с оператором плотности, определенным
в G.111), величину gW нетрудно вычислить в частном
случае, когда все пространственно-временные точки в
(9.46) одинаковы. Согласно расчету, степень
когерентности п-то порядка равна /г!, как и в классическом
результате E.108). Действительно, все квантовомеханические
свойства хаотического света идентичны свойствам,
полученным в классической теории когерентности.
Теоретический анализ интерференционных экспериментов с
использованием хаотического света можно проводить равным
образом с помощью двух этих теорий.
Комбинации операторов ё~ и £+, усредняемые в
определениях степеней квантовомеханической
когерентности, всегда образованы таким образом, чтобы операторы
Ё+ находились справа от операторов ё~. Тогда, согласно
(9.9) и (9.10), операторы уничтожения стоят справа от
операторов рождения. Говорят, что произведение
операторов, обладающее этим свойством, имеет нормальную
форму (см., например, [4]). Это обусловлено тем, что,
как обсуждалось в этой главе ранее, действие детекторов
света определяется операторами уничтожения фотонов,
которые могут дать отклик только при наличии фотонов
в месте нахождения детектора.
Близкое сходство между когерентным состоянием и
классической стационарной волной не столь очевидно на
фиг. 7.3, на которой изображено электрическое поле
когерентного состояния, обладающее в отличие от точно
определенного электрического поля классической волны
на фиг. 5.10 некоторой неопределенностью. Различие
обусловлено использованием в уравнениях, приводящих
к фиг. 7.3, полного оператора электрического поля ё и
соответствующего учета вклада нулевых колебаний.
Замена в G.73) оператора Ё2 на Ё~Ё+ сводит неопределен-
314
ГЛАВА 9
ность электрического поля к нулю и приводит к полному
согласию между фиг. 7.3 и фиг. 5.10. Такие же замены
могут быть сделаны в гл. 7 при рассмотрении состояний
\п) и |ф). Однако исключение эффектов нулевых
колебаний дает лишь незначительное изменение свойств этих
состояний, а потому качественные выводы о природе
состояний \п) и |ф) остаются справедливыми.
Счет фотонов
Квантование поля излучения и существование
фотонов не только сохраняют общую интерпретацию
классических интерференционных экспериментов, но также
дают новый тип эксперимента, в котором измеряются те
же параметры светового пучка, что и в обычной
интерференции и в спектроскопии. Этот экспериментальный
метод называется счетом фотонов и в простейшем
варианте производится следующим образом.
Исследуемый световой пучок направляется на
фотодетектор, соединенный соответствующей электронной
схемой со счетчиком, который регистрирует число
фотонов, создающих фотоэлектронную эмиссию в
фотодетекторе. Затвор перед фотодетектором контролирует
промежуток времени, в течение которого свет падает на
детектор. При счетчике, установленном на нуль, затвор
открывается на время Т. Затем затвор закрывается и
записывается число сосчитанных фотонов т. Через отрезок
времени, больший времени когерентности, затвор снова
открывается и повторяется прежний эксперимент с
записью второго числа сосчитанных фотонов. Эксперимент
повторяется в третий раз и т. д., пока не накопится
большое количество данных, относящихся к числу фотонов,
сосчитанных в точение одинакового промежутка времени
Т. Полное число данных за все время эксперимента
может быть, например, порядка 104. Результаты можно
выразить в виде распределения вероятностей Рт(Т) для
отсчета m фотонов за время наблюдения Т.
Постоянно предполагается, что все измеряемые
световые пучки стационарны. Измеренное статистическое
распределение Рт(Т) содержит информацию о
статистических свойствах светового источника. Мы проанализ**
ОПТИКА ФОТОНОВ 315
руем эту информацию, а также способ извлечения этой
информации из результатов эксперимента по счету
фотонов.
Скорость фотоэлектронной эмиссии пропорциональна
интенсивности пучка, которая, согласно (9.42),
определяется средним значением произведения операторов
£~£+. Уже упоминалось, что наблюдаемая квантовомеха-
ническая интенсивность аналогична усредненной за
период классической интенсивности l(t), определенной в
E.30). Детальное вычисление распределения счета
фотонов проще всего провести, используя классическую
световую интенсивность пучка T(t). Соответствующий кван-
товомеханический результат будет приведен позже без
детального вывода.
Пусть p(t)dt есть вероятность того, что под действием
светового пучка некоторый атом в фотодетекторе
испустит электрон, регистрируемый счетчиком в виде
одиночного отсчета в течение временного интервала между t и
t + dt. Тогда в соответствии с (9.14) и (9.26) можно
записать
p{f)dt=U(t)dt, ^ (9.49)
где величина dt предполагается достаточно большой для
применимости теории вероятностей перехода {см.
дискуссию, предшествующую формуле C.51)], но достаточно
малой, для того чтобы вероятность испускания
электронов более чем одним атомом за время dt была
пренебрежимо мала. Константа пропорциональности £
характеризует эффективность фотодетектора. Она содержит
матричные элементы для фотоэлектрических процессов,
обсуждавшихся в этой главе ранее, и множители,
зависящие от плотности и положений ионизуемых атомов в
фотодетекторе.
Рассмотрим определенный период счета, длящийся от
t до t-\-T. Пусть Pm(t, T) есть вероятность отсчета m
фотонов за этот период. Искомое распределение Рт(Т)
определяется путем последующего усреднения по
большому числу различных начальных моментов времени t.
Пусть t-\-t' есть момент времени, лежащий в
интервале между t и / + Т, как показано на фиг. 9.3, и пусть
dt' есть короткий промежуток времени, подобный исполь-
316
ГЛАВА 9
зованному в (9.49). По определению, вероятность
отсчета т фотонов в интервале времени между / и t -f- V +
+ dtf равна
Pm(t,t' + dt'). (9.50)
Существуют, однако, две различные возможности
отсчета т фотонов за данный временной интервал: 1) в ин-
0
t4 df t+T
I I—I I
/77 О
>•< >
/77-/ 1
> < &
Фиг. 9.3. Временные интервалы, используемые при вычислении
Рт ttf Т)> показывающие две возможности отсчета т фотонов за
период между t и t + V + dt'.
тервале между t и t -\-V отсчитывается т фотонов и ни
одного фотона — за время dt\ с общей вероятностью
Pm(t,n[l-pV)df]\ (9.51)
2) в интервале между t и t-\-t' отсчитывается т—\
фотонов и один фотон — за время df, с общей
вероятностью
Pm^(t,f)p(f)dt\ (9.52)
Согласно нашему допущению, вероятность отсчета более
одного фотона за время df пренебрежимо мала.
Эти два способа вычисления вероятности отсчета т
фотонов в интервале времени между t и t -\-tf -{-df
должны быть эквивалентны, поэтому из формул (9.50) —
(9.52) получим
Рт (*, f + df) = Pm (t, П[1-р (f) df] +
+ Pm_! (*, f) p (f) df. (9.53)
Используя (9.49) и определение дифференцирования,
выражение (9.53) можно преобразовать к виду
d?m$ П - С/(О [P»-i С П - Рт (*, f) I (9.54)
ОПТИКА ФОТОНОВ
317
Таким образом, вероятности Pm{t, t') для разных
значений т связаны цепочкой дифференциальных уравнений.
Первое уравнение цепочки для т = О отличается от
общего результата тем, что в нем, конечно, отсутствует
член, содержащий Рт-\\
*^Ы1 = _ ЩП Р0 (/, П. (9.55)
Цепочку уравнений для Pm{t, t') можно решить ме
тодом последовательных исключений, начиная с т = 0.
Вероятность Po(t, t') подчиняется граничному условию,
заключающемуся в том, что вероятность отсчета фотона
за нулевой интервал времени, конечно, равна нулю:
Р0(*,0) = 1. (9.56)
•
Используя это граничное условие, уравнение (9.55)
можно проинтегрировать и получить
/
Г t + T -1
I-г 5/юл7 J.
t + T
Р0 (t, T) = ехр I -1[ 7(f) dt' I. (9.57)
Удобно определить среднюю за время счета
интенсивность света 7(/, Т), падающего на фотодетектор, как
t+T
I(t,T) = -jr\l{f)df, (9.58)
и на основе этого определения переписать (9.57)
следующим образом:
P0(t, T) = exp[-U{t,T)T]. (9.59)
Остальные вероятности Pm{t> T) можно определить
из (9.54), начиная с m = 1 и переходя к более высоким
значениям т. Дополнительное к (9.56) граничное
условие имеет вид
Лп(*,0) = 0, тфО. (9.60)
318
ГЛАВА 9
Задача 9.14. Докажите, что общее решение уравнения
(9.54) с граничным условием (9.60) дается
выражением
Рт (t, Т) =
= {U {t'mT{] T)m exp [- U(t, T) T]. (9.61)
Вероятность Pm(ty T) описывает распределение
показаний счетчика фотонов, полученных в серии
экспериментов, каждый из которых начинается в одно и то же
время /. На практике обычно возможно одновременное
проведение лишь одного измерения по счету фотонов.
Последующие периоды счета протекают прследовательно,
а не одновременно. Интенсивность 7(/, Г), вообще
говоря, флуктуирует от периода к периоду, как это
описывалось в гл. 5 для случая хаотического света.
Измеряемое распределение отсчетов фотонов Рт(Т) является
средним по большому числу различных начальных
моментов времени t, а поэтому мы можем записать1)
Pm{T) = {Pm{t,T))=_
= ({е/(/^)ГГ:ехр[-гёГ)Г1). (9.62)
Здесь в соответствии с обозначениями, принятыми в гл. 5,
угловые скобки означают усреднение по t.
Распределения фотонов для когерентного
и хаотического света
Распределение, приведенное в (9.62) для РШ(Т),
применимо к любому стационарному световому источнику.
Оно содержит усреднение по времени, которое можно
точно вычислить в некоторых специальных случаях.
Рассмотрим сначала простейший случай, когда I(t, T) не
зависит ни от tt ни от Г, и мы можем положить
T{t, T)=T. (9.63)
1) Распределение Рт(Т) было впервые получено в работах [5]*
ОПТИКА ФОТОНОВ
319
Следовательно, величина, которую следует усреднить в
(9.62), не зависит от параметра усреднения t и угловые
скобки можно опустить:
Рт (Т) = -^ ехр (- т). (9.64)
Здесь была введена величина
т = ЙТ. (9.65)
Распределение фотонов РШ(Т) для постоянной
интенсивности является, таким образом, пуассоновским
распределением, аналогичным распределению G.62),
причем среднее число сосчитанных фотонов m определено
в (9.65). Статистика отсчетов подобна статистике
падения дождевых капель при «стационарном» дождевом
потоке или статистике поступления частиц, испускаемых в
процессе радиактивного распада долгоживущего изотопа.
Вид пуассоновского распределения для трех значений
среднего числа отсчетов m приведен на фиг. 9.4.
Величина флуктуации счета фотонов около среднего значения
фотонов определяется корнем квадратным из
среднеквадратичного отклонения распределения Am. Алгебраически
вычисление Am точно такое же, как в G.58) — G.60),
только |а|2 заменяется на т, и потому
(AmJ = m. (9.66)
Флуктуации в пучке постоянной интенсивности
называются флуктуациями частиц. Они обусловлены
дискретной природой фотоэлектрического процесса, в котором
энергию из светового пучка можно забрать только в виде
целого числа фотонов. Из формул (9.65) и (9.66) видно,
что флуктуации частиц Am пропорциональны корню
квадратному из интенсивности пучка. Флуктуации частиц
являются внутренне присущим, неотъемлемым свойством
экспериментов по счету фотонов. Световые пучки
различаются по степени превышения флуктуации отсчетов над
величиной (9.66), а флуктуации частиц имеются всегда.
Полученные выше результаты для пучка с
постоянной интенсивностью, очевидно, применимы к
классической стационарной волне E.39), изображенной на
фиг. 5.10, и, как будет показано в этой главе позже, та-
320
ГЛАВА 9
кое же распределение справедливо для квантовомеха-
нического когерентного состояния.
Другой важный случай применимости распределения
(9.64) следует из того факта, что интенсивность I(t, T)
0,4 г
0,3
0,2
0,1
Б О
си5 0,2
0,1
О
0,2
*П-~: }
И.
1л
I I' ' ' 1 I I \ I I
/77=5"
П П п „
1111
0,1 ~
О
m = 10
п п П
Ли
0 1 2 J 4 5 6 7 8 9 10 11 12 13 Н 15
/77
Фиг. 9.4. Пуассоновская форма распределения фотоотсчетов для
световых пучков постоянной интенсивности.
Значения m являются средними числами фотонов, сосчитанных за период Т,
Отметим, что для пуассоновского распределения Р _ —Р_ ,.
m m—i
может быть постоянной даже при флуктуации величины
/(/). Так, для хаотического светового пучка с временем
когерентности тс, как видно из (9.58), величина I(t, T)
не зависит от ty если Т много больше тс, и все
флуктуации усредняются за большой период счета Т. Следова-
ОПТИКА ФОТОНОВ
321
тельно, равенство (9.63) справедливо для хаотического
света при Г>тсив этом пределе для него справедливо
пуассоновское распределение.
Распределение отсчетов фотонов для хаотического
света можно также легко вывести в другом предельном
случае, когда время счета меньше времени когерентно*
сти, т._е. Т <С тс. В этом пределе мгновенная
интенсивность I (t) в течение одного периода счета в основном
постоянна и выражение (9.58) принимает вид
7(t, Т) = T(t), Т < v (9.67)
Распределение вероятности p[T(t)] для мгновенной
интенсивности хаотического света приведено в E.36).
С помощью обычной эргодической гипотезы, которая для
стационарного светового источника предполагается
справедливой, усреднение по времени в (9.62) можно
заменить усреднением по ансамблю с распределением
Р 17@1» чт0 Дает
Рт (Г) = I I exp (- if) ЩШ1 ехр [_ сГ@ Т] Х
X dl{t) = A +%+т . (9.68)
Здесь величина in определяется из (9.65). Таким
образом, распределение фотоотсчетов для хаотического света
в случае коротких времен счета сходно с распределением
фотонов в одной моде теплового источника,
приведенным в A.68) и изображенным на фиг. 1.9. Однако
распределение фотоотсчетов (9.68) применимо не только для
одной возбужденной моды, но и в общем случае
произвольного хаотического света.
Значительно труднее определить вид распределения
фотоотсчетов для времен счета Г, которые не малы и не
велики по сравнению с временем когерентности тс
хаотического света. Не давая здесь деталей таких расчетов,
мы приведем на фиг. 9.5 некоторые вычисленные
распределения фотоотсчетов [6] для фиксированного среднего
числа сосчитанных фотонов in = 4. Графики показывают,
как непрерывно меняется вид распределения
вероятностей от (9.68) для Т < Тс до (9.64) для Т > тс.
И Зак. 885
322 ГЛАВА 9
Хотя полная функция распределения для
произвольных значений требует длительного расчета, величину
флуктуации числа сосчитанных фотонов хаотического
Т/гс=0
ППППппп„
0,2
ПППППППг,
0,1 it
П П П п г, г.
JEL
0,1
0,1
z?ffl
0,1
о
П П п п „ _
д
20
я
Пп-
оо
П П П п
О 2 4 6 8 10 72
т
Фиг. 9.5. Вид распределения фотоотсчетов для хаотического света
при т = 4 и значений Т/хс, указанных на графиках.
Для значений Т/% , равных 0 и со, зависимости построены на основе формул
(9.68) и (9.64). Данные для промежуточных значений Т/% взяты из работы [6J.
света вычислить нетрудно. Из (9.62) среднее число
сосчитанных фотонов равно
оо
m = £ mPm (Т) = <£/ (t, Т) Т) = ЦТ,
(9.69)
ОПТИКА ФОТОНОВ 323
где усредненная за большой промежуток времени
интенсивность была обозначена через 7 и использована нор^
мировка распределения вероятностей
оо
£рт(Г) = 1. (9.70)
Среднее число отсчетов согласуется с результатом (9.65)»
полученным при более строгих условиях.
Таким же образом можно определить второй момент
распределения
00
m* = £m2Pm(Г) = <£/(*, Т)Т) + ([£/(*, Т)Т]2) =
т=0
= m + ([V(t,T)T]*>. (9.71)
Среднеквадратичное отклонение для распределения
можно записать в виде
(ДтJ = Л? - т2 = т + t?T2 [ (I2 (t, T)) - J2]. (9.72)
Первый член в выражении для среднеквадратичного
отклонения описывает те же флуктуации частиц, что и в
формуле (9.66) для случая пучка с постоянной
интенсивностью. Дополнительные флуктуации, описываемые
вторым членом выражения (9.72), обусловлены
случайными изменениями мгновенной интенсивности и
называются волновыми флуктуациями. Очевидно, что в
отличие от постоянного слагаемого, соответствующего
флуктуа-циям частиц, волновые флуктуации" зависят от
свойств исследуемого светового пучка. Более общий
результат (9.72) переходит в (9.66) в случае постоянной
интенсивности.
Волновые флуктуации в (9.72) могут быть вычислены
для хаотического пучка, имеющего лоренцев частотный
профиль с параметром ширины линии у, который, как и
в E.52), связан с временем когерентности соотношением
Y = l/V ; (9.73)
Интеграл, необходимый для нахождения среднего в
(9.72), уже был вычислен в E.94), где %г необходимо за-
И*
324
ГЛАВА 9
менить на Г. Тогда среднеквадратичное отклонение
дается выражением
т2
(ЛтJ-т + -^-гГ{ехр(~2уГ)~ 1 +2уГ}. (9.74)
На фиг. 9.6 показано, как меняется среднеквадратичное
отклонение в зависимости от времени счета Т.
Флуктуации частиц для постоянной интенсивности из (9.66)
включены для сравнения.
см
'i
Т/гс
Фиг. 9.6. Среднеквадратичное отклонение числа сосчитанных
фотонов для хаотического света с временем когерентности хс.
Среднее число сосчитанных фотонов сохраняется равным т=4 независимо от
времени счета Г. Горизонтальная прямая отмечает постоянный уровень
флуктуации частиц.
Для времени счета Г, меньшего времени
когерентности Тс, выражение (9.74) принимает вид
(AmJ = /ft + m2 {yT < 1). (9.75)
В этом пределе все хаотические источники дают
одинаковую статистику счета, определяемую формулой (9.68),
а среднеквадратичное отклонение такое же, как
найденное в A.71) для фотонов одной тепловой моды. Уже
отмечалось, что среднее, которое должно вычисляться в
(9.72), сходно с величиной, определяющей корреляции
Хенбери Брауна и Твисса. Среднеквадратичное
отклонение зависит от степени когерентности света второго по-
ОПТИКА ФОТОНОВ
825
рядка, и, следовательно, в пределе бесконечного времени
когерентности результат для хаотического света
отличается от результата для когерентного света, как
показано на фиг. 9.6 и как следует из формул (9.66) и (9.75).
Общий результат (9.74) принимает вид
(ЛтJ = /п + ^- (уГ>1), (9.76)
если время счета Т велико по сравнению с тс, и
переходит в выражение (9.66) в случае очень больших времен
счета, когда распределение фотоотсчетов имеет пуассо-
новскую форму, рассмотренную выше.
Квантовомеханическое распределение фотоотсчетов
Полученные выше распределения фотоотсчетов
основаны на полуклассическом выражении (9.62). Более
общая теория распределения фотоотсчетов получается при
полной квантовомеханической постановке задачи. Более
общая теория может учесть такие возбуждения поля,
которые не описываются классической теорией, а кроме
того, она дает более полные результаты для всех типов
возбуждения.
Кваитовомеханическая теория распределения
фотоотсчетов, как и полуклассическая теория, исходит из
анализа последовательности фотоэлектрических процессов,
связанных с детектированием совокупности фотонов при
помощи фотодетектора. Вычисления похожи на расчеты,
приведенные выше при выводе степеней
квантовомеханической когерентности, но распределение фотоотсчетов
носит более сложный характер вследствие появления в
вероятности отсчета m фотонов всех степеней
когерентности, как и в полуклассическом результате (9.62).
Квантовомеханическое распределение фотоотсчетов
было впервые получено Келли и Клейнером [7], в статье
которых можно ознакомиться с деталями довольно
длинного вывода. В том случае, когда размеры катода
фотодетектора малы по сравнению с длиной когерентности
излучения, их результат можно записать в виде
РЛТ) = Sp {рЛ*[еГ(уГехр[- U (Г) Г]}, (9.77)
326
ГЛАВА 9
где
00
7= -~ $ 2ejE~ (rt) Ё+ (г/) dt\ (9.78)
о
вектор г описывает положение детектора, а операторы
£+ и £~ определены в (9.9) к (9.10).
Квантовомеханическое распределение имеет явное
сходство с полуклассическим результатом (9.62), однако
в квантовомеханической формуле следует учитывать по-
рядок операторов. Оператор Jf обеспечивает нормальное
упорядочение [3] операторов электрического поля,
которые хледуют за ним. Иначе говоря, если экспоненту в
(9.77) разложить в степенной ряд, то для каждого члена
этого ряда операторы электрического поля должны быть
упорядочены таким образом, чтобы все операторы £+
находились справа от операторов £~, как, например, в
числителе выражения для когерентности n-го порядка
(9.46). Действительно, члены степенного разложения
(9.77) пропорциональны последовательным степеням
когерентности (9.46), включая интегрирование по времени,
вытекающее из определения I(t). Таким образом,
распределение фотоотсчетов определяется бесконечным
числом степеней когерентности. Нормальное упорядочение
операторов поля обеспечивает правильное описание
процесса детектирования на основе понятия уничтожения
фотонов. Использование оператора нормального упоря-
дочения JF позволяет записать распределение в
компактной форме (9.77), однако при разложении экспоненты
операторы Ё~ и £+, входящие в /(/), становятся
разделенными.
Квантовомеханическое распределение слишком
сложно для вычисления, и поэтому мы не приводим
результатов, полученных для общей формы распределения.
Можно показать [7], что квантовомеханические
результаты подтверждают полуклассические вычисления для
когерентного и хаотического света, описанные раньше в
этой главе. В действительности вычислить распределение
для чистого когерентного состояния |{ак}) весьма
просто. Когерентное состояние есть собственное состояние
оператора B{rt) с собственным значением, определенным
ОПТИКА ФОТОНОВ
327
в (9.47). Следовательно, каждый оператор JS+ в (9.77)
можно заменить его собственным значением, а каждый
оператор Ё~ — комплексно сопряженным собственным
значением. В результате распределение упрощается и
сводится к пуассоновскому распределению, сходному
с (9.64).
Главная цель записи квантовомеханического
распределения, приведенного в (9.77), помимо сделанных выше
замечаний о подтверждении некоторых полуклассических
результатов, заключается в демонстрации связи между
оператором плотности и распределением фотоотсчетов,
которое в принципе можно определить
экспериментально. Пусть фотоны принадлежат одной моде к, которая,
по нашему предположению, возбуждена в некоторое
стационарное состояние. Все произведения операторов Ё~~
и £+ упрощаются, как и в (9.19), а распределение
фотоотсчетов можно записать следующим образом:
Pm(T) = Sp{pJe^^-exp(-lufd)}. (9.79)
Здесь оператор JF располагает операторы а7 слева от
операторов а, которые являются операторами
рождения и уничтожения фотонов одной рассматриваемой
моды и
g = IchajV (9.80)
есть мера эффективности детектора, сходная с £, на
имеющая дополнительный множитель. Величину \ мы
назовем квантовой эффективностью детектора.
Распределение фотоотсчетов, приведенное в (9.79),
справедливо только для эксперимента, в котором
регистрируются фотоны одной моды резонатора и где р есть
одномодовый оператор плотности. В гл. 7 уже было
доказано, что стационарный оператор плотности для
индивидуальной моды не дает никакой информации о
временной зависимости возбужденной моды. Следовательно,
распределение Рт{Т) в (9.79) относится к вероятности
отсчета m фотонов за время Г, короткое по сравнению
с характерным временем флуктуации числа фотонов.
Оператор, среднее значение по ансамблю которого
необходимо вычислить в (9.79), имеет для состояний
328
ГЛАВА 9
с определенным числом фотонов \п) только
диагональные матричные элементы. Пусть диагональный
матричный элемент оператора плотности фотонного
возбуждения есть
Рл = (п|р|л>. (9.81)
Тогда этот элемент Рп определяет (полностью или
частично в зависимости от того, диагональна или не диа-
гональна матрица плотности р для состояний \п))
вероятностное распределение одномодовых возбуждений
среди различных состояний \п). Связь между Рп и
распределением фотоотсчетов, созданных этим
возбуждением, определяется ниже.
Если экспоненту в (9.79) разложить в ряд и для
вычисления следа использовать состояния с определенным
числом фотонов, то получим
оо
I I1 ( Д+\т+1А>П + 1
w=2>,,|f("'!(-oi-SK*t+v,+,i«). (9-82)
п 1=0
Вычисление матричного элемента по обычным
правилам F.86) и F.87) дает
оо п—т
^(D^S^irSt-^t-(»-m-/)i- <9-83>
п=т 1=0
Суммирование по / эквивалентно биномиальному
разложению и потому может быть записано в следующей
замкнутой форме:
оо
рт(т)=£ р«О^ и - $я~т > <9-84>
где
о-
т\ (п — т)\
(9.85)
Эта форма1) распределения фотоотсчетов эквивалентна
выражению (9.77) для одномодового возбуждения,
время флуктуации которого велико по сравнению с време-
*) Выражение (9.84) было впервые выведено в работе [8],
ОПТИКА ФОТОНОВ
329
ци Т. Распределение (9.84) называется распределением
Бернулли и интерпретируется просто как вероятность
гого, что пг фотонов сосчитаны, а п — m фотонов не за-
эегистрированы, причем вероятность регистрации од-
(п\
ного фотона за период счета равна |. Множитель I I
обусловлен тем, что нам безразлично, какие именно m
ротонов сосчитаны, а сумма по п учитывает возможные
числа фотонов, возбужденных в одну моду.
Из (9.84) следует, что распределение фотоотсчетов
Рт(Г) совпадает с распределением фотонов Рп,
определяемым диагональными матричными элементами
оператора плотности, только в том случае, когда квантовая
эффективность равна единице и
Pm(T) = Pn6nm A=1). (9.86)
В случае квантовых эффективностей, меньших
единицы1), распределения Рт(Т) и Рп(Т) различны и
экспериментальное распределение фотоотсчетов дает лишь
косвенную информацию о фотонном возбуждении.
Реальные квантовые эффективности имеют порядок 10~2,
поэтому экспериментальная ситуация обычно далека от
идеальной, описываемой соотношением (9.86).
Существуют два важных случая, когда
распределение Pm(T) легко вычисляется по данному фотонному
распределению Рп.
Задача 9.15. Рассмотрите одномодовый когерентный
свет, где, согласно формулам G.58) и
G.97),
Рй =-^ ехр (-я),' (9.87)
и, используя выражение (9.84), докажите,
что
Рт(Г)=-^1ехр(-1п). (9.88)
1) Выражение (9.80) для квантовой эффективности £
справедливо только тогда, когда ее величина много меньше единицы.
Более точное выражение, приведенное в [8], показывает, что, как только
правая часть выражения (9.80) становится большой, £ стремится к
максимальному значению, равному единице»
330
ГЛАВА 9
Задача 9.16. Как и в задаче 9.10, рассмотрите
фильтрованный одномодовый хаотический свет,
где, согласно формуле G.107),
*•-■«£?*• (9-89)
и докажите, что
^m = 7rfg^r. (9.90)
Эти результаты согласуются с выражениями (9.64) и
(9.68), полученными полуклассическим методом. В
обоих примерах среднее число сосчитанных фотонов in
связано со средним числом фотонов в моде п соотношением
т = 1п, (9.91)
а распределения Рп и Ят(^) имеют одинаковую
математическую форму. Однако это не является общим
свойством распределения фотоотсчетов, которое по
форме может отличаться от распределения фотонов Рп.
Эксперименты с фотонами
Из фиг. 9.5 видно, что распределение фотоотсчетов
чувствительно к времени когерентности тс в том случае,
когда время счета Т сравнимо с тс. Следовательно,
измерение РШ(Т) для хаотического света можно
использовать для определения времени когерентности на основе
согласования экспериментального распределения с
теоретическим. Этот метод определения тс называется
спектроскопией флуктуации интенсивности. Для
хаотического света он дает в принципе ту же информацию,
что и измерение методом обычной спектроскопии
параметра ширины линии у, связанного с тс соотношением
(9.73).
Минимальное время счета Т в спектроскопии
флуктуации интенсивности ограничено временем разрешения
фотодетектора. Самые быстродействующие из
имеющихся фотодетекторов обладают временем разрешения
порядка Ю-9 с. Время когерентности такой величины
соответствует ширине 2у порядка 108 Гц в единицах часто-
ОПТИКА ФОТОНОВ
331
ты (но не угловой частоты). Таким образом,
спектроскопия флуктуации интенсивности пригодна для
хаотического света с шириной частотного распределения,
меньшей 108 Гц. Практически таким способом можно
исследовать интервал от 1 до 108 Гц.
С другой стороны, обычная спектроскопия,
использующая дифракционные решетки, способна разрешать
спектральные линии с шириной 1010 Гц и больше, в то
время как интерференционная спектроскопия Фабри—•
Перо пригодна для спектральных линий, ширина
которых лежит в интервале от 107 до 1012 Гц. Отсюда видно,
что спектроскопия флуктуации интенсивности
превосходно дополняет область частотных ширин,
перекрываемую более привычными методами. Спектральные
линии, слишком узкие для разрешения методами
спектроскопии, измеряющей частоту, можно легко изучать
методами временного разрешения, применяемыми в
спектроскопии флуктуации интенсивности.
На фиг. 9.7 изображено экспериментальное
распределение фотоотсчетов, использованное для определения
ширины линии хаотического света на основе
спектроскопии флуктуации интенсивности [9]. Эксперимент
проводился с помощью лазерного пучка, рассеянного на
суспензии из сферических частиц в воде при комнатной
температуре. Теория броуновского движения показывает,
что такой рассеянный свет имеет лоренцево частотное
распределение [10]. Случайное движение частиц
обусловливает временные свойства рассеянного света,
характерные для хаотического источника, а потому
экспериментальное распределение на фиг. 9.7 сходно с
распределением на фиг. 9.5. Весь эксперимент включает серию
времен счета от 10~2 до 2-Ю-1 с. Время когерентности
тс, полученное из сравнения теории с экспериментом,
составляет Ю-1 с. Соответствующая частотная ширина
линии в 20 Гц, конечно, не могла быть измерена методом
обычной спектроскопии.
В экспериментах по счету фотонов другого типа
величины тс или y Для хаотического счета измеряются
посредством определения степени когерентности второго
порядка падающего света. При падении света на
фотодетектор измеряется корреляция между числами фото-
332
ГЛАВА 9
нов rti\ и гп29 сосчитанных за два коротких временных
интервала 6^ и 6t2i разделенных временем т. Если оба
временных интервала имеют одинаковую длительность,
меньшую т и времени когерентности тс, то корреляция
{т{т2) определяет введенную в (9.38) степень когерент-
0,2
5 о,1
О
п
о
П П п
6
/77
8
10
1Z
Фиг. 9.7. Экспериментальное распределение фотоотсчетов для
лазерного света, рассеянного на суспензии сферических частиц в воде.
,-i
Время счета Т равно 10 с, а среднее число отсчетов т = 3[9].
ности второго порядка g^f для света в одной и той же
точке, но в разные моменты времени. Выражение (9.38)
можно переписать через числа сосчитанных фотонов:
tfB)
&12
(m^/m2,
(9.92)
где in — среднее число отсчетов за короткий интервал
б/i = 8t2. Следовательно, для хаотического света с ло-
ренцевым частотным распределением выполняется
соотношение
•
(mim2) = m2{exp(- 2у |т |) + 1}. (9.93)
Здесь были использованы формулы (9.37) и (9.45). С
помощью классического результата E.77), справедливого
ОПТИКА ФОТОНОВ
333
также при квантовомеханическом рассмотрении,
корреляция фотоотсчетов для хаотического света с гауссовым
частотным распределением может быть записана в виде
(mi/n2) = т2 {ехр (- б2т2) + 1}. (9.94)
Зависимость корреляционных функций (9.93) и (9.94)
от т показана на фиг. 5.18.
Существование корреляций в счете фотонов за
время, меньшее времени когерентности тс, для хаотического
света можно приписать тенденции фотонов к
группировке. Группировка фотонов представляет собой просто
другой способ описания на квантовом языке флуктуации
интенсивности определенного вида, существующих при
классическом описании хаотического света (фиг. 5.7),
Необходимо подчеркнуть, что группировка фотонов не
является общим свойством света: из (9.94) и (9.92)
видно отсутствие корреляций для когерентного света.
В действительности возможны корреляции с
антигруппировкой фотонов, как, например, в случае
возбужденного состояния с определенным числом фотонов, для
которого степень когерентности второго порядка дана в
(9.39).
Измерение корреляций, обусловленных группировкой
фотонов, было использовано для определения времени
когерентности одной из линий испускания ртутной
лампы [11]. Путем согласования теоретической корреляции
(9.93) с экспериментальными результатами для
нескольких различных времен задержки т было найденр,
что это время когерентности близко к нижнему пределу
возможностей экспериментов по счету фотонов и равно
1,7- Ю-9 с.
Результаты аналогичных экспериментов [12] для
лазера и хаотического света с гауссовым частотным
распределением приведены на фиг. 9.8. Хаотический свет
получался путем пропускания лазерного излучения через
вращающийся диск из матового стекла, который
создавал гауссово частотное распределение у исходного
монохроматического лазерного света. Видно хорошее
согласие экспериментальных результатов с теоретическим
выражением (9.94),
334
ГЛАВА 9
За годы, прошедшие после изобретения лазера, бы*
стро развивались методы спектроскопии флуктуации
интенсивности. Существуют изощренные способы
извлечения спектральных данных из измерений распределения
фотоотсчетов, дающие более удобное и точное
определение времени когерентности по сравнению с простым
способом подгонки необработанного набора данных по
Фиг. 9.8. Корреляции между парами отсчетов фотонов,
разделенных временем т, как функции х для лазерного света и хаотического
света с гауссовым частотным распределением.
Черные кружочки относятся~к результатам измерений для лазерного света,
остальные экспериментальные точки относятся к хаотическому свету.
Теоретические кривые точно такие же, как на фиг. 5.18 [12].
счету фотонов (фиг. 9.7) к теоретическим
распределениям типа показанных на фиг. 9.5. Подробности методов
спектроскопии флуктуации интенсивности можно найти
в специальных статьях и монографиях [13].
Эксперимент Хенбери Брауна и Твисса, который
можно считать первым экспериментом в области
квантовой оптики, легко описывается на языке счета фотонов.
Пусть числа фотонов, сосчитанных за время Т двумя
детекторами на фиг. 5.16, равны Ш\ и т^. Допустим, что
средние числа отсчетов двух детекторов равны
mi = m2 = т.
(9.95)
ОПТИКА ФОТОНОВ
335
Измеряемая в эксперименте корреляция получается
путем переписывания формулы E.83) через числа
фотонов
({тх — т) {т2 — т)) = (ш^) — /п2, (9.96)
где (т\т2) —точно такая же корреляция, что и в (9.93).
Однако в этом случае она должна быть
проинтегрирована по времени счета Г, как и в E.94), чтобы для
хаотического света со временем когерентности 1/у
получить следующее выражение: *
((/Я! - т) (т2 - т)} = —^ X
X{exp(-2Yr)-l+2Y71 (9.97)
Отметим, что в (9.97) корреляции полностью
обусловлены волновыми флуктуациями хаотического света,
поэтому они стремятся к нулю для большого времени
счета 7\ Эксперимент поставлен таким образом, чтобы
он не был чувствителен к флуктуациям частиц, которые
не содержат информации об исследуемом свете и
которые в противном случае сделали бы измерение
полезных волновых флуктуации более затруднительным.
Величина корреляций для нехаотическог© света может
быть вычислена из соответствующего выражения для
степени когерентности второго порядка, рассмотренного
раньше в этой главе.
Кроме описанных выше экспериментов, где главную
роль в измерениях играет детектирование фотонов, в
рамках теории квантованного поля излучения можно
теоретически проанализировать все эксперименты
классической оптики. Однако это не очень благодарное занятие,
поскольку (как мы уже видели) когерентные свойства
первого порядка хаотического света одинаковы и й
квантовой, и в классической теориях, причем
классические оптические эксперименты обычно легче
рассматривать на основе классической теории. Однако с
методической точки зрения интересно проанализировать, каким
образом можно согласовать обычное описание
классического интерференционного эксперимента с
корпускулярной теорией светового пучка.
336
ГЛАВА 9
Проанализируем интерференционный эксперимент
Юнга, изображенный на фиг. 5.11, рассматривая
падающий свет как поток фотонов. Источник света можно
считать настолько слабым, что фотоны проходят через
прибор по одному. Классические интерференционные и
дифракционные эксперименты в действительности
проводились [14] с такими слабыми источниками. Было
найдено, что если время записи достаточно велико для
компенсации слабости источника, то интерференционная или
дифракционная картина при регистрации фотонов по
одному в точности совпадает с полученной для светового
источника с обычной интенсивностью. Отсюда
необходимо сделать вывод о том, что интерференция является
однофотонным эффектом и совсем не зависит от
взаимодействия фотонов друг с другом.
В эксперименте Юнга каждый фотон должен
обладать способностью интерференции с самим собой таким
образом, чтобы вероятность его соударения со вторым
экраном в определенной точке была пропорциональна
интенсивности в той же точке, вычисленной классически,
например по формуле E.71). Этого можно достичь
только в том случае, если каждый фотон проходит частично
через оба отверстия и благодаря этому может
«чувствовать» полную геометрию отверстий при своем
соударении с экраном. В действительности нет способа,
посредством которого можно одновременно определить
прохождение фотона через определенное отверстие и
записать интерференционную картину. Если, например,
позади одного из отверстий помещен фотодетектор для
обнаружения проходящих через отверстие фотонов, то
при этом невозможно избежать частичного закрывания
отверстия с соответствующим искажением картины
интерференции.
Эти замечания согласуются с принципами квантовой
механики. Поскольку фотоны между собой не
взаимодействуют, то все интерференционные эффекты следует
искать в том способе, каким каждый отдельный фотон
попадает из источника на второй экран. С квантовоме-
ханической точки зрения интерференция происходит
между амплитудами вероятности Прохождения
расстояния от источника до экрана двумя путями, соответ-
ОПТИКА ФОТОНОВ
ствующими двум отверстиям. Интенсивность на втором
экране пропорциональна квадрату модуля суммы двух
амплитуд вероятности. Схема квантовомеханического
вычисления точно такая же, как для классического
вычисления, которое тоже основано на квадрате модуля
суммы двух амплитуд, как в E.43), поэтому два вычисления
дают одинаковое распределение интенсивности.
Эти идеи можно применить к модификации
эксперимента с двумя отверстиями, где два световых пучка
получают, не устанавливая перед одним источником пару
отверстий, а посредством двух совершенно независимых
световых источников. В поле, образованном наложением
света от двух источников, возможно наблюдение
интерференционных эффектов [15], причем их объяснение
сходно с объяснением эксперимента Юнга.
Интерференция происходит между амплитудами вероятности
испускания одним или другим источником фотона,
попадающего на детектор. Не существует способа, посредством
которого фотон может участвовать в
интерференционных эффектах и при помощи которого можно
одновременно 'определить принадлежность фотона к одному из
двух источников.
ЛИТЕРАТУРА
1. Bethe H. Л, Salpeter E. £, Quantum mechanics of one- and two-
electron atoms, Springer-Verlag, Berlin, 1957, Ch. IV, Pt. b. (См,
перевод: Г. А. Бете, Э. Солпитер, Квантовая механика атома с
одним и двумя электронами. Физматгиз, 1960).
2. Quantum optics and electronics, ed. С. DeWitt, A. Blandin, C. Co-
hen-Tannoudji, Gordon and Breach, New York, 1965, p. '63. (См,
перевод в сб. «Квантовая оптика и квантовая радиофизика», изд-
во «Мир», 1966.)
3. Quantum optics, ed. S. M. Kay, A. Maitland, Academic Press,
London, 1970, p. 53.
4. Ziman J. M.y Elements of advanced quantum theory, University
Press, Cambridge, 1969, p. 70.
5. Mandel L., Proc. Phys. Soc, 72, 1037 A958); 74, 233 A959).
6. Jakeman £., Pike E. /?., Journ. Phys., Al, 128 A968).
7. Kelley P. L., Kleiner W. #., Phys. Rev., A136, 316 A964).
8. Scully M. 0, Lamb W. £., Jr., Phys. Rev., 179, 368 A969).
9. Jakeman £., Oliver C. /., Pike E. R., Journ. Phys., Al, 406 A968).
10. Pekora /?., Journ. Chem., Phys, 40, 1604 A964).
11. Morgan B. L., Mandel L., Phys. Rev. Lett., 16, 1012 A966),
12. Arecchi F, T.t Gatti £., Sona Л., Phys. Lett., 20, 27 A966),
338
ГЛАВА 9
13. Pike E. R., Rev. nuovo cim., 1, numero speciale, 277 A969).
14. Taylor G. /., Proc. Camb. Phil. Soc, 15, 114 A909).
15. Pfleegor R. L.t Mandel L.t Phys. Rev., 159, 1084 A967); Journ.
Opt. Soc. Amer., 58, 946 A968).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Наиболее подробное и всестороннее рассмотрение различных
проблем квантовой оптики можно найти в трудах трех летних школ,
а именно:
1. Quantum optics and electronics, ed. С. DeWitt, A. Blandin, C. Co-
hen-Tannoudji, Gordon and Breach, New York, 1965.
2. Quantum optics, ed R. J. Glauber, Academic Press, New York, 1969.
3. Quantum optics, ed. S. M. Kay, a Maitland, Academic Press,
London, 1970.
Статьи Р. Глаубера во всех трех томах, и особенно в первом,
являются хорошим введением в данную область физики.
Экспериментальное изучение статистики фотонов рассмотрено
Ф. Арекки в [2] и Е. Пайком в [4]. См. также:
4. Pike E. R.y Rev. nuovo cim., 1, nuovo speciale, 277 A969); Rev.
Phys. Technol., 1, 180 A970).
Кроме того, имеются две книги, где основное внимание уделено
математическим аспектам данного предмета:
5. Klauder J. /?., Sudarshan E. C^ G., Fundamentals of quantum
optics, Benjamin, New York, 196$. (См. перевод: Дж. Клаудеру
Э. Сударшан, Основы квантовой оптики, изд-во «Мир», 1970.)
6. Perina /., Coherence of light, Kan Nostrand Reinhold, London,
1972. (См, перевод: #. Перина, Когерентность света, изд-во «Мир»,
1974.)
Глава 10
Теория лазера
Световой пучок, генерируемый лазером,
характеризуется не только высокой интенсивностью, но также
своими когерентными свойствами. Высокую интенсив*
ность можно объяснить на основе простой теории
лазера, изложенной в гл. 2. Объяснение когерентных
свойств требует довольно детального рассмотрения
влияния взаимодействия излучения с атомами на
статистические свойства светового пучка. Настоящую главу мы
начинаем с описания тех изменений статистических
свойств световых пучков, которые обусловлены
поглощением и переизлучением фотонов при взаимодействии
света с двухуровневыми атомами. Затем теория
обобщается на случай трехуровневой схемы лазера. В
отличие от полуклассической теории, строго применимой
только к усилению внешнего излучения, общая
квантовая теория, изложенная в настоящей главе, учитывает
спонтанное излучение и может применяться для анализа
самовозбуждения обычного лазерного источника света*
Теория лазера ограничена случаем непрерывных
стационарных световых пучков, импульсные эффекты не
рассматриваются.
Кинетические уравнения для фотонов
Рассмотрим газ в объеме У, состоящий из N
одинаковых двухуровневых атомов. Пусть частота атомного
перехода есть шо, и мы будем рассматривать
взаимодействие с одной модой к оптического резонатора. Посколь-
340
ГЛАВА 10
ку необходимо рассмотреть только одну моду
резонатора, то индекс к у переменных поля излучения может
быть опущен и в результате укороченный гамильтониан
(8.103) для системы «излучение + атом» принимает вид
$$ = Нщл^п + Н<*й*й + % (nfd — affc). A0.1)
» ^
Допустим, что в моде резонатора имеется п фотонов.
Вероятность поглощения в единицу времени фотона
невозбужденным атомом, согласно формуле (8.76), дается
выражением
2я/яб (со0 — со). A0.2)
После подстановки ^г из (8.70) и обычного углового
усреднения по случайным ориентациям атомов
выражение A0.2) преобразуется к виду
(яАо | D12 Р/Зе,ЙУ) nb (со0 - со). A0.3)
В результате спонтанного излучения атома во все
моды резонатора присходит уширение узкого атомного
перехода на частоте соо (фиг. 8.2). Поэтому б-функция
в A0.3) должна быть заменена нормированным
распределением для излучательно уширенной линии перехода.
Если пренебречь всеми источниками уширения линии,
кроме излучательного, то получаемая из (8.143)
замена б-функции запишется следующим образом:
6(co-a>o)^(@j_y2 + Y2 . (Ю.4)
Здесь параметр ширины линии у находится из
выражения (8.137), вычисленного при со = ©о, а множитель я
обеспечивает нормировку. Подстановка замены A0.4)
в выражение A0.3) дает вероятность в единицу времени
поглощения фотона
e2co|D12|2
■п. A0.5)
Зе0ЙУ (©о - соJ + y2
Допустим, что частота выбранной моды резонатора
со совпадает с центром атомной линии поглощения на
ТЕОРИЯ ЛАЗЕРА
341
частоте щ. Используя формулу (8.137), определим
величину
ф е2(й01 D1212 2ж?3
3e0hVy V(o
2 • (Ю.6)
о
Тогда вероятность поглощения A0.5) запишется просто
как
9п. A0.7)
Отметим, что эта величина пропорциональна
пространственной плотности фотонов n/V.
Вероятность испускания фотона с частотой со = (Оо
атомом, находящимся в возбужденном состоянии,
определяется таким же образом'из (8.81). Эта вероятность
дается выражением
9{п+1). A0.8)
Два члена п и 1 соответствуют вынужденному и
спонтанному испусканию; 9 есть скорость спонтанного
испускания в данную рассматриваемую моду резонатора,
тогда как коэффициент Эйнштейна А или величина
1/тя из (8.84) является полной скоростью спонтанного
испускания во все моды.
Состояние поля излучения в одной моде резонатора
определяется оператором плотности фотонов р,
рассмотренным в гл. 7. Состояние фотонов мы будем описывать
диагональными элементами Рп матрицы плотности р
в представлении состояний с определенным числом
фотонов, введенных в (9.81). Согласно (9.87) и (9.89),
Рп=^ехр(-п) A0.9)
для одномодового когерентного возбуждения и
A+я)
для одномодового хаотического света. Как было под-*
черкнуто в предыдущей главе, если недиагональные
матричные элементы (п|р|п') отличны от нуля, то значение
Рп дают лишь частичное описание состояния фотонов.
Кроме того, использование одномодового оператора
Рп= „ .*".+„ A0.10)
342
ГЛАВА 10
плотности приводит к тому, что теория может
предсказывать только мгновенное распределение фотонов по
состояниям с определенным числом фотонов. Однако
использование Рп достаточно для описания основных
статистических свойств излучения. Временной масштаб
флуктуации числа фотонов рассматривается другим
методом позже в этой главе.
Поглощение и излучение фотонов двухуровневыми
атомами изменяет распределение фотонов Рп. Временные
изменения Рп могут быть описаны с помощью
кинетических уравнений. Кинетические уравнения уже
использовались для нахождения вероятностей населенности
атомных состояний в гл. 1 и 2. Для фотонных
вероятностей кинетические уравнения можно вывести
аналогичным образом.
На фиг. 10.1, сходной с фиг. 1.4, показана схема
энергетических уровней моды резонатора. Величина Рп
есть вероятность нахождения фотонного поля в п-ы
возбужденном состоянии. Предположим, что средние числа
атомов в основном и возбужденном состояниях равны
N\ и N2. Излучательные переходы, конечно, стремятся
изменить как РПу так и вероятность атомного
возбуждения. Однако мы будем предполагать, что некоторое
внешнее воздействие поддерживает значения N^ и N2
постоянными. Таким образом, во времени меняется только
распределение фотонов Рп, а флуктуации значений N\
и N2 исключаются из рассмотрения.
Существует четыре типа переходов, изменяющих Рп.
Если в моде реально имеется п фотонов, то каждый из
N\ атомов в основном состоянии поглощает фотоны со
скоростью, приведенной в A0.7), а каждый из N2
возбужденных атомов испускает фотоны со скоростью,
определенной в A0.8). Оба процесса уменьшают величину
Рп с общей скоростью, равной *
-N$aPn-N£{n+\)Pn. A0.11)
Имеются также два положительных вклада в
скорость dPJdt. Если с вероятностью Рп-\ возбуждено
п—1 фотонов, то N2 возбужденных атомов могут
испустить фотон и перевести поле в его /г-е состояние.
Скорость этого процесса определяется из A0.8) при замене
ТЕОРИЯ v!A3FPA
343
п на п— 1 и равна
N2$nPn-{. A0.12)
Аналогично если с вероятностью Pn+i имеется п + 1 фо*
тонов, то N{ атомов в основном состоянии могут погло-»
07+;
Рп
Рп-
1
1
1
1
i
Nz$(n+1)Pn
Л/,9пРп
f
■
п+1
п
п-1
о
О
Фиг. 10.1. Схема энергетических уровней для фотонов в
выбранной моде резонатора.
Указанные скорости переходов дают вклады в величину dPnJdt. Расстояние
между уровнями равно Ао>0.
тить фотон и перевести поле в п-е возбужденное состоя^
ние, при этом Рп возрастает. Скорость процесса
получается из выражений A0.7) при замене п на /г+ 1
и равна
N{$(n+l)Pn+i. A0.13)
344
ГЛАВА 10
Суммирование вкладов A0.11), A0.12) и A0.13)
дает полную скорость
dPJdt = - N2S (n + 1) Рп + N& (п + 1) Рп+, -
-Nx9nPn + NgnPn-x. A0.14)
Четыре перехода, дающие вклад в скорость dPn\dt,
показаны на фиг. 10.1.
Рассмотрим сначала стационарное распределение
фотонов; при этом правая часть уравнения A0.14)
принимается равной нулю. Получающаяся цепочка уравнений
для различных значений п решается следующим
образом. При п = 0 только два типа переходов дают вклад
в скорость dPofdt, поэтому уравнение A0.4)
преобразуется к виду
dP0/dt = - N2SP0 + NX9P{. (ЮЛ5)
Стационарное решение этого уравнения можно
использовать для упрощения уравнения A0.14) при п= 1,
которое в свою очередь можно использовать для
упрощения уравнения A0.14) при п = 2 и т. д. Общее условие
стационарного состояния имеет вид
N$nPn-x - N{$nPn = 0. A0.16)
Этот результат является примером выполнения
принципа детального равновесия в стационарных условиях.
Можно показать в общем случае [1], что состояния,
связанные малыми неисчезающими вероятностями
переходов, должны иметь точно такие же вероятности населен-
ностей в стационарных условиях. В данном случае
вероятности населенностей равны N2Pn-\ и N\Pn.
Решение цепочки уравнений A0.16) имеет вид
Рп = (Wi) Pn-i = (N2/N{)nPQ. A0.17)
Оставшаяся неизвестной вероятность Яо определяется
из условия нормировки
ЕЛг=1> A0.18)
п
а конечный результат дается следующим выражением:
Pn = (N2/Nl)n{l-(N2/Nl)}. A0.19)
Это фотонное распределение точно такое же, как в
A0.10), с
«=т5&т- A0-20>
ТЕОРИЯ ЛАЗЕРА 345
Следовательно, стационарное распределение фотонов
такое же, как распределение фотонов хаотического
света. Оно имеет точно такой же вид, как определенное
в A.75) распределение фотонов света,
взаимодействующего с атомами при тепловом равновесии. Приведенный
здесь более общий анализ показывает, что свет,
генерируемый источником, в котором уровень возбуждения
атомов поддерживается отличным от уровня,
соответствующего тепловому равновесию, имеет точно такую ,
же хаотическую природу, что и тепловой свет.
Временная зависимость когерентности фотонов
Довольно трудно получить общие зависящие от
времени решения бесконечной системы связанных
дифференциальных уравнений, одно из которых есть A0.14)*
Однако много полезной информации о временном раз*
витии распределения фотонов можно извлечь из анализа
первого и второго моментов распределения,
определяемых соответственно как
n = ZnPn A0.21)
п
И
n? = Zn2Pn. A0.22)
п
Умножая уравнение A0.14) с обеих сторон__на п
или п2 и суммируя по я, можно получить для п и п2
простые дифференциальные уравнения. Если использовать
A0.18) и A0.21), то для п получим следующее
уравнение:
•f- = £ 9 {- N2n (n + 1) Рп + N{n (п + 1) Рп+1 -
-N1n2Pn + N2n2Pn-l} =
^=Z^{-N2n(n + l) + N1(n-l)n-
- JV,n2 + N2(n + lJ} Pn = {N2 — JV,)&n + Nr$. A0.23)
Его решение имеет вид
,, _ {tt0 (A/, - Nt) + N2) exp {(N2 - JV,) St) - N2
346
ГЛАВА 10
где по — начальное значение среднего числа фотонов п
в момент / = 0. Отметим, что величина Ш2— N\)S9
определяющая скорость изменения Я, пропорциональна
плотности атомов Л^/V.
Дифференциальное уравнение для среднего квадрата
числа фотонов имеет вид
dJ?/dt = 2 (jV2 - NY) Зп2 + № + Nx) 9n + N23. A0.25)
Это уравнение можно решить непосредственно,
подставляя значение п из A0.24), однако такой путь является
довольно длинным. Результат может быть записан в
более компактной форме с помощью комбинаций из п2
и п:
/? — 2й2 — й = (я* — 2h\ - /г0)ехр {2 (N2 - Nx) Щ} A0.26)
где п2 — значение п2 в момент t = 0.
Уравнения A0.24) и A0.26) описывают временное
развитие статистических свойств светового пучка,
обусловленное его взаимодействием с атомами.
Статистические свойства в момент t = 0 определяются
соотношением между п2 и п0. Распределение фотонов
когерентного света приведено в A0.9), и, согласно формулам
G.58) и G.59), среднее число фотонов и средний
квадрат числа фотонов удовлетворяют уравнению
п2 — п2 — п = 0 (когерентный свет). A0.27)
Распределение фотонов хаотического света приведено в
A0.10), и из A.70) получим
п2 — 2п2 — д = 0 (хаотический свет). A0.28)
Общую картину влияния взаимодействия излучения
с атомами на статистические свойства света можно
лучше всего понять путем рассмотрения ряда частных
случаев, определяемых начальными статистическими
свойствами и относительными величинами N\ и N2.
1. п0 = 0, N\ > N2. Если в момент t = 0 не имеется
фотонов в моде излучения, то выражения A0.24) и
A0.26) принимают вид
n = {N2/(Nl-N2)}[l-&Lp{-(Ni-N2)9t}] A0.29)
ТЕОРИЯ ЛАЗЕРА
347
и __
я2-2Д2-п = 0. , A0.30)
Следовательно, при малых значениях t число фотонов
в моде резонатора возрастает линейно во времени со
скоростью N2S. При больших значениях t число фотонов
приближается к равновесному значению N2I(N\— N2),
полученному в A0.20). Сравнение формул A0.28) и
A0.30) показывает, что распределение фотонов для
всех / является хаотическим.
2. п0 = 0, N\ <C N2. При инверсии населенностей
верхнего и нижнего уровней результаты A0.29) и A0.30) по-
прежнему применимы. Свет остается хаотическим,
однако теперь среднее число фотонов п неограниченно
возрастает. Инверсная населенность атомов является одним
из условий действия лазерной системы, однако для
получения полной теории лазера требуются некоторые
дополнительные детали, описанные позже в этой главе.
Более реалистичная теория предсказывает совершенно
иные статистические свойства света, генерируемого в
условиях инверсной населенности атомов.
3. по хаотических фотонов. Первоначально
имеющиеся фотоны удовлетворяют соотношению A0.28):
/г| — 2Д2 _ я0 = 0. A0.31)
Тогда из A0.26) следует, что свет остается хаотическим
во все последующие промежутки времени. После
прохождения достаточно длительного времени среднее число
фотонов снова приближается к равновесному значению
A0.20), если Ni>N2, или неограниченно возрастает,
если N\ < N2. Временные зависимости величины Я для
случаев, когда фотоны первоначально отсутствуют и
когда первоначально имеется Я0 хаотических фотонов,
показаны на фиг. 10.2. Кривые относятся к случаю
нормальной населенности атомов, когда N\>N2.
4. по когерентных фотонов, N\ > N2. Теперь при
t = 0 фотоны удовлетворяют соотношению A0.27)
й~о- nl-n0 = Q. A0.321
348
ГЛАВА 10
Величину п удобно разделить на два слагаемых и
переписать выражение A0.24) в следующем виде:
n = ne + fitt A0.33)
где
ne = n0exp{—{Nx — N2)9t) A0.34)
и
ni = {N2/{Nl-NJ}[l--exv{--{Nl--N2)9t}]. A0.35)
На основе этих определений уравнение A0.26) можно
переписать в любой из двух форм:
n?-2h2-h = -h2c A0.36)
или __
п2 - п* - п = п\ + 2niiic. A0.37)
Два слагаемых в выражении для числа фотонов,
имеющихся в моде резонатора в момент времени t9
объясняются следующим образом. Из A0.35) видно, что
составляющая й* совпадает с выражением A0.29) для
числа фотонов в момент времени t9 если первоначально
фотоны отсутствуют. Фотоны h\ являются хаотическими,
или некогерентными; если в A0.36) или A0.37)
пренебречь величиной Яс, то эти уравнения переходят в
условие A0.28) для хаотического света. Хаотическая
составляющая й{ присутствует всегда, независимо от
начальных условий.
С другой стороны, фотоны пс являются когерентными; ,
если пренебречь niy то видно, что уравнения A0.36) и
A0.37) становятся идентичными условию A0.27) для *
когерентного света. Действительно, в общем случае
можно показать [2, 3], что выражения A0.33) и A0.36)
или A0.37) дают первый и второй моменты для смеси
когерентного света (со средним числом фотонов пс) и
некогерентного, или хаотического света (со средним
числом фотонов hi). Следовательно, первоначально
имевшийся когерентный свет остается когерентным, однако
его вклад уменьшается, согласно A0.34), и полностью
исчезает при больших временах, когда остается только
стационарная хаотическая составляющая, определенная в
A0.20). Временная зависимость хаотической составляю-
ТЕОРИЯ ЛАЗЕРА
349
щей иллюстрируется кривой, отмеченной Яо = 0 на
фиг. 10.2. Разность ординат этой кривой и кривой для
конечного значения Я0 характеризует когерентную
составляющую пс в полном среднем числе фотонов.
^
i
1С
1,5
- 1,0
0,5
no>Nz/(N,-N2)
n0<N2IW,-m
О
2 3
-Фиг. 10.2. Временная зависимость среднего числа фотонов в одной
моде резонатора, взаимодействующей с атомами, большинство
которых находится в основном состоянии (JVi > N2).
Три кривые соответствуют различным начальным значениям среднего числа
фотонов л0. Для всех значений п0 среднее число фотонов при больших временах
стремится к NdiNi — Nt).
5. Яо когерентных фотонов, N\ < N2., Решения
A0.32) — A0.37) остаются справедливыми для случая
инверсии населенностей атомов; при этом формулы
A0.34), A0.35) можно переписать таким образом,
чтобы подчеркнуть экспоненциальный рост как пс, так и Яг-;
пе = п0 exp {(N2 — NJ 9t)
A0.38)
и
щ = {NQ/(N2 - tf,)} [exp {(N2 - Nx) 2t}-\]. A0.39)
Величина некогерентной, или хаотической,
составляющей fii остается независимой от начальной величины
когерентной составляющей. Временная зависимость хао-
350
ГЛАВА 10
тическои составляющей иллюстрируется кривой Яг- на
фиг. 10.3.
При больших временах статистические свойства
света зависят от относительных величин п0 и N2/(N2 —
/ 2
Фиг. 10.3. Рост среднего числа фотонов в случае инверсии
атомных населенностей (N2 > N\).
Кривая Пц отражает временную зависимость хаотической компоненты. Дзе
остальные кривые характеризуют временную зависимость когерентной
компоненты пс для двух значений начального числа nQ когерентных фотонов,
большего (верхняя кривая) или меньшего (нижняя кривая) величины JV2/(N2—-Ni).
—N\). В случае слабого начального возбуждения
когерентного света, когда
n0<N2/(N2-Nl), A0.40)
т. е#
h0(N2-N{)<N2y A0.41)
спонтанн9е испускание фотонов, происходящее со
скоростью, пропорциональной N2, преобладает над
суммарным эффектом процессов поглощения и вынужденного
ТЕОРИЯ ЛАЗЕРА
351
испускания, протекающих с общей скоростью,
пропорциональной n0(N2— N\). В результате при больших вре-
менах доминирует хаотический свет.
• С другой стороны, при сильном начальном
возбуждении когерентного света, когда
n0(N2-Nl)> N2, A0.42)
доминирует вынужденное испускание, которое при
больших временах приводит к преобладанию
когерентного света. На фиг. 10.3 показаны типичные кривые для
двух случаев, когда йд больше или меньше N2/(N2— N\).
Для больших времен отношение когерентных фотонов
к числу хаотических фотонов имеет вид
J£.= Mtf2--^)y- \tf2-.N)$t^>l. A0.43)
til ™ 2
Здесь были использованы формулы A0.38) и A0.39).
Эти результаты показывают, что вынужденное
испускание стремится сохранить когерентные свойства
стимулирующего излучения. Следовательно,
экспоненциальные члены в A0.38) и A0.39) описывают соответственно
генерацию более когерентного света при действии
когерентного стимулирующего излучения и генерацию более
хаотического света при действии хаотического
стимулирующего излучения. В то же время спонтанное
излучение всегда дает хаотический свет. Эти свойства
вынужденного и спонтанного испускания проводились без
доказательства в гл. 2.
Задача 10.1. С помощью выражения (9.43) выведите
временную зависимость степени когерент-
. ности второго порядка для светового
пучка с произвольными статистическими
свойствами, взаимодействующего с
двухуровневыми атомами. Покажите, что в
хорошем приближении когерентность не
меняется при взаимодействии. Иначе
говоря,
{}? - т2=к - »о)/йо. о°-44>
если либо число возбужденных атомов
пренебрежимо мало и N2 ж N, либо ато-
352
ГЛАВА 10
мы имеют инверсную населенность, а
световой пучок обладает большой
интенсивностью, так что
n0{N2—N{)> N2.
Пороговое условие для лазера
Для реалистического описания работы лазера
изложенную выше теорию необходимо несколько развить.
Уже отмечалось, что получение инверсной населенности
на основе возбуждения переходов только между двумя
уровнями атома обычно невозможно. В простейшей
модели лазера, похожей на схему, рассмотренную в
элементарной теории лазера в гл. 2, используется три
уровня. Перейдем теперь к изучению статистических
свойств светового пучка, взаимодействующего с газом
из одинаковых атомов, у которых значительно заселены
три уровня.
Схема атомных уровней приведена на фиг. 10.4. Она
совпадает со схемой на фиг. 2.6, Предполагается, что
эти три уровня не вырождены, а соответствующие
скорости переходов указаны на фиг. 10.4. Типы переходов,
которые необходимо рассмотреть, точно такие же, как
на фиг. 2.6, однако обозначения скоростей переходов
изменены. Действие лазера начинается с возбуждения
внешним световым пучком атомов из основного
состояния |3) в верхнее возбужденное состояние |2) с
постоянной скоростью Л/>, где величина г определена в
B.46). В соответствии с обозначениями гл. 8 полные
скорости спонтанного распада двух верхних уровней
обозначаются через 2yi и 2у2-
Мы конкретно рассмотрим взаимодействие между'
атомами и фотонами одной моды оптического
резонатора. Как и в двухуровневом случае, мы предположим,
что частота моды резонатора совпадает с частотой,
соответствующей максимуму линии испускания или
поглощения для атомного перехода между состояниями |1)
и |2). Взаимодействие между атомом и выделенной
модой резонатора описывается, как и в случае вычисления
для двухуровневой системы, величиной ^. Однако по-
ТЕОРИЯ ЛАЗЕРА
353
скольку уровень |1) уже не является основным уровнем
атома и имеет конечное время жизни, то в A0.6)
параметр у следует заменить полным параметром ширины
линии перехода Yi + Y2- Тогда модифицированная
величина & для трехуровневого атома определяется
выражением
9= ^l*'2'2 =2ncl ^ . A0.45)
3sQhV (Yj + Y2) уЩ Yi+Y2
Здесь была использована формула (8.149). Если учесть
это изменение, то скорости поглощения и испускания
>
г
*
t
1
;—
2Гг
)
>
г 1
г
,
9п
2У<
'
Фиг, 10.4. Схема энергетических атомных уровней для
трехуровневого лазера, показывающая скорости основных переходов.
фотонов при наличии в моде п фотонов точно такие же,
как в A0.7) и A0.8). Они приведены на фиг. 10.4.
Условие работы лазера B.49) в используемых здесь
обозначениях принимает вид
Y2i<Yi. (l°-46)
Мы будем предполагать, что условие A0.46)
выполняется для трехуровневых атомов. Кроме скорости спон*
тайного излучения 9 в выбранную моду резонатора, на
фиг. 10.4 неявно представлены спонтанные переходы
в полный набор мод, определяющие полную скорость
распада узь Эффект уширения линий за счет этих пере-,
ходов включен в параметр Y2-
В реальном лазере число фотонов в резонаторе
определяется не только взаимодействием с атомами» но так-/
же несколькими механизмами потерь, связанными с
12 Зак. 885
354
ГЛАВА 10
самим резонатором.' Постоянный уход фотонов из
резонаторов в виде полезного выходного лазерного пучка
является одним из источников потерь. Потери фотонов
учитываются в теории путем введения вероятности С
ухода фотона из моды резонатора в единицу времени.
Скорость потерь в резонаторе С равна скорости
затухания фотонного возбуждения, определяемой всеми
процессами, кроме взаимодействия света с атомными
переходами между уровнями 1 и 2.
Для получения в моде разонатора значительного
числа фотонов необходимо, чтобы скорость излучения
фотонов атомами была достаточно велика для
компенсации потерь резонатора. Как только скорость накачки
г достигает величины, достаточной для того, чтобы
скорость воспроизводства фотонов равнялась скорости
потерь С, то говорят о пороговом режиме работы лазера.
Мы найдем условие порога для лазера, которое
определяет эту минимальную скорость накачки, необходимую
для увеличения числа фотонов в моде резонатора.
Рассмотрим лазер ниже порога, когда число
фотонов п в моде резонатора мало. Распад уровня 2
обусловлен в основном спонтанным испусканием со скоростью
2у2. Среднее число атомов N2 в состоянии |2)
определяется конкуренцией между скоростью возбуждения г
и скоростью распада 2уг> а поэтому
М2= Nr/2y2 (ниже порога). A0.47)
В действительности это соотношение справедливо даже
тогда, когда возбуждено весьма большое число фотонов
[см. A0.70)]. Отметим, что этот же результат следует из
B.51), если пренебречь величиной W ниже порога и
соответственно изменить обозначения. Следовательно,
скорость излучения фотонов в выбранную моду полости
дается выражением
N2$= Nr$/2y2 (ниже порога). A0.48)
Здесь вынужденное излучение не учитывается.
Величина, стоящая в правой части формулы A0.48),
часто встречается в уравнениях теории лазера, поэтому
удобно ввести обозначение
a==Nr$j2y2. A0.49)
ТЕОРИЯ ЛАЗЕРА
355
Для данного типа атомов все величины в определении а
фиксированы, за исключением скорости накачки г и
плотности атомов. В теории, изложенной ниже, мы
исследуем зависимость работы лазера от г или, эквива-
лентно, от а.
Лазерная генерация происходит тогда, когда
скорость спонтанного излучения A0.48) превышает
скорость потерь фотонов, или когда а больше С.
Пороговое условие для лазера имеет вид
а = С (порог). A0.50)
Лазер работает ниже или выше порога, когда
величина а больше или меньше С соответственно.
Численные значения лазерных параметров
существенны для использования приближенных методов в
теории лазера. Мы не будем пытаться в оставшейся части
главы изложить теорию, пригодную для всех типов
лазеров, а примем некоторые численные значения
параметров, которые позволят определить статистические
свойства лазерного света в простом приближении.
Определенные численные значения соответствуют
некоторым типам газовых лазеров, генерирующих в
видимой области спектра [4], например гелий-неоновому
лазеру. Параметр ширины линии 2у равняется
коэффициенту Эйнштейна Л, значения которого для переходов
в атоме водорода приведены на фиг. 3.5. Мы примем
типичное значение
2Y^3- 107c-\ A0.51)
которое будем использовать для оценок как величины
2уь так и 2у2- Допустим, что полное число атомов в
активном объеме V = 2- 10~5м3 есть
N = 2. 10!0.. A0.52)
Отсюда приближенно находится величина 2?,
определенная в A0.45):
З^Сбс-1. A0.53)
Здесь предполагалось, что частота принадлежит
видимому диапазону [формула B.14)], и было использовано
неравенство A0.46).
12*
356
ГЛАВА Ю
Типичная величина скорости потерь резонатора для
фотонов в газовом лазере может составлять
С» 106с-\ A0.54)
что соответствует добротности резонатора со/С порядка
3-Ю9. При пороге формулы A0.49) и A0.50) дают
Nr = 2у2С/$ « 6 • 1013c-J (порог). A0.55)
Здесь были использованы выражения A0.51), A0.53) и
A0.54). С помощью A0.52) находим пороговую скорость
накачки
г«3- lO'V (порог). A0.56)
Таким образом, для принятых здесь численных значений
порог достигается при возбуждении в верхнее
возбужденное состояние за одну секунду лишь одной
миллионной части полного числа атомов, находящихся в
резонаторе.
Кинетические уравнения для атомов
Внешнее воздействие, управляющее лазером в
приведенной выше модели, представляет собой накачку
атомов в верхнее возбужденное состояние. В реальной
лазерной системе накачка может осуществляться либо
внешним световым пучком, либо электрическим
разрядом. Величина г или, эквивалентно, а может на практике
меняться для изучения зависимости лазерных
характеристик от скорости накачки. Изложенные ранее
вычисления для двухуровневого атома основывались на
предположении о том, что населенности уровней N\ и Л^
могли быть фиксированы некоторым внешним
воздействием. Такое предложение значительно упрощает
проведение вычислений, но не соответствует реальной модели
лазера, поскольку фиксировать величины Ni и N2
практически невозможно.
Теория лазера довольно сложна, даже когда анализ
ограничен стационарным состоянием. Распределение
вероятностей Рп для фотонов в моде резонатора
определяется равновесием между генерацией фотонов при
атомных переходах и потерями фотонов в резонаторе,
ТЕОРИЯ ЛАЗЕРА
357
описываемыми скоростью затухания С. Сами стационар*
ные значения населенностей атомных уровней опреде*
ляются данной скоростью накачки г и распределением
вероятностей для фотонов. Следовательно, лазерная
система включает связанные движения атомов и фотонов,
а поэтому решить уравнения движения в общем случае
очень трудно.
Однако задача облегчается благодаря принятым
здесь относительным значениям лазерных параметров*
Из A0.51) и A0.54) видно, что скорость атомных излу-
чательных переходов на один или два порядка больше
скорости потерь фотонов из моды резонатора. Эти две
скорости определяют скорость движения атомной и
фотонной частей лазерной системы. Все скорости,
определяющие число фотонов в моде резонатора, примерно в
10 или 100 раз меньше скоростей атомных переходов.
Это свойство позволяет в адиабатическом прибли«
жении развязать атомную и фотонную системы. В
процессе временного развития распределения фотонов
более быстрая атомная система приводит населенности -
своих уровней в равновесии с мгновенным
распределением фотонов. Поэтому наши вычисления удобно
проводить в две стадии. На первой стадии мы выведем
кинетические уравнения для атомных населенностей при
стационарном распределении фотонов Рп. Стационарное
решение этих уравнений определяет атомные
населенности для данного распределения Рп. На второй стадии
мы исследуем значительно более медленное временное
развитие самого распределения фотонов, которое
определяется взаимодействием с атомами и скоростью потерь
в резонаторе.
Приближение зависит от относительных величин уи
у2 и С. Оно было бы несправедливо, если бы значение
С было порядка или больше ys, где s=l,2. Данное
приближение очень сходно с адиабатическим t
приближением в динамической теории кристаллической
решетки [5]. Электроны в кристалле движутся значительно
быстрее ядер, поэтому сначала решают уравнения
движения электронов, считая ядра неподвижными.
Движение ядер определяется на второй стадии вычислений,тде
электронные волновые функции используются для опре-
358
ГЛАВА 10
деления эффективного потенциала, в котором движутся
ядра.
Используемый здесь метод кинетических уравнений
является простейшим способом нахождения
распределения Рп лазерных фотонов. Он не является столь же
общим или строгим, как другие методы [6—10],
использовавшиеся для нахождения Рп. Однако в отношении
отдельных результатов, включая детальный вид
распределения фотонов, этот метод эквивалентен некоторым
более сложным вычислениям1).
Для проведения первой стадии вычисления мы
должны определить атомные населенности для данного
распределения фотонов. При расчете будем использовать
только средние числа атомов в состояниях 1 и 2 без
исследования флуктуации атомных населенностей.
Определим величину Rln как вероятность нахождения п
фотонов в моде резонатора и одновременного нахождения
произвольного атома в состоянии 1. Иными словами,
NR\jPn есть среднее число атомов в состоянии / при
наличии п фотонов. Поскольку вероятность нахождения
атома в состоянии 1 независимо от числа имеющихся
фотонов равна NJN, то
ZRn=-Ni/N. A0.57)
п
о
Определяя аналогично Rn для состояния 2, получаем
£ Rl = N2/N. A0.58)
tl
На первой стадии расчета распределение фотонов
зафиксировано, поэтому только атомные сЪставляющие
функций комбинированных вероятностей меняются со
временем. Факторизация величин Rn и Rn невозможна,
например
. Rln=£(Ni/N)Pn, A0.59)
*) Кинетические уравнения были впервые использованы для
определения флуктуации интенсивности лазерного пучка в работе [11];
вычисление, несколько сходное с последующим расчетом, было
приведено в [12].
ТЕОРИЯ ЛАЗЕРА
ооЭ
поскольку атомные вероятности зависят от числа воз-»
бужденных фотонов и не являются фиксированными, как
в случае вычислений для двухуровневых атомов,
проведенных в главе раньше.
•о
е
CD
+
о;
е
ч
л+/
/?;&(п+1)
п
п-1
О
гРп
СД("+/)
п+2
п+1
— п
2у2*1
LA
*0
Состояние 3
Фиг. 10.5. Схема комбинированных энергетических уровней для
трехуровневого атома и фотонов.
о
Стрелки указывают только те переходы, которые влияют на вероятности R
и R , |. Соответствующие скорости изменения этих вероятностей показаны
около стрелок, указывающих переходы.
Рассмотрим скорости изменения величин Rn и /?п-н»
На фиг. 10.5 показана схема комбинированных
энергетических уровней системы «атом + фотоны» с указанием
скоростей переходов, влияющих на R'n и Rn. Поскольку
накачка переводит атомы в состояние 2 со скоростью,
не зависящей от числа уже имеющихся в этом состоянии
атомов и от распределения фотонов, то ее вклад в R%
360
ГЛАВА 10
равен скорости роста гРп. Все остальные скорости
пропорциональны R2n или /?rt+i и анализ фиг. 10.5 дает
следующие кинетические уравнения:
dRl/dt = rPn + Rln+& (л + 1) -
-Rl$(n+l)-2y2Rlf A0.60)
dRln+ildt = — Rln+i9 (n + 1) +
+ R*9{n + l)-2ylR)l+l. A0.61)
Эти уравнения представляют собой более точный
вариант кинетических уравнений B.43) и B.44), в
которых излучение описывается только средней плотностью
энергии W и распределение фотонов не учитывается.
За промежутки времени, большие по сравнению с
временами распада атомного уровня A0~7—10~8 с), но
малые по сравнению с временем затухания моды
резонатора (Ю-6 с), атомная система достигает равновесия
со сравнительно статическим распределением фотонов.
В этом стационарном состоянии -значения Rn и Rn+\ не
зависят от времени и скорости, данные в A0.60) и
A0.61) можно положить равными нулю:
rPn + Rln+l$ (я + 1) - R\9 (п + 1) - 2y2Rl = 0 A0.62)
и
- Rln+l9 (n+l) + R\% (л + 1) - 2Yl*i+I = 0. A0.63)
Сложение уравнений A0.62) и A0.63) дает
^ = 2Y2^ + 2Yl^+1. A0.64)
Суммируя это равенство с обеих сторон по п и учитывая
A0.18), A0.57) и A0.58), получаем
rN = 2y2N2 + 2ylNl. A0.65)
Здесь мы отметим, что величина Ro равна нулю для
схемы переходов, приведенной на фиг. 10.5. Результат
A0.65) выражает равенство скоростей прямых и
обратных переходов для основного состояния 3 и
эквивалентен формуле B.48).
ТЕОРИЯ ЛАЗЕРА
361
Функции вероятностей для системы «атом + фотоны»
получаются непосредственно решением уравнений A0.62)
и A0.63):
2 _ гРп {9 (п + I) + 2У1] ПП fiftt
Кп~ 4YiY2+2(yi+Y2)S4>*+1) { }
И
pi гРп9(п+ 1) (}(\(\7\
«n+l— 4у1у2+2(у1+у2)$(п+\) ' { П
Это основные результаты первой стадии вычислений.
Отметим, что выражения A0.66) и A0.67) имеют
структуру, сходную со структурой выражений B.51) и B.50).
Относительные величины различных членов в
формулах A0.66) и A0.67) можно оценить, исходя из
приведенных ранее значений параметров. Рассмотрим два
члена в знаменателях. Удобно ввести новую величину
Из A0.51) и A0.53) следует, что
Р»3- 107. A0.69)
Из A0.66) и A0.67) видно, что для чисел фотонов /г,
много меньших р, первый член в знаменателе много
больше второго, а второй член в числителе много больше
первого, отсюда
*£«!§- (Ю.70)
и
, rPn9{n + \) R2„9(n+1)
*Ь* « 4YlY2 * 2Y, {П<®- A0J1)
Населенность атомного состояния 2 значительно
больше населенности атомного состояния 1. Суммирование
по п обеих сторон уравнения A0.70) показывает, что
величина N2 приблизительно равна Nr/2y2, что совпадает
с результатом A0.47), полученным на основе более
качественных рассуждений.
В то же время для чисел фотонов я, много больших
р, члены, содержащие &(п-\-1), доминируют в A0.66)
и A0.67), поэтому
R2a™K+i™rPnl2(Vi + yJ (п>®> <10J2>
362
ГЛАВА 10
Населенности двух возбужденных атомных состояний
теперь почти одинаковы и равны Nrj2(yi-\-y2). Это и
есть тот самый эффект насыщения, который описан в
гл. 2 и который, как будет показано дальше, важен для
определения статистических свойств лазерных фотонов.
Кинетические уравнения для лазерных фотонов
л
На второй стадии расчета лазера мы
проанализируем влияние атомных переходов на состояние фотонов
в моде резонатора. Рассмотрим действие показанных на
фиг. 10.5 переходов на число фотонов. Только два
горизонтальных перехода непосредственно влияют на РПУ
определяя скорость роста Rn+i$ (я + 1) и скорость
уменьшения #^(я + 1) для каждого из N атомов,
находящихся в резонаторе. Согласно A0.66) и A0.67),
Rl>Rln+i> A0.73)
поэтому суммарный эффект двух типов переходов дает
отрицательный вклад
(dP«/d%t n+l =N(Rln+{ - Rl)9(n + 1). A0.74)
Фотонная вероятность Рп также зависит от
горизонтальных переходов между соседней нижней парой
уровней на фиг. 10.5. По аналогии с приведенным выше
результатом эти переходы дают положительный вклад
{dPn/dt)nt n_, = N (/?'-! - Rxn) 9n. A0.75)
Вклады четырех типов переходов, определяющих РПу
показаны на схеме энергетических уровней,
изображенной на фиг. 10.6. Эта схема похожа на фиг. 10.1, но
теперь для скоростей переходов даны более общие
выражения, учитывающие влияние распределения фотонов
на населенности атомных возбужденных уровней.
Генерации фотонов за счет атомных переходов
препятствуют потери, определяемые скоростью С. ^Потери
фотонов приводят только к переходам вниз, показанным
на фиг. 10.6. Два таких перехода влияют на n-й энерге-
ТЕОРИЯ ЛАЗЕРА
363
тическйй уровень фотонов и дают следующую скорость
изменения:
(dPJdt)nmpa = - СпРп + С (п + 1) Рп+Х. A0.76)
Полная скорость изменения Рп определяется суммой
выражений A0.74) — A0.76). Учитывая общие
вероятности из A0.66) и A0.67), а также используя величины
^+/
п
Рп-1
л/СД("+/)
ШЦ.,9п
NR%9(n+1)
№1пУп
п+1
С(п+1)Рп+1
——- п
СпР,
П
п-1
Рг
Ро
О
Фиг. Ю.6. Схема энергетических уровней для фотонов, показываю*
щая скорости роста и распада Рп, обусловленных атомными
переходами и потерями резонатора.
аир, определенные в A0.49) и A0.68), получим
результат
dPn а$Рп(п + 1) . а$Рп-\п _
dt р + п + 1 "+" р.+ п
-СпРа + С{п+1)Рп+1. A0.77)
Отсюда видно, что динамические свойства распределения
фотонов определяются тремя параметрами: а, р и С.
Точно такое же уравнение A0.77) для распределения фо-
364
ГЛАВА !0
тонов получается при более строгих вычислениях1), в
которых используется метод оператора плотности.
Решение системы связанных уравнений для Рп
представляет сложную задачу. Даже моменты распределения
,фотонов трудно определить как функции времени в
отличие от соответствующих вычислений, основанных на
уравнениях, несколько сходных с уравнениями A0.14)
для двухуровневого атома. Наличие п в знаменателях
первых двух членов в правой части уравнения A0.77)
препятствует получению простых уравнений движения
для моментов. Временное развитие распределения
лазерных фотонов было исследовано в работе [13] методом
численного интегрирования уравнения A0.77), но здесь
эти расчеты не рассматриваются.
Однако стационарное распределение фотонов, для
которого временные производные в A0.77) принимаются
равными нулю, можно получить довольно просто. Как и
в случае стационарного решения уравнения A0.14),
полная скорость перехода между любой парой
энергетических уровней фотонов должна равняться нулю, а потому
для уровней мим— 1 на фиг. 10.6 получаем
NRl-&n - NR^Sn - СпРп = 0. A0.78)
Используя A0.49), A0.66) — A0.68), это уравнение
перепишем следующим образом:
Pn = j^Pn-u A0.79)
Величину Рп можно выразить через Pq посредством
итераций
р = №/0ПРо
' Л'~Ч"Л' " . A0.80)
п (Р + л)(Р + д-1)...(Р + 2)(р + 1)
(аР/С)яр! Яр
= (Р + я)!
Следовательно, распределение фотонов Рп полностью
определено, за исключением величины Р0> которая
является вероятностью отсутствия фотонов в моде резона-
1) Ср, A0,77) с формулой (86) из работы [6],
ТЕОРИЯ ЛАЗЕРА
365
тора. Оставшаяся неизвестная величина находится из
условия нормировки A0.18):
П П
Сумму по п можно выразить через стайдартную конф-
люэнтную гипергеометрическую функцию, определяемую
обычным разложением в ряд [14]
■'■fr-^-ni.Tiligiiii-g-- с»-82)
п
Сравнение A0.81) и A0.82) показывает, что исходное
уравнение можно переписать в виде
^A, 1+р;ар/С)Р0=1. (Ю.83)
Следовательно, полное решение уравнения A0.80) для
распределения фотонов дается выражением1)
Р = (*№ЯУ A084v
(Р + п)\ ХРХ A, 1 + р; ар/С) " UU.04J
Распределение лазерных фотонов
Наиболее важной характеристикой лазера, которую
необходимо получить из изложенной выше теории,
является среднее число фотонов, генерируемых при данной
скорости накачки. Скорость накачки пропорциональна а,
и из A0.84) видно, что распределение Рп зависит от а
только в комбинации а/С. Следовательно, для данного р
распределение фотонов можно исследовать как функцию
отношения а/С. Используя A0.80) и условие нормировки,
получим, что среднее число фотонов дается выражением
00
й-VnP У П WWP1 P° -
п п=0
оо
= 2,(Р + я-р) (р+пI -
= (ар/С)-рA-Р0), (Ю.85)
1) Эта форма распределения была впервые получена Скалли и
Лэмбом в работе [6],
366
ГЛАВА 10
где величина Р0 определяется из A0.83). Эти результаты
еще не являются окончательными, поскольку в них
входит величина Pq, выраженная через конфлюэнтную
гипергеометрическую функцию. Однако эту функцию
можно записать в простой
/7
форме для областей ниже
порога, при пороге и
выше порога, которые будут
по очереди нами
рассмотрены.
Последующий анализ
уже использован на
фиг. 10.7, где показано
среднее число фотонов п
как функция а/С для
значения р, данного в
A0.69). Отметим, что за
резким увеличением п при
лазерном пороге а/С = 1
следует медленный рост
при более высоких
скоростях накачки. Исходя из
этого, можно провести
аналогию между порогом
для лазера и фазовым
переходом второго рода [15].
1. Лазер ниже порога,
а/С < 1. Упрощения,
которые можно сделать в
выражении для
распределения лазерных фотонов,
зависят от различных
приближений конфлюэнтной гипергеометрической
функции, справедливых для разных значений а/С. Параметр
Р является очень большим числом,-поэтому
конфлюэнтную гипергеометрическую функцию удобно разложить
в ряд по обратным степеням р. Эти разложения
стандартны [14], и детали их математического вывода здесь
не приводятся.
Ниже порога второй аргумент функции i/7! больше
третьего, и соответствующее разложение дается выра-
107
10s
W5
10*
103
102
10
1
10~1
О
ос/С
Фиг. 10.7. Зависимость среднего
числа фотонов h в излучении
одномодового лазера от скорости
накачки, пропорциональной а/С,
для р = 3-107.
ТЕОРИЯ ЛАЗЕРА
667
жением
,ЛA, 1 + р; ар/С) = 1 _ }д/с) X
^'"tli-W^H' A0'86)
Пренебрегая членами порядка р~2 и подставляя найден*
ный результат в A0.83), получаем
а среднее число фотонов из A0.85) принимает вид
iJwc) (а/С<1). (Ю.88)
п =
Если только значение а/С не очень близко к единице,
'то число фотонов в моде резонатора всегда мало по
сравнению с р, а потому можно использовать
приближение
(Р + я)!=Р!Р* (Р»л). A0.89)
На основе этого результата и аппроксимации Ро первым
членом выражения A0.87) распределение фотонов
A0.80) можно записать в виде
р-=(■£)-т)-ТТ¥^ ыс<"• ('°•90)
где величина п определена в A0.88). Распределение
фотонов идентично распределению A0.10), и,
следовательно, ниже порога свет является хаотическим. На
фиг. 10.8, а показан график распределения A0.90) для
случая а/С = ]/2.
2. Порог а/С = 1. При пороге второй и третий
параметры конфлюэнтной гипергеометрической функции
почти одинаковы и разложение A0.86) больше не
пригодно. Функцию можно оценить с помощью
интегрального представления, детали вычисления которого даны
в приложении в конце этой главы. В результате получим
^(l, i+P;P)~(-f-I/2. (Ю.91)
о?
8
п
12 14 16
-8 0 8
(n-H)*10-J
Фиг. 10.8. Распределение фотонов Рп для лазера, работающего
соответственно ниже порога, при пороге и выше порога.
Распределения изображены в виде непрерывных кривых, хотя распределение Рп
строго определено только для целых значений п. Вертикальная черта на каждой
графике обозначает среднее число фотонов п. Численные данные для трех фигур
следующие: 0=3 • 107; а) а/С=7*. й=1, Р0=0,5; б) а/С = 1, й=»4400, Pfl = l,4-10~4;
в) а/С —2, й—3 • 107, Р0 —5,3 . 10,
ТЕОРИЯ ЛАЗЕРА 369
Следовательно,
Р°*(-£?УЯ (a/C=l) A0.92)
и среднее число фотонов из A0.85) есть
й*(^)и (<*/с=1). (Ю.93)
Для значения р, приведенного в A0.69), среднее число
фотонов при пороге приблизительно равно 4400.
Распределение фотонов при пороге определяется из A0.80) и
A0.84) и имеет вид
Эта зависимость показана на фиг. 10.8,6.
Описанный в приложении метод можно использовать
для изучения распределения фотонов при скоростях
накачки, близких к пороговому значению. Можно
определить некоторую околопороговую область, где
приближения, описанные в пп. 1 (выше порога) и 3 (ниже порога),
несправедливы. Можно, однако, показать, что эта
околопороговая область соответствует значениям а/С,
отличающимся от единицы на величину порядка нескольких
значений р~,/з. Данная область настолько мала, что на
фиг. 10.7 ее не видно. В дальнейшем она нами не
рассматривается.
3. Лазер выше порога, а/С > 1. Теперь третий
аргумент конфлюэнтной гипергеометрической функции
больше второго и соответствующее разложение по степеням
р-1 дается выражением {14]
iMl, 1+р;ар/С) =
-"«Р(*)(*Г[«+<>(£)]- <1М«
Эта величина" намного больше единицы и значение Pq
соответственно пренебрежимо мало. Следовательно,
среднее число фотонов из A0.85) имеет вид
Й = р{(а/С)— 1> (а/С > 1). A0.96)
Как указывалось выше, этот результат несправедлив в
области, очень близкой к порогу.
370
ГЛАВА 10
При сохранении в A0.95) только основного члена
распределение фотонов, приведенное в A0.84),
принимает вид
р __ (ар/С)Р+*ехр (-ар/С) _
Гп— (р + я)! ~
в№ + Л)Р(ГДГР"Я) (Ч/С>1). ХЮ.97)
Здесь была использована формула A0.96).
Свойства распределений фотонов выше порога
зависят от относительных значений р и Я. Отметим, что
согласно A0.96),
/г = р для а/С = 2. A0.98)
Значения /г, большие р, соответствуют скоростям
накачки, при которых населенность активных
возбужденных состояний приближается к насыщению, как
указывалось в обсуждении формулы A0.72). Для значения /г,
много большего р, приближенное выражение для Рп
имеет вид
рп = nnex?J-n) (a/c>2)> A0.99)
Выражение A0.99) совпадает с распределением фотонов
A0.9) для когерентного света. Отсюда видно, что только
при многократном превышении скорости накачки
порогового значения выходное излучение становится
когерентным. Вид распределения фотонов для а/С = 2 показан
на фиг. 10.8, е.
Задача 10.2. Докажите, что среднеквадратичное
отклонение для распределения чисел фотонов в
излучении лазера, работающего при
превышении порога, дается выражением
;?—Й2 = Р + Й (<х/С> 1). A0.103)
За исключением дополнительного
слагаемого р этот результат точно такой же, как
результат для когерентного распределения,
приведенный в A0.99). Следовательно,
распределение, данное в A0.97), имеет флук-
ТЕОРИЯ ЛАЗЕРА 371
туации, превышающие флуктуации
когерентного света. Отличие' от случая
когерентного света существенно для 1 < а/С <
< 2; при а/С > 2 величина отклонения
уменьшается.
Задача 10.3. Докажите, что степень когерентности
второго порядка лазерного пучка, описанного
выше, дается следующими выражениями:
д® = 2 A0.101)
ниже порога,
при пороге и
8$ = 1 + (Р/) A0.103)
выше порога. Степень когерентности
первого порядка для одномодового пучка,
конечно, всегда равна единице. Результаты
A0.101) и A0.103) снова несправедливы
в очень узкой околопороговой области.
График зависимости п от а/С на фиг. 10.7 ниже и
выше порога был получен на основе приближений
A0.88) и A0.96), а при точном пороге —на основе
приближения A0.93). Быстрое увеличение числа фотонов
примерно на пять порядков в области порога является
наиболее удивительным свойством этого графика.
Скорость накачки, в два раза превышающая пороговое
значение, имеет важное физическое значение. Это величина,
при которой начинают сказываться эффекты насыщения.
С теоретической точки зрения когерентное
распределение фотонов для лазера4, работающего при
значительном превышении порога, обусловлено наличием в
уравнении A0.77) первых двух членов, знаменатели которых
линейно зависят от числа фотонов п. Если в двух
знаменателях пренебречь членами, содержащими п и п+ 1, то
для всех значений а/С получается хаотическое
распределение фотонов A0.90). В свою очередь знаменатели
членов в A0.77) получаются из знаменателей атомных
функций вероятностей Rn и /?„+!, определяемых форму-
372
ГЛАВА 10
лами A0.66) и A0.67). Как уже указывалось выше, роль
этих знаменателей заключается в том, чтобы обеспечить
насыщение населенностеи двух атомных уровней при
Фиг. 10.9. Измеренные распределения фотоотсчетов для одномодо-
вого газового лазера.
Число около каждого распределения есть отношение измеренной интенсивности
пучка к интенсивности лазерного пучка при пороге. Следовательно, единица
соответствует точному порогу, а распределения слева направо соответствуют
переходу от допороговой интенсивности к интенсивности, значительно
превышающей пороговое значение. Время счета Т фиксировано и равно 3 • 10 с;
оно меньше периода флуктуации интенсивности для всех распределений (подан*
иым работы [16]).
значениях населенностеи порядка Nr/2(y\ + Y2).
Существование атомного насыщения является, таким образом,
важным фактором в распределении лазерных фотонов
и особенно в обеспечении перехода к когерентному
световому пучку при высоких скоростях накачки.
Распределения фотонов Рп> выведенные ранее для
различных областей значений а/С, могут быть изучены
ТЕОРИЯ ЛАЗЕРА
373
наиболее непосредственно с помощью экспериментов по
счету фотонов, описанных в гл. 9. На фиг. 10.9
представлены некоторые результаты экспериментов [16],
проведенных с одномодовым газовым лазером. Из этих
результатов можно видеть, что форма распределений
Рт(Т) для лазера ниже порога, при пороге и выше
порога качественно похожа на форму распределений
фотонов Рп, показанных на трех частях фиг. 10.8. Однако, как
было указано в гл. 9, распределения Рт(Т) и Рп обычно
не совпадают. Даже когда время счета фотонов Т много
меньше времени флуктуации света, распределение
фотоотсчетов должно получаться при подстановке A0.84) в
более общее соотношение (9.84).
Кроме того, конечное время счета Т может привести
к дальнейшим различиям между распределениями РШ(Т)
и РПу вид которых показан на фиг. 9.5. В гл. 9 было
показано, что в пределе времени Г, очень большого по
сравнению с характерным временем флуктуации
интенсивности пучка, распределение Рт(Т) всегда стремится к пуас-
соновскому распределению независимо от вида Рп.
Характерное для определенного светового источника
распределение фотоотсчетов можно получить только в том
случае, когда время Т сравнимо или меньше времени
флуктуации. Вычисление Рт(Т) для лазерного света при
произвольном значении Т довольно сложно [17] и здесь
обсуждаться не будет. Результаты экспериментов по
счету фотонов [16, 18, 19] с одномодовыми газовыми
лазерами находятся в очень хорошем согласии с теорией и
подтверждают выведенные выше распределения
фотонов Рп.
Задача 10А. Докажите, что в случае коротких времен
счета распределение фотоотсчетов для
лазера связано с распределением фотонов
соотношением 1)
рш (Т) = PJTFi [/» + 1, « + 1 + Р;
A-Е) ар/С], (Ю.104)
где величина Рт определена в A0.84) и
\ — квантовая эффективность детектора.
Щштттттщ I ■ —
х) Этот результат впервые был получен в работе [20].
374
ГЛАВА 10
Флуктуации лазерного света
Свет, излучаемый лазером ниже порога, обладает
свойствами хаотического света, детально
рассмотренными в гл. 5. Распределение вероятностей для
амплитуды электрического поля светового пучка показано на
фиг. 5.9. Эта вероятность имеет гауссову зависимость от
амплитуды, а наиболее вероятное значение амплитуды
равно нулю. Соответствующее распределение
вероятностей для интенсивности пучка имеет экспоненциальную
зависимость E.36), что на языке фотонов означает
экспоненциальное убывание Рп как функции числа фотонов
я, показанное на фиг. 10.8, а.
Чтобы рассмотрение, проведенное в гл. 5, применить к
хаотическому свету лазера, работающего ниже порога,
его необходимо немного модифицировать. Обычно лазер
имеет оптический резонатор, торцевые стенки которого
являются хорошими отражателями, тогда как «полость»,
описанная в гл. 5, была просто точно определенной-
областью пространства, через которую пучок мог проходить
без поглощения или отражения. Для последнего случая
в E.65) было показано, что временной масштаб т/
флуктуации интенсивности одной моды определяется
временем L/cy необходимым для прохождения светом
воображаемой полости длиной L. Отражающие стенки
лазерного резонатора обладают свойством пленять свет с
соответствующим увеличением времени, необходимого
для затухания первоначального возбуждения в
резонаторе.
Рассмотрим одномерный резонатор с длиной L, на
концах которого находятся зеркала с коэффициентом
отражения 91. Время между двумя последовательными
отражениями равно Цс\ часть интенсивности пучка,
уходящая из резонатора при каждом отражении, равна 1—91.
Следовательно, временной масштаб т/ флуктуации
интенсивности одной моды определяется из уравнения
\/Tf = c(l-9l)/L. A0.105)
Таким образом, время т/ увеличено по сравнению со
значением для открытой полости в A—91)~{ раз и
стремится к бесконечному значению для резонатора с идеаль-
ТЕОРИЯ ЛАЗЕРА
375
но отражающими стенками, в котором возбужденная
мода не меняется во времени. Для резонатора с длиной
порядка 1 м и коэффициентом отражения 99,5% время
флуктуации т/ порядка 10~6 с. Отсюда 1/т/ порядка
10б с-1, что находится в соответствии с оценкой скорости
потерь моды резонатора С, приведенной в A0.54). Уход
света через зеркала на концах резонатора дает основной
вклад в скорость потерь.
Теперь рассмотрим лазер выше порога, когда
распределение вероятностей для фотонов определяется
формулой A0.97). В этом случае вместо характерного для
хаотического света экспоненциального спада с ростом пу
показанного на фиг. 10.8, а, мы имеем приблизительно
гауссово распределение около большого среднего
значения я, показанное на фиг. 10.8, е. Из A0.96) и A0.100)
имеем
Тогда для а/С = 2 и р из A0.69) среднее значение этого
распределения примерно в 4000 раз больше его
среднеквадратичной ширины. В случае лазера, работающего
при превышении порога, распределение фотонов имеет
довольно ярко выраженный пик около среднего значений
Я, причем соответствующее среднеквадратичное
отклонение невелико.
Эти свойства распределения фотонов можно
использовать при нахождении распределения вероятностей для
электрического поля лазерного пучка, похожего на
аналогичное распределение для хаотического света,
приведенное на фиг. 5.9. В случае пучка, имеющего ft фотонов
с частотой со, амплитуда электрического поля,
измеряемая детектором, определяется из (9.21) как
E = (hv/2edV)l/2n/2. A0.107)
Разброс числа фотонов, описываемый формулами
A0.100) или A0.106), соответствует разбросу амплитуды
поля, который при значительном превышении порога
приближается к величине, данной в G.74):
Д£»(Йсо/280УI/2. A0.108)
376
ГЛАВА 10
Как и в случае распределения поля для хаотического
света, фаза электрического поля не определяется
расчетом точно, а потому все значения ф равновероятны,
A lm£(t)
Re EH)
Фиг. 10.10. Распределение вероятностей для амплитуды и фазы
электрического поля светового пучка лазера, работающего при
превышении порога.
Величина вероятности указана с помощью плотности затемнения. Амплитуда Е
и ширина АЕ распределения определены на основе формул A0.107) и A0.108).
Относительная ширина распределения АЕ/Е порядка й"/^ поэтому она была
сильно увеличена для простоты рисунка.
Следовательно, при значительном превышении порога
распределение поля лазерного пучка имеет вид,
показанный на фиг. 10.10.
Основные различия между распределениями поля для
хаотического и лазерного света на фиг. 5.9 и 10.10
обусловлены преобладанием в генерации лазерного света
ТЕОРИЯ ЛАЗЕРА
377
процессов вынужденного излучения, сохраняющих
когерентность. Выше было показано, что когерентный свет
с распределением фотонов, данным в A0.9), сохраняет
свою когерентность в фотонах, получаемых при
вынужденном испускании, и не сохраняет в фотонах,
полученных при спонтанном испускании. В хорошем
приближении это же рассуждение с небольшими изменениями,
обусловленными отличием распределения лазерных
фотонов в A0.97) от распределения для полностью
когерентного света, применимо к лазерному свету. Таким
образом, в любой момент времени фотоны лазерного поля в
основном когерентны и имеют одинаковую фазу. Общая
фаза поддерживается новыми вынужденными фотонами,
число которых превышает число новых спонтанных
фотонов в п раз. Вследствие постоянного ухода
фотонов из резонатора среднее число фотонов, конечно,
сохраняется постоянным и равным п.
Действие спонтанного излучения на поле можно
описать графически с помощью диаграммы Эргенда,
изображенной на фиг. 10.10. Допустим, что в некоторый момент
времени электрическое поле определяется большой
стрелкой на фиг. 10.10. Если теперь появляется спонтанный
фотон, то его вклад в поле описывается небольшим
вектором длиной (fi(D/2e0VI/2, ориентированным в
произвольном направлении. Повторное испускание спонтанных
фотонов заставляет конец большой стрелки на фиг. 10.10
двигаться поперек затемненной области в соответствии
с вычисленным распределением вероятностей.
Флуктуации, вызываемые спонтанным излучением,
можно разделить на две составляющие: а) амплитудные
флуктуации, изменяющие длину вектора поля- и не
меняющие его угол ф, и б) фазовые флуктуации,
изменяющие фазовый угол ф и сохраняющие неизменной длину
вектора поля. Амплитудные флуктуации определяют
относительно малую случайную модуляцию амплитуды
поля около ее среднего значения Е и вызывают
осцилляции, «размазывающие» значение амплитуды типа
показанных на фиг. 7.3. Фазовые флуктуации оказывают
более сильное действие на полевой вектор; они заставляют
фазовый угол ф принимать все значения между 0 и 2я.
Столь больших фазовых сдвигов не имеется в поле пол-
378
ГЛАВА 10
ностыо когерентного фотонного возбуждения |а),
описанного в гл. 7. Эти сдвиги определяют значительное
отличие состояния лазерных фотонов от полностью
когерентного состояния.
Скорость диффузии фазы лазерного излучения
Вероятностное распределение лазерного поля,
показанное на фиг. 10.10, строго говоря, относится к
ансамблю одинаковых лазеров, похожему на ансамбль
источников хаотического света, описанный в тексте за
.формулой E.36). Поскольку все значения ф равновероятны,
то из приведенного выше рассмотрения следует
равенство нулю вещественной амплитуды поля Е cos ф,
усредненной по ансамблю. Тогда, согласно эргодической
теореме, среднее по времени от Е cos ф для одного лазера
также равно нулю.
На языке квантовой механики это означает, что все
недиагональные матричные элементы оператора
плотности фотонов для лазерного света равны нулю1), а
потому ожидаемое значение электрического поля также
равно нулю согласно G.99). Напротив, оператор
плотности когерентного состояния имеет отличные от нуля
недиагональные матричные элементы, определенные в
G.100). Распределение лазерных фотонов РПу
соответствующее диагональным матричным элементам
оператора плотности, приближается к распределению
когерентного света при высоких скоростях накачки, однако
недиагональные элементы матрицы плотности остаются
весьма различными.
Несмотря на эти основные различия между лазерным
Светом и когерентным светом, свойства световых пучков
обоих типов часто почти неразличимы. Именно
небольшая скорость, с которой происходит изменение фазы
электрического поля лазерного пучка относительно ее
значения в некоторый момент времени, делает выходной
лазерный пучок очень похожим на когерентный фотон-
1) Это свойство оператора плотности стационарного состояния
здесь не доказано. См. [6], где имеется вычисление недиагональных
матричных элементов фотонного оператора плотности»
ТЕОРИЯ ЛАЗЕРА
379
ный пучок. Ниже мы покажем, что характерное время
изменения фазы порядка 100 с и больше. Следовательно,
для достаточно больших периодов времени лазерйый
пучок имеет -стационарную фазу и изменение его
электрического поля сходно с изменением электрического поля
когерентного света.
Скорость обусловленного спонтанным излучением
изменения фазового угла ср электрического поля можно
определить с помощью простого вычисления, основанного
на фиг. 10.10. Скорость, с которой фотоны покидают
резонатор, есть пСу в стационарном состоянии она должна
равняться скорости испускания фотонов атомами.
Поскольку вынужденное испускание должно относиться к
спонтанному как /г:1, то скорость испускания фотонов
можно разделить на спонтанную и вынужденную
составляющую следующим образом:
пС = (у^ + т^-т) 0С. A0.109)
Отсюда скорость спонтанного испускания фотонов
описывается выражением
т¥^-«С дляй»1. A0.110)
1 ""Г tl
Эта спонтанная составляющая не зависит от Я и ее
относительное значение уменьшается с увеличением п.
Рассмотрим влияние спонтанного испускания на
вектор поля Е на фиг. 10.10. Изменение Э фазового угла ср
за время t можно связать с расстоянием /, которое
проходит конец вектора поля,
£9 = /. A0.111)
Здесь величина Е определяется из A0.107). Поскольку
вклад каждого спонтанного фотона описывается
небольшим вектором длиной (йоо/2еоУ),/2, ориентированным в
произвольном направлении, то среднеквадратичный вклад
в расстояние i имеет вид
7^ = 1(йсо/2б0У). A0.112)
380
ГЛАВА 10
Среднее изменение фазового угла, обусловленное одним
спонтанным фотоном, можно получить из A0.111) и
A0.112), причем изменение ф может быть
положительным или отрицательным с равной вероятностью.
Нам необходимо найти изменение фазового угла,
обусловленное Ct спонтанными испусканиями,
происходящими за время t. Вычисление эквивалентно расчету
случайного блуждания конца вектора поля около
окружности радиуса Е. Согласно стандартной теории
одномерного случайного блуждания [21] *), нормированная
вероятность того, что расстояние / пройдено за Ct шагов,
среднеквадратичная длина которых равна /2, дается
выражением
р (/) = {2n72Cty42 exp (- /2/2/*Ct). A0.113)
С помощью формул A0.107), A0.111) и A0.112) это
распределение вероятностей можно преобразовать в
эквивалентное распределение для изменения фазового угла 9
за время t:
р (9) = (n/jiCtLz exp (- Q2n/Ct). A0.114)
Распределение вероятностей для фазового угла
удовлетворяет одномерному диффузионному уравнению
dp/dt = @{d2p/de2). A0.115)
Чтобы функция /7(9) из A0.114) была решением
уравнения A0.115), постоянная диффузии 2) должна быть
определена следующим образом:
2) = С/4п. A0.116)
Таким образом, фазовый угол диффундирует от своего
начального значения со скоростью, обратно
пропорциональной среднему числу лазерных фотонов.
Влияние диффузии фазы на электрическое поле можно
лучше всего продемонстрировать путем вычисления
средней проекции поля в момент времени t на поле при
/ = 0
Е @ • Е @) = £2 cosO. A0.117)
*) Статья [21] перепечатана в сб. [22],
ТЕОРИЯ ЛАЗЕРА
381
Здесь черта означает усреднение по фазовому
распределению. Используя стандартный интеграл [23], получим
оо
согГё= J p (G) cos 9 d9 = ехр (— Ct/4n). A0.118)
— оо
Определяя время диффузии фазы тр по формуле
1/тр = С/2й, A0.119)
выражение A0.117) можно переписать в виде
Е(/).Е@) = £2ехр(-//2т„). A0.120)
Точно такое же выражение A0.119) для времени
диффузии фазы может быть получено на основе более строгого
расчета [5, 24], в котором решается уравнение движения
для оператора плотности фотонов.
Наиболее замечательным свойством времени тр
является его большая величина; если значение С взять из
A0.54), а среднее число фотонов п положить равным р
из A0.69), то время диффузии фазы равно 60 с. Времена,
большие этого, легко достижимы при больших значениях
Я, соответствующих большим скоростям накачки.
Следовательно, скорость диффузии фазы примерно на семь
порядков меньше скорости потерь резонатора С, которая
в свою очередь меньше скорости атомных излучательных
переходов. В промежутках времени, меньших тР, фаза
лазерного пучка почти постоянна, поэтому для таких
промежутков изменение электрического поля пучка
сходно с изменением электрического поля классической
стабильной волны. Экспериментально период устойчивости
лазерного пучка может быть на несколько порядков
меньше тр вследствие эффектов, которые здесь не
рассмотрены, например механических колебаний резонатора.
Однако теоретический предел устойчивости пучка
определяется временем диффузии фазы.
Диффузия фазы вызывает эффективный разброс
частоты лазерного пучка около его центральной частоты соо.
Частотный профиль линии определяется фурье-преобра-
зованием электрического поля, обладающего
синусоидальным изменением на частоте соо и диффузией фазы.
Вычисление аналогично расчету ударного уширения,
приведенному в гл. 5, и ведет к лоренцеву частотному
382
- ГЛАВА 10
спектру с центром при частоте соо и шириной 1/хр, Для
лазера, работающего при значительном превышении
порога, ширина линии, связанная с диффузией фазы,
чрезвычайно мала.
Порог лазера имеет близкую аналогию с фазовым
переходом второго рода [15], например с
ферромагнитным фазовым переходом в магнитном кристалле [25].
В последнем случае при охлаждении кристалла до
температуры ниже точки Кюри магнитные моменты
парамагнитных ионов в кристалле ориентируются
параллельно друг другу. Для изотропного гейзенберговского
ферромагнетика направление ориентации магнитных
моментов не определяется гамильтонианом системы, а
потому все направления равновероятны. Однако, несмотря
на эквивалентность различных направлений, скорость
перехода кристалла из некоторого состояния, где полная
намагниченность ориентирована определенным образом,
в состояние с другой ориентацией намагниченности очень
мала. В реальном ферромагнитном кристалле в
действительности всегда существует некоторая поверхностная
или объемная неоднородность, ориентирующая
намагниченность в фиксированном направлении.
Электрическое поле лазерного пучка обладает
свойством, делающим его похожим на намагниченность в
ферромагнетике. Это свойство заключается в очень
медленной диффузии от данного фазового угла, даже если
все фазы в принципе эквивалентны. Проводя аналогию
с фазовым переходом, можно считать, что скорость
лазерной накачки играет роль температуры, а пороговое
значение скорости накачки является аналогом
температуры перехода. Эту аналогию между двумя системами
можно провести достаточно далеко {15].
Приложение
Здесь мы приведем этапы вывода формулы A0.91)/
Согласно формуле C.1.2) из [14], конфлюэнтная
гипергеометрическая функция может быть записана в виде
интеграла, Определяя
"-сТгЬр A°-А1)
ТР0РИЯ ЛАЗЕРА
383
из интегрального представления получим
1^A, 1+Р; ар/С) = ,7^A, 1+P;*+N= ,
1
= ^eV+Vxt{l-tf-ldt. A0. А2)
о
Произведем замену переменной интегрирования
s = t^7~a:, A0. A3)
тогда
оо
,f,(l; H-p;ap/C) = p(^-r-J ИтТГ/ ^-(Ю.А4)
Рассмотрим величину в фигурных скобках
подынтегрального выражения A0.А4). Легко,проверить, что при
5 = 0
{ } = 1, {d/ds) { } = 0, {djdsf { } = - 1/х2. A0.А5)
Таким образом, функция в фигурных скобках может
быть представлена с точностью до величин порядка s2
следующей приближенной формулой:
exp {s/(s + х)} x/(s + х)ъ ехр {— s2/2x2}. A0. А6)
Тогда выражение A0.А4) принимает вид
оо
iF,(l, 1 +р; ap/C)«p(ex-'/.v)p+I $ e-e,»+,>**'ds. A0.A7)
j
Возможность гауссова приближения A0.А6) для вычис*
ления интеграла обусловлена очень высокой степенью
р + 1, в которую возводится подынтегральная функция.
В случае порога вычисление интеграла особенно
просто, так как величину х в A0.А1) можно положить рав
ной единице. Тогда нижний предел в интеграле A0.А7))
384
ГЛАВА 10
обращается в нуль, и после интегрирования получим
,ЛA, 1+р;р)«(яр/2),7\ A0. А8)
Здесь мы снова пренебрегли единицей по сравнению с р.
ЛИТЕРАТУРА
1. Kittel С, Elementary statistical physics, Wiley, New York, 1958,
p. 171.
2. Lacks G, Phys. Rev., B138, 1012 A965).
3. Jakeman E., Pike E. R., J. Phys., A2, 115 A969).
4. Garrett С G., Gas lasers, McGraw-Hill, New York, 1967.
5. Ziman J. M., Principles in the theory of solids, University Press,
Cambridge, 1960.
6. Scully M. 0., Lamb W. E., Jr., Phys. Rev., 159, 208 A967).
7. Gordon J. P., Phys. Rev., 161, 367 A967).
8. Lax M., Statistical physics, phase transitions and superfluidity в кн.
1966 Brandeis summer Institute in theoretical physics, ed. M. Cre-
tien, Gordon and Breach, vol. 2, New York, 1968, p. 269.
9. Lax M., Louisell W. #., Phys. Rev., 185, 568 A969).
10. Haken H., Handbuch der Physik, ed. S. Flugge, Light and matter
lc, Springer-Verlag, vol. XXV/2C Berlin, 1970.
11. McCumber D. E., Phys. Rev., 141, 306 A966).
12. Fleck J. A., Jr., Phys. Rev., 149, 309, 322 A966).
13. Sargent M.t Scully M. O., Lamb W. E., Jr., Appl. Opt., 9, 2423
A970).
14. Slater L. /., Confluent hypergeometric functions, University Press,
Cambridge, 1960.
15. DeGiorgio K, Scully M. O., Phys. Rev., A2, 1170 A970).
16. Jakeman E., Oliver C. /., Pike E. R., Lax M., Zwanziger M., J.
Phys., A3, 152 A970).
17. Lax M.t Zwanziger M., Phys. Rev. Lett., 24, 937 A970).
18: Meltzer D., Davis W., Mandel L., Appl. Phys. Lett., 17, 242 A970).
•19. Arecchi F. Т. в сб. Quantum optics, ed. R. Glauber, Academic
Press, New York, 1969, p. 57.
20. Scully M. O., Lamb W. E., Jr., Phys. Rev., 179, 368 A969).
21. Chandrasekhar S., Rev. Mod. Phys., 15, 1 A943).
22. Selected papers on noise and stochastic processes, ed. N. Wax,
Dover, New York, 1954.
23. Dwight H. В., Tables of integrals, Macmillan, New York, 1961,
p. 236. (См. перевод: Г. Двайт, Таблицы интегралов, изд-во
«Наука», 1966).
24. Scully М. О., Lamb W. E., Jr., Phys. Rev., 166, 246 A968).
25. Anderson P. W., Concepts in solids, Benjamin, New York, 1963.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
По теории лазера имеется обширная литература. Более строгое
рассмотрение теории лазерной модели, сходной с описанной здесь,
можно найти в работах М, Скалли и В, Лэмба;
ТЕОРИЯ ЛАЗЕРА
385
Scully М. О., Lamb W. £., /л, Phys. Rev., 159, 208 A967); 166, 246
A968); 179, 368 A969).
См. также более простую статью М. Скалли в сб. Quantum optics*
ed. R. Glauber, Academic Press, New York, 1969.
Несколько отличные анализы теории лазера даны Г. Хакеном
и В. Вайдлихом, В. Люиселлом и Д. Гордоном в статьях последней
ссылки. Более широкое рассмотрение см:
Lax M., Statistical physics, phase transitions and superfluidity в кн.
1966 Brandeis summer Institute in theoretical physics, ed. M. Cre-
tien, vol. 2, Gordon and Breach, New York, 1968, p. 269.
Haken tf., Handbuch der Physik, ed. S.- Flugge, Light and matter la,
Springer-Veriag, vol. XXB/2c, Berlin, 1970,
13 In к В813
Глава 11
Рассеяние света атомами
Рассеяние света атомом представляет собой излуча-
тельный процесс второго порядка, поскольку при этом
должно иметь место двукратное взаимодействие поля
излучения с атомными электронами. В процессе рассеяния
поглощается квант йсо падающего светового пучка и
излучается квант fiats рассеянного света. При квантовоме-
ханическом рассмотрении рассеяния света необходимо
развить теорию возмущений, зависящих от времени, и
выйти за пределы первого приближения, которое было
адекватным для процессов, рассмотренных в предыдущих
главах.
Говорят, что рассеяние света является упругим, если
частота рассеянного света cos равна частоте падающего
излучения со. Рассеяние света без изменения частоты
иногда называется рэлеевским рассеянием. Неупругое
рассеяние, при котором частота ш8 отличается от о, на-
зывается рамановским рассеянием *)• При этом
рассеянии разность энергии между йсо и йсов поглощается
атомом, вызывающим рассеяние. Если атом первоначально
находится в своем основном состоянии, то, согласно
закону сохранения энергии, величина йсо— йсоз должна
равняться одной из энергий возбуждения атома.
*) Это рассеяние открыто в 1928 г« Раманом и Кришнаном в
жидкостях и независимо Г. С. Ландсбергом и Л. И. Мандельштамом
при изучении рассеяния света в кристаллах. В отечественной научной
литературе это рассеяние принято называть комбинационным.—
Прим. ред.
РАССЕЯНИЕ СВЕТА АТОМАМИ
387
Упругое рассеяние света можно приближенно рас*
сматривать на основе той же классической теории,
которая ранее использовалась при выводе .классического
выражения для зависящей от частоты восприимчивости в
гл. 4. Прежде чем перейти к более полной квантовомеха-
нической теории рассеяния света, удобно дать краткое
изложение классической теории.
Поперечное сечение рассеяния
Прежде всего мы сделаем некоторые общие
замечания относительно процесса рассения света. Сначала
рассмотрим геометрию эксперимента по рассеянию света.
х
м
Е
А
г(г,в^)
Рассеянный
свет
Падающий свет / ^том
•^z
У
Фиг. 11.1. Геометрия эксперимента по рассеянию света.
Рассеянный фотон имеет два независимых направления поляризации.
Система координат, которая будет использоваться,
показана на фиг. 11.1. Рассеивающий атом помещен в начале
координат, и на него падает параллельный световой
пучок, распространяющийся вдоль оси z с электрическим
полем Е, направленным по оси х.
13*
388 ГЛАВА И
N
Усредненный по периоду вектор Пойнтинга падающего
светового пучка дается выражением
1 = ^г,с\Е\\ A1.1)
где Е— величина комплексного вектора электрического
поля.
Согласно рассмотрению, проведенному в гл. 2,
рассеяние света в основном обусловлено поглощением
фотона атомом, за которым следует спонтанное
испускание второго фотона в процессе перехода атома в его
основное состояние. Таким образом, рассеянный свет в
принципе распределен в пространстве по всем
направлениям. Рассмотрим рассеянный свет с электрическим
полем Es в точке г. Его усредненый по периоду вектор
Пойнтинга определяется следующим образом;
Т3 = \г,с\Е3\\ (Ц.2)
Полная скорость рассеяния электромагнитной энергии
атомом получается посредством интегрирования
величины 7S по сфере с центром в начале координат.
Результат может быть записан в виде
$7>2rfQ. A1.3)
Здесь dQ — элемент телесного угла и интегрирование
ведется по полному телесному углу 4л. Полная рассеянная
энергия должна содержать вклады двух независимых
поляризаций рассеянного света в каждой точке г.
Эффективность рассеяния удобно описывать с
помощью поперечного сечения рассеяния сг, определяемого
аналогично поперечному сечению фотоэффекта в
выражении (9.29) как скорость потерь энергии падающего
пучка вследствие рассеяния, деленная на поток энергии
падающего пучка через единичную площадь,
перпендикулярную к направлению распространения пучка. Для
упругого рассеяния скорость потерь энергии в падающем
пучке равна скорости увеличения энергии рассеянного
света, определенной в A1.3). Это равенство не
выполняется в случае неупругого рассеяния, когда часть
энергии, теряемой падающим пучком, передается атому и
РАССЕЯНИЕ СВЕТА АТОМАМИ
389
только доля энергии, определяемая отношением частот
cos/o), превращается в энергию рассеянных фотонов на
частоте cos. Следовательно, в общем случае поперечное
сечение определяется выражением
а = (ф/) ^Т/2dQ. A1.4)
Очевидно, что поперечное сечение имеет размерность
площади и не зависит от г, поскольку интенсивность Т3
уменьшается обратно пропорционально квадрату
расстояния от атома.
Дифференциальное поперечное сечение можно
определить по аналогии с выражением (9.30). Оно относится
к части рассеянного света внутри элемента телесного
угла dQ и получается путем дифференцирования обеих
частей выражения A1.4) по Q:
do/dQ = co7,r2/co,7. A1.5)
Следует отметить, что по сравнению с поперечным
сечением фотоэффекта поперечное сечение рассеяния света
включает дополнительное суммирование вкладов двух
независимых поляризаций фотонов для каждого
направления рассеяния.
Поперечное сечение а, определенное выше, относится
к рассеянию света одним атомом. Однако во всех
реальных экспериментах по рассеянию света пучок
рассеянного света создается большим числом атомов N, поэтому
необходимо рассмотреть способ суммирования вкладов
отдельных атомов. В случае рассеяния видимого света
атомами газа среднее расстояние между атомами очень
мало по сравнению с длиной волны излучения, если
давление газа при комнатной температуре больше 100 Па.
Полное электрическое поле рассеянного света в точке
г определяется линейной комбинацией вкладов всех N
атомов.
Рассмотрим сначала рассеяние однородным
распределением атомов. Предположим, что падающий свет
представляет собой классическую электромагнитную волну с
точно определенными амплитудой и фазой. Компоненты
поля, рассеянного атомами, которые расположены в
пределах первой полуволны падающего излучения, нахо-
390
ГЛАВА tl
дятся в -фазе друг с другом, однако по отношению к
компонентам полей, рассеянных атомами, лежащими в
пределах следующей полуволны, они находятся в противо-
фазе. В случае однородного распределения
рассеивающих атомов вклады в рассеянное поле групп атомов,
расстояние между которыми равно полуволне, точно
компенсируют друг друга, поэтому никакого рассеяния нет,
за исключением рассеяния вперед при 9 = 0. Например,
свет не рассеивается идеальным кристаллом, в котором
атомы жестко фиксированы в регулярно расположенных
узлах решетки.
Рассеяние света может происходит только на неодно-
родностях распределения рассеивающих атомов. В
кристалле рассеяние света может происходить в том случае,
когда атомы имеют возможность совершать колебания
около регулярно расположенных узлов решетки. В
случае газа, к которому относится зсе последующее
рассмотрение, рассеяние света вызывается флуктуациями
плотности газа, обусловленными движением атомов.
Полную интенсивность света, рассеянного на флуктуа-
циях плотности, определить нетрудно.
Задача ILL Рассмотрите газ из N атомов, заключенный
в объеме V. Полный объем можно разбить
на меньшие объемы v таким образом, что
все атомы в объеме v будут создавать
рассеянное поле с одинаковой фазой, однако
соседние объемы будут давать рассеянные
поля с противоположными знаками.
Докажите, что если интенсивность света,
рассеянного одним атомом, определяется
правой частью выражения A1.2), то полная
интенсивность света, рассеянного всеми
атомами газа, есгь
7s = ±e0c\Es\HV/v)(^)\ A1.6)
где (AvJ — среднеквадратичное отклонение
числа атомов в объеме v.
Распределение N атомов между различными
объемами v определяется случайными движениями атомов.
РАССЕЯНИЕ СВЕТА АТОМАМИ 391
Вероятность нахождения v атомов в данном объеме
связана со средним числом атомов v в объеме v
распределением Пуассона, похожим на распределение (9.64). Тогда
по аналогии с (9.66) получим
(AvJ = v = Nv/V A1.7)
и выражение A1.6) можно переписать следующим
образом:
Ts=±e,c\Es\2N. A1.8)
Следовательно, сечение рассеяния для N атомов равно
сечению рассеяния для одного атома, умноженному на
N. Отметим, что этот результат был получен только для
газа и неприменим для жидкости или твердого тела.
В гл. 2 подчеркивалось, что поглощение и рассеяние
света представляют собой различные стороны одного и
того же процесса; свет, теряемый параллельным пучком
в процессе поглощения, вновь появляется в виде
рассеянного излучения. Если 1/т есть вероятность в единицу
времени поглощения кванта йсо, то временную скорость
потерь энергии в падающем световом пучке можно
записать с помощью формулы D.93) следующим образом:
А©/т = j©7x%l^l2= <*V%/c. A1.9)
Здесь было использовано выражение A1.1). Однако
поперечное сечение а определено в A1.4) таким образом,
чтобы скорость потерь энергии пучка при рассеянии на
одном атоме равнялась аТ. Следовательно, скорость
потерь энергии вследствие рассеяния на всех N атомах в
объеме V есть NaT. Приравнивая эту скорость
выражению A1.9) для точно такой же физической величины,
получаем
o = (®VlcN)x". (П.Ю)
Разумеется, величины сг и %" должны вычисляться на
частоте падающего света о.
Этот результат был получен на основе общего закона
сохранения энергии, и потому он справедлив как для
классического, так и для квантовомеханического
анализа рассеяния света. Полученный результат будет
392
ГЛАВА И
строго подтвержден вычислениями поперечных сечений
рассеяния, приведенными позднее в этой главе.
Другим общим соотношением, которому
удовлетворяет поперечное сечение, является правило сумм,
полученное путем подстановки выражения A1.10) в D.60):
оо
\ a dco = nZe2/2eQctn. A1.11)
Классическая теория упругого рассеяния
Поперечное сечение для упругого рассеяния света
может быть вычислено на основе той же самой
классической теории, которая использовалась для вычисления
восприимчивости в гл. 4. Предположим, что атом на
фиг. 11.1 можно описать с помощью классического
гармонического осциллятора, уравнение движения которого
имеет вид D.10). Падающая электромагнитная волна
возбуждает вынужденные колебания со смещением X,
определенным в D.12), и соответствующим ускорением
Х= ( 2 g(°22E -^ A1.12)
т (о>5 - со2 - /©Г) х J
В учебниках по теории электромагнитного поля [1,2]
показывается, что ускоряющийся заряд излучает
электромагнитные волны. В случае заряда, совершающего
гармоническое движение, частота этих волн равна
гармонической частоте. Следовательно, свет, излучаемый
вынужденными колебаниями осциллятора, соответствует
упругому рассеянию падающего излучения.
Если скорость осциллирующего заряда X мала по
сравнению со скоростью света, то классическая
электромагнитная теория дает следующие выражения для
электрического и магнитного полей испускаемого излучения
в точке г [1, 2]:
Е, = W4k60cV3) г X (г X X) A1.13)
И
Н,-(е0с/г)гХЕ, A1.14)
РАССЕЯНИЕ СВЕТА АТОМАМИ
393
Пусть 8 и Bs — единичные векторы поляризации,
параллельные полям Е и Es. Поскольку ускорение X
параллельно е, то из формулы A1.13) следует, что поле Еа
ортогонально г и имеет величину
| £,| = (e/4nsQc2r) г *е,| X |. A1.15)
Теперь дифференциальное поперечное сечение можно
найти из его определения A1.5), подставляя формулы
A1.1), A1.2), A1.12) и A1.15):
it=A^7) w - ®2J+co2f2 {г' *sJ' A1Л6)
Множитель
re = e2/47te0mc2, (П. 17)
квадрат которого появляется в выражении для
дифференциального поперечного сечения, имеет размерность
длины. Он называется классическим радиусом электрона
и имеет величину 2,8-1СН5 м.
Частотная зависимость дифференциального
поперечного сечения для рэлеевского рассеяния показана на
фиг. 11.2 для тех же значений параметров, которые были
использованы для фиг. 4.1.. Наиболее замечательным
свойством поперечного сечения является большой
максимум, получающийся при резонансе частоты падающего
света со с собственной частотой осциллятора соо- Этот пик
в рассеянии соответствует максимуму поглощения при
со = соо. При больших частотах, превышающих
резонансную частоту, дифференциальное поперечное сечение
стремится к постоянной величине
daJdQ = т\ (е . г8)\ (со > со0). A1.18)
При низких частотах
da/dQ = г\ (со/со0L (е . г8)*9 (со < со0), A Г. 19)
и поперечное сечение возрастает пропорционально
четвертой степени частоты. Таким образом, наибольшее
рассеяние видимого света атомами, у которых основные
частоты поглощения лежат в ультрафиолетовой области,
394
ГЛАВА II
соответствует фиолетовому краю спектра, чем
объясняется голубой цвет неба и красный цвет заката.
Дифференциальное поперечное сечение удобно
выразить через полярные углы относительно направления рас-
Фиг. 11.2. Частотная зависимость дифференциального поперечного
сечения упругого, или рэлеевского рассеяния для параметра
ширины линии Г = (й0/20.
Для получения дифференциального поперечного сечения ординату следует
2
умножить на ге (е*85J. Пик в сечении рассеяния при <o~GH соответствует
ординате, равной 400.
сеяния. Если плоскость рассеяния определить как
плоскость, проходящую через волновые векторы падающего
и рассеянного излучений, то два независимых
направления вектора поляризации рассеянного света es можно
выбрать перпендикулярно (-L) и параллельно (||)
плоскости рассеяния;
Г sin<p,'-cosq>, 0 A),
Нсозво— —а- — пп (".20)
cosq), cos 9 sin ф, —sin6
(II).
РАССЕЯНИЕ СВЕТА АТОМАМИ 395
Оба направления перпендикулярны вектору г.
Дифференциальное поперечное сечение пропорционально
коэффициенту (e-esJ, который для двух направлений вектора
поляризации имеет следующие значения:
Г sin2cp (±),
(8,8*)=lcos4cos'0 (||), AL21>
поскольку вектор г параллелен оси х. Два вклада в
дифференциальное поперечное сечение описываются выра*
жениями
deJdQ | _ ry ( sin2 Ф
Атц/dQ J (со2 - со2J + со2г21 cos2 0
J ~ (со2 - со2J + со2Г2 I cos2 0 cos2 ф. {11 *22)
Полное поперечное сечение определяется путем
сложения двух вкладов, приведенных в A1.22), и
интегрирования по Q правой и левой частей получаемого
выражения
** о / 2 2\2 , 2г»2 ' A1.23)
3 ^со0 — со J + © Г
-28
M'
Коэффициент 8яг2/3 имеет величину порядка 10
оставшийся зависящий от частоты множитель изображен
на фиг. 11.2.
Классическая постоянная затухания Г, появляющаяся
в формулах для поперечного сечения, может быть
определена по интенсивности рассеяния. Скорость потерь
энергии в падающем пучке вследствие рассеяния на од*
ном атомном осцилляторе определяется выражением
<,/„ t till A124)
' 12Jte0mV (со2} - со2J + со2Г2 ' v ' '
Здесь были использованы формулы A1.1) и AL23)'.
Применяя D.12), выражение A1.24) можно переписать
следующим образом:
оТ= (е2со4/12я80с3) | X |2. A1.25)
Другое выражение для скорости потерь энергии может
быть получено из D.36). При рассеянии на одном атоме
396
ГЛАВА 11
эта скорость равна
^тТа2\Х\2. A1.26)
Здесь предполагалось, что частоты всех осцилляторов
одинаковы и равны со0 (т. е. /0 = 1). Сравнивая
формулы A1.25) и A1.26), получаем
Г = е*(д2/6лг0тс3. A1.27)
С помощью A1.27) мнимую часть восприимчивости
из D.14) для случая /0 = 1 можно переписать в
следующем виде:
Ne1CD3 1
Х" = 6яв§У/и V (а>§ - со2J + со2Г 2 " (И*28)
Легко видеть, что точные классические результаты для
о и %", приведенные в A1.23) и A1.28), удовлетворяют
общему соотношению A1.10). Правило сумм A1.11)
также подтверждается для классического поперечного
сечения а.
Выражение A1.27) для константы затухания
приводит к трудности в классической теории восприимчивости,
зависящей от частоты. Трудность заключается в том, что
выражение D.14) для %(со), в которое подставлено
значение Г из A1.27), не* содержит все свои со-полюсы в
нижней половине комплексной плоскости. Это
противоречит общим требованиям причинности, налагаемым на
восприимчивость и рассмотренным в гл. 4. Указанную
трудность можно обойти, если в формуле A1.27)
заменить со на соо, как было сделано в выражении для Г,
использованном в D.11). Когда частота со близка к соо, это
приближение справедливо, однако необходимость такого
приближения является слабым местом классической
теории.
Задача 11.2. Докажите, что для
е2со0/6яе0тс3 < 1 A1.29)
классическое выражение D.14) для
восприимчивости имеет полюс приблизительно при
со « 4- / (блби/тгс3/^2). A1.30)
РАССЕЯНИЕ СВЕТА АТОМАМИ
397
Здесь была использована зависящая от
частоты константа затухания Г из A1.27).
Восприимчивость имеет два других полюса,
которые лишь немного смещены по
сравнению с их положениями, соответствующими
значению Г из D.11).
Рассеяние света свободными электронами называется
томсоновским рассеянием. Соответствующая формула
для дифференциального поперечного сечения может быть
получена, если в A1.6) частоту соо положить равной
нулю. Если затуханием Г пренебречь, то результат для
томсоновского рассеяния получится точно такой же, как
в A1.18), а явный вид угловой зависимости
дифференциального поперечного сечения определяется из A1.21):
do/d& = daJdQ + daJdQ = Z г2в(г • esJ =
= r\ (sin2q> + cos26 cos2<p). A1.31)
Томсоновское поперечное сечение часто приводится для
неполяризованного падающего света. В этом случае
необходимо усреднение по азимутальному углу ф, в
результате чего sin2(p и cos2cp заменяются на 72, а выражение
A1.31) принимает вид
dc/dQ = jr2e{l -f cos29). A1.32)
Классическая теория рассеяния свободными
электронами перестает быть справедливой, когда энергия фотона
йо) становится сравнимой с релятивистской энергией
массы покоя электрона тс2. Для столь больших значений
Ьы в процессе рассеяния значительная часть энергии
передается электрону. Поэтому рассеяние становится
неупругим, а энергия рассеянного фотона ficos—меньше
Ь®. Закон сохранения релятивистской энергии и им*
пульса приводит к следующему уравнению [3, 4]:
ф8 = 1 + {hco/mc2) A - cos 9). A1.33)
Неупругое рассеяние света свободными электронами
называется эффектом Комптона. В этом случае
дифференциальное поперечное сечение необходимо вычислять на
основе релятивистской квантовой механики, и эта теория
398
ГЛАВА 11
лежит за пределами настоящей книги. Мы приведем
лишь выражение для дифференциального поперечного
сечения для комптоновского рассеяния неполяризован-
ного света [3, 4]:
da со2, / со о„ п \
lQ=^l^t+^-1+COs2e)- (П-34>
Формула A1.34) называется формулой Клейна — Ни-
шины. Когда йсо много меньше тс2, из выражения
A1.33) следует, что рассеяние становится упругим и
o>s = со, а комптоновское поперечное сечение A1.34)
переходит в томсоновское поперечное сечение A1.32).
Общее выражение для скоростей
излучательных переходов
Прежде чем можно будет привести квантовомехани-
ческие расчеты дифференциального поперечного сечения
рассеяния, необходимо сделать отступление для более
подробного рассмотрения теории скоростей
излучательных переходов. Скорости переходов, определенные в
предыдущих главах, были вычислены на основе результата
C.72), полученного для двухуровневого атома, на
который действует гармоническое возмущение. Обобщение
этого результата — золотое «правило Ферми» — было
приведено без доказательства в (8.83). Эта обобщение
относится к системам, имеющим множество близко
расположенных энергетических уровней, как, например, в
случае спонтанного излучения, где для испущенного
фотона имеется некоторое распределение состояний, или
в случае фотоэффекта, где испущенный электрон также
имеет много возможных состояний.
Золотое правило Ферми применимо только для
излучательных процессов первого порядка, в которых
происходит однократное взаимодействие излучения с атомами,
как на диаграммах фиг. 8.1. Однако рассеяние света
является излучательным процессом второго порядка: одно
взаимодействие необходимо для поглощения падающего
фотона, а второе взаимодействие необходимо для
испускания рассеянного фотона в каждом элементарном акте
рассеяния. Описанные в следующей главе процессы,
РАССЕЯНИЕ СВЕТА АТОМАМИ . 399
имеющие место в нелинейной оптике, могут быть
процессами взаимодействия. второго или более высокого
порядка. Для анализа таких процессов необходимо
обобщение золотого правила Ферми.
Рассмотрим связанную систему «излучение + атом»,
описываемую в представлении Шредингера волновой
функцией Ф@э которая удовлетворяет уравнению (8.92):
MO{t) = ihdO/dt. A1.35)
Здесь Ж— полный, не зависящий от времени
гамильтониан связанной системы, определяемый в общем случае
выражением (8.44), где из гамильтониана
взаимодействия Mi исключена временная зависимость. Полный
гамильтониан можно записать в виде
Ж=Ж0 + Ж1. A1.36)
Здесь Жо— гамильтониан несвязанной системы
«излучение + электроны»:
Жо = Ж^ -f- Ж%. A1.37)
В электрическом дипольном приближении гамильтониан
Жг переходит в ЖЕв как в случае уравнения (8.92), од*»
нако мы используем более общий гамильтониан
взаимодействия.
Уравнение A1.35) легко решить, выразив формально
волновую функцию в момент времени t через волновую
функцию в более ранний момент tQ:
ф (/) = ехр {— 1Ж (t - tQ)/h} Ф (/0). A1.38)
Экспоненциальная величина в A1.38) называется
оператором временного развития системы. Если волновая
функция известна в некоторый произвольный момент
времени, то оператор временного развития определяет
волновую функцию во все последующие моменты
времени.
Пусть ф/ есть собственное состояние оператора Жц
с энергией ico/;
$о*/ = Аю/Ф/. A1.39)
400
ГЛАВА И
Вероятность нахождения системы в состоянии ф/ в
момент времени t определяется, как обычно, квадратом
интеграла перекрытия функций \f>/ и Q)(t):
1<%|Ф@>12 = 1<*/1ехр{--/3?(<-/о)/А}|Ф(«>12. (Н.40)
Здесь было использовано выражение A1.38). Присутст-
вие в экспоненте оператора Mi приводит, вообще говоря,
к отличию величины | (г|)/|Ф(£) )|2 от | (%|Ф(^о) )|2.
Физическая причина этого отличия связана с излуча-
тельными переходами, происходящими во временном
интервале от t0 до t.
Состояние связанной системы в момент времени t0
может быть записано в виде линейной суперпозиции соб-
ственных состояний гамильтониана Ж^ Пусть фи есть
одно из этих собственных состояний:
ЗД«==Л<М>в. A1.41)
Вероятность нахождения системы в состоянии ty/ в
момент времени t [формула A1.40)] может быть выражена
через вероятность наблюдения системы в различных
состояниях tyu в момент времени to. Коэффициент
пропорциональности, на который следует умножить вероятность
нахождения системы в состоянии tyu в момент времени t0
для определения соответствующего вклада в вероятность
нахождения системы в состоянии \f/ в момент времени t,
имеет вид
| <% |ехр {-Ж (t - tQ)/h) | г|з„> |2. A1.42)
Скорость перехода из состояния tyu в состояние г|?/
равна производной коэффициента пропорциональности
A1.42) по времени. В обычном эксперименте, где
переходы в некоторую область конечных состояний
наблюдаются одновременно, соответствующая скорость
перехода есть
Т"-й"Е|^|ехР^-/*('--'о)/А}|и>|2. A1.43)
f
Здесь обозначения для бра- и кет-векторов были
упрощены. Предполагается, что в стационарных условиях
скорость перехода не зависит ни от /, ни от t0.
РАССЕЯНИЕ СВЕТА АТОМАМИ
401
Выражение A1.43) для скорости перехода не очень
удобно для вычислений. Это выражение можно сделать
более полезным, разлагая его в ряд по степеням
матричных элементов 5^j. Мы видели в гл. 3, что матричные
элементы взаимодействия излучения с атомом малы по
сравнению с энергиями фотонов и энергиями атомных
переходов в видимой области спектра. Следовательно,
можно ожидать, что степенное разложение скорости
перехода быстро сходится. В большинстве случаев в
хорошем приближении это, разложение может быть ограни-
чено первым неисчезающим членом для
рассматриваемого типа перехода. Такое разложение позволяет
отчетливо разделять излучательные процессы первого,
второго, третьего и более высоких порядков.
Требуемый ряд получается разложением ехр{—1ЖA—~
~~-t0)/b} по степеням <9§/. Это разложение усложняется
вследствие некоммутации операторов <5#0 и 3$i. В
результате
ехр (- 1Жф) Ф ехр (- Жф) ехр (— №гЩ A1.44)
и нельзя воспользоваться обычным разложением
экспоненты. Однако эту трудность можно обойти следующим
образом. Тождество
ехр {Жоф) Жх ехр (— Ш/h) =
= ih jf {ехр (i%ot/h) ехр (- ШЩ A1.45)
легко доказывается прямым дифференцированием
правой части с использованием выражения A1.36).
Интегрируя обе части тождества A1.45) по t, получаем
t
\ ехр (Wi/A) &i ехр (- Шф) dtx =
= ih {ехр (Ж$Н) ехр (- Ш/h) —
- ехр (to) ехр (— Ш0/Н)}.
A1.46)
402
ГЛАВА II
Последнее выражение может быть преобразовано к виду
ехр(—/30//А) =
= ехр (- №ф) {ехр {i2e0t0/h) ехр.(— W/A) —
t
— y J ехр (ifSotJh) Жj ехр (— tf0/,/A) dt{}. A1.47)
Чтобы обеспечить достижение стационарных
состояний в момент времени /, в который вычисляется скорость
перехода, предположим, что момент времени t0 относится
к бесконечно далекому прошлому. Далее будем считать,
что начиная с момента времени t = —юо
взаимодействие постепенно возрастает до своего полного значения.
Для этого введем множитель exp(ef), где е — малая
величина, которая принимается равной нулю во всех
окончательных выражениях для скоростей переходов. По-
скольку скорость роста величины Звг бесконечно мала,
все переходные процессы отсутствуют. Эти процессы
могли бы возникнуть при внезапном включении возму-»
щения Жи действующего на систему, которая в
выражении для скорости перехода A1.43) описывается
собственными состояниями оператора Жо.
Учитывая эти изменения и замечая, что теперь
возмущение <9^i обращается в нуль в момент времени /0,
выражение A1.47) можно записать в виде
ехр (- Ш/А) = ехр (- iM0t/h) X
X I 1 —-g- S ехр(/5&о//А)^ехр(еОехр(—/^/А)^,}.
Правую часть последнего равенства можно с помощью
итераций разложить в ряд по степеням Mj. Мы
рассмотрим вклады членов этого ряда в скорость перехода 1/т
в порядке возрастания степени $б1%
РАССЕЯНИЕ СВЕТА АТОМАМИ 403
V
Теория возмущений, зависящих от времени
1. Нулевой порядок. Член нулевого порядка по S/ei
дает следующий матричный элемент:
</ |ехр (- тф) Iи) = ехр (— mut)(f \u). AК49)
Из понятия перехода вытекает, что ipu и ар/ должны
быть различными собственными состояниями, а потому
вклад нулевого порядка обращается в нуль.
2. Первый порядок. Чтобы получить член первого
порядка по Жи во втором члене выражения A1.48)
оператор Ж следует положить равным <#0. Тогда вклад
этого члена в матричный элемент формулы A143) имеет
вид
t
- (f | (Щ ехр (- 1Ж41Щ \ ^P Wi/й) X
— oo
X Ж j ехр Ш ехр (— i^0tjh) dt{\u) =
= - i/h ехр (— /cof0<J\3№j\u)X
t
X \ exp (i(Oft{ + zt{ — t(oJi) dt{ =
— oo
(t\*,\u) e»p(ef-/<oBQ
= Ь <»„-«, + /в • • <U-DUJ
Согласно формуле A1.43), скорость перехода имеет
вид
1 d у [</1^|«)|2 ехр Bе/) __
i~ dt 2.1 Ъ2 (соц - wfJ + е2
f
(С0и - ©f J + е2 *
Теперь для получения требуемого медленного включения
вазимодействия 36i устремим значение е к нулю. При
этом величина экспоненты в A1.51) стремится к единице,
а*оставшееся выражение, содержащее е, записано в фор-
404
ГЛАВА II
ме представления дельта-функции, приведенного в
C.68). Следовательно,
V—fZi^1*'1^126^"^- A1-52)
f
Это выражение является золотым правилом Ферми,
использованным в (8.83).
3. Второй порядок. Член второго порядка по Ж\
определяется посредством первой итерации выражения
A1.48). Иначе говоря, член ехр(—i26t\\b) в подынтег-
ральном выражении записывается через Жо и Ж\ путем
подстановки полного выражения A1.48), в котором
время / заменено на tu а оператор Ж в правой части
заменен на Ж$. Чтобы избежать путаницы, в
подставляемом выражении переменная интегрирования заменяется
на t2. В результате матричный элемент второго порядка
принимает вид
t и
— (f IЙ ехр (— i^ot/h) jj dt{ $ dt2 exp {1Ж4\1Щ %i X
—oo — oo
X exp (ef,) exp (- 1Ж, (/, - t2)/h) Жг X
X exp (et2) exp (— i$e0t2/h) \u). A1.53)
Теперь используем условие полноты D.100), чтобы
вставить единичный оператор Л I /}(/1 между двумя one-
раторами Ж\ в выражении A1.53). Суммирование по /
производится по полному набору собственных состояний
оператора Ж о. Присутствие единичного оператора не
влияет на величину матричного элемента, однако
позволяет записать A1.53) в более определенной форме;
-A-2J]exp(-/©f0</l^il/></l^/U>X
* и
X \ dt{ \ ехр [шfti + zti — /со/ (tx — t2) + et2 — i<dj2] dt2 =
(f\^j\ I) (l\Wj\ u) exp Bef - to J)
T2 (ш« ~~ to/ + ie) {®и "" ®/ + 2/e) #
A1.54)
— oo —oo
-I
РАССЕЯНИЕ СВЕТА АТОМАМИ
405
Поскольку 8 является произвольно малой величиной,
которая впоследствии полагается равной нулю, то 2г в
A1.54) можно заменить на е. Тогда, объединяя
матричные элементы первого и второго порядков из A1.50) и
A1.54), получаем
1 ехр (е/ — mj)
®и — ®1 + 1&
A1.55)
Выражение для скорости перехода, вытекающее из
'A1.58), аналогично A1.52), за тем исключением, что
матричный элемент первого порядка (f\2ei\u) заменен
величиной, . стоящей в круглых скобках выражения
A1.55). Предельный переход е->0 в знаменателе
матричного элемента второго порядка можно осуществить
обычным образом, просто положив величину е равной
нулю. Для большинства задач состояния |/), для
которых величина {f\3^i\l)(l\^i\u) отлична от нуля,
таковы, что частоты со/ не равна сои, а потому этот член не
приводит к дельта-функции. Таким образом, скорость
перехода с точностью до членов второго порядка по Жх
дается выражением
X ~ Ь2 la
(f\Zfj\u) +
tfl^l/X'l*/!*) 2
+;г
0) — CO.
и I
б (cott — co^). A1.56)
Справедливость исключения е из знаменателя
матричного элемента второго порядка необходимо проверять
для каждой задачи, в которой используется формула
A1.56). Ниже в этой главе мы опишем случай, где
частота со/ может равняться сои.
4. п-й порядок. Член п-то порядка по 36i получается
с помощью п—1-кратных итераций в правой части
A1.48). Вычисление аналогично проводимому в случае
второго порядка, но теперь необходимо выполнить п
интегрирований и использовать условие полноты п— 1 раз,
406 /
ГЛАВА 11
Результирующая скорость перехода с учетом члена я-го
порядка имеет вид
t-tL vi^/U>+tL ^r=^—+ •••
f i u i
X8K-(of), A1.57)
Состояния |/i), |/2) и т. д., входящие в члены
высшего порядка вероятности перехода, называются
виртуальными промежуточными состояниями для данного
перехода. Член первого порядка описывает скорость
прямых переходов из состояния \и) в состояние |/), тогда
как члены более высоких порядков характеризуют
переходы, при которых система переходит из состояния \и)
в состояние |/) через одно или несколько
промежуточных состояний. В формуле для скорости перехода
учитывается только условие сохранения энергии,
заключающееся в том, что частота сои должна быть равна со/. В
общем случае энергия промежуточных состояний не равна
энергии первоначального состояния, хотя для каждого
промежуточного состояния имеется зависящий от
энергии знаменатель й(сои— со/), уменьшающий вклад в
матричный элемент состояний, энергия которых йсо;
значительно отличается от Ьъ)и. Система проходит через
промежуточные состояния |/) виртуально. В
промежуточных состояниях сохранение энергии не требуется,
поскольку в эти состояния нет реальных переходов.
Последовательность членов в A1.57) обычно
уменьшается достаточно быстро, а потому следует
удерживать только член низшего порядка, дающий вклад в
скорость перехода для данного излучательного процесса.
Требуемый член можно обычно определить путем
подсчета числа фотонных состояний, изменяющихся при
переходе из состояния \и) в состояние \f). В случае
простого поглощения или испускания фотона меняется
только одно фотонное испускание, поэтому достаточно
учесть член первого порядка, как в вычислениях,
приведенных в гл. 3 и 8. В случае рассеяния света, когда один
РАССЕЯНИЕ СВЕТА АТОМАМИ
407
фотон поглощается и один испускается, требуется учет
члена второго порядка. В нелинейной оптике, рассматри*
ваемой в следующей главе, для описания процесса двух^
фотонного поглощения необходимо учитывать член вто-<
рого порядка. При описании генерации третьей гармо-
ники, когда поглощаются три фотона и испускается один
фотон, требуется учитывать член четвертого порядка.
Формула Крамерса—Гейзенберга
Теперь вернемся к теории рассеяния света атомом и
рассмотрим квантовомеханический вывод
дифференциального поперечного сечения. Основные члены мульти-
польного разложения гамильтониана взаимодействия из-
лучения с атомом 36i приведены в (8.47) и последующих
уравнениях. Мы применим электрическое дипольное
приближение и пренебрежем операторами ЖЕ<э, §6мв, а
также членами более высокого порядка по aok. Гамиль-
тониан электрического дипольного взаимодействия ЖЕц
определяется выражением (8.52), описывающим
рассеяние света во втором порядке теории возмущений. Га*
мильтониан нелинейного взаимодействия 36nu
приведенный в (8.52), имеет второй порядок относительно
операторов рождения и уничтожения фотонов. Следовательно,
он описывает рассеяние света в первом порядке теорий
возмущений, зависящих от времени, поэтому мы пока
его сохраним, хотя, как будет показано ниже, его вклад
пренебрежимо мал. Таким образом, гамильтониан
взаимодействия для процесса рассеяния света имеет вид
ml = XED + Жыь = ёЬ • Ег@) +
+ (^/8m) Z [Н @) X гу]2. A1.58)
Здесь D — сумма радиусов-векторов электронов,
определенная в (8.32).
Геометрия процесса рассеяния показана на фиг. 11.1»
В начальном квантовомеханическом состоянии имеются
падающие на атом фотоны с фиксированной частотой о
и волновым вектором к. В результате рассеяния
начальное состояние может превратиться в одно из возможных
конечных состояний, в которых падающий фотон за-»
408
ГЛАВА И
менен рассеянным фотоном с частотой а>8 и волновым
вектором ks. Следовательно, преобразование начального
фотонного состояния в конечное осуществляется в
результате действия на него произведения фотонных
операторов ак и а\ , или, в кратком обозначении, операто-
о
ров й и d£. В современных экспериментах по рассеянию
света обычно используется лазерный источник, световой
пучок которого может быть достаточно хорошо описан
на основе одномодового возбуждения. Имеющиеся в
рассеянном свете частоты cos определяются свойствами
атома и вытекают естественным образом из квантовомеха-
нического расчета, включающего как упругое, так и
неупругое рассеяния.
Допустим, что в начале процесса рассеяния атом
находится в своем основном состоянии |1), а в конце
процесса— в некотором состоянии |/). Энергия основного
атомного состояния принята за нуль отсчета энергии, а
энергия конечного атомного состояния обозначается
через йсо/. Для удобства предположим, что до акта
рассеяния имеется данное число фотонов п с частотой со.
Любой реальный световой пучок характеризуется
статистическим распределением чисел фотонов, которое для па«
дающего пучка может быть описано е помощью
матрицы плотности. Однако поперечное сечение не зависит
от распределения фотонов, поэтому при упрощающем
предположении об определенном числе фотонов
общность рассмотрения не теряется. Случай произвольного
распределения фотонов анализируется при обсуждении
вынужденного рамановского рассеяния в гл. 12.
Скорость перехода в случае рассеяния может быть
получена с помощью выражения A1.56),
преобразованного для данной задачи, где различные части оператора
Жг дают вклад в члены первого и второго порядков;
f ks
<rt-l, 1, f\$6NL\n, 0, 1> +
<«-i, \;пж£0\Г){1\%ЕВ\п,о, i)
ИС0 — CO,
X
X б (a — ю, — at). A1.59)
РАССЕЯНИЕ СВЕТА АТОМАМИ
409
Входящие в бра- и кет-векторы начальных и конечных
состояний первые, вторые и третьи обозначения
относятся соответственно к фотонам с волновым вектором
к, фотонам с волновым вектором ks и атомному
состоянию. Суммирование по /
производится по всем
состояниям объединенной
системы атомов и
излучения. Сумма по конечным
состояниям, стоящая
перед квадратом модуля,
отдельно учитывает
возможные атомные
состояния / и рассеянные
фотоны с волновым вектором
ks.
Вклады в матричные
элементы рассеяния
показаны на диаграммах
фиг. 11.3, где условные
обозначения точно такие
же, как на фиг. 8.1. На
диаграмме фиг. 11.3,а
показан вклад первого
члена квадрата модуля в
выражении A1.59). One-
ратор Жхъ имеет второй
порядок, и потому одно
взаимодействие <5§Vr,
уничтожает фотон с
волновым вектором к и
рождает фотон с волновым
вектором ks.
Второй член квадрата
модуля в выражении
A1.59) дает два вклада,
различающиеся видом промежуточного состояния |/). Из
двух операторов 2&Ed, имеющихся в этом члене,
выбираются только те слагаемые, которые содержат
произведение фотонных операторов й и dfsi причем явный вид
6
еп /
Фиг. 11.3. Диаграммное описание
трех видов взаимодействия,
дающих вклад в процесс рассеяния.
В тексте показано, что вклад
нелинейного взаимодействия, описываемого
диаграммой а, пренебрежимо мал.
Основные вклады обусловлены двумя
диаграммами второго порядка б и в.
410
ГЛАВА 11
оператора приведен в (8.93). Существуют две
очевидные возможности выбора фотонных операторов: первая
ведет к произведению операторов вида й\а и описывается
диаграммой фиг. 11.3,6, другая — к произведению
операторов вида йа\ и описывается диаграммой фиг. 11.3, е.
Промежуточное атомное состояние обозначается вектором
\i) и обладает энергией fico*. Диаграмма на фиг. 11.3,6
представляет собой комбинацию диаграмм фиг. 8.1, а и
8.1, г. Каждая из этих диаграмм в отдельности не может
описывать процессы с сохранением энергии, однако
возможны их комбинации, которые не противоречат закону
сохранения энергии. Второй член квадрата модуля в
выражении A1.59) можно записать в явном виде
следующим образом:
1 у| <я-1,1, /1#до1я-1,0, /)(я-1, 0, t\£ED\n,o9 1)
Ь Zj ( со — со ^
(п - 1, 1, f 1 MED 1 ft, 1, Q(n, 1, 11 MED | ft, 0, 1)
+ -co^-co.
Теперь можно оценить относительные величины
вкладов трех диаграмм. Поскольку ожидаемое значение one-
о '"ч о *<ч 2 / 2
ратора щН2 точно такое же, как Ет/с в свободном
пространстве, и все вклады содержат е2 и квадраты
матричных элементов вектора г,-, то основные различия
обусловлены соответственно знаменателями, зависящими от
энергии: 8пгс2, Ьш — Ьщ и —ficos— £со2-. Далее, величина
8тс2 имеет порядок 6- 10~13 Дж, тогда как типичные
значения атомной и фотонной энергий в случае рассеяния
света лежат в интервале Ю-18—Ю-19 Дж.
Следовательно, вклад первого члена квадрата модуля в
выражении A1.59) пренебрежимо мал. Два оставшихся
знаменателя значительно различаются по величине, если
частоты со и сог близки, однако в общем случае они являются
величинами одинакового порядка, а поэтому оба
соответствующих члена в A1.59) должны быть сохранены.
Теперь выражение A1.59) для скорости перехода
можно упростить, опуская нелинейный член, подставляя
выражение A1.60) во вклад второго порядка и используя
A1.60)
РАССЕЯНИЕ СВЕТА АТОМАМИ
411
формулу (8.93) для оценки матричных элементов
оператора Жеъ-
1 т-1 т-п яе4ако?/г ^ ( zs% D/i£ • D/i
~* \ СО; —• СО
2egfi^-
+
e-Df/Es-D/i \ P
СО. + С0^
) б(ф —О, —©;). A1.61)
Здесь е и 8S — краткие обозначения единичных векторов
поляризации падающих и рассеянных фотонов соответ*
ственно.
Поперечное сечение можно выразить через скорость
перехода тем же способом, который использовался в
(9.29) в случае фотоэлектронной эмиссии. Кроме того,
суммирование ео к8 можно преобразовать в
интегрирование
z
V
Bnf\\k2sdksdQ =
= [V/Bnf] J J (<*Цс*) dcos dQ, A1.62)
сходное с интегрированием в (9.27). Отметим, что
скорость перехода в A1.61) относится к рассеянному фо*
тону с данной поляризацией es, поэтому в A1.62) соот*
ветственно учитывается только одна поляризация.
В результате дифференциальное сечение принимает
вид
da
__ ^ g<<D((P-(PfK
f
Шг8$ С
X
IR
Dfi£-Dn g-DffCs»Dn
' CO ^. — CO, + CO
CO
]
A1.63)
Суммирование по f ограничено, так как дельта-функция
в A1.61) может быть отлична от нуля только для тех
конечных атомных состояний, энергия которых меньше
ft®. Полное дифференциальное поперечное сечение полу-»
чается суммированием вкладов двух независимых
поляризаций фотонов.
412
ГЛАВА II
Выражение A1.63) представляет собой формула Кра-
мерса — Гейзенберга для дифференциального
поперечного сечения, которая является основной в квантовоме-
ханической теории рассеяния. Данное поперечное
сечение учитывает как упругое рэлеевское рассеяние,
соответствующее случаю /= 1, со/ = 0, так и неупругое ра-
мановское рассеяние, соответствующее всем остальным
членам суммы по /.
Упругое рассеяние
Прежде всего рассмотрим упругое рассеяние, при
котором атом возвращается в свое основное состояние |1)
после процесса рассеяния. Если сохранить только члены,
описывающие упругое рассеяние, то дифференциальное
поперечное сечение A1.63) принимает вид
da __ е4со4 IV4 /e5*Due-Dn _,_ г . Duzs • Dn \ p
.2 '2*2^4
<Ш \6п%Ъ'с
у /ед-Рне-Рп +g,Pl^Pn>i .A164)
Полезно получить предельные формы поперечного
сечения для случаев, когда частота со много больше или
много меньше атомных частот возбуждения со*.
Сначала допустим, что частота со много больше всех
сог, но много меньше величины тс2/Ь. Это область томсо-
новского рассеяния, рассмотренного в главе ранее.
Зависящие от частоты знаменатели выражения A1.64) можно
разложить в ряд
1 * 1 / со. \
=БГ—-5-0+1Г+ --О' AL65>
1 1 / со. \
—т— = — A -+ ...). (П.66)
со^ + сосоч со1 / v 7
Подставляя в A1.64) формулы A1.65) и A1.66),
получим, что вклад первых членов разложения равен нулю,
а оставшиеся члены дают следующее выражение:
— 9 9 о а / <0/(ея • Dw8 • D£1 +
аа i6n2eg»V у
+ e.Due,-D/i)? (со » со,). A1.67)
CO.
I
РАССЕЯНИЕ СВЕТА АТОМАМИ
413
Суммирование по i в A1.67) можно провести,
используя некоторые результаты, полученные в гл. 4 в связи
с правилом /-сумм.
Задача 1L3. Докажите, что
Е ©Л • DHe . Dn = (ZA/2/и) е • е5. A1.68)
i
Таким образом, выражение A1.67) сводится к
do/dQ = Z2r2e (е • esJ (о > о.). (l 1.69)
Здесь Ti — классический радиус электрона, определенный
в A1.17). Это выражение точно совпадает с формулой
A1.18) для одноэлектронного атома, 2=1.
Классический результат для многоэлектронного атома также
пропорционален Z2, если длина волны падающего
излучения много больше размеров атома, как это предпо*
лагалось при использовании электрического дипольного
приближения в квантовомеханическом расчете. Таким
образом, при классическом вычислении для получения
поперечного сечения, в Z2 раз большего поперечного
сечения одноэлектронного атома, предполагается, что Z
электронов одного атома излучают синфазно.
Следовательно, при вычислении поперечного сечения для томсо-
новского рассеяния классическая и квантовая теории
полностью согласуются.
Теперь рассмотрим противоположный предельный
случай, когда частота со много меньше всех атомных
частот возбуждений o)i, а дифференциальное поперечное
сечение упругого рассеяния A1.64) принимает вид
do еА(й
i^i
d& lGjrejjfiV
У — (е, • Due . Dn) +
A—i ГЛ.
+ e.Du-es.DnJ (со <С со,). A1.70)
Это сечение пропорционально четвертой степени
частоты, как и в классическом результате A1.19).
Суммирование в A1.70) можно точно выполнить в
случае атома водорода. Возбужденные Р-состояния
атома водорода являются единственными состояниями,
дающими вклад в сумму по i, причем для каждого
414 глава и
Р-состояния только одна декартова компонента вектора
Ои отлична от нуля. Для каждого трио из Р-состояний
матричные элементы Хц, Уц и ZH равны между собой,
а потому выражение A1.70) можно переписать
следующим образом:
12
da е4©4
dQ 4я28пЙ2с4
о1
2
X2
(в-в,J (tt«4 A1.71)
С помощью подстановки суммы [5]
— = г. A1.72)
I
(й1 16mco£
где йоя — энергия основного состояния атома водорода
из C.29) ^
}Шя = те*132лЦ}12, A1.73)
выражение A1.71) принимает вид
это выражение очень похоже на классический результат
A1.19) для рассеяния света колеблющимся зарядом с
собственной частотой колебаний со0.
Общее выражение для поперечного сечения также
упрощается в том случае, когда частота со очень близка
к одной из атомных частот возбуждения со* и имеет
место резонансный пик. Очевидно, что в окрестности
резонанса первый член в скобках выражения A1.64)
превосходит по величине второй член, поэтому в первом
члене можно в хорошем приближении-принебречь всеми
вкладами, кроме одного, соответствующего резонанс-
пому уровню.
При точном резонансе, со = сог-, величина поперечного
сечения становится бесконечной. Разумеется, никакой
процесс рассеяния не может иметь бесконечное
^поперечное сечение, а расходимость вызвана тем, что при
выводе выражения A1.64) мы пренебрегли излучательным
затуханием. Более строгий расчет показывает, что учет
затухания добавляет мнимую часть к частоте со в зна-
РАССЕЯНИЕ СВЕТА АТОМАМИ
415
иёнателях выражения A1.64)» Согласно обсуждению,
следующему за формулой (8.143), требуемый мнимый
член есть /уг(со), где уг — та же самая функция, кото-
рея появляется в выражении для восприимчивости. Из
(8.146) получим
<*Ь <0>
*W-E 6nlofic3 ;) . (П.75)
и резонансное поперечное сечение из A1.64) принимает
вид
da _ e4Q4 !^-Du|2|e-I>ni2
Ль.2Л
dQ 16ne^V (со. - @J + [y( (со)]2
A1.76)
В окрестности резонанса поперечное сечение имеет ло-
ренцеву частотную зависимость, сходную с
классическим результатом A1.16).
Полное резонансное поперечное сечение а
полудается из дифференциального поперечного сечения
посредством интегрирования по телесному углу Q
(определяемому направлением волнового вектора
рассеянного фотона) и суммирования вкладов двух
независимых поляризаций фотона. Усреднение по углам подобно
гому усреднению, которое использовалось при переходе
от формулы A1.16) к A1.23), поэтому результат имеет
вид
£ $ | е,. DH I2 dQ = (8я/3) | Du P. A1.77)
по поляризации
Цо сих пор при вычислении рассматривалось рассеяние
на одном атоме, однако в любом реальном эксперименте
имеется много рассеивающих атомов, ориентации
которых распределены случайным образом. Для сравнения
геории с экспериментом удобно иметь дело с
теоретическим поперечным сечением, дополнительно усредненным
по всем возможным атомным ориентациям. Тогда рас*
сеяние на большом числе атомов N получается путем
умножения найденного поперечного сечения на N.
416
ГЛАВА II
Усреднение по ориентациям, точно такое же, как в
C.55), приводит к следующему выражению:
|e-D/il2=4[Dnp. A1.78)
Отсюда полное усредненное поперечное сечение есть
о д е^ LM A179)
18яе2Й2с4 (со. - соJ + [Y. (со)]2 # v
Рассмотрим частный случай, когда состояние \i) есть
первое атомное возбужденное состояние. Тогда
суммирование в выражении A1.75) для y* сводится к одному
члену с /=1, который можно использовать для того,
чтобы переписать формулу A1.79) следующим образом:
е2ю|Ои|2 Yt-H
а= Зе0Ьс ((of-(oJ + [Y.(co)]2- (IL8°)
В случае точного резонанса со = сог- выражение для
поперечного сечения с учетом A1.75) принимает вид
о = 2яс2/со2 = Я2/2я, A1.81)
где % — длина волны падающего излучения.
Этот удивительно простой результат связан с
аналогичным резонансным поведением мнимой части
восприимчивости в (8.144). Он показывает, что в случае
резонанса с первым возбужденным состоянием атома
поперечное сечение зависит только от частоты перехода и не
зависит от всех других свойств атома. Для резонанса в
видимой области спектра величина а, определяемая
формулой A1.81), порядка 6-104 м2. С другой стороны, вне
области резонанса, как следует из предыдущего
рассмотрения, типичное поперечное сечение порядка г],
или 7-Ю-30 м2. Таким образом, резонансное увеличение
поперечного сечения огромно.
Задача 11.4. Докажите, что если состояние |/) не
является первым возбужденным состоянием
атома, то резонансное поперечное сечение
определяется следующим обобщением вьь
ражения A1.81):
РАССЕЯНИЯ СВЕТА АТОМАМИ
417
где уц(ы)—частный вклад в ширину
линии, определенный в (8Л49). Отсюда
следует, что резонансное поперечное сечение
уменьшается для более высоких
возбужденных состояний.
Если частота падающего света со не очень велика,
не очень мала и не близка к одной из атомных частот"
возбуждения, то не удается аппроксимировать
поперечное сечение простой формулой и необходимо
использовать полное выражение A1.64). Численные результаты
получены только для рассеяния на атоме водорода [6] и
приведены на фиг. 11.4 и 11.5. Доводы, предшествующие
формуле A1.71) и показывающие пропорциональность
матричного элемента рассеяния величине e-es, в
хорошем приближении справедливы для всех частот со, а
потому дифференциальное поперечное сечение A1.64)
можно переписать следующим образом:
do/dQ = г2е\Ж{ |2 (е . esJ, A1.83)
где
mco2 v^ 2со. IX,. |2
Частотная зависимость величины М\ для всех частот
сэ, меньших сод, показана на фиг. 11.4. Вертикальные
пунктирные линии указывают положения частот
возбуждения о)г, в которых величина Ж\ расходится. Когда
частота со близка к од, частоты возбуждения сближаются,
поэтому численные результаты Гаврила [6] можно
продолжить только до возбужденного состояния с п = 5. На
фиг. 11.5 показана частотная зависимость \Ж\\2 для
частот со, меньших и больших (од. Область,
непосредственно примыкающая к сод со стороны меньших частот,
снова опущена. Следует отметить большие резонансные
пики и нули дифференциального поперечного сечения,
имеющиеся между соседними пиками. На высоких
частотах, когда со > сод, величина \М\\2 приближается к
единице, а дифференциальное поперечное сечение имеет
обычную величину для томсоновского рассеяния.
Как указывалось выше, введение излучательного
затухания устраняет бесконечности из поперечного сече-
1/214 Зак, 885
4 -
M,
О
-4
' ' '
0,2 0,4 0,6
V,o
-8L
Фиг. 11.4. Частотная зависимость безразмерного матричного
элемента Л\ для упругого рассеяния света атомом водорода в случае
частот, меньших ридберговской частоты со^.
Величина М^ не показана для области частот между 24/25©^ и <о^, где частоты
возбуждения очень близки друг к другу. Вертикальные пунктирные линии
указывают резонансы, соответствующие возбужденным состояниям с гс=2, 3, 4 и 5.
График построен на основе численных результатов М. Гаврила [6].
/7 = 2
J 4 5"
Фиг. 11.5. Частотная зависимость величины \JC\\2 для атома
водорода.
Вертикальные пунктирные линии показывают положения резонансов.
Горизонтальная пунктирная линия показывает предельное значение I <М^ |2 для о> > fi>/^
в области томсоновского рассеяния. График построен на основе данда* работы
РАССЕЯНИЕ СВЕТА АТОМАМИ 419
тя, а также устраняет нули между бесконечностями.
Эднако в масштабе фиг. 11.4 и 11.5 затухание ведет к
^значительным изменениям.
Задача 11.5. Докажите, что с учетом затухания
величина \JK\\2 для резонансного пика п = 2
в атоме водорода порядка 1014.
Неупругое рассеяние: эффект Рамана
Если частота падающего света со больше наимень-
лей частоты атомного возбуждения, то возможны такие
1роцессы рассеяния, в которых конечное атомное состоя-
1ие не является основным состоянием. Для анализа
этих процессов необходимо вернуться к общему выраже-
1ию A1.63) для дифференциального поперечного сече-
1ия. Рассмотренное выше упругое рассеяние
соответствует члену с / = 1. Оставшиеся члены соответствуют
неупругому рамановскому рассеянию, поскольку частота
рассеянного света, определяемая дельта-функцией в
A1.61), дается формулой
CDs = C0 — CDf. A1.85)
В общем случае рассеянное излучение содержит столько
частотных компонент cos, сколько имеется различных
энергетических уровней с частотой со/, меньшей со. Это
положение проиллюстрировано на фиг. 11.6. Поскольку
начальные и конечные состояния в выражении A1.63)
связаны парой электрических дипольных матричных
элементов, то правила отбора, определяющие эти
матричные элементы (рассмотренные в гл. 8), ограничивают
возможные конечные состояния для процесса рассеяния
[7, 8]. Например, из того, что величины Dfi и D^ могут
быть отличными от нуля только в том случае, когда
состояния |/) и \1) (и аналогично состояния \i) и |1))
имеют противоположную четность, следует, что
дифференциальное поперечное сечение не равно нулю только
для конечных состояний |/), четность которых совпадает
с четностью основного состояния.
Наиболее удивительное свойство неупругого
поперечного сечения снова заключается в наличии резонансов,
когда частота со близка к одной из частот переходов
7214
420
ГЛАВА II
©г. Резонансы обусловлены первым членом в
квадратных скобках выражения A1.63). Сохраняя только
соответствующий резонансный член, рассмотрим резонанс,
возникающий на данной атомной частоте. Полное
резонансное поперечное сечение
можно найти точно таким
же способом, какой
использовался в случае чисто
упругого рассеяния:
посредством введения ширины
линии yH03)» определенной в
A1.75). Тогда такое же
интегрирование, как в A1.77),
и такое же усреднение по
ориентациям, как в A1.78),
дают обобщение результата
A1.79), включающее
неупругое рассеяние:
О)
л А а л п
2
в ___;;
V
0O
^5
0>4
0J
0I
Фиг. П.6. Возможные частоты
рассеянного света ©<? для атома
с частотами возбуждения ©i,
©2, ©з и т. д.
Частота падающего света ©
показана слева. Длины стрелок
пропорциональны частотам рассеянного
света. Крайняя слева частота
соответствует упругому рассеянию
света, а остальные четыре частоты—
неупругому рассеянию.
Х/гл —
0)£<0)
■Z
f
Df, в
е4(о (со — ©Л*
18яф2с4
X
D,, 12
@. - ©J + [у{ @))]2 • A1.86)
В этом результате
поперечное сечение упругого
рассеяния [формула A1.79)]
соответствует члену с / = 1.
Из A1.86) видно, что
увеличение поперечного
сечения для всех частот
рассеянного света со<$ происходит в том случае, если частота
со резонансна с частотой атомного возбуждения.
Процессом, посредством которого атомы, возбужденные в
состояние |t), переходят на свои более низкие уровни,
является флуоресценция, рассмотренная в гл. 2.
Флуоресценция и резонансное рассеяние излучения являются
просто различными способами описания одного и того
же физического явления.
РАССЕЯНИЕ СВЕТА АТОМАМИ
421
С помощью выражения A1.75) полное резонансное
поперечное сечение A1.86) можно переписать
следующим образом:
e2co|Dn|2 у.(®)
° = Зг0Ьс (со. - @J + [Y. (со)]2 • AL87>
Этот результат совпадает с A1.80) и показывает, что
полное резонансное поперечное сечение, включающее
компоненты упругого и неупругого рассеяния, всегда
дается одним и тем же выражением. Поперечное сечение
можно выразить более компактно при помощи частных
вкладов в параметр полной ширины линии,
определенных в (8.149):
2лс2 у.{ (со) у. (со)
° = ~^ (СО; - С0J + [у. (С0)]2 • AЬ88)
В случае точного резонанса со = со* и
2лс2 Y-j (о)
со2 у. (со)
A1.89)
Поскольку полная ширина линии, как и в выражении
(8.148), определяется суммой отдельных вкладов
СОх: < СО
Y<(©)= E Y/f (со), A1.90)
f
то отсюда следует, что величина Yn(co) всегда меньше
Yi(co), за исключением случая, когда состояние \i) есть
низшее возбужденное состояние. Таким образом, полное
резонансное поперечное сечение A1.89) обычно меньше
2яс2/со2, однако это сечение по-прежнему велико по
сравнению с нерезонансным поперечным сечением.
Необходимо подчеркнуть, что описанная выше теория
основана на предположении о том, что существует только
излучательное уширение атомных переходов. Наличие,
например, значительного ударного уширения привело
бы к усложнению выражений для резонансных
поперечных сечений.
Полное резонансное поперечное сечение можно
записать в виде суммы отдельных вкладов:
а = 5>/, A1.91)
f
14 Зак. 885
422
ГЛАВА II
где Of — поперечное сечение рассеяния, при котором
излучается свет с частотой со — со/, соответствующей
данному конечному атомному состоянию. Используя
формулы (8.149) и A1.86), получим
°f ~~ & @)• - С0J + [Y/(С0)]2 ' \\IXI)
Таким образом, если частота падающего света
совпадает с частотой возбуждения состояния |i), то
интенсивность рассеянного света с частотой со — со/
пропорциональна скорости излучательного перехода из
состояния |/) в состояние \f). Отметим, что суммирование по
/ в правой части выражения A1.92) приводит с
помощью формулы A1.90) к прежнему результату для
полного поперечного сечения.
Проведенное выше рассмотрение поперечного сечения
для неупругого рассеяния было связано с упрощениями,
справедливыми для резонансных условий. В предельных
случаях больших и малых частот падающего света
также получаются простые результаты.
Задача 11.6. Рассмотрите аналог области томсоновского
рассеяния для случая неупругого
рассеяния. Докажите, что все вклады неупругого
рассеяния в поперечное сечение стремятся
к нулю в пределе высоких частот
падающего света (со <С со*) в отличие от вклада
упругого рассеяния, который стремится к
конечному высокочастотному пределу
A1.69).
В другом предельном случае низких частот (со «С сог)
поперечное сечение, конечно, также равно нулю,
поскольку частота падающего света должна быть больше
наименьшей атомной частоты возбуждения, для того
чтобы имело место неупругое рассеяние (ср. фиг. 11.6).
Поперечное сечение вблизи порога приведено ниже для
частотного случая атома водорода.
Если исключить специальные случаи, когда
выражение для поперечного сечения можно упростить, то обычно
несколько промежуточных состояний \i) в сумме A1.63)
дают сравнимые вклады в поперечное сечение. Поэтому
РАССЕЯНИЕ СВЕТА АТОМАМИ
423
частотная зависимость поперечного сечения может быть
определена только с помощью подробного вычисления
на основе известных атомных волновых функций и
собственных значений.
Численные результаты для поперечного сечения
неупругого рассеяния на атомах имеются для водорода.
Был вычислен вклад в дифференциальное поперечное
сечение процесса рассеяния, в котором атом,
первоначально находящийся в своем основном состоянии,
возбуждается в свое конечное состояние 2S [9].
Дифференциальное поперечное сечение A1.63) для этого процесса
может быть записано в виде
dQ e со
где
ж
^ тсо (со - <pf) у / 11 \
Ь Ал fl il \ a)t — со ~l~" cOj — со, + co J'
COr + CO
A1.94)
Здесь \f) есть 25-состояние. Отметим, что при упругом
рассеянии выражение для Ж2 переходит в выражение
для Ж и определенное в A1.84).
Частотная зависимость Жъ для частот, меньших 0я,
показана на фиг. 11.7. Отметим, что величина Жъ
конечна при пороговом значении частоты со = со/,
соответствующем началу рассеяния.
Задача 11.7. Докажите, что если частота падающего
света равна частоте перехода со/ в конечное
25-состояние, то
Ж2 = 16 X 21/2/27 (со = cof = co2s). A1.95)
При решении следует учесть, что только
промежуточное 2Р-состояние дает в мат-
ричцый элемент ненулевой вклад.
Волновые функции для состояний атома водорода
IS и 2РХ приведены в C.25) и C.26), а
волновая функция 25-состояния имеет вид
q2s = 2~W2 {1 - (г/2а0)} ехр (- г/2а0).
A1.96)
И*
424
ГЛАВА 1Г
На фиг. 11.8 показана частотная зависимость
дифференциального поперечного сечения для значений со, как
меньших, так и больших сод. Обратите внимание на ре-
Sr
II
с:
1 io
1 "
1 ^
Фиг. 11.7. Частотная зависимость матричного элемента Ж2 для
неупругого рассеяния света атомом водорода.
Конечным состоянием атома водорода является 25-состояние. Вертикальные
пунктирные линии указывают связанные состояния, соответствующие п = 2, 3,
4, 5. Реальное неупругое рассеяние из состояния с /2 = 2 имеет место только
для частоты о), большей 3/4 (о#, однако величина оЧ^ не имеет какой-либо
особенности на этой частоте. (По данным работы [9].)
зонансные пики и нули, сходные с резонансными
пиками и нулями величины \М\\2, показанной на фиг. 11.5.
При высоких частотах поперечное сечение стремится
к нулю в соответствии с теоремой, приведенной в
задаче 11.6. Из фиг. 11.8 видно, что дифференциальное
поперечное сечение обращается в нуль при частоте со =
РАССЕЯНИЕ СВЕТА АТОМАМИ
425
= o>2s и более низких частотах и линейно возрастает
пропорционально со— oJS в частотной области,
прилегающей сверху к частотному порогу неупругого рассеяния.
Учет излучательного затухания устраняет
бесконечности и нули из значений поперечного сечения, однако
1,0
1,1
Фиг. 11.8. Частотная зависимость дифференциального поперечного
сечения неупругого рассеяния атомом водорода для случая, когда
конечным атомным состоянием является 25-состояние.
На графике изображена величина (со — ©2S) I ^2 I Л0' за исключением области
(D < u>2S, гДе поперечное сечение обращается в нуль. Вертикальные
пунктирные линии показывают положения резонансов. (По данным работы [9].)
в масштабах фиг. 11.7 и 11.8 этот учет приводит к
пренебрежимо малым изменениям. Относительные и
абсолютные высоты различных резонансных пиков в
упругом и неупругом рассеянии на атоме водорода могут
быть получены с помощью формулы A1.92) и данных,
приведенных на фиг. 3.5. Например, когда частота
падающего света резонансна с частотой перехода на
уровень п = 3 атома водорода, видно, что пиковое значение
поперечного сечения упругого рассеяния в 160/22 раз
больше пикового значения поперечного сечения
неупругого рассеяния.
426
ГЛАВА 1Г
В качестве последнего вопроса теории рассеяния
рассмотрим проверку квантовомеханического вычисления
общего соотношения A1.10) между поперечным
сечением рассеяния и мнимой частью восприимчивости %".
Полный резонансный вклад в поперечное сечение всех
промежуточных состояний \i) с учетом ширин уровней
определяется из A1.63):
С0с<0)
а^ у *4<*> fa - «уK у |Pf<llpnl
Z-I 1Яттр.?Ъ2г4 Z-» (О, — СО— /V,
f
'О1
iy. (со)
A1.97)
Здесь усреднение по углам было проведено точно так
же, как в A1.77) и A1.78). Из сравнения с результатом
(8.145) для х" видно, что общее соотношение A1.10)
действительно выполняется.
Более полная проверка соотношения A1.10)
потребовала бы рассмотрения нерезонансных и кросс-членов
в поперечном сечении, обусловленных вторым
слагаемым в квадратных скобках формулы Крамерса — Гей-
зенберга A1.63). Это слагаемое связано с диаграммой
фиг. 11.3, в и определяется электрическими дипольными
переходами, не сохраняющими энергию, при которых
испускание фотонов сопровождается возбуждением
атома, а поглощение фотонов — релаксацией атома из
возбужденного состояния вниз. Такие процессы, однако,
были исключены из укороченного гамильтониана типа
(8.103), использованного для нахождения
восприимчивости, приведенной в (8.145). Согласованное сравнение
восприимчивости (8.145) с поперечным сечением
рассеяния требует расчетов поперечного сечения рассеяния
на основе точно такого же укороченного гамильтониана»
Полная резонансная часть поперечного сечения,
рассеяния A1.97) удовлетворяет этому условию.
ЛИТЕРАТУРА
1. Panofsky W. К. #., Phillips M., Classical electricity and magne-
tism, Addison-Wesley, Reading, 1955, p. 301.
2. Hewson A. C, An introduction to the theory of electromagnetic wa«
ves, Longmans, London, 1970, p. 69.
РАССЕЯНИЕ СВЕТА АТОМАМИ
427
3. Heitler №., The quantum theory of radiation, 3-rd ed., Clarendon
Press, Oxford, 1954, § 22. (См. перевод: В. Гайтлер, Квантовая
теория излучения, ИЛ, 1956.)
4. Sakurai J. /., Advanced quantum mechanics, Addison-Wesley,
Reading, 1967; p. 229.
5. Bethe H. A., Salpeter E. £., Quantum mechanics of one- and two-
electron atoms, Springer-Verlag, Berlin, 1957, p. 258. (См. перевод:
Г. Бете, Э. Солпитер, Квантовая механика атомов с одним и
двумя электронами,* Физматгиз, 1960.)
6. Gavrila M., Phys. Rev., 163, 147 A967).
7. Tinkham M., Group theory and quantum mechanics, McGraw-Hill,
New York, 1964, p. 249
8. Cracknell A. P., Applied group theory, Pergamon, Oxford, 1968,
p. 148.
9. Saslow W. M., Mills D. L., Phys. Rev., 187, 1025 A969).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Трудно указать работу, в которой проводится подробное
рассмотрение теории рассеяния света атомами. Обычной ссылкой служит
Placzek G., Rayleigh-Streuung und Raman Effect, in Handbuch
der Raddiologie, ed. by E. Marx,-vol. 6, Akademiche Verlagsgesellschaft,
Leipzig, 1934, part 2, p. 209.
С изобретением лазера стало возможным определение
электронных энергетических уровней атомов в криста'ллах с помощью
измерений неупругого рассеяния света. См., например,
Hougen J. 7\, Singh S., Proc. Roy. Soc, A277, 193 A964).
Kiel Л., Damen Т., Porto P. S.t Singh S., Varsanyi F.y Phys. Rev.,
178, 1518 A969).
В этих работах описывается применение теории, подробно
изложенной в данной главе, к экспериментальным наблюдениям.
Использование рассеяния света для определения энергий
возбуждения представляет широкую область исследований, в которой
электронные энергетические уровни играют лишь незначительную
роль. Обзор всей области исследований в этом направлении см. в
статье
Cummis И. Z., Laser light scattering spectroscopy, in Quantum
optics, ed. by R. J. Glauber, Academic Press, New York, 1969, p. 247.
Глава 12
Нелинейная оптика
В гл. 3 было показано, что скорость поглощения
энергии светового пучка двухуровневым атомом
содержит члены, пропорциональные всем четным степеням
амплитуды электрического поля -пучка Е. Иными
словами, скорость поглощения пропорциональна всем
положительным целым степеням интенсивности пучка. При
анализе поглощения мы вычислили только линейный по
интенсивности член, а вклады всех остальных членов
более высокого порядка не учитывались, поскольку они
обычно малы. Однако в случае света, полученного от
лазерного источника, члены более высокого порядка не
обязательно малы, поэтому в настоящей главе
рассматривается влияние нелинейных членов на оптические
свойства атомов.
На языке квантовой механики члены высших
порядков в выражении для скорости поглощения
соответствуют возбуждению атома, при котором поглощаются два
или больше фотонов. Однако нелинейные члены при
описании взаимодействия света с атомами определяют
кроме многофотонного поглощения также множество
других оптических процессов. Например, пучок
монохроматического света при взаимодействии с атомами может
частично преобразоваться в свет, частоты которого
являются гармониками основной частоты. С другой
стороны, пучки с двумя и большим числом различных
частот могут при взаимодействии создавать свет с
частотой, равной сумме или разности исходных частот. Кроме
того, мощный световой пучок может изменить показа-
НЕЛИНЕЙНАЯ ОПТИКА
429
тель преломления той среды, через которую он проходит,
причем величина изменения зависит от интенсивности
пучка. Характер рассеяния света, описанного в гл. 11,
меняется, если падающий световой пучок достаточно
интенсивен, т. е. начинает играть существенную роль
процесс вынужденного рассеяния.
Таким образом, нелинейная оптика включает в себя
целый ряд явлений и представляет широкое поле для
исследований. Цель настоящей главы заключается в том,
чтобы изложить теорию некоторых наиболее простых
процессов, а не в том, чтобы дать исчерпывающий обзор
нелинейной оптики. Наш анализ ограничивается
нелинейными процессами, происходящими в изотропных
средах, где атомные или молекулярные состояния имеют
точно определенную четность. Кроме того, в
гамильтониане, описывающем атомы и излучение, сохраняется
только электрический дипольный член и
предполагается, что световые пучки являются одномодовыми.
Большое число разнообразных нелинейных процессов
может происходить при взаимодействии света с
анизотропными молекулами или атомами, внедренными в
кристалл без центра инверсии. Члены высших порядков в
мультипольном разложении взаимодействия излучения
с атомами приводят к дополнительным нелинейным
процессам. Для анализа случая многомодовых пучков
изложенную здесь теорию необходимо обобщить. Мы не
будем рассматривать эти более общие задачи, поскольку
они изложены в специальных монографиях и обзорах
[1-4].
Двухфотонное поглощение (случай двух пучков)
Исследование нелинейной оптики удобно начать с
частного примера, поэтому сначала мы рассмотрим
одновременное поглощение двух фотонов, а затем покажем,
как этот процесс входит в более общую теорию
нелинейной оптики.
Расчет двухфотонного поглощения проводится
параллельно теории поперечного сечения рассеяния,
приведенной в гл. 11. Оба процесса обусловлены
взаимодействием двух различных фотонов с одним атомом. При
рассеянии света один фотон поглощается и один фотон
430
ГЛАВА 12
а
испускается, в то время как в рассматриваемом
процессе оба фотона поглощаются. Пусть поглощенные
фотоны имеют различные
частоты соь юг и волновые
векторы кь кг,
соответствующие двум однохмодовым
световым пучкам.
Предположим, что двухфотонное
поглощение переводит атом из
основного состояния 11)
в возбужденное состояние
|/) с энергией йсо/.
Взаимодействие
излучения с атомом в
электрическом дипольном
приближении описывается
выражением A1.58). На фиг. 12.1
показаны диаграммы трех
возможных вкладов в- теории
возмущений, зависящих от
времени, в случае двухфо-
тонного поглощения. Эти
диаграммы похожи на
диаграммы фиг. 11.3, но только
теперь волнистая линия
рождения рассеянного фотона
заменена линией
поглощения второго падающего
фотона. Диаграмма а
описывает часть матричного
элемента поглощения, соответст-
вующую оператору 3@NL>
С помощью рассуждений,
сходных с приведенными
после формулы A1.60),
можно показать, что оператор
3@nl Дает пренебрежимо малый вклад в скорость
перехода, и потому он в дальнейшем учитываться не будет*
Оставшаяся часть гамильтониана имеет вид
в
Фиг. 12.1. Диаграммное
описание трех вкладов в
двухфотонное поглощение в первом и
втором порядках теории
возмущений, зависящих от
времени.
Диаграмма первого порядка а дает
скорость перехода, пренебрежимо
малую по сравнению со скоростями
перехода, определяемыми
диаграммами второго порядка б и в.
ж
ED
еЬ • [Е, (г) + Ё2 (г)],
A2.1)
НЕЛИНЕЙНАЯ ОПТИКА
431
где Ei (г) и Е2(г)—операторы поперечных
электрических полей двух световых пучков в точке г. Двухфотон-
ное поглощение представляет собой эффект второго по-
рядка по <Жео, поэтому в его матричном элементе
имеются два вклада, определяемые двумя возможными
порядками расположения операторов уничтожения фо-
тонов: а2й\ и а\а2. Эти вклады описываются диаграмма*
ми фиг. 12.1,6 и в.
Скорость перехода в случае двухфотонного
поглощения определяется непосредственно с помощью членов
второго порядка выражения A1.57). При этом
матричный элемент очень похож на выражение A1.60) для
процесса рассеяния света, однако будет показано, что
когерентные свойства падающего света могут сильно
влиять на скорость двухфотонного поглощения. Поэтому
желательно вычислить скорость перехода для света с
произвольными статистическими свойствами, и
недостаточно использования в расчете только средних чисел
фотонов двух пучков. Соответственно пусть \R) и \Rf)
представляют собой состояния поля излучения до и
после двухфотонного поглощения. Выражение для
скорости перехода, получаемое из A1.57), имеет вид
1
т
2ле4
Й4 Zj
*f
у у /(V [D • Ч (г) \Rj> i)(Kj,i |Р-ЕГ(г)|/?,1)
Z-f /~d\ CD. — CD, "*"
Rt i l l
(Rf,f\D.E+(r)\Riii)(Riyi\D.E+(r)\Ri\)^V
)
X 6 (со, + co2 - cof), A2.2)
где E+ — часть оператора электрического поля,
описывающая уничтожение фотонов и определенная в (9.9),
\Ri) и \i) — промежуточные состояния излучения и
атома, два члена в матричном элементе описывают вклады
диаграмм, изображенных на фиг. 12.1,6 и е.
В формуле A2.2) суммирование производится по
конечным состояниям поля излучения /?/), так как
данное выражение определяет скорость двухфотонных
переходов независимо от конечного состояния поля. Сумми*
432 ГЛАВА 12
рование можно проводить по всем возможным состоя*
ниям поля излучения, поскольку физическое требование,
чтобы в состоянии \Rf) было на два фотона меньше, чем
в начальном состоянии \R), автоматически
удовлетворяется благодаря использованию в A2.2) тех частей
операторов поля Е+, которые описывают уничтожение
фотонов. Полную скорость двухфотонного перехода для
атома можно было бы получить с помощью дальнейшего
суммирования в A2.2) но атомным состояниям |/),
однако здесь рассматривается вклад данного конечного
атомного состояния.
Выражение для скорости перехода можно упростить
путем факторизации излучательной и атомной частей.
Рассмотрим излучательную часть. Использование
условия полноты ^
Х|*Ж1=1 A2.3)
«I
исключает суммирование по промежуточным состояниям
поля излучения. Тогда квадрат матричного элемента из
первого члена в A2.2) принимает вид
Б (RI ЕГ (г) ЕГ(г) | Rf) (Rf I Et (r) Et (r) | R) =
Rf
= </? IЁГ (r) E2~ (r) E2+ (r) Et (r) \R). A2.4)
Здесь снова было использовано условие полноты. Второй
член в выражении A2.2) содержит аналогичный
множитель; который может быть записан в форме A2.4), по-
скольку операторы Ei и Е2 коммутируют.
В более общем случае начальное состояние поля
излучения может быть статистической смесью
состояний, а не чистым состоянием \R). Тогда скорости
переходов для чистых состояний, образующих смесь, следует
просуммировать, причем каждая скорость берется с
весом, определяемым соответствующей вероятностью. Это
обобщение аналогично сделанному в (9.23) для случая
скорости однофотонного перехода, и результат удобно
записать через оператор плотности. В результате
скорость перехода A2.2) принимает вид
1/т = Bяе4/й4) | ЖТРА |2 б (щ + ©2 - cof) X
X Sp [рЁГ {т)Ё2 (г)£2+ (т)ЁГ (г)], A2.5)
НЕЛИНЕЙНАЯ ОПТИКА
433
где
•*Г/М-2Д со.-со, + со9-со. J* A2-6^
Здесь £i и £2 — единичные векторы поляризации двух
световых пучков.
Учет излучательного времени жизни состояния \f)
приводит к тому, что дельта-функция, входящая в
выражение A2.5), уширяется и превращается в лоренцеву
функцию
б (со! + со2 — cof) -> 7//Я 2. A2.7)
(ю/ - со, - to2)z + у<
Здесь у/ определяется формулой (8.146), в которой
соответственно изменены обозначения. В выражение
A2.6) можно также ввести параметры ширин линии для
промежуточных состояний, однако это уточнение не
столь важно для настоящего анализа, который относится
к тому случаю, когда частоты падающего света oi и оJ
не близки к какой-либо частоте атомного
возбуждения сог-.
Правила отбора для атомных состояний |/), которые
можно возбудить с помощью двухфотонного поглощения,
точно такие же, как и правила отбора для конечных
атомных состояний в неупругом рассеянии света,
рассмотренные в тексте после уравнения A1.85).
Следовательно, разрешенные состояния |/) должны иметь
такую же четность, что и основное состояние. Это условие
противоположно правилу отбора для однофотонного
поглощения в электрическом дипольном приближении,
где конечное атомное состояние должно иметь четность,
противоположную четности основного состояния. Далее
ясно, что величина .матричного элемента, приведенная
в A2.6), зависит от направлений векторов поляризации
£i и £2. Даже если состояние |/) удовлетворяет
правилам отбора для двухфотонного поглощения, матричный
элемент может обращаться в нуль для некоторых
относительных ориентации векторов £i и £2.
Скорость двухфотонного перехода, полученная в
A2.5), может быть использована для нахождения
характеристик распространения двух световых пучков
434
ГЛАВА 12
через газ, состоящий из одинаковых атомов. Допустим,
что два пучка распространяются параллельно оси z и
в точке z их средние интенсивности равны Т{ и 72.
Согласно B.32), пространственная скорость изменения
интенсивности пучка равна временной скорости
изменения его плотности энергии, следовательно,
d7l/dz = -Nh«)l/Vxt A2.8)
dJjdz = - Nh(D2/Vr. A2.9)
Здесь N— число одинаковых атомов в объеме V. В этих
выражениях т описывается формулой A2.5), в которой
необходимо провести усреднение по случайным ориента-
циям атомов и молекул. В уравнениях A2.8) и A2.9)
предполагается, что нет никакого линейного поглощения
света; затухание обусловлено лишь двухфотонным
поглощением.
Решить уравнения A2.8) и A2.9) в общем случае
довольно трудно, так как величина 1/т сложно зависит
от электрических полей двух пучков. Однако их решение
упрощается, если предположить, что два световых пучка
являются статистически независимыми, поэтому след в
A2.5) может быть факторизован в виде произведения
средних по отдельным пучкам. В этом случае,
используя (9.24) и исключая пространственные координаты,
получаем
Sp (рЁГЁ^ШЁ?) = (coico2/482//jife) ТЛ. A2.10)
Пучки, используемые в эксперименте по двухфотонному
поглощению, обычно получаются от двух разных
световых источников, поэтому в момент падения на
поглощающий газ они являются статистически независимыми.
Однако ниже будет показано, что нелинейный процесс,
вообще говоря, нарушает статистическую независимость
световых пучков, поэтому соотношение A2.10) не
выполняется строго в процессе поглощения. Тем не менее
это соотношение является хорошим приближением для
слабого поглощения, и здесь мы им воспользуемся.
Волновые векторы kj и к2 связаны с частотами «i и
со2 так же, как в уравнении B.4). Мнимой частью этого
уравнения можно пренебречь, если линейное поглощение
НЕЛИНЕЙНАЯ ОПТИКА
435
на частотах coi и сог отсутствует и скорость двухфотон-
ного поглощения мала. В общем случае показатели
преломления rji и т]2 на этих двух частотах отличны от
единицы, и мы имеем
&1с = т]1сй1 A2.11)
и
k2c = r}2®2. A2.12)
После подстановки выражений A2.5) и A2.10)
уравнение A2.8) принимает вид
d/j jte4 N cofcD2
~77 "ПГ* I ^тра I2 6 (®1 + оJ — of) /i/2-
^2 2e*fiV V k{k2
A2.13)
Здесь горизонтальная черта означает упомянутое выше
усреднение по ориентациям. Проведение некоторых
усреднений по ориентациям, встречающихся в нелинейной
оптике, довольно утомительно, поэтому здесь точные
расчеты не приводятся.
Для получения пары связанных уравнений для 1\ и 72
уравнение A2.9) можно записать в форме, аналогичной
A2.16). Однако в явной записи второго уравнения нет
необходимости, поскольку из A2.8) и A2.9) следует, что
J_^L = _!iJ.. A2.14)
Отсюда
QiM — (Г2/со2) = const = (Jio/щ) — (ГяМ. A2.15)
Здесь 7ю и 72о — значения 7\ и 72 при z = 0, где
начинается поглощающая среда. Поскольку отношение /i/coi
пропорционально скорости прохождения фотонов через
единичную площадь, то соотношение A2.15)
математически выражает физическое свойство процесса
поглощения, заключающееся в том, что в каждом акте
поглощения каждый световой пучок теряет по одному фотону.
Теперь можно с помощью соотношения A2.15)
исключить 72 из A2.13) и получить дифференциальное
436
ГЛАВА 12
уравнение только для Т\. Решение этого уравнения имеет
вид
/, =710 - G'о/-} " G2о/оJ) . A2.16)
(Ло/ffli) — (/го/в>2) ехр (— К2г)
Тогда из A2.15) получим
7"=7 №™1®д ~~ (^о/Д>2)} ехр (— К2г) A2 17)
(Ло/coi) — (/20/со2) ехр (— /С22)
где коэффициент двухфотонного поглощения /Сг
определяется следующим выражением:
я*4 ЛГ cofco?
2e*W У ~kjl
*2 = ГГ27з^--7Т^ I -*г/м Р X
X6(co1+co2~cof)(^--^). A2.18)
При выводе этого результата предполагалось, что в
первом пучке поток фотонов больше, чем во втором,
поэтому константа в соотношении A2.15) положительна.
Везде предполагалось также, что все N атомов
находятся в своих основных состояниях, а двухфотонное
поглощение достаточно мало, чтобы можно было пренебречь
насыщением атомного перехода.
Решения, приведенные в A2.16) и A2.17), остаются
справедливыми при равенстве потоков фотонов в обоих
падающих пучках. Однако предел, когда величина /20/0J
стремится к Ло/соь должен вычисляться с осторожностью,
поскольку при равенстве потоков фотонов
экспоненциальная зависимость от расстояния z в выражениях
A2.16) и A2.17) заменяется зависимостью вида z~K
Пространственная зависимость интенсивностей
пучков, предсказываемая формулами A2.16) и A2.17),
иллюстрируется на фиг. 12.2. Удобно изобразить
отношение интенсивностей пучков к их частотам; тогда,
согласно соотношению A2.15), при всех z между двумя
кривыми в вертикальном направлении сохраняется
постоянное расстояние. Двухфотонное поглощение
прекращается, когда более слабый пучок полностью поглотится; при
этом оставшаяся часть более мощного пучка распростра-
НЕЛИНЕЙНАЯ ОПТИКА
437
няется через остальной газ без последующего
поглощения.
Во многих экспериментах по двухфотонному
поглощению более мощный пучок создается лазером с
фиксированной частотой.
Более слабый пучок
получается от хаотического
источника, а его частоту
можно изменять для
изучения деталей двухфотон-
ного спектра. В этом
случае пучок 1 имеет
интенсивность, значительно
превышающую
интенсивность пучка 2, поэтому
относительное уменьшение
интенсивности пучка 1
невелико даже тогда, когда
пучок 2 полностью
поглощен. В хорошем
приближении выражение A2.17)
сводится к
lt/a)t
<1ю/со,Х120/сог)
19п/СО
/2 = /20 ехр (— K2z)
Gi>72), A2.19)
Фиг. 12.2. Зависимость интеисив-
ностей пучков от расстояния при
двухфотонном поглощении.
Вертикальный масштаб пропорционален
потоку фотонов в пучке, иными словами,
числу фотонов, проходящих через
единичную площадь в единицу времени.
Разность между величинами потоков
фотонов в двух пучках является по*
стоянной величиной, не зависящей от z%
и величиной 720 в
формуле A2.18) для /С2 можно
пренебречь. В пределе
1\ » 72 поведение
интенсивности пучка 2 сходно
с поведением интенсивности при обычном линейном
поглощении, описанном в B.11). Двухфотонное
поглощение можно экспериментально обнаружить только при
условии, что для коэффициента /С2 достигнуто
наибольшее значение, которое возможно получить за счет
использования лазера высокой мощности для генерации
пучка 1х).
1) Обзоры экспериментальных результатов по двухфотонному
поглощению сделаны А. Голдом [4] и Д. Уорлоком [5].
438
ГЛАВА 12
Двухфотонное поглощение (случай одного пучка)
Двухфотонное поглощение может также иметь место
при наличии одного светового пучка. При этом два
поглощенных фотона неразличимы, а частота света
должна равняться половине частоты рассматриваемого
атомного возбуждения. Двухфотонное поглощение,
достаточно сильное для экспериментального обнаружения,
существует только для световых пучков, генерируемых
лазером.
Теория двухфотонного поглощения, развитая для
случая возбуждения двумя пучками, требует некоторых
изменений при использовании ее для описания
двухфотонного поглощения при возбуждении одним пучком. В
случае одного пучка гамильтониан электрического диполь-
ного взаимодействия A2.1) сводится к одному члену,
поэтому никакого различия между диаграммами,
изображенными на фиг. 12.1,6 и в, больше нет. Теперь в
матричном элементе перехода имеется член только
одного вида, а скорость перехода A2.5) заменяется
следующем выражением:
1 2Jt£4 ^
grPflgi-Pn
со1 - со.
"б^-со^Х
X Sp [р£Г (т)ЁГ (r)£i+ (r)Et (г)]. A2.20)
След операторов электрического поля описывается
точно такой же функцией, какая встречается в
определении (9.38) степени когерентности второго порядка в
одной пространственно-временной точке. Обозначая эту
степень когерентности второго порядка через gB)(r) и
используя (9.24), получаем
Sp [рЕГ(т)ЁГ (г)E?(r)Et (г)] = (©?/4ek4*?) g%) /?. A2.21)
Появление степени когерентности второго порядка
составляет основное отличие от теории эксперимента, в
котором используются два пучка.
Здесь предполагается, что пучок распространяется
вдоль оси z и его интенсивность удовлетворяет уравне-
НЕЛИНЕЙНАЯ ОПТИКА
439
нию, сходному с A2.8), но только теперь в каждом акте
поглощения оба фотона поглощаются из одного пучка:
dJjdz = — 2тщ/Ут. A2.22)
С помощью формул A2.20) и A2.21) уравнение A2.22)
можно переписать следующим образом:
dfjdz = - Кк{2) (г) 7?/2Ло, A2.23)
где
б B^ - ©/) -^.
A2.24)
В этом выражении черта снова обозначает усреднение
по ориентациям, а дельта-функция, строго говоря,
должна быть заменена лорецдевой функцией, описывающей
излучательно уширенную линию, аналогичной функции
A2.7), Отметим, что коэффициент К'ч идентичен
коэффициенту Яг, определяемому выражениями A2.8) и
A2.6), если в формуле для Кч пренебречь величиной /2о
и считать фотоны 1 и 2 одинаковыми.
Уравнение распространения A2.23) трудно решить
строго, поскольку степень когерентности второго
порядка в общем случае является функцией г. Пренебрежем
на время этим усложнением и допустим, что величина
g^ постоянна. Тогда решение уравнения A2.23) имеет
вид
/i=7io(l+YgB)^)", A2.25)
или для малого поглощения, когда знаменатель может
быть разложен в ряд,
7"i«/io(l-|^B)^). A2.26)
Зависимость скорости двухфотонного поглощения для
одного пучка от статистических свойств света
учитывается коэффициентом g&\ Степень когерентности
второго порядка в случае когерентного света определяется
выражением (9.41):
§B)=1, A2.27)
Ki =
пе
1А4
2egfiV V k\
Z£l • Dfi£l D£
CO, — CD,
440
ГЛАВА 12
тогда как для одномодового хаотического света,
согласно формуле (9.42),
g® = 2. A2.28)
Следовательно, для малых г, когда справедлива
формула A2.26), скорость двухфотонного поглощения
хаотического света в два раза больше скорости
двухфотонного поглощения когерентного света 1).
Зависимость скорости двухфотонного поглощения
пучка от степени когерентности второго порядка можно
качественно объяснить следующим образом. Как
описывалось в гл. 5 и 9, значение g{2) связано с величиной
флуктуации мгновенной интенсивности пучка. Поскольку
скорость двухфотонпого поглощения пропорциональна
квадрату интенсивности в момент взаимодействия
излучения с атомом, то увеличенное поглощение имеет место
для световых пучков, интенсивности которых вследствие
флуктуации значительно превышают значения,
усредненные по большим промежуткам времени. Например,
пучок, интенсивность которого в течение одной половины
отрезка времени измерения равна 2/, а в течение другой
половины — нулю, имеет среднюю интенсивность 7 и
среднеквадратичную мгновенную интенсивность 272.
Скорость двухфотонного поглощения такого пучка в два
раза больше скорости двухфотонного поглощения пучка
с постоянной во времени мгновенной интенсивностью /.-
Этот вывод согласуется с формулой A2.26), поскольку
степень когерентности второго порядка прерываемого
пучка, как следует из E.109), равняется 2 при f=l/2-
Эти свойства далее иллюстрируются на фиг. 12.3, где
приведены результаты вычисления влияния
двухфотонного поглощения на флуктуации хаотического светового
пучка [7]. На фиг. 12.3, а представлена временная
зависимость мгновенной интенсивности исходного пучка,
которая похожа на временную зависимость, изображенную
на фиг. 5.7. На фиг. 12.3,6 и в показаны флуктуации
интенсивности той же самой части пучка после его
прохождения через среду с двухфотонным поглощением,
причем толщина среды в случае в больше, чем в случае
1) На это впервые было указано в работе [6].
НЕЛИНЕЙНАЯ ОПТИКА
441
б. Видно, что двухфотонное поглощение-и обусловленное
им ослабление светового пучка происходят
преимущественно в максимумах интенсивности. На фиг. 12.3 пики
Фиг. 12.3. Действие двухфотонного поглощения на флуктуации
интенсивности хаотического светового пучка.
Временная зависимость мгновенной интенсивности одной и той же части пучка
показана: а —для среды без поглощения; б — после прохождения в поглощающей
среде расстояния (Кп) I в — после прохождения в поглощающей среде
расстояния 4Г/С2) • Здесь величина /С2 определена в A2.24). Детали вычислений
описаны в работе [7]. Пунктирная линия на каждом графике указывает значение
интенсивности, усредненной по большому промежутку времени.
постепенно сглаживаются, в то время как минимумы
лишь слегка изменяются за счет двухфотонного
поглощения, пренебрежимо малого при небольшой интенсив-
442
ГЛАВА 12
ности. Это поведение противоположно поведению
интенсивности при однофотонном поглощении, когда
относительное уменьшение мгновенной интенсивности не
зависит от ее величин.
Таким образом, двухфотонное поглощение
сглаживает флуктуации интенсивности и изменяет
статистические свойства непоглощенной части светового пучка.
В частности, степень когерентности второго порядка g<2>
изменяется за счет значительного двухфотонного
поглощения, поэтому-анализ, который приводит к A2.25),
становится несправедливым. В более общем случае
двухфотонного поглощения двух различных пучков поглощение
нарушает статистическую независимость пучков,
поэтому результаты A2.16) и A2.17) необходимо
модифицировать, если величина /С22 порядка или больше единицы.
Теория этих эффектов довольно сложна и здесь не
рассматривается [7, 8].
Нелинейная восприимчивость
Исследовав довольно подробно частный нелинейный
процесс, мы теперь покажем, как двухфотонное
поглощение связано с общей теорией нелинейной оптики.
Линейная зависящая от частоты восприимчивость среды
Х)((о) полностью характеризует линейное
распространение электромагнитных волн в среде. Аналогичным
образом распространение электромагнитных волн через
среду, в которой происходят нелинейные процессы,
полностью описывается на основе нелинейной
восприимчивости среды.
Нелинейную восприимчивость можно вычислить,
сохраняя члены более высокого порядка по
электрическому полю излучения, которые не учитывались при
определении линейной восприимчивости. Приведенные в D.87)
и D.85) выражения для C\(t) и C2(t) являются лишь
первыми членами разложения по степеням
взаимодействия излучения с атомом. Разложение C\(t) содержит
все четные степени электрического поля (или
эквивалентно F12), тогда как разложение C2(t) содержит все
нечетные степени. Следовательно, поляризация,
полученная из D.69) и E.76), содержит члены, пропорциональ-
НЕЛИНЕЙНАЯ ОПТИКА
443
ные всем нечетным степеням электрического поля, а
потому обобщение связи между поляризацией и полем
D~5) приводит к выражению
Р = 8j (X(D£ + Х0)£3 + хE)£5 + л # #)> A2.29)
Здесь хA) совпадает с линейной восприимчивостью %(со),
вычисленной в гл. 4, а величины хC\ ХE) и т- Д- являются
компонентами нелинейной восприимчивости.
Общий вид различных компонент нелинейной
восприимчивости определяется довольно сложными
выражениями, которые можно найти в учебниках по
нелинейной оптике [1, 2, 9]. Мы ограничим наш анализ
рассмотрением только первого нелинейного члена, т. е. %C). Вид
этого члена будет получен позже в двух специальных
случаях путем сравнения с результатами вычислений
нелинейных процессов методом теории возмущений,
зависящих от времени.
Разложение A2.29) справедливо для атомов и
молекул, инвариантных относительно инверсии. Операция
инверсии изменяет знаки как Р, так и Е\ отсюда следует,
что при отсутствии четных степеней Е в правой части
выражение A2.29) строго инвариантно относительно
инверсии. Однако для молекул и кристаллов, не
обладающих центром симметрии, ограничения на вид
разложения A2.29) менее жесткие и в разложении могут быть
члены с нечетными степенями Е. Для того чтобы
получить такие члены в теории и действительно найти
правильный вид всех компонент нелинейной
восприимчивости, необходимо использовать многоуровневую модель
атомов или молекул, поскольку вычисления для
двухуровневой модели, проведенные в гл. 4, в этом случае
являются непригодными.
Линейная восприимчивость является величиной
второго порядка по электрическому дипольному
матричному элементу Dijf как, например, в D.89). Каждый
дополнительный порядок по £ в нелинейной части
поляризации дает дополнительный дипольный матричный
элемент, поэтому х(п) является величиной п + 1 порядка по
дипольным матричным элементам. Последовательные
компоненты нелинейной восприимчивости уменьшаются
444
ГЛАВА 12
в соответствии с приближенным правилом
x0»+*>/xW ъЕ-\ A2.30)
где электрическое поле Е0 является характерным для
нелинейной среды и обычно имеет порядок 1011 В/м. Ряд
в правой части уравнения A2.29) сходится для полей,
меньших Е0. Из табл. 2.1 видно, что. поле Е почти всех
световых пучков удовлетворяет этому условию. Как
правило, поле Е много меньше Е0, поэтому разложение
A2.29) можно часто ограничить членом третьего
порядка, много меньшим линейного члена. Поле Е0 сходно с
полем, определенным в задаче 3.1.
Частотная зависимость различных членов в A2.29)
явно не показана. Относительно линейного члена все.
очевидно: поле Е с частотой со создает осциллирующую
поляризацию на частоте со, величина поляризации
определяется восприимчивостью %A){(о). Если поле Е
содержит компоненты с различными частотами, то их вклад в
поляризацию просто аддитивен, как в выражении D.6).
Поведение нелинейных членов более сложно.
Рассмотрим, например, член третьего порядка. Если
электрическое поле содержит три различные частотные
компоненты
Е (/) = El [exp (— iaj) + ехр A@^)] + Е2 [ехр (— /ю2/) +
+ ехр (ш2/)] + Е3 [ехр (— mst) + ехр (ш30]> A2.31)
то величина Е3 содержит компоненты, имеющие 22
различные частоты:
«>1 + й>2+Ю3, COj + @2—С03,
2@! + С02,
202 + 0!,
20з + 01,
20i — 02,
202 — 0J,
203 — 0Ь
20J + 03,
202 + 03,
203 + 02,
20! — 03,
202 — 03,
203 — 02,
0, — 02+со3> ~оI+со2+еоз,
30!,
Зсо2,
303,
01,
02,
03.
A2.32)
НЕЛИНЕЙНАЯ ОПТИКА
445
Согласно формуле A2.29), поле E(t) создает
компоненты поляризации на всех этих частотах. Величина
нелинейной восприимчивости хC) зависит от частотных
компонент электрических полей, на которые умножается
восприимчивость. Кроме того, %C) зависит через
электрические дипольные матричные элементы от векторов
поляризации трех полевых компонент, имеющихся в
A2.31), а также от направления индуцированной
поляризации Р. Следовательно, хC) является функцией трех
частот и четырех пространственных направлений.
Физический смысл нелинейной восприимчивости
можно проиллюстрировать на примере ее применения к
процессу двухфотонного поглощения. Скорость линейного
или однофотонного поглощения, определяемая
коэффициентом Эйнштейна В, тесно связана с мнимой частью
линейной восприимчивости [как в формуле B.40)].
Аналогичные соотношения существуют между скоростями
многофотонного поглощения и мнимыми частями
компонент нелинейной восприимчивости.
В случае поглощения двух фотонов из различных
световых пучков полное поле Е представляет собой сумму
полей Е\ и Е2 с частотами coi и оJ- Из линейного члена
и члена третьего порядка выражения A2.29) получим
Р = воХ(|) (Ех + Е2) + 80ХC) (Е{ + Е2)\ A2.33)
Поле Е и поляризацию Р удобно разделить на их
компоненты Е+ и Р+, имеющие временную зависимость
вида ехр(—mt), и компоненты Е~ и Р~ с временной
зависимостью вида ехр(Ш). Это разделение похоже на
проведенное в (9.8)—(9.10) для операторов
электрического поля. Члены обеих сторон уравнения A2.33),
осциллирующие с одинаковой временной зависимостью,
могут быть приравнены друг другу по отдельности. Та
часть, которая имеет временную зависимость вида
ехр(—icoiO» Дает
Р+ (С0|) = 8о (ХA) (C0l) Et + 6%C) (- С02, @2, ©l) Е2Е?Et +
+ 3xC)(-cdi, coi, (oi)£f£i+£i+}. A2.34)
Здесь частоты компонент восприимчивости приведены в
явном виде, однако зависимость от поляризации опуще-
446
ГЛАВА 12
на для краткости. Аналогичным образом часть
выражения A2.35) с временной зависимостью вида ехр(—io^)
дает
Р+ (со2) = 8о (хA) (со2) Et + 6хC) (- @1, (oi, ш2) EiEtEt +
+ ЗхC) (- @2, @2, (о2) E2EtEl}. A2.35)
Вычислим величину двухфотонного поглощения на
частоте оJ в предельном случае, когда интенсивность
пучка / много больше интенсивности пучка 2. Если
линейное поглощение на частоте wi и двухфотонное
поглощение на частоте 2coi отсутствуют, то усредненная по
периоду интенсивность 7ю пучка /, определяемая
выражением
ETEt = (@1/2бэЛО 7ю, A2.36)
в процессе двухфотонного поглощения на частоте o)i+oJ
меняется очень мало. Кроме того, последний член в
формуле A2.35) много меньше среднего члена, поэтому ее
можно приближенно переписать следующим образом:
Р+ (оJ) = 8j {хA) ((о2) + Ccoi/sjC2&i) x<3) (— (oi, (Oi, @2) /ю} Е%.
A2.37)
Второй член в фигурных скобках имеет вид зависящей
от интенсивности добавки к линейной восприимчивости
на частоте оJ.
Допустим, что г\2 и Х2 являются показателем
преломления и коэффициентом экстинкции на частоте оJ при
наличии двухфотонного поглощения и определяются
формулами B.5) и B.6), в которые вместо
восприимчивости подставлено выражение из фигурных скобок
формулы A2.37). Допустим также, что линейное
поглощение на частоте о>2 отсутствует и, следовательно, мнимая
часть восприимчивости хA)((°2) обращается в нуль. Тогда
Х2 определяется выражением
2ri2^2 = C(o1/8Jc2^1O10ImxC)(--«b ©ь ©2)- A2.38)
Если вещественная восприимчивость хA) много больше
вещественной части второго члена в фигурных скобках
выражения A2.37), то т]2 мало отличается от своего ли-
НЕЛИНЕЙНАЯ ОПТИКА
447
лейного значения и из формул B.12), A2.12) и A2.38)
следует, что коэффициент поглощения /G на частоте о>2
определяется выражением
, ^2 = C01(о|/б/й1й2)/7о1п1ХC)(--оI,со1, со2). A2.39)
Следовательно, усредненная по периоду интенсивность
7г на частоте оJ убывает экспоненциально с расстоянием
2, как в формуле A2.11):
Г2 = 720ехр(-^). A2.40)
Отсюда видно, что характеристики распространения,
полученные для слабого пучка на основе вычисления
нелинейной восприимчивости, идентичны характеристикам,
полученным в A2.19) методом теории возмущений,
зависящих от времени. Сравнение выражений A2.18) и
A2.39) для коэффициента двухфотонного поглощения
К2 дает
ImxC)(— ®ь <°i> w2) =
= {nNe*/6e0h3V) E I ^тра Р 6 (©i + Щ - со*). A2.41)
f
Здесь интенсивность более слабого пучка в A2.18) не
учитывается, а суммирование в правой части ведется по
вкладам всех атомных конечных состояний |/). Этот
результат для мнимой части восприимчивости третьего
порядка, выраженной через дипольные матричные
элементы, согласуется с выражением, полученным на основе
прямого вычисления %C) в случае выбора частот,
соответствующих двухфотонному поглощению [1, 2, 9J.
Если интенсивность пучка 1 достаточно высока, то
вещественная часть второго члена в фигурных скобках
выражения A2.37) уже нельзя считать пренебрежимо
малой по сравнению с вещественной частью первого
члена; в результате показатель преломления на частоте cog
изменится. Рассмотрим две частоты coi и сог, сумма
которых не очень близка к резонансной частоте атома. При
отсутствии одно- или двухфотонного поглощения обе
восприимчивости хA) и ХC) вещественны, поэтому хг обра-
448
ГЛАВА 12
щается в нуль и модифицированный показатель
преломления у\2 дается выражением
Ч]= 1 +Х(Ч^2) + (Зсо1/8иЛ1O;0хC)(-оI, со,, со2). A2.42)
Здесь была использована формула B.5). Таким
образом, показатель преломления на частоте оог зависит от
интенсивности пучка на частоте ы\. у
Рассмотрим специальный случай, когда поле Е\
является не полем интенсивного светового пучка, а
приложенным статическим полем, которое обозначим через
Е0. Это поле имеет только одну компоненту на нулевой
частоте, поэтому первые два члена в правой части
выражения A2.36) преобразуются к виду
Р+ (со2) = 8о (хA) Ы + 3ХC) @, 0, со2) Е%] Е$ A2.43)
и модифицированный показатель преломления т]2
определяется формулой
Л; = 1 + Х(,)К> + 3хC>@, 0, со2)£2. A2.44)
Как и в случае других нелинейных процессов, величина
эффекта зависит от относительных ориентации векторов
электрических полей. В общем случае изменения
показателя преломления различны для света,
поляризованного параллельно и перпендикулярно приложенному
статическому полю, и потому изотропная среда становится
двоякопреломляющей. Это явление носит название
эффекта Керра.
Двухфотонное поглощение одного светового пучка
можно также проанализировать с помощью формализма
нелинейной восприимчивости. В случае одного пучка
света с частотой coi выражение A2.34) принимает вид
P+(coI) = 8J{x°)M£if +
+ Зх0) (- coi, coi, coi) ETEtEt). A2.45)
Мы не будем исходя из этого уравнения вычислять
двухфотонное поглощение, поскольку его полное описание
уже было приведено раньше в этой главе.
Однако в этом случае вещественные части восприим-
чивостей определяют один интересный эффект. Вне
областей одно- или двухфотонного поглощения, где вое-
НЕЛИНЕЙНАЯ ОПТИКА
449
приимчивости хA) и %C) вещественны, показатель
преломления ц\ на частоте (Oj получается из следующего
выражения:
ч\1=\+Х{1\*1) + Зх®\-®19®1,и>1)Е^Е?. A2.46)
Таким образом, показатель преломления для
интенсивного светового пучка изменяется на величину,
пропорциональную интенсивности данного пучка. Этот эффект
может иметь интересное следствие для лазерного
светового пучка, распределение интенсивности которого
обычно имеет максимум в центре пучка и спадает по
направлению к его периферии. Если величина %C)
положительна, то, согласно A2.46), показатель преломления в
центре пучка больше показателя преломления па краях
пучка и скорость света в центре соответственно меньше.
В результате происходит самофокусировка, в процессе
которой пучок фокусируется и самоканализируется в
более узкий и интенсивный пучок по сравнению с
исходным лазерным пучком. Самоканализация света
наблюдалась экспериментально и была объяснена
теоретически [10]2).
Приведенные выше вычисления, основанные на
нелинейной восприимчивости, являются полуклассическими в
том смысле, что поля описываются классическими
векторами, а компоненты восприимчивости вычисляются кван-
товомеханически. Теперь мы вернемся к полной
квантовой теории и исследуем некоторые другие процессы,
связанные с восприимчивостью третьего порядка %C)- Члены
более высокого порядка, т. е. %<5> и выше, здесь
рассматриваться не будут. Они соответствуют процессам такого же
типа, какие описываются восприимчивостью %C), но
включающим большее число фотонов. Эти процессы обычно
слабее, и их труднее исследовать экспериментально.
Вынужденное рамановское рассеяние1)
При выводе выражения для скорости перехода
A1.61) в случае рассеяния света атомом предполага-
1) Подробное рассмотрение вынужденного рамановского эффекта
см. в работе [12].
2) Впервые на возможность самофокусировки света было
указано в работе [15]. — Прим. ред.
450
ГЛАВА 12
\
лось, что падающий пучок имел определенное число фо-4
тонов и до рассматриваемого акта рассеяния
рассеянных фотонов не было. Такое же вычисление нетруд-^
но провести для более общего состояния поля излучения^
описываемого оператором плотности р, где
электрическим полям падающего и рассеянного пучков соответ-*
ствуют операторы Е(г) и Es(r). Этот расчет очень похожа
на расчет скорости перехода A2.5) для двухфотонного
поглощения. Для данного атомного конечного состояйия
\fY скорость перехода для процесса рассеяния имеет вид
1/т = Bяе4/А4) Е I JCsrb I2 б (со - 0, - ©f) X
X Sp [р£- (г)Ё? (г)Ё7 (г)Ё+ (г)]. A2.47)
Здесь
{ {-^~ + -ф^г} A2-48)
есть тот же самый матричный элемент неупругого
рассеяния, который использовался в гл. И, и
предполагается, что |f) не является основным атомным состоянием.
След операторов электрических полей легко
вычисляется в том случае, когда падающее и рассеянное поля
статистически независимы. Предположим, что
показатели преломления рассеивающей среды на частотах о и
cos суть т] и ц8 соответственно:
&с = т](о, ksc~x\s(us. A2.49)
Для вычисления следа в A2.47) необходимо небольшое
обобщение некоторых предыдущих уравнений, с тем
чтобы учесть существование показателя преломления,
отличного от нуля. Основной требуемый здесь результат —
это измененная форма выражения (9.22). Тщательное
рассмотрение предыдущих уравнений показывает, что
величину с в A2.22) необходимо заменить на скорость
света в среде с/г\
Т= {c2hk/rfV) n = {htflkV) п. A2.50)
НЕЛИНЕЙНАЯ ОПТИКА
451
В то же время выражение (9.24) справедливо без
изменения. Используя (9.24) и A2.50), получаем
Sp(рЕ~Ё+) = (co/2e0c2k)T= (ha>3/2e0c2k2V)Я. A2.51)
Следовательно, след в A2.47) дается выражением
Sp(pE~EtE7E+) = (h/2edc2kksVJ^Wsn{ns + I), A2.52)
где Я и ns — средние числа падающих и рассеянных
фотонов в объеме квантования V. Множитель ns + 1
возникает благодаря коммутационным свойствам операторов
рождения и уничтожения рассеянных фотонов,
используемых при вычислении значения оператора dsdfs в
левой части A2.52).
При рассеянии обычных световых пучков среднее
число рассеянных фотонов в одной моде поля излучения
всегда много меньше единицы, что можно видеть,
например, из табл. 2.1, где даже в самых мощных имеющихся
световых пучках, получаемых не от лазерных
источников, на одну моду приходится всего около 10 фотонов.
В этом случае можно в хорошем приближении
пренебречь величиной ils в A2.52), и тогда скорость перехода
A2.47) сводится к выражению A1.61), если показатели
преломления положить равными единице.
Скорость рассеяния, связанная с единицей в
последнем множителе выражения A2.52), определяется как
спонтанная, поскольку испускание рассеянных фотонов
происходит и в отсутствие фотонов, тождественных
рассеянным. Член ns в последнем множителе выражения
A2.52) увеличивает скорость рассеяния, если имелось
начальное возбуждение поля в виде рассеянных фотонов.
Это рассеяние называется вынужденным рамановским
эффектом. Такое рассеяние можно наблюдать
экспериментально, используя лазерные световые источники,
мощность которых достаточно велика, для того чтобы
генерировать более одного рассеянного фотона на одну
моду поля излучения.
Характеристики вынужденного рассеяния можно
исследовать наиболее просто, если рассмотреть рассеяние
фотонов в данную моду поля излучения ks, а рассеянием
во все остальные моды пренебречь. Сохранение члена Я3
452
ГЛАВА 12
в A2.52) делает уравнения распространения для
падающего и рассеянного пучков нелинейными, поэтому
вынужденный рамановский эффект явля_ется одним из
процессов нелинейной оптики. Если 7 и /s—среднир
интенсивности падающего и рассеянного пучков и
предполагается, что оба пучка распространяются вдоль оси г, то
уравнения распространения имеют вид
dJ/dz = — NhvjVx A2.53)
и _
dIJdz=Nh(oJVx. A2.54)
Здесь N— число рассеивающих атомов в объеме V, т
определяется формулой A2.47), где для получения
скорости, соответствующей одной рассеянной моде,
суммирование по ks не производится.
Общее решение этих уравнений связано с такими же
трудностями, какие встречались при рассмотрении
уравнений A2.8) и A2.9) для двухфотонного поглощения.
Скорость перехода 1/t зависит от характеристик пучков
сложным образом, так как даже первоначально
статистически независимые пучки не остаются независимыми
в процессе рассеяния. Влияние статистических свойств
света на вынужденное рассеяние рассматривается позже
в этой главе.
Однако в настоящем вычислении этими
усложнениями мы пренебрежем и допустим, что в процессе
распространения через рассеивающую среду пучки остаются
независимыми. Тогда след в A2.47) может быть легко
связан с интенсивностями пучков при помощи выражений
A2.52) и A2.50), и уравнение распространения A2.54)
принимает вид
dls = не* N ч,
dz 2e*fiV V
Здесь горизонтальная черта обозначает обычное
усреднение по ориентациям.
_ ^ _ 0f) / (у, + _Lj. A2.55)
НЕЛИНЕЙНАЯ ОПТИКА 45В
Из A2.53) и A2.54) следует, что
— ~-\- — 4т-= 0, A2.56)
© дг ' cos дг ' ч '
поэтому
G/со) + №,) = const = G0/(о) + Gs0/co5). A2.57)
Здесь нули обозначают начальные значения средних ин-
тенсивностей при z = 0. Таким образом, полный поток
фотонов сохраняется: каждый фотон, потерянный
падающим пучком, компенсируется дополнительным
фотоном в рассеянном пучке.
Теперь уравнение A2.55) можно решить, если
сначала с поМощью A2.57) исключить величину 7. Решение
уравнения A2.55) имеет вид
j ^ {GqM + (W*s)} fio + (K/^s)} exP <gg)j- (К7^М)
5 {(W©*) + (fico,/!^)} exp (Gz) + (/о/со)
A2.58)
Здесь коэффициент усиления для вынужденного рама-
новского рассеяния G определяется формулой
яе4 N со2©?
X6(co~co^cof)(A + b_ + ^). A2.59)
Общее решение A2.58) для интенсивности
рассеянного пучка имеет три различных вида зависимости от z
при различных значениях Gz. Для"'
Gz< 1, A2.60)
7>7„+ ДМЙ.+(-гК))<>' AМ1)
* *°^ (/о/СО) + (/S0/C05) + (ЙС05/П5)
и интенсивность пучка первоначально растет линейно с
расстоянием. В противоположном пределе очень боль-
454
ГЛАВА 12
ших значений «г, где
{(/soK) + (h<*JVk)} exp (Gz) > /о/со, A2.62)
Ts/(*s«Gо/о) + (/>>,), A2.63)
весь исходный поток фотонов превращается в поток
фотонов рассеянного света. Между двумя предельными
случаями, описываемыми выражениями A2.60) и
A2.62), имеется область значений «г, где интенсивность
рассеянного пучка возрастает экспоненциально с
расстоянием
7>{1 +К0/ш/0}{Г80 + (^/^5)}ехр(О2). A2.64)
Экспоненциальный рост является прямым следствием
наличия нелинейного члена в уравнении A2.55), а
решение A2.64) характерно для вынужденною рамановского
эффекта.
Рассеяние падающего света на частоте со можно
использовать для усиления первоначально имеющегося
пучка с интенсивностью 7s0 и частотой cos или для
генерации света на частоте cos в отсутствие внешнего
излучения, имеющего данную частоту. Если значение 7so
положить равным нулю, то общее решение A2.58)
преобразуется к виду
(h®slVks) (exp (Gz) - 1)
/ — v s' *'_ F v ' ' A2 65)
5 (hG>s(o/VksIQ) exp (Gz) + 1 *
Зависимость последнего решения от z приведена на
фиг. 12.4. Области линейной и экспоненциальной
зависимостей, а также область насыщения имеются и в
случае Tso = 0, где начальные фотоны с частотой со8
должны появиться за счет спонтанного рассеяния. Тогда
область экспоненциальной зависимости рбусловлена
усилением этих спонтанных фотонов благодаря
вынужденному рамановскому эффекту.
Во многих экспериментах по вынужденному
рассеянию длина образца достаточно мала, для того чтобы ,
первый член в знаменателе выражения A2.65) был
всегда много меньше единицы, поэтому можно записать
7,«(Аа>2/Уй,) [exp (Gz) - 1]. A2.66)
НЕЛИНЕЙНАЯ ОПТИКА
456
При очень малых значениях z спонтанное рассеяние в
линейной области точно такое же, как рассеяние,
исследованное в гл. 11. Поэтому можно показать (см.
ниже), что методы настоящей главы воспроизводят по-
ЮО
s 50
О
Фиг. 12.4. Зависимость интенсивности рассеянного" света от
расстояния для вынужденного рамановского эффекта, показывающая
области линейного и экспоненциального роста, а также
приближение к насыщению.
В качестве единицы измерения изображенной интенсивности выбрана
величина hap-jvk . Для простоты принятое значение Vk IQ/h(as равно 100. В обычных
условиях это значение было бы много больше, а область экс-поненциального
роста имела бы соответственно ббльшие размеры.
лученные ранее результаты для дифференциального
поперечного сечения da/dQ спонтанного рассеяния.
Рассмотрим объем V, содержащий N атомов и
имеющий в направлении распространения пучка длину г.
Площадь поперечного сечения объема равна V/z, а
скорость, с которой энергия падающего пучка теряется
вследствие рассеяния, есть ((uI(us)Ts(V/z). Тогда по опре-
Насьщение
Экспоненциаль -
ный рост
.< ^
Линейный,
рост
466
ГЛАВА 12
делению поперечного сечения рассеяния одного атома о
Na = Z G>7sV/<oj0z> A2.67)
Здесь введено суммирование для учета полного
спонтанного рассеяния. Используя линейный член из A2.66),
с помощью A1.62) получаем
do/dQ = [VlBnf] J ( h^2sG/T0c2N) das. A2.68)
Здесь показатели преломления были положены равными
единице, как и в гл. 11. Если в последних скобках
выражения A2.59) сохранить только главный первый член,
то уравнение A2.68) принимает вид
da е4ю (со — соЛ3
= 9 2.2 4 I ^SRE I2, A2.69)
где в JtsRE частота cos положена равной со — со/. Этот
результат идентичен вкладу состояния |/) в поперечное
сечение A1.63), но только здесь имеется усреднение по
атомным ориентациям.
Для больших значений г, когда интенсивность
рассеянного света возрастает экспоненциально,
коэффициент усиления G является в экспериментальном
Отношении более важной характеристикой, чем поперечное
сечение рассеяния. Излучательное уширение конечного
атомного состояния превращает дельта-функцию в
A2.59) в лоренцеву функцию:
Yf/я
6(©-©,-©,)-*7 1 ,о 2, A2.70)
(cof - со + со5) +Yf
как и в A2.7). Поскольку G входит в экспоненту
выражения A2.66), то интенсивность рассеянного света на
частоте, соответствующей максимуму G, для больших
значений z значительно превосходит интенсивность на
других частотах. Максимум усиления G
макс ПриХОДИТСЯ
на пик лоренцевой функции, где cos равна со — со/,
поэтому из A2.59) получим
ei Л^ со (со — cofJ — /0
°макс==^р¥7 kks |<ж^,^7- A2J1)
НЕЛИНЕЙНАЯ ОПТИКА
457
Здесь в последних скобках выражения A2.59) был
сохранен только главный член.
Максимум усиления для вынужденного рамановского
эффекта в газе можно выразить через поперечное
сечение A2.69) для спонтанного рассеяния одним атомом
следующим образом 1):
г da N 8я2/0 П979^
^макс — dQ у Ь(<й- C0f) kksyf # \i*.l*)
Значение GMaKc порядка 100 м-1 можно достичь при
рассеянии света от импульсного лазера с интенсивностью
1012 В-м-2, указанной в табл. 2.1.
Сделанное выше допущение о том, что при
вынужденном рамановском эффекте рассеянное излучение
принадлежит одной моде, является, конечно,
приближенным для реального эксперимента. В общем случае в
рассеянии участвует несколько конечных атомных
состояний |/) и для каждого конечного состояния имеется
несколько возбужденных мод ks. Однако часто бывает так,
что коэффициент усиления, соответствующий данному
атомному состоянию и данной моде рассеянного поля,
больше коэффициентов усиления для всех других
состояний и мод, поэтому большая часть рассеянного света
попадает в один пучок.
Приведенное выше краткое рассмотрение
вынужденного рамановского эффекта не учитывает многие
аспекты этого уже исследованного явления, описание которого
можно найти в специальных работах [1, 4, 12].
Генерация третьей гармоники
Двухфотонное поглощение и вынужденный раманов-
ский эффект являются в некоторой степени сходными
нелинейными процессами, включающими взаимодействие
двух фотонов с атомом, который переводится в
возбужденное состояние. Величина атомной энергии
возбуждения определяет связь между частотами фотонов,
участвующих во взаимодействии.
]) Это выражение впервые получено Хелворсом [11].
15 Зак. 885
458
ГЛАВА 12
В большинстве других процессов нелинейной оптики'
атомы играют более пассивную роль. Такие процессы
оставляют атомы в тех же самых состояниях, в которых
они находились первоначально, поэтому обмена энергией
Фиг. 12.5. Диаграммы для генерации третьей гармоники.
Все четыре взаимодействия в каждой диаграмме определяются электрическим
дипольным гамильтонианом &Cj7£S
между излучением и атомами нет. К этой категории
принадлежат эффект Керра и самофокусировка света.
Сейчас мы рассмотрим более важный пример: генерацию
света на утроенной частоте падающего
монохроматического светового пучка.
НЕЛИНЕЙНАЯ ОПТИКА
459
Пусть cos — частота светового пучка, падающего на
атом. Согласно схеме, приведенной в A2.32),
электрическое поле света индуцирует атомную поляризацию на
частоте соз = 3coi через нелинейную восприимчивость
третьего порядка. Эта осциллирующая поляризация в
свою очередь создает излучение света на частоте соз.
Скорость генерации третьей гармоники вычисляется
методом теории возмущений, зависящих от времени.
В одном акте взаимодействия требуется уничтожение
трех фотонов ki с частотой coi и рождение одного фотона
третьей гармоники, волновой вектор которого обозначим
через к3. Всего здесь имеется четыре электрических ди-
польных взаимодействия, поэтому необходима теория
возмущений четвертого порядка. До и после
взаимодействия атом находится в своем основном состоянии |1),
однако в процессе генерации гармоники он возбужден в
виртуальные промежуточные состояния.
Диаграммы для теории возмущений четвертого
порядка показаны на фиг. 12.5. Четыре различные
диаграммы соответствуют четырем' возможным
последовательностям испускания фотона к3 относительно
поглощений трех фотонов кь Скорость перехода для четырехфо-
тонного процесса получается непосредственно из члена
четвертого порядка выражения A1.57):
1/т = Bш« I I J(thg I2 6 (Зю, - ©з) X
X Sp (pErErETEtEsEtEtEti A2.73)
К
где матричный элемент имеет вид
THG
-.?.{
h, i, i
C(O1-cda)Bo1-(o.)@1-(o/)
+
(- °>i - %) Bcoi - °>/) @1 ~ °>/)
(» C01 - (DA) (- 2®, - CD,.) (©, - C0y) +
, gi'DiAgi-P^g-P//g3-D/i Д A2 74^
(— ш1 — ^a) (— 2<Di — ®i) (— 3®i — ^y) J
15*
460
ГЛАВА 12
Здесь Ё\ и Ёз — операторы электрического поля для
падающего света и света с утроенной частотой.
В случае генерации гармоник за счет взаимодействия
света с одним атомом все операторы электрического
поля в A2.73) вычисляются в точке нахождения атома г.
Однако скорость перехода при генерации третьей
гармоники обнаруживает новое свойство, которым не
обладают скорости двухфотонного поглощения и
вынужденного рамановского рассеяния. После окончания двух
последних процессов атом остается в конкретном
конечном состоянии и каждый отдельный переход приводит
к возбуждению определенного атома. Поэтому полная
скорость перехода равна сумме скоростей переходов для
отдельных атомов и все величины /С2> K'i и G в A2.18),
A2.24) и A2.59) пропорциональны числу атомов N.
Скорость генерации гармоник ведет себя иначе.
Поскольку речь идет об атомах, то их конечное состояние
точно такое же, как.и начальное состояние, и поэтому
нет различия между переходами, происходящими при
взаимодействии с различными атомами. Следовательно,
матричный элемент должен быть просуммирован по всем
вкладам различных атомов до того, как он будет
возведен в квадрат для получения полной скорости перехода.
Тогда полная скорость перехода определяется
выражением A2.73), где член, содержащий электрическое поле,
записывается в более общем виде:
Е Sp [рЁТ (г) ЁТ (г) ЁТ (г) Et (г) X
X Ёг (г') Ef (г7) Et (r') Et(r')l A2.75)
Г> Г'
/
Здесь суммирование по г и г' ведется по координатам
всех N атомов.
Используя в A2.75) координатные зависимости
операторов Ё+ и £", приведенные в (9.9) и (9.10), получим
координатную зависимость полной скорости перехода
Z ехр {«(к3 - 310 • (г - г')} = S ехр (/Акт) 2, A2.76)
г, г' г
где
Ak = k3-3ki. A2.77)
НЕЛИНЕЙНАЯ ОПТИКА
461
Следовательно, скорость перехода определяется
формулой A2.73), где все операторы электрического поля
вычисляются в одной и той же точке, но только вводится
дополнительный множитель, приведенный в A2.76).
Рост средней интенсивности третьей гармоники h
описывается уравнением
d73/dz = ha3/VT, A2.78)
которое сходно с уравнениями распространения,
приведенными раньше, однако теперь с учетом рассмотренных
выше изменений величина 1/т есть полная скорость
перехода для всех атомов.
Как и в других нелинейных процессах, довольно
трудно вычислить рост интенсивности пучка в общем случае,
где два пучка приобретают коррелированные
статистические свойства благодаря нелинейным
взаимодействиям. Эти трудности снова можно обойти, если
предположить, что длина пути света через среду достаточно
мала и начальная интенсивность падающего пучка 7-о
лишь слегка уменьшается. Тогда в хорошем
приближении два пучка остаются статистически независимыми и
операторы электрического поля в A2.73) могут быть
факторизованы и выражены через средние
интенсивности.
Произведение операторов поля, относящихся к
падающему пучку, точно такое же, как произведение,
встречающееся в определении (9.46) степени когерентности
третьего порядка g^ в том случае, когда все
пространственно-временные точки одинаковы. Операторы поля
для генерации третьей гармоники имеют такую же
форму, что и операторы для рассеянного пучка в
вынужденном рамановском эффекте. Тогда след в A2.73) может
быть вычислен и уравнение распространения A2.78)
принимает вид
д13 яе ^ со^соз
17 = eejcW £ lj*f' тиа' Х
V3O?o(^+lY A2.79)
Х6C<о, — <о3)
> ехр(г'Дк-г)
462
ГЛАВА 12
Здесь был введен координатный множитель,
определенный в A2.76), а черта обозначает обычное усреднение
по атомным ориентациям, которое теперь проводится до
возведения матричного элемента в квадрат.
Два члена в последних скобках выражения A2.79)
описывают соответственно вынужденное и спонтанное
испускания фотонов третьей гармоники. Если в третью
гармонику превращается малая часть падающего пучка,
то 7з не достигает достаточно большой величины, для
того чтобы вынужденное испускание играло заметную
роль. Поэтому в A2.79) мы сохраним только член,
описывающий спонтанное испускание.
Определение интенсивности третьей гармоники
завершается вычислением двух сумм в A2.79).
Суммирование по г зависит от формы пространственной области,
где протекает нелинейный процесс. Рассмотрим область,
имеющую объем V и ограниченную параллельными
плоскостями, расположенными перпендикулярно
направлению распространения при 2 = 0 и г = L. Площадь
поперечного сечения равна V/L, и мы предполагаем, что
размеры области в направлениях осей х и у много
больше г. Тогда
£ exp (i Дк - г) 2 -> {N/VJ J dr $ exp {I Дк • (г - г')} dr' =
= (N/VL2nJ6(AkxN(Aky)X
X
V
exp (i kkzL) — 1
i &kz
A2.80)
Здесь предполагалось, что пределы интегрирования по х
и у являются достаточно большими, для того чтобы
интегрирование привело к дельта-функции, как и в C.67).
Суммирование по к3 производится также путем
преобразования этой суммы в интеграл
£
> ехр (/ Дк • г)
г
-* [V/Bnf] \
б Coj — (о3)
V ехр (/ Дк • г)
г
4N2k<
2л1со<
б (За)! — со3) dk3 =
/\kL J
A2.81)
sin
ihkL)
№'-
НЕЛИНЕЙНАЯ ОПТИКА'
463
Здесь индекс z у Дй был опущен, так как
дельта-функции в A2.80) обращают остальные компоненты
волнового вектора в нуль.
После подстановки выражения A2.81) в A2.79) и
несложного интегрирования получим интенсивность
третьей гармоники на задней границе объема, который
занимает газ, т. е. при z = L
''-wp(t) ж|-*"""'-*Иль- (,2'82)
Интенсивность гармоники пропорциональна квадрату
числа атомов в единице объема в отличие от линейной
зависимости двухфотонного поглощения и вынужденного
рамановского эффекта. Кроме того, интенсивность
A2.82) пропорциональна кубу интенсивности падающего
пучка и его степени когерентности третьего порядка g^\
Величина g^ равна единице в случае
когерентного'падающего пучка в соответствии с E.107) или (9.48),
однако любые флуктуации интенсивности пучка вызывают
увеличение выходной интенсивности третьей гармоники.
Согласно E.108), величина g<3? для хаотического света
равна 6.
Зависимость интенсивности третьей гармоники от
длины пути определяется тригонометрическим
множителем в формуле A2.82). Наибольшая интенсивность
соответствует
Ak = 0, где { sin2 (у ЫгЬ) }/(Д&J = L2/4. A2.83)
Говорят, что световые пучки согласованы по фазе, если
условие A2.83) выполнено1). Условие фазового
согласования можно с помощью соотношения A2.77)
переписать следующим образом:
/53 = 3/5!- A2.84)
С другой стороны, поскольку соз = Зсоь получим
тъ = т|1, A2.85)
!) В отечественной литературе условие A2.83) обычно
называется условием синхронизма. — Прим. ред.
464
ГЛАВА 12
где г|з и T]i — показатели преломления на частоте третьей
гармоники и на основной частоте. Если условие
фазового согласования не выполняется и, в частности, если AkL
порядка единицы или больше, то интенсивность третьей
гармоники сильно уменьшается. Эта интенсивность
обращается в нуль, если величина AkL равна целому числу,
умноженному на 2я.
Требование фазового согласования является
основной особенностью таких нелинейных процессов, которые
не приводят к изменениям атомных состояний. Условия
фазового согласования экспериментально довольно
трудно выполняются, поэтому они часто ограничивают
эффективность протекания нелинейных процессов. В случае
генерации третьей гармоники показатели преломления
г\] на частоте coi и гK на частоте Зсоь как видно из
теории, изложенной в гл. 4, обычно не равны друг другу и
условие фазового согласования A2.85) в общем случае
не выполняется.
Эту трудность можно преодолеть в некоторых
специальных случаях. Например, если одна из частот coi
или 3coi лежит близко к атомной частоте перехода, где
показатель преломления довольно быстро меняется, как
на фиг. 4.2, то значения ц\ и гJ можно сделать равными
для отдельной частоты соь Однако этот метод обладает
тем недостатком, что пучок с частотой, близкой к
частоте перехода, может сильно поглощаться. Условие
фазового синхронизма часто выполняется в одноосных или
двуосных кристаллах, где изменение показателя
преломления с направлением может быть иногда использовано
для достижения равенства величин гц и ч\г за счет
выбора подходящей ориентации кристалла.
Наблюдения генерации третьей гармоники в газах и
жидкостях должны обычно проводиться в
экспериментах, в которых условие фазового согласования не
выполняется [13]. За характерную длину, на которой сильно
сказывается эффект фазовой расстройки, можно взять
величину л;/|Д&|, обычно имеющую порядок от 1 до
100 мм. Физически это расстояние равно длине пути, на
котором интенсивность третьей гармоники, описываемая
выражением A2.82), впервые достигает своего
максимального значения. Дальнейшее увеличение длины пути
НЕЛИНЕЙНАЯ ОПТИКА
465
приводит к осцилляциям интенсивности третьей
гармоники, при этом ее интенсивность никогда не может быть
больше интенсивности, получаемой после прохождения
расстояния я/|Д&|. Поэтому невозможно эффективно
использовать потенциальную возможность генерации
третьей гармоники остальной частью нелинейной среды.
С другой стороны, генерацию третьей гармоники
можно исследовать с помощью вычислений, основанных
на соответствующей компоненте восприимчивости
третьего порядка [2]. Было найдено, что интенсивность
гармоники пропорциональна _квадрату величины
ХC)(о)ь (Оь coi) и выражение для 7з совпадает с A2.82),
если установить связь
Х<3> К соь со,) = - (NeVe^V) Jt^. A2.86)
Последнее выражение для xC)(&>b coi, coi) в точности
совпадает с выражением, полученным прямым расчетом [2].
Обе формулы A2.41) и A2.86) представляют
специальные случаи общего выражения для %C)> которое
применимо тогда, когда все три входящие в него частоты
различны.
Статистические свойства фотонов
и нелинейная оптика
Из анализа двухфотонного поглощения,
вынужденного рамановского рассеяния и генерации третьей
гармоники видно, что статистические свойства фотонов
играют важную роль в определении скоростей переходов
для нелинейных процессов. В общем случае эти
скорости зависят от степеней когерентности рассматриваемых
световых пучков, а если пучков более одного, то и от
корреляции между пучками. Нелинейные процессы сами
вызывают изменения когерентности и корреляционных
свойств света, поэтому точная теория должна учитывать
эти изменения. Результаты A2.16), A2.17) и A2.25) для
двухфотонного поглощения, A2.58) для вынужденного
рамановского эффекта и A2.82) для генерации третьей
гармоники обычно справедливы в первом порядке по
расстоянию z или Z,, проходимому светом в нелинейной
среде. Они, вообще говоря, непригодны для более высо-
a
466 ГЛАВА 12
ких приближений по z, где начинает сказываться влия
ние нелинейного процесса на статистические свойств
пучков.
Эти эффекты иллюстрируются ниже с помощью рас*
смотрения некоторых простых проявлений статистиче-
ских свойств света в вынужденном рамановском эффект
те. Такие же рассмотрения можно провести и для других
нелинейных процессов [14]. Во многих случаях получаю-*
щиеся уравнения нельзя решить аналитически, поэтому
характеристики распространения световых пучков
должны определяться на основе численного расчета.
Для учета излучательного уширения подставим
A2.70) в выражение для скорости перехода при
рассеянии света A2.47) и предположим, что частота
рассеянного света cos равна со — со/. Наш анализ ограничен
рассмотрением одной моды рассеянного света ks. Если число
падающих фотонов равно л, а рассеянных nSy то
скорость перехода может быть записана с помощью
формулы A2.52) следующим образом:
1/т = /л(я5+1), A2.87)
где
е4 со3 (со — со^у
f= „2fc2 4T,2 \**.. l^SREl2- A2.88)
Здесь черта означает, что скорость относится к
«среднему» атому.
Параметр f скорости двухфотонного перехода
аналогичен параметру $ скорости однофотонного перехода
в A0.6), поэтому параметр ? можно таким же образом
использовать для определения временной зависимости
статистических свойств фотонов. Пусть Рп, ~ns есть
нормированная вероятность того, что одновременно имеется
п падающих и ns рассеянных фотонов:
£ Рп.п =1. A2.89)
п, ns
Рамановское рассеяние изменяет вероятностное
распределение фотонов со скоростями, приведенными на
фиг. 12.6. Эта диаграмма похожа на фиг. 10.1, но только
теперь каждый уровень относится к населенностям пары
S
НЕЛИНЕЙНАЯ ОПТИКА
' 467
мод полости, а расстояние между уровнями равно
й(со — cos)= йю/. Здесь предполагается, что почти все N
атомов находятся в своих основных состояниях, а
поэтому переходы вверх на фиг.^12.6 не учитываются. Полная
'"+f,ns-1
п,п.
'л-/.лс+/
n+Uns-1
^шш^швяа
Ng{n+1)
фп(п3+1)РПгП,
*' $
п,п<
П~1,П<;+1
Фиг. 12.6. Схема расположения энергетических уровней фотонов
в двух модах полости, которые соответствуют падающему и
рассеянному световым пучкам в римановском процессе.
Указанные скорости переходов являются вкладами в dPn^ n Jdt при условии,
что населенность атомных возбужденных уровней пренебрежимо мала.
скорость изменения величин Рп, ns, обусловленная
указанными переходами, имеет вид
dPn, njdt =
= Nf {(n + 1) п8Рп+1. ns-i ~n(ns+ 1) Pn, ns}. A2.90)
Теперь мы изучим временное развитие статистических
свойств света. Временная и пространственная
зависимости рассеянного света, конечно, просто связаны через
скорость света (ds/k8.
К сожалению, решить уравнение A2.90) для
распределения вероятностей или даже для
моментов-распределения не так просто. Рассмотрим, .например, средние
468
ГЛАВА 12
числа фотонов п и ns в падающем и рассеянном пучках
соответственно, определенные следующим образом:
n=ZnPn,ns A2-91)
п,п$
И
ns = Е »sP„, - . A2.92)
Тогда из A2.90) получим
dnjut = NfZ{(n + \) n>sPn+h - nns (n, + 1) />„, „J =
n, ns ^ s *'
= Nf Z /i(«s+l)P/i.v A2.93)
и поскольку в общем случае
S л^Ря, ns = шг* ¥= /m*, A2.94)
п. rcs
то найти ns без дополнительных сведений о
распределении Рп, п невозможно.
о
Свойство уравнений A2.93), заключающееся в том,
что временная зависимость первого момента п8 связана
со значением момента распределения более высокого
порядка nnSy является характерной особенностью
уравнений, описывающих временное развитие статистических
свойств в нелинейных процессах. Это свойство делает
уравнения неразрешимыми при помощи простых
методов.
Для двух статистически независимых фотонных
пучков неравенство в A2.94) можно было бы заменить
равенством. В этом случае Рп, п можно записать в виде
произведения распределения вероятностей для
отдельных МОД1
Pn,ns = PnPns, A2.95)
тогда уравнение A2.93) упрощается и принимает вид
dnjdt = Nfn {ns + 1). A2.96)
По существу это есть приближение, сделанное в данной
главе раньше при анализе вынужденного рамановского
НЕЛИНЕЙНАЯ ОПТИКА 469
эффекта. В начале нелинейного процесса два пучка
обычно независимы, поэтому факторизация, приведенная
в A2.95), может быть принята в качестве начального
условия. Однако временное развитие статистических
свойств одного пучка зависит от свойств другого пучка
таким образом, что статистическая независимость,
определяемая начальным условием, постепенно уменьшается.
Мы не рассматриваем математическую задачу,
связанную с общим решением уравнений для вынужденного
рамановского рассеяния. Вместо этого будет исследован
более простой специальный случай, когда интенсивность
падающего пучка в процессе рассеяния сохраняется
много большей интенсивности пучка рассеянного света.
Таким образом, данный анализ исключает область
насыщения, показанную на фиг. 12,4, однако он пригоден
*для областей линейного и экспоненциального усиления.
Если рассеивается только малая часть фотонов,
первоначально имевшихся в падающем пучке, то малым
изменением статистических свойств пучка можно
несомненно пренебречь. В этом случае, считая распределение
падающих фотонов Рп не зависящим от времени,
определим влияние формы распределения Рп на
интенсивность рассеянного пучка.
Дифференцируя уравнение A2.93) еще раз по t и
используя A2.90), получаем
d2ns/dt2 =Nf Z n(ns+ 1) dPn, nJdt =
n,ns
= N2f2 Z n(ns+l)X
n, ns
X {(П + 1) nsPn+\, ns-l — n(tls+ 1) Pn, ns} =
= N2f2 Z. n (ns + 1) (n -n8 - 2) Pn, n A2.97)
n, ns
На основе допущения об интенсивности падающего
пучка величиной ns + 2 можно пренебречь по сравнению с п
и переписать A2.97) следующим образом:
d2ns/dt2 = N2?2 Z n2 (ns + 1) Рп, па. A2.98)
tuns
470 ГЛАВА 12
Пусть в начале нелинейного процесса при £=0
среднее число рассеянных фотонов есть ns0. В начале
рассеяния факторизация в A2.95) справедлива, поэтому,
согласно A2.96) и A2.98), первая и вторая производные
по / при t = 0 имеют вид
(dnjdt)o = Nfn (ns0 + 1) A2.99)
и
(d%Jdt2H = N2?W(ns0 + 1). A2.100)
Такое же рассмотрение производных вксших порядков
показывает, что формулы A2.99) и A2.100) являются
частными случаями общего результата.
(drns/dtr)Q = Nrfrnr (ns0 +1) (п > л,), A2.101)
где __
nr = Y<nrPn. A2.102)
п
Временная зависимость п8 определяется путем
«суммирования ее разложения в ряд Тейлора с
использованием приведенных выше производных:
Я, = ("so + 1) Z exp (Nfnt) Pn - 1. A2.103)
п
Общие свойства этого решения можно сравнить со
свойствами результата, полученного в данной главе раньше
без учета влияния статистического распределения
фотонов. Если интенсивность падающего пучка всегда много
больше интенсивности рассеянного пучка, то формула
A2.58) приближенно запишется в виде
I = {/"о + (HIVK)} ехр № - (M\\Vkt). A2.104)
Переходя с помощью формул A2.50) и A2.104) от
средних интенсивностей к средним числам фотонов,
получаем
ns = (ns0+ l)exp(Gz) —1. A2.105)
Если G определяется выражением A2.59), где в
последних скобках сохранен только член 70/о), то из A2.50) и
A2.88) следует, что
G = Nfnks/a>s. A2.106)
НЕЛИНЕЙНАЯ ОПТИКА
471
Здесь в выражении для G была сделана замена A2.70),
а частота co's была положена равной со — со/.
Приближенное решение A2.105) очень похоже на
более точный результат A2.103). В решении A2.105)
можно перейти от координатной зависимости к временной,
заменяя z на ,cos^s. Тогда приближенный результат
A2.105) эквивалентен формуле
й, = (й,о + 1)ехр(ЛГ/й/) —1. A2.107)
Если два выражения A2.103) и A2.107) разложить в
ряд по степеням t, то видно, что в точном результате
коэффициент при tr содержит пг вместо величины пг,
имеющейся в приближенном выражении. В общем
случае эти две величины различны, поэтому только
постоянные и линейные по t члены решений, приведенных
в A2.103) и A2.107), согласуются между собой, в то
время как члены более высокого порядка по t различны.
Более точное решение A2.103) может быть записано
в замкнутой форме для некоторых частных видов
распределения падающих фотонов Рп-
Задача 12.1. Покажите, что для падающего одномодо-
вого когерентного света, где распределение
фотонов определяется формулой (9.87),
решение A2.103) можно записать
следующим образом:
ns = (ns0+ 1)ехр (tf/й/) —1. A2.108)
Выражение A2.108) является хорошим
приближением, если
Nft< 1. A2.109)
v Условие A2.109) хорошо выполняется вне
области насыщения для предполагаемого
большого значения п.
Задача 12.2. Покажите, что соответствующий результат
для одномодового хаотического света, где
распределение Рп определено в (9.89),
имеет вид
п3 = (nso + Nfht)j{\ - Nfht). A2.110)
472 ГЛАВА 12
Эти результаты показывают, что решения, полученные
ранее в данной главе, являются правильными для
мощных когерентных одномодовых световых пучков, однако
для пучков хаотического света они справедливы лишь в
линейном по t приближении, а вне его являются
неверными. Два последних случая проиллюстрированы на
2
О
Фиг. 12.7. Временная зависимость средних чисел фотонов ns,
получаемых при рассеянии когерентного и хаотического одпомодового
света.
фиг. 12.7, где приведены зависимости выражений
A2.108) и A2.110) от времени для нулевого начального
возбуждения рассеянных фотонов nso = 0. Из
приведенных зависимостей видно, что при малых значениях / обе
кривые имеют одинаковый наклон, однако при больших
значениях t хаотический свет рассеивается сильнее, чем
когерентный.
Рассмотрение, похожее на описанное выше, может
быть проведено для процесса двухфотонного
поглощения. Если интенсивность одного пучка много больше
интенсивности другого, то можно показать, что формула
A2.19) правильна только тогда, когда пучок с большей
НЕЛИНЕЙНАЯ ОПТИКА
473
интенсивностью является когерентным. В общем случае
эта формула справедлива только для постоянного и
линейного по z членов.
Вообще говоря, во всех нелинейных процессах
статистические распределения фотонов важны для
определения пространственных и временных зависимостей
различных эффектов. Изменения распределений,
вызываемые нелинейной связью между световыми пучками,
обычно влияют на коэффициенты при членах, имеющих
второй и более высокие порядки по z и /.
Задача 12.3. В предельном случае Т\ ^> Т2 проведите
анализ двухфотонного поглощения,
сходный с описанным выше анализом раманов-
ского рассеяния. Проверьте результат
A2.19) для случая, когда пучок / является
когерентным, и определите
соответствующую пространственную или временную
зависимость для случая, когда пучок /
является хаотическим.
ЛИТЕРАТУРА
1. Bloembergen N., Nonlinear optics, Benjamin, New York, 1965. (См.
перевод: Н. Бломберген, Нелинейная оптика, изд-во «Мир», 1966.)
2. Butcher P. N., Nonlinear optical phenomena, Ohio State
University Engineering Publications, Columbus, 1965.
3. Yariv A., Quantum electronics, Wiley, New York, 1967. (См.
перевод: А. Ярив, Квантовая электроника, изд-во «Сов. радио», 1973.)
4. Gold Л., Ducuing /., Shen Y. R., Giordmaine J. Л., статьи в сб.
Quantum optics, ed. R. J. Glauber, Academic Press, New York, 1969.
5 Worlock J. M., в книге: Laser handbook, ed. E. O. Schulz-Dubois
and F. T. Arecchi, North Holland, Amsterdam, 1972.
6. Teich M. C, Wolga G. /, Phys. Rev. Lett., 16, 625 A966).
7. Weber H. P., IEEE J. Quant. Electr., QE-7, 189 A971).
8. Agarwal G. S., Phys. Rev., Al, 1445 A970).
9. Ward J. F., Rev. Mod. Phys., 37, 1 A965).
10. Ахманов С. Л., Сухорукое А. /7., Хохлов Р. В., УФН, 93, 19
A967).
11. Hellwarth R. W.y Phys. Rev., 130, 1850 A963).
12. Bloembergen N., Am. J. Phys., 35, 989 A967).
13. Ward J. F, New G tf. C, Phys. Rev., 185, 57 A969).
14. Shen Y. R., Phys Rev., 155, 921 A967).
15*. Аскарьян F. Л., ЖЭТФ, 42 1567 A962).
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатическое приближение для
фотонов 357
Ансамбль, определение 35—36
— среднее по ансамблю 35, 230,
305
— — связь со средним по
времени 35, 149—150
электрическое поле 236
— хаотические световые пучки
147
Атом, вырождение уровня 31,
38, 58, 60—61
— гамильтониан 69, 123, 254—
255
вторичное квантование
258—263, 271
— запасенная энергия 53, 101—
103
— квадрупольный момент 251
— населенность уровня 31, 38
лазер 356—362
оптическое
возбуждение 51—55
— оператор рождения 259
углового момента 255
— ориентация 42, 86, 114
— переход, насыщение 54, 60,
362, 370—372
оператор 271
скорость, см. Перехода
скорость
— распределение скорости 130
— собственные состояния
энергии 69
— четность волновой функции
74, 257, 419, 433
— электрический дипольный
момент 74, 114—116, 251
V— вторичное
квантование 259, 260, 272
Атомный водород, см. Водорода
атом
Бсрпулли распределение 328, 329
Больцмана постоянная 27
— распределение 26, 27, 34, 60
Боровский радиус 74
Броуновское движение 151, 331
Ван-дер-Ваальса дальнодейст-
вующие силы 206
Векторный потенциал,
калибровочное преобразование 184,
252
классического поля
излучения 182—193, 210
оператор 202, 210
фурье-коэффициенты 191—
193
Видность интерференционных
полос 162
Вина закон смещения 28, 29
Водорода атом, боровскии
радиус 74
волновые функции IS-co-
стояния 75, 76
2£-состояния 423
2Р-состояния 75, 76
излучательное время
жизни 2Р-состояния 87
излучательный сдвиг
2 2Sl/2 -уровня 284, 285
~- — матричный элемент
перехода IS — 2Р 75, 76
— — неупругое рассеяние света
419—425
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
475
Водорода атом, сила осциллятора
124, 125
— — упругое рассеяние света
413, 414, 417—419
— — фотоэффект 294—298
Волновые флуктуации 323
Восприимчивость, зависящая от
частоты, см. Нелинейная
восприимчивость
— кваптовомеханйческая теория
275—291
двухуровневый атом 281
многоуровневый атом
287—291
резонансное значение
287
— классическая теория 95—100
— Крамерса — Кронига
соотношения 104—110, 119
— кросс-соотношения 95
— определение 45, 94
— полуклассическая теория 111—
112
— полюсы Г04—108, 119—121,
282, 396
— правило сумм ПО—111
— связь с коэффициентом В 59,
121, 122
поперечным сечением
рассеяния 391, 395, 396, 426
Временное усреднение, связь с
усреднением по ансамблю 35,
149, 150
Время запаздывания 187, 188
— отклика детектора 173
Вторичное квантование атомного
гамильтониана 258—263
Вторичные волны 154
Вынужденное испускание, см.
Эйнштейна коэффициент В,
Фотон
Вынужденный эффект Рамана
446—457, 465—473
временная зависимость
числа рассеянных фотонов
467—473
зависимость от
фотонного распределения 465—
473
кинетическое уравнение
для фотонов 467
Вынужденный эффект Рамана,
коэффициент усиления 453,
470
связь с
дифференциальным поперечным
сечением 454—457
— пространственная
зависимость интенсивности 453,
454, 470
Вырождение атомных уровней
31, 38, 58, 60, 61
Гамильтониан взаимодействия,
вторичное квантование 260,
261, 272
диагонализация 272—281
диаграммное описание 262,
263
магнитный дипольный 255—
257
мультипольное разложение
254—258
нелинейный 255, 407—410,
430
представление Шредннгера
268—270
теория возмущений 403—
407
четность 74
электрический дипольный
74—76, 112, 113, 254—258,
407—412, 430
электрический квадруполь-
ный 255—257
Гармонический осциллятор, кван-
товрмеханический 193—199
нормировка 198
т оператор числа часгнц
194
• рождения 193, 194, 198
уничтожения 193, 194,
198
условие основного
состояния 197
энергия 24—26, 196, 197
Гауссово приближение 383
свет 147, 148
форма линии 130—132
Гельмгольца теорема 186
Генерация третьей гармоники
457—465
476
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Генерация третьей гармоники
диаграммное описание 459
зависимость от
когерентности третьего порядка
463
нелинейная
восприимчивость 465
пространственная
зависимость интенсивности 461—
463
■— условие фазового
согласования 463
Граничные условия 20, 21
Де Бройля соотношение 65
Двухфотонное поглощение,
зависимость от
когерентности второго порядка 438—
442-
действие на флуктуации
интенсивности 440—442
диаграммное описание 430
нелинейная
восприимчивость 445—449
случай двух пучков 429—
437, 445—448, 472, 473
одного пучка 437—442,
448
Дельта-функция Дирака,
излучательное уширение 340, 433,
456
определение 89
представления 90
свойства 89—91
Дисперсионные соотношения, см.
Крамерса — Кронига
соотношения
Дифференциальное поперечное
сечение рассеяния света 389
классическая
теория 393—398
— — — комптоновское
рассеяние 397, 398
Крамерса — Гей-
зенберга формула 411, 412
неупругое
рассеяние 419—426
томсоновское
рассеяние 397, 412
упругое
рассеяние 412—419
Дифференциальное поперечное
сечение рассеяния света,
фотоэффект 302, 303
Диффузии уравнение 380
Диэлектрическая постоянная 45
Доплеровское уширение 128—132
Зависящая от времени волновая
функция 69, ИЗ
граничные
условия 78
линейная
суперпозиция состояний 72
■ Нормировка 72,
76, 118
Зависящее от времени волновое
уравнение 69
Запрещенный переход 257
Заряда плотность 16, 245
Излучательное время жизни
водородного атома 87
вычисление на основе
квантованного поля
излучения 267
затухание 96, 119—122,
395, 417, 418
связь с коэффициентом
А 54, 268
сдвиг частоты,
вычисление на основе
квантованного поля 282—286
Лэмба и Резер-
форда эксперимент 285, 286
уширение 120, 282—291,
340
ширина линии,
вычисление на основе квантованного
поля излучения 282—286
многоуровневого
атома 287—291
— отдельные
вклады 291
Излучения давление 65—67
— поле, см. Электромагнитное
поле, Квантованное поле
ускоренного заряда 392
Изотопов разделение 67
Интерференция, видность полос
162
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
477
Интерференция интенсивностей,
см. Хенбери Брауна и Твисса
эксперимент
— независимых световых пучков
337
—- Хенбери Брауна и Твисса
эксперимент 169—177, 308, 334,
335
— Юнга эксперимент 152—154,
162—164, 304, 336, 337
Калибровочное преобразование
184, 251—253
Квантованное поле излучения,
гамильтониан 203, 254, 255
— интенсивность 298—304,
326
когерентное состояние,
когерентность второго
порядка 3L0
, когерентность
первого порядка 305
неопределенность
фазы 225, 226
числа фотонов
224
ожидаемое
значение электрического поля
227—229
. — оператор
плотности 233—237
определение 222
— перекрытие
волновых функций 222
. — распределение
фотоотсчетов 329
_ . сравнение с
классической стационарной
волной 308, 312
. — магнитного поля
оператор 202
_ многомодовое
когерентное состояние 237
•— когерентность
второго порядка 310, 311
первого
порядка 306
/г-го
порядка 312, 313
, оператор
плотности 237
Квантованное поле излучения,
многомодовое когерентное
состояние, распределение
фотоотсчетов 326, 327
многомодовое состояние
с определенным числом
фотонов 201
оператор плотности 237
оператор векторного
потенциала 202, 210
числа фотонов 200
переход от
классической теории 201
Планка гипотеза 24—26
Пойнтинга вектор 204
рождения оператор 200
состояние с
определенным числом фотонов,
когерентность второго порядка 309
— —
первого порядка 305
—
ожидаемое значение
электрического поля 217, 218
—
оператор плотности 234
— фазовые
свойства 216
уничтожения оператор
200
фазовое состояние,
когерентность второго порядка
309
ожидаемое
значение оператора числа частиц
219
электрического поля 219, 220
оператор
плотности 234
определение 214
перекрытие
волновых функций 216
фазовые свойства
215, 216
электрического поля
оператор 202, 217, 296
энергия 203—204
нулевых колебаний
25, 204—207, 301
478
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Квантовая эффективность 327—
329
Керра эффект 448
Кинетические уравнения для
атомов двухуровневых 33, 40,
51—55
трехуровневых 62,
63
фотонов 339—345, 467
взаимодействия с
двухуровневым атомом 339—345
вынужденного эффекта
Рамана 467, 468
лазера 362—365
Классическая стационарная
волна, когерентность второго
порядка 176, 177
первого порядка 167
»- га-го порядка 178
определение 151
распределение
фотоотсчетов 320
Классический радиус электрона
393
Клейна — Нишины формула 398
Когерентности время 145, 151,
157, 165, 166
измерение 330—337
— длина 145, 156
— степень второго порядка,
временная зависимость 329
гауссова
хаотического света 176
двухфотонное
поглощение 438—442
квантовое
определение 309'
классическое
определение 175
классической
стационарной волны 176, 177
когерентного
состояния 310
лазер 367—371
лоренцева
хаотического света 176
многомодового
когерентного состояния 299—300,
311
— одномодового
состояния 299, 310
Когерентности степень второго
порядка, связь со степенью
когерентности первого
порядка 147, 175, 300, 311
счетом
фотонов 319—320, 332, 333
состояния с
определенным числом фотонов 298,
309
— фазового состояния
298, 309, 310
первого порядка, гауссова
хаотического света 166
двух мод полости
168, 306
двухмодового
состояния с определенным чис-
слом фотонов 306, 307
квантовое
определение 305
— классическое
определение 164
классической
стационарной волны 167
когерентного
состояния 305
лоренцева
хаотического света 164, 307, 308
. многомодового
когерентного состояния 306
общие условия
когерентности первого порядка
168, 306
одиомодовой
статистической смеси 306
— —. состояния с
определенным числом фотонов 305
третьего порядка,
генерация третьей гармоники 463
п-го порядка, квантовое
определение 312
классическое
определение 178
классической
стационарной волны 178
многомодового
когерентного состояния 312
прерываемой
стационарной волны 179
хаотического пучка
178, 313
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
479
Когерентный свет,
взаимодействие с двухуровневым атомом
347—351
— — второй порядок, условие
когерентности второго
порядка 175
вынужденный эффект Ра-
маиа 465—473
первый порядок,
физический смысл 164
Комптоновское рассеяние 65,
397—398
Копфлюэнтная
гипергеометрическая функция 365—369, 382—
384
Корреляционная функция
второго порядка лоренцева
пучка 176
определение 171
связь с
корреляционной функцией первого
порядка 172
первого порядка
классической стационарной волны 167
определение 155
связь со степенью
когерентности 164
счет фотонов 332—335
Коэффициент экстинкции' 46,
96—99
Крамерса— Кронига
соотношения 109, ПО
правило сумм 110, 111
Крамерса — Гейзенберга
формула 104—412
Крамерса — Кронига
соотношения, восприимчивость,
зависящая от частоты 104—110, 119
коэффициент
экстинкции 109, ПО
общие соотношения 108,
109
показатель преломления
109, 110
Коши главное значение
интеграла 105
— теорема 106
Кросс-соотношения для
восприимчивости 95
Кулоновская калибровка 185—
190, 245
Лазер, адиабатическое
приближение 357
— диффузия фазы, скорость
378—382
ширина линии 381, 382
— кинетические уравнения для
атома 356—362
— когерентность второго
порядка 371
— коэффициент усиления 63
— скорость накачки 61, 352—356
— скорость потерь резонатора
354—356, 375
— сравнение с когерентным
светом 378, 379
— среднее число фотонов 365—
370
— теория, учитывающая три
уровня 61—65, 352—365
— условие инверсии 60, 62, 351
порога 352—356
— флуктуации электрического
поля 374—382
— фотон, кинетические
уравнения 362—365
^распределение
вероятностей 365—373
отсчетов 373, 374
— эффекты насыщения 63—65,
362, 370—372
Лоренцева сила 246
— форма линии 98, 284, 287
Лэмба сдвиг, см. Излучательный
сдвиг частоты
Максвелла распределение
скоростей 130
— уравнения 16, 17, 183, 184,
188—190
Мода поля излучения 21
волновой вектор 21
плотность состояний
19—23
поляризация 21
Накачка 61, 352
— скорость 62
Населенность атомного уровня,
см. Атом
инверсия 60, 352
480
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Насыщение перехода, влияние на
поглощение 60
двухуровневый атом 54
лазер 63, 64, 362, 370—
372
Нелинейная восприимчивость,
генерация третьей гармоники
465
двухфотонное поглощение
445—448
Керра эффект 448
определение 442, 443
показатель преломления,
зависящий от частоты 447—
449
самофокусировка 449
частотные компоненты 444,
445
численная оценка 443, 444
Неоднородное уширение линии
139
Непрерывности уравнение 16,
186
Неупругое рассеяние света, атом
водорода 422—425
квантовая теория 419—
426
комптоновское
рассеяние 65, 397, 398
резонансное поперечное
сечение 419—423
Нормальная форма 313
— — оператор упорядочения 326
Однородное уширение линии 139
Оператор временного развития
399
— перехода 271
Оптическая полость (резонатор)
4, 19
возбуждение атомов 32—
35, 51—55
добротность 356
когерентность, см.
Когерентность
межмодовое расстояние
157
плотность мод 19—23
скорость потерь 354—356,
375
Отрицательной температуры
условие 40, 60
Первый порядок когерентности,
см. Когерентность
корреляционной функции,
Корреляционная функция
Перенормировка массы 285
Планка гипотеза о квантовании
24
— постоянная 15
— распределение 27
— формула для изучения 19,
26—30, 33, 34
Плотности оператор 229—243
многомодового
хаотического света 239—241
многомодового чистого
состояния 237
общие свойства 231—233
одномодового теплового
возбуждения 237—239
определение 231
чистого состояния 233—
237
Плотность мод полости 19—23
численная оценка 50
Поглощения коэффициент 47
классическое выражение
99
правило сумм 111
связь с коэффициентом В
59
Поглощение фотонов, см.
Эйнштейна коэффициент В, Фотон
Пойнтинга вектор 46, 101—103,
204
Показатель преломления 46,
96—99
— -— зависящий от
интенсивности 447—449
Крамерса — Кронига
соотношения 109, 110
Полноты условие 123
Полость, см. Оптическая полость
Поляризация 16, 45
— мультипольное разложение
251
— нелинейная 442—446
— фурье-анализ 94
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
481
Поперечное сечение рассеяния
света 387—392
квантовая теория
407—426
рассеяния света,
классическая теория 392—398
правило сумм 392
связь с
восприимчивостью 391, 395, 396, 426
— фотоэффекта 302
Постоянная тонкой структуры
256
Правила отбора для двухфотон-
ного поглощения 433
неупругого рассеяния
света 419
поглощение и
испускания 256, 257
Правила сумм для
восприимчивости ПО, 111
коэффициент
поглощения 111 ц
экстиыкции 111
поперечного сечения
рассеяния 392
/-значения 122—126
Томаса—Куна—Рейхе 111,
126
Представление 268
— Гейзенберга 269, 270
— Шредингера 269—271, 399
Прерываемая стационарная
волна, двухфотонное поглощение
440
когерентность /г-го
порядка 178, 179
Причинность 108
Промежуточное состояние 406
Пуассона распределение 225, 320,
321, 327, 391
— уравнение 186
Разрешенный переход 256, 257
Рамановское рассеяние света 386
см. Неупругое рассеяние
света, Вынужденный эффект Ра-
мана
Распределение вероятностей, см.
Хаотический свет,
распределение вероятностей для
фотонов
Рассеяние света, диаграммное
описание 409
Рассеяние света, квантовая
теория 407—426
классическая теория 392—
398
Крамерса — Кронига
формула 411, 412
поперечное сечение 387—■
392
природа коэффициента
поглощения 49, 55, 391
распределение атомов
389—391
Рождения оператор, см.
Атомный оператор рождения,
Гармонический осциллятор, Фотон
Рэлея формула для излучения
28
рассеяния 386
Самофокусировка света 449
Света волновой вектор 17, 21
— источник стационарный 146
хаотический 127, 128
численные данные 50
— скорость 17
— рассеяние, см. Рассеяние света
— усиление 62, 63, 347—351,
см. Лазер
Связь между суммированием и
интегрированием, одномерный
случай 159
трехмерный
случай 23, 301, 411
Сила осциллятора перехода (f-
значение перехода),
классическая теория 100
определение 122
правило сумм 122—126
связь между классической
и квантовой теориями 115, 119
численные значения для
водорода 124, 125
Скалярный потенциал 183—188
калибровочное
преобразование 184, 251, 252
Скорость перехода,
вынужденный эффект Рамана 449, 450,
466
482
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Скорость перехода, генерация
третьей гармоники 459
двухфотонное поглощение
431—433, 438—440
золотое правило Ферми
267, 398, 404
испускание 265—267
общее выражение 398—
402
поглощение 76—78, 264,
265
при действии переменного
поля 78—85
случай
большого времени 83, 84, 91
— короткого
времени 83
рассеяние света 407—412
фотоэффект 298, 301
Собственные состояния системы
атом + излучение, оператор
рождения 276
— —
уничтожения 276
— — — — определение
275
Соотношение неопределенностей
для времени и частоты 140
числа фотонов и фазы
213, 216, 226
Составная форма линии 137—
140
Состояние с определенным
числом фотонов, см.
Квантованное поле излучения
Спектроскопия временного
разрешения 175
— флуктуации интенсивности
330—335
Статистическая смесь 209, 229
230
Стационарный световой
источник 146
Степень когерентности, см,
Когерентность
Стефана — Больцмана закрой
излучения 30
Счет фотонов, волновые
флуктуации 323, 342
когерентный свет 319, 320,
326, 327, 329
Счет фотонов, лазер 373
распределение 314—319,
325—330
связь с распределением
фотонов 329, 330
флуктуации частиц 320
хаотический свет 320—325,
330
эксперименты 38, 314, 315,
330—335, 373
Теорема для среднего за период
23, 24
Теория возмущений, зависящих
от времени 76—85, 403—407
— случайного блуждания 147—
149, 379, 380
Тепловое равновесие, вероятность
возбуждения моды 26, 27
испускание фотонов 33—35
распределение фотонов
27—30, 36—38
Тока плотность 16, 185—190, 245
Томаса — Куна — Рейхе правило
. сумм 111, 125, 126
Томсоновское рассеяние 391, 392,
412, 413
Трехуровневая схема лазера, см.
Лазер
Ударное уширение 132—136, 141,
143
Упругое рассеяние света, атом
водорода 413, 414, 417—419
квантовая теория 412—
419
классическая теория
392—398 ^
резонансное поперечное
сечение 414—417
томсоновское рассеяние
397, 412, 413
Усреднение по ориентациям 42,
86, 114, 415, 416
Уширение за счет давления, см.
Ударное уширение
Фабри — Перо спектроскопия 331
Фазовый переход второго рода
366, 382
Фазы диффузия 378—382
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ'
483
Фазы согласование 463
— состояние, см. Квантованное
поле излучения
Ферми золотое правило 267
Флуктуации частиц 320
Флуоресцентное излучение 54,
116, 117, 420
Фотодетектор 294, 299—301, 314,
315, 330
Фотон, вынужденное испускание
32, 33, 266
влияние на лазерное
излучение 376, 377
« направленность 47, 48,
266
■ под действием тепловых
фотонов 32, 33
свойства импульса 65—
67
— группировка 333
— двухфотоиное поглощение в
случае двух пучков 429—433,
445—447
одного пучка
438—442, 448
— импульс 65—67, 129
— интенсивность 298—304
— интерференционные
эксперименты 336, 337
— когерентность, см.
Когерентность
— название 15
— оператор рождения 200
— ч— уничтожения 200
фазы 209—213
— плотность энергии 29, 30
— поглощение 30, 31
влияние атомного
насыщения 60
макроскопическая теория
45—47
" микроскопическая теория
55—60
свойства импульса 65—67
скорость перехода 76—85,
264—266
фотоэффект 294—304
— поток 435, 436
— пренебрежение тепловым
возбуждением 39
Фотон, распределение
вероятностей, взаимодействие с
двухуровневым атомом 345—352
второй момент 37, 224,
374—352
— когерентное состояние
224, 225, 329, 341, 346
лазер 365—373
связь с распределением
фотоотсчетов 329
— тепловое равновесие 26,
27, 36—38
хаотический свет 26, 27,
36—38, 330, 341, 346 '
— соотношение
неопределенностей для амплитуды и фазы
213, 226
— спонтанное испускание 32, 33,
266, 267
влияние на лазерное
излучение 377—381
излучательное
затухание 96, 116—122
направленность 47, 48
свойства импульса 65—
67
связь с рассеянием
света 49
сравнение с
вынужденным испусканием 34, 35
ширина линии 119
— среднее число, временная
зависимость 345—352, 467—473
вынужденный эффект
Рамана 466—473
лазер 365—370
оператор 200
тепловое равновесие 27
флуктуации 35—39
. численная оценка 50
— среднеквадратичное число,
временная зависимость 345—
352
когерентный свет 224,
346
лазер 370
тепловое равновесие 37
хаотический свет 37,
346
484
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Фогон, статистика и нелинейная
оптика 465—473
— схема энергетических уровней
26, 342, 343, 362, 363, 466, 467
Форма линии Фогта 139
Гаусса 130, 131
Лоренца 98, 131
неоднородная 139
однородная 139
составная 137—140
функция 55
Фотоэффект 15, 294—298
Хаотический свет,
взаимодействие с двухуровневым атомом
346—352
временная зависимость
140—145
время флуктуации 157—
160, 330—333
вынужденный раманов-
ский эффект 471—473
интенсивность,
усредненная по большому промежутку
времени 146
— — когерентность второго
порядка 175—177, 310, 311
первого порядка 164—
168, 305—307
д-го порядка 178, 312,
313
— ч— оператор плотности 237—
243
распределение амплитуды
147
интенсивности 148
фотоотсчетов 320—325,
328
фаза 142, 143
- распределение 147—149
флуктуации 142, 143
флуктуации интенсивности
143, 150, 169—175, 332—335
влияние двухфотон-
ного поглощения 440—442
фурье-коэффициенты 156
Хенбери Брауна и Твисса
эксперимент, квантовый анализ
308, 309, 334, 335
классический
анализ 169—177
Черного тела излучение 19
Четность волновой функции 74,
75, 257, 419, 433
Четность гамильтониана
взаимодействия 74
Чистое состояние 209
Ширина
спектральной линии,
влияние на скорость перехода
81, 82
— — —
— — —
287
291
130—
99
— — —
— — —
доплеровская 129, 130
естественная 120, 282—
излучательная 120, 282—
случай гауссовой линии
132
— лоренцевой линии 98,
ударная 132
численная оценка 50,
82, 120, 136
Эйнштейна коэффициент Л,
вычисление на основе
квантованного поля 267
— — — квантовомеханическое
выражение 87
определение 32, 33
связь с излучательным
временем жизни 54, 286
коэффициентом В
34
классическим
затуханием 119
флуоресцентное
излучение 54
численные значения 87
— коэффициент В,
квантовомеханическое выражение 86, 265
определение 32, 33
связь с коэффициентом
А 34
— — — — — коэффициентом
поглощения 59
— электрической
восприимчивостью 59, 121
— усредненный по ориен-
тациям 41, 42, 86
Электромагнитная волна, см.
Квантованное поле излучения
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
485
Электромагнитная волна в
диэлектрике 45—47
векторный потенциал 190—-
193
групповая скорость 104
интенсивность 47, 101 —
103
"СВЯЗЬ С ПЛОТНОСТЬЮ
энергии 57, 58
■ численная оценка 50
классическая стационарная
волна 151
координаты классического
гармонического осциллятора
192, 193
коэффициент поглощения
47, 59, 99, 111
■ экстинкции 46, 47, 93—
99, ПО, 111
плотность энергии 28—32,
101—103
— связь с,
интенсивностью 58
— — показатель преломления
46, 96—99, ПО, 447—449
поток энергии 101—103
связь между
электрическим и магнитным векторами
18, 46
скорость переноса энергии
103, 104
уравнение 17, 190
Электрическая восприимчивость,
см. Восприимчивость,
зависящая от частоты, нелинейная
восприимчивость
« дипольное приближение
254—258, 296, 407, 430
. дипольный момент атома
74, 113—116, 251
. квадрупольный момент
атома 251
Электрическая проницаемость !6
Электромагнитное поле,
классическая теория
в диэлектрике 45—47
взаимодействие с атомом,
гамильтониан 248—254
лагранжиан 246—
248
— — — — — мультипольное
разложение 249—254
калибровочное
преобразование 184, 251—253
координаты
гармонического осциллятора 192, 193
кулоновская калибровка
185—190, 245
лоренцева сила 246
Максвелла уравнения 16,
183, 184, 189
мода 21
описание с помощью
потенциалов 182—185
переход к квантовой
теории 200
поперечная часть 186—189
пренебрежение тепловым
возбуждением 39, 40
продольная часть 185—189
уравнения поля 183—189
энергия 23, 24, 193
плотность энергии 28—
30, 100—103
Эргодическая теорема 35, 149,
154, 321
Эрмитов оператор 199
Юнга интерференционный
эксперимент, квантовый анализ 305,
335—337
классический анализ
152—155, 162—165
Оглавление
Предисловие редактора 5
Предисловие автора к русскому изданию 8
Предисловие автора 9
Глава L Формула Планка для излучения и коэффициенты
Эйнштейна 15
Уравнения Максвелла 16
Плотность мод пол_я в полости 19
Квантование энергии поля 23
Формула Планка 26
Коэффициенты Эйнштейна Л и В 30
Случай теплового равновесия 33
Флуктуации числа фотонов 35
Случай высоких частот 39
Литература 42
Глава 2. Теория простых оптических процессов 44
Макроскопическая теория поглощения 45
Свойства микроскопических процессов ...*.. 47
Оптическое возбуждение атомов 51
Микроскопическая теория поглощения 55
Инверсия населенностей: лазер 60
Давление излучения 65
Литература 67
Глава 3. Квантовая теория коэффициента Эйнштейна В ... 68
Квантовая механика процессов, зависящих от
времени 69
Вид гамильтониана взаимодействия 73
Скорость перехода" 76
Выражение для коэффициента В 85
Дельта-функция Дирака 88
Литература 92
Глава 4. Восприимчивость, зависящая от частоты 93
Определение восприимчивости . . • 94
Классическая теория восприимчивости 95
Поток энергии 100
Соотношения Крамерса — Кронига 104
Правила сумм 110
ОГЛАВЛЕНИЕ
487
Квантовая теория восприимчивости , , , . , « .111
Учет затухания в квантовой теории 116
Силы осцилляторов 122
Литература 126
Глава 5. Теория хаотического света и когерентности . . . .127
Доплеровское уширение 128
Ударное уширение 132
Составная форма линии испускания ,,..,,, 137
Временная зависимость хаотического светового пучка . 140
Флуктуации интенсивности хаотического света . . . 143
Интерференционные полосы в эксперименте Юнга . .152
Вычисление корреляционной функции первого порядка 155
Интенсивность полос и когерентность первого порядка 162
Интерференция интенсивностей и когерентность
высших порядков 169
Литература 179
Глава 6, Квантование поля излучения 181
Описание классического электромагнитного поля с
помощью потенциалов ч . . 182
Кулоновская калибровка 185
Свободное классическое поле 190
Квантовомеханический гармонический осциллятор „ ,193
Квантование поля 200
Энергия нулевых колебаний 204
Литература 207
Глава 7, Состояния квантованного поля излучения 208
Операторы фазы фотонов ,•.,.....«. 209
Состояния с точно определенной фазой фотонов . . .214
Физические свойства одномодовых состояний с
определенным числом фотонов 216
Физические свойства одномодовых состояний с
определенной фазой 218
Когерентные фотонные состояния 221
Физические свойства одномодовых когерентных
состояний 224
Оператор плотности 229
Операторы плотности для чистых состояний .... 233
Статистически смешанные состояния поля излучения . 237
Литература 243
Глава 8. Взаимодействие поля излучения с атомом 244
Классический гамильтониан для взаимодействующих
полей и зарядов 244
Мультипольное разложение гамильтониана .... 249
Электрическое дипольное приближение 254
Вторичное квантование гамильтониана атома .... 258
Вычисление скоростей поглощения и испускания
фотонов 263
Переход к представлению Шредингера 268
488
ОГЛАВЛЕНИЕ
Диагонализация гамильтониана системы «атом +
излучение» 272
Излучательная ширина линии и частотный сдвиг 282
Восприимчивость многоуровневых атомов,
зависящая от частоты 287
Литература 291
Глава 9. Оптика фотонов 293
Фотоэффект 294
Измерение фотонной интенсивности 298
Когерентные свойства фотонов 304
Когерентность высших порядков 308
Счет фотонов 14
Распределения фотонов для когерентного и
хаотического света 318
Квантовомеханическое распределение фотоотсчетов 325
Эксперименты с фотонами 330
Литература 337
Глава 10. Теория лазера 339
Кинетические уравнения для фотонов 339
Временная зависимость когерентности фотонов . . 345
Пороговое условие для лазера . . 352
Кинетические уравнения для атомов 356
Кинетические уравнения для лазерных фотонов . 362
Распределение лазерных фотонов 362
Флуктуации лазерного света 374
Скорость диффузии фазы лазерного излучения . . 378
Приложение 382
Литература 384
Глава 11. Рассеяние света атомами 386
Поперечное сечение рассеяния 387
Классическая теория упругого рассеяния .... 392
Общее выражение для скоростей излучательных
переходов 398
Теория возмущений, зависящих от времени . . . 403
Формула Крамерса — Гейзенберга 407
Упругое рассеяние 412
Неупругое рассеяние: эффект Рамана 419
Литература 426
Глава 12. Нелинейная оптика : 428
Двухфотонное поглощение (случай двух пучков) 429
Двухфотонное поглощение (случай одного пучка) 438
Нелинейная восприимчивость 442
Вынужденное рамаповское рассеяние 449
Генерация третьей гармоники 457
Статистические свойства фотонов и нелинейная
оптика 465
Литература 473
Предметный указатель 474