Основы квантовой оптики - Клаудер Дж., Сударшан Э.

Автор: Клаудер Дж. Сударшан Э.
Теги: физика математическая физика оптика квантовая механика квантовая физика переводная литература квантовая оптика
Похожие
Квантовая оптика
Основы квантовой механики
Основы аксиоматического подхода в квантовой теории поля
Математические основы квантовой механики
Текст
                    Дж.Клаудер, Э.Сударшан
ОСНОВЫ КВАНТОВОЙ ОПТИКИ
Книга известных американских теоретиков Дж. Клаудера и Э. Сударшана
представляет собой современный курс теоретической статистической оптики, в
котором строго и вместе с тем достаточно ясно рассмотрены практически все
основные вопросы этого нового актуального раздела физики.
Книга носит характер учебника — изложению квантовой теории предпослано
рассмотрение классической статистической оптики, что облегчает знакомство с
предметом Вместе с гем она является первой монографией но этому вопросу и
содержит ряд новых оригинальных результатов, публикуемых впервые.
Вопросы, рассматриваемые в книге, имеют большое значение для разработки
теории оптических явлений, изучения процессов в лазерах, процессов
регистрации излучения, рассеяния света и ряда других задач.
Книга рассчитана на физиков, научных работников и инженеров,
специализирующихся в области квантовой оптики и радиофизики. Ее можно
рекомендовать также как учебное пособие для аспирантов и студентов-
старшекурсников соответствующих специальностей.
Оглавление
Предисловие редактора перевода	5
Литература	13
Предисловие	14
Глава 1. Частично когерентный свет	17
§ 1. Введение	17
§ 2. Описание аналитического сигнала	21
§ 3. Статистика частично когерентного света	25
§ 4. Временные и пространственные свойства функции взаимной	30
когерентности в процессе распространения сигнала
А. Теорема ван Циттерта — Цернике C4)
Глава 2. Распределение фотоэлектрических отсчетов	37
§ 1. Постоянная интенсивность	37
А. Распределение Пуассона C3)
§ 2. Случайные интенсивности	40
А. Статистика фотоотсчетов для малых временных интервалов D3)
§ 3. Нахождение распределения интенсивности из распределения отсчетов 46
А. Независимые вклады E0)
Глава 3. Полуклассическая теория фотоэлектрических отсчетов	55
§ 1. Случайные волновые поля	55
§ 2. Стохастические процессы	57
§ 3. Применения к частичной когерентности	61
А. Одиночные счетчики F4). Б. Несколько счетчиков F8). В. Полоса
пропускания, размер счетчика и значение сглаживающих функций
G4).

§ 4. Заключение	76
Глава 4. Статистика поля	78
§ 1. Постановка динамической задачи	78
А. Причины появления статистики G9)
§ 2. Преобразование флуктуационных уравнений	83
А. Усредненные уравнения для моментов (83). Б. Усредненное
уравнение для характеристического функционала (85)
§ 3. Марковские и немарковские процессы	88
А. Определения и различия (88). Б. Соотношения для марковских
процессов (91)
§ 4. Заключительные замечания	95
Глава 5. Статистические состояния в квантовой теории	97
§1. Введение	97
§ 1. Квантовый формализм и обозначения	98
А. Гильбертово пространство (98). Б. Линейные операторы A00). В.
Статистические состояния A05).
§ 3. Примеры статистических состояний в квантовой теории	109
А. Состояния поляризации монохроматического светового пучка A09).
Б. Статистические состояния гармонического осциллятора A12). В.
Статистические состояния нескольких осцилляторов A18). Г.
Статистические состояния для бесконечного числа осцилляторов A21)
§ 4. Заключение	124
Глава 6. Уравнения движения электромагнитного, поля	128
§ 1. Развитие во времени в квантовой теории	128
§ 2. Операторные уравнения для электромагнитного поля. Предварительные 132
замечания
А. Общий подход к уравнениям поля A33)
§ 3. Операторные уравнения для электромагнитного поля.	134
Нерелятивистский анализ
А. Формулировка в конфигурационном пространстве A34). Б.
Формулировка в импульсном пространстве A36). В. Операторы
рождения и уничтожения A42)
§ 4. Характерные свойства временной эволюции	144
А. Описание в конфигурационном пространстве A49)
§ 5. Характерные свойства пространственной эволюции	151
Глава 7. Представление электромагнитного поля по когерентным	156
состояниям
§ 1. Когерентные состояния. Основные свойства	156
А. Собственные состояния смещенного и сдвинутого осцилляторов
A57). Б. Волновые пакеты с минимальной неопределенностью A61). В.
Собственные векторы оператора уничтожения A62).
§ 2. Фундаментальные свойства когерентных состояний для одной степени 164

свободы
А. Предварительные замечания A64). Б. Непрерывное представление,
основанное на когерентных состояниях A69). В. Примеры и
специальные свойства представителей векторов и операторов по
когерентным состояниям A77). Г. Связь с пространствами Сегала —
БаргманнаA90)
§ 3. Когерентные состояния для нескольких степеней свободы	192
§ 4. Когерентные состояния для бесконечного числа степеней свободы.	195
Приложение к электромагнитному полю
А. Общие свойства A95). Б. Приложение к электромагнитному полю
B03)
Глава 8. Квантовая теория оптических корреляционных явлений	212
§ 1. Квантовые корреляционные функции	212
А. Идеальные детекторы и скорости счета квантов B12). Б. Разложение
по модам B19). В. Производящие функции B21)
§ 2. Полная и частичная когерентность	223
А. Определения и полная когерентность B23). Б. Частичная когерентность
B28).
§ 3. Распределения фотоотсчетов	241
А. Скорости и отсчеты для одной нормальной моды B41). Б. Распределения
отсчетов для поля излучения B50).
§ 4. Оптическая теорема эквивалентности	255
А. "Диагональное" представление для одной степени свободы B55). Б.
"Диагональное" представление для поля излучения B80)
Глава 9. Конкретные состояния поля излучения	289
§ 1. Хаотические и тепловые состояния	289
А. Квантовая центральная предельная теорема B89). Б. Обобщение на
случай многих степеней свободы B97). В. Хаотические и тепловые
поля излучения B99). Г. Распределение фотоотсчетов для хаотических
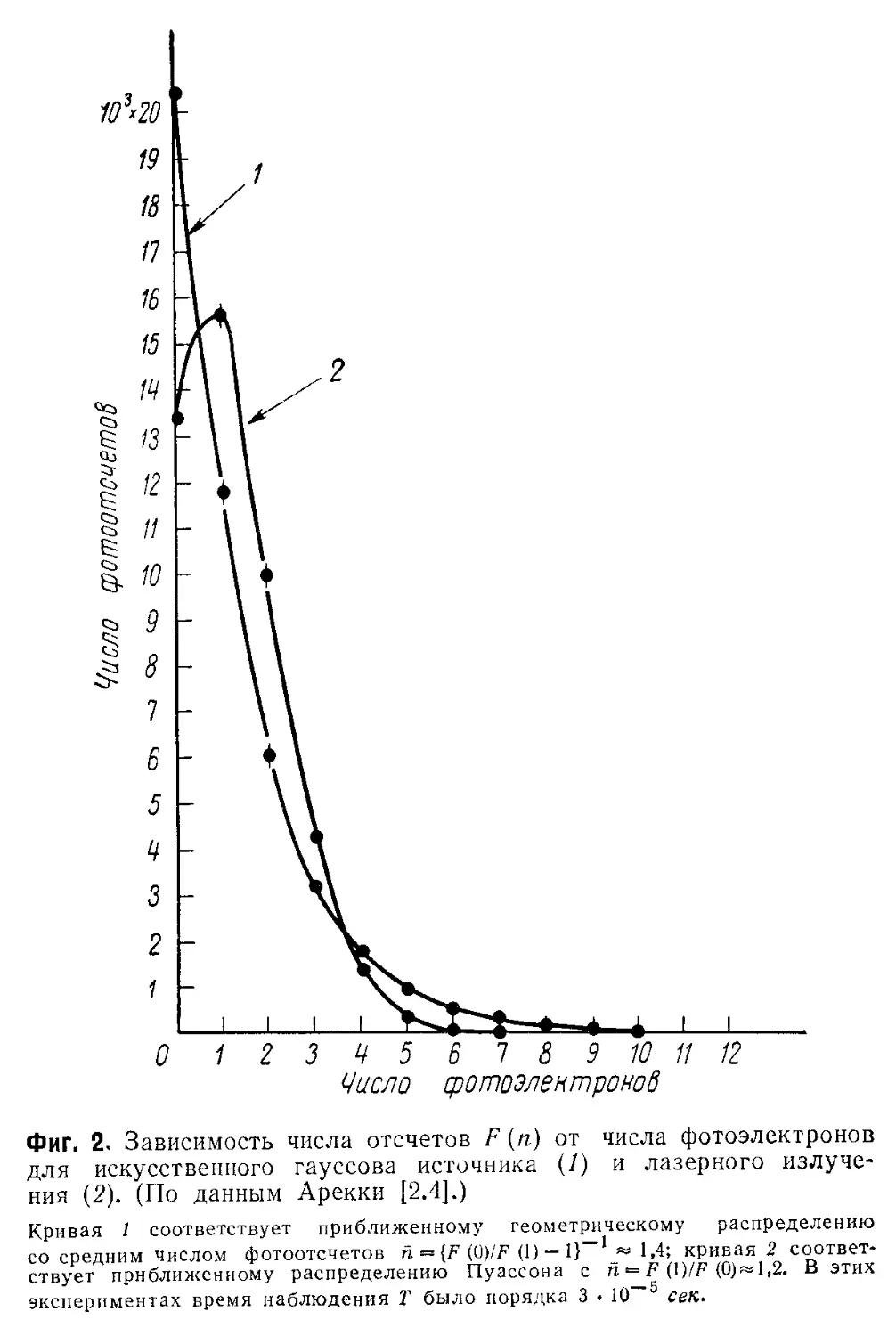
полей C09)
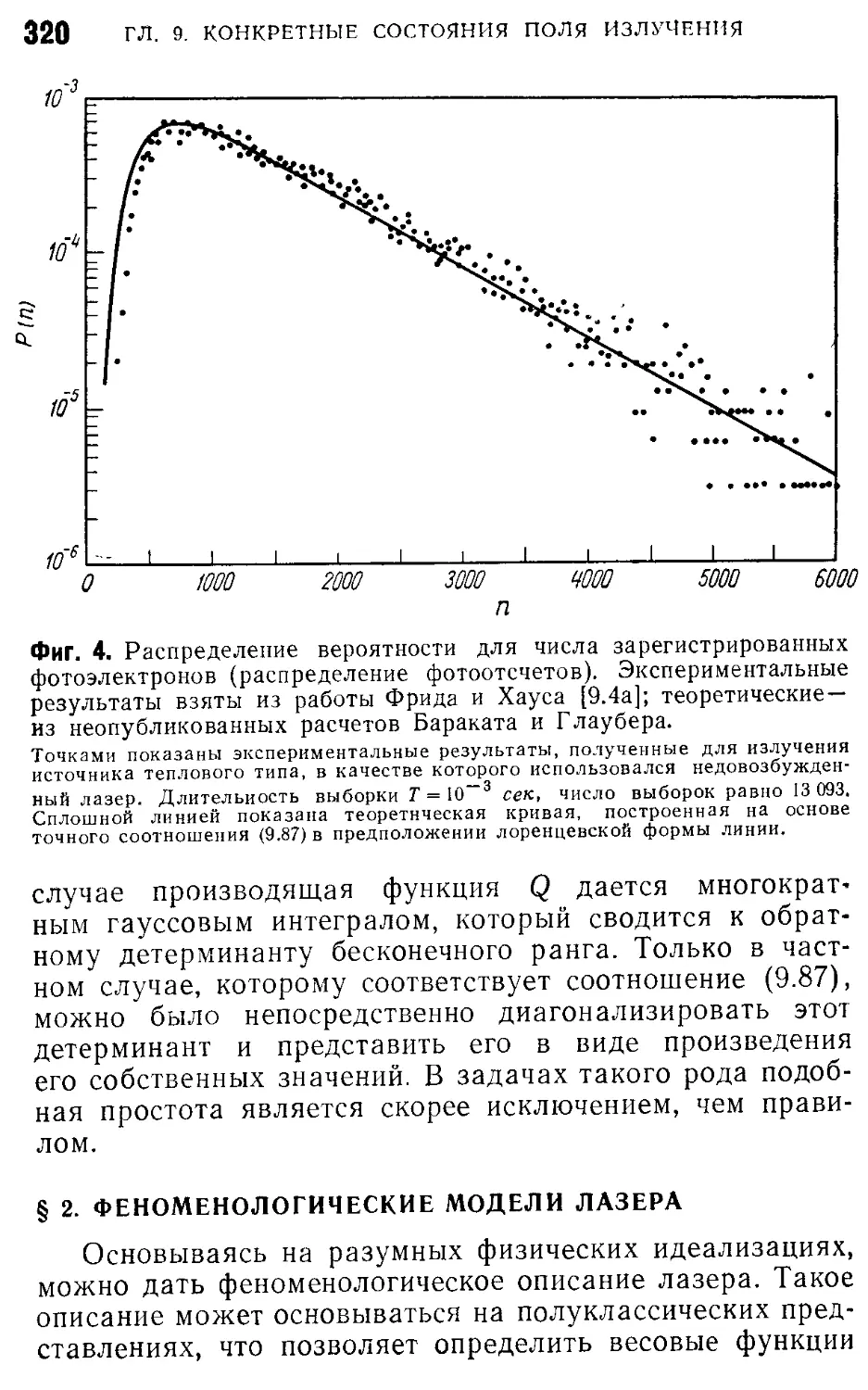
§ 2. Феноменологические модели лазера	320
А. Идеальная модель C21). Б. Модель колебания с диффундирующей
фазой C22). В. Модель, оперирующая с суперпозицией сигнала и шума
C27)
§ 3. Описание лазера с помощью модели связанных систем	332
А. Модель лазера C33)
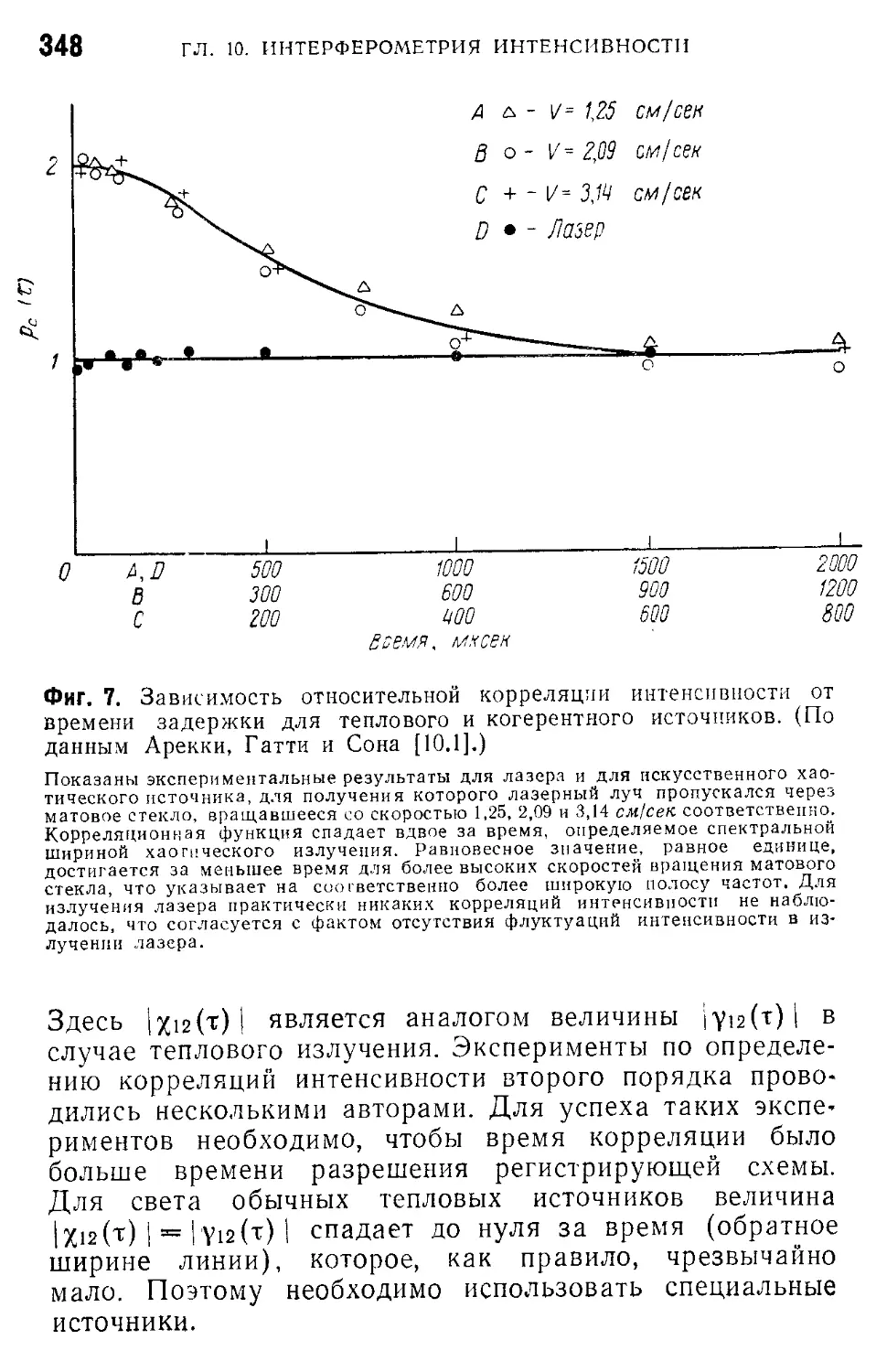
Глава 10. Интерферометрия интенсивности в квантовой оптике	344
§ 1. Интерферометрия интенсивности. Корреляция низшего порядка	344
А. Корреляция отсчетов C14). Б. Пространственная корреляция
интенсивности C50)
§ 2. Интерферометрия интенсивности в случае независимых источников 353
§ 3. Заключение	359

Библиография	362
Дополнение	332
I. Теория когерентности C83). П. Статистика фотоотсчетов;
интерферометрия интенсивности C88). Ш. Статистические явления в
нелинейной оптике C95). IV. Квантовая теория оптических полей;
динамика и статистика процессов излучения и эволюции поля D04). V.
Прием и гетеродинирование оптических сигналов D08). VI.
Флуктуации в лазерах D11)
Предметный указатель	422
Предметный
Аналитический сигнал 21—24, 30,
61, 147, 206, 288
Ансамбль световых нолей 20
—	стационарный 25, 76
—	тепловой 305
Бейкера — Хаусдорфа уравнение
162
Белый шум 91
Броуновское движение 90
Ван Циттерта — Цернике теорема 34
Видиость 18
—	индекс 240
Волновое уравнение классическое 78
Вынуждающая сила 88
Гамильтона оператор 128
Гармонический осциллятор
сдвинутый 160
	смещенный 157
Гельмгольца уравнение 151
Гильберта — Шмидта норма 266
	оператор 266
Гильбертово пространство, векторы
98
	норма 98
	полный ортонормированный
базис 99
	функциональное
представление 169
Грина теорема 32, 152
—	функция 32, 152
Гюйгенса принцип 34, 35
указатель
Даламбера оператор 77
Детектор распределенный 216, 251,
253
—	тензор адмитанса 354
—	точечный 213, 250
	идеальный 212
Диагональное представление по
когерентным состояниям 247,
255
Диффузионное приближение 95, 340
Закон сохранения тока 132
Излучение квазимонохроматическое
27
—	лазера 20, 320
—	поляризованное 21
—	тепловое 20, 289
Источники тепловые 17
	искусственные 45, 350
Когерентность, время 66
—	высшего порядка 232
—	квантовая теория 24, 212
—	определение 224
—	первого порядка 228
—	полная 223—225
	критерии 225, 226
—	свойство 224
—	степень 28, 237
—	частичная 20, 21, 37, 223
	интерференционный закон 26
	классическая теория 21
	модель 19

	скалярная теория 21
Когерентные состояния для
бесконечного числа степеней
свободы 195
	нескольких степеней
свободы 192
	непрерывность и
аналитичность 107
Коммутационные соотношения
канонические 140
Колмогорова — Чэпмена уравнение
92
Корреляционный объем 346, 351
Лазер, излучение 20, 320
—	модели 320—332
Лапласа оператор 31
Максвелла уравнение 132
Манделя формула 41
Марковские процессы 88
Матрица плотности, диагональное
представление 249, 251
	гильбертова пространства
106, 107
Норма Гильберта — Шмидта 266
—	оператора 100
—	следовая 105, 264
Оператор Гамильтона 128
—	Гильберта — Шмидта 266
—	Даламбера 77
—	дифференциальный 184
—	единичный 101
	разложение 101, 169, 200
—	Лапласа 31
—	наблюдаемой величины 100
—	норма 100
—	нормально упорядоченный 182
—	ограниченный 100
—	рождения 113, 142
—	с конечным следом 103
	каноническое
разложение 104
—	следовая норма 105
—	сопряженный 102
—	унитарный 102
—	уничтожения 113, 142
—	упорядочивающий во времени 131
—	числа частиц 113, 118
Отсчеты, группировка 43, 67
—	распределение 43
	для хаотических полей 309
	квантовомеханический вывод
241
	полуклассический вывод 38, 41,
55
	производящая функция 41
	случай тепловых полей 44
	формула Манделя 41
	характеристическая функция
40,42
Поле излучения, диагональное
представление 251, 280
	полностью когерентное
состояние 223
	распределение отсчетов 250
	свободное
	представитель основного
состояния 208
	стационарные состояния 304
	хаотическое 20, 290—320, 345
Поляризация круговая 21, 110
—	линейная 21, ПО
—	нулевая ПО
—	степень 52, 112
—	частичная 21
—	эллиптическая 21
Полярное разложение 104
Представление Гейзенберга 130 —
Шредингера 129
Преобразование Гильберта 23
—	Лапласа 41
—	Фурье 22
Приближение дальнего поля 35, 73
—	«волн вращающейся поляризации»
149, 334

Пробная функция 61, 259
Производящая функция для
распределения отсчетов 41
	нормально упорядоченная 221
Распределение гауссово 58
—	для идеального лазера 322
—	интенсивности 52
—	классическое, в фазовом
пространстве 181
—	кумулянты 94
—	многомерное 54
	нормальное 309
	отсчетов 39, 43
—	пуассоновское 39, 116, 122
	многомерное 122, 206
—	равновесное тепловое 305
—	связанные моменты 93
—	семиинварианты 93
—	с неопределенной фазой 76
—	стационарное 76
—	тепловое 54, 119
—	умеренное 257 Резервуар 81, 334
Скорость счета квантов 212
Случайное блуждание 90
Случайные функции 59
Случайный процесс 20, 62
Состояние, равновесное тепловое 307
—	смешанное 105,106
—	чистое 107
Стокса параметры 111
Теория возмущения 38, 212
Усеченная последовательность 199
Условие минимальной
неопределенности 161
Фаза 19 факториальные моменты 42
Флуктуационное (стохастическое)
уравнение 80, 95, 333
Фоккера — Планка уравнение 95
	обобщенное 333
Фотоотсчеты, квантовая теория
241—255
—	полуклассическая теория 55—
76
Функционал характеристический
60—64, 85
Функция автокорреляционная 65
—	вероятности 57
—	Грина 32, 152
—	квантовая корреляционная 212
—	пробная 59, 76, 259
—	производящая 41
—	характеристическая 34
8-функция Дирака 42, 47
Хэнбери Брауна — Твисса
эксперимент 71
Центральная предельная теорема
классическая 289
	квантовая 289—291
Шварца неравенство 26, 98
Шредингера уравнение 128
Электромагнитное поле, векторы
поляризации 138
	временная эволюция 144
	квантовый гамильтониан 141
	операторы рождения и
уничтожения 142, 204
	представление по когерентным
состояниям 203
	пространственная эволюция
151
Энтропия 305, 306
Эргодический процесс 20

Предисловие редактора перевода
I
Предлагаемая книга посвящена систематическому из-
изложению современной статистической теории оптиче-
оптических полей, лежащей в основе бурно развивающейся в
настоящее время статистической оптики.
Теоретические и экспериментальные исследования по
статистической оптике имеют долгую историю. То об-
обстоятельство, что обычные тепловые и газоразрядные
источники света являются по существу генераторами
случайных полей, было понято достаточно давно; выяс-
выяснение особенностей протекания таких фундаментальных
оптических явлений, как интерференция и дифракция
в поле случайно модулированных электромагнитных
волн, является предметом так называемой теории ко-
когерентности. Ряд важных результатов в этой области
был получен в работах Верде, Лауэ, Винера, ван Цит-
терта, Цернике и др., относящихся к началу и 20-м го-
годам текущего столетия; изложение классической форму-
формулировки теории когерентности является стандартным
разделом многих учебников по оптике (весьма полное
и последовательное изложение содержится в книге Бор-
на и Вольфа [1]).
Другой круг оптических задач, в которых статисти-
статистические явления играют решающую роль, связан с изу-
изучением рассеяния света — явления, многие черты кото-
которого получили ясную интерпретацию еще в работах
Рэлея, ранних работах Мандельштама, Бриллюэна, Ра-
мана и др. (см., например, [2—4]).
Важным разделом статистической оптики, тесно при-
примыкающим к изучению статистических явлений в источ-

6	ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
никах света, является теория формы и ширины спек-
спектральных линий (см., например, монографию [5] и
обзор [6]).
Следует отметить, однако, что в течение длительного
времени статистическое описание, использовавшееся в
перечисленных разделах оптики, не выходило, как пра-
правило, за пределы простой корреляционно-спектральной
теории для стационарных гауссовых процессов. Послед-
Последнее в значительной мере было связано с относительно
скудными экспериментальными средствами, которыми
располагала оптика; источники света были по существу
генераторами стационарного гауссового шума, и в подав-
подавляющем большинстве случаев речь шла только об из-
измерении спектральных плотностей излучения.
Сильное влияние на развитие статистической оптики
оказали поэтому выполненные в 1956—1957 гг. опыты
Хэнбери Брауна и Твисса [7], в которых впервые были
измерены корреляционные функции интенсивности. Эти
эксперименты по существу положили начало исследо-
исследованию корреляций высших порядков для оптических по-
полей; немаловажным оказалось и то обстоятельство, что,
помимо принципиального значения для оптики, эти из-
измерения позволяют усовершенствовать звездные интер-
интерферометры. Опыты Хэнбери Брауна и Твисса существен-
существенно стимулировали также интерес к вопросу о связи
между статистикой фотоэмиссии и статистикой света,
вызывающего фотоэмиссию, — области статистической
оптики, которую принято сейчас называть статистикой
фотоотсчетов.
Бурный период интенсивного и экстенсивного разви-
развития статистическая оптика переживает в течение послед-
последнего десятилетия: революция г. оптике, связанная с со-
созданием лазеров, коснулась буквально всех ее разделов.
Создание лазеров повысило прежде всего интерес к изу-
изучению статистических явлений в источниках света. Те-
Теперь оптика получила в свое распоряжение широкий
ассортимент источников с весьма разнообразными, в том
числе не гауссовыми, статистическими характеристи-
характеристиками.
Важной задачей современной статистической оптики
является изучение флуктуационных явлений в лазерах

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА	7
различных типов и разработка методов уменьшения ам-
амплитудных и фазовых флуктуации лазерного излучения.
Существенно подчеркнуть, что сказанное относится не
только к сравнительно маломощным лазерам непрерыв-
непрерывного действия, но также и к мощным и в особенности
сверхмощным импульсным лазерам. Работы самого по-
последнего времени показали, что статистические явления
играют чрезвычайно важную роль в работе многомодо-
вых твердотельных лазеров; в частности, наиболее аде-
адекватным описанием излучения оптических генераторов
мощных сверхкоротких импульсов является статисти-
статистическое описание.
Разумеется, проблемы, связанные с флуктуациями в
лазерах, во многом аналогичны соответствующим про-
проблемам, связанным с флуктуациями в автоколебатель-
автоколебательных системах радиодиапазона (ср. [9, 10]); имеются,
однако, и существенные особенности, обусловленные
квантовым характером флуктуации, распределенными
взаимодействиями, многомодовостыо и т. п. Новый класс
статистических задач в этой области связан с изучением
оптических генераторов со случайной обратной связью,
генераторов, принцип действия которых ближе к прин-
принципу действия ядерного реактора, нежели генератора
радиодиапазона [11].
Работы по оптической связи и локации с помощью
лазеров стимулировали весьма детальные исследования
чувствительности оптических приемников (обзор совре-
современного состояния вопроса см. в [8]) и исследования по
распространению световых пучков в статистически не-
неоднородных средах (в частности, в атмосфере и в воде).
Чрезвычайно интересные перспективы открылись и в
изучении молекулярного рассеяния света; возможность
выйти за пределы регистрации только спектров рассеян-
рассеянного излучения и использовать, в частности, статистику
фотоотсчетов позволяет получить новую информацию о
рассеивающей среде и процессе рассеяния.
Новым разделом статистической оптики, возникнове-
возникновение которого целиком обязано лазерам, является стати-
статистическая нелинейная оптика [12, 13]. Здесь можно ука-
указать по меньшей мере два круга статистических задач,
являющихся предметом многочисленных теоретических

8	ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
и экспериментальных работ, выполненных в течение по-
последних 4—5 лет. Прежде всего это задачи, связанные со
«статистикой излучения», т. е. с изучением влияния про-
пространственной и временной когерентности излучения на
протекание нелинейных оптических эффектов. Другой
круг задач связан с изучением нелинейных эффектов в
статистически неоднородных средах (нелинейное молеку-
молекулярное рассеяние, генерация оптических гармоник и па-
параметрические явления в неоднородных кристаллах, не-
нелинейная дифракция и т. п.) и с влиянием квантовых
шумов на протекание нелинейных эффектов.
Наконец, методы нелинейной оптики позволяют суще-
существенно расширить возможности интерферометрии ин-
интенсивности, широко используемой в последнее время
для изучения тонкой временной структуры излучения
мощных твердотельных лазеров.
Приведенный выше краткий перечень основных на-
направлений современной статистической оптики показы-
показывает, таким образом, что статистические методы, стати-
статистические задачи проникли почти во все важнейшие раз-
разделы физической и прикладной оптики — ситуация, во
многом сходная с процессом, происходившим в течение
двух последних десятилетий в радиофизике. Резкое рас-
расширение объема экспериментальных исследований, воз-
возникновение широкого класса новых задач стимулировали
исследования и по общей статистической теории опти-
оптических полей. Последнее десятилетие принесло ряд фун-
фундаментальных результатов, относящихся прежде всего
к ее квантовой формулировке. Правда, и здесь многое
было сделано еще в 30-х годах (принципиальное значе-
значение имеют, в частности, ранние работы Шредингера, в
которых были введены так называемые когерентные со-
состояния) ; кроме того, уже достаточно давно имелось
ясное понимание того факта, что квантовая теория опти-
оптических полей является частью квантовой электродина-
электродинамики. Тем не менее именно в работах, выполненных в
1961 —1966 гг., была развита эффективная квантовая
методика описания оптических полей, что позволило
придать квантовой оптике логическую завершенность и
выявить ее связь с теорией, использующей классическое
описание поля.

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА	9
Разумеется, стремление к завершенности теоретиче-
теоретической картины не является единственным аргументом в
пользу квантования поля в оптической теории. Необхо-
Необходимость в последовательной квантовой теории возникает
при рассмотрении флуктуации в лазерах, параметриче-
параметрических усилителях и генераторах оптического диапазона,
а также при исследовании статистики фотоотсчетов
и т. п.
Квантовая теория оптических полей развивалась в по-
последние годы Глаубером (который, в частности, ввел так
называемые квантовые корреляционные функции), Ман-
делем, Гордоном, М. Лэксом и др. Значительный вклад
внесли здесь и авторы этой книги — руководитель теоре-
теоретического отдела исследовательских лабораторий фир-
фирмы «Белл телефон» (США) Дж, Клаудер и профессор
Сиракузского университета (США) Э. Сударшан. Клау-
деру, в частности, принадлежит серия работ по исполь-
использованию теории когерентных состояний в квантовой
оптике; Сударшаном выполнены работы, позволяющие
установить связь между квантовыми и классическими
корреляционными функциями.
II
В предлагаемой книге в той или иной мере затронуты
ьсе основные вопросы современной статистической опти-
оптики. Однако в первую очередь — это книга по теоретиче-
теоретической статистической оптике, причем центральное место
в ней занимает квантовая формулировка статистических
характеристик оптических полей (представление поля по
когерентным состояниям, квантовые корреляционные
функции) и квантовая теория фотоэлектрических отсче-
отсчетов; именно в этих областях лежат и собственные науч-
научные интересы авторов.
Характерным для книги в целом является большое
внимание авторов к математическим вопросам и исполь-
использование весьма современного аппарата; следует отме-
отметить, что в оригинале книга вышла в серии «Монографии
по математической физике», выпускаемой издательством
«Бенджамин».

10	ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Вместе с тем изложение в книге построено достаточ-
достаточно систематично; в некоторых случаях изложению спе-
специальных вопросов предпосланы разделы, носящие учеб-
учебный характер.
Содержание книги условно можно разбить на три
части.
Первая часть, включающая гл. 1—4, содержит изло-
изложение основ классической статистической теории опти-
оптических полей и полуклассической теории фотоотсчетов.
Несмотря на сжатость изложения, материал этих глав
дает ясное представление о классической теории коге-
когерентности и теории фотоотсчетов (в последнем случае
авторы наряду с простейшим вариантом теории, опери-
оперирующей с распределениями интенсивностей, излагают и
теорию, использующую статистику самих полей), а так-
также методах вычисления статистических характеристик
полей в различных ситуациях.
Вторую — центральную часть книги — составляют
гл. 5—8, посвященные квантовой теории. По существу
это курс кинематики квантованного электромагнитного
поля. Изложению основного материала (значительная
часть которого носит оригинальный характер) авторы
предпослали гл. 5, являющуюся вводной и предназначен-
предназначенную для напоминания основных сведений из квантовой
механики.
В гл. 7 проводится систематическое изложение одно-
одного из центральных вопросов квантовой оптики — теории
когерентных состояний. Последовательно рассматривает-
рассматривается теория когерентных состояний для одной, двух и бес-
бесконечного числа степеней свободы — последний случай
соответствует когерентным состояниям поля излучения.
В этой главе, как и в следующей, содержится ряд не
опубликованных ранее результатов, принадлежащих
авторам.
В гл. 8 вводятся квантовые корреляционные функции,
играющие по существу центральную роль в рассматри-
рассматриваемой теории; здесь же с их помощью строится кван-
квантовая теория фотоотсчетов.
Третья часть (гл. 9 и 10) посвящена приложениям
квантовой теории когерентности к конкретным физиче-
физическим заДачам.

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА	11
Материал гл. 9 выходит за рамки формальной теории,
развивавшейся в предыдущих главах; здесь речь идет
о специфических статистических свойствах излучения,
генерируемого конкретными физическими системами.
Обсуждаются некоторые модели тепловых источников
и простейшие модели, описывающие статистические
свойства лазерного излучения (колебание с диффунди-
диффундирующей фазой, суперпозиция регулярного сигнала и
шума, модель одномодового излучения, связанного с ан-
ансамблем трехуровневых атомов), и вычисляются соот-
соответствующие распределения фотоотсчетов. Здесь же
кратко реферируются некоторые экспериментальные ра-
работы, посвященные изучению статистических свойств ла-
лазерного излучения.
Наконец, в короткой гл. 10 дана квантовая формули-
формулировка основных принципов интерферометрии интенсив-
интенсивности.
В целом предлагаемая книга является систематиче-
систематическим и современным изложением теоретической стати-
статистической оптики; ее можно рекомендовать студентам
старших курсов, аспирантам и научным работникам, спе-
специализирующимся в области квантовой радиофизики и
оптики. Ряд разделов книги, несомненно, представит
интерес и для физиков, занимающихся теорией кванто-
квантованных полей. Следует отметить, правда, что помимо
предлагаемой книги к настоящему времени в области
статистической оптики появился целый ряд других обоб-
обобщающих работ. Среди них следует указать переведен-
переведенные на русский язык обзор Вольфа и Манделя [14], мо-
монографию О'Нейла [15], небольшую книжку Франсона и
Сланского [16] и курс лекций одного из создателей со-
современной статистической оптики Глаубера [17]. Обстоя-
Обстоятельный обзор экспериментальных работ по флуктуа-
циям интенсивности излучения одномодовых и много-
модовых лазеров выполнен Армстронгом и Смитом [18].
Ряд обзорных докладов по различным проблемам ста-
статистической оптики был представлен на Нью-йоркском
симпозиуме по современной оптике A967 г.) [20]; содер*
жательные курсы лекций по теоретической и эксперимен-
экспериментальной статистической оптике были прочитаны в между-
международной летней школе по квантовой оптике в Варение

12	ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
A967 г.) Глаубером, Арекки, Хаусом, Хакеном и др. [21].
Укажем, наконец, книгу Луиселла [19], материал которой
во многом связан с теоретическими основами квантовой
оптики. Тем не менее книга Клаудера и Сударшана за-
занимает особое место в литературе по статистической
оптике.
Эта книга является, пожалуй, единственной в настоя-
настоящее время монографией, где получили достаточное отра-
отражение классический и квантовый аспекты теории; обзор
Вольфа и Манделя носит скорее справочный характер,
книги Франсона и Сланского и О'Нейла имеют дело
только с классической теорией, а наиболее близкие по
содержанию к книге Клаудера и Сударшана весьма
интересные и глубокие лекции Глаубера во многих пунк-
пунктах носят конспективный характер.
III
При переводе и редактировании книги встретились
определенные текстовые и терминологические трудности;
в некоторых главах изложение материала представля-
представлялось излишне конспективным.
Во всех этих случаях переводчиками и редактором
сделаны подстрочные примечания. Переводы терминов,
не имеющих общепринятого русского эквивалента, спе-
специально поясняются; одновременно дается и английское
написание (сказанное относится в особенности к гл. 5,
7 и 8, где речь идет о квантовых характеристических
функциях, теории представлений по когерентным состоя-
состояниям и т. п.).
Книга Клаудера и Сударшана и сравнительно крат-
краткий список литературы, составленный авторами, ни в
коей мере не претендуют на полноту освещения затро-
затронутых в книге вопросов; основная цель книги — изложить
идейную сторону статистической оптики. Поэтому нам
представлялось нецелесообразным загромождать основ-
основной текст ссылками на работы, не учтенные авторами
или вышедшими после издания книги в США. Вместо
этого к книге приложен список работ по статистической
оптике, опубликованных в период с 1966 по первую поло-
половину 1969 г. (подробная библиография работ, опублико-

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА	13
ванных до 1966 г., содержится в обзоре [14]). «Путеводи-
«Путеводителем» к нему служит краткое послесловие, написанное
редактором и переводчиками.
Перевод книги выполнили А. С. Чиркин (гл. 1—5),
Б. Я- Зельдович (гл. 6—8) и В. Г. Тункин (гл. 9, 10 и
библиография).
С. Ахманов
ЛИТЕРАТУРА
1.	Born М., Wolf E., Principles of Optics, London, 1965.
2.	Волькен штейн М. В., Молекулярная оптика, М., 1951.
3 Фабелинский И. Л., Молекулярное рассеяние света, М.,
1965.
4.	С у щи некий М. М., Спектры комбинационного рассеяния мо-
молекул и кристаллов, М., 1968.
5.	Собельман И. И., Введение в теорию атомных спектров, М.,
1963.
6.	Раутиан С. Г., Собельман И. И., УФН, 90, 209 A966).
7.	Н anbury Brown R, Twiss R. Q., Nature, 177, 271 A956);
Proc. Roy. Soc, A242, 300 A957); A243, 291 A957).
8.	Росс М., Лазерные приемники, изд-во «Мир», 1969.
9.	Р ы т о в С. М., Введение в статистическую радиофизику, М.,
1968.
10.	М а л а х о в А. Н., Флуктуации в автоколебательных системах,
М., 1966.
11.	Басов Н. Г., Летохов В. С, УФН, 96, № 4 A968).
12.	Бломберген Н., Нелинейная оптика, изд-во «Мир», 1966.
13.	Ахманов С. А., Чиркин А. С, Изв. ВУЗ, Радиофизика, 13,
№ 6 A970).
14.	Вольф Э., Манде ль Л., УФН, 87, № 3, 491 A965).
15.	О'Н е й л Э., Введение в статистическую оптику, изд-во «Мир»,
1966.
16.	Фра неон М., Сла некий С, Когерентность в оптике, М.,
1967.
17.	Глаубер Р., Оптическая когерентность и статистика фотонов,
в сб. «Квантовая оптика и квантовая радиофизика», изд-во
«Мир», 1966.
18.	Armstrong J. A., Smith.A. W., Progress in Optics 6, 213
A967).
19.	Louise 11 W. H., Radiation and Noise in Quantum Electronics,
New York, 1965.
20.	Modern Optics (Proc. Symposium, New York, 1967), New York,
1967.
21.	Lectures at the International School of Physics «Enrico Fermi»,
XL1I Course Quantum Optics, 1967, Varenna, Italy.

Предисловие
Некоторые достижения прошедшего десятилетия су-
существенно изменили предмет и перспективы дальнейшего
развития оптики — науки, история которой насчитывает
многие десятилетия. В области эксперимента сюда отно-
относится изобретение таких принципиально новых источни-
источников света, как лазеры, появление техники корреляции
фотоотсчетов и возникшей на основе этой техники интер-
интерферометрии интенсивности. Все это оказало существен-
существенное влияние на теорию частичной когерентности и пре-
превратило ее в законченную и весьма общую теорию слу-
случайных полей. В теоретической области развивалась
квантовая теория частичной когерентности, выявились
общие моменты и различия классической и квантовой
теории. Следует отметить, что, хотя исходные принципы
здесь совершенно различны, многие аспекты и форму-
формулировки классической и квантовой теорий когерентности
оказываются настолько близкими, что может даже воз-
возникнуть сомнение в целесообразности изучения обеих
теорий.
Настоящая книга по своему духу и по использован-
использованному в ней общему подходу во многом перекрывается с
циклом лекций, прочитанных Э. Сударшаном осенью
1963 г. в Бернском университете (Швейцария), а также
с конспектом этих лекций, составленным автором. После
начального периода квантовой формулировки теории
когерентности многое было сделано в разработке фор-
формальной и технической стороны вопроса. Мы попытались
включить в книгу эти более современные результаты на-
настолько полным и логически непротиворечивым образом,

ПРЕДИСЛОВИЕ	15
насколько это представляется разумным в настоящее
время.
Наша работа предназначена для аспирантов и науч-
научных работников, стремящихся понять основы современ-
современной квантовой оптики. Для успешного усвоения мате-
материала читатель должен располагать знанием классиче-
классической оптики и квантовой теории в объеме книг Джен-
кинса и Уайта и Шиффа1). Наша книга содержит изло-
изложение многих вопросов, ставших уже традиционными;
при этом в некоторых пунктах наше изложение отли-
отличается от общепринятого. Вместе с тем мы полагаем, что
многие моменты, затронутые в гл. 7—10, нельзя найти
в имеющихся в настоящее время учебниках. Некоторые
наши результаты, приводимые в книге, оригинальны и
не были ранее опубликованы.
Следует указать на несколько работ, которые являют-
являются основополагающими в квантовой оптике и могут по-
помочь читателю полнее понять предмет настоящей книги
и близкие к нему вопросы. Среди них должны быть от-
отмечены следующие:
1.	Born M., Wolf E., Principles of Optics, Oxford.
1965.
2.	G I a u b e r R. J., Quantum Optics and Electronics
(ed. С DeWitt, A. Blandin, С Cohen-Tannoudji),
New York, 1964. (См. перевод в сб. «Квантовая
оптика и квантовая радиофизика», изд-во «Мир»,
1966.)
3.	М a n d e I L, Wolf E., Coherence properties of
optical fields, Rev. Mod. Phys., 37, 231 A965). [См.
перевод: УФН, 87, 491 A965); 88, 347, 819 A966).]
В последней статье дана обширная библиография,
которую мы не пытаемся здесь воспроизвести. Иногда в
наш указатель литературы мы включали книги или
статьи, которые не цитируются в тексте книги, но в ко-
которых можно найти дальнейшее обсуждение рассматри-
рассматриваемых вопросов.
') Последняя книга имеется в русском переводе: Л. Ш и ф ф,
Квантовая механика, ИЛ, 1957. Книга Дженкинса и Уайта на рус-
русский язык не переведена. — Прим. ред.

16	ПРЕДИСЛОВИЕ
Необходимо сделать несколько замечаний относи-
относительно обозначений. Иногда вместо нескольких симво-
символов интегрирования или суммирования мы используем
один, а также часто опускаем пределы суммирования
или интегрирования, если они достаточно ясны из текста.
Так как наше рассмотрение носит в основном теорети-
теоретический характер, мы выбрали удобные электромагнитные
единицы Хевисайда, в которых, кроме того, скорость
света с = 1. Вместе с тем, поскольку наше обсуждение
охватывает не только классическую, но и квантовую тео-
теорию когерентности, в уравнения явно входит постоянная
Планка h (или Ь = /г/2л). Угловая частота обозначается
через со, обычная частота — через v; иногда обе эти ве-
величины входят в одно и то же уравнение; они неизменно
связаны соотношением ю = 2nv.
Мы благодарны всем лицам, предложившим различ-
различного рода поправки и высказавшим критические заме-
замечания по поводу предварительных вариантов книги. Нам
особенно хотелось бы выразить свою признательность
Блаунту, Вольфу, Глауберу, Гордону, Лэксу, Манделю,
Мак-Кенна, Мета, Пенделтону, Розенбергу и Уайтману.
Выражаем также благодарность Чилметти и Джордану
за составление конспектов лекций и А. Мерсье, благо-
благодаря которому авторы получили возможность приятно
провести свой годовой академичесий отпуск в Бернском
институте теоретической физики.
Наконец, мы хотим выразить нашу благодарность
миссис Н. Каллен, мисс Д. Домански и мисс С. Талада и
особенно миссис Б. Чиппендейл, миссис Де-Маттео и
миссис М. Свилар за помощь в работе и подготовку
машинописного экземпляра.
Рукопись этой книги была завершена в то время,
когда один из авторов (Дж. Р. Клаудер) был сотрудни-
сотрудником лаборатории фирмы «Белл телефон», которой мы
выражаем свою признательность за поддержку.
Джон Р. Клаудер
Э. К- Г. Сударшан
Сиракузы, Ныо-йорн
Октябрь 1967

1
Частично когерентный свет
§ 1. ВВЕДЕНИЕ
Хотя геометрическая, или лучевая, оптика адекватно
описывает многие явления, часто, как известно, важную
роль играют волновые свойства света. Эти свойства су-
существенны, например, для понимания экспериментов по
дифракции и интерференции типа классического экспери-
эксперимента Юнга с двумя отверстиями, показанного на фиг. 1.
Этот известный и наглядный интерференционный экспе-
эксперимент служит удобным исходным пунктом для обосно-
обоснования вводимого ниже представления о частично коге-
когерентном свете.
Согласно обычной классической волновой теории,
падение волны на два отверстия S\ и S2 приводит к по-
появлению интерференционной картины, причем в зависи-
зависимости от относительных интенсивностен может происхо-
происходить полное гашение излучения в некоторых точках
наблюдения Q. Возникновение такой резкой интерферен-
интерференционной картины тесно связано с существованием опре-
определенных фазовых соотношений; в таких случаях говорят,
что два пучка являются когерентными. Однако предста-
представление об интерференции, приводящей к полному гаше-
гашению излучения, не всегда соответствует эксперименталь-
экспериментальной ситуации. Так обстоит дело, например, для обычных
тепловых источников S, если угол, под которым виден
источник с экрана, не слишком мал, как на фиг. 1. Если
такой источник перемещать в направлении к экрану
(увеличивая таким образом опирающийся на него угол),
то обычно интерференционная картина постепенно сма-
смазывается; иначе говоря, максимумы и минимумы интен-
интенсивности становятся относительно менее выраженными.

18
ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
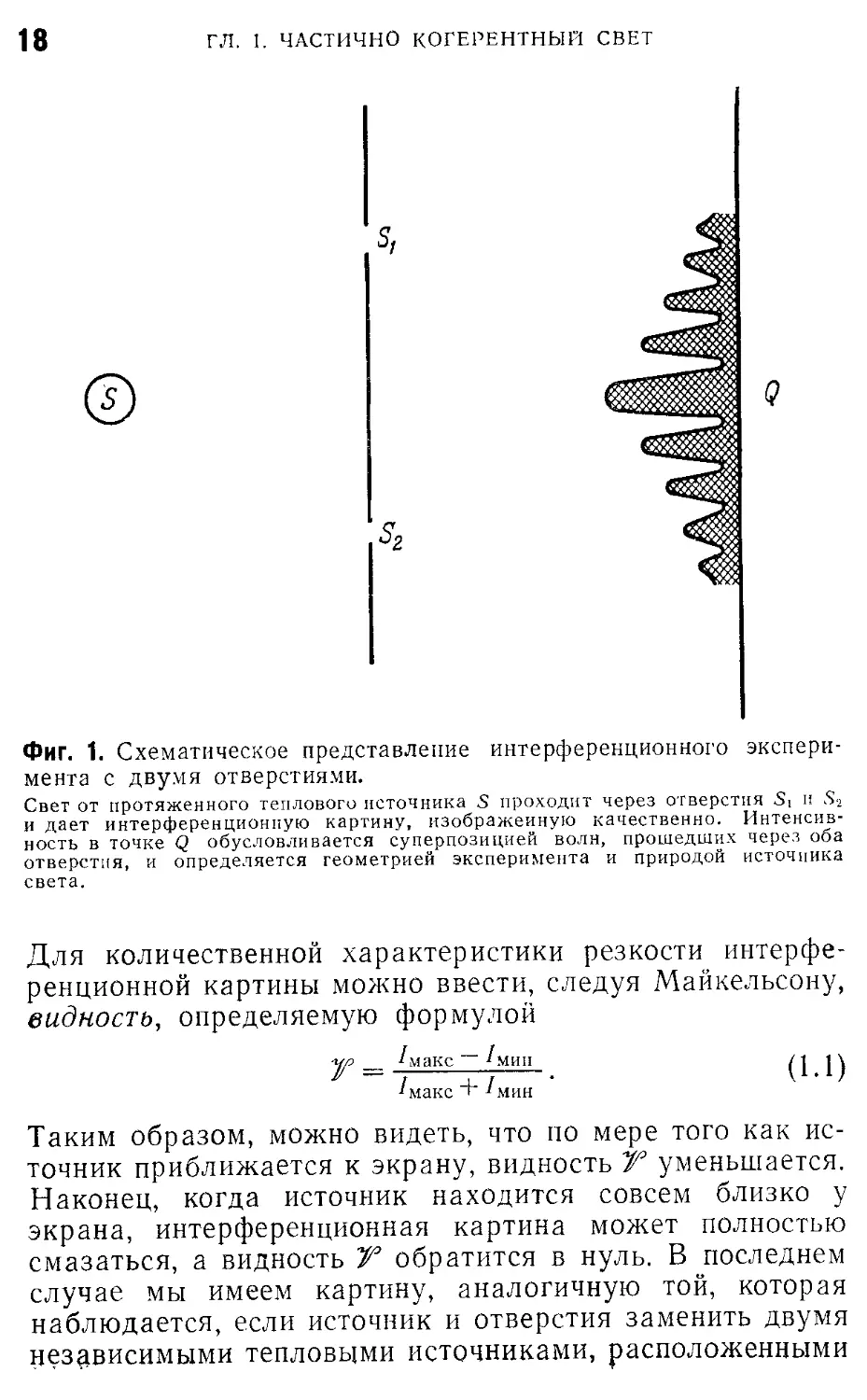
Фиг. 1. Схематическое представление интерференционного экспери-
эксперимента с двумя отверстиями.
Свет от протяженного теплового источника 5 проходит через отверстия Si и S2
и дает интерференционную картину, изображенную качественно. Интенсив-
Интенсивность в точке Q обусловливается суперпозицией волн, прошедших через оба
отверстия, и определяется геометрией эксперимента и природой источника
света.
Для количественной характеристики резкости интерфе-
интерференционной картины можно ввести, следуя Майкельсону,
видность, определяемую формулой
Лмакс 'мин
* макс 4" 'мин
A.1)
Таким образом, можно видеть, что по мере того как ис-
источник приближается к экрану, видность У° уменьшается.
Наконец, когда источник находится совсем близко у
экрана, интерференционная картина может полностью
смазаться, а видность Т обратится в нуль. В последнем
случае мы имеем картину, аналогичную той, которая
наблюдается, если источник и отверстия заменить двумя
независимыми тепловыми источниками, расположенными

§ 1. ВВЕДЕНИЕ	19
на месте отверстий. Другими словами, две достаточно
удаленные точки на поверхности теплового источника
типа лампы дают такую же интерференционную картину,
какую мы интуитивно приписываем двум совершенно
различным тепловым источникам. Это вполне естествен-
естественно, поскольку даже в одном источнике достаточно уда-
удаленные друг от друга отдельные атомные излучатели,
дающие вклад в суммарный оптический сигнал, имеют
практически независимые предыстории поглощения и ис-
испускания энергии. Очевидно, когда источник расположен
очень близко к экрану или когда источник и отверстия
заменяются двумя независимыми тепловыми источника-
источниками, интерференционная картина исчезает вследствие
полного отсутствия каких-либо определенных фазовых
соотношений между излучениями источников. В течение
времени, необходимого для фотографического наблюде-
наблюдения (которое, разумеется, превышает время характерных
атомных переходов, имеющее порядок 10~9сек), проис-
происходит много оптических колебаний (поскольку оптиче-
оптические частоты составляют примерно \0]5гц); этого вре-
времени достаточно для того, чтобы любая картина оказа-
оказалась смазанной из-за полной независимости фазовых
предыстории излучателей. В таком случае говорят, что
два световых сигнала некогерентны.
Промежуточной по отношению к рассмотренным вы-
выше интерференционным картинам является картина ча-
частичной интерференции, которая обычно имеет место,
когда источник S, как показано на фиг. 1, находится не
слишком близко и не слишком далеко от отверстий.
Тогда говорят о частичной когерентности сигналов. Ее
описание носит несколько более общий характер, нежели
описание двух предельных случаев, а именно полной ко-
когерентности и некогерентности. Представление о частич-
частичной когерентности соответствует самой общей классиче-
классической модели. Именно такую модель мы будем рассма-
рассматривать в первых четырех главах настоящей книги.
Основным предметом остальных глав книги являются
квантовые обобщения этой модели.
Вернемся к фиг. 1. Можно видеть, что свет, попадаю-
попадающий в различные точки, скажем в отверстия S) и S2, a
следовательно, и в точку наблюдения Q, представляет

20	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
собой очень сложную суперпозицию свободно распро-
распространяющихся сигналов, посылаемых всеми атомными
излучателями источника S. Для подробного и точного
описания этого процесса в любой момент времени необ-
необходимо знать поведение каждого атомного излучателя,
однако некоторые простые вопросы можно рассмотреть,
располагая только ограниченными сведениями об атомах.
Например, средняя интенсивность в точке 5) может за-
зависеть лишь от средних интенсивностей отдельных атом-
атомных излучателей, причем часто эти интенсивности мож-
можно считать одинаковыми для всех излучателей. Если не
ограничиваться нахождением средних значений интен-
интенсивностей, то необходимо применить статистический под-
подход и использовать статистическое описание оптических
полей, поскольку они создаются большим числом суще-
существующих в действительности макроскопических источ-
источников.
Говоря математически, мы выбираем в качестве мо-
модели частично когерентного света стохастический про-
процесс, т. е. предполагаем, что световая волна является
случайным полем, каждая из возможных реализаций
которого, если волны распространяются в вакууме, удо-
удовлетворяет классическому волновому уравнению. Усред»
нение по ансамблю возможных реализаций поля дает
наблюдаемые средние величины. В свою очередь опре-
определенный ансамбль возможных полей задается в конеч-
конечном счете источником, создающим излучение. Как мы
покажем, статистическое описание пригодно как для
лазерного, так и для теплового излучения, т. е. это опи-
описание применимо к самым разнообразным типам источ-
источников, если для каждого случая выбрать соответствую-
соответствующий статистический ансамбль.
Стало традицией при рассмотрении частичной коге-
когерентности применять теорию стационарных случайных
процессов, а именно рассчитывать рассматриваемые
средние величины при помощи усреднений по времени, а
затем, опираясь на эргодическую гипотезу, приравни-
приравнивать эти результаты к результатам, которые получились
бы при усреднении по ансамблю световых полей. Мы
применим с самого начала усреднение по ансамблю, по-
поскольку, с одной стороны, оно не связано со стационар-

§ 2. ОПИСАНИЕ АНАЛИТИЧЕСКОГО СИГНАЛА 21
ными эргодическими процессами, для которых средние
значения по определению не зависят от начала отсчета
времени, и поскольку, с другой стороны, оно является
самым удобным аналогом статистического описания, при-
принятого в квантовой теории.
Статистическое описание находит применение не
только при анализе эксперимента с двумя отверстиями
и протяженными тепловыми источниками; оно должно
применяться и при рассмотрении другого общего свой-
свойства света. Как известно, свет представляет собой попе-
поперечные волны, причем каждая волна обладает двумя
различными возможными состояниями поляризации. По-
Поляризованный свет можно описать точно, задавая компо-
компоненты линейной поляризации или компоненты круговой
поляризации. Можно также использовать более общий
подход и любую поляризованную волну рассматривать
как эллиптически поляризованную, В другом предельном
случае свет теплового источника содержит все поляри-
поляризации с равной вероятностью, т. е. является неполяризо-
ванным. Такой свет при отражении от некоторых метал-
металлов или при прохождении через некоторые кристаллы
приобретает определенную степень поляризации и ста-
становится частично поляризованным. Анализ частичной
когерентности и частичной поляризации во многих отно-
отношениях сходен. Для простоты ограничимся сначала рас-
рассмотрением скалярной теории частичной когерентности,
которая обычно соответствует световым волнам одина-
одинаковой поляризации. Более полное изложение классиче-
классической теории частичной когерентности можно найти в ра-
работах Борна и Вольфа [1.1], гл. X, О'Нейла [1.3] и Берана
и Паррента [1.2]!).
§ 2. ОПИСАНИЕ АНАЛИТИЧЕСКОГО СИГНАЛА
Электромагнитное поле или, более определенно, его
скалярный аналог, который мы здесь рассматриваем,
описывается действительными функциями координат и
времени; обозначим их через УЩг, i). Сосредоточим пока
') Цифры в квадратных скобках относятся к библиографии, по-
помещенной в конце книги.

22	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
внимание на поведении V^(r,t) в произвольной точке
пространства г, которую мы не будем задавать, и рас-
рассмотрим соответствующую действительную функцию вре-
времени V^(t). Для ряда целей в конечном счете физиче-
физический интерес может представлять не само волновое поле
1/М(/). Например, многие физические явления опреде-
определяются «огибающей», или «средней интенсивностью»,
поля V^(t). Последнюю величину можно определить
как среднее от '/г{Vм@}2 по интервалам времени (на-
(например, порядка 10~э сек), большим по сравнению с ти-
типичными оптическими периодами A0~15се/с), но малым
по сравнению с интервалами, на которых происходят из-
изменения огибающей. Именно на такие средние интенсив-
интенсивности реагируют фотографические эмульсии, фотосчет-
фотосчетчики, фотоэмиссионные процессы разного рода и т. д.
Можно привести аналогичный пример из радиотехники.
Так, на огибающую радиосигнала реагирует квадратич-
квадратичный детектор с последующим фильтром низких частот
(система, применяемая для приема амплитудно-модули-
рованных сигналов). Чтобы исключить высокочастотные
компоненты из члена '/2{V(r)@}2> не проводя усреднения
по малым временным интервалам, можно применить
математический прием, впервые введенный Габором [1.4].
Чтобы проиллюстрировать соответствующую процеду-
процедуру, рассмотрим следующий идеализированный пример.
Предположим, что для достаточно малого интервала
времени можно положить V(r)(t) = 2А cos 2n\t; тогда
средняя интенсивность А2 определяется выражением
V*(t)V(t), где V{t) = A exp(—i2nvt)— комплексный
сигнал с положительной частотой, связанный с исходным
сигналом таким образом, что V^r)(t) = 2 Re{V(t)}. Следо-
Следовательно, непосредственно используя V(t) и V*(t), мо-
можно сразу же рассчитать необходимые физические ха-
характеристики поля.
В том случае, когда функции V^(t) имеют более об-
общий вид, можно поступать следующим образом. По-
Поскольку скалярное поле V^r)(t) действительно, для
фурье-компоненты
e2niv1V:r(t)dt	A.2)

§ 2. ОПИСАНИЕ АНАЛИТИЧЕСКОГО СИГНАЛА	23
выполняется соотношение
t/W(-v) = t/w*(v).	A.3)
Таким образом, соотношение A.3) дает возможность
определить всю функцию F<r'(v) по ее значениям при
v ^> 0. Поэтому сопоставим действительному сигналу
V(r)(t) аналитический сигнал V(t), определяемый соот-
соотношением
со	+ оо
V(t)= j e~2nivtV<r) (v) dv ^ J e-2nMV{v)dv, A.4)
где F(v) = fM(v) при v > 0 и f (v) = 0 при v < 0. По
определению V(t) содержит только положительные ча-
частоты v. Действительный сигнал можно получить с по-
помощью соотношения VW(t) = 2 Re V(t). Из самого вида
выражения
V(t + h)^ \ e-2m(lt~x)V{r){v)dv	A.5)
ясно, что оно определяет функцию комплексного пере-
переменного z = t + it, которая является аналитической в
нижней полуплоскости т < 0, и что V(t)—граничное
значение этой аналитической функции при т->-0~. Кроме
того, действительная и мнимая части функции V(t) свя-
связаны друг с другом преобразованиями Гильберта. Это
значит, что выполняются соотношения
VW(t) = ±-P j^^zj-dt',	A.6a)
]/{r){t)=-JLg> [v^iD-df,	A.66)
— оо
где V(t)= 7г1У(г)@ + i№(t)] и где символ 9> указывает,
что главное значение интеграла следует брать в сингу-
сингулярной точке f = t. Эти два соотношения, очевидно, экви-
эквивалентны тождеству V (v) s= e (v) I/(v), где e(v)=±l,

24	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
v ^ 0, если выполнить фурье-преобразование по време-
времени. Впоследствии мы увидим, что в квантовой теории
удобнее всего рассматривать аналитические сигналы и
что их введение устанавливает связь между классиче-
классическим и квантовым описанием.
Аналитический сигнал, как и его действительную
часть, необходимо считать функцией координат и вре-
времени V(r,/). Волновое уравнение линейно; отсюда сле-
следует, например, что амплитуда в точке Q в эксперименте
с двумя отверстиями (см. фиг. 1) представляет собой
линейную комбинацию амплитуд (с соответствующей за-
задержкой во времени) двух волн, выходящих из отвер-
отверстий Sj и S2. Используя приближение, в котором поле
на протяжении отверстий Si и S2 принимается постоян-
постоянным, получаем, что поле в точке Q должно, очевидно,
описываться выражением вида
V (Q, t) = K,V (S,, t-U) + KZV (S2, t - t2). A.7)
Здесь К\ и K2— Два не зависящие от времени коэффи-
коэффициента, о которых мы будем подробнее говорить позже,
a t\ и t2 означают интервалы времени, в течение которых
волны (имеющие скорость с) проходят соответственно
расстояния S[Q и S2Q. Если, как было показано выше,
определить интенсивность / в точке (г, t) следующим
образом:
/(г, 0 = V*(r, t)V(r, t),	A.8)
то отсюда вытекает, что интенсивность в точке Q в мо-
момент времени t равна квадрату абсолютного значе-
значения A.7):
fi^K'KiV'iSu t-t^ViSu t-U) +
+ KIk-iV" (S2, t-t2)V [S2, t-t2)Ji
+ K1K2V" (Si, / - ti) V (S2, *-**) +
+ KtKiV'(S2, t-t2)V{Su t-h) =
= K*iKiV'{Sut-tl)V{Sut-ti) +
+ KlKzV* (So, f - U) V{S2,t- t2) +
+ 2 Re №#* (Si. t-ti)V(S2, t-t2)}. A.9)

§ 3. СТАТИСТИКА ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА	25
§ 3. СТАТИСТИКА ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА
Как показано выше, излучение тепловых источников
естественно рассматривать как суперпозицию случай-
случайных вкладов от большого числа атомов, причем вклад
каждого атома меняется и, кроме того, зависит от их рас-
расположения внутри источника. Математически такие све-
световые волны следует рассматривать как статистические
переменные, иначе говоря, как флуктуирующие поля.
В зависимости от особенностей источника флуктуировать
могут фаза, амплитуда, частота или все три величины
одновременно. Наш подход в принципе не отличается от
подхода, используемого при рассмотрении тепловых шу-
шумов, генерируемых в радиоприемнике, за исключением
того обстоятельства, что шумы радиоприемника лежат
в таком диапазоне частот, где их непосредственное на-
наблюдение не представляет труда.
Таким образом, мы будем считать, что скалярные ам-
амплитуды V(r, t) образуют статистический ансамбль, а
физические величины, представляющие непосредствен-
непосредственный интерес, могут быть определены путем статистиче-
статистического усреднения. Во многих практически интересных
случаях статистический ансамбль можно считать ста-
стационарным, что означает независимость средних значе-
значений от начала отсчета времени. Обозначим статистиче-
статистическое усреднение угловыми скобками; тогда свойство ста-
стационарности означает, например, что среднее
(V* (г„ т, + t) V (г2> т2 + 0) = (V (г„ т,) V (г2, т2)> A.10)
не зависит от времени t.
Используя эти обозначения и соотношение A.9), мо-
можно найти среднюю интенсивность в эксперименте с
двумя отверстиями:
(! (Si)) + KlK2 О (S2)> +
+ 2Re[KiK'2(V*(S2,t-t2)V(Sl,i-tl))}. A.11)
Чтобы выявить наиболее существенные особенности это-
этого выражения, предположим, что отверстия одинаковы,
и воспользуемся известным приближением Гюйгенса.
Как мы покажем позже, в этом случае коэффициенты

26	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
К\ и К-> таковы, что произведение KiKl действительно
и K.\K-i ~ I Ал I ~ I K-i I =i( ¦ При указанном условии, по-
полагая t = t2, получаем
</(Q)> = К2{A (S,)> + (I(S2)) + 2Re{V(S2, 0)V(Slt *2-Щ.
A.12)
Теперь введем в рассмотрение имеющую фундаменталь-
фундаментальное значение функцию
rij(x)^(Vt(ri,0)V(rhx)).	A.13)
При Xi = 1\ функция Г характеризует автокорреляцию
сигнала V'(rt-,/), а при г, ^ г,- — взаимную корреляцию
двух сигналов. Назовем Гг?-(т) функцией взаимной ко-
когерентности. Если положить 1{ = Гц@) и /2 = Г22@), то
соотношение A.12) можно представить в виде
K2Ui +/2 + 2 Re Г12(/2-/,)}.	A.14)
При этом
Re IV-rXIIVx)! <(/,//'.	A.15)
Последнее следует из требования, что (/(Q))>0 для
любого значения /1//2; этот результат является также
следствием неравенства Шварца. Таким образом, если
ввести величину
Yi,-(x) =	—,	A-16)
то
^XlYi/WKl	A.17)
и
</(Q)> = /С2 {/j + /2 + 2 (/,/2)'/г Re Yl2 (^2 - ^i)}- A.18)
Выберем систему единиц, в которой скорость света
с= 1; тогда время t, = sjy где Sj — расстояние от Sj до
Q. Соотношение A.18), впервые выведенное Цернике
[1.6], есть общий интерференционный закон для частич-
частично когерентных стационарных оптических полей.
Чтобы выяснить смысл величины yi2, обратимся пре-
прежде всего к идеализированному случаю строго монохро-

§ 3. СТАТИСТИКА ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА	27
матического света (флуктуации отсутствуют). Другими
словами, положим
V {S,, t - tf) = | A, \exp[-2niv(t - /,)]. A.19)
Тогда из A.13) и A.16) получаем
Yi2 (^2 ~ *i) = exp [ - 2n/v (t2 - f ,)]•	A -20)
Следовательно, в рассматриваемом частном случае
/ = К2 {/, + h + 2 (Л/г)"'''cos [2nv (*2 - *,)]}. A.21)
Выражение A.21) описывает идеальную интерферен-
интерференционную картину от двух отверстий. Даже если в неко-
некоторой точке Q косинусоидальный член принимает нуле-
нулевое значение, свет остается когерентным. Действительно,
достаточно поместить в любом отверстии идеальную од-
однородную фазосдзигающую пластинку, меняющую фазу
волны равномерно по всему фронту, чтобы интерферен-
интерференционный член возник вновь.
В качестве следующего шага при рассмотрении функ-
функции Yi2 предположим, что свет квазимонохроматический,
г. е. занимает полосу частот Av, которая гораздо меньше
центральной частоты v, т. е. Av/v <C 1. Согласно этому
предположению, можно принять
Y.2 (*2 -'.) = l Yi2 (h - Ь) I exp [ - 2mv (t, - f,)], A.22)
где огибающая |vi2| мало меняется на периоде второго
сомножителя в A.22). В этом случае из A.18) полу-
получаем
/ = /C2(/1 + /2 + 2(/1/2)'/2|Y12(^~^)!cos[2Jrv(/2-/,)]}. A.23)
При большом числе периодов это выражение описывает
интерференционную картину с гармоническим измене-
изменением интенсивности, аналогичную идеальной интерфе-
интерференционной картине от двух отверстий. Максимумы
(минимумы) интенсивности соответствуют, очевидно,
значениям косинуса, равным +1(—1). Таким образом,
видность такой интерференционной картины опреде-
определяется выражением
	 /макс ~ ^мин 	 2 (/j/2) 2 I Yi2 tt-2 ~ U ) |	/
— I д-/ —	I л. /	' \
1 макс ' ' мин	11 "г * 2

28	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
которое в частном случае /) = /2 принимает вид
^ = lYi2('2-'i)l-	A-246)
Следовательно, в рассматриваемом примере функция
IV1 зS совпадает с видностью Т. Если Ivi2|= 1, видность
когерентной волны максимальна; если |Yi2J — 0, интер-
интерференционные полосы отсутствуют (некогерентный свет).
Наконец, в случае 0<JYi2|< 1 картина интерференцион-
интерференционных полос соответствует частично когерентному свету.
Хотя в общем случае, которому соответствует соотно-
соотношение A.18), наблюдаемое распределение интенсивности
может и не иметь синусоидального характера, все же
IV12 S разумно рассматривать как меру когерентности
волновых полей. Действительно, помещая, как и в слу-
случае |Yi2|=l, однородную фазосдвигающую пластинку
на любое отверстие, можно получить любое значение
ReYi2(t), лежащее в пределах ± |Yi2(т) |. Если |у1г| = 1,
то волны V(Si,r) и V*(S2, 0) полностью коррелированы,
как и в выражении A.21), и их можно назвать когерент-
когерентными. При Yi2 = 0 (а не только при ReYi2 = 0) волны
некоррелированы и их можно назвать некогерентными.
Наконец, при 0<Jyi2|< 1 поля можно назвать частично
когерентными. Таким образом, во всех случаях yi2(т)
естественно определить как комплексную степень коге-
когерентности, а величину |yi2(t) |—как степень когерент-
когерентности.
В качестве следующего свойства функции взаимной
когерентности отметим, что Г^т) является аналитиче-
аналитическим сигналом в смысле( 1.4). Это свойство есть след-
следствие предполагаемой стационарности рассматриваемого
статистического ансамбля. Действительно, пусть
оо оо
= J J exp{- 2nt К (t + x)- v2/]} (V{v2) f/, (v,)>rfv, dv2 =
о о
oo oo
= J J exp {- 2ni [v,t + t(vi- v2)]} (vl (v?) V, (v,)> rfv, dv2.
о о
A.25)

§ 3. СТАТИСТИКА ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА	29
Тогда вследствие стационарности, которая помимо дру-
других свойств означает независимость выражения A.25)
от времени t, среднее значение, стоящее под последним
интегралом, должно иметь следующий вид:
где 6(v)—дельта-функция Дирака. В результате полу-
получаем
оо
Г12(т)= JV№vTI2(v)dv.	A.27)
о
Очевидно, Fi2(x) является аналитическим сигналом. Сле-
Следует отметить, что в ансамблях, которые не являются
стационарными, Fi2(x) может быть, однако, аналитиче-
аналитическим сигналом, если среднее значение A.25) не зависит
от t или справедливо соотношение A.26), что эквива-
эквивалентно.
На основе интерференционных измерений, проводи-
проводимых или с идеальной фазосдвигающей пластинкой,
или — в случае квазимонохроматического света — путем
измерения видности У, можно определить степень коге-
когерентности I Yi2(т) j. Однако представляющее физический
интерес спектральное распределение F^v), вообще го-
говоря, непосредственно связано с фурье-образом функции
Yi2(т), а не функции 1Y12 (т) 1. В связи с этим возникает
вопрос, в какой мере можно использовать jy^l Для оп-
определения величины
")]lYi2WI.	A.28)
Эту проблему, известную под названием «фазовой про-
проблемы», изучали, в частности, Вольф [1.7], Кано и Вольф
[1.8], Мета [1.9] и Нуссенцвайг [1.10]. Поскольку yvi(y)
представляет собой нормированную функцию взаимной
когерентности, она является аналитическим сигналом.
Последнее свойство можно применить для определения
фазовой функции ф1г(т). Если предположить, например,
что функция Yi2(t) не имеет нулей в нижней полупло-
полуплоскости комплексного т, тогда функция
lnvi2 W = In | Y12 ("О I + «Pi2 М	A-29)

30	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
остается аналитической в нижней полуплоскости и, сле-
следовательно, является аналитическим сигналом. Поэтому
действительную и мнимую части выражения A.29) мож-
можно связать преобразованием Гильберта и определить
ф1г(т) соотношением
Ф12(т) = —;
Jt	J	Т — Т
— оо
при условии, что интеграл сходится.
В основе этого расчета лежит предположение, что
функция yu(t) не имеет нулей в нижней полуплоскости
комплексного т. Если это предположение несправедливо,
то можно показать, что выражение для yi2 содержит
дополнительный коэффициент, называемый фактором
Блашке:
п
A.31)
где умножение распространено на все значения т^', в
которых функция "у12(т) в нижней полуплоскости обра-
обращается в нуль. Если мы не располагаем никакой до-
дополнительной физической информацией, которая позво-
позволяла бы точно определить положение нулей функции
Yi2(t) и таким образом вычислить дополнительный фа-
фазовый множитель A.31), то комплексная степень коге-
когерентности будет недоопределена. Нуссенцвайг рассмот-
рассмотрел отдельные спектральные распределения Г12(v), ко-
которые часто задают исходя из физических соображений,
и показал, что в этих случаях комплексная степень ко-
когерентности не только содержит большое число нулей
в нижней полуплоскости т, но и что значение фазы, свя-
связанное с фактором Блашке, сравнимо с «минимальным»
значением A.30).
§ 4. ВРЕМЕННЫЕ И ПРОСТРАНСТВЕННЫЕ СВОЙСТВА
ФУНКЦИИ ВЗАИМНОЙ КОГЕРЕНТНОСТИ В ПРОЦЕССЕ
РАСПРОСТРАНЕНИЯ СИГНАЛА
Рассмотрим теперь важное свойство функции взаим-
взаимной когерентности, а именно покажем, что она удовле-
удовлетворяет тому же волновому уравнению, что и скалярные

§ 4 СВОЙСТВА ФУНКЦИИ ВЗАИМНОЙ КОГЕРЕНТНОСТИ	31
поля. В свободном пространстве как реальные поля, так
и связанные с ними аналитические сигналы удовлетво-
удовлетворяют обычному волновому уравнению, которое в системе
единиц, где скорость света с = 1, имеет вид
'(г, 0 = 0,	A.32)
здесь
дх2 r ду2 г dz2
— оператор Лапласа. Умножая это уравнение на комп-
комплексно сопряженное решение V*(v',V), получаем
t) V* (г', П == 0.	A.33)
Поскольку уравнение A.33) справедливо для каждой
волны V(r, t) ансамбля, оно справедливо и для среднего
по ансамблю, т. е.
^), t;r', П = 0.	A.34а)
Возьмем уравнение, комплексно сопряженное уравнению
A.34а), и поменяем местами штрихованные и нештрихо-
ванные координаты. В результате приходим к уравнению
'2
V'2 - -?U Г (г,f, r', t') = 0.	A.346)
д? I
Впервые эти волновые уравнения для функции взаим-
взаимной когерентности были получены Вольфом [1.11]. Сле-
Следует подчеркнуть, что в отношении распространения
функция взаимной когерентности ведет себя как волна,
однако, если говорить о наблюдаемых величинах, то со-
согласно A.14) она ведет себя как интенсивность. Ни
амплитуда волны V, ни интенсивность / не обладают
одновременно обоими этими полезными свойствами.
Поскольку функция взаимной когерентности удовлет-
удовлетворяет золновым уравнениям A.34), для нахождения
интегрального представления функции Г в произвольной
точке пространства при помощи ее значений на некото-
некоторой поверхности можно применить теорему Грина. Что-
Чтобы получить интегральное представление функции Г,

32	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
исключим прежде всего t и V из Г и перейдем к часто-
частотам v посредством соотношения
сю
Г (г, /; г', /') = j f (r, r'; v) e~2niv «~{'> dv, A.35)
о
которое имеет место вследствие предполагаемой стацио-
стационарное ги ансамбля. В результате вместо A.34) полу-
получаем
(V2 + F)f (r, rVv) = 0,	A.36а)
(S"* + k2)l(r, r'; v) = 0,	A.366)
где k = k(v) з= 2kv. Пусть G(r, s) = G(r, s; v) —функция
Грина для уравнения A.36а); тогда применение теоре-
теоремы Грина к этому уравнению дает
f (r, r'; v) =
= J {С (г, s)-gj-(s, r'; v)--|§-(r, s)r(s, r^; v)}d5 A.37)
i
(более общее рассмотрение проведено в гл. 6, § 5).
Здесь s обозначает точку на поверхности S, dS — эле-
элемент площади поверхности и д/дп — производная по на-
направлению нормали к поверхности. Функцию Грина G
можно выбрать разными способами. В частности, удобно
выбрать функцию G так, чтобы она была равна нулю,
если любой аргумент попадает на поверхность S. В этом
случае в выражении A.36) остается только второй член.
Применяя теорему Грина с соответствующей функцией G
к переменному г', получаем
Г (г, г'; v) =
i?(r's) i!r (*¦''s/) г <s' s'; v)dS dS'- ^ -38)
Здесь существенно, что значение функции Г в двух точ-
точках пространства определяется линейным соотношением
из значений Г, взятых на поверхности S. Аналогичные
замечания, разумеется, относятся и к выражению A.35),
зависящему от времени.

§ 4. СВОЙСТВА ФУНКЦИИ ВЗАИМНОЙ КОГЕРЕНТНОСТИ	33
Для иллюстрации предположим, что поверхность S
является плоскостью 2 = 0 и что на этой плоскости
функция Г не равна нулю в области, соответствующей
конечной апертуре. В этом случае функцию Грина G
легко выразить через простейшую функцию Go
ik(r-r')
0-39)
Пользуясь, например, методом зеркальных изображений,
G можно взять в виде
G (г, г') = Go (г, х', у', z') - Go (г, х', у', - г'), A.40)
где в правой части равенства точно определена зависи-
зависимость от координаты г'. Очевидно, G = 0, если точка г'
находится на поверхности S, т. е. z' — 0. (Легко видеть
также, что G = 0, когда г находится на S.)
Функции dG/dn, входящие в A.38), определяют
коэффициенты К, введенные в выражении A.7). В обыч-
обычном интерференционном эксперименте с двумя отвер-
отверстиями мы имеем «светящуюся поверхность» 5, состоя-
состоящую из 5-образных источников, и квазимонохроматиче-
квазимонохроматическое распределение частот. Иначе говоря, спектральная
ширина функции Г гораздо меньше центральной часто-
частоты v. Положим
Я^[(х-хГ + (у-уГ + г2}''2	A.41)
и примем, что в пре-делах спектральной ширины функ-
функции Г произведение kR S> 1. В этом случае
eikR „ JM_ eikR = KeikR /i 42)
?	2kR2 e ~ Де ' ^Лг>
dn ~ dz \2nR
Здесь при переходе от первого приближенного выраже-
выражения ко второму используется то обстоятельство, что
спектральная ширина функции Г предполагается очень
малой. Из уравнения A.42) можно найти коэффициент
К в A.7); остающийся фазовый коэффициент expBmv/?)
определяет временное запаздывание в A.7). Таким обра-
образом мы непосредственно получаем свойства К, исполь-
использованные при выводе соотношения A.12).

34	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
А. Теорема ван Циттерта — Цернике
Важное свойство функции взаимной когерентности
состоит в том, что частичная когерентность приобре-
приобретается в самом процессе распространения. Это легче
всего можно показать с помощью соотношения A.38).
Предположим, что поверхность S является поверхно-
поверхностью оптического источника и что свет обладает свой-
свойствами излучения теплового источника, например звезды.
В этом случае, очевидно, поле в точке s не зависит от
поля в точке s', если расстояние |s — s'j превышает
«когерентную длину источника», которая составляет, на-
например, не больше метра. Физически это означает, что
световые источники статистически независимы на протя-
протяжении любого макроскопического интервала. Отсюда
следует, что функция f(s, s';v) должна обратиться в
нуль, если расстояние |S — s'| достаточно велико. Если
в этом масштабе оставшаяся часть подынтегрального
выражения в A.38) изменяется достаточно медленно, то,
не теряя точности, можно применить соотношение
тр/	/. \ А/	/\ Т*1 /	\	/1 у4О\
\ »	j /	о V	/ V * / *	\ * /
где 6s означает б-функцию, взятую на поверхности. Сле-
Следовательно, в этих предположениях A.38) приводится
к выражению
Г (г, г'; v) = f -g- (r, s) 4? (г', s) Г (s, v) dS, A.44)
которое, вообще говоря, при г ф г' не обращается в нуль.
Другими словами, поле, которое, скажем, статистически
независимо в различных точках поверхности звезды, при
распространении приобретает частичную пространствен-
пространственную когерентность. Теорема ван Циттерта — Цернике
утверждает, что выражение A-44) для функции взаим-
взаимной когерентности можно интерпретировать иначе, чем
это было сделано выше. Ван Циттерт и Цернике отме-
отметили, что формула для функции взаимной когерентно-
когерентности Г определяет также амплитуду поля в точке г. Эту
амплитуду можно построить с помощью принципа Гюй-

§ 4. СВОЙСТВА ФУНКЦИИ ВЗАИМНОЙ КОГЕРЕНТНОСТИ	35
генса следующим образом: 1) точечный источник нахо-
находится в точке г', излучение от которой затем распро-
распространяется [чему соответствует функция dG*ldn(r/, s)] к
различным точкам s, находящимся на «апертуре», опре-
определяемой поверхностью S; 2) в каждой точке s на по-
поверхности 5 излучение отражается, причем относитель-
относительный коэффициент отражения равен f(s, v); 3) наконец,
излучение от каждой точки s поверхности распростра-
распространяется [dG/dn(r, s)] в точку наблюдения г. Утвержде-
Утверждение о эквивалентности функции взаимной когерентности
и волновой амплитуды, построенной описанным выше
способом, и называют теоремой ван Циттерта — Церни-
ке. В некоторых случаях функцию взаимной когерентно-
когерентности можно определить, не проводя усреднения по ан-
ансамблю, только путем построения волнового фронта.
Дальнейший анализ теоремы ван Циттерта — Цернике
можно найти в книгах Борна и Вольфа [1.1] и Берана
и Паррента [1.2].
Интересно продолжить обсуждение соотношения
A.44) и получить приближение дальнего поля, особен-
особенно удобного для определения диаметров звезд. В этом
случае для dG/dn воспользуемся соотношением A.42)
и сделаем традиционные приближения дальнего поля:
Г2 _ г'2 _ ^2 ^ S2. ^2 ^> (г — г'J Отсюда следует, что
фаза в A.44) определяется выражением
k (R - R') = k (| г - s | - | г' - s |) « - -| s • (r - r'). A.45)
Используя это обстоятельство в A.42), получаем
, v)dS. A.46)
Это соотношение позволяет во всех практических слу-
случаях выразить функцию взаимной когерентности через
фурье-образ распределения интенсивности источника.
Применим этот результат к звезде, интенсивность кото-
которой имеет постоянное значение f(v) по всему круглому

36	ГЛ. 1. ЧАСТИЧНО КОГЕРЕНТНЫЙ СВЕТ
диску радиусом Ь; тогда, подставляя г' = 0, можно на-
написать
b 2JI
f (r, v) = | К I2 f (v) J J е-'(ад)sr cos (()s isdqp =
о о
(^), A.47)
где /о и Л — обычные функции Бесселя. Для рассматри-
рассматриваемого квазимонохроматического света зависимость от
частоты дается функцией Г(\>), в то время как другие
величины можно оценить для центральной частоты
v = k/2n. Таким образом, соотношение A.47) можно
привести к виду
Г(г,т) = 2л-^-|/С12Г(т)/1(-^);	A.48)
производя нормировку, получаем
Y(r,T) = v(T)-^-,	A.49)
где x = kbr/R и у(т) = Г(т)/Г@). Первый нуль функ-
функции взаимной когерентности соответствует такому рас-
расстоянию г в пространстве, для которого kbr ~ 3,83/?.
Это соотношение позволяет определить радиус звезды Ь,
если известно ее расстояние от Земли. Для звезды раз-
размером с Солнце F ~ 10" см), находящейся на расстоя-
расстоянии в один световой год (R ~ 1018 см), и для среднего
волнового числа к к» 10s см~{ (v ~ 1015 гц) расстояние г,
для которого у = 0, несколько меньше 4 м. К сожале-
сожалению, применение этого метода ограничено тем обстоя-
обстоятельством, что степень когерентности света от звезды,
наблюдаемого в двух точках, находящихся на расстоя-
расстоянии около 4.«в направлении, перпендикулярном направ-
направлению распространения света, значительно уменьшается
из-за атмосферных искажений. В гл. 3 описан способ,
позволяющий устранить это ограничение.
Более полное изложение классической теории частич-
частичной когерентности и связанных вопросов можно найти в
работах, приведенных в библиографии.

Распределение фотоэлектрических
отсчетов
В предыдущей главе было дано статистическое опи-
описание частично когерентных полей. В этой и следующей
главе мы проанализируем фотоэлектрические измере-
измерения, с помощью которых можно изучать статистику ча-
частично когерентного поля.
§ 1. ПОСТОЯННАЯ ИНТЕНСИВНОСТЬ
Существует несколько удобных способов, в которых
для детектирования света используется механизм взаи-
взаимодействия излучения с веществом. К ним относится, в
частности, регистрация света с помощью фотопласти-
фотопластинок и фотоэлектрических детекторов. Рассмотрим сна-
сначала безынерционное детектирование с помощью фото-
фотоэлектрических приемников, полностью пренебрегая огра-
ограничениями, связанными с конечностью полосы детектора.
Как впервые было показано Эйнштейном, фотоэлектри-
фотоэлектрический процесс имеет существенно квантовую природу.
Теория этого явления основана на представлении о кор-
корпускулярных свойствах электромагнитного поля (т. е.
о фотонах) и вследствие этого позволяет объяснить
статистические закономерности процесса фотоэмиссии.
При полуклассическом подходе можно считать, что
падающее электромагнитное поле изменяет статистику
фотоэмиссии; увеличение интенсивности света приводит
к увеличению средней скорости фотоэмиссии.
Количественную связь между интенсивностью и ве-
вероятностью фотоэмиссии (и, следовательно, отсчетов)
можно вычислить методами обычной нестационарной

38 ГЛ. 2. РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
квантовомеханическои теории возмущений. Результаты
при этом согласуются с интуитивными представлениями.
Пусть на фотоэлектрический счетчик падает излучение
интенсивностью I(t); тогда дифференциальная вероят-
вероятность dp появления одного отсчета в интервале времени
dt определяется выражением
dp(t)= al{t)dt = aV*(t)V(t)dt.	B.1)
Параметр а — коэффициент, характеризующий чувстви-
чувствительность детектора; он зависит от площади детектора,
средних спектральных характеристик падающего излу-
излучения и т. д.
Предположим пока, что интенсивность I(t) не испы-
испытывает флуктуации. Физически естественно также при-
принять, что вероятности отсчетов в различных интервалах
времени статистически независимы. Учитывая последнее
и пользуясь дифференциальным законом B.1), в этом
случае нетрудно вывести общее распределение для чис-
числа фотоотсчетов в заданном интервале времени. Для на-
наглядности рассмотрим некоторые свойства этого распре-
распределения.
А. Распределение Пуассона
Поскольку [1—dp(t')] представляет собой вероят-
вероятность отсутствия отсчета в интервале времени от ? до
/' + d?, общая вероятность того, что отсчет не произой-
произойдет во всем интервале t, t + T, вследствие статистиче-
статистической независимости событий определяется произведе-
произведением вероятностей, что символически можно представить
в виде
t + T	г t + T	-]
-d/> (*')]"->ехр - / dp(?)U
точное значение произведения в левой части раскрывает-
раскрывается правой частью выражения. Следовательно, вероят-
вероятность отсутствия отсчета в течение указанного интервала
времени просто равна
Pu@, T + t, 0 = exp -a J I{t')d?

§ 1. ПОСТОЯННАЯ ИНТЕНСИВНОСТЬ
39
Подчеркнем еще раз, что этот результат получен в пред-
предположении об отсутствии флуктуации интенсивности.
Подобным образом, вероятность Ро(\, Т + t, t) того, что
в интервале времени /, t + Т произойдет один отсчет,
определяется формулой
t + T
t + T	г- t + T
dp(t")exp -J dp{t')\,
t"	t
из которой следует
о]
t + T
I(t')dt'exp
t + T
-a
t')dt'\.
Из аналогичных соображений получаем, что в случае
постоянной интенсивности f(t') вероятность того, что
в интервале времени /. t + Т произойдет п отсчетов, оп-
определяется выражением
P0(n,T + t,t) =
= -7 <X
t + T
I(t')dt'\ exp
t+т
-a I(t')dt'
B.2)
которое представляет собой известное распределение
Пуассона. Формула B.2) дает распределение отсчетов,
соответствующее источнику электромагнитного поля
строго постоянной интенсивности, например идеальному
лазеру.
Если ввести обозначение
t + T
то B.2) запишется в виде
Пользуясь последним выражением, нетрудно рассмот-
рассмотреть некоторые классические свойства распределения

40 ГЛ. 2. РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
Пуассона. Среднее число отсчетов равно
оо	оо
п = 2] пР0(п, (х) = 2 (-тргТ)Ге~1г = И.
п = 0	/1 = 0
а для среднего квадрата имеем
оо	оо
~2 — V 2п /	\ _ У «ц" -A _
/1 = 0
Важной характеристикой любого распределения являет-
является дисперсия а2 = (п — hJ = t?— (пJ, которая представ-
представляет собой меру флуктуации п около среднего значе-
значения п; для распределения Пуассона
СТ2 = \12 + Ц — \12 = \1 = V.
Свойства распределения удобно описывать посредством
характеристической функции, которая для распределе-
распределения Пуассона имеет вид
п=0	п=0
Эта функция содержит всю информацию о распределе-
распределении Р0(п,\х.). Например, из B.3), производя повторное
дифференцирование относительно s и полагая s = 0,
можно получить различные моменты распределения.
Ниже мы часто будем пользоваться аппаратом харак-
характеристических функций.
§ 2. СЛУЧАЙНЫЕ ИНТЕНСИВНОСТИ
В гл. 1 при анализе частично когерентного света мы
интерпретировали волновые поля V(t), а следователь-
следовательно, и интенсивность /(/) как случайные переменные.
Чтобы учесть это свойство I(t), следует провести
усреднение пуассоновского распределения отсчетов

§ 2 СЛУЧАЙНЫЕ ИНТЕНСИВНОСТИ	41
Р0(п, T + t, /) по соответствующему распределению ин-
интенсивности. При расчете моментов и других величин
интенсивность входит фактически только в одной ком-
комбинации. Обозначим
T + t
?/= I I(f)dt'.	B.4)
t
Благодаря случайному характеру /(/') величина U са-
сама является случайной с некоторым распределением
p(U). Обобщенное распределение фотоотсчетов, учиты-
учитывающее случайность U, определяется формулой Ман-
деля [2.1]
со
Р(п, T + t, t)= | ~f-e~alJp{U)dU B.5)
о
и не является уже пуассоновским. Весьма удобная про-
производящая функция обобщенного распределения отсче-
отсчетов дается выражением
Q(X, T + t, t) = ^{l -A,)" P (n, T + t, 0 =
/1 = 0
= | e~XaUp{U)dU. B.6)
о
Видно, что производящая функция Q фактически свя-
связана с p{U) преобразованием Лапласа. Разлагая Q око-
около значения А, = 1, получаем с учетом B.5) и B.6)
- B.7)
тогда как разложение около значения А, = 0 приводит
к выражению
п{п-\) ... (n-k + \)^
со
= У,п{п-1) ... (n-k + l)P{n, T + t, t) =
/1=0
B.8)
A=0

42 ГЛ. 2. РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
где k = 1, 2, ... . Эти величины обычно называют «фак-
ториальными моментами».
Характеристическая функция для распределения от-
отсчетов
оо
C(s, T + t, t) = 2 ешР (п, T + t, t)	B.9)
/1=0
также может быть весьма удобной для вычислений.
Само распределение отсчетов дается фурье-преобразо-
ванием
2л
Р(п, T + t, t) = ~ | e~isnC (s, T + t, t)ds. B.10)
о
В результате многократного дифференцирования в нуле
получаем
kP{n, T + t, t) = (-i^)h C{s, T + t, t)
s=0
B.11)
Следует отметить, что, хотя соотношения B.5) и B.6)
сравнительно просты, распределение p(U), равно как и
U, являются производными величинами. Непосредствен-
Непосредственный же физический смысл имеет не величина U, а вол-
волновое поле V(/). Именно последняя величина входит в
микроскопические уравнения движения и именно ее ста-
статистику мы исследуем. В следующих главах эти вопросы
будут рассмотрены более полно как с классической, так
и с квантовой точки зрения.
Здесь же при анализе проблем фотоотсчетов выде-
выделим два круга вопросов. Далее в этой главе мы займем-
займемся непосредственно соотношением B.5) и рассмотрим
некоторые общие свойства, которыми обладает любое
распределение p(U). Этот анализ имеет одно физически
наглядное приложение. Пусть время Т достаточно мало,
так что в течение интервала Т величина I(t) остается
практически постоянной, I(t)^I. Разумеется, это зави-
зависит от природы источника; существуют искусственно син-
синтезированные тепловые источники, для которых такое
приближение имеет смысл для времен Г-^10 сек,

I 2. СЛУЧАЙНЫЕ ИНТЕНСИВНОСТИ	43
Если считать интенсивность / приблизительно постоян-
постоянной, то можно принять
T + t
U= J I(t)dt = IT.	B.12)
t
Таким образом, распределение величины U соответствует
распределению величины /, о которой мы имеем больше
физических представлений. Вначале рассмотрим именно
такую физическую модель.
В следующей главе мы проанализируем распределе-
распределения фотоотсчетов, базирующиеся на более глубоких фи-
физических моделях, которые содержат ансамбли волно-
волновых полей V(t), и, в частности, рассмотрим более под-
подробно, чем в настоящей главе, их зависимость от Т.
А. Статистика фотоотсчетов для малых временных
интервалов
Для более ясного понимания эффектов, связанных
с флуктуациями интенсивности в теории фотоотсчетов,
рассмотрим прежде всего случай, когда применимо со-
соотношение B.12). Если рассматривать интенсивность /
как случайную переменную с распределением рA), то
распределение отсчетов можно записать в виде
Р(п, Г) =J-*^e-°"> (/)<*/,	B.13)
о
где опущена несущественная зависимость от t.
Одним из самых важных общих свойств обобщенного
распределения Р(п, Т), является группировка отсчетов,
которая приводит к возрастанию дисперсии. Если при-
принять с физической точки зрения естественное предполо-
предположение о том, что рA) обладает всеми необходимыми
моментами, то среднее число отсчетов равно
{п, Т)= j
п (а1Т)п
\ е
а/г
п=0	0 п=0
оо
= J aTIp (/) dl = aT </>,

44 ГЛ. 1 РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
где различные моменты интенсивности определяются вы-
выражением
оо
(/") = J Inp(I)dI.	B.14)
о
Аналогично для среднего квадрата имеем [ср. B.8)]
оо	оо
J? = \] п2Р (га, Т) = | [а2Г/2 + а77] р (I) dl =
л = 0	О
следовательно, дисперсия ст2 равна
СТ2 = й2" - («J = аГ (/) + а2Г2 [(/2) - GJ] B.15)
и всегда превосходит га, если распределение р{1) не яв-
является б-функцией Дирака б(/ — /о).
Примером распределения, представляющего особый
физический интерес, является тепловое распределение
p(I) = Iole-'IJ\	B.16)
для которого моменты имеют вид
= /о | xne~xdx = n! /о.	B.17)
о
Поскольку « = аТ{1) = аТ10, соотношение B.15) приво-
приводит к дисперсии
ст2 = а770 + сх2Г2 [2/о-/?;] = га A + га),	B.18)
которая превышает значение, выведенное из распреде-
распределения Пуассона.

Z 3 Ч 5 6 1 8 9 10 11 12
Число сротоэлентронов
Фиг. 2, Зависимость числа отсчетов F (п) от числа фотоэлектронов
для искусственного гауссова источника (/) и лазерного излуче-
излучения B). (По данным Арекки [2.4].)
Кривая / соответствует приближенному геометрическому распределению
со средним числом фотоотсчетов п = {F @)/F A) — 1}~'_>* 1,4; кривая 2 соответ-
соответствует приближенному распределению Пуассона с п<= F (I)//7 @)^1,2. В этих
экспериментах время наблюдения Г было порядка 3 • 10~5 сек.

46 ГЛ. 2. РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
Из B.6) следует, что производящая функция этого
распределения определяется выражением
= A+Ка10Т)~1 = A+Ы)~1.	B.19)
Наконец, распределение отсчетов для рассматривае-
рассматриваемого случая вычисляется непосредственно из B.5):
/0«!
о
= A + aljy1 (l + -^)"" = A + д) A + й-')"",
B.20)
где гё = ос/о7".
В своих экспериментах по фотоотсчетам Арекки [2.4]
проверил характеризующее это распределение соотно-
соотношение Р(п, Т) ~ у™. гДе Y = A + ii~l)~[. Эксперимент был
поставлен таким образом, что условие B.12) выполня-
выполнялось. Арекки показал также, что распределение Пуас-
Пуассона приближенно описывает фотоотсчеты при возбуж-
возбуждении высокостабилизированным лазером (фиг. 2). Ряд
других распределений отсчетов, для которых условие
B.12) не выполняется, рассмотрен в следующей главе
и в гл. 9, где используется квантовый подход.
§ 3. НАХОЖДЕНИЕ РАСПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ
ИЗ РАСПРЕДЕЛЕНИЯ ОТСЧЕТОВ
Важные физические свойства частично когерентного
излучения содержатся в самой природе статистического
ансамбля. Естественно возникает вопрос, в какой мере
с помощью распределения отсчетов Р(п,Т + t,t) можно
определить общее распределение p(U) в B.5). Прежде

§ 3. НАХОЖДЕНИЕ РАСПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ	47
всего докажем, что полное распределение отсчетов един-
единственным образом определяет p(U).
Характеристическая функция для распределения
p{U) дается фурье-преобразованием
оо
C{s)= j eUup(U)dU.	B.21)
Как и выше, моменты распределения p(U), если они
существуют, можно найти из C(s) дифференцированием.
Однако поскольку интенсивности не могут быть отрица-
отрицательными, C(s) является фактически граничным значе-
значением (при /—»-0+) аналитической функции
оо
C{s + it) = J eisU~w p(U)dU,	B.22)
которая аналитична во всей верхней полуплоскости
t > 0. Частичные сведения об этой функции в верхней
полуплоскости содержатся в выражении
С (На) = | e~XaUp (U) dU =
п=0	0
оо
= ^(l-X)nP(n, T + t, t)	B.23)
при действительном значении X, лежащем в интервале
0^Л<^1. Однако благодаря особым свойствам анали-
аналитических функций функция C(s + it) во всей верхней
полуплоскости единственным образом определяется ча-
частичной информацией, содержащейся в B.23). Таким
образом, показано, что характеристическая функция, а
следовательно, и распределение определяются единствен-
единственным образом.
Явная связь распределения интенсивности с распре-
распределением отсчетов дается соотношением, полученным

48 ГЛ. 2. РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
Виддером [2.6]; она рассмотрена в книге Шохата и Та-
маркина [2.7]. Здесь мы изложим этот вывод в несколь-
несколько измененном виде. Введем для удобства обозначение
у = aU и определим величину р(у) = a p{U) так, что
оо
Р (п, T + t, t)= /-=?/} (у) е-У dy.	B.24)
о
Это соотношение естественно наводит на мысль о при-
применении полиномов Лагерра Lp(y) (/7 = 0, 1, 2, ...):
удовлетворяющих условию ортогональности
Lp(y)Lq(y)e~ydy=6pr	B.26a)
Это условие простой заменой переменных можно приве-
привести к виду
оо
2 J Lp By) Lq By) e^y dy = 6pq.	B.266)
Теперь определим конечные линейные комбинации рас-
распределения отсчетов
К^2 J LnBy)p(y)e-ydy
о
где п — любое число. В силу условия ортогональности
оо
2-y.	B.28)

§ 3. НАХОЖДЕНИЕ РАСПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ	49
Таким образом, в первоначальных обозначениях имеем
!-a".	B.29)
Соотношение B.29) определяет p(U) через P(k,T + t,t).
В связи с соотношением B.29) сделаем несколько за-
замечаний, которые относятся также к аналогичным раз-
разложениям, рассматриваемым ниже. Как и в отношении
любого разложения в ортогональные ряды, при интер-
интерпретации соотношения B.29) следует проявлять осто-
осторожность. Чтобы ряд B.29) сходился при любом зна-
значении U и. таким образом, определял функцию p(U),
достаточно выполнения условия 2|Ат|<оо, поскольку
т
т-0
для положительных аргументов all справедливо нера-
неравенство \LmBaU)\^l. Если сумма коэффициентов Хт
сходится абсолютно, функция p{U), определяемая соот-
соотношением B.29), непрерывна. Однако при расчете часто
приходится пользоваться сингулярными, или разрывны-
разрывными, распределениями p(U).B качестве примера можно
назвать часто применяемое прямоугольное распределе-
распределение: p{U) = Uo1npn 0<U<Uon p{U)=O при U> Uo.
В точке Uo, в которой функция p(U) сингулярна, или
разрывна, представление в виде ряда B.29), строго го-
говоря, может быть несправедливым. В этом случае сле-
следует обратиться к более общей интерпретации ряда типа
B.29), а именно рассмотреть сходимость «в среднем».
В частности, если ввести неполную сумму, зависящую
от М,
м
pM(U)^a^lmLmBaU)e-^,	B.30)
m=0
тогда справедливо представление( 2.29) интегрируемой
функции p(U) в том смысле, что
оо
Hm \\p(U)-pM(U)\dU = 0.	B.31)
Этот вид сходимости последовательности функций
Pm(U), M = 1, 2, ... часто называют L1 сходимостью.

50 ГЛ. 2. РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
Ее можно применять здесь, поскольку мы имеем дело
с плотностями вероятности. Такая сходимость означает,
что для каждой ограниченной функции b(U) последова-
последовательность приближенных средних значений
Ьм= j b{U)pM{U)dU, M = \, 2, ..., B.32а)
сходится к точному значению
b= j b(U)p(U)dU.	B.326)
Приведем примеры функций b(U), для которых прибли-
приближенные средние значения сходятся к точным значениям:
1)	exp(isU) для характеристической функции B.21);
2)	ехр(—XaU) для производящей функции B.6) и
3)	(«!)"' (aU)n ехр(—аО) для вероятности п отсчетов
B.5).
А. Независимые вклады
В заключение настоящей главы остановимся на при-
применении производящей функции (и в равной мере ха-
характеристической функции) для анализа распределения.
Опустим для удобства зависимость от времени и рас-
рассмотрим для простоты два распределения отсчетов и их
производящие функции
Q/(A)=i(l-A)"P,.(tt) (/=1, 2). B.33)
гс=0
Образуя произведение функций Q\ и Q2, находим
QM = Q,(A,)Q2(a,)= 2 A-А,)+Я1Р,(л1)Я2(л2)^
flu n2=0
оо
= 2A-Я)" Я (л),	B.34)
п=0
где
п
Р (п) = 2 Pi (п - т) Ро (т).	B.35)
т=0
Каждое значение Р(п), очевидно, положительно, и их
сумма равна единице, так что B.35) определяет «на-

§ 3. НАХОЖДЕНИЕ РАСПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ	51
стоящее» распределение. Таким образом, мы приходим
к важному выводу, состоящему в том, что произведение
производящих (или характеристических) функций дает
новое распределение. Таким способом часто удобно кон-
конструировать распределения или выводить новые, особен-
особенно если их статистика определяется несколькими неза-
независимыми причинами.
Вследствие прямой связи между Q(A) и характери-
характеристической функцией распределения p(U) распределение
интенсивности дается интегральным преобразованием.
В частности, из B.6) находим
= / J ехр [ - Ка (Ul + U2)] р, (?/,) р2 (U2) dUxdU2 =
О О
оо
= f e~^aUp(U)dU,	B.36)
о
где
и
p{U)= J Pl(U-W)p2{W)dW.	B.37)
о
Последнее соотношение представляет собой распределе-
распределение случайной переменной
?/==?/, + U2,	B.38)
равной сумме двух независимо распределенных величин
U\ и и2, имеющих соответственно распределения р\ и р2-
В качестве простого физического примера, иллюстри-
иллюстрирующего применение этих формул, рассмотрим фотоста-
фотостатистику для малых времен Т, для которых справедливо
приближение Uj = TIj. Предположим, что 1\ и /2 пред-
представляют интенсивности двух линейно независимых мод
поляризации падающей волны. Если эти моды статисти-
статистически независимы и характеризуются тепловым распре-
распределением B.16), то соответствующая производящая
функция получается из B.19):
7-) = Q,(A,, T)Q2(l, T) =
«(l + bft.r'U+bfta)-1,	B-39)

52 ГЛ. 2 РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
где для / = 1, 2 мы положили
п, = аТ (/,-) = аТ10!.	B.40)
Введем важный параметр
B.41)
ге,-«2
«1 + П2
^01 ~ ^02
'ol + '02
который, как показано в гл. 5, можно связать со сте-
степенью поляризации падающего излучения. Не ограничи-
ограничивая общности, можно положить /ш ^ /о2- Тогда
1 + &) п, B.42а)
\-@)п, B.426)
. = аТ10. B.43)
где
Из B.39), преобразуя дробь
1	1
(я, - п2) [ 1
, B.44)
можно получить распределение отсчетов и интенсивно-
интенсивности. В частности, из B.20) находим распределение от-
отсчетов
Р(п, т)=-^т{-
1
1
B.45)
[1 + 2/A +с5°)п]" + | [1+2/A-с56)
а из B.16) —распределение интенсивности
-ехр[- A_2^OJ}.B.46)
Кроме того, отметим, что для теплового распределения,
связанного с B.44), в силу свойства п2 = п(\ + 2п) по-
получаем для дисперсии отсчетов
а2 = (п, - п%
п\{\ +2й,)-/г|A +2«2)]-п2 =
= l("i + «?) + ("? + "i)J = « [1 + en],	B.47a)

§ 3. НАХОЖДЕНИЕ РАСПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ	53
где
е ==
= j[l+$>2].	B.476)
В гл. 5 показано, что для поляризованного света @ = 1
и е = 1 [и значение а2 согласуется с результатом B.18)],
а для неполяризованного света 9* = 0 и г — '/г-
Заметим, что если 53 = О, то Q(X) = A + ln/2)~2.
В более общем случае, если
^)~\	B.48)
что соответствует N статистически независимым «тепло-
«тепловым» переменным с одинаковыми распределениями, дис-
дисперсия отсчетов равна
здесь использован факториальный момент второго по-
порядка, определяемый соотношением B.8). Для эвристи-
эвристических целей часто оказывается полезной интерпретация
общего распределения как совокупности независимых
«тепловых» распределений, число которых (N для рас-
рассмотренного выше случая) можно найти, очевидно, не-
непосредственно из дисперсии. Параметр вырождения б
(который выше был равен n/N) представляет собой
среднее заполнение на одну независимую переменную,
или, как часто говорят, на одну «ячейку».
Если принять B.48) в качестве адекватного при-
приближения для полной производящей функции, то из

54 ГЛ. 2. РАСПРЕДЕЛЕНИЕ ФОТОЭЛЕКТРИЧЕСКИХ ОТСЧЕТОВ
B.6) следует, что соответствующее распределение пере-
переменной U определяется выражением
Помимо этого, из B.7) найдем распределение отсчетов
р=1
В последующих главах с этой точки зрения будет
интерпретировано несколько распределений.

Полуклассическая теория
фотоэлектрических отсчетов
§ 1. СЛУЧАЙНЫЕ ВОЛНОВЫЕ ПОЛЯ
Рассмотрим теперь распределение фотоэлектрических
отсчетов для произвольных частично когерентных свето-
световых пучков, падающих на счетчики. Для упрощения ана-
анализа будем по-прежнему использовать скалярное опти-
оптическое волновое поле. Ниже в основу расчета положена
статистика поля; при вычислении распределения отсчетов
P(n,T + t,t) будем рассматривать волновое поле
V(r, t) как случайную величину. Пусть в точке гг- нахо-
находится идеализированный «точечный» счетчик (перемен-
(переменную гг опускаем) и распределение отсчетов стационарно
(так что можно опустить и t). В этом случае соотноше-
соотношение B.5) имеет вид
Р(п, Г)=-^-!
X expl - a I V*(t')V(t')dt' I), C.1)
где угловые скобки означают усреднение по ансамблю
полей V. Из этого соотношения непосредственно полу-
получаем значения среднего числа отсчетов
п = JJ пР {п, Т) = | a J V* (*') V (f) dV ) C.2)
ff=O

56	ГЛ. 3 ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
и среднего квадрата числа отсчетов
ОО
п = 0
т J,
= (а2 J J V {t')V{t')V'{t")V{t")dt'dt" } + я. C.3)
о о	'
Из C.3) следует, что для полного расчета среднего
квадрата п2 недостаточно знать функцию взаимной коге-
когерентности Г, определяемую соотношением A.13). Если
для анализа интерференционных явлений в частично
когерентном излучении нам было достаточно только этой
корреляционной функции, то теперь необходимо исполь-
использовать корреляционную функцию четвертого порядка.
Для вычисления моментов высших порядков необходимо
знать корреляционные функции еще более высокого по-
порядка. Как и в гл. 2, моменты удобно рассчитывать с
помощью производящей функции
/1 = 0
C.4)
Для вычисления Р(п,Т) или Q(k, Г) необходимы корре-
корреляционные функции поля V(t') произвольно высокого
порядка.
В C.1) — C.4) усреднение проводится по ансамблю
случайных комплексных функций V'(/) (а не по одной
переменной V, как в гл. 2). Такие усреднения играют
важную роль для ряда физических и математических
приложений; существует обширная литература, касаю-
касающаяся их свойств. Здесь можно упомянуть книги Барт-
летта [3.4], Рамакришнана [3.5] и сборник статей под
редакцией Векса [3.2], в которых дано общее рассмотре-
рассмотрение проблемы. Более специальный математический ха-
характер носят книги Дуба [3.7] и Гельфанда и Вилен-
кина [3.6].

§ 2 Стохастические процессы	57
Ниже мы дадим краткий обзор свойств стохастиче-
стохастических процессов (случайных функций) и методов их опи-
описания, пригодных для последовательного вычисления
функции распределения отсчетов C.1) или ее произво-
производящей функции C.4). Свойства классических стохасти-
стохастических процессов не только непосредственно исполь-
используются в настоящей главе, но будут важны и при кван-
квантовом рассмотрении.
§ 2. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ
Напомним, что для описания распределения вероят-
вероятности конечного числа п случайных переменных обычно
задают функцию плотности вероятности рп(х\,х2, . . ¦ ,хп)
для п величин Ху
Как уже отмечалось ранее, эквивалентное описание
может быть получено с помощью характеристической
функции ')
= j
• • ¦ > Sn) ~
exp (i ^ XjS,^ p,, (x,, x2, . . ., xn) dxx ... dxn; C.5)
эта функция, определенная для всех действительных зна-
значений Sj, представляет собой фурье-образ р„. Независимо
от характера поведения р„ функция Сп всегда непре-
непрерывна и однозначно определяет рп. Более того, любое
среднее значение, которое существует, можно всегда
найти, пользуясь функцией С„. Вообще гоиоря, оба эти
свойства не имеют места, если р„ определять через мо-
моменты. При этом может оказаться, что некоторые или
все моменты бесконечны, однако даже в том случае,
когда все они конечны, они могут неоднозначно опреде-
определять функцию рп.
В качестве примера определим характеристическую
функцию, предполагая, что р„ представляет собой
') Мы будем опускать пределы интегрирования, если они ясны
из контекста или, как в данном случае, пробегают значения от
— сх> до + °о .

58	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
гауссово распределение с отличным от нуля средним
значением
р„ = я""'2 (det ajk)~lk exp [ - j ^ {x, - bt) ajk (xk - bk)\,
C.6)
где каждое суммирование производится от 1 до п. Тогда
в результате непосредственных вычислений получаем
выражение
Сп = (exp(t У x/s/)) = exp(j У s/b, -т У SjaJkSk),
C.7)
где ат^ — элементы матрицы, обратной по отношению к
матрице с элементами а,к- Замечая, что в экспоненту
C.7) входят только члены второго порядка и разлагая
в ряд левую и правую части, получаем
< 2 xjs,) = 2 s,bh	C.8a)
<B x,s,T) - <2 x,s,J = 2 siaTk'sk. C.86)
Поэтому С„ можно представить в виде
= exp (/ ^ s, (х,) - ~ ^. s/ (Ах,- Ад:&) sft), C.9)
где Axj ^ Xj—(х,). Это функциональное соотношение
характерно для гауссового распределения и его, соб-
собственно, можно рассматривать вместо C.6) в качестве
его определения.
Если перейти к бесконечному числу случайных пере-
переменных, то соответствующая плотность вероятности бу-
будет иметь, вообще говоря, только эвристическое значе-
значение. В то же время характеристическая функция (теперь
функционал) сохраняет смысл и является характеристи-
характеристикой случайного процесса в целом. В частности, если рас-
распространить пределы суммирования до бесконечности,
то соотношение C.9) можно рассматривать как харак-
характеристический функционал гауссова процесса с бесконеч-

§ 2. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ	59
ным числом случайных переменных. При этом следует
иметь в виду одно ограничение. Если для конечного
числа степеней свободы значение каждой величины s:;
могло быть произвольным действительным числом, то
теперь для сохранения свойств непрерывности и диффе-
ренцируемости последовательности Sj (/= 1, 2, ...) сле-
следует выбирать таким образом, чтобы выполнялись ус-
условия
со
2|в/<*/>1<°°.	C,10а)
оо
ILS,(iiX]^Xk)sk<oo.	C.106)
Чтобы подчеркнуть ограниченный характер последова-
последовательностей Sj, удовлетворяющих C.10), их называют
гладкими, или пробными, последовательностями. Здесь
нет необходимости конкретизировать какой-либо част-
частный набор гладких последовательностей. Многие инте-
интересные результаты можно получить, не задавая более
подробно полный набор подходящих последовательно-
последовательностей. Существенно то обстоятельство, что на допускае-
допускаемые последовательности Sj следует налагать некоторые
ограничения, иначе говоря, не каждая мыслимая после-
последовательность Sj пригодна.
Часто удобнее применять другое возможное описа-
описание формы последовательности. Пусть функции U;(t)
образуют полную ортогональную последовательность
действительных/функций одного переменного. Пользуясь
этими функциями и случайными величинами Xj, можно
образовать стохастическую переменную
оо
* (*) = 2 */«/@,	C.11)
которая является случайной функцией времени. Подоб-
Подобным образом каждой гладкой последовательности можно
сопоставить гладкую пробную функцию
со
).	C,12)

60	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
Пользуясь этими двумя величинами, характеристический
функционал гауссова распределения можно записать
следующим образом:
С {s (t)} = (exp [i J s (t) x (t) dt]) = exp [i J s (t) (x (t)) dt -
~l\ \ s(f)(Ax(f)Ax(t"))s(t")d?dt"}. C.13)
Условия, которым должны удовлетворять функции s(t),
очевидно, имеют вид
j\s(t)(x(t))\dt<oo,	C.14a)
s (?) (,\х (Г) &.х (П) s (П dt' dt" < со. C.146)
Как и в случае последовательностей Sj, обычно не тре-
требуется точно указывать полный набор гладких функций.
В большинстве интересных для физики случаев можно
считать, что подходящие гладкие функции бесконечно
дифференцируемы и при /—>-±оо спадают быстрее, чем
t~n, где п — любое положительное число.
Временное представление типа C.13) удобно для
анализа стационарных распределений, для которых
(x(t)) = (x@)) = m	C.15а)
и
<Д* (?) Ах (?')) = (Ах {? - t") Ax @)). C.156)
Последнее выражение можно записать в общей форме
(Ах (?) Ах (?'))= | exp[-2niv (?-?')] \х (v)dv, C.16)
где ji(v)<^0. Если применить эти соотношения и ввести
гладкую функцию, зависящую от частоты,
s(v)= j expBnivt)s(t)dt,	C.17)
то выражение C.13) принимает вид
С {§ (v)} = exp [ims @) - i- j Г (v) Д (v) s (v) dv]. C.18)
Полученный результат означает, что каждая спектраль-
спектральная компонента стационарного гауссова стохастического

§ 2. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ	61
процесса является величиной с независимым гауссовым
распределением и относительной дисперсией Д. (v).
Резюмируя анализ этого примера, отметим, что вы-
выражение C.18) содержит все величины, необходимые для
расчета произвольного момента стационарного гауссова
стохастического процесса; сказанное означает, что мо-
моменты зависят, следовательно, только от величины т
и одной функции Д (v). Следует также отметить, что
условия стационарности можно вывести из C.13), просто
требуя выполнения равенства C{s(t)} = C{s(t + t0)} для
любого t0 и любых гладких функций s(t).
В теории когерентности удобнее иметь дело не с дей-
действительными случайными волновыми полями, а с соот-
соответствующими аналитическими сигналами. Принимая во
внимание соотношение A.3), для действительных функ-
функций времени S<r) и V<r> прежде всего имеем
оо
у J S{n (t) Vх (t) dt = Re J S(r)' (v) V{r) (v) dv =
о
oo
= Re J S* (v) V (v) dv = Re J S' {t) V (t) dt, C.19)
о
где V = V2[V(r) + iVW] — аналитический сигнал соответ-
соответствующего волнового поля и S = 42[S(r) + /5<г')] — анали-
аналитический сигнал соответствующей гладкой функции. Та-
Таким образом, применяя аналитические сигналы V(t) и
S(t), характеристический функционал для любых рас-
распределений поля можно представить в виде
C{S(/)}^(exp[i Js(rV(r)^J) = (exp[i J (SV+ SV')dt]).
C.20)
Рассматриваемый ансамбль стационарен, если для лю-
любых V(t) и S(t) выполняется условие
C.21а)
В частотном представлении это условие принимает вид
С {S (v) exp {-2nivt0)} = С {S (v)}	C.21 б)
для любых ^0 и S (v).

62	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
Спектральные компоненты распределены независимо,
если для всех S,(v) и S2(v), для которых 5, (v) S2(v) = 0,
выполняется условие
С {S, (v) + S2 (v)} = С {S, (v)} C {S2 (v)}.	C.22)
Для комплексных волновых полей часто имеет место
другое условие, связанное с отсутствием достаточно пол-
полных сведений о фазе. Физически оно может появиться,
например, если поля V(t) и е^УA), где фаза ф постоян-
постоянна, рассматривать как равноценные. Равноправие фаз
в этом случае можно обеспечить, полагая, что условие
C{e~^S{t)} = C{S(t)}	C.23)
выполнено для всех действительных ф и S(t). В свою
очередь это условие будет выполняться, если для неко-
некоторого функционала С\ имеет место соотношение
C{S(/)} = C1{S*(OS(r)},	C.24а)
или, в терминах гладкой спектральной функции,
} = C1{S'(v')S(v")}.	C.246)
Наконец, отметим, что удовлетворить как условию рав-
равноправия фаз, так и условию стационарности можно
простым (но не единственным) способом, потребовав вы-
выполнения соотношения
C{S(v)} = C{S»S(v)}	C.25)
для некоторого приемлемого функционала С.
Применим эти условия к конкретным случаям. Пре-
Прежде всего рассмотрим опять случай гауссова распреде-
распределения. Обобщая очевидным образом выражение C.13),
получаем характеристический функционал комплексного
стационарного стохастического гауссова процесса с не-
неопределенной фазой
С {S (t)} = ехр [ - J J S* (П (V (П V (Г)> S (Г) dt' dt"'\ =
= exp [ - | J S* (*') Г (f -1") S {t") dt' d<"] =
- exp [ - J S* (v) f (v) S (v) dv];	C.26)

§ 2. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ	63
этот функционал удовлетворяет условиям C.21) — C.25).
Физически f(v) представляет среднюю энергию на ча-
частоте v, содержащуюся в волновых полях, которые обра-
образуют определенный гауссов ансамбль.
В гл. 2 с помощью перемножения характеристических
функций мы получили новые распределения. Покажем,
что новые распределения можно также получить, считая
некоторые параметры рассматриваемого распределения
случайными величинами и усредняя соответствующим
образом характеристический функционал.
Предположим сначала, что в C.26) F(v) имеет фор-
форму
f	/,	C.27)
где все члены положительны. Будем рассматривать G
и Н как заданные функции, а р— как новую дискретную
случайную величину (р = 0, 1, 2, . . .) с распределением
Пуассона, среднее значение которой (р) = ц. Получен-
Полученный характеристический функционал для нового моди-
модифицированного распределения (с учетом случайного ха^
рактера р) имеет вид
p=0
= exp|- J |S|2Gdv-n[l -exp(- J | S I2 tfdv)]} . C.28)
Хотя функционал C.28) является стационарным, усло-
условие C.22) не выполняется; таким образом, он не соот-
соответствует независимым распределениям для каждой ча-
частоты.
Рассмотрим другой пример. Возьмем теперь в C.26)
f(v) в виде
где опять_все _члены положительны. Предположим, что
функции G и К. заданы, а частоты vj будем считать не-
независимыми случайными переменными, каждая из ко-
которых равномерно распределена в интервале |

64	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
Грубо говоря, Г(у) представляет собой случайную вели-
величину, состоящую из большого числа независимых б-об-
разных вкладов (ситуация, аналогичная дробовому шу-
шуму), амплитуды которых определяются функциями К(х),
а центральные частоты распределены равномерно. В пре-
пределе, когда N-+co, F-+oo, причем величина N/F = р
остается конечной, можно получить результирующее мо-
модифицированное распределение (см. вывод Раиса [3.3])
с характеристическим функционалом
С {S (t)} = ехр { - | [ | S Р G + р A - ехр [- К I S |2])] d
C.30)
Как и для функционала C.26), мы имеем здесь незави-
независимое распределение для каждой частоты.
Вышеприведенное краткое рассмотрение должно дать
хотя бы грубое представление о применении характери-
характеристических функционалов для изучения случайных функ-
функций. В дальнейшем мы введем другие случайные про-
процессы и соответствующие характеристические функцио-
функционалы помимо уже рассмотренных. Однако во всех слу-
случаях основные понятия остаются неизменными.
§ 3. ПРИМЕНЕНИЯ К ЧАСТИЧНОЙ КОГЕРЕНТНОСТИ
А. Одиночные счетчики
Теперь обратимся к моментам числа отсчетов, рас-
рассмотренным в начале настоящей главы. Согласно C.3),
величину п1 можно выразить через корреляционную
функцию четвертого порядка, точное значение которой
зависит от статистики.
Будем рассматривать излучение теплового источника
(лампы, звезды и т. д.), описываемое стационарным
гауссовым распределением с неопределенной фазой (ла-
(лазерное излучение характеризуется иной моделью). Пу-
Путем непосредственного разложения функционала C.26),
содержащего всю информацию об ансамбле, получаем
^-([Re j St(t)V(t)dt]i) =
= ~{ j \ S< {t') (V {t')V {t"))S{t")dt'dt"^. C.31)

§ 3. ПРИМЕНЕНИЯ К ЧАСТИЧНОЙ КОГЕРЕНТНОСТИ	65
Это соотношение справедливо для произвольных глад-
гладких функций S(t). Приравнивая соответствующие коэф-
коэффициенты, находим, что соотношение C.31) будет вы-
выполняться, если имеет место равенство1)
(V (*,) V (t2) V (t3) V (t4)) = (V (f,) V (t2)) (V (t3) V {U)) +
+ (V4tl)V(ti))(Vt(t3)V(t2)). C.32)
Таким образом, для представляющего специальный ин-
интерес вычисления величины п2 находим
(V (П v (п v (п v (П) = (V (п v (П) (V (П v (П) +
= (I (П) (I (П) +1 г (? -1") I2,	(з.зз)
где введена автокорреляционная функция ансамбля в
точке г,-:
Г(*' - t") = (V (Г) V (/))	C.34)
[в гл. 1 она была обозначена через Гц(С — /")]. Из C.2)
и C.3) найдем дисперсию
т т
о2 = п2- {hf = a2 J J | Г (Г - t") |2 dt' dt" + п. C.35)
о о
Следовательно, имеется избыточный отсчет или группи-
группировка отсчетов, которая зависит от Т и функции взаим-
взаимной когерентности Г.
Введем нормированную функцию у (в гл. 1 уи), ко-
которая определяется соотношением
y(t'-t")= Г(^~0)П	C.36)
') В более общем случае соотношение C.26) приводит к ра-
равенству
(П V' «»/>-.> V{t2p)) = 2 П (v* {hp-x) v{hp{P))),
p=\	p p=l
где суммирование призводится по п\ перестановкам Р чисел
р-^-Р(р), р = 1, ..., п.

66	ГЛ. 3. ПОЛУКЛАССПЧЕСКАЯ ТЕОРИЯ
и, согласно A.17), удовлетворяет условию \y(t'— /
^ 1. Следуя Манделю [2.1], определим функцию
т т
о о
т
-f I {Т-т)\у{т)?йт.	C.37)
Функция %(Т) имеет размерность времени и представ-
представляет собой удобную неубывающую меру временной эво-
эволюции когерентности сигнала.
Из соотношения |уМ|^=-1 следует, что Ь,(Т)^~Т.
Если для некоторого начального интервала времени
функция y(t) близка к единице, то ?(Г)~7\ Если
|(Г)< Т, то это указывает на наличие конечного интер-
интервала, в течение которого имеет место частичная коге-
когерентность. Если y(t) спадает до нуля с характерным вре-
временем 0~ (например, как функция е~1'т или
ехр[—\l2(t/^rJ]), то для больших Т У? ZT функция ЦТ)
становится почти постоянной и имеет следующее зна-
значение:
Т	/со	\
I (Т) = -у J (Г - т) [ у (т) |2 dx - 2Г М | у (Гх) \2dx\,
о	\о	1
причем точная функциональная форма \(t) несуществен-
несущественна. Другими словами, l(T) ~ cZT, где с — постоянная по-
порядка единицы, конечно, при условии, что интегралы
сходятся. Предельное значение
(оо) = 2 j IyWNt	C.38)
представляет собой возможную меру введенного ниже
времени когерентности.

§ 3 ПРИМЕНЕНИЯ К ЧАСТИЧНОЙ КОГЕРЕНТНОСТИ	67
Поскольку
/¦
п = a j (V* (/') V (/')) df = aTV @),	C.39)
о
то вследствие стационарности дисперсию C.35) можно
представить в виде
[ Цр\	C.40)
где %(Т) определяется соотношением C.37). Обращаясь
к анализу, проведенному в гл. 2 [в частности, B.49)],
нетрудно видеть, что полученная дисперсия та же, что
возникает для распределения фотонов, разделенных по
Т/?,(Т) независимым «временным ячейкам», в каждой
из которых имеет место тепловое распределение, а сред-
среднее заполнение ячейки, или параметр вырождения, опре-
определяется как б = п/[Т/% (Т)] = п% (Т)/Т. Как показал
Мандель [3.12] в применении к фотоотсчетам, в случае
стационарных гауссовых ансамблей для достаточно боль-
больших Т правомерно предположить, что среднее число б
фотонов внутри интервала, соответствующего времени
когерентности, имеет тепловое распределение и что со-
соседние интервалы статистически независимы. При таких
предположениях распределение отсчетов C.1) переходит
в распределение B.51) с /V = ТЦ(Т). Более точные при-
приближения для стационарных гауссовых ансамблей и
больших времен измерения Т мы приведем в гл. 9, где
излагается квантовый подход к задаче.
Результаты вычислений группировки отсчетов, вы-
выполненных для гауссова случая, фактически являются
весьма общими. Любое классическое распределение при-
приводит к избыточным отсчетам по отношению к пуассо-
новскому случаю и, следовательно, к такой же группи-
группировке, как в C.40). Для сравнения приведем результаты
расчета, аналогичного выполненному выше, но относя-
относящегося теперь к распределению волновых полей, харак-
характеризуемому соотношением C.28). В этом случае сред-
среднее число отсчетов равно
,	C.41)

68	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
в то время как дисперсия имеет вид
т
а2 = п + 2а2 / (Т - х) | G (т) + цЯ (т) |2 dx +
о
+ cfy Г2Я2 @) + 2 / (Т - т) | Я (т) |2 йт . C.42)
Это выражение для а2 всегда содержит член, пропорцио-
пропорциональный Т2, тогда как выражение C.40) асимптотически
возрастает, в лучшем случае линейно, с увеличением Т,
поскольку время когерентности конечно. Как и следо-
следовало ожидать, эти два результата согласуются в пределе
Б. Несколько счетчиков
Вместо того чтобы рассматривать флуктуации отсче-
отсчетов в одиночном счетчике, можно анализировать корре-
корреляции отсчетов в двух или большем числе различных
счетчиков, освещаемых частично когерентным светом.
Пусть функция координат и времени V(r,t) представ-
представляет волновое поле от протяженного источника. В этом
случае естественно ожидать, что корреляции в стати-
статистике У(г, /) могут сохраниться, если различные сравни-
сравниваемые сигналы принадлежат к пространственно разде-
разделенным точкам. Предположим, что два безынерционных
счетчика находятся соответственно в точках п и г2 и
пусть
V,(t) = V(r{,t),	C.43)
It(t) = Vmi{t)Vt(t).	C.44)
Распределение отсчетов, соответствующее постоянной
интенсивности в точке г*, описывается выражением, сов-
совпадающим с B.2):
{
Poi(nt, П = ^т к/МОЛ) ехр
т	1
-а,//,@ Л .
о	J
C.45)

§ 3. ПРИМЕНЕНИЯ К ЧАСТИЧНОЙ КОГЕРЕНТНОСТИ	69
Поэтому, когда рассматриваемые интенсивности случай-
случайны, взаимная корреляционная функция отсчетов опреде-
определяется следующим образом:
«1«2= У^ rt1n,(P01(rt1) Г)РО2(П2, Т)) =
Т Т
f \(IAt')h(t"))dtrdt"\	C.46)
т т
= а^
о о
ее значение зависит от вида статистики.
Для иллюстрации рассмотрим комплексное волновое
поле У(г, /) со стационарным гауссовым распределением
с неопределенной фазой. В соответствии с анализом,
проведенным в начале настоящей главы, такое распре-
распределение можно описывать с помощью характеристиче-
характеристического функционала комплексных гладких функций
S(r,t), зависящих как от пространственной координаты,
так и от времени:
С {S (г, 0} = ехр { - J { S* (г„ *,) {V (г„ *,) V (г2, *2)> X
X S (г2, t2) d3r, d-V2 dtx dt2}.	C.47)
Для детекторов, расположенных в точках п и г2, поль-
пользуясь обозначением S;(/) = S (г,, /), i = 1, 2, получаем
С {S, @) = ехр j - \] J J S) (f,) <V, (/,) К*, (f2)> S, (f2) dtx dU_ \.
C.48)
Из C.48) можно найти все взаимные корреляционные
функции. Отсюда, в частности, следует, что
t")Vl(t').	C.49)
Подставляя последнее выражение в C.46), находим
т т
= п,й2 + сча2 J J | Г12 (*' - t") |2 dt' dt", C.50)
о о

70	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
где, как и в A.13),
r12(*'-n=<i/;(nv,(o> C.5D
означает взаимную корреляционную функцию, и
Щ = «J <У\ Ю Vt (O> dt' s= а/7Т„ @). C.52)
о
Введем нормированную функцию
h^lC.53)
NT,	C.54)
=
[ГП(О)ГМ(О)]1
и величину
г
которая, как и выше, является мерой временной зави-
зависимости функции взаимной когерентности сигналов. При
использовании этой величины корреляция избыточных
фотоотсчетов определяется выражением
^^	у >	C.55)
которое показывает, что в пространственно разделен-
разделенных счетчиках могут существовать корреляции интенсив-
интенсивности.
Помимо временной зависимости взаимной корреля-
корреляции фотоотсчетов, интересно подробно проанализировать
зависимость выражения C.55) от пространственных ко-
координат. Для простоты будем считать, что ансамбль не
только стационарен, но и однороден, т. е. на не слишком
больших расстояниях не зависит от выбора начальной
пространственной координаты. В этом случае можно
положить
(У (r2, t2) V (г„ *,)> = Г (г, - r2, f, - t2), C.56)
так что из соотношения C.52) получаем
т
щ = щ J Г @, 0) dt' = а,7Т @, 0)	C.57)

§ 3 ПРИМЕНЕНИЯ К ЧАСТИЧНОЙ КОГЕРЕНТНОСТИ	71
независимо от местоположения детектора. Полагая
Ti — г2 = г, находим пространственную и временную за-
зависимости взаимной корреляции избыточных фотоотсче-
фотоотсчетов
7"	- - 	 - — ь \f*> ' )	/о EQ\
где
т
l(r,T) = jr j(T-T)\y(r,x)\4x	C.59)
о
Примем для простоты, что для интересующей нас об-
области расстояний значение Т мало по сравнению со вре-
временем когерентности g(r, °°). Тогда можно положить
ЩЛ ~ I Y (г, 0) р;	C.61)
при этом корреляция избыточных отсчетов как функция
расстояния г счетчиков выражается через степень коге-
когерентности следующим образом:
пхп2 - пхп2 = п{п2| y (г, 0) |2.	C.62)
Хотя рассмотренные примеры соответствуют гауссо-
гауссовой модели, характеризуемой соотношением C.48), из
C.46) следует, что временная и пространственная корре-
корреляции отсчетов имеют место для любого ансамбля, об-
обладающего соответствующими корреляциями интенсив-
интенсивности.
Интерферометрия интенсивности. Измерение корре-
корреляций фотоотсчетов лежит в основе «интерферометрии
интенсивности». В отношении измерения параметров
звезд интерферометрия интенсивности, как показано
Хэнбери Брауном и Твиссом [3.9], иногда обладает опре-
определенными преимуществами по сравнению с традицион-
традиционной (амплитудной) интерферометрией. Предположим,
что в точках п и г2, где п — г2 = г, мы сравниваем
амплитуды света, пришедшего от звезды, и исследуем

72	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
пространственную когерентность этих волн, скажем по-
помещая в эти точки отверстия двухщелевого интерферо-
интерферометра. Таким образом, мы изучаем функцию C.56) или,
более точно, согласно A.14), ее действительную часть.
При прохождении света от звезды через атмосферу на-
наблюдаемый сигнал изменяется из-за турбулентного дви-
движения воздуха, что приводит к изменению показателя
преломления; возникают случайные, быстрые изменения
фазы. Этот эффект можно учесть, производя замену
y,{t)],	C.63)
где ф,-(/) = (p(i"j,/) означает фазу на /-м детекторе. Сле-
Следовательно, наблюдаемая функция взаимной когерент-
когерентности отличается от таковой для источника:
т(г, ? - П, C.64)
Гнабл, вообще говоря, уже не является функцией разно-
разности времен; более того, величина ЯеГНабт не равна
Re Гист.
Фазовые искажения играют очень важную роль в
точных оптических измерениях и ограничивают точность
измерений диаметров звезд с помощью интерферометра
Майкельсона, обсуждавшихся в конце гл. 1. Даже при
/' = /" быстро меняющийся фазовый коэффициент в
C.64) не обращается в нуль, поскольку функции ф1 и ф2
могут быть различными и в значительной степени неза-
независимыми, как, например, для расстояния более 5 или
6 м.
В интерферометрии интенсивности в пространственно
разделенных точках исследуется корреляция интенсив-
костей, а не амплитуд. В силу C.46) это можно осуще-
осуществить, измеряя за время Т корреляцию избыточных от-
отсчетов C.55), причем величиной, представляющей непо-
непосредственный интерес, является степень когерентности.
Из C.64) следует
I Унабл (Г, Т) | = | Уист (Г, т) |.	C.65)
Поэтому фазовые искажения, которые сильно затруд-
затрудняют амплитудную интерферометрию, здесь оказывают-
оказываются несущественными. Таким образом, интерферометрия
интенсивности позволяет исследовать корреляции вол-

§ Л. ПРИМЕНЕНИЯ К ЧАСТИЧНОЙ КОГЕРЕНТНОСТИ
73
новых полей, характеризующих источник, на гораздо
больших расстояний между точками наблюдения, чем
это было возможно ранее.
Рассмотрим пример. Пусть время Т мало по сравне-
сравнению со временем когерентности и применимо соотноше-
соотношение C.62). Если, как в гл. 1, мы имеем дело с квазимо-
квазимонохроматическим излучением от однородно освещенного
диска в приближении дальнего поля, то в качестве ком-
комплексной степени когерентности можно взять функцию
A.49). Для звезды радиусом Ь, которая находится от
О -
с/, мм
Фиг. 3. Зависимость квадрата степени когерентности | \12 @) |2 от
расстояния d между фотодетекторами. (По данным Хэнбери Брауна
и Твисса [3.9 в].)
Изображены теоретические и экспериментальные результаты, подтверждающие
эффект Хэнбери Брауна — Твисса и полученные для ртутной дуговой лампы,
а не для изображения звезды. Экспериментальные результаты представлены
точками с соответствующими вертикальными отрезками, характеризующими
доверительный интервал; сплошная кривая соответствует теоретически пред-
предсказанной зависимости, полученной с учетом спектрального распределения
света и характеристик электронных схем.

74	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
Земли на расстоянии R и излучает на средней частоте
v = k/2n, корреляция избыточных отсчетов при расстоя-
расстоянии между счетчиками г определяется выражением
' 2/, (*) \2
X
C.66)
где х = kbr/R. Измеряя функцию взаимной корреляции
C.66) в зависимости от г, можно определить размер
звезды, если расстояние R известно. Первый нуль корре-
корреляционной функции соответствует такому расстоянию г,
для которого kbr = 3,8SR. С помощью именно такой ме-
методики Хзнбери Браун и Твисс [3.9] увеличили базовое
расстояние своего интерферометра до 183 м, что в 30 раз
больше типичной базы в интерферометре Майкельсона,
ограниченной флуктуациями в атмосфере. Результаты
эксперимента по интерферометрии интенсивности излу-
излучения ртутной лампы представлены на фиг. 3.
В. Полоса пропускания, размер счетчика
и значение сглаживающих функций
Выше мы рассматривали идеализированные безынер-
безынерционные и точечные детекторы. Однако в разумных при-
приближениях можно легко учесть эффекты, обусловленные
конечной полосой пропускания и конечными размерами
детектора. Пусть 3*(v) —частотный адмитанс детектора,
т. е. относительное изменение амплитуды и фазы волно-
волнового поля V(r,/) на частоте v; аналогично а*(г)—про-
а*(г)—пространственный адмитанс (-го детектора, описывающий
относительное изменение амплитуды и фазы V(r, t) в
точке г. В этом случае эффективное волновое поле
У?фф@ на г'-м детекторе определяется выражением
К?фф {t) = \ at (г) S* (t - t') V (г, t') dh dt', C.67)
где S* (t) — фурье-образ функции 3* (v)—представляет
собой импульсную переходную функцию детектора. Эф-
Эффективная интенсивность Ii (t), определяющая ско-
скорость отсчетов г-го детектора, равна
/?фф@ = |К?ФФ(/)|2.	C.68)

5 3. ПРИМЕНЕНИЯ К ЧАСТИЧНОЙ КОГЕРЕНТНОСТИ	75
Для выяснения характера изменений, возникающих
в результате перехода к эффективному полю C.67),
рассмотрим для простоты только эффекты, обусловлен-
обусловленные конечной полосой частот, т. е. положим а,(г) =
= б(г — г<) для отдельного счетчика в случае гауссова
распределения.
Из C.32) получаем
We (f.) Ve (U) Ve (h) Ve (ti)) = We (*.) Ve (t,)) We (h) Ve (U)) +
+ We (ti) Ve (ti)) We (U) Ve (fe)>, C.69)
где введено обозначение
Ve (t) = 1/?фф (t) =js*(t- t') V (r(-, t') dt'. C.70)
Полагая Ie — \Ve\2, для первых двух моментов отсчетов
имеем
т
п = а j {Ie(t'))dt\	C.71a)
о
т т
tf = a2 J J (Ie (f) I, (t")) dt' dt" + n. C.716)
о о
Пользуясь этими выражениями, получаем для среднего
значения и дисперсии отсчетов
т
п = a J dt 11 S* (t - ti) S(t- t2) Г {ti - t2) dU dt2 =
о
= aT J | S (v) p f (v) dv,	C.72)
o2 = n2- (nf =
T T
= a2 J J dt' dt" J J J J S*(t'- t2) S (f - tx) S' (t" - Q X
о о
X S(t" - t3) Г (^2 - t3) Г (ti - ti) dtx dt2 dt3 dti + il =
T T
- a2 J J dt' dt" | J exp [-2rov (*' - t")\ X
о о
X\S(v)\2f(v)dv2 + n. C.73)

76	ГЛ. 3. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
Таким образом, формулы для моментов отсчетов, учиты-
учитывающие конечность полосы пропускания, качественно
аналогичны формулам, полученным выше. Если в обла-
области частот, где функция f(v) отлична от нуля, 5(v)~ 1,
то моменты отсчетов совпадают с таковыми для безын-
безынерционного детектора. Однако, когда функция S(v) уже
спектра функции F(v), статистика фотоотсчетов в значи-
значительной степени определяется характеристиками детек-
детектора и слабо зависит от свойств источника. Аналогичные
замечания справедливы, если учесть конечные размеры
детектора посредством функции аг{г).
В общем случае изменения волновых полей, описы-
описываемые соотношением C.67), можно отразить с помо-
помощью специальных сглаживающих функций
S],t{r, t') = ai{r)S*{t-t'),	C.74)
которые должны появиться в характеристических функ-
функциях C.47). Таким образом, можно считать, что глад-
гладкие функции S(r,f) отражают пространственные и
частотные ограничения, вносимые любым процессом из-
измерения. Следовательно, помимо сугубо формального
значения описание стохастических переменных с по-
помощью характеристических функционалов и гладких
функций имеет глубокое физическое обоснование.
§ 4. ЗАКЛЮЧЕНИЕ
В этой и предыдущих главах мы с классической и
полуклассической точек зрения рассмотрели описание
частично когерентных оптических явлений и соответст-
соответствующих моментов фотоотсчетов. Существенное значение
для анализа имело введение ансамбля классических ана-
аналитических сигналов V(r,t), подчиняющихся волновому
уравнению. Хотя мы рассматривали главным образом
стационарные распределения с неопределенной фазой,
эти специальные условия не имеют существенного зна-
значения. В следующих главах будут рассмотрены ансамб-
ансамбли, на которые не наложено таких ограничений.
Учет векторного характера полей в развитой теории
не представляет трудностей. Все особенности, связанные
с векторным характером поля излучения, мы обсудим

§ 4 ЗАКЛЮЧЕНИЕ	77
при квантовом рассмотрении. Соответствующие обобще-
обобщения нашего классического и полуклассического рассмот-
рассмотрения на случай векторных полей можно найти в рабо-
работах Борна и Вольфа [1.1], Манделя [2.1], О'Нейла [1.3],
Берана и Паррента [1.2] и Манделя и Вольфа [3.11].
В классической теории частичной когерентности воз-
возникает много других интересных вопросов. Среди них
следует отметить связь между формальным распределе-
распределением Бозе — Эйнштейна для фотоотсчетов, временем ко-
когерентности и т. д. и аналогичными понятиями стати-
статистической механики и теории информации. Рассмотрение
этих вопросов проведено в статье Габора [3.8] и в цити-
цитируемой в ней литературе.

Статистика поля
§ 1. ПОСТАНОВКА ДИНАМИЧЕСКОЙ ЗАДАЧИ
В предыдущих главах показано, как, применяя гео-
рию стохастических процессов, можно развить теорию
частичной когерентности и определить полуклассиче-
полуклассическую статистику фотоотсчетов. С физической точки
зрения открытым, однако, остается вопрос о выборе со-
соответствующего статистического описания поля. Во
многих случаях именно в этом заключается сущность
проблемы; число общих методов ее решения весьма
ограничено. Поэтому каждую конкретную задачу сле-
следует рассматривать отдельно в свете ее физического
происхождения.
В настоящей главе мы весьма кратко остановимся
на ряде характерных статистических задач и покажем,
каким образом следует формулировать уравнения, при-
приводящие к их решению. Прежде чем обратиться к дета-
деталям решения определенной задачи, предпочтительнее
сначала рассмотреть некоторые общие характерные
свойства, присущие большинству стохастических проб-
проблем, и сформулировать общие принципы их анализа.
Хотя здесь приводится классическое рассмотрение, мно-
многие методы и формальные соотношения имеют точные
аналоги в квантовой теории.
Упростим задачу, считая волновое поле скалярным
У (г, /) == V(x), и рассмотрим следующие уравнения об-
щего
вида '):
nV{x) = j{x) = J
n*k(x) = Fk{x)-l
(у У (лЬЛ)
п / . Т 7 / | \ \
D.
D.
1а)
16)
') Здесь ? = V2 — (d2/dt2) ~ оператор Даламбера.

§ I. ПОСТАНОВКА ДИНАМИЧЕСКОЙ ЗАДАЧИ	79
Физический смысл этих уравнений состоит в следующем:
поле V(х) динамически зависит от источника j(x), свой-
свойства которого в свою очередь определяются самим по-
полем V и конечным числом других полей {\|jft}. Аналогич-
Аналогичная интерпретация применима к второй группе уравне-
уравнений. Не совсем строго грь можно называть «материаль-
«материальными полями» (или «полями источников») для «поля
излучения» V.
В D.1) подразумевается локальная зависимость }
и Fk от полей V или г|)/г (по крайней мере локальная во
времени). При этом условии поле V(x) зависит от
источника j(х), который в свою очередь определяется
значениями поля в той же самой пространственно-вре-
пространственно-временной точке. Проблемы, которые описываются уравне-
уравнениями общего вида D.1), можно грубо разделить на ряд
категорий.
А. Причины появления статистики
1. Рассмотрим поле V в области, не имеющей источ-
источников; тогда для свободного поля получаем уравнение,
обсуждавшееся в гл. 1:
\JV(x) = 0.	D.2)
Функция V(х) удовлетворяет гиперболическому диффе-
дифференциальному уравнению второго порядка, которое име-
имеет единственное решение, определяемое начальными
условиями. Однако можно пренебречь точными значе-
значениями начальных условий и, таким образом, получить
правильные сведения только о некоторых частных во-
вопросах, касающихся поведения V(х). Например, для
гармонической волны, излучаемой генератором, нельзя
получить информацию о значении фазы в данный мо-
момент, если пренебречь начальным значением фазы.
Решение уравнения D.2), которое можно записать
следующим образом:
V(x)=zV(x;Vo),	.	D.3)
где Уо обозначает начальные условия (или их совокуп-
совокупность), представляет собой случайную величину с рас-
распределением, зависящим от распределения начальной
случайной величины Уо.

80	ГЛ. 4. СТАТИСТИКА ПОЛЯ
2.	Неопределенность, вводимую начальными усло-
условиями, можно распространить на все связанные уравне-
уравнения D.1). Предположим, как и раньше, что решение
таких уравнений имеет вид
V(x) = V (x; VQ, (W),	D.4а)
Ы*) = ФЛ*; v0, М-	D.46)
Если все или часть начальных условий остаются не-
неопределенными, то V(x) и все tyk(x) можно интерпре-
интерпретировать как случайные процессы с распределениями,
зависящими от распределений начальных случайных пе-
переменных Vo и {1|:м}-
В свою очередь источник j(x) можно рассматривать
как вторичный случайный процесс
/(*) = /(*; V, Ы),	D.5)
задаваемый случайными процессами V и всеми tyk-
3.	Рассмотренная выше картина для некоторых част-
частных случаев допускает существенное упрощение. Может
случиться, что число излучателей, создающих источник
j(x), так велико, что статистика источника ](х), опре-
определяемого соотношением D.5), не зависит от особенно-
особенностей распределений переменных V и tyk- Это обстоятель-
обстоятельство является следствием известной центральной пре-
предельной теоремы, или закона больших чисел, которая,
грубо говоря, утверждает, что сумма большого числа
независимых случайных величин обладает гауссовым
распределением. В гл. 9 эта теорема будет рассмотрена
более подробно в квантовой форме. Здесь мы хотим
лишь подчеркнуть, что свойства } (х) могут оказаться
более простыми. В рассматриваемом случае естественно
считать, что основное уравнение принимает вид
nv(x) = j(x)	D.6)
и что его решение
V(x) = V (x; D	D.7)
(здесь опущена явная зависимость от Vo) представляет
собой случайный процесс, определяемый некоторым
исходным процессом j (х). Уравнения типа D.6) назы-
называются «флуктуационными». Примером физической си-

§ ! ПОСТАНОВКА ДИНАМИЧЕСКОЙ ЗАДАЧИ	81
туации, для которой сделанные упрощения применимы,
является тепловое излучение, испускаемое большим чис-
числом атомных излучателей, как, например, это имеет ме-
место для лампы или звезды.
Хотя источник j (х) может и не обладать гауссовой
статистикой, такой случайный источник часто не совсем
строго связывают с «термостатом», или «резервуаром».
Независимость j(x) от реакции V(х) свидетельствует
об «устойчивости» термостата.
Рассматриваемый случай отличается от предыдущих
примеров в двух отношениях. С одной стороны, он зна-
значительно проще, поскольку поле V связано с / линейным
преобразованием [уравнение D.6) линейно]. С другой
стороны, исходная случайная переменная j(x) является
случайной функцией координат и времени, в то время
как в прежних случаях (только со случайными началь-
начальными условиями) основные величины были только слу-
случайными функциями координат. Иногда это слишком
дорогая цена за полученные упрощения.
4. В ряде случаев, когда предыдущее упрощение на-
налагает слишком жесткие ограничения, можно допустить,
что источник не реагирует на детали распределения не-
некоторых случайных величин {г|)/г}. Пусть имеется только
два источника; тогда уравнения запишутся в виде
DV(x) = j(x; V, ф„ ф2),	D.8а)
nnPl{x) = Fl{x;V,ibl,^,	D.86)
= F2(x; V, г|)„ ф2).	D.8в)
Можно принять, что эти уравнения детерминированы,
а флуктуируют только начальные условия. Предположим
также, что $2 описывает характерные черты термостата,
состоящие в том, что на него не оказывают возмущаю-
возмущающего влияния распределение V(x) или i|)i(*) и что он
представляет собой источник для V и \pi, статистика
которых в широких пределах не зависит от их началь-
начального вида. Предположим, что последнее уравнение для
ф2 можно решить с постоянными V и фь пусть решение
имеет вид f(x). Как характеристика термостата вели-
величина f(x) по предположению не зависит от V(x) и ^\{х).

82	ГЛ. 4 СТАТИСТИКА ПОЛЯ
Подставляя это решение в D.8), получаем систему флук-
туационных уравнений
nV(x) = j{x;V,$l,f),	D.9а)
П ф, (*) = Л (*: V, ip,, f),	D.96)
которые можно интерпретировать следующим образом.
Поле V определяется как решение связанной системы
уравнений, в которой источники зависят не только от
величин V и гр 1, но и от «внешней» случайной функ-
функции f(x). Нетрудно обобщить эти уравнения на несколь-
несколько «внешних» случайных функций f\(x) и /г (я) или
предположить, что каждое поле имеет свой собственный
термостат.
Как и в предыдущих примерах, основные уравнения
могут существенно зависеть от полной пространственно-
временной предыстории функции f(x). Сложным может
быть не только распределение функции f(x); в общем
случае может и не существовать простого линейного со-
соотношения между V (х) и случайным процессом f(x).
5. В качестве последнего примера рассмотрим кратко
атмосферную турбулентность, упомянутую в гл. 3.
Можно считать, что эффект этого типа обусловливается
случайными изменениями показателя преломления, кото-
которые влияют не на источник, а на условия распростране-
распространения. Таким образом, оператор Даламбера ? становится
случайным, поскольку скорость распространения в среде
испытывает флуктуации. Эту задачу можно проанализи-
проанализировать методом, описанным в гл. 3, где уравнение ре-
решалось для заданного показателя преломления п(х)\
при этом поле
V{x) = V{x; n)	D.10)
рассматривается как случайное, статистика которого
определяется случайной величиной п(х). В форме D.10)
задача не является более общей, нежели задача, опи-
описываемая уравнениями D.9), хотя причины стохастиче-
стохастического поведения в этих случаях физически различны.
Общая модель. Будем в дальнейшем исходить из об-
общих уравнений D.9) и для определенности запишем их

§ 2. ПРЕОБРАЗОВАНИЕ ФЛУКТУАЦИОННЫХ УРАВНЕНИП	83
в виде
UV(x) = V* (л) + ф2 (.г) + f (л-)),	D.11 а)
n$(x) = V(x)$(x) + g(x).	D.116)
Здесь у поля источника \р индекс 1 опущен и введены
две случайные вынуждающие силы / и g (в некоторых
случаях это может быть одна и та же сила). Эти урав-
уравнения напоминают уравнения классической электродина-
электродинамики или уравнения, описывающие волны в нелинейном
диэлектрике, и т. д. Существенной особенностью анали-
анализируемых уравнений является их нелинейность и нали-
наличие случайных сил.
В некоторых случаях эти уравнения можно линеари-
линеаризовать в «рабочей точке», иначе говоря, рассматривать
систему линейных уравнений, справедливых для малых
отклонений,
o{x) = V(x)-Va{x),	D.12a)
<p(x) = ipM-i|>oM.	D-126)
где Vq(x) и фо(я)—известные регулярные функции. Мы
не будем здесь подробно рассматривать довольно про-
простые результаты, получающиеся в таких случаях.
§ 2. ПРЕОБРАЗОВАНИЕ ФЛУКТУАЦИОННЫХ УРАВНЕНИЙ
А. Усредненные уравнения для моментов
Уравнения D.9) и D.11) не являются «обычными»
дифференциальными уравнениями в частных производ-
производных, поскольку в них имеются случайные члены. Для
решения этих уравнений в классическом смысле обычно
требуется найти прежде всего точное решение V(x) =
= V(x;f) при заданном f(x). На деле такая процедура
оказывается слишком сложной и фактически излишней.
Наблюдаемые величины и существенные свойства реше-
решений определяются усреднением по случайным членам
f(x). Мы можем преобразовать уравнение D.9) или
D.11) к дифференциальным уравнениям в частных про-
производных для наблюдаемых величин, переходя к усред-
усредненным уравнениям
(DV(x))=D(V(x)) = (j{x; V, ф„ f)>, D.13а)
(? ф, (х)> = D Ор, (х)) = (Fx (x; V, ъ, })). D.136)

84	ГЛ. 4. СТАТИСТИКА ПОЛЯ
Значение этой процедуры сразу выявляется наглядно,
если рассмотреть усредненные уравнения D.11):
?	(V (х)) = (V3 (х)) + W (х)) + (/ (*)), D.14а)
?	(Ф W) = (V (х) ф (*)> + (g (x)).	D.146)
Хотя эти динамические уравнения не содержат флуктуа-
ционных членов, они недоопределены, поскольку, напри-
например, (V(x)) зависит от величины (V3(x)), о которой мы
ничего не знаем, пока не решим самих уравнений.
Чтобы выявить наиболее существенные особенности
задачи, рассмотрим одно нелинейное уравнение
nV(x) = V3{x) + f{x),	DЛ5)
где f(x) — случайная вынуждающая сила. Чтобы полу-
получить информацию о (У3(х)), можно рассмотреть урав-
уравнение, получающееся при умножении DЛ5) на V(y)V(z)
с последующим усреднением по ансамблю
([ ? XV (х) - V3 (х) - f (х)\ V (у) V (г)) = О,
или в другом виде:
? х (V (х) V (у) V (г)) = (У3 (*) V (у) V (z)) + (f (х) V (у) V (z)).
D Л 6)
Таким, образом, для вычисления момента или корреля-
корреляции третьего порядка необходимо знать корреляцию пя-
пятого порядка и т. д. до бесконечности.
Эти уравнения можно в некоторой степени система-
систематизировать, вводя последовательность функций
Grs{xu ..., хг; уи .... ys) = (f{x1) ... f(xr)V (г/,) ... V (у,))
D.17)
Эти функции порознь симметричны по переменным х
и у и для любых г и s связаны основными динамиче-
динамическими уравнениями
DyfirsiXi, ..., xr; yu ..., ys) =
= Grs + 2(Xl, -.., X/, ljb . . ., tjs, yu y{) +
+ Gr+u-l{xl	xr, уx; y2, ..., ys).	DЛ8)

§ 2. ПРЕОБРАЗОВАНИЕ ФЛУКТУАЦИОННЫХ УРАВНЕНИЙ	85
Таким способом первоначальная задача сводится к бес-
бесконечной последовательности связанных уравнений.
Естественно, что аналогичный набор связанных урав-
уравнений имеет место для более сложного взаимодействия
в D.11).
Уравнения, подобные D.18), встречаются во многих
областях физики: нелинейной оптике, статистической
механике, теории турбулентности и т. д. Кроме того,
фактически аналогичные уравнения описывают средние
величины в квантовой теории. В библиографии приве-
приведен краткий обзор работ, в которых рассматриваются
такие проблемы, соответствующие уравнения и их при-
приближенные решения.
Б. Усредненное уравнение для характеристического
функционала
При помощи соответствующего характеристического
функционала можно дать удобную формальную клас-
классификацию связанных уравнений D.18). Будем рассмат-
рассматривать V(x) и f(x) для простоты как действительные
поля. В этом случае соответствующий характеристиче-
характеристический функционал можно взять в виде
C{S, s} = <exp{/ j[S(y)V(y) + s(y)f(y)]d4j}). D.19)
Предположим, что статистика вынуждающей силы за-
задана; тогда можно считать известным функционал
С {0, s} = (exp [i js(y)f (у) d*y]).	D.20)
С другой стороны, необходимые физические величины
определяются через V(x), поэтому попытаемся найти
функционал
С {S, 0} = (exp [i | S(y)V (у) d4y)]).	D.21)
Как заданные, так и неизвестные распределения опре-
определяются как частные случаи совместного среднего зна-
значения D.!9). Это обстоятельство является важной и
общей характерной чертой анализа флуктуационных
уравнений посредством характеристического функцио-
функционала.

86	ГЛ. 4. СТАТИСТИКА ПОЛЯ
Уравнение для C{S, s} можно вывести при помощи
соответствующих функциональных производных, кото-
которые вводятся как весовые функции, связанные с произ-
производными по направлению. Другими словами, функцио-
функциональные производные
6C(S, s)	6C{S, s)
6S (x) '	б.? (x)
определяются из соотношений
1с14х^ЖС^ + гЕ' S>U- D.22a)
где Е(х) и е(х) — заданные гладкие функции общего
вида. Как уже отмечалось в предыдущей главе, в каче-
качестве аргументов для характеристических функционалов
следует, вообще говоря, брать только подходящие глад-
гладкие функции.
В качестве простого примера рассмотрим прежде
всего функциональные производные от функционала
С, {S) = J 52 (x) d*x.
В этом случае
= 2JE(x)S(x)d*x,
причем при вычислении предполагается квадратичная
интегрируемость ? и 5. Следовательно, в рассматривае-
рассматриваемом примере
65 (х)	v '
Как и в классическом анализе, некоторые функцио-
функционалы могут быть недифференцируемыми. Например,
формально видно, что
= 2 -A. [S (Х) + тд(х- х%_0 = 26 (х - х'); D.23)

§ 2. ПРЕОБРАЗОВАНИЕ ФЛУКТУАЦИОННЫХ УРАВНЕНИИ	87
следовательно, в частности
Однако вторая функциональная производная в одной
точке не обязательно дает бесконечность. Например,
функция
С2{5} = ( f E0(x)S(x)d*x)\
где Eq(x) — заданная гладкая функция, приводит к зна-
значению
УС AS} _nF2M
-щ^-гьоКх).
Для правомерности выкладок будем считать, что функ-
функционалы имеют необходимые производные.
Теперь нетрудно преобразовать D.15) в уравнение
для характеристического функционала. Из D.19) эле-
элементарно получаются соотношения
= (V (х) ехр {/ J [S (у) V(y) + s (у) f (у)} d*y }), D.24а)
= (fq (х) охр {i | [5 (у) V (у) + s(y)f (у)} dhj}), D.246)
откуда ясно, что С удовлетворяет уравнению
= U г'^Ш +[~г'~бГпЛ( С
или, после сокращения на общий множитель i,
{S's]- D'25)
Решение, которое мы ищем, удовлетворяет уравнению
" D.20) и обладает хорошим поведением для больших
значений S(x). Функциональное дифференциальное урав-
уравнение содержит всю бесконечную цепочку связанные

88	ГЛ. 4. СТАТИСТИКА ПОЛЯ
уравнений D.18). Действительно, эти уравнения можно
получить непосредственно из D.25), разлагая экспо-
экспоненты в степенной ряд и приравнивая соответствующие
степени после выполнения необходимых функциональ-
функциональных дифференцирований
С практической точки зрения число точно разреши-
разрешимых нелинейных уравнений вида D.18) или D.25) очень
мало. Вообще говоря, уравнения D.18) предпочтитель-
предпочтительнее, поскольку в этом случае легче ограничить беско-
бесконечную цепочку уравнений и получить систему, допу-
допускающую приближенные решения. Способы решения
функциональных дифференциальных уравнений типа
D.25) пока не разработаны.
§ 3. МАРКОВСКИЕ И НЕМАРКОВСКИЕ ПРОЦЕССЫ
А. Определения и различия
В теории стохастических процессов существуют за-
задачи, описание которых во многих отношениях анало-
аналогично гамильтоновой формулировке классической меха-
механики или классической теории поля. Такое описание ха-
характеризуется набором N уравнений первого порядка
по времени, решения которых однозначно определяются
тем же числом начальных условий. Для анализа таких
уравнений обычно необходимо удвоить число основных
переменных величин, так же как в классической меха-
механике, в которой число координат Х\х удваивается при
переходе к переменным xh и ph в фазовом простран-
пространстве. Для наших целей такие уравнения первого порядка
можно записать в общей форме
{fj, t),	D.26)
где k=\, ..., Л'. Здесь поле V и его временная про-
производная представлены в виде двух полей, входящих в
совокупность {фй}. Функции fm соответствуют феномено-
феноменологически вводимым случайным вынуждающим силам.
В соответствии с гамильтоновым приближением предпо-
предположим, что все аргументы функций Fh берутся в одно
и то же время (хотя они могут относиться к различным
областям пространства). Далее будем рассматривать
только временные свойства уравнений D.26).

§ 3. МАРКОВСКИЕ И НЕМАРКОВСКИЕ ПРОЦЕССЫ	89
Для заданного набора вынуждающих сил уравнения
D.26) приводят к однозначной зависимости величин \|>й
от их значений в предшествующие моменты времени.
Если же силы {fm} имеют стохастический характер, то
уже нельзя считать, что поведение распределения вели-
величин \|зй в данный момент однозначно определяется их
распределением в некоторый предшествующий момент.
Чтобы сделать смысл этого замечания более ясным, вве-
введем обозначение
)	D-27)
для того решения уравнения D.26), которое соответ-
соответствует заданной предыстории вынуждающих сил и удов-
удовлетворяет при t = т начальному условию
гМт) = Ф*.	D-28)
не зависящему от {fm}. Тогда распределение величин \pft
в момент времени / формально определяется соотноше-
соотношением
Р Ш, 11Ы, т) = (П б [% - гЬ @1) =
х к
= (П б fok - % (/, {U; М, т)]). D.29)
При t = т распределение имеет следующий вид:
Р ({%}, т | Ы, т) = (П б (tfe - Фк)) = П б (% - Фк), D.30)
4 к	I	к
что дает нам основание рассматривать D.29) как услов-
условное распределение (см. следующую главу). Для времен
t > т распределение величин р в силу D.29) отражает
особенности ансамбля вынуждающих сил {/т}. Каждое
решение D.27) зависит от значений вынуждающих сил
только в интервале х, /. Однако эти значения, соответ-
соответствующие данному моменту времени, можно связать с
событиями в предшествующие моменты (т. е. для t<t).
В этом случае р ({\|з&}, / \ {ф&}, х) зависит не только от на-
начальных условий {фй} в момент времени х, но и от
свойств ансамбля в прошлом.
Для проверки этих зависимостей можно предста-
представить себе избранные изменения ансамбля случайных

SO	ГЛ. 4. СТАТИСТИКА ПОЛЯ
вынуждающих сил. Для этого будем отбрасывать преды-
предыстории, которые в прошлом не удовлетворяли какому-
либо условию, а затем рассчитаем значение D.29) в моди-
модифицированном ансамбле. Такие изменения будут влиять
на p({i|)ft}, ^|{ф,}, т) в большей или меньшей степени, что
может служить мерой независимости ансамбля случай-
случайных сил от свойств в прошлом.
Весьма важные процессы, для которых распределе-
распределение A.29) совершенно не зависит от изменений свойств
ансамбля в прошлом, называются марковскими. Все
другие процессы носят название немарковских. В неко-
некоторых случаях число начальных условий может быть
увеличено настолько, что немарковская система стано-
становится марковской. В качестве примера рассмотрим
объем, содержащий соударяющиеся молекулы газа. По-
Положение одной молекулы можно определить из урав-
уравнения
mx{t) = f(t),	D.31)
где случайная сила f описывает влияние других моле-
молекул. Очевидно, что поведение x(t) в будущем зависит
от предыстории случайной силы, поскольку рассматри-
рассматриваемые молекулы все время взаимодействуют с другими
молекулами. Тем не менее этот процесс можно, конечно,
представить как многомерный марковский, если ввести
примерно 1023 величин, необходимых для задания рас-
распределения начальных условий для всех молекул.
На практике эту трудность обходят, предполагая, что
соударения происходят упруго, а значение случайной
силы не зависит от ее предыстории (является б-корре-
лированным). Например, классическая задача о слу-
случайном блуждании (винеровский процесс) описывается
уравнением D.31), если предположить, что f(t) опреде-
определяется выражением
exp [i J s (/') f (f) dt']} = ехр [ - ~ a J s2 (/') dt'], D.32)
которое является частным случаем выражения C.18) при
m = 0 и ji (v) = 4.n2ov2. Классическое броуновское движе-
движение также подчиняется уравнению D.31), но связано с

§ 3. МАРКОВСКИЕ И НЕМАРКОВСКИЕ ПРОЦЕССЫ	91
другим стохастическим процессом, характеризуемым вы-
выражением
(exp [i / s (П f {?) dt']) = exp [ - 1 b J s2 (f) dl'], D.33)
гдеA(\') = 6. Этот процесс, характеризуемый постоянной
спектральной плотностью, часто называют «белым шу-
шумом». Что касается поведения переменных х, то для за-
задачи о случайном блуждании оно является марковским,
а для броуновского движения — немарковским. Чтобы
броуновское движение представляло собой марковский
процесс, необходимо рассмотреть условные распределе-
распределения как координат, так и скоростей молекул. Различия в
этих случаях физически ясны. Следует отметить, од-
однако, что когда протекание процесса f(t') зависит от
его предыстории (как это будет иметь место, если изме-
изменить с помощью фильтра его спектр, так что
/ \х (v)dv<oo), процесс х не будет марковским и его
нельзя превратить в таковой путем задания любого ко-
конечного числа начальных условий.
В некоторых случаях физическая задача удовлетво-
удовлетворяет марковским условиям или соответствующей идеали-
идеализации, относящейся к вынуждающим силам. Однако,
если эти условия не выполняются, следует учитывать
негдарковский характер процесса, включая эффекты
инерционности во взаимодействии между системой и
термостатом. Некоторые наиболее «очаровательные»
стохастические задачи соответствуют немарковским про-
процессам.
Б. Соотношения для марковских процессов
В частных случаях марковских процессов можно вы-
вывести несколько важных соотношений для условного
распределения. Обратимся опять к распределению
D.29), но изменим предысторию ансамбля, рассматри-
рассматривая среднее значение
(П
к
- 4rfe (/, {/;„}; {Ф(}, т)] И 6 [Фг - % (Т, {fj; {К,}, 0)}).
I
D.34)

92	ГЛ. 4. СТАТИСТИКА ПОЛЯ
Здесь наложено ограничение на предшествующее пове-
поведение вынуждающих сил, а именно мы считаем, что оно
согласуется с эволюцией параметров поля от значе-
значения {>„,.} в нулевой момент времени до значения {ф(}
в момент времени т. Согласно предположению о марков-
марковском характере процесса, это изменение не должно
влиять на результат D.29), за исключением возможного
появления численного коэффициента А, связанного с от-
отсутствием нормировки ансамбля. Таким образом, сред-
среднее значение D.34) должно иметь вид
РШ, t 1Ы- т)Л.	D.35)
Далее, полагая / = т и используя D.28) [ср. D.30)],
нетрудно получить
t|{U, 0).	D.36)
Интегрируя D.34) по переменным {ф;} и пользуясь
свойством б-функций в подынтегральном выражении,
получаем известное уравнение Колмогорова — Чепмена
Р(Ш.
= (II6 [% -'MMU; (U 0)]) =
= ?W,'I{UO).	D.37)
В дифференциальной форме это уравнение имеет вид
Ш, Ш) р (Ы) dN%, D.38)
где не играющие роли аргументы опущены и введено
интегральное ядро
К (Ы. Ш) = jrP Ш. 11 Ы, т) \x_t. D.39)
Для стационарного распределения К не зависит от вре-
времени.
Действие интегрального ядра можно представить так-
также другим образом, а именно посредством дифферен-
дифференциального оператора, который в некоторых случаях
можно адекватно аппроксимировать оператором конеч-

§ 3 МАРКОВСКИЕ И НЕМАРКОВСКИЕ ПРОЦЕССЫ	93
ного порядка. Общее выражение для такого дифферен-
дифференциального оператора можно получить следующим обра-
образом. Обозначим характеристическую функцию распре-
распределения p{{tyk)) через
С Ы зз exp [W({sk})} = (ехр
= J ... J ехр (г 5] skipk) p Ш) <*"%; D.40)
тогда
р(Ы) =
= Bя)"Л' J . .. J ехр [-/ \] 5Л + Г ({sk})] dNsk. D.41)
Из последнего соотношения непосредственно следует
др (Ш) _ д /г., п _
	g~t	. = Р \\W) —
= {2n)~N J ... JW ({sk}) ехр [ - i J
... J exp [ - i J] sfe^, + Г ({sfe})]
где IF = dW7/^. Как и в гамильтоновой формулировке
механики, уравнение определяет последующее распре-
распределение р по заданным начальным условиям. Для ста-
стационарного распределения W является постоянным, не
зависящим от времени оператором.
Удобно выразить W через кумулянты распределения
(называемые также семиинвариантами, или «связанными
моментами»), которые выражаются как нелинейные ком-
комбинации различных моментов случайных величин. Са-
Самое простое соотношение между обычными и связанными
моментами получается для производящего функционала,
который имеет вид
ехр [W (Ы)] = <ехр (/ 2 5Л)> =
= ехр {([ехр (г 2 зи*) - !]>„}, D.43)

94	ГЛ. 4. СТАТИСТИКА ПОЛЯ
где (...) и (...)св означают соответственно обычные и
связанные моменты. Из этого соотношения следует,
что W можно разложить в ряд
W({sk}) = ([exp (i V[ s.%) - 1])св =
оо
= 7 ¦	7 S-. .. . s- /^bi ... ibb N . D.44)
"-1	;'i	*n
Коэффициенты ряда представляют собой кумулянты.
С помощью D.43) их можно выразить через обычные
моменты. В частности, при разложении по степеням s\
несколько первых кумулянтов определяются следующим
образом (для одной переменной \j)i == г|з):
(г|з)св = (г|з),	D.45а)
('ф2)св= (^2) ~ (^J.	D.456)
(ф^св = ("Ф3) — 3 (г|з2) (гр) + 2 (фK,	D.45в)
('•I^cb = (Ф4) ~ 3 Aф2J — 4 (-ф3) (i))) +12 (о|г) (г|зJ — б (г|зL. D.45г)
Для гауссовых процессов кумулянты выше второго по-
порядка равны нулю. В случае приближенного анализа
распределения D.41) предпочтительнее, чтобы были
равны нулю кумулянты (а не моменты) высшего поряд-
порядка, поскольку это по существу соответствует анализу
корреляций низшего порядка и пренебрежению корреля-
корреляциями высокого порядка. Такое описание часто оказы-
оказывается адекватным или по крайней мере является удоб-
удобным отправным пунктом [хотя, строго говоря, если
^({Sft}) представляет собой полином, он должен быть
второго порядка, чтобы соотношение D.43) соответство-
соответствовало точной характеристической функции].
Как при точном, так и при приближенном рассмотре-
рассмотрении, комбинируя D.42) и D.44), можно получить соот-
соотношение
v
Г1г
X 1 I? (^'Ч • • • ^fen)cB \ Р {Ш)> D-46)

§ 4. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	95
которое известно под названием стохастического урав-
уравнения. Если суммирование обрывается при п = 2, тогда
D.46) представляет собой известное уравнение Фокке-
ра — Планка. В диффузионном приближении все члены
выше п = 2 опускаются, что и приводит к уравнению
Фоккера — Планка.
§ 4. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В заключение подчеркнем опять общность анализа
флуктуационных уравнений с помощью характеристиче-
характеристических функционалов. Даже в «чистых» случаях (см. вы-
выше п. 1 и 2), когда имеется неопределенность только в
начальных условиях, описанная методика приводит к со-
совершенно общим решениям. Например, для функционала
C{s} = (exp[/ \ s{t')x{t')dt'})	D.47)
простое уравнение х = 0 принимает вид
d2 6С {s} _ п	,. .„¦.
Чтобы найти общее решение этого уравнения, заметим,
что: 1) можно ограничиться рассмотрением функций
s(t'), которые обращаются в нуль для достаточно
больших положительных и отрицательных значений /';
2) для таких функций однозначно определяются и мо-
моменты
JVps(/')d*',	D.49)
а моменты в свою очередь однозначно определяют функ-
функцию; 3) функционал С можно рассматривать как функ-
функцию величин sp, р = 0, 1, 2, ... . Согласно правилу диф-
дифференцирования, получаем соотношение
_«_r = V -!!??_ J?.-у tpJ?. и чел
6s (t) L — Zt 6s (/) dsp - 2ul dsP '	^4-йи'
p=0	p=0
которое отображает полную временную зависимость.
В соответствии с D.48) С может зависеть только от So

96	ГЛ. 4. СТАТИСТИКА ПОЛЯ
и s\. В частности, вследствие того что С является ха-
характеристическим функционалом, имеем
{t')dt', JVs (*')<**') =
= | exp {i [jc0 f s (f) dt' + v0 J t's (*') dt']} p (x0, v0) dx0 dvQ.
D.51)
Естественно интерпретировать х0 и v0 как начальные
координаты и скорость. Заметим, в частности, что
С {s} = ехр [ - а [ s {t') dt') - Ъ (J t's (/') dt') J D.52)
является решением уравнения D.48), соответствующего
независимым нормально распределенным х0 и v0.
Хотя случай свободных частиц чрезвычайно прост,
следует подчеркнуть, что найденное общее решение
D.48) содержит все решения с произвольными распреде-
распределениями начальных значений. Все представляющие ин-
интерес временные корреляции также можно найти из
решения, полученного в виде характеристического функ-
функционала. Такие решения, как мы видели выше, пред-
представляют интерес даже в том случае, когда на частицы
действуют случайные силы. Отметим также то обстоя-
обстоятельство, что в своем анализе мы ограничились рас-
рассмотрением подходящего подкласса гладких функций и
выбрали соответствующую параметризацию (например,
{sp}). Это может оказаться полезным и в более общих
случаях.
К динамическим уравнениям и их анализу с помо-
помощью характеристических функций мы вернемся в гл. 9.

Статистические состояния
в квантовой теории
§ 1. ВВЕДЕНИЕ
До сих пор анализ электромагнитного поля (точнее,
его идеализированного представления в виде действи-
действительного скалярного поля УМ) был сугубо классиче-
классическим. Статистический ансамбль, обусловливающий как
эффекты частичной когерентности при интерференции,
так и непуассоновскую статистику фотоотсчетов, имел
строго классическое происхождение. Результаты клас-
классической, теории частичной когерентности хорошо под-
подтверждаются экспериментально; классическое рассмот-
рассмотрение удовлетворительно объясняет качественные осо-
особенности корреляции и флуктуации фотоэлектрических
отсчетов. Однако при строгом анализе следует, конечно,
принимать во внимание квантовую природу поля излу-
излучения. В конечном счете квантовый анализ, к которому
мы приходим в силу логической необходимости, должен
давать результаты, качественно подобные результатам,
получаемым в классической теории. Существует не толь-
только качественное сходство между квантовыми и класси-
классическими результатами; как будет показано в следующих
главах, имеет место тождественность в формулировках,
которая при использовании определенной схемы интер-
интерпретации позволяет изложить предшествующие класси-
классические результаты на квантовом языке.
В этой главе мы рассмотрим некоторые основные по-
понятия квантовой механики, лежащие в основе такого
анализа, а именно гильбертово пространство, линейные
операторы, вычисление следа, обращая особое внимание
на статистическое описание квантовых состояний. Ниже
будут рассмотрены примеры для систем с конечным

98	ГЛ. 5, СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
числом состояний, для систем, обладающих одной и ко-
конечным числом степеней свободы, и, наконец, для неко-
некоторых систем с бесконечным числом степеней свободы,
которые необходимы для описания поля излучения,
§ 2. КВАНТОВЫЙ ФОРМАЛИЗМ И ОБОЗНАЧЕНИЯ
Формулировка квантовой теории (как для самых
простых, так и самых сложных систем) влечет за собой
представление наблюдаемых и различных динамических
переменных в виде линейных операторов, действующих
в гильбертовом векторном пространстве. Сами же век-
векторы в свою очередь соответствуют чистым состояниям
системы.
А. Гильбертово пространство
Гильбертово пространство во многих отношениях
аналогично известному трехмерному эвклидову вектор-
векторному пространству. В элегантных обозначениях Дира-
Дирака [5.1] векторы гильбертова пространства обозначаются
символами «кет» (например, |ij?)) с разными индексами.
Как и в обычном векторном анализе, различные векторы
гильбертова пространства можно складывать или умно-
умножать на комплексные скалярные величины и таким об-
образом получать новые векторы. Число линейно незави-
независимых векторов определяет измерение D гильбертова
пространства, которое может быть конечным или счетно
бесконечным. Определим для каждой пары векторов
|г|з) и \Х) комплексное число
<Ь|Ч>),	EЛ)
называемое скалярным произведением по аналогии со
скалярным произведением в векторном анализе. Это
произведение линейно по вектору |ip) и подчиняется
двум условиям:
0,	E.2)
причем в последнем соотношении равенство имеет ме-
место в том и только в том случае, когда |-ф) = 0 (нулевой
вектор). Неравенство Шварца означает, что
t),	E.3)

§ 2. КВАНТОВЫЙ ФОРМАЛИЗМ И ОБОЗНАЧЕНИЯ	99
причем равенство имеет место, когда и только когда
IA) = a|ij)) для некоторого комплексного числа а. Если
|г|з)=О, то (Я|г|)) = О для всех \К) и наоборот. Если для
данных векторов \Х) и |г|з), ни один из которых не яв-
является нулевым вектором, (Л|г|)) = О, то такие векторы
называются ортогональными. Величина, или норма, каж-
каждого вектора конечна и определяется выражением
111^>!!=<г|^>'/2>0.	E.4)
Если норма равна 1, то векторы называются нормиро-
нормированными. Из E.3) непосредственно вытекает неравен-
11|Ь> 1>1К11и>|| + |||1>>||.	E.5)
В каждом гильбертовом 'пространстве может быть вве-
введен «полный ортонормированный базис», а именно на-
набор векторов {\п)\, и = 1, 2, ..., D, для которых
{п\т) = 8пт и которые накрывают1) гильбертово про-
пространство. Каждый вектор \ty) можно разложить по на-
набору векторов {\п)}:
I4>>=2i|>jn>=2ln><nl4>>	E-6)
в полной аналогии с разложением по ортонормирован-
ному базису в общепринятом векторном анализе. Квад-
Квадрат нормы, выраженный через коэффициенты разложе-
разложения E.6), имеет вид
Если D < оо, то коэффициенты tyn могут быть произ-
произвольными комплексными числами. Чтобы норма имела
конечное значение при D = оо, сумма квадратов коэф-
коэффициентов {г|)„} должна быть конечной. Далее, из свой-
свойства полноты гильбертова пространства следует, что
каждой последовательности с конечной суммой квадра-
квадратов отвечает определенный вектор |ip), причем этот
класс векторов полностью исчерпывает гильбертово про-
пространство.
') См. примечание на стр. 169. — Прим. ред.

100	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
Последнее замечание является ключевым моментом,
связанным с представлением абстрактных векторов гиль-
гильбертова пространства при помощи последовательностей
комплексных чисел; фактически именно такими были
первоначальный математический подход, развитый
Гильбертом, и первоначальная формулировка квантово-
механического описания, данная Гейзенбергом. Можно
сказать, что базисные векторы \п) «порождают» пред-
представление вектора |г|з) с помощью последовательностей
комплексных чисел г|з„ = (я|г|>). В обозначениях Дирака
скалярное произведение равно
<МЧ>)=2<Мп)<п|ч>)	E.8)
по аналогии со скалярным произведением обычных век-
векторов, выраженным через их компоненты.
Б. Линейные операторы
Наблюдаемые и динамические величины представ-
представляются линейными операторами, т. е. линейными пре-
преобразованиями, превращающими один вектор в другой.
Иначе говоря, если А представляет собой оператор,
тогда A\ty) является преобразованным вектором, а
(Х|Л|г|з)—его скалярным произведением с вектором
|Х). Операторы можно складывать, а также умножать
на комплексные числа или на другие операторы, получая
таким образом новые операторы. Единичный оператор /
оставляет все векторы и операторы без изменений. Для
краткости мы будем часто писать численный коэффи-
коэффициент с, в действительности означающий оператор с/1).
Если для всех нормированных векторов \Х) и |г|з)
\(Х\А |\)з) j ^C b < оо, то оператор А называется ограни-
ограниченным. Наименьшее значение Ъ называется нормой опе-
оператора А и обозначается ||Л||. В конечномерном гиль-
бертозом пространстве каждый оператор ограничен,
однако это не справедливо для пространства с беско-
') Динамические величины удобно обозначать как <«7-числа»
при квантовом рассмотрении и как «е-числа» при классическом рас-
рассмотрении. Часто оператор, равный произведению единичного опе-
оператора на число, также называют с-числом.

§ 2. КВАНТОВЫЙ ФОРМАЛИЗМ И ОБОЗНАЧЕНИЯ	101
нечным числом измерений. Детальное изучение неогра-
неограниченных операторов представляет собой серьезное ма-
математическое исследование, поэтому мы вынуждены
рассматривать такие операторы эвристически, обра-
обращаясь главным образом к физической интуиции. Появ-
Появление используемого ниже не вполне четкого понятия
«почти все» (suitably many) как раз и связано с труд-
трудностями, обусловленными неограниченными операто-
операторами.
В представлении гильбертова пространства последо-
последовательностями {г|)„} оператору А соответствует матрица
{Атп} с элементами
Атп = (т\А\п).	E.9)
Элемент Атп можно интерпретировать как т-ю компо-
компоненту вектора А\п). Из E.6) и E.9) следует, что век-
вектор Л|г|з) в свою очередь может быть представлен с по-
помощью последовательности {(^4i|))m}> где
= (т | А | ф) = 2 (т \ А | п) (п | ф> =
D
= 2
E.10)
Очевидно, что единичному оператору / соответствует
единичная матрица, поскольку {т\1\п) = {т\п)= Ьтп-
В обозначениях Дирака имеем следующее основное
соотношение:
D
/=Sl«>(nl,	E.11)
п = \
которое называют разложением единичного оператора.
Вектор \п), записанный в виде (п\ (соответствующее
обозначение носит название «бра»-вектора), называют
сопряженным. Из обозначения А =\п){т\ естественно
вытекает определение {k\A\\!p) = {X\n){m\ty). Подстав-
Подставляя единичный оператор в вышеприведенную формулу,
нетрудно видеть, что соотношения E.8) и E.10) яв-
являются простыми тождествами. Соотношение E.11)
справедливо для произвольного полного ортонормиро-
ванного базиса {\п)}.

102	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
Оператор Л+, сопряженный оператору А, опреде-
определяется соотношением
<х|Л+|ч>> = <Ч>|Л|Я>\	E.12)
которое должно выполняться для всех (или почти всех)
\Х) и |г|з). Если AAf = AfA = I, то А+= А и опера-
оператор А является унитарным. Для унитарного оператора А
имеем \\А |г|з) II = II |\|))|| для любого вектора |t|j). Если
Л+ = А, то оператор А называется эрмитовым. Из E.12)
следует, что значение (г|з|Л|г|з) для эрмитова оператора
всегда действительно. Эрмитов оператор А, удовлетво-
удовлетворяющий условию (г|з|Л |г|з)^О для всех (или почти всех)
|г|з), называют положительным. В конечномерном гиль-
гильбертовом пространстве каждому эрмитову оператору
соответствует полный набор ортогональных собственных
векторов и действительных собственных значений, для
которых имеет место соотношение
А\ап) = ап\ап).	E.13)
Если оператор Л положителен, то а„^>0. В представ-
представлении базиса \ап) оператор Л диагоналей, т. е.
(ат\А \ап) = ап8пт. В гильбертовом пространстве с бес-
бесконечным числом измерений можно таким образом
диагонализовать не каждый эрмитов оператор, даже
если он ограничен.
Два момента, относящиеся к используемым нами
эрмитовым операторам, заслуживают комментариев.
Будем предполагать, что эрмитовы операторы, с кото-
которыми мы имеем дело, обладают полными спектральными
разложениями и являются, таким образом, самосопря-
самосопряженными по математической терминологии. Это свой-
свойство означает, что эрмитов оператор А порождает
унитарное преобразование U(s) = exp(isA), где s — дей-
действительное число, и что величина (г|з|ехрA$Л) |г|з) до-
допускает представление
(г|з | eisA 11|>> = J eisa da (a),	E.14)
где а — некоторая (вероятностная) мера, определяемая
величинами ji|)) и Л. Чтобы найти пример оператора,

§ 2. КВАНТОВЫЙ ФОРМАЛИЗМ И ОБОЗНАЧЕНИЯ	103
который является эрмитовым в элементарном смысле,
но не удовлетворяет соотношению E.14), достаточно
рассмотреть оператор —ihd/dx, действующий в гильбер-
гильбертовом пространстве функций f(x), определенных для
х > 0. В физике обычно вводят ненормируемые собствен-
собственные векторы (нормировка на 6-функцию) \А') для зна-
значения А' эрмитовых операторов Л с непрерывным спек-
спектром. Мы не будем пользоваться такими векторами, под-
подчеркнем только, что неосмотрительное их применение
может иногда приводить к неприятностям. Пусть, на-
например, Л и В — эрмитовы операторы, которые удовлет-
удовлетворяют соотношению АВ = ВА + 1В, и пусть для не-
некоторого действительного А' имеет место соотношение
А\А') = А'\А'). Тогда В\А') также является собствен-
собственным вектором оператора Л с комплексным собственным
значением А' + i, что противоречит свойству эрмитово-
сти оператора Л. Чтобы избежать этих затруднений,
считают либо \А'), либо В\А') ненормированным.
Предположим, что в бесконечномерном пространстве
(D = оо) мы рассматриваем положительный эрмитов
оператор, который обладает полным набором собствен-
собственных векторов и собственных значений E.13). Тогда опе-
оператор Л можно представить следующим образом:
оо
А = Ъ\ап)ап(а,1\,	E.15)
где коэффициенты ап ^ 0 действительны. Если ап ^С
¦;С b < оо, то оператор Л ограничен, в противном случае
нет. Важный частный случай ограниченных операторов
мы имеем, когда
оо
2 ап<оо.	EЛ6)
В этом случае существует след оператора Л, а именно
оо	оо
Л1	\	^^	^	/Г* 1 *7\
\an)=2j й„<оо,	E.17)
<>
и А называют оператором с конечным следом (tra-
(traceable). В связи с этим результатом можно привести
несложную математическую теорему: для положитель-
положительных эрмитовых операторов Л значение 5р(Л) не зависит

104	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
от того, какой полный ортонормированныи базис
используется для оценки суммы (например, это могут
и не быть собственные векторы данного оператора).
Таким образом, значение следа Бр(Л) является свой-
свойством, присущим непосредственно самому оператору.
Далее, более сложная математическая теорема утверж-
утверждает, что если оператор А положителен и эрмитов, а его
след Бр(Л) конечен, то такой оператор обязательно об-
обладает полным ортонормированным набором собствен-
собственных векторов и соответствующих собственных значений,
для которых выполняются E.15) и E.16).
В случае пространства с бесконечным числом изме-
измерений класс операторов, у которых существует след
Бр(Л), не ограничен рассмотренными положительно
определенными эрмитовыми операторами. Однако каж-
каждый оператор Т с конечным следом имеет полярное раз-
разложение (polar decomposition) T = VA, где А — поло-
положительный эрмитов оператор с конечным следом вида
E.15) и оператор V—изометрический, т. е. обладаю-
обладающий свойством V'V = I. Такое разложение является
аналогом полярной формы z = ei(Pr, справедливой для
произвольного комплексного числа z. Оператор V обла-
обладает следующим свойством: он преобразует любой орто-
ортонормированныи набор векторов {|\|зп)} в другой орто-
ортонормированныи набор векторов {|л„)}. С учетом соот-
соотношения E.15) отсюда следует, что каждый оператор Т
с конечным следом допускает каноническое разложение
оо
7"=2|ЬП)РП<Ч>Л	E-18)
П = I
где р„^>0 — действительные коэффициенты, удовлетво-
удовлетворяющие условию 2 Рп<°°> а {\^п)} и {|г|зп)} — полные
ортонормированные базисы. Соотношение E.18) можно
также рассматривать как каноническое определение та-
таких операторов, для которых след можно найти одно-
однозначно. Отсюда, в частности, следует
оо
2pn<i>Jbn>.	E. i9)

§ 2. КВАНТОВЫЙ ФОРМАЛИЗМ И ОБОЗНАЧЕНИЯ	105
Этот ряд сходится абсолютно и в силу неравенства
Шварца E.3) ограничен величиной
Это выражение определяет полезное понятие «следовой
нормы» (trace-class norm), относящееся к операторам Т
с конечным следом; оно отличается от понятия нормы
оператора \\T\\. Соотношение E.17) показывает, что для
положительных эрмитовых операторов с конечным сле-
следом Бр(Л)= ||ДЦЬ тогда как в остальных случаях имеет
место неравенство. Каноническое разложение E.18) и
следовая норма ИЛЬ используются в гл. 8.
В гильбертовом пространстве с конечным числом из-
измерений (D < оо) каждый оператор имеет конечный
след. Следовательно, каждый оператор допускает кано-
каноническое разложение, подобное E.18), но содержащее
только первые D членов.
В. Статистические состояния
Чистые состояния. В квантовой теории нормирован-
нормированные векторы |\р) гильбертова пространства соответ-
соответствуют чистым состояниям системы. Пусть эрмитов опе-
оператор О соответствует наблюдаемой физической вели-
величине, тогда среднее значение О в состоянии \ty) равно
действительному числу
@) = №<У\Ъ).	E.20)
В свою очередь высшие моменты О определяются дей-
действительными выражениями
<(?"> = <4,|<?n|i|>>.	E.21)
Если оператор О неограничен, то для некоторых со-
состояний значения {(Уп) могут быть неопределенными.
Однако, как и в классической теории вероятности, ха-
характеристическая функция распределения О в состоянии
|\|з), задаваемая соотношением
Се(з) = <ф|е''в|Ч,>,	E.22)
где оператор exp(rs<?) унитарен, всегда определена для
любых О и |i|)).

106	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
Как обычно, каждая характеристическая функция
С© (s) представляет собой непрерывную функцию s и
является фурье-образом распределения наблюдаемых
значений, соответствующих оператору 0 х). Эти наблю-
наблюдаемые значения имеют разброс, т. е. обладают отлич-
отличной от нуля дисперсией, если состояние |\|з) не является
собственным вектором оператора О. Но даже если век-
вектор |г|)) есть собственный вектор для одного оператора,
он не может быть собственным вектором операторов,
соответствующих всем наблюдаемым физическим вели-
величинам (поскольку не все операторы коммутируют). Сле-
Следовательно, в любом чистом состоянии всегда некоторые
наблюдаемые величины испытывают случайный разброс,
описываемый определенным распределением. Таким об-
образом, вероятностный подход неизбежен.
Два состояния мы считаем физически эквивалент-
эквивалентными, если одинаковы средние значения всех наблюдае-
наблюдаемых величин (или все их характеристические функции).
Поскольку все эрмитовы операторы в принципе соот-
соответствуют наблюдаемым величинам, функции |i|)i) и \ty-i)
отвечают одинаковым состояниям, когда и только когда
|г|л) =eitpj\|J). Иначе говоря, |г|л) и |г|J) тождественны,
если не говорить о возможном скалярном коэффициенте
с модулем, равным единице.
Чистое состояние можно описывать также с помо-
помощью матрицы плотности
E.23)
при этом правило расчета средних значений определяет-
определяется следующим образом:
(О) ^ Sp (ptf) = 2 (п| ч>) <ч> | О In) = <ф| О I ч>> E.24)
в полной аналогии с E.20). Поскольку матрица р имеет
вид E.15), она, очевидно, является эрмитовой положи-
положительной матрицей с конечным следом. Более того, по-
поскольку функция ji|)) нормирована,
Р2 = I Ч>> <Ч> I Ч>> <i|> I = I Ф> ф ! = Р-	E.25)
') В дальнейшем всюду для краткости вместо этой полной
формулировки пишется «характеристическая функция О». — Прим.
ред.

§ 2. КВАНТОВЫЙ ФОРМАЛИЗМ И ОБОЗНАЧЕНИЯ	107
Матрицы плотности для двух физически эквивалентных
чистых состояний строго тождественны: pi = Hl)i)(^i I =
= |ij32)(i|J| = Р2- В качестве резюме отметим, что каж-
каждое чистое состояние системы может быть отождествле-
отождествлено с положительной эрмитовой матрицей плотности р,
для которой р2 = р и след Sp(p) = 1.
Смешанные состояния. В общей теории вероятности
обычно имеют дело с множеством условных распреде-
распределений. Предположим для примера, что p(T\S, М, Н)
означает условное распределение температуры Т наруж-
наружного воздуха для штата S Соединенных Штатов в те-
течение месяца Жив течение часа И дня. Однако если
имеется «размазанная» статистика, относящаяся к тем-
температуре Т утром Ж в течение лета 9* для всех штатов
Новой Англии JT&, то соответствующее (все еще услов-
условное) распределение определяется усреднением
Усреднение по Новой Англии
= I в летние месяцы и утренние ) р (Т \ S, М, Н).
{ часы	J
Такое усреднение («размазывание») более чистых усло-
условий неизбежно приводит к распределению, которое яв-
является более «широким», чем исходное.
Поучительно обратиться к более специальному при-
примеру. Распределения фотоэлектрических отсчетов, рас-
рассмотренные в гл. 2 и гл. 3, были выведены в два этапа.
Сначала с помощью соотношения B.2) мы определяли
условное распределение отсчетов для интенсивности,
имеющей значение I (t). Потом нашли окончательное
распределение отсчетов, усредняя условное распределе-
распределение по соответствующему распределению интенсивно-
стей; см., например B.10) или C.1). Как уже несколько
раз отмечалось, дисперсия отсчетов при усреднении по
интенсивности всегда возрастает1).
Способ, примененный для вычисления распределения
отсчетов, иллюстрирует удобный и наглядный метод
') Распределения D.29) и D.30) также, очевидно, являются
условными распределениями.

108	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
определения любого распределения вероятности. Сна-
Сначала необходимо определить чистые распределения, т. е.
такие условные распределения, в которых все осталь-
остальные существенные параметры постоянны, затем следует
провести усреднение по распределениям этих парамет-
параметров.
Применим описанный способ для нахождения рас-
распределения наблюдаемых значений произвольной вели-
величины О в квантовой теории. Каждое чистое распределе-
распределение, задаваемое своей характеристической функцией,
определяется соотношением
Се (S I Pa) = SP (Ра6) = <Фа | ^Ш I %)¦	E.26)
Как видно из обозначений, это распределение условно
по состоянию системы, задаваемому матрицей плотности
ра (или вектором |г|)а)). Если полные сведения о со-
состоянии системы отсутствуют, то следует провести усред-
усреднение распределения E.26) по различным ря. Обозна-
Обозначим через а набор неизвестных переменных величин
в ра я пусть ц(а) (с возможными б-функциями)—нор-
б-функциями)—нормированное распределение значений а. Тогда, пользуясь
линейными свойствами следа, найдем соответствующую
(и все еще условную) характеристическую функцию
С6 {s) = Се {s I р) = | ц (a) da Sp (Рае'*«) =
= Sp([ J(i (а) ра da]e'**) =
se),	E.27)
где
j	E.28)
Теперь независимо от того, какими являются фак-
фактически величины а или каков вид распределения (i(a),
имеет место примечательное свойство матрицы плотно-
плотности р. Очевидно, матрица плотности р положительна,
эрмитова и удовлетворяет условию Sp(p)=l. Таким
образом, в соответствии с замечаниями, сделанными в

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИЙ	109
связи с соотношением E.15), видно, что р всегда имеет
каноническое разложение
P=S 1Ц>„>Рп(Ча	E.29)
п = \
где Р„^0, ^ р„= 1, а {|г|з„)} образует полный ортонор-
п = \
мированный базис.
Таким образом, общее состояние системы соответ-
соответствует матрице плотности р в виде E.29). Среднее зна-
значение эрмитовой наблюдаемой величины О определяется
соотношением (О) = Sp(p(?), тогда как характеристиче-
характеристическая функция распределения наблюдаемых значений О
дается выражением
s6).	E.30)
Чистые состояния удовлетворяют условию р2 = р, но для
смешанных состояний, для которых в сумме E.29) со-
содержится более одного члена, это условие не выпол-
выполняется. Для конечномерного гильбертова пространства
полученные выше результаты изменятся только в том
отношении, что сумма в E.29) будет иметь конечное
число членов.
Для более наглядного пояснения этих свойств при-
приведем несколько примеров.
§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИЙ
В КВАНТОВОЙ ТЕОРИИ
А. Состояния поляризации монохроматического светового пучка
Рассмотрим состояния поляризации светового пучка
в качестве примера системы с конечным числом линейно
независимых состояний. Мы упрощаем задачу, фиксируя
дополнительные оптические степени свободы, соответ-
соответствующие направлению распространения и цвету (часто-
(частоте) волны. В этом случае пучок света имеет два незави-
независимых состояния, каковыми могут быть две линейные
поляризации. Как строго показано в следующей главе,
направления поляризаций перпендикулярны направле-
направлению распространения.

110	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
Статистические состояния такой идеализированной
системы не обязательно должны соответствовать поля-
поляризованному свету. В одном предельном случае, а имен-
именно в случае нулевой поляризации, когда никакое на-
направление не выделено, мы имеем смешанное состояние;
другому предельному случаю 100%-ной поляризации
отвечают чистые состояния. Смешанные состояния для
нашего рассмотрения можно образовать из чистых со-
состояний.
Поскольку возможны только два независимых со-
состояния поляризации, мы применим двумерное гильбер-
гильбертово пространство (D = 2). Таким образом, чистое со-
состояние можно представить нормированным двухкомпо-
нентным вектором
E.31)
4i i
Значения и, определяют характер поляризации. Напри-
Например, при и\ = 0, и2Ф0 (или наоборот) свет линейно
поляризован. Если и\ = ±ш2, свет циркулярно поляризо-
поляризован. В общем случае, когда ни одно из вышеприведен-
вышеприведенных условий не выполняется, свет поляризован эллипти-
эллиптически.
Матрица плотности чистого состояния E.31) пред-
представляет собой эрмитову матрицу второго порядка со
следом, равным единице:
u2ut \
. E.32)
и2и2}
Особенно удобное представление р, справедливое для
смешанных и чистых состояний, получается при исполь-
использовании стоксовых параметров1). Для чистого состоя-
состояния E.31) эти параметры определяются следующим об-
образом:
50 = ^ы1 + м*и2=1,	E.33а)
s, = и*и2 + и*м,,	E.336)
si = г' (и1и\ ~~ М1"г)'	E.33в)
s3 = u*ui — u'2ur	E.33r)
') См. книгу Борна и Вольфа [1.1], гл. X.

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИЙ	111
В любом случае (и в частности, для чистого состояния)
можно положить
' s0 + s3 s, — is2
Если ввести обычные матрицы Паули
'О 1\	/О -Л	/1 О
О/' °2 = [i О
и обозначить единичную матрицу через стс, то можно
написать
= j (SOCTO + S,CT, + S2CT2
E.35)
В свою очередь s,-, / = 0, 1, 2, 3, можно найти из р с по-
помощью соотношения
s, = Sp (pa,).	E.36)
Заметим также, что E.34) приводит к выражению
!(S2-s*).	E.37)
В обозначениях Стокса чистые состояния представ-
представляются единичными векторами s, s2=l. Это условие яв-
является следствием равенства нулю детерминанта матри-
матрицы р, записанной в виде E.32), откуда в силу E.37) вы-
гекает, что s2 = s^= I.
Смешанные состояния в свою очередь получаются из
чистых состояний. Пусть ра означает семейство чистых
состояний, определяемых соответствующим семейством
единичных векторов sa = Sp(paa). Тогда, согласно об-
общей формулировке E.28),
р = J A (a) pu da = у [l + о • | (j, (a) sa daj =
=1 A + s • а).	E.38)
Вследствие усреднения по различным единичным векто-
векторам значение s в E.38) всегда удовлетворяет условию

112	Г Л 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
s2<l, что является отличительным свойством смешан-
смешанных состояний. Следует иметь в виду, что различные
распределения ц(а), очевидно, могут приводить к оди-
одинаковым векторам s и, следовательно, к одинаковым
матрицам р. Короче говоря, одно и то же состояние мо-
жеть быть вызвано различными причинами.
Степень поляризации 53, независимо от вида поляри-
поляризации (линейная, круговая, и т. д.), определяется выра-
выражением
&>2=**2.	E.39а)
Если р! и р2— собственные значения матрицы р, то из
соотношений Sp (p) = pi + q2 = 1 и det(p) = pip2 в со-
сочетании с E.37) получаем
^ = 1 - 4 del (р) = (Pl + р2J - 4р,р2 = (р, - р2J. E.396)
Примем ,р( = ni/{nl + n2), t = l, 2; тогда из соотношения
E.396) следует, что параметр, определенный соотноше-
соотношением B.41), можно рассматривать как степень поляри-
поляризации.
Если перейти к общим формулировкам, то можно
сказать, что для чистого состояния степень поляриза-
поляризации 5s = 1, а для смешанного состояния 5s <1. Полно-
Полностью хаотическое состояние имеет степень поляризации
9* = 0 и задается матрицей плотности
/ 1 0 \
j	E-40)
Такое излучение можно разложить по любым двум орто-
ортогональным поляризациям с одинаковыми вероятностя-
вероятностями. Свет теплового источника неполяризован в том
смысле, что 9i = 0.
Б. Статистические состояния гармонического осциллятора
Гармонический осциллятор занимает центральное
место в квантовой механике вообще и в квантовой оп-
оптике в частности, поэтому рассмотрим его более под-
подробно. Введем эрмитов оператор координаты Q и
сопряженный ему эрмитов оператор импульса Р, удовле-

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИИ	113
творяющие каноническому коммутационному соотноше-
соотношению
[Q, P] = QP-PQ = ih.	E.41)
Разумеется, эти операторы вообще характеризуют одну
степень свободы и применимы не только к осциллято-
осцилляторам.
Операторы рождения и уничтожения. Свойства операто-
операторов Q и Р особенно удобно изучать с помощью опера-
операторов уничтожения а и рождения а+ , определяемых со-
соответственно соотношениями
В теории осциллятора ш интерпретируется как угловая
частота исследуемого осциллятора. Из E.41) следует
коммутационное соотношение
[а, «+] = аа+-а+а= 1.	E.43)
В результате умножения E.43) на а справа и на af сле-
слева получаем соотношения
Na = a(N-l),	E.44а)
ЛГа+= а+(ЛГ + 1).	E.446)
Здесь введен оператор числа частиц	(квантов)
N = а>а,	E.45)
который, очевидно, положителен и эрмитов. Повторное
применение этих соотношений приводит к выражениям
Nam = am (N - т),	E.46а)
Nafm = a+m (N + т)	E.466)
для всех т = 0, 1,2, ... . Далее, имеем
afmam ==M{N-l)(N-2) ...(N-[m-l])	E.47)
для любых т>-1. Левая часть соотношения E.47) за-
заведомо положительна для любых т. Следовательно,
распределение собственных значений оператора числа

114	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
частиц ;V не может быть непрерывным. Действительно,
если бы существовал непрерывный спектр собственных
значений, то существовали бы такие приближенные соб-
собственные состояния оператора Л/, для которых ни один
из множителей в правой части E.47) не был бы равен
нулю, причем при соответствующем значении т некото-
некоторые из множителей (например, один) могли бы стать
отрицательными.
Предположим поэтому, что для некоторого действи-
действительного числа оператор N имеет одно нормированное
собственное состояние
N]n) = n\n).	E.48)
Соотношение E.47) снова приводит к противоречию,
если п не является целым неотрицательным числом.
Чтобы показать, что п действительно целые положитель-
положительные числа, начнем для удобства с п = 0 и основного со-
состояния |0). Из E.466) следует, что
N(а*т 10» = a+m (N + m)\0) = m (a>m |О». E.49)
Следовательно, а+т|0) пропорционально \т) для каж-
каждого /п>-1. То обстоятельство, что данное утверждение
не бессодержательно, следует из ненулевого условия
нормировки
<0|ama+m|0) = m!,	E.50)
которое является следствием более общего соотношения
атаьп = (w + 1) (# + 2) . . . (ЛГ + т)	E.51)
для т^\. Поэтому в качестве нормированных собст-
собственных векторов оператора N с собственным значе-
значением п можно принять
Ц+'Ч0).	E.52)
Ути векторы удовлетворяют, например, соотношениям
flt | „) = уп + 11 п + 1),	E.53а)
а\п)=*У~п\п-1),	E.536)
которые отвечают соответственно увеличению	и умень-
уменьшению числа фотонов на единицу.

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИЙ	115
Наше предварительное рассмотрение оператора чис-
числа частиц N мы закончим нижеследующим замечанием.
Предположим, что существует дополнительный пара-
параметр вырождения, указывающий, например, что имеют
место L линейно независимых основных состояний
10, /), / = 1,2, ..., L, для которых N\0, /) = 0. Тогда,
как следует из предыдущего рассмотрения, существуют!
полных наборов состояний \п,1). Однако операторы а
и а не могут смешивать состояния с разными /. Что-
Чтобы избавиться от этого вырождения, постулируем, что
каждый оператор может быть представлен в виде функ-
функции операторов а и а . Другими словами, по предполо-
предположению квантование заключается в использовании не-
неприводимых представлений операторов Q и Р (в пред-
представлении Шредингера неприводимые операторы х и
—ib д/'дх появляются автоматически). При этом может
быть только один набор \п), п — 0,1,2, ..., который
образует полный ортонормированный базис для беско-
бесконечномерного гильбертова пространства. При рассмотре-
рассмотрении осциллятора удобно нумеровать состояния, соответ-
соответствующие собственным значениям оператора числа ча-
частиц N, начиная с нуля. Это приводит к очевидной и
простой модификации формул, полученных при общем
рассмотрении.
Статистические состояния. Важный набор матриц
плотности чистого состояния представляют собой мат-
матрицы, образованные из собственных состояний операто-
оператора N, а именно Qn = \n) (п\. В свою очередь важный на-
набор смешанных состояний определяется выражением
Р = 2 Р„1 п) (п |.	E.54)
л=0
Для гармонического осциллятора, находящегося в тепло-
тепловом равновесии при температуре Т (или обратной тем-
температуре р=1//с7\ где к — постоянная Больцмана), вес
равен
A Рй) ~п^На,	E.55)
поскольку (как показано в следующей главе) оператор
энергии, или гамильтониан, Ж = fiutN, и поэтому

116	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
собственные значения энергии Е„ = йсоп. Для среднего
числа заполнения в тепловом состоянии получаем
= Sp
п=0
E-56)
где, введя г/ = ехр(—рйш), мы использовали соотноше-
соотношение
d 1	у
dy 1 — у 1 — ;/ г/~' — 1 '
В результате находим
^C7-	E>57)
Характеристическая функция для оператора N имеет вид
оо
= Т1^Йтп-	E-58)
В следующих главах мы будем интересоваться слу-
случаями, когда рп в E.54) соответствуют распределению
Пуассона
pn==J_^e-ii.	E.59)
При этих условиях среднее число частиц равно
оо
(N) = Sp (p/V) = У ~ \апе-» = (х,	E.60)
мат fll

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИИ	117
а для характеристической функции оператора N имеем
оо
CN (s) = Sp (ре<**) = J] ~ y.neisne-» =
= ехр[(е"-1Ы,	E.61)
т.е. она похожа на чисто классическое выражение B.3).
Имеется большое число других матриц плотности,
которые тоже могут представлять интерес. Хотя все та-
такие матрицы имеют каноническое разложение E.29),
иногда удобно применять другую форму записи и вы-
выражать их через собственные состояния \т) оператора
числа частиц, имеющие важный физический смысл. Для
каждого вектора |г|зп), входящего в E.29), .можно на-
написать разложение
со
1Ч>„>= 2 Цп,т\т),	E.62)
так что
Кт\)К(€,т
п = \ т, т'=д
со
= 2 I m) p (m, m') <т' |,	E.63)
т, т'=0
где, очевидно,
со
р (т, т') = 2 Ч>„ тР„< т- = (т I P I т1). E.64)
Последняя форма в соотношении E.63) соответствует
матрицам самого общего вида. Чтобы матрица р была в
действительности матрицей плотности, она должна об-
обладать следующими свойствами: 1) матрица р должна
быть эрмитовой, р(т', т) = р(т, т')*; 2) должна быть
положительной сумма
2 C;P(m,m')cm,>0	E.65)

118	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
(при условии что сумма квадратов коэффициентов {с,,}
конечна); 3) след оператора р должен быть конечным:
оо
Sp(m, m)=l.	E.66)
т = 0
При р(т, т') = Pm6m m, приходим к рассмотренному выше
частному случаю E.54).
В. Статистические состояния нескольких осцилляторов
Рассмотрим К независимых осцилляторов с угловы-
угловыми частотами &h, k=\,2, ..., К- Каждый осциллятор
описывается своими операторами координаты Qh и им-
импульса Ph, удовлетворяющими соотношениям
[Qk, Qk'\ = [Pk, Pk'\ = 0.	E.67a)
[Qfc, PA = №kh..	E.676)
Введем для каждого осциллятора операторы уничтоже-
уничтожения и рождения
'/2 Pk,	E.68а)
)'/2 Pk	E-686)
и соответствующие операторы числа частиц
К каждому в отдельности из рассматриваемых ос-
осцилляторов полностью применим проведенный выше
анализ. Существенно отметить то обстоятельство, что
собственные векторы какого-либо одного оператора Nh
не накрывают всего гильбертова пространства (посколь-
(поскольку теперь представление для любого из операторов Qh
и Pi, приводимо). Если же предположить, что набор Qh,
Ph, k=\,2, ..., К, является неприводимым, то тогда

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИИ	119
набор единичных собственных векторов всех операто-
операторов Nk, обозначаемый
\щ,п2, ..., пк) = \{пк}),	E.70)
образует полный ортонормированный базис1)
Многие результаты, полученные выше для одного ос-
осциллятора, легко обобщить. Чистые состояния с опреде-
определенными числами заполнения определяются выраже-
выражением
а частный класс матриц плотности имеет вид
Последняя форма, конечно, эквивалентна общему выра-
выражению E.29), поскольку набор всех последовательно-
последовательностей {пк} счетен.
Особый интерес представляет тепловое распределе-
распределение К независимых осцилляторов, для которых гамиль-
гамильтониан имеет вид
к	к
Ж=Ъ h®kata,, = 2 йсо, N .	E.73)
В этом случае
к
Pr» i = П О - ехр [ - pficoft]) ехр ( - nftpfi©ft). E.74)
В результате получаем выражение
Д)-1' E-75)
') Эти соображения можно изложить несколько иначе, а имен-
именно исходить из того, что Л'ь Л^г, ..., Nk образуют полный набор
коммутирующих операторов, собственные векторы которых одно-
однозначно определяются (с точностью до несущественного общего фа-
фазового коэффициента) набором соответствующих собственных зна-
значений.

120	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
которое представляет собой сумму выражений E.57),
записанных для различных частот. Характеристическая
функция Е имеет вид произведения
k=\
что указывает на независимость вклада от каждого ос-
осциллятора.
Для многомерного пауссоновского распределения,
для которого
к
к
Ры = П iy № ехР (- >**)•
средние числа заполнения, очевидно, равны (Nk) = pft.
Следовательно, снова применяя E.73), получаем
_	к
2	E.78)
в то время как характеристическая функция для ? равна
Г К	1
= ехр 2 (exp [/fioofes] — 1) |ife . E.79)
Для нескольких осцилляторов можно получить формулу,
подобную E.63), пользуясь разложением единичного
оператора
оо
/= S I {«*» <{«*} I.	E.80)
Таким образом, любую матрицу плотности р можно
представить в виде
где
р(К1-К})-(К]1р1К}>- E-82)

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИЙ	121
Эти коэффициенты удовлетворяют очевидным требова-
требованиям эрмитовости, положительности и конечного значе-
значения следа, которые записываются по аналогии с E.65)
и E.66).
Г. Статистические состояния для бесконечного
числа осцилляторов
Теперь рассмотрим переход (К—+ °о) к бесконечному
числу осцилляторных степеней свободы Q/,, Ph, k =
= 1, 2, ..., при физически естественных предположе-
предположениях, что оператор полного числа частиц
N = 2 Nk	E.83)
и оператор полной энергии
со
2% = 2 ficufcWfc	E.84)
k=i
остаются хорошо определенными. Для правомерности
этого достаточно, чтобы полный ортонормированный ба-
базис в гильбертовом пространстве состоял из собственных
векторов операторов числа частиц
|«„«2> ...) = |К»,	E.85)
для каждого из которых собственные значения удовле-
удовлетворяют условию
k=\
E.86)
Это означает, что для любого такого базисного вектора
|{п^}) только конечное число собственных значений п^
положительно. Такие последовательности {ti]t} снова яв-
являются счетными, так что применимо общее рассмотре-
рассмотрение.
Следует отметить, что, помимо векторов, удовлетво-
удовлетворяющих условию E.86), в гильбертовом пространстве
существуют другие векторы, для которых числа запол-
заполнения для всех осцилляторов не равны нулю. Например,

122	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
если {nh} — {бы} (т. е. nt — 1, а все другие nh обра-
обращаются в нуль), то выражение
со
1Ф> = У 4-1 {**/»	E-87)
i=\
представляет собой настоящий нормируемый вектор, для
которого
(Nk)^(^\Nk\^) = ~>0	E.88)
при любом k^- 1. Разумеется необязательно, чтобы зна-
значение {Nk) стремилось к нулю для больших k. В качестве
контрпримера достаточно заменить Ьы на /46й;. Для
такого состояния (Nh) = k2 и, следовательно, (N) = оо.
Заметим снова, что для любой матрицы плотности р
и эрмитовой наблюдаемой О соответствующая характе-
характеристическая функция E.30) является непрерывной по s.
Применяя ее к оператору числа частиц N, получаем, что
функция
CN (s) = Sp (peiSN)	E.89)
должна быть непрерывна по s. В свою очередь это свой-
свойство может накладывать ограничение на набор парамет-
параметров, описывающих данную матрицу плотности. В част-
частном случае многомерного пуассоновского распределения
из условия непрерывности функции
CN (s) = exp ^2 (els - 1) щ | ^ exp [(ets - 1) (N)} E.90)
вытекает, что
k=\
E.91)
Таким образом, не всякая последовательность {\ik} сред-
средних (пуассоновских) чисел заполнения приводит к мат-
матрице плотности; это справедливо только для последова-
последовательностей, удовлетворяющих условию E.91).
Далее, чтобы установить непрерывность по s функ-
функции
)	E.92)

§ 3. ПРИМЕРЫ СТАТИСТИЧЕСКИХ СОСТОЯНИЙ	123
для многомерного пуассоновского распределения, сле-
следует рассмотреть функцию
СЕ (s) = ехр 2 (ехр [Шщэ] -\)цк\ . E.93)
Из неравенства
2 (ехр [iba>ks] - l)\ik
k~\
2 I exp [/ficofcs] - 1 \цк <
oo E.94)
fe-i
следует, что при выполнении условия E.91) функция
E.93) непрерывна. Отметим, что это условие не приво-
приводит к требованию о конечности значения
хотя несомненно, что в физических системах Е < оо.
Качественно аналогичные условия применимы к теп-
тепловому распределению бесконечного числа осциллято-
осцилляторов. Для характеристической функции оператора N из
E.58) находим
Функция Cjv(s) непрерывна, если произведение схо-
сходится к ненулевому значению. Для проверки сходимости
можно применить теорему фон Неймана, согласно кото-
оо
рой произведение \\ г», в котором все ?л Ф 0, сходится
к ненулевому значению, когда и только когда
оо
2H~2fe|<OO.
ft-1
Поскольку cos > 0, ни один множитель в E.95) не равен
нулю, и названная теорема применима. Рассматриваемая

124	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
сумма сходится, если
у
1 -
1 - exp ( - pficofe)
—exp
со
_ yi exp (
|П-е''
1 - exp ( - 0ficofe + is)
i
< oo. E,96)
Как нетрудно видеть, условие E.96) является необхо-
необходимым и достаточным. В следующей главе будет пока-
показано, что условие E.96) может выполняться и для ос-
осцилляторов поля излучения.
Наконец, по аналогии с E.96) нетрудно убедиться,
что для непрерывности характеристической функции
энергии
(l-exp[-pficoft])
i _ .vn r _ (л _ /ci fi™ I \ (р.97)
необходимо и достаточно выполнения условия
2j exp(-p/jcofc)<oo.	E.98)
k=i
Помимо рассмотренных примеров, существует много
других матриц плотности, часть из которых мы рассмо-
рассмотрим в следующих главах. Пока, имея в виду соотноше-
соотношения E.85) и E.86), можно считать, что соотношения
E.80) — E.82) определяют общую матрицу плотности в
представлении чисел заполнения.
§ 4. ЗАКЛЮЧЕНИЕ
Проведенный анализ и особенно последний пример
позволяют сделать выводы двоякого рода. Прежде все-
всего не только для одной или нескольких степеней сво-
свободы, но и при бесконечном числе степеней свободы
для построения квантовой теории вполне достаточно

§ 4. ЗАКЛЮЧЕНИЕ	125
определенного общепринятого сепарабельного гильбер-
гильбертова пространства (со счетным базисом). Хотя в лите-
литературе встречаются утверждения противоположного
толка, несепарабельные пространства (с несчетным ба-
базисом) не являются необходимыми для квантового рас-
рассмотрения, по крайней мере если речь идет об интере-
интересующем нас классе задач. Далее, последовательность
матриц плотности можно попытаться обобщить на слу-
случай бесконечного числа степеней свободы (К = оо) (как
это можно сделать, например, для последовательности
матриц q(K), каждая из которых соответствует первым К
степеням свободы). Тогда на параметры можно нало-
наложить такие ограничения, что предельная матрица будет
также представлять собой матрицу плотности. Простей-
Простейшим рассмотренным примером этого типа было много-
многомерное пуассоновское распределение, на которое нала-
налагалось ограничение E.91).
Сделанный здесь вывод можно сформулировать и в
более общем виде Предел матриц плотности не обяза-
обязательно должен представлять собой матрицу плотности
в обычном смысле, когда пределы определяются через
пределы ожидаемых значений соответствующих матриц.
Эта особенность присуща отнюдь не только проблемам,
связанным с бесконечным числом степеней свободы,—
с ней мы сталкиваемся в самых простых ситуациях. Рас-
Рассмотрим частицу, которая свободно движется внутри
ящика объемом Q < оо и гамильтониан которой имеет
вид Жо. = р2/2т. Для каждого значения объема Q теп-
тепловое распределение
E.99)
представляет собой	матрицу плотности (ненормирован-
(ненормированную, но с конечным	следом), тогда как предельная мат-
матрица
К	(ИУ E.100)
не является матрицей с конечным следом, хотя она и
ограничена.
Физическая система, характеризуемая полной про-
пространственной трансляционной инвариантностью, не

126	ГЛ. 5. СТАТИСТИЧЕСКИЕ СОСТОЯНИЯ
может обладать точным тепловым распределением, опи-
описываемым матрицей плотности. Для нас представляет
особый интерес одна из таких систем, а именно свободное
поле излучения, заданное по всему пространству. Чтобы
такой системе отвечало распределение, физически имею-
имеющее смысл теплового распределения (задача, весьма
важная для нас), можно идти двумя путями. С одной
стороны, можно определить поле излучения во всем
пространстве, но требовать, чтобы оно было тепловым
только в конечной области (например, в пределах Млеч-
Млечного пути!), а в остальной части пространства вакуум-
но-подобным. С другой стороны, можно представить
себе конечный объем квантования Q = L3 (кубический
ящик) с периодическими граничными условиями, яв-
являющийся в этом случае физическим пространством, в
котором рассматривается проблема. Мы будем, как это
обычно принято, пользоваться вторым способом, т. е.
рассматривать конечные объемы квантования. Именно
в этом смысле поле излучения удовлетворяет условию
E.98) и обладает тепловым распределением, опреде-
определяемым матрицей плотности.
При использовании больших объемов квантования
соответствующая матрица плотности позволяет рассчи-
рассчитать средние значения большого числа физических ве-
величин, которые во всех практических случаях не зави-
зависят от величины объема. При этом при переходе к пре-
пределу бесконечного объема результаты не только имеют
смысл, но часто и упрощаются (как, например, при вы-
вычислении средней тепловой энергии единицы объема).
Некоторые из наших результатов, касающиеся ожидае-
ожидаемых значений, приведены в форме, соответствующей
бесконечному объему квантования.
Наконец, следует отметить, что разрабатываемые в
настоящее время в квантовой статистической механике
математические методы1) позволяют непосредственно
рассматривать тепловые состояния в бесконечных объ-
') Представление об обобщенных состояниях квантовых систем
было введено Сегалом [5.8]. Рассмотрение этих современных мате-
математических методов (С*-алгебр) и их применение в квантовой тео-
теории дано также Гаагой и Кастлером [5.9].

§ 4. ЗАКЛЮЧЕНИЕ	127
емах. Это достигается путем обобщения понятия «со-
«состояний» системы, под которыми подразумеваются
теперь не только состояния, описываемые точными мат-
матрицами плотности, но и состояния, описываемые последо-
последовательностью точных матриц плотности, соответствую-
соответствующих конечным объемам. Физическая интерпретация
такого подхода аналогична интерпретации более извест-
известного (и используемого нами) подхода, при котором раз-
различные ожидаемые значения оцениваются сначала для
системы, находящейся в большом объеме, а затем совер-
совершается переход к пределу бесконечного объема.

Уравнения движения
электромагнитного поля
§ 1. РАЗВИТИЕ ВО ВРЕМЕНИ В КВАНТОВОЙ ТЕОРИИ
В предыдущей главе было подробно разъяснено, что
состояние квантовомеханической системы задается мат-
матрицей плотности р и с ее помощью определяются раз-
различные распределения вероятности. Матрица плотно-
плотности р может параметрически зависеть от ряда величин,
например температуры, времени и объема, в который
заключена система. Эти параметры характеризуют ус-
условные свойства матрицы плотности, подобно тому как
аналогичные параметры представляют собой условные
переменные в классических выражениях для плотности
вероятности.
В гл. 4 мы подчеркивали, что марковские процессы
играют важную роль в классической теории вероят-
вероятности. Для марковских процессов функция распределе-
распределения в будущем линейным образом определяется через
функцию распределения в настоящем. Другими слова-
словами, функция распределения подчиняется линейному
дифференциальному уравнению первого порядка по
времени — стохастическому уравнению.
В квантовой механике марковские системы играют
столь же фундаментальную роль. В этом случае состоя-
состояние системы подчиняется линейному уравнению первого
порядка, которое является просто обычным уравнением
Шредингера. В частности, для состояния |г|з) = |г|з(/))
уравнение Шредингера имеет вид
/й^|г|)) = ^|г|)>,	F.1)
где Ж — гамильтониан системы. Этот оператор эрмитов,
и, кроме того, здесь мы предполагаем, что он не зависит

§ 1. РАЗВИТИЕ ВО ВРЕМЕНИ В КВАНТОВОЙ ТЕОРИИ	129
от времени. Для матрицы плотности чистого состояния
р= |г|з)(г|з|; отсюда следует уравнение
ib-§fp=[3fS, p].	F.2)
В силу линейности отсюда непосредственно получаем,
что все (или почти все) матрицы плотности подчи-
подчиняются тому же линейному уравнению движения F.2).
Можно найти символическое решение уравне-
уравнения F.1):
| ф @) = е-»»'* | г|> @)) = U @ | г|> @)).	F.3)
Так как гамильтониан эрмитов, эволюционный оператор
U(t), преобразующий начальное состояние j^@)) в
1"ф(/)), унитарен и поэтому сохраняет норму состояния.
Из этого формального решения легко получить выраже-
выражение для матрицы плотности чистого состояния:
р @ = I ч> @) <i> {t)\ = u (о | ч> @)) а @) | и (О =
= U(t)9{O)U{t)-\	F.4)
Из линейности следует, что решение для произвольной
матрицы плотности дается тем же соотношением
р(*)=?/(*)р(О) ?/(*)"'•	F-5)
Отметим, что такой подход, в котором рассматривается
эволюционирующее во времени состояние системы, но-
носит название представления Шредингера; этот подход
наиболее соответствует понятиям классической теории
вероятности.
Существует, однако, альтернативный способ рассмот-
рассмотрения временной эволюции, который оказывается удоб-
удобным в ряде случаев. Происхождение этого способа свя-
связано с тем, что предсказания теории, которые могут
быть проверены на эксперименте, определяются исклю-
исключительно средними значениями различных операторов в
соответствующем статистическом состоянии. Имея это в
виду, можно следующим образом переписать выражение

130	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
для зависящего от времени среднего значения произ-
произвольной наблюдаемой:
(О @) ^ Sp [р (t) О] = Sp [U (t) pU (tyl0] =
= Sp [9U (t)~l OU @] = Sp [ptf (*)]. F.6)
Здесь использована инвариантность следа при цикличе-
циклических перестановках операторов. Кроме этого, в F.6) мы
просто положили р = р(О) и определили зависящую от
времени наблюдаемую О (t) соотношением
O(t) = U~!(t)OU(t).	F.7)
Следовательно, можно получить выражение для всех
средних значений, если вместо того чтобы рассматри-
рассматривать эволюцию оператора р, описываемую соотноше-
соотношением F.5), принять, что каждая наблюдаемая О эво-
эволюционирует согласно F.7). Такой способ описания вре-
временной эволюции в квантовой механике называется
представлением Гейзенберга.
Следует обратить особое внимание на различие меж-
между этими двумя эволюционными уравнениями. В диффе-
дифференциальной форме они имеют вид
fl>-J-p = [5B, р],	F.8)
-1Ь±.О= \Ж, О].	F.9)
Применимость того или иного уравнения в данной за-
задаче зависит от того, каким представлением мы поль-
пользуемся. Ниже в этой главе мы будем пользоваться
представлением Гейзенберга.
Когда гамильтониан зависит от времени (что вполне
возможно при наличии внешних источников), то почти
все предыдущие уравнения остаются справедливыми,
если под Ж понимать M{t). Существенно изменится
только определение эволюционного оператора ?/(/) че-
через M(t), Будем считать для простоты, что гамильто-
гамильтониан Ш{г) кусочно-постоянен, т. е.
t,^t<t,+l, ti+i-t,^,. F.10)

§ 1. РАЗВИТИЕ ВО ВРЕМЕНИ В КВАНТОВОЙ ТЕОРИИ
131
Тогда правильное выражение для унитарного эволюци-
эволюционного оператора U(t), ti^Ct < tt+l имеет вид
?/(*) = е-'('-'»)»//*Пе-'д/»//\	F.11)
/=о
Это выражение, вообще говоря, отличается от опера-
оператора
?/'(*)
Г
= ехр --?
L
г-i
(*-*,) 5В,--?
/=0
. F.12)
Истинное решение F.11) удовлетворяет уравнению
tt<t<t
l+l,
F.13)
как и следовало ожидать; в то же время U', вообще го-
говоря, не удовлетворяет этому уравнению.
Удобно ввести упорядочивающий по времени опера-
оператор Т, определяемый соотношением
U(t)^T{U'(t)}.	F.14)
Этот оператор формально упорядочивает различные чле-
члены, входящие в разложение U'(t), таким образом, что
во всех произведениях операторов множители берутся
в порядке возрастания временных аргументов. Исполь-
Используя конкретный вид U'(t), можно написать
exp --g-J
I L	о
F.15)
где в качестве начального момента мы произвольно вы-
выбрали ^о = О. В этом общем виде U(t) есть эволюцион-
эволюционный оператор для произвольного зависящего от времени
эрмитового оператора Гамильтона M{t); именно такой
оператор U(t) нужно подставлять в приведенные выше
формулы, начиная с F.3).
Стоит, пожалуй, заметить, что для большей нагляд-
наглядности мы вели рассмотрение без особых предосторож-
предосторожностей. Так как Ж в общем случае не является ограни-
ограниченным оператором, его нельзя применять к произволь-
произвольному вектору |г|)); нельзя и образовать его коммутатор

132	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
с произвольной матрицей р. Если гамильтониан Ж не
зависит от времени, то мы предполагаем, что он обла-
обладает требуемым свойством (называемым в математике
«самосопряженностью»), так что оператор е\р(—ИЖ/Ь)
может быть определен и фактически является унитар-
унитарным. Значительно меньше известно о том, какими свой-
свойствами должен обладать гамильтониан Ж{1) для того,
чтобы соотношение F.15) являлось определением уни-
унитарного оператора; такие случаи мы рассматриваем эв-
эвристически. Однако, когда оператор U(t) определен,
каждое состояние и каждая матрица плотности в пред-
представлении Шредингера или каждая ограниченная на-
наблюдаемая в представлении Гейзенберга будут эволю-
эволюционировать именно так, как указано выше.
§ 2. ОПЕРАТОРНЫЕ УРАВНЕНИЯ
ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ.
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
При наличии внешних источников /v электромагнит-
электромагнитное поле удовлетворяет уравнениям Максвелла, которые
в соответствующих (хевисайдовых) единицах и во всем
своем релятивистском великолепии имеют вид
= /v.	F.16а)
где eMVa6 — полностью антисимметричный тензор Леви-
Чивита. В квантовой теории антисимметричное тензор-
тензорное поле F^ и источники /v являются эрмитовыми опе-
операторными функциями, а F.16)—операторными урав-
уравнениями. Чтобы существовало какое-либо решение, ток,
очевидно, должен удовлетворять закону сохранения
<3и/и = 0.
Если мы сможем найти операторные решения урав-
уравнений F.16), то далее с помощью не зависящей от вре-
времени матрицы плотности р можно будет выразить раз-
различные ожидаемые значения, относящиеся к электро-
электромагнитному полю. В настоящей главе мы рассмотрим
первую часть этой общей программы.

§ 2. ОПЕРАТОРНЫЕ УРАВНЕНИЯ. ПРЕДВАРИТ. ЗАМЕЧАНИЯ 133
А. Общий подход к уравнениям поля
Здесь уместно обсудить общий подход к описанию
квантованного поля излучения, развиваемый в этой гла-
главе. Чтобы система уравнений F.16) представляла собой
правильно поставленную задачу для FPv, необходимо
предположить, что jtl есть заданное внешнее оператор-
операторное поле, динамически не реагирующее на распределение
того поля, которое мы намереваемся определить с по-
помощью jv-. Нетрудно понять, что такая задача является
в значительной степени модельной и что она взята нами
с педагогическими целями в силу ее математической
простоты. Существуют, однако, физические ситуации,
которые с хорошей точностью описываются как раз та-
таким набором уравнений. С подобной ситуацией мы
встречаемся, например, в случае существенно макроско-
макроскопического источника, когда поле не может заметно из-
изменить его или, точнее говоря, когда не возникает
когерентных и макроскопических эффектов поля, доста-
достаточных для возмущения источника. Такой подход при-
приводит к тому, что мы исключаем микроскопическое рас-
рассмотрение определенных явлений, но вполне согла-
согласуется с феноменологическим подходом к большинству
задач. Это нетрудно понять, поскольку можно предпо-
предполагать, что данное операторное поле ju совпадает с опе-
операторным решением, определенным из невыписанной
нами связанной системы «полных уравнений поля». Та-
Таким образом, выводы, которые можно сделать на основе
«половины» уравнений поля, не содержат какой-либо
принципиальной некорректности.
Тем не менее мы введем важное упрощающее пред-
предположение относительно процессов, обусловливающих
появление источников /v. Поскольку нас интересуют
главным образом поля, генерируемые тепловыми источ-
источниками или источниками типа лазера, можно считать,
что источник в значительной мере локализован в про-
пространстве и во времени. Конкретнее, если говорить о ло-
локализации во времени, то мы воспользуемся процедурой
«адиабатического включения», т. е. будем считать, что
в отдаленном прошлом и далеком будущем поле сво-
свободно и не связано с источниками. Поэтому наш подход

134	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
будет неправильно описывать связь поля излучения с
мириадами микроскопических виртуальных процессов
(например, с рождением электронно-позитронных пар),
так как обычно принято считать, что такие источники
присутствуют во всех точках пространства и времени.
Следовательно, мы не будем включать связь с виртуаль-
виртуальными полями в наши источники, а вместо этого скон-
сконцентрируем свое внимание на «конкретных» источниках
(атомах и т. д.), обусловливающих те процессы, которые
мы пытаемся исследовать Таким образом, мы прихо-
приходим к необходимости наложить на наши решения под-
подходящие граничные условия в отдаленном прошлом и
далеком будущем.
Наконец, рассматривая поле излучения в присутст-
присутствии заданных внешних источников, мы уже нарушаем
лоренц-инвариантность. Это просто означает, что внеш-
внешние источники можно считать выделяющими определен-
определенную лоренцеву систему координат. Поэтому уже нет не-
необходимости сохранять явную релятивистскую формули-
формулировку. Напротив, мы можем с выгодой воспользоваться
другой альтернативой— обычным нерелятивистским под-
подходом, который позволяет лучше понять физический
смысл получаемых результатов.
§ 3. ОПЕРАТОРНЫЕ УРАВНЕНИЯ
ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ.
НЕРЕЛЯТИВИСТСКИИ АНАЛИЗ
А. Формулировка в конфигурационном пространстве
Начнем наше рассмотрение, переписав уравнения
Максвелла в виде1)
= -V
V-
X
н
Е,
= 0,
E = V
V-E
X
=
н
р-
-j.
F.
F.
17)
18)
Здесь Н = dH/dt и т. д., и мы выбираем такую систему
единиц, в которой с—1. Первые два уравнения пред-
представляют собой самые настоящие уравнения движения,
') Не следует путать плотность заряда и матрицу плотности,
которые обычно обе обозначаются буквой р.

§ 3. ОПЕРАТОРНЫЕ УРАВНЕНИЯ. НЕРЕЛЯТИВИСТСКИИ АНАЛИ3135
тогда как два последних являются связями, т. е. усло-
условиями внутренней согласованности, налагаемыми в каж-
каждый момент времени. Эти условия должны выполняться,
чтобы уравнения имели какое-нибудь решение.
Связь V ¦ Н = 0 обычно «разрешают» с помощью со-
соотношения Н = V X А, но выбор А при этом не однозна-
однозначен, поскольку величина А определена с точностью до
произвольного градиента. Так как мы уже отказались от
явной ковариантности, мы вправе выбрать удобное и
важное для физики решение этого уравнения связи, а
именно такое, в котором присущая уравнению Н =
= V X А неопределенность была бы исключена с самого
начала.
Чтобы найти такое решение, отметим прежде всего,
что любое векторное поле V(x) с хорошим поведением
(операторное или с-числовое) можно разложить на по-
поперечную и продольную части
V = Vr + VL,	F.19)
которые обладают следующими свойствами:
V-Vr = 0, VXVL = O.	F.20)
Несколько ниже мы укажем, как производится такое
разложение, а пока предположим лишь, что оно спра-
справедливо. Тогда видно, что связь V- Н = 0 является усло-
условием для HL и не налагает никаких условий на Нт. Сле-
Следовательно, несвязанные переменные Нг можно одно-
однозначно выразить через новые переменные Ат:
НГ = УХАГ.	F.21)
(Тогда первое из уравнений Максвелла принимает про-
просто вид Ат = —Ет.)
Остающиеся уравнения Максвелла запишутся теперь
следующим образом:
tL=-]L, V-EL = p и ET = VXHr-f.
Первые два из этих уравнений представляют собой про-
просто формулировку закона сохранения заряда. В дейст-
действительности они не являются динамическими, поскольку,
как будет ясно из дальнейшего, EL определяется как

136	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
функция координат и времени непосредственно через р.
Третье же уравнение является динамическим. Пользуясь
общим операторным тождеством
V X (V X V) = V(V V)-V2V,
два основных динамических уравнения можно привести
к виду
Аг=-Ег,	F.22а)
Ёг= _v2Ar-f.	F.226)
Б. Формулировка в импульсном пространстве
Для наглядности проведем параллельный вывод
уравнений F.22) в импульсном пространстве. Введем
полевые переменные, зависящие от импульсов:
Э€(к)=О"'/2 J e-'k-x H (x)d3x,	F.23a)
~'k'xE(x)A,	F.236)
?(k)^Q~'h J е~*'х}(х)с13х,	F.23в)
р (k) = Q~'/2 | e~ik'xp (x) ix.	F.23r)
Пока мы рассматриваем й/2 как некий еще не опреде-
определенный нормировочный множитель. Для каждой точки к
импульсного пространства вводится тройка взаимно
перпендикулярных единичных векторов еДк), / = 1,2,3,
таких, что е3(к) -к = й= |к|. Это значит, что для каждого
к Ф 0 вектор ез(к) параллелен к, тогда как еДк) и вг(к)
ортогональны к. Всякое векторное поле
У (k) = Q~Vl Г е~/к'хУ {x)d3x	F.24)
допускает при каждом к разложение
= S еу (к) [е/ (к) • Г (к)]^У г (к) + У^ (к), F.25)

§ 3. ОПЕРАТОРНЫЕ УРАВНЕНИЯ. НЕРЕЛЯТИВИСТСКИЙ АНАЛИз137
где продольная и поперечная части определяются соот-
соотношениями
,(к).У(к)],	F.26а)
Ут (к)^е, (к) [е, (к) • V (к)] + е2 (к)[е2 (к) • Г (к)]. F.266)
Мы имеем два тождества
которые с точностью до множителя i являются просто
формой записи тождества F,20) в импульсном прост-
пространстве. Заметим также, что если положить
3fr(k\ = /k V <&? (U)	(Pi 2Я\
то для s4-T можно получить единственное решение сле-
следующим образом:
к X Пт (к) = ik X [к X / (к)] = ~ik2sf (к),
т. е.
ат (к) = ' х ^ •	F.29)
Полученные выражения можно непосредственно приме-
применить к уравнениям Максвелла, причем необходимо про-
произвести обычную замену V—> ik под знаком преобразо-
преобразования Фурье. Преобразованные уравнения имеют вид
3€=-/kxS, S = гкХ §?-<?,	F.30)
гк-§? = 0, ik-8 = p.	F.31)
Уравнения связей записываются следующим образом:
Пг . ЧР^ 	П !Ь . И^	п-	(Р\ 49^
i»v CJl' — 'J,	? IV U ~—* [J,	IVJ.O^jI
их решения можно написать сразу:
3tL(k) = O, oL (k) =	W~^'	F.33)
Эти уравнения выполняются в любой момент времени;
мы видим, что плотность заряда р(х, /) полностью опре-
определяет поле EL(x, t), как и отмечалось выше. Кроме

138	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
того, из F.30) и F.32) следует соотношение /к • ё>1 =
— — /к • &L = p, которое является формулировкой закона
сохранения тока в импульсном пространстве.
С учетом F.28) и F.29) два остающихся (динами-
(динамических) уравнения принимают вид
dT{k)=-&T(k),	F.34а)
8r(k) = fe2^r(k)-^r(k),	F.346)
где две компоненты ?т независимы и на них не нало-
наложено никаких связей. В этой формулировке видно фун-
фундаментальное преимущество перехода к импульсному
пространству: степени свободы поля, отвечающие раз-
различным значениям индекса к, являются динамическими
независимыми.
Необходимо, впрочем, сделать существенную оговор-
оговорку к высказанному утверждению. Поскольку Ат(х),
Ет(х) и ]'г(х) — эрмитовы поля, из соотношений F.23)
вытекает
= ^r(-k),	F.35а)
= gr(-k),	F.356)
= ^r (-k).	F.35в)
Следовательно, в этих переменных поведение вели-
величин с индексом —к полностью определяется поведением
величин с индексом + к. Это означает, что лишь поло-
половина всего к-пространства нумерует динамические не-
независимые переменные.
Векторы поляризации. Следует сделать несколько за-
замечаний по поводу единичных поперечных векторов ei и
е2. Они не определены однозначно и должны лишь удо-
удовлетворять условию ei(k)-e2(k) =0. Если ввести дру-
другую пару единичных векторов, повернутую по отноше-
отношению к первой на угол 0 в плоскости, ортогональной к, то
уравнение F.266) останется неизмененным. Для векто-
векторов, которые мы молчаливо предполагали действитель-
действительными, направления ei и е2 отвечают направлениям ли-
линейной поляризации k-й моды. Можно также работать с

§ 3. ОПЕРАТОРНЫЕ УРАВНЕНИЯ. НЕРЕЛЯТИВИСТСКИЙ АНАЛИз139
левой и правой круговыми поляризациями, введя век-
векторы
U	F.36a)
e_ (k) = 4= [e, (k) - /e, (k)]	F.366)
У 2
Такие векторы можно построить для любой пары дейст-
действительных векторов поляризации ei и е2. Этому комп-
комплексному базису отвечают две поперечные компоненты
поля
F±(k) = e*±(k) • F(k),	F.37)
которые в свою очередь соответствуют компонентам с
правой и левой круговой поляризацией. Если изменить
базис, повернув пару ej и е2 на угол 6, то мы получим
новые компоненты с круговой поляризацией, связанные
со старыми простым соотношением
Г'± (к) = е*"Г± (к).	F.38)
В любом случае два поперечных направления соответ-
соответствуют некоторому выбору ортогональных направлений
поляризации для поперечных мод поля излучения.
Индексы поляризации. Два ортогональных направ-
направления поляризации удобно обозначать индексами, и мы
условимся, что греческие индексы (как правило, X) при-
принимают значения 1,2 или +, — соответственно для ба-
базисных векторов с линейной или круговой поляриза-
поляризациями. Следовательно, любое поперечное векторное поле
Тт имеет компоненты Т\, где подразумевается, что ба-
базис выбран соответствующим образом. В частности, с
помощью поляризационных компонент наши динамиче-
динамические уравнения F.34) записываются в виде
slT\ (k) = — Ж\ (к),	F.39а)
<tl{k) = k2s4l{k)-fl{k).	F.396)
Таким образом, независимыми оказываются динамиче-
динамические переменные, отвечающие не только разным значе-
значениям к, но и разным поляризациям.

140	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
Для простоты ниже мы опускаем индекс Т у всех по-
поперечных полей.
Коммутационные соотношения. Прежде чем решать
динамические уравнения F.39), сформулируем соответ-
соответствующие граничные условия. В классической теории
граничные условия представляют собой просто началь-
начальные значения функций s&\ и &%. В квантовой теории все
эти переменные являются операторами, и мы должны вы-
выбрать операторы $?% и Ж\ в соответствии с канониче-
каноническими коммутационными соотношениями.
Для простоты и надежности представим себе, что
электромагнитное поле заключено в большой кубический
ящик размером L3, и наложим на наши решения перио-
периодические граничные условия. Интегрирование по объему
[как в соотношении F.23)] производится по ячейке
размером L3, причем нормировка выбирается так, что-
чтобы Q = L3. Чтобы выполнялось условие периодичности,
следует считать, что в разложениях Фурье могут фигу-
фигурировать лишь значения к с компонентами
*у = Х-«/,	F.40)
где tij, / = 1,2,3, — произвольные целые числа. Однако
мы принимаем, что любая компонента поля равна нулю,
если все ftjssO, т. е. полностью исключаем из рассмот-
рассмотрения точку к = 0.
В силу соотношений F.35) независимые динамиче-
динамические переменные нумеруются лишь половиной точек
k-пространства. Теперь важно обеспечить в таком полу-
полупространстве выполнение следующего обычного комму-
коммутационного соотношения между эрмитовыми канониче-
каноническими переменными:
[^(k)'k
Выделяя в явном виде зависимость от времени, нетруд-
нетрудно видеть, что эти соотношения будут выполняться для

§ 3. ОПЕРАТОРНЫЕ УРАВНЕНИЯ. НЕРЕЛЯТИВИСТСКИЙ АНАЛИЗ 141
всех х лишь в том случае, если положить
[s?k(k, t), <^,(k', Oj = Ht(k, t), <^,(k', /)] =
= -'"fiflu'flkk" F.41)
а все остальные одновременные коммутаторы считать
равными нулю. В этом последнем соотношении к и к'
могут пробегать все к-пространство. Предполагается, что
эти соотношения выполняются в любой момент /, в част-
частности они должны выполняться в качестве начального
условия для решения.
Наряду с этим мы будем предполагать, что для всех
совпадающих времен t имеют место соотношения
[.5#я(к, t), /v(k', t)] = 0,	F.42a)
[<Гя(к, t), /,,(k', 0] = 0.	F.426)
Эти соотношения не означают, что оператор $Ф (или <В)
должен коммутировать с f при несовпадающих време-
временах; они отражают лишь то обстоятельство, что источ-
источник f возникает за счет системы (например, совокуп-
совокупности атомов), динамически независимой от самого поля
излучения. Все физические модели строятся так, что эти
два условия выполняются1).
Гамильтониан. Соответствующий квантовый гамиль-
гамильтониан нетрудно найти, исходя из известного классиче-
классического выражения. Мы можем также вывести гамильто-
гамильтониан, опираясь на наши уравнения движения и комму-
коммутационные соотношения F.41) и F.42). Оба способа
приводят к выражению, которое можно записать в виде
M = j'2i[&t (k) &x (k) + ®2-&1 (k) ^ к М ~
— йсо — f\{k) ^(k) — fx(к) s4-[(к)], F.43)
где со2 = к2 и вычтена бесконечная постоянная (энергия
нулевых колебаний) для того, чтобы гамильтониан Ж
') Впрочем, соотношение F.426) может не выполняться в мо-
моделях, где свойства среды рассматриваются феноменологически и
оператор тока f или поляризации среды & выражается через опе-
операторы поля S, т. е. 3* = и&" + %& + 8cf3 +... . — Прим. ред.

142	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
был хорошо определен. Поучительно убедиться в том,
что динамические уравнения F.39) действительно яв-
являются операторными уравнениями в гейзенберговском
представлении, в котором записан приведенный выше
гамильтониан. Так как в общем случае внешний источ-
источник явно зависит от времени, наш гамильтониан также
зависит от времени, 3e = 2f6{)
В. Операторы рождения и уничтожения
Вместо того чтобы работать cl и Д можно ввести
соответствующие операторы рождения и уничтожения и
выразить через них различные величины. Введем опре-
определение
ак (к) = Bйсо)-'А [(о^ (к) - т% (к)],	F.44а)
а\ (к) = Bйт)-'/« [со^+ (к) + iS\ (к)]. F.446)
Если для ясности снова ввести зависимость от времени,
то из F.41) следует, что для всех точек к-пространства
[а, (к, t), а+(к', О] = виЛк'.	(
[а, (к, t), av(k', 0] = K(k, t), а+(к', t)} = 0. F.456)
Таким образом, мы пришли к одновременным коммута-
коммутационным соотношениям для бесконечного числа опера-
операторов рождения и уничтожения, которые обсуждались
в предыдущей главе.
В этих переменных преобразованный гамильтониан
принимает вид
Я. к
где
F.47)
есть оператор числа квантов на (X, к)-й моде. С помо-
помощью F.46) мы выразили гамильтониан всего электро-
электромагнитного поля в виде суммы гамильтонианов незави-
независимых осцилляторов с приложенными к ним внешними
силами, причем каждой точке k-пространства и поляри-
поляризации X соответствует один осциллятор. При этом на

§ 3. ОПЕРАТОРНЫЕ УРАВНЕНИЯ. НЕРЕЛЯТИВИСТСКИИ АНАЛИЗ 143
/ь(к) наложено ограничение /?(к) ¦= /л( — к); это яв-
является следствием того обстоятельства, что мы, как уже
говорилось выше, используем только половину к-прост-
ранства.
Как указывалось в гл. 5, для того чтобы гамильто-
гамильтониан Зё свободного поля был хорошим оператором, опе-
оператор полного числа квантов
N = 2 ЛГл (к)	F.48)
сам должен быть хорошим оператором. В данном случае
мы предполагаем, что как N, так и Ж — хорошие опера-
операторы. Это обеспечивает выполнение коммутационных
соотношений F.45) во все моменты времени.
Согласованность теплового распределения. В заклю-
заключение убедимся, что свободное поле излучения (в ящи-
ящике!) действительно удовлетворяет условию E.98), необ-
необходимому и достаточному для того, чтобы матрица плот-
плотности р теплового распределения была хорошо опреде-
определенной Используя соотношение со2 = к2, соотношение
F.40) и неравенство1)
можно показать, что
I, k	n
-pEl)~3- lj. F.49)
Таким образом, эта сумма конечна, что и требовалось
показать.
') Это неравенство эквивалентно утверждению, что
з
Г, S-1

144	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
§ 4. ХАРАКТЕРНЫЕ СВОЙСТВА ВРЕМЕННОЙ ЭВОЛЮЦИИ
Явное уравнение для .Я?*,(к, /) можно получить непо-
непосредственно из F.39), исключая &%{к, t)\ оно имеет вид
^(k)=-<o2^(k) + ffc(k).	F.50)
Это есть просто основное уравнение для осциллятора,
на который действует внешняя сила.
Еще более простой вид имеет уравнение для а^(к, t),
которое также следует из F.39):
ia% (k) = <аак{к) - BйсоГ''У„ (к).	F.51)
Оператор а? (к) подчиняется уравнению, сопряженному
с уравнением F.51).
Решение уравнения F.51) можно написать сразу:
t
а, (к, 0 = е~*Ч(к, 0) + iBficorV^ \еш'?К{к, t') dt',
F.52a)
где в качестве начального момента мы произвольно вы-
выбрали t = 0. Если же выбрать i = —оо в качестве на-
начального момента, то получается следующее важное
решение:
а, (к, 0 = аГ(к, 0 +«Bйа>Г V°* J em'fx{k, t')dt'.
F.526)
Здесь
аГ(к, t)^e-iata[n(k)	F.53)
обозначает форму оператора уничтожения в отдаленном
прошлом, когда влиянием источника по предположению
можно пренебречь. Поскольку здесь мы принимаем, что
ток f\{k, t) задан, в обоих случаях с тем же правом
можно считать «заданными» проинтегрированные по вре-
времени выражения. Например, можно положить
а, (к, 0 = <(М + Я\(к, 0,	F.54)

§ 4. ХАРАКТЕРНЫЕ СВОЙСТВА ВРЕМЕННОЙ ЭВОЛЮЦИИ 145
где заданный неэрмитов оператор Ж% связан с током со-
соотношением
Ж\{к, /) = /Bйсй)~'-е шг еш?х{к, t')dt'. F.55)
— оо
Мы видим, что Ж\ зависит от источников f% нелокаль-
нелокально по времени.
Мы уже отмечали сохраняющийся характер исход-
исходного четырех-вектора тока и предполагаемые свойства
коммутации F.42) поперечных компонент тока с пере-
переменными, характеризующими поле излучения. Другое
важное условие, которому должен удовлетворять внеш-
внешний ток, вытекает из следующих соображений. Наше ре-
решение для ак(к, t) должно удовлетворять одновремен-
одновременным каноническим коммутационным соотношениям
F.45) при всех /. Так как а%п уже удовлетворяют этим
соотношениям, отсюда следует, что для Ж% должны вы-
выполняться условия
[<(к, t), Ж{Лк', Щл-[Жк{к, t), а[?+(к', 0] +
+ [ЖК{к, t), ЖЬ(к', *)] = 0 F.56а)
и
[af (к, t), Жх,(к', Щ + \ЖК{к, t), akf{k', t)] +
+ \Жк(к, t), Жк,{к', t)] = 0 F.566)
вместе с сопряженными равенствами. Чтобы решение
F.52) действительно существовало, оператор Жх(к, t)
должен удовлетворять указанным условиям, а это нала-
налагает ограничения на внешний ток f\{k, t) при несовпа-
несовпадающих временах.
По существу предыдущие равенства дают формаль-
формальное решение выбранных нами динамических уравнений.
Однако два довольно очевидных и важных частных слу-
случая заслуживают специального рассмотречия. Если
внешний ток f% равен нулю при всех t, то равен нулю и
оператор Жъ и мы получаем просто решение для сво-
свободного поля
ак{к, 0 = е~"° а (к).	F.57)

146	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
Другая простейшая возможность состоит в том, что
внешний ток f\ пропорционален единичному оператору
при всех /. Следовательно, оператор Ж% тоже пропорци-
пропорционален единичному оператору, так что можно положить
Жк(к, t) = Cl(k, t),	F.58)
где ci есть заданная с-числовая функция. Это дает
обычное решение с с-числовым внешним источником
a, (k, 0 = e-to4"(k) + cx(k, ty	{6-59)
Очевидно, что в обоих частных случаях ах и at удовле-
удовлетворяют необходимым одновременным коммутационным
соотношениям F.45). Более того, только в этих случаях
(т. е. когда ток f%(k,t) пропорционален единичному
оператору при всех t) операторы поля $4--К (k, t) и
ё>к,{к', t) в один и тот же момент времени / могут со-
составлять неприводимое семейство операторов. То же са-
самое полностью относится и к операторам а% (к, t) и
а\, (к', t), а следовательно, и к их форме в отдаленном
прошлом а^ и afif. Если в некоторый момент t про-
пропорциональность между током f %{k, t) и единичным опе-
оператором нарушается, то из уравнения F.42) непосред-
непосредственно следует, что операторы М^(к, t) и ?V (k', /)
должны быть приводимыми, как и следовало ожидать.
Наконец, из F.54) и F.55) можно непосредственно
получить закон изменения других величин. Например,
для величины
(^)V(k, t) + a{ (-к, 0] F.60)
имеем
^(к, t) = (А)'/2 \е-ша1п (к) + ei»tatnt (_
cos corf (к) - со"'sin a>f«l" (к) +
, t')dt'.	F.61а)

§ 4. ХАРАКТЕРНЫЕ СВОЙСТВА ВРЕМЕННОЙ ЭВОЛЮЦИИ 147
Объединяя первые два члена, получаем
t
s4>K(k, t) = s$ln(k,t)+ J со-1 sin со (t- t') fK (к, t')dt'.
F.616)
Эти соотношения и дают искомые решения уравнения
F.50). Решение для электрического поля S\ получается,
согласно F.39а), дифференцированием по времени:
&х (k, t) = cos at&f (к) + со sin co^f (к) -
t
- J cos co(/ - t') fx (k, V) dt', F.62a)
— со
или, если объединить первые два члена,
Жк{к, t) = gi? (к, 0 - J cos о (/ - t') f% (к, /') dt'. F.626)
— оо
Средние значения и аналитические сигналы. Рас-
Рассмотрим теперь два трудных и часто возникающих во-
вопроса. Хотя мы уже потребовали, что наши решения
должны удовлетворять каноническим коммутационным
соотношениям, этим отнюдь не заканчивается физиче-
физическая конкретизация какого-либо частного решения На-
Например, наблюдаемые значения поля <§\ распределены
со средним значением
k, 01,	F-63)
которое определяется с помощью матрицы плотности р,
представляющей состояние системы. Особенно удобно
работать с полем ах(к, /), с которым линейно связаны
остальные величины. Для среднего значения этой вели-
величины имеем следующее основное соотношение:
t
\ш j"', t'))dV. F.64a)

148	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
Если бы матрицу плотности выбрать, например, так, что
(а^(к)\ = 0, то соотношение F.64а) будет иметь вид
классического (т. е. с-числового) решения волнового
уравнения с такими источниками (/>.), что решение об-
обращается в нуль в отдаленном прошлом. Основной вы-
вывод, который можно отсюда сделать, заключается в
следующем. В классической теории с помощью надле-
надлежащих граничных условий для самих полей можно подо-
подобрать физически подходящее решение, в частности та-
такое, которое обращается в нуль в отдаленном прошлом
до того, как были включены источники. В квантовой тео-
теории аналогичное операторное решение никогда не обра-
обращается в нуль, а принимает некоторый вполне опреде-
определенный вид в силу ограничения, налагаемого канониче-
каноническими коммутационными соотношениями. Здесь именно
конкретизация состояния р отбирает физически сущест-
существенный эффект однородного члена, в частности свойство
давать нуль при усреднении.
Продолжая аналогию между F.64а) и классическим
с-числовым решением, рассмотрим второй вопрос. Как
бы мы ни выбрали величину (a["(k)), вклад первого
члена в полное решение всегда является аналитическим
сигналом, так как co=jk|>0. При этом естественно за-
задать вопрос, при каких условиях, налагаемых на сред-
среднее от тока, выражение F.64а) представляет собой ана-
аналитический сигнал. Нетрудно совершить фурье-преобра-
зование по времени соотношения F.64а); это дает
+ iBnylBh(i>r4in6(v-vk) + i(v-vkrl](jK(k,v)), F.646)
где Vh = со/2л; = |к|/2я. Поскольку оператор j(x, /) эрми-
эрмитов, а векторы поляризации действительны, имеем
откуда
Bл)-1 Bйсо)-'/2 (| v | + v,)- </A (k, | v I))*. F.65)

§ 4. ХАРАКТЕРНЫЕ СВОЙСТВА ВРЕМЕННОЙ ЭВОЛЮЦИИ 149
Таким образом, если средний ток (/a (k, v)) не равен ну-
нулю для некоторого к и v > 0, то всегда найдется мода
(например, —к), в которой есть отрицательные частоты.
Поэтому, строго говоря, выражение F.64а) представ-
представляет собой аналитический сигнал лишь для исчезающего
среднего тока.
Однако в квазимонохроматическом приближении, ко-
которое часто является достаточным для квантовой опти-
оптики, разброс Д k разрешенных значений к в среднем токе
чрезвычайно мал по сравнению с центральным значе-
значением к. Следовательно, относительная амплитуда любой
отрицательно-частотной части выражения F.64) чрез-
чрезвычайно мала, а именно имеет величину порядка Ak/k.
Пренебрежение такими членами часто называют при-
приближением «волн вращающейся поляризации».
А. Описание в конфигурационном пространстве
Обратное преобразование наших основных оператор-
операторных решений в конфигурационное пространство произ-
производится наиболее изящно, если мы представим, что
объем квантования есть все пространство; тогда можно
положить, например,
А(х, 0 = Bя)-"' f e'k-x.s#(k, t)d3k	F.66)
[что соответствует выбору нормировки Q = BяK в
F.23)]. В этом случае из F.61а) следует
A(x, t)= -
+ | DR (x - y, t - t') J (y, /') d*y dt',	F.67)
где введены обозначения
D(x, f)=-Bn)-3
= - Dя|х|Г'[б(|х|-0-б(|хЦ-0], F-68)
= Dn|xir'6(|x|-0 />0,
= 0	*<0.	F.69)

150	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
Две D-функции, определенные выше, представляют со-
собой функции Грина для волнового уравнения. Аналогич-
Аналогичное уравнение выполняется также и для электрического
поля Е(х, t). Напомним, что все эти уравнения относятся
к поперечным операторным полям; как уже говорилось,
для простоты мы опускаем индекс Т, явно указывающий
на поперечность.
Первые два члена в F.67), очевидно, определяют ре-
решение однородного волнового уравнения (которое соот-
соответствует физическому решению в отсутствие тока J).
Следовательно, можно переписать F.67) в виде
А (х, 0 = А/п (х, t) + \ DR(x - y,t - f) J (у, П <Py dt',
F.70)
аналогичном F.616). Как указывалось выше, если ток
J(y, t) пропорционален единичному оператору при всех
у и t, то решение имеет вид
А(х, 0 = А'п(х, *) + С(х, 0,	F.71)
где С(х,t) есть некоторое поперечное с-числовое поле.
Заметим, что физический смысл средних значений
поля, таких, как (А(х,/)), непосредственно переносится
сюда из проведенного выше рассмотрения в импульсном
пространстве. В частности, хотя однородный член
Ain(x,/) необходим в операторном решении, его ожи-
ожидаемое значение может равняться нулю. В последнем
случае среднее поле полностью определяется полем, воз-
возникающим за счет источника. Вместе с тем следует от-
отметить, что однородный операторный член отвечает фи-
физически важным полевым флуктуациям вакуума, в том
числе и в тех областях, в которых не сказывается дейст-
действие источников.
Для большей ясности рассмотрение в конфигураци-
конфигурационном пространстве мы проводили довольно смело.
Строго говоря, А(х, t) не является эрмитовым операто-
оператором; для получения такового необходимо сначала вы-
выбрать гладкую пробную функцию f(x), которая при же-
желании может быть сильно локализована вблизи любой
точки, и образовать оператор
А,@= //(х)А(х,

§ 5. ХАРАКТЕРНЫЕ СВОЙСТВА ПРОСТРАНСТВЕН. ЭВОЛЮЦИИ 151
который уже является настоящим эрмитовым операто-
оператором. Имея в виду это обстоятельство, мы и впредь бу-
будем опускать требуемые процедуры сглаживания.
§ 5. ХАРАКТЕРНЫЕ СВОЙСТВА
ПРОСТРАНСТВЕННОЙ ЭВОЛЮЦИИ
Свойства операторов поля по отношению к эволю-
эволюции в пространстве столь же важны в квантовой опти-
оптике, как и по отношению к эволюции во времени. В гл. 1
обсуждались некоторые аспекты пространственной
эволюции для классических явлений. Для изучения кван-
квантового случая возьмем снова конечный объем квантова-
квантования (Q = L3) и перепишем основное динамическое урав-
уравнение F.22) для функций от х и v, которые опреде-
определяются следующим образом:
А(х, v)= | еышА(х, t)dt.	F.72)
— оо
Если, как обычно, положить со = 2itv, то (опуская по-
прежнему индекс поперечности Г) находим
-йоА=-Ё,	F.73а)
-коЁ= -V2A-j.	F.736)
Исключая Ё, получаем
(V2 + co2)A= -j,	F.74)
т. е. просто неоднородное векторное уравнение Гельм-
гольца.
Нам нужно найти решение этого уравнения, отве-
отвечающее распространению в пространстве для некоторых
не вполне общих условий. Пусть источник ограничен
определенной областью пространства (тепловой источ-
источник или лазер); нас интересуют значения поля вне
источника. Точнее говоря, нас интересует поле в тех точ-
точках пространства, где j(x, t) = 0 при всех / и где, следо-
следовательно, j(x, v)=0. Разобьем все пространство на ин-
интересующую нас область R, свободную от источников,
и дополнительную к ней область R', которая целиком

152	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
или частично заполнена источниками. Для точек, лежа-
лежащих внутри R, имеем, очевидно,
А(х, v)= J 6 (х-у) А (у, v)ePy,	F.75)
R
где интегрирование производится по области R.
Введем теперь функцию Грина G(x, у, v), для кото-
которой
(V2 + cu2)G(x, у, v) = (V2+co2)G(x, у, v)=-6(x-y).
F.76)
Существует несчетное количество таких функций Гри-
Грина, одна из которых есть, конечно, простейшая функция
Грина Go, введенная в гл. 1. Ниже мы выберем наиболее
удобную для нас функцию Грина Подставляя F.76) в
F.75) и учитывая, что в области R источников нет, по-
получаем
А(х, v)=|[G(x, у, v) (V2 + со2) А (у, v)-
R
-A(y,v)(V2 + co2)G(x, y>
-А (у, v)-(|-G(x,y,v)]^ =
= J [G (x, y, v) ^ A (y, v) - A (y, v) -~ G (x, y, v)] dS.
F.77)
В последнем выражении интегрирование по у проводит-
проводится по поверхности S, разделяющей R и R'. Обычно
источник сосредоточен в конечном объеме, так что об-
область R может содержать удаленные участки простран-
пространства.
В этом случае можно было бы ожидать, что поверх-
поверхностный интеграл в F.77) содержит вклад от «беско-
«бесконечно удаленной сферы». Напомним, однако, что, со-
согласно принятому предположению, система находится

§ 5. ХАРАКТЕРНЫЕ СВОЙСТВА ПРОСТРАНСТВЕН. ЭВОЛЮЦИИ 153
в большом объеме квантования L3 и на нее наложены
периодические граничные условия. Такое пространство
замкнуто и не имеет границ в полной аналогии с окруж-
окружностью в одномерном случае или с тором — в двумер-
двумерном.
Особенно удобно выбрать функцию G(x, у, v) таким
образом, чтобы она была равна нулю, когда точка у ле-
лежит на S [как в последней строке соотношения F.77)].
В рассмотренном в гл. 1 простом примере, в котором по-
поверхность S совпадала с плоскостью z = О, мы нашли
подходящую функцию G методом изображений. Однако
для более общей поверхности S этот метод не пригоден.
Наметим в общих чертах стандартное доказательство
того, что требуемая функция Грина (удовлетворяющая
однородным граничным условиям Дирихле) существует
в весьма общем случае. Пусть не содержащая источни-
источников область R, по которой происходит интегрирование
в F.77), является связной областью. Грубо говоря, это
означает, что любую пару точек в R можно связать не-
некоторой линией, целиком лежащей внутри R.
Будем теперь рассматривать область R как полость
в смысле теории электромагнитного поля. Тогда можно
попытаться найти (скалярные) собственные функции —
стоячие волны ipn(x), являющиеся собственными реше-
решениями уравнения
х) + ш^„(х) = 0	F.78)
с граничным условием, состоящим в том, что гр„ (х) об-
обращается в нуль на границе S области R. Можно также
рассматривать F.78) как уравнение на собственные зна-
значения для некоторой одночастичной квантовомеханиче-
ской задачи. В шредингеровском представлении уравне-
уравнение на собственные значения энергии в конфигурацион-
конфигурационном пространстве имеет вид
- J?- V2^ (x) + V (х) ^ (х) = ?Л (х).
Полагая теперь V'(x) = 0 в области R и V(x)= +oo в
области R', мы приходим к квантовой задаче о свобод-
свободной частице, заключенной в «ящик» (определяемый об-
областью R) с граничным условием ip(x) = 0 на «стенках

154	ГЛ. 6. УРАВНЕНИЯ ДВИЖЕНИЯ
ящика» (определяемых поверхностью S). Соответствую-
Соответствующее уравнение совпадает с F.78), где со« = 2тЕп\й2.
Для обеих задач, как известно, существует полная сис-
система ортонормированных функций if>n, п = 1, 2, ..., удо-
удовлетворяющих соотношению
Е<(х)Ф„(У) = в(х-у).	F.79)
Пользуясь этой информацией, мы можем сразу же
написать искомую функцию Грина нашей исходной за-
задачи
G(x, у, v)==>.
% М Уп (У)
Она удовлетворяет уравнению F.76) и, очевидно, обра-
обращается в нуль, если у (или х) лежит на S. Следует от-
отметить, что все обычные резонансные свойства полости
без потерь проявляются в членах, входящих в G. В кван-
квантовой задаче каждый такой член по-прежнему выпол-
выполняет свою традиционную роль выделения частот.
Теперь, убедившись в существовании нужной нам
функции Грина, легко вывести наиболее важные след-
следствия этого факта. В частности, уравнение F.77) упро-
упрощается и принимает вид
А (х, v) = - { ff (x, у, v) А (у, v) dS. F.81)
Последнее уравнение означает, что оператор поперечного
потенциала в произвольной точке х области R, свобод-
свободной от источников, линейно связан с операторами попе-
поперечного потенциала на поверхности S, окружающей R.
Кроме того, F.81) показывает, что поведение операто-
операторов определяется для каждой частоты независимо.
Столь же интересной является временная форма
уравнения F.81). Полагая
К (х, у, 0^ - j |f (х, У, v) е~шш dv, F.82)

§ 5. ХАРАКТЕРНЫЕ СВОЙСТВА ПРОСТРАНСТВЕН. ЭВОЛЮЦИИ 155
получаем, что операторы поля удовлетворяют соотноше-
соотношению
А(х, t)=jJK(х, у, t-t')k(у, Г)dSdt'. F.83)
s
Разумеется, нет ничего удивительного в том, что по-
поперечный векторный потенциал подчиняется таким соот-
соотношениям. Любая величина, подчиняющаяся волновому
уравнению для свободного поля в области R, удовлетво-
удовлетворяет аналогичным соотношениям. Например, путем сход-
сходных рассуждений можно показать, что электрическое
поле Е(х, /) в точке х, лежащей в области R, удовлет-
удовлетворяет соотношению
Е (х, 0 = J J К (х, у, t - /') Е (у, Г) dS dt'. F.84)
s
Эти фундаментальные выражения, устанавливающие
связь между полем в пустом пространстве и его значе-
значениями на поверхности S, без каких-либо изменений фи-
фигурируют и в классической теории, рассмотренной в пер-
первых двух главах. Следствия из этих законов распростра-
распространения, получающиеся в классической теории, имеют свои
аналоги в квантовой теории. В частности, теорема
ван Циттерта —Цернике, изложенная в гл. 1, имеет
прямой квантовый аналог.

Представление электромагнитного поля
по когерентным состояниям
§ 1. КОГЕРЕНТНЫЕ СОСТОЯНИЯ. ОСНОВНЫЕ СВОЙСТВА
Представление о когерентных состояниях, которые
будут играть столь важную роль в нашем квантовоста-
тистическом описании поля излучения, имеет свою боль-
большую и интересную историю. Суть ее содержится уже в
той части квантовой механики, которая относится к си-
системам с одной степенью свободы. Пусть, как в гл. 5,
величины Q и Р образуют (неприводимую) канониче-
каноническую пару операторов [Q,P] = ih; и кроме того (выби-
(выбирая для простоты круговую частоту равной единице),
положим а = (Q + iP)j V~2h, a+ = (Q - iP)jУ2/Г и N = afa.
Свойства этих операторов и собственных состояний \п)
оператора числа частиц (квантов) с п = 0, 1, 2, ...
были довольно подробно разобраны в гл. 5. Здесь мы
возобновим это рассмотрение, приступая к изучению ко-
когерентных состояний, т. е. векторов вида
от>>,	GЛ)
определенных для произвольных комплексных чисел г.
Следует сделать несколько замечаний по поводу обо-
обозначений. В правой части равенства G.1) фигурирует
линейная комбинация собственных состояний \п) опе-
оператора числа квантов с коэффициентами, зависящими
от г. Эта линейная комбинация определяет новый век-
вектор, который мы обозначаем самим комплексным чис-
числом z. Следует, однако, отчетливо понимать, что
состояние 11)—собственное состояние оператора N —

§ 1. КОГЕРЕНТНЫЕ СОСТОЯНИЯ. ОСНОВНЫЕ СВОЙСТВА 157
резко отличается от записываемого таким же образом
состояния |1), которое мы получаем, положив в G.1)
z=l.
С педагогической точки зрения представляется целе-
целесообразным ввести и другое обозначение для |г), в ко-
котором были бы явно выделены действительная и мнимая
части z. Полагая
где q и р — два произвольных действительных с-числа,
можно ввести определение
]?^1>. G.3)
Сопряженные когерентные состояния определяются ана-
аналогичными равенствами
lP)|_?l<n|,	G.4а)
G.46)
Особого внимания заслуживает то обстоятельство, что
сопряженное состояние также обозначается буквой г,
хотя в коэффициенты разложения в ряд фактически
входят степени z*.
А. Собственные состояния смещенного и сдвинутого
осцилляторов
Смещенный осциллятор. Наиболее важную роль, с
нашей точки зрения, играет соотношение между коге-
когерентными состояниями и собственными решениями для
смещенного (или сдвинутого) гармонического осцилля-
осциллятора. Рассмотрим подробнее решение для основного со-
состояния гармонического осциллятора, у которого, как
обычно, масса и круговая частота выбраны равными

158 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
единице. Это решение удовлетворяет уравнению
^|0) = -i{P2 + Q2-fi}|0> = 0.	G.5)
Здесь приведен гамильтониан системы, у которой в ос-
основном состоянии средние координата и импульс равны
нулю:
<0|Q|0> = <0|/>|0) = 0.	G.6)
Далее, одним из наиболее важных следствий комму-
коммутационных соотношений является такое свойство:
U [p, q}~1 (аР + pQ) U [р, q] = а (Р + р) + 0 (Q + q); G.7)
здесь а и J3 — произвольные параметры, a U[p,q] — уни-
унитарный оператор
U[p, <7] = е'(Р<г-?Р)/*.	G.8)
По существу действие U[p, q] на оба оператора Р и Q
выражается в их смещении на с-числа, равные соответ-
соответственно р и q. Ясно, что U[p,q]'1 = U[—p,—q]. Свойство
G.7) доказывается проще всего, если заметить, что для
двух произвольных операторов X и Y имеет место ра-
равенство
еуХе~у = X + [Y, X] + -~ [Y, [Y, X] ] + .... G.9)
В нашем случае этот ряд обрывается после второго чле-
члена.
Рассмотрим теперь соотношение
О = U [p, q] Ж | 0) = U [p, q] МП [р, q]~l U [p, q] | 0) =
= j{(P- Pf + (Q ~ qf ~b)V [p, q}\ 0),	G.10)
которое получается в результате повторного использо-
использования G.7). Очевидно, что состояние
\p,q) = U[p,q]\0)	G.11)
является основным состоянием аналогичного осцилля-
осциллятора, у которого координата смещена на q, а импульс—-

§ 1. КОГЕРЕНТНЫЕ СОСТОЯНИЯ. ОСНОВНЫЕ СВОЙСТВА 159
на р. В частности, средние координата и импульс теперь
уже не равны нулю и определяются выражениями
(р, q\ Q | р, q) = <01 U [р, <?Г' QU [p, q]\0) =
= (O\{Q+q)\O) = q,	G.12a)
(p,q\P\p,q) = p,	G.126)
второе из которых выводится аналогично первому. Ниже
мы подробно покажем, что определенные здесь состоя-
состояния \p,q) совпадают с когерентными состояниями G.3).
По очевидным причинам мы будем называть рассмотрен-
рассмотренный пример случаем «смещенного осциллятора».
Другое интересное свойство получается, если рас-
рассмотреть временную эволюцию основного состояния
\p,q) смещенного осциллятора под действием несмещен-
несмещенного гамильтониана Ш = '/г^2 + Q2 — Ь). Позже мы по-
покажем, что
e-"W*\p,q) = \pKX(t),qKJl(t)),	G.13)
где pKn{t) и <7кл(/) — решения для классического осцил-
осциллятора
<7кл@ = <7C0S^ + P sin/,	G.14а)
Ркл@ = — ^ sin / + pcost,	G.146)
удовлетворяющие начальным условиям ркл{0) = р и
<7кл@)= q. Другими словами, состояние \p,q) в процес-
процессе временной эволюции переходит в другое состояние
того же самого рода, определяемое зависящими от вре-
времени значениями параметров р и q. Образно говоря, со-
состояние \p,q) меняет со временем не свой вид, а лишь
средние координату и импульс, причем изменение по-
последних происходит в соответствии с классическими
уравнениями движения.
Эволюция состояний \p,q) согласно классическим
уравнениям движения имеет место для произвольно ма-
малых значений р и q. Это, однако, не означает, что полу-
полученным решениям можно дать строго классическую (т.е.
не вероятностную и т. д.) интерпретацию. Поскольку
Ь > 0, измеряемые значения импульса и координаты бу-
будут иметь отличный от нуля разброс.

165 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Сдвинутый осциллятор. Представление о когерент-
когерентных состояниях можно ввести несколько иным способом
с помощью следующих рассуждений. Рассмотрим ис-
исходный несмещенный гамильтониан типа G.5), но теперь
уже в присутствии внешних с-числовых сдвигающих чле-
членов р и д, связанных соответственно с операторами Р
и Q таким образом, что
3%' = j{P2 + Q2-h}- pP-qQ.	G.15a)
Это можно назвать случаем «сдвинутого осциллятора»
в противоположность рассмотренному выше случаю
«смещенного осциллятора». Тем не менее состояния \p,q)
по-прежнему являются собственными векторами гамиль-
гамильтониана Ж''. Чтобы понять это, достаточно заметить, что
W = \ HP ~ Р? + (Q- Я? ~Ь}-\ {р2 + q2}. G.156)
Следовательно, используя G.10), получаем
W\p,q)=-±{p* + q*}\p,q).	G.16)
Это значит, что \p,q) является собственным вектором
оператора Ж с собственным значением
?=~у{/>2 + <?2}.	G.17)
Более того, если сдвигающие члены зависят от вре-
времени [т. е. если в G.15а) p = p(t) и q = q(t)], то из
предыдущего следует, что состояние \p(t), q(t)) являет-
является собственным вектором зависящего от времени га-
гамильтониана Ж'= Ж'(t) сдвинутого осциллятора в
каждый момент времени /, и соответствующее собствен-
собственное значение ? = ?(/) = ~lh{p2{t) + q2(t)}-
Подводя итог, заметим, что когерентные состояния
\p,q) являются основными состояниями смещенных или
сдвинутых осцилляторов. В последующем рассмотрении
мы часто будем пользоваться этими свойствами коге-
когерентных состояний.

§ 1. КОГЕРЕНТНЫЕ СОСТОЯНИЯ. ОСНОВНЫЕ СВОЙСТВА	161
Б. Волновые пакеты с минимальной неопределенностью
Когерентные состояния возникают и в связи с совер-
совершенно другой задачей, а именно при рассмотрении усло-
условий минимальной неопределенности. Такой аспект имеет,
собственно, мало общего с квантовой оптикой, однако он
настолько традиционен, что мы считаем себя не вправе
не уделить ему некоторого внимания.
Для краткости обозначим снова среднее от опера-
оператора О по нормированному состоянию |г|:} через
($\С\Ъ)	G.18)
и, кроме того, положим
G.19а)
G.196)
Тогда (сначала с помощью неравенства треугольника,
а затем с помощью неравенства Шварца) получим
±Ь = j \([Q, Р]) I = \ | <[AQ, ЛЯ]) | <
< | (AQ АР) | < (AQ2)'/2 (АР2)''2,	G.20)
т. е. принцип неопределенности Гейзенберга в его обыч-
обычном виде. Чтобы получить состояние с минимальной
неопределенностью, нужно каждое из неравенств в G.20)
обратить в равенство. Неравенство Шварца переходит
в равенство при AQj\|)) =—irAP\ty); для того чтобы
превратить в равенство неравенство треугольника, ве-
величина г должна быть действительной; наконец, для со-
согласования с соотношением [Q, Р] = 1Ь величина г дол-
должна быть положительной. Для дальнейшего выберем1)
г = 1, что приводит к условию
(Q + IP) | г|)> = «Q> + I <P» | ф)	G.21а)
или, после деления на У^й, к условию
аК) = (а)К).	G.216)
') Случай гф\ отвечает осцилляторам с круговой частотой
со = г~', Здесь мы будем рассматривать случай единичной круговой

162 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Таким образом, состояния с минимальной неопределен-
неопределенностью являются собственными векторами оператора
уничтожения. Как мы сейчас покажем, эти собственные
векторы и есть когерентные состояния.
В. Собственные векторы оператора уничтожения
Третий аспект вопроса о когерентных состояниях, ко-
который мы хотим здесь обсудить, заключается в том
факте, что эти состояния являются собственными векто-
векторами оператора а — (Q + iP)\ \2h. Это свойство является
одной из причин (но отнюдь не единственной) их полез-
полезности в квантовой оптике.
Мы заведомо знаем один собственный вектор опера-
оператора а. Это основное состояние |0); соответствующее
собственное значение равно нулю. Поэтому рассмотрим
соотношение
0=U[p,q}a\0) = U [р, q] aU [p, <?]"' U [р, q) | 0) =
'>•	G-22>
пользуясь G.7) и определением а. В обозначениях G.2)
можно записать G.22) в виде
,q) = ^-\p,q)^z\z). G.23)
Тем самым мы установили, что состояния \p,q) =
— U[p,q]\0) действительно являются собственными век-
векторами оператора уничтожения.
Докажем, наконец, что состояния \р, q) представляют
собой когерентные состояния, определяемые соотноше-
соотношением G.1) [или G.3)]. Наиболее простой способ доказа-
доказательства состоит в использовании разновидности фор-
формулы Бейкера — Хаусдорфа, которая в том случае, когда
коммутатор Z = [X, У] коммутирует как с X, так и с У,
записывается следующим образом:
ех+ у = e-v, [х, YiexeYt	G.24)
Доказательство формулы G.24). Прежде всего из G.9) полу-
получаем
Yex = (eYexe-Y) eY
еYe
= (eYexe-Y) eY = ехр (еуХе-у) eY
ехр (А' + [Y, X] ) eY = e~zexeY,

§ 1. КОГЕРЕНТНЫЙ СОСТОЯНИЯ. ОСНОВНЫЕ СВОЙСТВА 163
так как Z = [X, У] коммутирует с X и У. Итерируя, находим
(е V)" - ехр (- М) en*enY = eYex (ЛТ~',
что приводит к рекуррентному соотношению р„ = п + |3,i-i для р„.
Так как р, = 1, то отсюда следует, что р„ = п(п + 1)/2. Заметим,
наконец, что
x** lim (e^V)" =- lim exp (- Щехеу = g-'/.K. ^ V
Л-»оо
Тем самым равенство G.24) установлено.
Представим показатель экспоненты в выражении для
U\p, q) в виде
i IpQ-qP] i[p(a + a+) + ig(a-g+)]
/p)gf (q-ip)a ^
/2Й
= 2a+-2'a.	G.25)
Применяя соотношение G.24), в котором положим
X = zaf и Y = — 2*а, получаем
?/ [р, ?] = ехр {zcv - z"a) =
= ехр (- -J \z I2) exp B<з+) ехр (- 2*<з). G.26)
Следовательно, учитывая свойство аР|0) = 0, /?= 1, 2, ...,
находим
U [р, q] I 0) = ехр [ - j | z |2) exp (za?) exp (- z*a) \ 0) =
= exp(- Uz
G.27)
где в последнем равенстве мы воспользовались соотно-
соотношением E.52) для того, чтобы ввести \п).

164 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Соотношение G.27) устанавливает искомую связь ко-
когерентных состояний G.1) с основными состояниями
сдвинутого осциллятора, состояниями с минимальной
неопределенностью и собственными состояниями опе-
оператора уничтожения; получение этой связи и было на-
нашей задачей. Сделав эти традиционные замечания, ко-
которые послужат для ориентировки, мы должны перейти
теперь к более широкому изучению свойств когерентных
состояний с тем, чтобы заложить надежный фундамент
для их использования в квантовой оптике.
§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТНЫХ
СОСТОЯНИЙ ДЛЯ ОДНОЙ СТЕПЕНИ СВОБОДЫ
Многие из обсуждаемых далее свойств когерентных
состояний являются простыми обобщениями таких
свойств, проследить которые легче всего на примере од-
одной степени свободы, и поэтому мы продолжим наш
анализ на этом уровне.
А. Предварительные замечания
Сосредоточим внимание на записи когерентных со-
состояний с помощью комплексной переменной в виде
оо
Yi-^T-\n)	G.28а)
~- (п!) -
и сопряженных состояний в виде
"!-^--	G.286)
Мы уже неявным образом установили, что все коге-
когерентные векторы \z) являются нормированными. Дей-
Действительно, в силу унитарности оператора U[p, q] из
G.3) следует
(г \г) = @\U [р, дГ1 U [p, q] |0> = <010> = 1. G.29)

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИЙ 165
Определим более общий матричный элемент (z\z') для
двух когерентных состояний:
я!
- еХР ( - j-1 2 I2 + 2*2' - \ I 2' |2) .	G.30)
Это соотношение можно записать также в виде
(z \z') - ехр { - j [ 12 p-zy -г'г +1 г' |2 - (гУ -глг)]} =
G.31)
откуда непосредственно вытекает, что
}	G.32)
Последнее выражение, очевидно, никогда не равно нулю.
Таким образом, совокупность когерентных состояний \z)
со всеми возможными комплексными z есть семейство
нормированных состояний, в котором никакие два со-
состояния не ортогональны друг другу, поскольку для лю-
любых z и z' имеем 0 < | (г|2') |-<1 1. Однако практически
можно сказать, что |(z|0)|««0, если |?J3> 1. С точки
зрения физики это означает, что величина энергии
|?|= lh{p2 + Я2} Для соответствующего сдвинутого ос-
осциллятора [ср. G.17)] должна быть много больше рас-
расстояния между квантованными энергетическими уров-
уровнями, которое для осциллятора с единичной частотой в
точности равно Ь,
Свойства когерентных состояний как собственных век-
векторов. Выше уже отмечалось, что состояния \г) являют-
являются собственными состояниями оператора уничтожения а
с собственным значением z, т. е.
a\z) = z\z).	G.33)

166 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Легко видеть, что когерентные состояния являются един-
единственными собственными состояниями оператора а. Из
G.33) следует
<г'|а|2) = 2(г'|г)	G,34а)
и комплексно сопряженное равенство
(z\af\z') = z(z\z'),	G.346)
Это соотношение формально можно представить в ряде
соотношения между сопряженными состояниями
<г|а+=г4г|.	G,35)
Заметим, однако, что G.35) имеет в точности тот же
смысл, что и более привычное соотношение G.33).
Если F(a) обозначает функцию от а более или менее
общего вида, то из G.33) следует
F(a)\z) = F(z)\z).	G.36а)
Аналогично для достаточно общей функции б(а+) из
G.35) следует
(z | G (о+) = G (z') (z I,	G.366)
что в сущности эквивалентно G.36а).
Рассматривая равенство G.33), естественно поста-
поставить вопрос, существует ли какое-нибудь собственное
состояние (назовем его |Я;?)), такое, что
а+|А,; ?> = А, |А,; ?).	G.37)
Легко показать, что ни одного такого состояния не су-
существует. Используя выражение, сопряженное E.536),
получаем, что из G.37) должно вытекать соотношение
</г|а+|Л; ?) = \гп(п-\\К; ?> = А, </г | А.; ?) G.38)
для п — 1,2, ..., тогда как для п = 0 из G.37) мы по-
получили бы
(O|a+U; ?> = А<0| А; ?) = 0.	G.39)
Если Я = 0, то из G.38) следует (п—1|Я;?)=0,
п = 1, 2, ..., т. е. |Я;?) = 0. Если КФО, то @\к; ?)=0.
что после повторного применения G.38) дает \п\к; ?) =0
для п = 1, 2, ..., и поэтому 1 А,; ?) =0. Следовательно, не
существует ненулевых состояний, удовлетворяющих со-
соотношению G.37).

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИИ 167
Непрерывность и аналитичность. Рассмотрим теперь
некоторые вопросы, касающиеся непрерывности коге-
когерентных состояний |г). Так как \z) = \p,q) есть основ-
основное состояние сдвинутого осциллятора G.15а), то физи-
физически правдоподобно, что состояния \г) и \z') прибли-
приблизительно совпадают для соседних точек в комплексной
плоскости, которые тогда, как легко представить интуи-
интуитивно, соответствуют почти идентичным сдвигающим си-
силам. В справедливости этих аргументов можно убедить-
убедиться, воспользовавшись нормой вектора [см. E.4)], на
которой основана обычная мера «расстояния» между
двумя векторами. В общем случае мы имеем соотноше-
соотношение
которое доказывается следующим образом. Если
А = - In (z \z') = '/21 z - z' |2 - i Im z'z', то
/ a a*\	1
2-e~A-e-A* = f+ f )e~xdx== f {Ae~Ax +A"e~A*-
¦00/	0
<2 f \Ae-Ax\dx<,2\ | A \dx = 2 | A |< 2 (| Re A \ +
о	о
+ I Im A I) - I 2 - z' |2 + I z'z' - z'z I < 2 (I 2 I + I z' I) I 2 - z' I,
откуда и вытекает G.40). Отсюда видно, что, когда г
сходится в комплексной плоскости к z', соответствую-
соответствующие векторы \z) сходятся к \z') «по норме», или, как
еще говорят, «сильно» сходятся.
Рассмотрим далее непрерывность векторов \z) в мат-
матричных элементах. Предположим, что |ф) означает про-
произвольный вектор гильбертова пространства, и рассмот-
рассмотрим функцию
л-0
где 2 принимает значения из комплексной плоскости.
Из неравенства Шварца [ср. E.3)] следует, что любая

168 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
такая функция ty(z) ограничена:
| г|)B) | = | (г |г|)> |<(г|) |г|))'/2 = || | -ф> ||< оо G.42)
и непрерывна по z в силу соотношения
|г|ф) - г|) (г') Ы ((г | - (г'|
2| + |2'Шг-2'|}1/2|||я|>)||, G.43)
вытекающего из G.40).
Функции г|)(г) имеют, однако, даже более сильные
свойства, чем непрерывность. Сумма G.41) абсолютно
сходится для всех комплексных г. Поскольку
1(/г|г|)) |-<|| |г|))||, это означает, что
п=0
последний ряд сходится, так как отношение n-го члена
к (п—1)-му стремится к нулю как | г' |/ У п. Но всюду
абсолютно сходящийся ряд по комплексной переменной
определяет целую функцию. Таким образом, выражение
ехр (^ | z |2) -ф B) = f (z) = 2 tS^ {П 'г|)) G'45)
определяет целую функцию от г* для всякого вектора
|г|)). Иначе говоря, можно положить
Чг)-	G.46)
Это означает, что любая функция ty(z) задается [за ис-
исключением общего множителя ехр(—'/г l^i2)] целой ана-
аналитической функцией. Отсюда с очевидностью следует,
например, что каждая функция a|)(z) есть бесконечно
дифференцируемая функция от 2 и от z* (или от р и q,
где 2 = (q + ip)lY2h). Допустима, однако, не всякая це-

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИИ 169
лая функция, так как на любую из функций f(z*) нало-
наложено ограничение
| f (г) | = | ф (г) ехр (| | г р) | < || | г|)) Цехр (\ \z\2). G.47)
Смысл функций ф(г) выяснится ниже при рассмот-
рассмотрении других замечательных свойств когерентных со-
состояний, к чему мы и переходим.
Б. Непрерывное представление,
основанное на когерентных состояниях
«Разложение единицы». При традиционном квантово-
механическом подходе часто отыскивают полный набор
коммутирующих наблюдаемых и в качестве базисной си-
системы векторов используют систему их общих собствен-
собственных векторов. Например, «n-базис» определяет полную
ортогональную систему векторов \п), я = О, 1, 2, ...,
являющихся собственными векторами оператора числа
квантов N. В свою очередь, как уже указывалось в гл. 5,
этот базис порождает каноническое функциональное
представление гильбертова пространства с помощью
функций от п (последовательностей), определенных ра-
равенством г|)„ =(/г|т|)). Такой подход, который во многих
случаях оказывается весьма плодотворным, основан на
фундаментальной теореме Стоуна и фон Неймана. Грубо
говоря, эта теорема утверждает, что всякий эрмитов
оператор порождает связанное с ним функциональное
представление гильбертова пространства.
Значительно меньше известно, вообще говоря, о «ба-
«базисах», порождаемых собственными векторами неэрми-
неэрмитовых операторов, таких, как оператор уничтожения а.
В действительности априори нельзя гарантировать, что
собственные векторы |г) накрывают1) гильбертово про-
пространство.
Например (правые) собственные векторы оператора
а+ не накрывают никакого пространства, поскольку,
') Термин «накрывает» (в оригинале span) здесь использован
для краткости, Речь идет о том, что соответствующий набор век-
векторов образует базис гильбертова пространства, т. е. любой вектор
пространства можно представить в виде линейной комбинации век-
векторов из указанного набора. — Прим, ред.

170 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
как было показано выше, оператор а+ не имеет соб-
собственных векторов. В качестве другого примера рассмот-
рассмотрим осциллятор Ферми, которому соответствуют опера-
операторы вида
/0 1\	/0 0\	/0 0\
af=U oj' aHi oh Nt=aiat=[o J-
Собственные векторы оператора Nf накрывают двумер-
двумерное гильбертово пространство; напротив, у оператора а<
есть всего лишь один собственный вектор I (соответ-
(соответствующее собственное значение равно нулю), и он, есте-
естественно, не может накрывать указанного пространства.
К счастью, однако, когерентные состояния |г) со
всеми возможными z накрывают гильбертово простран-
пространство. Впервые этот факт был отмечен, по-видимому, фон
Нейманом в его книге по квантовой теории [5.4]. Ней-
Нейман указывает, что подмножество всех когерентных со-
состояний \z), для которых 2 = jAt(/ + im), где / и т —
произвольные целые числа, уже накрывает гильбертово
пространство. Физический смысл этого состоит в том,
что полная система состояний определяется такими век-
векторами \p,q), для которых точки р и q образуют пря-
прямоугольную решетку в фазовом пространстве с плот-
плотностью одно состояние на «ячейку Планка» объемом
h = 2пЬ.
Далее, если уже подмножество когерентных состояний
накрывает все гильбертово пространство и, таким обра-
образом; по нашей терминологии, является полной системой,
то все множество когерентных состояний может быть
названо переполненным. Это значит, что должны суще-
существовать определенные линейные зависимости между
когерентными состояниями, и ниже мы приведем неко-
некоторые из них. Прежде чем демонстрировать это, мы еще
раз повторим утверждение о том, что система собствен-
собственных векторов \z) оператора уничтожения не только
полна, но и переполнена.
Из полноты когерентных состояний вытекает следую-
следующее фундаментальное следствие: обращение в нуль
функции г|)(г) ~{z\\p) для всех z влечет за собой обра-

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИИ \1i
щение в нуль вектора |г|з); обратное, разумеется, также
справедливо. Таким образом, абстрактные векторы |г|))
могут быть поставлены в одно-однозначное соответствие
с комплексными ограниченными функциями ty(z) =
= {z\ty). Аналогия с одно-однозначным соответствием
между векторами гильбертова пространства ц|э) и по-
последовательностями {tyn} (где г|)п =(«|^)) очевидна; она
наводит на мысль о том, что мы можем представить
абстрактное гильбертово пространство ^ с помощью ли-
линейного класса функций (скажем, 6), содержащего
г|)(г) = (z|\|)) для каждого |г|))е ?.
Чтобы окончательно определить наше представление,
мы должны превратить линейное пространство функций
<§ в гильбертово пространство, введя соответствующее
скалярное произведение. Как ¦ подчеркивалось в гл. 5,
при использовании канонической процедуры Дирака
ключевую роль играет формула разложения единицы
по одномерным проекционным операторам [см. E.11)].
В данном случае наши определения скалярных произве-
произведений и других подобных величин по внешнему виду
будут формально идентичны приведенным в гл. 5, если
мы сможем доказать основное «разложение единицы»
вида
/ = и>г|2)<2|,	G.48)
где
2
и интегрирование распространяется на всю комплексную
плоскость1). Разумеется, истинный смысл соотношения
G.48) определяется формулой для матричных элементов
>B|1>К2	G.49)
для произвольных \К) и |г|)). Потому для доказательства
соотношения G.48) сосредоточимся на соотношении
G.49), в котором подынтегральное выражение есть обыч-
обычная функция.
') Впервые разложение единицы вида G.48) с целью образо-
образования функционального представления гильбертова пространства
было использовано Клаудером [7.4]. В своем эвристическом выводе
соотношения G.48) мы следуем этой работе.

172 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Элементарное доказательство соотношения G.49)
производится непосредственно. Используя разложение
G.41), получаем, что желаемый результат имеет вид
(Мг|)) = ^| d2zexp(-\z\2) 2и -^у^у-ттг <Я 1 т> </г | гр>. G.50)
т, п=0 '
Если поменять местами суммирование и интегрирова-
интегрирование и ввести полярные координаты, т. е. z = ге'в, d2z =
= rdrdQ, то, очевидно,
A\т)(п\^)(т\п\Г1МХ
т, п=0
оо 2л
о о
G.51)
что и требовалось показать.
Строгое доказательство соотношения G.49) проводит-
проводится несколько по-другому, причем главным моментом яв-
является обоснование перестановки пределов. Покажем
сначала, что
С помощью стандартных теорем для любого конеч-
конечного R легко находим
R 2п	оо	R 2л
^ j | г dr d.Q\ (z \^,) \2 = ^ ^ I jrdrdQem (»-») X
0 0	m, re=0 0 0
X (\|)|m)(rt|i|))(m!tt!r'/2rm+nexp(- r2) =

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИЯ 173
где
R
yn(R) = 2{nl)~i / r2n+lexp{-r2)dr.
о
Очевидно, 0 < yn(R) < 1 для всех п и R, в то время как
lim Y«(^)= 1 Для всех п. Поскольку произведение (я|гр)
квадратично суммируемо (т. е. вектор |\р) нормируем),
то легко показать (в силу равномерной сходимости при-
приведенных ниже рядов), что
2
ft = O
oo
= ^ lim
oo
= lim 7,
таким образом, мы получили искомое соотношение. Со-
Соответствующий результат для (А,|г|з) получается в силу
линейности. Использованный способ доказательства со-
соотношения G.49) заимствован из работы Баргманна [7.6].
Соотношение G.48), которое, как мы показали, яв-
является искомым «разложением единицы» по одномер-
одномерным проекционным операторам, позволяет автоматиче-
автоматически получить (на основе канонической процедуры Ди-
Дирака) ряд свойств, перечисленных ниже и относящихся
к соответствующему непрерывному представлению гиль-
гильбертова пространства.
Представители (representatives) векторов: (г|г|)) для
всех |г|з).
Скалярное произведение
z<Mz><2№>.	G.52)

174 ГЛ. 7, ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Представители операторов: (г\Я\г') для произвольного
оператора 98.
Преобразование вектора
(z |Я |г|)) = - I' d2z' {г\Я\ z') (z' | -ф>.	G.53)
Преобразование оператора
Соответствующий канонический набор разложений век-
векторов и операторов дается следующими соотношениями:
Разложение вектора
>2|2X2|^>.	G.55)
Разложение оператора
Я = ~ \ d2Zld2z21 г,) (г, | Я | 22) <221.	G.56)
Соотношения G.55) и G.56) можно рассматривать
как формулы обратного преобразования от функцио-
функционального представления гильбертова пространства по
когерентным состояниям к абстрактному представлению.
Воспроизводящее ядро. Одна из главных особенно-
особенностей функционального представления, основанного на
переполненном наборе состояний, состоит в появлении
воспроизводящих ядер.
Пусть & в G.53) есть единичный ощератор /. Тогда
получаем
±j).	G.57)
Это означает, что представитель (г|г|з) любого вектора
удовлетворяет интегральному уравнению с воспроизво-
воспроизводящим ядром
G.58)
Далее, если положить |гр) =\z"), то из G.57) получаем
B | z") = 1 I d'2z' (z I z') (z' | z"),	G.59)
31 J

I 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИЙ 175
т. е. ядро является решением интегрального уравнения,
порождаемого им. По существу уравнение G.59) есть
условие идемпотентности, которому удовлетворяет яд-
ядро Ж. Это значит, что Ж ведет себя подобно проекцион-
проекционному оператору при действии на произвольные квад-
квадратично интегрируемые функции от г (и от z*)\ к пред-
представлению же гильбертова пространства ') относятся
лишь те из функций, которые удовлетворяют соотноше-
соотношению G.57).
Всякая функция, являющаяся представителем опера-
операторов (проще говоря, матричный элемент) {z\3S\z'),
удовлетворяет аналогичным интегральным уравнениям.
Полагая в G.54) либо ЗИ\, либо $ч равным /, получаем
(г | Я \г") = ~ j d2z' (z Iz') (z'\&\ z") =
= ~ J dV (г\Я\ z') (z' | z").	G.60)
Как и G.57), соотношения G.60) являются очевидными
следствиями основного разложения единицы G.48). Но
поскольку
(г\г')фО при гфг',	G.61)
то эти соотношения в действительности являются огра-
ограничениями, которым должны подчиняться представите-
представители векторов и операторов
Стоит отметить еще одно следствие представления
такого типа. Именно, положив 9& = I в G.56), получим
%d*z,\z,)(z,\z2)(z2l	G.62)
что следует сравнить с нашим исходным соотношением
/ = 1 ( d2z\z)(z\.
Мы имеем два явно различных разложения одного и
того же оператора по одной и той же системе состояний;
первая формула содержит суперпозицию «внешних про-
произведений различных векторов» !zi)(z2|, в то время как
рторая — суперпозицию «внешних произведений одинако-
') Обширная и общая теория гильбертовых пространств, осно-
основанная на воспроизводящих ядрах, была развита Аронсзайном [7.8].

176 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
вых векторов» \z)(z\, т. е. проекционных операторов.
¦ Возможность существования большого числа разложе-
разложений или представлений является следствием перепол-
переполненности системы когерентных состояний, что проявляет-
проявляется в свойстве G.61). Заметим также, что в следующей
главе будет, в частности, рассматриваться аналогичная
множественность разложения по когерентным состоя-
состояниям для ряда других операторов.
Линейные зависимости. Одним из наиболее характер-
характерных свойств переполненной системы векторов является
наличие линейной зависимости между базисными век-
векторами. Одно из таких соотношений получается из
G.55), если положить |i|)) = |z'):
).	G.63)
Это равенство выражает \z') через все когерентные со-
состояния.
Два других соотношения также представляют инте-
интерес. Выразим 2 в полярных координатах, так что [как и
в G.51)]
~-|«>- G.61)
(я!)/2
я = 0
Отсюда легко получить
2л
р=\, 2, ....	G.65)
Умножая на грг и интегрируя по всем г, имеем
zp\z)d2z = 0, p=l, 2,		G.66)
С другой стороны, любое конечное число различных
когерентных состояний \zi\, /=1, 2, ..., L, составляет
ряд линейно независимых векторов. Это значит, что ра-
равенство
L
2c,|z,) = 0	G.67)
(=1

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИИ 177
имеет место лишь в том случае, когда все ct = 0. Дока-
Доказательство этого свойства мы предоставляем читателю.
В. Примеры и специальные свойства представителей
векторов и операторов по когерентным состояниям
Примеры представителей векторов. Рассмотрим неко-
некоторые конкретные примеры известных квантовых состоя-
состояний, чтобы пояснить использование и свойства непре-
непрерывного представления по когерентным состояниям.
Один из простейших примеров — собственные состояния
гармонического осциллятора; каждое из них в соответ-
соответствии с G.4а) имеет свое функциональное представление
<z I п) = (п!)-'/2 zn ехр ( - у \г |2).	G.68)
Важно понимать, чему соответствуют эти функции:
их следует сопоставить с обычными функциями Эрмита,
которые являются собственными функциями осцилля-
осциллятора в шредингеровском представлении. Как мы уже
указывали, при использовании этого наиболее фунда-
фундаментального представления векторам |\|з) соответствуют
функции \\{х) одной действительной переменной, опера-
оператору Q — умножение на х, а оператору Р — дифферен-
дифференцирование —ibd/dx. Далее, уравнение на собственные
значения энергии для гармонического осциллятора с
единичными массой и угловой частотой имеет вид
(х) = Е^(х).	G.69)
В большинстве учебников по квантовой механике пока-
показывается, что это уравнение обладает (нормируемыми)
решениями, если Е = пЬ, п = 0, 1, 2, ...; эти решения
просто связаны с функциями Эрмита, определяемыми
следующим равенством:
exp(-у»). G.70)
В частности, для нормированных собственных реше-
решений уравнения G.69) имеем
ФгеМ = Й~Х(й~'/2*)-	G-71)

178 ГЛ. 7 ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Приведем в качестве примера явное выражение ф
при « = 1,2:
ФоОс) = (лй) "expl-^J,	G.72a)
Ф, (х) = (ли)" \f\ х ехр {-$-\	G.726)
Во всяком случае, главным здесь является то обстоя-
обстоятельство, что абстрактные состояния, представляемые
функциями Эрмита (в единицах Ь) ф„(х), для каж-
каждого п совпадают с состояниями, представляемыми
функциями (г\п).
Шредингеровское представление векторов является
столь традиционным и играет в физике столь важную
роль, что полезно иметь более общую связь между ним
и представлением функциями (г|г|з). Возьмем снова
запись в фазовом пространстве
= @ | e'WffP/VipQ/V^^ |г|)). G.73)
Последнее соотношение получается в результате двух-
двухкратного применения соотношения G.24). В шрединге-
ровском представлении G.73) принимает вид
(Р, Я 11>> = J Фо (х ~ j) е-МЧ? (х + |) dx =
= („«-'' J ехр [ - i^fH -4fc\t(x + ±) dx, G.74)
где мы воспользовались соотношением
ехр (^) о]) (х) = ехр (у <7 ?) Ч> (*) = г|) (х + f), G.75)
справедливым для произвольной функции г|)(х). Соотно-
Соотношение G.74) позволяет перевести любой шредингеров-
ский представитель в представитель (р, q\i!p) из фазового
пространства. Ясно, что и функцию ty(y) можно восста-
восстановить по {p,q\ty) с помощью преобразования Фурье
ф;(- у)\-'' J (p, 2y\$)dp.	G.76)

§ ¦!. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИЙ
Существует несколько соотношений такого типа, позво-
позволяющих определить г|)((/).
Можно воспользоваться свойствами аналитичности
для того, чтобы получить еще более простой способ на-
нахождения (р, q\ty). Рассмотрим
, 0 | г|>) = (пП)~'и J ехр (- ^- - ^f) г|, (х) dx ^
(p).	G.77)
Из сравнения с G.46) видно, что g(p) = f{— ipfY^h),
так что в силу аналитичности f можно непосредственно
найти (р, q\ty). В частности, имеем
(р, q | г|з) = ехр [ - -^ (р2 + ?2)] g (р + /?) G.78а)
или
/с [ ilA = ovn I — _
2
где
<z [ я|)> = ехр (- 4 | г ?) g (i VYh z%	G.786)
G.79)
В качестве иллюстрации выберем функцию
являющуюся основным состоянием осциллятора с про-
произвольной угловой частотой со. Тогда, воспользовавшись
основным гауссовым интегралом (при ReA>0)
BяГ'/2 | ехр (- ixB - ~) dx = У~А ехр (- \ АВ2),
получаем
^(p) = [~(^ + co-v2)]~1/2exp[-^|^-p2], G.81)
откуда (обозначая [ i|)) через | 0ш))
G.82а)

180 ГЛ. 1. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
ИЛИ
(р, ^|Ой)
i	G.826)
ХехР\~ 2fi(i + o>) [p2 + <*q2 + Hi-<*)pq]\-
Если со «= 1, то эти соотношения непосредственно сводят-
сводятся к приведенным выше соотношениям для |0i) = |0).
Замечание. Следует подчеркнуть, что G.82) не является «есте-
«естественным» непрерывным представлением по когерентным состояниям
для основного состояния осциллятора с частотой со; в естественном
представлении используются основные состояния сдвинутого осцил-
осциллятора, который сам имеет естественную частоту со. Действительно,
все такие естественные непрерывные представления по когерентным
состояниям являются формально идентичными, если они выражены
как функции г (т. е. все функции (z | я|з) совпадают), но отли-
отличаются по своему физическому содержанию в силу определения
г = (<в'2</ + l{u~>'-p)l\f 2h, используемого при построении (р, q [ я|з).
Ниже мы подробнее познакомимся с различными случаями такого
рода, когда будем иметь дело одновременно с несколькими различ-
различными осцилляторами.
Вероятностная интерпретация j(z|i|))|2. Сейчас са-
самый подходящий момент для того, чтобы расширить
наши представления о физическом смысле величины
jBjip)|2. Предположим, что мы имеем дело с мате-
материальной частицей в одномерном пространстве. Тогда,
как известно, шредингеровская волновая функция яр (л:)
есть амплитуда вероятности (более точно, р (х) = | яр (х) |2
есть плотность вероятности) нахождения частицы в точ-
точке х. Ясно, что такие события являются взаимоисклю-
взаимоисключающими, т. е. в результате измерения в данный момент
времени частица будет найдена в одной и только одной
точке х. Следовательно, распределение р(х) может быть
в принципе почти любым.
С другой стороны, заметим прежде всего, что вели-
величина i (p, q| яр) |2 не есть плотность вероятности того,
что частица находится в точке q и имеет импульс р.
Это скорее относительная частота того, что частица при
измерении будет обнаружена в состоянии, соответствую-
соответствующем основному состоянию осциллятора, у которого сред-
средняя координата есть q, а средний импульс равен р.
Квантовомеханически эти «события» не являются взаи-

§ Ч. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕГ-ЕНТ. СОСТОЯНИЙ 181
моисключающими, так как в силу G.61) два таких со-
состояния до некоторой степени схожи. Поэтому, исполь-
используя р(г) = | (?li|)) |2, мы имеем дело в сущности со сто-
стохастическим описанием на основе зависимых вероятно-
вероятностей.
В качестве грубой классической аналогии такого опи-
описания представьте себе, что Вы с завязанными глазами
стреляете, не целясь, в листы газет, лежащие на полу.
Пусть р(п) означает относительную вероятность того,
что страница номер п будет продырявлена. Если все ли-
листы лежат отдельно и не перекрываются, то события
(какой-то из листов оказался продырявленным) взаим-
взаимно исключают друг друга. Однако если некоторые из
листов перекрываются, то события, вообще говоря, ста-
становятся невзаимоисключающими и, как следствие этого,
появляются ограничения на величины р(п). Например,
если листы 1 и 2 лежат точно один над другим, то за-
заведомо будет р(\)=рB). Если не нарушены соответ-
соответствующие ограничения, то такой способ стохастического
описания с помощью зависимых вероятностей не содер-
содержит каких-либо неправильностей.
Возвращаясь теперь к распределению p(p,q) =
= | {р, q | г|з) |2, заметим, что для макроскопических уча-
участков фазового пространства с площадью Е 3> h = 2лй
выражение h~{ р{р, q)dp dq, несмотря на зависимость
Е
вероятностей, есть достаточно точная мера вероятности
найти частицу внутри ячейки Е. Именно благодаря этому
свойству p(p,q) обладает многими чертами обычного
классического распределения в фазовом пространстве
Ркл(р, q) ')•
Примеры операторов. Обратимся теперь к некоторым
операторам и посмотрим, как они выглядят и как дей-
действуют в непрерывном представлении по когерентным
состояниям. Сосредоточимся вначале на представлении
с помощью интегрального ядра {z\BS\z') для операто-
оператора Я [см. G.53) и G.54)].
') В таком духе распределение p(p,q) рассматривали Хусими
[7.11], Кано [7.12], Мета и Сударшан [7.10], а также Мак-Кенна и
Фриш [7.13].

182 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Для простоты предположим, что оператор $ диаго-
диагоналей в представлении по числам заполнения, т. е.
(п\3§\т)= ЬпЬПт- Воспользовавшись G.28а), получаем
Я I z') = ехр (- || z' |2) ^ -S Ьп I п), G.83)
и, следовательно,
оо
{\\)^^^p^ G.84)
есть как раз требуемое интегральное ядро. Если J? пред-
представляет собой эволюционный оператор осциллятора
ехр(—UN), то 6п = ехр(—Ш), и мы получаем
n=0
= expl-||Z»' ¦' -"¦' '
G.85)
Заметим, что матричные элементы эволюционного опе-
оператора получаются путем простого преобразования аргу-
аргументов у воспроизводящего ядра {z\z'). Следствием
этого является тот факт, что под действием эволюцион-
эволюционного оператора когерентное состояние \г) переходит в
новое когерентное состояние \гклЦ)) = \е~иг). Очевид-
Очевидно, что 2КЛ (t) = e~uz есть просто комплексное решение
для классического осциллятора, и мы предоставляем чи-
читателю сформулировать эти соображения, пользуясь
представлением о фазовом пространстве, в котором дол-
должны выполняться соотношения G.13) и G.14).
Рассмотрим теперь несколько более общие операторы
и соответствующие им интегральные ядра. Одними из
простейших являются ядра, соответствующие нормально
упорядоченным операторам. Пусть оператор J? зависит
от а+ и а [т. е. J? = ^(а+, а)] таким образом, что в каж-
каждом множителе все операторы рождения а+ стоят слева
от всех операторов уничтожения а. Если предположить,

§ 2 ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ СОСТОЯНИИ 183
что 33 разлагается в степенной ряд по а и а\ то этот
ряд имеет вид
оо
Я(а+, а)= 2 brs{a+)ras	G.86)
г, s = 0
с подходящими комплексными коэффициентами brs. То-
Тогда из G.36) сразу вытекает
af, а) | г') = Я (г\ г') (z \ г') =
= 2
г, s=0
2 Й„BТBТ<2|2'>, G-87)
причем последняя форма записи следует из G.86), если
это разложение существует.
Понятие нормально упорядоченного оператора столь
важно, что полезно ввести операцию нормального упо-
упорядочения, обозначаемую двоеточиями справа и слева.
Назначение этой операции состоит в такой перестановке
операторов уничтожения и рождения в их произведениях
(при полном пренебрежении их некоммутативностыо!),
чтобы все af встали слева от всех а. В рассмотренном
выше примере : 38 : =38, так как по предположению опе-
оператор j? уже был записан в нормальной форме. Однако
обычно :О : Ф О. Например, если О = aaf, то : aaj' : =
=^aLa = аа+ — 1 ф aaf, что следует из коммутационных
соотношений.
Важно понимать, что нормальное упорядочение есть
в сущности соотношение между символами, и что ре-
результирующий оператор зависит от исходного символи-
символического представления оператора О. Например, хотя
[а, а+]=1, но для : [a, cv]: имеем : [a, aJ'}: = 0, что от-
отличается от : 1 : = 1. Поэтому, чтобы определить : О :,
нужно принять некоторую конкретную символическую
форму для О. Проще и логичнее всего выбрать симво-
символическую форму для (У, отвечающую некоторой заранее
заданной функциональной форме (У = (У(а+, а). Тогда
будет выполняться соотношение
(г\:О {а\ a):\zf) = 0 (z\ zr) (z \ z').	G.88)
Поскольку произвольный оператор W может быть
представлен в виде 7f(af, а), то ясно, что подходящими

184 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
перестановками символов (учитывая должным образом
соотношение aaf = afa+\) оператор W можно превра-
превратить в нормально упорядоченный. Иными словами, для
каждого оператора W существует соответствующий опе-
оператор Wп{аУ, а), такой, что W = : Wn '¦¦ Это представле-
представление удобно для некоторых применений, и ниже мы опи-
опишем способ, который в ряде случаев помогает опреде-
определить Wn-
Для некоторых О мы можем записать : О : в явном
виде с помощью более привычных операторных выра-
выражений. Для этих целей оказывается полезной следую-
следующая производящая формула:
: exp (za+ — z" a): = exp (zaf) ехр (— г*а) =
= exp(j\z\2)exp(zaf-z'a), G.89)
выполняющаяся в силу G.26). Рассмотрим, в частности,
пример 0{af, a) = exp (та+а), для которого имеем
(z |: ехр (т. а+а) : [ z') = exp {xzz') (z | z') =
= ехр[- ^ I ^ Р + A + t)zV - -i-1 2' |2]. G.90)
Если сравнить это выражение с G.85) и положить
A + т) = e~u или —it = In A + т), то получим
: ехр(та+а): =ехр [ln(l +x)(afa)],	G.91а)
или, что эквивалентно,
:ехр[(е^"- \)аЧ\: = ехр[- it {а?а)]. G.916)
Очевидно, если х-* — 1 (или если it—*+oo), то
:ехр(- a+a): = | 0) @ |.	G.92)
Представление с помощью дифференциальных опера-
операторов. Помимо представления различных операторов с
помощью интегральных ядер существует другое весьма
важное их представление. Рассмотрим сначала оператор
а\ Из G.35) следует
Это показывает, что в пространстве представления функ-
функциями (z|ip) оператор af представляется умножением

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИИ 185
на z*. (Грубой аналогией этого является шредингеров-
ское представление, где Q представляется умножением
на х.) Чтобы найти столь же простое представление
для а, заметим прежде всего, что в силу явного вида
{z\z') имеют место следующие соотношения:
Y-r-^jexp^- -jlzr-TZz'-y |z |-j =
Hz').	G.93)
Но последнее выражение в G.93) справедливо, очевид-
очевидно, и для произвольной линейной суммы 2cp|Zp).
В свою очередь отсюда следует, что {z\a\ty) =
= (z/2 + д/dz*) (z\ty); это означает, что в пространстве
функций (г | \р) оператор а можно представить диффе-
дифференциальным оператором (z/2 + djdz*). (Грубой анало-
аналогией этого является оператор Р = —ihd/dx в шредин-
геровском представлении.) Следовательно, в этом
представлении основное коммутационное соотношение
принимает вид
(г | [а, аЧ |^) = [| + ~, *] (z |ф> = (z \у). G.94)
В более общей формулировке можно сказать, что
действие произвольного оператора If = W{а:, а) пред-
представляется с помощью соответствующего дифферен-
дифференциального оператора в частных производных, а именно
(z | W {а\ а) | г|>> = W (г\ | + -—¦) (z \ г),). G.95)
Далее, если воспользоваться записью (zn|)) =
= ехр(—l/2\z\2)f(z*) и операторным тождеством
/ 1 , ,2\ д	I 1 , ,о\ д z	,_ „„,
ехр тг I z I -ч-1г ехр — 7Г z I = ~г~ — -п-. G.96)
1 \ Z	I OZ	\	I	I OZ	Z

186 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
то легко получить
X ехр A1 z р) (z | ф> = ехр (- 11 z |2) Г (z\ Jr) f (z*).
В качестве примера применения этих формул полу-
получим еще раз свойства эволюционного оператора
ехр(—ita'a). В частности, с помощью тождества G.55)
находим
(z|exp[- rt(a+a)]|i|>) =
= ехр (- 11 г р) ехр ( - Hz -^-) f (г*) =
= ехр (- у | z р) ехр ( - г* -j^-г) f (ехр [In z']) =
== ехр ( - т/ I 2 Р j f (ехр [In 2* - г'/]) =
= ехр(- |1г|2)Пе-"г*) = <е"г|ф>,	G.98)
что справедливо в силу последнего равенства в формуле
G.85).
Запись через дифференциальные операторы G.95)
можно, разумеется, применить для получения матричных
элементов оператора If по когерентным состояниям,
если положить \ty) = \z'). В частности,
(z | W (а\ а) | г') = W (z, | + -~) {г I z'). G.99)
В этом выражении частные производные действуют на
все стоящие справа от них члены; среди таковых имеют-
имеются z* из {z\z'), а также, возможно, некоторые множи-
множители z* из самого оператора W. Поскольку для (z\z')
имеется явное выражение, можно воспользоваться опе-
операторным тождеством
((z | г'» ^(z |z'> = ^ - | + 2'	G.100)
[аналогичным G.96)], чтобы найти явные выражения для
некоторых производных. Именно, получаем
B | W (о+, а) |г') = <z !z') W [z\ z'+~), G.101)

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИЙ 187
где оставшиеся производные действуют как раз на тег*,
которые содержатся в самом Ж. Ясно, что если оператор
W нормально упорядочен (все а расположены справа),
то в выражении для Ж все производные стоят справа от
всех z* и дают нуль, поскольку действуют лишь на чле-
члены, не зависящие от z*. В этом случае мы лишь снова
получили выражение G.87) для матричных элементов
нормально упорядоченных операторов. Однако соотно-
соотношения G.99) и G.101) выполняются независимо от того,
является ли оператор W нормально упорядоченным.
Диагональные матричные элементы. Отметим теперь
еще одно фундаментальное следствие, вытекающее из
общих свойств когерентных состояний, которое легче
всего получить из свойств аналитичности. Предположим,
что диагональные матричные элементы оператора W
равны нулю;
(z\W\z) = 0	G.102)
при всех г. Что отсюда следует? Для операторов Ж ра-
разумного вида произвольные матричные элементы равны
откуда видно, что для выполнения условия G.102) це-
целая функция двух комплексных переменных г* и г'
(а именно двойной ряд) должна равняться нулю на
подмножестве z' = z. Однако из теории функций не-
нескольких комплексных переменных известно, что если
такая функция двух переменных равна нулю на подмно-
подмножестве г' = г при всех z (или даже при z из определен-
определенных последовательностей!), то она равна нулю тожде-
тождественно. Другими словами, если (z\W\z)= 0 при всех г,
то {z\7f\z') = 0 при всех г и z', и это просто означает,
что W = 0. Обратная теорема очевидна.
Отсюда следует важный вывод, состоящий в том, что
оператор Ж однозначно определяется своими диагональ-
диагональными матричными элементами Ж(г) = (г\Ж\г) или а
нашем фазовом пространстве величиной W(p, q) =
= (р, ц\Ж\р, q). Таким образом, операторы Ж могут

188 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
быть представлены соответствующими функциями W(z).
[Следует отчетливо понимать, что когда мы представ-
представляем операторы Ж функциямиW(г) = {z\W\z), мы име-
имеем дело с совершенно другим видом «представления»,
чем то, в котором мы представляем векторы |г|з) функ-
функциями г|>(г) =(г|г|)).]
Теперь, установив единственность диагональных мат-
матричных элементов как представителей операторов, от-
отметим некоторые их свойства. Для данного оператора
W{af, а) диагональные матричные элементы можно по-
получить непосредственно из G.101), если положить
z' = z:
Наряду с этим положим z' = z в G.88). Это дает
(z\:O(а+, а): |г) = О(г\ г).	G.105)
Содержание последних двух соотношений можно выра-
выразить одним соотношением, написав
(z\W{a\ a)\z) = l
= W„ (z, z) = <z | : Г„ (a+, a): | z>, G.106)
где Wn есть соответствующая функция z* и z, возникаю-
возникающая после выполнения дифференцирований д/dz* внутри
W [так, ка.к_если бы справа от W(z,z* + д/dz*) в G.104)
стояла «ели!™".3»] ('-пптнпгттрнир G IDfi) пярт лпгицргки
простой рецепт для перехода от оператора W(af , a)
к тому же самому оператору, но записанному теперь
в нормальной форме, а именно
:Wn{a\ a): = W{a\ a).	G.107)
Например, если W = aaf, то
(z |aa+ \z) = (z + -?,)z' = zz + 1 = Wn(z\ z) =
откуда следует уже известное равенство аа+ — а+а+ 1.

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ. СОСТОЯНИИ 189
Соотношения приведенного выше типа, позволяющие
получать нормально упорядоченные формы операторов,
фактически в квантовую теорию поля впервые ввел Ан*
дерсон [7.14]. В последние годы их использование в кван-
товых задачах теории когерентности изучали Луиселл
[7.2], Л экс [7.15] и другие. Главную особенность под-
подхода этих авторов можно охарактеризовать, если обра-
обратиться к операторному уравнению ifi (d/dt) U(t) —3@U(t)
[ср. F.13)], которому подчиняется эволюционный опера-
оператор U(t). Это операторное уравнение можно представить
в виде дифференциального уравнения в частных произ-
производных с помощью следующей цепочки равенств:
ujfUniz*. z, t)-ib-lr(z\U(a+,a,t)\z)~
G.108)
Используя решение этого уравнения Un, можно непо-
непосредственно записать нормально упорядоченную форму
оператора U:
U(af, a, t) = :Un(a*, a, t) : .	G.109)
На этом мы заканчиваем наше рассмотрение приме-
примеров и свойств векторов и операторов в непрерывных
представлениях по когерентным состояниям. Необходимо
добавить, что мы рассматривали операторы в основном
эвристически, игнорируя все вопросы об области приме-
применимости. Совершенно ясно, однако, что наши замечания
применимы ко всякому ограниченному оператору, а так-
также к неограниченным операторам с достаточно хорошим
поведением, например ко всем многочленам по а и af.
Нетрудно придумать операторы, к которым наше рас-
рассмотрение не приложимо; например, уже в G.83) и
G.84) возникают трудности для таких операторов J?, у
которых Ьп = (п\)а с а > '/г- Читателю предлагается так-
также обдумать менее очевидные трудности, возникающие
при 1 > о> '/г-

190 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Г. Связь с пространствами Сегала — Барг манна
Выше мы уже отмечали, что каждой функции ty(z)
с помощью определенного множителя сопоставляется це-
целая аналитическая функция 2*, а именно
<2г I ч>> =- Ч> (г) =- ехр (— -^ I г
Очевидно,/(г*) однозначно определяет $(z) и наоборот.
Следовательно, мы можем рассматривать саму аналити-
аналитическую функцию f(z*) как функциональный представи-
представитель абстрактного вектора |г|з). Каждый член этого
функционального представления является целой анали-
аналитической функцией. Если fj(z*) есть целая аналитиче-
аналитическая функция, соответствующая вектору |%), то скаляр-
скалярное произведение можно определить, очевидно, цепочкой
равенств
^ J [fi (**)]* М**) Ф.	GЛ10)
где мы положили
йц = (я) ехр (- | z |2) d (Re z) d (Im г). G.111)
Интуитивно ясно, что, приняв G.110) в качестве оп-
определения скалярного произведения, мы образовали
гильбертово пространство, составленное из целых функ-
функций f{z*). Такие пространства использовались Сегалом
[7.5] и Баргманном [7.6] в различных квантовых задачах,
их свойства подробно рассмотрены в статье Баргманна
[7.6]1).
Связь между пространствами Сегала — Баргманна и
непрерывными представлениями по когерентным состоя-
состояниям была отмечена Швебером [7.7]. Простая связь ме-
между (z|i|)) и /(г*) показывает, что многие черты непре-
непрерывных представлений по когерентным состояниям при-
') В цитированных работах обычно используется обозначение
f(z) для функции, которую мы обозначаем через f(z*).

§ 2. ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА КОГЕРЕНТ СОСТОЯНИЙ 191
сущи также и пространствам Сегала — Баргманна и что
не совпадают лишь очень немногие свойства. Из всех
этих характерных черт упомянем лишь, что свойства
аналитичности, находящиеся, очевидно, на первом плане
в формулировке Сегала — Баргманна, позволили Барг-
манну внести некоторую ясность в вопрос о переполнен-
переполненности системы когерентных состояний \г).
Баргманн называет характеристическим набором <5*
комплексных значений г* набор, удовлетворяющий сле-
следующему условию: если f{z*) = 0 при всех z* e ©*, то
fB*) = 0 для всех г*. Это означает соответственно, что
если ip(z) =0 при всех геб, то ji|)) = 0'). Баргманн
приводит два примера характеристических наборов,
а) Любой бесконечный набор точек в комплексной пло-
плоскости, сходящийся к конечному пределу. Этот пример
прямо вытекает из свойств аналитичности и включает в
себя в качестве частных случаев более привычные при-
примеры, а именно отрезок линии или открытую последова-
последовательность в комплексной плоскости, б) Любая бесконеч-
бесконечная последовательность av, avФ 0, такая, что
оо
<т=2 КГ2-*)	GЛ12)
v = l
для некоторого ц > 0. Этот пример построен с учетом
свойств, которыми обладают целые аналитические функ-
функции, удовлетворяющие условию G.47).
Заметим, что найденный фон Нейманом характери-
характеристический (т. е. «полный») набор, определенный соответ-
соответствующей квадратной решеткой точек в комплексной
плоскости (о котором мы уже упоминали), есть третий
пример характеристического набора, не являющийся
частным случаем примеров «а» или «б».
За недостатком места мы не останавливаемся на ин-
интересном использовании когерентных состояний и свя-
связанных с ними величин в качестве производящих функ-
функций для различных состояний и операторов. Эта идея
разрабатывалась еще Фоком на заре квантовой теории.
') По нашей физической терминологии набор векторов
{| г ) ; г е ©} является полным.

192 ГЛ. 7 ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Она же лежит в основе элегантного подхода Швингера
к квантовой теории поля, до известной степени сходного
с упоминавшимся в гл. 4.
§ 3. КОГЕРЕНТНЫЕ СОСТОЯНИЯ ДЛЯ НЕСКОЛЬКИХ
СТЕПЕНЕЙ СВОБОДЫ
Свойства когерентных состояний для нескольких сте-
степеней свободы являются прямыми обобщениями наших
предыдущих замечаний, относившихся к одной степени
свободы. Мы ограничимся некоторыми определениями и
вопросами размерности, предоставляя остальное вообра-
воображению читателя.
Пусть мы имеем дело с К степенями свободы; им
соответствуют операторы числа квантов Nk = a\ak, k =
= 1, 2, . . ., К и их общий набор нормированных соб-
собственных векторов
\щ, п.,, ...,
введенных выше [см. E.70)]. Тогда соответствующие ко-
когерентные состояния зависят от К комплексных перемен-
переменных и по аналогии с G.1) определяются соотношением
\zu z2, ...,
вместе с очевидным определением сопряженных векто-
векторов {{гь}\.
Эти состояния являются, разумеется, основными со-
состояниями К независимых сдвинутых осцилляторов при
соответствующих внешних силах. Аналогично \{zh}) яв-
является общим собственным вектором операторов ak>:
G.114)
для всех k' = 1, 2, ..., К.

§ 3. НЕСКОЛЬКО СТЕПЕНЕЙ СВОБОДЫ	193
Перекрытие двух когерентных состояний есть просто
= exp -
где последнее равенство следует непосредственно из G.31).
Нормированность и непрерывность состояний | {zk}) и
аналитичность функций f ({z*})=ехр ('/2 2 I zk |2) ({zfc} | ¦ф
также получаются сразу.
Основная формула G.48) для разложения единицы
записывается в следующей более общей форме:
к
I = ± J . . . | | {2,}) <Ы IП d%, G.116)
где d2zh = d(Re zh)d(\m zh) и интегрирование распро>
страняется на все 2Л>мерное пространство. Доказатель-
Доказательство этого разложения проводится аналогично доказа-
доказательству для случая одной степени свободы. Удобно за-
записать л"к и элемент объема более компактно:
я-*П dhk = dii({zk}),	G.117)
k=i
так что G.116) просто принимает вид
G.118)
Весь аппарат непрерывного представления можно
ввести с помощью G.118). Формула для скалярного про-
произведения записывается следующим образом:
= J <M {zft}> <{zft} 11> ф ({zfc}) G.119)

194 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
и т. д. У операторов существуют оба представления: с
помощью интегральных ядер и с помощью дифферен-
дифференциальных операторов. Заметим, что операция нормаль-
нормального упорядочения : : обобщается так, что все операторы
рождения а\ должны стоять слева от всех операторов
уничтожения ak> в каждом множителе.
Здесь мы хотели бы обратить внимание на ту роль,
которую играют круговые частоты аи в задаче с не-
несколькими гармоническими осцилляторами. Когда мы
имеем дело одновременно с несколькими гармонически-
гармоническими осцилляторами, мы, вообще говоря, не можем пу-
путем выбора единиц сделать все круговые частоты рав-
равными единице. Поэтому удобнее всего показать явно
роль каждой из частот a>h.
Операторы физических «координат» и «импульсов»
Qk и Pk связаны с ah и а\ соотношениями E.68). Анало-
Аналогичным образом можно ввести фазовое пространство
для К степеней свободы с помощью разложения
W)GЛ20)
для каждого k. Как обычно, определим \{ph, })
— \{zk}). В этих переменных функциональный представи-
представитель состояния |0) = |{0}), отвечающего основному со-
состоянию по каждому из К осцилляторов, имеет вид
I.	ft=i	J
Если переписать это выражение несколько иначе:
1
то оно принимает легко запоминающуюся форму:
Основное состояние =
1 V4 Г (Энергия классического осциллятора) 1 \
Р| 2 ~U [(Расстояние между квантовыми уровнями)] \
(	осцил	J
G.122)

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ 195
Стоит отметить небольшую отличительную особен-
особенность разложения единицы G.118), записанного в фа-
фазовом пространстве. В частности,
/= ||{Р*. Чк})({Рк, Ы1Ф((Рь qk}), G-123)
где, как непосредственно следует из G.117) и G.120),
^5П	<7Л24>
и интегрирование распространяется по всему /(-мерному
фазовому пространству. С помощью этого соотношения
нетрудно проверить, что функция G.121) удовлетворяет
соотношению
1 = J @ \{рк, qk)) {{Pk, Як) I 0) dpi {{pk, qk}) =
= {\<Po({Pk,qk})\2dii({pk,qk}).	G.125)
§ 4. КОГЕРЕНТНЫЕ СОСТОЯНИЯ ДЛЯ БЕСКОНЕЧНОГО
ЧИСЛА СТЕПЕНЕЙ СВОБОДЫ.
ПРИЛОЖЕНИЕ К ЭЛЕКТРОМАГНИТНОМУ ПОЛЮ
А. Общие свойства
Теперь произведем переход (Л'—*оо) к бесконечному
числу степеней свободы, необходимому для описания
электромагнитного поля. Как и в гл. 5, осуществим этот
переход в предположении, что
оо
N=2,Nk	G.126)
ft
3^=1ihakNk	G.127)
являются хорошо определенными операторами. Как уже
отмечалось в гл. 5, для этого достаточно, чтобы каждое
из общих собственных состояний операторов числа кван-
квантов
\щ, п2, ...) = [ {nk})	G.128)

196 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
удовлетворяло условию
оо
It пк<оо-	G.129)
иначе говоря, их множество должно быть счетным.
Чтобы определить когерентные состояния для беско-
бесконечного числа степеней свободы, рассмотрим сначала
состояние вида
Ё ffi|f^ !	С7.1ЭО)
и посмотрим, при каких значениях zh оно является на-
настоящим вектором. Из свойств ортогональности \{пь})
получаем
GЛ31)
Чтобы выражение G.131) было конечным, величины
{zh} должны удовлетворять неравенству
оо
2|zfe'|2<~. -	G.132)
w=\
Поскольку все векторы должны иметь конечную норму,
в последующем изложении мы будем считать условие
G.132) выполненным. Отсюда, очевидно, вытекает сле-
следующее фундаментальное следствие: допустимые после-
последовательности {Zk} сами образуют гильбертово простран-
пространство 3 (отличающееся от квантовомеханического гиль-
гильбертова пространства ?) со скалярным произведением

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ 197
и квадратом нормы
iizJ2.	G.1336)
4 1
Иными словами, аргумент {zu} вектора гильбертова
пространства \{zh})^& сам является вектором другого,
по-прежнему бесконечномерного, гильбертова простран-
пространства: {zft}e3. В некоторых случаях нам придется пред-
представлять вектор из пространства 3 не в виде последова-
последовательности {zh}, а в другой форме.
Имея постоянно в виду ограничение G.132), можно
теперь определить в качестве искомых когерентных со-
состояний векторы
\Zl,z,2, ...> =
наряду с их сопряженными ({}|
Состояния \{zk}) являются не только основными со-
состояниями сдвинутых осцилляторов, но и общими соб-
собственными векторами операторов
G.135)
для любого k' = 1, 2, .... В силу G.132) получаем
lim ak> \ {zk}) = lim zv I {zk}) = 0.	G.136)
Отсюда вытекает, что для достаточно больших значе-
значений k любое когерентное состояние имеет приблизитель-
приблизительно тот же вид, что и основное состояние осциллятора.
С другой стороны, для любого наперед заданного зна-
значения k' существуют когерентные состояния со сколь
угодно большим значением zk>.

198 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Перекрытие двух таких когерентных состояний опре-
определяется пределом выражения G.115) при /С->оо, от-
откуда получаем
к=\
ехр
( k
{
-S[Tlz*-
Все вопросы сходимости бесконечных произведений и
интегралов связаны, конечно, с выполнением фундамен-
фундаментального ограничения G.132).
Вычисления, аналогичные проведенным после соот-
соотношения G.40), показывают, что
^ 2 (| {zk} || + || {z'k} I) • j [zk ~z'k}\. G.138)
Следовательно, два когерентных состояния близки,
если отвечающие им последовательности {г/,} близки как
векторы в 3- Из этого свойства вытекает важное след-
следствие, имеющее физический смысл. Пусть задан вектор
\{zh}) с zh Ф 0 при всех k. Из физических соображений
можно предположить, что состояние \{zh}) приближенно
можно заменить на состояние | [z'k]), для которого zk = z'k
для k ^ М и z'k = 0 для k > М при достаточно боль-
большом М. Назовем такую последовательность усеченной
последовательностью и обозначим ее {z;,,M}. Это значит,
что
z ^= z (k <С М) z ^= 0 (k^> M) G 139)
Тогда из G.138) и из неравенства \}{zi,, M}\\JC\\{Zh}\\ сле-
следует
А\ G.140)

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ 199
Эту величину действительно можно сделать произвольно
малой при достаточно больших М, что подтверждает
наше интуитивное предположение.
Основные функции в непрерывном представлении
по когерентным состояниям даются выражением
4>«z*}) = <{z*}№>	G-141)
для любого |гр)еф. Поскольку состояния \{пи\) обра-
образуют полную систему, то таким свойством обладают и
когерентные состояния. В действительности, как и рань-
раньше, системы когерентных состояний переполнены. Для
одной степени свободы мы отмечали, что для нахожде-
нахождения полных правильных подмножеств когерентных со-
состояний можно воспользоваться соображениями анали-
аналитичности. Те же аргументы применимы, очевидно, и для
случая нескольких степеней свободы, а также и для
конечного числа из бесконечного множества степеней
свободы в проведенном выше рассмотрении. Мы хотим,
однако, заострить внимание на полном правильном под-
подмножестве состояний другого вида, которые возникают
лишь в случае бесконечного числа степеней свободы.
Пусть известно, что
Ч> ({**.*}) = О	G.142)
для всех {zh} и для всех М, т. е. для всех усеченных
последовательностей. Тогда для произвольного состоя-
состояния \{zk}) отсюда следует
I - ({zk, м) I Ж) К
S \zkf\\ G.143)
k=M + \
Последняя величина при достаточно больших М может
быть сделана сколь угодно малой. Короче говоря, из
{J)	)
G.142) вытекает, что ^({z/J), а следовательно, и |г|э)
обращается в нуль для всех последовательностей {z/J.
Нетрудно сформулировать более общее утверждение,
состоящее в том, что |г|з) определяется значениями

200 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
^(}) для любого множества последовательностей {zh},
которое плотно в 3-
«Разложение единицы». Перейдем к обобщению на-
нашего обычного разложения единицы по когерентным
состояниям на случай бесконечного числа степеней сво-
свободы и к определению соответствующего скалярного
произведения для функционального представления. По
аналогии с G.118) и G.119) естественно было бы ожи-
ожидать, что искомые соотношения запишутся следующим
образом:
/= J|{z,})({z.JI4i({2j)	G.144)
и
<М Ц>> = f <М {**}) ({zk} I Ц>> Ф ({zk}). G.145)
Однако в написанном виде эти соотношения совершенно
не определены, так как здесь необходимо вычислять ин-
интеграл по бесконечному числу переменных. Из интуи-
интуитивных соображений следует, что должно выполняться
соотношение
= Hm \
G.146)
где
,M})=K-Ml\dhk.	G.147)
Интуитивное обоснование соотношения G.146) состоит
просто в следующем. Поскольку мы имеем дело лишь
с непрерывными функциями ({^}|г|з) и т. д., всякая
функция, как отмечалось выше, полностью определяется
своими значениями на плотном подмножестве. Инте-
Интеграл G.146) определен просто как предел последователь-
последовательности интегралов, у которых подынтегральные выраже-
выражения вычислены на плотной последовательности при М,
становящемся сколь угодно большим.
Суть доказательства соотношения G.146) можно
сформулировать так. Введем сначала последователь-

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕН СВОБОДЫ 201
ность проекционных операторов Рм, М = 1, 2, ..., каж-
каждый из которых определяется свойством
°°	М	-1
-IV (\ z I2 + I г' \2) + У г'г'
2 Lk \\zk\ ^ | zk|) ^ Zu z*zk •
k=l	4=1	J
G.148)
Грубо говоря, это означает, что Рш есть оператор про-
проектирования на основное состояние для всех степеней
свободы с k > М. Отсюда ясно, что PMPw = Рм'Рм = Рм
при М ^.М' и что
lim PM = I.	G.143)
Далее, прямые вычисления гауссовых интегралов дают
-к] | Г/е, М)/ \{zk, м] | \zk I/ "f1 [[ги, Ml) ~ \\Zk\ I rM\ \Zk I/
G.150)
в силу определения G.148). Согласно стандартным тео-
теоремам, отсюда следует, что
Рм=\\ {2;(, м)) ({zk, м) I d\i {{гк, „}).	G.151)
Следовательно, для произвольных |\|з) и \Х) имеет ме-
место равенство
= Нт 1 (ЯКг,,^})^,,^}^)^^,^}), G.152)
что и доказывает справедливость соотношения G.146).
Наконец, сопоставляя G.149) и G.151), мы видим
/= lim \\{zk,M})({zk,M}\dyL{{zk,M}); G.153)
такой вид принимает наше обычное разложение еди-
единицы в данном случае. Соотношения G.152) и G.153)
и являются обобщениями соотношений G.119) и G.118)
на случай бесконечного числа степеней свободы. В ка-
качестве сокращенной записи точных предельных соотно-
соотношений мы часто будем использовать просто G.144) и

202 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
G.145), смысл которых определяется точными соотно-
соотношениями G.153) и G.152).
Непрерывное представление. Установив смысл нашего
обычного разложения единицы, мы можем взять весь
аппарат непрерывного представления по когерентным
состояниям из нашего предыдущего рассмотрения.
В частности, представление операторов может быть за-
задано с помощью интегрального ядра ({гй]| J?| (П
({z J | Я Ц.) = / ({гк} | Л | {<}> ф'к) | ф> ф ({4}). G.154)
Существует и представление дифференциальными опе-
операторами, аналогичное G.95). Если F3 ({«?}, {^Л) зави-
зависит от операторов рождения и уничтожения, то
Iw (К). к}) i^>=^э ({*;}. {т+-ц})
G.155)
Нормально упорядоченные операторы удовлетворяют
соотношению
G.156)
кроме того, имеет место соотношение [ср. G.106)]
<{zk}\W({at},{ak})\[zk}) =
связывающее Ж и :Жп: = W через их диагональные
матричные элементы.
Аналогичным образом
= Л
})	G.158)

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ	203
можно рассматривать соответственно как представления
абстрактных векторов |г|з) и операторов Jf. Нетрудно
обобщить на этот случай дальнейшие замечания, сде-
сделанные ранее при рассмотрении одной степени свободы.
Совершенно ясно, что всему нашему рассмотрению,
включая соотношения G.152) и G.153), соответствует
совершенно аналогичная формулировка в фазовом про-
пространстве В последнем случае основное внимание дол-
должно быть сосредоточено на величинах qh и ри, которые
для всех k определяются следующим образом:
Рк-	G.160)
Заметим, что в этой формулировке допустимые последо-
последовательности в фазовом пространстве в силу G.132)
должны удовлетворять условию
Представитель основного состояния получается непо-
непосредственно из G.137):
4>o(iPk, Qk}) = ({Pk> <7
= ехр
- G-162)
Очевидно, и это выражение имеет схематический вид
G.122). Рассмотрение свойства фазового пространства
мы продолжим после того, как будут разобраны свой-
свойства поля излучения.
Б. Приложение к электромагнитному полю
Как было показано в гл. 6, электромагнитное поле
можно рассматривать как совокупность гармонических
осцилляторов, находящихся под действием внешних сил.
Если считать, что система находится в большом куби-
кубическом объеме квантования Q = L3, то соответствующие
независимые нормальные моды обычно обозначаются

2U ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
индексами X и к, причем X представляет собой поляри-
поляризационный индекс, а к — переменную импульса, кванто-
квантованную в соответствии с F 40) Значение к = 0 исклю-
исключается явно Обозначение двумя индексами X, к соот-
соответствует использованному выше обозначению одним
индексом k
В настоящем рассмотрении мы ограничимся свобод-
свободным полем излучения и полем излучения при наличии
с-числовых источников Как уже отмечалось в гл. 6,
только в этих случаях возможно неприводимое кванто-
квантование, при котором собственные состояния операторов
числа квантов или когерентных состояний действительно
накрывают все гильбертово пространство. Тогда опера-
оператор уничтожения (X, к)-й моды в зависящей от времени
форме определяется в соответствии с F.59) выражением
ак(к, t) = e-iti>tu[n(:i) + cK{k, t),	G.163)
где круговая частота есть просто со = иц,, к = |к|. Из
F.55) получаем выражения для Cx(k,t) через с-число-
вой ток ff%(k, t):
t
ш'?к(к, t')dt'. G.164)
Будем считать |{«^(к)}) собственными состояниями опе-
операторов
N{n (к) = а[п + (к) < (к).	G.165)
Тогда когерентные состояния |{2х(к)}), определяемые
соотношениями типа G.143) для всех Я, и к, удовлетво-
удовлетворяют условию
а[п (к) | {zk (к)}) = гк (к) [ {zK (к)}).	G.166)
В свою очередь зависящие от времени операторы унич-
уничтожения удовлетворяют соотношению
а,(к, 01К(к)}) = [е-'^(к) + С,(к, t)]\{zK(k)}), G.167)
и, таким образом, когерентные состояния являются так-
также и собственными состояниями оператора ax(k,t). Вве-
Введем сокращенное обозначение
t)^e~'-%(k) + cK(k,t),	G.168)

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ 205
что является в действительности просто комплексной
формой классического решения уравнений Максвелла
с источниками.
Если по аналогии с формулой F.15) принять
^(Odt']\ G.169)
за эволюционный оператор с гамильтонианом Ж, за-
заданным соотношением F.46), то
ak(k,t) = U(t)-la[n(k)U(t).	G.170)
Умножая G.167) на U(t), получаем
ain(k)U(t)\{zM) = zAK t)U(t)\{zK(k)}). G.171)
Это означает, что
?/(OI{zfc(k)}> = e'?<»|{zA(k,O}>.	G.172)
где ф(/) — некоторая фазовая функция. Можно пока-
показать, что
t
Ф (*) = ]? J/я (k, nBM"'/2Re[2,(k, f)]dt', G.173)
I, k -<x>
где ф(/) зависит и от начального состояния, и от дей-
действовавшей силы. Резюмируя, можно сказать, что при
наличии внешнего с-числового источника fi(k, t) коге-
когерентное состояние переходит (с точностью до фазового
множителя) в другое когерентное состояние, полностью
определяемое классическим решением при наличии
источника.
Общим приложением этого фундаментального резуль-
результата является описание процесса испускания и погло-
поглощения фотонов с-числовым источником. Выясним, на-
например, какое распределение для {щ} будет обнаружено
в момент t за счет действия источника. Из G.134), оче-
очевидно, следует
р (К (к)} 10) = I (К (к)} I U (О I К (к)}} I2 =
ПыС	{7Л74)
К, к

206 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
Мы получили просто многомерное распределение Пуас-
Пуассона для любых /, причем
<nA(k)> = |zfc(k, t)f.	G.175)
Эти результаты приводятся обычно для излучения из
вакуумного состояния [для которого 2?-(к) = 0]; в этом
случае гк(к, t) = с%(к, t) при всех Я, к [см. G.164)].
Свободное поле. Рассмотрим теперь частный случай
свободного поля излучения без внешних токов. Тогда
для каждой из мод имеем просто
аК(Ы) = е-ша{п(к),	G.176а)
zK(k, 0 = e-'-'zfc(k).	G.1766)
Удобно ввести некоторые сокращенные обозначения для
соответствующих динамических переменных. Пусть ex(k)
обозначает поперечный вектор поляризации [входящий
в F.25) и последующие соотношения] и определим по-
поперечные векторы
a(k, 0 = Sex(k)afc(k, 0,	G.177а)
z(k, *) = 2еь(кJА(к, t),	G.1776)
которые, очевидно, удовлетворяют соотношению
а(k, Ol{z}> = z(k, t)\{z}),	G.178)
где I {z}) = [ {zx (к)}). Аналогично введем определения
-]'2е*-ха(к,Ъ G.179а)
к
V (х, t) = -L- У Ш'А e'k-xz (к, 0; G.1796)
А<+>(х,/) и V(x, t) являются положительно-частотными
функциями, или аналитическими сигналами в смысле

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕН СВОБОДЫ 207
гл. 1. Положим также
Е(+)(х, 0= - А(+)(х, 0 = ^?(-y)V«a(M), G.180а)
к
'el^z(k,t) G.1806)
n (x, t) = V X V (x, t).
Когерентные состояния, очевидно, представляют собой
собственные состояния всех этих положительно-частот-
положительно-частотных операторов, а именно
А(+)(х, *)|{z}) = V(x, *)|{г}>,	G.181а)
\) = e(x,t)\{z}),	G.1816)
> = n(x,OI{z}>.	G.181b)
Сопряженные операторы являются отрицательно-частот-
отрицательно-частотными операторами и обозначаются так:
[А(+> (х, Of = Ам (x, 0,	G.182а)
|Е(+)(х, оГ^Е^Чх, 0.	G.1826)
[Н(+)(х, t)f = Hl~\x, t).	G.182b)
Из формы записи ясно, что все положительно-частотные
(а следовательно, и все отрицательно-частотные) опера-
операторы коммутируют между собой.
Придерживаясь принятой нами системы, запишем
некоторые из приведенных выше выражений в фазовом
пространстве, что позволит связать их с более привыч-
привычными физическими величинами. По аналогии с F.44а)
и F.35) положим
z(U t) — (—V'2 а (к /1 — / ( —	V2 е (к Л Г

208 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
где разделение на первый и второй члены основано на
условии
а*(к, 0 = а(-к, 0,	G.184а)
е*(к, *) = е(-к, t).	G.1846)
В силу этих условий функции
a{x,t)^-~^eik^a(k,t),	G.185а)
е(х, О^р^^-Мк, 0	G.1856)
к
действительны. Нам представится случай воспользо-
воспользоваться соотношением
h{k,t) = ikXa.(k,t)	G.186)
и его действительной формой в конфигурационном про-
пространстве
h(x Л — ——- т pikxh (V t\	G ]R7\
Формулировку в фазовом пространстве легче всего дать
с помощью действительных поперечных векторов е(х)
и а (х); ей можно придать еще более привычный для фи-
физика вид, если использовать е(х) и «производную» от
а(х), а именно h(x).
Представитель основного состояния. Функции е(х) и
а(х) [или h(x)], очевидно, определяют последователь-
последовательность {гх(к)} и тем самым когерентное состояние. Чтобы
подчеркнуть этот факт, введем другое обозначение для
когерентных состояний:
|е, a)^|e,h)^|fe(k)}>.	G.188)
Хотя форма с независимыми модами наиболее удобна
для конкретных расчетов, представляется поучительным
привести запись в фазовом пространстве.
Рассмотрим основной пример, а именно выведем вы-
выражение для представителя основного состояния как

5 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ 209
функционала от е и h. Из G.1776) и G.183) следует
\ к к	/	V к
= ехр[- -^2 [со11 (к) Р + со| а (к) P]V G.189)
V	к	/
Воспользовавшись соотношением
| h (к) р = [к X а (к)*] • [к X а (к)] = к21 а (к) |2 G.190)
и равенством to2 = к2, перепишем G.189) в форме
\
Последнее выражение принимает наиболее элегантный
вид, если записать его в конфигурационном простран-
пространстве и перейти в пределе к бесконечному объему. Исполь-
Используя соотношения
е(к) =-^ j e-ik4(x)d3x,	G.192a)
h(k) =-\fr j e-ik-*h(x)d3x	G.1926)
(и комплексно сопряженные им!), а также соотношение
1 у е'-м*-у> _ 1 Г «<Их"у) J.U.., 1 '
™ю i' Ai |k|	BяK J |k| "" 2я» |х-у|"
G.193)
легко получить, что G.191) принимает вид
Фо(е, h) = (e, h|0> =
С физической точки зрения это есть выражение для
амплитуды вероятности найти основное состояние поля
излучения в таком смещенном основном состоянии, для
которого
<Е(х)) = е(х),	G.195а)
<H(x)) = h(x)	G.1956)

210 ГЛ. 7. ПРЕДСТАВЛЕНИЕ ПО КОГЕРЕНТНЫМ СОСТОЯНИЯМ
(как если бы оно получалось под действием внешнего
источника). Следует заметить, что с формальной точки
зрения вектор гильбертова пространства 3, представлен-
представленный ранее последовательностью {г^(к)}, здесь представ-
представлен парой действительных функций е(х) и h(x), квад-
квадрат нормы которых определяется двойным интегралом
в G.194) ').
Наш второй пример является простым обобщением
первого. Именно
<е, h |е', h') = ехр{ - S [ I z (k)-z'(k) ?-i Imz* (к) • z'(к)]},
G.196)
что следует из G.137). Здесь появился единственный
новый член, а именно
к
= Ть 2 i [~е*(к) • к Х h'(к) + к X й* (к) • е' (к)]. G.197)
к
В конфигурационном пространстве и в пределе беско-
бесконечного объема находим
Ф = ТЕ I [e(x)-a'(x)-a(x)-e'(x)]d3x. G.198)
Воспользовавшись соотношением
Лк-(х-у)
tf	Bя)» J |
1
х - у Г
G.199)
') Этот интеграл есть «число квантов» в классическом электро
магнитном поле е и h. См. работу: Я. Б. Зельдович, ДАН
СССР, 163, № 6, 1359 A965). -Прим перев.

§ 4. БЕСКОНЕЧНОЕ ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ	211
можно переписать G.198) в виде
G.200)
Ясно, что, должным образом комбинируя G.200) и
G.194), можно найти явное выражение для (е, h|e', h').
Разумеется, все эти выражения заведомо калибровочно
инвариантны
В последующих главах мы обсудим еще ряд свойств
когерентных состояний поля излучения.

8
Квантовая теория оптических
корреляционных явлений
§ 1. КВАНТОВЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
А. Идеальные детекторы и скорости счета квантов
Вернемся теперь к изучению взаимодействия поля
излучения с веществом, имея в виду описание систем
счета фотонов. Полное рассмотрение таких систем тре-
требует весьма сложного анализа, поэтому, следуя Глау-
беру [8.1], мы подойдем к проблеме в некотором роде
феноменологически. Системы, которые имеются здесь в
виду, «детектируют» фотоны с помощью процесса по-
поглощения фотонов. К числу таких систем относятся
обычные фотосчетчики, фотоионизационные схемы, фото-
фотопластинки и т. д. В процессе детектирования фотон по-
поглощается; соответственно меняется и состояние детек-
детектирующей системы. Идеализируя задачу, детектор мож-
можно рассматривать как совокупность огромного числа
идентичных независимых элементарных систем (напри-
(например, атомов), каждая из которых первоначально нахо-
находится в своем основном состоянии. После поглощения
(перехода в возбужденное состояние) данной элемен-
элементарной системой можно пренебречь, если (для простоты)
не учитывать на этом этапе процессы многократного
поглощения. Поскольку детекторы обычно размещаются
вне источников, поле излучения можно считать свободно
распространяющимся, если не говорить об его взаимо-
взаимодействии с детектором. Опять-таки для простоты мы рас-
рассматриваем взаимодействие с детектором в низшем не-
исчезающем порядке теории возмущений.
Анализ взаимодействия мы будем производить в до-
довольно общем виде, но полезно иметь ясное представ-
представление о некоторых положениях, лежащих в основе изло-
изложения. Исходный гамильтониан взаимодействия, харак-

§ 1. КВАНТОВЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ	213
теризующий поле и атом, равен —'/2е[р • А(г) + А(г)-р].
Оператор поля А отвечает однофотонному переходу в
поле, в то время как оператор р импульса отвечает со-
соответствующему атомному переходу. Этот переход мо-
может быть запрещен в силу правил отбора; тогда сле-
следует разлагать А(г) в ряд Тейлора вблизи центра атома
до тех пор, пока не появится первый неисчезающий
член. Для простоты будем считать, что для нашего рас-
рассмотрения достаточно пользоваться неразложенным га-
гамильтонианом взаимодействия.
Точечные детекторы. В качестве первого примера
предположим, что происходит поглощение фотона с век-
вектором поляризации е в точке г в момент времени t.
Оператор А<+>(г, ^.определяемый соотношением G.179а),
представляет собой оператор уничтожения, который со-
соответствует уничтожению фотона в точке г в момент t.
Для оператора, выделяющего фотоны с поляризацией е,
здесь можно просто написать
Согласно стандартным правилам квантовой меха-
механики1), вероятность перехода в единицу времени из со-
состояния \i) в состояние \f) поля излучения за счет по-
поглощения соответствующего фотона с требуемой точно-
точностью пропорциональна
|<ЛЛ(+)(г, t)\i)f.	(8.1)
Коэффициент пропорциональности — скажем а — содер-
содержит квадрат модуля матричного элемента перехода
атомной системы и, помимо этого, ряд несущественных
множителей. Если теперь предположить, что детектор
достаточно велик и имеет достаточно широкое распре-
распределение состояний, то коэффициент а можно считать
не зависящим от начального или конечного состояний
поля излучения, а также от того, в какой момент вре-
времени и в какой точке происходит детектирование. Сле-
Следовательно, полную скорость перехода (вероятность в
') См., например, учебник Шиффа [5.2]. Мы имеем в виду вы-
вычисление вероятности переходов в единицу времени в первом по-
порядке теории возмущений. См. также работу Глаубера [8.2].

214	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
единицу времени) из состояния \i) за счет поглощения
подходящего фотона можно определить как сумму по
полной системе конечных состояний поля излучения, ко-
которая при этом принимает просто вид
^r, t)\f)(f\Al+)(r,t)\i) =
(-)(г, t)A(+)(r, t)\i). (8.2)
Наше рассмотрение дает грубое представление о
том, какие предположения были сделаны при выводе
(8.2). Конечно, строго говоря, никакой реальный детек-
детектор не является столь простым, как предполагалось
выше; мы специально идеализировали рассмотрение,
чтобы сконцентрировать внимание на наиболее суще-
существенных моментах, которые допускают достаточно хо-
хорошее приближенное описание. Таким образом, наш ре-
результат применим к модели или, точнее, к идеализиро-
идеализированному детектору. Однако в дальнейшем мы не будем
делать этих различий и ниже будем называть подобную
систему просто детектором. Более того, временно будем
пренебрегать коэффициентом а (или выберем единицы
так, чтобы а = 1).
Имея в распоряжении такие детекторы, попытаемся
описать более сложные опыты по счету фотонов. Для
простоты обозначений сохраним и здесь предположение
о том, что мы имеем дело с фотонами с заданной поля-
поляризацией е. Пусть нас интересует амплитуда перехода,
отнесенная к квадрату временного интервала для про-
процесса поглощения фотона в (пространственно-времен-
(пространственно-временной) точке г,/| и поглощения другого фотона в точке
гг^2- По существу это совместная плотность вероятно-
вероятности появления двух событий. Короче говоря, речь идет
об описании корреляционного опыта типа известного
эксперимента Хэнбери Брауна и Твисса. Соответствую-
Соответствующий матричный элемент имеет вид
<ЛЛ(+)(г2, t2)Ai+)(ru *,)U>-	(8.3)
С помощью соображений, аналогичных изложенным
выше, приходим к следующему выражению для интере-

§ 1. КВАНТОВЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ	215
сующей нас скорости переходов:
(ЦА{-](ги /.М'-'^, t2)A{+)(r2, t2)A(+)(ru /,)!0- (8.4)
Поскольку все положительно-частотные операторы
A(+>(r, t) коммутируют между собой [так же, как и со-
сопряженные им операторы А<-'(г, /)], взаимный порядок
двух множителей с индексом ( + ) [как и двух множи-
множителей с индексом (—)] не существен. Важно отметить,
однако, что рассматриваемые операторы стоят в нор-
нормальном порядке: все операторы рождения расположены
слева от всех операторов уничтожения.
По аналогии с опытом по двухфотонным совпаде-
совпадениям можно рассматривать, по крайней мере в прин-
принципе, опыты с n-фотонными совпадениями, в которых
измеряется совместная вероятность того, что п фотонов,
каждый с вектором поляризации е, были поглощены в
точках rh, th, k=\, ..., п. По аналогии с предыдущим
получаем для искомой вероятности выражение
(/|П А(~\гк, дПЛ(+)(г„ tt)\i),	(8.5)
/г=1	/=1
которое, очевидно, снова является средним значением
нормально упорядоченного оператора. Подчеркнем, что
из-за некоммутативности операторов /1<+> и Л(-> это вы-
выражение, вообще говоря, отличается от
1Й
h)A<+)(rk, tk)}\i).	(8.6)
Произведем теперь еще два непосредственных обоб-
обобщения основного выражения (8.5). Первое связано с
рассмотрением фотонов различных поляризаций. Если
обозначить декартовы компоненты поперечного вектора-
потенциала индексом /, то вся возможная информация
о поляризациях содержится в выражении
<«-|П 4;'(rft, tk)flA^(rr t,)\i)t	(8.7)
k=i K	i=i *
являющимся тензорным обобщением выражения (8.5).
Теперь в действительности компонента jh играет такую

216	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
же роль, как и переменные rft, tk, поэтому тройку пере-
переменных (гь, 4, jk) удобнее сокращенно обозначать одной
индексной переменной xh. Имея это в виду, запишем вы-
выражение (8.7) в более простой форме
(ilUA^ixjUA^ixMi).	(8.8)
Заметим, наконец, что (8.8) есть в действительности
совместная плотность вероятности при условии, что в
качестве начального состояния системы было задано чи-
чистое состояние. Если начальное состояние точно не из-
известно, то необходимо произвести усреднение по воз-
возможным начальным состояниям. Как показано в гл. 5,
в результате мы приходим к обобщению выражения
(8.8):'
<й*м'
A(+\xi)\,
(8.9)
здесь p — матрица плотности, отвечающая начальному
состоянию.
Распределенные детекторы. Приведенные выше сооб-
соображения можно обобщить на тот случай, когда идеали-
идеализированные счетчики непосредственно чувствительны не
к самому полю в точке г и t, а к значению поля, усред-
усредненному по пространственному и временному интервалу.
Как и в гл. 3, можно предположить, что k-и детектор
реагирует на эффективное поле, определяемое, напри-
например, следующим образом:
;r(r-r', t-t')A{;}(/, t')dVdt'. (8.10)
Здесь тензор S/y — обобщенный адмитанс^-го детектора,
который «пробует» поле в различных точках простран-
пространства и времени и определяет таким образом «эффектив-
«эффективное поле». Для таких счетчиков искомая вероятность от-

§ 1. КВАНТОВЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ	217
счетов га-го порядка, отнесенная к п-\\ степени времен-
временного интервала, по-прежнему дается выражением типа
(8.9). Однако каждый оператор снабжен теперь индек-
индексом е, что в силу (8.10) отвечает учету свойств детек-
детектора. При таком обобщении можно учесть и то обстоя-
обстоятельство, что каждый из детекторов имеет различный
адмитанс.
Из линейности соотношения (8.10) следует, что все
свойства для счетчиков любого типа содержатся в кор-
корреляционных функциях
G{n, п) i	#	\
(Х\, х2, . . ., хп; хп+\, хп+2, . . ., х2п) =
b п
l = n+\
n	2n
= Sp рЦ A(-\xk) П A(+)(Xl)\, (8.11)
где каждая полевая переменная имеет свой собственный
аргумент. Зная эти корреляционные функции и соответ-
соответствующие адмитансы детекторов, можно вывести все
выражения для скоростей счета n-фотонных корреляций.
Легко убедиться и в обратном, а именно показать, что
функции (8.11) можно извлечь из информации о ско-
скоростях отсчетов при всевозможных расположениях счет-
счетчиков. Короче говоря, функции G<n'™> в (8.11) при всех
аргументах хи ..., х2п и для всех п можно рассматри-
рассматривать как информацию о поле излучения, которую можно
непосредственно извлечь из опытов по многократным фо-
фотонным совпадениям. Все эти выражения представляют
собой средние значения нормально упорядоченных про-
произведений операторов, причем в каждый член входит
равное число операторов рождения и уничтожения.
Поскольку каждая полевая переменная имеет теперь
свой собственный индекс х, можно получить выражения
<Й
А=1
Чхк) П ЕМ(х,)),	(8.12)
п	2п
(П Н{~\хк) И Hw{Xl))	(8.13)
fcI	ln+l
(П \ И
fc-I	l-n+l

218	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
или различные смешанные формы из А, Е и Я. При
этом мы взяли соответствующие производные и восполь-
воспользовались (поперечными!) уравнениями Максвелла
Е = —А и Н = V X А. Таким образом, все эти величины
тесно связаны друг с другом. Действительно, Глаубер в
своем рассмотрении использует скорости счета, опреде-
определяемые выражением (8.12), а не (8.11). На практике
различие между этими двумя определениями невелико.
Для квазимонохроматического излучения они пропор-
пропорциональны друг другу во всех задачах. Вместе с тем
выражение (8.13), по-видимому, наиболее подходит
(даже в квазимонохроматическом поле) для описания
n-фотонных скоростей счета в случае счетчика, в кото-
котором используются магнитные дипольные переходы (та-
(такие переходы возникают за счет первого члена разло-
разложения А(г) в ряд Тейлора вблизи центра атома). Для
простоты мы и в дальнейшем ограничимся рассмотре-
рассмотрением корреляционных функций, полученных с помощью
поперечного вектора-потенциала.
Корреляционные функции смешанного порядка. Функ-
Функции G<"'"' образуют, очевидно, подсемейство в целой
иерархии корреляционных функций G<n- m\ в которых
числа операторов рождения и уничтожения не обязатель-
обязательно совпадают. Эти функции определяются как очевидные
обобщения выражения (8.11):
и \Х	х; х	х)^
n-i-tn
(п	п+т	1
pIU^Oc*) П Л(+!(*г) (8.14)
4=1	/=л+1	I
и все являются средними значениями нормально упоря-
упорядоченных операторов. Для многих целей удобно анали-
анализировать всю совокупность корреляционных функций
для того, чтобы получить информацию о специальных
корреляционных функциях G<n> n\ относящихся к п-фо-
тонным корреляциям счета.
Все функции G<™-m) удовлетворяют довольно очевид-
очевидным свойствам симметрии. Эти функции полностью сим-

§ 1. КВАНТОВЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ	219
метричны по п переменным Х\, х2, ..., х» и, помимо
этого, полностью симметричны по т переменным хп+и
хп+2, ..., хп+т. Кроме того, очевидно, имеет место со-
соотношение
[G ' \Х\, ..., хп; xn+i, ..., хп+т)\ =
= G ' (xn+i, ..., хп+т\ хх, ..., хп), (8.15)
которое является отражением того факта, что [Л(+'(х)]'1'=
= А(~Цх). При п — т последнее соотношение устанавли-
устанавливает связь между зависимостью функции G'"-™' от первой
группы переменных Х\, ..., хп и ее зависимостью от вто-
второй группы переменных хп+\, ..., х2п-
Поскольку мы рассматриваем свободное поле излу-
излучения, каждая из функций G(n>m» по каждому из своих
аргументов удовлетворяет волновому уравнению свобод-
свободного поля
гь tt, ...) = 0. (8.16)
Поведение функции G'"'1™' в различающиеся моменты
времени можно получить, зная ее значения в какой-то
один общий момент, например при t = 0. Эти свойства
распространения выявляются наиболее четко, если сна-
сначала ввести описание в терминах нормальных мод, как
это было сделано в гл. 7.
Б. Разложение по модам
В соответствии с G.179а) операторы уничтожения,
отвечающие нормальным модам (которые появляются
при квантовании в «ящике» объемом L3), можно пред-
представить в виде
k)-a(k, 0 =
2(OV'2 f -lli-
/О 1-7 \
(8.17a)

220	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Сопряженное соотношение для соответствующих опера-
операторов рождения (Я, к)-й моды имеет вид
аЦк, 0 = еЛ(к).а+(к, t) =
А<~)(х>t)cfx- (8Л7б)
Для простоты обозначений переменную, характеризую-
характеризующую моду, будем кратко указывать с помощью индек-
индекса k; т. е. положим ak (t) = aK (k, t) и a\{t) — a\{k, t).
Предположим теперь, что мы выполнили многократ-
многократное преобразование функции Фурье G<n'm> и произвели
умножение на нужные векторы поляризации и нормиро-
нормировочные множители. В результате мы, очевидно, придем
к величине
?(«. m) .
\, t\, ..., kn, tn\ kn+\, tn+i, ..., kn+m, tn+m) —
{n	m+n	\
plUir(tr)Jl+iaks(ts)]. (8.18)
Зависимость от времени в этом выражении совершенно
элементарна. В силу G.176а) имеем
ак (t) = exp (-mkt) ak @) = exp (-mkt) ak, (8.19)
откуда следует
S(n'm)(ki, tu ..., kn, tn; kn+u tn+u ..., kn+m, tn+m) =
n	n + m
= Ilexv(i<ukrtr)II+iexp(-mksts)${n-m)(ku 0, ..., kn, 0;
kn+u 0, ..., kn+m, 0). (8.20)
Это выражение наглядно демонстрирует тот факт, что
все многовременное поведение функции С('г>пг> опреде-
определяется значениями, которые она принимает, если все
временные аргументы положить равными нулю. Следо-
Следовательно, чтобы получить информацию об общей

§ I. КВАНТОВЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ	221
(п,т)-н корреляционной функции, можно вообще опу-
опустить временные аргументы и рассматривать выражение
п	п+т
S	(Й,, .... Кп, Я +,, ..., И т)— \11 "ft 11 "ft / ~
п+т	1
(8.21)
Все нужные величины можно получить из выражения
(8.21), взятого при / = 0. В полной аналогии с G<n> m>
функции $(п'т\ очевидно, симметричны по п первым и
по т последним аргументам и удовлетворяют условию
r<g(ra, m) /.	Ъ ¦ h	b 'll* =
Iе-7	\№1' • • •> №/г> rt/z+l» • • •) №/г+т/]
<g("«, га) /t,	l . t,	t, \ со Г)о\
В. Производящие функции
Информацию, содержащуюся во всех корреляцион-
корреляционных функциях (8.21), можно весьма удобным способом
объединить, воспользовавшись нормально упорядочен-
упорядоченным производящим функционалом
V
- S чч)) =
= Sp I р exp f S tuali ехр ( - S и „а, ) ] ¦ (8.23)
Этот функционал определен для всех комплексных по-
последовательностей {«/;}, удовлетворяющих условию
оо
2!mJ2<oo.	(8.24)
Очевидно, что (8.23) содержит все корреляционные
функции. Действительно, дифференцированием функци-
функционала (8.23) получаем
«<«¦"») с и	и . и
/г+m

222
ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
С нормально упорядоченным производящим функциона-
функционалом тесно связана величина, которую можно назвать
«характеристическим функционалом» С({ик}) для матри-
матрицы плотности р. С учетом G.26) эту величину можно
определить так:
С (К)) = ехр [ -\ ЁI «ft I2) C.v
= ехр :
S("X - ulak) ) = Sp p ехр
L i	1
Г~ сю
S(
i
(8.26)
Следует отметить, что для любой последовательности
{uh}, удовлетворяющей условию (8.24), функционал
C{{uh}) есть среднее значение унитарного оператора [ко-
[который является непосредственным обобщением на случай
бесконечного числа степеней свободы оператора U[p, q],
определяемого соотношением G.26)]. Подобно тому как
характеристические функции (фурье-образы) полностью
определяют классические вероятности, аналогичный им
функционал С({ик}) полностью определяет квантовоме-
ханическую матрицу плотности р.
Разумеется, нет особой необходимости использовать
разложение по модам для образования производящих
функционалов. Снова ограничиваясь для простоты кор-
корреляциями при / = 0, мы можем с тем же правом рас-
рассматривать нормально упорядоченный производящий
функционал, задаваемый соотношением
С„ {S} = (ехр (S • Ам) ехр (- S* • А(+))>, (8.27)
где все операторы берутся при / = 0 и введено сокра-
сокращенное обозначение
s*(r)-A(+)(r)dW[S- A(-f. (8.28)
Наряду с этим можно рассматривать тесно связанный с
(8.27) характеристический функционал
C{S}-(exp(S-A(-)-S*.A(+>)>.
(8.29)

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	223
В дальнейшем нам представится возможность вос-
воспользоваться нормально упорядоченными производя-
производящими функционалами и связанными с ними характери-
характеристическими функционалами. Еще раз подчеркнем, что
любой из этих функционалов полностью определяет со-
состояние системы. Повторим также, что корреляции ско-
скоростей счета связаны лишь с функциями G("> n> и не
имеют прямого отношения к функциям G<n'm) при
п Ф т.
§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ
А. Определения и полная когерентность
Как мы видели выше, информация о скоростях счета
в корреляционных измерениях содержится в функциях
G(". n) (или <§(п, п)^ определенных для произвольных ар-
аргументов. На основе этой информации мы должны ре-
решить, какие из состояний системы заслуживают назва-
названия полностью когерентных.
Для классического случая в гл. 1 уже отмечалось,
что обычно различают когерентные, частично когерент-
когерентные и полностью некогерентные поля. Решающей вели-
величиной для свойств когерентности, которая используется
при описании всех классических интерференционных
опытов, является функция взаимной когерентности, ко-
которая для скалярного поля (или для заданной поляри-
поляризации) определяется следующим образом:
Г'1' »(г, <; г', О-Г(г, t; г', t') = {v\r', П V (г, ОХ
(8.30)
Используется также нормированная форма
которая называется комплексной степенью когерентно-
когерентности и удовлетворяет неравенствам 0-^|у|-^1 при всех
значениях аргументов. Ранее мы показали, что если для
двух пространственных точек гиг' при всех / и ? вы-
выполняется условие \у\ = 1, то наблюдаемая интерферен-
интерференционная картина будет такой же, как и для полностью
детерминированного поля, и поэтому поле можно считать

224	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
когерентным. Если |у| = 0 для всех t и У, то поле счи-
считают некогерентным, в то время как при 0<jy|< 1 —
частично когерентным.
В квантовом случае роль ГA-!) играет корреляцион-
корреляционная функция G*1''). Поскольку функция G(l'l)(r,t;r,t)
пропорциональна числу фотонов, попадающих в точку г
в интервале времени от t до t + dt, она также пропор-
пропорциональна интенсивности почернения фотоэмульсии при
такой экспозиции. Для различных пространственно-
временных точек функция G(X<X)(r,t\r',t') связана с ин-
интенсивностью, наблюдаемой в опыте с двумя щелями,
точно так же, как функция П1''>(г,/; г',/'). Обе эти ве-
величины удовлетворяют волновому уравнению для сво-
свободных полей и обе являются аналитическими сигна-
сигналами по t и по —/'.
Чтобы пойти дальше этого сравнения, постараемся
уточнить, ддвщшю неопределенное понятие «когерент-
«когерентности».. Умышленно придерживаясь общего подхода, бу-
будем говорить, что «свойство когерентности» статистиче-
статистического ансамбля есть наблюдаемый аспект, содержа-
содержащийся в каждом члене ансамбля. Различные ансамбли
будут иметь, вообще говоря, различные свойства коге-
когерентности:. Наряду с этим один и тот же ансамбль мо-
может иметь различные наборы свойств когерентности в
зависимости от того, какая группа величин считается
«наблюдаемой». Это наводит на мысль называть свой-
свойствами относительной когерентности такие свойства, ко-
которые удовлетворяют критериям свойства когерентности
для подгруппы наблюдаемых. Иначе говоря, критерии
свойства относительной когерентности являются необхо-
необходимыми, но, вообще говоря, не достаточными крите-
критериями свойства когерентности. Интуитивно ясно, что чем
большее число свойств когерентности имеется у данного
ансамбля, тем меньше наблюдаемые различия между
членами ансамбля. .Мщкдо. .сказать,, ..что полная коге-
когерентность существует в том случае, когда все члены ан-
ансамбля идентичны в отношении всех своих наблюдае-
наблюдаемых свойств,,1).
') Точное обобщение этих понятий на основе теории меры само-
самоочевидно. Мы ограничимся менее строгим изложением.

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	225
Для иллюстрации предположим, что в нашем распо-
распоряжении имеется система рулеток, каждая из которых
выдает комплексное число. Ансамбль состоит из чисел,
выданных совокупностью М одинаковых рулеток. Пусть
2ц обозначает число, зарегистрированное в ц-й рулетке,
ji=l, ..., М(М^> 1). Если мы можем наблюдать и
амплитуду, и фазу г^, то наш ансамбль будет полностью
когерентным в том случае, когда есть такое число г, что
z\x = 2 для всех |1. Чтобы проверить когерентность ма-
математически, мы можем при желании поступить сле-
следующим образом. Пусть а обозначает случайную ком-
комплексную переменную, которая, как обычно, принимает
значения, допустимые для ансамбля. Тогда полностью
когерентный ансамбль должен удовлетворять равенству
Zi 2ц = (а > = г = (а)
для всех п^- [. Если мы знаем лишь, что (а™) = {а)п,
скажем для п=1,2 и 6, то, имея только эту информа-
информацию, можно лишь сказать, что ансамбль относительно
когерентен. С другой стороны, предположим, что в прин-
принципе мы можем наблюдать только модуль z^. Тогда
для полностью когерентного ансамбля \zn\ = \z\ для
всех ji и для всех п выполняется равенство {а*пап) =
= z*nzn = (a*a)n. Последний пример не налагает в
сущности никаких ограничений на значение (а*пат) при
п Ф т.
Будучи безусловно грубым, наш пример тем не менее
позволяет мотивировать определение полностью коге-
когерентного состояния поля излучения. В квантовой теории
мы называем состояние поля излучения полностью коге-
когерентным, если корреляционные функции (8.11), соответ-
соответствующие наблюдаемым (в принципе) величинам — кор-
корреляциям отсчетов, — при всех значениях аргументов и
для всех п обладают свойством
G{n,n) ,	ч 	^
(х{, ..., хп; хп+и ..., х2п) —
II V(xi), (8.32)
l=n+l

226	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
где V(x)= V(r,t,j), или в векторном виде V(r,/)— не-
некоторая функция. Функция V должна, очевидно, удов-
удовлетворять свободному волновому уравнению и быть
аналитическим сигналом. Функция V полностью опреде-
определяется соотношением (8.32) с точностью до единствен-
единственного общего фазового множителя. Это условие фактори-
факторизации не налагается в явном виде на корреляционные
функции G<n>m> с пфт.
В каком-то смысле, конечно, вопрос о том, что счи-
считать в принципе наблюдаемым, а что нет, зависит от
определения. Основное правило квантовой теории ут-
утверждает, что эрмитовы переменные, например__элект-
рщщское или магнитное поля (должным~оЬраз6м усред-
усредненные по небольшой области пространства), р_ассм.ат-
б\\ что, проявив достаточное
тёрпениеГТз принципевозможно осуществить опыты по
измерению распределения средних значений Е(х) или
Н(х). Вполне правдоподобно (нам нет необходимости
вдаваться в детали), что эта информация даст нам воз-
возможность вывести (комплексное) среднее значение ве-
величины Л(+> (х), а именно G<0''>(*). Более того, можно
было бы вывести все G<">m>, обращаясь к аналогичным
мысленным экспериментам над подходящими эрмитовы-
эрмитовыми переменными. При таком подходе будем называть
состояние излучения «полностью когерентным», если
для всех тип при всех значениях аргументов выпол-
выполняется условие
п, т) /	t
\Х 1, . . . , Хп,
n	n + m
= П V* (xk) П V (xt). (8.33)
Нетрудно видеть, что такие полностью когерентные со-
состояния поля излучения представляют собой чистые ко-
когерентные состояния и ничего более. Однако мы будем
следовать общепринятой практике и называть когерент-
когерентными состояниями такие состояния, для которых вы-
выполняется лишь условие факторизации для G^n- n>. Это
соответствует наблюдаемой «на практике» информации,
для получения которой достаточно лишь экспериментов

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	227
со счетчиками1). Совершенно ясно, что когерентные со-
состояния являются также полностью когерентными и в
этом смысле, но помимо них существуют и другие со-
состояния, обладающие свойством (8.32).
Заслуживает упоминания и другая форма условия
полной когерентности. Функции (?("¦ '"•', определяемые
соотношением (8.18), получаются фактически из функ-
функций G(n>m) в результате преобразования Фурье по каж-
каждому из своих пространственных аргументов. Если функ-
функцию G<"' m> можно представить в виде произведения от-
отдельных членов, то, очевидно, это же справедливо и для
ее фурье-образа. Временная зависимость факторизован-
ной функции должна согласовываться с общим видом
временной зависимости в (8.20). Таким образом, мы сра-
сразу приходим к другому критерию полной когерентности.
Он состоит в том, что для некоторой последовательности
{zh} и при всех п должно выполняться соотношение
«<"¦ п> (ь	ь ¦ k	k ) -
"	Vе 1> • • • i №ra> "ra + li • • • > "rc/
ra	In	n	In
П zk . (8.34)
Отсюда видно, что полная когерентность есть свойство
состояния р в определенный момент, скажем при / = 0.
Если средние значения, взятые по состоянию р, удовле-
удовлетворяют этим требованиям согласованности, то поле из-
излучения полностью когерентно во всем пространстве и
в любой момент времени.
Приведем в заключение еще одну форму условия пол-
полной когерентности. Замечая, что GC- l\x, x) = V*(x)V(x),
') В оптическом диапазоне, безусловно, практически наиболее
удобно получать именно такую информацию. Это связано с тем,
что с помощью доступных схем даже с наносекундными A0~9) вре-
временами разрешения трудно определить что-либо, кроме поведения
огибающей сигналов с несущими частотами порядка 1015 гц. (При-
(Приведенное утверждение относится лишь к простым счетчикам. Си-
Системы, использующие биения изучаемого света с сигналом от опти-
оптического гетеродина, в принципе позволяют измерять фазу оптиче-
оптического колебания даже при сравнительно плохих временах разреше-
разрешения электронных схем. — Прим. перев.)

228	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
сразу же получаем соотношение
| Gin' п} (хи х2, ..., х2п) Г = П GA' ° (хк, хк), (8.35)
выполняющееся при всех п. Ниже мы покажем, что это
условие влечет за собой выполнение (8.32) и что, таким
образом, эти два условия эквивалентны.
Б. Частичная когерентность
Если условие (8.32) не удовлетворяется, то мы имеем
частичную когерентность того или иного рода. Было бы
идеально, если в каждом таком случае мы могли ввести
определенный параметр, характеризующий степень ко-
когерентности, подобно тому, как это оказалось удобным
при рассмотрении двухщелевого интерференционного
опыта. Однако в настоящее время ни одно из конкрет-
конкретных определений не является универсальным в этом от-
отношении. Нельзя надеяться, что с помощью одного или
нескольких параметров удастся отразить сущность всех
форм частичной когерентности, которые могут прояв-
проявляться во всех возможных экспериментах.
Когерентность первого порядка. Тем не менее инте-
интересно обсудить следствия одного особенно любопытного
случая, когда имеет место нечто меньшее, нежели пол-
полная когерентность. Выше мы определили свойство отно-
относительной когерентности как такое, для которого выпол-
выполняется ряд критериев свойства когерентности (но не
обязательно все). Следуя Глауберу [8.2], будем гово-
говорить, что поле излучения имеет «когерентность первого
порядка», если известно, что для некоторой функции
V(x) и при всех х и у выполняется соотношение1)
G<l-1\x,y) = V\x)V(y).	(8.36)
') Следует отметить, что экспериментатор, вооруженный интер-
интерферометром (а не фотосчетчиками), может извлечь информацию
лишь о GA' '>. Если он обнаружит, что соотношение (8.36) выпол-
выполняется, то будет считать (в той мере, в какой он может судить
об этом) поле «полностью когерентным» в соответствии с нашим
определением.

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	229
Выясним теперь, что можно получить, рассматривая
корреляционные функции G<n' ") высших порядков.
Обсуждение этого вопроса начнем с соотношения
|G(I-V y)?=Gll'l)(x, x)G«-%, у), (8.37)
являющегося прямым следствием соотношения (8.36).
Для простоты обозначений будем писать здесь G вместо
G*1''). Покажем сначала, что в действительности и
(8.36) следует из (8.37). Если положить
G{x, y) = ew^y)+i<f^y) = G'{y, x),	(8.38)
где w и ф — действительные функции, то из (8.37) по-
получим
w{x, y)=~[w(x, x) + w{y, у)].
Следовательно, вводя обозначение В (x)^exp[42w(x, х)],
можно написать
G (х, у) = В (х) В (у) et<f <*' v) = {А(~] (х) А{+) (у)).	(8.39)
В силу основного определения G(x,y) удовлетворяет ус-
условию (для всех конечных сумм с произвольными коэф-
коэффициентами Cft)
S c]ckG (хр хк) = S c]ckB (дсу) В (xk) ехр \щ (хр хк)\ =
= S d]dk ехр [щ (х xk)\ > 0, (8.40)
/, k
так как приведенное выражение есть среднее значение
положительного оператора. Для любого конечного набо-
набора точек матрица М с элементами Mjk=exp[iq)(Xj,xk)]
эрмитова и положительна, и каждый из элементов удо-
удовлетворяет условию \Mjk\~l. Взяв эти условия для
трех произвольных точек (т. е. для соответствующей
матрицы размерностью 3X3), получаем M12M23M3i = 1,
так как в противном случае мы имели бы det(M) =
= 2Re(M12M23^3i — 1) < 0- Но это условие означает,
что для трех произвольных точек должно выполняться
соотношение
ф(х, y)+q>{y, z)+q>(z, *) = 0;	(8.41)

230	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
это, как мы покажем, налагает жесткие ограничения на
вид функции (р(х, у). Если при фиксированном г поло-
положить а2 (у) ене —ф (у, г), то
ф(*. у) = аг{у)-аг(х).	(8.42)
В свою очередь а2(у) отличается от ао(у) (т. е. от az
при г = 0) на константу, так как разность
аг(у) — ао(г/) = аг(и) не зависит от у. Иными словами,
существует действительная функция а (у) = ао(у), опре-
определенная однозначно (с точностью до аддитивной кон-
константы) соотношением (8.41), так что (р(х,у) =
= а (у) —а(х). Отсюда следует, что
G{x, у) = В(х)В(у)е-^ам-а^ = У{х)У(у). (8.43)
Заметим, что с помощью этих соображений мы не
можем определить величину а(х) (даже с точностью до
константы), но можем сделать вывод, что она сущест-
существует, и отсюда заключить, что функцию G(x,y) можно
представить в виде произведения двух функций. Следо-
Следовательно, (8 36) и (8.37) эквивалентны.
Используя разложение по модам, перепишем (8.36)
в эквивалентном (при t = 0) виде [ср. (8.21)]. Для не-
некоторой последовательности {z,} имеем
K«,) = z;z,	(8.44)
для всех k и /. Будем предполагать, что последователь-
последовательность {zh} не равна тождественно нулю, тогда оператор
b ees 2 ufit = V' V/, Щ	(8.45)
\2j zmzm)
будет удовлетворять соотношениям
[b, ЬЦ = 2 «/И; \at, al] = 2«/И; = 1	(8.46)
и
W) = 2 щи', (alat) = 2 utukz\zt = 2 г^ > 0. (8.47)
Следовательно, b есть обычным образом нормированный
оператор уничтожения, для которого {bfb) ф 0.

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	231
Будем теперь считать переход от щ к b = bi	первым
в целой цепочке преобразований, которые возникают
при унитарной замене базиса типа
bm=I,umlah	(8.48)
где
SvirC	(8-49)
Ясно, что »u = W/=zJ/Q[j2^zft) \ и из соотношения орто-
ортогональности (8.49) получаем
(bfmbn)
= 2 umkzkunlzl =
(8.50)
В частности, для операторов числа квантов bmbm
(bibm) = 0 (/и#1). (8.51)
Так как оператор числа квантов имеет положительное
среднее значение в любом состоянии, кроме основного,
это условие означает просто, что моды, описываемые
операторами Ьт и bfm, совершенно не заселены при всех
тф \. Таким образом, все поле есть поле единственной
моды (не обязательно нормальной!), удовлетворяющей
единственному ограничению (8.47).
Введем определение нормированных собственных со-
состояний оператора числа квантов, соответствующего
этой единственной моде:
\n)~(n\)-'l2(bff |0>;	(8.52)
тогда матрица плотности р будет иметь следующий об-
общий вид:
оо
Р= 2 \n)pnm(m\,	(8.53)
п, т=*0
причем для нее должно выполняться условие
= 2 пР„„ =-!:*;&.	(8.54)
п=0	к

232	ГЛ. 8 КВАНТОВАЯ ТЕОРИЯ
Корреляционные функции высших порядков опреде-
определяются либо из (8.21), либо из аналогичного соотноше-
соотношения, содержащего Ь^т и Ьт. Однако в соответствии с
(8.51) или (8.53) лишь члены с b = Ъх могут давать не-
ненулевой вклад. Члены {Ь'пЬт) удобно описывать с по-
помощью относительных выражений
(b+nbm)
ёп, т =	y/.f/i + m) •	(8-55)
Из этого определения и соотношения al = '^ju*nlbm по-
получаем
(ьыьт)
) = uk ... uk и] ...и]
m'	1	и 1
Zfe • ¦ • ZkZl ¦ ¦ ¦ Z
knZl{ ¦ ¦ ¦ Zlm , у, г*?г у/„ (n+m)
4
Наконец, после умножения на требуемые множители и
многократного преобразования Фурье приходим к вы-
выражению
/7 («¦ "!)/	.	ч _
и	^Л], . . ., лп, Are+i, . . ., лга+т;
п	п+т
= gn.mll ГЫ П ^(*z). (8-57)
ft=l	l=n+l
Таков общий вид, который принимает (п,т)-я корреля-
корреляционная функция для поля, когерентного в первом по-
порядке.
Поскольку нас интересуют корреляции фотоотсчетов,
ограничимся вначале рассмотрением корреляционных
функций G(n-"'. Для них, очевидно, имеем1)
\Х\, ..., Хп\ Xn+i, ..., X<in) ==
П К(хг), (8.58)
') Этот результат для Gc- "' впервые был получен Титуламе-
ром и Глаубером [8.3].

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	233
где мы положили
gn^gn.n^jp^yr-	(8.59)
Все эти коэффициенты — действительные неотрицатель-
неотрицательные числа. Совокупность чисел {g,,} вместе с функцией
V(x), как нетрудно понять, характеризует скорости от-
отсчетов для поля, когерентного в первом порядке. Если
gn = \, п = 1, 2, . . . , М, то, следуя Глауберу, говорят,
что поле имеет когерентность М-го порядка. Это связа-
связано с тем, что если gn — 1 при всех п, то поле полностью
когерентно, так как при этом G(n- "> имеет канонический
вид (8.32). Условия (8.35) для п>2 вместе с (8.58),
очевидно, означают, что gn = 1 при всех п; поэтому вся
совокупность соотношений (8.35) указывает на полную
когерентность поля, как уже отмечалось выше.
Поучительно привести некоторые примеры матриц
плотности и посмотреть, каковы соответствующие выра-
выражения для gn. Если положить M = b+b, то из E.47) вы-
вытекает
(М- (М- 1) ¦ (Af — 2) ... (М- [п- 1] )) = (М1/(М-п)\)
gn—	(щп	—	(щп
(8.60)
Следовательно, если р= \т){т\—чистое собственное
состояние оператора числа квантов, то
д„——jr.	-г\	(8.61)
при всех п > т функции gn обращаются в нуль. Если
(8-62)
что имеет место для «теплового» (или хаотического)
распределения единственной возможной моды, то
gn = n\	(8.63)
Доказательство соотношения (8.63). Если положить А, = е~',то
оо	оо
{ (M)i-m \ Z-L (m-n)\ ~Л dkn ^ ~
m = 0	m = 0
%n dn	1	n\\n
dXn 1-Я A-Я)"

234	ГЛ. 8 КВАНТОВАЯ ТЕОРИЯ
Следовательно, для п = 0 и п = 1
Sp{e-P'M}=(l-^r1, Sp{Me-VM}^
Сопоставляя эти свойства, находим
что и требовалось.
Такое поле не может обладать когерентностью выше
первого порядка. Для полной когерентности необходи-
необходимо, чтобы gn = 1 и тем самым (bfnbn) = (bj'b) для всех п.
Следовательно, мы видим, что общее соотношение
оо
\. — (bfnbn) — ( : ехр {kbfb): ) = (ехр [in A + Я) bfb]) =
оо
U +л) pmm @.64)
приводит к частному случаю
2 A +^Гртт = ехр
откуда вытекает
1 d
p
m!
ехр (Л <6+
А,= -1
_ (Ь4)т
т\
¦&xp(-(bfb)). (8.66)
Таким образом, для полной когерентности необходимо,
чтобы диагональные матричные элементы ртт имели
распределение Пуассона.
Следует отметить, что результат (8.57) имеет пря-
прямой аналог в обычном классическом рассмотрении функ-
функции 14"'т>. Нетрудно видоизменить изложенный вывод
(или дать ему иную интерпретацию) и показать, что ус-
условие когерентности первого порядка |у| = 1, или
|Г<1-|)(*1у)|2-Г<1-1><*| х)^1){у, у),	(8.67)

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	235
приводит к соотношению
р(«, т) /	.	\
га	п+т
= Yra, т II V (Хк) II V (Xl) (8.68)
А=1	/=га+1
с некоторой функцией V(x). Здесь коэффициенты
Vra^^X^,	(8-69)
определены с помощью некоторого классического ан-
ансамбля для одной комплексной переменной v. По анало-
аналогии с (8.58) можно написать
Г("'
п	2га
= Yra П V (хк) П V (Xl), (8.70)
k\	il
(к) П
k=\	i=ra+l
где величины
(8.71)
являются, очевидно, действительными положительными
коэффициентами. Если же положить X = v*u и ввести
определение (при соответствующем о^-О)
оо
(Хп) = J Хпо (X) dX,	(8.72)
о
то Yra = (Хп)/(Х)п. Отсюда следует, чт
оо
Ях \ хп
Tin
о
^8.73)

236	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
т. е. уп образуют неубывающую последовательность
•- <Yn<		(8.74)
В силу этого свойства обычное классическое рассмотре-
рассмотрение, очевидно, не может дать адекватного описания ско-
скоростей отсчетов для всех когерентных в первом порядке
полей. Действительно, как мы уже видели, если в таком
поле содержится не более т фотонов, то gn = 0 для всех
п > т, что находится в прямом противоречии с требова-
требованием у„ > 1 при всех п.
Необходимо отметить одно важное обстоятельство:
при получении соотношений (8.58) [или даже их класси-
классических аналогов (8.70)], вытекающих из условия коге-
когерентности первого порядка, существенное значение имеет
тот факт, что G (х, г/)= V* (х) V(y) во всем пространстве
или что (а\а^ = z"hzl для всех мод. Если эти соотноше-
соотношения известны лишь приближенно, то простая запись
типа (8.58), вообще говоря, невозможна. Предположим,
например, что вместо (bj2b2) = 0 [ср. (8.51)] имеем
(Ь1Ь2) = *,	(8.75)
где е — произвольно малое, но положительное число, на-
например е = 10~137. Что касается заселенности второй мо-
моды, то матрицу плотности можно взять в виде
-VI Я2> <Л21.	(8.76)
Здесь а и |3 выбраны так, чтобы выполнялись соотно-
соотношения Sp (р) = 1 и Sp(p/?2&2) = e; это означает, что р —
малое (~е), но положительное число. Тем не менее
выражение для G(%2) [или ^B'2)] содержит член
оо
Sp lp {btf bl] = - e + p ? -i- = oo.	(8.77)
Следовательно, вклад второй моды, будучи совер-
совершенно незначительным в корреляционной функции
G*1'•>, полностью доминирует в G^2-2) и во всех корреля-
корреляционных функциях высшего порядка. Это, очевидно,

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	237
нарушает справедливость общего результата (8.58).
Если не исключить все примеры аналогичного типа на
основании физических соображений1), то для определе-
определения корреляционных функций высших порядков трудно
предложить что-либо другое, кроме прямых измерений.
Степени когерентности. В заключение приведем ряд
определений, которые использовались различными авто-
авторами при рассмотрении частичной когерентности. Глау-
бер [8.2] ввел ряд нормированных корреляционных функ-
функций
?<"> (*„ .... Х2п) = в^ (*.¦•¦•¦*,„) _	(878)
П {G'1-'>(**, **)}'''
fc= 1
Здесь мы можем рассматривать функции g(") как кван-
квантовые обобщения классической комплексной степени ко-
когерентности у- Если G^-^{x,x) =0 для некоторого зна-
значения х, то числитель тоже обращается в нуль; в таких
случаях мы будем определять g(") из условия непрерыв-
непрерывности (если это окажется возможным). Из (8.35) с оче-
очевидностью вытекает, что выполнение условия
lg<n)(*i. .... *2„)|=1	(8.79)
для всех значений аргументов и всех п обеспечивает
полную когерентность поля. Вместе с тем из (8.58) сле-
следует, что для поля, когерентного в первом порядке,
I ?<">(*„ ..., х2п)\ = ёп	(8.80)
при любых значениях всех координат. Выше при рас-
рассмотрении очень важного примера, а именно случая
1) В этой связи надо отметить следующее. Пусть в математи-
математическое ожидание случайной величины х вносят основной вклад «да-
«далекие хвосты» функции распределения, полная вероятность которых
~е <? 1. (В приведенном выше примере х — Ь^Ъ^) Тогда досто-
достоверное измерение этого математического ожидания требует чрез-
чрезвычайно большого числа опытов, N >¦ 1/е. (Более строго:
N 3> (Д*2) / (хJ.) Поэтому само утверждение о существовании та-
такого среднего (в приведенном примере (х) = G1-2-2'1 — <х>) не под-
поддается экспериментальной проверке с помощью конечного числа
опытов Л'о < 1/е и, следовательно, носит нефизический характер. —
Прим. перев.

238	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
хаотического поля, которое обладает когерентностью пер-
первого порядка, мы видели, что gn = n\, следовательно,
функции g<n> не обязательно должны быть меньше еди-
единицы.
Иной подход использовал Мета [8.5] в своем рассмот-
рассмотрении, проводившемся с целью обобщения классической
степени когерентности \\ Мета следующим образом оп-
определяет последовательность «комплексных степеней ко-
когерентности четного порядка»:
Jn<n)tv	v \ —G ' (хи ..., х2п)Гй ЯП
\Х	х)	\ооЧ
Чтобы эта величина была определена, поле должно со-
содержать п или более фотонов. Для определения всей
последовательности g(".n> нужно, чтобы в поле содержа-
содержалось бесконечное число фотонов. Даже при такой нор-
нормировке величина ?<"•"' все еще может быть сколь
угодно большой. В самом деле, чтобы знаменатель выра-
выражения (8.81) не обращался в нуль, в каждой точке дол-
должно присутствовать п или более фотонов. Однако это ус-
условие может и не выполняться. Отвлекаясь от этих труд-
трудностей, Мета показал, что если для данного п(=п0) и
для всех значений аргументов
I ?"••">(*„ ..., *2П)|=1,	(8.82)
то это условие выполняется для всех п > п0 и для всех
аргументов.
Приведенный результат можно получить примерно
так. Для п = 1 определения Меты и Глаубера совпа-
совпадают, т. е. gA' = g^1 '), поэтому условие
\g°'l)(x, у) 1=1	(8.83)
приводит к когерентности первого порядка. Отсюда сле-
следует, что функция G<"'") определяется соотношением
(8.58); если все gn Ф 0, то нетрудно видеть, что соотно-
соотношение (8.82) выполняется для всех п. Тогда, согласно
рассмотрению Мета, поле, когерентное в первом поряд-
порядке, будет считаться и «полностью когерентным в четных
порядках».

§ 2. ПОЛНАЯ И ЧАСТИЧНАЯ КОГЕРЕНТНОСТЬ	239
В заключение обсудим определение, которое было
введено и подробно исследовано Сударшаном [8.4]. При
этом он в значительной мере руководствовался жела-
желанием использовать такие величины, которые являются
более непосредственными обобщениями классической
степени когерентности и в то же время могут служить
удобной мерой чистоты возбужденных мод. Чтобы отли-
отличать настоящее определение от использованных преды-
предыдущих примеров, мы можем назвать эти степени «индек-
«индексами когерентности». Именно, рассмотрим «индекс коге-
когерентности порядка п», определяемый соотношением
S(rt, П) /	t	\
\Х\, ..., Хп\ Хп+\, ..., X2fl) =
s 	О(п-"'(*!, .... хп; хп+1,..., х2п)
[G(n- ">(*!	*„; *„,..., *,) G<n- n) (X2n,...,xn+1; хп+и .... x2n)]'h '
(8.84)
Если знаменатель обращается в нуль при некоторых
аргументах, то то же происходит и с числителем; тогда
S(".«) определяется из соображений непрерывности
(если это возможно). Чтобы величина S(n>") была опре-
определена при всех п, в поле должно присутствовать бес-
бесконечное число фотонов. Для п = 1 величина SC-') сов-
совпадает с grt1''' и g(l\ Следовательно, если IS*1- X){x\\ x2) \ =•-
= 1 при всех аргументах, то поле «когерентно в первом
порядке». Если к тому же все gn Ф 0, то «з (8.58) не-
непосредственно следует, что в этом случае
|S("-n)(*i, .... х2я)| = 1	(8.85)
для всех п. Более того, как и при рассмотрении соот-
соотношения (8.81), можно показать, что из справедливости
соотношения (8.85) для данного п(= п0) и для всех
значений аргументов вытекает его справедливость для
всех п ^> п0 и всех аргументов (для которых эти функ-
функции определены). В обоих случаях поле излучения есть
поле единственной моды, как в случае когерентности
первого порядка, плюс примесь других состояний, в
каждом из которых находится не более По—1 фотона.
Поскольку величина 5(п> "> чувствительна лишь к со-
состояниям с числом фотонов не меньше п, то указанная
примесь не повлияет на S("°'"°.

240	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Заслуживают упоминания две важных особенности
индексов когерентности. Прежде всего покажем, что
0<|S(n-n)(*i, ..., х2„)|<1	(8.86)
при всех п и при всех аргументах, для которых отно-
отношение (8.84) определено. Возьмем произвольные опе-
операторы si- и J? и вспомним разложение E.18) матрицы
плотности, а также неравенство Шварца E.3). Отсюда
следует
\К
= (s?s4>i:i {&&)'',	(8.87)
т. е. обобщенное неравенство Шварца. Полагая
sl = A(xn)A(xn-l) ... A{Xl),
Я = А(хп+1)А(хп+2) ... А{х2п),
получаем требуемое неравенство для S<n> n\
Вторая особенность индекса когерентности, которую
мы хотели бы подчеркнуть, связана с его интерпрета-
интерпретацией как индекса видности. Как уже говорилось, вели-
величина l±JYi2(t)| описывает относительные экстремумы
интенсивности в соответствующем эксперименте с двумя
щелями [см. A.23)]. Поэтому естественно считать, что
величина
l±|S(n-n)(*,, .... х2п)\
представляет экстремумы «-кратных корреляций интен-
интенсивности в указанных точках. Следовательно, величину
Г '==|Sl • '{хь . .., х2п)	(8.88)
можно рассматривать как обобщенный «индекс вид-
видности». Из сделанных выше замечаний следует, что

§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ	241
если для некоторого п0 измерения дают Т{п°' "о) = 1, то
можно с уверенностью утверждать, что в поле возбуж-
возбуждена одна мода, описываемая модовой функцией V(x)
и моментами gn,m [см. (8.55)], плюс примесь состояний,
в каждом из которых находится не более п0— 1 фотона.
Для того чтобы измерить такую величину интерферо-
метрическими методами, в общем случае необходимо
использовать системы, позволяющие осуществить нели-
нелинейное смешивание пучков и получить таким образом
волновые поля, пропорциональные произведению ампли-
амплитуд волновых полей в нескольких точках.
Согласно (8.11), любую из нормированных корреля-
корреляционных функций можно интерпретировать как норми-
нормированные формы скоростей многофотонных совпадений.
Измерение этих последних дает один из возможных спо-
способов определения величин gin\ g<n- ™> и рассмотренных
здесь индексов когерентности S<n- n\
§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ
А. Скорости и отсчеты для одной нормальной моды
Прежде чем переходить к выводу выражения для
распределения отсчетов (наблюдаемых на конечном от-
отрезке времени) для произвольного состояния поля, удоб-
удобно провести рассмотрение более простого случая в пред-
предположении, что возбуждена только одна нормальная
мода поля излучения. Обсудим на этом примере как
скорость счета, так и распределения отсчетов для ко-
конечных интервалов времени.
Введем следующие простые обозначения операторов
рождения и уничтожения для нашей выделенной нор-
нормальной моды:
aHt) = emaf,	(8.89а)
a(t) = e-iu>ta.	(8.896)
Скорости счета, соответствующие такому полю, можно
представить в виде
л (р) = ар0 <а+ (*,) ... а^ (tp) a (tp) ... а (*,)>• (8.90)

242	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Коэффициент ссо связан с множителем квантовой эффек-
эффективности а через разложение поперечного вектора-по-
вектора-потенциала по нормальным модам. В частности, непосред-
непосредственно из G.179а) следует, что
(8-91)
В силу (8.89) скорость п{р) в действительности не за-
зависит от всех временных аргументов:
п(р) = аР((а^ГаР).	(8.92)
Следовательно, в частности, п(р) есть скорость одно-
одновременного поглощения р фотонов, скажем при t = 0.
Интересно заметить, что величину п(р), рассматри-
рассматриваемую как скорость одновременного поглощения р
фотонов, можно вывести с помощью несколько иных
соображений. Если считать, что мы имеем дело с «со-
«событием», при котором само поле теряет р фотонов, то
возможно несколько взаимно исключающих способов
осуществления этого события. В частности, можно опре-
определить скорость в предположении, что имеется р или
р + 1, ... или в общем случае р + п фотонов с вероят-
вероятностью
n|}.	(8.93)
Заметим далее, что число способов, которыми можно
выбрать р фотонов из имеющихся р + п фотонов, равно
РЧ	) — (р + п)\/п\, если рассматривать каждый
определенный порядок выбора как отдельный способ.
Пренебрегая множителем пропорциональности ajj, ви-
видим, что скорость одновременного поглощения р фото-
фотонов описывается выражением
H~j~^- P(p + n).	(8.94)
В соответствии с E.52)

§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ	243
поэтому находим
({a+yaP),	(8.95)
т. е. ту величину, которую мы и намеревались получить.
Для ясности здесь предполагалось, что имеется лишь
одна мода, но это не играет существенной роли для
хода рассуждений.
Следующая наша задача состоит в выводе формулы
для вероятностей отсчетов из скоростей счета по-преж-
по-прежнему в предположении, что возбуждена только одна
нормальная мода. Иначе говоря, мы хотим знать вероят-
вероятность того, что детектор зарегистрирует m фотонов за
временной интервал Т. Приведем два различных спо-
способа вывода выражений для Р (пг, Т).
Многоатомный детектор. Первый метод нахождения
Р(пг,Т) приблизительно аналогичен использованному
Глаубером [8.2]. Представим себе детектор, состоящий
из N атомов, где /V — очень большое число, которое в
конце мы устремим к бесконечности. Предположим да-
далее, что sP(afPaP) есть скорость поглощения р фотонов
заданными атомами, число которых также равно р (под-
(подразумевается, что все атомы действуют как независимые
идентичные системы!). Здесь s — чувствительность от-
отдельного атомного детектора, которую мы считаем чрез-
чрезвычайно малой, порядка N~l. Так как скорость столь
мала, вероятность того, что р заданных атомов за вре-
время Т поглотят р фотонов, дается выражением
т т
s" J ... / <a+pap>df, ...dtp = spTp(afpap) = < : {sTa'a)" : ),
о	о
(8.96)
причем время Т должно удовлетворять условию
( : (sTafa)p '. ) <С 1. Из этого выражения следует, что ве-
вероятность события, в котором р—1 заданных атомов

244	ГЛ. 8 КВАНТОВАЯ ТЕОРИЯ
поглощают и один заданный атом не поглощает, есть
~sTa+a):). (8.97)
Методом индукции получаем, что вероятность события,
в котором р — г заданных атомов поглощают фотоны
и г заданных атомов не поглощают их, по истечении
времени Т есть
<	).	(8.98)
Теперь найдем вероятность Р(т,Т) того, что точно
m фотонов были поглощены в iV-атомном детекторе.
Она, очевидно, равна произведению числа различных
способов, которыми можно получить этот процесс, на
элементарную вероятность каждого события, а именно
В пределе, когда N —»• оо и s—*0, a Ns = oco является
конечным, находим
:). (8.100)
Так как мы перешли к пределу s—*0, это выражение
должно быть справедливым при всех Т.
Пределы применимости. Практически говоря, такое
заключение вполне верно, но в строгом смысле (8.100)
не может выполняться при всех Т. Чтобы понять, что
это довольно общее свойство, удобно воспользоваться
производящей функцией
= <: ехр (-
= (ехр (In [1 - Ха0Г] а*а)) = ^j A — kaj)n P (п). (8.101)

§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ	245
Здесь мы применили соотношение G.91а); Р(п) есть
распределение фотонов в нашей выделенной моде.
Чтобы функция Р(т,Т) представляла собой настоящее
распределение при всех Т, т. е.
оо
0<Р(т, Г)<1, SP(m, Г)=1, (8.102)
очевидно, должно выполняться условие 0 -^ Q (Я, 7") -^ 1
для всех Т, пока О-CX^Cl. Рассмотрим, однако, чистое
состояние с нечетным числом п0 фотонов, для которого
Р(по)= 1, а все остальные Р (п) равны нулю. В этом
случае при 0<^<1 получим Q(k, Т) = A - ка0Т)п"<0
при достаточно больших Т, а именно при всех
'1
Нетрудно показать, что ограничение этого типа яв-
является вполне общим и что для произвольного состоя-
состояния Р(т,Т) представляет собой настоящее распределе-
распределение лишь при условии
^ а0	ал	х	'
Кроме того, предельное распределение при 7 = а~' есть
как раз
Р(ш, а-1) = Р(пг).	(8.104)
Именно, в момент ао распределение отсчетов, приня-
принятых детектором, становится просто распределением фо-
фотонов в единственной нормальной моде поля.
Появление объема квантования в условии (8.103)
показывает, что верхняя граница а может быть сде-
сделана сколь угодно большой; таким образом, и вопрос
становится в значительной мере академическим. Тем не
менее поучительно понять причину ограничений этого
типа. Предположим, например, что в нормальной моде
содержится как раз один фотон, так что
Р(пг, T) = (l\: {a°T^a) exp (- aja^a): | 1), (8.105)

246	ГЛ. 8 КВАНТОВАЯ ТЕОРИЯ
или, конкретнее,
Р@, Т)=1-а0Т,	(8.106а)
Т) = а0Т,	(8.1066)
и все остальные члены равны нулю. Ограничение
аоТ 4^ 1 здесь совершенно очевидно, но более важен тот
факт, что этот результат по существу неправилен в лю-
любом случае: скорости, которые мы вывели с помощью
теории возмущений, не учитывают должным образом
распада начального состояния при временной эволюции.
Более удовлетворительный результат для примера
с одним фотоном можно получить следующим образом.
Начальные скорости, вычисленные по теории возмуще-
возмущений, по-прежнему верны, а именно
яA) = ао(а+а) = <хо, л(р) = 0, р > 2. (8.107)
В самом деле, осо есть правильная скорость поглощения
фотона в любой данный момент времени при условии,
что до этого не было зарегистрировано ни одного фо-
фотона. Поэтому величина 1 —ос0^влюбой данный момент
времени представляет собой вероятность того, что фотон
не будет зарегистрирован в интервале dt при условии,
что фотоны не были зарегистрированы и до этого мо-
момента. Отсюда вытекает (в духе вычислений, приведен-
приведенных в гл. 2)
t + T
11	(8.108а)
и как следствие
РA, Г)=1-Р@, Г) = 1 -ехр(-а0Г); (8.1086)
с физической точки зрения такой результат значитель-
значительно разумнее, нежели (8.106). Для времен, удовлетво-
удовлетворяющих условию ао^ "С 1, оба результата, очевидно,
совпадают.
Стоит, пожалуй, заметить, что аналогичные ограни-
ограничения налагаются на распределение (8.100) для любого
состояния, для которого скорости счета я(р) равны
нулю при р~^-М (для некоторого М>2). Поэтому еле-

§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ	247
дует остерегаться чересчур буквальной интерпретации
выражения (8.100) в применении ко всем состояниям и
произвольным интервалам времени, пока размер «ящи-
«ящика» L < оо. Тем не менее после того как мы обсудим
случай, когда поле обладает всеми модами, и более
физические состояния поля излучения, станет ясно, что
эти трудности не имеют значения с практической точки
зрения.
«Диагональное» представление по когерентным со-
состояниям. Наш второй способ вывода распределения
отсчетов Р(т, Т) несколько отличается от использован-
использованного выше, хотя приводит к такому же результату. На-
Напомним, что при выводе распределения Пуассона для
отсчетов в гл. 2 существенное значение имело предпо-
предположение о статистической независимости событий (т. е.
отсчетов), происходящих в различных временных интер-
интервалах. Здесь ответ на вопрос о статистических зависи-
зависимостях этих отсчетов содержится в выражении для ско-
скорости счета. Совместная вероятность того, что р фотонов
будут зарегистрированы в моменты t\, ..., tp в интер-
интервалах dt\, ..., dtv, есть
t{ ... dtp.	(8.109)
tp
События будут статистически независимы, если вероят-
вероятность можно представить в виде произведения элемен-
элементарных вероятностей для отдельных событий, т. е. если
для всех р
a?(a^aP)dt[ . .. dtp = Д {ao(cfia)dtt}. (8.110)
Это, очевидно, просто означает, что для всех р должно
выполняться условие
(а+РаР) = ({а+а))р.	(8.111)
Именно такое условие выполняется для матрицы плот-
плотности чистого когерентного состояния p = \z){z\.
Так как для когерентного состояния отсчеты в раз-
разных временных интервалах статистически независимы,

248	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
можно просто привести результаты вычислений гл. 2
для элементарной скорости яA) = dp(t)/dt, а именно
i^ = <xo(a+a) = ao<z|a+a|z) = ao|z|2. (8.112)
В частности, получаем, что распределение отсчетов [ср.
B.2)] имеет вид
Р(т, T\z)=(aoTlf) exp(-ao:r|zp). (8.113)
Это есть распределение Пуассона со средним значением
m = aoT\z\2, и оно справедливо при всех Т. Мы доба-
добавили индекс z, чтобы помнить, что имеем дело с коге-
когерентным состоянием.
Если воспользоваться общим соотношением G.105)
для диагональных матричных элементов упорядоченных
операторов, то можно написать
Р(т,Т\г) = (г |: Ка°[^а) ехр(- aja^a) :\z) =
= Sp {| z) (z | : (а°Г^аГехр(- aja+a) : }. (8.114)
Для тех матриц плотности, которые могут быть запи-
записаны в виде нормированной линейной суперпозиции опе-
операторов проектирования на когерентные состояния:
(z)\z)(z\d2z,	(8.115)
распределение отсчетов в соответствии с (8.100) можно
получить непосредственно из формулы
Р{ш, Г) = 1 (<p(z)P(m, T\z)d2z =
Если <p(z) есть обычная плотность вероятности, то опре-
определенное таким образом распределение Р(пг,Т) с не-
необходимостью будет настоящим распределением при
всех Т,

§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ	249
Ниже мы познакомимся с замечательным результа-
результатом (являющимся точным в смысле теории распределе-
распределений); он состоит в том, что всякую матрицу плотности р
можно записать в «диагональном» представлении
(8.115) по когерентным состояниям. Совершенно оче-
очевидно, что весовая функция ср не может всегда быть
положительной, так как иначе нельзя было бы построить
матрицу плотности любых чистых состояний, за исклю-
исключением когерентных. Необходимость отрицательных зна-
значений весовой функции видна также из того факта, что
в противном случае распределения отсчетов Р(т,Т)
были бы для произвольного состояния настоящими рас-
распределениями при всех Т, а мы уже приводили контр-
контрпримеры, показывающие, что это не так [см., например,
(8.106)].
Следует подчеркнуть, что такие отрицательные весо-
весовые функции не приводят к каким-либо трудностям до
тех пор, пока не нарушены основные правила. Поясним
роль отрицательных весовых функций на простом при-
примере. Предположим, что Pi{n) и Р${п) являются на-
настоящими распределениями вероятности; тогда такой
же является и их взвешенная сумма />,(/;) = '/г^г(«-) +
+ 1/2^>з(«)- Следовательно, соотношение
о
Р3(п) ^ 2Р, (п) - Р2(п) = 2 <Р«Р» (8Л 17)
а=1
определяет настоящее распределение вероятности и
включает нормированную Bфа= 0 линейную комбина-
комбинацию весовых функций с отрицательными членами. Все
свойства Ръ{п) можно вывести из (8.117). В частности,
моменты равны (прK = 2 Фа (пр)а и т- Д-
Стоит отметить, что «диагональное» представление
(8.115) для р приводит к выражению для квантовых
распределений отсчетов [первая строка в (8.116)], кото-
которое формально совпадает с выражением, получающимся
при стандартном классическом вычислении этого рас-
распределения. В этой формальной связи весовая функция
ф(г) является аналогом классического распределения.
Мы увидим, что эта аналогия может быть плодотворно
использована во многих приложениях.

250	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Б. Распределения отсчетов для поля излучения
Точечные детекторы. Руководствуясь рассмотрением,
проведенным для одной моды, не представляет большого
труда определить распределение отсчетов для поля из-
излучения. Рассмотрим вначале счетчик, чувствительность
которого локализована в точке х пространства и одина-
одинакова для всех поляризаций. Тогда, согласно (8.9), ско-
скорость счета для совместного наблюдения п фотонов в
точке г в моменты t\, ti, ..., tn дается выражением
а 2 (П^Ч^П^Ч^)/.	(8.118)
Поляриз. *=|	'='
Здесь мы опустили общую переменную г и не выписали
явно векторные индексы для А. Предположим, что эту
скорость можно представить в виде произведения
й{
а 2 '
Поляриз.
п
= 11 {a<A(~4'fe)-A(+4*fc)M (8.119)
k=\
для всех п и всех временных аргументов. В действи-
действительности это есть просто свойство когерентного состоя-
состояния поля излучения, для которого р = \{zx(k)})({zx(k)}\.
В таком состоянии отсчеты в отдельных временных ин-
интервалах статистически независимы; кроме того, в обо-
обозначениях G.181а) элементарная скорость счета имеет
вид
а <А(-' @ • А(+) @> = a ({zk (к)} \ A(~> (t) • А(+) (*) | {zx (k)}) =
= a\'(t)-V{t) = a\V(t)?.	(8.120)
Следовательно, здесь снова применимы те соображения,
которые были использованы в гл. 2 для вывода пуас-
соновской статистики, и для когерентного состояния на-
находим
Р{ш, T + t,
I T + t
ml
T + t
¦expl -a f \\{t')fdt'\. (8.121)
I т+t
-a J \V{t')

§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ	251
Это распределение, разумеется, не обязательно должно
быть стационарным (не зависящим от t).
Для тех матриц плотности, которые можно предста-
представить как линейные суперпозиции вида
р = { <р ({гк (к)}) | {г, (к)}) ({г, (к)} | dn ({zk (к)}) (8,122)
[ниже мы придадим этому утверждению точный смысл,
примерно аналогично тому, как это было сделано в
связи с формулой G.153)], получаем
Р(т, T + t, *)-
= / Ф (К (к)}) Р (т, Т + U 11 К (к)}) ф ({г, (к)}) -
X
<:-
exp
f Tp
•
V t
г
-
A(-
T + t
j
> (f) • A(+
m!
A(-J@
/
•A<+)@
¦ X
-.
(8.123)
что и представляет собой искомое решение. В действи-
действительности, так же как и в случае одной моды, любую
матрицу плотности р можно представить в виде (8.122)
в смысле теории распределений, о чем подробнее будет
сказано ниже. Следовательно, (8.123) представляет со-
собой искомое распределение отсчетов для точечного счет-
счетчика и произвольного состояния р. Далее, производящая
функция имеет вид
Q(X, Г + ^ 0 ^ У A - Я,I" Р (m, 7 + f, 0 =
:\. (8.124)
Распределенные детекторы. Рассмотрим теперь рас-
распределенный счетчик, который чувствителен в какой-то
области пространства и времени. Для начала предполо-
предположим, что можно рассматривать простой адмитанс

252	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
S*(r, t), который определяет относительную амплитуду
и фазу вклада, вносимого полем. Это просто означает,
что эффективное поле, входящее в выражения для ско-
скорости я-фотонных отсчетов, имеет вид
А(е+) (О = J S* (г, Г - *,) • А(г+> (г, t^tfrdt^. (8.125)
В дополнение к этому можно также предположить, что
специфические свойства S* не поддаются точному конт-
контролю, так что следует усреднить по различным возмож-
возможным адмитансам. Для однофотонной скорости счета от-
отсюда следует, что величину a(Af"")(r, t') • A(+)(r, t'))
необходимо заменить величиной общего вида
2a<A(e->(r, П-А<+)(г, П>^а(Аы-У-А(+)>, (8.126)
где суммирование производится по подходящим S' и
введено сокращенное обозначение
(-) (Гь h). Y (Гь t, _ h. Га> t, _ h) .
• А(+)(г2, 12)йАг{с(Аг2сИхсИ2.	(8.127)
Здесь тензор Y представляет пространственные и вре-
временные спектральные свойства детектора. Практически
наиболее важной идеализацией является случай, когда
Y = а (г,) б (г, - г2) б (Г - *,) б (Г - t2), (8.128)
где сг(г)—относительная плотность детектирующих ато-
атомов; она равна нулю вне детектора. В этом случае имеем
просто
Ан) • Y • А(+) = [ А(-) (г, Г) ¦ Аж (г, t') a (r) dh. (8.129)
Для когерентного состояния n-фотонные скорости от-
отсчетов по-прежнему могут быть представлены в виде
произведения элементарных скоростей
= a J V* (г,, t{) ¦ Y (г„ t'-tu r2> f ~t2)-\ (r2, /2) X
Xd:ir1d3r2dtldt2. (8.130)

ml
§ 3. РАСПРЕДЕЛЕНИЯ ФОТООТСЧЕТОВ	253
Отсюда следует, что распределение отсчетов этого
«Y-детектора» для когерентного состояния определяется
вместо (8.121) выражением
Ру(т, T + t,
г T+t
\а f (V.Y.V)df\	T+t
exp -a | (V-Y-V)df'. (8.131)
Тем не менее можно по-прежнему представить произ-
произвольную матрицу р в виде (8.122); тогда получаем, что
для Y-детектора и состояния р
Ру(т, T + t, 0 =
= / Ф (К (k)}) Py (m,T + t,t\ {zK (к)}) ф ({zx (к)}) =
T + t
-exp -aj A(->.Y-A(+)dr]
(8.132)
Модифицированная производящая функция, очевидно,
имеет вид
оо
Qy (Я, Т + t, t) = ^] A - k)m PY {X, T + t, t) =
= /:exp|-Xaf [A(-). Y-A(+)]df I :). (8.133)
4 I t	J '
Резюмируя, можно сказать, что, каковы бы ни были
спектральные свойства детектора, распределения отсче-
отсчетов являются по существу взвешенными распределе-
распределениями Пуассона с весовой функцией rp({z?,(к)}), описы-
описывающей состояние р, и совершенно не зависят от свойств
счетчика.
Случай нескольких детекторов. Обобщил! полученные
результаты на случай нескольких счетчиков, располо-
расположенных в различных местах. Для получения этого

254	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
результата заметим снова, что для когерентного состоя-
состояния отсчеты в разные моменты времени и в разных точ-
точках статистически независимы. Для такого состояния сов-
совместная вероятность того, что q-n счетчик (q — 1, 2, ...
..., Q) зарегистрирует mq отсчетов за отрезок времени
от tq до т7 == tg + Tg, равна
mQ\ Tj, ..., xQ;
К, г,, gfe(k)}), (8.134)
t,t
где последние выражения определены в (8.131). Следо-
Следовательно, совместное распределение отсчетов для про-
произвольного состояния имеет вид
Р (Ш, Т, t) = { ф ({Z, (к)}) Р (Ш, Т, 11 {Z, (к)}) d\l ({ZX (к)}).
(8.135)
Выражения для Р(ш,т, t) и для соответствующей про-
производящей функции Q(k,x,t) в виде средних от нор-
нормально упорядоченных операторов очевидны, и мы их
не выписываем. В последней главе мы еще будем иметь
возможность обсудить совместные распределения отсче-
отсчетов для некоторых случаев, представляющих экспери-
экспериментальный интерес.
Свойства в случае бесконечного объема квантования.
В заключение остается выяснить еще одну проблему,
относящуюся ко всем рассмотренным распределениям
отсчетов. Приведенные выше результаты все еще зави-
зависят неявным образом от величины объема квантования
через их зависимость от параметра L. Мы уже видели,
что некоторые распределения (для единственной нор-
нормальной моды) имели смысл лишь при временах, мень-
меньших чем 2ыЬ31(аЬ). Эти технические трудности исче-
исчезают при переходе к пределу L—юо. Чтобы окончатель-
окончательно определить общие распределения отсчетов и их про-
производящие функции для Y-детектора, можно считать,
что предельный переход L ~* оо включен в соотношения
(8.132) и (8.133),

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	255
Основное свойство, благодаря которому распределе-
распределения отсчетов асимптотически не зависят от L и тем са-
самым хорошо ведут себя в пределе L —* оо, состоит в
том, что поля излучения с конечной полной энергией
имеют вид волновых пакетов. Но сигнал типа волнового
пакета может находиться вблизи реального (конечных
размеров!) детектора лишь в течение конечного интер-
интервала времени. Как следствие этого, например, распре-
распределение для одного детектора Р(т,Т + t,t) принимает
при Т—у оо свой предельный вид, определяемый интер-
интервалом времени, в течение которого волновой пакет на-
находится вблизи детектора; оно не растет по величине до
бесконечности, как это имело место для единственной
нормальной моды в конечном объеме квантования.
§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ
Выше уже говорилось о том, что любую матрицу
плотности в определенном смысле можно представить
в «диагональном» виде (8.115) или (8.122). Полезность
такого представления была уже продемонстрирована;
так, с его помощью быстро выводится распределение
отсчетов. Действительно, как мы увидим, это представ-
представление оказывается чрезвычайно удобным вычислитель-
вычислительным инструментом в ряде приложений. Чтобы глубже
понять диагональное представление и придать ему точ-
точный смысл, особенно удобно начать с рассмотрения од-
одной степени свободы.
А. «Диагональное» представление
для одной степени свободы
Эвристические замечания. Общую проблему, которую
мы собираемся рассмотреть, можно сформулировать так:
необходимо представить оператор Т в диагональном
виде
r=J<p(z)|z)<z|4i.	(8.136)
Здесь мы положили d\i = n~ld2z, чтобы включить в за-
запись л~', и несколько обобщили соотношение (8.115),
чтобы рассматривать более общие операторы, нежели

256	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
просто матрицу плотности. Основной вопрос состоит в
следующем: какие операторы можно представить в та-
таком виде и каковы соответствующие весовые функции
q>(z)? Ясно, что если г = х + iy, то для функции вида
Ф (г) = яб B - г0) = лб (х - *0) б (у - Уо) (8.137)
получаем, что оператор T = \zo){z$\, т. е. представляет
собой оператор проектирования на когерентное состоя-
состояние. Если ф(г)=1, то мы приходим к основному разло-
разложению единицы G.48).
Для операторов более общего вида удобно начать
следующим образом. Рассмотрим диагональные матрич-
матричные элементы по когерентным состояниям
Т (z') = <z' IT | z') = j Ф (z) (z' \z)(z\ z') d\i =
= f <p(z)exp(-|z'-z|2)dH- (8.138)
В гл. 7 мы уже видели, что оператор Т полностью опре-
определяется этими диагональными матричными элементами.
Следовательно, если вес <p(z) удовлетворяет соотноше-
соотношению (8.138), то он автоматически удовлетворяет и более
общему соотношению (8.136). Выражение (8.138) есть
интеграл типа свертки, и это предоставляет нам возмож-
возможность применять преобразование Фурье ко всем встре-
встречающимся выражениям. С этой целью воспользуемся
формулировкой в фазовом пространстве, чтобы сосре-
сосредоточить внимание на действительной и мнимой ча-
частях z. Иными словами, рассмотрим
Т(р', q')^(p', q'\T\p',q')~
= J Ф(Р, q)^{~^\{p'-pf + {q'~qJ]\d\i, (8.139)
где теперь d\i = dpdql{2nti). Если ввести определения
Т (х, k) sa J el *p-WhT (p, q) d\i,	(8.140a)
ф (x, k) = J el ^p-^'/'cp (p, q) dn	(8.1406)

§ 4. ОПТИЧЕСКАЯ ТЕОРЕЛ\А ЭКВИВАЛЕНТНОСТИ	257
и заметить, что
ехр [ - ^ U2 + /е2)] = J е* &-»№ ехр [ - ± (р2 + <?2)] ф,
(8.141)
то из теоремы о свертке следует
Т(х, *) = ф(*.
Мы видим, таким образом, что
[±	]	(8.142)
Фактически мы пришли к утверждению, что вся-
всякий оператор Т имеет диагональное представле-
представление1) с весом qp(z), определяемым как фурье-образ от
T(x,k)exp[(\/2b)(x2 + k2)].
Следовательно, чтобы придать смысл соотношению
(8.136), нужно понять, что представляет собой преобра-
преобразование Фурье соотношения (8.142). Ясно, что если
(8.142) определяет абсолютно интегрируемую функцию,
то фурье-образ хорошо определен, но так будет отнюдь
не всегда. Чтобы глубже понять диагональное представ-
представление, нужно подробнее изучить величину Т(х, k). В этой
связи уместно напомнить некоторые положения тео-
теории распределений2), поскольку именно она придает
') Соображения, показывающие исключительную общность диа-
диагонального представления операторов, впервые были высказаны
Сударшаном [8.7].
2) Употребляемый авторами термин «distribution» переводится
здесь и ниже как «распределение». В советской математической
литературе ему соответствует термин «обобщенная функция» — см.,
например, книгу Гельфанда и Шилова (И. М. Г е л ь ф а н д,
Г. Е. Шилов, Обобщенные функции, вып. 1, М., 1958). Употребле-
Употребление при переводе термина «распределение» связано еще и с тем,
что в том же тексте авторы пользуются выражением generalized
function (обобщенная функция), придавая ему смысл, несколько
отличный от смысла термина distribution. Заметим также, что встре-
встречающееся ниже выражение «tempered distribution» мы переводим
[следуя русскому изданию книги Шварца (Л. Шварц, Матема-
Математические методы для физических наук, изд-во «Мир», 1965)] как
«умеренное распределение»; в советской литературе иногда употре-
употребляется также выражение «обобщенная функция умеренного ро-
роста». — Прим, перев.

258	ГЛ. 8 КВАНТОВАЯ ТЕОРИЯ
точный смысл понятию 6-функции Дирака и его обоб-
обобщениям.
Распределения. Хотя большинство читателей интуи-
интуитивно представляют себе б-функцию как пикообразную
сингулярную функцию, правильнее рассматривать ее как
функционал или как разновидность оператора. Именно,
для заданного класса функций она сопоставляет этим
функциям комплексные числа, определяемые как зна-
значения функций, вычисленные при определенном значе-
значении аргумента. Символически обычно пишут (и мы уже
неоднократно пользовались такой записью!)
/(*„)= {6(x-xo)f(x)dx,	(8.143)
хотя, строго говоря, в правой части мы злоупотребляем
обозначениями, поскольку не существует какой-либо ве-
величины, которая могла бы служить подынтегральным
выражением при классическом определении интеграла
по Лебегу. Существуют два способа, позволяющих сде-
сделать понятие 8(х — Хо) точным. В первом из них ин-
интеграл уже не используют, а просто считают, что
6Хо {f} = f (х0), т. е. рассматривают 6XlJ как функционал,
который сопоставляет функции ее значение в точке х0.
Во втором подходе, более известном под названием тео-
теории обобщенных функций1), действие 8Х, определяется
с помощью равенства
f(xo)=um [6M(x-x0)f(x)dx,	(8.144)
ЛГ->оо "
где дм(х)—некоторая последовательность функций с хо-
хорошим поведением [например, буИ (х)~(М/лI2 схр( — Мх'2)};
для каждой из этих функций интеграл имеет смысл. Су-
Существует, очевидно, много последовательностей, которые
могут служить определением данного распределения. Во
всяком случае, удобно определить символическую пра-
правую часть равенства (8.143) с помощью одного из двух
способов; это, конечно, неявно всегда и подразумевается.
') См. примечание 2 на стр. 257. — Прим, перев.

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	259
Независимо от того, какое из определений было вы-
выбрано, б-фуккция не определена для всех функций f(x),
так как х0 может оказаться точкой разрыва. Отсюда бе-
берет начало понятие пробных функций (это как раз те
самые гладкие функции, о которых шла речь в гл. 3!),
т. е. понятие класса функций, на которых может быть
определено данное распределение. Например, для
б-функции допустимые пробные функции должны быть
непрерывными. Во многих случаях, однако, в качестве
пробных функций удобно брать не все те функции, для
которых определено данное распределение. Благодаря
этому можно будет рассматривать одновременно не-
несколько распределений, а также их линейные комбина-
комбинации. Классическим примером здесь является множество
таких пробных комплексных функций f(x) действитель-
действительной переменной х, каждая из которых бесконечное число
раз дифференцируема и спадает на бесконечности бы-
быстрее любой отрицательной степени х (часто это кратко
обозначается термином «быстро убывающая функция»).
На каждой такой функции можно определить распреде-
распределения, включающие любое конечное число производных
б-функции, или такие распределения, которые растут
на бесконечности, как некоторый полином. В связи с та-
таким свойством подобные распределения называют «уме-
«умеренными распределениями»1), а пространство пробных
функций называют пространством пробных функций для
умеренных распределений и обозначают символом 9*.
Иначе говоря, умеренные распределения являются ли-
линейными функционалами2) в пространстве 9*: каждому
элементу из З1 они ставят в соответствие комплексное
число. Отсюда не вытекает, что любое данное распреде-
распределение (скажем, б-функция) не может быть определено
на более широком классе функций; это скорее значит,
¦) Интерпретация понятия «полиномиального роста» требует
осторожности. Хотя ех не является умеренным распределением,
функция ехехр(!ех) является умеренным распределением, поскольку
это есть производная от ограниченной функции —iexp(iex).
2) Строго говоря, умеренные распределения суть непрерывные
линейные функционалы; однако мы пренебрежем этим усложне-
усложнением, так как определение непрерывности по пробным функциям
требует рассмотрения неоправданно сложных топологий.

260	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
что удобно ограничиться рассмотрением некоторых кон-
конкретных пространств (например, 9"), свойства которых
поддаются подробному анализу.
Другое классическое пространство пробных функций,
обозначаемое символом 3), состоит из комплексных
функций f (х) действительного переменного х, каждая из
которых бесконечное число раз дифференцируема и рав-
равна нулю вне конечной области. Примером такой функции
является f(x) = exp[—A—х2)'2] при |jq<ll и f(x) = 0
во всех остальных точках. Поскольку этот класс проб-
пробных функций уже, чем 9", соответственно класс допу-
допустимых распределений будет в данном случае шире.
В частности, функция ф(х) = ехр(х2) является распреде-
распределением в 2) [так как / q>(x)f(x)dx = cp{/} определяет
линейный функционал в Ю], но это не умеренное распре-
распределение.
Фурье-преобразования от распределений определяют-
определяются с помощью соответствующих фурье-преобразований
их пространств пробных функций. Например, для каж-
каждой пробной функции f(x) из 91 можно ввести функцию
e-^{x)dx.	(8.145)
Нетрудно видеть, что это преобразование отображает
пространство 9* само на себя, так как фурье-образ бес-
бесконечно дифференцируемой быстро убывающей функции
обладает теми же самыми свойствами. Следовательно,
если по аналогии с формулой Парсеваля определить рас-
распределение ф таким образом, чтобы равенство ф{/*} =
= ф{/*} выполнялось для всех f(x) из 9? (где ф — уме-
умеренное распределение), то и само это распределение бу-
будет умеренным. Например, если ср = б(х — х0), то
ф = BяI/зехр(—iyxo); последнее распределение, очевид-
очевидно, хорошо определено на всем пространстве 91.
Конечно, очень удобно, если преобразование Фурье
оставляет инвариантным заданный класс пробных функ-
функций (а вместе с ними, следовательно, и соответствующие
им распределения). Однако это не означает, что так
должно быть всегда. Мы можем рассматривать также
фурье-преобразование пробных функций из SD, каждая
из которых обращается в нуль вне конечного интервала.

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	261
Соответствующие фурье-образы этих функций, опреде-
определенные согласно (8.145), не могут также обращаться в
нуль вне конечного интервала (поскольку являются гра-
граничными значениями целых функций). Следовательно,
образуемое ими пространство (обозначаемое символом
Z) не имеет с пространством 2) ни одной общей функ-
функции, за исключением нулевой функции / (х) = f(t/) = 0.
Следует отметить, однако, что так как 2) является под-
подпространством по отношению к 9*, то то же самое отно-
относится к пространству фурье-образов SZ. Распределения
в 2 [например, ехр(—'А^2)] могут быть также распре-
распределениями и в ?, но поскольку пространства различны,
то так будет, вообще говоря, не всегда. Тем не менее
каждое распределение ф в ?? получается путем фурье-
преобразования распределения ср в 2 с помощью тож-
тождества (p{f*} = cp{f} для всех f (х) из 2). На основе этого
процесса можно ввести новые распределения, однако
они полностью определены своими значениями на своем
собственном пространстве пробных функций 9L (даже
если их и нельзя определить на 2)). Подчеркнем еще
раз, что распределения характеризуются тем классом
пробных функций, на котором они определены.
Как уже отмечалось, обычно распределения опреде-
определяются не через значения их функционалов (и соответ-
соответствующих интегралов), а скорее, скажем, с помощью
последовательности функций. В некоторых случаях даже
затруднительно наглядно представить себе распределе-
распределение в виде функции. Например, хотя функция 6"(х)
равна нулю при х ф О, невозможно указать ее значение
при х = 0. Еще труднее наглядно представить себе рас-
распределение на SZ, являющееся фурье-образом от ехр(х2).
Этот пример лишний раз показывает, насколько полезно
определять распределения последовательностями настоя-
настоящих наглядных и интегрируемых функций. Все наши
распределения могут быть определены с помощью после-
последовательностей, и именно таким способом мы будем
пользоваться для придания различным распределениям
точного смысла.
Приложение к «диагональным» представлениям. Ха-
Характер функции T(p,q) [см. (8.139)] зависит от конкрет-

262	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
ного вида оператора Т. Если Т — ограниченный опера-
оператор, то T(p,q)—ограниченная непрерывная бесконечно
дифференцируемая функция. Особый интерес представ-
представляют для нас те случаи, когда Т — оператор с конечной
следовой нормой (это включает случай матрицы плот-
плотности). Любой такой оператор может быть записан в
канонической форме E.18). В частности, для этих опе-
операторов
Т(р, q) = (p, q\T\p, q) =
оо
= 2Р/</>, q\h)<$l\P> Я), (8-146)
где Р; — некоторая абсолютно суммируемая последова-
последовательность, a \kj) и j\|)j)—ортонормированные базисы.
Для таких операторов из неравенства Шварца в непре-
непрерывном представлении вытекает, что
Т{р,
(8.147)
Следовательно, фурье-образ — функция T(x,k) —являет-
—является непрерывной ограниченной (величиной \\T\\\) функ-
функцией для каждого оператора с конечной следовой нор-
нормой. Отсюда получаем, что
ф(*. k)^f(x, k)exp[-±-(x2 + k2)]	(8.148)
является непрерывной функцией для каждого оператора
с конечной следовой нормой. Существует верхняя гра-
граница этой функции
|ф(х, fc)K||71,e<*J+*>V2*.	(8.149а)
В действительности, как будет показано ниже,
Г ||, е^*4*')'4*.	(8.1496)
Ясно, что все такие функции ф(х, k) определяют распре-
распределения на 3>2 — пространстве функций f{x,k) двух пе-

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	263
ременных; эти функции бесконечно дифференцируемы
и равны нулю вне конечной области пространства х,
k '). Это очевидно, поскольку интеграл
J ф(х, k)f(x, k)d\a	(8.150)
(где dn = dxdkl2nh) хорошо определен для всех таких
}(x,k). В связи с диагональным представлением опера-
тороз с конечным следом для нас наиболее интересны
фурье-образы таких функций. В общем случае такой
фурье-образ является распределением, а не функцией.
Чтобы придать смысл такому фурье-образу в общем
случае, воспользуемся представлением с помощью по-
последовательностей. Именно, введем функции ц>м(х> ?)>
которые стремятся (в некотором смысле) к ф (х, fe) при
М —юо; кроме того, предположим, что у каждой из этих
функций существует фурье-образ q>M{p,q)—функция с
хорошим поведением. Иными словами, с помощью ве-
весовых функций фм(р, у) мы определяем последователь-
последовательность операторов
\Лр, q)\p, q)(p, q\d\x,	(8.151)
стремящуюся к заданному оператору Т. Если бы нас
интересовали только матричные элементы общего вида
(А,|Г|г|)), то было бы достаточно построить такую по-
последовательность 7л/., чтобы для всех \'к) и |)
Mm <А,|7-Л|1|>> = <А,|П1|)>.	(8.152)
/И-»оо
В действительности, однако, нам требуется значительно
более сильное ограничение, поскольку мы хотим вычис-
вычислять следы различных выражений, содержащих матри-
матрицу плотности.
Те операторы, средние значения которых нужны нам
для нахождения распределений отсчетов, являются в
действительности ограниченными операторами. Средние
') Хотя этот результат нам и не понадобится, отметим, что
если Т — любой ограниченный оператор или полином по а и а, то
ф(х, k) всегда является распределением на Z>2, хотя и не обяза-
обязательно задается функцией.

264	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
значения ограниченных операторов определены для
каждого состояния системы, и с общей квантовомехани-
ческой точки зрения они составляют максимальный об-
общий класс наблюдаемых физических величин. В самом
деле, такой класс содержит унитарный оператор, опре-
определяющий характеристическую функцию Сь (s) = Sp(petsfi)
для распределения любой мыслимой наблюдаемой. Если
нас интересует представление матрицы плотности с по-
помощью последовательности, то для того, чтобы такая по-
последовательность имела практическую ценность, она
должна допускать прямое вычисление среднего значе-
значения каждого ограниченного оператора. Иначе говоря,
мы хотели бы, чтобы для каждого ограниченного опера-
оператора В выполнялось соотношение
SpGB)= lim Sp {TMB),	(8.153)
М-><х>
а это значительно более сильное ограничение, нежели
(8.152).
Чтобы дать практически более удобную формулиров-
формулировку этого требования, рассмотрим последовательность
операторов с конечной следовой нормой, определяемую
равенством
*м = Т-Ти^ ? yf > | A,w»> ($™ \, (8.154)
где последнее соотношение является следствием кано-
канонической формы E.18). Тогда, очевидно, для всякого
ограниченного оператора В имеем
Следовательно, если операторы Тм_ сходятся к Г по так
называемой «следовой норме», а именно так, что
II Г-Гл, Ik-*0	(8.156)
при М —>¦ оо, то для каждого ограниченного оператора
будет обеспечено выполнение формулы (8.153) для
средних значений, к чему мы и стремились.

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	265
Нетрудно придумать последовательности операторов
Тм, которые просто сходились бы к Т. Для этого доста-
достаточно заменить ф (х, к) последовательностью функций
(fM(x< k), которые стремятся к ц>(х, k). Суть проблемы
состоит в отыскании такой последовательности, для ко-
которой выполнялось бы условие (8.156). Имеется два до-
доказательства существования таких последовательно-
последовательностей1). Мы не будем повторять целиком ни одно из них,
а наметим в общих чертах метод, принадлежащий Рок-
ка [8.10], поскольку это проливает свет на некоторые ин-
интересные аспекты задачи.
Нам понадобятся некоторые дополнительные свой-
свойства; приведем их в основном без доказательств и лишь
покажем, что эти свойства вполне правдоподобны. Из
G.8), G.88) и (8.140) следует, что
(p,q\T\p,q) = \f (х, k)el(ftv-W*ф =
= jf{x, k)(p, q\:U[k,x]:\p,q)d\i. (8.157)
Поскольку диагональные элементы однозначно опреде-
определяют Т, получаем
Т= J f(x, k): U[k, х]:ф = j" t(x, k)U[k, x]d^ (8.158)
где
= f{x'k)exp[i(x2 + k2)]¦ {8Л59)
Следует отметить, что t(x, k) является «весовой функ-
функцией Вейля» в известном вейлевском представлении опе-
операторов, Если перемножить два оператора, записанных
в этом представлении, то в силу правил коммутации
AB= a {x, k) b (xf, k') U [k, x] U \k', x'\ dpi dpi' =
= f a(x, k)b {x\ k') expГ^ (kx' - xk')] X
X U[k + k', x + x'\ dp, d\x' = f (a * b) (x, k) U [k, x] dpi,
		(8.160)
') Главный результат, о котором ниже будет идти речь, полу-
получили независимо Клаудер [8.9] и Рокка [8.10].

266	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
где величина
(а * Ь) (х, к) =
^j a{x-xf, k-Wbix', kf)exp[-±r{kx' - xk^dp' (8.161)
носит название «свертки с умножением» (twisted convo-
convolution product).
Из классического анализа известно, что всякая
функция х(х) из L1 дается произведением двух функций
а(х) и |3(х) из L2, а именно х(х) = а(х)$(х). Далее, из
неравенства Шварца вытекает
\\x(x)\dx= J |a
{JJ[/2. (8.162)
Для определенного типа операторов, действующих в
гильбертовом пространстве, выполняются примерно ана-
аналогичные соотношения. В частности, всякий оператор Т
с конечной следовой нормой является произведением
двух операторов А и В (так называемых операторов
Гильберта — Шмидта): Т = АВ. Далее, имеет место со-
соотношение, аналогичное (8.162):
l|71i = MflHi<Mlb-l|fllb.	(8.163)
где величина
M||2={SpU^)}'/2	(8.164)
носит название «нормы Гильберта—Шмидта» (она, во-
вообще говоря, отличается от [|Л|| и от ЦЛ^). Всякий опе-
оператор, для которого величина (8.164) конечна, принад-
принадлежит к классу операторов Гильберта—Шмидта. Этот
класс замкнут по отношению к сложению операторов и
умножению их на с-число и может быть превращен в
гильбертово пространство (составленное из операто-
операторов!), если определить скалярное произведение соотно-
соотношением
(A, B)^

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	267
Предположим, что мы аппроксимируем Т = АВ по-
последовательностью 7'м = АМВМ, где Ам и Вм — опера-
операторы Гильберта — Шмидта. Тогда
\\ТМ-Т ||, = || АМВМ - АМВ + АМВ - АВ ||, <
< || Вм -В1-1| Ам ||2 + || Ам - А ||2 • || В ||2. (8.165)
Следовательно, чтобы обеспечить сходимость Тм по сле-
следовой норме, достаточно, чтобы как Ам, так и Вм схо-
сходились по норме Гильберта—Шмидта; это и является
ключевым пунктом в рассуждениях Рокка.
Как мы сейчас покажем, такая характеристика тре-
требуемой сходимости особенно удобна. С учетом (8.157) и
(8.147) получаем
SpG-)=J<P, q\T\p, q)dvL = f(O, 0) = t@, 0). (8.166)
Для оператора Гильберта—Шмидта В находим
|| В \f, = Sp {В1'В) = (V * b) @, 0) = J | Ь (х, k) |2 ф, (8.167)
где bf(x, k) = b (— x, —k). Это соотношение наглядно
показывает, что класс операторов Гильберта—Шмидта В
связан с пространством L2 функций b(x,k), причем связь
отдельных элементов дается представлением Вейля
(8.158). Отсюда видно, что если весовые функции Вейля
ам(х, k) —*а(х, к) и bM(x, k) —> b(x, k) сходятся в смыс-
смысле нормы в L2, то операторы Тм = АМВМ-—Т = АВ схо-
сходятся по следовой норме. Интуитивно ясно (это яв-
является также классическим результатом), что a(x,k)
[или b(x,k)] можно аппроксимировать (по норме в L2)
последовательностью пробных функций ам (х, k) e 3)<i
[или Ьм(х,к) Eft], каждая из которых бесконечно диф-
дифференцируема и равна нулю вне конечной области.
«Свертка с умножением» двух таких функций
tM(x, k) =
= \aM{x-x',k- k') bM (x', k') exp [ -± (kx' - xkr)\ d\i'
(8.168)

268	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
также бесконечно дифференцируема и равна нулю вне
конечной области. Следовательно, функция
= tM (х, /г)ехр [-^-(х2 + &]
[±	] (8.169)
бесконечно дифференцируема и спадает на бесконечно-
бесконечности быстрее любой обратной степени (х2 + к2) (посколь-
(поскольку в действительности она равна нулю вне конечной
области!). Как отмечалось ранее, фурье-образ q>M(p,Q)
любой такой функции тоже бесконечно дифференцируем
и быстро убывает на бесконечности. Так как ц>м(р,я) —
весовая функция в диагональном представлении, мы
полностью выполнили намеченную программу. Подве-
Подведем итог.
Всякий оператор Т с конечной следовой нормой
может быть представлен последовательностью опе-
операторов с конечной следовой нормой
, q\d[x, (8.170а)
где функции (pM(p,q) бесконечно дифференцируемы
и спадают на бесконечности быстрее любой обрат-
обратной степени и где
\\Т~Тм1-+0.	(8.1706)
Конкретный пример последовательности срм приведен
ниже.
Несколько расширяя рассуждения Рокка, можно по-
получить нужный для физики результат, относящийся
к матрице плотности. Так как всякая матрица плот-
плотности положительна, ее можно представить в виде
р = В+В, где В —оператор Гильберта — Шмидта. Сле-
Следовательно, можно взять такую аппроксимирующую по-
последовательность Ам = В« [т. е. ам(х, k) = bM( — x, — k)\,
что рж = В'мВм будет положительным оператором при
всех М. При таком выборе q>*M{x, k) = q>M(— x, — к),
откуда следует, что функция q>M(p-q) действительна.
Поскольку нормировку можно обеспечить тривиальным

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	269
способом, всякую матрицу р можно рассматривать как
возможную матрицу плотности. Таким образом, можно
утверждать следующее:
Всякую матрицу р можно представить последо-
последовательностью матриц плотности
9м = j 4>м(р, Я)\Р< q){p, ?1Ф. (8.171а)
где действительные функции q>M(p,q) бесконечно
дифференцируемы и спадают на бесконечности бы-
быстрее любой обратной степени и где
Ilp-P*lli-O.	(8.1716)
Ниже мы рассмотрим примеры матриц плотности, пред-
представляющие интерес для физики, хотя большая часть
результатов применима к произвольным операторам с
конечной следовой нормой.
Отметим еще раз то свойство, о котором говорилось
в самом начале наших рассуждений. Именно, для лю-
любого ограниченного оператора В имеем
= Sp(pfl)= lim Sp(pMB) =
М->оо
= lim Sp I (f>M(p, q)\p, q)(p, q\Bd\x =
= lim [ <pM(p, q)(p, q\ B\p, ^>ф =
= { Ф(P. q)(p> q\B\ p, q)d\x =
^ Jq>(z)<z|fl|z>4i.	(8.172)
При получении третьей строки было использовано нера-
неравенство
J
<оо,
тогда как два последних выражения определяют рас-
распределение (f(p,q)—или в комплексной форме qp(z) —
с помощью хорошо определенной предельной процедуры.
Разумеется, не всякое распределение tp(z), определенное
таким образом, являе1ся «ненадежным»; многие из них

270	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
соответствуют функциям с хорошим поведением, для
которых последнее выражение можно рассматривать как
определенный в обычном смысле интеграл.
Следует отметить ту роль (на первый взгляд не су-
существенную), которую играет в нашем основном ре-
результате (8.172) свойство единственности оператора В
при заданных диагональных элементах {z\B\z). Ясно,
что если бы для некоторого В Ф0 все эти диагональные
элементы обращались в нуль, то из (8.172) вытекал бы
абсурдный результат для многих матриц плотности.
Приведем другую формулировку нашего основного
результата (8.171), выявляющую практическое удобство
аппроксимации. Ограничимся такими операторами, для
которых ЦВЦ-^.1. Это подмножество ограниченных опе-
операторов включает все унитарные операторы или опера-
операторы проектирования. Оно включает также такие пред-
представляющие физический интерес операторы, средние
значения которых дают распределения отсчетов.
Из свойства
| Sp(pfl) - Sp (РмВ) | <|| р - рЛ ||, • || В ||<|| р - рД1 II,, (8.173)
справедливого при всех ||В||-^1, видно, что средние зна-
значения всех таких операторов могут быть равномерно
аппроксимированы.
Иными словами, для любой матрицы плотности р,
описывающей систему, среднее (B)=Sp(pfi) лю-
любого ограниченного оператора (||В|| =С 1) может быть
равномерно (т. е. независимо от конкретного вида
В) с произвольной точностью представлено с по-
помощью интеграла, понимаемого в обычном смысле:
J4(p,q)(p,q\B\p,q)d\i,	(8.174)
где q> (/?,</)—бесконечно дифференцируемая дейст-
действительная быстро убывающая функция.
Конкретные представления последовательностями.
Выше уже отмечалось, что функция ф(г) может быть
представлена последовательностью весовых функций
фм(г) с хорошим поведением. Чтобы в реальных слу-
случаях выбрать подходящую последовательность, можно

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	271
обратиться к проведенному выше построению. Напри-
Например, пусть состояние задано в виде р = S* В. Не теряя
общности, можно выбрать единственный оператор В,
исходя из требования, что В = В'Х), а именно
В = p'/s.
Заметим, что из (8.140а) следует
Т (х, k) = | e-nkq-KP)ih (p> q\T\p, q) d\x =
= f ехр[-(ыг*-н*г)]<р, ?|Пр, ?>Ф. (8.175)
где
	 (х + ik)		 (q + ip)	,,
BbI k '	~ BЙI'2
Используя свойства когерентных состояний как собст-
собственных векторов и соотношение G.26), можно написать
f(x, k)= J (р, <7|ехр(— иа") Г ехр (м'а) \р, q) d\i =
= Sp [ехр(— иа:) Т ехр (и*а)} =
— Sp{T ехр {и*а) ехр(— ма+)} =
= Sp {Т ехр (и а - uaf)} ехр (~ | и |2).	(8.177)
Учитывая (8.159), получаем
= 2 Р/ (^/ I U+ [k, x] | г|з;->.	(8.178)
Этот ряд абсолютно сходится и определяет ограниченную
непрерывную функцию. Очевидно, [ t (x, k) \ ^ 211 P/1 =
= iJTIli, откуда с учетом (8.159) и (8.148) сразу следует
неравенство (8.1496). В свою очередь весовая функция
Вейля для В — pI/s имеет вид
Ъ (х, k) = S Pj2 <^;. I Uf [k, x] | %).	(8.179)
Здесь в общем случае имеет место сходимость в смысле
L2. Заданный элемент b(x,k) из L2 можно в принципе

272	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
непосредственно аппроксимировать пробными функция-
функциями из 3*>2 с тем, чтобы с помощью (8.168) определить
подходящую последовательность.
Можно, однако, аппроксимировать непосредственно
t(x,k) вместо того, чтобы использовать аппроксимации
для b(x,k). В этом случае устанавливают существова-
существование в последовательности с тремя индексами такой под-
подпоследовательности
tM(x, *) = да. i м (*, k),	(8.180)
которая обеспечивает желательные свойства q>M(p,q) и
Тм, а именно \\ТМ — 7"||i—»-0. Основная последователь-
последовательность с тремя индексами имеет вид
t'Nt L (x, k) = exp [ - WL {x, k)] t'N (x, k) =
^exp[-WL(x, k)\ SP/^y; N\Uf[k, x]\$,; N), (8.181)
где мы положили
11>/;ЛГ>=2|л><л|1|5/>-	(8-182)
п = 0
Здесь 1 п ) — обычные собственные состояния осцилля-
осциллятора и введена функция (в системе единиц, в которой
s = l)
WL(x, k) = f(x-L) + f{-x-L) + f{k-L) + f(-k-L)
(8.183)
Такая последовательность, весьма запутанная и гро-
громоздкая с точки зрения практического применения, удо-
удовлетворяет, тем не менее, требуемому критерию сходи-
сходимости по следовой норме. Усечение ряда и аппроксима-
аппроксимация состояний [см. (8.182)] введены для того, чтобы
сделать t'N(x, k) пробной функцией из ^2 (бесконечно
дифференцируемой и быстро убывающей); множитель

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	273
ехр(—WL) обеспечивает быстрое убывание (и бесконеч-
бесконечную дифференцируемость) функции
] (8.185)
Заметим, что если t(x,k) сама уже оказывается
пробной функцией из 5^2, то достаточно рассматривать
просто
tM (х, k) = exp [ - WM (x, k)\ t{x, k) (8.186)
или, иными словами,
фл (х, k) = exp [ - WM (x, k)] ф (x, k). (8.187)
В этом случае ум(р,я) является пробной функцией из
&>2 и \\ТМ — 7|li—»0, что и требовалось.
Сразу же добавим, что приведенные здесь конкрет-
конкретные последовательности не единственны; в некоторых
случаях могут оказаться полезными и другие последо-
последовательности.
Смысл и некоторые примеры. Каким бы ни было со-
состояние р системы, среднее любого ограниченного опе-
оператора определяется соотношением (8.172). Особенно
просты выражения для нормально упорядоченных опе-
операторов В = : О (а+, а) : , именно
<:С(а+, а):) = ± J q> (z) <z |: <? (а+, a):\z)d2z =
= ^г f (f,(z)O(z\ z)d2z.	(8.188)
Нормально упорядоченная производящая функция [см.
(8.23)] имеет вид
<exp(ua+)exp(-«*a)) = ^ J cp (z) exp {uz" - uz) d2z. (8.189)
Можно считать, что она связана с фурье-образом функ-
функции ф. Именно, если
	 x + ik
то
(ехр(ма+)ехр(-«*а)) = ф(-д;, - k). (8.190а)

274	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Умножая слева на ехр(—'/г!"!2), получаем общее соот-
соотношение для характеристической функции состояния р:
(ехр (иа+-и'а)> = <[/[?, х]) =
] (8.1906)
В качестве другого примера рассмотрим еще раз
производящую функцию (8 101) при 0 <11а0Т < 1. Соот-
Соотношение (8.101) означает, что производящая функция
для распределения отсчетов есть среднее от
^ = ехрAп[1 -А,СС(Л а+а)(= : ехр (- Xajaa) :). (8.191)
Поскольку 1п[1 — ).а0Т]^С0, этот оператор удовлетво-
удовлетворяет условию ||??;J| = 1. Так как Qy, — ограниченный опе-
оператор, наверняка имеем
Q(l, Т) = (&> = (: ехр(- Xaja^a) : ) =
= ~ [ (?,(z)dxp{-la0T\z\2)d'2z. (8.192)
Распределение отсчетов дается соотношением
оо
Q(A, T)= S(l-A)mP(m, T),	(8.193а)
т=0
или, в операторной форме,
оо
SA.)m^m,	(8Л936)
m=0
где
дт, 	 . (a0Tafa)
ехр(-а0Га+а): .	(8.194)
Эти операторы неотрицательны при ао7'^ 1, как это
следует из замечаний, сделанных ранее в связи с
(8.103). При к = 0 имеем QQ = 1 = %&т, так что || @т ||< 1
т — 0
при всех т. Свойство ограниченности позволяет утвер-
утверждать, что
Р{т,Т) = (&т) = (: {аоТ?а)"г ехр (- aja+a) :) =
= i J * ^ 1TL°:!- ехР (~ «оП z I2) d22. (8.195)

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	275
В действительности можно утверждать даже большее,
если обратиться к результату, полученному в связи с
(8.174). Из него следует, что для любого состояния р
определенной нормальной моды величины Р(т,Т) мож-
можно вычислять при всех пг и всех Г^сс^1 с произволь-
произвольной точностью (например, с точностью ± 10~137) с помо-
помощью соотношения (8.195), где ср(г) — бесконечно диф-
дифференцируемая быстро убывающая функция. Это
свойство дает нам значительно больше, чем мы могли бы
получить, рассматривая скорости отсчетов a™(afmam).
Мало того, что в общем случае их нельзя равномерно
аппроксимировать; для многих состояний поля эти ско-
скорости или большая их часть даже не существуют1)!
Соотношения (8.188) и (8.195) со всей ясностью по-
показывают, что диагональное представление позволяет
вычислять нормально упорядоченные квантовомеханиче-
ские выражения с помощью соотношений, формально
похожих на классические выражения, если последние
записаны в терминах аналитических сигналов. Такое
сходство по форме играет важную роль не только пото-
потому, что может служить мнемоническим правилом и об-
облегчать построение требуемых выражений, — оно дает
нам в руки сравнительно простое и мощное средство
изучения различных величин в квантовой теории коге-
когерентности. Сходство по форме отнюдь не означает, что
квантовая теория физически эквивалентна классиче-
классической, но говорит лишь о том, что ее можно привести к
формально эквивалентному виду Именно в таком смыс-
смысле следует сформулировать «оптическую теорему экви-
эквивалентности» и именно так ее следует интерпретировать
в общем случае.
Для большинства физических примеров, обычно
встречающихся в тепловых или лазерных задачах, q>(z)
фактически является положительной действительной
функцией, так что ее можно интерпретировать как нор-
нормальную плотность вероятности. В следующей главе в
связи с конкретными моделями мы обсудим примеры,
очень похожие на классические, а пока подробнее рас-
рассмотрим частный случай матрицы плотности, когда
') См. примечание на стр. 237. —Прим. перев.

276	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
вес cp(z) в самом деле является распределением рас-
рассмотренного выше типа и вида.
В качестве такого примера ') возьмем матрицу плот-
плотности ра = |0(й)@(й| —чистое состояние, отвечающее ос-
основному состоянию осциллятора с частотой со=?1. Что-
Чтобы найти для этого состояния вес y(p,q), записанный
в фазовом пространстве, заметим прежде всего (обо-
(обозначив рм=Гш), что в соответствии с G.826)
(р, q\TJp, q) = \(p, q\Qa)\2 =
|T	J	(8Л96)
Далее,
fjx, fe) = exP{-4[(l + oo)x2 + (l+cD-')?2]}; (8.197)
нормировочный множитель легко определяется из усло-
условия fa,@,0) = Sp(pw) = 1. Наконец, фурье-образ иско-
искомого веса, согласно (8 148), имеет вид
^[(ш-1)*2 + ((о-1-1)А2]}. (8.198)
Это выражение при ш< 1 (или при ш > 1) растет как
экспонента от квадрата х (или k). Таким образом, во-
вопрос о нахождении распределений ф (х, k), определенных
на пробных функциях в Фч (бесконечно дифференци-
дифференцируемых и равных нулю вне конечной области), является
отнюдь не академическим.
Чтобы придать этому примеру смысл распределения
в диагональном представлении, возможны два подхода.
В прагматическом подходе исходят просто из общих вы-
выражений (8.190) для средних значений. В частности, по-
получаем
{U [к, х]) = @J U [k, *]|0ш> =
(8.199)
') Отметим, что этот пример имеет непосредственный физиче-
физический смысл. Процесс нарастания колебаний одномодового парамет-
параметрического генератора из квантовых флуктуации приводит именно
к таким состояниям, Подробнее об этом см. в работе: В. R. М о 1-
low, R. J. Glauber, Phys. Rev., 160, 1076 A967). — Прим. перев.

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	277
По случайным причинам это выражение совпадает с
G.121) при К= 1 для осциллятора с круговой частотой
ыф\. Средние значения операторов, отличающихся от
операторов Вейля U[k, х], можно теперь извлечь в силу
линейности из той информации, которая содержится
в (8.199). Во многих отношениях при таком прагмати-
прагматическом подходе распределение ф(г) рассматривают как
функционал и задают теми значениями, которые он при-
принимает для производящего ряда ограниченных операто-
операторов, Линейные суммы таких операторов позволяют по-
построить все ограниченные операторы. В качестве про-
производящего ряда при этом используются нормально
упорядоченные производящие функции или характери-
характеристические функции.
Наоборот, в систематическом подходе стараются опи-
описать распределение непосредственно, скажем с помощью
последовательности весовых функций фм(г). Так как
функция t(x, k)=(U[—k,—х]), заданная выражением
(8.199), является, очевидно, бесконечно дифференцируе-
дифференцируемой и быстро убывающей, то для адекватного описания
достаточно рассматривать весовые функции, являю-
являющиеся фурье-образами от
фм(х, k) = exp{-WM(x, й)-^[(со-1)х2 + (со-'-1)й2]},
(8.200)
где WM (при М = L) определяется соотношением
(8.183). Разумеется, отнюдь не легко явно найти функ-
функции ц>м(р,ч), хотя мы совершенно уверены в том, что
они существуют и обладают соответствующими свойст-
свойствами.
Комбинации типа свертки. В некоторых случаях при
рассмотрении случайной переменной удобно разделить
ее на два (или даже большее число) члена: z = а + р,
каждый из которых обладает собственными флуктуаци-
ями, описываемыми соответствующими распределения--
ми. Здесь можно рассматривать
Р2 = J Фа (Р) I а + р> (а + р | rf|i (P)	(8.201 а)

278	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
как матрицу плотности, получающуюся за счет флуктуа-
флуктуации только величины |3, входящей в г. Аналогично мож-
можно рассматривать
Pi = J Ф1 (а) | а + р> <<х + р | ф («)	(8-201 б)
как матрицу плотности, получающуюся за счет флукту-
флуктуации только величины а, входящей в г. Совместные
флуктуации величин а и |3 приводят к матрице плот-
плотности
р=
= J Ф1 («) * Ф2 («) I «> (а I ф (а),	(8.202)
где
Ф (а) == ф! (а) * ф2 (а) = ф, (а - р) ф2 (р) ф (р). (8.203а)
Это выражение напоминает обычную комбинацию типа
свертки плотностей вероятности в классической теории
вероятностей.
Переходя к представлению в фазовом пространстве,
имеем
ф(р, q) зз j (fi(p — р', q — q')<p2{p', q')d\if, (8.2036)
что после преобразования Фурье дает
ф(А-, k) = ^i(x, /г)ф2(х, k).	(8.204)
В общем случае, когда ц>(г) представляет собой распре-
распределение, можно начать рассмотрение с соотношения
(8.204). Если распределения цц, ф2 и ср таковы, что
рь р2 и р суть настоящие матрицы плотности, то соотно-
соотношение (8.204) будет справедливо; при этом все три
функции ф), ф2 и ф являются непрерывными функция-
функциями рассмотренного выше типа. Однако, даже если
Ф, и ф2 описывают матрицы плотности, функция ф(х, k),
определяемая равенством (8.204^, не обязательно отве-

i 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	279
чает матрице плотности1). В качестве примера можно
ВЗЯТЬ фуНКЦИЮ ф1 = ф2 = Фи(-Г. ^) ИЗ (8.198) ССО<72ИЛИ
со > 2; при этом <р не удовлетворяет неравенству
(8.1496). С другой стороны, важно отметить, что если
Ф1 и ф2 отвечают матрицам плотности, то модифициро-
модифицированная свертка, определяемая соотношением
ф (х, k) == ф,(s,.Y, s{k)qJ(s2x, s2&), -s? + s| = 1, (8.205)
всегда приводит к диагональному весу ф(а), описываю-
описывающему матрицу плотности2).
Описание с помощью двойного интеграла. Выше мы
стремились придать точный смысл диагональному пред-
представлению
1 J>(z)|z}(z|fl!2z,	(8.206)
в котором р записывается в виде суперпозиции «внеш-
«внешних произведений одинаковых векторов», или операто-
операторов проектирования на когерентные состояния. Всегда
существует другое представление. Именно, согласно об-
общему правилу G.56), можно написать
р = ± J J | z,) <Zl I о | г2) (г2 \ d%d%. (8.207)
Это выражение есть суперпозиция «внешних произведе-
произведений различных векторов» |zi)(z2|. Следует отчетливо
') Смысл этого замечания состоит в следующем. Матрица плот-
плотности должна обладать тремя свойствами (см. гл. 5): 1) эрмито-
востью, 2) нормированностыо и 3) неотрицательностью. Из компо-
композиционного закона (8.203) или (8.204) легко видеть, что свойства
1 и 2 для результирующей матрицы автоматически следуют из тех
же свойств составляющих. В то же время неотрицательность ре-
результирующей матрицы может нарушаться и при выполнении этого
свойства для каждой из составляющих. Иначе говоря, хотя кванто-
квантовая теория и позволяет весовой функции принимать отрицательные
значения, свойство 3 налагает в этом случае некоторые ограниче-
ограничения на вид функции ср(г). Как раз эти ограничения могут не вы-
выполняться для произвольных сверток вида (8.2036). В отличие от
этого в классической теории эквивалентом свойства 3 является
простое неравенство ф(г) ^г 0; такое неравенство, очевидно, сохра-
сохраняется при композиционном законе (8.2036).—Прим. перев.
2) Показать это легче всего с помощью техники «сокращения»,
которую рассматривали Клаудер и Мак-Кепна [7.20]; однако ана-
анализ такого подхода увел бы пас слишком далеко от основной темы.

280	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
понимать, что это два совершенно различных представ-
представления одного и того же оператора; подобная ситуация
встречалась уже для случая единичного оператора [см.
G.62)]. Ясно, что весовая функция (z\\p\z2) в общем
случае обладает значительно лучшим поведением, чем
распределение cp(z). В этой связи Глаубер считает, что
в том случае, когда функция ср(г) сингулярна, представ-
представление двойным интегралом предпочтительнее диагональ-
диагонального представления. Мы считаем, однако, что лучше, как
говорится, заплатить дороже и использовать распреде-
распределения cp(z) (что было нами тщательно и точно огово-
оговорено). В итоге это оказывается выгодным из-за значи-
значительного упрощения и большой эвристической ценности
формул, получаемых в диагональном представлении.
Можно было бы возразить, что использование последо-
последовательностей для определения распределений вносит в
описание дополнительный предельный переход и что та-
такая последовательность, вообще говоря, не единственна.
Хотя такие критические замечания, безусловно, справед-
справедливы, они в равной мере относятся и к представлению
(8.207) с помощью двойного интеграла. Достаточно на-
напомнить, что лишнее интегрирование само определяется
с помощью предельного перехода и что из-за перепол-
переполненности когерентных состояний подынтегральное вы-
выражение (а тем самым и последовательность, связанная
с определением интеграла) не единственно.
Б. «Диагональное» представление для поля излучения
Основываясь на приведенных выше рассуждениях,
займемся исследованием диагонального представления
для операторов в случае бесконечного числа степеней
свободы; это представление символически может быть
записано в виде
Т= U ({zk}) | Ы) ({zk} I d» ({zft}).	(8.208)
Здесь мы использовали сокращенное обозначение k для
индексов моды Я, к и написали г* вместо Zj.(k). По-
Поскольку мы будем применять это диагональное пред-
представление главным образом к матрице плотности, вна-

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	281
чале ограничимся рассмотрением операторов Т с конеч-
конечной следовой нормой.
Как и при рассмотрении одной степени свободы, по-
постараемся охарактеризовать Т такой последовательно-
последовательностью операторов с конечной следовой нормой Тм, для
которой || 7" — 7"M||i—»0, чтобы соотношение
Sp(rB)= lim Sp{TMB)	(8.20Э)
Af->°o
выполнялось для всех ограниченных операторов В. Сле-
Следует отметить, что записанные в абстрактном виде эти
требования в точности совпадают с соответствующими
требованиями в случае одной степени свободы. Грубо
говоря, единственное отличие состоит в том, какое пред-
представление операторов рождения и уничтожения исполь-
используется. В случае одной степени свободы принималось,
что сами операторы а и а+ образуют неприводимую си-
систему, тогда как в рассматриваемом случае мы требуем,
чтобы весь набор операторов (afe} и [a?J образовывал
неприводимую систему.
Существует, конечно, промежуточный случай, когда
можно ограничиться конечным числом степеней свобо-
свободы, т. е. когда состояния \zi ..., Zk) накрывают все
гильбертово пространство. Тогда диагональные пред-
представления полностью аналогичны таковым в случае од-
одной степени свободы, за исключением очевидного уве-
увеличения числа рассматриваемых переменных. Мы не
станем обсуждать полное описание случая конечного
числа степеней свободы, поскольку читатель сам без
труда сможет должным образом модифицировать при-
приведенные выше рассуждения. Тем не менее для рассмот-
рассмотрения поля излучения нам потребуются некоторые из
этих обобщений; ниже они будут приводиться без под-
подробных доказательств.
Подобно тому как это делалось при доказательстве
основного разложения единицы G.153), определим снача-
сначала интегрирование бесконечного порядка с помощью по-
последовательности, каждый член которой включает лишь
чонечное число переменных из всего бесконечного мно-
множества. Для этого вспомним операторы проектирования

282	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Ру [см. G.148)], которые определяются следующим
образом:
<{**}! pn I {<}> - ехр I - -i 2 (;2;г р +1 ^ |2) + i zX I •
I	k = l	/г = 1	J
(8.210)
Действие оператора Рх сводится к проектированию на
основное состояние для всех степеней свободы с k > N.
Вооружившись этими операторами проектирования, оп-
определим последовательность операторов с конечной сле-
следовой нормой соотношением
jn~PnTPn	(8.211)
для всех N. Покажем прежде всего, что операторы TN
при N—> оо сходятся к Г по следовой норме.
Воспользовавшись соотношением ||B7"||i ¦< 11ЛЫ1В11,
выполняющимся для произвольного оператора Т с ко-
конечной следовой нормой и произвольного ограниченного
оператора В, получим
<Ц7-(^-/I!1+11(Рл'-/O!„	(8.212)
так как Ц/VII-*С 1. Рассмотрим второй член в (8.212);
первый член полностью аналогичен ему. Если Т = АС,
где как А, так и С — операторы Гильберта—Шмидта, то
из (8.163) имеем
|| (Р„ - I) АС ||, < II (PN - /) А ||2 • || С ||2. (8.213)
Используя запись А в общем виде
оо
Л = 2 ex; | ц,) <Ф/1,	(8.214)
j ~ 1
где |(ij) и (ф;)—векторы двух полных ортонормироваН'
ных базисов и [ср. (8.164)]
IMIIj^lllcz^oo,	(8.215)

4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ
283
получаем
| (P
I) А ||2 = 2 I <*/ I2
| (/ - Р„) | цу>. (8.216)
Сопоставляя этот результат и условие (8.215) со сходи-
сходимостью матричного элемента общего вида (/, |PN \ф) —>
->(Л}\|)) [ср. G.152)], с очевидностью получаем, что для
достаточно больших N величина (8.216) может быть сде-
сделана сколь угодно малой. Поскольку те же рассуждения
приложимы и к первому члену в (8.212), то отсюда вы-
вытекает
II TN - Т ||, = || PNTPN - Т ||, -> 0.	(8.217)
Таким образом, последовательность TN сходится к Г по
следовой норме, что и требовалось доказать.
Покажем, далее, что для оператора 7"л" фактически
существенны лишь первые N степеней свободы. Для это-
этого заметим, что соотношение
PNTNPN = PN (PNTPN) PN = PNTPN = TN (8.218)
в непрерывном представлении записывается в виде
(8-219)
4}) = 1 J
X
где каждый из интегралов определен в смысле G.152).
Не нужно явно вычислять такой интеграл, чтобы понять,
что (8.210) влечет за собой соотношение
V
** + zk
К fv(z,, ..., ziV; zf,
oo
1
z'N) =
X
'^К.л-))-	(8.220)
Здесь {z/i, л} обозначает усеченную последовательность
Bft, jv ^ 0 при k> N), подробно обсуждавшуюся в связи

284	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
с G.139). Таким образом, как и предполагалось, в 7"Л'
фактически входят лишь первые Л' степеней свободы.
В диагональном представлении оператор TN будет,
очевидно, иметь характерный вид
TN = / <р" ({гк, „}) ] {гк. N)) ({г,, Л.} | ф (fe, ,v}). (8.221)
Здесь интегрирование проводится лишь по конечному
числу BЛТ) переменных. Совершенно ясно, что это выра-
выражение удовлетворяет условию РNTN = TNP/V = 7"^, необ-
необходимому для выполнения соотношения (8.220). Из этого
свойства оператора TN следует, что диагональные мат-
матричные элементы по когерентным состояниям, комплек-
комплексные амплитуды которых образуют усеченную последо-
последовательность, удовлетворяют соотношению
Ф V (К л-}) I (К n) \ К л-}) |2 dp ({г,, „}). (8.222)
Это соотношение есть просто аналог основного уравне-
уравнения свертки (8.138) для случая N степеней свободы.
С этого соотношения должен был бы начинаться анализ
диагонального представления для N степеней свободы.
С помощью вычислений, аналогичных проведенным вы-
выше, можно показать, что непрерывные функции
<pN(xu ..., xN; k\, ..., kN), являющиеся фурье-образа-
ми функций (fN ({zh, n}) , представляют собой распределе-
распределения на пробных функциях из 3>2n- Исходя из аналогии
с рассуждениями, с помощью которых было получено
соотношение (8.169), мы утверждаем, что каждое из
требуемых распределений можно представить последо-
последовательностью пробных функций Ф^(х,, . . ., хдг; /г,, . . ., kN}
из Э'ъя (т. е. бесконечно дифференцируемых и быстро
убывающих) и что операторы
П s J Ф?(К n}) I К ,v}><K n} | Ф ({«*. м}) (8-223)
определены с помощью функций <p^({zk д,}), каждая
из которых принадлежит 9J.v. Более того, можно утвер-
утверждать, что для любого N
i|rv-7ff,^0	(8.224)

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ	285
при L —> оо. Отсюда следует, что двойная последователь-
последовательность операторов Т?, заданная соотношением (8.223),
удовлетворяет условию
lim lim \\Т-Т?{ = 0	(8.225)
в силу неравенства
N
vl
II Т TN\\ <г\т TN\ J_llr-V Tvll	(о nnm
Чтобы довести наши рассуждения до конца, заметим,
что из последовательности с двумя индексами всегда
можно выбрать подпоследовательность с одним индек-
индексом, сходящуюся к тому же пределу. Например, для
любого заданного N выберем L = L[N] как такое наи-
наименьшее целое число, для которого
IIт" - ЧII, <ит - TN lli +1 ¦ (8-227)
Ясно, что при таком выборе последовательность, опреде-
определяемая соотношением
Тм^Чшг	(8-228)
обладает требуемым свойством сходимости, поскольку
II7"	Т II — I Т — TN I! <Г 9II Т — TNII, -j- —	> Г)
Следовательно, если ввести функции
Ф*({2*.*}) = Фмлп({2*.лг}).	(8-229)
то можно сформулировать следующее фундаментальное
утверждение:
Всякий оператор Т с конечной следовой нормой
можно представить последовательностью операто-
операторов 7"л-, каждый из которых обладает диагональным
представлением
TN = J Фд, ({z*. л-}) I {2Л, лг» <{Zft. w) IФ ({zft, „}), (8.230a)
где q>N ({Zh, n})— бесконечно дифференцируемая бы-
быстро убывающая функция, причем для этой после-
последовательности
НГ-ЗД-^О.	(8.2306)

286	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Если Т = р — матрица плотности, то p-Y = PNpPN —
эрмигов неотрицательный оператор. Из нашей последо-
последовательности всегда можно опустить любые начальные
члены (число их по крайней мере конечно), для которых
pjV = 0; впредь мы будем пренебрегать ими. Как и в
случае одной степени свободы, мы можем выбрать каж-
каждый член двойной последовательности р^ эрмитовым и
неотрицательным. Более того, в последовательности с
одним индексом pw = p^[jV], определяемой, например, в
смысле условия (8.227), действительные функции
ф^ == ф^,у. можно нормировать так, чтобы Sp(pjv)=l.
Тем самым мы установили следующее:
Всякую матрицу плотности р можно представить
последовательностью матриц плотности рЛ*, каждая
из которых обладает диагональным представлением
P.v = f <Pjv ({«ft. л-» I fe, v}> ({Zfc. Л'} I dp ({2;e, N}), (8.231 a)
где флг({•?&, Л.-})—бесконечно дифференцируемая бы-
быстро убывающая действительная функция, причем
для этой последовательности
I! Р - P.v Hi -* 0.	(8.2316)
Ниже мы сосредоточим свое внимание на матрицах
плотности.
Условие сходимости (8.2316) и интегрируемости
функций фх позволяет утверждать, что для произволь-
произвольного ограниченного оператора В
= Sp(pB)= lim Sp(piVB) =
= lim [ фл, ({zk, w}) ({гк, v}' В \ {z,, л,}) d\x {{zki iV}) =
= J Ф ({zk}) ({zk} IВ I{z J) dp ({zk}),	(8.232)
где распределение (на функциях ({zh}\B \{zh}) бесконеч-
бесконечного числа переменных) в последней строке определено
с помощью предыдущей строки. Более того, теперь мы
можем определить правую часть соотношения
Р = j Ф {{гЛ}) I fe}> <{гв} I dpi ({z J)	(8.233)

§ 4. ОПТИЧЕСКАЯ ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ
287
с помощью предела выражения (8.231а) при /V—>оо,
или с тем же правом с помощью формулы (8.232) для
среднего значения произвольного ограниченного опера-
оператора. Именно в таком смысле следует понимать диаго-
диагональное представление при его использовании в прове-
проведенном выше выводе распределений отсчетов.
Существует также и аналог утверждения, высказан-
высказанного в связи с (8.174). Именно, если рассматривать толь-
только такие ограниченные операторы, для которых ||В||^С 1,
то средние значения всех таких операторов могут быть
равномерно и с произвольной точностью аппроксимиро-
аппроксимированы выражениями типа
J
<P,v
. л-}) <{гк. м)\В\К N}) dv {{zk, N}), (8.234)
где N — конечное число, a <pv — пробная функция из
Как обычно, формула для среднего значения прини-
принимает особенно простой вид для нормально упорядочен-
упорядоченных операторов В = :??((а?}, (aj)-"- В этом случае
(8.235)
В частности, нормально упорядоченный производящим
функционал (8.23) определяется соотношением
n ({"Л) = \ ехр ( X uka\ ) ехр ( - >] u\a\ j =
(uizk — u[i
Сравнивая с (8.190а), получаем
). (8.236a)
. ., — xN; —ku..., — &jV)==
}),	(8.2366)
где uk = (xk + ik/g), V 2fi.

288	ГЛ. 8. КВАНТОВАЯ ТЕОРИЯ
Нет необходимости повторять вывод распределений
отсчетов P(m,T + t,t) и т. п., который был проведен ра-
ранее. Читатель может легко убедиться в том, что опера-
операторы, средние значения которых определяют, например,
P(m,T + t,t) и Q(l,T + t,t), в (8.132) и (8.133) действи-
действительно являются ограниченными операторами. В самом
деле, оператор, среднее значение которого в произволь-
произвольном состоянии не превосходит единицы (а из физических
соображений следует, что Р и Q должны удовлетворять
этому условию), по определению является ограниченным
оператором с нормой, не превосходящей единицы. Тем
самым проведенный анализ придает сделанным ранее
выводам точный смысл.
При рассмотрении поля излучения существуют пря-
прямые аналоги тех комбинаций типа свертки и представ-
представлений с помощью двойного интеграла, которые обсужда-
обсуждались для случая одной степени свободы, однако мы не
будем приводить здесь эти довольно очевидные обобще-
обобщения.
В заключение этой главы сделаем следующее заме-
замечание. Диагональное представление позволяет дать та-
такую формулировку квантовой теории оптической коге-
когерентности, которая по существу во всех отношениях эк-
эквивалентна формулировке классической теории, если в
последней проводить описание в терминах аналитических
сигналов. Именно этот замечательный результат состав-
составляет сущность оптической теоремы эквивалентности1).
') Оптическая теорема эквивалентности была открыта Судар-
шаном [8.7].

Конкретные состояния поля
излучения
§ I. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ
Подавляющее большинство макроскопических полей,
возникающих естественным путем, являются по своим
свойствам тепловыми. Рассмотрим этот важный случай
несколько подробнее. Начнем с вывода соответствующих
состояний, а позднее обсудим некоторые свойства полу-
полученных решений.
А. Квантовая центральная предельная теорема
Классическая центральная предельная теорема. Один
из основных результатов классической теории вероятно-
вероятности заключается в том, что распределение случайной
величины
х = N 2j xn,	(9.1)
равной сумме независимых и «подобным образом» рас-
распределенных случайных величин хп, при больших N яв-
является гауссовым. Как следует из соотношения C.9),
среднее и дисперсия такого распределения определяются
выражениями
(x) = N-'''^(xn),	(9.2а)
'? [<**>-<*„>*]	(9.26)

290	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
соответственно. Так как среднее и дисперсия гауссова
распределения обязательно должны быть конечными,
то для того, чтобы распределение величины х приближа-
приближалось к нормальному, необходимо существование и
(хп) и (•*•«)• Наличие множителя N гарантирует сходи-
сходимость выражения для дисперсии при больших N в слу-
случае «подобным образом» и, в частности, одинаково рас-
распределенных величин х„. Если среднее (х) становится
исчезающе малым, то без потери общности можно счи-
считать, что среднее каждой величины хп равно нулю. Как
мы сейчас покажем, аналогичная центральная предель-
предельная теорема справедлива в квантовой теории при сход-
сходных и не очень сильных предположениях. Начнем ана-
анализ со случая одной степени свободы.
Квантовый аналог для случая одной степени свободы.
Как было показано в гл. 7, состояние одной степени сво-
свободы (не обязательно нормальной моды) переводится
из основного |0)@'| в когерентное \z){z\ внешним вы-
вынуждающим источником, характеризуемым величиной z.
Далее, если мы представим, что z состоит из большого
числа N вкладов, то можно положить
|г><гЧлГ1А22|1><ЛГ1А2;*„|.	0-3)
Интуитивно ясно, что тепловое или хаотическое поле —
это такое поле, амплитуда которого складывается из
очень большого числа малых вкладов, причем распреде-
распределение каждого из них можно считать независимым.
Пусть rn(zn)—распределение (в смысле гл. 8) эле-
элементарного вклада zn- Предполагая, что каждый из
вкладов zn может флуктуировать, мы приходим эвристи-
эвристически к матрице плотности
s J1 N
Следовательно, выражение для qp(z) дается многократ-
многократной сверткой, аналогичной обсуждавшейся в гл. 8. Ис-
Используя соотношение (8.204) и учитывая множители N~'12,

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	291
мы получаем выражение для фурье-образа стоящей в
(9.4) весовой функции
П(й (9-5)
Это выражение представляет собой простое обобщение
многократной свертки (8.205). Итак, мы убеждаемся в
том, что если rn(zn)—диагональный вес для матрицы
плотности р„ при всех п (что мы предполагаем), то <p(z)
представляет хорошую диагональную весовую функцию,
дающую правильное выражение для матрицы плотности
р при всех N. Тогда из (8.1496) вытекает, что
(9.6)
так как ||p||i = Sp(p)= 1; но это сразу следует из (9.5)
при учете соотношения
\rn(x, fe)|<exP[^(x2 + fe2)].	(9.7)
Чтобы понять суть дела, остановимся на случае оди-
одинаковых распределений rn, rn = r. Тогда мы, очевидно,
имеем
Н^)Г (9-8)
Предполагая, что для достаточно малых х и k
г(х, *)« 1-^(х2 + П	(9.9)
получаем
Последнее выражение для бесконечно больших /V при-
принимает вид
[^	]	(9.10)
для всех х и к. Для справедливости этого выражения
достаточно, чтобы функция г была дважды дифферен-
дифференцируема в начале координат и имела там исчезающе

292	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
малые первые производные. [Иначе говоря, это есть ус-
условие, налагаемое на первые два момента г; точнее,
(а) = 0, (а* а)< оо, где матрица плотности определяется
распределением r(z).] В дальнейшем будем считать, что
эти условия для г выполнены. При этом не обязательно
предполагать, что r(x, k) зависит только от х2 + k2.
Например, следующим членом в возможном разложе-
разложении f в степенной ряд может быть (х2 + 2k2J + х4. Тем
не менее результирующая функция ф зависит только от
х2 + k2. Более того [ср. (8.190а)],
(9.11)
откуда следует, что А > 0. Если А — 0, то <р (х, k) = 1 и
для матрицы плотности имеем р = |0)@|. Мы можем
поэтому исключить этот случай и принять А > 0. Тогда
получаем, что весовая функция ф (х, k) является стан-
стандартной гауссовой и поэтому таковым же является диа-
диагональный вес (p(p,q). Точнее говоря,
Ф(р, </) = Л-'р[
что при использовании комплексной величины z прини-
принимает вид
^(^)	(9.13)
где мы положили A ={\z\2) = {N). Нормальное распре-
распределение (9.13) для ф(г) аналогичным путем вывел Глау-
бер [8.1].
Общее решение. Соотношение (9.13) представляет
собой основной результат настоящего параграфа, но
пока мы только коснулись вопроса о его фундаменталь-
фундаментальной роли. По-прежнему будем считать, что распределе-
распределение г одинаково для всех вкладов zn, так что соотноше-
соотношение (9.8) остается в силе. Как и раньше, будем полагать,
что функция г дважды дифференцируема в начале коор-
координат, а ее первые производные обращаются там в нуль,

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	293
но теперь для малых х и k заменим соотношение (9.9)
выражением с квадратичным членом общего вида
г(х, Jfe)« \-±-{Bx2 + 2Cxk + Dk2).	(9.14)
Повторяя вывод, приведенный выше, получаем для про-
произвольно больших N
ц>{х, k) = ехр [- ~ (Вх2 + 2Cxk + Dk2)], (9.15)
что справедливо при всех х и k. Однако в отличие от
соотношения (9.10) теперь нельзя утверждать, что квад-
квадратичная форма в экспоненте обязательно положитель-
положительна. Иными словами, ф может возрастать в некоторых
направлениях [естественно, в согласии с (9.6)]. Действи-
Действительно, легко привести примеры диагональных распре-
распределений r(x, k) (являющихся пробными функциями в
9^2), для которых результирующее «тепловое» распре-
распределение (9.15) характеризуется отрицательным значе-
значением В. Это объясняется тем, что функция ф (х, k) в ко-
конечном счете чувствительна к поведению r(x,k) только
вблизи начала координат и возможен случай, когда
r(x,k) при возрастании х сначала, скажем, достигает
значения больше единицы, а затем быстро падает до нуля.
Нужно подчеркнуть, что, несмотря на такое странное
поведение, результирующие распределения получаются
строго тепловыми! Положим сначала С = 0, поскольку
в этом простейшем случае сохраняются нужные свой-
свойства. Соответственно для достаточно малых х и k при-
примем
Цх, *)« \-±-{Bx2 + Dtf).	(9.16)
Для некоторой матрицы плотности ро имеем теперь [ср.
(8.169) и (8.178)]
Sp {Рэ{/+ [k, х]} = г (х, k) ехр [ - -^ (х2 + k2)] «
i)] (9л7)

294	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
последнее выражение справедливо для достаточно ма-
малых х и k. Применяя к (9.17) принцип неопределенности,
получаем
|й2.	(9.18)
Поскольку каждый сомножитель положителен, имеем
В + {>0, D + \>0 и [b + \){d + \)>\- (9.19)
Если В = D, то В ^> 0; но если В Ф D, то либо В, либо
D может быть отрицательным (например, В = —1/8,
D — 2). Если положить
ft = l+2B и d=l+2D,	(9.20)
то
ft >0, d>0 и ftrf>l.	(9.21)
Далее, из (8.169) и (8.178) в общем случае следует
ф (х, k) = Sp{pt/^ [k, x}} exp [^ (x2 + k2)] , (9.22)
где ф — весовая функция, связанная с матрицей плог-
ности р. В нашем случае мы приходим с помощью (9.15)
и (9.20) к точному соотношению
Sp {р?/+ [к, х]} = ехр [ - --g- (bx2 + dk2)]. (9.23)
Вышеприведенные условия для bud, как легко пока-
показать, означают, что р есть истинная матрица плотности,
описываемая выражением
Здесь «гамильтониан»
Ж'= \{P2 + <u'2Q2-h<uf) = h&'N',	(9.25)
«угловая частота»

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	295
а «обратная температура» определяется из соотношения
[ср. E.56)]
-1].	(9.27)
Если b = d (т. е. В = D), то мы получаем определенные
тепловые распределения, описываемые соотношением
(9.10) при A={N'). Когда b ф d, получаются другие
тепловые распределения. С таким случаем мы сталкива-
сталкивались ранее [см. (8.198)], где имели b = со и d = со. Так
как при этом BD = —Dсо)~'A — соJ ^0, то значение
либо В, либо D должно быть отрицательным, если аф\.
В этом примере, очевидно, со' = со и |У = оо, т. е. р' соот-
соответствует вырожденному тепловому ансамблю при нуле-
нулевой «температуре» и является как раз оператором проек-
проектирования на основное состояние гамильтониана Ж'', что
соответствует примеру, приведенному для иллюстрации
соотношения (8.198).
Совершенно аналогичные выводы справедливы, если
множитель С в (9.15) отличен от нуля. В этом случае
соответствующий осцилляторный гамильтониан Ж' со-
содержал бы произведения Р и Q.
В результате мы видим, что при очень общих усло-
условиях (по существу достаточна двойная дифференцируе-
мость г, или, что эквивалентно, существование первых
двух моментов г) квантовомеханическая матрица плот-
плотности для бесконечного числа подобным образом рас-
распределенных вкладов строго соответствует тепловому
распределению.
Тот странный факт, что В или D могут принимать
отрицательные значения, вовсе не указывает на ошибку
в наших рассуждениях. Появление отрицательных В и Ь
означает, что мы разложили матрицу плотности для рас-
рассматриваемого хаотического источника в ряд не по наи-
наиболее «благоприятным» когерентным состояниям. На-
Например, если бы мы снова разложили состояние ра в
(8.198) по когерентным состояниям для частоты со, то по-
получили бы op(x,k) = 1. Этот результат имеет более ясный
смысл, чем другой, возрастающий экспоненциально.
Вообще, применяя произвольные линейные преобразова-
преобразования операторов Р и Q, согласующиеся с соотношением

296	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
[Q, Р] = ih, и используя соответствующие когерентные
состояния, мы можем перевести все тепловые весовые
функции вида (9.15) в основную гауссову форму (9.10)
с неотрицательной дисперсией.
Если предположить, что там, где это необходимо,
был произведен переход к «благоприятным» когерент-
когерентным состояниям, то мы можем следующим образом
подытожить наши результаты: при наличии очень боль-
большого числа независимых и подобным образом распреде-
распределенных вынуждающих членов матрица плотности для
одной степени свободы определяется с помощью весовой
функции
откуда для канонической диагональной весовой функции
получаем
^(^)	(9.28)
где A =(\z\2) = {N). При {N) = 0 этот результат можно
представить в виде qp(z) =я6(,г), где 6 — двумерная
6-функция, определяемая соотношением (8.137). Отсюда
вытекает важное следствие: результирующее канониче-
каноническое распределение является фазоинвариантным, ф(г) =
= cp(|z|), независимо от того, как оно возникло.
Довольно легко понять, что то же самое распределе-
распределение <p(z) применимо даже в тех случаях, когда индиви-
индивидуальные распределения rn(zn) не идентичны, но в до-
достаточной мере «схожи» (аналогично тому, как это тре-
требуется для вывода центральной предельной теоремы).
Мы не будем здесь приводить доказательство этого по-
положения. Закончим рассмотрение случая одной степени
свободы прямой демонстрацией того, что гауссова весо-
весовая функция <p(z) ведет к знакомому оператору плотно-
плотности для теплового состояния. Конкретнее, мы можем
написать
J exp [ — | z p A
n, m-0

(N)
п=0
§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	297
-^ J | г I2"ехр[- \г |2(l + <#>'')] I л) (n \d\ z f =
«=o
n=0
т. е. мы получаем распределение, имеющее такой же
вид геометрического ряда, что и распределение Бозе —
Эйнштейна. Положим
тогда
oo
Так как уровни энергии осциллятора Еп = яйсо, то соот-
соотношение (9.31), как это показано ниже, описывает рав^
новесное тепловое состояние.
Б. Обобщение на случай многих степеней свободы
В качестве предварительного шага для получения
тепловых или хаотических состояний поля излучения
проведем непосредственное обобщение нашего преды-
предыдущего анализа на случай многих степеней свободы. Как
и раньше, будем считать, что они могут и не быть нор-
нормальными модами поля излучения. Пусть r({zh}),
k = l, ..., К, обозначает диагональное распределение
идентично распределенных элементарных вкладов. Тогда
для фурье-образов гиф выполняется соотношение, ана-
аналогичное (9.8), а именно
(9.32)
Если на г наложены соответствующие условия, анало-
аналогичные рассмотренным ранее, то эта функция при

298	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
N —» оо имеет предел, который можно записать в общем
виде
Ф ({-^fc}. {h)) = exp I - 2j- 2j (xrBrsxs+2xrCrsks + krDrsks)\.
[	J
r, s	J
(9.33)
Здесь В, С и D — определенным образом выбранные
матрицы. Элементы этих матриц имеют вид
Brs = BST = \ (PrPs) - j 6rs,	(9.34a)
Drs = Dsr = j (QrQs) — -i б„,	(9.346)
Crs = ~ W (Pr®s + &рг)-	(9.34b)
Они действительны, так как являются средними значе-
значениями эрмитовых переменных. В очевидных матричных
обозначениях показатель экспоненты в (9.33) записы-
записывается в виде
В С
где Ст — транспонированная матрица С. Отсюда видно,
что полная квадратичная форма действительна и симмет-
симметрична и поэтому может быть диагонализована путем
ортогонального преобразования переменных х и k. Если
новые переменные, возникшие в результате этого преоб-
разования, обозначить тоже х и k, то (9.33) принимает
вид
I	к
Наконец, изменением масштаба, сохраняющим соотно-
соотношение [Qs, Р,] = ibbrs, приводим это выражение к кано-
каноническому виду
(9.35)
где 4ft > 0 для любого k, в соответствии с проведенным
выше обсуждением. Суть этих замечаний состоит в еле-

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	299
дующем: используя возможность свободного выбора уг-
угловых частот (Ой и канонических переменных, мы всегда
можем, как и раньше, выбрать такие «благоприятные»
когерентные состояния в диагональном представлении
для хаотического поля, для которых функцию <р можно
представить в каноническом виде (9.35). Для таких
«благоприятных» когерентных состояний диагональная
весовая функция записывается в виде
() (9-36)
где /lft =(\Zh\2) = (Nh). Если (Л^) = 0 для некоторого k,
то, очевидно, множитель в (9.36) можно представить в
виде nd(zk).
Прежде чем переходить к пределу X—>oo, заметим,
что из (9.36) вытекает следующий результат:
Как подчеркивалось в гл. 7, эти диагональные элементы
однозначно определяют матрицу р.
В. Хаотические и тепловые поля излучения
В гл. 8 было доказано, что любую матрицу плотности
поля излучения можно представить в виде (8.231), т. е.
как предел последовательности записанных в диагональ-
диагональном виде операторов, каждый из которых отвечает ко-
конечному числу степеней свободы. Здесь было бы есте-
естественным принять
к
(9.38)

300	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
в качестве усеченного диагонального веса для К степе-
степеней свободы и определить
р = lim pK = lim f ер* ({zk, K}) \ {zk, K}) ({zk, K) \ d\i {{zki K})
(9.39)
как матрицу плотности для хаотического поля. Однако
при такой процедуре, как было отмечено в гл. 5, нельзя
ожидать, что всякая последовательность средних чисел
заполнения {Nh) определяет истинную матрицу плотно-
плотности р. Для выбора подходящих последовательностей не-
необходимо иметь в виду, что в соответствии с (9.37)
<{z*} IР IЫ> = lim ({zk, K}\pK\ {zk, K}) =
к
Очевидно,
Щ
Если это бесконечное произведение сходится к нулю, то
все диагональные элементы р для когерентного состоя-
состояния обращаются в нуль и, следовательно, обращается в
нуль и сама матрица плотности р. Поскольку это заве-
заведомо нежелательно, многократное произведение должно
сходиться к некоторому не равному нулю числу. Это
имеет место при
S (Nk) < оо,	(9.42)
что можно вывести из замечаний, сделанных в связи с
E.95).
При выполнении условия (9.42) для последователь-
последовательностей {Nh) не только р является истинной матрицей
плотности, но, более того, в (9.39) имеет место сходи-
сходимость по следовой норме ||р — pxlli—*0. Из этого, в ча-

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	301
стности, следует, что для любого ограниченного опера-
оператора
= lim
к
= lim Г ер* ({z*. к}) ({zk, K)\B\ {zk, к})ф({zfc. K}). (9.43)
к->°° J
В частности, в соответствии с (8.236) и (9.35) нормаль-
нормально упорядоченная производящая функция CN({uh}) за-
записывается в виде
Cn (К}) = SP (р ехР [2 "X J ехР [ - S "X J j =
= exp(-|<^)|«fc|2).	(9.44)
Если ввести оператор
то оказывается, что (9.44) имеет довольно простую
структуру
<е/+е-/) = е-(^).	(9.46)
Эта формула особенно удобна, так как позволяет сразу
найти результат для оператора
/f = J S (r, t) ¦ А(-' (г, t) d*x,	(9.47)
который в силу уравнений свободного поля является опе-
оператором типа (9.45). При этом нормально упорядочен-
упорядоченный производящий функционал для поперечного потен-
потенциала принимает вид
= ехР {- S Js/ fo ') Gik (r- ь т'< О К (г
(9.48)
где /, k = 1, 2, 3 и
G/* (г, /; г', О ш, <Л<-' (г, 0 Л(/> (/, П) (9.49)

302	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
является корреляционной функцией второго порядка.
Следует еще раз отметить, что в настоящих примерах
распределение полностью определяется корреляционной
функцией второго порядка.
Из G.179а) вытекает, что эти выражения, используя
нормальные моды поля излучения, можно записать в
виде
Gjk(r, t; r', 0 =
= — У	^Ц- {exp [i (k' • х' - к • х) - i (соТ - at)] X
L3 ¦*¦ 2 (coco') '2
X<a}(k)afc(k'))}. (9.50)
Входящая сюда сумма для произвольно больших объемов
квантования переходит в интеграл V —> (L/2nK dzk :
Ik	J J
Gjk (r, f, т', t') = -—¦ [ \ d3kd:ik'	^—n-{- ¦ •}
!K	' Bnf J J	2 (ш@') '2
(9.51)
где выражение в фигурных скобках совпадает с входя-
входящим в (9.50). Если ввести функцию
S (k, v) = 2 ея (к) S, (к, v) = Bя)-3/2 | е-л-x+^S (х, 0 d4x,
х	(9.52)
то можно написать
(9.53)
Очевидно, только поперечные компоненты S(k,v) вносят
вклад в (9.53), и мы далее будем считать поле S чисто
поперечным. Эти соотношения применимы в общем слу-
случае; при этом не обязательно, чтобы состояние было
стационарным или однородным и изотропным в про-
пространстве и т. д.
Однако в тех случаях, когда состояние можно считать
стационарным, однородным и изотропным, соотношение

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	303
(9.53) существенно упрощается. При этих условиях
имеем
L3
Bл)
где
^ D (к) ак, (к'))« би, б (к - к') N (v), (9.54)
(9.55)
для любой поляризации X и значения к, удовлетворяю-
удовлетворяющего соотношению \k\ = a = 2nv. Используя эти свой-
свойства, находим, что
. (9.56)
Ограничимся в дальнейшем более узким классом
пробных функций, пригодных для описания детектора,
локализованного в точке R и чувствительного к фото-
фотонам произвольной поляризации. В частности, ограничим-
ограничимся пробными функциями вида
S(k, v) = BnrVlefc(k)e'k"R S(v).	(9.57)
В этом случае CN становится независимым от k, R и К.
Таким образом, мы можем рассматривать CN как функ-
функционал, зависящий от 3(v). Производя подстановку
d3k-+4jik2dk, k = 2nv и полагая
),	(9.58)
легко получаем
- j\S(v)fT(v)dv . (9.59)
Это интегральное выражение становится точным при
стремлении объема к бесконечности.
Полученное соотношение выражает существенное
свойство важного класса состояний. Подчеркнем, что
проведенное выше рассмотрение хаотических полей при-
приводит к гауссовым случайным процессам, однако при
этом дисперсия остается неопределенной. Даже в ста-
стационарном однородном и изотропном случае, в котором

304	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
выполняется соотношение (9.59), конкретная (действи-
(действительная, неотрицательная) функция F(v) остается про-
произвольной.
Следует отметить, что нормально упорядоченные ха-
характеристические функции для хаотических полей имеют
ту же общую структуру, которая была указана в гл. 3
для случая классических полей. Величина Ь может по-
появиться только либо в функции Gjh в общем соотноше-
соотношении (9.48), либо в функции F(v) в производном соотно-
соотношении (9.59).
Стационарные состояния. Особое значение во многих
отношениях имеют стационарные состояния поля излу-
излучения. В представлении Шредингера, в котором со вре-
временем изменяется только матрица плотности, условие
независимости от времени можно записать в виде
р (t) = e-txtihpetacm = p>	(9.60)
т. е. матрица плотности р должна коммутировать с Ж.
Представим себе снова, что поле излучения ограничено
большим, но конечным объемом квантования L3 и нало-
наложены периодические граничные условия. В этом случае
спектр Ш дискретен и имеет конечную кратность. Вве-
Введем ортонормированные собственные состояния гамиль-
гамильтониана Зв:
Ж\Еп,ат) = Еп\Еп,ат),	(9.61)
где Еп — собственные значения энергии, а параметр вы-
вырождения ат отмечает состояния с фиксированной энер-
энергией. Стационарные матрицы плотности диагональны в
энергетическом представлении; следовательно, они
имеют каноническую форму
P=!iVnm\En, ат)(Еп,ат\,	(9.62)
п, m
где величина
р„т = <?п, ат|р|?„, ат>	(9.63)
удовлетворяет условиям 0 ^ pnm ^ 1 и
SpmB=l.	(9-64)

§ !. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	305
Нужно подчеркнуть два момента. Соотношение (9.62),
вообще говоря, не означает, что р = /7(<5^), так как то-
тогда величина
рпт = <?„, ат \FC®)\ Еп, ат) = F (?„)	(9.65)
не зависела бы от переменной т. Далее, стационарные
состояния типа (9.62) включают значительно больше
случаев, чем обсуждавшиеся выше стационарные хаоти-
хаотические поля.
Энтропия и равновесное тепловое распределение. Выде-
Выделим состояния поля излучения, соответствующие равно-
равновесным тепловым распределениям. Равновесие означает,
что состояние не меняется во времени, т. е. что р — мат-
матрица плотности стационарного состояния. Тепловой ха-
характер состояния проявляется в том, что это есть состоя-
состояние с наибольшим беспорядком или с максимальной
энтропией.
Энтропия S(p) какого-либо состояния системы опре-
определяется соотношением ')
S(p)=-Sp(plnp).	(9.66)
Если матрицу плотности представить в канонической
диагональной форме
P
оо
0<Р„<1, 2Р„=1,	(9.67)
п=\
то вышеприведенное соотношение принимает вид
5(р)= - Sp{ S Р„1прв 14>„><4>„ I }= - S Р„1прв. (9.68)
Для любого чистого состояния мы можем выбрать Pi = l,
р„ = 0, п > 1, поэтому S(p) = 0. Для любого смешанного
состояния
S(p)>0.
') См., например, книгу фон Неймана [5.4].

306	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
Интуитивно ясно, что чем больше энтропия какого-то
состояния, тем меньше мы о нем знаем. Рассмотрим
матрицу размерностью 2x2, которая использовалась в
гл. 5 при обсуждении поляризации монохроматического
пучка. Если Pi = [5 и |3г = 1 — Р, то состояние с матри-
матрицей плотности
/р о
Р \0 1-
обладает энтропией
S(p)==S(p)= -pinp-(l-C)ln(l -p.).
Энтропия максимальна, когда
S' (Р) = - 1 - In р + 1 + In A - р) = 0,
т. е. при р = '/г. и, таким образом, соответствует матрице
плотности, содержащей наименьшую информацию: р=7г-
В общем случае для двух матриц плотности pi и р2
и параметра а, лежащего в пределах O^Ccc^Cl, выпол-
выполняется соотношение
S (ар, + A - а) р2) > aS (р,) + A - а) S (p2), (9.69)
т. е. энтропия смеси превышает взвешенные суммы эн-
энтропии составляющих эту смесь компонент. Рассмотрим
теперь составную систему, которую удобно описывать с
помощью двух индексов п и т. Для такой системы
Р
= 2 Уп, т I Ф«, т)
и энтропия равна
S(p)= — 2 Уп, mlnYrc, га-
я, m
В частном случае, когда две системы независимы, что
характеризуется соотношениями
Уп, т = KV-,m
Ух = у и =i
п	т

§ 1. ХЛОТИЧЕСКПЕ II ТЕПЛОВЫЕ СОСТОЯНИЯ	307
энтропия равна сумме энтропии, рассчитанных незави-
независимо для каждой системы:
S (р) = — 2 КРт ln (b,,Vm) =
п, т
= - 2^„1пА„-2цт1п(л,„.	(9-70)
п	т
Можно предложить обозначение, подчеркивающее, с
одной стороны, независимость этих систем, а с другой
стороны, то обстоятельство, что матрица плотности всей
системы равна произведению матриц плотности отдель-
отдельных компонент
S(Pi®p2) = S(Pl) + S(p2).	(9.71)
Определим равновесное тепловое состояние как со-
состояние с максимальным значением энтропии S(p) при
данном среднем значении энергии Е = (Ж) = Sp(p<5^).
Чтобы найти это состояние, обратимся к общему пред-
представлению матрицы плотности (9.62) для равновесных
состояний и рассмотрим
S (р) = - Sp (р 1п р) — р [Sp (рЖ) - Е] + ix [Sp (р) - 1] =
= — ZJ ?>nm In Km —
Здесь |3 и ц — множители Лагранжа, обеспечивающие
выполнение необходимых связей и позволяющие найти
экстремум величины S путем независимой вариации каж-
каждого множителя \inm- Должно выполняться условие
S(p)=-l
"Prem
Отсюда для prm получаем решение
1-p?J; (9.73)
оно не зависит от т [следовательно, р = F(Ж)].
Используя нормировку Sp(p)= 1, определяем Z:
Z= 2 ехр(-р?„) = 2^„ехр(-р?„), (9.74)
re, m

308	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
где Nn — степень вырождения уровня Еп. Величина Z на-
называется статистической суммой и играет важную роль.
Основываясь на сделанных ранее замечаниях, находим
(9.75)
p = Z~Vp3f.	(9.76)
Энергия системы записывается следующим образом:
Е = Sp (рЖ) = Z~' Sp {е~тШ) =
= 2 КтЕп = Z~l S ехр (- р?„) Еп, (9.77а)
п, т	п, т
что можно представить в виде
?=--lnZ(P)
Преобразуя E.75), получаем для поля излучения выра-
выражение
к, к
которое для больших, но конечных объемов квантова-
квантования L3 можно аппроксимировать выражением
Е -2 L3 Г rfaA= Д|к|	L* Г х3 Л* (979)
*	BяK J dft ee*lkl_i ~ Я2йзр4 J ex! dJf- iy-7^
Можно показать1), что последний интеграл равен л4/15,
и мы приходим к классическому решению (р = 1/кТ)
где к —постоянная Больцмана, а Г —абсолютная тем-
температура. Интегрируя (9.776) с учетом условия норми-
нормировки Z(oo)= 1, получаем для Z(p) приближенное вы-
выражение
ЩЛ	(9.8D
') См., например, книгу Ландау и Лифшица [9.1].

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	309
Из (9.80) вытекает, что Е однозначно определяет р и
поэтому полностью определяет равновесное тепловое со-
состояние.
Наше тепловое состояние является, очевидно, част-
частным случаем описываемых соотношением (9.56) хаотиче-
хаотических состояний, для которых yV(v) = (ePft@—I). Поня-
Понятие теплового состояния является настолько важным и
фундаментальным, что различные хаотические состояния
часто нестрого называют «тепловыми». Это отчасти
оправдано, так как вполне общие хаотические состояния
могут возникнуть и чаще всего возникают как отфильт-
отфильтрованные тепловые состояния, например при поглоще-
поглощении атмосферой излучения Солнца.
Г. Распределение фотоотсчетов для хаотических полей
Для простоты ограничимся обсуждением точечного
детектора, расположенного в точке R стационарного
поля излучения. Чтобы можно было сравнить наши фор-
формулы с формулами, полученными другими авторами,
будем считать, что присутствует только одна мода поля-
поляризации &х- Положим
Ai+)(t) = eK-A{+)(R, t),	(9.82a)
V(t)^tb-V(R,t).	(9.826)
Тогда, приняв в соотношении (8.124) / = —Т/2 и вос-
воспользовавшись диагональным представлением для мат-
матрицы плотности, получим
/
Q (Я,, Т) = ( : ехр ^ - *а J Л<~> (*') Л<+> (<') dt'J )
Г	тп	Л
= J ф ({zfc}) ехр \-Ы \ V (Г) V (f) dt' d» ({zk}). (9.83)
L	-Г/2	J
Здесь А<+) и V связаны между собой соотношением
G.181а), a q>({zh}) —нормальное распределение, которое
благодаря разложению по когерентным состояниям име-
имеет вид (9.38). Для таких нормальных распределений

310	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
расчет среднего, входящего в (9.83), является типичной
задачей теории шумов.
Удобнее, не пользуясь соотношением (9.83), вывести
пригодное для настоящего случая распределение непо-
непосредственно из (9.59). Так как при выводе выражения
для Q(h, T) нас интересует временной интервал только от
—7/2 до 7/2, в соотношении (9.59) можно ограничиться
функциями S(v), для которых S(t) обращается в нуль
при \t\^T/2. Это позволяет нам разложить все нужные
величины в ряд Фурье на временном интервале Т. Поло-
Положим
S(t)^T
V (t) EEE T-
T(t) = T~
I
i
'2гг
гехр(-
/exp(-
exp(-
2nivi
2niv
2nivj
,t),
it),
t),
(9.
(9.
(9.
84a)
846)
84b)
где v; = l/T. Так как и V(t) и T(t)— аналитические сиг-
сигналы, индекс суммирования / пробегает значения от / = 0
до +оо. Чтобы найти распределение 0 для переменных
Vi, можно написать, используя (9.59) и (9.84),
CN {§} = exp Г - 2 (sjs.rjl = /exp
Г L
Г	1
- lim [е? ({»/}) exp ^iftvt-srf) Пф(о,), (9.85)
где, как обычно, rfu.(o) = л <i2o. Замечая, что интеграл
- |s I2 Г)
распадается на два действительных интеграла, получаем
L
A)	(9'86)
таким образом можно определить искомые весовые
функции для переменных уг. Следует отметить, что это

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	311
распределение в общем случае отличается от (9.38). На-
Наконец, соотношение
J "г-ехР(~ ~1Г -^a\v\2)n-ld2v= 1+ЯлГ
(которое получается просто из условия нормировки и
замены переменных) позволяет определить Q{k, T) с по-
помощью усреднения:
\ [ Т II
V
= lim
П
exp - la
V
l +;
(9.87)
Условие сходимости выражения (9.87) имеет просто вид
2Г;< оо. Важные величины Г;, входящие в это выра-
жение, определяются соотношением
Т/2
Гг= J Г@ехр(^)^.	(9.88)
-Г/2
Общее и точное соотношение (9.87) имеет несколько
простых предельных форм. Когда Т значительно меньше
времени когерентности, можно заменить Г(/) на
Г@)ехр(—2nivot), где vo — центральная частота излуче-
излучения. В нашем рассмотрении с помощью гармонического
анализа [ср. (9.84в)] vo = lo/T для некоторого /03>1.
Следовательно, из (9.88) вытекает, что 1\ = 7Т@), а все
другие Г; равны нулю. Тогда получаем
это выражение представляет собой производящую функ-
функцию для бозе-эйнштейновского, или геометрического рас-
распределения фотоотсчетов [см. B.20)]. Из B.19) следует,
что
Р{пг, Г) = A +т)~'A +/«-')"'".
где m = аТГ(О).

312	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
В следующем приближении для малых Т мы можем
учесть медленные изменения модуля Г(^). В частности,
если положить
Г (t) s Го @ ехр (- 2juv00 = Г @) Yo @ ехр (- 2niv0t), (9.90)
где Г0(О~Г@) в интервале |/|-^7"/2, то наибольший
член в (9.88) имеет вид
Г/2
Г/о= J V0(t)dt.
-Г/2
Остальные члены
Г/2
-Г/2
предполагаются очень малыми при всех / ф 0. Можно
разложить логарифм в выражении (9.87) для Q(X,T)
в ряд по степеням этих малых членов. Если в разложе-
разложении оставить только члены первого порядка малости, то
получим
7
(9.91)
где штрих у знака суммы означает, что член / =0 из
суммы опущен. Однако для определения соответствую-
соответствующих параметров не нужно в явном виде проводить сум-
суммирование в экспоненте. Из соотношения
оо
Q (А., Т) = 2 A - А-Г Р (т, Г)	(9.92)
т=0
и соотношения C.39) вытекает, что в общем случае
m = - -^ Q (К, Т) \к_0 = аГГ @).	(9.93)
С помощью (9.91) получаем
m = m, + tn2 = o.l i @);	(9.94)

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	313
далее, принимая во внимание (9.90), имеем
Г/2	Г/2
т, = a J Го (*) dt = аГ @) J Yo @ dt, (9.95a)
-Г/2	-Г/2
Г/2
/п2 = а7Т@)-т, = аГ@) j [\ - у0 {t)} dt. (9.956)
-Г/2
В правой части соотношения ( 9.91) стоит произведе-
произведение производящих функций для распределения Бозе —
Эйнштейна и для распределения Пуассона. Отсюда ре-
результирующее распределение фотоотсчетов в соответ-
соответствии с B.35) дается сверткой
т
P{m,T)='2iPl(m-n,T)P2(n,T),	(9.96)
где распределения Pi и Яг имеют вид
Рх(т, Т) = A +т,)A +Щ1)т,	(9.97а)
р (т Т\ =	е	('Q Q76">
г2 Vni 1 )— ™i •	yv.viv)
Дисперсия результирующего распределения определяет-
определяется выражением
a2 = (AmJ = m + m\ = т + (\ +г)/п2, (9.98)
где г = mzlmi.
Для иллюстрации предыдущих соотношений возьмем
в качестве примера yo(t) = ехр(—y\t\). В этом случае
имеем
т, = аГ @) Т A уГ)~' [1 - е~™*] « аГ @) Г [l - | у^]
(9.99 а)
и
т2 = аГ@)Г-/п, «|-аГ@)уГ2;	(9.996)
последние выражения в (9.99а) и (9.996) получены в
предположении, что \Т<^. 1. В (9.98) множитель гТ/

314	I Л. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
Обратимся теперь к рассмотрению соотношения
(9.87) для другого предельного случая, в котором время
Т больше времени когерентности. Тогда можно считать
Гг медленно меняющейся функцией /. Если это так, то
можно перейти к непрерывному приближению и заме-
заменить сумму 2 интегралом Т \ dv аналогично тому, как
это было сделано прн выводе соотношения (9.79) для
больших объемов квантования. В этом случае
Q(K, Г)-ехр Г- У 1пA +ЯаГ(I =
= ехр | —Т dvln[l + WT (v)H , (9.100)
\ о	J
где можно выбрать [ср. (9.88)]
ОС
f(v)= J Г (t) e2nivt dt	(9.101)
в качестве спектра мощности для стационарного гаус-
гауссова процесса.
В общем случае полное распределение фотоотсчетов
Р(m, T) сложным образом зависит от формы спектра
мощности. Из определения (9.92) вытекают два метода
нахождения распределения фотоотсчетов. В первом ме-
методе
pim Т\ = -!——-— —	О О Т) \	W 1П91
I	\l I i . 1 ) 		,	-.л 11] \i/ \'«Ч ¦* / 1	1 *	l^llUill
\	'	/	JJJT	/)/"^	у Л == J	^	'
Во втором методе 1—7. заменяется на eis. Тогда для
Р(ш, Т) получаем интеграл
Л	/	оо
Р {пг, Т) = Bл) [ ехр - ism - Т j dv In [1 +
-IX	I	(Г
+ A -eis)aT(y)] Ids. (9.103)
Можно упростить последнее выражение при следую-
следующих разумных предположениях. Выведенные выражения

§ I. ХАОТИЧЕСКИЕ II ТЕПЛОВЫЕ СОСТОЯНИЯ	315
справедливы при больших Т и относительно широком
спектре Г(\'). И то и другое способствует тому, чтобы
величина m была значительно больше единицы. Тогда
разумно предположить, что Р(пг,Т) является медленно
меняющейся функцией т. Мы можем аппроксимировать
ее (с помощью интерполяции) гладкой функцией р(х, Т),
проходящей через точки p(xm,T) ^ mP(m,T), где
xm = m/m. При этом для функции р(х,Т) во всех слу-
случаях выполняется условие нормировки
оо	оо
j p(x,T)dx=^ p{xm, T)j- = l. (9.104)
0	m=0
Чтобы идти дальше, заметим, что
fh
P (m, T) = Bл) m exp J — ismxm —
-я	{
-Т I dvln[l+(l-eis)af(v)]\ds =
о"	J
= BяГ' J exp -iyxm-	(9.105)
-Ящ
-Т [ dvln[l +A -е1«1т)аУ(\)] \dy.
о	J
Аппроксимацию гладкой функцией получаем, заменяя
пределы интегрирования по y( = sm) на ±оо и оставляя
под знаком логарифма только первые члены разложения
по степеням у. Иначе говоря, мы полагаем
оо	.
р {х, Т) = Bя)"' J exp - iyx -	(9.106)
-оо	{
оо
-Т j dv\n [I -/т-'г/af (v)] dy.
о
Так как соотношение (9.106) можно рассматривать как
предел соотношения (9.105) при т—>оо, т-*оо,
f (v) —>оо, xm->x и фиксированном /«"^(v), то, очевид-

316	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
но, что р(х,Т) обращается в нуль при х < 0 и что
р(х, Г)>0 для х>0. Предыдущее условие представ-
представляется также правдоподобным в силу хорошего поведе-
поведения подынтегрального выражения (аналитического в
верхней половине плоскости у). Очевидно, результирую-
результирующее распределение удовлетворяет условию нормировки
(9.104). При m У>> 1 для всех практических целей можно
взять в качестве распределения фотоотсчетов
Р(ш, Т)^(тГ1р(^, Т),	(9.107)
где р(х,Т) определяется соотношением (9.106).
Приведем два примера для иллюстрации предыду-
предыдущих соотношений, выведенных для значений Т, превы-
превышающих время когерентности. Предположим сначала,
что спектр f(v) имеет прямоугольную форму, т. е. равен
постоянной величине b в некотором интервале положи-
положительных частот у. С помощью (9.94) можно связать аЬ
со средним числом отсчетов:
m = аГ J Г (v) dv = aTby.
Введем также среднюю скорость счета w = fn/T. Следо-
Следовательно, параметр
выражается через измеримые величины. Вооруженные
этими определениями, мы можем написать
Q{K, Г) = е-^1п[1+ад=е-(т/„Iп[1+ад = A +J4i)-*/n<
(9.108)
Так как
m (m — 1) = -ajjT Q(^> 71) l^=o = /и (ц + m),
дисперсия отсчетов равна
(9.109)
Сравнивая с C.40), получаем, что время когерентности
[ср. C.38)]
оо
jY(T)|2rfT.	(9.110)

§ 1. ХАОТИЧЕСКИЕ И ТЕПЛОВЫЕ СОСТОЯНИЯ	317
в настоящем случае равно у- Непосредственным разло-
разложением по теореме биномов находим
Г (m/ц)
Если ц = т, то Р(т,Т) есть распределение Бозе — Эйн-
Эйнштейна
Соотношение (9.106) можно использовать для нахожде-
нахождения подходящей гладкой функции, определяющей рас-
распределение при М^> 1. В настоящем случае имеем
р(х, Т) = Bя)-' | ехр{ - н/х - у In [l - и/ f ]}dy =
-Bя)-'J [l-ij-b] e-4'dy-
Следовательно, из (9.107)
)]-1^-^. (9.1126)
В качестве второго примера, физически, по-видимому,
более интересного, возьмем спектр, имеющий лоренцев-
скую форму
f(v)-(m.^ + Y>,	(9Л13)
где coo 5?> Y- Постоянная ab' связана со средним числом
отсчетов соотношением
пг
= шГ = аТ j f (v) dv = у -^—,

318	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
в котором мы нижний предел интегрирования заменили
на —оо. Отсюда ab' = 2wy, так что можно положить
(9.114)
С помощью интеграла общего вида
f
J
соотношение (9.114) можно представить следующим об-
образом:
Q (I, Т) = ехр {- Т [(у2 + 2kwY)'' - Y]}. (9.115а)
Это соотношение впервые было получено Гренандером,
Поллаком и Слепяном [9.2], а затем заново выведено
Глаубером [8.2] в связи с задачами квантовой оптики.
Введем опять величину [i = w/y; тогда
} (9.1156)
Для линии с лоренцевской формой |y(t)| =
= ехр(—vlTl)> поэтому в данном примере время коге-
когерентности
= 2 J e-^dx^y-1. (9.116)
Таким образом, дисперсия отсчетов опять определяется
соотношением (9.109). Распределение отсчетов, вытекаю-
вытекающее из (9.115), является довольно сложным, и мы только
приведем результат, полученный Глаубером [8.1]:
^. (9.П7)
Здесь мы ввели обозначение
Q = (y2 + 2wyL\
а Кт-у>2 — модифицированная функция Ганкеля полуце-
полуцелого порядка.

§ 1. ХАОТИЧЕСКИЕ II ТЕПЛОВЫЕ СОСТОЯНИЯ	319
По сравнению с выражением (9.117) более простои
и наглядной является асимптотическая форма для глад-
гладкой функции р(х, Т), характеризующей это распределе-
распределение при больших in. Из (9.106) вытекает соотношение
р(х,Т) =
= Bл) ехр | - /г/.v -Т j dv In [1 - itfr^yaT (v)] \ dy =
= BяГ! ' ехр { - iyx - -f [A - Щ ^f - l] } dy, (9.118)
что является табличным преобразованием Фурье. Отсю-
Отсюда получаем выражение
[ЦШ (9Л19а)
которое было выведено Гренандером, Поллаком и Сле-
пяном [9.2]. Следовательно, с помощью (9.107) находим
Pirn, Т) =	п-ехр	{} m	т=- , (9.1196)
Bя)лт3)/2	L 2ц \	]' m I J
что было получено Глаубером [9.3] как асимптотическая
форма выражения (9.117).
Эксперименты по счету фотонов для излучения теп-
тепловых источников были выполнены Фридом и Хаусом
[9.4]; результаты приведены на фиг. 4. Данные Фрида и
Хауса сопоставлялись с некоторыми теоретическими фор-
формулами. Наилучшее совпадение имело место с рассчи-
рассчитанной Баракатом и Глаубером [9.5] для лоренцевского
спектра формулой, вытекающей из точного соотношения
(9.87). Время счета в этих экспериментах слишком мало,
чтобы можно было применить соотношение (9.117) или
(9.1196).
Выведенные нами выражения для распределения от-
отсчетов и их производящих функций справедливы не толь-
только для рассмотренного нами случая точечного детектора.
Например, Глаубер показал, что аналогичные выраже-
выражения справедливы для плоскополяризованной волны, па-
падающей на тонкий плоский детектор. Если детектор
имеет более сложную структуру или если в течение вре-
времени Т поле нельзя считать стационарным, то выраже-
выражения имеют значительно более сложную форму. В любом

320	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
3
о юоо 2000 зооо то то бооо
Фиг. 4. Распределение вероятности для числа зарегистрированных
фотоэлектронов (распределение фотоотсчетов). Экспериментальные
результаты взяты из работы Фрида и Хауса [9.4а]; теоретические —
из неопубликованных расчетов Бараката и Глаубера.
Точками показаны экспериментальные результаты, полученные для излучения
источника теплового типа, в качестве которого использовался недовозбужден-
ный лазер. Длительность выборки Г = 10 3 сек, число выборок равно 13 093.
Сплошной линией показана теоретическая кривая, построенная на основе
точного соотношения (9.87) в предположении лоренцевской формы линии.
случае производящая функция Q дается многократ-
многократным гауссовым интегралом, который сводится к обрат-
обратному детерминанту бесконечного ранга. Только в част-
частном случае, которому соответствует соотношение (9.87),
можно было непосредственно диагонализировать этот
детерминант и представить его в виде произведения
его собственных значений. В задачах такого рода подоб-
подобная простота является скорее исключением, чем прави-
правилом.
§ 2. ФЕНОМЕНОЛОГИЧЕСКИЕ МОДЕЛИ ЛАЗЕРА
Основываясь на разумных физических идеализациях,
можно дать феноменологическое описание лазера. Такое
описание может основываться на полуклассических пред-
представлениях, что позволяет определить весовые функции

$ '-'. ФЕНОМЕНОЛОГИЧЕСКИЙ .МОДЕЛИ ЛАЗЕРА	321
в диагональном представлении для матрицы плотности.
Основная идея сходна с топ, на которой базировались
наши выводы для общих хаотических полей. Как и
раньше, источник г, возбуждающий поле излучения, раз-
разлагается на несколько компонент zn\ при этом должны
быть проведены соответствующие усреднения по их инди-
индивидуальным распределениям. Хотя для некоторых из
этих моделей можно ввести очень простые эквивалент-
эквивалентные гамильтонианы, мы не будем здесь этого делать.
Значение этих моделей заключается в их интуитивной
связи с классической теорией случайных процессов, и
именно такой подход мы будем использовать. Ниже бу-
будет проведено краткое обсуждение более реалистиче-
реалистических моделей, когда оправдано полное квантовое рас-
рассмотрение.
Начнем с замечания, что в том случае, когда стаби-
стабилизированный внешний источник го возбуждает одну нор-
нормальную моду, система находится в состоянии ]2о)Bо|.
Это соответствует диагональному весу
Ф (z) = яб (z - z0) = яб [X - х0) б (у - г/о).
где z = х + iy. Заметим далее, что в шредингеровском
представлении матрица плотности имеет вид
р (t) = | ехр (- гсо00 zo) (ехр (- ia>at) zo \
и не соответствует стационарному состоянию, так как,
например, величина (а(/))=ехр(—uuo/)zo зависит от '.
А. Идеальная модель
На оптических частотах мы едва ли можем распола-
располагать какими-либо сведениями о начальной фазе осцил-
осциллятора, поэтому приведенную выше матрицу плотности
нужно усреднить по фазе Go величины го = ехр((8о) \zo\.
Сравнение с разложением G.1) показывает, что резуль-
результирующая матрица плотности имеет вит,
р = ехр (- | zQ Р) ^ ifi zo I2" I n/ <« i	(9-120)

322	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
н, очевидно, является стационарной. Это состояние удоб-
удобно также характеризовать с помощью диагонального
веса
л
Ф (г) = Bл)-1 f лб (г - exp (/90)| z0 \) dQ0.
Вспомним, что если х + iy = reiS, то для углов 6 в ин-
интервале —л < 6 -^ л можно положить
б (х ~ х0) б (у - %) = г-!б (г - г0) б (8 - 90).
Множитель г'1 нужен только для того, чтобы исклю-
исключить г в выражении для элемента площади dxdy = rdrdQ.
Следовательно, можно написать
, (9.121)
Мы можем рассматривать это выражение как идеальное
распределение для лазера. Очевидно, амплитудные
флуктуации в этой модели отсутствуют, поэтому стати-
статистика отсчетов является пуассоновской. Далее, все кор-
корреляционные функции четного порядка совпадают с кор-
корреляционными функциями для чистых когерентных со-
состояний, как, например, в случае
Б. Модель колебания с диффундирующей фазой
Перейдем теперь к следующему примеру, а именно
рассмотрим корреляционные функции для одной моды
G = (a4h) ... a4tn)a(tn+1) ... a{Un)). (9.122)
Если интересующее нас состояние является когерентным
|20), а рассматриваемая мода представляет собой нор-
нормальную моду с частотой шо, то
/ п	2ге	\
G = exp i 2 oV, - i 2 о»о*< I zo \2n •	(9-123)
V 1	i I

§ 2. ФЕНОМЕНОЛОГИЧЕСКИЕ МОДЕЛИ ЛАЗЕРА	323
В предлагаемой модели мы будем считать, что вели-
величина |2о| стабилизирована, но существуют фазовые
флуктуации. Предположим прежде всего, что вместо
а(/) = ехр(—/соо/)а мы имеем
f) dtr ао,
a (t) = ехр - i j со (f) dtr \ а0,	(9.124)
где со (О—некоторая заданная функция, принимающая
значения, близкие к too- Изменения частоты могут воз-
возникнуть, например, из-за флуктуации параметров резо-
резонатора.
С квантовомеханической точки зрения это означает,
что феноменологический гамильтониан для такой систе-
системы имеет вид Ж = /но(/')а+ а, т. е. явно зависит от вре-
времени. Такая модель, конечно, слишком искусственна, но
мы можем интерпретировать ее следующим образом.
Так как полный гамильтониан излучения содержит су-
суперпозицию по множеству осцилляторов, флуктуации в
стенках резонатора — медленные по сравнению с оптиче-
оптическими частотами — могут адиабатически переводить ре-
резонанс с одного осциллятора на другой. Поскольку з
данной модели мы пренебрегаем амплитудными флун-
туациями, вместо нескольких осцилляторных перемен-
переменных можно использовать одну.
Если мы примем во внимание возможный случайный
характер функций a(t'), то соответствующая корреля-
корреляционная функция G определяется как среднее по ан-
ансамблю этих функций. Обозначая это среднее угловыми
скобками, получаем, что нам необходимо рассмотреть
величину
1 0	гс+10
G = ( ехр
= (ехр [/ J s (?) со (*') df'] ) | z0 \2n.	(9.125)
Здесь функция
V Г л	2л	П
-оо L 1	п + 1	.1

324	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
равна нулю, если t' меньше или больше, чем t\, . . ., tin,
в противном случае она принимает целые значения. На-
Например, если п = 1 и /j > t2, то
s(t') = Q (t'<t2),
s(t')=l (*,<*'<*,),	(9.127)
s (O = 0 (U < tr).
В данном случае непосредственный физический интерес
представляет характеристический функционал случай-
случайного процесса, а не рассматриваемое обычно распреде-
распределение вероятности.
Среднее, входящее в (9.125), аналогично средним,
возникающим в ряде различных по своей природе фи-
физических задач. Искомое решение легко получить для
очень большого класса стационарных случайных процес-
процессов, включающих в качестве частных случаев процессы,
обычно встречающиеся в физике. Каждое рассматривае-
рассматриваемое здесь распределение характеризуется двумя дейст-
действительными функциями f(t) и G(t)\ последняя играет
роль причинной функции Грина в том смысле, что
G(t) = O (t<0).
Характеристический функционал любого процесса дает-
дается в случае произвольной гладкой функции s(t) выра-
выражением
(ехр[г
s(f) со (f')d
= ехр { ко0 J s (/') dt' - [ f [ J s (Г) G (t" - tr) dt"] dt'}.
(9.128)
Мы можем рассматривать в данном случае f(y) как до-
довольно произвольную функцию1), для которой /(*/) =
=,/(-(/)> 0 и ДО) = Г@)=0.
') Точнее говоря, функция—}(у) должна быть показателем
экспоненты так называемого бесконечно делммого процесса. Доста-
Достаточно широкий класс таких функций дается выражением, указываю-
указывающим на их общий характер:
f (у) = ktf + | [1 - cos (Я,//)] а (Я) d%,
где ft^O и величина ?.2а(л)/A + К2) неотрицательна и интегрируе-
интегрируема. Функция, входящая в соотношение C,30), является функцией

§ 2. ФЕНОМЕНОЛОГИЧЕСКИЕ МОДЕЛИ ЛАЗЕРА	325
Для ознакомления приведем без доказательства не-
несколько основных свойств указанных выше распреде-
распределений. Из (9.128) в общем случае следует
<©(*)> = ©о,	(9.129а)
оо
С @ = (Д© (/) Д© @)) = \" @) J G (/') 6 {t + t') dt\ (9.1296)
о
где Д©(/)=©(?)— (со@)- Эти результаты можно полу-
получить, подставляя в (9.128) s{t')= ЬЬ{?— t)+cb{f), за-
затем разлагая (9.128) по степеням Ъ и с и анализируя
члены первого порядка по b и с. При f(y)~ ky2 процесс
является гауссовым и (9.129) определяет весь ансамбль
[ср. C.13)]. Если для произвольной функции f принять,
что
G(t) = Ae-Bt (t>0),
G(i)sO	(t<0),	(9.130)
то
е-«'Г@)-^-	(9.131)
и процесс является марковским; для любой другой функ-
функции G(l) процесс будет немарковским. Особый интерес
в случае марковского процесса представляет условное
распределение
Р (оо, * | со,) = Bл) \ exp \iy (со - ю^-*') -
-е-**)- $f (Aye-*1') dt'] dy, (9.132)
которое можно вывести из (9.128). Стационарный мар-
марковский гауссов процесс обычно известен физикам под
названием процесса Орнштейна — Уленбека.
именно такого типа. В этом случае а(Х) есть плотность вероятно-
вероятности нормального распределения. Более глубоко с затронутым вопро-
вопросом можно ознакомиться по работам Лукача [3.1] И Гельфанда и
Виленкина [3.6].

326
ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
Малое время корреляции. С помощью соотношения
(9.128) точное выражение для нормально упорядоченной
корреляционной функции целого ряда процессов сводит-
сводится к квадратурам. Существенное упрощение можно
провести, когда время корреляции процесса a(t) очень
мало. В случае марковского процесса это имеет место
при большом R, а вообще в том случае, когда область,
в которой локализована функция G(t), достаточно мала.
Предположим, что
(9.133)
тогда можно подставить в (9.128) G(t)^xb{t). При
этом получаем
(ехр[/ j s(t')a(t')dt']) =
= ехр{»ш„ \ s{t')dtr- j f[xs(t')]dt'Y (9.134)
В частном случае, когда п = 1, функция s(t') опреде-
определяется соотношениями (9.127). Полагая ti — t>0 и
t2 = 0, имеем
г t
(ехр г J со {t') dt'
= exp [uoo/ - tf (т)].
Результат для / < 0 можно получить, учитывая стацио-
стационарность процесса,
/ехр / J со (Г) dt'\\ = /exp It J со (f) dt'\\ =
-!¦
= (ехр| -i I e>(t')dt'
) = /exp t j (o(t')dt' \*.
Отсюда видно, что для произвольного
' ехр г J со {V) dt'
ia>ot-\tU{i)\. (9.135)

§ 2. ФЕНОМЕНОЛОГИЧЕСКИЕ .МОДЕЛИ ЛАЗЕРА	327
При этих условиях мы неизбежно приходим к лорен-
цевской форме спектра для корреляционной функции
(а+ (/)а@)) с шириной линии /(т).
В том случае, когда т можно рассматривать как «ма-
«малый» аргумент функции /, ширине /(т) лоренцевской
линии можно дать более ясное физическое толкование.
Из (9.1296) вытекает, что
J С @ dt = \" @) j J б (У) G(t + t') dt dt' =
= f"@)T2.	(9.136)
Мы говорим, что аргумент т мал, если в разложении
/(т) можно положить
f (тW @) + тГ @) + ~ хЦ" @) = -j J С W dt' &Л 37^
где мы сохранили только первый неисчезающий член.
Для гауссовой диффузии соотношение (9.137) является
точным. В этом случае из (9.135) следует
<а+ (/) а @)) = ехр (ко0* - g \t \) | z012, (9.138)
где ширина линии
оо
S = yJ C(t)dt= J <Aw@Дсо@))d*. (9.139)
о
Таким образом, ?, есть интеграл по времени от автокор-
автокорреляционной функции частотных флуктуации.
Конкретные примеры, приведенные выше, должны
иллюстрировать корреляции различного типа, содержа-
содержащиеся в (9.128). Однако нужно подчеркнуть, что в этом
анализе предполагается наличие только фазовых флук-
флуктуации, т. е. принимается, что какие-либо корреляции в
статистике фотоотсчетов отсутствуют.
В. Модель, оперирующая с суперпозицией сигнала и шума
Простая физическая модель, в которой имеются ам-
амплитудные флуктуации (и, следовательно, корреляция
отсчетов!), состоит в следующем. Предположим, что в

328	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
любой фиксированный момент времени амплитуда на-
нашей нормальной моды может быть записана в виде
2 @ = ехр (- ио0* + *0о) z0 + Zn @- (9. НО)
Здесь zq и too рассматриваются как постоянные вели-
величины, фазы Оо распределены равномерно, a zn— незави-
независимый шумовой источник с гауссовым распределением.
Диагональный вес ф, соответствующий такой сумме, оп-
определяется как свертка распределений входящих в нее
слагаемых. В частности, в соответствии с (8.203а) мож-
можно написать
<рB)=
X ехр (- |г~е(У |) | z' \d | z' |dQ' =
Разложим экспоненту в подынтегральном выражении
1 z - е*' | z01 Р = | z |2 + | z012 - | zQ | BV9' + ze-'8') -
= |2|2 + |z0|2-2|20IMcos(e'-e).
Вспоминая определение модифицированной функции
Бесселя первого рода
я
10{х) = {2л)~1 J e*cosed9,
—я
нетрудно видеть, что1)
)[(^^]. (9.141)
Распределение отсчетов. Для времен Т, малых по
сравнению с временем когерентности, производящая
') Этот результат был впервые получен Райсом [3.3].

§ 2. ФЕНОМЕНОЛОГИЧЕСКИЕ МОДЕЛИ ЛАЗЕРА	329
функция Q(X, T) для распределения отсчетов дается вы-
выражением [ср. (8.101)]
Q{K,T) = (: ехр (- ХаТа+а) : ) =
= J ф (z) ехр (- КаТ \ z |2) d\i (z) =
со
2 | г 1 | г0 |
	77
X
X exp[-),aT\z\2- ' г |2(^° P ] d \ z \\ (9.142)
С помощью известного интеграла
о
/0B
о
выражение (9.142) можно записать в виде
Очевидно, при (TV)-—»-0 распределение отсчетов становит-
становится пуассоновским, а при |2012—>¦ 0 — геометрическим
(Бозе — Эйнштейна).
Чтобы получить общее распределение отсчетов, поло-
положим сначала
г
+аТ (N) ' 6 1+аТ (N)
и перепишем знаменатель в (9.143) в виде
1 + каТ (N)=l+ aT (N) -{1-Х)аТ (N) =
= A + <хГ <iV» [1 - A - А) г].
Таким образом, получаем
_A1_Я)гехр[- 1_AЯ1Я)
{N} 1
Теперь, воспользовавшись тождеством
;vS=-rs(l -*,)(/•-'-l) + s[l -A -К) г],

330	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
о! Ю3
/
://
= //
: f /
¦-//
У
1 .
л
11
i
i
п
1
\\
\
1 1
\
\ ^
\
\
\
\
\
\
\
\
1 1
Эксперимент -
распределение
Пуассона
Теория
-
лг =
\ *
\
1
_
\
1 1
/о
20
J0
50
- 1000
- 100
-= 10
- 1
60
п
Фиг. 5. Распределение вероятности фотоотсчетов для гелий-неоно-
гелий-неонового лазера, работающего в режиме, близком к пороговому, при
длительности выборки 10~5 сек. (По данным Фрида и Хауса [9.46].)
Экспериментальные результаты показаны точками и вертикальными прямыми,
определяющими доверительный интервал; число выборок равно 15894, Av»260 гц.
Теоретические результаты, полученные иа основе модели сигнала, иа который
налагается шум [см. (9.144)], показаны сплошной линией. Для сравнения штри-
штриховой линией изображено пуассоновское распределение.
находим
e	1
i+aT(N) 1 — (I — A)r exp
f s(r-'-l)(l
L 1 —A —
Производящая функция для полиномов Лагерра [опре-
[определяемых соотношением B.25)] записывается следую-
следующим образом:
-2 <%»(*).

2. ФЕНОМЕНОЛОГИЧЕСКИЕ МОДЕЛИ ЛАЗЕРЛ
331
г -
п = 31825
	 Эксперимент
—	Теория
31
31,5
32
п ¦ Ю~'
32,5
Фиг. 6. Распределение вероятности фотоотсчетов для гелий-неоно-
гелий-неонового лазера, работающего в режиме, близком к пороговому, при
длительности выборки 10~ сек. (По данным Мейджила и Сони [9.10].)
Экспериментальные результаты представлены гистограммой, проведенной
сплошной линией, а теоретические результаты, полученные на основе модели
сигнала, на который налагаются шумы [см. (9.14!)), показаны пунктирными
линиями.
Искомое распределение отсчетов при учете (9.92) имеет
вид
v ' 1 +аТ (N)	m\ \	и
(И-аГ(ЛОI
STT ехр -
Х
|Zol
(9.144)
что впервые было показано Глаубером [9.3]. Это распре-
распределение можно представить как функцию его среднего
значения и дисперсии, воспользовавшись соотношениями
m
аТ {(N) + | z01
а2 =
a2T2
2),
z012 + (N)\.
(9.145а)
(9.1456)

332	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
Фрид и Хаус [9.4], а также Мейджил и Сони [9.10]
провели эксперименты по фотостатистике с использо-
использованием гелий-неонового лазера, работающего в режиме,
близком к порогу генерации; полученные результаты
сравнивались с приведенными выше выражениями
(фиг. 5 и 6). Обе группы получили удовлетворительное
согласие с распределением (9.144). Кроме того, в тех
случаях, когда время наблюдения 7" удовлетворяло усло-
условию aT(N) ~>,\, но было достаточно малым по срав-
сравнению с временем когерентности [чтобы выполнялось
соотношение (9.142)], были обнаружены измеримые от-
отклонения от статистики Пуассона. В экспериментах Мейд-
Мейджил а и Сони время изменялось в пределах 10~4 сек ^С.
,<! Т ^. Ю*1 сек. При Т .< 10~4 сек наблюдаемые рас-
распределения следуют закону Пуассона, в то время как
при Т ;>, Ю сек результаты не согласуются с (9.144).
Согласно оценке авторов, в их экспериментах величина
(N)/\zo\2 составляла около 5- 10~5.
§ 3. ОПИСАНИЕ ЛАЗЕРА С ПОМОЩЬЮ МОДЕЛИ
СВЯЗАННЫХ СИСТЕМ
Ряд авторов в качестве модели лазера рассматри-
рассматривали совокупность взаимодействующих идеализирован-
идеализированных систем. Подробное изучение таких моделей прово-
проводили Лэкс [9.11], Скали и Лэмб [9.14], Хакен [9.12], Зауер-
ман [9.13] и другие авторы. Модели, для которых можно
получить решение, были рассмотрены Шваблом и Тир-
рингом [9.15]. Несколько упрощенных динамических мо-
моделей для различного рода систем обсуждаются в по-
последней главе книги Луиселла [7.2].
Мы не сможем уделить здесь достаточно внимания
всем этим работам, а остановимся лишь на одной фун-
фундаментальной модели. Эта модель не только представ-
представляет интерес сама по себе, но и позволяет обратить
внимание читателя на общее свойство подобных задач,
которое, как нам кажется, недостаточно освещено в
имеющейся литературе. Это свойство заслуживает из-
изучения не только в связи со статистической теорией
лазеров, но и в связи с другими задачами квантовой
статистики.

§ 3. ОПИСАНИЕ ЛАЗРРА	333
Прежде чем переходить к непосредственному обсуж-
обсуждению, сформулируем в общем виде суть наших заме-
замечании. Б тех случаях, когда рассматриваемая задача
является существенно марковской даже при наличии
взаимодействия с «резервуаром», можно написать для
полной матрицы плотности уравнение первого порядка
по времени. Если матрицу плотности в диагональном
представлении выразить с помощью веса <р = ф(/), то
тогда можно искать уравнение первого порядка, описы-
описывающее изменение во времени функции ф. В той степени,
в какой ф ведет себя как классическое распределение,
такое уравнение первого порядка, согласно гл. 4, соот-
соответствует стохастическому уравнению (или, как его ча-
часто называют, обобщенному уравнению Фоккера — План-
Планка). Мы видели в гл. 8, что диагональные веса ф часто
представляют собой распределения, а не «добрые ста-
старые» плотности вероятности классического тина. Это
свойство может привести к необычному виду стохасти-
стохастических уравнений, в которых отдельные коэффициенты
диффузии могут оказаться отрицательными. Может так-
также оказаться, что матрица диффузии в диффузионном
приближении [которое получается, например, если в
сумме в D.46) ограничиться членами с /г-^2] не поло-
положительна. Такое поведение характерно не только для
лазера, но имеет место в очень простых моделях; можно
полагать, что оно является довольно общим. По нашему
мнению, такие стохастические уравнения представляют
самостоятельный интерес, особенно потому, что они яв-
являются весьма удобным уравнением для с-числа.
А. Модель лазера
Модель, которую мы кратко рассмотрим ниже,
изучали несколько авторов, в особенности Лэкс [9.11].
В этой модели предполагается наличие одной существен-
существенной моды поля излучения, описываемой оператором
уничтожения Ь. Предполагается также наличие N(N^>\)
трехуровневых атомов, описываемых операторами унич-
уничтожения а,т, / = 0, 1, 2, m = 1, ..., /V. Рассматривается
только взаимодействие этих атомов с полем, но не
друг с другом. Как поле, так и атомы испытывают

334	ГЛ. 9 КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
воздействие со стороны индивидуальных «резервуаров»,
имитирующих действие других мод излучения, фононов
в стенках резонатора, накачки и т. д.
В шредингеровском представлении матрица плотно-
плотности для комбинированной системы, включающей поле и
атомы, удовлетворяет уравнению движения
р = - j- \{Жа + Жъ\ р] + ц [{Mbf - мЧ), р] +
N 2
+ S S Wii { (aimfl/m) P {a]malm) ~
т=\ I, 1=0
- -J { [hbbf + (« + 1) ЪЧ\ p + p [iibbf + (« + 1) ЬЧ] } +
+ y{(n+l)bpbf + nbfpb).	(9.146)
В этом уравнении
Жь = ЪщЬЧ, Жа=Ъ ч,а)та,т	(9.147)
m, j
— гамильтонианы соответственно для свободного излу-
излучения и для свободных атомов (е;- — энергия /-го атом-
атомного уровня). Член
ihn{Mbf-M4)	(9.148)
описывает основное взаимодействие между полем и по-
поляризацией
N
Al = 2aLa2m,	(9.149)
интенсивность которого определяется величиной ц (гру-
(грубо говоря, атомным дипольным моментом). Нужно
иметь в виду, что члены вида Mb и Mfbl, строго го-
говоря, тоже являются членами взаимодействия, но для
квазимонохроматического излучения они далеки от ре-
резонанса и ими в приближении «волн вращающейся поля-
поляризации» можно пренебречь [см. обсуждение в связи с
соотношением F.65)].

§ 3. ОПИСАНИЕ ЛАЗЕРА	335
Модель лазера будет полной, если учесть эффекты,
связанные с наличием резервуаров. Эти эффекты опи-
описываются оставшимися членами в (9.146). Первые из
этих членов соответствуют переходам с уровня i на уро-
уровень у, вызываемым взаимодействием с резервуаром и
характеризуемым вероятностью wtj. Отрицательные
члены этого типа уменьшают заселенность уровня / за
счет перехода на уровень i и, как можно показать,
обусловливают затухание атомной поляризации. Нако-
Наконец, у — коэффициент затухания поля. В представле-
представлении чисел заполнения для мод поля можно получить
следующий результат: отрицательные члены дают затуха-
затухание рпт, пропорциональное рпт, в то время как положи-
положительные члены дают увеличение рпт„ пропорциональное
рп+1,тп+1 и рп-\,т-\- Параметр п есть среднее число фо-
фотонов при равновесии с резервуаром. Дальнейшее об-
обсуждение и обоснование настоящей модели можно
найти в статьях Лэкса, особенно в статье [9.11].
Интересный подход к этим уравнениям был развит
Гордоном [9.16]. В его методе используется диагональ-
диагональное представление для полевой моды и аналогичное
представление для атомной системы. Поскольку все
атомы можно рассматривать одинаковым образом, об-
общее воздействие на атомную систему можно описать
с помощью четырех макроскопических параметров. При-
Примем
ат = N~l [(N - Л\ - /С2) atmaQm + Л\а\таХт +
+ ^2<Чп + Л1а\таХт + JCa\ma2n\ (9.150)
в качестве элементарной матрицы плотности для т-го
атома и
N
ай = Цсгт	(9.151)
в качестве канонической матрицы плотности для N ато-
атомов. Каждая элементарная матрица плотности описы-
описывается одними и теми же параметрами yf,, /Г2> J% и
Ж\ которые для краткости будем обозначать SBh,
k — 1, 2, 3, 4. Используя каноническую матрицу плотности

336	ГЛ. Я. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
(9.151) и диагональное представление для полевой моды,
Гордон приходит к рассмотрению величины
р(*)== J(pB, %k,t)o(z, %k)d\i{z, BSk), (9.152)
где
a{z,8Bk) = \z)(z\aa	(9.153a)
и
= п~Ч (Re z) d (Im z) dS°x dA°,2d (Re Jl) d (Im .#). (9.1536)
Выражение (9.152) представляет собой разумное обоб-
обобщение понятия диагональных представлений, позволяю-
позволяющее включить в рассмотрение атомные переменные дан-
данной модели.
Приведенная матрица плотности только для одной
моды поля излучения равна частичному следу по атом-
атомным матрицам плотности. В свою очередь каждая из
них определяется так, что
2
Spm am = ^ (jm I am | jm) = 1.	(9.154)
/=о
Здесь | jm) = а],п\ 0) — одночастичное состояние, озна-
означающее, что атом т находится на уровне /. Эти состоя-
состояния удовлетворяют соотношению
a]~lnaim\fm) = bn,\j"m).	(9.155)
Очевидно, приведенная матрица плотности для одной
полевой моды b принимает вид
рь @ = { ф (z, %к, t) \z)(z\ d\i (z, SBk) =
= |фB, t)\z){z\dyi(z),	(9.156)
где
ф (z, t) = \ ф {z, S6k, t) d4^k.	(9.157)

§ 3. ОПИСАНИЕ ЛАЗЕРА	337
Соотношение (9.157) определяет диагональный вес, что
представляет интерес в тех случаях, когда рассматри-
рассматривается только мода поля излучения.
Основное уравнение (9.146) для матрицы плотно-
плотности можно преобразовать в уравнение движения для
веса ф(г, 96 и, 0- Такое уравнение, очевидно, линейно
по весу ф и состоит из суммы членов, соответствующих
слагаемым в уравнении (9.146). Чтобы получить это
уравнение, необходимо поступать следующим образом:
1) сначала выполнить каждое действие в правой части
(9.146) так, как будто матрица плотности есть элемен-
элементарный оператор a(z, 96 ъ); 2) затем произвести усредне-
усреднение по ф; 3) наконец, опять представить результирую-
результирующий оператор в форме (9.152). На практике действия в
(9.146) могут быть описаны дифференциальными опера-
операторами, содержащими частные производные по перемен-
переменным z и 96ъ и действующими на элементарную матрицу
плотности с. Путем последующего интегрирования по
частям можно перейти к производным, действующим на
вес ф. Если следовать этому пути, то для ф получается
дифференциальное уравнение, являющееся обобщением
уравнения (9.146). Мы не будем выполнять соответ-
соответствующих расчетов, а только приведем результат, полу-
полученный Гордоном для представляющего физический
интерес случая, когда Ny>\cZ?k\ для любой переменной
96h- Таким образом, уровень / = 0 макроскопически за-
заполнен и действует как атомный резервуар.
Пусть йо)а = 62 — ei представляет собой энергетиче-
энергетический интервал между уровнями 1 и 2; кроме того, вве-
введем обозначения Rt = Nwi0 и
Г,= S и>ц (' = 1, 2),	(9Л58а)
Г12 = 1 У (ш,, + w,,)	(9.1586)
для различных скоростей перехода, относящихся к рас-
рассматриваемому вопросу. Тогда основное уравнение для

338	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
<p(z,cH?b,t) принимает вид
, - л°,) - (г12
?! + Wl2,f 2 - Г,Л", + Ц B*^ + ZJT)] ~
ny + [	+
дгдг* ny + [dz доМ* + дг"
дг
Хотя это уравнение имеет форму уравнения Фоккера—
Планка, довольно очевидно, что не все коэффициенты
диффузии положительны; действительно, некоторые диа-
диагональные члены вообще отсутствуют.
В принципе решение уравнения (9.159) дало бы
весьма общую формулу для рассматриваемой лазерной
модели. До сих пор, однако, решения этого уравнения
не были получены. Несколько более простые уравнения
получаются в тех частных случаях, когда та или иная
вероятность перехода значительно больше остальных.
При этом можно считать, что рассматриваемая перемен-
переменная выражается мгновенно (а не динамически) через
оставшиеся переменные и затем исключается из урав-
уравнения. Таким образом, мы опять сталкиваемся с приме-
примером адиабатического приближения, встречающегося во
многих разделах физики.
Такую процедуру можно, в частности, осуществить
в том случае, когда выполняется соотношение Fi2 >?> у/2.
Это позволяет исключить как динамическую перемен-
переменную поляризацию Ж (и, таким образом, Ж*), выразив
ее через другие переменные. Приведем без доказатель-

§ 3. ОПИСАНИЕ ЛАЗЕРА	339
ства уравнение, получающееся из (9.159) при использо-
использовании этого предположения. Определим величину
а^ и>а~аь	(9.160)
и вероятность перехода
Тогда преобразованное уравнение имеет вид
^р- [л (Л 2 Л \) YJ С1
-	-д^Г [Rl + (О>12 + Я + Я2*2) ИС2 - (Г, + 7iZ*Z) Л\] ~
-	-^r [R2 - (Г2 + я + Я2*г) Л'з + (w2l + nzz) Jfx\ +
+ W [Vй + rf2] +
dz"
№1}ф.	(9Л62)
Как мы видим, это уравнение содержит частные про-
производные до третьего порядка включительно. Увеличе-
Увеличение порядка уравнения — это цена, которую мы должны
уплатить за исключение переменной Ж.
Особенно удобно ввести величину
ze=/V'9	(9.163)

340	ГЛ 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
в качестве возможного представления для амплитуды
моды г. Здесь l = \z\2 — интенсивность, а 0 — фаза
волны. Уравнение (9.162) непосредственно преобра-
преобразуется в уравнение движения для ср(/, 0, Jf\, Jf2, ()'¦
,?[?{* (И'2-.Г
[R-2 ~ Р2 + Л (/ + 1)} .Г2 + (?!•„ + nl)
~
Ф-	(9.164)
Можно провести дальнейшее сокращение атомных
переменных и получить уравнение только для полевой
моды. Если принять, что Ti и Г2 велики по сравнению
с вероятностями перехода W\2, w2i и я, то можно исклю-
исключить заселенности атомных уровней JC\ и Jf2- К сожа-
сожалению, полное исключение этих переменных приводит к
обобщенному уравнению Фоккера — Планка, содержа-
содержащему производные произвольно большого порядка. Мы
выпишем результат только для решения, проведенного
в «диффузионном приближении», когда удерживаются
производные порядка не выше второго. Для упрощения
записи этого уравнения положим
0 = Г,Г2 + я/(Г, + Г2),	(9.165а)
A2^SD~l[TlR2 + nI{Rl + R2)l	(9.1656)
Al^®-l\?2Rl+nI<<Rl + R2)\.	(9.165в)
Физически А2 и Л. есть средние адиабатические значе-
чения заселенностей соответственно уровней Jf2 и JC\.

5 3. ОПИСАНИЕ ЛАЗЕРА	341
При использовании этих переменных приближенное урав-
уравнение для диагонального веса ф(г,/) = ф(/, 0,/) приобре-
приобретает следующий вид:
-я/ (Л2 - Л,)}]
Кг <?" + яЛг) + ®~ (Т
}.	(9.166)
Таким образом, мы свели задачу к решению уравнения
только для одной полевой моды. Приближенная мат-
матрица плотности связана с решением уравнения (9.166)
соотношением
/, t)\z)(z\dlx(z),	(9.167)
где z = Р1'е'т. Теперь, чтобы получить рь(/), уже не
нужно, как в (9.157), интегрировать по какой-либо пе-
переменной.
Интересно отметить эффект насыщения основных
диффузионных членов при большой интенсивности I.
Коэффициент при фазовом члене минимален «при ре-
резонансе», когда а = 0, или [см. (9.160)] когда со& = соа.
При больших интенсивностях из (9.165) следует, что
коэффициент при сЯ/<362 принимает вид
± (уп + яЛ2) - ±- [уп + Я-(г%+г^]. (9.168)
Выражение для коэффициента при д2/д12 в случае боль-
большой интенсивности можно несколько упростить:
yhl + ЗГ'л/Г, {Г,Л2 - л/ (Л2 - Л,)} « yhl + -р^т- . (9.169)
1 1 + 1 2
Это значение меньше, чем то, которое можно было бы
ожидать, так как в него не входит величина ^2 —
вероятность перехода с уровня 0 на уровень 2 под дей-
действием накачки.

342	ГЛ. 9. КОНКРЕТНЫЕ СОСТОЯНИЯ ПОЛЯ ИЗЛУЧЕНИЯ
Некоторые из этих результатов можно получить не-
несколько иным образом. Рассчитаем (/) и (/2) для равно-
равновесного решения уравнения (9.166), каким бы это реше-
решение ни было. Это можно легко сделать, полагая dq/dt=O,
умножая (9.166) па / или /2 и интегрируя по частям,
в предположении, что поверхностные члены не дают
вклада. В (/) вносит вклад только первый член, и если
мы используем значения At и А2, отвечающие большим
интенсивностям, то получим
<^"»+Уг"Лг)а- (9Л70а)
В том же приближении для (/2) имеем
(/2) =</J + й (/) + _??_
Таким образом мы можем получить большую среднюю
мощность, если R2 имеет большую величину, и, кроме
того, малые флуктуации интенсивности, если п и R\
сравнительно малы.
Наконец, выведем приближенное выражение для ши-
ширины спектральной линии, обусловленной диффузией
фазы. В этом случае мы не будем предполагать распре-
распределение равновесным, а вместо этого попытаемся найти
поведение во времени величины (e~ie). Очевидно, вклад
в правую часть (9.166) дадут только те члены, которые
не содержат д/dl. Если выбрать а = 0 (соь = соа) и вос-
воспользоваться соотношением (9.168) для случая больших
интенсивностей, то получим
dt ^ '	\в 4/	, 2
В предположении, что распределение является прибли-
приближенно равновесным (в той мере, в какой это касается
интенсивностей), из (9.170) вытекает
1	=
4 1Уп (г, + г2) + (я2г, - я,г2)] ^ I —
Л(е-'е).	(9.171)

§ 3. ОПИСАНИЕ ЛАЗЕРА	343
Здесь мы использовали предположение о малости флук-
флуктуации интенсивностей. Решение этого уравнения
(е-ю)(==е-л<<е-«»)о	(9.172)
означает, что фаза диффундирует с постоянной скоро-
скоростью Л, а спектральная линия имеет лоренцевскую фор-
форму; ширина этой линии сопоставима с той, которая была
получена на основе обсуждавшейся ранее простой мо-
модели колебания с диффузией фазы.
Имеется, конечно, ряд других возможных постановок
вопроса и приближенных подходов, которые могут быть
рассмотрены в том же плане. В некоторых случаях це-
целесообразно ввести новые переменные. Дальнейшее об-
обсуждение этих вопросов читатель может найти в лите-
литературе.
Несмотря на то что изучение укороченных уравне-
уравнений, полученных в диффузионном приближении, оказы-
оказывается весьма ценным, по-видимому, нет причин счи-
считать бесполезным рассмотрение точного стохастического
уравнения второго порядка (9.159). Как было отмечено
раньше, неположительность диффузионной матрицы мо-
может быть частично отнесена за счет использования диа-
диагонального представления для р. Наше обсуждение не-
неположительных матриц должно было показать, что они
не так страшны. В настоящее время представляется, что
изучение таких уравнений и некоторых их свойств было
бы очень полезным.

10
Интерферометрия интенсивности
в квантовой оптике
§ 1. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ.
КОРРЕЛЯЦИЯ НИЗШЕГО ПОРЯДКА
А. Корреляция отсчетов
Здесь мы снова обратимся к вопросу о корреляции
интенсивности, который уже обсуждался в гл. 3. Исполь-
Используем соотношения C.46) и C.52) в качестве исходных
при определении корреляции отсчетов в двух счетчиках.
Для локализованных безынерционных детекторов эти
соотношения имеют вид
г
п, = а, \{Ч){П-М}{П)Ш',	A0.1а)
о
т т
Ti~nk = a,ak J J (У* (/') • V, (/') V; (Г) ¦ V, (П) dt' di".
о о
A0.16)
Здесь индексы /, k = 1, 2 представляют собой номера
двух детекторов, a Vj{t') = V(rj, f), где вектор г,- опре-
определяет положение детектора. Мы не исключаем случай,
когда Г1 = Гг- Имея в виду формальную эквивалентность,
следующую из оптической теоремы эквивалентности, эти
соотношения можно рассматривать как чисто кванто-
квантовые, если с помощью подходящего диагонального веса
cp({z?(k)}) es <j){V} провести необходимое усреднение.
Для анализа корреляций отсчетов типа обсуждав-
обсуждавшихся Хэнбери Брауном и Твиссом [3.9] введем
т т
ЩП2 = «i«2 + <*№ J J <ДЛ (О Д/2 (Г)) dt' dt", A0.2)
о о

§ 1. КОРРЕЛЯЦИЯ НИЗШЕГО ПОРЯДКА	345
где
A/, (f) EEE /, (/') - (Ij (О).
По аналогии с определением, введенным для тепло-
тепловых полей, положим
т т
i\i2(T)^T^- \\{ЫЛПЫЛП)сН'сИ", A0.3а)
Il\ll2 t J
о о
что для стационарных полей сводится к
т
412 (Т) = 7-(/,@)Н/,@)) J (Г ~ Т) <Д/' (Т) Л/2 @)) Л- (Ш-Зб)
о
В любом случае имеет место соотношение
пхп2 — П[П2 = ЯхЩ ^12~, ,	(Ю-4)
аналогичное соотношению C.55). В случае стационар-
стационарных полей и для больших времен Т можно принять
DO
Ли (?) ~ т!12(оо) = (/[@)J(/г@)) J (А/, (т) Д/2@)><*т. A0.5)
о
Для тепловых полей, рассматривавшихся в гл. 3, ве-
величина v\i2(T) = ?,i2(T) была положительной и изменя-
изменялась в пределах 0-^.%\2(Т)-^.Т. Это имеет место и при
квантовом рассмотрении тепловых или произвольных
хаотических полей, если диагональный вес по-прежнему
гауссов. Однако теперь, когда мы опираемся на изло-
изложенный ранее материал, нам уже не обязательно огра-
ограничиваться обсуждением только гауссовых полей. Если
принимать во внимание и другие распределения, то
можно предвидеть, что величина v\i2(T) может быть
отрицательной; в этом случае наблюдались бы отрица-
отрицательные корреляции отсчетов. Чтобы получить такой ре-
результат, не нужно, чтобы диагональные веса были отри-
отрицательными или имели какое-то странное поведение.
Например, если положить № = /](/) и Х = 12@), то
±	2)] A0.6)

346	ГЛ. 10. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
является распределением, для которого
(a/, (t) м2 @)) = </, @ /2 @)) - </, (/)) </2 @); =
= (WX)-(W)(X)=- 1,
где величины (WX), {W) и (X) рассчитываются с по-
помощью a(W, X).
Эффекты, специфические для квантовой теории, мо-
могут возникнуть (но не обязательно!), если измерять поле
внутри объема когерентности, т. е. на настолько малом
пространственном и временном интервалах, что
a (W, X)~o{XN(W-X).
В этом случае из (8.73) вытекает
<Л (t) 12 @)) = (X2) > (ХУ = </, (/)) </2 @)>.
Отклонение от такого поведения возможно в случае под-
подходящего отрицательного диагонального веса в диаго-
диагональном представлении. Наиболее важным примером та-
такого отклонения может служить случай, когда имеется
только один фотон. Тогда среднее nxti2, определяющее
совпадение двух фотонов, с необходимостью равно нулю.
Для хаотических полей общее поведение корреляции
интенсивности можно вывести из (9.48) или (9.53). Бу-
Будем считать поле пространственно однородным, стацио-
стационарным и линейно поляризованным; это равносильно
предположению о том, что
7gF<at(k)av(k'))-6,16ri6(k-k0^f (k, v). A0.7)
Последнее соотношение представляет некоторое обоб-
обобщение соотношения (9.54). Принимая во внимание (9.48)
или (9.56) (и опуская индексы, указывающие поляри-
поляризацию), можно написать
C,v {S} = ехр { - J J S* (г', ?) Г (г' -r;t'-t)S (r, t)d\x Л'}.
A0.8)
Из C.49) вытекает, что
(Д/ (г', V) А/ (г, /)) = | Г (г' - г; t' - t) |2. A0.9)

§ 1. КОРРЕЛЯЦИЯ НИЗШЕГО ПОРЯДКА	347
Итак, выражение для среднего числа отсчетов в кван-
квантовом случае качественно не отличается от C.56);
имеется только количественное отличие, так как в вы-
выражение для Г входит ft. Это особенно очевидно в слу-
случае истинного квантового теплового распределения при
температуре Т, для которого
r(k,v) = Bnyi7^~T.	A0.10)
В классическом пределе (й—»0) это выражение сходится
к Г(к, v) = кТ/2п. Если мы безоговорочно примем это
распределение, то не получим пространственные или
временные корреляции, кроме тех, которые обусловлены
частотными характеристиками самого детектора.
С другой стороны, для идеального лазерного поля,
в котором отсутствуют флуктуации интенсивности, оче-
очевидно, /(/)=(/(/)), поэтому тI2(Г) = 0, Следовательно,
корреляции отсчетов не наблюдаются: щп2 = пхп2. Ясно,
что в общем случае величину r\i2(oo) нельзя назвать
«временем когерентности».
Определение ширины спектра с помощью корреляции
отсчетов. Корреляции интенсивности второго поряд-
порядка также дают некоторую информацию о поле. Зная за-
зависимость от времени среднего числа совпадений A0.4),
можно определить функцию r)i2G"). В случае стационар-
стационарного поля из A0.36) следует
Экспериментально, однако, удобнее определять кор-
корреляцию интенсивности непосредственно путем измере-
измерения запаздывающих совпадений. Отнесенная к квадрату
временного интервала совместная вероятность того, что
один фотон наблюдается в момент / = 0, а другой в мо-
момент t = х, определяется выражением
= a2 [</, @)) </2 @)) + <Д/, (т) Д/2 @))] =
= a2(/i@))</2@)>[l+IXi2(T)P] =
= const [1+|5С12(т)|2].	A0.12)

348	ГЛ. 10. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
2
4
i
А Д -
ftteL Во-
1st. С +-
\. D • -
о—~~^л
a a • • ^Г —
! 1
V= 1,25
V- 2,09
V' 3,14
Лазер
—~
см/сен
см/сен
см/сек
о
1
o
I
KB
В
С
500
300
200
1000
600
UQO
Время. мх сек
1500
900
600
1200
Фиг. 7. Зависимость относительной корреляции интенсивности от
времени задержки для теплового и когерентного источников. (По
данным Арекки, Гатти и Сона [10.1].)
Показаны экспериментальные результаты для лазера и для искусственного хао-
хаотического источника, для получения которого лазерный луч пропускался через
матовое стекло, вращавшееся со скоростью 1,25, 2,09 и 3,14 см/сек соответственно.
Корреляционная функция спадает вдвое за время, определяемое спектральной
шириной хаотического излучения. Равновесное значение, равное единице,
достигается за меньшее время для более высоких скоростей вращения матового
стекла, что указывает на соответственно более широкую полосу частот. Для
излучения лазера практически никаких корреляций интенсивности не наблю-
наблюдалось, что согласуется с фактом отсутствия флуктуации интенсивности в из-
излучении лазера.
Здесь Ixi2(т) | является аналогом величины i Y?2(т) | в
случае теплового излучения. Эксперименты по определе-
определению корреляций интенсивности второго порядка прово-
проводились несколькими авторами. Для успеха таких экспе-
экспериментов необходимо, чтобы время корреляции было
больше времени разрешения регистрирующей схемы.
Для света обычных тепловых источников величина
Ixi2(т) I = 1 Y12(т) j спадает до нуля за время (обратное
ширине линии), которое, как правило, чрезвычайно
мало. Поэтому необходимо использовать специальные
источники.

I m
I
1
\
\
¦•. \
'. \
; \
\
I
a
	 Лоренцевскип спектр
с й V « 200 Мги
i i I i
/ г з ч 5 s
Интервал г,, нсен
!
I
IS
i	2	3	U	5	8
Интервал г,, нсен
Фиг. 8. Зависимость относительных корреляций интенсивности от
времени задержки для двух тепловых источников. (По данным
Моргана и Манделя [10.3].)
Экспериментальные результаты показаны точками и вертикальными линиями,
указывающими доверительный интервал, а — результаты для излучения высоко-
монохроматичной ртутной дуговой лампы. Этим результатам соответствует
функция взаимной когерентности с шириной спектра примерно 200 Мгц\ б — ре-
результаты для обычной лампы накаливания; здесь из-за очень широкой полосы
чостот время корреляции весьма мало и не могло быть измерено.

350	ГЛ. 10. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
Арекки, Гатти и Сона [10.1] измерили Р\г{т) для ко-
когерентных и хаотических источников (фиг. 7). В случае
когерентного излучения гелий-неонового лазера, в пре-
пределах экспериментальных ошибок, сопоставимых с флук-
туациями при нулевой интенсивности, имеет место ра-
равенство ри{х) = р 12@). В экспериментах с хаотическим
источником величина IXi2(т) j = j\Чг(т) | плавно спадает
от единицы до нуля за время порядка 10~3 сек. Чтобы
получить хаотический источник с такой узкой полосой,
авторы пропускали когерентное излучение гелий-неоно-
гелий-неонового лазера через вращающееся матовое стекло. Как
было отмечено в гл. 2, Арекки [2.4] показал, что для
такого искусственного источника распределение фотонов
в результирующем поле следует геометрическому за-
закону, характерному для хаотических источников.
Другой эксперимент такого типа был выполнен Мор-
Морганом и Манделем [10.3]. Они смогли определить, что
для излучения ртутной лампы низкого давления с ши-
шириной линии 200 Мгц, которая оценивалась другими ме-
методами, JYi2(t) | ~ ехр(—jTj/7c), где Тс «« 1,7 • 10'9 сек;
это согласуется с шириной лоренцевской линии, равной
200 Мгц (фиг. 8). Описанный эксперимент не так прост,
как может показаться на первый взгляд, поэтому инте-
интересующемуся указанным вопросом читателю мы сове-
советуем самому изучить эту работу.
Б. Пространственная корреляция интенсивности
Вернемся снова к соотношению A0.1) и рассмот-
рассмотрим его при временах Т, малых по сравнению с соответ-
соответствующим временем когерентности. Остановимся сейчас
не на временной, а на пространственной зависимости,
для чего явно введем зависимость от г. Следовательно,
если m(r')—случайная переменная, равная числу фото-
фотоэлектронов, зарегистрированных за короткий интервал Т
в момент времени t, то
m (г') - аТ (V* (г') . V (г')),	A0.13а)
m (г') m (г") = а2Г2 (V (г') • V (г') V (г") • V (г")). A0.136)

§ 1. КОРРЕЛЯЦИЯ НИЗШЕГО ПОРЯДКА	351
Здесь мы предположили, что эффективности детекторов
не зависят от положения в пространстве и не учли зави-
зависимость от общей переменной t.
Выражения A0.13) относятся к пространственным
изменениям среднего числа отсчетов или средних интен-
сивностей. Если мы рассмотрим пространственно одно-
однородное поле (но не обязательно стационарное!), то
т (г') — т для любых г, в то время как
т (г') т (г") = т(т'- г") m @).	A0.14)
Чтобы сделать аналогию с временной корреляцией еще
более тесной, введем величину
^),	A0.15)
где Am(R) = m(R) — m(R) и /? = |R|. Следовательно, мы
можем положить
m (R) m @) - m2 = m2 [^Ц^-].	A0.16)
Для излучения теплового источника непосредственно
вытекает, что величину r)(R) можно выразить через сте-
степень когерентности rj(R) = R \ y(R) |2. Таким образом,
для r)(R) выполняется условие 0 ^r\(R)^CR. Однако в
общем случае это может и не иметь места. В случае
идеального лазерного излучения нет корреляций отсче-
отсчетов ни во времени, ни в пространстве, поэтому r)(R) = 0.
Если мы просто положим m(R) = W и пг@)=Х, то
распределение, данное в A0.6), ведет к отрицательному
значению для r](R). Однако если R лежит в пределах
объема когерентности, то величина r)(R) может ока-
оказаться отрицательной, если имеют место отрицательные
диагональные веса, обусловленные квантовыми эффек-
эффектами. В однофотонном состоянии, как и раньше, вели-
величина m(R)m@) равна нулю.
Пространственные корреляционные эффекты типа
описываемых соотношением A0.16) в принципе воз-
возможны для ряда полей. В большинстве тепловых полей,
однако, их трудно или вообще невозможно наблюдать.
Это в основном обусловлено малым числом фотонов
в объеме когерентности. Хотя в тепловых полях длина

352	ГЛ. 10. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
пространственной когерентности может быть порядка
нескольких метров, соответствующий эффект нельзя на-
наблюдать, если число фотонов в объеме когерентности
пренебрежимо мало. Согласно B.18), фактором вырож-
вырождения 6 в данном случае является среднее число запол-
заполнения п. Из формулы Планка
eftco/Kr
следует, что для лучших тепловых источников б ~ 10~3.
Чтобы обойти эту трудность, Мадьяр и Мандель
[10.4] наблюдали свет, падающий из двух независимых
лазерных источников. Так как фактор вырождения для
лазеров б ~ 1012, то эффект, если он имеет место, дол-
должен быть более заметным.
Два независимо генерируемых поля могут комбини-
комбинироваться в одно поле каким-то одним из двух довольно
очевидных способов. Для простоты рассмотрим эти два
способа в случае только двух мод. С одной стороны,
предположим, что амплитуды складываются:
z = zi + z2.	A0.17)
Тогда распределение определяется выражением
я2б (г — Zi) * б (z — z2)
с последующим усреднением по фазе. Это приводит к
диагональному весу
B1 z \)~' б (| г I - | zx + z21) = б (| z I2 - | z, + z2 f), A0.18)
характерному для идеальной лазерной моды с амплиту-
амплитудой \Zi + z2\. При таком сложении флуктуации ампли-
амплитуды отсутствуют, и t)(R) = O. С другой стороны, если
состояния складываются некогерентно, как это харак-
характерно для случая их независимости и индивидуальной
фазовой неопределенности, то соответствующее состоя-
состояние дается выражением
Непосредственное вычисление свертки приводит к сле-
следующему выражению:
\ | Z | -f-1 z i z1 -+-1 Z i
121
\ \
ф \Z) — ке \А \ | z \ | Z( | -f-1 z i z21 -+-1 Z\ i z2\ \ —
iz I I z\ I IZ21 j •

§ 2. СЛУЧАЙ НЕЗАВИСИМЫХ ИСТОЧНИКОВ 353
Это выражение не равно нулю в области
HzJ-IZalKlzKlzJ + IZal,	A0.20)
что характерно для некогерентной суперпозиции. Дей-
Действительно, представим в соответствии с A0.20) \z\
в виде
где Ф — действительная величина. Тогда непосредствен-
непосредственно из A0.19) следует
q>(z) = B|z, П^ЫпФГ1.	A0.21)
Это соотношение непосредственно определяет область,
где весовая функция q>(z) отлична от нуля, что, есте-
естественно, ведет к амплитудным флуктуациям.
В экспериментах Мадьяра и Манделя [10.4] наблю-
наблюдалась неустойчивая интерференционная картина. Не-
Несмотря на неустойчивость интерференционных колец, их
«геометрия» определяется геометрией интерференцион-
интерференционного эксперимента и длиной волны света. Хотя усред-
усредненная интенсивность в любой точке постоянна, что сви-
свидетельствует о пространственной однородности, при ана-
анализе интерференционной картины неявно используется
корреляция интенсивности и, следовательно, величина
m(R)m@).
Итак, мы видим, что при регистрации интенсивности
могут наблюдаться как пространственные, так и вре-
временные корреляции. Фактически, рассмотренные нами
временные и пространственные корреляции низшего по-
порядка являются только двумя представителями целого
множества возможных в принципе корреляций интенсив-
интенсивности.
§ 2. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ В СЛУЧАЕ
НЕЗАВИСИМЫХ ИСТОЧНИКОВ
Основываясь на полученных выше выводах, нетрудно
указать общие свойства совпадений отсчетов в случае
независимых источников. Ограничимся рассмотрением
двух независимых источников Si и 52 и двух счетчи-
счетчиков Ci и С2; обобщение на случай М независимых источ-
источников и N счетчиков не представляет труда. В нашем

354	ГЛ 1П ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИГШОСТИ
рассмотрении будут использованы соотношения и идеи,
обсуждавшиеся в предыдущих главах.
Нас интересует производящая функция, определяю-
определяющая распределение отсчетов (8.135) в случае двух счет-
счетчиков. Ее можно записать в виде
со
Q=Q(X1,X2;t1,t2;^1)/2)= \] A - X,) A - К2)п> X
п,, пг=0
X Р(пи п2; хи т2; tu t2) =
= exp
-SV/ J \V{r,f)Yot{T)cPr
dt
X
A0.22)
Здесь мы приняли, что адмитансы детекторов являются
простыми тензорами типа (8.128) и, в частности, не за-
зависят от поляризации.
Представление о независимых случайных источниках
было использовано в гл. 9 при обсуждении общих хао-
хаотических полей. Интуитивно ясно, что в этом случае
поле V(r,/) состоит из линейной суммы членов, каждый
из которых имеет независимое распределение в диаго-
диагональном представлении. Напомним, что соотношения
вида F.83) и F.84) справедливы для любого поля, ко-
которое вне источников удовлетворяет волновому уравне-
уравнению. В частности, мы можем связать поле волны анали-
аналитического сигнала V(r, /) с его значением на источнике.
Используя ядро К, выраженное в F.82) через общие
функции Грина F.80), получаем
V (х, 0 = J J К (х, у, t-t')\ (у, ПdS dt' =
s
= S J J № У. ' - '') V (У. П dSj dt'. A0.23)
I si
Последнее соотношение отражает тот факт, что в нашем
случае «поверхность» источника состоит на самом деле
из двух поверхностей. Существенно, что поле в некото-

§ '2. СЛУЧАЙ НЕЗАВИСИМЫХ ИСТОЧНИКОВ 355
рой точке х и момент / определяется величинами, за-
задаваемыми на поверхностях источников Si и S2.
Схематически запишем A0.23) в виде
V(x, 0 = /CiV, + /C2V2,	A0.24)
где Vi и V2 — значения поля на поверхностях источни-
источников, а К\ и /С2 — линейные ядра, описывающие распро-
распространение. В этом случае удобно рассматривать диаго-
диагональный вес в A0.22) как функционал полей Vi и V2
в пространстве, ограниченном поверхностями Si и S2:
1, VJ.	A0.25)
Как обычно в теории вероятности, из предположения
о независимости источников следует, что распределение
можно представить в виде произведения
{V2}.	A0.26)
Однако, как неоднократно подчеркивалось выше, в опти-
оптическом случае обычно нельзя знать или контролировать
суммарную фазу волн, испускаемых каким-либо источ-
источником. В этом случае вес фь например, одинаков для
полей вида ехр (Юг) Vj (у, ^) при всех действительных Qt;
иными словами, ф] не зависит от суммарной фазы 0ь
Как и в гл. 3, мы можем назвать распределение, имею-
имеющее место в этом случае, распределением с неопреде-
неопределенной фазой. Для квазимонохроматического излучения,
для которого
V,(y, 0 = v,(y,
где Vi — медленно меняющаяся функция, распределения
с неопределенной фазой и стационарные распределения
эквивалентны. В общем случае, однако, эти распределе-
распределения не вполне эквивалентны, и мы будем рассматривать
здесь только распределения с неопределенной фазой.
Аналогичные соображения относятся также к стацио*
нарным случаям.
Если принять, что каждый независимый источник
правильно описывается диагональным весом с неопре-
неопределенной фазой
Ф/ {ехр Щ) V;} = Фу {V/},	A0.27)

356
ГЛ. 10. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
то нетрудно получить соответствующие соотношения для
совместного распределения отсчетов или для его про-
производящей функции. Согласно нашим предыдущим за-
замечаниям, можно, очевидно, формально написать
Q = J / ехр { - ^ V/ {
о, (х) d3x dt} X
.	A0.28)
Раскроем члены в показателе экспоненты и явно вве-
введем дополнительную фазу 0 между полями Vi и V2.
В этом случае находим общее выражение вида
Q = J J ехр {
- V2 • Л2У2 -
X фЛУ^ф^ЫцОМФОМ.	A0.29)
Здесь Aj и В — линейные операторы, включающие про-
пространственное и временное интегрирование и линейно
зависящие от множителей 1.\ и Х2\ их можно легко
вывести с помощью A0.28). Существенным моментом
является тот простой факт, что хотя производящая функ-
функция Q определяется с помощью вспомогательного пара-
параметра 0, она на самом деле не зависит от 0 из-за
индивидуальной фазовой неопределенности каждого
источника. Поэтому можно, не меняя значения функ-
функции Q, усреднить ее по фазе 0. С помощью соотношения
для функции Бесселя 1о(х), использованного при выводе
соотношения (9.141), находим
Q= J Jexp{-
X
(Ю.30)
Целесообразно также представить	линейную зависи-
зависимость Aj и В от ).k в явном виде:
А^ЪКАщ,	A0.31а)
B^S^Bfe,	(ю.316)

§ 2. СЛУЧАЙ НЕЗАВИСИМЫХ ИСТОЧНИКОВ 357
где /lftj и Bh не зависят от Kk- Подставляя эти соотно-
соотношения в A0.30), приходим к соотношению
Q= f Г ехр{ -У lk{v] ¦ AkiVi) }lo( y\lkV*-BkV2 ]x
I ^^	I v ^^	/
X ф[{Vi^2{V2}d[i{Vi)d\i{V2}-	A0.32)
В это соотношение неявно входят корреляции не-
нескольких типов. Даже если множитель /0 не играет
роли, как например когда V) и V2 имеют ортогональную
поляризацию, в общем случае отсчеты в двух счетчиках
будут коррелированы, так как <2(/чД2) нельзя пред-
представить в виде произведения Qi(X])Q2().2). [Вообще та-
такая факторизация Q(Ai,?»2) имеет место при Ahj = 0,
k ф j. Это означает, что в счетчик 1 не попадает излу-
излучение из источника 2 и наоборот; если это так, то
Bh — 0 автоматически. Физически это эквивалентно на-
наличию «стенки», полностью отделяющей один источник
и его счетчик (Si и Ci)ot другого источника и счетчика
(S2 и С2).]
Имеется, однако, существенное исключение, когда
множитель /0 полностью определяет ситуацию. Если в
излучении источников Si и S2 отсутствуют флуктуации
интенсивности, то только член /0 ведет к корреляциям.
Если считать, что cpj{Vj} имеет вид б-функции с пиком
при некотором значении поля (не говоря о неопределен-
неопределенности суммарной фазы), то можно легко оценить
A0.32). Для простоты обозначим поле, выделяемое
6-функцией, снова через V. Тогда получаем
Q = expJ- 2MVJ- AwV/H/oflSA.ftVl-fijMh. A0.33)
Если множитель /0 несуществен (например, как в уже
упоминавшемся случае ортогональной поляризации),
результирующая производящая функция имеет вид
Qi(?4)Q2(iU)> откуда вытекает, что корреляция совпаде-
совпадений отсчетов отсутствует. Таким образом, все корреля»
ции возникают за счет множителя /0.
Следует отметить, что, даже если пренебречь вторым
счетчиком С2, два независимых источника дадут непуас-
соновскую статистику отсчетов счетчика Сь Чтобы

358	ГЛ. 10. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
показать это, достаточно только, согласно A0.22), поло-
положить в A0.33) Л.2 = 0. Устраняя все временные перемен-
переменные, находим
= ехр{-Я,?}/0(А,,С).	A0.34)
Отсюда [ср. B.8)] получаем, что Е = п\, в то время как
С — {2 {а'\ — й,)}'2 является мерой отклонения от стати-
статистики Пуассона. Распределение отсчетов, описываемое
соотношением A0.34), неявно содержится в B.7), хотя
не в очень простой форме. Однако, используя B.6), мы
можем получить распределение p{U) для интегральной
интенсивности [ср. B.4)]
= J
A0.35)
a
2it
— ОО
= \ a Re
>]¦}-.
A0.36)
Это соотношение определяет распределение U как функ-
функцию времени счета, полей и геометрии источников. Флук-
Флуктуации в U имеют место, если С > 0.
Проведенное рассмотрение касалось статистики от-
отсчетов в счетчиках, освещаемых независимыми источни-
источниками. Конечно, совершенно не обязательно, чтобы все
(или какие-либо!) источники действительно не зависели

5 3. ЗАКЛЮЧЕНИЕ	359
друг от друга. Имеется ряд типов корреляции источни-
источников, которые также можно было бы рассмотреть. Все
эти возможности в неявном виде содержатся в формулах,
выведенных нами для общего совместного распределе-
распределения отсчетов при любых конкретных корреляциях источ-
источников, если эти корреляции существуют.
§ 3. ЗАКЛЮЧЕНИЕ
В этой книге мы рассматривали классическую и
квантовую теории частично когерентных свободно рас-
распространяющихся волн, которые представляют собой со-
соответственно разделы классической и квантовой стати-
статистических теорий. Была показана целесообразность
использования в классической теории аналитического
сигнала, особенно для квазимонохроматических полей.
В свою очередь благодаря использованию нормально
упорядоченных полевых операторов, которые, как было
показано, позволяют характеризовать скорость много-
многократных совпадений в квантовой теории, представление
о когерентных состояниях оказалось очень удобным и
естественным для квантового рассмотрения. Являясь
собственными векторами операторов уничтожения, эти
состояния включают в себя аналитические сигналы, что
позволяет установить тесную связь с классической фор-
формулировкой статистической теории. Последовательное
изучение когерентных состояний показало, как и в ка-
каком смысле применять диагональное представление для
матрицы плотности, чтобы использовать эту формаль-
формальную связь с классической теорией. Целесообразность
такого представления должна быть ясна из рассмотре-
рассмотрения, изложенного в книге, и приведенных примеров.
Полезно в заключение перечислить ряд других общих
вопросов, разрабатываемых в настоящее время.
В нашей книге речь шла только о волнах в свобод-
свободном пространстве; мы лишь кратко коснулись проблем,
связанных с атмосферными искажениями. Вместе с тем
для приложений все возрастающее значение имеют об-
общие аспекты распространения света в несвободном про-
пространстве, в среде, характеристики которой меняются
по случайному закону, в нелинейной среде и т. д., не
говоря уже о вопросах детектирования и генерации. Эти

360	ГЛ. 10. ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
задачи связаны с вопросами об искажении сигнала
(такие же проблемы возникают и в теории информа-
информации), а также о передаче сигнала по шумящему каналу.
В дополнение к этому остается множество нерешенных
проблем, связанных с разработкой более точного опи-
описания процессов детектирования, которое позволило бы
лучше отразить роль нелинейных явлений.
Мы обсудили, особенно подробно в этой главе, воп-
вопрос о реакции нескольких счетчиков на излучение не-
нескольких источников. Очевидно, здесь возможна и об-
обратная постановка задачи: каким образом, используя
информацию об отсчетах, вывести статистические свой-
свойства источников. Если, с другой стороны, рассматривать
один или несколько «источников» как рассеивающие
центры, расположенные в поле излучения других источ-
источников, то можно получить информацию об их рассеи-
рассеивающих свойствах. В частности, при соответствующем
использовании нескольких счетчиков можно получить
информацию об относительной фазе, недоступную в слу-
случае одного счетчика. Эти вопросы подробно рассматри-
рассматривались Гольдбергером, Льюисом и Уотсоном [10.6].
Еще одна проблема, заслуживающая нескольких об-
общих замечаний, заключается в описании статистических
состояний в случае бесконечного числа степеней сво-
свободы. И при классическом и при квантовом рассмотре-
рассмотрении мы подчеркивали полезность характеристических
функционалов. Независимо от того, является ли задача
классической или квантовой, имеет ли распределение
конечные моменты или не имеет, характеристический
функционал представляет собой хорошо определенную
и непрерывную функцию своих аргументов. Это особен-
особенно важно при квантовом рассмотрении, так как форму-
формулировка задачи с бесконечным числом степеней свободы
связана с некоторыми трудностями. Мы попытались
облегчить подход к этим задачам путем квантования
поля излучения в «ящике». Если, например, с самого
начала квантовать поле излучения в бесконечном объ-
объеме, то для рассмотрения равновесного теплового со-
состояния— или любого другого состояния, обладающего,
вообще говоря, пространственно-трансляционной инва-
инвариантностью,— необходимо такое представление опера-

§ 3. ЗАКЛЮЧЕНИЕ	361
торов уничтожения и рождения, которое было бы
унитарно неэквивалентным по отношению к использо-
использованному нами представлению (так называемое пред-
представление Фока). Действительно, при различных тем-
температурах или при изменении какого-либо другого
макроскопического параметра все представления не
эквивалентны одно другому. Грубо говоря, физическая
причина этого заключается в том простом факте, что
нельзя указать процедуру, которая бы изменяла макро-
макроскопические свойства равномерно по всему простран-
пространству (или, говоря более формально, нельзя придумать
«гамильтониан», эволюционный оператор которого мо-
может воздействовать на унитарную эквивалентность). При
квантовании в ящике эти вопросы не возникают, а при
использовании характеристического функционала они
играют второстепенную роль. Желательно, конечно, из-
избавиться от ящика (чтобы уменьшить на единицу число
не относящихся к делу параметров). В связи с этим
изучение состояний поля «без ящика» с помощью опе-
операторов представляет собой интересную, хотя и нетри-
нетривиальную задачу. Как было отмечено в гл. 5, рассмот-
рассмотрение этих вопросов как раз ведется в настоящее время.
Разумеется, центральным пунктом любой задачи как
в классической, так и в квантовой оптике является рас-
рассмотрение нелинейных уравнений взаимодействия и на-
нахождение соответствующих состояний поля, основываю-
основывающееся на использовании только исходных принципов.
Эта процедура (в тех случаях, когда ее применение
возможно) дает, конечно, наиболее глубокие сведения
о рассматриваемых связанных системах. Беглое изло-
изложение возможной формулировки таких задач было дано
в гл. 4. В гл. 9 приведено краткое описание идеализиро-
идеализированной лазерной модели. Другие системы и соответ-
соответствующие уравнения, так же как и методы, используе-
используемые для их анализа, обсуждаются в литературе.
С помощью изложенных нами методов квантовой
оптики возможно изучение ряда новых интересных и
актуальных проблем в этой области физики, области,
имеющей славную историю и внесшей большой вклад
в другие разделы физики, например в волновую меха-
механику.

Библиография
ГЛАВА 1
Классическим учебником оптики, в котором наряду
с другими вопросами рассматривается и частичная ко-
когерентность, остается книга:
1.1.	Born M., Wolf E., Principles of Optics, 3 rd
ed., Oxford, 1965.
В этой книге особого внимания заслуживает гл. X.
Частичная когерентность обсуждается также в двух
недавно вышедших работах:
1.2.	Вегап М. J, Parrent G. В., Jr., Theory of
Partial Coherence, New Jersey, 1964.
1.3.	O'Neill E. L., Introduction to Statistical Optics,
Reading (Mass), 1963. (См. перевод: Э. О'Н е й л,
Введение в статистическую оптику, изд-во «Мир»,
1966.)
Мы предполагаем, что читатель имеет основные пред-
представления о свойствах преобразований Фурье. Аналити-
Аналитические сигналы были введены и широко использованы
Габором:
1.4.	Gabor D.,Journ. Inst. Electr. Eng., 93,429A946).
Общие вопросы, связанные с интегралами Фурье,
включая преобразования Гильберта, которым подчи-
подчиняются аналитические сигналы, рассмотрены в книге:
1.5.	Т itch marsh E. С, Introduction to the Theory
of Fourier Integrals, 2d ed., Oxford. 1948. (См.
перевод: Э. Титчмар ш, Введение в теорию
интегралов Фурье, ИЛ, 1948.)

БИБЛИОГРАФИЯ	363
Понятие степени когерентности и ее связь с вид-
ностыо обсуждалась Цернике:
1.6.	Zernike F., Physica, 5, 785 A938).
Так называемая «фазовая проблема» в оптике была
в общем виде сформулирована Вольфом:
1.7.	Wolf E., Proc. Phys. Soc, 80, 1269 A962);
для частного случая излучения черного тела она обсу-
обсуждается в работе:
1.8.	KanoY., Wo HE., Proc. Phys. Soc, 80, 1273
A962).
Интересный подход к фазовой проблеме предложил
Мета:
1.9.	Mehta С. L., Nuovo Cimento, 10, 202 A965).
Несколько конкретных примеров форм спектра рас-
рассматривается в работе:
1.10.	Nussenzveig H. M., Journ. Math. Phys., 8,
561 A967),
где было показано, что в этих случаях «минимальное»
решение фазовой проблемы является неадекватным.
Волновые уравнения для функции взаимной когерент-
когерентности были впервые получены Вольфом:
1.11а. Wolf E., Proc. Roy. Soc, A230, 246 A955).
1.116. Wolf E., Proc. Phys. Soc, 71, 257 A958).
Векторные волновые уравнения, соответствующие
полю излучения, даны в работе:
1.12. Roman P., Wolf E., Nuovo Cimento, 17, 462,
477 A960).
ГЛАВА 2
Полуклассический вывод формулы распределения
отсчетов для излучения теплового источника имеется
в работе:
2.1. М a n d e I L., в книге Progress in Optics, ed.
E. Wolf, Vol. 2, Amsterdam, 1963.

364	БИБЛИОГРАФИЯ
Полуклассический вывод, справедливый для более
общих распределений светового излучения, приводится
в работе:
2.2.	М a n d е 1 L., S u d a r s h a n E. С. G, WoHE,
Proc. Phys. Soc, 84, 435 A964).
Обзор методов, используемых в теории вероятности,
дан, например, в книге:
2.3.	Cramer H., Mathematical Methods of Statistics,
Princeton, 1946. (См. перевод: Г. Крамер, Ма-
Математические методы статистики, М., 1948.)
Упоминаемые в нашей книге эксперименты по опре-
определению распределений фотоотсчетов для излучения теп-
тепловых источников и лазеров были выполнены Арекки:
2.4.	Arecchi F. Т., Phys. Rev. Lett., 15, 912 A965).
Вопрос о нахождении распределения интенсивности
по распределению фотоотсчетов в сеязи с квантовой оп-
оптикой рассмотрен в статье:
2.5.	W о 1 f E., M e h t а С. L., Phys. Rev. Lett., 13, 705
A964).
Идентичная математическая задача решается
в статье:
2.6.	Wi d der D. V., Duke Math. Journ, 1, 126 A935).
Вопрос о моментах распределений, возникающий,
в частности, в указанной задаче, подробно обсуждается
в книге:
2.7.	Shohat J. A., Tama r kin J. D., Problem of
Moments, Rhode Island, 1943.
ГЛАВА 3
Аппарат характеристических функций изложен в ра-
работе:
; 3.1. Lukacs E., Characteristic Functions, London,
1960,

БИБЛИОГРАФИЯ	365
С рассмотрением стохастических процессов под уг-
углом зрения физики можно познакомиться по работам,
воспроизведенным в сборнике:
3.2.	Wax N., ed., Selected Papers on Noise and Sto-
Stochastic Processes, New York, 1954.
Статьи, входящие в сборник, весьма содержательны
как с математической, так и с физической точек зрения.
Особенный интерес среди них для классической стати-
статистической оптики представляет статья:
3.3.	Rice S. О., Bell Syst. Tech. Journ., 23, 282
A944); 25,46 A945).
Различные приложения к физическим задачам рас-
рассматриваются в книге:
3.4.	Bartlett M. S., An Introduction to Stochastic
Processes, London — New York, 1955 (См. пе-
перевод: M. С. Барт лет, Введение в теорию слу-
случайных процессов, ИЛ, 1958.)
и в книге:
3.5.	Ramakrishnan A., Probability and Stocha-
Stochastic Processes, Handbuch der Physik, Hrsg. S.
Fliigge, Bd. III/2, Berlin, 1959.
Теория гармонического анализа с некоторым акцен-
акцентом на характеристические функционалы в доступной
форме изложена в книге:
3.6.	Гельфанд И. М., Виленкин Н. Я., Неко-
Некоторые применения гармонического анализа, М.,
1961, гл. 2 и 3,
а более полное математическое рассмотрение дано в
книге:
3.7.	Doob J. L., Stochastic Processes, New York,
1953. (См. перевод: Дж. Л. Дуб, Вероятностные
процессы, ИЛ, 1956.)
Вопросы теории информации и связь со статистиче-
статистической механикой в применении к теории оптической коге-
когерентности обсуждались ГабороМ:
3.8.	G a b о г D., в книге Progress in Optics, ed.
E. Wolf, Vol. 1. Amsterdam, 1961.

366	БИБЛИОГРАФИЯ
Эксперименты по многократному совпадению фото-
фотоотсчетов были предложены и успешно выполнены Хэн-
бери Брауном и Твиссом:
3.9а. Hanbury Brown R, Т w i s s R. Q., Na-
Nature, 177, 27 A956).
3.96. Hanbury Brown R, Twiss R. Q., Proc.
Roy. Soc, A242, 300 A957).
3.9b Hanbury Brown R., Twiss R. Q-, Proc.
Roy. Soc, A243, 291 A957).
Классическое объяснение наблюдавшихся в этих эк-
экспериментах эффектов в терминах корреляции интен-
интенсивности второго порядка содержится в статье:
3.10.	Purcell E. M., Nature, 178, 1449 A956).
Обстоятельный обзор того же вопроса дан- Манде-
лем [2.1], а также Манделем и Вольфом:
3.11.	Man del L., Wolf E., Rev. Mod. Phys., 37,
231 A965). (См. перевод: УФН, 87, 491 A965);
88, 347, 619 A966).)
Применение независимых совместных тепловых рас-
распределений для приближенного представления инте-
интегральной интенсивности в обсуждавшихся в тексте слу-
случаях было разработано Райсом [3.3]; приложение к рас-
распределению фотоотсчетов дано в работе:
3.12.	Man del L., Proc. Phys. Soc, 74, 233 A959).
ГЛАВА 4
Связанные нелинейные дифференциальные уравне-
уравнения в частных производных со случайными вынуждаю-
вынуждающими силами и (или) случайными начальными усло-
условиями встречаются практически во всех областях фи-
физики.
В квантовой оптике такие уравнения возникают при
рассмотрении сред с нелинейными электрическими и
магнитными восприимчивостями.
Это было показано в книге:
4.1. Bloembergen N., Nonlinear Optics, New
York, 1965, (См. перевод: Н. Б л о м б е р г е н.
Нелинейная оптика, изд-во «Мир», 1966.)

БИБЛИОГРАФИЯ	367
В приложении к равновесной и неравновесной кванто-
квантовой статистической механике аналогичные нелинейные
уравнения рассмотрены Кадановым и Беймом:
4.2.	Kadanoff L. Р., В aym G., Quantum Stati-
Statistical Mechanics, New York, 1962. (См. перевод:
Л. К а д а н о в, Г. Бейм, Квантовая статисти-
статистическая механика, изд-во «Мир», 1964.)
Сходные проблемы в теории турбулентности осве-
освещены Бэтчелором:
4.3.	В a t с h е 1 о г G. K-, The Theory of Homogeneous
Turbulence, London — New York, 1963. (См. пере-
перевод: Дж. Б э т ч е л о р, Теория однородной турбу-
турбулентности, ИЛ, 1955.)
Содержательный обзор математических методов и
физических задач теории случайных систем дается
в книге:
4.4.	Bharucha-Reid А. Т., Elements of the The-
Theory of Markov Processes and their Applications.
New York, 1960.
Изящное изложение метода, основанного на приме-
применении функционалов к стохастическим проблемам для
классических случайных систем, дано в работе:
4.5.	Кае М., Probability and Related Topics in Phy-
Physical Sciences, New York, 1959;
аналогичный метод для квантовых систем изложен Но-
Новожиловым Ю. В. и Тулубом А. В.
4.6.	Н о в о ж и л о в Ю. В., Т у л у б А. В., The Method
of Functionals in the Quantum Theory of Fields,
New York, 1961.
Техника дифференцирования функционалов была
введена в теорию нелинейных динамических уравнений
в работе:
4.7.	Hopf E., Journ. Rational Mech. Anal., 1, 87
A952).
Уравнения движения, описывающие классические
статистические явления применительно к линейным и

368	БИБЛИОГРАФИЯ
нелинейным задачам теории шумов, рассмотрены
в книгах:
4.8.	С тр а то но вич Р. Л., Избранные вопросы
теории флуктуации в радиотехнике, М., 1961.
4.9.	Davenport W. В., Jr., Root W. L.. Random
Signals and Noise, New York, 1958. (См. пере-
перевод: В. Да вен порт, В. Рут, Введение в тео-
теорию случайных сигналов и шумов, ИЛ, I960.),
а также в нескольких статьях по классической теории
шумов, ссылки на которые можно найти в работе:
О 4.10. Lax M., Rev. Mod. Phys., 38, 541 A966).
Применение метода характеристических функциона-
функционалов к динамическим проблемам квантовой оптики рас-
рассматривалось Сударшаном:
4.11. Sudarshan Е. С. G., Internat. Journ. Theor.
Phys., в печати.
ГЛАВА 5
Укажем несколько стандартных учебников по кван-
квантовой механике:
5.1.	Dirac P. A. M., The Principles of Quantum
Mechanics. 4th ed., Oxford, 1958. (См. перевод:
П. А. М. Дирак, Принципы квантовой механи-
механики, М., 1960.)
5.2.	Schiff L. I., Quantum Mechanics, New Vork,
1955. (См. перевод: Л. Ш и ф ф, Квантовая меха-
механика, ИЛ, 1957.)
5.3.	Messiah A., Quantum Mechanics, New York,
Vol. I, 1961; Vol. II, 1962.
Более математическое рассмотрение квантовомеха-
нических задач, в особенности важных для нас стати-
статистических вопросов, дано в книгах:
5.4.	Von Neumann J., Mathematische Grundla-
gen der Quanten Mechanik, Berlin, 1932. (См. пе-
перевод: И. фон Нейман, Математические ос-
основы квантовой механики, М., 1964.)

БИБЛИОГРАФИЯ	369
5.5.	Mackey G. W., Mathematical Foundations of
Quantum Mechanics, New York, 1963. (См. пере-
перевод: Дж. М а к к и, Лекции по математическим ос-
основам квантовой механики, изд-во «Мир», 1965.)
Более полное обсуждение свойств гильбертова про-
пространства, общих свойств различных операторов и т. д.
можно найти в книгах:
5.6.	Riesz F., S г. - N a g у В., Functional Analysis,
New York, 1955
5.7.	Колмогоров А. Н,, Фомин СВ., Элементы
теории функций и функционального анализа, М.,
1960.
Свойства чистых и смешанных состояний поляриза-
поляризации для монохроматического света аналогичны свойст-
свойствам поляризации в классической теории (см. [1.1],
стр. 541).
Читателю, интересующемуся применением С-алгебры
в квантовой теории и в квантовой статистической меха-
механике, т. е. применением метода, позволяющего рассмат-
рассматривать более общие квантовые состояния, чем те, кото-
которые описываются матрицами плотности, рекомендуем
обратиться к статье:
5.8.	S e g a I I. E., Ann. Math., 48, 930 A947)
и к подробному рассмотрению, содержащемуся в работе:
5.9.	Н a a g R., К a s 11 е г D., Journ. Math. Phys., 5,
848 A964),
а также к литературе, цитированной в этих работах.
ГЛАВА 6
Квантование поля излучения является основным
предметом рассмотрения почти всех учебников кванто-
квантовой механики, кроме самых элементарных. В дополнение
к [5.1; 5.2; 5.3] читатель может обратиться к соответст-
соответствующим главам в любой достаточно известной книге, на-
например:
6.1. Ахиезер А. И., Берестецкий В. Б., Кван-
Квантовая электродинамика, М., 1969.

370	БИБЛИОГРАФИЯ
6.2.	Н е i t I e r W., Quantum Theory of Radiation,
New York — London, 1954. (См. перевод:
В. Гайтлер, Квантовая теория излучения, ИЛ,
1956.)
6.3.	Jauch J. M., Rohrlich F., The Theory of
Photons and Electrons, Reading (Mass.), 1959.
6.4.	S с h w e b e r S. S., An Introduction to Relativistic
Quantum Field Theory, New York. 1961. (См. пере-
перевод: С. Ш веб ер, Введение в релятивистскую
квантовую теорию поля, ИЛ, 1963.)
6.5.	Т h i r r i n g W. F., Principles of Quantum Elect-
Electrodynamics, New York, 1958. (См. перевод:
В. Е. Т и р р и н г, Принципы квантовой электро-
электродинамики, М., 1964.)
6.6.	U m e z a w a H., Quantum Field Theory, Am-
Amsterdam, 1956. (См. перевод: X. Умэдзава,
Квантовая теория поля, ИЛ, 1958.)
6.7.	Wentzel G., Quantum Theory of Fields, New
York, 1949. (См. перевод: Г. Вентцель, Вве-
Введение в квантовую теорию волновых полей,
М.—Л., 1947.)
ГЛАВА 7
Элементарные свойства когерентных состояний рас-
рассматриваются в распространенных учебниках, например
[5.1—5.3], при обсуждении волновых пакетов с мини-
минимальной неопределенностью. Когерентные состояния
были введены в квантовую механику Шредингером:
7.1.	Schrodinger E., Naturwissensch., 14, 644
A927)
для изучения смещенных и сдвинутых осцилляторов.
Когерентные состояния неоднократно использовались
многими авторами для различных целей. Краткое изло-
изложение элементарных свойств таких состояний дано в ра-
работах:
7.2.	L о u i s е 1 1 W. Н., Radiation and Noise in Quan-
Quantum Electronics, New York, 1964. (Готовится рус-
русский перевод.)
7.3.	Carruthers P., Nieto M. M., Am. Journ.
Phys., 33, 537 A965).

БИБЛИОГРАФИЯ	371
Свойство полноты когерентных состоянии было впер-
впервые отмечено фон Нейманом [5.4] (стр. 299 русского
издания). Основное свойство когерентных состояний, от-
относящееся к разложению единицы, было впервые уста-
установлено в используемой в настоящее время форме Клау-
дером:
7.4. Klau der J. R., Ann. Phys. (N. Y.), П, 123
A960).
В этой статье неявно используется соответствующее
гильбертово пространство ограниченных непрерывных
функций, но не изучаются его конкретные свойства. Эти
свойства для тесно связанных с ним пространств Се-
гала — Баргманна были впервые систематически изуче-
изучены в работах:
7.5а. Segal I. E., Illinois Journ. Math., 6, 500 A962).
7.56. Segal I. E., Mathematical Problems of Relati-
vistic Physics, Rhode Island, 1963
и особенно в работе:
7.6.	Bargmann V., Comm. Pure Appl. Math., 14,
187 A961).
Связь этих пространств с соответствующим гильбер-
гильбертовым пространством ограниченных непрерывных функ-
функций — «непрерывное представление» — была отмечена
Швебером:
7.7.	Schweber S. S., Journ. Math. Phys., 3, 831
A962).
Все эти пространства, будучи гильбертовыми про-
пространствами с воспроизводящимися ядрами, являются
важным частным случаем пространств, теория которых
развита в работах:
' 7.8а. Aronszajn N., Proc. Cambr. Phil. Soc, 39,
133 A943).
¦ 7.86. Aronszajn N., Trans. Am. Math. Soc, 68,
337 A950).

372	БИБЛИОГРАФИЯ
В связи с разработкой квантовой оптики некоторые
свойства когерентных состоянии были заново открыты
Глаубером:
7.9.	Glauber R. J., Phys. Rev., 131, 2766 A963).
В важной и часто цитируемой работе Глаубера коге-
когерентное состояние, для которого у нас используется обо-
обозначение |г), обычно обозначается через |а).
Свойство однозначности диагональных матричных
элементов когерентных состояний для различных опера-
операторов в наиболее простой форме показано в работе:
7.10.	Mehta С. L., Sudarshan E. С G, Phys.
Rev., 138, В274 A965).
Исследование матрицы плотности с помощью ее диа-
диагональных матричных элементов по когерентным состоя-
состояниям дано в работе [7.10], а также в работах:
7.11.	Ни si mi K-, Proc. Phys. Math. Soc. Japan, 22,
264 A940).
7.12.	К a no Y., Journ. Math. Phys., 6, 1913 A965).
7.13a. M с К e n n a J., FrischH. L, Ann. Phys., 33,
156 A965).
7.136. M с К e n n a J., F r i s с h H. L., Phys. Rev., 145,
93 A966).
С представлением с помощью дифференциальных
операторов легче всего познакомиться по работе [7.6].
Различные дифференциальные операторы, позволяю-
позволяющие получать нормально упорядоченные операторы,
были введены в теорию поля в статье:
7.14.	Anderson J. L., Phys. Rev., 94, 703 A954).
В более простом виде, используемом в квантовой оптике,
они подробно обсуждаются в [7.2], а также в лекциях
Лэкса:
7.15.	Lax M., Brandeis Summer Institute Lectures
1966, vol. 2, New York, 1968.
Когерентные состояния для бесконечного числа сте-
степеней свободы были формально введены в самых первых

БИБЛИОГРАФИЯ	373
работах. Основы теории таких состояний даны в работе:
7.16.	Bargmann V., Proc. Natl. Acad. Sci. U. S.,
48, 199 A962),
где используется в элементарной форме техника функ-
функционального интегрирования, детально изученная Фрид-
рихсом и Шапиро:
7.17.	Friedrichs К- О., Shapiro H. N., Integra-
Integration of Functional, Lecture Notes, New York,
1957.
Можно отметить, что используемые в данной главе
представления по когерентным состояниям имеют много
общих свойств с более широким классом представлений
(непрерывные представления в фазовом пространстве),
частным случаем которых они являются. Основные свой-
свойства этих представлений рассматриваются Клаудером:
7.18.	Klauder J. R., Journ. Math Phys., 4, 1055,
1058 A963); 5, 177 A964).
Строгий анализ этих представлений для большого, но
конечного числа степеней свободы дан в работе:
7.19.	М с Ken na J., Klauder J. R., Journ. Math.
Phys., 5, 878 A964)
а для бесконечного числа степеней свободы — в статье:
7.20.	Klauder J. R., McKenna J., Journ Math.
Phys., 6, 68 A965).
В каждой из этих статей рассматриваются частные
случаи когерентных состояний.
ГЛАВА 8
Правильное квантовое выражение для скорости счета
многократных совпадений в виде среднего от нормально
упорядоченных фотонных операторов дано в следующих
работах:
8.1а. Glauber R. J., Phys. Rev. Lett., 10, 84 A963).
8.16. G 1 a u b e r R. J., Phys. Rev., 130, 2529 A963).
8.1b. Glauber R.J, Phys. Rev., 131, 2766 A963).

374	БИБЛИОГРАФИЯ
8.1г. Glauber R. J., Quantum Electronics (Proc.
3rd Intern. Congr.), ed. N. Bloembergen, P. Gri-
vet, New York, 1964.
8.2.	Glauber R. J., в книге Quantum Optics and
Electronics, ed. C. DeWitt, A. Blandin, C. Cohen-
Tannoudji, New York, 1964, (См. перевод в сб.
«Квантовая оптика и квантовая радиофизика»,
изд-во «Мир», 1966.)
Последняя работа в особенности отличается своей
полнотой. В ней перепечатаны две основные статьи из
[8.1а —8.1 г].
Теория возмущений первого порядка излагается, на-
например, в книге Шиффа [5.2].
Определение полностью когерентных состояний дано
в некоторых из статей [8.1]. Когерентность первого по-
порядка в наиболее полном виде рассмотрена в статье:
8.3.	Titulaer U. M., Glauber R. J., Phys. Rev.,
140, В676 A965); 145, 1041 A966).
С более общей точки зрения частично когерентные со-
состояния обсуждаются в работе:
8.4.	S u d a r s h a n E. С. G., Quantum Theory of Par-
Partial Coherence, Intern. Journ. Theor. Phys., в пе-
печати.
Иерархия корреляционных функций, нормированных
на произведение интенсивностей, была рассмотрена
Глаубером [8.2]. Другие нормализации, введение кото-
которых объясняется отчасти стремлением обобщить понятия
классической комплексной степени когерентности, были
рассмотрены Мета:
8.5.	Mehta С. L., Journ. Math. Phys., 8, 1798 A967)
и Сударшаном [8.4].
Распределение отсчетов в квантовом случае при
очень специальных условиях выведено в работе
8.6.	Ghi elmetti F., Phys. Lett., 12, 210 A964);
в более общем виде оно получено Глаубером [8.2]. В на-
нашем основном выводе распределений отсчетов ши-

БИБЛИОГРАФИЯ	375
роко используется диагональное представление матриц
плотности. Таким образом, хотя этот вывод является
полностью квантовомеханическим, он очень похож на
аналогичный вывод в классической теории. Благодаря
использованию диагонального представления выраже-
выражение для скорости счета для произвольного поля излу-
излучения становится формально аналогичным соответ-
соответствующему выражению в классической теории. Этот
замечательный результат был впервые получен Судар-
шаном:
8.7а. Sudarshan E. С. G., Phys. Rev. Lett., 10,
277 A963).
8.76. Sudarshan E. С. G., Proceedings of the
Symposium on Optical Masers, New York, 1963,
p. 45.
При использовании такого диагонального представ-
представления сохраняется вид классических формул для рас-
распределения отсчетов, выраженных через плотности рас-
распределений. Нужно учесть, что это уже полностью
квантовомеханическое описание, и, следовательно, плот-
плотность распределения не обязательно должна быть поло-
положительно определенной. В диагональном представлении
ф(г) формально соответствует классическому распреде-
распределению. Среди возможных весов cp(z) имеются такие, для
которых выполняется условие ф(г)^>0. Таким свойством
обладают все обычные классические распределения.
В частности, тепловые состояния представляются в клас-
классической теории гауссовым распределением. Квантовое
описание этих состояний с помощью линейной комбина-
комбинации проекций на когерентные состояния с гауссовой ве-
весовой функцией было дано Глаубером [8.1а].
Первоначально диагональный вес записывался
в виде формального бесконечного ряда, состоящего из
дираковских 6-функций и производных возрастающего
порядка. Методы записи диагонального веса без исполь-
использования такого бесконечного ряда рассматриваются в ра-
работе Клаудера и др.:
8.8. К 1 a u d e r J. R., М с К е n n a J., С u r r i e D. G.;
Journ. Math. Phys., 6, 733 A965)

376	БИБЛИОГРАФИЯ
и в работе Мета и Сударшана [7.10] , В последней статье
роль диагонального веса как распределения характери-
характеризуется с помощью линейного функционала. В обеих
статьях содержится хорошо разработанная процедура
определения матриц плотности как предела последова-
последовательности, каждый член которой имеет диагональное
представление. В [8.8] эти веса представляют собой функ-
функции, квадратично интегрируемые, в то время как в [7.10]
они составляются из большого, но конечного числа про-
производных б-функций. В любом случае матрица плот-
плотности однозначно определяется как предел диагонально
представимых операторов. Но последовательности опе-
операторов в работах [8.8] и [7.10] сходятся по норме Гиль-
Гильберта — Шмидта, поэтому правильное среднее значение
гарантируется только для операторов Гильберта —
Шмидта. Существование более строгих свойств сходи-
сходимости по следовой норме, необходимых для получения
правильных средних значений любого ограниченного
оператора, образуемого последовательностью представ-
представленных в диагональном виде операторов с очень глад-
гладкими весовыми функциями, было продемонстрировано
независимо Клаудером и Рокка:
8.9.	Klau der J. R., Phys. Rev. Lett., 16, 534 A966).
8.10.	Rocca F., Compt. Rend., 262, A547 A966).
Первоначально диагональный вес записывался в виде
суммы производных б-функций, порядок которых пол-
полностью определялся максимальным числом фотонов
в соответствующем состоянии. Однако в том случае,
когда в состоянии имеется бесконечное число фотонов,
такой способ записи диагонального веса не дает распре-
распределение в 3D г. Это было доказано в работе:
8.11.	С ah ill К- Е, Phys. Rev., 138, В1566 A965).
С другой стороны, Миллер и Мишкин в работах
8.12а. Miller M. M., Mi sh kin E. A, Phys. Rev.,
164, 1610 A967).
8.126. Miller M. M., Journ. Math. Phys., 9, 1270
A968),

БИБЛИОГРАФИЯ	377
показали, что бесконечный ряд, составленный из произ-
производных б-функций возрастающего порядка, может дать
распределение в 2Г2, являющемся фурье-образом 3J-
Представление Вейля для операторов, использован-
использованное нами при анализе диагонального представления, об-
обсуждается в классической книге:
8.13.	Weyl H., The Theory of Groups and Quantum
Mechanics, New York, 1931, p. 274.
Эти представления и их применение для статисти-
статистического описания в квантовой теории изучались в клас-
классической статье:
8.14.	Moyal J. E., Proc Cambr. Phil. Soc, 45, 91
A949).
Этот же вопрос рассматривается и в работе Вигнера:
8.15.	Wi gner E., Phys. Rev., 40, 749 A932)
и далее развит Сударшаном:
8.16а. S u d a r s h a n E. С. G., Lectures in Theoretical
Physics, Vol. II, New York, 1961.
8.166. Jordan T. F, Sudarshan E. С G, Rev.
Mod. Phys., 33, 515 A961).
Тщательный анализ математических аспектов пред-
представлений Вейля содержится в статьях:
8.17.	Loupias G., Miracle -Sole S., Comm.
Math. Phys., 2, 31 A966).
8.18.	Pool J. С. Т., Journ. Math. Phys., 7, 66 A966).
Свойства операторов, необходимые для полного по-
понимания доказательств диагонального представления,
приведенных в нашей книге, можно найти в книге [3.6],
стр. 40—78 или в работе:
8.19.	Schatten R., Norm Ideals of Completely
Continuous Operators, Berlin, 1960.
Свойства распределений можно найти в классической
работе:
8.20.	Schwartz L., Theorie des distributions, Vol.
I, II, Paris, 1951.

378	БИБЛИОГРАФИЯ
Конкретные распределения и пространства пробных
функций, представляющие для нас более непосредствен-
непосредственный интерес, рассмотрены в книге:
8.21.	Гельфанд И. М., Шилов Г. Е., Обобщен-
Обобщенные функции и действия над ними, М., 1959.
Более популярное изложение свойств распределений
можно найти в книге:
8.22.	L i g h t h i 1 1 M. J., Introduction to Fourier Ana-
Analysis and Generalized Functions, London — New
York, 1959.
Исходя из того, что имеющие физический смысл диа-
диагональные веса должны допускать произвольные свертки
и обладать конечными моментами произвольного по-
порядка, авторы работы:
8.23.	Bonifacio R., Narducci L. М., М о n-
taldi E., Phys Rev. Lett., 16, 1125 A966)
предложили определенный подкласс имеющих физиче-
физический смысл диагональных весов. Для конструирования
сверток получаемый таким путем подкласс диагональ-
диагональных весов слишком узок. Техника «усечения», исполь-
используемая для быстрого доказательства самой общей фор-
формулы свертки [см. (8.205)], неявно используется в статье
[7.20], раздел 2Е.
ГЛАВА 9
Вывод нормального распределения для случайной пе-
переменной, состоящей из большого числа аналогично и
независимо распределенных вкладов, является класси-
классическим примером применения теории вероятности. Эта
стандартная процедура была использована Глаубером
[8.1 в] при выводе нормального распределения диагональ-
диагонального веса в том случае, когда каждый из независимых
вкладов равномерно распределен по фазе.
Энтропия в квантовой теории рассматривалась фон
Нейманом [5.4]. Классические свойства теплового рас-
распределения для поля излучения можно найти в книге:
9.1. Ландау Л. Д., Лифшиц Е. М., Статисти-
Статистическая физика, М., 1964.

БИБЛИОГРАФИЯ	379
Выражение для среднего значения, соответствующего
производящему функционалу распределения отсчетов
в случае нормального распределения по полю, было уже
рассмотрено Райсом [3.3], который вывел приближенные
соотношения, справедливые для произвольных форм
спектра. Точные и асимптотические выражения, справед-
справедливые для определенных форм спектральных линий,
включая лоренцевскую, получены в статье:
9.2.	G г е n a n d е г U., Р о 1 1 а к Н. О., S 1 е р i a n D.,
Journ. Soc. Ind. Appl. Math., 7, 374 A959).
Распределение отсчетов для хаотических полей
в случае лоренцевской формы линии приведено в первом
сообщении Глаубера [8.1а] и выведено в работе [8.2].
Асимптотическое выражение, справедливое при большом
среднем числе отсчетов, также получено Глаубером:
9.3.	Glauber R. J., в книге Physics of Quantum
Electronics, ed. P. L. Kelley, B. Lax, P. E. Tan-
nenwald, New York, 1966.
Распределение отсчетов для таких полей исследова-
исследовалось в экспериментах Фрида и Хауса:
9.4а. Freed С, Н a u s H. A., Phys. Rev. Lett., 15,
943 A965).
9.46. F r e e d С, Н а и s H. A., IEEE Journ. Quantum
Electronics, QE-2, № 8, 190 A966).
Сравнение этих данных с результатами, полученными
с помощью точного выражения (9.87), было выполнено
Баракатом и Глаубером:
9.5.	В а г a k a t R., G 1 a u b e r R. J., неопубликован-
неопубликованные вычисления.
Начальные данные, относящиеся к модели лазера
с диффундирующей фазой, можно найти в работе:
9.6.	Townes С. Н., Nuovo Cimento Suppl., 5, 222
A957).
Более детально свойства такой модели рассматрива-
рассматривались Лэксом:
9.7.	Lax M., Proc. Durham Conf. on Quantum Optics,
1964 (не опубликовано)

380	БИБЛИОГРАФИЯ
и Глаубером в [8.2]; область ее применения определена
в работе:
9.8. Lax M., Phys. Rev., 160, 290 A967).
Общий класс стохастических процессов, используе-
используемый нами при обсуждении модели с диффундирующей
фазой, взят из работы:
. - 9.9. К 1 a u d e r J. R., A n d e r s о n P. W., Phys. Rev.,
125, 912 A962),
в которой рассматриваются физически родственные и
математически эквивалентные задачи, касающиеся спи-
спиновой диффузии. Фундаментальный процесс Орн-
штейна — Уленбека обсуждается в оригинальных ста-
статьях, вошедших в сборник [3.2].
Распределение интенсивности для случая сигнала, на
который накладывается шум, дано Райсом [3.3]. Распре-
Распределение отсчетов, вытекающее из этого диагонального
веса, получено Глаубером [9.3]. Экспериментальная про-
проверка этих распределений была осуществлена Фридом и
Хаусом; ее результаты приведены в работе:
9.10.	Magi 11 P. J., Soni R. P., Phys. Rev. Lett.,
16, 911 A966).
Литературу по более реальным лазерным моделям
можно найти в ссылках, приведенных в [7.15] и в работах:
9.11.	LaxM., Phys. Rev., 145, ПО A966).
9.12.	Haken H., Zs. f. Phys., 190, 327 A966).
9.13.	Sauerman H., Zs. f. Phys., 188, 480 A965);
189, 312 A966).
9.14.	Scully M., Lamb W. E., Phys. Rev. Lett.,
16, 853 A966).
9.15.	Schwabl F., Thirring W.. Ergeb. Exakt.
Naturw., 36, 219 A964).
Более полное обсуждение содержится в [7.2] и в дру-
других работах.
Наше изложение модели связанных систем для ла-
лазера основывается главным образом на работе Гордона:
9.16.	Gordon J. P, Phys. Rev., 161, 367 A967).
Авторы благодарны д-ру Гордону за разрешение ис-
использовать его материалы до их опубликования.

БИБЛИОГРАФИЯ	381
ГЛАВА 10
Прямые наблюдения совпадений отсчетов для раз-
различных задержек во времени были проведены Арекки
и др.:
10.1.	Arecchi F. Т., Gatti E., So na A., Phys.
Lett., 20, 27 A966);
при этом применялись устройства типа описанных в ра-
работе:
10.2.	Ma r t i enssen W., S pi Her E., Am.
Journ. Phys., 32, 919 A964);
Арекки [2.4] усовершенствовал эти приборы, приспо-
приспособив их для работы с подходящими для этих экспе-
экспериментов источниками. Аналогичные совпадения отсче-
отсчетов для обычных тепловых источников наблюдались
Морганом и Манделем:
10.3.	Morgan В. L, Mandel L., Phys. Rev. Lett.,
16, 1012 A966).
Пространственные корреляции в поле двух незави-
независимых лазеров наблюдались в работе:
10.4.	Magyar G., Mandel L., Nature, 198, 255
A963);
их квантовомеханический анализ выполнен Манделем:
10.5.	Mandel L., Phys. Rev., 134, А10 A964).
Методика исследования корреляций интенсивности,
очень похожая на рассматриваемую в данной книге,
обсуждается в работе:
10.6.	Goldberger M. L., Lewis H. W., W a t-
son К. М., Phys. Rev., 132, 2764 A963); 142,
25 A966).
Указанные авторы применили также эти методы при
рассмотрении рассеяния и информации относительно
рассеивателя, которая при этом может быть получена.

Дополнение')
Приводимый ниже материал представляет собой
прежде всего дополнительный список литературы2) по
статистической оптике, охватывающий работы, опубли-
опубликованные в период с 1966 по первую половину 1969 г.
Весьма полная библиография работ, появившихся до
1966 г., содержится в обзоре Вольфа и Манделя [УФН,
87, № 3, 491 A965)]; следует подчеркнуть, что библио-
библиография, приведенная ниже, не претендует на такую пол-
полноту. Вместе с тем была сделана попытка отразить но-
новые направления исследований, обратить внимание на
работы, не отмеченные в основном тексте книги. Крат-
Краткие комментарии, которыми снабжена дополнительная
библиография, преследуют те же цели.
Тематически дополнительная библиография располо-
расположена в том же порядке, что и основной материал книги,
и разбита (разумеется, с определенной долей услов-
условности) на следующие разделы, примерно отвечающие
рубрикации основного текста:
I. Теория когерентности.
П. Статистика фотоотсчетов; интерферометрия интен-
интенсивности.
III.	Статистические явления в нелинейной оптике.
IV.	Квантовая теория оптических полей; динамика и
статистика процессов излучения и эволюции поля.
V. Прием и гетеродинирование оптических сигналов.
VI. Флуктуации в лазерах.
!) Составлено редактором перевода и переводчиками. — Прим.
ред.
2) В составлении этого списка значительная помощь была ока-
оказана кафедрой научной информации МГУ.

ДОПОЛНЕНИЕ	383
Внутри каждого раздела работы имеют независимую
нумерацию и расположены по темам; в ряде случаев
близкие по тематике работы выделяются подзаголовком.
I ТЕОРИЯ КОГЕРЕНТНОСТИ
В течение рассматриваемого периода появился еще
ряд работ, посвященных общей теории когерентности.
Значительное внимание уделялось влиянию частичной
когерентности на работу интерферометров, дифракции
частично когерентного света, голографии при некогерент-
некогерентном освещении. Литература по вопросу о распростране-
распространении световых волн в статистически неоднородных сре-
средах весьма обширна, поэтому из-за недостатка места
мы включили в список лишь монографии Татарского
[44] и Иванова [45] и некоторые статьи, посвященные ис-
исследованию преобразования корреляционных функций
в неоднородной среде. Обратившись к этим работам, чи-
читатель может получить более полное представление об
указанной области.
Общие вопросы
1.	Меа dors J. G., Chang W. S. С, Journ. Opt. Soc.
Amer., 56, № 7, 865 A966).
Properties of partially coherent light.
2.	Mehta С L, Journ. Opt. Soc. Amer., 58, № 9, 1233
A968).
New approach to the phase problem in optical cohe-
coherence theory.
3.	N u s s e n z v e i g H. M., Journ. Math. Phys., 8, № 3,
561 A967).
Phase problem in coherence theory.
4.	M and el L, Journ. Opt. Soc. Amer., 57, № 5 613
A967).
Complex representation of optical fields in coherence
theory.
5.	Boileau E., Picinbono В., Compt. Rend.. 265,
№ 25, В1408 A967).
Remarques sur l'etude des proprietes statistiqueb de
la lumiere coherente.

384	ДОПОЛНЕНИЕ
6.	В о i 1 е a u E., Picinbono В., Journ. Opt. Soc.
Amer., 58, №9, 1238 A968).
Coherence properties of optical fields. II. Study of
experiments described by fourth-order coherence fun-
functions.
7.	Martinssen W., S p i 1 1 e r E., Phys. Rev. Lett.,
16, № 12, 531 A966).
Intensity fluctuations in light beams with several deg-
degrees of freedom.
8.	P e r i n a J., M i s t a L., Czechosl. Journ. Phys.,
B18, № 6, 697 A969).
Normal and antinormal correlations for the superpo-
superposition of thermal and coherent fields.
9.	Karczewski В., Zardecki A., Phys. Lett.,
A28, №9, 627 A969).
On the temperature functions of optical fields.
10.	Kano Y., Journ Phys. Soc. Japan, 24, № 4, 869
A968).
An application of Green's function in the theory of op-
optical coherence.
11.	Zardecki A., Phys. Lett., A24, № 9, 468 A967).
On the multipole coherence effects.
12.	Picinbono В., Proc. Sympos. Mod. Optics, New-
York, 1967, p. 167.
Coherence properties of optical fields: weakly and
strongly coherent fields.
13.	Летохов В. С, ЖЭТФ, 50, № 3, 765 A966).
Об исследовании статистических свойств некогерент-
некогерентного света.
14.	Arecchi F. Т., Nuovo Cimento, Suppl., 4, № 3, 756
A966).
Proprieta statistiche della radiazione coerente.
15.	Paul H., Ann. Phys., 16, № 7—8, 403 A965).
Koharenz der Laserstrahlung in semiklassischer Nahe-
rung.
16.	Di a let is D., Met ha С L., Nuovo Cimento, B56,
№ 1, 89 A968).
Stationarity homogeneity and isotropy in the coherence
theory of the electromagnetic fields.
17.	M e h t a C. L., Journ. Math. Phys , 8, № 9, 1798 A967).
Degree of higher-order optical coherence.

ДОПОЛНЕНИЕ	385
18.	Jakeman Е., О 1 i v е г С. J., Pike E. R., Journ.
Phys. (Proc. Phys. Soc), Al, № 4, 497 A968).
Measurements of the factorization properties of hig-
higher-order optical correlation functions.
19.	Con way J., Phys. Rev., 156, № 5, 1365 A967).
Fluctuations of beam intensity in space and time.
20.	P i с i n b о n о В., В о i 1 e a u E., Journ. Opt. Soc.
Amer., 58, № 6, 784 A968).
Higher-order coherence functions of optical fields and
fluctuations.
21.	D i a 1 e i i s D., Wolf E., Nuovo Cimento, B47, № 1,
113 A967).
The phase retrieval problem of coherence theory as a
stability problem.
22.	Chandra N., V а с h a s p a t i, Ind. Journ. Pure
Appl. Phys., 4, № 7, 257 A966).
Degree of coherence of an extended source.
23.	Surdin M.. Braffort P.. Taroni A., Nature,
210, № 5034, 405 A966).
Blackbody radiation law deduced from stochastic ele-
electrodynamics.
24.	D a v i e s R. D., P о n s о n b у J. E. В., Po i n t о n L.,
J a ge r G. D., Nature, 222, № 5197, 933 A969).
The Jodrell Bank Radio Frequency Digital autocorrela-
autocorrelation spectrometer.
Дифракция и интерференция в поле частично
когерентного света
25.	Shore R. A., Journ. Opt. Soc. Amer., 58, № 11, 1484
A968).
Effect of the phase term in the mutual coherence fun-
function on aperture diffraction patterns.
26.	Shore R., Thompson B. J., Whitney R. E.,
Journ. Opt. Soc. Amer., 56, № 6, 733 A966).
Diffraction by apertures illuminated with partially
coherent light.
27.	Thompson B. J., Journ. Opt Soc. Amer., 56, № 9,
1157 A966).
Multiple-beam interference with partially coherent
light.

386	ДОПОЛНЕНИЕ
28.	М i e 1 е п г К. D., Journ. Opt. Soc. Amer., 57, № 1,
66 A967).
Spectroscope slit images in partially coherent light.
29.	Grimes D. N., Thompson B. J., Journ. Opt. Soc.
Amer., 57, № Ц, 1330 A967).
Two-point resolution with partially coherent light.
30.	McCutchen С W., Journ. Opt. Soc. Amer., 56,
№ 6, 727 A966).
Generalized source and the van Cittert — Zernike
theorem: a study of the spatial coherence required
for interferometry.
31.	Konjaev K. V., Phys. Lett., A24, № 9, 490 A967).
Interference method of two-dimensional Fourier trans-
transform with spatially incoherent illumination.
32.	Burgess T. J., Appl. Optics, 5, № 7, 1239 A966).
Effect of high-velocity mirror translation on optical
coherence in laser interferometers.
33.	Boileau E, Piconbono В., Compt. Rend, 265,
№25, В1408 A967).
Remarques sur l'etude des proprietes statistiques de
la lumiere coherente.
34.	Gouyet J. F., Compt. Rend., AB262, № 3, B189
A966).
Autocorrelation d'une onde electromagnetique statio-
nairs.
35.	H a i g N. D., S i 1 1 i t t о R. M , Phys. Lett, A28, № 6,
464 A968).
An interference experiment with two independent ther-
thermal light sources.
36.	F r a n 5 о n M, M a 1 1 i с к S, Compt. Rend, AB262,
№ 7, B483 A966).
Coherence longitudinale de deux points eclaires par
une source. Applicationsen interferometrie.
Когерентность в голографии
37.	Bert о 1 о t t i M, Gori F, Gu attar i G, Journ.
Opt. Soc. Amer, 57, № 12, 1526 A967).
Coherence requirements in holography.
38.	Man del L, Journ. Opt. Soc. Amer, 55, № 12, 1697
A965).
Color imagery by wavefront reconstruction.

ДОПОЛНЕНИЕ	387
39.	Ma Hick S., Appl. Optics, 6, № 8, 1403 A967).
Degree of coherence in the image of a quasi-monochro-
quasi-monochromatic source.
40.	Mandel L., Journ. Opt. Soc. Amer., 56, № Ц; 1636
A966).
Wavefront reconstruction with light of finite coherence
length.
41.	Lefrancois G., Nguyen Ngoc Chau, Onde
electr., 48, №492, 245 A968).
Influence de la coherence de la source de lumiere dans
1'holographie.
42.	Huhn D., Spiller E., Wagner U., Phys. Lett.,
A27, № 1, 51 A968).
Improved holographic correlation measurements by
use of an additional spatial filter.
43.	LurieM, Journ. Opt. Soc. Amer., 58, № 5, 614
A968).
Fourier-transform holograms with partially coherent
light; holographic measurement of spatial coherence
Изменение когерентности при рассеянии
44.	Татарский В. И., Распространение волн в турбу-
турбулентной атмосфере, М., 1967.
45.	Иванов А. П., Оптика рассеивающих сред, Минск.
1969.
46.	McLennan J. A., Helv. Phys. Acta, 40, № 6, 645
A967).
Space and time dependent fluctuations in a continuous
medium.
47.	H о T. L., Beran M. J., Journ. Opt. Soc. Amer., 58,
№ 10, 1335 A968).
Propagation of the fourth-order coherence function in
a random medium.
48.	Сотский Б. А., Оптика и спектроскопия, 24, № 6,
979 A968).
О рассеянии света с заданной функцией когерент-
когерентности.
49.	S u z u k i Т., Н i о к i R., Japan Journ. Appl. Phys.,
5, №8, 807 A966).
Coherence of light from random medium.

388	ДОПОЛНЕНИЕ
50.	S t r e i f e r W., Journ. Opt. Soc. Amer.,56, №11, 1481
A966).
Spatial coherence in periodic systems.
51.	Fried D. L., Journ. Opt. Soc. Amer., 58, № 7, 961
A968).
Diffusion analysis for the propagation of mutual
coherence.
52.	Фейзулин З. И., Кравцов Ю. А., Изв. ВУЗ,
Радиофизика, 10, № 1, 68 A967).
К вопросу о расширении лазерного пучка в турбу-
турбулентной среде.
53.	Кон А. И., Диссертация на соискание ученой сте-
степени канд. физ.-мат. наук, Институт физики атмо-
атмосферы АН СССР, М., 1969.
Влияние геометрических факторов на статистиче-
статистические характеристики волн, распространяющихся
в турбулентной атмосфере.
54.	С е г n e v a I e M., Crosignani В., D i Porto P.,
Appl. Optics, 7, № 6, 1121 A968).
Influence of laboratory generated turbulence on phase
fluctuations of a laser beam.
П. СТАТИСТИКА ФОТООТСЧЕТОВ;
ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
В основном тексте книги рассмотрены лишь теорети-
теоретические и экспериментальные основы этой области ста-
статистической оптики. Последние годы характеризуются
здесь рядом важных методических достижений (можно
отметить измерения нестационарных законов распреде-
распределения фотоотсчетов, см. например [1]), детальным иссле-
исследованием новых объектов (в частности, модулированных
и многомодовых пучков, см. [18—23]) и дальнейшим раз-
развитием теории фотоотсчетов.
Однако наиболее интересными следует признать но-
новые направления исследования, возникшие в последние
годы. Среди них отметим работы по статистике фотоот-
фотоотсчетов при многоквантовом фотоэффекте (см. например
[16] и работы, цитированные в разделе III настоящего
дополнения). Использование нелинейных преобразований
излучения позволяет предложить ряд новых схем интер-

ДОПОЛНЕНИЕ	389
ферометров интенсивности, пригодных, в частности, для
исследования широкополосных источников. Некоторые
варианты таких схем обсуждаются в работе [17], где рас-
рассмотрена схема измерителя автокорреляционной функ-
функции интенсивности, в которой используется удвоение ча-
частоты света.
Весьма важными представляются исследования, в ко-
которых методы фотостатистики используются в опытах
по рассеянию света. Здесь наряду с работами [33—36],
где высказаны интересные предложения на этот счет,
следует отметить экспериментальную работу Арекки
и др. [37], в которой исследовалось рассеяние света на
специально введенных дискретных рассеивателях в воде,
работы Пайка, Камминса (см. [6]), и работу [38], в ко-
которой измерения автокорреляционной функции интенсив-
интенсивности G<2> (/)=(/(/)/(/ + т) I{1J использовались для
определения ширины линии концентрационного рассея-
рассеяния вблизи критической точки. Сравнение этой методики
с методом гетеродинирования показало, что измерения
автокорреляционной функции интенсивности позволяют
получить более точные данные о ширине линии.
Значительный интерес в самое последнее время вы-
вызывает использование методов интерферометрии интен-
интенсивности для определения формы и длительности сверх-
сверхкоротких световых импульсов. Речь идет о технике так
называемых пикосекундных импульсов (длительностью
10~12 сек), непосредственное исследование которых с по-
помощью фотодетекторов и электронных схем крайне за-
затруднительно. В работах Армстронга [40] и Джордмэйна
и др. [41] на основе наглядных соображений предла-
предлагается определять длительности таких импульсов путем
измерения корреляционной функции интенсивности
GB>(%) (для этого можно использовать различные не-
нелинейные оптические явления, в частности генерацию
второй гармоники и двухфотонную люминесценцию).
К сожалению, современное состояние техники пикосе-
пикосекундных импульсов таково, что в большинстве случаев
речь идет не столько об измерении параметров импуль-
импульсов известного вида, сколько о выяснении вопроса, су-
существуют ли пикосекундные импульсы в излучении дан-
данного многомодового лазера. На языке статистической

390	ДОПОЛНЕНИЕ
оптики речь идет, таким образом, о задаче определения
статистики огибающей на основе измерения одной (или
некоторого набора) корреляционных функций интенсив-
интенсивности
ГШ,	\	(/(/)/(/+ Т,) /(< + Т2) ... /(< + Tn-i))
lt 'Ui, т2 . . . т„_,)	(/(О/1	'
Именно такая постановка вопроса наиболее характерна
для современных работ этого направления. Теоретиче-
Теоретические исследования, выполненные Вебером [45], Клауде-
ром и др. [46], Харрачем [53] и Кузнецовой [47], позво-
позволяют оценить необходимые требования, предъявляемые
к точности измерения функции G<2)(t) в том случае,
когда такие измерения используются для выявления
пикосекундных импульсов. Гораздо более полные све-
сведения об огибающей могут быть получены из измере-
измерений функции G<3)(ti,T2) (см. [50, 51]).
Общие вопросы
1.	Arecchi F. Т., Lectures at the Intern. School oi
Physics «Enrico Fermi», XLII Course Quantum Op-
Optics, Varenna, Italy, 1967.
Photocount distributions and field statistics.
2.	HausH. N., Lectures at the Intern. School of Phy-
Physics «Enrico Fermi», XLII Course Quantum Optics,
Varenna, Italy, 1967.
The measurement of G<2> and its signal to noise ratio.
3.	A r e с ch i F. Т., В e r n e A., Son a A., Burla-
macchi P., IEEE Journ. Quant. Electron., 2, 341
A966).
Photocount distributions and field statistics.
4.	Morawitz H., Journ. Phys., 195, № 1, 20 A966).
Photon correlations in a multiple coherent and over-
overlapping chaotic radiation field.
5.	Scarl D. В., Phys. Rev. Lett., 17, № 12, 663 A966).
Measurement of photon time-of-arrival distribution
in partially coherent light.
6.	Pike E. R., Inaugural Conference of the European
Physical Society, Florence, April, 1969.
Photon Statistics.

ДОПОЛНЕНИЕ	391
7.	Korenman V., Phys. Rev., 154, № 5, 1233 A967).
Dynamical computation of photon correlations and
counting statistics.
8.	Bedard G., Phys. Lett., A24, № 11, 613 A967).
Photon counting statistics of laser light.
9.	Bedard C, Phys. Rev., 151, № 4, 1038 A966).
Photon counting statistics of Gaussian light.
10.	Clausen H. D., Acta Phys. Austriaca, 25, № 3 266
A967).
Zur Photonstatistik der Laseistrahlung.
11.	AlkemadeC. Th. J., В о 1 w i j n P. T. Va n der
Veer J. H. C., Phys. Lett., 22, № 1, 70 A966).
Single-beam measurement of Bose-Einstein fluctua-
fluctuations in a natural Gaussian radiation field.
12.	Martienssen W., Spiller E., Phys. Rev., 145,
№ 1, 285 A966).
Fluctuation measurements in mixed light fields.
13.	ГерценштейнИ.Е, ДАН СССР, 166,317 A966).
К вопросу о флуктуациях фототека.
14.	Скачков Ю. Ф.," ЖЭТФ, 52, № 3, 637 A967).
Исследование временной корреляции фотонов, излу-
излучаемых возбужденными атомами аргона.
15.	N u s s b a u m G. Н., Р i p k i n F. M., Phys. Rev. Lett.,
19. № 19, 1089 A967).
Correlation of photons in cascade and the coherence
time of the 63P, state of mercury.
16.	T e i с h M. C, D i a m e n t P., Journ. Appl. Phys.,
40, №2, 625 A969).
Two-photon counting statistics for laser and chaotic
radiation.
17.	A x м а нов С. А., Ч и р ки н А. С, Тункин В. Г.,
Journ. Opioelectron, 1, 196 A968).
Transformation of photo — counting statistics by non-
nonlinear light conversion.
Статистика фотоотсчетов для модулированных и
многомодовых световых пучков
18.	Magi 11 P. J., Soni R. P., Phys Rev. Lett., 16,
№20, 911 A966).
Photoelectric counting distributions for a noise-modu-
noise-modulated system.

392	ДОПОЛНЕНИЕ
19.	F г а у S., Johnson F. A, Jones R., McLean
Т. P., Pike E. R., Phys. Rev., 153, Al> 2, 357 A967).
Photon-counting distributions of modulated laser
beams.
20.	Ma gill P. J., Journ. Appl. Phys., 37, № 5, 2198
A966).
Influence of small signal modulation on photoelectron
counting of He — Ne laser intensity fluctuations.
21.	Pearl P., TroupG. J. Phys, Lett. A27, № 8, 560
A968),
Modulated laser beam photon counting distribu-
distributions.
22 В e r t о 1 о 11 i M., С г о s i g n a n i В., D i Porto P.,
Sette D., Phys. Rev., 150, № 4, 1054 A966).
Coherence and statistical properties of two-mode laser
beam.
23.	В e r t о 1 о t t i M., С г о s i g n a n i В., D i Porto P.,
S e 11 e D., Zs. Phys., 205, 129 A967).
Photostatistics of an /V-mode laser field.
Методика
24.	Johnson F. A., Jones R., McLean T. P., Pike
E. R., Phys. Rev. Lett., 16, № 13, 589 A966).
Dead-time corrections to photon counting distribu-
distributions.
25	Chang R. E., Korenman V., Detenbeck
R. W., Phys. Lett., A26, № 9, 417 A968).
Photon statistics for threshold laser light with finite
counting time.
26	D a v i d s о n F., M a n d e 1 L., Journ. Appl. Phys. 39,
№ 1, 62 A968).
Photoelectric correlation measurements with time-to-
amplitude converters.
27	Goetz K., UnangstD, Phys. Lett., 23, № 11,
667 A966).
Rotierende Mattscheiben zur Anderung der Koharenz
von Laserlicht.
28	Bedard G., Proc. Phys. Soc, 90, № 1, 131 A967).
Dead-time corrections to the statistical distribution of
photoelectrons.

ДОПОЛНЕНИЕ	393
Интерферометры интенсивности, корреляционная
спектроскопия
29.	Go I d berg er M. L., Lewis H. W., Watson
K. M., Phys. Rev., 142, № 1, 25 A966).
Intensity-correlation spectroscopy.
30.	Phi Hi ps D. Т., Kleiman H., Davis S. P.,
Phys. Rev., 153, № 1, 113 A967).
Intensity-correlation linewidth measurement.
31.	Артемьев В. В., Оптика и спектроскопия, 25, № 5,
635 A968).
Корреляционная спектроскопия оптических излуче-
излучений.
32.	Gamo H., Journ. Opt. Soc. Amer, 56, № 4, 441
A966).
Stellar intensity interferometer. I. Signal-to-noise ra-
ratio for the high-intensity radiation.
Методы фотостатистики и интерферометрии
интенсивности при исследовании рассеяния света
33.	Bertolotti M., С г о s i g n a n i В., D i Porto P.,
S e t t e D., Phys. Rev., 157, 146 A967).
Photostatistics of light scatterted by a liquid.
34.	Bertolotti M., De Pasquale D., Sette D.,
Nuovo Cimento, B52, № 2, 560 A967).
Effects of second-sound excitations on the photosta-
photostatistics of a laser beam.
35.	Gori F, Sette D., Phys. Rev. Lett., 17, № 7, 361
A966).
Spatial coherence of light scattered from liquids.
36.	Зельдович Б. Я-, Клышко Д. Н., Письма
ЖЭТФ, 9, 69 A969).
Статистика поля при параметрической люминесцен-
люминесценции.
37.	А г е с с h i F. Т., Giglio M., Tartari V., Phys.
Rev., 163, 186 A967).
Scattering of coherent light by a statistical medium.
38.	Chen S. H., Polonsky-Ostrovsky N.. Journ.
Phys. Soc. Japan, Suppl., 26, 179 A969).
Intensity correlation measurements of light scattered
from a two-component fluid near the critical point

394	ДОПОЛНЕНИЕ
39.	MillerS. A., Rev. Sci. Instr., 39, № 12, 1923 A968).
Inexpensive photon counting system for Raman spect-
roscopy.
Измерение длительности сверхкоротких световых
импульсов методами интерферометрии интенсивности
40.	ArmstrongJ. A., Appl. Phys. Lett., 10, 16 A967).
Measurements of picosecond laser pulse widths.
41.	GiordmaineJ. A., Rentzepis P. M., Sha-
Shapiro S. L., Wecht K. W. Appl. Phys. Lett., 11,
216 A967).
Two photon excitation of fluorescence by picosecond
light pulses.
42.	R e n t z e p i s P. M., Duguay M. A., Appl. Phys.
Lett., 11, 218 A967).
Picosecond light pulse display using two different
optical frequencies.
43.	D u g u а у M. A., Shapiro S. L., R e n t z e-
pis P. M., Phys. Rev. Lett., 19, 1014 A967).
Spontaneous appearance of picosecond pulses in ruby
• and Nd: glass lasers.
44.	Shapiro S. L., D u g u а у М. А., К r e u z e r L. В.,
Appl. Phys. Lett., 12, 36 A968).
Picosecond substructure of laser spikes.
45.	Weber H P., Phys. Lett., 27A, 321 A968).
Comments on the pulse width measurement with two-
photon excitation of fluorescence.
46.	Klauder J. R., Duguay M. A., G i о г d-
maine J. A., Shapiro S. L., Appl. Phys. Lett.,
13, 174 A968).
Correlation effects in the display of picosecond pul-
pulses by two-photon techniques.
47.	Кузнецова Т. И., ЖЭТФ, 55, 2453 A968).
К проблеме регистрации сверхкоротких световых им-
импульсов.
48.	Кузнецова Т. И., Препринт Физического инсти-
института АН СССР, № 47 A968).
Об особенностях некоторых методов измерения дли-
длительности сверхкоротких импульсов.

ДОПОЛНЕНИЕ	395
49.	Weber H. P., Dandliker R., Phys. Lett. 28A,
77 A968).
Method for measurement the shape asymmetry of pi-
picosecond light pulses.
50.	Weber H. P., Dandliker R., IEEE Journ.
Quant. Electr., 4, № 12, 1009 A968).
Intensity interferometry by two photon excitation of
fluorescence.
51.	В 1 о u n t E. J., К 1 a u d e r J. R., Journ. Appl. Phys.,
40, 2874 A969).
Recovery of laser intensity from correlation data.
52.	Klauder J. R., Appl. Phys. Lett., 14, 147 A969)
Spectral criterion for mode locked signals.
53.	Harrach R. J., Appl. Phys. Lett., 14, 148 A969).
Determination of ultrashort pulse widths by two
photon fluorescence patterns.
III. СТАТИСТИЧЕСКИЕ ЯВЛЕНИЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
В статистической нелинейной оптике можно выде-
выделить два круга задач.
1.	Задачи, связанные с выяснением влияния про-
пространственной и временной когерентности излучения на
протекание нелинейных оптических явлений («стати-
(«статистика излучения»).
2.	Задачи, связанные с изучением нелинейных опти-
оптических эффектов в статистически неоднородных средах,
с исследованием влияния собственных квантовых флук-
флуктуации, возникающих в среде, на протекание нелиней-
нелинейных оптических явлений («статистика среды»).
Эффекты, обусловленные «статистикой излучения»,
впервые наблюдались в опытах по генерации оптических
гармоник, проводившихся с твердотельными лазерами
еще в 1963—1964 гг. [10, 11]. Речь шла о неожиданно
сильных, так называемых избыточных флуктуациях мощ-
мощности второй гармоники, генерируемой многомодовым
рубиновым лазером. В работах [10—12] эти флуктуации
нашли удовлетворительное объяснение на основе до-
довольно простой статистической модели — многомодо-
вого излучения со случайным (в интервале 0—2я) раз-
разбросом фаз в эквидистантных модах. Вместе с тем,

396	ДОПОЛНЕНИЕ
в последующих работах было показано, что в ряде слу-
случаев надо учитывать дополнительные факторы — флук-
флуктуации числа мод, флуктуации расходимости и т. п.
Значительным стимулом для дальнейших исследова-
исследований проблем, связанных со «статистикой излучения», по-
послужили успешные опыты по генерации гармоник и сме-
смешению частот с использованием нелазерных источников'
света [13, 14]. Здесь речь идет по существу об исполь-
использовании в нелинейной оптике источников гауссового
шума, обладающих к тому же сравнительно небольшими
масштабами временной и пространственной корреляции.
Вслед за указанными экспериментами появились теоре-
теоретические работы, в которых исследовались влияние вре-
временной и пространственной когерентности основного из-
излучения на протекание нелинейных оптических процес-
процессов [15—18], фотостатистика оптических гармоник,
получаемых от лазерных и нелазерных источников [19]
и т. п. При изучении статистических эффектов в нели-
нелинейной оптике оказалась полезной пространственно-вре-
пространственно-временная аналогия [20], позволяющая дать наглядную ин-
интерпретацию влияния пространственной и временной не-
некогерентности излучения на протекание того или иного
нелинейного оптического явления.
Отметим, что некоторые общие вопросы теории нели-
нелинейного взаимодействия случайно модулированных волн
применительно к волнам в плазме рассматривались Цы-
товичем [8].
Наконец, в самое последнее время в связи с техникой
синхронизации мод возродился интерес к изучению ум-
умножения и смещения частот в поле многомодовых гене-
генераторов, обладающих статистическим разбросом фаз
в модах [21]. Частично возникающие здесь проблемы
связаны с разработкой интерферометров интенсивности,
предназначенных для регистрации пикосекундных им-
импульсов (см. также раздел II настоящего дополнения).
Практические схемы таких интерферометров служат на-
наглядной иллюстрацией эффективности методов нелиней-
нелинейной оптики при измерении высших корреляционных
функций оптических полей. Подобные измерения пред-
представляют значительный интерес для статистической оп-
оптики вообще.

ДОПОЛНЕНИЕ	397
Сходные статистические задачи возникают и при ис-
исследовании многофотонного поглощения. Высокие сте-
степени нелинейности, которые здесь удается использовать
(напомним, что в настоящее время зарегистрирована
шести- и семифотонная ионизация газов), позволяют
ставить вопрос об измерении корреляций весьма высо-
высоких порядков. Представление о современном состоянии
этой области статистической нелинейной оптики можно
получить из работ [23—31]; следует отметить, правда,
что здесь дело пока не вышло за рамки теоретического
рассмотрения вопроса.
Среди работ, в которых исследуются эффекты, обус-
обусловленные «статистикой среды», следует отметить ра-
работы [32—34], где изучались генерация гармоник и па-
параметрическое усиление в слабо неоднородных и поли-
полидоменных кристаллах, генерация оптических гармоник
в кристаллических порошках [35, 36], вынужденное ком-
комбинационное рассеяние в порошках [37]. Однако в рас-
рассматриваемой области наиболее интересными, несом-
несомненно, следует признать работы по так называемому
нелинейному рассеянию и работы, посвященные кван-
квантовым флуктуациям в параметрических процессах.
Под нелинейным рассеянием здесь понимается не-
некогерентное рассеяние, при котором интенсивность рас-
рассеянного света нелинейно зависит от интенсивности рас-
рассеиваемого излучения').
Впервые нелинейное рассеяние было обнаружено
Терхьюном и др. [38] (теория явления развита в работах
[39—41]). Речь идет о возникновении рассеяния на уд-
удвоенной частоте (и близких к ней частотах) падающего
излучения в средах, в которых когерентная генерация
второй гармоники невозможна (в средах с центром ин-
инверсии); последнее открывает интересные перспективы
исследования нелинейных свойств отдельных молекул
(нелинейное молекулярное рассеяние).
Другим примером нелинейного рассеяния, связанного
уже с макроскопическими неоднородностями, является
') Нелинейная (экспоненциальная) зависимость имеет место,
как известно, и при вынужденном рассеянии; однако в последнем
случае процесс является существенно когерентным, что связано с
сильным воздействием рассеиваемого излучения на среду.

398	ДОПОЛНЕНИЕ
нелинейное рассеяние на неоднородностях, возникающих
вблизи критической точки. Такое рассеяние (на второй
гармонике падающего излучения) было исследовано
недавно Фрейндом [42] в кристаллах NH4C1 вблизи точки
фазового перехода второго рода. Исследование указан-
указанного рассеяния позволяет получить новую информацию
о явлениях вблизи критической точки; интересно, что
обычная методика линейного рассеяния оказывается
здесь неэффективной (линейные оптические свойства
NH4CI практически не меняются вблизи рассматривае-
рассматриваемой критической точки). В работе [43] детально иссле-
исследована угловая структура такого рассеяния.
Изучение статистических явлений в параметрических
процессах в значительной мере стимулируется послед-
последними успехами в создании эффективных параметриче-
параметрических световых генераторов непрерывного действия. Инте-
Интересно, что лишь в 1967 г., через два года после запуска
параметрических генераторов света, появились работы,
в которых были зарегистрированы собственные шумы
параметрических устройств. Речь идет о специфическом
спонтанном рассеянии в прозрачной среде, которое при-
принято называть «параметрической люминесценцией» ').
Среди работ по параметрической люминесценции необ-
необходимо отметить теоретические исследования Клышко
[44], Клеймана [49], Джалоренци и Танга [48]; экспери-
экспериментальные данные об эффекте содержатся в работах
[45—47]. В работах Хакена и др. [52—54] рассмотрены
статистические явления в оптическом параметрическом
генераторе, работающем в установившемся режиме;
здесь вычислены, в частности, ширина спектральной ли-
линии и уровень амплитудных флуктуации.
Аналогичные вопросы возникают, разумеется, и при
рассмотрении других аналогичных процессов — выну-
вынужденного комбинационного рассеяния, вынужденного
рассеяния Мандельштама — Бриллюэна и т. п. Источ-
Источники флуктуации в этих процессах детально исследованы
') Следует отметить, что использование термина «люминесцен-
«люминесценция» здесь не совсем удачно; фактически речь идет не о люминес-
люминесценции, а о процессе, аналогичном спонтанному рассеянию (комби-
(комбинационному или рассеянию Мандельштама — Бриллюэна).

ДОПОЛНЕНИЕ	399
уже достаточно давно. Исчерпывающую информацию
о них дают многочисленные работы, посвященные спон-
спонтанным вариантам указанных видов рассеяния.
Следует отметить, однако, что в обсуждаемом на-
направлении сделано пока сравнительно мало; больший^
ство работ, в которых рассматриваются статистические
эффекты при вынужденном рассеянии, не выходит, как
правило, за рамки вычисления ширины линии в режиме
заданного поля накачки. Ширина линии для одномодо-
вой накачки вычислена Тангом [55], а для накачки об*
щего вида — Дьяковым [57]. Лишь недавно Дьяков [56]
оценил ширину линии вынужденного рассеяния Ман-
Мандельштама — Бриллюэна в существенно нелинейном ре-
режиме.
В заключение упомянем работы, в которых иссле-
исследуются статистические явления при самофокусировке
[58, 59]. По мнению Шимоды [59], в некоторых астрофи-
астрофизических явлениях определенную роль может играть са-
самофокусировка белого света в межзвездной плазме.
Общие вопросы
1.	Shen Y. R.. Phys. Rev., 155, № 3, 921 A967).
Quantum statistics of nonlinear optics.
2.	Prakash H., Chandra N., Vachaspati,
Nuovo Cimento, B57, № 1, 161 A968).
Coherence properties of optical fields in a nonlinear
dielectric.
3	Teich M. C, Wolga G. L. Phys. Rev. Lett., 16,
№ 14, 625 A966).
Multiple-photon-processes and higher order correla-
correlation functions.
4	Lambropoulos P., Phys. Rev., 156, № 2, 286
A967).
Quantum statistics of a two-photon quantum amplifier.
5	В e r a n M. J., D e V e 1 i s J. В., Journ. Opt. Soc.
Amer., 57, № 2, 186 A967).
Propagation of the coherence function on nonlinear
dielectrics.
6. BeranM., D e V e 1 i s J., ParrentG,, Jr., Phys.
Rev., 154, №5, 1224 A967).
Measurement of fourth-ordei coherence functions.

400	ДОПОЛНЕНИЕ
7.	Гладун А. Д., Барашев П. П., УФН. 98, 493
A969).
Внешний многоквантовый фотоэффект.
8.	Цытович В. Н., Нелинейные эффекты в плазме,
М., 1967.
9.	А х м а н о в С. А., Ч и р к и н А. С, Изв. ВУЗ, Радио-
Радиофизика, 13, № 6 A970).
Статистические явления в нелинейной оптике,
Статистические явления при умножении
и сложении частот
10.	Ах м а нов С. А., Ковригин А. И. Хохлов Р. В.,
Чу на ев О. Н., ЖЭТФ, 45, 1336 A963).
О длине когерентного взаимодействия световых волн
в нелинейной среде.
11.	DucuingJ., BloembergenN., Phys. Rev., 133,
A1493 A964).
Statistical fluctuations in nonlinear optical processes.
12.	АхмановС. А., КовригинА. И., Ч и р к и н А. С,
Ч у н а е в О. Н., ЖЭТФ, 49, 829 A966).
Статистические эффекты при генерации оптических
гармоник.
13.	Smith A., Bra si a u N., Journ. Appl. Phys., 34,
2105 A963).
Observation of an optical difference frequency.
14.	McMahon D. N., Journ. Appl. Phys., 37, 4832
A966).
Quantitative nonlinear sum-frequency experiments
using incoherent light.
15.	Ахманов С. А., Чиркин А. С, Радиотехника и
электроника, 11, 1915 A966)
Об удвоении частоты спектральной линии конечной
ширины при волновых взаимодействиях в нелиней-
нелинейной среде.
16.	Ахманов С. А., Су хор у ко в А. П., Чир-
Чирки н А. С, Изв. ВУЗ, Радиофизика, 10, № 12, 1639
A967).
Об апертурных ограничениях эффективности опти-
оптических удвоителей частоты.

ДОПОЛНЕНИЕ	401
17.	Сотский Б. А., Докл. АН БССР, 12, № 10
A968).
О влиянии пространственной когерентности первич-
первичного излучения на интенсивность гармоники.
18.	Ma t h i eu E., Weber H P., Zs. angew. math,
Phys., 2, 19, 980 A968).
Per Einfluss der Linienbreite beirn optischen Mischen.
19.	Тункин В. Г., Чиркин А. С, ЖЭТФ, 58, № 1,
191 A970).
Статистика фотоотсчетов нелинейно преобразован*
ного светового излучения.
20.	Ах м а нов С. А., Сухоруков А. П., Ч и р.
кин А. С, ЖЭТФ, 55, № 10, 1430 A968).
Нестационарные явления и пространственно-времен-
пространственно-временная аналогия в нелинейной оптике.
21.	Grutter A. A., Weber H. P., Pandliker R.
Phys. Rev., 185, № 2, 629 A969).
Imperfectly mode-locked laser emission and its effects
on nonlinear optics.
22.	Zuckerman J. L., DeVelis J. В., Journ. Opt. Soc.
Amer., 58, №2, 175 A968).
Classical coherence formulation of second-harmonic
generation in the optical parametric amplifier.
Влияние когерентности излучения
на многофотонное поглощение
23.	В г и п n e r W., P a u I H., R i с h t е г С, Ann. Phys.,
16, № 7—8, 343 A965).
Quantenmechanische Koharenz bei mehrphotonen Pro-
zessen.
24.	Lambropoulos P., Kikuchi C, Osborn
R. K., Phys. Rev., 144, № 4, 1081 A966).
Coherence and two-photon absorption.
25.	Meadors J. G., IEEE Journ. Quant. Electron., 2,
№ 9, 638 A966).
Coherence effects in multiphoton absorption processes.
26.	Menegozzi L., Nuovo Cimento, Suppl., 4, № 1, 15
A966).
Coherence properties of two-photon systems.
27.	Lambropoulos P., Phys. Rev., 168. 1418 A968).
Field-correlation effects in two-photon processes.

402	ДОПОЛНЕНИЕ
28.	Mollow В. R., Phys. Rev., 175, № 5, 1555 A968).
Two-photon absorption and field correlation func-
functions.
29.	С h a n d r a N, V а с h a s p a t i, Ind. Journ. Pure
Appl. Phys., 6, №3, 111 A968).
Effect of coherence on three-photon absorption.
30.	С a r u s о 11 о S., For пае a G., Polacco E.,
. Phys. Rev., 165, № 5, 1391 A968).
Multiphoton absorption and coherence.
31.	Gardner J. W., Internal Journ. Electron., 21,
№ 5, 479 A966).
The role of photon statistics in laser sparks.
Нелинейные оптические эффекты в неоднородных
средах
32.	Б е с п а л ов В. И., Изв. ВУЗ, Радиофизика, 9,
1117 A966).
Удвоение частоты света в нелинейной среде со слу-
случайными неоднородностями.
33.	Беспалов В. И., Изв. ВУЗ, Радиофизика, 10, 74
A967).
Параметрическое усиление света в нелинейной среде
со случайными неоднородностями.
34.	Чир кип А. С, в сб. «Нелинейная оптика», М.,
1968.
Удвоение частоты в полидоменных кристаллах.
35.	Kurtz S. K-, Perry Т. Т., Journ. Appl. Phys, 39,
3798 A968).
A powder technique for the evaluation of nonlinear
optical materials.
36.	Филимонов А. А., Суворов В. С, Рез И С
ЖЭТФ, 56, 1519 A969).
Исследование генерации второй гармоники излуче-
излучения ОКГ в мелкодисперсных кристаллических сре-
средах.
37.	Сущи н.скй М. М., Спектры комбинационного рас-
рассеяния молекул и кристаллов, М., 1969.
38.	Т е г h u n e R., M a k e r P., SavageC, Phys. Rev.
Lett,. 14, 681 A965).
Measurements of nonlinear light scattering.

ДОПОЛНЕНИЕ	403
39.	Kielich S., IEEE Journ. Quant. Electron., 4, 744
A968).
Molecular interactions in optically induced nonlinea-
rities.
40.	Ax м а нов С. А., Клышко Д. Н., Письма ЖЭТФ,
2, 15 A965)..
Трехфотонное молекулярное рассеяние света.
41.	С т р и же век и й В. Л., Клименко В. М, ЖЭТФ,
53, 244 A967).
Трехфотонное рассеяние света в изотропной среде.
42.	Freu n d I., Phys. Rev. Lett., 19, 1288 A967).
Critical harmonic scattering in NH4C1.
43.	Freund I., Phys. Rev. Lett., 21, 1404 A968).
Nonlinear diffraction.
Статистические явления в параметрических процессах
44.	Клышко Д. Н., ЖЭТФ, 55, 1006 A968).
Рассеяние света в среде с нелинейной поляризуемо-
поляризуемостью.
45.	Ахманов С. А., Фадеев В. В., Хохлов Р. В.,
Чу наев О. Н., Письма ЖЭТФ, 6, № 4, 575
A967).
Квантовые шумы в параметрических усилителях
света.
46.	Byer R. L, Harris S. E., Phys. Rev., 168, 1064
A968).
Power and bandwith of spontaneons parametric emis-
emission.
47.	Wei n berg D., Appl. Phys. Lett., 14, 31 A969).
Four-photon optical parametric noise in water.
48.	G i a 1 1 о r e n z i T. G., Tang С L., Phys. Rev., 166,
225 A968).
Quantum theory of spontaneous parametric scattering
of intense light.
49.	Kl ei ma n D. A., Phys. Rev., 174, 1027 A968).
Theory of optical parametric noise.
50.	Зельдович Б. Я-, Клышко Д. Н., Письма
ЖЭТФ, 9, 69 A969).
Статистика поля при параметрической люминесцен-
люминесценции.

404	ДОПОЛНЕНИЕ
51.	Louise 11 W. H., Экспресс-инф. «Радиотехника
СВЧ и квантовая радиотехника», № 8, 1 A968).
Квантовый шум в оптических параметрических уст-
устройствах.
52.	Graham R., На ken H., Zs. Phys., 210, № 3, 176
A968).
The quantum-fluctuations of the optical parametric
oscillator. I.
53.	Graham R., Zs. Phys., 210, № 4, 319 A968).
The quantum-fluctuations of the optical parametric
oscillator. II.
54.	Graham R., Zs. Phys., 211, № 5, 469 A968).
Photon statistics of the optical parametric oscillator
including the threshold region. Transient and steady
state solution.
55.	Tang C, Journ. Appl. Phys., 37, 2945 A966).
Saturation and spectral characteristics of the Stokes
emission in the stimulated Brillouin process.
56.	Дьяков Ю. Е., Письма ЖЭТФ, 10, 545 A969).
О ширине линии вынужденного рассеяния Мандель-
Мандельштама— Бриллюэна при насыщении.
57.	Дьяков Ю. Е, Письма ЖЭТФ, 9, 487 A969).
Влияние немонохроматичности накачки на форму
спектра вынужденного рассеяния Мандельштама —
Бриллюэна.
Статистические явления при самофокусировке света
58.	Б е с п а л о в В. И., Л и т в а к А. Г., Т а л а н о в В. И.,
в сб. «Нелинейная оптика», М., 1969.
Самовоздействия световых волн в нелинейных сре-
средах.
59.	Shi mod а К., Journ. Phys. Soc. Japan, 24, 1380
A968).
Self-trapping of white light and the redshift by non-
nonlinear optical effects in a stellar plasma.
IV. КВАНТОВАЯ ТЕОРИЯ ОПТИЧЕСКИХ ПОЛЕЙ;
ДИНАМИКА И СТАТИСТИКА ПРОЦЕССОВ ИЗЛУЧЕНИЯ
И ЭВОЛЮЦИИ ПОЛЯ
Здесь приведены работы, освещающие теоретические
вопросы квантовой оптики. Отметим прежде всего книгу

ДОПОЛНЕНИЕ	405
Луиселла [1], посвященную основам теории квантовых
процессов в радиофизике и оптике. Сходные вопросы
рассмотрены в книге Пантелла и Путхоффа [2]. В ра-
работах [3—17] обсуждаются различные вопросы, относя-
относящиеся к способам описания квантованного электромаг-
электромагнитного поля. В частности, в [14, 15] подробно рассмо-
рассмотрены различные типы распределений квазивероятностей
и квантовых характеристических функций.
В работах [18—36] рассматриваются конкретные зада-
задачи динамики и статистики квантованного электромагнит-
электромагнитного поля. Здесь следует отметить большой цикл работ
Лэкса [29—34] под общим названием «Квантовый шум».
В работе Моллоу [36] аппарат квантовых характе-
характеристических функций применяется для решения наибо-
наиболее общих задач квантовой механики с гамильтонианом,
билинейным по осцилляторным переменным.
1.	Louise 11 W. H., Radiation and Noise in Quantum
Electronics, New York, 1965.
2.	P a n t e 1 1 R., P u t h о f f P., Fundamentals of Quan-
Quantum Electronics, New York, 1969. (Готовится русский
перевод.)
3.	Mandel L, Proc. Sympos Mod. Optics, New York,
1967, p. 143.
Some recent work on coherence properties of photon
beams.
4.	M i 1 1 er M. M., Phys. Lett., A27, № 3, 185 A968).
Quantum and classical descriptions of two-mode laser
field.
5.	MehtaC. L, Nuovo Cimento, B45, № 2, 280 A966).
Degree of coherence of an arbitrary order.
6.	В a r a k a t R., Journ. Opt. Soc. Amer., 56, № 6, 739
A966).
Theorem in coherence theory.
7.	KanoY, Journ. Math. Phys., 6, № 12, 1913 A965).
A new phase-space distribution functions in the sta-
statistical theory of the electromagnetic field.
8.	Mandel L., Phys. Rev., 152, № 1, 438 A966).
Antinormally order correlations and quantum coun-
counters.

406	ДОПОЛНЕНИЕ
¦9. Miller M. M., Mishkin E. A., Phys. Lett., A24,
№ 3, 188 A967).
Anti-correlation effects in quantum optics.
10.	Paul H., Fortschr. Phys., 14, № 3, 141 A966).
Beitrag zur Quanteniheorie der optischen Koha-
renz.
11.	Roc с a F., Journ. Phys., 28, № 1, 113 A967).
Coherence optique et convolution gauche un theoreme
d'equivalence optique.
12.	Man del L., Wolf E., Phys. Rev., 149, № 4, 1033
A966).
Photon statistics and classical fields.
13.	Glauber К. Е., Proc. Sympos Mod. Optics, New
York, 1967, p. 1.
Photon fields and classical fields.
14.	С о h i 1 1 K. E., G 1 a u b e r R. J., Phys. Rev., 177, № 5,
1857 A969).
Ordered expansions in Boson amplitude operators.
15.	Cohill K. E., Glauber R. J.( Phys. Rev., 177,
' №5, 1882 A969).
Density operators and quasiprobability distributions.
16.	Ledinegg E, Zs. Phys., 191, № 2,"l77 A966).
Zur Koharenz n-ter Ordnung in der Quantenelektrody-
namik.
17.	Paul H., Ann. Phys., 19, № 3—4, 210 A967).
Quantenmechanische Beschreibung der Interferenz
zwischen unabhangigen nichtmonochromatischen
Lichtstrahlen.
18.	Шелепин Л. А., ЖЭТФ, 54, № 5, [463 A968).
К теории когерентного спонтанного излучения.
19.	Морозов В. А., Оптика и спектроскопия, 22, № 2,
325 A967).
К теории ширины линии спонтанного когерентного
излучения.
20.	Теплицкий Э. Ш., ЖЭТФ, 55, № 4, 1272 A968).
О возможности резонансного изменения когерентных
свойств света при рассеянии в многоуровневой си-
системе.
21.	Летохов В. С, ЖЭТФ, 53, № 6, 2210 A967).
Квантовая статистика многомодового излучения ан-
ансамбля атомов.

ДОПОЛНЕНИЕ	407
22.	Зельдович Б. Я., Переломов А. М., По-
Попов В. С, ЖЭТФ, 55, № 2, 589 A968).
Релаксация квантового осциллятора.
23.	Зельдович Б. Я., Переломов А. М., По-
пов В. С, ЖЭТФ, 57, 196 A969).
Релаксация квантового осциллятора при наличии
внешней силы.
24.	Бел а вин А. А., Зельдович Б. Я-, Перело-
Переломов А. М., Попов В. С, ЖЭТФ, 56, № 1, 264
A969).
Релаксация квантовых систем с эквидистантным
спектром.
25.	Bergman S. M.( Journ. Math. Phys., 8, № 2, 159
A967).
Induced and spontaneous emission.
26.	Robl H. R., Phys. Lett., A24, № 5, 288 A967).
Conservation of Gaussian distributions of coherent
states.
27.	Lachs G., Journ. Appl. Phys., 38, № 9, 3439 A967).
Quantum statistics of multiple-mode, superposed co-
coherent and chaotic radiation.
28.	Fleck J. A., Jr., Phys. Rev., 149, № 1, 322 A966).
Quantum theory of laser radiation. II. Statistical as-
aspects of laser light.
29.	Lax M., Phys. Rev., 145, № 1, 110 A966).
Quantum noise. IV. Quantum theory of noise sour-
sources.
30.	Lax M., IEEE Journ. Quant. Electron., 3, № 2, 37
A967).
' Quantum noise. VII. The rate equations and ampli-
amplitude noise in lasers.
31.	Lax M., Lou is el 1 W. H., IEEE Journ. Quant. Elec-
/ tron., 3, № 2, 47 A967).
' Quantum noise. IX. Quantum Fokker-Planck solution
for laser noise.
3?. Lax M., Phys. Rev., 157, № 2, 213 A967).
/ Quantum noise. X. Density-matrix treatment of field
and population-difference fluctuations.
33. Lax M., Phys. Rev., 172, № 2, 350 A968).
- Quantum noise. XI. Multitime correspondence between
( quantum and classical stochastic processes.

49Й	ДОПОЛНЕНИЕ
34.	Lax М., Phys. Rev., 172, Л» 2, 362 A968).
Quantum noise. XIII. Six-classical-variable descrip-
description of quantum laser fluctuations.
35.	Mo How B. R.. Glauber R. J., Phys. Rev., 160,
№ 5, 1076, 1097 A967).
Quantum theory of parametric amplification, I, II.
V. ПРИЕМ И ГЕТЕРОДИНИРОВАНИЕ ОПТИЧЕСКИХ
СИГНАЛОВ
В первую часть настоящего раздела вошли работы,
посвященные общей теории приема оптических сигна-
сигналов в присутствии флуктуации [2—8] (здесь отметим, в
частности, теоретические работы Караваева [4—6], где
дано весьма общее рассмотрение вопроса), шумам кван-
квантовых счетчиков [14—19] и супергетеродинным прием-
приемникам оптических сигналов [20—25]. Отметим также
весьма детальное рассмотрение вопросов приема в книге
Росса [1]. Во вторую часть отнесены некоторые работы,
посвященные шумам усилителей.
Прием и гетеродирование
1.	Росс М., Лазерные приемники, изд-во «Мир», 1969.
2.	Дерюгин И. А., в сб. «Квантовая электроника»,
Киев, 1966, стр. 259.
Шумы квантовых устройств.
3.	Митюгов В. В., Морозов В. П., Изв. ВУЗ, Ра-
Радиофизика, II, № 2, 260 A968).
Квантовый электромагнитный канал связи с адди-
аддитивным шумом.
4.	К а р а в а е в В. В., ЖЭТФ, 51, № 2, 490 A966).
Потенциальная чувствительность энергетических
приемников излучения.
5.	Караваев В. В., Радиотехника и электроника, 14,
№ 10, 1890 A969).
К вопросу о минимальном уровне шумов линейных
усилителей.
6.	Караваев В. В., Автореферат диссертации, Физи-
Физический институт АН СССР, Москва, 1969.
Вопросы приема электромагнитного излучения в
присутствии квантовых эффектов.

ДОПОЛНЕНИЕ	409
7	Hisdal E., Journ. Opt. Soc. Amer., 57, № 1, 35
A967).
Detectable information in a photon beam.
8	Hisdal E., Journ. Opt. Soc Amer., 57, № 1, 111
A967).
Threshold signal-to-noise ratio for a photon beam.
9. Козлов В. П., Оптика и спектроскопия, 24, № 5,
840 A968).
По поводу нового метода регистрации слабых свето-
световых сигналов.
10 О 1 i v е г С. J., P i k е Е. R., Journ. Phys. (Brit. Journ.
Appl Phys.), Dl, № 11, 1459 A968).
Measurement of low light flux by photon counting.
11.	Pao Yoh -H an, Z i t t er R. N., Griffiths J. E.,
Bull. Amer. Phys. Soc, 11, № 1, 111 A966).
New photodetection method for use with light of low
intensity.
12.	Артемьев В. В., Гуськов Л. Н., М и х а й-
лов В. Н., Изв. Сиб. отд. АН СССР, № 13, сер.
техн. н., вып. 3, 106 A968).
Регистрация когерентных световых потоков.
13.	Peters W. N., Arguelio R. J., IEEE Journ.
Quant. Electron., 3, № 11, 532 A967).
Fading and polarization noise of a PCM/PL sy-
system.
14.	Eberhard t E. H., Appl. Optics, 6, № 2, 251 A967).
Threshold sensitivity and noise ratios of multiplier
phototubes.
15.	Whiting J. S. S., Journ. Appl. Phys., 38, № 1, 415
A967).
Noise limitations in quantum counters.
16.	Gandrud W. B, MoosH. W, Journ. Appl. Phys.,
39, № 10, 4777 A968).
Thermal noise in IR quantum counters.
i7 Schemel R. E., Экспресс-инф. «Радиотехника
сверхвысоких частот и квантовая радиотехника»,
№ 27, 15 A968).
Отношение сигнал/шум в квантовых детекторах ко-
когерентных оптических систем.
18. Thomas С. Е., Appl Optics, 7, № 3, 517 A968).
Coherent optical noise suppression.

410	ДОПОЛНЕНИЕ
19.	Ducot С, Acta electron., 9, № 3, 215, 293 A965),
A966).
Problemes de bruit lies a la transmission de signaux
aux radiofrequences tres elevees et aux frequences op-
tiques.
20.	M a n d e 1 L., Journ. Opt. Soc. Amer., 56, № 9, 1200
A966).
Heterodyne detection of a weak light beam.
21.	H e 1 s t г о m С W., Journ. Opt. Soc. Amer., 57, № 3,
353 A967).
Detectability of coherent optical signals in a hetero-
heterodyne receiver.
22.	Hani on J., Jacobs S. E., Appl Optics. 6, № 3,
577 A967).
Narrowband optical heterodyne detection.
23.	F r i e d D. L., S e i d m a n J. В., Appl. Optics, 6, № 2,
245 A967).
Heterodyne and photon-counting receivers for optical
communications.
24.	Bell D. A., Proc. IEE, 114, № 2, 211 A967).
Noise in optical superheterodyne reception. Discussion
on the paper: «Experimental study of the theory of
optical superheterodyne reception» by M. P. War-
Warden.— Author's reply.
25.	Ерофеичев В. Г., ФТП, 2, № 2, 277 A968).
Гетеродинирование света на фотосопротивлениях из
InSb.
Шумы усилителей
26.	D'Haenens I. J., Ciuliano С. R, IEEE Journ.
Quant. Electron., 1, № 9, 393 A965).
Noise properties of pulsed ruby laser amplifiers.
27.	Kluver J. W., Journ. Appl. Phys., 37, № 8, 2987
A966).
Laser amplifier noise at 3,5 microns in helium-xe-
helium-xenon.
28.	Мазанько И. П., Радиотехника и электроника, 13,
№ 3, 483 A968).
О флуктуациях в газовых оптических усилителях и
генераторах.

ДОПОЛНЕНИЕ	411
29.	М их нов С. А., Рубинов А. Н., Журн. прикл.
спектроск., 8, № 1, 42 A968).
Исследование шумов в стеклянных неодимовых ла-
лазерах.
30.	Самсон А. М., Котомцева Л. А., Изв. АН
БССР. Сер. физ. мат. н., № 3, 76 A968).
Расчет шумов в матированном генерирующем
стержне за счет проникновения радиации накачки.
31.	Басов Н. Г., Г р а с юк А. 3., Зубарев И. Г., Т е-
в ел ев Л. В., Труды ФИАН им. П. Н. Лебедева, 31,
74 A965).
Регенеративные оптические квантовые усилители.
32.	Карлов Н. В., Маненков А. А., Квантовые уси-
усилители, М., 1966.
33.	Карлов Н. В., Труды ФИАН, 49, 3 A969).
Исследования по квантовым усилителям.
VI. ФЛУКТУАЦИИ В ЛАЗЕРАХ
Статистические свойства лазерного излучения суще-
существенно различны для лазеров непрерывного действия
(как правило, газовых) и для мощных импульсных ла-
лазеров типа неодимового или рубинового. Из работ об-
общего характера отметим обзор Армстронга и Смита [1].
Лазеры непрерывного действия чаще всего исполь-
используются в режиме генерации единственной моды с опре-
определенными поперечным (как правило, равным нулю) и
продольным индексами. При этом амплитуда, фаза и
частота излучения подвержены флуктуациям, которые
классифицируются по вызывающим их причинам и по
характерным временам корреляции соответствующих
процессов. Эта классификация весьма близка к той, ко-
которая дается в хорошо известной в радиофизике задаче
о флуктуациях томсоновского генератора.
Именно, имеются так называемые «технические»
уходы частоты и амплитуды, связанные со сравнительно
медленными изменениями параметров резонатора и ак-
активной среды; их в принципе можно устранить, улучшив
экспериментальные условия. Этому вопросу посвящены
работы [6—15]. Напротив, «естественные» флуктуации
фазы (частоты) и амплитуды возникают в результате

412
ДОПОЛНЕНИЕ
действия принципиально неустранимого шума спонтан-
спонтанного излучения. Характерное время корреляции этого
шума отвечает обратной ширине линии лазерного пере-
перехода и, таким образом, весьма мало. Работы по теории
естественных флуктуации одномодовых лазеров ведутся
несколькими группами исследователей; отметим, в част-
частности, работы Хакена и др. [17—24], Берштейна и др.
[33, 34] (в [33] содержится также обзор экспериментов
этой группы), работы группы Климонтовича (ссылки
см. в [35], работы Казанцева, Сурдутовича и сотр. (см.
например [31]). В работах Лэкса (см. раздел IV) также
развивается теория флуктуации в лазерах. Из интерес-
интересных результатов отметим решение нестационарного урав-
уравнения Фоккера—Планка для процесса установления
амплитуды при включении лазера [18]. Эксперименты по
флуктуациям одномодовых лазеров ведутся группой
Арекки [36—38], Берштейном и др. [52—57] и рядом
других. Необходимо особо упомянуть работу [54], где из-
измерена естественная ширина линии излучения гелий-нео-
гелий-неонового лазера.
Ряд работ посвящен флуктуациям излучения коль-
кольцевых газовых лазеров [58, 59], лазеров с нерезонансной
обратной связью (обратной связью за счет рассеяния)
[60—65] и полупроводниковых лазеров [66—70].
Наиболее интересные статистические и динамические
свойства мощных импульсных лазеров связаны с их мно-
гомодовостью. В частности, фазировка этих мод может
привести к образованию мощных сверхкоротких импуль-
импульсов света. В виду большой практической важности во-
вопроса представляется целесообразным, кроме списка ли-
литературы, привести формулировку основных относя- .
щихся сюда понятий.
В ширине спектра, генерируемого активной средой
(Дсо = 2-1012 сек~1 для рубинового лазера и Аи =
= 5• 1013 сек'1 для неодимового) помещается большое
число М мод, отличающихся продольным индексом (так
называемых аксиальных мод). При этом М = Aco/Q, где
Q = 2п/Г = яс/L, а Т — период межмодовых биений;
типичные значения длины резонатора L « 1 м.
В отсутствие связи между модами их фазы незави-
независимы, и излучение при М ^> 1 приближенно представ-

ДОПОЛНЕНИЕ	413
ляет собой гауссов процесс. При этом временной ход
пола E(t) и интенсивности /(t) = \E(t) \2 отвечает функ-
функции с характерным временем корреляции т = (Доо)~' ~
~ Т/пМ. Одномерный закон распределения мгновенной
интенсивности I(t) имеет вид
(что соответствует рэлеевскому распределению для оги-
огибающей). Независимость фаз различных мод приводит
к тому, что временной ход интенсивности представляет
последовательность всплесков, причем эти всплески в
среднем равномерно заполняют весь период Т, а число
их /V имеет порядок числа М возбужденных мод.
В определенных условиях работы лазера при том же
спектральном составе поля временной ход интенсивно-
интенсивности может отвечать картине со значительно меньшим
числом всплесков (N <С М) и соответственно с большей
мгновенной интенсивностью. Это происходит, в частно-
частности, если в лазере установлен просветляющийся фильтр;
такой фильтр на определенном этапе развития поля в
лазере ускоряет рост наиболее интенсивных выбросов
начальной флуктуационной картины по сравнению со
средней скоростью роста.
Случай с N <с М на языке разложения по модам от-
отвечает частичной синхронизации фаз различных мод;
такая синхронизация происходит в результате взаимо-
взаимодействия мод в нелинейном фильтре.
Особый интерес представляет случай так называемой
полной фазировки спектра, когда подавляющая часть
излучаемой за период энергии сосредоточена в един-
единственном мощном импульсе; при этом фазы мод яв-
являются линейной функцией продольного индекса п:
Ф„ = nQt0 + 'ф,
где t0 — положение импульса на периоде.
Вопросам генерации коротких импульсов света в ла-
лазерах с самосинхронизацией мод посвящен обзор Де-
Мариа и др. [71], где приведена библиография работ на
эту тему (около 120 названий).
Статистические аспекты процесса фазировки спектра

414	ДОПОЛНЕНИЕ
оптического излучения рассмотрены в работах [77—82].
Отметим, в частности, работу [78], в которой для опре-
определенной модели лазера получены условия того, когда
следует ожидать полной фазировки спектра, а когда —
лишь частичной.
Регистрация пикосекундной структуры излучения та-
таких лазеров является трудной задачей. Здесь обычно
применяются методы нелинейной интерферометрии (на-
(например, люминесценция при двухквантовом возбужде-
возбуждении). Литература по этому вопросу приведена в раз-
разделе II.
Общие вопросы
1.	Armstrong J. A., Smith A. W., Progress in Op-
Optics, 6, 213 A967).
2.	Chen D., Ready J. F., Bull. Amer. Phys. Soc, 11,
№ 4, 454 A966).
Measurement of the mutual coherence function of
He—Ne laser light.
3.	Leonard D. A., Zinky W. R., Appl. Phys. Lett.,
12, № 4, 113 A968).
Coherence properties of the supperradiant 5401 A pul-
pulsed neon laser.
4.	Кал лас Х., Чайка М., Оптика и спектроскопия,
22, № 3, 517 A967).
Поляризация спонтанного излучения газового ла-
лазера.
5.	А р т е м ь е в В. В., Оптика и спектроскопия, 23,
№4, 637 A967).
Корреляция фотонов лазера.
Технические флуктуации в газовых лазерах
6.	Р res cot t L. J., Van der Ziel A., IEEE Journ.
Quant. Electron., 2, № 7, 173 A966).
Gas discharge modulation noise in He—Ne lasers.
7.	G u b 1 e r W., S t r u 11 M. J. O., Appl. Optics, 5, № 4,
659 A966).
Experimental and theoretical investigations of the
spontaneous infrared radiation fluctuations of a high-
pressure, high current argon discharge.

ДОПОЛНЕНИЕ	4t5
8.	К u b о U., К a w a b e K., I n u i s h i Y., Technol,
Repts Osaka Univ., 16, № 716—747, 505 A966).
Noise and modulation of He—Ne laser.
9.	Kubo U., К a w a b e K., I n u i s h i Y., Japan. Journ.
Appl. Phys., 5, № 8, 731 A966).
Effect of plasma fluctuations on gas laser noise.
10.	Forgo G., Strutt M. J. O., IEEE Journ. Quant.
Electron., 3, № 10, 417 A967).
Discharge modulation noise in a He—Ne lasers.
11.	Bolwijn P. Т., Phys. Lett., A24, № 5, 285 A967).
Discharge modulation noise in He—Ne laser radiation.
12.	Mas G, Brun J., Compt. Rend., 266, № 26, B1583
A968).
Modulation spontane a l'allumage du faisceau emis
par in laser helium-neon.
13.	Suzuki Т., Экспресс-инф. «Радиотехника СВЧ и
квантовая радиотехника», № 43, 16 A968).
Подавление шумов газового лазера, обусловленных
модуляцией тока.
14.	Алякшев С. А., Гордеев Д. В., Остапчен-
ко Е. П., Пятакова Л. М., Радиотехника и элек-
электроника, 12, № 10, 1769 A967).
Экспериментальное исследование шумов излучения
газового ОКГ на гелий — неоне при различных спо-
способах возбуждения разряда в активном элементе.
15.	Лебедева В. В., Одинцова А. И., С а л и-
м о в В. М., ЖЭТФ, 38, № 8, 1373 A968).
Флуктуации частотного состава излучения аргоно-
аргонового ОКГ.
Естественные флуктуации в одномодовых
лазерах (теория)
16.	Scully М. О, Lamb W. E, Phys. Rev., 159, 208
A967).
Quantum theory of an optical maser. I. General
theory.
17.A r t z V., H a k e n H., R i s k e n H., S a u e r m a n n H.,
S с h m i d Ch., W e i d 1 i с h W., Zs. Phys., 1907, № 3,
207 A966).
Quantum theory of noise in gas and solid state lasers
with an inhomogeneously broadened line. I.

416	ДОПОЛНЕНИЕ
18. R i s к е n H., V о 1 1 m e r H. D., Zs. Phys., 204, № 3,
240 A967).
The transient solution of the laser Fokker-Planck
equation.
19 Risken H., Zs. Phys., 191, № 3, 302 A966).
Correlation function of the amplitude and of the in-
intensity fluctuation for a laser model near threshold.
20.	Risken H, Schmid C, Weidlich W., Phys.
Lett., 20, № 5, 489 A966).
Fokker-Planck equation for atoms and light mode in
a laser model with quantummechanically determined
dissipation and fluctuation coefficients.
21.	Risken H., Vollmer H. D., Zs. Phys., 201, № 3,
323 A967).
The influence of higher order contributions to the cor-
correlation function of the intensity fluctuation in a laser
near threshold.
22 RiskenH, SchmidC, WeidlichW, Zs. Phys.,
194, №4, 337 A966).
Fokker-Planck equation distribution and correlation
functions for laser noise.
23.	Schmid Ch., Phys. Lett., A27, № 8, 484 A968).
A generalized Van der Pole equation for laser noise
not limited to threshold region.
24.	H a ken H., Zs. Phys., 190, № 3, 327 A966).
Theory of intensity and phase fluctuations of a homo-
homogeneously broadened laser.
25.	Fleck J. A., Phys. Rev., 152, № 1, 278 A966).
Intensity fluctuations and statistics of laser radi-
radiation.
26.	Fleck J. A., Journ. Appl. Phys., 37, № 1, 188 A966).
Nonlinear laser noise and coherence.
27 S i 1 1 i t t о R. M., Phys. Lett., A27, № 9, 624 A968).
A statistical model of laser light.
28.	В runner W., Ann. Phys., 20, № 1—2, 53 A967).
Quantenmechanische Berechnung der Photonenzahl
und Amplitudenfluktuation einer Laserstrahlung.
29.	Pauwels H. J., IEEE Journ. Quant Electron., 2,
№3, 54 A966).
Phase and amplitude fluctuation of the laser oscilla-
oscillator.

ДОПОЛНЕНИЕ	417
30 PauwelsH. J., Physica, 36, №1,1 A967).
Equivalent classical models for quantum noise in the
laser oscillator.
31.	Казанцев А. П., Сурдутович Г. И., ЖЭТФ,
58, 245 A970).
Квантовая модель лазера с нелинейным поглоще-
поглощением.
32.	L о u i s е 1 1 W. Н., М а г b u г g е г J. H., IEEE Journ.
.- Quant. Electron., 3, № 8, 348 A967).
Solutions of the damped oscillator Fokker-Planck
equation.
33.	БерштейнИ. Л., ЗайцевЮ. И., Proc. of the con-
conference on laser measurements URSI Committe I.,
Sep. 1968 (Warsaw).
Radiation fluctuations of gas lasers.
34.	Б ер штейн И. Л., Андронова И. А., 3 а й-
цевЮ. И., Изв. ВУЗ. Радиофизика, 10, 59 A967).
Флуктуации интенсивности и частоты излучения оп-
оптического генератора.
35.	Климентович Ю. Л., Л а н д а П. С, ЖЭТФ, 56,
№ 1, 275 A969).
К теории естественной ширины линии и флуктуации
амплитуды газового лазера.
Естественные флуктуации в одномодовых лазерах
(эксперимент)
36.	А г е с с h i F. Т., G i g 1 i о М., S о n a A., Phys. Lett.,
A25, № 4, 341 A967)
Dynamics of the laser radiation at threshold.
37.	Arecchi F. T. R о d a r i G. S., S о n a A., Phys.
Lett., A25, № 1, 59 A967).
Statistics of the laser radiation at threshold.
38	Arecchi F. Т., Be r net A., Phys. Rev. Lett., 16,
№ 1, 32 A966).
High-order fluctuations in a single-mode laser field.
39	A r m s t г о n g J. A., Journ. Opt. Soc. Amer., 56, № 8,
1024 A966).
Theory of interferometric analysis of laser phase noise.
40	Smith A. W., Armstrong J. A, Bull. Amer.
Phys. Soc, 11, № 1, 128 A966).
Laser photon counting distributions.

418	ДОПОЛНЕНИЕ
41.	S m i t h A., A r m s t г о n g J. A., Phys. Rev. Lett., 16,
№25, 1169 A966).
Laser photon counting distributions near threshold.
42.	A r m s t г о n g J. A., S m i t h A. W., Bull. Amer.
Phys. Soc, 11, № 1, 112 A966).
Interferometric analysis of laser phase noise.
43.	Davidson F., M a n d e 1 L., Phys. Lett., A25, № 9,
700 A967).
Correlation measurements of laser beam fluctuations
near threshold.
44.	Boersman S. L., Proc. IEEE, 8, 1070 A966).
Statistics of laser radiation.
45.	ChangR. F., DetenbeckR. W, KorenmanV.,
Alley С. О., Jr., Hochuli U., Phys. Lett., A25,
№3, 272 A967).
Photon bunching in a laser at threshold.
46.	Siegman A. E., Dai no В., Manes K- R., IEEE
Journ. Quant. Electron., 3, № 5, 180 A967).
Preliminary measurements of laser shortterm frequency
fluctuations.
47.	A r r a t h о о n R., Siegman A. E., Journ. Appl.
Phys., 40, №2, 910 A969).
Further measurements of quantum phase noise in a
He—Ne laser.
48.	Freed C, Haus H. A., Solid State Res. Lincoln
Lab. Mass. Inst. Technol., 34, № 3, 19 A965).
Photoelectron statistics produced by laser operating
below threshold of oscillation.
49.	Freed C, Haus H. A., IEEE Journ. Quant. Elec-
Electron., 2, №8, 190 A966).
Photoelectron statistics produced by a laser operating
below and above the threshold of oscillation.
50.	D a i n о В., IEEE Journ. Quant. Electron., 2, № 9, 351
A966).
The measurements of the frequency fluctuations of a
laser field.
51.	D i t с h f i e 1 d С R., Conf. Phys. Aspects Noise Elec-
Electron. Devices, Nottingham, 1968, p. 162.
Noise in masers and lasers.
52.	Зайцев Ю. И., ЖЭТФ, 50, № 3, 525 A966).
О флуктуациях излучения газового лазера.

ДОПОЛНЕНИЕ	419
53.	А н д р онова И. А., 3 а й цев Ю. И., Изв. ВУЗ. Ра-
Радиофизика, 11, № 1, 149 A968).
Экспериментальное исследование флуктуации интен-
интенсивности одночастотных Не—Ne лазеров на волнах
0,63 и 3,39 мк.
54.	3 а й ц е в Ю. И., С т е п а н о в Д. П., ЖЭТФ, 55, № 5,
1645 A968).
Флуктуации частоты газового лазера и определение
естественной ширины его спектральной линии.
55.	Андронова И. А., ЖЭТФ, 56, № 2, 417 A969).
Экспериментальное исследование флуктуации интен-
интенсивности одночастотного газового лазера на волне
3,39 мк.
56.	С т е п а н о в Д. П., Изв. ВУЗ. Радиофизика, 11, № 4,
514 A968).
Стабилизация частоты и частотные флуктуации ге-
гелий-неонового лазера.
57.	Зайцев Ю. И., Изв. ВУЗ. Радиофизика, 12, № 1,
60 A969).
Флуктуации интенсивности излучения Не—Ne лазера
на волне 0,63 мк.
Флуктуации в кольцевом газовом лазере
58.	Беленов Э. М., ЖТФ, 39, № 1, 133 A969).
Влияние амплитудных флуктуации на стабильность
частоты биений бегущих волн кольцевого лазера.
59.	К л и м о н т о в и ч Ю. Л., Л а н д а П. С, ЖЭТФ, 56,
№ 1, 275 A969).
К теории естественной ширины линии и флуктуации
амплитуды газового лазера.
Лазер с нерезонансной обратной связью
60.	Л е т о х о в В. С, Письма ЖЭТФ, 4, № 11, 477 A966).
О стимулированном радиоизлучении межзвездной
среды.
61.	Летохов В. С, Письма ЖЭТФ, 5, № 8, 262 A967).
Стимулированное излучение ансамбля рассеиваю-
рассеивающих частиц с отрицательным поглощением.
62.	Летохов В. С, ЖЭТФ, 53, № 4, 1442 A967).
Генерация света рассеивающей средой с отрицатель-
отрицательным резонансным поглощением,

420	ДОПОЛНЕНИЕ
63.	А м б а р ц у м я н Р. В., Крюков П. Г., Лето-
хов В. С, ЖЭТФ, 51, № 6, 1669 A966).
Динамика сужения спектра излучения квантового
генератора с нерезонансной обратной связью.
64.	А м б а р цу м я н Р. В., Басов Н. Г., Крю-
Крюков П. Г., Летохов В. С, ЖЭТФ, 51, № 3, 724
A966).
Оптический квантовый генератор с нерезонансной
обратной связью.
65.	А м б а р ц у м я н Р. В., Крюков П. Г., Лето-
Летохов В. С, Матвеец Ю. А., ЖЭТФ, 53, № 6, 1955
A967).
Статистические свойства излучения лазера с нерезо-
нерезонансной обратной связью.
Флуктуации в полупроводниковых лазерах
66.	S m i t h A. W., A r m s t г о n g J. A., IBM Journ. Res.
Developm., 10, № 3, 225 A966).
Intesity noise of multimode GaAs laser emission.
67.	Скоморовский Ю. А., Зборовский А. А., Ра-
Радиотехника и электроника, 13, № 1; 160 A968).
Шумовые характеристики и искажения при модуля-
модуляции излучения полупроводникового ОКГ по интен-
интенсивности.
68.	Haug H., На ken H., Zs. Phys., 204, № 3, 262
A967).
Theory of noise in semiconductors laser emission.
69.	Haug H., Zs. Phys., 200, № 1, 57 A967).
Quantummechanical theory of fluctuations and relaxa-
relaxation in semiconductor lasers.
'70. Haug H., IEEE Journ. Quant. Electron., 4, № 4, 168
A968).
Noise in semiconductor lasers.
Многомодовые лазеры и синхронизация мод
71.	D е М а г i a A. J., G 1 е n n W. Н., Jr., В г i е п г а М. J.,
Mack М. Е., Proc. IEEE, 57, № 1, 2 A969).
Picosecond laser pulses.
72.	Tar g R., Yarborough J. M., Appl. Phys. Lett.,
12, № 1, 3 A968).
Mode-locked quenching of He—Ne and argon lasers.

ДОПОЛНЕНИЕ	421
Berklay D. A., W о 1 g a G. J., Journ. Appl. Phys.,
38, №8, 3231 A967).
Transient interference studies of emission from a pul-
pulsed ruby laser.
Haken H., Sauermann H., Schmid Ch.,
Vollmer H. D., Zs. Phys., 206, № 4, 369 A967).
Theory of laser noise in the phase locking region.
Haken H., Zs. Phys., 219, № 3, 246 A969).
Exact stationary solution of a Fokker-Planck equation
for multimode laser action including phase locking.
H о d a r a H., George N., IEEE Journ. Quant. Elec-
Electron., 2, №9, 337 A966).
Excess photon noise of multimode lasers.
Fleck J. A., Appl. Phys. Lett., 13, № 11, 365 A968).
Evolution of a Q-switched laser pulse from noise.
Кузнецова Т. И., ЖЭТФ, 57, 1673 A969).
К статистике возникновения сверхкоротких световых
импульсов в лазере с просветляющимся фильтром.
Кузнецова Т. И., Письма ЖЭТФ, 10, № 3, 153
A969).
Фазировка спектра и короткие световые импульсы
при вынужденном комбинационном рассеянии.
Караваев В. В., Радиотехника и электроника, 12,
№ 1, 144 A967).
Фотонный ансамбль Кастлера и статистические свой-
свойства излучения лазера в многомодовом режиме воз-
возбуждения.
Летохов В. С, ЖЭТФ, 54, 1392 A968).
Динамика генерации импульсного лазера с фази-
ровкой мод.
Летохов В. С, ЖЭТФ, 55, 1077 A968).
Генерация ультракоротких импульсов света в лазере
с нелинейным поглотителем.
Малютин А. А., Щелев М. Я., Письма ЖЭТФ,
9, №8, 445 A969).
Исследование временной структуры генерации нео-
димого лазера в режиме самосинхронизации мод.
Летохов В. С, ЖЭТФ, 55, 1943 A968).
Флуктуационные ультракороткие импульсы света
в лазере.

Предметный указатель
Аналитический сигнал 21—24,
30, 61, 147, 206, 288
Ансамбль световых полей 20
—	стационарный 25, 76
—	тепловой 305
Бейкера — Хаусдорфа уравне-
уравнение 162
Белый шум 91
Броуновское движение 90
Даламбера оператор 77
Детектор распределенный 216,
251, 253
—	тензор адмитанса 354
—	точечный 213, 250
	идеальный 212
Диагональное представление по
когерентным состояниям 247,
255
Диффузионное приближение 95,
340
Ван Циттерта — Цернике теоре-
теорема 34
Видность 18
—	индекс 240
Волновое уравнение классиче-
классическое 78
Вынуждающая сила 88
Гамильтона оператор 128
Гармонический осциллятор сдви-
сдвинутый 160
	смещенный 157
Гельмгольца уравнение 151
Гильберта — Шмидта норма 266
	 оператор 266
Гильбертово пространство, век-
векторы 98
	 норма 98
—	— полный ортонормирован-
ный базис 99
—	— функциональное пред-
представление 169
Грина теорема 32, 152
—	функция 32, 152
Гюйгенса принцип 34, 35
Закон сохранения тока 132
Излучение квазимонохроматиче-
квазимонохроматическое 27
—	лазера 20, 320
—	поляризованное 21
—	тепловое 20, 289
Источники тепловые 17
—	— искусственные 45, 350
Когерентность, время 66
—	высшего порядка 232
—	квантовая теория 24, 212
—	определение 224
—	первого порядка 228
—	полная 223—225
	критерии 225, 226
—	свойство 224
—	степень 28, 237
—	частичная 20, 21, 37, 223
—	— интерференционный за-
закон 26
—	"— классическая теория 21
—	— модель 19
—	— скалярная теория 21

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
423
Когерентные состояния для бес-
бесконечного числа степеней сво-
свободы 195
¦	нескольких степеней
свободы 192
—	— непрерывность и анали-
аналитичность 107
Коммутационные соотношения
канонические 140
Колмогорова — Чэпмена уравне-
уравнение 92
Корреляционный объем 346, 351
Лазер, излучение 20, 320
—	модели 320—332
Лапласа оператор 31
Максвелла уравнение 132
Манделя формула 41
Марковские процессы 88
Матрица плотности, диагональ-
диагональное представление 249, 251
	 гильбертова простран-
пространства 106, 107
Норма Гильберта — Шмидта 266
—	оператора 100
—	следовая 105, 264
Оператор Гамильтона 128
—	Гильберта — Шмидта 260
—	Даламбера 77
—	дифференциальный 184
—	единичный 101
	разложение 101, 169, 200
—	Лапласа 31
—	наблюдаемой величины 100
—	норма 100
—	нормально упорядоченный
182
—	ограниченный 100
—	рождения 113, 142
—	с конечным следом 103
—	— — — каноническое раз-
разложение 104
—	следовая норма 105
—	сопряженный 102
—	унитарный 102
—	уничтожения 113, 142
—	упорядочивающий во вре-
времени 131
—	числа частиц 113, 118
Отсчеты, группировка 43, 67
—	распределение 43
•*- — для хаотических полей
309
-- — квантовомеханический
вывод 241
—	— полуклассический вывод
38, 41, 55
-¦	производящая функция
41
	случай тепловых полей 44
	формула Манделя 41
	 характеристическая
функция 40, 42
Поле излучения, диагональное
представление 251, 280
	полностью когерентное
состояние 223
—	— распределение отсчетов
250
—	— свободное
	 — представитель основ-
основного состояния 208
	 стационарные состояния
304
	хаотическое 20, 290—320,
345
Поляризация круговая 21, ПО
—	линейная 21, НО
—	нулевая ПО
—	степень 52, 112
—	частичная 21
—	эллиптическая 21
Полярное разложение 104
Представление Гейзенберга 130
.— Шредингера 129
Преобразование Гильберта 23
—	Лапласа 41
—	Фурье 22
Приближение дальнего поля 35,
73
—	«волн вращающейся поля-
поляризации» 149, 334
Пробная функция 61, 259

424
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Производящая функция для
распределения отсчетов 41
— — нормально упорядочен-
упорядоченная 221
Распределение гауссово 58
—	для идеального лазера 322
—	интенсивности 52
¦•— классическое, в фазовом про-
пространстве 181
—	кумулянты 94
—	многомерное 54
—	нормальное 309
—	отсчетов 39, 43
—	пуассоновское 39, 116, 122
	многомерное 122, 206
—	равновесное тепловое 305
—	связанные моменты 93
—	семиинварианты 93
—	с неопределенной фазой 76
—	стационарное 76
—	тепловое 54, 119
—	умеренное 257
Резервуар 81, 334
Скорость счета квантов 212
Случайное блуждание 90
Случайные функции 59
Случайный процесс 20, 62
Состояние, равновесное тепловое
307
—	смешанное 105, 106
—	чистое 107
Стокса параметры 111
Теория возмущения 38, 212
Усеченная последовательность
199
Условие минимальной неопреде-
неопределенности 161
Фаза 19
факториальные моменты 42
Флуктуационное (стохастиче-
(стохастическое) уравнение 80, 95, 333
фоккера — Планка уравнение 95
—	— — — обобщенное 333
Фотоотсчеты, квантовая теория
241—255
—	полуклассическая теория
55—76
Функционал характеристический
60—64, 85
Функция автокорреляционная 65
—	вероятности 57
—	Грина 32, 152
—	квантовая корреляционная
212
—	пробная 59, 76, 259
—	производящая 41
—	характеристическая 34
б-функция Дирака 42, 47
Хэнбери Брауна —¦ Твисса экспе-
эксперимент 71
Центральная предельная теоре-
теорема классическая 289
	квантовая 289—291
Шварца неравенство 26, 98
Шредингера уравнение 128
Электромагнитное поле, векторы
поляризации 138
—	— временная эволюция 144
—	— квантовый гамильтониан
141
—	— операторы рождения и
уничтожения 142, 204
—	— представление по коге-
когерентным состояниям 203
—	— пространственная эволю-
эволюция 151
Энтропия 305, 306
Эргодический процесс 20

Оглавление
Предисловие редактора перевода 	 5
Литература	,	 13
Предисловие , . . ,	 14
Глава 1. Частично когерентный свет	 ...	17
§ 1. Введение		17
§ 2. Описание аналитического сигнала		21
§ 3. Статистика частично когерентного света		25
§ 4. Временные и пространственные свойства функции взаим-
взаимной когерентности в процессе распространения сигнала . .	30
А. Теорема ван Циттерта — Цернике C4).
Глава 2. Распределение фотоэлектрических отсчетов .... 37
§ 1. Постоянная интенсивность	 37
А. Распределение Пуассона C3).
§ 2. Случайные интенсивности	 40
А. Статистика фотоотсчетов для малых временных интер-
интервалов D3).
§ 3. Нахождение распределения интенсивнэсти из распреде-
распределения отсчетов	 46
А. Независимые вклады E0).
Глава 3. Полуклассическая теория фотоэлектрических от-
отсчетов 	 55
§ 1. Случайные волновые поля	 55
§ 2. Стохастические процессы	 57
§ 3. Применения к частичной когерентности	 6-1
A.	Одиночные счетчики F4). Б. Несколько счетчиков F8).
B.	Полоса пропускания, размер счетчика и значение сгла-
сглаживающих функций G4).
§ 4. Заключение	 76
Глава 4. Статистика поля	 78
§ 1. Постановка динамической задачи	 78
А. Причины появления статистики G9).
§ 2. Преобразование флуктуационных уравнений	 83
А. Усредненные уравнения для моментов (83). Б. Усред-
Усредненное уравнение для характеристического функциона-
функционала (85).

426	ОГЛАВЛЕНИЕ
§ 3. Марковские и немарковские процессы	 88
А. Определения и различия (88). Б. Соотношения для
марковских процессов (91).
§ 4. Заключительные замечания	 95
Глава 5. Статистические состояния в квантовой теории ... 97
§ 1. Введение	 97
§ 2. Квантовый формализм и обозначения	 98
А. Гильбертово пространство (98). Б. Линейные опе-
операторы A00). В. Статистические состояния A05).
§ 3. Примеры статистических состояний в квантовой теории . . 109
А. Состояния поляризации монохроматического светового
пучка A09). Б. Статистические состояния гармонического
осциллятора A12). В. Статистические состояния не-
нескольких осцилляторов A18). Г. Статистические состоя-
состояния для бесконечного числа осцилляторов A21).
§ 4. Заключение	124
Глава 6. Уравнения движения электромагнитного поля. . . 128
§ 1. Развитие во времени в квантовой теории 	 128
§ 2. Операторные уравнения для электромагнитного поля.
Предварительные замечания	132
А. Общий подход к уравнениям поля A33).
§ 3. Операторные уравнения для электромагнитного поля.
Нерелятивистский анализ 	 134
A.	Формулировка в конфигурационном пространстве A34).
Б. Формулировка в импульсном пространстве A36).
B.	Операторы рождения и уничтожения A42).
§ 4. Характерные свойства временной эволюции	144
А. Описание в конфигурационном пространстве A49).
§ 5. Характерные свойства пространственной эволюции	151
Глава 7. Представление электромагнитного поля по когерент-
когерентным состояниям	156
§ 1. Когерентные состояния. Основные свойства	156
А. Собственные состояния смещенного и сдвинутого осцил-
осцилляторов A57). Б. Волновые пакеты с минимальной неопре-
неопределенностью A61). В. Собственные векторы оператора
уничтожения A62).
§ 2. Фундаментальные свойства когерентных состояний для
одной степени свободы	164

ОГЛАВЛЕНИЕ	427
A.	Предварительные замечания A64). Б. Непрерывное
представление, основанное на когерентных состояниях A69).
B.	Примеры и специальные свойства представителей век-
векторов и операторов по когерентным состояниям A77).
Г. Связь с пространствами Сегала — Баргманна A90).
§ 3. Когерентные состояния для нескольких степеней свободы 192
§ 4. Когерентные состояния для бесконечного числа степеней
свободы. Приложение к электромагнитному полю .... 195
А. Общие свойства A95). Б. Приложение к электромагнит-
электромагнитному полю B03).
Глава 8. Квантовая теория оптических корреляционных явле-
явлений 	212
§ 1. Квантовые корреляционные функции	212
А. Идеальные детекторы и скорости счета квантов B12).
Б. Разложение по модам B19). В. Производящие функ*-
ции B21).
§ 2. Полная и частичная когерентность	223
А. Определения и полная когерентность B23). Б. Частичная
когерентность B28).
§ 3. Распределения фотоотсчетов	241
А. Скорости и отсчеты для одной нормальной моды B41).
Б. Распределения отсчетов для поля излучения B50).
§ 4. Оптическая теорема эквивалентности	255
А. „Диагональное" представление для одной степени сво-
свободы B55). Б. „Диагональное" представление для поля из-
излучения B80).
Глава 9. Конкретные состояния поля излучения	289
§ 1. Хаотические и тепловые состояния	289
A.	Квантовая центральная предельная теорема B89).
Б. Обобщение на случай многих степеней свободы B97).
B.	Хаотические и тепловые поля излучения B99). Г. Рас-
Распределение фотоотсчетов для хаотических полей C09).
§ 2. Феноменологические модели лазера	320
А. Идеальная модель C21). Б. Модель колебания с диф-
диффундирующей фазой C22). В. Модель, оперирующая с
суперпозицией сигнала и шума C27).
§ 3. Описание лазера с помощью модели связанных систем . . 332
А. Модель лазера C33),

428	ОГЛАВЛЕНИЕ
Глава 10. Интерферометрия интенсивности в квантовой
оптике	344
§ 1. Интерферометрия интенсивности. Корреляция низшего
порядка	344
А. Корреляция отсчетов C44). Б. Пространственная корре-
корреляция интенсивности C50).
§ 2. Интерферометрия интенсивности в случае независимых
источников	353
§ 3. Заключение	-	359
Библиография	362
Дополнение	332
I. Теория когерентности C83). П. Статистика фотоотсчэтов;
интерферометрия интенсивности C88). III. Статистические
явления в нелинейной оптике C95). IV. Квантовая теория
оптических полги; динамика и статистика процессов излу-
излучения и эволюции поля D04). V. Прием и гетеродинирова-
ние оптических сигналов D08). VI. Флуктуации в лазерах
D11).
Предметный указатель	422